diff --git a/.gitattributes b/.gitattributes
index a6344aac8c09253b3b630fb776ae94478aa0275b..3ffcbbdca9c236f6b98437613141d71641b756ec 100644
--- a/.gitattributes
+++ b/.gitattributes
@@ -33,3 +33,28 @@ saved_model/**/* filter=lfs diff=lfs merge=lfs -text
*.zip filter=lfs diff=lfs merge=lfs -text
*.zst filter=lfs diff=lfs merge=lfs -text
*tfevents* filter=lfs diff=lfs merge=lfs -text
+EfficientSAM/LightHQSAM/example_light_hqsam.png filter=lfs diff=lfs merge=lfs -text
+GroundingDINO/.asset/GD_GLIGEN.png filter=lfs diff=lfs merge=lfs -text
+GroundingDINO/.asset/GD_SD.png filter=lfs diff=lfs merge=lfs -text
+GroundingDINO/.asset/hero_figure.png filter=lfs diff=lfs merge=lfs -text
+VISAM/thirdparty/segment_anything/assets/masks1.png filter=lfs diff=lfs merge=lfs -text
+VISAM/thirdparty/segment_anything/assets/notebook2.png filter=lfs diff=lfs merge=lfs -text
+VISAM/visam.gif filter=lfs diff=lfs merge=lfs -text
+assets/acoustics/gsam_whisper_inpainting_demo.png filter=lfs diff=lfs merge=lfs -text
+assets/acoustics/gsam_whisper_inpainting_pipeline.png filter=lfs diff=lfs merge=lfs -text
+assets/demo9.jpg filter=lfs diff=lfs merge=lfs -text
+assets/gradio_demo.png filter=lfs diff=lfs merge=lfs -text
+assets/grounded_sam_demo3_demo4.png filter=lfs diff=lfs merge=lfs -text
+assets/grounded_sam_inpainting_demo.png filter=lfs diff=lfs merge=lfs -text
+assets/grounded_sam_new_demo_image.png filter=lfs diff=lfs merge=lfs -text
+assets/mask_3dbox.png filter=lfs diff=lfs merge=lfs -text
+assets/osx/grounded_sam_osx_demo.png filter=lfs diff=lfs merge=lfs -text
+assets/osx/grouned_sam_osx_demo.gif filter=lfs diff=lfs merge=lfs -text
+assets/ram_grounded_sam_new.png filter=lfs diff=lfs merge=lfs -text
+segment_anything/assets/masks1.png filter=lfs diff=lfs merge=lfs -text
+segment_anything/assets/notebook2.png filter=lfs diff=lfs merge=lfs -text
+voxelnext_3d_box/images/image_boxes1.png filter=lfs diff=lfs merge=lfs -text
+voxelnext_3d_box/images/image_boxes2.png filter=lfs diff=lfs merge=lfs -text
+voxelnext_3d_box/images/image_boxes3.png filter=lfs diff=lfs merge=lfs -text
+voxelnext_3d_box/images/mask_box.png filter=lfs diff=lfs merge=lfs -text
+voxelnext_3d_box/images/sam-voxelnext.png filter=lfs diff=lfs merge=lfs -text
diff --git a/.gitignore b/.gitignore
new file mode 100644
index 0000000000000000000000000000000000000000..b029c3b31ebd4001cadfb44e6b12a8f26597f72f
--- /dev/null
+++ b/.gitignore
@@ -0,0 +1,135 @@
+# Byte-compiled / optimized / DLL files
+__pycache__/
+*.py[cod]
+*$py.class
+
+# C extensions
+*.so
+
+# Distribution / packaging
+.Python
+build/
+develop-eggs/
+dist/
+downloads/
+eggs/
+.eggs/
+lib/
+lib64/
+parts/
+sdist/
+var/
+wheels/
+pip-wheel-metadata/
+share/python-wheels/
+*.egg-info/
+.installed.cfg
+*.egg
+MANIFEST
+
+# PyInstaller
+# Usually these files are written by a python script from a template
+# before PyInstaller builds the exe, so as to inject date/other infos into it.
+*.manifest
+*.spec
+
+# Installer logs
+pip-log.txt
+pip-delete-this-directory.txt
+
+# Unit test / coverage reports
+htmlcov/
+.tox/
+.nox/
+.coverage
+.coverage.*
+.cache
+nosetests.xml
+coverage.xml
+*.cover
+*.py,cover
+.hypothesis/
+.pytest_cache/
+
+# Translations
+*.mo
+*.pot
+
+# Django stuff:
+*.log
+local_settings.py
+db.sqlite3
+db.sqlite3-journal
+
+# Flask stuff:
+instance/
+.webassets-cache
+
+# Scrapy stuff:
+.scrapy
+
+# Sphinx documentation
+docs/_build/
+
+# PyBuilder
+target/
+
+# Jupyter Notebook
+.ipynb_checkpoints
+
+# IPython
+profile_default/
+ipython_config.py
+
+# pyenv
+.python-version
+
+# pipenv
+# According to pypa/pipenv#598, it is recommended to include Pipfile.lock in version control.
+# However, in case of collaboration, if having platform-specific dependencies or dependencies
+# having no cross-platform support, pipenv may install dependencies that don't work, or not
+# install all needed dependencies.
+#Pipfile.lock
+
+# PEP 582; used by e.g. github.com/David-OConnor/pyflow
+__pypackages__/
+
+# Celery stuff
+celerybeat-schedule
+celerybeat.pid
+
+# SageMath parsed files
+*.sage.py
+
+# Environments
+.env
+.venv
+env/
+venv/
+ENV/
+env.bak/
+venv.bak/
+
+# Spyder project settings
+.spyderproject
+.spyproject
+
+# Rope project settings
+.ropeproject
+
+# mkdocs documentation
+/site
+
+# mypy
+.mypy_cache/
+.dmypy.json
+dmypy.json
+
+# Pyre type checker
+.pyre/
+
+# checkpoint
+*.pth
+outputs/
+
+.idea/
diff --git a/.gitmodules b/.gitmodules
new file mode 100644
index 0000000000000000000000000000000000000000..b1096c0f07b94e0b7b1c735e9b26225baefe4b6d
--- /dev/null
+++ b/.gitmodules
@@ -0,0 +1,7 @@
+
+[submodule "grounded-sam-osx"]
+ path = grounded-sam-osx
+ url = https://github.com/linjing7/grounded-sam-osx.git
+[submodule "VISAM"]
+ path = VISAM
+ url = https://github.com/BingfengYan/VISAM
diff --git a/CITATION.cff b/CITATION.cff
new file mode 100644
index 0000000000000000000000000000000000000000..0c3221a96e68e96b5fd69a8abae833895fb7923d
--- /dev/null
+++ b/CITATION.cff
@@ -0,0 +1,8 @@
+cff-version: 1.2.0
+message: "If you use this software, please cite it as below."
+authors:
+ - name: "Grounded-SAM Contributors"
+title: "Grounded-Segment-Anything"
+date-released: 2023-04-06
+url: "https://github.com/IDEA-Research/Grounded-Segment-Anything"
+license: Apache-2.0
diff --git a/Dockerfile b/Dockerfile
new file mode 100644
index 0000000000000000000000000000000000000000..010d8312e154027a0307806ef1cd97ee122226d9
--- /dev/null
+++ b/Dockerfile
@@ -0,0 +1,30 @@
+FROM pytorch/pytorch:1.13.1-cuda11.6-cudnn8-devel
+
+# Arguments to build Docker Image using CUDA
+ARG USE_CUDA=0
+ARG TORCH_ARCH=
+
+ENV AM_I_DOCKER True
+ENV BUILD_WITH_CUDA "${USE_CUDA}"
+ENV TORCH_CUDA_ARCH_LIST "${TORCH_ARCH}"
+ENV CUDA_HOME /usr/local/cuda-11.6/
+
+RUN mkdir -p /home/appuser/Grounded-Segment-Anything
+COPY . /home/appuser/Grounded-Segment-Anything/
+
+RUN apt-get update && apt-get install --no-install-recommends wget ffmpeg=7:* \
+ libsm6=2:* libxext6=2:* git=1:* nano=2.* \
+ vim=2:* -y \
+ && apt-get clean && apt-get autoremove && rm -rf /var/lib/apt/lists/*
+
+WORKDIR /home/appuser/Grounded-Segment-Anything
+RUN python -m pip install --no-cache-dir -e segment_anything
+
+# When using build isolation, PyTorch with newer CUDA is installed and can't compile GroundingDINO
+RUN python -m pip install --no-cache-dir wheel
+RUN python -m pip install --no-cache-dir --no-build-isolation -e GroundingDINO
+
+WORKDIR /home/appuser
+RUN pip install --no-cache-dir diffusers[torch]==0.15.1 opencv-python==4.7.0.72 \
+ pycocotools==2.0.6 matplotlib==3.5.3 \
+ onnxruntime==1.14.1 onnx==1.13.1 ipykernel==6.16.2 scipy gradio openai
diff --git a/EfficientSAM/EdgeSAM/common.py b/EfficientSAM/EdgeSAM/common.py
new file mode 100644
index 0000000000000000000000000000000000000000..be321e5384b3e65c77cb3acf1a4e4b68d8de823d
--- /dev/null
+++ b/EfficientSAM/EdgeSAM/common.py
@@ -0,0 +1,118 @@
+# Copyright (c) Meta Platforms, Inc. and affiliates.
+# All rights reserved.
+
+# This source code is licensed under the license found in the
+# LICENSE file in the root directory of this source tree.
+
+import torch
+import torch.nn as nn
+import torch.nn.functional as F
+
+from typing import Type
+
+
+class MLPBlock(nn.Module):
+ def __init__(
+ self,
+ embedding_dim: int,
+ mlp_dim: int,
+ act: Type[nn.Module] = nn.GELU,
+ ) -> None:
+ super().__init__()
+ self.lin1 = nn.Linear(embedding_dim, mlp_dim)
+ self.lin2 = nn.Linear(mlp_dim, embedding_dim)
+ self.act = act()
+
+ def forward(self, x: torch.Tensor) -> torch.Tensor:
+ return self.lin2(self.act(self.lin1(x)))
+
+
+# From https://github.com/facebookresearch/detectron2/blob/main/detectron2/layers/batch_norm.py # noqa
+# Itself from https://github.com/facebookresearch/ConvNeXt/blob/d1fa8f6fef0a165b27399986cc2bdacc92777e40/models/convnext.py#L119 # noqa
+class LayerNorm2d(nn.Module):
+ def __init__(self, num_channels: int, eps: float = 1e-6) -> None:
+ super().__init__()
+ self.weight = nn.Parameter(torch.ones(num_channels))
+ self.bias = nn.Parameter(torch.zeros(num_channels))
+ self.eps = eps
+
+ def forward(self, x: torch.Tensor) -> torch.Tensor:
+ u = x.mean(1, keepdim=True)
+ s = (x - u).pow(2).mean(1, keepdim=True)
+ x = (x - u) / torch.sqrt(s + self.eps)
+ x = self.weight[:, None, None] * x + self.bias[:, None, None]
+ return x
+
+
+def val2list(x: list or tuple or any, repeat_time=1) -> list:
+ if isinstance(x, (list, tuple)):
+ return list(x)
+ return [x for _ in range(repeat_time)]
+
+
+def val2tuple(x: list or tuple or any, min_len: int = 1, idx_repeat: int = -1) -> tuple:
+ x = val2list(x)
+
+ # repeat elements if necessary
+ if len(x) > 0:
+ x[idx_repeat:idx_repeat] = [x[idx_repeat] for _ in range(min_len - len(x))]
+
+ return tuple(x)
+
+
+def list_sum(x: list) -> any:
+ return x[0] if len(x) == 1 else x[0] + list_sum(x[1:])
+
+
+def resize(
+ x: torch.Tensor,
+ size: any or None = None,
+ scale_factor=None,
+ mode: str = "bicubic",
+ align_corners: bool or None = False,
+) -> torch.Tensor:
+ if mode in ["bilinear", "bicubic"]:
+ return F.interpolate(
+ x,
+ size=size,
+ scale_factor=scale_factor,
+ mode=mode,
+ align_corners=align_corners,
+ )
+ elif mode in ["nearest", "area"]:
+ return F.interpolate(x, size=size, scale_factor=scale_factor, mode=mode)
+ else:
+ raise NotImplementedError(f"resize(mode={mode}) not implemented.")
+
+
+class UpSampleLayer(nn.Module):
+ def __init__(
+ self,
+ mode="bicubic",
+ size=None,
+ factor=2,
+ align_corners=False,
+ ):
+ super(UpSampleLayer, self).__init__()
+ self.mode = mode
+ self.size = val2list(size, 2) if size is not None else None
+ self.factor = None if self.size is not None else factor
+ self.align_corners = align_corners
+
+ def forward(self, x: torch.Tensor) -> torch.Tensor:
+ return resize(x, self.size, self.factor, self.mode, self.align_corners)
+
+
+class OpSequential(nn.Module):
+ def __init__(self, op_list):
+ super(OpSequential, self).__init__()
+ valid_op_list = []
+ for op in op_list:
+ if op is not None:
+ valid_op_list.append(op)
+ self.op_list = nn.ModuleList(valid_op_list)
+
+ def forward(self, x: torch.Tensor) -> torch.Tensor:
+ for op in self.op_list:
+ x = op(x)
+ return x
\ No newline at end of file
diff --git a/EfficientSAM/EdgeSAM/rep_vit.py b/EfficientSAM/EdgeSAM/rep_vit.py
new file mode 100644
index 0000000000000000000000000000000000000000..b8e9ed2e3efe0df679325cd95d9be8a192b734bf
--- /dev/null
+++ b/EfficientSAM/EdgeSAM/rep_vit.py
@@ -0,0 +1,370 @@
+import torch.nn as nn
+from EdgeSAM.common import LayerNorm2d, UpSampleLayer, OpSequential
+
+__all__ = ['rep_vit_m1', 'rep_vit_m2', 'rep_vit_m3', 'RepViT']
+
+m1_cfgs = [
+ # k, t, c, SE, HS, s
+ [3, 2, 48, 1, 0, 1],
+ [3, 2, 48, 0, 0, 1],
+ [3, 2, 48, 0, 0, 1],
+ [3, 2, 96, 0, 0, 2],
+ [3, 2, 96, 1, 0, 1],
+ [3, 2, 96, 0, 0, 1],
+ [3, 2, 96, 0, 0, 1],
+ [3, 2, 192, 0, 1, 2],
+ [3, 2, 192, 1, 1, 1],
+ [3, 2, 192, 0, 1, 1],
+ [3, 2, 192, 1, 1, 1],
+ [3, 2, 192, 0, 1, 1],
+ [3, 2, 192, 1, 1, 1],
+ [3, 2, 192, 0, 1, 1],
+ [3, 2, 192, 1, 1, 1],
+ [3, 2, 192, 0, 1, 1],
+ [3, 2, 192, 1, 1, 1],
+ [3, 2, 192, 0, 1, 1],
+ [3, 2, 192, 1, 1, 1],
+ [3, 2, 192, 0, 1, 1],
+ [3, 2, 192, 1, 1, 1],
+ [3, 2, 192, 0, 1, 1],
+ [3, 2, 192, 0, 1, 1],
+ [3, 2, 384, 0, 1, 2],
+ [3, 2, 384, 1, 1, 1],
+ [3, 2, 384, 0, 1, 1]
+]
+
+m2_cfgs = [
+ # k, t, c, SE, HS, s
+ [3, 2, 64, 1, 0, 1],
+ [3, 2, 64, 0, 0, 1],
+ [3, 2, 64, 0, 0, 1],
+ [3, 2, 128, 0, 0, 2],
+ [3, 2, 128, 1, 0, 1],
+ [3, 2, 128, 0, 0, 1],
+ [3, 2, 128, 0, 0, 1],
+ [3, 2, 256, 0, 1, 2],
+ [3, 2, 256, 1, 1, 1],
+ [3, 2, 256, 0, 1, 1],
+ [3, 2, 256, 1, 1, 1],
+ [3, 2, 256, 0, 1, 1],
+ [3, 2, 256, 1, 1, 1],
+ [3, 2, 256, 0, 1, 1],
+ [3, 2, 256, 1, 1, 1],
+ [3, 2, 256, 0, 1, 1],
+ [3, 2, 256, 1, 1, 1],
+ [3, 2, 256, 0, 1, 1],
+ [3, 2, 256, 1, 1, 1],
+ [3, 2, 256, 0, 1, 1],
+ [3, 2, 256, 0, 1, 1],
+ [3, 2, 512, 0, 1, 2],
+ [3, 2, 512, 1, 1, 1],
+ [3, 2, 512, 0, 1, 1]
+]
+
+m3_cfgs = [
+ # k, t, c, SE, HS, s
+ [3, 2, 64, 1, 0, 1],
+ [3, 2, 64, 0, 0, 1],
+ [3, 2, 64, 1, 0, 1],
+ [3, 2, 64, 0, 0, 1],
+ [3, 2, 64, 0, 0, 1],
+ [3, 2, 128, 0, 0, 2],
+ [3, 2, 128, 1, 0, 1],
+ [3, 2, 128, 0, 0, 1],
+ [3, 2, 128, 1, 0, 1],
+ [3, 2, 128, 0, 0, 1],
+ [3, 2, 128, 0, 0, 1],
+ [3, 2, 256, 0, 1, 2],
+ [3, 2, 256, 1, 1, 1],
+ [3, 2, 256, 0, 1, 1],
+ [3, 2, 256, 1, 1, 1],
+ [3, 2, 256, 0, 1, 1],
+ [3, 2, 256, 1, 1, 1],
+ [3, 2, 256, 0, 1, 1],
+ [3, 2, 256, 1, 1, 1],
+ [3, 2, 256, 0, 1, 1],
+ [3, 2, 256, 1, 1, 1],
+ [3, 2, 256, 0, 1, 1],
+ [3, 2, 256, 1, 1, 1],
+ [3, 2, 256, 0, 1, 1],
+ [3, 2, 256, 1, 1, 1],
+ [3, 2, 256, 0, 1, 1],
+ [3, 2, 256, 1, 1, 1],
+ [3, 2, 256, 0, 1, 1],
+ [3, 2, 256, 1, 1, 1],
+ [3, 2, 256, 0, 1, 1],
+ [3, 2, 256, 0, 1, 1],
+ [3, 2, 512, 0, 1, 2],
+ [3, 2, 512, 1, 1, 1],
+ [3, 2, 512, 0, 1, 1]
+]
+
+
+def _make_divisible(v, divisor, min_value=None):
+ """
+ This function is taken from the original tf repo.
+ It ensures that all layers have a channel number that is divisible by 8
+ It can be seen here:
+ https://github.com/tensorflow/models/blob/master/research/slim/nets/mobilenet/mobilenet.py
+ :param v:
+ :param divisor:
+ :param min_value:
+ :return:
+ """
+ if min_value is None:
+ min_value = divisor
+ new_v = max(min_value, int(v + divisor / 2) // divisor * divisor)
+ # Make sure that round down does not go down by more than 10%.
+ if new_v < 0.9 * v:
+ new_v += divisor
+ return new_v
+
+
+from timm.models.layers import SqueezeExcite
+
+import torch
+
+
+class Conv2d_BN(torch.nn.Sequential):
+ def __init__(self, a, b, ks=1, stride=1, pad=0, dilation=1,
+ groups=1, bn_weight_init=1, resolution=-10000):
+ super().__init__()
+ self.add_module('c', torch.nn.Conv2d(
+ a, b, ks, stride, pad, dilation, groups, bias=False))
+ self.add_module('bn', torch.nn.BatchNorm2d(b))
+ torch.nn.init.constant_(self.bn.weight, bn_weight_init)
+ torch.nn.init.constant_(self.bn.bias, 0)
+
+ @torch.no_grad()
+ def fuse(self):
+ c, bn = self._modules.values()
+ w = bn.weight / (bn.running_var + bn.eps) ** 0.5
+ w = c.weight * w[:, None, None, None]
+ b = bn.bias - bn.running_mean * bn.weight / \
+ (bn.running_var + bn.eps) ** 0.5
+ m = torch.nn.Conv2d(w.size(1) * self.c.groups, w.size(
+ 0), w.shape[2:], stride=self.c.stride, padding=self.c.padding, dilation=self.c.dilation,
+ groups=self.c.groups,
+ device=c.weight.device)
+ m.weight.data.copy_(w)
+ m.bias.data.copy_(b)
+ return m
+
+
+class Residual(torch.nn.Module):
+ def __init__(self, m, drop=0.):
+ super().__init__()
+ self.m = m
+ self.drop = drop
+
+ def forward(self, x):
+ if self.training and self.drop > 0:
+ return x + self.m(x) * torch.rand(x.size(0), 1, 1, 1,
+ device=x.device).ge_(self.drop).div(1 - self.drop).detach()
+ else:
+ return x + self.m(x)
+
+ @torch.no_grad()
+ def fuse(self):
+ if isinstance(self.m, Conv2d_BN):
+ m = self.m.fuse()
+ assert (m.groups == m.in_channels)
+ identity = torch.ones(m.weight.shape[0], m.weight.shape[1], 1, 1)
+ identity = torch.nn.functional.pad(identity, [1, 1, 1, 1])
+ m.weight += identity.to(m.weight.device)
+ return m
+ elif isinstance(self.m, torch.nn.Conv2d):
+ m = self.m
+ assert (m.groups != m.in_channels)
+ identity = torch.ones(m.weight.shape[0], m.weight.shape[1], 1, 1)
+ identity = torch.nn.functional.pad(identity, [1, 1, 1, 1])
+ m.weight += identity.to(m.weight.device)
+ return m
+ else:
+ return self
+
+
+class RepVGGDW(torch.nn.Module):
+ def __init__(self, ed) -> None:
+ super().__init__()
+ self.conv = Conv2d_BN(ed, ed, 3, 1, 1, groups=ed)
+ self.conv1 = Conv2d_BN(ed, ed, 1, 1, 0, groups=ed)
+ self.dim = ed
+
+ def forward(self, x):
+ return self.conv(x) + self.conv1(x) + x
+
+ @torch.no_grad()
+ def fuse(self):
+ conv = self.conv.fuse()
+ conv1 = self.conv1.fuse()
+
+ conv_w = conv.weight
+ conv_b = conv.bias
+ conv1_w = conv1.weight
+ conv1_b = conv1.bias
+
+ conv1_w = torch.nn.functional.pad(conv1_w, [1, 1, 1, 1])
+
+ identity = torch.nn.functional.pad(torch.ones(conv1_w.shape[0], conv1_w.shape[1], 1, 1, device=conv1_w.device),
+ [1, 1, 1, 1])
+
+ final_conv_w = conv_w + conv1_w + identity
+ final_conv_b = conv_b + conv1_b
+
+ conv.weight.data.copy_(final_conv_w)
+ conv.bias.data.copy_(final_conv_b)
+ return conv
+
+
+class RepViTBlock(nn.Module):
+ def __init__(self, inp, hidden_dim, oup, kernel_size, stride, use_se, use_hs, skip_downsample=False):
+ super(RepViTBlock, self).__init__()
+ assert stride in [1, 2]
+
+ self.identity = stride == 1 and inp == oup
+ assert (hidden_dim == 2 * inp)
+
+ if stride == 2:
+ if skip_downsample:
+ stride = 1
+ self.token_mixer = nn.Sequential(
+ Conv2d_BN(inp, inp, kernel_size, stride, (kernel_size - 1) // 2, groups=inp),
+ SqueezeExcite(inp, 0.25) if use_se else nn.Identity(),
+ Conv2d_BN(inp, oup, ks=1, stride=1, pad=0)
+ )
+ self.channel_mixer = Residual(nn.Sequential(
+ # pw
+ Conv2d_BN(oup, 2 * oup, 1, 1, 0),
+ nn.GELU() if use_hs else nn.GELU(),
+ # pw-linear
+ Conv2d_BN(2 * oup, oup, 1, 1, 0, bn_weight_init=0),
+ ))
+ else:
+ assert (self.identity)
+ self.token_mixer = nn.Sequential(
+ RepVGGDW(inp),
+ SqueezeExcite(inp, 0.25) if use_se else nn.Identity(),
+ )
+ self.channel_mixer = Residual(nn.Sequential(
+ # pw
+ Conv2d_BN(inp, hidden_dim, 1, 1, 0),
+ nn.GELU() if use_hs else nn.GELU(),
+ # pw-linear
+ Conv2d_BN(hidden_dim, oup, 1, 1, 0, bn_weight_init=0),
+ ))
+
+ def forward(self, x):
+ return self.channel_mixer(self.token_mixer(x))
+
+
+from timm.models.vision_transformer import trunc_normal_
+
+
+class BN_Linear(torch.nn.Sequential):
+ def __init__(self, a, b, bias=True, std=0.02):
+ super().__init__()
+ self.add_module('bn', torch.nn.BatchNorm1d(a))
+ self.add_module('l', torch.nn.Linear(a, b, bias=bias))
+ trunc_normal_(self.l.weight, std=std)
+ if bias:
+ torch.nn.init.constant_(self.l.bias, 0)
+
+ @torch.no_grad()
+ def fuse(self):
+ bn, l = self._modules.values()
+ w = bn.weight / (bn.running_var + bn.eps) ** 0.5
+ b = bn.bias - self.bn.running_mean * \
+ self.bn.weight / (bn.running_var + bn.eps) ** 0.5
+ w = l.weight * w[None, :]
+ if l.bias is None:
+ b = b @ self.l.weight.T
+ else:
+ b = (l.weight @ b[:, None]).view(-1) + self.l.bias
+ m = torch.nn.Linear(w.size(1), w.size(0), device=l.weight.device)
+ m.weight.data.copy_(w)
+ m.bias.data.copy_(b)
+ return m
+
+
+class RepViT(nn.Module):
+ arch_settings = {
+ 'm1': m1_cfgs,
+ 'm2': m2_cfgs,
+ 'm3': m3_cfgs
+ }
+
+ def __init__(self, arch, img_size=1024, upsample_mode='bicubic'):
+ super(RepViT, self).__init__()
+ # setting of inverted residual blocks
+ self.cfgs = self.arch_settings[arch]
+ self.img_size = img_size
+
+ # building first layer
+ input_channel = self.cfgs[0][2]
+ patch_embed = torch.nn.Sequential(Conv2d_BN(3, input_channel // 2, 3, 2, 1), torch.nn.GELU(),
+ Conv2d_BN(input_channel // 2, input_channel, 3, 2, 1))
+ layers = [patch_embed]
+ # building inverted residual blocks
+ block = RepViTBlock
+ self.stage_idx = []
+ prev_c = input_channel
+ for idx, (k, t, c, use_se, use_hs, s) in enumerate(self.cfgs):
+ output_channel = _make_divisible(c, 8)
+ exp_size = _make_divisible(input_channel * t, 8)
+ skip_downsample = False
+ if c != prev_c:
+ self.stage_idx.append(idx - 1)
+ prev_c = c
+ layers.append(block(input_channel, exp_size, output_channel, k, s, use_se, use_hs, skip_downsample))
+ input_channel = output_channel
+ self.stage_idx.append(idx)
+ self.features = nn.ModuleList(layers)
+
+ stage2_channels = _make_divisible(self.cfgs[self.stage_idx[2]][2], 8)
+ stage3_channels = _make_divisible(self.cfgs[self.stage_idx[3]][2], 8)
+ self.fuse_stage2 = nn.Conv2d(stage2_channels, 256, kernel_size=1, bias=False)
+ self.fuse_stage3 = OpSequential([
+ nn.Conv2d(stage3_channels, 256, kernel_size=1, bias=False),
+ UpSampleLayer(factor=2, mode=upsample_mode),
+ ])
+
+ self.neck = nn.Sequential(
+ nn.Conv2d(256, 256, kernel_size=1, bias=False),
+ LayerNorm2d(256),
+ nn.Conv2d(256, 256, kernel_size=3, padding=1, bias=False),
+ LayerNorm2d(256),
+ )
+
+ def forward(self, x):
+ counter = 0
+ output_dict = dict()
+ # patch_embed
+ x = self.features[0](x)
+ output_dict['stem'] = x
+ # stages
+ for idx, f in enumerate(self.features[1:]):
+ x = f(x)
+ if idx in self.stage_idx:
+ output_dict[f'stage{counter}'] = x
+ counter += 1
+
+ x = self.fuse_stage2(output_dict['stage2']) + self.fuse_stage3(output_dict['stage3'])
+
+ x = self.neck(x)
+ # hack this place because we modified the predictor of SAM for HQ-SAM in
+ # segment_anything/segment_anything/predictor.py line 91 to return intern features of the backbone
+ # self.features, self.interm_features = self.model.image_encoder(input_image)
+ return x, None
+
+
+def rep_vit_m1(img_size=1024, **kwargs):
+ return RepViT('m1', img_size, **kwargs)
+
+
+def rep_vit_m2(img_size=1024, **kwargs):
+ return RepViT('m2', img_size, **kwargs)
+
+
+def rep_vit_m3(img_size=1024, **kwargs):
+ return RepViT('m3', img_size, **kwargs)
\ No newline at end of file
diff --git a/EfficientSAM/EdgeSAM/setup_edge_sam.py b/EfficientSAM/EdgeSAM/setup_edge_sam.py
new file mode 100644
index 0000000000000000000000000000000000000000..4fa99254fb901f6606e37d8e319efced8ff86223
--- /dev/null
+++ b/EfficientSAM/EdgeSAM/setup_edge_sam.py
@@ -0,0 +1,90 @@
+# Copyright (c) Meta Platforms, Inc. and affiliates.
+# All rights reserved.
+
+# This source code is licensed under the license found in the
+# LICENSE file in the root directory of this source tree.
+
+import torch
+
+from functools import partial
+
+from segment_anything.modeling import ImageEncoderViT, MaskDecoder, PromptEncoder, Sam, TwoWayTransformer
+from EdgeSAM.rep_vit import RepViT
+
+
+prompt_embed_dim = 256
+image_size = 1024
+vit_patch_size = 16
+image_embedding_size = image_size // vit_patch_size
+
+
+def build_edge_sam(checkpoint=None, upsample_mode="bicubic"):
+ image_encoder = RepViT(
+ arch="m1",
+ img_size=image_size,
+ upsample_mode=upsample_mode
+ )
+ return _build_sam(image_encoder, checkpoint)
+
+
+sam_model_registry = {
+ "default": build_edge_sam,
+ "edge_sam": build_edge_sam,
+}
+
+def _build_sam_encoder(
+ encoder_embed_dim,
+ encoder_depth,
+ encoder_num_heads,
+ encoder_global_attn_indexes,
+):
+ image_encoder = ImageEncoderViT(
+ depth=encoder_depth,
+ embed_dim=encoder_embed_dim,
+ img_size=image_size,
+ mlp_ratio=4,
+ norm_layer=partial(torch.nn.LayerNorm, eps=1e-6),
+ num_heads=encoder_num_heads,
+ patch_size=vit_patch_size,
+ qkv_bias=True,
+ use_rel_pos=True,
+ global_attn_indexes=encoder_global_attn_indexes,
+ window_size=14,
+ out_chans=prompt_embed_dim,
+ )
+ return image_encoder
+
+
+def _build_sam(
+ image_encoder,
+ checkpoint=None,
+):
+ sam = Sam(
+ image_encoder=image_encoder,
+ prompt_encoder=PromptEncoder(
+ embed_dim=prompt_embed_dim,
+ image_embedding_size=(image_embedding_size, image_embedding_size),
+ input_image_size=(image_size, image_size),
+ mask_in_chans=16,
+ ),
+ mask_decoder=MaskDecoder(
+ num_multimask_outputs=3,
+ transformer=TwoWayTransformer(
+ depth=2,
+ embedding_dim=prompt_embed_dim,
+ mlp_dim=2048,
+ num_heads=8,
+ ),
+ transformer_dim=prompt_embed_dim,
+ iou_head_depth=3,
+ iou_head_hidden_dim=256,
+ ),
+ pixel_mean=[123.675, 116.28, 103.53],
+ pixel_std=[58.395, 57.12, 57.375],
+ )
+ sam.eval()
+ if checkpoint is not None:
+ with open(checkpoint, "rb") as f:
+ state_dict = torch.load(f, map_location="cpu")
+ sam.load_state_dict(state_dict)
+ return sam
\ No newline at end of file
diff --git a/EfficientSAM/FastSAM/tools.py b/EfficientSAM/FastSAM/tools.py
new file mode 100644
index 0000000000000000000000000000000000000000..d43c4ea51ff16e7a9a595692e05ad78a40c69bd3
--- /dev/null
+++ b/EfficientSAM/FastSAM/tools.py
@@ -0,0 +1,413 @@
+import numpy as np
+from PIL import Image
+import matplotlib.pyplot as plt
+import cv2
+import torch
+import os
+import clip
+
+
+def convert_box_xywh_to_xyxy(box):
+ x1 = box[0]
+ y1 = box[1]
+ x2 = box[0] + box[2]
+ y2 = box[1] + box[3]
+ return [x1, y1, x2, y2]
+
+
+def segment_image(image, bbox):
+ image_array = np.array(image)
+ segmented_image_array = np.zeros_like(image_array)
+ x1, y1, x2, y2 = bbox
+ segmented_image_array[y1:y2, x1:x2] = image_array[y1:y2, x1:x2]
+ segmented_image = Image.fromarray(segmented_image_array)
+ black_image = Image.new("RGB", image.size, (255, 255, 255))
+ # transparency_mask = np.zeros_like((), dtype=np.uint8)
+ transparency_mask = np.zeros(
+ (image_array.shape[0], image_array.shape[1]), dtype=np.uint8
+ )
+ transparency_mask[y1:y2, x1:x2] = 255
+ transparency_mask_image = Image.fromarray(transparency_mask, mode="L")
+ black_image.paste(segmented_image, mask=transparency_mask_image)
+ return black_image
+
+
+def format_results(result, filter=0):
+ annotations = []
+ n = len(result.masks.data)
+ for i in range(n):
+ annotation = {}
+ mask = result.masks.data[i] == 1.0
+
+ if torch.sum(mask) < filter:
+ continue
+ annotation["id"] = i
+ annotation["segmentation"] = mask.cpu().numpy()
+ annotation["bbox"] = result.boxes.data[i]
+ annotation["score"] = result.boxes.conf[i]
+ annotation["area"] = annotation["segmentation"].sum()
+ annotations.append(annotation)
+ return annotations
+
+
+def filter_masks(annotations): # filte the overlap mask
+ annotations.sort(key=lambda x: x["area"], reverse=True)
+ to_remove = set()
+ for i in range(0, len(annotations)):
+ a = annotations[i]
+ for j in range(i + 1, len(annotations)):
+ b = annotations[j]
+ if i != j and j not in to_remove:
+ # check if
+ if b["area"] < a["area"]:
+ if (a["segmentation"] & b["segmentation"]).sum() / b[
+ "segmentation"
+ ].sum() > 0.8:
+ to_remove.add(j)
+
+ return [a for i, a in enumerate(annotations) if i not in to_remove], to_remove
+
+
+def get_bbox_from_mask(mask):
+ mask = mask.astype(np.uint8)
+ contours, hierarchy = cv2.findContours(
+ mask, cv2.RETR_EXTERNAL, cv2.CHAIN_APPROX_SIMPLE
+ )
+ x1, y1, w, h = cv2.boundingRect(contours[0])
+ x2, y2 = x1 + w, y1 + h
+ if len(contours) > 1:
+ for b in contours:
+ x_t, y_t, w_t, h_t = cv2.boundingRect(b)
+ # 将多个bbox合并成一个
+ x1 = min(x1, x_t)
+ y1 = min(y1, y_t)
+ x2 = max(x2, x_t + w_t)
+ y2 = max(y2, y_t + h_t)
+ h = y2 - y1
+ w = x2 - x1
+ return [x1, y1, x2, y2]
+
+
+def fast_process(
+ annotations, args, mask_random_color, bbox=None, points=None, edges=False
+):
+ if isinstance(annotations[0], dict):
+ annotations = [annotation["segmentation"] for annotation in annotations]
+ result_name = os.path.basename(args.img_path)
+ image = cv2.imread(args.img_path)
+ image = cv2.cvtColor(image, cv2.COLOR_BGR2RGB)
+ original_h = image.shape[0]
+ original_w = image.shape[1]
+ plt.figure(figsize=(original_w/100, original_h/100))
+ plt.imshow(image)
+ if args.better_quality == True:
+ if isinstance(annotations[0], torch.Tensor):
+ annotations = np.array(annotations.cpu())
+ for i, mask in enumerate(annotations):
+ mask = cv2.morphologyEx(
+ mask.astype(np.uint8), cv2.MORPH_CLOSE, np.ones((3, 3), np.uint8)
+ )
+ annotations[i] = cv2.morphologyEx(
+ mask.astype(np.uint8), cv2.MORPH_OPEN, np.ones((8, 8), np.uint8)
+ )
+ if args.device == "cpu":
+ annotations = np.array(annotations)
+ fast_show_mask(
+ annotations,
+ plt.gca(),
+ random_color=mask_random_color,
+ bbox=bbox,
+ points=points,
+ pointlabel=args.point_label,
+ retinamask=args.retina,
+ target_height=original_h,
+ target_width=original_w,
+ )
+ else:
+ if isinstance(annotations[0], np.ndarray):
+ annotations = torch.from_numpy(annotations)
+ fast_show_mask_gpu(
+ annotations,
+ plt.gca(),
+ random_color=args.randomcolor,
+ bbox=bbox,
+ points=points,
+ pointlabel=args.point_label,
+ retinamask=args.retina,
+ target_height=original_h,
+ target_width=original_w,
+ )
+ if isinstance(annotations, torch.Tensor):
+ annotations = annotations.cpu().numpy()
+ if args.withContours == True:
+ contour_all = []
+ temp = np.zeros((original_h, original_w, 1))
+ for i, mask in enumerate(annotations):
+ if type(mask) == dict:
+ mask = mask["segmentation"]
+ annotation = mask.astype(np.uint8)
+ if args.retina == False:
+ annotation = cv2.resize(
+ annotation,
+ (original_w, original_h),
+ interpolation=cv2.INTER_NEAREST,
+ )
+ contours, hierarchy = cv2.findContours(
+ annotation, cv2.RETR_TREE, cv2.CHAIN_APPROX_SIMPLE
+ )
+ for contour in contours:
+ contour_all.append(contour)
+ cv2.drawContours(temp, contour_all, -1, (255, 255, 255), 2)
+ color = np.array([0 / 255, 0 / 255, 255 / 255, 0.8])
+ contour_mask = temp / 255 * color.reshape(1, 1, -1)
+ plt.imshow(contour_mask)
+
+ save_path = args.output
+ if not os.path.exists(save_path):
+ os.makedirs(save_path)
+ plt.axis("off")
+ fig = plt.gcf()
+ plt.draw()
+ buf = fig.canvas.tostring_rgb()
+ cols, rows = fig.canvas.get_width_height()
+ img_array = np.fromstring(buf, dtype=np.uint8).reshape(rows, cols, 3)
+ return img_array
+ # cv2.imwrite(os.path.join(save_path, result_name), cv2.cvtColor(img_array, cv2.COLOR_RGB2BGR))
+
+
+
+# CPU post process
+def fast_show_mask(
+ annotation,
+ ax,
+ random_color=False,
+ bbox=None,
+ points=None,
+ pointlabel=None,
+ retinamask=True,
+ target_height=960,
+ target_width=960,
+):
+ msak_sum = annotation.shape[0]
+ height = annotation.shape[1]
+ weight = annotation.shape[2]
+ # 将annotation 按照面积 排序
+ areas = np.sum(annotation, axis=(1, 2))
+ sorted_indices = np.argsort(areas)
+ annotation = annotation[sorted_indices]
+
+ index = (annotation != 0).argmax(axis=0)
+ if random_color == True:
+ color = np.random.random((msak_sum, 1, 1, 3))
+ else:
+ color = np.ones((msak_sum, 1, 1, 3)) * np.array(
+ [30 / 255, 144 / 255, 255 / 255]
+ )
+ transparency = np.ones((msak_sum, 1, 1, 1)) * 0.6
+ visual = np.concatenate([color, transparency], axis=-1)
+ mask_image = np.expand_dims(annotation, -1) * visual
+
+ show = np.zeros((height, weight, 4))
+ h_indices, w_indices = np.meshgrid(
+ np.arange(height), np.arange(weight), indexing="ij"
+ )
+ indices = (index[h_indices, w_indices], h_indices, w_indices, slice(None))
+ # 使用向量化索引更新show的值
+ show[h_indices, w_indices, :] = mask_image[indices]
+ if bbox is not None:
+ x1, y1, x2, y2 = bbox
+ ax.add_patch(
+ plt.Rectangle(
+ (x1, y1), x2 - x1, y2 - y1, fill=False, edgecolor="b", linewidth=1
+ )
+ )
+ # draw point
+ if points is not None:
+ plt.scatter(
+ [point[0] for i, point in enumerate(points) if pointlabel[i] == 1],
+ [point[1] for i, point in enumerate(points) if pointlabel[i] == 1],
+ s=20,
+ c="y",
+ )
+ plt.scatter(
+ [point[0] for i, point in enumerate(points) if pointlabel[i] == 0],
+ [point[1] for i, point in enumerate(points) if pointlabel[i] == 0],
+ s=20,
+ c="m",
+ )
+
+ if retinamask == False:
+ show = cv2.resize(
+ show, (target_width, target_height), interpolation=cv2.INTER_NEAREST
+ )
+ ax.imshow(show)
+
+
+def fast_show_mask_gpu(
+ annotation,
+ ax,
+ random_color=False,
+ bbox=None,
+ points=None,
+ pointlabel=None,
+ retinamask=True,
+ target_height=960,
+ target_width=960,
+):
+ msak_sum = annotation.shape[0]
+ height = annotation.shape[1]
+ weight = annotation.shape[2]
+ areas = torch.sum(annotation, dim=(1, 2))
+ sorted_indices = torch.argsort(areas, descending=False)
+ annotation = annotation[sorted_indices]
+ # 找每个位置第一个非零值下标
+ index = (annotation != 0).to(torch.long).argmax(dim=0)
+ if random_color == True:
+ color = torch.rand((msak_sum, 1, 1, 3)).to(annotation.device)
+ else:
+ color = torch.ones((msak_sum, 1, 1, 3)).to(annotation.device) * torch.tensor(
+ [30 / 255, 144 / 255, 255 / 255]
+ ).to(annotation.device)
+ transparency = torch.ones((msak_sum, 1, 1, 1)).to(annotation.device) * 0.6
+ visual = torch.cat([color, transparency], dim=-1)
+ mask_image = torch.unsqueeze(annotation, -1) * visual
+ # 按index取数,index指每个位置选哪个batch的数,把mask_image转成一个batch的形式
+ show = torch.zeros((height, weight, 4)).to(annotation.device)
+ h_indices, w_indices = torch.meshgrid(
+ torch.arange(height), torch.arange(weight), indexing="ij"
+ )
+ indices = (index[h_indices, w_indices], h_indices, w_indices, slice(None))
+ # 使用向量化索引更新show的值
+ show[h_indices, w_indices, :] = mask_image[indices]
+ show_cpu = show.cpu().numpy()
+ if bbox is not None:
+ x1, y1, x2, y2 = bbox
+ ax.add_patch(
+ plt.Rectangle(
+ (x1, y1), x2 - x1, y2 - y1, fill=False, edgecolor="b", linewidth=1
+ )
+ )
+ # draw point
+ if points is not None:
+ plt.scatter(
+ [point[0] for i, point in enumerate(points) if pointlabel[i] == 1],
+ [point[1] for i, point in enumerate(points) if pointlabel[i] == 1],
+ s=20,
+ c="y",
+ )
+ plt.scatter(
+ [point[0] for i, point in enumerate(points) if pointlabel[i] == 0],
+ [point[1] for i, point in enumerate(points) if pointlabel[i] == 0],
+ s=20,
+ c="m",
+ )
+ if retinamask == False:
+ show_cpu = cv2.resize(
+ show_cpu, (target_width, target_height), interpolation=cv2.INTER_NEAREST
+ )
+ ax.imshow(show_cpu)
+
+
+# clip
+@torch.no_grad()
+def retriev(
+ model, preprocess, elements, search_text: str, device
+) -> int:
+ preprocessed_images = [preprocess(image).to(device) for image in elements]
+ tokenized_text = clip.tokenize([search_text]).to(device)
+ stacked_images = torch.stack(preprocessed_images)
+ image_features = model.encode_image(stacked_images)
+ text_features = model.encode_text(tokenized_text)
+ image_features /= image_features.norm(dim=-1, keepdim=True)
+ text_features /= text_features.norm(dim=-1, keepdim=True)
+ probs = 100.0 * image_features @ text_features.T
+ return probs[:, 0].softmax(dim=0)
+
+
+def crop_image(annotations, image_path):
+ image = Image.open(image_path)
+ ori_w, ori_h = image.size
+ mask_h, mask_w = annotations[0]["segmentation"].shape
+ if ori_w != mask_w or ori_h != mask_h:
+ image = image.resize((mask_w, mask_h))
+ cropped_boxes = []
+ cropped_images = []
+ not_crop = []
+ filter_id = []
+ # annotations, _ = filter_masks(annotations)
+ # filter_id = list(_)
+ for _, mask in enumerate(annotations):
+ if np.sum(mask["segmentation"]) <= 100:
+ filter_id.append(_)
+ continue
+ bbox = get_bbox_from_mask(mask["segmentation"]) # mask 的 bbox
+ cropped_boxes.append(segment_image(image, bbox)) # 保存裁剪的图片
+ # cropped_boxes.append(segment_image(image,mask["segmentation"]))
+ cropped_images.append(bbox) # 保存裁剪的图片的bbox
+
+ return cropped_boxes, cropped_images, not_crop, filter_id, annotations
+
+
+def box_prompt(masks, bbox, target_height, target_width):
+ h = masks.shape[1]
+ w = masks.shape[2]
+ if h != target_height or w != target_width:
+ bbox = [
+ int(bbox[0] * w / target_width),
+ int(bbox[1] * h / target_height),
+ int(bbox[2] * w / target_width),
+ int(bbox[3] * h / target_height),
+ ]
+ bbox[0] = round(bbox[0]) if round(bbox[0]) > 0 else 0
+ bbox[1] = round(bbox[1]) if round(bbox[1]) > 0 else 0
+ bbox[2] = round(bbox[2]) if round(bbox[2]) < w else w
+ bbox[3] = round(bbox[3]) if round(bbox[3]) < h else h
+
+ # IoUs = torch.zeros(len(masks), dtype=torch.float32)
+ bbox_area = (bbox[3] - bbox[1]) * (bbox[2] - bbox[0])
+
+ masks_area = torch.sum(masks[:, bbox[1] : bbox[3], bbox[0] : bbox[2]], dim=(1, 2))
+ orig_masks_area = torch.sum(masks, dim=(1, 2))
+
+ union = bbox_area + orig_masks_area - masks_area
+ IoUs = masks_area / union
+ max_iou_index = torch.argmax(IoUs)
+
+ return masks[max_iou_index].cpu().numpy(), max_iou_index
+
+
+def point_prompt(masks, points, pointlabel, target_height, target_width): # numpy 处理
+ h = masks[0]["segmentation"].shape[0]
+ w = masks[0]["segmentation"].shape[1]
+ if h != target_height or w != target_width:
+ points = [
+ [int(point[0] * w / target_width), int(point[1] * h / target_height)]
+ for point in points
+ ]
+ onemask = np.zeros((h, w))
+ for i, annotation in enumerate(masks):
+ if type(annotation) == dict:
+ mask = annotation["segmentation"]
+ else:
+ mask = annotation
+ for i, point in enumerate(points):
+ if mask[point[1], point[0]] == 1 and pointlabel[i] == 1:
+ onemask += mask
+ if mask[point[1], point[0]] == 1 and pointlabel[i] == 0:
+ onemask -= mask
+ onemask = onemask >= 1
+ return onemask, 0
+
+
+def text_prompt(annotations, args):
+ cropped_boxes, cropped_images, not_crop, filter_id, annotaions = crop_image(
+ annotations, args.img_path
+ )
+ clip_model, preprocess = clip.load("ViT-B/32", device=args.device)
+ scores = retriev(
+ clip_model, preprocess, cropped_boxes, args.text_prompt, device=args.device
+ )
+ max_idx = scores.argsort()
+ max_idx = max_idx[-1]
+ max_idx += sum(np.array(filter_id) <= int(max_idx))
+ return annotaions[max_idx]["segmentation"], max_idx
\ No newline at end of file
diff --git a/EfficientSAM/LightHQSAM/example_light_hqsam.png b/EfficientSAM/LightHQSAM/example_light_hqsam.png
new file mode 100644
index 0000000000000000000000000000000000000000..179b8c8d9961b7bd7cc4441daf8e806c6aceef19
--- /dev/null
+++ b/EfficientSAM/LightHQSAM/example_light_hqsam.png
@@ -0,0 +1,3 @@
+version https://git-lfs.github.com/spec/v1
+oid sha256:866820ace9a150b791c00f955c2b436fc72a2e6a43b36187aba975be196161c4
+size 2324039
diff --git a/EfficientSAM/LightHQSAM/grounded_light_hqsam_annotated_image.jpg b/EfficientSAM/LightHQSAM/grounded_light_hqsam_annotated_image.jpg
new file mode 100644
index 0000000000000000000000000000000000000000..5a0af6b52022de48dcdcf2d34ef15914ee141fe4
Binary files /dev/null and b/EfficientSAM/LightHQSAM/grounded_light_hqsam_annotated_image.jpg differ
diff --git a/EfficientSAM/LightHQSAM/setup_light_hqsam.py b/EfficientSAM/LightHQSAM/setup_light_hqsam.py
new file mode 100644
index 0000000000000000000000000000000000000000..3a34cf7512223c330e8d724104fb9e893058330c
--- /dev/null
+++ b/EfficientSAM/LightHQSAM/setup_light_hqsam.py
@@ -0,0 +1,45 @@
+from LightHQSAM.tiny_vit_sam import TinyViT
+from segment_anything.modeling import MaskDecoderHQ, PromptEncoder, Sam, TwoWayTransformer
+
+def setup_model():
+ prompt_embed_dim = 256
+ image_size = 1024
+ vit_patch_size = 16
+ image_embedding_size = image_size // vit_patch_size
+ mobile_sam = Sam(
+ image_encoder=TinyViT(img_size=1024, in_chans=3, num_classes=1000,
+ embed_dims=[64, 128, 160, 320],
+ depths=[2, 2, 6, 2],
+ num_heads=[2, 4, 5, 10],
+ window_sizes=[7, 7, 14, 7],
+ mlp_ratio=4.,
+ drop_rate=0.,
+ drop_path_rate=0.0,
+ use_checkpoint=False,
+ mbconv_expand_ratio=4.0,
+ local_conv_size=3,
+ layer_lr_decay=0.8
+ ),
+ prompt_encoder=PromptEncoder(
+ embed_dim=prompt_embed_dim,
+ image_embedding_size=(image_embedding_size, image_embedding_size),
+ input_image_size=(image_size, image_size),
+ mask_in_chans=16,
+ ),
+ mask_decoder=MaskDecoderHQ(
+ num_multimask_outputs=3,
+ transformer=TwoWayTransformer(
+ depth=2,
+ embedding_dim=prompt_embed_dim,
+ mlp_dim=2048,
+ num_heads=8,
+ ),
+ transformer_dim=prompt_embed_dim,
+ iou_head_depth=3,
+ iou_head_hidden_dim=256,
+ vit_dim=160,
+ ),
+ pixel_mean=[123.675, 116.28, 103.53],
+ pixel_std=[58.395, 57.12, 57.375],
+ )
+ return mobile_sam
\ No newline at end of file
diff --git a/EfficientSAM/LightHQSAM/tiny_vit_sam.py b/EfficientSAM/LightHQSAM/tiny_vit_sam.py
new file mode 100644
index 0000000000000000000000000000000000000000..65f04aa374599f6bb70fe69c81660df9d4e786e1
--- /dev/null
+++ b/EfficientSAM/LightHQSAM/tiny_vit_sam.py
@@ -0,0 +1,724 @@
+# --------------------------------------------------------
+# TinyViT Model Architecture
+# Copyright (c) 2022 Microsoft
+# Adapted from LeViT and Swin Transformer
+# LeViT: (https://github.com/facebookresearch/levit)
+# Swin: (https://github.com/microsoft/swin-transformer)
+# Build the TinyViT Model
+# --------------------------------------------------------
+
+import itertools
+import torch
+import torch.nn as nn
+import torch.nn.functional as F
+import torch.utils.checkpoint as checkpoint
+from timm.models.layers import DropPath as TimmDropPath,\
+ to_2tuple, trunc_normal_
+from timm.models.registry import register_model
+from typing import Tuple
+
+
+class Conv2d_BN(torch.nn.Sequential):
+ def __init__(self, a, b, ks=1, stride=1, pad=0, dilation=1,
+ groups=1, bn_weight_init=1):
+ super().__init__()
+ self.add_module('c', torch.nn.Conv2d(
+ a, b, ks, stride, pad, dilation, groups, bias=False))
+ bn = torch.nn.BatchNorm2d(b)
+ torch.nn.init.constant_(bn.weight, bn_weight_init)
+ torch.nn.init.constant_(bn.bias, 0)
+ self.add_module('bn', bn)
+
+ @torch.no_grad()
+ def fuse(self):
+ c, bn = self._modules.values()
+ w = bn.weight / (bn.running_var + bn.eps)**0.5
+ w = c.weight * w[:, None, None, None]
+ b = bn.bias - bn.running_mean * bn.weight / \
+ (bn.running_var + bn.eps)**0.5
+ m = torch.nn.Conv2d(w.size(1) * self.c.groups, w.size(
+ 0), w.shape[2:], stride=self.c.stride, padding=self.c.padding, dilation=self.c.dilation, groups=self.c.groups)
+ m.weight.data.copy_(w)
+ m.bias.data.copy_(b)
+ return m
+
+
+class DropPath(TimmDropPath):
+ def __init__(self, drop_prob=None):
+ super().__init__(drop_prob=drop_prob)
+ self.drop_prob = drop_prob
+
+ def __repr__(self):
+ msg = super().__repr__()
+ msg += f'(drop_prob={self.drop_prob})'
+ return msg
+
+
+class PatchEmbed(nn.Module):
+ def __init__(self, in_chans, embed_dim, resolution, activation):
+ super().__init__()
+ img_size: Tuple[int, int] = to_2tuple(resolution)
+ self.patches_resolution = (img_size[0] // 4, img_size[1] // 4)
+ self.num_patches = self.patches_resolution[0] * \
+ self.patches_resolution[1]
+ self.in_chans = in_chans
+ self.embed_dim = embed_dim
+ n = embed_dim
+ self.seq = nn.Sequential(
+ Conv2d_BN(in_chans, n // 2, 3, 2, 1),
+ activation(),
+ Conv2d_BN(n // 2, n, 3, 2, 1),
+ )
+
+ def forward(self, x):
+ return self.seq(x)
+
+
+class MBConv(nn.Module):
+ def __init__(self, in_chans, out_chans, expand_ratio,
+ activation, drop_path):
+ super().__init__()
+ self.in_chans = in_chans
+ self.hidden_chans = int(in_chans * expand_ratio)
+ self.out_chans = out_chans
+
+ self.conv1 = Conv2d_BN(in_chans, self.hidden_chans, ks=1)
+ self.act1 = activation()
+
+ self.conv2 = Conv2d_BN(self.hidden_chans, self.hidden_chans,
+ ks=3, stride=1, pad=1, groups=self.hidden_chans)
+ self.act2 = activation()
+
+ self.conv3 = Conv2d_BN(
+ self.hidden_chans, out_chans, ks=1, bn_weight_init=0.0)
+ self.act3 = activation()
+
+ self.drop_path = DropPath(
+ drop_path) if drop_path > 0. else nn.Identity()
+
+ def forward(self, x):
+ shortcut = x
+
+ x = self.conv1(x)
+ x = self.act1(x)
+
+ x = self.conv2(x)
+ x = self.act2(x)
+
+ x = self.conv3(x)
+
+ x = self.drop_path(x)
+
+ x += shortcut
+ x = self.act3(x)
+
+ return x
+
+
+class PatchMerging(nn.Module):
+ def __init__(self, input_resolution, dim, out_dim, activation):
+ super().__init__()
+
+ self.input_resolution = input_resolution
+ self.dim = dim
+ self.out_dim = out_dim
+ self.act = activation()
+ self.conv1 = Conv2d_BN(dim, out_dim, 1, 1, 0)
+ stride_c=2
+ if(out_dim==320 or out_dim==448 or out_dim==576):
+ stride_c=1
+ self.conv2 = Conv2d_BN(out_dim, out_dim, 3, stride_c, 1, groups=out_dim)
+ self.conv3 = Conv2d_BN(out_dim, out_dim, 1, 1, 0)
+
+ def forward(self, x):
+ if x.ndim == 3:
+ H, W = self.input_resolution
+ B = len(x)
+ # (B, C, H, W)
+ x = x.view(B, H, W, -1).permute(0, 3, 1, 2)
+
+ x = self.conv1(x)
+ x = self.act(x)
+
+ x = self.conv2(x)
+ x = self.act(x)
+ x = self.conv3(x)
+ x = x.flatten(2).transpose(1, 2)
+ return x
+
+
+class ConvLayer(nn.Module):
+ def __init__(self, dim, input_resolution, depth,
+ activation,
+ drop_path=0., downsample=None, use_checkpoint=False,
+ out_dim=None,
+ conv_expand_ratio=4.,
+ ):
+
+ super().__init__()
+ self.dim = dim
+ self.input_resolution = input_resolution
+ self.depth = depth
+ self.use_checkpoint = use_checkpoint
+
+ # build blocks
+ self.blocks = nn.ModuleList([
+ MBConv(dim, dim, conv_expand_ratio, activation,
+ drop_path[i] if isinstance(drop_path, list) else drop_path,
+ )
+ for i in range(depth)])
+
+ # patch merging layer
+ if downsample is not None:
+ self.downsample = downsample(
+ input_resolution, dim=dim, out_dim=out_dim, activation=activation)
+ else:
+ self.downsample = None
+
+ def forward(self, x):
+ for blk in self.blocks:
+ if self.use_checkpoint:
+ x = checkpoint.checkpoint(blk, x)
+ else:
+ x = blk(x)
+ if self.downsample is not None:
+ x = self.downsample(x)
+ return x
+
+
+class Mlp(nn.Module):
+ def __init__(self, in_features, hidden_features=None,
+ out_features=None, act_layer=nn.GELU, drop=0.):
+ super().__init__()
+ out_features = out_features or in_features
+ hidden_features = hidden_features or in_features
+ self.norm = nn.LayerNorm(in_features)
+ self.fc1 = nn.Linear(in_features, hidden_features)
+ self.fc2 = nn.Linear(hidden_features, out_features)
+ self.act = act_layer()
+ self.drop = nn.Dropout(drop)
+
+ def forward(self, x):
+ x = self.norm(x)
+
+ x = self.fc1(x)
+ x = self.act(x)
+ x = self.drop(x)
+ x = self.fc2(x)
+ x = self.drop(x)
+ return x
+
+
+class Attention(torch.nn.Module):
+ def __init__(self, dim, key_dim, num_heads=8,
+ attn_ratio=4,
+ resolution=(14, 14),
+ ):
+ super().__init__()
+ # (h, w)
+ assert isinstance(resolution, tuple) and len(resolution) == 2
+ self.num_heads = num_heads
+ self.scale = key_dim ** -0.5
+ self.key_dim = key_dim
+ self.nh_kd = nh_kd = key_dim * num_heads
+ self.d = int(attn_ratio * key_dim)
+ self.dh = int(attn_ratio * key_dim) * num_heads
+ self.attn_ratio = attn_ratio
+ h = self.dh + nh_kd * 2
+
+ self.norm = nn.LayerNorm(dim)
+ self.qkv = nn.Linear(dim, h)
+ self.proj = nn.Linear(self.dh, dim)
+
+ points = list(itertools.product(
+ range(resolution[0]), range(resolution[1])))
+ N = len(points)
+ attention_offsets = {}
+ idxs = []
+ for p1 in points:
+ for p2 in points:
+ offset = (abs(p1[0] - p2[0]), abs(p1[1] - p2[1]))
+ if offset not in attention_offsets:
+ attention_offsets[offset] = len(attention_offsets)
+ idxs.append(attention_offsets[offset])
+ self.attention_biases = torch.nn.Parameter(
+ torch.zeros(num_heads, len(attention_offsets)))
+ self.register_buffer('attention_bias_idxs',
+ torch.LongTensor(idxs).view(N, N),
+ persistent=False)
+
+ @torch.no_grad()
+ def train(self, mode=True):
+ super().train(mode)
+ if mode and hasattr(self, 'ab'):
+ del self.ab
+ else:
+ self.register_buffer('ab',
+ self.attention_biases[:, self.attention_bias_idxs],
+ persistent=False)
+
+ def forward(self, x): # x (B,N,C)
+ B, N, _ = x.shape
+
+ # Normalization
+ x = self.norm(x)
+
+ qkv = self.qkv(x)
+ # (B, N, num_heads, d)
+ q, k, v = qkv.view(B, N, self.num_heads, -
+ 1).split([self.key_dim, self.key_dim, self.d], dim=3)
+ # (B, num_heads, N, d)
+ q = q.permute(0, 2, 1, 3)
+ k = k.permute(0, 2, 1, 3)
+ v = v.permute(0, 2, 1, 3)
+
+ attn = (
+ (q @ k.transpose(-2, -1)) * self.scale
+ +
+ (self.attention_biases[:, self.attention_bias_idxs]
+ if self.training else self.ab)
+ )
+ attn = attn.softmax(dim=-1)
+ x = (attn @ v).transpose(1, 2).reshape(B, N, self.dh)
+ x = self.proj(x)
+ return x
+
+
+class TinyViTBlock(nn.Module):
+ r""" TinyViT Block.
+
+ Args:
+ dim (int): Number of input channels.
+ input_resolution (tuple[int, int]): Input resolution.
+ num_heads (int): Number of attention heads.
+ window_size (int): Window size.
+ mlp_ratio (float): Ratio of mlp hidden dim to embedding dim.
+ drop (float, optional): Dropout rate. Default: 0.0
+ drop_path (float, optional): Stochastic depth rate. Default: 0.0
+ local_conv_size (int): the kernel size of the convolution between
+ Attention and MLP. Default: 3
+ activation: the activation function. Default: nn.GELU
+ """
+
+ def __init__(self, dim, input_resolution, num_heads, window_size=7,
+ mlp_ratio=4., drop=0., drop_path=0.,
+ local_conv_size=3,
+ activation=nn.GELU,
+ ):
+ super().__init__()
+ self.dim = dim
+ self.input_resolution = input_resolution
+ self.num_heads = num_heads
+ assert window_size > 0, 'window_size must be greater than 0'
+ self.window_size = window_size
+ self.mlp_ratio = mlp_ratio
+
+ self.drop_path = DropPath(
+ drop_path) if drop_path > 0. else nn.Identity()
+
+ assert dim % num_heads == 0, 'dim must be divisible by num_heads'
+ head_dim = dim // num_heads
+
+ window_resolution = (window_size, window_size)
+ self.attn = Attention(dim, head_dim, num_heads,
+ attn_ratio=1, resolution=window_resolution)
+
+ mlp_hidden_dim = int(dim * mlp_ratio)
+ mlp_activation = activation
+ self.mlp = Mlp(in_features=dim, hidden_features=mlp_hidden_dim,
+ act_layer=mlp_activation, drop=drop)
+
+ pad = local_conv_size // 2
+ self.local_conv = Conv2d_BN(
+ dim, dim, ks=local_conv_size, stride=1, pad=pad, groups=dim)
+
+ def forward(self, x):
+ H, W = self.input_resolution
+ B, L, C = x.shape
+ assert L == H * W, "input feature has wrong size"
+ res_x = x
+ if H == self.window_size and W == self.window_size:
+ x = self.attn(x)
+ else:
+ x = x.view(B, H, W, C)
+ pad_b = (self.window_size - H %
+ self.window_size) % self.window_size
+ pad_r = (self.window_size - W %
+ self.window_size) % self.window_size
+ padding = pad_b > 0 or pad_r > 0
+
+ if padding:
+ x = F.pad(x, (0, 0, 0, pad_r, 0, pad_b))
+
+ pH, pW = H + pad_b, W + pad_r
+ nH = pH // self.window_size
+ nW = pW // self.window_size
+ # window partition
+ x = x.view(B, nH, self.window_size, nW, self.window_size, C).transpose(2, 3).reshape(
+ B * nH * nW, self.window_size * self.window_size, C)
+ x = self.attn(x)
+ # window reverse
+ x = x.view(B, nH, nW, self.window_size, self.window_size,
+ C).transpose(2, 3).reshape(B, pH, pW, C)
+
+ if padding:
+ x = x[:, :H, :W].contiguous()
+
+ x = x.view(B, L, C)
+
+ x = res_x + self.drop_path(x)
+
+ x = x.transpose(1, 2).reshape(B, C, H, W)
+ x = self.local_conv(x)
+ x = x.view(B, C, L).transpose(1, 2)
+
+ x = x + self.drop_path(self.mlp(x))
+ return x
+
+ def extra_repr(self) -> str:
+ return f"dim={self.dim}, input_resolution={self.input_resolution}, num_heads={self.num_heads}, " \
+ f"window_size={self.window_size}, mlp_ratio={self.mlp_ratio}"
+
+
+class BasicLayer(nn.Module):
+ """ A basic TinyViT layer for one stage.
+
+ Args:
+ dim (int): Number of input channels.
+ input_resolution (tuple[int]): Input resolution.
+ depth (int): Number of blocks.
+ num_heads (int): Number of attention heads.
+ window_size (int): Local window size.
+ mlp_ratio (float): Ratio of mlp hidden dim to embedding dim.
+ drop (float, optional): Dropout rate. Default: 0.0
+ drop_path (float | tuple[float], optional): Stochastic depth rate. Default: 0.0
+ downsample (nn.Module | None, optional): Downsample layer at the end of the layer. Default: None
+ use_checkpoint (bool): Whether to use checkpointing to save memory. Default: False.
+ local_conv_size: the kernel size of the depthwise convolution between attention and MLP. Default: 3
+ activation: the activation function. Default: nn.GELU
+ out_dim: the output dimension of the layer. Default: dim
+ """
+
+ def __init__(self, dim, input_resolution, depth, num_heads, window_size,
+ mlp_ratio=4., drop=0.,
+ drop_path=0., downsample=None, use_checkpoint=False,
+ local_conv_size=3,
+ activation=nn.GELU,
+ out_dim=None,
+ ):
+
+ super().__init__()
+ self.dim = dim
+ self.input_resolution = input_resolution
+ self.depth = depth
+ self.use_checkpoint = use_checkpoint
+
+ # build blocks
+ self.blocks = nn.ModuleList([
+ TinyViTBlock(dim=dim, input_resolution=input_resolution,
+ num_heads=num_heads, window_size=window_size,
+ mlp_ratio=mlp_ratio,
+ drop=drop,
+ drop_path=drop_path[i] if isinstance(
+ drop_path, list) else drop_path,
+ local_conv_size=local_conv_size,
+ activation=activation,
+ )
+ for i in range(depth)])
+
+ # patch merging layer
+ if downsample is not None:
+ self.downsample = downsample(
+ input_resolution, dim=dim, out_dim=out_dim, activation=activation)
+ else:
+ self.downsample = None
+
+ def forward(self, x):
+ for blk in self.blocks:
+ if self.use_checkpoint:
+ x = checkpoint.checkpoint(blk, x)
+ else:
+ x = blk(x)
+ if self.downsample is not None:
+ x = self.downsample(x)
+ return x
+
+ def extra_repr(self) -> str:
+ return f"dim={self.dim}, input_resolution={self.input_resolution}, depth={self.depth}"
+
+class LayerNorm2d(nn.Module):
+ def __init__(self, num_channels: int, eps: float = 1e-6) -> None:
+ super().__init__()
+ self.weight = nn.Parameter(torch.ones(num_channels))
+ self.bias = nn.Parameter(torch.zeros(num_channels))
+ self.eps = eps
+
+ def forward(self, x: torch.Tensor) -> torch.Tensor:
+ u = x.mean(1, keepdim=True)
+ s = (x - u).pow(2).mean(1, keepdim=True)
+ x = (x - u) / torch.sqrt(s + self.eps)
+ x = self.weight[:, None, None] * x + self.bias[:, None, None]
+ return x
+class TinyViT(nn.Module):
+ def __init__(self, img_size=224, in_chans=3, num_classes=1000,
+ embed_dims=[96, 192, 384, 768], depths=[2, 2, 6, 2],
+ num_heads=[3, 6, 12, 24],
+ window_sizes=[7, 7, 14, 7],
+ mlp_ratio=4.,
+ drop_rate=0.,
+ drop_path_rate=0.1,
+ use_checkpoint=False,
+ mbconv_expand_ratio=4.0,
+ local_conv_size=3,
+ layer_lr_decay=1.0,
+ ):
+ super().__init__()
+ self.img_size=img_size
+ self.num_classes = num_classes
+ self.depths = depths
+ self.num_layers = len(depths)
+ self.mlp_ratio = mlp_ratio
+
+ activation = nn.GELU
+
+ self.patch_embed = PatchEmbed(in_chans=in_chans,
+ embed_dim=embed_dims[0],
+ resolution=img_size,
+ activation=activation)
+
+ patches_resolution = self.patch_embed.patches_resolution
+ self.patches_resolution = patches_resolution
+
+ # stochastic depth
+ dpr = [x.item() for x in torch.linspace(0, drop_path_rate,
+ sum(depths))] # stochastic depth decay rule
+
+ # build layers
+ self.layers = nn.ModuleList()
+ for i_layer in range(self.num_layers):
+ kwargs = dict(dim=embed_dims[i_layer],
+ input_resolution=(patches_resolution[0] // (2 ** (i_layer-1 if i_layer == 3 else i_layer)),
+ patches_resolution[1] // (2 ** (i_layer-1 if i_layer == 3 else i_layer))),
+ # input_resolution=(patches_resolution[0] // (2 ** i_layer),
+ # patches_resolution[1] // (2 ** i_layer)),
+ depth=depths[i_layer],
+ drop_path=dpr[sum(depths[:i_layer]):sum(depths[:i_layer + 1])],
+ downsample=PatchMerging if (
+ i_layer < self.num_layers - 1) else None,
+ use_checkpoint=use_checkpoint,
+ out_dim=embed_dims[min(
+ i_layer + 1, len(embed_dims) - 1)],
+ activation=activation,
+ )
+ if i_layer == 0:
+ layer = ConvLayer(
+ conv_expand_ratio=mbconv_expand_ratio,
+ **kwargs,
+ )
+ else:
+ layer = BasicLayer(
+ num_heads=num_heads[i_layer],
+ window_size=window_sizes[i_layer],
+ mlp_ratio=self.mlp_ratio,
+ drop=drop_rate,
+ local_conv_size=local_conv_size,
+ **kwargs)
+ self.layers.append(layer)
+
+ # Classifier head
+ self.norm_head = nn.LayerNorm(embed_dims[-1])
+ self.head = nn.Linear(
+ embed_dims[-1], num_classes) if num_classes > 0 else torch.nn.Identity()
+
+ # init weights
+ self.apply(self._init_weights)
+ self.set_layer_lr_decay(layer_lr_decay)
+ self.neck = nn.Sequential(
+ nn.Conv2d(
+ embed_dims[-1],
+ 256,
+ kernel_size=1,
+ bias=False,
+ ),
+ LayerNorm2d(256),
+ nn.Conv2d(
+ 256,
+ 256,
+ kernel_size=3,
+ padding=1,
+ bias=False,
+ ),
+ LayerNorm2d(256),
+ )
+ def set_layer_lr_decay(self, layer_lr_decay):
+ decay_rate = layer_lr_decay
+
+ # layers -> blocks (depth)
+ depth = sum(self.depths)
+ lr_scales = [decay_rate ** (depth - i - 1) for i in range(depth)]
+ #print("LR SCALES:", lr_scales)
+
+ def _set_lr_scale(m, scale):
+ for p in m.parameters():
+ p.lr_scale = scale
+
+ self.patch_embed.apply(lambda x: _set_lr_scale(x, lr_scales[0]))
+ i = 0
+ for layer in self.layers:
+ for block in layer.blocks:
+ block.apply(lambda x: _set_lr_scale(x, lr_scales[i]))
+ i += 1
+ if layer.downsample is not None:
+ layer.downsample.apply(
+ lambda x: _set_lr_scale(x, lr_scales[i - 1]))
+ assert i == depth
+ for m in [self.norm_head, self.head]:
+ m.apply(lambda x: _set_lr_scale(x, lr_scales[-1]))
+
+ for k, p in self.named_parameters():
+ p.param_name = k
+
+ def _check_lr_scale(m):
+ for p in m.parameters():
+ assert hasattr(p, 'lr_scale'), p.param_name
+
+ self.apply(_check_lr_scale)
+
+ def _init_weights(self, m):
+ if isinstance(m, nn.Linear):
+ trunc_normal_(m.weight, std=.02)
+ if isinstance(m, nn.Linear) and m.bias is not None:
+ nn.init.constant_(m.bias, 0)
+ elif isinstance(m, nn.LayerNorm):
+ nn.init.constant_(m.bias, 0)
+ nn.init.constant_(m.weight, 1.0)
+
+ @torch.jit.ignore
+ def no_weight_decay_keywords(self):
+ return {'attention_biases'}
+
+ def forward_features(self, x):
+ # x: (N, C, H, W)
+ x = self.patch_embed(x)
+
+ x = self.layers[0](x)
+ start_i = 1
+
+ interm_embeddings=[]
+ for i in range(start_i, len(self.layers)):
+ layer = self.layers[i]
+ x = layer(x)
+ # print('x shape:', x.shape, '---i:', i)
+ if i == 1:
+ interm_embeddings.append(x.view(x.shape[0], 64, 64, -1))
+
+ B,_,C=x.size()
+ x = x.view(B, 64, 64, C)
+ x=x.permute(0, 3, 1, 2)
+ x=self.neck(x)
+ return x, interm_embeddings
+
+ def forward(self, x):
+ x, interm_embeddings = self.forward_features(x)
+ #x = self.norm_head(x)
+ #x = self.head(x)
+ # print('come to here is correct'* 3)
+ return x, interm_embeddings
+
+
+_checkpoint_url_format = \
+ 'https://github.com/wkcn/TinyViT-model-zoo/releases/download/checkpoints/{}.pth'
+_provided_checkpoints = {
+ 'tiny_vit_5m_224': 'tiny_vit_5m_22kto1k_distill',
+ 'tiny_vit_11m_224': 'tiny_vit_11m_22kto1k_distill',
+ 'tiny_vit_21m_224': 'tiny_vit_21m_22kto1k_distill',
+ 'tiny_vit_21m_384': 'tiny_vit_21m_22kto1k_384_distill',
+ 'tiny_vit_21m_512': 'tiny_vit_21m_22kto1k_512_distill',
+}
+
+
+def register_tiny_vit_model(fn):
+ '''Register a TinyViT model
+ It is a wrapper of `register_model` with loading the pretrained checkpoint.
+ '''
+ def fn_wrapper(pretrained=False, **kwargs):
+ model = fn()
+ if pretrained:
+ model_name = fn.__name__
+ assert model_name in _provided_checkpoints, \
+ f'Sorry that the checkpoint `{model_name}` is not provided yet.'
+ url = _checkpoint_url_format.format(
+ _provided_checkpoints[model_name])
+ checkpoint = torch.hub.load_state_dict_from_url(
+ url=url,
+ map_location='cpu', check_hash=False,
+ )
+ model.load_state_dict(checkpoint['model'])
+
+ return model
+
+ # rename the name of fn_wrapper
+ fn_wrapper.__name__ = fn.__name__
+ return register_model(fn_wrapper)
+
+
+@register_tiny_vit_model
+def tiny_vit_5m_224(pretrained=False, num_classes=1000, drop_path_rate=0.0):
+ return TinyViT(
+ num_classes=num_classes,
+ embed_dims=[64, 128, 160, 320],
+ depths=[2, 2, 6, 2],
+ num_heads=[2, 4, 5, 10],
+ window_sizes=[7, 7, 14, 7],
+ drop_path_rate=drop_path_rate,
+ )
+
+
+@register_tiny_vit_model
+def tiny_vit_11m_224(pretrained=False, num_classes=1000, drop_path_rate=0.1):
+ return TinyViT(
+ num_classes=num_classes,
+ embed_dims=[64, 128, 256, 448],
+ depths=[2, 2, 6, 2],
+ num_heads=[2, 4, 8, 14],
+ window_sizes=[7, 7, 14, 7],
+ drop_path_rate=drop_path_rate,
+ )
+
+
+@register_tiny_vit_model
+def tiny_vit_21m_224(pretrained=False, num_classes=1000, drop_path_rate=0.2):
+ return TinyViT(
+ num_classes=num_classes,
+ embed_dims=[96, 192, 384, 576],
+ depths=[2, 2, 6, 2],
+ num_heads=[3, 6, 12, 18],
+ window_sizes=[7, 7, 14, 7],
+ drop_path_rate=drop_path_rate,
+ )
+
+
+@register_tiny_vit_model
+def tiny_vit_21m_384(pretrained=False, num_classes=1000, drop_path_rate=0.1):
+ return TinyViT(
+ img_size=384,
+ num_classes=num_classes,
+ embed_dims=[96, 192, 384, 576],
+ depths=[2, 2, 6, 2],
+ num_heads=[3, 6, 12, 18],
+ window_sizes=[12, 12, 24, 12],
+ drop_path_rate=drop_path_rate,
+ )
+
+
+@register_tiny_vit_model
+def tiny_vit_21m_512(pretrained=False, num_classes=1000, drop_path_rate=0.1):
+ return TinyViT(
+ img_size=512,
+ num_classes=num_classes,
+ embed_dims=[96, 192, 384, 576],
+ depths=[2, 2, 6, 2],
+ num_heads=[3, 6, 12, 18],
+ window_sizes=[16, 16, 32, 16],
+ drop_path_rate=drop_path_rate,
+ )
diff --git a/EfficientSAM/MobileSAM/setup_mobile_sam.py b/EfficientSAM/MobileSAM/setup_mobile_sam.py
new file mode 100644
index 0000000000000000000000000000000000000000..49d8c17cb207dd5c0022bfa8e4f60b53d48cd6e9
--- /dev/null
+++ b/EfficientSAM/MobileSAM/setup_mobile_sam.py
@@ -0,0 +1,44 @@
+from MobileSAM.tiny_vit_sam import TinyViT
+from segment_anything.modeling import MaskDecoder, PromptEncoder, Sam, TwoWayTransformer
+
+def setup_model():
+ prompt_embed_dim = 256
+ image_size = 1024
+ vit_patch_size = 16
+ image_embedding_size = image_size // vit_patch_size
+ mobile_sam = Sam(
+ image_encoder=TinyViT(img_size=1024, in_chans=3, num_classes=1000,
+ embed_dims=[64, 128, 160, 320],
+ depths=[2, 2, 6, 2],
+ num_heads=[2, 4, 5, 10],
+ window_sizes=[7, 7, 14, 7],
+ mlp_ratio=4.,
+ drop_rate=0.,
+ drop_path_rate=0.0,
+ use_checkpoint=False,
+ mbconv_expand_ratio=4.0,
+ local_conv_size=3,
+ layer_lr_decay=0.8
+ ),
+ prompt_encoder=PromptEncoder(
+ embed_dim=prompt_embed_dim,
+ image_embedding_size=(image_embedding_size, image_embedding_size),
+ input_image_size=(image_size, image_size),
+ mask_in_chans=16,
+ ),
+ mask_decoder=MaskDecoder(
+ num_multimask_outputs=3,
+ transformer=TwoWayTransformer(
+ depth=2,
+ embedding_dim=prompt_embed_dim,
+ mlp_dim=2048,
+ num_heads=8,
+ ),
+ transformer_dim=prompt_embed_dim,
+ iou_head_depth=3,
+ iou_head_hidden_dim=256,
+ ),
+ pixel_mean=[123.675, 116.28, 103.53],
+ pixel_std=[58.395, 57.12, 57.375],
+ )
+ return mobile_sam
\ No newline at end of file
diff --git a/EfficientSAM/MobileSAM/tiny_vit_sam.py b/EfficientSAM/MobileSAM/tiny_vit_sam.py
new file mode 100644
index 0000000000000000000000000000000000000000..fb0062b0e1b982a3004c92c8573c4c3754d4aeaa
--- /dev/null
+++ b/EfficientSAM/MobileSAM/tiny_vit_sam.py
@@ -0,0 +1,716 @@
+# --------------------------------------------------------
+# TinyViT Model Architecture
+# Copyright (c) 2022 Microsoft
+# Adapted from LeViT and Swin Transformer
+# LeViT: (https://github.com/facebookresearch/levit)
+# Swin: (https://github.com/microsoft/swin-transformer)
+# Build the TinyViT Model
+# --------------------------------------------------------
+
+import itertools
+import torch
+import torch.nn as nn
+import torch.nn.functional as F
+import torch.utils.checkpoint as checkpoint
+from timm.models.layers import DropPath as TimmDropPath,\
+ to_2tuple, trunc_normal_
+from timm.models.registry import register_model
+from typing import Tuple
+
+
+class Conv2d_BN(torch.nn.Sequential):
+ def __init__(self, a, b, ks=1, stride=1, pad=0, dilation=1,
+ groups=1, bn_weight_init=1):
+ super().__init__()
+ self.add_module('c', torch.nn.Conv2d(
+ a, b, ks, stride, pad, dilation, groups, bias=False))
+ bn = torch.nn.BatchNorm2d(b)
+ torch.nn.init.constant_(bn.weight, bn_weight_init)
+ torch.nn.init.constant_(bn.bias, 0)
+ self.add_module('bn', bn)
+
+ @torch.no_grad()
+ def fuse(self):
+ c, bn = self._modules.values()
+ w = bn.weight / (bn.running_var + bn.eps)**0.5
+ w = c.weight * w[:, None, None, None]
+ b = bn.bias - bn.running_mean * bn.weight / \
+ (bn.running_var + bn.eps)**0.5
+ m = torch.nn.Conv2d(w.size(1) * self.c.groups, w.size(
+ 0), w.shape[2:], stride=self.c.stride, padding=self.c.padding, dilation=self.c.dilation, groups=self.c.groups)
+ m.weight.data.copy_(w)
+ m.bias.data.copy_(b)
+ return m
+
+
+class DropPath(TimmDropPath):
+ def __init__(self, drop_prob=None):
+ super().__init__(drop_prob=drop_prob)
+ self.drop_prob = drop_prob
+
+ def __repr__(self):
+ msg = super().__repr__()
+ msg += f'(drop_prob={self.drop_prob})'
+ return msg
+
+
+class PatchEmbed(nn.Module):
+ def __init__(self, in_chans, embed_dim, resolution, activation):
+ super().__init__()
+ img_size: Tuple[int, int] = to_2tuple(resolution)
+ self.patches_resolution = (img_size[0] // 4, img_size[1] // 4)
+ self.num_patches = self.patches_resolution[0] * \
+ self.patches_resolution[1]
+ self.in_chans = in_chans
+ self.embed_dim = embed_dim
+ n = embed_dim
+ self.seq = nn.Sequential(
+ Conv2d_BN(in_chans, n // 2, 3, 2, 1),
+ activation(),
+ Conv2d_BN(n // 2, n, 3, 2, 1),
+ )
+
+ def forward(self, x):
+ return self.seq(x)
+
+
+class MBConv(nn.Module):
+ def __init__(self, in_chans, out_chans, expand_ratio,
+ activation, drop_path):
+ super().__init__()
+ self.in_chans = in_chans
+ self.hidden_chans = int(in_chans * expand_ratio)
+ self.out_chans = out_chans
+
+ self.conv1 = Conv2d_BN(in_chans, self.hidden_chans, ks=1)
+ self.act1 = activation()
+
+ self.conv2 = Conv2d_BN(self.hidden_chans, self.hidden_chans,
+ ks=3, stride=1, pad=1, groups=self.hidden_chans)
+ self.act2 = activation()
+
+ self.conv3 = Conv2d_BN(
+ self.hidden_chans, out_chans, ks=1, bn_weight_init=0.0)
+ self.act3 = activation()
+
+ self.drop_path = DropPath(
+ drop_path) if drop_path > 0. else nn.Identity()
+
+ def forward(self, x):
+ shortcut = x
+
+ x = self.conv1(x)
+ x = self.act1(x)
+
+ x = self.conv2(x)
+ x = self.act2(x)
+
+ x = self.conv3(x)
+
+ x = self.drop_path(x)
+
+ x += shortcut
+ x = self.act3(x)
+
+ return x
+
+
+class PatchMerging(nn.Module):
+ def __init__(self, input_resolution, dim, out_dim, activation):
+ super().__init__()
+
+ self.input_resolution = input_resolution
+ self.dim = dim
+ self.out_dim = out_dim
+ self.act = activation()
+ self.conv1 = Conv2d_BN(dim, out_dim, 1, 1, 0)
+ stride_c=2
+ if(out_dim==320 or out_dim==448 or out_dim==576):#handongshen 576
+ stride_c=1
+ self.conv2 = Conv2d_BN(out_dim, out_dim, 3, stride_c, 1, groups=out_dim)
+ self.conv3 = Conv2d_BN(out_dim, out_dim, 1, 1, 0)
+
+ def forward(self, x):
+ if x.ndim == 3:
+ H, W = self.input_resolution
+ B = len(x)
+ # (B, C, H, W)
+ x = x.view(B, H, W, -1).permute(0, 3, 1, 2)
+
+ x = self.conv1(x)
+ x = self.act(x)
+
+ x = self.conv2(x)
+ x = self.act(x)
+ x = self.conv3(x)
+ x = x.flatten(2).transpose(1, 2)
+ return x
+
+
+class ConvLayer(nn.Module):
+ def __init__(self, dim, input_resolution, depth,
+ activation,
+ drop_path=0., downsample=None, use_checkpoint=False,
+ out_dim=None,
+ conv_expand_ratio=4.,
+ ):
+
+ super().__init__()
+ self.dim = dim
+ self.input_resolution = input_resolution
+ self.depth = depth
+ self.use_checkpoint = use_checkpoint
+
+ # build blocks
+ self.blocks = nn.ModuleList([
+ MBConv(dim, dim, conv_expand_ratio, activation,
+ drop_path[i] if isinstance(drop_path, list) else drop_path,
+ )
+ for i in range(depth)])
+
+ # patch merging layer
+ if downsample is not None:
+ self.downsample = downsample(
+ input_resolution, dim=dim, out_dim=out_dim, activation=activation)
+ else:
+ self.downsample = None
+
+ def forward(self, x):
+ for blk in self.blocks:
+ if self.use_checkpoint:
+ x = checkpoint.checkpoint(blk, x)
+ else:
+ x = blk(x)
+ if self.downsample is not None:
+ x = self.downsample(x)
+ return x
+
+
+class Mlp(nn.Module):
+ def __init__(self, in_features, hidden_features=None,
+ out_features=None, act_layer=nn.GELU, drop=0.):
+ super().__init__()
+ out_features = out_features or in_features
+ hidden_features = hidden_features or in_features
+ self.norm = nn.LayerNorm(in_features)
+ self.fc1 = nn.Linear(in_features, hidden_features)
+ self.fc2 = nn.Linear(hidden_features, out_features)
+ self.act = act_layer()
+ self.drop = nn.Dropout(drop)
+
+ def forward(self, x):
+ x = self.norm(x)
+
+ x = self.fc1(x)
+ x = self.act(x)
+ x = self.drop(x)
+ x = self.fc2(x)
+ x = self.drop(x)
+ return x
+
+
+class Attention(torch.nn.Module):
+ def __init__(self, dim, key_dim, num_heads=8,
+ attn_ratio=4,
+ resolution=(14, 14),
+ ):
+ super().__init__()
+ # (h, w)
+ assert isinstance(resolution, tuple) and len(resolution) == 2
+ self.num_heads = num_heads
+ self.scale = key_dim ** -0.5
+ self.key_dim = key_dim
+ self.nh_kd = nh_kd = key_dim * num_heads
+ self.d = int(attn_ratio * key_dim)
+ self.dh = int(attn_ratio * key_dim) * num_heads
+ self.attn_ratio = attn_ratio
+ h = self.dh + nh_kd * 2
+
+ self.norm = nn.LayerNorm(dim)
+ self.qkv = nn.Linear(dim, h)
+ self.proj = nn.Linear(self.dh, dim)
+
+ points = list(itertools.product(
+ range(resolution[0]), range(resolution[1])))
+ N = len(points)
+ attention_offsets = {}
+ idxs = []
+ for p1 in points:
+ for p2 in points:
+ offset = (abs(p1[0] - p2[0]), abs(p1[1] - p2[1]))
+ if offset not in attention_offsets:
+ attention_offsets[offset] = len(attention_offsets)
+ idxs.append(attention_offsets[offset])
+ self.attention_biases = torch.nn.Parameter(
+ torch.zeros(num_heads, len(attention_offsets)))
+ self.register_buffer('attention_bias_idxs',
+ torch.LongTensor(idxs).view(N, N),
+ persistent=False)
+
+ @torch.no_grad()
+ def train(self, mode=True):
+ super().train(mode)
+ if mode and hasattr(self, 'ab'):
+ del self.ab
+ else:
+ self.ab = self.attention_biases[:, self.attention_bias_idxs]
+
+ def forward(self, x): # x (B,N,C)
+ B, N, _ = x.shape
+
+ # Normalization
+ x = self.norm(x)
+
+ qkv = self.qkv(x)
+ # (B, N, num_heads, d)
+ q, k, v = qkv.view(B, N, self.num_heads, -
+ 1).split([self.key_dim, self.key_dim, self.d], dim=3)
+ # (B, num_heads, N, d)
+ q = q.permute(0, 2, 1, 3)
+ k = k.permute(0, 2, 1, 3)
+ v = v.permute(0, 2, 1, 3)
+
+ attn = (
+ (q @ k.transpose(-2, -1)) * self.scale
+ +
+ (self.attention_biases[:, self.attention_bias_idxs]
+ if self.training else self.ab)
+ )
+ attn = attn.softmax(dim=-1)
+ x = (attn @ v).transpose(1, 2).reshape(B, N, self.dh)
+ x = self.proj(x)
+ return x
+
+
+class TinyViTBlock(nn.Module):
+ r""" TinyViT Block.
+
+ Args:
+ dim (int): Number of input channels.
+ input_resolution (tuple[int, int]): Input resulotion.
+ num_heads (int): Number of attention heads.
+ window_size (int): Window size.
+ mlp_ratio (float): Ratio of mlp hidden dim to embedding dim.
+ drop (float, optional): Dropout rate. Default: 0.0
+ drop_path (float, optional): Stochastic depth rate. Default: 0.0
+ local_conv_size (int): the kernel size of the convolution between
+ Attention and MLP. Default: 3
+ activation: the activation function. Default: nn.GELU
+ """
+
+ def __init__(self, dim, input_resolution, num_heads, window_size=7,
+ mlp_ratio=4., drop=0., drop_path=0.,
+ local_conv_size=3,
+ activation=nn.GELU,
+ ):
+ super().__init__()
+ self.dim = dim
+ self.input_resolution = input_resolution
+ self.num_heads = num_heads
+ assert window_size > 0, 'window_size must be greater than 0'
+ self.window_size = window_size
+ self.mlp_ratio = mlp_ratio
+
+ self.drop_path = DropPath(
+ drop_path) if drop_path > 0. else nn.Identity()
+
+ assert dim % num_heads == 0, 'dim must be divisible by num_heads'
+ head_dim = dim // num_heads
+
+ window_resolution = (window_size, window_size)
+ self.attn = Attention(dim, head_dim, num_heads,
+ attn_ratio=1, resolution=window_resolution)
+
+ mlp_hidden_dim = int(dim * mlp_ratio)
+ mlp_activation = activation
+ self.mlp = Mlp(in_features=dim, hidden_features=mlp_hidden_dim,
+ act_layer=mlp_activation, drop=drop)
+
+ pad = local_conv_size // 2
+ self.local_conv = Conv2d_BN(
+ dim, dim, ks=local_conv_size, stride=1, pad=pad, groups=dim)
+
+ def forward(self, x):
+ H, W = self.input_resolution
+ B, L, C = x.shape
+ assert L == H * W, "input feature has wrong size"
+ res_x = x
+ if H == self.window_size and W == self.window_size:
+ x = self.attn(x)
+ else:
+ x = x.view(B, H, W, C)
+ pad_b = (self.window_size - H %
+ self.window_size) % self.window_size
+ pad_r = (self.window_size - W %
+ self.window_size) % self.window_size
+ padding = pad_b > 0 or pad_r > 0
+
+ if padding:
+ x = F.pad(x, (0, 0, 0, pad_r, 0, pad_b))
+
+ pH, pW = H + pad_b, W + pad_r
+ nH = pH // self.window_size
+ nW = pW // self.window_size
+ # window partition
+ x = x.view(B, nH, self.window_size, nW, self.window_size, C).transpose(2, 3).reshape(
+ B * nH * nW, self.window_size * self.window_size, C)
+ x = self.attn(x)
+ # window reverse
+ x = x.view(B, nH, nW, self.window_size, self.window_size,
+ C).transpose(2, 3).reshape(B, pH, pW, C)
+
+ if padding:
+ x = x[:, :H, :W].contiguous()
+
+ x = x.view(B, L, C)
+
+ x = res_x + self.drop_path(x)
+
+ x = x.transpose(1, 2).reshape(B, C, H, W)
+ x = self.local_conv(x)
+ x = x.view(B, C, L).transpose(1, 2)
+
+ x = x + self.drop_path(self.mlp(x))
+ return x
+
+ def extra_repr(self) -> str:
+ return f"dim={self.dim}, input_resolution={self.input_resolution}, num_heads={self.num_heads}, " \
+ f"window_size={self.window_size}, mlp_ratio={self.mlp_ratio}"
+
+
+class BasicLayer(nn.Module):
+ """ A basic TinyViT layer for one stage.
+
+ Args:
+ dim (int): Number of input channels.
+ input_resolution (tuple[int]): Input resolution.
+ depth (int): Number of blocks.
+ num_heads (int): Number of attention heads.
+ window_size (int): Local window size.
+ mlp_ratio (float): Ratio of mlp hidden dim to embedding dim.
+ drop (float, optional): Dropout rate. Default: 0.0
+ drop_path (float | tuple[float], optional): Stochastic depth rate. Default: 0.0
+ downsample (nn.Module | None, optional): Downsample layer at the end of the layer. Default: None
+ use_checkpoint (bool): Whether to use checkpointing to save memory. Default: False.
+ local_conv_size: the kernel size of the depthwise convolution between attention and MLP. Default: 3
+ activation: the activation function. Default: nn.GELU
+ out_dim: the output dimension of the layer. Default: dim
+ """
+
+ def __init__(self, dim, input_resolution, depth, num_heads, window_size,
+ mlp_ratio=4., drop=0.,
+ drop_path=0., downsample=None, use_checkpoint=False,
+ local_conv_size=3,
+ activation=nn.GELU,
+ out_dim=None,
+ ):
+
+ super().__init__()
+ self.dim = dim
+ self.input_resolution = input_resolution
+ self.depth = depth
+ self.use_checkpoint = use_checkpoint
+
+ # build blocks
+ self.blocks = nn.ModuleList([
+ TinyViTBlock(dim=dim, input_resolution=input_resolution,
+ num_heads=num_heads, window_size=window_size,
+ mlp_ratio=mlp_ratio,
+ drop=drop,
+ drop_path=drop_path[i] if isinstance(
+ drop_path, list) else drop_path,
+ local_conv_size=local_conv_size,
+ activation=activation,
+ )
+ for i in range(depth)])
+
+ # patch merging layer
+ if downsample is not None:
+ self.downsample = downsample(
+ input_resolution, dim=dim, out_dim=out_dim, activation=activation)
+ else:
+ self.downsample = None
+
+ def forward(self, x):
+ for blk in self.blocks:
+ if self.use_checkpoint:
+ x = checkpoint.checkpoint(blk, x)
+ else:
+ x = blk(x)
+ if self.downsample is not None:
+ x = self.downsample(x)
+ return x
+
+ def extra_repr(self) -> str:
+ return f"dim={self.dim}, input_resolution={self.input_resolution}, depth={self.depth}"
+
+class LayerNorm2d(nn.Module):
+ def __init__(self, num_channels: int, eps: float = 1e-6) -> None:
+ super().__init__()
+ self.weight = nn.Parameter(torch.ones(num_channels))
+ self.bias = nn.Parameter(torch.zeros(num_channels))
+ self.eps = eps
+
+ def forward(self, x: torch.Tensor) -> torch.Tensor:
+ u = x.mean(1, keepdim=True)
+ s = (x - u).pow(2).mean(1, keepdim=True)
+ x = (x - u) / torch.sqrt(s + self.eps)
+ x = self.weight[:, None, None] * x + self.bias[:, None, None]
+ return x
+class TinyViT(nn.Module):
+ def __init__(self, img_size=224, in_chans=3, num_classes=1000,
+ embed_dims=[96, 192, 384, 768], depths=[2, 2, 6, 2],
+ num_heads=[3, 6, 12, 24],
+ window_sizes=[7, 7, 14, 7],
+ mlp_ratio=4.,
+ drop_rate=0.,
+ drop_path_rate=0.1,
+ use_checkpoint=False,
+ mbconv_expand_ratio=4.0,
+ local_conv_size=3,
+ layer_lr_decay=1.0,
+ ):
+ super().__init__()
+ self.img_size=img_size
+ self.num_classes = num_classes
+ self.depths = depths
+ self.num_layers = len(depths)
+ self.mlp_ratio = mlp_ratio
+
+ activation = nn.GELU
+
+ self.patch_embed = PatchEmbed(in_chans=in_chans,
+ embed_dim=embed_dims[0],
+ resolution=img_size,
+ activation=activation)
+
+ patches_resolution = self.patch_embed.patches_resolution
+ self.patches_resolution = patches_resolution
+
+ # stochastic depth
+ dpr = [x.item() for x in torch.linspace(0, drop_path_rate,
+ sum(depths))] # stochastic depth decay rule
+
+ # build layers
+ self.layers = nn.ModuleList()
+ for i_layer in range(self.num_layers):
+ kwargs = dict(dim=embed_dims[i_layer],
+ input_resolution=(patches_resolution[0] // (2 ** (i_layer-1 if i_layer == 3 else i_layer)),
+ patches_resolution[1] // (2 ** (i_layer-1 if i_layer == 3 else i_layer))),
+ # input_resolution=(patches_resolution[0] // (2 ** i_layer),
+ # patches_resolution[1] // (2 ** i_layer)),
+ depth=depths[i_layer],
+ drop_path=dpr[sum(depths[:i_layer]):sum(depths[:i_layer + 1])],
+ downsample=PatchMerging if (
+ i_layer < self.num_layers - 1) else None,
+ use_checkpoint=use_checkpoint,
+ out_dim=embed_dims[min(
+ i_layer + 1, len(embed_dims) - 1)],
+ activation=activation,
+ )
+ if i_layer == 0:
+ layer = ConvLayer(
+ conv_expand_ratio=mbconv_expand_ratio,
+ **kwargs,
+ )
+ else:
+ layer = BasicLayer(
+ num_heads=num_heads[i_layer],
+ window_size=window_sizes[i_layer],
+ mlp_ratio=self.mlp_ratio,
+ drop=drop_rate,
+ local_conv_size=local_conv_size,
+ **kwargs)
+ self.layers.append(layer)
+
+ # Classifier head
+ self.norm_head = nn.LayerNorm(embed_dims[-1])
+ self.head = nn.Linear(
+ embed_dims[-1], num_classes) if num_classes > 0 else torch.nn.Identity()
+
+ # init weights
+ self.apply(self._init_weights)
+ self.set_layer_lr_decay(layer_lr_decay)
+ self.neck = nn.Sequential(
+ nn.Conv2d(
+ embed_dims[-1],#handongshen
+ 256,
+ kernel_size=1,
+ bias=False,
+ ),
+ LayerNorm2d(256),
+ nn.Conv2d(
+ 256,
+ 256,
+ kernel_size=3,
+ padding=1,
+ bias=False,
+ ),
+ LayerNorm2d(256),
+ )
+ def set_layer_lr_decay(self, layer_lr_decay):
+ decay_rate = layer_lr_decay
+
+ # layers -> blocks (depth)
+ depth = sum(self.depths)
+ lr_scales = [decay_rate ** (depth - i - 1) for i in range(depth)]
+ print("LR SCALES:", lr_scales)
+
+ def _set_lr_scale(m, scale):
+ for p in m.parameters():
+ p.lr_scale = scale
+
+ self.patch_embed.apply(lambda x: _set_lr_scale(x, lr_scales[0]))
+ i = 0
+ for layer in self.layers:
+ for block in layer.blocks:
+ block.apply(lambda x: _set_lr_scale(x, lr_scales[i]))
+ i += 1
+ if layer.downsample is not None:
+ layer.downsample.apply(
+ lambda x: _set_lr_scale(x, lr_scales[i - 1]))
+ assert i == depth
+ for m in [self.norm_head, self.head]:
+ m.apply(lambda x: _set_lr_scale(x, lr_scales[-1]))
+
+ for k, p in self.named_parameters():
+ p.param_name = k
+
+ def _check_lr_scale(m):
+ for p in m.parameters():
+ assert hasattr(p, 'lr_scale'), p.param_name
+
+ self.apply(_check_lr_scale)
+
+ def _init_weights(self, m):
+ if isinstance(m, nn.Linear):
+ trunc_normal_(m.weight, std=.02)
+ if isinstance(m, nn.Linear) and m.bias is not None:
+ nn.init.constant_(m.bias, 0)
+ elif isinstance(m, nn.LayerNorm):
+ nn.init.constant_(m.bias, 0)
+ nn.init.constant_(m.weight, 1.0)
+
+ @torch.jit.ignore
+ def no_weight_decay_keywords(self):
+ return {'attention_biases'}
+
+ def forward_features(self, x):
+ # x: (N, C, H, W)
+ x = self.patch_embed(x)
+
+ x = self.layers[0](x)
+ start_i = 1
+
+ for i in range(start_i, len(self.layers)):
+ layer = self.layers[i]
+ x = layer(x)
+ B,_,C=x.size()
+ x = x.view(B, 64, 64, C)
+ x=x.permute(0, 3, 1, 2)
+ x=self.neck(x)
+ return x
+
+ def forward(self, x):
+ x = self.forward_features(x)
+
+ # We have made some hack changes here to make it compatible with SAM-HQ
+ return x, None
+
+
+_checkpoint_url_format = \
+ 'https://github.com/wkcn/TinyViT-model-zoo/releases/download/checkpoints/{}.pth'
+_provided_checkpoints = {
+ 'tiny_vit_5m_224': 'tiny_vit_5m_22kto1k_distill',
+ 'tiny_vit_11m_224': 'tiny_vit_11m_22kto1k_distill',
+ 'tiny_vit_21m_224': 'tiny_vit_21m_22kto1k_distill',
+ 'tiny_vit_21m_384': 'tiny_vit_21m_22kto1k_384_distill',
+ 'tiny_vit_21m_512': 'tiny_vit_21m_22kto1k_512_distill',
+}
+
+
+def register_tiny_vit_model(fn):
+ '''Register a TinyViT model
+ It is a wrapper of `register_model` with loading the pretrained checkpoint.
+ '''
+ def fn_wrapper(pretrained=False, **kwargs):
+ model = fn()
+ if pretrained:
+ model_name = fn.__name__
+ assert model_name in _provided_checkpoints, \
+ f'Sorry that the checkpoint `{model_name}` is not provided yet.'
+ url = _checkpoint_url_format.format(
+ _provided_checkpoints[model_name])
+ checkpoint = torch.hub.load_state_dict_from_url(
+ url=url,
+ map_location='cpu', check_hash=False,
+ )
+ model.load_state_dict(checkpoint['model'])
+
+ return model
+
+ # rename the name of fn_wrapper
+ fn_wrapper.__name__ = fn.__name__
+ return register_model(fn_wrapper)
+
+
+@register_tiny_vit_model
+def tiny_vit_5m_224(pretrained=False, num_classes=1000, drop_path_rate=0.0):
+ return TinyViT(
+ num_classes=num_classes,
+ embed_dims=[64, 128, 160, 320],
+ depths=[2, 2, 6, 2],
+ num_heads=[2, 4, 5, 10],
+ window_sizes=[7, 7, 14, 7],
+ drop_path_rate=drop_path_rate,
+ )
+
+
+@register_tiny_vit_model
+def tiny_vit_11m_224(pretrained=False, num_classes=1000, drop_path_rate=0.1):
+ return TinyViT(
+ num_classes=num_classes,
+ embed_dims=[64, 128, 256, 448],
+ depths=[2, 2, 6, 2],
+ num_heads=[2, 4, 8, 14],
+ window_sizes=[7, 7, 14, 7],
+ drop_path_rate=drop_path_rate,
+ )
+
+
+@register_tiny_vit_model
+def tiny_vit_21m_224(pretrained=False, num_classes=1000, drop_path_rate=0.2):
+ return TinyViT(
+ num_classes=num_classes,
+ embed_dims=[96, 192, 384, 576],
+ depths=[2, 2, 6, 2],
+ num_heads=[3, 6, 12, 18],
+ window_sizes=[7, 7, 14, 7],
+ drop_path_rate=drop_path_rate,
+ )
+
+
+@register_tiny_vit_model
+def tiny_vit_21m_384(pretrained=False, num_classes=1000, drop_path_rate=0.1):
+ return TinyViT(
+ img_size=384,
+ num_classes=num_classes,
+ embed_dims=[96, 192, 384, 576],
+ depths=[2, 2, 6, 2],
+ num_heads=[3, 6, 12, 18],
+ window_sizes=[12, 12, 24, 12],
+ drop_path_rate=drop_path_rate,
+ )
+
+
+@register_tiny_vit_model
+def tiny_vit_21m_512(pretrained=False, num_classes=1000, drop_path_rate=0.1):
+ return TinyViT(
+ img_size=512,
+ num_classes=num_classes,
+ embed_dims=[96, 192, 384, 576],
+ depths=[2, 2, 6, 2],
+ num_heads=[3, 6, 12, 18],
+ window_sizes=[16, 16, 32, 16],
+ drop_path_rate=drop_path_rate,
+ )
\ No newline at end of file
diff --git a/EfficientSAM/README.md b/EfficientSAM/README.md
new file mode 100644
index 0000000000000000000000000000000000000000..b93bdacbca1df347d5365e882f14c8ad4353a55a
--- /dev/null
+++ b/EfficientSAM/README.md
@@ -0,0 +1,194 @@
+## Efficient Grounded-SAM
+
+We're going to combine [Grounding-DINO](https://github.com/IDEA-Research/GroundingDINO) with efficient SAM variants for faster annotating.
+
+
+
+
+### Table of Contents
+- [Installation](#installation)
+- [Efficient SAM Series](#efficient-sams)
+- [Run Grounded-FastSAM Demo](#run-grounded-fastsam-demo)
+- [Run Grounded-MobileSAM Demo](#run-grounded-mobilesam-demo)
+- [Run Grounded-LightHQSAM Demo](#run-grounded-light-hqsam-demo)
+- [Run Grounded-Efficient-SAM Demo](#run-grounded-efficient-sam-demo)
+- [Run Grounded-Edge-SAM Demo](#run-grounded-edge-sam-demo)
+- [Run Grounded-RepViT-SAM Demo](#run-grounded-repvit-sam-demo)
+
+
+### Installation
+
+- Install [Grounded-SAM](https://github.com/IDEA-Research/Grounded-Segment-Anything#installation)
+
+- Install [Fast-SAM](https://github.com/CASIA-IVA-Lab/FastSAM#installation)
+
+- Note that we may use the sam image as the demo image in order to compare the inference results of different efficient-sam variants.
+
+### Efficient SAMs
+Here's the list of Efficient SAM variants:
+
+
+
+| Title | Intro | Description | Links |
+|:----:|:----:|:----:|:----:|
+| [FastSAM](https://arxiv.org/pdf/2306.12156.pdf) |  | The Fast Segment Anything Model(FastSAM) is a CNN Segment Anything Model trained by only 2% of the SA-1B dataset published by SAM authors. The FastSAM achieve a comparable performance with the SAM method at 50× higher run-time speed. | [[Github](https://github.com/CASIA-IVA-Lab/FastSAM)] [[Demo](https://huggingface.co/spaces/An-619/FastSAM)] |
+| [MobileSAM](https://arxiv.org/pdf/2306.14289.pdf) |  | MobileSAM performs on par with the original SAM (at least visually) and keeps exactly the same pipeline as the original SAM except for a change on the image encoder. Specifically, we replace the original heavyweight ViT-H encoder (632M) with a much smaller Tiny-ViT (5M). On a single GPU, MobileSAM runs around 12ms per image: 8ms on the image encoder and 4ms on the mask decoder. | [[Github](https://github.com/ChaoningZhang/MobileSAM)] |
+| [Light-HQSAM](https://arxiv.org/pdf/2306.01567.pdf) | 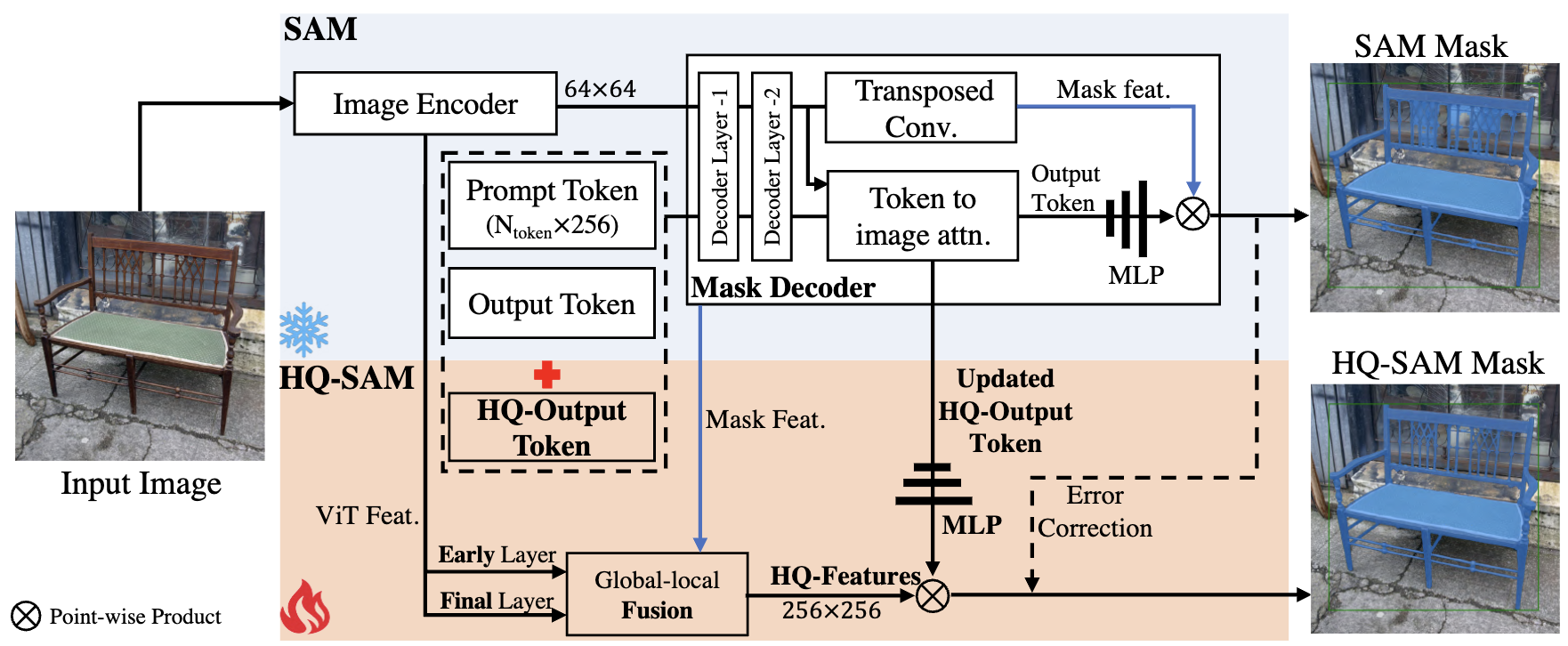 | Light HQ-SAM is based on the tiny vit image encoder provided by MobileSAM. We design a learnable High-Quality Output Token, which is injected into SAM's mask decoder and is responsible for predicting the high-quality mask. Instead of only applying it on mask-decoder features, we first fuse them with ViT features for improved mask details. Refer to [Light HQ-SAM vs. MobileSAM](https://github.com/SysCV/sam-hq#light-hq-sam-vs-mobilesam-on-coco) for more details. | [[Github](https://github.com/SysCV/sam-hq)] |
+| [Efficient-SAM](https://github.com/yformer/EfficientSAM) | 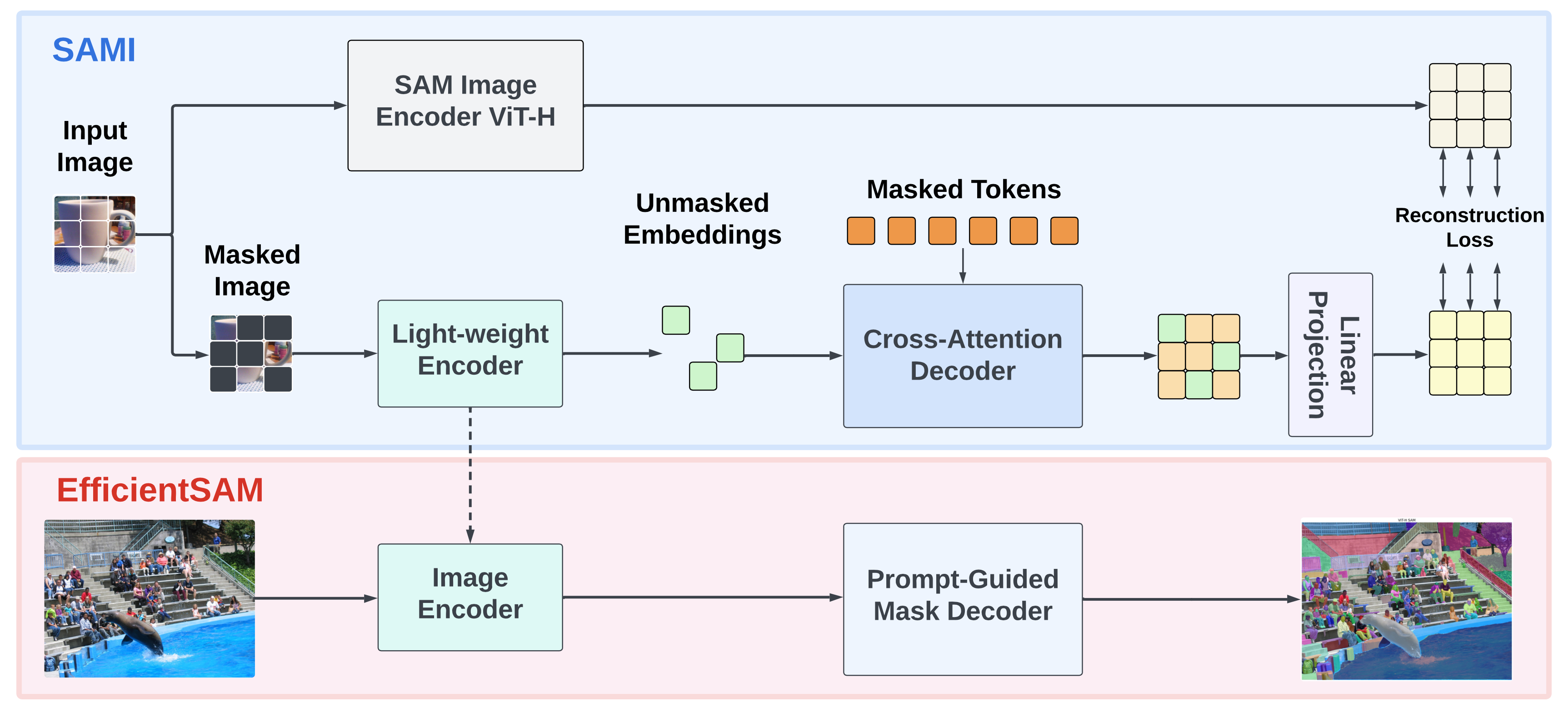 |Segment Anything Model (SAM) has emerged as a powerful tool for numerous vision applications. However, the huge computation cost of SAM model has limited its applications to wider real-world applications. To address this limitation, we propose EfficientSAMs, light-weight SAM models that exhibit decent performance with largely reduced complexity. Our idea is based on leveraging masked image pretraining, SAMI, which learns to reconstruct features from SAM image encoder for effective visual representation learning. Further, we take SAMI-pretrained light-weight image encoders and mask decoder to build EfficientSAMs, and finetune the models on SA-1B for segment anything task. Refer to [EfficientSAM arXiv](https://arxiv.org/pdf/2312.00863.pdf) for more details.| [[Github](https://github.com/yformer/EfficientSAM)] |
+| [Edge-SAM](https://github.com/chongzhou96/EdgeSAM) | 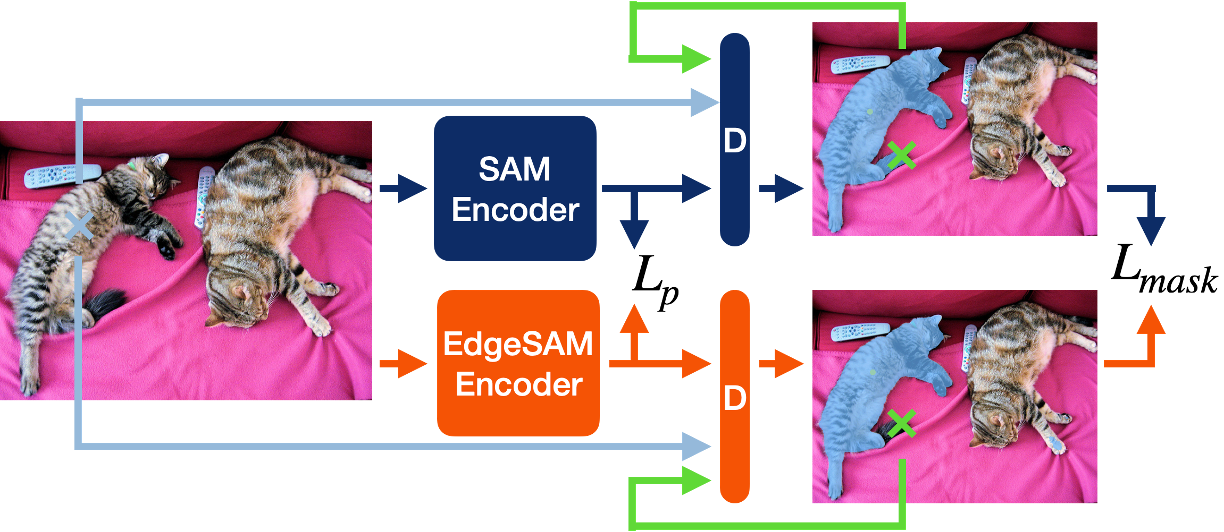 | EdgeSAM involves distilling the original ViT-based SAM image encoder into a purely CNN-based architecture, better suited for edge devices. We carefully benchmark various distillation strategies and demonstrate that task-agnostic encoder distillation fails to capture the full knowledge embodied in SAM. Refer to [Edge-SAM arXiv](https://arxiv.org/abs/2312.06660) for more details. | [[Github](https://github.com/chongzhou96/EdgeSAM)] |
+| [RepViT-SAM](https://github.com/THU-MIG/RepViT/tree/main/sam) |  | Recently, RepViT achieves the state-of-the-art performance and latency trade-off on mobile devices by incorporating efficient architectural designs of ViTs into CNNs. Here, to achieve real-time segmenting anything on mobile devices, following MobileSAM, we replace the heavyweight image encoder in SAM with RepViT model, ending up with the RepViT-SAM model. Extensive experiments show that RepViT-SAM can enjoy significantly better zero-shot transfer capability than MobileSAM, along with nearly 10× faster inference speed. Refer to [RepViT-SAM arXiv](https://arxiv.org/pdf/2312.05760.pdf) for more details. | [[Github](https://github.com/THU-MIG/RepViT)] |
+
+
+
+
+### Run Grounded-FastSAM Demo
+
+- Firstly, download the pretrained Fast-SAM weight [here](https://github.com/CASIA-IVA-Lab/FastSAM#model-checkpoints)
+
+- Run the demo with the following script:
+
+```bash
+cd Grounded-Segment-Anything
+
+python EfficientSAM/grounded_fast_sam.py --model_path "./FastSAM-x.pt" --img_path "assets/demo4.jpg" --text "the black dog." --output "./output/"
+```
+
+- And the results will be saved in `./output/` as:
+
+
+
+| Input | Text | Output |
+|:---:|:---:|:---:|
+| | "The black dog." |  |
+
+
+
+
+**Note**: Due to the post process of FastSAM, only one box can be annotated at a time, if there're multiple box prompts, we simply save multiple annotate images to `./output` now, which will be modified in the future release.
+
+
+### Run Grounded-MobileSAM Demo
+
+- Firstly, download the pretrained MobileSAM weight [here](https://github.com/ChaoningZhang/MobileSAM/tree/master/weights)
+
+- Run the demo with the following script:
+
+```bash
+cd Grounded-Segment-Anything
+
+python EfficientSAM/grounded_mobile_sam.py --MOBILE_SAM_CHECKPOINT_PATH "./EfficientSAM/mobile_sam.pt" --SOURCE_IMAGE_PATH "./assets/demo2.jpg" --CAPTION "the running dog"
+```
+
+- And the result will be saved as `./gronded_mobile_sam_anontated_image.jpg` as:
+
+
+
+| Input | Text | Output |
+|:---:|:---:|:---:|
+| | "the running dog" |  |
+
+
+
+
+### Run Grounded-Light-HQSAM Demo
+
+- Firstly, download the pretrained Light-HQSAM weight [here](https://github.com/SysCV/sam-hq#model-checkpoints)
+
+- Run the demo with the following script:
+
+```bash
+cd Grounded-Segment-Anything
+
+python EfficientSAM/grounded_light_hqsam.py
+```
+
+- And the result will be saved as `./gronded_light_hqsam_anontated_image.jpg` as:
+
+
+
+
+### Run Grounded-Efficient-SAM Demo
+
+- Download the pretrained EfficientSAM checkpoint from [here](https://github.com/yformer/EfficientSAM#model) and put it under `Grounded-Segment-Anything/EfficientSAM`
+
+- Run the demo with the following script:
+
+```bash
+cd Grounded-Segment-Anything
+
+python EfficientSAM/grounded_efficient_sam.py
+```
+
+- And the result will be saved as `./gronded_efficient_sam_anontated_image.jpg` as:
+
+
+
+
+### Run Grounded-Edge-SAM Demo
+
+- Download the pretrained [Edge-SAM](https://github.com/chongzhou96/EdgeSAM) checkpoint follow the [official instruction](https://github.com/chongzhou96/EdgeSAM?tab=readme-ov-file#usage-) as:
+
+```bash
+cd Grounded-Segment-Anything
+wget -P EfficientSAM/ https://huggingface.co/spaces/chongzhou/EdgeSAM/resolve/main/weights/edge_sam.pth
+wget -P EfficientSAM/ https://huggingface.co/spaces/chongzhou/EdgeSAM/resolve/main/weights/edge_sam_3x.pth
+```
+
+- Run the demo with the following script:
+
+```bash
+cd Grounded-Segment-Anything
+
+python EfficientSAM/grounded_edge_sam.py
+```
+
+- And the result will be saved as `./gronded_edge_sam_anontated_image.jpg` as:
+
+
+
+### Run Grounded-RepViT-SAM Demo
+
+- Download the pretrained [RepViT-SAM](https://github.com/THU-MIG/RepViT) checkpoint follow the [official instruction](https://github.com/THU-MIG/RepViT/tree/main/sam#installation) as:
+
+```bash
+cd Grounded-Segment-Anything
+wget -P EfficientSAM/ https://github.com/THU-MIG/RepViT/releases/download/v1.0/repvit_sam.pt
+```
+
+- Run the demo with the following script:
+
+```bash
+cd Grounded-Segment-Anything
+
+python EfficientSAM/grounded_repvit_sam.py
+```
+
+- And the result will be saved as `./gronded_repvit_sam_anontated_image.jpg` as:
+
+
+
+## Results
+
+
+
+COCO Object Detection Results
+
+
+
+
+
+
+ODinW Object Detection Results
+
+
+
+
+
+
+Marrying Grounding DINO with Stable Diffusion for Image Editing
+
+
+
+
+
+
+Marrying Grounding DINO with GLIGEN for more Detailed Image Editing
+
+
+
+
+## Model
+
+Includes: a text backbone, an image backbone, a feature enhancer, a language-guided query selection, and a cross-modality decoder.
+
+
+
+
+## Acknowledgement
+
+Our model is related to [DINO](https://github.com/IDEA-Research/DINO) and [GLIP](https://github.com/microsoft/GLIP). Thanks for their great work!
+
+We also thank great previous work including DETR, Deformable DETR, SMCA, Conditional DETR, Anchor DETR, Dynamic DETR, DAB-DETR, DN-DETR, etc. More related work are available at [Awesome Detection Transformer](https://github.com/IDEACVR/awesome-detection-transformer). A new toolbox [detrex](https://github.com/IDEA-Research/detrex) is available as well.
+
+Thanks [Stable Diffusion](https://github.com/Stability-AI/StableDiffusion) and [GLIGEN](https://github.com/gligen/GLIGEN) for their awesome models.
+
+
+## Citation
+
+If you find our work helpful for your research, please consider citing the following BibTeX entry.
+
+```bibtex
+@inproceedings{ShilongLiu2023GroundingDM,
+ title={Grounding DINO: Marrying DINO with Grounded Pre-Training for Open-Set Object Detection},
+ author={Shilong Liu and Zhaoyang Zeng and Tianhe Ren and Feng Li and Hao Zhang and Jie Yang and Chunyuan Li and Jianwei Yang and Hang Su and Jun Zhu and Lei Zhang},
+ year={2023}
+}
+```
+
+
+
+
diff --git a/GroundingDINO/demo/gradio_app.py b/GroundingDINO/demo/gradio_app.py
new file mode 100644
index 0000000000000000000000000000000000000000..15e08323f485291df8b53eefd4691c087d7863f7
--- /dev/null
+++ b/GroundingDINO/demo/gradio_app.py
@@ -0,0 +1,125 @@
+import argparse
+from functools import partial
+import cv2
+import requests
+import os
+from io import BytesIO
+from PIL import Image
+import numpy as np
+from pathlib import Path
+
+
+import warnings
+
+import torch
+
+# prepare the environment
+os.system("python setup.py build develop --user")
+os.system("pip install packaging==21.3")
+os.system("pip install gradio")
+
+
+warnings.filterwarnings("ignore")
+
+import gradio as gr
+
+from groundingdino.models import build_model
+from groundingdino.util.slconfig import SLConfig
+from groundingdino.util.utils import clean_state_dict
+from groundingdino.util.inference import annotate, load_image, predict
+import groundingdino.datasets.transforms as T
+
+from huggingface_hub import hf_hub_download
+
+
+
+# Use this command for evaluate the GLIP-T model
+config_file = "groundingdino/config/GroundingDINO_SwinT_OGC.py"
+ckpt_repo_id = "ShilongLiu/GroundingDINO"
+ckpt_filenmae = "groundingdino_swint_ogc.pth"
+
+
+def load_model_hf(model_config_path, repo_id, filename, device='cpu'):
+ args = SLConfig.fromfile(model_config_path)
+ model = build_model(args)
+ args.device = device
+
+ cache_file = hf_hub_download(repo_id=repo_id, filename=filename)
+ checkpoint = torch.load(cache_file, map_location='cpu')
+ log = model.load_state_dict(clean_state_dict(checkpoint['model']), strict=False)
+ print("Model loaded from {} \n => {}".format(cache_file, log))
+ _ = model.eval()
+ return model
+
+def image_transform_grounding(init_image):
+ transform = T.Compose([
+ T.RandomResize([800], max_size=1333),
+ T.ToTensor(),
+ T.Normalize([0.485, 0.456, 0.406], [0.229, 0.224, 0.225])
+ ])
+ image, _ = transform(init_image, None) # 3, h, w
+ return init_image, image
+
+def image_transform_grounding_for_vis(init_image):
+ transform = T.Compose([
+ T.RandomResize([800], max_size=1333),
+ ])
+ image, _ = transform(init_image, None) # 3, h, w
+ return image
+
+model = load_model_hf(config_file, ckpt_repo_id, ckpt_filenmae)
+
+def run_grounding(input_image, grounding_caption, box_threshold, text_threshold):
+ init_image = input_image.convert("RGB")
+ original_size = init_image.size
+
+ _, image_tensor = image_transform_grounding(init_image)
+ image_pil: Image = image_transform_grounding_for_vis(init_image)
+
+ # run grounidng
+ boxes, logits, phrases = predict(model, image_tensor, grounding_caption, box_threshold, text_threshold, device='cpu')
+ annotated_frame = annotate(image_source=np.asarray(image_pil), boxes=boxes, logits=logits, phrases=phrases)
+ image_with_box = Image.fromarray(cv2.cvtColor(annotated_frame, cv2.COLOR_BGR2RGB))
+
+
+ return image_with_box
+
+if __name__ == "__main__":
+
+ parser = argparse.ArgumentParser("Grounding DINO demo", add_help=True)
+ parser.add_argument("--debug", action="store_true", help="using debug mode")
+ parser.add_argument("--share", action="store_true", help="share the app")
+ args = parser.parse_args()
+
+ block = gr.Blocks().queue()
+ with block:
+ gr.Markdown("# [Grounding DINO](https://github.com/IDEA-Research/GroundingDINO)")
+ gr.Markdown("### Open-World Detection with Grounding DINO")
+
+ with gr.Row():
+ with gr.Column():
+ input_image = gr.Image(source='upload', type="pil")
+ grounding_caption = gr.Textbox(label="Detection Prompt")
+ run_button = gr.Button(label="Run")
+ with gr.Accordion("Advanced options", open=False):
+ box_threshold = gr.Slider(
+ label="Box Threshold", minimum=0.0, maximum=1.0, value=0.25, step=0.001
+ )
+ text_threshold = gr.Slider(
+ label="Text Threshold", minimum=0.0, maximum=1.0, value=0.25, step=0.001
+ )
+
+ with gr.Column():
+ gallery = gr.outputs.Image(
+ type="pil",
+ # label="grounding results"
+ ).style(full_width=True, full_height=True)
+ # gallery = gr.Gallery(label="Generated images", show_label=False).style(
+ # grid=[1], height="auto", container=True, full_width=True, full_height=True)
+
+ run_button.click(fn=run_grounding, inputs=[
+ input_image, grounding_caption, box_threshold, text_threshold], outputs=[gallery])
+
+
+ block.launch(server_name='0.0.0.0', server_port=7579, debug=args.debug, share=args.share)
+
diff --git a/GroundingDINO/demo/inference_on_a_image.py b/GroundingDINO/demo/inference_on_a_image.py
new file mode 100644
index 0000000000000000000000000000000000000000..207227b7419df8db7a6f0206361670287cf4d9fa
--- /dev/null
+++ b/GroundingDINO/demo/inference_on_a_image.py
@@ -0,0 +1,172 @@
+import argparse
+import os
+import sys
+
+import numpy as np
+import torch
+from PIL import Image, ImageDraw, ImageFont
+
+import groundingdino.datasets.transforms as T
+from groundingdino.models import build_model
+from groundingdino.util import box_ops
+from groundingdino.util.slconfig import SLConfig
+from groundingdino.util.utils import clean_state_dict, get_phrases_from_posmap
+
+
+def plot_boxes_to_image(image_pil, tgt):
+ H, W = tgt["size"]
+ boxes = tgt["boxes"]
+ labels = tgt["labels"]
+ assert len(boxes) == len(labels), "boxes and labels must have same length"
+
+ draw = ImageDraw.Draw(image_pil)
+ mask = Image.new("L", image_pil.size, 0)
+ mask_draw = ImageDraw.Draw(mask)
+
+ # draw boxes and masks
+ for box, label in zip(boxes, labels):
+ # from 0..1 to 0..W, 0..H
+ box = box * torch.Tensor([W, H, W, H])
+ # from xywh to xyxy
+ box[:2] -= box[2:] / 2
+ box[2:] += box[:2]
+ # random color
+ color = tuple(np.random.randint(0, 255, size=3).tolist())
+ # draw
+ x0, y0, x1, y1 = box
+ x0, y0, x1, y1 = int(x0), int(y0), int(x1), int(y1)
+
+ draw.rectangle([x0, y0, x1, y1], outline=color, width=6)
+ # draw.text((x0, y0), str(label), fill=color)
+
+ font = ImageFont.load_default()
+ if hasattr(font, "getbbox"):
+ bbox = draw.textbbox((x0, y0), str(label), font)
+ else:
+ w, h = draw.textsize(str(label), font)
+ bbox = (x0, y0, w + x0, y0 + h)
+ # bbox = draw.textbbox((x0, y0), str(label))
+ draw.rectangle(bbox, fill=color)
+ draw.text((x0, y0), str(label), fill="white")
+
+ mask_draw.rectangle([x0, y0, x1, y1], fill=255, width=6)
+
+ return image_pil, mask
+
+
+def load_image(image_path):
+ # load image
+ image_pil = Image.open(image_path).convert("RGB") # load image
+
+ transform = T.Compose(
+ [
+ T.RandomResize([800], max_size=1333),
+ T.ToTensor(),
+ T.Normalize([0.485, 0.456, 0.406], [0.229, 0.224, 0.225]),
+ ]
+ )
+ image, _ = transform(image_pil, None) # 3, h, w
+ return image_pil, image
+
+
+def load_model(model_config_path, model_checkpoint_path, cpu_only=False):
+ args = SLConfig.fromfile(model_config_path)
+ args.device = "cuda" if not cpu_only else "cpu"
+ model = build_model(args)
+ checkpoint = torch.load(model_checkpoint_path, map_location="cpu")
+ load_res = model.load_state_dict(clean_state_dict(checkpoint["model"]), strict=False)
+ print(load_res)
+ _ = model.eval()
+ return model
+
+
+def get_grounding_output(model, image, caption, box_threshold, text_threshold, with_logits=True, cpu_only=False):
+ caption = caption.lower()
+ caption = caption.strip()
+ if not caption.endswith("."):
+ caption = caption + "."
+ device = "cuda" if not cpu_only else "cpu"
+ model = model.to(device)
+ image = image.to(device)
+ with torch.no_grad():
+ outputs = model(image[None], captions=[caption])
+ logits = outputs["pred_logits"].cpu().sigmoid()[0] # (nq, 256)
+ boxes = outputs["pred_boxes"].cpu()[0] # (nq, 4)
+ logits.shape[0]
+
+ # filter output
+ logits_filt = logits.clone()
+ boxes_filt = boxes.clone()
+ filt_mask = logits_filt.max(dim=1)[0] > box_threshold
+ logits_filt = logits_filt[filt_mask] # num_filt, 256
+ boxes_filt = boxes_filt[filt_mask] # num_filt, 4
+ logits_filt.shape[0]
+
+ # get phrase
+ tokenlizer = model.tokenizer
+ tokenized = tokenlizer(caption)
+ # build pred
+ pred_phrases = []
+ for logit, box in zip(logits_filt, boxes_filt):
+ pred_phrase = get_phrases_from_posmap(logit > text_threshold, tokenized, tokenlizer)
+ if with_logits:
+ pred_phrases.append(pred_phrase + f"({str(logit.max().item())[:4]})")
+ else:
+ pred_phrases.append(pred_phrase)
+
+ return boxes_filt, pred_phrases
+
+
+if __name__ == "__main__":
+
+ parser = argparse.ArgumentParser("Grounding DINO example", add_help=True)
+ parser.add_argument("--config_file", "-c", type=str, required=True, help="path to config file")
+ parser.add_argument(
+ "--checkpoint_path", "-p", type=str, required=True, help="path to checkpoint file"
+ )
+ parser.add_argument("--image_path", "-i", type=str, required=True, help="path to image file")
+ parser.add_argument("--text_prompt", "-t", type=str, required=True, help="text prompt")
+ parser.add_argument(
+ "--output_dir", "-o", type=str, default="outputs", required=True, help="output directory"
+ )
+
+ parser.add_argument("--box_threshold", type=float, default=0.3, help="box threshold")
+ parser.add_argument("--text_threshold", type=float, default=0.25, help="text threshold")
+
+ parser.add_argument("--cpu-only", action="store_true", help="running on cpu only!, default=False")
+ args = parser.parse_args()
+
+ # cfg
+ config_file = args.config_file # change the path of the model config file
+ checkpoint_path = args.checkpoint_path # change the path of the model
+ image_path = args.image_path
+ text_prompt = args.text_prompt
+ output_dir = args.output_dir
+ box_threshold = args.box_threshold
+ text_threshold = args.text_threshold
+
+ # make dir
+ os.makedirs(output_dir, exist_ok=True)
+ # load image
+ image_pil, image = load_image(image_path)
+ # load model
+ model = load_model(config_file, checkpoint_path, cpu_only=args.cpu_only)
+
+ # visualize raw image
+ image_pil.save(os.path.join(output_dir, "raw_image.jpg"))
+
+ # run model
+ boxes_filt, pred_phrases = get_grounding_output(
+ model, image, text_prompt, box_threshold, text_threshold, cpu_only=args.cpu_only
+ )
+
+ # visualize pred
+ size = image_pil.size
+ pred_dict = {
+ "boxes": boxes_filt,
+ "size": [size[1], size[0]], # H,W
+ "labels": pred_phrases,
+ }
+ # import ipdb; ipdb.set_trace()
+ image_with_box = plot_boxes_to_image(image_pil, pred_dict)[0]
+ image_with_box.save(os.path.join(output_dir, "pred.jpg"))
diff --git a/GroundingDINO/groundingdino/__init__.py b/GroundingDINO/groundingdino/__init__.py
new file mode 100644
index 0000000000000000000000000000000000000000..e69de29bb2d1d6434b8b29ae775ad8c2e48c5391
diff --git a/GroundingDINO/groundingdino/config/GroundingDINO_SwinB.py b/GroundingDINO/groundingdino/config/GroundingDINO_SwinB.py
new file mode 100644
index 0000000000000000000000000000000000000000..f490c4bbd598a35de43d36ceafcbd769e7ff21bf
--- /dev/null
+++ b/GroundingDINO/groundingdino/config/GroundingDINO_SwinB.py
@@ -0,0 +1,43 @@
+batch_size = 1
+modelname = "groundingdino"
+backbone = "swin_B_384_22k"
+position_embedding = "sine"
+pe_temperatureH = 20
+pe_temperatureW = 20
+return_interm_indices = [1, 2, 3]
+backbone_freeze_keywords = None
+enc_layers = 6
+dec_layers = 6
+pre_norm = False
+dim_feedforward = 2048
+hidden_dim = 256
+dropout = 0.0
+nheads = 8
+num_queries = 900
+query_dim = 4
+num_patterns = 0
+num_feature_levels = 4
+enc_n_points = 4
+dec_n_points = 4
+two_stage_type = "standard"
+two_stage_bbox_embed_share = False
+two_stage_class_embed_share = False
+transformer_activation = "relu"
+dec_pred_bbox_embed_share = True
+dn_box_noise_scale = 1.0
+dn_label_noise_ratio = 0.5
+dn_label_coef = 1.0
+dn_bbox_coef = 1.0
+embed_init_tgt = True
+dn_labelbook_size = 2000
+max_text_len = 256
+text_encoder_type = "bert-base-uncased"
+use_text_enhancer = True
+use_fusion_layer = True
+use_checkpoint = True
+use_transformer_ckpt = True
+use_text_cross_attention = True
+text_dropout = 0.0
+fusion_dropout = 0.0
+fusion_droppath = 0.1
+sub_sentence_present = True
diff --git a/GroundingDINO/groundingdino/config/GroundingDINO_SwinT_OGC.py b/GroundingDINO/groundingdino/config/GroundingDINO_SwinT_OGC.py
new file mode 100644
index 0000000000000000000000000000000000000000..9158d5f6260ec74bded95377d382387430d7cd70
--- /dev/null
+++ b/GroundingDINO/groundingdino/config/GroundingDINO_SwinT_OGC.py
@@ -0,0 +1,43 @@
+batch_size = 1
+modelname = "groundingdino"
+backbone = "swin_T_224_1k"
+position_embedding = "sine"
+pe_temperatureH = 20
+pe_temperatureW = 20
+return_interm_indices = [1, 2, 3]
+backbone_freeze_keywords = None
+enc_layers = 6
+dec_layers = 6
+pre_norm = False
+dim_feedforward = 2048
+hidden_dim = 256
+dropout = 0.0
+nheads = 8
+num_queries = 900
+query_dim = 4
+num_patterns = 0
+num_feature_levels = 4
+enc_n_points = 4
+dec_n_points = 4
+two_stage_type = "standard"
+two_stage_bbox_embed_share = False
+two_stage_class_embed_share = False
+transformer_activation = "relu"
+dec_pred_bbox_embed_share = True
+dn_box_noise_scale = 1.0
+dn_label_noise_ratio = 0.5
+dn_label_coef = 1.0
+dn_bbox_coef = 1.0
+embed_init_tgt = True
+dn_labelbook_size = 2000
+max_text_len = 256
+text_encoder_type = "bert-base-uncased"
+use_text_enhancer = True
+use_fusion_layer = True
+use_checkpoint = True
+use_transformer_ckpt = True
+use_text_cross_attention = True
+text_dropout = 0.0
+fusion_dropout = 0.0
+fusion_droppath = 0.1
+sub_sentence_present = True
diff --git a/GroundingDINO/groundingdino/datasets/__init__.py b/GroundingDINO/groundingdino/datasets/__init__.py
new file mode 100644
index 0000000000000000000000000000000000000000..e69de29bb2d1d6434b8b29ae775ad8c2e48c5391
diff --git a/GroundingDINO/groundingdino/datasets/transforms.py b/GroundingDINO/groundingdino/datasets/transforms.py
new file mode 100644
index 0000000000000000000000000000000000000000..91cf9269e4b31008a3ddca34a19b038a9b399991
--- /dev/null
+++ b/GroundingDINO/groundingdino/datasets/transforms.py
@@ -0,0 +1,311 @@
+# Copyright (c) Facebook, Inc. and its affiliates. All Rights Reserved
+"""
+Transforms and data augmentation for both image + bbox.
+"""
+import os
+import random
+
+import PIL
+import torch
+import torchvision.transforms as T
+import torchvision.transforms.functional as F
+
+from groundingdino.util.box_ops import box_xyxy_to_cxcywh
+from groundingdino.util.misc import interpolate
+
+
+def crop(image, target, region):
+ cropped_image = F.crop(image, *region)
+
+ target = target.copy()
+ i, j, h, w = region
+
+ # should we do something wrt the original size?
+ target["size"] = torch.tensor([h, w])
+
+ fields = ["labels", "area", "iscrowd", "positive_map"]
+
+ if "boxes" in target:
+ boxes = target["boxes"]
+ max_size = torch.as_tensor([w, h], dtype=torch.float32)
+ cropped_boxes = boxes - torch.as_tensor([j, i, j, i])
+ cropped_boxes = torch.min(cropped_boxes.reshape(-1, 2, 2), max_size)
+ cropped_boxes = cropped_boxes.clamp(min=0)
+ area = (cropped_boxes[:, 1, :] - cropped_boxes[:, 0, :]).prod(dim=1)
+ target["boxes"] = cropped_boxes.reshape(-1, 4)
+ target["area"] = area
+ fields.append("boxes")
+
+ if "masks" in target:
+ # FIXME should we update the area here if there are no boxes?
+ target["masks"] = target["masks"][:, i : i + h, j : j + w]
+ fields.append("masks")
+
+ # remove elements for which the boxes or masks that have zero area
+ if "boxes" in target or "masks" in target:
+ # favor boxes selection when defining which elements to keep
+ # this is compatible with previous implementation
+ if "boxes" in target:
+ cropped_boxes = target["boxes"].reshape(-1, 2, 2)
+ keep = torch.all(cropped_boxes[:, 1, :] > cropped_boxes[:, 0, :], dim=1)
+ else:
+ keep = target["masks"].flatten(1).any(1)
+
+ for field in fields:
+ if field in target:
+ target[field] = target[field][keep]
+
+ if os.environ.get("IPDB_SHILONG_DEBUG", None) == "INFO":
+ # for debug and visualization only.
+ if "strings_positive" in target:
+ target["strings_positive"] = [
+ _i for _i, _j in zip(target["strings_positive"], keep) if _j
+ ]
+
+ return cropped_image, target
+
+
+def hflip(image, target):
+ flipped_image = F.hflip(image)
+
+ w, h = image.size
+
+ target = target.copy()
+ if "boxes" in target:
+ boxes = target["boxes"]
+ boxes = boxes[:, [2, 1, 0, 3]] * torch.as_tensor([-1, 1, -1, 1]) + torch.as_tensor(
+ [w, 0, w, 0]
+ )
+ target["boxes"] = boxes
+
+ if "masks" in target:
+ target["masks"] = target["masks"].flip(-1)
+
+ return flipped_image, target
+
+
+def resize(image, target, size, max_size=None):
+ # size can be min_size (scalar) or (w, h) tuple
+
+ def get_size_with_aspect_ratio(image_size, size, max_size=None):
+ w, h = image_size
+ if max_size is not None:
+ min_original_size = float(min((w, h)))
+ max_original_size = float(max((w, h)))
+ if max_original_size / min_original_size * size > max_size:
+ size = int(round(max_size * min_original_size / max_original_size))
+
+ if (w <= h and w == size) or (h <= w and h == size):
+ return (h, w)
+
+ if w < h:
+ ow = size
+ oh = int(size * h / w)
+ else:
+ oh = size
+ ow = int(size * w / h)
+
+ return (oh, ow)
+
+ def get_size(image_size, size, max_size=None):
+ if isinstance(size, (list, tuple)):
+ return size[::-1]
+ else:
+ return get_size_with_aspect_ratio(image_size, size, max_size)
+
+ size = get_size(image.size, size, max_size)
+ rescaled_image = F.resize(image, size)
+
+ if target is None:
+ return rescaled_image, None
+
+ ratios = tuple(float(s) / float(s_orig) for s, s_orig in zip(rescaled_image.size, image.size))
+ ratio_width, ratio_height = ratios
+
+ target = target.copy()
+ if "boxes" in target:
+ boxes = target["boxes"]
+ scaled_boxes = boxes * torch.as_tensor(
+ [ratio_width, ratio_height, ratio_width, ratio_height]
+ )
+ target["boxes"] = scaled_boxes
+
+ if "area" in target:
+ area = target["area"]
+ scaled_area = area * (ratio_width * ratio_height)
+ target["area"] = scaled_area
+
+ h, w = size
+ target["size"] = torch.tensor([h, w])
+
+ if "masks" in target:
+ target["masks"] = (
+ interpolate(target["masks"][:, None].float(), size, mode="nearest")[:, 0] > 0.5
+ )
+
+ return rescaled_image, target
+
+
+def pad(image, target, padding):
+ # assumes that we only pad on the bottom right corners
+ padded_image = F.pad(image, (0, 0, padding[0], padding[1]))
+ if target is None:
+ return padded_image, None
+ target = target.copy()
+ # should we do something wrt the original size?
+ target["size"] = torch.tensor(padded_image.size[::-1])
+ if "masks" in target:
+ target["masks"] = torch.nn.functional.pad(target["masks"], (0, padding[0], 0, padding[1]))
+ return padded_image, target
+
+
+class ResizeDebug(object):
+ def __init__(self, size):
+ self.size = size
+
+ def __call__(self, img, target):
+ return resize(img, target, self.size)
+
+
+class RandomCrop(object):
+ def __init__(self, size):
+ self.size = size
+
+ def __call__(self, img, target):
+ region = T.RandomCrop.get_params(img, self.size)
+ return crop(img, target, region)
+
+
+class RandomSizeCrop(object):
+ def __init__(self, min_size: int, max_size: int, respect_boxes: bool = False):
+ # respect_boxes: True to keep all boxes
+ # False to tolerence box filter
+ self.min_size = min_size
+ self.max_size = max_size
+ self.respect_boxes = respect_boxes
+
+ def __call__(self, img: PIL.Image.Image, target: dict):
+ init_boxes = len(target["boxes"])
+ max_patience = 10
+ for i in range(max_patience):
+ w = random.randint(self.min_size, min(img.width, self.max_size))
+ h = random.randint(self.min_size, min(img.height, self.max_size))
+ region = T.RandomCrop.get_params(img, [h, w])
+ result_img, result_target = crop(img, target, region)
+ if (
+ not self.respect_boxes
+ or len(result_target["boxes"]) == init_boxes
+ or i == max_patience - 1
+ ):
+ return result_img, result_target
+ return result_img, result_target
+
+
+class CenterCrop(object):
+ def __init__(self, size):
+ self.size = size
+
+ def __call__(self, img, target):
+ image_width, image_height = img.size
+ crop_height, crop_width = self.size
+ crop_top = int(round((image_height - crop_height) / 2.0))
+ crop_left = int(round((image_width - crop_width) / 2.0))
+ return crop(img, target, (crop_top, crop_left, crop_height, crop_width))
+
+
+class RandomHorizontalFlip(object):
+ def __init__(self, p=0.5):
+ self.p = p
+
+ def __call__(self, img, target):
+ if random.random() < self.p:
+ return hflip(img, target)
+ return img, target
+
+
+class RandomResize(object):
+ def __init__(self, sizes, max_size=None):
+ assert isinstance(sizes, (list, tuple))
+ self.sizes = sizes
+ self.max_size = max_size
+
+ def __call__(self, img, target=None):
+ size = random.choice(self.sizes)
+ return resize(img, target, size, self.max_size)
+
+
+class RandomPad(object):
+ def __init__(self, max_pad):
+ self.max_pad = max_pad
+
+ def __call__(self, img, target):
+ pad_x = random.randint(0, self.max_pad)
+ pad_y = random.randint(0, self.max_pad)
+ return pad(img, target, (pad_x, pad_y))
+
+
+class RandomSelect(object):
+ """
+ Randomly selects between transforms1 and transforms2,
+ with probability p for transforms1 and (1 - p) for transforms2
+ """
+
+ def __init__(self, transforms1, transforms2, p=0.5):
+ self.transforms1 = transforms1
+ self.transforms2 = transforms2
+ self.p = p
+
+ def __call__(self, img, target):
+ if random.random() < self.p:
+ return self.transforms1(img, target)
+ return self.transforms2(img, target)
+
+
+class ToTensor(object):
+ def __call__(self, img, target):
+ return F.to_tensor(img), target
+
+
+class RandomErasing(object):
+ def __init__(self, *args, **kwargs):
+ self.eraser = T.RandomErasing(*args, **kwargs)
+
+ def __call__(self, img, target):
+ return self.eraser(img), target
+
+
+class Normalize(object):
+ def __init__(self, mean, std):
+ self.mean = mean
+ self.std = std
+
+ def __call__(self, image, target=None):
+ image = F.normalize(image, mean=self.mean, std=self.std)
+ if target is None:
+ return image, None
+ target = target.copy()
+ h, w = image.shape[-2:]
+ if "boxes" in target:
+ boxes = target["boxes"]
+ boxes = box_xyxy_to_cxcywh(boxes)
+ boxes = boxes / torch.tensor([w, h, w, h], dtype=torch.float32)
+ target["boxes"] = boxes
+ return image, target
+
+
+class Compose(object):
+ def __init__(self, transforms):
+ self.transforms = transforms
+
+ def __call__(self, image, target):
+ for t in self.transforms:
+ image, target = t(image, target)
+ return image, target
+
+ def __repr__(self):
+ format_string = self.__class__.__name__ + "("
+ for t in self.transforms:
+ format_string += "\n"
+ format_string += " {0}".format(t)
+ format_string += "\n)"
+ return format_string
diff --git a/GroundingDINO/groundingdino/models/GroundingDINO/__init__.py b/GroundingDINO/groundingdino/models/GroundingDINO/__init__.py
new file mode 100644
index 0000000000000000000000000000000000000000..2af819d61d589cfec2e0ca46612a7456f42b831a
--- /dev/null
+++ b/GroundingDINO/groundingdino/models/GroundingDINO/__init__.py
@@ -0,0 +1,15 @@
+# ------------------------------------------------------------------------
+# Grounding DINO
+# url: https://github.com/IDEA-Research/GroundingDINO
+# Copyright (c) 2023 IDEA. All Rights Reserved.
+# Licensed under the Apache License, Version 2.0 [see LICENSE for details]
+# ------------------------------------------------------------------------
+# Conditional DETR
+# Copyright (c) 2021 Microsoft. All Rights Reserved.
+# Licensed under the Apache License, Version 2.0 [see LICENSE for details]
+# ------------------------------------------------------------------------
+# Copied from DETR (https://github.com/facebookresearch/detr)
+# Copyright (c) Facebook, Inc. and its affiliates. All Rights Reserved.
+# ------------------------------------------------------------------------
+
+from .groundingdino import build_groundingdino
diff --git a/GroundingDINO/groundingdino/models/GroundingDINO/backbone/__init__.py b/GroundingDINO/groundingdino/models/GroundingDINO/backbone/__init__.py
new file mode 100644
index 0000000000000000000000000000000000000000..76e4b272b479a26c63d120c818c140870cd8c287
--- /dev/null
+++ b/GroundingDINO/groundingdino/models/GroundingDINO/backbone/__init__.py
@@ -0,0 +1 @@
+from .backbone import build_backbone
diff --git a/GroundingDINO/groundingdino/models/GroundingDINO/backbone/backbone.py b/GroundingDINO/groundingdino/models/GroundingDINO/backbone/backbone.py
new file mode 100644
index 0000000000000000000000000000000000000000..c8340c723fad8e07e2fc62daaa3912487498814b
--- /dev/null
+++ b/GroundingDINO/groundingdino/models/GroundingDINO/backbone/backbone.py
@@ -0,0 +1,221 @@
+# ------------------------------------------------------------------------
+# Grounding DINO
+# url: https://github.com/IDEA-Research/GroundingDINO
+# Copyright (c) 2023 IDEA. All Rights Reserved.
+# Licensed under the Apache License, Version 2.0 [see LICENSE for details]
+# ------------------------------------------------------------------------
+# Conditional DETR
+# Copyright (c) 2021 Microsoft. All Rights Reserved.
+# Licensed under the Apache License, Version 2.0 [see LICENSE for details]
+# ------------------------------------------------------------------------
+# Copied from DETR (https://github.com/facebookresearch/detr)
+# Copyright (c) Facebook, Inc. and its affiliates. All Rights Reserved.
+# ------------------------------------------------------------------------
+
+"""
+Backbone modules.
+"""
+
+from typing import Dict, List
+
+import torch
+import torch.nn.functional as F
+import torchvision
+from torch import nn
+from torchvision.models._utils import IntermediateLayerGetter
+
+from groundingdino.util.misc import NestedTensor, clean_state_dict, is_main_process
+
+from .position_encoding import build_position_encoding
+from .swin_transformer import build_swin_transformer
+
+
+class FrozenBatchNorm2d(torch.nn.Module):
+ """
+ BatchNorm2d where the batch statistics and the affine parameters are fixed.
+
+ Copy-paste from torchvision.misc.ops with added eps before rqsrt,
+ without which any other models than torchvision.models.resnet[18,34,50,101]
+ produce nans.
+ """
+
+ def __init__(self, n):
+ super(FrozenBatchNorm2d, self).__init__()
+ self.register_buffer("weight", torch.ones(n))
+ self.register_buffer("bias", torch.zeros(n))
+ self.register_buffer("running_mean", torch.zeros(n))
+ self.register_buffer("running_var", torch.ones(n))
+
+ def _load_from_state_dict(
+ self, state_dict, prefix, local_metadata, strict, missing_keys, unexpected_keys, error_msgs
+ ):
+ num_batches_tracked_key = prefix + "num_batches_tracked"
+ if num_batches_tracked_key in state_dict:
+ del state_dict[num_batches_tracked_key]
+
+ super(FrozenBatchNorm2d, self)._load_from_state_dict(
+ state_dict, prefix, local_metadata, strict, missing_keys, unexpected_keys, error_msgs
+ )
+
+ def forward(self, x):
+ # move reshapes to the beginning
+ # to make it fuser-friendly
+ w = self.weight.reshape(1, -1, 1, 1)
+ b = self.bias.reshape(1, -1, 1, 1)
+ rv = self.running_var.reshape(1, -1, 1, 1)
+ rm = self.running_mean.reshape(1, -1, 1, 1)
+ eps = 1e-5
+ scale = w * (rv + eps).rsqrt()
+ bias = b - rm * scale
+ return x * scale + bias
+
+
+class BackboneBase(nn.Module):
+ def __init__(
+ self,
+ backbone: nn.Module,
+ train_backbone: bool,
+ num_channels: int,
+ return_interm_indices: list,
+ ):
+ super().__init__()
+ for name, parameter in backbone.named_parameters():
+ if (
+ not train_backbone
+ or "layer2" not in name
+ and "layer3" not in name
+ and "layer4" not in name
+ ):
+ parameter.requires_grad_(False)
+
+ return_layers = {}
+ for idx, layer_index in enumerate(return_interm_indices):
+ return_layers.update(
+ {"layer{}".format(5 - len(return_interm_indices) + idx): "{}".format(layer_index)}
+ )
+
+ # if len:
+ # if use_stage1_feature:
+ # return_layers = {"layer1": "0", "layer2": "1", "layer3": "2", "layer4": "3"}
+ # else:
+ # return_layers = {"layer2": "0", "layer3": "1", "layer4": "2"}
+ # else:
+ # return_layers = {'layer4': "0"}
+ self.body = IntermediateLayerGetter(backbone, return_layers=return_layers)
+ self.num_channels = num_channels
+
+ def forward(self, tensor_list: NestedTensor):
+ xs = self.body(tensor_list.tensors)
+ out: Dict[str, NestedTensor] = {}
+ for name, x in xs.items():
+ m = tensor_list.mask
+ assert m is not None
+ mask = F.interpolate(m[None].float(), size=x.shape[-2:]).to(torch.bool)[0]
+ out[name] = NestedTensor(x, mask)
+ # import ipdb; ipdb.set_trace()
+ return out
+
+
+class Backbone(BackboneBase):
+ """ResNet backbone with frozen BatchNorm."""
+
+ def __init__(
+ self,
+ name: str,
+ train_backbone: bool,
+ dilation: bool,
+ return_interm_indices: list,
+ batch_norm=FrozenBatchNorm2d,
+ ):
+ if name in ["resnet18", "resnet34", "resnet50", "resnet101"]:
+ backbone = getattr(torchvision.models, name)(
+ replace_stride_with_dilation=[False, False, dilation],
+ pretrained=is_main_process(),
+ norm_layer=batch_norm,
+ )
+ else:
+ raise NotImplementedError("Why you can get here with name {}".format(name))
+ # num_channels = 512 if name in ('resnet18', 'resnet34') else 2048
+ assert name not in ("resnet18", "resnet34"), "Only resnet50 and resnet101 are available."
+ assert return_interm_indices in [[0, 1, 2, 3], [1, 2, 3], [3]]
+ num_channels_all = [256, 512, 1024, 2048]
+ num_channels = num_channels_all[4 - len(return_interm_indices) :]
+ super().__init__(backbone, train_backbone, num_channels, return_interm_indices)
+
+
+class Joiner(nn.Sequential):
+ def __init__(self, backbone, position_embedding):
+ super().__init__(backbone, position_embedding)
+
+ def forward(self, tensor_list: NestedTensor):
+ xs = self[0](tensor_list)
+ out: List[NestedTensor] = []
+ pos = []
+ for name, x in xs.items():
+ out.append(x)
+ # position encoding
+ pos.append(self[1](x).to(x.tensors.dtype))
+
+ return out, pos
+
+
+def build_backbone(args):
+ """
+ Useful args:
+ - backbone: backbone name
+ - lr_backbone:
+ - dilation
+ - return_interm_indices: available: [0,1,2,3], [1,2,3], [3]
+ - backbone_freeze_keywords:
+ - use_checkpoint: for swin only for now
+
+ """
+ position_embedding = build_position_encoding(args)
+ train_backbone = True
+ if not train_backbone:
+ raise ValueError("Please set lr_backbone > 0")
+ return_interm_indices = args.return_interm_indices
+ assert return_interm_indices in [[0, 1, 2, 3], [1, 2, 3], [3]]
+ args.backbone_freeze_keywords
+ use_checkpoint = getattr(args, "use_checkpoint", False)
+
+ if args.backbone in ["resnet50", "resnet101"]:
+ backbone = Backbone(
+ args.backbone,
+ train_backbone,
+ args.dilation,
+ return_interm_indices,
+ batch_norm=FrozenBatchNorm2d,
+ )
+ bb_num_channels = backbone.num_channels
+ elif args.backbone in [
+ "swin_T_224_1k",
+ "swin_B_224_22k",
+ "swin_B_384_22k",
+ "swin_L_224_22k",
+ "swin_L_384_22k",
+ ]:
+ pretrain_img_size = int(args.backbone.split("_")[-2])
+ backbone = build_swin_transformer(
+ args.backbone,
+ pretrain_img_size=pretrain_img_size,
+ out_indices=tuple(return_interm_indices),
+ dilation=False,
+ use_checkpoint=use_checkpoint,
+ )
+
+ bb_num_channels = backbone.num_features[4 - len(return_interm_indices) :]
+ else:
+ raise NotImplementedError("Unknown backbone {}".format(args.backbone))
+
+ assert len(bb_num_channels) == len(
+ return_interm_indices
+ ), f"len(bb_num_channels) {len(bb_num_channels)} != len(return_interm_indices) {len(return_interm_indices)}"
+
+ model = Joiner(backbone, position_embedding)
+ model.num_channels = bb_num_channels
+ assert isinstance(
+ bb_num_channels, List
+ ), "bb_num_channels is expected to be a List but {}".format(type(bb_num_channels))
+ # import ipdb; ipdb.set_trace()
+ return model
diff --git a/GroundingDINO/groundingdino/models/GroundingDINO/backbone/position_encoding.py b/GroundingDINO/groundingdino/models/GroundingDINO/backbone/position_encoding.py
new file mode 100644
index 0000000000000000000000000000000000000000..eac7e896bbe85a670824bfe8ef487d0535d5bd99
--- /dev/null
+++ b/GroundingDINO/groundingdino/models/GroundingDINO/backbone/position_encoding.py
@@ -0,0 +1,186 @@
+# ------------------------------------------------------------------------
+# Grounding DINO
+# url: https://github.com/IDEA-Research/GroundingDINO
+# Copyright (c) 2023 IDEA. All Rights Reserved.
+# Licensed under the Apache License, Version 2.0 [see LICENSE for details]
+# ------------------------------------------------------------------------
+# DINO
+# Copyright (c) 2022 IDEA. All Rights Reserved.
+# Licensed under the Apache License, Version 2.0 [see LICENSE for details]
+# ------------------------------------------------------------------------
+# Conditional DETR
+# Copyright (c) 2021 Microsoft. All Rights Reserved.
+# Licensed under the Apache License, Version 2.0 [see LICENSE for details]
+# ------------------------------------------------------------------------
+# Copied from DETR (https://github.com/facebookresearch/detr)
+# Copyright (c) Facebook, Inc. and its affiliates. All Rights Reserved.
+# ------------------------------------------------------------------------
+
+"""
+Various positional encodings for the transformer.
+"""
+import math
+
+import torch
+from torch import nn
+
+from groundingdino.util.misc import NestedTensor
+
+
+class PositionEmbeddingSine(nn.Module):
+ """
+ This is a more standard version of the position embedding, very similar to the one
+ used by the Attention is all you need paper, generalized to work on images.
+ """
+
+ def __init__(self, num_pos_feats=64, temperature=10000, normalize=False, scale=None):
+ super().__init__()
+ self.num_pos_feats = num_pos_feats
+ self.temperature = temperature
+ self.normalize = normalize
+ if scale is not None and normalize is False:
+ raise ValueError("normalize should be True if scale is passed")
+ if scale is None:
+ scale = 2 * math.pi
+ self.scale = scale
+
+ def forward(self, tensor_list: NestedTensor):
+ x = tensor_list.tensors
+ mask = tensor_list.mask
+ assert mask is not None
+ not_mask = ~mask
+ y_embed = not_mask.cumsum(1, dtype=torch.float32)
+ x_embed = not_mask.cumsum(2, dtype=torch.float32)
+ if self.normalize:
+ eps = 1e-6
+ # if os.environ.get("SHILONG_AMP", None) == '1':
+ # eps = 1e-4
+ # else:
+ # eps = 1e-6
+ y_embed = y_embed / (y_embed[:, -1:, :] + eps) * self.scale
+ x_embed = x_embed / (x_embed[:, :, -1:] + eps) * self.scale
+
+ dim_t = torch.arange(self.num_pos_feats, dtype=torch.float32, device=x.device)
+ dim_t = self.temperature ** (2 * (dim_t // 2) / self.num_pos_feats)
+
+ pos_x = x_embed[:, :, :, None] / dim_t
+ pos_y = y_embed[:, :, :, None] / dim_t
+ pos_x = torch.stack(
+ (pos_x[:, :, :, 0::2].sin(), pos_x[:, :, :, 1::2].cos()), dim=4
+ ).flatten(3)
+ pos_y = torch.stack(
+ (pos_y[:, :, :, 0::2].sin(), pos_y[:, :, :, 1::2].cos()), dim=4
+ ).flatten(3)
+ pos = torch.cat((pos_y, pos_x), dim=3).permute(0, 3, 1, 2)
+ return pos
+
+
+class PositionEmbeddingSineHW(nn.Module):
+ """
+ This is a more standard version of the position embedding, very similar to the one
+ used by the Attention is all you need paper, generalized to work on images.
+ """
+
+ def __init__(
+ self, num_pos_feats=64, temperatureH=10000, temperatureW=10000, normalize=False, scale=None
+ ):
+ super().__init__()
+ self.num_pos_feats = num_pos_feats
+ self.temperatureH = temperatureH
+ self.temperatureW = temperatureW
+ self.normalize = normalize
+ if scale is not None and normalize is False:
+ raise ValueError("normalize should be True if scale is passed")
+ if scale is None:
+ scale = 2 * math.pi
+ self.scale = scale
+
+ def forward(self, tensor_list: NestedTensor):
+ x = tensor_list.tensors
+ mask = tensor_list.mask
+ assert mask is not None
+ not_mask = ~mask
+ y_embed = not_mask.cumsum(1, dtype=torch.float32)
+ x_embed = not_mask.cumsum(2, dtype=torch.float32)
+
+ # import ipdb; ipdb.set_trace()
+
+ if self.normalize:
+ eps = 1e-6
+ y_embed = y_embed / (y_embed[:, -1:, :] + eps) * self.scale
+ x_embed = x_embed / (x_embed[:, :, -1:] + eps) * self.scale
+
+ dim_tx = torch.arange(self.num_pos_feats, dtype=torch.float32, device=x.device)
+ dim_tx = self.temperatureW ** (2 * (torch.div(dim_tx, 2, rounding_mode='floor')) / self.num_pos_feats)
+ pos_x = x_embed[:, :, :, None] / dim_tx
+
+ dim_ty = torch.arange(self.num_pos_feats, dtype=torch.float32, device=x.device)
+ dim_ty = self.temperatureH ** (2 * (torch.div(dim_ty, 2, rounding_mode='floor')) / self.num_pos_feats)
+ pos_y = y_embed[:, :, :, None] / dim_ty
+
+ pos_x = torch.stack(
+ (pos_x[:, :, :, 0::2].sin(), pos_x[:, :, :, 1::2].cos()), dim=4
+ ).flatten(3)
+ pos_y = torch.stack(
+ (pos_y[:, :, :, 0::2].sin(), pos_y[:, :, :, 1::2].cos()), dim=4
+ ).flatten(3)
+ pos = torch.cat((pos_y, pos_x), dim=3).permute(0, 3, 1, 2)
+
+ # import ipdb; ipdb.set_trace()
+
+ return pos
+
+
+class PositionEmbeddingLearned(nn.Module):
+ """
+ Absolute pos embedding, learned.
+ """
+
+ def __init__(self, num_pos_feats=256):
+ super().__init__()
+ self.row_embed = nn.Embedding(50, num_pos_feats)
+ self.col_embed = nn.Embedding(50, num_pos_feats)
+ self.reset_parameters()
+
+ def reset_parameters(self):
+ nn.init.uniform_(self.row_embed.weight)
+ nn.init.uniform_(self.col_embed.weight)
+
+ def forward(self, tensor_list: NestedTensor):
+ x = tensor_list.tensors
+ h, w = x.shape[-2:]
+ i = torch.arange(w, device=x.device)
+ j = torch.arange(h, device=x.device)
+ x_emb = self.col_embed(i)
+ y_emb = self.row_embed(j)
+ pos = (
+ torch.cat(
+ [
+ x_emb.unsqueeze(0).repeat(h, 1, 1),
+ y_emb.unsqueeze(1).repeat(1, w, 1),
+ ],
+ dim=-1,
+ )
+ .permute(2, 0, 1)
+ .unsqueeze(0)
+ .repeat(x.shape[0], 1, 1, 1)
+ )
+ return pos
+
+
+def build_position_encoding(args):
+ N_steps = args.hidden_dim // 2
+ if args.position_embedding in ("v2", "sine"):
+ # TODO find a better way of exposing other arguments
+ position_embedding = PositionEmbeddingSineHW(
+ N_steps,
+ temperatureH=args.pe_temperatureH,
+ temperatureW=args.pe_temperatureW,
+ normalize=True,
+ )
+ elif args.position_embedding in ("v3", "learned"):
+ position_embedding = PositionEmbeddingLearned(N_steps)
+ else:
+ raise ValueError(f"not supported {args.position_embedding}")
+
+ return position_embedding
diff --git a/GroundingDINO/groundingdino/models/GroundingDINO/backbone/swin_transformer.py b/GroundingDINO/groundingdino/models/GroundingDINO/backbone/swin_transformer.py
new file mode 100644
index 0000000000000000000000000000000000000000..fa8837e4001e41dfed6af99e6619f8b03b989824
--- /dev/null
+++ b/GroundingDINO/groundingdino/models/GroundingDINO/backbone/swin_transformer.py
@@ -0,0 +1,802 @@
+# ------------------------------------------------------------------------
+# Grounding DINO
+# url: https://github.com/IDEA-Research/GroundingDINO
+# Copyright (c) 2023 IDEA. All Rights Reserved.
+# Licensed under the Apache License, Version 2.0 [see LICENSE for details]
+# ------------------------------------------------------------------------
+# DINO
+# Copyright (c) 2022 IDEA. All Rights Reserved.
+# Licensed under the Apache License, Version 2.0 [see LICENSE for details]
+# --------------------------------------------------------
+# modified from https://github.com/SwinTransformer/Swin-Transformer-Object-Detection/blob/master/mmdet/models/backbones/swin_transformer.py
+# --------------------------------------------------------
+
+import numpy as np
+import torch
+import torch.nn as nn
+import torch.nn.functional as F
+import torch.utils.checkpoint as checkpoint
+from timm.models.layers import DropPath, to_2tuple, trunc_normal_
+
+from groundingdino.util.misc import NestedTensor
+
+
+class Mlp(nn.Module):
+ """Multilayer perceptron."""
+
+ def __init__(
+ self, in_features, hidden_features=None, out_features=None, act_layer=nn.GELU, drop=0.0
+ ):
+ super().__init__()
+ out_features = out_features or in_features
+ hidden_features = hidden_features or in_features
+ self.fc1 = nn.Linear(in_features, hidden_features)
+ self.act = act_layer()
+ self.fc2 = nn.Linear(hidden_features, out_features)
+ self.drop = nn.Dropout(drop)
+
+ def forward(self, x):
+ x = self.fc1(x)
+ x = self.act(x)
+ x = self.drop(x)
+ x = self.fc2(x)
+ x = self.drop(x)
+ return x
+
+
+def window_partition(x, window_size):
+ """
+ Args:
+ x: (B, H, W, C)
+ window_size (int): window size
+ Returns:
+ windows: (num_windows*B, window_size, window_size, C)
+ """
+ B, H, W, C = x.shape
+ x = x.view(B, H // window_size, window_size, W // window_size, window_size, C)
+ windows = x.permute(0, 1, 3, 2, 4, 5).contiguous().view(-1, window_size, window_size, C)
+ return windows
+
+
+def window_reverse(windows, window_size, H, W):
+ """
+ Args:
+ windows: (num_windows*B, window_size, window_size, C)
+ window_size (int): Window size
+ H (int): Height of image
+ W (int): Width of image
+ Returns:
+ x: (B, H, W, C)
+ """
+ B = int(windows.shape[0] / (H * W / window_size / window_size))
+ x = windows.view(B, H // window_size, W // window_size, window_size, window_size, -1)
+ x = x.permute(0, 1, 3, 2, 4, 5).contiguous().view(B, H, W, -1)
+ return x
+
+
+class WindowAttention(nn.Module):
+ """Window based multi-head self attention (W-MSA) module with relative position bias.
+ It supports both of shifted and non-shifted window.
+ Args:
+ dim (int): Number of input channels.
+ window_size (tuple[int]): The height and width of the window.
+ num_heads (int): Number of attention heads.
+ qkv_bias (bool, optional): If True, add a learnable bias to query, key, value. Default: True
+ qk_scale (float | None, optional): Override default qk scale of head_dim ** -0.5 if set
+ attn_drop (float, optional): Dropout ratio of attention weight. Default: 0.0
+ proj_drop (float, optional): Dropout ratio of output. Default: 0.0
+ """
+
+ def __init__(
+ self,
+ dim,
+ window_size,
+ num_heads,
+ qkv_bias=True,
+ qk_scale=None,
+ attn_drop=0.0,
+ proj_drop=0.0,
+ ):
+
+ super().__init__()
+ self.dim = dim
+ self.window_size = window_size # Wh, Ww
+ self.num_heads = num_heads
+ head_dim = dim // num_heads
+ self.scale = qk_scale or head_dim**-0.5
+
+ # define a parameter table of relative position bias
+ self.relative_position_bias_table = nn.Parameter(
+ torch.zeros((2 * window_size[0] - 1) * (2 * window_size[1] - 1), num_heads)
+ ) # 2*Wh-1 * 2*Ww-1, nH
+
+ # get pair-wise relative position index for each token inside the window
+ coords_h = torch.arange(self.window_size[0])
+ coords_w = torch.arange(self.window_size[1])
+ coords = torch.stack(torch.meshgrid([coords_h, coords_w])) # 2, Wh, Ww
+ coords_flatten = torch.flatten(coords, 1) # 2, Wh*Ww
+ relative_coords = coords_flatten[:, :, None] - coords_flatten[:, None, :] # 2, Wh*Ww, Wh*Ww
+ relative_coords = relative_coords.permute(1, 2, 0).contiguous() # Wh*Ww, Wh*Ww, 2
+ relative_coords[:, :, 0] += self.window_size[0] - 1 # shift to start from 0
+ relative_coords[:, :, 1] += self.window_size[1] - 1
+ relative_coords[:, :, 0] *= 2 * self.window_size[1] - 1
+ relative_position_index = relative_coords.sum(-1) # Wh*Ww, Wh*Ww
+ self.register_buffer("relative_position_index", relative_position_index)
+
+ self.qkv = nn.Linear(dim, dim * 3, bias=qkv_bias)
+ self.attn_drop = nn.Dropout(attn_drop)
+ self.proj = nn.Linear(dim, dim)
+ self.proj_drop = nn.Dropout(proj_drop)
+
+ trunc_normal_(self.relative_position_bias_table, std=0.02)
+ self.softmax = nn.Softmax(dim=-1)
+
+ def forward(self, x, mask=None):
+ """Forward function.
+ Args:
+ x: input features with shape of (num_windows*B, N, C)
+ mask: (0/-inf) mask with shape of (num_windows, Wh*Ww, Wh*Ww) or None
+ """
+ B_, N, C = x.shape
+ qkv = (
+ self.qkv(x)
+ .reshape(B_, N, 3, self.num_heads, C // self.num_heads)
+ .permute(2, 0, 3, 1, 4)
+ )
+ q, k, v = qkv[0], qkv[1], qkv[2] # make torchscript happy (cannot use tensor as tuple)
+
+ q = q * self.scale
+ attn = q @ k.transpose(-2, -1)
+
+ relative_position_bias = self.relative_position_bias_table[
+ self.relative_position_index.view(-1)
+ ].view(
+ self.window_size[0] * self.window_size[1], self.window_size[0] * self.window_size[1], -1
+ ) # Wh*Ww,Wh*Ww,nH
+ relative_position_bias = relative_position_bias.permute(
+ 2, 0, 1
+ ).contiguous() # nH, Wh*Ww, Wh*Ww
+ attn = attn + relative_position_bias.unsqueeze(0)
+
+ if mask is not None:
+ nW = mask.shape[0]
+ attn = attn.view(B_ // nW, nW, self.num_heads, N, N) + mask.unsqueeze(1).unsqueeze(0)
+ attn = attn.view(-1, self.num_heads, N, N)
+ attn = self.softmax(attn)
+ else:
+ attn = self.softmax(attn)
+
+ attn = self.attn_drop(attn)
+
+ x = (attn @ v).transpose(1, 2).reshape(B_, N, C)
+ x = self.proj(x)
+ x = self.proj_drop(x)
+ return x
+
+
+class SwinTransformerBlock(nn.Module):
+ """Swin Transformer Block.
+ Args:
+ dim (int): Number of input channels.
+ num_heads (int): Number of attention heads.
+ window_size (int): Window size.
+ shift_size (int): Shift size for SW-MSA.
+ mlp_ratio (float): Ratio of mlp hidden dim to embedding dim.
+ qkv_bias (bool, optional): If True, add a learnable bias to query, key, value. Default: True
+ qk_scale (float | None, optional): Override default qk scale of head_dim ** -0.5 if set.
+ drop (float, optional): Dropout rate. Default: 0.0
+ attn_drop (float, optional): Attention dropout rate. Default: 0.0
+ drop_path (float, optional): Stochastic depth rate. Default: 0.0
+ act_layer (nn.Module, optional): Activation layer. Default: nn.GELU
+ norm_layer (nn.Module, optional): Normalization layer. Default: nn.LayerNorm
+ """
+
+ def __init__(
+ self,
+ dim,
+ num_heads,
+ window_size=7,
+ shift_size=0,
+ mlp_ratio=4.0,
+ qkv_bias=True,
+ qk_scale=None,
+ drop=0.0,
+ attn_drop=0.0,
+ drop_path=0.0,
+ act_layer=nn.GELU,
+ norm_layer=nn.LayerNorm,
+ ):
+ super().__init__()
+ self.dim = dim
+ self.num_heads = num_heads
+ self.window_size = window_size
+ self.shift_size = shift_size
+ self.mlp_ratio = mlp_ratio
+ assert 0 <= self.shift_size < self.window_size, "shift_size must in 0-window_size"
+
+ self.norm1 = norm_layer(dim)
+ self.attn = WindowAttention(
+ dim,
+ window_size=to_2tuple(self.window_size),
+ num_heads=num_heads,
+ qkv_bias=qkv_bias,
+ qk_scale=qk_scale,
+ attn_drop=attn_drop,
+ proj_drop=drop,
+ )
+
+ self.drop_path = DropPath(drop_path) if drop_path > 0.0 else nn.Identity()
+ self.norm2 = norm_layer(dim)
+ mlp_hidden_dim = int(dim * mlp_ratio)
+ self.mlp = Mlp(
+ in_features=dim, hidden_features=mlp_hidden_dim, act_layer=act_layer, drop=drop
+ )
+
+ self.H = None
+ self.W = None
+
+ def forward(self, x, mask_matrix):
+ """Forward function.
+ Args:
+ x: Input feature, tensor size (B, H*W, C).
+ H, W: Spatial resolution of the input feature.
+ mask_matrix: Attention mask for cyclic shift.
+ """
+ B, L, C = x.shape
+ H, W = self.H, self.W
+ assert L == H * W, "input feature has wrong size"
+
+ shortcut = x
+ x = self.norm1(x)
+ x = x.view(B, H, W, C)
+
+ # pad feature maps to multiples of window size
+ pad_l = pad_t = 0
+ pad_r = (self.window_size - W % self.window_size) % self.window_size
+ pad_b = (self.window_size - H % self.window_size) % self.window_size
+ x = F.pad(x, (0, 0, pad_l, pad_r, pad_t, pad_b))
+ _, Hp, Wp, _ = x.shape
+
+ # cyclic shift
+ if self.shift_size > 0:
+ shifted_x = torch.roll(x, shifts=(-self.shift_size, -self.shift_size), dims=(1, 2))
+ attn_mask = mask_matrix
+ else:
+ shifted_x = x
+ attn_mask = None
+
+ # partition windows
+ x_windows = window_partition(
+ shifted_x, self.window_size
+ ) # nW*B, window_size, window_size, C
+ x_windows = x_windows.view(
+ -1, self.window_size * self.window_size, C
+ ) # nW*B, window_size*window_size, C
+
+ # W-MSA/SW-MSA
+ attn_windows = self.attn(x_windows, mask=attn_mask) # nW*B, window_size*window_size, C
+
+ # merge windows
+ attn_windows = attn_windows.view(-1, self.window_size, self.window_size, C)
+ shifted_x = window_reverse(attn_windows, self.window_size, Hp, Wp) # B H' W' C
+
+ # reverse cyclic shift
+ if self.shift_size > 0:
+ x = torch.roll(shifted_x, shifts=(self.shift_size, self.shift_size), dims=(1, 2))
+ else:
+ x = shifted_x
+
+ if pad_r > 0 or pad_b > 0:
+ x = x[:, :H, :W, :].contiguous()
+
+ x = x.view(B, H * W, C)
+
+ # FFN
+ x = shortcut + self.drop_path(x)
+ x = x + self.drop_path(self.mlp(self.norm2(x)))
+
+ return x
+
+
+class PatchMerging(nn.Module):
+ """Patch Merging Layer
+ Args:
+ dim (int): Number of input channels.
+ norm_layer (nn.Module, optional): Normalization layer. Default: nn.LayerNorm
+ """
+
+ def __init__(self, dim, norm_layer=nn.LayerNorm):
+ super().__init__()
+ self.dim = dim
+ self.reduction = nn.Linear(4 * dim, 2 * dim, bias=False)
+ self.norm = norm_layer(4 * dim)
+
+ def forward(self, x, H, W):
+ """Forward function.
+ Args:
+ x: Input feature, tensor size (B, H*W, C).
+ H, W: Spatial resolution of the input feature.
+ """
+ B, L, C = x.shape
+ assert L == H * W, "input feature has wrong size"
+
+ x = x.view(B, H, W, C)
+
+ # padding
+ pad_input = (H % 2 == 1) or (W % 2 == 1)
+ if pad_input:
+ x = F.pad(x, (0, 0, 0, W % 2, 0, H % 2))
+
+ x0 = x[:, 0::2, 0::2, :] # B H/2 W/2 C
+ x1 = x[:, 1::2, 0::2, :] # B H/2 W/2 C
+ x2 = x[:, 0::2, 1::2, :] # B H/2 W/2 C
+ x3 = x[:, 1::2, 1::2, :] # B H/2 W/2 C
+ x = torch.cat([x0, x1, x2, x3], -1) # B H/2 W/2 4*C
+ x = x.view(B, -1, 4 * C) # B H/2*W/2 4*C
+
+ x = self.norm(x)
+ x = self.reduction(x)
+
+ return x
+
+
+class BasicLayer(nn.Module):
+ """A basic Swin Transformer layer for one stage.
+ Args:
+ dim (int): Number of feature channels
+ depth (int): Depths of this stage.
+ num_heads (int): Number of attention head.
+ window_size (int): Local window size. Default: 7.
+ mlp_ratio (float): Ratio of mlp hidden dim to embedding dim. Default: 4.
+ qkv_bias (bool, optional): If True, add a learnable bias to query, key, value. Default: True
+ qk_scale (float | None, optional): Override default qk scale of head_dim ** -0.5 if set.
+ drop (float, optional): Dropout rate. Default: 0.0
+ attn_drop (float, optional): Attention dropout rate. Default: 0.0
+ drop_path (float | tuple[float], optional): Stochastic depth rate. Default: 0.0
+ norm_layer (nn.Module, optional): Normalization layer. Default: nn.LayerNorm
+ downsample (nn.Module | None, optional): Downsample layer at the end of the layer. Default: None
+ use_checkpoint (bool): Whether to use checkpointing to save memory. Default: False.
+ """
+
+ def __init__(
+ self,
+ dim,
+ depth,
+ num_heads,
+ window_size=7,
+ mlp_ratio=4.0,
+ qkv_bias=True,
+ qk_scale=None,
+ drop=0.0,
+ attn_drop=0.0,
+ drop_path=0.0,
+ norm_layer=nn.LayerNorm,
+ downsample=None,
+ use_checkpoint=False,
+ ):
+ super().__init__()
+ self.window_size = window_size
+ self.shift_size = window_size // 2
+ self.depth = depth
+ self.use_checkpoint = use_checkpoint
+
+ # build blocks
+ self.blocks = nn.ModuleList(
+ [
+ SwinTransformerBlock(
+ dim=dim,
+ num_heads=num_heads,
+ window_size=window_size,
+ shift_size=0 if (i % 2 == 0) else window_size // 2,
+ mlp_ratio=mlp_ratio,
+ qkv_bias=qkv_bias,
+ qk_scale=qk_scale,
+ drop=drop,
+ attn_drop=attn_drop,
+ drop_path=drop_path[i] if isinstance(drop_path, list) else drop_path,
+ norm_layer=norm_layer,
+ )
+ for i in range(depth)
+ ]
+ )
+
+ # patch merging layer
+ if downsample is not None:
+ self.downsample = downsample(dim=dim, norm_layer=norm_layer)
+ else:
+ self.downsample = None
+
+ def forward(self, x, H, W):
+ """Forward function.
+ Args:
+ x: Input feature, tensor size (B, H*W, C).
+ H, W: Spatial resolution of the input feature.
+ """
+
+ # calculate attention mask for SW-MSA
+ Hp = int(np.ceil(H / self.window_size)) * self.window_size
+ Wp = int(np.ceil(W / self.window_size)) * self.window_size
+ img_mask = torch.zeros((1, Hp, Wp, 1), device=x.device, dtype=x.dtype) # 1 Hp Wp 1
+ h_slices = (
+ slice(0, -self.window_size),
+ slice(-self.window_size, -self.shift_size),
+ slice(-self.shift_size, None),
+ )
+ w_slices = (
+ slice(0, -self.window_size),
+ slice(-self.window_size, -self.shift_size),
+ slice(-self.shift_size, None),
+ )
+ cnt = 0
+ for h in h_slices:
+ for w in w_slices:
+ img_mask[:, h, w, :] = cnt
+ cnt += 1
+
+ mask_windows = window_partition(
+ img_mask, self.window_size
+ ) # nW, window_size, window_size, 1
+ mask_windows = mask_windows.view(-1, self.window_size * self.window_size)
+ attn_mask = mask_windows.unsqueeze(1) - mask_windows.unsqueeze(2)
+ attn_mask = attn_mask.masked_fill(attn_mask != 0, float(-100.0)).masked_fill(
+ attn_mask == 0, float(0.0)
+ )
+
+ for blk in self.blocks:
+ blk.H, blk.W = H, W
+ if self.use_checkpoint:
+ x = checkpoint.checkpoint(blk, x, attn_mask)
+ else:
+ x = blk(x, attn_mask)
+ if self.downsample is not None:
+ x_down = self.downsample(x, H, W)
+ Wh, Ww = (H + 1) // 2, (W + 1) // 2
+ return x, H, W, x_down, Wh, Ww
+ else:
+ return x, H, W, x, H, W
+
+
+class PatchEmbed(nn.Module):
+ """Image to Patch Embedding
+ Args:
+ patch_size (int): Patch token size. Default: 4.
+ in_chans (int): Number of input image channels. Default: 3.
+ embed_dim (int): Number of linear projection output channels. Default: 96.
+ norm_layer (nn.Module, optional): Normalization layer. Default: None
+ """
+
+ def __init__(self, patch_size=4, in_chans=3, embed_dim=96, norm_layer=None):
+ super().__init__()
+ patch_size = to_2tuple(patch_size)
+ self.patch_size = patch_size
+
+ self.in_chans = in_chans
+ self.embed_dim = embed_dim
+
+ self.proj = nn.Conv2d(in_chans, embed_dim, kernel_size=patch_size, stride=patch_size)
+ if norm_layer is not None:
+ self.norm = norm_layer(embed_dim)
+ else:
+ self.norm = None
+
+ def forward(self, x):
+ """Forward function."""
+ # padding
+ _, _, H, W = x.size()
+ if W % self.patch_size[1] != 0:
+ x = F.pad(x, (0, self.patch_size[1] - W % self.patch_size[1]))
+ if H % self.patch_size[0] != 0:
+ x = F.pad(x, (0, 0, 0, self.patch_size[0] - H % self.patch_size[0]))
+
+ x = self.proj(x) # B C Wh Ww
+ if self.norm is not None:
+ Wh, Ww = x.size(2), x.size(3)
+ x = x.flatten(2).transpose(1, 2)
+ x = self.norm(x)
+ x = x.transpose(1, 2).view(-1, self.embed_dim, Wh, Ww)
+
+ return x
+
+
+class SwinTransformer(nn.Module):
+ """Swin Transformer backbone.
+ A PyTorch impl of : `Swin Transformer: Hierarchical Vision Transformer using Shifted Windows` -
+ https://arxiv.org/pdf/2103.14030
+ Args:
+ pretrain_img_size (int): Input image size for training the pretrained model,
+ used in absolute postion embedding. Default 224.
+ patch_size (int | tuple(int)): Patch size. Default: 4.
+ in_chans (int): Number of input image channels. Default: 3.
+ embed_dim (int): Number of linear projection output channels. Default: 96.
+ depths (tuple[int]): Depths of each Swin Transformer stage.
+ num_heads (tuple[int]): Number of attention head of each stage.
+ window_size (int): Window size. Default: 7.
+ mlp_ratio (float): Ratio of mlp hidden dim to embedding dim. Default: 4.
+ qkv_bias (bool): If True, add a learnable bias to query, key, value. Default: True
+ qk_scale (float): Override default qk scale of head_dim ** -0.5 if set.
+ drop_rate (float): Dropout rate.
+ attn_drop_rate (float): Attention dropout rate. Default: 0.
+ drop_path_rate (float): Stochastic depth rate. Default: 0.2.
+ norm_layer (nn.Module): Normalization layer. Default: nn.LayerNorm.
+ ape (bool): If True, add absolute position embedding to the patch embedding. Default: False.
+ patch_norm (bool): If True, add normalization after patch embedding. Default: True.
+ out_indices (Sequence[int]): Output from which stages.
+ frozen_stages (int): Stages to be frozen (stop grad and set eval mode).
+ -1 means not freezing any parameters.
+ use_checkpoint (bool): Whether to use checkpointing to save memory. Default: False.
+ dilation (bool): if True, the output size if 16x downsample, ow 32x downsample.
+ """
+
+ def __init__(
+ self,
+ pretrain_img_size=224,
+ patch_size=4,
+ in_chans=3,
+ embed_dim=96,
+ depths=[2, 2, 6, 2],
+ num_heads=[3, 6, 12, 24],
+ window_size=7,
+ mlp_ratio=4.0,
+ qkv_bias=True,
+ qk_scale=None,
+ drop_rate=0.0,
+ attn_drop_rate=0.0,
+ drop_path_rate=0.2,
+ norm_layer=nn.LayerNorm,
+ ape=False,
+ patch_norm=True,
+ out_indices=(0, 1, 2, 3),
+ frozen_stages=-1,
+ dilation=False,
+ use_checkpoint=False,
+ ):
+ super().__init__()
+
+ self.pretrain_img_size = pretrain_img_size
+ self.num_layers = len(depths)
+ self.embed_dim = embed_dim
+ self.ape = ape
+ self.patch_norm = patch_norm
+ self.out_indices = out_indices
+ self.frozen_stages = frozen_stages
+ self.dilation = dilation
+
+ # if use_checkpoint:
+ # print("use_checkpoint!!!!!!!!!!!!!!!!!!!!!!!!")
+
+ # split image into non-overlapping patches
+ self.patch_embed = PatchEmbed(
+ patch_size=patch_size,
+ in_chans=in_chans,
+ embed_dim=embed_dim,
+ norm_layer=norm_layer if self.patch_norm else None,
+ )
+
+ # absolute position embedding
+ if self.ape:
+ pretrain_img_size = to_2tuple(pretrain_img_size)
+ patch_size = to_2tuple(patch_size)
+ patches_resolution = [
+ pretrain_img_size[0] // patch_size[0],
+ pretrain_img_size[1] // patch_size[1],
+ ]
+
+ self.absolute_pos_embed = nn.Parameter(
+ torch.zeros(1, embed_dim, patches_resolution[0], patches_resolution[1])
+ )
+ trunc_normal_(self.absolute_pos_embed, std=0.02)
+
+ self.pos_drop = nn.Dropout(p=drop_rate)
+
+ # stochastic depth
+ dpr = [
+ x.item() for x in torch.linspace(0, drop_path_rate, sum(depths))
+ ] # stochastic depth decay rule
+
+ # build layers
+ self.layers = nn.ModuleList()
+ # prepare downsample list
+ downsamplelist = [PatchMerging for i in range(self.num_layers)]
+ downsamplelist[-1] = None
+ num_features = [int(embed_dim * 2**i) for i in range(self.num_layers)]
+ if self.dilation:
+ downsamplelist[-2] = None
+ num_features[-1] = int(embed_dim * 2 ** (self.num_layers - 1)) // 2
+ for i_layer in range(self.num_layers):
+ layer = BasicLayer(
+ # dim=int(embed_dim * 2 ** i_layer),
+ dim=num_features[i_layer],
+ depth=depths[i_layer],
+ num_heads=num_heads[i_layer],
+ window_size=window_size,
+ mlp_ratio=mlp_ratio,
+ qkv_bias=qkv_bias,
+ qk_scale=qk_scale,
+ drop=drop_rate,
+ attn_drop=attn_drop_rate,
+ drop_path=dpr[sum(depths[:i_layer]) : sum(depths[: i_layer + 1])],
+ norm_layer=norm_layer,
+ # downsample=PatchMerging if (i_layer < self.num_layers - 1) else None,
+ downsample=downsamplelist[i_layer],
+ use_checkpoint=use_checkpoint,
+ )
+ self.layers.append(layer)
+
+ # num_features = [int(embed_dim * 2 ** i) for i in range(self.num_layers)]
+ self.num_features = num_features
+
+ # add a norm layer for each output
+ for i_layer in out_indices:
+ layer = norm_layer(num_features[i_layer])
+ layer_name = f"norm{i_layer}"
+ self.add_module(layer_name, layer)
+
+ self._freeze_stages()
+
+ def _freeze_stages(self):
+ if self.frozen_stages >= 0:
+ self.patch_embed.eval()
+ for param in self.patch_embed.parameters():
+ param.requires_grad = False
+
+ if self.frozen_stages >= 1 and self.ape:
+ self.absolute_pos_embed.requires_grad = False
+
+ if self.frozen_stages >= 2:
+ self.pos_drop.eval()
+ for i in range(0, self.frozen_stages - 1):
+ m = self.layers[i]
+ m.eval()
+ for param in m.parameters():
+ param.requires_grad = False
+
+ # def init_weights(self, pretrained=None):
+ # """Initialize the weights in backbone.
+ # Args:
+ # pretrained (str, optional): Path to pre-trained weights.
+ # Defaults to None.
+ # """
+
+ # def _init_weights(m):
+ # if isinstance(m, nn.Linear):
+ # trunc_normal_(m.weight, std=.02)
+ # if isinstance(m, nn.Linear) and m.bias is not None:
+ # nn.init.constant_(m.bias, 0)
+ # elif isinstance(m, nn.LayerNorm):
+ # nn.init.constant_(m.bias, 0)
+ # nn.init.constant_(m.weight, 1.0)
+
+ # if isinstance(pretrained, str):
+ # self.apply(_init_weights)
+ # logger = get_root_logger()
+ # load_checkpoint(self, pretrained, strict=False, logger=logger)
+ # elif pretrained is None:
+ # self.apply(_init_weights)
+ # else:
+ # raise TypeError('pretrained must be a str or None')
+
+ def forward_raw(self, x):
+ """Forward function."""
+ x = self.patch_embed(x)
+
+ Wh, Ww = x.size(2), x.size(3)
+ if self.ape:
+ # interpolate the position embedding to the corresponding size
+ absolute_pos_embed = F.interpolate(
+ self.absolute_pos_embed, size=(Wh, Ww), mode="bicubic"
+ )
+ x = (x + absolute_pos_embed).flatten(2).transpose(1, 2) # B Wh*Ww C
+ else:
+ x = x.flatten(2).transpose(1, 2)
+ x = self.pos_drop(x)
+
+ outs = []
+ for i in range(self.num_layers):
+ layer = self.layers[i]
+ x_out, H, W, x, Wh, Ww = layer(x, Wh, Ww)
+ # import ipdb; ipdb.set_trace()
+
+ if i in self.out_indices:
+ norm_layer = getattr(self, f"norm{i}")
+ x_out = norm_layer(x_out)
+
+ out = x_out.view(-1, H, W, self.num_features[i]).permute(0, 3, 1, 2).contiguous()
+ outs.append(out)
+ # in:
+ # torch.Size([2, 3, 1024, 1024])
+ # outs:
+ # [torch.Size([2, 192, 256, 256]), torch.Size([2, 384, 128, 128]), \
+ # torch.Size([2, 768, 64, 64]), torch.Size([2, 1536, 32, 32])]
+ return tuple(outs)
+
+ def forward(self, tensor_list: NestedTensor):
+ x = tensor_list.tensors
+
+ """Forward function."""
+ x = self.patch_embed(x)
+
+ Wh, Ww = x.size(2), x.size(3)
+ if self.ape:
+ # interpolate the position embedding to the corresponding size
+ absolute_pos_embed = F.interpolate(
+ self.absolute_pos_embed, size=(Wh, Ww), mode="bicubic"
+ )
+ x = (x + absolute_pos_embed).flatten(2).transpose(1, 2) # B Wh*Ww C
+ else:
+ x = x.flatten(2).transpose(1, 2)
+ x = self.pos_drop(x)
+
+ outs = []
+ for i in range(self.num_layers):
+ layer = self.layers[i]
+ x_out, H, W, x, Wh, Ww = layer(x, Wh, Ww)
+
+ if i in self.out_indices:
+ norm_layer = getattr(self, f"norm{i}")
+ x_out = norm_layer(x_out)
+
+ out = x_out.view(-1, H, W, self.num_features[i]).permute(0, 3, 1, 2).contiguous()
+ outs.append(out)
+ # in:
+ # torch.Size([2, 3, 1024, 1024])
+ # out:
+ # [torch.Size([2, 192, 256, 256]), torch.Size([2, 384, 128, 128]), \
+ # torch.Size([2, 768, 64, 64]), torch.Size([2, 1536, 32, 32])]
+
+ # collect for nesttensors
+ outs_dict = {}
+ for idx, out_i in enumerate(outs):
+ m = tensor_list.mask
+ assert m is not None
+ mask = F.interpolate(m[None].float(), size=out_i.shape[-2:]).to(torch.bool)[0]
+ outs_dict[idx] = NestedTensor(out_i, mask)
+
+ return outs_dict
+
+ def train(self, mode=True):
+ """Convert the model into training mode while keep layers freezed."""
+ super(SwinTransformer, self).train(mode)
+ self._freeze_stages()
+
+
+def build_swin_transformer(modelname, pretrain_img_size, **kw):
+ assert modelname in [
+ "swin_T_224_1k",
+ "swin_B_224_22k",
+ "swin_B_384_22k",
+ "swin_L_224_22k",
+ "swin_L_384_22k",
+ ]
+
+ model_para_dict = {
+ "swin_T_224_1k": dict(
+ embed_dim=96, depths=[2, 2, 6, 2], num_heads=[3, 6, 12, 24], window_size=7
+ ),
+ "swin_B_224_22k": dict(
+ embed_dim=128, depths=[2, 2, 18, 2], num_heads=[4, 8, 16, 32], window_size=7
+ ),
+ "swin_B_384_22k": dict(
+ embed_dim=128, depths=[2, 2, 18, 2], num_heads=[4, 8, 16, 32], window_size=12
+ ),
+ "swin_L_224_22k": dict(
+ embed_dim=192, depths=[2, 2, 18, 2], num_heads=[6, 12, 24, 48], window_size=7
+ ),
+ "swin_L_384_22k": dict(
+ embed_dim=192, depths=[2, 2, 18, 2], num_heads=[6, 12, 24, 48], window_size=12
+ ),
+ }
+ kw_cgf = model_para_dict[modelname]
+ kw_cgf.update(kw)
+ model = SwinTransformer(pretrain_img_size=pretrain_img_size, **kw_cgf)
+ return model
+
+
+if __name__ == "__main__":
+ model = build_swin_transformer("swin_L_384_22k", 384, dilation=True)
+ x = torch.rand(2, 3, 1024, 1024)
+ y = model.forward_raw(x)
+ import ipdb
+
+ ipdb.set_trace()
+ x = torch.rand(2, 3, 384, 384)
+ y = model.forward_raw(x)
diff --git a/GroundingDINO/groundingdino/models/GroundingDINO/bertwarper.py b/GroundingDINO/groundingdino/models/GroundingDINO/bertwarper.py
new file mode 100644
index 0000000000000000000000000000000000000000..f0cf9779b270e1aead32845006f8b881fcba37ad
--- /dev/null
+++ b/GroundingDINO/groundingdino/models/GroundingDINO/bertwarper.py
@@ -0,0 +1,273 @@
+# ------------------------------------------------------------------------
+# Grounding DINO
+# url: https://github.com/IDEA-Research/GroundingDINO
+# Copyright (c) 2023 IDEA. All Rights Reserved.
+# Licensed under the Apache License, Version 2.0 [see LICENSE for details]
+# ------------------------------------------------------------------------
+
+import torch
+import torch.nn.functional as F
+import torch.utils.checkpoint as checkpoint
+from torch import Tensor, nn
+from torchvision.ops.boxes import nms
+from transformers import BertConfig, BertModel, BertPreTrainedModel
+from transformers.modeling_outputs import BaseModelOutputWithPoolingAndCrossAttentions
+
+
+class BertModelWarper(nn.Module):
+ def __init__(self, bert_model):
+ super().__init__()
+ # self.bert = bert_modelc
+
+ self.config = bert_model.config
+ self.embeddings = bert_model.embeddings
+ self.encoder = bert_model.encoder
+ self.pooler = bert_model.pooler
+
+ self.get_extended_attention_mask = bert_model.get_extended_attention_mask
+ self.invert_attention_mask = bert_model.invert_attention_mask
+ self.get_head_mask = bert_model.get_head_mask
+
+ def forward(
+ self,
+ input_ids=None,
+ attention_mask=None,
+ token_type_ids=None,
+ position_ids=None,
+ head_mask=None,
+ inputs_embeds=None,
+ encoder_hidden_states=None,
+ encoder_attention_mask=None,
+ past_key_values=None,
+ use_cache=None,
+ output_attentions=None,
+ output_hidden_states=None,
+ return_dict=None,
+ ):
+ r"""
+ encoder_hidden_states (:obj:`torch.FloatTensor` of shape :obj:`(batch_size, sequence_length, hidden_size)`, `optional`):
+ Sequence of hidden-states at the output of the last layer of the encoder. Used in the cross-attention if
+ the model is configured as a decoder.
+ encoder_attention_mask (:obj:`torch.FloatTensor` of shape :obj:`(batch_size, sequence_length)`, `optional`):
+ Mask to avoid performing attention on the padding token indices of the encoder input. This mask is used in
+ the cross-attention if the model is configured as a decoder. Mask values selected in ``[0, 1]``:
+
+ - 1 for tokens that are **not masked**,
+ - 0 for tokens that are **masked**.
+ past_key_values (:obj:`tuple(tuple(torch.FloatTensor))` of length :obj:`config.n_layers` with each tuple having 4 tensors of shape :obj:`(batch_size, num_heads, sequence_length - 1, embed_size_per_head)`):
+ Contains precomputed key and value hidden states of the attention blocks. Can be used to speed up decoding.
+
+ If :obj:`past_key_values` are used, the user can optionally input only the last :obj:`decoder_input_ids`
+ (those that don't have their past key value states given to this model) of shape :obj:`(batch_size, 1)`
+ instead of all :obj:`decoder_input_ids` of shape :obj:`(batch_size, sequence_length)`.
+ use_cache (:obj:`bool`, `optional`):
+ If set to :obj:`True`, :obj:`past_key_values` key value states are returned and can be used to speed up
+ decoding (see :obj:`past_key_values`).
+ """
+ output_attentions = (
+ output_attentions if output_attentions is not None else self.config.output_attentions
+ )
+ output_hidden_states = (
+ output_hidden_states
+ if output_hidden_states is not None
+ else self.config.output_hidden_states
+ )
+ return_dict = return_dict if return_dict is not None else self.config.use_return_dict
+
+ if self.config.is_decoder:
+ use_cache = use_cache if use_cache is not None else self.config.use_cache
+ else:
+ use_cache = False
+
+ if input_ids is not None and inputs_embeds is not None:
+ raise ValueError("You cannot specify both input_ids and inputs_embeds at the same time")
+ elif input_ids is not None:
+ input_shape = input_ids.size()
+ batch_size, seq_length = input_shape
+ elif inputs_embeds is not None:
+ input_shape = inputs_embeds.size()[:-1]
+ batch_size, seq_length = input_shape
+ else:
+ raise ValueError("You have to specify either input_ids or inputs_embeds")
+
+ device = input_ids.device if input_ids is not None else inputs_embeds.device
+
+ # past_key_values_length
+ past_key_values_length = (
+ past_key_values[0][0].shape[2] if past_key_values is not None else 0
+ )
+
+ if attention_mask is None:
+ attention_mask = torch.ones(
+ ((batch_size, seq_length + past_key_values_length)), device=device
+ )
+ if token_type_ids is None:
+ token_type_ids = torch.zeros(input_shape, dtype=torch.long, device=device)
+
+ # We can provide a self-attention mask of dimensions [batch_size, from_seq_length, to_seq_length]
+ # ourselves in which case we just need to make it broadcastable to all heads.
+ extended_attention_mask: torch.Tensor = self.get_extended_attention_mask(
+ attention_mask, input_shape, device
+ )
+
+ # If a 2D or 3D attention mask is provided for the cross-attention
+ # we need to make broadcastable to [batch_size, num_heads, seq_length, seq_length]
+ if self.config.is_decoder and encoder_hidden_states is not None:
+ encoder_batch_size, encoder_sequence_length, _ = encoder_hidden_states.size()
+ encoder_hidden_shape = (encoder_batch_size, encoder_sequence_length)
+ if encoder_attention_mask is None:
+ encoder_attention_mask = torch.ones(encoder_hidden_shape, device=device)
+ encoder_extended_attention_mask = self.invert_attention_mask(encoder_attention_mask)
+ else:
+ encoder_extended_attention_mask = None
+ # if os.environ.get('IPDB_SHILONG_DEBUG', None) == 'INFO':
+ # import ipdb; ipdb.set_trace()
+
+ # Prepare head mask if needed
+ # 1.0 in head_mask indicate we keep the head
+ # attention_probs has shape bsz x n_heads x N x N
+ # input head_mask has shape [num_heads] or [num_hidden_layers x num_heads]
+ # and head_mask is converted to shape [num_hidden_layers x batch x num_heads x seq_length x seq_length]
+ head_mask = self.get_head_mask(head_mask, self.config.num_hidden_layers)
+
+ embedding_output = self.embeddings(
+ input_ids=input_ids,
+ position_ids=position_ids,
+ token_type_ids=token_type_ids,
+ inputs_embeds=inputs_embeds,
+ past_key_values_length=past_key_values_length,
+ )
+
+ encoder_outputs = self.encoder(
+ embedding_output,
+ attention_mask=extended_attention_mask,
+ head_mask=head_mask,
+ encoder_hidden_states=encoder_hidden_states,
+ encoder_attention_mask=encoder_extended_attention_mask,
+ past_key_values=past_key_values,
+ use_cache=use_cache,
+ output_attentions=output_attentions,
+ output_hidden_states=output_hidden_states,
+ return_dict=return_dict,
+ )
+ sequence_output = encoder_outputs[0]
+ pooled_output = self.pooler(sequence_output) if self.pooler is not None else None
+
+ if not return_dict:
+ return (sequence_output, pooled_output) + encoder_outputs[1:]
+
+ return BaseModelOutputWithPoolingAndCrossAttentions(
+ last_hidden_state=sequence_output,
+ pooler_output=pooled_output,
+ past_key_values=encoder_outputs.past_key_values,
+ hidden_states=encoder_outputs.hidden_states,
+ attentions=encoder_outputs.attentions,
+ cross_attentions=encoder_outputs.cross_attentions,
+ )
+
+
+class TextEncoderShell(nn.Module):
+ def __init__(self, text_encoder):
+ super().__init__()
+ self.text_encoder = text_encoder
+ self.config = self.text_encoder.config
+
+ def forward(self, **kw):
+ # feed into text encoder
+ return self.text_encoder(**kw)
+
+
+def generate_masks_with_special_tokens(tokenized, special_tokens_list, tokenizer):
+ """Generate attention mask between each pair of special tokens
+ Args:
+ input_ids (torch.Tensor): input ids. Shape: [bs, num_token]
+ special_tokens_mask (list): special tokens mask.
+ Returns:
+ torch.Tensor: attention mask between each special tokens.
+ """
+ input_ids = tokenized["input_ids"]
+ bs, num_token = input_ids.shape
+ # special_tokens_mask: bs, num_token. 1 for special tokens. 0 for normal tokens
+ special_tokens_mask = torch.zeros((bs, num_token), device=input_ids.device).bool()
+ for special_token in special_tokens_list:
+ special_tokens_mask |= input_ids == special_token
+
+ # idxs: each row is a list of indices of special tokens
+ idxs = torch.nonzero(special_tokens_mask)
+
+ # generate attention mask and positional ids
+ attention_mask = (
+ torch.eye(num_token, device=input_ids.device).bool().unsqueeze(0).repeat(bs, 1, 1)
+ )
+ position_ids = torch.zeros((bs, num_token), device=input_ids.device)
+ previous_col = 0
+ for i in range(idxs.shape[0]):
+ row, col = idxs[i]
+ if (col == 0) or (col == num_token - 1):
+ attention_mask[row, col, col] = True
+ position_ids[row, col] = 0
+ else:
+ attention_mask[row, previous_col + 1 : col + 1, previous_col + 1 : col + 1] = True
+ position_ids[row, previous_col + 1 : col + 1] = torch.arange(
+ 0, col - previous_col, device=input_ids.device
+ )
+
+ previous_col = col
+
+ # # padding mask
+ # padding_mask = tokenized['attention_mask']
+ # attention_mask = attention_mask & padding_mask.unsqueeze(1).bool() & padding_mask.unsqueeze(2).bool()
+
+ return attention_mask, position_ids.to(torch.long)
+
+
+def generate_masks_with_special_tokens_and_transfer_map(tokenized, special_tokens_list, tokenizer):
+ """Generate attention mask between each pair of special tokens
+ Args:
+ input_ids (torch.Tensor): input ids. Shape: [bs, num_token]
+ special_tokens_mask (list): special tokens mask.
+ Returns:
+ torch.Tensor: attention mask between each special tokens.
+ """
+ input_ids = tokenized["input_ids"]
+ bs, num_token = input_ids.shape
+ # special_tokens_mask: bs, num_token. 1 for special tokens. 0 for normal tokens
+ special_tokens_mask = torch.zeros((bs, num_token), device=input_ids.device).bool()
+ for special_token in special_tokens_list:
+ special_tokens_mask |= input_ids == special_token
+
+ # idxs: each row is a list of indices of special tokens
+ idxs = torch.nonzero(special_tokens_mask)
+
+ # generate attention mask and positional ids
+ attention_mask = (
+ torch.eye(num_token, device=input_ids.device).bool().unsqueeze(0).repeat(bs, 1, 1)
+ )
+ position_ids = torch.zeros((bs, num_token), device=input_ids.device)
+ cate_to_token_mask_list = [[] for _ in range(bs)]
+ previous_col = 0
+ for i in range(idxs.shape[0]):
+ row, col = idxs[i]
+ if (col == 0) or (col == num_token - 1):
+ attention_mask[row, col, col] = True
+ position_ids[row, col] = 0
+ else:
+ attention_mask[row, previous_col + 1 : col + 1, previous_col + 1 : col + 1] = True
+ position_ids[row, previous_col + 1 : col + 1] = torch.arange(
+ 0, col - previous_col, device=input_ids.device
+ )
+ c2t_maski = torch.zeros((num_token), device=input_ids.device).bool()
+ c2t_maski[previous_col + 1 : col] = True
+ cate_to_token_mask_list[row].append(c2t_maski)
+ previous_col = col
+
+ cate_to_token_mask_list = [
+ torch.stack(cate_to_token_mask_listi, dim=0)
+ for cate_to_token_mask_listi in cate_to_token_mask_list
+ ]
+
+ # # padding mask
+ # padding_mask = tokenized['attention_mask']
+ # attention_mask = attention_mask & padding_mask.unsqueeze(1).bool() & padding_mask.unsqueeze(2).bool()
+
+ return attention_mask, position_ids.to(torch.long), cate_to_token_mask_list
diff --git a/GroundingDINO/groundingdino/models/GroundingDINO/csrc/MsDeformAttn/ms_deform_attn.h b/GroundingDINO/groundingdino/models/GroundingDINO/csrc/MsDeformAttn/ms_deform_attn.h
new file mode 100644
index 0000000000000000000000000000000000000000..c7408eba007b424194618baa63726657e36875e3
--- /dev/null
+++ b/GroundingDINO/groundingdino/models/GroundingDINO/csrc/MsDeformAttn/ms_deform_attn.h
@@ -0,0 +1,64 @@
+/*!
+**************************************************************************************************
+* Deformable DETR
+* Copyright (c) 2020 SenseTime. All Rights Reserved.
+* Licensed under the Apache License, Version 2.0 [see LICENSE for details]
+**************************************************************************************************
+* Modified from https://github.com/chengdazhi/Deformable-Convolution-V2-PyTorch/tree/pytorch_1.0.0
+**************************************************************************************************
+*/
+
+#pragma once
+
+#include "ms_deform_attn_cpu.h"
+
+#ifdef WITH_CUDA
+#include "ms_deform_attn_cuda.h"
+#endif
+
+namespace groundingdino {
+
+at::Tensor
+ms_deform_attn_forward(
+ const at::Tensor &value,
+ const at::Tensor &spatial_shapes,
+ const at::Tensor &level_start_index,
+ const at::Tensor &sampling_loc,
+ const at::Tensor &attn_weight,
+ const int im2col_step)
+{
+ if (value.type().is_cuda())
+ {
+#ifdef WITH_CUDA
+ return ms_deform_attn_cuda_forward(
+ value, spatial_shapes, level_start_index, sampling_loc, attn_weight, im2col_step);
+#else
+ AT_ERROR("Not compiled with GPU support");
+#endif
+ }
+ AT_ERROR("Not implemented on the CPU");
+}
+
+std::vector
+ms_deform_attn_backward(
+ const at::Tensor &value,
+ const at::Tensor &spatial_shapes,
+ const at::Tensor &level_start_index,
+ const at::Tensor &sampling_loc,
+ const at::Tensor &attn_weight,
+ const at::Tensor &grad_output,
+ const int im2col_step)
+{
+ if (value.type().is_cuda())
+ {
+#ifdef WITH_CUDA
+ return ms_deform_attn_cuda_backward(
+ value, spatial_shapes, level_start_index, sampling_loc, attn_weight, grad_output, im2col_step);
+#else
+ AT_ERROR("Not compiled with GPU support");
+#endif
+ }
+ AT_ERROR("Not implemented on the CPU");
+}
+
+} // namespace groundingdino
\ No newline at end of file
diff --git a/GroundingDINO/groundingdino/models/GroundingDINO/csrc/MsDeformAttn/ms_deform_attn_cpu.cpp b/GroundingDINO/groundingdino/models/GroundingDINO/csrc/MsDeformAttn/ms_deform_attn_cpu.cpp
new file mode 100644
index 0000000000000000000000000000000000000000..551243fdadfd1682b5dc6628623b67a79b3f6c74
--- /dev/null
+++ b/GroundingDINO/groundingdino/models/GroundingDINO/csrc/MsDeformAttn/ms_deform_attn_cpu.cpp
@@ -0,0 +1,43 @@
+/*!
+**************************************************************************************************
+* Deformable DETR
+* Copyright (c) 2020 SenseTime. All Rights Reserved.
+* Licensed under the Apache License, Version 2.0 [see LICENSE for details]
+**************************************************************************************************
+* Modified from https://github.com/chengdazhi/Deformable-Convolution-V2-PyTorch/tree/pytorch_1.0.0
+**************************************************************************************************
+*/
+
+#include
+
+#include
+#include
+
+namespace groundingdino {
+
+at::Tensor
+ms_deform_attn_cpu_forward(
+ const at::Tensor &value,
+ const at::Tensor &spatial_shapes,
+ const at::Tensor &level_start_index,
+ const at::Tensor &sampling_loc,
+ const at::Tensor &attn_weight,
+ const int im2col_step)
+{
+ AT_ERROR("Not implement on cpu");
+}
+
+std::vector
+ms_deform_attn_cpu_backward(
+ const at::Tensor &value,
+ const at::Tensor &spatial_shapes,
+ const at::Tensor &level_start_index,
+ const at::Tensor &sampling_loc,
+ const at::Tensor &attn_weight,
+ const at::Tensor &grad_output,
+ const int im2col_step)
+{
+ AT_ERROR("Not implement on cpu");
+}
+
+} // namespace groundingdino
diff --git a/GroundingDINO/groundingdino/models/GroundingDINO/csrc/MsDeformAttn/ms_deform_attn_cpu.h b/GroundingDINO/groundingdino/models/GroundingDINO/csrc/MsDeformAttn/ms_deform_attn_cpu.h
new file mode 100644
index 0000000000000000000000000000000000000000..b2b88e8c46f19b6db0933163e57ccdb51180f517
--- /dev/null
+++ b/GroundingDINO/groundingdino/models/GroundingDINO/csrc/MsDeformAttn/ms_deform_attn_cpu.h
@@ -0,0 +1,35 @@
+/*!
+**************************************************************************************************
+* Deformable DETR
+* Copyright (c) 2020 SenseTime. All Rights Reserved.
+* Licensed under the Apache License, Version 2.0 [see LICENSE for details]
+**************************************************************************************************
+* Modified from https://github.com/chengdazhi/Deformable-Convolution-V2-PyTorch/tree/pytorch_1.0.0
+**************************************************************************************************
+*/
+
+#pragma once
+#include
+
+namespace groundingdino {
+
+at::Tensor
+ms_deform_attn_cpu_forward(
+ const at::Tensor &value,
+ const at::Tensor &spatial_shapes,
+ const at::Tensor &level_start_index,
+ const at::Tensor &sampling_loc,
+ const at::Tensor &attn_weight,
+ const int im2col_step);
+
+std::vector
+ms_deform_attn_cpu_backward(
+ const at::Tensor &value,
+ const at::Tensor &spatial_shapes,
+ const at::Tensor &level_start_index,
+ const at::Tensor &sampling_loc,
+ const at::Tensor &attn_weight,
+ const at::Tensor &grad_output,
+ const int im2col_step);
+
+} // namespace groundingdino
diff --git a/GroundingDINO/groundingdino/models/GroundingDINO/csrc/MsDeformAttn/ms_deform_attn_cuda.cu b/GroundingDINO/groundingdino/models/GroundingDINO/csrc/MsDeformAttn/ms_deform_attn_cuda.cu
new file mode 100644
index 0000000000000000000000000000000000000000..d04fae8a9a45c11e4e74f3035e94762796da4096
--- /dev/null
+++ b/GroundingDINO/groundingdino/models/GroundingDINO/csrc/MsDeformAttn/ms_deform_attn_cuda.cu
@@ -0,0 +1,156 @@
+/*!
+**************************************************************************************************
+* Deformable DETR
+* Copyright (c) 2020 SenseTime. All Rights Reserved.
+* Licensed under the Apache License, Version 2.0 [see LICENSE for details]
+**************************************************************************************************
+* Modified from https://github.com/chengdazhi/Deformable-Convolution-V2-PyTorch/tree/pytorch_1.0.0
+**************************************************************************************************
+*/
+
+#include
+#include "ms_deform_im2col_cuda.cuh"
+
+#include
+#include
+#include
+#include
+
+namespace groundingdino {
+
+at::Tensor ms_deform_attn_cuda_forward(
+ const at::Tensor &value,
+ const at::Tensor &spatial_shapes,
+ const at::Tensor &level_start_index,
+ const at::Tensor &sampling_loc,
+ const at::Tensor &attn_weight,
+ const int im2col_step)
+{
+ AT_ASSERTM(value.is_contiguous(), "value tensor has to be contiguous");
+ AT_ASSERTM(spatial_shapes.is_contiguous(), "spatial_shapes tensor has to be contiguous");
+ AT_ASSERTM(level_start_index.is_contiguous(), "level_start_index tensor has to be contiguous");
+ AT_ASSERTM(sampling_loc.is_contiguous(), "sampling_loc tensor has to be contiguous");
+ AT_ASSERTM(attn_weight.is_contiguous(), "attn_weight tensor has to be contiguous");
+
+ AT_ASSERTM(value.type().is_cuda(), "value must be a CUDA tensor");
+ AT_ASSERTM(spatial_shapes.type().is_cuda(), "spatial_shapes must be a CUDA tensor");
+ AT_ASSERTM(level_start_index.type().is_cuda(), "level_start_index must be a CUDA tensor");
+ AT_ASSERTM(sampling_loc.type().is_cuda(), "sampling_loc must be a CUDA tensor");
+ AT_ASSERTM(attn_weight.type().is_cuda(), "attn_weight must be a CUDA tensor");
+
+ const int batch = value.size(0);
+ const int spatial_size = value.size(1);
+ const int num_heads = value.size(2);
+ const int channels = value.size(3);
+
+ const int num_levels = spatial_shapes.size(0);
+
+ const int num_query = sampling_loc.size(1);
+ const int num_point = sampling_loc.size(4);
+
+ const int im2col_step_ = std::min(batch, im2col_step);
+
+ AT_ASSERTM(batch % im2col_step_ == 0, "batch(%d) must divide im2col_step(%d)", batch, im2col_step_);
+
+ auto output = at::zeros({batch, num_query, num_heads, channels}, value.options());
+
+ const int batch_n = im2col_step_;
+ auto output_n = output.view({batch/im2col_step_, batch_n, num_query, num_heads, channels});
+ auto per_value_size = spatial_size * num_heads * channels;
+ auto per_sample_loc_size = num_query * num_heads * num_levels * num_point * 2;
+ auto per_attn_weight_size = num_query * num_heads * num_levels * num_point;
+ for (int n = 0; n < batch/im2col_step_; ++n)
+ {
+ auto columns = output_n.select(0, n);
+ AT_DISPATCH_FLOATING_TYPES(value.type(), "ms_deform_attn_forward_cuda", ([&] {
+ ms_deformable_im2col_cuda(at::cuda::getCurrentCUDAStream(),
+ value.data() + n * im2col_step_ * per_value_size,
+ spatial_shapes.data(),
+ level_start_index.data(),
+ sampling_loc.data() + n * im2col_step_ * per_sample_loc_size,
+ attn_weight.data() + n * im2col_step_ * per_attn_weight_size,
+ batch_n, spatial_size, num_heads, channels, num_levels, num_query, num_point,
+ columns.data());
+
+ }));
+ }
+
+ output = output.view({batch, num_query, num_heads*channels});
+
+ return output;
+}
+
+
+std::vector ms_deform_attn_cuda_backward(
+ const at::Tensor &value,
+ const at::Tensor &spatial_shapes,
+ const at::Tensor &level_start_index,
+ const at::Tensor &sampling_loc,
+ const at::Tensor &attn_weight,
+ const at::Tensor &grad_output,
+ const int im2col_step)
+{
+
+ AT_ASSERTM(value.is_contiguous(), "value tensor has to be contiguous");
+ AT_ASSERTM(spatial_shapes.is_contiguous(), "spatial_shapes tensor has to be contiguous");
+ AT_ASSERTM(level_start_index.is_contiguous(), "level_start_index tensor has to be contiguous");
+ AT_ASSERTM(sampling_loc.is_contiguous(), "sampling_loc tensor has to be contiguous");
+ AT_ASSERTM(attn_weight.is_contiguous(), "attn_weight tensor has to be contiguous");
+ AT_ASSERTM(grad_output.is_contiguous(), "grad_output tensor has to be contiguous");
+
+ AT_ASSERTM(value.type().is_cuda(), "value must be a CUDA tensor");
+ AT_ASSERTM(spatial_shapes.type().is_cuda(), "spatial_shapes must be a CUDA tensor");
+ AT_ASSERTM(level_start_index.type().is_cuda(), "level_start_index must be a CUDA tensor");
+ AT_ASSERTM(sampling_loc.type().is_cuda(), "sampling_loc must be a CUDA tensor");
+ AT_ASSERTM(attn_weight.type().is_cuda(), "attn_weight must be a CUDA tensor");
+ AT_ASSERTM(grad_output.type().is_cuda(), "grad_output must be a CUDA tensor");
+
+ const int batch = value.size(0);
+ const int spatial_size = value.size(1);
+ const int num_heads = value.size(2);
+ const int channels = value.size(3);
+
+ const int num_levels = spatial_shapes.size(0);
+
+ const int num_query = sampling_loc.size(1);
+ const int num_point = sampling_loc.size(4);
+
+ const int im2col_step_ = std::min(batch, im2col_step);
+
+ AT_ASSERTM(batch % im2col_step_ == 0, "batch(%d) must divide im2col_step(%d)", batch, im2col_step_);
+
+ auto grad_value = at::zeros_like(value);
+ auto grad_sampling_loc = at::zeros_like(sampling_loc);
+ auto grad_attn_weight = at::zeros_like(attn_weight);
+
+ const int batch_n = im2col_step_;
+ auto per_value_size = spatial_size * num_heads * channels;
+ auto per_sample_loc_size = num_query * num_heads * num_levels * num_point * 2;
+ auto per_attn_weight_size = num_query * num_heads * num_levels * num_point;
+ auto grad_output_n = grad_output.view({batch/im2col_step_, batch_n, num_query, num_heads, channels});
+
+ for (int n = 0; n < batch/im2col_step_; ++n)
+ {
+ auto grad_output_g = grad_output_n.select(0, n);
+ AT_DISPATCH_FLOATING_TYPES(value.type(), "ms_deform_attn_backward_cuda", ([&] {
+ ms_deformable_col2im_cuda(at::cuda::getCurrentCUDAStream(),
+ grad_output_g.data(),
+ value.data() + n * im2col_step_ * per_value_size,
+ spatial_shapes.data(),
+ level_start_index.data(),
+ sampling_loc.data() + n * im2col_step_ * per_sample_loc_size,
+ attn_weight.data() + n * im2col_step_ * per_attn_weight_size,
+ batch_n, spatial_size, num_heads, channels, num_levels, num_query, num_point,
+ grad_value.data() + n * im2col_step_ * per_value_size,
+ grad_sampling_loc.data() + n * im2col_step_ * per_sample_loc_size,
+ grad_attn_weight.data() + n * im2col_step_ * per_attn_weight_size);
+
+ }));
+ }
+
+ return {
+ grad_value, grad_sampling_loc, grad_attn_weight
+ };
+}
+
+} // namespace groundingdino
\ No newline at end of file
diff --git a/GroundingDINO/groundingdino/models/GroundingDINO/csrc/MsDeformAttn/ms_deform_attn_cuda.h b/GroundingDINO/groundingdino/models/GroundingDINO/csrc/MsDeformAttn/ms_deform_attn_cuda.h
new file mode 100644
index 0000000000000000000000000000000000000000..ad1311a78f61303616504eb991aaa9c4a93d9948
--- /dev/null
+++ b/GroundingDINO/groundingdino/models/GroundingDINO/csrc/MsDeformAttn/ms_deform_attn_cuda.h
@@ -0,0 +1,33 @@
+/*!
+**************************************************************************************************
+* Deformable DETR
+* Copyright (c) 2020 SenseTime. All Rights Reserved.
+* Licensed under the Apache License, Version 2.0 [see LICENSE for details]
+**************************************************************************************************
+* Modified from https://github.com/chengdazhi/Deformable-Convolution-V2-PyTorch/tree/pytorch_1.0.0
+**************************************************************************************************
+*/
+
+#pragma once
+#include
+
+namespace groundingdino {
+
+at::Tensor ms_deform_attn_cuda_forward(
+ const at::Tensor &value,
+ const at::Tensor &spatial_shapes,
+ const at::Tensor &level_start_index,
+ const at::Tensor &sampling_loc,
+ const at::Tensor &attn_weight,
+ const int im2col_step);
+
+std::vector ms_deform_attn_cuda_backward(
+ const at::Tensor &value,
+ const at::Tensor &spatial_shapes,
+ const at::Tensor &level_start_index,
+ const at::Tensor &sampling_loc,
+ const at::Tensor &attn_weight,
+ const at::Tensor &grad_output,
+ const int im2col_step);
+
+} // namespace groundingdino
\ No newline at end of file
diff --git a/GroundingDINO/groundingdino/models/GroundingDINO/csrc/MsDeformAttn/ms_deform_im2col_cuda.cuh b/GroundingDINO/groundingdino/models/GroundingDINO/csrc/MsDeformAttn/ms_deform_im2col_cuda.cuh
new file mode 100644
index 0000000000000000000000000000000000000000..6bc2acb7aea0eab2e9e91e769a16861e1652c284
--- /dev/null
+++ b/GroundingDINO/groundingdino/models/GroundingDINO/csrc/MsDeformAttn/ms_deform_im2col_cuda.cuh
@@ -0,0 +1,1327 @@
+/*!
+**************************************************************************
+* Deformable DETR
+* Copyright (c) 2020 SenseTime. All Rights Reserved.
+* Licensed under the Apache License, Version 2.0 [see LICENSE for details]
+**************************************************************************
+* Modified from DCN (https://github.com/msracver/Deformable-ConvNets)
+* Copyright (c) 2018 Microsoft
+**************************************************************************
+*/
+
+#include
+#include
+#include
+
+#include
+#include
+
+#include
+
+#define CUDA_KERNEL_LOOP(i, n) \
+ for (int i = blockIdx.x * blockDim.x + threadIdx.x; \
+ i < (n); \
+ i += blockDim.x * gridDim.x)
+
+const int CUDA_NUM_THREADS = 1024;
+inline int GET_BLOCKS(const int N, const int num_threads)
+{
+ return (N + num_threads - 1) / num_threads;
+}
+
+
+template
+__device__ scalar_t ms_deform_attn_im2col_bilinear(const scalar_t* &bottom_data,
+ const int &height, const int &width, const int &nheads, const int &channels,
+ const scalar_t &h, const scalar_t &w, const int &m, const int &c)
+{
+ const int h_low = floor(h);
+ const int w_low = floor(w);
+ const int h_high = h_low + 1;
+ const int w_high = w_low + 1;
+
+ const scalar_t lh = h - h_low;
+ const scalar_t lw = w - w_low;
+ const scalar_t hh = 1 - lh, hw = 1 - lw;
+
+ const int w_stride = nheads * channels;
+ const int h_stride = width * w_stride;
+ const int h_low_ptr_offset = h_low * h_stride;
+ const int h_high_ptr_offset = h_low_ptr_offset + h_stride;
+ const int w_low_ptr_offset = w_low * w_stride;
+ const int w_high_ptr_offset = w_low_ptr_offset + w_stride;
+ const int base_ptr = m * channels + c;
+
+ scalar_t v1 = 0;
+ if (h_low >= 0 && w_low >= 0)
+ {
+ const int ptr1 = h_low_ptr_offset + w_low_ptr_offset + base_ptr;
+ v1 = bottom_data[ptr1];
+ }
+ scalar_t v2 = 0;
+ if (h_low >= 0 && w_high <= width - 1)
+ {
+ const int ptr2 = h_low_ptr_offset + w_high_ptr_offset + base_ptr;
+ v2 = bottom_data[ptr2];
+ }
+ scalar_t v3 = 0;
+ if (h_high <= height - 1 && w_low >= 0)
+ {
+ const int ptr3 = h_high_ptr_offset + w_low_ptr_offset + base_ptr;
+ v3 = bottom_data[ptr3];
+ }
+ scalar_t v4 = 0;
+ if (h_high <= height - 1 && w_high <= width - 1)
+ {
+ const int ptr4 = h_high_ptr_offset + w_high_ptr_offset + base_ptr;
+ v4 = bottom_data[ptr4];
+ }
+
+ const scalar_t w1 = hh * hw, w2 = hh * lw, w3 = lh * hw, w4 = lh * lw;
+
+ const scalar_t val = (w1 * v1 + w2 * v2 + w3 * v3 + w4 * v4);
+ return val;
+}
+
+
+template
+__device__ void ms_deform_attn_col2im_bilinear(const scalar_t* &bottom_data,
+ const int &height, const int &width, const int &nheads, const int &channels,
+ const scalar_t &h, const scalar_t &w, const int &m, const int &c,
+ const scalar_t &top_grad,
+ const scalar_t &attn_weight,
+ scalar_t* &grad_value,
+ scalar_t* grad_sampling_loc,
+ scalar_t* grad_attn_weight)
+{
+ const int h_low = floor(h);
+ const int w_low = floor(w);
+ const int h_high = h_low + 1;
+ const int w_high = w_low + 1;
+
+ const scalar_t lh = h - h_low;
+ const scalar_t lw = w - w_low;
+ const scalar_t hh = 1 - lh, hw = 1 - lw;
+
+ const int w_stride = nheads * channels;
+ const int h_stride = width * w_stride;
+ const int h_low_ptr_offset = h_low * h_stride;
+ const int h_high_ptr_offset = h_low_ptr_offset + h_stride;
+ const int w_low_ptr_offset = w_low * w_stride;
+ const int w_high_ptr_offset = w_low_ptr_offset + w_stride;
+ const int base_ptr = m * channels + c;
+
+ const scalar_t w1 = hh * hw, w2 = hh * lw, w3 = lh * hw, w4 = lh * lw;
+ const scalar_t top_grad_value = top_grad * attn_weight;
+ scalar_t grad_h_weight = 0, grad_w_weight = 0;
+
+ scalar_t v1 = 0;
+ if (h_low >= 0 && w_low >= 0)
+ {
+ const int ptr1 = h_low_ptr_offset + w_low_ptr_offset + base_ptr;
+ v1 = bottom_data[ptr1];
+ grad_h_weight -= hw * v1;
+ grad_w_weight -= hh * v1;
+ atomicAdd(grad_value+ptr1, w1*top_grad_value);
+ }
+ scalar_t v2 = 0;
+ if (h_low >= 0 && w_high <= width - 1)
+ {
+ const int ptr2 = h_low_ptr_offset + w_high_ptr_offset + base_ptr;
+ v2 = bottom_data[ptr2];
+ grad_h_weight -= lw * v2;
+ grad_w_weight += hh * v2;
+ atomicAdd(grad_value+ptr2, w2*top_grad_value);
+ }
+ scalar_t v3 = 0;
+ if (h_high <= height - 1 && w_low >= 0)
+ {
+ const int ptr3 = h_high_ptr_offset + w_low_ptr_offset + base_ptr;
+ v3 = bottom_data[ptr3];
+ grad_h_weight += hw * v3;
+ grad_w_weight -= lh * v3;
+ atomicAdd(grad_value+ptr3, w3*top_grad_value);
+ }
+ scalar_t v4 = 0;
+ if (h_high <= height - 1 && w_high <= width - 1)
+ {
+ const int ptr4 = h_high_ptr_offset + w_high_ptr_offset + base_ptr;
+ v4 = bottom_data[ptr4];
+ grad_h_weight += lw * v4;
+ grad_w_weight += lh * v4;
+ atomicAdd(grad_value+ptr4, w4*top_grad_value);
+ }
+
+ const scalar_t val = (w1 * v1 + w2 * v2 + w3 * v3 + w4 * v4);
+ *grad_attn_weight = top_grad * val;
+ *grad_sampling_loc = width * grad_w_weight * top_grad_value;
+ *(grad_sampling_loc + 1) = height * grad_h_weight * top_grad_value;
+}
+
+
+template
+__device__ void ms_deform_attn_col2im_bilinear_gm(const scalar_t* &bottom_data,
+ const int &height, const int &width, const int &nheads, const int &channels,
+ const scalar_t &h, const scalar_t &w, const int &m, const int &c,
+ const scalar_t &top_grad,
+ const scalar_t &attn_weight,
+ scalar_t* &grad_value,
+ scalar_t* grad_sampling_loc,
+ scalar_t* grad_attn_weight)
+{
+ const int h_low = floor(h);
+ const int w_low = floor(w);
+ const int h_high = h_low + 1;
+ const int w_high = w_low + 1;
+
+ const scalar_t lh = h - h_low;
+ const scalar_t lw = w - w_low;
+ const scalar_t hh = 1 - lh, hw = 1 - lw;
+
+ const int w_stride = nheads * channels;
+ const int h_stride = width * w_stride;
+ const int h_low_ptr_offset = h_low * h_stride;
+ const int h_high_ptr_offset = h_low_ptr_offset + h_stride;
+ const int w_low_ptr_offset = w_low * w_stride;
+ const int w_high_ptr_offset = w_low_ptr_offset + w_stride;
+ const int base_ptr = m * channels + c;
+
+ const scalar_t w1 = hh * hw, w2 = hh * lw, w3 = lh * hw, w4 = lh * lw;
+ const scalar_t top_grad_value = top_grad * attn_weight;
+ scalar_t grad_h_weight = 0, grad_w_weight = 0;
+
+ scalar_t v1 = 0;
+ if (h_low >= 0 && w_low >= 0)
+ {
+ const int ptr1 = h_low_ptr_offset + w_low_ptr_offset + base_ptr;
+ v1 = bottom_data[ptr1];
+ grad_h_weight -= hw * v1;
+ grad_w_weight -= hh * v1;
+ atomicAdd(grad_value+ptr1, w1*top_grad_value);
+ }
+ scalar_t v2 = 0;
+ if (h_low >= 0 && w_high <= width - 1)
+ {
+ const int ptr2 = h_low_ptr_offset + w_high_ptr_offset + base_ptr;
+ v2 = bottom_data[ptr2];
+ grad_h_weight -= lw * v2;
+ grad_w_weight += hh * v2;
+ atomicAdd(grad_value+ptr2, w2*top_grad_value);
+ }
+ scalar_t v3 = 0;
+ if (h_high <= height - 1 && w_low >= 0)
+ {
+ const int ptr3 = h_high_ptr_offset + w_low_ptr_offset + base_ptr;
+ v3 = bottom_data[ptr3];
+ grad_h_weight += hw * v3;
+ grad_w_weight -= lh * v3;
+ atomicAdd(grad_value+ptr3, w3*top_grad_value);
+ }
+ scalar_t v4 = 0;
+ if (h_high <= height - 1 && w_high <= width - 1)
+ {
+ const int ptr4 = h_high_ptr_offset + w_high_ptr_offset + base_ptr;
+ v4 = bottom_data[ptr4];
+ grad_h_weight += lw * v4;
+ grad_w_weight += lh * v4;
+ atomicAdd(grad_value+ptr4, w4*top_grad_value);
+ }
+
+ const scalar_t val = (w1 * v1 + w2 * v2 + w3 * v3 + w4 * v4);
+ atomicAdd(grad_attn_weight, top_grad * val);
+ atomicAdd(grad_sampling_loc, width * grad_w_weight * top_grad_value);
+ atomicAdd(grad_sampling_loc + 1, height * grad_h_weight * top_grad_value);
+}
+
+
+template
+__global__ void ms_deformable_im2col_gpu_kernel(const int n,
+ const scalar_t *data_value,
+ const int64_t *data_spatial_shapes,
+ const int64_t *data_level_start_index,
+ const scalar_t *data_sampling_loc,
+ const scalar_t *data_attn_weight,
+ const int batch_size,
+ const int spatial_size,
+ const int num_heads,
+ const int channels,
+ const int num_levels,
+ const int num_query,
+ const int num_point,
+ scalar_t *data_col)
+{
+ CUDA_KERNEL_LOOP(index, n)
+ {
+ int _temp = index;
+ const int c_col = _temp % channels;
+ _temp /= channels;
+ const int sampling_index = _temp;
+ const int m_col = _temp % num_heads;
+ _temp /= num_heads;
+ const int q_col = _temp % num_query;
+ _temp /= num_query;
+ const int b_col = _temp;
+
+ scalar_t *data_col_ptr = data_col + index;
+ int data_weight_ptr = sampling_index * num_levels * num_point;
+ int data_loc_w_ptr = data_weight_ptr << 1;
+ const int qid_stride = num_heads * channels;
+ const int data_value_ptr_init_offset = b_col * spatial_size * qid_stride;
+ scalar_t col = 0;
+
+ for (int l_col=0; l_col < num_levels; ++l_col)
+ {
+ const int level_start_id = data_level_start_index[l_col];
+ const int spatial_h_ptr = l_col << 1;
+ const int spatial_h = data_spatial_shapes[spatial_h_ptr];
+ const int spatial_w = data_spatial_shapes[spatial_h_ptr + 1];
+ const scalar_t *data_value_ptr = data_value + (data_value_ptr_init_offset + level_start_id * qid_stride);
+ for (int p_col=0; p_col < num_point; ++p_col)
+ {
+ const scalar_t loc_w = data_sampling_loc[data_loc_w_ptr];
+ const scalar_t loc_h = data_sampling_loc[data_loc_w_ptr + 1];
+ const scalar_t weight = data_attn_weight[data_weight_ptr];
+
+ const scalar_t h_im = loc_h * spatial_h - 0.5;
+ const scalar_t w_im = loc_w * spatial_w - 0.5;
+
+ if (h_im > -1 && w_im > -1 && h_im < spatial_h && w_im < spatial_w)
+ {
+ col += ms_deform_attn_im2col_bilinear(data_value_ptr, spatial_h, spatial_w, num_heads, channels, h_im, w_im, m_col, c_col) * weight;
+ }
+
+ data_weight_ptr += 1;
+ data_loc_w_ptr += 2;
+ }
+ }
+ *data_col_ptr = col;
+ }
+}
+
+template
+__global__ void ms_deformable_col2im_gpu_kernel_shm_blocksize_aware_reduce_v1(const int n,
+ const scalar_t *grad_col,
+ const scalar_t *data_value,
+ const int64_t *data_spatial_shapes,
+ const int64_t *data_level_start_index,
+ const scalar_t *data_sampling_loc,
+ const scalar_t *data_attn_weight,
+ const int batch_size,
+ const int spatial_size,
+ const int num_heads,
+ const int channels,
+ const int num_levels,
+ const int num_query,
+ const int num_point,
+ scalar_t *grad_value,
+ scalar_t *grad_sampling_loc,
+ scalar_t *grad_attn_weight)
+{
+ CUDA_KERNEL_LOOP(index, n)
+ {
+ __shared__ scalar_t cache_grad_sampling_loc[blockSize * 2];
+ __shared__ scalar_t cache_grad_attn_weight[blockSize];
+ unsigned int tid = threadIdx.x;
+ int _temp = index;
+ const int c_col = _temp % channels;
+ _temp /= channels;
+ const int sampling_index = _temp;
+ const int m_col = _temp % num_heads;
+ _temp /= num_heads;
+ const int q_col = _temp % num_query;
+ _temp /= num_query;
+ const int b_col = _temp;
+
+ const scalar_t top_grad = grad_col[index];
+
+ int data_weight_ptr = sampling_index * num_levels * num_point;
+ int data_loc_w_ptr = data_weight_ptr << 1;
+ const int grad_sampling_ptr = data_weight_ptr;
+ grad_sampling_loc += grad_sampling_ptr << 1;
+ grad_attn_weight += grad_sampling_ptr;
+ const int grad_weight_stride = 1;
+ const int grad_loc_stride = 2;
+ const int qid_stride = num_heads * channels;
+ const int data_value_ptr_init_offset = b_col * spatial_size * qid_stride;
+
+ for (int l_col=0; l_col < num_levels; ++l_col)
+ {
+ const int level_start_id = data_level_start_index[l_col];
+ const int spatial_h_ptr = l_col << 1;
+ const int spatial_h = data_spatial_shapes[spatial_h_ptr];
+ const int spatial_w = data_spatial_shapes[spatial_h_ptr + 1];
+ const int value_ptr_offset = data_value_ptr_init_offset + level_start_id * qid_stride;
+ const scalar_t *data_value_ptr = data_value + value_ptr_offset;
+ scalar_t *grad_value_ptr = grad_value + value_ptr_offset;
+
+ for (int p_col=0; p_col < num_point; ++p_col)
+ {
+ const scalar_t loc_w = data_sampling_loc[data_loc_w_ptr];
+ const scalar_t loc_h = data_sampling_loc[data_loc_w_ptr + 1];
+ const scalar_t weight = data_attn_weight[data_weight_ptr];
+
+ const scalar_t h_im = loc_h * spatial_h - 0.5;
+ const scalar_t w_im = loc_w * spatial_w - 0.5;
+ *(cache_grad_sampling_loc+(threadIdx.x << 1)) = 0;
+ *(cache_grad_sampling_loc+((threadIdx.x << 1) + 1)) = 0;
+ *(cache_grad_attn_weight+threadIdx.x)=0;
+ if (h_im > -1 && w_im > -1 && h_im < spatial_h && w_im < spatial_w)
+ {
+ ms_deform_attn_col2im_bilinear(
+ data_value_ptr, spatial_h, spatial_w, num_heads, channels, h_im, w_im, m_col, c_col,
+ top_grad, weight, grad_value_ptr,
+ cache_grad_sampling_loc+(threadIdx.x << 1), cache_grad_attn_weight+threadIdx.x);
+ }
+
+ __syncthreads();
+ if (tid == 0)
+ {
+ scalar_t _grad_w=cache_grad_sampling_loc[0], _grad_h=cache_grad_sampling_loc[1], _grad_a=cache_grad_attn_weight[0];
+ int sid=2;
+ for (unsigned int tid = 1; tid < blockSize; ++tid)
+ {
+ _grad_w += cache_grad_sampling_loc[sid];
+ _grad_h += cache_grad_sampling_loc[sid + 1];
+ _grad_a += cache_grad_attn_weight[tid];
+ sid += 2;
+ }
+
+
+ *grad_sampling_loc = _grad_w;
+ *(grad_sampling_loc + 1) = _grad_h;
+ *grad_attn_weight = _grad_a;
+ }
+ __syncthreads();
+
+ data_weight_ptr += 1;
+ data_loc_w_ptr += 2;
+ grad_attn_weight += grad_weight_stride;
+ grad_sampling_loc += grad_loc_stride;
+ }
+ }
+ }
+}
+
+
+template
+__global__ void ms_deformable_col2im_gpu_kernel_shm_blocksize_aware_reduce_v2(const int n,
+ const scalar_t *grad_col,
+ const scalar_t *data_value,
+ const int64_t *data_spatial_shapes,
+ const int64_t *data_level_start_index,
+ const scalar_t *data_sampling_loc,
+ const scalar_t *data_attn_weight,
+ const int batch_size,
+ const int spatial_size,
+ const int num_heads,
+ const int channels,
+ const int num_levels,
+ const int num_query,
+ const int num_point,
+ scalar_t *grad_value,
+ scalar_t *grad_sampling_loc,
+ scalar_t *grad_attn_weight)
+{
+ CUDA_KERNEL_LOOP(index, n)
+ {
+ __shared__ scalar_t cache_grad_sampling_loc[blockSize * 2];
+ __shared__ scalar_t cache_grad_attn_weight[blockSize];
+ unsigned int tid = threadIdx.x;
+ int _temp = index;
+ const int c_col = _temp % channels;
+ _temp /= channels;
+ const int sampling_index = _temp;
+ const int m_col = _temp % num_heads;
+ _temp /= num_heads;
+ const int q_col = _temp % num_query;
+ _temp /= num_query;
+ const int b_col = _temp;
+
+ const scalar_t top_grad = grad_col[index];
+
+ int data_weight_ptr = sampling_index * num_levels * num_point;
+ int data_loc_w_ptr = data_weight_ptr << 1;
+ const int grad_sampling_ptr = data_weight_ptr;
+ grad_sampling_loc += grad_sampling_ptr << 1;
+ grad_attn_weight += grad_sampling_ptr;
+ const int grad_weight_stride = 1;
+ const int grad_loc_stride = 2;
+ const int qid_stride = num_heads * channels;
+ const int data_value_ptr_init_offset = b_col * spatial_size * qid_stride;
+
+ for (int l_col=0; l_col < num_levels; ++l_col)
+ {
+ const int level_start_id = data_level_start_index[l_col];
+ const int spatial_h_ptr = l_col << 1;
+ const int spatial_h = data_spatial_shapes[spatial_h_ptr];
+ const int spatial_w = data_spatial_shapes[spatial_h_ptr + 1];
+ const int value_ptr_offset = data_value_ptr_init_offset + level_start_id * qid_stride;
+ const scalar_t *data_value_ptr = data_value + value_ptr_offset;
+ scalar_t *grad_value_ptr = grad_value + value_ptr_offset;
+
+ for (int p_col=0; p_col < num_point; ++p_col)
+ {
+ const scalar_t loc_w = data_sampling_loc[data_loc_w_ptr];
+ const scalar_t loc_h = data_sampling_loc[data_loc_w_ptr + 1];
+ const scalar_t weight = data_attn_weight[data_weight_ptr];
+
+ const scalar_t h_im = loc_h * spatial_h - 0.5;
+ const scalar_t w_im = loc_w * spatial_w - 0.5;
+ *(cache_grad_sampling_loc+(threadIdx.x << 1)) = 0;
+ *(cache_grad_sampling_loc+((threadIdx.x << 1) + 1)) = 0;
+ *(cache_grad_attn_weight+threadIdx.x)=0;
+ if (h_im > -1 && w_im > -1 && h_im < spatial_h && w_im < spatial_w)
+ {
+ ms_deform_attn_col2im_bilinear(
+ data_value_ptr, spatial_h, spatial_w, num_heads, channels, h_im, w_im, m_col, c_col,
+ top_grad, weight, grad_value_ptr,
+ cache_grad_sampling_loc+(threadIdx.x << 1), cache_grad_attn_weight+threadIdx.x);
+ }
+
+ __syncthreads();
+
+ for (unsigned int s=blockSize/2; s>0; s>>=1)
+ {
+ if (tid < s) {
+ const unsigned int xid1 = tid << 1;
+ const unsigned int xid2 = (tid + s) << 1;
+ cache_grad_attn_weight[tid] += cache_grad_attn_weight[tid + s];
+ cache_grad_sampling_loc[xid1] += cache_grad_sampling_loc[xid2];
+ cache_grad_sampling_loc[xid1 + 1] += cache_grad_sampling_loc[xid2 + 1];
+ }
+ __syncthreads();
+ }
+
+ if (tid == 0)
+ {
+ *grad_sampling_loc = cache_grad_sampling_loc[0];
+ *(grad_sampling_loc + 1) = cache_grad_sampling_loc[1];
+ *grad_attn_weight = cache_grad_attn_weight[0];
+ }
+ __syncthreads();
+
+ data_weight_ptr += 1;
+ data_loc_w_ptr += 2;
+ grad_attn_weight += grad_weight_stride;
+ grad_sampling_loc += grad_loc_stride;
+ }
+ }
+ }
+}
+
+
+template
+__global__ void ms_deformable_col2im_gpu_kernel_shm_reduce_v1(const int n,
+ const scalar_t *grad_col,
+ const scalar_t *data_value,
+ const int64_t *data_spatial_shapes,
+ const int64_t *data_level_start_index,
+ const scalar_t *data_sampling_loc,
+ const scalar_t *data_attn_weight,
+ const int batch_size,
+ const int spatial_size,
+ const int num_heads,
+ const int channels,
+ const int num_levels,
+ const int num_query,
+ const int num_point,
+ scalar_t *grad_value,
+ scalar_t *grad_sampling_loc,
+ scalar_t *grad_attn_weight)
+{
+ CUDA_KERNEL_LOOP(index, n)
+ {
+ extern __shared__ int _s[];
+ scalar_t* cache_grad_sampling_loc = (scalar_t*)_s;
+ scalar_t* cache_grad_attn_weight = cache_grad_sampling_loc + 2 * blockDim.x;
+ unsigned int tid = threadIdx.x;
+ int _temp = index;
+ const int c_col = _temp % channels;
+ _temp /= channels;
+ const int sampling_index = _temp;
+ const int m_col = _temp % num_heads;
+ _temp /= num_heads;
+ const int q_col = _temp % num_query;
+ _temp /= num_query;
+ const int b_col = _temp;
+
+ const scalar_t top_grad = grad_col[index];
+
+ int data_weight_ptr = sampling_index * num_levels * num_point;
+ int data_loc_w_ptr = data_weight_ptr << 1;
+ const int grad_sampling_ptr = data_weight_ptr;
+ grad_sampling_loc += grad_sampling_ptr << 1;
+ grad_attn_weight += grad_sampling_ptr;
+ const int grad_weight_stride = 1;
+ const int grad_loc_stride = 2;
+ const int qid_stride = num_heads * channels;
+ const int data_value_ptr_init_offset = b_col * spatial_size * qid_stride;
+
+ for (int l_col=0; l_col < num_levels; ++l_col)
+ {
+ const int level_start_id = data_level_start_index[l_col];
+ const int spatial_h_ptr = l_col << 1;
+ const int spatial_h = data_spatial_shapes[spatial_h_ptr];
+ const int spatial_w = data_spatial_shapes[spatial_h_ptr + 1];
+ const int value_ptr_offset = data_value_ptr_init_offset + level_start_id * qid_stride;
+ const scalar_t *data_value_ptr = data_value + value_ptr_offset;
+ scalar_t *grad_value_ptr = grad_value + value_ptr_offset;
+
+ for (int p_col=0; p_col < num_point; ++p_col)
+ {
+ const scalar_t loc_w = data_sampling_loc[data_loc_w_ptr];
+ const scalar_t loc_h = data_sampling_loc[data_loc_w_ptr + 1];
+ const scalar_t weight = data_attn_weight[data_weight_ptr];
+
+ const scalar_t h_im = loc_h * spatial_h - 0.5;
+ const scalar_t w_im = loc_w * spatial_w - 0.5;
+ *(cache_grad_sampling_loc+(threadIdx.x << 1)) = 0;
+ *(cache_grad_sampling_loc+((threadIdx.x << 1) + 1)) = 0;
+ *(cache_grad_attn_weight+threadIdx.x)=0;
+ if (h_im > -1 && w_im > -1 && h_im < spatial_h && w_im < spatial_w)
+ {
+ ms_deform_attn_col2im_bilinear(
+ data_value_ptr, spatial_h, spatial_w, num_heads, channels, h_im, w_im, m_col, c_col,
+ top_grad, weight, grad_value_ptr,
+ cache_grad_sampling_loc+(threadIdx.x << 1), cache_grad_attn_weight+threadIdx.x);
+ }
+
+ __syncthreads();
+ if (tid == 0)
+ {
+ scalar_t _grad_w=cache_grad_sampling_loc[0], _grad_h=cache_grad_sampling_loc[1], _grad_a=cache_grad_attn_weight[0];
+ int sid=2;
+ for (unsigned int tid = 1; tid < blockDim.x; ++tid)
+ {
+ _grad_w += cache_grad_sampling_loc[sid];
+ _grad_h += cache_grad_sampling_loc[sid + 1];
+ _grad_a += cache_grad_attn_weight[tid];
+ sid += 2;
+ }
+
+
+ *grad_sampling_loc = _grad_w;
+ *(grad_sampling_loc + 1) = _grad_h;
+ *grad_attn_weight = _grad_a;
+ }
+ __syncthreads();
+
+ data_weight_ptr += 1;
+ data_loc_w_ptr += 2;
+ grad_attn_weight += grad_weight_stride;
+ grad_sampling_loc += grad_loc_stride;
+ }
+ }
+ }
+}
+
+template
+__global__ void ms_deformable_col2im_gpu_kernel_shm_reduce_v2(const int n,
+ const scalar_t *grad_col,
+ const scalar_t *data_value,
+ const int64_t *data_spatial_shapes,
+ const int64_t *data_level_start_index,
+ const scalar_t *data_sampling_loc,
+ const scalar_t *data_attn_weight,
+ const int batch_size,
+ const int spatial_size,
+ const int num_heads,
+ const int channels,
+ const int num_levels,
+ const int num_query,
+ const int num_point,
+ scalar_t *grad_value,
+ scalar_t *grad_sampling_loc,
+ scalar_t *grad_attn_weight)
+{
+ CUDA_KERNEL_LOOP(index, n)
+ {
+ extern __shared__ int _s[];
+ scalar_t* cache_grad_sampling_loc = (scalar_t*)_s;
+ scalar_t* cache_grad_attn_weight = cache_grad_sampling_loc + 2 * blockDim.x;
+ unsigned int tid = threadIdx.x;
+ int _temp = index;
+ const int c_col = _temp % channels;
+ _temp /= channels;
+ const int sampling_index = _temp;
+ const int m_col = _temp % num_heads;
+ _temp /= num_heads;
+ const int q_col = _temp % num_query;
+ _temp /= num_query;
+ const int b_col = _temp;
+
+ const scalar_t top_grad = grad_col[index];
+
+ int data_weight_ptr = sampling_index * num_levels * num_point;
+ int data_loc_w_ptr = data_weight_ptr << 1;
+ const int grad_sampling_ptr = data_weight_ptr;
+ grad_sampling_loc += grad_sampling_ptr << 1;
+ grad_attn_weight += grad_sampling_ptr;
+ const int grad_weight_stride = 1;
+ const int grad_loc_stride = 2;
+ const int qid_stride = num_heads * channels;
+ const int data_value_ptr_init_offset = b_col * spatial_size * qid_stride;
+
+ for (int l_col=0; l_col < num_levels; ++l_col)
+ {
+ const int level_start_id = data_level_start_index[l_col];
+ const int spatial_h_ptr = l_col << 1;
+ const int spatial_h = data_spatial_shapes[spatial_h_ptr];
+ const int spatial_w = data_spatial_shapes[spatial_h_ptr + 1];
+ const int value_ptr_offset = data_value_ptr_init_offset + level_start_id * qid_stride;
+ const scalar_t *data_value_ptr = data_value + value_ptr_offset;
+ scalar_t *grad_value_ptr = grad_value + value_ptr_offset;
+
+ for (int p_col=0; p_col < num_point; ++p_col)
+ {
+ const scalar_t loc_w = data_sampling_loc[data_loc_w_ptr];
+ const scalar_t loc_h = data_sampling_loc[data_loc_w_ptr + 1];
+ const scalar_t weight = data_attn_weight[data_weight_ptr];
+
+ const scalar_t h_im = loc_h * spatial_h - 0.5;
+ const scalar_t w_im = loc_w * spatial_w - 0.5;
+ *(cache_grad_sampling_loc+(threadIdx.x << 1)) = 0;
+ *(cache_grad_sampling_loc+((threadIdx.x << 1) + 1)) = 0;
+ *(cache_grad_attn_weight+threadIdx.x)=0;
+ if (h_im > -1 && w_im > -1 && h_im < spatial_h && w_im < spatial_w)
+ {
+ ms_deform_attn_col2im_bilinear(
+ data_value_ptr, spatial_h, spatial_w, num_heads, channels, h_im, w_im, m_col, c_col,
+ top_grad, weight, grad_value_ptr,
+ cache_grad_sampling_loc+(threadIdx.x << 1), cache_grad_attn_weight+threadIdx.x);
+ }
+
+ __syncthreads();
+
+ for (unsigned int s=blockDim.x/2, spre=blockDim.x; s>0; s>>=1, spre>>=1)
+ {
+ if (tid < s) {
+ const unsigned int xid1 = tid << 1;
+ const unsigned int xid2 = (tid + s) << 1;
+ cache_grad_attn_weight[tid] += cache_grad_attn_weight[tid + s];
+ cache_grad_sampling_loc[xid1] += cache_grad_sampling_loc[xid2];
+ cache_grad_sampling_loc[xid1 + 1] += cache_grad_sampling_loc[xid2 + 1];
+ if (tid + (s << 1) < spre)
+ {
+ cache_grad_attn_weight[tid] += cache_grad_attn_weight[tid + (s << 1)];
+ cache_grad_sampling_loc[xid1] += cache_grad_sampling_loc[xid2 + (s << 1)];
+ cache_grad_sampling_loc[xid1 + 1] += cache_grad_sampling_loc[xid2 + 1 + (s << 1)];
+ }
+ }
+ __syncthreads();
+ }
+
+ if (tid == 0)
+ {
+ *grad_sampling_loc = cache_grad_sampling_loc[0];
+ *(grad_sampling_loc + 1) = cache_grad_sampling_loc[1];
+ *grad_attn_weight = cache_grad_attn_weight[0];
+ }
+ __syncthreads();
+
+ data_weight_ptr += 1;
+ data_loc_w_ptr += 2;
+ grad_attn_weight += grad_weight_stride;
+ grad_sampling_loc += grad_loc_stride;
+ }
+ }
+ }
+}
+
+template
+__global__ void ms_deformable_col2im_gpu_kernel_shm_reduce_v2_multi_blocks(const int n,
+ const scalar_t *grad_col,
+ const scalar_t *data_value,
+ const int64_t *data_spatial_shapes,
+ const int64_t *data_level_start_index,
+ const scalar_t *data_sampling_loc,
+ const scalar_t *data_attn_weight,
+ const int batch_size,
+ const int spatial_size,
+ const int num_heads,
+ const int channels,
+ const int num_levels,
+ const int num_query,
+ const int num_point,
+ scalar_t *grad_value,
+ scalar_t *grad_sampling_loc,
+ scalar_t *grad_attn_weight)
+{
+ CUDA_KERNEL_LOOP(index, n)
+ {
+ extern __shared__ int _s[];
+ scalar_t* cache_grad_sampling_loc = (scalar_t*)_s;
+ scalar_t* cache_grad_attn_weight = cache_grad_sampling_loc + 2 * blockDim.x;
+ unsigned int tid = threadIdx.x;
+ int _temp = index;
+ const int c_col = _temp % channels;
+ _temp /= channels;
+ const int sampling_index = _temp;
+ const int m_col = _temp % num_heads;
+ _temp /= num_heads;
+ const int q_col = _temp % num_query;
+ _temp /= num_query;
+ const int b_col = _temp;
+
+ const scalar_t top_grad = grad_col[index];
+
+ int data_weight_ptr = sampling_index * num_levels * num_point;
+ int data_loc_w_ptr = data_weight_ptr << 1;
+ const int grad_sampling_ptr = data_weight_ptr;
+ grad_sampling_loc += grad_sampling_ptr << 1;
+ grad_attn_weight += grad_sampling_ptr;
+ const int grad_weight_stride = 1;
+ const int grad_loc_stride = 2;
+ const int qid_stride = num_heads * channels;
+ const int data_value_ptr_init_offset = b_col * spatial_size * qid_stride;
+
+ for (int l_col=0; l_col < num_levels; ++l_col)
+ {
+ const int level_start_id = data_level_start_index[l_col];
+ const int spatial_h_ptr = l_col << 1;
+ const int spatial_h = data_spatial_shapes[spatial_h_ptr];
+ const int spatial_w = data_spatial_shapes[spatial_h_ptr + 1];
+ const int value_ptr_offset = data_value_ptr_init_offset + level_start_id * qid_stride;
+ const scalar_t *data_value_ptr = data_value + value_ptr_offset;
+ scalar_t *grad_value_ptr = grad_value + value_ptr_offset;
+
+ for (int p_col=0; p_col < num_point; ++p_col)
+ {
+ const scalar_t loc_w = data_sampling_loc[data_loc_w_ptr];
+ const scalar_t loc_h = data_sampling_loc[data_loc_w_ptr + 1];
+ const scalar_t weight = data_attn_weight[data_weight_ptr];
+
+ const scalar_t h_im = loc_h * spatial_h - 0.5;
+ const scalar_t w_im = loc_w * spatial_w - 0.5;
+ *(cache_grad_sampling_loc+(threadIdx.x << 1)) = 0;
+ *(cache_grad_sampling_loc+((threadIdx.x << 1) + 1)) = 0;
+ *(cache_grad_attn_weight+threadIdx.x)=0;
+ if (h_im > -1 && w_im > -1 && h_im < spatial_h && w_im < spatial_w)
+ {
+ ms_deform_attn_col2im_bilinear(
+ data_value_ptr, spatial_h, spatial_w, num_heads, channels, h_im, w_im, m_col, c_col,
+ top_grad, weight, grad_value_ptr,
+ cache_grad_sampling_loc+(threadIdx.x << 1), cache_grad_attn_weight+threadIdx.x);
+ }
+
+ __syncthreads();
+
+ for (unsigned int s=blockDim.x/2, spre=blockDim.x; s>0; s>>=1, spre>>=1)
+ {
+ if (tid < s) {
+ const unsigned int xid1 = tid << 1;
+ const unsigned int xid2 = (tid + s) << 1;
+ cache_grad_attn_weight[tid] += cache_grad_attn_weight[tid + s];
+ cache_grad_sampling_loc[xid1] += cache_grad_sampling_loc[xid2];
+ cache_grad_sampling_loc[xid1 + 1] += cache_grad_sampling_loc[xid2 + 1];
+ if (tid + (s << 1) < spre)
+ {
+ cache_grad_attn_weight[tid] += cache_grad_attn_weight[tid + (s << 1)];
+ cache_grad_sampling_loc[xid1] += cache_grad_sampling_loc[xid2 + (s << 1)];
+ cache_grad_sampling_loc[xid1 + 1] += cache_grad_sampling_loc[xid2 + 1 + (s << 1)];
+ }
+ }
+ __syncthreads();
+ }
+
+ if (tid == 0)
+ {
+ atomicAdd(grad_sampling_loc, cache_grad_sampling_loc[0]);
+ atomicAdd(grad_sampling_loc + 1, cache_grad_sampling_loc[1]);
+ atomicAdd(grad_attn_weight, cache_grad_attn_weight[0]);
+ }
+ __syncthreads();
+
+ data_weight_ptr += 1;
+ data_loc_w_ptr += 2;
+ grad_attn_weight += grad_weight_stride;
+ grad_sampling_loc += grad_loc_stride;
+ }
+ }
+ }
+}
+
+
+template
+__global__ void ms_deformable_col2im_gpu_kernel_gm(const int n,
+ const scalar_t *grad_col,
+ const scalar_t *data_value,
+ const int64_t *data_spatial_shapes,
+ const int64_t *data_level_start_index,
+ const scalar_t *data_sampling_loc,
+ const scalar_t *data_attn_weight,
+ const int batch_size,
+ const int spatial_size,
+ const int num_heads,
+ const int channels,
+ const int num_levels,
+ const int num_query,
+ const int num_point,
+ scalar_t *grad_value,
+ scalar_t *grad_sampling_loc,
+ scalar_t *grad_attn_weight)
+{
+ CUDA_KERNEL_LOOP(index, n)
+ {
+ int _temp = index;
+ const int c_col = _temp % channels;
+ _temp /= channels;
+ const int sampling_index = _temp;
+ const int m_col = _temp % num_heads;
+ _temp /= num_heads;
+ const int q_col = _temp % num_query;
+ _temp /= num_query;
+ const int b_col = _temp;
+
+ const scalar_t top_grad = grad_col[index];
+
+ int data_weight_ptr = sampling_index * num_levels * num_point;
+ int data_loc_w_ptr = data_weight_ptr << 1;
+ const int grad_sampling_ptr = data_weight_ptr;
+ grad_sampling_loc += grad_sampling_ptr << 1;
+ grad_attn_weight += grad_sampling_ptr;
+ const int grad_weight_stride = 1;
+ const int grad_loc_stride = 2;
+ const int qid_stride = num_heads * channels;
+ const int data_value_ptr_init_offset = b_col * spatial_size * qid_stride;
+
+ for (int l_col=0; l_col < num_levels; ++l_col)
+ {
+ const int level_start_id = data_level_start_index[l_col];
+ const int spatial_h_ptr = l_col << 1;
+ const int spatial_h = data_spatial_shapes[spatial_h_ptr];
+ const int spatial_w = data_spatial_shapes[spatial_h_ptr + 1];
+ const int value_ptr_offset = data_value_ptr_init_offset + level_start_id * qid_stride;
+ const scalar_t *data_value_ptr = data_value + value_ptr_offset;
+ scalar_t *grad_value_ptr = grad_value + value_ptr_offset;
+
+ for (int p_col=0; p_col < num_point; ++p_col)
+ {
+ const scalar_t loc_w = data_sampling_loc[data_loc_w_ptr];
+ const scalar_t loc_h = data_sampling_loc[data_loc_w_ptr + 1];
+ const scalar_t weight = data_attn_weight[data_weight_ptr];
+
+ const scalar_t h_im = loc_h * spatial_h - 0.5;
+ const scalar_t w_im = loc_w * spatial_w - 0.5;
+ if (h_im > -1 && w_im > -1 && h_im < spatial_h && w_im < spatial_w)
+ {
+ ms_deform_attn_col2im_bilinear_gm(
+ data_value_ptr, spatial_h, spatial_w, num_heads, channels, h_im, w_im, m_col, c_col,
+ top_grad, weight, grad_value_ptr,
+ grad_sampling_loc, grad_attn_weight);
+ }
+ data_weight_ptr += 1;
+ data_loc_w_ptr += 2;
+ grad_attn_weight += grad_weight_stride;
+ grad_sampling_loc += grad_loc_stride;
+ }
+ }
+ }
+}
+
+
+template
+void ms_deformable_im2col_cuda(cudaStream_t stream,
+ const scalar_t* data_value,
+ const int64_t* data_spatial_shapes,
+ const int64_t* data_level_start_index,
+ const scalar_t* data_sampling_loc,
+ const scalar_t* data_attn_weight,
+ const int batch_size,
+ const int spatial_size,
+ const int num_heads,
+ const int channels,
+ const int num_levels,
+ const int num_query,
+ const int num_point,
+ scalar_t* data_col)
+{
+ const int num_kernels = batch_size * num_query * num_heads * channels;
+ const int num_actual_kernels = batch_size * num_query * num_heads * channels;
+ const int num_threads = CUDA_NUM_THREADS;
+ ms_deformable_im2col_gpu_kernel
+ <<>>(
+ num_kernels, data_value, data_spatial_shapes, data_level_start_index, data_sampling_loc, data_attn_weight,
+ batch_size, spatial_size, num_heads, channels, num_levels, num_query, num_point, data_col);
+
+ cudaError_t err = cudaGetLastError();
+ if (err != cudaSuccess)
+ {
+ printf("error in ms_deformable_im2col_cuda: %s\n", cudaGetErrorString(err));
+ }
+
+}
+
+template
+void ms_deformable_col2im_cuda(cudaStream_t stream,
+ const scalar_t* grad_col,
+ const scalar_t* data_value,
+ const int64_t * data_spatial_shapes,
+ const int64_t * data_level_start_index,
+ const scalar_t * data_sampling_loc,
+ const scalar_t * data_attn_weight,
+ const int batch_size,
+ const int spatial_size,
+ const int num_heads,
+ const int channels,
+ const int num_levels,
+ const int num_query,
+ const int num_point,
+ scalar_t* grad_value,
+ scalar_t* grad_sampling_loc,
+ scalar_t* grad_attn_weight)
+{
+ const int num_threads = (channels > CUDA_NUM_THREADS)?CUDA_NUM_THREADS:channels;
+ const int num_kernels = batch_size * num_query * num_heads * channels;
+ const int num_actual_kernels = batch_size * num_query * num_heads * channels;
+ if (channels > 1024)
+ {
+ if ((channels & 1023) == 0)
+ {
+ ms_deformable_col2im_gpu_kernel_shm_reduce_v2_multi_blocks
+ <<>>(
+ num_kernels,
+ grad_col,
+ data_value,
+ data_spatial_shapes,
+ data_level_start_index,
+ data_sampling_loc,
+ data_attn_weight,
+ batch_size,
+ spatial_size,
+ num_heads,
+ channels,
+ num_levels,
+ num_query,
+ num_point,
+ grad_value,
+ grad_sampling_loc,
+ grad_attn_weight);
+ }
+ else
+ {
+ ms_deformable_col2im_gpu_kernel_gm
+ <<>>(
+ num_kernels,
+ grad_col,
+ data_value,
+ data_spatial_shapes,
+ data_level_start_index,
+ data_sampling_loc,
+ data_attn_weight,
+ batch_size,
+ spatial_size,
+ num_heads,
+ channels,
+ num_levels,
+ num_query,
+ num_point,
+ grad_value,
+ grad_sampling_loc,
+ grad_attn_weight);
+ }
+ }
+ else{
+ switch(channels)
+ {
+ case 1:
+ ms_deformable_col2im_gpu_kernel_shm_blocksize_aware_reduce_v1
+ <<>>(
+ num_kernels,
+ grad_col,
+ data_value,
+ data_spatial_shapes,
+ data_level_start_index,
+ data_sampling_loc,
+ data_attn_weight,
+ batch_size,
+ spatial_size,
+ num_heads,
+ channels,
+ num_levels,
+ num_query,
+ num_point,
+ grad_value,
+ grad_sampling_loc,
+ grad_attn_weight);
+ break;
+ case 2:
+ ms_deformable_col2im_gpu_kernel_shm_blocksize_aware_reduce_v1
+ <<>>(
+ num_kernels,
+ grad_col,
+ data_value,
+ data_spatial_shapes,
+ data_level_start_index,
+ data_sampling_loc,
+ data_attn_weight,
+ batch_size,
+ spatial_size,
+ num_heads,
+ channels,
+ num_levels,
+ num_query,
+ num_point,
+ grad_value,
+ grad_sampling_loc,
+ grad_attn_weight);
+ break;
+ case 4:
+ ms_deformable_col2im_gpu_kernel_shm_blocksize_aware_reduce_v1
+ <<>>(
+ num_kernels,
+ grad_col,
+ data_value,
+ data_spatial_shapes,
+ data_level_start_index,
+ data_sampling_loc,
+ data_attn_weight,
+ batch_size,
+ spatial_size,
+ num_heads,
+ channels,
+ num_levels,
+ num_query,
+ num_point,
+ grad_value,
+ grad_sampling_loc,
+ grad_attn_weight);
+ break;
+ case 8:
+ ms_deformable_col2im_gpu_kernel_shm_blocksize_aware_reduce_v1
+ <<>>(
+ num_kernels,
+ grad_col,
+ data_value,
+ data_spatial_shapes,
+ data_level_start_index,
+ data_sampling_loc,
+ data_attn_weight,
+ batch_size,
+ spatial_size,
+ num_heads,
+ channels,
+ num_levels,
+ num_query,
+ num_point,
+ grad_value,
+ grad_sampling_loc,
+ grad_attn_weight);
+ break;
+ case 16:
+ ms_deformable_col2im_gpu_kernel_shm_blocksize_aware_reduce_v1
+ <<>>(
+ num_kernels,
+ grad_col,
+ data_value,
+ data_spatial_shapes,
+ data_level_start_index,
+ data_sampling_loc,
+ data_attn_weight,
+ batch_size,
+ spatial_size,
+ num_heads,
+ channels,
+ num_levels,
+ num_query,
+ num_point,
+ grad_value,
+ grad_sampling_loc,
+ grad_attn_weight);
+ break;
+ case 32:
+ ms_deformable_col2im_gpu_kernel_shm_blocksize_aware_reduce_v1
+ <<>>(
+ num_kernels,
+ grad_col,
+ data_value,
+ data_spatial_shapes,
+ data_level_start_index,
+ data_sampling_loc,
+ data_attn_weight,
+ batch_size,
+ spatial_size,
+ num_heads,
+ channels,
+ num_levels,
+ num_query,
+ num_point,
+ grad_value,
+ grad_sampling_loc,
+ grad_attn_weight);
+ break;
+ case 64:
+ ms_deformable_col2im_gpu_kernel_shm_blocksize_aware_reduce_v2
+ <<>>(
+ num_kernels,
+ grad_col,
+ data_value,
+ data_spatial_shapes,
+ data_level_start_index,
+ data_sampling_loc,
+ data_attn_weight,
+ batch_size,
+ spatial_size,
+ num_heads,
+ channels,
+ num_levels,
+ num_query,
+ num_point,
+ grad_value,
+ grad_sampling_loc,
+ grad_attn_weight);
+ break;
+ case 128:
+ ms_deformable_col2im_gpu_kernel_shm_blocksize_aware_reduce_v2
+ <<>>(
+ num_kernels,
+ grad_col,
+ data_value,
+ data_spatial_shapes,
+ data_level_start_index,
+ data_sampling_loc,
+ data_attn_weight,
+ batch_size,
+ spatial_size,
+ num_heads,
+ channels,
+ num_levels,
+ num_query,
+ num_point,
+ grad_value,
+ grad_sampling_loc,
+ grad_attn_weight);
+ break;
+ case 256:
+ ms_deformable_col2im_gpu_kernel_shm_blocksize_aware_reduce_v2
+ <<>>(
+ num_kernels,
+ grad_col,
+ data_value,
+ data_spatial_shapes,
+ data_level_start_index,
+ data_sampling_loc,
+ data_attn_weight,
+ batch_size,
+ spatial_size,
+ num_heads,
+ channels,
+ num_levels,
+ num_query,
+ num_point,
+ grad_value,
+ grad_sampling_loc,
+ grad_attn_weight);
+ break;
+ case 512:
+ ms_deformable_col2im_gpu_kernel_shm_blocksize_aware_reduce_v2
+ <<>>(
+ num_kernels,
+ grad_col,
+ data_value,
+ data_spatial_shapes,
+ data_level_start_index,
+ data_sampling_loc,
+ data_attn_weight,
+ batch_size,
+ spatial_size,
+ num_heads,
+ channels,
+ num_levels,
+ num_query,
+ num_point,
+ grad_value,
+ grad_sampling_loc,
+ grad_attn_weight);
+ break;
+ case 1024:
+ ms_deformable_col2im_gpu_kernel_shm_blocksize_aware_reduce_v2
+ <<>>(
+ num_kernels,
+ grad_col,
+ data_value,
+ data_spatial_shapes,
+ data_level_start_index,
+ data_sampling_loc,
+ data_attn_weight,
+ batch_size,
+ spatial_size,
+ num_heads,
+ channels,
+ num_levels,
+ num_query,
+ num_point,
+ grad_value,
+ grad_sampling_loc,
+ grad_attn_weight);
+ break;
+ default:
+ if (channels < 64)
+ {
+ ms_deformable_col2im_gpu_kernel_shm_reduce_v1
+ <<>>(
+ num_kernels,
+ grad_col,
+ data_value,
+ data_spatial_shapes,
+ data_level_start_index,
+ data_sampling_loc,
+ data_attn_weight,
+ batch_size,
+ spatial_size,
+ num_heads,
+ channels,
+ num_levels,
+ num_query,
+ num_point,
+ grad_value,
+ grad_sampling_loc,
+ grad_attn_weight);
+ }
+ else
+ {
+ ms_deformable_col2im_gpu_kernel_shm_reduce_v2
+ <<>>(
+ num_kernels,
+ grad_col,
+ data_value,
+ data_spatial_shapes,
+ data_level_start_index,
+ data_sampling_loc,
+ data_attn_weight,
+ batch_size,
+ spatial_size,
+ num_heads,
+ channels,
+ num_levels,
+ num_query,
+ num_point,
+ grad_value,
+ grad_sampling_loc,
+ grad_attn_weight);
+ }
+ }
+ }
+ cudaError_t err = cudaGetLastError();
+ if (err != cudaSuccess)
+ {
+ printf("error in ms_deformable_col2im_cuda: %s\n", cudaGetErrorString(err));
+ }
+
+}
\ No newline at end of file
diff --git a/GroundingDINO/groundingdino/models/GroundingDINO/csrc/cuda_version.cu b/GroundingDINO/groundingdino/models/GroundingDINO/csrc/cuda_version.cu
new file mode 100644
index 0000000000000000000000000000000000000000..64569e34ffb250964de27e33e7a53f3822270b9e
--- /dev/null
+++ b/GroundingDINO/groundingdino/models/GroundingDINO/csrc/cuda_version.cu
@@ -0,0 +1,7 @@
+#include
+
+namespace groundingdino {
+int get_cudart_version() {
+ return CUDART_VERSION;
+}
+} // namespace groundingdino
diff --git a/GroundingDINO/groundingdino/models/GroundingDINO/csrc/vision.cpp b/GroundingDINO/groundingdino/models/GroundingDINO/csrc/vision.cpp
new file mode 100644
index 0000000000000000000000000000000000000000..c1f2c50c82909bbd5492c163d634af77a3ba1781
--- /dev/null
+++ b/GroundingDINO/groundingdino/models/GroundingDINO/csrc/vision.cpp
@@ -0,0 +1,58 @@
+// Copyright (c) Facebook, Inc. and its affiliates. All Rights Reserved
+
+#include "MsDeformAttn/ms_deform_attn.h"
+
+namespace groundingdino {
+
+#ifdef WITH_CUDA
+extern int get_cudart_version();
+#endif
+
+std::string get_cuda_version() {
+#ifdef WITH_CUDA
+ std::ostringstream oss;
+
+ // copied from
+ // https://github.com/pytorch/pytorch/blob/master/aten/src/ATen/cuda/detail/CUDAHooks.cpp#L231
+ auto printCudaStyleVersion = [&](int v) {
+ oss << (v / 1000) << "." << (v / 10 % 100);
+ if (v % 10 != 0) {
+ oss << "." << (v % 10);
+ }
+ };
+ printCudaStyleVersion(get_cudart_version());
+ return oss.str();
+#else
+ return std::string("not available");
+#endif
+}
+
+// similar to
+// https://github.com/pytorch/pytorch/blob/master/aten/src/ATen/Version.cpp
+std::string get_compiler_version() {
+ std::ostringstream ss;
+#if defined(__GNUC__)
+#ifndef __clang__
+ { ss << "GCC " << __GNUC__ << "." << __GNUC_MINOR__; }
+#endif
+#endif
+
+#if defined(__clang_major__)
+ {
+ ss << "clang " << __clang_major__ << "." << __clang_minor__ << "."
+ << __clang_patchlevel__;
+ }
+#endif
+
+#if defined(_MSC_VER)
+ { ss << "MSVC " << _MSC_FULL_VER; }
+#endif
+ return ss.str();
+}
+
+PYBIND11_MODULE(TORCH_EXTENSION_NAME, m) {
+ m.def("ms_deform_attn_forward", &ms_deform_attn_forward, "ms_deform_attn_forward");
+ m.def("ms_deform_attn_backward", &ms_deform_attn_backward, "ms_deform_attn_backward");
+}
+
+} // namespace groundingdino
\ No newline at end of file
diff --git a/GroundingDINO/groundingdino/models/GroundingDINO/fuse_modules.py b/GroundingDINO/groundingdino/models/GroundingDINO/fuse_modules.py
new file mode 100644
index 0000000000000000000000000000000000000000..2753b3ddee43c7a9fe28d1824db5d786e7e1ad59
--- /dev/null
+++ b/GroundingDINO/groundingdino/models/GroundingDINO/fuse_modules.py
@@ -0,0 +1,297 @@
+# ------------------------------------------------------------------------
+# Grounding DINO
+# url: https://github.com/IDEA-Research/GroundingDINO
+# Copyright (c) 2023 IDEA. All Rights Reserved.
+# Licensed under the Apache License, Version 2.0 [see LICENSE for details]
+# ------------------------------------------------------------------------
+
+import torch
+import torch.nn as nn
+import torch.nn.functional as F
+from timm.models.layers import DropPath
+
+
+class FeatureResizer(nn.Module):
+ """
+ This class takes as input a set of embeddings of dimension C1 and outputs a set of
+ embedding of dimension C2, after a linear transformation, dropout and normalization (LN).
+ """
+
+ def __init__(self, input_feat_size, output_feat_size, dropout, do_ln=True):
+ super().__init__()
+ self.do_ln = do_ln
+ # Object feature encoding
+ self.fc = nn.Linear(input_feat_size, output_feat_size, bias=True)
+ self.layer_norm = nn.LayerNorm(output_feat_size, eps=1e-12)
+ self.dropout = nn.Dropout(dropout)
+
+ def forward(self, encoder_features):
+ x = self.fc(encoder_features)
+ if self.do_ln:
+ x = self.layer_norm(x)
+ output = self.dropout(x)
+ return output
+
+
+def l1norm(X, dim, eps=1e-8):
+ """L1-normalize columns of X"""
+ norm = torch.abs(X).sum(dim=dim, keepdim=True) + eps
+ X = torch.div(X, norm)
+ return X
+
+
+def l2norm(X, dim, eps=1e-8):
+ """L2-normalize columns of X"""
+ norm = torch.pow(X, 2).sum(dim=dim, keepdim=True).sqrt() + eps
+ X = torch.div(X, norm)
+ return X
+
+
+def func_attention(query, context, smooth=1, raw_feature_norm="softmax", eps=1e-8):
+ """
+ query: (n_context, queryL, d)
+ context: (n_context, sourceL, d)
+ """
+ batch_size_q, queryL = query.size(0), query.size(1)
+ batch_size, sourceL = context.size(0), context.size(1)
+
+ # Get attention
+ # --> (batch, d, queryL)
+ queryT = torch.transpose(query, 1, 2)
+
+ # (batch, sourceL, d)(batch, d, queryL)
+ # --> (batch, sourceL, queryL)
+ attn = torch.bmm(context, queryT)
+ if raw_feature_norm == "softmax":
+ # --> (batch*sourceL, queryL)
+ attn = attn.view(batch_size * sourceL, queryL)
+ attn = nn.Softmax()(attn)
+ # --> (batch, sourceL, queryL)
+ attn = attn.view(batch_size, sourceL, queryL)
+ elif raw_feature_norm == "l2norm":
+ attn = l2norm(attn, 2)
+ elif raw_feature_norm == "clipped_l2norm":
+ attn = nn.LeakyReLU(0.1)(attn)
+ attn = l2norm(attn, 2)
+ else:
+ raise ValueError("unknown first norm type:", raw_feature_norm)
+ # --> (batch, queryL, sourceL)
+ attn = torch.transpose(attn, 1, 2).contiguous()
+ # --> (batch*queryL, sourceL)
+ attn = attn.view(batch_size * queryL, sourceL)
+ attn = nn.Softmax()(attn * smooth)
+ # --> (batch, queryL, sourceL)
+ attn = attn.view(batch_size, queryL, sourceL)
+ # --> (batch, sourceL, queryL)
+ attnT = torch.transpose(attn, 1, 2).contiguous()
+
+ # --> (batch, d, sourceL)
+ contextT = torch.transpose(context, 1, 2)
+ # (batch x d x sourceL)(batch x sourceL x queryL)
+ # --> (batch, d, queryL)
+ weightedContext = torch.bmm(contextT, attnT)
+ # --> (batch, queryL, d)
+ weightedContext = torch.transpose(weightedContext, 1, 2)
+
+ return weightedContext, attnT
+
+
+class BiMultiHeadAttention(nn.Module):
+ def __init__(self, v_dim, l_dim, embed_dim, num_heads, dropout=0.1, cfg=None):
+ super(BiMultiHeadAttention, self).__init__()
+
+ self.embed_dim = embed_dim
+ self.num_heads = num_heads
+ self.head_dim = embed_dim // num_heads
+ self.v_dim = v_dim
+ self.l_dim = l_dim
+
+ assert (
+ self.head_dim * self.num_heads == self.embed_dim
+ ), f"embed_dim must be divisible by num_heads (got `embed_dim`: {self.embed_dim} and `num_heads`: {self.num_heads})."
+ self.scale = self.head_dim ** (-0.5)
+ self.dropout = dropout
+
+ self.v_proj = nn.Linear(self.v_dim, self.embed_dim)
+ self.l_proj = nn.Linear(self.l_dim, self.embed_dim)
+ self.values_v_proj = nn.Linear(self.v_dim, self.embed_dim)
+ self.values_l_proj = nn.Linear(self.l_dim, self.embed_dim)
+
+ self.out_v_proj = nn.Linear(self.embed_dim, self.v_dim)
+ self.out_l_proj = nn.Linear(self.embed_dim, self.l_dim)
+
+ self.stable_softmax_2d = True
+ self.clamp_min_for_underflow = True
+ self.clamp_max_for_overflow = True
+
+ self._reset_parameters()
+
+ def _shape(self, tensor: torch.Tensor, seq_len: int, bsz: int):
+ return tensor.view(bsz, seq_len, self.num_heads, self.head_dim).transpose(1, 2).contiguous()
+
+ def _reset_parameters(self):
+ nn.init.xavier_uniform_(self.v_proj.weight)
+ self.v_proj.bias.data.fill_(0)
+ nn.init.xavier_uniform_(self.l_proj.weight)
+ self.l_proj.bias.data.fill_(0)
+ nn.init.xavier_uniform_(self.values_v_proj.weight)
+ self.values_v_proj.bias.data.fill_(0)
+ nn.init.xavier_uniform_(self.values_l_proj.weight)
+ self.values_l_proj.bias.data.fill_(0)
+ nn.init.xavier_uniform_(self.out_v_proj.weight)
+ self.out_v_proj.bias.data.fill_(0)
+ nn.init.xavier_uniform_(self.out_l_proj.weight)
+ self.out_l_proj.bias.data.fill_(0)
+
+ def forward(self, v, l, attention_mask_v=None, attention_mask_l=None):
+ """_summary_
+
+ Args:
+ v (_type_): bs, n_img, dim
+ l (_type_): bs, n_text, dim
+ attention_mask_v (_type_, optional): _description_. bs, n_img
+ attention_mask_l (_type_, optional): _description_. bs, n_text
+
+ Returns:
+ _type_: _description_
+ """
+ # if os.environ.get('IPDB_SHILONG_DEBUG', None) == 'INFO':
+ # import ipdb; ipdb.set_trace()
+ bsz, tgt_len, _ = v.size()
+
+ query_states = self.v_proj(v) * self.scale
+ key_states = self._shape(self.l_proj(l), -1, bsz)
+ value_v_states = self._shape(self.values_v_proj(v), -1, bsz)
+ value_l_states = self._shape(self.values_l_proj(l), -1, bsz)
+
+ proj_shape = (bsz * self.num_heads, -1, self.head_dim)
+ query_states = self._shape(query_states, tgt_len, bsz).view(*proj_shape)
+ key_states = key_states.view(*proj_shape)
+ value_v_states = value_v_states.view(*proj_shape)
+ value_l_states = value_l_states.view(*proj_shape)
+
+ src_len = key_states.size(1)
+ attn_weights = torch.bmm(query_states, key_states.transpose(1, 2)) # bs*nhead, nimg, ntxt
+
+ if attn_weights.size() != (bsz * self.num_heads, tgt_len, src_len):
+ raise ValueError(
+ f"Attention weights should be of size {(bsz * self.num_heads, tgt_len, src_len)}, but is {attn_weights.size()}"
+ )
+
+ if self.stable_softmax_2d:
+ attn_weights = attn_weights - attn_weights.max()
+
+ if self.clamp_min_for_underflow:
+ attn_weights = torch.clamp(
+ attn_weights, min=-50000
+ ) # Do not increase -50000, data type half has quite limited range
+ if self.clamp_max_for_overflow:
+ attn_weights = torch.clamp(
+ attn_weights, max=50000
+ ) # Do not increase 50000, data type half has quite limited range
+
+ attn_weights_T = attn_weights.transpose(1, 2)
+ attn_weights_l = attn_weights_T - torch.max(attn_weights_T, dim=-1, keepdim=True)[0]
+ if self.clamp_min_for_underflow:
+ attn_weights_l = torch.clamp(
+ attn_weights_l, min=-50000
+ ) # Do not increase -50000, data type half has quite limited range
+ if self.clamp_max_for_overflow:
+ attn_weights_l = torch.clamp(
+ attn_weights_l, max=50000
+ ) # Do not increase 50000, data type half has quite limited range
+
+ # mask vison for language
+ if attention_mask_v is not None:
+ attention_mask_v = (
+ attention_mask_v[:, None, None, :].repeat(1, self.num_heads, 1, 1).flatten(0, 1)
+ )
+ attn_weights_l.masked_fill_(attention_mask_v, float("-inf"))
+
+ attn_weights_l = attn_weights_l.softmax(dim=-1)
+
+ # mask language for vision
+ if attention_mask_l is not None:
+ attention_mask_l = (
+ attention_mask_l[:, None, None, :].repeat(1, self.num_heads, 1, 1).flatten(0, 1)
+ )
+ attn_weights.masked_fill_(attention_mask_l, float("-inf"))
+ attn_weights_v = attn_weights.softmax(dim=-1)
+
+ attn_probs_v = F.dropout(attn_weights_v, p=self.dropout, training=self.training)
+ attn_probs_l = F.dropout(attn_weights_l, p=self.dropout, training=self.training)
+
+ attn_output_v = torch.bmm(attn_probs_v, value_l_states)
+ attn_output_l = torch.bmm(attn_probs_l, value_v_states)
+
+ if attn_output_v.size() != (bsz * self.num_heads, tgt_len, self.head_dim):
+ raise ValueError(
+ f"`attn_output_v` should be of size {(bsz, self.num_heads, tgt_len, self.head_dim)}, but is {attn_output_v.size()}"
+ )
+
+ if attn_output_l.size() != (bsz * self.num_heads, src_len, self.head_dim):
+ raise ValueError(
+ f"`attn_output_l` should be of size {(bsz, self.num_heads, src_len, self.head_dim)}, but is {attn_output_l.size()}"
+ )
+
+ attn_output_v = attn_output_v.view(bsz, self.num_heads, tgt_len, self.head_dim)
+ attn_output_v = attn_output_v.transpose(1, 2)
+ attn_output_v = attn_output_v.reshape(bsz, tgt_len, self.embed_dim)
+
+ attn_output_l = attn_output_l.view(bsz, self.num_heads, src_len, self.head_dim)
+ attn_output_l = attn_output_l.transpose(1, 2)
+ attn_output_l = attn_output_l.reshape(bsz, src_len, self.embed_dim)
+
+ attn_output_v = self.out_v_proj(attn_output_v)
+ attn_output_l = self.out_l_proj(attn_output_l)
+
+ return attn_output_v, attn_output_l
+
+
+# Bi-Direction MHA (text->image, image->text)
+class BiAttentionBlock(nn.Module):
+ def __init__(
+ self,
+ v_dim,
+ l_dim,
+ embed_dim,
+ num_heads,
+ dropout=0.1,
+ drop_path=0.0,
+ init_values=1e-4,
+ cfg=None,
+ ):
+ """
+ Inputs:
+ embed_dim - Dimensionality of input and attention feature vectors
+ hidden_dim - Dimensionality of hidden layer in feed-forward network
+ (usually 2-4x larger than embed_dim)
+ num_heads - Number of heads to use in the Multi-Head Attention block
+ dropout - Amount of dropout to apply in the feed-forward network
+ """
+ super(BiAttentionBlock, self).__init__()
+
+ # pre layer norm
+ self.layer_norm_v = nn.LayerNorm(v_dim)
+ self.layer_norm_l = nn.LayerNorm(l_dim)
+ self.attn = BiMultiHeadAttention(
+ v_dim=v_dim, l_dim=l_dim, embed_dim=embed_dim, num_heads=num_heads, dropout=dropout
+ )
+
+ # add layer scale for training stability
+ self.drop_path = DropPath(drop_path) if drop_path > 0.0 else nn.Identity()
+ self.gamma_v = nn.Parameter(init_values * torch.ones((v_dim)), requires_grad=True)
+ self.gamma_l = nn.Parameter(init_values * torch.ones((l_dim)), requires_grad=True)
+
+ def forward(self, v, l, attention_mask_v=None, attention_mask_l=None):
+ v = self.layer_norm_v(v)
+ l = self.layer_norm_l(l)
+ delta_v, delta_l = self.attn(
+ v, l, attention_mask_v=attention_mask_v, attention_mask_l=attention_mask_l
+ )
+ # v, l = v + delta_v, l + delta_l
+ v = v + self.drop_path(self.gamma_v * delta_v)
+ l = l + self.drop_path(self.gamma_l * delta_l)
+ return v, l
+
+ # def forward(self, v:List[torch.Tensor], l, attention_mask_v=None, attention_mask_l=None)
diff --git a/GroundingDINO/groundingdino/models/GroundingDINO/groundingdino.py b/GroundingDINO/groundingdino/models/GroundingDINO/groundingdino.py
new file mode 100644
index 0000000000000000000000000000000000000000..052df6220595a1b39b7e2aea37ca4872d113dfd2
--- /dev/null
+++ b/GroundingDINO/groundingdino/models/GroundingDINO/groundingdino.py
@@ -0,0 +1,395 @@
+# ------------------------------------------------------------------------
+# Grounding DINO
+# url: https://github.com/IDEA-Research/GroundingDINO
+# Copyright (c) 2023 IDEA. All Rights Reserved.
+# Licensed under the Apache License, Version 2.0 [see LICENSE for details]
+# ------------------------------------------------------------------------
+# Conditional DETR model and criterion classes.
+# Copyright (c) 2021 Microsoft. All Rights Reserved.
+# Licensed under the Apache License, Version 2.0 [see LICENSE for details]
+# ------------------------------------------------------------------------
+# Modified from DETR (https://github.com/facebookresearch/detr)
+# Copyright (c) Facebook, Inc. and its affiliates. All Rights Reserved.
+# ------------------------------------------------------------------------
+# Modified from Deformable DETR (https://github.com/fundamentalvision/Deformable-DETR)
+# Copyright (c) 2020 SenseTime. All Rights Reserved.
+# ------------------------------------------------------------------------
+import copy
+from typing import List
+
+import torch
+import torch.nn.functional as F
+from torch import nn
+from torchvision.ops.boxes import nms
+from transformers import AutoTokenizer, BertModel, BertTokenizer, RobertaModel, RobertaTokenizerFast
+
+from groundingdino.util import box_ops, get_tokenlizer
+from groundingdino.util.misc import (
+ NestedTensor,
+ accuracy,
+ get_world_size,
+ interpolate,
+ inverse_sigmoid,
+ is_dist_avail_and_initialized,
+ nested_tensor_from_tensor_list,
+)
+from groundingdino.util.utils import get_phrases_from_posmap
+from groundingdino.util.visualizer import COCOVisualizer
+from groundingdino.util.vl_utils import create_positive_map_from_span
+
+from ..registry import MODULE_BUILD_FUNCS
+from .backbone import build_backbone
+from .bertwarper import (
+ BertModelWarper,
+ generate_masks_with_special_tokens,
+ generate_masks_with_special_tokens_and_transfer_map,
+)
+from .transformer import build_transformer
+from .utils import MLP, ContrastiveEmbed, sigmoid_focal_loss
+
+
+class GroundingDINO(nn.Module):
+ """This is the Cross-Attention Detector module that performs object detection"""
+
+ def __init__(
+ self,
+ backbone,
+ transformer,
+ num_queries,
+ aux_loss=False,
+ iter_update=False,
+ query_dim=2,
+ num_feature_levels=1,
+ nheads=8,
+ # two stage
+ two_stage_type="no", # ['no', 'standard']
+ dec_pred_bbox_embed_share=True,
+ two_stage_class_embed_share=True,
+ two_stage_bbox_embed_share=True,
+ num_patterns=0,
+ dn_number=100,
+ dn_box_noise_scale=0.4,
+ dn_label_noise_ratio=0.5,
+ dn_labelbook_size=100,
+ text_encoder_type="bert-base-uncased",
+ sub_sentence_present=True,
+ max_text_len=256,
+ ):
+ """Initializes the model.
+ Parameters:
+ backbone: torch module of the backbone to be used. See backbone.py
+ transformer: torch module of the transformer architecture. See transformer.py
+ num_queries: number of object queries, ie detection slot. This is the maximal number of objects
+ Conditional DETR can detect in a single image. For COCO, we recommend 100 queries.
+ aux_loss: True if auxiliary decoding losses (loss at each decoder layer) are to be used.
+ """
+ super().__init__()
+ self.num_queries = num_queries
+ self.transformer = transformer
+ self.hidden_dim = hidden_dim = transformer.d_model
+ self.num_feature_levels = num_feature_levels
+ self.nheads = nheads
+ self.max_text_len = 256
+ self.sub_sentence_present = sub_sentence_present
+
+ # setting query dim
+ self.query_dim = query_dim
+ assert query_dim == 4
+
+ # for dn training
+ self.num_patterns = num_patterns
+ self.dn_number = dn_number
+ self.dn_box_noise_scale = dn_box_noise_scale
+ self.dn_label_noise_ratio = dn_label_noise_ratio
+ self.dn_labelbook_size = dn_labelbook_size
+
+ # bert
+ self.tokenizer = get_tokenlizer.get_tokenlizer(text_encoder_type)
+ self.bert = get_tokenlizer.get_pretrained_language_model(text_encoder_type)
+ self.bert.pooler.dense.weight.requires_grad_(False)
+ self.bert.pooler.dense.bias.requires_grad_(False)
+ self.bert = BertModelWarper(bert_model=self.bert)
+
+ self.feat_map = nn.Linear(self.bert.config.hidden_size, self.hidden_dim, bias=True)
+ nn.init.constant_(self.feat_map.bias.data, 0)
+ nn.init.xavier_uniform_(self.feat_map.weight.data)
+ # freeze
+
+ # special tokens
+ self.specical_tokens = self.tokenizer.convert_tokens_to_ids(["[CLS]", "[SEP]", ".", "?"])
+
+ # prepare input projection layers
+ if num_feature_levels > 1:
+ num_backbone_outs = len(backbone.num_channels)
+ input_proj_list = []
+ for _ in range(num_backbone_outs):
+ in_channels = backbone.num_channels[_]
+ input_proj_list.append(
+ nn.Sequential(
+ nn.Conv2d(in_channels, hidden_dim, kernel_size=1),
+ nn.GroupNorm(32, hidden_dim),
+ )
+ )
+ for _ in range(num_feature_levels - num_backbone_outs):
+ input_proj_list.append(
+ nn.Sequential(
+ nn.Conv2d(in_channels, hidden_dim, kernel_size=3, stride=2, padding=1),
+ nn.GroupNorm(32, hidden_dim),
+ )
+ )
+ in_channels = hidden_dim
+ self.input_proj = nn.ModuleList(input_proj_list)
+ else:
+ assert two_stage_type == "no", "two_stage_type should be no if num_feature_levels=1 !!!"
+ self.input_proj = nn.ModuleList(
+ [
+ nn.Sequential(
+ nn.Conv2d(backbone.num_channels[-1], hidden_dim, kernel_size=1),
+ nn.GroupNorm(32, hidden_dim),
+ )
+ ]
+ )
+
+ self.backbone = backbone
+ self.aux_loss = aux_loss
+ self.box_pred_damping = box_pred_damping = None
+
+ self.iter_update = iter_update
+ assert iter_update, "Why not iter_update?"
+
+ # prepare pred layers
+ self.dec_pred_bbox_embed_share = dec_pred_bbox_embed_share
+ # prepare class & box embed
+ _class_embed = ContrastiveEmbed()
+
+ _bbox_embed = MLP(hidden_dim, hidden_dim, 4, 3)
+ nn.init.constant_(_bbox_embed.layers[-1].weight.data, 0)
+ nn.init.constant_(_bbox_embed.layers[-1].bias.data, 0)
+
+ if dec_pred_bbox_embed_share:
+ box_embed_layerlist = [_bbox_embed for i in range(transformer.num_decoder_layers)]
+ else:
+ box_embed_layerlist = [
+ copy.deepcopy(_bbox_embed) for i in range(transformer.num_decoder_layers)
+ ]
+ class_embed_layerlist = [_class_embed for i in range(transformer.num_decoder_layers)]
+ self.bbox_embed = nn.ModuleList(box_embed_layerlist)
+ self.class_embed = nn.ModuleList(class_embed_layerlist)
+ self.transformer.decoder.bbox_embed = self.bbox_embed
+ self.transformer.decoder.class_embed = self.class_embed
+
+ # two stage
+ self.two_stage_type = two_stage_type
+ assert two_stage_type in ["no", "standard"], "unknown param {} of two_stage_type".format(
+ two_stage_type
+ )
+ if two_stage_type != "no":
+ if two_stage_bbox_embed_share:
+ assert dec_pred_bbox_embed_share
+ self.transformer.enc_out_bbox_embed = _bbox_embed
+ else:
+ self.transformer.enc_out_bbox_embed = copy.deepcopy(_bbox_embed)
+
+ if two_stage_class_embed_share:
+ assert dec_pred_bbox_embed_share
+ self.transformer.enc_out_class_embed = _class_embed
+ else:
+ self.transformer.enc_out_class_embed = copy.deepcopy(_class_embed)
+
+ self.refpoint_embed = None
+
+ self._reset_parameters()
+
+ def _reset_parameters(self):
+ # init input_proj
+ for proj in self.input_proj:
+ nn.init.xavier_uniform_(proj[0].weight, gain=1)
+ nn.init.constant_(proj[0].bias, 0)
+
+ def init_ref_points(self, use_num_queries):
+ self.refpoint_embed = nn.Embedding(use_num_queries, self.query_dim)
+
+ def forward(self, samples: NestedTensor, targets: List = None, **kw):
+ """The forward expects a NestedTensor, which consists of:
+ - samples.tensor: batched images, of shape [batch_size x 3 x H x W]
+ - samples.mask: a binary mask of shape [batch_size x H x W], containing 1 on padded pixels
+
+ It returns a dict with the following elements:
+ - "pred_logits": the classification logits (including no-object) for all queries.
+ Shape= [batch_size x num_queries x num_classes]
+ - "pred_boxes": The normalized boxes coordinates for all queries, represented as
+ (center_x, center_y, width, height). These values are normalized in [0, 1],
+ relative to the size of each individual image (disregarding possible padding).
+ See PostProcess for information on how to retrieve the unnormalized bounding box.
+ - "aux_outputs": Optional, only returned when auxilary losses are activated. It is a list of
+ dictionnaries containing the two above keys for each decoder layer.
+ """
+ if targets is None:
+ captions = kw["captions"]
+ else:
+ captions = [t["caption"] for t in targets]
+ len(captions)
+
+ # encoder texts
+ tokenized = self.tokenizer(captions, padding="longest", return_tensors="pt").to(
+ samples.device
+ )
+ (
+ text_self_attention_masks,
+ position_ids,
+ cate_to_token_mask_list,
+ ) = generate_masks_with_special_tokens_and_transfer_map(
+ tokenized, self.specical_tokens, self.tokenizer
+ )
+
+ if text_self_attention_masks.shape[1] > self.max_text_len:
+ text_self_attention_masks = text_self_attention_masks[
+ :, : self.max_text_len, : self.max_text_len
+ ]
+ position_ids = position_ids[:, : self.max_text_len]
+ tokenized["input_ids"] = tokenized["input_ids"][:, : self.max_text_len]
+ tokenized["attention_mask"] = tokenized["attention_mask"][:, : self.max_text_len]
+ tokenized["token_type_ids"] = tokenized["token_type_ids"][:, : self.max_text_len]
+
+ # extract text embeddings
+ if self.sub_sentence_present:
+ tokenized_for_encoder = {k: v for k, v in tokenized.items() if k != "attention_mask"}
+ tokenized_for_encoder["attention_mask"] = text_self_attention_masks
+ tokenized_for_encoder["position_ids"] = position_ids
+ else:
+ # import ipdb; ipdb.set_trace()
+ tokenized_for_encoder = tokenized
+
+ bert_output = self.bert(**tokenized_for_encoder) # bs, 195, 768
+
+ encoded_text = self.feat_map(bert_output["last_hidden_state"]) # bs, 195, d_model
+ text_token_mask = tokenized.attention_mask.bool() # bs, 195
+ # text_token_mask: True for nomask, False for mask
+ # text_self_attention_masks: True for nomask, False for mask
+
+ if encoded_text.shape[1] > self.max_text_len:
+ encoded_text = encoded_text[:, : self.max_text_len, :]
+ text_token_mask = text_token_mask[:, : self.max_text_len]
+ position_ids = position_ids[:, : self.max_text_len]
+ text_self_attention_masks = text_self_attention_masks[
+ :, : self.max_text_len, : self.max_text_len
+ ]
+
+ text_dict = {
+ "encoded_text": encoded_text, # bs, 195, d_model
+ "text_token_mask": text_token_mask, # bs, 195
+ "position_ids": position_ids, # bs, 195
+ "text_self_attention_masks": text_self_attention_masks, # bs, 195,195
+ }
+
+ # import ipdb; ipdb.set_trace()
+
+ if isinstance(samples, (list, torch.Tensor)):
+ samples = nested_tensor_from_tensor_list(samples)
+ features, poss = self.backbone(samples)
+
+ srcs = []
+ masks = []
+ for l, feat in enumerate(features):
+ src, mask = feat.decompose()
+ srcs.append(self.input_proj[l](src))
+ masks.append(mask)
+ assert mask is not None
+ if self.num_feature_levels > len(srcs):
+ _len_srcs = len(srcs)
+ for l in range(_len_srcs, self.num_feature_levels):
+ if l == _len_srcs:
+ src = self.input_proj[l](features[-1].tensors)
+ else:
+ src = self.input_proj[l](srcs[-1])
+ m = samples.mask
+ mask = F.interpolate(m[None].float(), size=src.shape[-2:]).to(torch.bool)[0]
+ pos_l = self.backbone[1](NestedTensor(src, mask)).to(src.dtype)
+ srcs.append(src)
+ masks.append(mask)
+ poss.append(pos_l)
+
+ input_query_bbox = input_query_label = attn_mask = dn_meta = None
+ hs, reference, hs_enc, ref_enc, init_box_proposal = self.transformer(
+ srcs, masks, input_query_bbox, poss, input_query_label, attn_mask, text_dict
+ )
+
+ # deformable-detr-like anchor update
+ outputs_coord_list = []
+ for dec_lid, (layer_ref_sig, layer_bbox_embed, layer_hs) in enumerate(
+ zip(reference[:-1], self.bbox_embed, hs)
+ ):
+ layer_delta_unsig = layer_bbox_embed(layer_hs)
+ layer_outputs_unsig = layer_delta_unsig + inverse_sigmoid(layer_ref_sig)
+ layer_outputs_unsig = layer_outputs_unsig.sigmoid()
+ outputs_coord_list.append(layer_outputs_unsig)
+ outputs_coord_list = torch.stack(outputs_coord_list)
+
+ # output
+ outputs_class = torch.stack(
+ [
+ layer_cls_embed(layer_hs, text_dict)
+ for layer_cls_embed, layer_hs in zip(self.class_embed, hs)
+ ]
+ )
+ out = {"pred_logits": outputs_class[-1], "pred_boxes": outputs_coord_list[-1]}
+
+ # # for intermediate outputs
+ # if self.aux_loss:
+ # out['aux_outputs'] = self._set_aux_loss(outputs_class, outputs_coord_list)
+
+ # # for encoder output
+ # if hs_enc is not None:
+ # # prepare intermediate outputs
+ # interm_coord = ref_enc[-1]
+ # interm_class = self.transformer.enc_out_class_embed(hs_enc[-1], text_dict)
+ # out['interm_outputs'] = {'pred_logits': interm_class, 'pred_boxes': interm_coord}
+ # out['interm_outputs_for_matching_pre'] = {'pred_logits': interm_class, 'pred_boxes': init_box_proposal}
+
+ return out
+
+ @torch.jit.unused
+ def _set_aux_loss(self, outputs_class, outputs_coord):
+ # this is a workaround to make torchscript happy, as torchscript
+ # doesn't support dictionary with non-homogeneous values, such
+ # as a dict having both a Tensor and a list.
+ return [
+ {"pred_logits": a, "pred_boxes": b}
+ for a, b in zip(outputs_class[:-1], outputs_coord[:-1])
+ ]
+
+
+@MODULE_BUILD_FUNCS.registe_with_name(module_name="groundingdino")
+def build_groundingdino(args):
+
+ backbone = build_backbone(args)
+ transformer = build_transformer(args)
+
+ dn_labelbook_size = args.dn_labelbook_size
+ dec_pred_bbox_embed_share = args.dec_pred_bbox_embed_share
+ sub_sentence_present = args.sub_sentence_present
+
+ model = GroundingDINO(
+ backbone,
+ transformer,
+ num_queries=args.num_queries,
+ aux_loss=True,
+ iter_update=True,
+ query_dim=4,
+ num_feature_levels=args.num_feature_levels,
+ nheads=args.nheads,
+ dec_pred_bbox_embed_share=dec_pred_bbox_embed_share,
+ two_stage_type=args.two_stage_type,
+ two_stage_bbox_embed_share=args.two_stage_bbox_embed_share,
+ two_stage_class_embed_share=args.two_stage_class_embed_share,
+ num_patterns=args.num_patterns,
+ dn_number=0,
+ dn_box_noise_scale=args.dn_box_noise_scale,
+ dn_label_noise_ratio=args.dn_label_noise_ratio,
+ dn_labelbook_size=dn_labelbook_size,
+ text_encoder_type=args.text_encoder_type,
+ sub_sentence_present=sub_sentence_present,
+ max_text_len=args.max_text_len,
+ )
+
+ return model
diff --git a/GroundingDINO/groundingdino/models/GroundingDINO/ms_deform_attn.py b/GroundingDINO/groundingdino/models/GroundingDINO/ms_deform_attn.py
new file mode 100644
index 0000000000000000000000000000000000000000..489d501bef364020212306d81e9b85c8daa27491
--- /dev/null
+++ b/GroundingDINO/groundingdino/models/GroundingDINO/ms_deform_attn.py
@@ -0,0 +1,413 @@
+# ------------------------------------------------------------------------
+# Grounding DINO
+# url: https://github.com/IDEA-Research/GroundingDINO
+# Copyright (c) 2023 IDEA. All Rights Reserved.
+# Licensed under the Apache License, Version 2.0 [see LICENSE for details]
+# ------------------------------------------------------------------------
+# Deformable DETR
+# Copyright (c) 2020 SenseTime. All Rights Reserved.
+# Licensed under the Apache License, Version 2.0 [see LICENSE for details]
+# ------------------------------------------------------------------------------------------------
+# Modified from:
+# https://github.com/fundamentalvision/Deformable-DETR/blob/main/models/ops/functions/ms_deform_attn_func.py
+# https://github.com/fundamentalvision/Deformable-DETR/blob/main/models/ops/modules/ms_deform_attn.py
+# https://github.com/open-mmlab/mmcv/blob/master/mmcv/ops/multi_scale_deform_attn.py
+# ------------------------------------------------------------------------------------------------
+
+import math
+import warnings
+from typing import Optional
+
+import torch
+import torch.nn as nn
+import torch.nn.functional as F
+from torch.autograd import Function
+from torch.autograd.function import once_differentiable
+from torch.nn.init import constant_, xavier_uniform_
+
+try:
+ from groundingdino import _C
+except:
+ warnings.warn("Failed to load custom C++ ops. Running on CPU mode Only!")
+
+
+# helpers
+def _is_power_of_2(n):
+ if (not isinstance(n, int)) or (n < 0):
+ raise ValueError("invalid input for _is_power_of_2: {} (type: {})".format(n, type(n)))
+ return (n & (n - 1) == 0) and n != 0
+
+
+class MultiScaleDeformableAttnFunction(Function):
+ @staticmethod
+ def forward(
+ ctx,
+ value,
+ value_spatial_shapes,
+ value_level_start_index,
+ sampling_locations,
+ attention_weights,
+ im2col_step,
+ ):
+ ctx.im2col_step = im2col_step
+ output = _C.ms_deform_attn_forward(
+ value,
+ value_spatial_shapes,
+ value_level_start_index,
+ sampling_locations,
+ attention_weights,
+ ctx.im2col_step,
+ )
+ ctx.save_for_backward(
+ value,
+ value_spatial_shapes,
+ value_level_start_index,
+ sampling_locations,
+ attention_weights,
+ )
+ return output
+
+ @staticmethod
+ @once_differentiable
+ def backward(ctx, grad_output):
+ (
+ value,
+ value_spatial_shapes,
+ value_level_start_index,
+ sampling_locations,
+ attention_weights,
+ ) = ctx.saved_tensors
+ grad_value, grad_sampling_loc, grad_attn_weight = _C.ms_deform_attn_backward(
+ value,
+ value_spatial_shapes,
+ value_level_start_index,
+ sampling_locations,
+ attention_weights,
+ grad_output,
+ ctx.im2col_step,
+ )
+
+ return grad_value, None, None, grad_sampling_loc, grad_attn_weight, None
+
+
+def multi_scale_deformable_attn_pytorch(
+ value: torch.Tensor,
+ value_spatial_shapes: torch.Tensor,
+ sampling_locations: torch.Tensor,
+ attention_weights: torch.Tensor,
+) -> torch.Tensor:
+
+ bs, _, num_heads, embed_dims = value.shape
+ _, num_queries, num_heads, num_levels, num_points, _ = sampling_locations.shape
+ value_list = value.split([H_ * W_ for H_, W_ in value_spatial_shapes], dim=1)
+ sampling_grids = 2 * sampling_locations - 1
+ sampling_value_list = []
+ for level, (H_, W_) in enumerate(value_spatial_shapes):
+ # bs, H_*W_, num_heads, embed_dims ->
+ # bs, H_*W_, num_heads*embed_dims ->
+ # bs, num_heads*embed_dims, H_*W_ ->
+ # bs*num_heads, embed_dims, H_, W_
+ value_l_ = (
+ value_list[level].flatten(2).transpose(1, 2).reshape(bs * num_heads, embed_dims, H_, W_)
+ )
+ # bs, num_queries, num_heads, num_points, 2 ->
+ # bs, num_heads, num_queries, num_points, 2 ->
+ # bs*num_heads, num_queries, num_points, 2
+ sampling_grid_l_ = sampling_grids[:, :, :, level].transpose(1, 2).flatten(0, 1)
+ # bs*num_heads, embed_dims, num_queries, num_points
+ sampling_value_l_ = F.grid_sample(
+ value_l_, sampling_grid_l_, mode="bilinear", padding_mode="zeros", align_corners=False
+ )
+ sampling_value_list.append(sampling_value_l_)
+ # (bs, num_queries, num_heads, num_levels, num_points) ->
+ # (bs, num_heads, num_queries, num_levels, num_points) ->
+ # (bs, num_heads, 1, num_queries, num_levels*num_points)
+ attention_weights = attention_weights.transpose(1, 2).reshape(
+ bs * num_heads, 1, num_queries, num_levels * num_points
+ )
+ output = (
+ (torch.stack(sampling_value_list, dim=-2).flatten(-2) * attention_weights)
+ .sum(-1)
+ .view(bs, num_heads * embed_dims, num_queries)
+ )
+ return output.transpose(1, 2).contiguous()
+
+
+class MultiScaleDeformableAttention(nn.Module):
+ """Multi-Scale Deformable Attention Module used in Deformable-DETR
+
+ `Deformable DETR: Deformable Transformers for End-to-End Object Detection.
+ `_.
+
+ Args:
+ embed_dim (int): The embedding dimension of Attention. Default: 256.
+ num_heads (int): The number of attention heads. Default: 8.
+ num_levels (int): The number of feature map used in Attention. Default: 4.
+ num_points (int): The number of sampling points for each query
+ in each head. Default: 4.
+ img2col_steps (int): The step used in image_to_column. Defualt: 64.
+ dropout (float): Dropout layer used in output. Default: 0.1.
+ batch_first (bool): if ``True``, then the input and output tensor will be
+ provided as `(bs, n, embed_dim)`. Default: False. `(n, bs, embed_dim)`
+ """
+
+ def __init__(
+ self,
+ embed_dim: int = 256,
+ num_heads: int = 8,
+ num_levels: int = 4,
+ num_points: int = 4,
+ img2col_step: int = 64,
+ batch_first: bool = False,
+ ):
+ super().__init__()
+ if embed_dim % num_heads != 0:
+ raise ValueError(
+ "embed_dim must be divisible by num_heads, but got {} and {}".format(
+ embed_dim, num_heads
+ )
+ )
+ head_dim = embed_dim // num_heads
+
+ self.batch_first = batch_first
+
+ if not _is_power_of_2(head_dim):
+ warnings.warn(
+ """
+ You'd better set d_model in MSDeformAttn to make sure that
+ each dim of the attention head a power of 2, which is more efficient.
+ """
+ )
+
+ self.im2col_step = img2col_step
+ self.embed_dim = embed_dim
+ self.num_heads = num_heads
+ self.num_levels = num_levels
+ self.num_points = num_points
+ self.sampling_offsets = nn.Linear(embed_dim, num_heads * num_levels * num_points * 2)
+ self.attention_weights = nn.Linear(embed_dim, num_heads * num_levels * num_points)
+ self.value_proj = nn.Linear(embed_dim, embed_dim)
+ self.output_proj = nn.Linear(embed_dim, embed_dim)
+
+ self.init_weights()
+
+ def _reset_parameters(self):
+ return self.init_weights()
+
+ def init_weights(self):
+ """
+ Default initialization for Parameters of Module.
+ """
+ constant_(self.sampling_offsets.weight.data, 0.0)
+ thetas = torch.arange(self.num_heads, dtype=torch.float32) * (
+ 2.0 * math.pi / self.num_heads
+ )
+ grid_init = torch.stack([thetas.cos(), thetas.sin()], -1)
+ grid_init = (
+ (grid_init / grid_init.abs().max(-1, keepdim=True)[0])
+ .view(self.num_heads, 1, 1, 2)
+ .repeat(1, self.num_levels, self.num_points, 1)
+ )
+ for i in range(self.num_points):
+ grid_init[:, :, i, :] *= i + 1
+ with torch.no_grad():
+ self.sampling_offsets.bias = nn.Parameter(grid_init.view(-1))
+ constant_(self.attention_weights.weight.data, 0.0)
+ constant_(self.attention_weights.bias.data, 0.0)
+ xavier_uniform_(self.value_proj.weight.data)
+ constant_(self.value_proj.bias.data, 0.0)
+ xavier_uniform_(self.output_proj.weight.data)
+ constant_(self.output_proj.bias.data, 0.0)
+
+ def freeze_sampling_offsets(self):
+ print("Freeze sampling offsets")
+ self.sampling_offsets.weight.requires_grad = False
+ self.sampling_offsets.bias.requires_grad = False
+
+ def freeze_attention_weights(self):
+ print("Freeze attention weights")
+ self.attention_weights.weight.requires_grad = False
+ self.attention_weights.bias.requires_grad = False
+
+ def forward(
+ self,
+ query: torch.Tensor,
+ key: Optional[torch.Tensor] = None,
+ value: Optional[torch.Tensor] = None,
+ query_pos: Optional[torch.Tensor] = None,
+ key_padding_mask: Optional[torch.Tensor] = None,
+ reference_points: Optional[torch.Tensor] = None,
+ spatial_shapes: Optional[torch.Tensor] = None,
+ level_start_index: Optional[torch.Tensor] = None,
+ **kwargs
+ ) -> torch.Tensor:
+
+ """Forward Function of MultiScaleDeformableAttention
+
+ Args:
+ query (torch.Tensor): Query embeddings with shape
+ `(num_query, bs, embed_dim)`
+ key (torch.Tensor): Key embeddings with shape
+ `(num_key, bs, embed_dim)`
+ value (torch.Tensor): Value embeddings with shape
+ `(num_key, bs, embed_dim)`
+ query_pos (torch.Tensor): The position embedding for `query`. Default: None.
+ key_padding_mask (torch.Tensor): ByteTensor for `query`, with shape `(bs, num_key)`,
+ indicating which elements within `key` to be ignored in attention.
+ reference_points (torch.Tensor): The normalized reference points
+ with shape `(bs, num_query, num_levels, 2)`,
+ all elements is range in [0, 1], top-left (0, 0),
+ bottom-right (1, 1), including padding are.
+ or `(N, Length_{query}, num_levels, 4)`, add additional
+ two dimensions `(h, w)` to form reference boxes.
+ spatial_shapes (torch.Tensor): Spatial shape of features in different levels.
+ With shape `(num_levels, 2)`, last dimension represents `(h, w)`.
+ level_start_index (torch.Tensor): The start index of each level. A tensor with
+ shape `(num_levels, )` which can be represented as
+ `[0, h_0 * w_0, h_0 * w_0 + h_1 * w_1, ...]`.
+
+ Returns:
+ torch.Tensor: forward results with shape `(num_query, bs, embed_dim)`
+ """
+
+ if value is None:
+ value = query
+
+ if query_pos is not None:
+ query = query + query_pos
+
+ if not self.batch_first:
+ # change to (bs, num_query ,embed_dims)
+ query = query.permute(1, 0, 2)
+ value = value.permute(1, 0, 2)
+
+ bs, num_query, _ = query.shape
+ bs, num_value, _ = value.shape
+
+ assert (spatial_shapes[:, 0] * spatial_shapes[:, 1]).sum() == num_value
+
+ value = self.value_proj(value)
+ if key_padding_mask is not None:
+ value = value.masked_fill(key_padding_mask[..., None], float(0))
+ value = value.view(bs, num_value, self.num_heads, -1)
+ sampling_offsets = self.sampling_offsets(query).view(
+ bs, num_query, self.num_heads, self.num_levels, self.num_points, 2
+ )
+ attention_weights = self.attention_weights(query).view(
+ bs, num_query, self.num_heads, self.num_levels * self.num_points
+ )
+ attention_weights = attention_weights.softmax(-1)
+ attention_weights = attention_weights.view(
+ bs,
+ num_query,
+ self.num_heads,
+ self.num_levels,
+ self.num_points,
+ )
+
+ # bs, num_query, num_heads, num_levels, num_points, 2
+ if reference_points.shape[-1] == 2:
+ offset_normalizer = torch.stack([spatial_shapes[..., 1], spatial_shapes[..., 0]], -1)
+ sampling_locations = (
+ reference_points[:, :, None, :, None, :]
+ + sampling_offsets / offset_normalizer[None, None, None, :, None, :]
+ )
+ elif reference_points.shape[-1] == 4:
+ sampling_locations = (
+ reference_points[:, :, None, :, None, :2]
+ + sampling_offsets
+ / self.num_points
+ * reference_points[:, :, None, :, None, 2:]
+ * 0.5
+ )
+ else:
+ raise ValueError(
+ "Last dim of reference_points must be 2 or 4, but get {} instead.".format(
+ reference_points.shape[-1]
+ )
+ )
+
+ if torch.cuda.is_available() and value.is_cuda:
+ halffloat = False
+ if value.dtype == torch.float16:
+ halffloat = True
+ value = value.float()
+ sampling_locations = sampling_locations.float()
+ attention_weights = attention_weights.float()
+
+ output = MultiScaleDeformableAttnFunction.apply(
+ value,
+ spatial_shapes,
+ level_start_index,
+ sampling_locations,
+ attention_weights,
+ self.im2col_step,
+ )
+
+ if halffloat:
+ output = output.half()
+ else:
+ output = multi_scale_deformable_attn_pytorch(
+ value, spatial_shapes, sampling_locations, attention_weights
+ )
+
+ output = self.output_proj(output)
+
+ if not self.batch_first:
+ output = output.permute(1, 0, 2)
+
+ return output
+
+
+def create_dummy_class(klass, dependency, message=""):
+ """
+ When a dependency of a class is not available, create a dummy class which throws ImportError
+ when used.
+
+ Args:
+ klass (str): name of the class.
+ dependency (str): name of the dependency.
+ message: extra message to print
+ Returns:
+ class: a class object
+ """
+ err = "Cannot import '{}', therefore '{}' is not available.".format(dependency, klass)
+ if message:
+ err = err + " " + message
+
+ class _DummyMetaClass(type):
+ # throw error on class attribute access
+ def __getattr__(_, __): # noqa: B902
+ raise ImportError(err)
+
+ class _Dummy(object, metaclass=_DummyMetaClass):
+ # throw error on constructor
+ def __init__(self, *args, **kwargs):
+ raise ImportError(err)
+
+ return _Dummy
+
+
+def create_dummy_func(func, dependency, message=""):
+ """
+ When a dependency of a function is not available, create a dummy function which throws
+ ImportError when used.
+
+ Args:
+ func (str): name of the function.
+ dependency (str or list[str]): name(s) of the dependency.
+ message: extra message to print
+ Returns:
+ function: a function object
+ """
+ err = "Cannot import '{}', therefore '{}' is not available.".format(dependency, func)
+ if message:
+ err = err + " " + message
+
+ if isinstance(dependency, (list, tuple)):
+ dependency = ",".join(dependency)
+
+ def _dummy(*args, **kwargs):
+ raise ImportError(err)
+
+ return _dummy
diff --git a/GroundingDINO/groundingdino/models/GroundingDINO/transformer.py b/GroundingDINO/groundingdino/models/GroundingDINO/transformer.py
new file mode 100644
index 0000000000000000000000000000000000000000..d554215ecfaa7ad5a7661fa50757e5de713f0b32
--- /dev/null
+++ b/GroundingDINO/groundingdino/models/GroundingDINO/transformer.py
@@ -0,0 +1,960 @@
+# ------------------------------------------------------------------------
+# Grounding DINO
+# url: https://github.com/IDEA-Research/GroundingDINO
+# Copyright (c) 2023 IDEA. All Rights Reserved.
+# Licensed under the Apache License, Version 2.0 [see LICENSE for details]
+# ------------------------------------------------------------------------
+# DINO
+# Copyright (c) 2022 IDEA. All Rights Reserved.
+# Licensed under the Apache License, Version 2.0 [see LICENSE for details]
+# ------------------------------------------------------------------------
+# Conditional DETR Transformer class.
+# Copyright (c) 2021 Microsoft. All Rights Reserved.
+# Licensed under the Apache License, Version 2.0 [see LICENSE for details]
+# ------------------------------------------------------------------------
+# Modified from DETR (https://github.com/facebookresearch/detr)
+# Copyright (c) Facebook, Inc. and its affiliates. All Rights Reserved.
+# ------------------------------------------------------------------------
+
+from typing import Optional
+
+import torch
+import torch.utils.checkpoint as checkpoint
+from torch import Tensor, nn
+
+from groundingdino.util.misc import inverse_sigmoid
+
+from .fuse_modules import BiAttentionBlock
+from .ms_deform_attn import MultiScaleDeformableAttention as MSDeformAttn
+from .transformer_vanilla import TransformerEncoderLayer
+from .utils import (
+ MLP,
+ _get_activation_fn,
+ _get_clones,
+ gen_encoder_output_proposals,
+ gen_sineembed_for_position,
+ get_sine_pos_embed,
+)
+
+
+class Transformer(nn.Module):
+ def __init__(
+ self,
+ d_model=256,
+ nhead=8,
+ num_queries=300,
+ num_encoder_layers=6,
+ num_unicoder_layers=0,
+ num_decoder_layers=6,
+ dim_feedforward=2048,
+ dropout=0.0,
+ activation="relu",
+ normalize_before=False,
+ return_intermediate_dec=False,
+ query_dim=4,
+ num_patterns=0,
+ # for deformable encoder
+ num_feature_levels=1,
+ enc_n_points=4,
+ dec_n_points=4,
+ # init query
+ learnable_tgt_init=False,
+ # two stage
+ two_stage_type="no", # ['no', 'standard', 'early', 'combine', 'enceachlayer', 'enclayer1']
+ embed_init_tgt=False,
+ # for text
+ use_text_enhancer=False,
+ use_fusion_layer=False,
+ use_checkpoint=False,
+ use_transformer_ckpt=False,
+ use_text_cross_attention=False,
+ text_dropout=0.1,
+ fusion_dropout=0.1,
+ fusion_droppath=0.0,
+ ):
+ super().__init__()
+ self.num_feature_levels = num_feature_levels
+ self.num_encoder_layers = num_encoder_layers
+ self.num_unicoder_layers = num_unicoder_layers
+ self.num_decoder_layers = num_decoder_layers
+ self.num_queries = num_queries
+ assert query_dim == 4
+
+ # choose encoder layer type
+ encoder_layer = DeformableTransformerEncoderLayer(
+ d_model, dim_feedforward, dropout, activation, num_feature_levels, nhead, enc_n_points
+ )
+
+ if use_text_enhancer:
+ text_enhance_layer = TransformerEncoderLayer(
+ d_model=d_model,
+ nhead=nhead // 2,
+ dim_feedforward=dim_feedforward // 2,
+ dropout=text_dropout,
+ )
+ else:
+ text_enhance_layer = None
+
+ if use_fusion_layer:
+ feature_fusion_layer = BiAttentionBlock(
+ v_dim=d_model,
+ l_dim=d_model,
+ embed_dim=dim_feedforward // 2,
+ num_heads=nhead // 2,
+ dropout=fusion_dropout,
+ drop_path=fusion_droppath,
+ )
+ else:
+ feature_fusion_layer = None
+
+ encoder_norm = nn.LayerNorm(d_model) if normalize_before else None
+ assert encoder_norm is None
+ self.encoder = TransformerEncoder(
+ encoder_layer,
+ num_encoder_layers,
+ d_model=d_model,
+ num_queries=num_queries,
+ text_enhance_layer=text_enhance_layer,
+ feature_fusion_layer=feature_fusion_layer,
+ use_checkpoint=use_checkpoint,
+ use_transformer_ckpt=use_transformer_ckpt,
+ )
+
+ # choose decoder layer type
+ decoder_layer = DeformableTransformerDecoderLayer(
+ d_model,
+ dim_feedforward,
+ dropout,
+ activation,
+ num_feature_levels,
+ nhead,
+ dec_n_points,
+ use_text_cross_attention=use_text_cross_attention,
+ )
+
+ decoder_norm = nn.LayerNorm(d_model)
+ self.decoder = TransformerDecoder(
+ decoder_layer,
+ num_decoder_layers,
+ decoder_norm,
+ return_intermediate=return_intermediate_dec,
+ d_model=d_model,
+ query_dim=query_dim,
+ num_feature_levels=num_feature_levels,
+ )
+
+ self.d_model = d_model
+ self.nhead = nhead
+ self.dec_layers = num_decoder_layers
+ self.num_queries = num_queries # useful for single stage model only
+ self.num_patterns = num_patterns
+ if not isinstance(num_patterns, int):
+ Warning("num_patterns should be int but {}".format(type(num_patterns)))
+ self.num_patterns = 0
+
+ if num_feature_levels > 1:
+ if self.num_encoder_layers > 0:
+ self.level_embed = nn.Parameter(torch.Tensor(num_feature_levels, d_model))
+ else:
+ self.level_embed = None
+
+ self.learnable_tgt_init = learnable_tgt_init
+ assert learnable_tgt_init, "why not learnable_tgt_init"
+ self.embed_init_tgt = embed_init_tgt
+ if (two_stage_type != "no" and embed_init_tgt) or (two_stage_type == "no"):
+ self.tgt_embed = nn.Embedding(self.num_queries, d_model)
+ nn.init.normal_(self.tgt_embed.weight.data)
+ else:
+ self.tgt_embed = None
+
+ # for two stage
+ self.two_stage_type = two_stage_type
+ assert two_stage_type in ["no", "standard"], "unknown param {} of two_stage_type".format(
+ two_stage_type
+ )
+ if two_stage_type == "standard":
+ # anchor selection at the output of encoder
+ self.enc_output = nn.Linear(d_model, d_model)
+ self.enc_output_norm = nn.LayerNorm(d_model)
+ self.two_stage_wh_embedding = None
+
+ if two_stage_type == "no":
+ self.init_ref_points(num_queries) # init self.refpoint_embed
+
+ self.enc_out_class_embed = None
+ self.enc_out_bbox_embed = None
+
+ self._reset_parameters()
+
+ def _reset_parameters(self):
+ for p in self.parameters():
+ if p.dim() > 1:
+ nn.init.xavier_uniform_(p)
+ for m in self.modules():
+ if isinstance(m, MSDeformAttn):
+ m._reset_parameters()
+ if self.num_feature_levels > 1 and self.level_embed is not None:
+ nn.init.normal_(self.level_embed)
+
+ def get_valid_ratio(self, mask):
+ _, H, W = mask.shape
+ valid_H = torch.sum(~mask[:, :, 0], 1)
+ valid_W = torch.sum(~mask[:, 0, :], 1)
+ valid_ratio_h = valid_H.float() / H
+ valid_ratio_w = valid_W.float() / W
+ valid_ratio = torch.stack([valid_ratio_w, valid_ratio_h], -1)
+ return valid_ratio
+
+ def init_ref_points(self, use_num_queries):
+ self.refpoint_embed = nn.Embedding(use_num_queries, 4)
+
+ def forward(self, srcs, masks, refpoint_embed, pos_embeds, tgt, attn_mask=None, text_dict=None):
+ """
+ Input:
+ - srcs: List of multi features [bs, ci, hi, wi]
+ - masks: List of multi masks [bs, hi, wi]
+ - refpoint_embed: [bs, num_dn, 4]. None in infer
+ - pos_embeds: List of multi pos embeds [bs, ci, hi, wi]
+ - tgt: [bs, num_dn, d_model]. None in infer
+
+ """
+ # prepare input for encoder
+ src_flatten = []
+ mask_flatten = []
+ lvl_pos_embed_flatten = []
+ spatial_shapes = []
+ for lvl, (src, mask, pos_embed) in enumerate(zip(srcs, masks, pos_embeds)):
+ bs, c, h, w = src.shape
+ spatial_shape = (h, w)
+ spatial_shapes.append(spatial_shape)
+
+ src = src.flatten(2).transpose(1, 2) # bs, hw, c
+ mask = mask.flatten(1) # bs, hw
+ pos_embed = pos_embed.flatten(2).transpose(1, 2) # bs, hw, c
+ if self.num_feature_levels > 1 and self.level_embed is not None:
+ lvl_pos_embed = pos_embed + self.level_embed[lvl].view(1, 1, -1)
+ else:
+ lvl_pos_embed = pos_embed
+ lvl_pos_embed_flatten.append(lvl_pos_embed)
+ src_flatten.append(src)
+ mask_flatten.append(mask)
+ src_flatten = torch.cat(src_flatten, 1) # bs, \sum{hxw}, c
+ mask_flatten = torch.cat(mask_flatten, 1) # bs, \sum{hxw}
+ lvl_pos_embed_flatten = torch.cat(lvl_pos_embed_flatten, 1) # bs, \sum{hxw}, c
+ spatial_shapes = torch.as_tensor(
+ spatial_shapes, dtype=torch.long, device=src_flatten.device
+ )
+ level_start_index = torch.cat(
+ (spatial_shapes.new_zeros((1,)), spatial_shapes.prod(1).cumsum(0)[:-1])
+ )
+ valid_ratios = torch.stack([self.get_valid_ratio(m) for m in masks], 1).to(src.dtype)
+
+ # two stage
+ enc_topk_proposals = enc_refpoint_embed = None
+
+ #########################################################
+ # Begin Encoder
+ #########################################################
+ memory, memory_text = self.encoder(
+ src_flatten,
+ pos=lvl_pos_embed_flatten,
+ level_start_index=level_start_index,
+ spatial_shapes=spatial_shapes,
+ valid_ratios=valid_ratios,
+ key_padding_mask=mask_flatten,
+ memory_text=text_dict["encoded_text"],
+ text_attention_mask=~text_dict["text_token_mask"],
+ # we ~ the mask . False means use the token; True means pad the token
+ position_ids=text_dict["position_ids"],
+ text_self_attention_masks=text_dict["text_self_attention_masks"],
+ )
+ #########################################################
+ # End Encoder
+ # - memory: bs, \sum{hw}, c
+ # - mask_flatten: bs, \sum{hw}
+ # - lvl_pos_embed_flatten: bs, \sum{hw}, c
+ # - enc_intermediate_output: None or (nenc+1, bs, nq, c) or (nenc, bs, nq, c)
+ # - enc_intermediate_refpoints: None or (nenc+1, bs, nq, c) or (nenc, bs, nq, c)
+ #########################################################
+ text_dict["encoded_text"] = memory_text
+ # if os.environ.get("SHILONG_AMP_INFNAN_DEBUG") == '1':
+ # if memory.isnan().any() | memory.isinf().any():
+ # import ipdb; ipdb.set_trace()
+
+ if self.two_stage_type == "standard":
+ output_memory, output_proposals = gen_encoder_output_proposals(
+ memory, mask_flatten, spatial_shapes
+ )
+ output_memory = self.enc_output_norm(self.enc_output(output_memory))
+
+ if text_dict is not None:
+ enc_outputs_class_unselected = self.enc_out_class_embed(output_memory, text_dict)
+ else:
+ enc_outputs_class_unselected = self.enc_out_class_embed(output_memory)
+
+ topk_logits = enc_outputs_class_unselected.max(-1)[0]
+ enc_outputs_coord_unselected = (
+ self.enc_out_bbox_embed(output_memory) + output_proposals
+ ) # (bs, \sum{hw}, 4) unsigmoid
+ topk = self.num_queries
+
+ topk_proposals = torch.topk(topk_logits, topk, dim=1)[1] # bs, nq
+
+ # gather boxes
+ refpoint_embed_undetach = torch.gather(
+ enc_outputs_coord_unselected, 1, topk_proposals.unsqueeze(-1).repeat(1, 1, 4)
+ ) # unsigmoid
+ refpoint_embed_ = refpoint_embed_undetach.detach()
+ init_box_proposal = torch.gather(
+ output_proposals, 1, topk_proposals.unsqueeze(-1).repeat(1, 1, 4)
+ ).sigmoid() # sigmoid
+
+ # gather tgt
+ tgt_undetach = torch.gather(
+ output_memory, 1, topk_proposals.unsqueeze(-1).repeat(1, 1, self.d_model)
+ )
+ if self.embed_init_tgt:
+ tgt_ = (
+ self.tgt_embed.weight[:, None, :].repeat(1, bs, 1).transpose(0, 1)
+ ) # nq, bs, d_model
+ else:
+ tgt_ = tgt_undetach.detach()
+
+ if refpoint_embed is not None:
+ refpoint_embed = torch.cat([refpoint_embed, refpoint_embed_], dim=1)
+ tgt = torch.cat([tgt, tgt_], dim=1)
+ else:
+ refpoint_embed, tgt = refpoint_embed_, tgt_
+
+ elif self.two_stage_type == "no":
+ tgt_ = (
+ self.tgt_embed.weight[:, None, :].repeat(1, bs, 1).transpose(0, 1)
+ ) # nq, bs, d_model
+ refpoint_embed_ = (
+ self.refpoint_embed.weight[:, None, :].repeat(1, bs, 1).transpose(0, 1)
+ ) # nq, bs, 4
+
+ if refpoint_embed is not None:
+ refpoint_embed = torch.cat([refpoint_embed, refpoint_embed_], dim=1)
+ tgt = torch.cat([tgt, tgt_], dim=1)
+ else:
+ refpoint_embed, tgt = refpoint_embed_, tgt_
+
+ if self.num_patterns > 0:
+ tgt_embed = tgt.repeat(1, self.num_patterns, 1)
+ refpoint_embed = refpoint_embed.repeat(1, self.num_patterns, 1)
+ tgt_pat = self.patterns.weight[None, :, :].repeat_interleave(
+ self.num_queries, 1
+ ) # 1, n_q*n_pat, d_model
+ tgt = tgt_embed + tgt_pat
+
+ init_box_proposal = refpoint_embed_.sigmoid()
+
+ else:
+ raise NotImplementedError("unknown two_stage_type {}".format(self.two_stage_type))
+ #########################################################
+ # End preparing tgt
+ # - tgt: bs, NQ, d_model
+ # - refpoint_embed(unsigmoid): bs, NQ, d_model
+ #########################################################
+
+ #########################################################
+ # Begin Decoder
+ #########################################################
+ hs, references = self.decoder(
+ tgt=tgt.transpose(0, 1),
+ memory=memory.transpose(0, 1),
+ memory_key_padding_mask=mask_flatten,
+ pos=lvl_pos_embed_flatten.transpose(0, 1),
+ refpoints_unsigmoid=refpoint_embed.transpose(0, 1),
+ level_start_index=level_start_index,
+ spatial_shapes=spatial_shapes,
+ valid_ratios=valid_ratios,
+ tgt_mask=attn_mask,
+ memory_text=text_dict["encoded_text"],
+ text_attention_mask=~text_dict["text_token_mask"],
+ # we ~ the mask . False means use the token; True means pad the token
+ )
+ #########################################################
+ # End Decoder
+ # hs: n_dec, bs, nq, d_model
+ # references: n_dec+1, bs, nq, query_dim
+ #########################################################
+
+ #########################################################
+ # Begin postprocess
+ #########################################################
+ if self.two_stage_type == "standard":
+ hs_enc = tgt_undetach.unsqueeze(0)
+ ref_enc = refpoint_embed_undetach.sigmoid().unsqueeze(0)
+ else:
+ hs_enc = ref_enc = None
+ #########################################################
+ # End postprocess
+ # hs_enc: (n_enc+1, bs, nq, d_model) or (1, bs, nq, d_model) or (n_enc, bs, nq, d_model) or None
+ # ref_enc: (n_enc+1, bs, nq, query_dim) or (1, bs, nq, query_dim) or (n_enc, bs, nq, d_model) or None
+ #########################################################
+
+ return hs, references, hs_enc, ref_enc, init_box_proposal
+ # hs: (n_dec, bs, nq, d_model)
+ # references: sigmoid coordinates. (n_dec+1, bs, bq, 4)
+ # hs_enc: (n_enc+1, bs, nq, d_model) or (1, bs, nq, d_model) or None
+ # ref_enc: sigmoid coordinates. \
+ # (n_enc+1, bs, nq, query_dim) or (1, bs, nq, query_dim) or None
+
+
+class TransformerEncoder(nn.Module):
+ def __init__(
+ self,
+ encoder_layer,
+ num_layers,
+ d_model=256,
+ num_queries=300,
+ enc_layer_share=False,
+ text_enhance_layer=None,
+ feature_fusion_layer=None,
+ use_checkpoint=False,
+ use_transformer_ckpt=False,
+ ):
+ """_summary_
+
+ Args:
+ encoder_layer (_type_): _description_
+ num_layers (_type_): _description_
+ norm (_type_, optional): _description_. Defaults to None.
+ d_model (int, optional): _description_. Defaults to 256.
+ num_queries (int, optional): _description_. Defaults to 300.
+ enc_layer_share (bool, optional): _description_. Defaults to False.
+
+ """
+ super().__init__()
+ # prepare layers
+ self.layers = []
+ self.text_layers = []
+ self.fusion_layers = []
+ if num_layers > 0:
+ self.layers = _get_clones(encoder_layer, num_layers, layer_share=enc_layer_share)
+
+ if text_enhance_layer is not None:
+ self.text_layers = _get_clones(
+ text_enhance_layer, num_layers, layer_share=enc_layer_share
+ )
+ if feature_fusion_layer is not None:
+ self.fusion_layers = _get_clones(
+ feature_fusion_layer, num_layers, layer_share=enc_layer_share
+ )
+ else:
+ self.layers = []
+ del encoder_layer
+
+ if text_enhance_layer is not None:
+ self.text_layers = []
+ del text_enhance_layer
+ if feature_fusion_layer is not None:
+ self.fusion_layers = []
+ del feature_fusion_layer
+
+ self.query_scale = None
+ self.num_queries = num_queries
+ self.num_layers = num_layers
+ self.d_model = d_model
+
+ self.use_checkpoint = use_checkpoint
+ self.use_transformer_ckpt = use_transformer_ckpt
+
+ @staticmethod
+ def get_reference_points(spatial_shapes, valid_ratios, device):
+ reference_points_list = []
+ for lvl, (H_, W_) in enumerate(spatial_shapes):
+
+ ref_y, ref_x = torch.meshgrid(
+ torch.linspace(0.5, H_ - 0.5, H_, dtype=torch.float32, device=device),
+ torch.linspace(0.5, W_ - 0.5, W_, dtype=torch.float32, device=device),
+ )
+ ref_y = ref_y.reshape(-1)[None] / (valid_ratios[:, None, lvl, 1] * H_)
+ ref_x = ref_x.reshape(-1)[None] / (valid_ratios[:, None, lvl, 0] * W_)
+ ref = torch.stack((ref_x, ref_y), -1)
+ reference_points_list.append(ref)
+ reference_points = torch.cat(reference_points_list, 1)
+ reference_points = reference_points[:, :, None] * valid_ratios[:, None]
+ return reference_points
+
+ def forward(
+ self,
+ # for images
+ src: Tensor,
+ pos: Tensor,
+ spatial_shapes: Tensor,
+ level_start_index: Tensor,
+ valid_ratios: Tensor,
+ key_padding_mask: Tensor,
+ # for texts
+ memory_text: Tensor = None,
+ text_attention_mask: Tensor = None,
+ pos_text: Tensor = None,
+ text_self_attention_masks: Tensor = None,
+ position_ids: Tensor = None,
+ ):
+ """
+ Input:
+ - src: [bs, sum(hi*wi), 256]
+ - pos: pos embed for src. [bs, sum(hi*wi), 256]
+ - spatial_shapes: h,w of each level [num_level, 2]
+ - level_start_index: [num_level] start point of level in sum(hi*wi).
+ - valid_ratios: [bs, num_level, 2]
+ - key_padding_mask: [bs, sum(hi*wi)]
+
+ - memory_text: bs, n_text, 256
+ - text_attention_mask: bs, n_text
+ False for no padding; True for padding
+ - pos_text: bs, n_text, 256
+
+ - position_ids: bs, n_text
+ Intermedia:
+ - reference_points: [bs, sum(hi*wi), num_level, 2]
+ Outpus:
+ - output: [bs, sum(hi*wi), 256]
+ """
+
+ output = src
+
+ # preparation and reshape
+ if self.num_layers > 0:
+ reference_points = self.get_reference_points(
+ spatial_shapes, valid_ratios, device=src.device
+ )
+
+ if self.text_layers:
+ # generate pos_text
+ bs, n_text, text_dim = memory_text.shape
+ if pos_text is None and position_ids is None:
+ pos_text = (
+ torch.arange(n_text, device=memory_text.device)
+ .float()
+ .unsqueeze(0)
+ .unsqueeze(-1)
+ .repeat(bs, 1, 1)
+ )
+ pos_text = get_sine_pos_embed(pos_text, num_pos_feats=256, exchange_xy=False)
+ if position_ids is not None:
+ pos_text = get_sine_pos_embed(
+ position_ids[..., None], num_pos_feats=256, exchange_xy=False
+ )
+ pos_text = pos_text.to(src.dtype)
+
+ # main process
+ for layer_id, layer in enumerate(self.layers):
+ # if output.isnan().any() or memory_text.isnan().any():
+ # if os.environ.get('IPDB_SHILONG_DEBUG', None) == 'INFO':
+ # import ipdb; ipdb.set_trace()
+ if self.fusion_layers:
+ if self.use_checkpoint:
+ output, memory_text = checkpoint.checkpoint(
+ self.fusion_layers[layer_id],
+ output,
+ memory_text,
+ key_padding_mask,
+ text_attention_mask,
+ )
+ else:
+ output, memory_text = self.fusion_layers[layer_id](
+ v=output,
+ l=memory_text,
+ attention_mask_v=key_padding_mask,
+ attention_mask_l=text_attention_mask,
+ )
+
+ if self.text_layers:
+ memory_text = self.text_layers[layer_id](
+ src=memory_text.transpose(0, 1),
+ src_mask=~text_self_attention_masks, # note we use ~ for mask here
+ src_key_padding_mask=text_attention_mask,
+ pos=(pos_text.transpose(0, 1) if pos_text is not None else None),
+ ).transpose(0, 1)
+
+ # main process
+ if self.use_transformer_ckpt:
+ output = checkpoint.checkpoint(
+ layer,
+ output,
+ pos,
+ reference_points,
+ spatial_shapes,
+ level_start_index,
+ key_padding_mask,
+ )
+ else:
+ output = layer(
+ src=output,
+ pos=pos,
+ reference_points=reference_points,
+ spatial_shapes=spatial_shapes,
+ level_start_index=level_start_index,
+ key_padding_mask=key_padding_mask,
+ )
+
+ return output, memory_text
+
+
+class TransformerDecoder(nn.Module):
+ def __init__(
+ self,
+ decoder_layer,
+ num_layers,
+ norm=None,
+ return_intermediate=False,
+ d_model=256,
+ query_dim=4,
+ num_feature_levels=1,
+ ):
+ super().__init__()
+ if num_layers > 0:
+ self.layers = _get_clones(decoder_layer, num_layers)
+ else:
+ self.layers = []
+ self.num_layers = num_layers
+ self.norm = norm
+ self.return_intermediate = return_intermediate
+ assert return_intermediate, "support return_intermediate only"
+ self.query_dim = query_dim
+ assert query_dim in [2, 4], "query_dim should be 2/4 but {}".format(query_dim)
+ self.num_feature_levels = num_feature_levels
+
+ self.ref_point_head = MLP(query_dim // 2 * d_model, d_model, d_model, 2)
+ self.query_pos_sine_scale = None
+
+ self.query_scale = None
+ self.bbox_embed = None
+ self.class_embed = None
+
+ self.d_model = d_model
+
+ self.ref_anchor_head = None
+
+ def forward(
+ self,
+ tgt,
+ memory,
+ tgt_mask: Optional[Tensor] = None,
+ memory_mask: Optional[Tensor] = None,
+ tgt_key_padding_mask: Optional[Tensor] = None,
+ memory_key_padding_mask: Optional[Tensor] = None,
+ pos: Optional[Tensor] = None,
+ refpoints_unsigmoid: Optional[Tensor] = None, # num_queries, bs, 2
+ # for memory
+ level_start_index: Optional[Tensor] = None, # num_levels
+ spatial_shapes: Optional[Tensor] = None, # bs, num_levels, 2
+ valid_ratios: Optional[Tensor] = None,
+ # for text
+ memory_text: Optional[Tensor] = None,
+ text_attention_mask: Optional[Tensor] = None,
+ ):
+ """
+ Input:
+ - tgt: nq, bs, d_model
+ - memory: hw, bs, d_model
+ - pos: hw, bs, d_model
+ - refpoints_unsigmoid: nq, bs, 2/4
+ - valid_ratios/spatial_shapes: bs, nlevel, 2
+ """
+ output = tgt
+
+ intermediate = []
+ reference_points = refpoints_unsigmoid.sigmoid()
+ ref_points = [reference_points]
+
+ for layer_id, layer in enumerate(self.layers):
+
+ if reference_points.shape[-1] == 4:
+ reference_points_input = (
+ reference_points[:, :, None]
+ * torch.cat([valid_ratios, valid_ratios], -1)[None, :]
+ ) # nq, bs, nlevel, 4
+ else:
+ assert reference_points.shape[-1] == 2
+ reference_points_input = reference_points[:, :, None] * valid_ratios[None, :]
+ query_sine_embed = gen_sineembed_for_position(
+ reference_points_input[:, :, 0, :]
+ ) # nq, bs, 256*2
+
+ # conditional query
+ raw_query_pos = self.ref_point_head(query_sine_embed) # nq, bs, 256
+ pos_scale = self.query_scale(output) if self.query_scale is not None else 1
+ query_pos = pos_scale * raw_query_pos
+ # if os.environ.get("SHILONG_AMP_INFNAN_DEBUG") == '1':
+ # if query_pos.isnan().any() | query_pos.isinf().any():
+ # import ipdb; ipdb.set_trace()
+
+ # main process
+ output = layer(
+ tgt=output,
+ tgt_query_pos=query_pos,
+ tgt_query_sine_embed=query_sine_embed,
+ tgt_key_padding_mask=tgt_key_padding_mask,
+ tgt_reference_points=reference_points_input,
+ memory_text=memory_text,
+ text_attention_mask=text_attention_mask,
+ memory=memory,
+ memory_key_padding_mask=memory_key_padding_mask,
+ memory_level_start_index=level_start_index,
+ memory_spatial_shapes=spatial_shapes,
+ memory_pos=pos,
+ self_attn_mask=tgt_mask,
+ cross_attn_mask=memory_mask,
+ )
+ if output.isnan().any() | output.isinf().any():
+ print(f"output layer_id {layer_id} is nan")
+ try:
+ num_nan = output.isnan().sum().item()
+ num_inf = output.isinf().sum().item()
+ print(f"num_nan {num_nan}, num_inf {num_inf}")
+ except Exception as e:
+ print(e)
+ # if os.environ.get("SHILONG_AMP_INFNAN_DEBUG") == '1':
+ # import ipdb; ipdb.set_trace()
+
+ # iter update
+ if self.bbox_embed is not None:
+ # box_holder = self.bbox_embed(output)
+ # box_holder[..., :self.query_dim] += inverse_sigmoid(reference_points)
+ # new_reference_points = box_holder[..., :self.query_dim].sigmoid()
+
+ reference_before_sigmoid = inverse_sigmoid(reference_points)
+ delta_unsig = self.bbox_embed[layer_id](output)
+ outputs_unsig = delta_unsig + reference_before_sigmoid
+ new_reference_points = outputs_unsig.sigmoid()
+
+ reference_points = new_reference_points.detach()
+ # if layer_id != self.num_layers - 1:
+ ref_points.append(new_reference_points)
+
+ intermediate.append(self.norm(output))
+
+ return [
+ [itm_out.transpose(0, 1) for itm_out in intermediate],
+ [itm_refpoint.transpose(0, 1) for itm_refpoint in ref_points],
+ ]
+
+
+class DeformableTransformerEncoderLayer(nn.Module):
+ def __init__(
+ self,
+ d_model=256,
+ d_ffn=1024,
+ dropout=0.1,
+ activation="relu",
+ n_levels=4,
+ n_heads=8,
+ n_points=4,
+ ):
+ super().__init__()
+
+ # self attention
+ self.self_attn = MSDeformAttn(
+ embed_dim=d_model,
+ num_levels=n_levels,
+ num_heads=n_heads,
+ num_points=n_points,
+ batch_first=True,
+ )
+ self.dropout1 = nn.Dropout(dropout)
+ self.norm1 = nn.LayerNorm(d_model)
+
+ # ffn
+ self.linear1 = nn.Linear(d_model, d_ffn)
+ self.activation = _get_activation_fn(activation, d_model=d_ffn)
+ self.dropout2 = nn.Dropout(dropout)
+ self.linear2 = nn.Linear(d_ffn, d_model)
+ self.dropout3 = nn.Dropout(dropout)
+ self.norm2 = nn.LayerNorm(d_model)
+
+ @staticmethod
+ def with_pos_embed(tensor, pos):
+ return tensor if pos is None else tensor + pos
+
+ def forward_ffn(self, src):
+ src2 = self.linear2(self.dropout2(self.activation(self.linear1(src))))
+ src = src + self.dropout3(src2)
+ src = self.norm2(src)
+ return src
+
+ def forward(
+ self, src, pos, reference_points, spatial_shapes, level_start_index, key_padding_mask=None
+ ):
+ # self attention
+ # import ipdb; ipdb.set_trace()
+ src2 = self.self_attn(
+ query=self.with_pos_embed(src, pos),
+ reference_points=reference_points,
+ value=src,
+ spatial_shapes=spatial_shapes,
+ level_start_index=level_start_index,
+ key_padding_mask=key_padding_mask,
+ )
+ src = src + self.dropout1(src2)
+ src = self.norm1(src)
+
+ # ffn
+ src = self.forward_ffn(src)
+
+ return src
+
+
+class DeformableTransformerDecoderLayer(nn.Module):
+ def __init__(
+ self,
+ d_model=256,
+ d_ffn=1024,
+ dropout=0.1,
+ activation="relu",
+ n_levels=4,
+ n_heads=8,
+ n_points=4,
+ use_text_feat_guide=False,
+ use_text_cross_attention=False,
+ ):
+ super().__init__()
+
+ # cross attention
+ self.cross_attn = MSDeformAttn(
+ embed_dim=d_model,
+ num_levels=n_levels,
+ num_heads=n_heads,
+ num_points=n_points,
+ batch_first=True,
+ )
+ self.dropout1 = nn.Dropout(dropout) if dropout > 0 else nn.Identity()
+ self.norm1 = nn.LayerNorm(d_model)
+
+ # cross attention text
+ if use_text_cross_attention:
+ self.ca_text = nn.MultiheadAttention(d_model, n_heads, dropout=dropout)
+ self.catext_dropout = nn.Dropout(dropout) if dropout > 0 else nn.Identity()
+ self.catext_norm = nn.LayerNorm(d_model)
+
+ # self attention
+ self.self_attn = nn.MultiheadAttention(d_model, n_heads, dropout=dropout)
+ self.dropout2 = nn.Dropout(dropout) if dropout > 0 else nn.Identity()
+ self.norm2 = nn.LayerNorm(d_model)
+
+ # ffn
+ self.linear1 = nn.Linear(d_model, d_ffn)
+ self.activation = _get_activation_fn(activation, d_model=d_ffn, batch_dim=1)
+ self.dropout3 = nn.Dropout(dropout) if dropout > 0 else nn.Identity()
+ self.linear2 = nn.Linear(d_ffn, d_model)
+ self.dropout4 = nn.Dropout(dropout) if dropout > 0 else nn.Identity()
+ self.norm3 = nn.LayerNorm(d_model)
+
+ self.key_aware_proj = None
+ self.use_text_feat_guide = use_text_feat_guide
+ assert not use_text_feat_guide
+ self.use_text_cross_attention = use_text_cross_attention
+
+ def rm_self_attn_modules(self):
+ self.self_attn = None
+ self.dropout2 = None
+ self.norm2 = None
+
+ @staticmethod
+ def with_pos_embed(tensor, pos):
+ return tensor if pos is None else tensor + pos
+
+ def forward_ffn(self, tgt):
+ with torch.cuda.amp.autocast(enabled=False):
+ tgt2 = self.linear2(self.dropout3(self.activation(self.linear1(tgt))))
+ tgt = tgt + self.dropout4(tgt2)
+ tgt = self.norm3(tgt)
+ return tgt
+
+ def forward(
+ self,
+ # for tgt
+ tgt: Optional[Tensor], # nq, bs, d_model
+ tgt_query_pos: Optional[Tensor] = None, # pos for query. MLP(Sine(pos))
+ tgt_query_sine_embed: Optional[Tensor] = None, # pos for query. Sine(pos)
+ tgt_key_padding_mask: Optional[Tensor] = None,
+ tgt_reference_points: Optional[Tensor] = None, # nq, bs, 4
+ memory_text: Optional[Tensor] = None, # bs, num_token, d_model
+ text_attention_mask: Optional[Tensor] = None, # bs, num_token
+ # for memory
+ memory: Optional[Tensor] = None, # hw, bs, d_model
+ memory_key_padding_mask: Optional[Tensor] = None,
+ memory_level_start_index: Optional[Tensor] = None, # num_levels
+ memory_spatial_shapes: Optional[Tensor] = None, # bs, num_levels, 2
+ memory_pos: Optional[Tensor] = None, # pos for memory
+ # sa
+ self_attn_mask: Optional[Tensor] = None, # mask used for self-attention
+ cross_attn_mask: Optional[Tensor] = None, # mask used for cross-attention
+ ):
+ """
+ Input:
+ - tgt/tgt_query_pos: nq, bs, d_model
+ -
+ """
+ assert cross_attn_mask is None
+
+ # self attention
+ if self.self_attn is not None:
+ # import ipdb; ipdb.set_trace()
+ q = k = self.with_pos_embed(tgt, tgt_query_pos)
+ tgt2 = self.self_attn(q, k, tgt, attn_mask=self_attn_mask)[0]
+ tgt = tgt + self.dropout2(tgt2)
+ tgt = self.norm2(tgt)
+
+ if self.use_text_cross_attention:
+ tgt2 = self.ca_text(
+ self.with_pos_embed(tgt, tgt_query_pos),
+ memory_text.transpose(0, 1),
+ memory_text.transpose(0, 1),
+ key_padding_mask=text_attention_mask,
+ )[0]
+ tgt = tgt + self.catext_dropout(tgt2)
+ tgt = self.catext_norm(tgt)
+
+ tgt2 = self.cross_attn(
+ query=self.with_pos_embed(tgt, tgt_query_pos).transpose(0, 1),
+ reference_points=tgt_reference_points.transpose(0, 1).contiguous(),
+ value=memory.transpose(0, 1),
+ spatial_shapes=memory_spatial_shapes,
+ level_start_index=memory_level_start_index,
+ key_padding_mask=memory_key_padding_mask,
+ ).transpose(0, 1)
+ tgt = tgt + self.dropout1(tgt2)
+ tgt = self.norm1(tgt)
+
+ # ffn
+ tgt = self.forward_ffn(tgt)
+
+ return tgt
+
+
+def build_transformer(args):
+ return Transformer(
+ d_model=args.hidden_dim,
+ dropout=args.dropout,
+ nhead=args.nheads,
+ num_queries=args.num_queries,
+ dim_feedforward=args.dim_feedforward,
+ num_encoder_layers=args.enc_layers,
+ num_decoder_layers=args.dec_layers,
+ normalize_before=args.pre_norm,
+ return_intermediate_dec=True,
+ query_dim=args.query_dim,
+ activation=args.transformer_activation,
+ num_patterns=args.num_patterns,
+ num_feature_levels=args.num_feature_levels,
+ enc_n_points=args.enc_n_points,
+ dec_n_points=args.dec_n_points,
+ learnable_tgt_init=True,
+ # two stage
+ two_stage_type=args.two_stage_type, # ['no', 'standard', 'early']
+ embed_init_tgt=args.embed_init_tgt,
+ use_text_enhancer=args.use_text_enhancer,
+ use_fusion_layer=args.use_fusion_layer,
+ use_checkpoint=args.use_checkpoint,
+ use_transformer_ckpt=args.use_transformer_ckpt,
+ use_text_cross_attention=args.use_text_cross_attention,
+ text_dropout=args.text_dropout,
+ fusion_dropout=args.fusion_dropout,
+ fusion_droppath=args.fusion_droppath,
+ )
diff --git a/GroundingDINO/groundingdino/models/GroundingDINO/transformer_vanilla.py b/GroundingDINO/groundingdino/models/GroundingDINO/transformer_vanilla.py
new file mode 100644
index 0000000000000000000000000000000000000000..10c0920c1a217af5bb3e1b13077568035ab3b7b5
--- /dev/null
+++ b/GroundingDINO/groundingdino/models/GroundingDINO/transformer_vanilla.py
@@ -0,0 +1,123 @@
+# ------------------------------------------------------------------------
+# Grounding DINO
+# url: https://github.com/IDEA-Research/GroundingDINO
+# Copyright (c) 2023 IDEA. All Rights Reserved.
+# Licensed under the Apache License, Version 2.0 [see LICENSE for details]
+# ------------------------------------------------------------------------
+# Copyright (c) Aishwarya Kamath & Nicolas Carion. Licensed under the Apache License 2.0. All Rights Reserved
+# Copyright (c) Facebook, Inc. and its affiliates. All Rights Reserved
+"""
+DETR Transformer class.
+
+Copy-paste from torch.nn.Transformer with modifications:
+ * positional encodings are passed in MHattention
+ * extra LN at the end of encoder is removed
+ * decoder returns a stack of activations from all decoding layers
+"""
+from typing import Optional
+
+import torch
+import torch.nn.functional as F
+from torch import Tensor, nn
+
+from .utils import (
+ MLP,
+ _get_activation_fn,
+ _get_clones,
+ gen_encoder_output_proposals,
+ gen_sineembed_for_position,
+ sigmoid_focal_loss,
+)
+
+
+class TextTransformer(nn.Module):
+ def __init__(self, num_layers, d_model=256, nheads=8, dim_feedforward=2048, dropout=0.1):
+ super().__init__()
+ self.num_layers = num_layers
+ self.d_model = d_model
+ self.nheads = nheads
+ self.dim_feedforward = dim_feedforward
+ self.norm = None
+
+ single_encoder_layer = TransformerEncoderLayer(
+ d_model=d_model, nhead=nheads, dim_feedforward=dim_feedforward, dropout=dropout
+ )
+ self.layers = _get_clones(single_encoder_layer, num_layers)
+
+ def forward(self, memory_text: torch.Tensor, text_attention_mask: torch.Tensor):
+ """
+
+ Args:
+ text_attention_mask: bs, num_token
+ memory_text: bs, num_token, d_model
+
+ Raises:
+ RuntimeError: _description_
+
+ Returns:
+ output: bs, num_token, d_model
+ """
+
+ output = memory_text.transpose(0, 1)
+
+ for layer in self.layers:
+ output = layer(output, src_key_padding_mask=text_attention_mask)
+
+ if self.norm is not None:
+ output = self.norm(output)
+
+ return output.transpose(0, 1)
+
+
+class TransformerEncoderLayer(nn.Module):
+ def __init__(
+ self,
+ d_model,
+ nhead,
+ dim_feedforward=2048,
+ dropout=0.1,
+ activation="relu",
+ normalize_before=False,
+ ):
+ super().__init__()
+ self.self_attn = nn.MultiheadAttention(d_model, nhead, dropout=dropout)
+ # Implementation of Feedforward model
+ self.linear1 = nn.Linear(d_model, dim_feedforward)
+ self.dropout = nn.Dropout(dropout)
+ self.linear2 = nn.Linear(dim_feedforward, d_model)
+
+ self.norm1 = nn.LayerNorm(d_model)
+ self.norm2 = nn.LayerNorm(d_model)
+ self.dropout1 = nn.Dropout(dropout)
+ self.dropout2 = nn.Dropout(dropout)
+
+ self.activation = _get_activation_fn(activation)
+ self.normalize_before = normalize_before
+ self.nhead = nhead
+
+ def with_pos_embed(self, tensor, pos: Optional[Tensor]):
+ return tensor if pos is None else tensor + pos
+
+ def forward(
+ self,
+ src,
+ src_mask: Optional[Tensor] = None,
+ src_key_padding_mask: Optional[Tensor] = None,
+ pos: Optional[Tensor] = None,
+ ):
+ # repeat attn mask
+ if src_mask.dim() == 3 and src_mask.shape[0] == src.shape[1]:
+ # bs, num_q, num_k
+ src_mask = src_mask.repeat(self.nhead, 1, 1)
+
+ q = k = self.with_pos_embed(src, pos)
+
+ src2 = self.self_attn(q, k, value=src, attn_mask=src_mask)[0]
+
+ # src2 = self.self_attn(q, k, value=src, attn_mask=src_mask, key_padding_mask=src_key_padding_mask)[0]
+ src = src + self.dropout1(src2)
+ src = self.norm1(src)
+ src2 = self.linear2(self.dropout(self.activation(self.linear1(src))))
+ src = src + self.dropout2(src2)
+ src = self.norm2(src)
+ return src
diff --git a/GroundingDINO/groundingdino/models/GroundingDINO/utils.py b/GroundingDINO/groundingdino/models/GroundingDINO/utils.py
new file mode 100644
index 0000000000000000000000000000000000000000..27da9bbd88843598238467951c8339d5f92c95a4
--- /dev/null
+++ b/GroundingDINO/groundingdino/models/GroundingDINO/utils.py
@@ -0,0 +1,270 @@
+# ------------------------------------------------------------------------
+# Grounding DINO
+# url: https://github.com/IDEA-Research/GroundingDINO
+# Copyright (c) 2023 IDEA. All Rights Reserved.
+# Licensed under the Apache License, Version 2.0 [see LICENSE for details]
+# ------------------------------------------------------------------------
+
+import copy
+import math
+
+import torch
+import torch.nn.functional as F
+from torch import Tensor, nn
+
+
+def _get_clones(module, N, layer_share=False):
+ # import ipdb; ipdb.set_trace()
+ if layer_share:
+ return nn.ModuleList([module for i in range(N)])
+ else:
+ return nn.ModuleList([copy.deepcopy(module) for i in range(N)])
+
+
+def get_sine_pos_embed(
+ pos_tensor: torch.Tensor,
+ num_pos_feats: int = 128,
+ temperature: int = 10000,
+ exchange_xy: bool = True,
+):
+ """generate sine position embedding from a position tensor
+ Args:
+ pos_tensor (torch.Tensor): shape: [..., n].
+ num_pos_feats (int): projected shape for each float in the tensor.
+ temperature (int): temperature in the sine/cosine function.
+ exchange_xy (bool, optional): exchange pos x and pos y. \
+ For example, input tensor is [x,y], the results will be [pos(y), pos(x)]. Defaults to True.
+ Returns:
+ pos_embed (torch.Tensor): shape: [..., n*num_pos_feats].
+ """
+ scale = 2 * math.pi
+ dim_t = torch.arange(num_pos_feats, dtype=torch.float32, device=pos_tensor.device)
+ dim_t = temperature ** (2 * torch.div(dim_t, 2, rounding_mode="floor") / num_pos_feats)
+
+ def sine_func(x: torch.Tensor):
+ sin_x = x * scale / dim_t
+ sin_x = torch.stack((sin_x[..., 0::2].sin(), sin_x[..., 1::2].cos()), dim=3).flatten(2)
+ return sin_x
+
+ pos_res = [sine_func(x) for x in pos_tensor.split([1] * pos_tensor.shape[-1], dim=-1)]
+ if exchange_xy:
+ pos_res[0], pos_res[1] = pos_res[1], pos_res[0]
+ pos_res = torch.cat(pos_res, dim=-1)
+ return pos_res
+
+
+def gen_encoder_output_proposals(
+ memory: Tensor, memory_padding_mask: Tensor, spatial_shapes: Tensor, learnedwh=None
+):
+ """
+ Input:
+ - memory: bs, \sum{hw}, d_model
+ - memory_padding_mask: bs, \sum{hw}
+ - spatial_shapes: nlevel, 2
+ - learnedwh: 2
+ Output:
+ - output_memory: bs, \sum{hw}, d_model
+ - output_proposals: bs, \sum{hw}, 4
+ """
+ N_, S_, C_ = memory.shape
+ proposals = []
+ _cur = 0
+ for lvl, (H_, W_) in enumerate(spatial_shapes):
+ mask_flatten_ = memory_padding_mask[:, _cur : (_cur + H_ * W_)].view(N_, H_, W_, 1)
+ valid_H = torch.sum(~mask_flatten_[:, :, 0, 0], 1)
+ valid_W = torch.sum(~mask_flatten_[:, 0, :, 0], 1)
+
+ # import ipdb; ipdb.set_trace()
+
+ grid_y, grid_x = torch.meshgrid(
+ torch.linspace(0, H_ - 1, H_, dtype=torch.float32, device=memory.device),
+ torch.linspace(0, W_ - 1, W_, dtype=torch.float32, device=memory.device),
+ )
+ grid = torch.cat([grid_x.unsqueeze(-1), grid_y.unsqueeze(-1)], -1) # H_, W_, 2
+
+ scale = torch.cat([valid_W.unsqueeze(-1), valid_H.unsqueeze(-1)], 1).view(N_, 1, 1, 2)
+ grid = (grid.unsqueeze(0).expand(N_, -1, -1, -1) + 0.5) / scale
+
+ if learnedwh is not None:
+ # import ipdb; ipdb.set_trace()
+ wh = torch.ones_like(grid) * learnedwh.sigmoid() * (2.0**lvl)
+ else:
+ wh = torch.ones_like(grid) * 0.05 * (2.0**lvl)
+
+ # scale = torch.cat([W_[None].unsqueeze(-1), H_[None].unsqueeze(-1)], 1).view(1, 1, 1, 2).repeat(N_, 1, 1, 1)
+ # grid = (grid.unsqueeze(0).expand(N_, -1, -1, -1) + 0.5) / scale
+ # wh = torch.ones_like(grid) / scale
+ proposal = torch.cat((grid, wh), -1).view(N_, -1, 4)
+ proposals.append(proposal)
+ _cur += H_ * W_
+ # import ipdb; ipdb.set_trace()
+ output_proposals = torch.cat(proposals, 1)
+ output_proposals_valid = ((output_proposals > 0.01) & (output_proposals < 0.99)).all(
+ -1, keepdim=True
+ )
+ output_proposals = torch.log(output_proposals / (1 - output_proposals)) # unsigmoid
+ output_proposals = output_proposals.masked_fill(memory_padding_mask.unsqueeze(-1), float("inf"))
+ output_proposals = output_proposals.masked_fill(~output_proposals_valid, float("inf"))
+
+ output_memory = memory
+ output_memory = output_memory.masked_fill(memory_padding_mask.unsqueeze(-1), float(0))
+ output_memory = output_memory.masked_fill(~output_proposals_valid, float(0))
+
+ # output_memory = output_memory.masked_fill(memory_padding_mask.unsqueeze(-1), float('inf'))
+ # output_memory = output_memory.masked_fill(~output_proposals_valid, float('inf'))
+
+ output_proposals = output_proposals.to(output_memory.dtype)
+ return output_memory, output_proposals
+
+
+class RandomBoxPerturber:
+ def __init__(
+ self, x_noise_scale=0.2, y_noise_scale=0.2, w_noise_scale=0.2, h_noise_scale=0.2
+ ) -> None:
+ self.noise_scale = torch.Tensor(
+ [x_noise_scale, y_noise_scale, w_noise_scale, h_noise_scale]
+ )
+
+ def __call__(self, refanchors: Tensor) -> Tensor:
+ nq, bs, query_dim = refanchors.shape
+ device = refanchors.device
+
+ noise_raw = torch.rand_like(refanchors)
+ noise_scale = self.noise_scale.to(device)[:query_dim]
+
+ new_refanchors = refanchors * (1 + (noise_raw - 0.5) * noise_scale)
+ return new_refanchors.clamp_(0, 1)
+
+
+def sigmoid_focal_loss(
+ inputs, targets, num_boxes, alpha: float = 0.25, gamma: float = 2, no_reduction=False
+):
+ """
+ Loss used in RetinaNet for dense detection: https://arxiv.org/abs/1708.02002.
+ Args:
+ inputs: A float tensor of arbitrary shape.
+ The predictions for each example.
+ targets: A float tensor with the same shape as inputs. Stores the binary
+ classification label for each element in inputs
+ (0 for the negative class and 1 for the positive class).
+ alpha: (optional) Weighting factor in range (0,1) to balance
+ positive vs negative examples. Default = -1 (no weighting).
+ gamma: Exponent of the modulating factor (1 - p_t) to
+ balance easy vs hard examples.
+ Returns:
+ Loss tensor
+ """
+ prob = inputs.sigmoid()
+ ce_loss = F.binary_cross_entropy_with_logits(inputs, targets, reduction="none")
+ p_t = prob * targets + (1 - prob) * (1 - targets)
+ loss = ce_loss * ((1 - p_t) ** gamma)
+
+ if alpha >= 0:
+ alpha_t = alpha * targets + (1 - alpha) * (1 - targets)
+ loss = alpha_t * loss
+
+ if no_reduction:
+ return loss
+
+ return loss.mean(1).sum() / num_boxes
+
+
+class MLP(nn.Module):
+ """Very simple multi-layer perceptron (also called FFN)"""
+
+ def __init__(self, input_dim, hidden_dim, output_dim, num_layers):
+ super().__init__()
+ self.num_layers = num_layers
+ h = [hidden_dim] * (num_layers - 1)
+ self.layers = nn.ModuleList(
+ nn.Linear(n, k) for n, k in zip([input_dim] + h, h + [output_dim])
+ )
+
+ def forward(self, x):
+ for i, layer in enumerate(self.layers):
+ x = F.relu(layer(x)) if i < self.num_layers - 1 else layer(x)
+ return x
+
+
+def _get_activation_fn(activation, d_model=256, batch_dim=0):
+ """Return an activation function given a string"""
+ if activation == "relu":
+ return F.relu
+ if activation == "gelu":
+ return F.gelu
+ if activation == "glu":
+ return F.glu
+ if activation == "prelu":
+ return nn.PReLU()
+ if activation == "selu":
+ return F.selu
+
+ raise RuntimeError(f"activation should be relu/gelu, not {activation}.")
+
+
+def gen_sineembed_for_position(pos_tensor):
+ # n_query, bs, _ = pos_tensor.size()
+ # sineembed_tensor = torch.zeros(n_query, bs, 256)
+ scale = 2 * math.pi
+ dim_t = torch.arange(128, dtype=torch.float32, device=pos_tensor.device)
+ dim_t = 10000 ** (2 * (torch.div(dim_t, 2, rounding_mode='floor')) / 128)
+ x_embed = pos_tensor[:, :, 0] * scale
+ y_embed = pos_tensor[:, :, 1] * scale
+ pos_x = x_embed[:, :, None] / dim_t
+ pos_y = y_embed[:, :, None] / dim_t
+ pos_x = torch.stack((pos_x[:, :, 0::2].sin(), pos_x[:, :, 1::2].cos()), dim=3).flatten(2)
+ pos_y = torch.stack((pos_y[:, :, 0::2].sin(), pos_y[:, :, 1::2].cos()), dim=3).flatten(2)
+ if pos_tensor.size(-1) == 2:
+ pos = torch.cat((pos_y, pos_x), dim=2)
+ elif pos_tensor.size(-1) == 4:
+ w_embed = pos_tensor[:, :, 2] * scale
+ pos_w = w_embed[:, :, None] / dim_t
+ pos_w = torch.stack((pos_w[:, :, 0::2].sin(), pos_w[:, :, 1::2].cos()), dim=3).flatten(2)
+
+ h_embed = pos_tensor[:, :, 3] * scale
+ pos_h = h_embed[:, :, None] / dim_t
+ pos_h = torch.stack((pos_h[:, :, 0::2].sin(), pos_h[:, :, 1::2].cos()), dim=3).flatten(2)
+
+ pos = torch.cat((pos_y, pos_x, pos_w, pos_h), dim=2)
+ else:
+ raise ValueError("Unknown pos_tensor shape(-1):{}".format(pos_tensor.size(-1)))
+ pos = pos.to(pos_tensor.dtype)
+ return pos
+
+
+class ContrastiveEmbed(nn.Module):
+ def __init__(self, max_text_len=256):
+ """
+ Args:
+ max_text_len: max length of text.
+ """
+ super().__init__()
+ self.max_text_len = max_text_len
+
+ def forward(self, x, text_dict):
+ """_summary_
+
+ Args:
+ x (_type_): _description_
+ text_dict (_type_): _description_
+ {
+ 'encoded_text': encoded_text, # bs, 195, d_model
+ 'text_token_mask': text_token_mask, # bs, 195
+ # True for used tokens. False for padding tokens
+ }
+ Returns:
+ _type_: _description_
+ """
+ assert isinstance(text_dict, dict)
+
+ y = text_dict["encoded_text"]
+ text_token_mask = text_dict["text_token_mask"]
+
+ res = x @ y.transpose(-1, -2)
+ res.masked_fill_(~text_token_mask[:, None, :], float("-inf"))
+
+ # padding to max_text_len
+ new_res = torch.full((*res.shape[:-1], self.max_text_len), float("-inf"), device=res.device, dtype=res.dtype)
+ new_res[..., : res.shape[-1]] = res
+
+ return new_res
diff --git a/GroundingDINO/groundingdino/models/__init__.py b/GroundingDINO/groundingdino/models/__init__.py
new file mode 100644
index 0000000000000000000000000000000000000000..e3413961d1d184b99835eb1e919b052d70298bc6
--- /dev/null
+++ b/GroundingDINO/groundingdino/models/__init__.py
@@ -0,0 +1,18 @@
+# ------------------------------------------------------------------------
+# Grounding DINO
+# url: https://github.com/IDEA-Research/GroundingDINO
+# Copyright (c) 2023 IDEA. All Rights Reserved.
+# Licensed under the Apache License, Version 2.0 [see LICENSE for details]
+# ------------------------------------------------------------------------
+# Copyright (c) Facebook, Inc. and its affiliates. All Rights Reserved
+from .GroundingDINO import build_groundingdino
+
+
+def build_model(args):
+ # we use register to maintain models from catdet6 on.
+ from .registry import MODULE_BUILD_FUNCS
+
+ assert args.modelname in MODULE_BUILD_FUNCS._module_dict
+ build_func = MODULE_BUILD_FUNCS.get(args.modelname)
+ model = build_func(args)
+ return model
diff --git a/GroundingDINO/groundingdino/models/registry.py b/GroundingDINO/groundingdino/models/registry.py
new file mode 100644
index 0000000000000000000000000000000000000000..2d22a59eec79a2a19b83fa1779f2adaf5753aec6
--- /dev/null
+++ b/GroundingDINO/groundingdino/models/registry.py
@@ -0,0 +1,66 @@
+# ------------------------------------------------------------------------
+# Grounding DINO
+# url: https://github.com/IDEA-Research/GroundingDINO
+# Copyright (c) 2023 IDEA. All Rights Reserved.
+# Licensed under the Apache License, Version 2.0 [see LICENSE for details]
+# ------------------------------------------------------------------------
+# -*- coding: utf-8 -*-
+# @Author: Yihao Chen
+# @Date: 2021-08-16 16:03:17
+# @Last Modified by: Shilong Liu
+# @Last Modified time: 2022-01-23 15:26
+# modified from mmcv
+
+import inspect
+from functools import partial
+
+
+class Registry(object):
+ def __init__(self, name):
+ self._name = name
+ self._module_dict = dict()
+
+ def __repr__(self):
+ format_str = self.__class__.__name__ + "(name={}, items={})".format(
+ self._name, list(self._module_dict.keys())
+ )
+ return format_str
+
+ def __len__(self):
+ return len(self._module_dict)
+
+ @property
+ def name(self):
+ return self._name
+
+ @property
+ def module_dict(self):
+ return self._module_dict
+
+ def get(self, key):
+ return self._module_dict.get(key, None)
+
+ def registe_with_name(self, module_name=None, force=False):
+ return partial(self.register, module_name=module_name, force=force)
+
+ def register(self, module_build_function, module_name=None, force=False):
+ """Register a module build function.
+ Args:
+ module (:obj:`nn.Module`): Module to be registered.
+ """
+ if not inspect.isfunction(module_build_function):
+ raise TypeError(
+ "module_build_function must be a function, but got {}".format(
+ type(module_build_function)
+ )
+ )
+ if module_name is None:
+ module_name = module_build_function.__name__
+ if not force and module_name in self._module_dict:
+ raise KeyError("{} is already registered in {}".format(module_name, self.name))
+ self._module_dict[module_name] = module_build_function
+
+ return module_build_function
+
+
+MODULE_BUILD_FUNCS = Registry("model build functions")
diff --git a/GroundingDINO/groundingdino/util/__init__.py b/GroundingDINO/groundingdino/util/__init__.py
new file mode 100644
index 0000000000000000000000000000000000000000..168f9979a4623806934b0ff1102ac166704e7dec
--- /dev/null
+++ b/GroundingDINO/groundingdino/util/__init__.py
@@ -0,0 +1 @@
+# Copyright (c) Facebook, Inc. and its affiliates. All Rights Reserved
diff --git a/GroundingDINO/groundingdino/util/box_ops.py b/GroundingDINO/groundingdino/util/box_ops.py
new file mode 100644
index 0000000000000000000000000000000000000000..781068d294e576954edb4bd07b6e0f30e4e1bcd9
--- /dev/null
+++ b/GroundingDINO/groundingdino/util/box_ops.py
@@ -0,0 +1,140 @@
+# Copyright (c) Facebook, Inc. and its affiliates. All Rights Reserved
+"""
+Utilities for bounding box manipulation and GIoU.
+"""
+import torch
+from torchvision.ops.boxes import box_area
+
+
+def box_cxcywh_to_xyxy(x):
+ x_c, y_c, w, h = x.unbind(-1)
+ b = [(x_c - 0.5 * w), (y_c - 0.5 * h), (x_c + 0.5 * w), (y_c + 0.5 * h)]
+ return torch.stack(b, dim=-1)
+
+
+def box_xyxy_to_cxcywh(x):
+ x0, y0, x1, y1 = x.unbind(-1)
+ b = [(x0 + x1) / 2, (y0 + y1) / 2, (x1 - x0), (y1 - y0)]
+ return torch.stack(b, dim=-1)
+
+
+# modified from torchvision to also return the union
+def box_iou(boxes1, boxes2):
+ area1 = box_area(boxes1)
+ area2 = box_area(boxes2)
+
+ # import ipdb; ipdb.set_trace()
+ lt = torch.max(boxes1[:, None, :2], boxes2[:, :2]) # [N,M,2]
+ rb = torch.min(boxes1[:, None, 2:], boxes2[:, 2:]) # [N,M,2]
+
+ wh = (rb - lt).clamp(min=0) # [N,M,2]
+ inter = wh[:, :, 0] * wh[:, :, 1] # [N,M]
+
+ union = area1[:, None] + area2 - inter
+
+ iou = inter / (union + 1e-6)
+ return iou, union
+
+
+def generalized_box_iou(boxes1, boxes2):
+ """
+ Generalized IoU from https://giou.stanford.edu/
+
+ The boxes should be in [x0, y0, x1, y1] format
+
+ Returns a [N, M] pairwise matrix, where N = len(boxes1)
+ and M = len(boxes2)
+ """
+ # degenerate boxes gives inf / nan results
+ # so do an early check
+ assert (boxes1[:, 2:] >= boxes1[:, :2]).all()
+ assert (boxes2[:, 2:] >= boxes2[:, :2]).all()
+ # except:
+ # import ipdb; ipdb.set_trace()
+ iou, union = box_iou(boxes1, boxes2)
+
+ lt = torch.min(boxes1[:, None, :2], boxes2[:, :2])
+ rb = torch.max(boxes1[:, None, 2:], boxes2[:, 2:])
+
+ wh = (rb - lt).clamp(min=0) # [N,M,2]
+ area = wh[:, :, 0] * wh[:, :, 1]
+
+ return iou - (area - union) / (area + 1e-6)
+
+
+# modified from torchvision to also return the union
+def box_iou_pairwise(boxes1, boxes2):
+ area1 = box_area(boxes1)
+ area2 = box_area(boxes2)
+
+ lt = torch.max(boxes1[:, :2], boxes2[:, :2]) # [N,2]
+ rb = torch.min(boxes1[:, 2:], boxes2[:, 2:]) # [N,2]
+
+ wh = (rb - lt).clamp(min=0) # [N,2]
+ inter = wh[:, 0] * wh[:, 1] # [N]
+
+ union = area1 + area2 - inter
+
+ iou = inter / union
+ return iou, union
+
+
+def generalized_box_iou_pairwise(boxes1, boxes2):
+ """
+ Generalized IoU from https://giou.stanford.edu/
+
+ Input:
+ - boxes1, boxes2: N,4
+ Output:
+ - giou: N, 4
+ """
+ # degenerate boxes gives inf / nan results
+ # so do an early check
+ assert (boxes1[:, 2:] >= boxes1[:, :2]).all()
+ assert (boxes2[:, 2:] >= boxes2[:, :2]).all()
+ assert boxes1.shape == boxes2.shape
+ iou, union = box_iou_pairwise(boxes1, boxes2) # N, 4
+
+ lt = torch.min(boxes1[:, :2], boxes2[:, :2])
+ rb = torch.max(boxes1[:, 2:], boxes2[:, 2:])
+
+ wh = (rb - lt).clamp(min=0) # [N,2]
+ area = wh[:, 0] * wh[:, 1]
+
+ return iou - (area - union) / area
+
+
+def masks_to_boxes(masks):
+ """Compute the bounding boxes around the provided masks
+
+ The masks should be in format [N, H, W] where N is the number of masks, (H, W) are the spatial dimensions.
+
+ Returns a [N, 4] tensors, with the boxes in xyxy format
+ """
+ if masks.numel() == 0:
+ return torch.zeros((0, 4), device=masks.device)
+
+ h, w = masks.shape[-2:]
+
+ y = torch.arange(0, h, dtype=torch.float)
+ x = torch.arange(0, w, dtype=torch.float)
+ y, x = torch.meshgrid(y, x)
+
+ x_mask = masks * x.unsqueeze(0)
+ x_max = x_mask.flatten(1).max(-1)[0]
+ x_min = x_mask.masked_fill(~(masks.bool()), 1e8).flatten(1).min(-1)[0]
+
+ y_mask = masks * y.unsqueeze(0)
+ y_max = y_mask.flatten(1).max(-1)[0]
+ y_min = y_mask.masked_fill(~(masks.bool()), 1e8).flatten(1).min(-1)[0]
+
+ return torch.stack([x_min, y_min, x_max, y_max], 1)
+
+
+if __name__ == "__main__":
+ x = torch.rand(5, 4)
+ y = torch.rand(3, 4)
+ iou, union = box_iou(x, y)
+ import ipdb
+
+ ipdb.set_trace()
diff --git a/GroundingDINO/groundingdino/util/get_tokenlizer.py b/GroundingDINO/groundingdino/util/get_tokenlizer.py
new file mode 100644
index 0000000000000000000000000000000000000000..f7dcf7e95f03f95b20546b26442a94225924618b
--- /dev/null
+++ b/GroundingDINO/groundingdino/util/get_tokenlizer.py
@@ -0,0 +1,26 @@
+from transformers import AutoTokenizer, BertModel, BertTokenizer, RobertaModel, RobertaTokenizerFast
+
+
+def get_tokenlizer(text_encoder_type):
+ if not isinstance(text_encoder_type, str):
+ # print("text_encoder_type is not a str")
+ if hasattr(text_encoder_type, "text_encoder_type"):
+ text_encoder_type = text_encoder_type.text_encoder_type
+ elif text_encoder_type.get("text_encoder_type", False):
+ text_encoder_type = text_encoder_type.get("text_encoder_type")
+ else:
+ raise ValueError(
+ "Unknown type of text_encoder_type: {}".format(type(text_encoder_type))
+ )
+ print("final text_encoder_type: {}".format(text_encoder_type))
+
+ tokenizer = AutoTokenizer.from_pretrained(text_encoder_type)
+ return tokenizer
+
+
+def get_pretrained_language_model(text_encoder_type):
+ if text_encoder_type == "bert-base-uncased":
+ return BertModel.from_pretrained(text_encoder_type)
+ if text_encoder_type == "roberta-base":
+ return RobertaModel.from_pretrained(text_encoder_type)
+ raise ValueError("Unknown text_encoder_type {}".format(text_encoder_type))
diff --git a/GroundingDINO/groundingdino/util/inference.py b/GroundingDINO/groundingdino/util/inference.py
new file mode 100644
index 0000000000000000000000000000000000000000..7c9b8a0b382f615bcda0ef8220f79afc0892e641
--- /dev/null
+++ b/GroundingDINO/groundingdino/util/inference.py
@@ -0,0 +1,257 @@
+from typing import Tuple, List
+
+import re
+import cv2
+import numpy as np
+import supervision as sv
+import torch
+from PIL import Image
+from torchvision.ops import box_convert
+
+import groundingdino.datasets.transforms as T
+from groundingdino.models import build_model
+from groundingdino.util.misc import clean_state_dict
+from groundingdino.util.slconfig import SLConfig
+from groundingdino.util.utils import get_phrases_from_posmap
+
+# ----------------------------------------------------------------------------------------------------------------------
+# OLD API
+# ----------------------------------------------------------------------------------------------------------------------
+
+
+def preprocess_caption(caption: str) -> str:
+ result = caption.lower().strip()
+ if result.endswith("."):
+ return result
+ return result + "."
+
+
+def load_model(model_config_path: str, model_checkpoint_path: str, device: str = "cuda"):
+ args = SLConfig.fromfile(model_config_path)
+ args.device = device
+ model = build_model(args)
+ checkpoint = torch.load(model_checkpoint_path, map_location="cpu")
+ model.load_state_dict(clean_state_dict(checkpoint["model"]), strict=False)
+ model.eval()
+ return model
+
+
+def load_image(image_path: str) -> Tuple[np.array, torch.Tensor]:
+ transform = T.Compose(
+ [
+ T.RandomResize([800], max_size=1333),
+ T.ToTensor(),
+ T.Normalize([0.485, 0.456, 0.406], [0.229, 0.224, 0.225]),
+ ]
+ )
+ image_source = Image.open(image_path).convert("RGB")
+ image = np.asarray(image_source)
+ image_transformed, _ = transform(image_source, None)
+ return image, image_transformed
+
+
+def predict(
+ model,
+ image: torch.Tensor,
+ caption: str,
+ box_threshold: float,
+ text_threshold: float,
+ device: str = "cuda"
+) -> Tuple[torch.Tensor, torch.Tensor, List[str]]:
+ caption = preprocess_caption(caption=caption)
+
+ model = model.to(device)
+ image = image.to(device)
+
+ with torch.no_grad():
+ outputs = model(image[None], captions=[caption])
+
+ prediction_logits = outputs["pred_logits"].cpu().sigmoid()[0] # prediction_logits.shape = (nq, 256)
+ prediction_boxes = outputs["pred_boxes"].cpu()[0] # prediction_boxes.shape = (nq, 4)
+
+ mask = prediction_logits.max(dim=1)[0] > box_threshold
+ logits = prediction_logits[mask] # logits.shape = (n, 256)
+ boxes = prediction_boxes[mask] # boxes.shape = (n, 4)
+
+ tokenizer = model.tokenizer
+ tokenized = tokenizer(caption)
+
+ phrases = [
+ get_phrases_from_posmap(logit > text_threshold, tokenized, tokenizer).replace('.', '')
+ for logit
+ in logits
+ ]
+
+ return boxes, logits.max(dim=1)[0], phrases
+
+
+def annotate(image_source: np.ndarray, boxes: torch.Tensor, logits: torch.Tensor, phrases: List[str]) -> np.ndarray:
+ h, w, _ = image_source.shape
+ boxes = boxes * torch.Tensor([w, h, w, h])
+ xyxy = box_convert(boxes=boxes, in_fmt="cxcywh", out_fmt="xyxy").numpy()
+ detections = sv.Detections(xyxy=xyxy)
+
+ labels = [
+ f"{phrase} {logit:.2f}"
+ for phrase, logit
+ in zip(phrases, logits)
+ ]
+
+ box_annotator = sv.BoxAnnotator()
+ annotated_frame = cv2.cvtColor(image_source, cv2.COLOR_RGB2BGR)
+ annotated_frame = box_annotator.annotate(scene=annotated_frame, detections=detections, labels=labels)
+ return annotated_frame
+
+
+# ----------------------------------------------------------------------------------------------------------------------
+# NEW API
+# ----------------------------------------------------------------------------------------------------------------------
+
+
+class Model:
+
+ def __init__(
+ self,
+ model_config_path: str,
+ model_checkpoint_path: str,
+ device: str = "cuda"
+ ):
+ self.model = load_model(
+ model_config_path=model_config_path,
+ model_checkpoint_path=model_checkpoint_path,
+ device=device
+ ).to(device)
+ self.device = device
+
+ def predict_with_caption(
+ self,
+ image: np.ndarray,
+ caption: str,
+ box_threshold: float = 0.35,
+ text_threshold: float = 0.25
+ ) -> Tuple[sv.Detections, List[str]]:
+ """
+ import cv2
+
+ image = cv2.imread(IMAGE_PATH)
+
+ model = Model(model_config_path=CONFIG_PATH, model_checkpoint_path=WEIGHTS_PATH)
+ detections, labels = model.predict_with_caption(
+ image=image,
+ caption=caption,
+ box_threshold=BOX_THRESHOLD,
+ text_threshold=TEXT_THRESHOLD
+ )
+
+ import supervision as sv
+
+ box_annotator = sv.BoxAnnotator()
+ annotated_image = box_annotator.annotate(scene=image, detections=detections, labels=labels)
+ """
+ processed_image = Model.preprocess_image(image_bgr=image).to(self.device)
+ boxes, logits, phrases = predict(
+ model=self.model,
+ image=processed_image,
+ caption=caption,
+ box_threshold=box_threshold,
+ text_threshold=text_threshold,
+ device=self.device)
+ source_h, source_w, _ = image.shape
+ detections = Model.post_process_result(
+ source_h=source_h,
+ source_w=source_w,
+ boxes=boxes,
+ logits=logits)
+ return detections, phrases
+
+ def predict_with_classes(
+ self,
+ image: np.ndarray,
+ classes: List[str],
+ box_threshold: float,
+ text_threshold: float
+ ) -> sv.Detections:
+ """
+ import cv2
+
+ image = cv2.imread(IMAGE_PATH)
+
+ model = Model(model_config_path=CONFIG_PATH, model_checkpoint_path=WEIGHTS_PATH)
+ detections = model.predict_with_classes(
+ image=image,
+ classes=CLASSES,
+ box_threshold=BOX_THRESHOLD,
+ text_threshold=TEXT_THRESHOLD
+ )
+
+
+ import supervision as sv
+
+ box_annotator = sv.BoxAnnotator()
+ annotated_image = box_annotator.annotate(scene=image, detections=detections)
+ """
+ caption = ". ".join(classes)
+ processed_image = Model.preprocess_image(image_bgr=image).to(self.device)
+ boxes, logits, phrases = predict(
+ model=self.model,
+ image=processed_image,
+ caption=caption,
+ box_threshold=box_threshold,
+ text_threshold=text_threshold,
+ device=self.device)
+ source_h, source_w, _ = image.shape
+ detections = Model.post_process_result(
+ source_h=source_h,
+ source_w=source_w,
+ boxes=boxes,
+ logits=logits)
+ class_id = Model.phrases2classes(phrases=phrases, classes=classes)
+ detections.class_id = class_id
+ return detections
+
+ @staticmethod
+ def preprocess_image(image_bgr: np.ndarray) -> torch.Tensor:
+ transform = T.Compose(
+ [
+ T.RandomResize([800], max_size=1333),
+ T.ToTensor(),
+ T.Normalize([0.485, 0.456, 0.406], [0.229, 0.224, 0.225]),
+ ]
+ )
+ image_pillow = Image.fromarray(cv2.cvtColor(image_bgr, cv2.COLOR_BGR2RGB))
+ image_transformed, _ = transform(image_pillow, None)
+ return image_transformed
+
+ @staticmethod
+ def post_process_result(
+ source_h: int,
+ source_w: int,
+ boxes: torch.Tensor,
+ logits: torch.Tensor
+ ) -> sv.Detections:
+ boxes = boxes * torch.Tensor([source_w, source_h, source_w, source_h])
+ xyxy = box_convert(boxes=boxes, in_fmt="cxcywh", out_fmt="xyxy").numpy()
+ confidence = logits.numpy()
+ return sv.Detections(xyxy=xyxy, confidence=confidence)
+
+ @staticmethod
+ def phrases2classes(phrases: List[str], classes: List[str]) -> np.ndarray:
+ class_ids = []
+ for phrase in phrases:
+ try:
+ # class_ids.append(classes.index(phrase))
+ class_ids.append(Model.find_index(phrase, classes))
+ except ValueError:
+ class_ids.append(None)
+ return np.array(class_ids)
+
+ @staticmethod
+ def find_index(string, lst):
+ # if meet string like "lake river" will only keep "lake"
+ # this is an hack implementation for visualization which will be updated in the future
+ string = string.lower().split()[0]
+ for i, s in enumerate(lst):
+ if string in s.lower():
+ return i
+ print("There's a wrong phrase happen, this is because of our post-process merged wrong tokens, which will be modified in the future. We will assign it with a random label at this time.")
+ return 0
\ No newline at end of file
diff --git a/GroundingDINO/groundingdino/util/logger.py b/GroundingDINO/groundingdino/util/logger.py
new file mode 100644
index 0000000000000000000000000000000000000000..18145f54c927abd59b95f3fa6e6da8002bc2ce97
--- /dev/null
+++ b/GroundingDINO/groundingdino/util/logger.py
@@ -0,0 +1,93 @@
+# Copyright (c) Facebook, Inc. and its affiliates. All Rights Reserved
+import functools
+import logging
+import os
+import sys
+
+from termcolor import colored
+
+
+class _ColorfulFormatter(logging.Formatter):
+ def __init__(self, *args, **kwargs):
+ self._root_name = kwargs.pop("root_name") + "."
+ self._abbrev_name = kwargs.pop("abbrev_name", "")
+ if len(self._abbrev_name):
+ self._abbrev_name = self._abbrev_name + "."
+ super(_ColorfulFormatter, self).__init__(*args, **kwargs)
+
+ def formatMessage(self, record):
+ record.name = record.name.replace(self._root_name, self._abbrev_name)
+ log = super(_ColorfulFormatter, self).formatMessage(record)
+ if record.levelno == logging.WARNING:
+ prefix = colored("WARNING", "red", attrs=["blink"])
+ elif record.levelno == logging.ERROR or record.levelno == logging.CRITICAL:
+ prefix = colored("ERROR", "red", attrs=["blink", "underline"])
+ else:
+ return log
+ return prefix + " " + log
+
+
+# so that calling setup_logger multiple times won't add many handlers
+@functools.lru_cache()
+def setup_logger(output=None, distributed_rank=0, *, color=True, name="imagenet", abbrev_name=None):
+ """
+ Initialize the detectron2 logger and set its verbosity level to "INFO".
+
+ Args:
+ output (str): a file name or a directory to save log. If None, will not save log file.
+ If ends with ".txt" or ".log", assumed to be a file name.
+ Otherwise, logs will be saved to `output/log.txt`.
+ name (str): the root module name of this logger
+
+ Returns:
+ logging.Logger: a logger
+ """
+ logger = logging.getLogger(name)
+ logger.setLevel(logging.DEBUG)
+ logger.propagate = False
+
+ if abbrev_name is None:
+ abbrev_name = name
+
+ plain_formatter = logging.Formatter(
+ "[%(asctime)s.%(msecs)03d]: %(message)s", datefmt="%m/%d %H:%M:%S"
+ )
+ # stdout logging: master only
+ if distributed_rank == 0:
+ ch = logging.StreamHandler(stream=sys.stdout)
+ ch.setLevel(logging.DEBUG)
+ if color:
+ formatter = _ColorfulFormatter(
+ colored("[%(asctime)s.%(msecs)03d]: ", "green") + "%(message)s",
+ datefmt="%m/%d %H:%M:%S",
+ root_name=name,
+ abbrev_name=str(abbrev_name),
+ )
+ else:
+ formatter = plain_formatter
+ ch.setFormatter(formatter)
+ logger.addHandler(ch)
+
+ # file logging: all workers
+ if output is not None:
+ if output.endswith(".txt") or output.endswith(".log"):
+ filename = output
+ else:
+ filename = os.path.join(output, "log.txt")
+ if distributed_rank > 0:
+ filename = filename + f".rank{distributed_rank}"
+ os.makedirs(os.path.dirname(filename), exist_ok=True)
+
+ fh = logging.StreamHandler(_cached_log_stream(filename))
+ fh.setLevel(logging.DEBUG)
+ fh.setFormatter(plain_formatter)
+ logger.addHandler(fh)
+
+ return logger
+
+
+# cache the opened file object, so that different calls to `setup_logger`
+# with the same file name can safely write to the same file.
+@functools.lru_cache(maxsize=None)
+def _cached_log_stream(filename):
+ return open(filename, "a")
diff --git a/GroundingDINO/groundingdino/util/misc.py b/GroundingDINO/groundingdino/util/misc.py
new file mode 100644
index 0000000000000000000000000000000000000000..d64b84ef24bea0c98e76824feb1903f6bfebe7a5
--- /dev/null
+++ b/GroundingDINO/groundingdino/util/misc.py
@@ -0,0 +1,717 @@
+# Copyright (c) Facebook, Inc. and its affiliates. All Rights Reserved
+"""
+Misc functions, including distributed helpers.
+
+Mostly copy-paste from torchvision references.
+"""
+import colorsys
+import datetime
+import functools
+import io
+import json
+import os
+import pickle
+import subprocess
+import time
+from collections import OrderedDict, defaultdict, deque
+from typing import List, Optional
+
+import numpy as np
+import torch
+import torch.distributed as dist
+
+# needed due to empty tensor bug in pytorch and torchvision 0.5
+import torchvision
+from torch import Tensor
+
+__torchvision_need_compat_flag = float(torchvision.__version__.split(".")[1]) < 7
+if __torchvision_need_compat_flag:
+ from torchvision.ops import _new_empty_tensor
+ from torchvision.ops.misc import _output_size
+
+
+class SmoothedValue(object):
+ """Track a series of values and provide access to smoothed values over a
+ window or the global series average.
+ """
+
+ def __init__(self, window_size=20, fmt=None):
+ if fmt is None:
+ fmt = "{median:.4f} ({global_avg:.4f})"
+ self.deque = deque(maxlen=window_size)
+ self.total = 0.0
+ self.count = 0
+ self.fmt = fmt
+
+ def update(self, value, n=1):
+ self.deque.append(value)
+ self.count += n
+ self.total += value * n
+
+ def synchronize_between_processes(self):
+ """
+ Warning: does not synchronize the deque!
+ """
+ if not is_dist_avail_and_initialized():
+ return
+ t = torch.tensor([self.count, self.total], dtype=torch.float64, device="cuda")
+ dist.barrier()
+ dist.all_reduce(t)
+ t = t.tolist()
+ self.count = int(t[0])
+ self.total = t[1]
+
+ @property
+ def median(self):
+ d = torch.tensor(list(self.deque))
+ if d.shape[0] == 0:
+ return 0
+ return d.median().item()
+
+ @property
+ def avg(self):
+ d = torch.tensor(list(self.deque), dtype=torch.float32)
+ return d.mean().item()
+
+ @property
+ def global_avg(self):
+ if os.environ.get("SHILONG_AMP", None) == "1":
+ eps = 1e-4
+ else:
+ eps = 1e-6
+ return self.total / (self.count + eps)
+
+ @property
+ def max(self):
+ return max(self.deque)
+
+ @property
+ def value(self):
+ return self.deque[-1]
+
+ def __str__(self):
+ return self.fmt.format(
+ median=self.median,
+ avg=self.avg,
+ global_avg=self.global_avg,
+ max=self.max,
+ value=self.value,
+ )
+
+
+@functools.lru_cache()
+def _get_global_gloo_group():
+ """
+ Return a process group based on gloo backend, containing all the ranks
+ The result is cached.
+ """
+
+ if dist.get_backend() == "nccl":
+ return dist.new_group(backend="gloo")
+
+ return dist.group.WORLD
+
+
+def all_gather_cpu(data):
+ """
+ Run all_gather on arbitrary picklable data (not necessarily tensors)
+ Args:
+ data: any picklable object
+ Returns:
+ list[data]: list of data gathered from each rank
+ """
+
+ world_size = get_world_size()
+ if world_size == 1:
+ return [data]
+
+ cpu_group = _get_global_gloo_group()
+
+ buffer = io.BytesIO()
+ torch.save(data, buffer)
+ data_view = buffer.getbuffer()
+ device = "cuda" if cpu_group is None else "cpu"
+ tensor = torch.ByteTensor(data_view).to(device)
+
+ # obtain Tensor size of each rank
+ local_size = torch.tensor([tensor.numel()], device=device, dtype=torch.long)
+ size_list = [torch.tensor([0], device=device, dtype=torch.long) for _ in range(world_size)]
+ if cpu_group is None:
+ dist.all_gather(size_list, local_size)
+ else:
+ print("gathering on cpu")
+ dist.all_gather(size_list, local_size, group=cpu_group)
+ size_list = [int(size.item()) for size in size_list]
+ max_size = max(size_list)
+ assert isinstance(local_size.item(), int)
+ local_size = int(local_size.item())
+
+ # receiving Tensor from all ranks
+ # we pad the tensor because torch all_gather does not support
+ # gathering tensors of different shapes
+ tensor_list = []
+ for _ in size_list:
+ tensor_list.append(torch.empty((max_size,), dtype=torch.uint8, device=device))
+ if local_size != max_size:
+ padding = torch.empty(size=(max_size - local_size,), dtype=torch.uint8, device=device)
+ tensor = torch.cat((tensor, padding), dim=0)
+ if cpu_group is None:
+ dist.all_gather(tensor_list, tensor)
+ else:
+ dist.all_gather(tensor_list, tensor, group=cpu_group)
+
+ data_list = []
+ for size, tensor in zip(size_list, tensor_list):
+ tensor = torch.split(tensor, [size, max_size - size], dim=0)[0]
+ buffer = io.BytesIO(tensor.cpu().numpy())
+ obj = torch.load(buffer)
+ data_list.append(obj)
+
+ return data_list
+
+
+def all_gather(data):
+ """
+ Run all_gather on arbitrary picklable data (not necessarily tensors)
+ Args:
+ data: any picklable object
+ Returns:
+ list[data]: list of data gathered from each rank
+ """
+
+ if os.getenv("CPU_REDUCE") == "1":
+ return all_gather_cpu(data)
+
+ world_size = get_world_size()
+ if world_size == 1:
+ return [data]
+
+ # serialized to a Tensor
+ buffer = pickle.dumps(data)
+ storage = torch.ByteStorage.from_buffer(buffer)
+ tensor = torch.ByteTensor(storage).to("cuda")
+
+ # obtain Tensor size of each rank
+ local_size = torch.tensor([tensor.numel()], device="cuda")
+ size_list = [torch.tensor([0], device="cuda") for _ in range(world_size)]
+ dist.all_gather(size_list, local_size)
+ size_list = [int(size.item()) for size in size_list]
+ max_size = max(size_list)
+
+ # receiving Tensor from all ranks
+ # we pad the tensor because torch all_gather does not support
+ # gathering tensors of different shapes
+ tensor_list = []
+ for _ in size_list:
+ tensor_list.append(torch.empty((max_size,), dtype=torch.uint8, device="cuda"))
+ if local_size != max_size:
+ padding = torch.empty(size=(max_size - local_size,), dtype=torch.uint8, device="cuda")
+ tensor = torch.cat((tensor, padding), dim=0)
+ dist.all_gather(tensor_list, tensor)
+
+ data_list = []
+ for size, tensor in zip(size_list, tensor_list):
+ buffer = tensor.cpu().numpy().tobytes()[:size]
+ data_list.append(pickle.loads(buffer))
+
+ return data_list
+
+
+def reduce_dict(input_dict, average=True):
+ """
+ Args:
+ input_dict (dict): all the values will be reduced
+ average (bool): whether to do average or sum
+ Reduce the values in the dictionary from all processes so that all processes
+ have the averaged results. Returns a dict with the same fields as
+ input_dict, after reduction.
+ """
+ world_size = get_world_size()
+ if world_size < 2:
+ return input_dict
+ with torch.no_grad():
+ names = []
+ values = []
+ # sort the keys so that they are consistent across processes
+ for k in sorted(input_dict.keys()):
+ names.append(k)
+ values.append(input_dict[k])
+ values = torch.stack(values, dim=0)
+ dist.all_reduce(values)
+ if average:
+ values /= world_size
+ reduced_dict = {k: v for k, v in zip(names, values)}
+ return reduced_dict
+
+
+class MetricLogger(object):
+ def __init__(self, delimiter="\t"):
+ self.meters = defaultdict(SmoothedValue)
+ self.delimiter = delimiter
+
+ def update(self, **kwargs):
+ for k, v in kwargs.items():
+ if isinstance(v, torch.Tensor):
+ v = v.item()
+ assert isinstance(v, (float, int))
+ self.meters[k].update(v)
+
+ def __getattr__(self, attr):
+ if attr in self.meters:
+ return self.meters[attr]
+ if attr in self.__dict__:
+ return self.__dict__[attr]
+ raise AttributeError("'{}' object has no attribute '{}'".format(type(self).__name__, attr))
+
+ def __str__(self):
+ loss_str = []
+ for name, meter in self.meters.items():
+ # print(name, str(meter))
+ # import ipdb;ipdb.set_trace()
+ if meter.count > 0:
+ loss_str.append("{}: {}".format(name, str(meter)))
+ return self.delimiter.join(loss_str)
+
+ def synchronize_between_processes(self):
+ for meter in self.meters.values():
+ meter.synchronize_between_processes()
+
+ def add_meter(self, name, meter):
+ self.meters[name] = meter
+
+ def log_every(self, iterable, print_freq, header=None, logger=None):
+ if logger is None:
+ print_func = print
+ else:
+ print_func = logger.info
+
+ i = 0
+ if not header:
+ header = ""
+ start_time = time.time()
+ end = time.time()
+ iter_time = SmoothedValue(fmt="{avg:.4f}")
+ data_time = SmoothedValue(fmt="{avg:.4f}")
+ space_fmt = ":" + str(len(str(len(iterable)))) + "d"
+ if torch.cuda.is_available():
+ log_msg = self.delimiter.join(
+ [
+ header,
+ "[{0" + space_fmt + "}/{1}]",
+ "eta: {eta}",
+ "{meters}",
+ "time: {time}",
+ "data: {data}",
+ "max mem: {memory:.0f}",
+ ]
+ )
+ else:
+ log_msg = self.delimiter.join(
+ [
+ header,
+ "[{0" + space_fmt + "}/{1}]",
+ "eta: {eta}",
+ "{meters}",
+ "time: {time}",
+ "data: {data}",
+ ]
+ )
+ MB = 1024.0 * 1024.0
+ for obj in iterable:
+ data_time.update(time.time() - end)
+ yield obj
+ # import ipdb; ipdb.set_trace()
+ iter_time.update(time.time() - end)
+ if i % print_freq == 0 or i == len(iterable) - 1:
+ eta_seconds = iter_time.global_avg * (len(iterable) - i)
+ eta_string = str(datetime.timedelta(seconds=int(eta_seconds)))
+ if torch.cuda.is_available():
+ print_func(
+ log_msg.format(
+ i,
+ len(iterable),
+ eta=eta_string,
+ meters=str(self),
+ time=str(iter_time),
+ data=str(data_time),
+ memory=torch.cuda.max_memory_allocated() / MB,
+ )
+ )
+ else:
+ print_func(
+ log_msg.format(
+ i,
+ len(iterable),
+ eta=eta_string,
+ meters=str(self),
+ time=str(iter_time),
+ data=str(data_time),
+ )
+ )
+ i += 1
+ end = time.time()
+ total_time = time.time() - start_time
+ total_time_str = str(datetime.timedelta(seconds=int(total_time)))
+ print_func(
+ "{} Total time: {} ({:.4f} s / it)".format(
+ header, total_time_str, total_time / len(iterable)
+ )
+ )
+
+
+def get_sha():
+ cwd = os.path.dirname(os.path.abspath(__file__))
+
+ def _run(command):
+ return subprocess.check_output(command, cwd=cwd).decode("ascii").strip()
+
+ sha = "N/A"
+ diff = "clean"
+ branch = "N/A"
+ try:
+ sha = _run(["git", "rev-parse", "HEAD"])
+ subprocess.check_output(["git", "diff"], cwd=cwd)
+ diff = _run(["git", "diff-index", "HEAD"])
+ diff = "has uncommited changes" if diff else "clean"
+ branch = _run(["git", "rev-parse", "--abbrev-ref", "HEAD"])
+ except Exception:
+ pass
+ message = f"sha: {sha}, status: {diff}, branch: {branch}"
+ return message
+
+
+def collate_fn(batch):
+ # import ipdb; ipdb.set_trace()
+ batch = list(zip(*batch))
+ batch[0] = nested_tensor_from_tensor_list(batch[0])
+ return tuple(batch)
+
+
+def _max_by_axis(the_list):
+ # type: (List[List[int]]) -> List[int]
+ maxes = the_list[0]
+ for sublist in the_list[1:]:
+ for index, item in enumerate(sublist):
+ maxes[index] = max(maxes[index], item)
+ return maxes
+
+
+class NestedTensor(object):
+ def __init__(self, tensors, mask: Optional[Tensor]):
+ self.tensors = tensors
+ self.mask = mask
+ if mask == "auto":
+ self.mask = torch.zeros_like(tensors).to(tensors.device)
+ if self.mask.dim() == 3:
+ self.mask = self.mask.sum(0).to(bool)
+ elif self.mask.dim() == 4:
+ self.mask = self.mask.sum(1).to(bool)
+ else:
+ raise ValueError(
+ "tensors dim must be 3 or 4 but {}({})".format(
+ self.tensors.dim(), self.tensors.shape
+ )
+ )
+
+ def imgsize(self):
+ res = []
+ for i in range(self.tensors.shape[0]):
+ mask = self.mask[i]
+ maxH = (~mask).sum(0).max()
+ maxW = (~mask).sum(1).max()
+ res.append(torch.Tensor([maxH, maxW]))
+ return res
+
+ def to(self, device):
+ # type: (Device) -> NestedTensor # noqa
+ cast_tensor = self.tensors.to(device)
+ mask = self.mask
+ if mask is not None:
+ assert mask is not None
+ cast_mask = mask.to(device)
+ else:
+ cast_mask = None
+ return NestedTensor(cast_tensor, cast_mask)
+
+ def to_img_list_single(self, tensor, mask):
+ assert tensor.dim() == 3, "dim of tensor should be 3 but {}".format(tensor.dim())
+ maxH = (~mask).sum(0).max()
+ maxW = (~mask).sum(1).max()
+ img = tensor[:, :maxH, :maxW]
+ return img
+
+ def to_img_list(self):
+ """remove the padding and convert to img list
+
+ Returns:
+ [type]: [description]
+ """
+ if self.tensors.dim() == 3:
+ return self.to_img_list_single(self.tensors, self.mask)
+ else:
+ res = []
+ for i in range(self.tensors.shape[0]):
+ tensor_i = self.tensors[i]
+ mask_i = self.mask[i]
+ res.append(self.to_img_list_single(tensor_i, mask_i))
+ return res
+
+ @property
+ def device(self):
+ return self.tensors.device
+
+ def decompose(self):
+ return self.tensors, self.mask
+
+ def __repr__(self):
+ return str(self.tensors)
+
+ @property
+ def shape(self):
+ return {"tensors.shape": self.tensors.shape, "mask.shape": self.mask.shape}
+
+
+def nested_tensor_from_tensor_list(tensor_list: List[Tensor]):
+ # TODO make this more general
+ if tensor_list[0].ndim == 3:
+ if torchvision._is_tracing():
+ # nested_tensor_from_tensor_list() does not export well to ONNX
+ # call _onnx_nested_tensor_from_tensor_list() instead
+ return _onnx_nested_tensor_from_tensor_list(tensor_list)
+
+ # TODO make it support different-sized images
+ max_size = _max_by_axis([list(img.shape) for img in tensor_list])
+ # min_size = tuple(min(s) for s in zip(*[img.shape for img in tensor_list]))
+ batch_shape = [len(tensor_list)] + max_size
+ b, c, h, w = batch_shape
+ dtype = tensor_list[0].dtype
+ device = tensor_list[0].device
+ tensor = torch.zeros(batch_shape, dtype=dtype, device=device)
+ mask = torch.ones((b, h, w), dtype=torch.bool, device=device)
+ for img, pad_img, m in zip(tensor_list, tensor, mask):
+ pad_img[: img.shape[0], : img.shape[1], : img.shape[2]].copy_(img)
+ m[: img.shape[1], : img.shape[2]] = False
+ else:
+ raise ValueError("not supported")
+ return NestedTensor(tensor, mask)
+
+
+# _onnx_nested_tensor_from_tensor_list() is an implementation of
+# nested_tensor_from_tensor_list() that is supported by ONNX tracing.
+@torch.jit.unused
+def _onnx_nested_tensor_from_tensor_list(tensor_list: List[Tensor]) -> NestedTensor:
+ max_size = []
+ for i in range(tensor_list[0].dim()):
+ max_size_i = torch.max(
+ torch.stack([img.shape[i] for img in tensor_list]).to(torch.float32)
+ ).to(torch.int64)
+ max_size.append(max_size_i)
+ max_size = tuple(max_size)
+
+ # work around for
+ # pad_img[: img.shape[0], : img.shape[1], : img.shape[2]].copy_(img)
+ # m[: img.shape[1], :img.shape[2]] = False
+ # which is not yet supported in onnx
+ padded_imgs = []
+ padded_masks = []
+ for img in tensor_list:
+ padding = [(s1 - s2) for s1, s2 in zip(max_size, tuple(img.shape))]
+ padded_img = torch.nn.functional.pad(img, (0, padding[2], 0, padding[1], 0, padding[0]))
+ padded_imgs.append(padded_img)
+
+ m = torch.zeros_like(img[0], dtype=torch.int, device=img.device)
+ padded_mask = torch.nn.functional.pad(m, (0, padding[2], 0, padding[1]), "constant", 1)
+ padded_masks.append(padded_mask.to(torch.bool))
+
+ tensor = torch.stack(padded_imgs)
+ mask = torch.stack(padded_masks)
+
+ return NestedTensor(tensor, mask=mask)
+
+
+def setup_for_distributed(is_master):
+ """
+ This function disables printing when not in master process
+ """
+ import builtins as __builtin__
+
+ builtin_print = __builtin__.print
+
+ def print(*args, **kwargs):
+ force = kwargs.pop("force", False)
+ if is_master or force:
+ builtin_print(*args, **kwargs)
+
+ __builtin__.print = print
+
+
+def is_dist_avail_and_initialized():
+ if not dist.is_available():
+ return False
+ if not dist.is_initialized():
+ return False
+ return True
+
+
+def get_world_size():
+ if not is_dist_avail_and_initialized():
+ return 1
+ return dist.get_world_size()
+
+
+def get_rank():
+ if not is_dist_avail_and_initialized():
+ return 0
+ return dist.get_rank()
+
+
+def is_main_process():
+ return get_rank() == 0
+
+
+def save_on_master(*args, **kwargs):
+ if is_main_process():
+ torch.save(*args, **kwargs)
+
+
+def init_distributed_mode(args):
+ if "WORLD_SIZE" in os.environ and os.environ["WORLD_SIZE"] != "": # 'RANK' in os.environ and
+ args.rank = int(os.environ["RANK"])
+ args.world_size = int(os.environ["WORLD_SIZE"])
+ args.gpu = args.local_rank = int(os.environ["LOCAL_RANK"])
+
+ # launch by torch.distributed.launch
+ # Single node
+ # python -m torch.distributed.launch --nproc_per_node=8 main.py --world-size 1 --rank 0 ...
+ # Multi nodes
+ # python -m torch.distributed.launch --nproc_per_node=8 main.py --world-size 2 --rank 0 --dist-url 'tcp://IP_OF_NODE0:FREEPORT' ...
+ # python -m torch.distributed.launch --nproc_per_node=8 main.py --world-size 2 --rank 1 --dist-url 'tcp://IP_OF_NODE0:FREEPORT' ...
+ # args.rank = int(os.environ.get('OMPI_COMM_WORLD_RANK'))
+ # local_world_size = int(os.environ['GPU_PER_NODE_COUNT'])
+ # args.world_size = args.world_size * local_world_size
+ # args.gpu = args.local_rank = int(os.environ['LOCAL_RANK'])
+ # args.rank = args.rank * local_world_size + args.local_rank
+ print(
+ "world size: {}, rank: {}, local rank: {}".format(
+ args.world_size, args.rank, args.local_rank
+ )
+ )
+ print(json.dumps(dict(os.environ), indent=2))
+ elif "SLURM_PROCID" in os.environ:
+ args.rank = int(os.environ["SLURM_PROCID"])
+ args.gpu = args.local_rank = int(os.environ["SLURM_LOCALID"])
+ args.world_size = int(os.environ["SLURM_NPROCS"])
+
+ print(
+ "world size: {}, world rank: {}, local rank: {}, device_count: {}".format(
+ args.world_size, args.rank, args.local_rank, torch.cuda.device_count()
+ )
+ )
+ else:
+ print("Not using distributed mode")
+ args.distributed = False
+ args.world_size = 1
+ args.rank = 0
+ args.local_rank = 0
+ return
+
+ print("world_size:{} rank:{} local_rank:{}".format(args.world_size, args.rank, args.local_rank))
+ args.distributed = True
+ torch.cuda.set_device(args.local_rank)
+ args.dist_backend = "nccl"
+ print("| distributed init (rank {}): {}".format(args.rank, args.dist_url), flush=True)
+
+ torch.distributed.init_process_group(
+ backend=args.dist_backend,
+ world_size=args.world_size,
+ rank=args.rank,
+ init_method=args.dist_url,
+ )
+
+ print("Before torch.distributed.barrier()")
+ torch.distributed.barrier()
+ print("End torch.distributed.barrier()")
+ setup_for_distributed(args.rank == 0)
+
+
+@torch.no_grad()
+def accuracy(output, target, topk=(1,)):
+ """Computes the precision@k for the specified values of k"""
+ if target.numel() == 0:
+ return [torch.zeros([], device=output.device)]
+ maxk = max(topk)
+ batch_size = target.size(0)
+
+ _, pred = output.topk(maxk, 1, True, True)
+ pred = pred.t()
+ correct = pred.eq(target.view(1, -1).expand_as(pred))
+
+ res = []
+ for k in topk:
+ correct_k = correct[:k].view(-1).float().sum(0)
+ res.append(correct_k.mul_(100.0 / batch_size))
+ return res
+
+
+@torch.no_grad()
+def accuracy_onehot(pred, gt):
+ """_summary_
+
+ Args:
+ pred (_type_): n, c
+ gt (_type_): n, c
+ """
+ tp = ((pred - gt).abs().sum(-1) < 1e-4).float().sum()
+ acc = tp / gt.shape[0] * 100
+ return acc
+
+
+def interpolate(input, size=None, scale_factor=None, mode="nearest", align_corners=None):
+ # type: (Tensor, Optional[List[int]], Optional[float], str, Optional[bool]) -> Tensor
+ """
+ Equivalent to nn.functional.interpolate, but with support for empty batch sizes.
+ This will eventually be supported natively by PyTorch, and this
+ class can go away.
+ """
+ if __torchvision_need_compat_flag < 0.7:
+ if input.numel() > 0:
+ return torch.nn.functional.interpolate(input, size, scale_factor, mode, align_corners)
+
+ output_shape = _output_size(2, input, size, scale_factor)
+ output_shape = list(input.shape[:-2]) + list(output_shape)
+ return _new_empty_tensor(input, output_shape)
+ else:
+ return torchvision.ops.misc.interpolate(input, size, scale_factor, mode, align_corners)
+
+
+class color_sys:
+ def __init__(self, num_colors) -> None:
+ self.num_colors = num_colors
+ colors = []
+ for i in np.arange(0.0, 360.0, 360.0 / num_colors):
+ hue = i / 360.0
+ lightness = (50 + np.random.rand() * 10) / 100.0
+ saturation = (90 + np.random.rand() * 10) / 100.0
+ colors.append(
+ tuple([int(j * 255) for j in colorsys.hls_to_rgb(hue, lightness, saturation)])
+ )
+ self.colors = colors
+
+ def __call__(self, idx):
+ return self.colors[idx]
+
+
+def inverse_sigmoid(x, eps=1e-3):
+ x = x.clamp(min=0, max=1)
+ x1 = x.clamp(min=eps)
+ x2 = (1 - x).clamp(min=eps)
+ return torch.log(x1 / x2)
+
+
+def clean_state_dict(state_dict):
+ new_state_dict = OrderedDict()
+ for k, v in state_dict.items():
+ if k[:7] == "module.":
+ k = k[7:] # remove `module.`
+ new_state_dict[k] = v
+ return new_state_dict
diff --git a/GroundingDINO/groundingdino/util/slconfig.py b/GroundingDINO/groundingdino/util/slconfig.py
new file mode 100644
index 0000000000000000000000000000000000000000..3f293e3aff215a3c7c2f7d21d27853493b6ebfbc
--- /dev/null
+++ b/GroundingDINO/groundingdino/util/slconfig.py
@@ -0,0 +1,427 @@
+# ==========================================================
+# Modified from mmcv
+# ==========================================================
+import ast
+import os.path as osp
+import shutil
+import sys
+import tempfile
+from argparse import Action
+from importlib import import_module
+import platform
+
+from addict import Dict
+from yapf.yapflib.yapf_api import FormatCode
+
+BASE_KEY = "_base_"
+DELETE_KEY = "_delete_"
+RESERVED_KEYS = ["filename", "text", "pretty_text", "get", "dump", "merge_from_dict"]
+
+
+def check_file_exist(filename, msg_tmpl='file "{}" does not exist'):
+ if not osp.isfile(filename):
+ raise FileNotFoundError(msg_tmpl.format(filename))
+
+
+class ConfigDict(Dict):
+ def __missing__(self, name):
+ raise KeyError(name)
+
+ def __getattr__(self, name):
+ try:
+ value = super(ConfigDict, self).__getattr__(name)
+ except KeyError:
+ ex = AttributeError(f"'{self.__class__.__name__}' object has no " f"attribute '{name}'")
+ except Exception as e:
+ ex = e
+ else:
+ return value
+ raise ex
+
+
+class SLConfig(object):
+ """
+ config files.
+ only support .py file as config now.
+
+ ref: mmcv.utils.config
+
+ Example:
+ >>> cfg = Config(dict(a=1, b=dict(b1=[0, 1])))
+ >>> cfg.a
+ 1
+ >>> cfg.b
+ {'b1': [0, 1]}
+ >>> cfg.b.b1
+ [0, 1]
+ >>> cfg = Config.fromfile('tests/data/config/a.py')
+ >>> cfg.filename
+ "/home/kchen/projects/mmcv/tests/data/config/a.py"
+ >>> cfg.item4
+ 'test'
+ >>> cfg
+ "Config [path: /home/kchen/projects/mmcv/tests/data/config/a.py]: "
+ "{'item1': [1, 2], 'item2': {'a': 0}, 'item3': True, 'item4': 'test'}"
+ """
+
+ @staticmethod
+ def _validate_py_syntax(filename):
+ with open(filename) as f:
+ content = f.read()
+ try:
+ ast.parse(content)
+ except SyntaxError:
+ raise SyntaxError("There are syntax errors in config " f"file {filename}")
+
+ @staticmethod
+ def _file2dict(filename):
+ filename = osp.abspath(osp.expanduser(filename))
+ check_file_exist(filename)
+ if filename.lower().endswith(".py"):
+ with tempfile.TemporaryDirectory() as temp_config_dir:
+ temp_config_file = tempfile.NamedTemporaryFile(dir=temp_config_dir, suffix=".py")
+ temp_config_name = osp.basename(temp_config_file.name)
+ if platform.system() == 'Windows':
+ temp_config_file.close()
+ shutil.copyfile(filename, osp.join(temp_config_dir, temp_config_name))
+ temp_module_name = osp.splitext(temp_config_name)[0]
+ sys.path.insert(0, temp_config_dir)
+ SLConfig._validate_py_syntax(filename)
+ mod = import_module(temp_module_name)
+ sys.path.pop(0)
+ cfg_dict = {
+ name: value for name, value in mod.__dict__.items() if not name.startswith("__")
+ }
+ # delete imported module
+ del sys.modules[temp_module_name]
+ # close temp file
+ temp_config_file.close()
+ elif filename.lower().endswith((".yml", ".yaml", ".json")):
+ from .slio import slload
+
+ cfg_dict = slload(filename)
+ else:
+ raise IOError("Only py/yml/yaml/json type are supported now!")
+
+ cfg_text = filename + "\n"
+ with open(filename, "r") as f:
+ cfg_text += f.read()
+
+ # parse the base file
+ if BASE_KEY in cfg_dict:
+ cfg_dir = osp.dirname(filename)
+ base_filename = cfg_dict.pop(BASE_KEY)
+ base_filename = base_filename if isinstance(base_filename, list) else [base_filename]
+
+ cfg_dict_list = list()
+ cfg_text_list = list()
+ for f in base_filename:
+ _cfg_dict, _cfg_text = SLConfig._file2dict(osp.join(cfg_dir, f))
+ cfg_dict_list.append(_cfg_dict)
+ cfg_text_list.append(_cfg_text)
+
+ base_cfg_dict = dict()
+ for c in cfg_dict_list:
+ if len(base_cfg_dict.keys() & c.keys()) > 0:
+ raise KeyError("Duplicate key is not allowed among bases")
+ # TODO Allow the duplicate key while warnning user
+ base_cfg_dict.update(c)
+
+ base_cfg_dict = SLConfig._merge_a_into_b(cfg_dict, base_cfg_dict)
+ cfg_dict = base_cfg_dict
+
+ # merge cfg_text
+ cfg_text_list.append(cfg_text)
+ cfg_text = "\n".join(cfg_text_list)
+
+ return cfg_dict, cfg_text
+
+ @staticmethod
+ def _merge_a_into_b(a, b):
+ """merge dict `a` into dict `b` (non-inplace).
+ values in `a` will overwrite `b`.
+ copy first to avoid inplace modification
+
+ Args:
+ a ([type]): [description]
+ b ([type]): [description]
+
+ Returns:
+ [dict]: [description]
+ """
+ # import ipdb; ipdb.set_trace()
+ if not isinstance(a, dict):
+ return a
+
+ b = b.copy()
+ for k, v in a.items():
+ if isinstance(v, dict) and k in b and not v.pop(DELETE_KEY, False):
+
+ if not isinstance(b[k], dict) and not isinstance(b[k], list):
+ # if :
+ # import ipdb; ipdb.set_trace()
+ raise TypeError(
+ f"{k}={v} in child config cannot inherit from base "
+ f"because {k} is a dict in the child config but is of "
+ f"type {type(b[k])} in base config. You may set "
+ f"`{DELETE_KEY}=True` to ignore the base config"
+ )
+ b[k] = SLConfig._merge_a_into_b(v, b[k])
+ elif isinstance(b, list):
+ try:
+ _ = int(k)
+ except:
+ raise TypeError(
+ f"b is a list, " f"index {k} should be an int when input but {type(k)}"
+ )
+ b[int(k)] = SLConfig._merge_a_into_b(v, b[int(k)])
+ else:
+ b[k] = v
+
+ return b
+
+ @staticmethod
+ def fromfile(filename):
+ cfg_dict, cfg_text = SLConfig._file2dict(filename)
+ return SLConfig(cfg_dict, cfg_text=cfg_text, filename=filename)
+
+ def __init__(self, cfg_dict=None, cfg_text=None, filename=None):
+ if cfg_dict is None:
+ cfg_dict = dict()
+ elif not isinstance(cfg_dict, dict):
+ raise TypeError("cfg_dict must be a dict, but " f"got {type(cfg_dict)}")
+ for key in cfg_dict:
+ if key in RESERVED_KEYS:
+ raise KeyError(f"{key} is reserved for config file")
+
+ super(SLConfig, self).__setattr__("_cfg_dict", ConfigDict(cfg_dict))
+ super(SLConfig, self).__setattr__("_filename", filename)
+ if cfg_text:
+ text = cfg_text
+ elif filename:
+ with open(filename, "r") as f:
+ text = f.read()
+ else:
+ text = ""
+ super(SLConfig, self).__setattr__("_text", text)
+
+ @property
+ def filename(self):
+ return self._filename
+
+ @property
+ def text(self):
+ return self._text
+
+ @property
+ def pretty_text(self):
+
+ indent = 4
+
+ def _indent(s_, num_spaces):
+ s = s_.split("\n")
+ if len(s) == 1:
+ return s_
+ first = s.pop(0)
+ s = [(num_spaces * " ") + line for line in s]
+ s = "\n".join(s)
+ s = first + "\n" + s
+ return s
+
+ def _format_basic_types(k, v, use_mapping=False):
+ if isinstance(v, str):
+ v_str = f"'{v}'"
+ else:
+ v_str = str(v)
+
+ if use_mapping:
+ k_str = f"'{k}'" if isinstance(k, str) else str(k)
+ attr_str = f"{k_str}: {v_str}"
+ else:
+ attr_str = f"{str(k)}={v_str}"
+ attr_str = _indent(attr_str, indent)
+
+ return attr_str
+
+ def _format_list(k, v, use_mapping=False):
+ # check if all items in the list are dict
+ if all(isinstance(_, dict) for _ in v):
+ v_str = "[\n"
+ v_str += "\n".join(
+ f"dict({_indent(_format_dict(v_), indent)})," for v_ in v
+ ).rstrip(",")
+ if use_mapping:
+ k_str = f"'{k}'" if isinstance(k, str) else str(k)
+ attr_str = f"{k_str}: {v_str}"
+ else:
+ attr_str = f"{str(k)}={v_str}"
+ attr_str = _indent(attr_str, indent) + "]"
+ else:
+ attr_str = _format_basic_types(k, v, use_mapping)
+ return attr_str
+
+ def _contain_invalid_identifier(dict_str):
+ contain_invalid_identifier = False
+ for key_name in dict_str:
+ contain_invalid_identifier |= not str(key_name).isidentifier()
+ return contain_invalid_identifier
+
+ def _format_dict(input_dict, outest_level=False):
+ r = ""
+ s = []
+
+ use_mapping = _contain_invalid_identifier(input_dict)
+ if use_mapping:
+ r += "{"
+ for idx, (k, v) in enumerate(input_dict.items()):
+ is_last = idx >= len(input_dict) - 1
+ end = "" if outest_level or is_last else ","
+ if isinstance(v, dict):
+ v_str = "\n" + _format_dict(v)
+ if use_mapping:
+ k_str = f"'{k}'" if isinstance(k, str) else str(k)
+ attr_str = f"{k_str}: dict({v_str}"
+ else:
+ attr_str = f"{str(k)}=dict({v_str}"
+ attr_str = _indent(attr_str, indent) + ")" + end
+ elif isinstance(v, list):
+ attr_str = _format_list(k, v, use_mapping) + end
+ else:
+ attr_str = _format_basic_types(k, v, use_mapping) + end
+
+ s.append(attr_str)
+ r += "\n".join(s)
+ if use_mapping:
+ r += "}"
+ return r
+
+ cfg_dict = self._cfg_dict.to_dict()
+ text = _format_dict(cfg_dict, outest_level=True)
+ # copied from setup.cfg
+ yapf_style = dict(
+ based_on_style="pep8",
+ blank_line_before_nested_class_or_def=True,
+ split_before_expression_after_opening_paren=True,
+ )
+ text, _ = FormatCode(text, style_config=yapf_style, verify=True)
+
+ return text
+
+ def __repr__(self):
+ return f"Config (path: {self.filename}): {self._cfg_dict.__repr__()}"
+
+ def __len__(self):
+ return len(self._cfg_dict)
+
+ def __getattr__(self, name):
+ # # debug
+ # print('+'*15)
+ # print('name=%s' % name)
+ # print("addr:", id(self))
+ # # print('type(self):', type(self))
+ # print(self.__dict__)
+ # print('+'*15)
+ # if self.__dict__ == {}:
+ # raise ValueError
+
+ return getattr(self._cfg_dict, name)
+
+ def __getitem__(self, name):
+ return self._cfg_dict.__getitem__(name)
+
+ def __setattr__(self, name, value):
+ if isinstance(value, dict):
+ value = ConfigDict(value)
+ self._cfg_dict.__setattr__(name, value)
+
+ def __setitem__(self, name, value):
+ if isinstance(value, dict):
+ value = ConfigDict(value)
+ self._cfg_dict.__setitem__(name, value)
+
+ def __iter__(self):
+ return iter(self._cfg_dict)
+
+ def dump(self, file=None):
+ # import ipdb; ipdb.set_trace()
+ if file is None:
+ return self.pretty_text
+ else:
+ with open(file, "w") as f:
+ f.write(self.pretty_text)
+
+ def merge_from_dict(self, options):
+ """Merge list into cfg_dict
+
+ Merge the dict parsed by MultipleKVAction into this cfg.
+
+ Examples:
+ >>> options = {'model.backbone.depth': 50,
+ ... 'model.backbone.with_cp':True}
+ >>> cfg = Config(dict(model=dict(backbone=dict(type='ResNet'))))
+ >>> cfg.merge_from_dict(options)
+ >>> cfg_dict = super(Config, self).__getattribute__('_cfg_dict')
+ >>> assert cfg_dict == dict(
+ ... model=dict(backbone=dict(depth=50, with_cp=True)))
+
+ Args:
+ options (dict): dict of configs to merge from.
+ """
+ option_cfg_dict = {}
+ for full_key, v in options.items():
+ d = option_cfg_dict
+ key_list = full_key.split(".")
+ for subkey in key_list[:-1]:
+ d.setdefault(subkey, ConfigDict())
+ d = d[subkey]
+ subkey = key_list[-1]
+ d[subkey] = v
+
+ cfg_dict = super(SLConfig, self).__getattribute__("_cfg_dict")
+ super(SLConfig, self).__setattr__(
+ "_cfg_dict", SLConfig._merge_a_into_b(option_cfg_dict, cfg_dict)
+ )
+
+ # for multiprocess
+ def __setstate__(self, state):
+ self.__init__(state)
+
+ def copy(self):
+ return SLConfig(self._cfg_dict.copy())
+
+ def deepcopy(self):
+ return SLConfig(self._cfg_dict.deepcopy())
+
+
+class DictAction(Action):
+ """
+ argparse action to split an argument into KEY=VALUE form
+ on the first = and append to a dictionary. List options should
+ be passed as comma separated values, i.e KEY=V1,V2,V3
+ """
+
+ @staticmethod
+ def _parse_int_float_bool(val):
+ try:
+ return int(val)
+ except ValueError:
+ pass
+ try:
+ return float(val)
+ except ValueError:
+ pass
+ if val.lower() in ["true", "false"]:
+ return True if val.lower() == "true" else False
+ if val.lower() in ["none", "null"]:
+ return None
+ return val
+
+ def __call__(self, parser, namespace, values, option_string=None):
+ options = {}
+ for kv in values:
+ key, val = kv.split("=", maxsplit=1)
+ val = [self._parse_int_float_bool(v) for v in val.split(",")]
+ if len(val) == 1:
+ val = val[0]
+ options[key] = val
+ setattr(namespace, self.dest, options)
diff --git a/GroundingDINO/groundingdino/util/slio.py b/GroundingDINO/groundingdino/util/slio.py
new file mode 100644
index 0000000000000000000000000000000000000000..72c1f0f7b82cdc931d381feef64fe15815ba657e
--- /dev/null
+++ b/GroundingDINO/groundingdino/util/slio.py
@@ -0,0 +1,177 @@
+# ==========================================================
+# Modified from mmcv
+# ==========================================================
+
+import json
+import pickle
+from abc import ABCMeta, abstractmethod
+from pathlib import Path
+
+import yaml
+
+try:
+ from yaml import CLoader as Loader, CDumper as Dumper
+except ImportError:
+ from yaml import Loader, Dumper
+
+
+# ===========================
+# Rigister handler
+# ===========================
+
+
+class BaseFileHandler(metaclass=ABCMeta):
+ @abstractmethod
+ def load_from_fileobj(self, file, **kwargs):
+ pass
+
+ @abstractmethod
+ def dump_to_fileobj(self, obj, file, **kwargs):
+ pass
+
+ @abstractmethod
+ def dump_to_str(self, obj, **kwargs):
+ pass
+
+ def load_from_path(self, filepath, mode="r", **kwargs):
+ with open(filepath, mode) as f:
+ return self.load_from_fileobj(f, **kwargs)
+
+ def dump_to_path(self, obj, filepath, mode="w", **kwargs):
+ with open(filepath, mode) as f:
+ self.dump_to_fileobj(obj, f, **kwargs)
+
+
+class JsonHandler(BaseFileHandler):
+ def load_from_fileobj(self, file):
+ return json.load(file)
+
+ def dump_to_fileobj(self, obj, file, **kwargs):
+ json.dump(obj, file, **kwargs)
+
+ def dump_to_str(self, obj, **kwargs):
+ return json.dumps(obj, **kwargs)
+
+
+class PickleHandler(BaseFileHandler):
+ def load_from_fileobj(self, file, **kwargs):
+ return pickle.load(file, **kwargs)
+
+ def load_from_path(self, filepath, **kwargs):
+ return super(PickleHandler, self).load_from_path(filepath, mode="rb", **kwargs)
+
+ def dump_to_str(self, obj, **kwargs):
+ kwargs.setdefault("protocol", 2)
+ return pickle.dumps(obj, **kwargs)
+
+ def dump_to_fileobj(self, obj, file, **kwargs):
+ kwargs.setdefault("protocol", 2)
+ pickle.dump(obj, file, **kwargs)
+
+ def dump_to_path(self, obj, filepath, **kwargs):
+ super(PickleHandler, self).dump_to_path(obj, filepath, mode="wb", **kwargs)
+
+
+class YamlHandler(BaseFileHandler):
+ def load_from_fileobj(self, file, **kwargs):
+ kwargs.setdefault("Loader", Loader)
+ return yaml.load(file, **kwargs)
+
+ def dump_to_fileobj(self, obj, file, **kwargs):
+ kwargs.setdefault("Dumper", Dumper)
+ yaml.dump(obj, file, **kwargs)
+
+ def dump_to_str(self, obj, **kwargs):
+ kwargs.setdefault("Dumper", Dumper)
+ return yaml.dump(obj, **kwargs)
+
+
+file_handlers = {
+ "json": JsonHandler(),
+ "yaml": YamlHandler(),
+ "yml": YamlHandler(),
+ "pickle": PickleHandler(),
+ "pkl": PickleHandler(),
+}
+
+# ===========================
+# load and dump
+# ===========================
+
+
+def is_str(x):
+ """Whether the input is an string instance.
+
+ Note: This method is deprecated since python 2 is no longer supported.
+ """
+ return isinstance(x, str)
+
+
+def slload(file, file_format=None, **kwargs):
+ """Load data from json/yaml/pickle files.
+
+ This method provides a unified api for loading data from serialized files.
+
+ Args:
+ file (str or :obj:`Path` or file-like object): Filename or a file-like
+ object.
+ file_format (str, optional): If not specified, the file format will be
+ inferred from the file extension, otherwise use the specified one.
+ Currently supported formats include "json", "yaml/yml" and
+ "pickle/pkl".
+
+ Returns:
+ The content from the file.
+ """
+ if isinstance(file, Path):
+ file = str(file)
+ if file_format is None and is_str(file):
+ file_format = file.split(".")[-1]
+ if file_format not in file_handlers:
+ raise TypeError(f"Unsupported format: {file_format}")
+
+ handler = file_handlers[file_format]
+ if is_str(file):
+ obj = handler.load_from_path(file, **kwargs)
+ elif hasattr(file, "read"):
+ obj = handler.load_from_fileobj(file, **kwargs)
+ else:
+ raise TypeError('"file" must be a filepath str or a file-object')
+ return obj
+
+
+def sldump(obj, file=None, file_format=None, **kwargs):
+ """Dump data to json/yaml/pickle strings or files.
+
+ This method provides a unified api for dumping data as strings or to files,
+ and also supports custom arguments for each file format.
+
+ Args:
+ obj (any): The python object to be dumped.
+ file (str or :obj:`Path` or file-like object, optional): If not
+ specified, then the object is dump to a str, otherwise to a file
+ specified by the filename or file-like object.
+ file_format (str, optional): Same as :func:`load`.
+
+ Returns:
+ bool: True for success, False otherwise.
+ """
+ if isinstance(file, Path):
+ file = str(file)
+ if file_format is None:
+ if is_str(file):
+ file_format = file.split(".")[-1]
+ elif file is None:
+ raise ValueError("file_format must be specified since file is None")
+ if file_format not in file_handlers:
+ raise TypeError(f"Unsupported format: {file_format}")
+
+ handler = file_handlers[file_format]
+ if file is None:
+ return handler.dump_to_str(obj, **kwargs)
+ elif is_str(file):
+ handler.dump_to_path(obj, file, **kwargs)
+ elif hasattr(file, "write"):
+ handler.dump_to_fileobj(obj, file, **kwargs)
+ else:
+ raise TypeError('"file" must be a filename str or a file-object')
diff --git a/GroundingDINO/groundingdino/util/time_counter.py b/GroundingDINO/groundingdino/util/time_counter.py
new file mode 100644
index 0000000000000000000000000000000000000000..0aedb2e4d61bfbe7571dca9d50053f0fedaa1359
--- /dev/null
+++ b/GroundingDINO/groundingdino/util/time_counter.py
@@ -0,0 +1,62 @@
+import json
+import time
+
+
+class TimeCounter:
+ def __init__(self) -> None:
+ pass
+
+ def clear(self):
+ self.timedict = {}
+ self.basetime = time.perf_counter()
+
+ def timeit(self, name):
+ nowtime = time.perf_counter() - self.basetime
+ self.timedict[name] = nowtime
+ self.basetime = time.perf_counter()
+
+
+class TimeHolder:
+ def __init__(self) -> None:
+ self.timedict = {}
+
+ def update(self, _timedict: dict):
+ for k, v in _timedict.items():
+ if k not in self.timedict:
+ self.timedict[k] = AverageMeter(name=k, val_only=True)
+ self.timedict[k].update(val=v)
+
+ def final_res(self):
+ return {k: v.avg for k, v in self.timedict.items()}
+
+ def __str__(self):
+ return json.dumps(self.final_res(), indent=2)
+
+
+class AverageMeter(object):
+ """Computes and stores the average and current value"""
+
+ def __init__(self, name, fmt=":f", val_only=False):
+ self.name = name
+ self.fmt = fmt
+ self.val_only = val_only
+ self.reset()
+
+ def reset(self):
+ self.val = 0
+ self.avg = 0
+ self.sum = 0
+ self.count = 0
+
+ def update(self, val, n=1):
+ self.val = val
+ self.sum += val * n
+ self.count += n
+ self.avg = self.sum / self.count
+
+ def __str__(self):
+ if self.val_only:
+ fmtstr = "{name} {val" + self.fmt + "}"
+ else:
+ fmtstr = "{name} {val" + self.fmt + "} ({avg" + self.fmt + "})"
+ return fmtstr.format(**self.__dict__)
diff --git a/GroundingDINO/groundingdino/util/utils.py b/GroundingDINO/groundingdino/util/utils.py
new file mode 100644
index 0000000000000000000000000000000000000000..e9f0318e306fa04bff0ada70486b41aaa69b07c8
--- /dev/null
+++ b/GroundingDINO/groundingdino/util/utils.py
@@ -0,0 +1,608 @@
+import argparse
+import json
+import warnings
+from collections import OrderedDict
+from copy import deepcopy
+from typing import Any, Dict, List
+
+import numpy as np
+import torch
+from transformers import AutoTokenizer
+
+from groundingdino.util.slconfig import SLConfig
+
+
+def slprint(x, name="x"):
+ if isinstance(x, (torch.Tensor, np.ndarray)):
+ print(f"{name}.shape:", x.shape)
+ elif isinstance(x, (tuple, list)):
+ print("type x:", type(x))
+ for i in range(min(10, len(x))):
+ slprint(x[i], f"{name}[{i}]")
+ elif isinstance(x, dict):
+ for k, v in x.items():
+ slprint(v, f"{name}[{k}]")
+ else:
+ print(f"{name}.type:", type(x))
+
+
+def clean_state_dict(state_dict):
+ new_state_dict = OrderedDict()
+ for k, v in state_dict.items():
+ if k[:7] == "module.":
+ k = k[7:] # remove `module.`
+ new_state_dict[k] = v
+ return new_state_dict
+
+
+def renorm(
+ img: torch.FloatTensor, mean=[0.485, 0.456, 0.406], std=[0.229, 0.224, 0.225]
+) -> torch.FloatTensor:
+ # img: tensor(3,H,W) or tensor(B,3,H,W)
+ # return: same as img
+ assert img.dim() == 3 or img.dim() == 4, "img.dim() should be 3 or 4 but %d" % img.dim()
+ if img.dim() == 3:
+ assert img.size(0) == 3, 'img.size(0) shoule be 3 but "%d". (%s)' % (
+ img.size(0),
+ str(img.size()),
+ )
+ img_perm = img.permute(1, 2, 0)
+ mean = torch.Tensor(mean)
+ std = torch.Tensor(std)
+ img_res = img_perm * std + mean
+ return img_res.permute(2, 0, 1)
+ else: # img.dim() == 4
+ assert img.size(1) == 3, 'img.size(1) shoule be 3 but "%d". (%s)' % (
+ img.size(1),
+ str(img.size()),
+ )
+ img_perm = img.permute(0, 2, 3, 1)
+ mean = torch.Tensor(mean)
+ std = torch.Tensor(std)
+ img_res = img_perm * std + mean
+ return img_res.permute(0, 3, 1, 2)
+
+
+class CocoClassMapper:
+ def __init__(self) -> None:
+ self.category_map_str = {
+ "1": 1,
+ "2": 2,
+ "3": 3,
+ "4": 4,
+ "5": 5,
+ "6": 6,
+ "7": 7,
+ "8": 8,
+ "9": 9,
+ "10": 10,
+ "11": 11,
+ "13": 12,
+ "14": 13,
+ "15": 14,
+ "16": 15,
+ "17": 16,
+ "18": 17,
+ "19": 18,
+ "20": 19,
+ "21": 20,
+ "22": 21,
+ "23": 22,
+ "24": 23,
+ "25": 24,
+ "27": 25,
+ "28": 26,
+ "31": 27,
+ "32": 28,
+ "33": 29,
+ "34": 30,
+ "35": 31,
+ "36": 32,
+ "37": 33,
+ "38": 34,
+ "39": 35,
+ "40": 36,
+ "41": 37,
+ "42": 38,
+ "43": 39,
+ "44": 40,
+ "46": 41,
+ "47": 42,
+ "48": 43,
+ "49": 44,
+ "50": 45,
+ "51": 46,
+ "52": 47,
+ "53": 48,
+ "54": 49,
+ "55": 50,
+ "56": 51,
+ "57": 52,
+ "58": 53,
+ "59": 54,
+ "60": 55,
+ "61": 56,
+ "62": 57,
+ "63": 58,
+ "64": 59,
+ "65": 60,
+ "67": 61,
+ "70": 62,
+ "72": 63,
+ "73": 64,
+ "74": 65,
+ "75": 66,
+ "76": 67,
+ "77": 68,
+ "78": 69,
+ "79": 70,
+ "80": 71,
+ "81": 72,
+ "82": 73,
+ "84": 74,
+ "85": 75,
+ "86": 76,
+ "87": 77,
+ "88": 78,
+ "89": 79,
+ "90": 80,
+ }
+ self.origin2compact_mapper = {int(k): v - 1 for k, v in self.category_map_str.items()}
+ self.compact2origin_mapper = {int(v - 1): int(k) for k, v in self.category_map_str.items()}
+
+ def origin2compact(self, idx):
+ return self.origin2compact_mapper[int(idx)]
+
+ def compact2origin(self, idx):
+ return self.compact2origin_mapper[int(idx)]
+
+
+def to_device(item, device):
+ if isinstance(item, torch.Tensor):
+ return item.to(device)
+ elif isinstance(item, list):
+ return [to_device(i, device) for i in item]
+ elif isinstance(item, dict):
+ return {k: to_device(v, device) for k, v in item.items()}
+ else:
+ raise NotImplementedError(
+ "Call Shilong if you use other containers! type: {}".format(type(item))
+ )
+
+
+#
+def get_gaussian_mean(x, axis, other_axis, softmax=True):
+ """
+
+ Args:
+ x (float): Input images(BxCxHxW)
+ axis (int): The index for weighted mean
+ other_axis (int): The other index
+
+ Returns: weighted index for axis, BxC
+
+ """
+ mat2line = torch.sum(x, axis=other_axis)
+ # mat2line = mat2line / mat2line.mean() * 10
+ if softmax:
+ u = torch.softmax(mat2line, axis=2)
+ else:
+ u = mat2line / (mat2line.sum(2, keepdim=True) + 1e-6)
+ size = x.shape[axis]
+ ind = torch.linspace(0, 1, size).to(x.device)
+ batch = x.shape[0]
+ channel = x.shape[1]
+ index = ind.repeat([batch, channel, 1])
+ mean_position = torch.sum(index * u, dim=2)
+ return mean_position
+
+
+def get_expected_points_from_map(hm, softmax=True):
+ """get_gaussian_map_from_points
+ B,C,H,W -> B,N,2 float(0, 1) float(0, 1)
+ softargmax function
+
+ Args:
+ hm (float): Input images(BxCxHxW)
+
+ Returns:
+ weighted index for axis, BxCx2. float between 0 and 1.
+
+ """
+ # hm = 10*hm
+ B, C, H, W = hm.shape
+ y_mean = get_gaussian_mean(hm, 2, 3, softmax=softmax) # B,C
+ x_mean = get_gaussian_mean(hm, 3, 2, softmax=softmax) # B,C
+ # return torch.cat((x_mean.unsqueeze(-1), y_mean.unsqueeze(-1)), 2)
+ return torch.stack([x_mean, y_mean], dim=2)
+
+
+# Positional encoding (section 5.1)
+# borrow from nerf
+class Embedder:
+ def __init__(self, **kwargs):
+ self.kwargs = kwargs
+ self.create_embedding_fn()
+
+ def create_embedding_fn(self):
+ embed_fns = []
+ d = self.kwargs["input_dims"]
+ out_dim = 0
+ if self.kwargs["include_input"]:
+ embed_fns.append(lambda x: x)
+ out_dim += d
+
+ max_freq = self.kwargs["max_freq_log2"]
+ N_freqs = self.kwargs["num_freqs"]
+
+ if self.kwargs["log_sampling"]:
+ freq_bands = 2.0 ** torch.linspace(0.0, max_freq, steps=N_freqs)
+ else:
+ freq_bands = torch.linspace(2.0**0.0, 2.0**max_freq, steps=N_freqs)
+
+ for freq in freq_bands:
+ for p_fn in self.kwargs["periodic_fns"]:
+ embed_fns.append(lambda x, p_fn=p_fn, freq=freq: p_fn(x * freq))
+ out_dim += d
+
+ self.embed_fns = embed_fns
+ self.out_dim = out_dim
+
+ def embed(self, inputs):
+ return torch.cat([fn(inputs) for fn in self.embed_fns], -1)
+
+
+def get_embedder(multires, i=0):
+ import torch.nn as nn
+
+ if i == -1:
+ return nn.Identity(), 3
+
+ embed_kwargs = {
+ "include_input": True,
+ "input_dims": 3,
+ "max_freq_log2": multires - 1,
+ "num_freqs": multires,
+ "log_sampling": True,
+ "periodic_fns": [torch.sin, torch.cos],
+ }
+
+ embedder_obj = Embedder(**embed_kwargs)
+ embed = lambda x, eo=embedder_obj: eo.embed(x)
+ return embed, embedder_obj.out_dim
+
+
+class APOPMeter:
+ def __init__(self) -> None:
+ self.tp = 0
+ self.fp = 0
+ self.tn = 0
+ self.fn = 0
+
+ def update(self, pred, gt):
+ """
+ Input:
+ pred, gt: Tensor()
+ """
+ assert pred.shape == gt.shape
+ self.tp += torch.logical_and(pred == 1, gt == 1).sum().item()
+ self.fp += torch.logical_and(pred == 1, gt == 0).sum().item()
+ self.tn += torch.logical_and(pred == 0, gt == 0).sum().item()
+ self.tn += torch.logical_and(pred == 1, gt == 0).sum().item()
+
+ def update_cm(self, tp, fp, tn, fn):
+ self.tp += tp
+ self.fp += fp
+ self.tn += tn
+ self.tn += fn
+
+
+def inverse_sigmoid(x, eps=1e-5):
+ x = x.clamp(min=0, max=1)
+ x1 = x.clamp(min=eps)
+ x2 = (1 - x).clamp(min=eps)
+ return torch.log(x1 / x2)
+
+
+def get_raw_dict(args):
+ """
+ return the dicf contained in args.
+
+ e.g:
+ >>> with open(path, 'w') as f:
+ json.dump(get_raw_dict(args), f, indent=2)
+ """
+ if isinstance(args, argparse.Namespace):
+ return vars(args)
+ elif isinstance(args, dict):
+ return args
+ elif isinstance(args, SLConfig):
+ return args._cfg_dict
+ else:
+ raise NotImplementedError("Unknown type {}".format(type(args)))
+
+
+def stat_tensors(tensor):
+ assert tensor.dim() == 1
+ tensor_sm = tensor.softmax(0)
+ entropy = (tensor_sm * torch.log(tensor_sm + 1e-9)).sum()
+
+ return {
+ "max": tensor.max(),
+ "min": tensor.min(),
+ "mean": tensor.mean(),
+ "var": tensor.var(),
+ "std": tensor.var() ** 0.5,
+ "entropy": entropy,
+ }
+
+
+class NiceRepr:
+ """Inherit from this class and define ``__nice__`` to "nicely" print your
+ objects.
+
+ Defines ``__str__`` and ``__repr__`` in terms of ``__nice__`` function
+ Classes that inherit from :class:`NiceRepr` should redefine ``__nice__``.
+ If the inheriting class has a ``__len__``, method then the default
+ ``__nice__`` method will return its length.
+
+ Example:
+ >>> class Foo(NiceRepr):
+ ... def __nice__(self):
+ ... return 'info'
+ >>> foo = Foo()
+ >>> assert str(foo) == ''
+ >>> assert repr(foo).startswith('>> class Bar(NiceRepr):
+ ... pass
+ >>> bar = Bar()
+ >>> import pytest
+ >>> with pytest.warns(None) as record:
+ >>> assert 'object at' in str(bar)
+ >>> assert 'object at' in repr(bar)
+
+ Example:
+ >>> class Baz(NiceRepr):
+ ... def __len__(self):
+ ... return 5
+ >>> baz = Baz()
+ >>> assert str(baz) == ''
+ """
+
+ def __nice__(self):
+ """str: a "nice" summary string describing this module"""
+ if hasattr(self, "__len__"):
+ # It is a common pattern for objects to use __len__ in __nice__
+ # As a convenience we define a default __nice__ for these objects
+ return str(len(self))
+ else:
+ # In all other cases force the subclass to overload __nice__
+ raise NotImplementedError(f"Define the __nice__ method for {self.__class__!r}")
+
+ def __repr__(self):
+ """str: the string of the module"""
+ try:
+ nice = self.__nice__()
+ classname = self.__class__.__name__
+ return f"<{classname}({nice}) at {hex(id(self))}>"
+ except NotImplementedError as ex:
+ warnings.warn(str(ex), category=RuntimeWarning)
+ return object.__repr__(self)
+
+ def __str__(self):
+ """str: the string of the module"""
+ try:
+ classname = self.__class__.__name__
+ nice = self.__nice__()
+ return f"<{classname}({nice})>"
+ except NotImplementedError as ex:
+ warnings.warn(str(ex), category=RuntimeWarning)
+ return object.__repr__(self)
+
+
+def ensure_rng(rng=None):
+ """Coerces input into a random number generator.
+
+ If the input is None, then a global random state is returned.
+
+ If the input is a numeric value, then that is used as a seed to construct a
+ random state. Otherwise the input is returned as-is.
+
+ Adapted from [1]_.
+
+ Args:
+ rng (int | numpy.random.RandomState | None):
+ if None, then defaults to the global rng. Otherwise this can be an
+ integer or a RandomState class
+ Returns:
+ (numpy.random.RandomState) : rng -
+ a numpy random number generator
+
+ References:
+ .. [1] https://gitlab.kitware.com/computer-vision/kwarray/blob/master/kwarray/util_random.py#L270 # noqa: E501
+ """
+
+ if rng is None:
+ rng = np.random.mtrand._rand
+ elif isinstance(rng, int):
+ rng = np.random.RandomState(rng)
+ else:
+ rng = rng
+ return rng
+
+
+def random_boxes(num=1, scale=1, rng=None):
+ """Simple version of ``kwimage.Boxes.random``
+
+ Returns:
+ Tensor: shape (n, 4) in x1, y1, x2, y2 format.
+
+ References:
+ https://gitlab.kitware.com/computer-vision/kwimage/blob/master/kwimage/structs/boxes.py#L1390
+
+ Example:
+ >>> num = 3
+ >>> scale = 512
+ >>> rng = 0
+ >>> boxes = random_boxes(num, scale, rng)
+ >>> print(boxes)
+ tensor([[280.9925, 278.9802, 308.6148, 366.1769],
+ [216.9113, 330.6978, 224.0446, 456.5878],
+ [405.3632, 196.3221, 493.3953, 270.7942]])
+ """
+ rng = ensure_rng(rng)
+
+ tlbr = rng.rand(num, 4).astype(np.float32)
+
+ tl_x = np.minimum(tlbr[:, 0], tlbr[:, 2])
+ tl_y = np.minimum(tlbr[:, 1], tlbr[:, 3])
+ br_x = np.maximum(tlbr[:, 0], tlbr[:, 2])
+ br_y = np.maximum(tlbr[:, 1], tlbr[:, 3])
+
+ tlbr[:, 0] = tl_x * scale
+ tlbr[:, 1] = tl_y * scale
+ tlbr[:, 2] = br_x * scale
+ tlbr[:, 3] = br_y * scale
+
+ boxes = torch.from_numpy(tlbr)
+ return boxes
+
+
+class ModelEma(torch.nn.Module):
+ def __init__(self, model, decay=0.9997, device=None):
+ super(ModelEma, self).__init__()
+ # make a copy of the model for accumulating moving average of weights
+ self.module = deepcopy(model)
+ self.module.eval()
+
+ # import ipdb; ipdb.set_trace()
+
+ self.decay = decay
+ self.device = device # perform ema on different device from model if set
+ if self.device is not None:
+ self.module.to(device=device)
+
+ def _update(self, model, update_fn):
+ with torch.no_grad():
+ for ema_v, model_v in zip(
+ self.module.state_dict().values(), model.state_dict().values()
+ ):
+ if self.device is not None:
+ model_v = model_v.to(device=self.device)
+ ema_v.copy_(update_fn(ema_v, model_v))
+
+ def update(self, model):
+ self._update(model, update_fn=lambda e, m: self.decay * e + (1.0 - self.decay) * m)
+
+ def set(self, model):
+ self._update(model, update_fn=lambda e, m: m)
+
+
+class BestMetricSingle:
+ def __init__(self, init_res=0.0, better="large") -> None:
+ self.init_res = init_res
+ self.best_res = init_res
+ self.best_ep = -1
+
+ self.better = better
+ assert better in ["large", "small"]
+
+ def isbetter(self, new_res, old_res):
+ if self.better == "large":
+ return new_res > old_res
+ if self.better == "small":
+ return new_res < old_res
+
+ def update(self, new_res, ep):
+ if self.isbetter(new_res, self.best_res):
+ self.best_res = new_res
+ self.best_ep = ep
+ return True
+ return False
+
+ def __str__(self) -> str:
+ return "best_res: {}\t best_ep: {}".format(self.best_res, self.best_ep)
+
+ def __repr__(self) -> str:
+ return self.__str__()
+
+ def summary(self) -> dict:
+ return {
+ "best_res": self.best_res,
+ "best_ep": self.best_ep,
+ }
+
+
+class BestMetricHolder:
+ def __init__(self, init_res=0.0, better="large", use_ema=False) -> None:
+ self.best_all = BestMetricSingle(init_res, better)
+ self.use_ema = use_ema
+ if use_ema:
+ self.best_ema = BestMetricSingle(init_res, better)
+ self.best_regular = BestMetricSingle(init_res, better)
+
+ def update(self, new_res, epoch, is_ema=False):
+ """
+ return if the results is the best.
+ """
+ if not self.use_ema:
+ return self.best_all.update(new_res, epoch)
+ else:
+ if is_ema:
+ self.best_ema.update(new_res, epoch)
+ return self.best_all.update(new_res, epoch)
+ else:
+ self.best_regular.update(new_res, epoch)
+ return self.best_all.update(new_res, epoch)
+
+ def summary(self):
+ if not self.use_ema:
+ return self.best_all.summary()
+
+ res = {}
+ res.update({f"all_{k}": v for k, v in self.best_all.summary().items()})
+ res.update({f"regular_{k}": v for k, v in self.best_regular.summary().items()})
+ res.update({f"ema_{k}": v for k, v in self.best_ema.summary().items()})
+ return res
+
+ def __repr__(self) -> str:
+ return json.dumps(self.summary(), indent=2)
+
+ def __str__(self) -> str:
+ return self.__repr__()
+
+
+def targets_to(targets: List[Dict[str, Any]], device):
+ """Moves the target dicts to the given device."""
+ excluded_keys = [
+ "questionId",
+ "tokens_positive",
+ "strings_positive",
+ "tokens",
+ "dataset_name",
+ "sentence_id",
+ "original_img_id",
+ "nb_eval",
+ "task_id",
+ "original_id",
+ "token_span",
+ "caption",
+ "dataset_type",
+ ]
+ return [
+ {k: v.to(device) if k not in excluded_keys else v for k, v in t.items()} for t in targets
+ ]
+
+
+def get_phrases_from_posmap(
+ posmap: torch.BoolTensor, tokenized: Dict, tokenizer: AutoTokenizer
+):
+ assert isinstance(posmap, torch.Tensor), "posmap must be torch.Tensor"
+ if posmap.dim() == 1:
+ non_zero_idx = posmap.nonzero(as_tuple=True)[0].tolist()
+ token_ids = [tokenized["input_ids"][i] for i in non_zero_idx]
+ return tokenizer.decode(token_ids)
+ else:
+ raise NotImplementedError("posmap must be 1-dim")
diff --git a/GroundingDINO/groundingdino/util/visualizer.py b/GroundingDINO/groundingdino/util/visualizer.py
new file mode 100644
index 0000000000000000000000000000000000000000..7a1b7b101e9b73f75f9136bc67f2063c7c1cf1c1
--- /dev/null
+++ b/GroundingDINO/groundingdino/util/visualizer.py
@@ -0,0 +1,318 @@
+# -*- coding: utf-8 -*-
+"""
+@File : visualizer.py
+@Time : 2022/04/05 11:39:33
+@Author : Shilong Liu
+@Contact : slongliu86@gmail.com
+"""
+
+import datetime
+import os
+
+import cv2
+import matplotlib.pyplot as plt
+import numpy as np
+import torch
+from matplotlib import transforms
+from matplotlib.collections import PatchCollection
+from matplotlib.patches import Polygon
+from pycocotools import mask as maskUtils
+
+
+def renorm(
+ img: torch.FloatTensor, mean=[0.485, 0.456, 0.406], std=[0.229, 0.224, 0.225]
+) -> torch.FloatTensor:
+ # img: tensor(3,H,W) or tensor(B,3,H,W)
+ # return: same as img
+ assert img.dim() == 3 or img.dim() == 4, "img.dim() should be 3 or 4 but %d" % img.dim()
+ if img.dim() == 3:
+ assert img.size(0) == 3, 'img.size(0) shoule be 3 but "%d". (%s)' % (
+ img.size(0),
+ str(img.size()),
+ )
+ img_perm = img.permute(1, 2, 0)
+ mean = torch.Tensor(mean)
+ std = torch.Tensor(std)
+ img_res = img_perm * std + mean
+ return img_res.permute(2, 0, 1)
+ else: # img.dim() == 4
+ assert img.size(1) == 3, 'img.size(1) shoule be 3 but "%d". (%s)' % (
+ img.size(1),
+ str(img.size()),
+ )
+ img_perm = img.permute(0, 2, 3, 1)
+ mean = torch.Tensor(mean)
+ std = torch.Tensor(std)
+ img_res = img_perm * std + mean
+ return img_res.permute(0, 3, 1, 2)
+
+
+class ColorMap:
+ def __init__(self, basergb=[255, 255, 0]):
+ self.basergb = np.array(basergb)
+
+ def __call__(self, attnmap):
+ # attnmap: h, w. np.uint8.
+ # return: h, w, 4. np.uint8.
+ assert attnmap.dtype == np.uint8
+ h, w = attnmap.shape
+ res = self.basergb.copy()
+ res = res[None][None].repeat(h, 0).repeat(w, 1) # h, w, 3
+ attn1 = attnmap.copy()[..., None] # h, w, 1
+ res = np.concatenate((res, attn1), axis=-1).astype(np.uint8)
+ return res
+
+
+def rainbow_text(x, y, ls, lc, **kw):
+ """
+ Take a list of strings ``ls`` and colors ``lc`` and place them next to each
+ other, with text ls[i] being shown in color lc[i].
+
+ This example shows how to do both vertical and horizontal text, and will
+ pass all keyword arguments to plt.text, so you can set the font size,
+ family, etc.
+ """
+ t = plt.gca().transData
+ fig = plt.gcf()
+ plt.show()
+
+ # horizontal version
+ for s, c in zip(ls, lc):
+ text = plt.text(x, y, " " + s + " ", color=c, transform=t, **kw)
+ text.draw(fig.canvas.get_renderer())
+ ex = text.get_window_extent()
+ t = transforms.offset_copy(text._transform, x=ex.width, units="dots")
+
+ # #vertical version
+ # for s,c in zip(ls,lc):
+ # text = plt.text(x,y," "+s+" ",color=c, transform=t,
+ # rotation=90,va='bottom',ha='center',**kw)
+ # text.draw(fig.canvas.get_renderer())
+ # ex = text.get_window_extent()
+ # t = transforms.offset_copy(text._transform, y=ex.height, units='dots')
+
+
+class COCOVisualizer:
+ def __init__(self, coco=None, tokenlizer=None) -> None:
+ self.coco = coco
+
+ def visualize(self, img, tgt, caption=None, dpi=180, savedir="vis"):
+ """
+ img: tensor(3, H, W)
+ tgt: make sure they are all on cpu.
+ must have items: 'image_id', 'boxes', 'size'
+ """
+ plt.figure(dpi=dpi)
+ plt.rcParams["font.size"] = "5"
+ ax = plt.gca()
+ img = renorm(img).permute(1, 2, 0)
+ # if os.environ.get('IPDB_SHILONG_DEBUG', None) == 'INFO':
+ # import ipdb; ipdb.set_trace()
+ ax.imshow(img)
+
+ self.addtgt(tgt)
+
+ if tgt is None:
+ image_id = 0
+ elif "image_id" not in tgt:
+ image_id = 0
+ else:
+ image_id = tgt["image_id"]
+
+ if caption is None:
+ savename = "{}/{}-{}.png".format(
+ savedir, int(image_id), str(datetime.datetime.now()).replace(" ", "-")
+ )
+ else:
+ savename = "{}/{}-{}-{}.png".format(
+ savedir, caption, int(image_id), str(datetime.datetime.now()).replace(" ", "-")
+ )
+ print("savename: {}".format(savename))
+ os.makedirs(os.path.dirname(savename), exist_ok=True)
+ plt.savefig(savename)
+ plt.close()
+
+ def addtgt(self, tgt):
+ """ """
+ if tgt is None or not "boxes" in tgt:
+ ax = plt.gca()
+
+ if "caption" in tgt:
+ ax.set_title(tgt["caption"], wrap=True)
+
+ ax.set_axis_off()
+ return
+
+ ax = plt.gca()
+ H, W = tgt["size"]
+ numbox = tgt["boxes"].shape[0]
+
+ color = []
+ polygons = []
+ boxes = []
+ for box in tgt["boxes"].cpu():
+ unnormbbox = box * torch.Tensor([W, H, W, H])
+ unnormbbox[:2] -= unnormbbox[2:] / 2
+ [bbox_x, bbox_y, bbox_w, bbox_h] = unnormbbox.tolist()
+ boxes.append([bbox_x, bbox_y, bbox_w, bbox_h])
+ poly = [
+ [bbox_x, bbox_y],
+ [bbox_x, bbox_y + bbox_h],
+ [bbox_x + bbox_w, bbox_y + bbox_h],
+ [bbox_x + bbox_w, bbox_y],
+ ]
+ np_poly = np.array(poly).reshape((4, 2))
+ polygons.append(Polygon(np_poly))
+ c = (np.random.random((1, 3)) * 0.6 + 0.4).tolist()[0]
+ color.append(c)
+
+ p = PatchCollection(polygons, facecolor=color, linewidths=0, alpha=0.1)
+ ax.add_collection(p)
+ p = PatchCollection(polygons, facecolor="none", edgecolors=color, linewidths=2)
+ ax.add_collection(p)
+
+ if "strings_positive" in tgt and len(tgt["strings_positive"]) > 0:
+ assert (
+ len(tgt["strings_positive"]) == numbox
+ ), f"{len(tgt['strings_positive'])} = {numbox}, "
+ for idx, strlist in enumerate(tgt["strings_positive"]):
+ cate_id = int(tgt["labels"][idx])
+ _string = str(cate_id) + ":" + " ".join(strlist)
+ bbox_x, bbox_y, bbox_w, bbox_h = boxes[idx]
+ # ax.text(bbox_x, bbox_y, _string, color='black', bbox={'facecolor': 'yellow', 'alpha': 1.0, 'pad': 1})
+ ax.text(
+ bbox_x,
+ bbox_y,
+ _string,
+ color="black",
+ bbox={"facecolor": color[idx], "alpha": 0.6, "pad": 1},
+ )
+
+ if "box_label" in tgt:
+ assert len(tgt["box_label"]) == numbox, f"{len(tgt['box_label'])} = {numbox}, "
+ for idx, bl in enumerate(tgt["box_label"]):
+ _string = str(bl)
+ bbox_x, bbox_y, bbox_w, bbox_h = boxes[idx]
+ # ax.text(bbox_x, bbox_y, _string, color='black', bbox={'facecolor': 'yellow', 'alpha': 1.0, 'pad': 1})
+ ax.text(
+ bbox_x,
+ bbox_y,
+ _string,
+ color="black",
+ bbox={"facecolor": color[idx], "alpha": 0.6, "pad": 1},
+ )
+
+ if "caption" in tgt:
+ ax.set_title(tgt["caption"], wrap=True)
+ # plt.figure()
+ # rainbow_text(0.0,0.0,"all unicorns poop rainbows ! ! !".split(),
+ # ['red', 'orange', 'brown', 'green', 'blue', 'purple', 'black'])
+
+ if "attn" in tgt:
+ # if os.environ.get('IPDB_SHILONG_DEBUG', None) == 'INFO':
+ # import ipdb; ipdb.set_trace()
+ if isinstance(tgt["attn"], tuple):
+ tgt["attn"] = [tgt["attn"]]
+ for item in tgt["attn"]:
+ attn_map, basergb = item
+ attn_map = (attn_map - attn_map.min()) / (attn_map.max() - attn_map.min() + 1e-3)
+ attn_map = (attn_map * 255).astype(np.uint8)
+ cm = ColorMap(basergb)
+ heatmap = cm(attn_map)
+ ax.imshow(heatmap)
+ ax.set_axis_off()
+
+ def showAnns(self, anns, draw_bbox=False):
+ """
+ Display the specified annotations.
+ :param anns (array of object): annotations to display
+ :return: None
+ """
+ if len(anns) == 0:
+ return 0
+ if "segmentation" in anns[0] or "keypoints" in anns[0]:
+ datasetType = "instances"
+ elif "caption" in anns[0]:
+ datasetType = "captions"
+ else:
+ raise Exception("datasetType not supported")
+ if datasetType == "instances":
+ ax = plt.gca()
+ ax.set_autoscale_on(False)
+ polygons = []
+ color = []
+ for ann in anns:
+ c = (np.random.random((1, 3)) * 0.6 + 0.4).tolist()[0]
+ if "segmentation" in ann:
+ if type(ann["segmentation"]) == list:
+ # polygon
+ for seg in ann["segmentation"]:
+ poly = np.array(seg).reshape((int(len(seg) / 2), 2))
+ polygons.append(Polygon(poly))
+ color.append(c)
+ else:
+ # mask
+ t = self.imgs[ann["image_id"]]
+ if type(ann["segmentation"]["counts"]) == list:
+ rle = maskUtils.frPyObjects(
+ [ann["segmentation"]], t["height"], t["width"]
+ )
+ else:
+ rle = [ann["segmentation"]]
+ m = maskUtils.decode(rle)
+ img = np.ones((m.shape[0], m.shape[1], 3))
+ if ann["iscrowd"] == 1:
+ color_mask = np.array([2.0, 166.0, 101.0]) / 255
+ if ann["iscrowd"] == 0:
+ color_mask = np.random.random((1, 3)).tolist()[0]
+ for i in range(3):
+ img[:, :, i] = color_mask[i]
+ ax.imshow(np.dstack((img, m * 0.5)))
+ if "keypoints" in ann and type(ann["keypoints"]) == list:
+ # turn skeleton into zero-based index
+ sks = np.array(self.loadCats(ann["category_id"])[0]["skeleton"]) - 1
+ kp = np.array(ann["keypoints"])
+ x = kp[0::3]
+ y = kp[1::3]
+ v = kp[2::3]
+ for sk in sks:
+ if np.all(v[sk] > 0):
+ plt.plot(x[sk], y[sk], linewidth=3, color=c)
+ plt.plot(
+ x[v > 0],
+ y[v > 0],
+ "o",
+ markersize=8,
+ markerfacecolor=c,
+ markeredgecolor="k",
+ markeredgewidth=2,
+ )
+ plt.plot(
+ x[v > 1],
+ y[v > 1],
+ "o",
+ markersize=8,
+ markerfacecolor=c,
+ markeredgecolor=c,
+ markeredgewidth=2,
+ )
+
+ if draw_bbox:
+ [bbox_x, bbox_y, bbox_w, bbox_h] = ann["bbox"]
+ poly = [
+ [bbox_x, bbox_y],
+ [bbox_x, bbox_y + bbox_h],
+ [bbox_x + bbox_w, bbox_y + bbox_h],
+ [bbox_x + bbox_w, bbox_y],
+ ]
+ np_poly = np.array(poly).reshape((4, 2))
+ polygons.append(Polygon(np_poly))
+ color.append(c)
+
+ # p = PatchCollection(polygons, facecolor=color, linewidths=0, alpha=0.4)
+ # ax.add_collection(p)
+ p = PatchCollection(polygons, facecolor="none", edgecolors=color, linewidths=2)
+ ax.add_collection(p)
+ elif datasetType == "captions":
+ for ann in anns:
+ print(ann["caption"])
diff --git a/GroundingDINO/groundingdino/util/vl_utils.py b/GroundingDINO/groundingdino/util/vl_utils.py
new file mode 100644
index 0000000000000000000000000000000000000000..c91bb02f584398f08a28e6b7719e2b99f6e28616
--- /dev/null
+++ b/GroundingDINO/groundingdino/util/vl_utils.py
@@ -0,0 +1,100 @@
+import os
+import random
+from typing import List
+
+import torch
+
+
+def create_positive_map_from_span(tokenized, token_span, max_text_len=256):
+ """construct a map such that positive_map[i,j] = True iff box i is associated to token j
+ Input:
+ - tokenized:
+ - input_ids: Tensor[1, ntokens]
+ - attention_mask: Tensor[1, ntokens]
+ - token_span: list with length num_boxes.
+ - each item: [start_idx, end_idx]
+ """
+ positive_map = torch.zeros((len(token_span), max_text_len), dtype=torch.float)
+ for j, tok_list in enumerate(token_span):
+ for (beg, end) in tok_list:
+ beg_pos = tokenized.char_to_token(beg)
+ end_pos = tokenized.char_to_token(end - 1)
+ if beg_pos is None:
+ try:
+ beg_pos = tokenized.char_to_token(beg + 1)
+ if beg_pos is None:
+ beg_pos = tokenized.char_to_token(beg + 2)
+ except:
+ beg_pos = None
+ if end_pos is None:
+ try:
+ end_pos = tokenized.char_to_token(end - 2)
+ if end_pos is None:
+ end_pos = tokenized.char_to_token(end - 3)
+ except:
+ end_pos = None
+ if beg_pos is None or end_pos is None:
+ continue
+
+ assert beg_pos is not None and end_pos is not None
+ if os.environ.get("SHILONG_DEBUG_ONLY_ONE_POS", None) == "TRUE":
+ positive_map[j, beg_pos] = 1
+ break
+ else:
+ positive_map[j, beg_pos : end_pos + 1].fill_(1)
+
+ return positive_map / (positive_map.sum(-1)[:, None] + 1e-6)
+
+
+def build_captions_and_token_span(cat_list, force_lowercase):
+ """
+ Return:
+ captions: str
+ cat2tokenspan: dict
+ {
+ 'dog': [[0, 2]],
+ ...
+ }
+ """
+
+ cat2tokenspan = {}
+ captions = ""
+ for catname in cat_list:
+ class_name = catname
+ if force_lowercase:
+ class_name = class_name.lower()
+ if "/" in class_name:
+ class_name_list: List = class_name.strip().split("/")
+ class_name_list.append(class_name)
+ class_name: str = random.choice(class_name_list)
+
+ tokens_positive_i = []
+ subnamelist = [i.strip() for i in class_name.strip().split(" ")]
+ for subname in subnamelist:
+ if len(subname) == 0:
+ continue
+ if len(captions) > 0:
+ captions = captions + " "
+ strat_idx = len(captions)
+ end_idx = strat_idx + len(subname)
+ tokens_positive_i.append([strat_idx, end_idx])
+ captions = captions + subname
+
+ if len(tokens_positive_i) > 0:
+ captions = captions + " ."
+ cat2tokenspan[class_name] = tokens_positive_i
+
+ return captions, cat2tokenspan
+
+
+def build_id2posspan_and_caption(category_dict: dict):
+ """Build id2pos_span and caption from category_dict
+
+ Args:
+ category_dict (dict): category_dict
+ """
+ cat_list = [item["name"].lower() for item in category_dict]
+ id2catname = {item["id"]: item["name"].lower() for item in category_dict}
+ caption, cat2posspan = build_captions_and_token_span(cat_list, force_lowercase=True)
+ id2posspan = {catid: cat2posspan[catname] for catid, catname in id2catname.items()}
+ return id2posspan, caption
diff --git a/GroundingDINO/groundingdino/version.py b/GroundingDINO/groundingdino/version.py
new file mode 100644
index 0000000000000000000000000000000000000000..b794fd409a5e3b3b65ad76a43d6a01a318877640
--- /dev/null
+++ b/GroundingDINO/groundingdino/version.py
@@ -0,0 +1 @@
+__version__ = '0.1.0'
diff --git a/GroundingDINO/pyproject.toml b/GroundingDINO/pyproject.toml
new file mode 100644
index 0000000000000000000000000000000000000000..24dcc68d94ea5aaee6bb7a903a0e1638cf14e6b1
--- /dev/null
+++ b/GroundingDINO/pyproject.toml
@@ -0,0 +1,8 @@
+[build-system]
+requires = [
+ "setuptools",
+ "torch",
+ "wheel",
+ "torch"
+]
+build-backend = "setuptools.build_meta"
diff --git a/GroundingDINO/requirements.txt b/GroundingDINO/requirements.txt
new file mode 100644
index 0000000000000000000000000000000000000000..f9060c414d631f872d3401a1cfeb8ab3875d8a20
--- /dev/null
+++ b/GroundingDINO/requirements.txt
@@ -0,0 +1,10 @@
+torch
+torchvision
+transformers
+addict
+yapf
+timm
+numpy
+opencv-python
+supervision
+pycocotools
\ No newline at end of file
diff --git a/GroundingDINO/setup.py b/GroundingDINO/setup.py
new file mode 100644
index 0000000000000000000000000000000000000000..a58340d44eca86b09cb69630465dfbdfe8acb742
--- /dev/null
+++ b/GroundingDINO/setup.py
@@ -0,0 +1,216 @@
+# coding=utf-8
+# Copyright 2022 The IDEA Authors. All rights reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+# ------------------------------------------------------------------------------------------------
+# Modified from
+# https://github.com/fundamentalvision/Deformable-DETR/blob/main/models/ops/setup.py
+# https://github.com/facebookresearch/detectron2/blob/main/setup.py
+# https://github.com/open-mmlab/mmdetection/blob/master/setup.py
+# https://github.com/Oneflow-Inc/libai/blob/main/setup.py
+# ------------------------------------------------------------------------------------------------
+
+import glob
+import os
+import subprocess
+
+import torch
+from setuptools import find_packages, setup
+from torch.utils.cpp_extension import CUDA_HOME, CppExtension, CUDAExtension
+
+# groundingdino version info
+version = "0.1.0"
+package_name = "groundingdino"
+cwd = os.path.dirname(os.path.abspath(__file__))
+
+
+sha = "Unknown"
+try:
+ sha = subprocess.check_output(["git", "rev-parse", "HEAD"], cwd=cwd).decode("ascii").strip()
+except Exception:
+ pass
+
+
+def write_version_file():
+ version_path = os.path.join(cwd, "groundingdino", "version.py")
+ with open(version_path, "w") as f:
+ f.write(f"__version__ = '{version}'\n")
+ # f.write(f"git_version = {repr(sha)}\n")
+
+
+requirements = ["torch", "torchvision"]
+
+torch_ver = [int(x) for x in torch.__version__.split(".")[:2]]
+
+
+def get_extensions():
+ this_dir = os.path.dirname(os.path.abspath(__file__))
+ extensions_dir = os.path.join(this_dir, "groundingdino", "models", "GroundingDINO", "csrc")
+
+ main_source = os.path.join(extensions_dir, "vision.cpp")
+ sources = glob.glob(os.path.join(extensions_dir, "**", "*.cpp"))
+ source_cuda = glob.glob(os.path.join(extensions_dir, "**", "*.cu")) + glob.glob(
+ os.path.join(extensions_dir, "*.cu")
+ )
+
+ sources = [main_source] + sources
+
+ # We need these variables to build with CUDA when we create the Docker image
+ # It solves https://github.com/IDEA-Research/Grounded-Segment-Anything/issues/53
+ # and https://github.com/IDEA-Research/Grounded-Segment-Anything/issues/84 when running
+ # inside a Docker container.
+ am_i_docker = os.environ.get('AM_I_DOCKER', '').casefold() in ['true', '1', 't']
+ use_cuda = os.environ.get('BUILD_WITH_CUDA', '').casefold() in ['true', '1', 't']
+
+ extension = CppExtension
+
+ extra_compile_args = {"cxx": []}
+ define_macros = []
+
+ if (torch.cuda.is_available() and CUDA_HOME is not None) or \
+ (am_i_docker and use_cuda):
+ print("Compiling with CUDA")
+ extension = CUDAExtension
+ sources += source_cuda
+ define_macros += [("WITH_CUDA", None)]
+ extra_compile_args["nvcc"] = [
+ "-DCUDA_HAS_FP16=1",
+ "-D__CUDA_NO_HALF_OPERATORS__",
+ "-D__CUDA_NO_HALF_CONVERSIONS__",
+ "-D__CUDA_NO_HALF2_OPERATORS__",
+ ]
+ else:
+ print("Compiling without CUDA")
+ define_macros += [("WITH_HIP", None)]
+ extra_compile_args["nvcc"] = []
+ return None
+
+ sources = [os.path.join(extensions_dir, s) for s in sources]
+ include_dirs = [extensions_dir]
+
+ ext_modules = [
+ extension(
+ "groundingdino._C",
+ sources,
+ include_dirs=include_dirs,
+ define_macros=define_macros,
+ extra_compile_args=extra_compile_args,
+ )
+ ]
+
+ return ext_modules
+
+
+def parse_requirements(fname="requirements.txt", with_version=True):
+ """Parse the package dependencies listed in a requirements file but strips
+ specific versioning information.
+
+ Args:
+ fname (str): path to requirements file
+ with_version (bool, default=False): if True include version specs
+
+ Returns:
+ List[str]: list of requirements items
+
+ CommandLine:
+ python -c "import setup; print(setup.parse_requirements())"
+ """
+ import re
+ import sys
+ from os.path import exists
+
+ require_fpath = fname
+
+ def parse_line(line):
+ """Parse information from a line in a requirements text file."""
+ if line.startswith("-r "):
+ # Allow specifying requirements in other files
+ target = line.split(" ")[1]
+ for info in parse_require_file(target):
+ yield info
+ else:
+ info = {"line": line}
+ if line.startswith("-e "):
+ info["package"] = line.split("#egg=")[1]
+ elif "@git+" in line:
+ info["package"] = line
+ else:
+ # Remove versioning from the package
+ pat = "(" + "|".join([">=", "==", ">"]) + ")"
+ parts = re.split(pat, line, maxsplit=1)
+ parts = [p.strip() for p in parts]
+
+ info["package"] = parts[0]
+ if len(parts) > 1:
+ op, rest = parts[1:]
+ if ";" in rest:
+ # Handle platform specific dependencies
+ # http://setuptools.readthedocs.io/en/latest/setuptools.html#declaring-platform-specific-dependencies
+ version, platform_deps = map(str.strip, rest.split(";"))
+ info["platform_deps"] = platform_deps
+ else:
+ version = rest # NOQA
+ info["version"] = (op, version)
+ yield info
+
+ def parse_require_file(fpath):
+ with open(fpath, "r") as f:
+ for line in f.readlines():
+ line = line.strip()
+ if line and not line.startswith("#"):
+ for info in parse_line(line):
+ yield info
+
+ def gen_packages_items():
+ if exists(require_fpath):
+ for info in parse_require_file(require_fpath):
+ parts = [info["package"]]
+ if with_version and "version" in info:
+ parts.extend(info["version"])
+ if not sys.version.startswith("3.4"):
+ # apparently package_deps are broken in 3.4
+ platform_deps = info.get("platform_deps")
+ if platform_deps is not None:
+ parts.append(";" + platform_deps)
+ item = "".join(parts)
+ yield item
+
+ packages = list(gen_packages_items())
+ return packages
+
+
+if __name__ == "__main__":
+ print(f"Building wheel {package_name}-{version}")
+
+ with open("LICENSE", "r", encoding="utf-8") as f:
+ license = f.read()
+
+ write_version_file()
+
+ setup(
+ name="groundingdino",
+ version="0.1.0",
+ author="International Digital Economy Academy, Shilong Liu",
+ url="https://github.com/IDEA-Research/GroundingDINO",
+ description="open-set object detector",
+ license=license,
+ install_requires=parse_requirements("requirements.txt"),
+ packages=find_packages(
+ exclude=(
+ "configs",
+ "tests",
+ )
+ ),
+ ext_modules=get_extensions(),
+ cmdclass={"build_ext": torch.utils.cpp_extension.BuildExtension},
+ )
diff --git a/LICENSE b/LICENSE
new file mode 100644
index 0000000000000000000000000000000000000000..0d2de3722b12c47ba035ffc621509ed1379799ff
--- /dev/null
+++ b/LICENSE
@@ -0,0 +1,201 @@
+ Apache License
+ Version 2.0, January 2004
+ http://www.apache.org/licenses/
+
+ TERMS AND CONDITIONS FOR USE, REPRODUCTION, AND DISTRIBUTION
+
+ 1. Definitions.
+
+ "License" shall mean the terms and conditions for use, reproduction,
+ and distribution as defined by Sections 1 through 9 of this document.
+
+ "Licensor" shall mean the copyright owner or entity authorized by
+ the copyright owner that is granting the License.
+
+ "Legal Entity" shall mean the union of the acting entity and all
+ other entities that control, are controlled by, or are under common
+ control with that entity. For the purposes of this definition,
+ "control" means (i) the power, direct or indirect, to cause the
+ direction or management of such entity, whether by contract or
+ otherwise, or (ii) ownership of fifty percent (50%) or more of the
+ outstanding shares, or (iii) beneficial ownership of such entity.
+
+ "You" (or "Your") shall mean an individual or Legal Entity
+ exercising permissions granted by this License.
+
+ "Source" form shall mean the preferred form for making modifications,
+ including but not limited to software source code, documentation
+ source, and configuration files.
+
+ "Object" form shall mean any form resulting from mechanical
+ transformation or translation of a Source form, including but
+ not limited to compiled object code, generated documentation,
+ and conversions to other media types.
+
+ "Work" shall mean the work of authorship, whether in Source or
+ Object form, made available under the License, as indicated by a
+ copyright notice that is included in or attached to the work
+ (an example is provided in the Appendix below).
+
+ "Derivative Works" shall mean any work, whether in Source or Object
+ form, that is based on (or derived from) the Work and for which the
+ editorial revisions, annotations, elaborations, or other modifications
+ represent, as a whole, an original work of authorship. For the purposes
+ of this License, Derivative Works shall not include works that remain
+ separable from, or merely link (or bind by name) to the interfaces of,
+ the Work and Derivative Works thereof.
+
+ "Contribution" shall mean any work of authorship, including
+ the original version of the Work and any modifications or additions
+ to that Work or Derivative Works thereof, that is intentionally
+ submitted to Licensor for inclusion in the Work by the copyright owner
+ or by an individual or Legal Entity authorized to submit on behalf of
+ the copyright owner. For the purposes of this definition, "submitted"
+ means any form of electronic, verbal, or written communication sent
+ to the Licensor or its representatives, including but not limited to
+ communication on electronic mailing lists, source code control systems,
+ and issue tracking systems that are managed by, or on behalf of, the
+ Licensor for the purpose of discussing and improving the Work, but
+ excluding communication that is conspicuously marked or otherwise
+ designated in writing by the copyright owner as "Not a Contribution."
+
+ "Contributor" shall mean Licensor and any individual or Legal Entity
+ on behalf of whom a Contribution has been received by Licensor and
+ subsequently incorporated within the Work.
+
+ 2. Grant of Copyright License. Subject to the terms and conditions of
+ this License, each Contributor hereby grants to You a perpetual,
+ worldwide, non-exclusive, no-charge, royalty-free, irrevocable
+ copyright license to reproduce, prepare Derivative Works of,
+ publicly display, publicly perform, sublicense, and distribute the
+ Work and such Derivative Works in Source or Object form.
+
+ 3. Grant of Patent License. Subject to the terms and conditions of
+ this License, each Contributor hereby grants to You a perpetual,
+ worldwide, non-exclusive, no-charge, royalty-free, irrevocable
+ (except as stated in this section) patent license to make, have made,
+ use, offer to sell, sell, import, and otherwise transfer the Work,
+ where such license applies only to those patent claims licensable
+ by such Contributor that are necessarily infringed by their
+ Contribution(s) alone or by combination of their Contribution(s)
+ with the Work to which such Contribution(s) was submitted. If You
+ institute patent litigation against any entity (including a
+ cross-claim or counterclaim in a lawsuit) alleging that the Work
+ or a Contribution incorporated within the Work constitutes direct
+ or contributory patent infringement, then any patent licenses
+ granted to You under this License for that Work shall terminate
+ as of the date such litigation is filed.
+
+ 4. Redistribution. You may reproduce and distribute copies of the
+ Work or Derivative Works thereof in any medium, with or without
+ modifications, and in Source or Object form, provided that You
+ meet the following conditions:
+
+ (a) You must give any other recipients of the Work or
+ Derivative Works a copy of this License; and
+
+ (b) You must cause any modified files to carry prominent notices
+ stating that You changed the files; and
+
+ (c) You must retain, in the Source form of any Derivative Works
+ that You distribute, all copyright, patent, trademark, and
+ attribution notices from the Source form of the Work,
+ excluding those notices that do not pertain to any part of
+ the Derivative Works; and
+
+ (d) If the Work includes a "NOTICE" text file as part of its
+ distribution, then any Derivative Works that You distribute must
+ include a readable copy of the attribution notices contained
+ within such NOTICE file, excluding those notices that do not
+ pertain to any part of the Derivative Works, in at least one
+ of the following places: within a NOTICE text file distributed
+ as part of the Derivative Works; within the Source form or
+ documentation, if provided along with the Derivative Works; or,
+ within a display generated by the Derivative Works, if and
+ wherever such third-party notices normally appear. The contents
+ of the NOTICE file are for informational purposes only and
+ do not modify the License. You may add Your own attribution
+ notices within Derivative Works that You distribute, alongside
+ or as an addendum to the NOTICE text from the Work, provided
+ that such additional attribution notices cannot be construed
+ as modifying the License.
+
+ You may add Your own copyright statement to Your modifications and
+ may provide additional or different license terms and conditions
+ for use, reproduction, or distribution of Your modifications, or
+ for any such Derivative Works as a whole, provided Your use,
+ reproduction, and distribution of the Work otherwise complies with
+ the conditions stated in this License.
+
+ 5. Submission of Contributions. Unless You explicitly state otherwise,
+ any Contribution intentionally submitted for inclusion in the Work
+ by You to the Licensor shall be under the terms and conditions of
+ this License, without any additional terms or conditions.
+ Notwithstanding the above, nothing herein shall supersede or modify
+ the terms of any separate license agreement you may have executed
+ with Licensor regarding such Contributions.
+
+ 6. Trademarks. This License does not grant permission to use the trade
+ names, trademarks, service marks, or product names of the Licensor,
+ except as required for reasonable and customary use in describing the
+ origin of the Work and reproducing the content of the NOTICE file.
+
+ 7. Disclaimer of Warranty. Unless required by applicable law or
+ agreed to in writing, Licensor provides the Work (and each
+ Contributor provides its Contributions) on an "AS IS" BASIS,
+ WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or
+ implied, including, without limitation, any warranties or conditions
+ of TITLE, NON-INFRINGEMENT, MERCHANTABILITY, or FITNESS FOR A
+ PARTICULAR PURPOSE. You are solely responsible for determining the
+ appropriateness of using or redistributing the Work and assume any
+ risks associated with Your exercise of permissions under this License.
+
+ 8. Limitation of Liability. In no event and under no legal theory,
+ whether in tort (including negligence), contract, or otherwise,
+ unless required by applicable law (such as deliberate and grossly
+ negligent acts) or agreed to in writing, shall any Contributor be
+ liable to You for damages, including any direct, indirect, special,
+ incidental, or consequential damages of any character arising as a
+ result of this License or out of the use or inability to use the
+ Work (including but not limited to damages for loss of goodwill,
+ work stoppage, computer failure or malfunction, or any and all
+ other commercial damages or losses), even if such Contributor
+ has been advised of the possibility of such damages.
+
+ 9. Accepting Warranty or Additional Liability. While redistributing
+ the Work or Derivative Works thereof, You may choose to offer,
+ and charge a fee for, acceptance of support, warranty, indemnity,
+ or other liability obligations and/or rights consistent with this
+ License. However, in accepting such obligations, You may act only
+ on Your own behalf and on Your sole responsibility, not on behalf
+ of any other Contributor, and only if You agree to indemnify,
+ defend, and hold each Contributor harmless for any liability
+ incurred by, or claims asserted against, such Contributor by reason
+ of your accepting any such warranty or additional liability.
+
+ END OF TERMS AND CONDITIONS
+
+ APPENDIX: How to apply the Apache License to your work.
+
+ To apply the Apache License to your work, attach the following
+ boilerplate notice, with the fields enclosed by brackets "[]"
+ replaced with your own identifying information. (Don't include
+ the brackets!) The text should be enclosed in the appropriate
+ comment syntax for the file format. We also recommend that a
+ file or class name and description of purpose be included on the
+ same "printed page" as the copyright notice for easier
+ identification within third-party archives.
+
+ Copyright 2020 - present, IDEA, Inc
+
+ Licensed under the Apache License, Version 2.0 (the "License");
+ you may not use this file except in compliance with the License.
+ You may obtain a copy of the License at
+
+ http://www.apache.org/licenses/LICENSE-2.0
+
+ Unless required by applicable law or agreed to in writing, software
+ distributed under the License is distributed on an "AS IS" BASIS,
+ WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+ See the License for the specific language governing permissions and
+ limitations under the License.
diff --git a/Makefile b/Makefile
new file mode 100644
index 0000000000000000000000000000000000000000..e2b0d1ae1d38d447e8a8d3e44826ad845878dc43
--- /dev/null
+++ b/Makefile
@@ -0,0 +1,43 @@
+# Get version of CUDA and enable it for compilation if CUDA > 11.0
+# This solves https://github.com/IDEA-Research/Grounded-Segment-Anything/issues/53
+# and https://github.com/IDEA-Research/Grounded-Segment-Anything/issues/84
+# when running in Docker
+# Check if nvcc is installed
+NVCC := $(shell which nvcc)
+ifeq ($(NVCC),)
+ # NVCC not found
+ USE_CUDA := 0
+ NVCC_VERSION := "not installed"
+else
+ NVCC_VERSION := $(shell nvcc --version | grep -oP 'release \K[0-9.]+')
+ USE_CUDA := $(shell echo "$(NVCC_VERSION) > 11" | bc -l)
+endif
+
+# Add the list of supported ARCHs
+ifeq ($(USE_CUDA), 1)
+ TORCH_CUDA_ARCH_LIST := "3.5;5.0;6.0;6.1;7.0;7.5;8.0;8.6+PTX"
+ BUILD_MESSAGE := "I will try to build the image with CUDA support"
+else
+ TORCH_CUDA_ARCH_LIST :=
+ BUILD_MESSAGE := "CUDA $(NVCC_VERSION) is not supported"
+endif
+
+
+build-image:
+ @echo $(BUILD_MESSAGE)
+ docker build --build-arg USE_CUDA=$(USE_CUDA) \
+ --build-arg TORCH_ARCH=$(TORCH_CUDA_ARCH_LIST) \
+ -t gsa:v0 .
+run:
+ifeq (,$(wildcard ./sam_vit_h_4b8939.pth))
+ wget https://dl.fbaipublicfiles.com/segment_anything/sam_vit_h_4b8939.pth
+endif
+ifeq (,$(wildcard ./groundingdino_swint_ogc.pth))
+ wget https://github.com/IDEA-Research/GroundingDINO/releases/download/v0.1.0-alpha/groundingdino_swint_ogc.pth
+endif
+ docker run --gpus all -it --rm --net=host --privileged \
+ -v /tmp/.X11-unix:/tmp/.X11-unix \
+ -v "${PWD}":/home/appuser/working_dir \
+ -e DISPLAY=$DISPLAY \
+ --name=gsa \
+ --ipc=host -it gsa:v0
diff --git a/README.md b/README.md
index a1e39bf8c5ed4f8c4e63fb4151d60599e2689e4c..e8d15b62d4923fdccf9a2db6a8fa292561082988 100644
--- a/README.md
+++ b/README.md
@@ -1,12 +1,786 @@
---
-title: Grounded Segment Anything
-emoji: 📈
-colorFrom: red
-colorTo: yellow
+title: Grounded-Segment-Anything
+app_file: gradio_app.py
sdk: gradio
-sdk_version: 4.23.0
-app_file: app.py
-pinned: false
+sdk_version: 3.50.2
---
+
-Check out the configuration reference at https://huggingface.co/docs/hub/spaces-config-reference
+# Grounded-Segment-Anything
+[](https://youtu.be/oEQYStnF2l8) [](https://colab.research.google.com/github/roboflow-ai/notebooks/blob/main/notebooks/automated-dataset-annotation-and-evaluation-with-grounding-dino-and-sam.ipynb) [](https://github.com/camenduru/grounded-segment-anything-colab) [](https://huggingface.co/spaces/IDEA-Research/Grounded-SAM) [](https://replicate.com/cjwbw/grounded-recognize-anything) [](https://modelscope.cn/studios/tuofeilunhifi/Grounded-Segment-Anything/summary) [](https://huggingface.co/spaces/yizhangliu/Grounded-Segment-Anything) [](https://github.com/continue-revolution/sd-webui-segment-anything) [](./grounded_sam.ipynb) [](https://arxiv.org/abs/2303.05499) [](https://arxiv.org/abs/2304.02643) [](https://arxiv.org/abs/2401.14159)
+
+
+We plan to create a very interesting demo by combining [Grounding DINO](https://github.com/IDEA-Research/GroundingDINO) and [Segment Anything](https://github.com/facebookresearch/segment-anything) which aims to detect and segment anything with text inputs! And we will continue to improve it and create more interesting demos based on this foundation. And we have already released an overall technical report about our project on arXiv, please check [Grounded SAM: Assembling Open-World Models for Diverse Visual Tasks](https://arxiv.org/abs/2401.14159) for more details.
+
+We are very willing to **help everyone share and promote new projects** based on Segment-Anything, Please check out here for more amazing demos and works in the community: [Highlight Extension Projects](#highlighted-projects). You can submit a new issue (with `project` tag) or a new pull request to add new project's links.
+
+
+
+
+
+**🍄 Why Building this Project?**
+
+The **core idea** behind this project is to **combine the strengths of different models in order to build a very powerful pipeline for solving complex problems**. And it's worth mentioning that this is a workflow for combining strong expert models, where **all parts can be used separately or in combination, and can be replaced with any similar but different models (like replacing Grounding DINO with GLIP or other detectors / replacing Stable-Diffusion with ControlNet or GLIGEN/ Combining with ChatGPT)**.
+
+**🍇 Updates**
+- **`2024/01/26`** We have released a comprehensive technical report about our project on arXiv, please check [Grounded SAM: Assembling Open-World Models for Diverse Visual Tasks](https://arxiv.org/abs/2401.14159) for more details. And we are profoundly grateful for the contributions of all the contributors in this project.
+- **`2023/12/17`** Support [Grounded-RepViT-SAM](https://github.com/IDEA-Research/Grounded-Segment-Anything/tree/main/EfficientSAM#run-grounded-repvit-sam-demo) demo, thanks a lot for their great work!
+- **`2023/12/16`** Support [Grounded-Edge-SAM](https://github.com/IDEA-Research/Grounded-Segment-Anything/tree/main/EfficientSAM#run-grounded-edge-sam-demo) demo, thanks a lot for their great work!
+- **`2023/12/10`** Support [Grounded-Efficient-SAM](https://github.com/IDEA-Research/Grounded-Segment-Anything/tree/main/EfficientSAM#run-grounded-efficient-sam-demo) demo, thanks a lot for their great work!
+- **`2023/11/24`** Release [RAM++](https://arxiv.org/abs/2310.15200), which is the next generation of RAM. RAM++ can recognize any category with high accuracy, including both predefined common categories and diverse open-set categories.
+- **`2023/11/23`** Release our newly proposed visual prompt counting model [T-Rex](https://github.com/IDEA-Research/T-Rex). The introduction [Video](https://www.youtube.com/watch?v=engIEhZogAQ) and [Demo](https://deepdataspace.com/playground/ivp) is available in [DDS](https://github.com/IDEA-Research/deepdataspace) now.
+- **`2023/07/25`** Support [Light-HQ-SAM](https://github.com/SysCV/sam-hq) in [EfficientSAM](./EfficientSAM/), credits to [Mingqiao Ye](https://github.com/ymq2017) and [Lei Ke](https://github.com/lkeab), thanks a lot for their great work!
+- **`2023/07/14`** Combining **Grounding-DINO-B** with [SAM-HQ](https://github.com/SysCV/sam-hq) achieves **49.6 mean AP** in [Segmentation in the Wild](https://eval.ai/web/challenges/challenge-page/1931/overview) competition zero-shot track, surpassing Grounded-SAM by **3.6 mean AP**, thanks for their great work!
+- **`2023/06/28`** Combining Grounding-DINO with Efficient SAM variants including [FastSAM](https://github.com/CASIA-IVA-Lab/FastSAM) and [MobileSAM](https://github.com/ChaoningZhang/MobileSAM) in [EfficientSAM](./EfficientSAM/) for faster annotating, thanks a lot for their great work!
+- **`2023/06/20`** By combining **Grounding-DINO-L** with **SAM-ViT-H**, Grounded-SAM achieves 46.0 mean AP in [Segmentation in the Wild](https://eval.ai/web/challenges/challenge-page/1931/overview) competition zero-shot track on [CVPR 2023 workshop](https://computer-vision-in-the-wild.github.io/cvpr-2023/), surpassing [UNINEXT (CVPR 2023)](https://github.com/MasterBin-IIAU/UNINEXT) by about **4 mean AP**.
+- **`2023/06/16`** Release [RAM-Grounded-SAM Replicate Online Demo](https://replicate.com/cjwbw/ram-grounded-sam). Thanks a lot to [Chenxi](https://chenxwh.github.io/) for providing this nice demo 🌹.
+- **`2023/06/14`** Support [RAM-Grounded-SAM & SAM-HQ](./automatic_label_ram_demo.py) and update [Simple Automatic Label Demo](./automatic_label_ram_demo.py) to support [RAM](https://github.com/OPPOMKLab/recognize-anything), setting up a strong automatic annotation pipeline.
+- **`2023/06/13`** Checkout the [Autodistill: Train YOLOv8 with ZERO Annotations](https://youtu.be/gKTYMfwPo4M) tutorial to learn how to use Grounded-SAM + [Autodistill](https://github.com/autodistill/autodistill) for automated data labeling and real-time model training.
+- **`2023/06/13`** Support [SAM-HQ](https://github.com/SysCV/sam-hq) in [Grounded-SAM Demo](#running_man-grounded-sam-detect-and-segment-everything-with-text-prompt) for higher quality prediction.
+- **`2023/06/12`** Support [RAM-Grounded-SAM](#label-grounded-sam-with-ram-or-tag2text-for-automatic-labeling) for strong automatic labeling pipeline! Thanks for [Recognize-Anything](https://github.com/OPPOMKLab/recognize-anything).
+- **`2023/06/01`** Our Grounded-SAM has been accepted to present a **demo** at [ICCV 2023](https://iccv2023.thecvf.com/)! See you in Paris!
+- **`2023/05/23`**: Support `Image-Referring-Segment`, `Audio-Referring-Segment` and `Text-Referring-Segment` in [ImageBind-SAM](./playground/ImageBind_SAM/).
+- **`2023/05/03`**: Checkout the [Automated Dataset Annotation and Evaluation with GroundingDINO and SAM](https://colab.research.google.com/github/roboflow-ai/notebooks/blob/main/notebooks/automated-dataset-annotation-and-evaluation-with-grounding-dino-and-sam.ipynb) which is an amazing tutorial on automatic labeling! Thanks a lot for [Piotr Skalski](https://github.com/SkalskiP) and [Roboflow](https://github.com/roboflow/notebooks)!
+
+
+## Table of Contents
+- [Grounded-Segment-Anything](#grounded-segment-anything)
+ - [Preliminary Works](#preliminary-works)
+ - [Highlighted Projects](#highlighted-projects)
+- [Installation](#installation)
+ - [Install with Docker](#install-with-docker)
+ - [Install locally](#install-without-docker)
+- [Grounded-SAM Playground](#grounded-sam-playground)
+ - [Step-by-Step Notebook Demo](#open_book-step-by-step-notebook-demo)
+ - [GroundingDINO: Detect Everything with Text Prompt](#running_man-groundingdino-detect-everything-with-text-prompt)
+ - [Grounded-SAM: Detect and Segment Everything with Text Prompt](#running_man-grounded-sam-detect-and-segment-everything-with-text-prompt)
+ - [Grounded-SAM with Inpainting: Detect, Segment and Generate Everything with Text Prompt](#skier-grounded-sam-with-inpainting-detect-segment-and-generate-everything-with-text-prompt)
+ - [Grounded-SAM and Inpaint Gradio APP](#golfing-grounded-sam-and-inpaint-gradio-app)
+ - [Grounded-SAM with RAM or Tag2Text for Automatic Labeling](#label-grounded-sam-with-ram-or-tag2text-for-automatic-labeling)
+ - [Grounded-SAM with BLIP & ChatGPT for Automatic Labeling](#robot-grounded-sam-with-blip-for-automatic-labeling)
+ - [Grounded-SAM with Whisper: Detect and Segment Anything with Audio](#open_mouth-grounded-sam-with-whisper-detect-and-segment-anything-with-audio)
+ - [Grounded-SAM ChatBot with Visual ChatGPT](#speech_balloon-grounded-sam-chatbot-demo)
+ - [Grounded-SAM with OSX for 3D Whole-Body Mesh Recovery](#man_dancing-run-grounded-segment-anything--osx-demo)
+ - [Grounded-SAM with VISAM for Tracking and Segment Anything](#man_dancing-run-grounded-segment-anything--visam-demo)
+ - [Interactive Fashion-Edit Playground: Click for Segmentation And Editing](#dancers-interactive-editing)
+ - [Interactive Human-face Editing Playground: Click And Editing Human Face](#dancers-interactive-editing)
+ - [3D Box Via Segment Anything](#camera-3d-box-via-segment-anything)
+ - [Playground: More Interesting and Imaginative Demos with Grounded-SAM](./playground/)
+ - [DeepFloyd: Image Generation with Text Prompt](./playground/DeepFloyd/)
+ - [PaintByExample: Exemplar-based Image Editing with Diffusion Models](./playground/PaintByExample/)
+ - [LaMa: Resolution-robust Large Mask Inpainting with Fourier Convolutions](./playground/LaMa/)
+ - [RePaint: Inpainting using Denoising Diffusion Probabilistic Models](./playground/RePaint/)
+ - [ImageBind with SAM: Segment with Different Modalities](./playground/ImageBind_SAM/)
+ - [Efficient SAM Series for Faster Annotation](./EfficientSAM/)
+ - [Grounded-FastSAM Demo](https://github.com/IDEA-Research/Grounded-Segment-Anything/tree/main/EfficientSAM#run-grounded-fastsam-demo)
+ - [Grounded-MobileSAM Demo](https://github.com/IDEA-Research/Grounded-Segment-Anything/tree/main/EfficientSAM#run-grounded-mobilesam-demo)
+ - [Grounded-Light-HQSAM Demo](https://github.com/IDEA-Research/Grounded-Segment-Anything/tree/main/EfficientSAM#run-grounded-light-hqsam-demo)
+ - [Grounded-Efficient-SAM Demo](https://github.com/IDEA-Research/Grounded-Segment-Anything/tree/main/EfficientSAM#run-grounded-efficient-sam-demo)
+ - [Grounded-Edge-SAM Demo](https://github.com/IDEA-Research/Grounded-Segment-Anything/tree/main/EfficientSAM#run-grounded-edge-sam-demo)
+ - [Grounded-RepViT-SAM Demo](https://github.com/IDEA-Research/Grounded-Segment-Anything/tree/main/EfficientSAM#run-grounded-repvit-sam-demo)
+- [Citation](#citation)
+
+## Preliminary Works
+
+Here we provide some background knowledge that you may need to know before trying the demos.
+
+
+
+| Title | Intro | Description | Links |
+|:----:|:----:|:----:|:----:|
+| [Segment-Anything](https://arxiv.org/abs/2304.02643) |  | A strong foundation model aims to segment everything in an image, which needs prompts (as boxes/points/text) to generate masks | [[Github](https://github.com/facebookresearch/segment-anything)] [[Page](https://segment-anything.com/)] [[Demo](https://segment-anything.com/demo)] |
+| [Grounding DINO](https://arxiv.org/abs/2303.05499) |  | A strong zero-shot detector which is capable of to generate high quality boxes and labels with free-form text. | [[Github](https://github.com/IDEA-Research/GroundingDINO)] [[Demo](https://huggingface.co/spaces/ShilongLiu/Grounding_DINO_demo)] |
+| [OSX](http://arxiv.org/abs/2303.16160) |  | A strong and efficient one-stage motion capture method to generate high quality 3D human mesh from monucular image. OSX also releases a large-scale upper-body dataset UBody for a more accurate reconstrution in the upper-body scene. | [[Github](https://github.com/IDEA-Research/OSX)] [[Page](https://osx-ubody.github.io/)] [[Video](https://osx-ubody.github.io/)] [[Data](https://docs.google.com/forms/d/e/1FAIpQLSehgBP7wdn_XznGAM2AiJPiPLTqXXHw5uX9l7qeQ1Dh9HoO_A/viewform)] |
+| [Stable-Diffusion](https://arxiv.org/abs/2112.10752) |  | A super powerful open-source latent text-to-image diffusion model | [[Github](https://github.com/CompVis/stable-diffusion)] [[Page](https://ommer-lab.com/research/latent-diffusion-models/)] |
+| [RAM++](https://arxiv.org/abs/2310.15200) |  | RAM++ is the next generation of RAM, which can recognize any category with high accuracy. | [[Github](https://github.com/OPPOMKLab/recognize-anything)] |
+| [RAM](https://recognize-anything.github.io/) |  | RAM is an image tagging model, which can recognize any common category with high accuracy. | [[Github](https://github.com/OPPOMKLab/recognize-anything)] [[Demo](https://huggingface.co/spaces/xinyu1205/Recognize_Anything-Tag2Text)] |
+| [BLIP](https://arxiv.org/abs/2201.12086) |  | A wonderful language-vision model for image understanding. | [[GitHub](https://github.com/salesforce/LAVIS)] |
+| [Visual ChatGPT](https://arxiv.org/abs/2303.04671) |  | A wonderful tool that connects ChatGPT and a series of Visual Foundation Models to enable sending and receiving images during chatting. | [[Github](https://github.com/microsoft/TaskMatrix)] [[Demo](https://huggingface.co/spaces/microsoft/visual_chatgpt)] |
+| [Tag2Text](https://tag2text.github.io/) |  | An efficient and controllable vision-language model which can simultaneously output superior image captioning and image tagging. | [[Github](https://github.com/OPPOMKLab/recognize-anything)] [[Demo](https://huggingface.co/spaces/xinyu1205/Tag2Text)] |
+| [VoxelNeXt](https://arxiv.org/abs/2303.11301) |  | A clean, simple, and fully-sparse 3D object detector, which predicts objects directly upon sparse voxel features. | [[Github](https://github.com/dvlab-research/VoxelNeXt)]
+
+
+
+## Highlighted Projects
+
+Here we provide some impressive works you may find interesting:
+
+
+
+| Title | Description | Links |
+|:---:|:---:|:---:|
+| [Semantic-SAM](https://github.com/UX-Decoder/Semantic-SAM) | A universal image segmentation model to enable segment and recognize anything at any desired granularity | [[Github](https://github.com/UX-Decoder/Semantic-SAM)] [[Demo](https://github.com/UX-Decoder/Semantic-SAM)] |
+| [SEEM: Segment Everything Everywhere All at Once](https://arxiv.org/pdf/2304.06718.pdf) | A powerful promptable segmentation model supports segmenting with various types of prompts (text, point, scribble, referring image, etc.) and any combination of prompts. | [[Github](https://github.com/UX-Decoder/Segment-Everything-Everywhere-All-At-Once)] [[Demo](https://huggingface.co/spaces/xdecoder/SEEM)] |
+| [OpenSeeD](https://arxiv.org/pdf/2303.08131.pdf) | A simple framework for open-vocabulary segmentation and detection which supports interactive segmentation with box input to generate mask | [[Github](https://github.com/IDEA-Research/OpenSeeD)] |
+| [LLaVA](https://arxiv.org/abs/2304.08485) | Visual instruction tuning with GPT-4 | [[Github](https://github.com/haotian-liu/LLaVA)] [[Page](https://llava-vl.github.io/)] [[Demo](https://llava.hliu.cc/)] [[Data](https://huggingface.co/datasets/liuhaotian/LLaVA-Instruct-150K)] [[Model](https://huggingface.co/liuhaotian/LLaVA-13b-delta-v0)] |
+| [GenSAM](https://arxiv.org/abs/2312.07374) | Relaxing the instance-specific manual prompt requirement in SAM through training-free test-time adaptation | [[Github](https://github.com/jyLin8100/GenSAM)] [[Page](https://lwpyh.github.io/GenSAM/)] |
+
+
+
+We also list some awesome segment-anything extension projects here you may find interesting:
+- [Computer Vision in the Wild (CVinW) Readings](https://github.com/Computer-Vision-in-the-Wild/CVinW_Readings) for those who are interested in open-set tasks in computer vision.
+- [Zero-Shot Anomaly Detection](https://github.com/caoyunkang/GroundedSAM-zero-shot-anomaly-detection) by Yunkang Cao
+- [EditAnything: ControlNet + StableDiffusion based on the SAM segmentation mask](https://github.com/sail-sg/EditAnything) by Shanghua Gao and Pan Zhou
+- [IEA: Image Editing Anything](https://github.com/feizc/IEA) by Zhengcong Fei
+- [SAM-MMRorate: Combining Rotated Object Detector and SAM](https://github.com/Li-Qingyun/sam-mmrotate) by Qingyun Li and Xue Yang
+- [Awesome-Anything](https://github.com/VainF/Awesome-Anything) by Gongfan Fang
+- [Prompt-Segment-Anything](https://github.com/RockeyCoss/Prompt-Segment-Anything) by Rockey
+- [WebUI for Segment-Anything and Grounded-SAM](https://github.com/continue-revolution/sd-webui-segment-anything) by Chengsong Zhang
+- [Inpainting Anything: Inpaint Anything with SAM + Inpainting models](https://github.com/geekyutao/Inpaint-Anything) by Tao Yu
+- [Grounded Segment Anything From Objects to Parts: Combining Segment-Anything with VLPart & GLIP & Visual ChatGPT](https://github.com/Cheems-Seminar/segment-anything-and-name-it) by Peize Sun and Shoufa Chen
+- [Narapi-SAM: Integration of Segment Anything into Narapi (A nice viewer for SAM)](https://github.com/MIC-DKFZ/napari-sam) by MIC-DKFZ
+- [Grounded Segment Anything Colab](https://github.com/camenduru/grounded-segment-anything-colab) by camenduru
+- [Optical Character Recognition with Segment Anything](https://github.com/yeungchenwa/OCR-SAM) by Zhenhua Yang
+- [Transform Image into Unique Paragraph with ChatGPT, BLIP2, OFA, GRIT, Segment Anything, ControlNet](https://github.com/showlab/Image2Paragraph) by showlab
+- [Lang-Segment-Anything: Another awesome demo for combining GroundingDINO with Segment-Anything](https://github.com/luca-medeiros/lang-segment-anything) by Luca Medeiros
+- [🥳 🚀 **Playground: Integrate SAM and OpenMMLab!**](https://github.com/open-mmlab/playground)
+- [3D-object via Segment Anything](https://github.com/dvlab-research/3D-Box-Segment-Anything) by Yukang Chen
+- [Image2Paragraph: Transform Image Into Unique Paragraph](https://github.com/showlab/Image2Paragraph) by Show Lab
+- [Zero-shot Scene Graph Generate with Grounded-SAM](https://github.com/showlab/Image2Paragraph) by JackWhite-rwx
+- [CLIP Surgery for Better Explainability with Enhancement in Open-Vocabulary Tasks](https://github.com/xmed-lab/CLIP_Surgery) by Eli-YiLi
+- [Panoptic-Segment-Anything: Zero-shot panoptic segmentation using SAM](https://github.com/segments-ai/panoptic-segment-anything) by segments-ai
+- [Caption-Anything: Generates Descriptive Captions for Any Object within an Image](https://github.com/ttengwang/Caption-Anything) by Teng Wang
+- [Segment-Anything-3D: Transferring Segmentation Information of 2D Images to 3D Space](https://github.com/Pointcept/SegmentAnything3D) by Yunhan Yang
+- [Expediting SAM without Fine-tuning](https://github.com/Expedit-LargeScale-Vision-Transformer/Expedit-SAM) by Weicong Liang and Yuhui Yuan
+- [Semantic Segment Anything: Providing Rich Semantic Category Annotations for SAM](https://github.com/fudan-zvg/Semantic-Segment-Anything) by Jiaqi Chen and Zeyu Yang and Li Zhang
+- [Enhance Everything: Combining SAM with Image Restoration and Enhancement Tasks](https://github.com/lixinustc/Enhance-Anything) by Xin Li
+- [DragGAN](https://github.com/Zeqiang-Lai/DragGAN) by Shanghai AI Lab.
+
+## Installation
+The code requires `python>=3.8`, as well as `pytorch>=1.7` and `torchvision>=0.8`. Please follow the instructions [here](https://pytorch.org/get-started/locally/) to install both PyTorch and TorchVision dependencies. Installing both PyTorch and TorchVision with CUDA support is strongly recommended.
+
+### Install with Docker
+
+Open one terminal:
+
+```
+make build-image
+```
+
+```
+make run
+```
+
+That's it.
+
+If you would like to allow visualization across docker container, open another terminal and type:
+
+```
+xhost +
+```
+
+
+### Install without Docker
+You should set the environment variable manually as follows if you want to build a local GPU environment for Grounded-SAM:
+```bash
+export AM_I_DOCKER=False
+export BUILD_WITH_CUDA=True
+export CUDA_HOME=/path/to/cuda-11.3/
+```
+
+Install Segment Anything:
+
+```bash
+python -m pip install -e segment_anything
+```
+
+Install Grounding DINO:
+
+```bash
+pip install --no-build-isolation -e GroundingDINO
+```
+
+
+Install diffusers:
+
+```bash
+pip install --upgrade diffusers[torch]
+```
+
+Install osx:
+
+```bash
+git submodule update --init --recursive
+cd grounded-sam-osx && bash install.sh
+```
+
+Install RAM & Tag2Text:
+
+```bash
+git clone https://github.com/xinyu1205/recognize-anything.git
+pip install -r ./recognize-anything/requirements.txt
+pip install -e ./recognize-anything/
+```
+
+The following optional dependencies are necessary for mask post-processing, saving masks in COCO format, the example notebooks, and exporting the model in ONNX format. `jupyter` is also required to run the example notebooks.
+
+```
+pip install opencv-python pycocotools matplotlib onnxruntime onnx ipykernel
+```
+
+More details can be found in [install segment anything](https://github.com/facebookresearch/segment-anything#installation) and [install GroundingDINO](https://github.com/IDEA-Research/GroundingDINO#install) and [install OSX](https://github.com/IDEA-Research/OSX)
+
+
+## Grounded-SAM Playground
+Let's start exploring our Grounding-SAM Playground and we will release more interesting demos in the future, stay tuned!
+
+## :open_book: Step-by-Step Notebook Demo
+Here we list some notebook demo provided in this project:
+- [grounded_sam.ipynb](grounded_sam.ipynb)
+- [grounded_sam_colab_demo.ipynb](grounded_sam_colab_demo.ipynb)
+- [grounded_sam_3d_box.ipynb](grounded_sam_3d_box)
+
+
+### :running_man: GroundingDINO: Detect Everything with Text Prompt
+
+:grapes: [[arXiv Paper](https://arxiv.org/abs/2303.05499)] :rose:[[Try the Colab Demo](https://colab.research.google.com/github/roboflow-ai/notebooks/blob/main/notebooks/zero-shot-object-detection-with-grounding-dino.ipynb)] :sunflower: [[Try Huggingface Demo](https://huggingface.co/spaces/ShilongLiu/Grounding_DINO_demo)] :mushroom: [[Automated Dataset Annotation and Evaluation](https://youtu.be/C4NqaRBz_Kw)]
+
+Here's the step-by-step tutorial on running `GroundingDINO` demo:
+
+**Step 1: Download the pretrained weights**
+
+```bash
+cd Grounded-Segment-Anything
+
+# download the pretrained groundingdino-swin-tiny model
+wget https://github.com/IDEA-Research/GroundingDINO/releases/download/v0.1.0-alpha/groundingdino_swint_ogc.pth
+```
+
+**Step 2: Running the demo**
+
+```bash
+python grounding_dino_demo.py
+```
+
+
+ Running with Python (same as demo but you can run it anywhere after installing GroundingDINO)
+
+```python
+from groundingdino.util.inference import load_model, load_image, predict, annotate
+import cv2
+
+model = load_model("GroundingDINO/groundingdino/config/GroundingDINO_SwinT_OGC.py", "./groundingdino_swint_ogc.pth")
+IMAGE_PATH = "assets/demo1.jpg"
+TEXT_PROMPT = "bear."
+BOX_THRESHOLD = 0.35
+TEXT_THRESHOLD = 0.25
+
+image_source, image = load_image(IMAGE_PATH)
+
+boxes, logits, phrases = predict(
+ model=model,
+ image=image,
+ caption=TEXT_PROMPT,
+ box_threshold=BOX_THRESHOLD,
+ text_threshold=TEXT_THRESHOLD
+)
+
+annotated_frame = annotate(image_source=image_source, boxes=boxes, logits=logits, phrases=phrases)
+cv2.imwrite("annotated_image.jpg", annotated_frame)
+```
+
+
+
+
+**Tips**
+- If you want to detect multiple objects in one sentence with [Grounding DINO](https://github.com/IDEA-Research/GroundingDINO), we suggest separating each name with `.` . An example: `cat . dog . chair .`
+
+**Step 3: Check the annotated image**
+
+The annotated image will be saved as `./annotated_image.jpg`.
+
+
+
+**Step 4: Running the updated grounded-sam demo (optional)**
+
+Note that this demo is almost same as the original demo, but **with more elegant code**.
+
+```python
+python grounded_sam_simple_demo.py
+```
+
+The annotated results will be saved as `./groundingdino_annotated_image.jpg` and `./grounded_sam_annotated_image.jpg`
+
+
+
+### :golfing: Grounded-SAM and Inpaint Gradio APP
+
+We support 6 tasks in the local Gradio APP:
+
+1. **scribble**: Segmentation is achieved through Segment Anything and mouse click interaction (you need to click on the object with the mouse, no need to specify the prompt).
+2. **automask**: Segment the entire image at once through Segment Anything (no need to specify a prompt).
+3. **det**: Realize detection through Grounding DINO and text interaction (text prompt needs to be specified).
+4. **seg**: Realize text interaction by combining Grounding DINO and Segment Anything to realize detection + segmentation (need to specify text prompt).
+5. **inpainting**: By combining Grounding DINO + Segment Anything + Stable Diffusion to achieve text exchange and replace the target object (need to specify text prompt and inpaint prompt) .
+6. **automatic**: By combining BLIP + Grounding DINO + Segment Anything to achieve non-interactive detection + segmentation (no need to specify prompt).
+
+```bash
+python gradio_app.py
+```
+
+- The gradio_app visualization as follows:
+
+
+
+
+### :label: Grounded-SAM with RAM or Tag2Text for Automatic Labeling
+[**The Recognize Anything Models**](https://github.com/OPPOMKLab/recognize-anything) are a series of open-source and strong fundamental image recognition models, including [RAM++](https://arxiv.org/abs/2310.15200), [RAM](https://arxiv.org/abs/2306.03514) and [Tag2text](https://arxiv.org/abs/2303.05657).
+
+
+It is seamlessly linked to generate pseudo labels automatically as follows:
+1. Use RAM/Tag2Text to generate tags.
+2. Use Grounded-Segment-Anything to generate the boxes and masks.
+
+
+**Step 1: Init submodule and download the pretrained checkpoint**
+
+- Init submodule:
+
+```bash
+cd Grounded-Segment-Anything
+git submodule init
+git submodule update
+```
+
+- Download pretrained weights for `GroundingDINO`, `SAM` and `RAM/Tag2Text`:
+
+```bash
+wget https://dl.fbaipublicfiles.com/segment_anything/sam_vit_h_4b8939.pth
+wget https://github.com/IDEA-Research/GroundingDINO/releases/download/v0.1.0-alpha/groundingdino_swint_ogc.pth
+
+
+wget https://huggingface.co/spaces/xinyu1205/Tag2Text/resolve/main/ram_swin_large_14m.pth
+wget https://huggingface.co/spaces/xinyu1205/Tag2Text/resolve/main/tag2text_swin_14m.pth
+```
+
+**Step 2: Running the demo with RAM**
+```bash
+export CUDA_VISIBLE_DEVICES=0
+python automatic_label_ram_demo.py \
+ --config GroundingDINO/groundingdino/config/GroundingDINO_SwinT_OGC.py \
+ --ram_checkpoint ram_swin_large_14m.pth \
+ --grounded_checkpoint groundingdino_swint_ogc.pth \
+ --sam_checkpoint sam_vit_h_4b8939.pth \
+ --input_image assets/demo9.jpg \
+ --output_dir "outputs" \
+ --box_threshold 0.25 \
+ --text_threshold 0.2 \
+ --iou_threshold 0.5 \
+ --device "cuda"
+```
+
+
+**Step 2: Or Running the demo with Tag2Text**
+```bash
+export CUDA_VISIBLE_DEVICES=0
+python automatic_label_tag2text_demo.py \
+ --config GroundingDINO/groundingdino/config/GroundingDINO_SwinT_OGC.py \
+ --tag2text_checkpoint tag2text_swin_14m.pth \
+ --grounded_checkpoint groundingdino_swint_ogc.pth \
+ --sam_checkpoint sam_vit_h_4b8939.pth \
+ --input_image assets/demo9.jpg \
+ --output_dir "outputs" \
+ --box_threshold 0.25 \
+ --text_threshold 0.2 \
+ --iou_threshold 0.5 \
+ --device "cuda"
+```
+
+- RAM++ significantly improves the open-set capability of RAM, for [RAM++ inference on unseen categoreis](https://github.com/xinyu1205/recognize-anything#ram-inference-on-unseen-categories-open-set).
+- Tag2Text also provides powerful captioning capabilities, and the process with captions can refer to [BLIP](#robot-run-grounded-segment-anything--blip-demo).
+- The pseudo labels and model prediction visualization will be saved in `output_dir` as follows (right figure):
+
+
+
+
+### :robot: Grounded-SAM with BLIP for Automatic Labeling
+It is easy to generate pseudo labels automatically as follows:
+1. Use BLIP (or other caption models) to generate a caption.
+2. Extract tags from the caption. We use ChatGPT to handle the potential complicated sentences.
+3. Use Grounded-Segment-Anything to generate the boxes and masks.
+
+- Run Demo
+```bash
+export OPENAI_API_KEY=your_openai_key
+export OPENAI_API_BASE=https://closeai.deno.dev/v1
+export CUDA_VISIBLE_DEVICES=0
+python automatic_label_demo.py \
+ --config GroundingDINO/groundingdino/config/GroundingDINO_SwinT_OGC.py \
+ --grounded_checkpoint groundingdino_swint_ogc.pth \
+ --sam_checkpoint sam_vit_h_4b8939.pth \
+ --input_image assets/demo3.jpg \
+ --output_dir "outputs" \
+ --openai_key $OPENAI_API_KEY \
+ --box_threshold 0.25 \
+ --text_threshold 0.2 \
+ --iou_threshold 0.5 \
+ --device "cuda"
+```
+
+- When you don't have a paid Account for ChatGPT is also possible to use NLTK instead. Just don't include the ```openai_key``` Parameter when starting the Demo.
+ - The Script will automatically download the necessary NLTK Data.
+- The pseudo labels and model prediction visualization will be saved in `output_dir` as follows:
+
+
+
+
+### :open_mouth: Grounded-SAM with Whisper: Detect and Segment Anything with Audio
+Detect and segment anything with speech!
+
+
+
+**Install Whisper**
+```bash
+pip install -U openai-whisper
+```
+See the [whisper official page](https://github.com/openai/whisper#setup) if you have other questions for the installation.
+
+**Run Voice-to-Label Demo**
+
+Optional: Download the demo audio file
+
+```bash
+wget https://huggingface.co/ShilongLiu/GroundingDINO/resolve/main/demo_audio.mp3
+```
+
+
+```bash
+export CUDA_VISIBLE_DEVICES=0
+python grounded_sam_whisper_demo.py \
+ --config GroundingDINO/groundingdino/config/GroundingDINO_SwinT_OGC.py \
+ --grounded_checkpoint groundingdino_swint_ogc.pth \
+ --sam_checkpoint sam_vit_h_4b8939.pth \
+ --input_image assets/demo4.jpg \
+ --output_dir "outputs" \
+ --box_threshold 0.3 \
+ --text_threshold 0.25 \
+ --speech_file "demo_audio.mp3" \
+ --device "cuda"
+```
+
+
+
+**Run Voice-to-inpaint Demo**
+
+You can enable chatgpt to help you automatically detect the object and inpainting order with `--enable_chatgpt`.
+
+Or you can specify the object you want to inpaint [stored in `args.det_speech_file`] and the text you want to inpaint with [stored in `args.inpaint_speech_file`].
+
+```bash
+export OPENAI_API_KEY=your_openai_key
+export OPENAI_API_BASE=https://closeai.deno.dev/v1
+# Example: enable chatgpt
+export CUDA_VISIBLE_DEVICES=0
+python grounded_sam_whisper_inpainting_demo.py \
+ --config GroundingDINO/groundingdino/config/GroundingDINO_SwinT_OGC.py \
+ --grounded_checkpoint groundingdino_swint_ogc.pth \
+ --sam_checkpoint sam_vit_h_4b8939.pth \
+ --input_image assets/inpaint_demo.jpg \
+ --output_dir "outputs" \
+ --box_threshold 0.3 \
+ --text_threshold 0.25 \
+ --prompt_speech_file assets/acoustics/prompt_speech_file.mp3 \
+ --enable_chatgpt \
+ --openai_key $OPENAI_API_KEY\
+ --device "cuda"
+```
+
+```bash
+# Example: without chatgpt
+export CUDA_VISIBLE_DEVICES=0
+python grounded_sam_whisper_inpainting_demo.py \
+ --config GroundingDINO/groundingdino/config/GroundingDINO_SwinT_OGC.py \
+ --grounded_checkpoint groundingdino_swint_ogc.pth \
+ --sam_checkpoint sam_vit_h_4b8939.pth \
+ --input_image assets/inpaint_demo.jpg \
+ --output_dir "outputs" \
+ --box_threshold 0.3 \
+ --text_threshold 0.25 \
+ --det_speech_file "assets/acoustics/det_voice.mp3" \
+ --inpaint_speech_file "assets/acoustics/inpaint_voice.mp3" \
+ --device "cuda"
+```
+
+
+
+### :speech_balloon: Grounded-SAM ChatBot Demo
+
+https://user-images.githubusercontent.com/24236723/231955561-2ae4ec1a-c75f-4cc5-9b7b-517aa1432123.mp4
+
+Following [Visual ChatGPT](https://github.com/microsoft/visual-chatgpt), we add a ChatBot for our project. Currently, it supports:
+1. "Describe the image."
+2. "Detect the dog (and the cat) in the image."
+3. "Segment anything in the image."
+4. "Segment the dog (and the cat) in the image."
+5. "Help me label the image."
+6. "Replace the dog with a cat in the image."
+
+To use the ChatBot:
+- Install whisper if you want to use audio as input.
+- Set the default model setting in the tool `Grounded_dino_sam_inpainting`.
+- Run Demo
+```bash
+export OPENAI_API_KEY=your_openai_key
+export OPENAI_API_BASE=https://closeai.deno.dev/v1
+export CUDA_VISIBLE_DEVICES=0
+python chatbot.py
+```
+
+### :man_dancing: Run Grounded-Segment-Anything + OSX Demo
+
+
+
+
+
+
+
+- Download the checkpoint `osx_l_wo_decoder.pth.tar` from [here](https://drive.google.com/drive/folders/1x7MZbB6eAlrq5PKC9MaeIm4GqkBpokow?usp=share_link) for OSX:
+- Download the human model files and place it into `grounded-sam-osx/utils/human_model_files` following the instruction of [OSX](https://github.com/IDEA-Research/OSX).
+
+- Run Demo
+
+```shell
+export CUDA_VISIBLE_DEVICES=0
+python grounded_sam_osx_demo.py \
+ --config GroundingDINO/groundingdino/config/GroundingDINO_SwinT_OGC.py \
+ --grounded_checkpoint groundingdino_swint_ogc.pth \
+ --sam_checkpoint sam_vit_h_4b8939.pth \
+ --osx_checkpoint osx_l_wo_decoder.pth.tar \
+ --input_image assets/osx/grounded_sam_osx_demo.png \
+ --output_dir "outputs" \
+ --box_threshold 0.3 \
+ --text_threshold 0.25 \
+ --text_prompt "humans, chairs" \
+ --device "cuda"
+```
+
+- The model prediction visualization will be saved in `output_dir` as follows:
+
+
+
+- We also support promptable 3D whole-body mesh recovery. For example, you can track someone with a text prompt and estimate his 3D pose and shape :
+
+|  |
+| :---------------------------------------------------: |
+| *A person with pink clothes* |
+
+|  |
+| :---------------------------------------------------: |
+| *A man with a sunglasses* |
+
+
+## :man_dancing: Run Grounded-Segment-Anything + VISAM Demo
+
+- Download the checkpoint `motrv2_dancetrack.pth` from [here](https://drive.google.com/file/d/1EA4lndu2yQcVgBKR09KfMe5efbf631Th/view?usp=share_link) for MOTRv2:
+- See the more thing if you have other questions for the installation.
+
+- Run Demo
+
+```shell
+export CUDA_VISIBLE_DEVICES=0
+python grounded_sam_visam.py \
+ --meta_arch motr \
+ --dataset_file e2e_dance \
+ --with_box_refine \
+ --query_interaction_layer QIMv2 \
+ --num_queries 10 \
+ --det_db det_db_motrv2.json \
+ --use_checkpoint \
+ --mot_path your_data_path \
+ --resume motrv2_dancetrack.pth \
+ --sam_checkpoint sam_vit_h_4b8939.pth \
+ --video_path DanceTrack/test/dancetrack0003
+```
+||
+
+
+### :dancers: Interactive Editing
+- Release the interactive fashion-edit playground in [here](https://github.com/IDEA-Research/Grounded-Segment-Anything/tree/humanFace). Run in the notebook, just click for annotating points for further segmentation. Enjoy it!
+
+
+- Release human-face-edit branch [here](https://github.com/IDEA-Research/Grounded-Segment-Anything/tree/humanFace). We'll keep updating this branch with more interesting features. Here are some examples:
+
+ 
+
+## :camera: 3D-Box via Segment Anything
+We extend the scope to 3D world by combining Segment Anything and [VoxelNeXt](https://github.com/dvlab-research/VoxelNeXt). When we provide a prompt (e.g., a point / box), the result is not only 2D segmentation mask, but also 3D boxes. Please check [voxelnext_3d_box](./voxelnext_3d_box/) for more details.
+ 
+ 
+
+
+
+
+## :cupid: Acknowledgements
+
+- [Segment Anything](https://github.com/facebookresearch/segment-anything)
+- [Grounding DINO](https://github.com/IDEA-Research/GroundingDINO)
+
+
+## Contributors
+
+Our project wouldn't be possible without the contributions of these amazing people! Thank you all for making this project better.
+
+
+
+
+
+
+## Citation
+If you find this project helpful for your research, please consider citing the following BibTeX entry.
+```BibTex
+@article{kirillov2023segany,
+ title={Segment Anything},
+ author={Kirillov, Alexander and Mintun, Eric and Ravi, Nikhila and Mao, Hanzi and Rolland, Chloe and Gustafson, Laura and Xiao, Tete and Whitehead, Spencer and Berg, Alexander C. and Lo, Wan-Yen and Doll{\'a}r, Piotr and Girshick, Ross},
+ journal={arXiv:2304.02643},
+ year={2023}
+}
+
+@article{liu2023grounding,
+ title={Grounding dino: Marrying dino with grounded pre-training for open-set object detection},
+ author={Liu, Shilong and Zeng, Zhaoyang and Ren, Tianhe and Li, Feng and Zhang, Hao and Yang, Jie and Li, Chunyuan and Yang, Jianwei and Su, Hang and Zhu, Jun and others},
+ journal={arXiv preprint arXiv:2303.05499},
+ year={2023}
+}
+
+@misc{ren2024grounded,
+ title={Grounded SAM: Assembling Open-World Models for Diverse Visual Tasks},
+ author={Tianhe Ren and Shilong Liu and Ailing Zeng and Jing Lin and Kunchang Li and He Cao and Jiayu Chen and Xinyu Huang and Yukang Chen and Feng Yan and Zhaoyang Zeng and Hao Zhang and Feng Li and Jie Yang and Hongyang Li and Qing Jiang and Lei Zhang},
+ year={2024},
+ eprint={2401.14159},
+ archivePrefix={arXiv},
+ primaryClass={cs.CV}
+}
+```
diff --git a/VISAM/.gitignore b/VISAM/.gitignore
new file mode 100644
index 0000000000000000000000000000000000000000..559c6cec67ed36247e55449487568c05c0b5ed8b
--- /dev/null
+++ b/VISAM/.gitignore
@@ -0,0 +1,8 @@
+__pycache__/
+*.pth
+*.train
+exps/
+build/
+*.egg
+*.egg-info
+*.mp4
diff --git a/VISAM/LICENSE b/VISAM/LICENSE
new file mode 100644
index 0000000000000000000000000000000000000000..fdaf436e9548250539b3ccabdf204dbd10eadba6
--- /dev/null
+++ b/VISAM/LICENSE
@@ -0,0 +1,270 @@
+MIT License
+
+Copyright (c) 2022 megvii-research
+
+Permission is hereby granted, free of charge, to any person obtaining a copy
+of this software and associated documentation files (the "Software"), to deal
+in the Software without restriction, including without limitation the rights
+to use, copy, modify, merge, publish, distribute, sublicense, and/or sell
+copies of the Software, and to permit persons to whom the Software is
+furnished to do so, subject to the following conditions:
+
+The above copyright notice and this permission notice shall be included in all
+copies or substantial portions of the Software.
+
+THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR
+IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY,
+FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL THE
+AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER
+LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING FROM,
+OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER DEALINGS IN THE
+SOFTWARE.
+
+
+MOTR
+
+MIT License
+
+Copyright (c) 2021 megvii-model
+
+Permission is hereby granted, free of charge, to any person obtaining a copy
+of this software and associated documentation files (the "Software"), to deal
+in the Software without restriction, including without limitation the rights
+to use, copy, modify, merge, publish, distribute, sublicense, and/or sell
+copies of the Software, and to permit persons to whom the Software is
+furnished to do so, subject to the following conditions:
+
+The above copyright notice and this permission notice shall be included in all
+copies or substantial portions of the Software.
+
+THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR
+IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY,
+FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL THE
+AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER
+LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING FROM,
+OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER DEALINGS IN THE
+SOFTWARE.
+
+
+Deformable DETR
+
+Copyright (c) 2020 SenseTime. All Rights Reserved.
+
+ Apache License
+ Version 2.0, January 2004
+ http://www.apache.org/licenses/
+
+ TERMS AND CONDITIONS FOR USE, REPRODUCTION, AND DISTRIBUTION
+
+ 1. Definitions.
+
+ "License" shall mean the terms and conditions for use, reproduction,
+ and distribution as defined by Sections 1 through 9 of this document.
+
+ "Licensor" shall mean the copyright owner or entity authorized by
+ the copyright owner that is granting the License.
+
+ "Legal Entity" shall mean the union of the acting entity and all
+ other entities that control, are controlled by, or are under common
+ control with that entity. For the purposes of this definition,
+ "control" means (i) the power, direct or indirect, to cause the
+ direction or management of such entity, whether by contract or
+ otherwise, or (ii) ownership of fifty percent (50%) or more of the
+ outstanding shares, or (iii) beneficial ownership of such entity.
+
+ "You" (or "Your") shall mean an individual or Legal Entity
+ exercising permissions granted by this License.
+
+ "Source" form shall mean the preferred form for making modifications,
+ including but not limited to software source code, documentation
+ source, and configuration files.
+
+ "Object" form shall mean any form resulting from mechanical
+ transformation or translation of a Source form, including but
+ not limited to compiled object code, generated documentation,
+ and conversions to other media types.
+
+ "Work" shall mean the work of authorship, whether in Source or
+ Object form, made available under the License, as indicated by a
+ copyright notice that is included in or attached to the work
+ (an example is provided in the Appendix below).
+
+ "Derivative Works" shall mean any work, whether in Source or Object
+ form, that is based on (or derived from) the Work and for which the
+ editorial revisions, annotations, elaborations, or other modifications
+ represent, as a whole, an original work of authorship. For the purposes
+ of this License, Derivative Works shall not include works that remain
+ separable from, or merely link (or bind by name) to the interfaces of,
+ the Work and Derivative Works thereof.
+
+ "Contribution" shall mean any work of authorship, including
+ the original version of the Work and any modifications or additions
+ to that Work or Derivative Works thereof, that is intentionally
+ submitted to Licensor for inclusion in the Work by the copyright owner
+ or by an individual or Legal Entity authorized to submit on behalf of
+ the copyright owner. For the purposes of this definition, "submitted"
+ means any form of electronic, verbal, or written communication sent
+ to the Licensor or its representatives, including but not limited to
+ communication on electronic mailing lists, source code control systems,
+ and issue tracking systems that are managed by, or on behalf of, the
+ Licensor for the purpose of discussing and improving the Work, but
+ excluding communication that is conspicuously marked or otherwise
+ designated in writing by the copyright owner as "Not a Contribution."
+
+ "Contributor" shall mean Licensor and any individual or Legal Entity
+ on behalf of whom a Contribution has been received by Licensor and
+ subsequently incorporated within the Work.
+
+ 2. Grant of Copyright License. Subject to the terms and conditions of
+ this License, each Contributor hereby grants to You a perpetual,
+ worldwide, non-exclusive, no-charge, royalty-free, irrevocable
+ copyright license to reproduce, prepare Derivative Works of,
+ publicly display, publicly perform, sublicense, and distribute the
+ Work and such Derivative Works in Source or Object form.
+
+ 3. Grant of Patent License. Subject to the terms and conditions of
+ this License, each Contributor hereby grants to You a perpetual,
+ worldwide, non-exclusive, no-charge, royalty-free, irrevocable
+ (except as stated in this section) patent license to make, have made,
+ use, offer to sell, sell, import, and otherwise transfer the Work,
+ where such license applies only to those patent claims licensable
+ by such Contributor that are necessarily infringed by their
+ Contribution(s) alone or by combination of their Contribution(s)
+ with the Work to which such Contribution(s) was submitted. If You
+ institute patent litigation against any entity (including a
+ cross-claim or counterclaim in a lawsuit) alleging that the Work
+ or a Contribution incorporated within the Work constitutes direct
+ or contributory patent infringement, then any patent licenses
+ granted to You under this License for that Work shall terminate
+ as of the date such litigation is filed.
+
+ 4. Redistribution. You may reproduce and distribute copies of the
+ Work or Derivative Works thereof in any medium, with or without
+ modifications, and in Source or Object form, provided that You
+ meet the following conditions:
+
+ (a) You must give any other recipients of the Work or
+ Derivative Works a copy of this License; and
+
+ (b) You must cause any modified files to carry prominent notices
+ stating that You changed the files; and
+
+ (c) You must retain, in the Source form of any Derivative Works
+ that You distribute, all copyright, patent, trademark, and
+ attribution notices from the Source form of the Work,
+ excluding those notices that do not pertain to any part of
+ the Derivative Works; and
+
+ (d) If the Work includes a "NOTICE" text file as part of its
+ distribution, then any Derivative Works that You distribute must
+ include a readable copy of the attribution notices contained
+ within such NOTICE file, excluding those notices that do not
+ pertain to any part of the Derivative Works, in at least one
+ of the following places: within a NOTICE text file distributed
+ as part of the Derivative Works; within the Source form or
+ documentation, if provided along with the Derivative Works; or,
+ within a display generated by the Derivative Works, if and
+ wherever such third-party notices normally appear. The contents
+ of the NOTICE file are for informational purposes only and
+ do not modify the License. You may add Your own attribution
+ notices within Derivative Works that You distribute, alongside
+ or as an addendum to the NOTICE text from the Work, provided
+ that such additional attribution notices cannot be construed
+ as modifying the License.
+
+ You may add Your own copyright statement to Your modifications and
+ may provide additional or different license terms and conditions
+ for use, reproduction, or distribution of Your modifications, or
+ for any such Derivative Works as a whole, provided Your use,
+ reproduction, and distribution of the Work otherwise complies with
+ the conditions stated in this License.
+
+ 5. Submission of Contributions. Unless You explicitly state otherwise,
+ any Contribution intentionally submitted for inclusion in the Work
+ by You to the Licensor shall be under the terms and conditions of
+ this License, without any additional terms or conditions.
+ Notwithstanding the above, nothing herein shall supersede or modify
+ the terms of any separate license agreement you may have executed
+ with Licensor regarding such Contributions.
+
+ 6. Trademarks. This License does not grant permission to use the trade
+ names, trademarks, service marks, or product names of the Licensor,
+ except as required for reasonable and customary use in describing the
+ origin of the Work and reproducing the content of the NOTICE file.
+
+ 7. Disclaimer of Warranty. Unless required by applicable law or
+ agreed to in writing, Licensor provides the Work (and each
+ Contributor provides its Contributions) on an "AS IS" BASIS,
+ WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or
+ implied, including, without limitation, any warranties or conditions
+ of TITLE, NON-INFRINGEMENT, MERCHANTABILITY, or FITNESS FOR A
+ PARTICULAR PURPOSE. You are solely responsible for determining the
+ appropriateness of using or redistributing the Work and assume any
+ risks associated with Your exercise of permissions under this License.
+
+ 8. Limitation of Liability. In no event and under no legal theory,
+ whether in tort (including negligence), contract, or otherwise,
+ unless required by applicable law (such as deliberate and grossly
+ negligent acts) or agreed to in writing, shall any Contributor be
+ liable to You for damages, including any direct, indirect, special,
+ incidental, or consequential damages of any character arising as a
+ result of this License or out of the use or inability to use the
+ Work (including but not limited to damages for loss of goodwill,
+ work stoppage, computer failure or malfunction, or any and all
+ other commercial damages or losses), even if such Contributor
+ has been advised of the possibility of such damages.
+
+ 9. Accepting Warranty or Additional Liability. While redistributing
+ the Work or Derivative Works thereof, You may choose to offer,
+ and charge a fee for, acceptance of support, warranty, indemnity,
+ or other liability obligations and/or rights consistent with this
+ License. However, in accepting such obligations, You may act only
+ on Your own behalf and on Your sole responsibility, not on behalf
+ of any other Contributor, and only if You agree to indemnify,
+ defend, and hold each Contributor harmless for any liability
+ incurred by, or claims asserted against, such Contributor by reason
+ of your accepting any such warranty or additional liability.
+
+ END OF TERMS AND CONDITIONS
+
+ APPENDIX: How to apply the Apache License to your work.
+
+ To apply the Apache License to your work, attach the following
+ boilerplate notice, with the fields enclosed by brackets "[]"
+ replaced with your own identifying information. (Don't include
+ the brackets!) The text should be enclosed in the appropriate
+ comment syntax for the file format. We also recommend that a
+ file or class name and description of purpose be included on the
+ same "printed page" as the copyright notice for easier
+ identification within third-party archives.
+
+ Copyright 2020 SenseTime
+
+ Licensed under the Apache License, Version 2.0 (the "License");
+ you may not use this file except in compliance with the License.
+ You may obtain a copy of the License at
+
+ http://www.apache.org/licenses/LICENSE-2.0
+
+ Unless required by applicable law or agreed to in writing, software
+ distributed under the License is distributed on an "AS IS" BASIS,
+ WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+ See the License for the specific language governing permissions and
+ limitations under the License.
+
+
+DETR
+
+Copyright 2020 - present, Facebook, Inc
+
+Licensed under the Apache License, Version 2.0 (the "License");
+you may not use this file except in compliance with the License.
+You may obtain a copy of the License at
+
+ http://www.apache.org/licenses/LICENSE-2.0
+
+Unless required by applicable law or agreed to in writing, software
+distributed under the License is distributed on an "AS IS" BASIS,
+WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+See the License for the specific language governing permissions and
+limitations under the License.
diff --git a/VISAM/README.md b/VISAM/README.md
new file mode 100644
index 0000000000000000000000000000000000000000..a89c00b80f50d5f43bdf0f5cd2274e0afe756217
--- /dev/null
+++ b/VISAM/README.md
@@ -0,0 +1,104 @@
+# MOTRv2: Bootstrapping End-to-End Multi-Object Tracking by Pretrained Object Detectors
+
+
+This fork from https://github.com/megvii-research/MOTRv2 [MOTRv2](https://arxiv.org/abs/2211.09791), and after we will release our code CO-MOT.
+
+## Main Results
+
+### DanceTrack
+
+| **HOTA** | **DetA** | **AssA** | **MOTA** | **IDF1** | **URL** |
+| :------: | :------: | :------: | :------: | :------: | :-----------------------------------------------------------------------------------------: |
+| 69.9 | 83.0 | 59.0 | 91.9 | 71.7 | [model](https://drive.google.com/file/d/1EA4lndu2yQcVgBKR09KfMe5efbf631Th/view?usp=share_link) |
+
+### Visualization
+
+
+|VISAM|
+||
+
+
+## Installation
+
+The codebase is built on top of [Deformable DETR](https://github.com/fundamentalvision/Deformable-DETR) and [MOTR](https://github.com/megvii-research/MOTR).
+
+### Requirements
+* Install pytorch using conda (optional)
+
+ ```bash
+ conda create -n motrv2 python=3.9
+ conda activate motrv2
+ conda install pytorch==1.12.0 torchvision==0.13.0 torchaudio==0.12.0 cudatoolkit=11.3 -c pytorch
+ ```
+* Other requirements
+ ```bash
+ pip install -r requirements.txt
+ ```
+
+* Build MultiScaleDeformableAttention
+ ```bash
+ cd ./models/ops
+ sh ./make.sh
+ ```
+
+## Usage
+
+### Dataset preparation
+
+1. Download YOLOX detection from [here](https://drive.google.com/file/d/1cdhtztG4dbj7vzWSVSehLL6s0oPalEJo/view?usp=share_link).
+2. Please download [DanceTrack](https://dancetrack.github.io/) and [CrowdHuman](https://www.crowdhuman.org/) and unzip them as follows:
+
+```
+/data/Dataset/mot
+├── crowdhuman
+│ ├── annotation_train.odgt
+│ ├── annotation_trainval.odgt
+│ ├── annotation_val.odgt
+│ └── Images
+├── DanceTrack
+│ ├── test
+│ ├── train
+│ └── val
+├── det_db_motrv2.json
+```
+
+You may use the following command for generating crowdhuman trainval annotation:
+
+```bash
+cat annotation_train.odgt annotation_val.odgt > annotation_trainval.odgt
+```
+
+### Training
+
+You may download the coco pretrained weight from [Deformable DETR (+ iterative bounding box refinement)](https://github.com/fundamentalvision/Deformable-DETR#:~:text=config%0Alog-,model,-%2B%2B%20two%2Dstage%20Deformable), and modify the `--pretrained` argument to the path of the weight. Then training MOTR on 8 GPUs as following:
+
+```bash
+./tools/train.sh configs/motrv2.args
+```
+
+### Inference on DanceTrack Test Set
+
+1. Download SAM weigth fro [ViT-H SAM model](https://dl.fbaipublicfiles.com/segment_anything/sam_vit_h_4b8939.pth)
+2. run
+```bash
+# run a simple inference on our pretrained weights
+./tools/simple_inference.sh ./motrv2_dancetrack.pth
+
+# Or evaluate an experiment run
+# ./tools/eval.sh exps/motrv2/run1
+
+# then zip the results
+zip motrv2.zip tracker/ -r
+```
+
+if you want run on yourself data, please get detection results from [ByteTrackInference](https://github.com/zyayoung/ByteTrackInference) firstly.
+
+
+## Acknowledgements
+
+- [MOTR](https://github.com/megvii-research/MOTR)
+- [ByteTrack](https://github.com/ifzhang/ByteTrack)
+- [YOLOX](https://github.com/Megvii-BaseDetection/YOLOX)
+- [OC-SORT](https://github.com/noahcao/OC_SORT)
+- [DanceTrack](https://github.com/DanceTrack/DanceTrack)
+- [BDD100K](https://github.com/bdd100k/bdd100k)
diff --git a/VISAM/configs/motrv2.args b/VISAM/configs/motrv2.args
new file mode 100644
index 0000000000000000000000000000000000000000..0b4d7d46d08dd2a4ec84a75b18c9c6eab1d3cb60
--- /dev/null
+++ b/VISAM/configs/motrv2.args
@@ -0,0 +1,23 @@
+--meta_arch motr
+--dataset_file e2e_dance
+--epoch 5
+--with_box_refine
+--lr_drop 4
+--lr 2e-4
+--lr_backbone 2e-5
+--pretrained /mnt/dolphinfs/hdd_pool/docker/user/hadoop-vacv/yanfeng/project/MOTRv2/MOTRv3/checkpoints/r50_deformable_detr_plus_iterative_bbox_refinement-checkpoint.pth
+--batch_size 1
+--sample_mode random_interval
+--sample_interval 10
+--sampler_lengths 5
+--merger_dropout 0
+--dropout 0
+--random_drop 0.1
+--fp_ratio 0.3
+--query_interaction_layer QIMv2
+--query_denoise 0.05
+--num_queries 10
+--append_crowd
+--det_db det_db_motrv2.json
+--use_checkpoint
+--mot_path /home/aiot/yanfeng/data
diff --git a/VISAM/datasets/__init__.py b/VISAM/datasets/__init__.py
new file mode 100644
index 0000000000000000000000000000000000000000..759fcc1ffc37c65e80f86ca924b571af2da9b5ed
--- /dev/null
+++ b/VISAM/datasets/__init__.py
@@ -0,0 +1,20 @@
+# ------------------------------------------------------------------------
+# Copyright (c) 2022 megvii-research. All Rights Reserved.
+# ------------------------------------------------------------------------
+# Modified from Deformable DETR (https://github.com/fundamentalvision/Deformable-DETR)
+# Copyright (c) 2020 SenseTime. All Rights Reserved.
+# ------------------------------------------------------------------------
+# Modified from DETR (https://github.com/facebookresearch/detr)
+# Copyright (c) Facebook, Inc. and its affiliates. All Rights Reserved
+# ------------------------------------------------------------------------
+
+from .dance import build as build_e2e_dance
+from .joint import build as build_e2e_joint
+
+
+def build_dataset(image_set, args):
+ if args.dataset_file == 'e2e_joint':
+ return build_e2e_joint(image_set, args)
+ if args.dataset_file == 'e2e_dance':
+ return build_e2e_dance(image_set, args)
+ raise ValueError(f'dataset {args.dataset_file} not supported')
diff --git a/VISAM/datasets/dance.py b/VISAM/datasets/dance.py
new file mode 100644
index 0000000000000000000000000000000000000000..ba3f0ddb8acc09975315dd44aae88ceb7e888e36
--- /dev/null
+++ b/VISAM/datasets/dance.py
@@ -0,0 +1,308 @@
+# ------------------------------------------------------------------------
+# Copyright (c) 2022 megvii-research. All Rights Reserved.
+# ------------------------------------------------------------------------
+# Modified from Deformable DETR (https://github.com/fundamentalvision/Deformable-DETR)
+# Copyright (c) 2020 SenseTime. All Rights Reserved.
+# ------------------------------------------------------------------------
+# Modified from DETR (https://github.com/facebookresearch/detr)
+# Copyright (c) Facebook, Inc. and its affiliates. All Rights Reserved
+# ------------------------------------------------------------------------
+
+"""
+MOT dataset which returns image_id for evaluation.
+"""
+from collections import defaultdict
+import json
+import os
+from pathlib import Path
+import cv2
+import numpy as np
+import torch
+import torch.utils.data
+import os.path as osp
+from PIL import Image, ImageDraw
+import copy
+import datasets.transforms as T
+from models.structures import Instances
+
+from random import choice, randint
+
+
+def is_crowd(ann):
+ return 'extra' in ann and 'ignore' in ann['extra'] and ann['extra']['ignore'] == 1
+
+
+class DetMOTDetection:
+ def __init__(self, args, data_txt_path: str, seqs_folder, transform):
+ self.args = args
+ self.transform = transform
+ self.num_frames_per_batch = max(args.sampler_lengths)
+ self.sample_mode = args.sample_mode
+ self.sample_interval = args.sample_interval
+ self.video_dict = {}
+ self.mot_path = args.mot_path
+
+ self.labels_full = defaultdict(lambda : defaultdict(list))
+ def add_mot_folder(split_dir):
+ print("Adding", split_dir)
+ for vid in os.listdir(os.path.join(self.mot_path, split_dir)):
+ if 'seqmap' == vid:
+ continue
+ vid = os.path.join(split_dir, vid)
+ if 'DPM' in vid or 'FRCNN' in vid:
+ print(f'filter {vid}')
+ continue
+ gt_path = os.path.join(self.mot_path, vid, 'gt', 'gt.txt')
+ for l in open(gt_path):
+ t, i, *xywh, mark, label = l.strip().split(',')[:8]
+ t, i, mark, label = map(int, (t, i, mark, label))
+ if mark == 0:
+ continue
+ if label in [3, 4, 5, 6, 9, 10, 11]: # Non-person
+ continue
+ else:
+ crowd = False
+ x, y, w, h = map(float, (xywh))
+ self.labels_full[vid][t].append([x, y, w, h, i, crowd])
+
+ add_mot_folder("DanceTrack/train")
+ vid_files = list(self.labels_full.keys())
+
+ self.indices = []
+ self.vid_tmax = {}
+ for vid in vid_files:
+ self.video_dict[vid] = len(self.video_dict)
+ t_min = min(self.labels_full[vid].keys())
+ t_max = max(self.labels_full[vid].keys()) + 1
+ self.vid_tmax[vid] = t_max - 1
+ for t in range(t_min, t_max - self.num_frames_per_batch):
+ self.indices.append((vid, t))
+ print(f"Found {len(vid_files)} videos, {len(self.indices)} frames")
+
+ self.sampler_steps: list = args.sampler_steps
+ self.lengths: list = args.sampler_lengths
+ print("sampler_steps={} lenghts={}".format(self.sampler_steps, self.lengths))
+ self.period_idx = 0
+
+ # crowdhuman
+ self.ch_dir = Path(args.mot_path) / 'crowdhuman'
+ self.ch_indices = []
+ if args.append_crowd:
+ for line in open(self.ch_dir / f"annotation_trainval.odgt"):
+ datum = json.loads(line)
+ boxes = [ann['fbox'] for ann in datum['gtboxes'] if not is_crowd(ann)]
+ self.ch_indices.append((datum['ID'], boxes))
+ # self.ch_indices = self.ch_indices + self.ch_indices
+ print(f"Found {len(self.ch_indices)} images")
+
+ if args.det_db:
+ with open(os.path.join(args.mot_path, args.det_db)) as f:
+ self.det_db = json.load(f)
+ else:
+ self.det_db = defaultdict(list)
+
+ def set_epoch(self, epoch):
+ self.current_epoch = epoch
+ if self.sampler_steps is None or len(self.sampler_steps) == 0:
+ # fixed sampling length.
+ return
+
+ for i in range(len(self.sampler_steps)):
+ if epoch >= self.sampler_steps[i]:
+ self.period_idx = i + 1
+ print("set epoch: epoch {} period_idx={}".format(epoch, self.period_idx))
+ self.num_frames_per_batch = self.lengths[self.period_idx]
+
+ def step_epoch(self):
+ # one epoch finishes.
+ print("Dataset: epoch {} finishes".format(self.current_epoch))
+ self.set_epoch(self.current_epoch + 1)
+
+ @staticmethod
+ def _targets_to_instances(targets: dict, img_shape) -> Instances:
+ gt_instances = Instances(tuple(img_shape))
+ n_gt = len(targets['labels'])
+ gt_instances.boxes = targets['boxes'][:n_gt]
+ gt_instances.labels = targets['labels']
+ gt_instances.obj_ids = targets['obj_ids']
+ return gt_instances
+
+ def load_crowd(self, index):
+ ID, boxes = self.ch_indices[index]
+ boxes = copy.deepcopy(boxes)
+ img = Image.open(self.ch_dir / 'Images' / f'{ID}.jpg')
+
+ w, h = img._size
+ n_gts = len(boxes)
+ scores = [0. for _ in range(len(boxes))]
+ for line in self.det_db[f'crowdhuman/train_image/{ID}.txt']:
+ *box, s = map(float, line.split(','))
+ boxes.append(box)
+ scores.append(s)
+ boxes = torch.tensor(boxes, dtype=torch.float32)
+ areas = boxes[..., 2:].prod(-1)
+ boxes[:, 2:] += boxes[:, :2]
+
+ target = {
+ 'boxes': boxes,
+ 'scores': torch.as_tensor(scores),
+ 'labels': torch.zeros((n_gts, ), dtype=torch.long),
+ 'iscrowd': torch.zeros((n_gts, ), dtype=torch.bool),
+ 'image_id': torch.tensor([0]),
+ 'area': areas,
+ 'obj_ids': torch.arange(n_gts),
+ 'size': torch.as_tensor([h, w]),
+ 'orig_size': torch.as_tensor([h, w]),
+ 'dataset': "CrowdHuman",
+ }
+ rs = T.FixedMotRandomShift(self.num_frames_per_batch)
+ return rs([img], [target])
+
+ def _pre_single_frame(self, vid, idx: int):
+ img_path = os.path.join(self.mot_path, vid, 'img1', f'{idx:08d}.jpg')
+ img = Image.open(img_path)
+ targets = {}
+ w, h = img._size
+ assert w > 0 and h > 0, "invalid image {} with shape {} {}".format(img_path, w, h)
+ obj_idx_offset = self.video_dict[vid] * 100000 # 100000 unique ids is enough for a video.
+
+ targets['dataset'] = 'MOT17'
+ targets['boxes'] = []
+ targets['iscrowd'] = []
+ targets['labels'] = []
+ targets['obj_ids'] = []
+ targets['scores'] = []
+ targets['image_id'] = torch.as_tensor(idx)
+ targets['size'] = torch.as_tensor([h, w])
+ targets['orig_size'] = torch.as_tensor([h, w])
+ for *xywh, id, crowd in self.labels_full[vid][idx]:
+ targets['boxes'].append(xywh)
+ assert not crowd
+ targets['iscrowd'].append(crowd)
+ targets['labels'].append(0)
+ targets['obj_ids'].append(id + obj_idx_offset)
+ targets['scores'].append(1.)
+ txt_key = os.path.join(vid, 'img1', f'{idx:08d}.txt')
+ for line in self.det_db[txt_key]:
+ *box, s = map(float, line.split(','))
+ targets['boxes'].append(box)
+ targets['scores'].append(s)
+
+ targets['iscrowd'] = torch.as_tensor(targets['iscrowd'])
+ targets['labels'] = torch.as_tensor(targets['labels'])
+ targets['obj_ids'] = torch.as_tensor(targets['obj_ids'], dtype=torch.float64)
+ targets['scores'] = torch.as_tensor(targets['scores'])
+ targets['boxes'] = torch.as_tensor(targets['boxes'], dtype=torch.float32).reshape(-1, 4)
+ targets['boxes'][:, 2:] += targets['boxes'][:, :2]
+ return img, targets
+
+ def _get_sample_range(self, start_idx):
+
+ # take default sampling method for normal dataset.
+ assert self.sample_mode in ['fixed_interval', 'random_interval'], 'invalid sample mode: {}'.format(self.sample_mode)
+ if self.sample_mode == 'fixed_interval':
+ sample_interval = self.sample_interval
+ elif self.sample_mode == 'random_interval':
+ sample_interval = np.random.randint(1, self.sample_interval + 1)
+ default_range = start_idx, start_idx + (self.num_frames_per_batch - 1) * sample_interval + 1, sample_interval
+ return default_range
+
+ def pre_continuous_frames(self, vid, indices):
+ return zip(*[self._pre_single_frame(vid, i) for i in indices])
+
+ def sample_indices(self, vid, f_index):
+ assert self.sample_mode == 'random_interval'
+ rate = randint(1, self.sample_interval + 1)
+ tmax = self.vid_tmax[vid]
+ ids = [f_index + rate * i for i in range(self.num_frames_per_batch)]
+ return [min(i, tmax) for i in ids]
+
+ def __getitem__(self, idx):
+ if idx < len(self.indices):
+ vid, f_index = self.indices[idx]
+ indices = self.sample_indices(vid, f_index)
+ images, targets = self.pre_continuous_frames(vid, indices)
+ else:
+ images, targets = self.load_crowd(idx - len(self.indices))
+ if self.transform is not None:
+ images, targets = self.transform(images, targets)
+ gt_instances, proposals = [], []
+ for img_i, targets_i in zip(images, targets):
+ gt_instances_i = self._targets_to_instances(targets_i, img_i.shape[1:3])
+ gt_instances.append(gt_instances_i)
+ n_gt = len(targets_i['labels'])
+ proposals.append(torch.cat([
+ targets_i['boxes'][n_gt:],
+ targets_i['scores'][n_gt:, None],
+ ], dim=1))
+ return {
+ 'imgs': images,
+ 'gt_instances': gt_instances,
+ 'proposals': proposals,
+ }
+
+ def __len__(self):
+ return len(self.indices) + len(self.ch_indices)
+
+
+class DetMOTDetectionValidation(DetMOTDetection):
+ def __init__(self, args, seqs_folder, transform):
+ args.data_txt_path = args.val_data_txt_path
+ super().__init__(args, seqs_folder, transform)
+
+
+def make_transforms_for_mot17(image_set, args=None):
+
+ normalize = T.MotCompose([
+ T.MotToTensor(),
+ T.MotNormalize([0.485, 0.456, 0.406], [0.229, 0.224, 0.225])
+ ])
+ scales = [608, 640, 672, 704, 736, 768, 800, 832, 864, 896, 928, 960, 992]
+
+ if image_set == 'train':
+ return T.MotCompose([
+ T.MotRandomHorizontalFlip(),
+ T.MotRandomSelect(
+ T.MotRandomResize(scales, max_size=1536),
+ T.MotCompose([
+ T.MotRandomResize([800, 1000, 1200]),
+ T.FixedMotRandomCrop(800, 1200),
+ T.MotRandomResize(scales, max_size=1536),
+ ])
+ ),
+ T.MOTHSV(),
+ normalize,
+ ])
+
+ if image_set == 'val':
+ return T.MotCompose([
+ T.MotRandomResize([800], max_size=1333),
+ normalize,
+ ])
+
+ raise ValueError(f'unknown {image_set}')
+
+
+def build_transform(args, image_set):
+ mot17_train = make_transforms_for_mot17('train', args)
+ mot17_test = make_transforms_for_mot17('val', args)
+
+ if image_set == 'train':
+ return mot17_train
+ elif image_set == 'val':
+ return mot17_test
+ else:
+ raise NotImplementedError()
+
+
+def build(image_set, args):
+ root = Path(args.mot_path)
+ assert root.exists(), f'provided MOT path {root} does not exist'
+ transform = build_transform(args, image_set)
+ if image_set == 'train':
+ data_txt_path = args.data_txt_path_train
+ dataset = DetMOTDetection(args, data_txt_path=data_txt_path, seqs_folder=root, transform=transform)
+ if image_set == 'val':
+ data_txt_path = args.data_txt_path_val
+ dataset = DetMOTDetection(args, data_txt_path=data_txt_path, seqs_folder=root, transform=transform)
+ return dataset
diff --git a/VISAM/datasets/data_prefetcher.py b/VISAM/datasets/data_prefetcher.py
new file mode 100644
index 0000000000000000000000000000000000000000..07ea9cd12ebff04dccb0ee03ac51d29e2ef397d5
--- /dev/null
+++ b/VISAM/datasets/data_prefetcher.py
@@ -0,0 +1,114 @@
+# ------------------------------------------------------------------------
+# Copyright (c) 2022 megvii-research. All Rights Reserved.
+# ------------------------------------------------------------------------
+# Modified from Deformable DETR (https://github.com/fundamentalvision/Deformable-DETR)
+# Copyright (c) 2020 SenseTime. All Rights Reserved.
+# ------------------------------------------------------------------------
+# Modified from DETR (https://github.com/facebookresearch/detr)
+# Copyright (c) Facebook, Inc. and its affiliates. All Rights Reserved
+# ------------------------------------------------------------------------
+
+
+import torch
+from functools import partial
+from models.structures import Instances
+
+def to_cuda(samples, targets, device):
+ samples = samples.to(device, non_blocking=True)
+ targets = [{k: v.to(device, non_blocking=True) for k, v in t.items()} for t in targets]
+ return samples, targets
+
+
+def tensor_to_cuda(tensor: torch.Tensor, device):
+ return tensor.to(device)
+
+
+def is_tensor_or_instances(data):
+ return isinstance(data, torch.Tensor) or isinstance(data, Instances)
+
+
+def data_apply(data, check_func, apply_func):
+ if isinstance(data, dict):
+ for k in data.keys():
+ if check_func(data[k]):
+ data[k] = apply_func(data[k])
+ elif isinstance(data[k], dict) or isinstance(data[k], list):
+ data_apply(data[k], check_func, apply_func)
+ else:
+ raise ValueError()
+ elif isinstance(data, list):
+ for i in range(len(data)):
+ if check_func(data[i]):
+ data[i] = apply_func(data[i])
+ elif isinstance(data[i], dict) or isinstance(data[i], list):
+ data_apply(data[i], check_func, apply_func)
+ else:
+ raise ValueError("invalid type {}".format(type(data[i])))
+ else:
+ raise ValueError("invalid type {}".format(type(data)))
+ return data
+
+
+def data_dict_to_cuda(data_dict, device):
+ return data_apply(data_dict, is_tensor_or_instances, partial(tensor_to_cuda, device=device))
+
+
+class data_prefetcher():
+ def __init__(self, loader, device, prefetch=True):
+ self.loader = iter(loader)
+ self.prefetch = prefetch
+ self.device = device
+ if prefetch:
+ self.stream = torch.cuda.Stream()
+ self.preload()
+
+ def preload(self):
+ try:
+ self.next_samples, self.next_targets = next(self.loader)
+ except StopIteration:
+ self.next_samples = None
+ self.next_targets = None
+ return
+ # if record_stream() doesn't work, another option is to make sure device inputs are created
+ # on the main stream.
+ # self.next_input_gpu = torch.empty_like(self.next_input, device='cuda')
+ # self.next_target_gpu = torch.empty_like(self.next_target, device='cuda')
+ # Need to make sure the memory allocated for next_* is not still in use by the main stream
+ # at the time we start copying to next_*:
+ # self.stream.wait_stream(torch.cuda.current_stream())
+ with torch.cuda.stream(self.stream):
+ self.next_samples, self.next_targets = to_cuda(self.next_samples, self.next_targets, self.device)
+ # more code for the alternative if record_stream() doesn't work:
+ # copy_ will record the use of the pinned source tensor in this side stream.
+ # self.next_input_gpu.copy_(self.next_input, non_blocking=True)
+ # self.next_target_gpu.copy_(self.next_target, non_blocking=True)
+ # self.next_input = self.next_input_gpu
+ # self.next_target = self.next_target_gpu
+
+ # With Amp, it isn't necessary to manually convert data to half.
+ # if args.fp16:
+ # self.next_input = self.next_input.half()
+ # else:
+
+ def next(self):
+ if self.prefetch:
+ torch.cuda.current_stream().wait_stream(self.stream)
+ samples = self.next_samples
+ targets = self.next_targets
+ if samples is not None:
+ samples.record_stream(torch.cuda.current_stream())
+ if targets is not None:
+ for t in targets:
+ for k, v in t.items():
+ v.record_stream(torch.cuda.current_stream())
+ self.preload()
+ else:
+ try:
+ samples, targets = next(self.loader)
+ samples, targets = to_cuda(samples, targets, self.device)
+ except StopIteration:
+ print("catch_stop_iter")
+ samples = None
+ targets = None
+
+ return samples, targets
diff --git a/VISAM/datasets/joint.py b/VISAM/datasets/joint.py
new file mode 100644
index 0000000000000000000000000000000000000000..70c71336d112c78a2a73a741caa0cf42dc59ce17
--- /dev/null
+++ b/VISAM/datasets/joint.py
@@ -0,0 +1,290 @@
+# ------------------------------------------------------------------------
+# Copyright (c) 2022 megvii-research. All Rights Reserved.
+# ------------------------------------------------------------------------
+# Modified from Deformable DETR (https://github.com/fundamentalvision/Deformable-DETR)
+# Copyright (c) 2020 SenseTime. All Rights Reserved.
+# ------------------------------------------------------------------------
+# Modified from DETR (https://github.com/facebookresearch/detr)
+# Copyright (c) Facebook, Inc. and its affiliates. All Rights Reserved
+# ------------------------------------------------------------------------
+
+"""
+MOT dataset which returns image_id for evaluation.
+"""
+from pathlib import Path
+import cv2
+import numpy as np
+import torch
+import torch.utils.data
+import os.path as osp
+from PIL import Image, ImageDraw
+import copy
+import datasets.transforms as T
+from models.structures import Instances
+
+
+class DetMOTDetection:
+ def __init__(self, args, data_txt_path: str, seqs_folder, dataset2transform):
+ self.args = args
+ self.dataset2transform = dataset2transform
+ self.num_frames_per_batch = max(args.sampler_lengths)
+ self.sample_mode = args.sample_mode
+ self.sample_interval = args.sample_interval
+ self.vis = args.vis
+ self.video_dict = {}
+
+ with open(data_txt_path, 'r') as file:
+ self.img_files = file.readlines()
+ self.img_files = [osp.join(seqs_folder, x.strip()) for x in self.img_files]
+ self.img_files = list(filter(lambda x: len(x) > 0, self.img_files))
+
+ self.label_files = [(x.replace('images', 'labels_with_ids').replace('.png', '.txt').replace('.jpg', '.txt'))
+ for x in self.img_files]
+ # The number of images per sample: 1 + (num_frames - 1) * interval.
+ # The number of valid samples: num_images - num_image_per_sample + 1.
+ self.item_num = len(self.img_files) - (self.num_frames_per_batch - 1) * self.sample_interval
+
+ self._register_videos()
+
+ # video sampler.
+ self.sampler_steps: list = args.sampler_steps
+ self.lengths: list = args.sampler_lengths
+ print("sampler_steps={} lenghts={}".format(self.sampler_steps, self.lengths))
+ if self.sampler_steps is not None and len(self.sampler_steps) > 0:
+ # Enable sampling length adjustment.
+ assert len(self.lengths) > 0
+ assert len(self.lengths) == len(self.sampler_steps) + 1
+ for i in range(len(self.sampler_steps) - 1):
+ assert self.sampler_steps[i] < self.sampler_steps[i + 1]
+ self.item_num = len(self.img_files) - (self.lengths[-1] - 1) * self.sample_interval
+ self.period_idx = 0
+ self.num_frames_per_batch = self.lengths[0]
+ self.current_epoch = 0
+
+ def _register_videos(self):
+ for label_name in self.label_files:
+ video_name = '/'.join(label_name.split('/')[:-1])
+ if video_name not in self.video_dict:
+ print("register {}-th video: {} ".format(len(self.video_dict) + 1, video_name))
+ self.video_dict[video_name] = len(self.video_dict)
+ # assert len(self.video_dict) <= 300
+
+ def set_epoch(self, epoch):
+ self.current_epoch = epoch
+ if self.sampler_steps is None or len(self.sampler_steps) == 0:
+ # fixed sampling length.
+ return
+
+ for i in range(len(self.sampler_steps)):
+ if epoch >= self.sampler_steps[i]:
+ self.period_idx = i + 1
+ print("set epoch: epoch {} period_idx={}".format(epoch, self.period_idx))
+ self.num_frames_per_batch = self.lengths[self.period_idx]
+
+ def step_epoch(self):
+ # one epoch finishes.
+ print("Dataset: epoch {} finishes".format(self.current_epoch))
+ self.set_epoch(self.current_epoch + 1)
+
+ @staticmethod
+ def _targets_to_instances(targets: dict, img_shape) -> Instances:
+ gt_instances = Instances(tuple(img_shape))
+ gt_instances.boxes = targets['boxes']
+ gt_instances.labels = targets['labels']
+ gt_instances.obj_ids = targets['obj_ids']
+ gt_instances.area = targets['area']
+ return gt_instances
+
+ def _pre_single_frame(self, idx: int):
+ img_path = self.img_files[idx]
+ label_path = self.label_files[idx]
+ if 'crowdhuman' in img_path:
+ img_path = img_path.replace('.jpg', '.png')
+ img = Image.open(img_path)
+ targets = {}
+ w, h = img._size
+ assert w > 0 and h > 0, "invalid image {} with shape {} {}".format(img_path, w, h)
+ if osp.isfile(label_path):
+ labels0 = np.loadtxt(label_path, dtype=np.float32).reshape(-1, 6)
+
+ # normalized cewh to pixel xyxy format
+ labels = labels0.copy()
+ labels[:, 2] = w * (labels0[:, 2] - labels0[:, 4] / 2)
+ labels[:, 3] = h * (labels0[:, 3] - labels0[:, 5] / 2)
+ labels[:, 4] = w * (labels0[:, 2] + labels0[:, 4] / 2)
+ labels[:, 5] = h * (labels0[:, 3] + labels0[:, 5] / 2)
+ else:
+ raise ValueError('invalid label path: {}'.format(label_path))
+ video_name = '/'.join(label_path.split('/')[:-1])
+ obj_idx_offset = self.video_dict[video_name] * 1000000 # 1000000 unique ids is enough for a video.
+ if 'crowdhuman' in img_path:
+ targets['dataset'] = 'CrowdHuman'
+ elif 'MOT17' in img_path:
+ targets['dataset'] = 'MOT17'
+ else:
+ raise NotImplementedError()
+ targets['boxes'] = []
+ targets['area'] = []
+ targets['iscrowd'] = []
+ targets['labels'] = []
+ targets['obj_ids'] = []
+ targets['image_id'] = torch.as_tensor(idx)
+ targets['size'] = torch.as_tensor([h, w])
+ targets['orig_size'] = torch.as_tensor([h, w])
+ for label in labels:
+ targets['boxes'].append(label[2:6].tolist())
+ targets['area'].append(label[4] * label[5])
+ targets['iscrowd'].append(0)
+ targets['labels'].append(0)
+ obj_id = label[1] + obj_idx_offset if label[1] >= 0 else label[1]
+ targets['obj_ids'].append(obj_id) # relative id
+
+ targets['area'] = torch.as_tensor(targets['area'])
+ targets['iscrowd'] = torch.as_tensor(targets['iscrowd'])
+ targets['labels'] = torch.as_tensor(targets['labels'])
+ targets['obj_ids'] = torch.as_tensor(targets['obj_ids'])
+ targets['boxes'] = torch.as_tensor(targets['boxes'], dtype=torch.float32).reshape(-1, 4)
+ return img, targets
+
+ def _get_sample_range(self, start_idx):
+
+ # take default sampling method for normal dataset.
+ assert self.sample_mode in ['fixed_interval', 'random_interval'], 'invalid sample mode: {}'.format(self.sample_mode)
+ if self.sample_mode == 'fixed_interval':
+ sample_interval = self.sample_interval
+ elif self.sample_mode == 'random_interval':
+ sample_interval = np.random.randint(1, self.sample_interval + 1)
+ default_range = start_idx, start_idx + (self.num_frames_per_batch - 1) * sample_interval + 1, sample_interval
+ return default_range
+
+ def pre_continuous_frames(self, start, end, interval=1):
+ targets = []
+ images = []
+ for i in range(start, end, interval):
+ img_i, targets_i = self._pre_single_frame(i)
+ images.append(img_i)
+ targets.append(targets_i)
+ return images, targets
+
+ def __getitem__(self, idx):
+ sample_start, sample_end, sample_interval = self._get_sample_range(idx)
+ images, targets = self.pre_continuous_frames(sample_start, sample_end, sample_interval)
+ data = {}
+ dataset_name = targets[0]['dataset']
+ transform = self.dataset2transform[dataset_name]
+ if transform is not None:
+ images, targets = transform(images, targets)
+ gt_instances = []
+ for img_i, targets_i in zip(images, targets):
+ gt_instances_i = self._targets_to_instances(targets_i, img_i.shape[1:3])
+ gt_instances.append(gt_instances_i)
+ data.update({
+ 'imgs': images,
+ 'gt_instances': gt_instances,
+ })
+ if self.args.vis:
+ data['ori_img'] = [target_i['ori_img'] for target_i in targets]
+ return data
+
+ def __len__(self):
+ return self.item_num
+
+
+class DetMOTDetectionValidation(DetMOTDetection):
+ def __init__(self, args, seqs_folder, dataset2transform):
+ args.data_txt_path = args.val_data_txt_path
+ super().__init__(args, seqs_folder, dataset2transform)
+
+
+
+def make_transforms_for_mot17(image_set, args=None):
+
+ normalize = T.MotCompose([
+ T.MotToTensor(),
+ T.MotNormalize([0.485, 0.456, 0.406], [0.229, 0.224, 0.225])
+ ])
+ scales = [608, 640, 672, 704, 736, 768, 800, 832, 864, 896, 928, 960, 992]
+
+ if image_set == 'train':
+ return T.MotCompose([
+ T.MotRandomHorizontalFlip(),
+ T.MotRandomSelect(
+ T.MotRandomResize(scales, max_size=1536),
+ T.MotCompose([
+ T.MotRandomResize([400, 500, 600]),
+ T.FixedMotRandomCrop(384, 600),
+ T.MotRandomResize(scales, max_size=1536),
+ ])
+ ),
+ normalize,
+ ])
+
+ if image_set == 'val':
+ return T.MotCompose([
+ T.MotRandomResize([800], max_size=1333),
+ normalize,
+ ])
+
+ raise ValueError(f'unknown {image_set}')
+
+
+def make_transforms_for_crowdhuman(image_set, args=None):
+
+ normalize = T.MotCompose([
+ T.MotToTensor(),
+ T.MotNormalize([0.485, 0.456, 0.406], [0.229, 0.224, 0.225])
+ ])
+ scales = [608, 640, 672, 704, 736, 768, 800, 832, 864, 896, 928, 960, 992]
+
+ if image_set == 'train':
+ return T.MotCompose([
+ T.MotRandomHorizontalFlip(),
+ T.FixedMotRandomShift(bs=1),
+ T.MotRandomSelect(
+ T.MotRandomResize(scales, max_size=1536),
+ T.MotCompose([
+ T.MotRandomResize([400, 500, 600]),
+ T.FixedMotRandomCrop(384, 600),
+ T.MotRandomResize(scales, max_size=1536),
+ ])
+ ),
+ normalize,
+
+ ])
+
+ if image_set == 'val':
+ return T.MotCompose([
+ T.MotRandomResize([800], max_size=1333),
+ normalize,
+ ])
+
+ raise ValueError(f'unknown {image_set}')
+
+
+def build_dataset2transform(args, image_set):
+ mot17_train = make_transforms_for_mot17('train', args)
+ mot17_test = make_transforms_for_mot17('val', args)
+
+ crowdhuman_train = make_transforms_for_crowdhuman('train', args)
+ dataset2transform_train = {'MOT17': mot17_train, 'CrowdHuman': crowdhuman_train}
+ dataset2transform_val = {'MOT17': mot17_test, 'CrowdHuman': mot17_test}
+ if image_set == 'train':
+ return dataset2transform_train
+ elif image_set == 'val':
+ return dataset2transform_val
+ else:
+ raise NotImplementedError()
+
+
+def build(image_set, args):
+ root = Path(args.mot_path)
+ assert root.exists(), f'provided MOT path {root} does not exist'
+ dataset2transform = build_dataset2transform(args, image_set)
+ if image_set == 'train':
+ data_txt_path = args.data_txt_path_train
+ dataset = DetMOTDetection(args, data_txt_path=data_txt_path, seqs_folder=root, dataset2transform=dataset2transform)
+ if image_set == 'val':
+ data_txt_path = args.data_txt_path_val
+ dataset = DetMOTDetection(args, data_txt_path=data_txt_path, seqs_folder=root, dataset2transform=dataset2transform)
+ return dataset
+
diff --git a/VISAM/datasets/panoptic_eval.py b/VISAM/datasets/panoptic_eval.py
new file mode 100644
index 0000000000000000000000000000000000000000..a870e4fa5f307fab63c99bd0e744c57a6e141483
--- /dev/null
+++ b/VISAM/datasets/panoptic_eval.py
@@ -0,0 +1,54 @@
+# ------------------------------------------------------------------------
+# Copyright (c) 2022 megvii-research. All Rights Reserved.
+# ------------------------------------------------------------------------
+# Modified from Deformable DETR (https://github.com/fundamentalvision/Deformable-DETR)
+# Copyright (c) 2020 SenseTime. All Rights Reserved.
+# ------------------------------------------------------------------------
+# Modified from DETR (https://github.com/facebookresearch/detr)
+# Copyright (c) Facebook, Inc. and its affiliates. All Rights Reserved
+# ------------------------------------------------------------------------
+
+
+import json
+import os
+
+import util.misc as utils
+
+try:
+ from panopticapi.evaluation import pq_compute
+except ImportError:
+ pass
+
+
+class PanopticEvaluator(object):
+ def __init__(self, ann_file, ann_folder, output_dir="panoptic_eval"):
+ self.gt_json = ann_file
+ self.gt_folder = ann_folder
+ if utils.is_main_process():
+ if not os.path.exists(output_dir):
+ os.mkdir(output_dir)
+ self.output_dir = output_dir
+ self.predictions = []
+
+ def update(self, predictions):
+ for p in predictions:
+ with open(os.path.join(self.output_dir, p["file_name"]), "wb") as f:
+ f.write(p.pop("png_string"))
+
+ self.predictions += predictions
+
+ def synchronize_between_processes(self):
+ all_predictions = utils.all_gather(self.predictions)
+ merged_predictions = []
+ for p in all_predictions:
+ merged_predictions += p
+ self.predictions = merged_predictions
+
+ def summarize(self):
+ if utils.is_main_process():
+ json_data = {"annotations": self.predictions}
+ predictions_json = os.path.join(self.output_dir, "predictions.json")
+ with open(predictions_json, "w") as f:
+ f.write(json.dumps(json_data))
+ return pq_compute(self.gt_json, predictions_json, gt_folder=self.gt_folder, pred_folder=self.output_dir)
+ return None
diff --git a/VISAM/datasets/samplers.py b/VISAM/datasets/samplers.py
new file mode 100644
index 0000000000000000000000000000000000000000..7a4ede1e4ccbf050539eb475c7cfbb268f624b2e
--- /dev/null
+++ b/VISAM/datasets/samplers.py
@@ -0,0 +1,142 @@
+# ------------------------------------------------------------------------
+# Copyright (c) 2022 megvii-research. All Rights Reserved.
+# ------------------------------------------------------------------------
+# Modified from Deformable DETR (https://github.com/fundamentalvision/Deformable-DETR)
+# Copyright (c) 2020 SenseTime. All Rights Reserved.
+# ------------------------------------------------------------------------
+# Modified from DETR (https://github.com/facebookresearch/detr)
+# Copyright (c) Facebook, Inc. and its affiliates. All Rights Reserved
+# ------------------------------------------------------------------------
+
+
+import os
+import math
+import torch
+import torch.distributed as dist
+from torch.utils.data.sampler import Sampler
+
+
+class DistributedSampler(Sampler):
+ """Sampler that restricts data loading to a subset of the dataset.
+ It is especially useful in conjunction with
+ :class:`torch.nn.parallel.DistributedDataParallel`. In such case, each
+ process can pass a DistributedSampler instance as a DataLoader sampler,
+ and load a subset of the original dataset that is exclusive to it.
+ .. note::
+ Dataset is assumed to be of constant size.
+ Arguments:
+ dataset: Dataset used for sampling.
+ num_replicas (optional): Number of processes participating in
+ distributed training.
+ rank (optional): Rank of the current process within num_replicas.
+ """
+
+ def __init__(self, dataset, num_replicas=None, rank=None, local_rank=None, local_size=None, shuffle=True):
+ if num_replicas is None:
+ if not dist.is_available():
+ raise RuntimeError("Requires distributed package to be available")
+ num_replicas = dist.get_world_size()
+ if rank is None:
+ if not dist.is_available():
+ raise RuntimeError("Requires distributed package to be available")
+ rank = dist.get_rank()
+ self.dataset = dataset
+ self.num_replicas = num_replicas
+ self.rank = rank
+ self.epoch = 0
+ self.num_samples = int(math.ceil(len(self.dataset) * 1.0 / self.num_replicas))
+ self.total_size = self.num_samples * self.num_replicas
+ self.shuffle = shuffle
+
+ def __iter__(self):
+ if self.shuffle:
+ # deterministically shuffle based on epoch
+ g = torch.Generator()
+ g.manual_seed(self.epoch)
+ indices = torch.randperm(len(self.dataset), generator=g).tolist()
+ else:
+ indices = torch.arange(len(self.dataset)).tolist()
+
+ # add extra samples to make it evenly divisible
+ indices += indices[: (self.total_size - len(indices))]
+ assert len(indices) == self.total_size
+
+ # subsample
+ offset = self.num_samples * self.rank
+ indices = indices[offset : offset + self.num_samples]
+ assert len(indices) == self.num_samples
+
+ return iter(indices)
+
+ def __len__(self):
+ return self.num_samples
+
+ def set_epoch(self, epoch):
+ self.epoch = epoch
+
+
+class NodeDistributedSampler(Sampler):
+ """Sampler that restricts data loading to a subset of the dataset.
+ It is especially useful in conjunction with
+ :class:`torch.nn.parallel.DistributedDataParallel`. In such case, each
+ process can pass a DistributedSampler instance as a DataLoader sampler,
+ and load a subset of the original dataset that is exclusive to it.
+ .. note::
+ Dataset is assumed to be of constant size.
+ Arguments:
+ dataset: Dataset used for sampling.
+ num_replicas (optional): Number of processes participating in
+ distributed training.
+ rank (optional): Rank of the current process within num_replicas.
+ """
+
+ def __init__(self, dataset, num_replicas=None, rank=None, local_rank=None, local_size=None, shuffle=True):
+ if num_replicas is None:
+ if not dist.is_available():
+ raise RuntimeError("Requires distributed package to be available")
+ num_replicas = dist.get_world_size()
+ if rank is None:
+ if not dist.is_available():
+ raise RuntimeError("Requires distributed package to be available")
+ rank = dist.get_rank()
+ if local_rank is None:
+ local_rank = int(os.environ.get('LOCAL_RANK', 0))
+ if local_size is None:
+ local_size = int(os.environ.get('LOCAL_SIZE', 1))
+ self.dataset = dataset
+ self.shuffle = shuffle
+ self.num_replicas = num_replicas
+ self.num_parts = local_size
+ self.rank = rank
+ self.local_rank = local_rank
+ self.epoch = 0
+ self.num_samples = int(math.ceil(len(self.dataset) * 1.0 / self.num_replicas))
+ self.total_size = self.num_samples * self.num_replicas
+
+ self.total_size_parts = self.num_samples * self.num_replicas // self.num_parts
+
+ def __iter__(self):
+ if self.shuffle:
+ # deterministically shuffle based on epoch
+ g = torch.Generator()
+ g.manual_seed(self.epoch)
+ indices = torch.randperm(len(self.dataset), generator=g).tolist()
+ else:
+ indices = torch.arange(len(self.dataset)).tolist()
+ indices = [i for i in indices if i % self.num_parts == self.local_rank]
+
+ # add extra samples to make it evenly divisible
+ indices += indices[:(self.total_size_parts - len(indices))]
+ assert len(indices) == self.total_size_parts
+
+ # subsample
+ indices = indices[self.rank // self.num_parts:self.total_size_parts:self.num_replicas // self.num_parts]
+ assert len(indices) == self.num_samples
+
+ return iter(indices)
+
+ def __len__(self):
+ return self.num_samples
+
+ def set_epoch(self, epoch):
+ self.epoch = epoch
diff --git a/VISAM/datasets/transforms.py b/VISAM/datasets/transforms.py
new file mode 100644
index 0000000000000000000000000000000000000000..a0b902dc6656ef654b9c1f4d83c5fe4f20dce377
--- /dev/null
+++ b/VISAM/datasets/transforms.py
@@ -0,0 +1,616 @@
+# ------------------------------------------------------------------------
+# Copyright (c) 2022 megvii-research. All Rights Reserved.
+# ------------------------------------------------------------------------
+# Modified from Deformable DETR (https://github.com/fundamentalvision/Deformable-DETR)
+# Copyright (c) 2020 SenseTime. All Rights Reserved.
+# ------------------------------------------------------------------------
+# Modified from DETR (https://github.com/facebookresearch/detr)
+# Copyright (c) Facebook, Inc. and its affiliates. All Rights Reserved
+# ------------------------------------------------------------------------
+
+"""
+Transforms and data augmentation for both image + bbox.
+"""
+import copy
+import random
+import PIL
+import cv2
+import torch
+import torchvision.transforms as T
+import torchvision.transforms.functional as F
+from PIL import Image, ImageDraw
+from util.box_ops import box_xyxy_to_cxcywh
+from util.misc import interpolate
+import numpy as np
+import os
+
+
+
+def crop_mot(image, target, region):
+ cropped_image = F.crop(image, *region)
+
+ target = target.copy()
+ i, j, h, w = region
+
+ # should we do something wrt the original size?
+ target["size"] = torch.tensor([h, w])
+
+ fields = ["labels", "iscrowd", "obj_ids", "scores"]
+
+ if "boxes" in target:
+ boxes = target["boxes"]
+ max_size = torch.as_tensor([w, h], dtype=torch.float32)
+ cropped_boxes = boxes - torch.as_tensor([j, i, j, i])
+ cropped_boxes = torch.min(cropped_boxes.reshape(-1, 2, 2), max_size)
+ cropped_boxes = cropped_boxes.clamp(min=0)
+ target["boxes"] = cropped_boxes.reshape(-1, 4)
+ fields.append("boxes")
+
+ if "masks" in target:
+ # FIXME should we update the area here if there are no boxes?
+ target['masks'] = target['masks'][:, i:i + h, j:j + w]
+ fields.append("masks")
+
+ # remove elements for which the boxes or masks that have zero area
+ if "boxes" in target or "masks" in target:
+ # favor boxes selection when defining which elements to keep
+ # this is compatible with previous implementation
+ if "boxes" in target:
+ cropped_boxes = target['boxes'].reshape(-1, 2, 2)
+ keep = torch.all(cropped_boxes[:, 1, :] > cropped_boxes[:, 0, :], dim=1)
+ else:
+ keep = target['masks'].flatten(1).any(1)
+
+ for field in fields:
+ n_size = len(target[field])
+ target[field] = target[field][keep[:n_size]]
+
+ return cropped_image, target
+
+
+def random_shift(image, target, region, sizes):
+ oh, ow = sizes
+ # step 1, shift crop and re-scale image firstly
+ cropped_image = F.crop(image, *region)
+ cropped_image = F.resize(cropped_image, sizes)
+
+ target = target.copy()
+ i, j, h, w = region
+
+ # should we do something wrt the original size?
+ target["size"] = torch.tensor([h, w])
+
+ fields = ["labels", "scores", "iscrowd", "obj_ids"]
+
+ if "boxes" in target:
+ boxes = target["boxes"]
+ cropped_boxes = boxes - torch.as_tensor([j, i, j, i])
+ cropped_boxes *= torch.as_tensor([ow / w, oh / h, ow / w, oh / h])
+ target["boxes"] = cropped_boxes.reshape(-1, 4)
+ fields.append("boxes")
+
+ if "masks" in target:
+ # FIXME should we update the area here if there are no boxes?
+ target['masks'] = target['masks'][:, i:i + h, j:j + w]
+ fields.append("masks")
+
+ # remove elements for which the boxes or masks that have zero area
+ if "boxes" in target or "masks" in target:
+ # favor boxes selection when defining which elements to keep
+ # this is compatible with previous implementation
+ if "boxes" in target:
+ cropped_boxes = target['boxes'].reshape(-1, 2, 2)
+ max_size = torch.as_tensor([w, h], dtype=torch.float32)
+ cropped_boxes = torch.min(cropped_boxes.reshape(-1, 2, 2), max_size)
+ cropped_boxes = cropped_boxes.clamp(min=0)
+ keep = torch.all(cropped_boxes[:, 1, :] > cropped_boxes[:, 0, :], dim=1)
+ else:
+ keep = target['masks'].flatten(1).any(1)
+
+ for field in fields:
+ n_size = len(target[field])
+ target[field] = target[field][keep[:n_size]]
+
+ return cropped_image, target
+
+
+def crop(image, target, region):
+ cropped_image = F.crop(image, *region)
+
+ target = target.copy()
+ i, j, h, w = region
+
+ # should we do something wrt the original size?
+ target["size"] = torch.tensor([h, w])
+
+ fields = ["labels", "area", "iscrowd"]
+ if 'obj_ids' in target:
+ fields.append('obj_ids')
+
+ if "boxes" in target:
+ boxes = target["boxes"]
+ max_size = torch.as_tensor([w, h], dtype=torch.float32)
+ cropped_boxes = boxes - torch.as_tensor([j, i, j, i])
+ cropped_boxes = torch.min(cropped_boxes.reshape(-1, 2, 2), max_size)
+ cropped_boxes = cropped_boxes.clamp(min=0)
+
+ area = (cropped_boxes[:, 1, :] - cropped_boxes[:, 0, :]).prod(dim=1)
+ target["boxes"] = cropped_boxes.reshape(-1, 4)
+ target["area"] = area
+ fields.append("boxes")
+
+ if "masks" in target:
+ # FIXME should we update the area here if there are no boxes?
+ target['masks'] = target['masks'][:, i:i + h, j:j + w]
+ fields.append("masks")
+
+ # remove elements for which the boxes or masks that have zero area
+ if "boxes" in target or "masks" in target:
+ # favor boxes selection when defining which elements to keep
+ # this is compatible with previous implementation
+ if "boxes" in target:
+ cropped_boxes = target['boxes'].reshape(-1, 2, 2)
+ keep = torch.all(cropped_boxes[:, 1, :] > cropped_boxes[:, 0, :], dim=1)
+ else:
+ keep = target['masks'].flatten(1).any(1)
+
+ for field in fields:
+ target[field] = target[field][keep]
+
+ return cropped_image, target
+
+
+def hflip(image, target):
+ flipped_image = F.hflip(image)
+
+ w, h = image.size
+
+ target = target.copy()
+ if "boxes" in target:
+ boxes = target["boxes"]
+ boxes = boxes[:, [2, 1, 0, 3]] * torch.as_tensor([-1, 1, -1, 1]) + torch.as_tensor([w, 0, w, 0])
+ target["boxes"] = boxes
+
+ if "masks" in target:
+ target['masks'] = target['masks'].flip(-1)
+
+ return flipped_image, target
+
+
+def resize(image, target, size, max_size=None):
+ # size can be min_size (scalar) or (w, h) tuple
+
+ def get_size_with_aspect_ratio(image_size, size, max_size=None):
+ w, h = image_size
+ if max_size is not None:
+ min_original_size = float(min((w, h)))
+ max_original_size = float(max((w, h)))
+ if max_original_size / min_original_size * size > max_size:
+ size = int(round(max_size * min_original_size / max_original_size))
+
+ if (w <= h and w == size) or (h <= w and h == size):
+ return (h, w)
+
+ if w < h:
+ ow = size
+ oh = int(size * h / w)
+ else:
+ oh = size
+ ow = int(size * w / h)
+
+ return (oh, ow)
+
+ def get_size(image_size, size, max_size=None):
+ if isinstance(size, (list, tuple)):
+ return size[::-1]
+ else:
+ return get_size_with_aspect_ratio(image_size, size, max_size)
+
+ size = get_size(image.size, size, max_size)
+ rescaled_image = F.resize(image, size)
+
+ if target is None:
+ return rescaled_image, None
+
+ ratios = tuple(float(s) / float(s_orig) for s, s_orig in zip(rescaled_image.size, image.size))
+ ratio_width, ratio_height = ratios
+
+ target = target.copy()
+ if "boxes" in target:
+ boxes = target["boxes"]
+ scaled_boxes = boxes * torch.as_tensor([ratio_width, ratio_height, ratio_width, ratio_height])
+ target["boxes"] = scaled_boxes
+
+ if "area" in target:
+ area = target["area"]
+ scaled_area = area * (ratio_width * ratio_height)
+ target["area"] = scaled_area
+
+ h, w = size
+ target["size"] = torch.tensor([h, w])
+
+ if "masks" in target:
+ target['masks'] = interpolate(
+ target['masks'][:, None].float(), size, mode="nearest")[:, 0] > 0.5
+
+ return rescaled_image, target
+
+
+def pad(image, target, padding):
+ # assumes that we only pad on the bottom right corners
+ padded_image = F.pad(image, (0, 0, padding[0], padding[1]))
+ if target is None:
+ return padded_image, None
+ target = target.copy()
+ # should we do something wrt the original size?
+ target["size"] = torch.tensor(padded_image[::-1])
+ if "masks" in target:
+ target['masks'] = torch.nn.functional.pad(target['masks'], (0, padding[0], 0, padding[1]))
+ return padded_image, target
+
+
+class MOTHSV:
+ def __init__(self, hgain=5, sgain=30, vgain=30) -> None:
+ self.hgain = hgain
+ self.sgain = sgain
+ self.vgain = vgain
+
+ def __call__(self, imgs: list, targets: list):
+ hsv_augs = np.random.uniform(-1, 1, 3) * [self.hgain, self.sgain, self.vgain] # random gains
+ hsv_augs *= np.random.randint(0, 2, 3) # random selection of h, s, v
+ hsv_augs = hsv_augs.astype(np.int16)
+ for i in range(len(imgs)):
+ img = np.array(imgs[i])
+ img_hsv = cv2.cvtColor(img, cv2.COLOR_RGB2HSV).astype(np.int16)
+
+ img_hsv[..., 0] = (img_hsv[..., 0] + hsv_augs[0]) % 180
+ img_hsv[..., 1] = np.clip(img_hsv[..., 1] + hsv_augs[1], 0, 255)
+ img_hsv[..., 2] = np.clip(img_hsv[..., 2] + hsv_augs[2], 0, 255)
+
+ imgs[i] = cv2.cvtColor(img_hsv.astype(img.dtype), cv2.COLOR_HSV2RGB) # no return needed
+ return imgs, targets
+
+
+class RandomCrop(object):
+ def __init__(self, size):
+ self.size = size
+
+ def __call__(self, img, target):
+ region = T.RandomCrop.get_params(img, self.size)
+ return crop(img, target, region)
+
+
+class MotRandomCrop(RandomCrop):
+ def __call__(self, imgs: list, targets: list):
+ ret_imgs = []
+ ret_targets = []
+ region = T.RandomCrop.get_params(imgs[0], self.size)
+ for img_i, targets_i in zip(imgs, targets):
+ img_i, targets_i = crop(img_i, targets_i, region)
+ ret_imgs.append(img_i)
+ ret_targets.append(targets_i)
+ return ret_imgs, ret_targets
+
+class FixedMotRandomCrop(object):
+ def __init__(self, min_size: int, max_size: int):
+ self.min_size = min_size
+ self.max_size = max_size
+
+ def __call__(self, imgs: list, targets: list):
+ ret_imgs = []
+ ret_targets = []
+ w = random.randint(self.min_size, min(imgs[0].width, self.max_size))
+ h = random.randint(self.min_size, min(imgs[0].height, self.max_size))
+ region = T.RandomCrop.get_params(imgs[0], [h, w])
+ for img_i, targets_i in zip(imgs, targets):
+ img_i, targets_i = crop_mot(img_i, targets_i, region)
+ ret_imgs.append(img_i)
+ ret_targets.append(targets_i)
+ return ret_imgs, ret_targets
+
+class MotRandomShift(object):
+ def __init__(self, bs=1):
+ self.bs = bs
+
+ def __call__(self, imgs: list, targets: list):
+ ret_imgs = copy.deepcopy(imgs)
+ ret_targets = copy.deepcopy(targets)
+
+ n_frames = len(imgs)
+ select_i = random.choice(list(range(n_frames)))
+ w, h = imgs[select_i].size
+
+ xshift = (100 * torch.rand(self.bs)).int()
+ xshift *= (torch.randn(self.bs) > 0.0).int() * 2 - 1
+ yshift = (100 * torch.rand(self.bs)).int()
+ yshift *= (torch.randn(self.bs) > 0.0).int() * 2 - 1
+ ymin = max(0, -yshift[0])
+ ymax = min(h, h - yshift[0])
+ xmin = max(0, -xshift[0])
+ xmax = min(w, w - xshift[0])
+
+ region = (int(ymin), int(xmin), int(ymax-ymin), int(xmax-xmin))
+ ret_imgs[select_i], ret_targets[select_i] = random_shift(imgs[select_i], targets[select_i], region, (h,w))
+
+ return ret_imgs, ret_targets
+
+
+class FixedMotRandomShift(object):
+ def __init__(self, bs=1, padding=50):
+ self.bs = bs
+ self.padding = padding
+
+ def __call__(self, imgs: list, targets: list):
+ ret_imgs = []
+ ret_targets = []
+
+ n_frames = self.bs
+ w, h = imgs[0].size
+ xshift = (self.padding * torch.rand(self.bs)).int() + 1
+ xshift *= (torch.randn(self.bs) > 0.0).int() * 2 - 1
+ yshift = (self.padding * torch.rand(self.bs)).int() + 1
+ yshift *= (torch.randn(self.bs) > 0.0).int() * 2 - 1
+ ret_imgs.append(imgs[0])
+ ret_targets.append(targets[0])
+ for i in range(1, n_frames):
+ ymin = max(0, -yshift[0])
+ ymax = min(h, h - yshift[0])
+ xmin = max(0, -xshift[0])
+ xmax = min(w, w - xshift[0])
+ prev_img = ret_imgs[i-1].copy()
+ prev_target = copy.deepcopy(ret_targets[i-1])
+ region = (int(ymin), int(xmin), int(ymax - ymin), int(xmax - xmin))
+ img_i, target_i = random_shift(prev_img, prev_target, region, (h, w))
+ ret_imgs.append(img_i)
+ ret_targets.append(target_i)
+
+ return ret_imgs, ret_targets
+
+
+class RandomSizeCrop(object):
+ def __init__(self, min_size: int, max_size: int):
+ self.min_size = min_size
+ self.max_size = max_size
+
+ def __call__(self, img: PIL.Image.Image, target: dict):
+ w = random.randint(self.min_size, min(img.width, self.max_size))
+ h = random.randint(self.min_size, min(img.height, self.max_size))
+ region = T.RandomCrop.get_params(img, [h, w])
+ return crop(img, target, region)
+
+
+class MotRandomSizeCrop(RandomSizeCrop):
+ def __call__(self, imgs, targets):
+ w = random.randint(self.min_size, min(imgs[0].width, self.max_size))
+ h = random.randint(self.min_size, min(imgs[0].height, self.max_size))
+ region = T.RandomCrop.get_params(imgs[0], [h, w])
+ ret_imgs = []
+ ret_targets = []
+ for img_i, targets_i in zip(imgs, targets):
+ img_i, targets_i = crop(img_i, targets_i, region)
+ ret_imgs.append(img_i)
+ ret_targets.append(targets_i)
+ return ret_imgs, ret_targets
+
+
+class CenterCrop(object):
+ def __init__(self, size):
+ self.size = size
+
+ def __call__(self, img, target):
+ image_width, image_height = img.size
+ crop_height, crop_width = self.size
+ crop_top = int(round((image_height - crop_height) / 2.))
+ crop_left = int(round((image_width - crop_width) / 2.))
+ return crop(img, target, (crop_top, crop_left, crop_height, crop_width))
+
+
+class MotCenterCrop(CenterCrop):
+ def __call__(self, imgs, targets):
+ image_width, image_height = imgs[0].size
+ crop_height, crop_width = self.size
+ crop_top = int(round((image_height - crop_height) / 2.))
+ crop_left = int(round((image_width - crop_width) / 2.))
+ ret_imgs = []
+ ret_targets = []
+ for img_i, targets_i in zip(imgs, targets):
+ img_i, targets_i = crop(img_i, targets_i, (crop_top, crop_left, crop_height, crop_width))
+ ret_imgs.append(img_i)
+ ret_targets.append(targets_i)
+ return ret_imgs, ret_targets
+
+
+class RandomHorizontalFlip(object):
+ def __init__(self, p=0.5):
+ self.p = p
+
+ def __call__(self, img, target):
+ if random.random() < self.p:
+ return hflip(img, target)
+ return img, target
+
+
+class MotRandomHorizontalFlip(RandomHorizontalFlip):
+ def __call__(self, imgs, targets):
+ if random.random() < self.p:
+ ret_imgs = []
+ ret_targets = []
+ for img_i, targets_i in zip(imgs, targets):
+ img_i, targets_i = hflip(img_i, targets_i)
+ ret_imgs.append(img_i)
+ ret_targets.append(targets_i)
+ return ret_imgs, ret_targets
+ return imgs, targets
+
+
+class RandomResize(object):
+ def __init__(self, sizes, max_size=None):
+ assert isinstance(sizes, (list, tuple))
+ self.sizes = sizes
+ self.max_size = max_size
+
+ def __call__(self, img, target=None):
+ size = random.choice(self.sizes)
+ return resize(img, target, size, self.max_size)
+
+
+class MotRandomResize(RandomResize):
+ def __call__(self, imgs, targets):
+ size = random.choice(self.sizes)
+ ret_imgs = []
+ ret_targets = []
+ for img_i, targets_i in zip(imgs, targets):
+ img_i, targets_i = resize(img_i, targets_i, size, self.max_size)
+ ret_imgs.append(img_i)
+ ret_targets.append(targets_i)
+ return ret_imgs, ret_targets
+
+
+class RandomPad(object):
+ def __init__(self, max_pad):
+ self.max_pad = max_pad
+
+ def __call__(self, img, target):
+ pad_x = random.randint(0, self.max_pad)
+ pad_y = random.randint(0, self.max_pad)
+ return pad(img, target, (pad_x, pad_y))
+
+
+class MotRandomPad(RandomPad):
+ def __call__(self, imgs, targets):
+ pad_x = random.randint(0, self.max_pad)
+ pad_y = random.randint(0, self.max_pad)
+ ret_imgs = []
+ ret_targets = []
+ for img_i, targets_i in zip(imgs, targets):
+ img_i, target_i = pad(img_i, targets_i, (pad_x, pad_y))
+ ret_imgs.append(img_i)
+ ret_targets.append(targets_i)
+ return ret_imgs, ret_targets
+
+
+class RandomSelect(object):
+ """
+ Randomly selects between transforms1 and transforms2,
+ with probability p for transforms1 and (1 - p) for transforms2
+ """
+ def __init__(self, transforms1, transforms2, p=0.5):
+ self.transforms1 = transforms1
+ self.transforms2 = transforms2
+ self.p = p
+
+ def __call__(self, img, target):
+ if random.random() < self.p:
+ return self.transforms1(img, target)
+ return self.transforms2(img, target)
+
+
+class MotRandomSelect(RandomSelect):
+ """
+ Randomly selects between transforms1 and transforms2,
+ with probability p for transforms1 and (1 - p) for transforms2
+ """
+ def __call__(self, imgs, targets):
+ if random.random() < self.p:
+ return self.transforms1(imgs, targets)
+ return self.transforms2(imgs, targets)
+
+
+class ToTensor(object):
+ def __call__(self, img, target):
+ return F.to_tensor(img), target
+
+
+class MotToTensor(ToTensor):
+ def __call__(self, imgs, targets):
+ ret_imgs = []
+ for img in imgs:
+ ret_imgs.append(F.to_tensor(img))
+ return ret_imgs, targets
+
+
+class RandomErasing(object):
+
+ def __init__(self, *args, **kwargs):
+ self.eraser = T.RandomErasing(*args, **kwargs)
+
+ def __call__(self, img, target):
+ return self.eraser(img), target
+
+
+class MotRandomErasing(RandomErasing):
+ def __call__(self, imgs, targets):
+ # TODO: Rewrite this part to ensure the data augmentation is same to each image.
+ ret_imgs = []
+ for img_i, targets_i in zip(imgs, targets):
+ ret_imgs.append(self.eraser(img_i))
+ return ret_imgs, targets
+
+
+class MoTColorJitter(T.ColorJitter):
+ def __call__(self, imgs, targets):
+ transform = self.get_params(self.brightness, self.contrast,
+ self.saturation, self.hue)
+ ret_imgs = []
+ for img_i, targets_i in zip(imgs, targets):
+ ret_imgs.append(transform(img_i))
+ return ret_imgs, targets
+
+
+class Normalize(object):
+ def __init__(self, mean, std):
+ self.mean = mean
+ self.std = std
+
+ def __call__(self, image, target=None):
+ if target is not None:
+ target['ori_img'] = image.clone()
+ image = F.normalize(image, mean=self.mean, std=self.std)
+ if target is None:
+ return image, None
+ target = target.copy()
+ h, w = image.shape[-2:]
+ if "boxes" in target:
+ boxes = target["boxes"]
+ boxes = box_xyxy_to_cxcywh(boxes)
+ boxes = boxes / torch.tensor([w, h, w, h], dtype=torch.float32)
+ target["boxes"] = boxes
+ return image, target
+
+
+class MotNormalize(Normalize):
+ def __call__(self, imgs, targets=None):
+ ret_imgs = []
+ ret_targets = []
+ for i in range(len(imgs)):
+ img_i = imgs[i]
+ targets_i = targets[i] if targets is not None else None
+ img_i, targets_i = super().__call__(img_i, targets_i)
+ ret_imgs.append(img_i)
+ ret_targets.append(targets_i)
+ return ret_imgs, ret_targets
+
+
+class Compose(object):
+ def __init__(self, transforms):
+ self.transforms = transforms
+
+ def __call__(self, image, target):
+ for t in self.transforms:
+ image, target = t(image, target)
+ return image, target
+
+ def __repr__(self):
+ format_string = self.__class__.__name__ + "("
+ for t in self.transforms:
+ format_string += "\n"
+ format_string += " {0}".format(t)
+ format_string += "\n)"
+ return format_string
+
+
+class MotCompose(Compose):
+ def __call__(self, imgs, targets):
+ for t in self.transforms:
+ imgs, targets = t(imgs, targets)
+ return imgs, targets
diff --git a/VISAM/engine.py b/VISAM/engine.py
new file mode 100644
index 0000000000000000000000000000000000000000..988cbd41a9f6cafbab54a819424f795a91069029
--- /dev/null
+++ b/VISAM/engine.py
@@ -0,0 +1,80 @@
+# ------------------------------------------------------------------------
+# Copyright (c) 2022 megvii-research. All Rights Reserved.
+# ------------------------------------------------------------------------
+# Modified from Deformable DETR (https://github.com/fundamentalvision/Deformable-DETR)
+# Copyright (c) 2020 SenseTime. All Rights Reserved.
+# ------------------------------------------------------------------------
+# Modified from DETR (https://github.com/facebookresearch/detr)
+# Copyright (c) Facebook, Inc. and its affiliates. All Rights Reserved
+# ------------------------------------------------------------------------
+
+
+"""
+Train and eval functions used in main.py
+"""
+import math
+import os
+import sys
+from typing import Iterable
+
+import torch
+import util.misc as utils
+
+from datasets.data_prefetcher import data_dict_to_cuda
+
+
+def train_one_epoch_mot(model: torch.nn.Module, criterion: torch.nn.Module,
+ data_loader: Iterable, optimizer: torch.optim.Optimizer,
+ device: torch.device, epoch: int, max_norm: float = 0):
+ model.train()
+ criterion.train()
+ metric_logger = utils.MetricLogger(delimiter=" ")
+ metric_logger.add_meter('lr', utils.SmoothedValue(window_size=1, fmt='{value:.6f}'))
+ # metric_logger.add_meter('class_error', utils.SmoothedValue(window_size=1, fmt='{value:.2f}'))
+ metric_logger.add_meter('grad_norm', utils.SmoothedValue(window_size=1, fmt='{value:.2f}'))
+ header = 'Epoch: [{}]'.format(epoch)
+ print_freq = 10
+
+ # for samples, targets in metric_logger.log_every(data_loader, print_freq, header):
+ for data_dict in metric_logger.log_every(data_loader, print_freq, header):
+ data_dict = data_dict_to_cuda(data_dict, device)
+ outputs = model(data_dict)
+
+ loss_dict = criterion(outputs, data_dict)
+ # print("iter {} after model".format(cnt-1))
+ weight_dict = criterion.weight_dict
+ losses = sum(loss_dict[k] * weight_dict[k] for k in loss_dict.keys() if k in weight_dict)
+
+ # reduce losses over all GPUs for logging purposes
+ loss_dict_reduced = utils.reduce_dict(loss_dict)
+ # loss_dict_reduced_unscaled = {f'{k}_unscaled': v
+ # for k, v in loss_dict_reduced.items()}
+ loss_dict_reduced_scaled = {k: v * weight_dict[k]
+ for k, v in loss_dict_reduced.items() if k in weight_dict}
+ losses_reduced_scaled = sum(loss_dict_reduced_scaled.values())
+
+ loss_value = losses_reduced_scaled.item()
+
+ if not math.isfinite(loss_value):
+ print("Loss is {}, stopping training".format(loss_value))
+ print(loss_dict_reduced)
+ sys.exit(1)
+
+ optimizer.zero_grad()
+ losses.backward()
+ if max_norm > 0:
+ grad_total_norm = torch.nn.utils.clip_grad_norm_(model.parameters(), max_norm)
+ else:
+ grad_total_norm = utils.get_total_grad_norm(model.parameters(), max_norm)
+ optimizer.step()
+
+ # metric_logger.update(loss=loss_value, **loss_dict_reduced_scaled, **loss_dict_reduced_unscaled)
+ metric_logger.update(loss=loss_value, **loss_dict_reduced_scaled)
+ # metric_logger.update(class_error=loss_dict_reduced['class_error'])
+ metric_logger.update(lr=optimizer.param_groups[0]["lr"])
+ metric_logger.update(grad_norm=grad_total_norm)
+ # gather the stats from all processes
+
+ metric_logger.synchronize_between_processes()
+ print("Averaged stats:", metric_logger)
+ return {k: meter.global_avg for k, meter in metric_logger.meters.items()}
diff --git a/VISAM/main.py b/VISAM/main.py
new file mode 100644
index 0000000000000000000000000000000000000000..13859a86d005ab05b58b95abd6fd03473d7b7588
--- /dev/null
+++ b/VISAM/main.py
@@ -0,0 +1,332 @@
+# ------------------------------------------------------------------------
+# Copyright (c) 2022 megvii-research. All Rights Reserved.
+# ------------------------------------------------------------------------
+# Modified from Deformable DETR (https://github.com/fundamentalvision/Deformable-DETR)
+# Copyright (c) 2020 SenseTime. All Rights Reserved.
+# ------------------------------------------------------------------------
+# Modified from DETR (https://github.com/facebookresearch/detr)
+# Copyright (c) Facebook, Inc. and its affiliates. All Rights Reserved
+# ------------------------------------------------------------------------
+
+
+
+import argparse
+import datetime
+import random
+import time
+from pathlib import Path
+
+import numpy as np
+import torch
+from torch.utils.data import DataLoader
+
+from util.tool import load_model
+import util.misc as utils
+import datasets.samplers as samplers
+from datasets import build_dataset
+from engine import train_one_epoch_mot
+from models import build_model
+
+
+def get_args_parser():
+ parser = argparse.ArgumentParser('Deformable DETR Detector', add_help=False)
+ parser.add_argument('--lr', default=2e-4, type=float)
+ parser.add_argument('--lr_backbone_names', default=["backbone.0"], type=str, nargs='+')
+ parser.add_argument('--lr_backbone', default=2e-5, type=float)
+ parser.add_argument('--lr_linear_proj_names', default=['reference_points', 'sampling_offsets',], type=str, nargs='+')
+ parser.add_argument('--lr_linear_proj_mult', default=0.1, type=float)
+ parser.add_argument('--batch_size', default=2, type=int)
+ parser.add_argument('--weight_decay', default=1e-4, type=float)
+ parser.add_argument('--epochs', default=50, type=int)
+ parser.add_argument('--lr_drop', default=40, type=int)
+ parser.add_argument('--save_period', default=50, type=int)
+ parser.add_argument('--lr_drop_epochs', default=None, type=int, nargs='+')
+ parser.add_argument('--clip_max_norm', default=0.1, type=float,
+ help='gradient clipping max norm')
+
+ parser.add_argument('--meta_arch', default='deformable_detr', type=str)
+
+ parser.add_argument('--sgd', action='store_true')
+
+ # Variants of Deformable DETR
+ parser.add_argument('--with_box_refine', default=False, action='store_true')
+ parser.add_argument('--two_stage', default=False, action='store_true')
+ parser.add_argument('--accurate_ratio', default=False, action='store_true')
+
+
+ # Model parameters
+ parser.add_argument('--frozen_weights', type=str, default=None,
+ help="Path to the pretrained model. If set, only the mask head will be trained")
+ parser.add_argument('--num_anchors', default=1, type=int)
+
+ # * Backbone
+ parser.add_argument('--backbone', default='resnet50', type=str,
+ help="Name of the convolutional backbone to use")
+ parser.add_argument('--enable_fpn', action='store_true')
+ parser.add_argument('--dilation', action='store_true',
+ help="If true, we replace stride with dilation in the last convolutional block (DC5)")
+ parser.add_argument('--position_embedding', default='sine', type=str, choices=('sine', 'learned'),
+ help="Type of positional embedding to use on top of the image features")
+ parser.add_argument('--position_embedding_scale', default=2 * np.pi, type=float,
+ help="position / size * scale")
+ parser.add_argument('--num_feature_levels', default=4, type=int, help='number of feature levels')
+
+ # * Transformer
+ parser.add_argument('--enc_layers', default=6, type=int,
+ help="Number of encoding layers in the transformer")
+ parser.add_argument('--dec_layers', default=6, type=int,
+ help="Number of decoding layers in the transformer")
+ parser.add_argument('--dim_feedforward', default=1024, type=int,
+ help="Intermediate size of the feedforward layers in the transformer blocks")
+ parser.add_argument('--hidden_dim', default=256, type=int,
+ help="Size of the embeddings (dimension of the transformer)")
+ parser.add_argument('--dropout', default=0.1, type=float,
+ help="Dropout applied in the transformer")
+ parser.add_argument('--nheads', default=8, type=int,
+ help="Number of attention heads inside the transformer's attentions")
+ parser.add_argument('--num_queries', default=300, type=int,
+ help="Number of query slots")
+ parser.add_argument('--dec_n_points', default=4, type=int)
+ parser.add_argument('--enc_n_points', default=4, type=int)
+ parser.add_argument('--decoder_cross_self', default=False, action='store_true')
+ parser.add_argument('--sigmoid_attn', default=False, action='store_true')
+ parser.add_argument('--crop', action='store_true')
+ parser.add_argument('--cj', action='store_true')
+ parser.add_argument('--extra_track_attn', action='store_true')
+ parser.add_argument('--loss_normalizer', action='store_true')
+ parser.add_argument('--max_size', default=1333, type=int)
+ parser.add_argument('--val_width', default=800, type=int)
+ parser.add_argument('--filter_ignore', action='store_true')
+ parser.add_argument('--append_crowd', default=False, action='store_true')
+
+ # * Segmentation
+ parser.add_argument('--masks', action='store_true',
+ help="Train segmentation head if the flag is provided")
+
+ # Loss
+ parser.add_argument('--no_aux_loss', dest='aux_loss', action='store_false',
+ help="Disables auxiliary decoding losses (loss at each layer)")
+
+ # * Matcher
+ parser.add_argument('--mix_match', action='store_true',)
+ parser.add_argument('--set_cost_class', default=2, type=float,
+ help="Class coefficient in the matching cost")
+ parser.add_argument('--set_cost_bbox', default=5, type=float,
+ help="L1 box coefficient in the matching cost")
+ parser.add_argument('--set_cost_giou', default=2, type=float,
+ help="giou box coefficient in the matching cost")
+
+ # * Loss coefficients
+ parser.add_argument('--mask_loss_coef', default=1, type=float)
+ parser.add_argument('--dice_loss_coef', default=1, type=float)
+ parser.add_argument('--cls_loss_coef', default=2, type=float)
+ parser.add_argument('--bbox_loss_coef', default=5, type=float)
+ parser.add_argument('--giou_loss_coef', default=2, type=float)
+ parser.add_argument('--focal_alpha', default=0.25, type=float)
+
+ # dataset parameters
+ parser.add_argument('--dataset_file', default='coco')
+ parser.add_argument('--gt_file_train', type=str)
+ parser.add_argument('--gt_file_val', type=str)
+ parser.add_argument('--coco_path', default='/data/workspace/detectron2/datasets/coco/', type=str)
+ parser.add_argument('--coco_panoptic_path', type=str)
+ parser.add_argument('--remove_difficult', action='store_true')
+
+ parser.add_argument('--output_dir', default='',
+ help='path where to save, empty for no saving')
+ parser.add_argument('--device', default='cuda',
+ help='device to use for training / testing')
+ parser.add_argument('--seed', default=42, type=int)
+ parser.add_argument('--resume', default='', help='resume from checkpoint')
+ parser.add_argument('--start_epoch', default=0, type=int, metavar='N',
+ help='start epoch')
+ parser.add_argument('--eval', action='store_true')
+ parser.add_argument('--vis', action='store_true')
+ parser.add_argument('--num_workers', default=2, type=int)
+ parser.add_argument('--pretrained', default=None, help='resume from checkpoint')
+ parser.add_argument('--cache_mode', default=False, action='store_true', help='whether to cache images on memory')
+
+ # end-to-end mot settings.
+ parser.add_argument('--mot_path', default='/data/Dataset/mot', type=str)
+ parser.add_argument('--det_db', default='', type=str)
+ parser.add_argument('--input_video', default='figs/demo.mp4', type=str)
+ parser.add_argument('--data_txt_path_train',
+ default='./datasets/data_path/detmot17.train', type=str,
+ help="path to dataset txt split")
+ parser.add_argument('--data_txt_path_val',
+ default='./datasets/data_path/detmot17.train', type=str,
+ help="path to dataset txt split")
+ parser.add_argument('--img_path', default='data/valid/JPEGImages/')
+
+ parser.add_argument('--query_interaction_layer', default='QIM', type=str,
+ help="")
+ parser.add_argument('--sample_mode', type=str, default='fixed_interval')
+ parser.add_argument('--sample_interval', type=int, default=1)
+ parser.add_argument('--random_drop', type=float, default=0)
+ parser.add_argument('--fp_ratio', type=float, default=0)
+ parser.add_argument('--merger_dropout', type=float, default=0.1)
+ parser.add_argument('--update_query_pos', action='store_true')
+
+ parser.add_argument('--sampler_steps', type=int, nargs='*')
+ parser.add_argument('--sampler_lengths', type=int, nargs='*')
+ parser.add_argument('--exp_name', default='submit', type=str)
+ parser.add_argument('--memory_bank_score_thresh', type=float, default=0.)
+ parser.add_argument('--memory_bank_len', type=int, default=4)
+ parser.add_argument('--memory_bank_type', type=str, default=None)
+ parser.add_argument('--memory_bank_with_self_attn', action='store_true', default=False)
+
+ parser.add_argument('--use_checkpoint', action='store_true', default=False)
+ parser.add_argument('--query_denoise', type=float, default=0.)
+ return parser
+
+
+def main(args):
+ utils.init_distributed_mode(args)
+ print("git:\n {}\n".format(utils.get_sha()))
+
+ if args.frozen_weights is not None:
+ assert args.masks, "Frozen training is meant for segmentation only"
+ print(args)
+
+ device = torch.device(args.device)
+
+ # fix the seed for reproducibility
+ seed = args.seed + utils.get_rank()
+ torch.manual_seed(seed)
+ np.random.seed(seed)
+ random.seed(seed)
+
+ model, criterion, postprocessors = build_model(args)
+ model.to(device)
+
+ model_without_ddp = model
+ n_parameters = sum(p.numel() for p in model.parameters() if p.requires_grad)
+ print('number of params:', n_parameters)
+
+ dataset_train = build_dataset(image_set='train', args=args)
+
+ if args.distributed:
+ if args.cache_mode:
+ sampler_train = samplers.NodeDistributedSampler(dataset_train)
+ else:
+ sampler_train = samplers.DistributedSampler(dataset_train)
+ else:
+ sampler_train = torch.utils.data.RandomSampler(dataset_train)
+
+ batch_sampler_train = torch.utils.data.BatchSampler(
+ sampler_train, args.batch_size, drop_last=True)
+ collate_fn = utils.mot_collate_fn
+ data_loader_train = DataLoader(dataset_train, batch_sampler=batch_sampler_train,
+ collate_fn=collate_fn, num_workers=args.num_workers,
+ pin_memory=True)
+
+ def match_name_keywords(n, name_keywords):
+ out = False
+ for b in name_keywords:
+ if b in n:
+ out = True
+ break
+ return out
+
+ param_dicts = [
+ {
+ "params":
+ [p for n, p in model_without_ddp.named_parameters()
+ if not match_name_keywords(n, args.lr_backbone_names) and not match_name_keywords(n, args.lr_linear_proj_names) and p.requires_grad],
+ "lr": args.lr,
+ },
+ {
+ "params": [p for n, p in model_without_ddp.named_parameters() if match_name_keywords(n, args.lr_backbone_names) and p.requires_grad],
+ "lr": args.lr_backbone,
+ },
+ {
+ "params": [p for n, p in model_without_ddp.named_parameters() if match_name_keywords(n, args.lr_linear_proj_names) and p.requires_grad],
+ "lr": args.lr * args.lr_linear_proj_mult,
+ }
+ ]
+ if args.sgd:
+ optimizer = torch.optim.SGD(param_dicts, lr=args.lr, momentum=0.9,
+ weight_decay=args.weight_decay)
+ else:
+ optimizer = torch.optim.AdamW(param_dicts, lr=args.lr,
+ weight_decay=args.weight_decay)
+ lr_scheduler = torch.optim.lr_scheduler.StepLR(optimizer, args.lr_drop)
+
+ if args.distributed:
+ model = torch.nn.parallel.DistributedDataParallel(model, device_ids=[args.gpu])
+ model_without_ddp = model.module
+
+ if args.frozen_weights is not None:
+ checkpoint = torch.load(args.frozen_weights, map_location='cpu')
+ model_without_ddp.detr.load_state_dict(checkpoint['model'])
+
+ if args.pretrained is not None:
+ model_without_ddp = load_model(model_without_ddp, args.pretrained)
+
+ output_dir = Path(args.output_dir)
+ if args.resume:
+ if args.resume.startswith('https'):
+ checkpoint = torch.hub.load_state_dict_from_url(
+ args.resume, map_location='cpu', check_hash=True)
+ else:
+ checkpoint = torch.load(args.resume, map_location='cpu')
+ missing_keys, unexpected_keys = model_without_ddp.load_state_dict(checkpoint['model'], strict=False)
+ unexpected_keys = [k for k in unexpected_keys if not (k.endswith('total_params') or k.endswith('total_ops'))]
+ if len(missing_keys) > 0:
+ print('Missing Keys: {}'.format(missing_keys))
+ if len(unexpected_keys) > 0:
+ print('Unexpected Keys: {}'.format(unexpected_keys))
+ if not args.eval and 'optimizer' in checkpoint and 'lr_scheduler' in checkpoint and 'epoch' in checkpoint:
+ import copy
+ p_groups = copy.deepcopy(optimizer.param_groups)
+ optimizer.load_state_dict(checkpoint['optimizer'])
+ for pg, pg_old in zip(optimizer.param_groups, p_groups):
+ pg['lr'] = pg_old['lr']
+ pg['initial_lr'] = pg_old['initial_lr']
+ # print(optimizer.param_groups)
+ lr_scheduler.load_state_dict(checkpoint['lr_scheduler'])
+ # todo: this is a hack for doing experiment that resume from checkpoint and also modify lr scheduler (e.g., decrease lr in advance).
+ args.override_resumed_lr_drop = True
+ if args.override_resumed_lr_drop:
+ print('Warning: (hack) args.override_resumed_lr_drop is set to True, so args.lr_drop would override lr_drop in resumed lr_scheduler.')
+ lr_scheduler.step_size = args.lr_drop
+ lr_scheduler.base_lrs = list(map(lambda group: group['initial_lr'], optimizer.param_groups))
+ lr_scheduler.step(lr_scheduler.last_epoch)
+ args.start_epoch = checkpoint['epoch'] + 1
+
+ print("Start training")
+ start_time = time.time()
+
+ dataset_train.set_epoch(args.start_epoch)
+ for epoch in range(args.start_epoch, args.epochs):
+ if args.distributed:
+ sampler_train.set_epoch(epoch)
+ train_stats = train_one_epoch_mot(
+ model, criterion, data_loader_train, optimizer, device, epoch, args.clip_max_norm)
+ lr_scheduler.step()
+ if args.output_dir:
+ checkpoint_paths = [output_dir / 'checkpoint.pth']
+ # extra checkpoint before LR drop and every 5 epochs
+ if (epoch + 1) % args.lr_drop == 0 or (epoch + 1) % args.save_period == 0 or (((args.epochs >= 100 and (epoch + 1) > 100) or args.epochs < 100) and (epoch + 1) % 5 == 0):
+ checkpoint_paths.append(output_dir / f'checkpoint{epoch:04}.pth')
+ for checkpoint_path in checkpoint_paths:
+ utils.save_on_master({
+ 'model': model_without_ddp.state_dict(),
+ 'optimizer': optimizer.state_dict(),
+ 'lr_scheduler': lr_scheduler.state_dict(),
+ 'epoch': epoch,
+ 'args': args,
+ }, checkpoint_path)
+
+ dataset_train.step_epoch()
+ total_time = time.time() - start_time
+ total_time_str = str(datetime.timedelta(seconds=int(total_time)))
+ print('Training time {}'.format(total_time_str))
+
+
+if __name__ == '__main__':
+ parser = argparse.ArgumentParser('Deformable DETR training and evaluation script', parents=[get_args_parser()])
+ args = parser.parse_args()
+ if args.output_dir:
+ Path(args.output_dir).mkdir(parents=True, exist_ok=True)
+ main(args)
diff --git a/VISAM/models/__init__.py b/VISAM/models/__init__.py
new file mode 100644
index 0000000000000000000000000000000000000000..c621adca73917d93b8197f59890f688b234ce789
--- /dev/null
+++ b/VISAM/models/__init__.py
@@ -0,0 +1,20 @@
+# ------------------------------------------------------------------------
+# Deformable DETR
+# Copyright (c) 2020 SenseTime. All Rights Reserved.
+# Licensed under the Apache License, Version 2.0 [see LICENSE for details]
+# ------------------------------------------------------------------------
+# Modified from DETR (https://github.com/facebookresearch/detr)
+# Copyright (c) Facebook, Inc. and its affiliates. All Rights Reserved
+# ------------------------------------------------------------------------
+
+from .motr import build as build_motr
+
+
+def build_model(args):
+ arch_catalog = {
+ 'motr': build_motr,
+ }
+ assert args.meta_arch in arch_catalog, 'invalid arch: {}'.format(args.meta_arch)
+ build_func = arch_catalog[args.meta_arch]
+ return build_func(args)
+
diff --git a/VISAM/models/backbone.py b/VISAM/models/backbone.py
new file mode 100644
index 0000000000000000000000000000000000000000..9f7b6476108296ccba9fd3c5707e006187d2e535
--- /dev/null
+++ b/VISAM/models/backbone.py
@@ -0,0 +1,138 @@
+# ------------------------------------------------------------------------
+# Copyright (c) 2022 megvii-research. All Rights Reserved.
+# ------------------------------------------------------------------------
+# Modified from Deformable DETR (https://github.com/fundamentalvision/Deformable-DETR)
+# Copyright (c) 2020 SenseTime. All Rights Reserved.
+# ------------------------------------------------------------------------
+# Modified from DETR (https://github.com/facebookresearch/detr)
+# Copyright (c) Facebook, Inc. and its affiliates. All Rights Reserved
+# ------------------------------------------------------------------------
+
+
+"""
+Backbone modules.
+"""
+import torch.nn as nn
+import torch
+import torch.nn.functional as F
+import torchvision
+from torch import nn
+from torchvision.models._utils import IntermediateLayerGetter
+from typing import Dict, List
+
+from util.misc import NestedTensor, is_main_process
+from .position_encoding import build_position_encoding
+
+
+class FrozenBatchNorm2d(torch.nn.Module):
+ """
+ BatchNorm2d where the batch statistics and the affine parameters are fixed.
+
+ Copy-paste from torchvision.misc.ops with added eps before rqsrt,
+ without which any other models than torchvision.models.resnet[18,34,50,101]
+ produce nans.
+ """
+
+ def __init__(self, n, eps=1e-5):
+ super(FrozenBatchNorm2d, self).__init__()
+ self.register_buffer("weight", torch.ones(n))
+ self.register_buffer("bias", torch.zeros(n))
+ self.register_buffer("running_mean", torch.zeros(n))
+ self.register_buffer("running_var", torch.ones(n))
+ self.eps = eps
+
+ def _load_from_state_dict(self, state_dict, prefix, local_metadata, strict,
+ missing_keys, unexpected_keys, error_msgs):
+ num_batches_tracked_key = prefix + 'num_batches_tracked'
+ if num_batches_tracked_key in state_dict:
+ del state_dict[num_batches_tracked_key]
+
+ super(FrozenBatchNorm2d, self)._load_from_state_dict(
+ state_dict, prefix, local_metadata, strict,
+ missing_keys, unexpected_keys, error_msgs)
+
+ def forward(self, x):
+ # move reshapes to the beginning
+ # to make it fuser-friendly
+ w = self.weight.reshape(1, -1, 1, 1)
+ b = self.bias.reshape(1, -1, 1, 1)
+ rv = self.running_var.reshape(1, -1, 1, 1)
+ rm = self.running_mean.reshape(1, -1, 1, 1)
+ eps = self.eps
+ scale = w * (rv + eps).rsqrt()
+ bias = b - rm * scale
+ return x * scale + bias
+
+
+class BackboneBase(nn.Module):
+
+ def __init__(self, backbone: nn.Module, train_backbone: bool, return_interm_layers: bool):
+ super().__init__()
+ for name, parameter in backbone.named_parameters():
+ if not train_backbone or 'layer2' not in name and 'layer3' not in name and 'layer4' not in name:
+ parameter.requires_grad_(False)
+
+ if return_interm_layers:
+ return_layers = {"layer2": "0", "layer3": "1", "layer4": "2"}
+ self.strides = [8, 16, 32]
+ self.num_channels = [512, 1024, 2048]
+ else:
+ return_layers = {'layer4': "0"}
+ self.strides = [32]
+ self.num_channels = [2048]
+ self.body = IntermediateLayerGetter(backbone, return_layers=return_layers)
+
+ def forward(self, tensor_list: NestedTensor):
+ xs = self.body(tensor_list.tensors)
+ out: Dict[str, NestedTensor] = {}
+ for name, x in xs.items():
+ m = tensor_list.mask
+ assert m is not None
+ mask = F.interpolate(m[None].float(), size=x.shape[-2:]).to(torch.bool)[0]
+ out[name] = NestedTensor(x, mask)
+ return out
+
+
+class Backbone(BackboneBase):
+ """ResNet backbone with frozen BatchNorm."""
+ def __init__(self, name: str,
+ train_backbone: bool,
+ return_interm_layers: bool,
+ dilation: bool,):
+ norm_layer = FrozenBatchNorm2d
+ backbone = getattr(torchvision.models, name)(
+ replace_stride_with_dilation=[False, False, dilation],
+ pretrained=False, norm_layer=norm_layer) # is_main_process()
+ assert name not in ('resnet18', 'resnet34'), "number of channels are hard coded"
+ super().__init__(backbone, train_backbone, return_interm_layers)
+ if dilation:
+ self.strides[-1] = self.strides[-1] // 2
+
+
+class Joiner(nn.Sequential):
+ def __init__(self, backbone, position_embedding):
+ super().__init__(backbone, position_embedding)
+ self.strides = backbone.strides
+ self.num_channels = backbone.num_channels
+
+ def forward(self, tensor_list: NestedTensor):
+ xs = self[0](tensor_list)
+ out: List[NestedTensor] = []
+ pos = []
+ for name, x in sorted(xs.items()):
+ out.append(x)
+
+ # position encoding
+ for x in out:
+ pos.append(self[1](x).to(x.tensors.dtype))
+
+ return out, pos
+
+
+def build_backbone(args):
+ position_embedding = build_position_encoding(args)
+ train_backbone = args.lr_backbone > 0
+ return_interm_layers = args.masks or (args.num_feature_levels > 1)
+ backbone = Backbone(args.backbone, train_backbone, return_interm_layers, args.dilation)
+ model = Joiner(backbone, position_embedding)
+ return model
diff --git a/VISAM/models/deformable_detr.py b/VISAM/models/deformable_detr.py
new file mode 100644
index 0000000000000000000000000000000000000000..2a2c90d73509622c5c4088d2a7d65e1836078dd8
--- /dev/null
+++ b/VISAM/models/deformable_detr.py
@@ -0,0 +1,235 @@
+# ------------------------------------------------------------------------
+# Copyright (c) 2022 megvii-research. All Rights Reserved.
+# ------------------------------------------------------------------------
+# Modified from Deformable DETR (https://github.com/fundamentalvision/Deformable-DETR)
+# Copyright (c) 2020 SenseTime. All Rights Reserved.
+# ------------------------------------------------------------------------
+# Modified from DETR (https://github.com/facebookresearch/detr)
+# Copyright (c) Facebook, Inc. and its affiliates. All Rights Reserved
+# ------------------------------------------------------------------------
+
+
+"""
+Deformable DETR model and criterion classes.
+"""
+import torch
+import torch.nn.functional as F
+from torch import nn
+
+from util import box_ops
+from util.misc import (nested_tensor_from_tensor_list,
+ accuracy, get_world_size, interpolate,
+ is_dist_avail_and_initialized)
+
+import copy
+
+
+def sigmoid_focal_loss(inputs, targets, num_boxes, alpha: float = 0.25, gamma: float = 2, mean_in_dim1=True):
+ """
+ Loss used in RetinaNet for dense detection: https://arxiv.org/abs/1708.02002.
+ Args:
+ inputs: A float tensor of arbitrary shape.
+ The predictions for each example.
+ targets: A float tensor with the same shape as inputs. Stores the binary
+ classification label for each element in inputs
+ (0 for the negative class and 1 for the positive class).
+ alpha: (optional) Weighting factor in range (0,1) to balance
+ positive vs negative examples. Default = -1 (no weighting).
+ gamma: Exponent of the modulating factor (1 - p_t) to
+ balance easy vs hard examples.
+ Returns:
+ Loss tensor
+ """
+ prob = inputs.sigmoid()
+ ce_loss = F.binary_cross_entropy_with_logits(inputs, targets, reduction="none")
+ p_t = prob * targets + (1 - prob) * (1 - targets)
+ loss = ce_loss * ((1 - p_t) ** gamma)
+
+ if alpha >= 0:
+ alpha_t = alpha * targets + (1 - alpha) * (1 - targets)
+ loss = alpha_t * loss
+ if mean_in_dim1:
+ return loss.mean(1).sum() / num_boxes
+ else:
+ return loss.sum() / num_boxes
+
+
+class SetCriterion(nn.Module):
+ """ This class computes the loss for DETR.
+ The process happens in two steps:
+ 1) we compute hungarian assignment between ground truth boxes and the outputs of the model
+ 2) we supervise each pair of matched ground-truth / prediction (supervise class and box)
+ """
+ def __init__(self, num_classes, matcher, weight_dict, losses, focal_alpha=0.25):
+ """ Create the criterion.
+ Parameters:
+ num_classes: number of object categories, omitting the special no-object category
+ matcher: module able to compute a matching between targets and proposals
+ weight_dict: dict containing as key the names of the losses and as values their relative weight.
+ losses: list of all the losses to be applied. See get_loss for list of available losses.
+ focal_alpha: alpha in Focal Loss
+ """
+ super().__init__()
+ self.num_classes = num_classes
+ self.matcher = matcher
+ self.weight_dict = weight_dict
+ self.losses = losses
+ self.focal_alpha = focal_alpha
+
+ def loss_labels(self, outputs, targets, indices, num_boxes, log=True):
+ """Classification loss (NLL)
+ targets dicts must contain the key "labels" containing a tensor of dim [nb_target_boxes]
+ """
+ assert 'pred_logits' in outputs
+ src_logits = outputs['pred_logits']
+
+ idx = self._get_src_permutation_idx(indices)
+ target_classes_o = torch.cat([t["labels"][J] for t, (_, J) in zip(targets, indices)])
+ target_classes = torch.full(src_logits.shape[:2], self.num_classes,
+ dtype=torch.int64, device=src_logits.device)
+ target_classes[idx] = target_classes_o
+
+ target_classes_onehot = torch.zeros([src_logits.shape[0], src_logits.shape[1], src_logits.shape[2] + 1],
+ dtype=src_logits.dtype, layout=src_logits.layout, device=src_logits.device)
+ target_classes_onehot.scatter_(2, target_classes.unsqueeze(-1), 1)
+
+ target_classes_onehot = target_classes_onehot[:,:,:-1]
+ loss_ce = sigmoid_focal_loss(src_logits, target_classes_onehot, num_boxes, alpha=self.focal_alpha, gamma=2) * src_logits.shape[1]
+ losses = {'loss_ce': loss_ce}
+
+ if log:
+ # TODO this should probably be a separate loss, not hacked in this one here
+ losses['class_error'] = 100 - accuracy(src_logits[idx], target_classes_o)[0]
+ return losses
+
+ @torch.no_grad()
+ def loss_cardinality(self, outputs, targets, indices, num_boxes):
+ """ Compute the cardinality error, ie the absolute error in the number of predicted non-empty boxes
+ This is not really a loss, it is intended for logging purposes only. It doesn't propagate gradients
+ """
+ pred_logits = outputs['pred_logits']
+ device = pred_logits.device
+ tgt_lengths = torch.as_tensor([len(v["labels"]) for v in targets], device=device)
+ # Count the number of predictions that are NOT "no-object" (which is the last class)
+ card_pred = (pred_logits.argmax(-1) != pred_logits.shape[-1] - 1).sum(1)
+ card_err = F.l1_loss(card_pred.float(), tgt_lengths.float())
+ losses = {'cardinality_error': card_err}
+ return losses
+
+ def loss_boxes(self, outputs, targets, indices, num_boxes):
+ """Compute the losses related to the bounding boxes, the L1 regression loss and the GIoU loss
+ targets dicts must contain the key "boxes" containing a tensor of dim [nb_target_boxes, 4]
+ The target boxes are expected in format (center_x, center_y, h, w), normalized by the image size.
+ """
+ assert 'pred_boxes' in outputs
+ idx = self._get_src_permutation_idx(indices)
+ src_boxes = outputs['pred_boxes'][idx]
+ target_boxes = torch.cat([t['boxes'][i] for t, (_, i) in zip(targets, indices)], dim=0)
+
+ loss_bbox = F.l1_loss(src_boxes, target_boxes, reduction='none')
+
+ losses = {}
+ losses['loss_bbox'] = loss_bbox.sum() / num_boxes
+
+ loss_giou = 1 - torch.diag(box_ops.generalized_box_iou(
+ box_ops.box_cxcywh_to_xyxy(src_boxes),
+ box_ops.box_cxcywh_to_xyxy(target_boxes)))
+ losses['loss_giou'] = loss_giou.sum() / num_boxes
+ return losses
+
+ def _get_src_permutation_idx(self, indices):
+ # permute predictions following indices
+ batch_idx = torch.cat([torch.full_like(src, i) for i, (src, _) in enumerate(indices)])
+ src_idx = torch.cat([src for (src, _) in indices])
+ return batch_idx, src_idx
+
+ def _get_tgt_permutation_idx(self, indices):
+ # permute targets following indices
+ batch_idx = torch.cat([torch.full_like(tgt, i) for i, (_, tgt) in enumerate(indices)])
+ tgt_idx = torch.cat([tgt for (_, tgt) in indices])
+ return batch_idx, tgt_idx
+
+ def get_loss(self, loss, outputs, targets, indices, num_boxes, **kwargs):
+ loss_map = {
+ 'labels': self.loss_labels,
+ 'cardinality': self.loss_cardinality,
+ 'boxes': self.loss_boxes
+ }
+ assert loss in loss_map, f'do you really want to compute {loss} loss?'
+ return loss_map[loss](outputs, targets, indices, num_boxes, **kwargs)
+
+ def forward(self, outputs, targets):
+ """ This performs the loss computation.
+ Parameters:
+ outputs: dict of tensors, see the output specification of the model for the format
+ targets: list of dicts, such that len(targets) == batch_size.
+ The expected keys in each dict depends on the losses applied, see each loss' doc
+ """
+ outputs_without_aux = {k: v for k, v in outputs.items() if k != 'aux_outputs' and k != 'enc_outputs'}
+
+ # Retrieve the matching between the outputs of the last layer and the targets
+ indices = self.matcher(outputs_without_aux, targets)
+
+ # Compute the average number of target boxes accross all nodes, for normalization purposes
+ num_boxes = sum(len(t["labels"]) for t in targets)
+ num_boxes = torch.as_tensor([num_boxes], dtype=torch.float, device=next(iter(outputs.values())).device)
+ if is_dist_avail_and_initialized():
+ torch.distributed.all_reduce(num_boxes)
+ num_boxes = torch.clamp(num_boxes / get_world_size(), min=1).item()
+
+ # Compute all the requested losses
+ losses = {}
+ for loss in self.losses:
+ kwargs = {}
+ losses.update(self.get_loss(loss, outputs, targets, indices, num_boxes, **kwargs))
+
+ # In case of auxiliary losses, we repeat this process with the output of each intermediate layer.
+ if 'aux_outputs' in outputs:
+ for i, aux_outputs in enumerate(outputs['aux_outputs']):
+ indices = self.matcher(aux_outputs, targets)
+ for loss in self.losses:
+ if loss == 'masks':
+ # Intermediate masks losses are too costly to compute, we ignore them.
+ continue
+ kwargs = {}
+ if loss == 'labels':
+ # Logging is enabled only for the last layer
+ kwargs['log'] = False
+ l_dict = self.get_loss(loss, aux_outputs, targets, indices, num_boxes, **kwargs)
+ l_dict = {k + f'_{i}': v for k, v in l_dict.items()}
+ losses.update(l_dict)
+
+ if 'enc_outputs' in outputs:
+ enc_outputs = outputs['enc_outputs']
+ bin_targets = copy.deepcopy(targets)
+ for bt in bin_targets:
+ bt['labels'] = torch.zeros_like(bt['labels'])
+ indices = self.matcher(enc_outputs, bin_targets)
+ for loss in self.losses:
+ if loss == 'masks':
+ # Intermediate masks losses are too costly to compute, we ignore them.
+ continue
+ kwargs = {}
+ if loss == 'labels':
+ # Logging is enabled only for the last layer
+ kwargs['log'] = False
+ l_dict = self.get_loss(loss, enc_outputs, bin_targets, indices, num_boxes, **kwargs)
+ l_dict = {k + f'_enc': v for k, v in l_dict.items()}
+ losses.update(l_dict)
+
+ return losses
+
+
+class MLP(nn.Module):
+ """ Very simple multi-layer perceptron (also called FFN)"""
+
+ def __init__(self, input_dim, hidden_dim, output_dim, num_layers):
+ super().__init__()
+ self.num_layers = num_layers
+ h = [hidden_dim] * (num_layers - 1)
+ self.layers = nn.ModuleList(nn.Linear(n, k) for n, k in zip([input_dim] + h, h + [output_dim]))
+
+ def forward(self, x):
+ for i, layer in enumerate(self.layers):
+ x = F.relu(layer(x)) if i < self.num_layers - 1 else layer(x)
+ return x
diff --git a/VISAM/models/deformable_transformer_plus.py b/VISAM/models/deformable_transformer_plus.py
new file mode 100644
index 0000000000000000000000000000000000000000..9e48f3d863422b960765834665743d6e871d31b9
--- /dev/null
+++ b/VISAM/models/deformable_transformer_plus.py
@@ -0,0 +1,489 @@
+# ------------------------------------------------------------------------
+# Copyright (c) 2022 megvii-research. All Rights Reserved.
+# ------------------------------------------------------------------------
+# Modified from Deformable DETR (https://github.com/fundamentalvision/Deformable-DETR)
+# Copyright (c) 2020 SenseTime. All Rights Reserved.
+# ------------------------------------------------------------------------
+# Modified from DETR (https://github.com/facebookresearch/detr)
+# Copyright (c) Facebook, Inc. and its affiliates. All Rights Reserved
+# ------------------------------------------------------------------------
+
+
+import copy
+from typing import Optional, List
+import math
+
+import torch
+import torch.nn.functional as F
+from torch import nn, Tensor
+from torch.nn.init import xavier_uniform_, constant_, uniform_, normal_
+
+from models.structures import Boxes, matched_boxlist_iou, pairwise_iou
+
+from util.misc import inverse_sigmoid
+from util.box_ops import box_cxcywh_to_xyxy
+from models.ops.modules import MSDeformAttn
+
+
+class DeformableTransformer(nn.Module):
+ def __init__(self, d_model=256, nhead=8,
+ num_encoder_layers=6, num_decoder_layers=6, dim_feedforward=1024, dropout=0.1,
+ activation="relu", return_intermediate_dec=False,
+ num_feature_levels=4, dec_n_points=4, enc_n_points=4,
+ two_stage=False, two_stage_num_proposals=300, decoder_self_cross=True, sigmoid_attn=False,
+ extra_track_attn=False, memory_bank=False):
+ super().__init__()
+
+ self.new_frame_adaptor = None
+ self.d_model = d_model
+ self.nhead = nhead
+ self.two_stage = two_stage
+ self.two_stage_num_proposals = two_stage_num_proposals
+
+ encoder_layer = DeformableTransformerEncoderLayer(d_model, dim_feedforward,
+ dropout, activation,
+ num_feature_levels, nhead, enc_n_points,
+ sigmoid_attn=sigmoid_attn)
+ self.encoder = DeformableTransformerEncoder(encoder_layer, num_encoder_layers)
+
+ decoder_layer = DeformableTransformerDecoderLayer(d_model, dim_feedforward,
+ dropout, activation,
+ num_feature_levels, nhead, dec_n_points, decoder_self_cross,
+ sigmoid_attn=sigmoid_attn, extra_track_attn=extra_track_attn,
+ memory_bank=memory_bank)
+ self.decoder = DeformableTransformerDecoder(decoder_layer, num_decoder_layers, return_intermediate_dec)
+
+ self.level_embed = nn.Parameter(torch.Tensor(num_feature_levels, d_model))
+
+ if two_stage:
+ self.enc_output = nn.Linear(d_model, d_model)
+ self.enc_output_norm = nn.LayerNorm(d_model)
+ self.pos_trans = nn.Linear(d_model * 2, d_model * 2)
+ self.pos_trans_norm = nn.LayerNorm(d_model * 2)
+
+ self._reset_parameters()
+
+ def _reset_parameters(self):
+ for p in self.parameters():
+ if p.dim() > 1:
+ nn.init.xavier_uniform_(p)
+ for m in self.modules():
+ if isinstance(m, MSDeformAttn):
+ m._reset_parameters()
+ normal_(self.level_embed)
+
+ def get_proposal_pos_embed(self, proposals):
+ num_pos_feats = 128
+ temperature = 10000
+ scale = 2 * math.pi
+
+ dim_t = torch.arange(num_pos_feats, dtype=torch.float32, device=proposals.device)
+ dim_t = temperature ** (2 * (dim_t // 2) / num_pos_feats)
+ # N, L, 4
+ proposals = proposals.sigmoid() * scale
+ # N, L, 4, 128
+ pos = proposals[:, :, :, None] / dim_t
+ # N, L, 4, 64, 2
+ pos = torch.stack((pos[:, :, :, 0::2].sin(), pos[:, :, :, 1::2].cos()), dim=4).flatten(2)
+ return pos
+
+ def gen_encoder_output_proposals(self, memory, memory_padding_mask, spatial_shapes):
+ N_, S_, C_ = memory.shape
+ base_scale = 4.0
+ proposals = []
+ _cur = 0
+ for lvl, (H_, W_) in enumerate(spatial_shapes):
+ mask_flatten_ = memory_padding_mask[:, _cur:(_cur + H_ * W_)].view(N_, H_, W_, 1)
+ valid_H = torch.sum(~mask_flatten_[:, :, 0, 0], 1)
+ valid_W = torch.sum(~mask_flatten_[:, 0, :, 0], 1)
+
+ grid_y, grid_x = torch.meshgrid(torch.linspace(0, H_ - 1, H_, dtype=torch.float32, device=memory.device),
+ torch.linspace(0, W_ - 1, W_, dtype=torch.float32, device=memory.device))
+ grid = torch.cat([grid_x.unsqueeze(-1), grid_y.unsqueeze(-1)], -1)
+
+ scale = torch.cat([valid_W.unsqueeze(-1), valid_H.unsqueeze(-1)], 1).view(N_, 1, 1, 2)
+ grid = (grid.unsqueeze(0).expand(N_, -1, -1, -1) + 0.5) / scale
+ wh = torch.ones_like(grid) * 0.05 * (2.0 ** lvl)
+ proposal = torch.cat((grid, wh), -1).view(N_, -1, 4)
+ proposals.append(proposal)
+ _cur += (H_ * W_)
+ output_proposals = torch.cat(proposals, 1)
+ output_proposals_valid = ((output_proposals > 0.01) & (output_proposals < 0.99)).all(-1, keepdim=True)
+ output_proposals = torch.log(output_proposals / (1 - output_proposals))
+ output_proposals = output_proposals.masked_fill(memory_padding_mask.unsqueeze(-1), float('inf'))
+ output_proposals = output_proposals.masked_fill(~output_proposals_valid, float('inf'))
+
+ output_memory = memory
+ output_memory = output_memory.masked_fill(memory_padding_mask.unsqueeze(-1), float(0))
+ output_memory = output_memory.masked_fill(~output_proposals_valid, float(0))
+ output_memory = self.enc_output_norm(self.enc_output(output_memory))
+ return output_memory, output_proposals
+
+ def get_valid_ratio(self, mask):
+ _, H, W = mask.shape
+ valid_H = torch.sum(~mask[:, :, 0], 1)
+ valid_W = torch.sum(~mask[:, 0, :], 1)
+ valid_ratio_h = valid_H.float() / H
+ valid_ratio_w = valid_W.float() / W
+ valid_ratio = torch.stack([valid_ratio_w, valid_ratio_h], -1)
+ return valid_ratio
+
+ def forward(self, srcs, masks, pos_embeds, query_embed=None, ref_pts=None, mem_bank=None, mem_bank_pad_mask=None, attn_mask=None):
+ assert self.two_stage or query_embed is not None
+
+ # prepare input for encoder
+ src_flatten = []
+ mask_flatten = []
+ lvl_pos_embed_flatten = []
+ spatial_shapes = []
+ for lvl, (src, mask, pos_embed) in enumerate(zip(srcs, masks, pos_embeds)):
+ bs, c, h, w = src.shape
+ spatial_shape = (h, w)
+ spatial_shapes.append(spatial_shape)
+ src = src.flatten(2).transpose(1, 2)
+ mask = mask.flatten(1)
+ pos_embed = pos_embed.flatten(2).transpose(1, 2)
+ lvl_pos_embed = pos_embed + self.level_embed[lvl].view(1, 1, -1)
+ lvl_pos_embed_flatten.append(lvl_pos_embed)
+ src_flatten.append(src)
+ mask_flatten.append(mask)
+ src_flatten = torch.cat(src_flatten, 1)
+ mask_flatten = torch.cat(mask_flatten, 1)
+ lvl_pos_embed_flatten = torch.cat(lvl_pos_embed_flatten, 1)
+ spatial_shapes = torch.as_tensor(spatial_shapes, dtype=torch.long, device=src_flatten.device)
+ level_start_index = torch.cat((spatial_shapes.new_zeros((1, )), spatial_shapes.prod(1).cumsum(0)[:-1]))
+ valid_ratios = torch.stack([self.get_valid_ratio(m) for m in masks], 1)
+
+ # encoder
+ memory = self.encoder(src_flatten, spatial_shapes, level_start_index, valid_ratios, lvl_pos_embed_flatten, mask_flatten)
+ # prepare input for decoder
+ bs, _, c = memory.shape
+ if self.two_stage:
+ output_memory, output_proposals = self.gen_encoder_output_proposals(memory, mask_flatten, spatial_shapes)
+
+ # hack implementation for two-stage Deformable DETR
+ enc_outputs_class = self.decoder.class_embed[self.decoder.num_layers](output_memory)
+ enc_outputs_coord_unact = self.decoder.bbox_embed[self.decoder.num_layers](output_memory) + output_proposals
+
+ topk = self.two_stage_num_proposals
+ topk_proposals = torch.topk(enc_outputs_class[..., 0], topk, dim=1)[1]
+ topk_coords_unact = torch.gather(enc_outputs_coord_unact, 1, topk_proposals.unsqueeze(-1).repeat(1, 1, 4))
+ topk_coords_unact = topk_coords_unact.detach()
+ reference_points = topk_coords_unact.sigmoid()
+ init_reference_out = reference_points
+ pos_trans_out = self.pos_trans_norm(self.pos_trans(self.get_proposal_pos_embed(topk_coords_unact)))
+ query_embed, tgt = torch.split(pos_trans_out, c, dim=2)
+ else:
+ tgt = query_embed.unsqueeze(0).expand(bs, -1, -1)
+ reference_points = ref_pts.unsqueeze(0).expand(bs, -1, -1)
+ init_reference_out = reference_points
+ # decoder
+ hs, inter_references = self.decoder(tgt, reference_points, memory,
+ spatial_shapes, level_start_index,
+ valid_ratios, mask_flatten,
+ mem_bank, mem_bank_pad_mask, attn_mask)
+
+ inter_references_out = inter_references
+ if self.two_stage:
+ return hs, init_reference_out, inter_references_out, enc_outputs_class, enc_outputs_coord_unact
+ return hs, init_reference_out, inter_references_out, None, None
+
+
+class DeformableTransformerEncoderLayer(nn.Module):
+ def __init__(self,
+ d_model=256, d_ffn=1024,
+ dropout=0.1, activation="relu",
+ n_levels=4, n_heads=8, n_points=4, sigmoid_attn=False):
+ super().__init__()
+
+ # self attention
+ self.self_attn = MSDeformAttn(d_model, n_levels, n_heads, n_points, sigmoid_attn=sigmoid_attn)
+ self.dropout1 = nn.Dropout(dropout)
+ self.norm1 = nn.LayerNorm(d_model)
+
+ # ffn
+ self.linear1 = nn.Linear(d_model, d_ffn)
+ self.activation = _get_activation_fn(activation)
+ self.dropout_relu = ReLUDropout(dropout, True)
+ self.linear2 = nn.Linear(d_ffn, d_model)
+ self.dropout3 = nn.Dropout(dropout)
+ self.norm2 = nn.LayerNorm(d_model)
+
+ @staticmethod
+ def with_pos_embed(tensor, pos):
+ return tensor if pos is None else tensor + pos
+
+ def forward_ffn(self, src):
+ src2 = self.linear2(self.dropout_relu(self.linear1(src)))
+ src = src + self.dropout3(src2)
+ src = self.norm2(src)
+ return src
+
+ def forward(self, src, pos, reference_points, spatial_shapes, level_start_index, padding_mask=None):
+ # self attention
+ src2 = self.self_attn(self.with_pos_embed(src, pos), reference_points, src, spatial_shapes, level_start_index, padding_mask)
+ src = src + self.dropout1(src2)
+ src = self.norm1(src)
+
+ # ffn
+ src = self.forward_ffn(src)
+ return src
+
+
+class DeformableTransformerEncoder(nn.Module):
+ def __init__(self, encoder_layer, num_layers):
+ super().__init__()
+ self.layers = _get_clones(encoder_layer, num_layers)
+ self.num_layers = num_layers
+
+ @staticmethod
+ def get_reference_points(spatial_shapes, valid_ratios, device):
+ reference_points_list = []
+ for lvl, (H_, W_) in enumerate(spatial_shapes):
+
+ ref_y, ref_x = torch.meshgrid(torch.linspace(0.5, H_ - 0.5, H_, dtype=torch.float32, device=device),
+ torch.linspace(0.5, W_ - 0.5, W_, dtype=torch.float32, device=device))
+ ref_y = ref_y.reshape(-1)[None] / (valid_ratios[:, None, lvl, 1] * H_)
+ ref_x = ref_x.reshape(-1)[None] / (valid_ratios[:, None, lvl, 0] * W_)
+ ref = torch.stack((ref_x, ref_y), -1)
+ reference_points_list.append(ref)
+ reference_points = torch.cat(reference_points_list, 1)
+ reference_points = reference_points[:, :, None] * valid_ratios[:, None]
+ return reference_points
+
+ def forward(self, src, spatial_shapes, level_start_index, valid_ratios, pos=None, padding_mask=None):
+ output = src
+ reference_points = self.get_reference_points(spatial_shapes, valid_ratios, device=src.device)
+ for _, layer in enumerate(self.layers):
+ output = layer(output, pos, reference_points, spatial_shapes, level_start_index, padding_mask)
+
+ return output
+
+
+class ReLUDropout(torch.nn.Dropout):
+ def forward(self, input):
+ return relu_dropout(input, p=self.p, training=self.training, inplace=self.inplace)
+
+def relu_dropout(x, p=0, inplace=False, training=False):
+ if not training or p == 0:
+ return x.clamp_(min=0) if inplace else x.clamp(min=0)
+
+ mask = (x < 0) | (torch.rand_like(x) > 1 - p)
+ return x.masked_fill_(mask, 0).div_(1 - p) if inplace else x.masked_fill(mask, 0).div(1 - p)
+
+
+class DeformableTransformerDecoderLayer(nn.Module):
+ def __init__(self, d_model=256, d_ffn=1024,
+ dropout=0.1, activation="relu",
+ n_levels=4, n_heads=8, n_points=4, self_cross=True, sigmoid_attn=False,
+ extra_track_attn=False, memory_bank=False):
+ super().__init__()
+
+ self.self_cross = self_cross
+ self.num_head = n_heads
+ self.memory_bank = memory_bank
+
+ # cross attention
+ self.cross_attn = MSDeformAttn(d_model, n_levels, n_heads, n_points, sigmoid_attn=sigmoid_attn)
+ self.dropout1 = nn.Dropout(dropout)
+ self.norm1 = nn.LayerNorm(d_model)
+
+ self.self_attn = nn.MultiheadAttention(d_model, n_heads, dropout=dropout)
+ self.dropout2 = nn.Dropout(dropout)
+ self.norm2 = nn.LayerNorm(d_model)
+
+ # ffn
+ self.linear1 = nn.Linear(d_model, d_ffn)
+ self.activation = _get_activation_fn(activation)
+ self.dropout_relu = ReLUDropout(dropout, True)
+ self.linear2 = nn.Linear(d_ffn, d_model)
+ self.dropout4 = nn.Dropout(dropout)
+ self.norm3 = nn.LayerNorm(d_model)
+
+ # memory bank
+ if self.memory_bank:
+ self.temporal_attn = nn.MultiheadAttention(d_model, 8, dropout=0)
+ self.temporal_fc1 = nn.Linear(d_model, d_ffn)
+ self.temporal_fc2 = nn.Linear(d_ffn, d_model)
+ self.temporal_norm1 = nn.LayerNorm(d_model)
+ self.temporal_norm2 = nn.LayerNorm(d_model)
+
+ position = torch.arange(5).unsqueeze(1)
+ div_term = torch.exp(torch.arange(0, d_model, 2) * (-math.log(10000.0) / d_model))
+ pe = torch.zeros(5, 1, d_model)
+ pe[:, 0, 0::2] = torch.sin(position * div_term)
+ pe[:, 0, 1::2] = torch.cos(position * div_term)
+ self.register_buffer('pe', pe)
+
+ # update track query_embed
+ self.extra_track_attn = extra_track_attn
+ if self.extra_track_attn:
+ print('Training with Extra Self Attention in Every Decoder.', flush=True)
+ self.update_attn = nn.MultiheadAttention(d_model, n_heads, dropout=dropout)
+ self.dropout5 = nn.Dropout(dropout)
+ self.norm4 = nn.LayerNorm(d_model)
+
+ if self_cross:
+ print('Training with Self-Cross Attention.')
+ else:
+ print('Training with Cross-Self Attention.')
+
+ @staticmethod
+ def with_pos_embed(tensor, pos):
+ return tensor if pos is None else tensor + pos
+
+ def forward_ffn(self, tgt):
+ tgt2 = self.linear2(self.dropout_relu(self.linear1(tgt)))
+ tgt = tgt + self.dropout4(tgt2)
+ tgt = self.norm3(tgt)
+ return tgt
+
+ def _forward_self_attn(self, tgt, query_pos, attn_mask=None):
+ q = k = self.with_pos_embed(tgt, query_pos)
+ if attn_mask is not None:
+ tgt2 = self.self_attn(q.transpose(0, 1), k.transpose(0, 1), tgt.transpose(0, 1),
+ attn_mask=attn_mask)[0].transpose(0, 1)
+ else:
+ tgt2 = self.self_attn(q.transpose(0, 1), k.transpose(0, 1), tgt.transpose(0, 1))[0].transpose(0, 1)
+ tgt = tgt + self.dropout2(tgt2)
+ return self.norm2(tgt)
+
+
+ def _forward_self_cross(self, tgt, query_pos, reference_points, src, src_spatial_shapes, level_start_index,
+ src_padding_mask=None, attn_mask=None):
+
+ # self attention
+ tgt = self._forward_self_attn(tgt, query_pos, attn_mask)
+ # cross attention
+ tgt2 = self.cross_attn(self.with_pos_embed(tgt, query_pos),
+ reference_points,
+ src, src_spatial_shapes, level_start_index, src_padding_mask)
+ tgt = tgt + self.dropout1(tgt2)
+ tgt = self.norm1(tgt)
+
+ # ffn
+ tgt = self.forward_ffn(tgt)
+
+ return tgt
+
+ def _forward_cross_self(self, tgt, query_pos, reference_points, src, src_spatial_shapes, level_start_index,
+ src_padding_mask=None, attn_mask=None):
+ # cross attention
+ tgt2 = self.cross_attn(self.with_pos_embed(tgt, query_pos),
+ reference_points,
+ src, src_spatial_shapes, level_start_index, src_padding_mask)
+ tgt = tgt + self.dropout1(tgt2)
+ tgt = self.norm1(tgt)
+ # self attention
+ tgt = self._forward_self_attn(tgt, query_pos, attn_mask)
+ # ffn
+ tgt = self.forward_ffn(tgt)
+
+ return tgt
+
+ def forward(self, tgt, query_pos, reference_points, src, src_spatial_shapes, level_start_index, src_padding_mask=None, mem_bank=None, mem_bank_pad_mask=None, attn_mask=None):
+ if self.self_cross:
+ return self._forward_self_cross(tgt, query_pos, reference_points, src, src_spatial_shapes,
+ level_start_index, src_padding_mask, attn_mask)
+ return self._forward_cross_self(tgt, query_pos, reference_points, src, src_spatial_shapes, level_start_index,
+ src_padding_mask, attn_mask)
+
+
+def pos2posemb(pos, num_pos_feats=64, temperature=10000):
+ scale = 2 * math.pi
+ pos = pos * scale
+ dim_t = torch.arange(num_pos_feats, dtype=torch.float32, device=pos.device)
+ dim_t = temperature ** (2 * (dim_t // 2) / num_pos_feats)
+ posemb = pos[..., None] / dim_t
+ posemb = torch.stack((posemb[..., 0::2].sin(), posemb[..., 1::2].cos()), dim=-1).flatten(-3)
+ return posemb
+
+
+class DeformableTransformerDecoder(nn.Module):
+ def __init__(self, decoder_layer, num_layers, return_intermediate=False):
+ super().__init__()
+ self.layers = _get_clones(decoder_layer, num_layers)
+ self.num_layers = num_layers
+ self.return_intermediate = return_intermediate
+ # hack implementation for iterative bounding box refinement and two-stage Deformable DETR
+ self.bbox_embed = None
+ self.class_embed = None
+
+ def forward(self, tgt, reference_points, src, src_spatial_shapes, src_level_start_index, src_valid_ratios,
+ src_padding_mask=None, mem_bank=None, mem_bank_pad_mask=None, attn_mask=None):
+ output = tgt
+
+ intermediate = []
+ intermediate_reference_points = []
+ for lid, layer in enumerate(self.layers):
+ if reference_points.shape[-1] == 4:
+ reference_points_input = reference_points[:, :, None] \
+ * torch.cat([src_valid_ratios, src_valid_ratios], -1)[:, None]
+ else:
+ assert reference_points.shape[-1] == 2
+ reference_points_input = reference_points[:, :, None] * src_valid_ratios[:, None]
+ query_pos = pos2posemb(reference_points)
+ output = layer(output, query_pos, reference_points_input, src, src_spatial_shapes,
+ src_level_start_index, src_padding_mask, mem_bank, mem_bank_pad_mask, attn_mask)
+
+ # hack implementation for iterative bounding box refinement
+ if self.bbox_embed is not None:
+ tmp = self.bbox_embed[lid](output)
+ if reference_points.shape[-1] == 4:
+ new_reference_points = tmp + inverse_sigmoid(reference_points)
+ new_reference_points = new_reference_points.sigmoid()
+ else:
+ assert reference_points.shape[-1] == 2
+ new_reference_points = tmp
+ new_reference_points[..., :2] = tmp[..., :2] + inverse_sigmoid(reference_points)
+ new_reference_points = new_reference_points.sigmoid()
+ reference_points = new_reference_points.detach()
+
+ if self.return_intermediate:
+ intermediate.append(output)
+ intermediate_reference_points.append(reference_points)
+
+ if self.return_intermediate:
+ return torch.stack(intermediate), torch.stack(intermediate_reference_points)
+
+ return output, reference_points
+
+
+def _get_clones(module, N):
+ return nn.ModuleList([copy.deepcopy(module) for i in range(N)])
+
+
+def _get_activation_fn(activation):
+ """Return an activation function given a string"""
+ if activation == "relu":
+ return nn.ReLU(True)
+ if activation == "gelu":
+ return F.gelu
+ if activation == "glu":
+ return F.glu
+ raise RuntimeError(F"activation should be relu/gelu, not {activation}.")
+
+
+
+def build_deforamble_transformer(args):
+ return DeformableTransformer(
+ d_model=args.hidden_dim,
+ nhead=args.nheads,
+ num_encoder_layers=args.enc_layers,
+ num_decoder_layers=args.dec_layers,
+ dim_feedforward=args.dim_feedforward,
+ dropout=args.dropout,
+ activation="relu",
+ return_intermediate_dec=True,
+ num_feature_levels=args.num_feature_levels,
+ dec_n_points=args.dec_n_points,
+ enc_n_points=args.enc_n_points,
+ two_stage=args.two_stage,
+ two_stage_num_proposals=args.num_queries,
+ decoder_self_cross=not args.decoder_cross_self,
+ sigmoid_attn=args.sigmoid_attn,
+ extra_track_attn=args.extra_track_attn,
+ memory_bank=args.memory_bank_type == 'MemoryBankFeat'
+ )
+
+
diff --git a/VISAM/models/matcher.py b/VISAM/models/matcher.py
new file mode 100644
index 0000000000000000000000000000000000000000..38a2418986b2a0ea43b070ca45b50250db65dc8e
--- /dev/null
+++ b/VISAM/models/matcher.py
@@ -0,0 +1,122 @@
+# ------------------------------------------------------------------------
+# Copyright (c) 2022 megvii-research. All Rights Reserved.
+# ------------------------------------------------------------------------
+# Modified from Deformable DETR (https://github.com/fundamentalvision/Deformable-DETR)
+# Copyright (c) 2020 SenseTime. All Rights Reserved.
+# ------------------------------------------------------------------------
+# Modified from DETR (https://github.com/facebookresearch/detr)
+# Copyright (c) Facebook, Inc. and its affiliates. All Rights Reserved
+# ------------------------------------------------------------------------
+
+
+"""
+Modules to compute the matching cost and solve the corresponding LSAP.
+"""
+import torch
+from scipy.optimize import linear_sum_assignment
+from torch import nn
+
+from util.box_ops import box_cxcywh_to_xyxy, generalized_box_iou
+from models.structures import Instances
+
+
+class HungarianMatcher(nn.Module):
+ """This class computes an assignment between the targets and the predictions of the network
+
+ For efficiency reasons, the targets don't include the no_object. Because of this, in general,
+ there are more predictions than targets. In this case, we do a 1-to-1 matching of the best predictions,
+ while the others are un-matched (and thus treated as non-objects).
+ """
+
+ def __init__(self,
+ cost_class: float = 1,
+ cost_bbox: float = 1,
+ cost_giou: float = 1):
+ """Creates the matcher
+
+ Params:
+ cost_class: This is the relative weight of the classification error in the matching cost
+ cost_bbox: This is the relative weight of the L1 error of the bounding box coordinates in the matching cost
+ cost_giou: This is the relative weight of the giou loss of the bounding box in the matching cost
+ """
+ super().__init__()
+ self.cost_class = cost_class
+ self.cost_bbox = cost_bbox
+ self.cost_giou = cost_giou
+ assert cost_class != 0 or cost_bbox != 0 or cost_giou != 0, "all costs cant be 0"
+
+ def forward(self, outputs, targets, use_focal=True):
+ """ Performs the matching
+
+ Params:
+ outputs: This is a dict that contains at least these entries:
+ "pred_logits": Tensor of dim [batch_size, num_queries, num_classes] with the classification logits
+ "pred_boxes": Tensor of dim [batch_size, num_queries, 4] with the predicted box coordinates
+
+ targets: This is a list of targets (len(targets) = batch_size), where each target is a dict containing:
+ "labels": Tensor of dim [num_target_boxes] (where num_target_boxes is the number of ground-truth
+ objects in the target) containing the class labels
+ "boxes": Tensor of dim [num_target_boxes, 4] containing the target box coordinates
+
+ Returns:
+ A list of size batch_size, containing tuples of (index_i, index_j) where:
+ - index_i is the indices of the selected predictions (in order)
+ - index_j is the indices of the corresponding selected targets (in order)
+ For each batch element, it holds:
+ len(index_i) = len(index_j) = min(num_queries, num_target_boxes)
+ """
+ with torch.no_grad():
+ bs, num_queries = outputs["pred_logits"].shape[:2]
+
+ # We flatten to compute the cost matrices in a batch
+ if use_focal:
+ out_prob = outputs["pred_logits"].flatten(0, 1).sigmoid()
+ else:
+ out_prob = outputs["pred_logits"].flatten(0, 1).softmax(-1) # [batch_size * num_queries, num_classes]
+ out_bbox = outputs["pred_boxes"].flatten(0, 1) # [batch_size * num_queries, 4]
+
+ # Also concat the target labels and boxes
+ if isinstance(targets[0], Instances):
+ tgt_ids = torch.cat([gt_per_img.labels for gt_per_img in targets])
+ tgt_bbox = torch.cat([gt_per_img.boxes for gt_per_img in targets])
+ else:
+ tgt_ids = torch.cat([v["labels"] for v in targets])
+ tgt_bbox = torch.cat([v["boxes"] for v in targets])
+
+ # Compute the classification cost.
+ if use_focal:
+ alpha = 0.25
+ gamma = 2.0
+ neg_cost_class = (1 - alpha) * (out_prob ** gamma) * (-(1 - out_prob + 1e-8).log())
+ pos_cost_class = alpha * ((1 - out_prob) ** gamma) * (-(out_prob + 1e-8).log())
+ cost_class = pos_cost_class[:, tgt_ids] - neg_cost_class[:, tgt_ids]
+ else:
+ # Compute the classification cost. Contrary to the loss, we don't use the NLL,
+ # but approximate it in 1 - proba[target class].
+ # The 1 is a constant that doesn't change the matching, it can be ommitted.
+ cost_class = -out_prob[:, tgt_ids]
+
+ # Compute the L1 cost between boxes
+ cost_bbox = torch.cdist(out_bbox, tgt_bbox, p=1)
+
+ # Compute the giou cost betwen boxes
+ cost_giou = -generalized_box_iou(box_cxcywh_to_xyxy(out_bbox),
+ box_cxcywh_to_xyxy(tgt_bbox))
+
+ # Final cost matrix
+ C = self.cost_bbox * cost_bbox + self.cost_class * cost_class + self.cost_giou * cost_giou
+ C = C.view(bs, num_queries, -1).cpu()
+
+ if isinstance(targets[0], Instances):
+ sizes = [len(gt_per_img.boxes) for gt_per_img in targets]
+ else:
+ sizes = [len(v["boxes"]) for v in targets]
+
+ indices = [linear_sum_assignment(c[i]) for i, c in enumerate(C.split(sizes, -1))]
+ return [(torch.as_tensor(i, dtype=torch.int64), torch.as_tensor(j, dtype=torch.int64)) for i, j in indices]
+
+
+def build_matcher(args):
+ return HungarianMatcher(cost_class=args.set_cost_class,
+ cost_bbox=args.set_cost_bbox,
+ cost_giou=args.set_cost_giou)
diff --git a/VISAM/models/motr.py b/VISAM/models/motr.py
new file mode 100644
index 0000000000000000000000000000000000000000..f1b661115af3d724e1107a56931b813f158ec183
--- /dev/null
+++ b/VISAM/models/motr.py
@@ -0,0 +1,776 @@
+# ------------------------------------------------------------------------
+# Copyright (c) 2022 megvii-research. All Rights Reserved.
+# ------------------------------------------------------------------------
+# Modified from Deformable DETR (https://github.com/fundamentalvision/Deformable-DETR)
+# Copyright (c) 2020 SenseTime. All Rights Reserved.
+# ------------------------------------------------------------------------
+# Modified from DETR (https://github.com/facebookresearch/detr)
+# Copyright (c) Facebook, Inc. and its affiliates. All Rights Reserved
+# ------------------------------------------------------------------------
+
+"""
+DETR model and criterion classes.
+"""
+import copy
+import math
+import numpy as np
+import torch
+import torch.nn.functional as F
+from torch import nn, Tensor
+from typing import List
+
+from util import box_ops, checkpoint
+from util.misc import (NestedTensor, nested_tensor_from_tensor_list,
+ accuracy, get_world_size, interpolate, get_rank,
+ is_dist_avail_and_initialized, inverse_sigmoid)
+
+from models.structures import Instances, Boxes, pairwise_iou, matched_boxlist_iou
+
+from .backbone import build_backbone
+from .matcher import build_matcher
+from .deformable_transformer_plus import build_deforamble_transformer, pos2posemb
+from .qim import build as build_query_interaction_layer
+from .deformable_detr import SetCriterion, MLP, sigmoid_focal_loss
+
+
+class ClipMatcher(SetCriterion):
+ def __init__(self, num_classes,
+ matcher,
+ weight_dict,
+ losses):
+ """ Create the criterion.
+ Parameters:
+ num_classes: number of object categories, omitting the special no-object category
+ matcher: module able to compute a matching between targets and proposals
+ weight_dict: dict containing as key the names of the losses and as values their relative weight.
+ eos_coef: relative classification weight applied to the no-object category
+ losses: list of all the losses to be applied. See get_loss for list of available losses.
+ """
+ super().__init__(num_classes, matcher, weight_dict, losses)
+ self.num_classes = num_classes
+ self.matcher = matcher
+ self.weight_dict = weight_dict
+ self.losses = losses
+ self.focal_loss = True
+ self.losses_dict = {}
+ self._current_frame_idx = 0
+
+ def initialize_for_single_clip(self, gt_instances: List[Instances]):
+ self.gt_instances = gt_instances
+ self.num_samples = 0
+ self.sample_device = None
+ self._current_frame_idx = 0
+ self.losses_dict = {}
+
+ def _step(self):
+ self._current_frame_idx += 1
+
+ def calc_loss_for_track_scores(self, track_instances: Instances):
+ frame_id = self._current_frame_idx - 1
+ gt_instances = self.gt_instances[frame_id]
+ outputs = {
+ 'pred_logits': track_instances.track_scores[None],
+ }
+ device = track_instances.track_scores.device
+
+ num_tracks = len(track_instances)
+ src_idx = torch.arange(num_tracks, dtype=torch.long, device=device)
+ tgt_idx = track_instances.matched_gt_idxes # -1 for FP tracks and disappeared tracks
+
+ track_losses = self.get_loss('labels',
+ outputs=outputs,
+ gt_instances=[gt_instances],
+ indices=[(src_idx, tgt_idx)],
+ num_boxes=1)
+ self.losses_dict.update(
+ {'frame_{}_track_{}'.format(frame_id, key): value for key, value in
+ track_losses.items()})
+
+ def get_num_boxes(self, num_samples):
+ num_boxes = torch.as_tensor(num_samples, dtype=torch.float, device=self.sample_device)
+ if is_dist_avail_and_initialized():
+ torch.distributed.all_reduce(num_boxes)
+ num_boxes = torch.clamp(num_boxes / get_world_size(), min=1).item()
+ return num_boxes
+
+ def get_loss(self, loss, outputs, gt_instances, indices, num_boxes, **kwargs):
+ loss_map = {
+ 'labels': self.loss_labels,
+ 'cardinality': self.loss_cardinality,
+ 'boxes': self.loss_boxes,
+ }
+ assert loss in loss_map, f'do you really want to compute {loss} loss?'
+ return loss_map[loss](outputs, gt_instances, indices, num_boxes, **kwargs)
+
+ def loss_boxes(self, outputs, gt_instances: List[Instances], indices: List[tuple], num_boxes):
+ """Compute the losses related to the bounding boxes, the L1 regression loss and the GIoU loss
+ targets dicts must contain the key "boxes" containing a tensor of dim [nb_target_boxes, 4]
+ The target boxes are expected in format (center_x, center_y, h, w), normalized by the image size.
+ """
+ # We ignore the regression loss of the track-disappear slots.
+ #TODO: Make this filter process more elegant.
+ filtered_idx = []
+ for src_per_img, tgt_per_img in indices:
+ keep = tgt_per_img != -1
+ filtered_idx.append((src_per_img[keep], tgt_per_img[keep]))
+ indices = filtered_idx
+ idx = self._get_src_permutation_idx(indices)
+ src_boxes = outputs['pred_boxes'][idx]
+ target_boxes = torch.cat([gt_per_img.boxes[i] for gt_per_img, (_, i) in zip(gt_instances, indices)], dim=0)
+
+ # for pad target, don't calculate regression loss, judged by whether obj_id=-1
+ target_obj_ids = torch.cat([gt_per_img.obj_ids[i] for gt_per_img, (_, i) in zip(gt_instances, indices)], dim=0) # size(16)
+ mask = (target_obj_ids != -1)
+
+ loss_bbox = F.l1_loss(src_boxes[mask], target_boxes[mask], reduction='none')
+ loss_giou = 1 - torch.diag(box_ops.generalized_box_iou(
+ box_ops.box_cxcywh_to_xyxy(src_boxes[mask]),
+ box_ops.box_cxcywh_to_xyxy(target_boxes[mask])))
+
+ losses = {}
+ losses['loss_bbox'] = loss_bbox.sum() / num_boxes
+ losses['loss_giou'] = loss_giou.sum() / num_boxes
+
+ return losses
+
+ def loss_labels(self, outputs, gt_instances: List[Instances], indices, num_boxes, log=False):
+ """Classification loss (NLL)
+ targets dicts must contain the key "labels" containing a tensor of dim [nb_target_boxes]
+ """
+ src_logits = outputs['pred_logits']
+ idx = self._get_src_permutation_idx(indices)
+ target_classes = torch.full(src_logits.shape[:2], self.num_classes,
+ dtype=torch.int64, device=src_logits.device)
+ # The matched gt for disappear track query is set -1.
+ labels = []
+ for gt_per_img, (_, J) in zip(gt_instances, indices):
+ labels_per_img = torch.ones_like(J)
+ # set labels of track-appear slots to 0.
+ if len(gt_per_img) > 0:
+ labels_per_img[J != -1] = gt_per_img.labels[J[J != -1]]
+ labels.append(labels_per_img)
+ target_classes_o = torch.cat(labels)
+ target_classes[idx] = target_classes_o
+ if self.focal_loss:
+ gt_labels_target = F.one_hot(target_classes, num_classes=self.num_classes + 1)[:, :, :-1] # no loss for the last (background) class
+ gt_labels_target = gt_labels_target.to(src_logits)
+ loss_ce = sigmoid_focal_loss(src_logits.flatten(1),
+ gt_labels_target.flatten(1),
+ alpha=0.25,
+ gamma=2,
+ num_boxes=num_boxes, mean_in_dim1=False)
+ loss_ce = loss_ce.sum()
+ else:
+ loss_ce = F.cross_entropy(src_logits.transpose(1, 2), target_classes, self.empty_weight)
+ losses = {'loss_ce': loss_ce}
+
+ if log:
+ # TODO this should probably be a separate loss, not hacked in this one here
+ losses['class_error'] = 100 - accuracy(src_logits[idx], target_classes_o)[0]
+
+ return losses
+
+ def match_for_single_frame(self, outputs: dict):
+ outputs_without_aux = {k: v for k, v in outputs.items() if k != 'aux_outputs'}
+
+ gt_instances_i = self.gt_instances[self._current_frame_idx] # gt instances of i-th image.
+ track_instances: Instances = outputs_without_aux['track_instances']
+ pred_logits_i = track_instances.pred_logits # predicted logits of i-th image.
+ pred_boxes_i = track_instances.pred_boxes # predicted boxes of i-th image.
+
+ obj_idxes = gt_instances_i.obj_ids
+ outputs_i = {
+ 'pred_logits': pred_logits_i.unsqueeze(0),
+ 'pred_boxes': pred_boxes_i.unsqueeze(0),
+ }
+
+ # step1. inherit and update the previous tracks.
+ num_disappear_track = 0
+ track_instances.matched_gt_idxes[:] = -1
+ i, j = torch.where(track_instances.obj_idxes[:, None] == obj_idxes)
+ track_instances.matched_gt_idxes[i] = j
+
+ full_track_idxes = torch.arange(len(track_instances), dtype=torch.long, device=pred_logits_i.device)
+ matched_track_idxes = (track_instances.obj_idxes >= 0) # occu
+ prev_matched_indices = torch.stack(
+ [full_track_idxes[matched_track_idxes], track_instances.matched_gt_idxes[matched_track_idxes]], dim=1)
+
+ # step2. select the unmatched slots.
+ # note that the FP tracks whose obj_idxes are -2 will not be selected here.
+ unmatched_track_idxes = full_track_idxes[track_instances.obj_idxes == -1]
+
+ # step3. select the untracked gt instances (new tracks).
+ tgt_indexes = track_instances.matched_gt_idxes
+ tgt_indexes = tgt_indexes[tgt_indexes != -1]
+
+ tgt_state = torch.zeros(len(gt_instances_i), device=pred_logits_i.device)
+ tgt_state[tgt_indexes] = 1
+ untracked_tgt_indexes = torch.arange(len(gt_instances_i), device=pred_logits_i.device)[tgt_state == 0]
+ # untracked_tgt_indexes = select_unmatched_indexes(tgt_indexes, len(gt_instances_i))
+ untracked_gt_instances = gt_instances_i[untracked_tgt_indexes]
+
+ def match_for_single_decoder_layer(unmatched_outputs, matcher):
+ new_track_indices = matcher(unmatched_outputs,
+ [untracked_gt_instances]) # list[tuple(src_idx, tgt_idx)]
+
+ src_idx = new_track_indices[0][0]
+ tgt_idx = new_track_indices[0][1]
+ # concat src and tgt.
+ new_matched_indices = torch.stack([unmatched_track_idxes[src_idx], untracked_tgt_indexes[tgt_idx]],
+ dim=1).to(pred_logits_i.device)
+ return new_matched_indices
+
+ # step4. do matching between the unmatched slots and GTs.
+ unmatched_outputs = {
+ 'pred_logits': track_instances.pred_logits[unmatched_track_idxes].unsqueeze(0),
+ 'pred_boxes': track_instances.pred_boxes[unmatched_track_idxes].unsqueeze(0),
+ }
+ new_matched_indices = match_for_single_decoder_layer(unmatched_outputs, self.matcher)
+
+ # step5. update obj_idxes according to the new matching result.
+ track_instances.obj_idxes[new_matched_indices[:, 0]] = gt_instances_i.obj_ids[new_matched_indices[:, 1]].long()
+ track_instances.matched_gt_idxes[new_matched_indices[:, 0]] = new_matched_indices[:, 1]
+
+ # step6. calculate iou.
+ active_idxes = (track_instances.obj_idxes >= 0) & (track_instances.matched_gt_idxes >= 0)
+ active_track_boxes = track_instances.pred_boxes[active_idxes]
+ if len(active_track_boxes) > 0:
+ gt_boxes = gt_instances_i.boxes[track_instances.matched_gt_idxes[active_idxes]]
+ active_track_boxes = box_ops.box_cxcywh_to_xyxy(active_track_boxes)
+ gt_boxes = box_ops.box_cxcywh_to_xyxy(gt_boxes)
+ track_instances.iou[active_idxes] = matched_boxlist_iou(Boxes(active_track_boxes), Boxes(gt_boxes))
+
+ # step7. merge the unmatched pairs and the matched pairs.
+ matched_indices = torch.cat([new_matched_indices, prev_matched_indices], dim=0)
+
+ # step8. calculate losses.
+ self.num_samples += len(gt_instances_i) + num_disappear_track
+ self.sample_device = pred_logits_i.device
+ for loss in self.losses:
+ new_track_loss = self.get_loss(loss,
+ outputs=outputs_i,
+ gt_instances=[gt_instances_i],
+ indices=[(matched_indices[:, 0], matched_indices[:, 1])],
+ num_boxes=1)
+ self.losses_dict.update(
+ {'frame_{}_{}'.format(self._current_frame_idx, key): value for key, value in new_track_loss.items()})
+
+ if 'aux_outputs' in outputs:
+ for i, aux_outputs in enumerate(outputs['aux_outputs']):
+ unmatched_outputs_layer = {
+ 'pred_logits': aux_outputs['pred_logits'][0, unmatched_track_idxes].unsqueeze(0),
+ 'pred_boxes': aux_outputs['pred_boxes'][0, unmatched_track_idxes].unsqueeze(0),
+ }
+ new_matched_indices_layer = match_for_single_decoder_layer(unmatched_outputs_layer, self.matcher)
+ matched_indices_layer = torch.cat([new_matched_indices_layer, prev_matched_indices], dim=0)
+ for loss in self.losses:
+ if loss == 'masks':
+ # Intermediate masks losses are too costly to compute, we ignore them.
+ continue
+ l_dict = self.get_loss(loss,
+ aux_outputs,
+ gt_instances=[gt_instances_i],
+ indices=[(matched_indices_layer[:, 0], matched_indices_layer[:, 1])],
+ num_boxes=1, )
+ self.losses_dict.update(
+ {'frame_{}_aux{}_{}'.format(self._current_frame_idx, i, key): value for key, value in
+ l_dict.items()})
+
+ if 'ps_outputs' in outputs:
+ for i, aux_outputs in enumerate(outputs['ps_outputs']):
+ ar = torch.arange(len(gt_instances_i), device=obj_idxes.device)
+ l_dict = self.get_loss('boxes',
+ aux_outputs,
+ gt_instances=[gt_instances_i],
+ indices=[(ar, ar)],
+ num_boxes=1, )
+ self.losses_dict.update(
+ {'frame_{}_ps{}_{}'.format(self._current_frame_idx, i, key): value for key, value in
+ l_dict.items()})
+ self._step()
+ return track_instances
+
+ def forward(self, outputs, input_data: dict):
+ # losses of each frame are calculated during the model's forwarding and are outputted by the model as outputs['losses_dict].
+ losses = outputs.pop("losses_dict")
+ num_samples = self.get_num_boxes(self.num_samples)
+ for loss_name, loss in losses.items():
+ losses[loss_name] /= num_samples
+ return losses
+
+
+class RuntimeTrackerBase(object):
+ def __init__(self, score_thresh=0.6, filter_score_thresh=0.5, miss_tolerance=10):
+ self.score_thresh = score_thresh
+ self.filter_score_thresh = filter_score_thresh
+ self.miss_tolerance = miss_tolerance
+ self.max_obj_id = 0
+
+ def clear(self):
+ self.max_obj_id = 0
+
+ def update(self, track_instances: Instances):
+ device = track_instances.obj_idxes.device
+
+ track_instances.disappear_time[track_instances.scores >= self.score_thresh] = 0
+ new_obj = (track_instances.obj_idxes == -1) & (track_instances.scores >= self.score_thresh)
+ disappeared_obj = (track_instances.obj_idxes >= 0) & (track_instances.scores < self.filter_score_thresh)
+ num_new_objs = new_obj.sum().item()
+
+ track_instances.obj_idxes[new_obj] = self.max_obj_id + torch.arange(num_new_objs, device=device)
+ self.max_obj_id += num_new_objs
+
+ track_instances.disappear_time[disappeared_obj] += 1
+ to_del = disappeared_obj & (track_instances.disappear_time >= self.miss_tolerance)
+ track_instances.obj_idxes[to_del] = -1
+
+
+class TrackerPostProcess(nn.Module):
+ """ This module converts the model's output into the format expected by the coco api"""
+ def __init__(self):
+ super().__init__()
+
+ @torch.no_grad()
+ def forward(self, track_instances: Instances, target_size) -> Instances:
+ """ Perform the computation
+ Parameters:
+ outputs: raw outputs of the model
+ target_sizes: tensor of dimension [batch_size x 2] containing the size of each images of the batch
+ For evaluation, this must be the original image size (before any data augmentation)
+ For visualization, this should be the image size after data augment, but before padding
+ """
+ out_logits = track_instances.pred_logits
+ out_bbox = track_instances.pred_boxes
+
+ # prob = out_logits.sigmoid()
+ scores = out_logits[..., 0].sigmoid()
+ # scores, labels = prob.max(-1)
+
+ # convert to [x0, y0, x1, y1] format
+ boxes = box_ops.box_cxcywh_to_xyxy(out_bbox)
+ # and from relative [0, 1] to absolute [0, height] coordinates
+ img_h, img_w = target_size
+ scale_fct = torch.Tensor([img_w, img_h, img_w, img_h]).to(boxes)
+ boxes = boxes * scale_fct[None, :]
+
+ track_instances.boxes = boxes
+ track_instances.scores = scores
+ track_instances.labels = torch.full_like(scores, 0)
+ # track_instances.remove('pred_logits')
+ # track_instances.remove('pred_boxes')
+ return track_instances
+
+
+def _get_clones(module, N):
+ return nn.ModuleList([copy.deepcopy(module) for i in range(N)])
+
+
+class MOTR(nn.Module):
+ def __init__(self, backbone, transformer, num_classes, num_queries, num_feature_levels, criterion, track_embed,
+ aux_loss=True, with_box_refine=False, two_stage=False, memory_bank=None, use_checkpoint=False, query_denoise=0):
+ """ Initializes the model.
+ Parameters:
+ backbone: torch module of the backbone to be used. See backbone.py
+ transformer: torch module of the transformer architecture. See transformer.py
+ num_classes: number of object classes
+ num_queries: number of object queries, ie detection slot. This is the maximal number of objects
+ DETR can detect in a single image. For COCO, we recommend 100 queries.
+ aux_loss: True if auxiliary decoding losses (loss at each decoder layer) are to be used.
+ with_box_refine: iterative bounding box refinement
+ two_stage: two-stage Deformable DETR
+ """
+ super().__init__()
+ self.num_queries = num_queries
+ self.track_embed = track_embed
+ self.transformer = transformer
+ hidden_dim = transformer.d_model
+ self.num_classes = num_classes
+ self.class_embed = nn.Linear(hidden_dim, num_classes)
+ self.bbox_embed = MLP(hidden_dim, hidden_dim, 4, 3)
+ self.num_feature_levels = num_feature_levels
+ self.use_checkpoint = use_checkpoint
+ self.query_denoise = query_denoise
+ self.position = nn.Embedding(num_queries, 4)
+ self.yolox_embed = nn.Embedding(1, hidden_dim)
+ self.query_embed = nn.Embedding(num_queries, hidden_dim)
+ if query_denoise:
+ self.refine_embed = nn.Embedding(1, hidden_dim)
+ if num_feature_levels > 1:
+ num_backbone_outs = len(backbone.strides)
+ input_proj_list = []
+ for _ in range(num_backbone_outs):
+ in_channels = backbone.num_channels[_]
+ input_proj_list.append(nn.Sequential(
+ nn.Conv2d(in_channels, hidden_dim, kernel_size=1),
+ nn.GroupNorm(32, hidden_dim),
+ ))
+ for _ in range(num_feature_levels - num_backbone_outs):
+ input_proj_list.append(nn.Sequential(
+ nn.Conv2d(in_channels, hidden_dim, kernel_size=3, stride=2, padding=1),
+ nn.GroupNorm(32, hidden_dim),
+ ))
+ in_channels = hidden_dim
+ self.input_proj = nn.ModuleList(input_proj_list)
+ else:
+ self.input_proj = nn.ModuleList([
+ nn.Sequential(
+ nn.Conv2d(backbone.num_channels[0], hidden_dim, kernel_size=1),
+ nn.GroupNorm(32, hidden_dim),
+ )])
+ self.backbone = backbone
+ self.aux_loss = aux_loss
+ self.with_box_refine = with_box_refine
+ self.two_stage = two_stage
+
+ prior_prob = 0.01
+ bias_value = -math.log((1 - prior_prob) / prior_prob)
+ self.class_embed.bias.data = torch.ones(num_classes) * bias_value
+ nn.init.constant_(self.bbox_embed.layers[-1].weight.data, 0)
+ nn.init.constant_(self.bbox_embed.layers[-1].bias.data, 0)
+ for proj in self.input_proj:
+ nn.init.xavier_uniform_(proj[0].weight, gain=1)
+ nn.init.constant_(proj[0].bias, 0)
+ nn.init.uniform_(self.position.weight.data, 0, 1)
+
+ # if two-stage, the last class_embed and bbox_embed is for region proposal generation
+ num_pred = (transformer.decoder.num_layers + 1) if two_stage else transformer.decoder.num_layers
+ if with_box_refine:
+ self.class_embed = _get_clones(self.class_embed, num_pred)
+ self.bbox_embed = _get_clones(self.bbox_embed, num_pred)
+ nn.init.constant_(self.bbox_embed[0].layers[-1].bias.data[2:], -2.0)
+ # hack implementation for iterative bounding box refinement
+ self.transformer.decoder.bbox_embed = self.bbox_embed
+ else:
+ nn.init.constant_(self.bbox_embed.layers[-1].bias.data[2:], -2.0)
+ self.class_embed = nn.ModuleList([self.class_embed for _ in range(num_pred)])
+ self.bbox_embed = nn.ModuleList([self.bbox_embed for _ in range(num_pred)])
+ self.transformer.decoder.bbox_embed = None
+ if two_stage:
+ # hack implementation for two-stage
+ self.transformer.decoder.class_embed = self.class_embed
+ for box_embed in self.bbox_embed:
+ nn.init.constant_(box_embed.layers[-1].bias.data[2:], 0.0)
+ self.post_process = TrackerPostProcess()
+ self.track_base = RuntimeTrackerBase()
+ self.criterion = criterion
+ self.memory_bank = memory_bank
+ self.mem_bank_len = 0 if memory_bank is None else memory_bank.max_his_length
+
+ def _generate_empty_tracks(self, proposals=None):
+ track_instances = Instances((1, 1))
+ num_queries, d_model = self.query_embed.weight.shape # (300, 512)
+ device = self.query_embed.weight.device
+ if proposals is None:
+ track_instances.ref_pts = self.position.weight
+ track_instances.query_pos = self.query_embed.weight
+ else:
+ track_instances.ref_pts = torch.cat([self.position.weight, proposals[:, :4]])
+ track_instances.query_pos = torch.cat([self.query_embed.weight, pos2posemb(proposals[:, 4:], d_model) + self.yolox_embed.weight])
+ track_instances.output_embedding = torch.zeros((len(track_instances), d_model), device=device)
+ track_instances.obj_idxes = torch.full((len(track_instances),), -1, dtype=torch.long, device=device)
+ track_instances.matched_gt_idxes = torch.full((len(track_instances),), -1, dtype=torch.long, device=device)
+ track_instances.disappear_time = torch.zeros((len(track_instances), ), dtype=torch.long, device=device)
+ track_instances.iou = torch.ones((len(track_instances),), dtype=torch.float, device=device)
+ track_instances.scores = torch.zeros((len(track_instances),), dtype=torch.float, device=device)
+ track_instances.track_scores = torch.zeros((len(track_instances),), dtype=torch.float, device=device)
+ track_instances.pred_boxes = torch.zeros((len(track_instances), 4), dtype=torch.float, device=device)
+ track_instances.pred_logits = torch.zeros((len(track_instances), self.num_classes), dtype=torch.float, device=device)
+
+ mem_bank_len = self.mem_bank_len
+ track_instances.mem_bank = torch.zeros((len(track_instances), mem_bank_len, d_model), dtype=torch.float32, device=device)
+ track_instances.mem_padding_mask = torch.ones((len(track_instances), mem_bank_len), dtype=torch.bool, device=device)
+ track_instances.save_period = torch.zeros((len(track_instances), ), dtype=torch.float32, device=device)
+
+ return track_instances.to(self.query_embed.weight.device)
+
+ def clear(self):
+ self.track_base.clear()
+
+ @torch.jit.unused
+ def _set_aux_loss(self, outputs_class, outputs_coord):
+ # this is a workaround to make torchscript happy, as torchscript
+ # doesn't support dictionary with non-homogeneous values, such
+ # as a dict having both a Tensor and a list.
+ return [{'pred_logits': a, 'pred_boxes': b, }
+ for a, b in zip(outputs_class[:-1], outputs_coord[:-1])]
+
+ def _forward_single_image(self, samples, track_instances: Instances, gtboxes=None):
+ features, pos = self.backbone(samples)
+ src, mask = features[-1].decompose()
+ assert mask is not None
+
+ srcs = []
+ masks = []
+ for l, feat in enumerate(features):
+ src, mask = feat.decompose()
+ srcs.append(self.input_proj[l](src))
+ masks.append(mask)
+ assert mask is not None
+
+ if self.num_feature_levels > len(srcs):
+ _len_srcs = len(srcs)
+ for l in range(_len_srcs, self.num_feature_levels):
+ if l == _len_srcs:
+ src = self.input_proj[l](features[-1].tensors)
+ else:
+ src = self.input_proj[l](srcs[-1])
+ m = samples.mask
+ mask = F.interpolate(m[None].float(), size=src.shape[-2:]).to(torch.bool)[0]
+ pos_l = self.backbone[1](NestedTensor(src, mask)).to(src.dtype)
+ srcs.append(src)
+ masks.append(mask)
+ pos.append(pos_l)
+
+ if gtboxes is not None:
+ n_dt = len(track_instances)
+ ps_tgt = self.refine_embed.weight.expand(gtboxes.size(0), -1)
+ query_embed = torch.cat([track_instances.query_pos, ps_tgt])
+ ref_pts = torch.cat([track_instances.ref_pts, gtboxes])
+ attn_mask = torch.zeros((len(ref_pts), len(ref_pts)), dtype=bool, device=ref_pts.device)
+ attn_mask[:n_dt, n_dt:] = True
+ else:
+ query_embed = track_instances.query_pos
+ ref_pts = track_instances.ref_pts
+ attn_mask = None
+
+ hs, init_reference, inter_references, enc_outputs_class, enc_outputs_coord_unact = \
+ self.transformer(srcs, masks, pos, query_embed, ref_pts=ref_pts,
+ mem_bank=track_instances.mem_bank, mem_bank_pad_mask=track_instances.mem_padding_mask, attn_mask=attn_mask)
+
+ outputs_classes = []
+ outputs_coords = []
+ for lvl in range(hs.shape[0]):
+ if lvl == 0:
+ reference = init_reference
+ else:
+ reference = inter_references[lvl - 1]
+ reference = inverse_sigmoid(reference)
+ outputs_class = self.class_embed[lvl](hs[lvl])
+ tmp = self.bbox_embed[lvl](hs[lvl])
+ if reference.shape[-1] == 4:
+ tmp += reference
+ else:
+ assert reference.shape[-1] == 2
+ tmp[..., :2] += reference
+ outputs_coord = tmp.sigmoid()
+ outputs_classes.append(outputs_class)
+ outputs_coords.append(outputs_coord)
+ outputs_class = torch.stack(outputs_classes)
+ outputs_coord = torch.stack(outputs_coords)
+
+ out = {'pred_logits': outputs_class[-1], 'pred_boxes': outputs_coord[-1]}
+ if self.aux_loss:
+ out['aux_outputs'] = self._set_aux_loss(outputs_class, outputs_coord)
+ out['hs'] = hs[-1]
+ return out
+
+ def _post_process_single_image(self, frame_res, track_instances, is_last):
+ if self.query_denoise > 0:
+ n_ins = len(track_instances)
+ ps_logits = frame_res['pred_logits'][:, n_ins:]
+ ps_boxes = frame_res['pred_boxes'][:, n_ins:]
+ frame_res['hs'] = frame_res['hs'][:, :n_ins]
+ frame_res['pred_logits'] = frame_res['pred_logits'][:, :n_ins]
+ frame_res['pred_boxes'] = frame_res['pred_boxes'][:, :n_ins]
+ ps_outputs = [{'pred_logits': ps_logits, 'pred_boxes': ps_boxes}]
+ for aux_outputs in frame_res['aux_outputs']:
+ ps_outputs.append({
+ 'pred_logits': aux_outputs['pred_logits'][:, n_ins:],
+ 'pred_boxes': aux_outputs['pred_boxes'][:, n_ins:],
+ })
+ aux_outputs['pred_logits'] = aux_outputs['pred_logits'][:, :n_ins]
+ aux_outputs['pred_boxes'] = aux_outputs['pred_boxes'][:, :n_ins]
+ frame_res['ps_outputs'] = ps_outputs
+
+ with torch.no_grad():
+ if self.training:
+ track_scores = frame_res['pred_logits'][0, :].sigmoid().max(dim=-1).values
+ else:
+ track_scores = frame_res['pred_logits'][0, :, 0].sigmoid()
+
+ track_instances.scores = track_scores
+ track_instances.pred_logits = frame_res['pred_logits'][0]
+ track_instances.pred_boxes = frame_res['pred_boxes'][0]
+ track_instances.output_embedding = frame_res['hs'][0]
+ if self.training:
+ # the track id will be assigned by the mather.
+ frame_res['track_instances'] = track_instances
+ track_instances = self.criterion.match_for_single_frame(frame_res)
+ else:
+ # each track will be assigned an unique global id by the track base.
+ self.track_base.update(track_instances)
+ if self.memory_bank is not None:
+ track_instances = self.memory_bank(track_instances)
+ tmp = {}
+ tmp['track_instances'] = track_instances
+ if not is_last:
+ out_track_instances = self.track_embed(tmp)
+ frame_res['track_instances'] = out_track_instances
+ else:
+ frame_res['track_instances'] = None
+ return frame_res
+
+ @torch.no_grad()
+ def inference_single_image(self, img, ori_img_size, track_instances=None, proposals=None):
+ if not isinstance(img, NestedTensor):
+ img = nested_tensor_from_tensor_list(img)
+ if track_instances is None:
+ track_instances = self._generate_empty_tracks(proposals)
+ else:
+ track_instances = Instances.cat([
+ self._generate_empty_tracks(proposals),
+ track_instances])
+ res = self._forward_single_image(img,
+ track_instances=track_instances)
+ res = self._post_process_single_image(res, track_instances, False)
+
+ track_instances = res['track_instances']
+ track_instances = self.post_process(track_instances, ori_img_size)
+ ret = {'track_instances': track_instances}
+ if 'ref_pts' in res:
+ ref_pts = res['ref_pts']
+ img_h, img_w = ori_img_size
+ scale_fct = torch.Tensor([img_w, img_h]).to(ref_pts)
+ ref_pts = ref_pts * scale_fct[None]
+ ret['ref_pts'] = ref_pts
+ return ret
+
+ def forward(self, data: dict):
+ if self.training:
+ self.criterion.initialize_for_single_clip(data['gt_instances'])
+ frames = data['imgs'] # list of Tensor.
+ outputs = {
+ 'pred_logits': [],
+ 'pred_boxes': [],
+ }
+ track_instances = None
+ keys = list(self._generate_empty_tracks()._fields.keys())
+ for frame_index, (frame, gt, proposals) in enumerate(zip(frames, data['gt_instances'], data['proposals'])):
+ frame.requires_grad = False
+ is_last = frame_index == len(frames) - 1
+
+ if self.query_denoise > 0:
+ l_1 = l_2 = self.query_denoise
+ gtboxes = gt.boxes.clone()
+ _rs = torch.rand_like(gtboxes) * 2 - 1
+ gtboxes[..., :2] += gtboxes[..., 2:] * _rs[..., :2] * l_1
+ gtboxes[..., 2:] *= 1 + l_2 * _rs[..., 2:]
+ else:
+ gtboxes = None
+
+ if track_instances is None:
+ track_instances = self._generate_empty_tracks(proposals)
+ else:
+ track_instances = Instances.cat([
+ self._generate_empty_tracks(proposals),
+ track_instances])
+
+ if self.use_checkpoint and frame_index < len(frames) - 1:
+ def fn(frame, gtboxes, *args):
+ frame = nested_tensor_from_tensor_list([frame])
+ tmp = Instances((1, 1), **dict(zip(keys, args)))
+ frame_res = self._forward_single_image(frame, tmp, gtboxes)
+ return (
+ frame_res['pred_logits'],
+ frame_res['pred_boxes'],
+ frame_res['hs'],
+ *[aux['pred_logits'] for aux in frame_res['aux_outputs']],
+ *[aux['pred_boxes'] for aux in frame_res['aux_outputs']]
+ )
+
+ args = [frame, gtboxes] + [track_instances.get(k) for k in keys]
+ params = tuple((p for p in self.parameters() if p.requires_grad))
+ tmp = checkpoint.CheckpointFunction.apply(fn, len(args), *args, *params)
+ frame_res = {
+ 'pred_logits': tmp[0],
+ 'pred_boxes': tmp[1],
+ 'hs': tmp[2],
+ 'aux_outputs': [{
+ 'pred_logits': tmp[3+i],
+ 'pred_boxes': tmp[3+5+i],
+ } for i in range(5)],
+ }
+ else:
+ frame = nested_tensor_from_tensor_list([frame])
+ frame_res = self._forward_single_image(frame, track_instances, gtboxes)
+ frame_res = self._post_process_single_image(frame_res, track_instances, is_last)
+
+ track_instances = frame_res['track_instances']
+ outputs['pred_logits'].append(frame_res['pred_logits'])
+ outputs['pred_boxes'].append(frame_res['pred_boxes'])
+
+ if not self.training:
+ outputs['track_instances'] = track_instances
+ else:
+ outputs['losses_dict'] = self.criterion.losses_dict
+ return outputs
+
+
+def build(args):
+ dataset_to_num_classes = {
+ 'coco': 91,
+ 'coco_panoptic': 250,
+ 'e2e_mot': 1,
+ 'e2e_dance': 1,
+ 'e2e_joint': 1,
+ 'e2e_static_mot': 1,
+ }
+ assert args.dataset_file in dataset_to_num_classes
+ num_classes = dataset_to_num_classes[args.dataset_file]
+ device = torch.device(args.device)
+
+ backbone = build_backbone(args)
+
+ transformer = build_deforamble_transformer(args)
+ d_model = transformer.d_model
+ hidden_dim = args.dim_feedforward
+ query_interaction_layer = build_query_interaction_layer(args, args.query_interaction_layer, d_model, hidden_dim, d_model*2)
+
+ img_matcher = build_matcher(args)
+ num_frames_per_batch = max(args.sampler_lengths)
+ weight_dict = {}
+ for i in range(num_frames_per_batch):
+ weight_dict.update({"frame_{}_loss_ce".format(i): args.cls_loss_coef,
+ 'frame_{}_loss_bbox'.format(i): args.bbox_loss_coef,
+ 'frame_{}_loss_giou'.format(i): args.giou_loss_coef,
+ })
+
+ # TODO this is a hack
+ if args.aux_loss:
+ for i in range(num_frames_per_batch):
+ for j in range(args.dec_layers - 1):
+ weight_dict.update({"frame_{}_aux{}_loss_ce".format(i, j): args.cls_loss_coef,
+ 'frame_{}_aux{}_loss_bbox'.format(i, j): args.bbox_loss_coef,
+ 'frame_{}_aux{}_loss_giou'.format(i, j): args.giou_loss_coef,
+ })
+ for j in range(args.dec_layers):
+ weight_dict.update({"frame_{}_ps{}_loss_ce".format(i, j): args.cls_loss_coef,
+ 'frame_{}_ps{}_loss_bbox'.format(i, j): args.bbox_loss_coef,
+ 'frame_{}_ps{}_loss_giou'.format(i, j): args.giou_loss_coef,
+ })
+ if args.memory_bank_type is not None and len(args.memory_bank_type) > 0:
+ memory_bank = build_memory_bank(args, d_model, hidden_dim, d_model * 2)
+ for i in range(num_frames_per_batch):
+ weight_dict.update({"frame_{}_track_loss_ce".format(i): args.cls_loss_coef})
+ else:
+ memory_bank = None
+ losses = ['labels', 'boxes']
+ criterion = ClipMatcher(num_classes, matcher=img_matcher, weight_dict=weight_dict, losses=losses)
+ criterion.to(device)
+ postprocessors = {}
+ model = MOTR(
+ backbone,
+ transformer,
+ track_embed=query_interaction_layer,
+ num_feature_levels=args.num_feature_levels,
+ num_classes=num_classes,
+ num_queries=args.num_queries,
+ aux_loss=args.aux_loss,
+ criterion=criterion,
+ with_box_refine=args.with_box_refine,
+ two_stage=args.two_stage,
+ memory_bank=memory_bank,
+ use_checkpoint=args.use_checkpoint,
+ query_denoise=args.query_denoise,
+ )
+ return model, criterion, postprocessors
diff --git a/VISAM/models/ops/functions/__init__.py b/VISAM/models/ops/functions/__init__.py
new file mode 100644
index 0000000000000000000000000000000000000000..08d47add93a709a50357c0fc894895c8f2a25fe6
--- /dev/null
+++ b/VISAM/models/ops/functions/__init__.py
@@ -0,0 +1,13 @@
+# ------------------------------------------------------------------------
+# Copyright (c) 2022 megvii-research. All Rights Reserved.
+# ------------------------------------------------------------------------
+# Modified from Deformable DETR (https://github.com/fundamentalvision/Deformable-DETR)
+# Copyright (c) 2020 SenseTime. All Rights Reserved.
+# ------------------------------------------------------------------------
+# Modified from DETR (https://github.com/facebookresearch/detr)
+# Copyright (c) Facebook, Inc. and its affiliates. All Rights Reserved
+# ------------------------------------------------------------------------
+
+
+from .ms_deform_attn_func import MSDeformAttnFunction
+
diff --git a/VISAM/models/ops/functions/ms_deform_attn_func.py b/VISAM/models/ops/functions/ms_deform_attn_func.py
new file mode 100644
index 0000000000000000000000000000000000000000..f57e425c440dded083cfb9dc7a601e3270c35bb0
--- /dev/null
+++ b/VISAM/models/ops/functions/ms_deform_attn_func.py
@@ -0,0 +1,64 @@
+# ------------------------------------------------------------------------
+# Copyright (c) 2022 megvii-research. All Rights Reserved.
+# ------------------------------------------------------------------------
+# Modified from Deformable DETR (https://github.com/fundamentalvision/Deformable-DETR)
+# Copyright (c) 2020 SenseTime. All Rights Reserved.
+# ------------------------------------------------------------------------
+# Modified from DETR (https://github.com/facebookresearch/detr)
+# Copyright (c) Facebook, Inc. and its affiliates. All Rights Reserved
+# ------------------------------------------------------------------------
+
+
+from __future__ import absolute_import
+from __future__ import print_function
+from __future__ import division
+
+import torch
+import torch.nn.functional as F
+from torch.autograd import Function
+from torch.autograd.function import once_differentiable
+
+import MultiScaleDeformableAttention as MSDA
+
+
+class MSDeformAttnFunction(Function):
+ @staticmethod
+ def forward(ctx, value, value_spatial_shapes, value_level_start_index, sampling_locations, attention_weights, im2col_step):
+ ctx.im2col_step = im2col_step
+ output = MSDA.ms_deform_attn_forward(
+ value, value_spatial_shapes, value_level_start_index, sampling_locations, attention_weights, ctx.im2col_step)
+ ctx.save_for_backward(value, value_spatial_shapes, value_level_start_index, sampling_locations, attention_weights)
+ return output
+
+ @staticmethod
+ @once_differentiable
+ def backward(ctx, grad_output):
+ value, value_spatial_shapes, value_level_start_index, sampling_locations, attention_weights = ctx.saved_tensors
+ grad_value, grad_sampling_loc, grad_attn_weight = \
+ MSDA.ms_deform_attn_backward(
+ value, value_spatial_shapes, value_level_start_index, sampling_locations, attention_weights, grad_output, ctx.im2col_step)
+
+ return grad_value, None, None, grad_sampling_loc, grad_attn_weight, None
+
+
+def ms_deform_attn_core_pytorch(value, value_spatial_shapes, sampling_locations, attention_weights):
+ # for debug and test only,
+ # need to use cuda version instead
+ N_, S_, M_, D_ = value.shape
+ _, Lq_, M_, L_, P_, _ = sampling_locations.shape
+ value_list = value.split([H_ * W_ for H_, W_ in value_spatial_shapes], dim=1)
+ sampling_grids = 2 * sampling_locations - 1
+ sampling_value_list = []
+ for lid_, (H_, W_) in enumerate(value_spatial_shapes):
+ # N_, H_*W_, M_, D_ -> N_, H_*W_, M_*D_ -> N_, M_*D_, H_*W_ -> N_*M_, D_, H_, W_
+ value_l_ = value_list[lid_].flatten(2).transpose(1, 2).reshape(N_*M_, D_, H_, W_)
+ # N_, Lq_, M_, P_, 2 -> N_, M_, Lq_, P_, 2 -> N_*M_, Lq_, P_, 2
+ sampling_grid_l_ = sampling_grids[:, :, :, lid_].transpose(1, 2).flatten(0, 1)
+ # N_*M_, D_, Lq_, P_
+ sampling_value_l_ = F.grid_sample(value_l_, sampling_grid_l_,
+ mode='bilinear', padding_mode='zeros', align_corners=False)
+ sampling_value_list.append(sampling_value_l_)
+ # (N_, Lq_, M_, L_, P_) -> (N_, M_, Lq_, L_, P_) -> (N_, M_, 1, Lq_, L_*P_)
+ attention_weights = attention_weights.transpose(1, 2).reshape(N_*M_, 1, Lq_, L_*P_)
+ output = (torch.stack(sampling_value_list, dim=-2).flatten(-2) * attention_weights).sum(-1).view(N_, M_*D_, Lq_)
+ return output.transpose(1, 2).contiguous()
diff --git a/VISAM/models/ops/make.sh b/VISAM/models/ops/make.sh
new file mode 100644
index 0000000000000000000000000000000000000000..c3649ac63afd85c62b61295fede41e3311d630e7
--- /dev/null
+++ b/VISAM/models/ops/make.sh
@@ -0,0 +1,9 @@
+# ------------------------------------------------------------------------------------------------
+# Deformable DETR
+# Copyright (c) 2020 SenseTime. All Rights Reserved.
+# Licensed under the Apache License, Version 2.0 [see LICENSE for details]
+# ------------------------------------------------------------------------------------------------
+# Modified from https://github.com/chengdazhi/Deformable-Convolution-V2-PyTorch/tree/pytorch_1.0.0
+# ------------------------------------------------------------------------------------------------
+
+python setup.py build install
diff --git a/VISAM/models/ops/modules/__init__.py b/VISAM/models/ops/modules/__init__.py
new file mode 100644
index 0000000000000000000000000000000000000000..487445a5811c6687e5589666bedaae7b7edda9ea
--- /dev/null
+++ b/VISAM/models/ops/modules/__init__.py
@@ -0,0 +1,12 @@
+# ------------------------------------------------------------------------
+# Copyright (c) 2022 megvii-research. All Rights Reserved.
+# ------------------------------------------------------------------------
+# Modified from Deformable DETR (https://github.com/fundamentalvision/Deformable-DETR)
+# Copyright (c) 2020 SenseTime. All Rights Reserved.
+# ------------------------------------------------------------------------
+# Modified from DETR (https://github.com/facebookresearch/detr)
+# Copyright (c) Facebook, Inc. and its affiliates. All Rights Reserved
+# ------------------------------------------------------------------------
+
+
+from .ms_deform_attn import MSDeformAttn
diff --git a/VISAM/models/ops/modules/ms_deform_attn.py b/VISAM/models/ops/modules/ms_deform_attn.py
new file mode 100644
index 0000000000000000000000000000000000000000..42832285736a6ee68aaa0ef1d029762b1c04028e
--- /dev/null
+++ b/VISAM/models/ops/modules/ms_deform_attn.py
@@ -0,0 +1,121 @@
+# ------------------------------------------------------------------------
+# Copyright (c) 2022 megvii-research. All Rights Reserved.
+# ------------------------------------------------------------------------
+# Modified from Deformable DETR (https://github.com/fundamentalvision/Deformable-DETR)
+# Copyright (c) 2020 SenseTime. All Rights Reserved.
+# ------------------------------------------------------------------------
+# Modified from DETR (https://github.com/facebookresearch/detr)
+# Copyright (c) Facebook, Inc. and its affiliates. All Rights Reserved
+# ------------------------------------------------------------------------
+
+
+from __future__ import absolute_import
+from __future__ import print_function
+from __future__ import division
+
+import warnings
+import math
+
+import torch
+from torch import nn
+import torch.nn.functional as F
+from torch.nn.init import xavier_uniform_, constant_
+
+from ..functions import MSDeformAttnFunction
+
+
+def _is_power_of_2(n):
+ if (not isinstance(n, int)) or (n < 0):
+ raise ValueError("invalid input for _is_power_of_2: {} (type: {})".format(n, type(n)))
+ return (n & (n-1) == 0) and n != 0
+
+
+class MSDeformAttn(nn.Module):
+ def __init__(self, d_model=256, n_levels=4, n_heads=8, n_points=4, sigmoid_attn=False):
+ """
+ Multi-Scale Deformable Attention Module
+ :param d_model hidden dimension
+ :param n_levels number of feature levels
+ :param n_heads number of attention heads
+ :param n_points number of sampling points per attention head per feature level
+ """
+ super().__init__()
+ if d_model % n_heads != 0:
+ raise ValueError('d_model must be divisible by n_heads, but got {} and {}'.format(d_model, n_heads))
+ _d_per_head = d_model // n_heads
+ # you'd better set _d_per_head to a power of 2 which is more efficient in our CUDA implementation
+ if not _is_power_of_2(_d_per_head):
+ warnings.warn("You'd better set d_model in MSDeformAttn to make the dimension of each attention head a power of 2 "
+ "which is more efficient in our CUDA implementation.")
+
+ self.im2col_step = 64
+ self.sigmoid_attn = sigmoid_attn
+
+ self.d_model = d_model
+ self.n_levels = n_levels
+ self.n_heads = n_heads
+ self.n_points = n_points
+
+ self.sampling_offsets = nn.Linear(d_model, n_heads * n_levels * n_points * 2)
+ self.attention_weights = nn.Linear(d_model, n_heads * n_levels * n_points)
+ self.value_proj = nn.Linear(d_model, d_model)
+ self.output_proj = nn.Linear(d_model, d_model)
+
+ self._reset_parameters()
+
+ def _reset_parameters(self):
+ constant_(self.sampling_offsets.weight.data, 0.)
+ thetas = torch.arange(self.n_heads, dtype=torch.float32) * (2.0 * math.pi / self.n_heads)
+ grid_init = torch.stack([thetas.cos(), thetas.sin()], -1)
+ grid_init = (grid_init / grid_init.abs().max(-1, keepdim=True)[0]).view(self.n_heads, 1, 1, 2).repeat(1, self.n_levels, self.n_points, 1)
+ for i in range(self.n_points):
+ grid_init[:, :, i, :] *= i + 1
+ with torch.no_grad():
+ self.sampling_offsets.bias = nn.Parameter(grid_init.view(-1))
+ constant_(self.attention_weights.weight.data, 0.)
+ constant_(self.attention_weights.bias.data, 0.)
+ xavier_uniform_(self.value_proj.weight.data)
+ constant_(self.value_proj.bias.data, 0.)
+ xavier_uniform_(self.output_proj.weight.data)
+ constant_(self.output_proj.bias.data, 0.)
+
+ def forward(self, query, reference_points, input_flatten, input_spatial_shapes, input_level_start_index, input_padding_mask=None):
+ """
+ :param query (N, Length_{query}, C)
+ :param reference_points (N, Length_{query}, n_levels, 2), range in [0, 1], top-left (0,0), bottom-right (1, 1), including padding area
+ or (N, Length_{query}, n_levels, 4), add additional (w, h) to form reference boxes
+ :param input_flatten (N, \sum_{l=0}^{L-1} H_l \cdot W_l, C)
+ :param input_spatial_shapes (n_levels, 2), [(H_0, W_0), (H_1, W_1), ..., (H_{L-1}, W_{L-1})]
+ :param input_level_start_index (n_levels, ), [0, H_0*W_0, H_0*W_0+H_1*W_1, H_0*W_0+H_1*W_1+H_2*W_2, ..., H_0*W_0+H_1*W_1+...+H_{L-1}*W_{L-1}]
+ :param input_padding_mask (N, \sum_{l=0}^{L-1} H_l \cdot W_l), True for padding elements, False for non-padding elements
+
+ :return output (N, Length_{query}, C)
+ """
+ N, Len_q, _ = query.shape
+ N, Len_in, _ = input_flatten.shape
+ assert (input_spatial_shapes[:, 0] * input_spatial_shapes[:, 1]).sum() == Len_in
+
+ value = self.value_proj(input_flatten)
+ if input_padding_mask is not None:
+ value.masked_fill_(input_padding_mask[..., None], float(0))
+ value = value.view(N, Len_in, self.n_heads, self.d_model // self.n_heads)
+ sampling_offsets = self.sampling_offsets(query).view(N, Len_q, self.n_heads, self.n_levels, self.n_points, 2)
+ attention_weights = self.attention_weights(query).view(N, Len_q, self.n_heads, self.n_levels * self.n_points)
+ if self.sigmoid_attn:
+ attention_weights = attention_weights.sigmoid().view(N, Len_q, self.n_heads, self.n_levels, self.n_points)
+ else:
+ attention_weights = F.softmax(attention_weights, -1).view(N, Len_q, self.n_heads, self.n_levels, self.n_points)
+ # N, Len_q, n_heads, n_levels, n_points, 2
+ if reference_points.shape[-1] == 2:
+ sampling_locations = reference_points[:, :, None, :, None, :] \
+ + sampling_offsets / input_spatial_shapes[None, None, None, :, None, (1, 0)]
+ elif reference_points.shape[-1] == 4:
+ sampling_locations = reference_points[:, :, None, :, None, :2] \
+ + sampling_offsets / self.n_points * reference_points[:, :, None, :, None, 2:] * 0.5
+ else:
+ raise ValueError(
+ 'Last dim of reference_points must be 2 or 4, but get {} instead.'.format(reference_points.shape[-1]))
+ output = MSDeformAttnFunction.apply(
+ value, input_spatial_shapes, input_level_start_index, sampling_locations, attention_weights, self.im2col_step)
+ output = self.output_proj(output)
+ return output
diff --git a/VISAM/models/ops/setup.py b/VISAM/models/ops/setup.py
new file mode 100644
index 0000000000000000000000000000000000000000..a0131bc21cf1b45b90fcf174e2c53e4c08e9c641
--- /dev/null
+++ b/VISAM/models/ops/setup.py
@@ -0,0 +1,71 @@
+# ------------------------------------------------------------------------------------------------
+# Deformable DETR
+# Copyright (c) 2020 SenseTime. All Rights Reserved.
+# Licensed under the Apache License, Version 2.0 [see LICENSE for details]
+# ------------------------------------------------------------------------------------------------
+# Modified from https://github.com/chengdazhi/Deformable-Convolution-V2-PyTorch/tree/pytorch_1.0.0
+# ------------------------------------------------------------------------------------------------
+
+import os
+import glob
+
+import torch
+
+from torch.utils.cpp_extension import CUDA_HOME
+from torch.utils.cpp_extension import CppExtension
+from torch.utils.cpp_extension import CUDAExtension
+
+from setuptools import find_packages
+from setuptools import setup
+
+requirements = ["torch", "torchvision"]
+
+def get_extensions():
+ this_dir = os.path.dirname(os.path.abspath(__file__))
+ extensions_dir = os.path.join(this_dir, "src")
+
+ main_file = glob.glob(os.path.join(extensions_dir, "*.cpp"))
+ source_cpu = glob.glob(os.path.join(extensions_dir, "cpu", "*.cpp"))
+ source_cuda = glob.glob(os.path.join(extensions_dir, "cuda", "*.cu"))
+
+ sources = main_file + source_cpu
+ extension = CppExtension
+ extra_compile_args = {"cxx": []}
+ define_macros = []
+
+ if torch.cuda.is_available() and CUDA_HOME is not None:
+ extension = CUDAExtension
+ sources += source_cuda
+ define_macros += [("WITH_CUDA", None)]
+ extra_compile_args["nvcc"] = [
+ "-DCUDA_HAS_FP16=1",
+ "-D__CUDA_NO_HALF_OPERATORS__",
+ "-D__CUDA_NO_HALF_CONVERSIONS__",
+ "-D__CUDA_NO_HALF2_OPERATORS__",
+ ]
+ else:
+ raise NotImplementedError('Cuda is not availabel')
+
+ sources = [os.path.join(extensions_dir, s) for s in sources]
+ include_dirs = [extensions_dir]
+ ext_modules = [
+ extension(
+ "MultiScaleDeformableAttention",
+ sources,
+ include_dirs=include_dirs,
+ define_macros=define_macros,
+ extra_compile_args=extra_compile_args,
+ )
+ ]
+ return ext_modules
+
+setup(
+ name="MultiScaleDeformableAttention",
+ version="1.0",
+ author="Weijie Su",
+ url="https://github.com/fundamentalvision/Deformable-DETR",
+ description="PyTorch Wrapper for CUDA Functions of Multi-Scale Deformable Attention",
+ packages=find_packages(exclude=("configs", "tests",)),
+ ext_modules=get_extensions(),
+ cmdclass={"build_ext": torch.utils.cpp_extension.BuildExtension},
+)
diff --git a/VISAM/models/ops/src/cpu/ms_deform_attn_cpu.cpp b/VISAM/models/ops/src/cpu/ms_deform_attn_cpu.cpp
new file mode 100644
index 0000000000000000000000000000000000000000..e1bf854de1f3860d20b6fef5c1a17817c268e70a
--- /dev/null
+++ b/VISAM/models/ops/src/cpu/ms_deform_attn_cpu.cpp
@@ -0,0 +1,41 @@
+/*!
+**************************************************************************************************
+* Deformable DETR
+* Copyright (c) 2020 SenseTime. All Rights Reserved.
+* Licensed under the Apache License, Version 2.0 [see LICENSE for details]
+**************************************************************************************************
+* Modified from https://github.com/chengdazhi/Deformable-Convolution-V2-PyTorch/tree/pytorch_1.0.0
+**************************************************************************************************
+*/
+
+#include
+
+#include
+#include
+
+
+at::Tensor
+ms_deform_attn_cpu_forward(
+ const at::Tensor &value,
+ const at::Tensor &spatial_shapes,
+ const at::Tensor &level_start_index,
+ const at::Tensor &sampling_loc,
+ const at::Tensor &attn_weight,
+ const int im2col_step)
+{
+ AT_ERROR("Not implement on cpu");
+}
+
+std::vector
+ms_deform_attn_cpu_backward(
+ const at::Tensor &value,
+ const at::Tensor &spatial_shapes,
+ const at::Tensor &level_start_index,
+ const at::Tensor &sampling_loc,
+ const at::Tensor &attn_weight,
+ const at::Tensor &grad_output,
+ const int im2col_step)
+{
+ AT_ERROR("Not implement on cpu");
+}
+
diff --git a/VISAM/models/ops/src/cpu/ms_deform_attn_cpu.h b/VISAM/models/ops/src/cpu/ms_deform_attn_cpu.h
new file mode 100644
index 0000000000000000000000000000000000000000..81b7b58a3d9502bbb684dc84687a526dedf94cae
--- /dev/null
+++ b/VISAM/models/ops/src/cpu/ms_deform_attn_cpu.h
@@ -0,0 +1,33 @@
+/*!
+**************************************************************************************************
+* Deformable DETR
+* Copyright (c) 2020 SenseTime. All Rights Reserved.
+* Licensed under the Apache License, Version 2.0 [see LICENSE for details]
+**************************************************************************************************
+* Modified from https://github.com/chengdazhi/Deformable-Convolution-V2-PyTorch/tree/pytorch_1.0.0
+**************************************************************************************************
+*/
+
+#pragma once
+#include
+
+at::Tensor
+ms_deform_attn_cpu_forward(
+ const at::Tensor &value,
+ const at::Tensor &spatial_shapes,
+ const at::Tensor &level_start_index,
+ const at::Tensor &sampling_loc,
+ const at::Tensor &attn_weight,
+ const int im2col_step);
+
+std::vector
+ms_deform_attn_cpu_backward(
+ const at::Tensor &value,
+ const at::Tensor &spatial_shapes,
+ const at::Tensor &level_start_index,
+ const at::Tensor &sampling_loc,
+ const at::Tensor &attn_weight,
+ const at::Tensor &grad_output,
+ const int im2col_step);
+
+
diff --git a/VISAM/models/ops/src/cuda/ms_deform_attn_cuda.cu b/VISAM/models/ops/src/cuda/ms_deform_attn_cuda.cu
new file mode 100644
index 0000000000000000000000000000000000000000..d6d583647cce987196d5ad1968a8a365a379e774
--- /dev/null
+++ b/VISAM/models/ops/src/cuda/ms_deform_attn_cuda.cu
@@ -0,0 +1,153 @@
+/*!
+**************************************************************************************************
+* Deformable DETR
+* Copyright (c) 2020 SenseTime. All Rights Reserved.
+* Licensed under the Apache License, Version 2.0 [see LICENSE for details]
+**************************************************************************************************
+* Modified from https://github.com/chengdazhi/Deformable-Convolution-V2-PyTorch/tree/pytorch_1.0.0
+**************************************************************************************************
+*/
+
+#include
+#include "cuda/ms_deform_im2col_cuda.cuh"
+
+#include
+#include
+#include
+#include
+
+
+at::Tensor ms_deform_attn_cuda_forward(
+ const at::Tensor &value,
+ const at::Tensor &spatial_shapes,
+ const at::Tensor &level_start_index,
+ const at::Tensor &sampling_loc,
+ const at::Tensor &attn_weight,
+ const int im2col_step)
+{
+ AT_ASSERTM(value.is_contiguous(), "value tensor has to be contiguous");
+ AT_ASSERTM(spatial_shapes.is_contiguous(), "spatial_shapes tensor has to be contiguous");
+ AT_ASSERTM(level_start_index.is_contiguous(), "level_start_index tensor has to be contiguous");
+ AT_ASSERTM(sampling_loc.is_contiguous(), "sampling_loc tensor has to be contiguous");
+ AT_ASSERTM(attn_weight.is_contiguous(), "attn_weight tensor has to be contiguous");
+
+ AT_ASSERTM(value.type().is_cuda(), "value must be a CUDA tensor");
+ AT_ASSERTM(spatial_shapes.type().is_cuda(), "spatial_shapes must be a CUDA tensor");
+ AT_ASSERTM(level_start_index.type().is_cuda(), "level_start_index must be a CUDA tensor");
+ AT_ASSERTM(sampling_loc.type().is_cuda(), "sampling_loc must be a CUDA tensor");
+ AT_ASSERTM(attn_weight.type().is_cuda(), "attn_weight must be a CUDA tensor");
+
+ const int batch = value.size(0);
+ const int spatial_size = value.size(1);
+ const int num_heads = value.size(2);
+ const int channels = value.size(3);
+
+ const int num_levels = spatial_shapes.size(0);
+
+ const int num_query = sampling_loc.size(1);
+ const int num_point = sampling_loc.size(4);
+
+ const int im2col_step_ = std::min(batch, im2col_step);
+
+ AT_ASSERTM(batch % im2col_step_ == 0, "batch(%d) must divide im2col_step(%d)", batch, im2col_step_);
+
+ auto output = at::zeros({batch, num_query, num_heads, channels}, value.options());
+
+ const int batch_n = im2col_step_;
+ auto output_n = output.view({batch/im2col_step_, batch_n, num_query, num_heads, channels});
+ auto per_value_size = spatial_size * num_heads * channels;
+ auto per_sample_loc_size = num_query * num_heads * num_levels * num_point * 2;
+ auto per_attn_weight_size = num_query * num_heads * num_levels * num_point;
+ for (int n = 0; n < batch/im2col_step_; ++n)
+ {
+ auto columns = output_n.select(0, n);
+ AT_DISPATCH_FLOATING_TYPES(value.type(), "ms_deform_attn_forward_cuda", ([&] {
+ ms_deformable_im2col_cuda(at::cuda::getCurrentCUDAStream(),
+ value.data() + n * im2col_step_ * per_value_size,
+ spatial_shapes.data(),
+ level_start_index.data(),
+ sampling_loc.data() + n * im2col_step_ * per_sample_loc_size,
+ attn_weight.data() + n * im2col_step_ * per_attn_weight_size,
+ batch_n, spatial_size, num_heads, channels, num_levels, num_query, num_point,
+ columns.data());
+
+ }));
+ }
+
+ output = output.view({batch, num_query, num_heads*channels});
+
+ return output;
+}
+
+
+std::vector ms_deform_attn_cuda_backward(
+ const at::Tensor &value,
+ const at::Tensor &spatial_shapes,
+ const at::Tensor &level_start_index,
+ const at::Tensor &sampling_loc,
+ const at::Tensor &attn_weight,
+ const at::Tensor &grad_output,
+ const int im2col_step)
+{
+
+ AT_ASSERTM(value.is_contiguous(), "value tensor has to be contiguous");
+ AT_ASSERTM(spatial_shapes.is_contiguous(), "spatial_shapes tensor has to be contiguous");
+ AT_ASSERTM(level_start_index.is_contiguous(), "level_start_index tensor has to be contiguous");
+ AT_ASSERTM(sampling_loc.is_contiguous(), "sampling_loc tensor has to be contiguous");
+ AT_ASSERTM(attn_weight.is_contiguous(), "attn_weight tensor has to be contiguous");
+ AT_ASSERTM(grad_output.is_contiguous(), "grad_output tensor has to be contiguous");
+
+ AT_ASSERTM(value.type().is_cuda(), "value must be a CUDA tensor");
+ AT_ASSERTM(spatial_shapes.type().is_cuda(), "spatial_shapes must be a CUDA tensor");
+ AT_ASSERTM(level_start_index.type().is_cuda(), "level_start_index must be a CUDA tensor");
+ AT_ASSERTM(sampling_loc.type().is_cuda(), "sampling_loc must be a CUDA tensor");
+ AT_ASSERTM(attn_weight.type().is_cuda(), "attn_weight must be a CUDA tensor");
+ AT_ASSERTM(grad_output.type().is_cuda(), "grad_output must be a CUDA tensor");
+
+ const int batch = value.size(0);
+ const int spatial_size = value.size(1);
+ const int num_heads = value.size(2);
+ const int channels = value.size(3);
+
+ const int num_levels = spatial_shapes.size(0);
+
+ const int num_query = sampling_loc.size(1);
+ const int num_point = sampling_loc.size(4);
+
+ const int im2col_step_ = std::min(batch, im2col_step);
+
+ AT_ASSERTM(batch % im2col_step_ == 0, "batch(%d) must divide im2col_step(%d)", batch, im2col_step_);
+
+ auto grad_value = at::zeros_like(value);
+ auto grad_sampling_loc = at::zeros_like(sampling_loc);
+ auto grad_attn_weight = at::zeros_like(attn_weight);
+
+ const int batch_n = im2col_step_;
+ auto per_value_size = spatial_size * num_heads * channels;
+ auto per_sample_loc_size = num_query * num_heads * num_levels * num_point * 2;
+ auto per_attn_weight_size = num_query * num_heads * num_levels * num_point;
+ auto grad_output_n = grad_output.view({batch/im2col_step_, batch_n, num_query, num_heads, channels});
+
+ for (int n = 0; n < batch/im2col_step_; ++n)
+ {
+ auto grad_output_g = grad_output_n.select(0, n);
+ AT_DISPATCH_FLOATING_TYPES(value.type(), "ms_deform_attn_backward_cuda", ([&] {
+ ms_deformable_col2im_cuda(at::cuda::getCurrentCUDAStream(),
+ grad_output_g.data(),
+ value.data() + n * im2col_step_ * per_value_size,
+ spatial_shapes.data(),
+ level_start_index.data(),
+ sampling_loc.data() + n * im2col_step_ * per_sample_loc_size,
+ attn_weight.data() + n * im2col_step_ * per_attn_weight_size,
+ batch_n, spatial_size, num_heads, channels, num_levels, num_query, num_point,
+ grad_value.data() + n * im2col_step_ * per_value_size,
+ grad_sampling_loc.data() + n * im2col_step_ * per_sample_loc_size,
+ grad_attn_weight.data() + n * im2col_step_ * per_attn_weight_size);
+
+ }));
+ }
+
+ return {
+ grad_value, grad_sampling_loc, grad_attn_weight
+ };
+}
\ No newline at end of file
diff --git a/VISAM/models/ops/src/cuda/ms_deform_attn_cuda.h b/VISAM/models/ops/src/cuda/ms_deform_attn_cuda.h
new file mode 100644
index 0000000000000000000000000000000000000000..c7ae53f99c820ce6193b608ad344550348a0b42c
--- /dev/null
+++ b/VISAM/models/ops/src/cuda/ms_deform_attn_cuda.h
@@ -0,0 +1,30 @@
+/*!
+**************************************************************************************************
+* Deformable DETR
+* Copyright (c) 2020 SenseTime. All Rights Reserved.
+* Licensed under the Apache License, Version 2.0 [see LICENSE for details]
+**************************************************************************************************
+* Modified from https://github.com/chengdazhi/Deformable-Convolution-V2-PyTorch/tree/pytorch_1.0.0
+**************************************************************************************************
+*/
+
+#pragma once
+#include
+
+at::Tensor ms_deform_attn_cuda_forward(
+ const at::Tensor &value,
+ const at::Tensor &spatial_shapes,
+ const at::Tensor &level_start_index,
+ const at::Tensor &sampling_loc,
+ const at::Tensor &attn_weight,
+ const int im2col_step);
+
+std::vector ms_deform_attn_cuda_backward(
+ const at::Tensor &value,
+ const at::Tensor &spatial_shapes,
+ const at::Tensor &level_start_index,
+ const at::Tensor &sampling_loc,
+ const at::Tensor &attn_weight,
+ const at::Tensor &grad_output,
+ const int im2col_step);
+
diff --git a/VISAM/models/ops/src/cuda/ms_deform_im2col_cuda.cuh b/VISAM/models/ops/src/cuda/ms_deform_im2col_cuda.cuh
new file mode 100644
index 0000000000000000000000000000000000000000..6bc2acb7aea0eab2e9e91e769a16861e1652c284
--- /dev/null
+++ b/VISAM/models/ops/src/cuda/ms_deform_im2col_cuda.cuh
@@ -0,0 +1,1327 @@
+/*!
+**************************************************************************
+* Deformable DETR
+* Copyright (c) 2020 SenseTime. All Rights Reserved.
+* Licensed under the Apache License, Version 2.0 [see LICENSE for details]
+**************************************************************************
+* Modified from DCN (https://github.com/msracver/Deformable-ConvNets)
+* Copyright (c) 2018 Microsoft
+**************************************************************************
+*/
+
+#include
+#include
+#include
+
+#include
+#include
+
+#include
+
+#define CUDA_KERNEL_LOOP(i, n) \
+ for (int i = blockIdx.x * blockDim.x + threadIdx.x; \
+ i < (n); \
+ i += blockDim.x * gridDim.x)
+
+const int CUDA_NUM_THREADS = 1024;
+inline int GET_BLOCKS(const int N, const int num_threads)
+{
+ return (N + num_threads - 1) / num_threads;
+}
+
+
+template
+__device__ scalar_t ms_deform_attn_im2col_bilinear(const scalar_t* &bottom_data,
+ const int &height, const int &width, const int &nheads, const int &channels,
+ const scalar_t &h, const scalar_t &w, const int &m, const int &c)
+{
+ const int h_low = floor(h);
+ const int w_low = floor(w);
+ const int h_high = h_low + 1;
+ const int w_high = w_low + 1;
+
+ const scalar_t lh = h - h_low;
+ const scalar_t lw = w - w_low;
+ const scalar_t hh = 1 - lh, hw = 1 - lw;
+
+ const int w_stride = nheads * channels;
+ const int h_stride = width * w_stride;
+ const int h_low_ptr_offset = h_low * h_stride;
+ const int h_high_ptr_offset = h_low_ptr_offset + h_stride;
+ const int w_low_ptr_offset = w_low * w_stride;
+ const int w_high_ptr_offset = w_low_ptr_offset + w_stride;
+ const int base_ptr = m * channels + c;
+
+ scalar_t v1 = 0;
+ if (h_low >= 0 && w_low >= 0)
+ {
+ const int ptr1 = h_low_ptr_offset + w_low_ptr_offset + base_ptr;
+ v1 = bottom_data[ptr1];
+ }
+ scalar_t v2 = 0;
+ if (h_low >= 0 && w_high <= width - 1)
+ {
+ const int ptr2 = h_low_ptr_offset + w_high_ptr_offset + base_ptr;
+ v2 = bottom_data[ptr2];
+ }
+ scalar_t v3 = 0;
+ if (h_high <= height - 1 && w_low >= 0)
+ {
+ const int ptr3 = h_high_ptr_offset + w_low_ptr_offset + base_ptr;
+ v3 = bottom_data[ptr3];
+ }
+ scalar_t v4 = 0;
+ if (h_high <= height - 1 && w_high <= width - 1)
+ {
+ const int ptr4 = h_high_ptr_offset + w_high_ptr_offset + base_ptr;
+ v4 = bottom_data[ptr4];
+ }
+
+ const scalar_t w1 = hh * hw, w2 = hh * lw, w3 = lh * hw, w4 = lh * lw;
+
+ const scalar_t val = (w1 * v1 + w2 * v2 + w3 * v3 + w4 * v4);
+ return val;
+}
+
+
+template
+__device__ void ms_deform_attn_col2im_bilinear(const scalar_t* &bottom_data,
+ const int &height, const int &width, const int &nheads, const int &channels,
+ const scalar_t &h, const scalar_t &w, const int &m, const int &c,
+ const scalar_t &top_grad,
+ const scalar_t &attn_weight,
+ scalar_t* &grad_value,
+ scalar_t* grad_sampling_loc,
+ scalar_t* grad_attn_weight)
+{
+ const int h_low = floor(h);
+ const int w_low = floor(w);
+ const int h_high = h_low + 1;
+ const int w_high = w_low + 1;
+
+ const scalar_t lh = h - h_low;
+ const scalar_t lw = w - w_low;
+ const scalar_t hh = 1 - lh, hw = 1 - lw;
+
+ const int w_stride = nheads * channels;
+ const int h_stride = width * w_stride;
+ const int h_low_ptr_offset = h_low * h_stride;
+ const int h_high_ptr_offset = h_low_ptr_offset + h_stride;
+ const int w_low_ptr_offset = w_low * w_stride;
+ const int w_high_ptr_offset = w_low_ptr_offset + w_stride;
+ const int base_ptr = m * channels + c;
+
+ const scalar_t w1 = hh * hw, w2 = hh * lw, w3 = lh * hw, w4 = lh * lw;
+ const scalar_t top_grad_value = top_grad * attn_weight;
+ scalar_t grad_h_weight = 0, grad_w_weight = 0;
+
+ scalar_t v1 = 0;
+ if (h_low >= 0 && w_low >= 0)
+ {
+ const int ptr1 = h_low_ptr_offset + w_low_ptr_offset + base_ptr;
+ v1 = bottom_data[ptr1];
+ grad_h_weight -= hw * v1;
+ grad_w_weight -= hh * v1;
+ atomicAdd(grad_value+ptr1, w1*top_grad_value);
+ }
+ scalar_t v2 = 0;
+ if (h_low >= 0 && w_high <= width - 1)
+ {
+ const int ptr2 = h_low_ptr_offset + w_high_ptr_offset + base_ptr;
+ v2 = bottom_data[ptr2];
+ grad_h_weight -= lw * v2;
+ grad_w_weight += hh * v2;
+ atomicAdd(grad_value+ptr2, w2*top_grad_value);
+ }
+ scalar_t v3 = 0;
+ if (h_high <= height - 1 && w_low >= 0)
+ {
+ const int ptr3 = h_high_ptr_offset + w_low_ptr_offset + base_ptr;
+ v3 = bottom_data[ptr3];
+ grad_h_weight += hw * v3;
+ grad_w_weight -= lh * v3;
+ atomicAdd(grad_value+ptr3, w3*top_grad_value);
+ }
+ scalar_t v4 = 0;
+ if (h_high <= height - 1 && w_high <= width - 1)
+ {
+ const int ptr4 = h_high_ptr_offset + w_high_ptr_offset + base_ptr;
+ v4 = bottom_data[ptr4];
+ grad_h_weight += lw * v4;
+ grad_w_weight += lh * v4;
+ atomicAdd(grad_value+ptr4, w4*top_grad_value);
+ }
+
+ const scalar_t val = (w1 * v1 + w2 * v2 + w3 * v3 + w4 * v4);
+ *grad_attn_weight = top_grad * val;
+ *grad_sampling_loc = width * grad_w_weight * top_grad_value;
+ *(grad_sampling_loc + 1) = height * grad_h_weight * top_grad_value;
+}
+
+
+template
+__device__ void ms_deform_attn_col2im_bilinear_gm(const scalar_t* &bottom_data,
+ const int &height, const int &width, const int &nheads, const int &channels,
+ const scalar_t &h, const scalar_t &w, const int &m, const int &c,
+ const scalar_t &top_grad,
+ const scalar_t &attn_weight,
+ scalar_t* &grad_value,
+ scalar_t* grad_sampling_loc,
+ scalar_t* grad_attn_weight)
+{
+ const int h_low = floor(h);
+ const int w_low = floor(w);
+ const int h_high = h_low + 1;
+ const int w_high = w_low + 1;
+
+ const scalar_t lh = h - h_low;
+ const scalar_t lw = w - w_low;
+ const scalar_t hh = 1 - lh, hw = 1 - lw;
+
+ const int w_stride = nheads * channels;
+ const int h_stride = width * w_stride;
+ const int h_low_ptr_offset = h_low * h_stride;
+ const int h_high_ptr_offset = h_low_ptr_offset + h_stride;
+ const int w_low_ptr_offset = w_low * w_stride;
+ const int w_high_ptr_offset = w_low_ptr_offset + w_stride;
+ const int base_ptr = m * channels + c;
+
+ const scalar_t w1 = hh * hw, w2 = hh * lw, w3 = lh * hw, w4 = lh * lw;
+ const scalar_t top_grad_value = top_grad * attn_weight;
+ scalar_t grad_h_weight = 0, grad_w_weight = 0;
+
+ scalar_t v1 = 0;
+ if (h_low >= 0 && w_low >= 0)
+ {
+ const int ptr1 = h_low_ptr_offset + w_low_ptr_offset + base_ptr;
+ v1 = bottom_data[ptr1];
+ grad_h_weight -= hw * v1;
+ grad_w_weight -= hh * v1;
+ atomicAdd(grad_value+ptr1, w1*top_grad_value);
+ }
+ scalar_t v2 = 0;
+ if (h_low >= 0 && w_high <= width - 1)
+ {
+ const int ptr2 = h_low_ptr_offset + w_high_ptr_offset + base_ptr;
+ v2 = bottom_data[ptr2];
+ grad_h_weight -= lw * v2;
+ grad_w_weight += hh * v2;
+ atomicAdd(grad_value+ptr2, w2*top_grad_value);
+ }
+ scalar_t v3 = 0;
+ if (h_high <= height - 1 && w_low >= 0)
+ {
+ const int ptr3 = h_high_ptr_offset + w_low_ptr_offset + base_ptr;
+ v3 = bottom_data[ptr3];
+ grad_h_weight += hw * v3;
+ grad_w_weight -= lh * v3;
+ atomicAdd(grad_value+ptr3, w3*top_grad_value);
+ }
+ scalar_t v4 = 0;
+ if (h_high <= height - 1 && w_high <= width - 1)
+ {
+ const int ptr4 = h_high_ptr_offset + w_high_ptr_offset + base_ptr;
+ v4 = bottom_data[ptr4];
+ grad_h_weight += lw * v4;
+ grad_w_weight += lh * v4;
+ atomicAdd(grad_value+ptr4, w4*top_grad_value);
+ }
+
+ const scalar_t val = (w1 * v1 + w2 * v2 + w3 * v3 + w4 * v4);
+ atomicAdd(grad_attn_weight, top_grad * val);
+ atomicAdd(grad_sampling_loc, width * grad_w_weight * top_grad_value);
+ atomicAdd(grad_sampling_loc + 1, height * grad_h_weight * top_grad_value);
+}
+
+
+template
+__global__ void ms_deformable_im2col_gpu_kernel(const int n,
+ const scalar_t *data_value,
+ const int64_t *data_spatial_shapes,
+ const int64_t *data_level_start_index,
+ const scalar_t *data_sampling_loc,
+ const scalar_t *data_attn_weight,
+ const int batch_size,
+ const int spatial_size,
+ const int num_heads,
+ const int channels,
+ const int num_levels,
+ const int num_query,
+ const int num_point,
+ scalar_t *data_col)
+{
+ CUDA_KERNEL_LOOP(index, n)
+ {
+ int _temp = index;
+ const int c_col = _temp % channels;
+ _temp /= channels;
+ const int sampling_index = _temp;
+ const int m_col = _temp % num_heads;
+ _temp /= num_heads;
+ const int q_col = _temp % num_query;
+ _temp /= num_query;
+ const int b_col = _temp;
+
+ scalar_t *data_col_ptr = data_col + index;
+ int data_weight_ptr = sampling_index * num_levels * num_point;
+ int data_loc_w_ptr = data_weight_ptr << 1;
+ const int qid_stride = num_heads * channels;
+ const int data_value_ptr_init_offset = b_col * spatial_size * qid_stride;
+ scalar_t col = 0;
+
+ for (int l_col=0; l_col < num_levels; ++l_col)
+ {
+ const int level_start_id = data_level_start_index[l_col];
+ const int spatial_h_ptr = l_col << 1;
+ const int spatial_h = data_spatial_shapes[spatial_h_ptr];
+ const int spatial_w = data_spatial_shapes[spatial_h_ptr + 1];
+ const scalar_t *data_value_ptr = data_value + (data_value_ptr_init_offset + level_start_id * qid_stride);
+ for (int p_col=0; p_col < num_point; ++p_col)
+ {
+ const scalar_t loc_w = data_sampling_loc[data_loc_w_ptr];
+ const scalar_t loc_h = data_sampling_loc[data_loc_w_ptr + 1];
+ const scalar_t weight = data_attn_weight[data_weight_ptr];
+
+ const scalar_t h_im = loc_h * spatial_h - 0.5;
+ const scalar_t w_im = loc_w * spatial_w - 0.5;
+
+ if (h_im > -1 && w_im > -1 && h_im < spatial_h && w_im < spatial_w)
+ {
+ col += ms_deform_attn_im2col_bilinear(data_value_ptr, spatial_h, spatial_w, num_heads, channels, h_im, w_im, m_col, c_col) * weight;
+ }
+
+ data_weight_ptr += 1;
+ data_loc_w_ptr += 2;
+ }
+ }
+ *data_col_ptr = col;
+ }
+}
+
+template
+__global__ void ms_deformable_col2im_gpu_kernel_shm_blocksize_aware_reduce_v1(const int n,
+ const scalar_t *grad_col,
+ const scalar_t *data_value,
+ const int64_t *data_spatial_shapes,
+ const int64_t *data_level_start_index,
+ const scalar_t *data_sampling_loc,
+ const scalar_t *data_attn_weight,
+ const int batch_size,
+ const int spatial_size,
+ const int num_heads,
+ const int channels,
+ const int num_levels,
+ const int num_query,
+ const int num_point,
+ scalar_t *grad_value,
+ scalar_t *grad_sampling_loc,
+ scalar_t *grad_attn_weight)
+{
+ CUDA_KERNEL_LOOP(index, n)
+ {
+ __shared__ scalar_t cache_grad_sampling_loc[blockSize * 2];
+ __shared__ scalar_t cache_grad_attn_weight[blockSize];
+ unsigned int tid = threadIdx.x;
+ int _temp = index;
+ const int c_col = _temp % channels;
+ _temp /= channels;
+ const int sampling_index = _temp;
+ const int m_col = _temp % num_heads;
+ _temp /= num_heads;
+ const int q_col = _temp % num_query;
+ _temp /= num_query;
+ const int b_col = _temp;
+
+ const scalar_t top_grad = grad_col[index];
+
+ int data_weight_ptr = sampling_index * num_levels * num_point;
+ int data_loc_w_ptr = data_weight_ptr << 1;
+ const int grad_sampling_ptr = data_weight_ptr;
+ grad_sampling_loc += grad_sampling_ptr << 1;
+ grad_attn_weight += grad_sampling_ptr;
+ const int grad_weight_stride = 1;
+ const int grad_loc_stride = 2;
+ const int qid_stride = num_heads * channels;
+ const int data_value_ptr_init_offset = b_col * spatial_size * qid_stride;
+
+ for (int l_col=0; l_col < num_levels; ++l_col)
+ {
+ const int level_start_id = data_level_start_index[l_col];
+ const int spatial_h_ptr = l_col << 1;
+ const int spatial_h = data_spatial_shapes[spatial_h_ptr];
+ const int spatial_w = data_spatial_shapes[spatial_h_ptr + 1];
+ const int value_ptr_offset = data_value_ptr_init_offset + level_start_id * qid_stride;
+ const scalar_t *data_value_ptr = data_value + value_ptr_offset;
+ scalar_t *grad_value_ptr = grad_value + value_ptr_offset;
+
+ for (int p_col=0; p_col < num_point; ++p_col)
+ {
+ const scalar_t loc_w = data_sampling_loc[data_loc_w_ptr];
+ const scalar_t loc_h = data_sampling_loc[data_loc_w_ptr + 1];
+ const scalar_t weight = data_attn_weight[data_weight_ptr];
+
+ const scalar_t h_im = loc_h * spatial_h - 0.5;
+ const scalar_t w_im = loc_w * spatial_w - 0.5;
+ *(cache_grad_sampling_loc+(threadIdx.x << 1)) = 0;
+ *(cache_grad_sampling_loc+((threadIdx.x << 1) + 1)) = 0;
+ *(cache_grad_attn_weight+threadIdx.x)=0;
+ if (h_im > -1 && w_im > -1 && h_im < spatial_h && w_im < spatial_w)
+ {
+ ms_deform_attn_col2im_bilinear(
+ data_value_ptr, spatial_h, spatial_w, num_heads, channels, h_im, w_im, m_col, c_col,
+ top_grad, weight, grad_value_ptr,
+ cache_grad_sampling_loc+(threadIdx.x << 1), cache_grad_attn_weight+threadIdx.x);
+ }
+
+ __syncthreads();
+ if (tid == 0)
+ {
+ scalar_t _grad_w=cache_grad_sampling_loc[0], _grad_h=cache_grad_sampling_loc[1], _grad_a=cache_grad_attn_weight[0];
+ int sid=2;
+ for (unsigned int tid = 1; tid < blockSize; ++tid)
+ {
+ _grad_w += cache_grad_sampling_loc[sid];
+ _grad_h += cache_grad_sampling_loc[sid + 1];
+ _grad_a += cache_grad_attn_weight[tid];
+ sid += 2;
+ }
+
+
+ *grad_sampling_loc = _grad_w;
+ *(grad_sampling_loc + 1) = _grad_h;
+ *grad_attn_weight = _grad_a;
+ }
+ __syncthreads();
+
+ data_weight_ptr += 1;
+ data_loc_w_ptr += 2;
+ grad_attn_weight += grad_weight_stride;
+ grad_sampling_loc += grad_loc_stride;
+ }
+ }
+ }
+}
+
+
+template
+__global__ void ms_deformable_col2im_gpu_kernel_shm_blocksize_aware_reduce_v2(const int n,
+ const scalar_t *grad_col,
+ const scalar_t *data_value,
+ const int64_t *data_spatial_shapes,
+ const int64_t *data_level_start_index,
+ const scalar_t *data_sampling_loc,
+ const scalar_t *data_attn_weight,
+ const int batch_size,
+ const int spatial_size,
+ const int num_heads,
+ const int channels,
+ const int num_levels,
+ const int num_query,
+ const int num_point,
+ scalar_t *grad_value,
+ scalar_t *grad_sampling_loc,
+ scalar_t *grad_attn_weight)
+{
+ CUDA_KERNEL_LOOP(index, n)
+ {
+ __shared__ scalar_t cache_grad_sampling_loc[blockSize * 2];
+ __shared__ scalar_t cache_grad_attn_weight[blockSize];
+ unsigned int tid = threadIdx.x;
+ int _temp = index;
+ const int c_col = _temp % channels;
+ _temp /= channels;
+ const int sampling_index = _temp;
+ const int m_col = _temp % num_heads;
+ _temp /= num_heads;
+ const int q_col = _temp % num_query;
+ _temp /= num_query;
+ const int b_col = _temp;
+
+ const scalar_t top_grad = grad_col[index];
+
+ int data_weight_ptr = sampling_index * num_levels * num_point;
+ int data_loc_w_ptr = data_weight_ptr << 1;
+ const int grad_sampling_ptr = data_weight_ptr;
+ grad_sampling_loc += grad_sampling_ptr << 1;
+ grad_attn_weight += grad_sampling_ptr;
+ const int grad_weight_stride = 1;
+ const int grad_loc_stride = 2;
+ const int qid_stride = num_heads * channels;
+ const int data_value_ptr_init_offset = b_col * spatial_size * qid_stride;
+
+ for (int l_col=0; l_col < num_levels; ++l_col)
+ {
+ const int level_start_id = data_level_start_index[l_col];
+ const int spatial_h_ptr = l_col << 1;
+ const int spatial_h = data_spatial_shapes[spatial_h_ptr];
+ const int spatial_w = data_spatial_shapes[spatial_h_ptr + 1];
+ const int value_ptr_offset = data_value_ptr_init_offset + level_start_id * qid_stride;
+ const scalar_t *data_value_ptr = data_value + value_ptr_offset;
+ scalar_t *grad_value_ptr = grad_value + value_ptr_offset;
+
+ for (int p_col=0; p_col < num_point; ++p_col)
+ {
+ const scalar_t loc_w = data_sampling_loc[data_loc_w_ptr];
+ const scalar_t loc_h = data_sampling_loc[data_loc_w_ptr + 1];
+ const scalar_t weight = data_attn_weight[data_weight_ptr];
+
+ const scalar_t h_im = loc_h * spatial_h - 0.5;
+ const scalar_t w_im = loc_w * spatial_w - 0.5;
+ *(cache_grad_sampling_loc+(threadIdx.x << 1)) = 0;
+ *(cache_grad_sampling_loc+((threadIdx.x << 1) + 1)) = 0;
+ *(cache_grad_attn_weight+threadIdx.x)=0;
+ if (h_im > -1 && w_im > -1 && h_im < spatial_h && w_im < spatial_w)
+ {
+ ms_deform_attn_col2im_bilinear(
+ data_value_ptr, spatial_h, spatial_w, num_heads, channels, h_im, w_im, m_col, c_col,
+ top_grad, weight, grad_value_ptr,
+ cache_grad_sampling_loc+(threadIdx.x << 1), cache_grad_attn_weight+threadIdx.x);
+ }
+
+ __syncthreads();
+
+ for (unsigned int s=blockSize/2; s>0; s>>=1)
+ {
+ if (tid < s) {
+ const unsigned int xid1 = tid << 1;
+ const unsigned int xid2 = (tid + s) << 1;
+ cache_grad_attn_weight[tid] += cache_grad_attn_weight[tid + s];
+ cache_grad_sampling_loc[xid1] += cache_grad_sampling_loc[xid2];
+ cache_grad_sampling_loc[xid1 + 1] += cache_grad_sampling_loc[xid2 + 1];
+ }
+ __syncthreads();
+ }
+
+ if (tid == 0)
+ {
+ *grad_sampling_loc = cache_grad_sampling_loc[0];
+ *(grad_sampling_loc + 1) = cache_grad_sampling_loc[1];
+ *grad_attn_weight = cache_grad_attn_weight[0];
+ }
+ __syncthreads();
+
+ data_weight_ptr += 1;
+ data_loc_w_ptr += 2;
+ grad_attn_weight += grad_weight_stride;
+ grad_sampling_loc += grad_loc_stride;
+ }
+ }
+ }
+}
+
+
+template
+__global__ void ms_deformable_col2im_gpu_kernel_shm_reduce_v1(const int n,
+ const scalar_t *grad_col,
+ const scalar_t *data_value,
+ const int64_t *data_spatial_shapes,
+ const int64_t *data_level_start_index,
+ const scalar_t *data_sampling_loc,
+ const scalar_t *data_attn_weight,
+ const int batch_size,
+ const int spatial_size,
+ const int num_heads,
+ const int channels,
+ const int num_levels,
+ const int num_query,
+ const int num_point,
+ scalar_t *grad_value,
+ scalar_t *grad_sampling_loc,
+ scalar_t *grad_attn_weight)
+{
+ CUDA_KERNEL_LOOP(index, n)
+ {
+ extern __shared__ int _s[];
+ scalar_t* cache_grad_sampling_loc = (scalar_t*)_s;
+ scalar_t* cache_grad_attn_weight = cache_grad_sampling_loc + 2 * blockDim.x;
+ unsigned int tid = threadIdx.x;
+ int _temp = index;
+ const int c_col = _temp % channels;
+ _temp /= channels;
+ const int sampling_index = _temp;
+ const int m_col = _temp % num_heads;
+ _temp /= num_heads;
+ const int q_col = _temp % num_query;
+ _temp /= num_query;
+ const int b_col = _temp;
+
+ const scalar_t top_grad = grad_col[index];
+
+ int data_weight_ptr = sampling_index * num_levels * num_point;
+ int data_loc_w_ptr = data_weight_ptr << 1;
+ const int grad_sampling_ptr = data_weight_ptr;
+ grad_sampling_loc += grad_sampling_ptr << 1;
+ grad_attn_weight += grad_sampling_ptr;
+ const int grad_weight_stride = 1;
+ const int grad_loc_stride = 2;
+ const int qid_stride = num_heads * channels;
+ const int data_value_ptr_init_offset = b_col * spatial_size * qid_stride;
+
+ for (int l_col=0; l_col < num_levels; ++l_col)
+ {
+ const int level_start_id = data_level_start_index[l_col];
+ const int spatial_h_ptr = l_col << 1;
+ const int spatial_h = data_spatial_shapes[spatial_h_ptr];
+ const int spatial_w = data_spatial_shapes[spatial_h_ptr + 1];
+ const int value_ptr_offset = data_value_ptr_init_offset + level_start_id * qid_stride;
+ const scalar_t *data_value_ptr = data_value + value_ptr_offset;
+ scalar_t *grad_value_ptr = grad_value + value_ptr_offset;
+
+ for (int p_col=0; p_col < num_point; ++p_col)
+ {
+ const scalar_t loc_w = data_sampling_loc[data_loc_w_ptr];
+ const scalar_t loc_h = data_sampling_loc[data_loc_w_ptr + 1];
+ const scalar_t weight = data_attn_weight[data_weight_ptr];
+
+ const scalar_t h_im = loc_h * spatial_h - 0.5;
+ const scalar_t w_im = loc_w * spatial_w - 0.5;
+ *(cache_grad_sampling_loc+(threadIdx.x << 1)) = 0;
+ *(cache_grad_sampling_loc+((threadIdx.x << 1) + 1)) = 0;
+ *(cache_grad_attn_weight+threadIdx.x)=0;
+ if (h_im > -1 && w_im > -1 && h_im < spatial_h && w_im < spatial_w)
+ {
+ ms_deform_attn_col2im_bilinear(
+ data_value_ptr, spatial_h, spatial_w, num_heads, channels, h_im, w_im, m_col, c_col,
+ top_grad, weight, grad_value_ptr,
+ cache_grad_sampling_loc+(threadIdx.x << 1), cache_grad_attn_weight+threadIdx.x);
+ }
+
+ __syncthreads();
+ if (tid == 0)
+ {
+ scalar_t _grad_w=cache_grad_sampling_loc[0], _grad_h=cache_grad_sampling_loc[1], _grad_a=cache_grad_attn_weight[0];
+ int sid=2;
+ for (unsigned int tid = 1; tid < blockDim.x; ++tid)
+ {
+ _grad_w += cache_grad_sampling_loc[sid];
+ _grad_h += cache_grad_sampling_loc[sid + 1];
+ _grad_a += cache_grad_attn_weight[tid];
+ sid += 2;
+ }
+
+
+ *grad_sampling_loc = _grad_w;
+ *(grad_sampling_loc + 1) = _grad_h;
+ *grad_attn_weight = _grad_a;
+ }
+ __syncthreads();
+
+ data_weight_ptr += 1;
+ data_loc_w_ptr += 2;
+ grad_attn_weight += grad_weight_stride;
+ grad_sampling_loc += grad_loc_stride;
+ }
+ }
+ }
+}
+
+template
+__global__ void ms_deformable_col2im_gpu_kernel_shm_reduce_v2(const int n,
+ const scalar_t *grad_col,
+ const scalar_t *data_value,
+ const int64_t *data_spatial_shapes,
+ const int64_t *data_level_start_index,
+ const scalar_t *data_sampling_loc,
+ const scalar_t *data_attn_weight,
+ const int batch_size,
+ const int spatial_size,
+ const int num_heads,
+ const int channels,
+ const int num_levels,
+ const int num_query,
+ const int num_point,
+ scalar_t *grad_value,
+ scalar_t *grad_sampling_loc,
+ scalar_t *grad_attn_weight)
+{
+ CUDA_KERNEL_LOOP(index, n)
+ {
+ extern __shared__ int _s[];
+ scalar_t* cache_grad_sampling_loc = (scalar_t*)_s;
+ scalar_t* cache_grad_attn_weight = cache_grad_sampling_loc + 2 * blockDim.x;
+ unsigned int tid = threadIdx.x;
+ int _temp = index;
+ const int c_col = _temp % channels;
+ _temp /= channels;
+ const int sampling_index = _temp;
+ const int m_col = _temp % num_heads;
+ _temp /= num_heads;
+ const int q_col = _temp % num_query;
+ _temp /= num_query;
+ const int b_col = _temp;
+
+ const scalar_t top_grad = grad_col[index];
+
+ int data_weight_ptr = sampling_index * num_levels * num_point;
+ int data_loc_w_ptr = data_weight_ptr << 1;
+ const int grad_sampling_ptr = data_weight_ptr;
+ grad_sampling_loc += grad_sampling_ptr << 1;
+ grad_attn_weight += grad_sampling_ptr;
+ const int grad_weight_stride = 1;
+ const int grad_loc_stride = 2;
+ const int qid_stride = num_heads * channels;
+ const int data_value_ptr_init_offset = b_col * spatial_size * qid_stride;
+
+ for (int l_col=0; l_col < num_levels; ++l_col)
+ {
+ const int level_start_id = data_level_start_index[l_col];
+ const int spatial_h_ptr = l_col << 1;
+ const int spatial_h = data_spatial_shapes[spatial_h_ptr];
+ const int spatial_w = data_spatial_shapes[spatial_h_ptr + 1];
+ const int value_ptr_offset = data_value_ptr_init_offset + level_start_id * qid_stride;
+ const scalar_t *data_value_ptr = data_value + value_ptr_offset;
+ scalar_t *grad_value_ptr = grad_value + value_ptr_offset;
+
+ for (int p_col=0; p_col < num_point; ++p_col)
+ {
+ const scalar_t loc_w = data_sampling_loc[data_loc_w_ptr];
+ const scalar_t loc_h = data_sampling_loc[data_loc_w_ptr + 1];
+ const scalar_t weight = data_attn_weight[data_weight_ptr];
+
+ const scalar_t h_im = loc_h * spatial_h - 0.5;
+ const scalar_t w_im = loc_w * spatial_w - 0.5;
+ *(cache_grad_sampling_loc+(threadIdx.x << 1)) = 0;
+ *(cache_grad_sampling_loc+((threadIdx.x << 1) + 1)) = 0;
+ *(cache_grad_attn_weight+threadIdx.x)=0;
+ if (h_im > -1 && w_im > -1 && h_im < spatial_h && w_im < spatial_w)
+ {
+ ms_deform_attn_col2im_bilinear(
+ data_value_ptr, spatial_h, spatial_w, num_heads, channels, h_im, w_im, m_col, c_col,
+ top_grad, weight, grad_value_ptr,
+ cache_grad_sampling_loc+(threadIdx.x << 1), cache_grad_attn_weight+threadIdx.x);
+ }
+
+ __syncthreads();
+
+ for (unsigned int s=blockDim.x/2, spre=blockDim.x; s>0; s>>=1, spre>>=1)
+ {
+ if (tid < s) {
+ const unsigned int xid1 = tid << 1;
+ const unsigned int xid2 = (tid + s) << 1;
+ cache_grad_attn_weight[tid] += cache_grad_attn_weight[tid + s];
+ cache_grad_sampling_loc[xid1] += cache_grad_sampling_loc[xid2];
+ cache_grad_sampling_loc[xid1 + 1] += cache_grad_sampling_loc[xid2 + 1];
+ if (tid + (s << 1) < spre)
+ {
+ cache_grad_attn_weight[tid] += cache_grad_attn_weight[tid + (s << 1)];
+ cache_grad_sampling_loc[xid1] += cache_grad_sampling_loc[xid2 + (s << 1)];
+ cache_grad_sampling_loc[xid1 + 1] += cache_grad_sampling_loc[xid2 + 1 + (s << 1)];
+ }
+ }
+ __syncthreads();
+ }
+
+ if (tid == 0)
+ {
+ *grad_sampling_loc = cache_grad_sampling_loc[0];
+ *(grad_sampling_loc + 1) = cache_grad_sampling_loc[1];
+ *grad_attn_weight = cache_grad_attn_weight[0];
+ }
+ __syncthreads();
+
+ data_weight_ptr += 1;
+ data_loc_w_ptr += 2;
+ grad_attn_weight += grad_weight_stride;
+ grad_sampling_loc += grad_loc_stride;
+ }
+ }
+ }
+}
+
+template
+__global__ void ms_deformable_col2im_gpu_kernel_shm_reduce_v2_multi_blocks(const int n,
+ const scalar_t *grad_col,
+ const scalar_t *data_value,
+ const int64_t *data_spatial_shapes,
+ const int64_t *data_level_start_index,
+ const scalar_t *data_sampling_loc,
+ const scalar_t *data_attn_weight,
+ const int batch_size,
+ const int spatial_size,
+ const int num_heads,
+ const int channels,
+ const int num_levels,
+ const int num_query,
+ const int num_point,
+ scalar_t *grad_value,
+ scalar_t *grad_sampling_loc,
+ scalar_t *grad_attn_weight)
+{
+ CUDA_KERNEL_LOOP(index, n)
+ {
+ extern __shared__ int _s[];
+ scalar_t* cache_grad_sampling_loc = (scalar_t*)_s;
+ scalar_t* cache_grad_attn_weight = cache_grad_sampling_loc + 2 * blockDim.x;
+ unsigned int tid = threadIdx.x;
+ int _temp = index;
+ const int c_col = _temp % channels;
+ _temp /= channels;
+ const int sampling_index = _temp;
+ const int m_col = _temp % num_heads;
+ _temp /= num_heads;
+ const int q_col = _temp % num_query;
+ _temp /= num_query;
+ const int b_col = _temp;
+
+ const scalar_t top_grad = grad_col[index];
+
+ int data_weight_ptr = sampling_index * num_levels * num_point;
+ int data_loc_w_ptr = data_weight_ptr << 1;
+ const int grad_sampling_ptr = data_weight_ptr;
+ grad_sampling_loc += grad_sampling_ptr << 1;
+ grad_attn_weight += grad_sampling_ptr;
+ const int grad_weight_stride = 1;
+ const int grad_loc_stride = 2;
+ const int qid_stride = num_heads * channels;
+ const int data_value_ptr_init_offset = b_col * spatial_size * qid_stride;
+
+ for (int l_col=0; l_col < num_levels; ++l_col)
+ {
+ const int level_start_id = data_level_start_index[l_col];
+ const int spatial_h_ptr = l_col << 1;
+ const int spatial_h = data_spatial_shapes[spatial_h_ptr];
+ const int spatial_w = data_spatial_shapes[spatial_h_ptr + 1];
+ const int value_ptr_offset = data_value_ptr_init_offset + level_start_id * qid_stride;
+ const scalar_t *data_value_ptr = data_value + value_ptr_offset;
+ scalar_t *grad_value_ptr = grad_value + value_ptr_offset;
+
+ for (int p_col=0; p_col < num_point; ++p_col)
+ {
+ const scalar_t loc_w = data_sampling_loc[data_loc_w_ptr];
+ const scalar_t loc_h = data_sampling_loc[data_loc_w_ptr + 1];
+ const scalar_t weight = data_attn_weight[data_weight_ptr];
+
+ const scalar_t h_im = loc_h * spatial_h - 0.5;
+ const scalar_t w_im = loc_w * spatial_w - 0.5;
+ *(cache_grad_sampling_loc+(threadIdx.x << 1)) = 0;
+ *(cache_grad_sampling_loc+((threadIdx.x << 1) + 1)) = 0;
+ *(cache_grad_attn_weight+threadIdx.x)=0;
+ if (h_im > -1 && w_im > -1 && h_im < spatial_h && w_im < spatial_w)
+ {
+ ms_deform_attn_col2im_bilinear(
+ data_value_ptr, spatial_h, spatial_w, num_heads, channels, h_im, w_im, m_col, c_col,
+ top_grad, weight, grad_value_ptr,
+ cache_grad_sampling_loc+(threadIdx.x << 1), cache_grad_attn_weight+threadIdx.x);
+ }
+
+ __syncthreads();
+
+ for (unsigned int s=blockDim.x/2, spre=blockDim.x; s>0; s>>=1, spre>>=1)
+ {
+ if (tid < s) {
+ const unsigned int xid1 = tid << 1;
+ const unsigned int xid2 = (tid + s) << 1;
+ cache_grad_attn_weight[tid] += cache_grad_attn_weight[tid + s];
+ cache_grad_sampling_loc[xid1] += cache_grad_sampling_loc[xid2];
+ cache_grad_sampling_loc[xid1 + 1] += cache_grad_sampling_loc[xid2 + 1];
+ if (tid + (s << 1) < spre)
+ {
+ cache_grad_attn_weight[tid] += cache_grad_attn_weight[tid + (s << 1)];
+ cache_grad_sampling_loc[xid1] += cache_grad_sampling_loc[xid2 + (s << 1)];
+ cache_grad_sampling_loc[xid1 + 1] += cache_grad_sampling_loc[xid2 + 1 + (s << 1)];
+ }
+ }
+ __syncthreads();
+ }
+
+ if (tid == 0)
+ {
+ atomicAdd(grad_sampling_loc, cache_grad_sampling_loc[0]);
+ atomicAdd(grad_sampling_loc + 1, cache_grad_sampling_loc[1]);
+ atomicAdd(grad_attn_weight, cache_grad_attn_weight[0]);
+ }
+ __syncthreads();
+
+ data_weight_ptr += 1;
+ data_loc_w_ptr += 2;
+ grad_attn_weight += grad_weight_stride;
+ grad_sampling_loc += grad_loc_stride;
+ }
+ }
+ }
+}
+
+
+template
+__global__ void ms_deformable_col2im_gpu_kernel_gm(const int n,
+ const scalar_t *grad_col,
+ const scalar_t *data_value,
+ const int64_t *data_spatial_shapes,
+ const int64_t *data_level_start_index,
+ const scalar_t *data_sampling_loc,
+ const scalar_t *data_attn_weight,
+ const int batch_size,
+ const int spatial_size,
+ const int num_heads,
+ const int channels,
+ const int num_levels,
+ const int num_query,
+ const int num_point,
+ scalar_t *grad_value,
+ scalar_t *grad_sampling_loc,
+ scalar_t *grad_attn_weight)
+{
+ CUDA_KERNEL_LOOP(index, n)
+ {
+ int _temp = index;
+ const int c_col = _temp % channels;
+ _temp /= channels;
+ const int sampling_index = _temp;
+ const int m_col = _temp % num_heads;
+ _temp /= num_heads;
+ const int q_col = _temp % num_query;
+ _temp /= num_query;
+ const int b_col = _temp;
+
+ const scalar_t top_grad = grad_col[index];
+
+ int data_weight_ptr = sampling_index * num_levels * num_point;
+ int data_loc_w_ptr = data_weight_ptr << 1;
+ const int grad_sampling_ptr = data_weight_ptr;
+ grad_sampling_loc += grad_sampling_ptr << 1;
+ grad_attn_weight += grad_sampling_ptr;
+ const int grad_weight_stride = 1;
+ const int grad_loc_stride = 2;
+ const int qid_stride = num_heads * channels;
+ const int data_value_ptr_init_offset = b_col * spatial_size * qid_stride;
+
+ for (int l_col=0; l_col < num_levels; ++l_col)
+ {
+ const int level_start_id = data_level_start_index[l_col];
+ const int spatial_h_ptr = l_col << 1;
+ const int spatial_h = data_spatial_shapes[spatial_h_ptr];
+ const int spatial_w = data_spatial_shapes[spatial_h_ptr + 1];
+ const int value_ptr_offset = data_value_ptr_init_offset + level_start_id * qid_stride;
+ const scalar_t *data_value_ptr = data_value + value_ptr_offset;
+ scalar_t *grad_value_ptr = grad_value + value_ptr_offset;
+
+ for (int p_col=0; p_col < num_point; ++p_col)
+ {
+ const scalar_t loc_w = data_sampling_loc[data_loc_w_ptr];
+ const scalar_t loc_h = data_sampling_loc[data_loc_w_ptr + 1];
+ const scalar_t weight = data_attn_weight[data_weight_ptr];
+
+ const scalar_t h_im = loc_h * spatial_h - 0.5;
+ const scalar_t w_im = loc_w * spatial_w - 0.5;
+ if (h_im > -1 && w_im > -1 && h_im < spatial_h && w_im < spatial_w)
+ {
+ ms_deform_attn_col2im_bilinear_gm(
+ data_value_ptr, spatial_h, spatial_w, num_heads, channels, h_im, w_im, m_col, c_col,
+ top_grad, weight, grad_value_ptr,
+ grad_sampling_loc, grad_attn_weight);
+ }
+ data_weight_ptr += 1;
+ data_loc_w_ptr += 2;
+ grad_attn_weight += grad_weight_stride;
+ grad_sampling_loc += grad_loc_stride;
+ }
+ }
+ }
+}
+
+
+template
+void ms_deformable_im2col_cuda(cudaStream_t stream,
+ const scalar_t* data_value,
+ const int64_t* data_spatial_shapes,
+ const int64_t* data_level_start_index,
+ const scalar_t* data_sampling_loc,
+ const scalar_t* data_attn_weight,
+ const int batch_size,
+ const int spatial_size,
+ const int num_heads,
+ const int channels,
+ const int num_levels,
+ const int num_query,
+ const int num_point,
+ scalar_t* data_col)
+{
+ const int num_kernels = batch_size * num_query * num_heads * channels;
+ const int num_actual_kernels = batch_size * num_query * num_heads * channels;
+ const int num_threads = CUDA_NUM_THREADS;
+ ms_deformable_im2col_gpu_kernel
+ <<>>(
+ num_kernels, data_value, data_spatial_shapes, data_level_start_index, data_sampling_loc, data_attn_weight,
+ batch_size, spatial_size, num_heads, channels, num_levels, num_query, num_point, data_col);
+
+ cudaError_t err = cudaGetLastError();
+ if (err != cudaSuccess)
+ {
+ printf("error in ms_deformable_im2col_cuda: %s\n", cudaGetErrorString(err));
+ }
+
+}
+
+template
+void ms_deformable_col2im_cuda(cudaStream_t stream,
+ const scalar_t* grad_col,
+ const scalar_t* data_value,
+ const int64_t * data_spatial_shapes,
+ const int64_t * data_level_start_index,
+ const scalar_t * data_sampling_loc,
+ const scalar_t * data_attn_weight,
+ const int batch_size,
+ const int spatial_size,
+ const int num_heads,
+ const int channels,
+ const int num_levels,
+ const int num_query,
+ const int num_point,
+ scalar_t* grad_value,
+ scalar_t* grad_sampling_loc,
+ scalar_t* grad_attn_weight)
+{
+ const int num_threads = (channels > CUDA_NUM_THREADS)?CUDA_NUM_THREADS:channels;
+ const int num_kernels = batch_size * num_query * num_heads * channels;
+ const int num_actual_kernels = batch_size * num_query * num_heads * channels;
+ if (channels > 1024)
+ {
+ if ((channels & 1023) == 0)
+ {
+ ms_deformable_col2im_gpu_kernel_shm_reduce_v2_multi_blocks
+ <<>>(
+ num_kernels,
+ grad_col,
+ data_value,
+ data_spatial_shapes,
+ data_level_start_index,
+ data_sampling_loc,
+ data_attn_weight,
+ batch_size,
+ spatial_size,
+ num_heads,
+ channels,
+ num_levels,
+ num_query,
+ num_point,
+ grad_value,
+ grad_sampling_loc,
+ grad_attn_weight);
+ }
+ else
+ {
+ ms_deformable_col2im_gpu_kernel_gm
+ <<>>(
+ num_kernels,
+ grad_col,
+ data_value,
+ data_spatial_shapes,
+ data_level_start_index,
+ data_sampling_loc,
+ data_attn_weight,
+ batch_size,
+ spatial_size,
+ num_heads,
+ channels,
+ num_levels,
+ num_query,
+ num_point,
+ grad_value,
+ grad_sampling_loc,
+ grad_attn_weight);
+ }
+ }
+ else{
+ switch(channels)
+ {
+ case 1:
+ ms_deformable_col2im_gpu_kernel_shm_blocksize_aware_reduce_v1
+ <<>>(
+ num_kernels,
+ grad_col,
+ data_value,
+ data_spatial_shapes,
+ data_level_start_index,
+ data_sampling_loc,
+ data_attn_weight,
+ batch_size,
+ spatial_size,
+ num_heads,
+ channels,
+ num_levels,
+ num_query,
+ num_point,
+ grad_value,
+ grad_sampling_loc,
+ grad_attn_weight);
+ break;
+ case 2:
+ ms_deformable_col2im_gpu_kernel_shm_blocksize_aware_reduce_v1
+ <<>>(
+ num_kernels,
+ grad_col,
+ data_value,
+ data_spatial_shapes,
+ data_level_start_index,
+ data_sampling_loc,
+ data_attn_weight,
+ batch_size,
+ spatial_size,
+ num_heads,
+ channels,
+ num_levels,
+ num_query,
+ num_point,
+ grad_value,
+ grad_sampling_loc,
+ grad_attn_weight);
+ break;
+ case 4:
+ ms_deformable_col2im_gpu_kernel_shm_blocksize_aware_reduce_v1
+ <<>>(
+ num_kernels,
+ grad_col,
+ data_value,
+ data_spatial_shapes,
+ data_level_start_index,
+ data_sampling_loc,
+ data_attn_weight,
+ batch_size,
+ spatial_size,
+ num_heads,
+ channels,
+ num_levels,
+ num_query,
+ num_point,
+ grad_value,
+ grad_sampling_loc,
+ grad_attn_weight);
+ break;
+ case 8:
+ ms_deformable_col2im_gpu_kernel_shm_blocksize_aware_reduce_v1
+ <<>>(
+ num_kernels,
+ grad_col,
+ data_value,
+ data_spatial_shapes,
+ data_level_start_index,
+ data_sampling_loc,
+ data_attn_weight,
+ batch_size,
+ spatial_size,
+ num_heads,
+ channels,
+ num_levels,
+ num_query,
+ num_point,
+ grad_value,
+ grad_sampling_loc,
+ grad_attn_weight);
+ break;
+ case 16:
+ ms_deformable_col2im_gpu_kernel_shm_blocksize_aware_reduce_v1
+ <<>>(
+ num_kernels,
+ grad_col,
+ data_value,
+ data_spatial_shapes,
+ data_level_start_index,
+ data_sampling_loc,
+ data_attn_weight,
+ batch_size,
+ spatial_size,
+ num_heads,
+ channels,
+ num_levels,
+ num_query,
+ num_point,
+ grad_value,
+ grad_sampling_loc,
+ grad_attn_weight);
+ break;
+ case 32:
+ ms_deformable_col2im_gpu_kernel_shm_blocksize_aware_reduce_v1
+ <<>>(
+ num_kernels,
+ grad_col,
+ data_value,
+ data_spatial_shapes,
+ data_level_start_index,
+ data_sampling_loc,
+ data_attn_weight,
+ batch_size,
+ spatial_size,
+ num_heads,
+ channels,
+ num_levels,
+ num_query,
+ num_point,
+ grad_value,
+ grad_sampling_loc,
+ grad_attn_weight);
+ break;
+ case 64:
+ ms_deformable_col2im_gpu_kernel_shm_blocksize_aware_reduce_v2
+ <<>>(
+ num_kernels,
+ grad_col,
+ data_value,
+ data_spatial_shapes,
+ data_level_start_index,
+ data_sampling_loc,
+ data_attn_weight,
+ batch_size,
+ spatial_size,
+ num_heads,
+ channels,
+ num_levels,
+ num_query,
+ num_point,
+ grad_value,
+ grad_sampling_loc,
+ grad_attn_weight);
+ break;
+ case 128:
+ ms_deformable_col2im_gpu_kernel_shm_blocksize_aware_reduce_v2
+ <<>>(
+ num_kernels,
+ grad_col,
+ data_value,
+ data_spatial_shapes,
+ data_level_start_index,
+ data_sampling_loc,
+ data_attn_weight,
+ batch_size,
+ spatial_size,
+ num_heads,
+ channels,
+ num_levels,
+ num_query,
+ num_point,
+ grad_value,
+ grad_sampling_loc,
+ grad_attn_weight);
+ break;
+ case 256:
+ ms_deformable_col2im_gpu_kernel_shm_blocksize_aware_reduce_v2
+ <<>>(
+ num_kernels,
+ grad_col,
+ data_value,
+ data_spatial_shapes,
+ data_level_start_index,
+ data_sampling_loc,
+ data_attn_weight,
+ batch_size,
+ spatial_size,
+ num_heads,
+ channels,
+ num_levels,
+ num_query,
+ num_point,
+ grad_value,
+ grad_sampling_loc,
+ grad_attn_weight);
+ break;
+ case 512:
+ ms_deformable_col2im_gpu_kernel_shm_blocksize_aware_reduce_v2
+ <<>>(
+ num_kernels,
+ grad_col,
+ data_value,
+ data_spatial_shapes,
+ data_level_start_index,
+ data_sampling_loc,
+ data_attn_weight,
+ batch_size,
+ spatial_size,
+ num_heads,
+ channels,
+ num_levels,
+ num_query,
+ num_point,
+ grad_value,
+ grad_sampling_loc,
+ grad_attn_weight);
+ break;
+ case 1024:
+ ms_deformable_col2im_gpu_kernel_shm_blocksize_aware_reduce_v2
+ <<>>(
+ num_kernels,
+ grad_col,
+ data_value,
+ data_spatial_shapes,
+ data_level_start_index,
+ data_sampling_loc,
+ data_attn_weight,
+ batch_size,
+ spatial_size,
+ num_heads,
+ channels,
+ num_levels,
+ num_query,
+ num_point,
+ grad_value,
+ grad_sampling_loc,
+ grad_attn_weight);
+ break;
+ default:
+ if (channels < 64)
+ {
+ ms_deformable_col2im_gpu_kernel_shm_reduce_v1
+ <<>>(
+ num_kernels,
+ grad_col,
+ data_value,
+ data_spatial_shapes,
+ data_level_start_index,
+ data_sampling_loc,
+ data_attn_weight,
+ batch_size,
+ spatial_size,
+ num_heads,
+ channels,
+ num_levels,
+ num_query,
+ num_point,
+ grad_value,
+ grad_sampling_loc,
+ grad_attn_weight);
+ }
+ else
+ {
+ ms_deformable_col2im_gpu_kernel_shm_reduce_v2
+ <<>>(
+ num_kernels,
+ grad_col,
+ data_value,
+ data_spatial_shapes,
+ data_level_start_index,
+ data_sampling_loc,
+ data_attn_weight,
+ batch_size,
+ spatial_size,
+ num_heads,
+ channels,
+ num_levels,
+ num_query,
+ num_point,
+ grad_value,
+ grad_sampling_loc,
+ grad_attn_weight);
+ }
+ }
+ }
+ cudaError_t err = cudaGetLastError();
+ if (err != cudaSuccess)
+ {
+ printf("error in ms_deformable_col2im_cuda: %s\n", cudaGetErrorString(err));
+ }
+
+}
\ No newline at end of file
diff --git a/VISAM/models/ops/src/ms_deform_attn.h b/VISAM/models/ops/src/ms_deform_attn.h
new file mode 100644
index 0000000000000000000000000000000000000000..ac0ef2ec25f7d0ee51ca2d807b159ddf85652017
--- /dev/null
+++ b/VISAM/models/ops/src/ms_deform_attn.h
@@ -0,0 +1,62 @@
+/*!
+**************************************************************************************************
+* Deformable DETR
+* Copyright (c) 2020 SenseTime. All Rights Reserved.
+* Licensed under the Apache License, Version 2.0 [see LICENSE for details]
+**************************************************************************************************
+* Modified from https://github.com/chengdazhi/Deformable-Convolution-V2-PyTorch/tree/pytorch_1.0.0
+**************************************************************************************************
+*/
+
+#pragma once
+
+#include "cpu/ms_deform_attn_cpu.h"
+
+#ifdef WITH_CUDA
+#include "cuda/ms_deform_attn_cuda.h"
+#endif
+
+
+at::Tensor
+ms_deform_attn_forward(
+ const at::Tensor &value,
+ const at::Tensor &spatial_shapes,
+ const at::Tensor &level_start_index,
+ const at::Tensor &sampling_loc,
+ const at::Tensor &attn_weight,
+ const int im2col_step)
+{
+ if (value.type().is_cuda())
+ {
+#ifdef WITH_CUDA
+ return ms_deform_attn_cuda_forward(
+ value, spatial_shapes, level_start_index, sampling_loc, attn_weight, im2col_step);
+#else
+ AT_ERROR("Not compiled with GPU support");
+#endif
+ }
+ AT_ERROR("Not implemented on the CPU");
+}
+
+std::vector
+ms_deform_attn_backward(
+ const at::Tensor &value,
+ const at::Tensor &spatial_shapes,
+ const at::Tensor &level_start_index,
+ const at::Tensor &sampling_loc,
+ const at::Tensor &attn_weight,
+ const at::Tensor &grad_output,
+ const int im2col_step)
+{
+ if (value.type().is_cuda())
+ {
+#ifdef WITH_CUDA
+ return ms_deform_attn_cuda_backward(
+ value, spatial_shapes, level_start_index, sampling_loc, attn_weight, grad_output, im2col_step);
+#else
+ AT_ERROR("Not compiled with GPU support");
+#endif
+ }
+ AT_ERROR("Not implemented on the CPU");
+}
+
diff --git a/VISAM/models/ops/src/vision.cpp b/VISAM/models/ops/src/vision.cpp
new file mode 100644
index 0000000000000000000000000000000000000000..2201f63a51dca16d0b31148ed2c9e8e47ec15bdc
--- /dev/null
+++ b/VISAM/models/ops/src/vision.cpp
@@ -0,0 +1,16 @@
+/*!
+**************************************************************************************************
+* Deformable DETR
+* Copyright (c) 2020 SenseTime. All Rights Reserved.
+* Licensed under the Apache License, Version 2.0 [see LICENSE for details]
+**************************************************************************************************
+* Modified from https://github.com/chengdazhi/Deformable-Convolution-V2-PyTorch/tree/pytorch_1.0.0
+**************************************************************************************************
+*/
+
+#include "ms_deform_attn.h"
+
+PYBIND11_MODULE(TORCH_EXTENSION_NAME, m) {
+ m.def("ms_deform_attn_forward", &ms_deform_attn_forward, "ms_deform_attn_forward");
+ m.def("ms_deform_attn_backward", &ms_deform_attn_backward, "ms_deform_attn_backward");
+}
diff --git a/VISAM/models/ops/test.py b/VISAM/models/ops/test.py
new file mode 100644
index 0000000000000000000000000000000000000000..8dbf6d5547d131f01a8c5c28b76557bd27a9334b
--- /dev/null
+++ b/VISAM/models/ops/test.py
@@ -0,0 +1,89 @@
+# ------------------------------------------------------------------------------------------------
+# Deformable DETR
+# Copyright (c) 2020 SenseTime. All Rights Reserved.
+# Licensed under the Apache License, Version 2.0 [see LICENSE for details]
+# ------------------------------------------------------------------------------------------------
+# Modified from https://github.com/chengdazhi/Deformable-Convolution-V2-PyTorch/tree/pytorch_1.0.0
+# ------------------------------------------------------------------------------------------------
+
+from __future__ import absolute_import
+from __future__ import print_function
+from __future__ import division
+
+import time
+import torch
+import torch.nn as nn
+from torch.autograd import gradcheck
+
+from functions.ms_deform_attn_func import MSDeformAttnFunction, ms_deform_attn_core_pytorch
+
+
+N, M, D = 1, 2, 2
+Lq, L, P = 2, 2, 2
+shapes = torch.as_tensor([(6, 4), (3, 2)], dtype=torch.long).cuda()
+level_start_index = torch.cat((shapes.new_zeros((1, )), shapes.prod(1).cumsum(0)[:-1]))
+S = sum([(H*W).item() for H, W in shapes])
+
+
+torch.manual_seed(3)
+
+
+@torch.no_grad()
+def check_forward_equal_with_pytorch_double():
+ value = torch.rand(N, S, M, D).cuda() * 0.01
+ sampling_locations = torch.rand(N, Lq, M, L, P, 2).cuda()
+ attention_weights = torch.rand(N, Lq, M, L, P).cuda() + 1e-5
+ attention_weights /= attention_weights.sum(-1, keepdim=True).sum(-2, keepdim=True)
+ im2col_step = 2
+ output_pytorch = ms_deform_attn_core_pytorch(value.double(), shapes, sampling_locations.double(), attention_weights.double()).detach().cpu()
+ output_cuda = MSDeformAttnFunction.apply(value.double(), shapes, level_start_index, sampling_locations.double(), attention_weights.double(), im2col_step).detach().cpu()
+ fwdok = torch.allclose(output_cuda, output_pytorch)
+ max_abs_err = (output_cuda - output_pytorch).abs().max()
+ max_rel_err = ((output_cuda - output_pytorch).abs() / output_pytorch.abs()).max()
+
+ print(f'* {fwdok} check_forward_equal_with_pytorch_double: max_abs_err {max_abs_err:.2e} max_rel_err {max_rel_err:.2e}')
+
+
+@torch.no_grad()
+def check_forward_equal_with_pytorch_float():
+ value = torch.rand(N, S, M, D).cuda() * 0.01
+ sampling_locations = torch.rand(N, Lq, M, L, P, 2).cuda()
+ attention_weights = torch.rand(N, Lq, M, L, P).cuda() + 1e-5
+ attention_weights /= attention_weights.sum(-1, keepdim=True).sum(-2, keepdim=True)
+ im2col_step = 2
+ output_pytorch = ms_deform_attn_core_pytorch(value, shapes, sampling_locations, attention_weights).detach().cpu()
+ output_cuda = MSDeformAttnFunction.apply(value, shapes, level_start_index, sampling_locations, attention_weights, im2col_step).detach().cpu()
+ fwdok = torch.allclose(output_cuda, output_pytorch, rtol=1e-2, atol=1e-3)
+ max_abs_err = (output_cuda - output_pytorch).abs().max()
+ max_rel_err = ((output_cuda - output_pytorch).abs() / output_pytorch.abs()).max()
+
+ print(f'* {fwdok} check_forward_equal_with_pytorch_float: max_abs_err {max_abs_err:.2e} max_rel_err {max_rel_err:.2e}')
+
+
+def check_gradient_numerical(channels=4, grad_value=True, grad_sampling_loc=True, grad_attn_weight=True):
+
+ value = torch.rand(N, S, M, channels).cuda() * 0.01
+ sampling_locations = torch.rand(N, Lq, M, L, P, 2).cuda()
+ attention_weights = torch.rand(N, Lq, M, L, P).cuda() + 1e-5
+ attention_weights /= attention_weights.sum(-1, keepdim=True).sum(-2, keepdim=True)
+ im2col_step = 2
+ func = MSDeformAttnFunction.apply
+
+ value.requires_grad = grad_value
+ sampling_locations.requires_grad = grad_sampling_loc
+ attention_weights.requires_grad = grad_attn_weight
+
+ gradok = gradcheck(func, (value.double(), shapes, level_start_index, sampling_locations.double(), attention_weights.double(), im2col_step))
+
+ print(f'* {gradok} check_gradient_numerical(D={channels})')
+
+
+if __name__ == '__main__':
+ check_forward_equal_with_pytorch_double()
+ check_forward_equal_with_pytorch_float()
+
+ for channels in [30, 32, 64, 71, 1025, 2048, 3096]:
+ check_gradient_numerical(channels, True, True, True)
+
+
+
diff --git a/VISAM/models/position_encoding.py b/VISAM/models/position_encoding.py
new file mode 100644
index 0000000000000000000000000000000000000000..27acc10780ae3bf53d24b0d6ddd45b454b3647c3
--- /dev/null
+++ b/VISAM/models/position_encoding.py
@@ -0,0 +1,99 @@
+# ------------------------------------------------------------------------
+# Copyright (c) 2022 megvii-research. All Rights Reserved.
+# ------------------------------------------------------------------------
+# Modified from Deformable DETR (https://github.com/fundamentalvision/Deformable-DETR)
+# Copyright (c) 2020 SenseTime. All Rights Reserved.
+# ------------------------------------------------------------------------
+# Modified from DETR (https://github.com/facebookresearch/detr)
+# Copyright (c) Facebook, Inc. and its affiliates. All Rights Reserved
+# ------------------------------------------------------------------------
+
+
+"""
+Various positional encodings for the transformer.
+"""
+import math
+import torch
+from torch import nn
+
+from util.misc import NestedTensor
+
+
+class PositionEmbeddingSine(nn.Module):
+ """
+ This is a more standard version of the position embedding, very similar to the one
+ used by the Attention is all you need paper, generalized to work on images.
+ """
+ def __init__(self, num_pos_feats=64, temperature=10000, normalize=False, scale=None):
+ super().__init__()
+ self.num_pos_feats = num_pos_feats
+ self.temperature = temperature
+ self.normalize = normalize
+ if scale is not None and normalize is False:
+ raise ValueError("normalize should be True if scale is passed")
+ if scale is None:
+ scale = 2 * math.pi
+ self.scale = scale
+
+ def forward(self, tensor_list: NestedTensor):
+ x = tensor_list.tensors
+ mask = tensor_list.mask
+ assert mask is not None
+ not_mask = ~mask
+ y_embed = not_mask.cumsum(1, dtype=torch.float32)
+ x_embed = not_mask.cumsum(2, dtype=torch.float32)
+ if self.normalize:
+ eps = 1e-6
+ y_embed = (y_embed - 0.5) / (y_embed[:, -1:, :] + eps) * self.scale
+ x_embed = (x_embed - 0.5) / (x_embed[:, :, -1:] + eps) * self.scale
+
+ dim_t = torch.arange(self.num_pos_feats, dtype=torch.float32, device=x.device)
+ dim_t = self.temperature ** (2 * (dim_t // 2) / self.num_pos_feats)
+
+ pos_x = x_embed[:, :, :, None] / dim_t
+ pos_y = y_embed[:, :, :, None] / dim_t
+ pos_x = torch.stack((pos_x[:, :, :, 0::2].sin(), pos_x[:, :, :, 1::2].cos()), dim=4).flatten(3)
+ pos_y = torch.stack((pos_y[:, :, :, 0::2].sin(), pos_y[:, :, :, 1::2].cos()), dim=4).flatten(3)
+ pos = torch.cat((pos_y, pos_x), dim=3).permute(0, 3, 1, 2)
+ return pos
+
+
+class PositionEmbeddingLearned(nn.Module):
+ """
+ Absolute pos embedding, learned.
+ """
+ def __init__(self, num_pos_feats=256):
+ super().__init__()
+ self.row_embed = nn.Embedding(50, num_pos_feats)
+ self.col_embed = nn.Embedding(50, num_pos_feats)
+ self.reset_parameters()
+
+ def reset_parameters(self):
+ nn.init.uniform_(self.row_embed.weight)
+ nn.init.uniform_(self.col_embed.weight)
+
+ def forward(self, tensor_list: NestedTensor):
+ x = tensor_list.tensors
+ h, w = x.shape[-2:]
+ i = torch.arange(w, device=x.device)
+ j = torch.arange(h, device=x.device)
+ x_emb = self.col_embed(i)
+ y_emb = self.row_embed(j)
+ pos = torch.cat([
+ x_emb.unsqueeze(0).repeat(h, 1, 1),
+ y_emb.unsqueeze(1).repeat(1, w, 1),
+ ], dim=-1).permute(2, 0, 1).unsqueeze(0).repeat(x.shape[0], 1, 1, 1)
+ return pos
+
+
+def build_position_encoding(args):
+ N_steps = args.hidden_dim // 2
+ if args.position_embedding in ('v2', 'sine'):
+ # TODO find a better way of exposing other arguments
+ position_embedding = PositionEmbeddingSine(N_steps, normalize=True)
+ elif args.position_embedding in ('v3', 'learned'):
+ position_embedding = PositionEmbeddingLearned(N_steps)
+ else:
+ raise ValueError(f"not supported {args.position_embedding}")
+
+ return position_embedding
diff --git a/VISAM/models/qim.py b/VISAM/models/qim.py
new file mode 100644
index 0000000000000000000000000000000000000000..f13f96fa30e6d67dc73869e77a0e5ccf0e0e1415
--- /dev/null
+++ b/VISAM/models/qim.py
@@ -0,0 +1,200 @@
+# ------------------------------------------------------------------------
+# Copyright (c) 2022 megvii-research. All Rights Reserved.
+# ------------------------------------------------------------------------
+
+import math
+import torch
+from torch import nn
+
+from util import box_ops
+from models.structures import Boxes, Instances, pairwise_iou
+
+
+def random_drop_tracks(track_instances: Instances, drop_probability: float) -> Instances:
+ if drop_probability > 0 and len(track_instances) > 0:
+ keep_idxes = torch.rand_like(track_instances.scores) > drop_probability
+ track_instances = track_instances[keep_idxes]
+ return track_instances
+
+
+class QueryInteractionBase(nn.Module):
+ def __init__(self, args, dim_in, hidden_dim, dim_out):
+ super().__init__()
+ self.args = args
+ self._build_layers(args, dim_in, hidden_dim, dim_out)
+ self._reset_parameters()
+
+ def _build_layers(self, args, dim_in, hidden_dim, dim_out):
+ raise NotImplementedError()
+
+ def _reset_parameters(self):
+ for p in self.parameters():
+ if p.dim() > 1:
+ nn.init.xavier_uniform_(p)
+
+ def _select_active_tracks(self, data: dict) -> Instances:
+ raise NotImplementedError()
+
+ def _update_track_embedding(self, track_instances):
+ raise NotImplementedError()
+
+
+class FFN(nn.Module):
+ def __init__(self, d_model, d_ffn, dropout=0):
+ super().__init__()
+ self.linear1 = nn.Linear(d_model, d_ffn)
+ self.activation = nn.ReLU(True)
+ self.dropout1 = nn.Dropout(dropout)
+ self.linear2 = nn.Linear(d_ffn, d_model)
+ self.dropout2 = nn.Dropout(dropout)
+ self.norm = nn.LayerNorm(d_model)
+
+ def forward(self, tgt):
+ tgt2 = self.linear2(self.dropout1(self.activation(self.linear1(tgt))))
+ tgt = tgt + self.dropout2(tgt2)
+ tgt = self.norm(tgt)
+ return tgt
+
+
+class QueryInteractionModule(QueryInteractionBase):
+ def __init__(self, args, dim_in, hidden_dim, dim_out):
+ raise NotImplementedError
+
+
+class QueryInteractionModulev2(QueryInteractionBase):
+ def __init__(self, args, dim_in, hidden_dim, dim_out):
+ super().__init__(args, dim_in, hidden_dim, dim_out)
+ self.random_drop = args.random_drop
+ self.fp_ratio = args.fp_ratio
+ self.update_query_pos = args.update_query_pos
+ self.score_thr = 0.5
+
+ def _build_layers(self, args, dim_in, hidden_dim, dim_out):
+ dropout = args.merger_dropout
+
+ self.self_attn = nn.MultiheadAttention(dim_in, 8, dropout)
+ self.linear1 = nn.Linear(dim_in, hidden_dim)
+ self.dropout = nn.Dropout(dropout)
+ self.linear2 = nn.Linear(hidden_dim, dim_in)
+
+ if args.update_query_pos:
+ self.linear_pos1 = nn.Linear(dim_in, hidden_dim)
+ self.linear_pos2 = nn.Linear(hidden_dim, dim_in)
+ self.dropout_pos1 = nn.Dropout(dropout)
+ self.dropout_pos2 = nn.Dropout(dropout)
+ self.norm_pos = nn.LayerNorm(dim_in)
+
+ self.linear_feat1 = nn.Linear(dim_in, hidden_dim)
+ self.linear_feat2 = nn.Linear(hidden_dim, dim_in)
+ self.dropout_feat1 = nn.Dropout(dropout)
+ self.dropout_feat2 = nn.Dropout(dropout)
+ self.norm_feat = nn.LayerNorm(dim_in)
+
+ self.norm1 = nn.LayerNorm(dim_in)
+ self.norm2 = nn.LayerNorm(dim_in)
+ if args.update_query_pos:
+ self.norm3 = nn.LayerNorm(dim_in)
+
+ self.dropout1 = nn.Dropout(dropout)
+ self.dropout2 = nn.Dropout(dropout)
+ if args.update_query_pos:
+ self.dropout3 = nn.Dropout(dropout)
+ self.dropout4 = nn.Dropout(dropout)
+
+ self.activation = nn.ReLU(True)
+
+ def _random_drop_tracks(self, track_instances: Instances) -> Instances:
+ return random_drop_tracks(track_instances, self.random_drop)
+
+ def _add_fp_tracks(self, track_instances: Instances, active_track_instances: Instances) -> Instances:
+ inactive_instances = track_instances[track_instances.obj_idxes < 0]
+
+ # add fp for each active track in a specific probability.
+ fp_prob = torch.ones_like(active_track_instances.scores) * self.fp_ratio
+ selected_active_track_instances = active_track_instances[torch.bernoulli(fp_prob).bool()]
+
+ if len(inactive_instances) > 0 and len(selected_active_track_instances) > 0:
+ num_fp = len(selected_active_track_instances)
+ if num_fp >= len(inactive_instances):
+ fp_track_instances = inactive_instances
+ else:
+ inactive_boxes = Boxes(box_ops.box_cxcywh_to_xyxy(inactive_instances.pred_boxes))
+ selected_active_boxes = Boxes(box_ops.box_cxcywh_to_xyxy(selected_active_track_instances.pred_boxes))
+ ious = pairwise_iou(inactive_boxes, selected_active_boxes)
+ # select the fp with the largest IoU for each active track.
+ fp_indexes = ious.max(dim=0).indices
+
+ # remove duplicate fp.
+ fp_indexes = torch.unique(fp_indexes)
+ fp_track_instances = inactive_instances[fp_indexes]
+
+ merged_track_instances = Instances.cat([active_track_instances, fp_track_instances])
+ return merged_track_instances
+
+ return active_track_instances
+
+ def _select_active_tracks(self, data: dict) -> Instances:
+ track_instances: Instances = data['track_instances']
+ if self.training:
+ active_idxes = (track_instances.obj_idxes >= 0) | (track_instances.scores > 0.5)
+ active_track_instances = track_instances[active_idxes]
+ active_track_instances.obj_idxes[active_track_instances.iou <= 0.5] = -1
+ else:
+ active_track_instances = track_instances[track_instances.obj_idxes >= 0]
+
+ return active_track_instances
+
+ def _update_track_embedding(self, track_instances: Instances) -> Instances:
+ is_pos = track_instances.scores > self.score_thr
+ track_instances.ref_pts[is_pos] = track_instances.pred_boxes.detach().clone()[is_pos]
+
+ out_embed = track_instances.output_embedding
+ query_feat = track_instances.query_pos
+ query_pos = pos2posemb(track_instances.ref_pts)
+ q = k = query_pos + out_embed
+
+ tgt = out_embed
+ tgt2 = self.self_attn(q[:, None], k[:, None], value=tgt[:, None])[0][:, 0]
+ tgt = tgt + self.dropout1(tgt2)
+ tgt = self.norm1(tgt)
+
+ tgt2 = self.linear2(self.dropout(self.activation(self.linear1(tgt))))
+ tgt = tgt + self.dropout2(tgt2)
+ tgt = self.norm2(tgt)
+
+ if self.update_query_pos:
+ query_pos2 = self.linear_pos2(self.dropout_pos1(self.activation(self.linear_pos1(tgt))))
+ query_pos = query_pos + self.dropout_pos2(query_pos2)
+ query_pos = self.norm_pos(query_pos)
+ track_instances.query_pos = query_pos
+
+ query_feat2 = self.linear_feat2(self.dropout_feat1(self.activation(self.linear_feat1(tgt))))
+ query_feat = query_feat + self.dropout_feat2(query_feat2)
+ query_feat = self.norm_feat(query_feat)
+ track_instances.query_pos[is_pos] = query_feat[is_pos]
+
+ return track_instances
+
+ def forward(self, data) -> Instances:
+ active_track_instances = self._select_active_tracks(data)
+ active_track_instances = self._update_track_embedding(active_track_instances)
+ return active_track_instances
+
+
+def pos2posemb(pos, num_pos_feats=64, temperature=10000):
+ scale = 2 * math.pi
+ pos = pos * scale
+ dim_t = torch.arange(num_pos_feats, dtype=torch.float32, device=pos.device)
+ dim_t = temperature ** (2 * (dim_t // 2) / num_pos_feats)
+ posemb = pos[..., None] / dim_t
+ posemb = torch.stack((posemb[..., 0::2].sin(), posemb[..., 1::2].cos()), dim=-1).flatten(-3)
+ return posemb
+
+
+def build(args, layer_name, dim_in, hidden_dim, dim_out):
+ interaction_layers = {
+ 'QIM': QueryInteractionModule,
+ 'QIMv2': QueryInteractionModulev2,
+ }
+ assert layer_name in interaction_layers, 'invalid query interaction layer: {}'.format(layer_name)
+ return interaction_layers[layer_name](args, dim_in, hidden_dim, dim_out)
diff --git a/VISAM/models/structures/__init__.py b/VISAM/models/structures/__init__.py
new file mode 100644
index 0000000000000000000000000000000000000000..6ae8dda900614e4476cd25cd9c421ee4a38132fd
--- /dev/null
+++ b/VISAM/models/structures/__init__.py
@@ -0,0 +1,8 @@
+# ------------------------------------------------------------------------
+# Modified from Detectron2 (https://github.com/facebookresearch/detectron2)
+# Copyright (c) Facebook, Inc. and its affiliates. All Rights Reserved
+# ------------------------------------------------------------------------
+from .boxes import Boxes, BoxMode, pairwise_iou, pairwise_ioa, matched_boxlist_iou
+from .instances import Instances
+
+__all__ = [k for k in globals().keys() if not k.startswith("_")]
\ No newline at end of file
diff --git a/VISAM/models/structures/boxes.py b/VISAM/models/structures/boxes.py
new file mode 100644
index 0000000000000000000000000000000000000000..47204390a2ca1277e5cd751958f01b2763e8c4df
--- /dev/null
+++ b/VISAM/models/structures/boxes.py
@@ -0,0 +1,412 @@
+# ------------------------------------------------------------------------
+# Modified from Detectron2 (https://github.com/facebookresearch/detectron2)
+# Copyright (c) Facebook, Inc. and its affiliates. All Rights Reserved
+# ------------------------------------------------------------------------
+
+import math
+import numpy as np
+from enum import IntEnum, unique
+from typing import List, Tuple, Union
+import torch
+from torch import device
+
+_RawBoxType = Union[List[float], Tuple[float, ...], torch.Tensor, np.ndarray]
+def _maybe_jit_unused(x):
+ return x
+
+
+@unique
+class BoxMode(IntEnum):
+ """
+ Enum of different ways to represent a box.
+ """
+
+ XYXY_ABS = 0
+ """
+ (x0, y0, x1, y1) in absolute floating points coordinates.
+ The coordinates in range [0, width or height].
+ """
+ XYWH_ABS = 1
+ """
+ (x0, y0, w, h) in absolute floating points coordinates.
+ """
+ XYXY_REL = 2
+ """
+ Not yet supported!
+ (x0, y0, x1, y1) in range [0, 1]. They are relative to the size of the image.
+ """
+ XYWH_REL = 3
+ """
+ Not yet supported!
+ (x0, y0, w, h) in range [0, 1]. They are relative to the size of the image.
+ """
+ XYWHA_ABS = 4
+ """
+ (xc, yc, w, h, a) in absolute floating points coordinates.
+ (xc, yc) is the center of the rotated box, and the angle a is in degrees ccw.
+ """
+
+ @staticmethod
+ def convert(box: _RawBoxType, from_mode: "BoxMode", to_mode: "BoxMode") -> _RawBoxType:
+ """
+ Args:
+ box: can be a k-tuple, k-list or an Nxk array/tensor, where k = 4 or 5
+ from_mode, to_mode (BoxMode)
+
+ Returns:
+ The converted box of the same type.
+ """
+ if from_mode == to_mode:
+ return box
+
+ original_type = type(box)
+ is_numpy = isinstance(box, np.ndarray)
+ single_box = isinstance(box, (list, tuple))
+ if single_box:
+ assert len(box) == 4 or len(box) == 5, (
+ "BoxMode.convert takes either a k-tuple/list or an Nxk array/tensor,"
+ " where k == 4 or 5"
+ )
+ arr = torch.tensor(box)[None, :]
+ else:
+ # avoid modifying the input box
+ if is_numpy:
+ arr = torch.from_numpy(np.asarray(box)).clone()
+ else:
+ arr = box.clone()
+
+ assert to_mode not in [BoxMode.XYXY_REL, BoxMode.XYWH_REL] and from_mode not in [
+ BoxMode.XYXY_REL,
+ BoxMode.XYWH_REL,
+ ], "Relative mode not yet supported!"
+
+ if from_mode == BoxMode.XYWHA_ABS and to_mode == BoxMode.XYXY_ABS:
+ assert (
+ arr.shape[-1] == 5
+ ), "The last dimension of input shape must be 5 for XYWHA format"
+ original_dtype = arr.dtype
+ arr = arr.double()
+
+ w = arr[:, 2]
+ h = arr[:, 3]
+ a = arr[:, 4]
+ c = torch.abs(torch.cos(a * math.pi / 180.0))
+ s = torch.abs(torch.sin(a * math.pi / 180.0))
+ # This basically computes the horizontal bounding rectangle of the rotated box
+ new_w = c * w + s * h
+ new_h = c * h + s * w
+
+ # convert center to top-left corner
+ arr[:, 0] -= new_w / 2.0
+ arr[:, 1] -= new_h / 2.0
+ # bottom-right corner
+ arr[:, 2] = arr[:, 0] + new_w
+ arr[:, 3] = arr[:, 1] + new_h
+
+ arr = arr[:, :4].to(dtype=original_dtype)
+ elif from_mode == BoxMode.XYWH_ABS and to_mode == BoxMode.XYWHA_ABS:
+ original_dtype = arr.dtype
+ arr = arr.double()
+ arr[:, 0] += arr[:, 2] / 2.0
+ arr[:, 1] += arr[:, 3] / 2.0
+ angles = torch.zeros((arr.shape[0], 1), dtype=arr.dtype)
+ arr = torch.cat((arr, angles), axis=1).to(dtype=original_dtype)
+ else:
+ if to_mode == BoxMode.XYXY_ABS and from_mode == BoxMode.XYWH_ABS:
+ arr[:, 2] += arr[:, 0]
+ arr[:, 3] += arr[:, 1]
+ elif from_mode == BoxMode.XYXY_ABS and to_mode == BoxMode.XYWH_ABS:
+ arr[:, 2] -= arr[:, 0]
+ arr[:, 3] -= arr[:, 1]
+ else:
+ raise NotImplementedError(
+ "Conversion from BoxMode {} to {} is not supported yet".format(
+ from_mode, to_mode
+ )
+ )
+
+ if single_box:
+ return original_type(arr.flatten().tolist())
+ if is_numpy:
+ return arr.numpy()
+ else:
+ return arr
+
+
+class Boxes:
+ """
+ This structure stores a list of boxes as a Nx4 torch.Tensor.
+ It supports some common methods about boxes
+ (`area`, `clip`, `nonempty`, etc),
+ and also behaves like a Tensor
+ (support indexing, `to(device)`, `.device`, and iteration over all boxes)
+
+ Attributes:
+ tensor (torch.Tensor): float matrix of Nx4. Each row is (x1, y1, x2, y2).
+ """
+
+ def __init__(self, tensor: torch.Tensor):
+ """
+ Args:
+ tensor (Tensor[float]): a Nx4 matrix. Each row is (x1, y1, x2, y2).
+ """
+ device = tensor.device if isinstance(tensor, torch.Tensor) else torch.device("cpu")
+ tensor = torch.as_tensor(tensor, dtype=torch.float32, device=device)
+ if tensor.numel() == 0:
+ # Use reshape, so we don't end up creating a new tensor that does not depend on
+ # the inputs (and consequently confuses jit)
+ tensor = tensor.reshape((-1, 4)).to(dtype=torch.float32, device=device)
+ assert tensor.dim() == 2 and tensor.size(-1) == 4, tensor.size()
+
+ self.tensor = tensor
+
+ def clone(self) -> "Boxes":
+ """
+ Clone the Boxes.
+
+ Returns:
+ Boxes
+ """
+ return Boxes(self.tensor.clone())
+
+ @_maybe_jit_unused
+ def to(self, device: torch.device):
+ # Boxes are assumed float32 and does not support to(dtype)
+ return Boxes(self.tensor.to(device=device))
+
+ def area(self) -> torch.Tensor:
+ """
+ Computes the area of all the boxes.
+
+ Returns:
+ torch.Tensor: a vector with areas of each box.
+ """
+ box = self.tensor
+ area = (box[:, 2] - box[:, 0]) * (box[:, 3] - box[:, 1])
+ return area
+
+ def clip(self, box_size: Tuple[int, int]) -> None:
+ """
+ Clip (in place) the boxes by limiting x coordinates to the range [0, width]
+ and y coordinates to the range [0, height].
+
+ Args:
+ box_size (height, width): The clipping box's size.
+ """
+ assert torch.isfinite(self.tensor).all(), "Box tensor contains infinite or NaN!"
+ h, w = box_size
+ x1 = self.tensor[:, 0].clamp(min=0, max=w)
+ y1 = self.tensor[:, 1].clamp(min=0, max=h)
+ x2 = self.tensor[:, 2].clamp(min=0, max=w)
+ y2 = self.tensor[:, 3].clamp(min=0, max=h)
+ self.tensor = torch.stack((x1, y1, x2, y2), dim=-1)
+
+ def nonempty(self, threshold: float = 0.0) -> torch.Tensor:
+ """
+ Find boxes that are non-empty.
+ A box is considered empty, if either of its side is no larger than threshold.
+
+ Returns:
+ Tensor:
+ a binary vector which represents whether each box is empty
+ (False) or non-empty (True).
+ """
+ box = self.tensor
+ widths = box[:, 2] - box[:, 0]
+ heights = box[:, 3] - box[:, 1]
+ keep = (widths > threshold) & (heights > threshold)
+ return keep
+
+ def __getitem__(self, item) -> "Boxes":
+ """
+ Args:
+ item: int, slice, or a BoolTensor
+
+ Returns:
+ Boxes: Create a new :class:`Boxes` by indexing.
+
+ The following usage are allowed:
+
+ 1. `new_boxes = boxes[3]`: return a `Boxes` which contains only one box.
+ 2. `new_boxes = boxes[2:10]`: return a slice of boxes.
+ 3. `new_boxes = boxes[vector]`, where vector is a torch.BoolTensor
+ with `length = len(boxes)`. Nonzero elements in the vector will be selected.
+
+ Note that the returned Boxes might share storage with this Boxes,
+ subject to Pytorch's indexing semantics.
+ """
+ if isinstance(item, int):
+ return Boxes(self.tensor[item].view(1, -1))
+ b = self.tensor[item]
+ assert b.dim() == 2, "Indexing on Boxes with {} failed to return a matrix!".format(item)
+ return Boxes(b)
+
+ def __len__(self) -> int:
+ return self.tensor.shape[0]
+
+ def __repr__(self) -> str:
+ return "Boxes(" + str(self.tensor) + ")"
+
+ def inside_box(self, box_size: Tuple[int, int], boundary_threshold: int = 0) -> torch.Tensor:
+ """
+ Args:
+ box_size (height, width): Size of the reference box.
+ boundary_threshold (int): Boxes that extend beyond the reference box
+ boundary by more than boundary_threshold are considered "outside".
+
+ Returns:
+ a binary vector, indicating whether each box is inside the reference box.
+ """
+ height, width = box_size
+ inds_inside = (
+ (self.tensor[..., 0] >= -boundary_threshold)
+ & (self.tensor[..., 1] >= -boundary_threshold)
+ & (self.tensor[..., 2] < width + boundary_threshold)
+ & (self.tensor[..., 3] < height + boundary_threshold)
+ )
+ return inds_inside
+
+ def get_centers(self) -> torch.Tensor:
+ """
+ Returns:
+ The box centers in a Nx2 array of (x, y).
+ """
+ return (self.tensor[:, :2] + self.tensor[:, 2:]) / 2
+
+ def scale(self, scale_x: float, scale_y: float) -> None:
+ """
+ Scale the box with horizontal and vertical scaling factors
+ """
+ self.tensor[:, 0::2] *= scale_x
+ self.tensor[:, 1::2] *= scale_y
+
+ @classmethod
+ @_maybe_jit_unused
+ def cat(cls, boxes_list: List["Boxes"]) -> "Boxes":
+ """
+ Concatenates a list of Boxes into a single Boxes
+
+ Arguments:
+ boxes_list (list[Boxes])
+
+ Returns:
+ Boxes: the concatenated Boxes
+ """
+ assert isinstance(boxes_list, (list, tuple))
+ if len(boxes_list) == 0:
+ return cls(torch.empty(0))
+ assert all([isinstance(box, Boxes) for box in boxes_list])
+
+ # use torch.cat (v.s. layers.cat) so the returned boxes never share storage with input
+ cat_boxes = cls(torch.cat([b.tensor for b in boxes_list], dim=0))
+ return cat_boxes
+
+ @property
+ def device(self) -> device:
+ return self.tensor.device
+
+ # type "Iterator[torch.Tensor]", yield, and iter() not supported by torchscript
+ # https://github.com/pytorch/pytorch/issues/18627
+ @torch.jit.unused
+ def __iter__(self):
+ """
+ Yield a box as a Tensor of shape (4,) at a time.
+ """
+ yield from self.tensor
+
+
+def pairwise_intersection(boxes1: Boxes, boxes2: Boxes) -> torch.Tensor:
+ """
+ Given two lists of boxes of size N and M,
+ compute the intersection area between __all__ N x M pairs of boxes.
+ The box order must be (xmin, ymin, xmax, ymax)
+
+ Args:
+ boxes1,boxes2 (Boxes): two `Boxes`. Contains N & M boxes, respectively.
+
+ Returns:
+ Tensor: intersection, sized [N,M].
+ """
+ boxes1, boxes2 = boxes1.tensor, boxes2.tensor
+ width_height = torch.min(boxes1[:, None, 2:], boxes2[:, 2:]) - torch.max(
+ boxes1[:, None, :2], boxes2[:, :2]
+ ) # [N,M,2]
+
+ width_height.clamp_(min=0) # [N,M,2]
+ intersection = width_height.prod(dim=2) # [N,M]
+ return intersection
+
+
+# implementation from https://github.com/kuangliu/torchcv/blob/master/torchcv/utils/box.py
+# with slight modifications
+def pairwise_iou(boxes1: Boxes, boxes2: Boxes) -> torch.Tensor:
+ """
+ Given two lists of boxes of size N and M, compute the IoU
+ (intersection over union) between **all** N x M pairs of boxes.
+ The box order must be (xmin, ymin, xmax, ymax).
+
+ Args:
+ boxes1,boxes2 (Boxes): two `Boxes`. Contains N & M boxes, respectively.
+
+ Returns:
+ Tensor: IoU, sized [N,M].
+ """
+ area1 = boxes1.area() # [N]
+ area2 = boxes2.area() # [M]
+ inter = pairwise_intersection(boxes1, boxes2)
+
+ # handle empty boxes
+ iou = torch.where(
+ inter > 0,
+ inter / (area1[:, None] + area2 - inter),
+ torch.zeros(1, dtype=inter.dtype, device=inter.device),
+ )
+ return iou
+
+
+def pairwise_ioa(boxes1: Boxes, boxes2: Boxes) -> torch.Tensor:
+ """
+ Similar to :func:`pariwise_iou` but compute the IoA (intersection over boxes2 area).
+
+ Args:
+ boxes1,boxes2 (Boxes): two `Boxes`. Contains N & M boxes, respectively.
+
+ Returns:
+ Tensor: IoA, sized [N,M].
+ """
+ area2 = boxes2.area() # [M]
+ inter = pairwise_intersection(boxes1, boxes2)
+
+ # handle empty boxes
+ ioa = torch.where(
+ inter > 0, inter / area2, torch.zeros(1, dtype=inter.dtype, device=inter.device)
+ )
+ return ioa
+
+
+def matched_boxlist_iou(boxes1: Boxes, boxes2: Boxes) -> torch.Tensor:
+ """
+ Compute pairwise intersection over union (IOU) of two sets of matched
+ boxes. The box order must be (xmin, ymin, xmax, ymax).
+ Similar to boxlist_iou, but computes only diagonal elements of the matrix
+
+ Args:
+ boxes1: (Boxes) bounding boxes, sized [N,4].
+ boxes2: (Boxes) bounding boxes, sized [N,4].
+ Returns:
+ Tensor: iou, sized [N].
+ """
+ assert len(boxes1) == len(
+ boxes2
+ ), "boxlists should have the same" "number of entries, got {}, {}".format(
+ len(boxes1), len(boxes2)
+ )
+ area1 = boxes1.area() # [N]
+ area2 = boxes2.area() # [N]
+ box1, box2 = boxes1.tensor, boxes2.tensor
+ lt = torch.max(box1[:, :2], box2[:, :2]) # [N,2]
+ rb = torch.min(box1[:, 2:], box2[:, 2:]) # [N,2]
+ wh = (rb - lt).clamp(min=0) # [N,2]
+ inter = wh[:, 0] * wh[:, 1] # [N]
+ iou = inter / (area1 + area2 - inter) # [N]
+ return iou
diff --git a/VISAM/models/structures/instances.py b/VISAM/models/structures/instances.py
new file mode 100644
index 0000000000000000000000000000000000000000..94429c8ec3be65a44cd0e0b55879ffc2bed8c396
--- /dev/null
+++ b/VISAM/models/structures/instances.py
@@ -0,0 +1,204 @@
+# ------------------------------------------------------------------------
+# Modified from Detectron2 (https://github.com/facebookresearch/detectron2)
+# Copyright (c) Facebook, Inc. and its affiliates. All Rights Reserved
+# ------------------------------------------------------------------------
+
+import itertools
+from typing import Any, Dict, List, Tuple, Union
+import torch
+import numpy as np
+
+
+class Instances:
+ """
+ This class represents a list of instances in an image.
+ It stores the attributes of instances (e.g., boxes, masks, labels, scores) as "fields".
+ All fields must have the same ``__len__`` which is the number of instances.
+
+ All other (non-field) attributes of this class are considered private:
+ they must start with '_' and are not modifiable by a user.
+
+ Some basic usage:
+
+ 1. Set/get/check a field:
+
+ .. code-block:: python
+
+ instances.gt_boxes = Boxes(...)
+ print(instances.pred_masks) # a tensor of shape (N, H, W)
+ print('gt_masks' in instances)
+
+ 2. ``len(instances)`` returns the number of instances
+ 3. Indexing: ``instances[indices]`` will apply the indexing on all the fields
+ and returns a new :class:`Instances`.
+ Typically, ``indices`` is a integer vector of indices,
+ or a binary mask of length ``num_instances``
+
+ .. code-block:: python
+
+ category_3_detections = instances[instances.pred_classes == 3]
+ confident_detections = instances[instances.scores > 0.9]
+ """
+
+ def __init__(self, image_size: Tuple[int, int], **kwargs: Any):
+ """
+ Args:
+ image_size (height, width): the spatial size of the image.
+ kwargs: fields to add to this `Instances`.
+ """
+ self._image_size = image_size
+ self._fields: Dict[str, Any] = {}
+ for k, v in kwargs.items():
+ self.set(k, v)
+
+ @property
+ def image_size(self) -> Tuple[int, int]:
+ """
+ Returns:
+ tuple: height, width
+ """
+ return self._image_size
+
+ def __setattr__(self, name: str, val: Any) -> None:
+ if name.startswith("_"):
+ super().__setattr__(name, val)
+ else:
+ self.set(name, val)
+
+ def __getattr__(self, name: str) -> Any:
+ if name == "_fields" or name not in self._fields:
+ raise AttributeError("Cannot find field '{}' in the given Instances!".format(name))
+ return self._fields[name]
+
+ def set(self, name: str, value: Any) -> None:
+ """
+ Set the field named `name` to `value`.
+ The length of `value` must be the number of instances,
+ and must agree with other existing fields in this object.
+ """
+ data_len = len(value)
+ if len(self._fields):
+ assert (
+ len(self) == data_len
+ ), "Adding a field of length {} to a Instances of length {}".format(data_len, len(self))
+ self._fields[name] = value
+
+ def has(self, name: str) -> bool:
+ """
+ Returns:
+ bool: whether the field called `name` exists.
+ """
+ return name in self._fields
+
+ def remove(self, name: str) -> None:
+ """
+ Remove the field called `name`.
+ """
+ del self._fields[name]
+
+ def get(self, name: str) -> Any:
+ """
+ Returns the field called `name`.
+ """
+ return self._fields[name]
+
+ def get_fields(self) -> Dict[str, Any]:
+ """
+ Returns:
+ dict: a dict which maps names (str) to data of the fields
+
+ Modifying the returned dict will modify this instance.
+ """
+ return self._fields
+
+ # Tensor-like methods
+ def to(self, *args: Any, **kwargs: Any) -> "Instances":
+ """
+ Returns:
+ Instances: all fields are called with a `to(device)`, if the field has this method.
+ """
+ ret = Instances(self._image_size)
+ for k, v in self._fields.items():
+ if hasattr(v, "to"):
+ v = v.to(*args, **kwargs)
+ ret.set(k, v)
+ return ret
+
+ def numpy(self):
+ ret = Instances(self._image_size)
+ for k, v in self._fields.items():
+ if hasattr(v, "numpy"):
+ v = v.numpy()
+ ret.set(k, v)
+ return ret
+
+ def __getitem__(self, item: Union[int, slice, torch.BoolTensor]) -> "Instances":
+ """
+ Args:
+ item: an index-like object and will be used to index all the fields.
+
+ Returns:
+ If `item` is a string, return the data in the corresponding field.
+ Otherwise, returns an `Instances` where all fields are indexed by `item`.
+ """
+ if type(item) == int:
+ if item >= len(self) or item < -len(self):
+ raise IndexError("Instances index out of range!")
+ else:
+ item = slice(item, None, len(self))
+
+ ret = Instances(self._image_size)
+ for k, v in self._fields.items():
+ ret.set(k, v[item])
+ return ret
+
+ def __len__(self) -> int:
+ for v in self._fields.values():
+ # use __len__ because len() has to be int and is not friendly to tracing
+ return v.__len__()
+ raise NotImplementedError("Empty Instances does not support __len__!")
+
+ def __iter__(self):
+ raise NotImplementedError("`Instances` object is not iterable!")
+
+ @staticmethod
+ def cat(instance_lists: List["Instances"]) -> "Instances":
+ """
+ Args:
+ instance_lists (list[Instances])
+
+ Returns:
+ Instances
+ """
+ assert all(isinstance(i, Instances) for i in instance_lists)
+ assert len(instance_lists) > 0
+ if len(instance_lists) == 1:
+ return instance_lists[0]
+
+ image_size = instance_lists[0].image_size
+ for i in instance_lists[1:]:
+ assert i.image_size == image_size
+ ret = Instances(image_size)
+ for k in instance_lists[0]._fields.keys():
+ values = [i.get(k) for i in instance_lists]
+ v0 = values[0]
+ if isinstance(v0, torch.Tensor):
+ values = torch.cat(values, dim=0)
+ elif isinstance(v0, list):
+ values = list(itertools.chain(*values))
+ elif hasattr(type(v0), "cat"):
+ values = type(v0).cat(values)
+ else:
+ raise ValueError("Unsupported type {} for concatenation".format(type(v0)))
+ ret.set(k, values)
+ return ret
+
+ def __str__(self) -> str:
+ s = self.__class__.__name__ + "("
+ s += "num_instances={}, ".format(len(self))
+ s += "image_height={}, ".format(self._image_size[0])
+ s += "image_width={}, ".format(self._image_size[1])
+ s += "fields=[{}])".format(", ".join((f"{k}: {v}" for k, v in self._fields.items())))
+ return s
+
+ __repr__ = __str__
diff --git a/VISAM/requirements.txt b/VISAM/requirements.txt
new file mode 100644
index 0000000000000000000000000000000000000000..c85f109e578081abf481bb073b7fede61a5941f0
--- /dev/null
+++ b/VISAM/requirements.txt
@@ -0,0 +1,3 @@
+tqdm
+scipy
+opencv-python
diff --git a/VISAM/submit_dance.py b/VISAM/submit_dance.py
new file mode 100644
index 0000000000000000000000000000000000000000..15e6377606740af6408a5ec3e9526879e12e4500
--- /dev/null
+++ b/VISAM/submit_dance.py
@@ -0,0 +1,271 @@
+# ------------------------------------------------------------------------
+# Copyright (c) 2022 megvii-research. All Rights Reserved.
+# ------------------------------------------------------------------------
+# Modified from Deformable DETR (https://github.com/fundamentalvision/Deformable-DETR)
+# Copyright (c) 2020 SenseTime. All Rights Reserved.
+# ------------------------------------------------------------------------
+# Modified from DETR (https://github.com/facebookresearch/detr)
+# Copyright (c) Facebook, Inc. and its affiliates. All Rights Reserved
+# ------------------------------------------------------------------------
+
+from copy import deepcopy
+import json
+
+import os
+import argparse
+import torchvision.transforms.functional as F
+import torch
+import cv2
+import numpy as np
+from tqdm import tqdm
+from pathlib import Path
+from models import build_model
+from util.tool import load_model
+from main import get_args_parser
+
+from models.structures import Instances
+from torch.utils.data import Dataset, DataLoader
+
+
+import sys
+sys.path.append('thirdparty/segment-anything')
+from segment_anything import build_sam, SamPredictor
+
+class Colors:
+ # Ultralytics color palette https://ultralytics.com/
+ def __init__(self):
+ # hex = matplotlib.colors.TABLEAU_COLORS.values()
+ hexs = ('FF3838', 'FF9D97', 'FF701F', 'FFB21D', 'CFD231', '48F90A', '92CC17', '3DDB86', '1A9334', '00D4BB',
+ '2C99A8', '00C2FF', '344593', '6473FF', '0018EC', '8438FF', '520085', 'CB38FF', 'FF95C8', 'FF37C7')
+ self.palette = [self.hex2rgb(f'#{c}') for c in hexs]
+ self.n = len(self.palette)
+
+ def __call__(self, i, bgr=False):
+ c = self.palette[int(i) % self.n]
+ return (c[2], c[1], c[0]) if bgr else c
+
+ @staticmethod
+ def hex2rgb(h): # rgb order (PIL)
+ return tuple(int(h[1 + i:1 + i + 2], 16) for i in (0, 2, 4))
+
+
+colors = Colors() # create instance for 'from utils.plots import colors'
+
+
+class ListImgDataset(Dataset):
+ def __init__(self, mot_path, img_list, det_db) -> None:
+ super().__init__()
+ self.mot_path = mot_path
+ self.img_list = img_list
+ self.det_db = det_db
+
+ '''
+ common settings
+ '''
+ self.img_height = 800
+ self.img_width = 1536
+ self.mean = [0.485, 0.456, 0.406]
+ self.std = [0.229, 0.224, 0.225]
+
+ def load_img_from_file(self, f_path):
+ cur_img = cv2.imread(os.path.join(self.mot_path, f_path))
+ assert cur_img is not None, f_path
+ cur_img = cv2.cvtColor(cur_img, cv2.COLOR_BGR2RGB)
+ proposals = []
+ im_h, im_w = cur_img.shape[:2]
+ for line in self.det_db[f_path[:-4] + '.txt']:
+ l, t, w, h, s = list(map(float, line.split(',')))
+ proposals.append([(l + w / 2) / im_w,
+ (t + h / 2) / im_h,
+ w / im_w,
+ h / im_h,
+ s])
+ return cur_img, torch.as_tensor(proposals).reshape(-1, 5)
+
+ def init_img(self, img, proposals):
+ ori_img = img.copy()
+ self.seq_h, self.seq_w = img.shape[:2]
+ scale = self.img_height / min(self.seq_h, self.seq_w)
+ if max(self.seq_h, self.seq_w) * scale > self.img_width:
+ scale = self.img_width / max(self.seq_h, self.seq_w)
+ target_h = int(self.seq_h * scale)
+ target_w = int(self.seq_w * scale)
+ img = cv2.resize(img, (target_w, target_h))
+ img = F.normalize(F.to_tensor(img), self.mean, self.std)
+ img = img.unsqueeze(0)
+ return img, ori_img, proposals
+
+ def __len__(self):
+ return len(self.img_list)
+
+ def __getitem__(self, index):
+ img, proposals = self.load_img_from_file(self.img_list[index])
+ return self.init_img(img, proposals)
+
+
+class Detector(object):
+ def __init__(self, args, model, vid):
+ self.args = args
+ self.detr = model
+
+ self.vid = vid
+ self.seq_num = os.path.basename(vid)
+ img_list = os.listdir(os.path.join(self.args.mot_path, vid, 'img1'))
+ img_list = [os.path.join(vid, 'img1', i) for i in img_list if 'jpg' in i]
+
+ self.img_list = sorted(img_list)
+ self.img_len = len(self.img_list)
+
+ self.predict_path = os.path.join(self.args.output_dir, args.exp_name)
+ os.makedirs(self.predict_path, exist_ok=True)
+
+
+ self.sam_predictor = SamPredictor(build_sam(checkpoint="thirdparty/segment-anything/sam_vit_h_4b8939.pth"))
+ _ = self.sam_predictor.model.to(device='cuda')
+
+ fps = 25
+ size = (1920, 1080)
+ self.videowriter = cv2.VideoWriter('visam.avi', cv2.VideoWriter_fourcc('M','J','P','G'), fps, size)
+
+ @staticmethod
+ def filter_dt_by_score(dt_instances: Instances, prob_threshold: float) -> Instances:
+ keep = dt_instances.scores > prob_threshold
+ keep &= dt_instances.obj_idxes >= 0
+ return dt_instances[keep]
+
+ @staticmethod
+ def filter_dt_by_area(dt_instances: Instances, area_threshold: float) -> Instances:
+ wh = dt_instances.boxes[:, 2:4] - dt_instances.boxes[:, 0:2]
+ areas = wh[:, 0] * wh[:, 1]
+ keep = areas > area_threshold
+ return dt_instances[keep]
+
+ def detect(self, prob_threshold=0.6, area_threshold=100, vis=False):
+ total_dts = 0
+ total_occlusion_dts = 0
+
+ track_instances = None
+ with open(os.path.join(self.args.mot_path, 'DanceTrack', self.args.det_db)) as f:
+ det_db = json.load(f)
+ loader = DataLoader(ListImgDataset(self.args.mot_path, self.img_list, det_db), 1, num_workers=2)
+ lines = []
+ for i, data in enumerate(tqdm(loader)):
+ cur_img, ori_img, proposals = [d[0] for d in data]
+ cur_img, proposals = cur_img.cuda(), proposals.cuda()
+
+ # track_instances = None
+ if track_instances is not None:
+ track_instances.remove('boxes')
+ track_instances.remove('labels')
+ seq_h, seq_w, _ = ori_img.shape
+
+ res = self.detr.inference_single_image(cur_img, (seq_h, seq_w), track_instances, proposals)
+ track_instances = res['track_instances']
+
+ dt_instances = deepcopy(track_instances)
+
+ # filter det instances by score.
+ dt_instances = self.filter_dt_by_score(dt_instances, prob_threshold)
+ dt_instances = self.filter_dt_by_area(dt_instances, area_threshold)
+
+ total_dts += len(dt_instances)
+
+ bbox_xyxy = dt_instances.boxes.tolist()
+ identities = dt_instances.obj_idxes.tolist()
+
+
+ masks_all = []
+ self.sam_predictor.set_image(ori_img.to(torch.device('cpu')).numpy().copy())
+
+ for bbox, id in zip(np.array(bbox_xyxy), identities):
+ masks, iou_predictions, low_res_masks = self.sam_predictor.predict(box=bbox)
+ index_max = iou_predictions.argsort()[0]
+ masks = np.concatenate([masks[index_max:(index_max+1)], masks[index_max:(index_max+1)], masks[index_max:(index_max+1)]], axis=0)
+ masks = masks.astype(np.int32)*np.array(colors(id))[:, None, None]
+ masks_all.append(masks)
+
+ self.sam_predictor.reset_image()
+ if len(masks_all):
+ masks_sum = masks_all[0].copy()
+ for m in masks_all[1:]:
+ masks_sum += m
+ else:
+ masks_sum = np.zeros_like(img).transpose(2, 0, 1)
+
+ img = ori_img.to(torch.device('cpu')).numpy().copy()[..., ::-1]
+ img = (img * 0.5 + (masks_sum.transpose(1,2,0) * 30) %128).astype(np.uint8)
+ for bbox in bbox_xyxy:
+ cv2.rectangle(img, (int(bbox[0]), int(bbox[1])), (int(bbox[2]), int(bbox[3])), (0,0,255), thickness=3)
+ self.videowriter.write(img)
+
+
+ save_format = '{frame},{id},{x1:.2f},{y1:.2f},{w:.2f},{h:.2f},1,-1,-1,-1\n'
+ for xyxy, track_id in zip(bbox_xyxy, identities):
+ if track_id < 0 or track_id is None:
+ continue
+ x1, y1, x2, y2 = xyxy
+ w, h = x2 - x1, y2 - y1
+ lines.append(save_format.format(frame=i + 1, id=track_id, x1=x1, y1=y1, w=w, h=h))
+ with open(os.path.join(self.predict_path, f'{self.seq_num}.txt'), 'w') as f:
+ f.writelines(lines)
+ print("totally {} dts {} occlusion dts".format(total_dts, total_occlusion_dts))
+
+class RuntimeTrackerBase(object):
+ def __init__(self, score_thresh=0.6, filter_score_thresh=0.5, miss_tolerance=10):
+ self.score_thresh = score_thresh
+ self.filter_score_thresh = filter_score_thresh
+ self.miss_tolerance = miss_tolerance
+ self.max_obj_id = 0
+
+ def clear(self):
+ self.max_obj_id = 0
+
+ def update(self, track_instances: Instances):
+ device = track_instances.obj_idxes.device
+
+ track_instances.disappear_time[track_instances.scores >= self.score_thresh] = 0
+ new_obj = (track_instances.obj_idxes == -1) & (track_instances.scores >= self.score_thresh)
+ disappeared_obj = (track_instances.obj_idxes >= 0) & (track_instances.scores < self.filter_score_thresh)
+ num_new_objs = new_obj.sum().item()
+
+ track_instances.obj_idxes[new_obj] = self.max_obj_id + torch.arange(num_new_objs, device=device)
+ self.max_obj_id += num_new_objs
+
+ track_instances.disappear_time[disappeared_obj] += 1
+ to_del = disappeared_obj & (track_instances.disappear_time >= self.miss_tolerance)
+ track_instances.obj_idxes[to_del] = -1
+
+
+if __name__ == '__main__':
+
+ parser = argparse.ArgumentParser('DETR training and evaluation script', parents=[get_args_parser()])
+ parser.add_argument('--score_threshold', default=0.5, type=float)
+ parser.add_argument('--update_score_threshold', default=0.5, type=float)
+ parser.add_argument('--miss_tolerance', default=20, type=int)
+ args = parser.parse_args()
+ if args.output_dir:
+ Path(args.output_dir).mkdir(parents=True, exist_ok=True)
+
+ # load model and weights
+ detr, _, _ = build_model(args)
+ detr.track_embed.score_thr = args.update_score_threshold
+ detr.track_base = RuntimeTrackerBase(args.score_threshold, args.score_threshold, args.miss_tolerance)
+ checkpoint = torch.load(args.resume, map_location='cpu')
+ detr = load_model(detr, args.resume)
+ detr.eval()
+ detr = detr.cuda()
+
+ # '''for MOT17 submit'''
+ sub_dir = 'DanceTrack/test'
+ seq_nums = os.listdir(os.path.join(args.mot_path, sub_dir))
+ if 'seqmap' in seq_nums:
+ seq_nums.remove('seqmap')
+ vids = [os.path.join(sub_dir, seq) for seq in seq_nums]
+
+ rank = int(os.environ.get('RLAUNCH_REPLICA', '0'))
+ ws = int(os.environ.get('RLAUNCH_REPLICA_TOTAL', '1'))
+ vids = vids[rank::ws]
+
+ for vid in vids:
+ det = Detector(args, model=detr, vid=vid)
+ det.detect(args.score_threshold)
diff --git a/VISAM/thirdparty/segment_anything/.flake8 b/VISAM/thirdparty/segment_anything/.flake8
new file mode 100644
index 0000000000000000000000000000000000000000..6b0759587aa5756e66a13ef034c6bcdd76a885f5
--- /dev/null
+++ b/VISAM/thirdparty/segment_anything/.flake8
@@ -0,0 +1,7 @@
+[flake8]
+ignore = W503, E203, E221, C901, C408, E741, C407, B017, F811, C101, EXE001, EXE002
+max-line-length = 100
+max-complexity = 18
+select = B,C,E,F,W,T4,B9
+per-file-ignores =
+ **/__init__.py:F401,F403,E402
diff --git a/VISAM/thirdparty/segment_anything/CODE_OF_CONDUCT.md b/VISAM/thirdparty/segment_anything/CODE_OF_CONDUCT.md
new file mode 100644
index 0000000000000000000000000000000000000000..08b500a221857ec3f451338e80b4a9ab1173a1af
--- /dev/null
+++ b/VISAM/thirdparty/segment_anything/CODE_OF_CONDUCT.md
@@ -0,0 +1,80 @@
+# Code of Conduct
+
+## Our Pledge
+
+In the interest of fostering an open and welcoming environment, we as
+contributors and maintainers pledge to make participation in our project and
+our community a harassment-free experience for everyone, regardless of age, body
+size, disability, ethnicity, sex characteristics, gender identity and expression,
+level of experience, education, socio-economic status, nationality, personal
+appearance, race, religion, or sexual identity and orientation.
+
+## Our Standards
+
+Examples of behavior that contributes to creating a positive environment
+include:
+
+* Using welcoming and inclusive language
+* Being respectful of differing viewpoints and experiences
+* Gracefully accepting constructive criticism
+* Focusing on what is best for the community
+* Showing empathy towards other community members
+
+Examples of unacceptable behavior by participants include:
+
+* The use of sexualized language or imagery and unwelcome sexual attention or
+ advances
+* Trolling, insulting/derogatory comments, and personal or political attacks
+* Public or private harassment
+* Publishing others' private information, such as a physical or electronic
+ address, without explicit permission
+* Other conduct which could reasonably be considered inappropriate in a
+ professional setting
+
+## Our Responsibilities
+
+Project maintainers are responsible for clarifying the standards of acceptable
+behavior and are expected to take appropriate and fair corrective action in
+response to any instances of unacceptable behavior.
+
+Project maintainers have the right and responsibility to remove, edit, or
+reject comments, commits, code, wiki edits, issues, and other contributions
+that are not aligned to this Code of Conduct, or to ban temporarily or
+permanently any contributor for other behaviors that they deem inappropriate,
+threatening, offensive, or harmful.
+
+## Scope
+
+This Code of Conduct applies within all project spaces, and it also applies when
+an individual is representing the project or its community in public spaces.
+Examples of representing a project or community include using an official
+project e-mail address, posting via an official social media account, or acting
+as an appointed representative at an online or offline event. Representation of
+a project may be further defined and clarified by project maintainers.
+
+This Code of Conduct also applies outside the project spaces when there is a
+reasonable belief that an individual's behavior may have a negative impact on
+the project or its community.
+
+## Enforcement
+
+Instances of abusive, harassing, or otherwise unacceptable behavior may be
+reported by contacting the project team at . All
+complaints will be reviewed and investigated and will result in a response that
+is deemed necessary and appropriate to the circumstances. The project team is
+obligated to maintain confidentiality with regard to the reporter of an incident.
+Further details of specific enforcement policies may be posted separately.
+
+Project maintainers who do not follow or enforce the Code of Conduct in good
+faith may face temporary or permanent repercussions as determined by other
+members of the project's leadership.
+
+## Attribution
+
+This Code of Conduct is adapted from the [Contributor Covenant][homepage], version 1.4,
+available at https://www.contributor-covenant.org/version/1/4/code-of-conduct.html
+
+[homepage]: https://www.contributor-covenant.org
+
+For answers to common questions about this code of conduct, see
+https://www.contributor-covenant.org/faq
diff --git a/VISAM/thirdparty/segment_anything/CONTRIBUTING.md b/VISAM/thirdparty/segment_anything/CONTRIBUTING.md
new file mode 100644
index 0000000000000000000000000000000000000000..263991c9496cf29ed4b99e03a9fb9a38e6bfaf86
--- /dev/null
+++ b/VISAM/thirdparty/segment_anything/CONTRIBUTING.md
@@ -0,0 +1,31 @@
+# Contributing to segment-anything
+We want to make contributing to this project as easy and transparent as
+possible.
+
+## Pull Requests
+We actively welcome your pull requests.
+
+1. Fork the repo and create your branch from `main`.
+2. If you've added code that should be tested, add tests.
+3. If you've changed APIs, update the documentation.
+4. Ensure the test suite passes.
+5. Make sure your code lints, using the `linter.sh` script in the project's root directory. Linting requires `black==23.*`, `isort==5.12.0`, `flake8`, and `mypy`.
+6. If you haven't already, complete the Contributor License Agreement ("CLA").
+
+## Contributor License Agreement ("CLA")
+In order to accept your pull request, we need you to submit a CLA. You only need
+to do this once to work on any of Facebook's open source projects.
+
+Complete your CLA here:
+
+## Issues
+We use GitHub issues to track public bugs. Please ensure your description is
+clear and has sufficient instructions to be able to reproduce the issue.
+
+Facebook has a [bounty program](https://www.facebook.com/whitehat/) for the safe
+disclosure of security bugs. In those cases, please go through the process
+outlined on that page and do not file a public issue.
+
+## License
+By contributing to segment-anything, you agree that your contributions will be licensed
+under the LICENSE file in the root directory of this source tree.
diff --git a/VISAM/thirdparty/segment_anything/LICENSE b/VISAM/thirdparty/segment_anything/LICENSE
new file mode 100644
index 0000000000000000000000000000000000000000..261eeb9e9f8b2b4b0d119366dda99c6fd7d35c64
--- /dev/null
+++ b/VISAM/thirdparty/segment_anything/LICENSE
@@ -0,0 +1,201 @@
+ Apache License
+ Version 2.0, January 2004
+ http://www.apache.org/licenses/
+
+ TERMS AND CONDITIONS FOR USE, REPRODUCTION, AND DISTRIBUTION
+
+ 1. Definitions.
+
+ "License" shall mean the terms and conditions for use, reproduction,
+ and distribution as defined by Sections 1 through 9 of this document.
+
+ "Licensor" shall mean the copyright owner or entity authorized by
+ the copyright owner that is granting the License.
+
+ "Legal Entity" shall mean the union of the acting entity and all
+ other entities that control, are controlled by, or are under common
+ control with that entity. For the purposes of this definition,
+ "control" means (i) the power, direct or indirect, to cause the
+ direction or management of such entity, whether by contract or
+ otherwise, or (ii) ownership of fifty percent (50%) or more of the
+ outstanding shares, or (iii) beneficial ownership of such entity.
+
+ "You" (or "Your") shall mean an individual or Legal Entity
+ exercising permissions granted by this License.
+
+ "Source" form shall mean the preferred form for making modifications,
+ including but not limited to software source code, documentation
+ source, and configuration files.
+
+ "Object" form shall mean any form resulting from mechanical
+ transformation or translation of a Source form, including but
+ not limited to compiled object code, generated documentation,
+ and conversions to other media types.
+
+ "Work" shall mean the work of authorship, whether in Source or
+ Object form, made available under the License, as indicated by a
+ copyright notice that is included in or attached to the work
+ (an example is provided in the Appendix below).
+
+ "Derivative Works" shall mean any work, whether in Source or Object
+ form, that is based on (or derived from) the Work and for which the
+ editorial revisions, annotations, elaborations, or other modifications
+ represent, as a whole, an original work of authorship. For the purposes
+ of this License, Derivative Works shall not include works that remain
+ separable from, or merely link (or bind by name) to the interfaces of,
+ the Work and Derivative Works thereof.
+
+ "Contribution" shall mean any work of authorship, including
+ the original version of the Work and any modifications or additions
+ to that Work or Derivative Works thereof, that is intentionally
+ submitted to Licensor for inclusion in the Work by the copyright owner
+ or by an individual or Legal Entity authorized to submit on behalf of
+ the copyright owner. For the purposes of this definition, "submitted"
+ means any form of electronic, verbal, or written communication sent
+ to the Licensor or its representatives, including but not limited to
+ communication on electronic mailing lists, source code control systems,
+ and issue tracking systems that are managed by, or on behalf of, the
+ Licensor for the purpose of discussing and improving the Work, but
+ excluding communication that is conspicuously marked or otherwise
+ designated in writing by the copyright owner as "Not a Contribution."
+
+ "Contributor" shall mean Licensor and any individual or Legal Entity
+ on behalf of whom a Contribution has been received by Licensor and
+ subsequently incorporated within the Work.
+
+ 2. Grant of Copyright License. Subject to the terms and conditions of
+ this License, each Contributor hereby grants to You a perpetual,
+ worldwide, non-exclusive, no-charge, royalty-free, irrevocable
+ copyright license to reproduce, prepare Derivative Works of,
+ publicly display, publicly perform, sublicense, and distribute the
+ Work and such Derivative Works in Source or Object form.
+
+ 3. Grant of Patent License. Subject to the terms and conditions of
+ this License, each Contributor hereby grants to You a perpetual,
+ worldwide, non-exclusive, no-charge, royalty-free, irrevocable
+ (except as stated in this section) patent license to make, have made,
+ use, offer to sell, sell, import, and otherwise transfer the Work,
+ where such license applies only to those patent claims licensable
+ by such Contributor that are necessarily infringed by their
+ Contribution(s) alone or by combination of their Contribution(s)
+ with the Work to which such Contribution(s) was submitted. If You
+ institute patent litigation against any entity (including a
+ cross-claim or counterclaim in a lawsuit) alleging that the Work
+ or a Contribution incorporated within the Work constitutes direct
+ or contributory patent infringement, then any patent licenses
+ granted to You under this License for that Work shall terminate
+ as of the date such litigation is filed.
+
+ 4. Redistribution. You may reproduce and distribute copies of the
+ Work or Derivative Works thereof in any medium, with or without
+ modifications, and in Source or Object form, provided that You
+ meet the following conditions:
+
+ (a) You must give any other recipients of the Work or
+ Derivative Works a copy of this License; and
+
+ (b) You must cause any modified files to carry prominent notices
+ stating that You changed the files; and
+
+ (c) You must retain, in the Source form of any Derivative Works
+ that You distribute, all copyright, patent, trademark, and
+ attribution notices from the Source form of the Work,
+ excluding those notices that do not pertain to any part of
+ the Derivative Works; and
+
+ (d) If the Work includes a "NOTICE" text file as part of its
+ distribution, then any Derivative Works that You distribute must
+ include a readable copy of the attribution notices contained
+ within such NOTICE file, excluding those notices that do not
+ pertain to any part of the Derivative Works, in at least one
+ of the following places: within a NOTICE text file distributed
+ as part of the Derivative Works; within the Source form or
+ documentation, if provided along with the Derivative Works; or,
+ within a display generated by the Derivative Works, if and
+ wherever such third-party notices normally appear. The contents
+ of the NOTICE file are for informational purposes only and
+ do not modify the License. You may add Your own attribution
+ notices within Derivative Works that You distribute, alongside
+ or as an addendum to the NOTICE text from the Work, provided
+ that such additional attribution notices cannot be construed
+ as modifying the License.
+
+ You may add Your own copyright statement to Your modifications and
+ may provide additional or different license terms and conditions
+ for use, reproduction, or distribution of Your modifications, or
+ for any such Derivative Works as a whole, provided Your use,
+ reproduction, and distribution of the Work otherwise complies with
+ the conditions stated in this License.
+
+ 5. Submission of Contributions. Unless You explicitly state otherwise,
+ any Contribution intentionally submitted for inclusion in the Work
+ by You to the Licensor shall be under the terms and conditions of
+ this License, without any additional terms or conditions.
+ Notwithstanding the above, nothing herein shall supersede or modify
+ the terms of any separate license agreement you may have executed
+ with Licensor regarding such Contributions.
+
+ 6. Trademarks. This License does not grant permission to use the trade
+ names, trademarks, service marks, or product names of the Licensor,
+ except as required for reasonable and customary use in describing the
+ origin of the Work and reproducing the content of the NOTICE file.
+
+ 7. Disclaimer of Warranty. Unless required by applicable law or
+ agreed to in writing, Licensor provides the Work (and each
+ Contributor provides its Contributions) on an "AS IS" BASIS,
+ WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or
+ implied, including, without limitation, any warranties or conditions
+ of TITLE, NON-INFRINGEMENT, MERCHANTABILITY, or FITNESS FOR A
+ PARTICULAR PURPOSE. You are solely responsible for determining the
+ appropriateness of using or redistributing the Work and assume any
+ risks associated with Your exercise of permissions under this License.
+
+ 8. Limitation of Liability. In no event and under no legal theory,
+ whether in tort (including negligence), contract, or otherwise,
+ unless required by applicable law (such as deliberate and grossly
+ negligent acts) or agreed to in writing, shall any Contributor be
+ liable to You for damages, including any direct, indirect, special,
+ incidental, or consequential damages of any character arising as a
+ result of this License or out of the use or inability to use the
+ Work (including but not limited to damages for loss of goodwill,
+ work stoppage, computer failure or malfunction, or any and all
+ other commercial damages or losses), even if such Contributor
+ has been advised of the possibility of such damages.
+
+ 9. Accepting Warranty or Additional Liability. While redistributing
+ the Work or Derivative Works thereof, You may choose to offer,
+ and charge a fee for, acceptance of support, warranty, indemnity,
+ or other liability obligations and/or rights consistent with this
+ License. However, in accepting such obligations, You may act only
+ on Your own behalf and on Your sole responsibility, not on behalf
+ of any other Contributor, and only if You agree to indemnify,
+ defend, and hold each Contributor harmless for any liability
+ incurred by, or claims asserted against, such Contributor by reason
+ of your accepting any such warranty or additional liability.
+
+ END OF TERMS AND CONDITIONS
+
+ APPENDIX: How to apply the Apache License to your work.
+
+ To apply the Apache License to your work, attach the following
+ boilerplate notice, with the fields enclosed by brackets "[]"
+ replaced with your own identifying information. (Don't include
+ the brackets!) The text should be enclosed in the appropriate
+ comment syntax for the file format. We also recommend that a
+ file or class name and description of purpose be included on the
+ same "printed page" as the copyright notice for easier
+ identification within third-party archives.
+
+ Copyright [yyyy] [name of copyright owner]
+
+ Licensed under the Apache License, Version 2.0 (the "License");
+ you may not use this file except in compliance with the License.
+ You may obtain a copy of the License at
+
+ http://www.apache.org/licenses/LICENSE-2.0
+
+ Unless required by applicable law or agreed to in writing, software
+ distributed under the License is distributed on an "AS IS" BASIS,
+ WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+ See the License for the specific language governing permissions and
+ limitations under the License.
diff --git a/VISAM/thirdparty/segment_anything/README.md b/VISAM/thirdparty/segment_anything/README.md
new file mode 100644
index 0000000000000000000000000000000000000000..6256d2b7f5a387988338d538df4e699eb17ba702
--- /dev/null
+++ b/VISAM/thirdparty/segment_anything/README.md
@@ -0,0 +1,107 @@
+# Segment Anything
+
+**[Meta AI Research, FAIR](https://ai.facebook.com/research/)**
+
+[Alexander Kirillov](https://alexander-kirillov.github.io/), [Eric Mintun](https://ericmintun.github.io/), [Nikhila Ravi](https://nikhilaravi.com/), [Hanzi Mao](https://hanzimao.me/), Chloe Rolland, Laura Gustafson, [Tete Xiao](https://tetexiao.com), [Spencer Whitehead](https://www.spencerwhitehead.com/), Alex Berg, Wan-Yen Lo, [Piotr Dollar](https://pdollar.github.io/), [Ross Girshick](https://www.rossgirshick.info/)
+
+[[`Paper`](https://ai.facebook.com/research/publications/segment-anything/)] [[`Project`](https://segment-anything.com/)] [[`Demo`](https://segment-anything.com/demo)] [[`Dataset`](https://segment-anything.com/dataset/index.html)] [[`Blog`](https://ai.facebook.com/blog/segment-anything-foundation-model-image-segmentation/)]
+
+
+
+The **Segment Anything Model (SAM)** produces high quality object masks from input prompts such as points or boxes, and it can be used to generate masks for all objects in an image. It has been trained on a [dataset](https://segment-anything.com/dataset/index.html) of 11 million images and 1.1 billion masks, and has strong zero-shot performance on a variety of segmentation tasks.
+
+
+
+
+
+
+## Installation
+
+The code requires `python>=3.8`, as well as `pytorch>=1.7` and `torchvision>=0.8`. Please follow the instructions [here](https://pytorch.org/get-started/locally/) to install both PyTorch and TorchVision dependencies. Installing both PyTorch and TorchVision with CUDA support is strongly recommended.
+
+Install Segment Anything:
+
+```
+pip install git+https://github.com/facebookresearch/segment-anything.git
+```
+
+or clone the repository locally and install with
+
+```
+git clone git@github.com:facebookresearch/segment-anything.git
+cd segment-anything; pip install -e .
+```
+
+The following optional dependencies are necessary for mask post-processing, saving masks in COCO format, the example notebooks, and exporting the model in ONNX format. `jupyter` is also required to run the example notebooks.
+```
+pip install opencv-python pycocotools matplotlib onnxruntime onnx
+```
+
+
+## Getting Started
+
+First download a [model checkpoint](#model-checkpoints). Then the model can be used in just a few lines to get masks from a given prompt:
+
+```
+from segment_anything import build_sam, SamPredictor
+predictor = SamPredictor(build_sam(checkpoint=""))
+predictor.set_image()
+masks, _, _ = predictor.predict()
+```
+
+or generate masks for an entire image:
+
+```
+from segment_anything import build_sam, SamAutomaticMaskGenerator
+mask_generator = SamAutomaticMaskGenerator(build_sam(checkpoint=""))
+masks = mask_generator_generate()
+```
+
+Additionally, masks can be generated for images from the command line:
+
+```
+python scripts/amg.py --checkpoint --input --output
+```
+
+See the examples notebooks on [using SAM with prompts](/notebooks/predictor_example.ipynb) and [automatically generating masks](/notebooks/automatic_mask_generator_example.ipynb) for more details.
+
+
+
+
+
+
+## ONNX Export
+
+SAM's lightweight mask decoder can be exported to ONNX format so that it can be run in any environment that supports ONNX runtime, such as in-browser as showcased in the [demo](https://segment-anything.com/demo). Export the model with
+
+```
+python scripts/export_onnx_model.py --checkpoint --output
+```
+
+See the [example notebook](https://github.com/facebookresearch/segment-anything/blob/main/notebooks/onnx_model_example.ipynb) for details on how to combine image preprocessing via SAM's backbone with mask prediction using the ONNX model. It is recommended to use the latest stable version of PyTorch for ONNX export.
+
+## Model Checkpoints
+
+Three model versions of the model are available with different backbone sizes. These models can be instantiated by running
+```
+from segment_anything import sam_model_registry
+sam = sam_model_registry[""](checkpoint="")
+```
+Click the links below to download the checkpoint for the corresponding model name. The default model in bold can also be instantiated with `build_sam`, as in the examples in [Getting Started](#getting-started).
+
+* **`default` or `vit_h`: [ViT-H SAM model.](https://dl.fbaipublicfiles.com/segment_anything/sam_vit_h_4b8939.pth)**
+* `vit_l`: [ViT-L SAM model.](https://dl.fbaipublicfiles.com/segment_anything/sam_vit_l_0b3195.pth)
+* `vit_b`: [ViT-B SAM model.](https://dl.fbaipublicfiles.com/segment_anything/sam_vit_b_01ec64.pth)
+
+## License
+The model is licensed under the [Apache 2.0 license](LICENSE).
+
+## Contributing
+
+See [contributing](CONTRIBUTING.md) and the [code of conduct](CODE_OF_CONDUCT.md).
+
+## Contributors
+
+The Segment Anything project was made possible with the help of many contributors (alphabetical):
+
+Aaron Adcock, Vaibhav Aggarwal, Morteza Behrooz, Cheng-Yang Fu, Ashley Gabriel, Ahuva Goldstand, Allen Goodman, Sumanth Gurram, Jiabo Hu, Somya Jain, Devansh Kukreja, Robert Kuo, Joshua Lane, Yanghao Li, Lilian Luong, Jitendra Malik, Mallika Malhotra, William Ngan, Omkar Parkhi, Nikhil Raina, Dirk Rowe, Neil Sejoor, Vanessa Stark, Bala Varadarajan, Bram Wasti, Zachary Winstrom
diff --git a/VISAM/thirdparty/segment_anything/assets/masks1.png b/VISAM/thirdparty/segment_anything/assets/masks1.png
new file mode 100644
index 0000000000000000000000000000000000000000..559e20feb4ab76b0833d4d52bd16c6be8731eef8
--- /dev/null
+++ b/VISAM/thirdparty/segment_anything/assets/masks1.png
@@ -0,0 +1,3 @@
+version https://git-lfs.github.com/spec/v1
+oid sha256:094650248317c2b41ca0279d402253a8d1ae3801f8809e69480561dddd7d9f64
+size 3703371
diff --git a/VISAM/thirdparty/segment_anything/assets/masks2.jpg b/VISAM/thirdparty/segment_anything/assets/masks2.jpg
new file mode 100644
index 0000000000000000000000000000000000000000..29360eb40414747e5e6c6cb1e72f9bd3f6098863
Binary files /dev/null and b/VISAM/thirdparty/segment_anything/assets/masks2.jpg differ
diff --git a/VISAM/thirdparty/segment_anything/assets/model_diagram.png b/VISAM/thirdparty/segment_anything/assets/model_diagram.png
new file mode 100644
index 0000000000000000000000000000000000000000..ba24e42d793346047f258bf5c3cfe9d1653c6d9b
Binary files /dev/null and b/VISAM/thirdparty/segment_anything/assets/model_diagram.png differ
diff --git a/VISAM/thirdparty/segment_anything/assets/notebook1.png b/VISAM/thirdparty/segment_anything/assets/notebook1.png
new file mode 100644
index 0000000000000000000000000000000000000000..8fb19cb8a1a68d2b53948ca4d27658d06a5e977c
Binary files /dev/null and b/VISAM/thirdparty/segment_anything/assets/notebook1.png differ
diff --git a/VISAM/thirdparty/segment_anything/assets/notebook2.png b/VISAM/thirdparty/segment_anything/assets/notebook2.png
new file mode 100644
index 0000000000000000000000000000000000000000..15bfd9ffbbbf8a8b2172571da09a4d9c9e13ba8f
--- /dev/null
+++ b/VISAM/thirdparty/segment_anything/assets/notebook2.png
@@ -0,0 +1,3 @@
+version https://git-lfs.github.com/spec/v1
+oid sha256:bdffadfdddee81d090ec130566eae7de6de0c6d6b2be85974860327c5d860fcc
+size 1221706
diff --git a/VISAM/thirdparty/segment_anything/linter.sh b/VISAM/thirdparty/segment_anything/linter.sh
new file mode 100644
index 0000000000000000000000000000000000000000..df2e17436d30e89ff1728109301599f425f1ad6b
--- /dev/null
+++ b/VISAM/thirdparty/segment_anything/linter.sh
@@ -0,0 +1,32 @@
+#!/bin/bash -e
+# Copyright (c) Facebook, Inc. and its affiliates.
+
+{
+ black --version | grep -E "23\." > /dev/null
+} || {
+ echo "Linter requires 'black==23.*' !"
+ exit 1
+}
+
+ISORT_VERSION=$(isort --version-number)
+if [[ "$ISORT_VERSION" != 5.12* ]]; then
+ echo "Linter requires isort==5.12.0 !"
+ exit 1
+fi
+
+echo "Running isort ..."
+isort . --atomic
+
+echo "Running black ..."
+black -l 100 .
+
+echo "Running flake8 ..."
+if [ -x "$(command -v flake8)" ]; then
+ flake8 .
+else
+ python3 -m flake8 .
+fi
+
+echo "Running mypy..."
+
+mypy --exclude 'setup.py|notebooks' .
diff --git a/VISAM/thirdparty/segment_anything/main.py b/VISAM/thirdparty/segment_anything/main.py
new file mode 100644
index 0000000000000000000000000000000000000000..55bdd28ca9de346269f3c001a39ce962c34788bd
--- /dev/null
+++ b/VISAM/thirdparty/segment_anything/main.py
@@ -0,0 +1,110 @@
+from segment_anything import build_sam, SamPredictor
+import os
+import cv2
+import numpy as np
+from collections import defaultdict
+
+class Colors:
+ # Ultralytics color palette https://ultralytics.com/
+ def __init__(self):
+ # hex = matplotlib.colors.TABLEAU_COLORS.values()
+ hexs = ('FF3838', 'FF9D97', 'FF701F', 'FFB21D', 'CFD231', '48F90A', '92CC17', '3DDB86', '1A9334', '00D4BB',
+ '2C99A8', '00C2FF', '344593', '6473FF', '0018EC', '8438FF', '520085', 'CB38FF', 'FF95C8', 'FF37C7')
+ self.palette = [self.hex2rgb(f'#{c}') for c in hexs]
+ self.n = len(self.palette)
+
+ def __call__(self, i, bgr=False):
+ c = self.palette[int(i) % self.n]
+ return (c[2], c[1], c[0]) if bgr else c
+
+ @staticmethod
+ def hex2rgb(h): # rgb order (PIL)
+ return tuple(int(h[1 + i:1 + i + 2], 16) for i in (0, 2, 4))
+
+
+colors = Colors() # create instance for 'from utils.plots import colors'
+
+
+
+predictor = SamPredictor(build_sam(checkpoint="sam_vit_h_4b8939.pth"))
+_ = predictor.model.to(device='cuda')
+# image = cv2.imread('/home/hadoop-vacv/yanfeng/data/dancetrack/train/dancetrack0001/img1/00000109.jpg')
+# image = cv2.cvtColor(image, cv2.COLOR_BGR2RGB)
+
+# predictor.set_image(image)
+
+# bbox = np.array([0,0,100,100], dtype=np.int32)
+
+# masks, _, _ = predictor.predict(box=bbox)
+
+# masks
+
+input_path = '/home/hadoop-vacv/yanfeng/data/dancetrack/val/dancetrack0004'
+targets = [f for f in os.listdir(os.path.join(input_path, 'img1')) if not os.path.isdir(os.path.join(input_path, 'img1', f))]
+targets = [os.path.join(input_path, 'img1', f) for f in targets]
+targets.sort()
+
+bboxes_all = defaultdict(list)
+gt_path = os.path.join(input_path, 'gt', 'gt.txt')
+# gt_path = os.path.join('/home/hadoop-vacv/yanfeng/project/MOTRv2/MOTRv3/exps/motrv2ch_uni5cost6g/run2/tracker0', 'dancetrack0004.txt')
+for l in open(gt_path):
+ t, i, *xywh, mark, label = l.strip().split(',')[:8]
+ t, i, mark, label = map(int, (t, i, mark, label))
+ if mark == 0:
+ continue
+ if label in [3, 4, 5, 6, 9, 10, 11]: # Non-person
+ continue
+ else:
+ crowd = False
+ x, y, w, h = map(int, map(float, (xywh)))
+ bboxes_all[t].append([x, y, x+w, y+h, i])
+
+fps = 25
+size = (1920, 1080)
+videowriter = cv2.VideoWriter('tmp.avi', cv2.VideoWriter_fourcc('M','J','P','G'), fps, size)
+
+
+for t in targets:
+ print(f"Processing '{t}'...")
+ image = cv2.imread(t)
+ if image is None:
+ print(f"Could not load '{t}' as an image, skipping...")
+ continue
+ image = cv2.cvtColor(image, cv2.COLOR_BGR2RGB)
+
+ masks_all = []
+ bboxes = np.array(bboxes_all[int(os.path.basename(t)[:-4])])
+ # predictor.set_image(image)
+ # masks, _, _ = predictor.predict(box=bboxes[:, :4])
+ predictor.set_image(image)
+
+ for bbox in bboxes:
+ masks, iou_predictions, low_res_masks = predictor.predict(box=bbox[:4])
+ index_max = iou_predictions.argsort()[0]
+ masks = np.concatenate([masks[index_max:(index_max+1)], masks[index_max:(index_max+1)], masks[index_max:(index_max+1)]], axis=0)
+ masks = masks.astype(np.int32)*np.array(colors(bbox[4]))[:, None, None]
+ masks_all.append(masks)
+
+ predictor.reset_image()
+
+ if len(masks_all):
+ masks_sum = masks_all[0].copy()
+ for m in masks_all[1:]:
+ masks_sum += m
+ else:
+ masks_sum = np.zeros_like(img).transpose(2, 0, 1)
+
+ img = image.copy()[..., ::-1]
+ img = (img * 0.5 + (masks_sum.transpose(1,2,0) * 30) %128).astype(np.uint8)
+ for bbox in bboxes:
+ cv2.rectangle(img, (int(bbox[0]), int(bbox[1])), (int(bbox[2]), int(bbox[3])), (0,0,255), thickness=3)
+ # cv2.imwrite('tmp.jpg', img)
+
+ videowriter.write(img)
+
+videowriter.release()
+
+
+
+
+
diff --git a/VISAM/thirdparty/segment_anything/notebooks/automatic_mask_generator_example.ipynb b/VISAM/thirdparty/segment_anything/notebooks/automatic_mask_generator_example.ipynb
new file mode 100644
index 0000000000000000000000000000000000000000..261323d85b3aa9b9d1793077857269e77ff2479d
--- /dev/null
+++ b/VISAM/thirdparty/segment_anything/notebooks/automatic_mask_generator_example.ipynb
@@ -0,0 +1,454 @@
+{
+ "cells": [
+ {
+ "cell_type": "code",
+ "execution_count": 1,
+ "id": "5fa21d44",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "# Copyright (c) Meta Platforms, Inc. and affiliates."
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "b7c0041e",
+ "metadata": {},
+ "source": [
+ "# Automatically generating object masks with SAM"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "289bb0b4",
+ "metadata": {},
+ "source": [
+ "Since SAM can efficiently process prompts, masks for the entire image can be generated by sampling a large number of prompts over an image. This method was used to generate the dataset SA-1B. \n",
+ "\n",
+ "The class `SamAutomaticMaskGenerator` implements this capability. It works by sampling single-point input prompts in a grid over the image, from each of which SAM can predict multiple masks. Then, masks are filtered for quality and deduplicated using non-maximal suppression. Additional options allow for further improvement of mask quality and quantity, such as running prediction on multiple crops of the image or postprocessing masks to remove small disconnected regions and holes."
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 2,
+ "id": "072e25b8",
+ "metadata": {},
+ "outputs": [
+ {
+ "data": {
+ "text/html": [
+ "\n",
+ "\n",
+ " \n",
+ "\n"
+ ],
+ "text/plain": [
+ ""
+ ]
+ },
+ "metadata": {},
+ "output_type": "display_data"
+ }
+ ],
+ "source": [
+ "from IPython.display import display, HTML\n",
+ "display(HTML(\n",
+ "\"\"\"\n",
+ "\n",
+ " \n",
+ "\n",
+ "\"\"\"\n",
+ "))"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "c0b71431",
+ "metadata": {},
+ "source": [
+ "## Environment Set-up"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "47e5a78f",
+ "metadata": {},
+ "source": [
+ "If running locally using jupyter, first install `segment_anything` in your environment using the [installation instructions](https://github.com/facebookresearch/segment-anything#installation) in the repository. If running from Google Colab, set `using_collab=True` below and run the cell. In Colab, be sure to select 'GPU' under 'Edit'->'Notebook Settings'->'Hardware accelerator'."
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 3,
+ "id": "4fe300fb",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "using_colab = False"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 4,
+ "id": "0685a2f5",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "if using_colab:\n",
+ " import torch\n",
+ " import torchvision\n",
+ " print(\"PyTorch version:\", torch.__version__)\n",
+ " print(\"Torchvision version:\", torchvision.__version__)\n",
+ " print(\"CUDA is available:\", torch.cuda.is_available())\n",
+ " import sys\n",
+ " !{sys.executable} -m pip install opencv-python matplotlib\n",
+ " !{sys.executable} -m pip install 'git+https://github.com/facebookresearch/segment-anything.git'\n",
+ " \n",
+ " !mkdir images\n",
+ " !wget -P images https://raw.githubusercontent.com/facebookresearch/segment-anything/main/notebooks/images/dog.jpg\n",
+ " \n",
+ " !wget https://dl.fbaipublicfiles.com/segment_anything/sam_vit_h_4b8939.pth"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "fd2bc687",
+ "metadata": {},
+ "source": [
+ "## Set-up"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 5,
+ "id": "560725a2",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "import numpy as np\n",
+ "import torch\n",
+ "import matplotlib.pyplot as plt\n",
+ "import cv2"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 6,
+ "id": "74b6e5f0",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "def show_anns(anns):\n",
+ " if len(anns) == 0:\n",
+ " return\n",
+ " sorted_anns = sorted(anns, key=(lambda x: x['area']), reverse=True)\n",
+ " ax = plt.gca()\n",
+ " ax.set_autoscale_on(False)\n",
+ " polygons = []\n",
+ " color = []\n",
+ " for ann in sorted_anns:\n",
+ " m = ann['segmentation']\n",
+ " img = np.ones((m.shape[0], m.shape[1], 3))\n",
+ " color_mask = np.random.random((1, 3)).tolist()[0]\n",
+ " for i in range(3):\n",
+ " img[:,:,i] = color_mask[i]\n",
+ " ax.imshow(np.dstack((img, m*0.35)))"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "27c41445",
+ "metadata": {},
+ "source": [
+ "## Example image"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 7,
+ "id": "ad354922",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "image = cv2.imread('images/dog.jpg')\n",
+ "image = cv2.cvtColor(image, cv2.COLOR_BGR2RGB)"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 8,
+ "id": "e0ac8c67",
+ "metadata": {},
+ "outputs": [
+ {
+ "data": {
+ "image/png": "iVBORw0KGgoAAAANSUhEUgAABiIAAAQeCAYAAABVBSJEAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjcuMSwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/bCgiHAAAACXBIWXMAAA9hAAAPYQGoP6dpAAEAAElEQVR4nOz93ZbkOrImiH0GgKS7R2Tmzl27qk6fVk+vkWaNrqU1egjpvaUnkNa8gy66T1ftnRnuJGBzYWaAgaRHeERG7r9yy+XJcDoJgoDBYP9GzMy4wx3ucIc73OEOd7jDHe5whzvc4Q53uMMd7nCHO9zhDnf4DhB+6w7c4Q53uMMd7nCHO9zhDne4wx3ucIc73OEOd7jDHe5whz8v3A0Rd7jDHe5whzvc4Q53uMMd7nCHO9zhDne4wx3ucIc73OG7wd0QcYc73OEOd7jDHe5whzvc4Q53uMMd7nCHO9zhDne4wx2+G9wNEXe4wx3ucIc73OEOd7jDHe5whzvc4Q53uMMd7nCHO9zhu8HdEHGHO9zhDne4wx3ucIc73OEOd7jDHe5whzvc4Q53uMMdvhvcDRF3uMMd7nCHO9zhDne4wx3ucIc73OEOd7jDHe5whzvc4bvB3RBxhzvc4Q53uMMd7nCHO9zhDne4wx3ucIc73OEOd7jDHb4b3A0Rd7jDHe5whzvc4Q53uMMd7nCHO9zhDne4wx3ucIc73OG7Qbr1wv/X//ZfN+eYGUDxZ+pfpB8AKAwUZsg/u1cuZ7Z29D4ixJhAFIBAABGIqP5en8ksj9N7mblrp/WodP3yUNvldY/bs7iUeq3vx3Ng/Sic9Y0DwBEMQmHSsSggYhCxPpbB2cZS7EOZL2AGygJwAXIGgAiiCXEYMRw+YJhOmB5/wHR6wOnjDzicTjicHvAwPeBhfMDhcMA0TTgcjxinEcMwIKWElBJijEgpIYSAGCOICCklgAAOaLO1Gp/tOOhk1uGket7Ggu0aLm3yFSOYM5gZpSyGECilYJ4vKCXjks8oJWPJZ3DJKHlGKRklLyjLgrLMyEtGyRklX/T3glIKGAWsz+Qi7dq8Mpf63Y6ZF3BhLEvRPswozMiloBRGXgpyKVgKI+dcn1OY5dXKFtcIQAAp2rL0sxScz2eUUrBcpL9fL4ylZDydn5BLxnm+IOeCy2XGkgsuc67DFwNhSIRxHDBOCQ/HCafjiGkMmMaIYwLGoONdGHkBSgFmTmCKGE4fEIcRp48/YJyO+Pzjf8Y4Tnh4eMCQEo6HE4aUcDocEWPCOEwIIYCi4EoIASAS1CgBXAKWsmDJCxbOyCUj63HR98056/gQCIQQFOdIcHAcR4QQME3yrGEYEGPsjyEihlBxkFIExbBZn0YPPE1Y0weus7PCZ6Ut7GjLHlTcwvZa7uiSXMfI/fXZfhf8Bxs+zchlxrI8IecFS74gLzMW96GSQaXhH5esOK3vjaJrrR+LnBc5IgptKf16BApKyXJdKeCi/Udrg0oBMSMFIEXCIRLGGHCIwBAJUwJiJIxDQIyEYYoIMSCEgECEAwYEIsEnIqE9ils2jxQCKEQQRQj9hK7PomPFrW/s1rCOQV172l4ibTsO8l3Qt5t9ec/ixqogF8blcsHlcsHX86yfJzxdzvh6OeO8zLjodSDZt4ZhQgwJx+mElBI+fHhAGgY8HB4RY8I0TUJ7xwExJQyHI2IakKYTYhyR0hExTkjpAAoJoIiSRnAcQAiyNxKBgvaeCAyyrVDmtZt32aV7nNzul1QJ+ArvqcD2+fW+zbquSylYFqHTl1mPlzNKXjBf/inHWej2fH4SHFuEvi+Lo+dG03Ve8zIjL0ulH8uSlSZesCwLLk9n5GXB09MTlmXB+fxVaM6yoJQMxgUERgqEFAjHMWIIAYckuJgICIEQA9k2jHkRmnWeZ1wWob3LknFeMual4Lww5lxwXgqWDMwZyIWwFNnfbTRHwzGiSittzeXCWHKpfFGbAUHKEAJCIKQUkVLEOIwYUkKKJPTP5ouMDTKcleMFC5Zc8PMvZ+Sl4HwuyLng6TJjHBM+fjzi8+fP+J/+y3/Bxw8/4C9/+Rsejh/x4fQDHh4ecDo9YJomjOOIw+mIcZowTGPlHRr9p4pbOQsdW5ZL2ztL0fktMic5Y1kuOpeLo2kLcha6k8sCzoYPWeYxy3wuF6WJikt5FlxaZvl9Xs4oXGpf7OjB6E7/sfP9bzIP7UNyIShQt+fUvce+O5pSSq6L0mhq5Rv0s+S50mbD9WxHx2ewp9WNzQLc+l//TkQdnSN3vl6/Obe+Fqvz7b0j7f++P87r9re/7fLZAUrq1m2ESrfW97ej3bvt40s8/V5/v+V6//0WceL6uGzPv9S39b743PGWNtb3PTeeezzUtWvXfen6HQEwUJYEAiPGRR8gMmZGRmZgYeD//H/5v+H//r/9P1F4QCkD/vf/7/8b//v/7/+Dpy9nnJ8uIBIZ7MPjgGlKmAbha7nScF1HUWVIL+reCHvv8NK1b/39tdd9S1u3vM9L110bm628/zxc7+N2wq7h+zVe/3rb6xOA5yYzMopKwuEKDbhKG0y38Q7w0vh96zyu36VQQeGCyBHR/FyJwfpp9LrI6gpHMI1Y0n9CoRPm4a84hyP+/4e/4hIHnNMJREDUxVcogAMDxIjESAACJxASxlAwBkZwdIgbM1y/Z84oXEQu9fKYk909jywyknxY27KZVo4Ny7w4HqaXyxoPlFHKovoIaJ/k+aPDHdE3ZNUBzMoPLBUvyN5FeYmlzCicpSlTdzEws/AQT8uCJWfMXBxvVICs7zU/ASWD5gVUCqDyJfJF5coZXDLATT+DInoFKjOozE2e4CZ31o7Y9da5qgTcx7X1kpN1vHMxJYASPj4+4vHhAZ8+POJ4OGCehZ/8xz//gfPljJ9/+SfmRd7BdEG1bT2mmPDh8SPGccTj4yNyzlXu+/LlC4riTNvnAkCh6tCGYURKQ9WvNX5R1oDhw9evX7EsS+WNbe2M41ivy3nB5XKp9xgvVWXd0tM1r7+y9rZjStovkSWY4fjzRWWQ4uigjHlb93IMFEEIEElZdZhg6JKsV+YQnR4QiIBcJ0pMFADDww/4y//1/4H04S+Y/u1/FR68XLBcnnD+8k/MJeDMEZkJGUDIZ8RyBrGwgxEAkekQC5Yi+F4Uz6E6jHyRNZcNF6Fy6zwLXi5zG6eKf7reTeeBDLDoWFAyiBnEBeAs+G4Kth00lXXhn+Fokh573myNnbfQabfWduBb9/G3Qim3MU03GyJ6+HYmZO/a5xgoItpRnGx7sm+M2Gcu+mvp6iS2dq70bef5cvQ95E5B366XxdR/ty/UGBwCKIpiLsYJcZgwHo4YpiMOxyOmwxGH6YBpnDCNkyguBiWMw4A0pM4AYcpkL2CTauaICEwMgo45aV+wRegqGJNukvrKxW9EYN1DbZPSc7oxlWKGCBHYzUiQVfmQlwWFTTkq37k4RYV+cs7gbMJ9VuJsxKQpAMwY0BkickFBQdb7cjVELMq0qCEiqyEimwJBlOuFS2eIsNkHgEhBlZ4BpAJTwxNjehRP9bjBWf+Hb7zb1RlXV5BS2EABTEEU+tHjQ6hK/lCPspEGaoqX4BhPQ02P4fWlKm7YoxW/AkAcnKJCnmvGsBDkE2PQv7eKIFJFHMjYQDcE5AcJXT9a1+y7vsN6ZVcm8bqAUmfpynXczbEavcwgBtmwSjbczKrUzRu8z2UR5Zwp6fQYSgFxw3NpqzEppRo32kbnFXNZ+cGcM+oGpn1jVuaExThqG729byi6CUcVuiggg1ECoRRCYYAKgZlsqTskocaxdIjc6ITRetJ1a/NZleA7UybosNU2dYYNIgTD42AKQ79mmjBg/QD6fakq5iqaCC3JtuFSABBQAiPFCxiMyzyDAVzijMSMmKK8eYlAYURj4phUCWKfAIYyvXAP9sfVWLy0Qz6/JzchobtOp8nWDuvCN6PPWqnafThXem74WexYr2nrowk0bf3sKbvavK6/Bxm1yryv7l3PNjX6hPo81GP37KrNNLxVvNRB4oqnBKrjBHcdObrgmMZGjmR5XNljjacQxphUsN9SfL/10qqNGAgpRjFgK38wDAOGNDgjQ3T0WfBvPXbs/3IPlHlu9G/zgf/u5lv7WEdzJQC1Ud724Cp4FHb85TVes98bep7T99PmttIpu46oKQmudmqPa1WFhmsPOwro1h9PQ1uTHY9ccZhq+1dpAe1h0a3Q+Bj/vKtXPyMsf1/w6/E6/Pr9+n3BLQrH5/aQ7zu/be9pfJ6c36WDLI4X5iBg/KLQsyB+bsHRBf9/3Te+scfvKOjfriTv52DPAPVS/15jQHlveEkXsHe9h3bvPq31z/h+76e842tu+RXH+rvOax12/YOhvIo+u/6/5cVgPNbOwFUxQtur/ChY+Wfdp0l3O8dDXMVz2c2fwZQbYWe/tj7vvYN/vY1IvwOmhhEZrR2fnUdeHZ+7xn2tY1FlgZ3O3AJ89cvNcPX9bEAIVbbrDeGO17yhD2x38DVcoc31ldfjZrCyI5HIRwgOL+xzZS9tfHF77zXfym7+93nY/vyWll7hg7jx2O19r1zojuwQZnNHd4I7vKGYENKAEBNCjE7y1htNlmdScuBkPHetfMtgonZf1xcbf5XvnJy3C1XEo9XbN/mHybdFSkOonq9kDK/fX0zn8K8GbzREAO8xWBWlX5isrfcCKbK8zEysFbrXL9xuBSZcWl+vbRTr91gzfoXN/q/n7C4WJWBVXrNvh8Al6bsmUIxIwwFxmHB8/AHT4QEffvgJh8MJjx9+wDQdcDw9YhxGjNMBh+mIw+GIaZwwjEMXCeGVutXLTzf/ECxbV3FjR/r+2/GRqAOGN8UzN+cCdsrN5rGtildeqrAgv4vSKqv3gHkRzBYRUcRCvywzULJ6TWaURSyfJWdwWcA8d54JfpNo3rtqLV1M+SuKsMsyi+Fh0evmjFwYc85qiFiQM2NWz9xcDRpNISeESJT2gQKGmBDV4z/GKB4bIOTCKAwsRQwhy6IWXY2+0GYQQkBhIATd8KCRNF6xxeZ9Y9bnHsS7PGCIB1AccHz8iGE64PHjJ4zjAQ+nRwzDiNPxASklHKYJKSZM46FGI3RK3RAFQ9hmXzwGCkyhmOvKoBAQmGGRPkn7EuMg4zJMiEGeIZERA4hCF60jngdyX3CGCDGEuLc1vCuk8254uFqzxmnVPapfu8Tbc51yjBilmKK8v6ZXtDljmOE5ZxRmzJdZccc8YbMY2spFPIfzGaWI13DJC/J80QiJGcRiiOiictRLxeO7reO6Dhb1WlYjgRkmil+bbl0UziumlxFQEJgxpoAUCXmKmFIA54gxBqDI+UgDqERwVAMGiRd6Ya6CCQURIqiYco0qI1fI6G8W6kNALozMYqToNK4KMUZdN4ITRt8GVa76iAiB0hgXfV8xLgCZMhgyvmIky3VNAkBRz+yvX7/iMs9Y1PE5hhEhREzTASklPD09IqUBDw9fkYYBj4+y1o78AWkEMDASEWKJYIogTgAnBAwgRAADQBGg6Iwt6mFfDScm3nkhHLrm+jF6ab9d/15x2QIRuRm1hEYKXs4WEXF5QimLRkYsyPo9X2b1NHpSY696tavHValROBltDaHOo8yvvFtKSZl9BoWIkVnmnmQdxRilz1nmOKAgEJQmN2a2CcCo9ISM+SUzvgYU4sYEO1nZ+EZm6BoCsgmNRa8LRsup/t6hbzdf+3PReAO5VLwtqZ6QeaFKa0oRvkLWSUHOM4gIp+OIx8cH/Nvf/4YffviMn376CR8ePuHHTz/icHjA6fixRkLYcRyNd4giNNiAGe0vzdPOPLoaTVIHAd2fLRLC9nfbp+t+nXPlAyRypBmtPF5UqAKorfkgK4NpI1g+L6RdF+rsfqNLpBNvv3cCMK25JCcIUQEFoLAZydr9IQQwhFaVUhD1mYb36/eAKlBq300AoyZA1S51NOH9hRzHJndj5hWia574VcrGXkpd/XCH18If1djCDJScQSBEGiGyhnncNVrNDFAWj89//vMfOJ4CHh4+IsUEQPhKTIQQGIEYKRFCABgSoQZecdDVI/cqIt7hDwivNXi8BmQn2q613ef9CfVORAHgAOHdsVKgXHthcktsFeHurvJODeKmJPyt6VhERkaVi1GcC6iTz3x3XqkvvApeEW4N+2duH7SXHb1XSHsekOwPf+zu9PqoF96LWx+hPL5EOujHos99q/XZz7W56tEbB/dZIwQkkjkMCeM44HA4aCYV4XFE5l1EtqgOL8/3u+SCHHJzwnP8S3t9pRnK9JSc6/jlKBEj4uApDpUpoukrQIgh6q09/+iNGWudVSkZkqlAeGxzCF3zp2s+d+980UweQJP9bS15uKqvZ4asaa7rub/O8ZpEYogBQMssYwQgxITp40+YPnzG9PgJ6fiAFGXWCkMijuMot4PVaSAiUEEojMAShWHJZArUAajqBZT6UgQCIyQdk6KRHzXxjK69IHKjjKvo0LgwUMyhrKh6swAUlM/W56kxgvU8ggjJaymgCooAzKmbAfgwkn1Z5E+4OezAKw0RW2Q1Zaie0ctWigz/t//tjTTK5vTdPBpuaOI5hmWvD0IMfPNGBdfCIOu7rLrBAFjCoCiOCGlAOj4ijQccHj9hOj7g+OETDtMRx8cPmMYJp+MDhjRgHEZMmpJpHEcNHRuq9zsFYdirRymo98RcCbB1v0IvZPae0ltDhG1i1SO8po9pqZiKeoA3BVTBMp/BpWDW1B2zpmTKRRVXyyzW5rxIJIMZHHKGGDfMi9wUGKrQYG4GBk0XkWdRoOdFjudlRimMJUuKpnleUArjsrT0QrkUzHPeREQUTb1gDFWAbBhLSki6AcUYkVSZk3NTIGcNs+Syz7CQw0HaeMLqhslF8IUaxlVHFBJPsJASQhwwjBOGccI0HjBMh+oVO6QkG2mU4zpipipV2mN1A3FpgSrT5bCICFE96GMcECggRTE8DEmOzfDQpwtbe+ba+3TIyls6w9zW5p5y1frumYza1ur3hsswK0VlFup52DNd+i9NdSTKbWWKNIphXi6KmxZ9oCloykWYKEtdky9qiJglZHeZAS4gzopDcrSony4FGVZMTZb0XnORvpohzdYH1wiLFjG0fr9IBZEYzAGlBKRQQBwwEMsxBBACSg7IAEqOQmMCS8q3OmXc4RBq9AOBOYCo1HkmAGxGDJ0PYkPCxjB6A4TgmuGQHmOLjKhIw1DGMoCKnCBqnskV32i1D+h9Vcm6aNQUMUIQZUbOWelvRkgDBmaM8wKmiJGBwKImZw5gxPYh+Yg3Z5S+VQ14rxAR701uI+G8OZ7b2tZej2zv062VZvysgpEa4LKmzVmyGso0vczSpVxaJFVezlg0gs0ifhaNcLNw9ZpaqzRagmro6/sttIARYkRkRogBzLHONwDZTygBnCWcVw0RVK0INpy90Fv3xaC0JzCC4mOjgxVV20g3mU72wIo2gte2xzcBU0UmR85rc2QzCrf2jO6slbl7/Ic7qw+lEDCMA6bDqOmXjpq68YBxnGp4eY2cTOKtZJFpHf2tzdr+7o2ZvPu9v3bvfNn5e1+Q37xxXZ+2HlwngTpWe8La2jjh8WBj+GgT0t2/bt9+l6kk2TPUSEDuuP4A5nggQpU3WPg2N6KONCjX2vPc9dKP26FXqDwDuh/aa18b02tjdYsikDaLY/frs11c81ObZ9yiMMSWj/j1lPrf/pw1jXtv8PPZKXFe0a/bgNz/dsYMc/pbCMK3Xy4Yhln3pqz8DGnULyMEcfCxFBN9v/S9nOz2Uk/X7/8ecA3nXhrja3Lpa575rXiyJ6P/WmvG9BOvu+db+6bj1jpwnba8H4rcDNfm/z3x1StugTUf40S3/ibheVY6CLm/62hVoahEpitf9Q6QNDFyqfELvBnrxrrdGhHRMgCsL2Trvp9v5d/WbV7di3h7bXcdr06t5dvVhU0WwNV+r26sN1R655lZY1yv9c9/vxGX+vXp3uDa/dxfR85JURzFqMOtXd4N7pkqBniesOM1u74KTl/jbywFTQ5iKC96PYdQ+fXV0zdtrHlmPxZNZmi42unidvha/721Zfy1H5+KLTfCet5Xuhi7huuybo+gAIoDhuMjhuMj0jghpgGBugxqYozQtcwgcCAEJtFvcW+IkJtMV2BCABz9FWc8CgEiTwbpssnSmuKYguEFq/+eey+7lpsOTBzB5DxBaBexvbDRQHbD4s510PB2gxPoz78nnf49wRsiIm4cCH/ZN+7tzwksrzVGbNt5uV73W5kTb6EX0NVIrAtClHw98kH3AAKXCSEOODyI9/rpx79hOJzw8PknTIcjPnz8jGmc8Hh8xGEYcJoOGGLClBLSNCGpEcITa1rlN95DcBNm11vjVrnQajAYcQMYhS1VkbyneBm3lDNsnt+qeLXIB1Ns5eUJXHLN6zcvZ2nfaj8sfQRFyQWs0QmgDMB7WTZLcmGuOcbnWQQTMyjMmof8fNE+ZTFAWB69Wb9bjYh5WcQ7O3slDExvBsASqzCizsFxmiTaYBwRY6hjLh6ikjM8F0bJXNM3caNEMEt8gJZPCeoVQECAKKaJJTWM3oRSNW4DQkgYjw9IwwGPHz9iPJzw8YfPGIYDHo6PSHHA4XBE0jyCIQYXQZPcrmK4IBbsnCWnevPOt+gI2wgiQkCt/TKmSQ0PIyJpbQiiLgJi3wDS42I9rjZeAFc3dH+/MbKbdivT1RT5dt5f7xVmtU1mqfXCXL3rl2yRPBeXo1M9w1ny3lskELMZ2lotlCWf1eBmhgpZC1wW54VsY+8NDNIXr/iz9XDJ3pCmR40M8oY75lI3fFvfKQEpEaYhYEwRyxwxDRFlkSNKwpgCAudqdEuxIDABIaAM1HiAEISJ66Y3QFzZqfsQifdD0RRnVSVHTanX1Z3QYyCqUTgUI0CkzhBS7wKMqvwmkIvoCRJ5FSyBU89wETMoM7BIVNb8dBZDp6xQDOMZMQ7IeUEcRjwVxjhNoHHCARFjCQAPmHBAoQMKHUFhAocTOExAPIrXBiVUBzMz1NR1WEdBRQirRcBNlsBtUI1nq/1Kcm56Y5b3aF9wmZ80r+lXlLzgrDUgrMYPX76glJYX1SIiSp5bJJur5WNRPX20iuGf4IHNr/EGhQtCzIIjWSIAmAsCCy5RngGImSeQfgIqnYmx5wMKJP9wcc+NsSBx0VoQLLSXncMBm8eRrkGdrRC1pkNodLnSnzo5DL8IeH0sAAdWBbW20tG9Xlip+YLrE4EhRnz6+IDPP/6Av//97/j44SN+/PQjjscPeHj4iGmQSMphGjEcWmrHmvc2trpAhisFXKMJq1Hdpz2s0Q0Z2dVuupbGq7CmXzR6lgu8kcqeg0rbCbWAQG8Z2uD/NT7yOaPEHn/JxRlIqUVwwcLvVkJnk0OERhUAoZO6IDwhxW7PWhsfujzAW7VpE3gJaJFQL7Pf38KemwLoJRb5tcaHa/Cme5m/7SV/M9jB6Xr+t4P3cAB70zyS5ag2TSS3H/RYmEEUMcQJXBi//PMfKDmglIRffv4ZX748YUgDYkgYhoCUCCnNCCG3XP6d0q4pa/6QKPQHhW+lE7fBe7fv6fnb9QZ/JLidrl/ThLdf7Ypi/BScLvC5Pui9BQzlJEXWaGkZAKhUrOoXsMVOct1Ly5X+ieMAV14bxE25urquyjNVOlEnHnBHM/2W5BWO9bv1Wfta9HmNt18ry5u+pjhZtYDBpJ7mpOpTarJcY5JUeVEYKFkjIvRcY759J52cvKMgfVd9aR2p7mxKUm9vOhw0IsIKScnvjRd9uTMMiRQIIWBZlo73CiFInc31PW4OzBDBTMhBnumzjohjms211DHxdftqrbCl1dvodW1Op4HrBhE7ro0Rdo6Iseh0emdFPxLAGre2YCV8KxpAa0KwYCIVqR8RidpKIAKGE+LxEY9/+58xPX7C4cNfEJLUx1hY9V4UENKIVDKABUzmKB3F3sBFjRHSXSoQA0ApYCbF+SKRDgyAJHtEKKgyBAokvN7v+XUoG96zGhuqrEFmfAjtPkAMJ0UcgQ1NdabRKNTemLYo+zWwu/PPDq8wRDyziewps9HP66a1DV17fiPzyhGzCtrcPscYy3W0OrdSal555jVPhueUm9153QzaU3UXtOs2PbVRE4/POEyIacLh8IDheMLD4ycMhxNODx8xTgdMhxOmYVRvRomEGNUQEVNCUAV4iEGUIVeMEH4cqtUUvXXYZOxGvJrnIsCOEJviyjxbzSO8NEWEFZHR78tsnt+qhJjPqqC1Qk0X9ZRdekNEdoaIIlEN0HQqZoiwotNWmGpZRNl6cYaIXIoWvyw4W6TDYgaKWQqLqrHAFLlzLYbpNouuDpIwRQTWvb0gUEDWMNEYm3dp0WgIb3zwSqWeibE8t5YmqSlfmzrGrz7ZmEOMoJC0oNKIYVAPWKslkgYki4QIQTxhybxgzRsbVelfKl5YOGFu886GyUK4De8k0sEKpEeJhKCAFFuNCK9MJtNW26fD0YazMEZOxwqMGqFR1yD3663heb9269/Ffr9m0GjGODvf8KBF/FjB3eoh7gxytbDqrDVQZk3VlOdaC6WURddJRtGonZK1oHWenaFN10YWRrSo4Y2z4pY3RHDBeVk6PM95kSJpzhABbopPzzSL8C6RDjllBCRwKRgCg1AwByAgYlblbl4WEBg5R4C5eptXz2ArumzcMlpdCCgjIDQeYApt1lQBZkyfoHtbG5u6ImSe9I7/UCHD+lJ1HJUKKtNmuKZrmmwl2rPq2gMsSqzkAkBoEEKuRhSmBA4JFAb5xFE+YWznQlQjhB11KLyymuQ/JhNO1pEQ7Ovvdfi7a5hjV8fECSpmWK4K4xrRMGskyIwlL1JYeh0ZkTN4VZQ6azFqo+O1NhB03fmQcPdC6y2+n2dl9M1AQQVgQuSkXirSQJAZqIonT0e1VfFE54AQGDFElCCeOTEE5CDnA4sBWGj4eixbXxmQ1ABE1VMPDq8aVb8OrDSsCaBbnoc3EjvVfth+k4aIw/GA4+GAo6VtVLovjgoJIaSVl5muoUB1bVXhiRsN9IJTFZKvRDVsIx6cEWp1Ldx7ewHJ8NNf50Z8NYBeFHje6PAS2J5S/8Z1/rN5vvL2vKX60ohUKl6J0XB772Nv2UWswnsDsj1oNSQ7/ZBbnzEkPK9Aqpe49p5zHug8A1eGFn/dpo87wO6/5wTzukSfmd73UHzuvdtzwHWabn3u69q/qcU3tnPrfWuj2ns8W2hqqWvZZEGvcIlBi2qqQfzLl19wmS9KD+X3EK1mlO+ri4yo2sYX8H/nff8s8Nz83Qrvde/rx/aW51675qpWQP7vcGbbDF3TLr2iB6+FW+nmtXu+5bl1D6S1fkUzLjxLgOsGYgqbNvomdrLyvtQiS10PjKOSvjilPO3tvQwTHKo8u/temz66/Yp3riHl7F4Y+tZD4SX89sS15z30uzDVzcP4yHWfvcy618burt42VDghqPJee29iz7r2pt8KjbeqEiiMYRFnxogUXbpmdv1et+Oa8K3ZH8bDllI6HYQVit7nV7xDjKVGdemFi0VD9+Nq+5bxtoWbE5g48OrVzA6bezncG5S8XqIOQ0cP2veiDl4ip26vuzIT136oTzW8JqMAJjgDABMoRKTDCePpA8aHjxiOHxDSJLKuPUF5WVAASAw2LCqAqgciNSHWHlGT/UFSq6HWWiRGlc5JUiuxZVogfY4JZtoBGRNrp716dUak2iFdSKoNqLRFx1QniCFGzzoxuvquRfrKfLrzfy6WYhfexRDxVrBF8NJm2P/eCPA3ig3fdPctYEp50oWipEot72ZMIYjvvCC/IHVCCCOmhx8xTif8+Ne/4XB6xOe//zuGwxGHD59FoTxNGGPCcRwxpYTTNGGMEcdhAKcIHtKmFsQ1C2pVLNumQ71VVnRFfU2IXmHQlAu5iKKqGSD0uxogFvWEFUVVwTw/VYMEa0RELU7NBXlZxDPZUnhUA4SkT5JaEZrjj63ArxgiZo2KWNRb3AwP58uCXAouF414sMiHRZS2y6K/mzFkaXUgTAHPsPHS8VRtZRtXORGpgEBYloIQA87jgBildoQYEmROltJwxrxARQnoGAglyIECQiCtnZB0M7boCCN8ooAFkRi14oTj8RHj4YTTwwdMhyOOxwcMw4TTdFIvsZYmSeoxxIo7IFIxTSI3siqsZ61bUMdGn23pPJKm+BiHETEmDGnSfqshIkntAI+rIMJ61YtXSM/8FO5Ztx4n95mkNc1ZX2uGiH08R1OcoW3wrIwEmJuBbRHDwjKfkUvGMp/VGDajcMacv4iC9mI4ZgY3iRha5qXiuRggFN9LwZwvuOSL1ikpriYK18idUpohohapzoJfTxetv6LK4GVxv5eWp9IruYzpiYEQIzANEWMKOB8TDlNEWQbMU0TggjxGBAA5FcQA5BxBzIghYIEwjpmTpiEpbh1QpZd14qsQoMxkLTRtyidbG1TxKDrjViBCtGKVIegaQqVzBEi0QakzjgyW6KQCPTaDKpg11Q8hhoAhRJSQMIcFHFjHUqKqArOMcUg4hAlIJ4T0gDA8IBw+Ik4nxPED4nBAHB8R4oCQDqCUgDgCIYgniatX3eEyed7bcuO2T1E8NW+wvTVR6brR1NX6sIiIxRvU8qKp8xZczl+Q84zz5StynjGfzyh50ciHjHyW1HpLviitVTq+zDCDtvDnLETUrN6ur8LcbqMXzXg5DAmlaD79UkCZAC6YEEFcwDkCXEBFjGJRcTpqVJmkjVP2lqCGsoAAo02LeusQsg7NHIWpDyGroLwyJNs7KN9r8q9NxVpMfI4j6WlQr3Rtwoir1MRBmOAsY3k4Jjw8HPHTj5/x+fNnfP70CYfDCdN0xDgcMMQRKY1qpG6REOLIEKshT/BhncvWRcLVdeKLmC/uWrvOR8/Jfo5NakJvtFjnztX9WHkWq9fznEzsx/85eFFBvlpHJnR6hUyLlLiydIkkfy7LTi15aVHvY73GnuFrRZhw263jTrOwq2b4biAsSRszz2deU4hdM1a8BJ3BoL7/86mxfg34Hs96rWHjXwIYwn9m8VqNGqUFaBBYYaQYMI5HxJjAXPDLLz/jP/7HF/zy8y8AJEf1MIwYkjhFMl9gtbuqukEdFhqlZkj1tTvc4dvhX24107U9idxH+RdTOprTpHJ+okimel/wSnNX05K9kq97iu5JgYRf07SHNR3UuntmbzA9Zb0u6FOMN11tvbuNudO8/fXabt3tk9aZen8/prb1WVpsdsf+tRyv6/rUNcR25KbY6BrhnRvfAi/f34xcBHCovOg4jDgdDpjGAUMKYHXKM2/5akhQ5XTFwZ1HMrjWX7AaCj5DA0NqDPT9Fr5T+FSRF0rRqOwibbTUmnqX8rWBAkS3oHKaRQAvLu6CGeCsuk6dtWAe9nKvjI3JS75e5RY3SrGoiFBx422w1r42fJL6e1LHgZmBbKskIsYRjz/9O6YPP+L01/+KdDghHU4ACspyhq1cBrXUTCrrmxqAQ6i4WUV4QBwTKENytEh0Rk23SKb41wwuJegSltoQRn7U5RehFBRzeKyO42Z4UD4cDKtFQdVxUmiWGWSZGRxs3YYq08jEtVq8tf1qCGkR8/8q8A3FqhtcR+jvaNK5sUmh3U44MWXWrzzL3cZYdzfRIlUyr2l1Ujogpgmnhw8YDw84PX7E4fSAh9MDhumIw3RETAnDOCLFiGkcMaaIYVCFdApiiNjxCG59MMufLIzm3agEhLynvynH0TxmYZEQRhSb0qBo2iVeGyJchIM3PNSIiMU8wdUgURZVoi4AF3CxVB6qwMhZNp+cNXVNwVIWUfpqjYhZDQqLKlgva0PEPKsxZFZlm7zvol67s4uEkD1ZlSG6WVs4pylFjdZsGAQCliLeuDQDpQRwUSVYEmWE5NxvBqGmUPTI6tLaOMVrCEEiGYKcg244YlmOiGkQRZPWhhiGCcnlBDeDQ58SqaGrraMC6HhqfnhNo7Ho5l1pqjNipCiGiBQHOerzYkza/5XHpykxVs+WvjRlkBmCXjQqrOA5Q0RnRFI8b7itPdDvtgvWdZKlwNei0QbeIFHKUhWxVaGbvad4QZ4vut6skLpFELm6DcUicmbM2QxuFtmQ1ZDAUvNEDRK9IUIUeE+L9cX6qtfV/P/mNVEntNKMqHNWMiPHIPkdS8EYAHDBlCIAxqCeJEMUuhFDQIkBvCSEIO0GK+RbCCGq0FEdHJqA4mYP3utpo5/ZUYj10TXuMm74ZRt/9a0yNLO51etM8VlXveK5FChLYAAZJMXlo6RDS2lCGg4YxgcM4wlpkE9MB8R4QIgWCZFAIUFzBilvw30+S9iCcH1FLzts8J7bH3u/d6lvXDiw3ZO5Rd1IpIMYIsSQPGNZpFh11qOcb7UiiuJ9K2K81D1F9h6rKK8e9c4QsZr5nv01QaNGREj6JEmlxSBWlpQB1gKkxpxKSiVJz2TROYYcwvwGTScHZNbKHbEgFtbnSXqnSEFTPZW6x7OOszHPjuVsNXvgaJl7Hy+Uk0rCrI1VPDSZrDLIbf7l78bg2BoZpwmHw4TT6YTj4aiKuBExtoiIZLQ5Rsc3bBXG0o/GK1SccXujRUPuRT7032WT4/UH7Xw3UhV/XV9qfwzHrzB3dN3I0C6RMd/8zu5QnyPHRot6AxH5G3aUyv3R7Xs7tGv9YaaKA1XHQw3/dl69veEzWrD1e7+s//Y09frF36JUZ4fca2ODMfN7ERH1ktbTm561ecYr+vx7Mn48F2nyvZ5ZDcffwzDjcS0Yr9AMdHaVeKQKD385P+E8A09n4DJfAIgTjzgqyB4AwKVUZb9w4TjQXXgJT5qx+OWxf+maa2P6Pcf89wSvGcvXwrU2X7vGanvP3fNOepHnxuF7jNEe7NNb4471uy3bF2mHXMOVT2+GiBr5pHutGPclNWbjl9Z90zbcFeQ61JxcUHu8Ky+u261EqKXJlH6jnjdeo+OdOnnG+u14RTcOvOo11Y5a3+umr4pLN4amO1hxAps3MwXDVVjTPm73NEboGbiuaNtKdVdua6/ZjqQ1flKsjpPyOqXyoF37nnd9pleep/U01XQhni/w8lHjO7hry35jd40ZAohYIrXX4+J1Hzt7yZo38f1Yv80ebKfbn7C2X5hXL4T4VhhSIxoEYuGK1V0TKY1I4wmHh08YH35Amo6Iw9QMC8r/VjzX+8T+ptEjjnISkZVdk1RNjoeW6Bcx9FS+mmvn0GQspTOGP8QgNnnbeY9ZG2Q1JuReBtVILSI1oOi4eNnMr9v23Y19HUeHnVeQ9KU98Nrvv9Z+8FZ4F0PErXD7UNjEv7BxAS8QUrmoboykBNsEyO/EuO0JMrU7nohIL5BrSp+EEAZMp08YDyf8+Pd/x+H4gL/89a84HE748fNfkYYJ43RCjEKEY4qYxgExBQyDKKNjICBESf9hG2HNT42mLHBKhC4fHRhrT/Cac36lrN0UmYREOizq3Q12itdqcDg7z1r1FM/ZFTl9krYWn+LGK2hVIbv4WhAWAbFgybnVgljUMLGIkvV8mdUAITUeLvMCqxHBhZsiV993WRYw++Lbe4u6eYz7n4yJMpQrOQMZyItYzYchIwTx5iUKIE4Ai+Kv92jgju6TClOBAmKIGl0QMCSqaY5CUC9WVYaOhwcM4xHHx4+YjiccTo+S3ms6SHRNSgjUir12DJTOrRghpKbFZZHUVkvRMS+L9imKci5IxEOMCeMwyXEcWySE9luMKVzX+1YB1Ma8bupuDnze7GvrbH3uJUOEKD48vq8VaHq9JmKvCjnFy+Y5Lh7jhu/z/CTROosY6S7LL3pe8XqeezyfzUhghjbzIi645BlzniueV4PCYpE/htdZhfJS13EpVpTdaktIXRI4upDz2rtCEJwB8eLlgGEAYiScLwnTGJCXGV8nyXN+nBK4ZIxDRMGCIUUwZ8QYMbLWCNGcnCmb54koP1NCVTBXtt/4CZsnW1+0NWR5g1qNstGICKZuIdWIgkoX0eoCVI9rqLclSzSbeWCLN0RESiOAgEKQd1pYDRFHUBxwfPiMYTrh9PhXTIcHHB9+wjQdMY2fMYwT0vCImAZQOkgNi5SAqF4bxPJBhGffS8V/1HmrQo2jGbbfFRMiYHJEw+NmHCirfUCMbVb/ZZ4vyMuMeTkj5wXz/BUlz7VGxHL5ipwXnM9yvJyl1k9ZZk3Fl9s6YW/kY1gkxDVBwGisCKWhTmGMsVu/5iEUozCNSXOKQguVUQkgZOUzxUuGVkXu7HkSqSX4QoGQNTTNjHSpGtgkcoZ0rtjwRZXaxrqGIm2ZTw0cX9JokaKnCZx2vtOE93IA6zNk3DwHK7QrpYQPHz7g06dP+PHHH/HhwyeJjBuPmMYTxvGIcZgwjpPQ6CEipICQWk2pnj4qHfLpuhzuZI2yMsNTq2PTatpwyZqLOGskhN0vPIMvWN79XfG2Fxpz99uWxt+mCKf+yEZ0yC+9KouwGhiKplliWhlG2ckyK35zvcdyYSlwiOZFx0T177XCtQrc1JQQL8N1xcBbwXRGLxl42vWv47nXxoXtvq6GIH6Gn2feaj6eedazbf3KsDYC2rl/VQhRohKCVuCRqAfW6FMAJJXZlqXg6ekJ/+N//Dd8+Zrx85cFX3/5GQSJ0BUFVgZRQc4QxYOp/6gpEbxa5uVqgne4w78uiDLubfuL8apVVjZFH4ljXdTVJ/7gAZktzSZgjLyt2GqysDSs+owaFaybsjcQNPWv9sf93ylG63kCWBWbndBfubr+BetGac1ajUg5UdCU5xKVK22HECTqtkjkuDegrB5QB9BkpKK6BPUDF1mnH3X0Z9Z/u9+rkGQf3rmn784tqHD1EnK/rxS3gQghJYzjpLUhIqoOq7SaEGbAag9bz2f/QC4sddhKaal+IXNAuedBvOwkUBq+qVGCLbaeGaZqFf0K1yja9pbCO/rnAowSWi1RLwu9RbEsfI3o7fpBeGEuFYw3qtNfUymbTM4gaG1GzFUOAgXRaT58wqe//U8YHj9jfPwMxKj1GhbJiMDqMG2EQJ7qbFDy7hYlYes5mD4gBEiUA0BB6jWIjGcGgghJZbzA0rzBrTWrSVgL7KmTta3Xbrw0ew3X3plM6iIcVAAQBwolcKHpl3RQ1Zjp7vkXhG8yRFyzutDOWF7boK4p7f0S3b/x+o9rZX9P1d4O+5ZI1yVnjaoWOp+YrlJV1POyqCV3eEoTUppwePiIw+FRIiGOD/KZDlILIg0Yk6RLGDSP8xCjeMKrF62lLzOpWPC87/vuB16h1SuFinIKdmS7plg9iIyi6ZlyXjTFh+ab73KKL81DfLYICMs1LrnyLYVTyc4Q4Tx289JqRVRjQ60JkTGXjGVW5dmiholckLMYHnIuuJihwor2auRDsfRIvshvP3zYw04ZNvONlGvcFHQ4Yzn6KGeEEkCUQSTpQoS+6xgzd89tDBaqYhZALV69V1shhIgQE9I4YpgmDKOk37Ai5ha1YIyS9b7hjBad1hQ1i47Veb7UlFe5ZGTOagDTAkU1IqLlG49BPsEiN4KN0ZYz8AqlhpO9EaJ6MJSt4uAlQ2A72nlhKFqe8+c8ebU/6M+XsmjRdMF/qw0h+N9qPWStAVH094bvanBbFaBelkXSji1NsTfnBZeyVDy3VGJ5kcigecn1mAtXg4Mpg2eN+KnKYVVoV8Ve9uNkBEVpGyAeD4t8fzovKIUwBFk3Q4pYckEkxrRIxMSYixihGECQdE1MJAWkUBCCrLWghaFDCMKYqHJPjG8unJh6ZV4zOOwYs3S2iOWZcAo8r9z0HjGWEq2lrBMBwYQEpghQBAVGDAUcAwaGFExO4tUV0gNCHHF6/AHDdMLh+BHTdMIwnjCM4hES0lgjIUTp6wq0q2d/NUY4lK6C24qG2xz1+G/Mj/u9U+QW987Ou11pvEQ7aC0I/WT75LnWhrBICV8rgosZlH2R4dL3wc4X3ul7P4s9g6eo4BS2MQYNqIggJgQ92t5LVAR3SWhbrf9tbdlTSDOAWeomFiN/cbSrRqQRVWNGY5urXOjKBusa03exsOFQr28GbUFh278b3bOoipaWgGq7ba5RaRaRFMs+HERom6YDhmFCiANiGBCjGItjSohRjIGSO92lyXOjb/tTFfzqsaVLWuOj71ffV/taE0pt2q3j1Qh11xd2AipWawLY7gNtD92JNPDjWb8Z3fONNIOfh6DzTzpH6Oay8YVe2W1GhsKlo1t7hlWgpYHyAqngzDPK6RVe7vz8jLKbr5z3dzfYMxx4Hv8tSnS2hfTG+1/7rLVMsvfM38IY8K3RCM/xWb/GuL7Hc1gVP6ycQHH8F4WIMQ0gGkE0oGTG09NXnJ8yLk9LrQPHzI2lscXKtubamm/yGimav73vz733LUqlt4zbc/P9UrtvUXRdu++3MpztreHv15e98Xr+WS95t1590hvn5i19uHW82nUvXU9uXfXnyZ1rURCautBuJU1FQ6T8nTorEWkgcWjZVvx+TNTqRbCLXgCq3NP4Nm4q+E7+tp7pD8asvaytqgpqi+rqxpvcnbWemTXbxsXzDZ2uCebwqPJCY4eMq+q7V4WHVZdfnGtGd5M2s7M7Pj8eL6KUjevqsTYONR21RPECEDl27ZRYu8GVh67n/WU7uoNrckjlS+u9q66u5LFaOxVayBhrxznj+6UPxueZUvvWPf/14Pnj2/cf3cXlLwZA3I2B6R5N5GIQKETEwwOG0weE4yPC4UEj/h3iqzGANLE3WCPMqx7Vrmv9qSNjvDDaNc4c6bZxNUxoaqpNwWmC4oqmUQqxeZFVpt7uMZnc+APPUPgR1r/YOPBuwbW2PFLyLTPyPLx2b3lvPuC18F0iIjxpfo4o2dC/jjno0OtV97wOrvf75smFem+uCJW1LfsBIbOkz0nTI8bphE+f/w2nh4/44ae/4XA44ePHj5iGEQ/HE1IUZjvEKF7sKSINCVYcgAlaJNmhtm481aLJLn+z5v/eEtC8OecNFkAzQjRlq+Z7zjM4zy2qYL6oB+0TFk3lUfKCMq8iJTSdU1kuqgBTBVZV0JaqmDXl67JkXPz3LErUWYtRX+YZS01dszVELGbc0L6CnYJytRn1eNqNcD/nWBOc9iszY9G8goUlz20pUpQnaTJprvkuueLLNfE/aI77poBVto0CECLCMCKmUQqbHx5wPJwwHk4YJy1WrQYCCkJYC1vuvbbZlsLIDIl+WBZc5hlPl7OcN0MNAUOUmhCgIKlq4oCUBoya/mnQSAgpnE6OOdO1gba2eoXw1lPaRsiYzj0FyBrWbXvd1rbg6joCaJtSxCKAJB8kI88LWCN7LEVNLhklP7kICXecz1qcfRaP2EXw3Oo0GJ7nueG3HS85Yy6Sb1/OSeHqZc41IkKMdFLHo3kll+4d7Hs/PvbxWOw8MyzssjDCIhEyXwNjniUyYs4ZhylinkccxohSGNMoXv5DSigcpbaCKuFS5mpIjTEgFWhEjeCIKOIgwgcZ3jdFaYx9BMS1ejhVsCBSY58zIsEiHUpHGzMDWcdCvDsIHCIQGBSsnkpACAVxGIWWxgQOEfHwCTFNePzwNwzjCceP/4ZhOuD08FHS6o0PEh00HCQPfxJjRFCDhLwsV6VLP0dN6ftSVBCDa7RBG4sen1tu/9yNATNX48NlfsKyzJgvT8h5xjI/oeQZ8yIREXJ+wXx+apFupQBL2XmmM4642jvPGyFk5TdmUNPQoXmRA1H/1poQSxbiFAKIC4TMFaAI0wvNC+7pnTYtRggCEiTMd0gBzAEpRxTWVE2sRokSUD1fFLJWCmfF2wIzqsn7EEGE46A5kG19ebzVT4vGKTWku0VWNNop8qXWZeAMBEIaIh4fH/D4QZ0bDg+aLmyS+hDDQdL0DQNSIsHF2KLjQNQigsq6VlKpOJNrfZFGO/t5VT4ExY03d59GhzNqLZ7uWYa/1TwDXcqCStUocg2XaGc3bb9dg7aWGoJ4owCR1KGp4ght96TuSU4xJkpUwc/6ewgdTpiAWiMj0PL8mmL1Zbb0Ck97i2LgDaKRV+pvnXTeBt96/+/lGXd4PTBaTm7RYUgkp9A8RooRDw8fwCVhWUYsmfHlH//A+Zzx9JQxX75iyTOy8mvdh1h1IcaEewn2XhviDu8Df3aqYhkArr/pWm6m9j+tryRJAwtC1OuLKRTBwssVUzlKfcTqQMKA1Phye62XzLnnrSrvxM3po2mZuHbV9faWDdee0L/+zm2svL4cyB1dZEQpm/20GjesTaWFwitKxHTlDcHt/fTt2A+E79/VV+OXLnhfWD+OCCkmTJNE7w4pamaMRV/WIgtQ9QsMSAHoWx63o+/a+33NHvSOGwWSHrDxd6VkUARiSGAW5yZzHjEZtzUGiIASEUvsZLFrjtvWh9t0k3zl71vAvzj3p1Uhw9Rq1RWKCGnE+OknTB//gvTxJ8TDAxBN9SyRjRwiUNTxkLNbclGf5I0/VPGeCKBMbU2bnL+SocQQoCmbKKiTn0P2SoAYCH69ksiIxJCoSSt8LTwDArfIEI2Q8rKJ0ZvArbaHQMC1dfQrrazfFdxsiFhb/jxcR/63bbt+kW8FAq6HW8Sja0LndUGDVse3owURELhZqdnIPwMMzYUIQkoTKAw4aiTEw8cfcTw94nh8xDQdMI4HDMOANCTxKh/UszypUjf6HRiafmSdOxVtI1KBvRZ5RLPc+mLMwCplE9t1TalkhSez1gyQug4LkCUlkuXKz0UKGpsHbcnqGa5HqSFhKR1yO6qnuKSPyZpuRpSu8yzRDmc1OsyzpakRw8OSM+Z51lRNLWWNFFjOTZFuNSDAsMQZ1ZLtlEPMZuDxDI3jADbmNxnrtaejMWOkytTGELmirWCw87xc4zHX9vXaYtdqUSIluiEkxDQiDaOmgRklJzhpEVZlHdkoORVUY4yOQy6SnmUpMtbzsuB8udR0IETBpf7S8LrgIyAk7ZOl+ajGB7Jn+uLEPa4Zbnoh1PpmClpibBi0azSpZzJQ33vjheuNDTbGHv9N4QZLI1LcWljax9VLkYiGrKmZFsF3LUzNptwrElWQNfLH6j8Ifmt0zzzjkgsuWQpa2zmJABI8t1RN8r0Z2nLjTOX9c9s2/bh5plwmyhUQ1r9rUTQwqDCe5gWZA1KS1AiRGOdZvFYOS0FMA8YBoDIjhYAC9QaODApS+DmWAGapHVEYWpQ9SlFJUK2DwuC6fnxExNoA0d6JKu74ReRxrRb6LqV+Kl6wMlhBDHwUgRAJsQhjUkpBoCT6i2ECxYTh+BExHXF8+CRp0U6PGMYJ0+Ek6dBcZJIV17YC71Vgq3S8rXejz1tF74ZAwJT9/hp7n4b3zvDgDLNG18UQccEyX+rfEhEhNSKyGpqX+aIREWqUzqUWXxe6tmeIQJ965wZGmrk4hWyv1F0biylIOC64KO8YNSJC6ByVhv0e29sg+rarvb8d6w3c3WXpvawFi34QwylX42mgRmvZzZn8TXWdtqPOqd7nLFTt6axRd8QYR0mJdzgeMR0OGLRWUAwjYhw1IqJFqVH9RJPk3LibMOuNBQ0X94U4T0sbHe3fs5tc164ZIVzERY3Y2QqL1/uAOodtVm0PXkdErLtzRVDgtZJ9i7t2Xr9tG694C/HutJRM1m9VPviIiIb3BKkppYWrYZ5pTbyqjwE93xdua+BWb/pbPPWe87Lai5r4Fnj5/oZrtzxrbRS8tY/r+/4ocK3f+3vp299vzU+/rq2mUCQSBUYpTTANROJUE0dM0yO+Pp1xXr6AubQ9Sfk3I22ktLuUojQaukwqde8F0nWPfsfzfNteusXz792PW8bsvSJAXoLn35d6QqqnVi081/qzl1yRUJ572DfDtXl+buxeExXBtJZVTd7lnRd2BgLy1zZvcZiyUR6ACFQbIUH5fhCAgEClmgyFV6u7fJPHoXsneVWhOrZxM0K08WlcIb1iPdWWacWf6rv2SmVVwIJqmpZnsXJDO6k6jAjKGsdZ6vvVLkknQSYDMJpS1V28q/3yjKpnN2+lGc+wQlev9UDiJJOGAdPUUjKJs94ssmHFVTfr7Gf65Qfu8o9uDl13oKx43xJb6iXbZ0Llk4PVJLoi6zQ+bX+QSjWi3wbvvz8JnpGZGtayj8NfBokj7HTA8PAR6eETkCZwGMTphjWGhwBGqKlNiUwLF8S52oyNJPdYXdRKLWg9BzqGdlKFMTNMhiDGnaZ/MtyQAtUWoECkfDGpHB7EuU3wX89xafori6xUmadfRCZj7q4seP50d52sLv+e+/VvAd+xRgS5422DtadEeukRhNfnS3veCPG+C1cUDk5PANv4CCx5HzBMR6ThiI8//BXH00d8+su/4Xh8xOPjDxiGUYpLpiSK5BgwJFUcaA5nRF0UuiJlP+prQvgNVhRRvddrp/xlVbLunDelMNByOjelqzD7XGagzJqixnmIz2fx3J4vmorJIiGkmOk6l7gobFvR3kXrPVi6pXmWv8+zREbMi6RkMkNE1iLUZojIpeXSt9QrbKmY1PBAtI9LvSBaNUbrq3R3eu5edApUMUSQ0koVhgDU9A++Da8iY5dGyr1LLqw1eQJIrdHDcMA4nTQtjBaqVmMEQelnVeZk6ZN6n85ZClNf5gvmZcHTfMG8ZJyXRdZfCIhB2mIiicIISYv3DhjTWIuhtrRMUIZJGbV+VFd42vA1723e3O55ySNgT2FlY9hHRFiuyeZdK/f1St9qiMgtBVnOC2Y1tlmNiJqiSSN/staMKFpHhWudBlGG50XWwDI3Q8SyLLhcxAg0zwsuS8ZlUfxelg2e+wgIv86LCgQRUiRK1rMOI63GaT3IFbTIsJ5fFj2WghAJJReMKWBeIqYhgplwmBI4JhyGApoZKQZMRSIKlqG0iIgQsSQWfFmKKukZsTAGEBCVflf+sK8J4VMbdXihzJ3Hj1qk2dG4rMbJpUhRe/MCZwCFCBwIiBEUpeAlSgGFhMIZpJE+4fCAMEyYTj8hDUccHv+KNB5xevwBaRhxPD4gpoTpcKyMddD2qNLwJkJxjUbxXuF9RMR6TQiPJRvP+hrD94YXzYjGpdXbWSzl0iw1f+bljLxcMM9nNURoZMSlrxFhKTDMsIxV1M1LymOD3ZBpRVNT0PJKgWzKXHnfAISkAmQGoUVEUGGpTwAGsWHyOrJEeJdq7CLxuvNGCAuI92uksJjtcudVC2WG2302WVxYIzZaxM8aqvzntx6VhHq6aXuC5CCdpgmn0wEPHx5xengQx4ZhQkoHpDghDiNiEmMEaWpHClE/vl12eNIMVS2SZuu0YMJXjWyA7/+a6/bP0jYdLa74yVmjOC1qyfEnWgDdG7a2bXNN1bUeay/UP8uHKhKulQn7e0/b3TrhgdzGBzH+dF7YIYAUx33O4kojUGqRd2aufAyZgWqnC80Joq29b4W9YbpFae/H7r2E5Vvm7C3wXn39PSutf21461ha3ucmWMlZWUMBKY0YhhOOhx9A4R/45ekXMOeaTpA1Aq55zBpdEB6sKj/1WTDlIfhbUOib4T3XyR1uhfV4v5fS54+jPHqNEeKZX/W43fPFYQ7dd0m4JElaSHU8wcu+UDpgefmVoxLnOk17bDybPd3J0qCmS+zqvq340jWYPnH3Tdc8LVicQdz41H1/s58oj7l9mhp3sGnHHBjbi1E/wmx6JuuLKlX3dBb28QqHq3DlAt5re33ba/De6Q213RACotaGOB5PSMnqA4n8exgl4wKIUBCr0yPYHK9eeLMdWcTjgckWzUjmIyN6HlB4Xn0TEmMJAJSgRiLHE8s1fvbbu3tHO4sS3l7/awJBFEy9Sr0awmARRnI+Tgek4yOmH37C+OEn8PCAEgeEcoZpQQHGgggGS3pvXZsiWSWpq5CzGiOFF44rg1A3em4P73quTmlBjQcFuZpMbLUAWk9QxUdxVMvNGCFvqPpWrumbTFKv1qm6Hja92B1V6cFa73K77vyPDq8yRNjcvyzA0Oq435ZXrb5eKOo3t9vDkl5i6hrydHZp9zirB8nPoAzrBtE/RYhK1QkpkRnHI8bDA06PH3F6kEKSh8MJh+mEYRjUABERhyRei0MSIhtjtZ00VYgSOu1FMYWVEz73lAbFNk87t4qI6NJ12BbH3Ckj6u85o1iUQy5NsVWLSi8aEbHUSAjppxWMtqK/mhN/1hoTmgff0i1d5kWV44tsRkvGMkue/OpFXgtaNwVtVZAAsOKeXGeo4Ug3c8783SszveKsfd9sLNxIY10dujmzMRLUZhHgyoCoDtIZ3QwJ9Xk6Z5kLiINEiimuxZSQhgHDkCSiJkYtCtzeiblouLripPaysNQSWJaMp4saIi5nzCXjsmSEGDTNUkTSKAgKUr8kxlQ9bXuPW6UjbnhsCJtSSd+nNNyUMFOu68oGsuUDvW1j7vYIxxCYwqyuC/Wc85ExpiTrvmudCDglXS0qnVuERK2RYkXaSwas6LqtsVrHwa8ZqYGyzMJszYtE+Vxmb4iYa7SE4LnVghCctzEVeqCKXOUUioWsUts3t4YIQw0b4yJRV0Zn1DAgtUQI54WROSN8lTU6JCloHWPEYUhIDxPGFFGgOf1ZQlVTjCjRIrPESNTqtgBELX9mAGlx1z5tguHCNjpC8Lo4hDOBodI97DOiDFtnFnIqTBdFkpDLQiCOiKOktBmPDwjDAdPpEWk44XD6gDQcMB2OYpwbRzXUuSLd1evZLQ6NTLL5KrpG14p87MyW0QVfb8b/1vaBpkQ2nPVGCMMvi4aQiLZFU4/Zce6+10i2ooWHLdLLj7v/e682hJFb7O+zdb9n1tRHjR42Ay80UkvrQiCAis6dpmuSfMEkzKRFL3ZP2q4BMiRUIbnKS4o/Xt5j15IJxPZGZk/zT+I6Tk6wNMbe42jrUL1PMaUy1yEETMcR0/GAw2HCNE01Oi4NCXHQ6IiUEGJUY5jRaKrNr+fNR03uCWzXjBItcqyPqOjXmhoL3Lvj2rpcfaoAxNjt1/4eQfWf7Zneg/E5WF+3yzNsOItNI60fnXBFm09NzxAEf6n4vvaC8K8Kb5SJPR++zzftPGr1+1rc/L0qa38P/XqNF921SIi935677xbYXzc7bXd/Cb6bk0FhcZj5+vSEEKSe3jiMGGIC4aL1i4QfM0an1vrRVH5EqhjhZmbu92O3O9zMb942bq9t65b29tbUtTbW59f9voYzm/X4DN4816/XwHsox2+nk72e4VWwuuXFXm8Y7tXP70jbXzv2N485NCqCqClKgMpn91qf/j7jq0w+XEnQ7i/jn6S+Vot70P+75rfztzEYVD6BN79vW1L5s5ORPIe65sd35kyHxTsxtD57+Vb1Bq3oJ7zy2q7ZyjvUmMvaBWr0qwnA1/vof9pc/xLwzp9797u5sfY3Cvl2jkJoDo7jCCJoOm6RQTCkWu+SjLcwOYDXTT6/F67PW+rrmgLWnJfYDNQO17nNIYMlfU9lTOWs8c7Xnt2nIupx8lv2kVvftz17O07dCt6wt8qvQ+SyOEwYDgcMhwekwwk5RDAIicUxzOYnl9YIkTh7SRLXKOne4Z3BWkSEXN879oqc5XhL5Y2t0H0g+Uv2e+stOhTtqUaTDUTnoevL1icZ7QGsxovpt/fWTZPdTOa0s3sy574c+mvBr8W3foeICFodV7864tuJae/wwl4wvLaZGPRC0OZX/Z87PlQar3xsd19P1o0KcUfDvUcaqyaCKOJwOOLw8AEfPn0WQ8TDBxymE07HBylOPQ4IiRAHURaEIdYUCkbDLRUEtPK8KUjXUQ/27p2iQMmeKbNhhNYpHszDujdEaJ55rQ3RvCUXsEvPkRdNy7Q0ZVXJrXivFevNavHNi6ZgUs9a8SQvWveh4LIsmHPGeV5w0YiIWY0Sy8woC1cv8iXnmmKljYVNmBCNqsNhnTteMeKGR/R8+h/5bY1LPQu1+bk4jCFgXemdDVe4lo2u11dlFzePjqxKHCixFkOEFKi2VDAhRcmxrx2QOiVL6522a0afeV7w9emMeVnwdT5jKRlLKYgpIvGANAAhJoSYutoQvbJVcDasDBEMSHogbuGxpfQeKpaT3HustPV0O7TxksHu10EfEQF3rq2b/rvlR/deuy0dU0vR1BsgFszLBVwywpyB6t3bUjJZNI9F9sxqhLgYns8LzheLBGoGisWt0fqBG7P63hXZdSy47oPMaPSrDfQKJzOqV0DNmSgiQWbgaS4IS0GeGSkC4IJplDDa45gw8YJpSMiFkVJELowYAsYhargtpOZClrzPKQGVGYAwKZEIHMIGH/aMEC1I1+bfCyLYGmF3PoAZAxpzbNGaFMQYksYBcUg4PHxAGo+YHj6JIeLhE1I6YDyeEDW/aYwRcRjEAKHe6G1/aHS9rpPce0C3o3nk9zPU11XZeW82w9vKEKH0W1IwKX5dLljmM3K+1EifJc9a+2duNYBqyr3FGSJkc1rvx31ftrLOVqC0N2v02IwN3fa8otGCu5JTmNQTRkhs0NyeAVQACqIoDxyayLyiN+4hndBrZLsbb4baitd95PYO9V2g9MbS6+zRNd47dEjSjSFLzvPj8YjTwwnH4wmHw1H2AP3IfjAiJTMeB8VnagoBJ1zV6KA1/7D67DovlL4guY/E6dZZx0g1+n/VAIHm0Sh02MbhuqDnJlInoQkavfHyZWg0RugDMbf0SX4Buxfba1+6sOUr1kaIoN5aTBq2Xq/tBRbxz/p1BJhfR1TZe27j9+/wrwE1OkHxnkLQWnXiNPPl61dM00ccDkecL2eMw6AKqxklS0REYcsjLtG5MQaI8QGQNWTfLSRsu4b/SPAeyqtfc439Ptbzt/XhreqjPzKmiff+XmqmJl+80IBRdOWtSNPurm8lSdmKIrETqqgP5Pe/7ePWOhBTAxgPYXyD/b66u/uLVr+YTgT12H7s2qqMnwhbvbMC2suqMr09eYdnuHLe2JrGF1J9X3Rt+hd4K8bx/r21zSu/vwaqIUIcHIdhwDRNTRbRGnYMqbUnj+daR7B16MY3WuEAEanuQuRN4cW4q7tXsaJU5ZKcLeqEVVjSgVkqzSt1zKouAlzpLjM6Xvzb4e3tbFbFCnVrLU09kaYDhuMDxocPGE4f8BSSooYYIogkSiGzyFA1XTgRsq5wW1PGB0vmhFA7ZEaiKvKBgOCpkKypYLJhiSBoRD2XqwaDeq/Kj/aSRpuUidA6NW09cjUc8qqd1VcW6V2+isPc7vNNR/MnhjcaIlZCz1qhTz3x7cex5UdeTw6vjr7RzZV7tM8v7DcRv/4e8qfJn9ecvGthz/bb6llpob1VOtb+ScGU4fgBcTzi9OlvOD5+wunxB5xOH3A6HjGNI6ZBCraOg3iepyiREKHmEA+1X6bQYC4oiwXiNcXIVUF+JdRXpVH1Su8VD8UUr5q6qRogsssLvjBKhhTdzZobP2tO/Oxy49di1FqE2lLczBoJcZmlnsNFvGzPZoiotSEkCuJS09UsWOaCZVEliHqHm2JblBR0fV13e+Z2gzeice2aXtmp53QD6ber/c2RefUbd9glRNQhWkHAUoC5EJYiBiEUAjJhZACISHHEOIjXa4xC1MVTfgEjgJdYvcqYmzEgA8g542k+4zIv+PnpS42IgBLiMQQkIkSKSCFhjAOmYcCQkkTwxCDKWhJ1nHgPkyPCGumgYYxdmg1uylT7DtacgnWN65yslY9XYE8JWiwFWVXIZl2npiAz5lIniL1CTdOBqAFiUcNDKQuY5QNegGUBihjnOGdg1tRGNRpD2mH1JM/Zap5YCrIFl3nBec4SCXGRguEXNURIWrLFGQs9g0OV3rJjDktX6nY1Tmvc31ykeVk7umgMGFW8XbLUD/vliXFeGIyMaQCAJ0xjwsclYBgSHjOQUsSpMGIoKJlFMZoKcknITFiYkIplphQaylRAmaVwdBQGRkI6bd4IISh+19q4PqJFv7JG23ATJZgJhQm5AKUQCgcQBgREMBWEWCT0OgBWoD0dH5GGCcPxR6ThiOn4A6JGQsRhxKB5TcMwCAOjxd0pujwRQF2LQo/lmNmiWvqtjTVqojL9hqaqPDEv8VZfZa0sVnpQ6bdEPSy5MfhLfsJcnsQQYUXY84xlOWtNCPU2tbR3i9J12+/yngHFH6FrrldCkCnx1/hnxhn3LtUTxkaBzM896gTLjdUMQCypiBgAad5V0r+5F568Uj2XgswZCxcsrNFHLGmYmK2AsNAzsjnUeWprpRkwupeq8ygCjARtkBqNbR3LXAotNz5M66WAtc5QQQAjUcBxOuE4PWAcHjCko9SGCEnqsQRCDIwYgBQDQkygYJ8mLPkUXhthvvsYnW7ODK0wta1JC0l3Y2zjbbye4bQMBFpUjaeZZuzK1SBsv/l+2r5wzcjQnVdXrJ7/7P9Y24hY+88kmLZ+RkeHnaGhV9UQ6kapEQ+WAZfZChvKsRSW+jklaDRg2awb69daUc/9C3X4SHJhL7yhkqR6pr+iLsQNf+zf/9Z9ud6/d73xU27hVGXVTYpLd42bxLWxZh3lcq3t9Xt5pcXtYOO3FVJ/K11sU37073NrhMRNc/mGa9tFRjuE/hGE1kWNJsy54DzP+OeXL2CK+OHz3/HLlwLCf0MpM5b5C3L+ilyekKBRiAywFpPUVQcQo/Ai20IAjOf+PcNzOPiyUbaH947e+J7Peg3c3q+VbGb8bZXrrM/X+r7hol+GX20cbhgD2RA8JX/xBmbjRfR+reVmnGkVF9x2wXZv/ZvRcusLaSwEZCds+J6QyoAE4de9OVF0NMZboMmT5kCZmxOY6UgAVFlzO2beqcec1bi2aTXmPDtTo/mNb7I1CnTz3cSoZjCoY2LjSconwMmk1k6QTBtZxH+UoBHqFIUfAqoziPFU4IwmGFGVQcjSzpCkwWssUHEf1472V9ZH03XJudJ+c0O5wSaW+RVex3jFOlAAJCX56XjENIyIFLGUJ1zmJ5FR1DlyKVnSM1XZwWg6NeRzfHkbf6mpITJfARUxWIcg4xGQECMADuCyCN9lWMGo0nSTraRdc7w0GcUyLJjeAZbg2MakoohNuvxt+7I5uXiHq/We3Q/rdh+/hQZej0qU2hfSuBkJACI5X4uChwBKAw4//AXTp79hOXwGD48IyCBmZIookhsNRVOSE1jT7cqrU4EoEKiAqegsGX7GGmFd6zkydE053sS/u+FAIC2MrQ8qVGUO4mYAhPIBoAIOltJVqIpE2rPWrybYmuTCVSdFpp+tMhM7Htv0kKWtkzr5q72H7D+08b4yO/sz+3rG5Tkc+R779TdERDQLVEN2953UOChn7Id2uxKD7n1142kGpZUQw9uh3rNgbzaSZ4SJF8GEvNWlnTHCKVSoHrUGRPWqyXVDAEUQRQyHjxhOH3D64e94ePyE08MPOB5POB0PmIYR0xiQongKUwyIKdbFI89VQwcpYXXpYbyf7FpxsE03wy2vsil9zZm15ni2DdyUnUv7niW3eEtJU1AWoFih3UXT06hBgjU1E6unZC0Su2g6m1lrS6gh4nwWxezTRVMyXRatW6AFqdVrXAwSUqDXv9vVgq46v9egF+D3r31ZyLbr2u28w9CaYa4q3cxrfdV8qYRKrMgLEy4ZmErBUkjqFZBsqGaIsJoQIai3LxfZCDXtDVVsBmb1GJshoe6/XJ5wvlzwj6efsSwLzucLQogS8TAMskkHNUSkhGkYMaakdUxIN3I0Rw95a3mXImtn9kwabw0QVaGk4+SZS/HEt7F+fj3vGiIsT2BVXrW85HXzqIojNYSYh68aEFoqm1nrpMwoLAWpuSzgPIPzAsyLKJoWBoo92fKbl2qcK3lGtogew+054zwXnC8Z58tSoyRaPn8xSnjS1wlLyjGxMbp7yPzCWujbNWKv49I4afm/ALOOW/nKCKHgvGQMibFQwWFccC4R05BRQBhTBhWpHcE5I6aIWAqWxEgcEJkQivMupyz1SIowA4ndXu09o5SxNo+n2kduOGT8tDivEIwtEqcXMUIIKkTxzwgzGLMS+wKKCRQTkqZiGo6fMQxHjIdPSMOE8XhESAPGaZL0ZVE9dYIWeQ8tZsNWd3GFnYsyWaUaU9Z7ILp598rPot5Qtb6K4njFOUaNgjCD8pJn5HxRY8QFc/6KOT+pgWxBXi6SnkkjInKNhDCjtKZmgtI65zm0d/T7KzM2e359mxcULOvriICAhCbcqcBLRYralYya202LO1NQo5UasuwZZoRYsgg8maVmzcJmiICOdRBmtDRepdEn6RSjJf7QaXJSCNWXFmE3QrIg257PaB43jekmFVQt8iOAkQJ1hoiUTghhRAyDRBoFQgxFjRFa6JVGGRtCxY0W1bA1PGwjI7aCKqEZdBtNXQmw9jG6zo4/cSm+zPhgEWhccju3Y4jocOwZPOqMER6v1pd2qLlKIVVzyK4FRfeq7m4w6v5YFQGBQKV4hyuNhLAjoRQNLydxRiD1FrvW0etegW033o0uIPed16JxO8/+/Eop/ZLMcosC3/fBP9vPV//M/bGg1WTa/O09b89g5fu76durQQXV3V+s7St3vvGZ3ii399v6On/+JYPCW6KIbuXXGh/OqpCAaNqUbyUAiQIKCItG8f789QsO0wM+/fAj/vt/+6eomfJFDBHLF5TyAGBEoCQKhkKAFcwMgBhMRf0ZqaV/XOPQLe/5XuPx2nnfa/dblQhvuf+149Dg2njc1t5rjS87LbRH3Tg3nvd6LfROGK4XN6zBW+HlMZF33u/JC/fperRhq05BVhiaSaMXWquWycF4RdljHC1Sx4AsnVcWqY0xAbXOsvcpJr2eseZZeicccVLseec9Q4TJnu18LzNafTm7xLftI60rq+P7SdQU2da0vS81vhGk2S5K23FN18aQVLUZXI0RNWI8EKQ0jgoRbOYhzYnfKd0IZoAAibNXU164e8zBpCpSvUzl+L+dPbbn2KmOCRFrSh4g20wyVKHLGGLC6SBOuoGkZsLl8lSzXixFHIQiO0c5BqyKiGGWT3sE9A4ihSUzBxVSBbnqMRCREMBlVkW8pAuSeUWNBGoGB8Mn4eGsRgQZb13EccYUhi2Qws3DShba27uvGSH21vlzxtM1aXnOECEPiGBEiNxkH3kXZgINA0Iacfj0E6bPf8d8+Iw8HHHIP4M4o5CkaOI8g7kgwHhecR7jEJCXBeCsbbPgP0UQIghB58pSrpcqOlS6ALtttWsT1fSmzKb9ompokBaM9nOlN/aLTgyq85CuHeYidSStkDW5topyKobgRQweZm5ksBpA1utFr+j48D0afo1ZtGa+dS/8vvAdi1Vv4VZrnL/+vdt8C+wx2nsGkE3fwJCiw3atoFAcD4jDAY8fP+P48AkfP3zC6eEjHh8ecTwccTocpDbEMCAGy8MfWv67YPZDKBGTZ7T6B3uGiG0qBQDNQuuPDFfwsWAr4Psip6ocMOWTS0mTVTm7LDPKYp6zs3rO5urBnWep/bDMsxgvLhr5oMfz5SIREGcpyHuuhohFc+hnLdSbJQqj9O931QjxDvBaIez5xpQZU6uuN1j4i2QeqM65eM8DlwCMCKCgTKFTjDSlDquSM4OoAMi6YYtCf+YFmRmXIl74//jyC54uF/zj539WPmYaA9I4IIUBQxowxIRBczfGGBFTXxuiKl6JWt0L2MbvjGDKyOyl/7B3sPcna+SqsLIzvK4dNiZVq3xfTzVSHC03ZZhE+tTUZzUSoSlia22I3Iq256r81SLXcIyxK5BsaZlmjfg5W02Ii6Zh0s/SRUHoRszea+d6GrHXQofnxj/uKC88PVYeufaRiJAz4T/+B2MYAvLCOIwJnDPGIWI5jhhiwHFMSClimhgpFYwjkEpGGkYsgTETI4SIEDJSzFgQMKtnYxiTeJDHZrRt8oNL4bISSqqCFI2NIWXIq9d0AAKbATiC1EARxgMojhjHE4bhQY8njNNJU+BMkoc/JTHc6XoIVljbqfgYjZ73OInKTOwxnRsaZ2vDOFzzKPdrq+Ku0E4uRreXlpap4tkidFp/t2skIsIbIPRYhUBoOPL1PZN5P2/wc7h4DToF8K0NkhfEUAUzVkEyZxMolYcsEuSx5OI+rZYNk6QoaIwxAKfUoEDtXD0JwAnYz72fN7T4te7ndxwHTOOE6XDANB0wjANGqxWUtH6P0WeXHixEi7Lc7pmM9by1ZzdeYUvTe/xsxlD77nESxjOhp9W+MLuvSdXxPFeiNrw32Eue7t8Cxo99q7K6i9K4cr77hNDSODB3ePGbgUPtl2BtvLimMN8Vwr+1nzvwnoq/Vz55NWbfAUdv4Fd//fd+DdjchEpcjZZQDDgMB4QQ8PXrV8QwgE7A6eGEv/3tb/iP/17wH/kLmIF5njHEoHqBfr9gNsWM8uFv5PHfVTa4wx1+FXgNJ9bu6f++bfMhKL9GXgm+aq+wFpW2fO7q6KFRrLbvSa+t+K2130cteJ7fp5vmlQzgDQ6NU1MeGjCCgxrZWTQlI0s6405BX4ooHI153AOu6kbHNzceST659Q3uferf20jQ+k6FNXWoG3v/XSbC8aAM78xVr+HV3PgX6P5297+ACkZnjVfe6mpEDkvDgDRYbQhJU2kySl5KVwM0oOnLpCZmVL7Uauw936dtH0mN04QYo/KcAYXX8u7aKED1fdaGCEtxbnxOCGZ8oK4t03lf7ZeTd0zG/p76UIu0JwICeQObnNfAc0wnScV0+vAXTI+fkVPQ4s+yVv0Y1VRHgNbt07Vn8nHlc0kjpES7mSHOYFVaIIgxwcgJ7+AgoxoeAKuVqsyq0iExYlk/HF0iUm9AK1RNVSgs1YAgfS1mrwBq217OBxzds377Tv6LwTcZIvYUCv3fbXDfukCa8uvbFWlvhWt932+zbcSC4LJZlUpoCTFNGKcTHh4+4vThBzw8POL08IDT8YjDdMBhmpBSxJBSzU1H9qnKXJE2vdKqcPNatBz7rrfYFNp95tM2cN3gsLPRFXd0CoKshXlz6RVXNUVT9grbxhBkLSx9WeS3y6wpmS7i+S1FqkUxKylrco2MKOqZro7qm/d8Dr5VcXBLWy+fN7zpcW2t/DHc8qF+y7JgiYR5BmJkRKXKZojo50wrTXidJQNcpDj1AlGGP+UZ58sFv/z8M76ez/jnzz/rxj5gTCMiJAoixQEpppqOSWpCxE2h6o2yAUK8i1O84qryqldisilZ7fjKufGKs2vPXH9MTWxGA1lvise1Por75Kx1UNTg9gzTK+vVrPtacFo/NeLHlMJzUw5bMfeWjknnckOH91Boi1nXYOsdic28rK+pjLQx6npNzlJgLEVR4h+GhAA5ggvGFJFLxpgSmIFhMJolHhM5EBYipFRqFFUgKVBPIIyDMRiakolRUUTGZjvfZWeMLNVNxwjB+PWAQLEyFiEdENKEYThiGA4YxyPSIAUzLRd/iBHQVExhxWB1zL2n5844bHO7N6frtVKNdA0h7ER9/2qIUMOX4awUSNcoNo3K6Y0OPS3PWeh9yS4SYhUBsbeON7hl35+7ZoVr6/Z6L3SrlbOZ2nYvsDJCOIOQGnqLGhhyaYYGi07JhSUcPLfQYO8DZsYIe4z8sU/Pba08Z5LpFdB+1LbrMaVBjA/TiGEaMaggF9UIEWNEDM0ghkCVxwAVp5TzPMF6Ptd0EnWPuU7Ha8Pd93W727Z9XYm+9tW6DtY1XPPj6I/vBixS47XnevrZ8GyL08/BniEiQD1GgUrz9tq7+ow3sMb9u7ytUWbe8AbXYM8w4fth11y795b299p+jva8H6zG6oVH3NqX1/T5JaPPa+GWuXjTM+pQKQ3UfY4hdaPGcQKDcH56wjQeQQCOhwP+8pe/YL78Ez//nMBgrR8XERZp1K9JqAFddAS0eu4ru8tr5VSDa2P+Wln12jh+i8z7Utu33tfxJa9sq3Xfcwf++7fDa+jut9z/e4Eez9+jvZ5/fVGqYM9laRvu+/o3GN+ha5JRhK9ShTlxqXw4k3hW9/c2Y8TawW3NR8gtqrPx+4r22zi02ifjVVbpiHwKJOq+r8bGy2mmwEc7WL+v8lxA1fNc47k2aTB3oRJS/crYnUZqegNHKVFlcce7+fY2dKhOtimhUT2+TebpnkWh1pu0mpPNAXN2Nh+dzyCGlxBCdbrxsvcaXqKT5kQZVd8i7VlMMzX8qHJxL594Wc74GKv31/i40PBY3wWv2CvX+8xLvNJbgVWJHwkgcuPZHQjD8QHT40ccTj9gOn7EOUVJb7SiPY0eUXeSSCKDrS4HG2+txogMifLPXFS3yu5ea0d75GUMPU9osnelYTrPqPoxOy9Rx4DiKaPDzzY23O4x44U8uHtPdm2LQwXr5aVvk+rtf3r4LhERW4Q3QufOEGD54m9dIHSlrdf353XgBZJb2mwEQTc1QMs5JAAJx4dPOD78gE+f/4bHD5/x4eNnHA4nHA8HjOOIlAgxEsIgStyg3r1WRBKqrLZNyLwDRTnalGuWJ117XPv93IZVczFXg4bzcnRENVuO5rzUNAk1GmK5IC8Xl0v8IpEQtTi18xgvRSMnMubLRSMgNBXT+YJlyTifL1hqZITkgF0WNVTUsCxJM2Rhli8pI74H9FvQW++uXMguU2f8jIUHGswhYKAAKaYbEULSmiKh4qPU4Zg1/2HbvOU3yXqYWVMynZ/w9XLBf/vv/4HLvODL1yeM44THhwOGMOJ0OOE0nXCaHnGcrKbJiCkNGIdmmPBK16IbAbMYILLiqxW1ZX05nzqsHfsPV8an1HHZg96O2fLsm/fthjnl3PrAbT2wMpxVEVbToC2SjomzHK1OhEUCae0IdkV8USQpU9a2rDj1PEsqpvNFCoQ/naU+x9P5okcpyH6pyuAMn9/0FiWcjso3iXLM5nXL3TkZ7/UKaM/KOQu9z8CcGfh5wdfEyMtXjEPAL+cZ0xDx4TDiMCY8HDMO04AHBkb1jDIlbJiFJgZ9XlAv82UuIJZIhkBuPa029YpJddywO47dm6izeGQpzI0wgELCcPiAkA44HD5iGE+YDo9IwwHDdBJGOI3iaR5TU6itFGtV2cqWb3YtIPV0bT3uldG1N9b10dF4OIEsS2hwF71Wlq74m//k5eIiImZNzdSMEy26QlLzVRHFra06jqYIBm1ppvuyt+/6d/bMty8kV8/bWBAagwmgGR5C+5vUQ6Wm4pJQezMESuRdwbwwLkvBZZHvy8KYM2PJwFI0RRPUN8/Lcx1558rrqn8NChutKmqMCFonYB8X/W7ThAGuazONkgrscBDHhmEYRJBzAl1MK4Ox/t2y3/Zjvi3m3n4zHmItEPtC052xwN23H42mkWOVPvfRZt6rsWtjFUXn8a1DM2eM+J7KpOdweL3+9xSTZijy9NWfNyHbilm7u2u7dt8e31zPf2c26do4PHc98MdT9H0b2CT8K73z7UCQtIn2twDX/4lE8ZQz4TwvuJzP+PLlFxABHz4+4suXR3z5+ohxSBoFOKMmYnT7w3vj3q8pg/z5gFd/39fG7wc2ZoOX7zC9T4Wt4lpOsziJBXPGye0qYhRiBHWOlHSUohg1Q4ToIFV2U1muOPmSmYVvZZFD6/OrLqRlUTFDiGPCa99FZm2peqsSIpsywtJTNpmWsKefMP0LtK8WcZ87WYDZnM5U1wPniKHP5GIOqfb+TqYpYryBN9jUVEtYveOWD7wO167dOS/EWhUZaz7T/qLKL4cYME0TpnHCOI4ohbusAGaIWOYZlxirk1iMvSGicHYKaAbz87hrfBWpwYRCQClR9Sg9Dhs/G9TLvr1oqG3VIzl5TXm5WvONPR93jffv4XsZHa48DXViiGuBePbCTgw4fPorTp//juHxR4TDR9FX8aLzLXMv8p/WWtBXsBoh8reOfQiCs6RGCF1DYohQZ1YZCG1E+in1QVifzbX+qX8V1SapnGjREI6ukRkUSN/a+GiVH2tkxGqUqNVjBbZUcn929nj01+u7/4hwsyGiepcCeB1xagVNrB1ACc5rx7hef8ONfnG+w6K8jSC0x0lYlaa+0eLUUhtiwDA94HD6iIeHT3h4/ITj8aGmTxiGllvf0iWYMrkpU3QMAVVosttQXVGmss0dfM0Q0YheU1jt/d6UBC0VDXsFQTZl7KyFTVVRq0aIarQoluvZlGEtImLW3PjnWZStloKp1oSYRTl0mc0j3IQRyc33XkT4VoGkXgfueCxhOPpre8X41RZRBaydC1kbyLn9tsQoxYEZAInHthXqtXZMoQNIKhHmls4rK++RS8acM75+/YovT2f88svPmBepyxEpgTgghSRpP4YDDsMBY5okRVMSA8QQmxHCiivVt3IbQuGCPn9mY/LWRgjm+uad4q39tj9We8re5z5+87d1UIulguGLWnf473KVW1RQS8/kr23eMUUVdRL9IOlx7GN1T4zhusyLGOg0AsY81j0urZnbfjwIPRq3cdsbq+7KzYV1KmobDa/3FYCmyEQBFgBUGIyMNAujPKSApTAOYwQX4LIow8ZAjBEgQkwBMYgnd4oLAhFSlMK7JRdkKshZmKOYAQRhloSXoMoNrEXbzUttfjOGUQvFsiiKKY0IccAwHBGHE8bxhDSeMGrqvTSMiDEhqkEQ3vt35UkGoBqPm/LVG+QsxdSWOW3rp29xzwhh68zqoGyjeNSgrLS4GSpWR42G6CIhskXlFWPtRNnuDBE+aqExd/v4s8XZ/t02ERB7Rz+91qYKIVR/aAxx4QApWid5frt0aZkl+iHLml00IiIXXyuCahbdDZ41Htx422qEsChfQdN9I3T//rXV/hkyyBL5MCSMg0RDCB5GxCjpl4w2m0JbPpo7VaPjNrTxOVrJaswDdq9p87oiHCua7nkMc6xo0TtZaxt54dwE83XfXgZvhPitjBG+L3vf10egpWOC8ncUtLR19wzaPPeqQcZ48e78G192B14yQrxF8VvXtjDbb+oX7dCXmz2kVwO2iWPi+oMqxTYNYEMhXny0a/Qb4LVGoT147f2vitC5rUVHVNupGMUZp2jdrvP5CTEAx+OE4/GA0+mIGGXXKTkjk9THEWXTas/X/7+XGmBNp15Li167Xl4D3xpl8Ry9e6nt5/u6Q6xe2Y9fC17jvHhLO+8j1xqOvUNTbh46Xl//I0YtebV/l79D554h6ZYqzyq/VyMCJDULk2VpyLL3MSFQQUFL2yv1KkpVzBv/shcZodoD9DxNkwoY7L0ctd9Oubz+MOvRpWliX+dwLad57/KmY9lPiW3pt03X03ghLs0Y0WpYNCOEjasf8/pOlYFrcrdOLrBS2te9d3v26txuTjudYuVv6hZH9cKgBuakaUUvF8sIIBHbpjheckv3zYEhkRROD6G8jthAqNpC9mDNR/Z8cnOutL56nYG921oWM551L0KuRkSQ1hhww2m89Xocn6Nt30p7rtFiS2nEWuEyuPVdGDWyenz4iOnDj4jTB4ThuJFpjH9rcnmo41VZUh3zwiz8LmSqBTVL1Z+YQc4cFasNgfs5KO6duD7I/tbvRYwRrO2wnZeXr32zW4AtdhsvXpfztTFetVNfXn99F3L/B4E3RURshaOrV76xW1egLsb2zPdSOn8PYBSAM5ikXM4wPSKND3j89Bd8+PRXPH74jIfHH3A6PGAcR4zjgCFFpNjqQpgCi3WxMprX7FKjE3JdkLah+E3Oz9NW+dpvvr7vTXllaWj6PPjsjBCtkOnSCvcuF/WYnWuRataUNYWtnkRGnmVDmbUWxNP5gnnJeLKaEBoRYamaLsuiiiGtZ2F59X5j6+E68GxLoJ4Xalpx01450z2jKhb1exbviUsAIoDDwsiFAIqgmABICpxlmbVlIejLIoTcokkWFvyRNEAz/uPnn/F0vuCXX74ACIhxxDhMeDw94uH0iMfDI06HB5ymE47TAYdhwjRMGJIoXwNFydWP5pnMWoIqq+JoKax52NUbw3sN1PffM4QZw6TEmtZMnY7nij7tGx/W9ShaLn2oslaercWrWYwQ8l2KKbEWpi5lRikLiuK7KW2LFQLWKCJ79qyGNIsAOp/lnqezRkRcxAhxPl9wWTRywtVW8XwbDCccbqxx8N1IpQkY8JtmP+7+qF/0RiBoqV6r55LLjBgIT3PGOAR8fbpgGhN+/jrgeBjx8XzG8TDh4XzEpwdVchOQkRFUqWDM4TwvyjCoR8ygHik13LoJdVw5ENS+wZ1rjJFGYQRZI1K8MiKNE0I6aATEA8bDI9JwxDAeENOElBIoRkgcqzCb/eMazlpqrtLh4tbIds0QYbUg2L1fu75UgSVrbRMrTi10O7uP4e1cfyuLGtP0mK3ejxapNkNEdqmZHKqg5LZnG4OpEmcd361yjFafPfC/UTeflREkvzeoZw1LWUM2xl85Tts+JeWSfKwWxKz7zmVecNbC8fMCzJkkbZM6wEmYvLRz3egsOMusERFkERFUhd+WK3Z/z2bux6Uae5R5n8YJh0nSg43jVKMhQkiIQWtEBFcjIkjasD2xsQlZ6/PrvvWRL9U40eHilalcPa9Uz76sBmsX9bn6NCG7jyIyYXFNm9ZRELcpqwjbtFqrK75Bu7OnHF5HRIhRv6AUiQQr+hvUc6/uWzD8e54/b4I0fjO26dp7r6/x17aIqt+S22u2hG6bW1+0+r374c3Q9rE76N6qFt75cgFjwHQ4gMuCf/zHf0NMwJAIITA+ffpY+TEi9Xoly9e8UvRUIzXfR/wOr4I/fyTXdZ7MMrAbfewudbUDiBq30WSXJi3CeAoAgV2cJovBIcDJbChaR0K93vU6Yq5RCsanbNI4srW8SqHk55CFv2i6FdYualSGGiCoZEkXVQqCOkkEFu/tamxY801efrI+ep6aW+Qns4ua3nsfaDQFLLK6GSV83YrGsPrfVF/FWcbOam1uIijgmFo3X20mN1+3oOMAn7VjDQSEgDgMOBxPGMap8kKiY1ra+xdgvlwQiEQHEeKqu25eIU5l+6xRjye1vmEIep/0NVBz4rH6D1UvY/uRGwDB0RbZyoWr3mKPR1sby1o7+04Entd7WS/7diCy+rRN0R5IIsEBYHj8AfH4iMOP/47p878hpwkFAeBFDX2rcVE9QtWMBT3JjRLIOlTDgMO3woI9TAQOAa0wgxojdD0ETTXbZEIvYzU5SgwI5jhv54Ky/qU7vzMym986YwQDpHJNpSG/JfP6O4NXGSK8YP2cMWKrUMCbF0ZdXLBNqP6yueZKA2967rdCIzC2qQWkQWpDTIdHTMdHTIcTpumIcZykiKTmbRaPRfVOtEXlFCrsNyGzDOqR6gbJm/nZU8Qa4bXf3RvU37bKBrO2m/duaZ60eXHK0tylbuLcvBl9rmfxrC1ixNCIiHkpuNSaEWJ4mGsOc1+c1/r7dsbv1oiHa/f1G8D1Z/T4u/69Y8k2z9x+b+eZGXmR3PnZHDJAIIowBV3JGRlAUY/dZdFICI2MWHQ+zovU4vj69QnnywXz5SJ1IQapWSKREBOm8YBxmDCmEUOUotUpirIr+mgMUh4OXOerOpZU45l7vxWuCg7upGpitM1qhb8e718XEWGMojKN9dlOwdMxCJo+xB3XURJVWeY8eE3RZgW2LDWTeHiUGhGxZIlOmRerG5Fb2p7Vu+/iyApX1r9cU/i8uB7QGK3O7OEetN+GKH4DotqdZFyWLEqBpRRcloBSMiYzOuYMJsZcGAUBQ4o4TgkxBlAA5jxIREQZHT2RDwCkREAQmtn62iuw/VvZTmMRaGaEMDIcjBZr3tKYBgzDAWk4IA0T4jAhJsnFT9UTBx0N9+NmgoXhRBUe2EV6ubXuj928sZlhe3xoyuBGq1tR34abzNyiGmpEj1P41rRLPj2OGaPXOG5rl7p+oBuCXvFTlfDk52R/+2641Rsh/Pn+u3+eO6oCypT6DKo1ILJGOpSihglXmFpSMXFLxeQ+VRjp+tu/k3LUda4KxFbF1TtnzdSuhT57x+1cC44SUhr0IxE5IUSQMzwQWZSleXcF61YVjP287e+B2z1pe936/uv8WPdMNVJXurwT9eDptm0ue4LdNXq2Nkj4Id/e4yWY6/AWBdQ1Ptra8/tY7bMzqNSifvX5GvbOa6H12tj/1ir9Bps5UdgVwG8c66v72jvoCtfGiN0KL7ztKr/h+YYera0NpVmdX39fX7ddr9e8r7+Hl/6tUPtyFZWp4nvOC0KIGIaI5ZLx9ekXDAOhDILjx+MB8+WMZYZGBzd6t2eK+DXhVv7re8KfTYH+kuz23vAaL+Vr8NLa+7Xf6TVg6jvPoZXuN0D46yZFdG9T+dX26b2pnbue7fVVXiumIkXgdk3lja/wD9qcPIMdj8WoxNbc6bprTAZVhT5tIiF8BETry24/4Oa1eP6n56lLKTWt8VVeCE2Wlbb7qAyXl7kfaO6/e6VvHY/1UcfATW37wY/lLuwx9/0XCgEhJqRhlFTTyt+IM6DJ5C2rgBkOLMpl/bRb9JB+rNsY9rJK9dZfRTisd97G/8rf7TpG09O5K/1Q7sh5/txbec233is36r0MlZtcH4mQphOG00ekh09Ip48oMaHK1E4mbAyTKog8b61FsEFogTgUdPU1eaL9EzkGpPVi1uIhHF0yHXYdEH+hUKuqt9LrCUHnJnetubfpG/WKcvfjcxKQ70F31w34+meA71IjosH7bYz9pPcC+O8H1u8bAASEeEBMRzx8+Izjh7/g4w8/4cOnHyUl03jApDmcp0FSJwxJUjIxhaoogNoTJXd1dpEQzcre7ZFG3FbKCu/53TaulRKg3YEuL756dfeFeZfqIdtyip9bjYhlqZERZZlbrnwumC9S4+F8vmBZlhoJ8eVpxlxrQ2Scz5KSZl4WWIHazf7Hq3X/G8CusHzDb/I7lDl7Hqe3m5N8Losoa6bzjDTOuJgie1kQ57la9ZcsBhzV08KURxmCG1KPYMbXr1+x5IIQIqZxwg+fPuHj4yf88PEHfHj4iNPhhMN0wmE8YhoHjEmNEU4B21g3rQnBlo7IcE9xMmePsCumCrs4aqG2puRtuMs6lk1x04+XNyT47wtMGSuCaVbc15oRejTmsCpyWSN8ikX+iKe4pWRi5yVeLAJEvXzFq0NrQ2hR9iVniYRYFpwvC+bZirb3hog1vu/jzK8lmHjFasPhtfexzU9growBQMhqmJizpLqZl4IYF/zz6wWHXxL+45cLjocRj6czni4X5HzBpw+PeMBR8nZy1hBOLW4FRiySq7No/AXDPIqC8uBc51v65plIzb/OAEegee+rL0hIoDBiOByRhhPG4wnDeMJwOCKmA9IkKZviELWuTz9avQDCGiFkUQu2LtSssKLjaxpdGUvuFeA9M621fPRodUkqzmq+bKHhQrdLjXhYXOqlpX3USOxrn/T5+l1fVv3qnRhM2Wqh0i1k+q28sn9G8XyyMawwmmK+ewHMAbmQGh0Y88JaAyLjMhdcFsZ5Zlxm1u9aM0JTNGUvVNicmIKsis47HLIfJDLRPHQ/NFrYjCh+P7ExB4AYAmJKOJ5OOJ4eMB6OGMYJMQ6axiwiuU8MksZPGH3CniHlW8BofH9u+4ymEBABuRp2ncNCy31sNDjLtcoLeWPFfpTNrw+3ODns9dX/bekNZZ5bGplugXSGCJHgiN6RPya8FBCyuv73Y9z448N6HK/h1Fo03ojKLz/pd7BmXgKjqlD+DQSEAHApOJ+fME4RxyGClwU5n7HMM34pFxyOEdNBnBjAASULL9bsOqo47Aw9v++xuMMdftdg7C8JH7TdQ0xmqJne3TmL368rXvc+akdTCu6SSFUksno5r2SRjo82w0J93mrvJoJF0sJdu37udr9VuYFZ03Aq3coiZ9YUmNoYAzW10rXoz3VEBNinhEITZljGtfvOBSgi29ZPWfTe1flVWikvIfWqU7fXk2mP/fdnZFO7zHgcZ/SgEMTRaxxxOBwQU+wjXrWNohEj87KASNLyeWiRDcJT3rK9VaOPfgKxpJyw3ocg0cURAFq0SpXTvKGNGZKinZR/a0PQ6zoIXKib667NFc6uU69v9Xfbd/pWkOllmeMSUSxF0zAgDiM+/9t/xfHzf8Lhh78jPnzGEhKYgJDlhbmuH/9urV8996Iahc18NdwirZMGNqcyZyxUGsAh6t7unlOKBF4QNE6DqnEUbKn0SflekvW4PyIQ+VFwLjSPYu0qqf6I2zri/n2JGi5XHuSGufgzwbsaIq4rYd/WXscU39DI3kLjK+dvgWsh488v9r4vDCFYIY4YphMOx0ccjidMhyOGYXQFJKVwZAxUvRazueI6JDXBvpjS1M7Zy4Kw9iBvfdtaz9eEbnufKXf3LPprj1mXE9/nxs/mSdtSSZniSlIsNc/v9cciIMRDtVSv4XVqClSlHW82mvU4vJegtYtvzzzrObxp+/XeHLwMWV1zZx3LrLnNLf2VtEeYcxZdD4fufkmZpFEpsxiXCrPk408DjocjjocjDtMB0ygpmMzwkGLqcjGaxybDcPOaF4h7V6eIEry0MdhuxEU9Obiw6RV38Hhf6bfbD25pyIoya7aZcWkeJvDX12NxxoHiGMi8us7uRb3ePPfbR3PzF/W+XpoXdl1ndR1u8arHmbfjeGX0njWcPc/wXA0PrXNNGoXZhAzbrHNh0CJK33kRRe9lkYLAxzHgYQoYxxHDNGBeZsQALHlBXAJyyYgcHY4ZQ2NzHCq9rCyQCQAGyhhQIARunhgM9boIASFEjYgYkdKAmMYaCRFi1NR60gZMebweijoc60LAbaj8WK8ZUz+m7G/AHp63mjzryAhfBNii0ywCoru2Ckg+b7+PhrD16fq4YxDsjRB45sgrNHY1JdxxjXvWiJeBnIpX0nBYFERNgSTzk1kiIOyzFDU0ZPksmbvfZT/y64Fr51oVChcpR/6sXF+/S5JT45/RC37762299s0IPAwjhlHT5MXUUjBRQCBJ7bPOd1v3n7cybO8AW/rqcLj0+FwFuI4XauNxyz7vDdbf862vCYnryOK1MWLLTxj5bMi9UgXAFDCyFG4L09+PAHG/q0ZpO6L7bfvrXstv3bL/6IX2gFe139p9jh97qU2/Nt8Hrs/B3jPYvf5zxoc9Kvny/n29T8/DzXOH7Rq9xfN7G3Hixoi1AO1QEAMg6TcyluWCef6CNBxxoKQ6Bk23WFFhpQwxWc/jCLfvv4ax5hZ587Xwkiz0Xs+6Bb+ec9r6vcOvaaz7I4xH4/e6Q/1bqND+mJHxTKK1rYy5456c8nZriKgpkbsu2H1Owej3eu4dOSwN22rjckZK6x/Vr/0b+npk1D7Gw7Leq0x/1aWs5Fs7XvvUDBil1YggMxgY78aodTbaeHL7Hf43M0Bw/4G/3o0Bu3epk12ZEjdQBCkS4jFgO/PtfwNXU5ZIZalY9Qs2Dt0OZ2Ozicjuf+/P79O9tXNPbc/NUx8RYcapPc6o35ukXUkJS43Jh9/LOx52Z8TWfd17T/8e7w+m0Df5SeTqmBLiOOL4+BkPn35Cmh5BwwEm35rkZuizadUtPUcCbDOu8tA6vblEBIucXp0TCjupCg5NqbYPItcXh7cOZytd6eYKiu/uttpRR0OYd95z5809/2N6gj8AvX9v+CZDxFqI+u7A9b/rl3xjP9YL2xfbfW0bjIiCBBpOGI4f8PDxMz59/gmPH3/A4+NHHA4HTKNEQgxJvRODWvaqEUJt8LYJFa6e0dk8o30U2pX37wX4fWsrYPn5LfTNFAAFlt++pVyyj9aGKOJRW+YZOV/EMzzPaMWrm5FimSUS4nK5IOeMrxYRcdFIiMssObln9RhfpKZEXlpaG6Antq+Z9peY8d8CRGnQz8UW2ubfchzqvGkbFx2/82XG5bLg6Xzu5nhepBBriINak1NjuCyNPggxRiSKGA5HPDx8wOfPP+Lx4SMeHz/gdDhhmib9HDCMEgqfBlF41UI/StN9JESncK3RBT0DZDj4HGOG2gYA6q97Dnz9CWM2LMrIcF02ES0s7dLYWPEvKcibkYvgeDZv8nlGnmcx4uSMsli6Mk13o8V8lzlrhI8YHpZ5kZooFhFxnjHPtg4WzC7c1J5PWmdhj4kV/Ph+OH1dUbFViW2uh23xjKLCRNDQx4LmFcPM+t6MeZnx5angH19mzPMZX778E09zxqwoUwiI8YzCjGE4gChiSAUgQloymAkhCvNY1HJFJDcXmBGkbHCHKCAEwUkRahIWIsQ0IcSjREGMJ6ThhJiOSMOEkEaEFEFRvDU8o2G2IyuuZeHVgns+UnqfNl8zQkDvAW/XjOWYlUg2qw1RhDaXFs5sdX0Wqw1RtL5JcTVOeNFc/YszOCtudukCuXaNGNVY2CCgY9y0v3vKWOPz6hkvkBI0tzc2imQvbhCaeBPsjKsJwYU0vBtaEwIS7TBnoadzxmXOOC8Fl5qayQwWUG80aDqA9jDyc+F/qH2Ttwuw2ElqI8P9m68jvNaGHYvYCoM4NUyHA6bpKOmZrFB1MGNxMxoHTQUp4/dONOOKF5zgpL37jdAJcD4i0xvBfC7dW7tIu2P53rDB550+vmSM6I8BIUiqRZgBCZD0TM5Djtj24Ov8+YvGGnr2az1L10IlaB9fn4P1/nU9srEpK34L6GjSr/3sl+btDwSvehcGQD4ybA/vCrgsmC9nEBUcTwOevkpURF4IX7/mxizDHFm4NnVNZXaHO9zhBqgKVVXtM3qPZlvrezo52KpuvE8IIiMkRFEehgC2ktQsNRnAQT/C2wXyJgopWgxuefdNidwc9KCMYGx/UzNSql5RmEPlZUV8KAhBPNhBDASpAyCMvHGdUaOVqdIciUKQ71RMfjftK6+im53CH9RIF5w84PPOuztIZQNa00rrhp2ukQ8aEWGppUrr05afW3/vc+ujOvv499h+9aaIrvfMCBTV4VEcaghUZSS5vukCwJJZYSGq8kcwb/k6Vv5VekNUfauqU2m/5ZwRKIJj4022e1aTfU2vUKNTqVUP5brvxK4N0UuQBqBo/xXf5Z0z1rCOiPCwt6++j56WIdEdIrEUfcT08UccPv2IT//pf8bDT/8F5+MH5JBAvAhuLkXlbZOn4WxZal5QnacUoQdMcqOg61hxlSE0ABRQwOJ0IGe0FouuNa3DAdURkcrdIqu2DGWN4pjxQecQTVLVEUSjUi6Ch7TvWsOXbJhk0LHFfZdyX/tLbG1Y//14//nhZkMEc1ucnSX5RWPE+7F2zzH/r1lgr732LZ4pzAzWoqaSpmPCMB4wWk2IcZSaEDHIJ+ima0YIvwHpxlSVoGxFT4CqiEL7W75z35crH/9e7QgIQXXWZXbfnaesKAKa96x53XYhhS4dTtHIhqoAy5YLv7g83Fo4VaMnWt70fj/czsfbhLNrholr8/2cF9FrPYy8d17bBNf37b2Xy3dn8wbLZ56dgnGRDU3bNkNEQpAUOSEpprV1SgRRWsWIaRxxmCY1mk0axTOIYiuqV3gI4rmgii0pIATF24a79ciegUDtu+eOruNn702CnTF7acyfWw/StjfUOY9bcMN7bvje0oaU7u8+jYgZEi2yp7QIIYuI6CIhss5jH5LblHn9+l6/t+xrRq+x+f0WuOX6fcPHCzh/5boafg0jbSQ5+AtjKUIjfo4FA2Z8/HjGw9OMh+OCKScZr5Br1FQujFDkXgRlG9ZMwVUFiIV0m0cVROBQ4UQUuZZ7f5CIt5BaDn7PaKzpgX7MGNGnY7pGj/ePleGp9Ln9vv8p3acP+86rj6PvO/f6VFJl9RzACwuO38K+QnLLR8idJkAaX0bu2I2tKWN323b9MGOFi4Io6qUm4e7QaA+uONTWpouCcEyskqTaHbO5MKFVcLMxWClsiVpRR4Lg1g7bepOizmhj0IjKGAU/pRZEqwnRjs2rq36HiggOF7sXuBFEtrh+w2ujDzq6jyu4/Y08Zt3zv6mVffDr0mw0a5p8qzK23d/47aqmqAIyVyK6t67Wfdv3VO33jnZ2fa0KUh1ZdQLVi++zXxNifY0/vhf0PM8+3/Zez97O83Pr47b2XvIo/7WcEeRZ9S+7ovv+HI98rc3N71VVZbvo9gqTW3IWBUhKATEKrS2csSyEAPN/dm1QrxTzioQ9fuW3GOPXwksGUH/+z2LY+t7wWoPqa+65dv01+fS3gVuIk7/GJah0W5NeeL1VRyeJpDhwM0To2jU+kQNQgrtVeRvmRivWsvIOD2FGgUpnjL2UG3TzFWFCrg+QVD8BTKV3IDVmsKaFAqxaxnOruteW+b2CYN7ajdux754HWDXILh0Wr5/N9ZruU+lsG4v1La2L2rc6PuReYp+H2H1/zxTp00nr8Em9yVAvq7IO2zxaE41HlOeueYst73OtK1s+s9xAK/vZY2bdV3o6vOahetnPyUP1HZocs+3rdk/qnrVjjPgm8M8g+y8gHk4YHz7K5/QBl5AktTzQggzYYVNlEU3qaLJc24xdSrYAoMj3osIWkWVVCILn5NY7DB/bs4wHZjRfhG7EiLpMZtZfrro561tlFjpcb6md1mNk19nakL6RvX9dO9ytvH8leGVExG3CRYPtIvhW5urqk140iLwdnmP6r10vnRqAcMR4+AEPH/6Ch8fPeHj8iNPphONhwmFKGIeAFCFWvRCksKpuuvZEUwbVSAhNr2Pp1jpF1HrfqATOK5GuGyMs7U2voPKFpTUfvkZC1DoQsx7zgqIe4bxo0V5NO7NoyqbLMiMvGV8vM5Zl0WPGl1kjIuaL5s5Xr93F5xxfqWp21vwfF/q56H5xSoStFzqE2hOw5Blfz8CXr18xTb+AS8Y4JLG0A1JbgQIoDCCKiHEUZVTJoEIYKCHEABwj4jDi8dMPOJ0e8fDwiOPhiHEc62cYBkkplkINnaQQqkWZIVblqkhXHEJxBSqK5QNXi3VlLq4xjBadIOPRb+Lt6BUIW8+D1m7hFgnBzDW/JFWjSFPEFktvU1MruQLt+jdrJETOS42MyItcv2japXmWa88XwfOzRQI9LZiXBV+fzjUyqKgitCqrHabQBldeVnL8OlDVsbu/lu6o9TkA5TaakpQo1bnJC7AsBf99Kfj6CxDSP7FkUbAiRKSwgCjiMi8gLBhiBiHgcgmIBepRgxYdbUxJh1tAU09xVc4GqVANCgNSDIjpESGdMI6PiMMD0nBAHEaEmEAxScJqzbkvLWpdCjRvGcMf+15lABu5HZz268Izd+vfW5uMZZHaELlYjYisuCie5XkxOq6REPOl4nMr/NbS7i1ZonRytoiJUqOILP/tukxcy+RLq/nd4mmTR94Ph/ew0FjWWreFWQ2BjKVIxMNlKXiaNSJiWXBZMubF0jMBltYphKBGKydMAFokHY3BpEq2bGAqCLZkSZnUjZeNixOYO61vYwSISPLpmuF4mqrBOMUBKQ5dCj3/kbaoCZMraHO4DyYwAZb6qq8RY/0WD0K430K9fw8YngY3IzSh+kUBxFXmeI5/v8YX1md/A8pV0eGVvOLN7XeKGZ8aQKioL5zor/HFFJ8TaG/qw42GBf0Df2Zh6rfeYX872JvTtbLnuvLn20euVGGdVEkpFCLDMsrnPON8/gUxSqT5MBAOxyR7cJ5ViSG1o0ynsMNRuzch/f7nxec73OG7QKch9zGXXpJp+7nuXpo6Up0qCEjBlPsRIJa1zgVUgigoSVPkcNH1betamDFiRgkr3lhT/dSUPyUCEH6wowcMcGQwZWnParqhIEA98Inl0aWAs9StEUYHQFFuUw0mxIRAAAdR4pqDWx0mGK9UUEpECCLzEoIoWwkAZ6yLBVcfBNoxSABVT9Q+0rc6T/VjHupc9abX6ba8A0g1uHtGiJcYs3oJo3qXx4AwJEynE4ZpgmfwhKXuUyehO8d1XokIKSXEFEH5dt2gl6NyzgghVl6rvffeW+n5Og9q9Fb8NcU2qYOcGU4sIkIitd0O5+Sk5yJbfzUwfSMWEIA4nhCGCR9++j/h49//C9LHH8GHB5RZo0LaTWCLDCFC0HVqA9icskT+YUQQSZh5YK0vA4CYNBopSx1dxWMilpqOLEXjS5XigWjGA6UZnJu+VIbOhexXw5q+Lkv91PYziWzPFvXk+G1t3xagSoftGVTa+qzGB32cl/0Nx/+F+I1XRUTc6im+b8HvF9FbhKKXWNj1QqX2Qz13i7Fi7UmyafeqoMndOxFFUByRhgnjKEUj0zBJXv0UECNJJAQ1/Hd/uGa5RRm4BdQpqyqBqF2piLxn/d9T9rq36K/rFoTbzDce4KUqdNvR/c0tRY9FO1jth0U/1Vvcp17Q9/Ue3uzf1xSIjX58E7xms3r/ZzVl1t61XqnTdn3jQFphpnlZMM8z5hjFMODSLllaGsDyhEegaIoQEmPYQAFpGDGNk0ZCSD0IU2yFKCk9govkaYosrm9yTZFqzJD/55Wq144e703Bd+16YH/z7r8LybeDP0dtBVUF2NqQty4qVT+q4FzjfYsKMm/rtgasHkqLaGlFrrfIsN2omgJ3nz6t6dqLirlXwFpBWrFyPRdAVR4au1/fQxlZE/4JZCrWOvczM5AZX77O+PnLE57OMy6zpb2yvP2l826nLEXAuhrAbna3A9CUbuROhhDBISHGAdFFQgRKQuutPoqlzcJKqcv7tNjmt6H1Fl8N//oL+9+f/Vj6pB366o0NPrJnHQ1RXD2UVjDPFbOz9Ynma1oFkSs41XiGdn2/h2734mvfXwO2fRj9YIZGOljdB0Zmi4Jo67BF5lEVeIPicpOVDLNoQ1rk9y3u2dYvqQS4Kui7Pnc0lLeDhVasOiqt7iIhQvvbxjYENXs4hdzbdzWnbHB7tT1LaHGL+tzzNqfVd7h9wZ1p17sheK7vt/B9ey101zepfIt3DdG3rXaGt76G1S0RAevHMLc/usiIlbFizS/cNgbXntuoMvAy77P3RvuGx5f56nW/9/aZTT9vGVN6215Xb16f+Q4GqFtgb1ye/30fTz287l3W7TU56JZ29uXF555lFxo+Ko3QtE0M4aVkiQi/G2MQh47Cuh1x1Y95A5s9uuvRjmF23fdvmftb5+3Ne90b1vvr5uR7wbfLV+/V729p51tx5P3H/i3j+gK96BSzvP5xw01f7VInvlBT5hqtDhJhwMTqe2e0p0XPGv9Ra0QU5ZWKGikgc2KOQZUP134Q9WVpCRD6EozOmD6CwRRAkHQx8rt0hTjo7wQKEPmDXa58VVySKSdBXZ78jldiU3Ryk7Od7G8Ka+EH+kG3q1aibeVTr8+k561e4gr9pG0lp6v7Ddf/VoMt7xhCrNkXjL/yQcWmp6rfVzKP8blBa6O9hMO1Vcdv7OnLAJsCal8qf9u9XPe7Hwuuk9Ce6W+rDiXOGLHHv71E26/xV9+ku3LzFmJEGieMxw+YTh8RhgkcI3heYIhG7KpKkMdboFIGG0o0fK9jKtKVyCvahUIS8cSQCAn5PaOWg/HDa4IZkaQs3eAB1SliZ1xYQ5sTdKnz7RH1fdhLd369uo41Rl6GdEemr0KqH6A/KbwqIoIroXvfQamLayWUbf9mYGUFvtrmThtvFchuVXismxumI8bTZ3z89BM+f/4rPnz8hIeHB0zTiGFoxgjioto5mQ5J6aQIzVw9UyUioveg7ZRUnkhr3nvrv0/HsTZCAM1T3CIisjMqWD9M8WrpZCxHeC6Lflo/rfBuqyWRpRByXmoh6su8YMkZ53nBYt+XLJ7jmlZIntnm0tYvOWHnzwGNXdh7Lz9fRGti2W5YFolA+fLlC8aUwHnBmBKgxaljGBBjAnOoORhjiADEo9IUv1MMGKYJHz9+xOF4wvF4xDSKl+04TRing6RpGhJCpLbZUqOfW4VrM1KBGSU7nIQLjb3CADQ8bsop5t4Y4cdrb42vIyJs+LaKeTcfmzkoQJFonz2FfjM+uMiJIgaGuj6WjHmWiKDL5aKRQDPmecGs6yBrjYTMbrZfpL+/7ob1nMBaFab+ekCV10CMqhANRussbEf9rykgMtRDgpTxLDgz47//8yuWMuPThyOOhwEfjyccR0JeGAsxSiaUECEBLgXLwlo4Wh6RK+41XNU3gDEmICB4r4c0gdIRaXhETA9IwwPCcEJIB1CcQGFUjy317SrGfMh7ljK7iDZvxJJe+aHc7E06lH3+WKzWBnd0nJnBuUhKiiz4uiwzih2Vxi6L4KFEPGSt6SORb1wWLCVj0d/k+kVybuelrmXpg8e9xmDVkPwb99BbeK7XGiGYSGXEyumtaBK01oArUq2pAucs9VxmrQ+RdbuW0HGoR50Kxaz4DUZgEX4KuNJE3/+2PriOGBEQHWn3zh1+jsX429ozo0KNWJsmDIcRaUxIQ1J+I1VjsoW7i3BPtuw2Y9xBVQq8MO66SQfNb+u99SUiYt8IUQfBf93shU6pTy0yoI6PpsPqlf/vBMw3kddrPGz7/i2MiyklUN9/7TUnArvuxa/kdd/Wn9vbvmaMWI/Z805Nbl1cuf8Of05gw20FU8CZkhFBvBULL8oLLwAv4uwVA0qwFB9rXm+1TqXxfcXqrwzfYnC/wx8TrtG/3ze8vLetJdf1HbRSvoZgvA0hUABZRAQRQpGIBEmJFCA1DjxtYM2O1HgCOxpf2uqZMQhR5clS+2Z8OTHXXPNMrDWZAihYilK0NwkAEHWfzpKFIAjvQEUyzwfl4yvvIp1wfW8Rj3JNrHTPqJLXZQVzjIEoaQuZJ7kpNRlWB0J4dudA1I2+6uFAMpZX6Q6h1YVwxZrZz6wbk9WdjKB62RY/LcpdmeM4TBgPBxyPR4yD6Cgs6ji4tbEfEVGU32zRvzFGBCLl21tfNmIWC97Y+RYRkdW4TRpBTLVdG1+r5bpnuDDwURU295WHYj9u2tHf6/LXfh1ODzh8+gseP/8bHn78zyhxwmL6HDBCETwKUQ1Bfn2aocL9DdvrdmSgGAJiYWQSvCtkmGTrWuqnUdG14ArLEwEBESUQQBkSRS0RUFKDQmycDKjTojovAk0oJdSIDKq8QXsbOSh/QYbX0o99tbXhMZp8D4+Tv9fJf3/4pmLVr4VeSWUEiTe/9fcAppQnsySuYCMvbxbwbRN6G7PnvD3hN9L1WUKIA9JwwDgdMB6OGIYRQ9Kc+qRFlQzXsSXdTaHJ1QO1WsrgFVj1jmpnXLfxnHLX7q3tgevq4FUbtnl1aZ5WufD9tf73lnu7OC/w9nfJ3kPXPE/buD8/LXz1sluZ+NcYpr61jdfBXptrjKG2GYLFsHO5IAXNn2dMRbL0SVrMST+goHKceB9QSlIoahgxpAEpRil6qtfXSIgQ1Aahig8oijjF6taYwF20gOGbMWPr+/p73Rjbd6dcrKAC6lbEBBpitbXUjesK9+uacPeuDXQthyS39tZrrjhD3noN+Loo2Xlfr+ee11QCe2/4m8FGcdT9pkdUlrfSq9UOLL9xmz23DaBAirJ/PTPOlwXzZUFZWm0IKyIcC9c0MLXOHHk8gjNwOAa6dtoYcfVeCgkhjvoZQDEhRI2E8LUh4Ii6PRMNZ8BrmoqK+6vBXOGqo9WrMfeK7SoUGV5qVJqlFvO1e6wWhI9oK/4+1nutIHBZ4zP3/XU0ifC8UtboBdwdt2PyipfwjN5OI9Yzv+zrh1uNCKNH9pvVgvA1IepjyPZ/ZVIVq0shM10B2GRQrFAY6DhU43crC0HVOFGHrnvZfmyJSNIw1YgIza+rRoegH8HVUJX59WW60UJF/4bS/nntexOI9VztY1sPpPuLXGcpBrzHo19/XrlOdRxfo4yrrdV30DlaKbL3FNtdO1WJ74lX3w/nQ+hv7P/u+LwVjdFjHTaFZ3kJU8Bib1wqYr7aCEF7eLB3piHkZjxEgcuNlO4aY7b9fk7h+pIytp+B65Skw4vuAdsLSc8TueM77bWeXG1aZXv+ah/p+rYz5zd+t/2hp83rHq45p+s49Ny88FUc3V5j1+3ha0O3nXY2g8eAKgcLlabsUgWbKB37O6yZ+tarxzy3gr6Xp/v3NSDeDt/LCHLzu+3i5t4Pa97z+/T7rfDSWtj7/b1w4HWGjdePW8fHEbSwrDTVClbrHztdIKNp5Pd/+Rr0Y39LS1R1KMxqjKi6FwFLvbaGQKIYDFpYugSS9E5BhAv2e5tGVDkKJbW+bG8FuX9BIzV6R4nKxLkoWqYeOwO17PZ1z/S8nrVn/9we2nLNO7zxclOdoF3t2XYifD+ugvEY3J1q0b7Kb/kwj71He2Lr3slqnA0pIUWrESEGFIavrdf3v5fFZcwsRRN2urK3LmTYedWmPouMF7F7jT+9tqZtKnmDi33fG8/2Gng7fdCHmazoT3ue1J+GX9diSIrTEePpA+LhETScUELQgtEFlt5a0D8AJHUbm6zbnGr6/ZgdDegY4p13sL9aO/ZhvaRbaZ2h0pamEKktx9RwuXWD2m+eTmx+NQl4vSfZ/7y6c//7Bhzf/xzUvaR78rX7nuHNdq66Fdtes4vcbIgIoVWfvxWMINy0sSqxtg1oPQTV0wsEZp+DnCA5hMk11G2LN/e36w41lAHJurPiqdBNB6rGClQAKiglQMKKJlA4YDj+iOnTTzh9+hGPP/yAx4cTTtOI4zBgjAmRIogiWNwq1cIHFF7ATOqty1g0R3wuRWmHV37279i2GkVsNiNARvPAZTBnudY0JHpHzZWvfpylWF0K8ZAt6jHLVgtinlHyjDwvtWYE5wWwoqe1KLV40s7Lgsv5gsu84PxVcuM/Pc0SGXGZpTbEOWu+8dARSo82bBzON8/0HxNkDWV3gmS8SDw6fvnyFTkvOJ/PGAc1foWAD48BIUUMQ8Q4JIwpSUQEM3IhqfkVIsbjCeN0wMPxA6bpgON4wjRMOKQJQ0gILJ7qRCR7UgCgeFms8PKSJf2WeoCbF/qyWF0Gzb7nLM/M5HDWF0vX35VdK6ogJTg08HSGyy4jFIrmGC4a+1EywCw5O9GeWZThacxOAXgBygyUDJQFnGdguYDnGWWZUeaLro2+YHv11NDIoFlrQnxdMual4JezeKQ/XS61ULUZIwBUDxA32XiLsPDrwz6DFiB7Ccp6zQY77YC7ZlgroT9dGEte8M9/POGfxy84f3hCHgZ8DUcsHBGHMxYueAgRQMR5GaUGj62ZEsEIqmEu1Ysd5HCOCJJeT2o/0PABGD4B4xEYJtA4ASkhDoQQGVraR3JKmj4EVneEBS9YjmCNANJnEfdiQv2u/dsxScl46Nqw2iXtu0Qr5HLRCAg55sXq7pzV20dxtsxgi2xbFqHnRaMl5hnLZcYyS0Sb1DyRJVSHraIkV0IdojBkgWJlKr03e/c+xhevBCGJ1WpVE4w53irpQsdEm7KXqdQ7zYglfxMKAgpFFDAWZixcMAPIROAYNDJxcAYbmVQTjD3WEoAYnLe6dq7RFFTjus00m9Cm6GJ9qzwHAZYT2AvirSgaaZutTsDx4YjT4wMO0wdM4wPGeMAQplojIqUBKSaEFEApNMN0XQpKU4NEA+VuCStzS2ZYoFW0Q1RDjfJ9EeASECLJ+qKijJQZ9qBebkvDjVqxW79rasGgNU7WOFT5Sf14uZ8IIJ2TEMWj0tfEuBqV8SyQ0mPntQ9LR6XeUIaDpBwrCV5381uFlXZum4xr//kWIwYQQmi5eLm+C2OXWLwSanowXde7TTq2u3LodR1auol+DwYAL2T2SoDGt24jPdBdR0QSPQTb+mV9VsVM18Xe9C0en26cNte7vppOY7XtfusO7Od7ozRl9wzaXsfP4iytjnvAK9ls79o9MXT1pFcrqbnSCyLzqN17VsMDeU7QeUv1aqGZOqdxaGxCyQA/uev8M9ZKA9S573qidGz1tpu3+d6RCr91JMT3ef4rdAjSi835l7D1uet+73CL8e6W+6+34c9dV+698qkAWJT0AeCsqZOMdhaWCASoBz/Mc1hWbaAo0cTqOJFUD5RIPJWTZefR/cRMAAEkyk8EWMbh5pPI9Tpv5S+h7bqSWkn6nRFQXGVntsbMCwVQXqvUYSLIT5EiAgdkiijIAAgFWp8pSN56ELSGnEv9oxHFgcSzfi6aBYKVR1RjBwsjDYI4sQ4URFeDgsxZo3T1PnVuCcoIFWItps1AKC3FVNE3MH1aEP4PpvM3elkZ6BWa8HPHtv/LPttHmRj3XylsjDAjVQgJp9MDHh4ecDo+IAXZ55elYJ6fMOcz5jJLxo/SHLCgvEcuC+Z8QcoDIiJCHJGGgoBfRPp7cVsraOmBtJ9csJQZEREUZV2lMCBTQd7dF9rubvI/EWo0hVxDlR8lEl2XpQfTG/c6t/MsJ3G8ydDIVdYCBB0KCKXqWSXdIXFBYEYCkMcJPE44/Pv/gsf//L9i+fG/4OfDjwBloGQkvoA4gzmCOSAPB4CAgAvIFf4OUAdYk5W4OZEI32gRQ+IotrDWHa3v3QwQUQgMUpb1JutH0kcBEP0Wy7uAGEmZx0AscojWfcn6LKFLSUQWZDBngEVX5iMeREwXw0uq/G4EULCUBbVAq74xyNq3N2Gla0Zn3ByuDDLMjp7dAJ2s/Cravt4jXrsvvO76mw0RPgzsLRa4axb55yMh1gOgok7tw3PU0GDb15fepesTmQDjmoef4KragJFuCREaEOOINIxIw4BhGDS/vo+GUDueKWZq27bwqG1Kzvq75yn+HHRe2f4DbsWK/LVo11Tv2Hrfuh5EKw7kc4qbYsA/z7xqLed28wr3hVFblMXufPh5/Y2Z9PeH6+/z3Kt2RlI95pwxz4Q5XgAUjWaIqhCyTZCqUo1tUwSDYssznmKq98YQ1avWe6k25gJY51Xcq5/g8BFoSiS0d/DXoV5jFyjeOvwXVFgRZ2OA3Jqt4O5rl/uLnFe5v97+rsaRPod+vy7Z3dKvpxoZxIzMfWREn5t/3wvUuvMtQuJ7CZgvtfMcZerG+Ma77UwpjAWQ9DmLpLqycQw6tgtLdARRabKDZ6qtMBgTvCGbVQVB+n7RGIuQpMh7SOJlbgykLoKqHLXm9TmmmN37uIHYMheG77YO9sZD18Vem/06bGnQfF0I5qwF24vzMlrVk8jy4VVEhPFNxI5BclAVQ8+Bnw/a/Nn4Mr8ldxf2/EGvuNznBbjrXfNEY/e3ZwD9e6k82H/XbsRoOUwbbWRWw0YdHzW22jNZLuoZxtY4dR+9y0VF+TknIsSkEREhIiqeBqXbpJ8Qgijog3tHImHGgRakYTi9HmbrHvk8xo7/IidKkN0sDDjUgMFubDvjgrZL5I/9mFJ7Uj/3bnZ9pyuNegkZaTsHjbfaxzP/ZHumzaWhZxsZbud9T1eszDV+rqe1rgUbpJ371m3dyrtv5v0qnbccvujf1wvHeH7ob/EM9+B5d8OTnjFf8wJr+WDvLdbft7Rs77q9ft0E3EalOT1dkYV2ercPL+zFHuFeCbfKba9s9Up/XpZrNqS/Uhy7oNRW133tVlGlDdfWfQ/X5dXb7v814D3m6iWv/be1/boxeYkz3Dz6Owz5e0S7fC9ceAvObfUw7yMHdP1Aq/5WDwTnN2j7Vu2VUycaL637P1CLWPsJlhQpV97X8QhrJ7Vu79CfRO9Odf8n08XYNrLiw7t3ANr1QP8e606tjp2/OW2poZN266cqx/1j2HhXJ8ewf9Zqaexug8/ubHpYHQl1bF4DjXv1ZyqjB6JQa5zFGLV2ZY1d77ODdK8jk1blHC4IHGubIDNhbfu7Xeftvep8mG7M8RKEnofdW4NNj+Hffm9gqBruel3fbfvR6/WzW0TYsgjb/jKAkAbQdMJweMRw+gBKEzhEiKNfxUY3tY0v7uQp4810rbe1qcZGavhcgKYLvfI2AVTTtVkaLos2ArjVl3Y8t2VK6JaVyRx1XkvPR6psYrLiukN1ZE13ZWevsaArgYCsXWAHN6/zsdfgtftYHXbHp75a3/qK61+VmulbjRFvBxHe33PL9O9yYxdghKdtFJ5hbgskxoRxmHA8HvH4+Ijj6YTDNGEcRwzDgJAiKDolFhrSMmyxATmrwtLlFLfnbRRP1qeOgFkkRIuG8B7fsrr7+zsPbi7iLctqKNDc9nmRXOFFoxxyXlpqmZwh5vmmUG2/LbX2wzwvuCziGS458a0ti/K4w9tACN88z5ofN2OYIw5acBoQ3I9RPhQ0R14Sj5JUCBQTxmGQXOPDIJ8oIZJyn3i5hqqRczgH7BbFbfjYlPZWj4Rd3sRrRgwj6MziBeKVoXZfjZpSBvK5Nb5dO2uGarvZ+Xdo6cPcZ/XOfk1YIeqWhmmp68BqRfgC1X4d/xpCzR8NpBg1cJkLzpcF53nG5TIjTQVUGHMuQCh4mgmxAEMsoEggc6HNMpYl67wbn6E8RQHEUAcCQkRAAmgA4gBKA2KS9EwhJs1bG1BWKiOuUWWNDvYG261xud7rztffO4wkHYeiXkHbIupmbLDopFINvo0ez/NFcHEWD6NlkYiIZbkofs7I86znskZEtIgfW4MbVmmlXP4W8Ir2PeiU6f4a2mfYzJ+uY7DcXmxthBCQUkBKhJyBYjwI977rduugaeqMUYwBADOWIoKqOtNAeAVztHNGWdfXAsMn6Wf/6rKvE5HU6WDWug8BwyA1IlIaETUKQsLcYxPs7O8QXdg6oTpxrRyBr0cOmFfz/jx3hgWsUjHV99p+6j31e/+3CAGSD9ZyKBfKlea3Z94GL/GBt/CKt+J5r0Tf25f2+ff1PVVQ4caR3qo8vBnek+F+6VFrZfEz7+Llj6oTeRfF+B8InHz4mzz+BTx+T/i1nvNCL37DZ9/hXwn+VLSMd5hDKK+zcqiArnEXs2bqzNaM5Xnidq7qYW5UznklH/TvdcZ319H6Gu7rzVCd5lZ3iu5SlZwme+7IA3s6ntaTlcxqWtaN1QGra1wbncjr2zOZW69ZGyFe4ileM1DWJSIgRoRhwOEg9SiTRsSi5KYrU52YKJNF+W0KU2bCovUXh2Gp7ysKaXHCEcerV/Tvua6T1ijTDCl7chytDAtreZ6ZVZdCtY6h1M3s9Su39MWO1x1QdvgsHaNs66j43zVCWoU8RsDChMcPf8HxL3/Hh89/w8PjD+BxBAKkJqMZEigiDEmMAmx1GEjlJ1ZDYtPbsO+T/NHh2VZm7t/GIp1jSghcaqIN0locOS9q1FQ86owPIleEIFlBAoAYrC8STc2mL+UCSdfWOmCOXL6vxefzVRtEjaollUEtY8cNCNnh0ItX/7Hgu0dEbC3wb4W10tCOK+K5urZT3az6covgRrB1qhikyGvqjI7oVOE6IMaEpMrcIQ2uSKSmBiCqyKkPrbkH2RQVxYpSN0WT9W+txPJj0+65/qmb4w7B2r++zyXu01VwpwhrhZDWirGs9SFKsUK+vKuwvsNbgNCKRxn+SJqkQlTnSwi/5SsUlavZnwHbWKW4UAgBweGsRfHYdQJsNjpU7421gp77nI4bPNxsNttrjaAz1uf17avxgatCao9ebfCrY75WwGi/7TKI5kW+7W/ZedfeUMGuJkqft1+u91183zXxa6yxd1eKXYHCLZpkyUJjQmEsYofAoiHhVAQ3fKEzLjVDlzK1ij+wgEkCgqTwYcs/pun0JO++5S61tWdNGWPFnSHC5tUfpS/t04+VlwX2BBITyHqaX9+v4p3DV1fvodJwwzuLcHO0eW1cY/cu9hzjo94kQN+ADjtv/Tw42tQ30qJVfCvGiJpnk+3hQWlhDKS1cYoy0Y15h+IMkTDZZA8jqqHxEf08Wh5dKoIrXAxT/EvTqmfo+QWjtW4uiCQiIqbU6LcL/TahqUVHUDNCEGkRNrhx2Bta6v5ugtZLs0L9kXSadgwR+0aI3jjhC6ALDsrgdLzd7n61DywIvMsjdgaANyqJ9trrhFLdym5uviFy1+4zPXhtj/u76j673f/fCteUy8+N9UsGCvv7uWufe/at0MkIK8XC3rNvedYt/RbF1W33r/HhvRWcu3h8A9w6T+vzL73fS8+51u5zbb3nmH1LW6/Bn1vuv5UPe+m6a3O4d9/6FW4ec7us7n/Un68/r9bclT7/2nDrvH9PA8SvJVd7PpVN6VZV7ZZaG86ogGcmSvkkV3TWlOKFTX8nrbJtoNyhy7ZFo5+22XK72rj2+i5V9LPeNxl0tf12I1BHgrn2x19vf2/bkHZNdqwybzd3JqzYX8b7+8fTG7bl9TP0yKsP/PE1be6c3ZkgooAQQ3WeCSGgasbX8rTcAHDPr5rzbincFSq3CGCr+1EUl+z35zr7HK3a+1gfvRFi07RfJzYcjveh+uyez7/WD9/u89/XtHiN+XbWNJoy3wSWqAdKSNMDDqcfkKYTYhpRQhCcVrm68rLBJBhbv87oR/7ZpDJB4ycIO3zti3u+yGHMoeGXjaneb9+sfZO0AHL12anvA0ijplZ8sbVvL2w63PVasR5Qewf3+i9CHYMrvMwfXW/6qxarfhZWgmMPV4hkPfKV8+8IDClEtDJGAOg2HCAgDQOm0wkPj4/4+OEDPjw84HQ8YRpHpCQFJKsnYmibrFlBC0x5n7uIiK3CdrtBbZW9+wpg80b37QF9xARXRZXUhfAREMsitSFaRITUkEDJkvu/RmKo9+1SNApiwbxkyfe3zM4jvCAvZnhpY3uH20A22egKzDIKAXnJIC7IQ5Qc5pIJE4QFgRYwzzr3QdIzkeTTHoaIYUwYhuSMaC3Xu4DiVyHJL8kAs6XaKrX48lKy9Mel37IPANUGw+Fn3uCrIMUWl6tFmxpfeVXZgy3BXit45R6nZDFmheGKrpda9yTnuUUEqUEhc/NEzzljKfLbrN7k8yyRQJfLjMu8dBFBLcrie2DJnwwYWBapLfN0WfA0Z8SFkROQZvPwYMRcMCfBlahuEkXr75QFxtc35SiE7YqRkEIAcQJjAsIBMR4R4gSKk+SlDgkISeoJUKPlzISsBlfDf9gzi9Fq9yqM3Tm/dt7awDP0vdR0X0qPc4vUqRESrhZEyVnq/hhNXxbk+SI1ImbBc1vDdQ/RPppQ+DZh+hmF4Y1XmuLZcZXyBwcnUXY3KC0L7m8CISIERggFKWWgEDhFUEkIBOSYsXoIbO+NmsfcWNWoY5GUSa/GBjbhsUX/dcIVM2YmzMXTWqoftkda3RlmjOOImBKmwxHT4Yg0DEhDkpoQKSHGoDRcigDGkCoPQuoYQQFA5vpqzykI+99a8enNnNj1WEVE6CfoHHSGkhBQ6ndCKdLHwFbfgWXPsTZCAKvXk1eM9QaNraLqVvieCqL3gk4I3n1PzyO/1Nirnnx7u743LwjLu0/a4Nfzbf5acIsB4T2g4fG7Szf/UvBb4ckdvg3WNVrusA8vG6W/P5iDijsBcxToOac9Wcf4nFZXybElSvwKghUu1rzuBO7q7lR0WRHMqsMBaopIEwKaE4Yw3ly5OZU/7TvvoyI7ObUqIrkp7S29phlENopEFk/xjh/s3qjt4/LucH1yCk8r9LAzrqseOyHD/i6rT+6/o7h38gpSx2NYwY7t02pPOigFFAgpJQzDiOPxKBERKaEsC5YiGULy0hz46vtKbmnlqxnLsiCEgGWZ1elG6peFqJ7yS4vkfgk6HcQOhCB8tbmu+awla/Dr0uZdInrbnmRe/TJWBVbU4lp7147NyLG3163WnC4S70xkGFRTLCku0nQApg84/fSf8fnf/xccPv0N8fgIhIjCGWTZUIKkR0pRGiMpyyAZBtiiAaQvdYHWNbKVI4xuSFf36ZsYIAiJkqwNk+WrrkhoRgKrH1lo7+fHlIL4m+X/g70/3ZIc19UFwQ+kZGbuMeWwz1S3u+77P1v3WlVd5+yd4W4i0T8wEKQkG3zIiMwIZirMTSZxBEHM0Nx3AKryKcySPbftGVVWJPK8jkwWtSPuk25EjU5/ZzT9Vzku/3RFxK5mceveOxCLozB/q52tg5xtw8jptTrctCYABEoTplk8IeZ5xjRlTxYcmXHvQwzKrOIKEyY3zTh6xO44Px6UW4qI7Uv2UhzjgJz82Tp8slvONk8IRezBEr4PxzN6PvDqMqEM82Vq8z0IrG9NtL1ZCYSI6Lg4xAJHuBqsyAFaPDkP0uTCqVFI1IRI8ihDk/RoAtImoDSLa7OqVg+YAA8rJQNfgt+esIv32x7sD+Hx06dIDzzbL42A2pvSuFdC2+4NFKzHw3i6XVnZr3EfNKFxm5dYooXFeP97Lu+1p9jgVL6BWS1gmDVHBCNVhE80QoiaJXWtQK2EKiEtAbT94RIuIlBNqKyJi80bwjwhSEIymQbD0LFCyi7OjURinK9Lc9aj5sYMtR84fMZ9UwNcDXvK8fiIy3vviIbr+77T0Jde8ccuEN1Pwkubf68F3TtvbzyzfXps3xlsY0Duui1eA0xJPCGyXBMnUPOtbW2yAJmPs1uTxvRKS3KPiRvhz31uHZDCprprD3S6tskdjEGF9h5+ybwgUsgNoXjcCOFIh/Rz2sYXPeX25rzhJ1Jl8AbTNNZnddHYFztzTDE0fEblgn3yzjiG9/bIigZv5EzOS/Dr63Fyo8Eu1bUnjo6C6nvbbVJ9bv9uzOulsscYx3qBnjl+yVyP9UY6/rVC5te8e0/bW8YR97V9G6zcXNuL+vCy+m2dtuYr4o5RsDLSc9f6uvXcJdpwLG8BT99beT+67PqacHcuvrCuiKp+kHIvTnlPmL2JD9lb53tBj038P4o/ep4xpI11qtO/Ew0KLN7py9oj4tYiNE/sdjMmcxHNBps5nuDjTHIY50oeFehwRkhuzbw5htYWr/sz8ODd3/F7d6H91j3Xen/zgofHKCXJb5bFYMYMhTqvcrRzRGQPbdWFJq4ud2gCfrko0MC34KFIz448WkfnDDzLtXOq5/1W07BzYx9/7+33bR7JOJ9G640ezWI41MInuUxpPiE9fsT08AnT6RNoOoDF5xvQhM29vMXqilRr42soToB0GODeI8LG0RkV0cAUefcbj9WNMcC0s/eBkg4DD+y/Gub6TVJPrEAj2ztMHQntf2o/SeNA0d5a75RblcqjQvOvRrO8WBHxJlr3HVxwqyDi1iYwLNL49+Z7W0yUYEDQ0G9HxUQAZcyHIx4eP+Hx4QM+nB5w1Pj8OcVQHu2wFKYieEJwL8TlDQFl27zhELD7owCs66mFTarDfeuHCUc1kWntY4qXekapC3iRnBG1FLBeMcQMq+WthGQqWIpc57NY4y5LQTmLF4TFxv/bKAS+QZHwHlU12YQpEXJizFPClBNmvVJigCqYxRuCICbhS60AMtI0ASmBcgZ5XPHU70kSpMpUpcXKIEriEcAslv/D+osQvn2KoqIIvFYAaMoog8NGfBSH70YUKPkZT4MdZQTiI06mcSP0Ls/sihDxcDVLkatLtD6E4QGH0EHiFfG8FJyXBUsxTwjLDWF9s3GsmfGfBfCDg8SNuVQWD5OlYC4FWCqeC8AEpCSHXC1JCA8W1/BaVIFxNkKMkYiRzKOTgJkzjnnGxAdUnMB0BNIsF8nFlDVsk8EfiUcMj+GPOHhEjJZKPZE7WrTE0pyIDN8LPpfvLbRXxNtV96X3qVb1bjAvHIPhglLFG4L1d/vNQvKNfdIt5fejUNqfS3vn+fUzfpsAXROozaU2zulWG0KoWkxXSUUu+CuRegwwwImRcsWk8bsIjJwItaauLlmL3oOrlKYkEGK7ufm210j7IgqMUWnVLGyo4//EGqcJ5kzhm7Ik+DscJEdEDp4PzQPCwuw1Js6YqH7i7LP10eba1nhrXcRiiN3CK16VKxISKliVPRzmJHhIqDdEooxKVRQpVZXpHD0pssSeJQaS5InYZBRHLuNS+Y5o9z1hEpFZUqLRoo3tASWhF28+L0YBzc2T0Nd9WQlh9f48v96q/CgzOTLYrxGyjnVcq+vW5/6M8j304W3KjwK5P8tLihklqKTCBX+LCb6VZ0ts+1lDD1MCGCYSVSWEVYqQKPtS40qVJeEryazsL760LXAf6R8Oz0UBa1WjwAQN/RLeb4IlGafjr6GNyuyyI+jjsdfkNFzgeVkEx7DIGMYUcW2f9gz2PCGaPCl0fD09W/OzMZOEhJzEi/d0OuEwS46zurQ8i8Y7CR2bneYUPl3qqZ4TT/hxMcwh5Dwp/5PFy5YKrtFI23K0VsyDIVVa+5/soOtYl3hE2BlzH27cOxM2DYHCc5LvABK9JIAZyBQK0pcs3IYYqaYEpIzDp1/x8B//Jx5+/1+Yv/wneH7EmRPIwn6zeiWpsTZryIqsuV1IL4HnrtPyAZOjrunJ6Pls42SPrQwnXU05lVQGU4vwrlQLqFYPz2xTwizeQ5Y9wh1sCMgk3wnWb+HH9B9HLGQKT51P56uMPjccpN/N+M0UFf2GUOXF3+K8v63crIjYA+7Ruulaae/IWr77ZN+4UftXHELlY3wf8WCjoIOTzZryhDxJqATPC6FA6fKqUJf/ZUjBEN9GN7u+sznmDYLSAXmaNtD2zt7B2XpiWmVVWIy5IIIlbZ/fIcQR76y9Wxx3CTVVPWxJ7SxtuVEPK6HS2xGwf0+BrswfKdLMCWLFmxPylDwxqREdLYl5AbFYjouAB6BkB/2GZSptePQQHF6aIFSFsfZ9sKpmJXIaUu8ZRbl6L4NGbNjf3IY+lFEQQxSJyrA3pEEHu23Y6Pty61VtzwQPEWY075DgBTGO5VZrvx+v9POikBCE7JrImi0ZsOR4kEhGJKF2WJQXXIFzyJ9AYKTEDt+UCBMnVGRwmoRQS+IZAZK0Vw2ph/4ok2Tr7YwIo1/rOI6N+91+gOHl/jdnIjDmJemTxBuB2fZVy0nScMHoJTHkhNDBmfA4Ev/dCl0903XehGLbf+qC8sE/afudsb0or23qvkDkkhC5ItDWEEApAYkEj1aJVVspuk7bP6rcqkaUQs9ymbORTnL+2BhfEqbXlpIZSAwku4fmZE9OfBhESJFEfNkv2vCIWOeFaILtfg7R4XtQU0Zcnmc4Xbeef1c52C1/wYTp47qa5ZqfP93fgeAPMYKjMs8+2xl2WWBudNz2uPZp3NES7uWlF9bfhuOVaQlvUvz0vb//tu1jgYUGs9vFcBLdxDi3ejgs+csFyfcKhq8pSO7ty0vP3REuV7TJRrm3b2/BS43ju7XOcXx75bV9/Csz5y+d2zdoecDJ+zD81mRlD+fre7G8dD7ukT/8CCXO41vNyV31XF3G/pwbWnIZiLQrd6vxfzDyh5HAgT7qc5VFaYbTCvK1CfJv6Tvt9XX7nN6Su6zb6ImkvbN7s1WX5WxcTXPhzzReNxCX3RUUEc68YP0cEGiJ2A6GMY693hrFapIBCL+Vc8Y0ZUzThClPYoAC6iIIEJHLM8wAhZghBpZrxY8I+kN+1tD+iHNWcG45AYa5NlrU64h0psse1jTSFo/XrjXPZ/XvGZbccm+b9tH6Lfl7YJC2qGBKGelwwvzwEcePvyIfH4HpIIZ4TJIEmgJvGHmzQL+3fLvrrdW1ukGvj4ZPJnsax7yWIzX+lYb62zvkHfDUNTYMkvEBomyK3BDZQLgKS+tbRcfo9LnyNBzmHtv73Ovs+tfji73yVz0LXx2aKW6QyCRcmgh/DuMivJ0nxFuWxqA2pMwwNxuCxRpDmkDTEdPhEceHjzgcHnCYZsx5krAIgQlnl0JYbSY464WW+4Iri0MWDj3AhU8tDE61nl+lMjshqsafZo0lXhe1kNVP8Y6QvBB2xTwRFr9a4pGL5e15KRITf6k4LwXnIvHTaxGhbJPsfH8w8P0XIcdEqEaY5oxpSjgeJkw54XCYMOUMMIsl9PkJ50w4z2IFvJQDKAOzJqqeJrFGSCmLpbBeW9awBm+WIKq4h8CYE6K4pwyL5G4Fv70gtYT7ZpUxjNoIJ6wJ8CgE2Tq0nKjT6WvHw0AsqCKiuvC2F/Z2V6maHyP+XbrfFs2bsQQrj5iM/jL8G4FFV577mxcdvuAqUW6el4qlMFIBFhZBbkUGccaZSZMDC9GxLCI4fj7L3JciMZrEuUHyQ9REyDxhoQNqOoHzEUgHVJqkXrdrkDPAWCWHk8GTrVcM9GWLkIp/yx6D4/MuvwqzepS1UErFEqHzEpSAVXB1WdSTZ0FZzuoZcdY8EmfB8SEvENs+DMSckVcu1N8gFK8u3tYv9wrlBibg1kKaayClZqUPZHDNSgMyCAWS/CYhI2NJkDMRULwhdEEpsh5nVQah9MSg4KL2GeGGCBLdC9wMzljnlkmVlTJbVXkG4XF6JjGnCVOekSe91LU92RU8IiglUCJRtOCyWABA7K2vheHXyCTJZ3xTvU7ICPuqnitRqWCwA6+7tdnocfEbSU7Q+5pDJrDFXg4E+wgPV4TSrylvVRftCj72ngeM4U0wGrKBRxffd6/awDxdU0DE78y3j7vxpOs1uEeRM/IXtzS/qXT6DvmMewoF3PtXKS+Z878aQ/39llvnce+5v/Z++Vm+j7I2aegLB8G20byAsn4ktDUBmExhDqCwhGcyasbPMeX5jPVjFwJu0+Ak5Ep/XoSXN6h2tP3CfkVBuMtdjEdVzO1tcDPMJSWUPO/h3hxhLWRlNhmKzJEY+bV8bn2Yb71UTiMeEHZP+1s5eEb4woTPMSJBnIt+Pi4Xk/ZKFIbj4YDj8YSHhwdMKSPrLCzngqJeDgTCNM0oU8GSF2mNGeblXAFQrd6yhHiCeFcUBtGz9qtc7BnrPFQSuUqtNdC6DU48r1kd+R/j03lVr8Fo9OQVnq4EkBJPbdL2vU8b/bwmb/VParQD10WWXWlINkJdBJTd6uXDCYdPv+HD7/+Fz//5vzF//gfq/IhCEq5ognhQCF3fjLhAMleZMgCg6Lo4r2CKiY3ub9GGKXhEAOwOPeM8CMxXz03KtYJU6RaVSI4LuMqYuclzjeNIJPwYEYv3FRRkBVmoEgywKB3cOhQUM+hDxL2KrPn70UR3KCIig6d3eP3dGO4eQW+h1I17V2QXspC3upxThwJutdiJz+52acS3ABiCjPKkCSLngwpzs1orpoYQ0NwP2eqww667emFG61/1DbTafMwrgdeuZn4LoP1AMga270v73LmME15ZxmvuAA6eEG4RHucx9OONy9+ZqTE4TUTIGg/R8pLknBQGZUdULljKGcuScD5PoFSwQJ6BHiSePLQTGulv6K0K2NdVwhC5UN7oGU+gXZ1Is0Q+o9DVBPw9/NZdGL5klOl1O/Ln4bdGKGpLrV29uj0Vwo51MSuHa1ROuKKGo5cEgodI7FpPcIwESJyCv4IsZW/PvakgaAMvNeFaIygZFaA8rJcQUqUq81A1zAslFCZUymL1YR4R1FJ4+Vh0f0QYCp2Dc0PDnNyCj7yf4NV7Ps6uueF5ZSIYbY6qMim9l88I3/b74JU0jGNrHdu9kZ26TXnWBNypg/GurV29RNsvQovQiviL9iyG4ySeUPVkyDlngBOIs8yJzidB9y/51KIaL0Xw8EHSXsCRgSdhI2BDpyiMyerJIEm4Rib0ZWVSqdHu+mKaMvI0IeWMlNU7QnNcpHB13hHKBDY6xNZ2f432xAiN2dE5jxOO8JVHZcW6jo03lV+V/poCw/5GgMPOYn5QmtPQxu4Yb6Ux7ywX2w5gusb5L+tLp9zRM66jig1ML9bylvPQj39UXsb7d9X6QgH3Pe/dwz+8e7F1fbFweC0c2StvNe4eL1N3773KW/X5W5W32wf7a30bbrl/n2z/dtu7tygj43Pf1d4M5Xvrzz3lNedfby/M7fsGs2Z0T6CCwEALN6S/eEhKfcLMK0UIqILVhhjDQHxA/fdXFKMDI3/YokU0mhveW+0TR7zL4bIJGM8k9v9GfnT7il7MGkpVk027Id9mAmpun701TBuL0/76rPUpjmWEmWtzHclNpffzNLs3RKIELjUYOValg8np2ZwnsPFsQiyDurmFy97MEOdWPsRXIPD1onCoSFnVXp1Mrz/XmNeTsE3T9bxFLKbwSCmpsRw23r+nGO9anRZ0at35FoRP4Y3y8YTjx8+YHz9hOn0ETQdUosDiaL0EV7SZ4sN+N1AXJwzFChz2bTfujVyfMIxiiqAdWn3gi4ltzxrfACeOufIKvONcOd+h+MfabOvd1pNg68L+KfNrHWn7/FIxXuyvfH7cW944WfU4wVc2S8TLVybdAeje/edCxlDXTlub2sbQfmPWaf0MEVKeMM8nzMcHHB4+4Hg84TBJsuqO6YpSBz1qRZiLJsj0zTEisuYJMV4AOuFnP6YeOY/jbgeqatM1RwRzgWWAH4XEfdvtUGONJ+i5JapZgTOWwljUE0KsxrcWdD3HP8vlYoKWnIApE6YkYZmmKUmy9CzKicoFpRCenv4A8wJQRUozeJowQUN6JMkLkVIGwQRXkqQ3QRUR3A6WyoxaWCz8LQyXegC0ROUt9Es1wijEyh9hqVNCYFsRcR1RbyOLTqgf9o7DcThcZD+yhxezT7tvz7XY+2V1LZWxVJZcKbXAElOXGixWGABr2Bfq+/ojHUj3FlPyVLUcN+0XtdhMQkOUIt+n5HiVGahMKJXwXNTjhQtyzjjQhJkTKk3gdADSAUiTS5zNimRUynmfOmWVkiMb+PqW8ZliofseKKdNfGy/2X/uEdHDqed+qEW8JZainm3iCRfjyMY+b/V/9IgwYhHdHN0Ky9eYBfLcE1sCTbO4oS2awdbOLGzAAEt81MxV+8wgTBCvCIm9T2CURSykmOFxebOGtas6ZrOaMRO7GvrhtD1MudDmpRHWFdnHIc+bJwQ5YatrrOOeDzMOxwOmeUae1SNCPSOmPIUk1jF8E/rJ2Zys/TWJ896YBp/gHm8xYB4SaKT5hdIrFFsPSOpR4br1e8vCPioj2vjeVkC0Wxfd+Nwd5SXMZ6eYeWEd/SJ8P2fRz2PxxylvqRy8RRHyk+Z6r/I2a/izfN9ltAynTubhTzmBY/Si81xoxlsAQkhKoc+URINFd291RUVIK00KEgWFq97cfKgYjd0rAdiVAEaidSIutH6boWZsm5yciX1Y86PjFaNfsOV0MxlOLWCLUsGL0vMWtWL0iIjfPUW49qHawOG0p8/sxp6+eZuLgBeUQXnC8XgSudnhBFTG8/krlqXg+fkZbIFxKGkIpxl1sjmoYIiSQGTeAhVMQJ4ycpJwT6UUyT+mdV3tKKsMglObY51vSoHmTASq5IqKWIFN1Rbf160jGOQKArS6Y0jVrS5eOBe3zk3N4oAQo0V5lgxZZ/HKqAwVKM04fPyCj//2f+Dh13/H/Ol3YDqFKOoM8+Amdedxmz1Td3DS/dC8ou1tbMho+0Egbu+gjOj5j2Ysh0FWpDn+iFokGli4NzRd3AjKNOIUluTVScJ91Uq2AAonJrsKijrfR6Ygu6W0/T4aWMUZ+DuVVykiKKzD9Wd7Rsj4yNsJvia4t/oubsAb+mLlJgLXNXj2j24Hk3YQIaUJ0yzeEPMh5Igwy8S4+QZho4KeV08c3BI7pB8FpLX7viXoGjWvYTib68b+jh201j9TQoQwMh4uJwj8TDDWWYWHw9qFhu0A9TnB33GL/UmFDDEbbcdycI9woSGzlvMZRBC4zAyiBZQrJGlrcuuBMb549OyxRKru5RIEsObx0h3eXbz5YOkBOwjWyXBjWd83BE/rZ2gbB3T7YiVYNThuJ1Lca9FS3D0dar8nOsJiDNtUA+yH70NXQp9sn/7cEasSUCIFAS0jEAOOm5TSIMGrQKMxRDmnX5gkiS5L8jumDEoTkCQh9WhxZULiaOnVw4DRIvtWTFeHac+iCb5X+H2DKRnrj3jXFRv+XIPdtUdEwxu+R4b+3bJYt5z1vSdEb3HSHho+bymEDbdYbpxhIiR1xOWU9GFRuBIkZwSQwaXK77B512RuZKGF+nAp5urMAa8YP24EMbOEEEuxg2pxkwBPwi3dZIFVWHVWX8KUJ7EkmzQkk9Ib7gmRUjevdla0eZTz2+9fmdCXW2O3IiRDTMy+8cy1nvhZtHE/MDztbNzvN6Otwd5zW/c37/k//e+77Uf4DM82Bc9Az43bIjxzC03NrhV7WXmNoHZkqjuBzIVx3DSPN5Q9JWr87RrT/z0Jqu+B1fdq655yTXBy62+3rtXW+/d6ZUhdt+DGtyuX+n/v+9+y3+GXi7+v17d/71ZPiUt1vlf5nvDBS8p78BhR3HFHT+CyBzQYcGcCkvxZnhPCGhiNDSKxd2VobPXblytPM1fQJXqe++e3yFhnX0xuEkU8vPa4uOSBD6Ph0Wj7RtePglHhJHo+N/C+8e/Og4LRKydsrJEneAFNETyWE5Hkh1DDmcJLF74YxEhJ87lxRk4Tcq5I5ey53TAmM2YJu5pyU0RcEupvdpHha2CKhkrVQzZFC3mTkUgYJ6iw+vKkWP1wmO4F0Ea3rg2trvOQW7LAjvajxga16pWpZoBIFBH59IjDhy/Ix4+g6QRQFvmSyUVJcjECVYIUM4MqgJQ854I1GMOnsvYh9tf7DW6Q5vNh/e09ny3DdORRjTNIqoDglAKkmnwqROzgxtm0hNlN0dFGAOctxjOq7WPrg+Gl7b1h+3+vjLTxJpP0Nyhv7BFxX3mp0HkFGAMTEX54o4UzxMC+icdziyBuYvPhhMPphMPxhMPhoG5m2ZPrkAoyanifAd8IfkA4nuf+SbKDay2QGg+s2P9rM03ertVjQi07zMQzonLxGITtwKxwgQuaMMvj44fDpNr9JSYv/msTcd9DEbyplrtu6apwYEoBVJSlgAA8Pz2L5USpSFPBnD4h5SKKiGSHvLhHpqCcMGEWoOBCaGGHbG01Zv8qP4QJNNEIm9UhOQpcvPDwiU64eZPwZdgrI27oDxUh2Fx5U6t6MDSLExtT8/gYc2JY3gjzjlDPEc0PEZUSQmSvxyBjvDq0H7Nww1sEjRFrSiK1BpIA++S4jTTGbFKKJiVCYgIogYlhDloVCZwykGdwmjREU1uIpHH2k+41Q9m9Ekr2HQZFRPRY86FsnGeI9ZmKZVA+ozb49PBKXFEh+FqeRceUeOzMUYGm3krVLaksrNiQ9Bpb+xONMFzdvweGKVzwc7f7Pd0mDI41qlmO9agJibNYMoEySCMNp8oolDQnTgYpfNUs8yUMRgVqUqaBTY/lF1iIWVmzdrYbnCZicAISEhgJTKKMcKYDGvGW1A5MwzIZ0WTMJkg83ebDjOPxiHk+Yp4OYgDRXRMoZ1BOGropqaOKnRNoc3N1hfrQZC8qrGsc+dm4RKE7zv9e6tPGOUAY723BJq/ev0Uocysj+1oB1aZF207/onXYfn06ld8pP7OHQ2Jpa/Vn9Oj7LC/lnaR828W/T/h//3s/y7cr7yHQ/ll+jCLnUjO8Edqz/Wjb3wyR1Zd1pfCPZhKXMIbTvXeIiVgPTzahsdPOo0JilL+sB9v40NafwEj4e84DDDKfVpX9Z9EDBh5oFYrJPBysvRieyYgt84Su62e25EmrMd9TROhLKWE2I96cUUvB+fkZ5/MZy7JgmjQUk0ZkqBNjKoxSzihlERlVpcB/Cd+ScsY0T5gPBzBL2NVSy+1naMfT1U4RkVKLYmBKiChnIPWe9pFuKBOIGsyMSgiQCO7H0EwvKQZrFaw8DVvXAWjyd5cxaqdzBh1OmD98xunX/8D08VfQ/AFczwAXWLhu2Yci8K8AssJWquIaUTtaPAFkfkyqQBj7ebHIyjmtS41f1KEIr6XJs4kSOKmpIkc+OhqTsr8qBmitpa5OtvtNMeQoyvaA8nkI/Nr2glwZ5g9UXqSIuNXN+5L12HvRK97mhqDxUr+vjwUqMG8nox8KKtQSl7HJrRNzzi1GM4Xj0boY2rYD7iVlPJxGYe64DLKB21jsr/4gtRBNJugyBQNLIurakrJyHTX2NYT3qB6Cpru4JeTuJuUdduePQByLcLWtNcHOk6relgxokl7mgufnhFonMFfkwsgPFn/RLGhN6aDCuOAdEQWFBruRABsF/s1qw6w1+r5vae31l9U41/uEXbk3vrclW9tTdHBQPKzGhQb7nVcH0B9iG/uwu0YvoSGZsR6vqzHvzcVfubxuT4Y5MiuUzmKkEY7gKrblbkkhLIQbUqSExGJpwyCHcYd33QdQ4lf6TWMvvE3Df6YkAI+4ca1AvjZPtVZ3VTeYdMWvhk0yRUSpxogYvDUPnoZ7Wx+tPs/fY7i5msKi+N4dmY1LygibJ6cTb1rTZoESPSKiNVAzfBtmn3sBZt+38QBEJ9Q3k7WUCFwlSXlCQmICcUId8iyAFeewOXjL+918opEgPt+1qrWN7nPR4oJI3bLNAif0OHr7yMDssrNd4V8VDjlLTiDq9kUa5nSIb+pz9LY4ZpMuMfi1+cK4J8Y+9Lj81h5uekRc6Stxr7i4JPCPnzs92IXV6+/u1HijkuRScQUWIn14m4XgOO57lP9bj16al4ueK45jtuvdwgX3zt21te/ObRcorD1Y7rHw3+vD+rmeVn6NwP6Wfr6mbCum93H1S7w7rq3VXrvx3Vu8Kt5Cqfie5SW44VZe/t423nLexjp/VIXUPXKX74bntX5cXDJuSoiVkFsMFV2BHgtRIOGUpo9GLGMfbuhqmzcO1/icEnaB7410zGa5KN5guHUAhTZDfyIP7Z+xf8QDBcftC4f6VwqSkCMgVsnhvYvzt+YL7ioubBdPh5wtLLTw9GbIanK2aZo0YTmhLhUlFdCQLHrks9y40sOTaj5MwkZOhj0eot3b8oiwd0dlxF7dW99jHY1+tbBmL8d7I70X6Wz34R7Jf7IwSwnIEzAdQMcTaDqC8gxgAUpR+RCrGkMYKyJoTkap2JQVY46YXpq6pk3tnn0n6xeMVlfeEC3/g4xF4dp4O8UTNSUQSx5TKP1obLpvI6/JPD1CT7t5E5/5YoKE1d6idvvtWavd8t3g/TvLu3lE/BmH4Xgwv7TNS4R8T1BFnLxGvpSSJKieZkxZ4zTn4AmxwfC1g2U8CF9X+gO1H5vPV7hfQ7ty9ohAyixjq37CBFSmpOBgMevhaiTOeCkLlmVBWYp8lqaEKLUlsf5ZXl9cEQHJu6rnmKwdAUupSJXAqEgaWz3nM87LhOlQcayCMUXYph48FD0iJMSY5IxYw3AXqmilmBqtORzYByFUVyucMHsJiNgBMPQzfvYEVu0OvVZJIDY3lBB9iKa1sDm+W2rwjHCB8Nbg9qnWHgf9iKVfm94l1sLnsYbRaRZAGq4SRngTAEqSEJgB5KzW7cmUbuTKCGhYpp5OMwJEe8NRiB8UEjVaXNymiIgCkwhfFaxGSgF+2RQPpuwVj7XmtWPKiBBqKYTLa32KHjztPdSWI6LnYSKZuC+Mu492Xp+PxmD6nKMn/LfKVUbdLLAYQmiTxfQlSVKtCqSUEohFsM81JHy29UgkuUi6bjRlq1EI1eCgiIdKIvXIYQKnpgQBCFndhx1GwR5OTAfXcKc9Q0ni4M6T0xxN+ZAc3/fKiI15s+sd8UvDsaHR+DsDPe4cmPArpbM4wwAnd/Jxl+jJW5nCb6WEMPf3nka+Z2EvjzvC0Wtp1lsY9FXvnOYHLi3siJPeo2zjvbdZ979y+dHG+7P8mOUnnF8ufMu5s3OG8MDHcRCcS1HhM/RMMjFiLxN8oSBw68xk/9ji86TPPa1MAJgsesR+W2TeBtSUG14fsNHO0CedGOc9nM+2h5Wfdl2N8eL6kwmC7RrGe/sc3VOaIoISdaFFAXiOUWbW0E0TKoSXdqVCSj1d6zyOXBIaXQyE61SGpNUXeqbCalDj76ydSrxSRNg7powQq/v+t7H+YSY2vq95nnvprZHXbCxLx9C1S4X7SJAcEWkC5iPo+Aiaj6A0A/xVowsEToUkNBZRAVdWUJMgs2S5+Gwz+lphpQjZkr/086L9o6Ay4JEPC02p8VgOsiiTuVYGimoiEqxbyev3XjC3XCrehxG1cNe0/EGv2x4/SLlZEXHN+qsBDbrPrXp2mTv9TJ1NoLP2Cmv7yJw94BGaAJNCtMArTOXqdzbxE4E1kSyZMKsW7ZmlmJmAfMR8+oj5cMJxnjFPE1LOTQmRRKhFlKGBROTQMd1fx2z3CH77mX70fgBZsqTh0La/VZ6jeV1VkKVX4aLhl9phaBadJuTyEB/doQyIhScgSXctKayEpqiFQwLfFh7kPTfpX0s7+NK+jkIWOTxL0TXjhFwttiIjQ2Rv5WlBSgkHzjgQwESgTJ7QlFjTUqsiwmAGSRF0UssDV0YJQo8wxR6OqSmxmkvoehSO8BsJFgRvA3HZoLlb5w5PdTSU4ac+T4V4/vR9EZgNQlxzUUUbVy1LsxavLemvh76Jcfe5JV+rzC2Ztx6GltR2JCwN14wz9WPzPUZ6CDFSasHzUrCgoqQKpmex0kgPQjClCaBJE3MRKmUAhKzKiQRGoopCjJwJhIw0zTgcTpimAyjNIJpBmqyaXTGhXhIgD71Ta8uPbfkmzLIDiLEoe8bC/t4q/nsIExaZICgebjkd1JNNn2X1vLFE3JUXVC4AlwDHC2oRCxcfQJUxyNaT3dmTrdsENpsAf0Pozfa7adP8bO6fbRZBFJgm+zvSBhEHjDDSdba77wQxGT8mSgFrLFEW72FkEGekxGIUxAVEjEIMKur14HPTcJUoOkQZ5p5U3FjowpI+rRYgV0ZNQM7AFAhqG34lOU65OFYQ5RifgVpBWfL8HA4Jx0MCZWEIcpox0QFZFcgpqaKOFN2o4gNUm9eFMqy0saabMLliHGy6uYOWSNMQs7fXxTUO8NwY4TanhqojcyPTWRtsDUsfwg+vyghrrvAyfsaP1Qgz7bufRXug5vPTC6VJfxi9Y2l4b43j2WFCxmbz07NCbSyWGDzSk+SLtrWm9ypX9gx4Rsa8jUD60Nmwdc9ut7Nd7IwcvSHX70UFwfV636ZsKSXG9sc53+wnreHax74mDYb7F/iscQq4q2L1+6rOC0rgvfHdUr4Xmv3aeRzLd2WB/sKy3jP+F3r8Mv4en9uod/VwC1vRoVDqYczP0I06VwJYw8krULsd9rbaIVyGxy08eOneqs0d/Lnbxxth7BpNOTy98/eOTCQ+sQf3ZHQpIBbdcR2TkjipNUn6joZrYQCZCZWFjhSxAvtjiYBMYswheTfVQM7OzQBbA/jqcUlK7skZmZglBGaHn82KG6hUPeQMw8JSmkQm/q1/RdqBJcimwLbR52N4VgIgBoNMpDQfKSnkRJaPn9HCIS8aWUIZb6VgW8hsz5Vnz/izMn45Y8zrOSSldmKDerBQGqJ5AYc1XBUOH3ZuhPOaGKhnECakeUY+nnB6+ITj8RETE6hWPC1/4MzPWDJQc0bKRw23WyRpcGZQeobkLNC1MWVBLViWFhY854w8zcjTjFSLG/+4Ydem8YCNWuezCgxVShK+NefGl3Q0V/Cup0YRG0sTJ0wM9KvyHKa8aPNuBjl2X9inba/CPVqjPcvItAAMkVmChb8ASVhvBqgmGI+ZKCHNYtw05YScGImK7ocWJguQvCkpyd6mJHBSlWhv4dcLzKSvo05Z95LNl8p8Wl5ZrV8XJWXNw6E8RdIx5pxQVa4oYcAD/cvSkIM1MZgqqtLSFeLXkSE4K+k2kcwXuu9g/QSgCcoJcOWGbwhb52qya6PZNKQ9d6PvMMgIgP4sR0zTlz0ezaCGr5wttxSBOcXJhluMjTS4cxH8iDcul1d6RDTgjn+3OegHf+2gJf+v5XNvSgg7XH3sXb0uCOh+QBfubLfdDcbFGstaz1JFmZCJQCgAnh0oKiYUTOB8xHT8gMPhAYdJFBHTNIGSppAn1cRSVktIHRCa0DICUDzUEH7fUkZ0SgidC3uVEKxTA+MrG6i4Ja8ITdvfJkRtyXlVCBuTH4XamAngJHH6qnwXwSt7XohlEVe7Wur1hflZvOxtHT8oTTkAmdZFBT61MkqSAyIlkkRCicStLjFOqChJCB/KLblpYkLihEwWVkyQs1CCSvEZXeM5IdhDwrAJRmu7WgzKYQxoGMSPqEiA1fadht2/PS3bXHbbI4MiwueyJTtybwe1JjdrETsUXRGhVuNc9pURTQnRvIGKJ2wHJMZif8CEbX/D+L7f8uZMujEJIGQI3D2dF5y5YKEK0LMc3qkiJRZcS5OG2SGwKiLIiAGqKFRREzAxiSfQNCPPR8zTEZSmpoyg2ZURTKbGIPeCcF0bm3twI1AEbtZKiJFp3GMiBRfrnip9zgY5HyP8qUUQDzDL5hkRrnoWWFb4pWoMi/EvSZ7Tue9QfhOnroSPJgx1AkUGAZAmBA8GAvFE76zXCe6dMgDB5qf1bVRGruGPDH3JN24wBRIziJQJ4AUcmA3GJIw1CgoqCivdQYpH2Bg8UtxbWogrR2fCath2zyTKiEmZtUyisEjZ6BpoKCd1ISYl/LmCuIAIyIlwPBCOx6xucQmZDsjpgJwm9WaTrWPeETDBOxJY86aQEuIl4KFL8Ais4VcnFMD6eXMDJxs/TBnRCGxXXEeDB2WexXBB9rHglcZ0WX8aB7BfRubM4VWZbIWQ7pndSh2IxnaNcejbtJoibTb+bjR0O9vh42zMilxEfd/i3pN8JsZGhbByl5iW1TCHOdohRLbmdD0uzZmie61C8vNQA4iLdW/18VKfYnmJUPxSuafNS0KCPWUEEGbE1h/GzBoMDX1ga4MRK9j0zriySfZ+byDUj6l/5vpcx2d2DcGsL9f4xlf+fmvZG9dbw9ZLyx4f+7K+XabZxirHpXPc1bGw/UMjugyyMnQyhVX3mywgtsX8Bmsd+hClGlvlNev+noqrl9V9/ztbyhaC0kBgABbTnsO/PW7xs59EYGmiQ+E/xRCukAg0EyT2fGJCThBZDCUkJDWcM2H6un+9qEoNbBy8TNgntEg15QaxKixIhZb2TguWKS3IWVudlrEGFT5Yv5txkvJ/jkz1jQqgqlDYlBI6ECepEuB0fUXFAhamYyneI+sdc+2towJtD2YQZSBVoKhixsStzpAbEa43fDolLGlbVDJ2oMnhekhp96IeAgD4LGfZYUY+PuD4+BnHwwkTRBHxXL7imc8oE4FzRkoHzW9QJadarqA0CZ+HpDlFpM+lVCxLS3id8oSJgTTPSGURRQS3nCPYOYeMPjEeTtZVwvY2kxszLFaVmSklPCRR8bllKC/qzbDn/kupKSIMDVbnHwgpZdRaduVBrc9r+stkgAlF+DAcnL+QkEpCmSVOCi4VoIQ0ZeQpISdCTgyis+wRmn1eYDwEt7BXIEbxfKBtVP38mmJP+5uarNJCcrlnC2QPmqLQFGzJZsvWExIaq9Ql4APtgyOhpoSoqfHTlicj62YjblvItw8jJLOG7ydWZQmxysqU2o2yLHbMofNh6MFpe9tSYYE5huZ9AZ722b2/jPKbpFEiislv7YC38Og+jD6CxLXyKkUEUTv8x0PprQ9ar5MCMIX7gfx+08LGUGqySNeDOxWkYRamLImp1bUsqwJijM9sGn7TKGODwWPetgRZ9W0QZl16Tj7RDgwjUm1z8lif3TRhQEte2j/Tz1b1pNYhXI2/p0KF96PBfqgywkytcvAxV83nKgQU1aIIBEBJjuRSSpimSQ7plJHSJJ8UYjuBVvDbt1l3cWOEu+GP7vfXjP8tGcBR0edJgC2htIep6e/Xuj0OOcxjkquWyL1uKGT+juXtGa54qEvIsefzgufnM56fzlgeCqZaVcxlBFJVRgeiTHABnpSUCDkLo8CUkecZ0+GAwzzjOB9wmCbMU1YLGqy58DDWSDhFhZfhPyPcrishBqU015Z0PuBSOymqhk+K3m0NRk15VkN4PIXvVVL5dWi1u1foyju37dntvb0t4Nxu/7IQYWMZo3Zis0cN56SUkJVpyCmBk3h61MRAkXkzSxbWeKnVrdfJ6c6q9Kx5WTAJsc+FRF8M8zZTQtgSX0PeTyRWQFOeMU0H5HxEzgfxanMPzD4s5NbUvek+dVqiDjBscF1hHj5AH35shYOH/rU9Zs/Ehq9RgbSCn7c4P1aC49iddyp7wtvLiiNszmmsbyyjMH2r7TQoC99yTl/7zPjstxQYbwnfx7ISzm/Vg33QMib+vQohmm5cefZPgoM/q3xPfflZtstbKoXea7XfUwnxvRXDVdzR7SazCee10kPGdtJA/9HqIlj8fGKNouECjjjHW3IKrTPcdonHBgnR0yTtDHUZyOZ6rnnfFd0PNBpxU56yX5z2uRhVIshxvEuhv2x/j23f0RcVAvJY32CAEDoOO0XMMIIgIc3n+YDT8YT5MKNCvD2WpaBW1vwOE/KUxUMF6HNDKuAQqecKi7f8siw4Pz8jKz0sdkLUaBbyLAn37XfqaUkJepId/zSadgGQJC8B1MDE2tuRk15SyFvfjba+V9bKBgPQz12NcvSqYTesBIvHO5eqbVsVbUzdjo/0P4AYZnbkL+NY4n5oaorYR8EeiYTTdw9gintJVR8aISZIrjrwbrJYwyVWVc9zjDx75L91AIpTAhKh0aQjfKcBddB44zZe9r1Lvy5V+0NAymBSuYMa4OmP6DSON5RXJqu2uVsD05taH4kerWmXqS3MrgLkrc96hmjFGehIcSKJNe7JcDQcU06uPYrKCAFMcs369iEGv/+2RIshB2uCh8MoNh8FXr2Ft/dto3YThBVuyoj4aZt3ZJivWWj9qGXcRmvrQN8JYo2dTGEGSBJUPaPF/w8I9q4pJxyWIw61al6ICUQZ5pEkxF5rJ9g/C9hgjaS3hazcEyuB0HkpfEclxKgouWZhZ8V/3Tgc4xU9hOBbJiRrv3BIMeJz5nXEqyRZf7fybsyWEe6Ky0qpOC8Fz8+ijChLAc/Ridq8cMQ6K1mWYj9D5CmPGUoZeZowzxPm2bzaMrKHtiEXSMexXtwHDhv3KSHs0Pd3TIlVq+Pa8fcWOi/Abm3KCfduszwR0YtiA95vX0d77jY8fit9sKVs3BPmrfu6a9fbfYx1cziXt0TbzhDoeZ6JNKG1OIvFM5X8u+HLdZ+LE68VnMTLJpNZjwOFGbUSaiXHPUZYJ1OK5Fk8IPJBrMaSerKpK0Q/ZxeUOBfw8q3wEETdq9kTvFixBfcG83WgNbpnh71khQJDGe9tlbcQSq/eDeew3uhvtwfvbuteVLpWQlxfu5Fmd7psg54f63mJEqKvs99le+tD3Rzf1p+t+vas2u/p/1guKXLG36+Nz+/v0DGrcGGrtvdg73Jfr/0Wqn5RGefi2rrd3KedckmRfeu7t/bxeyx/pb6+pmzB1avH7jKV++oZz6QfrZhkoM1bENY5WcD+Sy8nt7CQ6PCMfLX/EK52fsSZbmvQKt8+nfuzlTfFMWspRzcG3nqm8cZOp+zxBesqr5cwj8zNWnp1xjNjHeoyvNspKsY5u5F3BnQyObRj98Os298+4PAsEXKeME8zjscD5mnySB3LIvkGRK4muQaISTyWyeQTkY5opZaKQgvO57MoMeYDKsNztjbe4rK8YGtPGw/YzmwRhOecUavUyVw9cXWjcFipl316YYvmikqIWhv9c1XGMdIfPFLJaD1jwELRG/8McKPHNRy9yTGlXqXGqI1wlKdHYTpbQ0P7lxUq5PxO947Wl6xtVYwkIjX6WvM6I6T7E6RRP/QHf4uDDLTjQ4ZPb4l6aKQ2o4i/k3h0O/xtjL/HY9fX+r3KWkGkRp1txsLEGmzcZyT8bsmq37LYoXOz5vKN1otIXPYG8PDDh3WyKU1I0xHzfMDhcMB8mEV4NSbTsbAISTR4lXXz6IKyMtMWj+xWwNsTGvXfFQHqrqg1uD1ZPP/KGqJDE1RrPgeJsVdQLBFqEGaZgsJi6Uud0pdSK0rIDVHHmNnfaGN9n2Ut8opKgGvF3rRERETQsGTsBB5cASZnQa4GwwmHacZhnjHlEW6jEs3eVRJm8HSJAnh/LhInb4xY9xQRF+fJu7JNxEk4lRZX0uDWvtcouK3R+t3oMA3DVA3+K2qxHCmMpfYeEj/3wctLBbDUivMCfH16xh9fv2JZnlHLLCGzIJe40Sb1aNAwJWPURyX8KCXknDGrF8Q8ZWQasxYNxI3DzoZ3QWQ6tpgR9Pug309N4b2uU5UR1WLOFsW5EtamLIu4gC+LwLOHxJMwTJ7YWussivdHj4h7yzgWIPAjw/6kQLCsFYvb9d9D3HDHEK9/dazpzAz1KJioe59URSsaAHiM2WnKICKcpwwQYSkCU1NKYr1VJJijmmp1uNr6UhiYGBJGj4BMLAoOWFg3DfPluZeEDsl5wpwPmKcjpumInA5IaRbcnZPmh0jOxHT4PIwszsglZUR3n9f3R+Jc7lt+nWiE0LzJtvbN6JFjn6tQkdzWkLDmcfqzYXM4q+e3/n5N6eAaWMf2f3XdHJIjbgm4h3eaFnZjv4ql6V7ZEvLdI6zdPat1HLcJo9e00o9UTJTxVyo/aZyf5c8sb6KM+FnuL4qa5Ig3odv1vR+NKzz0HAWaC6yZIBJaUFQxLIp5Q7eUELGYoBFbvw682CX6h/3TxMt747K2Rh44CGX13BVblNCHKADXF1hjw/DAW8SreUvHlixEDPeffiFcl+cw9CiO5OJTPH63qikh5QkPp0c8PDzgcDwiAfjXP/8H//r6FU9Pz6CcMB9OmOYDpvmAmipqWjCdM9K5ySqSytVMKWB8zfPzM4gSjlnC8qYkBsOUJnGUp0VW6JVnVKSzS1k090NCSgxGAjOhsyjHPj010qGjguL1xym5wo8VuEysnGBeJQpvyi+296hJ8DmI3kmUAGvBtdQv8sdBNrRlkMmskSc4JF0cey/FsnJIyFqdm5BEnEjCxANBWWIsg/Y9u4eJellADchq2Cc7+R2r7zNClyOEWw8l54UmuAtDaYqZhiI53I9U7remn6KSnznkgTS0EkMzQUMb30Gjvosi4hKjcu+Ekv/LnTLi8vOhbX8v9musY2Skwu1xLEDXC4IgnilPck3TSpgriSI13I0FazbNEVuNLeagsut9u9eEAgiHHnM3D66Zt1rZAKoJVE2g5UqIYH0bQ3ashM5+cEUBgeUKGIQMHMKC2Ls/aFkTyduTcav1ZtRMMhqCtrWQn3qiSWBBDu9pypimqIDow4qNvYzC15VwlRG+WyzJrtVNYmt7XNtzshZcXlBCDJV0wuGhT11scoNlbjDd509Ze0R0B5Qr6Uwxwf53jN/fzcdfvPxZ47CDulTGslScz2c8Pz9jWRbUuoC5wMMyoYBoUgGbxeAMFkFspASphTmpd1tI8mtPKBHmoxwIk01lwwaDM657T+C0UDVWonC284jghqfbfmyKYSGIg5Kh1Pa39dHf2Q7HdOuaMq+Fnlb2sNdKSLohCF4JVqMVRv9H64g+eZFeoNAvIsWFBDuPCSY8blSIqk6UCZYbUxLydcoZzJL3we6XmrBQRTJmT/sn4QmURawQZoWBVEURUYklTjDgcZPdBijwjs0Tc0bOksdEQuylzvKrhc8ZCcSmhDBmjPn6ml/6fT3nkbnu328wOCok1uHB2pnTPts+fn3ZOkNuF2bx8PxIU9p96uHu5nKJUV6ff3HvNMur0Nd4pnf18u4+jsxwbEfoTYOjcR68h6u/zeOy24Nb767u97j0duVF/Gzvb7V5b7m3ntueu7zHojDjljpfomRb8XJX6NRvWe4Z/1j25vB7GNf3WP4u9Op7lrfCLX+5clm80t3k7lwTokboLnYaqxKCjz5MZ+2CU7vHRiEx4xLu3OtTdwo6zTE8w+MfbSS7TUWeGD2vALtgsp/2TpQxRVq264PWQ1196zO9EV76T2yb0Q/Uvl9NsEq9cDVKTrFFZXaToj9IroXD4YjD4Yh5msF1wdfzM57OzzgvZ0x0EI+GPCHlCUQFRIxkUUfMwFezBZAKhY0fOi8LUl5wqKzPJg1BncFJciPIfJWxl74W66H39JOF7XXhN4tgNiWjvyxXVy+wfakS4rIHwf4YpOqeFuqlO0qfhvxrqKXBSuguw3L9+WCabDO0Cd+Po/yx5wm6/kYYDd0LNvjynWGb3+WpK1rYxmljH2A0UTMGF0WJALLls7C9NVDJYT9bKxT2wNAOAZ03vGuBhr1BKqvmZm5yy+kRFQXx+1sVU+Lsghx3gIGYH/KW8s08Igx24mL1m8WfxCakbpW984d4teVWsgvwesEbhxQYKY1PZ8CGDKJJtLXTAfN0QJ4ky3zKJshNjhxFa0YDUOu/G0KgW0rb1IFpdwGbbZaWtEUQ9NIJrNyjwS3CF9SyoJaQzNTvqWVtrXKv9vkjarWEvBYShD2+dQwdMkzyD17WcH6rEiLW4YheceIYQrLfIoTpcMB8POEwn3CYj5rcdPIjfasws4cMKSzC4FHo2guQxCL22j4eCUgnrC6N+Ma58V3RCX7jIdMLwWxP+FVEwC3fbT9sKSHgQjRJ0h4sf7klqObaevWz3FFcFiV/1AosFXg6V/zxvODr1yccpozn5z/EovwwI6WDvEgTUpoBiGUKQ9ZDYKBKAmoiEGUnfKdpckXESpSlErurFt1bcA24oqHhwnWs/PhOp2jwJL5B8cBVYFMVEJIUr+FzU0p4EnbziOiEu/ueEG8lfOgVhzseEVFYeUulY9cMEe4f6sM9YwCMUWCAsp7Zl3uQEmECME8TEhHKUpBqAZgk+XOqKGCkWtWzQdVjkRcsmi9C6ZCJKiZKEoPTApcGoS1pGKhpSiGMmOaG0ATbzRDC4nVSS4Bo08RmoBCJTF4985KyPgesnQGWO2VuUASHe5WLJ2uXfRK8LIxpfoPyYgLeuIZvVDoLsMCMjPtKn/b52lIubJWRGe7aRsSJ9r2FUo2Pt/AaPU69c7RoEz7WsqVwGEM4hM5+z4V7/u5n+Vl+lnvKN0bKP8u2XGXrOY95r+eWnyMkRnXUkUGqwBYhaCJTUlgYFOODB37a/7VDqecFwT0NbPSKGYK8bAKCPCZ+5/67PgR0SYy7jpt4V85W5u7k617hqJAJ1Th/bs+JIROh+thj44MB922F2iz7OLnJ38wrtJogdj4hHx/x8cNHPJ4eRHHw/Iz/53/+G//841+olZEo4XQ44TAdkKaMWuRgpJzlGoWeREBKCjnioZyWgsqMDCDljFwz8nQAiER+odELbpNR9Dxc42N6mstkf0mTDjAnzQ3J4G2dh7835t3aos/uVUbE93o6KcCi7rEO5m0slmdUHo41uly9jVv2YTVadHgtyopMLiMGSbW70MHPMA5rG0onKT9uWeXNm4qTeksMAmfxbifJiWq/EEBcnIb152MHfE8bT9PvQ5EPy1/ZX2nMnvHtIixabzKnbn1975CBv0NpeBkganIusHj5aAZxuWoFJcLpdETOt+eJeJEi4jVC5Ka5sendmuCXERBby9WxI/rF1raz7Bof7n6xQ27r8Gga1pwnjbWvQgANCSKWX6KEYIoa0Shoat+uaQt3Szzc9BC1z6iskI0fwxtshFiqwvhXE7j6fUMQFczFY5BHoUOXG4JbWAkLM+GA/LN42WaU18qI8eDx79SUEILsmtQqbtfubSKkaUKeZlWeWbJqagQFGRMfYBXo1ndFvA0HTPsMTYe64jhugYst6894b/tw5rA92t5qB2IUfg2CsbBPWjibctEjQg7VnU/2ZXoRIRHH3Y3wB9hUtk1YgblClGFLqTifC85niQm6nJ9Rpgm1nsFMYJqUoBKrFCITv8Y8C1I5KXGSgkeQE1dbgtwrlzyI1Xvx/XavF9RaacqNpoSoiocNfmMuktrBq15sigfD31HhEZXYYR+Oe+aNyyj39X1MDfeMqojdvqzu25r29MpK1hxwLyEpcaKMQEpAbUzu9hgkWd2khNeUEwjq0UBVYpaO+L3RpQjL7IoIITtYtA2pIrExJoGwJ2h+CFOcZYFZBAOIiBvtPFjBsNEfHL5vKBEiPN9Z9vdB+71XRmztpaZ86JgXGPGkc/NCZcIlr7qrgvrxuU54MDwZaL14Zt3S7701WCnygtLA8FbXBhGAur5/pe2t54mHPeXMU5P3UJiPeF0i9fc9HaymWOPW8/397fpug+drZ+29MHdpziNN9xay1JdY+b9kPOP7cYzvaRX+Ek+Q96aV/j5W8COlvvPUHn8Skd3d5eVyhlcXP662O/+a9b3Ky71BG3t1fAse4bYW5Uzv5DU8ym+EUBm96wjNqtmkQCt6zeuSwyjKQlwmsupNJClvO/83f1OGz4SWozDbGvH22GhRuDIfRG5c6BczEho/2deJpoxgBCGsKSnCKLu56MtNIlBa/RGISvYzjMITBAJTAuUZaTrgeDxhng9grlhKwdevT3h+PsuzJBFHcs5Kx6pwmQiUciA+zCil92E2w1grYpwjnsSSxyFrhKDbcF0UohsfZkZM67NWYlPYZyJbr31a+hId+vpiKxpXA4hj7nYOtf6YLNOe9fNdANVl0fLahjf6wEvavx1vsMF7GJ0oCjg4LNkfzMYzDd66NlJaj7PtI831Z6oHl7j3FCaUD2VTJOl/OqBuPPb7pRWMb1yCN9n/fz7OtuL4I9s6B9j3s50AakoHAnCYJ+TpdvXCm3pEvFRDNxZDkhQQjNy/sGC4tJyvKQqkFBF4AFyIBe00HTBNM+b5oAJdNPV9ClAd6+02nB1W5AOJRn7EIsz3zaiHi13tPNkm/EzxYO24wKoEzwgTXJWCZVFPCLMCN6vEMVTTliC2SuJkD0PTWZrrUfh+C/a3KfccRsb7i+DcDr5oXTEesoI8pvmA+XDEYT5hntQjImVY2AS4MC8cIBuW32DuBPbWVNsz1vZ60df7+vIhfU/pFRxrJYO5HZrg1vOhmAdEiJ1falmPu2tDYb2ULqfEuA+6+J4/y52lwS+DJOQVGE9LwddzwR9/PGEi4F/H/wGXiuN8BFAxnzMARs4LCMnxVCnqubIwkDMSC0EpOFwvygNxqLgbxjw0gnQrvn0j9O1rr2hogtXeIyIqIvwdbpbkqAyG5vrhpiDjWlCWs8BsOUuOnsXgeWnwWYKSwkPvNcakP+vuWKE9uN4ksNceEfLoWxHiI3sZ8CDDhfI98a3EaLVDPAHIQMpy3tai+LX444CE8JqYkHNSAlis9XLOAKowIdDk0xyNYpoFX0/zVI+FDO1StjBh+s/pdMDpdMThIAnWxRMzK+xGuA35IYT87onpjjl52dw3vNozE6Myowu9BLv2ni3dnqpBmSu91rPHGIwgAF0JzuPy31lu8hoYv/xJ8jMi+LwAa0bu/dtfC7rfl5neb/va/b9D+fuO7Gf5WUL5E3Hoz/JWZTgLXE5Stx8HMNJoHhjTBJsEFcJLjgihq3qhp4cipg2DEQ5CQRJhotFsBPHVh/OHjQZu/GyjaQCowfV9AsLdJzfObDbZF7Vxtd66nNQ/mwHJRitkT1ShcTU8LSm/4cmsLRa/EaYmUHIm59oIVaAzynVMlqV9r85bMCgB+fiAw+kDPjx+wun4iOfzGU9PT/jj+SsKV5xOD3g4PeB0OGGaDug8lMMnk1PKPYlPcJ4JEMXFPM9IRDjPJyTKwkMSeX69FqJpW5Ym4xDv89YFyQXhw+Z2ye9CD1UFNqKiz/WyA0tufUu5l77raCKTfwBAqrDgRIlkj1UVPiZKyNOMNM2gNIMpCbXuba+RtMv1QUhhj0ZFQacwIJJcFAaT2FEsRLnoxrmw4jkoWeoIgGw/29gtrBSQKbn6YJMH5aD8tE03tu3jTI63iNkVGKaYMT7PLra9Fvbcdy8XiuMn91HT7xIy7dffPuN4PN5c5c2KiBFw9G537z0n8C2UEPf3j7q/ePVbE0ylJMy/5IYI1rMj0hzq1Y41pGW4j/snbe8pbHc9IBsbjzESuWPw5eCBA7vd2/KMaIlL19az/aG5RgC90IyDgMsQ8x2Jx/9i5V7+t3+eVu9vWc9sWtIogHayT62zPajfg2Qrp6lZ0+YmuOqtDhVx4/Kat4MkwGAgPOQA3p6Hl+KO654QUdBr+D8Is4wQY4PTuBfawdAn8Y2uu60Nh/md/RAJzVvHe48F359l7bdV/sw2aYBzyafF4hWxLDg/Zzw/P2NKGctyRl4keRglAkKIOoNXC5sFZk9gZUnPCL0C4h6PCPvdm9so/d7ZUlBst2OEJGOA2c6rpynW+lBMlvuE+3e6/R26zX1/u7V4Y4HfVn2X9/Ut97mr238OfEtHgDrna6GMDBY0HpITXz0vaiEEEqmVjXKLiQg1JZBm9rL51SPR87UpvSx/E1BRO6tAIydSIiQlCPKUMc0hFGQib5+Ga6Agh9lZ3395Wa9Lz7iETx5hew3rvWKvfVoFHNrbU0LIGXk5zJe1cUkhdhHPdQzSAGQ7j8X2rO57tpSMrZ+ze4sraaQTjdgNn9cCpN2rEBjn+SV17/1+jxX+t1BYdDAZ+jB+H0tjjN++T99ScXOt7b15+XP7fF9bW/vwvfr7Ui+urTrupUuvllfA6rcWx+zIuzbLSzwP3otev9uA7a0LKf20ll7cUUejd9joF3UJaAqIDVp0HLvJUcZz2ehz69nQPaeD/S1unyJl7Hi/SMdsNI9Gt4T6AxPD2J4dt0D3+ZB5bQYlw3C79u3txjAFjh7GAxmP3oh94y+CfCnM2VYvx97b86v+xfYApGlGng84zCdMeUIt4hGx1IIKlpCj86yGYUHoaR/UfweR5DcI8os218LX5ZwBZuRpAjOr8D+jARdtjjXuV6NLJbdbG8/+XpY5uuWs26JD43ej+fqxXS7tXX3P4JHQBPsdvaclSZhXSmKIxUq3OK9oNDWZLAY+F44Bwrz1fJb8xjx46XCvOIzwYsHXWgX2yh79S60KYLXPCM2bqiLgF0c+3MJj7rHyEfwN/uJkt55078c1HCuO4/h2lNm6dVk/7udi4C0pER4ej3h4eLi5lW+WI2KrNIKzJwEubbQ7j7d7ewRmEZpXssNGwgOQt56R04xpEteyaZrVhexirWCQWkYOgkvETfeCHu8JZyQ+kguvJN59davYEpOb6sUhrjiXAq6LWpDLOyZNiQcyM0vuALU2lkNFrY53LMHjgfqtic/Xle3ebzPxG4fSDQu+InQiEqO2H0Zmt+sjAzRNSNMk3hCHI+bpgDnPGptQM0RQfKtqmt/ih/CeBfhaGLs3lmZtElt6C8J8FASbsMbqN2FuVbNkH0tpFuItV0pvOe4W6U6cylWqCH5LqShF94BfZgUMwSkj5fuz3FVs9qrG9D8Xwvm54vl5wVNK+PrHV6QK/PHwT3BdkOaEuczISeLogzW/xMJYKnBegKQW7M0+xFHcUORGy6+w4SGEuDcb0T8KWPt7F3JECNZue8Y8a2AKB/NmE3y9LNGzx3JENE+I5hFRW7LrEELMaI0axvvSfTkyiL2A/EVV3lgYrnhyXFjQcJs1bsyMjJhNEaHeEJSEcUnIMkf6HTgDsD3dznEjy5LmeEgpIUFiZxIb3tPcOqCVraBjBoJkvs6ENImiYcoZmZLGRWacjkecjkfM84RpSsiJkDJ1+SHIc5/8eZbqVkZ4X+0XN4QoGHNDmEv96Ekm9QKyd1o7APzM6zwhXtDnrfcuCZv2sPlaIbI+5l8ilB/P2vH3ZoFXu3XvmGZ7noXBc17KaInxs+u0bumeVL+5vA0MflsW7TXlpbD5Vyl/v/G9ENB/lp/luy/vwIfssjcm4LvWHz+NXDAoMs5RlGhUqvAB8XxMJoZXgWJDRxtnO5uBSE+ndDmsNsbl5/A4ID+T96SX7TkGvA3LqTme6YZ9Oh9dAmpKYiA3zgkxiNjDOTn2MmEvqrrk6lU1OoApCpzx2en4LsEzjJ+kA+y3GgGUpoyPn3/Bp0+/4vH4gGma8Pz8jHJeQClhPhxwOB1dSUGkEfeTRv/38Ex9eHR240LpKEM9MUjo4mk+oc4V5+czKE1YagEtZ+Tzs0zDXgKHOMxaUamqMiJfebrJYWydI30m09UboZlnxFsaeG8akIffLdcKs3hEVEA8qw8PwHREpUlBR2ly5V7EXyD5OCK/J+Gc1vKoRBJqjKuFUWMDFadJDfqqqxy34dGf83y0uhuT1mN7jNkdf5z2tb4B6BSbzhr2AoDVWhABlISLoyS5W1KCB4pTmDcBPnf1mBwKm3styg++HeUha8maRwZo+KjhNgZ4AQDMpwkPD0f8/o9f8PHj482tvIEiosdIoxbvr1wcccI2xhpYzHpW8kLk4BExCnJbpWpb7gdfrx2XWptp5Av73o0jCMFgVsB9vHHLAWFhmNZWtjW4T8nmdMXJhhC6blwNKXDXwb8Led/rBWPZY8qCNeROnaMVxXiva5+Hei7sPyJyeJ08N0RyuO0FdaY66wWpUfi2ddl6G8wQjX0KQpGOuGsz4ufBC6y++vnaaCfA7qXLhGX9WCvGtdm+Qogyg/+NLl+zjrqHqf8zPSO+LY63dFLi8lqqeEbUUlCWgiUvWM5nnHPCcn4GEVDKWWEx+XoI8UmOm5uG36yNgXFnG3GzCffY2KuMzfvtnQ2489ijugO34As9PDYlRlSOFA3d0oS/bY9GeLRTqdFG/n3o971CpktPb1VlOICxVlaMMLcLg7z9jPClQrdsWeiAQ7xhcwVPCWBlAWmEkd5bsNWFpgBwdbvNb4Af9PMpOJiF4TJlgiefloTY4Aoi9qTqrnQI3phep/bjinVE9+W99nXbN1t7ZyPP0AY+bftl3dfI8NxnGdrauPR+x7xEWnfrBDfSMdap9+3p97SSbu32OSMMAjvzDx4VDdyEP4gqu56ote5fwwtbXib9s9fhrWek971HL7X93uUl+PGlOPUty937/RVdfatx3jpv8bm/Mk96L5y8hg5cC61uq2vV5q5A+s+A9z9/P90z198CFt/N82V4fqR39KZ8OD099iHKV/TvRkgJTRTqWo2ANv9sVYT769FH2izQu13vAg3ssozhu9Pljdfr5npr2vX53rRNaWBXougcoPHnRL3nq9GRcjr2FAl1UxvmOPAf9n3o2uper9nYGFN8XvtZmfsHE4FydkPIKU/IlCQUMlehewHM84R5mh2enBfTSYjzkkhoYInCxNiKBkZESHmSvGt5Rq6MlCekYLBxjRSJcoE4KmcJdt+LeLGt6wgf9lz0fLBGzEO/947YgOar+7bRT63bKnR2+lQjA+RJvSGS8tpRFkIuR7FxRR6IhnF2nhkK32x8WKRBO3oRLtg32PbzyK/ITzFW9HiY1wESvS2XnwX4bjxw65zV0b9PmitN1CoUaWeOmyV0ySu5hou/Hc0S5YAuw0Nbngaf8ts0ZczHCY+PRzw+nm5u5008IsZN8fYH7AVq5k8uzKyABchGlZBM83zENB2Q83xBQ2oAqdup1m0kYgevAv9aaBWevYEINwGVIBDNBbFI8lKJHV7BFtN+OaPUglLOKtAzi1qzsA3WiT0K8OeWZdGrqGCwCcB8GrpZ6RNQ/d3KWxDcK8Hm+glpyz6pHQbjEyBgnmccDwc8PDzgdDphmjS2uMcSb4lODesYIm/eAybEZZhFa+tjL1iS+9XnQ+qx56h7LwII8xYKv32+Yj1bAt+W1LdZ54pHQ4ih75bjpRtnbKsXIHNXz7KccT4vWM4LlqV6bPif5eXFHEoY5tlQcT5D8ROjLAuWlPCvf/0L52VBJcZ8mAFIzMspH8FMeF4IpRKWMmHKgITdSUASoqvZt4e2FSYNf49eQWbVYp/Ehh97C6uqFkgjji6leR11wmSwtFmiIllz/CgBb3h6Wc7yWZ47T4liOU/c06cpLKCeEJUZnpKLG5F5z7l+O84zJnNbwHtv6Yl6hnlE8ECjGAMDXGCHiUDI8PhIpH+7TZrUIXhEzz/1fipKfAqYipdN7XDPxkwQIaeMKWfMc8I8Z8xTRs4Jc1alMSVl2M4gYjwcHnE6PGCeDpjyrImrxXvCvSIoMB2G05NT2W0deH/eb/ekCEox7vdHNWOHzsOsh8HRs6gxPLX7rNEoIqz7Vh9fopR4LyHZS88zYxwv7UExLki9ApO5WztThlzeyfcdTvfM17YSAs6Zjr9v12tCqb8vzfi9llsh4+/lDfGzvLSshNF3vfu9cP1vX/7KCrGbikv0blvF3tBgrIgBUstrFV52dY5HydgNrcMFg4Myxsm7oa8rj4hICwelhNMl0WOzF3fTiAABAABJREFUNlqvPd8Mh/Rlp296L4yoHHDSX8fAsLSwiQg5SdjPUtWb245Fkd72c4wKshyONV46LqWp0PHhDKDesRHX8ikRMquaRfuWH46YHx7x6ctv+PjhCzIyoLIiMHA6npAT4XE6IEHkEsy6JqgAGQ/e5BUpZ2SWaCS1ViCpZzvbUMXDdkqEzBnzfAABmJeD9DVP0j0XrsPBt+lllUeiQEcRwElpauMriMR4SeUnPpNqNZ9VDsMAmFiNfE2QLbS4GJDA5SNwaOjlKKMy4rpBhiquakJLNCu/VZZ/KgNMGWk+4PDwiHw4gfOMwgCpR30pRXJAkHhvVMiyJFUccNhztvQbagCYR4QDrCsvzM9pyDATWfK2lXRrEjRILszzfFFv/0V55EVllzL3a3zD0DkJPV1LpqSflNQLokoeQCL1jOg7tb0eXh+t7nw/JYGQfQUE3sJaGQ+ZE1JO+O33L/jyy0f89vuXP9sjokfsWxr3S5Yot1ipRK3MuLD3LNvorXHNe2ONBIbf9SGi1CwX1U1sr4MO2INyoW+/KSsujXBv7lzgOghdVwJYz9/QlAsucPWD1A7j9iyYHVH7ATsIDOKB2guj28FMbRb9YP+7lPEwuJcx21/Xi29pW21WyVUT1pEm8BKhl1jURsVDtLrY6gP75976ssKIwXcUgMTeRKvWW2ZlZ9Q7L/f3rX87dezsld4LwirY31e9sqPtKU/QqofTS8f7vXicfdO27Q+1orCEZCUQ/ybwXJYFRITz8zMYjOfzEyauACcwEkqVyxiBRuWYkHkkFrQPG/h7C8/ZPmj/9Ptk7931mQDYPlm3WYe/AwPlIW0uW5tr7dvzvUFQXRI+vlYIxcz9mX/hua3vm7DJQmzrhw9H8FJjCrxo+54Ej3rlQ3jI6/e5bWSu/ORn5GV6RQTJkuw6TxOmecI0ZUwpYZom5JQwUUYGoSp3mvOEKU1Ke2wokY0pwr4igboxvVHRwba1MJokhiPbyTu1CaP9WWJ1SFP7s3oJTu8pe5ak3fcLzbjQY+OhsX8NRtt5bvdv7WsvyF/T5a1uclLTzzh5YlDa3dbu1ueqvdV7/R/XlBGGG8aqLrWx39/73tmuY13u7cstpcGQt37fe2+i7DUAefm43npu3mOur7U1lr+q4mWPT7l1nFefewH+8Lpveuv1vNY95dp+v/TsdTnHXxOGtkujtW4ro8gv3g9SR4PPjbeNiuGtB3Z72X+OHe56Emgap0P26HenTzi81yo0Phqhjnb4XpL5wHl4Ebk2D1jLpbHi+dsAnMZv7Ag7rYZ4D2NfbphQrcfkYoif3SCAPE3I84z5IOHMfdk1VI/QuyQhmTiBaogigurjkOoanUCJIMSx0L1G2zJM5lUdWJLmP5D8rkIzB2IEZiLfhkI+hxTGMo6V7W/jOdCGB0CNoqjVHUC8o9vRQEKq0vXlfY+I23gye9cHAONSiM2wFJBkz1mMq/MEKC/EG7I9T97uvJUFNw57N35dFZ0hV0K0+toEcDfP/qbvx20amX1MGg3A+A+fjl4e0+7bd25rioHeCGtPmlfQuxnnddg/jfJEeL/tzf4cXj29W66d3y8uLCPpvNJiu4mQcsLDwwmPjyecHg44ng43V/+mOSL2NHT7L2Bzfh2QI1LYWYjW1i0bcOu9y8/ZRjWGLZLhonCwkEyyWSll0bLt9vh6cTcl1TzdBlQDo6l3XaBaTesetfwFpS5qMXtuOSKqxmuuNXhCLGD7NK36qo3axR5vXhi3CbyaL907CEa+83IN1VyFAe7fb0RghId2eE1TwnyYcDwecDwekGhCQhaE6AfhdkxxZkaBCtV3xtKPqa07AbD8Cm1Mb7/W14RU40G6aZVrigR/rjaCcqOOXmAWvSKil4VZzbzxQfHDlQAzLJ4Qy8LNS6dUVCp4/voVy/mMggV5mlDBmKYZp+MZwISCGRUZZxzBWT24NJRWtGrqV6zHy3tKCCdYHB5K+NzOl7OCJ1hIM/t9JAKj4rd59KxznrAS4QVwuG6w+MpIgLeVDVzyVmV77pv3IgcC1+gLuZKTiuv+JuVnstSnaLFCCVuIfVrlHmas6sqMwm3/x3BukbkhQJTCU8Y8zzjMMx4eTjiejqKIyBr6kRImZCQm1PoEoOJ4fMDh+IApH8UjIk3IyRTLSa2ycse4jMzOW5RL6xrxIdcGq8wcvIp6PCy5rILHqK9r7xFxS7/uhbnbrPL7s+Wt943Q0ft9G+k7u4yuXSl0hro72vdiH67PnSSRbP27BgvjWPQLbl1Prenqs3/XcpGf/5Pax42w8T2Vt1JK/ljldiHIz/KzWBHqiK4jK2ZwEG4x6bVxbsVnLjQcaGUON9ddsXBFTfDoUtT2/gZtH+nunrbpZSLxeVhd2KpL6KDmMdva3hqqKCAQxOFNsLwzY3APgq4/wRsiXu4BwXsV7patY7wT7GpIpuOHBzx8+ICH0wccDieURXNUMCMlwunxARmEA2WgAOUZYtXOCxgLKolH92piiPpFZmgkDsLz+SwGw2cx3Mk5ATxhyjNqKZKXoRKqDqIHv305Yk/zrJ9zLwcE2Z4aP11THGzuA53ju+WtXmwnUBPue1v6SQRKGdN8xOnxI+bjI/J0wsLccg3Wilpb7hYiEo8JNOcQMn2OenxUrMPYxtyH3aQP+3E1Cv2tsvJkCHSxKoAq4DzFEqJe2Dw0WQz7f1HI01R3Vq9KKcMaaGdVmaA7k2y0Uktidt7HccpVmfb3XGzeBI5PxwOOD0f827//A7/99hmfv3zAw8Px5tpuVkR02yXID13WSe055n4jAW84ucHSot2KiCNiQrr46i0WCzQOMD6PgIgSbSClrvLdk4IQkYr2j8axxKf7e50iN7THvumjRexgMdsJpcbEkCYsYLfsbgcWvB+OvOxQZnHtWiXitv29BQbjmfcKfuGbbmJbuw5kGrK6zEbHu7ftl71HvAvU9iSMOIQo0ZIleEq5xZq091cw1R+0hkjj4bEl8LA+MkePiAYE3IB9RTjGVtuO3t6zW9aX15QR4/Pt70A4dkSaP9TeGeEb0d3Wko/1cfk3wf9GmP0zYPv7PwRHLMieb624xzFriKYCZuD8vKBWxvPXJ5SZQXQAEaNSQiXCQhUpxvwMuEqSi1tL1uQ2jI2CcHD4e4D9VtVasWCfq3HyzhV+cwIrEncBllmtQho8t5GtoPMaKIRz7X1kPCND0O73v68/uyEGPAOgU/I7bUKtZvMlizjL9vdItDKjC7tkuUcKS4imloCwoRE25AzBaSkFL7VpwjTNmKejJKCeEjJl5JSQOSOBsBQhvUmNH8QbIub5WdMjm9bow3z6PEVCJDJ3NL5xW2k0Qsw7pTMYYXaEcfvus95gdIRVigt4RfjROObGxIcH2u+uMWpfHZQGmmVPZLcSgDpth3bQXsK5N030Pt0rfWhNjLMG6gUel9H/OOKd3tyADMZ5ufbOnufI1jP9s/vzYhVcGvIeFd73ZZjVq2O59GsAsM3OyX40+I8eXWvjk7YvuudfXLahfNvT5XI7jQ+73N74+95c79Et9ygfXqKsiHN+4Sl/5iXk1S3KvZcoWbbH+4a0qKI2QXlX4OGmVjca0M8tfuXWufHVudKJe+b6NevyZ5VrR88ral7dcaxGCOGtoYbnHfG1fknrbF/1QVKsZud1oHVlPUM72F7e2CRt9lyfi/RlQM3c4dtG4LHzjEHoOPIJsX07o0de00ceYGrjWq0jtz+61jp+lteXtaH0VyMcNmaPg923L+7YfmxHPHfn+YTD/IBZc0NI7r6qZ1jCNM3IICQmFWI3S/aKMYSV7bEotGB4Hji9Y6GZbF0kwbWFrhy8iO1Ata4H8OzGFNaj+8XPtubFMIhQYPkeNssesO6UW73ChNeR8SVNZt54QfPeEMKKUkKaZkzzCTnPwmOUgrYBGN1mQPhzIF944x3LOdqI0wBrdnB0MLdHC4z8r/42zKHzaD7eYYK7rxYwKtCnGH4P8rK4tj05wDqsNpZNObP9w+H7DeWqbGurndsq9hqc1w3WioaVAIGp+TDjeDzg8eEBjw8POEwT5nwtiXsrt3tEBGP1cdKAupkYxjop47q+q2zTNgMrWzhpsG2uukGbS74GQUBRMw00d5KXEGrVp9ySkDCApVRQYqTM4AnIh4xsYRRAmBnI2mxlBixub6R4WCw23c1OBTpMLSafII2k/KrExpXY4qvh+/zJhlRvB9dcnlF5aR4OFkPcPxf/zrVgOT/Ju5oroi56UCgiSo4/GCjVY7PXyliYcEbCcyWcK3AuFeelqhUjkDSmXL/KuLDp/yrFTivSfXKJrMEaGXpILx4+Q937FQ13yPcpwYgKeZQYyJQxpYxDnnDIk1vT+tvJulO1Ek1UxEBx2KxgLKi8Heubq1pfs8TCr6azrgHJMcC8bI6ngwYfzEgKNByxZeU7Hk5+SHBp3g7hORnHguqx9WU/ABUr9zrWGIaqqFvKgufzguel4Hkp+KqfT0vBeSlY6uLWGT/Ly4sTvuFaCvD0TPjX14KMgocJfmBmKjg/MZAIT3+ckacDHj5nYDqgHjI4ATxPeOSKDzmJcqJmMGcAk+6k6vjJLTEGYtiKhZ+JigD5MIVGkvpccF3Uk0HzPXDROqvTZyTSbs1Twq4odgVykX3WYvGfwXUBF8HvrB5vEnaveE4JQwhMKjDXgzxB9pRB6+bpHYkmai7iSQn7bImex/VbKQ1lHlJKLhgxIeOIAb3P3fvrTyOkeq8tgxcLn2hELKFqNFICqTWNr7auzxlcn4F6BngBcQHzGaUumlOp4lwkP8TTuWCpFX+UM0plPC+iIHuuGYXlfDTijihhyhnTNONweMDpeMLD6QEPx0ecjo+YJkKeCHmSvA+UsvTx6V+odQFPD6j5CJrEI3NKhDmReGhOs7udy0WgZARlBbh28+JxQHUmlFVos53U7b/CGRhXurqygABu8Xxrtbwt5n25tNwQLLlKuCySs4TVG1NzSbi1HhhMprgI/WF4nw1AyLkPk4Ap05H0vp8fep8sC4wyOdQqd1I7HqSA94FDBM4AcsPN9hsle1fpg1HbH0kBGnddqCgID23PRJwE9LkWxvCiMtYMEzIQ+m60/Rff4/WxJYQFKls4x/1zbdsjp42rsxi8qdjzaf3LZh2299v7I5VxpanV99t6alAUP9vb+8NVPLXzm8NQqBGmXB26OoKlBZi7vYS183auvPFi4es1gcoGrfsC5cHL+vKWdV+fw768vPFtYfP6DL2n3buMVej+0d5XdjboC2rZ47g6HoJoF+bukXd8H2Xb4/3Vtao8hlVRUBMBSfcqGExFZR8HweGcgZrFioiUjiVGsVj5nJ2bJq5y7hjvR4YtGQSRjUhugB7n03CE2bFYxE4bSel2k23klFAqAM7C69biwu3AwcJDBVGjZ11ATSLjKSxyqZYfTj4Xz4WlcfbrYqyDLUYTnhrVyEK7UalIpSLVgqT8ADYuXQGIN3QBeJF5hvK1vOhztT0H6G862lFWoauRQZgYWIhRqIIpC2FkvAEXOZFUBoBpRpqP+O3T/8bHD7/g8/wJRMD/8/X/AwCYjydM+YCH4wcABVyfUOgZpTyjLgWsMq2yVJyfzjg/fwWzeLlzXUCVsdQFpQBEBQBhmiRszFIK6HwGkJDSBMoJVBbgDwmpPqcZlKH5UguKRUBQYJHPFp6VbKHKAtbQrQwhjk0RRpSQMylsVA/NrAQgSIWd0ZvG4bPbS72nq4DGwPNcKCJX1b6nI4gYhyQ84dPTAiCB8hFAQcEz0nTC/PABp4+/4NPn/8L8+AU0ZVAV+ElgJAIyVSSwZvFIMFUGFVVQWa4FV2CUJhVjBpe2H5polEWmYmOtLYy7fLVoHI137XmEQK8kQs4TQBW8SEhb84hI2qL1p+qqSl7AquQUoyCBHDeIF7zgzASgSB+6MDiNv+JSgCp7FLWCzCPC/TdEptuT+mpNafP02tOzJ7XvKyw4AlS0KpJR6/pgJtCU8eX33/DLl0/4X7/9A799+YDP6YCZ30MRoSVanbVDd+fZVxzKzcrkFkaBtD/W1sBA2V83dqMTknt9kYHQzeXYVhlKZ1CaK1aTfK46PfSfG9Mb+Gj5+bILFg3PmrLELF9FeDMkexw8IGJIBHFfUkGVe00ExMAhYXdAjvGyCBXNEtSQ5s6cvzOp+p7FCbluCHpYXSXy1qhmkKVtttXXc0EA4O/1jYjAUBKZphBX3J7dY7pa3xT576x/E8CG5xxTj4QNd2OlvqPKdreNMcJK3BtbHhOt3fhD+KM70O277ZUNl8FYCVv/G5xbLojxsmpGpua9yl+PKbq3tHWtLF4QS2EspcqVGJkqOCkMEYGpIlcgPS9ATahUgJxAuaKw1UhoPuKxLfiGukYEuiWR/94TkNtXY1QwhL8TmqvBpeHzyKjYewj3DZ63fmtX7Dh7e/6d90ViVqi7gmdVmLNYQxREdvvXP8PUmcCtwz393+M9I3Tjb7HudobrFFHLp2NJypUO9T4yjEY2qyz23CSlMpbwKXBov6mnDpN6CjbQcOVNysh5kkTq8wHTdMCUD6KIyE0RYQnwUpmEj0xZLg8jpbMfBL/tMwg/R7gdljdgav2+v/6rHdCh24b/Gyw26zYYc71zlsTKeky+se8aEdQm18m3cKh2v3OYq/1zz494p824m7M1GlhXNHYpzlC/N4b39hvZaXNrEI0AiPTK3lzuetF0X20y1k3GPXe1yw00X1X2rQJ3zu5As18qjC24uKfDDoTde6upHavcmcO2ZtStn9nwtR7STt/v7X/oA+lZ8Kr1Gl/eW7dvX/Zg6H7hbVz7l9Fjr5mXFU65sQukB/iLacg/dS3vb2sVueGOdy8pwLZ49Xvp8fd8/rXKh71xN/wTcQTBlKRB2mi/+M4gr6FRHXbgr1rbOHPau4YHuR/XMERu1a+f6WhWMtLF35PP1kZHKxksWQNjez3B3dFarP+MtHtH6zO63/3F4WpmGxsDj3O8ovb6Z8h7uS6EtrTtJmE9qbqIKSPlGYf5AYf5Qc6oWvB8/goQIR8OSACmNIFBKPysMoAWqjOG9zShsnk1OBRp/8OxFXKgyhymRIB7Qmie15qEf2FgDWBrJNpFFtHcg90bHSkavJNH2dDWftrYk6zrvbdfbzsjjLZjuDes8g2se5USIc0HTPMR8+EBeTq4t3UCgvJPL6WdDebJicu2aZgrKBoOdTxp7UByLUtqXXfegQzOQ5Xe3nq8/XdeffOVMV6JzJS4Eam2bg3m9e2+ymHtDHn0+6y9Tg1QQt9fRy2sy+2QEdvcwB+hJM1neHo44uHhAafTEcfDARMlSch+Y7lLEXHPofuWhXzF3r6M/d4UcoCbxaQJqKDzQebFQZ7wZmTitpg5SVS/gYz4dfO5ek+/jzGYa7F44mYhe0Yt1T0jytJyQ1iccXatO4tNL3OLlx3r3rg2+/Y3LS9jGJpAMGq9X9yHkaIafjV4naYJOYfQTBSR7tjD1r/Yz7USqsDi/oFbPG+uvTWz/d0Pdb0f10JK6n7vnoMKFDlg80AwjgeEnXFdcvWNscW2YleNMJLPqvHia/BEinHPB6Hvz3J/MZokytxYBL5g4I+nMxIYj4cZpTLORWDbiMF0BtK04In+CUwL+JyQDgWHNOFQxOLJPBcaXcSb22gLTjjA2d4+MSVvKeLdUOrSfa+OZxvRRgy11IqwGAS4tbR8EGXwUGJWPN9yFbR8FRvKtoCHXlo6y2fzjBjPuziXq33e0+ZstN6wF/f25lbfV7gD/bJu/S7nW0JFQqkkVwFKYfxxZpyXiq9PC5ZS8XyuKBV4ehYX8OeloDDj+SzKh6UkFF0LQMiIRIQ8zZgPR5wePoo3xMMHHOcHHOYT8kyYMpBnVUToXIqb+YI8HyQ3VZzvtKY/5Hrp2UTh2i9b+LLBGINq2xfi8VDc2yzmOom4ONItI0Pu8Erb6/nasku//SnlZXvPPCm2PRBaiLm3KK70eoOyd75fa/+e53+Wv2d56/X/CVN/lfLnr9HfHS7ejkc3T3r5RkxC72j19snEAFUQVSDVXuDMUg+5t2orTSxoFs2NHuiE9VYPk/SpoymVDotyQhXv2Pvx03lIBFLZ52ugQ71dtYB2D0/tfzAGEI96OJ1jOdwABnFvcGRJdxnmwWyRBroI+VaxXNUuDtEI4jxwm4Q7179C8kU20eoorLcVAkCE6fSIw8MnPDx8xOn4gOfnrzgvT/i//p//W/g0JDycgPwxgxmoNYEBzUsgdPVSFpyXM4orIeJlAt3qa1fqAhBjWSaACOfzM4iAnB+QSBJj11pAeRKaVGUAfWyfqNEweQJJ6F9NGlAruwfy6HdoAnxouJo8TPPmvjMZ9yDv2FJwbr2/rWxkMC8AAQsAQsI0ZZj3s61/ng94/PwLHj7/iscvv4AePyDNM6gWUCnqtV+RkxizZkrqdGz1qMzPaH6LjhGiuXR0fWkyQpn7tUGShZSy/HHOp9ba9X21Zjo6WRfdGwrr5kEt3hNJ7leGGaJF2LUQuuAEUFWeVBBG2z7s+3yTXzHFy6UyKjXeqryg3va4zL3JfIEEJMLDh0ecHk/4t99/we+//oJPnz/i4cNJk5u/gyIiAvX4d2QiukG8JdfzwrKlxLisfOjeFoFQOFDtwDKml8J/0h6pMk1/7ZhZChrSvk+OQF0xZu+tD7utsqVAsTdWArGQtMXcxVpOiJAzwnNFcPtkSzgc6ox1h8ute4fnt8rfjcC7ZnGyKSgbiZkXt9nIgv53hVtqAgoL20Gm/Q1Cq4hIbM2VHhuItLX2uhfGNiFtv8F6oq71mf3ffSVEJA7Dc7Cjhg340RqxX6IWPR7skSBDu9CPw+rlMK44Psbe3LS1/TPg/XvAv+9ZnObUta+QkHnnUvFcKtJShHgIuFVIxAScFxBn8LRIXH5jHKjh+ga/8D3RweDW/Bq8eBUj4Rj2w4UL43vccg+s4BXmdRM81+pWvUOSeMfJAS5tCDevwRqOV2db+2HnHTlN+32+xgutn2vl4Io438C3I0HvPEX4Pe5Va1mUEeQeDYXFw8E8H86lfYryS0MUFlXWuzdEwBM+bI3FmibkaULKs14TKGcNpwQJyaRWW/JOFibcY+gpExjojHVpCgUf69ZjYY3uxlPdejQcDR5woM/F9hmy2g8Ia93/0wC26+rq9PN7cl6sn2NGMNzU8fcaT/906/M/A8Xejcc3aMvw98vOhR4zrIxoQhn32kvLJcOnt6hXjnLe/O1qn3jnfnfv5X18j9J5wvi55r9eeVthny8/en1tLofwuqVcg4s9WjvC/t6z1+j213T9tfTY2Pf3pCE3+dONPrwHjXlr3deGf8v8XKPH936/pe7Xeh38GeXePt00p8QhDBK1hdKmWmQ3oRHayTL2peXo6mUtev7oORxDLnU1OC0dcoCF8Tptsmp161vjXde8oF2Brub2ucX79TIdHjjTwCtHvnKgoZjR0ZQdXcVhfNa/9kffz50JuILq27TYk0p7xjwRjaYigBJyPiBPB0waNrSUM87LM56eviIlQlkW1FpVKaHGM4HvaTPUn917e02WXJIqNwPB4sZAjf7OKgcROrsFpdV/IwiTwBRCv2oVZZqFygQ1g6rYRwu/bmzmyB92Z5T2L46pW2v0dW99XxttWsNh55HsocpVw6Ul5DxjPj1iPp6Q54MqULiNAWF9iDQ5NalnuS2QASE7rMV+r3ndXqbT1rvBLWu9K55a62l8n0mSTKUQ5sZqM3xkc2JzpWvEzjK4bynck0US3cS0Ces/2ia0CQld3voeO9k4j0s4+vZzeBNDrsqFlvqvSfbN4TDj4XTE48MRj6cjpsOElDMYY1jky+Xu0Exd1wKwR0b+peV9DurLopW1IKNnTAF0G9+jJuvGIg1rk1ISy3JFaki5zU9QKshni8FrFxt33CEu+HN+8N3K+YZxGaLsPCEWiYVfPDdE6XJF2IHQLLtLQBbBIyLWbWEoCmsuiqqabKvjtq7/3csWnHcCqnco7UASgiGRwOs0TZjnCVNOkgyVCJkGgs/hOPSVTbC5MS6uXYy/asmmzDNi571kSDX0Oe5POeRNc25j0kPRhVQ9HqrWVm1WJDHk0ugpxDFGuR5srJYkTbirdTrd2YS/bS+oBUdplunfIyPyly3EHYNTFQa+nsW74DhNeJ4LjsfaFBEA0gRQrjjgK2iuSDzhUAnHj1DCKsMssASaKoDe3bbB1iAwDdZckXGwd3omQuEuKoQ9DF4JsCJ7pgZrcgDuZWSwVsuCUhYs6sFWRq8IVSqbR0RP+IxnoE5xdy5dJoaicrPd0ytd94gYizNR4bsR7kA/r1t9jyPbfIbsPG9rOwpQdYrVEwI4a+il58JYFuCPM+P5ueJfzwXLUvF0VkXEWc7C5SzrXapYjgkaYTdKE94sY5pPmI8POB4fMR8fkedHpOkAygdQBpBJQjLlJMmpiZCmBVwTKM+gNKHShIossWpVMdGtgV0aGdU7cKFcp+eicL8pFqKHpOct4R4P+t7ZCA0p75YOT9ueEm3c6Fm33af2956QKdJY8Qdj1oZPp+TEsqoPhXMfbo/08m174nL9I+MpdGmgW0nCD9Qq7QnjbOt7mUbujWu42+c9vdzaujqam8f91yzf/9DW/M4t7wSRyZv25vZyGVb/nsXG/N0D1c/yo5d45LKJ7pJnn2o/ywOJjcZWoZ7SL5RYLqqdAiI1ztQ4P5j9uQlHmeA5qwAViHWiEyUmb8AjTj/6Mc/xY3yyeT0oneo5ATZlN8YziLi0+vNo9A5YeNcaDES5qnELo6CiOI0U88SpF4TR+kY3hfCsrd87Y7k6M+Hsj9L6+BQDzATQDEoZD6dPeHj8gsPpEXk+4J///f/Dv/74b/xf//f/FzlNeDx+xGE+YM5JxrcIgVaKeBdXAJXY01DUjr4hp1WscQZLPlQqICTNifAVDOBB5XeH6QhiwmE+gZhwzl9lPWrL1bc9L+RyL5FBQOWAaQVfxmfkJP3Lyq/aWt1iLKKjcZp47/lriuqkgndGAoM1YkAFljOQEvLhiOOHT/j8j//Eh1//gePHz1jyjKVKvo+cCakmcIGGa4KH+WbqDYxgUTAM5krzXjC5qvHBxvOtx95/Ny8L3x8GA/ZpsxX2HvnV+BN/jxSbuEdEVaxSoIODuUmRjlfGqS+zKHJETjR4HykuEHlS6ff1uAffgaxxMHwh6ZAsYbPylKYYosOEPGX89stn/PblE/7z91/w6y+fcXo8Is8Tzsv5LnnXixURWxo4Z65eMLGXGZNe4RHfGeu41sbW9/X97fYBHRK3+x4zzJl/NIFLJ/vVw3PQknpNyhE7e9DJfvbG1SPGXijWDrPufifw4uD10HtEtIMttsOrlnlVf6+ciPfHufw7lv6Y6kBF8Y+t8bCmo5pWb663BO/8TRt/rwUDJtBTuaBaAbSQYg639sDYuq2jE3dbAtfxvgpg0eBxqHRzRLE0jwe3v7iIXlo/rd3WVi/M7A+GeDhGAVgcy7qxNh16wndtbQl437P8OAqPfi8wxEo9lYqnpQiQWJJebjQFQZJGUWHkwuImawwQESiFEGWRuOn2LzpY6uCo3fHnEO62LTTAVvjuv/s74289bq2DoqzViVAvvP01Xt4ue0TuxpM2S5vPCJ9y+Xzvi/Y9HIQjoXpJGdFjwI269an4bu8RoXNWTcGoigTN91A45ITwvCTsnhKmlGcWDwrDQ/E8MHwr1lhZQyxlwBUKBDY8TMkT4snLGUTV4RaAPIuAv/cK9bPTjp3tdy5Zv8vcxb/j6dbj2ktXhP3NdQ04tZvE0Frsw76F67bygRlDXOD+01QQIjKArE038N3p2ejDRrjB7qzfquw+AWw0YtlsL3y2eL4X6vN6afM+YBN6/ZOtnmGJ9pQz294G+/B4s7LzhmdeflYbLrz9jXsUOePkdXIP2oPifer7tSTJrfO09di9724dWX+2Umtcq5d4CNzX57cd31t5NFwbw1b9t6/3LSFHLuOG13glfCs6+rWwvPX+rWN5/T6Sg5Rc5tErLxuVCJiC35/q+M6maBB5iiox/DE1fkFTbth7cn6MveIOP45IpJHKO/N0iZyy6kY6NNCrNgtb02u/Ntqp0eqxTv+Px9yD3BlFobu8cwMNFX6/cBJehhv2ZOT9BDFs/dzqPmVQmiTnwHQUY10ClnLG+fyM5fwM5IpSFnBtyqe+L41M9dzAEQ+Pez3wZAwx2KKSxLhWDQRTyuIRkTOmeQbXipxnhSHxjJDE52Poq8CXaD9MKZGSCr036GZKyQXfpOs1Go1szXP8fMkZ0/NwCDxCpOBkr02T5IU4PHxAPpzAmq+jqhEbhYpsp0bSlbS9uPsb9drzsR0sXhob2auxvvYeecORTmjz1vHPzO5lo4gDniuDg3yOrT7yv53+9/Fy1w/fzT6m8Bn7NH5ulHtOn2vnXFyzS89h67koP1SYydOE6TDh8XTEh4cTHk4zjocJKZki+OLQVuVVHhFjiUwV3zKNCgy3bKze+2KjqlcRDZcOXzsO2TeZFBMImHX5JMgVTaC76xGBHshW31cEGGMNllv3wq92QA0Wh6Wol0NZ3IrWLGq7+OJ6IMRE1aGDejBKkYSdLZO6ub79sJbghggDQ2jHIcLn6jXTsnp5+byNEO2ISqtMiZATIeeMPIk7ooVoSpTcykQEFRRfbYIh/wz3/UlGS5CuV233un7q9+YM2e8B+bt6zYlbEkYjYJm9tkHxojE6PUl72xftN90nHJVyUbDLQBeHc1wXo4wsVqDkGWgKOfY8KX9nK9A/o/jMjzhFkejXwniuDPr6hMOScSoax1IFffOckCZCmQsyCqbKmCqBkoTEmSbB48boAPAk0eO6OwHKCjvgDt5HZoCD5dLaMpwbzYJ4LspVa1MQx9+j50MJrscx7wN5n3qr81bXy9bCYDkpcZ3S+uzz567A/WpfKK3ffUc/P+NnxCudz1UQvDvu5bWwYhSA1lrB5axnpHgRLqXgvFSczxXP54Lnc8HX54LzueDpXEVBUSDKiyL9dk9AQnNdlgkTBmiaME0z8nRESjMYGYyMioyEBI1wKnQVTaKQSAepMM1A0nuyGMpAref3skLhNXhprUCI8GsJAt2zUi+33CvVvc6ccexglF1Y7kzCRt+NjurAZiTId4Q09wsF//40ze1zEghjAiQWdyB2tz77llpNfF0J8aOXXnyw8btugvHz7wqye0ZxP8tfv3yrtXxpm/efJX+zshp6E0cDQJMgi5CX1NjCSEROCZwkJGVNEvJFxSwwm9wYBjuR+Hhmq14RXlGBpNOLCHz3pvxIjEs6Gt5GQMLb9XRiozW2IYWV5gciHW+eG5VaW1HA2tH9G7QuAygwT4iCUk1eI7R/S5occ0NIPi6LVND4EvOQwMuZAJ9QApC8z5oHGRLXPwP5CJqPeHz8jA8fPiPnWfi1r//E16//jfMf/wOeZyzLM0opHv4nUQuJ69SfKyLWfa4U6E+PwCCW7Us5g8E4Pz+BACzLgpyBNM2YUsLD4wdM04TzsiCdMyqbjGzIcUoq+EaIvFAW5a8yaiVMKYTxQaO/cxY6PpkMjQHjVoxH28Y9l+V9txTvwwSR4VGWNktFBaEwY5pmnD79gofP/8Djr/+F+cOvqGlCKRVLeVZuBB6SyGgLrgyiBluWs8UMrE160/ZDlCPZ0PbkYhZcSZ63fW1yZvvV9qTPl/aFLQ+uRrqgwvpeVQPFBPOsYmZUFPXgLqt9YbIA0rWrrLnuQih71CJeFbYHLam6R9KIzOw6Z0RUdYxhpf7swtB9bDeIgJxw+vCAhw8n/OP3L/j3X7/gl8+P+PjhCMpARcXCq2FdLG8Smsk7zdfDM8Xf9p66zzLocokIbK8IYK+lHlFDbe748j0KSfUfE1wN1hq9xUz0iAh9CidmPDxjXy6McJjvppGzg6sTBqMdgBwOI/eMqH1YnajN35g0R6ZR8THGJ29z+Tcn0Gj99zh31xR0t4L8peeaDGDNoJG5wVI7mOywt2dC9/fb6L6NGu5G6/QnDXf318JHmZ21EiJ6QujhMyjDWlu9wqXThEPg3f5eKfvifon7ZBxfmIRtHBWJyvbdD9AfmVF5q7JFuOj8VgDnwgBV5FJRWVxhSWnlTFW8IBiYWBmhDc+gqIQzuG68jAFyhG2OXQn0VYOh0UssKi3ipxGlbbABF3MLKRaVG/5OqAu83d6mwgQG+3Yr/L5TGizviccGfLKy0BnPyO61rmwpH7zPwz1XPVDPKm7uVn3fz+busrmPysmmRDJlY/FLFBAGLt6iMdSAKCOiYiDgYpCGF9CrAg0OlYmPZCpgjDwBJExOzBmxp3xYkxjaQSXw6cp67pWRvnO0iS34HuG+oi1Aw90jD9ahYOrvmwXltT5G75d4llwVJIWzNb4b69t8bRCud4Yq9tveNnNgvjisu8pIp++Nee++j9mh3PbZSEfTzqe3cLGP71leIptv+OW++dqr5553Vm1d2oubU95oqr9CuURbXXr+Fj70vcpbeRpcqnss13HOPqTfCwv3ehi8Baxdq+PS77euw63PfYu9c2+b98DeW4+nOwHI7oSv3TMq/lPapXl8ykVqfCH9hHpDhDCgygcSy9OsGgtiQiIRNZJJTSM/2PW23W983sb5RPIPEVSIrLQatf6ta0UkgIz5a085bcOwPBYrZQn3u9deqWyCUAv3GaJZdObIHdMSmZKBf0H4Hp4Zx+HT0sZhuqU4AU496j8pT8jTAfN8wmE+yhzWimV5xrI8azLjDFM6UUpIDOQ8iZFvzqjGvwO9HIUGWtWUFyoYZzRZldDqosApi6ZrTgmJEqZpAtcqnhFcJA8bM7icQ91oAu/A3zNHeViFKatI+2MhbiQHRevtSAs2McO4h3t6YaQ1r9Fp4wXnExiFJd04p4Q0HXB4+IT54QPS8RGYDlhYAoh5fTZuAVv5DoFFivxiANzICyDIT53u3ux9mHO07TN+Am2Lk/6htYf1CKG20UT9ykGpYiXuoZYwXgYnCgZRROj6+h4WuHRZavxuigbjcaw+nUAK89D2JNoAx79vLNfo+XvOCMvZzswSZjknHI8HPD6e8Pj4gMeHE+ZJlMeCQ21/3H62vI9HhE7ca4lB28zXmN+Xl4bApMs7fXXAJkeCdmhIAkkJ5wFyfeG6GQTcvUcXOoYLDd/JKvkGDIdLryRomkGPL14LWD0g4HHy18qEVVv2++h10cV83n//Z3nr0iNYYH3QQQ9z84BIKXVCWHvnJUXAeljrgKgbLETCZ2MUnTCokR1kGDHgFQ7vWC84COxYDwOL3d9ibK5D2zSPCAZzAXPpujnCMQ3td6RfIAS7s9mk4QAGu+2f5d7Slry7xQx8XQrOVdxqp5QwkVhXLZyQOSEVBiaAleFJKSOnDKKsHkGRDRobtK9m8dALwi2vyChstfwM5n1TubT8IzxeSjxZU7pvjMgtGr+0hBw+tS4eSkiszIc8EaWCywj/vWdQU54ROsDdKFsE7ugVYUzjnnDYCclN3HNdwLClhGgrtXV+bpzP/m4g0uPeDEyeWJ5J7hdPjL4UnJdFc0MEDwjk1lxQOrjiNygfJCxYhodZgnmIKQwygTmBq7xTOaFyozco5XZ1HhH9eJniHA/zYOseIi5vz10jZm3eujYMp3LIgVLDvRDD2PGtfR8Jc5gSeqRF9oVr7f3Q8w0h5XjvVmLfWh6VEC8pbyUI6vcP3zSU1u/Lc7lXript3rHc1/bLxvc9l7+KMuF7KT/n6+9Yfq7pd1toh3Z0KZWtXQZjAmMCMIHVwxNKx2RK/mhSQwsnmQhIYMlriOazLjnhCNWkl9a0/2f3Wx+NBjH6N57nKSWRKSZ9ngBOag3tyoiBWlKe13iBXuAoHRWvAalT+E/hO8G91bn0XeeMSR0bWHImMJSeWsDVZDjm/TDGq+cw7q7isaGbS09h0/CLibQI0+EBh9NHfPzwBR8+fEFKGUtZ8PTH/+Dpj/8G1zPAGSkBKSfkaZIVo0cslXE4/gs4L1jqM4CkbJfSqk3YEdpvphG2xqUsYGYsyzOICF+fnjBXxjzPSCnhdHxAThLfPiXC0/MTzngCzs9ruQZ6OGEWBVgtBYXQvOpTbnIWIo+agqoW+UFJIbkiWh7M1uTLaBc3miDzxshofFmS3HJV+OTKAPIB+eEjPvz+Xzj9+h+YPv4Knk/4WsJeHqI7dHwvIDAP81oiMIoqKdZjaCISdnZznGPAJbS98oFF6cA8ZnBs8lnxTGBUFm8VUuUABbyQFIeYXIxrEQ+KsqDWxeVIVBcgeEhQFZkSTHbql+YXVe8kk6eiLusBcg+fW8vcJHrvQ79e5V1IFbyKtyln5MMBX758wq+/fcbvv/2C3375hNPxgCknPBks3aGEAN5IEbHH5F1i0lZrcjNDd9+C9OLK2wQb8dMPTT8/7Xe5b1uFNKZzKxT+agKOqKQRWURgIHmN7rbnZN3XqIndzM1gBIALxvrERVGpwN37JqSCWyDEGY1KDomL/VP5EA+A8d749xaDJLq3DVjdgA97nofvDlcwKA3wOAoKo5VJEFK5GNZ+uySUBJq2N1A57P/GcbRnfGdS37845vjiHt3UwRt7ZMq2R4Igqwl1++9Gl66Em/bdCY9Ifm30lVvb4/NNufr25UfYcy4o5t6yAej3gITGIsFJkLidIE0ZxujwMblCzu2vVu1WtsR6kYJvcCRtxrMh9sssIXrlxFiPf9tghkzxHfF7C7NUPbl6l+tHmaAY0qm1gdZ3a2vYa9t/x3UY761uYe/M7fDMoIQQS+v2at/6MCd757a+zsEa7pI1J1FzK3dljOGphh4Qz3y7enzKSMnwpnkmwPErwGBqTKslJ69V3IHBBQQLo1iE+S3kcFFZCPBlkedLzeod0/rWY/swGQTH6UJX9PPSlDDjaXJvCXvD/mK+6cKgGLOFGHHb6oz1wdzQu0Brdn9jhImts5laDuuRZrVzZ9guUo2rjDp1zo5K6E3LJSGsWZbeSlZv0TbvVfbaulcBIo9uPE/747il/reagXGct87xS9fgWyqQtso43rFv987L+N57lpv7tIUTbtxzprTea/s9y55Cd+/7S/r01srYe57dO1de06/vbX/9ucUAexw/O90kT2h0CM1xxSnLpWEpgShPCWcmWcgbgKg6D5v8uSTCd6XFzPhDRDjUnfFG6zceMdAp1rKRciRGNqLpSKi1WZonIhStwOhpp1t26eieprGk1UYwRdogcjmjzCfmhoj0Elb0vNXb87OvL2G9TfhIADSnAlsekDwh5Rl5kvC3lSuWsuD5+QnnZ/GIILCEis4ZOU/Cj03AwgWH0wlMz5qHTUM3idZCyXSDuehpvLHHXVZVsCxnECWUsgA5I+mVpxl5KsjTLOF5KIFQV9O5LgxGRWWCJA0X5RmMx9JukvZD/k6Aw/G2LKiDWVN6BV6le34Hr9lvth8YDMTwqJSQjw+YTh9x+Pgr5ofPoFnyQ9SqyoWwT3zVGUHugwZzzqa3PWx7gXeutkQRB+s8+T60hsn3iX9GftyvJuNMTuNX75HR5GBuPLTxyxq2TMbJzcKMRWEo/LWFmm18NzRpvD0Hy7Xb4R3t78C3bskzDO/Fcu85e5GmMr7U+cHWEzes14me54zDccaHhyM+PZ5wOh4wzzPM+I2NF125SV0ub+oRMZZbLcUicr12gN9P53C3oKF3Ye/w5qdLQ3yfsR82DBIlsx6k4t4V2cpekAvqw984AHATmo5lXwnRtm7rs1rZqqVsjLHsigmzTCwVrAl7uNTBo2EJ3gzB1cjICO13nLvmCVFQgjLih80RoWWE58sKmh4Rbe4CVV6t6iBqsEo9Y5Si4K69gJxS0JCjwSrg91wBcY3l7g6hJkS1T98zhtwvlH7/b89VfygPQtthPzXCUvaEwfWuR8TGvukSgdkwh8/xHYR32ly0Pv2wfMqriyp91eVxnEdb9wrxjFmqEIeJAFRxBRfaOCGREp5Z9kJOGVvQ7vDjwlXu1rzDsb4HIswIUV6HMEnNaKwnlONIVozHgFtbjgjF52zxLaPHm4bbs1w/YZ8C8YR84YoMRPSo6Lz8bnun/xx2f9h7mwLsMFf+CrhPPLPRb2bNadURYaHNwEAwE4yENThM5kGTEqbEMHsgEIHS1LVlRfKJqEUNVyzLGUt5xnl5xgRCShOWqn5cRKhIoFrVcqoATDgvz2BecFqyetrYsipDGNfEBFnKhEQl0Fb/wgyh5b25BUaMeJU953jQPICip2TcL0OidWEAjICvboE1rrctkdDIivV31noUMMWz2f8e4WeLHqXAhA30mbuHrxqX38y4swlV8OL4/ZdpiV6518bRxBsvosl4f37HvlnbP8vP8rNIibuBNhHF3vNNzPLitm/kxX+Wn+X1xYTShC6vnvOo8lmJJBFumsHpAE4H1DTrlcGUXXAqJh0EIDldmRKQqHlEJIjxkZlIJwYqqQV0CNnSKGxVwqsyoiqdX4ezNSWlD2vSSisSJTCRhoRC814IvJ94eGKgK9Y0a5TXkNKc7bROYKormYvW1Pe3u1QAW+OgW/gYUxS8WWGRg1ljTsvpYqTpgHw44XCU0EzL+Yzn8x/41z//G1//9T9gXkBgzNOE+XDAfDxhmjKQT6Ap47mckaavWCqJEuP8hJIZyOweIlHuJnAjfjJExdeBIV7kwIKnp6+oteJ4nME8i2fENONwfAQz4XD4A8yMlL+iFgawhAGv+RWAVXHBKCUp3SUQYrDssjSnkdTvXmG2lKKkuhKFb7REokiTvVMhMsJaZC7KsiAfTjh++gUPv/wbPvzj/8Th829Ix0/OQxJEPcg6w26MA7gywnmocBncOt9EDRzlUrj2ca73ShiFDUZ5/0azUwiDRL4fQngkVKS2Y1o/meS+8ikoRT0piiseCPDIB65gq5pTdzmjlrPm1C2Ael+ANceux+kdF7Llhrh+Lr/vue2101ZrQRGRCI+nAz5+POH3Lx/xb79+xuePj3h4OIFSElRTVHHk+/G2crMi4iVMxVsSPvfU1WuaESY4TA63Ayi+s1ZGtOelrl7waQxlE04oYgqIqgm3aJPhdQEzycF4baijEGYUcMUEuU2IaslUx5jhtbtMGNvFO9tqXz+bx1+vld9br0sa279jeck4tyyEY32bTIXLYXqFl5yPhvaDF0QXjqkJrkaPCAdt70D72mA8PhLyT8AYIHi7jOhZ0Q7jfrzb7Y2lExBv4XoM+7m74HDaknsNAk4YMVXD90Zo+dR2o5G/GFb/OIHWL6zH+sLyo+wlKY2SUdpvY3o3JlWfM8smv0iSs2dVJK8E6Lo9oqLrGoHYwDsS5SMcjt0zAinAX21s06iEWAnjQ+ibHg+jB1IEuminLzZ07u6MdWwZDewIs8c73Xtrjwi/jwG2x3m88Om9VgZ0FD5rdTDvC0+6FttQxrZC4xenJJZd0wGZEg4Lg/KEwsC0FMxTEbdU9Y6klJzVtREZvrHQXBI3d8I0JaQM9dypEGs+OCMulkGsZzKhmNIpWKB0bQWlw3i1dQhTqxNGPTK/UJpQu82n4buB0Q5r1+iPthc65izg5Qi3u/REW+muP5fO0LHPWx4RW3RKE+YDewjgLnRuXV5VNbTxSvS+aWn3HQgm13O7/j32c88q7LpXw9441/CyX8deDbvUifbxtnpeUm4f/+117ZXG12zP5q3KJ8G5t/XlLXmF94b3sc9j39fY8k5csVHnrc8Zf/oWc/D9KRlf1o+XzoPhpGtrsU0f3de3bzHH1/j264WGT6An2AGxkhcaiSkDNIFpBtOsf0uIVKasMpGhjwh4KMgmOwF+Z3RR/T0bIzNU1hLp355+Geei8QTkIS5FINvDgvOI1j1lWaB5BKyPfjYAzYhVPxMs/wWLcmWcAyeZIl+CQNzHVRjoq9Vs3lA2aX3qBkhMQm9bvVxh1hcpT0jzjJQlR8KyPOP5/IRyfkJZznowAJSTeiVMSPOElBnTcsY0HzAvBYfpgDqdUeYDzhVABgrX1h/tq0Qo4XCfXZ7BlcFUsZQziAjns3zWKn2f8oQyzTjMR9RaME2zJAevZ62TXcjer4nS9gUoqvxIqSicikBajIlkXaN8pD8h2hli/boVW23hjpHuNxq7FulTnibMxxMev/yGhy+/Yf74K9LpkygIIQZBxmsTiTLOFC/yv20+hqjm4L8LD1tFa1j1k1XoDxL5SmTklT4YFRDxq3M5vglizobGV5gyjjhm3WNVWhk8WF2qfDCvdA0xZfuJawHVpe1t94TQEExchH/n9k7bd00Za/5gW+UyhTU8u0ML7zx9qaLLzxhvOSWkTHh4OOLThwd8fjzh08MJ0zyBcnIv/6Trz5fa3Cgv8oh4swOSr01gePDGga3r49VX9rZr9874rnwVxt/ACsz+HgBdSHMVtFsD86s7c5dhCCO8toDtvOkVCVvKCNYNP1rHbl3uXqTPmOvR9py2vjADo3vgyl3wZ7l7HrYER3Z/ZNCZ7WBEUwKQJqHuOlH98DMrcMkVQS6EbW0D4USBVi+WKTuCk62+Ci3QYlFTO2n0GXTvxi1zW9GDwTdov+N7pUIT2DaBmBwkFpJszG0irpZ9uDHeaQcO8/IQ+1ONGFq/+bPcVXjjNLDpJMBcurmD3Ub8u+vvlOTS3BCT54iwfSCbaWulHIa2cjuEnBFdiKTw26XBOck5MBQclBCbFzdLc4/J71pioMfH/WYhh9W+vITZXhPAF4aL9f7fLd08rxUxu/00+nbjGUFDRo6u360AJFASoVIC5RkJhPmYkbgC+YBSCvJ8lJwRZ1bmIylTpV2oCk9VVrhq/NClakK8acLxMGGeRBFBVJDMNT03oh5gTYbNWM5n8XwpVQ13FDuztGGKECRyxqzPHRHmPeL6yK/swmqkeQaCGEEpFmmQiGvDGta6XsMVDXNhz7gQYOu3G5URb1bCubZV2AjP1Wu39OtlNFVPL7zz+IfyEoHaFoO1p6S4t+6/U3mNoPNVc/YXnO64/3/yIz9Gee1a/6h45W3KOHfc/0RCkUs0iRlMByAdwemImmbJE0GTEFCeI6JXJlSGWjijycNb9fp347kaTSEXlCd0DsHCp7gywu6HjhM5PelW9+NIlfdzpQi1/npVSn4bLy68uvpWJKEhkglBiZA0113taJ21h8TAkIbLDEtb37qO7JYbhKIqeCDXtsg77HXLOZXnGfPhKDKHRHh6+oqvf/wT56//Qnn6qkJsksTU04Q8HzAdZqQJmDU0U62M83EBuIDLGVRJ5Me1aEx+GSZBaV3SLGvUAmKKIbDIws7nJzBXPD8fAQCnU0VKGfN8BEAoD88gYpyfv+KcAPCiuTjK7jlYixgRLSCl5RNSYjAnUGKUovOhfclZYCAhdzOdUupgBB1M3obXHLZSy//ZZCEVdTkDIMzzAQ8fPuDX//hfePj9f+Hh9/8DdTqipCMYz0i8tCTUKZo7eYfgYY46mZPITyyRt/yQdZMofjYZMEEES0wup/Jhdvy9gZV5/Kj3tClrjL8NsJ98xzRjbPnOsOTWsDwOdQEpn0L2bK2A5WCx+VMviFoXj0TQFBkt7D25EqLfvVvD2lq/t6FXLp9ll3e5vJunjPk04cunR/zbr5/w+5dP+P3zRxyPB1DOwoMyI+vzBdjkqffKm4Rmemvi7qVMRuyH/01D/xRZjoKJfWWEpUokF4JJuILhcG3cfPe+IUH/hcxSPCAZ6j0ijMlf92XdV7bPQUjl3+23UWAWpwOtnjWOCYKxKBh3xNLqaXWMwgV//Ycvl2Cahme2lBGjEmK/Hb1YvsT9QCqYEgVEA9+VxWy8XHPPQztrJZxd3I03eETszEn71P1v/n/Y35/6a/htFDqFgwk9cuwEO352rYXLUZAbCbwbyDR0m+TGN24tPy5TTeFfKX6oKzBmzfmQM5AJSKl6IuUeYAMBtaW8i/ViZ84NFTo/0Ihwe2d9bYUHGzweWtZjT/I7KhTGemv4LbrFb8N1wNXo4f3WZFO9YPTKO5sC4fV5GabS27ilH5vPhr6thZyNbdrEy5SANCFNwJQyUp4wcUUlWeHjsqDUguPxQRQRS1NEEAEp9+efZk/0dVy4KCwmTPMJx9MDQBOIJlA+gNIBOWtsYl0WOgOFGLQQqELzm5CHGBMYTx0eHpVDbfyRffcHEOmju8tAQkTFmh0fAjNwj5+OIcEdjNbWvasguH5gtHCNwvu9hs27xZ/Vn14ya1ZPf2Y10N04dr3ft9ADUcm/ib746s79U8qewmhci16ZeGWtXtmX9ypvUf+49vco3F7e/uX33kL5dLmufRrqFrxxSXG+dW/ck39m2ToLrz07FqOJ3xqc31IR+Nq69tb0Un17sPKW+35vX34PdPu9fbh1jVyCQSQW8naP1PLZeDQiwDxNKalnhF5IcpF+glv6ATYxqCkMTLgwyjSiXISVftZPvU9KJwvt3ozIOloYRifZ+LXJKPsIc0MUf2vynESWn4Kc1xa6wfgOqFVxlXAxmggbLOE5I94lH9v2eb4qTTjjxMTaG2S1kP1k7hYZjy5BExgArlihlJDnSS41flzKgmVpFuYmFHPZAWkYVA55tkEgiPHYPM1YUoGHNvK+SgeIDH6gigBZtCa/giaWTliWBSllTxY9zRnME6bDAVM5Y54O4LqgpAzW+P8qVvEyJnCmVD2RuPRHeTlVKrCzoJH2HmbWeFFq+cz25ZQ9TeTvDzwAQ2X3KjhOOeH0cMTjx4/49OtvOHz+Ffn4AUwZiy1LAhInCW+MIPfgZjg3tmn7Ul6pIFYjKW45MyRklXpXcILDJSRht7WzD4o6FwYgzmu0sLA2567kq0ar6/Msz0MNtT3Bu/LflrwatYBqcZzjRoU2maZ4UFiOoatg/OXeZqXuw/+6B0dv0cz9990X40f/DgDDxfNhxul0wMePD/j86QM+PJ7wcDwgpdTSQXCQy5hHyY3lXXNE/KnlJmEF/MCR79c3tZRgMRmUEH4Awfh3w8IGWSb4QhOA2QuGyZi7DceuhNgmXFZ9Dt9HodYYk7mzMOw++/lbWbxrHy0/hAzNA/fAnZ68S9zFdf4WRPxfszSG4ZogaTyYxmIknB1iXr/WkTRBrwiu9glMYvg67/OgStAN9TTlhUL2jpA3jssOZ0Po10Enkp9tnL5PoFr5QeDFG/sGOwLbziPCr1v61hOQ7d7P8vqyrzCglCXUTSJMWeiPDCCnXtngsKpJ7dR4fKPevTULMFFbfFdTNKyedpiq6783lBBxb6/wOZvn2uAdYMnHLPkdYjuDIiOcA74/urHZnN7I8MQ12MMnNzL6BIC7/b+9N1fKla5ETk2TaXUEu+CHPaxEKYEyCfPEFZPBRzYLI5nP8/OCWipKUdLNFRFqF2LdKOGMBKPURfJAVCDlGWk6AsiSEyIdAZqRtS1jqMWKR/JFMAsOz6kl+Gs4fftaF2UAdp55mdBkQ4krlXWKCSH2G562d2PbW+2Tf47nYs8UvbRcU0Y08u3PtbDeE8BvMaERZ7Xn9kKK/HXps5cqIcxQ4qXleznF30MJ83cq76Vw+Z7Kj7v+P+q4v+PicgETSsV48qyhexiejFoTVUtcygniCTGJggJRxoBQp7FfSluRCH25am44NcA0L+HCFUU/PTmv8XAIso0onNRigsdxjO2BrUkIvQ3CZJP5RMVFUs1FStTeYpYAJ4E+d/ps1WaUN4Xmu2cizxp410Hu86IShOkcGjYLeSRCmhKmecZ0mJFzRkoJy/KM8/m5cxURobd4MzAlMAiFGUXYK52njJwmzHnGOS+icFDZk8mgJDxQU2KR5a4gl4CIVKAsYADn8zNSSpIEW8NCAcDheEKtBYfDEcwLlvMkEUPizA40qqwVPK9CUU8NQkVimQ/JLZK6qY+ykSYDiTupb/OmpaHmDRHpxBJ4v5wSPnx4xMcvn/HLv/8X8sd/Bz18QVkKlqc/kAmYUpLZrBHuWXknViGRhjlO8RF2eE0AmJPzncQSlsnyM0g1DFAF1arrX1sy7NCuAQwzr3M3RN42zIPlloErBLVjrPIhDbNULaeDKiRYczBSWYDAP1uEGeaWrBpcurUSA7dvTVu/8oxUY7z5eMTjxwd8/vwRv/3yCZ8/POLDwwnPKaGg7c/JwCHyejeUF+WI2LW+8Afky2gt5orLDrn3WJM5bLSOWWhA3bUZBIo1CHZMAOB40p+TGytlRFd1O/yYWx+s30yEqkmWoG6EAuqMhKYJakdx251tjpqywg6r2t0DsJZlxUlq4WSKxSqzjbH432B1ZWOLKb2gsiZa4YJSS0u8YkKwuKHDWDpBcpf018KDMAqzd3sLYf6ZjPu1Mq731i+x+Dm/IxCI9zbbuzB2AYNGoJjeyl3e5BRthFmjU/oDTf+JoZagxFl7mJETeVz8RKKltnbMxoDQQLGRhKGlUfEW+iDabpsfux8opYEg25w322/X4Kg7wWkgJJuANgpk4X83nMNhT6GYSx57MlXvi1sXtMPP2m+CnlWX4TiJqPv+rcv3tCfXZYCJsMZmM2FwmkgT2KWKKQlRJDAOZXhIQt7kSULiUBLCV5Vyht/a8sRAeRF2/a/2Uwe73P3uSoUAf71yIBBTzFgn+GsMib9TWy4fsiR0aJYZLeSNEESVi+f/McWanyMwtKAKdx5HggDzbcjs4+Ru63F4hbGFIYBeYEorHBBnkNB1CXZ+bysiAsVARhT17tkIZ3rgo+SdsBeSetX4d7XmEvfy5u5cHgSP1NKsnggMyjHJMjQ0E3yeLW9TZYAog1KWsUGIP6IZFlJJQjBVfM1nnM8LKh9RS8bxcMJ8OIIoC6GvDBjtKiMsoWBbrzjBbEQTNQWFJ57cQRM9jq0tKbpCg51ltqSrvFRKyBv9YXVG5skZGKmxMUA9WPizkQG7TSGDhrRN87Z1tuu/Qp5ZTwZBQKvQt68dl1v9WPdppE+52wmjEsLOW6MJDV+YzIeg+2DoXSKSeLmUFH+0frcpsXYiybo+r+M8Xfp9S3C+qWxarVGkA6z+1WsXhLKRPhvvoKH1QGN1ba2r0XAAkWazs9+w3u1KgnuEyRdheKfOcY73zvyr9TID6fa+7lRirW2u4aXnbylvI5iP/OI2rN3Xl8CWG3hsvhB7MDK726/s0298wzN/3dLWJI4t8hXyfXfibirju0r5cA8f6z6t996KxrmyJtt4Mdb98nG9mxLd8j8Y76ZQ7FIRI4RoErkIHQA6oNCMShMSq8lISuAksccBCXHCEW8AEnmHgUoJZyTjxrAwUKuEwSm1gosmjY3WzlFgqWds8nCR7Zle+KP3KnsI62o0dqTlEejKyCRE2NBxsTIuEpHJ+MtA2rDx8mHVyS4KlvURFrndCONzvqJL4stYAbH1kfcgjdoYtG6jx8TzJdAsKid7mB/wYXpEgtAalRdUnGFBXKDhuVI+ilEOSTCqUhYsz0/419d/4vnpCV+f/oWkycKnnHGYZ3BdAFQsy9zkYATUwhIWtZ51nHBohArCmeBysGWpSIlRKwGUMU1HzHPF8fgI5oLz07/AtaAsz8oz9fu6zXmY7iSyg5oWcE0agUKZ1YHOk6W3gGMNRutqfQiuZNHVcRgIy9PR9wSHsVzUE2WakU8f8PDv/2+c/vG/kD79B/j0BQtXVFRMFEIuAWbZimYhFmn8QJOQzAMRgZN4QyTj2bLm4qyBznJCVWnYpHNgYZp0Ts2DAqweM5TAyQzp4HvPNl8mUQRQARii3Gi6lLDBKgc5ajPc5oBzPCLOCndEHpJcsSZDso0KtBBz6/3GkUnwXoVnKF084zd3r/PR1Nq1CAtO02j4L0roEInypuCKNDPyxPj08YTfvnzC589f8OHjF+T5CEYGVQkjZ/iKrd1E2OzYTnnzZNV28PTPt8kflgBR2i4WW+HXCDTBF07c4lttTQlhQBmsSZk6pI6wsXuhYjwz7NAEii2aj84OgAmcD+B8EKGBsqRREQGokNeEC3au6SGEDWJAkDd54p/9WWe4IkC1eQhKCPACYAFQwBrbrikhxs/S8kcMMZx97Ctky57c14ReldX2PKxFc1nbHcibl/uIrK2OddyA3tqub2TAX2tR6goIQx5E4TAI3gsKQ5aYXH+V3xOtcACB3IVNBDWQsB+kSXqVmPCEvT4L1OpuGEwEZDCN70h0G3Fiz2LcYIYlwrh7Ij3SUpcwGjtusb2mOGglpFSlneY+aUqEQK+ZEiISraqIcMLUp0T6WWu52L+ur39DZvAtylqA47+sn9VkX1yjgguYSDwepszICZiyWI3nDAlto67eaZIQOymJMiJRS9ouSgltyM8PZ3sagcdtxQWWyOkNF/5zg5lOwcXGCASGICoj/PwwoavBnSVNN8Gt4XxjKiw+JauSeARfiXvp8O8MCrTj5PO/CafjUth3UqqLZE8TtXkSOuDi0jtjvRZeKizofHa4IzCFfR4BI2j1bSZxCR6Iikj30WDBE0tWWBG8mpCnA1KekPOMnLIKuyUPQ1v7QGxQE1SuBRfbwoiGY0wxkQBOKKWilIqU/sBzJgAHlDrheDzhMD8AmCSptjKIaSM8UzufqCfaeaTXukOowcdGf63PAuPc5U1xipzaAroCZlRGGHy6R0+r2xUUzvj5rw3mYt/jtxsUECuG0uhCbjTaWhkBYa6EsnO6rjEA4QC7sAf2hPZxXsPDXmenjACaRae7iCttArgSopsley8lmd9VJ1u7Pn7a7u8944q02RadNtZLa+JhpRDZK1uCgn4d16M25njXSyrcrxvnfoOz8SzbqGtzrLc9f6+w/V7B46X6V/wAbqdt4mttHffrWfGRb1yuz2Pj5W59f3MM3cD7mm8qzMPcrY3ptvo2Nn1veQmcfdsS8ZZ83+rTeGs9hXurc8146Pbx78/VBX7nwphe0t7t+/a29ogJYBU2o7g8yCMmeJ5CQEIzHQA6SrJqTHpOqTAy5Sb2qUV+SYzEhBTkQQUJhTIqVfcwLYWxKM1k9LLzdFu0I7MIw5hVmN3Ob2PFm7GFWLp7LjY2xcfSmMlwZglt4DMEo1Gh0mEGOQ0h9m7sT3bnbrhMCQGLaIAmezE5l8f1ZxMsCn1g9wmNPu2A2mifQQrgYzH6EKEdYiA3PsXHnjI4z3iYH/Fx/oCMBFTxBi4s8ikQA0kUEZSPSOmAnARW6nLG8/kJ//z6T5y/fsXT079woAmnNKsiYgLzDKBing/qAaOKCAx8kcoaSWlfS1pssq+iXs3ipJsxTQ+oM3A8PaHWM85zC9FUWGCNVrSzLaRME1cGJWlDPJmlbuPxRlqPzCjE5Wq1C9HbYMjgqHagJXcVRnQpjc8hAqiaIoJQDwfkhw94/Pf/jdPv/wvpy3+hpiPOEPnIRA0OQRB5JEdPk8ZvmexJHo10sz4rLhGaWFzmRCyw7Hlps5pxR4bCKoE8NleRfUj6KpF4TiSbK+lAAoFIjG0TMwoJlV6Hw7Df1wwuMeJAM+qzJbWt6UoK3UMy42FNlGc1ZYTQ2ZYbY8+6fKT/w743fiSC2IqfHKsLfIjLNGKOSlK+L8kcI8HCxslPMo6cGYcT8OnjCb//8gVfPn/Bx8+/YJqPqMiguiB7fh0FfQJAlpnjtvI2OSIQ2cxwf1zEzZfXE+wMhDNxNqm+1Fc61NBmXCjTnHV900q7foe/LcFj0taF+Uggyi7AatQeYSsh5KXSITHb2GyA0M61KFA14fMYmmPMDRE3VUsO2XsycFAisB+sdQPArzNWhljXwpe3ZyAu9uJW4gojxA5MzwgUG8O/1TrtWmE/NfaLtSVhOXSPUEJKgfYZ61ClAgcEZMqMUUDjMrD+9V4exQaXPDwTBA/axxg3ESag3BlX/PROsBx2W8vZrEFVALqh1NDRwgknCq6+PaJCH8pmPc6GyxpcNG35z/Ka0u/XcFBubDquVQ85I5KE6EgaHz/nhJySugCTh7YBWMPWZLd0XxOQ2ytpeFfiWN6y18O553i7wU+vIMPwPVhkRS+eIT9Ep2AzQiq+U5uCI557CH1SDqrvH79HvPX+j9fUf5UAi88ao7Xa69YdwwW9wNdwbE4T8jQjpQkpZUzzAVOeMU0H5Dwh58k9akRnYjhDcckocNroc7S0afQKa+xkcphbzgWlCDM+TROQCKUUnE4nHE9HzPOMaZJ+klrfXBPAO5NJtJrPJsS6JMBfn7XdCRrhMsKgj3VQiF0pDDR7gGAY8BKYfSsYX1vCv6yslB2R7rWz3p4d3hvnr1NShHr3aOfY1v44Al069Pc9hI99/2Nf728r9vUt8dufIXR9zXjHcX/vZU/J+e2F27eX9xzD3nreq2T60cq3gaFb+OVX1P6CMf1587CW+Chp1GZEeTtSGpW4gLCAeAF4AvOitLAIMhO3qmPt4tEnUt+qyo+iAsWihpU1KAt62lc+hbZXwXWgqaGCZrZ2jZZWb3lJVitW+83LuM3CNgezj9OJJRoBIALUJvkUY1qJXiBXViFsNYm3JWdOJsgWZQX2LpCGv2KAS1u2UQayu75dz9vCjJK+PIHmA+bDEcfjEfM8ybwaHgu8AZEa0KhyxXih5+dn/M9//w+ev/6Br//8Jz6dPuDh8YB5PiBPk/NypRbxYCZGygRPLO1CNBF6l7rAZQKAeCzUilKKXtUNMlOSRNvTfECej0jLAqIn6XMtOuQNL08IHFEtKp/IgR5XXtTyI6B5eK/hROnLTkzFYb4H+pDI5ZIJWWEqIzFJuBwWHxTKGQ9ffsfjr/+Oxy//jsOHXwCalB8pIFRRFsCMuZRXGWUoBF1PaF9VJjOeRyoXlMgerLAZ5o0EGDp+g4HEoqAQ+b2GszJ41fGCzICQZC3axMi+Mb6YUmhT8lAAhBJzxwS5QvMFGeQTV4TQ/dMmu75kVL5XTLp14Ylbzv4mHLT/0fa54gLoXjTjOVIYOZ3w6fMjfvn8Cb98+YwPj484Hg/IGvq65W8xftvGjbtG/EY5InqB3DgxA37erkGRWGdBFSptCthrw/MH/RCIOD32zw+0MTFnWKPkTJwKs2SLgpA8PMNKGXHrAqi2qwemcaZ6pn0lgBoFXfbd44kHbwdXQpj1IffPB0GWtWkTMfCql0sQUHzvBPJ4fPTftg7cnXpuIPBuYxhG4Wh/q2f+Cclczmp/GG2VXhkRL/SbDVHAEsQfvm/C54ZgzxB1G6/tkWGkQz9760nAqMC9eSPqlRDtgBz7FPZnH3gepjhjRJgfxjnAcrzfEZ+jwG2n/NWY629THHv3d9Vd0wqReDy4EiLnQRHRW9uPMfRbvZdWTfHtHQdrFBB2OHpFn61xO6DEMTOg+Lpys9aormToFdAGe6zEW2SoDCeP54QR6VuEcJtk+FjanDVry+uwHN12Lz877g1mrOdmdT7ps/ElbJNxXOtKAeH4RZtNpLkXsiTFS3lGnmYc5iOmacY8HzHlGWmakTTmrcGq1FmcnN0a7wrPMa3HKLfNgA/naUFZCipLiCgGNFH2EcfDAdM8YZoE5imtaZA9hcKWEiL8unm39XODcRrXzuYEDdaUd+n2SKxqa0/Ys22N+6l9rWA8vnuz9ecN5/mtdEEr7Yy2v/3nnbbi3S0lhH8G2vQSfbY3roEU8Wdeaoxh/br2rnWloZD95y+N59J7r4GZ175ziQ7ae+cS3I1rP75zL4xfa2+vj7eWa3Xv/f4tFUGvVfBcW7+9Nrbw3E968nrZFvLdX76neY77OZYo3Nx7563a2ngyXPo9Hmn+J8M8eSlc9l3CSJthufmesURhIKmyAqhsSghChYSbdjqZTRnBK1lH/DS6pKI4LRxp9zAJcA9m9bCwuPKtLvT5JoaiIp8ON8dgC6R+lt074UopIdeErEoIM7SzpN9ucR1Z96EW7mocn4mnfBQtjiXKG2x64rj1vZSBacY8H3A4HDBNM5hLTxYTnD+PMglmyY13Pj/jf/75P3j++hVP//wnjmkGHoFpnkE5C2/EjEMtAAGFC5CA56c/UEzIyuK5CpYoBgwAeRY4YuHvmqysACm5UmSaJ+R5Rp4PSOdnUJpApbbpWs0M2yKjcgFpgmSihFKKhn+SPlJNq0rI+QZdC52TXkYo7XeKMgRlDiVYrowkfij+WoV4ez98+RWPX37Dw6ffMT1+gSSKJ4igv0jueAbAWWn5IAeM9LcrTEwGs8eX2btWTy8TMv684ZoEYvPurcr7I/C4WjeZPBaN9wtzJV7rAKopaWSfMJPiEAsp3xOahIRmCBulRMO4Ln0n2oSRS6XhWJ2wHZoWuPHsr9ZrjWxiINcxDnEMsrgpJZxOR3z59BGf9Xp4PIkiQpVoVBuW8JD8Kwx2vbxZsmpfnKsHXQNU7r96MZFPGjmf0BaHOhiQmGFBQNFkPtwBr/RxvQ6mi+gZePNwIA+LasvJsGS/YzxmKO4YmcsK2Q37hK2BvwiabPNxp0Dok5Y2xFm5qrtgUzzYuzF8k4UIYUvGYnkm6iDQUuEBRYS4WocmkPA5fyGh81cstzCM9xTBdwyom5QjG0DwEQRpZuqwt1pLhP20KcCNDD2BKCNRDoJ6r84PFjtc/MDohqfWI1vCKI03FwUNHquOjea4JMSxWHYbxOBO2fOIENBtg+uFV/qAwTBae+0aLMZvQbHc74cfaU+8bdmaN7UAUtyUsoRkmqcJOSVMU0LOSYWyqUueJd5DCvdoe6tbW6f9NqzJLVb+Zr/ac022GgSorMoBjLDVvB5aiDvzVgvhaoIiQpgoZZ5KyxmBcDbw8HeE7Ziwj0vx+91oVnsI/lyP596GMY/1RqXA1nM8Mpar/dn+pkCcCwpiv8+ogqdQ4XmcCMIgZNIwXrNaXh1wOJyUoTohTzOm+SheE9kS7Gm7tSpcBSLUx9MrCRoKigJ7sc4za75agZTOWNKCUlkVEeyKCGHwJk8EaAyU0ycBjjsG+NVrdhk3s/efe8+IYQ2raVtualQ/dzp/zxk87vHVu28srL3eP2PAjI91Tg9w5Ra6tlq+oy1l3dA2sFPHdj9uLW8pnIsCr9sErNfb/l4Eta9RlL2k7MHj9zIfP1JZnW8/y8/yzuWaovx94FB5KYv3bn0xfhLKSrLIRKgsYDwD5av8kp8BSkA5S3z9IAQEkccel60kCWKNbqq1oPAoI6nBuLLrYmOK/Qq5IYCgINCxaMQIl8OU4nHlW6iWTflea9p4g3Hum8Cq62f0tJAQKhZOWeVPlSSMVVXhtSkkCCIlTBABMwGg0u575zhcxluN4WMuwcn2OSIkvCSXTjmroczkkRJMfuVCC+135IWM51nOC/741x94+uMPfP3nv/Dx9AGgBMoZeRIFwVQqpnJG5YLpPKGWIiF484JUMiqzhmTyBVAr+YK6nFEoYTk/g4hwfn5CnjJoPoABpDxhmg+Yjycsy4Kn+RmJgHquztOB4/neaGMxYIOHEhPlio1Rd0SQO7v4xpRGvBU+sk07EQGVgtCb1E5PvEISCFnlPFwLGAn5eML88BEf//H/wuOv/4nD5/8AHT+gsHoJlDOINPdgVFpZ0j1U15PEMe/Bgc83BjqVWdqIMsQIa7pHe5lkCDdsyivjsStgeSZApAJ4qCyK9D1u86R8dClFc/DpSG0wYY82rrJ9b38Eg7crOJW8P7fj3lsMnvbbawFI20oafyzyaJHPqVKXGaCCaZowH2d8/PSAX3/9iF++fMSnT484HSYNm6YwzNxk5wz1surlcbeUVykiVtaGFwWHYbd1dfRr1y/22oKrf44cQFh3ccTnTfjaM1z2jLPjprXyj8AweKxlCNBD4DvBmNgU4jFbr/XZsDv3xFfrOeoFKk0ZEQVXw4X2tysoPH8Et8M4aO49nrMLCdZKCJ/3K0xLW5oNZPIdll7juI871sNW6Ijr+mYMnQIlkeNRVpi0UsGe9McPAFAz8g9nhrjHWZ+1BTv0oRpkCsK3NiJFxhbSZgulcPjcELSHQ2ol9HItOHfrsCcM2cIp/rdV5QfHqqNRqhMm1C5Lb2YHoxEP8IMyYoreIoF8jPtlo88/yyuLrIcps2I4piln9YogF8oaTgYQcHVqIBDhq4FVXygSJ1t9UiINEZ4b/HC4Z7H514qI+AyrIqHAFQfclBDuERGVEo7L9RkX9lq8S6DD79pGZLxWoxrw5Oa4byQ4rAbSsTehjPy6EjzyNn3RhK17wtfh/PHq7F6FeUq0yLwAO9EtPFHKJEnMNSfEbFZd8xGzKiIO80lDNKlXBBk9U5Wv7eemzWfTjsW+x7EUXiSJXhFFBDQJ9TyL8mSpC3ItmOcZ8zxrH7bDjo0C0FH5fHPhcc4v4TQO79T1Wg1nB2/B5y7OvELsv+JM3lRAvlPp12OgfP3Yal6FK9p5C96BYT+0MRk9vZ7Xfq79/MP+XN5rhHGvN4LhAvlc/xbfuw1PdTXoe/ePY1Xzncqqe+bhe1AWjHP9UirmklfHW43zvbwXtspL6rr3nWvP/6QpX17Wc/d+e+299/F6H11v771gh8O/sTROkjRnEUMUCRaO6RngDNQFTAuYFxUsJuPQJF0Wq7jc6Q/h4WqV+POli/4g9C9t0SsmA3GhUOD5ohDJH+dGy7hcxgyFSjMeBasCI5ynwwxtyrIYq/dcJsBBJqX/ZUooSsEWFeSLYFFC1ypzCldOgNEUEslZWPnDfofzQ75oHPqy6rT9bYJwbn22tVaDmJwzpkkNHwkuq2pDtlyqgRbU9SnLguevT3h6esLT0zOWRYwyKCXQNCFNM/JckM8zUlk0lOoiYUo1VGkii19Nre9cJddgKahpQSlnpJJQyjOAWUKvAkhJeIBpPiLPZ+T5gFoXMT7q4Iobv+Hkrwjb2RURFGCAxWMirK0JyW0ByITtRsON8hSgyRqDsgMQ5YeE8hJZTlFj6DQfkU+PePjyDzx8+Qemx1/A0xGLCueJFzSAtJwQzjC7INvQzfi5uXf0/igfND4giFnC720vurJRf22+QG0y2OW45uEeuc4GW9ZF4ZOboZ+923jGvv/dd+5xR1f5xbKm419S7sPf5KDpOV1X3Wi4FCxKrPk44eHxiE8fH/HhwwmPDyfM8yRKOJMtxNU0eeELzrtXe0QM6P2+YvMRJ4UN+Pukdl2bA6NqFnXV8vFwD3Berd8gB+jAritQm3DWmHWJ1RxTP0hCmSRuZ6lHFBFx2M5sG9WQ8DANW0KuIEyya9T0b3tHxBjh4V3/3H7fBWGexDfMPXPAMlvF2olz/NchlKMj0TWmJd59awu3agSahg/pL5aYbHqYEIYQJgGuVmy3IXKuIMryTCJJdGUxxX1MaMh43HfQTApGtO3t/LuXvSe+IqLfF0gxhg28WWRPxxXuidK+rZg8mBuyFamiiC+ZFW816xcXaMR9b/jDCDJ6uVb7Z4lF5lDCMQGHSQjceZowZfGISLnlhiClVDwBrgsZnYzR29T91hQdfdLfdQnu0K02mJWBrHnLPwK0vePEqHk+BGUyD8yUWUZJzFN1H45h9thwvzJI0RNu8KZrygz2RGgm+HsZLuvnM54dI8h3yoYLpSNGQ51RcD3eF2K1t35L6hLTC1r7sCXynrQVBbUpZWVADpiPooCY5iPmSRQR83xCnibM00EVADIFrOdpHZVT3VyxozCwKUPtb/h5vpSCslS1ckooarZT6oJSF8kNofkhpilLaDLzjNiAXRN6Cxq7tg588Vs7V7jNofEU4XgguxHXkOO8Xy/kOJwxhtez38dx3iv8fkmJCrR7cPw27bAekzCyW0fq7ZT3a86dtleukIC7773O+r7N094YbB7uaeN9BYM/y8/ynuW1e+pnuaW8jcDo25R78eFbtx3PJuuHRpbQZzw0UzUPiCd5ZnoGsSRBJSIgFa/GrJojRWUhU6vJNkzWgZ5vlLNIQq2QesISmWGpUmZOU/YjIqPV1OCnlhZJgpUOj2Pm8J7RREb/NGv4GO2i0UGk1uywvBbKOyywRNy9URKUjpOwPElDNFmuCA1Jk4Tnh4YuQpLxo2hbK03/1ppuF6NP2hpve7eyjn1ZnrEszzifzyjlLM8mAmXxcBB5hOR7qKXI85qDg4g8FKoY/siVphkTM6bzGaVWUP4KkNLukyS8roAbdkEF1pY/YlmeAGI8n7+CwZimA6apAImQ1dANKWE6nDCXimORBNuVF2A5o5azy0w0NbHTK+TKHuX5IMmla61NTAD12O7mOvCIgxzExYVGUkdpvP2ACsoTUmKYp0upBcgZH37/T5w+/46H3/4L86d/YJkewCkLb8EseaK1C+NO7rnmILencH/krYSh8bF4bpbKQInGcKxe5W3sZMZ1Hm4t7usgUCcSvlfboDCNi+6zZTEZqSou7ZPZ63Bd0CA33d0B/XJtb5XuKPnzzxTyf6vyfX1hMjirsqVywsPjEV9+/YTffvmC33/9gk8fHvFwnJEJYC6eH8fr6BtznHpruUsRsVX1Lc1tChMJLb4ZemAf/xrrWn0PzK/BufzWmG7ADhhFQgrE0evCt1lU8VnSyNAlUqTfNM52qAUmODVhVhRM3ULgNKZ+bSF46eoTUTeN8pZgd7xgCAPrQ9wQiwl1L/QcXsMgONorW0qmdy/Whh4SfRd6ZD/+0ja1VrEzH/eOIz6+jfYItSoDkmoHtWP/urpM4MPDTgvCc5egOfyjm4DYGztOTRPq/w6H5bWyVvj08DLWsok/lIgy3TiPzzaKtR8A2rz4mOx7UER0iEMPSqMr+nXvocJnsqGHn2UohmusjIK5UXAsv7W5TAQnEqec3RvCklanYBXeMST6L0VY735bofuAx5twsCfJ+gU23W2D7DWF0p9JcTcpoxKYFP90ZYTAaFM8tPBO0b18PAP6cyJadPR7bzVvNI5wLCN5atUOuNWYgP6p7t3+3Bn2affZnzFNGN7joK1zyNbQ50AJT1NCuCKCEnLKyNOkl+SKyHlGTvqpbtvijSBEjYXCqkNy80hAb4+pfbqVHRaQJmBkBnKeUGtFzhmU4CGZcmoeER4jdhDGR4tJM4poSrn12q3PjjjXtnZbJcy1I1evQJ9YYfj+4NoojmUHofS2suVCPZtzcl+Je2RLAdH6erl9+77GUdvneSt7XM9LCjnz1ZQOPYy2Lq/7bs/EsewpIV4y38asb7/qs7TqW//MZs1392VV84Azby2vFSS/dm5X8LpDh6/PgvV631NGPPySuu4d90vm6i0F/fG8eau6t8a01e5L6n2ruv6KZc8Q7VY+9S3n6V7eub0H7OG8vTrX4121Zk9e6hHiudTCn/Z0UPJOSpJqrguIzwBP6h0hxjZAVpoR8DyekodZ47mz/s8oSveZjW7jTeEEuRvG2HdsnBpsYoHxPNc6XVYyWL06Ld3myP8Mz6xlL1XlVdS9YzU0n310ChYPybglJjbpsHkBRD6fGM3YNhhQUevDlqFHm5/1fR/tBdCw8ZZSsJQFpSxC0wLeP6Hh1AhZQzNJuPHqdac85GaFKCcmTEjThHSeQClDQjdNSLXIdw+XGsZZK5gYtS4oJWFZziAiLMszAEYuE4AssryUNBzrAfPhhLI8YTlPYhBW0jjasH/YaW3zGDEeT+alY5CG+QqkM4f6dAQtZbPNhcGh1J2IkRJAJFBSIEmyTx9/wcOn3zA9fkE+fUTNkqSaUWTcJM3VQfWQKHwLPHITl/a4M47BYF+/dPtizbsZboCGHGZXQjThd+DHQ1u1VqWZm6ymWjJqM8aLvHA8l1MM2Kz4Y+CRY/Fd0uGAgY9RpVe3wlfwuvfHerHBz95anA/pYKv9oi00GQURUk6YDzMeHx/w4cMDPjw+4uF4wGESbwge5QeD1N6h/I6+3u0R8VasD6CbsGEHP8JsWzcmWfXoVbTfrLvTcnBUjrCgUaD3YIhtK8d+wBGgHDnqwg5J9QJI+Ju2ASW0TWP4kxwYhLZb4dX1G9U5y3ZgM5pGvQlZoqCpoI8l3nI62OZsMbNjXMQmpPLNtxJMBaCqa+FD9Ih4y7X/NmUbmQANicblk5WIG7b/49b5uGdDMgNswgCwJOvRgzqFw7cXcG8RpL2gzmKNC21i5JcIbJMSAJLgSMM2AbLm4cAxIaZZnQhhtJ4HI47WygPaJmS6g8sOLLi1drNmjwgaSkS+lPDXflR2N98I+5VbfH7oPmrDoO4zjm+0rP+phdgqFwjdofSHMCDGKYRZPSEO84Q5T5jmjJwIk3pCJCOK9HClsH9IqSdTKEfrcTjdoLs/YUPQaQnlmlVVrHdjEB2BJbBU0XB9UxA0r4WmfKhm6eEeDuzWWTC8PYZkKuYVUZQBGJTU8YDcmPNLDPW+QKURrav6sDM3O232xHePI3RKL96P1hqx/pVCKdHq91L+/+z9W5fkOpIuiH0GkHSPiMzcl6rqntM6I2ktvej//ys9SGtmTnftDCcB04NdYABJd4/M3LuqugqZHnQnQVwNBrvAzApKKWAwSN18TdOCeZrltNR8kd/zpVNEiBWO+drc0xmtffs+xD237eOMnDdsW/E2F95AiVEwoxTy4OzJP80l2bPWAedpgI9H+5gzE5pXs9saYdsvwrOuqnoOk54IaMTYPnDr2OdzZcwdPH7YtcfBjntG7BjHPS0Q7eC7nTI8pSWo3wvHfHG9HykLorB0fC7vw/HYUZt/tKDyR8zJR8r68en5Pe4fKjGLC4R/sPRRBv5HpX8WAf4/fjKc/a90nJ4ZnybXsKM+vuqMbwUrajQ3IAWoG1BXEE0gVP2IaJSS8qnEftfojCbyUmEkhbrCHuziMnau11kzkRZpnLRRCaW0mgnVGu3cH/Y5H4uw73aHioJFhNHr6i7JTumzxc1SS+lin9q+q41E6KH31DrnQn4QKa1LcDeyJry2AJNxigcB6uN594lGo0RI6WKLRcnYtg3btqHyBuYCk+9ldX+0LAvmeUZKCaUA6+2Gsm1gMOZ5xjLPeLm+YJ4Wt/QQq+cJy3IBQFi3mxwK4oo1ZXAtKCnLyfhUULabwp20spYCYMV6+w1cC3KeUOosBjrTBOAKIkLOEy6XF6GxUYEqzrFuLKfxoW67xlUiYFRdvpCIUakgkeZOGvsEPR1m8jun23yECQk5eHUJEhFiTFktOSYgJcbGRWSZLxfML5/w5X/7f+H6058xffoZuLxgc9lGRSJCTovAZa3eJqglEWl72qHrPe1LpO7X9ANm1CCXhfXNeGCTswA7iwhzcxP5Y68v1FmruGUrtbR1bnXXilqqWkA0a6ZqfAi5TZHDcnN7H9dWVVmtKSGh4xEsogx1uJsybUzlQ9iQMTy2pD7L/5HE0FjLAEptLq2l4KSwabwBY5rEHdNPP33Gv/3lT/j1l5/x85fPeLleMOUU5BPG3JkbAO+MYPl6Dzfu09OKiK5IHZ1RGBC/jyfeujyhvHZbseAo2+sqJwcADvNs17gNehuiQGA3LtR9N11jA0sJSt1lp5ZHBj34e/Z8hoZNOAXX3Hk5I6OINnFN6370GWoLQi7uvseTsqE87MvrBSE9w8vMIpDmDywKfp7w/9EMwkfKa3uuueWivSJCN+S4R/ew3Y/KoQDgg+3SIXdaysa+OuOdAn0xMrx7YUSbZ3RWSAKm5ILa7nSsC3INXCNKZv99BKP35t/4srNx8t82yk50AlDzzH7zvZPuDLkLy6wOIzrZ5rfVe2/qDoUy/uxfrM15OhbUHO0l/obCewqWEFkFwDlRs4awOSE449IIl0Yo98o8BOBsaw9op1u69YEw917I0WzzwfeI68dsvYIY4fsujg9zM3Md8Dw6/H+ghPhocqQRbvGRIPBbIF4Guy9vpCBGfDbsl34dFbCCMzoCFsF0+sA1lRNbECKSgpA/p6xB8Cb1RZs9IF+esuDSQQnS9zTQL3f6VGtF8mCNhG2bME0FuWRUlpgo4mrAlMiDKz9nFD4+H0cw8gzMsP3h/dy1zbM98X1X749jcFS+bVn2/r3rt6RnhdsxjYyE7FEj7rpfpmHDjt41eL5DS9u7JlL5aJvjeuvbOjJH7HTJ2JbvFbZaPY+UNPv94MfUG8s6a8uzZTUYBB7hwkd1PDsuj/I/W98zZRpNtgOED9XlVGV8w+/fL/pg/30yfS9e+FFl/agyzmnsXij0r/R8Ot17Pkwz7fmwZ+fi2ap2a/POfP8YPrvJH85xjG9bwwoP/GVsC5tgz1wcjfwTufyEuMdBro6Ip/yVCNnvwdoabr97Txhy3e2h3V5sNxjY7bUxYK3VFunxY3mO0UrGT1ej3VHbATkwTOFQA11fjam38vaz4XKNpjym+Hj4TYqChzl6kMj6zv14C68mdHOjKSQwsMmiwMaLJY8lIe6XpF1uEQFROMzThGkWS2TWA8DyPikNPmFeFjBXzPM7uFZMeQaYUbcNAKHWTQ5yaT/dte22ohChbDcQQa4A6lSczs95AlHCNl8wTwu2vCLlDbUE2ccRHcbsspxq8jmdd7Hy4TDsgf/Tdzs21Sm+Yer03ZwkTmJSpy2mHknLjHy94vL5V1w+/YK0XMF5VnffYkFBgLjHqgGXEFQiWrt1sDugp2vV8RJMdmSv6KowBBH5VV/NIbZpgG97r3JFQurwj60lc1lGAIjN8gqudHB80a29eEguxndhIBwQ9zkM79LwuzF1oYxuAPo04u0djg6w9M34O6Itp+G1XhN31NbHnAjzPOHluuDT6wteX664Xi+YpknpsnEPaMGw9W5f75Pp2xQRZ3mMqR6W4oFIoc9vV5I/Dohd/v3Gx/oO2wk5Hsb9MA3MDXq3NIQM3zTjp5lpoDVWTow/GptOKED3X4iLkrkESwfbhMzPWRHk6dYSFtshjM0grGHmYBFhlhb2aad09wuC5ZQ++rLjph77+Y8gfTUhcVJzrKQBbLP6FG9IQmeDZWwresHDPfzwI4g/QxzWDgJES0xN4Hp84tNgoQXDNXzT8GZzH+YbisY8OWuMCzd9s6zf1U8RFraNZhSyWj1x0XyEuTKM1Ii1uPFZn6Cnzdvz6MvTSjmrdRzDTqkz3PsxDME/ejJXIC1YcExHY2Soc5oSlilhnjOmKWGeJS7ElDMykQQZRpt3UsLaBLbiQ78JkOUkjv4ms5LYtSi0cxSg3Es9wyJrLv62E03tdEinOOgs4QyxV4VVhU2znqgVXKr7r3WLOX1uFhEjE9QTs3t80vps/Rl6qGX179h+Oposn6Xz9XykdIifqFxpe2Qk4nVfD2vUgCkl89gqXZPbCUQFiTas64atrjIPqFpUWM85S7C8PAnDpSe/OOleGa2oZGD1e4udcdYXQALh5RyvE/KWUVldMHGIg2L4xsY9MgjfKIx6hKoMnkfCXgkEb9eowDss6+5YRFqx559jH2no87gvjnnOBDffKsAbhdkffBuHNqdD/wHzry1D4Hv6N9T40fYd1fKjBZ3n5R3jnr1C5V/p7zr5NPHx/d3WM9z4F/n0ofSvtfGPmr4N0GWf+NvPt8r1wq7GGt2w7WNOP5CpBSywbkbSeAc5i3yGyPg0o++NvnRRdBN8aoDrlFgPK9thIvNskUDG48H4kFYOtM3mqYKUX27no9XFUaqiHDk4d+I85iCsHGkat4hIso8V3kYXH0K/ewzQTayc6wqqckJdLAvMnZUqdFgFxyKJlYDdYPhx8QheLtOyP8dxHp5LxlckJBIrhcv1istywTzPWNet43WcJlb6OecJU5rEEwk3RQQRYV4WfHp9xcvrC+bLglXHRNw8Fckzz3h5ecM8X8ClIucJAKNsN+SUUcoK/g1AWQHzelAqWONRMFfccoYEo2a9EqZpxrxckVLGlGeUyxVlfUVRXmtliTnAsKDHOrQ+rhBeROVotRQwVeU7mszJcLVbdAdaUp4luAWBBeEmq05keKZiK7WCE8DLG9J8wS//4/8uSohf/yem1y+g6QLkDMKqa8/4I4l3lzjrGhCXTQSZB1MeWf+i9K+zTjpQFrDyocbDusWDEbQhf7cODLYsXxCKF3P1tQms5EiHs8F/lbFKuu7VXMP4QlnnWn6ot9HkZp3S1hQ0PowoaOyjkiW3aPrbEywM6HglZQ/J50mGVA/pTROuL1f8/NMX/PLTF/z68xd8envBMs9IRGixhIEuaHLooqklptQg45n0vGumJ8uMwx6Zx04AAyBqp1pe2tXjbx1NqOw6D2VD/pjinfCdmgVE3IzM6sEXlC0uFW6dEs9N/Nn6HZni86bKe8ZcRsEvd6O2+8Q8VkjUqDqjb3njv67ssS26WcR5GuZChoV0KP/2RJCvld2dIZHYs4jmXnKnYCIH2By07ZkQiHsF2ShU8hp3AoSTtsbnFIzsHGzGgK/s7WgWEq2sUdCCMN8tXzcId9tndaIrg7uyI/w97O/J3SNhI7zs4xPGLtg/XNeh9CCoCUsi9In9d8s8vMRHq+N+vRFFxDb/K0k6Oo17Twlh6zTn5B+xgkhIZHEhtFxdtyAjkRBckEWhZNrdO25ra/PzzD0Pf8e+jbh0VMbtLSB2e4Ldq/1vr/WkrDDgp63v+8jt8rDrkQh5PE7GJB6ncyXE4cfiMzghL8ouIzbFjJuFGOMECn5yZf7VjLcY8xcChdseqXSAwY/sFxY8TxmLwGS13pmSK7llGikzilrFDUGVnThsuSCCxzzx2CeHip898fetJ7vj72cF6xz/WNvRX0/rHOYxtiVej8p59sT4UR4r+9G6/vDpa/s7vHZafvg77jT9OEQa7z7pezRv3Vg+oTg5wtHPpm/d68b3WvN49/xbBK1Hcx7vxTxnbfpo+pH7/tjWP6LO722LpXNUz761OP1uAoIoKLu7V3x/+lFj9i046dkyP6rojPn/HmDm7zdF4ubj+O68LL1zsla+TXH9belH47V9BbHXkQPv6dzdS1CShsxFanN7bduoi1+4lW3eK8Yd1GU6kaGm1j4vwrfSSKkM89O1eDjQYN/RYox5jyKPfECXW7tcJhPzaEyDZtncf0zwSWwHE8yyJLqO0bK4tWXPc5zNyXOPdp4JgtyCyNyaTsiTuGhatyOakjSmqlhQRF/90Q1MTgnLsmCaZjn0wy1WXrR4ztMMUMI0L6i1YppnAIypbgJLSd5NKUksCm10raLMKNsKImDbJhARtryCKGFSYbZYbkyYphmTxokrKaPS5uIDOuOTfNpFilNZjkKlA7pbv/h4Gkshsnt22HNtByHMOcHsi2hakJYXXD//guuXX5FfPoOWV0AtVcgE0ZSDDHTgyxhtpXV8DdlyQ8gNt5IZOt/JdoxHDxs/UXDhpLBKPMKswLzd8gN35kbbD8A1mCelI46tScjXiNVl64pjXT62dz7O+7TfzscNw/Et8sJvSobnjH4Ic9ryyFqd5xkv1wuu1wterhcs04ycckMh8f2OWpNJtCfJxvTJ9OEYEc+kA/anu+/zpsKToshYkOt4Ys1e7AN+2YZB1Jfva9GSEbP+jt1Pmr8XJNjpPXKBtCxWV/AQ1F2PbJaH/ef+C1v9po32ZFYMR0Lcdq/zKxhOuvaxIU5m3RAZ0C3Eg4xel7wWiCZmt4joN2UbS7S8ONic/tD0HCGZSAPe6ilW87Gd1b+2lcB6aqJWPVVQA8I4kQJ8M1KJa9f3lVHZIA9d6WA3GbJ2EsPcjjTFU0AiDlNaBuQEClOLB3GaGB2sGgzu3cM0uB4GRouJMNYsIgz2StEwTGYpcTKXUYCA0L949RPSIWaKryfuT423IEatTz007TfWk4b5Wnsk4P5Xup+IgJyhJ84T5nnCskh8iClnzDlhCgGqLR0xXGa6OwWLCAt8llIjhinEjDg6zd3BnVTm1/av+bbs3SQ1fD6uoz42xLDGrJzgp5ZR9HRUQVHLtmK/i56Uqs2qwsuy8eFesPtYqHf+7AjnncH9eFL9frkIYzbinjKMHaPULYwtALb9XdpP6nvP2rZte/dGhi/n96+Yvv4V07yo1cwFhAkpbWBk5KkAypgwgDSZYuJk7MIziwcYr4LGdb9h1vgewToGzRKyWTG2mSH784245tF+dfa0Yy6MICWdt9GiBw32MMSripWcKSOeTU6L0DkOfiiUezLfmEfaekIcPJkUCrq9L5C63bgcfbqyTp4/GtMezzWG9xlh5pGw7WNK3DE9HsuPlv39berTP8Me/31Q/Tj9qLn4V/pX+lukf3b4dcHkAU0nO1oFkUR7UEJM+KWUQWlCohkpLUhpBicNPAwgkZzGFQGv8LvEZkVBqEhwCwASiwdKWfY7jZPWGqniVjuUwi1wsJAlKvNQdxdNRap0TSIQEhJn6VSGEHBVLZvDYXar1twoRev/anEDAD8ZTirjgQlVq8Z6K6tbQFOtSGYNXYTGl48qIvQ31yJuQi34dzVriRho2068h/s+Yda4Tmx7MOv7HYEgMpVlXnC5XDz2w29fOVgxbDLHlLBcXjBfxOKAoHHaNJ6EyQNynnC9vGBZrpimBVstIDDqtuL2/o6UJ+fdcs64vrwiJ7FuyHkSGKAMmt7FoCVLnIWUxOqYy4bCFSsxapnAtWBbF5RSsS0rmCuW+QJaXpDThOvlDWUrErdD+wPentggTSbDYN46WjVRvscNhY+WgwZkbuxSJXg7pgVpuuDTn/93XD79jF//5/8b89svqK8/oeQZhIpUGXNSOZAKORmkhVUkjQthlh7UtQVgrkrrJ6elTulRhvKragkR4nMmGYAW/s3kn7XIytO6c8ruPr2qx5haNpRt81iKbsXAYcyI1YMIoQYFouAChXv3fqHKPAQrCYsPwWE9+bqqYW01BQZcaQFAY2QcWT3/rkoIG4aoVBpbkRKWy4LPnz/hT7/+hP/t3/6CP//yMz6/veFyuQgeVWufFlx9T98DjFpqqOr5ffCbFBGHmhwM145R0t/kYBEWYkPMTWAQ6xq/aCLVuoWN35QQfRm2iQD9MopCJnIlRLuX+ueh4ntj/JiBHpjEY9H+LmdbyzzcO1dCuDLhGSbu4D3/3o4h7ObBFTcBmf4tk+MeYDdH43bqyhlTRFA4cQrFTUmQiQn9Y/fuaTTP5v9DjDKaMqK932C8F4a6JKtrEx+0s605GYkPz5ivXTSh0m7TGcahNUB/R7jdC1CsjeBjRcTRacb7QpqGc3pCoF0R8sa+xjLjzXbL1hm669HAfg88/DMmIoiCIJESmDEwrzAh9hkVBC4QDILnRKZwsMDsbU274kh+wPAahfd3SohQV6N7Iswfw+++iLYP2prqcEjganq4bgG/uit4yLfHAXvcMioIojDSnoW1tturn2fCz4TCR/vlPaGrB/0zZaIGmW4WEegaSpw6eBBcav5U5V4pFSlVbFvBtq0omxC6pWzYyoapFqR4GECJ2Ihbpb0NthyX9z1TuAl9Oulnm+umjArUVMNAvw8te0pjdHmgfda2NBS+XwO+Lxne9ft7Qfm3EugfUT6cwe6zJ4jHdTT29+G62El4zxXwx3vSkOVozWA/phFeve3c769dpR/cr0YFzUcE//u98seV/ajOj5ZxRv8eFTPCzLN1jfmfpSXOcevz8B1ufCz/LkPcU74tnb37t+BBPlLXt+CSmJ6Fl3vz/C/6U9LxGDf5w0jbe46n8VZD6EdK2Qcl3Cl335Z7cPE96+xeOq2TG0fpI8CshzdZfOHH/ikB3g6DJEgwaftOLQ+Hg6l2G2b5QLCTdEK6m8yixRQUQaAUEOVpbQdsc9a3kvSOlkUSc0EOrzIoVVANlqoEsB6o3dMzkcbXAQt0kH3YXNaE4LqmaCC1hACH0+JK+7drfxAqEGOIdGP/CZPY/Q7j6vNvj+Jc2hyQ7xN2uNP4NQDtACCLi2lKCXkyF7niVlTy9BYRQqdnL48MpqrR/XKsOKfsVgt1rsjTLDHX8oRUK4iyKLhG+pCrer4VxQdtq8x6EouIbZqR0wRWC4KcZ/1MasmRQKXBzbga433jDeQwUWrXUwJ+oNsi7a/39MiVT3FKE1JesLx8xuXTz1jefsH0+hPeLdA33wAwEhvYBlfzDJD6JOvWKwNO3Sqxz5r3Earxdzo4hM+teq5q5Qx8a5TBEUEPMulh7OgRYBxwx8PwODNGhxge4dgnXY8WL6Ljvx99hjgaIy5vY2Bd/LH4ebfPO/8ZaOX9S8jThOvlgpfrFW+vL3i5XLHME3LOEMgqYKbG4w1CrmYBo9iWsV8Ad9J3WUTERaFLor/fTYjvCzuArTVokMJ7VTeeXlSq24/BUxCUEMQvYK3VTxraoJAKltRIR7VjCezlybW55tFIL3ZCPh8IYtBuObB2tw/y3k0KyGFRCANZg7ACg2CiH+PjMsPoUXPzcMh4C25BOShFgHBfT5wL+XLWv78PoleQWTAFJHLLiJxTt5ipVj0cHzB0KKdXDI1w/8F0sHjHW1Y0s7nvUAa8CvJMIHEj6Guzf68vJ/jI40bIPdNMa0MkdLrf3bjUkA8wiwiLvxCFifF+53MvpI8pIZqrlmgN4aemY2yIMC6tzHNF39Ga883tn5TB+1HJiA0PSj2Jie88kcaEsMBmJB5xBqGUC6rlhqxzwJUYPf7rT01TSmqCe4YnG8PSJcfXbT8QsB9P9I+wGJR6ugeMcNwxFlpXPFHuMU0C82KEmjM1cY1q2feg9BiG6RBPPZVOx/JxGsdDTlUVbNuGWqv4kuUqPmAdlxDaaTdWpqcJqyL+b8qt5OXlZUaaM+bpgpQyGDO2AjDP2DYGkDDNFaVW2T8SaxkGvzn2wBkc67MT0caYBRipeiKsFOvninVdsW43ua4rStkwzxuIMspWUbK4lMqpfoDm+EAaYXKshDsqEIY7I8wBSuDb/WBR1xd1vwOR5jj69Hnv/35UySjgvPf+R4WszwjOCQj7W3tv3DNHxVXMZ3jH7sVnIy2dUh/D5KjN8bswK9+Xfs/98nuVEz8y/Yh2nPXnRylj/oj0vcqIf6V/pd8/fQ98fiuR9Pule+strscfgTq8CBf61I69ZM9k7pcyEmUkmkA0gSAKCafXIq+qri8JeqUEOVM94D1VXgBJLDEA9Q2v1urV+msufklF2WZpqkJ1843vWqqEREAlO02fTVQkRvwkAvbISzYlRL//Gr0O9bhAxRQQReO+iWUDb3LiOlWhc4krSC0fyP3Wq/zI3TMV5ROC1US0iKjhu70b+O7zmaUm+2AVGAWFUXxXglCL1QPQLB3WbcW2baKEmCe8vr7i9fUF8zwj5ySHfrYV2/sN2211Ot8E/sk9V1TNu4l1CCXgSpgxY5oXpJyxrSuIMm7rDcSimGAw+CZzmlIS65TKAArqxqi0odSCvK5i9bBtACegEhLEhc3lushBpVqw3r6KhYdaZJt1jsGjkGkcF4bDApHAsIC2Wle7xq2HIeEvpRxX5iic5SwWFTK3hMvlE5bXn/Cnv/w/cP35L1je/h24vIGXq8zNbQWBMZmMNWVUIhQV8qMUECTuiKgEJ5WTGD+JMP/Nqqhra0ePNrmKy3RJFHwpkYugfJmNkKeyS1tXXBl1K2IRUTdd6wg8nypNAs8oc6Pr3qWaYf34OlB8wQy3Prf+stUR1tpAoJO2oXovknF93p+/B/pHvEwseHt9xZ9+/RV/+fMv+Le//AVfPr/i7SoWSoDNa1M22dUPaiaZPFeKpY/tfs8Hqx4ZRWc3ZWLOlBBNyIKmhAh8J7cCj1vediy0hR0E3gyFXNN2V1nUumQ8N0U9vWxmhFiWad/1nKy5aXKfzAjvq8C+27FHTRzBFRShgx0w7uCQR9yD/Q3uf3EbY18Eumn2J1zh/SVvRxvZqNjerQ+WDLEFowKkEwwMiqKuqLtrLz78mIDqfrKzDPs9E7qIjM44EjoQtz4S9QvS2j3Cc3veCy0f9v9AGXC6NFj3/Th3AYZam/aVmmIutvm8VS3fiAXsZhOYciNQQjvjxtXjigC7HIS4oYxOiAVltHHAyNoGFdrjijz/jf65v9Y2y9bPMM+6BqwVnknXeiNUj1bXcfpbCQv+HjbAXbKNDe1KRG6llPVkTU6EnJoFhLnU8YUdcGtcgmQLnuL82K0WW4WQ+hmMeO10vgYc7XB9JLDtAAftcVTkxeccXjk+ndHDdqca7fFSGON4P/ZqJ7TVQejXIHAE2x+H5/P8HGiKdq9XvFQOHxXkW1DuytxPh9U4BK8WRiD1+6imbduwqdB/XVfkaQWlFVNZQWnCVjY5qJCE2ti2jJzZGQlhUuH0SStb5q25Vaw7RZLHp/AghQWVN9RS+ntqgt8YSsQY2Sdr/QQHD2M1zlG/799LAc9amYd7VKBluMF6VwUfQpr8/QC4fRQ2z/bcOzXADgYcPfP+9yTjcSWKxvzEn23yAU90beXje/HZEV1+ry+PqYKPp3OFzjg4H6vblli8dvV6vr6ee/Pb4Ts6OPjgz6wkmcxRmBcZtn277ZRta9cxnXdvPOKz1o72bLTOsXtDbopljLlDh4CeWfBWa86xrXT35++SnqVvfqQ1w++fdHzJvj+T39LZeh7v036C/g5JxTHt1+TBWnsSJu4K64EPjgfvGbTvSHG2urbspm3kT2O/zvGF8bYfa9H43bANodu2bM8nw48EdvfWGUzxk5w/p6Ea48eZ3BYCgLjO5pPmH/X8qCd8tB7ib5ehQHnvICMw3i/wge2z3/zDdr6vqaPpg/JiR//Dv5sLmY53ZiUGx4+5enUB6jGN2H8/I1SMWIlDRsNzPQw80HsASbDkEG8hpdzo8dosJ4w29LGmIJMw+h8EEPvp+Jyz8I7TJFbMOYNKVsuIgkIJZkfQz5W4iOdSUJhAtCKlSRQjqniYMSHlJAfktP05T9jSBEpF+7ePbWnrtuPSbH41IDKZEovimA3yN4QybPhZLHXkKyHPF0zXFywvn7C8fAbNV/C0KF1ZocN1khgeyM5aTur+zKttcN0fTkEHhx4a2eG09asNil24u91RRkTdg+6AjTI9bsUAaIB2bRBae6yRXeyJMQ/r+ydrrcm44lrTuTpnpk7TEV3eY9du9exQChnhyy2/ZbTVG6fSc6WEeZpwuSx4e7niRT/LIrEhoGvxcXcOkO8HSKanFRF1rASAdfK+EsIEjamZz3hKDUiHZGY4UpD5eVZgtA0AYfOxRctiFUEMJEN2USDvLW/bmC8yAswSwoPn0AQQ3C9ZSknrqM0ki5oJXq2MwqJPq15XAFgHmAbUxKwaSNGEYyvN1UM3jgdC1oHRbFsAwU8boIIgwrspJRROqBoTo4B0FqyJ0taov2Mwim/5Ya6YkfSjtYkYz+J2JjSkupuBnrfpBXbfQ/SzBoenbn9M2iONfSWWDwnIWYVSuSARac8jYWYtEojJAKoSPW3MYt+M8Yub0JHfcN7V8Tzasrr630ZHujBypBMNIxEhZQkgVSGWR5xk83I4YtJ2i4Ze9OJs3iQ9T2KoVn5Fj+zb1RG3a82bJQS4vxpRIRX0G7mb11aAqYLUlNHmIXaXq2iqawmnz7VNUge6+CoW7MjXV3R/YhMTD8okQJyDkq50g/6Aq6wtvq4QntmEfGzW/9GTjEMB0GI6NL+DAqAEIBNhyhnTlHCZJ7WGmDDPhFl98YvVgpyksuGtxXCh4iuP+wCkpH4iCahlRUpATivmVHHJhDlNSHxB4llmkhigFUQLZKsk74MTQNBYDLwBqACp//5SUOsGrlX2IggeNTc+ML//LL5iW8CtHh7aHih7RKosp66q/K5FzJJr0RNUbsFd1R+tLkM9dZ601HE/d8XOWKfdO1DE2A6RYO/qP7YlokxiOoub0PVQftl+YXtpifGQarMQ0M+qJ6X8qr50Pc4MZ6/H2Q3d56MlhFjCJeRcQZv0h4nEioEzSgG2QliuGwoIc1mxpYq5LFiKxJAovCKnhHnKGtNkglnYGNyARTEKRov3geZyqailRymMrZhv4A239Te1ivgN6+2Gsn6VcbgBCSuo/oTEGblWZAZKFXcBMvUV1XfwZmXW4NfoCtvY+jlpdLYKD8KuOibJp2tC8ZuhO1OslFpQIc9ZgYVJYp644q3CcfUORXbMrkJ02sPnDtJ2hyJaEHMlIDv6Mgqfj64tJRW6iBWOFKnzfNaW8PENLOQ3IU7S05+1s4oNe2Toi+9j/txgC4jK+B+Z+pO05+N/eMDDx57DmHYYyN4+LacDx3DtaAGcU5bPUJrn886NpGeE/oQTkMDuXSLy6B9NJbDvxpj6usP8k/whaGMCV0ZHg0LW+v56OhbDmKeO69MSuM9vPep79pjaubuGSXDTucLv29LfXslwnhzOP0Irtg1cURujm12yP2N5Z+Xf27//O6WBJnryrUi97os8oOe+A94O3/SFzE9mjL+P4ODDLfBkou1EhIQkQhil+QlV5AVEABYQTdjSG2p+wbZ8wja94X/lTyj5ijRn1VFU4VGr7MuzMfEQ/pM4t32RCEgZmwqvq/KdhmudL65GfzVeQWKGVuHySV3kcDkY2mE+yeREGeaOCZRQSKQuYjmhipIg46ioEovCoEzd4FRtY2GAIf7smQhFFTfFeNOifAPYrUrJLByKWkGXVSwm9Mrbps/14IrNVgm4pRMccI9LEIShjkNMkC8SAlJ6rSChcsJGcsKeuCDXgkwie5nnF8xzQUVCXha8vHzG9fqGJc2YaAJTQgHwXgtW5W/A1fkUEe8kVCRsFVhL42i2ckPOwNvrK6acUbcV7ynh/XYD0YxtBXK64H29oaw31PJXMBfh91BBJLRp1bHczDqFGYSKec5YFkLKM5brDMqfUAHQdEGlCXz7DaX8FVxXd6NFYZplBG3MjXYssFPnwpdI/JHd3kQJFSJjzKiYUEE0gTihcEapCXVhpCXj8pc/49PP/4bll3/D9PlP2F5egJRxqV8BrioLSygm6+QNADBzWCtqyaJBHIzF7VZBtzO5tc0KcMXEm8gy9WAV86ZlKySRWeSSj0/iIGdT63JDU8IWCO9iFvHmDcToaHZXZEZ/yO+k64KL8t8q80lGMxtvrlZGrJZHqFVglwtKlcNgVFUa5t4/Gh3bTZf9PaBXxoMt5zRNWI+8vx/1M8dvK7Rl5W3Y1uyM5bLg158/4y9/+oL/+R8/4ZdfPuGXL1fkaQEwyzgFzzu9zBboGkQtwznnc5yed810MEgc7w8YuxOQcwsAeTAdRkLDmJDIkATxgSsJ+hEPTMpOYogAxX3e3XdzyZQGpUcyCwlrofoHDGVEBrGTwR6RKEe0wLDJ8fh898Lwe7jlvaV+PP2Kxmy3EaaTenWDR/CR6OU3tjHWSaDu+oN537upn9U2S+Rtg8saGmP4HG3o78YF6J2LDCXvp+0utbpv+/MpICPu750BBqMRUOeN6M6N70rj4Ud/kjt8H64G4X4SF+3deGqHh0raqbvWflfUwfzdx46EOgKO4jhv3NreTkOH9cSBeAx4zbXP2g5QxFkBrsYhhcFZGNkg9PrnSm29WNcdIxE0JoRYQiQSS4iUTXCslhD2T/f5cQgdsxFCbIgI9yKYJ+LmhskxYmhntITxtuu3JqVt98NeKMRr7HOfxyE47gFdmehgtQ3YsG6MeHQ4RXe18lyZdzAj/diF71EhO9LFbda6fWBXziGCHdYLmX/6kCX0K37Mf2ytjNIpKoRwKqpUjOuUALdkNCuYOGamLzEY2bYN623F7XbDNL9jmt+BlDEtN7luN0BhtbKYRnNSM/1akZWeMIHGGM9DlE5G6FUnruVTUYoEYqtV3DCVugoh3FlJqMKLG1G8G6+IOztSZFgwA43GIyj6eB7gqgPioVMisNXY8GnYDVr+gH/3+0LD+xHfHuHTR9e+rdTISurv74XP91LchI/wyMErNp4UnhvRf5y5/RqYmHEPYR7H9qDFPeHQ3R9PuSGQ3s+MyVmejwp+H2a3raRtKWMJH6jre/ZjPvweYcjLjbTYR6s5fMEQZ6CRHNePcxxpfYO14cSd3aVAbw1Vn7abY1v28LXbp4cJPlcYtuI+DkPHrqDO6r6/Xr4vfVRhKvc+UL5eOU7YuG9/BKWh7fO/B516Nh736vqjlEf0EdzxbEYX6ny0D8/lj0KgR/N1rkT+IID0pYa/h5XqewlME5gm1JRR04RCGRUZ2ZlybvKKQBt2vD2zHgy0GA6t8ohv2WjohyB8vCee9ZtUKBBxbrdZWn7i4f2GexFq7FW86kCGmv9+29fZaOORz+YYOyK4X0K81xF0p308OiQcu89GtlB81JzeMNsZKG2X8mI5aUyIqhYKeqDMDggZX82I/TPaPOJphLriCApPl7O49C2lYJ5mcGXM8wICsOZZDopZrA89LuaTwQCbdUTdUDVOXNmEHq+1gEjrmGfMpWKaF7VmfgeT0uQGCpHEG4aT2VxtW8yIYwvMNsjUldnBUCIgZ+RlwXS5Ii8L0jSjJAInQlL3X77kXSCmUMm9PKXB9cFqp7FPTe7icAiBOVHKtEnjtmIBsC8Pih9q332+B/6m1ROAjg0O4G3xvHooh9Rtt8nzWhlBnhWZn7imIkyy93yYXQrjOD6zob83x/qne3WgV0aI2hFXVo/9sXty8G6aJrxcL3h5kc/1smCe2zq08ba2ShXcyhza+q278gcUEUf3hkH1uQoCRvTj2E+R3Tf/flkFBpMGIDVtXBa2Tv1VxREgAFVdMZHWXR1I0ZDaICZpaLgFIAIgPtZAbgKRTPuOYeA1xZOa7qf3wSZmiOPepMWtqF94DamPZcZ+7IShDpDh5KsJ51jcSyQkdfOgp9x1fJwC0A3A1oeXdUDMpxT8O9J+fQBwfiWeFPjRyVsWxiUlqJ9BCuNxPCNxU7RGt/3OCAmb8RLesywDUTPQJzsN6h9EYLf6Qp3U4NIE5nb6IG52lk7nLWwEli+e0uwDzHI7GexrZ1+uMdTjBh1xTBy7bqMKv+XQg1EvvW/2GlykdOuY0dc1CKecKA5j6WvLLKxG6eq/kuOzuCskAqZZ3DDNs8SCmOeMacpyTdQrIny8ecAxptAQPDTNM6Ys5rQpJSCpNUVOGtwst9M2u829bzedIDRXSKPhanDE26HfHV6PJ9MHQniwkIh5j+CorasA1/Vj8HYutG09DbkP37+Hx2g3zrHO473Ca9b+beoXdl3VR+sqlhA3tYwY++4n1wJNEONC2JqO8UMYjG1dsVXC1/cV72vB5eUdGwOX6w2VK+Zlwba8YMoZ4BdMaULZxFJyWoTJybkxTUaUO95DHyukFIkLsa2b+KatK2pdcVu/qkXETfu+inXBJieaShFLg61soJRRygyipP1nlMQQsKdTIVTb1nrcGamlSIN0NMkJThvXBHbv9nAf18jZ/Ef8b76CI8w9q4Q4HgcOnLUwSY+VEZEwt7Ydt3+kyx6ncez3CocudxzbsP/G67NpVNSd5Xm03s/eu/f7LMX5twMBxsxGG2cgTKP95uH3h1p8nM5h62OC77/PNAwYjA77oUU+9xr3Jyc/kv6+x/iZZIP2L7rxKN0V5vwr/W0ScydDa3hZ6D6mDEYG0gzkBUwzGDOACaCMaiftDb+GJSB2+sZIs+dh1gMhuv+OEOFiZur3dDJa+8Fe19rfjnaMsOfWF9FvPNAUJZSU/SxizZd0kMRIXPKxCIy5cjNQDWPJBLMnlfq4AigeC06sI1hPd7tQTk95m0+DvQzp+xIByCCqwoup4qRUia9QVT5mQaSX+YKtbCi0YZomCaysPJjkyTtL6kafq4Ux9BQ7Rt6/We4SEa7XK+Z5BhFhXVfM84zb7Sto+ytut4yy3cTyeNPT+iEcgMCXnITH9o7be8JvidxQYJ4kYPXr6ysulyuAinma8FesWFeFwqrWyEH2I7KM+zTlSAs7nCVgSkksYBC3VPHDMk0XTMuCy/UNl5fPmJcXTMsFK0Hp7baebEx3tQ9yk57eGufdVrUqQakJ8k2JZDLZlpsbCDI3lzPAgCkC7rAyFZZqKc3NGAPug8ZlClaH8VubWzyAuXdpq4fCYOtDFXgt3mIBLFZEnIshPeJf76WP7mMO8/qK2QQNnLXgOwJiAI6UCNfrgs+fX/CnP/+EX//0E3755We8vb1iWa4wu9cqqOV3T98cI+LofkPkvQCw4bwG0I1Vs8GxjwULFt8+ZFcyoR6ClFe+O6CqT7PEzcWKCZk5Cj5GgRWsHMCC6hgXExlHeU4O+Ah92mnppPPdOHyYHuYj9v6AuQl3d/NEbVl3wlPrr3+aQuaZxdAxoDb84erC/Qfl/R4EJA1fmnDdTj6GvtPwYm3vuQDF2hrau1cgtCKiEsL0EKxIscvM389etHbQrt/HaWTVabjb1iMdFTjAeCd0abu3XxnjujjADWh5ffMK9VkbGMenBEbhVGvMAXFpvw+EYvD2+ddToZJv/mRDFsayW3NtPXTdAT6OD/6bpd0aAtSFklk/SPD4+LtZNeg6JrgSoo1zApkFmyou/BMUiyMOi8LwM0H5cx1rXwx67FunaAhfjtZUt3dEpsZhNiw39LDfE7E/HsfG9MzYCB3UI9tnhXdA63OzhNADAO7KqHQHAsx1TSlytWDlVu+4F9ZaO6EiEaFsRWjk9xtAGXn5DUiE5f0FlBKmeQHAyJQAnlHyDGR1U6hB9cTCMimeN6TSK2IliJr2q2zYSnGFRCmiiKhlQy1bC2KoRHJVF1+Vm0KjOv2DAZfZWMZZ2Y30jm7x+zHP+M7BT8PvsdKmuAjfT/aH59M5/D2jjBjpmL5IfgJR+26A87XW9tORoTujDdn+cJyzBy0ZxxJtjO35Yeti2wL+GFpzNx3hgXGdHdd7PDdeszbm8P2WKRJerfBx+p6ZzjttOal9996ovNrBXZBKjAzlx9pw0rI7735kdY201ffSLN9H694nbePYnz2/B0tHZX1r+ntXfuz5lx/b3ntz8Wxdj3jHs7V29P54SOnvId2Dxe9qIz2/XxzXR04/360EOMAL3ONkGO0X3oGojKFBqk0pwerPmW0vDjQ4E8TFjT1qJTvvWvW70/VGYyriaLZhQZmt1cj2sd/7OhbYDxUeyGUiixn4WbZ3I6Pvv2l41awfrBbqrxSeUTjcEa7SeLO8lY9PZUfLWf7Y/mPe5H6y3loHezqKWZUzViWRB5sWxUPqBeHUDgnZfLT9vNFqxsP5O4n0oPpeFmflz/Ms12kCV4npYAoPdnc11A8TaSdUiVP1ENC6vuN2m0AQt1wEICc5YT5NE3KaUNKEWldxP7ob3vMDQQ0GT/Yxp2FI46nYUQyZCxvbPM3I0wzKE2CHuCOtGtdYIJ0OZZnAjg9tctfG3fSIZ2Q+ekgZBlkXORRmpTzSeyLabTDNw7XhmgjXgeZVfskPgcUDUNo2Gspr3+vBfRuswxnyYTHa/hE+7g7XdGPTLndpuqF8GdU4PzbBsm5yTliWjMtlwsvLgut1wbIsmCYJLG/w90dtlc9bRNxp1MjkRCGICXPjAq++FtTagGSRUMqKYCZFVuZjWRa8+1pOYVBh/IZubo70GiCLIgK+UAxG47JqjGryoqMAse3LbTdhhvrorti2rbOKiDl7ZcSxsdtTwn+O7RgLiF96bbz0q/XTPyYsYQ4WEeQnRG0T5YMFQKEs20zEL7b4ABQE/0iV9kdAuc6fxYZQYWbWk9KJkseyQIQfyJxE65qGF/p220aXEiMTw5RpVRFX2SQmgXnNlsJsTH9vhmUcY4KZZZHPGzkBQKr8s/EYkV+DbDuJ0dZ5kDABYLeqGf1Wd7+Z5eSHwu0hRBhSRFtDozAxCsyI0PvQ1s2Euvm0QFgaBNZdnjQ3KV3UVxs6m7qA2wM9NAgzh/XmjFGc/38lwKxJdYOcMybdKKecsSwZOYtFRKLeLofUd2XKABjIWfYSE/qaAmLOkxOelITpSUmtIbK4fxrn6kx4+SiNyjcRGvfBiZvP9h73H+2hxlgQ9kRiW3toZXOziLC1+iPSOAzjGB0J+CPTQFpIXBvWx6i8O2qvxYuQuBAF600sIm43sRC4rStKlX2YhzVueMwZHEispForcs6uuLA9zNqybhuYEt63gum3v+LresPl+leUWvBye0OpNyzLFbV8xjLNSFwx5RklL0gpodRNLCOmHGh9g4OgODDlCYsv3K0U1E0UD6XeUMqKst1Qtg1lFbdNdZP+li1hS8BWVmx1ReGCVAtqER+rtdj4SQSbaoy8+XyNiGwY92MlxJ5Z6VPD01aGBxavgQkI32MNpmiyOELPCmTurdF7Soj7hT5Vtaa4/zS4jm2I9VEH5vs+djT16VgftGKHG7R8eo7G1Nb1bTJTZ3825H4CV34rLv1HT79ff4/x5O9RpwXQ/NvTLH8QV/yv9HedPnKA4ez9R/n/1pD+Xem72YtnCojjdyQfELq1CUnttSRylzSDaUHNCzhfUJJ8WK2VWePvNRkNA0Sw8MLJnipjT6R0RmFY5GpmAhWJ0VBZ90CoPIPbISF3f288b6oar7jJmYx2a9y//tXT0pHWb3YRgCmFpF4bCAIjgYlRqWgV5mpY2+YyThmDSgkVFYWgSgirhdsp76onxKue7HYhaghQbSfAvYJA4wXe/Tm+Ic4s21A119XMGguDPWZHShk5T5jnGXOZcCtiCWE1mUXENE3IOQV+XNwg2X2j5dOUkaeMNE3gdUNldj5gXVeRdqSEKWdcLxdx07RtIALmZQHXgmlaAACV3mFxvhw/sPL1XIG6YV2/orK4Sb3dvuLt9Qvqyxvm6YKcJlymGbS8YFteARBuzKi0AWWFHRLyNXKyTws/ZCdij/IYBBJAGRKrMoGwIjNjShPmacFy/YT55TPScgVNC9w1rCog3P2OLgyZ/kabn814l0bBOUMscgzuLP6d/ksq/6SufEYM9kvMSBjcLUHKZWaN81DEokGtGgjcYNcDVyvtvG36ziZtKUX7qRYOvHZriNXtLZcCLhtQNl3jjWejJ/ebj+xN+7znNN5JCWj4qcn0oIoyGV5TQsz46acrfvnlFX/+yxf88uUz3j59wpRlLcohv49Gevj29OEYEY+VES17/DTREBzwJUVBhlk/xGjHCe6yyeM4UKiLnMl3N0ustbEsT2JTRATGzJQYoQ9ObLvQRNsFKbRXApBvsiZ4ar6eo6bteJyeSkSd37RQitcZRzYKtkYm2MfYfpswyIQ0YR5cMMTcI5qDtncCnujqiMjHrxco/FEkni1HOwWt1l/UTkV3WnUdAYkx2IQAnVBLPyb0A9CVlRMjJyWOQD4fxEUICAs0G9aDJPci/l39lekax5d2sLAXGvbC3ShgJ/hSwQhjPkbyJcC8nwUZBFaDwgKBtGN/o18jThy1NvkaPtioo4ueI+FNrzRtCKopTE9w3OmeoHDm2oijPOfv/YOzPD8kGU6ymBCTBg/OKbklRMrkykTBu7aQTMDX8E3cjlNqaz4F4gtH6yAIW0ZheZc3wMGY7yix7UcRZwc8IL95B5tNaQX/vT+tMgLlo98fS34qSX61sd7leVAO4IzdKNS6R5Db8nfF4Yk1RClVY0XE0y4taKwdujJCvLI4hKxVnlUzzYWdBlT/tPq91or8/hUMxtevFxAB0zyDmbHkGVQr1mkRpWqFnPZKACdxGwnbatiUodUVn7WU9rvYR6wfalnBddVg5EZ8m8mwxYrIrSwLYOj7VRX6h0UZnhI52DVBdcCLI20R8hzMUIMNh3E0fMoNdls2bm/GveQEto/omNOmDOs1plFBdpwO7oe9Lz63dj0F+7aRxvwKh6c+mEMd92jGYyXmOY44KutsTRsdyLx7HN7zktE2yY9cf0w6m+978/703H0gncHF/f0hwPiJomd4wx7czXvWBt7B3I+lQb5VEfLcew03+3vyMhotdvCO7tvtWYTDVlJg489aebd1f4+Ktmfa9BF89pG6vqW8I0Xuo/KevT/28y4/Hva0ezTKM+24l/dHjb3X8yPK+EC/jPcEhtXB7GvTVlXD+gSxfhCLiEoTqlpFsEhtPD9bwWH9Gh9gSgQnKUm4aQ8QTQR32ae0nMSUaHuyCc9tHyS/0XWx6xfi3npIu5yNlH4c9VgchOa1g6n12wNuc6PLIs2E0Ib20UDU7mMIIQ8eAwi3L4Hy7x+euRXyKsKEeBlQqVmUOenHuuK5bKhNoK1lDHxblOE4TVlr4wlS7fi9TMJj5pSR84w8bciT0PFFT7NxFSdeooBvMCcKHTnkU7YVW0rY1hu2PEtg9ixtTykhTzNmrqhllTDtVWJFiGus+/ik0V42HocZA9Cr+2cmMMnhKrGEWEB5UYsjX3Vdmb4LBvlNdbhqqdGtvssi3OrbFd8PsHTaD5OkEgVLCPjV3o0wzxpw3ntj62mAd1dchMOlEhic/Xe3bg6uJhvqZEZosSVGMiLOG3fE8/EYHB/Ie7A3neTp5pmO7otSbp4mvFwXvFwXXK8zlmUSeUtKAU20Q3yxrqf2zg+mbwxWfby5M3cu6fwznsuMxJ4JJYiSWD5QBqVJT7JK0Iw0iX83uD9gkSrUVoqUqwDBbMjdNOfyQNo3CIOG1JQRTdMOYBfIJIM0wLX0X6whSjjN97G0I+BgTdCT1ETa46oA0rSN8N4C58CeQFTVAqKKZtLN4hg1CUKj2nzGuZCZbM4Y7QRjkgj31Hxt59QsIXpB99Oj8MH8j0tKSciarL6xmzY9uxuYrq0DM1+LIObN3GnECPIQEEgqNJ0zsGS4X3qBQ+C2bthKxbpueoq1hSkAzHFH3PZ/dGrUWzOLbOaRlHQj64SD+ociSSit7DYGGzOhAhxpxzH0sayC3LlGhQQjniBpZaKVHZIga26vKu4Amgmca5bZzO3iCVz7qFBP287afj85cm8od3AdqGNUmNNRMjQigSm6seve+ydKRxutonYsc8acMy7LjJwT5kUUEtOc1FoiFGQ0gTIZto6nKYuFT6hD7mtZUwZRRuG0C2DdQD5YB1FTfIdeeLvjb3CAXxh4G/w1QsZOhhO3uEbjmIwgKPCsJzkOGJ+oRHO8/WAeOBB5z6QR7CPe7JkDhX2/NjwCGsfuOLXlL/0rVawhtk1jQ2wr1m3DurbfVfdhQG2rfLkRag1MLAFIjMqEyZlow1Gtb4KjCSsVgBhrWZEnMbe+vlyxlRXX6wtQNlyWKypXTHnBMl2QU0atC1LOmJV+kfpNUWLWG8I0gU2xoL/1dE4pN9R6a1YTpcqeVFbUumHbpC9recdUFmy8IvGErWwAzL1UjH+h3xF4hbDnHc/CyRwZbBv8HcBehM/IRLfPGCOit4iwubB0rEhveCDm/3FCwchM7BmGMfXtxR00//zaO1zzuzFr11JKN5/eJMJw/z6TZHnGd9paYpjibl+G+iOmvQ/iozr69jyfxnd//Pz/+MQDTMUn30oXfKy/41w98+5jeP29x5wdqVtb6HHTabiG0s5/HxX69wtP/11TxD1/5Ho2dPe3mPEfKeD545OKvBgwCX/cYdhy0ATQDE5XlHTFSnItaQI7T2r5+/FwqwhqhwuFD6ygpEJ9aP0MUNXdKRkskfKq8nyrACeRZcjjpDJ8pWkq+XdrCjM3CwQVWjZrZFMcNIxSIbInu4pcjFFJrCNAFcyk1hsk3v6ZUdgO3ZgrziCDYGOClL/k8Kn2XXzbeztNQPeNcyvpEfFujG/ySeoPf8EPhkkgaAuKC7hSCeKydNvEVal5T5BDZWq5nBOQU5PDQcZr1RPwt9tNC51FyAqhReY8AXPFy8srUkpY1xVrfgerK1Sru5bVeRjpu7hFLbxJXWUDMaFsG67XgnnekFLGNC14uX7CMl9AIGzbO25gOVzEESpOho+jMsJkiZHerWAUEM0Azd18JBDmyxXX6yfkyyfQ8oZKE0RiqbJCLUeso5ulfrNYFh4qPaSjuJErNoEhBoPDWm3f3auLyYSU97Jj3aT0aQEGl2KtLC4FKAXJASbBvQz4Omh8FheziFCrlLppe62dZgkh+eD816oKj+YOFxxjZGlnujk9Hivp12Na+3sSx+p1vTEILURkxpQy3q4XfP50xZ//9Am//vyGn39+xavGUQFsKi04RIJY3Py+6QMxIiIeDoIT/cPgAHujkETDiDD6t11+Z/7ZLD6DWUNkRV7qsimpNlUtIxp7ozpvE0R6W023LkySPLMANyaAGBQAzmFp6cRBWye/qwqRDLHK+HCbwMAkdh09SEeL3Fi6XjQ8JF3MwHB60DF6X4cL2GDMMYX7QVg0MP1ATwjY6QKC7jdoVhZRQ/1HEY3H9Rjhqu3TPpr1QgtIijDCNurtdEcPx/uhtU3RFDBTBqaoiABko7WNpQrM1FI665pzpvT70pFciUzpZ5ZHCHBGxtQpYWejMjRtFII0WAzEG7jLd0xS9uPd3bZNrr/Z6tQka74/MeFtOxzSXnhma6c/Y9e325UwZzBNsY9xL7izfv+ZU5BZEYxWldMqHssh98GEmzBbiVcINBG1q7zbgtADDVZEQaoB0CjpqSc/n6NT23BBxJnt9/fMJvf7wtH66QTCgfjq8Hx73u0xO9rGyjgSEPbpoRyHWhmH+1V3b4/LnPx6+O4etzhTN1pC1ConnoIlRHWhtuIfQFwzHnRQtm8OlhFV57g6Dmk+emUOtm1D5Yr3998AMK7X30AAbpcXEIB5uoAzg5hQc0ZagVyzEtjkcQmhJtpFlSdmEQHWvighTCzEcTXLhyIKrchwitVEErdNqpwo9g4lMQWvzVUd62mNWs1KYi/U9t8D2LBsIMNcGwyHwxAd7ddlDV96xYSXcwCrPWP27Wvwu9bvk6/u2knjthH3ldCuhz65j9ORcqIxlCMN2ghwRvT9HxULLb+te1krR2v3+LvhgDYOEQ/t6zpTIDwjkNuXdZ5nnyKuam1u79zDnXu8Fdve6j6pnPfUEDml8X1w/lQ6oOm6xw/q/9bncUSPcP/jMo6IRS31bpuOx3RXJ3qeJ54E/d70CK5/9PNvgaHdu44yPgYfz6Rny3h6Tf2B6R9bWXCePooHDhMhMJ9BKCO7jt7XeBDQGBFmEaGnuw8a5vwojK/q9p92yt641yiXSGjhH1llN1YPkVlq2G90beh2CQKCW4PQvJE+R0fTR9reRqJR+Yb1wyfSvsNHyg0Bpw8/dqBu+DgCbrTAc8jNeFsKv3TsjVQk66Yxd72soeOlbIYO0Kv0W2n9snkMtZh8XlNqiolBBmXuXEuRsUgqMcw5g+uEZbkAAG6XKxIRyvoO2gi1vEs76jb0P4xZrWCqKGXFumZM+QaihGmCup/KIIIGyWbU7YbCQKUNzxxUPpIf+oGPjkbzEOw+xtNyxXR5RZ6vSNNFYq9IoUMlPaxFWZfIVU7cjEaQ1snvFGMKl+04uLYVwBjEHUOXmkWEvGu/wazW5s2CQWQHbe3WUKjIdgKfFN1tc3jm/FS757Ekassf6zyYrbsrSMayHUR7RDvu9hZfYPB3e2lV+9vodv0QwXzCpUTIU8JVLSE+vV7x+nL12BBPiAqGfv24ffhpRURcOg3hGiBrHtZzvzu8aBtQ3IQAGyxypcOkvjQmgJLGjEjIWe93p9ctJoQmCme2A9JPlFyzd3yirKkzGEeD2+wuJFNtAtqUXLjCUVhipnGPZlUgtGNe/ZNId046jw0RcSOz1DlMCvm4RE6N1CLCNgoJ6MMAKsmWbXEirJ44g5GBJkJTfA/WBY/FsB+E/A8k0uCkrW1qtZGbcLNrIwMc2sMM92ttJxjYdlt9IZEoIOZpwjxPuGRgSQBlib1hgvC8JZQqVihrqeDC2FBFeWyV97P0sb4StUV4muS5CWtjoCap1GyHhlkj6t7vSjSYC8IV+TvmbdrkoJ4FuyXEQdsPu3PWhoaEpck2jxyQOHs7XBFRWdoQT5KENoNP2naYesIhClUizvq94P0fLlG7TEl89s9TxjRltYTImOfJFROUlFphApAa8aD4hzSwtVhEtPVteHWeZ6Q0YZpmgDK4pOZOzlz+BRTZ4bHdomwE24fSAE6+T+k/cgs3hHXB3XtRCTESLP1vydcrWI4SfRvSwThGZglBu48xfcZE3k9t77ZrVWuIUopYQWwb1rVgXTfc1EJi0xPg/SEDPyzVSg9j1EaancDpA+cJs1xrAYNRqp2WWjHNM4iA9fUVU8rYLi9AJUzTgnIpGnvihpQS5nlBSgLnsU+lNEWEtcMsIogrEipquYlyYZNTOXUTN1KsrpvKJmXebl+RcsZ6+wpCwpZWAMC2Tc6kiTVgs44wn6fx0zHUaHRMw7Ptt9F2Ydb8XxhwRKWv04OepZ/vs7kCetqsh7Hdq9+WflA5nTKiEY4hB3d5vyWdKSDMEsIsg8Z6vLqO0ewZIX9HeVw5lBfHvpXzrQraUenwPelcCTEyff0evU/j8z3T+N8z2dqO1P2/0r+Spf+e6+C/qzLhb5l6DMoOOr1YQoh2pgk1zai0oNCCQnMIWD3ic5M/qLqW9tIFw14S5VDlM/Y2t2C09nEFhCoqmEzmUbWtQiMlKGtI1oFemtXt7C4zcYEBXPnAemY7+Mx36wZjj6vQd1spclgluu/U+A/me78TkppAFWoF4bEiwtXpt4MZO1sKj7bMs1fUEsJiQlDOoJyRism3ND6pKyb6MTQr5/fbV6zrOsjsJOWUJWbEPCHNE7LSr0LvJvFiUTbgXQTW8zwjEWGaZlFG4Gds6wqihPX2FSDGentXevvWLJXVQkBYJd0rawGDsN7eldYilFJwfXnDPEsdRDMILFYWtWJL7xLvrULm0ob1zrga3S00JTp6zfoJFv4hTTPSlHD59CtevvwF88vPyJcv4DQ5ryOeXZoFyl65ZfWqeBIjBRXg29uHBpdsMRuCVTOxl4VxDRrABNf3pEqMZMoIlcF1MVAQ6FA97MslKipqi+vARebQYkOwWqZofAmUEBPCYr7EumofE8Jiancs+sle0s8bdOx/zL7DB9+kTlPmqoxc5bzzPOF6XfDzT5/w88+v+Le//IrPn17x6e0VU1oMs0p5DmZ/zL7/AYuIXvDSNLvUABq9RURzgxQG3820g/a6Y0qi8EIXWgoaVSJ1vdErIjiUY20Bt1PwBuxgc4dRvT+9/7QxtWek7Wdm8f1MSYX5hA5JhvHoGC0TcEG7h2MmjojkxK51LHyxfjWEEF60IT7pRazb6/E2EUyBtmPeRi2IyQS5fe/KtH53Ar0/juiLbXDNOcXYEC2fpSZI0avPYSMi7Kpve//Et71+sglNkwaVYlf6pERILM/dW88P6Ku1x+bSe2QEoK89QUjxpLmtQyg8BiBAuHOQIlxwoMoO5pmHq717kNX05qCIsBm7zLGeYQ35aTbP1t7vhDcwYnFUpoTvzPtmDoSTr+dT+Pre0/T/fdJI1wqaJ/8kDSDfXL71Y9oTM6o+o+aayS0qdI8wSio53Jv13InAfDez9/tweP9UgcXD+jAC0LamQNyF33vsafskXPB+1qojhYWX8gAkI+6+dyqRnCo7csHS1srYikdrYhS0FrOIKMEqovYWEfJeqO1OHcwsMSCYUNEOBIQcXo4R64yKsm0AGNt6w3qbsN5uyCljW28AAyXPAE/YMsQknAA2PwLawMpy2os9KJgpIsTygdTUuFY1C9a+N+JX21ULagXKdsO2ztjKirytKNMKIkIpK5gzchapcm8tdOLmi3n3LAzsgJfD2HB/z+mwbvLjHhsVE41W9IMmXm0guQ9hOcIiHV7ju2dwRyfPuj1VbtwtZ/eO0lRd26nP6/vRB1OviBgP2Ry2bGhjYz/6dlve/d7l7kqDEuKUjh3yHL0zKpiO24LDd47zxF/c9Xm8fzSFj/DS334v/zZ6OtKBd3LhbN/7ntTToNTfgz2iw3f+9uMd051xv8PnPILro7yR16BvtJj6e0jfOn/fO+8Rn1L8wm0POq/cHn8v7A04v1uDfJyTIJaP35qolfVs6x/V9mgttucy7pFDamO9o/5F+E9iCcEuQOvTyN3Z5MRadqWrzIfu4BtW/tj7FOn2uD93N9qveEdr6OQnnbwg0E5RNsZsZ/PaffsYzWfxwJpglMNJbvmYkqW5FtbPM2BkdJtfz/mJ4aUmpwKUmWt1msLB5Q2U3FpgnifM24RpmtRSPXeHxyTGwyZWwE7XN7oU0KDWecKUJ8zTDHbLhyaTq7Vi4835SagbbTAhTxMYGrQajHm5gJk1ZkQFpazigaNDxTpfZQMD2NYbCFImAMzzBWIhIYfp5nkBmOVwNRuvEhUMcRgfr1qXaaLR3TTNSMuC+eUzltefkJcXCVJN1FgGE9oh0u09DxmtXsjy6Z1ObBPxaFSKaVltpXAPYkOZca1FGO7aF75Lu8J7HZPR1oW75K5qSQ4rC62tbK2z38Nh1bAWCFBvc2dro42tzWFlaafJtQzfRFx0hp/O0smuAQ+iGeR4tstQAuY5YblMeH254PXlipfLBZdlQU7ZYwcywngP5Z/RZz8iPW8RUeFA4AITqHd3JoVDPeOs/Wju6OIE2R9zmiRuMsTEpllHkAWpzmoZkXrzKyvVoZH6CTLfWKLt7id6ZNbuD6j6n4cCv9VKhEpJg1E2RYSdKjxKtsApkfgtTASqBwIxy++IA62dxrAOVcTYSoe1+66pzGUidVuhpyQTAdXc9QS/z7st3lsDO12Jod1e5UG/fiDsHqYoOBMFRApWAIRdTIjYIx1vgWOoj0Y2fBUEK+1ERCIgJ8KUE6YpYc6NmKoQTW5WoWie9KTHJAFMZeP8cf0+IREtB8Dkp8KnSYgAIjk/kswfvp4nsdPiTjDzUGbw/TlWbIjWES6js4QYYaqhSy+g5XyKKOrb1lu5jJtKyMkiWKxR6BbiVZzWwOLb0xzKYYTz8H10FdS6+PfEXP/BiQEEYVbOCXlKLY6DuTrTUzMNHtSKKBCnILN0ypjyFKyeMgyyCIQpTxp7KAOUUZg6AjkqkXYraU+Dngj8GqHU9r3wNOKRQLAliDdGIO6tfFh3E8CFOvUE1+FQPxRMPp+OhICxPUTo9mhXIB3C+gP41/aOganXTSwh1m3DbVs1ZoQoJY66mGi/5u1KRO6SSegRBnXKlHCSB1A8UbHebti2hK9//Q2owMvlr0CtyDSJn1hSeMOMkhK4zgrnWXtugbe3RjMoNWX97Xz8glUhwXrojZUqET+1FZu4iyLC7etvICbM+QXMVWOrZJ0bCcZn60XGouLYPVOPN0f6JioRZKTkb7xn89gJ2X2PRairh09jzsb5ivNmV1+zdAyfrbxvc3fTvWP0/TOK5YPHe0XX9ydTQOz9/N6vp+31KjxA3Y2bdThax5qgxbIc0a2xjDOFwb25utfm/nq3i3fTvTbfq/uHpTvF/U1oAwIin/avdJTurKmzYaN7D59LTbj5OzNP/+1S5B0iHucA6sd01u6db6n76LBVoNsO3/nueq2cj5YV22Pc7bfUHPm6UPY4FJSAlME0g9OMmiZUmhoh+URrzSmLs5ZeQdgn+OiAScvOkW4Ish2AgcR6WFAUgWy8XUrumtuCXicySZF8oj1ipJ38U9Q9p8nNlN4q6oazVLOAldPZvG2NHjSlRKlA3UAe/yFYSVgQyiDEbWBxAHsMNC8AdwY9CoC7NdXjJ7N4yFNGntT7Qs6YeELFjOv1CkbFb9s7EmVMeUZOE8BC86+3G9ZV6PtSitDhXLFtq7sZndKE63LFdtnAhZGZsNpBYRZL440ZpSqtCALzhOk6CY3OAKWMy+sb0jxh3W6glPH1q9DSUtemwlkAXBxtiAxODxHpgaLb+hXMjG3ekD4lpLRguVxBAErZkPKE377+VWg1rD7Wkd49Av0d3eNCbZnXqgcp0+UF89snvPz873j99T8wvfyEtLyiUBIucVgoTamD1hb7jCywwmdSmpHBPgYmwHdLguAWzFeWyy0jbcodCDGbxQ+7AsH5h8gnmBInyidZrT3UgoWVv5L11pR4HNeCj0VbI82ColfoGR/YXEW190cZVc8zxA42BdmHeYERLhy9U7uqHMMOWsbnKROuLwve3i749Zc3sYr4/BmXywXLNIORutgzP5pPeZQ+oIjolRAWjKdZQBhCHe834taYHlJfQ6IAbeLuwOk1hE+jYCMI+/wdSRwQpFWboEqOgYE1i4hDoAhCXblNepix+SwjDW5UdCPaM/J8iNSJSEyPFDF+9PRVhHlbAE1LeEzeSBmRade6rT2DAFX2WFl5bH7pDgGzP4WfqJVpZmMpJdS6H2Pdx7uymonA9wgMmksE0chH2iYKLdq7ES82vBSFLUfd3yNIC95tMMxsm994utR2HYQJe57ROGKgI00d2zim3jXTNAhhyWEDaDBybz6o6y/6eWbbiPp2jCRv943sVduk79NGUp4pH+6tgpZXCIvmY7MjmE+SIHhucBsFMXYlU34Z7hrGk/Zz98+XIrFqazG5xVIKY9awsBFeJL5D3acj2poN+Mthl5rpL3wWLHtTFJHFlgiwPLb1mT65ENbwsj5q+GMggiIe74S3gQBD21cetyHuovR0649ShFNnzML9Hb7FGWz3BNFx2VpS3D/9av5im0WEWUXEqwlihV6A7//RoN9GhnmPJSrkJFWNY53Ed147MaOXCoArtnXDmlfc3m9IlLAsNwCQ01lckbMI/y0oOrgG/FY9eB3XYhAUXCQJIS5hC1XAXCX+hPUkgURRXhllXbGlG9b1HUQZy3QDA5hKBmNCKgmZK4gQBMtGPzRlrNU9Bj/uhdtx4QHj3mbroCnuj9L+IMgI5wYbj5UIe3i6l78Xqrf3pfm8g8ldWQH3n5YvXMv4xGHz+V3gubXfxhzDXO2T0XZOI1E/blERQZSCsi4yW9jlf0a5MCoueqUC+fVu23fv9c/P8Muj3/feO7v3TBsP83T7zHD/URk+RifM78l7jTm9xyeExP39Rus8gK2T+zwAfqQV7733bPnx+iwj/TQ99kS286IaD/yR1LftfK7P3vseYUL/7tkhpz82Pdsvfx4aPe5EEfePcKkvdL1+dixb3dyWqdf0bPo2eDlMzxbTde/x3uk5B1h098aGY3QvZAp8L0iIfwQXIh4XFL4vjXTG2F6GyqFs7+imkWC+0U0G5V7rG4kOiTcX3VfbNwqzwLHl1nEkkuDSkXcxyt+UFu70IAgSetlCbS6g1a23KSXip1dClOZWxpUPjZ/1zrk7po+mnpcYnzh8Ok+zp/FligkpN0XENGVMNKGi4rIsqLVgWSSgc84aoBwCY6aIATWZBdAOJrHKlHLKmPQQ2pYzUskeU8IP9bDIB7ZagCqKKzkbSoAeyql1Qsoz8rQhTzMqF6RpBgpQ6iaQE8fT+k4yt6awWDeJL7FtF3HLqhYRk/IE0zyDUVE1cPIRLo+ysbt0gArdKQHICdPlBfPrJ8yvXzC9/ASaLgBNbR0e0p6RjjBot1/9gSF5ZmspyDhZYI1GuKHAO9nHSUt2MLJbRn/3fMd4jTyx9anxifaMEayJunVgferXhfGbYHi/uv7FoeoED3HeBl7BO7afuvG9u0mZBi+bIZ54YkUkODXK4zzljDRlXF9mvL4ueHu54OW6YJ5mPTCXmuwC4dCYc5pnzfp+OsPS04qIUiPjCBRteLSAEEWE+taPAhRWFzDqK0zXvwioE3U2B7Ipke4hGlh0OGWZUtvA2qiEJcD6PixYdSN6ffAAdMoIRKK4FTqKxMwMjiihBoI+ar1bMNwhBeQi3aPOIqLLesCQ+eILi6PBwH1gcN4zMoIqIElI7k9RXJpYoG4jxo7LJtskTKBHep5eF0R2s7ymjbUN+PdKEYEnVRalnKAevsJYD8Se4xYTwJj5ZBtjVsIG6jajbXYFzEJYkSMFiG/lCvfdXKtpWq2x1oQTzvCwf88wZifEG5ESBBOWecE8LZ2bJveZT/G0JMEClN/htLwtPVIyYmjfvkfIS+bJBP+pzx+++1lwI0aBFkxprJUZUL/nZinR8h+1x/offzcqYRTeNHdCGTnVbkzT6Kz+X8n2TiS1YMiUkCmpTU7bDwBZe3aqQ/xFst+3wHdmPddbOuQggAkzSaaQyx4rRXBYaKBvzmcpMhSRWApElecJJ/aN0DlaByPxMxKCZ+3ROojgp7R+tNLraI8aCWb73j4hv72EY1QyCoAjHi61YtuKWkBs2LYV67qibEX96cq4mOstWdKBprBrbXuhMchGajCUVDGYKxWgEtrWCFUGcHtfASb8dvkraq2YpllOPqWEqUxIYGGwoNYXue3zfvJGfZJackWLMqgJ6qO4FIX5DGJCJlkhqxLbt9tXMANf//pfqKViylfMdZXYFNMEgJGSMGnut5eMxmWvOzIB8WqxkiKD0FLbb3ZEfsd472miPVwbDRZPifV49igR7Z8/gv/I8N3PN8Y+uUee+1s7EqNrV1jHxkidtfFozfeHIBSeak+Lx/qsD5EG7vpDjdn350hg1GA9s6crzhULxwz0Pj/u5t+N20mZz9b9TLnPtOFRelj3ARAJhgrq97P22vsfrdPfPwbgozbuFSOPeIJ9wb2yoVeQ/4gxPypjpEV/9F541obTZ9/D8/yLdPxd055vsQf4vnn71mT7xt+i7u9NZLKc2HzlA90JPNDkOsqYpwlISqs3BAh3mzvS5QhbKDOQ5JBoCuQzmywI5Ly8xWCQDHZS22JFSOMMHpIJXMmaoARTSi4YzIlQuVdEVJUnEUiNDVujnK412rYIXbUVCWK81c1dMZkgFUYj1gJwAdl3PYnvroMi7+CWEXZi/SNz+ER+FiBlPkZPdgh1mmdMy4xpWTDPC2oW96CvL69IifDbdgMzSayHpHa+LONSaoF53TCr3m3bREnBIjucUsY8zVjmDWUTV05Go5YqblRFvgfkMqEScOEKcEJVWl9cMQHzchE6/nIFEzBtK8qW5KBQAUCjUFvGgQngsgJ1xfu7WFIsywWJEnC5ICUJjJ1SwuXyKi6fyuoKk3hwJKKhM96KzXKlFBFHTDPSNOHy6Qtefv4zrj/9Oy5f/h20vIHzArDEtmsUts3viGTIn8uY7YMzxyUHZrVaKLDYEKhRITF8FAcIPxTbEYdzVEI0eap7rjALbtiaUv4EwlNVaGwIW0PRbZQzfgdAi0ZX20R02ZTOlrsq3MN+3n50Gum9Xtlh8o8m0zUayxTsNE/I1xmff3rBl88v+PmnN3x+e8XLfJX4y9xsuQTfKb3GRyv790nPKyJUgGoD7oh9d4UjWmOvSJkYIj0xroJp9RQgQiZuIOvJmEsogR6ZGDIhg+VVoYduQPbOoKtoSiomSDCihgj2xCQBnAaeoS3W/WmABrwRmLv6qWna7Xefo+vSqbDnKO1PLtowkY8f0DON7cx7H9Q6JVLrvrBonUE14q21SwSxzQ+7KyZSAlENxF5buMYAW9t/TBoEBQ/GzuV9A6HQlFR9QTFfRUUloNYkioY8Ca5N8ImLTEhY6nvBwwfX/Gl/DDkrUdXBAqKv/KQC2KxB4cNJdFtLAT7uNpEaMd8JEx/0YWzbbj2xtIOZu4DzsWyCzRF3k+7a3Ti/aELjo52DhqvpHRDaxjB4N+Xq+See7g+9Gmv550sBrzVBGAJeD7CjHIIpuRvmHAScRsAkI6KG/UIZA+4KR8Bb+/lrm/sImyPs8HAZFAyBAGrK+ZCfue0Zdt1thg2Gj9O413yfRcSY7gmMHgqK9Dq2ZyyTmRHXRVuzvesZOxHFtdEdraa2y9tea0yj4EXqgcuqrHIVq29b9EYXyC1KDZakWFEwl62gZFGQpJRQygoiRimiACjFFLzN7ZPA7Kb9CIoIDmb7zNIGeQAURla8LKQNOSG+rRuAFbf1HaCMdRXrjGma9US7KPsIhJQaDpKhl9+1lt5NXUdPRJwZ4DSKGwYce3gYw5/389ve79PRvmL3z9K3Cx17puJuOU5jjHuW7fJaHjccZy+yET889Plus++t5v5wBzuePH+nV0bsf1uNj85Cj0xyK+NYaXSstNg/e6bdT11DBfG7dJB9Pz9691EbegH7cZ7Tez1T0W4fjPhxWT2uPMp32o+h7rsKC/RzQid1363vG+r+aNnfNAc/IH0EL31zHXr91v38j1DI7Gn376c+jpSpPyqdrWGv4z76PC3nh7VPCv+md8+U2s9X3PD+vX7FOWn8UY9TbQ80+pYolC0vItJtkfcCOFg7cLcOoqzcaLyEQGrrvXjdC30j/aG7XdiLfBu1ZkZaR+8xGw8hBy9rlZMu3JtntLYa7dPFc1IriNoLXENmuDuaKh93MxOVEP2IDNdm9zHyQEe88L7llgb6GbSHN5tnc5mrbqCnaUKp4mp0nhdstailAFQOkbQbDabsoJgoIlReV4UPSCkj5f4wWVuP8PE0OtR4h62IBXLKEuOVeUJiRsqTfJJ9MljdxLPS7r0S3uiK6iNb6waAxDI5JSzr1WldIsI0L5Jvnl1uxMx+dX4jlN/o3yaAZ8BdQ+eUkOcJy/UVl9fPyNdX5OWKShnMJHJqqPPZsGb7td3Wr8PKQL83upD7v4xo4NCK62jSqAix8pR/sbqCJfb5Wm1WDwbXNSgrvAIOcVhk9p+WuLRyGs8Tx6qTHz1cOvwUHX2USHFf+2vFDqWR4SOdQ1IoVbhZlhnX6wVvby/49OkVr29XXK8XdWWdvYBofSLHkNNTO8mP2AOfd81kDL/OgVk8WOwIi58TXTK5uJU1CjoROOmpxMR6uFhHkW05t0VuRLkMycDgBIGAjoZRyRaTWibDsjSrP+1DOgH2OKAEUDubG5daUvRjz0x4FAXV+9SAyjdhHn0da9+84QOzdgbQvnZGZQT1lwFopSoZOyKzkFBBKtiX7zDafZuo+VvPfrK4KSNGBvMH02x9m7Rdh4LhsFHF1ITbdgK3nS6U+yORrWugMgoKSiHUmsR3va7r0XrdhaWsWPsHBp8jIj0tG4VGoyBS4Mo3bjWXzIqMfJxcIGvB4QOJ+ACXjszCKAxtm0K8edCXrry2YWkvAlHX7vUxUtqm1cbEiug3q6ig8zoNXpXa9JVIcARNaLB0qozYuZa7P37/bMnXJcU12547ARbocbBtkI0QEeK0Kk6vQnyR4SUhwQCFx0CwE4lizoTEca4kf9/OyIwwB/zADbY7Isr6Ia0M+YM68oBZsrckWo+B6qgkbe8dCnwDDvzRTDKw55GP4P80szUQ+/Xe+Nc2HtFdkFmXlRqs1nxfbmvX9gF71IS/Fdjhcw71Uxi3aps7QEBCs64hIsH/pWBdV6SUsK43EAHbNgOo2PIkRF1qcOhEm55yazGlpI4WE0PnlFjIwcKAKrkTNXxssL+u76jMeP/6G7gSlstXVK5u/QBAT7+QWkZwmCdhfoygr8os+tjrSaMG35FW6me1w7EYv9vPtgbjmmhXY8j0ZGI4qf9IWP39grZGNx0pQPrKTl89IXJsrKljUvqXT1oVxry/f6Q0OmrcQWt8PCP826vcdeMjAuN787QX+vfv3atr/66t8/39e+9ZMrx6r+7vUjbcaQPTPn/kT+4l5xMe1H06Z8E687S9JrrYlWnPBurywZp0uHyi7o+mj8Dmv9I/ZnqIi0OK8Pat9M+3CI7+btJ3Nf35l4/mhONHkZl5DwDQ9hdBYmhBqtWqOZTHAdeM8oeetkbjEdDT3/Ha3F7u6W5pW+ABh/vsAqVjWBI+hlq/SNribXa5mMoOrD1s1hFF5Q41KCniqWux+BALC1VMuLVDzBdiRHSj1crZTVj/5SA9QVNYx/Rj8pZpmjDPs39qraAELMsFlSuWZUGtLHH9bG/0MU2dEoOI1LOEjFOmyZUQEhQ6uczAXLmW0g75SKwJwrqtYDCuy0uj9SH0cZ4mcc1UC6Y8AbWgpKzuU2M0Pz3Y5i7HpNW1bqjM+Hr7DZUZy3wFL6zx4RKW+SJWNNtFDyxRcyGFnq9sfGrkW0NEQAXJacqY5xnXt094+fwz5pfPSJc3FEwCgboOE+Vj3vNwOpUG97nwb94yk3kaD0qH3i/6Mj2RynQSOcz4uh3WaLy29d1kO+xeSXq5s695LgAD+W7r4ojjeJ1HGPc8USlyp7xvSns6a0d9Kb5Jjjv3a+j6csXb2xU//fwJP31+w5fPb7herljmBQxS70alG1e41P1AtvA7pA+5ZgK3E4MWxLeowNYtIdTzjLlKEGa6EdlUWfacKhuNWEcJsz0VQaq1VBcatX9RW64qCudi7E/wUpbCI2tImMEmaorABF3crVwXc1hBFW0Ruai1guuqSKiKkoYgAn7YSUjTX8pgEMHdMqlETE6mg0Ao4hmazEVVG0dusAb2ugvcl6BtWt67MzCydingqlUKWN52tGcEBBsT0pcBggryfE0gE2FOCVsS08XVxzEQI5GCCFMUSv7mJHJ+hlIDSgQQmKNA0fptSE6RH5lBWhi5gbCxltr2vlYGr5sLNTMn0bZzEOa4pg4SnB0JSS0qHhHKRzK9QK5J+8Z3FIqr9UQ3TMoSNHueMuYpI4OQvT2q/EsEznKVjQLSft343AzVCLew9mRFRCKuWcTYvIc91ftyLAwIc+Rrbt/Pniy198I9MmKtbZw+eixzY/4+aeib7bUuICDpqds1RaEINRNdczM0efyBFqyEVWn0RzPGv4dA+qPJxpFgCh3fGcR3Z8B7DFNEIcyZ4mu0tVVKwbYlnZEEzoSUqphMM0AkwmciMd2W/WtDrknBI4FUyMxgMLEozCkBNME3E+2Bx4FDxJWtHw1pExCHnLjf0yJBw21c2l4m//pQ1Lan2HpJDRYR47OMrNuD+Y8I/FGKSMgZyqZ0bESS5Y1rpSk5j4R+JnCNjKMI5uWz2afI1dCq1Zy0j4l07N29W/MV3JTAFP42jG88Z8RDoqSGuzF2IliZyFI21FJQt4KyriAGyrQBEHPynBLI/EYbzi6bMqIl1N2IXd9zdAzlr+VV4r8mUM3AKjEn1t/+C9g2vC8L6nZBTow8zaAM5DrJGssZs/qnTSkctFDEXM31YK3eb2ZqcemYAE4Qc+woABdc2++QcPrP4Ra6/smUKnIdaUZWwsvprwBv8l1xOwEecMZBdKBUut/3KA3bOQOuUvxzJJSOxTK3Eny/Goq3/cohMMJlFH44LfZEYqApEyKNEuDZYIgareaVoA8yb+tDBE376gL55H01usEUZO3gQhtLovHZ8P0AJ3idA23QKYsPCaS9KJGH/ESE6aC+UTl6Lz0r/D8S6HPXj9if++/L/NEuX4/N9uVYHXyC5mnI14aSDvKN9wgHtyVxK4vRr4lHyqezNAoKn0kdz/iD0nhA5+44RHoWrd1H+/J+zNV9sLzR1xVST3v7bnMXj3xk7FvOQLyDsKvh3jA8SP147HHow8ZxaB/6/o3CrdM2PFFv5HV4OFhGT9Rxf9y/nVbvDJaepPnjvDJ6ODp/Qeed2vwTN0mHb6DQuKBgyNOMihmVF7li8j2fiMT1ERjuEwmke2HYN71k9mdGP3SHd4BwYCW846UxfAmr1w8K9LiSak6X8wDrfZnNcmE8NFT9IE1x4WjlcLX7ZdNA1OJ+icomFrN+f2vBqsUk2IXAFA+1dB9rLDf6EuHRKEjlvn9txPVjciObzuCuGMgAJdQ8ocwTck6YE4EywJmRkcA1I+UZaSqYpwWVGfO0YJonFHVXyigoZUUtQluv6w1b2bAxo6YEul6AeQbNE5BvYAqnt1VJkyAgtKkyotQCKnKAWOBDeJF5npEI2K4XECr+ukzgmvGe1G1YzqAa3MGzjqW7DfPNTUeKUbcVKwO//fX/wnqbMc/iBnvKhJwW8MsXlLLh6/tvKNuGrUi7E0qgy2yeTFYg9WSGCP2JUakALy9IP/0MfPoz8PZnlOmKDVldvlYQb5I3C19dqypr9DREdE1NthD1qLXINOQ5GU3Lexhxft72Nn8WqApK4u6WIQex4joxayBdjyK+U08IMLexzQ2UyG3UBVORQO72G+auTONW2C5ojkqMB3dLoyprh2pB4ho8L7DOJmDuvK1HpoQ5UkJEBa1x5zZej/YfBrrDGg4CIQ8RtXJBoKQyCn2tsirLJkKeCb+8JHx5nfDr2xu+vL5hWa6Y8qIqtYhTCUTipoj0MOfRNjDSLT9CrvSxYNWmaOAWC6KYAtby1APdK8npYIExBlWNRVBFS0VJJ6+IOxw5raf1qXCiEvu5VkSC0gnytlA9G/pFBg30yB2ghXQ0niSnIlktI4BoWm8mTAW13FDrisIFBYyqbSJkEBKSmnj1TJPWmQiosgGTIXryrU1An4KpILUYGCwDBuYCtsWigteebB26RQ2ULU+3bFVwrz+kWoYKUxqVaUMvwlYjMwgTJUwpYU0iADRxWqSRnE6xFvwAHoEM4YD8arBhXu96Ar4tpqaISE3TrcRQdwo5vFkYqKViZfF9SImROSNzdgRop3dRBZyyCiiTwlDTQd7pF/XXuEnt8nIKfeR2pYqUCWlKokWfJvXJn5D0pLkrxrIH1fAyCOgE7UxVYouwjSsC/NgagQsYOoEO99r27pSjdzI5HjCi0vuoec2FVh9Acfxuczn4y2SogsUsI1r/JaCrnq4P8XGa4kNNcAMuUnGMmOgmgf+ScrASsnVdQ1n/bCnCU1ultj4rRCEUVy7raRFSJQ7X4nAvsWcq1rWgViBREXhIomSjQBRQypgqC1FWC2rNGvxX8LRs5mr6SVCGSE2cNJyxgU/1PVDwZkWk59teFK2pmlrBlMZxE28sjpgCSxtOzjF5HU6gmiK5K/Mb4YuoX2sU1qWtY1/Ttl9Rx6vYPmVEZY+/YtslNf/2DR9bMGqxgCjYasFWKtZSsVa52kEII5T3J9ka8WmKJhuXgX8IYyf4IJHtx9LmypCDFLrP7RQR24ZKCdttBSqwzRuY4bgk2dhJh8UPMBdhvsa9xZQRaLgVBDBCXmbB9ZVRtwrQijX9L/Dyjq/LhLJckGfGVC+gKSOlCWtl5Dxhq1VMulMe1IFAhTDH1g4xhVfUqVZJHJT8CMxtR4qR0Qvck2xWn45HVp2GH38Yg/w4LJEfehhhzU+2hfUe4eAsxfyCjZr1lFMKYb84WlJN4McN5ny+egsIfyd2z+ByZPJ4FHscdsBzmLCHesKq76crb1hbXDvXdJ5/eN/ZnoEOkWk5VizGwYqu7/osRwcQxiy0u47CRTpq3FCP9Ku1yqx44+m7s7acMVtnCpJnUnrynVMlzAeF6u09HApO2657rw7bb44qiF/p8H60Bv7Wftg745w8HMcmIv1h6bDOOzjirIwjvNUXKWu3CYrOytyPSw3ZjpSpZ22KZd7Ne0Sd+CvpAQK7lxpPSMPvXZkHzf0GsBpqvz8n94T18TTxh5Mj/W8dOP6OMdf3rfHeiX1vyPMpViUoPW3bmO1HcpofxCIwpgmFFxRcsGFGwQzrNMX4nyzlMjeZQ4WKS7rWKq3EQFGZkYiyjU5vrj3bgUi1IojdKsoLxj24jQgalgz3TUal9JxKeOGxJrk/UGMKh6KHVk3wXkoFlwLemsKBagHXVWNCbH6FxSG12BN235URzUKCDBaMRDtQQozrt/tFIyAEnogA5Aok1uFUIi8R6jyD5xk5JyyZQJmBiZGqyIbyNCPXinlewMxY5sVdN8lBrxXbdkMpG8q2Yt1uWMuGtVbUnECXBTTNQJ7AaVLPHdrGKmNCrO66qro6LRMQhNuMBFDGvCRMOaG+XkBUcPnrLMGkicCqiEDNoI0CWBgM2ZCSjxIBKNsNXAv+q25IKePl+oppmvH58xeknJHygq0UbJwAWoFNYn+InLSCsam4QtaA0csAIbPEhihUURKB3t6Qfv4z6Mu/AZ/+HSW/YENCqkUUFrUIP5knVLJ4KSopU4VKo46kFyK0z0hk9KSuT1V+NZrfjuBRy2Mj0e1VwgNRNZ7iyAVs8ImTxOKcQbqG1epBlQ4ic5XDX66AQG1la6wK46AAiFtbXw76V+WnVHX8a0W2NyjELGFR6sh9Vq873NaV9rnjJ1xGrLz/ieDeaRlfapF2Ip2jlhKZ3EQ5VZoAVcQxGKyB02nKyEvCn14zfn6b8adPn/D29obL8iouhId177yP8iOjzM379DukpxUR2ybNtsWhONstI4xRLdr4yoHkJwDBFYAR/8SqnNDOVaogJvVpbFcpK7ExU20y7XRdTAH2DwfNntsCD3pxnfSQmeBAYcykEYQdkgf2C6r73YC2icFDRUYcaj6jQfbb3tAX31jjxr/P06dwKlGZyH5bt7Gz9w3NVH9/lxd9kGoTVLsAGsY4trb8TvC8S3tkJ3i09W947r4XDclokFlXysDH3H6DRQF3WzegMqZckXNRORxJICo9xSsmg+rv3pmCRmj10zUC48GviMT4Prxo9jYv4wft2YNStCzbcsjbYfOddOMxiYzdf3bi2/yc1P4E8/a4Eu1DgFMnsIbGtD2iH59RODL2s60zW/t/EOCH9CM01j8qxbaY3K25oTvPb/iNETZu2EmJ6Mal7R+llO6kb0oM0nVpqeEnB1VfIwet8avhcFMqOM4ffx98dn2Le8RJ6rGnj8jh+ojlHxE/e0KoHw+7+hhwY7pN0Bpb81CIYusi7eOqtDytL2NgZA/qFxi6kZAd+8ZEx8gjtDe2O5ZhroBGhY61MTLazAwuFZxUYZKM0ZTA2sxATgSkhAKLNyVMjJkTyxVw5RQQ8E0KLgq0bmcmG61hJuh0W1GYkX77DVspoDxhmjYUTkhpxjRtyHnCslQ9oTVD7DWlBrEGk/hHNgai/IsusvQkksO4tclOGiEIzHqi2hVnh7QZdYDO7cswvy3TCN9HuDlU7/P5SPB8mJ5E3Z1iItDAxKFzQ51n6/hQQRW+38Mxe6Vc713WaPHj9a/+roV4h7OagY67N3b35qG7d1DGvfzjdcQ91Hfm9P177X9Ux7NtO8v36P1H7z477mfldBYRIXsy/kbvNyUssKNbnlgvR23p3e8ONNGzpBE/aMJ4P6DxZsn6ZF1jGaF8Gn7Hn3uuK/ylvbLgTKlglcd2f4Tmvbs+ht8jvng23c3L+7F4pjwXwFGP744KO14Hj8p+rh3flb6H7P6eqp/gAx+8/tRdl1MQ+b4vDwjRLt7pGUU8gleaOyZfj1bOGa8b4UEIIcR/bde1uu9NAEGPk2jbbNCEbpQ+9bV7v7XeRp9WpcUOPqYAcZpWhKpKNAWLBm78kEs35UqWl8P9GvCo3475bHwM5z0aj6Mhso2C+ldjMA7tgxy2TeqynZCQkWnCnBfM+aK+6MXZdyGAckKeMpZFFBHzJIqIlDOYC9bbhnVd8fXrV7zfbti2Tfg6iHxpSlmNMcSbSiKEeBQZXDNq3cCqGEuKlZlZ6OLULIuNX5/yhHlecLm8gCvj+vKGdZ0ArihccVsTwAm1iOtS3yN76BCavFaXmDFXbNsKAFjXFbkyKM/ISLgsFyQirOuk8ceLzxMpPDbZkPK8UPp6WpCXGcv1M66vXzBfXiQGBempeF7VXZL0tWyQQ35Vx8IO+HEvsO8ODvl+M8CO0ZlO67cDRw4XnjXQpOOnWy97mtZ4waI8X+T93NLJFCO6ELj2/Lf1ydaI8+e1uAKx59fbeo7j3u8bxzt8P0TPrzfHN4dkwABldvDP6DWdK+fHCKBEEhfiuuDT58/49OkN1+sVy7LsXNRHt2D36IOPpo+8+7wiojTtX1REVMDd1YkmGh4kBC7YYzCaUEgERgkVglhMcGQMcARCyV9hHr6s/sbsaadPR2P/VAS3pvXRMpwx6nL2xLhKq0iZMxqQhAtPXPtuLTwA4IFYMEbeN8XTbXCfBv72eAHF/dv7K5/ooqkfBFEx9HoxCs8bwrTAvC7407fJNzNfOzjCa793akjGNiRp/xgcx2HXkWLAqdz324aVdGdYt4qyqSJCg3ZLPjO/hAh0uLmh6HmiDiLud8iFhPuTwHdfw7ESou08d1/W/A3JGGPr31XYwWauyWyXHYd2D1Hxg3x7YWIs/PFYdAoyGwcNjg1uY9LO9+xJjlOBgNPVYTcHdSvnj0h/TwqIfWqEg/y8v5Eb0YKhT5bHgn2tK6mVBInfUcVHOWdxS1NqCDqsyfYIY5JOZikyPM70cFA8YFRGnAsI98TNEbHTj1bf77ZnPMp/TEjt04eEsh9IjmMCrjlW6PXj0hQPSnR2J8t63L1LzMZThlvsdUX8sX+1zyfftUhixwaxjVyrmJGn4r5ot00UDFMmgBMyZcGdYJipr9ELsS8VLPsHyd7r8zJ0yBjd6PsY6w2FK+jrb5hKASVRRDASUp4xzRXTJCcQc8qoWSw1sjJ4BJJDrOHAB7gx1LWaAiKOfdsPO7pmoKydqjgAL6dJFPf+Prir7d8j7I3wePSsHagY2h7gxe+hF/q7fOVev6jN7ylcHzwb8cvZO2cCUNvP7bs31wk1g7/GHMf3x76P5Z89v6eMuPf7aSXHyXsfeecs/9n731rHj/j9THuNhzkacyIT2DxX1jNp1+bw155/uI4PZu9EoiTXH1XnWTFHtyOv+BGYMjxK4/0Hydf8vXbScZs+Oj5n+WXP/FhZrS0HTMMH01j32dgf4fCj32P+03pBp2P+e6fvWbP8DWN9Ds9N5Gi7IXUxITJajAjBS6LyHqxJKF5oKL+1wQWN9o/P5inAucoBKP6NfCWPI9Lvz+7fn8+UEdWFqS4gbcFU0YRodrC1HcgxywyX3wzsLcX+eZ5Qrr+Pu3QHx0I7Uc8BL0RxMpqHgURiTWpKoEQZOU2Y8oI5L+4RRLkkUE5InDEvC8CMKc8ScDonlFKxbQW324b393est5vHhjBOWmhVwDx/JEjQ5mmakKeMWpqwNRGpvEXobqPT20ADRAk5T5imGZfliloZl+u7HJreVtzKBkoZHGJOtCEx3sXWgigCyGnmjC0XAIR1XSV2xDQj5YRlnkEEvL9P2FRZ0KaK1DmK7QNNRkUAUp6Rl1cs10+4Xr9gXl6Qp0X5norKG0jdp4LE25d7BGHAXavGWTbywOWPPZ1gfDiPsBYBVFH2EU3Kw78jSPRfkRfkYBVRZS2VsPaoVofHqADs+CVzVB55dldKBH4m8DU2p8b3s87Do2RyMOvzs0nI62HNcXsY5XXOFeoyZVNyEkAp4XpZ8PJyxae3N3z69MkVEVbGkRxi5CukOff3kx8hL3haEbEW1R9qEMVqV8Ol3W8DMgI0wIu8UztlBCqBU0T8CRntdN+2bQBkIRORvg8wN5/d/cSZ2PB4Y+yEp2GQreyjvG0TTOEnw4RWtr2ybjSlbMGtgSyUpMBOPh5WkC5erqAQjLO5AYpAcT43TelxDFBWnwiNTSgE3/x7flldGFF/yuGQmNUpJh2vROSBOd29nrlsSuqyjhjmIisW86OS7ItHBAH7HDci11y7HOcHG6HS0wDt7EXfiU3dS1SuyKlZAMnkCfKX8VX4SeqzngyGgHYy+DEj+y2pCyjeBRNv80hEB7X37eiEN/qJjM/hpP7AiT4WJh4xLQfEVCiDfMu1blCHT87LPSqvldlhByKJt2FNcZj450sNB8PxDyuRUWoFCqEUPZXgGbsS/NoL9lvgXyNaUzLFqLgiS2kC0oaUGNM86TpsZXbwf2et7fCE+qTcndhgdZk34KBnBIfjeD2b2BYfx33kcfq9lBBnay8mI2w75k7nsJTq11LYr9FaglksYSLjGdd0HIJx3z8SxJwLba2Qfo9pcUoKiDalW4C83QDOKAlASthQ1X2he6ltjKle2Z8APCrM4OdiW/91jrdaUCtjrQVpXVEIyNOMrRRM04LbuiFPM5bLDdO8oJSCKc+YpwU5NQvGpBYYnaPpA+ba1plY+hWHfXOxZUtL1pTECUrGQFJS68kkgbOpIKWMlIRRsEDao9ucZ9KPhN9nyjoTwtgBFm+7byHHe0l/hvSwpsO6exz4PD4xt0R7RYS0w1xpRAZzdOFAijuJ0r5XbAHaB4FcoHfkwELfrrGd8fszwv6j/sZ1/oyw9RH+b3jirH2eM7xz9Pu43KO2Pat0eKbdwgfs80aHno/KeiYdr4vzPD9679kpnu8Ih7+l7ntzsl+L1OQ0H6jLeDXi5+d5TImOsEdfzsgTfyTdzW+O2k/SEc7qyusCHuzfeQz/w/PwO+LbQ46HzvFppBWOM+DHMrb/0MmRPEAZIHGnw5Q0SJTuIdQ8VOzfZt862HnpQDP6PHCTSUVaSvkN4ugBgkP5cIRu8pTufYbTPUbfFz2UUWt1qwVzBWUxzUqV0/SlqOA00lFqaWqxKZpwV93pmKsnZoDNzU6zpvDWmSsmj4PIrRztySkwUhsHJy49xl3qxsUyJbKodUFGVRlyAIsASlimBdflBdflKqf+U5bJU9dDeZrABFyuVzADU5qRKCPlCaUU3NYVt/WG221Vy+LWJ+H1tlZ1LQAB05QAnrDNE1Bn3N7fhaoKwuYKUusExrq+A1ywpep0as4zrpc3EE0oW8X7NPuYr7e/ArWgbjjewHUAZa8RnpRJvLis2zsqb8hfE6Z5RppmpJQxzRkgCdpNYKzvbWLOJBesLp7n6yuWTz/j9dOveP38J8zLG1K6qOLrBqo3EAvPAQYqJ59imVZZB8mEeF5144ePk8GsfBjRmqKNhOc+2gthx7k5rOM9bx0PWbkFBJtldlt7TrMyu6WDxw0gXZvVYtrV5kpN3ePKYeHN+RvhzULbTR6Ixt/cSzR8d+x0h0YngscmvVeiKbuiupYAxRcVeSbMU8aXtzd8+fyKn3/+gi+f3nC5LJjnyQ9I++G1TroZ97X93vt7pQ8pIoARUFyZ25C/TlhzMtDMPoyxTBYvIkk0c3OFUKsFlan6u6IU6gGT2QOiABAiLS5Z/31OpIyEzCkzSa1MgJwmovA8MpxNY1cdcfZKhRGCbSPxXaj79AKrYwBu+++xMmInTPGStCMuSO5atGup0dFdeUFgSwSQCf6SCF4lnkALSAni3w2s2xxyt6zG5+OY3Du5LD2DEz09cdkjBg4VCpGiIRYUXfgQK7Kx9sgQWqAlATAiG+c7MBn7Fpv0CEESgdRaw6xYpF3HyoXh7Y5xaYKLPTNznJ4TlhiivdMJgPlg7Rrcx4EgREaob7c8jv3olHVQrfZJm/cz1DZw8i9tjAUGVLP+g5nurl0fENz9rZIpaYxwM/xJTKilQuKD1AaLti4AR5lx05Q+NzdNpvQ2YVutE3IGaN6QMyFPSlAE3Ac0WLDvrb0NDI7whVvBBYIKB7jF3vf0gbl6Zj9wAipg8I8qIw4eNGEl0PaNO+VEBedZ6tvV71mVTaFUXLFUS7OEiK6b5L2+SX3ZtBuzhn8P8GmYK8MDVg4d5POA2uoKzCwiyibHm0oWk+6coPHLY+QP7umFDoeFoQntjPV2yhA7IUQaUytPKFWCVZfCyLMEBpy2C4CEeRJ/wyUqp41GwgAPA03hiojAEDRGweJahFM7TqWZ0EH981eJn5WoeiyNIwXRI+FwTN8qnI33jva5cTuONIULDDtWLLxj8KgLaLcmA5gd4hc+X8dn9x8Jr03Z07Z7OzgBcNfdtgfuKIJIb+9rOqarHRo0TpmR2Sfz9kgB8RG4eEaJcQ/W2v0etx2Xe5yn/T6v/1EbP5r/TAkx7nGjRcSj8j6autH54DyOz3e8TcAZYz7bix6N+UfT8XvkzL63oeLuntmnQLtC1xfRwdp7brwYuKcLeLq8b3/nOM8Z3/3k6/7wdI2ZQPWgLFNMndfBJ/efS8QfmO4n00fo+mfn8khI6DTeN6am+Iu8qfBVpogAJcCE04HGdzpQ/3bUF9muykJHKV9uwn/rj+2VyhF43tbDscdwHt/eiwdCrF3dfW6xJ+SkvgpElY8pzK6EqKaMCN4y0H1wcK9ZWdinE4oi5DtUQlieUMau02hMbHdNLZMzXFByJhzDJBs0HbdaZX5BmKcZ1+WCy7RgnmaP/WGx91LOyARMfAHAyJg0VpXAxLZt2NYN27b6wWTvrx5UirQvIHLFacqY8oSaN11/qiCBHvhBRVFFRNlWEBhbpmYVnCYsywuAhPW6gSihrCvKdkPOM2qS2BGEMzpBIZSrAqweFNpWMFfc1q+oXHG5Co8wTRmAuJSqpQie7/CW0kcdABOQEvJyxeXlEy6vX3B9+YI0vYDSrNY3m8QVCfEofW3spHtK7BltekC3teobbJkLI2KrY5/OaVMcyNT2+3bP6zTLIrPMlrXXuy8ziwn7TUN7TZEBl9X27pThcqqw3uIaOqE7dn087NW91GRx/TjA15/zHLECHytRsGSaMOWEt5cLPr+94NOnN7y9vWJZZkzTJGPvhVrr2rXNWU+H/J7pg4qIyBTph8J3wJS76EXOPSKtqj0FBDGlIogvKiSICKWar+/qzxMATk1IwLZOnfXFnokefp8BzqigCG/vMxsDFpjHGhZIX14bt4MDHl3994gN2zAP37X3T9/WfAQgNcFSLJ2dGAj3jCSojVZwApL7zkhsCDld2awjkgq+UzgJetaN7wN4ZlZLjuBHT2EzA+7qa/dOwDFJA1VXDWTlXYywcbf9EtQUYLBY44kihjVgo9Tav2UxIjTgjABKOPF9r89HTTh7QQUPWU+Jy0Y6WkY0pqdnURt+tHwppeY+7bBxHC87WuhxeuaFscNRkYPh/h6+okXEw9aMGxBbwOpGriYTs9gY0T5myj97Mhgz6DZz7FplLZjlUqKs/g6VcNEAuWwbj5fX1rHsFc09kwVJLaUiZwamFdMETNOEpuwb9gqoQGYk6j3pb/FH2Agm/179t2noXdA8fnBOrKF7NhJpsS0BrzIaQRb2k3sE4ang9TS1vPHaYYyDe9a+R0ugI0CZnamLAm/2INXju3KtinN3bILheYWZUWB01LY2RoeNdcK4lA0pEUoRi4g5ZxBLQDnkhEKmhFT4oZ4uknYJU9BcHJLTGWz7EEOF/nCwMMWMmH5X3LZ3UEqYb+9Iecbt/YY8L1jXG+blCq4F67SgXq7IOSPnyRV3sDpd+GU4tZ8fi3FhColivlbNQsisPGpcGz6qkFWm/UwJVMUqgrn63tIdXgHCtYfVEW7PBclSdxSC/SPh5CP8YemhcD01uEqpt4bUXK0cHtiQFPCh73dxjff7sLSlWS4PrQmf4+c2T+O1L+MxLnkMG/v1T0rojmWP75uy8FkFSa/EMH5qrMOex+tp707yHeG0kEdxTI+vsTt1f5ZGnHk/9XmT7fe7Iu6t1/1Yyj5Cu3ytLN5diWhfy9G9XRab7+cEEMPbPtQfESRLqt4xd43/TTiLjEja3Y6r+FnFzqO6npxamMD6XlnO9HKj81yIFYs+nNvzyp+q+4QziFj3DHroyUN336pcuCsnOJF1HL0zPpch6/H2sMscCxz1r1MMLpuxcZRIVKAJTBOYZlTY96CQOCnZcGXkNY3Uje2PwtYa9kfnaxOpUrCCq8KXyaX8faHrLY6jBb/tXHCGmGVWL0Fo1QpuBzMGK2m2U+S6j4oANVgudMI04zEsQPCRwiEO0QNYOn0eVxN1MyzyCKMCuXvKKnWTHxVgAs0XpPmCT58/48tPP+H1esVlmsVydtu8/5kAEGHKQm9OeUEiiVm2ldVd8ViTTZBetoJtXbHdbk0grf6MCBD5U2r0TQSUKkESAFRwKfht/i9MeQLVgpySKEyQMM8XEGVUJqSUUTZRRPw2X+VwEX09WN/dRAAd3ANcCwoq3t8l3u48/SemeQbxVehdYuQETCmLe/voocXm2WYpZSBnzNfPuH76E5a3XzC//oKaFzDIXacmsgDLhApST0wMQvHptvXOsLWqM1yhNB8BSXElQ1xTVQkULW6q1HqAmrV2gweF0cAjh1608XJSkJy/j/FXohyMrUa29c2+nhLb92a51OhVdqVD1YDXrHDDGvBaLCbg70Q4B/r2P5TTdr8fWTsbfsL9A6qCUENZil19nQg/+/JywcvLBT9/+YSfv3zC6+srrlfh82zfeyRr/qPTx2NEAMo8x42AmgBAM0VHRx2hw4AdF6iVgaQnYWsIUs2iZeNaUYl0oPcD6ERJYCpHovxoU372BJkxJC3tF1IsMy6c2MYoNOJnJDFn6UCwMjx+DGRKIDQKv73rmIlb/0DtGevC9xMPA3FLENcOJnzdnZTbjWfHut7vu+V/xAyQoR3y8kVBAUdyZ2XauJAxOTZVigDAYXhCixualP6xEs62FpDCcJ9MvzOL+sM1n7rBjkqJo3F4SNMT3FolCiHIxpHCfJ2shSOm3t5nHgbI28nD9XGKa+bs4ZGyof/Opz9j9kdMXXxtvxkdmL360qIgTEQbt3Me558iRfhRqGj43U4Y6f5Awa+AoRvR81LbS+Spb8btlExTuAo9RJg2OeXS8PIeJ3k7AYgP0gRf5Ww4tp1ih+Fc9ELC+Aw4mfKIe+6kVm+/luxft8ZwDrP30pngLMIuNYTR56E21uO9rhPU2nN33dl+qgyJnX7Zxyc4fNlxucHEWHZVHG9ugOw93+cY3h/vC/aWWra/xEDOpVQQVT1QAZQqBHsN+4AA1z5ImCgvg7A4sH5OP7EpsBpxbm2QoH4Fdd0AImxbRVbLiGleABBqKZhzRp03YYDUN26zIGoKgjZPgTnlHs6bm6jSlBB1XAdG3/f0Aoi8PomJkTolhOGC/Qc7ePNyT4R1cZ6P8jwS5H9fMrzfw+Iza/NhHtofwDnqu7OZ1DPqe4WE0Xax6dz60PUqwsa4//bd7ZWTx/R6zHd23efDnTQ+HOf7PuzcVya08p5RRvR5OHxw+M6zQuczBcsZHxTxd8jttODj9NEDFa0tFXyqnjp9e+if8X3j85aMFu+vEZ+fv/u4HR99v833cTpe38bs2boLaj+nxYHniEnBsUfCkH5MT+igD+K+Pv+3E7odv07DPvmdbXyyBbs7wo/RvSx6u7krOUv3xvx73/uowsr5TbR92e+f4MihAERc2OQDpII4Aiip0iGDYVcjisK7XlEsu7UzVKo0d3tmynkXUjbJBqC8ufARun5CcdVoaWeyoXxDpHWa+6VIkyPm8e+1a5Pxi+xCWmsRRN4VeIZG3DnhFJn/ds/ux2ffkwynGM8VcOhIz1v/pX7Jk6aMvMy4vlzx9vqKZVkwT5PMlR5cAZrSoKilRJ7EIiKnjJzSbv6SMn+1FNStoKybKnm0zOp+GVQONTa0HXCuGwOpYr19BU8zVkqoeUKmLFYVeQKmhGUR2nZe/oppuSBPM1JWax5iP8zEYHAUeCrwNKoMAguVwLyBK+N2ewdzxaIugmVL1naTHQoOc65lggCkBMoT8nLFfH3DfPmEvLyhplnPvYkFCBQHuRyqqgswlAb7pGsCQc1kyoeqTFDVsWcW/+q1Ce6TzVFKfQhVY9TDQby4dm3vchyv89v1duAzGNbefk2C4dZIfV3aBoWBMSYE/Bp5ZykjUqpj8OrYvjEZjX2WXE52/HR35z7tb7gvKOwScJlnXC8L3l6veHu54rIsmOe5t3h3ucMP2p/vPH8mPW8R4fNpWD+uEWXgd/fbU4AU+e8FRrXIAjGNjTPwLBoqM83KWQJWpziIfG/aj1PcpMfYEHfeQk/0tcm3W2PgyBoWB8wfILFaRfRkypECgQA/1XnHXeWujH2P7gGKCNmakEkIBpsf3++GeroyhudWjLtlss/jLnx/0n0zLrQK6OGiwBS6ZOQ4NYJXJiC3/VgQoVZlxTQ0Vj2TEf61NsGJMBSGgNnr8k3IyuHoAz8QdzibzSfGheGbvZ0Uj7Nim6ExPQ4Tu3EaiFwXZNBgVghvfxuNDzbYyzjbBM5gu7WztdkYuECyEPn43sUkYW3aVRSoCERIIA7VNyRB10BqAd2f0ZD/d05NkJ4Ol6Cc6lBmjhlU5QQpEdSnaniJdWG5FZr8EV/1NTAeInyetw2g5O5+eEBw93FUmF8YvlXhOOwkuPhpBI8ETvNreV+IfrwXHD3jHUxGl4DPn3rYKw+ew9R7Zpd2z3y9EYl5NgCi50VRsqcCu2DVxuRpnclYJjYlwhnBZ9QInBnaM/Z9f0yxHt+Xp01JbK6ZAHHJRAxsicC1gFBRcwKhiHVUd6K47QFm8Zk0UDXtvLaH+nviweu/3VZsZcNWvoIJyPkmvmjf3zHPC7Ztw+1yBbhgni9icj5NmOcFOSWlwexje1Xqxsd9NGv8k2YmLUxWLcIkls1cawnDWGvRfMeHNmwcwA1+zCLiniLC3utm8FSoFuf3Ud7nhDk/Vgj2mNnZ1Q+oRcne4tPzEDWXmemedV6jc/ut3zlXtGNGPSNyJDCOv8fvbd2N7Yjrb49b2vs2n0fvhn77nB/Vk0IZ1H0f8zbm+bg9jxUm7SpDI/vaPj1T17385/0xGvSozrM0Zj+es4+k52mfozG9t96O8jU4/NFr9XEbwt0d7Os3tLXV5zdBkf6SMtDo1ljXXsjTEiuyvIdLjvbLR4KGZ1InlP6dyji6/7113muLlX83n34ejfm3tuFh/Qdln9U3KnjMM8LZGD6zHxKg8Ku0XsoAJdSUJT5EmkVwShkVCaxBJQn7A46HVFwQTvYU2QFnZbhRA/+KIbsKhgE1RGg8d1X3P6UILV+D0LIONDwrv+tUPnPwCtLcRrV3dDhseEgOPm5O6fmbaFIGhrlgIpcvGN0UD8Lx8Hk2kY8RoDw8BbiglsfHh4dxvszANOPzr7/g7dNP+Pf/8e/4069/wl9+/YLX1zdkpf3XdVWZm9CCdhZ/cnmE0IrbdnMLY+MXEiWxVCkVdRPf/lVlhAz2OH3Se0LKE3KeXG64mkUGqWVtlngRVFksI0CYJ2CeLphyBl1fQASUckPZVvzX9Q3buiLlGQkVRNzieByh8C7ZnEnE3K/vf8W6TTKnyr/WWqWtBOcX9+u8CvBMGfnyguX1C6bLG6blFRtNABptZ8eYuCisVJPrNBkkMbfA34C6MapqUk7qSlbXR2WxIihFrQiq2lsE8NEyqsascyvpEuCfTcbVH2ZCWCf3YinuuScObZe+EQPFeOMqa6eUTduicFDNRdPmsAOT1yL0W/n8bjYHOe33pHt4+TQ/iYxElGCCcOZJXJP99OUVXz6/4defJEbEsiy+Bo5kBx+p+/dKTysiSg1TfiKY7B9FJqQxE64nDANhcR/aSdjqm+3ZB1pGjBdBRrvZD79/zBiYwOJRit31JdsxaNof6AIa/ADaM98m+SHW6ut4JmuQT5jA2u7cE3u68sHfUCXEQTMIjfmLgBrz9gItuEAbQxm79n/jah6ZXdY/Rss4rAzEWzINgrfKZzKUp0iW0UymqI0Oc+g7t3c939BRP4UxMIw2BUnfq92uJt/vC9esK31/jpIJJLzSozzWqNA+u9+EQP08PwLRsdnPI1/ePwvrf2jq0AsefpPDBekmC7I+0B1lX1sPXftsfXf9a4SgrSpZB+R1wX7/4PRHbx7fmqSdNj/9OLTRC6caNF/DqS2/LlNhCPQZM1zYyWqGKuOemmsfboGO98Db9pkOTrnfyCVfUDi4cNx64KXB1vDHxwmhrvZ7r4QIvz9WjacjIY6M28FYHOSjsJbiPSBQAAeCpVHB5wymEq69a582Zw19h3Nb3CzJjpI8lzFKu/yNLrDXTXBnze3uhzqNeE6ksSyooFbZS8WViVhEgPYKT2Z2SwTAFJaijIjj4jzp0f6pJ/W2UkTZsK1gMFKqoJQwVXGhlPIEcMUyz9LeTJjKDLAoS2qdkCiDaGp4kVrbWq8JURFh1iBcTelgAeHaCaR+3TRc/oxQ5UwRYc+7ScFwv797uF+MirhnlRChVIdZvTGkhmcO5y+wVM8wCodtGNbvkWBx7N/Yi/G7Z/O2yzppr5sif98GS+05de94uTy+e3zlXT4M94Fxfo/K9PZwfyjh3r68h4dIM9qXE/ouCHr2z+/Takf97co9qntsU/jd3jnA5Xdac8ZDfTR1YPDsO4/6HwpvY31Uzre3+yPpXhu6xI0C6jmunuZAhFF/Hg8SPRC6GxH6oC3n4/btY9YJub+xnEdKhT0++Nu73bu3lr43PaNk+eaxRtvLPqL42T03HhwEcwkgQXYzOH5AEBspg2ltBR3wM5G+jfuH1GrSlbE1ux4KD9jWTqPQ9/svs7haQncPA91iFtfstKOQqNzuI/CrsS2RT/WOHX30PWc2IzEYNlGMv09S93iPR8Fh/+lK5v70v9Fi8wS6XvDy6Q2ff/qML18+4cvnT3h7fcHrdWlBhgupgJhRdOZBzSUp6wGyqu4+235phwaHQyxh7EblkMWcMMtaUySJwqgiadyGlTKYGctWkEkCXxMlTJRQasG8XDHNF0yTWEVQyhAqvgKkAbpPUxw94QO4SsyIWituU/aDTrauExEqEZpQjHw9WB5KCWmakZcL0nQB5cVdK3bKI1sXLN90acGzeC4EWarJK8n3KFcW1OpKCK7VpYVJC7VV2BQKFsujtrkZWO4jvvaYx+1Tv1waHIQVJesUTZEoPEuzSupkDFYO17aaDtoS232MC9nnrDX0mbSXEYiMO/CMYV6NjzJ+OKWEeZrwcr3g9UU+18uCacru0vZu7Xd4ZuB4n/1R6cOKiDFFpArsGx0nK65XQpvkmqoo+tTywSwgtm3rftuVq0YCxp6A2wtFZSMcCX87YVv1tG2txiAP/SNoPu4WL+sZTEI7hcbK7BdjxCPG1j1DhNrN194zBIMRnL1SR/vy4HVblHFxmnDBJK+G2IgBSqz51dSKW6CgU+JkN2aqjSWLDWHuJmpcQ79bYogVmuB9OZl+2uQjhOz9AKZEnokAUIpIDkBwGVYqo7CZvzXXjvZGshPy5hrJYMBiR+gCSejUVijalh429wTWw0TweB1+auUjabeGaHzQtSWKYiUXOUP0GIk1YmrcjAiP35fHbd0I/o64wE77khJT4RNbcEh4Wh2mjdYNn1u/bXOwNS5z3JN05z60/5unDo3pHsBVfc2bYNhgTFG9CUS5h7Ygzxw+TdkAQNziFEgQea3P4ZMMJ8IJFCC6fxiJFatTy7a6jGBxJYiayJrlxRGh1XpylwDjrs6j58Ym2Ekq7dqd9fZIMHOPwb+Xxral1NbY2YYVGYyjT6mKXwv7d2P2wKwn5yHxj7jNnTMJvvTanmdMIgG9KXdrlb7KGNvNzA2XqXWkBafecgZzRkpAyglARS0JCewBmgUnjFURCHtLiK5mSg6nsr0xNq5Ytw3rumJdV2zbitu26fgXECXktWCdbmBmrDcJELgsC2p5xzTNuFwuGisiI9GMlCbZv402sEAt2kYQ6VqBuGRSXOjXyihF3UTptZQipvW1CEOAgnby675l6plg6VkBaXv/+bLPUoNrs/DR9w7M8/fvHt8Hh33joK4jZu0o3VVAhO9du++mDtt2/WjMjTCYo6VTr7ToKKtdeffSc3hnLDvWu88ry1fbJIQthgjd3sQOb3XsRl8nDdf4JJaHO3jw+M17fd/XOZaELocJC55PP1aYe973s9zP5R9Hn/2v/f49Dn+ctWJ3n4LI0fdq+FyQ37HE3XsdLUvwtXZvT211e+N2/G1ouJM3gVPUXx+Dl77uR217fLr/W5PzuZ56/v4xXJ+361G7CQMdAtwZ/I+lDy/HB7xeT4U+xsr3DqT47xRF7IyaJoAmIM1AXsB5AacFnGZwynI4LpEfvgCzHh7UCHJB0Ng1dt8ZBEDu8g1nmpuCAWZnoNSz8hDF6flwepqbsiEWrvJLsX6AxjXj9tto/eBJVjBxFTousQp/jc3YMzTt47yI8SOBCYrjciTM2sEgoSNETyZfaGU19YBYryAnvHx6xcvbKz79/BNeP33Cn379Ez5/+oz/+Pc/4efPX/CXX97wcn0Bk4zF+/uCshWsv33FVir+j9/eIeFnN9TCeH9f8dtv/4X399+wrreA70LMUZ1MUnjhKmNbWeU+KSHlCfNyAYiwlQIg4f12Qy2MWiWQ9ZYSOBW8F0adNsyUAK54KW9IE5CnjBkzXvEJpdzw9befwFzErdL2FXX9iua21+RpzUra6G/A8JBPDMq2otKGr6gat3MKih/tV4IHYfdVaixrSkhTBhtp6f8AAQAASURBVE0zkLO4RrI4Igr/HhtCLX6SjqXxEFafWF9b4TzAk66RyuJaqxTwtjmtbyBUUVX2Ku+UsufnbI3IO5IvWkC0fHX3G2FMXQ7EapPuzYwWDToPRG7xZGXZ4SgyC4gQwyUu7j2tbftHWCR71nC4RQiI8G5ScvmJ/VD2fPP4AN1nri8LXl+u+PXnL/j5yyf89PaG19crJuXrWj33FTx/i/S0IqIeNLgXrA1JGXWngUahhuZxLSf1gGv3RxMdF97od2LTJLZWRcA4Z7zsnvkSN8n1GYOHBmEcyF7VTpBmaO3c+xB3d0D8cdcshzLfs+9Av+EYviBZ/xxe6oTJJuwT7gvPmCk4sxmaQFaXXWl/CnQkdn9U4lgs82lsiJbN/Eb2LI8xscZr+4aYeiRDPsVihrYxOS4rBJALzGws2ph4WNDIp3JfvrRtmE4d892SvEdFUuuXz8c3MJiRMLDfu8SG7B4juvvPe2TJPMTLcPzR8vZlH7ffLFNYicHdOOy6dIK4D4hdU0Ds6kWPi35k+nvZTD6SIh0fYcVwviiMGClxg3foCZrD7aYxCO3TGE+uAKf2oiyVo3EztluJHb3bcLe+eXBt+5MporiVx8+z86dKhu4Kr6NTVnDf/vvpMSw2eP0+GOvxap9GXLHb7w0uWFU7SgM0Qjj6JEYncHExz8FaBQnzkmy/Q4/XSBpz0JthLzH6pTIqajs4UQsYLMGqoYHUmVEhhx9GnGC76OgKqdEq8p1tMwmwJq6Zqh6EkO82rkSNhsq3dwCM27tYQUw5gWtBJkbNGZwzUipIaRZFRCKxkEgEYbZEUdLG2NZrCzLfzLDb6SMj9M33r7V7JIo7ocgw9s+e0LyX70ej34/j8/0+0uOMPQP0UaZh3Ju9jUFo2T97bCHR464jYtT6EvEF+b1+nw3ENDur4NdIZ8f67aR5WPaIVqbHbYvEVbtla03qbOMyDrGPzxGudMVFLwTfj+XwdjdGT8Avn9wfSt+10ft7Z0y6jAdlUH/fcj4CxdNVEeb16bXzdP4epo1eDH+O5/EHp7t4SoG8V7warRHe64qg4Yat2efHsFtfJ+mQjCbg91Lh2P5x1gcXOH0Qx3Z7eHj3Uf+H2nGPPnqkHPU4g99W+Q9P98dw5I357nw/dXgSbcXJO0ksIpLQEBYrQhhqCWTtB/OA4DO+IQzH+yc9MJcsHDJHPmOk7cHtl99Vmsndntg+zOP+bPt23J8x3A9l6L94Kt16ZyfR+34d0PBWaOwZj9dxYB7RDBG3HMOB+9TwxxKjIM0zLi9vePvyBT/98gu+fPkJv/z8Ez69veLz2xVv1wWvlxkvlwmc5DjPlCCKCDDWreC3bcNaGFsVhU8pK8q2iRud4GrS5CbeZh0eSrZv67zpc0oZKWfkKq6ZatVDsIHOqqWAmFGU1i/bipInVC4glsM2KWdM84x5WbBcLpiXC6blgsIbeHMJjq+Yxi4dMRzxUQEzoRQSy+ksuMoExqQCik6B0e2D1AaF3Ems4pkG+y6OYCjPIfnJaCCKENBkq77bO1Bb7DcL6twr19hoM52YI/erkR+PHYoy08q1c3FvvIXLVRwMh/3cyj5bBwFGfB1D115XbiyDfRAjNvF9Sf8c0Yy2Xo5Q5allwUFZ1pnG83nXG55TOmCeJ1wuM16uF7xcL7gsE5Zpesoa4pn0rfvxM+l5iwi2ddyIJhPgCvHd8jpgn0xEo48jkcAoCrTRAoKIUKJiQoHbfAc/RLPUTjrHe/F7E2je0xRpgBq2gdDgX9p5K9N8NW/bhlr6RaiOz/v2xXEJm95pf0Kf/L3DnAGJxLdVCE1JTCIpJSRmB1arX05DMprx1XOxNLx9CciZkItpsslpDnbN+u9HmNn8VQ1sy+rw6O4ioha3Q6wGVNlMwJREKDPlBEqErIFE7QQHMWHjDWtdYYrp21awlYptq2pRJHWbLY+fGRmG9hmRpQlnP5rSYBHxI4XjUWAYlXGHAtSD61AaImSfKSOeaNXJ/aZwM2GEjwO3dXAmFAIgpzKCdINNEOfEpz45wD9PN/+/YSI91WJEfFWrko3FaoiZHb+nlJDzpLjDPIruUWScI60FIoxowhdT/cmOTwDbOmjzExUIRpDZKaVG+4uJ5+jiyT9mXuwnMHrC7FC5zjiEsxHOG400rjVueMOpzzAaA5HzfULZKPA5vo57e3urT5EI7QjX7kTMiEvQr69Qh1MnZMygslJBGLfHnMMvb3+cAzrI2fpQa8WGDZmz+8GVPTALpklivlyJUIuegpoyciLkKSOlCSkL8yT+lIPwx5iGgxbUyqKAiGNVJR6KnBATnFRKQS4bwBVlvSExY1sWoKyY5xnldtGg1Rkpzch5QkpZGLqUYa6iXKAQ5tuIboNBoXvUwqlWDSxYUMuq19LF+ihQpQXKHbhvv89OZD6rqPjedFpeA5mjl5Su6k/S+vdhXd9TRnTPjsoa2ug0MIxvpV2ep5I5DPbfdipDGdfu4Ioxy9Y9O7QxWEgoMm/CTmWuR+sEYxztpjFlSL5/M6tgwt7tTLDDePwgunNU4jSc+qj8e4Dy+yXncw7bE6/j/V1B9yu6K+3e80B/XCL83lao4/yPSjJBA4YHQpxBxBOzsTxdt2ynWMcr4d6Akq7PXnDOvmaAKGDwt/oynuBH7qd7b99r+7gHfzTt9/WPvfuxPaivC52r13GsH6WPCn2O6K3x2SOFDxDkXE9Ue1SP0aDEymExAK5gdZNDaQHSBUgTOCmtkyZQzqCUkJNtCVUsIqrsDZWbWLznDEP9kFUU4zeCm/DT+dAaFf9Gqzd6unKI5xbcS9qRe6frndaXd+SQTB1+H+zXzKCq4v2w9kQ4bLyytF0DpMkYWowIo+89Fp1aQdvVPg9hjcIHaIIIG0E9xQ7bawk0L8iXV7x++ozPX37Gf/z7X/Af//5n/PSnn/Hpyye8XGdclozP84LLNOFtZlzyhnS5ACnh8+sse/n6Geu6IV3+T7yvG/7zv264rRu2lbBMhMsyYb1lTDmJNa271IWPuUlTKgoKV3VMQJhmqUNo8CxxAUGYptnHxGjWUiv4tqKmit8gssbl+oJluYAmgcnlsuCyvuL17Yu4PX1/xzsY79vNXf22caNGwjgQjknqJgB1KyCq2JhFlsQ9r9LTcQlQV8OAyEnXsmItN0z11urTk/4FAHMSYTsxEppiSSmXoVkKnzUozcDwoNO1dNb9thYB4TfIYBZtXWDgcavKQC1MnvOxOo4SM7hgsxgUxRQRVdcNkMwSwmWW5LjC6msMOwvZGtxwHgXG7vrv38NVJ+yILzlVLAxFP0qBzRwehA/QDnPJJo5pmTFPE37++Sf89OkNv/7yBT99fsPbdcGyZN/Xj/iKv5f0tCIiMky2HThTpUzBjoy1vXzkT7o8/QbKwC5GRATm/YxG4kCrGwDj9IRYfLFWv45NdqKN9zR2ZEbY+hCY7G7yATHXhG2q5+mIXbiTWdqJ/koHwGaIyCilqKhxZl6vFrTqHiEZhapGGPsV6APhdK37/dJeIGnEyHFfmgCau71ZAjtKH3JWRcSUkFOSYEbqekpEnIS1EiajHZhBNyBtCnNFfAlGBsC3hE6I5r1ovxUROk5EfEAx0xMpnO77wQIaAMN6RbiG58AOGZ4jxgOk/i1tOkoPCfTjdvvrXVuMgIyTtCfUHQd9qAfH6e9tM/lwYiiRoMxFZXCqqjw0HEJg0wRQI4+Ax/0/enzIvI/02PAueWE9XPt8o9/g2dfqeO9ee/droV8rLd+hkNIJlVFoYA+OFA/nyohurzzaR+4oIR6nx3naWDX8Yf18DPe8a3IjGBszS9ZeR4fjPihlnfVg7EVUNAFAreJLtmYxW64lAcEqJ1V1f6j0A3UurHBAV+3H7UhwLfBLDW5Y3RBA3F0mArb1hkSM9ZYBFrPtmgu4Tsi56mGP7B9RRMg1mAmOsmIws7tYk1NtHGJH9LEieKSPujX1Y9M3C98flBfuDAKcgVhUOvmsb44rztY3sLvfvT/cO6SBqe39e+H5E8lpqP6en5aPODPCseYT2rzR003QSO1ht7KO4L3R4hz60u6bFID614P1Qut/4+7O9oqj+tszOoCr5+HMWaeuzPO2jPlifQCdPo/3AxvXlz9Q5/FQxj7/g77t6NRWXtydRmHr2dr46Jo9K/dHHrq5n8Y1FU/N+gij8SZhHQAQV7KDUqtDLnGNpEM4jTUzapfH4E7qosP7fs9ohwc9Pksy9sdvP54KefdI2PNMarTet6S+3R9tAx2M5dM1D3U9U+9jxcgH9r8nshyNR9dmKNQoXvcDDAcfeS/BDj+2PcEGMcZSGOh2pbNtWTnJdsh37mlxo9U9j1bfeNfmwslOdxzSXIEujXTqjr7hENf0gE80LNmUf22PQqTzmXvrD+aQN/w+5X2PfkT8ZKNjbTALgQl5ueD68obPX37GLz//ij//8id8+fknfPrpDZeZME+EFyLMRJgTI1NFSgzKJIfKQKBM2KYJr+9fQSnhdhOaccpJPpO6CU2kehijHUN3rcWBJiKFNQLkYI/RsVn85FPKoBSUNCwupwhKG+cN27YiqRVFTmJdkXPGNM2YpwXTtGDLk8d1M/qjx5+mdL439AaT0r9KcA8A/doi/xvlopWruIH3oN3UxgONBwBIg1PzUBp8XfkaUril0D6BtarWAxHW0K4cy2j5+u6fEB/huchN2XkFs4gA2K0XzKojEYFTAlcyVqmtcyD0wQYPPkZtAzxry0Hrwvp2bHSHpt8fOnpQ9im82Lyik5dYymq1c71c8HK94nq54KKxIbIe3ozt/0hfrR9nz35UeloRIQ0ASAfBBnm3GeH5ud3tib6Aeiass4A42ABi7eOJH/M9uKvUNmbPHHy9gdWXmQK+MkhE5KfZmSWojZyIJ5MBqT9rOw04TFhAfpFIOiKQ93PdlAT30mMQ0ZPgGttCEGmziJCxtvsAkZxWZiKcKUdGhOvCHIuF8IgBoP0W+KOSwShXaGyOPXwyt/5TEr/YKSUkUquORJgn0c4vs5wavc6zbk4mpCHI2c6CTf2Y//Z+w+224a+/ic/ubWPV+mq95ozSOk6BsAB6pN4a++2DQaoY8hgVYSxOBBzPVdmvyb1FRC9wchcep/UZUfGRvvYQdKQ48JwGj0wdvnGCsiNYx0CrfTvjGh43iH+l42TjlAh+SpbBbZNlWSdixlwBFGdsSONF7OeifT/FObquj3DRmJ+NOAPrJhHfYc8DgxE9jSQ+71swLxFMl2ZyeiB8jYzMkfCx1XmwRh8szmdO4j1S3BuCf6R8OFJq74T7QXhn6+dsriTPDlvf7a+R2uS/I9nd+hf3sihmIcP9KcE8B+9pnP1uZXiNVbmfc8K2JtRckXJCYTntJK51CTllr0v2SrH8yTkPQoixKlX0D/WaNYRYGzGwJWcqEAh7YjGvJmKUMoNQsW0Tarm1GBF5QcozMtkpxUn3xRziRYQ4QzZXFMaBWU25GaVu4FrEL26tLXaErY3a1su3UAEOQ0/k+8PSfuKeSyfr/0gZ8VHBLekfGy+Dc6344239hvStQsX7ZTYa/ZgDoYNrwPVupTGmNFz9jTvvPN/mvu4HdP1pvr3AYp8G3uLpVv59pR8DO/fe/9H4YT83bd7tvvGdEV9Q+KplcITFJmyjAwuPcceTIhrNPfLu8fdOoamqjL8lzNwT9oz57v3+YK2IK+XZNsT8R3zmUZuOlMijMm18/qjucX6ffZ8AcDrO3wni7pThz1nlL2zBiE0QnAHSmBEQt0wiJBaay0Ze4gpYI9RFcQ2Qrc8St7P8tpIoPO/3SzucYaw1SQyHwPNVdRETfcpDXQeNHwx7sbgP7ePG2acpOhjmNsFPjkclQuxffMduBl5jGHnrcH99mAzHhLEj23N0vIiANGG5vuLLL3/Gv/9v/4H/+b//P/F/++kL/uPnz/jp1y+iiLgkzDMhlxty3SR+WF1RN4A5Yc5vSCljnibMOeGXLz/hdd2QacbttmHKE+Y54z//6/8EUPD//f8lrGvF169fsUwv2G4rapG4C8ys7pyKek8RmnSaJiQirEXipOUpo/KEeVpAEO8cEji7xTarteC2voOJ8dev/4nCBXm5YMaCPIl18DxfMM8XLPMVZVqwTZPXvXNrMfBMngyg3TWr3q4VRIxtA+yAK/x5wwUmBy3bhtvtHe/vv+G2vmMu74C6U3UwYfUI4PKWKrxBmmEyS+awViqCHIhBXFwexRaAw/CSdidhlAuOuExyOw5JzSUt0OMWs4iwMa1mEaHKyay7neBWwScM8d5SqdGxbMJYHWBikfUkiKU5Ewufrm6vmCJP1dxsHVFKTYEJV/r0yvw2V76n4v5SbHg1DOwwiKRCUusaTIicEl5eX/H68oKff/kFv3z5hC+fP+Pz28XdMm0Mx2d/r+l5RUQbgS5FWUWvAaD+epjo9LkJCP13RPiOuA/Kw7jRngs5DEgIkFO3kR60BXRQfntCAFW00NPWTjXt49qEsk1sJW/ySOr0fT+/e/A00K/+OSxEHpC3N1gvmGBagb4TDoVF2rejJ3Z3gifQ8b2DLfR70z0iUbSN5LjJcwomEeRkeUIiEq1rIlLhUULOYg0xTfKZJw3qmQwxZmzm85AFTratKjwXGLFhSqoOhRv9oH+6LvF+Sh3hjkn7tSeFSf8HxEl7EugD5DZsOdp6tfVpRJfD/bBmeehc/CkIPCD1o+4dtKaV0Qjm/v5BQZEa6F/vBqWn7Q42G2bftLt+2vdhDTi++WdMYT2yUkFi/ivXxjA0Yp5qBSmbYsTYWbH3E3X47ryN8IUoVUULPa2Muc1vXEWO7w3jtz2g5Q1ldIwIemALeTqhpO+DGMq8g/5xLmrZKRXCRx+0PYHG/E3J8CjF+ekZZvJ/Vs4jfmrc548qMjLZiOXWbuz6E/e8tvWN5cb7bc93cQ0HoporJFa5ukdKkNM7Ol42p63u1Co4wN6RPu7wbZhtUvy+U+4ofqq1ggqhbAVbStg2CdxXUgKrmT8zNKZKQaIMTlUUEWoZQSQE/Ris2faS6kHgTKlY1Ldsc3PQAltHRTW6vozCmCMhWj/ve/g7E8b86ET+R1IPsuPOOu5PDW6Yh/t+vXdQ4PyE1pGS8E4Pdq0fq4ykpha8z7ibEtqV3v0+wdtdka3Cg0qO59fep25yBsymjWE/KTeWYrD3Mfjp6z7JAzvpRkrvNHp71wrS/HqN2ey9NhX9bwz5AlUSyu7I4buM84BW7iYbe8+3g89YxtHOdUT9Hadxvnew+2AOvwVFPCMUlsptL2q0bt++MDds63hcOfuxOFU67vbGwOsiWgdq4wJvyPtVfj42TnZw9zu0sH/+odTa1wt7WkUmoNnXaN9PGv7BuX6OthyriHTMuRLiLgxR7M3x/fF5a6uNzX6M4u89bh6fB7w0Iu8hGeyCASIl8AmAunUExDKCidRCgkJfmgiQHCkp5MS6Oebl/rZ98zUWFPdGmx8hLd+aT/bY4Z/zBb5fWx0hb+ADRlrN5EC9POuYTtjxBbuGGz8Q8tigje8EfNTdjtcOwWsZKt9I04z5csHl8oLX6ysuy4JJXXpOOeMyZyxLxlQYqRLWFXpqv2qYgaLVC62bc8LEGcs8gxi4LjPWdcKyiKLCaMWybahFDrR0vHZw6Zpzo3HiAR/7pJyRmJHRTt6jilsnYpHDi1v1FTlPKNsqvKYekEnqXiznGSlPoDSBaIPHdOM4lhHjRTx7MOiBQxEYEe8ZZvLSULXgswq4i9OybaJQqSKwd/pgXO8Od1oYxycj/MnYsl8ZsT8i6zXO6oBAdLodMH501+XDew2GI68AHx0bAzjeIDDqjh7hXbP6IWl73yPPNMeJ/S9hVFAbzX5AR92h74bXQ77+Hem9urZXl/ceG+Ky4OWyYJknkUumtKO3vJpHhNtBo8758MO7H6rjaUWEkb7OoJvgOjSEXJN+vAHuTqO2wgDoPJFobyygs/jZK6AKj3ZfqlojJNtYRPNXvV3R3G/oh94YA3icnRoINhAN2YPEryEY4KygIYRjqRtKWbGVr1jrC268gZA1ooT6kOMqGzOzIsa2xxIYRCyCSioAVb0WMDaACywIZD8/0u/ksyJA4KcTdSKSnaChDAaBSXxZ15QFGRdpW0rSqiKOreFBc1TIYhYVMRo7UT/HROKyaEoJS04oap65HiGwrtXfno6YcLtPROLLzpG60zQyM8yoVMQlk1o5TJQxUcKSJkw54zrNmOeM62VBnhKWZQonC2VzNW3uTBMu04qMjPfbir/iHTcquK0bClVUc5ihgZyqBbrWNldFqPuwdkf9bt9N0RPVPcQJqWagZnBNqBUolVFQpS0yzShKGJGOn1nGCNwqgQlC88YpyFxgaVxsFWA9LUAWC0BPGfsMwN2GOHHn10YYjbhuz2SfjYxtOGfkna5v25tZ+saqbWcmcDWGIrg7sfaSKfPgQiRTRpqvThutZMqslEFV/J7+syWfd2VYWrB3YCXBfYkTKFVVQCSkWt2Kp6aMakRm+PiJJDXfNX+i4ykATuJaJhlhqq7VzP9lJkIG3AxVBLLB7ywaScYqbEVVs1H152oxJCywV+UNFVVOB7HtalEAK/hc9gN5RnoKi5qzf1lLtp68RaxWinpCyto9MFzdcvGOKDJMjTSjMS/ghHazlFMi0PAoWaDBjKZsJt/Qbe76BkTWJ+x+TM31LaONpe93QZkXyhH8SyC1SEgah8S7qydKSWmYlG3dquVbgsYyMs9DVazHvJ8c2tsK5rErBBQWxos2UtdGq4wdsvBzWawQK08A2v6RjVGvxnwoXGsdzuCQ0Blb2VDrBuaCnAg1J2TRRGAhqI9YPRClCK4qfl1XBqFizRWoG6gyUk6oKSHlTdqcJS6ExaxIDgeTMnfUdd7pZuOFa2MSK1fUsomCZpNAhOYH1nw2NxKrYsTnoxKClQ7z/slwIZ/Qe/b8UeqVUf0L1v9GG+q1ga/DRb/LxO/q89aoW1urusZH6zth3I3m2q9nz6t7ZKP3+v4IU976MuKHYRTC95bHfesavR5zj/vxjszveQFnbceYEYcYqD3fz+eoQNy/24Rj2oYQNwig0JFIO7eFHYWQck1D2ftr3+5di/y+Y7VujfevS5Opu34fodzPb5RdEQZa8qhBPaCfNKZ/sdVBXaFRCXFUV5tjy9/XdU8BdVTmvZPmZ7yDtVz2oOeV7kfJlRG6fXdKmLCQOuWUT0p/yv15JasFA7Ydc1ALjGMa6XAAFm/pPMVN0H6HfuGZ0apjq/ZlBFhoPO2dkpnQIb2DMg9qsZd7/umsDrJ9YMjf7QFjCW28zuaOR2vwLp/RVrHo+Ju7qtnb2Gq3F3ev4ryvz0C8x57kFeBN6DEGCBMqXwC+oPIFtzxhnTK2icCZMfEK1ARM4s7ShM0tWgEaqjapcRTUGj0A8VdfgM4aoRrxw2hrSYXaKEJsJuXbk1mOary6TffKYkRpK0LomWIHlPREd2UUPYy4VWBlYGPjFwrAUj6BkZLStusG1ALmtbO26AQCruBpe5bsoYFgtgnvZq2ezx4BwqcDs4jd5MAMlJ/fWAPEErAsoJcrps+fMOWM+b9u+G0C/j9zwe0/V3yl/8L/mL/g0/UVb5cL5vSC375uuG0V2+2Gda347f0/AVQsWXiGG09gTnibM0oi5LQhYcLrteL/SDf89X/9n3j/+o7tr7+hXF7AvKKUFe+3FZQqKBdVUogiIlFCJkZCRU6MmoCcE5gnLC+vyKW4Re5vv/0vlLXg63oDGLhME5iB9//8L/Btw1QTyuWCvG4oVcZoyhdcX77gdttA74xU/i/kmpAVfzM2ABLzAQAqxDWOhbU2EWln+0vCj7QZFVgjqMcVo99AYGSAC7Bt4K9/Rf3P/wK+3kDvBWUh1CkDiRUENhBXqZMJhRcpk4XPdvyOoCRTZYbBuPHShhhSSkhMerjIaNjqnmVMOWHclq1ZV8hRVTo9+32CuH4Sflv5gWJxWYrLV6x058lIy1V5S6N9I28s64aYxO0bV3+nhJgSkQay1rqHA5VQOd9vf7nD5Cf8hRXsIzI+CfKLAyKaAE6MkiqoJrlXhdCcLxOmy4Q//fSKn7+84X/88oqfP7/gy4soI25t8Hd7/McSn3wfe3T2zuP0QUWEfh8UCEeZz4ik/ca7z9eTt0at9cKVaCIzMhLxlCbReRt6psYIwME/owF/I9M9f8d86EqNFhF2mrdp0QOxy70ubkcA+A/uPiOxZu+xt/UeADRkZ+0lMrdLUbAHHzfyH8ewPJ5OHAWEVp4JdZKWFfbSwxb+vsnmWn+ZYMMRG/ZEgI6YWUhQJ5gRzb4gGyUWoNr+Ki6dSs7IOSHXGhBrTxQe4Yz4e4T92JeYItLs8zXEZF3rofPovbEUIYLbegn9GF7tNe1tDe8a233h3WMJtjS0Y6j/botJFApd7xwAIxV+D/ra2t81fdcO7p/aWjLA71Zt35+zdCQ0+v+z96fPluNKniD2c4DkOecusWS+fO9VdU+3jaQv+v//kjGTzMbGZkZSSz091VX1tsyIuPeQgOuDuwMOkDzLjcilFmSe4CUJYnX4Crj339xn5f61UsdMU8UhRowzWI5bs9yBAcpqiIAIGWUNdqcj8gbR3Ri5RpC3da9vUGBC4YM3yvC7mAtHoh/1e0jW68B/UhdkgQhTljT33NCOWohvXb8Y99aaf8RydBX7MFjHqtKDRiHiaInbnuB+ftyszHrtfWRvJZnWdk153OzpfXlibWSheLUvtU+e3rU8AwqdWo0HDE5c4xy9tuEX92J2JJaQsxhlmt1xpb06rq6GAhqlu7X/hcdwcNH0GWYMkufeS6Tw/BpAPTMyZWkbTDGadJ6iCA66LjmoMBTFQGgxLdDBjw1FdoYI5hrEWgx0XE9HFPhG05/tExD3J8+fyP31vNfqWxkj9HkhKau15ubO0cJ6ymqDt/VKjy3aCWw+821s1+nt/erLLn+6hVvAvv7TFdaWuV/3ZZxhea6Vc7FvdRE1vGz7TaVJPcy0be3HyfBYe91P27wEsW5sYJftYtpu2/59rWuVh9vnXhmBjef+3RYIbn1fhO2LcLD3rMO3+qicZNkpbvN9Q270hjfeu9Ss3hvccpEb1732N+PX1dnAkZHya3VeaBRzuwCoe17xV7dQujZvlLzzfdOy0qf9ttVS+qq2aXC3bjfTHi7pv/d1aRu4y3MD+WnLrONQ10K7sHeNEBfG0DV0owEO5laf73RgD5du574Og3CuTUh5S2KIISyA7UdB9Gn2YzQxLbfAraGtW1egyrXlypWnsBfGN5d7lGe0UTTgaHHhuVFVBA0dR9X7OCVnkbHrR4BsT9K6/e6bqkjdTezKsnL9wO0wIgVGN9ETd7RH587TfhI+MOeM5Tzjy5eEJZ4RhwSEGR8eD3g8jngYR4QwIETCgIywZAROyPlVNlck2VS8gAEOIBY3oQGqlM4JnGbk+Yy8zEDSnf8aFyGlpPkr/1hWe8FpqnvSjT7DMBSeKKUOB9o85oxlXhAoYD6/Sjy1cdLthAQKEcMwYRgPGIYDljghhFcgBDAHeCPQagbZZsAxCB7FOB2kvbQNOkROCW/8Y0rIywzWUxFFhiTRedQ5tGqiQmGCTz2JkjHUuTbdC6MSJf+ljZ221uahltwiDCL3rNOB1nVV1yh52lzotTapBklpeWSDB3Zrzq1b393mSdO/XhPG5aO7nVlwPwob32/po2DrlWseFAhCjAHjMOAwDTgdRhymAYdxkJNBQTcHg8u2Gb9h81rapk17WLnN+xY91F0xIu5N14wQ5H57ySN7AIWoMNAafrs6ekVD/967FWDmotCy+8K4+R1bBNnc7eqogbW1dczFH5f/9UaUzYkmK9sYspaYrftFAF0ewV1rW6mSQIigkIQIaMyIelWEtFtDW5cpB/tf85zI7YL/7SSzkjIBIUkL55TAYAwpyMmRnJHZKz8JdgKHDEmRKHSC+vqLccAwAMM4gkGYtWzBMRWR923Zum+VE7cnM5hUuHNMksKuq63B/V5xtzlu3VdF8dooMtaKliKQfQNYuIxkqclXn1KxdWvDGqbyLe1q16aOu1+zuLRa/20kYw6KkhECA34O7USDV0QSycLKpCeFCepXFpsCldEJ2Hvn+/byjmDFi52y8Wq/vOCxoWRcwZbPc6HMOmhrPFDX8eXfRVC+KxbLThEb4284seAXYxApuLnVvJvf+jno3ru/fF6b4kZpSdQYW0Q4UcpneJu44Me3Kr0LnVUakknU+suSECMhBRG6IrX43Rv7r2EHm0/PV6xTI1E4/qEaBUISvLQsCwgBqcSfJgl8l3LhbYgWgEh3ZwWQOLIFkcWz6HgkB6PeENHEjOCWL6r8Uz2ObWVszcnehgcrpxfqLs3prcaHb5HKqu3pO9p1XeMo1fzcjesaF3T0re/XBm/cf3NLanlsYAtm27LfvqZ+S+kt43XNiLbCa4IY6/OCHwW3OPPPr5K26FV/3/Ni9wjAW/U1MkzDptLlodh770/G2NUXvPkdYR0r5OtTpe+ttqLtN2BCwtcaZe9NIvKuVDZdjv7+Ak3aLSe074xn2NWH/BJjcFV99JX5L5fEzR11b28o4wqcbPJsN5V8PSnVlaXEAaAIphobohgkmpoljpZwia38dQl62P0HbMnKbg0V5WmV+7x+RUozF5Udf+55+ex2cLt8JQac6X6Mn6mCthYlJyOynpBIJaacU6YyHF8Ix1fJdqxVuZ2sUNOl9QuZGxbPI6Dq56AdeXmW84LX1xf8yD/hvy8B858+Ycmf8f6793h+/4Tz64zP598hfT/iw+MBwzhiGgkPccCwLEifFpznM3769CNyysjhDCLxPJFTxuvLK15+/Cs+/enPePnLX5BffgTPi4xResXr6wteXj7j8+vfijuoEAJiGKFn2YunB2ZCoAHTNGEYJP5azhnnecY8n/EZQm9DCEBW41FakJYF8zwjp4zzfEQGifFhOmKaJGYE8wJCQsCCz3lGwozESXf2A0R6on0TVnVke12ee95uAmlprmjsAtL8itfPf8P5y98wf/kbhsOIIURwiAAFMI0CzUvSNqmsrKc7ytxyrnwaGOCEctrIoIca8L2YnEalXVsENB5mgE0dKanynInVa4SX9lybWP9h8RZQ3LyqK616lXmJulbK5vCyLDra0/VljX9tRW3z3e39utyuS3W8tD1rvr31mUMDEBHwcDri4eGAj++e8PHdMx4fTzg8HEBDFLdNAJgJ6Lzn/BbTmw0RdbD6+y2hxP7yk2JKORtgdoKSz7/DjDQVaHkbgpYpUft229+XGTsHgKWj629NRACq65aGKF1RNq0Tt6v5SrKmNYaO5r3dUWV4C+TbHgb913QibuzucY+7NQf+FIEXTN8om9xU/6W0JyQRVdcVmRkpZ2SWnayJM2IOcsyz+L424QDSJ9iO4AKS8iRQMcD4MdAWFKVkD+j7DNX9qVcY8MZfq3Sr7NErRRwf1cN+r1hdPd9rignkXd1V+eTXwcWi1mXfUO/uHFxQdJHDHd4w8W8xlX47dM5wvs2xJXxrPnefURV0RKiKG1PeNHDOZVk1zFHfuGu49qumbG3OKmuka0IDuH5NaSlb+OB25tBV2JKy8tc+LfQf9vTaJpSxqmDz7q2pp+frDQZljWGLH+n5Az1VA0J1VbzeQd4LcUTUTFw/XjbbBs/ykxMHOVtpcYWkVmNUBPJaMrTMZmODo10NT7ZihLlrT3YbJpRvyQwOytiTtFc2aMh4ZZvnYOPGdV5ApU5WIZ+NlhahvRoaVoYytAY8P77+2VX8+QZe5aZygaYN9yoE/freMiiYUNWv8/p3iwcNNrbo5p4xwtbFJWPFHh3eF7T2jQx92W9RjF377lvR01U5a3asyXet3h5WdjJtVVCJW3ntcK67FlzTzd21uSz1dHkc53oXr3nJ6HCLEeK+Odyapwvf776v/MhmuSsapmO/U9X+ZoW1vLluYmEyV3k939TyNjWfv27XX+Gmwgaa58xt/pKvrXw3tf3azrsPBn0bbviuocEXm4aeV9iuv69rJeRcreNa/tvh3K/EvfJvwZfX+731njo43Ep7a3rFxxo+AQGy1VFd+OqvKBzc91rGuqz9duwZ53u59Jo6yeC9yOSV0JZ747vYeLSOl2naUq5dLex5oeqSsdSz3bDCK5Fe0X/Tf1vYwBtgj3qPGi0HCrZgwjPm5YzXeMb5/ILX+TPiNAIx4K+fvuD06QXvH2eM44KHKWJQl64hRozjBCJCXhKWtODLvCCljCW9IqeM+TxjPr8inc/gtCBSRiTGQqJYPp9nnOdXzPMLgKnh+xmivzFVNxGpu1Vx95UjgyghLEm8WUDgO9jwaHy0pK66zjGCQsA0zwAFDGBQCBjjiOkw4XA+4HUcEYcBeQ7tqPVT6OjttnzS0u3+75WxHwROCWk5I80vyPMLkGeQ+AsAdHOsKNyrC3CDBc9J1l33ivsBlDhTjQ4UDX+6AUANvKyyeTKyweu39M/fMsoEExpYr0bB/nR1XR/etFm/dU22Cq2P7Pvi5sf9seb/e1y6Xm89ClhnWW8O8ricAT2oIqfRxzHiMI04HiYcDxPGUWK1WENIrUdbs3UvXr+UNnmaO8v5qhMRZe5uFDjscej4uSrQin8y3XhX6VQpsy6wai1SoZjqbnwikp2yFBolg2+bjxGxFoodAbNIKLW6JhW3C4wSI4OZJU5AyiVewCVjhPXPrdEN9dXOd92zdR1trmoFtPEIQLDxqCdDLOaBGBICMu0zi7YoTcETY0TMWa4xY4gDxiEjhgVJT0XkFXH+dVKP9JnFUjovCYlkJ22KjEDiuzxEMUqEIPljlACe1heBUnEhExQ5xRCQI9RfOINIfYUzA2yqVUPy2IbDGxh9n7YEwuB2hBckzpdhrVd23qSwsX83FCp2L724lTH/+kQbQlxtUOU5++eVqO0j17UIK7FRyro23EQBRPmW6fvXnwhopYKe8UK5lyDvNpYW9A71GaBxCKCu3yp9yOrX2SKT9MINs9tN9QYiDO3GJmzY2mEzXHaGab+2GkHDyT+3VH9LuzeAW6luKePy2ja/okKnZYyFiSWbRz0OTEH9jFIugiaZwKn0yCvNt9aeV8D6RM5PfzVCBbfG7MSDD6SsK9LRqBC7ExHa5uZX6lQG3bUZvIMLDacSF6hbEhAzsFAAx4AxBeQYy7iQr6woGbfRxOqkpRuXEIRu5+L+z8bZdtpljVlChbdKw4BAQEoa8yc5fouD8D+ln7oOQxXiZC6FWQsl1lHH62g7WeO3NAL4FRy7B5fXeKl70r357zVCdB+XMuzKrJtW4HZrmfFG8+VcvQo3uATt2vF0f8WPd23+Vkr8reTp3i11vaUttylh6+aQO0q+uy176W6DlVM8GN7Zf/5t5++eEt8isP572kkbIlurgNJZ0ZhLFhPRZOIWvrZmcQteuHvO3fNLDfwF081Vb0Guxe27Je8tFe59t6nqcfnvGT9TC94q7637dyu+2conYpKLN3Dh28s4QPuvMfdAulM7yMkI/zMlDQfhHYo63OhbIy8af9Tx8Eo3M1Bi763b590gGf9d4d5OQmTzU59bOmxKT065xHHIWWJ2FvqdLSaWxvLMJlfUmIHmnpJz1gDMuQQcNhc7sO82mWP5kfJ0X70+uQa/FcYxN/UEKO+2zFheX/Dl8yeMEzBxxPnlE85ffsJChE9zQjz+M/52BpY04XefE/743Uc8HA8AAkIgfPjwPWIgTOOI13nG//y//6/46dOP+PM//TfkJYEW4NNPn7B8+YKwzHg+RrwoiC/LGX/605+AEHA4TTgen8H8DIwAxgBOSWKuRvVEMUQQBhAF5Z8Cck6Y51S8VQSSuI05ZeRFYkecX18RQsR5nnFWI8Tp4RHjJEG6j6cHhMAYxoCUXjAvr1jmT8hnFHenLQ+mLsltTIGbeSOvOzH9pvkzS6+v4PBXvPz0T5hOE8bHI8I0SEy3MGgweIsRlwuqYNaNUCUQdKlN7tjiCRncSi5t7S62c91z7a/8quUosi2vvcYQY+OAvtusoy3LhBK8PKdF9KwWS9DiTbCspaxXyuJm1nBFbbziqaJX0EYYDS7GmVafdlu6J1+FhyIvEwB1+ZX1v2mKGMeI988P+PjuEd9/fMZ3H97h8ekBh8Mkc84ssX135uvnTG/hDe82RKyNDnvP3aCqokKInD3bLrMaFEjxok2IC9piyid/pb5Of90WWla7TrY73FxXLB7VExFVl+CEyx0Dx05lF96tUyGhnVBrFnjSdlOXb697VbFQx5PIn4jYVgj0Y0qopyD8KYBiJCowcIu55dullVVZ2701LllN60kNTUsSDc2wyHjOcQFRwDAsINIYEQXxCyNj7mVa44LMjfEXqodRxNy20++4gHu/lfwcbMOY27kKuHHfYHSsMtoer906uP5R+rfX6L3H/Rxp1q9Xmnhha6dBTgl8U7K2atErJVjBGXVN6T/3NPxfVyJ36WiHpd4Y0QrLrdGgGJZRcVVxKQcTbPQrEz5g645r8WUZfAuMxM2/a77KcID2h0uLLqT93RLl2uVvy2wND/elqpww8C1Tdgc4U/vPbd84OrRN73veoXXlU79TgSAEEKEaLCjAArT1v9pSZ4Tw44A1DbF/q4FHGXEITQm0Ycx3w2FwWfgKKx9VcM4utoKNQCBCpropYz3GFe7J6JHSqFzKZYTQCvht0mCtOStPoPVIQ8umjYbRL4Rte7dgXXj1WtBqqYMVJ9QR3n5eJ25byPPfrtPPqZgH6rhs8Wurn5vv+r3vw37a68de77aUSvcKE5tKrYtz8XVl3lQHt/ihf+/xxHb57FGfPFkZBK6nLQH2tvFdz4lXTlv1veGpv99u03ZVt8/6Fj+1ko4ul/CV6+3nXq+3J9r52z29p60Kc70x6nK962ceHrZgo4WnvTJvhYi2nfvg7dvX19H39ZYx87TuEvxtr/OtDVKbtWzwqNv5XH6+TG8up/2+1Kbs49U3GyOK7sCQi1S4BRVltjx+g5tBM0LAnK2EerUdovpV5ZiEe+pUhRVei7B1+XRRr2+p7ar3bZ+9bFFpsx+TNZ12+h3Hx7PLD7i4C14GsV+uBg5vICnyaJEN3L2TY4qgvZtsvNDka8aOC9DWurQ+YpnBDBZjSUpYlgV5zEAkjNOESI8YpyPiOGHJwJfzgh8/v2AcJjwcj0jMGIeAYQh4OBwxTSMeTyfM84z3796DCPjbX/4ROSW8LmeclzNyWgACpmlCpoQzL1iYMCc5MfHy8hkhTIjxKC5V3cbioHHYgupjTPdU3K/rfwG6ObDw6vWkMDJk0472N6WElMVNN2m8iWmaMI7yi3EEhQHICyS4cR3wdont8xtbPNjWM1JDhCjhZ6TzF8znz8jpFciLbnAFoHECTOYq06z/VHlQVO01PgiVuWeFjxInztpR5MnaJYIYyAucd6nwtK5v6z66devWUH3ljJTFgFHdn0ngbAfD3brxskmDCUj7bTIEw+l25fNbUOqWl2PWAsj+Xn9V2lH13VVfJN2h0r4hBkzTgNNhwsPxgONhwjSOiENAiKRBxLm0u6npLv5z+9tV/95QVp/uMkTcY4TwTL64QODV8/JekYgpqqP6fQshIoYgQW9CRI05UP+mEFZlru/XbWx3TLaLvvmbbMUqYmFPMiUxxOrolV92IsL7cd6dsNJmNNC+hYjAUKthK6iuENaNDKS0OQBBrKCCxG2XqZ6MYNZxuFxqHVtCpIAYAmIUJX2MUe/1BEGxtP52kvRN/JcLIWIwL4hEYM4YloCcFpyHiGVZcDgsSDnheDiAmTHEgBgIKWXkxFhSwpIy5kWs8CllLEtGMgUQ2PZoFISxaVTCGqFc7Uv3QVD3UIW/ZL+rsoedVjQAtgX5PXi+VWFSCcJ+3kLsfqHUMIo3riFThhnbXYxvqKdiZH0HBMoNfvq3lmyc6v114mbwJHkzQC1eJKISzLrAqco55ud+yhmB1Wer7XLSeuw/mXfcv9hcm5nN+NiWx8xul1Ot496q/Dr0BhsxwtSdFKbErQryynxdg7y1AqSj7yvlf/vbanNhsG5ezVaH7m4KQWgKBUSI0j1LhlK+bF5ojd5C5+uJCDNEDMH3QYiqNL0ysC3uW0/UZUVfzZ9VcR+S4AMBDW2L7kJj9w1hW9EpODsh2Q6gnEBAGRsQYwgB4OhORpiBzoQAltOb2e3eS4SUUqkzEBACK1yFyv/oDqqsrprMlSPr+a+sc9zGeJAx3TZCuJ2X/bXAALsr3DXrc/EFLJ+JT+BrCvBryuS976/B+XYyvrFtvtHfVUBvo8l22sV2K7q2N/k2hblvk75GWHmrEWIv/6UxX9VllJi2892eLsPNPcaIb5W+aZ1fDTJb7eiffePx2UbF//qSoj1WDUjPM30LGFgbIfbSvg/ty+mitNjlIXe9ta5b4O+2tD8Ovrxb+nNL3ittuVrHz41z/HwTNpnGnhyX5NqovAEQwTQg0yB+62kEIyIjIheXFa485S3WUqnABpEoRpnEEc3KeNw3ijee2XNmobFZfPpDT0F4Jad/z8ozcXcSotBlTqKIVsWoqIIzyOQOPQlRYkjoSQikVOuxNvkTHM2Z7p5XugZrNm4bWYvyCuDBTYLKK8TAGCJSBs7nM9LrC/LrF6SHR8SHCe8O7/B8OCKPEXmIwDDg08uC//ZPf8Vff3zB5y8zHk8nfPfxGY8PJ/zdf/wO75+f8MPHDwBnxMMBf/rLn/Dy+gl//etf8Oc//xd8fvkJ5/QKisD7Dx8wzQn0MuPzS8LrpzM+f/4R9N8Z8/uMlAKW5YjDYSmxIEzXwSp3mwEixiicAYk7piEMYEqlzynLiQjOSTah54SUZpzPL4jjgMP5BdPhAARgnEbE+IAvj0+Yz684v37CvMxqxFBTGnso1msvAF9JW3jJjCi8zMAr4/zpz/h8iHj87gccTg+I8QFEEygSOMhJlMyMZPpLEh2inQDIEH2iiD9tfX1gZtOKrBTcRV5rWXmThfOGDNDzwK3xAUVmti1UJlurWQxpqSciWOetBH1H3axVXTfZ2pHvbS4IAZSBrFYEDtr4IsYwNrX6nQ5CB6KfQUVdrUzZFtHzyvqIHC5VQwQFwul0wPPTEd9/eMYPH97hw/Mj3j0eMY4RFEnjzQAD20a127d8384TfNt0syFiX8BYv98yNoiM6twj6EP/vCgRKCCGqK5MLNhxG/jYXC8F9Ze1EhJL2dhsT//3brLAZRaF2H1bhAK2cdD3naBYFFG+WA/E7q+W4fRtbBGaRwZXAUcJUAEyU0wYgCuRYluYhM3xRDdeW0KRzG17qqKcjAjtczv+1I/CL5XW41aRiYyTnowgYEnCCMxk/ZZ8MaqiiwJSFGtlViXPsmTMKWNZUjFKpGRW97rz0+DKFDi9calt5noObkvd/Pmy9fdmBLQhGO0VVWEQN/HqhLcoELZSR2Cpj32yhvHbdo+3ijLf1FZha3TP9mb/204NvkSd4z08WYmpjHWbjTfyyy/rWi1HrRmN4FA+5wvgePcLbv7lG8q4Kko0jMkNeXfTllRZ362VbJK/N+xvrfm31rqVvDGh/JpNB2pAsPz2r+NHKq9hhnWL1ePXpNK/sC2sKlS2fAPWuKGMWQ+n5RuqNqhasPZDx8h939D9wt3bLjwL6Mzl1TVeB6hwb9OqfH6Je0QkfAsFM5b0+SuOY9esun8xwGCoqdfzQMUIsR7rbaHLxnf1apXvGnxZ8VRo+PqLexTpt7yreGZbENv7VfcS8k+BhhZ4rqZb+nMv3b+27m8Zl3u/v51vr5BwzXBx6Vm73vfHp64J2rzfy/9zpFvbcomfvDXdCgP9faGFW/xfx4/R3t034QffmBpxhdz9LW0i4CKmcjjfLkW+3D69s7Uu9janbeW5PV3Frl0eky9vKW7juze1i9bPrBns3lC7Brw+t5MSHG3eqnctu9Z8ZZ91M523pq28tDNmnq4VjqUr4Nq3/t2WY8gtcPF99Q2vI1PjQYhKVk5EZH3ORCvVnOGHleKMfbsq89HzqnUM+u/bTrTig9FnR6/Lz9ZK3ZxmV3GjWF1RNpuQYCvdXJquy6itMAGkrRdNFp9n1YN18vwjILvo1z1vxkfkcmUKdwQiguhyhjhgmg44nB5wOj1iCUAiQiJGBmFeEl4w46fPr8hMeHh6xJgBGibE8aCnFQhPD09IKeG7738AhYB//Mf/jnGZcXg8IR5GxMMB07yAvrwifpmR6QWBBuQ5YdF4EkMMGEJAUve8OUektOYBbFOtyQMxRKQY13jV3PwGgaOcE9KyYFnOWJZZTmuwnowYRxyOR4yHI8bXg8RrSIv6QyoDW4eSTAOwwSP3U9LpDauMAQQE2cjKEidiOb8gLzM4ZXlPujFIvyOo8W574tEAm4c1u2/WToXlLVnIl13Ww018L0S2Adcg8GX8cuGFbftuG2/OThTltv36jooLs7o2WxReN+8VGhlCGbNr7Mo+v2dLcRun1uo9vK5pfYbCZZS4EKfjAQ8n+R00NoSEBrDvtS8MgNrN81+zmWWPp9iC03vSz3IiwucvRgeYHc98pRP8SQhAdvYFChiHETFEjMOEECNiHDTegF2jnpYYEGIAxQjSUxIUggRTJGmfN1L4urba6hk4WxgUbA0SQC0wrZQTeptZYkNYfIjcTcouIPhCygOXSnDkijwu7+Sg9pZdP027AKhy1BkcgsUTaH1v5zKOvSLQjwc5RG67WSNiyLJzM5hSyCOGX1GwaFJti+A8VQpAdpHOCzDPC2IgvJwJh/OI8znhcFjw8rpgHALGwY6iEuYlI+WMl9cZy5Lw8jpjXuSERGrcNhlS4gYG5fpteia7hUMpuzJMXP7bS72C61I+4LKYxVA4Yf/8gsX2GwmdnkH09VrDiJyYSLaLGGVNsOKxFuF6QmP3XMYLdtVKAgIiZV1LAeZz/d/T9SQ4T1VCBSSqAFHmzOYny/zmnBECISVGTNycUiu/Av/bMGiwyfVBs4bWQpNnvqDM0/WFrCduAdT+2G4e0G2+HgUGDZJvqJN7GmLjYEedqWmL/F13GzfG6gt12Nqp2db5i6EghOrnNQZHRwJCuc8S60Cba9xFNTK0bR4ouvuK02zMQJW5LW0uvIuNy+XkjRGm7LBZEME1IyMUX7zWtso4Sr5W6aZPmZHUkG2nF7yiUQ9ECO3Nl02oougWJj7nhJSBJQuDXw031KwRj8e8sUpap3iMs+rNKu/R0DNONzGoKwZf58HmwwQt40uo+31t2lLa75Vf7nerben4ptFh52SE5Qd0NSryk++867pt5v8eo8reOOyV+ZZn1+q69932847vfUNaK3ft/hsxYzfW/a862QavkvbmEriMzX7p1Ldlv937+W+FUTKGeYWD/vXAydb49PzIXv4bx8AX0RXP/fs+727dW3Lrmg9c5VlVuE5VabndkLX+4No43AErV1DcTQomp9wDi+yU9QREoohMg94HmFrVuM7sCvAK/TapDqJU4/i47Q9cu5SfccpRFfZbf/V6OgJcT0JooyC7rVk3cHTumRppQYwQhCy8T7a4EUl66uM7NDEh3K8oVFH0P4Xw7/HSt7H+TXbA4lBlAEuFXSbdPy65QhD93Ol0wvO793j39B7vHz/gNZ0x5wWv8yuWZcZ8nrGcE1KOmH6aMT1/RDhF0PSIeHxEyhkBwPfvP+Lx9IhEAf/9n/4B//TXP2N8PIGmAOKIEA54OZ/xl08/4dOnL/jrn3/ET3/+CT/+04+YP3/GZ4qgvABpBnAC8wQixjCMyFniQwwxIoAwhCCxO3UD8zhOYOYq17Cw5oN6ZBkG2eyUljPmc8DnzxHDMOB4PGAcRwzDgNPDI0CE1/OL8PhpFriYGTnrTn0n/4VoobRR4Q8buokLytxAhIECZiRwXjC/fAJ+GrC8vCLPi2zk1qDFmQAKQGCAUy+F2imB7EDJYAy1XVVBVV2JFd7f6XWwxduq7NLxt1Z2+5PYKuVUiq4PdqcbMnN5nm1N5aQxVpLK2hZnRU5IcFrKyvQrJchAg4MpeSP8ae6cqZaDimfKvBjewTbKafF0d8qs3Hl9ktPBumd6vgNjDBimgHfPD/j+u3f43cf3+P7DMx4fjjhOI2CngEIEssB5nc638669kWGvn19jjLj7RET3dDPf6geA2O7tdIP87XfKR4oIQayt4n7JXDM5twolCHVw5W0zaluM2zVhrCfyVdHoBM6N8TVBWSXxTYFzrfRpCzBbqaen9uwtcLTNUxFMYbrbkKJ82hPC/fhsxIgo894rCtqTL+1QbjF2v1JyTWH9W0NFYMkeEWUQzeXQ5JIIy1IjrS9ZgoTOS9JTERkpJw1oZIE6ja9gd8+1HfB5uod7zd+YW1k/BZq2+9wWUirti1utpfL3ZYUBdzNe9wzdouRbl+fv2SYKW35vt7+zNpRV1xGBdtWYTNjD/kYdfr2QX0to7/FLqDZ+3XRNYF6/r0ofLsywshAMYMvHfkncrJ2ye4mp+P4U10zVL77ltd8eLN5r4X97IqerkL4TObdLuFVZtd3e/W/NoKNtUCS4STfp1ja4Ou9QnlTlfDUmlB+5U5FEFS7q1+Vfo58BLQ2TMn199o9+acofrBmqHn+u8UE1qpqwoVgJ9WHbR82m4+/wkDUFLo5DF3eKO6ejdfWgEY5rG2tbcxGmRUAIFPRkBDReoQnTBRpwGb+avNJhNvbXLRqwIjCrPhm/sK6zwmUPXz2DvMen9O/6cm9LVJau1d0Kme39tkGCG0HPj3GFn37c64xv9aHpJ637fbVXWzTzyrO9vy+XT3Xl6vrzT9uV5/ICJT+zQdf+vMOXQfXvvj2rsezyGc9meffq2oLJvbRd91pB8VtIfX/vaxd1V7u7DdZ2S/1Zx+Z6W9t8a75mPfc2dnJX32+tn61yjYbY99stuo112eNGb+VSt/D6lS+3XhY+3mXqh9LTPCNOO23iZiyxopee19ls2LYQ3d+sM7p+tOP/Vjm3Gp6JeiM0Nupp39/DvvbuWPp0sSxTmttYE8FiQ9QTERYjIuiJCTWsAy0Dg7oDXO5sPNcKr1b+5OKX3TUMhcf1/IjxSA6fawlOfrj8yzk3ytKivBVFkOpv5O8VbWdXLdc2bf6azGVQOtCz9XD7hDf4h7RQQllnmYFMAMKAYZpwOj7gdHzA8XDEOBxU8Uml3wQWLxhB3FwnZrycZ3x+OeOnLy84Hic8PIwYA+mGY2gQ6Ec8Pj9jHEe8f3pEoBFjfMTfPn/C8Kd/wviXv2KZEzAz+EsGTSMAMRScX2ViU5qlLzkDExBiBFg3J0N1jjEgxIgQB4SwIFAs7t4lNChDvFircjzNWJagLphecH59ARHE1VMQg8agP4pi/IDx91D+vUxWXaymT9jTC16UOcl4+Fz4eGj/EAIoRN3YVtePbERlZOICIn7VgKAewBy/6uCZbL1w3WBHZa2VbrXrY2MdWd+2DBFtnWh+ttbMgMLFs0h1hQZ38qF5VtbP5lAqzwiYTFZwShWKS7tv4TNYv3NfNrRnd2rJb0prT9HHIeIwDTgdD3jU2BDHw1QMZxkEYlIDC8q++Z53vZWi35K8jPU1/Nfdwarfkszg4GNANFenYAi6sGOMGMdRd0XWmBAxGAIJmz8K1VWT1F2VGUA9EbHdzooUyt+wSZMYCj0fYX6Y5bmz7Dvrut/xtldvQKgKERMWjfQ6Xqwu2u0+BMcArrOYEYL2cxRBtY0RkckLsNvMVBlr/UUiJFDx2WcxIkIMCDk4DslT4j1G/pdK3FyMGWIIQSYAC4A5Mc7LjPOcML4ueHlNGAbCEO3Ej8EC4TwvSDnjdV6QExcfbobzBdk45A9DVPsC6T3JK/Pq2vAEBYVY9LX1MLspeN6KgFZME+7u1p7iujdGrL8zmkLNpxXeK1GuhrS2gGY2eF8hJ7iMdedFLuu6rI1ACLYj8FtRhH9NiT2OAmDKKTTyXfsJG6xy8wxAUbSmlJGWhBST7nqqxz+LwvaSEGZr842Tdk0pJQYHYWBY6QDbcUu+TeFTx6HWcZ1JsDzAHl5v7jtFyUrhufGu4ojruCIE26ggvMFgdL85ERFAtkPM1wmjp0I9o9KyZjMDtYYIf9KRdF1mhyv21vnWOIngLEK17a0JKtwUGV3HIwSLl6QtN9hrhqjuKEpZTkMsy9LtLNpojONdRGao+J4BoKyJhEBAzgEJVVgBqjfiih+5GRNgDWtUpBmyQSlDzM2uIC6vSRUWuvepk6tbXq6fx/633khynUG+9P5exX2f+jm6ZITISQVKvS/iKxESTKEBJwy2yLBvYj82FqD9bcrjWubWtX9/e1mNKAzbKU+Fk/Xl2ZMtAiBvvBFivy1tvaQDe3lctp5VofqtY7nHX7X1cvfu1+KNf750q8Hrt53uaa/An/Cl+3KhvwK0vWbemIp+84oy3ujZpbTNylqZfbk7pTVtsXQpPgWtm30hMdMKR5ZyVvdGrF3dvexysZw9fHHrvDne93KlTmm2nfXeTTRbreyL2Cuy0jkoTY9gyAmIhAGZIpjkNIT8pLKkAX6D03UUnM5oINBD637P/JtcOQuv2NdTCGL8zzVmVpEN2k0f5dQC4Oi2C5gLd1rVR4C0MrKLRaF8euHSqsCtdXhXM7new35G7bSvRZdyfzL6J/EpAMToymfMnIE4AIcDDg9P+P7j9/j4/jt8fP6IIR4AGsAZSCkBKYFyxnQYMMQRmUS5/7dPX5Ao4B/++U/IvODd4QfEYcIhjgBFHB+e8bgs+N0f/h5jIPzx+48YhyMOhw/4h3/+J/zP/9v/in/8h/8DyAuehhPexQd8Op/xeZ6xnD/h/JLx8jIhDAOens84HB/wQBkjJnCMKn8HRCKMwwgwcB4mxJQRhwnMQBrOCCyyIWn/cxYvFlljvg5EmIYBBKieckA4RhyOj3g9nxHjAaAvAAfdfG0QC/DG+l1vWNmbI7dpCQLRiRNyXvSkNYAQQWFEGCaEYQLzWWJWkEZqoQgGsNAscOODlDd1c4E1H+9EYNa7QhIoNwnGYNyvm6xw3p+E8LHQtnSlpR2o61zyLkXOt5MTsF+/VizGSznp43CqocvSbYdfyL0s9HbN5+3NF2+OaaVj1QjZfW9KKF+WoYYAHA4jnh6P+PD8iO/fv8OH5yc8PTxgUj25GC4IUWHOigoifdYyiTSg93binb+3kue1r/Oy++lmQ8Tmjh+hEGsFHzaEIFhMh6oYCBoHInZBqr0rpjY4ddwVQIuyY0vQIioCNfd9WHdU8jshT+ZV7lcsiwIqoa5rIWq5CPo18FErfDbt1nobto3aOiojihXAAsYwmmsIRaVOEG5YGlLEaGuiK8eKaMcY2sZ2d0Z/bRQFdoKlK6cHI2vTfczaN057jNxWNuUfKDFAGTQnpExIkUCBESgXwjMvxuTYzlYUpacvz9CuWYPfyFc0yRuWypxsEkSPIPfL2iy7PLitPWXnhZtqwrbygOBha7sdaL7lBjarwqwqYSriRIXzCvCuUQ62mXdwx1pJJUchHbxDrNTGk1T4v8xK/2tKdYzWp0hKWg3FtmDc5+kNEFJfywsUIYOroFFORbBfi+uymiZ+zaJklLA4FcocbTK4LHRB14WtsS2ahw73Wuff0rgbFvAtSsxN5aRD+utdibVm/22hrVSN2fVEREAg3d3jpoQBYbJ2mlfpz7qNVXg2P7IVZn2B2xi06wg8ze14CaybV4zCqxd2UeF2Q2hp6DQcrKzqqN+Ju8Hg5HJurqIQJyDn4h6MlIEVpnd7iIWuCV7ztMGJAOWvAku9kmGLDtwB05u86g3pUv5ryua+nxsloGxs2TFGeLovQpzFAKljjuZfa/dtffDv9/JdU4pulfEW40RT3qYiUN9cHPPrOKj9vipyPf5s81/BbWVFv1Xpc9/YbOHlyjv8S0yOv0IPN30+bDz/LSWv2N7D7JIuK5sqvly9uaHztyqJ9+uv9dT3az78YhtM7nT3fr11tW2WsKYS221ZP9tr3a119+2QfERbVI77bHeUewcNc/JhDwNcBNDKU1S6+/VpD3x62NmEJa6YkRssGSDbMcQQwSSnIrzsK/RxHaGCtNymhY5nB1q+rvD+ClPsP7OyVGYoO7CdkaFMcUOX645tv5ZtkwhzavQ+WRW19fvc1Au2HebyI33m22rjuXetS1UFHS/wrCem6dfGWzfYKpdmbU8IiNMBh+d3eHp+j+enD3g8PmIaJlnzGuQ5p6TVy0mHaRiRdK6X+YwvX4D//k//iCW94nfvHpEBTMdBx3ABgfF4esBhHPD9++8xjkccpnfgDPzl9z+Blxl/+ed/xJgiwmtCGAOGOeDL6ytezwlpecWynPEyDMicMIwSnDqPB0SOhZDEGHUDsbp0jxEhy6mIrMHCGXpaWDevmT7w9fUFL18+Y5gOGI8nFO8uMSIOo2ySjgNyCOBMusmGNUZH3dzj/tmeLW43RvgN1JkzEicgABQCpumI4+kR03RCHI+gMMjaYoCJxRMsgGibnpSfZ5Yg5bJviBBUYAlksV3aFhazmcG/argyuxhm29qyzf6164NRB6cmOU3C6I0isnG2BoovdTVrzcWMYHHlRHC0rmmiGiQLToC6Y+PVellz4OtebuJKrl96WQBocbyNpsliFAkhBhyOI54ejng8HvFwOGAssSHkdJngE6V5jejaufs1XPENkjdCbPHTt6a7T0Q0AyzYvghLu0ppCiBEVSIQYhgQY1BDA6lBgjTivZyIEB9to16H5t6fkAg+BgRh1Qb4q1OGbPYNkABKniA4RoOw/tyOnwVUm1vOLDsX0yKxIjr/aD3wNcol9R9dlAqNgISav05CuW9gD/UDQ6Lt0lBi080pEckxtiTHWlvFlxiSGHtCXDfvIdQd4P7Uyo4yqBGu8WulywKmvU2shlhmLDlhWYAQCTHWvgPSx6xMTkrijilD40HB8yU6R831Umt2GGSfw81dG+h9zaA3CpGdsr42FUOZ4o2t5ysmqRNStwwB9ryH4737VnGrx7epii2eoQ0hyE6WTlCr7VivA1EaMUIkhKzGVxVabVfxtxjPf11Jx2PFiXfv71QAmdCWs8bsSbnsLu/xMcpafEv7ryfSuoK2K0D8r7bGsZaOlrbtwIsp0L0iXf9AJ6nd1LFrCtet+veeNwaTwvzRblN6pWFTjtEPfyIi5GbDovZgU5ht29TWp6sWpMZj0kBwvi3lG8t/cShbdSWXvyov4nFAzoAcPMyQoIxWgZ3QVMNZrsJu7VPXN6W1RZ60UfGCtzY+5ywxU0KQNpDfxSQNoxDKqc8CG07wWM1/EbAuwZAZZ63xrj/22+CNLm5Ccf381rj1m5bZKTF6pUaNEaHvTamypYhpkleK6pMLa/Ot6VsYIZr3KyX79rx+TVvb+2tGiLtqwL306GJp/wZ4Aurkh+0+XxuHrxvzbzfObyvHr+VLJHlrjHqDxs+B737etNfWrYG4p1/fdgyoENC9Cdqq7xJc+vy3wO+F/myxxrfp/25It5lYdw1rhZW2/0ynEgEMkNMRAxh2KkJ5IFWCMkRpW/iAzbqbqhyf3MpktnnD+B47EVGUgkZj9ZRCVj6LmGuMiGwxImynd43dZEYIcbcsu7ONRytGC9vhnSVOBDjp31x/qvRvkAHbM9R3fYyIN6RdI4TJDlCazAAnBigAw4Dp4REff/g9vvvdH/CHH/6I94/vcRpPGsD5jLzMSMsCgEEUMA0jjtOEDNmF//LlE15ff8L/+v/OePenJ3z38QPOmfFuPIA5Y1leAUr48P49no4P+I+//0+YxgMO0wOeHp5A04TjOODHv/4JPw1/xpQSHucFr/OMP/0lIy8veH15wct5xpIXjC8HxBjAnHA8nMBxKDEfh3EEIG6bKAx6IoIRYwRg8TszFiziUntegGXGsiwgYgRi0DAiHB4wTRPGMCIOA8bpgGGcEIcJOdgpDAI4FHySivFw63zEOnm+1+5tIx1iQIwjHh6f8fz+e5wePmA6PIPipMY+gZUQGIGBIUflcey0Dpp1AYIaTMT7S2Y5oZRJ9TNOdjAoyr4fpsD3uiTehrmSXdcAMeQHx/+zYSOLCWGGCFmjsl5TNR749cq5nJIgXW85p6IFXRneXdv98yp/26xt6MZKf9Y4kWtHXb8VK/V6153xCUNAOA54fn7Adx+e8fHdEz48PeJ0nDCMAyhGaUWGyI8mV+qgUneqcFPPtpHY5Lwd/uJbGSGAb3QioiD+nYZ55r/ujq/XEniwiwfR35tCohVU9siVa6a1tTTnjoEyLE1lj0czJmWxqdLAAhiVQNXdcaNLAEDuv6IZxZ4A5ZQojPIVw5j9agWrVa6VecYo2Dj2dXlF0q2I01AZkd2rkOyUOXa9dVH8MqmG2TT0mj0i8sOnf4tvS0IybxQkuxgT57qIjdfQj6sRgstUXBNpV0abC3O6JYBbTJZvLbQU2CAq8/nV5W2/aZZtj1/8Tq614manHnMDQW0/bm3bHgJu1461qmRCsxj+zaUdhZniUJu7NV6o+K7ZAWHJzb/8b/m94JCLsFGNbrWUe9bflS5eTA0Dggoz2/12dW8qYSvOtSuoKvvLt3Kz2QZDaHtKjV5heu8aN4bG+wOu70onAWek864cKw1RfsE9V4DYaJMXTPvk1myBR8vfjwOvvkE7lKWPPlcR7voqyeVxjDozIzEjuLGGg84qRNtw9UYrVNc7ZTzXNMMbIlYSvfWDAc4ABanT9mIFrOd/c5S5GuHZDUQzRs1HhXNROG5xqb9upb1NMNe+uyWt+rvL46LwSFu7obi79u+9EFS+cWDAtIEbShuucQ/7fdrqxxb+2cpXxth4x4Jzwwoo1jBSX1w1Vmy87+d3a5NB++2at92uY0PO2WqTSO24huw35aZShhMvaOOKVmypH/FVXuVy469/t1f2Lbz6pfliXJqja+XcNjfXk+H8Ne9s72sbNEfBY9TludaWWke/vuvf5S+t8376ek+eizJot5723vdl7a3DVuy+BFO0Mdb63VVkcutcXE9tG/v1vV7v1MAQFWq9DUMbvMRm2pmf3Wn7hrLEmiXYz9qxEdISLt3nbrlwFbaczsHKMBWf8oEdX3gt3b1mAJgLl6KMhXFc/t9Kn62j7SaCPsh1NULAlKdN/IiN3rCnBbyB9N0QlLas+8/G49+lT3GGmcqYFuMHxYDhdMLp6QnvvvsOz+/e4+HhEdM4yvClhLScwXkBc0YchuKCO4YgimwwAiRG5p///Gd8/vIZ/9t/+f/ibz/+iPcUEAPjbz/+Ba/LGcjAQBEP0wHjMGEIhNM04t3TE94/v8PHj98jLgvy5x+xLIwlaSjtIO4rU85Y5lcsy4LPpwcwCI8PZ9n0TBGgUOcPBFi8WXVbjSS6G84LOC/qkmkp3y3zgPPrC15fXzG+vNSN0nHAOE2YDgdMhwPyawRSkDESBk4nWuBq30H8el49v2JzlZnFXe0w4PjwiKd373E4PWCcjkghFpdnRITIomONQdxFMaXKj2aoG2CooUHwcG7kiMqze70rG9Q24Nbxjmhpfquk704bkO+v1F3Eldzma6u09WoIyda1rsdsJyOSWyOo66R81sopTfmkYs3W0vT0u+BEwycOd7hvs6uj12W1ZTPiEDEdDzidDnh8OOF0mHCYRo0NoXiUglNROp4DEoC9x7XX8GWRc1Yt6t7vlHUvPn5zjIhmQnFZsCnKhY2YDnHrWXPiITiXTbExTmjp7tcC0dcydAWIUBG17Zm0/JW4sBrjWJCX7Tbc2nnbJbK2uq7Ird851I9nvdppDBvnexT7dfeoKQ9ktfXCGgEuYKoFItrrTxVNre21vVSFqK8WKL598gRi3T1qLgApzVZ4yLboK6dQlIOuzAYWPP3/Nl2orXVErAaI//qdhqs66o1ev1nxu3W6O/f8Th5M15gZnVb96OrcUxT3+UIgsMZ8Mbg3mC9L/LcH+r9IKiCyq8Trx3qjDL32Ary9q8bc+loYEi442YwRxvg3CtpVm1sifkMvnYJwO/XGiN0TQbUR3Xr2hn1Hi8siuG5Usz4bTrqFOdG/0K67vbat6VFhXjewnucTqGxAoPbal++1dk1jjQ27nDoKV5nsvWnAzbLxhSydAK6CBeUMkHj07N9bHj+WxgsB1Q9oIAKZHziqsNsLz8wAh7pT0BvmjHzpyeSiYjEBKpu7pjJqtUfk/mI3NVvMfSugmKDWGrQ9veqFMit3V0F+AZ53jX0X0jXm+8rHzXXTWMHtqdmiACESISm4su4idNt9ANZ0bQv/XOqv23bi7u8Zm7cTwoY/3fi7XmVBbMHUum83tqcId2+bh7JKHEolaq+bNXBXwL310nV//1+T9g0836L+b8U00cb1loF9A5zA1hjQw4rHx2+Fo3tx0T2yoaW3Q7nv+y219Ok2XuvnS29v09e2ynjCXyPtKZ+aPC05a54bH4/CA4uM5Tc82jOrqTVEuFFm//TbJaGtvf97o6vt6Qn70UaHOVe6XTac+hMR5W9132S6pELfa50Eru3ZbnTHa3W8l9H1Oxcs2wlb4y/0BAhYTgkcn57w9PEDfveHP+Dd80e8e/cOY45AhpyEmF9EWQ9GVIX8EAd1BSTlnDljSTP+z3/4R2Qi5CHi9x8/4I+HCYcx4J9+/AdwZkzxiAER7w4PiEFiVeTDAd+/f4/P332PP/z+7zDxAn79K8ADkCPGccDhMGJOM+Z5xt8+fcbLvCCOE+Yl4fn5A2IcEcMoHj2Mx9LAziFI0GoEAhOwJDFC8HKWuIIpyShTwlllkHj8hHh8wjCO0t9hBI4POJ4ekOYz0pcRnM7ImYosYpuV29nbT3tyVFbYGmLAcBjx+O4dPnz3PR6e3mE8PeJLHJCdfi0iIDJhCFFOG4UIBiExg82FOCufxLKjlpiAEJCZ9bQ2AbnqHauM1PaD0dEY2saGhbdFlflN9pO1EJC4undtjGXc40a3bmxdZ/F+wBK8RK5IKAKNq9/aYEuzTwLFfGG6+rI6Hp9RAwbC47r2GZXxdOUCGMYBp8cjnp4e8V7jQjwejxiHQdwyIcDOPZTvCUg36DNWPeFOl4/tbm/pw75Gr3inIaJnKszf93YDvCDaKuHcDk7q3MbUD+oiFBdYKIf9SkBPaYMgeZSAiI3yQ90LFMOJW6DbbfYCO4oxQvyLWZsM0EoOWG4hJgnL8oolybG1lBYsKSGlXI/cZ0ECIBJ3CgBokbEMpMFFfHuJAFU6NQK5+zEAJmuRtqZhgP3ViF9Z265uoAarjoKkwgBCgrhRIOM0wG6FlZEgFCtza2SSeRRXTe1uXint52Qqb0jU4Iv1AlSq71QtEAG3jiurvz0Zzr3+1IXu68lurjxq35BhXDktLNpy1KWhwcElQDhF2RFQ1haCxDJgD0MKEb1s5I6OVqVDi1QrHlXYNPxcytKcRLJYM5Uvy9z3CiJ4glzHrrx3ygVBjFKenUAyg5l4VyKlVeX4irrUIx0XBkIAsRwvLfZgotouNtOd6/NqVuS/gCD/UkDUtRRdEOsQqMQuKF9uD4M+qw/vV47/zMnzHgUGUGGxXKlZFk0/UGHKoRgU5YyrxtP4rnoITXC3Ou85G61wH5dfVcrCaIz+zZxRsVSrrCNl2oQ2hILPtjbL5nJ1tMWtb7/zyolvHYXpk61JO1CLi/RNxq6WVxnLNjVGgQ0FsJ+TrW9rXUAMgnNaBzz1b1mPSo8cvyCu/SIiRQQERHd60ngCs8Kba0w7bZFJXV+xHKWu//maPXDqhDGqwMw1p29b33fdW+Vwofwb9E9R9NcPbH0YSpXT/gyKJM0wEktOUWXH+Y2rLdpKGzBZM5nVqKH/CUiZIqB2SdCzQpcXuFXhLe1gMLIIKER1SBjgzFpGXde15zYe7kmv5HbMrp8RD+F7imafbmF+23Lqs024dr3YLofL1a8hof0OQNj4gwI9tXRl1GTjFju8lNBRU82v9KvBKVVVZZ6H7XW7gcX3UQ20FhycrTEG//AVdKu08hREVI/RK7IruL30dGe+6mBii+P7GmFmP3E3d/KsNKN5Lve9nFP4GnvCplpoeZC9PmwKa1ywv/AmHdxRw2k0U79Zdnm9s25K+9BgjnX5F1LLZ+33d2WAMJ4XHnf6tbRVznodfg181DlAI5tu1Xm5LYSttl2tV8sx2h6okPtasp+vcq2ztWeM3Uuedf2aFDo+bdVebu+9bHPbnHm8X/7awBCr3LeUeBW2r8Fev1Flnb/Fekzc1LlWEF+flCoTrd/4ulZpg85ezLPx7haQWSncYF1kYxcctEcJWE2hunpBRomeR6GQIaM1PR/p+eD6AlWXb/01Gq9SGGs93l0S2Lk/NEMDl4rUVYw/oerpK/S+cvALM2Z1wcTeGKEnBUqwXgugWwwOQtgLe2iMk7lyKsF41+6cDKuw7obmogRTZsHjHXJGiuKSQesMCphJT48TaXDqI4anZzz97o94/vgDnh4/4uHwiIECMi94WV7wunzB6/ICpoghDpjGCdNwlGDJMWr/RQEcwBhSxpIS/vJ//J9If/0b/qfThDgG/J8//QnDMOD3P/wReXzAJwCHAEwkAaMTf0EYMh4ejsjvvgN9Tsj5jJzOIMyYxoxl+YQxLgh0xk+fZtDygvSFcP70CQMHUJY4s8siLtPBGUTAOA0gjHgJUWU4UewaL82cCm+T84zl/AXz6ye8fvkbjlPEMg4IIeIwHXF6kJgWL19+xMyMlGeNtybzHouMFgrsiPpB9TAFDgkRAUMY4L1sZE4IQdzxPL7/PR6//x1OH/4e4en3yNMJSwgAZQRmdYplm7cCclS4JgIg+jnh5SVWhMCl8h2dbpEAgbPACAjSDiI5RVGEGJEXtnjIQGLU4LxoH20tyxrISGBI/xgSAyMjIXOS76w8t9hFvCCVrcQNl18jZAGrNf5IkTNVLmF3yqIYIpqFUaX+PWRb8E6PT60OxSch22PHXygDLSELhsKjS/MZFCKGccDTacLHhwnvThMeTgeMkwQjBwaA1S1TMc7kgksrBfE87z7tWG+02upTOz7Sl66gN7BodxgiHFvkBp03ajVYKAwf0LpfMmYKqM9CPSLlpEVZBBZtxRyJOcELqIaInBgU6ukAZgny5yOEF4OE75ljnhojhDNGeMVmz9ZU4BJky3nGMldjxKyGiKy7ctUVtAjzgRFiACtBljGRQJzQ0wnokUIvRAcVKgNJ5wPUEusAxhEmGz8TYEsdQDVEQNoQKYICYQliiEHIem5LgZ5DFcrYFjtgR94aF1uBEKIZIpzfOxtRlgXEjTngl0ydMNhIbNZGGyoTvv2ipQLvhrz36qjq7PrvVt2XGULe/Nt0CgR2RwcjKMociJJd4DhwQGC5r8TRGmCMsCH3WlsAIVnNRrChylaFy4obHOyRKVCoHHVr/Lx3klMveF3acefXcQhofKnXgKsmRCvBJFPQUTnxQ0R6jBPIlBxjzu3P4epGOGRTTqsRIkRwBIYQwUEUs5xDOVaXC0FsWd1/icmvEfsB66v83c+lEzZsKJhWw1GEko01UsWFduVkhgTjSiYMGA60Mr2i11ajMn4MwXlsvjXdbmUGLBCfUroqSFkfSztb4QWllYq/7Tg069q1QpiVTWNtlZbTGURsTE1RZAxNO3b2Xdb8YfXeyundJJa1aHSqYu7yzZZhkCiW2amJVs9sA5XFfrLg1JEiBgqI6Oge1WE3ZrGOpxg+so52NUbU+g0CxJDskJEQUxD17VWVfgdeBqY6gKVbdYNZViV1LF/YdItbU0Ykx94kAIHByuuIQMvgJD0qPBARKh4D4AwugtSoDEq21pOrH9VwkXOWnWpgHWftRAaYsu68UXxpskbQkjolbh2cqtBteUa9LwzvGheUse1gasuAcKtysuKgS0YI30rL62i+Tn7DqOs7TvVroX9w68R4SojQoGBmp8azCpme1DZjxm37S4fY4GRNObZppfw4G74lQzHNN71i3uP1wPq+8Drctc2vsvavNt8GUdhod5/epoz2c9eUVt7vfdfAs/3FlUuN2Bu3neKsJMdfcpkJV0vDf/om3wrva97I0j2uIe41dGy2wxA0AL+22g5e5nZdiXfmt2RrcOtkU9/2vs9+jdxTr/bVrMAMELKIao1yu92g4eWHvdm+xXBTp66ly7emrTasuas+t+C8srHjCrh2LH9TxiUTwvqTrbw9bbon8c7f931d13rF09c+3ERR3c1bsOBGVd2D2/q5ZYSw8ogUvyh9yQhgisg0ICGon/zCgQAIQBC1aegCypaVTu2myuatl003xop0t4ro6G3DRUZSY0RWohvV9zwpY0ZqMAgFI5PD0lVKYAALM84pa2yJDPACViNCvRqx925itBRSJakxgcUIsVQmgbUPTReVnjNQjRA2Ed182vNGlicgKm5KonBHjMAQgadnDB++x/Mf/ge8e/8d3j/9DodBePEXfsWX5Se8Lp9xTi+YhpPEdBgPOEwnhGEAh4BMGneDRP4aUkJ6PeOf/8t/xV/GiHn5DB4C/vHzZ5wen/B/H55Ap3f4CQwOjCFkpDRj4U+IQ8Lj0wnT8gOelneYlz9hXv6MaUx4fCAQf8bDISGdfwQtwHn+gmVe8PrjjwgJII4IccCSUzEwEDEO0whCBoUI6I9TUnFMZD5TSXNizLzg/PIj4jjgfBixTBMeHt5hOpxwfvoACiP+9umvoJSRzl+QckZISVeCpMRRYBoJIIkvKnOgpjszRFCEbP5NyJDNKnGYMIwnvPvu7/Ddf/i/4OH7/4z4/HdIhwfkKDIBgTFkLSuKbkfeAQNkIwnHIGAV7DSswbVyrbbxOUQ1VugqCEAQBSaMYeWc1ODUcqFUSpTNl2ILYDUP1hWUi4QrfHBGVp5YXZsRRI9rOh1mO2yj8E+lLQbflHNZQ7KZkMt6MPljD4/59VUwTqb2HfeLERvvJU/QzWYJshZIY4iAoHH9BveJuG8fYsR4HPF8OuCHxwkfHg94fjzhcDwijAeRq3PFgcVYrlPQcBAN/9X2z/9ZdQd6ze3GW+mFpLDD791PKd9kiPDVXSeF5LRRl5SI/fP62y63UeU6gDItvzGZZom+RZHpy/IAakfvLqVybErdFgBAWhbM84yUFqS8aFCj3Lk2qAJaIEI2BnRD6G4E5+5ZVbTaM92v5Yh3z1j1AEOkltAS8IRgxpBWASS/4k6hKdXahtIuChawut1ha4GsZWfCxeFt2ujH+9unG2H0yvs+X9Ne/+elbuxz/OusXTNsZ4m46ujcnFnAV6+ELGDVEpI28VeNOzew2LW3ubkg0F75uwqZ20qmdh05YmvPy4kIUqNNhXe/q8+X159UKOW5uBy1fDSuZ/41plv6dWvfr+7Noir0rr6tWtCdstcPto5N7lZNHRyqMuG6CsGV4RpSsLQyL5UWbdEeauDcaIZc2rVRjO83KJTugclitNjhx8itmfU7K2PVq/otOZqxZdQOAZRUkFSFfIYYAcXI19Jzb7wxRXHTci9hbrZXaCOcMpO7yavjrU1yhRmfWPlldkf7GUQi8FBQRbGdAmXbbFGP7a8VaFzL7H/Ym9eOCS8XaY/xFL0bxjJujrntjWK3rCKvDPRXP2ZbuP1amf137u3Fb259vlPzmgbD5P5tnrLhLTeHy8bW7rcBU05K5DofZW3xlfFr526tnL0tbdLZdTPvKufanHybObulXTaeG7iTt7Zhte1Y06UVwtv+e/P92/iFlcxz4d317xvuZzPP5t8mV0BltybP1SZ07dGWvJEV3YKh2+DzbfUBJq9WvNjyjFsf8NdVeCHdbYy4YX33T6vq9jZXXOsqVHb15NnW1M437OiR/eX1rf7Jz8V7t6f+7OFmi25Ol4wxWunb3mE9j18vVassT81oN7+CNQsPhfJNaVc3P3VcDYPst1YlO9iJ4sp4lcJQZVkzJdRTuQ3gOTzulZdyklF3bFuAajg+zU5G2GkGb0yA2y5VjsWiMoZu1PqetZsVO1gvpybqOyJXR7Y+Uls46w513QTMMSKOBxyf3uHduw/4/v1HvH98xnGYEJCR5hnz+RWvry+YlwVpyeBBZN1AESFEuZJssLVNtrLpJyKGiBgjOBP+/I9/RSbgy+sZy08z/j9P/xU5Z/zP//Df8IenR/zfPn4ALQHjKyHOAJaM6TDh+LsD5tcF82sCU0IIjPP5I8ZxwMvrgsPhiD/95RUvrxmvr5/E+ABCHEaEYQBAiFFcFmXKGDSmRQy6kczrA3JwehxxuX4+vwCfP+FweMA4TBiHI4ZhwhAjjscDTscH5OWM+cskivC0NHNn7lOrgSOXEzkE3TwaIhAjGAGZAmgYMRLh4fl3eHj+Hs+//494+PgHjA/vEcYTclCXTGpQa9eDWzVbcoKezF0HaLc8BnKk7q20UD01rYPWYLiWn2zXKnewTH2bfID24irMGRNMLi6/hGoYqSeSyoY7VBzyFh1Wv3HK96Smltf2ebjJ7XVLcgoHVJc/kcTzOBwmnB5PeDidcDoecTwcMU2TwkYoZdgYF48IKvuS0tAt+nEz/WsmVGWIjmnt+bG3UNa7XDNtMdXNNFxQ2nrmr1GoX03rfMVaY9b0xhDBaoFthSozDtxS75bgeEuwaZ+XmbGkpMfAFiFaq3gRnYAQCMTmOkeJKe38unfWt/rTsVi1T58X6o/yLZtgRSZoretpFLPUuuqqe051zE2ZpO0J9nfx+y2WQvbleH7jN53qArwkQG/uSMaaP3yrgr/WV5VJShPkGmhtjAhyyoVCVRQ2a/RqrW9nV1uG8npaCdFXlBXtut9+v2+IkNNaIDPs5Qbet9u8bg95eLfxJzFCUHYngm4agX8hyeCtKJJ/4ervrNAYi+5pd+2Yo9267Q/9h+5vj9H7qhOubdlqq+VXfZj+0cJ/v55bAX6fObl7LK093Bmst6uRbzbwHVEdOyIzWgdHQ5zhXZ97JaEctTWmrtLuLUNEYag22ldwR9PGfhS3v2sV6v20OWOBGSD02D4RIWelt4CckmQ4Q4QKuat2wtXTGyC22+rbtsmcM1emk6iUV3vR/tEbYq+NkW/H1pj5ObmmGN/iJd8Kx3vtvFy3/g2hte0wrg33zTh6HvMGmsr9wJsYq2v/lnHzRgeVeja/qfmuNquWd8fzS4ze3vzdaoT4FkrGFV+1wdddqmePn7NpqrjrUt33tvXn/eaWcnbnTv9huj6//dhdm+9beect3vHnUkivkuHaPZy79xGAa7zyllx+ae3fki7x3Ztl2ftGT3qbQfpSMgNOU+cuPJS/SlMcdmtknK9NDR7dzdS2B53Mf2k+7mnntfXyVtnynroafocqf4pieBAZytxeugNC8h2obGip00iNAtHyXeQv9N8KAZ0xovSjXnllgNDvaG2w6zeGWDDccq87uotLpZR1Z7YqTK3s0iR2v1KJv6jo2ffb4bKG6cjldVEYsq9fx9WPNTtDRJDTKXGc8PD8Ds/P7/Hx/Uc8HR5wHEbk5YxlnrGcz3h9fVGdFgAmMUDYj2SjY3aujgBzQxMRwoCUEv78T39FThnLkvFyfMXr9F+xION/+Yf/hjn9Dv/j+49AChjPAfEMIGVMhyMe3j3g/GnB/HlB5hmEhMwfcTwe8HpeMB0OOJ//CTm94PXlE/j1BaCAYTzgcJQTG9N4AIiQU0S24NpFxlCdIbPEktCxzzaW5zMyfcbLl8+YxgNOpzOmJSEOAw4EnI4n5OUVn4cJeTkjkW4as6kLTvPCkDgGOukUCUMcygkNJj03NA4YpxGP3/8BH374T3j+4T/g4ePvER/egaYH5DCgbD7m9U720odikOiNEagnetSotcX3G8/NxVuBrmntj8cJW2tIyiLU1Qp3h9J+OZWkbdD2EOcaK68YHPQ0BtspJn1nRybc2rrXGLEp9+zn1m/2vlVqaDyQ+RemzgUnEUIMmKYRjw8nPJyOeDiecDwccDgcMAwDYoyN/rGR+bW8wKEp822pygj7PO912fhaenOwakueVdoVfgD1W6xXBSzbfbwlsPmvxYWRuVrRAXfEhlVoNsRBuh28toWKsA/sT4pvgzc8+PZdYootnwHEPJ/x+voF5/ODnIxYFqRBXTRxBnOswiVD3biIApNViVl2vPpfCAiqJDVljXSdURWrepyJGOY/zBZDGVfss7hEqMGpu/qZqHh98PPUAqQSHr97VXeBRyLEJnBy26bfair8wN77DaWIT9VY1t5/G0axjmNmIBaFXdTYBEL8Y9SfMgsw999ufreAwlvF72mSrItahisR1wSsVrF/WTDqhUxZ72FFbO00khgaANbgSBYkiSnqmCygouwUCwI7wtlpdbu+URnToAafkNXQoSdRgsZaqUT9twz5b0sF+76RCG4NydeMk4gA7OCx4new8T+8wvk+3a9wA1q86MrNtSG1Ptce35Y7+rm1blqmUHBFT1f6b9+S1kppgrC+e+VVuipthFs7QXYtaZybGMUP7TBkxGWWnVWU1RVhFTQbBS/XQIII6p6r1FxxUKtH0TW5MkbspbrTt+lZx58xqzsoH+CQ8uZpS4kVV91b1NgmdbxEmVz7mzNX148G0BcTb8J7EZCtd0TNeEJ9Egfe4/ku80pNzl5YaVxItkz2bzVRN8/AdTyyUcrGMzNc1TJJQbIZDuaq61KYuHm4toTEZrwrh79Jc5tHb8chv6SR4b5kffw29PmXav1veb0Al/m3W57/W0i2zk227Wn1zlf67fo01LdMWzyrGfbvr2tHkdHrXm8qh5o73rn7t5J+DbmC2dxjKz2ioG5oCNAd8sxyzaYnsI9NKae0pTFCGfFzZgao2xb7hlTZK7KvlJ17vozlaxkb8xuvu7Cz47cL8TW+XE4+2AkIH6Dado/nZCch1CWR6npMQVp843uFqQ8WxrU9pb3uXx2k5r7h15wHi7W7WSe/6ocMcUklI0miux0C4jDi+eEdnh+e8e70iEOcEBlYloSXL1/w8iI/Ijn9QBTLZl/TtTEzUpITI2nOWOasMRFZPUgFnMYHYJR5zpHw+umMH//hT/h//E//T/z5u++Av/yEIwWcmHFezjiNB0zDgCkQwjRi4Aecz1+wLGe8zq9IecbT0xGZF/z44QEhEv7244x5mXH+8jcs5xHEGcM4SfBmouI6S9SGpHqRATSMYkiBnX7JBT7SMiPRZ7x8+UniQxweEUMN1H06PgCc8OX0iADGS1qQ0iwxEgDknEBU9TQUIszAJXoIBoaAcDhiHA44HE44Pjzh4d0HPH3/93j8/u9xev87DM8fwccn8DCB1eATSHWDxW2PwTsK7BWZQfU6Yn9Qxb5zIca2Lrz+k0gMKRx003dAyk53ZKBI5pEGMKNdhm3EbfVJ5d6f3slZ4pYUl2nyrBon1G1ZslNHYpCgcvrIOt/K3W/Ruxk+KKvoAg32FMjkbXOJS8Qydk6Xa44ypfsZQ4gYp4jjccLT4wlPT494fHzE6XjCNE5qhJD1nX0fCqvKru6KQ29JXt5aG5IaoePmMm9JNxsi1krE9jljmznx+ZqfKe5RQWX7G9LFQerLTN0EZMhzVRK2VqFcCJlXiN+T7hEke4bP7pdlxnl+xbLMSCkhNScirNNKRYlLwBpPRFfMJ5mhwpSpGlAaKGNDhRgBWzsI2vp3e7VphDBrMdy7YuLQsSK1lJYmU+2TXYNTflfmGfL3DevGK9h+sVT6s27HnpDQt6/APG+/X1W5089dY5prLFEA6Q4FuQaEqPEiyE6mVMWfN9zdm7a+8JC3Godr5V1QPOy921K69nlCCM4oScUAUQ14wngYnBfiakrV0qm6Hvt6vLKIyLvHIlBW+C9Uo02Fn7wCR792Ws3LqnlrHHBPqkrd9XdfPxa90r87dcDb63Y/Xe5bAR8rXApsr+geeyWkb9uVtMlIaBsqnFahpP/WX/3zshZqaZtlrMv0c4ndehsDRqinhsydXCx/B8RkBj0RGsTMwY7WdYpztPS8jA06HEF+J53R5Wtz64Xi9RytnjAKI26GiJTSGr+HSs+zExzaAj3f4fl3hZ2LLbdv2hMUMh5r2G/waRnTPZ7PMbAFTdo4GXNc+2D5DEbt+8267aurCjk3SnfgnsLf3P7F7hs/LldxVqEpGzDUwHALkmacWDdpTT9WiskC77sNWqUVbuhKuM+gWXnIS9+s3l9s4XYqQlkHQ6sW9c96MndlHq/zaXXEfg749fnfosS//o2Vfdt35bnCtwfNW40P19q0ywv/DDzTz2EY2Wun4L2rJGhVThnygjuv1+XrvOV+zVvXeW5lluv49GvnaWuNaVM8hbz4zVvbsIVXdvN8ZV175b4l77X+v3V8WrUClaC3wqHV0xEMQubqpqn5jqCh4Soe83wGo2au+qNKGzydsF8vfUpRufA8QKtwLQxUqayehJC/vX/8rK5tdINpUgWqBabOqcScYDUylKC7xQhRmH2UkwvWCQA1NirBOPo6J1zzEqkrfyvL9YlQDDWlD+ByoqKOkQTPPR0f8HB8xMN0wkgBlBm8JMyvZ5xfX/F6fsU4HBCGEaQnHRh1E68ponPOSCkjJXYHQxhgwjQeEClgDBEzZ7x++YzP/CP+9//l/4Ufv/sz4pLx4fSAv3/3DlMkHOKIKQ6YCAjDgIgDpsMR0/kF0zRiThGn0wEpJTw9HcGc8eXLWdykv34GKGKMYozgw1EUwTp/YDWVWXxTjBLPRINt55S1fyxK8Dnj9fUzQhjw+vIZh+mIYRwQ44jD4QhwwuHwgJwS5tfPAj9ZYx5YYOg4gCAGCYmUICmTGp+nA+LxEYfHj3h6/z3ef/8HnD7+Eafv/oDh4R3i8REpTkg0VFAl517aIKTIuSgw2DxzsoDBusGnA5/Cp8MkrsKbV+hEg/8rrDEYfolVqcmvOda1UttMuRohStB2NUBw7/qsBIO3TqGpY88IsYfvalNtPQGm4LmLF/A8GVWcVmil1smqtx2GgMM04OF0xOl4xMPphMNhwjSOiEXfy8X7D5HNiTXaIUg/xjv9vdJ4AFXO4CKr+Hvs3t+SvuJEhAlF7UAaYPpfzkkDUTK4BIGM5ZnEgw1yDwnkyuByzTZhC8AhF2CQXSLqTNkJNYUQlWifqGXc1rUCFP1uxcpk+Wf6nNsJn8+veB1GnM+vmOcXLMsJSxqR86RBWNRwwLKAAwgou7VzPRGh5FT6Fpp+9gDtr14R4Pt2SzJ9gyAzK7+24+oAOoElEBX/e0OIGGJEzowhLOAALCTKj59BbvhmyXm2RO3bfQLffcrNr0umyIshINhO4jhiHAaMw4g4jIjBfM25uB3B3BNtqVhsTbdtX4kBuh72d0HjZjjcS5cEJls/rEfTWlyUi3IzZwLzImvP4rqEBbodWd2kBUgQWA3k1RFRWw+9oZZI8A9lkhMWesxQeUVRtpLEhPnXkm5VsFxSHGwrXO9ow4oJqs+Dw2GSp4MN9jvPN5iWtwqrRiuVkfF63sKAdEygtK36fG0ZxduGp2F0mravRTP/zVYPJBXHoHBiNUqg5/LM3pvxv3fR0Csw1m0x5qrEhdATEbGcjIjIOWMJGdGNnR1DsO9NkSNMG4OD31jg29zW7XmZ7mXL6LUvS12C/9q5MhjLOSPpzjB/IsLT8pxJToHqseOygWElUgPM1MCPPkQRkh1M911p5tvxriu2wfN2BNRtiGsFN+npsVZJvT3W/nmDQZ2CZ6308n24jwZbn+8xZNzaFp+//221d8W3GYPP7OMAapn1am0QPlqNhEHWnIXtqm2sG3BuabtPlnXP+HCrInmn9PJvjw2ANaRslegxx30GkN9Cuta+W0Zg46tftN/3CrO/jfRrwsY1hcilL4Fb8E8nl/Me3v3XmFps0nIWtEFlftn0S81Ez7v8nHLmfqL2RxFM1d99BlX6xha4vdIvQPlm5R1NC1PlA+WFuKWTBOGvNTx1lWtJNj8Ke8ilEvPLj5xFxuMsgXdzVt6rnqiVn79fJI8GEWYLTF1807MYITiD81ICv5Ly9AQu1NkCZlflaW3jbWPt+CiuSlk5elAottB0PYldXA+xqysGhOMDpocnPD29w+n4gAgCspxumNMZr8sZ57wgIWOigCGOEg+CGfP5BTOdy6bTlGfknPDl5TPmecbL6xcs84z5fAaYwDkjhIg0yEicGMgvZ/z0f/x3zH/6K376pz/j/bsn/P0ff8Dv373Hf/rhd3g/TnicJsyZsdiBEgTd1S9jPISM4xiwHAJOE4ETIy1n5ExI588AL3hVA0rOCfMyY1lm5JRE70ainyQwcgqCPSx2ginCSfoLJnz+9DfxPBEjiBkBhHGYcDo9gMBI5y+YKeCVk54GSQWeCQa/BKKIYZhweHrG9Pgej7/7I8aHDzi++z0enj/i8d3vER+f1R3TERwnZAT1OCNzGNXVdOAgsKdQkpxcAHanITysFTmzB7+el/cyVC1XNYSArV0rzwxSxVCQy9piPcltpxosULs/AVHblarbqOwDuvvA7m2Ad8clesXmZXm+4KFGKsEeBm9ocqnC1rKudOXZxUNMNOUowCRLUkXmOEQcDhMejgc8nQ54Oh3lNMQwIVKocl1Sd1RFd9e24VK6d0PNJZ1Bj3+0hMsN6NLXu2ZyDS6nHLpf5gw7pJAzIwcRugILoGb178WsyISzWsSy0ggnsDEBlDqBQwoXI4cT9FyU83sET983b4gQ5cK631sKH2bGssyY5zOW5aynIhYhYGoN5W4tE1EJMmyK/3I1ogpUy6RTHhd/9sB2PzuB+HLqyikCqV/Hzq+ZrjevhLE2eqNJpKAGiYgYMiIFZLJ2/3oM4rW0NZzXBN49o8NbecJbjD+eeBhckO0cDuabUYJV2w5ji4vQrA9SYrJbZe3LJYPEdhsdUTDAQRXQ3iIkrpUQ+63xJyJCIKRMCqNqICUqMAvzb2nIqwC57mxxim3bj+376tesDacuCf10q41V4HzrePwqqYCOn4Pb0x5u2lagvnVM6u48dkyGLBsVblgFoE6IEyXw1wl1ZoCojOc6VZpQmS+7v0WwXK2vvg0F134LxZaV46/9+669uhhquWsDtO0aCaHSNzNGBD1ZFCkgkvxd+ANuKiltKsywswDJfds3aZo/SdIr06GMn1NrOAm4+N3tDRitfqQITGKIqDyGV06HYEy8naJUgwV1a6sbO4NfHVlnk9hSiJt46r+/4ETLlGCMCsygVbn1bAp36p/+vnZib2/+Lcrzn1P57Ou/V5G/lyqdradO7V4263i4rTihwVncrTkWKlSELClwsz9NG+qbUh7RFk3t1soVWntpo4B7usmXl9bvPHeFNs9uMUbcTVd1zFcGwLLuaf1sp/wtYXX3/Q33e+Xvfef7frvhbgtO3tDGfZD82XicS+X+GnyVbbC4XUHscWy9v4UHaXHV7fTe0t2wyM3lats2nt706JZU4B19r/fpTL9G7k3fWtn/tbTmlzZClLY6OC2yEVHnoqmwt8Z8yz0xxBV17X9Ro5L7Bma4sKrMDRGUDqKBnUol/ey7DCo4cyG47rSDO43Kdu9c1pTYEHbyoQTPdeX43dylPmsruQFwg9K5qPSJfRnaQdIBKu9ybQepfAsnb7uJK2MDkpP7cTpgmI44Hh9wmCbl+Rg5LWqMmJE4iXEoBIlnoDyvGB5yoTEWG1U244oBwvRiwqroxltEBCKMFDAvC15+/IzPAfjHP/0z3n18j895xrws+O7dM04gUBjAnLEwI2m3bAgJjEDAMBCmMWAcgDECxAuQgby8AhAjghgishghlkVdJqk+AACzGCaSwV+ZuwzOQFpmAAGvr18wjgfMp0cMwwACIQaJQ8Fpwcs4gXPG+fwFILe5ucicMgchBIRhxHh4wPHpGU8ff4fp6TucPvwdDg8fcXz6HWg6gKYDEEdwGAosSr+FfwsF2tUtuwMxKrDtZYU1lBkf2rEtqK1Vc5tbN6F5q4YJhgaclvWSXf7GsGgKLHYnhrjeZ65GDIHvVIwRZAY/b4ArrsnKIqn8ccMn7yyyRqTl7oVfQi3fxexdqOr5JQ1IrcJjw/d7D1pEEkR9GgccphGnacJBf8MgngEAFAMOOBe3jc0McTdbbyADvgzBj56f6N/3m/bak5jX0lcbInxiVsu1IcLyAuDAyFBf7IkQtZXVvZDGD4hRdyXHqoSIsqiK4rQoEnWXshfkisZPzhjI4/t2wDX96ZQE/p0le9corZgRzq+gIeA8v4pBQhF5TuKOIQ4BzJXJFD975m6inoiwMar9iIJwEBCIizJ/s48rBpHRP9noeYt0gcYPYx1vF5OeuVnbRFRiXcQQwCHILlbOmEYBu9dxFqNTQN2Z8BtLjkzL1Y3xrfC0Zgp/JsFLGiVEMI4YhhFjHDHo38MwYhwnjOOhxopQ5V5jwCNqlG13tUHr15XY4PJ2ej1C3593v7unX3+XhP3CF3f5quFOjokGJRAUkh5nDKCQuzUXHCOXVyuIS0/1ztoQZFdCCAEhcz0hoWvIDERfKwT9e7qePH70gmplooznycWH/zXjSH2tDNTNyeIPVVphvmcbjnGj/tqmvg2rnKXfACTeT/memvd76+gWxZdXaPdt3Pv+FrxJsLUqvxiFfgwxYowD5hiRcsZA4rIxZ2HobJdcbUzbvEvz6tsnCnmC+DTu53eNtwi0prG61O2kvRm46nF1EXqWnGUXkx7uDCzGCspoduKtR6j2qcSH0P4b87m1McT30/se75u/l6QOKpVs8UUe796Cty8pXvr2/1JKxLvrohYuDGrUAUS5cnnnFNxEAKvChiVvhm0uqGpw4xXthggAEyIU/jtYF1gG7PRE18Ou+Vt5/HtHW/2yF8bjTuX2Gm/4Ot6afhZjVH+/g5dvxWul0F8GjP89faP0Sxsvqs5kw/3az5B+DePML5mokUb+7aafc54FXgk1EKv5QBf/9RmErAYJU4IzoH7fRU8kz4KiSJmz6tJad0NzpYFemYmex7Hylf+VjZ52MkH9z8PFb3C/rDEhUl6QU8KiG0lFj7MUl0ym75LYp27HvDMGVENEB3+W305Q9BYU8s+24Vc2vClvYHo3IoBi4UqZASxqKEmO57CXIYBODxhPj/j4+z/iw8fv8e7DRzwcTqKITwvO8yu+nF/wZX7BjAyKA4ZxwDhGAAnL8oLX11ec57noIuRkCePzpx+xnGd8/vQTUpqxnGcwZ/yIv4BAGPWk8/j4AGZGmpPwvJ+ALzPjvzIjfXkFM+N/fP8R48ffYYkLlrDg5TXh5cxIicAcAQ7CCOUEzgsCJcSQMA0yBDm9gjlhfh0ABKS0YEkL5vMX0Ue5eZCpM/666gJt41rOC2ghvL58QiDCNI7IaS5+/Ic4ANMRh+MDKBDO8xdg0ckyWIZstg4xIB5OOD5/wMe/+x/w8PEHfPyP/1fE4zsMT78DDQ/A8AQaI8IQVKbLCCzcJUFgMGRzlaSxP1THWPhOrdsM46VPIagRT3QijFSMULt8S4nNYHCnspDT25isI8rzpHKJnWrQ2BF2Cin1pxuSrktzcWYnj3J3EsJ9A/1dkPP2dLn+fbMJSWVBMoOd1wP6teTKlo1pIkfmYPps1WUr7svFWMAIUfTfp9OE58cTnh9PePd4wuPpiON0wOBcMhU8x2t83msZ71UrbeVnParWv1tvuEaVP+9It8eIcH9vkbFGac1196gFiWRVwHHOEkwF68k2S6ocrzKXBeyAW4QlD+RAVbKYgq/6F9xSsHat17buEecaIDt0n7UCvVcm2i+lBcsyY0mzELGkOxuLJdCPLBU6Q6R+5Z1wV5pX6rJAumsFW9NOrBUvvTLr5mTEvHlmxVBRfFgGa1PQ72JQF00xYshqfIpB+ybfFSXWryalVUxrw2mwigvXvbHsjRDNOqLeivg1iQCqR+Mk8HmspyCCuTUx44MZvWQXBFbwc8v41z41SNkeVsq3jbDgGMW+ZKfM7Nd7/9zu9xSqe0ox+VNjQsAZYGw9wa+t0BBbS2VnDmlPPB/p16YPUGTv1DCxhoM6Ir8F48TPKbj8ov3zc9vpXU0pyLyNMyVjfyqBCx7/2m4YLVjVbfLWZpsu4xyfvEB2acwv0ZLdfALQF3Kvzwu1ZTl8UJBuPRlgeKoGeq8u5CTeSqdkKLv1bYfYxa7s9k//gjC1Wppw+KXQlRGxWf9QnkWpGXv+oB5NlhOjAZmSGB86vLA7Xw3cVSPEqsNeWN/urMvasrErQzArbrp0ImIDX/fv957fg2u+Bi9t0YO3pY7tp/bvFd2z11TvqzlCHEoY71xxyzbttFVV10/dhdTO25pf7du/4jN3kq33yrN1vNKNeEPv1mXfUMa1dOv3W/C2vUY2TkR0f9NOeTstvPyWtsfl1vxvLefWPP8yEl2FZWBDiO/m/5cYjz28XI2It31HHvegxeV93J+tumoZfZnrfN+Wb/v5ecAqy92y3stX+CXaVmq7E9Yu5b91M8it83h7/laG6mNEOEVGfabl2t4G+5XNHbwSJ8vDZoOCU9Bdbie3P/Y/K9pJBaqzsd39pjRlc9Vj8QVcDAg4RXPz2+DNqvsYRmEU63Aa416fV/Z2o2tVHi34IFdZpcak0DJt8wEFhOmA4XjC47t3eHx6xukk7mCEf8iYlxlzmnFeZnCkckI5DhGAnJg4nyV2RG2O1Pv68gXzfMbr62csy4K0zKqgXgAGxjAgjgMOI0AIwALRJ58ZM14xj3/DOEQcn054QsDfHR+BgcEj47xkLInFuwHLT2LLytgSGCEwoni1wZISmIG8nMEg9VaSkdKsDLuDk376VCfAqAYmpoS0nHE+v+D19QsCBUzTATFqXLthwDCOyHmRGJ05Scxbky2gG48QEMYJ4/GE07uPeHj/HR7e/w7h8AQ6vQfThEwHUARCKNvZxBhhhghTbTtQMadNBtErfUzB/UE2sujO4MLvF5nHw50rsZxGMthDMUbs/eCuxSDTGSfqqYb6q65mxWUt2Bsm1icher5ti95v6k1Xz91Zj05GXn9PZZjMQa/XsZXsBdfoPFLAMESMw4DjNOlvxGEYMA6DnIbQfmVdw0bPmjZ0Ignc1NySet1bX0ZfVq+68jLIreluQ8RqyHcmMQNqdGgHKoSAhVJh7YN21nbm5SwuexCj5idQMoFLJjOodckU8a4x5UrlqmqKBgjsvevcDk0XCyk03gQawPHMbmFwCBK4iDMQgRQyvnz5jNPhM84PL5jnI9KyYAkRwxDVR7yUE4OMkwGcBa/2p0YAgN09g9U1hew6kKtzXeWIuZ9IdvcmRFUi3o8CQazMNlCG8KWuPokxoj1JYq41BmYMMYCz7G5NKUtwIOLNsn7pZCikVVhvIx2vfL+VZf25WVtxtRQwDAOGYRAi6E5CTPobhuhcndTflhKyV4r0yhGvVii/Dbzgl1spu1NR9gRgpQjbyXf7+NR5lNNGQsYt0FYIAwACUwIHlGDWxZDK1hMzTO7PZoH9SIhMiFECtA2K24Y4gBllXaf068P/16SeKF4Tfvt0XYC4oQ07ApMYRD18b5s6/S6Rb55ou86uBai7o+CUjKvCcAun0Sv2zdgv/OUax23hukvPSyNvSdRjyqps7/vp6UaMQBwGxJSFZsQBQ4jIccAcInKQzQ0MQmIzKSUpHz5OTAdjjhYar92p7iBsvJkqRdAUmXALm218W5g5Ki6ZliUhUMCyLBW/xVDaGtyehxocsa3HG8SE/yb5FaHJ3Adk9QXbnihofqUnlbOxsleGBROIL8aIuM14/C3TbUrWy9/cer+qiwGJI1R3gPnrrjDWli5FGYyWXXi2Lup8lyuZAZ1FdiQqsdCIIoi4wFIjp3DFAbf0c2242BPA7knfFgb+ZSnQLwgcv0D6+nn7OTnYW+p/a/t/zXZbCzbW8S3fbeDV2+fxFnj7dWFyL/16G9L+Pb0lFd1lMTOIrCR8hq1dz+DIUVZSviJnLqyVh++sik4u/B2KkcAU7OaWxVy4mN/5mkcUl8Qsu8hVTxNUCWrRKCyYsO3ktt+yyImItCxIOSFluVrAXGIUv/ackgSsZnPXxGVMqhKJy6ZUO/jApt+9J/lTF24iymmNpH714wAMhFFl3GVZAADDGBEPBzz/8Ec8PL/D3/3df8Dz0zs8PTxiUJ/0S17wef6Mz+cXfDnPOBwOOByOGIcJMUZ1QT7j8+ef8PnLp4rfxHcPPn/6Ccs848vnT3KiZDmDWQwRRIQpHhCXAXMICBQRMWCkiNNwAIeANGd8/stP+C/p/wf+6xcsP73i+fmI5+cj0vyKvGScF8KcBix5QOYI0IAQRIEbKYAoiVFC4SovX8DMmM8zlpQwn2cZu1Ak2XIKhkAIYShurBlJZQyB5eX8RU5CEHB++YTHx3cYxwMG3fQ5jQcAjHGSa36dYZ6gGXJIAuOA8ekDDh9+wOMP/xHH97/D8Pw7IB6RhxMQRgSaEGgBISFAXNdHNUTYKQATYQu02b3CVj2YozKm5+do5QPEXYz398ppp/B3WXujwspYqK6U8jKDc0JeZom5kmYJQq0nIyS2ihgXcp7llJKdjEjyMwOE1WlqB4s3c2k53WaE0PXkZR2ve26Ya6+PtoueNnHyFulk5Ky4LIiue5pGnE4HvHs84f3DEe9OB5ymEWOIAmk5N/IAIHosr8/t678VnVySMfv3PZ5iffhW9c3trpkc/9mzLL0g6pO5agowodnFMoCbTHBRxHkfc8yEUJTaXokCrE4pbApQooxYGSJuZOJYlePBBb5thmVDMW39TGkGFrG4zstcXTPlVIVR+ylGIlLjTOiUBSTGBrJANN17q7+/Z7vyuu0oAGZ97dPWGHl1s9wbWwCYNqcK2jJPdQcrkfj3ziG7OAXr3UvXdnRsjXn/7P7kUTAX+OnLbea8u+6qpUo739i0q+XW8VoZFzQ+RA32OpSdxXtKxtKXpsEttiuvdI7rf/V5/2eH6jb7dE159a2UXAU/KFFZr7Vc+0WkYL+N65ixWi2kdQRbr+ZmRv3aW0BxP/5WVoHFX1HBcv9YdkwN9pV/W0Tv2+6ya+s0HFOvG437mdNahcPNu3aNtMp5Qo/XufSj4O8L43evEmNPGflWY0SLE9yRV670qc6POzVEAUEDuxs+M7ohp7lc/mb0tsaiY6Adc23taPqkNK2SZ6pxPshw4HpWrcxmrJX+ZqdkridAM4jEtU6NeZGRs5XdcZlsPe1PVdZcRaGtg3xxfXX4x8ZnE0ZY6Tzt572mNOvvrxkAbk3Xv6s4YL/uy2Xu0kngInH343+Jwfd5xUVcncs2r/GNbdVtvgunT8AqMO73tf3Genr7XF2a1/rn9bm+Ch8bc3KtbbfzCt+OJtmcCNpZj+W1dCvOviXPrWtsne+2dq/mQv/dxsv3pNtlt+10ma/6Jfite40QX/udT5e7V+f22jBs83FbtPArE1We0tK+jGVtqK2pHbncrnsMQm2d98PLvxSe/i3f26aSkh96KkJ1PbSaTWDFl2GbJnqlotFI8zfPThlZn5v7GaO98re5gQK4uIT2e8bt5zcNtAGrUzkdUXdvS7lkLnws+G5x/+TK7vgyT4RvX0E1J1tfrXw/wIWBAEIcQDFiGA4yj+czGMBwGDEeDnh4esbj0zs8PT3j4eEB0zCKkWaRoNznZcacFqScAYjboRiGslE2pYR5PuN8fq2xVbPwIPP5rO/OSGlBSmKIyLyAEBBpAFIALQlMkGC+AYhRgpszA/PrGWde8Cca8RAPmPEEigBxAnEWt0tZ3Z1DNvYQosrylZfWqAngPCNnC2KdkPOiGFA2L4PJxYil5jR2mU2Fo5wkKPfr62fknDGNBxAIMRyKnF88VMQI2yBs7WICEMQ1Uzw8YHx4h+H4jDA+IIcJiCPEsKJupyqTLy7GzAhhUMDaS7t266hZW1Q3bnsdR6EGjDVB2OJJ2fGJ3K4h/52126/ZesrIgrvbCQg15BWDohkZ9Zl7bmWXU0llhZiXnOvpIl+4J/OW/O21kSJpC/95Hl5k2WGIJT7EYRxwGKK4LaNWh1va2fH/zeTan3QbTtnSobLDlb0qsCeZVQa5obIu3R0jwvXtZqLGLEEZZdFUVzwzy4mJkEO1UmYJyGEBGqWeyjzK4C8yoeozy9rFDSPlr15xb/X3CtO9vrSMq1f4egWi32lohGt5zaA84/OXTzhMJ7y+vmA+zljmBUNYkIdR4zsE+N3DtkM6hLpjmpkFOTPAQUyadiIiqLsjGbNQAvJKO7UHhW5tIA+7v6awQMWBZcy5miHMRQYzkJCLWloMK0EWU5DjRwxgHEcwCON4BoiR1Bf2z6SPvCkVVLKncOvy1sOl2AehXyAZ7MUYMcQB4zhimg4YxwnDMGKaJkzThMPxiMPhgDgMQhC9i5MLJyJymZs6PwUPo/yB7g8A1flRxtena8qtLSPFVjIGwAe7JSIZD2Zksh30EjNC7JEEc5+xRWQLy1IGSHY3Rz0BMcYBxIQlZmQQhkHg38ej+LmU8T9n2jdCtGz1Hr34OY0Qvm6L9eEN2FWJbQYn3L2OTblpxoJSzoW2GGE3V4Pe1Y3RrGZMdCgrjAuzWfK7dVv7WpXd3Cu9czs39bvtX233vUqsKoReGhTpTx1LY/ZjFD40xiCu/aK69osReYiF7sUowlEGV3dpaBk3+WWJDRMCmG/vxzZ8OqWHK4rZTlHUfpU25IxlkV1g87KUtuZMQA5gjgAimHNz8tPTazZeiqj0p8XPreC8v7buV6pUDms/bcHLvYq/X1NZ06drRjjj3ZIb+16J4e+33qWUy2mZnJJcc0ZK26cojIcNehICTAgkbZBnuRt3Kt95YXRTLbSisd2s93PT3W/N9724Yy/15fwWqOVvB1Ivp193TVUe4e3GiH8pI/3t0x5f/svM6Q1rVwXNt/Gwa17kbenfLnx8bfLz9jUwRURV/gFQlL/G/olCZ01DlCZxkGsJaOvfVzWrPjKDfT0FgeI+idV/vek1srjG1tMKnPXEQs5iPGCo8YDV3VI1OIjrnoSku+PthEROGZykDkoMShmUcj0Jgdzu1i6KcONLGeX0s/W/9HsjnsRNEwCtk8vv8PiMcRrx/uP3OByOOB5PCCFgPi9gMIYxYhgnvPv+9zg+POL79x9xGCeMzMgpYZ6/4Hz+jM+vcpohxojDOOFpesQ0jghhRM5fcD7PePnygs+fPpVTuIFE6b4strHGNTUEHMdHxDji4fgOwzDhdHpCCKLDAGDhRUADZE5eZvyVfwLOhC8vX/D5yyc8Hg84Hg4IKQJ8AOMA5hkhHDBEMXSAoQaQrLDHSPMZKWfM8xkpS1wKBhUvJaK5EKNIoAiEwWEYCbCds8HEGYnlNM35/AUxEJbliMyPiCHivJyxpCSnLULEEAYwSIJ7kxrrhgnD03tM777H4d0fMTx8QB7fgzXWimhRxJvMwoC4oHKyjkFU1vVDIkOZjMGLGsYaLS7qvYNBduUBotMQ7zVVX2hrr6wbNtnHyx/mQknh0U5CJAkMnmYxAqXlVVwspVlPPNiJiNkZHFKpk51s0wSK90YIVXxWU9K2vHOJXjVGB8dLFx3ySnfc88bKY0ugY1OawivDTG93mCY8PTzg6fER79494fHxhNNhwqj6I3Ar21rbEouuNbpQBNYvNs3sBZS+1f/CWygQlBgRwCZa4mbM70/3GSJo96ZJa8tKPS4EZDA7FxFEhTh5pQkTISVVSjhDRLlS3Z0IeENEbVtrKDAlay+g+XZu90Wqq9HKt5Q0W4YIJAaTKB6WZUZaUg3aUoRLbb1TirTl+yM93f2Goqj/sSmqnPWgKjVa4Hk7K8gbFxsPWb+m7Jb5DOKzL0bEzIgxIGXr169riKjIZV/xILna69bdL5lsrOtJiC4+RJCTEBbw1Z9Q8UjW4EzS9bkgW7/YVmrsfof74W3P2LAloPnr5Va09wRZitYvU6ZW5fCFOnxgMVMWAxXmKYCCGD9C3l7D/1KEqV1FUyO0XheUbzMYXc63Zclv2lTGeC3/aAaYvvy+8V8zHfV6vRxRCha+uFH6MVPbbm77I3i9npooX5I3VPh7f7Vx2FYw3GKMsFRGfkcpsnp0AR58m+HqNQOpxIqwU15GSzqXW3QBC7Ebb31Qdim7j9rx2YM7G481AybzU3ece+Vbq4RmyMkHNRIRq1FB+BSokXK3O55/gL9ChW8VDja/2+5XhcGvS1tGiFuU03v8zM+Z1uWv+7/HC1yDk7UhbP+Xi4DljUkVViq8VpeBFT+q6oIZmYHQCWNNe0pz23Z7HHFxvDbGbO+bfb66/LWb9yq8XFrrd7TlW6Tby+YyJ/c2p1+ze+uqz3/rXF17dylt0d3N8uhr6njTZ9333wYG9njOPv1cGyy2Nq68ZXxunYse1lawJczHGkaxxoy3jt1bU2njNy11O92mvHejcKlR3xA93TuvPd6/he/erM/ylzlo1Jkw6XIHYxn7u67XK1wdT2NK03IyQpV1mbMLPr3eCFAK0V8fqBq8QZu5KliLQtSXl/33rs1ctHllRCod8OOz4tRs2G4QmFl4UXPTYnAZAg7HI6bTCe/ef8DxdMLx9CCuQWdR7MYhYBhHPD69w+F4wmE6iCsYhhhjNDj3nGZk5rK7f4wDIg0ICOAsmykWc2Gl4xIDQJBNP2WjlvsN44RhmHA4nDAMBxwPj3VjLTLmPIOCup5kAjKwzAmfP59xOERMEyQeZhzE/THqZh5xTyknItDAuc2pBCEX9z9qrGKNsqB8sMjtUaYgVuCrhiTSuczgXF1OzcsrQiCJDRFi8YQClQcCAjJynddAoCgusuLhiHh4BI1HcDjoYmHIbkiFQ6iw5IROOwGRTS6gdp2UdVCACsVoWPhUt2K5flx5Q+VB2XhRG4vygbyr68StEVsDrOPVnXAw44IIQRb/oT3p1G/K4VKenmpq+F6AO0yzhRYv6ZLKMyKg88Czpok2rD3P4xQPBXlVJEaQDbAxRt1APOIwTZjGUXR1RA59aCVdFR4abVzKXBM3uvL+u0Z4dW0uBimPxnCJ12mv96S7T0RIqoL1FkHZY5Az67G9nBqkxMj1yBMzlii+k6NOAtMaSEgDqliqC8l4ohbh5ZxXO76vM+i2axXwu6AB2Znpy6qE3IK0ZKSFkRLj9eUFL4cXsbymuVrUbeGxWbzkYicIzEVTHyMiO7cxRbkfWgOFnYqQ8fU9ascLJpcaAa2DAYBX43gp2YkUU8JYO2IU5B9jRGZgGABQwHESi/lxOoNAmJdcEfavlG7h3wiNl8vfRBLjA2EcB4zDhHEc5TeMiMOAcTrgMB0wTQdMhwPGcZQYEs7NSVF69UiOK/Hx6a3K84Is7+/mm9MWEZPnLVtM1O5s16cQuG6Z88ziUVTeGjGrjCj7Mm0tsBjeMmw9cHMiojKo/3JSwac7iu3fQpI5CC0zbO2FiUh3lgkUnL9dp/6KgYsaJV7ddVCIDLyhoBFUlGFtDQ3acq2opWudsI+K5+u3FdD2lMJ17C4ol/aExzpKVxFrqwRVP64hQEKz5GpgjQEhBYkREeTYKmdGNBqZqShkS/Ns3VPHxK478AZtTh3HLeHdjBKlHSA5Dp6yxoiIOi9KVUjcMzFbmCwxXPa8J0OETuNJtpTaFgi7+Eju0h5jSdel3jZ/BxuXjBDXlMu/BdxhMLhvfNhf77Yee/izq82L5wHl76y/pLCRyj2zwIuwaMKHxhi1HVFO+yIgEJCJETLEP3RgsLoUtT4V6bQIt9S0857xX+f9+YxGe3Pwa5FKj8/vScz3cku/teRxw47Q/u/pF0n3rte3pj3lTLsJh7YX483Nu4/m/MtItPH3Xh/7gfoW58dvT98ajugGXorIh4CVxN3OicIf1yfGyLbGCPaG/BpIGsz11EOqCk9kcaME1ngRDFXg+qDU7a/dRCrucOpVg+bqSQgqylntjilU6wDVQdD3sp4unIQoS6Tj3bGGHgZwfHzCdDzhP/2n/4z3Hz7ghx/+gMPxiBhHAMF0wiBOkGDVR8Q44BAGMULMZ6T5Fecvn/H68hnn+QVEAw7TAYdhwoEOIIoABuRMWOaE+bzg/LqUeQyHCSEMmCY5TRAISHlBzhNCILx7/ohpOuLj4w+I4wQ6PYNJYlIs5xcsP/0FIRLGQwRTRA4jhjkgzgGvX874E52RE5BmxmkcMMWAjAFEB4BGIIyI44QxJYzTGYwZLy+znnT5UhXmuc5X5lDgjDQYt3DnhJwysunuUkLWuHHiGiiB8xmZF7y+fEJOC5YkJ5tNrzUvsxg/UhavXSAgEIbDAYenRzx9+B1O775HPL4DpkfkMIqCHRmcZ6T0BZlGZAwKBhm2irLyh0nhmVTWIxb3TQnJVhiqtG7QAu0H1JtYq1VuOUX3fGUQEPj1vK3feG3uluxUko1LTovEikgLoEGoizGCGUBaxbrLrHE6OJcmkWtTbvQ3tZ9vS73cUmMPXyq7GjFIVUOp4h4QhjAgDFFco51OeHp6wvPTE54eH/F4POE0TWDVkRcjxg5a9ejWdN4AnKuOXm6/MB5OPwysNxhs1O4/vpJ3nd5kiGj7c1mwLKloQloFgDBTGmrFFOfFYibPA1qgN+NF2WnIcFdsGiK8Yt6UUOwMGSvGyvVMbA/ahixHu3q3DvXbaiHnLCciUkoS4ChJcKPMpiCQ1ha2ntkJOFyBGLTqjynWQO0JDT8f5DqhpaDZodBYD3s184VEzQWVMFYjhM8sbePiI99OR1RXGwFDjMV3ftHN6XjKvwR3i/6mzNUGP3yHaC3/XviAdG6a/q1a0yvWWvhYI8Z9we4S40rdnfkgjFEDUUdV3LnYEDGK67Oopya8ctbaDTfWZvnmrikexVN3v9lKxzvtiRy9Aq/2fz0uDS7oBCJffoMf+jLg4b/MfgUA8nndPDLK2vVwb4W1aKQqn+tPmXBbCyEU1znCv19eib8JYV8FjTL3DZ5BM3YE/8CNjzHVjuj1Pd8kgJ2Qs4W7mwKLAaBt1yYH36V+XRBbb6gF/s1y9AVVhmSlpHZWB48zGvqiAF13k10/EbHVkvrehq/2beu37v96XPo6JLGNEPbWr29V22+92ugVPs6dgCgnJIKekFC6wiQnJbwMzw6n9a6Yyjp2LS23ZdA7xI4KVju9qmOxdkPCUH6SLVAiCZ/DUL7A+JTgmHcrdJu2l3Lh8DWz+7v2tcy90fyVUabvxXYvmbn0UZrWUaMrNHTr/pKivzy70WBRs6/LLmxVyVfp76XvrrWxpE2jDxfBvzUY1asYjvyuTme4cG63FKgRiJCZgKzuL60eABmssFV5Z7KmVWSgvb6ULkP69lzptYWQdT7cJrJ8O2PVep77nXCbdKRfbP6x50tX7aJN1q4f0cv9ad/Vb982BqWuSyznxe+7jxqcSu2V/HNHHXijnFVj1nP11tSO7w3zfUN603cO4P3XWyVJVr5hrvfX5yW42jem3j7Ym7yGm/P6Z8tn12RzgZ33lmtrTd6KC67w0qjxtkwOXn17Za7J5ymdqTDf80WXqO31Fl9Kfs2sx+UtMHsZL7Y9617utO9yzsp/6R+8Mweax8unYkyotNYILnX8UOWFuLB4VkClzdldq1sl/VjyGsdVFLC5qa8S/NqWZiy28MFKNuqGzQC1EaJcBmOaETAejjg+POL5+T3ev/uId+/e43g8Qbb2m4zB4LSAQWCN9xCUUcguSHdaEjgzQoToDizGpMlBvrs2vtqcEAhDEBdNKY2gHJCyuCyWExgnnE4PCOMEnI5IzMjLC0KKIicTYYgRHAbkOCJmQljktMZ5zng9zxjjGQMkKgQzgSlKPykixBFxSKr/yGA+F11cCejtB9/dm67H60i8fq96QajwymAxQlAA0RkUorjxcu7BjP+WKQ0I44RhPGA8PmCYjqBhAtR9k7XDDGUMBoJtjKxyDcPg3+nhPE5j184ibHML9w2wOXj1cmrhZf36q+WAc+FdG57VyrGFWoyCGnDaxVTx8V1KMPbyrgU21nLttEbb8sv867VU5P6yrtw7f1OGzI2Zz9/pOGx5Q0/4jzFiGgYcpwHTKL84iOeSBLh+3cITdMnNXfv4FnpATd1dwVrOFt9234baN56IsB3hrZLN0r4RgiptacZFglmboSDlBWblIyLk0DIdVXlQF3Rdb/J3UVaoSxRxg2C7R1EQqLl1WAUzcYpQBmThWN0k1se+vH6igi7a/PqCl88/4svLJ3x5/Yzj8oiYBhzyATFFjFktl+rvdyA59RCGgJAsuHeAHDMDKKiFNsgcZMrIVF0h2ZgT4A6N2Iy1pgJme2ZEVXfeZQt+JAvRXAFEjbHBIQHEiOrP2oxvbIRdvytonEiO8ukxPgLjHBkDM6ZJfOCNi/jjF7zkR7MKOB7NbLBam09vSdcsm13um2ra3xmZm/uagiu1Im+T2YxvMaWChWOiEDDGEUMccRiPmA4HDNMIGiPG04hxmvDwcMDD4wEPxwmnw4TjOOEwTIg0IJKcPIpE4gLGtagoTAqMoBASyhnEGSHbjpJ+lILsQlblJ1Moi17a3zFmzRj17mXaq41vZjEMmoJ4jSuzazfkOCTkmpHFqs7VTVyNERFV0StX+QbioZHNVx8jUJ1P13GtTxhJC3wdgzANg9Z1iBERAE8jZjWUppQwL4sbFYY/f/NbMEKQ4mvb9aSkuqwK2gnEaSxVZve+0K2WOdpdhSzHDMvaUfxr2lV2t5WfZERiDORogLYg6kki4+lCPcXbtbxkkTXnX5ExpM1D+Y8JARFMhEypFd6Yu3444TUQiCVQM3IAaEHGUsa59I8zqNtFVZSrxMhJ3lnxakcv/lq9oX7rVF1vlFgpkeHWYzlQJRFh7Dh2fdF+X9d0P3bGfitNjEAYCDHL7qSYxa8tI2FYApgClhxAAcgkJw7mWSoIOueRxegaOICYwInBgcDmY1/9wdbEtT0qDBV2zBhgroJK+cb4CAVl4jrlNi+JFyAzQlJqHAgDBXCOyImRSFw2BVqAMACIBcRk97u6tAR0j5P4CU05YdFfKsIAkBMjL6rk1naIy1IqXTR5JitPRZkQQqX/jvogG5TqYlsZ6wq+2qel+wau9uqNTmaIKhs0FF8LP2/8TVsGERqYrvWu17nhrWqsuI5rvYxligjxi8tlc6NhSGbha5Y566kHOwXBMm9pQUoiwJ3TgmVJOM9ziR/BhcklxCRuAwYGIhHGKCdnEjNiIHGtoP6I60YegSHOBIru9GM3PpeUlLvvlV4bBFjR5du+LHdl/003MV9vfFhXXOiTp0OXUgfGBWUHh8t8r0unfC9XzbhSc6UhW80JO5sVLikObe7qq77sOyTHvq3W367feyWK68GtNlhbQ/furW377ST2P+bVnncDG8sLNvaGiwuN7TVY13dT3oV1fEtay0T73zHntj+OJ3PCOe6ax64621RkAtG6H5fr8KuxHT0dP2Jtrl6NryfC/kq+U+rc3WTUSbta4D3KnKtVd7znvd+2X2xjMNbGC2sgnKDwubJ7WXYEL5AAtFTotsmygXKl2TDQEfnTNV4u9rOxgvC3yIrbGSXeA5CRKYODXkn8+YMzyALkIkFqkvwhyy7tkGX3dmDJl7AAqCchMi8AEggLxIf/AvBSA+3qbvlGgVqGUIwClPQ5aYdY+sDJrz2Rrdi7AAa0zclGEDwdgDjgww9/j48fv8ff//4/47t3H/Dh3XeYDgekqF8vetoS4nIpJdkkmzQmxuv8gtfzK3788gXnecHEIwYMmEAYQgaGGQgJhIgYMsYYMI0jDocDXl5fkNKCEAnDFHE6PYongE8By7IA6YQhDnj++Accj0c8vvsgpzzjIJ5D/jYDIWM8HhBixBRGkcUxgAfoLnHCPC/48dMZL+eE5WnBw2GS3eY5gvGIEAY8ngIOwyvSS8YLPuHT8ifk84yZAxjq5pUBpEWZadkIFCMQmUF5BjMhMYqrIHACYRb4YkagQWLWKg+c0lKCLwcKBQeSxu+wTdCBGSEOOD5/h8f3v8fpw3/A4fn3oOEkej6eASSAFmTKmOOgYTMSqkSiMpSCT1Q6TApPVc6UfkbTP2WHsVWBYy6qbBs9EUpA95wWRJJTLTkvgJ1mYJMtuJxwSMussVvsFEYq8hIxg9OMvCzIry8aE+IMcEbQkxGcFueiiRVfLECe1dqSQcWQ0Z6IUAzkuI8aJeI6prZ1hi7vDidW6u6JbyjPCQxSY19CEBk1iB51iIRhDHh3ivjuYcQf3x3w8fmAp8cJwzjgrJtUzfBT6uKqywjGJxa2tsPUJpB6nMF9/7aTcSn7GpkqF/pxuJe+vNkQsT0x62Q7Psv+SGWu+l3MriuNpU04gtYRTiFKnQJwU+kLXg+icQ4MCY5Ub13vanv6sguzUvKujRA1I2vwwUUFzbp4G0WUq9cqJ6pCrM8hAGiBSfS+Y8wagdAzbLQnfvhx4uayrlsZBTbBxq422orY0Qo9XpFAZHEj4E5GEHKJFQGYtbOUYYxtN1vUaB3dcN24FrxyYv+dFzpdn1b5Nc+bOEi/U4/gj+f2jHARU6nuEt4+DSG+5+IQMWhw1yHEupu4cVfTtsbkBxOc7Fr6VyanFzbWaevN/rqxMai4wuCrv2IbJJqa+7ngLVgHyjryhjpbY37VFMHF/+sERWt7U273C+4XQ0CO4o4md4paFCJyWUG02fMrMPhW5Y4fjX50WkXitgJmrWDoJ3FfAUG4MNVGY7rvDNdszUP5dX2q367XRX1ev9seynZ0RCm/P+bCP2r+AuNU6EDTXh2mvbYyqK5Nhw8NVfbGhT1jw9ZY7bXdX0uFbiR8mdtGCP++nT8iEoGhxMBZ/yJrQDVSYxgTqBzQJTRLXnEXM6FvQslPZSR1GKmDrS2aw+WeDC1Sm8nviG99n/bv6q+Ou+Ol3DB7/Ox3CBZ+qhGAPXfgk21HoDI22/PZr9GvT+TGqMKS4zUM9uy38bGsxxYPX64LAHrf2BXerpVj7228bR4MwHrILkZ9thMQdW5yrr6tbTdZ0t+SvSECMIMvUwZlgfeguCNkAhAQs8FtkU7qxdHQ28epxQ29wnvLQKnD2z5o7pWu9d9cTR0H9iY65pDhig9Zz90mS8m+auV7/drYWCbkO1umpuVBRHilNl/fEN+MjTm4DLcu3w6z3LepPt8rUfEr1esOO6Zlev6uK6vwXG0NtU3X1/heWhs+34bHbuXvrfzMVcKy36rMG5/Vsq0tl9uwt0Yvpa8y/HXs26W5vpbY4+ebyE7NtJW1UE8P31ZPd61FrtcCd9/3eS9qR24aWmnFPdPwJpHz1rTbkO654QBswG7hQdy1K8VWvtf4bE17UTr29KXcUllo7Oqzf/1d3YhpBfr21Z/FkaC+D4w2b9fPZjl0eiTPG1L3ov2yEoKeJHgULhtbAmgY5ETE6QGHwwmH8YhxmDCEAYja90yidCbZUMhqHJLNdrm6HQJAJO5QhyAeFQTNZ9cQgVXRNQyISwSDi95hGNVbwzCIVoMYcRgxTgeM0xHDNOlmEyAlgun2ijeHMMBWbyaom1XRAy8pA8Q4LwnDkMR4wABD3EbFOAHMGIcJSzzr5jOAlzoFVTFbJLDKZet8coZzdZrbeS4TUZEyQwwR2fvoL0rk+kUIhHE6YJiOGKcj4nCQOSQdB9k9IjNh9NVBgPH6DZvQyyN96hXGTkZoSrbX4Oa7mt+6ZJtR62lef8KiUD67qDGhBnPXex1XO6nSniyy/N077ccWx3ENfe7T8Q28tvNgpXx3hLk35ot9UWDYu9WfxgGHccBxHDENETHKBsnc1bFGeEbbfT520942vJbjGNAracUNb7OM63G4I32FIeLtqRWs63DIxAQ3qBlg9Y8FxwQo5rAjIVsKDYsJkXUB97s9e0Z7Tygj2h9YP/BbQSU5i2C5LAvO51ecX1/x8vqCeVEXTU3k945AQXcJ6NGdWgerst6fgKAavPNaHAyYW499HOXHxE6plLpDUN9zUidyZTC9EgRO2HUoHVlvyS3CcRwBIkzTAUQL5nP1l9wixq4/Do6ax/vduprIE/wblRE3l007ynStuSbPAGHjvZRlsCHEX4j6MB4wagCoYRgxDgeM04TD4Yjj8YhpPGAYJ4QYQUNQRmEo8+SNQNKSViEmD1uEs8KRuzNgfVqxlTcjr378rLgep+x92681UoXjnlJ0K5kitdDVXem8MpemLGUW/94MYNRdycngf5ATT8nhBevft4HAb5VMSHqbUO9xz/Za2GC2+7qxXh0MiMTvyg9BGD2D8yEOEhsljohxFKOdGeb0dAR1OPTSKFQDgc1v0PgGVK6UeiaxxSvVoNYztS2s9z9mKA5uXQ+qN1MANb5Qz7z6+vfuv1US1EKyHlzfRTmxjRNJgcT6OgwSR2mZM3LU+Co5YhjFV+qSkuRLslOII8smg7IZJgMUmjqqEeJWiuHF5UvEE27dOqNRq7GAKKCFzhFYj7rLKSud1upOMkYbwjJ+rqRSlgWIQ8F1SncbOlr5Brju8424lMr39p2fN4Cdd9Z7MZfv39YapO5d8+vGZa8PzNt6lb31cNOV0e7ahFG7uqmmGoQqLSo+qDVGxJISUpZTcfOScZ4TlpTLXBpii0EN1+By0i4I4a6CNgfEALCejDAeW/Bn29f1Lqp2HP0YX0pVGMOqjp0v3HUtHJkxbH8H/dfgLGurr3tD8FprubBqCm1lVSXO9ksAVNZc+cLWkrXIrcUy/aqEuRdd38Ij3f9dP19+k8h+XStcf6XOt23s+deXvmYcro355bSdv5nrC23b4/Pelr4ln1KV0L89GLvCZ3x1/p8rbbSBueysFh1B9W1vchIBiLC/DecJfvG0tbBsGQhODjM202CxYl3Fp5xB6nO+BMZNqbiI4aSulTKLe8+svHUm0QeXuBLKTmr9EZDd8r7vhY+xLuoD48fdKWF5LGNRT9friFCAnbSUfvJ6nZF4y+CFgZQxHgYM4xGPDw94enySuBCHSXRRaa5GURbYT6ugwtJeC577+PiIZV4wxqH0IwQ92QCRfSSuJ2OaJjzyIw6HCZwzHh4fMU4ia4mMOyBSQDgMGMcJj6dnHI9HnA6PABjn+RWcJCYWAIzjWNohvPIiMdac3izlDCyEl9dXICcMJN4WbMd/HEYQEU4PTwgx4PnLBwwvX/D615+E39IhJdbT7tGgEWVO6gYS5dc1jqmdRRcPHtzIjoLrTLleY3UFIoRBNpmdU0AYRjw8vsfj0zs8PD5hOB7BFCs3kqsBu5w1djBwM94yGMwdP4pON+KuRYDQfJkZ0I0x6l0JKFltMxU1PG5Za8ygzvWSfQeDQT1FwuqpQuJuaJuyl2vatn+7JJjkGo3s614bpnv+pzetCi9+GCNOxwPePT/j+Z38Hh4eMA4jQoguv9uUXOQO5S6rlWvVlmv9/K2kmw0R7aSsO9owzA6ZuQzlS8+MNHn6iWeU45LdY/T4eGvwb1msvh33APS+Qtm3UxevIq8lJUWkNYBL7chG3bTeEViNDyWT5IGNpe0cRKP88cqrjYau623GptTUKgLciQjLYVyBF75rsVQQcSbdxc9cFeohIBeFLSSojzcMlH9ggNQ3fLs/F1IjIura3ENA6+dW0dsX9HZd20qBLaVk2Q0cI0IcnGK1xosw5esQB7W0BtiJGgpBiWc7nExw89cif9+65v0Fg8JKThEAK0zktdSv0yoAmR5hXxCyqho2fWfJXUoG+1bNVn/X/d9W6AjMi494OdGiway9C7miIUSBy55ZvNjeDh9/q0ROyXSrMru2pZZhbduiB1zWfFe+YYQijchTwPlOdN0lN7ahwHrdRV/WQVkA19dynZ8dBV2vdyJgFZ+gHxvm4laqjpGD9Y4O1LGqC7feM+B2s5txlfs6sS5z6/1um29KXqz0/Vqv5U1jRPedGdx7/BdCEEGRssBIgaO1cF7Xg+Eug7+etnbdWOGM9YkusmdEOg1uDfs2oGX+14HYOpzLrL4Ye0S9bpfJDqWvirMvMdeGS21e/PMGFzUDglW+YozgNYzs0botxf7mGuuJVJ+U7+lh7VLaMy5ce3+t3F0ayRX++vmVec8qaJuRwnztovmWkOXkTxb+K4DAQTeOACq85uKCzeCbwdWNoZYkbdses1U/N/rt6UwDO6gGjxV+7/jCZsyadwZLta238ltNneWT7vvmecWS3Lehayua3BXHosO1hg9WONhcETZMbdN6La2TLVx7/Rq7ROs9fq9jst449TVpJUcRbc7xW8q8pc5fOt3PW90nW/o69vNtl/stx+M6P9duGqjjYXC5w8/swKmVeU9b7klc+ES7R1PnrTB3Wz33tbfvn+Hs25PxMLfxsOu6LhW95nRqnVvPYQSrE7p8a7n5wtB0y4U7/GltYBSgIr33Hq9Wvbc21MmWujX2Q6N0LUGL+2vtjz8ZIa6MW5mltIGo8uHFoF4NzQ0tpdrUloFBpRV7OqLulSnux2HEOAyyWYkkSDSra+wi34OR1W1Or68xvcI4juK4tNs0y0V+T4XvG2LENE4YYgBzxjiOZaMjM8qJ5SFGiQuq+gqjkzmp2+OCMyp/X9tWXQf5lDNjUc14cR0MIFBEiMAwTsicME1HpJwRwxewfcMAQU96KN9ZeQHjwyyOl8gYJrNtoWGCk+t0YisPA1DtICgEDJPEiIjjhBiHks/MpMafQ+Xba3qH9nTmDTjNeNOyHlCedQKFO/EA5Vnt6gwZNbtvlJbpYY1Lf1byTjl5ArSbq1q9lK+o4JQ7SUVLt24zmK/WAjz/s8aQvgaCbDaLMWIcBhymCYdpwjSOGGLUTWkofex5giLbF7xR27qGja22l78u9tHX+a31SD69LVj1DnBfEnThvujz2aIti7fkZ4eEDXE6hN+5bPKTVSZM/2NuT0VYPvum7ibtGaZ9oN5iqrb6n1IC5hkvL1/w+fNnzOdXpDQj5QU5jyp8ep+90m5TyMcYSzleEQ3yQrr5UtbdsSEAQY7ue0GevVQlnUDzIBjnaPMhjQohSADEEJWgylV8wEHHNyOlOjb2sxExgpJZLMeLjvmocTAOY0JAwDImzLSIIUL91glycMpGMr7AEPqafl9LVHp5+zc/byoHscqTPQVICAEhDohxwDBOGKcTjofHQvjlVMSIw+GE4/GEh+MDHo4PmKZD2WXglbMSKyXI/DvFAHPrQsIzRF5oXyNlhu0XEHhZs/9G+G5BhuVL5mZ92g544SQ67OzqImW6qLOubzHkK5abemXGza2F9F/WZowRRCT4gBKGJG0f8gAQYZoSKMwY84Jl4bKWfuvpXgHRC6dvr1SZo243QLt2gDgMyhwfMI4HDBpLZRhGPRkhzDAF538e20zGVj8ApTEkOxMER1WDscX9oSJd9YYEYzKpoXX9GBEqvgfklEeW853rExEsdECKVYa68L2dAqHpz/b9rcrX9fiYIR22iDoa29H7fm13dFUEo4A4yAkJ5gFDXgDoCQlm3QlOJVCv7DCrLKGNhTHQQfOUwH3cUQUll5s9t0ltdrFVEQIENdZjJa0IXtXj53oiIikPFAMhJyBRpZnlOzLYIKV/VHgiK5OZ9YSzM2pk2VNo8GCg41vVC8Gr+dhJe3zQlkLtmmLL8yrGzwDuXuHIxqTN3/EAO3DbN+GasWGrbXvjYDxq/6zS0NzMU9mkkjOWzFgWO0E7Y54TzssiMSLYWDUpf9F2DDmLcB9JTkZAlAExEDgGubKdlGUAAdA4OGx8FNpxW/HnF/p8Pe2unpuyX4O92wu9XuYevv+aNty6hja+hKzqGpGol+mttF9DEd8mw3/tibNdwenfcPpmim7m3+TwXlPgXDNG/BKJ+TpG+rXa9ltNG9oebI0iFRWop4Mt31N+2dypkOPj6+ZL/QBE1J3o7OuEF0sBVRQXbZH6vecmOK6dhEjVz3yC5E0+X/2OM4u8mZwRomtUuXU6GulD0Ksqd7vFa+ofE53JeMsQ1B1N32MqOg+W4IUl/+n0gKfnd3g+PeDxcAQFYOYZy+tZ2qDjshjtp5aGmBwxjiPGccTpcERaFpwPB8zzjPP5DGaWExGmiVf92ul4xPFwAEjwU4gSN+E8L+KlhETxfpik7KgnNed5RuaE19dXzPOssoG5kw6qA2OkLDx7ZolNwWzvCZmBeZENv8QZMQMBAYcpIhLj9PQe43LCy/mMOH3C5y8zXl9f8dPnTwCAqONA6rFgSQI3KYuBZFlScZ9pY2ibc00l2sc0s5MbQeE8yJYRDRDOACIoTjg+f8Dp3QccHp5BhwdkCsrTV9DOTh1KHj/1uKoXXnbSSvHv5MRacVtA1vVhJ3mXnDS+iAvGzdWVqKjuzIME6+kIO/FgLuqTrkOJDcE5AWnWNasxIjKD8wLkpfJpGpSUyghdwtm3EkuZp1t5RJPh/HvRZbf4seJDXVtEmMaIx4cDnp9O+O79O3x494Snx0ccplFiBjKDF4014trTyyG/Nj39FultJyI2GHXLc4nhrmqW9bfrnHIl6HEg/41N8k47tu6J+trtnrt73wcDuq51F5QnTZ2qPGJAArikRQwQGieC1bpafM51basKLVoBn89qStLNvE4BRKro4J35adq9Usc6hVoxkmQECqoc0eCkIuHCjAQmkJAbN+9qKrC4EshZXAzk5mQEVaaxcBubUOT4oqpEulVAa3eu9DBzeyJ4WKlzWFtdmbSKRNo6a91WxoZCBFR9peuOghgGhDCooSgiBDVSDKP4hhzkPnZBaY2nKb/SGmXiVDHvLdAmIkv7vQXbI+q2nGaQasc3+l0ylPL791trbk+B6cu6SKc2sm+0rrujTWG7abPBLXcKNpIgWUFd+YTgYn0URZtZIu5U5vStdgTrnvz7aQtee2VfW2dbt+486XDmbcRUuX83JFtTHhQfxhAQQyy+RlexBQperFGqCf201oWxOTK9NLKRybDBauyogoiteVPSr9bN5tB45X5tdw+CDeXbUDLuKYJvN0bsNVAQC1kDgdK/nl8wmuufbym4y8/WjFs/8q4arG3M+3azCpKCu+qJiFoXlS4JSdviH1CerXfFbeGhrbqdscDhWpMBvEGsfI+ynwoFTLxcov9lX4eru0H29oXS6fJ61WbtFfXPd040XVW8er7Lyt6CvTU/08NqTVTXkytzfWVdK/vwfQ3ub8Opaxppcypv6263Bhb87juLHaHsodHZrFHQKcnmkkQEQPioTPIdkZQDMleltGpHy1/dmDbmdXuuPb/2dvq1l8rIX+UlJLetlUt0Zote9fz+Vj17wuAmf1LaQ24Br2HKYNVLFAx4nd3VtIn3UHd77spqd/K+WjoKDjWifBNcbMllt6at/JUelidfCX578LI1vnv3e4aua3W8Nd1T3r3zvSrbZMsC6+WF40laPm9v7G5ry9dN6M+utGH8TGvs26QtXLOF867Tt731bVfPmFSZ13gSc9cEk0XLF8bcVzrFQOGTvC/6XL5xGx+lEqUN7E4NmCxom1Jsc0BWo0NrKFnTS94omwtGrXwuuT4JLhSUKPxp20drkw1+N5x2X3Cq1eF5TQINEWEYcDyd8Pj4iOPhiGkcQUE3n6hhxWJczCSbUwLVTR0+hSBq8yBbtxFjFLdEDWxoX5QPpxhlDkycIqNZMl42HMaBpkWCFKe0IHPGfH7BsiyV/0flA0G2wSogsIRsZrY4mOKOtugq1FeWwIzKeWFAiFk2bi4LpnEE54whRuTMVSYfgh6MyWKfSgyGd1+VjXOTkyJ+3AofrRBpMKReyJh0h3/OshyGAWEYMUxHhPEAiiOgbpkUutpV5GG4zAEcOfVtUdi6cBr/lqRUXdcMmvVn/GrhW70c4773vFqzjuytc9fk8zAzyi4cJwsZ7DVl7La9/r3FK65xXOVjtni/Xibb4xX7Ev3yjoEwRIsNMWKaJtlEHIeyHmVYeLNrvVxyP996m+GC98XYzTa9la7+KjEiriXB37TCxwAKkMvohPa5I6qtkAmsiebefc8UX0/bgoa1I2icCMb5/IqXly84n18wz2ekNCOnESklBApIXd0USAlB3WlkJx6YWa9r4Tx4ZbP6Dyb9QeM6XOxb5QGKMCQ7TQGOUXdbBgCDTAMt8IaU6ssNm3MS1Uo+pAQQYVwyCIQ5RgQG5kmOEy7LgoCMlJMuBhWcveLjphna7eIND+8t1aM9Kk+5qLLqtc+3hXG88qXEUEFAjPXUw1QCPh0lUFSMGMYTxsOE4/EJDw8POB4fcTye9Bu3E7y0cb3iMjMWXscxYWX+2oBEWYk1Kyz0R+kqu1g7x7djORuhbq3tXd0X5Tshlj447PW6W8WYmxMZtD3617caIPMDCj2qmjCmBAIwhAgw1A8+YxpGAAtiWMoRSIOTr0H23zrtKecuJY9l+/m6iTB2V4NaoqqctbUiQaAOYozTgGjDMCIOA8ZxaNZBiBVnmiDR0g8Ug0Flfnyr1keFLYkQVI24DRPBAKvinBxzoK+uznfV98jO54qDZJTruHD33XqurgnMF98Tyhrp14wJJH1ZPS7X0kq7t3CD0Y9hENYlLTOYGUMIugNcThEGUrwUqlLEaJno/1rh0vLYM9IdXRRMeHSNKIx9pW3o+2C40sad2r6yMpmMjEwZRKIs5iyCFnPLvLZjxPX7nFs3ThA4WFygY9uV5cddw281oMwdS3RtPZe13K3hIkS+QdGy5t16A241wq/ztST8slFhzbBfMzrcMh7NLCkslTgQtiMTAhdGQxOqACdxIjLmZcF5WbAkEYbNENHvwBIBWgzaOWbEEIDMmAOBWQyvERrMupz6qfNlASJv6WeZh43nW3/Lg4tD9g1Sz8f370xB1AplW4q3a4ri3Rbs8h77/ModpevPCafF0HpbWrUJvCNdfW3yova1PFv879b9vWktw5kv5X9Pv530dXzst5xLrzL7t50uzcnNog4AFPVp86goMYtC19zccLAooEgQXB18ScxIMHoqPz2YoM8rLQW6QMLMGog5AexPOHA5+ZDTUq45Z6Ql1d3ebve3lyHrTm5f19aAGT+rbVE6rHrpFTb0NEsnBXDK7n7DiyhuCUDE9PCM6ekBP/zx7/GH73/A9x+/w9PDIyjIaeFlOSOnhKABgr/wrGMmegC/mz+GgGkYQSofAdVVU2+IAMTlkn+nPqsavofzgqhGmAgG0oK//e2fAQaWpJGjwQAFUJDYb6oBAxAQaMAQgRCSxFnkAHAoslxOM3JesOQFKTFCFjoZYkSOhCGMIBDG4yOYIp6f3mEavmBZZuWrhLeM44DMwLIkzEtCymckzkj57HTiouMorsRVp0Y5IwBIuo7yol5MBumP6LIy8rwAMWJ8fsL4+AHT8/eYHj8AwwEch6oLpICMoCcLdEX0C7HAmocqdgfse55sj/pXPnvPdsHKr6ackPQ0b86s3lrstENW44HTtVhAibzU0w85gZS5tRMSdiJCTj9wiR0BxRemU5LGuAAVb0y30iAznPY84q3f2xkagngzOE4DHo4jPj4/4P3zA949P+LxdMI0joimF8gZOSVTxL6pb7uGkV7Y2y3ktmxfm+4yRDTKX3Z7/64MkuhfqlL2pkROeNiYbO6e94rFyvTfDqf9joweyLZ2EfhvdwUNHaucEpYSqFqDVbM7GZEZHKqQUEhPI5yvkUoxHKjWZ0uIZ1Qh0hRH5VsGQLwab17VQUWp1CoI2gA9IO9fT0rKQHOcjIC6IzyIK40YIjgwYojIoQb1DYsgxlwUJm5eeuWDtfeG5NFxr5xoh/j2lVhgwFlzGsG31WG5snsupr5vxzmoz8MaAyLEem9KGgnOO+rxymp8CDHqDnFxx9SOnxIxruuLN37yyrWX1QK+k3etolmPVy2qVbj1z24xQmxZuO8SesrUdQqpYggw5aNqKi+0t7ZbfsF83FvcAua6q9v5w4yhrtd2rO+Dx7YN356i3GuMuE+gqanSnm3FeoVjUmIfdH3IqSA5DSS7DQKFum5C1DUVurW2fTLAhI7ChG91d9207lFlFkFur73DCSt6wivRbpUMxnrwIyio7rGfFxS/15S0vo6dVqHUvCrj+omI2iaUd36d1BNE8jNDRKJU6EXbZq4X97jwtmxjaH/UMa1UeWMm7mE0SkvMcFBhqv1B+ez9cgueNhxX/q48EZeadphS/7cKLtsK1bu6dzXdAmsC0y1vsVeO3HT8wCb8Xji1uwPnl+DfC+T1GdDSwXYuKm/VfQOUuW+upcxGTSGuBglIOUOCRjJy0ECCRQgUgwUAhNBuEGFmMFmg69tpxJYif+vvdTfbhfcWmlTrpeayU2H5pufXt8q8RzAtVV3pwzZ/opSsfLp9qsi9bXlHp1zfM+bvwSq5RdLz0ujacK3v67qsXS3GqX2zPIZr9w1CtySPdtc8fBFuuueX+7KXtuTBre+3YOtO0lDreNtnv8m0J1f37y1dhuXrI3NpvZfnV769Bh+35rslfW1Z9+DSW+fg3jbR5uYy4QHZ/4qMCeV9bCsbIYCRXb0Zbvd1CRyc3U+NG6aUtJ8pZLl7zgzzP5+dy6akSvOk7mPMDY+UvFWv7cC3QLze6K0/RT2F/1VGkj3Df3FoDbnpn8qTlldKS0AB43TA6fSIx8cnPD0943Q84TBOyFG8VuQoimoJ5FzLEbedVFwyBSJwiOJESGmLKJxz2QhR4MF4tEAgDp6cNUn2w1YasSxngYmXz2IkmWfJFwIoRIzTETzIDnGiQTSVLDqQoOWz9rvVPwWVyavBa04JzAQOuusedUPsMAyYxqn0i0JAGOSEBFiMTpHETaqfhmaGbA4MRp2b96IHs6udHgAQQsR0esL08ITh8IAwHsEhgKkaAgovb/wC+zpXUFJTgTWni9PWh438RjvLtKLKm20MEuNjK3+bs7ljyiWwdi+tcrfu9taojwVhpyTKc7hvbP3s4qWvoZzbvPBbjRBAHT6CGO3GIeIwDjhOE47ThHEcMA4aG8LxYXV9d+Xxvgyz1eb1fTvfu99v6ROu0Ii38PRvOhHRGCS+MomSHAW49aEq4cpq3GuJm69W2ViBxSkWLqQtQeXeAV1/Y4sJABPO5zNeXl5wPp8xLzOWNCMteiIiRKScgCTHdswQE0iOfzG1JyPKz6oidzXC4PKFQMgsFl/SXXSZqBwZc9RRy6kKPeYMBAlyhICqPIHt8mZk200MRx/1zoRgZm58O8eyQ1ziTUzjiEAB45QlhsSySLtTQtKgQgInrSDbCzuX0qbMSn7w3s5QGixvwdFtSKvW7xUfFlRXAlAHhDCIn/txwmCGhnFCGEfEQYwMh8MRp9MJTw+PeHx4wOl4xOFwkEBSGshqGPQYWNNe2RnAoMrglR+7PNWd2KbCpfOFvSe8XjIeWNnNU25hac8YYWU0J3U28MNWm8zgAKcEs9NH9e8MWQy+HGFY95Q0IQoDHgcC5Yi0CG4wP95jFH+Zy5TAxBjmWX0v2nFjLQ9fA6XfPt2HJ/fzeoImjNCGkA/ArfjVE5uvGEfEMOBweMA4TpgOD3oaYlQD3SRrQe+jGeiKezNya+9S/9oTNu28oyhPpQgCkCtnd/FEkMzyrbhD8nm8KGUYTgrqcxRYMwzbCuC37Wjvv/dj4OuQtsm17Z9JbkKP2vUG8SkbCTwMiAQssxzPHuIAMOEwApES0izjzG6J+qs1w8+bb09hBj1u6duoiRt4vDwuPgnvbcz8jsF3r0yueFZiQLjdeipY13gRIsibEpDaYuoysq6tqrqfF7Lvtvp9S/KCZcvHbBsM5Zu2+Zfg29bWtTbcmvxcbv0qDwTnSsL11Rg3K8cEULZj8PJtYm4+FveYJLuooDxSAgYVrOOyADFoPJCg7RBXT0Qa//zCeG3hgkt44q04421JhbTN57/1tIHzLtBG3cpTdVANq76vEL/MY60+uCrU3cbHZtgZvy0jgweRe+SuPUNAwzfs8N5fC5eXxvdSvkv8602Jfuk19dtLbzFC/Hv65ZM3BFYNkSiGWYmzKFlN5wNkPZqpG+hBIDFG6PJYVI5MnBp50p8ytGeUMwI7ZaXtttbd10iyU5uTbQSVOJR2EuKsO+PTMothYpHnCy/InGRXPGcs0N3fnCqPhVzMDz1m18HxyqjC1zmNieAEcztbH1f9DEE0g3b62ngBCkAc8Pj0Ht//7vf44+//iL/74Q94nA4Y44iZEhIyQsjIywKeZ3BOGJYBS5bTl7arHYDoh2JEmiaEEDCOo4zDsiClVNwz+dhlJZh04V1JRRw50xD11H/AGUtO+PzlM5Zlxk8//UXiT5zPICJM04hhOODx6T2m6QFgwjQdEeNUNiAx5cK4MANRT7OD7eTGCI4BWeMMfH45g5AxhgWkbisZEgODwHj3/LwysKScNOB1xhwJKYuBJlul/USrfCJ8VbupwMsOdiICISBOB7z74e/x8PGPOLz/PeLTB6QYxRgBcZuVnYzLuk5WlKOnJbYODdbIVJC2HhVWV3hV44eZUjAXIamvsYxVVqOdudOy+CySAcX1GucMThlY5NQDshkZdDwsHkSu93B6JmYGcQJ0nZU2bLasa+cNeWrq5dR9/mr1ZcMPr2kWQeKQjDHg6XjEu4cHfPf+Ce+eHvH0cMRB11vBCRfG/et5gsv85r3ZLN2u62zTzYaItxRevgXqbviVQqL2sygubmyLKV62lED2vGdMS506YB5hbDLu1h7qMc9aUdYqyKgQxCJQpoS0zPpb9ETE9m7GOjDVKENodwj68VSOVdqwIagz9c8teKHNjzIKSixJ+25qPttFJQYMtO3Q8pjNEtwKTNKfLUWdIPeofp9iILDtanUnIqJa8pONZwlQ7PpuSrsN6FnvbHd/+wW9A3j7CpVWAcpdnk1BSMfCFFxNWW6Xm8FcnSvbARydz3uLCzGIgYksoGvUgNUjhnEowamjGjIsTkTZBa5za7V7JUiPxWUOTVmCEkTMG/7suqtEuyEZzPh6fboV4fXlXEqNImZjDXkis0UIZPwCjFHcMkYAZrzLOleMEAlRAwzLyaDw/yfvX5skx3U0YfABScndIzKzzqVvc3m312xszXb//39a2w87031OVWaEu0RiPwAgQUpy94is6p6xZZWnwuUSryCuBFA/wk/b6WivfXhqSPvlznRs0Fz3Y/tjHP4RYdyfJ9k394xIdp5yd42tk8ag679+r6TYcqSkSZNTx6ka85pHhDKxdc1RDVF7yviKC7SX4/R0aMn1jXeeP5qvhm+c7LJ9EmZ86BWI/n6bf6Y2n0dKRX/1v3co8oCe3hnRliWriqNt3bV/AyPv+2JrZvFhQ1GvuthCFwY17hUmgBjbrnZEVvtjMKnNd/x8J3V4LO3uORpqNEn5hI1hjbQPNT/FkRJ75Eep1lVRgnu+GiXQ8LKnxUeIo3Z5c3+rxGSdoJqqZfj9PpO8nXd75yMK77F4Y8T+fX8dvXA+hr+APdgfadWW3xFhcFt//dg9/S9QNU+06tm3TabCQPV819N4kitC4CEXRmSAihkgevgSGN+bj+fWqH09xiHdd/fveH9vfu6WvZ/pGA4elY8InUcG3b1nN1fbl/Wfxv/t8ToABvp/bGA44kF92aer0sajOXiKFxtwZsPt9+nGs21v5LSfKM++/ywPujfXHo9/2BjxZL8aXb0/f3uwe6TcGGWUDc/zYX7g+fIIj2xA7oBXu/vSk314NLZnn7tX7u3jz9b9LP36eFs9fWh8+0APKh0x2dx5RVDTE+gZRzG3uiPYxtOUapBongn+O7MmBK54VTecnb4u/kCdT0BdqjK1RqkokkS3XUuNXmHPVG8K7UslpBsNhIapcnuegKoPs3+bN4fe7Zg2dsRRv7v1CTEhxBmn0xkv5xfM0wlTMlmHNI+nhk6yOS2EBIBKAWeSJMOa1NuU8suyVAMDM3deEXYgRH7TOXXzb+GDjI+wA6tggEvB7XrFstzw/uM78rrgttwAApYlIqUTACCfM+bpAoIYIxADIsmhVYuj73lqkdsssTVJ6C0G1iWDy4IVNwAZKO9AWfVwTsA8zx3PnfPa1okkrKV4XUcdn+Dz4mDUxkaDrDHix6ICXZrPmF6+4PTlzzh9+QXh9AqazmBYfginF6z8AVUY6LlKVBgh3y7z43yw3e8yBlkpcoKn21OwNtrYK64w74W2w+GNCuyujLZnyO0fM2ZUuG9EE03gOeq/G8lP4OFH/Nwz73Sz6vjrGMQQcZrMI2LCPCekKFEw2kt1p99V9ezR7ef1Yo/L3mNNB/L8/Dwqv2uOiJ+x1LT3ZAP4Qe4z0gCw7xHxDHO6Z6TYKsVal7YgMdZPMHdpRRuws/uy8YB1veF2fcein1wzosvGLMwiLA59M+EvEIHRTgTaKe0QQhVAD5Wngr1BCEKwA0FOyJWq9G5DamMPigsCh6rckHn3eSoEoTcE1TPao2BeNyWpwiiK10eOKwKAOQnBlERLAeuaAZLTDkIkS1sOpvs79U7Zh9Uts330Xhi2Yp1nHMGTB6hRiGKYoUkr00vzhoiqSE1RFatplkTUcUYISQhcSpjnCefzGS8vL7icLzifz5inGVNKmFKqSlphYCS0CatCwWIlendXv47GeDTmbO93IyhNCPu9y3OEpsHi+M6e8qyulTIeIKfw7K6o8O9PUlS1EQFwnhGjMjWlJMzsxMgErClhBWl4DaqnXtcpY6EVuXAzRvyBZRfNbb/2zM4nWrEd5udks57GkB/sIdIT/g21kYZcEo+G03xGmiacLxfM8wmn06sw4iFUI900TS1kmb5PmrBsVLh19GVnTvx9Y2Clb0IXiBjmCTEqKDf16DtG49yE7D9bjQ/cvuNovo4VV48UvnuKgaf2oUzI5uYe/TVG3sOY71MIwuJKPFpgiglgxpoiQEBKRa43mYcMUjzUx9aXE0dhaF/6VRlH4y267u/QfbvnBIW6kapHI4bYrj1eYkbFJ30emyrK2qzBRHbDzZIkrgnUeQgrIDjan9RxlNrwc4W1Y57I/SD70kb/NN/3iK12szrApP97l7/BFsR2FcD1emyM+Ahe69bJ0T7v4SKVoirZ98eAKvASJGpzrntE+ciCjQRRPSXU42LNwmvmVU4gRgI4AiEIvFNpdKl+DgwOFkbQx44m9Guis7CZ82e/2+tHc393TSo87359eh0f4bV7+PBRv8fvx32quwlHe8RzM7bnfBiIz8petXZFvB8V4g+FYTKcG4b53G/jET3xvx3ipgflWZr1s88cGyN49/ffozw7F/eMDvffvwObfzRz+sFyb509f/HHdQCPxMj/48qzQ2JVCAuPF4EQwaTJhTXev3lJWFqzmpNVQ5UW87aH8DFZZU3LdzV6QzAzEjOiviWbrQAlA1m8IXhVL4hVPSH0mjVc9prFI2LVnBE5L/Wac8aSb52hooajYVGmVsUrADGp2Olw6w9L+Ca9Av4Qn2XJaJPcw2+b/aacltvpNGM+f8W3r7/gz9/+hC+XV5ymkxzgJNIwvwzMJ+lviGAuIDUsTCTje2PGuq5Y8g1Zw4gTkeZjGA6RAkAIkpNBPUqYueZKkFxepAYD6XspADGjrCt++/XvuL6/4dd///8i5wVLvlZ+NqUJP77/ipeXbwgIyOs3zOmENE0IJzEMxCDhplj5a4nDShK2eo5IOt8LAdffrrhd37DefgWz5F4MxDgzI4aAl9Or8vuSNPvt7YfMj/ZcDm9GTEl1c7lIc0UPxfp10ogScJ68QAuTmcEIIWH+5R9w+eWv+PYv/4rTL/+A+PUfQNMZmZLOw2ocvsx3lfPUO9zTQntG/604nDRk2AF/UHV3QvTBFEBBjFQms7ETWthgeMACBv+mG2qciuqQNNcB5wzkFWx5Ijjre2qsqLq9lmNUG3B1/rHlI7yUf2aja915PwTCnCLOc8LXlxO+vZ7w7csZL5cTTtOEFCv26kd70JWf0bejtvSHU8Knyn9MsmrWrUIHNhS9XxfTvzoK7LvVbzdGV4MTEluTxwtQmVz4dNh4sGayqGymLJHQ4YlHXlcsyw23ZcHtdsOaV+Sy9uEUQhAixYJwxS5zLHyjbpzWR5nD9lx1mwPrCVGSE/Rg8YRwg5PnDliOHUG6/US1XTv5IPjN0KkxGAyJPNULcTXedxHiwJEleS8BS0oArVizSPO5m/IBUQ59embpNkL1DmzsKysGeD5AQNuisDIgEiN8HpnJ3MT6iUGMCLEaE9zJ7ii5IaZ5wjz3itYYhZiae2NbvxZT0XqxMSgAdQ29a6wRnt5y37/zkfKMkPYRY6N7a/funsKBqJ0g2e65oEY/rsa/MTyU1gSJdOqZiP5aPYEiVwIUs+ZEyUE9XiTJWAgZgDDhta+Ho3q+HEHq8f2Gaxr6+RjBVgRVFeVAT1C79d3pS1OmAmRJngm6N0i8HmKs4crm6YRpOiGpgYJiQIga2iymmtydgjNADEpyT0NsJ9wtIl1017ojBmXKcQUfL6bQtCqqoga08YjYM0bsMVZjvXvrVN857LcanzZ0g3b2M1nnt3uKqNJW83gw74cQAqLuy2BXBkLRoCYk9W6nnJzgp0oKsu9ewECjf0BV3noTgVwYPeC6BRnbdRUbDjXBdPtBTTBtijxmH7NYTw4OCvDn9UPSD9KX/HtN4Tf024ZK/TruM/PHTO8R3O09Q+P3zfXgvU2d2/efVSrXETn8VY9ocKOFdT2xL1SM9MXynUTFRSEQqDRjRB0fa0XcaCwX8aQvzAiMeqjF876sgjMHrrRL6HhvMH/qU8fQYGzkjY7mr/vOqIvW+B7sPr+7Dpu6+3tbGOye7p47wsdj+3u4714/D/uvGlHe+22n/3Rw//D5O7R5O16b92cQxvDe4WOGTEf57EHtTyKtI1pWe3bw20fq/5ky0vpRDr1Xv6fdI+rsceRW9vXrvkfn/XMj/3t/Tj0e6vfCti3/++f5GV88L3DvOf/srsFr4APY/btt635fDp8zQn2nPGpj0++dOf89yj16W9sb6K978uB7U8rJNTS9AGxuAkBGIz2fbLye7RlU/gcMTXwrf9uZRAMzhir70V5kb7QYrjXxdL2X3TXrff+3fq9GCEu4LfTW2qTilKsu7j2bPMBFYdA63u8T9gOHyDoAa8JeVLpJIWA+n/H67Stev7zi9fKClJLuYc27URiS40KbogCGnM4mBGASpfSieRrqQTltu+ZPGHkl5Tdzzu5AYsNXVIw/bocXbV1s7uV8Ftd5YpYwUrf374gh4O3tVxAFnE9fMOUZjIIYCCGaFztQVD6hqtdQXVKMSEVDHHHB+/UdOd8QaEEkIKYAjgHzLPNF6vGQYkTJRasnEAORJHSyHPgIyBKjSQ8AjftRD565vcMq00xpQpxPeP3TX3H55R8wvf4J6fINSGdwnHWPCGCT7YsqM0N5NqDyl8YLgrElFTIvA2brbpB7t/L9zONLPfzqHjNWKxBUJ8dolwbX3hPJElj7+prs4+Rjbu9XY17t1BFt2pZncewR3+TlDsKWbu7xdp4y2/oTESIFzNOE0zzjcppxPs2YpwlzSmosbO/Y4fUd8n9YnqELezT6Xtlyb39M+V0NEXvE+kih1L0nL28YLOYmaLlKf78O3ymVCQyPn+3e8YzeIJzelhsKA29vP/D29obb7YrldMJaVoSSRNHo4xwSQC4uvcXKthPsvUdEU6IBqPPZ55UIkqwQDGYxRAR2RA+oBMbKRqhSRGj1jte2hi58hFZZWBIqkgvJQUQaeglIIQIRmKakOS0YMQfkXBBXQl4zCKinIgwR3xNGgOc28b2yp/Qgoo1HBMippe4ylbK9O4RWFVvkQsUApKe8o3pCxJiQppOGnJEk1CEmhCSx06fTjMvlgvPlgpeXC+bT3AwSSZNbh5bgCcEnd0K9liLKDL3TKciqMYKzMjjNK0CYFr67HvdKe+/++3vK652nZE539Rf7px5DCHJWWsOFjR4RHILW15i0UYAjRJ0xteyjhweb90lP4udJlEJrYVAIWDTh0zRNYBCmwljXrPxsm9tHcP+/Q9kQajIjzbHga9/3k2rZCRspMYhRZ1LDzZRmxJhwOb9o8rYv4jk0ncS1NgBTSpjnE+b51PZGcAa66hEBwBh4qPAA7tbgsCiDTcaUVabxUXkO/pvwYvPi55L672AROBw9ekbx9ux9+Q1Kc/rn6zxu6PtWuWfPekWnr1/2DSTNhtKyEAMixxbGb8kurB8hlMb0SjvDFBZoHgmbEzceGG1sNzxjP/axVr3l/jfzNx6wgKPDI3yJErn1U4Q4ueZcsDqBupSseWXK/pjvFIvTXPsy9N3pI+p4PXO+N9amRN8y7+Pf4/vjRxIZ9jki+ra2dexd99o6+vvRu01wgpvvIedH1b2YOLNtX3BPQQwRMRTEGJFLEaNasYjBzfzVOiAXs1GXAhRiFZgZWSRm5JBBYA3fRCjFGdKdMcL3xwx83fxTS2zd+u8M5CQKpkdz3eEBdt/D/vz077ih0/a5o++jWDWuxx5O3BU0d8Z21MdH8LPHnMqjj/fIUXn4vOtTHe/PMsl3y8eE3w/VPOCejQz2kEfEU7///PONd2t8cl/2xsHMd2H8Z/p4NHe7ynuHx59r61n1yWfKEQUentobv8mMtSav4Pr/v/IMPJlO4KlZsuoCASQHfKqMaVcyrwg7tMiSwwBA1ID2JhWL8RzVCFFFKnZXLU3RX0BmPFhzzQORs88Jofd9WCY92W85InhdhafKq57m1jrVU4LNiIHSXDpMKV30tHeR3BZQhbjn7+rxBa4Dbt/9iXC4uquuRg+TpojXr9/w13/6J/zlL3/Fn3/5E86zhDYqonRpSbUhHASHCHBABBCJkUKsYZeWZen+tnn1PICn/7lkTQbd9iRREB4dXI02rLypyVA255IQm0B5BTgDZUFZCe/rgpIXxHjCsiyIYcZ8PuOSXxFjkLyimthaZAMgJtGDTKnltpDDvIxcVvz241fcbm+gckUMhPjlFadpwvlyQiCIAQLAnCZwEYNHJPFORYhAisgs/NiaAayshjDz3tkWNj0mARQI55cLTi9f8Nf/+q84//JPePnLf0F4+QU4fQUToahKP6DnqQjqZaLpMTZJw9GJKbulyjJV51Qb2PzWVQpPu0yuYBCKHLeklk6CdP+ZDoirQS47g554Q0h+CDXwMat3iRnvrC8Vauv3PwpbH/Hn4zMj3XzI4zEjUESKES/nM75cTvjl6yu+vr7g9XzG6TRV7yU7VFYN+PSYih4fBvgdyh/KF7byOUMEYQgz0JdRUSZ89T4xq4uIjvV2CPm4fh4Cyu4JxM+W4/focHM/WnRlgRvjua4oDNxuV1xvEiNvXVasOSPGrMmqCYFZjBEKhXtCeRWSx00w/g4Mz7dnAgWUmieC+o47obq7jYbs9oQu+8QooQEKA8gNgXApCGRWbFt7qif1I4QggAipiOYjJUHOKSVRLmXnEkn7ShMd1P79+wt2/5FxbnspoaukU053CGyfSSe2+s1I0NapyxGhp7tDiOKKaEmsY8Q0Jcwn84hISGp8iKEZIWoyXrQ8EYbwRSGBigi9ksxW0RuBxquMe5wzmamKXN38fKZ85L0a6uUDeIHsxI5+xn0EMxbt9Mevc+H9da67jSyckCpRNaF8DIRip7yjrTuDqOzC+mfmca9XH1FAP6uY8X9XpQDR5nTBeK14ba/nZF4L0BiopF4/UT2AzEhnIcxaHpUQSZ+REGUSpszvjeC8hswA1RTD/qTQOO+VujmGye+VvdLX9Xgdn1eoDAo3ndMtLurLszDwUbjzb3sl5IZXoNbfPUU0Z4bfnrZmMQYUNdITaZ4hVs+J4ts87vOouJJTTOr6PY7G1k06Xw8djOM9am07ywYH9xQoDg5dWABTrlQZFQ0nm3xcxUTjAfba1n9YvTqO4MSe87j1mPcSHPgR3uwzcNmuTzVR4WyXR/pEqSc6vRCx1+5uXwQfRiLV15DGJA4IVESZQ0V5HeVHlbRsWmEHQ17pwVwFHDOSmDHLGyFGWjbODWFvLcY1sOv+KZ6t4EZNRthMkl/XxoszKz/asV/3adJeP0ZF7B6sbvvblC7tGd+/vs/j330ntn3yP+zuPes7epx1BMOb70e/HfZF264wIj0Z+zq2cRSf+hHt2Pvd4+WPlD1l+6PnP1L3B3rS7cXx/XHMTXb+OD66169n2hxLu7+VhTc8EG/3xkf695nnPQ8xPr87HuzwYw+m+dk+17789Lrdq6HxH/3tLQ082kf38ONH9stu38jJwcargyChmcT4IDkrxSPCELnRUCK0HAPslqYxON345Vlbe3fquh4GMEVnO6Bh8qyv04wY0CubUlQTMEkyXU26y0VCPoEhClVoWCKpj0qR2Pel1QfXLvuxgDdGFThFdFf8uENATBPSPGM+nTHNcsJawvdgGDeDI2niYuMB1UsaqPx1jBHTNCGrccE+MQRR9FMLBV6KHJhISO1ZG656Cqzr0rxLuOghGW6HHBAgJ2z80Bgokk/1/e03EAKm9O843c7IeZHoDjEipgkhTpobLmA6zYicECgqPAjul+dFPsh5RV7eEQm4TROIGcttBVKUCAUkeqZcMqaUkLMcNAwgpEji9aLeKUSEFUulw3Wu0baAzXWIETElvLy+4vzlK7786S84ffsz0llyQ+SQtMsWEqrhEWHZqe4NBomhr0uMfQffuv7t7Z8GWg42Bz2Nr4NLM5KZHEaQLrGFFLY6mJtNre5F24PWTDOTWdvkQjzVA921b3fKDl6zd7zOpn/F800Odw3vP1P28SohkiRsP80zzqcTLqcTzvOMOSWkGDUKh7NjlgIidudy9vjyYZz1mZ6O/Gw5pBUVlLb09qN041OGCDJE9mEi1UrHIFZo3hMMsDuXXuD2z35WuXlUPiqX9oxv61NhFkv7mvH+/oa3t++4Xq+4ncUYEcKKlFdJKlSyzm/EI0NEIwx65QwMBox+PDLPIRAKCMRBrfV6cpa8Ino7GU0Ylnr3PCJCCA1xlW2dWRVGQohMcaTGCyKxZBeJw0chYFqFGExrBoiwZHUE4+y6diwUfayYlP/Mkz1TtxdreaNkxb5wYXIqoRkKxBARQORCM2mSalOmhpiqMjumiPk04XI543yecTp7bwiNhW8hahAhJxej9mutazTSKnZwrOSiZ/C4EZD9/adzamFLfqfy7F4XmH1OEVb3h7s27yMLZ9ErSXfrAIBSJErogWBEQRgcn5S9gNUQEdTwBiRNupVDcXPdt/d74717pdNdPJjTjeDj5mzcHy2EHBT4PE6y/SOMAikOi6qEThpjcZpnpDjhNJ8wzScJ0ZQmxJRAFJAmQkotdNmU5DMaI6z+TjHtPkVPbXTwb9/RJ+MalZN7a/io+Kf9Ht191sOYwYZsgt8VVu4pLh7vtQF3Dn0b3yYyzwobn3wx4SnGqCHTDC5EGAlZ8gsx275tAl5jrmWpxvFwNdLvUxU2jF8lj5/gh9ALABslKRrcEVEfVsDBH9Dgq3A7defHsEd/9tZxpF19b23OdtbOdBEfNkL0AtCIY/f4H7tv7d6t/aAfzyhn7v1e9/6OstG9rbTlqG4R5CIR1iAxkKMdPijtAAOZDsrQqavf8CX8+jt8FQiNTyws3rHDc36sxst5r4j9vR3q3PdzeX+ujwwHvPPs3nzZs888v1f2BdMG29YO0VjnYxh6ZAzYWcAND7s7buv7Tjv3eJKxfhr4Euyu3/Z92UNe9DsGaI8R9+ZnhLe9to768p9dPqNMHz/j76Ps+0eP+9k2P9cXQ1L/cXzppgd7a6T0fott/ncrd+ab7feh712+xPvjGtfz9+AJPX8OInAgI0swnFM9IijCDBHCZwk/TYAaH1R5CNT1qj10MkI3CpeImmoYJeWTsiWabgp2cOONqpK2sHpTWEimIvklshge2PJN1JBL4qLR9KZmcCg1PBNp7PvN3m8CttodbDQ9H1SJkIWWUMYrhCiyzOmM8+UF59MF8zTLAdNcNJG3GU5Y5jyQnl4n9T5p7UjeNVJPW9OxNEPENE2VvlgOiTQlIEEPNTDyWqRt9UR5v75jXZcW2kq9LSTXZcQNUWhRGfR9XJCXK3779d9wuy1YV+B0vuD1+gUhEFKKSNMZ03yRSA8p4VQK5tOshgiBnRBIf4/gUrCuC97ffyCA8RYncC64zjfwnMSrPmgkAmacphklM0K4gliyqxIBKAUxBBQU3HQ+bFwZaDleNQQWiBCnCdM84euffsHrL3/BX/7pv2D68lfg9Rs4XZDTJPBccg2XTqQBWaiZ8hryMnmoyU/bsj2EYrzhBrvY69zzP6PManDPlsfBjAUV9Rgwt0NS5uXgE8R3hhGWd8yzBCq30LgP7pYjKe33Kb4Xe3Jvx3dteBkghog5JbycL3i9nPHl5YLXywXnSQ5LxhBER4wWcUSX2VXUPjUwhA8BhuHZvc5/uDw/pz+jg3/aEOEnnwFNttM6sMdYbienR3yVqYbmDdCJZSVK7YRpa4fdu7LJFaCJq6KlCsFNXwGzYtqOaXJSQ37VwGKbniDuQrvCQuuT+9aNrFg/dbOZYuB6fcfb23cs6xVrXpDLglKSbPLCCCxEolpBtUemJDUCLmMN9WM9F+VpkLjgJAKnEW2JEQxwCWptYzmdwARGaMlpKLQ1cEiKa4ekbTmp506s2jg3fJInsoJ2yHOEBMQUQYWQdB2nkEHMmGMAccRJCWHOGSsRrhpn0ZCsCeso7WQauTa73rh2d0RghwSou0ew8ATqEjioArbttJAWFfEO/WhCta6pGiDEIBEQQ9KcAZOc9tZwTBSDaS/ECDFPmKdJk1JPmOKEWT9TSEiU6olhitJOsUS6MIZsy5jJVVxNoUm57FMTDbEYnaQiJValT1z0jB2izpOtyIDc9gS4sfSCkxd8tytFqIsDQFPAksAvB4gxiFvCcPHo0b0YCkC5J6ywPaNGOWr5WSocFAg+UnN3b5BgTEnCppUsp0XWSEAJyFFmvZReyJNm92eWuvG6BdhRFDEaLHa/0J7xrCPNPV4kPWWjSW6a8kGDmQ3Plp219UY7M1LIkC1UlveE0PBlKVXDwzSfkOYTQppAMQEhAYEQIiNOYuyc5rnuqUgTIiVECmoUFYW2InBNjGaQrP8p3BO44tL6K4u7eVUEE/fMdh2vKcK9QaPfKB3sc7eaPT1tMmDHSBpaxB5NRmOi9hSD7X6Dl0NFV/fXFl6MRpkSzfDNtvDQLwlbI2SKlfwRzGjLDISQECM0sR6Qoxjko7jf1XxLpXbLaCnqqWq/q9o8ESxHsPEn3egaiFSm0IQHQSB28s6Nq1KlHhYYQssKJPxg1jCNR/hQQIX0wJ7kkMkMZKaW4L70fJEx94FUUKO2s412E8tvo5IKkHYC2b42nNbDRcNHpOveGyOoE6zqMmhfxmcbTDCXltOqovfWBkw42yk9PBvd3TeK7hfjixRCKn/aPm0PK8nU03HsXj02olBl7UIgzREhYRACkSY8Jz0x5QRJx88GsuMksvYBDC6kuSMcKVc+LrPEaI4chCZF73nZwjfafJlhVvC4W2/rj8FSvW4V/eNz3X3/28669Q/qqgz4457C1HjCrjeO/5PTi1sj72PFvlX1AD8Oz9cxwE/F/Xft1214rC08HbbP1O1b24iPjSe2T8rubxVHdkx1a6OOoOKJnt4f9tf9vafEfzTf49z5tkfys2dw2pPxduXbg7Vr9ZYOBg/Hb3gCQD1PTmPfjvni9pznD7ftPLPe+kPVcbPi9Q0fvvvi8YGJe7oKmyOjI8eKjX7MPtxVO6zwsX4dVC9tbG/tFllprvzAptInKiEweOy+5wmHSqrZj7UHnnbv9tBfh+c2k8ONz3EPerpW14sAMCHzCcwnLOUXrPyK93TBFTMyARwKIhXVERiHLHsjmpxN9fibJidu+hAQkAtXvsu8JkjxGoyfVuVm0b9qGGHl2Y2nL0YT2VNz9HTc5Fm5oWGXnDFC35fwQkWTUhcNVSN/m1xQJ4+Hq1uFegrcJjUI3vWraf0nAlIgTCFgDlEP0YnX7IpcdWsRhk/Q2iChe0yqCiYgpqmG4LZDDFEjKRQuWFcNbcUZRAFTOAFB1mvBFSszVl6R8w3ff/t3XK9X0R0QMGni60ASVpXmAKIErEkSDdTT9gITKDeU23dcAeTbCfn2q4alnjCdXzGtN6R5RkxJHSsYIU4AiQyt7tAIKeH88gpGwXJ7A+cVb8uKwoTz7YrCBVMKSDHgPCdMU8Tr6wUhBtzWFUsuuC0aPiwm4Z8DkChiCROuyxXrukiYVOWhq1mOCGE6I55fEH/5vxB/+Ufw6z+jXH5BCBNAhIibyokW1ihUmBD5kpUnFw9toqBQHfRQnAG+8mMqBJJ9wA0WFf6MhlmOlJJXhfMM0/nUfCkKeyZHef2e59Uzc90TxC0EVy4rSl7gQzKBW6gm5KxeRI63NWSzQ/Ofp7yNW9472LCVe4d3dV5N3111AIrz9tplZjBpqCXIoaLzDFxOhJdLwvkiYcam0wyaou7tXEOpEetat4ZE7i2kaXVI5SZ3oMS2zM7o79O6LY/gS2VXBrLVOCov5wHtoMozlLKVz4VmYq7Nt1t3XGB3GEGgCTDigiIKUZHzWqIOtP1V3yKQKszZIS1WuUepEqv1TmPdmpAnivkmXFUiS02I9cBoJ1/vnTRqY5V+GJPPSpyLEcYioRLe338gpYTb8oa1XLGWBYlTTaIUGYgMBMeJcF16U8xowlw2I0TzkEAI0hbZqbeiIXiAElRIpYDCQCBxzYcm1y1kMe01zr0xCpW4G68TlD5GMPW5IkrJSv6bgaCDDZtb23D6W0wRgSNmhrjwxYzAwBoiQiTwJEoQLhk3AtYi+SPYDKlgVVDJTIWdeMO1OF6Nhl1G3V/k7phoEGGeBA4KWl1DQ0oTKnz4NrwwyNUPVRQRMU7i7RAslMyseSImUIxCCWNAiYQ0JVxOM07zjHmeMacZJ/uYISKkGoqJ7F01l3nRpfFKlROrH1OMBSU6NQlVNuLFHfFilN1xN8TlZoqGtneu98qxgOrX0Eap94nUIKanSdWg6bQvADNiVFQZWJlbIR5siKq0EyRwQkg1IKIpqUyXVQhAFMISKCAl8VApOcpJoCI5VUqJAArWEiSGZPZjGP/ega1+kvSNnd+Mzx9+qniygxL/O/VwbC+5jxDN2HaUJ/5FoNBCORiDJKyknS6BrlWEhBRrp+FTEjfdmBKSekFM57PkhZhmUIjgkES5l1akFHA6nXCaT0hpRowzQhBjRKJQjRFB6QlTj/sKGJmVOSu5MmdVz6MK3WL/DXDuFmOgHdgwFOMpKhG40DFnFeagAtyexc8xjo/KVqnlw7ftP9uaEQOBwX2Dnbbu3Rs7ij/f5b6eDAokXnYqmIaQACbEIIJIiglgiPEOhBQIxISs9D9Y6DmVrFkN+gU1/USH/4n7czkGvwHdg42G+MGRChMmpCrvUgV3pZFWChcUSK6YyKIoji4UWH2uFOcCL3x/LqwfiYS4ZkbOXAFPojKrcIJmPKsHQCACCYqcyscAA56hZXgjxLBmVUHXmFTPnHqloMAyAwUIMSBo7hirx06se8aWLc+Ux0WKH46o/Vb5b59xjHvCCg9sgOFP5fUU1zPYGaRtbVxoLLZ9BITQPFu6tgg1SXUMATkInxZQqtDhT4rWMRBgoZsqD6p5JYrI4Zo7QmCDWPAXwFiZkThBcoZR53kpa0Aa2rt5iNlhjH4fjzhjfzXuGwpo93ubn+0id6E7HpR7bdfqD8JJjTjqGcW/vMf7z1HDKaNRYe/de/LHx+echj+fM0K038IGJ8n94zVsN/o9/lx/+98e8YRHayNDbXN6nxw2nrHhn/bGVt6tLdzp+4NnPJh3e9tgALUPfujbeRh4Cl957ct9mNnrV62t4y/uvd/3i7t39ma/r6vJTM/UPfJDUp/t560ia6h304xk1Wr3TVvxhBxS9ROfLyzxCoZ7x3XaoZ3Kw3tg8rByTCXbMyZQo6fv/m/288INllj5pcxnZP6Gt/Jn3OgLvvMrbjQjRwJiQQgZCY63Dark1QN+NiYGA4GRLGq+xcYHV/1BBRNhzqvy3OTPyolzEeV55dWsr0Kni/anHh+qYYrtJLfQeMv9QNw8L2r8GVWqyonm/oR3Xb+qOGT1hOD2fuWVdd0st0QZFkCXrChuSCFgCgEnzXNgMsrKWWUacodPTEbTrhDA6inBAOI0IZQELqHOJSlvwqvkjrC5TfEk8hMBRAzKGcgruCxYljf8+vf/hR/fv0NShQR8eXnVA5aQkEqnBAoFuE0CgrcV1b2EC6jckPOCt9t3UEj48WvCNJ9xOr9gennD9PoV03pCmk6i9wIhprnNFRdwCIjThMvrF1AI+P7bb1jKFT+uC5a14Px+RS4ZcwrAHEHniClEzNMLUopYcsbb9YalXBEgHj1zipgiIYWCJYoSOWskk3oQhOzwDxBPF4TLL0h//h+If/pn8Jf/Bj5dwFEU0ZGvstxkcBjqPMialTokPc4lz5KFOh/wpR4YBUuYo8DK3xtzCsOZliNFDBHVsFZEtrV91OimTq3xDfqnqSrNqCHwXABewSUj5xtKWQFeAWSgrDXfCkoWuCkFsfaPYDKHo7obfPa4UCU3xcJedbLAHh3k7m8RfW1vyoEg1jFXSYSdjAKIUYwIGQEUCC8z4fVEeH2d8PIy4/RihgjRK2XOcmismA6TtE7Xh3oAT71z2snI7Zxwdzkg03zvx/YM909R9w2OHxiNEXeqHcrThoiRyBM3svgUM7NT2sC2impybQ0d2c65e64CGaEeyPIeG88IDPdO6oynEz2Dahu7F8ahCssmpK7rimW94Xa74Xq9YV1X5JyRc0akglyyCIHclHAiwIr7TqAADs0ToRNUSNQpJsjX00v2Ybg6K5eLqmg6AJ7dtai8TtvM9vGhmtq8G9OyJ8TYPMv4EOR0K2DJq8W0QQRkFkKTuWBdM+DPHlvCG1gojp1uu6F6wdB0Dn4sllTLXjTh3I+1U7yQHx9tNmPfn6aUkqa0fkgiJlEGOEOEhpCRpJ16YjJFpGnCfJpxPp9xOp3EEDG3BNUhRYT6nkv4aT1t2v+qQGnX8VPctcXArPeccq0aMjpO+Ehoul/aPMunr+aj+MdQaSMc8r3tIarGNVEmchDmgEkIkSjDxMBXe6VGGUCYCBF2HQGr+7nhBjAjqoIqRVHUrxaqKRckBqYkYcrWVRVMUZPVbpRmWmxAw+lhMkRij+ztDVfBVqng6kE7hewrMmEIdY5MeeWIP9pVBCgxOVQUxYx6mswWuu63oHlRAmIIFc4nTdw+myGi5oZQQ63WPc0T5tmFLKshmWKLW1pDMul1hNmmadSv3ljQiHJjEBRmwcOzqO9j2CvjMzbLBU3g2y9tvuHW8kiRNv5d+6PFK4O9AuG+8lYfHWDDt1db4AZLPd31/ChjZHLso3ZCxBjACIhJrilJWMO4StLqyCwGLwttVJVM2/7ZabqA6BA2N5qBdhCjwyBEPV9kY/WMWb8sWqfhM69kM9SqwnExHOT6yIIP7FRTDdVU9uHMxtvtRfediNSL6bny7JNE+8z/o1of8W2f4zofv7kVUtoYrF92bUoPz5fuSQb322o9c/yrSTg774Q6p/qcecR6Hoyo0noLrzTOg90zqj3uQYMJ4z/3DBGjHHAPt+yO+SPflbbUwtvVfEYe2ePz7/H9+8SSsG2qwczOC/U3jwqOcNA4j/fm8mhv7X0XdOrvl4Ph7Q3C9/y4HMGAYvKH7++2zx22PZrk7t2j+ej43uNa3HtdFza4QL7uG7FQW9zy05tnjMdy+/joc9jrykdtx7K3Ls/J7/2e29y7U3iDKR69u/f854pXqsv3Z+WPsX/3cToP3z6ihDms86OVKEOyx7K6Sv1ltwr/Y/3T4F//aXmFenzHCMgUkBGxImJBkA8RFhBWELLyX0yk+beah6bnXKGyRAD0wIgYbVlzFJBFwzC9ywHvLP1rR2SK0mrx/GxheGnn2j4tPGExGsQ7e4LdDfN8rxPpYKgJjcP6tKGbvCB/0wb8nGjUcAKJacZ4T1uwKs+jAEjyTpRKMgqoMEKI2icCUIbDpZJf4Xq94fv37yLrcsblAlzCJM6/tfuEkkU3sywZy22R9gIhBZG5xEEiIKUZAGGez8hrwJrXFhLLDZQBUYwzsK434AqUGJEpqr6ekOcVOakubc0CkwwQIgJNSNMZc2acL18QQ8Ly/hsyM95uNzAY60tBMr+RIN4RJxC+MTBfF4T4hgJCITngNMWA21SwzgyEjJgABEZYFnBucw8A03TC6XzB5XLB+XLRqBaxevo3UZ2r96tAp9Pzufr2S4MXW4wKoZ2OxxttSzPa2f3q6dMMaAaL3r5KpP2s/CrB9iycXFINGeqSa17a9XAfm6zsDtzt6J4qLO/Qjrbt9uZH+3dn6vZkjY7PB2Cn1Yz/rp4WrZXWvM59jIQUI06nWcKlzyec5rnqHtr6oB+r8RJP0ebPl0ckRgyqQzngy+z5o8fulQ8bIqzh59jRR6UJXX1jQLMeu5vu+mgCZU8Ytn8+TvEzxorN6YqKIOS+dxGV3/sELTmvWBYxRNxuV6xZkGcpYoQouaBYYloy4RQQJZyeBuV7TKqd7fQESmdCBRFTAjptClAVR/uTuzfnnUJjYJL9905Z/6CYG2bNGVFKNUQgELLWXbiAaFFrdKkMhs15HWtdzl4gGtndpiiFY0aaIWKPKfHv2fRxN5+txYqoD+Yv2ClEiAHCEkuHIKGYJCeEPkNBiWXCPM84nU5iiFCPiGmSGPhR80O0RLyN8fLSFderEZ0eMfZGN0dcNs+V7tmGyB6t+/7vnij0yoKGsJ9BePeVDHavnSoK6poagjNElAC25MW6llW5bwxg1TLUszpd/6H7wCCVAFEWAUjKCFrOiJTkWXMbXpMoGnOJWNasSeA3I6kMWPWiagDuOZOdOQDaW+Pc7MwT2omz+htp+2QKzmaM0N61ebPvZCe0m9K2KPx0S0USEi3WXClRjA7TJIaImDDPZ8kXoSGa5DivrSlJ6DI1XlRDRPDhSMjF3+7noTFE7BLh+Y+jBdywaV3tO0RrICHbX8ffDlCp3e4wzwPhcxxjravDb7ruh3un/U117Y+ZkfZOzwA2eqHvdgLckTGCECIhQvKFMKtBgoAYxGtJDCpyuluxxjBL6HCLCYJN2tO+Gu9DTZitvzP0tEwfvqmNpxdOjubeYMma3yquyN0vLV9EMQPlTjxioCWPtcsOnd77frCCwJ31PXyrvnD/RT8XzynK9D308/65vg1zg/1xHisV/WY9pmv7e8l+23+3LqHScnleRt3ebUYI8Rx7Zj2hlL/x3h4OrA5LMNnN1TAufx3v783DvSSCff/6Bo1W36NXR2VT9wGc3YXXO0a7R0revTl7ti9Hc/vM3BORhoZs+Fek68Oh7Pb80RQf9aHsbIeP7tMa2u+AoD0Le6j82L3ykb7dhwdT6I398njd49Rj+e6xIcJffd8ewc6zZdwX42GEir8Vf1b6h3vrtvd9P5zkc2V7wOEZ+dOe450+HT++z4t/pjwa7yP9hH77VNuusv3b+s+ejMvMKIGQKWGlhJUiVgq4kRkjAlYSQ4W9axEREgWXytq3Jt8CCUNo8lcgMs0OGM4jwfUFA13uZo0bj2a8YJNf2rXJ+8OBTviPzYtri6VvpssSXtIr1+GWaDvXTfHaTcPmcdOr+IMGXjTwZh07uBZ0TDFK30JewXrgkZnBGXLau6PLjGXJuN1ueHt701A7GTHOOJ+c7MMyJ7mIIWJdVizLCuPdI0X1Yp8hSagnBCKs8wkrEfJyldbKMgyVUQ/0ruLtUUJCgSQiaWUxAAEAAElEQVT6DRSwrosaIVbkmNw+iSCaME1nMAPny1cEiljef6CUjPfbDUTNM4ZVtxJTwikmSQb+fkWMCZkljr8kHw6YJ8a6MAoWUGBkXgAqyFdGyVxTf0zzjNPpjPPLBefLuR4oNdnUxiimB93jJDukhtMe4WMLNaiyYp2zpvA3PY9PNj0eaPLyrVvUuhKdTGTARg3ObMq5tl0gYZh0L6hnEaqMY7JtB9S72Mu3Pf5+TOOr6CZ7eqzT0a2tjgndnOiTirVcL5ysZo2a0YgCIaWA82nC+XTC+SSGiEmTVJtM2PQHplsvVV4zA+1R+Qh93D7bY4vn6qh/7db9GXr9OUMEPkdiG4PdD9yfyHuyJq1vf9BNoeSQ8x1B6N7vvu/+2i9CI3hbI4Sz5ilAr8sNt/eA97c3vL+9IS8ryqyJlIokGQr1HWhIKU84RNlSBU5qSQUFqTRrtk+wGwI03EsTVosnvqb440a0RiV0G4ojuiOTHAiB+yTWPhFtp9vZWQ9bv4kZsRCYkyTqBVfiGIOEtjAFU86reJaALEqOa0QpOTVF81GppNyywWwEgFCv1t8mRwjD0Rhuk3VGwdJgzsVaJtQk1YEsLIKFSXCJqYPBdUAMEVOacJ5POJ/OguROJ8zDaW9JUh1Bdg2h0r9KYhzj1iHF7jMqvVwIps2zjgBiq9z25RkEZvO48zb2FnSDr57CLUpkiAEN4casAiQV9SZxsE3ioURBw5rZHqv7xXtHyXdtBgAkzJUqkFg9YAD1jGBCiUqSlMjl7CgeE4oxa3vExekZGsbiQ4Jmp4nuzVJvTHBhVoY9YqckApnyN3TvB/Z7hyXOKZO4OpOIFoGpMjP1XWX+JCSTwneaEOKEGGcNz3RCSpPkUAlR9y/Uw4pwOZ9xOZ+b95DmVIlRc7KID3GNg98XEXpGYxhX99WWyKv3HBqv+0nHayuGa9XgV7gJWrKnyuGeMVoz1vwsb3Ck1Gr751gx3N33f9IOjOy829MUw5/Dew6XxhAAZebq3kkigMiJuYw0F9AqRupMpeYTqnz20USMvJmiGbnIXtc0SjI+VkWw3egqaZPC3W5EzwcCW9hirsaFXCwskUsOWJMxlhrakYtLQCyVqgJ5h1a7NXtawXX4xPj8Fj/0s3G/zaeMEE/zjK1PHZg+8/6DR472cr1XvPC0D3FVv4Fhjeo7DMtPAqh9FT5vg3VVA6ORMwRWQbGrrfvXFBrWPogqvYuKF2PY8j79GPa/34epfUPE5p0q4PYl4H4f7rU7lvuK7bE/VL2HjniN8bpX/3NKxeO5PMbT+/ULfYabSENa98rAtz/ckrT7N4DuJOHRM3frdnTv0Xt34U6vNczCQwLZ5nfPWN/XulWeNxmshQoaFR5WhdFLq5/IGxVDre8YnvZCIzwPH2MZjQz+2QYTtPtsfxzHnr3Pj/TNPIaNo/75ftpz/pmHCv+HLf/vWT5qvPfvAbvSlOgE7FdVsjETyHt3AygckTFhoYSFE96R8IaAH0y4FUgM/VzE6MCMSfPjJa2LqAnvzC5UpgqskhdBTySTHfpQRapilk55OPCUIHI5JaCp+kh5/oASxDOAQZIDEAwOAeCIoOF5uRSUoLwcUz2UZvOymbu9+RwL2dw+yajLZAOFUXLGsq5Y1ow1S/hSkOoPSMKRBuVLGXKwjSofTyCKkkstCY7KvCIigDSfQ1Gjwo8fb3h/f8f7+xWGY/IqOSMsz+S6ZuRc6qH6ECfE6VQNTEWSUSCpjiWECWASzwgGUprErJTlAKDlsWh8MgPIApL5hrJcUdIEjglluSLfJixpAhfjeaky+iHMSIlwOn8BUcTbj78j5xtuSwbRivfboocACRQj5tNJ+Z6Iy/mE8zxjyRlLzlWOzrPom5hWxERYeQUIeFuuKFmTDrPIJdNsuQtn1cOYvNxgwnaT8TUSPlXCBbOFrDeQkSnsQYbtMIkEW+/1OqXKq35vFC+TFvtdw47VME2MGme0tu/3vRgc7BBU0WTvdsBaDB2qLyq55p/gIvkiqvxcVPbV0KGmT61yLXPbKx8pygMfvXVkhGjXRtsB462D5oFz4aO9+pcIp2nCeZ7w5eUVX18lQfXL+aw6ilDxVOGaxQbktTHU8MqI05/igXBHxpVahiefmddROH6Gf7pfPmWI+ASN8zVJHfVv6sZ+KMMf1CPvbBnfPWH7SAjfW+DdFjvAbOKc3qyohLlda136DoGxrguICNfrO27Xd+S81mzyhbMqSoywqlAIYT4Dh80Y6mn3EDUZtbku+jGa0qRXGJrQqbOHCvw788CmOaljakLaXp8EiTQF0t56jYUgAh4zI8WIQuL5EEgJaJAkVxTMI0KeXRZ0/erWSBF9Y9L7DVS/dxfqAN0EcBqNW8oUAcEyB9Q+WPzz7XB9DHUa6jehI1RDRPuEdrKXNK9AjNXdyxSrc5qQTFFr70X5kJ38HhGONx7wkSFixzBxzwjBbU32bdy+ee6ue8Xm8TM4z6/z/TY0tJnziDBjA7EaI5jVGKGhmUpRcDGOyS6jJ9YAZw42iCS8DMDiGRGBmKMwugngwsipMQtrLgi57fOOgHYDGubB49/ht9rLnf1Z4VT/aScg9k7rSRzNXVxrcO/mwpjFwAF2HkCY0H5cFc9FO1WTqpEuRks8LVeqRgWdYzVEnOa5nkqYpwmTvR8igiZ/r4o4Nw2s+Lg3urU9UkozMjTaYInH9j9W716x0x/ceR+57+jr6BQb+uxIRJ9lFvaUW4Y7jxQa/t1ufeXu9rnaOzXE8T2PiKFvxjSindqymPYppfodMMOEMMQEIAcJc4biVoj7ufHb2CuITDBqAq9TqhA3I4QjAf0aNObm3kpw5SHaUjbhWlhVwQOCFywkU1GvQI+T0Y1r2I8DWurmeFMaHzHujXvlEE6ee/2n2vjM7+Pfj8Z5zCu2P9rJSOzytZ5XaayIXyNG9e6lto6imPS42e9XWyuuAhgNbXpOvBs/UVVmiDGieY0dKb4fKQHHefXKw9EQsalr4M+6vTqM+249B/3b0M7Nmh7ICgeGCHuux2dbfP9RZeHR+I7W4IiOb/t7rx+C8wU/36/7qO2O3wY+b4hwCPfZd/rntutUcelQ3/6+vg/r/rkxdKIZIaryx+WIGWWQxhM6eWqPl7rHp23W6v7+PPr+s8+35+TalDqP+fzfl0r05VllfaXYD3inZ2SL/51LxU/6fTPuIe+YhVhmpg5eGQEZCSsnLJRwQ8AVAVcGrgysBeDAiEXyV06WmwgWpik3PI92DaonktC4GqKJLMWCMXQDf10/1usmw1RjRK3b5deshghRhrJ6xYcoeTNDzVMRXBvFA3nX/yYPuK+b0vPXdx70iwBkMewsa8ZaMnIpcpAxABpboeaFqD1hwEIAgcyoaXijgHORNQLqgcOcM65XCSV+uy0IgZBSVCPFWse45oxcTB6SHG7i/aBzUtRIAcNrEQhAihNQNBdj0fwoyvtU9GW8NkRhzXkBLzfwtIDzKn+nK9brLEaQoN4SZrylCTEGTPMrGAFhmlEgOS9oybjeMqYpS+itEJBmOaR2mmYs84R5SrgtK663perkSyaUAqx8AwLj7fYuc0U3qD8EGCze+5pkO06TRqVoIYNHmaB65cMy7qHSvke6FIONKkMyu71Rai4zeUzl2jGca2nXCr6unr4pMzI0ucOMDwY/JhvXUE2ac7STmb3QsyPftrYb/TjCu7u0Eff5+VFH1PFsxlBX+jsKT7JGnuwTgCkmnKYJL+czXs9nvJxPOJ9mpBT1oGvDFcX9XfGvVnTE4x7RmzqOA1g54m+oc/HH3fka6/oZ2ve5ZNW/U9kqsBpxgDHMd3mWXsjvGbVPMrtWc90UZfjB/rHJl+/sNxL6Z+qmsQ27LlgBXN9/4O39B9b1hpzXzproN7UhpUBNGccs4XskaXJECOoFEQJKUes+tVwR9bR2zk3YtHmqf2+VJqZ48/OyEWPIlOiAJB6Pyiywxg7sEUqnNHNt6Y6T+hiAJnpJEANEASMUTZIdxG4YY0AA4WahCixnhPIG9xU+0iazMjZQ4gDoaTeqin9vgLAxdxSSmvLN4JYs470CcUMm7VRTmz85mQAlziEEOe1NUcIrqUHB1jPGhGmacJrF3es8n3Ca5mqESGaEiD7EU68cBlFN/tWtL8OdHM4dkZHERvqpxEWs2natxKUqZe+XEZFtEdo9oeX+vvYKj+eLg0PNF0FUdE8pk8eiOC/MAAVQkP1eNPkYoRmhWD0j7DdoQvigjJVFcTKG1+LbW8IrBsCTJg2DJtVloIDEDbUUlJxdThSucHxnZnSkjwVPb4ToSPBGKNU9UsPgRL3KW/J4rxYjsJ5y7Jl1UkbECzlmhGifhBASKEzu7wSEBKijt4QoIcxTwjxPOJ8vOJ8vmKcZs+aVMO8hS35dcaz2yRLeOe2i3OcMhjuJ7pg4MibOTpcYwzfgUlddw43q8VA63Fsf0nd7Y8RAamDKfL/eAoMCe1tDdTMgHwvV9xUIP1P2FWTHz/p3bN2AZoDIOYMoYE6MlQLWWABkESKLpC8EBpLdWtjuC+UOuf3ZdMN6vxCqcVGekQdamOBBINW2QAZpLTCBwYrAAdcDScF+tRiso0eEwQxz31dH84lUwewl/o+xR0+Vezj3qMk9CNtTGlW8rnLSIyXttm89bjt61oT2vTbsHYNDtvCQuzyOx53cre+mzoDt5AyP1TNT1DxEDZuPfHWry896EKmpgmSDzfqEeVuEHnY8Lm9zsJ0XPz/jb54u31sD6z+P94Ypau+R/f9E6ceButY0PqX8Xbtj/AHQ8y3juEc4bOP+CE+yJxTuz9k95fTe98c4V3nXD/BP99rz61T5gaOqeRSkHb5y93n47p8/mrOuGW5eEVUM35vHvsGd5lr/RE9rb8hBluJo/H44Mq6NWPvmyRYODnYYzPU4kpRn9SFxPwYX/rvxDEe/++kY6fgGjZEwvXbd6dT+vTtwOta1+T4+/0Sd2y7c509GOYOsjU+W/IRi7ahf+6vd+rRLc3CPszMiu31rC5MJwAmMGYwJKxIWRLxxwHsBllJQMmHmjFgYKYrcc+a022nzWpDE1KweEdAEvco1kfHj3mu4DcxRBkO80l+IESIqvxdjABXpDwPibatXAAglA4j14FkBI2jfoAfTlDA0eFCazNYREwqH6d182UF7m1VhBueCZV3xvixYshyykbBBURIUoyDoHLJ5Ztr8RI2KwYDk25CT/k2JKXv/er3ier3idruhlIJpmjDPE04nycfn+R3z1A0UkdKE19cvmOe56rDer+96ilzCN1mybyJCiAFTmkW+XWfRJ+Slk3EqGBJJzoh8RVki1sC4BkLJC5ZlQUwzQpxBQcL3Wu4/AEjTDKDg8vIFyy3ibc1gAr6/vYMC4f26IMUEWOSJGEA0IQYgpYAYqfLqJYtHRCkrAhHe39/BueA9vSOvGYvCRCmMtTCWXJBy0XQD/aYiPzbF2y0D5Yiv9g0S5GHHKe+ZNaxsEWnWy44GD3UdLXRTEbkVTm6xHnuDQ87iiWN5bmukjJxFL1G9IsQDAlk8Iqx//TBKxxt3BoG6N3b20N3S6PBHS8OVBGj+kLFW+WKrJ+OhQIiR8HKZ8OXlhK8vF3x5ueCsh4UDAOKWQLywrYqvVQ87PpBlfp/ix/kfXz5niDjo84YY702ce3djiBiqJMcsPAtCnVHjQBjw/T1Wuui9QVHrB8LclAtN7O8qGO6pe1oW90PJE/GuRoi82XwdYwxoWJjmbWCxC0VBGjSEjLkYivdEKU2IYfdHZTw6DuRJINzlH1uCXyFErH1BTTQluQVsHsa2BgGFNLRL4ZorIpq7GCz+n65fdecqNV8Eip523QtKu+09unODVdj2cNPfa2TDnjd4bUMRfNmIij2zJ1DI1TwlxMDkvSF80kn7mBJ11uS8EneuGSFi9awIsES8drKql+lGksZOCGwEr4WVaZbt8bspw6oRYlP3fjkyRrQtu0N0D4T8R23UNTwUKPUfanBtiryaAL56RigxgTwbgg/PFlStMQiKnWDe2rREbCEERGakKMJqYgZzQE6xEu4lFywu1mPJTTFNyo0Y3B4ZdozdbPA9TINTvuiWrNER9xQu8vHeEIPhq77X2mPWE8ODIszjU68k914Rsi+SXvWjhtm2X2VeUwqYUhRj3aQxGlPczRHR+orKKDCPDJJ913BMnRLYhqNMCe8ZqrulcGi4Z/xsjuRe60MVvOz3o/qdEut4jz3G+4ZvRzj5NHNEPQV4xghRnx+UMNaP5jFmBgkJ2cRMNe8KrWvlDdgkmzut9f3i7ROWKwJU0Txzg+GGvvb4GDenRJUeVzkCAyg5XGpwUA0Rzlhcca7BjVOOdLzWHX7o9yrH9bV561/o39lXtPlaPEQOgt0hH3oMw/fauAuj2scmOPV7rGt1jy3+qBzQ2I4Njm0xhft5bNDYrq1dP7ZWX8WJzhjR8Twy9M28HSnk7V43LwfrVPkU2kDJ/pR8QmDzNM6UtjuU8HB89veIi2rdw9g/Y4g4fm7bp3sKy7Hc3+89PHym3IOJvete//baHu8fPXev7r4+Ga2ELDkuZA/fmWNuyB+g0PeN2gGAY1zC7XHPV7k9OfJTW9jr9xZXQa/v673vvjwKndb+3I+zvYH/Ok8fgKs7z4517X53dYzfnynjXnmKX/kkLT2C5r36du+59x+905R893f5OFpfradD4AhgAmNCQWpJq1k8IpbCKCS8ayJgJTUwdL1vcoB9s6yXok9AS25NbRymRN3oYgay17gu+ctyRAQSD+pghggicHB5KewapceBJXQRsXoUMBlT2K6+H6wd9pO9+Zsc/9YvSnuMKmNYSsGaC26LHEizfot8GhxZb3hJVONOpq14qgAm67IafZixrmv9MGuYoWnG+XyBHYQYDRGkIaXP5wumaao4RJJNr8h5ARcGadhZ0n7EmAAuCDEChZGLjZWdeCPrxSWDcUPJEXkBlhBRioSGCnFGnM8IMYFR6sFNIgvjOmOeTwAY1/QGlIzrbcWUFtyWjDW3aB7yTkAMk9BtMJgCmALyApQVWOYZzEXCNy03pJgQwgrSPI6FoZ4iRdeJx+WtEClrRY0pZOOWjY/j7vuuDFNFQseTGghUHhWuDSd1cPvOQEu1a7IF+/VuYbqzHk4tTg/E1QDRDulVebaUJuDAxsitDza+e+N8otSt+EQ5xusEOFgPuo/J9EQe6yp+ioFwmiLOc8L5NONsURhS0kOo7UDZKGWOx2GOwqEe9be7Tw1+Hoy+8goNrx6TyWdo4LPlJzwiWDt5LCSOz/eFIO5hfUgGoE12ZSgeDnjLpN3rj5/AQwHXhMkuuZiMo+F2D0R9H/s6WeUpd9o1F9yub7i+vUmIptsNeV2QQ9I4f2psMJ86Ux4EGpRmPh9GRIxCjEOR/A82FxsWuwpCQoxGBrZ7EKhKtqYE68cq82gn/Qsstr5sWvFiKCxeEoaGjUjeF2Jl7EGVbhKOKWtMd4nfF4iQYsCk4VrSsqp1tiCv2XmXoFoXuQodwuQHTUpNoWf626lu84wYuJqduSKHkNr8tPE07xFLtKzELkyyvqpkTWmuY/RzklLC6TTj5XLB68sFL5czXi5nXFyeiGlqCXkthE3LDyFIVGLz92ybsiMoegq8EZzcER3m3AhM/Z7R4uRXStgJKvfKqCCVv2XfbGb6rjD3keK5wIMnSCgLMQGFROHNYmYozBr3uI3T8kSIz4ImVSOLd2iEi8HBNoDApiWvMqaXKCCsGQajyJCEvFiRwShEiERY1wXggnUpdS1bFH7amSvandO9maFaV0ssZ3NCLgdExUVBPy6M2ZaIDsQUXjjYzr1XMps3xJQmpDRjmmekNCNNJ2H+YtsrDNZ9FHC+qOfQ+YzzfMI0nzClWfNMRAQ1SlRltnebNAaqmIeP7JC6N1j3SikS+1I9g2wvVIWwG/A4Tq71KpvJ/Ye6Hcp1brxQTW5dfGxNImpK6p2yd3+PHo+C1ccE7Z3TnGjkfauc0vu7Le/UrvWmEGV1opxzS5JYCSkKJKcQBLMxakKxkRE8LG1L6WopXdclITKeZYBlQrfgppsibiPzCpw9nrvCmv7SDBAmDDQhJ7swTU/hSEendn9+cp1HBezPliMjRK/cd/fRDKVjn7Z/H/MdY6EB+nbn1OioF/z6gLHtrwp7O4UHYBn7Qh63W2XGS5AmbpR9EFw8BoOryqP4+XTYRzGZws7YNg1SCVmH+i4PcGDvkf5WH2VnGhnn3uODnenwMsLRGj8q99a/r3db/7127vXH47eP9mnn6U/3a29PjTLLM/XcK8/Nw3M84fjekVH9XnvH9A8ALC/V8cjJmOaBU9mXH+0PrY8JXMwwvt9nqazRdqB5RMQdL2qr45EM3owRfX8fzf0418+84/ELd7x/3xej7/fbb/WN/djWyR/6/qjOvTb884/aGNv5UCECDQcg9+ry6zgavA/xqiuPYKf/vcnOjUY1w7S9Hyli4gkrJRRKCJSEH6WADOBWCjKgsgtjjhHMwA2MBCB5dK9AQoDwV8ZntdZ70lBp7zAOr6ERJrmnS5r3L0CSfhkPCT28UmgV78AQ9OCZyH8auxfgAGikBhiNZDOdWPuOdvowV93f+p64LyhrSGi6GqBDToWBIDkisuYtiDFimhLSNGHN6p1QZK4KWZaPJjPYHFelsp1qzxnrcsP1esWPH9+xLDeEAEzThGl6kWgMp5PmgxhzgYo3BAFiCChFww5LuKRlWfDjx3es64Ll+g7OGWteNMpCFm/lEADIQTPzmGeGHiw1BpzBvGC9ASUvWNcFIc4I6TsoTNUQMZ9ekFLC+fLSkkRzwTzPIGLczheJUnJ7x/uy4m+//kBh4OXlgvM8gZmRAiFF8e4/nyYwIpgCFhSsYJxOMygCX68vIGK8f78iIOD77R0ZIqPfbu9Y1gVJoxiAixyis+Wvyz0KC20/2rUdSPNiieYr6cIDQ70aRKPj9zpXGEOTASp0UN1zZG23DQRm8fLIuWDNLSxYF+JJvSVKXlHyCi5rzT9hxgjiAjLZWe/Zb52xZac8g19lTu2553D9cZtNDmC20Iq2BqRzJ/gqpYB5jvjycsKX1zNezqKbm/Tgo5Uqp9NR7/a0Ih8tPFyfffZn232+fNoQYd08ImZbZmdH2QEnx9D2lN4u8+g26sjo9G3uCEPWk6HOI0G3bpZuBD2ryvWUf98Pr4itkqcRdBZF/bouWBY1QOS1KnjNqsh9U434kv+0MYYQwEWNFCGAyj2jjG4i8m2MIje6zdbmR9/fZe5MAdnCQtk6ySNFFLoV8Y3v999lKSOoEDgyigoLVGw2UNfIkA5TEKt7yFgB5NwUcYKifVvDaSP4+eqZLHvGv++fpdrhOlPuOdS6xo/dt3VrSaot/JZjmohqfPzTPElOCM0LIUyCGiB8ourhxHfto60fbyHbEzr7pSpddyzenSdEVby2Op4VKkYhTfbLlsFve3ZvLfbr3QgT7t8Nfqq8Iynf3ebf1qoU8ZYQcDYXYSHSbbw2HreXDJ4s4VkbAAJzjXdvtD9ZUjJ1FSZmzJywMlfjTw4BHAi5tBr9yDwubbDYD3mLq9nh5f6ZBr/BzYnBaejuj3toLAMvtOmPD0lWwydFlx/CQivFVHGiDcMSPJo7sRgwWg6V4PZHDS010gJlqoRJMjOqh2/uYN8bbOtcDnic2Zg+98wI65Upa/3YVDZ8px4t79NQ/+aOEOppRn/drtJPCduwfbHlI5jdMjyhLKgwqPAnCd5Y119hp7CGsIF6C5oRsVcZW9nOm84BA+YJUUmonx4Gup1NbZ5Y322n58zQ5IwQxjoYdHQCiJQaOq8aHMZcPceGp2Hi6vz5q5/Xdn1uHY6KH8dorK/ve4Ed+/B5VPejMbTv937baYu2tOOzRvCeYvX0t4OvR5UclEBUP54+jryk54+tJ9z95550/EdPNLR+cjSnEYrus8EpusH7+Wh1VJkX99dou16NJ763Rvfo0T4sPYKpx3zIPTh8tm7p31jHffo61nXPCHGE5x/18d4zj+bjGZzh39nSin0atvfecRuN3yruOc8Ttby8PUwcwZBcdVcXLwvdMxxwB/fdB/0+GufjaPyN99z+/pF1vHfv6DDDrtzftv8T5fG+emRUe6Rof6Ycj6+v62NGm8PGDnDF8Vx0/L178lEfnjNC2FEkh9trSz0sBSZECogUJcSw8mMMMT5kMFa2o27AygURhFVljeTrVVlJd2cbF7u+6HyNvFL9afirp2tQGiRwKgpqACTRJpjaYU7BsUF5AdVvVPeMYLGiAONfiCBH1TIw4lLH+7nhOmYYlRUY59qPjMEaZ7/J2RaGOYaAUCz3hjxPSqv9jPgd6g+25JKxLDeN2nHVUKfiDXE+n+sBR0APXcHwlcjEFiKVgoVMlUOXpYh3wu221Lx6mVfksoJL1gOQDOOZJVy1HMTiYuG4bLoywBl5ZZQiyn2iBRQXUEiIeUEICaUUSQ4cCGkSbw5Z74gYRR7MYKw3YM0Fb9cb0pTw9n4DwJinAI5BQ2YTUkxgBDBFDT1UME0JFIDT6YQ1r3JdCq55BTMjlxU56wFZ9RwgZgQFhwbzAzzUP52OhlsUhmMeh/u/O/mxgdTGmEqOP+sflYNXTqxl9X7J5hHho2DYnqxySXEytI2N6/OjrHzfWP8B+kW9sfIZY/F+27anzZjjf288tH2NwfK3SrLqabIIDKEdELL20Mt2pnO5RyQf6c98t1srzxYz5vY6ts18/I7l04aIZ7pxjwH1iqVOSdrVLwsusZfN2jQo72qdfZuP4HPPGLH3neoZRNQNNtS0W7fAkJf+NEcDYJgHWS3Ct+s7bu9vaozwm7GgsHlGhHqa3U4bC2Prrqw5IqiF5BmZ2f+IYmu7t6FZT1MwGKQhlTyzX/9lSLJZCI0XJKmeESEgloIYmmdEPf1/KjhnxrIuWNcVt+uiboVi6V8L19Ojsvl7ZtIEEqqMgrJgVUkZRpG0+5sqstpnFvtP6P6OMdXkkH7tTBFOgRBSrPEZL5cLLuczzqcZp5Mmqzb3r2qUUIPGsL8q8uP+JGfLBWGJkZsXROHmFcHuHrPE/GPnNdEn7bUTWcqUudi5YNQd1sOLqkZcMrRxLj+rDPJzoOfLIA664rFEle0FLOi7wTSCnjAH9O2mTGrMoId5BphApHHpDScwg7NTfyrxJ5I1RgmIRDWRhPGnYRUlUyZoQjHGEgICxBVwWfVkQl3bDFScqXvvCSEw1Kf34HbHgFavAXAeETK00J4H9ISC7hHhaDqh1fpme8jqFu8FMT5Ug8Ik+z4EYbIZkisjRGl3miLm04QvlzMulzMuJ/GMkBBNYpiIMTUaFELd0lXRW/OirBL7sjKBzSjnc/qYJ0Q9kc4WUVSpGpkSvsFId8KlvufkhqpcLsMzDf7cpRavnN4r9xixLd2QNXpG2UXGLH6Q5nj6vcuDeoHb9S0oLPIQminFDLAwhohAignimcgoQZK+FzZvl48Xhvg9AQbLEJ4VLoxZkyz0GioeYFZXeRNKDA+7dTM49DBT1OOvuUUzcoHDz1xh5V7xSuv2kb6OzL7tUVOKmFfVCCfP8Bvs9sNHil/73d+eFVCeKB0vqYKHwZ+nkTnnbj9u95wX942v1L2rOUscGellxs1eRFVI+ukzCiZGN413TaqEoDYG603dn8P8FccfZZZDI3HD4xouv8/f7/GeGxgBNvVwP7S2Bjvtbfl9Xz9wLIAdywn7Qu4xPO0ph4+e68u+UHxPqVzfZN92698x2Hu8ur93Rj78sKYn9tZH5uOZ+o72/T2FxUfq9YaDiHG3Vs5pp4bjMXR1E2mOwDsKFqAS/HGfRJU7jsa0VbC479z6KX+R0qidjdbVqS9TPwu73dZ+bYf1pMLksGxhsvara7vh2BG+n1ba3Cm9DLsv84+/fZYESZifxx4Rm0LDGg/vHe2Re/eNDyMAXD3sqmSAEf4DiVIpksgmkQgTAYnEyBCU5y/IYDBuRZJTX8sKJkIKQDTY9HwVyZVKzzcUk19tfB3xrCNvW8BkKks0DdGtyBgDAgMIQXgyCqBQwBTaHiD1WyahuM1NI6hBovGAdeJUxnGLo20TJCmFXz/1mjfPCPs+4mbWOjQvIEVShrOFiLVDgmCZMUmOSwBnMCD6JlCV29dV5Js1L1huN3z//ive3t7x97//TXBQFMwo8laoXZYDaKavAHKOes0azon1GeB0viBNM3LOSFPE7f3fkDOwVi+MVXNtSaLr+SRhnaYUUXLBukidy7LAjg8VU3DnK0A3EN0kasHyDqKI2+0NMSaU8o40TTifLtp/SZg8RfG6KOkEoODX335I/2LAl8sZvBbMc8TllHA5nTC/vNjAkUsAl4yQAgoXLHnFlBLevy+IFHHNN/C6Yr3dgLc3XN/fEK9XXIoZIewA666w06FPT5NMZnDA4PSiWznSwA7c+PhS6s6B4XnSrVGL2Ra0VbZ8h6YnMljzvaT2bIXDLIYmWNQMvZqHRBuY46G3M/KhYnSheXI9fueIPpvuz/9uGmkmFlygzwUinE8zXi4nfH0948vrGeezHISMkVqUG6ClaWPXPje+znIOtvE8SQseFS+SfKoYkvt9yucMEcr4dmz6M8wpmoJiV1CpDH2/+0gXm+rSHzHsd9o2WHya+XAEBfcYyOP6jJA34d2YP6lYXJdWSTi7rjXOeFerIZImeRzOX1MObg0Qrf0/thz1ywhXz5yX2iO/dpVGw60xkehkC0nKmPpCC3sEAIEZSU++rmr58UpTrAVZE88K+t0XL6roURGB1jF21jP4rk9HAm7/cafJqfdYaHuiNl3nMaaIlDQMVYpIFpIqxrueEJXpHBj5kXHjhhU13h93yi0hLk0x2j7+hLgncjuzxX1bvRseO3DfN+q0+T4Wjj5SCO3UD3skq2tg61Lzs1gMTio1oTQpFW/7njZt+KrrzCi3T64eQkFAc3cNQRKz25QmzkgcwUnWc80rCqc6b0XjUOa61nvCk5/HB/MzCMbdnsIRHt/iJttDbMOGF3poaKu1V2GZQk3cbkbIGlaNlIFRpi4Qasi2eZ5wmoY8KtFysNi+c2szKBS7kx2b30blo3667w0aOgpX5Qvur37ugc2pd3uWTaGJYybKSi8k93M9Kk/3aUsD3iMB1+NAP7y9YnV6OGzK3p4B80rgTsnl/+Ce3jA7jwgKKJrDiCG5XcCSbBCloFAvkD/kE0zZYbICN5jutlqHB/ofTHzwbT77Kd4FmjUvuv7NKjhUOfhwAdp1XOftXvT3vWJ5qPIBT2Z9Njyx945/9meY7mOa8Zip735vXe33H4Z9swMz/lZPG9HvW792vG2n66v1rVMuGr40PkEMBT2ncjCXwxzUMcEOKXQP90qiDi30e3+8kr+S1kRUE1nafjhacaOPfsx231/7v+/DzxF4beHiuJ62b+7TUv/MPcX5dg/twfH9d47qbu/2+Lvfzz/HT31kHM8+t2eIOKIJz7S5937j2wCA0KQTu3MEm/s0satbbj6k0XuGCACdsfhoHO7Opn/j3n8GbipP3hHZj+2np8Xtw/psr4zj247Hichd2+MYj4xaYzlao6P929f5MwO3vAV79T5bnsMLD3uifFiVbyqTY20Mcj4EbiSMq4TetnwO/nCTKTYzF2QmrFzkICXUo1zrb00FDePSYNlm2KtgSfs8KnC7gw9EqDFniPRcCEmkhm48bYxdIcUE7rr5mALDMw9V6PU9I1e9wTUPc9xuy2I0xq7CIelMVF6C+3ZMhrZ6AMnlAJPt3aGWLKf3bzfxhrje3lXmOgFAPdFtbUtEYeO55QBQKUmveohG+xvTBAoB0yzJqMnCEesa1QM4IIAkFG9KEfM0Ia8ZpAfNmJduSeSdLFMTGMgrKGdQiChcsMaEaY4oZZZk3qofEYWy6V80TNhyQwgBP368IwB4Oc1gTogBmOcTiKIafgJiBDhR9eSY5xmlFJxOM27LInKmekHYvIoByJkNKpx0Ky4z4vcvN6NbBaM9eVOZtl4e9XDnWvEVGtgayBtzx31bZiSwtnpcyPU/z9B6j4iuz8PH+E3mVlftMRkP+QGcRv3TI1a+Z1Tu6/Ht6phIUo5DD8mDlE4HwpQSppQwzwmnyfQNzVjHvt5ODgBAXMP2GqpqqGuflj1dHpCnj9T34bbvlJ/IEdHKY2K3FaiICCGGTml6SMQJLpwPYe+k3yCjDW0zShmZuKYA2e0xqysgleH+x08qSApirsxk0biAnBesyxXv7z/w/n7Bst4wlRMyF4k/XxgUJExT4FC3oFcwM0dIGCQGodT+euVd8SGajMhif1N2xN0pOvYhuK+lMd5BT4UTNMWUEiO1qJKESgL17LEhzQJ2ep6m/IiUNPF1BIeCGApyLIjJn9qXeTMviNN8xbKuWG4rci64LXKSdNHcEe30uPSX3YYflasdk/FBGGjz1QwQ/UlyZ6TT74Z/SAnn6XTC5Tzj5eWCl5czXi4zLpeTxr+fcZ5mnNJUE1fHlBA0bn7vDrYV97mLNy6x/bgUie9XipwGVzdEuWefrSdEi0ffXNiqwhNc46BUoaxjqrjbY8wern6Oqd6Uxs/VvCUG976I4iQCBHBgkEQThbDWUU7HlHY6oyrENV5LHU9RqlIkErd4/JinBLX9RwAF8YgwwkthBQEooYiBLQAUJOb9PEXESFjWCdfbFeuaa/Iyynpql9nt7wfCpOKrI6Vd2xfNM4uUkZO9YoYBhWsnsNhcE9qajgK2/9v2htGJFGbEMCHRJO7fJrJxQSmkxgnG+ZQwTxO+vn7B+XzC19cvuJzOeDm/YJ7EI6KGdHKGOkDxIJsnhMa5tGRcDs5ZQ2aJgSCrt4Q7HY1jM6cMVE9VdCiVQGxG93vFmMuRtsoKPlO269mvxfaewOs9RVF7D6g5cDxuc/i0weJWoVTlrQH2xhJIDAuse9PW0upKSZJTT1MEBdKYuQwm8RwquuFCwcYYcWfmbNQH9yvXIX/T3orw7jdTfo2GoWaA6L0gqtJaDROFfXz/pnDp9hgPjWK7vzHs/yaY7z+3t4+7mdmDqZ3fj8qhcrP7e1vHPl45qGunj+3xYwPEaKxswpetXXvHBPP2ETd9T3+z0tmcjYYEmKju973ILKG2YTyr5fIRxdCOoLW5435zcGau9wx0StkRn1c4q7+E7iqEkxy/166jXHloLNnrK9DF2wWe48V6mHimpccwvXd99Pyj+/eeGZWpHxt3v087ZcVOXSNOPDSQHfT16Pej/n2Uz3tWIK61mq6G+v3crvLkNkWzvrzTR5NR9vrDzJLz7wlDhFc1+fmILpb4UenrdLkNVQLd9ve5wlUGpuH63NwfjvXBu/fgcOQ39ut+3M9nYeehAWn3mc8ran5OybO/j+7t4/vzo1Ap5B5tXi1vos9bUgBaAFoRqSBRQULBHAJmIpyCQGOWFwAwCmesJSCgIFMSsmD55yqNYD3Rzxo6zTyug8gbKkP5Yt4SEA1h1WOwOR3YUPS9aNTSTvuHACql8qs+rLPkkoyVLhMnmasYIJ7/WbwdSb3mbfJU0dg0ruoRUQ9lEponhE266yu7q5a8rsjLDctNcjpMKSFN4vlLJPlISfUyOhWSD4ozUBjrsqCUgtvtilIybtd3XK/v+P5DPCLefnxHTBGlrAC4ymLiSW56JtLIFIQYBRbMGyLnjNW8Ru1UfQyI04TT5StimkFxQskZy3RFyStut3cZJgEICXGaav+XlcCSJdFYM1nPyhppVIOywnJXEgW8EyOmBF7EsBLjSeSQInJ/jBElAysHLEvB33/9gXWR3BuvlxOAV8xzQUGQUNhzwhyBfIIYGjjjttxQSsb5dMK6rDifZ0kXMk8IuiaSYJLEw4hMONjbf9TgVEGId9bf85ciC6iXQcmVF0WnP3H8qcEgBl7a8QoMVm++1m7lEyvFYu0rq97IRxLIIiurnAwuIOubGSesz5yBWuPP4MCPlz0c3/RWdoPbggBoJjTxqgqqd3t5PePr6xlfX054fZkxn2ZMU3Jo4EDPhBYCcmCNu36ajPtTpWff/1PLTxsijhRIm+eAqoywZ/vPMOl1kqkipLpQhwwuMM5qY9ifI7z+dyF3j5/b9kH7XYV3USyJ0pnk+CIJwswlY80r1rxURVe1OFaO2W+ErdKoF+7371fm5O5o/MCeeIZ0nG4u2ppIrECfxKgUIYb2HTvhMLj717CuCrhK1EMwAZ2E0FOu7dj8BSIVUvVEOQJyLgCJIYJI3RHzqgoAabYME7SnnBsmYP8r7/xeUYuOaXeNdD6b1qfCjXhBTJhczLn6cZ4QsQt5Rp0rmKxTm13f3d74pN4QVfnFNYRJYeeSd+AJIbDgYGLDBNvV96OdCvXCmEe8XlHp69krzwlbvAvr/b5WKzYZ42DKN1F6cwFYwzGZx8TQEzcPqPumgcfYTxf+JIjBFhp2DQzECESOSBr+igiYSxLsWDIILgmSwnZhY3DrqHdxwYgp7ilb2mfICaEfD9f1JIMOe29Nax+GNjqDXZBYnbVNGF/W8LwooCVp2zxPNZeKhCqbqmtxHAwQbd0bXG9ClXk4HxSRdv8pBqrOQxtz2yfNEOQ/lSI6gcSDqb3+M0zKHp5rc9SgZpyz7V5rxoc64O0UyDy4Nu8xWbYnWuHKlNvTtv+MHkR1Rw8hILIYLkoo9QScjYtIDEBjq+M4B7RQF2A7zi1+9fX0vAptn0G/tiOs9R/H2PJQkV/PDZz3Pd4b95b+NV6uHzcw7qXj2u88fwdl79Lg3Tb333OvHP4+jnfsjzcObcs4+SYDNgHnngGDizcojbSxN032+LvtzQqFZDwTuTfQ4S3/dj9H9ixMZgVg3np+dI2Gkf+n26eNomx+Nxo+zOLReh7N+rNK1T060/iI/drv4S//+6ES3e4fPH/33Tv9/8z7/vnteu/T4BG336PXR/159Pxnx/Govk2p5ELUiV0q+V1eZKx32HWbcYXj+Rr23bEhovfDsH0cNmvm3tnQIJFc2ygIdGBWeTx3LKFp+rcqzX30/t58PN/2tq/bsW7r6ts8PsR0dH94quOp7q1B/8wRh/1c+ajxb1t+fm6bDOeqJKC5yMiNcd8y6YFIPSAZSMItJSIkkrwLYKNmAkhFw1AbC9OGQJVcsPN4Fbzq5OaKZ1vf/Rgq8XI0h/39NhrNC7FDF2tTXs+i4ZuYQBwrfW2T5g8VGX9gDbe2PT3sHvHtb5h9ucelIK+r5MXUnAQEiOwoR1p1Hrir03gPH3425xXrumj+UrmueYUp6hfNa1qKeN+nZIccDXbk8FHN5WchunOuyZJZNhSIAmKawAxMhVGiKP1zXpCzhu7xB39rDkJGSwSuq+50Bn7u5f8MpoJ1uYLLioWAEiNK3MKT5DMJKAwsy4pbDHi/3pBSxJoLctEV1XDgTAEpEm7rDcioOQBilBwBU0pYSsGUEigl1c3IWCTmuFtyHmCiAX41QrDuv0pTiJrexuBe55gqLLap6WDZ3fbHwtqmJ4Vf4wUdDfMyL5r53MsiPmpGlV9gIY0YzQDSGE0bQ4fv7qCyZ/HiETbe0wnv4nlGPbjQwh56xKj8t+prTPcwTQlzzQ1h2Vq2eoIm+zc85J22jvp9RF+P6KPXh8v37TwclVEntn//c+WnckQ8YigP3yWHxEmVLv4BPvhiBEA34HGbBvDU0wT/xDOTx6wn8PeZ5COmyvAaCV5rHhHREroKwc05A7cb3t/e8OP0huvtijTfcF5XUIh1Q4pHRM+cNo+IprAaJsTN84hwoYhgbw7uCdpj6ed8ZNZGpZDsNVM2a2aAEZEI241GVHqmg8yKzM2NL3ED41IKOBfkSbwd5tOpxhbMpdQY+rdbRi6Mm54GKFnqW0o70SwfIwr9Rj4qz8ycR2PkgIWCJpqMoSI0IXgTTqcZr1++4OV8wtcvcsr75eUFL5cLXs4t7r1PWC0eEVGTcAkSLIYAbVx6GqA3OrhPzh2jYh4QWyXtECcfypwZFauYT5MBskOmjlKyZygeFc+4fbJUROz/84zMbrNCSgNJTPpGo80NVU/o1E46YgfATrjGiEaY2RJQOYUiKcNDEucwImjczQKKhBgJa4nIJSOFgEUV7CkL/lhzwW1Z1DMio7Akljrc+oqHHabpx11xYABR7PB4TfZsJ5RqXgjb0w1HFdUIOF6n1t8rPZshwpjaGMbQY8LMBcUL8yyxGL9+ecX5fMK3r7JXLucLTvPckrlrrgkv4HvFYM7Z7QHBKTUZtYXFkXNFLs57+3iBpDKEfh55UHrvMYvD3MfQ6Bk73N/2XNsQVQAogmeLM9T6sbZYr9TN90EvYHh+7JtngEzB14xPTeHn4ej+tu33jeO7+2eI5NBZpRmMGh4NQElykmpKBYSMEDNCAUIpKGE0lgw9eCTsM99nkk0QMmHYjcjfe6a09wBm6kMx6QNNLLBuUc2vZAqt+8MZwl7t8ljbVdso7929Z579TLk3JoPrzyi6HvVtNCrYe7vGBt17zD6vxA6NLUUOsBUgZ5bki1l5knowxQk9lWahwnkVBg1BFG6CuxN8BHasXRGYRXPgx70dfyew1asKXxB2IiidIrKQFXYfNcSAeQd5L6FnV2kk9z8HQb9DIXJzMWKsfnzjc/W3Qa74vZS2D7rd0Tw74DO2uf/ucT+OxvLMO0d1jPfN89R2/t29ClS6y2hyUh3jnjKgb3Wvxjt93a6db4v27o/Pjz1QHPcIn/X19czEPUNE3/+jBxydq/w5YS/XyF6/njqYcef9e99rF3fG0J6lp+7vv2/7BNijfezmw9f9s8qZvff37t3jXbZz569bPs5+Nw8HLwcx0HlEsF7t0/YCFF7kY0aIKYo3RAkRiQgLi7JX0v5K46WwHhIMyFH8DewQne0B5gjSPH2kylwqTc7wuLVXZlLNDcFKlyyLYVWL5DZ3YmiQw5SN1xAlO0UGleoPD9asMibxVW0WQZXLDOLQ6zssPyAR+lPWtteUQJZhDAZrbmw/3n6g/M//iV+//RlvX3/BL9++4Xw+YwonFDDef/0N602U+4VZDs2BkVfxxFzzgpIzbrcb1nXB29sP3K7vWJYbcpZcDKUA1+tVPCQLME2Sk3Ka5MCXeEeIh7nJhjFGpElCMS05g7JEqpBckzKOFC+IYcb5/CpzWG5Yblf8jf4nbrcr3r7/ilIyiIri0AJG1lwcBGCS6VKdg5v9qleUPJbAci1YQVivN4QQkaZVQ11LH2OSfqdpBrhgKSvotiJ8/4GYIjIsBCqBSD1CphmBEvBGwE1gruQiuVFSwpeXF8ynM/Kf/gHh9Rv+8uc/Yfr2TfJAEkmQBED1MG0j7uIzt/wVcD1f5uRXLkXzqQw4Q9+t/KvJqwZeTxYvx/i2c8mifytZc5Swaw+VLyb1hLC8SeT7M7Tx2VJ5Y5fjyHSQe8+OuHvUKW9nwOF9yPrEGDGliJeXM15fLni9nHHR5O4hGp5grKX41617sv2pakwGfcy2z3WcG1z+B0QQ6Vu407OPlw8YIprQcbd58hddUGwVEVVZQX2dJlTt1Tn2xxSCu33l/d+MCD+0pHnCsPNMr6wkGALsFf9KZ8By+rJVVJlSSRK0YF3E8iwJq7PLMG8ahr4fGwPDMFfPgEjHqCvBfGb399Y1HTvtn2bt+2ehPcYETAN+1RFUhFBPrtopvwAmjfMNdIij5CInMkpBYDGClMgIQRSKIWaN8Z+RczvBLok/GaQnCmrIpmJQYG2Rm6Z2WqbOp01g5Yao8hR769YpAElPfAfSq8RIjJoPYp5SVaROaao5ImJMGsMx1vj5XaJykGMibb4d81Pp0c4pTbi/uf/biJhfA4/Q/fx0+62+prNqRqn6O3+AKvo3HTO8+a2v3i9R2+v3i52CYWVO2UiFwWa3H5vkZgaZShxcmDmptRktKk/awbsy/kHmM0QgQk/fyANISXbOWgqYgKTeP4WL5kNjUFWgc0MndwQZuz79MYGkhmZqdddxdHe4Et5+RRxtGBK6kxpyFbEqGuHqLZGmKAmqZzHe1eTtmhsihliNc2bUHPH67sfmbOd+20Dbeaz4zMsbNu+7ZK7RrQ6eCKLMc4jS+NAN6eJGj+D+PdgN7Zk7W+5IMSTt7XtEtH/3iwdBwxNbZXb/uzbYNcNuLqw+IgDmNs68n5S57j/jU+6MszLrHpc1ilWXhVtdfvAfQmmtN/18scFgH0qu8QkDr6C4oY6hoaquZh7bqH1Xns+R6g/ztgPft/vbeN2UkeEeeTdXIe+00z17v9G9cVZq9kC55FGAZw+rEYKbJ2HxYbUY+hswJin37EQlU368XtTcwSeVdvg+8t6zyqfcXWDP59gctYo6Hu4DcDIKfuP3nr/agsmWA9i51wsg/cu0w6M8W47q9d9HZKBfaXzsDo7d+/7sb9vfPY6Va8Od+20+lJewXa+je4/6fu97laKo/3u3XjaayY1PIxrkjEfFQ9Sdfm3wyn4tz7fX6rV9/FnFAhmfeu+Zu+vTd8so3GPTdu918vHy3Cpt9re7/4kdvd+G4y+euf9HlD0cdc8QcVzuz2sIpDxGe5bgowXQ7tw2fo0BDQtEBDVGSML1GMRYLQZxQmB/Ul9pZOVsFHegzTPpvu/ljV7f0jrUOtn1t8PZ+g+PLxjQU3vG3WtGiqCGdgYiV/7JToHL2Fh+d/qSjtFoDNdu3/sbdm0/5nXF7XrFuizIecUUCC9zAgeRVfE+4cYFN5YDU1RlfhfloOYwyC0yR5VD1DBVGEWNCSEE5BwlP0TQeVHDpJxjanjfdBpiQ/Z6BMMOASlFXeeEgIApnVDWXBXXeV117aVfVNfNz0ubtIaymiGUSxaYYqBQAdECDupdDzUu6aE6JsmhkQtjWSTMd86lnjcDZFzRDseZvkX5byI5dDzPk9ChlxeEl1fM5zPiPIND04k2SG8cTh3JZpMp+Ay3jf/3vKOF/b3HL+m2UzDndtPJEU7K7drrdJNO/uj5VwbYMl6XxnzqVYwQDYeyjWWYj34Cni3U5tCBh42qm7uuXbdV4XCpl/sM5N2kEFC9YaYURV+n0UosWXsbvsLpk7SjdWFnQYEK43ul6fr68bbft391v/8H0LenDRHmVOKZj17hbBvKTteMs9U2XnXVC/KRfDXOeldxywgARRfStMO2qlArN8Es2B4hGTRydy0NGADUMB+OQBAA75XqlazWhuBcC73U4J3QvK+qGyJDQhlafZTBYPz227+hcMY/v/03nOYZeb2J69iaJRq9xTTUOQkUwQEIMYnBXBXXpqxraaHuFelMYbVcssRxIx1TPTDv4v23cQ/AXGNEmqJE4rzZs3bCttWVwFxQyCu1pU8EaGThLQY2tz+Z26Cn+OAYEULJXMMHmcAvJw2FqGX9bdUcEXJl5FWUttd1qXkmLNdE4YI120liWUuxE+lpRjejXilXr4q4glsjIkIMeoI9JfkeJyFgKYp71zwhpoTL5YJ5nvH65QXnecZFrayXywXn8xmn0xnTdEKaThJ6JibEOCFEI7Khg1sCoI6SLa8Gu1wQXJDLAot9L7Cxgsta80NgXcElAzlLLEJ4OHGUBRiczQHWkwsjQWjY33GdevVGrqpc8SD4kD6N8MS6AzwL4HBG/ctwHrt1JnXUkVBJwl+RJL4li1FfNGeAhRJr+6AeTivUCDHa1SKPti6wMC4TIaSAWAhxDYgxIecVKRfEEJFzQZwScs6Yp4R1zbjersg5431ZJDfKIgzWUqjFLO4IrClVye01CXNmxjFLPWeeEIEiCAGkp2vNO6LFN20GxMYcGhw0xbsxeLLXI1JMytCJR0RKEyglICZwJHHyiQyKjMtFEpr98u0Fp/MJf/7TV5xPZ/zp61ec5hmvL18wpQnz+ST7Y5oq0wm0UFbSj3ZyeV3VMAwInsziJZTXFXldUdYVnLPgPG7uxNXji5rXDKEg1rYkb1E19BEjQ+mgGlZyzh30Fq0PLChXQg41ZbQwos6bzJWgyf6MJ2HlZnsBTloRQ0aE90QBmkCyqTv0+FpCuTrmx53MtvnFQEfaVlejbNBkeg63d0bOyiqQoouePtWQgFHiDIdACBFIUd7LdsozEFaWeK2ZoTSwiTHeqb4qAjbzYDPaTmMxWPKXkKyTCU62vtB1f1ykL6WIIqDmK8ktl4/kFMgoq+TxsUMMBA1LSFR5Ln+1fghkxToOa1dwbQFzcPBhU0M171Bj09opPxt/XZMKZGRQ5uR7ktw7RJC4v4YDSPtIGLMUtO9O4AVanppxFncVsb6dUBUo4zgVBe8qgmTcztBQ0LzOIDj2llewnvYszOAsf68FKEXgbi2MZZVYyrkUrIWr55gcUhCDWbF9XsetvASr9wtESI8Jmqhd9kG20LtggIUn2CgSbWtVdEIKu+YB5/lKo5VUeWwCJBZ1IHfVqfTfCS0B356ocKeMj26p+vY5dsrnsTZy43lWmd9EhB18SMOs0v7wqvFTJ+KTOuauX89+l/L7SpfPGBzuvXevdIZu9/jTI6Dx6tax5vHa64s7sPHBNfKKU317w8PuF+Ep/XwS+r7t/d3jpZ45Fig/9ojY9v3OQB08b0O+7u2weyqSbWFTWunb2xWxe+SeoYpLBMU5bn5nKHuKp6P+P3v/U0bMg9If5vr8+96z1dOuR+OpPBQyNPkWGECsORQZoALQCgleHSCqpAQQI2BBpoxMBVMgTCFhTieUMIEDYSUgwbx7Gw9SCnAFYw3iHsiBla4xIloezECMiQAOYtzgEMGBwST8crSoEzmiEMCrzudKwkQVoIa3QcPFalEAcRB6FcWznVMUxTSl6kmIwqASMDEwJVa5eUWJcho9h6nyYmKcsNjPFrd/bYSWCKAkf69XEIAYEhilyh6CUByQs9DUgIJye8f7bwFrfgNPV/zffpnw//rHr4g6vv/3OeDX2xX/n3/7FW/XBd9Vm76ooh/lBs4Lltub5HIAg2LEPL+AaEJZLF+HyntI4BKxLgDnjHxl5MSIsajClWoSagpAIuB8iigTQBSxLoxf365Ylhve3v8uUx++Yk4zvr3+gmW6ga8ZP5Bw+/U3cFmxXq9VYpek1RGykMtWUUpySLAeqhm0D4wVQEGgBUE9LXgF1kwABcQkatHAwFoyfqyMeZrw269v+PLyqrJARMKEhIAIIBSAMoFKRCgJUwAwAdPlK5Am4J//FXj5M8Iv/wycv4JTEkZc4b+yEsVkJ26hmmBskqy/sakiv5eaZ4FzAat8AC7m4CN6Cd1rhQtuRRNHlyJ1FcdJM1ewNC1N09SQxQDAWjJyXsCaFDwWMeSUDFBGlZNZYYvzD6BkhLxIGy5HhOggXH61LWbSC1W95F1SbHyqo2OyA00m99Wa3OzbDVVW8TJGQNaaCKY6l1wr8ngg4HWOeL0k/HI+4ZfzCV+mGZdpElyseiGAVS/MtQueSBbmela1gBAJzueqHaCrjPdBsV+epXP/meV5j4jKPPXGiPozdMn2AKWupVPW+yv1iooxu+M4oVw3y0hYvXRTu62CJG/qQN1gQy4ILygNbQNwzCTcfOxLVCbEmq4Ibo5YFUPLIu5oyyqucWwhcNhbOKEMqvavCtD+NIBjWqkR2tbv1n9fmr3zEYA+YrzU6qfKsrGtXljxyg2uvQDMEDGwsG48HcwQ6SlpOyXBYAo1HEomRgguTJQqDCxnRQyq0FFPCcSgoQugYaVEmRByhlcuCO6XREzWe+666wQJpxzzaxbVGt8MEUlCMmmInWkWr4fTbHkhpi60jIWXiS4/xBivv54aYbOSN/yL2m/n8QBvydbfUNwzpd5HB589DDVRAg3hOjhqyud9mKp91mtvhOifayDWM9J79frnquDS3z0oApNV6NFxdfvMlBAVvsckf7XTii4URtgYYnLKONd33fSkJ5UCAYEDojsNItUJE2lK7ECEwhkhEDIzAmlSVGJkAqhoqCbfS8MhtT8Nhk19xdYfvwfHe1Yh2+gdHsDYb89/eJzmDXc+B4XigDCcQJgTTqcJ53nGaZ5wMm+ISYxzsl+ChDxT76O69gMctlM7vP2oZwnK9jfZNyPo7MGw45McrhiVFQ2WjbFqIQcFjLjO8T34bXDZNelodk+/NsqIEcbbbPkW2nerk8dnj1nIo/Fv9r7N550xezzR+I0GiXKPO/gm5q53mykAaoiZzXj3e7Fzx/MKfR3bKZcbXNkan4x6/JQqQHQIXrvhe+2bYduH7Namw6fbWe74PEeTm4LN9vYOr+hgTU62tef880S+jc007hfPF4w/be75mdjui1YeM+1V4HWPGj/gcyxVL0tung8WXstyMI3r6/vFvF0L428rT1hxduOTuEpfjC6cCksFZB+9ud3fjm+H59Raf0hXsN3z+P54329CB9wpYw333hS6Qoff+1qfd2PfGiMOxnXAe+/de1TXo758tOz3ZVj1gWd6Zk89UpY/+32vVNzykTHT+McIbQ1W96vd3n/UvP3e6Lu7cfc9pXEOWdMAIB+Z0+4341s/UD66H+4bV54tIy+x3fN1JZXfNM2U8YXGH5h8/jx2+blyZKTee86XXeMN0U6euc/3a6/dx+80f4Sm4Qj9DqKRQ5BDDww76ND4+EABkdqhiARRKhYuMAW7Hstxf1Hlb1vfGl3rP81LmgIhFMn1EEhzUsAC9ejH5BbA6VUIltuyyhvB5AQJryRNNGVMYIgylyC6BQQUSSQAAqGQHD4g5LbWbEmsXYJt8geI/H71V8VVleYqwycnLREDME8Rr3PCL6cJUQ9+fS8zKAK//biCQMhrRsyMkjIyGBQJKHLoI9gs2TzqYSQCaW4+nRNAve0DQBL6F5CDFUSQOikgWYJsNQ7FEORQnfY9lxUESCQQPUQSiEReixOmNCEXRs4k/G/xfJFOvv1pAKJ4u0W1Mhrf4Fvg0LxDMgAJdwoqQIabf1Fgr+uKZVlqaG85VIsmD+qHdN1TlDBi0/kETGfg8gV8+YKcTuA4q9uIwqvB3w67vcdN1b+44Y9RBvWyT5st1fQpj2n8nlZQ9TS7Mq/KtdVrF00HJDwkugh+sLlR/RHsY887HRA213GknygjvlM0smeaGl7sfm87ktH3j4x9hvGPgQgpBcxJwjNNMSCFhhMxrBFQK9joDpnbZDas6GTacXh7dKQO4PgwwGOa5XbCE/Tts+VDOSIenehoFuaDZa44N9RQGk1hag+wMhStzaNPziOF6vshFcAttr/Kpz4bUPsh/4r1jJzlfG8+THHbCT32XXFcZUiLYJ2iyHMtDKaCH29vKAj47bffkNIZ377dEMOEnFcBYp7AbMp1AEEsqDEEiXPtCZcRWP145bcg6P4DMiaO5KBzOZ53P757xYiVr8fu+7nyOQbsO6AW3LEdNy4ZUyOWHo6gylpDOhO3kxeGgAtDlYnAumooJj0JsGqfshKWJa+a1FrzIijdtxPTTbkgioZcSj+/aAYIfwVQk+6aIcKS6E6TeDPM5xNSShLvcZ7x+vKK03zC6+UFp5PEvZ/nE6bJPs1IEWLUEx1UlRXs5jyroUviRmouCB0DlyyW9RorP6vHhHhHtFwQ+8zyffho8LAPUw0xmzECdIxzfrp4BZxrv/+7If9uaHrDr3OPE6LCt8y+nYRnSxwd0J16sP3B9ZSex7dR44yKUSgQUCKQc0QpWT17MlJMFQbXdUWMETlnTJPkilhuE3IpiDc9eavwX2OWdsMTZlI8GeyksZyORQigEFFzQVQlgVOy69zWta2EtTHX3o3X2qz7JO7QEq0qxoBpini5nDDPM759EU+IX75KfNRvX77idDrj5fKKaZpxPl8QY0JKkxrteq+xnqErNURezks9eV7juVt4lYobGw6QXCsHBowBj7Y59sKizd8Orrb7Q5839QEVhkD9DFa6ZEqWe3R8FJoJ42rcLZbcvQ+J5Po4tHFkfBiVHY2+br3PfF1cGedNz+rv7PgD//u2fAz3NIX8pmXr4J33tsviaWSFR9ZcAj6PgIOzOicmsFQPJVOcf4yxHPt01FfQALd3yrM85XjP8y+P+013v3+GtngYHetqa6Q8wSJel8JDtDVcllzXcl01f1W2z6peL7XFun+Mf618CxE4JNlP0fPWob6zVwQKmpBIKBBTsyVzz90VjjsGgKCKlGqEIFFmOJSm0ql6m9h3k77xQYTyO5efVc7+DD9SlX1toj5d11j+MF7JlWfn4lE//uh+3it/pGD9e5d7RoidpzEqTf7zyj4dPHqWOoWseHXtPmny7ODp0ckU1vxQ9nD2XvnI/WfrHH/3vI0vMcYP1Tc+u4cD7tHZsQ0xaCv/XoxXlrVhliPUTEIv1DUZjACmCQgnACcQzUCYgJAQYkCIhKS8vcW/4GJXAGBEcr56xlPDIku0cSBE8QjQ0JtEBRQjMM2gksFF2ilFM3TqKWkuGYQiihltw5TZkksRADKIMjIDsWQkAFQKCkWUwghBTnOTxr8PDDBWFJ7qCe+8iHfqqnLDqnoESSatxpdiBgntB0O8vVm9IRFknDBRyuRhmUteM/JywzTNmCbgv/zyFf+Pf/5n/MuffsEvLy8SaQSEPEf8sq54SWe83Vb87ccV12XFj9s7lrzi1zfC9XYFyg3X2w2//lgAzgi0IMaC+SyHJlOapKskuqs1Lyh6PG1lRtCT+EABVuEKTvOMFCW0dKCIOUwIkXBKJ8nJUQhLXrEuf8N7StVDgSZgfpnx9S9/xbq84/3tV6zLFdf3H8o/LTD2T0WahhMUvENouh/DLVW/EiQiBQiqCwHWrIp43CqnY/67UyL8+n3Cl98u+P79O1IipJmQwowYJrwtK643WdtIjJcvF4DOCF//BJpfsP75n5BPv+A6f0OJZ2TEpuQmQmA1SjmdSv0de35lDMtK4vUxJoNW3t4mx8kF1ZjDJi9opBlNLm3RMIp6TnDOqvTShOYsHthVB+TkYBSNkMGl6SthvNZ/Dh2qOhm0/gCozs8f4QKaMafADQ9zSpimhJfzGS+Xs+ajnKseNFdDXa/r7PC6I1gbHTZ6WenZcYM+ctTnoI6xn75Tv9O6fjpZ9Vhs3ipb7SfS/eaVEd4IYYz53hz3SqJGaOt9KFCFnUlj/YeHSbUM6PrplGVaIanCxnfKA4L2+HBOCjdEaTIXQRVBpPGCC6q19XZbcLvdkEuL09eFT1FlQkWSVQiU3mwUV90CYaOU6hbnJ8s4L7jD9Pgk2/67MAKeGdrpvxvbBo7qb8owQRVyBjOQUwvG+DA3T4kYJe1UUEu3IeuwRhQuiOrGaOE78uaUI1dLed8XqvHoq4LVFHSQhEUpRk1KLWFQ5mlGSBHzPCOmhFmR2jTNmJJ6RqTJhWESr4ga+56oeokoDR6KV6AO+R80wVCvPO0Vq70ib1/Rynx8Ypm59aG/3zpbw3wRdcnp7zHwzwi1u0KEUw42jGLX8ZS0JxBt93d7riar7uG7KmPq+4IUTPiyOoRIESwUXT+sUJvoFIEsXg4FBMqSKMtwqsW8jEU8LXIuWAoJ4whoUlXqxtMpgatmyfqLfi/63/vZ2l4bV91oxiBke2OEvGXPatgREiNsihFTmnCaJszzCaf5hHk+aV6IGfPeHrGwUegV3B5ube+Pydi57BkYhr1hzM0TzII3tLV58PhtazCmDTy0MWyZlP0duLdN7u4dv6zkbtb92rdJGPvg26iLPqAl3h/3Ud/4vgLb6hzxDLl/2zP+V8MvQ1X6075Q8FzZwkQ/d3QAByN81k8Nq6e4soHfUQ98Z7BH+4/BgHZ/3zNGbKZup9JuBYa13Fv/Zw0b98o9ZZ7xhHt9f0oh5XGnHmKoie793ww18PvE1ePV/t7nh3sSZHyOW0/FFe1BDxUjL1xf6a4HA97MW+Vvu+sIEx5PbK+fVfBvMM/Be/fW3Z98fKZto6nP9PVor1h7d/HbT5afNUY88+6jdXs0vj9y/Pul7ZEjAXsXL9TfgAc75KfKLp48gN37c9bjdqUmv0t/Pv7sPp05LsPzGz7Bt9f4Q+AA5v+DQGukEx9RGP1R5Wf3VQ09pyGLej7e8/zOUBEiQEk+SGA9rMSajy2QeFQbpS2KT0tH6xvFMvpWpakq00p9Ha9UvSICvAGcKejhTQJDY4EXkcda7QBpABQKqisIUYwgIaEgIwQGyA6oAqBST4KDWRJXU2h6GlL/AhKlbOX3pdI2n8a8wQwTDNHSWx0mn/q10dcKI0XCeU74cj7hT5cXnKcJMQZEPeR14gQQ4euZMccVKMAtRswBWPIK4IYpEt7eTkiBsK4LEjFKiiiBsAKIQZJSSy8ZIRdI8kGdfw2vXiz3g/Y1Z/GiscNIJiNZWNygXhvregO44P36Q8NQCtzNpxlEjJxvIhfbGtt8dLzHPn/o9Uw13Kx6ahgvZLyXiXCgFo4eXLCsopu73a64Xq+4LScs6wqOEYWDhCriAhBLCNg0gSIhnF+A+RWYLkA6g0IChajg23gPcvKUrXfPafDOp6djo2GgwpvVUPk+Rh2oPWvzoOtXD91ZGCcNAdV7Y/vQ6nbI0urm1nlGu0foeeUnZKk9aXLUA9mvdeZG3Ds2M/bPrnfIR+W10a72UAgBSQ9HzjV3a2j91RDuI9+xK6/fmZKPGCPa+j949kFddXr+QHr2KUNEU7jZ9+H3w/cE/8YYEKPEHfcKJys23mbB65U9OeuVvVWJxE2sq4e7vzslKQEAazgbc4sFqOhpe5dcukcarn6nqKRhY3jDyihIsxJAs8Ty2xvWzPjbr38DxQn/eHvHNM1YlgUEQj7NIA0RRIo0SIHfQvKYhe1QWFdlFo+/MeRUAtscPYTLnarbmD0z6L/7q62DKWj9+gLQFCCKVGXBMEKVjLPFqa8KTCK1QpqJphexLTIBa+at6iGAHrYAIU65nmhQ5QCX/r4pLXXizKBS+weS0yAkiafNCEFu3uz5OE0IUQwRMQZM5xNiiDjNZ6RpwuXygnkSj4h5mnE5X8QoMYuBIponhPM2YjMaWD4OZCUmdsLbTmWu/XVVq/i6yrN64t6IEzAQIjxCskBNf3b4O2BEtsZVN6bzDymMRu29EaJH3kY/j4rBdfWIIIDVE8dgwgwR3XzpP0GDOI77ptghCW57W0qEKUVzCODCWBUHTMpApCmKB8Q66elbOdm/aNKtmK5YS26ncte1KcKY1YKvp0gq7jBhICCEtFEO1u6ZgGIx5Cuzapuv7UmTG2x83gjh93WMhBiBaQqY5oTL5YTzacbXr19xebng29evuKhHxGk+4cuXr5jnGZfTC1KUGLUxmvdRyw0x0hgzOphHhOWIyGVVpWKLz19K2xOlOIWjY+SA/dMPjYYS7NizwI/ComMmpa8SE9WEHgd9tZ4e9zb48u1JGyJA1HibTyqEuj5b2xtFDuo6m1A50r9eSdqYK3L98bBgz/h5NCbriOa0z2YQrU9Knxl9u2Nh9+49YwQdGH7auhuPoHO3UWjqmFG3TgebQDtNbyft7NBCLozMzSPnaBysQvJeoSfh4XDf2zs787jH4/lbzypO92Bp7M+j94/6dO9Z6+MRT2qDksSKsi7LKl4N67pKksecURjIln9mad4ti3pFrKsmjMyCZyyUUoOZ/dL1wxux0EIrtjF5+vbcGj8qI8z8xyuZH5cNTDrDzd7vh++5vXrcVv/u/rN/jEfE710+uq/89/E6KhD25uePVuD+ZyuIny1+bn4Gb9nht4+2+/uUfZr46Pk69r0n7uzTDY81irsDnblHd/bw/2fu3yvjM78HbHre8SN1e/phWrkqpzKBOdb7INFjSE6TBEYCc0KmM0CvKHRBwQklzMhBDRJB+Pig+JNBkgCbuV6ND2QSaTFz6RKee2jyPGIQxRKYE0AFrCFRSgkuab0JVAmgoEYDU7Qy7DCWHHxiBCbEUhA5AqGghFXDEYkyn4oZIlja5bUy3THKYYSwLkL34xXIGUQ3iY8vSdCAorkh8irfoyh1S1EaHdWwUZwHRwCqR+Fa8PVyxj//y1/wf//nf8D/+Kd/wp9eXmSeNYfmCxJOMeE1nZCZ8f38jnVd8Z5XLHnF/3o74f12xZ/nhPfbDf/r1zOutxv+/rdZvDWXFSEGpHlCZmBhxm1ZJP9gCcgtizmWW8a6sspPjFvJWCngFiw6g/LkMSBOCZfTCYEY37//He9c8H77FVNKeHl5xZQmvHz9hrwumE4nxO9/x5IX8LUgr9cq39yjx00vFDBNM2KMOJ1OAFC9K5aseUJz8Ry5wqTkyXx7A/4WCKfTjMvLBUQFUySkeUWYTriuV6x8Q0iMM0W8vFwwzSfwt39Bmb/g76d/AMUveE8vQEhItKJlKm74mTXfbPG6ywP8Wferun2bPMql1xeYccJkW6hhocJ9tvwMlje1RQEQ2CvNI4Ilr2zJKzhrntBinhCl5hGteWc5Vz2R7C2GJriAGaWOycMHaYfCwd486e7e1ma42+fx7dnC3cJcdI0EZ52miMtpxtfXC769XvBynnE+JZDmh7RcsqPhaKhVMO4TvP526Pvjflge0YTB4LX3hPYAvs8fpWMfNkRslU52UbbeL+QOcxoqYuhPe3aF2ymvZoVCVfj6a29sKEM13P1tdQnBk34SFwQEtx5me5eBSJ1HQKFKU4zLsNO+PcMQpTD01D3EbWfNK5bqEbGqR4QlnnGKKWYzKra59KGJ3NUTbOsD7oym/vgEDO2t7Yb5sUG761YJ0047qwuK+jpSraRGq/RKpPoZhGb7G+3Usxf2arXqthcskWw1InA332sIkiNiLTXesySjChJ3P5eq7K9KP2WCmiFCDBDeEFHXwfZCIDUkiOtgjJJ8N4SEeZKT3VOaMNW8EPIJISKGdtJ7qzxQGOXttfvouKoVnNu1OA8JcJsfAA+vPaI7eGanEAEtyavO1ai9qtWyvdCuVgkavLN/3r7v9runjtS9LHeIjGxsjW2tRU12pt3a7A2FRxW9dF+7MVal0R6DJcQzUEAJBREuzF0gTAACFxCh5oEQb52AHAqWXBBzQIB4BC2EllC1eEVmn9fkSPm3YQbHobZdPIyHdumubRPBby1W6ZQi5inhNEkOiPNp1pwQs4Ypm5vHkMufcrQ/RsaguqRyOx2y2Ss+IfXwHeAO5p+D9e0cNuV8j+capFj9DbFW+Knz6uC8b9H+b3ukU3qM+H1c59YXoZE9Pm/rp+MZ2iblu/04e7Dfwti4x6i2zZs1tfnefOw3/ZcdPvS/jOtSf2GbLx+vcyCY9R1b9y1KOkJjNlsyPh0Tw/WzH5cZvSqP1INeX/FO2R/1duz3isHLXnNbhRjQBMed/jxgsD+jIHukGPcKUtL56/HRHoM//M3o4gRXjwYzWGqIppItoTVXQ4OEf2thnMwTIqtBGGy7zAxnKjjt8NgdpVUe1/PRfujCdm/Xbm+Oju4/+/3RGhyVR/Xzzm/P1N3B1BPGiG0//PW4vXGNHs/rx+H7qI/j/Udz+dn67z2z17bh8Gf79nsbDf5II8Qerur26082/fwaKsaopIg2BOfuaj6A63u/bofY8yuPS+N3x7d26cmdZ+7RtREGn4GLI2XPR+7/R5bPt288uuULUPipCmdjzgNqYle2vyOY1DBBCawKfybSUJ0Nb1rdwlspQ+r4J4aEQnYRo+vzDJ/7yNWjfSVYe9Q8OtRTQvoD+btWwZXOsukiNFQThSiyFgCwKasZQGgHQ5UHsLpCZFEqs2TWoJLlp6IhtyrvqKEZivUzyK3KcxtcmpeH9tUxlOfzjG9fX/HlfMZLEm+Ifr5ZclnEgMiMMkWsktoBKRO+lBOmGJCXBdf5CkLB9XbDVEQ3tSyLnPieJ2RmMUSsC663CWsG1ozKg15jwLqsWBaSaBG6PlkNKWZfsQPJp3kCeBVPjMxYlxuYC9IyASCcZpn/NM3ySRPKOmGhiJrg2IONQQ83PGKyn/eGN/muKu/ZIGDcBzLfJRcxvlyveH9/x/V6w3pbwBQRKaBwBhMjTiKnzqcT0nzCms7geAaHGSWkui7B8c097rG8KE1KaUxm+3ujr3B6marXqMJHnRUnP0hLqHKRvd9k2lITSjPkdHBpModFzqi/6bW4flae2o3BGNrWo9qPXox6zvN8kNgO5cD2LLtV7f+g7tehHXYPkeEe6WcIkNwQU8RpSpjnhEk9IuDWmF09R/SGjV4qCt6H677s8VSH/X9QNs9169Bk2g/X86A8bYjolU7ouAAzQhwxHDY3MYgXRAqhKk9DMPcVJ2DXxIv+u8btZ8aa1yqIS2lxJf1C9+58veGi8/AiY9y8ck0FN40xaGO3E5pt8ftkr6HOkUtvMkA8U39CNvOCzMBv339FTBOu1zec5hOWdRFF45olTVRSIljU1S1EcGAsIehJeImbKAHku17VBSMCmPxKmeIDjZAHgMq+kOAVQm19x2ddspXx6uCBdHNSsPXWa1WckmvT+mrDEcJNbj0EKQzeCOZxYwyK9VXnpKApcUyhYMiZWbxumJunRPWgsJwKmqxaxqewUg0R1ifxujHvm7GEIMAYkhDKeZ40RNNJckVMJ6Q04XQ6S7z7+ayJq0+aE2LahJ0BVbTfKa7q1QwqFvtePSHKKlbuvLg4gdxOfIN5s5fuGyFGZR/6Z+4We+YJhtpr/I4YcB6s4rv93uZKcKALS2Zm/ZLm3J5nBpF6RjCBOSBATgUQ2YkiYbIRGrNAEDoupwV07HREig1fqTGS7YR/Y0TyJOu1qDGzekQsss7T1Dwlcim4LXZ6t7RTIo0fcnNhAogvA0Fw/RQlddvPMlUD2dm82pjLGC0fhIQoe7m8yOf1BZfLGd++fsXL+YIvX75gPp3w+vKKaZpwPl2Q0oR5Eq+iGJMmKAsdfFSFrvOEYMegFs4u50Np3hHOUJxLBtuzlnR28PJ6pnhDhNGZNiOhJjX3i1JBHuMOe9AW9j0iDHce98/heRN0ijcIGKp19NTngqp4XE0J1N4d2/IfC6FnV0exuvc9n8Isnm4ZElKvMBTfa9ib6sFik2z7/wCeK+3oDSM2o1zfkntVeNYfVIbcRU/WolKtSpNtHGOOiPrJDoczt0TqWqk3alDtXTMqswkAd1Bnr7gd12bn2Y5XHNa1n8o/tDxrhOiKACVkQqhtLIZ4jhYyL3U9BMY1zFLOYmAwnCq4luv1ljNKAfLKVcA3o8NaCpaOHnM7FYkergHxj+roThB+SE6S9jS6FPGLIACRqIb1c2zRZp6MN9/zWO755FE22J/jjxohPlM+UnfdD23TPoSPXtGM9uJu/f07e+P/rFL80Th/1ujwmfKRPXYPXvae/SONB8+WR1P4R8/xx+ofuIGROfiZrj7z7k8t10c5mf+zyiOj20cMI0fPjbTiqO2xHtlrI71vh6uUEsGMD6LMD2BEEEeAI4AZmS8odNLPhEwJTFGSFKt4GpiFnyX1jAjGrwEw1Zfj2QrVloV/g4ShRe2T9oVCUwdxVPxexHEjqP4kcOVdwaqRV72D/E7SsCZVDiyeE5my6lemekqcTLFaAji3UCyF1COCIjhl9c5YZS5LBhaps542Z1bPaAIow2S5Fmff4v4XMIvXJIiA04w///XP+B//+t/xz3/+M77NZ6SQJExvkENpec1gFESl+6/nhFICIgJyKbhMklfwry+vWPOKH9d33JYFv/32G/K64nq9iiEiJRSI5+0tr7jlFeuSsSySAyOXjB9v73hfFrxdb1jWFT+uVyzrir//eJNQRnr4Nk4zUoo4x1fcrgnX91/x9v6Ov/36htv1htuy4nJ+QZrPSCHifLmAS8F6W0CIWJaCkm/gfK0StcXB6A5jqd5FZEDJyWle7styFe/TYvJ0kw2NL2IGOEsIqx9vP/D3X2fM84RLjPgWZ8QvBeFSEFIBTYzzecYpnHC5/IKYLvg+/RlLfMUtXHCjGUskcGDMjr8HSVJz09XUPdk0OPDK/RE9liqbcj24rBUoj9/0PsXBm8kKwWQB9fa3+VnXtcGoPlNy1hyia8sHod+5FKCsQF5BOYNyAXIBeU+MTqnAMGNSL2FY5/33e+VI/9BKncsPkJa+B/q+hfQioVMpSUim18uMb69nfPtyxrfXC86nCfM0qeqTxVDFT47HiddPDG1Xfv79igmvj+auySpsyPsD5UOGCLkCQC+AylwdMaJt3Yig7mL+lKcbSqfkRBfuht1m80pVNiRtdUhFQhtMsLb3PSCya5Pa3jDkYxOvb1V48KeFNwpWY5q1EiYfLbu1rctVLU0S+65gWW7yWReseWkn09md3uya65XvIDe3Zjxxk1wVXXDKAgfs7RQmu4l4jgneY6gebpDahnEOEhbLELIPy1HbqEMyhdn29Gw9+ex+QxWoDXbl3WbCMqG01DUyRkD60p9EjTFqstDslkTqD2E8RR70VPc9QwQ00aQkrY4hVu+HaZLT3f6Ud3CGvOBPepMxd0qed5TtniiNsQB3T3uX8d6Txog7hogGLCNMjD/S8c9jVSPc3WHm9/t953nY/vA3ewTWM/P+MbcfN6NphJcN+B0lOhLLmlrRC+vU4JZIDillQgnNNRMQvEokTGgg0uTWAaUw1ihJrMOa1ePT8GDjg4QYh743dWwODrEjA5Mwx+TG2PLyUaURQXOmRE10Ns8T5nnG6XTC2X1O8wmnkyRqn3V/pCj7p3oKuT3SVnOkN84TorR7/vetF8T4jMPTTxbSObD+2BzVuRrx+bAlTHBshoAnBHlyl522Nm3Ttk++sKcdvpmBwPf4F5VeegF4z6jQ7qNerf82HY35aWvAMGODjwHLnbHIXGaFR7YTVlZrqIbuNnX7RgjPhPUrwMrHVSJb75P+6//z8wTuTwV1cOV4pMrbcxNd/JrpQldGjNCvk2eKRmZ5o3zdxWE7t+2XyoP1MGTvjLS7e/8OzB2WZx/bwKVfs705asU4t0pLuYVsrLijsBoTNJSj/Z7NG0I9ISzUVpG/sxnIKm/b5rbjUf2821obPwfF8a6PNjWNRaAub9UzRoW9e3vPf5RfvHfvM+VePV1/Pc6i9vtRXSP9IHIv1sKb54/m5dH3vcM+R9/H8rPP33/2/v3x9/77dj6P2h7pob/32bInpzz7/KNn9vpZ7+30e4/e79Xt+bzn+rgzRxu0/ZN77eh9I4C12Y+0MyifHsK/0Mjfo/T0/Pep79nf9uD8mfJ7KaB6ucn60dai8Z2N42Ly3t/G5wUQBzE6UKzeEAhBQ0Ibx9OORrLyg2z8ia2BXmq2vApWepCk8njaS1IPgEDqueH65T5G91BIE1izgpBJeNDxAcYzURAvhUCMot4FbfIAAoNJwjc1yiLe0cQSGopiACGCouQHEKUtmdoDMANKya2/vljuCDuopody0umEry+v+OvXb3idz5gslC4kPwWbTOjlEkL1EpHclIRQ5Cx2LhKVYVlWRBByXrGcTggkOfkK5GDPomGd1mXFsorSei0Z5xRxXRb8mCcs64rTFHFbVhAKbkvEbRWFbJwSiICQTrgR8PXlBTEEXN+vwgtlCRe83G5ASog6JzHNSNMZ87xgXSCJk+FCa3nc46eQmoyQswsX5Gj5ZsrdLgDLQehlXXG93XC93nC73jDNE9IUEVNAioQ0RaQYgTSjpBOWMGOlCSVElBBUdHaeRtijadovbuvW6Vqa8rJ+xmfIfiN7pP/dt2M6rm1dFo1FE4g7OVmeLfXD9ncp3X0ZhAkovummV2hYBWgL6O4cojhq14/iwdod6r9qg+xlEsN77h0iyTdjURrO84TzaZLrPCHFiBAEB1XRtKtjZxwGvgyQHY7/wJB+L/65Kwy0EGLDD8McdoP7IC193hDh5PHGu/cT5QXMuplUuRzIckJQ/YyMW6cg5SaMmXC3asLgdV2d4gdghE09VaAm24xOGAM5QiekjjgIHahKTB0BF8XbApBBGR87gdwQmbp7kex8r5izUiPQsVN2Q9zWCgNv79+Rpgk/fvyKeZqQv6woZZI3WWL9FpZktlW5VsOWBD0teiDUBwIVAkGSHxFFFWKzMhXiAElEQAiStNli3jtl7SMBclQkPcNkbRDtXrtSSRX+rL6gpyx6T4imeGzJm9XrgKKsSbATuX3iWirWB4GBsoPEvSGsxvJjZdBwrNDzhoi9uaEoTI/FMjxPJ8SYcJrPiGnCPJ8RY0Ka5pp8N4aEEJLOw/GesmvNbWGx71fLCaEnwV18QDFCZNhJcHZEZ0vUNquKGqrmQekgg/du8N6T+61ulIRb+OyND+XBOI56TJVY+HaawtQ9rUnLQuhhyeJ/myeQ9LPU58wzYvSgsmc9M9ONsfYRNWfEFBMKa2x5bgqyVXNELBrT00KGLKsYJDKb4hYO5mkX57b5V/dX7SyjrQsRIUafXwJKsOH2iexb8fpJOJ1mzKcZ5/MZX16+4MvlFS8vLzhfLvjy+orz+Sz5UlLzhGjeQha+zE679AYEC0VlMU2Lg/fmDeTyqXBGqR4RzTOCu1wR29MtHy1tLjTReSBRZjs/dTM+AXuK8eN6R37oSLk40jDvDWhlpAlN5tsaiO13YxwNp4/GCA/TBhsAYIfAuDJqImYxGGJAFhEVKCi8Kp7LTvGrcfhzwbpkrDnLurO8xYrvrYh92HkTwuRx6oTgnhEbGf1KGjymqLW1QANtvWVvU3sXPj+GFyxEcZ0tdxFYZVtC8Gugwv599foHysBf9ALfAEs6DZVn7OBgD9b65x7d2zxzMMJ7St2dSuQdXTMmNfioAsQMD1nzceSSUXKDtXUtCmsrcvWEYKyLCMG3ZcW6ZvGUYDFArFk8IirfqqX6C7swhdY3AyMmzRdWD6QAaw0F0QwaoOblEGJL3riXk2fv3t0pG+jQs0LRzwpPhkN+qi3a/72H8Q7IGx570Mbz8/EAZ9/5/rPPf6SMVW2/qwD9aIt9sk8/ozBuitPHfOJYjto8Wt+jfo4HYB73Fxt8+7gYpfo/vAw8brvt+ZL788IfmIff2xjxM+U/si9NbvGwbDwP20NqJzC+RRk9k3lraKYEYAaHCZkiShQFLKLm3oSEawnGjZDK4SGIkjs3Guh5rKAKzcy2phoiRh6FGRhIFfAS6kiVpXqKmYKaNYwhs5CiAcr8ad2ad4+IxaCgUTtCG217RuPzs6ZykFOtQKCCElgU6KUggYGUsRKDy4osii0ZXCFQ1JBMFp4JSWPuF5uAXqGbs8g/X17x3//xX/D//G//in/68iecKSGR5MHLINP3AlCewNaRUHnFCQkAYTqfwGC8qny43hbJAbCuIIj+jrmgQOTIpWTk9Yacl5p78Pv1DbfbgvdlwZIzvr+947qs+Le//Q3X2w0/3q8SKjgop8YFy3LBHAK+/3hD5Igf7+/4X3//G9brDb/97d8xzzP45QUowGl+ReAJiS54f/83vL8x1nVRT3bhdSgo/4tGn0TWW8EM3G43lJJBJPAQNKm3yRrNQCGJtk3myLng/XrD33/9DX87veDbdMZrAC4ReDlfcJkmXC6St3OJvyCHF3ynV7zTGbc4ocSElFhtTlQPmct6bPf7Q9zFBhNmHGg5VRlA4Sy5D5xHhDc4QI0LknvQ9DoZPhqAhF+S34m5yrzIq9wr5hmxgnOuHhFcVjDrbxa6yQtXNZxTO+hdy5Okzods99f6+0Md1dDepiNwJIbcA6JnjAE4n064nGb86dsX/OnrC/787RVfLhec5kn2CwwvsGtkr3H0nvM73w+7/2H+4IOF3R/3VX56/Tjd+rBHRP1+dL/xTlXR1Cmd6j3tuZ76M6WuP/nvlXbVE8Keq0DW3rfS8LUglPa39Nx32clz6CrwXwE9rayogbwS+cFcVUTomQsFajLLqPQzryvW5YbldsWyXKtSjN2m9WpG3RK90GjK6G7e+xGO/WushZ1+2Ho0PDp9MT7fxnz4yu77prysVlr4lev77+EL1n9sFWB1Dvxc1Pu9IWIUSsnBoc0Ds0tM3MHKsSECQDVE+Dnt2krym3lExJSQNKxMihEpSjLqToEQtsYZX3ev+B5Pd/dhaey6f/JbiUa3946Q/UfY/35t99/bKlhp85t7mvu93u//PZzwfP+Atl62Z7bt93Dfng+KrYrCqVMSwfZO89GR/CXsvOLYPQtl5H3/9ve4/W0GTGGqxKgb1BMi5KChxiRUSFwysio62wlyC5MXxC1au1M6GLF+tAwF7PpBFJDi5PafJLBrvwtDKCcNJkxzwukkXg/nyxmX07l5QkxTlw9CQpTpHoktYbtOVu1NT1O2uR4s4W/vJWFJqHO9X9zvPiSO8B2fFyI9LvUGHMHNUFmqhUIyoa2vowmN2wb09g6e6nHqiGP7a8P3+7zB3rg8njKaKnXtt+Gft71MZEzaDvPe8QyaeF0Nq3b6vLiT6KXIUYRShVNXF3pcMnLLchJuUGbVNxsbQSRf7JQdtUfcW402dfmzKq5qAkXrm30ab9T1z9M02wOONxjnradLI193n5CPilo30t11bTygfq/3RyPHxxnszyvBjf+ALjd1MDDSUe9RmLur8amo4bIsBNP2wwqjio+sfemChqSwnjSaUWfY5pEaTJQiPCXBhD/jj/b2+XhvMIjtzOXR/O7v3+evHy3Gt7Zv/to/2Xik4doT0Luw17573n/LuRy9N75/jCk/0pfn3n/2neeeG/ONjO08qme77iNPfPT+IznkfqFd2nqvvb7NkcYew/HW0KHQukOzdnvqceWD/m3ftfbqHTyCtefqfR7mPmfg2eFXGjAN5Jec4uioft7w56PM9ej+o37fg5m+u5+nY7+nQeJo3NsHhz86lFUZMDQcSrpGbsZJT+STC1NtfBP3q8Y7f4EaD9XCZ7ZnfJd6Ob8JYF7uJ9dHVPlk06rqeZq8i7rW8qBBKfWvuF618dZx27tGz4laDov60UY6xpFcQ9zuAZjnGd++fsUvr1/wp/MrLtOMRBEBcmA2ZzmcYuFzjIuA5uyAefvGWNshUl8KO/hSQjUaBBCYSZTbBHCWA60hFIRI4s1JGSkGxBSw5oxIwLKuoLzgtkx4mWL1QmaIcWRdM0pmnKcJ7+83nKYJ1+u78E55RV6A23tAoIRIE2KacD5HML+DyzsAUj7LTuKrbGFryS75Nzd5tW2Fre5kD98zoIf0VlxvC75fb5jWjFNhABEhzOBwQg4nXMMJSzjhnSZcw4QcA0ogBFLZn2NXrwGyQl6n++1u2DAMRip42vdxPzt9jTGIWolB0g7WdXJy0z963pfQ9gbVZ4pbAzVe2K6v/dd91TXW7+c6GR0ueJ6XOH7O1Wn0Q38iHbNsgKYv7AQV1w/S/ZpSlMOS84TzacYpJcwpIllYtBpup+6+neKwif3pZJBuFHf48Xu4/YiXOqrLP1O5VieX9L0fMOkeQD0oH05W7cs+g9Tc+7wCIQQgUNBPU6oIwI/KHhOst/H5C1vcfqgBUDbVRiFc96VNEzuYagqvQCTWSU8LulEKRFhIJotVeKQ48eP2hKn2zDO+inakzYLb7Q3v7xE/vv8dp2nCmhfkoqFSCmtiJB04i0XV4p63UD0RehzycK2MMFpIDXNDYtb49yGA1PXP5tX/XWdmYMYak93W3b9yLMD2dVZkPCp4djZWvRpT5MIUEVGLTx5crg9SJWUgSNx+1zdujIsf49HYO2FmCBU1lnaieC/kFKnylPQUd8A8zUghYZ5PNURTCBEhWaJq8TCyQ7u+j0W9EcwDol3X4bvFude4gHlRxar3hBDtxtYIIaePK6RXgqLE7mFcuW2RdfZfulk/+MHa988YPNrzzfjwUcb+kAQqM9n12Xrk4KIZrWR/BLa9pEYGDjqXCv9sV7sn8FJPRTtctkuY0GAtxghmrldWw2/JpeY4aTkNoB4QBheMNXvcLPFBC1MdCyDJsGuic20DDDndA3TzQBSqR4Qpu6KdliIzTEhIpkkNDefzGafTCZfLBZf5jMvp0u6dXzRk00VCOJ1mMeBN4glBMeg6ycx1eVKY635on6w0qN2XZ/T0fF5dHPfmFdGP/4NAf6eMCkLb56NCZefNKpARBjhhwUFjjojuXX9/pCUj4+OYOgJqDPr98bQ/SK9tHNtxN1ote8ZyRMg4Gt7xymHzfrBT6WvOuK2LnEa/LTUOqv3OMMHFxC3UeTblfu0fCQvPddzbuefaN4d3PHPWsUv+/VB5pDZ/lQ2seEG8buTVThGec62P3NpW0ZsqlRwWo3XlET/vFWNHv8O18UjpTKQ+Jwc0c3zn6Lm6Bx70/yPF0/iGC/Lmb4El8Sozg1fOBavCT8sdsVZvs2XNuK1ZeV1gLXra0+gCsOVLyfGw6q7R8ILAZNaTnGbAbnMbK18z4hOPi/0hh6McEeOa7N1/9vpzhdwHO9cHfar7YKfmu/00Q8b2+We/79V5+MuH6/pY+Zn67u3r4+fp8Lljevbc7/f72tfx7Lh7XMy7vx2N46i/z/TB09ffe82fLZ9t9+Nza7ivzfER/wF///djtX7X8p+1Xj9diI7Fr/0XIJ4QEolAGSStRw4sZWiuB1InBXhvB6FBlrvLM5KV3+KWNg96JTjWSeu1L0U1K6braDqPoHWYN7d60Zq8YrKhnRx3si/BQmmqTFujzohi1bxqUYQ79BETLA8ltC/9AalQD6hYcumaXBv2t04zU6X7IMKXL6/4r//1X/Df//qP+L++/gV/Pr9gTglEEVQIyyryCcoCOfWu1cQJTAGkuqKiB8NMW0xEomeKQU41rJp7tGSR+zIQA4MpIHBASQGTZK3CPAfhqxfhs5eXE0rO+IfLjHVdcbuKR0RZRY/3W75hLQV//fYL3t5veJ0v+NuvvwLriu/vP/Bvv/5NDua+vWE+veBy+YZpPmN+fUGagWkm4Ne/IzOQ1xvYPGpKg6N1XXQ/mhwtOTgKN/5p3K+9EjfADFNrznh7v+Fvb2+Yvn/H9PUVLysjYEaKr8jhG5Z4xt/iN7yHM/4eX7CEE2iSQ6iJix41bJ7Wu7KBu2d/ktseqvXc6GTcCHp5gVlDbMtBSHAzRDSmsnvd1e0OQFlb3AwQkjMi1/yipeaOMEMEN4ce2w1Wx9Dmbqly74iRjjFUkwccv7HRD+21Q01/SkDV6UH47wI1xgVCiITTecbLy4yvrxf88nrB62XG5TRpomrZKwWia/Y66Y8Ug897hoNnefQ948TP81s/T4Sf94hAv1dGQVP+Zve74UtV9pMXquztQZGw0ea1SyNT9wfNe5sbtpiCVPo+DSfEYJvT3uzDUYyCnCWnNsVfl8y6KtS98ONGRPo3MYAgSYLzgtv1HdfruyDzaRWlYRChlURz2SMgQhMmgxCYUZCUjyZm0s3pBVFjCLyAu13fHnCPmS1DHPaMwQXt4A67wZWBsVXcnCoBOsXN0ZpsiEu9Npru+9E9R6q4cXWze7yOpvbDzQWJe+qRssQr1+zdOkcETTgeWnKlILkgzMtlhFU4fgVm0jKFnDvRvffxyhXmrDki7GS3uvrBKVY7gueV5I1YVSWpzfXRieyt1r7uWxoWZ2AP3Cu8e99+6wW9feUwD2u4LTRcaPMzVaDiDb55KOxWRttOtzdvCKC5hMop2OaFI3gHwhxvqalegm0lgS0V2myeM2VJGOc8e5gZuQCsIZyYGanGPHeGiEIanknGbAZk8wpgz0SjweuYtN0+MZmRsOVSiTEgqSGiekScZpzmE+Z5xjzPkjslTTVZe/WGCBGWeEwpTF1ryzvkjQabj+0F5yVUXOilzmDhcvjcK1uB+/DJCgMehtopqtEIYfijx9dtH217ZvI7tQcPcae0vcX1/Xioko/tM23X1O9GR6j91tHIvfEN98G9sZqHNd0YI1RZnLOEZCpq4M/F3Pv9HGuvGOqiD8VvfoTkGOO299n9izr6dte90THifo3vnUavBhdunqE+nOUhZHn4OEBJvjmPu3qY2n1zeG573cAUwbnPe8X48TsfLT+jDOqM+gPt3Br3G5zlbIkbLWSTCK9rFpy6ahgm85yQ9atymbat7aoxoRog2A4xWoCIBlE87gc11hWQhkVth2+EnxBc28KljrziPi7Ym9+fvY7lHq4Zfxvd8x+9t7kONP65fu7zv4++y71R49D9unPv+brvle374+8fqq6r8xF8bO/dWc8HPNNHDAhHbX++Do/Bx3q3NL6j3xu63TwdH/X5mee27/X9uAdbj+v6/LvPlqM1eYj/7/VthxjuwdtR/Y8UNI+efbZOg4d7bf0eh1vurWMHux2s3MNXfTH500JJN2293LacnaYNYJWbmCVEtjdEGG9Vc9Rxa2XTd/2HiNTn3Ovv3SEMas+NcCOyTKlXWHQADU1jxyO9Ypb1kBayhAJdOdfk0qb0zaUgQ3kFO2TrCb7J1vdk0Mo0kjHKoBhwupzxyy/f8Hq54KyHtzgKXyD91MTCLOFxosp/HBhsXiOa748IjSGD8L1Nv6DyvZ54LyxjYbIVq7NcQ4AH5aNTEFlxniJiAKIm8ZaDcAW0Aisz5lhwioTrLy+IlPHvv7xinoBlfce6FtxWlVchOrAQgWmawOUih4vWjCsXrKUl+tZTfgoh6gHBKpYOkNTkigZTxrn3eF34wVvOeFsX3ApjQcANJyx0wUqvyLjgnS54pxPWMKGEgOj4tMIEi4JiEO+jvHg9i8GHN0KA4XRh/gfDFeoVgl5vU4/42hjZVm9bjJdksOYbs33YYMHnhGANT8xlrYdYu/BLdTz9xFP/tWu/Ab5t3O3De7Sx8sDtodr/cd8T3D3SZ4mqcdCQxkhBQ5Rw+PMknhDnecJJc0OkSNXmSSGoEe8ez9PGus976zrtouCm43pEp70s7d/vR9ZPMBvO5n7q2L1GylN5Vvqj5OoDhojtSbh+UH3L5D9EjiCgG7dXjI4WPlZipQ5mnWV5r4f7t2QWq/AbAmIVwNAENPL9rQNUJL1luOWdFot5FOJsRmzjix6jUhSoOwMAtvzIyGXFcrvi+/dfMaUZ79d3pDRjWcSiW8oqQJEjwEAhVUyhhTOJpaghIqmXRK6eEiGwJq4tNeZ4IJK8FoE0M5QgYztBDWBAjtvv23mnYc9vIXm7IahbxaO6GwLu69lXduww8Upc97asgMtWCRTG9e/easnLKehphAPkuM+YtnGEJCfFp2lCoIApzQqvUU+NU5dgEh0xE4LSvIiEGFgOCFOkjkoUO/mdV2WUsnlCrG69LTfEvjGiURdHxR0C25aOBVBU6BlexTWHPPAxFvAw+hwDXw7uf0D4GghkQ9wPhF59sJ32tvArtseEYWFWb6ziYA1ccWtfRAEvp27kSU/ObQ8mp8QE4K7StjB0/Xza87kQVjdto5dBDXemSdjFOEsVhsdQTGaYCCHV75KsOmmi6hnzfML5fMJpumD+/7H3Z02S40q6IPgpQDNz94jIzJNn6VpuTU/PlRGZ//+r+qFF5nbVyYxwIwGdB12gAEFbPCJP1Z1uZFrQSYJYFboCqqcXD1D9cnnBcpJA1nlp7pnIdiSA9XQQXGho62M0SASFIzcjXYwNUSyugPnR1NMgHMq5Cy4HcGkMhfmDn8GwrPsetmZK47gIRzgRnoF2JyJmOHR2nbfb/u5pKAXmDuG5tSsy+rZm2v2xMcLWTqeIr7UzPKxbwbquWLcN1+sVpRS8r2LYX9cNpRasZdNy9bTOEAfD1iKFsTIm3d63NHDZbVS6OzPWNvRG3b9GQ8ZvoqspM4IVw+tV4rnwvjrn4RvueAK3WRE3PiE6hpVDmNJfGgo2JcEtOIzl/pGpw3luaBCYqrX6VWCr4ttVT92sq8d9KKXifRPj1/u2imFi4zZf1XauWZ0CGbKhj/V4O4bxYCSOhjDF30QoRQ1narxIKSERlD+MJx40thgl3fCwPwlxFD9ixlt99DqmR5Vl+qQXJO98t4dBW9T38+7qHR4f5e94/pkSzd/3MZceKfvRtG/T+H4URmdldHd32/bs/a3nO/r34bRv69FYH6VRcX2rHz39lnV9lydEjzPtZxvcZm0+aOnd/jwyln8Ejn1Uaf9HtuGR9Jj8cPztvecjXD9rjLj1zZRvfCgZZY6JG1O3qy4oGGHSXAVE/a58irkphLtocZ2q6n02LiLDMmCxG5hbjMbYjNhUc9EJbgrVRBrrU3uSAp6vxquQ8dhRnyG7uFHVN77GHahuiBBZuNrGvWK8P2OtG7a6wZTG7aSjxlSom25M2FRmsM5FrwJBqOr0MXHQGJQI+bTgy09f8M///E/4808/4XM+YVkyatbTIK4UXlF5A7giKd9feUHlBNmnLvE7QAR1DuEyaCWG7J5XJbO1nYvr4jQktxMIwVUA2w7wJKdV0nkBcwJdFtFd1Q1cGS/l5Cfvr+uGSwZ++bSAy+/4H/9+AeqG37++4//7H78hEQO8IVFFzoyXywXnJYluDQmVC7aySZwC01eQjhkDRCI/5ySnNzY78aLtFmAI8MIN5M2LBSA81rd1xb9f3/FbYXzDgq/pDUv6BV/pT1jpE/6D3nBNZ5R8Aue2cbDqiZm2IVjgz0Y0RtUcl7ZzEtpODPJrn8LGwBLcB5vhwflLp4pCa8IKq2jrk9m8N1SFiQqqaoDYNtTtKvFF11V0SGaMqM1dU+9i/jh5/4PmwloWNcC3ZAC2EWsCp1onB6VSlFPiSQjVPcdDGN4KInXJdMKnt1d8+fSGz2+v+Pz6gpdzxikn0c1CvNWA4TqIWZrJuPu+jWNmeXWkiDTPLTp6+KpLcXrcFSz17yNasja39yyGmCdI59MxImY7CO51cBSkLO0a+jGa3yqZaJitbhfGgiCWLaiNEichXEJYnVgNR9N7BhF+qiIKbJbPrclVBMOASoT5N0OE7QrQnbfX9R3X6zdsq+3k3FCKuVaxBU0NAXmAOFlsKSVwogPBUlwwJRIKUVMM0h2NQJCjVXcYxClzhAnDNWHcbyGRnT81bvMZCt7NSXef+meTHvRVDAvuaN7bl0ppDXbU9czozmC2ZnaKLCL/Nk0UA/5OdzJaQyuEgSIQEvrd7aa4asGJhx3d8d6Yq+AzH2xM5nzneJuauKPjtmD3KGM/CmtHhoVbQuWtup4R5u4J6Z6TxpvbR/PBbdSagJpCIUa80m48HAoJvWKRBIvtiRk5nnPoPZhXZkaqdhw19JHN/3lC5SYYV2NcORgiAo40t2hicIAeW2z9zhY7JWWF7+SGiLwsOKuh4XI+43ySn7htUuNDXpCyumIKrulsTOOOEOgup8jAeRAvoLvG7yQfd+vG89qUT9fAHYF0Cs9G/APs2NxxY8YiA7NfF1Y3D8p+O7JuO8Tm+LFbV+F+jr9HBoj9iWLIadndKDnzNxpVelg+wgMdzgs4ru1Wb7vWqwWv1vc25mI3K2JAU3dpY9+5XxIHyXruHXMBYIIJunEZ+Ysxzdaq76aq7bTjbZa08Tvx/n6fnksjzDQeqy9vRr+PyriXDGc9wmf4Nx0fsX8/O1EYT9wYfG3rKkEcNwl8v20aiFrdg5kvZDkRIXEhTKisTOp+osdDEYyMLyMo7eD2TBBBGFfFFx3v4Kct9W+9dxel9kupnRgG/Lr7GQz1TFmYMxxc4zjvB3w2X0dwwJjP8wz2ptcPGSP2/Nzt/PO0z3+spH627Nm3Le131z1S7FHdR2ttPj4BAzxQ6T2l/fOp0cFbbTjiWx/t67hJYDwREfPcbK3hRV1rM754X/+I/Wm4n7f5Vhv+s9Ox/NbP5/1v0OW/l+ePGqNZ2UeywrNtOWrTfbjRd3dLHvlbMr2m8PuunmZXPLIZzqn/1ly12H/kRgjj3VW+ZK+lkThzo2yCO5GI42FHPlJC5YoE4elAAKcKhmzAJKVzzNS1BIg7us2Fk6qKa3RFa38LP0mivVVeFP2GEXN1rApctbIEOTsO8TDGQRZPRDgtC14uZ3x6e8XlfBaZKhO2RcJ1JzvdQewbqUj1PpwItBBSzkDKLQi3xWtVtzpcSvup+x2Poadqc+M/WPtSlM+uttFR21FJx5BC34hx0ngTtmP99UIoJeOXz28gMP7++xeclhOuWwV0gxlRReUriICcTzidLrhcNry/X1DKiu0qceB6WLNqGaxBqk3Wdj5muvZMAW48i8gAstGkYGVgpYx3OmNJL/iWX7GmV2z5BTWdBCzZQVZiKwJIti50ak3G7PUrBh+hbeHqeXYtNplU63DY5cM+3lr1rguKcobObVwLTa9U/KREg+/WncN6npGbD55Ho/9Bxr4OAkhPBJHqbu1EfDRCjEZd2yBpsSsvlzPO55PolM0DHAeZJ8ivt/s13+hzqxs9HzLv9nHqx8pQ6fy9vTjWi/V8z+OteDpGxKMCnglHe6EkCsDD4sPMsnfUBm74GYIu+GBygHYSogljhEy9O7DxWyJF1pPnRsDEwLF3gwTAPPWgFkbdKppKRpT+lARdVO33da2oZcP7++/4+u0F79d3nK9XrNsVKRNqEYVzSeJnDlWJreEjFTpFAJWjerXmtmuXGbWKQSNlcQOTU3Z1p1k9YcSFBkXeREk3V4L1ZoRHBMSYlGTpvOrczMCCB9cWsZ7gh5Ea8KHN9Iw5b30c2zxFDiSttfuUMhLlqV/lIwGiGzp3zbQ4nDYFgsJYtn7pWKnhIJO4cIrKOFOSNH/2+1gRTjz8JERpcx2I4ZERAkdz4wP0POHbCVKKHX+UUNraf68NwB5G9OkA48Nb9H2YrI+BsDFH10sZpvTvCUN03aTIj4KaVxklU0BFo2h0GWbvgXaaoeHi/nRD+17RTK0ALeCBdDCzr9sdnhx21S6nFiMlPifk0HZxtZRzDqcizjifXnE6XXA6XbDkReKoqMEiBqq25Kc1oP7zC7r+jXitXQOT57xfcUaLzbVKHYx2DzBTR2mmqHgk7zxfv8YajlIYC/TyIYVQKHXPIM3Xs6+ALv9RXY3RB/aMX/zNjBBTRfFWsG4r1nXDumqsiOtVlMRrcfc5gJwotJQgwl5vYIUQprYx6k66peAAQP2RaOOKWj9n33Fj+m3HV2XE+CSmsDIa/lgbx7n8cWmmbJ1R3ln+Ga9wizkHsCMdH02jYWvv5ktORhSFqa0UvL+/Y6uys69WRtnkRMR1XWXH31WfW/BqnyDlsyJDa33x9igd0P65AUONT5yzynymlIFvSsk5ues6uSbk3GLx5JTd8JBTQrar/nyzzcgHAQMItcHvWK7h2qbvsYk65hVpinmOeMzd9UNGCP1yeHz8ndHWW/nbijjip4/bcpxuC+23scP3KmCPlaCPjK+k2/TtI+l7EUMbt4/yobE/t8auw3/2bPj+mB/u+c4GYx9r7637Wbo3X98zdsMTre/2upm17ZE2fA/sfXQMxvmd5Z/JDvfS42P+YD4abxrMkRkhEDdKQMlDjwfsselAhIxEvQOcC2Ovyf4toSx28V4OE/SyjuijdK87ZzFE2CmjWl3XIXxT2/UtDVCDAxqvL3JScWPEVjZstYCqnYjQk9dcm5tG9UAArkAxZS20DuvKgJt7MgIwi0uYJePt9Q0///QFr28vWJYMPhG2M5C2AtoKmApAFSuvKHUDYRE9wQLQKYHOJxBlpLo1vQ+z6AJKQd1WNURsfnXDgv5HGreiqrvTdVv11EdxN07sRhFx3+wnAhi4sCj2ExgZjM8vhEwnbH/+gtfLCVsBXv/jd6yFsDJjrRWggo2/4kQvWNIFl8srAOC6fpOT62WTcQ7JFMMiMleFjQXxDAA7PA0fBlxs01Uq41o2XBl4pwW/p1dw/oRv+QvW5TNKvgA5Y8EVCQWkO+ILREtt3Dn73/vNRabfIs+rm5kmMuvYZvNKVU1GUJiV9YnRRnOYmqpEYV4NaHIiaAO2DbyJ/sj1TWWTTczMgLoFc6Pbgzre70li7DqiiwP+p7Zh2fWFEFNqHHeXp1Svcjqd8fLygk+fPuHLp894e33Fy8sZy0LICeAqsWpIecXoVvu4/4rXRj77Bkq+h9dneshZnkgXH6GjfZtb2aMO49H0sCEideWOSrhxUbRJjo8oxGeR/AG/ejEBWHhQBHQtICc8rYQAXEFYImLd6UWq0G2+cffqxDYhROo6QIHTGEFAfPUSkRs3Ft9ZFhTFgqOFkJIcByMVIp20mp89ZiTIbuLy/o719Bu+ff0fOC9A2T6hZmArVwCMlBcpK8mCqbrwEsQXXQaBKQG0gJIcY5MgSiSIhCsKJSBVPZYn37sfNbCe4GCkJAKuCLyCjIgI3LmJGUaQDUJGJrb/o7dIU5s+JVyunPFyZ5I5wry0cW8Sr5VLoTm6s0E0QtrS2NamGEiUmnCvyly2+ggAcuhPiD2SUkcsomAxtRoSeZM17JX7YARZiys8YJVoGpxnYSoSxL1y23nBzZ9j4XhvR2Yt2G7b2QFTqhrnyHvCITAc761NNhvc/ozJp0zzmFIlHEndeyzcz07/2jUzaAK/ruGdooH6GnQXzJhGRQmj65XPRyTmkQ0XprjNdc9NUrsS0CFuhTNmJWEUd4GP89AMgX3bZ7uLG2wNcoCeVujL3DMLvaDByHCNrE8l+8h2RJ1k50kzMKiLpjGvYVjLR01xdjqJy6XzcsZpOckvi9smN9YZrocE8rXZaoY13e/kzJ4FkxOYb7EeTOCIMVZEcSjoWvB0AauPTQUY2wYhnCICcDsNowBPGOayEz4m85koibBE8GPbErhZAzgHRsLWGLMIYGRMKENiHsTZIjGmZ/UdP3XBov+lQAcnLfU+2BJs7iTMoEYNtia0o33NCquk/ehhJZHtuWs0wY53t0DAFWupWEsRgaGI0ngtpgwuGlPBmHsKcKEB7UjpIDfGhaoxMruGh3HYPex6KjuTCHbiyfiilGzu9uu8PRO8z5UQ0bUrhiHzTXba02q2uQu4YUwOO07bDlJg4uMQCO3au1vqyo9jEel0+MX23VNY9nwZOT9lrSKF9rb6Apw6buauPBvvZnCUa9Fg1KvGgrjq7r9vVzFOvK9FDQ8Sz2vdBH+sm+kdZM7kJITxGNJO5oE5bqMKWxMMcRsgbicSEpPApg28nYxlIJG4XVrUl+2yEHJG+znONJePsskh6YYHgwHHZJN5cuhyumJ0xmgOdc/bNcBAGP0o7M/u+3lvRTjc78FyBz8dHBGc5jhfcOPbfl72z+f57VlfeA/jWirv391vy3E6XueP5f+IMeKone050I1DYwpbMgLi8xvwEU+yPpVsPT0zjtr+Tj49VhA0bKPyhdFmINDdhpFmFRoOzb5JAx2v+JiwHxfEnt7eS22pzuH28LtIF5xAxTKPyojbz+6XH9mvxl/EfNOvD+ue5b1lzLjZxtC+o7bsSlG4FxmzuaWMGfp+zvEQhrqn7fMxnMg/3TXeJXiMG9L2eGXtFESytpnbId3sAYhyDgkwNTGjxYEAgNXET31fwa0z3M9eW8UEIjEuyGa8Iicj2GQ0+VBOA0D1SgROCyoqSjIlY1ZFtRkqdPe3yeOqTDXlrsTLs9O1jFpY62R1TcOoZQNzARVRRqe6yagFha4UrrTcleGDTMAEVIBWBp0y0pcL3l4v+PPpjNcsp8AzgBQ2R4nrKEbCAlAC5xNqysj5AqQTPI5eauvUNyOq/oCDLsG9cdiYcHFRR1wtVaCs8l6V0TB3VcbDKH9WS9GxFB8uGzM2VdYnAk4JuCzA2xlYL4QvLxnvW8XXjcFEqFUUvomATIQlZ5xPZ5TLC7btCgajlqvouxrQw8BVTjhUH+kI6uZOx3ULBtGEprtLCZTP4PyKmj6hpFds9AKkRTYNpwKGGqHAyGQUQfC/1ex1G5hXHVBuNMR5RH3evmnYMiUZR9NPscZ6hI08s6Nh/3GrC64P46ACavyXyEF6yqSLCVE8QLXEUpF+MzYADGKB+8oFUZcU8Q4P13G+YjoyJLc53G9OaXl73s8Y16ifcH6XRXaQ0J8MpoSNGRkiV70uwJcz8OVC+PyScD5nLKcFyHLSSg5GkeoLFHacUI0+Alrbet55zmMc8bRTvjHwKUc8w0hTmoaswd6Mbs741safTLp4Iz0VrDr2oYlG+2RrWHYVymSbbJOSKFP64CzWGRooaCNCLgz5lU1+aO0D++QlD84nk2E7yk1xNSqGW396JV6KO4lBcoxNV3JKwKI7zpaT7iALMSWEPAujLUrtVl+tda8E1dko71/xTsBvf/8/sOSCbf0ZWwa29Q1gIOWLkPvi9AkAISOjIiEjoSCD1RCREoMWIFMSK2atWJMqeLIo0qmSEFrY2MqIpGyKeNsVoLu36cYxI0d6EwbWcYIJwfuYDMS9NTumEZE1FKNj2yJgNoC1+UREUNXh1MxRpgyWnYmiLK26S5ur4Y/k82++8L18ymqISh1szRDFdMdvgo57dXhkVYZVIwDKw0gdzYWYuRHxHZyuRN1CPIiKUs2/vZ6I4E2P2JWOYSC09dnaKT/jnVqylYE2wha8OWArWa+BKOifJcIStwXtxqgD4tOqa8zX0Kzhj5mYE6FiJqTIs2p/dVk6xxDt/nBtWF2E6JfZELisCWWSGch0HKelrdFQOtHhT5sFw5sG74Ynx3J27eZgGEH7PgyF9isosnynQTvpQERYJmu+W8mkJ7rS4nEiPF7E6YJlOft9zllOQRCppztWBtl2NBdX0hveNYJju5p8bGFCRzRC6G5zPXKddF2QBUWzlhMBlH0NcYBjAiOCQ4+HOPzQvbHxEQaJZPdRglieE4Ixoorhs9YQb0T7ZMxB8EUvS0bqsXETQ0RymOjhQV3CkbnUGoSkaWoMlYJ2D7tDH3dgAPsm8Ab96zaCzNiqGCHe9fTDuxok3rcNa9nwvlmMiLXBQWwn0D0XVM+Oh0RI1LULthyYzduuI3rfcrLvkMpGS5LxLAaH+g2H0w6tZWAmMUZw47XAjSMztXai5lpHSJXh3dlIaq2G6GeM7YBTQHq03nFKKGNeOMJ09rjkEG+16+4HmZGoUPY5c2xqz4WiA1GRF/CwN4hhgR5th1etcsLGYo9sGm9k2zb89u2KbSt4f1dDxFUMEddNBHU5yU6oNWt8D+M5w+7X0JPI1DJbf6R9hRkJJC4gkqp91KUCmGAxKM3F0pIzlsUMEYSUWU8Di7EXyoOJESIjL+L+IOVmjECEB4cLqbu9Pp6rW/Aw85zbU+v9vf1NNnIdfQvlRJelQxuMn+/eOQDcgF9t0b6ueR19D26nIwXzjzAQ9GlPY8b7ezX43Ezm/Va50UjZaOKBHGHX1D/Z09IHpd5uPownOMgytNtRZkRekxTF+FiPBwZ1uWWOW8drHmTVGYzMdzCG9zhSJezT4fx/EOYozM4jRTRD8ON1PpP1Xr6+6nlm59exH/uY536TDmQEanBtPFArdw+zsc7Yh66mIEMdnbSwFnXwy4ZDjaOwt8GbPSnPjAIySsYqu+oGOFGwy2aayqTxB0JSQnDdjYqtGy0z9hcQGqRzRVa7KdbVJw7Z9nDKsu4SAVRB9YRKFStXOexKGZwIhUnikiZdywWmzHH+2eJerLoBpoR4ETC5ohZwuarORRSyZG6PzZVRMUX5aZjoML66+ZAKQFdG+rwg/fyGT59f8LfzBZ+WBZwTFgZORTbgbKVIPLzKyHQS//fLGTUvSKcLKC+iwAI190DRW0IpGiuj+KkGmJ6gVu9PZVU8K48ErRfBpZPTaDL2ilE2MchwOsm9upE2GeucGa8L4/MZ4BfCt7eM398FBjZOWDkhcwKx6LWWlHE5X8CoWMsKJuD6raihZ+CdZUGAUHSjMBROkuj7jL5XArE5rjJdnp6WyRnp9AIsn1GXn7Dlz9jSJ2A5Iy8JFQUFFZvCTE1ZNwaVbhVB2+LKKEXWyfFgw6DyapC9lBYkIlDOvnHOCFanN+DGo1uPfDOdx1GMDdOzTc6H6iKA6o+2FXXbUDfZacN1A/MGiXixQuJIlAY33uQed+7Q1QGSvm8AjryXXSPN3287JwvWnpK65DWBk5FC5g2CBhZinAj4dAJ+vgA/vyT8/Jrx8rJguZzAlBQzVt30p3grNR2P41GnNbd4J0LcXHVLNpqPSNigNuD+caxafXC9fLexa2hvSz09sQ3Wd6crpMddM1GsrjUunoIYCab9IYDfdlQmLS8W7sIGkVrWYCsGVNgXLxMEqYL8mRXnC5L0ZEJqVtPoIzfu+JLFud/1bW1PKtLL6QmooUGY40Qi3GXzZ54SlsA4VjRrP1uLfZLVn7+3Ho4wbKK/fv0dp9MZ396/glLGa1ll0ZQrEldURxSKONWQG11FoWY5+aB1ibsmcWGSEerTwSTVt9TaAxs1s14YngNWyxHhOM8+U/r/PsC3lLt3h+XApfM14+GUdqjPwVCxxw4JTyMu1zeG6AkRrivYlLBGjDUuRFxwtgDtJElPK0bWqicnRDSEN7FxDrnswuif60Mj8GPA3VKaawlXzHZuTDAdy93Y3mKAJ0VEWG8F7GnMjkG+Iyns1ilPQGzSvudy7L+YwTo51LQnR0LxVLkPwAVVFyIMI7AwwsH40AtAx8GPxnr364sUL/cxbY6+UfNrexa+b11oC95dk+UYuL35Hs9JBIIxAKOtI/kl5NRcM9nPXM61gO3UldHWCe9+APzUj52IaAaLOv3Gd/SFsu0P5r3hye77+eyRYdzVOJuvmWIhKs2gQq4wiIOSQmvpA15DEbgdSRb8fggb6N81ajtCrX8V2mywGuakK/sgTQoO3XXYQJhzVkHO/O+7r35zobNuWDd1y2S+a2vRkwSxXbWjF93c16pCeOzxgH9D+/dzOnasIXICK+3ejzeMCfT1ru0KsOewOY4v7ec2EYmIZfNpZHiYk0cVkV0KKB5s/Nk+9Upqm8rbyupb70aF3K0231IM7WgSALBsPpANgOpKqVaUwu72q6gCwuBuXeWkxLZtElS8CE6TuJS6gxJm9BwFspH22TPJYy5Em3sk56QgupXU4jukdiXfkNOek79PbsiNbiBnp6J2Yw87WTXwWrizzsexhwnH83m+BRP29/6bWPqkzhvte1bpf/T62XJm+Y7+/p4y7317tJ6cnk3exfe32nw0T7u2HOJSeRmzCw1+HN4izx3bcD81Y+5h2bEtY5eI3Jd9w1vzebk3ljte8c5cVpVH5jUef9dRgkl/Hkt7o92tvLOyRyho/X603Gfq3j8b08xYOCttnKd9nuF9hGvS03zGv2mG8X5a7o7/PIalWdv8VLcg5qHsmM8b22hFI1nex7GVnZw38g4wPdLAd7v8H/jproj2704GM4bHFrATTfnTdpObqyaq1T1oAC2WRGBqvXIKVVi7XZ6oEqvA/jaGwvhK6ZvJcdV5QjDrptC+C4DoF87nBb9+/oKfXj/h9fKCZVkAMn2TGUmq701nVbRCfw3upF5rm7lXKupqp27mvnnw+W/RNEzfYB4WXO/Qu7C1zRRAi2e2lVW6n6QhVY0fdVtR1var2xW8raC6IXFFtpPtlQF+R6niPorqhiURLssJ5fIqerjKWOmKsl3VpTB3oMNsCjOFHWpbQIkp6BmNS5EikijIhNerEiC71E2CgqsxSvRQeoKIwqZB3kFnB+OdrKp8ofH5ked3TYPCZVMAt9Y6j635muI/yKoNELr6amXXIUX4JY0P0dZmDb/QPhOXo4wy63sH5B/nI2MZR1+FbYMdbzt3pd7jRrsXt0wZL5cLXl9f8fLygpfLBae8+CZ0Ijn5TMn6TmIcag0B0OvLY3/HKw80tJej7vDNjG48jsb0UBeBJnOO8zPSllbE8/T5YUOE7wieNCSIwk2oao/QGSF2goMOciCcVf9ux42KLH4nJD1RdTpDNAhkCTmJ96FOyEoatCj049jalmEWUtk5artGLfh187W75Iwl1FN04bXdl/3Y9eOGYB2Xbn79+jvysuDb+zekfMKmhghsK1JiFLHKAJSQciP57pOdSIhPzUASgEppQc4aG4KrA7Psatzv3hcEJy6BZDGm3Xjtxi4qIqbAuHfNEpUoyTiEbsCMlkWkuReMqBvVnms6mmFXJ7MgKw7jwFxAGuyDDfESBkVfct6EjYEKYzOOj8fAMFxBA4KwspwXU0JmhGKiCGvKsxCodfCb3u3w7gjbwcDA5t/qu0lGNL+1p31vfXKiiLBDnIz5vM/cT5EluuF+LtEAI0fZDpC9FHFb2LDvnEnwMnrI7RSjyCqIqFV9x5ygJ2xDXbd+IePuebz2yijbJdJOO1hgJ1NTxwXrhD3lli+U2U5ENINjXCeGx4lyZ4jINxRmPqJhnKZGBfOXidqtmdEwMVP0GpM2MinDBIRZbTPa+tnDgwkvUXCcCrARR/gVioNCmWhMqD0XZptAAXen1Maahja3agYB7G7a46SGP6w/zygmrMz9DgvrhwWNK8V8928omxgetm3Duq6dIaKU6nOo2AOJEipVN4z1xqtWf6zbBUgiF6LHvusfmg/9fXyGsG4DRorj1n7zewLEqOFt6td1YLECjFK87ZrVr+jbyfNyDzvTvK0RB8/3z2bvZvRi5AUmBR696cqNOhCJA6Nxvoq6YtiaAUIMD1VjRoSA6NzktaYc0JPAwLAmpPV2WiNgC++V8XMNThqvY3x1NEA4jqR2Orh3kTcEsL5pjOjnwNc1zIB3PHf3njfR8Hi+b93v6FqXb/p4KCO24LjOe2U/2t9n6hjz3W/T4++Psu7G+k7Zz8yVVTyW9LDCwadqTysf/vwp2rNPR/zivba4nMV7GWuWL/59b10cKrojXSd0QVPvJfJ5arzGrOx7ZYwK1f/50oCvHoQ5wYofAzYx8jb3TM/W/Rz1PmoETddqgwflVMImP/j9fs17sZM+NMNFoyZRjWR0znQmNODspkuZy6jNm7EzxTK2pmhOCYkZrPxfSrKrOSX50GNMVHM/dbAO9R8zRNRirh2DIcKVuKXJF1K4lq0yiq0bnQNtCioxLqcT/vTpM768vuHlfMGynPR0pLh9lJgU4nFDPImS8P+6CcF5elY1o7lxdkOEGQXM7U5thojmFLWNfW39NAPEzhChegvTPWzb5kp/gIGyyQnUdVVjxBVlvaKuV/B2VUME6+ZZmYsNm+jYGEBlkSuXE/jyilM+YVsLGEnmQTRxMqS6E5q3ELNVr5JLTxm4rpGEt2V1PabzVqtuhDIvE2yByCE74AEgsbjQDOO1ExcMBjq5A23ctD575652g0GB0WTAsES1+TQIT8P6GOra65KaS65U7aRMiPsQ3XYFubmdtgh9tAZP1s+t9Aydn+VvMl/PT406hDF1c8GMnBeczgsuLxcxQrxccLlccMoZS8oGKq67hioeZQrCeODYfdGU3k/kqkd4g+HzDyTq2z6pY//u+dqeCFbd7/1tJGHylBrSSyn3wUCstE4Q6OtJiVQIVOU/m3sgdpoXjRomKImbCRPApA3REGHtSUQtMroj4zoFDKakhEDqWnIGEcTVE+lx9yQBhnMijRWhAQI1IKEpufoJChZNPWWwbe0oVSLC+/tX5CXj77/9OxiMt7cvWE4bTkyyW/hUkdKClE9giALfUJPsHBbLZMqKCwhYFjkql7cFlRkbmRsksTQLjm4KIxE2P8JU3ZQCbRL1moIynhBdzjiQe3FtH56NY1/r84ugM6pArOHmEkmQe0VKJC5QjDFIhkiUDJDGG+AkrrA6+DL+hxxRzRsSWtEpnUzxXJ242Hj5OjIGiJtFu1m22/2oZN0RxTiWRIcIaKckHcZxL4ACVOP7RpRv1XUvGd0dv31MeG+73O4Kc5Py4k6JyOTur/ZdrKNnDnrltDG7BE7CEJAStKasH+DWn8uJrXbSYXLqyPAz9Sci4k8ItCqk0CuwzPhJ1NabdLUx8kQkx39DvYZ7c3dSQmFbFXUNHsyQnJEWMWhQTntaokx/7BtIg8WBUUvbvQNlrtpunvEkRBMa+pMTzU/sqJiLxpPjtSI4rTdePnaEMcKFuWFCSuBiuCBJeAq2AMuWZDdO74KoBc0y0DShhNQVyxhYPCrnrT1HzAmrJLaD5W5sjOF9nAGVfhekJK5pmCReTuF2CmLd2umH67ZivV5x3TZc369YNcCwHVuO/ZcWNSGpjY/yBKS4fsdFK443uh660jOc3QghGpGVCqqbHELKSd3zBW5rFBo0iL3ssI8GNM2cks/r8W+E44mh8mAuYkcfpbQz3s/o2A9NcVJDXY+kOA61WpwQNXbZyQc9WWgncNZrPHnTYkeIsQtyYlXLMXdMs3obHeQ27wonJkdGV1tE4hfZN8Kkxp8mO6GbsrgKzVnwbkq752bkzYNhohfO+jmPY3pPOX2Ldtq9udt4jF7fL3PMN/vOfyYodlkfwUn33v9owL6fHh239vd9XivyZt2zB9fYM226994VLMOJ7I/wjM+0wevWvLZp5kPfTnCg3u3ac4S7j/pwxP/G0vcr+TiZnONfUP/u0TKEOXns9O5BKfrr9Qz/uPSxtazURP6+A6fz943PaGnOb81qj7zXzXZO6haWhoeAtmGLhPNNUNbHqZPyRJqb2saKXTsGdQiBAGruUIxPYo3NZoKeSMHmmTTSS7jy02J/VaC5HWotbu3Rn/F8yElkflZ3TzUL5KmHDusPuOraVZxELHwbw+u2WHM1bHCS9oXdCbArYP6fzOsCKe8JSrLDfisAb0CueHs54V9+/hP+/PYJb6cTTovEiKjKNxYAxfgPAihnUFY5Kmf1UMQoLCcd6iauo8omCvVtldgKZRP3OlyLKuH7Ux0VzTBhLrjEHZW56TEjh+QVXkpc5W7bpvKXuoRm+UZOQlxR13fU9R28XYHtCpR3YKvyY2iMtKo8sHgGSWlBThn5dEFZztjWDUtawNuGDYRSV22/AZ3EWk029u6DC6BotdX4qQRdEwyZn7Jivf6Ob7//O87f/gPp22cgn0GUwUsGJ4upwi7kje7FHNpdPg1Xg9mgs6nVgkDraRe07tg3DQZtbUFkPF8L8URDK7/frBpOkJcNYjgraowQowRzc9Fl8VPMONEZI1gX4gfx9kNyovbxvlBha3bCX3R/t5/hQxBwOi94fX3Bp7dXfPn8CW+vr3h9ecH5dMaSs3/l8Y25lRHRrFUxIwt73jWA7I6Pu/NM0OqHk9U96jvG9o4qr2fTw4aISfWDQrgRJtUttwB4qfkinzFk+5rkmRmV8gBgROb7uPm0JjR/mqboEqFK4zHTRLkCtAU+GT0XBUkCQEvZLeBqC3ptgp0aINQ3b6lCWHsfz90Qel9tAg0RgIDr9R0pZ3z9+nekRPj2/jtOtYIpI+czFiTkXEUotVMEJG1OlLBQRkmqhE5C1HPK4FzlRERqLincOq/4woEK2Ls6whEDo/eUdvkHnqbNJwmKd4XYHSB2mBv4NGsrrOjApHndB8zgiMiF16jSNpITD6akqrWiOeogxB0glVmP+Y2GCFI83DDKDIlw7IsRDRZFhmRT5SNkfXFcS8qs9cYIZRhqULIaUQtD5KcGh3bdY55jw2X3jr+dDLJ0Ku5ucSTHrW6OgyAV9feTNL7aKysOvsMe0c6SM6A05muiXQO5HiOHJY5uXGK+UM8oPFjsj8BNAxDXOnNDxC0FZBiXg+cNbyY1HOROOZWzBqoOBo7WDoIbL4jUNdPkRMSydH00xV8K8qq3JTcjBKinHQhj3hQVPV6PsUME7o9dMAkONMPDyJDEtBf0/O8poQaaEaKfZ7vv+hTm0vIRU7dG+vq1PUQBB45lG01Nu3VNqt2Mp1fadWLavYejh/aNxghmc3c0L2jkD/x7rZshR88rVwk6rUzzViQexOZGiRXXdRVlsQs++3GObHs8vcjKgPBuK6nQoJuCPg83bLSL4Q6RqRfUjc1x+sU97Nkj1r7XgOujeEPYr+9unQ/KgdiFPRPc4ztbz+3J7XSMV/f0z+5vKd2O0q25eEiQIcPljR9rwpka893NoZyCkFM3EovErm70h+GbIO9hL1C0dkejfMQBZmQI8T5IT+SSxBgRF0zmeYGcL3XeNBoZiALf3FwzjUaIe+6ZZvzLrfdHQhPd+OYjZc7yd/V1wG5/3JeextePtvFe/nvvnsn/eB2PKSgBdPRkyPChNvV457F+N9pqDRrXzmOpw5EPtiHWQROc9eg4gvffjbR5VuYja/DeOMRaHh2ttjZp1sQncOrk46eS0Zsefv+rpwPO6Tg/9Xy0pF6/su/3+L4v75G0gx1DhSocBUjs+sPkXERoszEvjSeN/RG5I1QUu0MQdzgQ1zdRPo0bO1o8Kg4ivtJKbqfH/eSh/0xiDzqOwCchiVcJRlJBhJz/S3piIiUxCki3WHk19i5TIqCiuV9kU9KLXGEKfDNGmJJWule0faLkJQs0rMwDFzNEMF7PJ/zt8xf8/PqKy5Kx6G5bJqBAXEDKGQAdrGiIsF3bxGDlZyyeQ91WPRGxqluprTEv8cQGzMxTQ9/YgxbXsvlmruoBr6MhomrcLUaRmMZI0NMXWzsRIW6ZruBy1SDY4oIJBeACVC4otQDIADLyiZAp43Q6gSnjel1BSPi2fNXNIMVlQIHHBXAotjgmBjGDu2wFG5dauAJlQ7l+w/X977i+/4b8/jvS+TNSvkB0YKoPIp1PlhHsdG5efDVgD8/79d4MDTqmzB5nlkMe6WEUpr1L8medGyKiscN/xQKXyzWF2CFejm3a0407evTXy/VNlA0V/DGJery30191Gvl5Q/o5sauYPJEIy2nB5XLB2+srPr2+4vXygsv5gpNu6Klg1QPaoM+MECYHI6z/oamxH7jPfx7yxtNeHtc3brIY657pBAeV14fSEyci+hQF9k6RBXZBaMnyk1MDJtzcbqwpUJo+kmDRyoyJzZ2wJM/8aDr1O7pyIo8RQaTKFjKFN0mgXhXuWYlaFOmNypgwmLOc8Fjs6gq6GINCdjeiAolZlYbVhdvQ2TYYWndKhMrS30oFW73iNzsR8du/43y+ooCQ8xVLKcjLCScuyHnBwicPusKmCCWz+CewKRU5I+cFJezwl77WbvHBFhXaztqo1OtTRJ7HDJKxA0FlthcKOka8femA3ilv0SkhaVjZDKiie2B8xnbbN8bkMBrXgwIQK6wkcE3gnL0n1hBmmbvE5nNOfsY0jcqOUcjI2lkbayKDyeKMKpFa5mv1Xe22ZuAMmPmoHI0RgcjNsN+QbGxlN/fILD+ZiITYj7RBR0imddI2bhT0ERznSh3npmNNY91iZHKGD+PqNwPZRDDTPo3lzhSvBw0NGNw7uyOkRFlxYD8+KavLNM/buml4EqBw/DgIBxEfDkJuc+uWQehxacShEoB69K1o+fRdMB50cJ6aIYJVumBoQPYhjYaCwoGpUyYoim3Q4WRl8u1kRFSCm5DAbGtNd+4g1rUPniJDSt14jEYD7ibj1vQ/diLiXhmGa609kZGN8CKgokwxAcw5kLc2Z/EkTMNVET+3dXULxo+MEP37hleOUxN8IpNsLnCi0WFdN6zrFdd1w/t6DS6Zqp+I340hmmK9M1iZoKjd7QX24/ZG8mT8kIsKbIxpKMvXE4XxnY9CpCXVxoJtt73ksx2FjrvG9kV8Rr1SujUp4Arcm5/5eOyNZR9LjygKH8nX8PfjdTQ5LQhoRQwSdvKhGSQ2Fww51sRqdlLA8DcRlDisNOVLjc+xeVlS2whDBCxZgscvp4ycCCflPxc7jau/RRUVy6IbZU6L8Irq6u52TIi5sNONKfVwMt7fmg+7PsJTHApakzbNv2+85D0h7tG2PPr8R6Rn2zj79unvPvTVH50+2BeisIGoPRvzAL1sE/OMCqTuXYDj8blckyq72nPn24c27GG8fz7r260UV/Ojo0dETW9DPfP93DqRvesfS6Ryw0dPS9/+5qNraYSPWT1KQT9UNgG++e/D8taNtt3KQyQ8xLj5kER7rXcmkxlEaQw51ZOoI1cfg707bvhCNJqXdXUuAFj1Mgz4BtFxH3nUNkDle+IqLpZUBm6nn5sBQOQN5e0tILQFtiCVk5J6wTCZadOTiHrqwcat9SDQPm9XkyPGUxvC0lZvvJB6Yzb0hEARpoCJgbIB169Ip4zTpwt+/vIJ//rTn/Dr6xvOugHWNhFVVZsWQAwpiZCWjLQsoGUR3ZC2slSJBYF1UyOAuWHiLg4AmScS20nfych6SqIUNWioW6dqBojivBOzxoLYGSJY40psWK/vuK7yW9d3lO0dpVzB5d3LRxEjSmunbI4Tua8gnWXz8afLCacFKNsr3peE379JIO5Srzpv6u2Di/xdDA5MTix+6iaZ3AmV2WpBXd/x/tv/wN//xwn5y6/g8wUvl89Ylhfk5aQrwMwCggMzFkQZqofmx5Lx/1FWtc1ZfjIlyrC6VIN3b7RNdwyEIOVFXWSJ6yWx+HApYNZTER6sXOfcglFzBUGDsTfn436CxFbKx7HZDVxrdPJIdop6r34UZXaZujwmx1fXCQMpE9Ip4fJyxtunC97eXvD29oLL+YRzzlhINvxsLJu7Kdk8FR37xjuMsr/Py9Cfdn88bnNeo+fDn3GPaDoFw6v3SWTcYClPPkKzHj8RcY+g6T9JCU92Y0RW10jkv+n3AxNowjCHHmYyg4OceMjJ3EnA7zuFmebP9rfmtxgGRAQLyszcu6AIDQOCAm80OGTbZRZORlCCuFnwCZLjY6L0CouJWiwEZohrJW5W/Q0VpW4erPrb+2+oXJGXC0ouqAzkugGkBhUiJGRFyc4GoEX4kB2NTdmUtV/kSEKUeab8aYqTODazhR3fBVDu87ikHVniiWDZJPJQjwnn+kmsLzArZCtIsxiRJ9yAYX/eFE9VEYWtMOYiyIQZlKJhIRSTkiBiNUTYkdWqY9p2AfeM2WgBN8MBkblfqWF8bHhIdoAEZbBbw1mt0+5eJswjx/7GWvu0Q5Z3mNq772/UFucIA6zZNzMi05R56PMqoPTzM1eIxV1u0oaBCMCY6bT71qKddW1V+IyIedZmx2vG0ztgw9+3OchhLhRGUbu2HhJoI0iDgDtTPPUEfZ7fYuy4sWHcIU1yRDbpUbRpGZR7mJWJFzzpKte+b5HpKlyEmaqTOQ1Em9mYszn+auui7UZpWJDDM/h1r6zrx1/o4O15iWN1a20dGX2N1srjGax7rmYsqRyES3JQE5QU6cJ+3kfYmWP3fToyRjRYjicjevj3Muy/MGdxx07z1W9xIkozTmybK40d92FWTd/GZsBp+NZzUvtmaCjGNwYLBB7ByNh0z+eojNpTHgp29N2NB/q+cYOPo9RtAhjvya6z0zGtXzNM2to5n/dnFFgzOPx+Re/t743njMnGN461x4vQHYV1G2KPEMAmeMAE27Z2PJlmlKBBEMOaY3PHFjbUJHEFSkRYFLcu7iI0Kc9NvhEm6bMuboQ9n8SFaGPcxuFIWYvY1hv5Hpmzu4rUkT7trp7zsLw5Le7p/+zbHXk5aOu9cbj17fh+h+8P+n2vnONnt2nSvbIeTc9+e9T/lkGvJj49XLwh1T0XeX+shsTzOY1yyFw50Ndu62wGXzv6i+/Df5EePVoC6Zg5LfkAXIgMRMCUd76fjKNifh6WHk0fKXfk16ZlcD/W9+QjINBNGEf0fUb8RzYBjHlMLGmciba/Y88Cv0YNuhKSz3njLIx/DN9zW8D22PzxJxjNtBOwo2QUeCCoFwKI14AUeHlTJkaZ15WvqO7v3/l8Cw5OFDZvwewT3lX5xfU58Cc2Hs6XSZ2BeTOmopfD1QABZj0RYYVUebddkc4XnF7P+PT6gj+/fcLny0U2+qpM5htTgBAbIslpCP1BZQ4O8RxMoezeONQdlrkuJAUAa1OvT2AN0Nx2yddamuHBDRLGHxXZIFnsauO0oZYN63bFtq3Ytiu2sqKUFVxWgDdw3YC6imK1FtkfWiCKb0pAURfffEZCxuWUkJcT3l8uIALW9QowUNVtVDOwlAYPDHddJTBkMUGbUh8gUcRvG9Zvv4N++z9x+frvyN9+wml9x1K3MLfcYE/XCfv66ZfDIzKVtSu6/LJ1YCelO6W61dZVGeRKP6lT+5geUSa2YNRVXHi5IaJzYxyMVMYHz+A8pA/hNlt7s7IIw8iOsj6ctxY9Aas7tdrltREy3MLMwlsvCefzgsvljMvlhMv5jJNu9MlJDLAJ6iJNGyL1abuDrN+u2hyX5fdjY59bW+bD0vMMHQ9yoHM/Tm2MrMw4fn0bGh/zrJwX0wdPRDDcZzZIkbUSFYoCjwhOOROW1Hbb9uWwMz3WsU6wRoNjd720NNdLRPG4uinYo9JLhLM4Qa5cQQweGE5EBIUFUe7objYBcFl8B5r3OQkRS0bMkvquUwJBukvdFMaj8oJS9g4zWI/jVXz9+huYGX//j/8Tl5crUpa4EHlbkfMJ13XF6XTB5aVgWU44nc8Qkq7BvgGloAkpyZQvWWJEpLwg14qaSKiXHbObKH+kaUfWRSAivzlWNQAXS+SoxPyetEO8AYkcKfQw5It9IZiCtDFEMORRK8jcWgXhqKQIh2owU+ZGSlKDgsfEaOshEaEkW09qhEBDnHLKJQOoLTZKakGErf3RLVPVAFTiu7ERHCc0dbbz27il53Yx3Wayo9rt+Nt78zQiuNmzjyoKjpRmt4MZ6Y5/V8w2QhwR8454EoHiVoHWIVgx8sl8XNi0XXQM20eEaXweY0RIG3u3Szu8CYXR2XO9Co5M4fTZ0JaJWAH3N2pPVTBQA2tVxrj4Rp22W7iDrCYHAGg7cXx4u5Npg+ASGGdntlyIaOxjFEZs7B8RNMfUMfSY49YOp3aJAoyE3Q86BGM8CjslZwJcYzR6I8QM3l3UtGdKO2fC+JNDgDb/B9hB3dmJO1LWHegV61qwXkNcCP2968mI63XFpq5yZJipq8chmY6VU5GHsG/8ryk+GBixyQkfmzIry3A8od9JyJ5b77QoiQ3BnVumWympcO8KrdDHUYg21z/J+xZbOXaTDqfsR6YfrYB6prQ4tg0/2N/h+DrXBmeT+ijijvCCAOcNUrJ5Uh6axD+18bLR4NCuciIiJcL5lLt7OwlxOp2Q9bosGafTgiUvcpJCTyvnYWPKEa20cSCVsmx8jIbsaMkH5u6IPh9dEUEVEcLn5R0wpk+1LfIMj+Sft+M4749O+7Ibhvmj2vDH9Yc/gHcMm9J3zP4+jfN7xI/68x2PuaeXI+0Z//5QO41DHab9bpkuBz/GY0/zUGpBS/sMQ11zWlmHrHvF+fGMjjzZPdngmfQIv9dxuRPYwMF7oQs6b0P7b91/JO3LDGKI8kykL/ozRdQ2toifYC9v/5/kj5JSrFDKl3oWXaOVbAMfeZwHGydoK5wmGx/EaoxQRXrjp/1jWYNRZorPKPzN3LeRGh2XMbGf8XT6jckMvlPcZMLmvqgFrYaXpxp5ldPR1swmLoDABW+XM/75f/kr/vUvf8G//Pwzfnn7hNNyQlJ3S5WUN0wEIOkJiCyx+kK8PgtAXTf1/182lXd0938inXvRN8ipDmmnG3PsV4rEYNhWPYG8qhvUePKcPX+xullcNBWWU+llvaKWFd/ev2K9XvHt/Sver+9Yyzu2ekWtK1gtD4kYmSoKaUBpVgPH9i75MgM443K64JIS+NMFr+cELiuua8LXrywunUj8QskhCELOZ+GD8oIKYGODM2hsQhh0Kswztm0Fv3/Ftn5D3d5BVHXzh+IV0pMainuryb8u6g56lp0eakDD3OYhGuNcdjX51dx/KZyboYVQNTwJg4ueoNhW3dS1SpDzusHiQZD+HGarnY7YIK6sBoOFYwdrc5CFviNORFcqjfcUxBFrC3Qc0GK8BA8GXIGkcWBNurbmC77pZatTTricT/j0csbn1wteXy54uZyxZNEDy8jGxvWyvbvOR88T7PH3nkYQPT9qjxihH0mRB5kbI+Y87rN06XFDhCvVRp6hMVVmBOh+2QJG94qvSND6TjCYqS+fm6BjgaA9cCqwU6L0JyIwN0RonWaIaCcj+gE044A9dR+88WSEubIg8dMLF+YFEVWiRvw0gKggo0AQlahb28xwATDW9R2UEt7ffwcIuKxfkeqGXBkpb66cS3kBQd1HUROCm+LA+i9CZ05VBF7d3Wy+8zh2uAMB3i3QMaMT/gOhvFun/TaLvrRYB3MPLSNTEq7E/f09Q0T3PViIMaE3ppDuymBCge5UnDDEpK6c7ESEIINofEuieEhSlvuiZEJFQrJovR6fogCUUNRiz6xIgHSnZOWOOewMR+pD0IwQzjhYnmiE2M1nTwxnY9dU77P5343woQh4ZISYKdbnis/9TrRHlRmz8u/lmX6nDKmdSpqN37xNzokqDhCKQw7ko/U8tlEY51uwvTMADIJz31djtEZDwbyssVzSxd3wixo00jD2vXimhTfaAoVPG1chOLKLpzKQattxUCcnIhwuILC5i89jfiyhO5wjwxB+ds/q+oldqLCG9nV+zAjRqoxMy/Q64LxQOzo40zsTKKn90XIwuwIUYb5HGulzvYOVgI/DOhzbctTnyRsY/BnMz8bI/fTrr5SKTX/tVESVYML6PI6dwWdsdxT+x+cjL+FCJ8HH0+Z+j6+sZ5N1aeXwAElWh3GeoUyG4feA59GPU1dBqKfrYwSFgYkkaps62jqfMbO3GNzHmV+XUab45PuUb8dN6zHQEb6fGgd9Dfa01n3j9iX01WIGY8aaCRXPitcotZPFJtAuegK3uWjK+lw2/Nj7xpdafLYUTj7IL7pukgDp5O7BGvBM+LJIe0a8c7Su7tDRR+jscdn9wDo8HQhHQ28Q8cG+DfM23Wt7fHerb7cUpM/C/TNj+N11P9C2W3N/Kz1GQz8uYCuVmb6jiDSPPsYxXBzxjs0IQR3/dgu/HcHYx/stmzqIj9u//2jPfz/03ZDo5hoLa2GSx/jq1qSJzHWjHUeGoVtteSbd4/seLXHXL/uW9nXcu3827cc08o6tF9GgALs2hOs5mvxAkcDBSMtoivB+armJRFq0spmU96fWVuPpOnm3imsY32hXjW82eVZ/na5g4PthPBN3raTu14wPZpggNFkB7jpWN54itIGDQtfkC1jTmvcCN0IwA6oQBirO5wV/+ukn/PL5E35+fcPb+ax0v8U8NX2WBIyy4NQ50PcwbrWKiyNrlxZCpp9AEjhAcIUL1Rv4bnhx71T1RLL8zD1Q2LwKc9HUrh57q1Y//bCuK9btinVbsW0rSt1QaoGG4IZ4h2CkVJFKRoLJ3ybrEbBlIDGW84KUE17PGUsCfj8vAFesSfRkxQwRVWOq5hMoZeTl0nQnLA58UiJQFvd65hpYvFLV5s6IC8SQI3x0EBYUpjlAT9SJ9PxlIza2rvSZI4bAmxrsubwq12Zsa/AcJGoFvzCHtqHG4mgwh+9gAhgseHk0djT4juuI+26AVOn/8WS8MsK1w9u2mOJ4MAc4DLQUkd9olMbELnN92+RAwnnJOJ8Wcce0LB4XgnSu2yY/ALONpiHtdTmz7K1Nt8oCejx+bOR4gm7fyde/H2SFO3R5lp44EWEApkRF/ZbbevNYDHoC4pQSFiIsUJdKQ3yIKPRQR3Aj42VX2VluO23tVEJWP/0mrMUTESZkZDuhMDB/dm0nIkblh1DijhEExC0JEbIi92SGiGwKi8hENH/bNjkG3Dskgn5sEiBR2JmxrisYwL//x//ARQNY5+WEZXlFyicsyxXb+i4I/XJB5YIlnZDzWebE2ANKAKlAm09gAMtyAjNjS1l2HK9l6lOsV+rf2YnJFQiL3v40fGXuOGScGA4Y+uvZgLEd0Prlas8MWY6Gh3uGiP4dg4OFultMA1NW1fAkCtO2+OQnuxUpFb0mfw4iUFWDWTXDhHy7Ue3KEFhJSLlIrcF/u8E7bF6NOYMxJIHgM6uVu4KLGSqMmBjSLk6cgBanYhYbRPJYPBFT9rWxjQjerg037/Pdjz/SI7ceid9OjyhIrLqZ0HeEN1q+9rczhDf60dWR+vfM4fSSwXSAdeY4/vqM/OMJg0/tan8L1w+zB6dkgeXJ85lhNbrsmPVd5qC5fWu4u+qa3LseYofQVkZ/jFf6F3Gh1KsnvAINGXfgxr+9tmLCgDIKfuIrjlt4Ho6buuHO8MJw7PW51AIl73BO2Ekylr9XcH9Q8EwqFHKWhVjLZP1QR7Ng+GpUnDgstfa1svZzMe6Yju+9XDI6wUHo6XHEGBti2wq2VeNElIK1VGyFsZUQL826H+qO/XYYCu8c9lXIszHpxyEwPz4WgZvUNSsMb3UOl6wOsphWut4oeRyqLnlxtnJakLrKuv4Tdb6LjX/oWEVq63tkHEOmg8eN7jVh6DjNcGf8RV7wnlLuRyXBf3M1ZKs7rsfqV+N3DE80AxDCJrAd9t3xMckEy6QYVz2Fkp6G6INR96d5lyX7vZ2IoGQncwmn04Kk+SgRThoTYlmy/oLxYYgJYfMe9+aR8b9o4WIbmlfeP0WYenwe7j0/osPT74mH99bU5+Hpe2FwhPt7eZ/B44f9v5H32fvd84Pyx1bPvv+j1/NH0r0W7d8HKKI5LY5/Hym+5TlU9rm9S/8W7pz34BEYsspbGx5OP3gaZ3X3vHgYG/T0teMjh7H+iNLl2fdP13FjnmOZs3VXcRtGHsEdzgvfyDuOIZHK09QUd436x02kIo/KJlGjITtThMAut1KGzuuV3Eu1KQSNh2FAjRFSZ9wAx0M5Lln4C23XeF81J2M4HWERFuS9GxoIoU+ExDo/anQgsCin9bSDPyNqRNX1C3ZfO/hw3sOUvxb4qwifnt/e8Msvv+D//S//in/7y9/wy9snvFzOoCWBE1C4ymmIIMdRzqAl68n01PS05k7HDSIGC8YnZeVzKlDNV77EcOBaULbNDRDlekVZV2zrhqp8eSnFx9BkV3MZFPn4WiW+VqkF1+0btm3Ft+s3bOtVjBFlkx36XBG4LlgcByIVa6iNqRhY3sFbAdUTEgOXBVgo4fPlhDMBqVRsNaFSAYiQzl+QlgtOr39GWk7I5zcUMDaLZ8Grg4/1g2oFlQr69Bnp9Q0vP/0Fl08/I5/PoCwrGLWC7XQKtTXGXJFCjyJ8jCmumiZetHVp40sqF3hZDIFD1c2wygww7xhVA5SH2CC1mNulIv1ji7lS1R2WMbzBeMVlAsva1gRQdYasxWr9QWmHn4M+tdcnsOojqn2ow2Tu2IA49tH8TSSb6S+nBZ8vCz6/nPH55YLXywmXc0ZeSBzPKE4sJr8rAjQdyC3ByfF5FEMeSLf0ZEcbI35c+rFlPmyIME99jTFTsqGDbYJ1ThKTweM5dMxUEBQ6hssI31Cn0r1MzfAQr6NA2yto4QJ/DoJXrDumqSFikrc7daHBsSnRoGxRQkZ9QNNRwVRdijUM07cxEYnCoRSUDXj/9hUA8P7+FUvZUCsh5wLWLcJ5OYFIDBhYCBZQlgM/576fkwSttl1ylBJQk1Nzx3mTZDjzEKkw9ohpuDEmk1kZGjDMldQtQ4Q1gL0hsU37OZwZIrp5GBVfjZ1pSuEhCXNVnRK6BZlMkZvBxILEqSKx+tNXns12fVAm7wvrC4HlBHIB2yaEhMkhcdEUkQ1RsNCTDX9/CsJdzviYBANCGKejsbp93Stn7Xk38zO4GOZqnJ845iOSdWTLrG6q+vk6UmKMStNbypFR2NwLBdNPD9NcWO9xDSnzLIxGc/MkV4lBYox5K4F3pOG4/63tpqAzyrkTfsPVPmoQa/M0UtAGEzO83hH9OP8eWLoFidqNeaoeSycadf11OHHHHOFK781w1hrguKQ/NVSHb5tCcgbvu54dvZ/Ae3w+5hnffST5184Nz9YC/H6klXuFSMPPvbC7V6TfVSTGvFHYCLVE3NQEGdtNJf76S2UVWmToK7e9a7HKQ8VPuHdDhPMSwxjoveHaOLRe0iAUgLmrg6i53Yk8jJcVtq/GeAPM8RooldL4tp5n4xv/pu5vAob2DXAA2pVxK91nfm/wYogcEdo4PFH/cZU9QopwGWlWXOee3Rkf3i1vuskxxbnpeV6y+GkwQ0RyXppSMzwsuglnUR4hZ4HNxU49xDgQKcBwInSuSn0H1x7PW9rR2TB0QcPUfnhkvue0j4c5mJV1/F5bRmO+Nua3IOYRen6LN3jk+U1856/muDPk7Mo6ytfjueN3scyxnbv2D18drcF7c9cK+D5a9mzq6ufjufA5aF/q9/qWZ31r+XrBf/KcG44ZcevRXNjfcr+HVaO59xKp/BBPRBzBZeM1Gk05atu0rgn8jPToVt3xXYd3sMdLR989kx7tz/N13J+bozKFlz/+9nv6e69MNlEz8oj6b782DPd3nEP3n9DaWEn/h62LoFTqeBC7msIQYFW29nLrQYd2a7mRaG5XzTt8DDj3GMldkJS4lUWsv1rb37FbXk2Qh7txifqI2EwW9ziZsFzOeHt9xZ9/+hk/v33Cy+mE07IAmYIrGfVrb5tnkv1krjp5QuUZ57nDENn8Mcnpc+Nf2WOzqRK7bKhVTiLLqQhRcleTlbx7TRYzl6LOx1eN7VZW/W3Y9BSEb6JsDFib0cB+UKhHlCBFu1dAXER/mIHzIjqu8ykjF0YliZ+RX99ApzecvvwZdLogXz6jgrGVFZU31HqFbEVTeYMZqRSkUkBvn5Be37C8fEI+v2ocDoMxgzOCeBwJ/KW9j3ASEzWe0WR74h5sHHa4lRXljfZcZXX7O8i4ZpjweKLVjBfVY4T0fK+VG09EzNx76zV2jvq3R4lsgpnv5u1qDDhh/AEQYwqR00P5rufldetYwysEUErimmnJuCwLLsviG32Md2ZbI8waArvvj6zrvjdHtIX7f+b9HXQDox6k499D+Tu55SYZcUw01L17cquQh9LjJyJIBjIpUksiQYBIOrnoqYDllLGkjGVZsGTZjSXBqnvGvwljIYD1cHTHhKbRENGMAa2M/nnb/ZgoiX+uJJ3wCSdDuJL2Sp/+OgrnbojIM9/a9k1vALH2N+Ka9PRBUWBpO6oZGsAJBKqMUjf8/e//gff3d1RmnE4XvL68Iy1nLMs7ztdvKNuGy8srSt1wOb+hnBinLPPhIUFJGR1t87KcADC29SzEZ9vAKIr0mu9jI7zctvX2V+81N9w1wE/LZ2OtLoysp7qo6/CBw0yjbLu6vWxWQqhjaMF33ODgVzREF67eE8NDyRCWEVR22EWYy7bYzfimOw9TktMzSvRAhKSWeK4LiAhV+01UXIiR+clSnq45MVQkD/bb7WxkY+OEglXduVk4BCJi9qN7VQMqyfhAglahXwejstQI6N5ogd23TnAjcmR0c3a7rh5BHxohDD6Mg+4gp/2dYt6uRw8IcjeF6xvugY6Y5KFNu/rULjfHTYRa92M71jdT+nTt1HgkLkwYk61xHZCME0IzZHbtrfowRFwdFHeyG6BjySVPMfiQix/XLUXLCHtzjdDXJL5PM8AJ4sqMQrttzM2VEoz5jTEh0JcN9t1RbnjogqvpDqkdnPbztZvngZbYeqh1/twx57A2dvl+kOxJip/a3yHGkcf22J8C6BUn/fFPw32xH804b/UGgW6Ez05mZYCE0RWhBSiFNTB11YDUxQNSr9uGba3YVjFKiP/PDE4EWqgx0EHZZ+iCSA53O1ugfMayLD4GJkj4eE0VKwMDC1tfDXcZ3bCAwqclebBB513CkoSPVYSL/tfqaj+re5y7/rfHkxNPia0fN1UjPz55U2y+qPEvQKPLcN5R3kU8v/tZH2b0Ayr7ADIQ3dHq+De8PiLyTSiJobvHJCsTC+5TPiGl6CJUUayfbsg+7+5+1F0wNUOEGyjQTkScNFZZHlwznc5ZT0qYO6YWmNpx/BH9mYwLpf75HicM8zcIV3+MopCcKZzSuKfr+p62fG8y+JrVEV1iYZJvHOt+IY/3Yzrq1+xpbMWHxkN5tWe+3dOZx7/rH9zLH8dpHNNZ/vA3x3FpzxOg8a1av3t+Yc47jif4Zv2eKrFnPKfBzghCk+Tts6VFmHf+4fQd6xHobEcj3w/s8cyYZuPxKAyN+GssaydLHPDfz+YhkMpv8zxHSqfvSW1sgyjVGe4I8USEbHDUjJ0bn5g/JC20kyaDzGblmu4jbkayvJ2caKcavLYJpPH8aryPsVXFFLWax3UdXq5xQKbQDQYH3Sku93A53NtDPOy41kxtv6quNZVDTDti47IVXF5e8de//Rn/+re/4b//7Z/xTz//gsuygJYMZNuU1XhPSqpgXxakZVF6r/yix6AAMghMCZwJYN3IxwywnGioGoDaXC/VdUMpq3vfqKVgW1eUdfUTDu5hJM4OAUX51U3LWvWb6/s7at1Qru8o24qyXlE2ie+2qbvVWll13QJnpLE8sqhHnBcm3TS0JPVIUQqATU/9Ay8LsEA24DITsHwGnV9w+vV/Bb38Avz638HLK+rLT9J/XIG6AuWbG2BqJXURXJC4IL28IZ9f8fKnP2P59BPq6RNWZKSqulEN4O6MIVao37ARWgN82LhFnibqTueAbjAsxgKAFS6tbjtlU1lgGLaO3CBR/KSExUgkO+Vj8nDn5jvIxmAgnPIQXpr8jdMe213efdeSGMDsKuNmOa2Yo2RGkv4kRFgXRqSd0QdcJ+jjHNpPhLwsOJ/P+Pz2hl+/fMYvn97w5dMLXs5nLMsCyrK2zBSj54iQHIf2cxR7eqMnk2c9zYvX8W+7N5yeUlb0O9b5OG2+xbP8iPT4iQhfHE2GER7FFBl2IiLu0DIBm3cKCPumez4YInIWtyEpZRfYmgIWbsCYxYqwlCBIiQND1QlUmm82uZJqV0dU3OBAyLeJmilcOvctlcGp7b7rGIqOCgth3soVXCu+fT2hloKcFqRSJb4FATmfRPG9LEh0Qk4rEtjZB1/cpHdkCig7GSE77pFYjgRaP2JDtG1H43U4jo6NWjmsBzBShSMfQQxiPbb5cfHAqz+aK2NYom/CdmRtVOz1CkpFQKEOIvKjle6ISA0xEW5HQwQTgUh2ridOuhNJd3UQuRK4onYwYq56Wrkmt9m51STlksFK9F9OIDZFm5TN6I9ENis43AJe7X5A2vMxZngckd1Yjvd1/71wmJP5msPTjNneXWG0pcHqzjAQyhiTjdej6UcoPEJpk3LMPVPf7p6wGLzxboyearPhKns+fS+N6ZlLbmvR2I3dvHGY63HOB0bMjn7GnRqxDURyArwSKlUQVT0erTt3YEbb1lZrxxS2uuZw42Q5GCRcJLC+WFYeC5jWhVBnNDi01xyyzddcdyVrHzd8+GRqDBm8hB3dUjw8GioiDHGY/wZTrT8zBSR1wtgsKcBzdaaVOfSZwwmIajuq7CSE/MxozlphIhG0RFiJzGbD70ZjKCg0W/wp8jXSr6FA4/WfuQJI+tErcE3ZTIFHMsNAGCtfmuSMcxPSJ/WEP+6htEHOkcShvuk3P575PKio+5nc4O+6a8Nb3D0+aKuO8dwIEXae0Th8Pfbz4hw8moHB84djqEQWqyye4IXDQE7JFf3REJGIkJeERMDiPK9gui5GWTgJ4QaJlJFyf0JiZkC4RzOso0dGiBlc3FIOHilPZ0rGuzTW1gz1+ff0/7gtu7xHoPPEeM3yzuj8PB2N3fj89v0hKZe7XemPztdIe+7N0Yh3KTTmUR7qe41az+Tvs943mNjrI/wTbJEdjPewN8Jgv9Ye7cfxuhNB4pEYEV6G0YOxow+2pePHb6w/q3PaFvS07CNGiGfw0L02zuWHg/eTsX40mYL+iJ49Mw73xmjMZzJnT3iBfhaNVjqTEr6LM65j0yoBmqr9uF2d3BDkCvT8YCxcYLbpC8JHfT42mBzxL4cWw/82GBx/gCl50ckPcUWPJ3z3jZKM5DJA/9zGYkkJb29v+PzpE355+4S3ywU5bBhjjVXgw0YkHi+Mj3Uk1W+4TDoK1RieUVZXOd52zLtBQo0OJfxtPx8KQtd3l48qh/wFtaxy+qFsofyg9HYDi8KV4TEov5RZdermAofa5uPKAFXnEzIByITLSXQn6ZzFEPH5J+D1F9Sf/op6esP68hMARqIrqK6g7au6MJIYFJUJxBsSCvL5Den8guXlJ9D5FZwWDUht00gIvqNgVq4jGc7pha0uIrTFZWtmgPMgK/nTAJP+vHvW5til+yirMnsMFVJ52I1lO28B+q0vstCMCMoUx2Hvit9gt0GN3jPHIZjybW58CfihwxMIwzhWO9w3/EvOY5+WBS/nMy5nORFh/LfJHo7Z4sS4fkrb5l2a09JOhqR2z9gbmo90oHM9Gfy6rxPTNNKXlvcBonbE2t5IDxsizKt/25wtDbLj5EvWCdOdV6dTRk5Zj443RiwKbHa0RU4VRIbE3qsrpuC32oQ1opZvNET0zJvs7kxa8JEQ5iTDiYJ+j2MBjogkgA3RtO7WBh2rlBU4JLZFJYnHQESdn3z726zMpA3brmItLrXidDpjWwtSPiOfvuFyeUPZGGVT1yWFUCtwWU6oy+IGGehJDtbAOTklIGecTmcx2GybEoetA2gfp7C4D5XWR4vG/nG6qK5VamPOQUBFUdhKzTqq5Y7XfbJd+/L33jqqeabXptDsjQvNN2ANSlJrcxwT4vY8ZXF5VTMjUUaqupPE3COwwCcpt82perkCLxobIqwdmb/JiQiBVG+b+Ec3Q0TVEw+2K5vF8s1GVNBiVU0RnBJQLXM27z1cRDc26MdmV3Yz7nhtA7zZtVMaGWyilfmsgCrAmO7nCsKj1T9L41qZEpi7yRguAKSMrS+r+fH/WMeMMM2rmOOzmFpZFUDyeTJ8W2tFSknXa2S4APJdxY1110J1N1MbLwluNhjL0PpPSABXwV+cwLVXkoch6ozQ1sbYly4iQMe41O7vtsfh+cRDndKGFiOiDUVg5LpnM5yKfhhhQs/QRmWCmRudBYSWyGsd0akRv98pfcQwzRPt4N1o/RED2dFUFVxGfFpKwboWrOvmv23bsG7yfLNn+nyrFaXKTiSQKHJnqVtLhmMBgBjLsiDnrAyg4ehQDg8MdhhXoMGcuaVs60ZoWs5ZXFgGn/1JeRTnj0gkVLL5tN8Bkz2ZjR1tsGeHvCS1S/+bfUAN9IwPs8E4GOdZehRvP6L4OuK//D0aXE+NEUF1AMW/TrTisyT4zYI8i/tNYaa5wykyjVnddy45u4KCNKZazglZ4z80A0JqrpeSxSSLfACwZDNULLL7T/nQ5WQnISx2RA4GCwlsbS7HUpZglnbyqRnFBh53Mmd+pSP4aHmfUYQ9kjplqZ+2OoDRf3C6xyN8b7lH9x/N+3Q78FGq+IPq/8Hj+j1lj7RsBsM9PDx+IuIj7dqX7S8afXuUF/3PnmhrQuj6jL9+jrd+sv4/ANYeaTMRPeVP/UeOg8sV4+ArFyGJm0yOOZiYxN/YV+GYOqlSlZdCVgVGq8vvkS+H01OOJyG4Kf5HSSNoHBrMs8m+g4ykrzzOlpL8Ct0SSdL6FORNPzCpJyLYr82fg+SLm0eO9RUeEyIyG0QgTricX/CXv/wFf/v1z/inLz/jl5dX4U+XBTXnJsvrd0bvc85IOSNuqUKUZbNt1ElobpsBbDL2pVbUUiVgtAaTLtuGsm4hOLWcWthq0XgKNtbG00u/KsvYbGVD2TZc11W+X6+oVfj4UjaUTWJQbKv8XbeixgjtG3LgwSooVXAhcAESnUBIWNJJvEYg6cF9MUZcMoMzcMoEUMLp8ob08hOWX/8Z5e0v+PqX/weuyyuuyyeAGCmtSLziVL4hlQqUCol6u4CwAShIpxek5QKcFnDOqIvKHepK02Oo1E0BS2VLEtnCvSIYs6j9NL5bcFACcxF5AqTasQje3ALiMZpLJTR3S2A54WKnedzAYGCnaykpzPpJihp+DZDbCmNGPAnheqJ+If6hyeXszvX4flMgpSgThe+DlaCjzCQx2C6XCz69vuLnt0/4/PKGt8srzssihi0E2Ywg8WxgMoNgkX8kHR11tsxAChucP5YMm/1xHXkiRoTu5otCCmTt9L5p1a+t3/e+kOGK1XiCQRecIlPbPZ7dFU2fz5QoTTDb/7zdBwq33aREhBDAVEP8dAobKwexfhNyw78R2m384FcGagIndoXekdULmp2ZwaViu14BBt7zN6RckasAypJPWPKCbb0g5QUpn5BJjUUwZYcE/mbVGrjSPCWwKkbAyd0FeV97YBgUZXuFfs/wju9becyMlIS1SUhGLQVR2yLW+g8NHgNf7zsnMFHcGMF2Rq+1Tf7vAw7Dy9ATBvXYEOEMjSvXjKBUdSGha0g+BlNF26bUXFK5Iqqy3kv/UyInGKT+eyL8sUPhaIhoilZTisL88bvS9GCMfYB5+l7G1ObCEPo41m2e7H6A9A5cZky1oofdvaHHJgi2OYjl7QXFfp3PkSwN+cZvHkszQcHbMfY1EEkKeMRbMAi7Uel7qMzZoaMHFRW+RuRmVBL3ylAdGw59rdVhGwjuFcI3nRHATts4V2CBsENcDIMrFuNI34857OyeDczUPQLbzb4ykKTt9HGf1hnx3ojbx+fjehuvre9Bqmht7BjaoZuYwUdTbDqOcbw1gfLJUrE+tLpbuf0nsa5O1HJewJvKPW5p/mQLStnHh7CTENVxvNWnCniazy2z4ValzdogaY8ol01enSqHvMVhLQZmjeJP13QiNFc+dh15F//a6ELX6G5S/e3YFOvHkHGKGgIf19el/XaU1xjbW7gm4qkIC2OdrT20ez4r7+j9URr5vb5xwA5I29Shn71J2cPnicS9YiKIT+Ua6BOhBSa3INVofHHyGA+Nb87JDFRimLDTEbZWiPREBGn8MzeIkMeKiDEjjL875JPJxsnKH/LcGnZD+2FMHP90HMkwgPH7o0Jv0NtYtuOwoZK4MltHh+pv0NNHkw/jZJ0diRmP8BF9G/q1RB1T0H0Vc/T5H6/6drukcY/nfyLvj/r+GeX9I9/dez4zbFpiRQQRb05l0EldzxtHYr367IF+7N7PePBY2vh6BC9fcsf9vNem/ervaeLR2r1X7lD78M1zbRzfN/yxx0hHuGVuPNp/f9SWGS3e8WY3Uvy+E6UHQ0TDN4ZvyfG+bNrocdLeTMBdHT1+JpcPJxw8nP/1TI0J3fObfd/sW0KUGQPPbjI1Bjk+tLMbxqhbcBlmVHwGPs15/VkDwyftC39nytBPr294e3nB6+mMk7qEYZethnlzut0zN+PYOm23cqJMwiw6AnPrbDEb/AREEUOFn4Twrbzd/Jq40gJJs+shuNiph+ACKpTpJ5yDHGrrKgFqjJDQppXJ9Vu2sYe59QloXjyRZXxOpzPS+YJ0+QR++Yxy+YyyvGDLr5CNJieAV6BmCUythgiiBUABqCAtF1A+A1nGm90V1wiNHOReE5WG9RUwXpQHIh7kroAwV+EnqvBexnb3S0EP1ooymWWAXw4GCf8O+ndbW10buvYd3u6TMcuz59PChvyDTmKnI+wS7b+l6Emhjb+4r884LwvOJ/mdltziDh9VEZsarjH/LdQ8frfrAQ0bxLuP29hE0+9zm328JrjfSQXGu3PZUP3D6WFDxJLD0XATgAAXoJZESJlwykBeCKcFuuMLnUAENMNEjJkg/RWgM9/fdvxMTmEQ1MsCUoagouEUwmgsAADbzTgTTHfEG2rZRmMOrKipIcKuhs97Vq21QZ9kzeuAqP79iOSkxLY1RGGBWM3XP5QglVpxXVdctw1f399BlJHTCefLC76+/Tuu7z8B/BWX7Re81A2lvGA9nTVOQcapnsKRPQClIjHjnBIqMnA6oSQC6ioWVBJLY1IfkJUqUBm1WECivQ91clLRE2nWwSGO40CqVCRUTt04GrK+tXSM4fL72twNxTYZsdwlajEvBMfabn6FiNKYDke6VlcgDxGPklrBmVn8FiYGpw2cFjmNAg02jS3AoxwXROhzIVWRDbCbip6IyMmDpXPAFcoZ6vyw8hSDi6ZaWr/YmKUAnIHw2zjuxt6wUpWgUEag3P9gmyAf330ZaHFHrFbLG+tURYlBF6ONm481CTMcr16ul9UTfx+vCZSZz2Bz2+IwAPIjlPEUytyIc5QmBNZZ+1jqKCjNBa95nbEOhSEz4kaB0oA3XJmru7MTggzUykgpoVQASeIEJT3N1GAOoKr4mNV9XTDuyU6MsBYjbojrbljXBrfEpMyRKdhyYLoJzL5fJIzZMCShrqa87sfYcZAvbFUgcBtVY+9tp5RddWWhj0cBuJ+3KKRQg6u+kbb+uBOKHEbiUkWEC8NF1L0zQ/eoCLETWb4rusO+hlQSwIQSXB+Jy+tqC9h5ARMUyE+zABzqsHJJ++YjzSx0pVZsGguibBXrumLdrni/XnG9rvj6vuF6Lfj6dcP7+4Zv3yrWjVFLAteMTBUpse9WacaqnpXvmUFVENvGB4uDRTaeEe83LqvRfvJBMRxOADIqiKABhkl3sQclMzXXPDnwRzLsItRUoAvuV0tF3QqoCt1O3PAwg2UDgu62lw0IIphE11NxPThf1Z/gd7gUXGpB4Y0BLjqc1ldnkhQcjHdqeHWmJIqnAaXvyeEhnuAwniAuY8OQUWCI9UwV7j5z+jcZfMq1MiCbxgjgBNZfZfELzJSE+cyEFsWxImXCAvGZ3dm9woaaRISU4acbUlK3S0lw2CknLLn1eVnsZER2I4SMafL3NneJgCUvCmO5nb5IDT+6MQIWwFLax6iNBtpc2MGocJLZ4T2OnyImYx2gMEu7q4y8zaEp0cm+C7yTn6Jz2usgBGtmn6hN4E1OMZbtHWj98PJnfMC8/0ITgMYjtGsPabN74JHTmK0Ng9yxa0mQEON4EJzfbph9xntM6jThZ8K7HY10N0ZB8B0Vtd+THjYyzJ489unT9UUjw608owLhKI0nO23z3cgXPZye/YTaWN3q/QeG87GCFO8bLRm4Vs/jPDdsl/6wzg4a+APA8A9Nj6yXuLbmsseD64QGuEqb8jNZM7hkKVeV0xMKmNRtMRE2nFBwAnhBpTMqX0RHwxUJgu3UoQ0IjMSMk2gdkFi9XzALHa5NLpUTCuaw2ZSsJuNrPjJu3PrBwee9KNTJTjorE59ZdBnJdnwX9pgPXIFa1bii41prxcb6qwUby0mAtaoCHeOGGLguq6ryirioPG7yjw5rynJTtW+bxHCkF8Lb5wv+29/+hr/9/Ce8LBfk0xnrRTaZnjbdiAPoqcjcYkAxwJEWsMWJVFdLKsVQXUDKW6ICKBu4bOBtRd3esX77DWVbcb2+o24F67a6a6aON05Ki+MatF3qm5yi4G0DbxuwSh1bWVHLhuv6jm3b8P7+DVspuBYxRFRKYKrKXsv8Gd99hvC/JWeUJYMLAYWRqCIRsGZh05SrwqkKzC2JkNKC0+kz6uVP+P3Lv+Hr26/4319+QhHlIhZKONEFjBO29CKwxAVLJZyYxKV6gsbtDD+Y8aCAUZFTEV412UkEkQw2o8JBJCQQMuTUbHa+V+SsWljHsqDFLpR78pMAamyAuO8uGrGg8ibPNR/x5t+LoUl0ZrVWcN2ECS4rqLzLZkJYDAkGFUYqAG9qSCpFvtG1lfz0v8nACg5BJ9XwTqSFLH3oTis1PtH5RrTsJqi46yhDZjG5Ug5AZl2DCcSEVJPyv7rhkRZU9bggG+AJl8sJX76c8fnzgi+fEt7eFry8nXC6nLCcTnoCKKx5jcthLvBr7ddDL0Wy88Le1qiDwZxXuGmEgMrboe/GGz68qWFCQnxZ00G+XSMfq8rS466ZdGBtB18i83tLaMfKw5X6EwzxyPdslxYAEAlxGZX+KfWCpbWFglFgJng2YbcR0SaI93+bAp3d/7p+QdiVefOK/t5Sfx+FllhGVJC0NpugZ4jOLMu1VBAVFJLgQmLlzXh5OYPyBfn06jvjmM01hCBCEwxNsxSFVWYJPA4waqqgKs9rFYa4gkDVfIXbLnTDOE0Q64wQJrSOcpoLhQAMIcQUNfwHaVTIRmTWWYCHRR2X8sjItasSwSmj15gJGQtDKiFvrWAi1EogKnIKhghIEnS4GeLERZUhbJ9rAL4DZQeHDCRRzkbRcqasbq5ngkEivE8dwuxKm/Q7jptCKE9+8uGN71t1UYC4pdCf4UMYE8rzvkchsRcWOZQVdshM1qpdR0Z/FNEfMUa4Ug+t3z6fsYcD4T5KN+sUTkYVOmGxTc5O+lhMhOW+jgpxkVRRkxkPw3gHxoNc2wcNkmUK+v2ae6g/LAFlWJEiWwCz2P5Zos68eTg/M1gx3NWPYWMkmnI/8hH7euLzniGLqGn/3EDDWFwY/Gh5ra0dH/OQUuT4F4Zc+y8KcXbBxoQpO+LbTktqHYjXSB85lB8ZOY3zoLTNT0DUilKLHwOXgNVqrKiMUtjhocePwTBgTJnjhDAW+qApa1Wc6LTKJkT0HYvL1ngJU5ILr8TOA2Xne4x/mvMtOqhg1r1N3AzKvVGkjWpTRDZhqM8z9LnL0OPMewxrxJmPcJwjrEqVPU/WzV3goSj0Z1BD7e5vJdpNuL/wntjLjnwhXKnBlTyzjRfxHRCV6ASd5xTmPbrloqQGB3Fvam3NublTsvVINPDOKcKXBbO2oOc2bmYEjGM6G59+bEbzT3/tSwgcH0wZeHRtoxzOFFF/7RAHYQePU/gMoLjv4cizhXV8h7we8fkjnu7aj3ENze4TxnG8l0YjRDQs7Po8sBJPdntYL9TT9zv4wdv4QL67dX9PPh5GeKDfz5Q9UwyPiuCZwcrHbJLv2TYAI69w7/vH8t0sAz3M3cu3fz55NjTMuzPJ3KPq4bvI+wQ80308GYRRpJwr7/tBPpqzmYF98vnTyZfshBefw0XkV5+b+45nHCSaxl/AlVERPTurz+LmhzmhamRKNn8SJCWI/p88mKtKVG3EuZU74iijL61N6HPwThKD85Uua7CXYviMnG9CkF1DY0x/gfa4apmV28/rCPwZDf9OWPxwH3gHhgQKJiAvCefzCV9eX/GqsSHMewUzg2wTn8J6dD/DPqiE5ksKaH8FEdM6p/oT1uDFXCR+QyniMqk/sRBj+UXYHzpoY+KBjrUOdWUVefutFIkZUVkNXGF4nIbppgaGbneVE6kKaK1nZGIudXPrbubzGZwvcgpiecE1ZdSUkFBlIxMRQBkcDDsgiHUjA5D9Wc7379dc23Alf5uuRmmADX4DtTaYYexsbhrvr8Y4Zpe9LFg6HFblecUoMzBgRgiEeIgcfxbIWgwQ4CZ76AKQZodvXAdk7ULbQMcBtkfQ6PDbjrAZkmjjsedzBkYdB7Ta10CUKOydKv3DE0BPQ+SE83nB+ZSxLAnLkrr4EDY23RoamjYjbCNvHBofCFTr28hTdPh+Rmz2TOk07WnqPk876d/zsDfZ7CfT44YI3a1lwrT7qE3ik3bJMlGns/hXXpZFfdW1oHqWXHCynflQxYTtiNfBaUIX/B6AlkVqRcZOkN8J9YjzIgOadru92g4Uduwcv29tivczhnUGNGOaMa5N4AxuTDBnRsRKWsBMKBV4v17x+9ev+PbtK37//Xf8+ueCP3EC6hcQgGWpQFqw1opCCUsSyznZDgGYMi3pcaSTxzJwX/C1IlX1Da9+BbkmuGJbr02SN2YgjCuNCALqgUXZEtKd1A8KaTuF39F1lywKtVmmJ7vyAxMCNuSPcO3Lrw5jFvsiN0beEUdC4urj7AScxMCDAYajwkaIXVOYzWOizMfN50fnJsbOmA3TbcY7MDVKDIlbeUdGnXlZPuDdmHZjq0o5OU0SIOPmurI67yDim2/7Mr1sA2ShEJO1eRsjc+gXhWdxnd8TWPe83kGdyg3s2uhB1+djKC8hzG3ou53UIqJwIm2ys5Og/kcb0W+W+XmbZ/DSlPy667lWYebY1pSsN9t1D8pz4juU2TWV+vFs5UY8bus0fku7eYvG5XtwMEtHygwxGrc1Zm2OLv2Y0dZIW6K7soFeoWnvpgpxQI9ksyv9x0Vjyk3ixlTJLiA0gSjkMzxmfdu2DbWynISoFetWJQ7EuuJ9XfG+XvHt/Yr39xXfvl1xvW54f3/H9aq+ZPVIt48TAXJ8GrAzHh1MH407KZvq/Tf8HBjx2bcK/tl35cv3i9Jzc8W05OiSSU+Q6NHfTMJDyQJhbEVPHbr8oILWkcIn8J2Njo+bPZpC2/v8QNrxPklw3wg7Y/4GTzN6Nq/jiK+61bYjHuzROo+e25w7TQvCGDOCmwF5likr3rM1IOs0mRsl5YWXnJFzwnnJ7ss5Z3NFKj+P6ZCiK9JgaMj9uC568kFOGYd4aUPMB+1h31/jLVREj4G2ZSD0XqXuZhhKR8vpbjqib8/O//ckmioPnqm7ff+PaK+lUST80enWuvgITQPu8zN/ROrYwKe+O25nxweih9ebfVSCfW8MZ7jrHz1u/6XSyJxNsxyMPc2nf87vjd9/EHhCHR/+fMJfPbPuHhiyafnGq5lLJufXlO3wvUtkNMNO9ieAMpgXFGSsWLByxioqXYhBom0+YsBjLcrWQ0JRElOUb60Im+tsLJVHc/XM2FGn07UfQjY9hKrUnIaz7vjWezspUNvJge40alSkD/oFeV68n5160NbwcOWh7Q4wDGDbsFxO+PKnn/Drr3/Cf/vzX/HXn37G5XSS+KuZgFKxlqInGwDTKTTvIwygBi8fYcc8dCd7lfECV9S6geuGUlfUsmLbrti21Xnx6/XqJyGsycaDjGvNZZKi4+JjWVDrhsobSpWTEOu64tu3b9i2DdfrVTcehV3mAU477yamMxjXvcIYK4wQVxCLHCNanISUMvD6M/D2M9bzBeuyYBMokbkjoGbdaJ3V6MGMVAFU3UZBtqFq2LjcXa2t8HUkBhStg8KcuzJcnRRzgEs+MAABneccubeTPeaOSWGgVpBu8jKXW+0kBHewXZlRuMFGZ0Di5vK76hwlMzcc4B1ZqoTmFWCXQ9f5R5Bm49f7OgNeD7gr6SYQ1egJfjLkpuswZ8LlfMKn1xf8/PkTPn96w9vbG87nM5Zl6eTXcXPYrA1P9WZHj/rF1eFrbh4ZrPm39Ub3T23GvOFNLGW439Vy4908PR4jIjBFyX/NH60F1zMByoK19IixldMrUvuudoonROE6MGb+a8qDsY6x/eN1/Kbl3TMqY7lHAlPHmCIoRtBP8CMA6m0M/RN/wKTBncgXQdmAUhjv6R0pZby+fcXrt684nc44LScpw2absoafZT8677v7dKzF73HyOXDC4m4YzOLa3Eh5v51TmI/nPjHAeoyfTdkcFYe4Cffs6HtkDvp7r8vaZXcHCtBnrvvSATkGmoa8VVw/UO19CTILQfV5hZr7WYX/0K6UnLAbcTYYM5cIuzFyxqu3gBvR7hDdrh9eiI80OqPMPEjQbDzHNvkIBEzaYK3Nn8FQ40nJx2zsbVMK+6gBw/rr3ndKynnvjemyqxVpsN53b2/5n6UDW/aD6Zj47Uqd4ZtnKjZYHFIzSuwXKBGJGze0cW54b0+g78FKe86w2DGsBFpwUosnYWqyWTdCYdK28Nxw9SGx9ucG3+1vo2Nj3xrTcBsHHjEHbojZwTAwbaKt/js48xb9G+u3o7t2AkE/6Og1SAzICWgBuyxHvARaaGMS8YYJOnGH1LZVvW5Y9Vd851QwgII7fgCuKr3FNNk4kl/9mUkUTE3o4P3S8e9tzJTvTSQGh5T7YMCymQPiVseUz8YjuUAz0L+bbZ8woPFPoi5v6+t83kd+qy9DBuERhfERr3RPsfbR989+d6Toa/hnT+sdzvQXcVUbXtL5V0NU4JNbHDXhkfvraIjYG3JSMhepPT/cx4AY+eVh7Mf5JWprMkhsPR4dxzbmey6Nhv17vPr4fNqKe7BF83xHrb8HS0d8wr029zxJX97dKrtvIu250cqD6Xt0rYyCqc3XjEbfK/Oe8enZ8u7mNxLEgcI/WOYj7exlHt7dx3w0wPz3pMhP3Wvzj0gHYZb+sDr3fPlt+DgaUz74dOSdZoale23byxj7yo/q6Nty8LyxAtM847rs23YbJxy1wRT1GGiB8yKOS9p6ApHweyyqyMoJRU9F1OYYUvMaDZVGVu2nSMXWFqWsSmfZnoX70PDWZjJdSAvG2+RIBJGVrUDY5oLmBx8IWV03YPXHv1ub9nkcL+v4wLh3as86EHdUTqGhomC8vLzg9fUFny8veD2dwmYFuBwPaieyI333ceTQMW8NfLzAEsTY40D4r05/De9I36wuojaGTR9QXXltf9daVQEe+Pxtw6Z8fe3GuYdtGc4In22O7V3THlDHPNvcM/T0znJBPb2gpAWFksNiLzzpiVOou1Crn9Ag25lpDNeGU5r8xsFwMsrj7PBgawQ6bhYI3E7f2Ds3QnBoNYdCbb3536b/Eddc7vEj6IR8rphDG+K38Vm3dHbdsmG4qw8h8jE4zoOwVsIzbu8aaMpN43Ete/vb1y/iPUEClcvGsNOyqPHvhGVZPJyA5Z9dP5r2epLBGDGpo609+64vKybXR2OgjRS4YH3hbUADZ9eNHHH8ZO17nid4PEbEIjsL24mI7EdXciIsp0Um7nSSY+Z6ImK287IPUh36oYMcXTOJ0NWu8T1bAGDc39UZGY1jAfs+U3yLIdi/A0ZkYwqDnQLbCZj5wWuLKKfkhofEEvi4lIpt3fQo24atbNjWim1d8fX331GRsNaKdX1HKe94e/2Ey/mCnM9IaQEvJ6Sa5LQJNSIi1lqS42hgeNwCqPBrrjMoKWHKSlC2titVgyqbYimOwXSpKux63OZdruMFvjNCfGARAAPBHu6fMkZ0c8sgqhqzd3+SxhADWbwOaz+pp/Z2xMKvBLi7J3kmDr7NJ12HVIb+yacaENiDVGsfatid7+1sTJU9xzBGgO5uCX7/7yHkMd/UcDIoepj7Hbj+7V3kf4wYzTAkQ3kPbky1urc+P2wQGFLlvud7pusY1zjLdNj/Ye5ivvCq3qlTHkJ2gRzg19Gf8XhCYsSRY/578BKVH0QMTnIqohIh1ewGU8lXMcPvrSvm93rsYohfQBaomAGULhdcwrTdVREG9sZwb3NgKiKjMRuj2dgRCOZQdMYwNkZR2s1WZw8G3q7xNNXMEGT4fC0FW9mwqrukqNQjGB1PAEtgXfiOE8BkMVIaI3XG04dqeKgV61qwlYp11dMQ1yu+Xld8fV/x+2/f8O3bO759k5MQ1/cVZZP8tQbsTwOv4Axc7FszOhwJ7MymSI642XCSjrFmjL705Sq70hfFbCnL5oE8GCLM5aS56JGYWFJHqYCY+Vv7G48AjGtwXJtzPueAJ5oPwR0eab5m93zWvKxn06wNt3i92fNH3wOAGeCigayL09EJ5TYWYgQ1l1uLGhPsRITxynnJWFLC6ZSRUpYTMeqKqa3NCFNhvSqsJYVLc8mUk6zFHIxeVojNQ+e2KfwSzWBlPvb7Hz7Kcn13MkPJIWyNtx+Ewe+F3ePEw99j+Xt6/1By3GZlNn50XvZBMTf4j0fp139qGtDUURMfafuRnHcLRxrPWkqRyid0f1bPLTz+UWXHR7931vj7dCwfT39A3XG6jX97tvL4zSNjejTvs7rZeMuDuu7Bq4Law6nxqYbMVRdgcQsgMaEEFpT/NcCgDGABY0HlEzaccMVJTkXAFLwJjA1yYsB2U8su9ZUSCqCnaRnQWIN+cl/pa90pSptC1GQY8eO/6e5vlh3htUqcCJVRARbZlxlcxLURFclHgbfqlK/d7m+LKWm+8yV2QNzp7Wsm/JESgdW1tRhtakP5DIkryWEnfN1wWl7xl7/9in/6y5/xb7/8CX96fVMeQkUyVBTe5OQ5bGOwxo2kiSHC+mcCoBohyvaOWgu27SpumNZvKGXFur1j21as2ybXdXVeKCXhWUiDkZkrHhv3Wjbn7Wut2LYVpYieqpQNm8Z++/btHet6xdevXyU2xPUqg5LzsPJsg0bsiYwVm48kT403h/OqLPABAGkBLy9YP/0F69uf8fX0hm/LBcU5CoHDCtYYnBmJgVMFaibUJIblxI2/VR8tEs9WZchkPBeCfKmwlRq0uWEgdElPBqnBQE+pWPxTrtVjERiEsS5NkxPsdA/rGohXOZGiHlWqeVaJxqZNT48UhxFZu3rl4icimpGL2ri3VdDuHGft8aDjxkdx/YD+WvwC/UP1jyCdT3ep0zbeCPgH06YbV2UeTgvh8+sZX95e8PPnz/jy6RM+ffqE8/ncGSPG2LP36PszKeoVbr3X7hzSBZfDEZeJuoYio4dWiBcOfXqzfzPa9JH+P+6aSReU+LlNQai2kxDi6za6XNorPaRrO0EmdIrsSu067v4iI4RKOM3KReiZtiOGcSbEz64x3RPSju4jDDlMDfN0pMDtBFF7wAnZCW9SZpfcx78p/q/Xd3z7+ju+vb7i5XIWoThIjVwInORkBJEtZiNOvfZKBGACqsw9J/ERH3ogxFUZ7xjwu43HbSHI5t26+Uekvtw9Yy6LaAwo+/jVFFRu/zafeEohdvNs/ta5xcYgKwuzUQq8ixNZa287VsuYfMxaKgciHa/e/sjI9nDQtT20c9+3VpYlG/v2fIasZgJzX7e0jcMX/T4ZA+OeuY7l0/A3N35ltzjjbEDnlQ/X71Gbj9L3yVhhDKb4Y7d/aFqEw8rNeXFK7z+OAFY7Cgai2n99IMQ/l1odZhxl0RbLeQg2pXNC39axJ/LurvGj67M9NHg/+CbQt3YPsDKs94TIm2NjRB5jr8ZvZvcDLp8olGaCdVTAFj2psNmxbGPSSQOsESMzuUDFpEzORFHYxsVwhZ660GPxpeoJiLK5UWINpyG2bRO/srpLiFtnAntv9xGvNkYs8gy7oYbtdGpxL8b3JkCAonKYnFaSih7C/wwxIpy/6XkbY5xBjfbLOO2a0M3fbm5HFmTMgzuwNpmzW/V2Y8PNYNzKulHVUOYIn7GuRxTC95U0x7yhm/GcnvUGvp0iJPQRBjNaXhrmvQWpTnrc34xP7XSx8cpxg47Dkp+cCc8D/EzjjRhMUd/vWb4jxef9cd3zbPfmawqzT6Tu+4MyJTF8QU2/ndCHh2HvDv34AJ3bb0S4mftmhvbqO2hOeP+oEtWf3cj/LE45asfdtreM/uQjdd/Lc+u50dYfdSIiCvo3xx97eLrV1pvpNqgd1v/9acYvPFNn3KAwoeN3+3WsBDqqv415wy+35qtvT5Az9mT8ofqlnMfnq8k/FO4jz6QNIUDkWGuY8rToT0QwJdmkaC6ZkrhKJTaOSN3jKCNdTSnCjX4CaAaIkQ4f/KTfwS305OebBtQdEQ/vRUwPO70Rdnzb9/b30CbTmbis2MlTTY5mGlDjCNJWVkpYTgu+fHrD59cXvC4Lzjk3mLC2GDfa0XEdxyDr+zqwsQ9jIq6T1GVSFUNBNXenZrTxMfaCAq/Q9AWm0G6K7XJ8DSefiynBbQ1YfVbdDKBVzoiaVju941IA25kcmwMC8gLkM8rygpJfsKUFhZrreOHb29yROgpz+CRSrWM7jWP8n7WVyAvRtrfTCzJgzX2YP+94SoFnjich9GSEwKr1kx0Wpld7j56nRYThDpbD5hq9t7xxHUr7gg6imxjqLqOSYY+vlCYKIDsszdLODZcqMTpjxEhjicI8kY1a+1fxma0jItk0dDplnE8LzqcFJz0NEb37HBlUHuedD5K2ty+rd8fUXeGgdlNWNGom8m3UJdh87fnqmW5g1r9Z255JDxsizifxd28KbY8NsYhR4ryckLIgT4kxsPikmmBlHWhBrPtd4ia+tjgOZgWdxIIgs+a0iTK3NlG4uXeNgxnrGJ/P8t7K488jE9Uwzo6QxhgL9kxcW3G4lzHKKaNo3IaURTGUqICLudAo+Prbv6OUKxKv4O0r6vYryttnvL5+wmk5g04XpJRV0B0Z/UBQbW6IIDv1hVER4dhORbT5LaXIblx129L5tDtAXLP5+nFJiUmTStqbQaiJim4jRMKkza6NufArswecNgQhR04kDkdldRtTbW3YsT9Dbqbc0vJsfZh6zYw/1hlHQrWv074KQ9ks143Qc7h2c8PzeXAChPGUy+3gw+O4tzGHM1Ntevp2ztpAVAUG49o3BTmnA4LQ0HB8Zn3thIWGoaf9v/fsVor5a+x3lwetLSEdEYDu23Fuxvez9gZKNu2OjZG1IeA16YeG/7qzdscTbU/hUcDXTJwrZpaTEZzk2rkoUcV4XPPS0qHsHue1MaLwY8DH9gjOleEMdM5lFDQ3eiMj8xAMJeoZFN0R0wlJAMwgzNSvSWdOfRx7nNsxlRwMEKVgLQVX3a10vV79eLBtODgvJ2HSCEBOqPmk/vFzFzzPGfShnk0NHO/bim0reL+ueH+XXVK/fb3it29XfP36TeJCvK9Y1013q7c5Sh2MQBW7kKBzPjfxKn/PQS4okIbnAPnY+vjpDnbZjQ6hq9ROY9gO9yWeDlWhyfijJI1uczXA7F75PbSY9rzP4fMP0tp7SrT4fpzvZ+u6xw+M/bz3fFb2mOJaimug6q6xmYuCCCdmdLNTCcsixobTkv1EREoJy0l45pPHgUhIWXwRN0OE9R8Q2bk/wSQoVOtCM3I1ntutY3of5yQhUZY1gmCsu8ETx7G9Ncb3+Ox76VF+HTA8ftCW2aMfyltaWc/R/39E+vE89Pen72nTiM+e5bmeKf/ZPA/3SwSLH9L+ozIe4Q//y6Y/BGRHfn94S7cVN/e+/8MSHdcc5/jYMIOQ54HqhnEwWdQnxeJ4mtLO5AWS2BDAoteEggUbnVHoBMYZpAb3VAFwAXSTEkOUqxszEipqkQZkVBDEbQyY/Yra0+ZRVyLKVT3V4EF2q0rUUakqSnBUBpeiJyKK8NKqdC9FYkQUU6gXRi1ap+0Qr1XiH9SgcGfbQa51Qds0+N4XF0XGb8DlKzCDNmkLvZ7x+afP+O///K/4t7/8FT+fL3hZsowfAygkgZ51KiLf0HOtTVdBOi5Ui5wSqQVcNtTtPZyEKFjfv0l/thW1bjC3pMbPuewd5EA/NWIblrZNPWWs4FqxrleUsmHdrijrhvf1ivV6xftVYkSsq/BXEoKOkZzXbTqNyHcYLyx9s/DT/UZFMz8QKhIzKjE4JaTLJ+D1J1xf/oz3y6/4ll9wTSfZJALGBbqpHiwwWysSi7J0A/mYk7VJWwAGcpA/MgX+xQ0lMs9JF6eLZVGGc6W/GW6KniwRGEtVxseCRhus24mH5v6KPb6En5CwzVsaK6JyRUXp6qq8yekRX0d26ofbj00GYhdXXG/RY5cO0RBu0CTSkSTt21HqwdtxkhuluhMR5Jt5bBePexGIm3gV51FOOC8LXt/O+PnnN/z05Q1f3l7x+nLx0xAGf33TfxwBayh2PKnWZKzbCv+PtOWYv5npSeN9fH6/bfP0sCHCBB3b3bXosayckhol5Gh59hMRewVEFJL2ypCg9nFha+/Oxr8hDAJ1KOeOMDMTpJ4RgI6e755NnWsGy+TEIDHm9Z8jMelqSoTMCZwYOWdwBcrCKLXoUDBq2bCu73h//4b3968SRDxnR9g5L0g1CLiRIyEjnqZ8mweZcXrUzc2xwkQQBODz5Y97IO7EvKAXnD7n8SF1D9u0tMUc2TzrdrtGBMDDu55pi8rE6fw5cWnlsgW0De3cIzZ4hcytT43QHqJ7fzA2xxW43BshZkwv+zz1/bEhHmf4UaVqnItpHdPPrWz41ebBlEetAmW6YJBwvOMbE0Vkb50fdyhMhL/jrh6nALwfFXMiou/bxYdz8+OScR52p8HZw1HVfcdEvCDSgNfSCfgIHgwkwVyYtRFj8XUmzJuWM16Rkr+nro4e2t3jIcWxjAr+2JmGN8YxHzvdGPaQ644id5Z8zYJ87Tv9a53aMwiBgbd7hO+P6NuIz6JCdvPYDMLAivEhafAvgHlpa9Tx+0x5Gcs24aV2vmLXdcXVftdVhZUWH8LWPlFyWHKWwGWkoAifDW6gM7txd4Fuj6CaUCEl+4YJV/o2gZCAsKu99kVfwAABAABJREFUuaT0+o2u2/gYckOA27s4dc9H3cyPY/7mRykMY20+B0+W/Uz+j/QjCrWSRn4Mwz377rRaq8+LwwEln08zLrkBQE9HpGw88/wEcUoNXjpYdrgxmOl5rtnPMh7ltTGY4YNH+WDp+XxcRwVyrO/WXD3chvHW721e5m3u2nVLMP4DUrfh4UaeiM8fXQcPr4En1sYzqftmglsflaXu1f1wfh662jXvR+CLx5Lj9e9Msf6b63GS78N4veN//gj6EFmZ5+Z9TI8aZ2Jeez1+2j57rL+7tRpFkgfb3ckoN+j4o3hB5v9mlibuh/7OFIru0oNxvKi6vMojIfA4aPyg59U2WMDlRIHuWl9Nth7osfXRNwS4XO+Cof4aGLNWOPrAR6hn9vPGHkhsra02qH2Z4JaHx1IU1xMAKuLa+vRywevrK379/AU/v75hsZOUtqnXffvvaSp7R7UtXINSnT0WBOvPFM2irDa3O9XbLeU3ryY93LV5qNEo43XEeztVLTz+VgqKuVZldhjwsYSbkZzHGuWarhm6Zho7pw87HVoC5TOwXFDzC2o+y6mdJK6UMoKbJbsyNEaE/ojcVTpB94hpHDnoN90KIW1DxAlt5DpocKMZzGjFIcZGNLqpnsNl3GaMa0Yw7mDBa+Kme2zrYyh795MSSPtBOidulLJJ0livATQCTpzguUCjWGUf2uEYBH52mHelrdzdN77XZ8P/hsB2pyVpM5YoYVkyLqcFL+czLucF5yX7JqKZHul7eIfptwpXTRdF03q96cNwTF/MWyU/WyaT9sx0Z7f4uFGP+2h62BDxcj6BiNw/1rIsSEQ4qRBlgTyWZRFBKu8FH/uNcSNMeZhMcA/5EO67v0nDk3bML1x4v8f0PiN4fa/1Kyp0RJitbpFkxm6XnVwbDugZQf2x7oQj8TO8LQV52fyom1g9V3z79hvMYnp9/4a6XfHy8oLzyxuWfELOJxAl38XX+i9zwrV4G6LAPu4OtnEham5bZswCAHfd5B1yRBmUbLMxnlCgMVhPyzhnGDDksR3WqrcEheDSXe4bgsThO5ZxMqWWle+BdbWf0ejhn4UOt3eMvioK1wQKxwu7jBNByEqM/GX4ePdEnnJ/jczOB1IUtsfnXflB0StrIvqYH7/XMQeGMZ+lOAKTt7df3wexJ9Izwu183NpOo6NyO0X1hODca5+JEhFux/I6vBlinBAACnEmAMhO8vhNSv1wBwbOWSmSExBWF7MEdYMRQA+g3WJG9O2TtTcKjHt8v495MsJ9f+3HQnkqvWo7Ux+4/jFBMhhnKcx91ueVXADr8G1oH9jNLYdzZn9bAHL724wDYhC44v393QWIZRHaw2DU0wmnusgpEOP9UgKp20bHM04L2Y0P5nrp/V3iP/z+9R1fv33D77//hr9/veK336/67iqCS2lxQJZ0anDU3OIj2S/2j44NDzH1sLB76+8tvpL75c/mvlJocxrGV3gnIKKjnXDn60pxus2bCw7HbW1lPMiGhjr75zfyU38ff7NnrYrneKajtnb17do9V6pbuic47BUQ/QmIUgrKtslPd01KebIpZ9HTCWaEWDIp/IvxYTllPT28SBy1UzsRYYCbEkkQcx1ra6sFsh554qzuGhL2PLZJ0yPPPcaHeWisw/3+g+Mynk2P8OP3C3k0W09Hnk8/kAEYS35SkPvPTmNbx5b/Z/TF2IeIF3/EjH0cXu6WPMGfoxH/H5xI//kOHv//Tk8mavLZ9PWD8PdROG1zdqMVh/OqvLApZZUHM/k6ESFBnN0Yz1rBdgYCZMGmTTEaTj34rm9VjLDGaWhKczlNYbHUCOiUqXFnOJSmk/2YwZsGbY76Gqvf/MlP+MGu585zA8TqWqq2n9zXJqeRICWL6ZbXitN5wU+//oK//u2v+P/807/iX37+E15OJ5yWjHzOUKWRtFVlMTLelkWvhAR3W8p6UqOWDVwrtlVjQVzfwXWTH/eumdqOd8KSMpAZZVlQakHdquJS0WMRIfBIK8omP3G/JLvry7qilILr+zeJ/6bX1eKc6k590R/plBnPa7wRACC1+RygU4wEaO6vXIEmXjqIFlBakC5fgJdfsJ1/xnb+CZzPoLTglEQheuIEIpF3T/YjucraMOW7ul+FGfxMfwnEGK9Hy4R4tsJ0PSjsVzsJoVc51WNZVYdl8Mm9gamacalbS+2khLnQspgTbW1wO5EQ1pVtCJSuJoAqKpF6Zk6tJ9w0RbveU09LDnHUTmfzOL7bx2P1HADD4800fsB7hWVJ+PR6wU+fX/GXnz/hT5/e8OX1gpchNsRR++P9bO7vvZ/363b3+9etLw+lOzquUS9ySy8e8z9Lex4/EWECj552WMzvre3qysl94lIidVewF0qJKLhrQFMOECEFpVAvAB0/nzLAocyZomkmWB1dpwLBTtCn2SXgi2FXXSCuZvXsSqNGpPs2tXIN8YEYi9XJcnKlpCQumtQPnQQiWnG9fsP79SzfpoS6FCzq4gmsBiTf1QdtgyG+foegxaJoBob+Z//Woc82QlHJNs5LG3fs0hS0A/Gf554viCOkYtcjg8SYL16lHO9mvEzbInR22Lk9mAhiMyJS7cfQGLNJHyfjM1PyDz1tdCU0locr4hVz1tWHYxjvZvEdWYrYpvkchJu5kGRrnzRPaNjYxtlcdmXs1PtjO/vmzBLdgwVr51gW9a9luIZKKMJN/H7WmD3leZxgxJEzuOTwfOydwJDsYqHQR0EwsqsnrBm2PTHkxLftxGq4o/1YGQsS72dGW5hU8Jnhd1vnkR7A79v49op9v86eoccVo2GiN2QYTrcxOqAl47iSjeOAb1qM7QGfqhs9eRE8no00ZY8DYxrplp1ekKsYXGqpqKkqMwyYJcKYclPIj4bpFnuiYtuKn4RY1xXrVU9CXFc/JVFK0ePELO7sfJwYicTYYpCRKAgF4Wr/HPJeOs4OXnvSb+DrfvpzSr7j3XkUkMfVMkFx9PPfxrznN/rx91pvpsYjPZB74Jv2+fcClMML2p60x5TFvTHiWSXbjEfr2z3/9ojWHJUlMLnn1Tr4NyHOf7GNaD+f5z5WRDz9kDp40fZQjB8Sn8u4+zubnwjbBu+hbuHzbis3j8Z+Nv+35vmRZ7M6j/jyW9euzPGPO8DflWE4dcbjD2nG5/1npqMxfOT+cfHwuAzgtiAK7KfiWeH0o+Ps33Fgjfyd/aUcd3d/s9QPt60pTm/X8WiRjyswGk25p/y4WSZPBvKJtvznrZfGMx6tiTYu/mb49rE0K2+2+ePWt13Lb9DxR/GVlX2r/hkd9LUhOToe1Xgj8mdR7pfciQsSClKqupXCAvaSbhAhD9qcuJd8TeyMa8aUqIjraAiWy8xuwJA9lEEu9DKaghdqgOAqbnu4tvw11OMnINHzAk1mVf7f9CM+JD2PYI/BbaNmmwTAdnEzgJQzPr19wpe3T/j55Q1v54vwkll+qBUo+mFgJiuL+yXWvY4udVh/hgDGtkHVDS36NwV5V3iJ5B5PGOwbGQxW5IRocbmghnrsVEQ87bxp8OttW8WwUUuYRx0rGvAW4uauNtY23saXNjhiNGfv3hmxiC0XcL6A8xmcZCMuoZ14ELGqlyUSWDc2ETKRL1CDayAo6bukm8C0X80ZUISV9kc0srFdQ6yOBmSxnyMctk1LbSm0d/266o0UVqefrGBWo0Q7cSQyUWtEwyHm8QONZoS2Oj7pUOwEN+1wW8BAgec2iTpmi1/2LGHDVmOKsJ5SwvkssSEu5xPOp4xTlhMRZojY6ylH3H/Mm424e6qDHN/xMZ9uMuoNznjyRiF1r3w4bNeu2js06Fk++YkYEYtPVCLCKYvielkakrKg1aQ7vHZCj7mtVdcEdjULlnl62wss5qMuHI0hcpfKcnsgtLAhMKtz7qd8KpTRbeZw/25AEgPxGuNAmB8389m274sigG4LZavCDpTUnFHrgvMSdu9xlV0GlcF1xfu331G2FUSMdX3Huq04nU44ny7IOeN0OiGlrP6txcAEQyjWm0lfALSARlUt7/ormqc4URoV5Q119/PQhGvLd7gOd0yWlLl/PmfGRlgblY9xrux+lmqVOBBSpjzzAz+hD+RI3IRagKGxI5CHUqMyspU0S7J7c48II+xbWawEgI8IwTh23Zg8IFCN99rx2XMhkF5ReBfhbtbE0KYZLbN/2Nz4xMUcWAclmD9W0TAbnxlx5UkWbq+HkWkqwPGz59prMXgOk1USB14Jv43VCAcyjMbK2TMO70ingmD/VRcQjTAac0fe39akUFZbUbKbicTHIxGBquCvtrOfOlzSTkrsGQC7Tg0Q2graPW/CRsOPdTdG0v457jikM61abZ8ZF9qpBeXMFXSiYdhOX9ixbHkfT2XcUkrEd92O8CJGbTvNkFLCSU9HcmFwhhiCAh23mAltdzm7q6dt3XC9rni/XvH193d8e7/i779/xdev3/Dbb1/x9f2Kr+9inNi2rbUxyT+kEUoSqXJX680eX8d4hzbGR8t7xgtEGG88BPQaTkKQuGYCIfS7370+Hu0d13+3nrrnwM4iMm2/c+ldm9vvbhHd5208+nf7uB+3ldS3no/vx7r374e1S/fLfrwtbV1HOG1xImSHWnFepq2jBmOMnO1EhJ0WlpMQy5LlJMQS3ZcaT9x44wg7FgvC4oykAMtSLyu/1s9FChmP5mo2trOxemR+j8b2iC9/9vpIXc8YIYjaKbFZHTMeJ/II8t3t+v6o9L38iXGU310OHSs5pzzgPzgZy2L193toI1/dfXVQ1h2e6U66zTH/F0/KY/xx5f9xRf9PmegYOj9U3I11evxNkz0bv61EiuGSCGlMh6QBfTM2LLhiwQkLTigMFCIxODCQKWNJjbdKqOYQQ/kc/cMupiwt1flZGF/b8buKn1WpGmM+uPtPcxO0SYwEKrL7O2m8NWIW/UXUz6gupQQ+wHl8VFigZ2buuPsKeD+i8wh2lTfQa2lJv0tYTmf801/+in/581/xrz/9CT+9vSKfEtIpIZ0zeCVwqXC3pCAIOyI6CK6MtqsXTclcWlwI+XvT+9rFBLCd+tBNqaaZq+oSN27GKLWisMaTUGODnRyVDbByvV7fsW0r3t+/4nq94tu3r1j1pLXpiZroa3qKIGPWJkP5vOt/YPRe0FWnwGr0YZDM7SkD+QRcvoAvP6OcP6GcXkHIaiqzEOvwWcr6NhMjUcWib5i4Q4lBiu31kgjAHX4U2krM3Xpn5hbDo3Oh5YsErtvwsehhdrbZ2YxCFtuE9R4lGo0sPkTRmBMBLnztsePsTn4HxC2T6lyaq7SYWt6pDmSaqF053muKpzfGLxVfwdupC9KbQbpYxWB6WjLe3i74/OmCL59f8On1gtfzgsvphGVZ2vyE8g95oIHXPtIt7Xhm9KNiOpOxzsiH9iqbW5u7DGM8TnRHXnzkg29982h64kSEugLKCebKJ6UWtDqrGwY7Zh5PRDThPApQe+FmlKP7vlB4rpR6ELhnV1kQcyH2SMBqf7cFd5RGpa/oNnuBdnY1RGqLsRWzn/RWl9bjzVPFaRKGQNzzyLdJkaXvIE0itNa6Yduu2NYM1gA0uWYArIakRQ1J2VBLWxTGGHg/EJRfeuyryq7VaB0vpYADcmw9pfCXCc3Q/jwmjGqz2jSRHpaLRAzGWM3n2ZU01AbXFOSk8yk7OO5cA2LtYKub06YUGuH8/tqNPWXv51Ga9VX17oqwDnZKUVM293Ufpzb+A1KdristcYLQxnXQp6AQDlKmnATRgGrRaOcEqK/Pxq7f6zOr7qDPN+fpSfGBukurclKHK5QtyxNKITN6PdQkHaKuJxFwiKdw54JCX9pDdTIbc4X91cv23DfKrbC98cRGtNvaS0m/jopd0vtAK2ZGCLtvuGX/d8t7YLCjm7cNx7P9LYNgO9GMYeoBQW6J4CdDWt2a1wxyeAxueqWmBhy03dyU9Kiz4m0Ou83CTjWuLAx7lV0yIhAKTYonIcS4USQGhBomrnZse7NAbdVhuO2sQ9htrrvPrc3Gdwx9iv2/r+zu2EGlEboBItY1nIiwMnJK7TtYmwhjyTGZ8C1/R2GnZ35vzp38seN3YluOlNLWhl7QiH/frvve9egXy5/lj/ddmbHf2nctpZt/H4+OEedm7x0mJBoUR8HOMxPBjITya6cuJB5E26STs/DM8fRMM1ShwZGXheHvwKfcGMudO1ODOf+l4Xp/jI/m15/j/rzP4GAs6953Y77Zu3v55X7Gb0gyvqg973HACCj32vJHpg/XZzjig2VE2eTW/AEz+na82eOoLbG+R9oVnvQ4oMt7VMbNKv6Q1I/hvdxHY3Db0MyO1Cc0bVdueO786B85MB8r+x5cNHJ1zFQfw/+Pc7/17BozXdv41dEGklk7x7G514apcTUoTFnlc1GJGA0Vhb8ZIRJVZKpYULBQRUYRvpErkiqNMxFqSqooZmQHS90gw6rkrdWVyU0H0Z9GiLw4s+7kj1fNaz7z405vZtbgzWq8YHZjSaT9TdcR3DSx8Q1xoxHEZSy3NdZGTwHR6LF9EAebK0AJOGXk8wm/vH3BL6+fcFlOOOkmXyJVaxNLnGICiExtDr/GKoxf8dPRNi7goLxvwp7EPjA/1TXQicZ/GA6XzaZFTjXoJo1aCkrZUGoBmyvLYiedr7qhaMVW5HlzH9VBI3ya9V10AeXPfE6T9kXlHGXRjBu0/5gSkDKQL8ByRk0ZTEn5eQDUxonif0QAiQzj/CJ6eXrGGXMT4vYpdnD/sslPCnuoNnfmFqvL3eqDm2d8rTTdXAhaHV0z+amLVqcOuhsj5LSRuT0LBgkDDoMjQ7qmP4vdcsBsa6aN3m1c28Zd0dCYfdD3Sb7AawR9hpDC2DqZ47wsOJ1OuFzOOJ/FFdppkRMRFvv4aCNyrM/+nr2/9e3hO9OPDn2yzZZxNGVsZnxzxDWtznm9cVzm/PQjxohn0sOGiGWRnaanIUaEBao2Ydz8QoOisCF9aycg9kIwoeHp+LO3phggQ74RQ+KGEGNWfM9+3IZZ+h7hwq3G6k/Yrp0xgm1XPBrSm7S1MVSNqRKDKCtAZoAqOCVQqe4qy4VonYNSVsi5voK8ZpRyRcoLSlmRkp2MSADOE4anKUo8WCP3/ZSdrgWrKpCYGWXrDRG+WGHdaoSaAKTcLwDzAX4vyaIkgJIzH/HdTPBuu1r7uW6KehHsxxMR4zUyLeP82XwZLFIa1kYgds5M3FOSS639XdRNDnDejdENxtX60iN7Hq6305EC4Sif+Q89EhQaY9iWcrvamhDf/8yyU6Qpn2Of9vE4/q+SIi49oh2N3MGnojccKstwCJojM5AwA4Ej+LtF1EaDgDSgP30h81p38CdXMaQzit73wjapEEGTEx3hAYBx7TcmsP2OheOPpEbLgsDhcG/3gjNIJyjiWWZW16qPMQ9RqZlSwpIzllyxLAu2bcOS2cdMytP+d7vICbUUEICS2njVWrGuRf3FisHh/V1+X79d8fXbN3z9+g1fv73j6/sV17W5ZWJm5TkIS5JNEYv5389qLPG272n7M4pSuaowFmjFeLVxGpWrRIQlGEW9LQQ/SrsHL979PfILRyShYxiVju5pXsv7bIr0yuqa0dN710fKt/sjXq3ni4Z2BLZ9pyDXJy3yRqMDUdDxDRThFFA0hnWMfEKIr1WQksRzSCkhn07IKeF0WhqMZjtB04I/xj620zaDYSH1494bLag7Nu5jtRufWO8eNm7N4zhP3T3dn/d7fPf38NnPpcgT7p89+q2WEMp6vv2P4OIfnYRH/r7vu7IGwfuRcZjl+UfMP9H3cH3/KPicr81R9fRcmvHvhONTHkP53zdw/3f6g9OPxiPOtriXBt3kJZXJiVeX4RlEFYkKMlWc0oZL3XBOG84o2JBQQKLEBGNJCcy6YZUZqQpsFdhZX+V1SHfgs/qht8Z1hoVR/u2NEMKTatwHVYybv33ZCV5UwYu2e5vjptGww7yUpsRVJXFUx7BK7FA5oklLxmPY37oxaLfsCMgEvJ5x+fyGf/v1r/jnn3/Fp9MFl9MZ+ZSAnFr8AFc/W7mNFrfCm/HFf2o8go5VUOr4SeZMWUsXH0+ssnVKyeP8VchJiKKnHsq2gkvBul1Rts3jUFzf31G2Dd++/oZ1XfHt2+9YtxXv63sIVD1gN+7xlD3rDdgEjv0BJO4HiuuASJ0tOTeYT6DlDDq/AedPqMsJNWd14yqTmdTgAED6avX7L+JSdyzsUiM1gAB0Xc5FZVPmz97BYzbUEl1pNYBj7a8ZKGwToAVitnDM4nFFYksUO1mxSfwIkalkHXAtci1yQga1gGp47sYrO4XRx4j18SGF8UH/dpyCb+EHU4QDlz0HQ0TU9TS5Keg+3BgBgAgpZ5xfLri8vuDT5zd8envF68sZL5cTLqfF9d/3cO3IH91Kj/LARv4jj8XM4iqNuYNL05FZEyngh1jgcdsi3rrd1h9pjHjcEGHuB3yXlwj+OQrjGh9C8IApR0xQORZeJQX78U0hiOKDaVt3wk/3Mu4u7Zno2Bb7ML6bWdxmz+3Z0W/eZmvpvk9NGA3tZQBZjslVRegWaLlanIcE2OkVrzVJ/7hWFACpbGBmrHq6hcgULNKosKwAQAmHEeJeCSeEpai/7+LuDQ4NEc7M9MRUiN1cAXFLie7wQXo6QVcloZWVUgIHAd/gTp16yC5WioogHa8kym0kZQI0eJUpHsEahHxg9oeZ1HamQXhvZKyHxeZjXJt6J0WlQgrX9rwpSmt3bfUK0zQq7vvrINIExYxd781ZS8IA8YAL7N8o6DL6+fTcfHsdj0aJSRPuypnGToZiv1M0JYCOYflHCRZ9t6MhptUzKurG50DfV0LgoW4MgjC6DV+RDiIFg7SlR/rbmDrL207CGJNhMG7UWOAPIA0az3HH0s734iDYIHYUKqf0OHze7sm8Tp8epx28DjEt4DSsr2VUM/m6jWaMg7UQ59x2ctdakWvFsjCWvOC0nNyNYLfubGxst00hN9gYfqu1+Ak58RPbaMW2mt9YNTxs4nPWd68p8NjOFN9lHvzt+4kIkO9ysjgNzHHIyMcwKmH7sSEQyS41MpzjQbFlF5qdcLA6Hdc6zzPyLzZHCgvhdWTs206mJm5yF3fjGLdaW+PC7/HxUPEcEm4w9cBMf7U39E74sCnf17d9pIFHzPrI23m+gzpnfws+CbwCBr5t2DDiIxLoqdyq26Ssp4NzRsqpj59GNMRNg8dxIJhrpjZHzlNbm4n9ubyjbrymvLX+Zu/GkxM93I/zQOEX+KyDdGvOxjk4+m6WZwY3t+h6/+3+PWOvJLjFJoxlP9ueXf2HfMtj9f/Ib45wyey7yKMczc9RTY/O10feT78Z7o6KuF+3XEdy/6P5tYPaAfBhG/Qpbq/J+f0z8P5fLR3Bq78P/8qrNkZH03XEk97imabffwc4jPT7Hp64pRB6ZN767wmgCtmUY0BiO8SldaJ2NdOB8NZ2IiKBsVDFAsZCrK5uVMYmICEhE4mhQN+T1ssgUJZgzL7bt8oO8ERWyxxXWV+dP3KS1b55KM146oFuJqhOhTPMJJCJUYiBanQX4ESy59OuLHQcUfNOJLxeKQAScD4hX874+eUNn8+vyEl2Y+ecwQnYlDerOmZEhESqe1MdHZQ+F65yernUthacgQvugIy3dL2Ejj1XMJPrfDqvHtFl5XBf9GRE1RMREvtNTkVs3aaOqvBmTZstmh6/Mtuc2DBycyXFQefj/LfAawKAlEApg9IJlBaRB0klSCJwMroO+KY0gyEiFJ/t2sGKc0kjbdDlZNDdEvt3dgLDeP7Ih5pBogWPVgPbJI4zAxhHj0PZ1edNjAnNqBZjhDS5o52GED5YZHlz0dTkFLY5OST4AdceIF2OmcPdLXzWy+C9XD7KIXGMHM5IN66a9k83YV8uZ7xeLrhcTjidsp+KyN/Bt9zKd4sH9meB9475rI+Ve9gSvUb8et6+R9p9zK/bpLfrXT3bjfSwIeK0hJMQqQXuyFHRaX5pg6/k2IFxJ2HslA3XfWEVsN3Pe7VLzEch//iyCXWiGfMXk7o+nqIQO8Ya2DEwIJjSI34PNMMApX58hFCz+utmpNJ2njIkTsOyLF2ZRQMullrEugnxr81ckEIwolK3IJAChNQWvB3fGvppBGbdCratusX7yBABboLgKNAc/e4ZImaw0wnfrpiDwywRhDkiwmlpS+KWwrE7CQHoUVKxRMfUf2ZBI2bwTcN1HBcCDt3GDH0EOiXGuN4iPLIeiW3zYkQ+7RhcjmM3rjzer/M4L+P4OdGAKGj6gTIrtuykMX+M7D4xH0F4Udl8J+uTqRe3Pyhx0Pd9f6Qk6PPEa5wLeT4SjkiyOmIeGCRX3GGE1IM2gIWpM1TrbTr+eqbUbPATOAoARgvat2j5SNoa1zv7OVzLn7q62omJ/Zpn5faYAyM2rMVjhQR1Y/fdifZjOCV11rewYncC+8DAGX0HBM8tLAHBL6W0gNRYvf9eWmXZlVQKKiGcALR6hD5cr1c5EXEV90vrVeNEvF/llMR105MQRQLwQWU7knYti+xQWXLCoicyF3Mbhbg2ZAPFrJ92HX/92ImRax9XKu2+ETybYUaXVlQvIjj8AypYR7gJ/AIPggGAttNuXP+jBNTzUrO6x3RLlpitx0ffH+GpR5lgu84YYhO6u3x3vhvvRxof+TV3KxnmIpZj7r/MKLCcBEbsVOlyWuT0jp2YSIQYTBrKz7V4Kq2sSLfFcMv6vm0IiuM0heUwPvE3O8GD0AY5yWYuH/aGio4CEjCjYffm+zbduk/bnkmzYh4t+yjf97TtR/Xrw/UDnXJuth4eWbez/P9VExGJ/+r/7DYc8ge3ZKAf347/KySiGWa6Rel+bN0fZvX+wfPT87+u1Q3DpLQJpr42ScE88CdYrIgFFSdinBJjAZDByMwoEH4nkXrk1zoWQvORzwDTqaO/qIxKoj+gCiCZt4PGo9twJQDJZA0S5bLRP+Y7wzrISHb1n+m8LI6drkvz/mHuqJFIjBFJd+wnkp3rSYJMu4JZR1E7ga0CSBV4OeP09oq/fvoZv75+lrhS6jJmQ0XlxnezarkT6WaHnH2Tl4lIpcoGLGND2d6q9p68JQmJsshH2fggQimqky5RjyUnS+JJ0aJ8v8WOK9uGsglfv20rrtd3d89k39TKAKVBnjtOpn8yntxlqajEV3iQmIEJGuFBeLW8gJYTsJhrpgRWF5mcGMgEOyVGnCCWCbUHALC95wl+/qXpLQEZU5/btoxMSduU/BHsWlk+cTzvlz+vaoww+QD7cltroUYIM0RIbBSJFaG8bTRIMOuENz2fPDd9YZNXrKm3Zo6hY3p3ej92MkJ+UBmz14ftPzD627uIBxHSkvH6+oq311d8/vyGt7cXvFxOeDmfcFkWcG7u5Dod5nekQz6XBtPBEB9w5Nd6WtOMdHYvZfTfPtFKmAyw/54Prs+nJ2JELCoIZfdvawjaBB4XCl14CkKOLdkJwvdk9y1IgPbPR1H94mlZaS94zsqdD34kqAhtm+WTNjjKmcG4LgizLFa2Y2c9wM/a5u0ey1e/5e2YfhQKKTDXFWbFFgV5QuUWNCfWmXrU6cilFgbXglUVUTWfvE5Hl8yIFtQI9NGVwbqJMaJsFRaUtJYwHo69TIgJYwEzfKjQDlWuU+jHCO/UiHorQ8sZhO+swbhPADjL0T2z+kuAx9p2GATXMmwERW+qOgxkpe6swWGjotEYBSP+7Gf+bP4CfFm/vJ/UHvKQD+TtsXvpd/PjLrsv9Wf3rvhqhohSjRhpvzQokhvOuIBYGBHqmhrWctytbVfq10lErcb0GjNrH3Z98jWR29eszFO3I6CtBVLmA9TGttOfgB0vjSX40vN6ra1oZe16uVcrU3i3q2eH70JZEb48LzcYm7TZ4eQAdYmyYf/c4a5xSlMaYgy8TFOAdz2pE2Y09GfXwdDv1tBbSsvx79YWaUw3HoHHab6/yYVQvwLKsLX6AUJKvFOk1toYog5/Bz5JHtfwIl4nyWGozfdsXrn/oF9PEwjs6VZbO1TZx8PoUr8ew9/DvMkOmBhzQYzSXMT/KkEMtyYs2uYEkNgitlrBhUBbQSJWdzPsgX6va8FWCt51l9S7/tbghgmoSLoTz041EIAlye6UJSVkPZEpJzNlZFOK+L9X4sz4hF45PeIN2bWH3XsoHhL6bDMlaHCMxdGOBpPmMVi0yZnJHeDGUyCQTM/rP8nTBzFWpNW57wo8lD1x5UMPZ0oh0E7wGd3ScqY8TOuvuccyziGN5YS6hackb3urqEPc/qybQ6f7gQb5OqGDssb3gNFTMTyIf+PIv8lpdPK50ZZAQR5ZT+QsSeBx0VMQmWSjjsRVIeWdY1yT0U0ShLgl46tbf0jh2waKBx4n+G7yH4VrD+fjWpjElrCqu+s4T5I8Hsuwrm79HWFnhI3xfsa/R14wklGbT9r9teffJ6WG8mf3+7w7Hu6g5F27D2kFh/aFtneIjANtn9XV6LErDI2fCPwC6VpuGIDj8Ph63wufx3PT5mXo3535fOTd0yl0pOerHv7Q0zN6B6vjaNPUuIFon/YKGWNbeVaGFNTfI+bvt9A+NcYGNh9Odz72fjU552itfVcrdnPRd2y2Lh8Zp3EuuvKfbnag1Xz/+5tGrWdq5DYaBAJq1kKUE3C+Omte+yA52U0oWOiKjU/IWJF5xYmuyGyaH5E/T8TIqO10gxoOFpDUV6S8DRLkumahbcQJVAGqDFQCV5LmWZwHxe9E6sPegzUTTIihVJFBYhBwwaAKrwygxV7LMKUxE6NWAlNC5SwyfCJQFb5zSQWUFqBWpCqbP+WnQYY3c60jRVfl6exghAXIRgVOmfC3n9/w337+E3799IIvrydQEt2OGDIArhZtQ2T6JSfkTMiZnC44r+jus5uQpNRAxoMSkBhkSn1bi0nkhVoLKm/Y6opSN6zbVfnzTVxVFQ18va2o6yq803pF2cTlaokGiOuKdVs1loS5gQKKgRKP8hZ1eNR5YX3HbAp8CdAthWSACZQyEiWI6oAlKDkxKF+A/AJOJ9R08hMRRYGOIIasE4DMjBOqbGwynpvEENU2BiGwkuqeieDEgsG+kaoZDZpJAzoXLbe5UlL9IRjFXCFBDCA+AlEWtbKUXySonq+yxEExV0t6ygF1c9dL4Aoudr+C6wbUFcwFqJsYneQ4j7TW3KKNNGoUYqyPphPT97Ot42E7VleWP28gAeYmc7eNWjFuBQDfRBNwGgigVZ5U0tnKAIkxKi+El0vC22XB5/MZn05nvCwnLEuGWEtNZpnT9xmtuMUzzPjem/TmFs/U0ZqeP2uPHqAIFCmQ4NPK1bU9UUcSC/8RLNvDhoikCtycFz1+roJP9MU8EXykfxa00YStNi5RqR7L6HoXV10naGFXV0wiNDqmcMa+V/zvr30h9k8rZ5qHDXkHJS7C8SXvi5SRbghn8Xn82SkUzQFADBEpyWkEooJSCMxFjjLuXI+I9dwJDjOAImtzk2d1ewdRwml5AZH4NAYJHfVdCq2VAJkQz24hv64Fa2F3s7G5mw01YAwGGpvSlHozyWhEOBqrYeQg1n1REMTvZeesxjTJBFAGcwbZjnsW5V3K7D7hmgunnlgeWUb7e3IewI5PGYodV2+b1X0fYz29MiesI1XYL8sJKS2yXlMGURalhgTBgAFrhRggtm2VtlUCKmNb36U+9acpfgV5wKqG5BXhJ3KiQzHLhJeWNpPPM0CoZIHJGhLtEHQwCFFiZzKZWXcuzJUt/j3pyLvCZGhkuHWFT/jEZyaUW8OpUs9kuOJALunb1NfNgWS2/Eb8I+virTnGWwdLpFcotsyNsQo4FvFP0m5Z35IzZ9b68VzqI0JcU0Y+sq4xCH2K/7w7EXYa7bWnTmC7Ncvq0q4ntIenG7ifsdvXaQ+Gu3H+J3npYI4RcIXDiuZXzXT8ogRmcGzNbuwpIacKcEbNFYlkpz+xGCAygDUl2dnE3E5cEaGCsZaKwroDLiUsJDRj2zaUWvG+irHhmwal/vr+jm/vVzkhsa2odQO4qnKdACaP/2BBf5eU5XSEnYQgNAW44W0fm76f+2v8BQFI8WWkAYFx6Xkfm8UO1/Rz2GCRd/MtU2M4QXb9qYtkvbZTiMytjBrWrBQhdRsvbrsH2YKxa32VWU9CNmNEW/fWOom3Y33VpnXjGZXhzqcYXLIpByK0NYZemNg8DJWV03bkw/nH2U7+OIhWEPl49niWnP70dEZmRjZRqHswNZrVwj4P0UgUle/LIsNz1qB252Vxw0RSg5kHek8yN7v4IgaualgbgFI3FjQY7Z+T0voAb/b+4BfHb8ZftXd9U8ZERjMP19bBXAUYuvX+bl7zY87xvc12LJOG+13pd+6P8j/+3bgO9rRiEO7DmtgLmE1472WCMfVGiGisl3+53XJTePfdOxBuH0kdH3eU5f7cfzT1Lf+eep7/9h7Mz9N+nhse02kKGycOy3P8C8eJ/ynpgWrd1YneYVi3H022AWBW4yPPRgOOl7nLNzEuPbo+DltwIEfcSA4H/Py3gC11Aqoq5PMmingUecvmmlLKZ8rOU0rA6ncsWJBxwonfceIspx/UCCGnIYQfKbqvvChsipqBkNWN0JXEFU5Zku7tMEPEIu5lCoNLBbHFCJDNM3IKQk9NEMCVVCFdkVkMEFQZTNIniRWxqS5bkCAlC0orrmkqJ9Hf0uJMQKoMyhWpMnKpyKg4c8WKig0FpcqGhnKt4I0hxg3bVQ2XqdNWgFoAqricM/77r3/D//brn/G3n97w89sJKW9AXkR+Z9JTFQAnRk5igFgWQsqEynoCglXfIIqZEOhYprXqGIGSXpLQAbPDQOC88oZSN2xFTzWsVzE26E8MLVfU7YqigajXqxgrrtdvGhNCru/XdzViiA5JapTYH8ZT9UDbNlv2Mltb0Dqa4jFBeUnQqfEyi9I7w4P5BbS8oeYX1CQnIgoBGySWXVYYuMAMEUWVNwAnVVzbGDZNjkcfNP5alr/Uy1DXYy7DC1zaXHTnITSPGSMKS8SLeB4ja522cdRPLKjsYRu1E4CkRggqG6io4aEW1CrxPFBXoFbQdhUYrCuobiBeZW7rJgY1jzjBENdM/QY8c7Fup+PbZuO2cdnyJ8z4SHMTxt2zNtvRUEEBJor3P8KOndIyZXorSQ1OVWAffJbHGVhOCW+vCz6/nvCn1xd8uVzwupyxnBbUk+LzeoPeHibLO9CHZ8ox9u3gXeMM4lVrvWUNifniX8qnMhjJ4baXo2Z1RfLzbHriRERTzDZBH7DoenFwd4olGoWCedorEPffHE3efIet1RtY0QcEpP2z47YfKad3i2NsG26P2Ux47I/UC9YRi31092RLN6Hy3A2UPTMBZa9Qr6jlXRBrIkeOdjQPcPZYib7smC9VhPd1k1MRmwasbgRI6yqGpGSMrNu289UDjqr06ztiU88YTmdFgxTZLkXzKb5kMUDQIh+6D0ptQ0q6s5FEcWI7Fs1FSRyfW8rKOAdyr7SrM0iNsNdD6cwQcZQaDC0gysh5kdNLaYEYkk7CxOVFx09aIfEsKtZtFWZrE6ImAc4L6rah1gTeGEwVskeljTxrYCsQoYP0Tqnt1Da8ojaG9on954KV+WBPjjuUb5L+6g5rKTA5g+zjQRNs40xCeE/CRsT5MFjrx558jqwfEq9FdjjM1nYHnSEoUt+kNhZ7wTKOD0Y9/x7HxvJalw/SQLqMgAzleGKAidux5P5VX+5AGOdtMOVlauvcSr1DJlRUaPePKL7mf0460FanybD3aKrN2+x6tyOzB8PzEUcADV6acoJ0oEcM01JKed6b0NYoyHIlfZeQK2uciKWjAUSEEgzTZoC3tjFLcOmqCu/iJyJWFVau/tu2tQ8IDMXBis+TrtllyY6XxaAsx64z9TTT+JNOtJnQ1/j3jg6T/WPK9GGuwt8duO0UPzGPIcN+Gtr6n/MjRC0PB0WDwxuColXLOYxFOnnWj4U08B4MHynCzGDZjbdk7BoxE0jGBh7xaY88nynWZ7S1438i3xYlRGmxu1Gy7hisedySFI0O/enhpK6Z0mSDhICZjvkAy/2v1XsEt8ffHhsjHuW1Z+N9Dwc/e52laVsm7+f5Rvo8r+cIln5UEiPYvfKVwk3HfpK7w2n7kgjz97O8u2GZ5b/PXEzfPzOWkS96JJ+lw/yHuPv59FGYmPESj665R9uy+9bG8YFvLT2quHgq3evSDSXLXQbsbsXzAh4d5hEWj2BuP/aPt7IVdrsNY53H6fGBo8lfUCb+dgm9fiN+K5sPzAAhMRUSieHB4hAwRHFuikIiiDEgScVJlfa5MpCApSaU1NwC11rFjVAljanc3D0Jnk3gauWJAhQ5i6K2VlHaRoRseQDdxS5GjkQJmWWDIpEopt1PvymDs3kPqFhQxBhRVhQuUs8JWDcWQ4EeISGxFgB8BRHwejrh57cX/G//9E/4X3/9Bb+8vuLT+aSibkWpEstz0VGvBIBlk+C2VSTOGnebNJh148fHXRTmKUegRJ9BeXWGb3rZPL6DnHbYtq1zyeQx3dY1xHdbWzyIbcNWxJCxc8utcy4b2eOG3Sj12p/c8cY+ZZG6GU8Egh1VFd6kzbG4w0xAzkDKUgNb+WiD0oqUeoj6FWVt0YE0I4AdOk/+igRW/BstVYVL8zLivQ11O48ffu2EALmMamMTZQLrTHvOXT77VYWNqoaqbo52OsGhbd4b7p89QD8sC3XP+nJ6fYdgCW7HydEGDW0svEwDEGp/U4MtImu1bLRalhMu55MEpz6fseRFfsui8qeVP2g77uDlri10QCcOnt3L4+PUZkDzAeaOvOkj7hbfJmNoCoO772/xmz4HH6B9TxkigMnuKfuFRs4UWY8S5j1zBSAIf12xHVLrFUD9da7AbgqHxwWgOOlNwdoWUbfQB2LdKTm0HR8WJlXMYJY5EXcWQnxSEgWRHSMbF/mo+Ny3HWAuPR60PqnFXRqZvA1cxRpfa8VairhmKi0YqVnCqx5TFNdOTekU+72k434fzYsl89Od3ABhgaVOaowQZFZrkWlnCcxluwtIXSfEoOxHSGBuhICPSZcXuu/HKc4eTgPaPBTGdsiOTLFxAqVTZ4hIKSNlOSEhhogmTdppnW27ivusqygBQWKIKPSOUpJY56n0g9z1gRpTJw0UIuZZ23N5FQhyKLAZIgIjG3bApkyg3CtkhAsQ91rjmByN1f7ar7lZPI1xzmqtSGwzqoZY402UiQ8loHtwQIh2ymsiECp0Y8/HsPuknoM3h/iZAI2xZhxAI+z+PnBRe6WPpX7n5h6XebbQ3n17jCmMGXz+xud9A3S9G5GOz/YwOesND7gc6HHpbB4fVaaMbR8a0rUsTeHYvtX4SWFKmdnpt/VEX0zbAgCckgY2YyQNWG00oFTdD0QEcn+vFbXoLrQ4FiBfndtW9ESE+Il9f5dj29frVYWd0hk5cs56EiL7iQczQPi1iw3R6KadYqiTObO/b9FaG8/252yB0OHft5Wr47gb82jSLQI+3Jc/Ks8jDLm89gTP1doxH4+nkstDA9wP43iLn5vxQveez/ox69fNpnf8D+/mwCiABM5sAaYNDs0QkT1odYzT1HiLSGfiiQgE2KURR5K5yezh/B7veCsdvX9kbdwb42eu9+bv5vNADx6d51tlPtqWPyzR/X482+YdTR7w4K1v7/Edz45PhyV/8Nh+T3lHPP6PS4aUn2tLvz6OlRmz739IH0Y0/geM0yGcP0jAjseD78Lv/TL+cenptXRjLo7Kemi+HmjGSOPNORJMboPuuEeG+Om3nWSqoHU5L5bDHi+QIAffMxio4pKTWOMwctVYEdBd/AzzdcR6Op6ZYewUudI5SxtzM0SwHW1n29+milsNvI1akLN4najVXFOhOekYdqZnFGQu2NKCUguwiOtnvK9Yi7j6calR4ypQYrxdzvjlyyv++7/8E/7t55/wp9cXvJwWaQNXFF5BTFiUCWECNhZXkmKoYNju+iiPN0V0daWiDXnbGsk6g/pOeflt27BuqxsiWkwIiwGxYtuuWO00xPAzw0QpW+dNw/HTAENQngvD8xnEiowB2HkE4Z3aaVI5KSrrn42e5gTkJEGrs5+naKzyTsYVIcqfso2bpbZQ3AiBJg/vXAvBnoe+U1MvtKUZ1kPX6fZH1MntftaGyM/O8lswagtePTNCMFyn4U3o9Ibt/q4xgmVEyPobhzHqhnjsOSP4tO3qdN5v1CFYJa6Li4oFgBSPEElMt8vpjLfLC14uZ5yXBadlcX7eJvFpUkfxQgGsnuSpeJ+/rSEbB6P5Jk9C8WAkgcd9MIPGCIM+jA+k7+E7nnDNFAQqY47sh/uDG5rbYOLgk76s43IlHyGCY3xOR6Noz8dXs+eBCYzja4ikKvIsIVgxowP7rk8dk4nGaEblibmVsBMBpMIW+b0qP2F+i9nngmoF1QKqpEcKa4d8mmslRcPheQzOWKq6XEKPvOzIX1Xsab6Ta3BLtRbxAV40eJEZIkpRxKdWcDKsHsyfRO1UQpvH/r5Ny3yByliKMmDJGTknvJzPGoj6AmZ1vQRGKasQLM4AZ7iJh8SynXNTCghokMOC7fyMKZA1H2ZD3hzfc4Mth41OOxoL7YkycztynUxxkU6gdMaynJCXBSmJASIv52CISN4Pm891FUPEuojfRzNqXXNCLkV8Y9aCsl0DoWrUU0dDA0o3Amlj0RG3au8CVSNonJOeUADQ3c5JDSuEvGTFPykMEU0RNTvFiqxFIAY2ztTjs+ynbhQx1xrm0Bgg8ufm2iy2nVoNHRH35uqfplAeDYPt7wTosVOlvv7+ViJMh6SNzROEwrMefHPLUNYIYWNUpO1xh8sxru6JaMPDPqFWXoSp+ByAGB7kPYVyWx2tbiPeR2muBzs2PuyMS+MY3qir8QMGw9RgS/HQXuEECMx0JYBGRq+x1of1d+2gpAbeKmsyZeQs+JyIUVHddR+D/bSZuL2CHw03Q8R1XbGVzQ0Q2yrxhMxwIWuQFAe3E25EzT3hMpzQjEyejwvFWR9ob1z3iIGoA042QnAnPau8NEGlXzv9hgGjLz3m73FrrK+5pdr3r60F7dIA54R2LuxIAd36FdzwHfS7HQCL34/KbUO/e6X3WOYtZfWR0m7e9v75yBcZfyPxIUxIs3kJ4w09+h5gMufspy5tE0M0NkTDxLiZxzZHgILLJhJOZGew0MEdYzoc9f0IzucxIUbDxy04iGO+n5Oj/EdzN76793zkmW6V+Uj5t+qYPZvR0Ht17/PupIRDjPzouPSl7fONfMajZR2X/EDuKZ36ny89Mj7PwMD/LOk/t0ffU/tj3/7/45x9OM3Qkr/QFPlnAuRUukSDkl8Wf/oWLJjMECF0jolQbYMVh0rJyjMzRUImMShUTrIZihlVN1rWpN5S3KCQ1LuQejuorB47hA9lmLwgboolzGWVE/8M32xFlZFYNpuBkrgnMT/0UP6GSWwfagBJJN8BwidTSSASV1DMhFQJKRX1KsziCgcAo+CUgP/nn3/Bv/3pJ/y//vpn/C+fPuHzsuCUk7a7oqxXUCWkQhqbYQWnKj8miK8eVcIDEvdB9QTV5AWtUfB/C1BM5nqHTQe0YduuEt9hW3F9/6bPVz0RsXng6fX9Hev7V1zXK1Y95bxpTIitFD0R0Z90lik3TwqjAsWemKcBk+8eT422ssMVQKCUgZxR84KqxqnKwkMQKw8cYrO00xQ+ctrG6nkU/JwHYtUJCqhz34TYTcuv+kM7xWK8v1kPaOgGsdeKFq+1nchpBoag97M5Z/uu182MvzqMt+sftA3NXsBtABB4oqY0aKo9V6DMJM8YOeLGXJsexudBB3JoL8U58/qbzEsqfCQinHLGp5cLPr+94qdPb/j0+orL+YTzSU5EjF5Ynk3KdUUwup3/O2kRUdRpAA61rlvEzSG2b+JfbVo1SHyQ/X4U7XziRIQJMIMhQlrTNeoJfcth2nfwWKHQv++FXoyKwNigsY7Zc4p/2IKTJ4ZIzRjx/2Pv3xokt5E0UfAzgO4RmamUVCWVqvrePTOnZ3d23/b//5TdfTh7OWfnTHeplBnh7iRg+2BmgAEE6fTIVFX3zEDyZJAEcTXYFTDLfrKBZsJHAjV1z3uhExuCNFB3bZdeZgIF8XNMmYCUBMFSDSraKjwNKbWGCDl+lzHrab7ekFGRpQRxMheE4nYJYklPCbNawc0YIT9GTrnoVOtIVEF/3N/ta5/suSmsTpMoCMDiOspiP6S0QI54RvH3z5O2R1yY2NzEVUBJ1+qDBNIIS6vO6Np9qKQ69tZX2x1M4YQQnxDVEBHDWQ0RTxLXJU5CiAtiZTXInJFzRow3CVRNhCUtEsQpLUgsQWZB7qin+syubbdAQY7ZcASwfscOqbmOV45UdjRI58RfdojSJ1X2eHdZIxiw+ttYJjsp1HXWrD1QA/+lTGZZayBVVNWdD8G1qVnljUagGpGMNbQ1SeSCKpZ/C5bpnu8ksi/bfD243gPfSstavDdK/VqofeoYNWVI5LmxJPbj5vuavyrgwG5XT6NQ53rRSo0hJfjraOyqEeKeMWL0eZPf4dhmPnUQPGkYDWclIXXMmSHbw5jKzumtfvhLC0uOLOm4r4SAPg/Vq61HyqZglWvW0xGZ1Rjf4Cbtw2LxaCRGxE3dMIlLpoTkYggBQAzOyIBqbPX0MVIfYBfK/Le0n/ywPEhbPI8zgu+9e0t1PNpRLnPQM/1OeDB3iMUw4Rl+gxPHi5HilE3aCIykgHW+jt5VuucAi9b5pQ66w3L10DgoY6P+LQX36LqXr09eADMjhOD96n+WNUgfIAZkhhrJQjVERN300BscSmwIGhshqiHC5UE1LlXY1xGmvTkav7s3TkfK2h9zHMpvc29rtYeBvXlarTmtmLr3974fvd96d3Sd9+/38EWhS3vrdEALt9qy3ab1mNfrul1N+zdKrCTm2ByNnt9BP3fTvTnYyrc371vPj/L4R9p0FHbs76P9dB8BqOi55aHemN4435Z6g/kwz9Za0Y5sm+fupcfn+16bjj7/mulr1nkXpri5KFtNTYZGGejoObMYIjJLEFgyYwTF4sYXpNNKdQe+Y2eKgtako6iuUaYQJfBuiLKTOZDFtS5GCGTxDa8PQRREbtJdzWQnIsIEQE46MOlJDpUzwEAg1iCtLEGoo8rcVAPimoKYlC+L0GDCpIp9JrAZIgCEBIibKuMpkvJ0GXEK+NvffIt//OF7/P0P3+O3T8/4EAEKhCVAZPBZTkQgAUgJOS8yExFgmG6nyjgejxP1fKYPYp3LVfidVFwy3WYzKtxEya0xI5PFjLjdMN/MECHx3W4aI2KevVvuVBTtBWa2wNABnknVIygf4nL3nIzZ5boDHxork/VnkRfMEGGB06vs6JpZxE8H/Z26r7aZ9X8uMNJ1zhkiqixo/L5/2PSyLJJ6iqHo53TjTM65yg1921Hl71JNI2O4TaMeXmx91o9q4/2YuOeei6A2e/m7xWPVxVBB/+4D6u6hc2b6gVIXKfwrHnBDhsL7OB71FAPeP5/FGPHuHd4/PeN8OpUTESDbsFTHza+vvp3rVOvsuaqj/Nw+mm9l3KprGeFsDNz19vzecLVVfQbzZt8f5ldceuBExHoHFgjl2NMqtXCMdTaqeQ60f7W7FOtdjP3frva75R8RVoGq4FztpBsoPsuiKGVbwEF7Ln+b3+F6TF/zrYJh9uW1u5uIqHHBYTtT/S+lRegyt/1tDRL1aickTOFkeEjeA0tizcclWPeSxRJupyRSkqN+KXmlivWmTo9HQAXRO5p1X/Cqhcg4asBIEuX6+SwKbVHAy9G9nKMGBJ3VV94EqHLZfrL70flzlkY2il6iijCo/cchaiNVnsjVDoYNhNMv/EbZpzsxKT6BpjPidFb3TE+IYcI0PSOECWE6C1ypks+UXdM0ixuvcJEjlAyEtIAhY5YRkdMiDGCSXRESHMpOBLCjqrWNotRJDbHMFrCc0a593XkQQwQC1N1KxBSlL+fzUzFIeHdZ9WQEFaLfGs0OMOpBmd4grG9wviMzZ/EnygLbIHM/k1CAk21Xjj5hLooqGZWMCuCu32BkoubRqrWO5q8JRptPxr2rY2eZNLC6XeRGhT6tCayUX/0T2trYE4xHBK7e19FkHn/v66h1VSGpvW61dd8v/gFogo3HyghEhNAzlq1I19ViDJCOr+7UMYbI8EvDblj7PcE1POWlPZAqVj0jYQaeulM8K8NbfM6iuzI3J+aKiyZPC926tzhBixmpF/VPClHuTiEWVFJo4VAhS43RD/5vCmVsYMPgBmlLGdvMQGGo23xfQ9ngeQUPbyuhQPFO4ux+3WYHrvxDORFhG0W6eo1f61PPH9TC38hUEopf1YZnPMiDPapk7Odx79fnHwphAEwK5OYqnfPl2QmI0zSpS6bQxYTw1zUPYYGgS7v8Nwb7q40Q0r57/dw6+dC/3yvHn4gYldEK/Y6vLZxNfy2z1725z9uNn5tB416+/XS0zn05436ZR9rWrkHuxtblM5eQw3XlxhX9umoNEW9JjyqGm3Hr7vdw6lvm8t97GsGcPHuM9nip13iiv0QiGm94+PPU/eio+W+/Dr3/95rasVO8bnJbJzzUkxBihMgc9EcAaXwvMhc6KlcrHatsKRcZDkBHjzUeoUrkREGV/AGZWDfXZQBRgu/qN6yBgZGNjxYaKz91FSWHzqVjufqOt3p7FMTQ8jSbb3N5r+6BoDxvYtkEyZzBWICckV4/g9KCDxH44fmE//L730tsiKcnvD9NsolHXRGDGekmpynE00WSYMIxgEJADPUEChy/UPn4hAwW11Y51Z8GnM5pRsoJy3zV2G2vmG833K4XMUTMV5EDckJOCUu64Xabcbtecbu+Yr5exGixLJjnpbjkzn5nPtCd0lc5LegLpxPosZ3nZ1tdop4Y0fgjUowGLS875fW0CwVQPAHTE/L0hBxPMN2DyRMR0Hgg1gJfa5e617rtcmU2qTEi2o+Nj0/K69tY+U3DVfGPKvL5UgrfWo0RyCxza4Yl2AYaE5zVXa7jmyrbK3nK5huT9Pzzosvipg1dQU6psSXdrvuyia25H75xPnPl3cr7fg6rPE0UJC7E0xO+//AB3314j48f3uGb9094ejrhdJoQYyjy7a9NwvZ1mniw/m0+VWDxbZ0ZbZp7RGbbSw8bIoCWWRaZ3zWkU5yVxweVPXvJf7t17f8+kvaEID/4/eLzCpg+r18Q9wTjlSHCfqFv01pB0JSjO1TtNAARFWOE9gA5K0HfAMaC2EwRkpbSR9Y25Aw97ZAxL2JgWGY56ZCzEN0lL/VeT0KYYaL2pRdiJTXH+JzSfWuO2lSDX4FcAOogMSzePT0hBMJznhAzlCiTWpQTLGaEXUmFft04r9fxPGxZB4sRq9z7/td86pBk3aNQucLeEBFjlCNk0wSaTnp6QH/hhGk6i5um6SzuVaIwLFYOhRNSlh0LtERMKQEhYNHdJykDKUggLCIJWJ3UHZEgaCqIjbV9dWcpN8TVjFrIDhcSwIFhO2eq4BzkREecEOMJIU6YphOC7jzt10txGaZr8fCJCGLlT82wEco4U84g0n5QVndMSZkLZX4KnebqHzKYgcFWDLc40garE9HWRMLWALB65XP5F8bMEW1/sKrhTpkPJC88mMLMGwhqvvab0fppFbU9HvbMoucK6/q0eu0drznC3bpWa/jYkErdPUNqQk0rw9XyXb+84dJfpU1cx7MghVELKo0ujFQPJg6XtErYioNth83KCKFsqt+1X0/VGSOs5aesJyagNMXiSoiBz9ZwMaL73eNl7LrgvtybemxzBLVrrXP7N7rupRHP4cs7ymv0cDMa92YcjeYa/uRcj147+LSxKT90/W9bvGp//66ugUf4qJYeBhrwOgcUt3uK3737Ld6qL3drHv2GEru3ExDtjl7tn/LCMcgJiClYkOpjBpDarraN5A0XGBngjvV7XNd2nnv86ZG6VnOyZYzo5saD6711OXpu+OFevlX7HoCto2XfS+tv13RmfD96vjb47NfXr4vDzR636Y4xYhsuPI55uyx4NB2FpRFOOJKvz/+WtEVX6q+8eaTUmv0BXL7K9xUUMPfq/towUOAL23B+Dy5GG2OO1LmXHoWRPRn9S8rd+8aMBe3EE9a+Xiufb9v1GAEZAYkjsv4t/Fj13W8cJBEXJW3lY30cxVZpaScqIgWAsmz2oqrzqMaIoHu/MljbXc5eGP9u/IidvtfTxk2EXLZT21Wpb40q8rzn4VSZLhtzy754PUEgJw1EIZ/AvIDnC7AsePf0hG/PJ/z9b36Dv/v+e3w4nfA0RVBgaZIMGXhJNbi3bg4iQOV5Cb4MCtX9MpyeSmfJTj8UJbUaJMTAsGjA6RnLrHEfbjd1rbSIfiQtSHkp7+bbVQwW89XFhEi6wUjcsBrPqorCNbzpeBGMFxjJTiUz/J/C+0YZcy3Hz1+vaKAwgeMkrpni5E7fCHwFVv2OtadMeOGOHVx2QMoVkqlcFQcx12Z4iDd+v7s2RohB8jKAGCBcoOlc57gKfe16rlyD76M/YWAwLg8YVS4h167VBp4ik43Gpn3U5OteNvNvMntfltHn0imjlYJnZB2OcLLqvQg4nSY8nU/45vkZ3zw/4f3TGc/nE05TRJx0M7iBUZEF7vOWj76/y/cOZLpN/N3xCmseqzeMtTNyJG3xRl/CAx02RIwEE8aAPu10qB8Uz5w+ko4IGu7B8N1xBUK36J2yYLyb7ghj2SlWykmJ4BAsaXDhimD35rkgdK3adiGEUAPEcBCmttml7o5yZTv9kDKYlhJ8uhpaVEEBd3JiUSWz5U1yIkJ2AOhiyNyNI5o+GaEnZRRSqoGVGiQ0ZMjZZWHYOQZz5UKKHHPOuJ5mnKaIJSecTgEZGedzFB+UeSkGFvOD1s/tPYF/a/470qXIvYNHm/P1xJYd9pVw5ZI/xiCnO04nhNOTnCKYTohRDBBTfCoumihEiRXhme2oQahyAoWIJWVQWJCYEFJCZkJYZmG6KCBlyKLPRpAYNSqY7Urg4msyZ4kXwjkjLQ6+gOreKYpyJ9iuDgqgGBGmCSGeyimPaTqL+4tpkpMRIRbm0Riu1jfi/UR2DEWZGSI5xpuzGCJ4WUAkQcWkb0lOx0JdklndmZFYADFmv6sClUkqy9ngKXag7JmUFnbAbh3oc9nxUMvr4QY4jlsLLDZr1OofqR3Wdba7g1h5f6rXoHhImXYy5vQBAqC6q801aNctH+g9sexpwpDOcZ1HCm/bKcdcd//Lg8pw9aUVPOlwIOvzquy0kzbZMcpjnLRqL9fdZx6GjOE0RWzO9ZoyS4C6cpJB5xESjI+ZitF5WXS9Kz0xxjrllnb2gakLf0A2F3Yqou4mN1d5hVnf6fd6Djq3Wd11/QFUeH2bwox1iuqnPR2sdKWhN7nSzNY9k6NFcIHfXCLU0yLND3Xd+GcaAannc7V9rtwh7e3TFvPf5SKqugC35uzdo9etX//+frvW5QU9UclBfD6HYGNFmKZYNgKYiyXP11k/QwBodVJiXF+pl2Re1iciWiGg719/EuLeyYfa8TIA9VSNC44Ny086x2RtoE3cs8cXvWU9rearqX2/3D38sNXOe3zdVl0j+tD3fVuQ9GVuq/vvGQJqvq12H6BhBTwem6uvMbdfmu7Bwdcs0971+Nx/Q7TFph1ZI4VxPNrSg/kOFvV2/cK/37r/B03cKGGBimk6GCQAwTjYAHHLFJEQMIMwc0DigKROi1B2Kxu/qrRRa8ycVe6q/OyWvqU2jZRHM0QlNBqBAA6wc+lbIFQlRFMdm94h6Wa6RTfUzarsTVXpq5sqjWeeMwOJkSgjgzFn4ZXnm7ghXSBye7q+IC8zwusveAqE//z7v8Lf/fAb/Iff/oifPn6D87NstuNJcEhaZuH7s/AXU5iQwwSKAE6kwZcniBsspYhKq3M2/juXHzgB5STEIgaI+Yq0LLhdXzDPMy6vL2pseJV4EfNVdDvmsul2xe12w/V6xXy7YNbTEMuylFPOyemVgP1lTKCiQqgQp8w3of7tpt2u1levljbTU9FXhQmIJ+D0DJzeYZmeMIczOAQgECIRpgCciBAJ7rSAbvqCawqAbnnIpSyLVuluxjYq42Cyl1zNUNMbI0Q2uoP8tIOsGz7Z6/TMjbTpaDZUBGbEkTHkMnYEjaFSvlXdBHNZm2WArS0b9TR1rjuh19zduz/LNXf1yN+eSnpYKZ+xvqV6XoViwPsPz/j4zTt8//E9vv3wDh+eTng+TzidpxKKADoWe+f6dvm50rpfh5ARsKuD35J330pbR/20cr+Et3ooWHVNTkCB7w9V+DiYCqN2/JPmu0PvdoQQn0aWni1DxCNGCLt64XZ0LflghNoFzi2K+pEizddf/2iVZqx4I4AN8Vh/mZF19+mUMxIRgiJQE2RbBqAdj6qwsp8FJ1KEwBsAjMpwWD4ALQFbKUbty/p3UdaxLUpDG6zIWMYl54zL9QYKhNvyhBhJTwMEJQh5OKejNFJ4+GvN17cXm/CytZi9QMKcQbkqGWIMiFNAmERxP012imBCCBMmvYZJrnYiwtqRFc6meAIzEOMEBiFG2V0S4yJwoG6bKCQJykUJ0CBfhZApffBwkVQhWU5ENEYw7RXL7tJ8st0TyrjaCY4gvxAndUV1LrEiGAxQna8hw7o7jywwU+YvCjyp+ylhkJLumqk+Py10WS7B2rN1XtruGZIa9gIFXkl8kbapEvtVO63sklMZS4zXVu3fEcxaFVzIa1gdlzGucw3bPlaDfFcNEfvUcNQvO5l0T0Fp3/bu+9oyWwXs1pq270h3Km+17V4yRnGvf+UdqqDU0prQ4QkLOCcf7ffXle/WS6lDhbDeWJAzI6f1SQZDsQXVqgJdTr/ZyYh1H3I3Dv60pbV9qJxVpXCBmruKwdbUQxgzZWWsBuO0qQjs6loroSpz5NvQ57e/jUaKm0AejtfIgDFq71ElpeWsgl0H72TKh/VXx+vYqXuw9nw7jlx7mrm1fkf3Pu3xcJU2VD6YSGNDBB+YuhWOy0dEzRgTtf3fhHfqjRDb3x0Zp9G7EFQ406kmi5nk+lPyj/rl1FR7bRiN6z38f5d2WR0HjBFbMLHftvswNMIDR+p4pI1b2OkQfN/p91YqufvvN6brkbX2SB6fxrLPY2UfrfPR7/2897SXyLvqvF9mv15reYeaPihv3dbDZWwpWHb4i4aOuH+PfNvkO2ps25wrrDv/YBlb+d7C/23xDP/2EhdgNX6icu9rnM1ilQZzQAYhgcqVQchmhCAqWjNyZVfv8HXTiumRGr7HN4+oxMAkwDyXIiAIbwpo8Gm4GpoeyrUpO5c2VOV96v6uBomUTJksiuCcMhISMmcsehpgWW4SA01l1Hx9Bc83hPmC82nCH777gL/9zbf48f0HfP/uvWxqiAE4BSlzWcCs7jcRQDEgRAKdAnIEOBKIJCC4dLZfNU6mLCchMuBcNOVlkbgP7qTDssxIyyybCZdFvFwsS4kZYT85RaEnIVJCMv6/1DmA847vY5MRqfLPjQLX8ectZgkOkuRCZTJV9wNAdAlijODphEQarFpxayTZkBOhm3hUIe+NcmQnZsh3gJul0GM9e13dM5lUV+ekwHd/teztcK2TlZGdDOHKUvXINu3Rn18FAVQcSlfdmgp4WLfT+lUa3A5LMy7UPZFbPY0Bt/bh51LrKG2w51qv8aEOFOx9F60CIP07EM5PJzw9n/Hu+Yx3T3IS6TxFdbHau768z6tu8SePcTnHEvVrYlVJpVMjeXdtjBjLlCsVlUu9HPoIf9anw4aIdhIECXh5uzRkbZ65mxqmC2ve4Z4QsV8u3WVGegHf19W7XepjRIy+MebRlCUmQPqj9ibI+vuG2afWCLAColVftQ7bzV8WtSFp2blK1Aav9lHQmRkxBo0ZEJBTxlXzL4u4aEpZrPOsvhi5uH4KCLCd4hkL144UJFDayRVn9UwGAPH9p9Zo8mPcK3MGVzZUr+jejCQ3xm1ZcDpPmNOM8zkiLQueThLI+ukkhPyUUhkjU7z5+R6lXjhHt2sxbKKi9cJdg2qraGGWrQNFWRHEl7OcFBCXTFPUExFxwhRPeiLiVBX7ahlmFgRARDidn0AhYF4SEBbMWZTuIZ2EOIeIsgvb1pVistI6FkYzZcaSJWh5WhLmRU5GzPNcTkZUZSSBpoA4TTg9vUNgcdMUlLkKFMWQosaVaZownVpDBDsYCY0xaTRZG4Sh4ApjZBMYGZSVGclimKiRQyxIO5CS/OxYZNCgYWYosLVpBglTHFNw8SMcPJT33L0xAC/Q7XCWEvCGeGMPZ7YclKl3jfGgfskVXo/W35cnjK5yJZJ2bSHmHjavfW6K1GPaKMwHuUktz2ztDeIINfkarnhNa1qcvOboHhImjTFve+j66rI2rGFlNr3RutZfx91wzZpmtlyazbPtmiqxHswNUPa/ugvMBLGcLfi0nHjKSQURfwpCkxkcR97StpSkthwDVdeFMj+ytoy2748/6ZqtdyhiqYrX1DKwDZi8gYNsaZXNhl+ra4OC9aMd8/U8rGiQ57/Y+qcAttpJf3zHytBIM1Cw9qUZ/2buIFdrr+F/jFzSqozR/b1rX9foRMBWX1tjWRtwnVTIKeOnPFMIQWJExICopyRGQaqJoKchatDqoCddG1dOwZT/mg+jOasG457XtDJHc771a8Z4gPuaeXXfrMYax+ZslEcW3Lb7s61UZAWsjZjrvICMjVzbNIDrB9tyJK3LqvzTXv9b/H28fC8Ev7kfozYRVjLe1xyn/ebcr+fXbMte2T2+/JI6Rr97ZT/Ch2zJkP69u1nxYPfKbu/31DeHSvwLffs/eOLKU5ZxZKhS1TFyyodlVrdMiFgwYUHEgoiMCKiLJiq8ekDkBKGBEHySxQyQYLEolVfmrDpI5yLUQFJpc9C2mdtkDqq0RAZnkZcz1sYI11nJYycIdCNl1hP9OS+6wUbcGFn8g2UxHo2RsrotWhZxS62yYFoWcMpaRgJ/+iNCmvG7D8/48eN7/N/+4W/wD7/7Cd++e4+n0xnx6QmIhBSBtCxYIH0KMQKBkAKBThPC81nKV0Vso4ezW6eMbhS5stsFnBbkJDEg5uWGy+UV86yxIZYFaZnFNdN8w5KSBKfW97dZAlOLsUJ0JUuqp6hLtY32px1xIqgC2ryrtPiuk/zWkqeJviYPM2vfKy/EgMSGiGfk0zuk6R1ewxk3msRDiMaknECYCOpwuZbr3TSRa0eV1/pWVqoOoAZq1lgNucgAdaMXs56M0JMNRbFgCn9U81/hGNhktwzVuqExFGQuui8zUJgMp64/UAOU1024UB4Ybt5sHAbdrfKnTfjd5PBKEZW0TVaOvqvijQFT3XxZ5HFw4QHN8MjkPC9YJQRY7BYiYJomvP/wHh8+vMfH9+/w4d0Tnk8Tzqeo8WNFA2Q1HOnaPbq69Y2//lppxEOsjRHH011d6IPpAUPEqilosZ9emgZSw4g0TeyEmyrwlddos+9M2OAj2ipo1cbx815ZMHq31b7SL6r1yzPZ0bl3IkIyr8seKQe0NdqmbmwCVDlRH/QCdm/YEKV7RsjqZoMSco7IWZQ2xVc+dCcdSwwGcEDW+qwdLf8qDRHlrHXQK9papYx8OyhjoHjqjRFNobDTFQCnhJSB621GIOB6nRFDwLIkLFH8OIbQKn5CCOKLsSi2FcnTxl4dN+cm81aB0H9zUAjQ5E8j1fFDcRNRlRERMUSEEFXpESWmgt6T/SgUX5yyI5KLa5QQIwIzAkVk4vJNOaWg7bN2rBgMI3pqtLKA5zmLkjKnhGWucUdAhIAJICpBcakQjND8HaKdjND+DQwRzEHL3iIfI2MPCtMCRGFbGXqSRk83UICxKT42RGaI25pC+LnsqjCCXsfMrlLTVnDy0XvWwWVlmvu81SDRoo9twtBqhb3C0QSOwSgNx662sT1OekQhdS9Zv10LYMtBcCwN+1uv1WiHnXzH2szw1qGHmY6OOe/TGrdpToKeQOCi5F1/YyyTGfP7fsR12cwiIKE9Erz1q8YLjR9kAlunKB8ZbXs8vVKEolNwkpwAtEDM8hzuaix/N4ZdpWuy4Nn5sdLkETjdZMiMhXZSS89DmCHW3vlf5t4tU1dXv84LfUQVRHdSeT+Apa3+K+lryxnxV5Z5VJ97UudzveZG8NHfv/W6x/95IaxvvIBdy7etTy2sf6YgqQaYtp8hGI3zPDGt8tV7DJ4fMzQNx8R4lp4fJzT8xe7YYj1f9/C+PK9AdQ8nDwpY1b2VfxOfY7/OR2nWXv57ZT3c/53v6ryMynhAYd6XXYbsWBvfKpi+tYwhPjpAp9/aTo9TdnGWPHyoDaN1N0pDI/EmDt/H8f3393Y57q01wOjpfh2bSWFtQ9q6XybtVH6wnK1dn/fa/iUw92gd9+ja10jWkiJ+UuWiisTDJMYIkl8m8b7AZKphnQ7TETCjOFAiKhsZ6+bEsnfch9zVNkhBBhsBALF6ZWJSZSQV+Ks8Y8sB1l75kxDt3yh/+6DCKs8y60mABUuecVtmzMsCUjcyWd2U8jIDaQGurwh5wcfvPuC3757w1999i7/67iOeThNijAhTBAdCChk5UBnvEAgcCDkonxwngMV98AAd174xHC+mo6fGCAlYLW1PPkaEnYTIboORnoZYlhmzy5dTkpMgmVV3zuVQvbhsZaybR93fplPpdVzVjNGvBS8RmlLaeN86uwaoGkMjTuB4wkIRM2J5bTJGbCCkrYdgm/PINd+tN5J7qn/W98b/N3DmTxS4/DZfeq26YlWuUy0DcPBq/xV4dXKD748pLswg1cSSqK00XZ71qRmRpv1c2luHpZP90Cfuntdy/MbK5ovS7v49F8ODjR9Vs4lLBQNJjPoYcDqdcD6fcD5POE8TTjFgUuMUyGLAEPw0+b9GcsVbeJUtGl/GQmngUO+M0fiu69jSHxdjxBemrc1rR9MXGiKAOsH2qAegKihVyab9lMi9A5xvWiUy/huf3Df9tRCbTvhv27Z+d89IMWLM1gIclT4x1WfmWiKSE2T70xDDbtKq/oIEJEcz+QVJeAWelmEnIHrFUQiygzulAOYMohNyTqKg1hMROWfMSZT2UwhIKWOZJg1aLTsF5iWpzpaQioXcK1OcccAhntYQ4WDqTYkciAVF0OI6Z54XEAGX2w0hEC7zrK6aEiQGQgbpbn4QSfBmQFxVsSC8wKzBcCQ5kodKGF0PvBDnW7kjeGw9641JjVLE/aK6MYqTGCaiBrUKUZT+oTSHQYkwRQlAfYoTwECIi6jdKQKUQYqdLTQEM7sjh/LMdkbM84LbfMPtJr4n59sVKS2YZ/GXmeal+jEkwtO796AQG8Rra8fWj52AENdTsdwbPukVeRz02o97D1ZkRiOZQdYA5ZkDiIPYX5jEPRMFABGybwdIDMwaH2VJCZz02GudrBbR6zxmterHENu8ei2ByBz7L3xJZYwlA9e+OYbDP+72i67kskbAcG1ZP4SDaR68XDMW5BYBuX/HlfZ19C3Uu8J0oMwbtRma56Qu52o+WZw9jWlrq7tnt8ZrlHgFbH0GZZS3Cinzxs181pd7hL01LK1PRrSGiJzlGLrfkePd6iU2gcutcW2XCWO2MywpbVgWOz1h+L1OtMdj4l6qPgf05IOu5boeDRXs00YpcwSsJooeZ4iOppGyoOEnDP4ZaA10rRBifyd3osTHXEo5a1BwN0+O9nt+w7NDsGdowa3QDTjlwF1aq7keJMk9L4SurX78jip+9xTiW7++XM9Ptak3ojljQgjgKKcnjf4YDZJYXGhosZ2CkHtPq+vGgib4utK8GjfMNub0/VuPwxb/eW8smusw34ExR4WfI3M5VGTS9vutZHUfzbtZ9wP3R9PjwmiLJ/fK2GrjEM53vxkItStityLG8oz32/iXSntj9qiS4NH6tnBKyUO0S4b21u9eGikWjtDLh5KCy5Fv17D2BdSXqOxyPZZ9Baxvrfl/8NTzTNVFdCNckP1jp8QJmSIyTXJFUDdNaPgQItXpRPHPTwwEdUmZlf5l3clt/GfWqph9y1oaEEhjTgTbkCGbWUASp0nETdKyVEYhVl2sbHYDA5lT6T8BIFY4zFyD1yYof8Yi93IN+pyXGUhJYwwm2a12fQHSgsgJz6eIf/7bv8I//vQ7/OP3H/HTN+8Qnk/IU5SNnQBoyaCUZWAY4CjGlRwyxDOBxImUuIoM7564zqI8L43OGUhZjA/LgnS7YVnkhMM8X/WqcnuSoNQpJXHDtMy4Xl+xzIu6ZFqQZo0Zx0DOpG6Kg9Wscy2T5vGgpz5Z+Z6Ydb5gG6KKBg+jdTwSo7j8hPcWgwiBwgkUn5CnZ+TpGdfwhGs4I4eMKZjbK4NyHSutgEDlIDzVUUV1Vta3y9xBKZnM0qJkIoDes8YXgS/b3rfCeGOMgNObVYMd3LXq/nKR4WTOOS/ikstihNgp9/JzpzLM0DHoY5XvgY0Mg1mx29xOqQmXWddcE0ex6kQY6OJdtPKwGDyhBEf1JWZRoDpzRIQwTYjnE85PE57OE56mUH5TFF5eTl+hGp+a/hzmPCuG6nwcHZF36jsq9PeYcn+/TM8j+DIfsBuU5OXgLWPHkfQFhgignZQ95laBofxgY9sIQfoB0AlgDpYGZa+vHoUBgBf6m9Z3yoBRnlWPO+W+/7v/eSNEFUSF4IXm/j7DOX7/yKKowOIBpgbF8a6bAqaYZUeDKqjkue5gJ/GRGENGoIAlpEJgwIw0RUwMQMP65kxC8ItCVZBCK/TXPjVHqvybA/NoS9/2Svh7BlfGQQM0J1W6pVx3ofpfIW5eya0wW+BXBreZkVo/mvcFgbs58X9vKU58GgXi9eumKkIUvvQUhD0vbWHdacGhKALtFILt9JR5tZ4o06nEEGaMKL9OmZnEbcuSFtlRsSxyImLRIGBJ4OnkfMYXvD+Sid06sp/hlJUhwhPrvSVi+AXBVNRyEqT87DQIwU6FWAMNRnxQd2+IsF3sXKZI/kgltoPCZoOHgOrSqcLMysBo3JFdNtZEUUi7/rbsXWFxCkyUtbeJCntBpfm4EN2uZtht6ZWvq2vf1n11jGWv2/L79bN2zeKU4n1dXZ2rsg+obPfoR4HFA8oFaakXuSrjtaVE9WPZGiJIhZeazBCRXCwIMUQvCtM1VkTDhnNlWHuleW9wlvxbc9QyQwSbK2Ns+vx9WtPMjtVb/Tui3aOyGyNDz0x0VXC7cMq9X1Xczc1oU4GNdW523amxaIUf6vqq/IPrU+nxOJF0bpPnMAX4Hg1q8g/KWq+dQS0dXhwp40Z17Clfj7Rve7NJO/ee5pDSRwYa+lPyuTFrf+u2D/vp8EJds+Px8OO2VfZoDHZGaNj2vq7RtbQZ4zm82xbHjtxr6/r5Pkxu3bd/H/9uLx1dK9vfVjeN9+B6j+btrbueBt4te0SrCuNwbO2tyn8k71ca+5FgfK//Wzhiq5w9g4DIWvfbvw2j47beq9M/v9ePrbyFonR4YC81deMuu7Od2Kp+y3rCIV6rVHVnvh/Z3fmXSn5931MQbs9jz/tTvRJA3J0zt/GBN0YE/dVnKLlq/XaCwd6IaOo91AMaTq7qHv26WPUJLiiw8UEifzlxCUTGl6IoebeGQepxsvxKXaE8mbrBKS51VPmLZAaABUgzpkA4TRE/fPsRP33/LT4+nfF+iqApSuBpUOH1TfHKAfIrfIK+hxpPKOvJWy/HFc1F+ZnsaPEuqjtVDTSdlnLvN8bYiYjk8piMn9lvPDI4qQNL7nhuz+/bHIBZeCuWfkLFWy+lli51895CQ4V76bHOGgWAIjhM4DAhUUQidf9tbWOFHapTbPw/GeA44JDTGwO86tpUT8ADboC0me0abavo1+BqS1orC7Cf2z7P6FcDWxd9gn1byljrRH3ecTv75OCuPFL53W1SK+0HA5zb4nLbhhJPxsE3aZxOcSHBmktGtJ6QcWMd/aZdQnQ/H65Q6hBYHtnDe/q7LU/pvxu85l1eTBTJQz5my1S0R7eI1kYDua5bvcu4WBuczOTLeyQdNkSMBkuUdoKmTeHQDlZV+Bytg2jgW7hXMWwIRSPmq1pX15MyXGgH2rjV5lXbiYDQCner4/y7tVlZtV1E5Nxz3APgdb/6vpqfuRCqYYIZmIJYSZdF3BMtqpgSgpUwn2eJBbCIb8B5XrDMC263G+KSMS2sPgUX3G4z5nkBcwalCvCj0RY8l7tn2/3o/y5jAGM6bKdtUJoUhSgVb4BqDydjetpyvbFkW1h3ygSguMYQNObm2CHFvXnfQ27rNWaN1bHzVZXvSQwQoSp/jF/ILPhb3DlxQc4UCJTVNRLIOKF2TPR4pwX6XhYxMsyLnH6Q+Z+x3G7lRETOuVzzkhBCxPkd60YAZR0Zw3Evyh+NrYJiYGm/WRki4Ah0jwNU0BEG2PCZxkEJBJDsSiHSGBlFuNHAbJmxJMaS8upERCX2BovC6KQsxHaymBusRrrCXPRuk/RdCQpfTHryvuEH1gyOhyMi3SPudyZY+9iJDBu40JiU4eotPhvRwPpGIXVdr8rqhA2/HoyRcRloICgb3AfFw/VUXRa0HJTpH9FbV6bH0MTcb2xo6tyiL+VeezpUHNF6RP194LpbaJ9eZSsOrUK5cljMZmTtXDGxxn/gakwUXCPrrFecI6/bYuu0GjHad+1VnvendnY425qrw8FZj6jnRhRQQyIq03jUGKGfC+xt+DoyQ6K1O+tCV/lFr1zWc627HUeLwSF+ifNKCOznvDLhtR8l3gA6mB3QrJ7vMDSwIh7dOLkH+keoqIBQyo0dT7THA/b80z2FYb92eqP8Fn/2SGrpDSOG2ISHmaZJYkRMkzPg930BQliPe6H/Ax4Cfhwwhk25545H3uZJVnU8NA7rcRnm69q6N+ar/jzUokE5vH5+D4bq8zttOzheR8Z39K7l41pe/y11f+nY9v3Y3oz+1lkD0OEeYFtYHt3vyWiPwvej6RH46GnNvTJH83gPd/l3vWLhL5XWY3SEmm8W9tCJiH9L6ej8/0q14wtGvStntVpRT9/6etToQEF/pHEZ1mdSrVRxnKDcXxCeNMYgisUMUVqyKNk5G2OlGwG1UNtfI/S50xNBdruD1cxLknElb5hiX4/gk+oKgukISD6OgUDIYF7AIMSsMjBncBZ9SIB4vJBXrP74pQHEhN9+/BY/fPsB/+U//kf8xz/8hO+ezngiQn6awHHS5jBOmZGYMRMhU8YcxFV0nE4SZwqs/QtIBCSkMj7tdDE4cZFNk3q3SKqrmZcrrpcLbvMN16sEqV7sJMQ8Iy0LbrdLkeeXRU5KmGuqxGJrMRnb1n9xJ20BPTq6ZopPk1EKL8wiE4dQZZ3CYpJBj3wfAiFQ0Dk2WU7mt0AuyQ54Op2QT0/A6QkpnpDiCROlCocGwcxySkNToIGL5O7OcXUNjEuJHvoFXuyQCvtiHH/J2r+6kamb0jK1dXy6Ka/vvHynrrFRNp85fYI/CWGeFywuppPlviwJ7mg22Elnqz7C6ReKrqE8gz5vjRtFH8pAxQJFqkHZ5JEg8BAl6HuJdQ5u+HWtpehcCg36ElJ0kJfe/Ja3aco9bL8l83qZ8kvp1cgY8Uj6IkOETHX1w8dcmXtDGkX2ovarUZkjocnhniHT1pYjU+LF/bKguZ2QRgnG7bMjfd8S+HrBEu553aE+VhrYdy3gSL+K3FUm2S+09feGhPs+rRn6DObgnknZxJCgT5g0TkJYBaEMWRQ9IaQyxcwZmTIycVHEpiUhhYBAWX3coVk5o2Gvz3Q+HcItMNEgKHlG+p/BpBnJJF6WBAgPMTRKgrLjfch4jdMIBrk0zjfS3jfNHP4NB8ctyI3m3+r2po6OcBUlBRQO7TmX9hqcWJ5SX3NbyzfCaoYIY8Sy/dSvpL9abAg7JZGUKcpWRhkJB5tbONEEWXJtdH8LEa7GukME1CEZAkrQLAEodyWg7vyRuhJzOVFjO8VtEnpDljFjZoioRA9KjAeGCALk+DCXMeMSOJsLA1OXC/tPh+MGKJPs4cUIyR4uLGtQv+2zUH+SY5R6o5BjOIapWwu9IUIFBW848DhTlOiGj2UsAWOUx4aIFufW0S2nnD0d8f1dMYVc0LRnR20eauwDga89mVv86da4AaWu1bAJXNiJCDPEUI1cAnANTp0UZsUA4V00WRwXC5BtkdYdhe3G4kiquEtGokUxdazZ5y/j6wsq/5R8xo/0GLZStSHFrPlW9ISUAcQ2eMI1rcB1R8e5Mra+IyOjaY3VsXafaPPuG+MV3FRgvh2bprctg+ZgF7aUyvtNxb7/rvlo+zv/zlW/yrunQB/xXE0fVmPSVN2BKqNdlah4wpVRjAx6hJ8ZJeB04eUG4yL31JRLVlbXxzJ/9q190+Aye88uP8q1dpeafmzBQTtWW21aw1IzV+4PguGZLs8GLdgqZ5WvNqK5p/6Djr6hr7dfE3a/At81LG2lyj/V/u90xbV7xMc12e7W3bdvs6y7JUiuVZ1lPK3BivepfDFsx/2a4PB5FV7HmVezfAyejMfpyj9i8Lif+nXhqbrWZ3TW568fbbZha93ca+OWEcL/3Y9Fn2f0nlWg72t/BC5NDruX6tw4fs8vsFEd91uxausjMv5e/j9XGrVray5djvETx6Rsc9vrv2oJoXlbTQz2l23uM6MEJH6fft+wV+zLsZ/TixDJxh8ijdVHFR4Z5ZSDZ+zICoLhYzgcQmV11h/qR4VcUinMThsQROHNuhshhoDMUTxDBCBmIFNAhMiOUQlyKvVpu0PAh3fv8N2Hb/Dbbz/iN998xCnKZgaOAYgETlx255PynsLb5lJG1R2N1pbUR1BZ2AabUfhHU0yn3G54sY0wZWNMfyrCn4TIFuCYVsAk/IPxvn5sW7618uu+9TJTuemYx6Uez1EpoaAMKt11dUVQmMDhhBxO4BDLPFO3HryM0OhVSAqvWJ51nDsZZsObBzXtqpDo6/RfdcvEZeg2WK5qcmWwqOAb2cLBQlG2l//g5Mq1fFnHxi06l6HFle0kFJzVyS9FhqxKAXvo7uu1ylFtXXVcfdtcB/oBJb0x923lof60/7aODjJSO6nVY2zyMT1DahA2oO+i5626ziYNAGPFEg/4g1UBY3DeTG/dEPGAayZqroYMBTBE/VGtnopidMdvKxiaSsT8FFM9IWBl2xiY8gNeuGoFsNomRlbLl4GQU5siq4LGAsoWA4TWGzYgbUv4He3E878SgNoEPQhhC5ZnNS7rOkc80EhIHBGjRsnnFIimbClKF5JFR0FOQkTNy5MRrQlmEbXATNms6imXY31y6mHG6UQ43TKe5oxLYFwjI3BCQMZFNW15YXekj5FKMIBgrbfWomUY6m7fQFUJ4Mc42E+DLEucZTv2CZzPE+IU8e37Z5yfzjg/nTGdT4inM+LphBhj4wN6NK/9iZ0CE918tu/doscI4aDfGtzMp11td3yde+sxA5TK4slapxznDCXeAii5ygz2uRz7JHXfxKTH24KdFsnIsJ3SCcwJnBOQFyx5wZITbssF8yK7LObbBWm5gecZab4iaQyRnLMGqwbCFBGmCefTM87TM07xjEgTchJfmIXYB8MtDNtn07K8WceOCn0BkVizBbyh7j9XjA/Y1kIurEUZHpZ6mSQexKK/W2ZcEnBZEq7zgut1xny7yY4CU/AbsW+U1i3TM3NCk3ra6YgvlJGwdzmz+jL137SMkRsRYWQHz3O/W7vgiuxwRduPwjy4Pq3K9o3I/vtKoLLugjD/9239fZmAbSNpcjjGghxtaWNAVBxpYTma9tQK1goZQBT1rEZYUBNEuCBpz2gGa5iMgxkcCsp1gqTHKYZXRsnYbTPu2ikko2Ve6dmNmtLOtuy6G7+6YGKWnVN+hI1dL0rRQr8UVyhO8vNdZJOgQqQL0l53YSjpsXLLjiZHjZV+VppeW0aZbHhLC1eJAXCl7HV5VSbbLSnBcyigoKdQsmtHN8AdgW5a4GhudoZFvwvFfLSmJDFmbnPGMmfMC6tLO/0tCxYz4LLxVk4YLWNMsnufnAIdtju/uoUk3x9U2CKlFT1D0fIbVinKhgqosc8yGBdma8tOI/X0cVTH1vN7CqX+RGpQemBLyrrscZqnL3ECQgoIYUIIGSnVszXB/tBohtNJj3JPupNKx3oqbZC6YqGppHOAhjds+Qs/7FzKDEFiUFh/7SRXmKJbLyiYb8Sb3JMHPC9u9+26t7+4vPc12w5SK+2RVGB49Z3j7XYLcHjaZBL7pmW7Vs2rOpI7dWwUYXiOlFey+agIZ7tU4rbONfw3EvMOz+/WMd2514fCK273z7VK/6WmW29Rzj6u8P/65Xr6+ngfCIVBZwY7ejWGXqXLNm6dD/exQcDh5+7vI9qAe2Px6ByU8cqPz7erFS2wtXBdcq2atlPn0W58RZAbKVd+LSNFLy9qbQ8UsPVioGzidQ7CBFAG8Vx5S9J94xQQ8wQiiQAByEbjTCfMeEbGE8AnndCETDMSZRAmBI7gTLKpUfUxmSTeXibSzTGyK5syEJgwQXBrhOlxTKPDRSblqN9ZyihtJmJwiLDAyYykdFxdwGQGEFXxzwBnxDAJn63vWV1UxyCxEKYAcbFEwJIS5pDwjBOQn3GlGbdpwQsRUozgWV0zRWAi4L/84z/hP/zuB/zTdz/iD+++xen5A3CaEBEBVvfRBHAI0tccQWBMTIiYMNEZFCIoTsggLJxByJhQz6kUsSSzxLWAGEcSyeDkPGNJN9zmV9xuN9wuCfPC4IXAWT0fJGBRnc7lYichksZDlFMQKclm1CkDYQqgSNWNVFnmyu+aVxKTwjV2H3GN4ckAKBOY5RSIBD+XzR/VPanyG8rvpqyyLTM4TECISEggMGK6gjgAp2/ATz/i5fQ7XKYfwDGCAuFEEyIxFjCYGAEZERAXPcYTCSMnchvkhE4wHRlQdXtw+lABLwDCGzJFGY+gMhBMRORSRjYeWt3Tiv4mKM4JsJMUUBhlJIHP0VpXZlNOqzCuSQxHs7owIk4AizwBNT6xuZXmuomZ2JhmeObZKmn0GX0zsgXBbmgHg8wVvI2hleme1xoqQJtOwmKjNGir6A56OlI9TgCq02LGcrsg3YIEereYHE6ml7m1WCc9bR/LI1vPSjytFS/1CHFqvTeI/NLKC6PkZdnB07YG451R//Fy8WYFXyk9bIhYCYaMssvddaWR2wsz5ktrBCUvHaAyvewn15izcTtMRW2CelFidzvwi/WvAK9UNp6e2tatercMEb3hoioHWiPE3k6M/tXWbpbRc281rUjE5qdeLdBRcG53vMBB6maDsiBgorrLPIRc2lhjTTDYEF2OyDliigEpBsQobp4oJ7X2m6GkG3+Dnf5IFAUVB7jsSkQR4mUsIwIiVeVejBJwOAZRKJxOYog4n084nyZMkxoeykmJY3E79uZ/nW+gKPMLREZ7s65uEBq48GNGZdFw910Z0EJTrM4Ry7suvOYXhsEpYU2hyak5FSGETdx+wU4LFOWt9paEqRC3UHXsK39cW0fNGHHfKhRFqSF6PcpbjHpNv/W7otRzxTomw8q23QRZGaJyzbKj3H6NayavrG7qcw3pFZldA73S0q72tymO+7x2ZLeW2dXdPe/d1tWdFtVAsTZE6BzuCGLk+shdHaYTz2q08X3pr2171+/63WHFEKGEh5oyCBazubrQ8vTKwYIXOHONk2O41Y619u0UuObCAUgzguPjuAY/M5ylrsam2AaUbvqvPavBpWVtlaBnru0jvDUycvSGCBRDRFuOD5zbGGVh/ezgwC3Tnq76+SrGiML96Phqj03RafdlgwFrvZ6m2Trv4WYIon7HatM43fVWcZDPRytmfB9r2/cjePW7lCzA9+rnmWPHJAMOfmy1O66xeV5yD0bB0xGjUyNmbfShY+zkU8/wWd8HFZW6xsnzPSP+5h5dbr9bVz+YQljza9nO0OO6arxGcV1o7+xUREDnqsm+OfJb0yevkPJ8sM1v0yk342t+tR3TXT61rLruv/K+tKLe03pOR4LW1rw1Qtog/yaP3PS/+7vH51ttoHHdW4mIWrcKjucovEd3HZaD9atWybl+vnXdKmPv/s4Scu1s69rb6XZkXXLbsYON6GHrWL1H+PeH37NvwfY8GImytdMqDsZ1eBzUyr37aYtvHOV5dKzIGtalLbq3npv2+xFcj1Ih7Vv1HIWdN343Ok3Trs/9HZ+P7ggdJ/ve8T2434fCH7UP22dFFtmoV3d2k+PxlEMr9KYRPiGBqsW7QqiPVd+SHe8bFH86jQHq9pe6fRRWn5Np3AyUOsS3P7vNdvqKUE63s71QQmsb9EBZrsiiIMhVdhCCnkVZzgCy6BLAYssom4JC1g18EYnFxBIjEJmQsrhxCtOEKRK+/+Yb/Pjtt/hwfsLzdALFCRSm0iW3DczJwOImSjaVqIwcqOQ3BbV6mHLMlzwgQNVcWrbJ69l+UMcEMkam+C8nIpY2LoTwopW3964ppYiqZCY/V04IN7xi/IZ6dyr8SgAVr06Wn+29KsizxSthVI6edAOlQhSBgTAB8YwU5Jctt22M1V3xBpPRMY6kcGCl+hMPHgc2y4hXf4xy1X7BYNW3X9tI5uHEKf7ZRPDNFsBmW/okbr7shE4xgjgZBMwOdsQo16Bgq7TrZFmrXPPZxklg8I3pF4r+1fL17mu73pTGSTktv1Zb2uPdikFdO7kG4wacvrN2v/3Y8jX47gAtLc0ymO+uD9AHT4fg+FqDjT6x9qtrQn3f0eEybkonCrkYNbGMz5fSt5oOGyKiKkkaYgzpcHBAeoRYjhinZjB20laegr5IFEQ1j+0UI+Ts3Rp1yrV22ZV23jv5sFLOOEV27/d4zWRupz0h4xGBpFd89Io+MmZhY/7M6FAUYKqUm6ap/L0sC06nk1rNZ5xOC27TAppk5x4DCDGCYsQ8JwSaZQcoiVWWks1rRTQglJMyIarCTq3ooggAorpYEkW2LM5TiJjcqYZpimqQkDKmKSCGgHfvnjCdJnz85j1O5xPePT/jNEWcpgkxRkx69b+9+VwL/3+p1HAiq0Sb2GVUFBclbErV16Ad00SWX2b1O5gW5GUuDIwFa5Z6K7NCQY6xTjEiThNOpxNOeholuB299p2dbhkKfCuipP0MQXaDNPhqJKA5ZofEgG+K5pRdUPPBMdVku5UV7vMiLqjMSNMbC2RIq0S6Yh024GasyJQd8f1zUVLp2jlQ5t5VlKhp/Z7XxoXNfhQGh0uZNg1mvOQB/tliSJjTKvZAU3dRAgEgavx7AtBTcxtlu38Li+jic0i/Ky7NJV6HO21nzBahCA39zmdjRaLGC4pRBIypiVvhr3U867FoPRVhMDbwLe7xUU+/q1JI5ifnrDvCeP1tCIhUDYW2Hluavz2HlUdt8/SKqRFduwe/997382/K/DyCARWifLkm/Byl2z6lQnOzgy0nANgpwyVrnKVZ/l58sMDcjFttq1eW9wptKj56iWiIH9uiunHv3m/zZX7HkcM95VTCMaP+qI4tWBjR2vVvt6ptAQKO3iidCqx+qwMDerrEeAEzINqvnEZxMSKg5dznHVHmru33oO1EK7pHWI9xO1a8OXb3xqm98ur7Zt4eHPMvSQS0wUv9mFEdu9G4NFdgiySsvqPm2raGhteDfdlo49F7/2wTvrt5PNqW/t1dmn+n7r0NDP92ExXewuOqo/2+97zH3+u1uT9n99rwRWO+1cU9PVit/E1tsXxfgjfIEMEw3WvD28f766S/lAxpitAA2xUMd8+qJJZ5DeXH1cu+KvPIlSVcvnFBGSpnAVj0eWI5gb1k2yoKVUSL0SBzLohaYkQEKY0ZrMfd2eI/ELq9eLqeAskO+VyNDhYtm1nfQXffhyCblliU0KZT4izeIygt2kaNDXY+gSbCNEfwkvD+iXB6Al5ef8FtueLb6T2+fZrwdz/9hL///e/x7Tcf8fzuHeLzWYNUK5+o8qPwfdWjCCI0vmUlbKZctY1wJvPYBkA7XcLEqgYT/JU5Y8kJc0pYckIIwDQFZJ6AWdyyLvMNr6+vuM03XC6vSFliRkjYC0aIQWR2BiJ0tzkBC2ekxCXuQAB045XJpdJ+45046zozHtLxxqYUrvKjZVM3qn6JqFjN1lUAkSICTQjTGXmSuBBLiJgV3s6sJgnSle5xDSlsGOworEkltlLq8jB+rGwUdLjD5N6sjSxlNc032OVKA3S9yVGKVFhttv4WX7627kjPDEDdMNmzIO7SdcBCaZfFN6kB1sEZyEn7k7TCDNKTNyIAJ1OUwJT6prg2WdDcdntxmgBwWpr5tiHsxwOlLMthmGSMF/syZCqpzcAZ5pUmkDv1ovgsO6MEkcqOtjHtzekYn/BrJYK5fPZ6Dffe0dnR9c+VHo4RUQR0GPhXH8yj/Kty4L73C3h1NVaAy1cjxqQMljJxpjjokx2lfZRx3Bd4j/98GXvjc7Qto+sjyY+VH7NewUOa0QOoHePJIZQgof4bw2mnfEJmxul0QlLFLgAsWZiKlGXhJ1WGVcFQ5ipEEeCLoi6aIkx+MYoRIsYomxcCiSEiRDFSxFACSxZDRBRDxNPTGdM06amI7mSEc5Uycs9kfd16vjcnb5urVojbLKNB3HapO0zqGmizb6lllaTY10UhVhRjTindvDPlqFLNMkaOGWGIccqPeTuWnYIG7fqR9nMTzK5ViHBhIqw3XjVglmX5zj+r41YHaN3volR3I9j3f+vUglV4BGcODRmoTMQ6vxbPWdeR4k9q85hCtC2zv1bXP60hoo5J30aiQVwOl59LGXUM2Y21b9uIQSnMk82Rq6K0oVypOqTS/GlliCCfoRvvAvkao4PVTVOrSJbTCezGS1JQ10Uh6lUB2eB4otgYUlOIBc5tziRvKO3LHWyVHUp2JlAZMKnKGGmIwZfQrC3ro8Ft2Vnl6KQx4WLIzyUQdascZ+zB096z1XoeMER7aev9kIniMstjnGdSjKaszHX5lcXl8u+k5kSDx6Rsxh8xJiVvXCpGph7nbPTJ4zzPfJNTlrrnjbIWlR9bP18NzvDpVjqiKO2zMLenQI/S2kfbtAlXW/Q9AJQP8HlBaRzVtYt735DPj1Xdo37u9XrMh6wVp6PxPFrOqF3lb3b4t2/3qJ6dPtzro95076RUP5Z7bSGiw7JmLYP8klo1pb1uFLw6tXqk31vtWT/b5z/fjlfvl71f5tbaGxmkh+V/oXDcl70lbG/BaiOnPNBfUhnHfzf+fjSn43dH2z4a857u3itjlZhXTT0CF/fa0ud7i7zkSt6BtXtzpxqOTh7eul9/v1/+W5Q8D/E666/h+d7afjTP19/ItRh82bQ+JC6LvJNcUoWoGSHUFQzbznWrj1FjlClnVE6a6zoxDq2cmiBS/s2djCWtw/Emppdi6WTL0BgzRND2G3Nk31PNo98LPc8Agvh11fiKxCyxMW1TDiJAGZQnxCxeGRgomxCezxM+PD/hm3fv8PHdO5xOE4LGhRBjSCdD2kCVZgXnCtOPp+OnCwmuPKbxu2BRhGeYW9cqv5K6UBXeVDbfLepyOy1L2YhnxgFrFFEdr6w865KznApJIhtFAMTiGir4qShwKE8KH1qed/cOKstsce0zOU7d3tkJEoQIxAlMARmEBIG7zCyxTMv4dbBCtcxC8E0G4Nrmqm7ZkX8G7S/z3b0X+uzyca26VGm0BP4EBQY/aq4etj0TU5sqsFJK4/6X3RX13spQuKVioGhqLWWOcdbWs3v4rYymjtVYJ21FFUOE/gbeaKVUB3y78Ru3cL2DzSM0b7ts8g/0D+lr1W+h4Y3qcy5rrGap/PGeEeIej/A109uCVZf1R6q4oHG++rB+qMjDk8WM1ghRLVN+BVbGbq8ueeZdXIiN0BQoAIrAXxJzAZZeUPO7++zqBbiRonr02xybQdoTGkfv+zQCojVytAW+9h0OVL/m5Xsdp6S+5HwgzX53+PV6w+l0w+kU8TTLTvfz0wmny4R5WTBdIuYlY7rckJas1n/pTyBxURKIECe5nqeTnG44iW+/qIq7ctphMsODWjkJ7YmI6Hcdy7cn/ebp+RlTFFdNMUacdWf+6aR1qiFjyzDRz9veWjg8/4Nv/HWsZPOEwwixPc+6ttYpbyBZm2/zHZhT0kBW2Rke1Meg5uGUwJqPU7WGR5J5ywEg20VLAe+fnnE6P+Hp/ITz+awnT/r1NHDdBIPxnXEK1JyICJU9PYRUjRleGV9QGQ6Crf+2zcI0d6yF+95wzzFo2GBsOhzWw1YwhmwDV7D6cNwzRhQFPBj9yQgdCLCDuVGbm3yaPO5Y5bU2KWO7fl8qqDBavluPaaEzxvBxQm1sy97KmPZMUoV1Oaac9SSC+EtlZiQL9NwZniwgdlSn8abwMpg5uZ3VYpAwg0XQE15t7Aii6popJXOpZLufuMH7Vrdd5XvAn9KwMg1heJdRzekvZkCDVuecEWMs8NfSmRam6vMW7nthvpmvg7TyiKDfCzNAnfmxUh9V0DRJgLkG/B7VuYFLGB2cE2AOJE1IFAMEl5MP87wgLUl88aakO8tUCOzqsXkqV3HfrHNssGT9qc/92FERtKvCvcjiq96Mx7vU39G9PRop1/Z+Ve6DPNPXSB72/eYFpO7kQxdDyq71REQtRxb8cUPEPV5PhP92nAjrMV7zsm8f091yqM+LRkDqy1iVCaxkiCPfWWVUKrVna9ja6ne7Du4nz0vIg25NNnXfL890Gkfz+3yjtdW3c+v+fh33878VP2/xr4fLG/BWR9Oj8lfzrCjf1vLVVhmP9LPFAyP8+XZFQN+WEXwcMQS95Zs3y0A7+Y7D82Mw+OdM+20YcbGW7rfbxxRqv+vLHfHB4pdfHhmmC6qf0Q0xRCgxIzCBMSFTREaU3dewSH5VAZp1BanZAYu6MFpYjBDGS88pOx4NRbdYW0xONjMWzQwe2ieu2iTAGUhIeeEop3kpS+wI8U6dkVjiNFBUHENJh01d83AEOCPkJPJlgAV+QmJCYuAUI85T0CAKGYRfQGD8/vuP+JvvPuLvf/wBf/3b3+L56QlxmpAn8RlNSZS72Z9mAORdCIinSYwa0eIxOQUtQZ5DeUtjXZ1Mk3PW+I03iTeWWU99BEwTYQFjnm+4Xi/4/PkTrtcLXl8/SwyMZZZyDIbUNaXJEImB12XBbUm4zjPmJamOAJhIjDLPpyixF4LEtmKFCNKgfRHiOQMmG5PNqW3uQ+kfWc8Jyr8GOUlBusHRdCBhAsUzcHoHnt5jjifcQsSVJVD3mRKYgVMIAtk6brmsCJlbg+F6Ekgr57pBbItDLnK09qNujBOALc+9nqHMrZrhLOBE6Xhdq9JGeyeGucworpiSrr0EwqK8/hQ04kqQ2BUc1EhRrH6ysS1A5N5QTk2YF4ylyOiFFpfYmHafVK+qLdXFbLFatpOjKY3WYJSs4+5Tssv2BpvTdMLT6YTnk7hnj6ojBFVXX6Vmgp6GfgsFPkYTN78uPM/g5QjghrxRyz8Q1THbMz54+uTfH27zg+l4jIi+AsKuADH6ntmV0302GhRfx0h5sccQkkcYrjJRpjBCqD7KFWzdd2OG0P/64Ih7eX17jjBso28eKcuX04/RCFbtfaPI0voaxaT97drifadbEsu5EVPGnE5giCU+REGUIQqRTzEX9xMU5NjUyXymq6FBDBGkRgEqirs4RXEbUp6rSwTIaYoYYkEyUedrCmLcqGVPCFHcOYXODdNe0OrR3IyEw+OMuDBPRcY9rKZ2qUysJwpsesYdTLqicIUBZFesU/kqIar1emWoJ1BlvThlvSlZpzhhitUFVjN+d9bfFpEpdSrDXGAb7dFJyScVbSLY8pjcv+6eWmUxe3c1DtmLwqEquX3TC5l4UDC6n18Z8Q0iYjtujHmv13a9e0aqFQrsnlsgGbStNaDUINXewNnnZ2y/19qVYeJS1jCPq9jjMMtB5MrieiS4ziOKYJCS7V7XeCgpqQuvaojwteYsjGvBkQyFf0YgOUkWius7ex40qFkNtLsaG3Y757O0raFlJN/LvLd0hWjEdNhYkDu26+YsA5ksLlCohrRuHe4ZIgQltGO74ilQV5qtzZWic+uG2/ku1H8D3x4zRChsbeCcvTXoDYUlH3WGiGRzWANXG46op27c7rYBDwQ3h5Vn0a50fHrT1RX9MuZ9PW72fj1ca9p2nA9t63oLz/RoujdfUlc/liOeb4MmlRMRbm3oRIxp2GDeVv1f8xqDodyE93p/nL6M6uurLc97YRAtDIz42ua+E37qO5Ryt54DqDsiB+0jfdFfa0vr/RF+q7aj5dX690fgVniCtu1HwLyfjyPyxDjfAJfs5t9vz9H3R5T4m2XVQt/UFp9nzxi+Wxbvw3TJNlAIbM3Zm8fj4HejMb83DvfK3prHo8++NB0vc51v1PYt2lDHCTAeyed/a9/ur4PRO+Hv+rbeW2NbdXkc5Gsw2bHoRGDyjAiSdT++4H42t01UXcSIUrfdhW3iKLi6ZxJNAcovGc/fNqg+M/ESni9q9aCqkRHZgFDaAr/+jK9DAGlgZJhiF0CNHcGieGeGtFbcf8svgogRQkbiBGbVTWACpRkS+Fr0Gd++e4fffvMeH57OeD6dEGIUQ0AwA4kxsK73hKL0tx80r1duFwpf5BuucVupyi/ZNhRy3eQlilsNZjzfJHj1fMM83+opiFKuKv2VD2KgnBCfl4TLPON6M0OEdilGZAo46caYojaw9RMqfHhZVcpXqOPWALyC/47nMH2HtDUihxM4TkgUkMhORGQk0wPCR5Socp9dbVpyNzX1L5OZK3w1bWxEzqof4Y1fowhvCvEnDAb4mmw9ov2RNoG0agoginKiKbC4NqNquNMRFfzQjQW5dvmx8c/rJLtBQX/dTp5j3cKCZQwaZtM9d+NSYb0aYqYosWvNQ0rZNER+7Fsej9z4HEl9riN8w2ZJVNeI9aWviwcIvcXV7mm/1jZoxrZeftDKA3zvVnrAELFdsf97pYToGjii973lpe603PdZdazDpATD6jEjREYIdWGbL+lqWJA6vW/tVhgdGyLeku4J4CMh/V55QMuAtAJpXeJb5cVOC9YrKD2BsrgBJbbCFHFKE6bThPN8QzxF3OYTnm9nLCnj/VViRFwvs8YeEIbCjkpNGjTaDA2n06kaKAJhipOcjLB8ZjBQQwQB6tdZ3pkRIsDtXtRv/MkHCgFnvW+e03oXZD9fo/nr52N/zuQfOoCoh6msDVMGCnk1w8AafXpFSKvoaov1TI9ndoDKJYpfQTsxYVyIHMUkhBjBAVhyAkDibz5GPL97h7OehrDx7mHddoqHLaNQaMe+rMfuRIQh6hbZ2thvGCPI5lYNc2WnbHCxQybEeMI0MQIiOMqxVHB2ikZTNidlmm1vSevCyK8xfx3NiQ8+/DYjht9xsn7vf3ICYFROd92IG9Er/zPGTJefh8YA0pXRzFdX59Ypil1jE5vhQ91kruZBg7Cz+rO1AOWpxkzx64JpPVgEQkRLQzLLbnubzxijfMvVVVmvzF4bIljbbXi9GgmAdZDq0ck+yy/KNfGHT263byrjw8U9kz+d1I9xb5Ao7kTvwHUzXqVdgN953DNLe98bSz1Kda7QKSodjlCg6HHSI+u0XF0/bA5TqteUMhY9Hehj0PjggG3/Ct+s7QoFVxFBd/Hs0/iKQyUrhTVPV38Odgw3O/zbw5Pv/1g5hebdl/BP99KIyW7eb9BcUvzfr5nKQ1QaVWhVz6vpr4eh2hyZJ6traxz6d9w/x/14HFtCh69jL22+PjBt27wRRN4jd7+Vb9AeZTF6U0gRUm19rMuUStnW/R2U1OBKq4Xa96N275U3yn+cv9+e57eU+SX5Hy37UX7l30b69cbkf6ZxMjj/Ncp9Gwx6GfrL2vW2NpgGaEMT9GBdo+dCSVj4oNJH+Su7cw5Qpb0435kgXijEIJEQkEk3ZilzwVKk6ijFWJEhLnKS8rHm2oe9fkKrs01VwpKZe9ZWJvUhr1Wclu8bIiM9BLHwSMxAjtXYwLb5ydUPmAa3uOcMIBBr0GrOSByATIinJ5ynZ3y+/gm324L3p4jT0xP+l9//Dv/LTz/gp28/4uO7J8TzBEwSN5PUgtK4wlW+LE5RFP+qhyjKZMsP9SbBVE5TmI6HKINJYz4ssxoYZqS0yGYqEmlhWWZcbxf86x//Ba+vr/jTn/4ocQ+XWU6rpASigBh10+ZpUhmIcZ1nXOcZn14ueLne8HKZcZuTnOpGwPvTCacYxVUVR5xPuvkrGN9T1zgRSaxJlXtsXMbLQGe50GSLVWLdZw1S/YR8fofl/B7XeMYlTLjCYkQkMAhnFv2gRuQo8R0Sc5GJirmMczk5brEoeu5DUpWBLJafBIU2uW3Rd7TWpxkMFv2K9CfrJjjKtiLVWEMM5qQMvBgWcvllWYdgcNYYKNNZPVmweLGYWGI3ZBkBDgvA7mRJMQkBGiEG1dEXdM1V3RUBxZWartw3abXWPLunB45pDG4mjF93fDtzluUcAsI04f3zMz48P+PD8xPePz+Jt5bTBFKvKW3y0sFR3qx58sX82NE0xvOeZtV7LwfsGa77fPb+a6c3n4g4MpRHyPWmgqmUgOFgDWurWoUy7lQWkHVB7mXzsrMwmq6gCInjXWxbhghr56OpF/z769bf91I/XtT80T0flNcrsHogtDkZzQtDiLztEF6yIgIixJQBIkwpI1AQZW05hSgC5BSDGhyECJ9OEwIFnKIFd43FEEF2QoJaZUhxpaTfyI78qkyIwVw3qcFB6xoFojx6ImI0h2WcD8GGEuc7uVbj7TXCRoRXRRtH10ntXyGZktIrHxu4KsoF2X0S9PRJjc0xMDD06w/9WsH+nCihKs+UgWyRrzSu4pyeZFZGvFVqrBkog5PKCJEqiPPaaMCetKN998C1/65PQzGOW3xqRt9K6Ln7ZQQNdtXWKXPApcPkGMTt5KADwLF+rMpweFullAfGaLvuTUOcF3acUr4xPti1Nmldh46vjXXOLC7L1IgQiOWYrAlsmq+vZ/STd7UmS737JLv3J9ls/gNJUMAAQqb6Xu4BuLJYAcDDF2sjqiECbqy256an+6t1PjgZci+1SsMusRsh8vnraSUyRtroWzdWTT+YsYIcNhbWVRbkhY2FNybVeCO5Oabd1DMSeHSR13Z7GlTzjXBli1vbcWu/6XgSo1HdNz2Ju0fzRrTyazPpe8z2ukE2fj19QXcKou3rLg/QwY4fT38dldM0rXvXQ1w/f/0aGpU1Sts85niO++9q7n2+tiQGiDpe9QG42OOJqXnvv9F1ZdPD2/1a14eqnOr7/EY4fguv2MPfl5b7Nn71eH5PN968xgdrdmut3EtH21Dybcy55dlS9Na/gZ4ajdvwdfHfdj33343y7RmX31Lu1y7rXurbv3W/niv/PY3A4M1teOy77bq3yt1ac5vPkStOdDwluSsVVazFiajxIlpXSADKl1xEDJaGop7Y5ZKnyhRObNWboqgvLmP9jn3W1hdWayAOU2kDiFSQAVBORJgcJHm9G3GqDA9AKu9l1TVkcSFMZSOTOKn65ukJH57O+PHjN/jh40c8nSbEUDd/wIwQRd7SpG6fLAZF4SXc3Nm3Jv+UwMPQvf1ZXMjmnJDTUu6LwjsnpLTger3icrnger3idrtKbIiUnFwvMFU3IIliO+eEeUm43hZc5wXXWYwQtyWV0BdzEBdMYmjqpOuOZzGZYo3nef03FWiBZ4CLS2oA0PgQOUxI4YREAQssoDMjsRgbMjMSitNokdtl9gXW2cW8BEt8EIUzX5+/ruW1GjNhKL8xw4wUJiNazD6793BO/RDBVW66k46hpXLaXgxv1TVTlHrKdZKA1WVpsvzNESZvVGi1+VCDGLKcxlHPAtTFcCHYFN+T9aku1YKn7AeUE0z6nDyuafhkayGJIULdr59PJ5yniNNk3lDqGiv03ATYDU32Fs90lCc5iv/bNTP+ZpumjOmZLLV9I4S/Xz3Xf74WbT5uiMAxZtXvSPULEuXvHplidb8lMO+1qxS9UrTKffAPCbA4EmJV5nIiwpIgXKx81veGiHuA0VuX+nbv9XdPsNkbD1MqeUAhpcy9xW9rgfSGCE8seiVJznVn8LIsSHlGyrJjfJ5PCNOE87JgWcSv+rLYUUDxJYgy7+KLMqqLAxv7aRJDwhSjG/sAC1pddsUHQqAIotj4We/ni8i5aDqdWuPGpEYQ3YEwmu9+fr5krmqm+1n2kzA/NYhQ/5aV1Mbhl3Bzei9RIQiFOxeY0Lks46XvMhQmQwQoIJ5OmKYJz8/POJ3POJ3OjUusYkAK7a8d5zr2o/crYqcMjiFVHzOmDr7tftY59X3uGEF074r1nWRXrJ0O8EKq1Vm8oJbdK206qlQ/Ol8+GZ7bitPQMlDms/S+Itwr4skxk56QAY6ZV/hhY5rL132feuGgra8/EbGmN+u/R/fyrK2zMuyMnLFSEG8n8x3q6i99qMKXN0CAJXAaIAx84XvByJnKfGz1szKw4zgM/bWNESHXDAkqlzMQuNK7DIHpZKPTCRDrccza/m3Y8mlPybEVSGwr9f08jNPKd/UEhHxqSve6QeHe+qvPW+NdsJ1JOjYW+yFlRk7upE3uj8S37WyU4sE2BIkRRXDhNv2RPIozVVjxsSXasajPPY7z+e/xab+2kukoj/homYarqdCK7E4+rDejyGaHjQ0K7vRQHdNx28fj1/XP+Nnm+7Aq495c7PGjXysdaRMdbMtWu+73y/7q1hKMXq1eDb+vuKG+KxzEg2P2JWNsMPE/evqacHqwxs02eB7H37f86jaQ3cdfd4D0v8v0P2F8O1V++G5OB1cjGO1TQCpmhvLdIBf0NATjDKYTGOKGJ4GQqXXLVMuxHf/G1Wv8BVXwouEbgaJrdwYHr9xl5I7fUl0OQzbOmFyK6p+ffbMKfTUJmlweHQHOdfUZ7Q5BdoxPE2znfsiEfGXclguIZzzFhH/86bf4q998wP/lH/4O//Tjb/Hxw3vEKUqQ6gjdhe76ElRSCHYS4iT6jdjqX8oAcXXpmXMC5yQ8CwNpviHnGbfrK5bbFTndwLyAOSHzguv1guv1gn/5l/+G19cX/Pzzv+J2u+F6vRbcVXg/jZuJEIEQkeaE223By8sFf3p5wafLDa/XG64zsCRAusiICOAMzIu4sDJjRM+zGDxSB6M+mecGJ14CyBo0vU4u2S+cgOmMJb7HHN/jgglXDlgoIxMwJ2nMnMVYMhMVA0QQrTrAEmcBbI7GJAKKmOBUxwbUjcwQPry6zE1FP5ZZjUOsJxEKHOvKYDnZwCJsVplOvUzYGtgyQpDy84ECmCaEsCAgImig7sgkbQpB47wSQIvqTPWqpyEQEjjNAEdwXlRXEQEWx1aiZ7LAHSgLVYyYDMYifQjJT5booDqdQNcL+LNYppORJMZO4ReBGv3crk6mpXImBQY0cTrh9PSEbz+8x3cf3uPj+2d8eKcnIs4TwhQrvw1vEPX6h0do0teSR76E8vd0Ys0r9zTBUq+7bvLhS9q0Tg8EqzbPe80//s8BkpAJrEqSo3WRK4tLmfU6ctdUhbT1bqyqROh5veJH3TqgqSpq2p30I5dMR/ozyntP8Dsi1G9+q//Idb2rcb/MNWPcA6gniCsmOglWnqLM+Uknj0JATIwQxAARQ24MEUENESLwu9MLqpSeQuzmwBkhtM2BJogrrvUJiUr8oIYIiVNQFNlh7W4hql/GEAzJu7EkN85+IRycuzZxM3Gj3GOG0i2+8ozLb12OR6r10Wpp3pGJiFAt5rJ4oENS14fBR2Bw1rnKEkg8amyOGKfio69hfMqc9QagFo77efbKmiavdru38Ho806BXrjvfvVK6+cGPdx1DUzRuMlRO9T4WbtFpSFwea/BgHnvcvK63TFXp674hou4O8DjcK8W3DBLYKBdYK/StbDiDhNXfj6Ed2WVSoA3GnNZrmUL9mxvWRvqdyzjUeRCCTyju0UKoJwf0yz5ocBlbFbyowEWbjwakuxp7CAgaUwKEHMikIlEUk9yMDCvtM6ye9cng3sd5kKu2kUgMIaB2nXiYIncZwBu7GCCAMYPdtRsZwM+Eq8PAve9Hd1+4kdIP7Ao1zbduDMpYKN9g/IbPB4zHv2kftzBQcYxCOlfhJGd3KsIEFfT4w7fBGUutbaj4sRKmNa5s+lLgui3P80qreoZ0rMVlW8rn0betsg6rfEd5oyNpZLzrmWsiCJ1iQsgAApV12dCnQnPQXK1tzXg3z9sxXeUd9n9taKmxEajAu/+2vfJ223BkfnfGFPuswnab9J1i3KO88aO8sn/c/k3lRAQ2cMxmW6hicxrkO9Lee++O5PsSueEteX/NfAcL233+tWoatrksMbepwsFFj8fWwv2RlbLVHteIN6QtRUP/blz3GD6qkqZ5O5yit8GADTjVkXtDOYW36ObM3z8yPn3+3bo3ytqig28tb+v9qI4eRtffKP9MDGSlLcYRmwaUbXeIBajWnwasZtj7oLjS6qByIZ3e6uamcCKFV7JVo431F+WR9L7hKUUOyIzq1okdR84d99mVpyPg8thGKWmouXoqRmkdd2JCYGBJC5Y54RQY56eIH7/5gD98/x2+//AB3zw/Y5qixnoQGm677cvefpuPchqiMAyNzGk77IlrfDHdLQVTWue0yG9ZkNIiyu+UkJYZyzzjdr3gennF6+srLpcLlmVR+Ur7VFxSipweQgSDkLK4Ep3nBbd5we2WxK1oVtlX54UJJR5F4oycTSfgNw1W2m/zI7dulhwgCGzoOLkJ43pMUWGV1GgygeMkpyIQkSiUsRbXYIQlixtpVVvpe4stYIp/LrBQ5GDjXbjUKs6huM4Pq15GjAlqiDBdaAFgGzCu9waF7K5s8Os3MPpvtvlK06dIMGsWJX5QQ0Ja5JqTDEA8QY7Ac32WMwAL3k4ohghG005iqm2lXANg2/gpbpH17fQgrBPd8WutJqy6YGL4/I7uELmRcfw9iZuzaZrwdD7h+XzCeZrEbVikZp3VjYQuNW3Z5pla3hab+Y6kui7W/PFx3N/KZqzjbNnHNOA+rXiE7z+SjhsinH18rCaFruJqd5adn9V6PWr69iDUa852FUVyzvJddTuxZoA8ogNIdwnWq0d2zGze5RpmgagqptcC6Bo4/Pej/u0JW3uC6SOpfGsLX8sY7YAdt8muYdW+UT9NmPenIqYUsSwzAkXEaUGIE07q+9orW1LSscr1uCcB6qutGnvMTVJriEDZsNC2M4KwdqsUQmzG9aT3VrZcgRAF1qI7fQHPcFC99mPWMjDtnByYOTj0+lgqsKx+DC2Y1maLamKmqtVoinSr3BHUmqEqWeq4QMdOT0OY6xGDxRARiHE6nTCdzzid5UTE5OJDCNPT/oI7ntrD5Pi0hNDZTB42oAqHtXsmY2ycGrwyrVyVhGU3gyoRy70FlM3CAbPtgBjsavazsYq7UIgd1WmFgy/mQnuNdS3re0MJWKerfV4YIzbGqm2Mb/uqD42P1seNERYQehT/QHqWSz7/XtqtTJ0fR/+9MkG98tvnZZYdL/b3an3qehIclZCJsPC63hWeLgJPXXdl3F37LPiaGU/AjCBSCQJngDIo11NFVck8wgxW1yCIx2Dsfdt9GRSqQDhkZJsTRL7uNaxt1dk/v4cX995v9ae9VlharYeez3Q4zO6NaevL3Tc+rO/NFYy5bjMGOauf1vLTWBEW92PYv+Di5thO/M4gH3Qut/iLgmsdzm7zQNvrvoejz13+PvV4enSV8anjvernAH/1db6VX1rNn+PVKcipMWbIrsWCj91pvcYIAeERixKlHWfLNB7n++Mk19UgrcvCvbLWsU6OtKGHicFgrts3SLvzuvF8lP+xsu/kNyVnZb3ulm3tle8d6ByEvb7ct6W3f7uHv/5n2p6Xhi9zebboguczrYR7vLh8t49b/22lo3LNW/M4WvEFpd+t/cE18WusoZYuHiu78ijAMdhq6xjXKXwoFd6noz8EiM98OQmR+YyEMxacsYQnZEwAyjHNyjOYIozMr73ymybP6AbBSCTKda+ktN61YkWjq/U8d+bqUiew+uj3Cly9kO06z36DFZfA16ZcNc7aeJ8yTCQ8EmfZtMAJSLdXXF5f8MOHZ3z7/Iz/01//Hv/pr3/C3/3wI3785j0CZxABHAAggxeJ65DBahgXHRc0NgSiuMOpkR+0ReaGSQ0QnJIFuAOnGZkTltsrlvmK5SrXNF+Qlxm3ywsu11f8/Md/xcvLC/7lX/8Ft+sV8zwj54wYRBdCxV31SeMjnjAvC+bbjMvlhk+fL/j8csXn1xtuKWNJekCdquZh4QzKaqAJQOYzADVumG6l0GMBnWJEciINoQ4+kXSViown722TmJz0jeB4BqZ3SNMzlukJc5hwQwTzAgZjVri5auzKRXVeiSosAL0epZ7eaY1oYsAJasgp3g7Mo0Beik6gGBQ6ORkO7qjILnrCgK1Mlb0V8E3K6WmP/CICARNF2dxGYoTIJCci6ARA40YgLwABnKLog/ICpABiBewsRizYfTEs5NJeMIOynIDgIP2u1il1GcZLWbTMrBv30AgDMqZtfwwKqmbT8Z3krmRD2OqsAhHO757w7v0TvvvmPb798B7fPD/h/dMJp5O4Cpf9gFa7AWCPV7cpzphe/6Xp+D7fsUXL1vxLRzMKzv066YETEWNBQdvk/qLB9fEkcGlKG1/OYNCMWCoS964LzIrWC1W1+aosgCAW7haACeN9UOpHBCWfb4uJ7cs+yohuCnDu/r7A6b8vf63aNarHK/NqHlXyaYGMgBASFt1hbIrbHA0ZyVfB2JUoc2YGh6CEsQSdJjNECOLxQri5ZvLKALmaYUHyTcUQ0ZYZglCXrZMvo7lpx2b8/N5cPrqoh+V5wuaYtQbRNIKTZrhfW/m2jKtMgPjdc7s35NRDAAVd/TmX9WaKuKgBzaPGivABp22OqCh9evhtFT2iiFsHzrU6+/XQGiHaMWhK4L0ZqYSx7sypBle/4z/3SnM30/07Kkz6GFa2DBp2/zC9az7wuwBYmOCi2K8EHYDserC+D3+lwU27C2Onu1KCMawObuU/dYtCoWXYUMwv7h51rswI0RsmKu1sxtwT4XbMhSmy+B7M4p4ls7hf4Q7X2c/6ZwKMSBzsxtn20LT00frEOYODGdwrjJK2L3QTXGFX4I65G48uUf+tWxuc7X2Ly4lkTdvuoGNprUjvYaG06Y1M2hbz1JRJQB+8u+TVfxvM3eEMgfEx7b7XphbnqsGznGSuuMHWS1k79l8nWKgkVudG4QL6aoXv7vAUVqZ90/46oabUe2y+DtWtI2F4xPMTZfoOjvuRtvSpN65K3nGbPQ4o9Ilk/TZ9XfGZNsBoxm80Hj2v0PZ9MHZDWB/P/17f+nH6KmOOrTasyzbQ3uIvj7Zjq2x/XZVHvq0PlK1rbyTdbLV39Nw/O4IX743F1hj29+tydgxN61oO5dkq7xG4uquQ7cs6gpsO1j0cf6OQHc8wytvzmR7X7dc1aqF9/7a0BUvDTRjjEgbfP9SCY7lG43iP5m58Jy/Xyqx+7kb834r2roo9Om5tOvJNLbvh1u7kfSztKpjAKLIAyQ5qYzLYjqdSAHNE4oiECQsmJJqQMOmJiBZPVi6rKk+JoE6ZjJ8XzjgSgcob0sC9mqcLoK0qRohL4n4c3HrrZeD7I1QUvSi1c9Naa0FmU6pmcMo4BQI9Rfzmm2f88M07/Pabd/ju3TNOU3T8E2tQZjS8OhHAKlNbbAhzP9PIFpnLhixOCVl/pLvUc17KyYe8LHqdMd9umOcrLq8veL284nq54ObcMFmszborKUI2pAaACcsi7pgulysu1xtut1ndbAPmbpaMppLJdlBe1+KfZWQOBaTJ990edlNFIB0rzWcilZNJqgip8ri2HyGCw4QcThq1w9ZWCT+NzD5WhMqJpWgukFYNEsKzExv06XunXCfONfg5c/H8YW7Ciqzq+kzs+t/L3tzWYbKt1zUUGPE/j8tKzztZzhak51lDAHSerE7ZoYP21D9T7attfi3t1UGCrW6tzOTWIe6iFblg4yfYm4SogZXikZ9tZh1QEEAh4HyacH464+l8xtP5JPEhpqj6JpvhajotP+pP7R7nw97ORTuc9QZe0JXSyOLy2SN0aKOuL+nYID0UI6K0oWdwcZRN2meULZkwKgjHBtLX4BeXQKAtIFFe+t3vQQib1qWG+qJgtgUbSrFVVShCZ8tw9gLcqoc7k7cnmG0L68fqGQkd5ATlvRMRa4FN2YeufVttAOoO6rprMCLmCVPKOE1yEmLJEiOC1TeffWN6j6gMWO7d9NgJCFqPFRGVXbzSz9jM/9qlFsp4EKjs3q995Sb/nrC+HodWcfV4os31fbjMMp5GAFqLfu2rjl/x/L7brGY8WX9SDCNzRGAzKgSEiEJvJHCY1B8nUeJOT2ecz2eczidMp5MyQHb6JSDGCVN3IqJXAvWxJNaMdYUXQJle8gTbK71M8evHDQ0R78dB8E2psTAcsushIad6IsLqsvlgvc+pjv29tb9ipJV5YEdsDRNTJ/B6odMTN1aOriqlHYNiDGXWk2yuPDMYbhkiVu1WpsuIInMqytaRscbuLdh9E/cgGDOH9diOro6JA4CFaLOthZNxijQ/LxIMLpR8mVWgYNvFnltaZRyzjTMwXN/CqOa682oAB4GwMkQ0ZZhHzJ7B9d3rv+fK5I9gxt2gIM5h+1vjzroOlDm4J+Svy15/dy+1a4mbQW/G1r0yAbHSwu0TEVt1DttqMEUAuYDv1RAhQ5Pdrrzi29SXDzPOGu4T3iYQXMyGtv89jV89xzg/lPE3nsHcEtYTiGM6vMXHPMLX/EXSYNyIZHOCBPeTuQhl/P04UeElxoYI6Nzf5/PWz6lcfV7SyW7GeMCv1Xus6hoOw+D7o9/UodzmccdXz5Nsl3uo7iGMjfENkblwaLJs1t2OtT5bf3o4jdo+Nor/GqnC1LG8j5a9l946Yl+evmRUbY3Z36O56p+3Cl6jL9vGCI+n/fOvnTws36erf0F8TfRla+zN1e6Py977Xg55S91lfRob2SgXt9rhYabm2YK1LT5MKZ0WF8EsGwkZEN6bApgiEp+wpDNuOOOKJ1zxhBuekChq/AfXnqK8ZZCqbcu2J8PDIAQwTiEW5aoohrOFgUNm0Wlkks06gQiJMwhRXP/qSQFSeaWRbb2SF9gO9gu/qUfaXfdgc1HC2k5wtkDQi+wYf/8UcX73hH/6w3f46998i3/48Tv81Xff4PlkhgiNvaHucApHqHopO4VA06SZlQ81eaU3QizieimnBEKS8Zlv4n7pdpXf9YJlvuLl0y+43i74+Y9/xOvrC375+Wfc5hugepvz+SxzlFVeUYYvM7AsGZfrDS+vV/z86TMulyteXy64LRk5yfxJc6ucIF56xPXskhOWRCUOmgO+yp+g44EMVh00jZdUldmZzBBBwDQB5yfk6Rk5PiPRhOz22ifl+Zcs+r9ZXK0gUVD5Vk4vBAWYoLy8Mx3VwOhZYaLE6EgSZ8JkzaQnGVI9TdAmz5NXw8XaCGGP6kamJs6IGqPsJANzKmWUOLkaj6QeDZIfBQJYTzNlBocomw4zQNHkV+VLmXWtMYhDWQ+CtzTYvXNPJS6bvFecsJKPi4wIxR+O1yoY0KO7ImavdSxNihFhinj/4RnffPMOHz++xzcf3uH98wlP54gY6wkuw1Zgo/dhNVNHUzVo/CXTcT56S2fk85Sk9t/+u7emr3gigtHPmOWRHWXAiAEeCfBvZb6KANkosltDBIWW6TNCY2Bn1jSvzPRlf4lAPRLGRkL76JsjZbXv1wJeX34dg7Ww2grC47bZ87JjWHcQQ76EnE7JCCGKG62UEDkjB0HwOdlxLSnLFG05yHFEUgE/RIsdISULQahxG8o4gjRgtZt/C8pJ9g4oCmWgGppsvNCehChBiBuh4vi8HE3U/bFlkhghDbs3JaR/9vWSwYoGQwpBLfjOXYUqyTIzAgJS5jq2oQbYjGYsjHqKAi3M2d+jGBFw8z1yk1bmSdduee4U9B7JNorjdZe1LQb/bcyRGMTnYE4JOWandK3zZ/PS4zmB53FA+K053kteIPGMW5+nL3ulPC0cumMKelhTXL9ngBi1v4w1UXP6rBfe+vmp18qz7AxE9339wJ4R9Pi2R/COuXS9VEFJYD6GAI62O9opd+2YcDNGVrQyZ3YlT9zrr05YNbwUttSKWHWc3V+Vud2Cm/659J9h243I6urysmMSPXO4rlsZ1A6H9bvSWPPQwCXcoNVO+HBtWvEa5S+FAfe8tGdAN62lhfeoMGk8yz0lYS/Y93kN9/j39dfJyFT/aNyldWNKho+piAaVnlPbz4q/Op7Dg7/rC1F1mVDoqueXBjxKyef6uU8Lt/P58ekZ4lHy+Mevrb7ue8qlkWy4ois22n1z3H0/xhi0pa+7p2PWB08TN6pb92N15Z0vxt8P3jRro7k2nXcwOoCT8XVc9xEeau+b/mTPZrmEIdzu1tXgj1Vxq4VV0dO6ni2l9n56JO/g6we/ebyOXSK9W/ajcuAjbfuSvHK7xkdrHLHmYzwd22/Drz+Xo2+HvAH8TGkdPD5t2XwrBWzWdbRNVv/b+9cqspqylf/0916FVfFmm47A5hGadTfpFl+RFQD3z9EChu3can95DtLd0IDsPAhgFsMEE4OJJBYERyRELIhYWK8UkRA6IwQKX+ln1ZxcEKhsnGOYW52qoM9EuhGbAOKq+DU5kwKYs2wOYOOErHLl3QCImWPsvtQxXc34Vf6r+874kyyBhcUIQJjihO8/PuO7DxP+8OP3+KvvP+LjuzPOGmg6sTl94eKSiUMEgsaeVI8CsCtR2ZRSZHtTbptr4GRxIYxnSlhmPQFxvWKZJQ7EfLvg9eUzrtdXXF9fMd+uIDBiIJzPZ9lAZwGUczXBpJSxLAuu1xs+f37Fy+WG19dX3G4LlpTUOKTeJMDIRT7gMqdVPVyNO1ViUKhTA0IzDdT/UeUHE+vKG8VLGWowCATECNJTEQhBg1qvN1RliDuurFKcesktMJvtK0KRlRR4Ybv0W/AQY464CDMGv86fyD/rjq7k6TLfKO7Dyvw798jw3/hyyimMNu4cZ3HjxVldLeUMyllde1kQai4nOqzMrpe2FMptM+/2bemLGSV0KNx3hovLaDBK0HBfK+s4GE9cDQ/6neFIq1uFa4uPMZ1OOJ1OcjLipJtdy4ZadeWtAFCMEJTRCejHU0d83q7fPs6/H00j/D/Sw/TflOc6vndlqoPpoRMRIwa+/tkyZu0uV5vIseINWHd81AluoLdn3NEIc9UPshwvsxTUgXJVSPctCwX8WVdNLyi9lYlvlQPr31vLGr/HSvGyLWCty74XI6LPX5R8OuaZGBGswThld/jkYkTkXAlos9OXCEl9B/anGUiJnJwQHY+hFMXVkKDWbTF41t2MRB5mtGoIw2JK4kcEQxmDr4ss3pa4uXyNJHAEnQtCZnV1pc8zC2Mag5xeAMsxzMIEkipzI0AUxDXTSYJVWzwQD7dmgPA+uc2Y5E9E9LBRRoDtsK+DUVQc0xsGhn2m1sgVQkBgNUDoKYw4RUx5Qk7ibiyDlCkFcqIGD/odDLbnmaI7orqxvkYKzr1UjAQYk66eWRmVa2toS+Q0Jqk9uTCuxxip1lihAgOt+zbG+y2ev5v8/HZjGA0mVzv8W2HEeD6HKISZRYCdfGjaykoDh1utPN0iFZBqsZXGZDCTxkCSNlVmixomuglY1jFyR1M1tovSveDhjnHKQHGR4HFtQ4/Jf9jiVWOEfZnlkwFDZGlvja6el/nw+M9gqpYX0NE5+asw0T6vGSKANVyOaJ+1q8ByLHuQVu31hgitWXeQtXBY29nxNs2JCKcYb+ian7NBH9oRdPRbeSI9ok9EpY49HiZWgF6N0720le+eMaLH5Xs0+x7OH7QKALs+2saFtswyP9jjsfZ5x/V8eR5s0O6dcV3XtYYpYCxsbLdNyvHro1wHRdznTyu9H+V7S2rL4I3nbf6eTt6dP7s/2qaD+UZ1/Vrp1y7/v4c0htsW5/f5Rs+33vdlexzj710ufFWm/oH0aK1rFdtfKt2R2VaqrtEYP9b7ni94W6LSFMNRW23Zg6k31V+FZYAn5Wn1lENgjfEQkWnCghNmPuHGE26YcKOIZGX4JrM3TahORR5LbDR7Q8AJhExAYio7wHPQNcUMIlXwaiRqzhkSNzShyBVuDKQ5ZoQY8FbuL3tbebPKY5elaPKMnnxPSU4jnEg2pf3V736Dv/3Dt/jPv/sWf/XxHX57fo93k2ysXJARWeLALdebxHh4OoMQEMMkGy/1RARC3YktEqMoc0tw6qTxJRZRJhPkhH1KC5bbFfP1guvrJ9yuF3z+9Auul1f86V//FZfLKz5/+hPmeQaIMU0Rp5OchEi32QWWFndKKd1wuVzx+eUV//IvP+NynfH59aKKe4AxIVIs/L83PZiUksHlL1NGWxyI6HkLdLyr4+E3wZVE75J1jFgni4hEv3CawNOEHE8AImQnvjEd1S1TAsRtlOoKuUAHt/f2iNb3pmSHjl0ovlgZlBV2yumFCnwVzTOauATOCFEGjSHyp/XY4LQzYmRnqMo5l/gZzBm8zPJNWqQ9KalhK0mMB2gciBKQ2ukKytrVNtlJCPvb4q6UGCZ2UsJOb2heP7XdPJfHK1TMDTisZCr71/QRClAhapDq5zOe3z3h3fMZz08arHqaQA4kajJcsjY0/XtLLS14nCL3fE3Z3Plm+rZOx09ExLjxQq8MIQ6qFDGlBgMgloN4DHKA5FaiRV9fKcRspXJxHwETfERSlvuAFjfoL8ZWgW1lmvBEsKsMbPUB6HbjabCZRtG5MQikgO/3YZDrx9Z11V/7eiV7tozpqjz/DmsDyrgN6+c9I9z/PUpeWSBBl3QMobu/dVwyZWRK4t4nV+D2pfogRkXx4ubRK2WKkGzKAAICsbuvBE5go7p5qnUTTIFYg7UCpoSwudiX31Sp11vc7aO7i/Y+gtAmlb8N5osazSkGi/W7/OdZQBRGkJvSyTEY8sh2qARlGiNkd3iOURtAII6gPEkw6hjBmRFszQYqwcizju0UIyb1RxkMVkEakLp1uSRKt1iCVQNmjGBVmInhqy457SllITBGk5xS2sOquf+xqSrw4BBvaVOOkOOvYhipxpEgLqQgO3gyEThwCc5uc1N2+RpOsbncAKzVDgevzDUcWGaPVgKAxz3usUBBRtnp7ne8t3iOCj73SfJw4zu9VTQ7DsMzW7ljNwZLojVY+N4VFki/5iI0wGDdaIj++vcACs6xeSnr2/1rjKIwdGpMLay0GOIMs3mC0+/Q8K2Xq++ojgnXNda8dPyaGxwrsOWHS+lrZs6/7VOhiVaQcsdbAmwDXt4IMaiwwGhfRj9OAwX9Kt9BhmelBEJr7Oqbs8dQ1bLGZft8ta2epoogTW4B2AwxV3wMBxsEVtolD7x/bIORqKf6JpITgs3JBaN5DQ3rlVuVPwLVd/WET20r9B08fLLQULg6S+tpPcZl7BseRPiDosSmQkocvtjnlUpjmvJtVFs+qeT2wloRkduj8rU3ZJ3t6tC3bnwNB5T3/S6XvuQBf2XPR+0ejgec8QlU3DpLFUrrCv9SFUEjXm7cnn6c10YIS7JbsMJIKPl8nf6+XmlYbotbGprEXRnNUHHDy61Gs4wdKr6jLk/zt2t0l/zGm0fSCs9jVAU37R1Kwj0xwf15W68XG89xBTSoYy+19e81usehW/mO1bvfjrd/tyrHgSc1ANh9w3C+7RXG7vB6QEtTGzyNCo97o0H9X/1yGrQX3XrqX60ev3Fsj6Tx2NAmCKx43tH7WopLrIqnyoObv/69/j5iuOVC0GqdbdsGidub4he/yPLd/CsfsSeTt0Vzgc/hc22Z8bdFhoMo+QkBOU+Y8xm3/ISX9B4XPOOGJyxhEiVuIPHsxEoXzK3q4Of7k0lXi9ch6s/88BuJty4EBVAG1K0Mu1hn+i4QGhsEUT2NQeogKkg7GRKoN6jL3Em3xYuLmXYsE4Ala3SAQPj4ccJvvznj7/7qO/z9H37AT99/xG/ev8O7EBEpiLsj1lMUGrDaxgqRJC6m6j24Iztkcg0YWb9PbOp9MYiIi6gbcrphmT9jnj/j9fJHXF9f8enzz7herni9XHCbZ2SOoABETABEjuackUOSAN5ZFNmXyw3XyxUvv7zgcrnidp2xLEl0BERuc5Lsnq9RBivdEtW/GgsYSKqkN3ktK49sc2sKbpt3c5jjHAnJvBYgygAH0UHwInxdmACKyPEDKHyLK51xoYA5ZiwhydyDEJAQiDGRGUSCwqTIm9VZT22LfBzle4thCIYei5f6KSMggTTQNDGQzUVSJ9iV9agD0Mj6zDXYtQUjz3puQ5X65WSMwSKby3ONx6HwkVlcYpVTNJyAZQE4g5ZFYnmmWepbZj0xMaOcmFA3T6R9oCwSMZn+RO+hpywksHU1ktS+Z/c33EQaIrbFiXUq3xGIqxm57t2y2SqLX2BjOiGcT3h3jnh3DjidJ0znCXSKEgw+RJDNdtMmK8ljo31c6zSU7mWTszave/04p7PdjpJY9SYeKaJuwOH6oWbvGAIdCm+Q6YpS7xa+vnJzuN3HT0Ts+Ij2rSNtTG3L+sjH6somtMPBow0IYAJdhTUuR9eYoApPRQKKDs2Xbw02rQBChlYqsFQBmEFquRP9BANYht31YOolKy+sik3buSsaMAy9EOgHdJ/poSZPA/p+ILt6RnWOrt5tzHYb130B0BgiAjOY1G0T2WmIqrjsv90Tkrd+Pr+ebFyVu9fv+r5jAMo49kKZpZ65vM+kjtrlS2h3FPg3o9x9netvzdjA2rlWRGcY4bWrBW9SciMnHEmOx0YAEwXB7ySkOnEC8QlICyhOoDDJPCOLKxslmrIyCRQIJ7VEB1KFvtYOEjdcFhtCDAARIU5lB7spzEQBx2oMcLiJWBk93QVDDn12RoiqpDbmtirmylckOCTGqK7HorZb/YKTvIPCOQc5bmtuyrwhwq4hLVWxuQEzo5MLTVk0hpMGPro1WxkcyAA648wawI3KGAxVakNk47yO71Dbzm1REByNDv/3342Uz+Tg1Urug3TVHRpu7GDz68rM3JRtfedBfjvBkjUAuTDRIqjlLMJmdkOF0j1P4gkEM+KnSh+VuzZ4a+CgKLUdDVwNF7d4zv07OstCG3+74tyYdd9u4Ev/XW26Z0MUxrvPvJFh9J3d79GbkUGgf1+npcV6q+/YMKEtCccXHGCmals75SRDd/HVe4bBOeCNwkTebzLqpi0tL5K6ByNxbTdFQnSn+4r7Qf0vOODwRojSENdWb4SoNJCUnwm1lYz6jMidxiDFmfrNzlitp9ROzbm2ohp4x3zHaE7qHFi57VXy+J2OLlwhYMIdO15qg3dY/9RI7k9RkikUfDvqz7v5s/KbMfHok7DKu+JrOmTAsBOJ1Rh2hO9b5/FjPuYBTWBvy/JtHz8/nhwupf7bhhMHXH/b576N7luu62+dHmrkg6lv96i+Hn92sIx+jvbrafk+lG97WNtPY8rieeWtVOP9PZKGWPvRQrZL36Ntbcb9JvXvLeYPRlz5dvJ0byTbCYYbl7at/Lg3M4MPXF1D9uPPlO7KVDsNG+kdVh8WSwS6Idjmg4bN6DcqEA15tmOp5Z0rH7NmBUdzsx3gm+qFR3hB/s44AWBkuoEoq4+ICM4n5HTCdX6PCz/jE3+DW3jCNTxjpiibC6PEVaKcEXIGq5LaemWbeXznGECirLv+61SIslhkUgpCn3VfG2xrq+8C52pzsHHgwlhV/VKdIy0lAMxUDBJhWRAycDL/PIwayFjLTCwxBQgMmgi//eGM//TXH/DPf/8D/un3f4Mf3n/AN+cncJollsPLKzAvYohICRRlVfNEQITEhDCdS5FHKk0LEDmEOSOpYjmzjG/OC7AsyMsFaXnF7fZHXG+/4PPn/4bXl8/4+edfcLnccLksSIkBRFCcMJEp3GfkkDEn2Q3PKWNJjNeXV7x8vuBP//oLrvOM6+sNM0usDpF1jafMCLnyThYQmohUgS/8TMr2Y+RsIqjJZjZpngdjROrmVCZW5s127GeCaCcWgxaAIjh8izz9Fq/0jE8UcZ0SlsAIqhY4acSIKUQdC41+qPUHYtmACckvXnqkb5PGtZQYGFnnKwOUACwIWECc6kkIJ5cCULdHUD2m9Y3qEHDtn7jfStV1UuZinMopafyJKuNyTmJ8QFYDxIKUE5ZlEXndjBrLDMoJMc2yXtOsrsYWOWGUZzUsJIClP9JRWWyhjL8/PbFIu72c7a/FKIH275LP4+MieejfYsQITllOVPVVYNPrqkGPg8D6+Qnx+Qkf3k345l3E89OE89MJdD6BpiiGKxBCUWWYycvzSRYZczvJ+1G+Osf94+GDXqb+Aj50LfnWMd3jS3opyn9jfHh5RkZSuGUoH2Aajhsi9pQCq6wtA7DFEPTKtsLLGjWywkkZIkUCJqCKsrIKTluCaysI1Z3VUrwbUfdHac+G0FYlovrcM46+/D1md08xvpeqQKYKhV4Ac4qHLcX9Vt332nO3nQGIFBoloSll7efnfksgPtL2kSGCGgTSw8I9Y8RaobWd1gq1zfyH5pabtvd1uVXkHquCoGi5fB6P2EdrjCqD1oxpKFfvJolDQIiya8SCmIEJMWtg6SBXxAio8lZ84nM5kSBKk3XcB18/mrq35z+E9rl00/mwc/PRGh/2xpe1OVSUbB7D2SkTNGOG0m4Qic9PrI1t5XtlwPoTEVvKWVtDMUaXh4uyaVRH6ZW2cYVrBwGf12VVhVhbpgxJZmFAzQhQ13sa4nmwjtzAiGBGjdI+bTM50ZuUzQRlBA7DMsBcYg8UQxPV+jNnEHcur1CxtdGZLXjhjb/XyY+lrDXv3oaoi2VjP7QrvdIUdEKUPBjiG4YbtUJCV2WuWnzvuW9LfWlV+urb7/1H7Gl5e1/nu61k1Cz/rGwcKJ9V1s02IOz1kZTDGvENfozv0XG7NrTUvTNxvBgDNwDIYKTdDGDK/xZver/99k3ddIHmnS+7wBrVvD0sFvzrILLNs/7Gno/Gq20DmjLq+IzHtzVQSr95MGdH0zYdWKe9ddHTplH+0RiN22T5Dzftbjs9Ttnj8fZhepvHeWNTXVnH343zdmJfi+ianIYf2GUz3MSr7N0cbrRxm5sYPWzxaNuSzY/W329kvwc3W+/v4de+PSte4IE2WBlvT8d2pR9qxQD275b9leu+16Ymn+GHewqRFdy7E1H9txtF+Y0yeyfdvhwD3E93jRFHyig0plXNbOHc1ji3Xf/KANFWarnsQft6XZpeQ8PLrIp15ReZri/pDq4Yt0ieTHmgEGRRMGfImfAEwgLCAmAmxkKMmeyraPvBi8I8c3WDY7pMwHSRbJu9Zde2dt6U1wyJr8CKe1QHC9vACuNhOKhvfymgSEocqqLYGC8mmIvVrPLAoq8oTJKXSQwg6vRHXBYlpOUKTjdEvuLju2d8++ED/un3P+Kf//a3+Lvf/R4/ff89Pp6f8XyakJYZOSdcc0YKhJQXZCY5JREI4XwSF70Gn+Voo3TSTidIQOoFOc3gtCAvN7mfF+TlCl5uuF4/Yb694k8//4zPn/+EX37+BZfXV1xer5hvqbgQjhoIW1z2ZNyWGTklXF6vSEvC7fWC223G66fPuF5uWPKCzBmIhMgqE4YACrLZL1MW40OW9heYYpkF85RSzSs1ZS7nyh086E9hSGZA7z38KNNvB1tIY4SIO/YaGyKbHJv1uAzXExeRCJHcyeJ+zRSGwXQT9X2AuBEjPQHEIDGKhIDA6nlDLBASz4TlKwbEbRFQNliy48fLL4iexa5ihaMSD4WznJBmUDlJJGMn781Vqm2DK+YSZvhYEDo4YNUpFAOIncAohgYzREDeM6sRglFcOeXqgssMMEC9Uom74jwYlORxM6F0qtzXVdxwoOT+BpX/kuqexHtFwClEnEKNDVHkbwd3Xo+qaK+szUf5jjWtvcOAOZdhXyuJXN22qqmDyz9dW/zzlt+v+i9fhtXFK1p7JB13zVSCEH+dNDwZARQlSu1j9wAAUaxuW3rheSAErvOtTygY8fIVcZfHK2SIwgpA26vt9N7a1Yedb+8nyeZ2Aeq1LiIqu+R6AbhXmtyr+03PnTJwZIx4y4mIQ+/R7hQetXN7zMcLZ1tx0AtFX7I6xpqpMr99LU1V8n59ZmnQH4dbKqLgZhxtjQiiri6SOIhLJVZXa5kzCAEp3dSdUiwGCw4BISjRgzAAQhdrbIe6ixdFUdIr2/yO23YtbweqFsssOvy643LGaByhqccCGt9fkw6OyDiTvIozUlK2CtdTtGeMaJ47X5K+/3up2aHQnQxoelPKQ3OtGQAmPe2kPiA513Wecx38IZ7fMETYHBWjAlADbrnG5I1YLIWBKbS0XVPCOKEqvvVtZZxVgOHWGFFeA6v2HUkmFnnFawPj/Q9o8DgA87biSsQ2g1SYahsIz+Bt48Ot+yN5ynjcgUW/Q7s2an0qpzIzefWsr3O8PO3deg2u7ivkrMrYozujVOkQrXlkaXQt224HZRKZEUXhBR3MwBT+eu1wt8HZbpvL85aOen4phNDCEnze9ruWTnfjsWpDf30k1VNsX5JGINqv7RGfsfXz6Sgf9/a2P6CQvQOr/bP1PLZzvfXtW9O6LH9/D8+S618nINUK2tJszVE7NIUWEGHFTQ3629COVbM23jTwT/t575V1MD0Cm/fw2hbcHYUHyffW/oxlhmN16t8b77ZoQlPzTnX3eLBHxmyFM51i5C3pLWu10t9Copu0xf7s1fXI2DyS9uSz8Qfrb+9tKNvmPbbq3mzuujmVWMq3TSN3CuLKx9Zn+9/cHWsGAtczC0y6mx0SHy2DsJAaIQiYA9QIwZgpA4hADkgsxoPsf7k6RJT/WT216GljZswpO6m0iCqqTDb+XMeHsxofGKCgO8bNAMIwdxlsvikYomTVspLqS0WEkVMOYEIMk7q0kQ0PsmMsgzlhyTPm+YqYbzjxDd89v8ff/fgt/tNf/x7/53/4W/z07W/w22++xXkSZeecZqSUkOYZmRjpdhMcqhtG4tNJN5zUE6WscwuVrzglcFrEAJEWpDQjp5uUuSxIywV5vuB6+YzL6yf8/K9/xM8//xGfP/+C2/WK5ZqQE8vBAdQYYzmLkeRyvSEtC64vFyzzjMunF8y3G14//YLbkrCkBYkZFAMCCGcQlCNFIvEZQhqDs9UtOz6qKKPblMEDbyjCHbPCn0m61VMDl/eFh4WdkpG2ibvmCKaoJ9h17vU0AUG8YUUqkSMQuMN1KouVq9VUeCGIiyAlacI2qEcWBN1hLwAcOYvcSijGNKvDChA2Xg0N6rqc1O0xhSB6eT0SFACwGShcIHaxMQRQYExatsZKl/gtUM8KxVBQDQeMemK4uFTKZpAwQ4P7jv0CcoGvtS11c6xb0ZxAK0BwSikYjhp4LgBQ9Ip1xORriVCuLpvsP5TyIgWcYsQpRsQ4yaZZkg2jq7CO5Gium6Y+rXDpFto9xH+tZYhHdAzbqcqJ200bbajWbw60YYs3fISuPxSsGrCFPmpNf7t60HTK+xUvZXfGiPLc7fqTaxuotro+aiMJlkUlNW4ydLZztmkDhABVhGFXs4x2zGJzVSTlkIt/vyXo9ukeo+rvKyrT992YHanvXh171yZxOz69srFn/u6VffQKQMf7eL8GOQ7n7+fyy5Ig33Xi7ooNnGKuJriB5/qpf86oAYANxrvyi6BuCqkIxAykSb/IivSDIPY4IcaIaTqpP0PGQsX3DExz1BsWvGBKJMo2M2hYzIiiXAvVXROp4cPK65XHFtD8ofnZUUyVn9u1z+WETyrB16vPRh4a3KxM5bbqff9+8HyVehS7gVtW74lAGCvT22+U0Pf5lOvLOYvRyfpT4i90Jw66/hgjVHY3mQukLvi1P+XACsOZozJKnmnidd6mznoSI0zSthK8y3WLzcihTBkRNac0gtKabLQnG+ytp2YvVRqxNrIBQqn8XJCun8owGX4f43ig7oKRWy7jcRSvP9aXMeyNYOAoTXNvNvPswftWfWvlTstwrvO2NOsw/ewYWZmt7IxZlR3yDFwxMBQhqD4z+KMGj0oZW4atvs1SjvnEtfI8ng/rvzturpQf1rxN/RvDduzlCRYJmmy8ZOSq0MFFCG09ltZTahvcaYvD69MWd3T96+fGvx/dD/mynd9b0hAOB0W9tfyatnnUnt+618ZfM/X0qt7uI2WZ11Vp8tvfAv7m1I/L23nH4agfzLvFZ+7U5ud7wFP9Oeb5ramF1W59Fhx9dDzv9/NLZYI/59o5kghF9/MXqv9XqJz57lR+6fi3fKHnAu5DkXIdzbMtiGqec6WJ/Wa8tl0+VgSBu9KrW0fhRzMFMEckjsgU1aENlCcV//FR2X9R5topCHUfZGpSMg6odtR0O4XPjos1VPtERUHa9EMZKJMepT8WcVBSVj4/ZXOtmsCZsaiidV5I7tOCnBmvS5T4BWlRN08ik8zqqmZZbkC6YcKMb54CfvP8Df7xDz/gP//DX+Of/uon/NVvf8A3T884nyT+IQiVTztFhBSRzxMoiGI0BNu9X10mF2nf5Mm0iCFiUWPEfAXPNyzXVyzzDcvtitv1E+brJ3z65Re8fH7Bn37+Ez5/esHr5yvmeRZIKqo1xsvLpzqeRHh+/oCcMjADyMDtesXtesX1ckFiYIqEEAlBPSHkTOqeOOLGquCXEQczmaMFIaMMVGOOymcWhyJkRG5jzxovluy0ip2IyWaQkhMsVX4zQ4bJ0wxQAMIkLpLDJMHPoZvm3LqKKicFyEkPovHpovLMeC0bUK03AMX1tSnE5T+FRpLBkGEQ3j93eD6rIc1O7yB4vQyBKUkdOYthzenT0GzWkz6IC+Es7lvzGSkkfZ4RMsBZ3C1J80RPU4wZOTXwUScH1fAAZ4Qwl1GcNZ6Kn+9mcjE6FdNWsMfH2PhCTr+onAQ1gpHJ1DrWUD47BvlNIWIKUQLLq4vtSLSq08tu5vr/PiUynrGVlgqvt/vxug3NW6LNEfvLp0rbRvL30fSAIcIN1AFlQkvIW6Cm1fvjDfeMWn/SwQOBFzpV91aboADTUfGqMDNLCHcAZN85A0PfJsvilQd7Y3OP8RwLS/45NRltMYJ8n7cVE+M6x++3vh8pwuDmoVdW7TF59+q4pxRwLvfu1mFpyyCyld9/1y6+43UOSsO45da2VYFtbiWOhank+phQeW+/Fko23+6yjhxCJjVEMAMxwQ7HEQchxBrTIcYJKSyIYQKHLKeoiv9EHYOBQqaokEgNDhTV6NAZLmDvzRgR4Xc8e2MEiPYnpHTXC459/vq8UWLp48w1IHVriKhGiqEhwnDNSmHu8mw8L3BkgdS6NXUPzgqOClR9tzr47xU7fh2XpE7BiagYDcBcfbEao7bRn941W2PcGfz8994wAFhZa2OE8ImdkpGFSRVGdy3cMDMom2DGK4MI5dzi0WacsCrLxnQ8D/7vHjcP6EtPw/pCfNmu3NIWH7T5IF7v+zLuR0vL9owRR1Jfd+Y1bHqYaGhvhwdqmeWvmhctfhvVbczVI7TTfbq6YfZjWZUGtXVUeIc1/YYo/sPohKe+H+DWvs2KggWn9zA3+H50IqLWv8djrOF61KbCT7k2yMfyyqiimSPs3zq89flwGkbwtwGTe4bZUfvvwcVoLvbS6Nu9fBUP7a/nI/Xea+Oj8P9IG+7hyntpjc8e+FgBzDDCFve41cZ7vGPfxn6O9/JuPe8VnEf51fp8mxZsPd/CrffK6dMX6OitptX8HoVFcG9SdTTgvprBCrvfwg08fI8Wbq6xB8fsretolIpUYk0p8F5q223D3saYrbSCvbsS3SNpPJhH11C/3rdohoggdb0VvR62RqwpoOEKtsBmS1pp4iT2/Sgyg75jmLq0ZA8F7FQpaqchKCDpqQiBC1E8BiQwizIpMMu9Bq/NyqczgH7rsfE0ACMHUVJOSKAySI4JKN+QBkZmmJpGTovqu1DzmRufhcUAsiQxjMwpIXHGPIsrqGWRd3+6Ainp8wRcE2NBxrws4LxgWS6IPONECz48PeGn7z7g7373G/zz3/4Bf//Tj/j9b35T4iUx68mPQCAEhCmAThPCaQKTGCAs7hfIcTSqqC6yZEpAWoCUwMsCXmbk+Yp8e8Vyu+B6ecXl9Y+4vP4Rf/r5Mz798oJf/vQJLy+vuKqrpdNpQogGrxmvLy9IKeF0PiFOJ7x/9y3AQLrMSPOCeZ5xvd1wu96AQJiezmAKiCDkJKHLA4kr5pyTnixRBThxY4wAmbFIZRCVz5gzWD0DFDSn/LEZkExEtpMQLtwCFKxUr8GwuF+igBbvDWaMSNDTLiarGv/LJMYI1jWjfbATE5bXgLXX0HhdCxnDTgHiDigghCzPWTfPCFCUsaqLwO5CY4iQFMEgjckpZxpKMPkSU8QMMSqnMiMnAljcgSFnpCAnh1JKoMneTzIHManhLcrYhgCocaJZrwo/q9MQxRAhbpqoTkyXuIkXs4UIK3vj6Z8iixCKkQEEdZ0ExZn6n+p/DIXYBi4zRMQQMVEQY6Aim1QqknKpFCxmVN/UMX2qmH1FO1xb2sf9ALQ0pdCY8m6PEfgyGvmIzF9r9Pxk/d42cT6SHjZEjBnue8zhgADphOvXW1lRqI3PqUAXNGC1KRYAGg5o/a8bsoIsu2vTjNB/1aR+F6vvz31FB4bvKyCux22dqsuPoH0istp1Udnfo7atGHHa7O49I8Je8n3sdyCO8mxd7y+Qewv2WDu37vt3a8Xb/TI3SsO43Q/2hxmZk3ki1P/8SYmSEcVK39VG9o8xdyRBpIEI8ISCnFU5O8UT8nRCmhbkSYJxsRG9wADVXS5khAF+3Ro9rsqvQP2JCOWQaayIq933u32OJT+PZiDwV2OQvPzf1m0GlcpMWlkrZTcktoKUnWtdrv3+utle9eX4qGKoJDti2eVZlxfWMJ5ZceVgHVf6vSrX8tppuGbXhQoYe0YIm1sfIDsEhXNeGzPALH5RXVnWNOqMIb78ugNLmM+gjHGIUfyKanDylIPGqkhrGGqGxMbV2qBBtfxpH+qVvi1NpdAyM1s7S7YVSHn4/J5i7Ai+HuWv9zaurrVF6nXfWeYuyfjmIWz2cNnjASl3xHtY/tqIEbtiedp1DvRzUzti82+P6kaItYHNt4kKjJRVF2SJVpwoZUY10AbXLnK4Gt0Y2dX4lBhq/+05EUq8nXupgZfumb/auPm6x/nq2G7xWN7AbOvyS2NE3EsexkZ0xt6Nvhnl3Xu+l2+r7qN4/22pFYT+sumtbTjAN5Uoe9hirr+s/F81fcnc7Lf9EZ73z536pj0EoyOcbTTgzwzq99Zz856wdh/xZ0p3IOXP15A/Q3oLvrsn0+sdjP2jO8dLRkaXcRVK600xi24TVvcN++/8PbUzzBBXO/IuaqyJCOIJE53AdMJ7TDhjwoknpBCxaJBqDgETMWJxAsNlfQUdk6C8QYjKdxQ+TBSYJ0zySTCdRctvGI8UioKb1PBCiJEQY9AAwOrqCBKXIkNdQzFjZgn2PM8SvHdeElLO+PmaMaeM6+WKJSW8Xm64LQm/XK64zTd8vjyD0oKw3PD9uzP+8PE9fv/dR3z//h3enU8NC2MuZXNaJFjwPCPPM8AsO/BDQFR+nxlgUlk96WmBZQFykm9SQp4v4OWGdH3BfH3B6+c/4XJ5wevLJ7x8/le8fP4Zv/zpBS+fr3h5ueJ2lVmMMUqg4pxxvV2QcgbRhNPpGT/88BPePb/HT7/9CUSE1999wqdPvyDGiF9++Rn8//l/y0a7lGQsNUB1ooCcGUteAM6qd6Jy2oWVN2ODeUL1XKCwKiTEokBUJb8pfanwzFXfLZvYuLj5Mri1mAdlN36YgHjGEs9YwrnEMmFOAIveUMMYI4LXLpms7bC1VZiEAouZMwITLLaCxTMocox33Q51Y8x1o2iJ4VIWN4EoA5jAlEWfmCUQN6vXhTpaACUCRdEfFOObDhYhgEMGAiHmDHBAyglEETllxHCTgNZLAOeEtERwTliWGQiLnjZQud9ilqQAYNaRmKER3nW8CXrkCTVtUA0avXULx2SBnv6BxLhEcoLGgtUTmcuxWjjrWMiJHK5u/CGumILK3EEDULPqHqoUQhvtHHWnlV025e9NtE/d9V6ePy8jILq0X7/O4zEiDNpxh2nq8khaH4NuBC2MCbB9231Zv+uEtLuMRCfvDo0Qbty5lLlfbjBFQte/UduOMC5VaTUat9G3guwsjocFs+kXx3FjBDcXGZMtI4RDpO3Xh/s7eveI4L2GtXr/FqFpq+4+9WOypxi5B5trha6NZzOa7fw7xRUBjtB5JaUpatdQzGgDRSmnh4peK3GgEBCYgTiVMnMWBWyMETFPejJiQooTQtITEX6daiXeCEGl4m5Nhy4YNZlPSKzzOuHY/r6DCdwQOgWyGxd/HeGg0n6qSjfhrUz5OFZKF8MocxOnYS//uM2ptO8ebA3f7xgiav6W8FVBB+VI9Xh91e/WeG2QQrDFszJG+Dq2FOLyLIyNEUCJX+Hb0Mx7b4jw3+pcBfdjdc/UjtN2Mhip3IgXstofKZPUl0gr3izX9Tmob/1sHUFmhFNHuG9r3LdSv6bEoE4FR/lm34MP4XU7RXYpt/223irmZBbfpiVPvdqa9Uxn04dS5iN03E4nKdw4ZsLjhFEiak9PFjcH5NwnBZTAa00frO+dcNO3NRScheH77bShGKdxWe14jevya4cc7G+tpZbWmhHiTrMfSFsz8yiP+Zhi1NHXDRjbq/v4/B1JVRXg52C77DFfvll6ZzTsn/c0XN5ZfgzvR2W0+Vr6NU5jHN6uVera4Mdnvy17acDyNc/XZff5j/Gpo3SPT73Hn/9lUotTytND7Wnxy+qbB/u0JxMc/eboejYa9eio743LVjv7b7hbP+syvyI+HCVet+GRsu+tx605ODo+e4mI3KL1tG3A53RPbSOZFtTW3QhCtlOclOMQQKkSkPG2fX2+NoffwMWMgCC8KGgC8YRIE8zvfuKIEzQeYAySNwacaMEUdAcxUdHHyu5/MRYEIkxqMJiMt4HwiScsIEB9/K/1AKJQ5OL5QHY7q+uVKWKa9Lug403BVMWi1wVjyRmJM5ZFDBFLylicIeL15YolLfh8ueKyLPj55YrL7YafXyZgWcC3Gd8+n/G7D8/4zTfv8PHpjPMURSaiOi/MrArfBXmRGA+mmLfNdjBLEqnMYq590wxOWU5BpAWcZuTlhjRfsVwvuL5+wuX1E14+/QmfP/2MT5/+iM+frnj5fMXtxkgLI6qL4znNWNKCl1c5CfHhw/eYTmd8/90P+ObDR/zV7/4aMUa8zi/49OkXvFxecHp+wh//9EfcLldcX16LPoBDQOSIKy/IKQFgcW/j+LOsPL7BgEKY8sUWeFrXZQephLVewuQP2XxvLpsYxf24GiLsRAMoAuGEFCYsYRLDSalTFPWB7JxPVUL3aMbvU/B/2dJkzjJv9YHTpRAk2Dn0ueQJQU8tRO+SSt+KzaCOiC6MrPy9c4ClZXopkkxYkiZmOdGQc5ag1hY/JcqmLs4JORByXqTsnOSkEwUEjeWC4srK84YSl8VOl3iDSp0vDJPNfx1Ggw19WQQK0lgb3cckp1yowEfWllUDD5WyuVRWdUnO1Wy51tjHobQDTra+R8/FvLF+3radSkdXpaxozpoG+2bcoz/H6NM9/qXSGj/39+q0lfI4zX/AELEWRu1vfx1/W/5qBNMykbTReAOkwat7wuFaSeSvtd4q4Aa9z0UoEjmmuufo+1+UAl0bjjI9/fMWID0qlnZX343jsTAFFjkNwdY87Qu3I8AzLCJogAyr+OvBPnuhc6svo+9HTOKaaUfT9n3YWD/7EsZZ+vX2b3NH9tD85dfO+nsh3kKQzcdfq5AV34KVnLW+Gc2UVvyQW/wVioiBMcUJTEF+SpCYIzJnJJ6R84LTdAafsuygYEZMszC2SVhbigEhqpHB0RywrT91u+Thufzt4XwNE/cEiNV4jRT8aOsJGqibODTBtc1AUoNzR5m24texekI1WG8QPLMq8uv8jJQzXjG+buw+uvffDL9PefVujFPXBmgQGkPEas3ktMmNbJ14aJTdG0YIAOW4dcmn19IwDPoTlEkDA2xrdIfRKEuu0oo1PjZ42aN7/huDLW2X7dIgaq5GU9Zl9W210GyjOkd4bG2MGeXbwo1r04jPUKqoF6q7nlwLHDeKbjg7I2tbZPsJtfhx1DIZevPgOqZ7VOqkvinrvDv8hsc9fr021wHcW0Wj8g3LCq5BY5St+LCj/R3O9P0MXR8fU6isx8MNU9eunk8ECrPfVWnvQfvryKd6ImLQTv1nxJYwF/kRTCLIlvumgLZ9u7xG325SwLR1b/waoYTNYvd6AMybMLfVhqbu7vtSDiqEj8psV9mBeRit0xEdeCCtNhJsltXj7YNt/uL0detYk8cVJv+q9R0rm+7k2aGZR2um2ve3wMv6kyNl/Dng47/PRFjHEPBv/10mavnEX6UKoPKnfd2jqstjw9Ruh7V72tML1WHXG5jCHU0mR8WMEpTSW5pRT1tKDL4ACmeAI55wBvOEjGcwJjCdxD1unDRfxBRRdvqDSE4uUI1hFVX2C04GLHwYESK9L7ywtbFh19WwIXwypLwQEKP87KRFJbKOUjAVRTjAjVI7M/BTEne683xDygnXecaSMl6WjFtKeLnNuN1mXD6/IqSMacn49vwOYQF4SUjLXHiZPC/IKWN+kVgOfJmBJWlsLjHcMEGCSINFZs5ZDBY5I883CU59u4KXWU5C3F7x+vIzXj9/wi8//ze8vHzCL59+xsvnT3h5+YTrNWGes+wxI+C6XJE543p5xZIXTNMZz+/O+Lu//Q/4+PF7/NM//DM+vP8Gv/n4LUIgXOcLXi8vCKcT/vjHf8H56Rl/+uMf8f/9X/9X3K43vLy8yrAG8a0/xYgMCYJMxMpTCT0240+ZX1UEy7ybgYvKDHt1J+lfYl/QeILm8jhpfD/biULGX2dxGE0Ejk/g6R3m+IRrPONGEQv05HpmxJD1NATJ5jLltymTyC1BFiMHCZJu0phHG5nlJIVsrPLyKjRGgcmmbu2SLd8Km1ZgYIBNJ0Ok+4hJ4Sm7cUlFNiDPRBCKDytCAIgRsIBCxsQW6zBIjIgQwTkjTRNyTghxQkoLOEygtCAjAmFGAgFh0Zp9e7Mj5FyucrFA2H7l2ZeqtHe4rvLANLiiXhWGQKQuwaF6o1zqYV3HFlhEDEk1hshbqBV1f1XZx7jqO0aIVUH3eKzxp78utbpXu2/Fr9OSw4aI4o+sKFT2hfM+DQWkve+NWQVgfubulTl87wiSe9P0xf7ujQ2CVcJKMGqE7p2+eeHKvxsJt2vlUCtgGZOwpSgSJfK20mVvvMbj55dg/VuN3fbhUOpvZfOdudlJe23eVf41Ld8v+16dW+83LZd8vF99qixrZZ4q+vftGhvmSimFEPREoLB0m4wwyBRZGcVq7GIyVG+PGUBA5gxCRkwSrDoEORERYkTIQa9JXfFEd0IChYnox6YwKCtFDDVtHStUHkvrddi54aBqcLRnPkix3XMQf5chEDJL/rzRPjtC7Ze3zzcyPvT3q/HY6NPoXh82yv6+7r5Nvg1EVTDtDSZWNrtjsys4HBghRs+3jBHc3Y/q8O2Fm1d2zeoZwVIWARYgz8pZ0yZuiuhft7gKzd893Vj/gqO1TaUdHEjfjB0a1X8PX23RktWzjeejjMx6kJl93wPKbj0rcPT5cL3kUu6R/PLc/R1aQxppBlImuA8MPqrjCJ/T0/yeEd9U5Tj81jC5ZPBSjRDexRGV92v4qfSiFD2kiyOaOoLLpm3+utGGvl/td6sRGI7jo7jd8HXPjqyWu7FWdiGMB2ejPZv8l9Eze1/q824HUGgfo48f1htwtus8yr+UfA6u9nnB6ubz7vg79HnUFLDJ+xTF9Igm7yuuPZ65d6LiXjt2Wj5ow5jO3iu7NUJS966t40sU9vfTPZjaq/PL2vOl8/FWmWKU5y2wAKxZjnExFX8eFeDf0odHyj0KpyW/p9vjnA+35d5moRb+t4SVrXeunp339+Bgs8+PdrdXFjo5uWRpyqYiY7cU1LXJ0zXHbwjfxWAXzLdmY6DZlEGOHtSf8BlqNIgn4UfjGUQRAWcAE0AnABKjL4SIGMR3e1DXSDFWPitow4ohgqoRwfgSuSrNCyfHA5tvfDNGqLuVIDxRJHXHFFTWjOau24+aDYBVSO0rp0vNKj/nNCNzwrwsyACuTFgy45oYl8sNf/rTJ8yvN9x+ecW76QRKDKSMnBZAN9KlRU4MpNsN6XoD5kVizMVYXIozkQRR5gxmjauR1bVxkpMQebkhzzcst1fM11dcXz/j8voJr58/4eXlF7x8+gWvr696ioOREsBqrVn0JMTldkVKCc/vPuD53Qf88MPv8f33P+Knn/4W79+9x4fnJxABt+WKd7cPyMR49/4DXl9fcT494Y//7V/B+TNyfgEFRuAMIiDGUOEvZyBAAiE7fV3LG2I1ByTTuoEh3eYdjcFYYxJmVdxXF0EFlotrphPmEJEoIDlmkFhP1LDoUkRRTaU9yCxw59q1WvbM5VSGPz2vnoJFQ8L92q5/eP646NQCI3IQmSeEom+R6iR+QwCDOJZY0HXlsmyEVLfJCBpEO2fECBBl5Aka5xBgncNsgalDRATAFASeQVBgAmKqY8wJsADjimvkGIce57D685q/kTHq1mfDo+ri1vGRNe9kYeWdCaTxvwnVhxaXDV/FEFKASmOHDCnCDo1QWDU9HDVzV40Qh3mKBteOXrvn3P7Z87i/Vur5BMPN8szybLXl7Xzh8RMRIWpVpIQlKE6pQn1537WrCNbddXSaYFh378i+FK+QRptT2yGAoMBT1A/wM14RJWBI0IC4BM3Ueos7pp2mjxSK/uqfr4XvRmu2KaDbvd9JW5kLabH1q702pXRjYPWP+3SUid26f/TdQ/Vx3oCFY238UkFgD0/s9tUhNveBvvO32zBHZHkyQFmuFkuAWYiEHYRQ4iuBoTJKECIjf4FEiafXECaAMigUT5DCtCEjJTkRMelR13hawJyxTDNyZlBcGuu9LCsGZQYFFXUKIaLq04/8rxoHVszkA2m1w153xZR22VjCr4VKLOsx0TxQsvu5oCYWgmdWiiqZ8nCZbSnqmz7QmHUblTF4uXILtb1bXjGeWx+s+Hj4HakS35gBl3zwZ1/v1g7y0ViUsbNnXUBww9kNE+vLyH297VVOXGx8yy5PN74eL64MPKqta074bJ6IaHe0+1KIPIMg86/RJpqcQpOBCrce6vbTUNG6UUfTOgcHrTGNJE7MYFyO1G3KiB5G+jHq4XBTYaw9oo4fGeNmruimMMEtWAtKdmuG7dg4ZIdVeT/qe21rWT7G9FLFhSPaX5fbyAhQ3TCVMhVnEnGXt/IKW8oXX1dbp43Nug192/z3aAy+wyp/lSRoxU7qPJ7W/d/ud//d1lj4ORt9e6hNpIHHB20wmC+KnkH9fh63+lva2FYjz4+206WKI8b57ytMj47TNp08NtZfB0AfOTHypadL/ntOXzIuf54xNXiT69fSG/zbhIZfu1Vbg8drJDRI+xzykTSqg3bfotSpugPqNhFpowqvOFRsMPxmmFx4aXeKj1WWyCaPVL41cUDmVpY0ZZbQAR+TjCBhiM27A2FSmWsiMQpEnCBHEUznkx0tSAi0SJmqW8laHqD+1wHA+NoQ5CRAee75LwKx1BW4+thnkOo1udCpTASOVGNTTBEMRipjRWW8qvqo5XPIGmDyXxBVb4wBEYxpWsAAniGi88IB89OC787PuHx6wScmTCDk1xfMIeGyXKUfAchLAqeMdL2B54RJjm+AThGIAYtqrBckMCeEJQE5gZcreEnIt1fkecZy+YzldsHrp59xvbzi0y9/xMvLJ/zpl5/x+vqCl5dX3K4LlgVIiZESY84Llpzxer1gSQkfP36H5+d3+Kf/8J/x3fe/xd/+zX/Eh/cf8c13P2KazsAkmwtDCDiFCb/5lvF8/oBIE374zU8I4YT/+n/8V1z/H/933C4XvL68IoaAc4iYSeMvBFOoq56hXxNsY8gIOWNJDBAjsfAfSUW+pHE8lpSRMmNeNN5kbmP9mY4OuZ48YIXbPJ2B8zvcpie8xidcKOIKktiMYFAGiAkhRDEcWFlqdmXj10uQi/LaGP4qC5Y1qSeYmdW9cDH7FTdiVR6ztYMGQRGg6yXIWJIVwkicSwBlgTFqZWx2vFpAPZFBagzMEg+jGCKyjEXgAAQgpgxQQAgzksovOc1iFMkLOMqmUzFEcvF6QCRunkBqjMgk1xBN0eM6SYJHHBM54kdL7l6FoHqBam/I0j5OFRZ0/KVaGaOcc4mTkrKceso563ba2jSJKdHORzAcZmOvb/aN8z5V+erfY1r3s8pwXzM9HCOiAEyJR7B/NGVb8Kq+4kfftWXwzlzu7RBv21GIHXydG4yA/AFDMYarGjbEhHv/afNlK4TWOrfatv0eWAd9bL53gmYV8LbHfi/tvq4S8+51Cw7Wxd1ryxH4aGfgMIq4A6u/RtoqW1V2m3nJwfme0qwBUlKhVhXDxtbVT1orsldWCr0VGCc9/irBrSv1zCxwF2PUHSkRQU9GyLHeCApJjRq+zS0SK0TaltRKceMIsLWrU6zcS/u78AcfNHXUMedCCMeq3ZHhcVU0DDcEjErxwsvoSsbB7EQwHBkw3EsUcWmgVG/bPjhlNUCbvZLU/OOvBLG3tHfvufVk9X2dJ19GVUa2x2lN2W3C3EYr2/aUMtbrdq/PIyVmE1DL4fkWnvw4y/HYEWn0yse21ffTkP64srby7fXZ4PUteJXUj+6e4WdU39b7egIC8DilCKVNQS0+Kn0ZrHHrv5OBHb7C5iTYXBVcAx1rkkYZbPi66rdjWCLU4JBdd5p59H2vJKMaQhqeyfWz/rbw9bifVtdovYz617//emkLx4zr7Od/9OuZptFY7PHC/RiP0h49QVffqo4dXnBvHnu8v2pCAfFj/Jn/e4Q7+zRWyj8KD9sLcB+2BoTubj3+2iZRLhwradTvo7vZv0b62nV5/mmrrj7vVhlH2zSkZQ/2p7bN469RvqYWfImgvoVLj0s2+2V/jVTLGcPoKO+bYGoz67HFNFakPMQRbZY36gezMy1Qu469TO4KgXtZPixcrPGoumcpwyvi6saY7BS1iTvXTK69BHG/TsZf6O55YjEiqClC/7JrRPEtCCCIJrfSDJgv+QDGCcyx8BR+r3mARTbznIjxG+o8MgeY934/FhlovhR6ZAaVCFCoLntkxFQGWWNxC+XA7GbT+BICAqLSOoLJWAxCQsBTjHiiCaeUkZ9ewTeJGZEuwAI5FcAB4JSBnMFzAlJGOJ8QyIJ6ExLZXEm+kMUQAT0JwYvGhLhdsFwvuF1ecL284vL6gsvlBdfrBbfbDbfbgmXJyIlKDIVlWTCnhGUR5evTuw/4+O33+OkPf4Pf/OZ3+O0PP+Hp6QPOTx9k7EICdLNiRMDzMyPGEzgzQpjwx19+wZwZz//7/yaK3M+fEdnMTrLpJRd+V41UqyVWYTWxBBAPWQwQhOJNB0uGGiLE+LCkjLLxD0ZD5SPKMocm60kKQIzIccISTpjDhAUkboZUzpMTEEFPRNTnrqmwANUCv+3a1AyF3/fGCFucpOK5HRIIPa4w2d3x3syqu9P1gLKu3G+DzlT9EdenJGsSFMSGGIIq1vX0CovBI2ICISHmSVxOxYiQRX8jAcoFqJlJTmMU10xiCCCC2mx0vTBVYxRX10nS3miLbZsfhuI9gnNxZZK+jT3EEGHlG4L0+pyCI53xIWfdeMtes6vNM1zcUo3Cn5uxp2t/m69PI6Z5Iz83l/WLzTq+fir1bMhEnpc9ot+5lx5wzaQnIkqgRLtWhsSETH9tBdAW6EzgLs+2+lP6XxVoa+GmVa71BQSK8gtTOfY3nlMNIESG+JwlVgG9EcR3mrvq34CR3hL86nugjmVYjXEpA0agUZCZyXnk8x+EYzM8rRWlZSLHVz8Ad+sY93lrd+sxAf0xdr0vc+wW5e3lHc0r0LuN2AhAoDXs1ySnIJpXTklpu2YCQ3a0cyWmmRkJYt0vWokQQJwRwiQEKMpJEypzY7vHM1KWExFpSuLz8rQAzDhNM8CMZZ5kDeWsp3aoMNLEKH4/baeODyBhiriVcPYF+Ljf7S7CQigMvtC17AhYm7cQtJTE2q6+RVOy47W5jK3V11zrpGy270uSH6dt5XBt08gQoblgc2DlAiibGrbKDsGYFEgflSkxZnJ0MmLUllbZ7+ojKoIXkYvB0TAtpHU5fAISIUHn0L6FMX/MIG7bth4Pa0JlMFYnIHrFCkbKYmUMqRoh7ERE7AwR0k9UAimcKjzGqEJavW/aRPttLH3a6vUGQzLM3ysedH0/Ate1Dm5p8J32rpla33DHREqmRhDt+Q/DRT19vteOyo+0aWudETQ2D3ocR4i6y8saWmljrcvjyBLLpn4CwG1iCKMTEWUIVn/tpQJrO3R5XJdXsj5C28f85DY/9RiRILKltX2Ste9Pg2upL08eePrV9+nRsdtrS/9t+RtjHFS/c0qlYR5gxMda8vFjRuNzPH0BUb9b7nhNflmZ7d/3+/p1+vc/6omJv2y/K0/xa6R/n/P567Z5RGv/vGlHHrs3Xw5fNn1Q3jSx8cKVN64bZYDkeB6T3TK3O8ONtRbZyuWlAPYxAI0GUIS4PcogCohR/ePHKLwDCf+ZThLbISRSvjJVFEqk8SAIFN2JdY0RgZDA5YQEFZoYSOog8RMDi8lpzKFtwjmR8OUS64GAEGUWAsrzwKSxFuB2XvtodjrUq1msOqJe6cdMSOpyRqIpMmIUhiCZEh0S8Pc0nfB0OuH904QlzZjzFXxJWOYZOEVgklgVIQTQRKDAmE7imviWU2M4Cou4bILGhEjXF6R5xvzyCUlPQtwuL/j0p3/F5XLBp19+weV6weX1itu8iPFBd2svKeM2L3idb7gtCb/54Xd4/823+Od//r/ihx9+wt/8zT/hw4ePeP/+I2KcgCwh0RPLaZbpfAIxY4pPmNIMxBPC+RlLCHj/7XfgQPiv//v/hv9X+H/idnnF7eUFPOmGQxLZSfgNz1drLAyF/WVJYAYuccESGTmcAEKRsZeUkZkxL7J7PaUK70Tm2isoz2GCqMwkq9Kcpyfg/A7z6QnX6QlLnJBCBDiK4SQnBGIwZTE0kKpDirylMiKpAYEACw3NqlQpHohYY3zA1mPVrWRVwgUCuMRN0fXAppwxHKF9KEqIDpa51gVmhOxkXmYAuYK3ukZmtlihqeRhZHAWjxWm46CcZe6y/dRbRVkjYnhUJRQIk8j3nOVEiTiMUqMAifGg6Be8IQJq8OzkMt9JNRDI61wNDC4/F28OqsNCKn/DdJ12y4x5XnCbZ1xuN1zmKy7LjGmJWHJCDEAMYmgtfLJj5GuYt6M8Xukp3kwf/5Ik71CyNVNlhy+l0w+fiAjdSYhjgpLt1r5jrNjtS7tw13Xa4ut34Sp4NS5exjsMJakVkrTOBpjqvQl4It+4heb+M8J9fJx6xQA1DI13hzUqq/V3XbXQWwLkbrJvNhbTsMyGUbtX/LgPXtjYum6Vhd0W32/L1v2DpX1B3S3yamFh23+/JF7hvjXktgaIqiy33eBWr/1s54kyn2zzWn0rZhCi+goNMcrpiBDrKYlsTGrr66/tgq3RpnJ4ZdJKSfJGJL+lNPa7M+1syAq32gNj+AtDmdtrbpmJlcK9L++hNm7nA7ZPqK2Me8E3ZCz01fHv4E4mf3OdsDIEtTwxSliVoeTj1bU3RIixquL1Un+X3+eF64u4onG+RTuc6EZO90esFZD1fo2va5+PEWLfB0JbXnCGCctbxqNs46pr0BPM4qKpov2mjd4QsafQGT5/wGjhPkKFmzp2jyTpvxmMjPHZb7PxFZYCbeddfdt8WRu+RZ/vd6BtiyUbmQoKa1iAuw/koLIjt0PlcSmv73uljhWPGs/i2jKYqzXMSC+2xmXr3s/PKM9YEb5X1nay98d5ZCprbq9to3sb8366R8qrIQ84qOcIzzgqv2+z9uxOG3bqdvR6c06wXfco/9YYWVvelPyH/WSUe27yHgENGuRvsUZHGwflWvVHQyZaS12LV6mn6V+Stsr6Gpsi/tzpa47H1vO9Oh4ds35dP5q+9px1pW+RsabuI+PS5z2S70vmktaCBg5reWw5D/Da6O97faq8PxVlG6MqYM1FrAVcnbMqN7NsxEiqoPWKWZFBRDnKzjUTU+wZGRDZ/i7WExHiFidQQGTD+SwGCIoIAQgsgWrdzindYC2GCDn1TkDQTZ4xq9tWPQdBwXSDIEogBFAUFzAyLyTHM1B536zBjAOr4cI2TqC6H+QggYUDAbKzqPY0wFzD2sxx96/9tcbQzLb5Uty2RK4bOk2dShDldCTCFMRN7cJZTjKYdpogG/mIXFBuMbwwyzxySnLiIGdQSuKPPy3IdhJivmKZr5ivL5ivr6L4v15wu10wzzcsS0JKJrFUWEq2cQ7Au/cf8f33P+J3v/tr/Pjj7/Hddz/g6fk9zqcnEBHmOUncBdPDxQnE6jI9RZw5IQH47rsr5mXGjz/+hOV2w7/8H/8/cF5weckAovYtoWx2cKvGgi5bG5NEE5aTDiBQEl1CMbQlUbjfkt1X/UQgiAFMBhjGuVbeWICcYwTihBTEAJFDBIeAkHWzD0g3VFY5n2RypK3M5tXHvfdyu1vXMH2BtJeyfJBVFrOTSXZQwMADWHtiKOqF5mYtI8PJxHLvFfaof6sRgBujpsYjKd9wuZJ34c3Q0wi2ZuxHoCIrq7u2IGuGTHVqG127sfKyKWwcnN5J1q3bCFjchbvxsHcmz7tZaLgyMjwgRt0lZyxJTwrlhMRZN+YaPwi0MR+cHsBK3uB9m3aZHsvJRncpzp0MRZe8qmvnmzu0tnT7AHkd8xdCL6yFj7RtlA4bIqJaza1he8LS+gf4CbK0+hZYKcdsIdWHgBz/6supCAtwg8GCtIIpS0OsJyKswFKUV5NlRULVqui1k1WI5wqgWmpVCOjyuCNYtkEovYijJSryLePY3Lucrlx2q/5RZm6PwRoZCtbfHyt/5HLCFAH++b362jzBk6bNRbFV1peciCBjrt7yLYBsFv5Sni9XiJmAKzUf6ioBkFaMczku6Oqx/PKYCyEmhgZc1t3ZLOu+HHFltX0rfy+7RBiZZzAWpLSAc0LOJ4AyTukMEOM030AEpGVRRq474VDkhRHu0Jc9DGwM80rZv5H8LgsrkO1DrgS/UXR3ZeSUMM8z0rIgLQlplgBlxVehIwbrMnizkUcQuYBah+vc33trmArJracTvjSNhOgyhmr1yFnd7ORQxta3b+va52VgGH/D8pZ8XOssJyhYlNp2n7Pg+XJcU+fen9qw+xACImTeuTmlgybvGn/Z+NRd69GdgjDaWk9GxILPW0MEHDOXmzUQbOXzYGlY+w4I4UO8aKd84NfpOpvtkLBKC2tIbzMbElHZaUREzZY3M6Ta+BvurcyfxrqhsWHu/8/dv3VJjiNpguAnAKhq5h6XzMqq6ev22d0zZ/dp//8f2p2ZruquqswIdzMlAcg+iAggAElVNfeIrKxGhDqNJIg7BHKX4RkGbKDXAUEfTKPdvn8kGDyCFUM+KWjAFeaYIZZ83VAEkDG6o5zhpQSG3J+hBjPOz+2zWdJ6h34/cxbvmeX2XT/bHtX910syPnsE/iN4iL0/PMfulnU+J0ffzzgjP/iGDs5Wnxfgw/dtXHCMGw17Z1fmt6YPfOuYXVL3/lg1BoDtufaeXP7dhqXDP+c62N3f63Jrw9PpaF3QYY7/FdIze+rfQzo7Gx6lPT37N5QOm/M31sa/cno0R1zEBUg1xrPhkUXwmcIicDA8NGdRYKq1oFTgrVTJo7REyUUtIhSnBoONUe7rhQgSKEQ0t0vSYLVKCKrQSIghNdzDzggQxBULqeIjoylWcS0C76PgKCkuEnw5JoSQEEPSYNWGs1igaYL6hgHFBRptGgKAY2tDCAHLIvyZmKIISVTYIcpuhEuMiDFgSRElRqG1org3WjSuIKCWGPMe3Jm8op8bYCy8NrybAKCSUtUASKwcUKEugzas729AybhEYIkLUryiLAE1BVCSWBAwCxall7kUccW0ZaAw0paBWrCWFaVs2N7fW0yIfHvD11//Bbf3d3z98gtu6w239zesuUgsBR2/XDa8r++4bSu2bcPPf/wTPv3wI/5f/+//D/63//Bf8J//y/+OH374I67XHxFiAlNFBaNgBaOKKyombJVlXq8vAFcsMQLpAgBYQsIFhJ8+fUakiv/+3/9P/H9DxbZVbFvRNWUxE6gJbxpuzmJhUFTgtq4ZIVSsenDaOq4sbp6K8qCLed5hhhioSLwQJqF5IonDLwCiCJkWhOUKvryClwvqcgHSAlBEog2RCQszIliDUgv/jpk1zgWDg+wtkNA0TBJLM3ZGhe41NAFLZXUzpZYEpSnfKYZUVXM8dL6h0VKdRXNATxzQouJGq4Ca9wVxrVVVgMAqiKjKuyxFYYd6cKhllT1dMsBVA6NX1E1cgvF2U9dgG7hmdStQYPwl4x6IpYTAiIAEogomiR0RLJr2jG+xrBD2rpu0T9bfPiA8ChyMD6T9PdrHcGNucLLkipwL3rYVr+sN67Zi3RIKF3FPZbSj56MeI4VPpr+ds1Ho1dO331u6Xp93wX2WvsE1kzQgBCP80a7nBJgRwSNDYkeUTfStEUiyFvcasSMuIHlbhJN2Ff9mZpbY3L/YsmsH9UhsA4ByQGwE4BfmKDCY2mEbBhjGZTdexkVu4xdcn9q2aP7lrIwwjZu1YUfctuF6fsEZ0iL9nzrn7s+Icjqcm30tIwOCDqv8JgaAf8Aj0dhr13/HYepvD58/kyaI+IHEDsC30uaxxnhvdco2IcALMvTwJs9dd7WZlovw83gqrzO0AhFYVBFAxOo+xMZVDgwT8HnLiFCjmKdWE/4V9TVoHZsFDa6/JyN5xM609TJr0j97hiiO5Mb3uQ9tRNkRC1UtIvaCCNV20itsTR4E9Xo2kUyJHrY9mcshg10zYSxMq77L7gnqOsOxHzTtuQx6yzt9jTaOZH/TUwyb8/6OfTG40f1ouvp8O2FzYf5AqZucNqEVQ3xgVtTaYc0zzMTnYOv+LOgMY/u7u2byz70gwpjrkgTxtzPE5BS7mbA1qHmf1aQYmt5UeTq7/rjb44FxDK+eT0QCEc0/sO9c1TN+HlP7zrr5jGBZIOdJGw/O0Lk/O0GfgymPyqR29eusZ2qoRNs4vH/X/u6C3fmMbczm3fwY/nPQwAfJ0Kye/XyMhvsBR/B7qJ9JZ0umj8+TDbQ/jbDxONxBXjroi2//XVyknV96vo0j3K9HcMS+eAB3xrXh53tsZ7+3rTudsSdr5EgQ4cflbC/PfTtrz720Az3Pfjosn3E8DjPR9GgnvT2ApHvAimGB3a3bZbL3h/Chf9xPXuwtxU/q2MOhOaO9/zZ4/D2pMyOOsDh7db9df11hxTS/APYE0ZRlfjXgK/vMHp+a99xw/wBNfIYB8HhtHKejUZDvW8lDeXull/6v5ObH/eK7t4dt9G0Yvtt9PPaorcY783hWdivJcHATOEC0utmCo3JXhBFBBCOr5UMpop1sgohSCgoz3rIJIgCuFbkUpTU83ooBIzS6QtyNAKKw2RUZAhntJnNQAwAKEvNB+8gACnWUDwzULMxCLllwsiD8oJQWhJgQkwkiFiwxIEVqyAlbJIGggohUQRSBEJqAgkCgKK6LKsR1dmJuVwoBNTCiWuUzc4PQpeFQ4qUpxuBOeWNoTmsC+kFT1tBxU+am0eEVZgnh4lWwuuTVYNTE3KyYY1ThQ6BmESFjYLg7C2e9FiAXUGUgiyCiloxaNpRtRd5W5PWGbbthW0W4sOVNrSBKW1NC5hIKs6wPABQjPn36AT///Hf4wx//Hn/84z/g8+efcX39jBgukLiEW1eacsudrb9R4kGGtCBxxfXyAn79jPzjH/D29Vf84Q9/xJe3L3j5l09g3JBzRZtpxdm78fJ4Jhq/wRTAUApAhApbD1ABm8QTac4FKoOCCASCPWv4Vt+jRAEICQgJNUTUEJR/QSAeo5T0BdFp5SYwol6HkLs00F/crmZVwbr/7WnHNqtbQW2TWvmHTDYbKLd+/b0y7ttPvTE0gaEy9Yt5aVBBhFwrahVhmAScrmqdYwKJDFT/U6Y/m9vi7vJNUKC+16ExQ3dKF+z/MBseNHhpQk7YOOq+JetnS8EX04ueKyPyensi4DX32Q0mK0+mzcoIR8d2Q5fxM2dmxx0fnVv9rBxPyXY8utfzCjlvC/tMU7umlj7bnQP6dqix0U7H1uTPpOcFEenakEii7jvNE9Ftsmg8uM1ncSd8OvFr00Z2GvikRYTxdve+pw4I+goTzQAyBo/5fHb1e+S4mTjWjrAQsYAScouH7k+OlBmaOWHr43Cd422Y30TLH1zZfexC8zdB7r3m0Qeiua5g8jGeukteSOIePvjIxvEY6TVthZaaA7Z+nWwC3OsOHTqj4rxBpzqp8+Y8vB+vJrDqhZ+V3oHQU4nGnobx0UF2apCXhrYBhAgBwhLoi1FReUPihMAkEnRDpKpYX1QAWy1i0qmHldHkC4kGCseEioIcuO17Q7yYVcKerqgMLFWQtqrtyLmAQYiXDdWQUkWeKhMQFqgNsJjgKr6qIXthwbGJQwum5oF8hYMNhkjAzimbIdN0H/0lMrJNpSaJEWFChQ6XRAADhSFkWL4G4BYNdpLzWttkpo9cbe95M0zWIFtiyjmvA8nr4NhJMn/yuzVipcw+afwa6lXBhEn3QMS81kKD+fqWPEwlmCZCq2YS7noLt8FaxAmT5rb29/O5qFYWplGxa7zMHxla0r7X4zyQIjyqBaMxJKgG8d2q5xoDqJkFcXbtC8GE23V43ttmY6gaPCAsqpWWQkQMwWmSJTmnLJrgAONEh6njqbrSddybRYRDUQRU9CBe1pB2JpyCq4Zewyhbc63G2B19HXw38o9bGwkmDKAdQtO/3z+3pjGS/myOZA3E2Ilnu+4YOQBSiMOInNn/HHl9CmRwxXruyqYe58bWnSlnACoArlX1ooSctfZF7i4WTRsxBGpBJJU/ADsuBewr3Dta4mRm6xJHqAnheI5PQACN1qQgNMKB2zx2+CJfnTCplWC0EJehne9K4BqBMtTXz3oa2tamqF9psghxGQxXMqFdEyTpWqdg+8fM2Esn4KwM+/Wtoe2em6yjYAydyT1pGzNSDVPF4cyVZnOp6f4bz27Suduv5b2AgN3zYRHs22TvCRBvHR1/t/dEYx1jnWjr9CzZ+ujj9Fz6LZjGXjAzFndGph2Lhs5Pv36mnbe2ny3Hueanvc6Jzj0t/7gHH0lH/fv28R/Olw+24g3fQ50AAQAASURBVKzWZwVYZwzv3yc9gUO1fLavLYCm4nh19JE9AjhAApQqaLJgpTwqspy35N9P6qBI52/37z4/gRRL97uoPrlv0ODXkJcAccFzyskyKHlaboEIGaq6YWF4S1r5Za7ItWsh55xRakEu+j5n1FqxFb1umzxXOiyri5rqgvV2Wr6fR42f4SzkYsiIIYllbVAFTASEoFiEait3/+0KkbQOYSszai7a1k1oGVVySlGsFlJKiDFiSQtSTEjLgkihKaRRjAhpAYWIdLmKYpq2mavhl8LepSg0Yy0BHIBwARCAuohro0IVNTBqrNgCYU0BKQa8LxExRaQl4hoTropLC96geBkZJu7OCUbj6ZgrGi4qgIiiJV3I8AGlBd5vKLcV2y9fkN/fkUpFoIj48gqOF2xxAWm7GI6eYUZR5i+vK7gU1HUF14J13YCaUW//iryteP/lL1jXG3755Res64qvbwXrWvFlC9hywHuJyAU9GHXOuG0Zt1zxh7/7D/jxp7/D/+2//e/409//J/zn//r/wM8//wmvP/6EZbmKy30W6xquFVQlvgZr/OAYAAoMrllolbQIZvcKUEhgjmBKCJTwcv0BVAj/+E//F/5p+7+Qi7hdokBYEGTtQ2MvQlxYCd9GkA5BqcUCiEHIJAhsShcEAhaSvXPTOBFrAZIyfmKoSFB6g4wuKgAt4AjU+Akl/oz3+Iq3cEFNDISCwgSuESUUEKoKGBwUUua0WVyACEEtIox2C2xKS1ViTDga2iPnfWepEEJpoWgxYdjwaoU5jdwyBrwKCWp320UlI3BR/oIJCJSpXkXA4K9ZhZwlS0wIE3qiiiUEstaxZZSakdd35Lyh5jdw2cDlXSwissT6VIAnljgOQhp51KF5VeWxTvvUKvg3G/3cPBDUXnajs3QuPEwmamUJNCOLDGEEC0yy0GhXFXKWnFG3DSFXhCJWZZkJHBJAEdF4Z1y6cIKCSDYtGb3dGoQxeWT7w+kYM2rG/BPP41ENMw+cTnhBve7z5OmFZ1Cub8Xrn48REbxrpk4EmCBiIKxmpDL0vL6xnYHRkYTDuj9E4CiS2ogtE0TMBB3gmQNGpFUSiakAUd86j0Dyrq173NSYdftYGjsGnhHTzcrEiMoRIRoZ+ufj0xgI1uxvWBvfuqD6dzzcz8S8+2BijIyk4lxuF0I8aOdpv2lETg/as283FKj5np2jz8+mue5wwJDzZRuDw6TQI5FMEK1pW8ncfmYgCzirAdeX6pEm17bOgLL9Y3tZED2JTcTNnUwIqZnphpDFMqJ0l2g11IZ4cuuTtLUxRRoJsicIWpsaMTNrifenAAaG/p7ZbQRE39/syuhHbScyB4aN/nYMuglcNCRlaCL3dxhXzM6y4ySdLe82r3XaKK78s2f3rCPA/QpFzNjeOeSyMUFP6xzXmZ+Te26izgQRve3n7e+Pu3bSkNM4AX69eRMDm1dtPw7mDTYWu0TDX6T5xM9sD05tV9lbUWqZzlJpoiH0I7OiMxl9fSZAZ3gOPMG57jsFV9xKkHO9YyPk1vfQ745ND+9afJiT6T0aNj9WDJ1/B9MsyMnMHJ7L8AI7xj6goT0/GoeOs+hYcD/TZqHHMBd+gHZrcmL4tvLGc9tgre9L229TG30eD4KO+jOcb74f1AuZjvDO7PBwbupT+52tpwMc5d69fzbjFFbcfB4QaEQQ2ti7daPP+6x2SM+tmfv+7XFXN4cOt9mtjQfftjLulL0XFPi12Soa2mn9Hs5Vcv11ZRwLIWhYC/fxwT3sOfrm3hyPz+5UdVT7PBYn5frnw/UO2rVfg5bGtdiv9+sdnu3ynLfD1/stgp9vTbs6ZoL4iSYYDB/IqIM6npvDvn6fai88XnD3wJvK2ZVyL/fJ38+UYWfLBMt3e/ug7AmXv5fOV+9JvgOY+93JlSk+02k6HwfWk99hwxiQU5xpx9bpXhiQkXYxN5JDHdO/Qync8SFztVSKuW/u+KsJIrbK6pe8oJaKLW8oRe6LE0SseWvvq+VnVUTm7jLU48aGjwmuKPhVcLiJ5BA1LQI3L0iVVfePR7zbUi1Z+4fGsDYhCUtjxEI+VqX/GBzVN3xUgT9FcCgIcUGoABAQksBYUo1pc6ZD6PQZVQaIwVWpQxNUFO7G/mAUUldPGjtA9dVEeIEganAEREKPach9Ce2oRe5/iHBEGZzEyEHGM3AFlQpsBXXdUNYVnIuUrwpprJr3dnY2NzMa1FfcmxbRPi8FXDJqLahlE6bvdhNriPWGvK7YtoycM3KWeAq5iGArV2GkyjpTC3wQQlzw8vIZP/74B/z449/hp5/+hNfXH3G5viLGBaSKg8a8Nvc9BAebde004pIIFCJCXBBTwXK54uXlE3744Sf88PlH/PD5R/zlz/+CGIK6IAMilNvQYL2s1cpGz4S2ds3FOOucktVHQFSzh873sXgofUuzm0Tj+REIlSI4LGBK4hZYJVFMWhe5dcDY8RC4lS/upKyi4NaPCFZs/8MI0NYuP5QMpzRpgL5p/7RG2MbsX7R5slgJ3OuZfjMdzWr5INfc1oqsRVkHpAILrrlZ5HDN7QdWiwjTsmQRUwqeaWPBOlJOsKk0YhfQuD3g41IA3fVSkwAYnBvPgt05pHjb+MYeGNWqV50XU6JtRBIInq8319rq6QtlfEZz1nYazaU8kSYEYG7Gs6XwSd6TAh4KF9wA71DB4cz5vvS0IOJyubRKDeE24qNL9uZrH5WZSLf1AJgW/J1JOMF4z/rP7p/ukumIIJzLlYPWE7BVy9kx67wGrLa/9VnrMDO1fb3HlhD9am3aCzHuXX3yfqK/Jd1nJuK03qPnZglx2m6X//uX9PmYHLft+P54bPV0oeN2muuvu63z9MVUt2lSnRO0utKO2mbmc+1QDydlHKfOtDccRDVOlcEXa0QgQlKtlhiCHGIcULgi1oIYE1JakOICrgVLugIALnmT9cii4dP3uh5qwblNaxZLZDjMsHeldfu+tfWp57h3yzMi3eqjUPtriNw4XoZQ6r4GQAduYGKMWJalHaKmAV6JBOm0ep2PRyldWapVkSC//sm547kzV2fJMxYPyd5vODxGFwOk5o17JrBHGs/ba4hWf2fv6zROcxl9je7bPsLn/bzP/S6l7L4zjTZGDzw+/1oedhYt5yMHOYNGrW4z407LghgCLpdL0zCzfWAr9WjcmiaJJ6MnBMQI57aik6KNuzbz+JchkBNzhRCGPXYM/+TFXEfbz+FwRbY2jAzcjgMx9vPkY2QcM8f1nVfzP8MyThDKjuug1Q10LX27n9cSoGu5MSqOcBdfxwkj2KX9nBhsDGpNoUwJkj4GGrX2W18OxowOnh3BiTPGuB8fmefzfjyTiDo83s+YF9rIAXE0fmO7Htd3/71cZ0uI8Xp/Ho/uH12PxtqsYfc41IF1CQjmhqPjqMdtOKrLFIgejdvRtn6Oqfzx787a/K1l2PUefnvc9nFsyG+uv0L62L4ySPrXS4djbngz84fnTJ86+HRUp+Q5astsYfDxZGN4cs7YWsHEQqF7PpoBTxsR9ThRx/XvPu5/36/k/N3DfL/N2tm56yD/R8crjHavxpDScytoPp4/x/294M+xjr9I/jqPKbVmyPtqePqxwCGrtUMp4v4klyzChpyRK2Nz77bcNdhLLVhzRil2Lz7MJWBv1XFQeKKcJTZYhx5Hql0tcLQqsRgzMEL96p/wuDze3QQrtWLLGZWraM4zo2y5j6HGN+PKGgdDZQJFXLzEKMGBl0WGM6SERIRF8d1lWUQpjWU2a+ERt6mi58wlg6tY1xMRKAZQJUSO4MASO0CFFsSidZ5LASKjpohU1VM8eZdUx/NtgpcWv0MXornUibUCuYJuKzhn1PcsNB1p/ACy1VRasF9SJjCXDbUUlLKBS0FZb+CSUW5yXdcbal6R335F3m54u33Ftm643d6wbRve3r5i2za8v72L9cN66+tGr58uP+KPP/6E//QP/w1//w//Cf/xH/4r/vCn/w2fPv+IdLmiEoPrhlJWdcGz6tjpAMVLG2OhTiUaAAPCxF8WRFS88CuYN9TyM3798kf86V//hF+//Av+9V9fcLvdcENXMiSSYN9V7w1HCsuCECNSugBE2ETlFyHIulguFwQwIgq2Kg6bhJ6Dlh1RiVBIPBiYhEP+E4VHxATEhEtKuKQLYiKUAIQNIFRkZDAqku70oHCncya4BWo2iwiAUDUeBbt9adY0H4WRBIyCMqiSZmPcK6yB/dRCCr2uPe3aLSMELsn+zep6ye7JrC2yrGPeNtSSJdZlkTiXtXRXT1KJCRBI4ZPRk2bpoPEmuPeDwKj6vtYs576zhAKruyf2kL1RfMbJA5nbfHI/Axme72O8N52PqvyYS0p4WRa8XC94uV5wSQuWKOswNJhgGLK2xeN2eAaze+wC+N8kfRfO89dLzwerDrET83aFEYTTc0MIyRgx8/uOHHQCCYd7+Qi59ITzWWJdjGNciMfEhWiVe8TypA7q5p2dWTm2y4jlfd1GSJ1d/eZ4jmjdt+97Ee+eztHv8zk4ItLO2z1iqXvXH3T4t307PrrfZ5rrmu9P2thl5ucis4eMF5q+ne+nNhy1fr/PLIk3dSZDwGw9Qdvvu8l6WLi/9bkFQOvEkbq2aUICf5XgUiEYEqyxWJpmd2ixI2qU4GMHMgTXtykdrIM+xoao90PMm8LaWWdM6bFIHu7OkQiDT/vm9WOrvyQi6TtXEELXYtoR2f76jcy6HUyc9tRU5CPhhRHqTwk5pnT27ZmlBZGfmzmv/97nsXn0mnLcpq4tZZ34ygdXmAXnXrA8CC1geNKBFc1wRbu/nwYA05kOjvHQglST7KeKLjjovfZtHceViAe46edDeEBywN6bYwKcoo4/3zqzROb6uMttW06pMVYOLSII4suYdk/v7orJIuJobfoT/GGw2JMz4PBoneC8BU6fMh1X44AJKYD2cKCVTWOfjqfs5OyjzsA/wj3Onu/OL1+2tqm1y9oI8oVaq6Y+3zu/px65NpyftL19YxPP8vOwn8/qBUarl/mdfz6P1R7f+b7r0c/XtYf3x/vAz+swtg/q7M8Oh2v89sH7s/tn8x2tn498c+/en3332nYIX2ac4AhROEkjfN637RnFn2fxhm9AL74rHY1Zt+47t+h4Bk48M8bzt35+fxuayM3PtO+tLvv1uuezd4T7R30Yn99p9xmneSzwcbcO8525HDv7/DwvHyIN6LgEUWfw7YaXd9kf1d0Vf9xzHr+fcUllnwkjujoGH3dLiFqqEx6olUMpyJsw8kwQkTWfWDxk0WrfTBCxoTSXTKLxztyVcWYlRESNpeBcL8oVCGohHyzY7skAHZ2VA22kfTSGJrdYBH3sjbZqhbFYElTUjiIwUGMB1aDMRhEkiUayBss2pjWpy+AK1TJXRmwtqMQI1XANEq12F1evEoMLoxKL2yYwCjFCFbfUzdVxsLbrEvOTrzQDM5AVRyjmJsb6XgqoFGDNEuC31r7nCCIkAkDc/do3DXAV7tRSVNO86K9bRJSyYdtW5G2TtVOckErXU1UGMfu50V8MCdflFS+XV7xeX3FZrljSosHGWSwwwGLxYrEBqu1r21EdxzFaSh0e6IIR96wxBsSUsKSEy0WuS4rIOSCW0PjyHd9W6wjlC8TlIoKI5SLzXwsqARTEhdeSEgJkDqt5UkHH3QozChNKNZwOTZFZeqSOe3SdNSUdgtLmtsep8dV7n63/nag0l1ItdoTlpcZgaNcW+wCt0ePwsq4VNjHjCJfafjRcFY4ePYCe/jwxvsdMs8pe7jDMCwrmddSU7UwA4X62vtv+txY5q41uvdHpZAvW3iycmtWEDfA8dg7W2P6F27cKCywYvcFATMKDVhQBKQUsS8SypOZOLsZjxR0Qq/IatcrbKeLXyjQP7fvD5x9Lu+94P/dPfws43uVz+Yf3E2ox8hzo8Pm3pKcFEcty3VUOQNwHsF84M4GD6eqeGwC3eT9YS/1b2t0/N8974sunHbPMAurKwxbGoDOgvG9qhgUMDfO4EFn4nVOib9Yk3mvYPWcRcdhrwsCy+3iatE/ujPVufvT7c6JxQrJ2FN3oe/neRI9rgRygtPfH3x4SQW0xHoz1gcTTDqXe/36Y+37t1+++TYQTheE5F40HWCs7CIC3Q5ZiAlGUsfRIJ1c9hPvBxKiKdGuvGP1INx/rURBdsYgISDG270utWJzGeC4XMBeUKloP5bJJHIUsUneyzlJFc4QuGB24ahyL1j7pX2cG2XwcjPeQ7HA81o4/Q9jPYJCMjPij5OGw3adA6ldSGZRmgs7ToWsIxhkBtavfwSpD7Ie2u4O17s6yCc6d9fFBPtK+eMOfsz12TzBBtL8KzBCLA0kVzYS+abYrgmDMeBtLK1v93HotNtcClCLwe7a+OFobXOfn1g/fn70wZR4vO+tA/Zn3sduvl/auun7JttT9Pc1Pv3b/mYdnqPbfgON+nk82A0z3xTHOpv52ON7Ln8cAOAfjR1ZktrMZaEKkYXynus7WYDxBDmfh5Gy0MDNhPTNrtoiw93Zfa3XEBnawwp//QYmtTjCRBJo0ZNvqxjiyndnlLCG0TI+P7JjKdA9HO2BWC1ge6u/x6ZzVHDmBE0brsY+kuQ3j9H2b0Nba9NHUx2EkWmaLCDubZmb+/LO8x8/RxszKPqrTK/G4hu5wyX6VdRtOlHHamjlqY8C+rnmMcHxePiRwTnHD+/jaWR+eKetevjMC66xNfq70Cc4xh+N0XO5xG599/631Pv8x7m6l0zFGd91Iz+Q/bePH+/9d/T2o28o0xYipsgP6w+GtNJ4lR/t9hJu/Vdv/NtIj/NPG9SNzdpY/NOtSp8yi/zbeGDqO1egXtWauufZ4Dlxb/IaSVRCxbSi1YNuErtka47hocNQee69koY82s4gwAUQWWqcM+Go7qBGjKKfEmNQNUJzgdkVMERGEGDvPADB3uWJ9G9T9p4yv4LA21rtf5Rbg1Z6Rzo25N4kkPvMJgMUKBItgoVAEM5AqsKSMFBOIa+eHQGkkQLWbudF7hSV4MdcCooCaizCw0yJnXARApEzxClRCrdqPVB2uaDG+gFBtT3U3MJ3dSU3TfGNpd82C/MfCoFrB2ypBpd9vCMwIXBCizA0Tg4lBqAgWa6KSaJXXgpI3FSKs6pppE2uPfEMtG7b3L8jbii9f5Pr+/i4WEHq93W4SrHpbhXap3LXwKwOlIoYFl+sPeHn5Aa+vn/GyXHChCL6tyFtGVW/6lTMsZiIBSEFdNpUMthhw5LhGmq/xJQTZQ4wBaYm4XCJergter1eJH8LdXVQhdfFFBKaAeHlFSAuun38UV1EpgUF43zapL8r8Xi4RVAuwveGNK94DxH6hivXNxowtE9ZoSpIBiRgJwIUDQKrwiIAUAi4x4BqTCOkSAVSAuoG5gIOxi0z8KHYgQWGFOGjvMELiUegKZmUUDIx15RKRjhl1WsnWHJP95CCl5sPK78GZv6C0jumGHZ4TaPCjzYHFiHBXgAFz2aQuwsp6Q60ZedtQa1ZrpIJm7lQaMSxzY9YRRo8eBc529w3gaN1nCITxRdrJN+MGwcdt0LFjmTsrXoZaBYkEhEj46afP+PGnH/DTjz/ixx9+wMvrFZfLRVwiuxh0LP4CW2vupt3rv9FzWum+j1M/Z8WdK8l8jzDi+RgRFCHz5ZEx2HnZJp6cgGAmsuAZxu17lfLDlePLx1hnY8TaddfQ+dby+pfnAyYBw9hVPhMbvm0CaeyQ7u/6txJQhxpDnQCRzOrAtfGift+fHxBfj/rfav4+iwjzsfZcGpk2MyAZ33smQx+X8evpnnC3p20dDbX7z88Jvt39Qdt6ucet6Gt6zDN879f9QTNbXw5rGDoz5nLroW1CqBjBNp7LLjk6Qt4OiYExb5CLWhmGhAqDwh+AoQVF69fQ7kOoYgJXU4sTcTAb2ippoTRn1kQfv2DWQ/7ugM3rd2aUNgxruh/zdAIBGE48+Db6tnXGqddUsO+5Xff762lgTvs1PL2e9pU+/44Do8EhjID6EdPE0hET3RORdh+CjVfDvBoBD117bVzruJ5MO4lp2kvyEEyGRB2319ojiOdRv6b9PZwJd6wN3HEyMBwaMtSRIgoBYSeIkH/OBRHyPuxa5dva99IYY6JvpD1DzmAFufGRT3ZMg5Pl2NfNnXE5aO/RCTx1aFfHvgw6fO/nijAK7gacgWBUey/T5g5tdToQ0jViG4I0tWqY/3av5Qb0bye4/YHjuOMaAw5xphxwhLNZG+7MrdbjYdHRfD5iCJ8xl9t3E5y/C/dOYM6c5ufGoDkqr83NAY43MsIf9++I2djrwC7fcTn7vjZc4yDvGS55Vse9Ph2lszeP8M/jtfj4PLk/NvfLOsp3xMh8vk3D3WGej6Zn1vfHcPt+hj5Tx902OUDEJ2vjaJ+YMJOmdvR2nT0/bM3h03t4zbfgPfsx6vhiOxK4t4eIOn7Xvt+frffX7H7s5v4ewa577++lx+ugHWwP3j/+/rhZNNXwcbp1hs1uAvSeWv2M7nLJlK+q4uLmukQCSJsgwqwYemDpUqq6YNpQSsG26VXd5ZScOzNf3S2ZYMIEEWYZUbIwz7Mq0BiWwU5wLAIEsbIOUAZokPaHoIIDzzeBMWkni1tl3IoODjvcYxLE4g6qYfvf8O/2nMUlLQnWXkIBBR2Ppm0tzHmg2/dKoF0JZluZhedJBpMDOAJUJXh0YImdJvwTQEzyK6gEsYiwcGhKP3onwIZPE0b0n8EDX9/WA1VogG4GGzO2dppt8NrQaEJqt2L9oHEhqjFk+49ZLCNKXpHzim3bkPMmQgd3zSU3IVXDtyDM1lrFamIrGVvN2Krkz3lD3laEkmW+VRAh4aN1HIjE3VXgNp5CG3WPCObHn2WzwLTe2Xz9o2o8B3HXlUJAYRbl5BoQiMHKE0jXK2JacL2KQAJR3HNVCmJ5EReEQLgsAagBXNfmBtr2gQRvN5oaoCDxT0TZQheOuVwgCw1BSKTufAKBOQAc3ArsK57cr+8QR+2r8KHxUBz9YM9k981rxPEVCA0O2bfQWZn5BSYk4aGSPQ45wz/jn7S5G+hGbYfjr5gVBNvVhA62rlmsmuyeuLu3RhOcuNgPw5X7/mh1t467pHREe9eQC3dP/Z76eLcBdbcENIHZy8sFry9XXC8XXJYFS0yytpoQYjynx2a504n9nPl3dnsPR/7AmbYDvvdwoeeKe3SmnuIM1Nu+Uzycvv/oue3T04KIlJaxfQeVdmJIFokhmF1jr+UaypifB9ThfWUeBvMeMm5t2N1bGW1B1ZHpBCgTTN0sBGXY8OgCovsCqx2BhkOwD1wiHbabqAXrIRekmuAPWrpzJZyubR4B4sfTXtv6bu55XieGb+u3OyTmzeHLYAT/0ArFUYdHIoZUUfYo32OgIdNimgGuzqFut053baKh7meJWfuU3PyO6UBjeLeXqqw9hgjTLO6Crk72h89wiBiiJAGJzB+iWYC0mWvIrGgcUIi6lypiTIjpglALIlfEeEGKFTUVEICarggI2C4rQAQuue2BdrboWSAHY3GmgmL2bPu0a6YrEVHrgWsUj2naYVg6ccAW5AsdPWVbc3CYqkna2ZXVi2fVeJp/XORgbuaQc+wDNf01fYszQvJo/TwiMk+1wyaN2TkwdGMYTAzuozykY/Kh9T218agN9m5AkCbGuG3vbmo6CoOYxUdudTE62rcsxKW0fXw/1GHM5EqyZogEqSX5LoSA6pC/xww3/ekeijGKT98k1xDMXDTKmRBj+7YLIs4tIsY+yJjuLCOm/cE8rcn2fBoPiK9cHw+DJOt+jZxYRPjvjpm5B2tN28y7tt+va2bOxtn6TtM8jsHXQX7s+ADhNMKN2j7gBjsZRgKLMNiX18/5ziDQv2NAiNLeKNRVNwdnBmqPGbKfs7H/ROP5PTO892M2fvsMnjXXNxNDZ588YiDv6rpDHzxC7kfi6/HzozbaXNm8AXPcDXvemT/zu3lMj59LZ+fnx5YOPOQxALMr03535vXefPt1cZb2jOXn0tl8n9U1t/m4vffL+tY6z+8BDGf4eIZ+JD0+Q87xyidKxxE+/i1t8uN/gGY/bgHRsG+/FYc4rOMEP/Lz/szcnLdhbDcf4voENHWA+rBN3rqq78cwrKd/96lx0vz1LNH013jOH/EBxm+p5WzoutIMWV0N1SICgqx0hjyvaqWg1gqlomwicFjX1VkxSKwHcZ0jAai3bRMf7C4gbGCxKDf8jTWuxFbERdO69XgSZhEhXVAXTGoJwcvSz5/AgGmCowuvWYlVQkSgpLH6JF7fsiyIISE6SwqLhUAM1ErINnq6N9u5B3PP4+ifKrEgKlUUHvk0/u/CFblmUEyoRECKWLggZVFMg8VBMyuUnMHM2LLGDIgiNIlxAVEUiwiNMyH4kuDLsSSkBCxMqAhYKDbLixChMT8hTOXGqDQ8TVJVmrmyut8qwoQNJnxQpXcawCgDKECpABftvKNNXVBqCQycxbqCMyqrAGK94e3LX7CuN/z65Vds24avGhPiy5cvTcjFLJ0Rd0MVWWOMvL+/48vXr9jSv+BrjFj+fAVdRbiQ37/iQglRXSsLz0XY7DUGIAQsl1eElHBhoaHDokIiijKC1XEPyoq63pDf37C+f0F+/4ry/g6qFZcUUZcEcEXJ1KwXGEC8viCkBa8//R3S5QXXH34CxQW5AoUZly3LkKo18JIAlA2FNqBuuMaINVQwEXJh3ErWdc/qJirjNQRcA6GAAIoN304EXALjUwByIHCIAAiZFoADYpWYHoGFV0YVjj/Inf7Y+ZQ9olccf1HXGikPzsaQgOZarJXsaAZu/BjPq3Hg8wEO2WmykS7etVbz8ew6rBRZyyqUEIsGHQ9tk7idLqPLJRM8KD/I4ESDGei/0bOB4fDHZx3re7siiKULEwss1BgxgSVyB9c+byDC6+cXvHx6wX/8hz/h559/wt/9/BM+f3rFp9cXXC8XpBgRm8sbcvN8QnQME27vH8eGoF3/Po4ffnP6K6EQz+JWZ+l5iwgXQMszwSc00tYXLMCIAA1juusX5L8bBRRtymwRwjb3Y8JDno2tavfiHA7GJBfdUWHIeOaTaXyKZQRwvihDK7sTfPLP0J+JmDsCImeEau/Dc4SXJWvxh6RwQ3oWaRyz9fq6VBnw7QwOsKAdGC5jyzd+N5czfzKvoYN2H9R12DsjAA7mzXrZ8851kevDuE+O7vdV00Hbj4F0Z0L4+9oetMDZ/pAC+sGgzOR+gFiGjv77NpNivfv1SY3BaqbAoVlDRHBQZitXeRYF6Z/hxnBc6UHZ3TNVPRjtgJZ+cpU4FQMzml3fXOrCC0fU6DeydBTSOCFEu7bGjnt6LH86/J2rKq/lAD28GZ2x6Nf104Q0Ha8lwWt0HarbOA+rW69mBv8Bg3tuQ4ORhlRNwohnpeK+rEf5dnn1EoLE4LjXdnM/5sszP7OmRTOvh+ZOi3m4t6CAnlkA2sNtq3dorE6BmbUTzbEh+k/M7zv8a8iomfAymlAROArwLfnCvMN2+0Hy2b7Qp4frLxjV2j6GnpFzXg3gd4KQNIgxjFt/NjVQiGbmY6H4A6FHqwf01Jqcv7v73vIowtsJgX4//1hh6+6st2d2NWuzaX+T7uUmJLvTxqOzlQzxP/nsCA+Zx+Isj3TdW1vg8Nv572fqdD06bfuIu1F75nJ0ODx+uRuDXtcxXnbUH2ub7/dZv85wPhwIIfbXfd27dngciEat1+fbcr/Offp2TPOwDyd1PbdW7pf3CHf+SLuoq+/dzfdsurunnxyj47THxb+v/9RotGeS4Axo5+Az83OWvlcr71v67WqwHBg6hGltMrWYGEewaa6nw50Jr3Znqe0wxj04KDk+so6+LT0oo20LN06Pvzp4z8OXvtizr4x2aMw2/VVmsUCoFaUIfr5psOmtiqXDTd3frOuKWiryKvnX2zq4UyqDVUNtTHR2+H4k6jgY99gLJfdAsmJZoUpXRouoNwbxzhhQg8arCEXsg4mBwJPmMPX/WkzMToelGFv8MfmvolYnBGNzkduHs6/CcXAZSttQ5860JcXo/pBqBhcglw0hJ8S8gQOhMCGU2FysWByOolYoWxGmPlWNSVABChURhMCqFBQDIoTaZQoAVVCsCJUQqghIQg0N7lQCzENEd+0/ur6U+et/o2qwW6WXO9xii8YIKhYLogAkMSsMP2eN52A06+DOlKu4wikZeVuxrTes6w3rtmFdV4kTkWVNstYbQmgKuQyIhU4uWNcNuL0hv/2KX77+gs+/fsKn5QWRCS9hQaKIGKm5C2YQOEYgBBATYkmoiYEYhRdAhErCsDflPAbEXU/JqDmjbhtqFvc9pLSRWURAlahkrAIu1xfE5YKXl1ek6wsu11dRYiyMwCzOkBgqiACWBDAqEIO6zjFFZiFrq+5tIgYHWccXAio7mkmRMYOqUReyvBOlH1ZeYBNEsFgXgcXNlq3+rnU/7oUD9n7fM+z/4CF/WwfDl5NFhP2Nfn/0Vft64lncR3O5rUn4OqYqqJXjXMwO32MoZ8Qx5B9mIxTdC/N9bQgz7SGNkaTyKblXYx7PNSLXBRABIeByveL19RWfnPDhsiwigFBBr8yt7SvqFe8STY+P2yXVnx3Qx/kfp/t07r063fH7Td/PcScP63A42bcKI54WRIS47BpDwImfckAQIsk1rDfLM30zJucHDFDg4MveX8/Kmoll818WtFxmknunVc1sASgxrIGGL/p7bUM4qjvYXhuRf0Naz2JEHPXhI4QIkRhx0p1xeZTs0PtQsv4BJ/Mrp4mtme6ObVxT3mf4PL9zmWdMi12bnhg/0vxEitpZ3eQJAMLcwzNmxb269nUrc/MQahyVqV+1NppAwQ52Q1Cja69I3j3HX0xHLRAbMDAlJ6ZMIJKgaco0NcZoShEVCyqLCWhRDaFaxZKhsvj5vKyrWEbYIQbTJDYkQZDLggrigq1sICIseRGt7GBmlapRQ8JQlUPTDkUxGfXMJ9v3pq3UgjF5JIFrGyfToBJmqK3JmYGMIU5CS6za+M1HI6v/VKfhrxYRcxyHXsQRg6xfG2P8DgEfjeiwb0O/Z2CnzeTLftQGH0fjPnG9fz7fP+rr/Ny08+e9Npfnx74jc4wAiQFUq1lO9HezMGn2nW7m0GbCWmpArWdMYYcU6n6MMSKmhLSItlpKopWRlkUQ+ZRAGgzO+tQFEdO8tPuya/ecCGKaPrRuKGe2kJgENOBBkEG9e2NZFoSQj+sSGnuEKR1XmOZb2xaA0RrD8tG+nft+iy/jo3S2zofvDz61dXFWjn8fQnCEJMDsz7VR8NAsI9SFwi5mRSBQHS04dzgVKSMiHFs0np1C9xi/vmzbD7NFgDHZTDB4hPMclTk/Pzs/j75n1WYwWscLJb+X2XYU+2Fu+9HP8p6/f9TvM9dZx+PQ9wIp3mLEt+FhUuZxXTg9Q/p1fH7YjgHL/P3S0Rh+dJ4fffeR5x0XbFT2U2V9NH0rPjl9gSMY+y11tfkmTKvrJH9bRHZ/HMXo2T49onu+RyvvcRsGgNt22dG3vY82SvNo+fcjnPD7koj0szB81Vlbh62b3k6E7HelJ8fopDp/dlo6w1vG+u7XaxqxVQUCEpehSAwGDdYqMR5qs2iQgNFFrRMKbrebXld5v25dMKECBxNEcO1a/GaxbTCBiJDCiHuYsGHT+BGbWkRsahFR3RQREUJMMlaVxYKAGSFWAMKEp5CEwtf1EtCVv0JIiCFhiQsu6YJLEuabrVmLWxEJKKqhXVA6D8S12zNHRTm6gliUMGf6hRhADOBICFxANaO+B9xqwYqKtF4Q4rt4fFDNdaujucXS9hAsOPJNXPssL2LpUSTYcUwLUkxIBUiVkUAoxGCyyBWiMBU5NHeXxqNpK03JwKJ9NFdcYtEucT2IJfZBIGhcRAClINQMLpvEvtCAyy2wMURQIJbwQiyJIgk3wcX6/ob396/49de/4P39DX/5y1+w5Yy3t7cWqBpELTbGsiwouWBdM5hvuN02fH17xy+/fkHZKuqXr+DKeP/6hvdfv+IvP/wBP1xe8JIWvC6LCAlIoDdHsa64vrwiLQuo/ICQImKSOalqgROQYNZZtWyo2xvy21dsb2INwduGAMYSI2pKSi/rekwyT59//jtcXj7h009/QLq8IFw+gSnifRNBHMKb4PdBrM5fEsARWHNCXiQQdooFIQagFnEypTQ8KZ2fKCFRknar2yc2XBXABTLPKUQQMUpYwFyRBSlHVPpcwmyyxuFQyxwI7WRQa4ZCO/p1B5lGDr9xGRq3ofFcOo9CFplTomNMIHwPK41nMQgy7DfTSSaEcN+YO6YBX9zVMvWbAYtNOHzEUEGX8WSszQSOsjcFZwV2TBRHl84n2JhHFFWptds1IASEJeEPf/wjfv75R/yHP/0JP//4A37+6Qe8XK/4dL0ipdT5kOjnZQvZcdp5ml4+g7f8NTDkk5rvH8dPFPCxj78VB3teEBH6VpwJ4Pa3ux8tImaifhZEnNW6R6DvEXVHz/YML/1+Ym7MmityHvPga1xozT2RRjA3PdN4kN6T9pgcMTgRuP1+Gl9X2TzWdwZOyvFmQzSP+nkS5olpPd/PO8+r/Tv2wTYvWcMnnN4TKzNpO0sie8V08J7nsm3cT57vilUgaeNrzR3b4oCRG9dDRsqz4046X2NneiH7hh70jRvjy5AOXbTzpw62yGHRnhkQnoYnBGGadWaUCjwogGp/F0IAxW4ZIUK+hBiqINe1IpTYgwk7hu0gMDC3TOpXtFZS/6IGiyy4WxiYzewOv0MS5iGM9IfqftyOmHOt346YtHlgP7YnMzDUPhFlM2yyPJ3p1+GbX3us89ieV2Uoa9skSPnYn9k6YGix7zf3sTjKNz8/O5xmJu7cx8NvrG9gB5uOGd9HH5MSKB3GH2f1bW9XUkZvC147zvnYBqnQbz/7JpC3gojiY7W5ZpK/+3igIZJHwgi/b06FSK0Jbk52gghCQ2AnwYNYJXhEdgJTLe9oETFor+p67GepF0QcnNv6bLaI6OeeCk4ao+aELUN76OvxzEfzP3zHI6PY7mcco6+VvmbE8nLuuzv3/TNyA4XzvWj9HL+fcI5pSM76e7aO5+dHuNf+2XjteI2HndM4HO6hSZt4IhA6jNuvRz8njD2sOYMR+37un5/hn3Oee2O3f78XQuzxW8LsxmyPb+zbf9qGR32QKg/aMaeDPfZgfP39WfmP693ne+bvjz47f37E3D8ez29N3zs2kvrGsb14VM6zddlsN8vmO/nb3x72HXz1veME7HGgb0lPf89Ka7hvhrMBHg8iOL8wTizRRYUd1e/OPAx/A9FeDMEHY0/2jvdj/MFhmc+0p9a18ZxOKvvI3LQzw+gDGyu2ehzdALM4cDEZakXeRBBh1gfmbz9rLAexgBBLh1KqE0TcRABxc66XuKKU3BjWPQisw8XVvQyIxDmj629RGkViRdR27YpRI5+RqQqbVa0PmHkwXrc5Mdran7GBAmIQfDLFKG6aYhRrXBBKCKhVtIiDtoMAxBABBjK2rlXuznRRTTNcc5zmto4ZKqGQluWSwTmAtg0VQKgS+4GCCiK03z5GBAAEiuqLXugNBHHhQ0XiRJiWJ9Ui1hO1oBRSOlHWAROjQq2DiRuTsSt5UKMXZXxrm09mBhcRQqAKI5qZEBTfDpWBWhFbzAexiDBUlAcFKIAURzchw7resN7ecbu94XZ7x00tIcwKQuItigCC1BVVlQHocxMiQkzicogDcq64rRu+vt+Q4htQGVsSV1BLCIhBV0wWS4OIAs4JYYHQ5kndgbWYdUncMMeIWjaU9R1luyFvNw3CXRwOLPMRQgRTwOXygrgseP30Ay4vn3B9+YS0XIF0AVNAYQKgAjwlKIhkWtEsz/v6MvqnexmoCIGVEQ2Aqa2rSiKIqKQqiTrH5rILBA2SLusvkjDNzdW0KLkEmJKjuFg1aN/5Yg/pLfZ/6K2D0fLMrw/Pv9B1iU7byRrlwXWTd1/sYeKQ2NXJfSwbMLnL5NvDbMmum8nh5e3M0QFiggoj0PKy43GNuF9XhKXWl6lduhel7S7mSksqQEsJcVlwfX3By+sLXq4XXC8LLmnBksQNclc2cv2xOCPk+BE2Cq1/8vMtO8QjPbHrCxm6c2/c75f/fCL377d9fVb9QO8e3H8kfUAQkbRBHskEBgLKfhNxoXBzl2yPilDs3qQ8Q6Th9LlnWAlyGMAwabVIRX3wTrlqeRavYaq7AUpy6MA8HjT7Fqbh3hgGwfux9hsaaqp5QjjcS027/oRQPU9qzm9g985meZ5wmTT9O+xq+Wlo23y1VwcbfkfYnj0/Xze9btIDTZ76OtsBdljWEWD9OOI95ifMarFHhNaw1prwiBHUvFLPWti6o6m8xngM1Hz/s+M0eiGLMU9jCAgq2WZmEAvSGGJErIL41rogscZ2qAUEwmXZQKBmmlxRwdX8s2sALwZK2UAE5LyBAGybCTScmxyi5mYnQBh9APe4A4ZAsriC+mjyw0wQp2KGyNuYxyB9NcSgIQWT6ynT6O5WV/3w78jD8T6bhRDz3NnczNcKBvHxmtfRPu37UVt8GTYWR+lZOO3ruSekmMuuygAYmd/9vT2vE1Ehhd47kO30mjQ8fF9AGiOl9OB/iMMe6e3yfauCJFOU7+OCEBOWRbS6lmVBjBGXy0ViBaTUFmDHSS1AnNu3jogyDZp762hMukarb6dZTHH3ZaoI+qCf0ijO/RjO67mt0T4kbaw6sXFsESH77hjuDX2i/b0hgp0EmMru5ngH/dinHVMcOL0vpTQ4EZQ4kzzdCmnGJcagktQJqJNkY2fxtwaXXzQ65vJMaX+1ZKbv8549ioVw9BvrUKK014529hzkd1ij/vZwjqgjDGy0T5sPuweAEYc7Ez4cCXbmeezX+33f44QfGadZAHOO5/a9Mgpx+hhCLY7m+d7jI0HxALsayTdYglC/zmM13FsNz9FUv2v6CE3wPfn+Wul7+3OW39b1/P6Zcj2zwe/WR+c+kfP1PJ0D99p6lO4JuZ4l7s++/0BmR6cdwPQdTqDnuQIrU3Bj+05/DGECsneVc9Al39Z7gmoRZDzfrW9P9ys5G9t7OOxcusB0uRZAgxyjxViw+A1GX6ybWDtIIODcfhZc+n29KVN4dZYQFbfbO0qu2G65lQXFgcSdi97VPu5EYvHKgRCDMMThvCyYICJncfeUS0bRWBWNV2djAqDkAiIRcAQGYkhArKil8yY6ZWLnlMVVSFjSBdflipfLBdfLFUtKSIobmDuoW1qRi+CyWykohbEhYwsrTAAGxSkarglu9FRlB/9b2014IO6RKgWEWrAxI6wJMSUQxSaIMJ/xpphmlvxRGfGhMihEFIjbpUqEUCMSCBEs7p4yoxIQiZGCMJYDBXWNJaebPxMbHxXWH24Bs7mKxQxXxrbWRqoFAAuJICXmilQLlpJxQUVUgUfp0LDRHaR1lirBqd/f37Cub/jllz/j69df8ec//zPe39/x65ebKN2EhBADLq8XxJhwub4AJFYbBRsKNoENKSG+vOBaGRxewOEFKAlf3wr+Z/yKLxvjl9cbrsuCn7YFlxTwEhiJgIXF50iNETEmbLefJSZJNNew0oaULkqXLCglI99ueHv7C96+/IL1/SvKtoJVCCeLMiCkBYEIn3/6I64vn/GHv/8HXD99Qrp+knghHISGoxUhbPj1/UujJQSPhbr9knVgtKoJ70z4BzCoVrESZrXeCBfQckVNF+S4YCPCRkKPhyrCI7NwYAJSkhVilhAUCFwKisLravtdok9ofASamN+HUG0HDdnWnq472TudF0DsaPrhZ0qZ0n/xtFBV8FYavWFr14SbQwxFeAsJDTZuP4tvctDeFs7BbRwvJAfrWQVuPFyiHt9QuuopR1Jep60Xq0nHH4CZhrV2Odrd4leACxhFrFbY7FasXQHLywuury/46Q9/wB/++BN+/OETfvz8gs+vLxKsWuPMjGfMwJE8OK9mnOkc5aUp7791+ttpyXn6QIwIPewwIgleQ4vITQF1NI38uvNl6j+P8b8uHX2ENJ8jk7LQBg0Po2AVQuw/HfuwIwINf2zjMubtC3omHveEv3/er0fMOCv7fpqFII/HR1IfHWvP3gS4lWX/0vx8fHYkiBj+bGvFFzSXsatkfO7v+fg9Hdbjb/tivLfO+hx1wGV5h70x/nM3SbbJs7uDdl4AMoxG20QmPFDdIZoB7bT2VNgm65dbmaYtPjUEAJq/RnMjAkAFA+557AF5a4hAqCghIkZGjAnMFTknAITKeajCH5ZiBZFRa9C/A0qR/KUUFerpmLAyUNHL6IxoPdxbUCU4RmrTR3D7jdqAD8tiHIqBWXPvF9T8c2AeN0EEN6a6Z4YdCRkepZkInuH0PJuEzjQ+S74NnthlOuFDY8+wfcQYeJ5xrnMLGlz1MIyK4zGfYzp2QYTTWFItprEebix374+1BbG72xP5nug+o8Svi/aLovEkP3HRpB+A2fzokv7GfjUCboj5MI6H5e9Pjasr57cJG/z37FwfGSILX/TR/EBgyRHTHgAmZW505uoe3npU7kgQwdxxj9O90pGRMR/6uX2ahvEa98CjPSmEe4UBWFIijWj8/i7s0HZ6IVrrljtnDhne89kHN9a074O92zPG9+UfpaO2HL1/JpGeYSdvhztjlhgKNzx3f/v1e29vHv/d6z1jlvVz9duEEOd1H317xnQ8a1u32vF76pTh59vj9ufZWAHYwd/DPI/KuPPuaHw+8v29cj5S7vj+/mnwPXvg2e+eL3OGn/fX3MM2GTyd0MSz/aE3Dk19PA+nPTk4C37L9HzZw25S+CmuCYm49dO3V7aJA1a7usb91s4chUFHLXtqPL5juB7uB7i+2d3JJ/sznA/f+b8NtFTF10qpLd5Drf1eGPvd2kEEEVl+64actyaAaIKI2w2ldEFEc8V0U1dMa1YGtSkQqOuZqXEN12YGVQYjgIPF71JBQ4sDUQdteSFJ2IFQOf/aGOgLVtqlMSonmpOoKz3EEMVtUdSA1WnBZUlIQawiilqqM4AQC4paKWxJ6KubCh5I8RdpVT9HW2y7gzlmhkW4BgfBTysqKGdFqUg12dHObsC737Q4kuKWijWoA9cqViJVlHqEkapXrcd+5oqrMiEwCd84dIi9g9xtDoRBXDXsQ9644d8BjIKKUCtSKSgsAXtDYCTSdu72rgyS0BAQ4UYp2LaCTYViJqAKQfptzP/lepG5TEkDaIuSHhOBUsJyfdH4iwkcXoHwguv1FcvlCg4RmYH3UlFDQcyEDAKiCFNsDAJEgJffvogrHfFd1Sy1l8sFMSVweUHVeBbr7Q3rdsNWxK1ZF7ISQKpEFROW6ydcP33G9fUzri+vCMsLEMSVbamMSBtKAESBSmI9MAMbATVnrGXTwO7GcK9KLaPhuClEpAAscUGKC2K6IKYrEBeUsGCjgA2k1g7ApdF0ch91L4eg5xIHcBRhExNJzA+o5RAYgaFlNWrJZrvzFoBeB2HIJQQS9/VmAhV43ofjD+hvVDpTC5xJ0c4Emn79+fUNGOxoCx6N+T9uBbD7V1FbmHIqNR4ZARZTo9EW+7Nfji9PSx34s2abkb5DO+3DjRcjfBxzve2FQWydBkJEXC5I1ysu1ysuJoSNESkGxBiaAo7VyOPAjX87fvFwjk9ZfZ/Rv9D8j2kOzO34rdIH+UgfSX2O+fD+I+lDwapnBpdttLlh/p4039k42PvHiP1Yx4CsHCA0flC8Rop+oQeFBDqCIXsDkqwMPRr7a/cjkYhpXHoZ/n6OATESplrnMLaP0+kCExu303E5Sl2CT+O3H2zDfkOaFNRtYn89aNNHCdnWP18Jjsf6vND20WlesjrUxMwbLRCOiYWRIeQrGjpwPNDk/mgnw/Sdvm6sZYJonKADXOtPZ5pwM0ckkoO22hzpfiTdnLp6FUEhxNjdxzAzIheEKs8ZAWlZlElaFJZXhEDIlytIgwyXkrFtxkwS7NXcLJnAYcsrAEaK0joLUCx9CYhR1muwKacOC0wzoCEx5rPTiANUhzsI8eAnwFANG6+jRBPzyRjL6hC+taMfqnaYygFe4JEP7K42Z3O6l89g7hys+KisM+31o/pmeLs7wE/q+t7Ddjc2MNcFklqwZhcXZP7+aHwHAcVQV23My8J1+A1aJjwifq6U4c7g6bxGmjumFBHVIiJd5Losi+7r4JBNjU8x1D/1Y2gQt7Yw8xCYz1/bfuBumrwfo2kMea7L9jG1vPPY+iN+XLceLrmzkjrUfCSsOl1TunV5yk/AjiF2UDhck9v3h3thWmM2z6Kh2C2hfDubKzdzaUcjLDGo05HfaTyHNeXxkfEMGnCVNgk8vDuyiJjn5PAsnNt8kO9ZBq/7Ag0Ze4ATAh42Gb5nffQw4/46OWtzMF/JgTC7YTsbo0djcu/7+bovX8anHfkneOaIQ051uyf36rbvH+Jhd98+Th8hkD6+lr6/zn/L9Fu1k8j2k92f4LbTOj0sa/q7E+X315LhtwaCHtEM9/ryDN7xuxD1wLjnyJBlv1dVEEHddeaMpxnMGn9yXoxlaX18vs+eGo/fYBndH8/zCu7N66M5Z4b6hGcROFTGtoqVwpo31GoWBgVrzsi5YFs3lJyxZRFC3DQA8LapIMIYwC4mhMWAKJsETM6bahdb4GRFbYz+gdOmDWT4RPWxaYW2CJ3RXjyDXGOMmRueOhx1E+NI6QVmVmEMNx6lnZVkrj6jxIa4pAteLi94ub7i5XLBp5eraALHiEChxatIKSGXAqIgsSsqI24b3m9v0rcQRCucuKF8rDiiYKdGkro1KuruFucYJWdxOgGAlJke1Fc/Ee3oNgSNS4Cq3pdEG52L+OyvWaxNOWZwJXBN8i4E1EKoOaDGghr1XnEsqhgdDChLiAGYm3mJT8jIBSgb43Zj1MLImzA+iSsCZyTecEUGUwEiEBOMHdBwkQBSFkpnFJcirpNutxW3dcVt20QQAWC5XEEU8XJ9RUwRl5crQAEVJLFNtooKid8QL1d8+inik+2j8IoQXlERwQgoFLCRMPy/bhkrZSyF8POFcAmEHwAsRChV1nZ9+6prSh4QATFGEWwsC7ZPn9XaaMP77Su+fv0F77c3rHVDrkWXbAQFRry8Il5e8PrTH/H5x5/x6ae/w/XltVnA5E0EC9u6ohYCo6Dwhi0LzV1LRd1ueH9/w9f3d9zWrcVTQZVYHaYI+bJEXFPEp8srXi6vuLx8Rnr5DL68Ii9X3MKCNwo6b4xUleHJFYGAK0VEECJ1Wh41iCu0WlGKnnBMsr8rmquuATed/iSlRsmEF7Z/wGrAz45Br5vZhAx6Tw2IdEVKrmoFcBCDkh1tuofHXphRpQ2eFoGy9fU8a70jbXNTXtKHFPTwd/SUeo6hxuM0forRyXZ1Hgp0Lhjo8SSgfBqN/9BimgIg5d+wCiIa2m+fxgiKCZfPn/Hyww94/fwDXj99xstywTUtuKSElBJimOmFfWou+Yn6fPh0enT9+8At/9bSh2NEjMKIc1cxkteIH29OeJDowKelq2OWuDwiSMbnhtTNvsS6aT+ogqqIRXdanNbnRpweEO1A69/Yto6kAmj+I3f9gCHp83XEQI82zUxs2jPxxRas9KFc9Ke9bPCksXrEynSEx1ijK9cNhv7tyV/FWQ764fLMyNhhot2aMoRobJzO1zS2Q9uP+jfNzVy3QcGBaD9cxUdt3bfdFXKcGG1cj/ccW2vb+vQuMvZ7yPKQW2dWxki09vxtSQnipQSlCScqB0RE+VstIjhUjRXBTdO7pAVE1BisrWzq9bEezFVjRJQSkEtGBKuPS3XTRNR3tiGWjjlozNvh0DZBBJTvSgQOojbDDTfgUz6YH/5jxvA45vMc7JjV30iseSJ0yOfX7lE5JCawM2P+EVHryzKY+Ii5d9T+wzZjP15HTAUTgvg8wkSntvWPmLZNYDExr8c6O5F3j/ndy5/rAfwG7sz53g7ZLz3gexNMqN/KqObSBl+YuWnYi6BOteqYB8GIVjj0ZUACDe6yEyKxO1/awrcg9HtBxFAP7+dlDiC9m+eD7wCR2/nxAUZBxFDHwf29NcsNZx61DI9iOrmCBSZgBMezIML+9oGSpT/mKk7rQCfY/fd+Hxle0HGmXrfB6LNz075vnXMn0czQbr7KMY732X6dmZO78nZDNwbzPirrIXP7AKfpfevLfF8OuTz+2vfsGYw5b+u9d/sxPhqjR2M449JHc9Df7WGnH69927itp3vpI+tgSNMef3R+zGNxr+zH6+T73v9bpLOz7/dIvQ6FCQ7mPTvmR/mMTnhkEXHSqqEdj+ryabfvuf0z5pvL8mvyyWG/i3c16GwDMAsi0M5vTztKU/bWKXDQft4f3M7oY3jIji540KHHeQ6TMsZO978Wf0gnWd3HD6iNnZ2tqljCwrRnQNwXMaPkjFK5Wy1sIjywQNOrChjE+iEjbxm3vKlFhAgisgkiSkFtlhEVecsDM29252nJhA5hWOeOSaW+irhUcNdFAoMcoxB96WhA19Bojpl87WujCyAOFFCA5pLRYo3FGJFCQIo9VkSMEZFIY05UFHUBusQEMJBiEmFEjBLMWpXNSqDGPhmpQzejwxybUov+WuBmUsUXAoKLhcLu5K7qatW00YMrh6eBYrGEQLDxrU3QI3MY+rgdtBnal7b2IBYRpTJKZeRNhAd5LarIlhGwIXEGh4wYCgIDiYCIgGReQ4JIXgL3tV5rbjRwWRKu1yuYCz7/8Bl5yyg1gRCwLOqedVnEErs4HJ8IIUYsQZSXjIYgugB0ReGAyoStEgqTuD5mxm1jlMJYmJCVVs9EyIAwgLetxWRk9b0fY0TZViyXCxji3riUgtv6hnVbsRWz5ujwligixgVpuWC5XJGWK+JyQUwLLCgxBbEaMvrCrrkU2fc5o2433N5vuN3WZr0ka5zUx39AShEvKeKaEl6WF1zTFUu6IsYrEC/guKCEiEIRgFm09KSOq9t+JlZ3w0HjgRAJrsUVzBFUdYVWsXTuGJWHe2z/K80BteiBrW6YBTqUjrRg1V7BiwAPPJrbJujzWfGpl36Mk54B5vbuFB9g256Or6cE1cDTpeZSjYKWp/mYu3UDMUuQcXJ4edvbal1Ti8KMouNZFZagWbaY82Qhewi19GYgkAhklyRKflFjMKqg39xrS9t2AzL3fhhT19vD/P39fbzmWYWoZ9JvrXDxTFtnXP9Z3P9eet4iwhNDjeHpEd1zxJJcnjlf287THPQ8hNn901HbjhB8It1FDVh4YYQhjWoZEXSx+7JcP8df3wTWdj8evd9ildCYKycWEYfPyMbM9/0xId3LkaBBh3VZYfNouH674AK7fGfJt10AxWRVYQv2sCABckRmi/Exgm2om8f1YnXPyPIRI4MOGtcAS1tONqbH7q8OGrf/ezdv9tcOOmodR0TMuE/8/cwM2jNWGurn1ppdabhva960PrxLPgZCDIgIYMihb3ETuCwAlLggwlIviDEALCbUhvQD2c7DNn8WHI5A2LasvEFCrUn3qZiPEsZ4BTZ93WSxYPCZ6NARZkap+kHUzkCCVPm5OIYB1No//2ZE4ZCJe7C5rMwjuHCWPLw6e7+HLdQ4sceClPuCiaAHu33vr4/afa+9R3Bc5nwUIhx91zAL2vvvPBI+zIScKw0270eM75Eg1Ov07WEfCVOQ6uAED0osJjOlv/RDBRj634Vz01o7QE5bu8HNNH3oO4+Inn3rLSO6ewH/HRoWN9TpVAJnGCyFHbWR25j53z1BBDdq/qAN05g3mO3fs4Y1O1qjSvA1BNrlmwURbbzcfDeYwKZcQXr2nJ/3rb8DjjXu3REmY/iWpvL56L0vh+b3Y5vmRGQWHv06t/8sfZTZOPZ13+eddOig3DMibb9OOpz3c3wE6+/9rP6z53d7OuTju+XJq4MxOSwLLb+uwru42187PYvX/W2n87n420pjO79n7ElxUQMje1r+g/j6h+oGvKU2n8GIwy/5iXzPtIGGNhjuMdKrKoBAcIyonn8PY85h6gzTdzd08PiAwfI9M968BnxDYoNZduzY2ISpf6XArFBr7fTBtgkzdlPt8dtN4hrcbje5rluzathyxk0FEdu2Yc0b1twFEWXLqMX5Vs9qmVDKMGaG43gb6XZGW0DqNjq6thgARPMdEPSJmzugLkgwfV6JfyAwWj9t78exFnZpx/2qs4xgt5ZmPDJhUbdMiwZpXdQtiXwXJHh0iMhZ3B1dLgVMwHJZAEJjAOciOtNURR2CQE2juq1Vcp0A5D2hCRa4BIilhAoiiNCsiYx2BaE0NmNUckz3LemvViB4P/dFg3gHcA07vJiZ21wcrM6GyjIzMksshi1X5K1ivVWUXLG+iZvgvN1EEBFuyLEiXLRuEF4ISIjDnvbrG1wRKeB6uYJQ8fmHH3C5RKQkwc9rEbMKIhGOFGbkWrCW97ZmQAFLWkApISyLzPGygBHBHJALkCvwvgFrhuwV3QvEFXUhLIHA1wUpEC4AiAvS11/BNWPbVjAXlLwihIjr5QWX6xXb9iZtAmPNG963G27biswVxRx1hYCAgOVyxVWDU19fP2G5vCIu1zbitXB32VU6bbFtqwhr8g1lveH91694f3/D+/s7tiLLJaaIa0i4LAmXZcFLXPASE16XT7imF1wvn7FcPoOWV/DyonEikqxdVGxtHJUTyBUBhEgRgcRVkxJqYIgbKeaKWgggiWkp8KHCILzwGzpd0cGB0FHGcG/rrW12gTlke0VGR7O5PaT3lk9Itj2tLmvNyBdq18a7OThvTeAibqjOTgieEMe+RuVW8ctm4R0GXh/B4KnAL2IXXLt1rwI1w9xOqR8zpUG5XQMHOVN1RM0duFk0CV8jIF0WLJcL0rI4t0xxiMEHQDlBz51rj0/Q/xXw2X+79LwgQin6mWgl97Af2u2jTlDfLXssE9O9Q/GG90ZmytlvhGSvX5hESuBpw2SzdkKX2SSf8ozbvpPSA/pGNgSqbW70Q5havz0jIaJ5lHRlNEZAQ9AmorV1mG0ntxbRUMM8bp4AVYuIlm0e2+kZmyaPtqzS+NrlgxEju9Swzdbf8a08bzgBzT0J7vHILDirbnczNnsYb1/n6X2L0DOttoG415J1nPtQ0iFcO13Xu0G0xbuTqY51H7RtnGaCIfy7tpjkWt0mmfsQqAlsQ78VV/S/AOFfB6hGge6DygQOUYiuwChhASdCLbJWijJSa1pAhZAWMdetdRFrh9pJSnIVMsR3aK4VXAoQcvPVH0JE4KoMSzMS9jBBtTWqEDhNMOHMHxkAVwMWNm5REX8xbTXE38ypJTA1GqI5IrwMmMm1muJ6n7ANaaiiDbEz+JsITIVI/bVjpNGd7wzu8cTgbQw4t+48Q933x9fXinZE8S7YtV/LwxnhemH/tH3v4B0Pn7quif9aakzw7nt1yGeg0tBDpTAs4FhTgWc+HFPfd5tbMeGsCAEIxAihopIGLHNA3wiPOe5Eh9Xat8CgAIQoWknBkKOYENWfb4yiyQE3Z8aklLIF+dq7ifICMGcJYd1ToFsnoUULvNbmXLE6liBkUf0Jw/dtKsPX2+esz7ePXcztnO1nsMcp+llrQ6yjOB7sfcEAaNp3U+qt0XlvmLqd3b3e/k0Xthix0eohnqrplAdRZ0LYl0LcTOHPDV8g59ahfQX317z3sINy7Rsm9P8kSGMwON/2YD+vPP5hPWxXhb1tHhpR3a+9Tfu/O643/uvraOeL/UltWDCsWdd3oKEe3qhjl46Ei4T98jgSlMkSi2PDQOgsqennmQ32O0l9re1/7f2EOA/dbG3ad54xCuNbPa2+B4IU3wbXQy3c7eWTvp2/0nLvjcvc7uO8eyFLP4ukDZ049qDC438mGhx26aPGn7arw68dZv5soU/X9X3fDXTJIa2w+2J6fjROZ9+ffdvz7+idZ5MAu5E0ONnvPjVhwEl1x3N7mFGKaQBJi6WOpzEE5+gnVGdKDnD7oO+jEHPE2bygdAIK+1bvBqDjI+0d77f0/r1+xx7utV0m73c03Dy3PFrO6BzatJVSUBnIOaNyxabWCVvOqKViXSW483oT64X3dxFAvL+vGnB6Q8lF/Nar0EGCUjsf8zmjZLGCqMUx80tXLBEU0Z9ncHH0DE4aXuLXeB9Itg/tezdaIHHjS4rDVUITVDBIcAcWBnSjRdoZNM2R4l/+ZPJXy8gB3fVjTKAYlXEnc5dAoFCxlApQQEobCjNSuoAZiLT2Nveudaafa5VbNop3AyhVkRa1kmQAXFrMBsMnOjWjro4pNKYv1apujmpzf2VsEWJ1L6zP2lSQCm/0TGBqPhYwpqHVUIdQ2kfGVjdZa7lbDAS1DiAuCMjIlZCZsDEjg3G9BCyxK2yILj6hUkCpFeFzRVo+4bUSlu2GmD6JK7FVlFdMyWjbVmQuElOiVhQGKgUgRVBcEOIFQa9MCUwJIRfEWrHwJuMcxKKkKGO3loDMhPcsQatzkHgIqRSgZJR1BdeCut1knZSCUjZZhupyOJeMkjfdR7J2mVqQBektS5ANLlmUCYvGuWDGtt3k+7oCdUXIGUGtlLYs+zqvN9y+3sSaicVV0pISolr4LEvA9UJYSAQr15eEy8sF+PQZ+eUn/Lq84s/xik35XwvLMtyoIINxUR5PBaEQIZLHgm3fCs0o/MHYySTSkOS1ANVobW50ZUfjqj7TgOe2nl3ciUZH2XLkKYKCnW/EEMFFlSu40WkDrmafEdRTBDeXR1QrAis/wsFw/xPrWYanWIymINg76iREQzBtbOSsFTzLKQ8yN0s3KiIU6zRkBalAEcxyBZrLYH++VzsTNRYTg4BK1mEgLUBKIKWnlyDWQyFGCcYeQjvDDWMMetY2+NC6M40qHTzb0SnP4TOP8t1TLP2W9Dye1fN9SxM8v+KjfXhaEAF0PPCQYMEwnf09UeMB+TTzxM6FEHToJMjwsarMjqOy9a41qAGbiZiTQYt7Bh9YFKU9kX1GzKGPj6VAEYNVwAnhftT/jlVwayMN+QxwHn/fGRB+XPgwrxU3lB1p6AvZ93TyvU9hCk4Nm2dyjArfzm9IR4g8oNydB2Xee08H70/maN/2vdrF80KI+218VPewthoCu19j9ndtDj6DAt/SgXDbk1ZeF0JEyNKI6PubLSZCiKAK1EQgRHAlECVBhEjiPNQQACqoRSwjSs1YV6iAQJIhkdUO65Kbn/4YI1KtiEk0fwhiktyZorUxZasiB55h282uBWulKnuoQLSCxKmjxLoozIOGTW0HqAoomdR3owkqOrFTSmnWGPvAUmbnHPv+3U2/Eb0yIr4fQEfGj5eOIiHkGdnTmnGEZuNJt+v9Q4TRg8sR0UDkd2Gq34fUEDWDAb6t9yvryAhpv+tBO3spuhaU2Ao6drFtB0O6aFgXVl4XRkQlihhcCTUAIYgwQtYHOSRMkRkTktjc0NxXluB2KXazUbWCiCkhLZf2zAuPRDPNEMYwtLOtK/R1P/drP6TzeTkKMwDuQbCBHr1vGiNBHPcWQK3HDQwpUklkVCy6VYONja3RPk+dLJCCWu6p/R2V3PerXWm6Wl3ocFFz6/oReGC1Wns7MW7t99r0ZSjP3MdFx8AyHoOdgw2nkk3VpBOs+9PaGtTfNCvh0vk8eqay/ILCwxD2Yyvt9/jIOIJNM1fxDiGm0Z7Pe9f31eNrVuJ470m9vm0MvvnTy81g/8vgGE9Zhvf7571MOW921EMrTPaW9Mn32zW0/YLu7QOL07aOfDM7rKS5KMs0Ick2x0xo5u5W6q4Hp/gJ9rFHDvDWwdXIjJ+1xuCb0jP4ziPhw3lZ8wj3ZPSBgOi+5rqfcGrzIfm/hfgj9MF53M9/u3Q+bo8n9uib87z35uy3GZmZ+r+Th+d8hPn7YyHEUaEHeA3B4TWSqqpoVLAalSvscUyVoz2x35thl+e4vc+kzrSae7SHVS61I7Wfg/7AIox97+W484A6xGrnK6BMV1bXShLzodSKbRNG7Pt6E8HDTSwebu8SA+Lt6w15K3h739QiIqvW9w05b1i3m8aA2BrujqouPQZt+dHKQ3AtNw8QfM3cSpMBk2Bm4X7QyDE05OJI92nQO6bSGOUsPPvKjNBIjNg/b2erq1a1i00pTCgWdFcvJLgEpYiQEmJahCEXQmOCLpQQUsXCBIoZl20DE+G6XAAGbvQmZwOjCWUYBA4NQXGDYC1T17fmR5+1HVXOUq4ZTCwoYVB81nAsQOJqEEAkOC9VVQqqFQhd6EDq4gVFzkdi4RQZ7QaKOgumWOfPUIx/60hHDm0aKxjvRYRbb9sq+4cZAVmCPBcJOL0k4FoC3ivhxgU/xITPV3EdFEJEhbgsroioIIT4iqUUxMuP4Lxie/kzSl7x9esXlJLxvt6w5VVciDFwywW5VmQAoAhSAQSFK0K8IqQrOFxQwwUxrqC8AlXiNlKsiLVgVahUiuy5r5CYjTEQAjOWLSPkDXh/B5cM3N4AIqzpDXG5YM2bWGovVxSuyFX2YmVC5SCeN0I1kQsCZ3DewNuKvG2oFJF1763vX1DzhlLewfWGuG2gbcMtb3hbN/zLr2/It3esv75JXAoOiCHhJb7gJQV8TgGXhXG9mFVCwPJ5QfzxBfXHn7F+/hP+fP0R/5ResQZRKnlhQgTwC2UwVaQqFudZPI+JQM5RG0HPiqB0nlhHiGufnMVjQlXPCUxKezn6o4MFCUzSsc6qtCEjNka8p2EVl2g4icCgFpzZhBHmvuiA5gGAgACm7lmE1HooWNzM4dsugAjEYBLrEbPOCDDrdIZJEFkQS6usQ3dikQsoLQrXx1oywBUp3wD3zoQRLVq5o/d7H2W/ViMOoyjqoag3PIqgEMHLBbhc1B3YBdew4KpumsKiAokQG2VpuG6keIz/6QH5GDP8W8T5JD2LW/MAy9tTHOFMj+rzPKdn0wcsIiak0iGW3ad/b0zPNz6bmQDydzh41g9f+bC/q0qkGzPtUAtuGAjS/z3h4F9zv9gr/du0FmHMBVKgpchIcFYHM6oddoT/OVJ5KIgw5Jnd2JCvRzIZsTwWsUeoh/E92zwNYd+/3zXxZLExjf3el/MAuTZkd//wtC3+xTOb4DgPjf/6efXjPj0/a+NZXd9CnD97Pwuq/PuBYUQ9cG49Ahxka2u/UmgqLwRlgNWO4HAMPXh1iQAqUBPE1eKCQoSUCkINegZV1daWGkjXPUywUOWQM9LOfFm2QOgw2CLEkWf6G2Is9wWmwQAAge17OdyM0YyQGrHUNdxtTNTfYAxIKTUCp7ggdtaeM8YwM5r0fxYmEnV3RLIda4N1/nsCdrBvXgena61aAY4oGtp3QrB7uH+wfndnBI1ua/w7e3ZvHxwzzU+zn7e752hMYf/eM/XbM7XUOYrlMLioobG8Q/oTJFY8ofvsNVdMZmItFhERSWOoyNjVxtCGO+t6e4u8VyRXhGWyn9iPuU52Fz6NV1lvsQszgj9wiwQGtDPXCyFCmMo66n2xyTmeo2G+pgcDHHP1z+NLU91sx8hxf31GY8DK+Op3ITjy5LkUgrgGaPFrgrh9bMGqXfsabmRxNQ7Gbd6PB6SOR7qGco9wC3s+41kjLBfttiOmdXctiV0dvp57qWnMAJ3w6m+n+7Myjs//xgtqQ+LPhbsl6gftn+F6xLz3aYZ5/e9xrM4EAR62WnsP4bb9PTHQdvkO0qO6d/i2HQy757uSARph+1Hd/voYRh9/f1T1sziXPpwe9PX2bQzeD9b/XfWcl/PMPnz07Flc9NnmfwS3/XAa0fCWdvv8MN+DeeHzfPzEmiIcEOJEwsg87PfvOE5Dq06qPYE1vIOJiud4HNSVvBcz23iS4uOiyFOqKAhlDT59WzfkUnHbVgnma4KHdUUuGV/f31Fywe0mVg1v7ytKrnJfKlb1Ib/lFaVkdfFSRBPb4WejEt14zhAURttVcdwEoAulSXE/arETuqGLW3cE5Q/MJ5sx14xnYRbfZuGr2suKg5TaMTaPw5iila+2VW/CJsbA1DN+heGvzdN1IIRasSyC816uV4AIl+UCZnWxy1Vi/pk1OAz/FuZkm2m3jprVq1sozJ4Gq2gMVvvGLyql7aS2KmPV6CeP53Eb20Y6znOJPp9+TvhoDWheC0qeIqFGQtA4FYGF35NIHBGDCwpXvK8ZXANKrgBlVM54fYlYFkJcBKcncdyEwgSmjJJehMG93AAKoGUFM+N9XfG+vuPPv3zBmld8uW2qUEegQIgmdrI+2TRDKWMKoJAQYkVcKpgiKiJKrYMHIQmcXkAlo24baFtR329AycC2gQIQkcRaYMuq/CW8gsLdssgCLFtw97ytCBRwe/8CpoAcL4jbpvu9Yrt9QS0r8vtXEVKUjFoy1rd3vN9u+PLrr6jrirqKJUZMEUtMuC4LLpFwWSJSLFA0FUAFpReEyx+xXv6A2+Un5HQFx4glEBIBKRAiByzq7SD0ldI3EHXOQsPVbcAa3BD+H4eAwFUCoROp4q3QXSaybStLtebEqohslg5poQPME+a+rC1sf3WJ0B3PD0qL3G2DuK2SWQDS22w0j9Ceiiva3m744Hywcuu/7VsTNrAKGNhigJjlA49t9H/P/WpjQd76BiLQZJZnarFDMSKkKMp+MUh8CP1NhM8h/6S/dn3kvg52ib8Xf3wuzeXfVSp/4vv9eyt3eIpGH3+gTd+Svi1GhP/b3mOP0FB/OZQzlzvej8/bweoYKBX3GAtzcguwIVXzYte6wr5tgTD0K+J4HI76EkBPT+Iu37BpjvLNYz3X00SV37BJOuJ5N9dZ30LXcnj2m7nqD393kO/jBK5WrjjKzCC2LIfPfRF36nqWefPo+VE549rYj4PPY8wxQ7zk4BkB7tH+tQedoSHjEQJJkK1aEaJYMcUkmik1RzURXFBrALggVAIvEoSaedZW6hi2uAzMgAWAjRGZKyJHcFWfgWzIrCHKHeHdx24oA8wI8IKIgBhYzVDFl2lF18AHhJlMymw0f6ylFCFSaC+I8EHw7Jm+FcR1mpf5e0McjlZDfXCInsMGO8T6ncDUw+IOy3/EAJsZXgPiQ3u4eFbeDN/rA0GEftTKmpkCdpQctaExSY05z2LBYMzlEAJY570Upw3t4AEbfcO9TM2kQoikVg8Ry7JgWZJe5WdrqrdvXMtWpv18YORZ4HV8RnbT3FmocXpfCWbE05DFyodCiMPzmPemml1AYuDlBLEiR3YqxUVzHQ1JOEBijSg/HQ/fCNEQs76Llt3zqROxJoiIYEYX9jqmQu8mQ71GD3CLXcVtPobGdvzo6Bw7Yh42eH0AH/w5IO4nxz087+czmmjECsfk91ffIh/Xnjkv+8Nf7Z6c9dnH9zqDX/P4+PE+H8f9QD5T19H9R8dxxiV/j3TUtu/B0Xb32M/it47Hs2nAle607VvKOevvfH4+yn/2TP6+T7fc//bs8B0FnP/LJdKz4AOdPJq7g2J/t3Xa6jiYG2vTHLdwbFu34OtsW10D09lI3moC/SPxVkoopaAUxpYLcqnYcmmulXIpzfLh7e2GnAvebzfkkvHr11+QS8GqgofbbUUtjG2rKEVcOBUVPJSSUevWcP2UElLswVVtjQor0gI0eHcqcjUvCGmA/+pOc1ZC6SM6jOOBUwCHf+gQsllCdKZaw/fY+KMzTlYb4+6obNg3nTvd2hVCQAyx82wCoTLjUgWPvGYR3lwvF4ArlsUEESJ4Eat1cnDAkDPVMTb8bBiR1sDOmCRRtAroTEVAeXqi4gyL9SaCCGcF7C1/pVWWC8YwJpBze6lM1mCeNaZxG1asrIyorlPlR+JSlUXDPIWAJSxKNFWULIGbcw64UUBFRi4ZjAs+kQSdjumCoD4EAhMqRdBSUCmALxtAEWERa4Sv6w1fv77hX3/5FWvOeN82iSeSksYwEOW+qmPPxdyg2g4VJTqKDIkRnVApgYq6S2Jxc1wro+QNKBvybQW2FeXtHSgZVFYRxJC4cMK2IckiBZPq55fSAoTLr4CrCCLAwNvXL8iVsSEgLFcUdW2V1zfUmlFvX1BLBpcNnDfc3r7i7e0dv/7lL+CcEeuGlCKWeMGyJFyvCdcYcIlBjZLUUgkVYfmE8PL32K5/xNv1D8jpCsSIhcSl7gICUcBFrVKoxcVz7pXdOjARGHgE98E8PzCjNJdAGj+FAqh2G5y+vljdDAVxSaTltj2xX4T+giaMuHtGdIAyMvh1lxrtYTCKe/8ar8vgHImFrAi+glgeBRFGIMQdni2CUh/LYbSEYI3Hw2oRUYrFfpjosQMhhGxXcrCZnGZ4AKjKFIYAhCiWEqbgt0SkGJBiwBIiksK9e/yKM+Y+EQ302NBAwnTufX+a8cLfGz/4W0hPCyJ88Fty+6IdvBjv+2GlEvmBm+4m72SPjWc8WwiH7ucZx4wFssY1REG0l8e2DTXpPU95tF+tOEPDyC1ocmbtrnO7vx4TCId5dj6tOrZE7v6QiTkzo8dGPk5eEntIfLj5270L9zcPnW9dBtRk8+iz++3vczS3lOYHd96H4f0ZUfu9xP/xd3vgc2/dDO+I3JTo3Hki0ibKnqkpK0X1/xcCgu0nx+wyxM5tq+EnTDdpOgcGUjSUH+AquP6yaKA31cIgDc7FgtAAgpiWIgHqLEiaR76N2VprBrmgvw35MmSCvUVE1cB0egCCUTVIVCPEVBBBIYFCRIoMChHkXDQBDjmBIbviAsVryAf1+x8bw1g0jSoKutubnszdyo7xZH1vc7ef+2cEsTNjfSac/Ke2B3gq8+xAvE9c9/V59M0RE+TePhrb4wVD/f3wvWM+z8lihMxtGZjAuj64douY5k6rVXDUb7T5866rPDNTfhExJBVKaFyI9otIcREYGWzuKqiy+viU+qtqp/lg0n6sjgQEXlA35+mChwMLHiYwx4YwtqsFZjTEch4XXcNc8jR0Y77ZhmSeyvZvq3+oxJUDMPw8YVgsvizBw4cNMPRbmOXqHfWE6D/aJ104NF5RK+q0xB3I1vu+TspOuORo9N1S56mM/nerx63D9s7gOLrwIegZ4b85TsfPBfarBh/p/dF16nvrwbyXcQLHdP4MH+zfHAkqFXYbSnrWIwKEzFZ3hURiHGdjakdomK4EiBVJ6OOK/bh/RBghf3rMecZiPHOx47CGdxsefF73rsqD8Xget3kaT3my3G/55iP5AKV9J7z/UZn3CNlvSc+W91GBw70yR7TxuXHuz8dNNOZ/fIb/eySqG47w+5T+u5Q61EAddtzDwTDladdg/Tfm1XzekPKT1X1gFZy9VmArVfzcbxu2UrCuG7YtY92KWj6oRYQKJG7vq95LUOqv73LdVvWdvxbRyi5iWWF2wwQSJjsJPwpg0YSNPbISalXc2rkBQVf0UZArFAERLlpe0LiQMUbRSg9Rz+lGcPnRa+V00wN53uQDnu9WAWJGLQxq40YgY8R3ssOVpEw/HhW3OqNe3hvz0eJaGo1i64FYYq8ttYIC4XpZQAAulwuYqwRC5ooYouJ7ANi5yjZmsB6OBGrua7lCtcA7jlgZII7CqySJiyGsGcPBoZao6PEfgglohMnZ4kO0M9b6BoyRIXpqeBbtT1FDCwBRHGUipBBQY8D1khCIUfMFABApIEXCNQVxMVVW5O2GbX0Xg38mZCTcKuGSGbQWcNywVBa3MERikV8Lblm+/fXLL1hvb/gf//JPeHv/in/8n/+M99sNf/7yhlIZBRJTbokJFQniSCgiIqpAIrh+EIgiEJLg7CkCoSKFglhZ2swVvL2LIIE3VCZsqql+W1cgZ1B+R4wB1wgUBjisKElcIbEsAREs5gIuomhXStE4L4ScC0pISLcVacsI6aKxYBhcJCA253dwFXiwrhtu72+4vd+w3lZAPSsQBVxSwpIiLingQiQMS+UJxMsL4vICfPoTyqf/hLeXf8Av179DXl5AkXAlYXBG8ZGHS4ioRAi1yDpy68Fwgc4BsY03IqoDLcehWYVDGfTdIoJAbLYXiruyWBm0GAzEjXbykQvI3Q/rWH/KLbAoDFDUTzthAdxlTrlkjTsi607aUTRotF6rxGmweCvBIKJW2N3MyQhZm/vAab0+wLQpfpai7quz5GtupazIk1OVyPGsbNzFtZK4PVS+MjMQzRoiICRxi2ZBqqMJjXHMi5j/PsV/tE1Dmpp+9u09XslZ+uviSd9X17f0b04fsoiwkR+JHriJnvPr30rS78szIu6cIGKWRcdKuZ5qAtg9OnCRxRsEOA91zldM1/7eu+c9QtrDVN+j9CyBwUA/cccHp9/tiIJvJObmus4W2j0mxT3XTPe/ZV/1B76DQ4jvp/vjsBeifAtR+KjOPZF+gHEe5tu/J7IgX+P8z3MwlEEq8Q6hm96dNh6Hc2IMDcMlYxR/iolN41UDf5akggixfCAwaswgZpQgwZ9KkeDZxvD1sRwEOZexURmFY6jMrpmMeVdUuFFGiwg4iwhD3hAQ0iIazCBQjap1oUidbcE2PQZXQkdKQtCgSOJuyjSioSNRK4A6Mkm92ffw08qaBtQ0f4LQTgzXk7Rj0p8kvwr9t0dlzYzBo7wzs+1Zzc97/ZD2UZuHXZkt8/jel10ni5gZOTEBBDN2QgjPFD5O1t99X/x6jSEhBCd4SPp3SIjqvsn2ptr/iZ9PR3TaPYUuYNiN1bQf7gkr+lo7EkQIaur3piG+Uvd+LQ5l+7llGyn/4B7QNhigvXTrfpjHg78Md7AUaA8nfKNmQYT4Rw3DXpv3wFF/Z0EEkTL6j9bNnXXv15uUf5CXlaKyq44BTXjLMQMcDU1oP2VawJgVHsfzhZ60l6jHtrl7baNuLT4tdSjbnjU/r67ffTkcDfS4R8ZzF63dxkAiPa9CmMdy/zNcuDH47R3OhQ++HfJoFCz4NnZRxPS+5YO7Orz8YBTGusfr3K5xnB6VdY6fHL0/Ohc+imfxk/meSWeM8seM+efSR/I/O/bf0s/GNPzGftpa/S3b9NdMD9tne3GP7D5VzrP4lpXh8b97+b4vdXx3148554wbDCXsaZRGGhhgZ3P7wmLBsGW8rxtu24p123C7rcJ4XAtyLhojouC2ZZQqrpmqfldKwdebuGzKm2pxl+IY+dxYzw0XV1o/BBGqD7GSmiZ0Z57BMa/JDQ8BWGKnW4gIs1vOEI72quIrqCNCOlVrXh24AqTuqkjpBA7NScwwLw0na4y/UXnEaCX0kMvtjPLuRZviEzMCM8qSQIFQygKAcbksqFUEEbVWxBDA7ITsNJ7e+ljL1Hq1/c0dUHMZKkxgrlX1x6jjhEQafFYLIosJIX2m1veef8Zn/Hr2zMdhnYJd87vggkhcL8UQsCQTRAA1lzb/S4q4LosKIjastwQKAXkT4VhGxFoDbhmgUEEho1ZGSqXVzVyx5hXresOfv/yKr29f8H/+8//A29tX/I9/+Ves24a3r+9gCgjLBYkI4ITKEXBCiAAJ5Gz7LigCEyippn4CqCJFW2ub0MWoCGFDKQRUYENFrgVvq1gn0HZDShG0RBFExFUsWLjjgLXmHvxdf6VUlLoCRNgqEOI70rqCoriGkjVaVLC0AVyx5Srw4PaO9XbDdltBBFwuCURBhBAx4BJJhQrcXLOHuGB5/Yzy+ncor/8Bby9/wq/XPyIvAEXGBcDF0Y2VosYZAAJVENKwYFj3BJxIokVqt7VDajlc5VoBUDVLITROZzAmuakw1gi125GVSKbs1DbNiOWd4NqeviQozqu0GCweZTVhROd9NIt6DbQu+0mEB6RKmwYDzSKCXXMkVqLSetwVRdu1xXnQeVbrGxRxqw0VRAxCjGHkse/vhHQL3BUrKkYVKwhAhBCBgBQQkuzRRWMwhhCbItHuTHd9eCbt+Q19Lj5a1lG6h1N8a9nP4w4jPTTWP5d5/Pzjdfb0AUEE4ImlkUAF0LeYa4gAXmrM3YnAamWNPepnhBCZdqgODLCBstV87ddNJ0NIIEq64Tujz/ejHbCWx11b2yx/o348ujqdgMe96eNC/TtPfPr5I6Nm+4Pd+O3vezkMOvVpetRUZtdW6j1jOInrUE5r5UEaN+hBE07fE/CNFhEGbO7V/FwZvoSPEsePks9/NG9HeZ8i8v2ibuWdt3X0Z97vTRO4E/n2c3NNbPE6O6LLQKUeHwLU9GKBReoZBBFFtDaimu6FUEAwQURGCKphUdGCPnvXTQ1RUMudmXlq2h9FzVB9GUBH8gkikFmWK2JcAIoIIYERIcHqbBBCIxyatZAbd4MjMUZllsoYhlqRs2jLessIZpYocwfz3OKIk/VtFmD0QLg+HR1Wc9l9DYxlmnurYKzlHbP2eO17Bs7vpfW4ZxzTONfDmjWi7xiGzEx7XwezaKYJ4ugtJM7cfE1r8SQJgRwQY0JqVg/ipimlBSnqTwMKxiSEIQWJrcLMiHHSfJvXe/PN6QlTtGemOziWgZa3/0ZrpFY2V8S5XpZV3veiIfE2DUI4clSNOn2+d610Pn5eONLa5QnJFnSyr2tf2hBrZSjX+u48q3K/NgECnEl2+9Y0gyaClmTdIAg5EpsWXAVVakKwY6FcFyYTEYgJFmDZ5qq6eCGNkdvaY+R/6LgDqQAE87WfGaR1+qDG2qpmjtyY9O1Nh08NBfP3x1P53anjf85YdII1xpDZfWsMok65tXceH2Ucw7kR393DVBNcNIWcdmZ2t06zGxQzMr5Hfx29l7VGh+8H5sxuTn+f9FvUcQ9XOcV/5OX+2cH7oxJ+r1H5nrF4VgjxLeX9rQsJ/r2kZ8bxe4VIv/VUGVOJuZFuVlP7mwdgLl8JKCP0AIr9XLDjL1fBj0pm5FywrZtct4z3dcXbtu4sIrYsjEuLFbFpIF27FzSbQGERvW+OGqDYXEuSMra4Mbgk4KoIH4RpNbo1bS5KvCsRZlg4WTLGoH6T9PzuvISgOL4oEHkvEZ1IltNRxqb2l2x4hZIPqh0d9DAjqkpmECRMnVio1xZHzs6v7prIrB4GmsKaUVUIULvLp0bH6c9wI+uHxSe7LBcRRKQFNWeEGBCZUEBgYtTGODWawcNqxQtJYipIzVXwGWbR1NZvmEULW84poUNJXeIaLjlaOTBa4F5BJGF6aHu9RzXJMAvHtnqnPdHabWc3N/c0y0WslwkS3DiqW9ZLWsAcwUUY/hwisGXwWlCpYq0Fv96+4n0DlhVIAYhJlFrzJoGo//l/iuDhH/+v/wNfv37Ff/+f/4Rt20QQxwAjIlBCClcgLAjhCg4LKC5gtZrmENRnvsSNUMy99TaoG5sYgvQJBeCCEgAuG4CMEgn1+kkGIyXUUrCVIsGU1xWJGUgLmAmRSoMdW5WA8HnLKHlTt2hZXbExkCtAAWF7B0JoFtzmKS0GiQn5663gy5rx5e0db7cNhYFEAaEpaUWkSFig9EdlYTaEBHr9I8LP/wVffvhP+PLp7/HL8hlfaQGQsTT7EUbhYIiy26MqTFQuXlNnNORWYZ7HZ7sQsO8jixlhxE3Q3RDamhVhkCx/0n3f3Y01XLph7/p3Vc4bKR/P+BzVVq7/qbcHHwdTLSJqzU1olLO4R4pV4jVwzsKrMGsJc7VVjVbT/lp8mKoKbciOz6JwxywdmrWZiw1RVehxSif3M6ij9Qf4n55dRBYrQrsfIhCirBmND7HEiBRk75m7LONHHSni3cM/mxLYdCZ3uve353n8ddK3tnmGot/f9w+4ZtovjL1AQYE55omRg2b/7d6vb9ucTdigB5V77yjG9l4K1SCywbQiAgKJ9qnV2RHy8WA+7xf3cT5cj5MAgeZJOmI6nF/HfPPROdepaOLBt7VxGQ6+PiDez/bRoyVGBxu0AfJ7393buOdN39dO85N9zc8CiY8KHY7KvQNq7aOTe1lcnQ90lg/D4Ni9LJd5z5231xDrwX0I1BKhtcd61Brl/hVEsO9NQiAGExAVVkQ9oDkmFBSAVKu6MioJc7JQQSkbqBBYCQ0JEg2EMMZWqHwk4afGOByYpE7w0N0+TQi7nu9iCQEkrojpogRZEaTaYBc5XMbPzDSmRIQQpbzIojERQhRmpGHmKqhQ/uw4R7u56mtiFgoc7eOj+T6GMb7c6QoHg++kQTC8K3/q1wf34BGyIG3D6Xtr87kGAe9gyyi88trn+7LMwqYJxQwJ4/tj1YRUIepPTORNY8O7ZhKrmthikBgj3rfX2tLbCMew7+6beq+NiD0Z09bPiuaCaahrdC3WLASYHazV7/V5Z+ozwE5oxnwidzgePylzH2OllVf7+Mij4L4dkSS/tqh9cO566ey+Vu/aoWWSvgWolRnULUQn9IP3dTzvGdphCm0c5zVpe44c/sPtK0LzGdT9Sh787E+FDcYkN1d7huU3VKsLGYb73RU4m8tnUx+b43cDc3X6xq/zERE4hgm+rN7+GVe8j7f13/Q9jr833M3nHdt0fJ3znH3f8hw+5btvz9Ij2P5b4Fhn776VqXv0/R4//1i6J5g/q/MsfaTd31KOfz+OwfNt2N8fj9kzuPHvnWbc4ZvKmKk7K/M72iNt2j//FvriUT33ktDOHX4DgD/BGyeOMJzr3eY4CEPNMAo9l3KtKIWxrhnbtuHt7Sbul24r3rYb3tZ3ZHXlsuaCrEKIwtwUaS1WQmGxDmACWJUxCEEY1MSIxgS3s48Nv6kIZF46gsY1qCDnzkcY94Bo9LLeqzsRO78VVyKgCR6svtkSwr9v9JAmYQqSu5/mzKimQCpg6Vq7w7ncDzgJzOoEESaMQHvuLSasP30egeMzLZBw6wTflNgaS1mQYkTWAN3VrYkBfgzO07uGNzHEGtXGHmbR0C0jgACuXmhueKy5umFttwnEvOKP/Vx7qLejz8nUd9fWdhISNTZS0zsNhJQsHoE8sxgbKSaAGTVGcTGFgEorCm2o+SZuirYNVDPSmhHUKoHAuN2+YltX/Pd//O/48uUL/s//4/+Hr1/f8D/+9S8ohZUGSLhcPyFSQggXUFiQaQEoibUDRXElTKLlL64kQ8OtK0RQxlDrl6TBt3U/BGTUHIByQSDGen1BLRUICTWsWEtFYAZtGQsI6VJACMgmiFALilwySs7IWayXSi0SjL5WodVBwHobUI0lSltY3T59ec/4dc14u624bVmWRyCli9TPfyBEtaQQQUQAxQS6/gT64T/g9ulP+OXlD/gaX/FOERdkJDBEnRDKO0CDF4Z7GX5mrth06So+7Wku+6cvM7J1Y/tJaYku1DAhIwAmcAvmDDATCqmA0QszbZ2zCHGo8VdUTOGXNdk552m3TpdWE0SwCSREKMGVEbiIq1jlicAEE42m8TAE7bkJKipnHReZD26WFgLMm6IZs7iwcO6nmssnnyZYR9PzIRnNZi7UBVAD3jW2xXfRuQ3UrZ7u0cBn6RE+4YUb35Ie4S3n/IxvLfMIX/Dr/bwug5W+rO/pu6WnBRExjln3RBA7QD8eqibNI104u0MWHakhskEn7IkmPSkYGC0V5CATrT6NnE6mxSDAuxN/nmjsDFx7v+tf83/dqx8HYmrhjtBxLIK+wyZi9Phd//lGEXpT22gP7SGI9P3ICOqMeBoXkyPwW1fG93O/fTq0xBjqO/vyvMzj5wc5d3BuRu7v1zq//wixcE8z2o4pa44nBuReEbFpLfTLOMe7dw3hOm7n/LwhoZMgogNmv/ZsHQuSyP5EdKQMkfC+OMgBwMqIY4g1BGVCDSqIUAZiCHJIhlgACii1gMEoNah7d/E7yiCRyEM0gyuzmHuqJlUXOJiwIsu1ZPVhmdvhzNJBaX0QK4ZPhbEsF1C4IkbGggiiCIoChyj03io9h+6eSRBBRQs0MFdFVjPJotfaGN16uJT9IegP4YbAH66r80PL5oKZDq/39p5Pj4QMA0P0Tjpi3hwxh84EK4OwgG2PmN9Nts21+2b+lhylMcM7G85nmDS9rJHBcyQEMYJVftT8DZsv0WDIcOj5UhTXTEIYOh/HMDDMqk09Wy0YYorhql/qv4aMGzNBkUw2Lf+6+95co42um7TMfkD0shsiWtEsB6w8TyjfhZjW36JIfNfSYUCJ2o6MG0NiiFfh3/cFMoyjR+SBfr4zxvdjm0zzaLQyMasyAALnEBBibTCBN4NVZaiTfZksJvC7Ol09XhjRILDCINJ1FGNoLiX8r2vn+z1H7h7oeMfR3ufd3t2didN359dn3Jh4PNC1xZ+jrm17pNjjYFPJu/ag7ekjhs35d/v8RuTuf3C/58p/ru37c52Gtt3Dfe6X+XunezjVt7bhnpDAPcHZ2vit6vy3Tkf783es7a9Uz2+bduNzHJnyqe7taanx+TOw5OnKPpBsHcxtuMdDaGcDM4SZJrC0VjnP1pyRs7h0WbcNX99uWNcNb+8rtpyxrhm5SjBpOYYJjISQCJQCkp0zTGpVwci5NrdOlVlc23DFUhQvqaohb1u3WTcUhCAW2TGQKHqQCCY8PiIMNRFEiN9ycWMCZmHIQc9Xq0PPwz0sJRcjqM9ZO5FDMIzIXmn1igcpX1Lc2pIEIiZR4iIGUiTVsZiwfzvOWowIdZViDMXmmsVojtGFE8BqgUENd44EUCWkJDye63UBUNVFU8aSIlAjSpA2eaWSjidaqjqr3bpkwMmtXgAWY0KYuSxXDWDNIcjUUtFvzPK1uvm0+guGgNYsgp+qOFqkqLiVc3m1W/deCUnmP4XQBDANXSSgcFdCKkqPcAhADNi2ii1v2G5fULYbqL4DNaPkN5Sy4S//+s+4vb/jH//HP+Ht7R1//stfkHNF5gQKCen6CSEmhOsnUEjgeAXHBEoXUFoQlhdQjBDJhjBgu1lIBAJ3jfYQASJwTGo9UUCooLIgECOWKygQXn/4ETEmXH/4EQiEr7/+gsziFu0KYMkiiFiCMqxLwVYL1iJxXXLJImgsBVlxWLOOoObbXHFCRFAllBKQGfjlVvHrmvHrTWLFsMbQuy4LrsuClyViIUaCehlgQrh+Rvj8I8qP/xlfPv/f8c8vf4d/XC64RQKjIHLBwhKTYoOuA1bLLWIEii0WQgA1a+EWroTbym2ro3dB/ggUxOohhOY9oG1026gGF6ri50Bj0hMFEOoQ85Zg8VdsP4hr3o7zkgEc9BiuXd8fcO02wWStA29E4kGIW2zOCjdUuY7VY0NV927Nh5wqj1pAcmazfkCDOUZDUrMy0yFwdBsAiw/exmZ/7u0PJHvSvBNQRI06WkRAEOU9c522LBGXFqxaecI2zkQ7uu3oXPY01qP0DA/kLD1bx1m9c1lH7z7StqO2+P7N/KDfQggBfMgiIvqmaWMADIzTiTiD+mVurky65n3L5w5vwCNGnsR0/soaU41b/W2TN40FCyYVECi2th8RhnAE2h4h7VqH7c0DHPVMEPEsAjoAnVkQMccvoFl/Z3y+i3V9Jw3lOuyJ4BCIe9/sXn6gPp8MR/nod67ah3kevr+f/4xQfshUO8h/dD883zfmpB0jS+ao3UfvDvfEvih0plxF13B2CIYh6KrhE4hQSQ75YKdPFISX1eTZyohpAUpAqRUgQomCfJYiTDyqQU14+4FrSGOp5p+ytIBZop2hQZryBq4VOWsg7JoHZnENpNroFzATri8ZoklSlNAoioQIoDDkRFlNCDTuycrGuNVf01Lw7nzQ2n8m7e7wEaADkSLZSX+Qxrk5vsr4t9Icbs+7ub+3/p9J/rA9Y/KdlTmPkYwboaIadBraeyqAkKcDUrwTRmDcbr6d05GvxOiutY7g25dj35D+YYJJI/jlzCIxy7cgW6Yxc8AM71eGCSyONT3s230Z49gyzqwP5Fd2+Y/aZMwC7w7KkFFmVqRWicoHiTkctknqmNrYBBEnbeRxHEchTp2XEiw+x9zP5u7JIWN+rTUkVrX9SkwAFZQSQdTrtLg3vmki4HDtp3HWBiEEM0xM2RnfPW6NxXuwNdffK67k+iACCodTHZ4l9eS5u9d/d3je7opvTq1O5Q7cP3fn+bO/D9olA3IIn87acAbPzvGf87E5Khs4JziewyGfSw/LmvLN6UxgfZT/UZ7f4ryZvzv++xDR+VCdv3Xbf8u2zM/63+fCie9t72/R3+9Nz7ThdJ7akjgYS8l4t457TIln9ruHJY/a/GyyM8CXscc5T9oEp5SmqEQtKohYN6xbxpe3G27ril++fsW6ZhFElIIt97hUoZ1LSQXlCT1+IyFkEzyIK9XYXDSpAlHUM1fPfXEBJAw3CWJsgghR+IgxqGsOGs55sAoiuKLWANSCWtQFYvVMIensPOL+/DJFS/mFXgcAJnEf0pn2woQzywijKYIgMSDSmBZaYSACAlArSZutAZ14UHyqu2mCMh69AAIDbuJ+gRS5UHcyRINFRCkFSQO+phBRQ+jftvGZ8UuoAIeFXPL4sNEVXMHSMVXuMo1vc5tCPT+OrTz6e+2/urD0fe3fQfFCh4eeJMtjeFAQrTqADC+zJSdCsVpZXREpvkSEzIxbKXi/rdhub+DtK7iseH/7C7b1Hf/8P/4Rb29f8E//85/xvq643TYwCJeXn0UBKV0Q0gJariCK4JiAsEiswpjkGqL8rfSBUaRtTBRnJAoigAhRBCX2PEQQJxFwgLG8vAIAlpcX5LyBVSEwlwLKBUWV6ppCXRM+ZORalPYWK6cKRjH6lxmBqYMWAkoxN8UVWwXeMuMtV9yyWFNEjY+XYsISI5ZIWNBZ7cwBYblief0J7y9/xPv17/Hr8hl/ThLPg1ARuCKoCzDWPVm5O/WSfWfwzeHObhX3q+1f3at6QATq8eOaqtiwuJxVhZ4n1GqTfcQGW4e2QAUXxp8UJ08Nbhvt2HghRyua3X+2F6pz2aRmaNWEDbXBUda9xWB9ji6IUIsIL3jgJoiwDeQs+HVQTPjS2Q33cMz+947uYrX4sX1MJGuZIsQTjsR3SaqIFaMKpW3AXZkz3+WMAf9U4vt5753nz9Zxlm+mOx/X4dtyv0xb/4/a+FsII56PEdEc2o7b1OVoRGxDqDRTgENn6ODbdpjZrzbgLwMpW7SxLcgmt29kW4iBxESHSIJ9RoqdqbMjGh/Qag3wjIN93P+jzztn4wj5JD+YuzwChEak2OefWjEUT7tHj3VP3ZeuHY+kfcfvzuo6EZx4ZNeN+b6u02a4kk6eP4nDhxPpzVMEtT98nizj6P0jJsjxO3dotvv739ncGuMTMCab13LZM2ONiThaTaiJLwBQRQ2MyJ3xVWtAJWHME8QHKVFAjEURFBU+1AIGiW9Uiig5C/IRMkARoWRQjqCQAcpg3lDrBoYgHrmKMGLbVpSSsa163VbUWlDy5ph4st5SWhBCQikV15fPSIlA4YrAhICqSKl36N3nZ0c8Gr6sY1lLQa4FXORvQWgFwS654HyvyCvS/dCnTYmfhowfp0eMpcG/rZa749miT++3MkNmyfysheDhy6P1bgIWgvqY7QO0q39mRNsKFlSZHCGnRXCHQtwYnIq9Wvuc1QLzGLhw/K63xTONW0C3UlBLQSkZsURdD5PbsCfHeWSq+X6PWh8+j2+r5el1110/RMOKAU5oIzMRoO0bRl+X3joBopEmFJxDdnVWzlITEviKHME4XtHHcV+QXKtrt7bVEPV56MUaYwxuDgaCxusI03y1GDvmig2diEMhxKgMAjDMbYONW/NS6wk3a+P0J4Od5pRZQJgpe2wmymQWOOhaXyCDH/o3oAILwPALE7LuhzAMrThKskMfJ1bmyxEc+JbU16Mh5kdtnAm3A9hINOCLPh0JHY6EEM3qhCbXXC2u0n1hh38+j8szQgiPfz/EcQ/SM/D4W9K3CCmeKPU7ypxxpg/W/KA/3zJ+3zr2H+n3bzyt/2slAo4sIuTx83jK0Vr4LQj23y6d9aXjsYCcT1sRBuS6iebz19s71m3DL1+/4LZm/Pr2jnXLeFP/9oWVdo0LlpAQw6KxsRLSckFSF5QhiFY3g5C3osKNFbVUtYyouORVzuZaFHxrXANYcFX7qWumGBDILCPEwsCUE2op4MooZVNaIIBrQd4ymIsE7+Vu6diDPs+JG1yd+QkdHskZ0jCRoEFbyfBqEsEEQ89weReUiywKXFXc2Bi+o6SH4V/CFOQez8xpQXf3LE4BiiDWEGF//jAzlpQQQBIDoVRclwU1S+yyWovEvAI0Bl4FqwumGX1r5w4D5uFCrFrFxz1RBVNSl1Si+R1CgIhEagdQbYxt2IWpSepznpgRwAiVQVVdp1ZGLtLWkjuPRQJul3G9e5e7IGWej3tY0AhSwYPhltQY79smlj+39Yb39Yb39xve3zPe3jas7xvW9xvK9o73r1+xre/4y68bbjdGrlcgJFw/C+35+vlHpHTBp0+fZW9EcbkUKCKmBel6lXhyy6Vpf1OjPQRvZJif/6IKcSwWMqUgcgVT1XgrguMFFWYExXk+//QziAh/eX0FrwHv719BRYQERAE5odFMlVn3UpV4MKUgl4qiy8FoYBA3q2+QvatYc8VaGL+swNe1CI4MwjUlvF4W/HC94uUSsAQJpUgV4HQFrj8AP/1H0J/+K94+/2f8z/R3+Nd4xV+o4hMyrrp/C4BVKQtTod5YBEcJESZjaoqFuudkugkm5zQcoeHMQSjPaOREIMXpnbKU7A54qyCrqcVKoVFxbKDiGo+BGo9CEXVALYakTZ0GGPE+47sEEFXh3dZO7zcLjoYy6x8Wx8EsrBS+yGQWoBYQ1JpM85P+3ft5kHZA1EQwz1ILvSCm4GJCRLFu0f1ySQmXFHFdIq5LQIrCC5Zg1iqwe0Bjn9Eh0t+zrt3vwyMhwqN0j6fyXB1hwvnu919rRVu3D8brt0gfEEQ4xIX3Qz8i0DQwdEVzeBrM9sfJ7DrLh16bJ9JNKmjIgPjvIxJf3FBBhAko9kzD0TrjeEClbsa0ODtO8CDtLUBa6x8QoQ0gHeSzOThHJk+68mTyzLxnmefP1vW9xNF3EVGP+nKS7+z5/lmTcd9pwln/9wyFe/n35T3WxDp63g8uz3g5r7NrHjumTzuGRPps2jAUWOOOOwaWYgYe2YuCnSLWCpSAmCqoBNUekoDWIJIAWjDEXH21hgoKpR3eZjZeckHOBesmgbRut5sQH9sGH7S6BsKyVGzrhhhEE4jItJUZoNq0hc0qYhi7Ce6hjYX8Z+bB3jLCENpc8uk4S+PMPHzPrCd0TYOzuT277uHdHpqxcuiZ7sHHfZ0zzPitiW87Ho/qPm0LG6JEEsqY2c2XI/Lat3osNWrTsnarhVqPtRfPuitrwQQOtf3d1oUTBgwCCWWqn+3Iec/amdmv1sexNcNxNtR54BaIentMqCD/j1xy9s8dgmv/kQkiduV9QBChVgT9+9FqYTa79WeZ1e0a3BDTIyFQw8Hn8ZjqskTUA0sTVdSoMDFEfabukhB0bxsM7cQkSBQvjtqzX/u6HqkLk5twrDEbIoj2gZJH5nvH76ye++dYX5G7Nj44n/u86HS4dToLLY/+HlvRCSobLzJ3DxPhMJZ9NA6Ajac9P/vN78dypnGFz4/zvC49OvufxhUOxvDeN/f6c9aGM/h+Nn/PzOtHn8/Q8dnvbc4/ks7m6uj+Kbz8Th3Pfv/sXPW/j3CA+2V/6/uP5vtrp938NRpzOtftyQf6MeNBv/dYnX/Hu/Owr/35G3JHoylQiMbzbd2w5YwvX99w2zb88stX3LYNv77dsOWC21bETUZIiCkhxgUxXnGJL0jLIrEHLspQVYsIc2m6JXGpGoL42I+b3MeUlOGeG2NVQGtRpyROEOFdM5EIIgIpDoHaBBHbJopRGYyqwodSNF9VfH/gO4xj6YfKBtOUDml8AQveLMe70BMqj4C54bUzi2DoprlWDgfrs+M/DTcxXKHhMWhay7u5pY7DQmkpc88bQwRFCdJdVKkhms/1EDVflQC9ho0cDBOBQFyhtqytHcKysDNbY0Ho3DH3MTQG2DCUw/A3xGz4cTW3uKrsVQNqqaiBAFQRwtiYkM2NirKYGwNdXuv53vgs3PCMwlKPuCUS64Atb1jXVeOkFKxbxW1j3NaCbc14f8/Ia8ZtZWwZYFqaK6YYE64vP0ig8OsnYRwbPgJRKglJ48cZjhdTP68Vb5TYKqxxKyz2idLkTEKPoyKxxnumaHGuAWZcrq/I64q4XBBKUaEi1BrCFIlkDMTdkbr8MQFQrRqFYt4faIu76jivpeCWGbcsf5fKiERqBRFxWRYsEQhUW9wGigtw+QR6+Qn06U/Yrj/ja/yENwq4EeOqNVcGSiWsJOsvafWFG/uh8d5BuiSpN5pAsldBbUF0HongyvY9QRj9pbBmV5qnVeDwTm5iD7cf3AL3NJUCBNY9wQpcuNGtR7Ab/VuYIgrZtm911VZ5r3iI69BgiY69CSW4iZn6AHJ3Hb1vjWt7G1337qT9Z1gJGz6t9I4pmwf926wh7Gfu+Snsx+rDwoij5jYS4zEe9Vun5/kqCrta4+/3e//t47p+Cx7PB1wzpQERs31qB28j5IyYc5NmC0I2aGs+oMEtdz9nDmf7jUAqyQXagTotykCxSXdNEGGmOcfEpLYDHUHbMejohLk84SOHKIsHxENyyK5Hej0wdJuuPaU22ofI8q7+E8L+2fSIWLlL+BxHJP2u9FQfzpgW9EhEoNv1wCJiWBHDuUFTdb2Oo3H7CBH70WT766PfGFLa/w7ChFdE3O+RzjAkZRDayo8I5tsT6EJH9Z9IJD7tayWxjEBBrYJk18riF7KIJUSsFRQjaikIMaOUDFIBwbatKLUg5g0hb6BtgwQ2I1RFKGPMKIVRsaIwY9skgN77+61ZRpibJBAhLglEUQLnQQSanaEXEUPSw05MyOEYekH7HVJEKBYoKaKyIImo3Mw3AaBQARNQIId8ccIcwHCezlyDQ2YGBpiOephg1/GaGOfa/z1+N1tIaP2ks35Qx54JOZZ59P6sjfO3MzweJPUTo9YjDrs95YkgzKjhs2lGYowAPMvdNeGYGTlnWQfbhhITcs5ISUybQwnIZUPIhJxXVE7gtg+rIlLB0byP5/qj/dFeKbwPw56X4astj/9+gKikY03ykdBGJmZQV01GJFN3q0S6F3Yts3nTNrWkAd/brBpyr/MRaCQEiKgxVaCEGjCu9k7Ej1YpgSUomu3LfjVhw7iaQrA8MnclA8wFgSKYILBEha4czOetaDDarm6WEu037yGtUYUNUbWBUpIgimlJwjxIZhEhlhamGOLocL02jGqoI7iz3zOxBhh1kJjRg1SSc1P1AUbcoyQMKaDRidxjDrU5mfpn/fLJ44FGYJqW4TO/2XJiUHiBt4iwOvZw9wgHePT+0XPpS8dLnxFCfGvyOOI9+P7s89+iPb93mY/m4Hva8dHvPpJ/pHu+Hb//Xz8drGP8PuyG33NvWvJn4VT7WJdqfucs7pC2bUMpBV/e3rHlgq9vb9i2jL/8+gu2reDr+w25MtZSQQiI6QXLcsX15RXL5Yrr9QVLesUSX5GWBTFFuQaxhghKowOEXEXwcLutguuvarWw3VTDXy2ZNb4DoYDAiGoZEcDq2ogbD0CsmfuZLnHiCrZEKCVjDYySgxsbYVrXovEXqs76btzYHRqeljeGj/IMHCpvsQ/k3FA6idXdSACICVTVMoJZ3QJ1IUFzB2lYFwFivVpQuft2F81stZQoYoXb6B2b9XbGmGsomXeKjAJgWRYwV1wuF+ScsaQELhkpRMHxolipc2VMIczaeWz7xQKFN0UQGx0mtdAQHM9oxo4TekUMwSK7lnYF1SJa3lV824MIJURUErrR5iyx6MOHGDT4eV/7QcwfVBAhdavthohHVCG8mpswFXTkqlYAWxaLiLxi21bkTdau4IYXhMSgtEn8jUtFCC/4kV5RqwjtKgOIC0IIuF6u4uN+WQBA/fRLN0wIZLG/hC5Vt2YU1NVpx6ElaHQW2hqMXGTNXEgEc69cEAlI8SI0JG+ghfDpxx8RCPjx5z8gpoSv71/BINw2oV9eisQWIK4o+ss6Hmup2Irg/ey2RW2sAFlvhQmlMt5XxttW8OvXG26lIhLjEgk/XBd8vi54XQJSlP3OFMHxCnr9A5af/xv4j/8Nbz/9P/Hl8vf4dXlBSRUJFRUVK4vAgYiQSfDnxAXEQFE6YoHRFUBT+mm71hQtDffubHTDpYLyRSoIpZLGRYBTKutrjPVftngQWqanqKj9rUx9pQlQLQC1WaE4EIQeO4Ybk9RihkQgoFm8xLAAUdzry3ruVg1NpNgOOG0ruqsmUl5tp0rc39QvrRyDA4afW9FuHFumE9qAHe+zjX+IoBCBlMS9d1hAJOdIDAFLiFhCxCXJLyW1iggBFDuP+kjx6duTn8HfJ30f7aQr8Mm+jtk6fXumjHdcxsfH9XlBhLM+kD/suUdm2jG5IwAp2ALoTBxu2x7DzxZnX4hadqvatYVIFihCiw3RpGXqFqZ7VTkSRPTEhkC4J2hM/ynN2XCQjQ4q8YPirh8jdmhq5z59bPEeLxxmq+/OwjoZntN+P0gj6Lnz7l7xj8b8TuIH2eb3/t7ad2/sv1UY8a2CpLN7zxw62hf39gizIT6h7Wko88UGxFZpgBNfUBBEOyh7kgU5DxzBIMRUQM08NojvTSLEygBJ8CtosOnKgiiWKIhnqBGh1n5YKXJZzEKiiIVEzqUxrUAESlFNFeVI3jGcGizphEdjRLFjXLVgxOIeDgGqCc0DU3lg6dII+D3zGgxlois70h+eRIg7FuX3paMYI72haELhhkqdHDb3DqxHgoizPDvh8AcEEbN4hadxO2a2dmZzQ6R4/MaIlrPkER0jJGst6qeztL/tedEfiJSY4bbW1GnPsGcfpXl6Po4bdPT4GURGcDxqyKVhog1B1fcEHgK0+XPdqlOStKF4TQvQ/dvLVPcAlp/M+qILTRtxAYM94wnaBREmYO3z5te6t4RoeIxrt1mORIU/Ajd4uAZIvloBCkpdTEdsR96nMR/gM/r6MJeUKjANarZs74BuEXEsHBwtZDz896nDoN7gQ4S+ESGjEGK/djvMOWZmn+EeJnyyX9+P1DS2ev/2woj53vKNOOKzP1/PUB/pOnN13LsetfcoPWaEe4Tkfp07AvAbiJ4zBvwzjPl7dT1ux3M4s6X9GpsVSe7U9CH8/Pz+e+p6Nv8TNTz89rzMY7zwUfpepahn0m9Sbts60754sq6z/TMceVNlz+BAv306hu/MaPHW1nVFzgVf3t+x5oyvX9+wbht+/fqGnAtua1F2lZw9KS4iiLi+4np9wcvLK5b0CUt6RVzMSkKUdYLz600kWtdiESFKRzGt4FJQYlArYrGMsPgOhKJa90XxI1YhBDf/7aTBeQ1fy3rugisCMWqJgOLnzCy4vMWeaoTtOCd8MnYtb9Okdq8cWmTnjylpkCo6CtzvLmD6dV4bI37klSiETlAhip2JA2P0YK05qprNMkLdZs3WEDJOJMp61Sl5jKto/3fj92BCqNlGut+zKYtMJbMxiBUpt35XBqgzbiUob0UJsnaICKFanwOo8etZGEMdVfDohDB+QW1P9B+La1WlKT0O32KQMCDSJYnpQHFBTFfhUVEUxZNF40uQ4Gkppoa/AZBA6nC0dcMLFOezANUIEL9FNkwqTHHW1tWtnQigBB1zsjhhFRwrLpcr6nXF9XrFtq1KRxv9LJYPgUV7vltFsBPSsAiWYPEUqNG51gAb11wYW2FsOaMUibMQA+GSgjCRY0AMGpOOIOO4vCJ++gO2l5+Rr3/Alj5hTQkcNjXqYBRUFHXGVNDHIrDRE6YkxrBgGm2VNYFEX2tkewx9v8geFJxe3gVUt49dge7fTgnx8LZfe139S4uHUF3behqdP3UYpHU1usNoEV0rmPatR7MJbm9KydRcNjk6avjZoelgJ2wfuDbPtLQCxh0NYe3HdBaq4JpVYUjulecLtYJzlhHNMty7MEOnWb77nD0jT37H9BGBAGDj5+bom+r7WCd/V0FESstwPxBg0AONZgTOAKceFtx/Pk+/3XeAQCCzxmgHc9D95jYcuomOaQHa4a7OCn2TJkza7cJhvghwkuazRIYd8H66j6bkiIj114MPxjZ1yva8TfzBBXHY0Dvv763r32B/f3vx9J2wwUPks3f2/nhQ/Dz+NQiwo/SIwDwSQthPwBbfXV9WhisZvf+ABJCTe3PXJN+gSwYB8fMpGDkqL6DKAIm2TYjiR58oItcMihIzQg6hrR14FFg1hGNj4qZF/JqGGEDZdKZoaGcgEuIpXdzvKtflIsh4WnRcoqck5HuNQSOIuwTY4iRjYsKOUDtyDwAxxhY423y6mr/N6oJAURtIh6AzGkIg/kOfm3P/zuY4qJa9IUlEI8t+WLfY74ajPTZrGhwx+ed2HjNG9+W6HPCCiPk86QSW/MpUVmnrsLfNl+EFEVU1nxrR0WI7FL3vPv/HPnh6SywiCMC63RACYbu9IxBh21aACMu26pRGxJCRShHrmpyalnWz9JvSfkzPEIcDi5c+wtpeP1+9jP2Z3fsJoKH2M6elMe793rfnO9jhW+8R/yko29wMj00r3JEkRKaq/KlfY0N8rfFkVumifUTiR9iITxlTR9RbhW2Nu5ba+U+svmdp2PMyvSJcFWOIoNpjrGtUmUCscUzIEd462AKTDbcxE31hFMSUkFJCTAKPLstV3TOZhYsjDiAMC8/cGM4zGZA78GSck51w4Q7eMQol+v1Z6oj0XBB0OlUbrflvNgJ+hHcmaDDLELvv/bcxGOs++s1urmZhj+HEwQKDUy9rLtuXc4YrHMI32rd17pf16PcUQpy14a+dfs86/y379W+RHgs+Dp/+Lm35W0knUOg702Pa4FhA+7E0w0IpV+pnRsOZt1WYgr/++ivWdcOXL1+w5ox//iqCiLe3N5QiQaqJCCldkNIFLy8/YLlc8en1My6XF3z69EMTSMR0QVwuKoSQWEY+nqNY7oV21t1u4prpdlsF17pt4FpRyioKHC1mxCZxApB7rAD9ATpfXABkjaEgroJKDQ0HkBhtYgECAKVGwS0NKbCYTx5ugyC+ZZ9ZDY7WCNI/s5oUZQldAdX0IxT3Z8VTW91y1rZz2ruXhOFTDt9SfFUsQGpjljfaYoJnAc4DBQNLWoDKuCwL8nLBsiTUsiBGcYZVqozy7JqyjTs8jODWr4Gi0P6GqnhbEE3swhlUAwjizjLGAoBQSUReJUich1ISQAEhlgZ5mDIYwoikEEDZrBNkvDnz4PFAjVIB5UEVxftqUbosVxU+iEsqXRLCdC9qeUKMmAKWFIBCKBkgqsKiigFR+WYRDNSLKNIxI+WKUoFNTQiWZk0pOI25BiZihFrAOWugYqjiewBYrHW5yryRRM5umvRmZdRwVRZBRIoEDoSXkMCqMBcALK+fAK749PlHlCJu0UrJuG0rAgO3mERggIqtbFi3FVup2EoPZi0CmE6DMUZN/oKAwoy1ApsK/VIIuF4TXpcLfrxe8HpJuEYpI7N4SIivn5F+/Dtc/vRfkD/9J7y9/D3ycgGWhEupQC24MfC1AiwuUNQaR2KGgCsSgAgCRbFAZo46v2KzXVniP1RlvEs8S9uHsk8MuoiVKwFB+sNVY6DAuXWCwQvjfxj/wO0FR9YwhB/CumehrpxZBV/NsqkJSOxbs+ohrdGEVYRKBIoBxAEUAwIHFN1+TPJdsKYxw23SVnKzRmoRQHo2A0UjhBwtPh6lPd55rOCDIL72jEfV5B+KX4dAiFHceyWlhxpNlJJNwo5P8UwiOunL6Yt/j+nbcYwzns+z6QOumUZGxv4wm4nalrMT8O5bkzLau85PMGYBte+7xoBuNGOaBdt4RzEgqDMcyJVtv6GZNN62xIdPD9MhoniMaN4TQjREcSj6nOhsNd1hFN3L0zOfP+KDYXhMrNxHrO9+iw7Az/OclE/PI+37fHuG4v3vP17HIwHBo3z33/s9eL+MERDrvmn/taLuEGCOoBm3e3fb5taybEU1fiSouxlBRMVUWS2aUAGOqMQtyFSMFUzGbAJCFYQ+hIoQE2JNGgiW5T6W5rLEtHnannNMKQoBUYPoBbuqRYVpp3RXHR3+ed4nGO2999MOqDkwWK4mjCAgslphKENdmKDKwHPz4omQrglk4zlrc97X7tzBGbmZQKDePWBIsTH6BuLi+X13D6qewYeOuHWiy4QFQ8u4j0MT3GBECNuZY0ioXrUXrR0W7M+Q+W56a0xPm5e5teOusTghWYnDXDJSySilIKhQA5QRcgZHZzUI8WUcAqFSQPB9bcea9deuZ/CV723mMacyosf7o3wY63T5WO+5/W1z4ZjrB+XuHlmzTz7Z3e/+AMxevK9WgkMKIG9oelenfA01GZ65QYCDdB6S9r+VOIJ70zZ0YyS4dTUxOzoc9fiDaP10f6hB4Zf5Eyb4ifdEKTDChT7PjULfpUcY0dnxPu/Db0sH64vtKsym7tJA8gZlcgWYRYiOn5Yj6KE7E6iPrx/rEbccx81gKTDPzfF5fHSdFQNkrHS8z/A/jMt86Bf27fLX3zLNuO3Zu4/k+Zb6P4KPeTLgufz3x+/eGDwq+/d67/N4eupoF/eiftu5OU7fSrl/3xoeYM9Hi3g6Pzlcgt3PtZsnRlTDtbWFR/SWfnfcJkEGzkZV4JivXy5Vgxybhve6bcg54+vbG9Z1xa9fvuK2Zfz6Lq6Z3m/vov1cBM9OFBDigsv1BdfLC15fP8v15TMuywWXywvCsiAsS7OEiKqlakqDaUnNhzezuFcqpQjOUwo2iuBaUDKJICJA7gsgVhEQOoJFU9t5qFcEMIhgnzteXgIhsFow19AslgMFCcBMnT8xjNsIbXfn8wiPR3zc8FIptuPPcvawsTLUv79YdTD5M2Cacm1OoxWUPvB4sb8avtpaN51J9oyCBHYuKjQyV0BBcQlzqQs9M+HKdVjGUIc8MQROXVMq3gXDvFgQvY6fVBUA2N89ILDh08S9j0SkLrxqj8un1gDSZnVz6smFYLi7WZfIr3LVOL1Ga2B6b33ktj7EGt4Y1B1zDCGAQwBSEldSLFY4lQqoMsTTmLj7mSe3jwXDLF5s5NoatSnlTiN25aralN3ArK6AgULBwoKrNZHsR1FmWSSOy7KAYgCq7MccJBh1VKudvr70p3VZMGa/RkEdj7bxK649FIAlJSwpyi8GBFXEkU0QEZZXhOtnhJefwJdPKPEFHMXlTmAgVcI7myJPH1NbWwYbZNWFtiZ5mN+Oeze9f/22PaE+TwR1YQqPu7l9wD0f2l4ZaYqWjc0lGVzd/f14kuyfWxpKbrhk5+/YpmS3OVlBme1dcmuq/XQjNB82/l3LjwEm7s6jAUDux6CNk/FpbE+4Zx1xI8y+7yUuECGGgEihKe91i4iO/8/Cj34eH5yi9/BLD5wHCDt3/RyBeIYnOgwb+/txv3kKd/juvMTpi30vHpZhF8Nr+HwcztLTgojYNMm8ht39ZjYoDmPe2Nrl8UtSLIrCgIQFXXSBEjrjzWmGOiKQQCIp1sO0HQYBDdGx78cF5SZgx4CjJgOt8+T4xeOwBDuSiSB+H3Uz7ZDgA4LVlze04jcm3D6afguC6Om6frOSvq325/vyb9vS80TT9X4KJhBQjf8Y1BSPTU8Xzc/+vkTZVxUVjA1kG08Pp+anWlSERfOJGawKRWYSzQAqVSQkQWhCQOWKTIRCAcSEWBLAEYQM5gjCAsIFRAlMCQk3gFYwB6R0BUBY0gVcKlJMKFvBCmqWQpfrghgTPv3wR9Xi+hnXl1fQ8gJKF3C8gkMERbGI6P3iBvhrBXJFi0+BKJo8IcjLoDFwYkpACEhUEWpQa9puLdGQOgr9kLfB1z86colGsA3A8nC6R4Ya3PUuF6YhAlbweLBEX507+TxS5A8lnwy5G6s7bss9hnUTgOsa6m2sYzuGU3uuQP6xOAWCJHfkvxTVLKsSlK7WDYwVhTMYeRRQGFMUpIRKt8wqEgkRv76/YasFy9uvyLVguV5xySuIWNdqQUwJ9SLWOCEtwmCOKuanPhakiJbNhB8PItoFbWYSIdiRIl8/Q6dxb2NtZ7h/z7vvj+apzczuldfO37epl23aOMdtk6rJvZv2jtMEBAzh7mszN9jW1zm3uVQ42Aem98e1hS3wfaNUxblwLUJosijzAUW1nYoJuNTapmYhGmtVJJMBM4fGhJcEBpSojiEqzFU4lRJCukhww3hRS4moy0ZaXs19gPfzOoytxP7hGgfQolAaxjBobxi7ckAuRkrPeYDT7AWeRGK10BkQ+jygEyYy2GCo3++J4QIY4W7xGWysbKbFtzIxIcJMu7ugWWznNLYYFKckwSMFp6RGvMvzoPhnaEwCqdssJUZC5khYYRZqczo7zefnugNgzEyrI8xw36Wdtu/viGf+fgxtctf5udXd/npw7J2P1dHzZ4Qsv186Xy2ePjtvzzkh+reb5nn+69R4fjzNu3DEPPz9vf0rx6vAdbPgCy0TufzC9GvMGQBmFjv4Dzfa1/A4dU0i5yChqO/72yqCh7ebWDx8efuK27rhX/7lL7i9r/jzL1/VF/4KgEEhIYSE5fIJabni5dNPuF5f8emHP+Dl5QU//vgTrpcrPn/6pIzFJBZ7USwfYogI0TRXoyoCqcsQxZfy9YJaKt5v78i54C2qZURO4FKQQwDXjLoBQARqhJxLetCacg9Y6AUmEMn7AAClIlbRgE5pAYiw1MUxp4Bacz9v7jBo0KZhwoXaxPapalaWit+LdSNLQG0GwMImBVdQBYp63qmVlLlrZy2BKgnhgQqZTGVSc/3/s/dva5LjSJog+AsAUtXM3SMyqrq6t7f3m29v9mrf/2H6ZqanZ3e6dyoPEeFuByUBkb0QERxIqpqau0dmZFXCXY2qJIgzIGcRoJSqOa3uaDNKVkteiMMFLTv0164/JQFRCKfThFLUIqLkhEQJIIFQApM6wRGiijMDat3ZQ/7KqLfxrcGrWZFRqZkszoi5vAlUlAFcCCxRA06LgKEWLWuJYAKElIEeQQjECMSQtUAQ1MIVhEIMmFWDtwcg1Tof8B+jx8wiorALdVyRiFHMosF0+RU/FAYjgWlGiIx5YpSyQkpWS45AYDqhuqyBgJYVgQumywK1wlUaoTBr0O2y2vhRixUHczkmAsm5LTLHQw0P4iK6HYoAxfeFafoTcEFEQUCUCTMIU1TXSJPMwMz4+PEH5JIxnc7IXPCSVwgRZlkxUQRCVOGKUk4oUiC8AlIgtl4DojGEE4KQjT9hzYxLKXgpCy6SgVNGoIjzdMLDfMKH8wPmyBD5AuVHTJjO/wEPf/h/g3/4X3B5/F+wzh+QT4QJgh9KwRcWvABIxMjmqpUtBgmrDQjIHDUxBK/GwDYjBkgUFIi6xoW7dBpx1yQCIVUYJHdzagFQouVKTFizo/8es0zXNxsn0YVb4M6qeBAeid8yyjRYxIZY26Ql80CEaxxOE8IEAqAuwBQL1jOSQGoZQRGBAA4aX6RGqJMmhCCPVM4C6ePMCCNYTBrd9iOe34jEXsmxKWVVcoG0f024YFh3iGb5E8yypVcyV1qUJIKKKoxKiFjFY9skPJ5mPE4BjwmYQkAiQhQVvKmQ2dzikh2b23QQI/ZmOsh+KMu4VcQV3Lx/eShyh0xsbtwpCJDNrw7daHdpzFjnb1NGo/fuqXmf7hZEVIY6jQShbFs6NM+2mvQflzhauZ10SqVVfaV98L9jbTS/9ou1Eo7U2nz0Xm1jZe5snjuhJrLpc/OPWJt6IEyo47Z93iGS19r0lobVyHw5Su9fEN9LM+2WhO/NOt5o9vcg9N4iKL+nMOJeovZr23Zczv11ErnmTbeHoBokIr2LoDE507UVpIi1I9098a+AhzpLCY0N4ZA1EFXgTqyFk6jfRQlqMREEiIHBQYUmEggpAoUnRCngqAhcSopMTNMMMGOeZggzpmmq2iEigmmakdKE0/yAeT4jpRNinFoAPfKPEXPkQa0a0ufaE1zPsx6w+tnjwFSqFQgFi53hQN/PAGNwVeuHYT4bsu9MPBydLZsV0AseDjUANmvh6Hs7xVrZlW22AZJt/o1A2a5X7E26bzHJxMuo49HmYuzPaK5aK3OkpxPu9BpuI/RyJqYzNjvrB/vuCGYFu5Vp3WAdfA670llEg1PngHVdEWNUP6wE5HUBBIhhqv0KUZkRREEReSgS5nW5H+RxDZAR9tQxZq1tZodOB2dzE/IfJyeae7PL/ox/67y8blEhN59r3aMgYpv/Giwf3rf7Hd4OF46o+fW+DBEnW3gQ3ogYci793I/EBNgEDizqck3MxyujumBjIzilBqRzN1+oZe2sUsgUI9zqhxruo/tbz6s+Rpb64kZdx8rg6gQqw9jqmq1L18ZX91bnTqlREmiMGN+rbeSxK3mb7l83GtxSOoKmnb291VLbk10AdKIqtHMcFLYeGt64dTflz7o8nr8+3/zuYGhft5d9DQ/1MvoA4UfpTVwA7bilbnRvMdh7S4xreW7dv+f5W7jsvWUdj01/ztJw/0jI9VZ7vocw4j3PvzavvXGzjOt9+Tpi8Xuk74C+H5R5Z6E3uv3183Tte59f66bhRnuj36vtTG3tNVSy3ZRWhuuV9y/08GzAkEyOXIqgFGBZVqzriueXV4v98IyLxYC4XFY8XxaUXCAlg4gwTYr5xTghxhkxnRDTCWk6I01nTPMZ83wyfFq1m6MJHlIyH/idIMKthxXGhNp2DoxSEogIy2pMWGH12R+jMrNjVGZ21WpnuL5467tjqqJXkqqYGMQ0Zbm5c65nNTUFx270rsCvDkYN9JB+HGY47KxrwZAKxy2qe5T+Y3hZwGDnobWMTBU43PPfIo6DtFgBTcnJGaRoV++uBXQO5v6nfXr60PEPh1uNHupXna9b/2wZX21koXgpsw2I4SUCjQlCJjQIBJYCiCqqkfWP2DTeRcxNkZirnGZVwdzo0xBoqN+HsyHLG6344Z/jh223VVrY45K6ggI15h6RxS0k7SJFs9wMAErDz9gEHR6HbOtStWI/ZllS7/T4p3eFGz7aK7YUYYAJmTUoep21oG4+nTYOUTV7szCyMIqYlwKrt/J7unFS6wFrl+jpRN4EkMab4BbsmkwYN8WEKSYLLqy4LyGpQs30iHD+A3j+AWV6REmTCuoYiMLVqkMVKnUsCSbYq7OseKzrBLFvIULDue1fDdFMhuOKgMn6IK2/lT9oe4CpCfcq28OWmJ8nehZ4a0f6uK5IX091xqm6UfJ2STcH/V7u8da2PtrH969j0lLn8ABmiO+F1ucxukSlIsY03OgVGu0cqGcOQZyG7a+6Sa0zoeuYt5oqqu5blqFrOcWAFAjJLJQqDtQ1TemhbaNbpnfjYX5s1Dk9zralM68Wt+FtcNe2q4W3l68gWbLLtm/gwc0O12jld23x39fQ8DvT3YIIbYQv2g6wSLsCNya5B0WWyQF002p1ANZfXdMMw9WfqyZay09tN9rG7xr3Fek2k8S/jCM/tP9wwo/6ebwB7t0UlWn3j/SP9M5ENPq9pu4gPGL6NYA5PvOlqhqtLQ9ZULDqHzW4T0ODJMmCOovGhshmKg0EhKIExpb5XCyQHRIQMiGmgLwmpCmh5FV98Z9PQCCclldQjFjWC5bLAhFBmhNimvDDp3/CNM14eHhEmmYTRiQz+d4OlDbXEfvsGkceN4AZ6tqxMSn7LUkW1yGQKGN4ExjXr3vm+/dPW+Hr0M33AuJN9oac3S7nHqZbP+91/oWG806/A4I9w/rw/a6Oozbs7jnV4ciP99ngja53OiC2xjLd//HnLzOWRTWBTvMJpahgLOeCGBOm+aTBho1YV1c7tm487kpnbtojpME0v93HbIdddcupYk4VPTyaqgE1JezW6pD31lxf8afsTHwx7fbW3FZWgPsp7d+7vS/G51z3kRMDXrnuT9Oc74kWJ+qIIeQWBOgokUaIKDJs4+K+hY1AXuxsWNZF/V6vC7gw1ry0fMJgKSa04EoKNSLAhGA2jtM0I8aOEBwIEoLGxlCtJ6LOtZyFt3fNO4GX21lGiLo3UDnxeLY3PM0M+gWVmQIEw3/domOf+tVRtUNtrkc8VzqhQnffSCcXYro7kXVdq09sJ9C1fBVIh2iWQyJGmEQT4O1bp4HteqWWUbAwCA4258hR3v27cljW0dXH4n6G+G088lbq4f/XpPcz0P+Rvi3R4Zj/25iHv0IfruAr7fGGKdORcT3MPWrr+Pydzbqy95Vh1rsjRmNwmWIsVZd0TWAKgyXMjJU1BkTOBS+vC5Yl49cvn/F6ecWvnz/jdVnw5eUF65rxellRiqjSPUjjpcWIaX5AjBPm84PFgDjjdDphnmecTiecz2c8nE54eDhjmiLmKVX3PrHiMnpWaayInpnpioihnuchBOSTxnLIIhp0tyRIMCtszqa9DogE14WqMFM9LDCIAyCEQAKYT3ygMdpjDHDXTSKCGIJZuDbGrjPv9tDNzvWjuaS2CmpAbDKBugmnQzCagk3/2TiZ0aymOZK6nA0uREfFp8T7ygzJBRwLCq8onMGSUTijlBU5L8h5AecVzBOAqa0Vai5snPEaQ4RErj7Wp5SQazDl0PFYrOd1k+xxBhyOmTUeAmEti+0dRgEFgRTrv5BeESzgcEAogEhUI6KQ1AWlJMUNSNcOEaGUCKLS0ba6f0Z6oG9Sr5UubXwPPo7jOe1X9ytpHA1XZGv71mKj+HpnFaxxUNqXs6jrMXcvVVYAhJACmGnjInYkTh2H0+hiik+KlMEtE7Uh1yhawlhWjUOwBlYm7jQhQvDw+ICX1zNCjBAQ8lpQAsMZ6ImC0ui1v6laB7Dh25nJ3KjpkZVN+PC0rLiUgqUIChM+0IQ5TPjD4wnnlEBwS5AZ6fQRpz/8F4Qf/h+Qf/rPWD/8hNfzCa8x4hKBBcDK0HaEqMqKjiuj4dPq/4qr0MGdNLEIiqhgRnddG69ua+taII2rwQwUFMCCIte11K37Ae/rzwO/BgcoB/SnHOwYamtXzzFzNRH0DBExa3eIWuCIWgFVhcBVXYLFGEGi/JXg56lQFUbA+iFugdW1Q+oIWZ1VNHEkoO3b3sq2TozwttIALojY8HB1lIaxrPWbQC1Az9eUIqapxYZIscXvJApgyd14N7qjKVi9hUO9BdObw7n3vPW3SPeiils21BGOcsRfeS8v+m5BRJWgbWDLwJzw2bzVEOvZWwyiej0gCt8i+MZ714m5bX3X2qrf38i/IwzJiPWD+5af/HoHAfkWQdqPZWvwX0cw8V0JIGt234ueOXW4ybvnN4u+NhdXft9bzu8tbdfCvWun7pmDvThWMO57c0hh+WEERc841gd+RmyLrEi6qDZCsLJVcKEaEjEGxBIgUZA4Oh5sJosJUpEJ9a/KJYMIyOczKBCWdVEXN0HjM6RJAxhNJw1OHVOqrk5q82RciIKGmKof0c7/as+U7AiYOmDwMWlaEdsxHq42Vvcc6LfmeWTWy3D/6Oy9L9GOZ3yN+Xh4/x31HQkhjsrR9oxA8j31VjlDt65HQrSWgh5h2u4bbet+vAEPIqjMUwLhclFLiGm6GLEZkVLRvoSAkNzPv5rSKtGqLRkFEYC7TAxuMm1Uh+bZnJ09z7/2iNqPsafKJKiT6VYA/bhqbr9u+03heA37nnG//o053VrgIeZb069wuvsyh+SMdvS9rOV4ftfH9DJUEFHgwq1KoAz7vFbaGAKipv0sUoWTVVDprr5Ks65h8WD1bC4OOs1FVoKRzW2HAIjRA146otX3vf/t6zFsxtSt0ZxR4yvB+kk0jvfRPoK7XvJFsdnpjSobb4iNe1dSfzZu6xzqtgXoQow+fktPpKsAotcoBBCCMnqoTaFx68Y9DKd/bgsh3kr7d67dv152fy7fI4y4Vsdb7/nvb8VpvhrH/o51fM+6/hplfmvd773/W6Z767xG1H5NWV+Taslv0QIbmNk/HvOO7zns33bBz5cep+jLvbVvewxEOhhGgLrt2TBqKtwWd9GjeMeyrlguGS8vr3i9rHh6esbL5YKn5xdclgteXy/IhZFXViavuWsli5tGIZlyRBdHzWM/JAsQOiVMkzKEpiqI6KwfqsLriL+IuVIJwXF/pQlCUJw/BALMikH5B8robfhN/7FxchzaiQXL2+Nq4UDwjA7PrDRSxUO289PP5fGa8nnv59it+2SzwNzaoH66fy6A6LqyoT+OmeW9ZUSPFza4RwOfIxAhGMPQ/axXi5GREdJouw6yN3/z26HqN7/DYc2smvSoANrb6f1iURdU6k4pKr7srpPEx2EcD48zUWNIdLhjZT72NNF2VkeEqvbhiEY4wpJ07zS3xG6lquNv3+tEcsUhfd6cThzmVMQEMmNfII05vF0PHnugnmmi7mlKKcikuJHYXEsMNcCvL0LXv3Emua8D33ti+cT2ja0wZfjb7ywq2FyLurhybwApREyUcIoBU3Q8lIAwgaYHxPOPoPMn4PQBMp9QYkQhQgYjg5BhgghvF7nVMOp4VLfq0tadCiWclY6RfWx0iPbZx1naewKIWYjXfMM5sEd994l2D9tJs89ZyxsK93NNv/t+JaK6X8UtdHg89xr+6+uC7D+1Slvt8PWs33vr4YMO9kcE2txoMeEgb1tL3cFnqZs0+LFcCS9UnlKAxbMxV4AxbASngPNjmwByC6R9iHu41NOOV/ASO0cI7l3kIN2gWd9K+5Xy3vQ1PB57U67gJBu+zNfxkVp6l0VEf2T7Qb29bhvraYvI9R30Z5XpE4KtSZ38GNJALMUYaznXrm1QrmyWN1J936SOdw3xESIi19uJcOW+t/wOJuS/ydQNw24ENhv96Pk/Et51MChhoADGgdm9dfTJBRJqRtj77+/2u4iVb6g9AWReFh2BotCQxxAFiIRSCCESSmFMKZn1QcFUJixlRc4zSlYNoMIZp4cJJa84nWes64Lp4Yw1r7hcLlp21EDVD6cf1Bw1Thonwww9G2OQzJVSVMYhBFkKMq9YOVfNXEf8FZmEIkLs9zoGWB3zPfNnIFQ2yM17047dd3CWXAMmd60dwsb+4Ljuw1e/4pwbkYPxvtiaqujJnefmSLRshUf79lUkPBCoWPDDGMGcAKjmGgM1iF7XSogAhdX0+svzM1JcwOY6bF1XTNOEl5dHFY7NE8j9+5P7UR5xOHUnoMib4lSjf/o+n+J2IwLYC6gqLotjWGS6egcj04QPFaHdLRvXP9riBvpM5Aj1Hssaiqz018FcHU3fwTLucVk/Z/o6G3FpvnvRrSknTAYmuRE0FuPBBRG5yBAE9NUsYnLOEKiGmMA1t7ycdli088MOFJIWcLMwYpCmuWkerJwgJ8efqntLb2/UcYe7hArdbwHgAtZegLMZZicKIN3ZIkY0Ay4s62mZQVDrtwcGUC88b2vTE5cmEBJRN2e9RUTOucbdcJyPSF2VxaDBD4EIQx0r8dyYUQBFOrSIaLEexqvjoS78277nDEmfi22f+7Rdpvcyabc49Cic+G2RoXvK/1sy8P/tpn+M6V8rOb+isiN6JtDBPBztz7fwkR0j/ACOF3M95FC4uSNxGG40M8gsdrNa7JaM58uKl0vGly/PeH5+wa+/vuDl9YKn52cs64J1uajA3FhzFDQQdYonUIiAa53HGSFMyiQME0KaTJkn4XSa8fh4wuPDCZ8+PmBKCfOUTGiRhvOwMtS7sWFpLm7YXKkSBaSk+djP2pgUx+KoWtjua10aU7dZ+REaMBS4+w8KGnMyxAQXdviHmStexdwpc+ENi4gtjR+cthnXQQuMrYxxt4gIor7/VeeguXGK5gWCg8Uw8zoIGN2kGP5RlC4qRS0iclmx5qzwsXSxIqStu2AMQDGcQ2NXBLWESBNOaUJJKlQqRV0kkflXoUBq1YAmVHEnMtaq7gM4c9y1sL0digEFCIpZYxrMtn6qtWkBqCDEDMQCcAFx0bgfBQAxKBQwB2O0hwF+w+hcv9cLI0Qa/uR0HMle6aaOdS8cYI0dUcRpRtiaiwhJXQhTnMyTh064FEYBIVMEUCA5g0s2vEZQOFfcjUMTJGUu5h7JXK1SUIta6MfHWiDVct/XoIdozsX33II5E9YUMREQkirqnR/PmJ/PiGkCUcQqGi7A8cnBVVcg40vr+eMWIGJxJAoiRAjPy4q1MJ6XBSszihACTfgwn/EwT/hwSkiBAKyQOEM+/AT64T9h+k//L+Djf4L8+J+B+RHrdMJrWfElL1g4YOGAHDSmCkHd8oSibk8ZOscLBYuNpsOTAxAZyObyWaD4YKhxDXSjBftqJ4mNmZhHOLNCcTeplZ5q06+orNP/bqFg6yOQup8uOj/i+2/Y05WNr0NMBKYumplbRgUjxoPGoQhRABa1gADU6iYy1ELaLL4QAXjcQLdkjmZVpjVwFJApQJEEgDWOi7urrcpcvRCmtnhMW7i2VfATdLGHaUMtuqKa0wUe48P4MVM4YUoTTvOEh/OM0zzhNE04zQnzFBGiCmMCmgWLtmHDh7CfWxrFhQze2ltKjtXYZfu8Ea7vT79DdO8a32j7/N70DouInvDuvjpReoOJ4wz5fkRv0ScVITMCrjJcNgTelhHi5feHwTCL945Lz0/ZlvHOdEtY0lWwu38vI3mQ6A8cOuz6uz0Evja91a7fmviUN+r4PRO/v9u2UYdQHzA1tmnHwG3cL2P0KaLdhI4jQG8LdK89Vve7xVIITApko/nZFIAKqd9GErD54oxEhmQQCEWDXnNBiAErF4Q1AWb6rW44ItKkAgj1pR4MCLbGat9o01/XLtpYROjA2PV4iF0g0xjBI09zn3d8fi3/W0dUHXsf7DfOgHGuNs/ecaTuzppKbG8IRXEIs81/o2HS5blGMNxojwC7+TsSSNR94LBnA4t6s/vGTFAnpj1d4ohPKQUEYF3VDPlyUUYAKCDmiFKyCspSbw6PQRDRfBo7OyIM8+vDNMDMfkwsg6ONVF/t96P3O9wURFwTpNe2diEMW7lO5B0TezvYvXkmtRO30p6hU58YAi3sxG7rwyiI6GKC+B9dOFpQh5CDPeC5XnNR64icS2UKcVGXbqMgQro6jBDRgowAFcCC05WixAEXAUcXVsjoDg5NO3AY82EoGk5VSQLxgW9ItxPq7Ry/JiQ92oTUxgtuRdHSrn0+oAfzuoU3Kuxx9whcBcJ9AMpeEOCahN6pxhRr877d173A4Nb1mjBgu5+ulem9vxczOBI27Ou+vSfvzXPr3a99795n31r+e/DUewU/3zO9t+wx//397IXO3zvdW+a30B7fq91k5/xw6mzX3HYXbvbX5ja2u3bE1RqRTtuH+4J2e3nTMLSzdFct/PxWMCRYS8GaVyzripeXBU+vC748PeP56QVfnl/w8nLB6+WiglzD31UIq8xIZTjqVYK7+nOXMxEIoVprxhirW4zJLCJSDEhJ3xsDjsqug9Ld8vO64lZEYLd8cPrC21GFAwEwt4Aj/CJUU86eNjk448ez0D7Ur4ZrA98Q0qswAiM9T9RbRIx0QOs7ho/yGqnvWdeU0YJgiDklnUWExwzw+d70RsdYKt4Y0CwimkJDn9+KIqp4x2ZFYgfPvf46ch3/SP1qHeCn/QyMeLozb/t+Of404vaCfq50sFv2vobW1C0tt6MmhjwVN6m0jCuCACFqkGcylXq1MDLtf18HIs3KngUUeldBB0pTurBq/+tYYMzvk+at9/2ughANBu5bJwRSd5ZRF57HJqj7gXydbFZPt4fEfoPMmgIahDvbGmTWOI8xBHOjExEJ6pILAMUIOj2CTh8QHtQaAtMZIUwgBDBIXc2JIIugiPICfL8GWziOkYZ+jLuZ9JHyvCM2NhKX/bqv+DW6PVDLlq6UnqZtC607FQ5PE1+/vd2xl7ah4rryWqvpGi7u/bRzVbo59fn1NSsk6M9cAFXQQU4r2Dj0ELWecZvq93B138TWV3dx5HtryxuQZkHVrdlkcCiFYIHSTVmQ/CDZ8poO2nQl+cn7Fl/2mkUEtc7t37nGb7izbVqIrsv6bnceb8eedrTg0Jjr+JGMX+ng2p4LbgzTLr0vRoRX8gbjBjjowK1JtrxN40wZjr5JQgx1A42CCWC/uLzMru5t+2/0jbbfr4zmtzLza0PeMVk3i/oe7flH+nebgmIhBqSav9Rb6+q6JnnT1BKR6gHEpfqGb3ZnhJ8lpuNjWEFkDdMmQU0MIwHFAA6LMqBSiZhzQpmKaQKtYC7I84zCGfM8I5eM6XTGmnNl+qqvcUIMMwihVYpYEbAK0i1QFwujSDGLCNVe8RgRDWFERYKBdmZRB+SJxAytio6Le0hB0wprgKT5Wm157ODoxt3Z0TdTTyB132+dc7fSV504IqrBgc6cWxq9+LWnmFtnOJLNHXwagOsGbvW+gK+t9X4OBQ1OiflQDbXMqP5ciYwYLEPZCtfUZY8w40VQNbpjDHh5eVKEyrTPUkpwywciMrcG/j1UM9yeeOZKmGjbXYgRBu2P9nyEoaMQon6niCNBRLO26NbVQQob25m3mFIDwd6v8dagw760fC2/BgkcGQF9kit7qBF13MbG/sqg5dSuzQOVtmnJyhxflgW5FFxeLyisFhFs50kjkgHUAIS4QkgDhAxhYEkaZyLGBBEg5xVEajFGQbAW9UFMrD6SI3XOp+owhlqX7kH1A4xhTQEw6wkid5fhAjY9g5QY6+fJTbe7yoY56gjCbj+O8z2W22sfiki1gFgXi8OxLCa0UUFECI4nJgCCwmGIg0DO0HLm244ZNV5d4Ag0IWAvDGxne/+O03F3CDR8Hq6kW0z6fr0fXb93+lohxG+dfo9t+tZ03Kd/e/386yTfF2/hGd9jfO8po+HJN3MRQMFZ7vaOwDTHnQkM06RmvK4Lnl9e8HJ5xdPzMz5/ecbnLy9qEfHyiufnCy7LarCLcHrQ4LTzadIzTaK1TX3c5zADFCBhMuuIhBAmxDQjzSecHx7w8OERHz4+4uE043w+IUZCigSRACBWl0wNfx1hxsjMa3Q+BVJFJLKg0xrASC01hCHBglZ3FnxE0uCTjZrCE6lwpp7n5jpKYanFqvOIs2z0iDFzHTvYC9AFW1iB/lzH3tLYYZv+FOuTGBNVNbXRMQsDR41R1YXg1da5QlQTPJSSLS7EhJyjWokX1bjnzoIbLNVyw9sOCgik7kGjM/Qszkcw4VPtANwdT8fUFYdlXewpoFpZVmUJi/Wkpj1UxwBhqusdQWpwcZBb6jf8CNYHdC5y67M+j6jffI8hUpmCFdUgw7cOaFrbW70wg1Cnt16ZBSWrtUG22BaKRyUEIsTpZJY4WlZcV8WdgtKbbBb+nFX5RTiDRa2hIRHV5JV1brjywKTGhNh+mLMq4plA0aLIqCIMm0KLBGRMYCKdawgkmfeBEFBCgFCEBHVdHMjZ+r09jiBaIHi2eGHuVYEhKCJYcsaS1VUpAJxMaPn46QGnFEC06njNCeHxA+J//C+In/4z4k//BWH+A+L8AxYERAkoBXjKjFU03gWqRaqdWsZjUDpex7tIQIZbN2tMkqJbvKZYOfUdvR10xuuWpk7UM5xZvuSkW3dXeCSk5xokqEWGW0TXQow69nPSX/PvwoAU+9i6AGrAdt0TJtRip3FdUFtDTWi8FA4qYGBlRBCTynXJZlgHtfahDpfT1Hbt6cdewDrQ3hCg8NCvuq96QXKlLTSX+NU3HDHILIIghCkFnOeEh9MJj6czztOMU5qQLF5EiAp8ggl42mh253mHExzSpfbqTSGEyHWLiJ4k2tTxJvy/+bTtwQZtxt/b0t6qbStQ3tY2llzFnlee35fuF0RsmDmVwVPvd0jE8Gv404aha6k+3mslkG0CR9aOtRfuafv48623dhKkCvvGxTMiUreJyJ7QHpASQ3L8+nsSKPweCLv3aLV9bZnv1er63nl/i/eP0nXNOP99vzunLTFRy+6KdKl4D18UEev2FNp3v1ERPfv0+z1A8TKwabCaOWEg9RUZSMBMCAQUVnPCGAJyYcSQAVD13a5wdlIgY4H5YAikd6QytM00trCZPZcWpFpME1dds2yYiz4ch+ebas17GgQSvB2Y/Tki6Mamjn2by74JI+NqQzR9TfIz62YW2p2TnqTL45oe9Xqr3B1w0S++rvq2bRG5Oi+VcOq0hyoU6383ZqgvibE/I0zyIIhad+9mxnXZfEOQ0VCqyb1mJToEglhCFUwwa9C9KnQIUEIgkBEXzhxt87gLsmim/aOGyl4QAdqun/7ZsUVE05Dz94/XUugWYs2/acf2ecsnFQEc3x37s08+L3GTpwlYHMHt3mgtkyaI6BFsfwYxKwRItWjox1jEhAEsWLOeF+5OqJQyCCKqdputf1/MPY7lfShcQAXIOYNCQCkFMeh5FoqeQ1wCCheAAObOjaW4p0lpxIWNgBIFBA9IOG403PzdaI7WzmF2tPBujx48B+Bm677fnGkBSA2+3rvB64NFqnDHfSsDzraTzfjV1jtu2Tb2Dtb49R6cs/GepK7VN4UP1N7FG0TOtu49DnN8/1abPb2LKNrAjOvj8fW40rfidO9p0/eo+7dK19ecYlLvbWvD/75f2977/NZ73zoX9xH04967WvdA1H99m9589+Ce48eeXwyH0NTgsFru6hlZCqMwY1kzXpYLvjy/4vn1BV+envHly7O5ZXrF6+uCZc3IWQXLeuyp5UIIETFEQILhYQr7VWBrWvEhIkT91KCg04QYVXkixGbB2bp3bTRbT7ZDQnYmO1O/v7pbvRYYWFCtIgyHd3g3jK/0QufeSiN0wuWmLATqMZpGn4/z6FTNhj/hMAUC6qzDG77uMNjHp2HBykwFQFJdMXl3qYxVO44yCCM8HgQ32kQFEAVi9EqPW9R1VuH4foZq34bqrQw0uG2IhH3nDn9p3xtc72CPNPjvD4exrx973n2kMlqPlIqO19w4s7fySldto5/r9HbtqzhjbRd1gpZuvYl0MSMM36r9aTghbftjTGdxFzOOg23yVWZ4N1a+/pryldIkzG2jhuCxQXTwNTZEc7TV8MRmqdvXpa/JsOd8jfjbkVRIMaeIFCOmGBBDW/1hmhFPZ0yPHzE9fECaHxCmWZUjQXU6uH7EcEt91q9P/x6gFkiB2rD4fNpyrfvVvIHVWGnSbeWG4+2XyG79dGtmh1/VCi3bFhah3xf9/KKNZTf21K0b2NyKKF0idh5Ibw2FVoav29YYqePQOu1x5Vo+adqk6I3cnH6pfSAa30PrVjsbur3tuM0+czdQovVbjYGoxoVQN6xKL4d63hrsaERuN9Ljz/353rfqeqp8mW0VXvRbBXxLEhkX5vb3ti03nvk+PH4RTjqOv+0Y2j1/R3qHRcR44PFWCu1tIz24qlZBbaW1HPuGVl1DapoQoCYBd6TsPUKIAcDd38mvSteZsrqJd8IHYPzN3Wz+jgihf6R/P2nLOOn31zXGcH8WhDBqs1Zg0t/xNV8Z7gbkQ+/uQ9EeElEGJgFiWgkK9AhBGBKCIklBtTWYizKiSqo+cpkLlmlCKYx5OmEtGZfLgsIFy6rMwGJ+YPNaVOGkQxLYkXxWIq9wwZoX5LyqBm7O4Jx3SKAzzfzc87GMpMxmsqDDWn4w6ww0ywobGPejesjIFw/Ieky8U0VaxvueXLv32jn6lkD0CGBfY7hty3SPj9cS3eg3gbDliWs+FepsBR/bMlrosq0QYi+M8EDH1TjZCIpt24Mz+4kgklBCVkTfEf9K+OlacrS+sKhv1+UCIkIMWlYyDTS1iNC9Gahpp4UQ1H9rH0TQmAq+hupnHKir43ozWSPaHn3Hq6CqRfW+Km+vrXtrd+HQVgi7XWOVuETrJwtDTIg04nm2jjsz+kqAdolNGOVug/p4Br4uanm23+vZa8SDr5VWp6iWHAVMpZhFhGBezoAA6zqpP9yLrhUiW1O2lmJs+17XR6ehVK9Ah+cPNK1ebxDAm/YOQrGDfTnCjONzbvzo+nZLtMvlgmyWbszqM5aIMKUINm1X9tgZPs8Vz7S9Y+bbFEZcc3tG7t7bfIBeCIHD9TYIIfp8PgRX0tcKIb5HuoYXfM+y/9Zl/N7Sv8U+/ftKx5v5CK71+8qFsGMeAJztvIgKo0iZd7kIcma8XlZclgWfn1/w9PyCn3/9rNYQn5/w/PSEl6dnlCLgIhBS/+BpcqGCCRLCSeNRmY9wEYV+Hpw6pQlpmnA6nXE6nfHw8IDHx0c8PHzA+XzGPM9IKaqmLaQKhf2s24+PbH77WaZnbBSYa0pRCXpgU6wQQKLSCDEaf7baxBoMdyWf7twMETC6gojBaQKIEIty91NSdkiMWofHurO34e4RRzjv5/5upu0vdblk+7jCDWWUqYVCECAZfYAQ1II7Gp9AnDfpVg2AlAAuGYWAEgg5JsSS1CpiDViXBet8wbpcsM4TSs7gqD78CQS2cWoxpjqctVujQ/BXn7UuPzOrlUXPH7JIx9U1VC1XF4W6viTVxIbiCJUW9XoEig+B1GoTymxlKdWSQEoGh4AgES6U0bIj+nTzXDUgvMMNBajRlVtB/cUbieYWy+dJeUCKn0ezOAJiSEDkFp/E8U1uZQCo7iZLWREiqYUDERATGnvU67aYZmLzUNeL+fo3Bahs+Ki63QI0HkfEaUoIUlCMmZpZsLJaE7AEFIYGs6eMtRQsJtxyK51GNUNxw0roq7VPjMDZ4t59eDhjnhI+TsmUBwsoRMw//AHzj/8BP/7H/zvmh3/Bx08/QnBGgSCylqvWDFEFEXaMkABk8TCCuDMpxZ8D6c6zkKwIpGuMRYN2NywfRoepchfELCrAZtHVmLThgK8otlYannxMbxEpTeSWOsJNuNpzS1vgN24WDiIuIYIUE0xx0biEruBkLmA5L0p7lFX3CBcTSmYVUhZzPcvugpaNEd1tCMeNbU5rf6TraNs62J7rA49YpLNeKuMzH0GvnKgrxmPkqXWdbUi4EDqlgHlKmFLAlAhTpOqeKQQXohMQuCvT93hHC2LP0+hz36J8nZ46soggYMc2uMXjeG/ansdfy9Ppy+rbtxOkbfJv+dtf06e7BRF6MDZfxE0Q4QiAEmBi2gjsUdr9iBLjZ2jWGnAE9bcM91yC5BoClq0lkR4KAL0EbZe+FqlvhPlYtfQ/2tU3ol31wpt2dq3a3d/nu8bM+9p8x/V+XXrPgv+t6/ze9XxtWV9b/3v79Z56tky47e+xXAwMkmuEUf/cGU/+qcg1uqVv24JoX2bV7fCyOuZw23z9Ow1gi/p7Mm0HixvBBA4AG0FVgvpjDyECohYRQEZhBhU90woJEARStF5nlnuQsCJqCbGuKohY8wLJxYKojYw4115wLZ06ALvBhp2LB0JK7IWXfdrmb3PTDXh/blL3vZ8YGu7u3r2WjpdfQ+a27RpzvV2+v3+ExI1BKgwOsJa5A6T+t+LsBDfdfxtomjCN9J3GnByZrSzSebkRiGiwPAoW4KsnqHpm3mYPWTxeMxceNavJhXGdeyYXTpBpgXjZvTCMvV4P+GVwStBd0a3O7kuHTiri6+PdZ21/DssACJECehR7n2/3o46/P2vaLFf1NQ5LGAURzapiON+sbOpbKe0c2u2ODZN93P+tLWJEYNPez+Yjt2n16zqyJd0zpYzwgBFTffkijFzcIiIjF40rEgJZIGwg5gwIUHIBoqCQaqK19UzWR18XtcF6vx5b7Xt/vrWXsOv/8Tno+/54DH1PAbDDpX/u67Zp8+WiY6qxN0olrlXQS4gSEPp+2OxuGX97IcOxsss98Pa60GF79bkeXn7zRLyFA/SPrrX76Putft3T/2tw6O32vm9sv6aNV+HPO+by3ne+H965P6O+d9qRTn/j9N6x+6sLaX6j6o6YEU4zVxSBzB1k12exc7AUxnLJWNaCp+dXvF5W/PqkAanVDdMLXl5esS4ruLAFFQ4WDy0hhFTjQQzaHRVPMm3TEEFRNZhTTMPHLTMV7xhpZUe5jqfriEZUHL6+SeN5rQLjZq2A4DErBNUdoDjHoLlXrV2qPIi+bMWdpBMuBwoQYowWyybIvoorX7GIEKAG5z7CT8nxEmnF9fNA3mZdA2NAVepgL3fX8cOcUXL7uHsmZnVX5bwWEXSuXGRjtdlNElobVNhgLmCYVYt/wyNqOMVeedV9vZOPleMC3Ts2UOoqixhCylANHJvLp8H10xYX2a6zzRwYDKvjQNtJ4GENH8NzjOdEt39ha7fi6VD3X0xUcc5GFxjt633w8TR8kIXN/Q4bg7XDxSqe5BMEU/6QNqxoc+vr05WFYgwahNnmNJeCwoIiQGFn3AtyYQ2Ebsp//aY30kU1wzs6P8Vga1nHYU4BUyAkUcUsIQLFiOn0gPn0gIfTGfN8whwjCqjifcVwVnW/ZFa2aEx68jUlSke5OmQl/3xgBB5mprXb8GPqNl611XA6zDqn68VfbuPbUnO75ku7WxZ2YyN4OEr9vKKjyrrfPX3Q9oFZQJlVlLAJqdiFG219Vdzbvlc8ndBcXEnHjzhs5/hlEFb0dMO27s5lVOuPj7oX1/GD0L1r8xeiuY8LbgmxcVu83ZtX0t5iYuzerSLq+BwVIb6+3m7Dt6QqSLm5oO5L34qTv1cYcbcgopR1AC5bi4g9QdcBdph5px3KzpCxF+zAaghDNfVxSwFqi78uzrqDb3X4O8z8rRVohwQNmxrdwWzbiahqOw6t24yZtrgD9N/e+n9X6a9OoPybSW29EqnmQAhkiGpbzm3L+qZwJhZhi2Bqvg5wEQag22etiFxFVs1PZtVIby9UD3aG6Ddgo/733T1SMaR0SQmZGSmpZcQlLchcMF0uyIXxuqyKWBX1rytFTU6LtaEYQHfhw+Xyot/XRS3B+RjZBUx4KzAkoBOwdITJdrz6qwO1ewR7u7VfJ2u4WRGuBvivpKOtNHLOrr15lVXsSEFw5HBDLFwbx5FQ77BHfyZipqLoKE69Ur8uxc1Yu7W5GbfKmG4o6yFM83YQlVpWsHkmQhME9EDZ6ooxNsSKjKCDwxEGpPmzd8RKUnPJFOOEKU2IMWKaphowkkKozFguqpnkpstSmiBCEffxWq7MhV5dZ2gD4oRtHvnGu4C4FufNOvbzX4mqg3naJtngAmKEFlHT7sRAUHTzvdl32/u32rh91p+D1XVT/T3iTnWutHb07iLEtAs9WLa/E0uua5GZ8TrPYADz8qJum8isHxCQUkEk9fU7TUmt1mLv0qudRXUQK+HbXMZxbUNHCKC5odt/jnBEAQl3Ve3HTIy4oLBfK7UtJtRZ3SJiXdQiYl2qFmEwyyEyzVwRKPMtRFAM+un2c3/tBRFbi4jrlhCo+e4TQoxH6T3Ew22BwfveuVdgck/d1/J8T6HAv8207ffx2N/37j/Sb5neZBbdka4S5ganKjOUHA40wYAKAyYIpApgL+uKZcn4/OsTXl4X/PmXL3h9veDXz094fV3w/PSMy7LidblU7d0YEogSQjqpECKq9QIoghGU3GbA4tQixghQRIozQow4nc5I04zH8xnzfMY0nwz/UFyIC2vcLHMrusXVbo2DCzKCWQurhXVQiw0BYkqKI8UIISBwAgTgMAEgSCgGvwh7q1WjI8iHWw9hV1LgpLRDjRURnJYoEKHOOkAOcEalg6jbv47nbqgha8PmrNVR6dkh6BlvZNrbkch0bYLqLddgBwpvmYsqYHGAcIYzIl15arm84vL6iikmLI8Xda0VU8NlRS10hRV3LAZjc/aYElzxpkqfuBuoYu4mS2na2jIKIxyfqVYdFfc1bJvZFJxZBQ5F51OXkir0gBiq5CNICCggxDiBC4FjBHEccI57hBEAajzE4AvEY2BJqFY9TjNQpd1uJyICgq5fMpdnwT5ka0w85oIx5+HxOjr8SxnJASVnxflyQRCzDgKZHM6RcnQ+i6Typ3Rju2BJqtKGCzmJEmJIOM0TUAQsGWtZ8XJZ8LKuWBlYWb0GLIERS8GlrHgtq7WzixnmYwrHv5XeO50SZgFSUKuQh5MGFT7lVdfBHDDNJzz++BM+/PgT/vnDj5hOj5jmgFcB1pLBUnCRDAFhMqav0upcu1vHoduAxWkPOwfV24LTVuT87Lq2w25/q+VIqARQsfetOqM9Kl7cMc37fS19iWYBFIwnKiA9RXravE6rdFepvx0wiU18sxBS3JizxoaRvEC4ACUDXEDMJpAwS4gaZ0JMuOPtP1jXNs4u4ILImLNaatmaMGWqKoAozYOE0xsDHdIFxN61oNIdrf8UCWmKmOeEOUbMISKRBapWzjPY+c5jYRj4CIe9vT/15/lmRKxq6hbo/r1tGs6sATbcaMOWL9K/LK2uW0KCr8HHr5X7HmHEOwQRqmHnATiZW6BGJ/Aboa9mR1smIYWOeDMuG4lpLhgDqJpD+oaUpm0xSCnqwXetsw40RqaXFn2bSJLxRDu435gkWz9+e+BHdiCbVPwKEXvYDsi375CvSF9DiH5t/q8lRL8HAft7II6/day/Z6pMus363DFN6n7fM9+2gsldHfAlLcPdY4aWDHlVcwKVma7HgWu6AuZEHyIBZKZ/DAHZWUWkAgoqhJwLgIIYlZkaghtyChiMbOaKhXNnCbFgXReND5FXjVNxY4uKCSJca6SdmQp8e7/nAOp1ANR9ef3541hV/T0ix3UeBoDuega73Fd6sO3QHQzhrrTDnE4rAqgYvhNpB29sW6rzvs/X1uVtho5rw91ep9LgU1eeIu79e82M3NeqEoUBIbgPZvMHKxYIeKjFEapxTgbwY/0NFBFDwhQnTGnGNE1IKWGaZ8Sofpr7YLy+1tgQZCmdMMzgdiUWpQvabTBn+A4z90ZbV1f368FZEBCuvru9v7s6MbWdocO9cYCIDUN+pM1jzAVA56cSG36hfVtpXIE87Odxf9ep3PR5m8gqNJFUq8/baDuLxZyQWXyEbATqumYQCDmvEAimrIojHmiSSIy5o3hZXStOWPsaFq7uFIb++XpBE444IcHSzq+rgggrA7WfbeyHsRFY8NHx7PfkrsfcNVMpjGKxOHwNNFzR8a6m3dtf+89WyFDn5SDvvYz7YyHElbwH5Rzlu3V/D6ff07brfXrrzL9XgHGtzK/Bed6Dz7+3PfeUde/z2/lvz83fU/qebf6afXBXeV9BS1XI/B36dwvn2OIZPXGv4ETP53UpyCXj6eUVy2XB589PeLmo4GFZMvKSgcJIFICYEJJ2QsFagCAC1NzrjPih3bM4CTEmpeWniBAT5pSQzLd7jMEYc6ja8MU+zEC0QNOuaKF9A2D4h43IwSg1XKi3Qq3XEJQJRoQav4KCuYHhit86PlitI9x1p3ZwN9bVRY4Jo0VcGMS17SJHc2dtrX8Nlnb9NfXwOr7jfNvYCExZUSCd1W4dN+roM3/f29KNccPpXDhRjDG5Iq+qQJXXFTktyGmy1zU4eSlNqFE2n95VkyG6Wtfgh77hDr1SAjez3HHOhQwnIGhU4IYnqMsY7bwLXYgARlFFJuaWr157HGsPH96E28Ns6vBWIUWA0po0CiOoezdQ+yie0VaGTZ6tP3S1dBrou9TGGCItFqG5GFMEX7qhlXatRfi9Dr+rbqt0nyRzYRlI3YEtywXLsmDJGaUwYAG1RVS5JnNGZq7KS0oD00Cs+W+t2nAwoGquR6ImLiRCnCek0wnn8xnn0wnnKSJFQiJVBlSBASNCMAE4kQoiClFHu9iQgIbtxoa3+olQhRAYaclhFjY4vs+vJqVoguPpdjg4GdfDi3qOU7f7BWgCi76OzW/a5OiXtQbFrGeA1Ie9NVTp9kZpn84qwj9U+Q2Op/c8CK/U6N9u/UDQuVxte0+4WdYAwCDw6HkbVTnJf98A0nW/NoEwmStjDUytsClY3JEBjm5ov1vVDEMure9v8z78XNjku8lrOK5zzCt18bzZhqO6usW3L/s4vRff2ZZ7bz2e7hZE5OUyEJfO6PAFtEWkBosIcnPQEalo77UjgYjU/KzfyKLveAAZB/TXUh0AMu/eNJqKvEWc7QQR3SQOV5bO59m1uBkdAevmeaHTeO2+/z0SIP9I/zYSGXJU12XnJ3bLPNsuU1/7Giti9EG+S7J9F3CNCi9jQHoV0qECvYrX2dkiiuRE0/RtbTYtnhjVBVOIauERgwWrFoRSUFiRkjVlSBEwaSyIS1mqJUTOK5bLC0pesC6v6mMxZ0jVvrqyd40xObpi6YjLDSNuz7gbx3iYC9pOhIHBBrPqe23eFNEk0F2QeH8e2vdN3T0RBrgW/oiot1bCBBFUfx/KRsaGdHU15HHsGwZC0QmIYcy665a5XD/VkmEff0OJCSAERbCICMzRhPMMCVQRL/ftWnkgvd/lytDtEQdnDAMVbRZFeVOImNKEeTrjfHrA6XTC6aTaiKeHs/ptfjgjpWRafm18ihODxqBmb8NGc6yuURnXpK5F80G6gX/bdV24ADIK1K7lvzr+u7p9TjDkPSp/W569ofO59fHbPRsJt7ZOxBbrEVzvcQyuGlkH+7u9saudyOfY+mn7hp1QdTzH94ZoiUWkxpm4XF7BXDDFiJLVWiLmBAKZz2s9k3OeLFaEW9bsmTHV7/TmDKnzCSdQjAipFh9lmFdXVtnOI7i7V4mmzV60MW3nnGuy6u8+3kYpBetq2l8stv9t7GBB61JEtKCq0Qlu08rbf5rFDIABR+uv14QSt4QUdHQYjothBxuHdfIV979WCHGrjnvLvDf/16Z/4Mp/f+kqTviO93/7tIX5d+b71lqp98HfLAnq2VsCShE8PV1wuVzw559/wevrBX/55Rcsy4qX5wukCKQIIggfpxNoIoQzkAEUApaVsa6MjKAseaHKD6uMPDIrhBAwz7NaW84nxJhwOp8R04R5npCmiEgEEkFZC3IsuCwrAgWUiUGUEMncIsJ9c/v892tgpJV9LPwTQ4SIWWcACCEBQiihgAQIKYGLgDjClSIbvtiEEM0dKJvBRLMKjMbYdYuIEPwaKo7mwX2PGD0Odwg0nPeyzQfZn3/OvbSx1HUAlIINLEJz38iA0x3SdbcJIYq6YyoZOUcsywIiwuvrM2IgvD4/qVY4RZQ0IUwJCIRi1t2cV5SccVkWtbzJGhNgZIpLxXG5FHDW69b9Uq+c0c99NcRkc11drTuKGVsWqAWECZdCABFb7FHRGBccAS6AhMZcrSYBbZ62/Kj+fr//vJ3ksb3QcFsw12gTujZGeB82n0gECdZus3wIFpNjWPJuJbIR0rjOUhtjjYHBOYPJXFLBl7TUbrtbLGcEex0CMcGUuggVCChMCJFwmiecpgkpAAsXPD99xtPTFzy/vOKyFlBMAEUUVlpAeMECwepMfQQ4okpQF0yM0AwzAATDO09pQqSA2eLqFYG6avrwEQ+fPuHHHz/hw8cP+OE0IcQAwgohxkzATIxTEDwK4RN0vxVAaRxmGwbF/cTxWbRYb8mY0QlAglSBSLdBFSulRrvW+SVYbJlg4s1GtopIVaYuTohaqnQoempgw08BQCSdx2HH/W2NYSABtE1u0SxcY0nCKDyRrFZRrLEgwKseKHYlLhZDxOOJdLEpxcqoFjXNfaxObBnzs3us4E5IIWbJ4zSRlSPtShjp9zoknStjReXJ2uQ32gsxEuIUcTrNeDjNOM36mVNESrFZN19FOW4xHX5HyWHE173cFs5vmI7w/Pfgeu+2iChOZLp2rzO2DBCDzJehdAc/RWPgqPQymPmNvmSAijSWiIoeA5ypJJUxcEPblfqLa0cbEkKosrBeSnMEhA5Tp/K8Y4KIVB/xWyZLW+Od1kWMVfK4Z+7uAaTcuXruYfjek94iIr9H+toy33rv1vNrY/3eOr4l/R4I5y0SfbRujpgs2+f94X3EPDw+hHqgs2UcNmS/+TX13/5uz9LTPe6aJwQX8LV2MSsgjwq5EVkZX07YhBBA3EnJDV6pqacGmM1dTIhluaDkFXld1GyYCzwg3nZMapEOq7eWDkPfrzBgW7MOUxuXTZ1teNu9K2vvrX2xE0D0dXcuXXQODiwajs4gP9PpuOxrqbatO4vHtt54x/OTEd82SEdr3PGWpgnVXQHDGgUIVIV1jqiJCCT0jMtOOMasMUuENYgczGrVu+SwSWBIrVZG1pYYolo+pAnTNGGaZszzjNPpjGme8fDwqMzWNA19KtVVkwVIFidKzErHidedIKJZ75CwCiIMU68M85pnDwNbvt7P8F7gNhKtB/edqAK6uhzB7fdPm4fx2rdJeqpdTxXX3DlY604313b1C61D7ooQAqTi2g65tV00bmLprFQqLtD1oxULkApaRYISmqER2GIWNqWoa7Cc1SKilAwAahkhjBj7oNUEQacQgsZ49zPb57Zvco1lUYUHTlRYu7EXRLT3mos6DPPrrvfGcxHUlEwUluhYOxPDBRE550PBtfat13CNB9+P3TJRx9Q5YrDfL3Q4wlP9Hg5TT/ReS9fxlut57xUE3MKLf0thxDUc5GvS1+Cv34Lz3iO4ufH2u/v5/fJ/P6r03jYN+WR4cP13z5DYHqLfqW27+d/nuPX2Xe3Y1jXU+QbdImKxIJYF65rx6+cnXC4XfP78hGVZsVxWlMJIISFEQiJ1TTHFhABCBOFVGBcWhNcVRBnIgpX79vshiwoXK00fCCkGhOjnZvMgI+yxjwqKufFZY8a6FgB2DlODMdfwPOU1Gd1ubXILZQqqFBVckaievRobAv1ZHAy/8wDBBqPYXNOol4ZOuBDcX3+AW0A4bHD+he9TVww55hs0hlaFpd3ouno2ofEgeoGF1uFvGPzdwKEQgjIHCZBgwn8rlWobBB7oWJWt7FMySknIOWNdVyzLghAT4rSARZBIAAqmTCHgUsza0N91q4iNgodIc+Po3ytsr6u4jjf6e8NCrwverF2kQ+idiBLrtz5rK3eTrxuze46mLY3g65Rs3fb4fxCYzIMHHMJhd48/VKENKZ7DwiZdChXfrFYc9V/DsrZnnPfbx8k/VeBQg4eM46nlEzSOARsu3lyNEQEpTkgxqXApZ1xeX7FcXtWFkwhCTOrmknQvFS4aixEA3OW6Ei5G1hGKqDeC1fqTAiw+xjgvZYoI04R0PmM+nfFwOuE8T5gTQEG9E0QETADORHgkwkLAGYwLqXUFMVc2HYvGe/TA3NKNqDlMQASpEBW2Ry2fr9ow0GGdeyX7hLr6Ds6zK/iM80krnupzus3blVxJjK4BHrPBc7py9jCo/foQNrxb40WgBonmLk+Xt8PvPUad0ygAzLVTabRQ977m7d7taDeCt4lbXJg6Bl3/rNe1n914eX/buIbqhjWZtV7cxIuAjf1wHh8kAjpB0H1pP302Y7ty6kxeKed+fOxIED7UtOPhDL/uOhM9bw/T3pPeauNRul8Qsa6GFI3abp56JIuNsAOZvzViJaKNIBSJ7Uz153aYEZEyPpwgFTeo1EVF2HfwGiEUQqjy8Xvy71PHdACGfldhTCeIqESxSxOJBndM0TTGxfx5O4CLpoHibaEOot0rjLja9n+kf6S3UrdUtoKIW0KL+vp2X8g1s6wO6RoYiO5qJDeNjV19drgZMVD9OoYAoqiar50gIohrIgQEVqZdCGwaOioUDDwCOYhpG7vv8bLi5fKMvC5YXp7BeQWvl+pjUhwt6cZpbDI1Zl1lbu6vh0KIr9y+A03/dUXsy9y2GW3eBsQdnTBi0/6eaOun9jpxev1M7gkbZ5Ievd+vw0oIkyKopM6Id5YTAiWG3Idq9aVqz2qQN2iQLCdAxFwM1qBpRBCZ7Lv6UlXrBHMV2DF3nXYIFflCRaR9fcWUTPhwwjyfcT6rZcTjhw+YTyd8/PgJ83yqLpocnmQ2QsjqG92ASSUuy0aY0JjigiBigX+P1/Bh7INuPLkoOeK4wzVXZEeCCgjXMb1HmLHdV32dIlLNiLflHFlx3FP+Ub89FSPKtskJHmfQM3fjaGuDba0p40SRW3EXB0Y0lCJYLTbCki4QZszzBGHBAjJze8ODSh5wjSYs6xgdmz7W9r7TIqIRuuM4YVDa0HW5xSGd8NqfC1zXkFtE9AIJz+8WD8msIFIavzeriICtMKLCmO7M8M9RfIht3lvXt9P3Oq27Et/Ak4/yXMv7XmHEvfluMSh/y/S1wo7v9/43vf73m7bU/iCoJaN/t4PT//62tXIfw+F7rI39ut/Trj0Tc8Qhe/i1rhl//tMXvL4u+PMvf8HrsuCXX35RV0ilIIWI8zzjNM34eH7AKU54nGZECpgo4Je84td1xefPz3h6fgUuGbxkcMXYTItY3M0gjNxW+n1KwWIKuHBBGUuFGVQKlmUBAMR4AQRIMRnsIsSogow2LuP8keNj5OPezgX1pCCm3BERIxDCqngbRXBQ/I3F+QoBTKEtHxEIK94vJoRowggBTEDPUfW6Y1TehFpfWEBhtvMfht/JlsmiQpHbPhq2/T2KFWHMSiUp4LEygNjwSdKYEcwdXgJnczkrVS26UQpiyYglIOcVMQRcLq8gEE7nF8OBI1KeMMlZ+REw5m1Ri4hlXVTYtbZYEb1SiWvzD8KInoaB8yodw+2TYZdVmUczqxcmY2hWBqWdC0yQqoxhLo0ETaepZm+KBcqGOlauuwabHBeKkSpuRiyAx7OIrszGHV6wOaWc4c+Gh+eMEIFoQha3TmDz7e+4suPc2/GqzGOz/FBf+9qOqp9fLZwcd/ZiHE+1AMYlwym5QKQ0xTRByoJ1WfH0+TOevnzBZVlQmBDSGRRtCoQhpaAEgviaQVPIYgDCgpULijAWUVz2HGckADKh8bYCYXWXTB8/4sOnj/jh8QEPjyecT7qjcimYSsADgI8U8JNZnb+CsRDwTIRIVrcYr09aoHW3jiEIKCq+O4WIySlVgTLqyfBy0pgSuk9NkAqzP6L+hLoOiY4FDL6/KzNxx542bkKz56EObgRASpeXqDHlqW+R2D4Ss0pQ6yiNG5O1EHa6qtR1ahu/rjGurp2k8jAAgLgg9Pg9tzykxEzF/6XuYzS2Nufa19b5dpaCGITuTLiRQtR4ePM8YT7Nep0nzClhSlPdm7YlbpdK2M3HLsNVvEC6v2/wkr8mGf33lS9/fb23/I5/53S3IILzal94WHi+5yr+WJnoUhnqpghaA2cCelBT3dk2yk4Q0la3VheBIysD0kKo5fRXIkDYN3VH7MJdPFE1ddzNcjf4DVYZs0AMkBiDhItGpS/sTFQDFCwGBZu5LXNS/2Vim0QHovp8hjG2oglxGhxpzK8B2NHmSwcMRTYduZKOCKodM/FwExy95699++q9l9C7J9+9ZX2NJO/3lLZCgy1AvNavHWFGLYiSA0Itq1+D3WIji60gjFwKLNRbJcjamjQUq5qKmua0Ce/cz6hhr+MqklYX2f4NRnSoUsZe+KEIqbUhUOfjk2qgKoQA5oAiFuCaM4RXSFnA64qyLOB1USFELuDShBB2Ilj/ewS3DWwdO9nPS0U+3W1M9aFeB6z72gtu/DzY7NMrqTHGtxo/o6n8LYbQwIwd7lsz7Mv2rK1HtSNeYutNNmV0iahbb44gdOsPd6zvY6a5jx/tEKzWZpi5uyGOgWy4zZrP2MgmsjB3w6q17gLvYD5VYx0zdfUkpaglOpQYDqREJrvvYu8bqbufwuYf1+ABBRVshxgRpwlxmpGmE6bphDSdEdOMaT6p9UTSNkwdsxg4tjpwAUtjEgNOvAigigHo1p+v2zqm3buABi0c7ucBOe2tLyrR1K2xoY1uGbUJru3nRG/BofPJFWYKVKjompsNOXYrDTQhxzAuvmd56Mf2eT3HegY7+v5s94q9uy3TGAvc/Wa4n2cv23ApG8fQnc0Ed8dAyGWFumPSvOuqDBbXLAVYmStOQPPIINOxGwUEvg7chZ504wIbexnmW110Cdr81vO9lt208vr9q/W3c6TiP7bjSinwgJrOkOmZDCkp42xKAdMUjSjZaEp1QogtY4Kc+LvCvBjOio6Z5HNR71PvUxgVWlALctSRX3tGhj/Z13l8f/+8z+N4gZ+tLV+HWo7t765HfW4vbPpd8fOWafv7ZplX37svvYW7bZ+/hfO99fxbcMXfCs8caZZNf9HP2Db/luo6oI2G/G+14yDjBvaPvvOPCO7xBT8XvnbkGhp5Zb6d6hqYO/sad48NtyC71659RoOf3YaraJwxmZW5ylgXjX/z/PyCy7Liz19+xetlwZeXZ7V+E2AOEafpjDkmfDyfcUozPpzPOKWE8zSr2xQBQo4qTMgFgQVZBFkYq8EnMsZ3DIQUgp2R0RBrVfnx/ohA4R0YFBgcHJYzCqv1Rs4FMQYUUcYyi3RMoI6G6Gjaiuf6N/Lx0XGJwRiDoQnm9VQ1AiBEqLZtHPBnIoYrc0C4w1VbDK9grplU2CEIUYUaeh9gUqZ4MCuMBhvbeiWoNnidTurxXP8yCiEAUxLgLhC0wTpjoYDIfwvcfRH5x/DkAFbFLAZQoK6A3IVKcRctUS26Y8Lr66vGL04TUhEwJYQYbQwBzqrkUDTcCEQ0UHYRQbGrM32FXAAiDccbND+lu0i9thFxmFExGR3rfr0IQciVBqgOstQPtXXaXZ3vQr54u3Frv4dW2rKR/U0/F8Zph5KQtpEHmlktid09jloTRKUnAHC5oPACd+vaK7ESYLRtY4QP1UsTWDiO5SOpLrxcLOXWGIZ3FmM6QwNwTxNhngkfJuAUBUu54Hl5xZ+fXvDry4JSdKBPkZAgEM7WhuqkqgturHy1IowCxisXjSMBgRBhZkACNfdV5IJK9e8/nx8xnz9gmh8xpRMmCiqkCRdMKDhD8BER/4QJEDY8UNdnhuAF1OIcSK6TU6eQGi6ZJGAy+iwQLM5kG+IqzCBBEI2gUuDWyQDEzoG6pKUL1aFrTypi1c6K0SLC+HvSiUqI1NLEriDjX27wswqiROtiRIAEjGzjT8jWjzr3DEghgAMgeaS5LYNUV01sQePNBRO3PkCcX6HfPUZuC15t1vMdzej7BGjnW7eDhq811RfaTXF4FCMkBIQpIc4T5mnGeZoxx4gpBCASEHW9EQGxHjuOBztt0cEioZEP1g9QQxowphE36OdHNvm+GdMbqqL97z7jtv6xMfvfb9V5Jb8Ph2zybPHLe9Ldggix4IetMuhCBIb7yjCpYWjMl5kuCrAxZKRUjbz2mgkIrmG5G+JIr6Pg4liLqzvB0R0UVqbHkLCHaKiENb9+22r5qXS5lGzmj6v9boGdxBCkYG41IifEkiCJNRAYBIgRxRgLingQQtIIYzwM62ZjUrcYtxu7debNtEWMxnR8//pC63fHvav9H+l3kRxxZqgPcZXSIVJQZIcaAtSh25XiEqgbGHf9Et0FiO+1HTOvMfCQ3d1b80MqjSRpDQTBbSGIAgLU7ySCgIIh62h7X0SqICJGe89MOSMFFLNOUkGiIHMBlxWcF5TlFWVdUF5fkLMKJIRFFQqgTOHKiMUmUA98j4xM1u11YO7LZr9sf9dzzAC/n32bHNdSX49rqnk1lfF6492+reMZ2QDffhw6d0Ob8m8xYVpWacxJjHjAWJ4TZa3cHSN1i1hUi4NNWSZ48EhqFc6LBQnupCh+BA/a5N5eVoLKTVMDMSRqgHQqrP5Gw6QIGxdb7U0rnyHILChQ/70U9RNSQJw0SPV8PuN0flT3TKdHTNMJp9MDYkyYTnM3FoCju0fMfn1q1wPLAH3vyALB3DVt1rkKHrp8UoYxHmMJtDr3z1kRaJZd3QQTROysMMa6Vl67sjyYJg/v6dDvrToIjlRvxs1kpbcsQfp0KGDxumt/x/JcEOEBqcUYFi50Cbb+ommoimQUFqzrK0QSiAAOERQEsSihokyPaIxz1xjcx7hpwQzH/bEXyLR10OctxbSkIPv++txhbyZMRC77qahYbyXSj2EuXRvJLSEI5zkipYDzKWGaEk7zhGlKmC2YXQz6ca3Jbf39mBwFsN4LLnqBUI+ejZ1zZkJjMPn9t5H2txi/W+HEW2frKIzQNpAVdEsIMVbaY3vX3zsWZnSF3JVu5etokncKIf626RvaMtBbb5Ul4zcCeucSu1bVMRrpoL66e4bx+lhLK2hLqxy+0nC6kZJ7xwi+gxS5lvW4roYNOy3sTHcRGA7tOTc4rZ01Uvn9zjTXjXV5vWBZMv78l1/xfLng//vzH7GsK/LzK4IAD0g4xwn/8vFHPEwn/OHhA04p4cPphCklzHOqinIf8oLnnDCxIAG4SMECjZMmAoSkLpfmaPGoQtJYDGGChFjPB2d65swIwiBiBFKBcCmCtRTEUrCsGSFFTCwmEJeq/OeLsOHIbXydfSoQU8BQnD4QoCEiqMZx0IOajL8Q1Y+9rxAmCK/1XKwKN6TCjOpjocatLCAAKakKVYwqmEghoQgpnoKgfPrOtU1PoTRhsruqNkEqOfzcKwLpMuiEK9xwaXV7I+ryEQKQMUZJIMSAuSkSggbxZfNhD1Zrb5lAJasSaFnBJWBdLzrQzwkpZzAlTHNBxoSYgDipr39ZGSUXrFmQs+K8LAGZocImcQazY4CdMgKPxxNsbwwfG7FQx4ngcUJF2AQ6ycaM4EIGULNycKkPE6ogos1nNLeofnUFA9Q5Un6Le+IYm6pXb+dIZ8D2dzH8xQUR6rpogw8wK+4LAcuitGdUmjnnV+UdifKPuJh3DcMJk/fFx8nGzmlwV4eqysBiay/o3ikoGu8QXJU2XGkWUkABOJ0DHh4ifjgTHpPg9fKMX1+/4H/8/Bl//PUFeVVrpodISOapIIgghAkgZXcHYWXQmzBmZcaFM545Y2EVAgYCzkxIovskQmM0gARzCupa9tOPOH/8EafTJ5zmB8yBVBBBL0rrhwVTOOEUBA8smFdBEgGx4JmBXwAVihSGMtoZkubGf6xrlTBLwAkBEao06aJWMcY/M8PdgwXS04Kh7lGj+KbWPMPS7t3dVd4jdWu+p4/16tYPTKT1RHMn766lwgG4bwcEUIUQQJGILAUrNC6QCyOqEGKNTdexLnSAqhKoWpuRiLm7Ml5m6egz77+5utb9wFaJu3bSc0iFEW3rEKACDuj+rTCBvOgG6wG47+3udwQoQWICUkQ4zZgeTng4n/BxPuGcJswxglIApwC296OdSQVO8zcaHv23I+C/1Zp8I/WzK7sn70BEDt+lzb0u7c7cN+5/j/Qdy7pfEMHrpgE9o6JPBOFQgTFYpdxcNRCc4OwGshck0J40awh0TxTuiZ/xeqxRpcF02gaoZm1djv7a9qtL/QHVKlRBRC4eFGpRU9mcTZOxQG3BTAgRIlKaEWPSQ5KLomNSgJiMgUUd0KSubeNCdGSmD24DiAZZou+50rz0YzR8z/Sz9vWU9vduy++AmLynDX9fRLEmAoaA8GoazRVQuhS/33uVOOzPBGZ1aR4C+CDGijOTqpu3ktW3owkyivkg9GU17HeCmhGbz1CwaaR0hEGvbdB65r4CDZETqXVldmGi7udcsgWpzsg5V+FipZcrEX19rwmkmgzfYvIfzUEbybfy+hx0BPFb72z27FHbrrW3WVDcn96b/973rzF736pPfGFUpH58Z89kRUWiPFXtLRkFL72bJ7LKtDoVxrmvfjYNf2dAN21+1wQ3wtXM8ItpG6pbKNRgw1Wzu8aQiGotESNSTOaKJxmca31VYV/H4AUqbGvCtR5ZbZov45jZbpIeNkpnXdCEA3WViseWkEOfwq19/j50rDwfe50+hyMTXzjX/SAiKIPbILVYVAbNpo1uldBZSLggwtvrcWvYGAZs59VOEMGjVUazANM2N6vKNhe1HFsX6t9Zib+UUhWesDPgbfybWyHqCKJ25qLObeuf4hh7pkjbA73lQpuTa9+rq6Z6r7lpADaxIiCVGCHq1hi686VrfnXjNKw/6NwYLCACppQQY8B8mowRN2OaVBgx7YJVjy6qRuuHPT457nsMgonhvrWsMcD06n213MfPsU9bFOH9OMU+/1Wc+Ubea+82Tb39eN0jkLjn2a18zuDrb78HN/tW2PQ16Vgwc9zmt9pXV86dqGQV6tN1nH4se/y2ad3VOt5uiOd9s/LbTXhPnfeWhSv8iM059Z7ktJy69tEKAtQaLZAy+gsLChjruqAUxi+/PuNyWfHLr19wWVbIJSMUxkOcMVHED6dHPEwn/PTpDzilCR9OZ0wx6lkXA8JkAW1jQAzAFIBpXjGtBfO0YC4MzuqmQwOx0g5m2BeFGyLQwKQMkFlXxoLCAaUUhBjgsQn8mktBMAE4RGHO4XlHVlFXpz9orgPVTVKP9wAC7ugQp+vdZapbKzdCwDXm/dzQ8lUTuYsRQc5Uhllb97yAeuhZn9pPdxvbeI2j8GFYDwd7u2dSOg09vocq3CDbwyJilnc2thXOF3AJKEQouSAHVWigEBHzCiLCui4ABaS8juNXYa4qjYrxMzzGADuO0ytWdHi0elW6xgnzgXRXNbLnsW3HxHBeZfrvXSRWeNzB0348+zl6K/XLRXo6oeIzUnGUvh4PRt2u1iYbS4agxRUEpBSNNSjH41Txx4pf9Tk6XKvbM25BqxrtMvDUQKI0BDMCqcDx4/kBH88PCAFgKXh+ecXT8wuenl5wWRZMKSK5KzZiiHQuk+vFhJRO68CY4qzKItH2UqSApOqJet4Z/pZOJ8zns35OJ6R5Qkgttp4KV4DAhBiBGYQ5AadJcBLCmQkTuRBOYCZYhgiPw8pibYMGIje52+gd0NeJAL2GvJ6B9Qfceq3iuP2S6PAiF4A2XkDXJsd1ZXgNu5U6vOM/lfFfraHFXXzx5lM5l1AX+E6v+d0qSqy0J6Gtq80QolqEkdKsRNLa3x+1NrDdyQvH3FsfG93SDja3/teAHlSVhUgFESGBYwRixJQmzPOMeZpM0agpGzUlI8Fmux6P8dXnsvne5bhShK+J9liGs+levHPEU4/x9C0PaNdWolb9kO++dNeZ+a4Sj9Pdgohq7gTU1XbMxIIxCv0AJMAjNdjvo6G4RiD5RtJ0XUPt6FoZmIN3sI6I9MV/OJSqNaQHjMAlfQI/8LMKInK2oLaXqr3oQgpQBIVGAE8pIyU1LZM02SZWDY8Qgh7SPTFM7UBGRa5QD7fWBz80ZLdQ/x7T75FJ//eU3sswVkQChojq2tL4KoxomrggQvPaucXsdA06I7K5XJIKELaasSKimr4iYLtmF1AYc7GvpO7nYDs2KCyMZk4s3BAK6T7bvW07WU2MWZDZBQ/Z9u+KnFesqwZ28/3syCcRDW26Os4O/H4DZseWEXZP/vE36lx9Td39mfnXZOZsibo9Q3R/v293zdMTGD16f6W8a3N5jZEbQqj+O92vsBAhSgQxGSEnIHPVxOxj2Z3lou54WMSCxpn1AQEhkrr4M8FDGAQQTRARY8LpdAYF0gBu2Pev968/9B+oxGUw/H4gxtC/c6WM6vu2XHm+JfKO23b0eyAIu2eOjG/bNgg/B0HEsUUDM5umzzYQc2e1cMMiwpkBYx/3/d6W58KG/kxS5o75FM4F7IJRWw9tPytSz+MyHda3CyJ8/R7hUtWX8JX52V/b/KOfm8O9JIanoI5H18KDtVCGNer5lMhGdbXkFg/n01ktIapm8IRkwewcD+uFED1j48if9DW8cvfc/l7DRz0d3f92dGevdHOL4b0XQuzzvdluwoALfK0Q4lsSdbjvb1nPcb1/nXoqUTvU6f2+l5huv69RO4evHgRTaGTHHvf5Lcblr08LHO+b/ly6u01dPjGGt/vaIAmICCAJICZVhhHG56dnXJYVf/nLZ1xeF3z5/IyyFvC6IILw4XTGeTrhn3/4JzyeTvjnH/6AKap1RAjqL10D6apGceCogghSQcS8FpzmGafCKAgAF0Q4M7ud19VXP1wI4QxOQHVtgcIZxIRSMigTYs5IMSDnjJQjcs6IISEKIfhaGbdsl0aWl+9td5+kQgJUIbLHcWiMVmNqkTp/UYXDrjxnCnY7gKhZvrk7Q2ZV7NAPqnBhbLwxd7rN5PCo0t/dedmvm7fw5XqmGVAfzl2BxcywvnKL8DGMpAkOStFzPJeMUHQ+QAExLYAAeV30+bpARMcjGPOcuYtjUN0HmTJGj+fwBmY7ExjY4IgY8YBuHK8KIaD4s7oJNssDY1JeE0Ycw+236aWjZXlILxzMn9fnVvahb4NIcw1KqDEjqnIbC3a6o9KoEsWhx3Wj25GbWy9x+psrfgtW1+d1f4Cq5dI0Rcxxwg/nD/jh4REhEAqv+PL8jM9PT/j85QmvrxdT7gBiEARhsGQbJ1f080iNRle7Qo2YNTcbw56ACLO0MpdTGfrs8XTGfH7A+eEBp4cHpNOEmFJ1RWKGUQABifUMPTHwMBEeSsBDDphILcz9DKkjNR4pFsjaXIw5V9HPPWrLsI8b7+8RidpRGXM9gHfx5lql49qo5450xXY01jb/vhTU9wFUl1uAxXNgHveqC79EFcALjIAz7kcbp14Y0bisvX26QGEXxN2pSZdD7H6zDkGlcZye1bbrCJBacwHofc00wbHvVfUVqGcwwS2iQkxASKAUISlinic8zDNO04R5UsvnlCa1iKJoc2Of3Xh+Tbq3lLfP+PvgwP3plrCbbuT7vaT7g1WXy+ZOk4T1iagFeGqHcQCxWyL42/ZXMADt/lprEmOBkoHd0CwayBeuIwHbq5n8dQ2s5XiZ9mC4DtIo0TY4Y0Y1FjO4FKx5RS4Zy/JqgcXWahFBGh1HJXUxAbNqGIQAEBglAIRkrhUixAUPzIq0blwHoGMFH12vLbJri/r2Yv9tCYCvJTDeIn7e0/+/p7Qlgt4iim71+fAg8r1Z96Bp2oYGbAkdL5acB9gha/Y7BALBA3mNQKtnuuWslhA5r4okuasW4Q6INUQvUNBgZebPlNR5o+YJqkFOZjroyJJrkufCyMx6LYy1FKwlY81r+6wL1nXFsrTvxV3Sue9OgZrRbwiOg1Ee4NG1w79nZm8BydF77xYyXWF8OTPXn71FMG0ZIZWufGP9bRmXt965J11jiF5rw3G9TuTq922/+/aJKPZIHZzSvOGw7r7fJGJmtgHMgIQIgBAjqzWPNYW4KOFAiuhyx0hX4VhB5qLa/QRz1aSIGnxvGFNVifSEGCekmJDiDIoBKYWGdKPt221was+hYE/XMBljYhxzE0bI5toxoWtA7MP4De3q50dtU/e9mfzzcL+dN522vRjz34gy7YS9b4KHwp1FBHorhv14EAogZbRYuHUtZslV7+fWB0G1pBAbK6+zOBFRmjCiWVpme2aapl2QZi8bUOFUj3MdCRBuMafbvGJ4d+tuaisQ2OYH3KJ674rC91J1i1bn39eczz/X9eVj6eSvW9Vq3AvCPE2IMeJ0mhFjxPl8QkrqkimlVJ/fI4hoPK23BRHbe7aVj++/gd/qvd2twzk6ft7Xvs9/JCQ4bsvb7w3frd4ji4hr7X7P2X9P3lt1fG9i72vfOS7nG+qzPTTeuK8MuVHxfv6ulX0b97y3LW/X/9vj7bUO8cvtPeCwFmi4wXadDWcuYNbuyuohOLPXePtZlQyeL69YyopfLEjs09MLyqraNSkm/JDOSCHiw/kB8zThD48fcZo0QHUyq3tl0irtK1E125kKhBMQPAZCRDQLsSSiMc/Ez1ajiW0k6j9hjSnABQhAg2lcmaz+KcXdnFrMCGaUori7MiZpjJ0zDn+lQXTs9meyBpRu7pOy+w0natdg3gWk788wq9CI0AKSoP7GEcylj9ItYvhVqHBzaOGwgd3RWX/+Vw8u0lwQ9t+3/d9e3UOoKxX4WLDRaUQBEqTFl+tG0T2dSlJpAAEAAElEQVQuqDvHDM4ZJQTkVYOKrzFBWLAsFwgIaVFBRFWgYVd28GC3PbOzYGR8eqymDq+ptM+WOXsLV9dxpo6h7Di6M9MrnkuEQ8sIXBNGtHk5gt/1GRouck/ymCD+frT4KhIiSojgUJC9XFb2sbteUjdJpfZ3i7t5PJNBCOF4rwcJh1h8OaN5pfnQCAByDSRuMT0MjzpPJzyeT/jp8SN+eHgABcG6rvjjX37Gn3/+FZdLBjPw+HCGOgy6QKQAnK02vQs719RyW7lTKoBwJT/RAPdESBSQnKdAhBIIMSWcHj/g4cMnnD98xOnhAXGaQDEas117SCAEYqSgVgBzFJyT4ByBx0CYiyDCYhI4XSe2gTrtRHVfpDElIlScak6OzdWpj2S3Se2MZ0NUGSakNbdpjQ+quGsNYdI2/cjzrHShWWzBNCpJZ41EABO8KtFp8ShI9FzTAIZge035MG2veOxL3SMEMIHd9VtKgBCoFHuRlD4iASQAhWx9MRD0DFELk94ixwUg0ugrR+LFAk1Lc0msY9Pjix5fhLozVAXIHgORQkBIk86Hu9SmAFXMViGFBEIyYcQ8JY0FF6PCwirA8PH5+vRb4SBbfst723Dt3o7fcYVH8T2EEd9ToHF/sGpe3myIdvDgwDcGzNG728m4Z1JGYOIBia4Qfejq1hPCv8A1IkYG1b7+LWGuCNeKUgoW06BelotqUue15iHzUTZNMzhNVjKruRsEHNV1jRBVNzMabchPmK28VLr2jVdljH0d8bZ7pw7X7bKuLsQB0fxtiYl7NsO9G/57pL9GHX3qGUzvPRiuHWYEAIHAaBYN6jPdpeIdaulMvF6z2gSRzD3i7YCruWQqOaMw47Iuqq3grpoan7G2MYSAaDFXiAWUVAZBZJpf5v5GEYImiGgaGk0IkU3jeC0Fa872cWFE++R1RSm5IhNkxH/VYPnGqb7KrLsj/xFj6Jrw4PhsHf3yb8u5tY6/B/z5HnvymjBiOx57oC+GRI9n3NV+a/YNUbkfL6+nd9GkARZtbovCBImdhncByILC0UHcipwLQlDNeIEixWq2GlQYUfeHCyOaICJG0xCJEXSaa6C8vr+9FtPVcWWp2j/tfhMU6BAJrltGjJ9rc7gTjEjT1hliOgzvbvLX993s3dwEldtChKO6Ibn6SXV3BO+xiBBeRtyhHPe34RSNuM95RWETRBT1IcylIKdULS/LgWVEJagP5nG7vrfnQp/vrbgXPXNhN7ddufvzTZ834ho6P6KCGhZGqa68eiGE6UwFAQVCTLreVeAQcTqrJt35fEaKEfM8G6EyI5gyyJEgojEXG9PimJlx5/XK2N4+i4dhezNdOzPfwuuO2tCIb1T8+Fa/+8ZSfamdo1/DTL4XBuzzHQOi98CWryECv6au2/D0fbDwWq4339/O95tl7LWtt2O+08aG7LNdqewafVHvX8MzvhJloEr/bVKt5/rIbPdMfbWj0fo361mqP2o+g/TGrAHWNSPngl+fnvGyXPDz51+xrAvWiwqaZ8yYQsJPp484pQmPj4+Y0oRPDx+QYsIpzcNZBiK1vgjmd5wBCcUYPc0tXUoJkRlJnIHU+u58JcXZFfYFFnBQ7WuqsMs/DX4VVoWfZK5ZEqsSRmF1sRIHGlaGr/0Pcvysg2tu6RGjxYpgQaCowaQtIwUP3RzMgsP7JI0x43S/wZgQAgSh4VAx6n0KEHILwoGotQFqo9avZZ0Hh4UNX2q4o1NQ7d7uamW5QMLxVXVzpe8ys/mQb7C4Ek8ujCCAS0bJASWuIBByWHTtLQsAqgKKaEFgyRQfxC0jeS9wqvNe6TXxxe6TOVz18X6n9DjLVggBG1df187nqRYRodf438Pttlf7Mt6Cb6MVSt0Hm7Q9KcjyR1LBVjR6VfmhUnGbmthdMxldvTlXfMz0a49TigmgHO+mup4BVAsCdeGvgsYaSNnm6DTNeJzP+PHhI354OAHhgpUX/Pnnn/Hnn39RV3AIeHw8Q8qKsjxDLTNKtQoAqeIs4O66lMlfigog3CICwdwymTsopV0AjoSQIs4PH/Hw+BHnxw+YHx4RJrWaUJrEmN4oaoFgMWlOATgnwUMAzoC5ZuK6fny/oOdCk8Y6KSQoIsggE0Q4a7zD/yxAILmVgJ3dxb5DoDFyKqzr9rJQi/faprKfVvjBJi6EkAAKogx/E0DouQZUd0rBlDOJqg6CuJUDtfrJ9kmwjxhsYAhEos2drzuThkOgko1gStDctaXFy9BUbJBUGOEkVlWSrvR1PSLr2Ooopg5J9qti9wqjAihGhJg6RTvl8bY8uvenFFUIMSXMKWIKUd0Smos0tBn6JmHEb5W+lm93lL6W9/fWe+/hr35Lut81Uy8V65AvYItLNIjqv6l0QYHEtSz8YOxK6gHKUGZXUwe4QE0KXhdsve9Xl3d2jaVmEVHf7XriKKQAFnxJlBEgjVmQi/ryXNYFuRSsi7pmWstSAYYG0gUgBZCMGAMCCUqKGgQnJUUWLViWCNkBbG02gYQiZaoh0tCfbTpaDO/H2L8LI73HNf+RfvP0FuP4a8tx5Mr3skCZRQ7uB+Yf75lWZMwKp/+cSehavspsY7yaRUQLXjsioUqEKCLDMQIydcwvmA91VOJFxAwQhWrcicWEHosJHpaSsZQVy7pgWS+4rBcsi37WdUFZlQEohTdng/aXiJo14Tekt4QPR/m/Tz5FGK4Jo4DvA2B+q9Qz/o8EOdcEO7W/DRwdvt/nddzK8/u9IyFgT8S4S4NKDAUCWIUFNcYJROMGEQPImpdJiUBplkOvlwvi0xPOD4+YZw1KPU2zatOLa6VJJbZCDd6nAftCjDW2RN9mDwbcM/g9iaiAorlp6J8BW8GDGCF8UxjRE1hWkBNJQ0Bie8b2D06E1fINB+ksFSFqXQAvCxaP4ICx3q7FnpvmJ3d9kAypflf7d5oQxsvYPgcYwqfKyHEcAmjnlpdRqiVEE0QUE0CUYu6ZOtdxbnnpbpsqY4PMVRG5X9/2cbdDGqS+rYPRdV5b02723wvVuknT9dwxVvo80Zj67gbK19Z2j7mLsj6mSJGCIrnSNGSETDQmlLoLcEuIgPN5RopRrylVX7HTpAKKlFIVRGxjQ6jWWDdOPX75BsOifxYO8NZr7/RXDHm1n/t0hGm/P91q/7Xyr7W3nh/+/MCFz99DagzGa3Buy2rafv/9wsdt6vG4q8/vK+nK9xvpKj1AV/JdK/c3GO9a5H196c+5AWb6WQh1/anBUVEZlr0TE4GoAtvK+PLlGZfLgl+ePmNZFqyXC4QZj2lSP+6nDzilGf9y+gFzTJhPs8YbjLOdzQQWAlHUuAaBTBlY3Y9mFiyZseaClTV2G5Fqb6cQINECmDouQ9RgG6sNhzBX9xzOdBMxVR8LUtrDyN4yohRGiQWBA9iCV+8YUdiuKmMB2uA1OOaBnYEYucIXIvUQTyEAEjrhhNHQHX/MCBGFQ9x4AEKuxKHuaEUiYtRA2DEGo08cb7L9IiYgp7EXA1Pb2aNWf0/HDx9ywYuGp2Ya8dhAUvN6VRSoKSb38NkDx0pRPQwu4JLBZUUBUKIGgs6LerlYl1dA2GBj1LhYrLiHu2XSIMeOh3FTPKu40sjKGTfN9sTcZnQN8G4TSRsdEal7p07Arpit94gRjrfZGWHfHsb5WCt9R53fpNDt+1YmKZ8YFSuqTOAUo1lIBGQiWwSOj0pdP/4BFJdgos1YjvuMuSiPSAQkKgwQW+DqWl+Z/4RiIRPYrJGAkAJ++PABf/j4AT+cz3iIEZ+f/i/88vOf8T//9Y/49ZcvmE8PCCHiw8MZ68J4elkBzgApM5zhgrxQ12kRZdQXAbKgCkhSSpiSucekFjt2enjA9PCIDx8+4eOHTzifHnCaZ0TS3SFcatf1/Gz0RSRgIsFEghlArOuro93q34C6c8yEQGNEMFYmMDXrqiagbMur7VVBz4wsAm2neE5V1oo2JsFwQTd8r+u5p422G6Zbg/6z53/qOdXOOTWY0PVKASoojoSScsW7KSTtAzMk2RoqyfatxZko5nrNlC5hAjLhovh5cetygSBD4EHPRdcFM8BFaUTPS0UDp9f+ex/8XPez1zpI0Swh/JoAEzr4DvFTIFAviIiYY8BkwuloQeqJOuYMdVje3w/K9u8qvUMQIU76N6DnlzrfOt1uFeVpp0Gy+WCTd0CKjZMpm7L213AFwIyCiPH5KLwY2qg9qVqMVQBhPuNzWZFLwbL2jIGMXDSoNzOru4Qa7EdQ8oQSAkpZ1fd+KWAKqiFL6pIjVKRCUVrfhHY8W1/uQdSPiN3byHYPXL9XeouZ+V0EH985vaWhduv5VcbnO+t4bzpioL6zAIN8Ug98L6vujwpEGcVNTE0I0WvM+L7WZjSg7PfXdQEz657hgou5aBq0nkURHSc+YgiQqAA0DOtT94cylNQqwoNSiXiALjH3Ns0tU7bA1GtZ9ZNXLHnBui5mCaFayD2y0GCqAnHXytmO/z3pvcz+Y6bRWMY1htFxeV7GPXW1OhrD8nY7bwnHvlVwdlTHvcKIQRBhhOlWmLGryxkklfHQOCtHYz+UVWESVUZnoAgJDDG4FGNSFwoQMDHU45gidS64W5YFIRJeX19xeViwmsZ88UBl8GBqinyTB80LCuOiuRrQgNkNTl7XeG/WRCqI2M9DH4thC89vCSPGMtrz/vzwVFwQYWdCz9RubWhlF86GRDemCeSaIMLdS7Tza+xDhkiudW6tMnphhsjmfRF4fAn/NFdNIzPr8JMLJCuewdwED+saNThoCNUyoi9vK4AYmTi9YHcUSgFUNR09v396wruSZ84zONhjveHNdk9pPjeit3m3OXBriIJSCXoiMzdPup7TpMFY51kFEbNbRJyU2J2nhBAjpintrB8O40KQt3kveHhLEFHzHdz39D5hxHjPx+ra82vpnjbs2g9UAvE2o6YW2oh92uOM7znfvzcutE3Xy3Vh9s233yjje7XlXaVcJwGu1EHkjM5ji4jdOzseyRbnutYyg4ubAu6mKaRVfTxWX89JUEbEuNaktu42nt7WwR62eXkCNI8g7RUApC49ISimbLbkjMuS1RLi5RVfvnzGuizK1CTCeXrAaZrxhw8fcU4n/HT+ASloHBwYQwposRjZaFk/W1UIAawFWItgyUW1lK0TgVQYobiDatlXVzMOo1gB/wjTmhCC7CqVQdoJI4xG0GDWjBS6ia1Chk4w1q1L6WgRIh1Th2MuiNi71TNLgaCxIwKi4gYUIJ31L9WyO7wsBO1PIBC7S6ZQhfAOLz2Gl1q09GzKBg/9TPH7DT6iE0Ls13DAuH4qmtqPg41TZb8YXlaVw8SHVnEP8+MJVaYI4KIMylIyAELOK4iCxYoAUp6BYPhUdcNkggiMuM0e3xuntpvp4cewywhwl0zDdvEXqZGl9bY0vKEvyMfmJty+A54Duv8EApALz+y+0T4unBjOUhv7QObYghR/iRTAFDRoM3wLmYWxwIQJMrRdPepsz+O2xyiY62/YuRrMWgbNclRgOLvh8EXUGjsGwoeHMz49PuLDdEKKwB9fnvDLl1/w57/8jJfnBdOs7i0fzieQXPCFMyAZHli8wGlw3VsesaCIxV9gdagkRDVuXXKPBiCAAuL5jPnhAY8Pj3g4q3JVmibjFdgas7EloMarIWFEqJ+TZJ9gfW1b0NeTn/G+mdTawDxbIZuibxGxOe9WoeE0FQeTDqbZunS3aPU8hDYk6M26p/1MhbT8FUZskq5T2NnYzij/7Q0g9O7oGaBo8TIFMU4ACCkxChVbPgyYJb6UaP3S31R0bVFxoYL+hllDoYjFHREwMhgZcIWvsgKlgKiAWC1YVFEzoLnH9Vb7vvG58L2n1hjVGiJEUIgtPgTpiW7+sapCXYqEOeo1Bf24IpbzguoEvJPP8l5+zvcu4610rexr97fYzVttu/X8vXXfk+4XRKBtzLZBvQW3GyQkAyPSEcL+e19UBRr1/b4qMqDsYg/UDemIGNUNigEoAei+dwTUhlB2YCFQ81IRNlcIyjxl5uqCac2r3i8ZrhXSUhiAFdFGiXrD4SG/dTD2jaBvEF/gSMpvQ8D9I/07S9JL+N1XZUNymWHm18rIF3GtVjXjdea9M9MwgHbzzy6MZVlUmLeoRcTLRhDh54H6bTW/9yFgShNymlBmRipZ/dwyI0VWs3MKZoZKlYm6WnsueUXmgqfXV6wl4/nyist6wevlgsvlgteXF7WIuFyQ1wxh3c8VyYQhzfeS1L5X7zybt8y8r01fw6y6Crw2bWrEB1BndUuMb86jraDgt0zb+p2J2qfv0wYjSK+MdSVeidRMO6p7ghANASQ1EzZUEzFyhVPM6tcZTA1OQnBZLshl1eDTFDDPJ/WNP58xpaSuAjmhlIwQoplLG4wgReQDVJuISLXWdRqjCkC2MNsQbyWadmyrDUOmZ+A3+GklwR269ZYOtR7vo/RCgoams5fl687GY1u3a+tViwjPx51FBKQGqa6xJHhkogh7H8TOgLX2rcao8HZaf7cWEY1gzwPRvg8AvReOVGFMUdP9UqbBAmJZFpRSzAqsYF3MFWR1RWVnZxfYc3RBpN9dINVbPGwZ1RoQFDWPU9sNRhyfNxYmDkVcO7gRYIALcLiNm88VoMQyNYHBlPTsT1NSCwgLPq2Ch9BiQ8wzYgxI84wQIiaLDTFN0zAOKSVjwjn+dwtHHH+/xZzflrNN7xFCvDe9RxByjyDinjL/3i0iPP01YNNvlpxvcue6+zvt5fdJlSuEPV525xJWnqEzg/Ultyrzgtsz/ShTkEAMLMuC1zXjz5+f8fT8is+fn3B5XRByQULAj+czTmnCT59+wGma8enxE6Y043x6QAgJMSUIlOkHdBqyUf37C6EyHguTfoSQ4X64VTg7paTMSQJKLlVDu3LI2JjRBIgEw/+DMdkUP0EXIyKYlnyNEZEZMRfkSJii4+NseM9tdbp+QghcNX4J6uZS3V2a+5Fgwhig0fGkDKyqZS/GmnUGMpT5JWpGrXNDHoNO8TVIqAGxR4uIUDXjBTp+1A7Pkb+AvYLLNfy0x/8AIHpwXCt7wLOhZ2/lr5GOr9bouJDOkyo9B7OMiOAClKxeG9blFcKMNJ9UCTIkg5PaTnaLiKocMrJPe17JsKGGs7R/1jZgnSp7Tk4r2ZoUixNIUuy+uuuhzhpDcazRnWkvHPF719IteNzyjDDTFRZ6i9IjuE+kQgm3TtCrK8mZNrr3pZm14EhM1fBHU4IpRYVlxtQXFiCYsEGawrCztsQCWD+cZjzME/75px/x08ePgKx4fX7F//7f/3f88U9/xK+fn8BM+MMPP1ocmxVSVnBeASkVRxBRYQRB9zRBsAphBZBF8b5AARMFnNOE86xx6iQIJCXQnPDxh5/w8PETPn36Az58+ITzNCPFqfLAAPVlogJGFTuIBMUpGRAhFAFWqCUGw/ARC73QmPjqhUSIQMSVd1igglqQgIOXoXsqkq9WXZ2MveBArM4WsNru+jImqLWF8wvsbG1u7bauT5slN5wG2K712gLtl/I8xQw5gpaPqPF8SEU0MTI4znV9AWLKS6i9qjRQMaunkq0dWeFAae7ZlM5clTZihtAKCdmEGBpHBCbEIIgJLNqoVZuTGoNU4QGZ264QmkCiIugOS42lEoJaOs9pwmlOOKWEKSUVeMWocSWo7aStNf8/0u8v3S2I2AohbrLj9iepaSizbVSp156obdl7H5G0eSz1/ngwGGOnfw8wP4Leh0Y8tY71iMMIzEQE2dwluABiWRb1g2muE3L1i1m6IhtgcjcJ7qVprN4Olx45pu66GQ/PI33GocD3MyHfk+4m1iqG9HZd7yUAv4Vgf6/m3bZt2/eO2v5WnmvPr0lR38r/PZN0e3NELAFHht3s2oEZCyCcwZyVoDF3Ic74a+vVrIqEqxuzvKh7s5fCNUYEANO08oBLzb+3A0xFvJMRN9qGQCaFh2oueXCupVgciqwWTJdVLSAu64JlXc0CQgNT52VFXjNKzpWB6eJOquNg4xJo2KZ7jUJ9eqT9tE23GCHXmd3X89y3Nvygua9tDRl2Ky1vx369boktz3cPw+d7MOSO6vpWZpPiQ+NBvRW6AGM/+zFwBMuJDTKtkUBQv7yV2CmKLGcNLumug3LOyKvg5fkFU5rx+vqC8/mMXFYLdqyfIgWRS2Xu9u1XYYShsT1QBA0RQxqTv0d8h5Fo89ohslslg/4VQbMg2I6XX3eMfMDcRtCuTdsg1a4xFjnWfFrmaIXAwZngfRwPrlr56PIK61kyrv3OEsKsMZjjrv2oRHK/d+Kmf9fjTUgpABfkrBYQRGRXmEWE/g4gnf+iZ4230f1pbzVHfe56IrpP/bNxjmRzvb5PXSPMBRBM2/nrxsRdaxke5NpOVXAwJYv5kEzwpoKI82lGTBojIsaIedJYKDFNu5gQO5dMwRkKY7+31+2Y3br279xKbwkjtmfWPWW9VfZb/TAyzzl0V/NtCq2sQv3/Nm50q+1/i/Q1TbiGp92bjmDGe+vu+Ez+YHy+zd/fu1bmYca92sW9+PxvOr9bsPSeqRiOrrry23wOz45Sb0Gzpx37Mj0GoQA1Uuq6rHi5LPj89IRfn5/x9PyCdcn4FBJiiPg4n/E4n/DTwwf15X5+QIwT0nxSZZuogghxNN32n7iLPTJXLOayiY1hp2whZQA5Az+GphgBtzwEGnJpzGANtEsI5qdc4bzBfIdh4oJ6c83EjFwKuBgT35/7WX+TVq0nC8iGTs8ws1qwPUSdhZ/uAYKbT1QhRE/fu5smp3Goz+9wT991pphsLCNgbdni9XtY0hiURO0KtB+7Mrc4o9H3OxrCYJe4x2uLjN3YpVLnTusrgAR1d0OkLlgA5LxAAKzrAhAhTwtE1M96xUVcoczg9l6U2X473uN5/K+3rI2R99F/2Xt1P+saoY2SCcQtdJtClHh3v/I8vimEcNhGNh+kgr/ebaVfiXgoy7Hjuq4wumqrm7jHOWubRlxgS3+R1QsKiL6n2MeFN8ejj1/BaXrAw/mMjx8e8eHxDOGM5fKMf/3Xf8Uf//wnPL9ekOKM01mDVJfXBVKUz9XY9GTxn02YYnOn1hDunkkQTAl3ShpImFS2p0HgLUj144dPeHh4xPn0oC43Q+hPT/tEqFVPVLqenbYnFBCy1cvWLoCaSYiV4WeHYylic8EiKDD3ZmSWLN0K95UsgAbkHlgiUufT55LEbK98XQv0zLI8JDKs157+6IVRjX7wc7hf75W9bv0RuPZyCNqRGLQnAqiAOCQ0HoYAoTh50tFO3X7vhAr6m5tAcr1AcgRTBkgtq1DdINnMSbFjjofRbG0GXJCC0Kz39Uw3Opl64X4T/AtgLvSiumaKel4lEyCH6PDAz4ZvOxfu4fF5usa7uxcX/poz7M13No+v5X/v/bvqfkd6hyBiBJY3G+GQ15LL6pvB4gYf3DHF/CgaMc22AN6B5NZ2UPtNXW2+se1PMQl1Mf9oa8mDG5nFBBI5W8Bd7g5+oo7YDZimGdM0qdlZmjDPD5jnE6bphJRUAhzj1JkixYpA6Rjb5iZr8LA5j9IB4fG3IPgqcvuPdG/6FgL1W+ps3zEidN21dAHpcslYc8Gy5urKo5QVXFazGlKBRCl7k95SsgkiFnApan3ABS+rBrtik567eXoyM73J/H7naUbKE7JpBKeUEOIEigkxJGOe6cddMl2qIGJB5oLnywvWkvHl5QnruuDl+Vm11F6esa4L1kV99Lo/d9dar+OESru8vcaNQXPPmXn32TrkH3//VmkrnN0CzreEZ/09or2Vwvdu67bevr1VKx/SEYjj2PftFyOQhjXgJvoH+QcCwph1TsjGGLu+2ziEoH5eRaqguvKbrOxSdF+wFLy+XkD0GafTSTXjpwmFGfN8BojsCqTyqm6e8oSEhJgBMauhnoCv89KPGZxOd6bDmKESkL6+qwBQ7AzhLf5Tx6afoy2htRV61cZw3zpHyE0IQC5QMP/FgSvBChGUsCXkzE0BK3ncEwLVL7YdhmKaVz0RWJnnwlBN0THeRGu7aBw6L196QYUT2KFrQ7uvQhCNTxNjrIKHnLMRvwUpRXApWGPQODilxRRxjKsXNgTzzxsqOamTXJkjcPN00wztRVO2T5qfa0eXDhgkB/fVhzJVhpLvvepOz/YYSANmhkRVkDBPvQAi1eDULpiYZyVg50nxqJjSziKCiEwQoabbRJ0gbrM+t4KIft3eK6w4Su8VUFyDAe8RPty6Hrfp7XeGNt7q0F8l3QPzvh4u/lYw9W+B6/3bSd24jdzN+9Ot90bCtNapAjsTzIRjJYcebjlz3JlKlyUjv1zw589f8PPzE/7462d8fn5BhLos+cOHT/hhPuM///gTPswnfHz4gBQnpGkGQkSZJ0iI4KT+/RUuEzSAp7bDrQcZaiHHpAw0CQlCGYgJQUS1SSus0GDGDd1vsANiGujGrHIllCDFhPQ9/HQBhGluF9bAtYWxFkYsjBiVmRfqGHd0YodkECnMUGsPzR9E3apEA0QhSAssLQzKoc1J9RW9FQxTe25wr3pSIEEwC8AYEwgeS0FhkjZXlaGKKKNvz5cYlxWhke4VcFIdaBCptrWDYHE4K2qx54ahAqCQ1HGx17Vs6gJaO8NflGlMohnINJTBFmyYsjL01hXCGiNCpFTBPZKGFOecIcaUJOGKO6AKOjrmaGOo1HHRbo1ipyYs2fAy3BVEv5irxwipEZhd6BVMebvV2RW1g1dtPo5SD3PbfKERxZvCej5PjK6EovFQ9soIbJ82Q1WQZ8I8SKkxEMgQoSNc2fcYMatVjjRnPSJShRpudaEKKgUpBEwx4D/+8z/hx08f8OnjGVMC/s//z/+Bn//yR/z3//7f8eXpCSmdMM9nxBTBa8br0y+4vD5BShOStOlhMC+K1RFjYWARYM06FnMgTBQwBUKKBEoBSAnz4wPmxwf84cf/gI+ffsCnxw84nU/VpY4uegIhQhAhSCgSkWVC5ohLiXhi4Nci+IWBnwV4BmFFNCGA6HiT1LY6mzxSs1Ihw2eFNB5LMfyUpSM3OlzXeZh1aRgWXfe25xM743zd2VHTXEvB5sjdwiqfBFWhqqilTLVKKI22EW5zPrDYDNYYUk0xKa5Lvi5MOclhU3T4IQMN5AHqS45abwkgLhBkdRcmol4njI6ogcslAOKCbmsPnDa0Q833oJ3zweAjBfdi0695/2NjbUGxmXTcKRDmlHCaIs4nvZ5m5RNNaTJaJ8DCi/8j/R2k+wURt5g127wOJWsGPVwc/6tAdMh2DCZ8Sdc1XvMd5xeR0VS2B5CVw+OXPUOELfhjyco0VbNVVr/xbgnBbIzWDuxSI/wdoE/TpMKINCOlCSlNiDHZx4KImgmpR4UfkSc7yerAoT7XOrs5ENWCHMbuDgL56LkP2QDkvjJ9bw2pe5iev1W6p+638tx6viVubuW/xXB9q03HeWD45agVpQjQ1u+rCuJ8H7ggwuOkrHk1F00ZrqWryJoJ9cy9yOXyisIFL2tndlqBOGGyfSIyVWsJttgMHqQXhUGxIISiPhLNP34uUn3xZhNEFC64rOpf/7JesC5qCeHXvK4GjLkOSI9M+F8BKpP5emrYzDUG93Y+b+UbSiays/N4v7+d3l4PRwKRI8HDvWfDtp/Xnr9135m8Y/J2jb/b++OJprhSG8Pt2B/NxTjb1/sy7GH4kd3O4V67rt1XfSky/8cw5NBd46gQT5kAOWe8vr7i5eUZMUY8Pz8jTROW9YJpnpFLRigRa8lACMicAQZK0bIKBwSE3frbMY+HHzIwkTFcnWnRrRkJmynSH33fleGhZKrSnyMzx4Uaymuhht92hK+IAMQGg4NxL2xeajlhKJPIr2gEIRNArLQAdeucBCJNeFTbbabfvYVHW5emiVgPVIELM1woWduO/spNmAOohQNxN25NMMActB9RmSGRGaUEWyeKv4QNk4Q6GoFA4zTWOafqH1m6FdDjbQORfrSPN6uHMO6DKnSAwyyrmQAKQEoBMQXVkLPg0zFFnKbZXDKpC6b51AQQMQYTOATEOAanrgyDEMzaghqjbdv2YU++fb2V/yjdy+B/K71HGHFXP9DRj2/k7wq/q633pG/F4d5+/xpe1LpxL/xp96+Xe1zX98WDv3fa4ZUbGulr1+b3TQdl++H0PcrCNcxId0gwho/eur3PHXQ53FnXgsvrqu6Yvrzg6fkVzy8XfJhPmFPE43zGp4cP+PHhIz6cTjjPZ4QQITFpsNsUNf5BjF3dhOYIz/D0ImqBRga/KEAodJqnsZ6HIRACUw2QW+duvMCFKaOwpYdvnUWkMWXd1aoHrGYTULQy6MbUKbCiysBS+BAAcFDGej1/q1JFMFxgA3uGChx/V4hE4mpGCnyCST0CBQjFwSICIptxklreW4xvgrpOwvgaXOgjTmc4DgUBW3+lX24b1EtENb01TIgYv6+xSMn1u33+mEHEEHOtpZruhJJXEAE5r4BYHBGYMgQ35meFE8MuaeuhdXGLS0r31rV9M+LNPf5UP16X/6z5fA72igTb+0fz1d/f0TObn76mHJdvFhF7N02KX9re3HXXhBAYac2GD41t7JVhQm9ZLK2RYgPj1ke+3xIRQoz49OERP3z8iHmKIBT8/Otf8Ke//BE///wzXi4Lzg//jJQ0TgMLY1lekJfF4sOq1QGU52zKuAIKilOvDKzcYhVHAhIpMzwSQDGAUkA6nTCfz3h4+IDH80ec5tncZxouKLZBzISCJYIRkTli5YiFI16Z8cLACwPPAiwgFI8JAMCldQJq+wWqDBPrHNZJr2IiEXWn1IaWWnlis98qacKJPjCQ02+WiwV1P7YSpc57FTJ095oFENfYDM1am2uTqld3P1e8TaQqRyG0ODkkYoIIVxyDngMASlWMMrrGI2y7xYvHx/E9Barbs63BlpwGGKmI9tCfV5vaXaYm0Pd2MatlNRMsELy6bZ2iCtk0RkSzrBiG5RvSe/CZa7yAe/ly13h735Z8HG/X/db9W3m+R3vfFSOiUqN+vfs1qof8EbP1nmqP8h+yAqm727VzRzjU08YIf3Nn4YKGFgvCA+uai6aSK2AhMk3DEEBRieA0TYjJfJhNZ8zphGmazSLijJQmTPMZMU6IaTZN7mQbKBgiogcx7VwqdDEwqJmivZcoejt12NI/0t8k/VZac1vNrXrlRnD0RAcXj7WggVHXdcWyrHh9vdTfOV+Q84I1L+ZCZrVYElk1s8w6IhuTfzEBxHK5qGumVX2ZMku1hlD/4MqMOs2z7qeT7qNpmhCSMqgozKBoAr6QQBQBCsb8A5ZSUISxmgub58sL1rzi6fkZ67Lg5ekL1mVBvlxQXAvBTAp9nykCQhWDIfLvXz8PW6S3R6D7ubmNNN9Xz8FduKHwUR1Hbbkn3cts+fZ1LVe+b+vBZoy7+az+QsN+L1Smddd/6dt9LKw4EtR4fqLe134b21aO+8x3lwIqTK8+/QOBWe/ldcWvv/6C18srEAhfnr6AQsSnywVCEWd+hMSEbMKIVCYAQAwRUxGEqIK6EFocgA6/Hoa2kTjj3B4ReleXSoewOq1B4uNUK9ltJ+lutiL6f6zufwijpqCgBtqkzp7aEdOephCB+q4VtUjpwlNov+TA/ze1mAkiPpdkRL4HaSM9i7qzVIfOmTBGaFijVQgRapkSAiQUxKjBPikAqQSUkpTBs6qARP1Xt3gLpXhMjNyNogtyehcUmwmBjVf1sdsSyeb3Zr1vt7MzLyr/ABbAmvRs56oo0syxQyCESJhiREqhs4iYTCBhLpjmJnjQa0KIZLEfNI6QCyKIWiyMaIRuoOOz7Zqg4dqzPs+9goUjZshbDPDtmfoeIcStOm8JIu5tm++hv2WMiN8rY/83Td1599umf390wMi86JA8aYw+P/BcKQbYwHyjO5kZl8sFLy8v+PkvT/j55y/4y+fP+PXpCcuagSL4+PCAHx8+4F8+/YQ/PH7Ax8dPOE1q5StEyBTBgZBDAAIhTorfhpgURwjJWVggFlBmUCmQNQNhNa1V1aCOACQQJl4hKJjMjaEaOrAJDBgUjGlGyk5yrXQXllOlE0wtnTtlJVNUosIgVouInBklM0pgcGSLZeFl2XgZbCQTrFSmmS12lQUQguH1bl0aq0VEhAZKhZkIqGIfDdaU1F1V6EASDAcEOKqAPya1iOAYEURQQkQRQGJCCAUOw11niwZ+CBleOfJIelzxljKOr6MYSftilpsgqrhCW6SOlzmMkArS26LlytCUoHQWTGkh0wVBCtZlAjMjpQlICQEzCKSutbiLW2Xe8kV6TepOaQRHJ4bUuwZeNEfl6WxHwVezFbSJo7kbs47x6K4oRzeMwZjc1xX1hvKgwh3H8be8rkr6VTyqCSP6T8UNWsF1H+nq6KxTyaxujF5h1nOlWubvcGCnUTxMdNPXF8DiwxTbN4QfPn7E+XzCP//4CR8/POCXX/+El+fP+K//63/FX/78J6wrI9KMjx9+REoJr5dnLC9f8PLlM8qymiUKoZDFeglcY764+cBrEVyYAYkgBEwh4pwSUlBcMz7MSA8n/PAf/wUfPv6Af/7pP+KDW0NMCWxKtAwxpnkAS8AiCStHvHBSa4iS8Gsp+HMu+NdC+CMDXyRgQaf/TgyQ9l8gSEKICJhIFXQSWajtYNYRZjNRjBZZabtWLbKBCQF0vfdnSbtW3qBNlMfSqNNvsxS4CSE8poIeQsW47qXFEOn3sPMm/AxmMbe8bG56de7FBRmiNBCJQIpTc/6qPs+ifJmSVREz54vWnxezzF40Xsyq8UJkXcxVUwGXFVIyiLPOQHXlViovCRVuwoQgzcsAFVGrCXLhss6FK2HBz1GniaD7+3Q64TzPOJ9mnKakLpqCfmC0pUB5pAEeEuDvA5d5L9/lzfRXwRW/Ld0tiHCz/HriUee7sG4wS7v5pnqefw3TXJmCThz1ZR4hGduX6fpE1JO9Y7xWLW/f3E3zu7k+gCI71Hx/q39iFUS42xi3hlBBhAkpKtPUo8OHQQihm9BNRo8I3WYRcY1AvjqObxDKu+F5p+Tr74UofO8mf0uieavfXysV3T77HtLSrcZxL5BgA1KOXbu2b8mKcGSPh2JXF0JclgV5vWDNF423kNcaWLWUVa0oLJC7C/mW5RVcCi6XCwozXhcLqlbM2Nz2RJ7UekiEEbMG4I0pI5esgr+UQDGDwoyYJsQQQSEpMBMVRqysgojMCqTXdcGaM9ZF29lbQrCrc6CdM+TnR0VK/OOZ3jpc9vPqc7Gd63uIlZb/DkbRld/eobcFHTcIgE1b703fekb0dMGGRtgzRKVpvo/1N8Lull1LHZ8K97y/eHOOtgKQfr6cgOmDAIsTln2HqquAaFpvqETh5bIgl4wvXz5DRPDl6QtCnPDh0wUhJczrCoCQ8goBsMasmi5ECKzIXghBg0f2hM5Bd6ov2Dp+TRiun3hAULZUEfAq1JFhjIaxcgJQlIGi0L89l80/UJvngQoetqYhwwRAnNBEXRtk5Zp0pN3v5q3NtdQ1o4SmBZVEe+6Vb9dWCLZ2vE9k9VYkuRMQe0nk8D6CSECkwioCzKzbmQXu/quYa0lUvGaYix2usBlDOK63wecOtvjI5PaplWGq+3wBrjxhhB1J5+JALSFSMJ+vLoiY52pdqle9789TighxE4x6w4wgADH4HBy7t7xH6LC9HgorKofFfnVLgDoGzJB3k+9a+lqhw1v9pNbcOpFv4pS1vzhcH98DX3kvrPgW2PLXxl07fvabaTeHm3Xkd7unVkn/aDwYj/CP75mO8J1rz7bpe7flnlTX63i3tVU68NK175ZmoSu0vb6+4svzC37+8oLPT694el5qvKZTmPCQznicz3g8PWCaZg1ITUE1QEHqfpAICBpMmWIEJRVEUJyM6Q0TvhfN49ymUkAc9SMRAaznJQe7CkJgZfypp0ioa5N2HAwQyRlL/ccYTiIekJqrRjZXAYVpaDMslgRZDKGDs0/IQLW7IaHajh7vqIxfczcpjiSZoGHPfO72gHTMDMdpgloQBBvrSCr8CUQQs6ZjDsZ8BoiapeRuPQF1g2+VT45w5i0+SUZjqNslqjhGf9b2eNFmt9mZ3luGOjOToH6NSBmJ8NhTGVyyMpuDMcKlxa7q4wHU5eAroOc1bnlBHft8y7+ooHJofI/EbcvqZpDGH/2a6GHzEZw+Ekq0/d/hbxsCo+L+2otdmQMfZ3dm9/2RoR+63EKts9IFFCqu2q+l8WOxG4jajnRhBhTnPJ9nfHx4wMNpxjxF/OmXJ3z+9Rf86ec/4pdff4awuiOb57O5AH3SuInLBZK5bXMEMAqK1ctOtwhZTBhGJFP8oIApBEQyBZApIp4mnD98wOPHj3g8f8DD6RFxSggxmNsdr0fHi0HIQliFsHDARQIuHPHCgqfCeGbgSYCLEIqQh0ppg0o+1gR32hxh8cEA80biEFPnlknPJyLUfHUduBtRaJ9FukaDOjpnc2b6yrLn5Hi+jN9dqNvcNLkQouWpcRc6QYMLIgoX+3SxVQCNRygClEbrNEGECS6qICKjrCaIKJ0gImdwXiBZA5hXa6ms3yEapHoQUm9pPoL55QNqhA3ReZK6L9EBnbbJK01IqAp0KUVMMSL2Fn51HxxYId1Idwkp38gi45+OJnpfnb81bnatzu+R52vTOywifAFtG3OjcRtAQ6GtxwpuurnY9rPRytK/8RVEQy2oq0u/u/mam4/m1Zit7gNfiiJR1vNqhhc1pkOcVKiQphlpSphPJxNCTJjiGVM8VeRySidlmEb3Z2zXqMxTMuGGS/lDUEMysoGqBH0w0yq/b1hjz/iQ4RD8R/p7T28xpm+911+3QVH9mld36QHbD8XuK2GRTSi35hWXy4LX11e8Xi54eX3FZXnC5WIxFtaMZb2g5GzWRKUGf15Xc8m0vKKUjMvlonuukCnuGPJkyJgL8E62p+bTWYmnlBBiVOHffEacHtTtWVDBBYUIICriJLpz16LWGS/LC3Je8fnlC/KyYHl9BVtsC6kaboRQmZUj0d8j0G8P/vVH1xj4X8vgv1XP/jdBpBwTUDcYSA3xdq+bfxumQZ/eAubXrRSOyzoSCG3remuOKpHgZu3UoaQdoZGSBhHTQGxcEUpnLJdICCUglGi+emNFNAtn5MuKn//yFzw9P2E+nfH6qu6Z1nWBIGCeT+BASGlGKRqcMqUVIUTMc66MW4cxikM1CO8EFYEtQGS7r58Gp5rgHMAGHgXq4S6sz/45GrvuWkNoKlHtQaWrduqG6GUzaWCxGDUlG2HQmCWOvKtbJo/r0MV3kK783QeqGSVq6ixA9e+L/i+h+uxVBL2RoIKmweb3G4ZiTyIBMcJdS4Wo7rX8LI3kFjLO6FFNTXfRxCXWcfZx7dduv05dueKa4sE2/zb1W5CIgBBrQFHNb8x/1240RgcFQowBKcVqRZpIGUB6L1UBRBNMmOulaQKFgDSpe8uY9DqnWOFHW6fNZ+9bgtcdMwh75sW1a/N7bffrtf3FJseYbsOD4zpxeP/W8+tChnfi13u0+ned/trCht820eYKVE7tNg33/eT526RvEhbhr9Xy+9vY76cex16WBc/Pz/j555/xpz/9Cf/zzy/4n395wfryirys+OF0xuM042N8wE/zR3w6fcCH06OdaxELBRQAC6krjTjPCDFhenhQvPd0Uu3SEMECjRPEDMkFoTBiTCgxKAOO1Nu6WxYwTyBoDAcSQmEYw7OoQBsZgDQmqLjFnlTmNJEr5TEomLZu0bqrZUQpKFk1qXMpSBJRhBHEXBXBdZHbuDtTVett8914jKYEEQOIzUe/WUZAGFKirZMDf/3GpCJ2HeVWJxFpHAqYa2fhaoXhVqNuyScSrIn+W4x5dn11voVTbvHOSOZeSyfM5kLMRcvb61LNGm0sRd1FMhdtdykgARgZJEDMKwhAzmpFWYIqlmjwWrM8dZwN0mI12PMen0M3sn1DG8zRe8F8wxvnER7YvZ1Txqjs3ve1QaS8pNDBZWfgu1vs/uNWESHG+k5rwxZmqqIKUYtlR5ZXmfu06WNtoLo/M+uLhoM0CwktIyCQwFC3ikenFMFmXcCs+CKTx5fQGvu2+5qxyuHhsAVAZsbKjPM8Y0oJ/+Gf/gmfPn5EioT19RX//b/9r/jjn/5/+B9//B+4XC746cNPmKcHnOYzCmc8vTxheXlSzfgCEJv1FUUICQo06DkSIIXAogKDLFB8LkScpgkP04QUCSkCpw8nPPz4Ef/0L/+CH374CT/++E84TSekGerJ1aySfWBZAgoIixAuHPDKAc8c8FkIvxbCrwX4uQh+ZsErh25P7rdHMPwvhYAIIEnUnRtMM1/aioOgKn3pcvB4BmpZIGCguPJRB5E2FhJOEYQO3wfQLMHN8wIzV8sHMGtMBubqIto/ThtKKVZei8uT84qci8XBzCZgAMhcPVFWAQetpdbp+1eVTD3urVo+5PwKSAHxCpQCmNWDrIsGorYg1sIClGyCiEbr2gQeTgZHm2OLWdesnYIf8EZ3BjRYYHRiVDphmieczzNOs36mlOo+JyIUq14631Xuuu43T0c48TciLt+LF/R7Tu9yzeQsip0w4h24JQEtVhQasaY/Dgixaz9o/HKtCdW1ckft94S1Mzaa5kYzL1VzxKp7Wf3CV1+bUYUIKSrBnNKEKU1I04R5mpDirJ80qxVEahYRHvndyyIDZCCYZoYzgfyK7ooqfGij4Myf1t+3lm7PnHgj5xvPfWylfv9rEX339+Hb6/C0restzfFbed7T7kEY0WHotMlz9N6WmdQzSzXQVrH9oKu9lAIuUmNBZGOArnnFmlcs64JlXXBZL3i9vOL19QXLovEX1ssFa16RLS5DWRVYLcsFpbSrCyIKk/HrFNFzJG6eM2JKYC6IKWEt3AQRISCkiFQEqQApZduLE0JIEFIhnhgTMnNWF02rapLn1YNrl+brXbr58HGldkJVf7JtZA/mt+2BXjruN3s4dQ0+3SOMULpHS7m2hHrG8fXUFpATek5XtX4daBD1XzbM1FupMqotNY3wXauOb8j1/vRD1cbn+PnYpmNisO032ZStSGi/H+WogrrnukZ1XXEtqMaQl2H9NXjbVorYp5grs2W5oHDB0/MTYprw8vyMGBNODx8AAqZ1gQgQsaprBBGEUNRkNQTzXUzdcvVaqTKLgyG+FdZWYtDcRrFUgoocNnX5pO+0deKYqe1CCK7CCDc+d3dpTUPP3+XhfTZi2LV9XIDgRDJXwllLZtc4GsrVM5DsTDgWSNhM+PPdCvZ8GJ7Zaupmsk9qK+F7kiAW7M0YEjYOGoJCx9pdD1EHf6vWFkZcB9294X5PT3WwYfv+br5srmkzt+Zvo+EvTogZ4ecEezBBxGRxIKIJIhL0jI8pYkrN1WUTSATEKakgIsZ61WDUTRDheAgBo2D5IL3FuH9LCNHZFdT91Pby1jYGB/f3FjR191cGCep1h/917T8SNNxqf3+W93u3K30HYwRd3vrHz7p2oF/peXs+jMFtCFJzHmTb3rpGFfT336czZ2k4yzd44e7OQd31/Q3Qu8bI7O/v1u62l9dGm9qVgGbe/kZjvyPte7QWt2kHA7fP/e9Xtqvv0pHW4XbN+/32y3apL0Np49+Xy8xY1oyX1wuenl/x65dn/Pr0gs/Pr5AlQ9YCSUBIAYkSpqDKbJECYNYPBcpQKRbfIcWIYGdkSAlxShb/IZnbDWUOKpQmUAKoqMVwiFEFFiEiiMeJ0PrYrQqYzRJAwIfrY8RTBsZ0BxMH+CHOsO781osrGAiceedjf33tynA2OZewxofoXO8QmZDB1KP7c1IMvlb+Qxe0WqQJJA4/HYOZ63lse7O/7sasrY+r13qA2l3pcYDNMdH9brgEOryh4YldK+Da0yqgYECCMQsbs1NKUesbKVCLiV6z2hGEutDRbnQfabU6HrClQxx+1bnq4KR3zE/oYUTrfWrj08Fa8nXRXe3rkA+ba4PhcLTFprPb304TmJACuz6N66Wvv64V76Kv9X5twYSG5sOSydejo1Qb3KDDy2w5wjFXT8ncGp/PJzycZ3BZkddX/PLrL/j5l5/xuqg74nk64XQ6mcWPVE8BRRgk7izN+0q1Tqr9am0LBNVQJ3XJFIL2b5pPmE9nnB8e8fDwAfM8Y54mUCzg6rKqTbRbAbFZO7hlxMU/rJYQrzgKSXwA9729MEXHfj0N2ZtNjM/bMHdolhcDCPeC7ExRHNyFEBvlI5+/njY5gv2+pcQFkN2eq3F5nGdZUEpG4WwWK2IuiQRUzGVSzubKKeu5bF5eVBBR1DMEZ5T8AhVEWKD6okHrJa8gKSBRq2sVoJgLKVe2quPgg9O57NWO6/3gu5sqXiS2N8T3je0BXx2BADJhY0oJKcYaF6LGhujP4IH2OoYud6dxmXflj1n0djuHAXTjcr1oYI/mDUdpV3rfrWv3vxfyNuDItoCv4c1fhU9bel+MiK9NzsySthH75Gs39BoG6JZQiAMEdtC7P0RwvDiMoVGl+CLIxYJRF91U2TflmlG4IHugXdtMFJ3UVERumtS6YT6dTWv7bJYQZhGRZsTphJRO1X99dMldTOaSyZgIIdlVmQtupqTE9MEKPry3GdkecfuqdEQUfUNx/0hvpvcKUwj7aRdB1dzoy9Og61KZc8LKfFsvFgPFY6RYQGnfB2te7arxHy7mjun55dWC5r7g5fkJLy9PeH55xuvrC9bLK/K6Ys1qAbFe7LpaXctqwo/m/sm2WW13cD/gadLAfTEiTnMV4EUT+sXzE8J5xmk+Y55OSNPcLIwq9CAUs2xa1osC6xeV/otpHmiwu0Y4DISFI7M9vi1c3bOhTsH28JHKl9PjyzVstGX5Gmf8ypoYNKk2dXor7nbX7RpIrSK7WCBcAZzJq77vvUYx1KDphCA4QeVnsgxncwibRvlPIgsY6AHSu2dot4bXNohvy7ghvYaBIFTtPiOQau6ej12bdTzmDekkgFTrW4F/C+oFAYJpsVcZuKh5c7RyxX3AdoilSDQ3ZIIYTRgezEIiMjivYFpBzIhSoIF5s+2vFX/61z/i6fMXpBDw6dOPIAAPDx/A64KUZqynC0JMSPNsGuXq0iZNU0fENOQQgMKsEBGDubYxJokzEzxfCgEBhGSWEcEw/Ohw29eBIf7BCflu7lQI2qwSxMZeBMoYsTGuCHnnt7qfHbaxdgEDSrHyuc6VOPHt98XPRRNMGAPBfV9Lveft5EoIVOYLBNWqwgjyZh/h+MzR77pEu/UNuHDD11gMQQko0vWjRKPGOWEuyHkUoDGNQkxve7F3fMgC6eYtUDyod60BaS31NvbXQMHwNtrsmVWfx1DPcyI04UNKqqUW9Vl0IUKMmOKEKUyGJ6mQIvWumKbYyvAAdWQWqkQqmOjH0ZrbmD37VJ+Rn20j4dmIUjtrD5gZylRo+Nq2DTcqtkHrENxhmG2veFtCY1CMma/DkreEKHWT6iFe4eY4gpsygd2y8O9XFZYO+9ZR87R9fu29o/tvA749ikyQfn43JV1rf8vRMejeaN+bbTlkZG7u94wIqiq1ltFI9m0Zw+QYHeZr6Y31OaIIneu5b4oJcgV+D8/HevsUDu59bTrSTFd8Rts4nJ9k7tBJEM01XhRR3I654s6vlwV/+fyMP//yhP/zX/+CP//8Bf/XH1/w8vSCl6dXnOcZ8+kB6eEB6eEMjgErGMtacFmy4hVBsFJBCYRwfkSYJpx++KTx0k5npR2TBa0mdROUWWMJxZWQSWFgkgmlCsybUJ9CAQVBTAoTp5JBwihlVbhm+BEb4kvGCFEXeKMvfNXS1nMzCDQmUxFQ1N8shBUBiQmhAKmYb3Y7KqsQou6HERMxhzUg6G6rsYYCIIFASXFICsH4BLGDvdHeZggKlB1o1gXk+9iRH7M8EEKhDAqCkGaAAlJhUCH1hw6pdAAbl1jpKjSlR7Qt4nyHtmb16laUdbVXHMz+mn97CjYOaqSh80foyhQrq2EWTmV46VUJo+i8h1D06EBQq85yQaGCkhMgGTkI3EKBhcGrul8JXBDASOr5FgmMQtK12zX4uzmsZw2aQIDaMRW6fvvIqJaMwzmzbEHRNWhBxclCDxOZq7JogdxDAAfSECEd/REDNF6B4SEENFhaLV0MFyR1TSauIr89J4KOHRker4I8dftTKIICI8SEUBghJMQgOtam0iMgSDTc6ZRATKC8mhZ3ADHArFfh1GgJQRU4arMMH6UVEqWGGZhwwhRO+JcffsKnj4/48dMJ05zx3/63/4q//Pwn/Lf/43/Dr7/+iok+4vE84aef/gOmlLCsL1hfn/HlLz9jXS5YSkIAYZpshdGCyIyJDc4EtYCYYkAMwEMOOE8Bc2LE8IqCiHD+Z0wfPuKn//D/xA//9M/44Q//N3z49BHnTxOmSOC1gESQiuhKphmMgJUnLCViXRIWTHjBCZ8l4E8c8bME/BkBfw7AXyJQIlU8XOcqQM01dAkUUuug2fAzp1OjRZKughzSM88c12ImtZwIphgFAIUAVlYBguUXEfdp17a4ON2nc9V4m+qGOngetsOiunmy+BWIjamPoCe3xaujjtbJnLGWFWsuyLkgFwZnUypldZckfAE4g9dXgAtkXdQVk+1rzmt1xRS4gPKiwsiiweuFGSQaJN3pHjLajCpdJX3Xj5MAlK0HbhHlPlMpIAiZtZqd/sH2tK21kCKmOeHD+YwfHz7gcTphDhPmacY0T6AYIAHVyq4/ce/FGK4rKvlcHGGFR6VvyzlgNGzz9a9IX26Pk2Knw1Jf397/PmiSwSajaTeVCHpY+vXpryOIAOpCvdbgSgYMxJlTOo5s79/a/gUZs2KTSxkEbpbkVg8tFoRbQBS2WBDww0fLDQY9g1kwpKRMUncfMxkDdEozYlTriBhn+8TqgikYwkShC0a98WsIl7jTMbEgNk6HTypC/W0Lox/SKz9vpm+1ANhrmv9+0nv69pbFxtHzo/K341Fx9qoy0b1rv/ty3OIHzoAz07qSiwnedN2vJavlw7JUAUQpGUvW2AqXZcFlWfDyaoKI1xc8vzzj5fkZT89f8PLyrMGo11VdMXlQ6lxqjIiyOqA0RmMxhr1RGR50jJkRiyHNMSKWovsoRKRUUCZGhCCaGbIyLdVPenCrIg9EZVL8kjV+BediQghFXqolQBvwfvT1vmsbSc+uHfM7kuD0uuer8+UP39hNR+t/ezbueA7+e1e0DA9kyNw96QpQYse0lnohhD4AteLQnza0PbNov/alf9m/d4N/CAMO2jwKHxrq4bfb+S3D89ou2z/bPbjTluz+9v1tpVKFMao1BfSCQLGFMGjQDakxFt0CBaCu/QQEhgRBoAIwEKMSfC7MW5YLRARPT08IIeDl+dkYswElZRDUGk9QQDGAERFKQJEMkBHMtl/ImKocBBKl3lNyKKBUH9Da5lJcU5DNr6oxDiJXOAYozklwgQy18RAYbFaz417zkt1ayoU9FbaLIUXNF6nAiUknAqT6W61EJlygUXRGud3XekutW6ogwkjlWnaBaxm2sq3uynjo9m4nsPK11CPvbZ11+6h/bnvd96QEgltEMIfKmBisRWqbtQhm9/vtBI+lACWEifbnR7/I+9VKPSFvAgn4/jEdMEJ1aeHWCX6uT9OktIVrmZrrBCVqE6Y4VVPrKcUxJkQMXUwIFUQQqaDGNVaPYO2bTNcKR2l/Hz1+ar9o+xw7fO2uOmsSXGPwjtYLNPyu79ZGXH/36rWe7/WtilPfh66NzPteE/C+Nzuc5rDUb7s/pO74PRRC9KDrhuUAHXx7b9r39758uweba50Lh619n6xL23V9rZLj29fxl/vw+2vvbmqRsZ6KW11lFtyz3t6iKZoW5jbJOJR6BirQAXPBuma8XlY8vbzi8/MLfv78il+fFnx5KcgLaxw2CzStjNOAAsHKjKUUrLkgJEYAUIJqBKeoQoc4TWYNYS4oVDMAVXHEtEE4BBUIeOzCEDXIp9OdFM0ircUnVOasWo15XIYtQ8OZyA63j9ZuPx4990fgrs9VsU+trhus8OVk2FIHFgW+QvuP46GNsU3D2SgHb6A/p7t15He9piY497GNFtupWUN43Ibo64S0H/3xLRBVKHS8tkdByXHF7QLrLt1aq72w/laLR4Ixn8ay2vxJq8eUN1zhAkLqYpI0FoS7fyFyF06Gyxq/RFjxJkLDRSqbwkawWZp0kw+M+es6atu40hr1Lar9a33azCqFcd7DrhIbL8/frxN01wO4Uc/IDdZPNIz11gpCq21xIqjGjAjteT1bunYGAkUVZoSKMxEYARQYYFtH3k7DT535bpwtuCVQimrt9HA64fF8AoHBJePXLz/jLz//CU9PT7i8LjhNH3CaTzibNcTr6zNKvmBdFnVNbq69Wrx3ddfWWO7Or1Lub4iEOQKTnSUgRpgmpNMZp4cPOD98wnw6m6vyoMK1jDEeOWkkBxbFcUUCGAEZESvcIiJgkYgFgrVXMNsitvabxc42W8EDyKvD2qugVEpIXYx2WEqPI1Pd33WRKc5ARpZ0Z1ubM1xJDR7L5hxrf0d4uFWkEjH6qForKI0inCGcwRbzAXmBlIK8LlUwAWFQuSi9VNTyQd3amlsnpymcrqp9OXBTdi3153qVqPrVY0b0Ah2fU12HgcyVa4xKF4SAaMpNZDSGtN21qxK4Fz+5lW/Edf3emGPb7Vv4RkNIa7kbdgVtsh/Wsbn/Ftt0x0/c/G4ZW/tvKRgJjryD3J/eJYioQJC+r//y7aTvFsE1xPPoZqXd7RBiBrvfSmFj3CjDtQWhlnY1zXDvXjTTf9eynqaEEBKm04O6wDBLiHk+q2umSQPnTnFCiDNCR1T7FS6IMEDUA1UApvZx/6b5R/r7T8euSv7/7P13l+RIkicI/kRVAZiZk2CZ1d0ze3t33/+z3L57u+/dviE9zaq7qpIFcXcjAFTl/hARJTCYuXtEVnZNTyHTAg6mXIUTOep9V95Hw1SlmAp4MG4TJEmGUsI8SbLmZLkf9P7xKKFdTpPkcxinSfM3HDHHWfM5RIya5Pl4OuF0OuHpaY/D6Yj9/oCnxwc8Pjxgv3/E4XgQr4jxJHXGOXsdFXdtbaYimGCxNIMmujJChCQWfkpRGStLRCqKvr7vEXiDDlFcDuOMOE85GTwRqcUCNMYiSxzEVMJCEV/SVFfjn89K8FYPGkJVrRmQifJM+gCL+QPOE6euhVF56XEZVpwjSwIqKyDOWGtppbnWPlmHziitszacK1SpgW3ClPIZolxb48v7q3jn1UN1vs8u1bl2vXbflFiW+8GRWBDlax1HcQc+78NSCWlCZfs+xoikOCgl8VSi6OBiAINkj80RMR7w008/4vHxEYDDze4G799/h74fsNmdxHNvO4gyrwsiSPYeDCAyad6ioHhsg64jOBcA8vChF2bJOUyasH6ajphn8SoCMzq1VvNOmS6ne4bUykevfRYaWP+5otGNuVJmPhWGqx5/UyhYgrQMBzmWMhjg2CZbtNBM2cPCYFL+pigioIR9tgYxpUmliCiKh+UZCluqua7XDhtBVxP1NYdU1mtdhsWtBpwoJSB9c540SbUaWswtg5K0H17poDqOt+2tkjDRGQmS5yTbVy6YfwLlcAI2l6QxpkMwT0/k8iUvSfGAkPvI8ZyD6xB8px4gDl23jPlM6lmhcZ+1DX4BZ9b21qWjpkNXraRr7hOFFWk8JBZ1r7Xlat0153Ghbett0nYpV32Npr747Mw5zpijZ7kZOX07K/DvchRBkxEkCwR4cQiudfhbGd1L5SzmGzXDjpapz/ep+szg7ZqY/YV8xlIS/5sfL1iTLynlAq0hh3q81fSSCTXzMjFvUELihNMU8XQ84U+fvuDT4xP+9Ydf8OXxgJ9/ecDpOGE+TnAuYHPboxs6uC4gOodTAh7GEeQPGJ6ecIgRN2DxUtxtQJ1HuNnBDQP6zYDgg+SQoJoOdVnYLcmTCVAPVmYx8kEMQArwmjcpxA5ICSmIlbkPYuk/e589Hh1zFkTWylZLrlpwahGyZtdfHUc5GU6s4pInAidRqOc8Bss5AjQsYREsiaJZZFWBGfBtjgjzNCVHZ6FsSqlqDcGpYpNMKO3UY0CEoV6965IXzwrxupP49WbMBRS6jzUGhwiSJGb/Erdck6HU76aq7IQk9HoSQTABGoLSekUrwiGlX9Q7RhLtqpJNPeYTknqTRACEOItHzJzjrfvGwMHOhu3LvGvbG2bo+l7NsEgLcFnwWoT4hXdA+Tsr2GpDTqVfqD3n3yJ01zI3RM0jEWlcfxLFmdGpmqoj83f2zRJ/ZzrHe7iUlGZneCd54CJmaCbGQieC4NwG4pE5I7kIgkeKMj+JxVAWRms5QEyHNEdYBBI8EIWOvLvb4nazxZs3G2w3Dh8//hue9p/xD//wD/jl55/x9HQEJ8KHt9/hZrvD3c0N4jTiD58+4fHpAcfDXvOQ6Typ54DMgUcIlt8DkBhwDr5joGM4kjXqhw26vsf9uw+4e/se799/wJt3b3F/e4PtRngQgJHIS2gmjZXE6jUCEgVq8h4zO4zJ4cjAUwIeE+MhAqNNWxF86IXhxpT3BYMQlSe3cLTRFX69XgkOJUR1g3VJDJIDEyI7laXrPrYoAOw0v4fS0o5bJZJWwoZPyJRuyjOpUVCq9laGwc5p3kErR+abwDkPRsVRAOa5HaN4TceouR4mVURooul51twPEZQiSKNEyHoSPicZPMk9qWni1+DkzOXJ18rrGQ9dapD9zzKkABF88Bj6Dn3fSQ7eLoiBkvPZEOkv9/h1aJf/qMeLFRFriPTFh/E1F8qtzxfeOieAub1VCyrqv7MCwjwdLA9ETIgK4Mt7tZDKhCmu8WYIQZKGhSCeECF0Gq+s0zwQkjNCQgdIHomMmAx5GpKtEGLLuJb+frsG79f95luP5zwElu+9ttxf83jt+Lx6X7yy3FVLbS6APWWBreIPVsFUrDx/NATZNIuAf5wnzEkUDZK/QXIoHI8HOZ/kfDqdME0zDqcjTscTnp6ecDyesD8c8Pj4gKfHR+wPTzidDjgej5IfYpI6bE+6CnmZ8EbCariccJRIBVSOBLk4EVQJsVuscZwJt4hKIlIbj8wkFS+J0v8ZKUZNTl23SVtWryMllhmciYb2aG1p6Oy+ESDn60JpoUYg/xpFLxGdgUSidUu+1e9Ro8VS1lIofg6bpPFr6/yaIqKutz43jcm4oKkqz61Ox8rYcP6uHtfLZyMez8ew7rcV3Vj5royPeI7oNSjnElqFB1yQ4XLMrV0pCePpKoVEvc8dGJLgmtXqXEILMgPjOAEg7Pd7gIHNZot5jmASLz5GlDBnURQR8B4MQmKJy98xlNnIjQORWFJ6JzgssrihEzkwQxWNCUzqMK8u8FCrOkdi5eXVgj6p5FO8JyprPirjreILTYxYJ1NWBYMqIihVCgW0iggwEGNSnnypiLCzMiv6jnk15Lni4p0hSgmoACLlNthzzmVq2xeKiHbZGtXN1TtK1DRClPp5GSdbM86Z5ZgKQgiyHtnoH1uHnBkmJNfs7QKfilKBz6TLxTLL3jElAC0UEc7L3PoQFFYXAcCZIsIVSyfLtyUhweRdr5ZPwfIC+eIxR2QwBzBl19coIgwOLNjFlklcvY/qeXlXH8mdZ6ov31zwIFi24WKbtPWrz4sQugI6Z0x206gC/q60vSLsbS0L4Du7beWuDcelOao+u3z/0tw8d6zgmrPKrvAt6y37yjZcfEzLG4vazykOEXLQ2TdniqwzkPKiFl9YEHRhnNbur9MNTRUXeIR1muhS3dePpdIQqLp2BgiQbzQer8yIiTHOMw7jhC+HEz4/yW9/GDGOURJCK00rXvLCEzKJIGtixikmHOYJbvJwc0TnHAIgOSM05EzNS4Ko2l8mRIfylgznDO8WuGu5IEpeBbnmrNA1y20LB9hu1nYuePGrh8kEcsqL45w3Nyvumtduxj+vUa7QIRUQhyKgdsYD0IoAuqKH804jKrSm7e+83iCCeTLvB7FIN6t2R0LbMTnAEvYuDmmiYpOK9l2j69fW96qCIuMW5D41NGMdalSJ3DyiebkaDaBXLEZYorCyKBHFIyKXXc1ZoZvagwiqT9Ixrfp/+TC8be3L6v2GfyDDrfX1a39Y3iv1L+GHrgTtp9GnLV92DocKDXWmANEflL6yyhoRN1H2viOSHFfeJRBHRO+AVK1jkn1pgdaEziUg6fr3hGEI2Gw7OJ/APOHp6QGfv3zE48MDnp6ewEnCrm42O2yGLRyAKUWcTkeMR4leADC8d0pHotBWthALISFzZ7nkSBVoIcB3PfrNBpvtFpuhxzD06IN4tdpYZzhDQFYg1LlbSPiryMDMAi+nBEy8yA3BF9YcVZBKh8pgEmMJH+RI9l7GA2aEI3IAgQ/c4Fn702bX2T7l7C9fra+qyTBwVMGlXCyVa9vXBSDmYSMUWJhzi9i4Np3nZj9Lgmy9r14PF8UOzX1a3HwpAuazP22Ic71s68y8zaSHrHgsqFd00DCBXvHXmnzlxc1aa+kKDVLD8rXriwct+vgXcCzbfPX6paThN3Twqz0iXnpw3jxtOctyL9VXXS0YjvWO1xalJniNMWropSKQnavE1MyMqGETjKG1WJih28BrTgjnPbpBLFOGYas5IoYqJFNQYlPOYhkoSoicE8IRzAOiMAnmZqsLm64zgH89/nos95TK3bKVTrIk0+MoYZFiROSEWUMvHUdRPBxOJ8xxxuHwhBhnHI6S3+Hp6RHTPGJ/eMI4juLOeTrh6fEJh+MRT497nE4nHA4HHE9HnE4HSXAVpxz+zAiyXsNq9BqfvvMdiBxC6NTqVfZa13c5REdD7DiLNe5yrogudJKPpR8Qho3ki/BBcrmQUw8MYJpnICXEeURSd8SYIuI8Cmxy3QKyLKlSPmPuXw7/invo5ePbdvpSwPBcjaRx3UmtQWy91HB9KRjPLTUinCGWFM+0aZVRY66UPe0izsyWvQshc42mqOmzQgO1xNN5layyf2m3Wwgd8nkNiXKuojCYDf+w8IjIVjCuYb7rvjcNpRXhopbnTGGh4dTIOfiUQI4QY1Fkk1rJTJPkcpnHCXGO+OWnn/A09JjGEX0/4ObmBqEL2G53kuR96KV8HwRP+R7DZovbWw8fBrjQIXQb9P0OXegQfK8JhAPIwrdNYjV5Oqn30ywuvl7zh5gHhNMcSOYJYQoJp0xha80ulDOrmF99mipFgxDOiWMmrmVsTdFQKyYYKRJqZUKZA3MxVkWFMtlNvpJKWcAmWNFvpJg2GvNZvooUz3gjKW6x1qheI83Su3iYt4nFijddVQ4T5c2a0cLgaaLyZLklLLRWgoV5kp64zJiUvSPPbI68d3k+HZX1a8R/CK4kkiZRNBNRVi6EUBlnkLj0e+dV6RCy96kpK4QB0dBLC+vG2ivB9lAeo8X1pftl77UCgvPvlXVegZMEi+5b2uHqb2lBvy4Odq0SeQ3WtJ1Ywtj1nD9YGZciTKivqzX4TFvP3muk2isr91phz1V06Xnug1u591yZNjbGpb+g7rXXVquiZ/q7AAYX+/dyHmuVHjHhRfU8n5d49xV1rTf4Av307Hdfc9Di/Jrj0lwbddHala/RVmATKkheh8M44YdPT/j4cMDf//EjHp5O+OmXI1JkJAzoOsJNT2KkpvQpnNBfiQiHyMAUEQ4n7GPCGDr0zLi5uUEPh53vQKGH73oJuRI8gIWHJjkNUc5gL3A4hISUPEKKQPJA6iQnWgiIISBxhEsejCQhGxPgveZFzLBfU187l69Zab8cdsjwZDOSlYjP8HYV+jjGEs4x4ztamVkVQtHiHaEtHDyALkSAPWIIQheEiDgDHBkiqqwoxwwSLb8Kq3BPgr5bniFGQEoEcJS4+ymIRXzs8n3mkv/BvBekihJ6hxe4Yl2IvX40a4+4eEQ4M6wow87at9qDxLonf+o4JG1HiiCnubdSAkXxcJ4dIaVZhecentRbdhZPGk5R14QagRA3aMgMwq6CVJtTQkXzOaWdpV7A8n2QhDAzGYp6RbrsHSkeMWYgs/arDSC8N/rBVeCVoKmL1YgFIA2rU+ie4tlSYUn5l0s5Rhs45+BdkFCqzsP5pCGFE2ZyWh7UIwiiaGCnsEWUib53WTEUOeacpsZbx5g0cwDD8QDiDjfbHtuhw7v7ATfbgMP+Ex4envA//uG/4Mcff8C//usfcNgf8P7+e9zs7vDh/d9g03c4fPw3PD58wi8//Ijj8YB4GjN9RtA2SraEPNl5jStd3AeHEJxRwhhubrG9vcOb77/H+w/f4d37e9zd7XAzdAjBS85KBsgFVXSoYoAp52owpd9MhCMzHhPweQY+R+BTEo+IFgvUc8SZNk62CxReTSSKgpjpHslnIytP/ExmVs8JsHoHq7+OKlqdF/o35920slR4l7gOT2mbVXkT40OYq3WoPTA5Dswcq3xdiUPgkgM7AfbJC7/FQVazRaxNs8Jt23MJcEmU56KA0AWsf696thJlHubXEKS7jGc580IWisoULAI3IXkkNJQgnESjudn02A0DtkOPTd9jGDp0IWSeBGii9/5FHJSlGH89Lh2v8oh47ZGFWwtmfK28i+XXsptGSlWmdin0SZWSoSaAUoo5F0QdT9m0o9YOSQQqyDCEDs6JYsE8Ibydg117eA3BZIjS5fBLlg+CGiWEIWRjnhrh3TO8zNXxWozJtXdf6p3wv+pxiWj82r1w9dtlVXQujGguDIkA1RouCC6mCI6VIs6Eh3oepxHzHHEaR8zzhONJwqzs93tM04iHpwdM04inp0eM4wmPj484nU54fHzC6XjC/umAcZrEU2IeMU0TWAk5CbnhsxBp6IWJGoZBlHqhg8t7SwgYr4oIEXQpQrE4gjoWpPF1fdehC73kZ+k2CP0gQlLn8/sxppx8FUpccCYoiqs4p+KG3wps2nk6m541zLw2tzUFsXzARrahLesFezeHSmmaXPXjykHNO+cMU/NuIySuSlgT8NXCvYWgbG0vGaEPM7mpvuVqbGryUhgdfWKfnjWl+pLLexnW6ltXXeX5rCTUwp16P1t8WzPZa63NqyKrxtbPm3eJ1MofmanJzSFRUMh+91aohFPQsAQpJRADcZ4wEoSxiBGOgNAFAMJwhziJgi90cL5D6BxCp4IHcnBO8J7zAeQCxFLLg+BF6I0EHzqEFEFOQjrMKSLFGY4lMaQpGLxThgoaz19D/+Tky265xjj/Z0IN81qwJNS2r00Dy6jvA5YjIkUq46RnOXSMq2RrnJmFeg20SgyDr+az0bCmTbgyZVBWUEhZZtco5pfhmLyGnDIgbMyhr+iiojAxqimHCzOlGclzENS7pbSNdL9nC1vzYMuht8q8AYQQxODiTBFhxh1evHG8F+s/5+Sd4L0keXQ+r33DIZQTTVqYL/MmXYzDAk6twYb2XnVdMUOl7Ayhz95v6yywtwhbXkjjlqIvvnvper3MZRuv9Hml7hcRoHXdNfwuAPu82MsFvfr5GT56TXn6/RI11zixWdJVkRfZyUt02tr6s3KKiff1AleeFyxWnZshaZ8/t16kUdfZ5WIB2DZKWLy1fVPGi9p/muOszhoPtFsPbNagK3U8d1x9e9GH0pTqntEkLMKc0zTjcJrwuD/h4XDC02HCYYyYkqQm9T4gOIfOadhDcjmJru3LZNa+iTFHxpQYzpIfZ0pNflWAvNyTRg5a0Wq10lY8IugsFyFRMWaon7WL/cJ4ZUl4Ras2LbN3yrsNv638i5VwYVVWe5RgEeOMDHOoPCLOFNTSj6LgqGgtExiqYIKUtpBCCaTW5UwiAHPkwKoYB4vVcQ3f6zXCVbvr8FAmlMzyECjfdjaua4Nt9KVODVdjk1+hQgwv5y3nutFwPnkOjFaKlYJJDCiIkUP2yXN7v05GbVVT0/ECDy7xz+18oFwiG2m6Moe2NpeeLy7nYjif+yVtvdwX7eg2o1zhThvH0hdqvuKzvy/xSc2+sr8tLNnKeBAcnGM4L17HjiRXBAAJ05St4kve0i4EbPpOaOo0Yb9/xNPjZ3z+/BmfP3/BPM0AOwzDFtvNDkHdnvf7Jzw9PWEcT/KOHpl+hBh8uHxfVwAXA53kAbDQaXCE0A/oN1sMW/lJOJ2g3tKUU8fb/rNwalSNGVf1GYwcGRiZMTEhgleF58uUV7ZaJVeEtR2IeU6LsRugCkaiEvyKGeLpVXkaKc6kpgH1OigdsG8K/1Hv+9KGwvcYbKgUl2ZwAzReW6z7gEn4LaiXW1IFNVMSJZ96dKUKNpICUjEoIYVX+strVN+p+iKg5jxqwMWjQVLczE3eH6ACpkBZeZLbQWLIlD0inM8eEbb/rx3c/vNi2ryV21WD0JR1ter8aqGf2rF6Vs64gicujXd7//wdvnJ1Xupvpz55dbLqM4HNM+/KGS+nFtfKATIRYochupa4EeuEeZa49PM8Iyb9O86IlisiVUoMQBa9ul+GEOC80+TTHv1wB+eC5obw6IcNfAgY+k3OEeFUEeHU68HO5CQfhGnmC7FnFt/LccpU02+2AP56/KUdBTCvHi1tX9a9xvGLuvbjPCPNeo4JoyZpfjoeMM0zHg57TPOMp+NeFBBPXzBNIz5//oLT6YiPH3/G6XTCl4dPooD48ohxHLHfHyS00TRnZikEh9A58VAIAZvNBl3XYRjKdQgBm36AdwFdJ3vFzkE9hUJwDbCOms8iqdWShUgLncQR70IP3w0IYcgEkOWiGKcJc4w4nk6Y5wkExhxnsFpkTSBNnjdld0vBuYIAM7FqCJErV8HlDwUuNsL4F8x0TQAJ89ISReuro7pexrV+9uDmtKo8WBxOBcdZPKyMwpkL+ZIxo/VQUZeEIkuvjKWiIH9vZa8pEKo6mDmHNarhParyrpaBl8HhumWMNjfEmhXcGrO01uf6+0wQeQ8XPdzswSkipQBOCSH0smfmCcwSenBKIz5//AjvPU77QXNEbMWyrO/hQkAYtuiGLXa3HqHfwYcNuv4Gw3CHvt8ihJ3kW9G4yYBZrQMMh64fcJonJAIe9w8YxxPieABxQp89IjoQiuKhcxJ72SsxHHzNIJoQkDVxpgkx5F6yuKeVkEMeWYilhfeDWf6cTZqOZ6XMlaMoE2ytWHkiiKqeZ0ZN2rgUWiFZmKjz6nOZYJhA8py+ubav2/dl7BhmtUbe1o56RvCMxAyfHFJK8DMhxgQfzFKz0Fecksbb1rJJBGvZwnDhneDMy0o/8GSKBwu1R/nalAvkChPhyBJQU/YiLUIDs2yEyonkj8bbALanoLRVe//SNVUCABtTMJ3fv2A5v9y/roKpVsZ5HevtsjquC4wvwc6yVtb6d6kN7XuXPJ1XN08pG4DEIT9n8K7xCc8xjs/139rxNUeNn1bnppn7+tpgybJfa+1YrLuz6xe39kL73Mo7yj+cjZ3BVapeX4pCyndFYLKsQp/XiHGtqsX1N7F/NT/Ei+tXlGFUdVE01v2/PBtcbX2vOGCKjOMY8cPnPT4/HvA//u1nfNmP+PHTAYkdXHeD3gdsuwGBCJ0jicMdZyQNo+NyyJaARB4zHCY4zOwQ2IGTkzxQswPNDnOUZLScrbnr9teCsaLATUlDN3oPDgF+Dog+iTFPmnPuAx88EicxoIMoQpCSCtzrsSg8toRltMTHgqed/sr4JvXoZHBkJJcQI2N2yq8oTZ0AFa5VU9Yiw3zPKZ5iFQh458GeEYPkiIhercsjmbMjsq8aMQDJi6HUvtBr1bpmkmgIssY9XAQ4eBAx4izpqVNSj+uUV1W91DIWTs19s5Bur7P5brW/iO0NWZupwq1ElEMwFjC2oJXrgcu0C4EpQTJDODF2kazmSERgjjKuyQMkeJo1cXLJESFe9mDxUnXGByQguYoySjXuOadxC+3g1KBAhaHK40FxPsiBvOQoc0EMYkLQ5O0+iFAyaG4p9bqvvSGKEYMIoEteqeIB2rQtWe6NpNPCYDbjH0MXBnvXcwuueUBnZYnKhcTryKtXqwcIcKogSrYenAMxwTuG4wSfPGJKmCeJ4Y95lpwxoUfXDei7Dd7cbnB/O+C4/wUfHx/xP/77f8GPP/4Jf/8P/4gvXx6w3dzj7vYef/d3/xvubu4AJOz3B/zTP/0jHh8+4/FxD4DR9xJSc04SfoycA7EDaZ4xAQ8W1hzqXOzB7DFsB3RDh5u373D//ju8+e53uH//AbubG2w3HYImsp7IlA6p8N5M4EiZLwBEWTAz4xQjjpHxNDP2ibAHFRqay1yu4ZvaxChBQjxZHgiZn5y1QzkcRmTJBSNcheVZUVhb092UxdENP1BIRqWNNASS/V3sqLjQToCutQRmDSWPBPP2ztCMJHQfefPWAKLyuY6izBMREkeBrd4jIQGhQyKCm6PotFIASGQsxJKgHhrJAhwL/5NK+DZDPUQt/7Mmr1oTn9sh249kj9saA4nHmXpA5M6R5Aftug67TYfNEDAMHkPXoQ+dGDC53zhHRF3Vs8TIV1M/z5Rzqdxr9V14Zq44F55/S9illxwv94gwwT+uMBFX2pqZ3Nd2qIIqreXBuhKijoUvIZkiZk3wKcCTc+6dWpjoLIySWlbnEEtdD++CKig8Qqe5IHynyC9kAakku7JYmy5vMkPIxXpwRYP3yk10SQj4Ne/+ORbZbwoUfuPjmnfDc54Pr/ZC4QuXbEK3Kg8K1x4QUUIR6VkE8zNO44hpnnAcjxinCfvDAdM8ZYuILw+fcTwe8fnzZ5xORzw8fsE0jtjv95hnSXAERqNw64YO/RAwDAO6rsNms0Xf93IdAobNBsEH9F2vYc4qRQSVEB4+x44UT4VZ8zikBM0V4VfCoPWSSFdj50qsU1FceE2S7YgwxwlEhNlPyjhlgKTEgFAwrNYGLNR/DfUy+1I4Ylf4B0YDq56TNJwxDWtlrH7XfrC6Bi/Ud60tF98z5FS/IzXnd5drOt+38VsI+18qbLt03wicNSXFWXuW+21hXbCmhFiKKkq9K200Irjmm1faBLTJvy8pIi4drXLCAz4HEVJFOgmx6xM4qZAAAKckxPckVm8UJriUkEBwCYCPcEHjupJTzz4JxeRcByINk0MOBGGObC1478Ek+NCFACZCZMlXgSSErQiMhbg1C0Z2Zp2j16m14MzDYNR8pSzgQsHnezINqcxt/Yx5ZUMwmljWeR61vrwASnnCKNWeEPkVFKa0qigzIZdmVBUUFoQ3b37r+6Xv2qOMVbWGGDlvg9FGxF6VLtIgr4k3RblUt500IV7xyrGQWkURUZQEdrZ3xUKvKB6oEQCU3BDnoRNEwdEwJ00dWeqSBQK1GKgIFmqB1tLy/9o1rXx/fS7yvl20oRYQrde7cu/Kt22dl56vtZ2qp3SxH+vl2t46/+gcTpV6Gxh5uTrUMPMCtF9/cIaf2pjpdRsajLUYlyywqO9nvkD+KVvL8BxQoZTr7bxQ50uO9rN1/E5YzEOZwKbNlyu58rzWSi7qXWskL4pbv35h59tGanMyA/gVZVRt0HV6tq4Nnixgta2AghqE1h6nhNM44/Ew4uEw4vEw4jDOiAkgchI21Afx/CUtx5uQRytxBHjJAUHOA04EwCAV51fJplNMSLHK81OGpnSAKId1rH+WH6J4PpgFuV6nIhB2zsFlbwDKuKTFa4JDzjwDM86110q+pSWfXiypy6/aeGezJriamv2nU1b1Uz3mqr5nuqjCraTzTAQxdMix+WtSV75zROJJQsbTa12QgJFGX9KyxWSC6xaWSt013KtCdqyO8/lUn/Pydq5oYetyXWJNY6QEdgBVNKKdhS6MSBVvYXRXEZoaTW3hagogb6zRMy23pgyvcSPld0sOE5tHp94RRkMUD5iscGjCMdXflvWgW6RaH6UNRGUNOCh9quOcUlUGCtw94zlsndfXQPXTgWkStIuMqKw/Wxu2fgEHn+8zJF8iM0RB4TTkcRewGTp4B3CacTzs8fTwGV++fFbDwgkxApthh5ubO2y3N+iHAafTEYf9E572exyORyRN4E5Ka1loIgIENiZZr4nFKyOmlB1kUhIrfPIewXJD7HboNxs1SJRcX3kt2piDtZ+iyDIVD1VrhrUtiSWEemQniiJbizV6YFXUrZMu1fwY1c6Si4/EE4K0LvNISEb7U6HXyx5cw0cZAFZn4yNKc2u4SfbeAkYW4FgOEnBYqFWq13qBi7pDZU3b/kKNGyznjWvWXD5zSRZt93URZhx6if+W7hQZy7lCouxHa7goo0oboNescJicRKnpLD+Ec+Jdc+ZNX+qvq3vueFaeWsO1pbx08eqvJU9ty1H8eomhXLbtuTbRyv0KbzT03YLXfll7X3e83iPimedrTfl68rEiOFaIlCyEXeSDkFj1cp7TjDnNgmSZ1UBSmWIisQ4hBx/MA2Ir2dmHAd532Gxaj4iu6yWsjHpMdF0PCUMTtKE+a/sNMuRkjgtrvTxeVP391+Ovx5WjQVTV2p9TxBRn8QIyr4gYMY2igHja7yXXw/EJ4zzhy9MjTtOIz1++YBxP+PTxFxwPB/z40w84Ho74+PPPmKYJx9Ne9k5MokTwHYbNBrvdDTabDTabDbY3W2x3G2w2WwzDgO1mh67r0fc9QvDog4RkyiE91HsodEEUEc6EYtK/rECcR8XFRnxqfFBVFnof4Eh+ZnFi1junccQUZ/Rhj2me0HmPaRLvh9N0wul4lPHjuQrhVBAxrwjZGMJIyJ4lidcqcWoyopczmrIuHWbF3PLZdfzf8u4ZXqQaMzZPnl1DLxF8n5XUIPvatkvvXEBCtRCiJly+WgmxQjCsKRJKS18OV4viwgillpE0wrSux/4wxtPaUxNqS0R+TfGzHKv6O1NEhBAwz16VjYLbOCaNSSvxfi03gI3FPCfNCTCBfEKIgA8M8ht0HeBdj67bYrO5xWa4xTDcwrsOjgZ4zdtCOqCUCHBA5wf40GOzuRGi3gckEMZpQponzBxBbLkIAK9j2jkRbndZMG1J6yuC2ohjG+daKZCZ4fO5KM/sWLdcgyXVaxZHYdbzUqiVDvVfNdGW52dRF1/Oo1J7dCypv7K3z+mF0n6u9mQR1JPCH1fRGrIGAxInTLPkGhFvs4S+t/AMVQ+VybP17JVpcSJVaxQIqwoJ3QvmEXGmcKhChiyFZpp3saq7NuA4h11n5zKKZ8KPa3stj38WUrRQY42Qp6bs8+sWgl6vmwhNgvDnYPTZc768Vpa089k1cd4Pa3UA67ArN/yc67GKnj+ewUHtu0K7U31Daezm/jNlltwWQOOzd8Z7XoPNaJNCP1P3S/NuvGo86m+MUcL5HL1WCbCGU/9DHLpHMy0BZezr/V+9bN5VkusnIU0Tpjnh4+MJX/Yj/vlPX/B5f8QfPh3EkpN69F2P2+2tGLP5IN73ZvnmSq1i1e3ge8k16PoB1HWA7wEfEJkwz4zpOMGBMG17EZR5haN0bgFqAinLsyZWyglI0g4XZvgU4UMnNH2aAE5iUMAph2qJDLGYn2XfJxOYMQAIjU0QnoBIkxw7KUNoEckhAR81r0DQ+Pak/AqJdbcKL9e4YqGfbE4qGMkm/JbbYumOrMg2TxARPjsweaUfYp5PopSFeJUWpBLESQWCz1h4e6jyHiy8AdRSmDRUU94v6wKtpdBubY9dul56xealSut1ial9ar7VIShNTARyXMbEOUQiUU7MPnsSNzQsmyGI4AzSsQdDPFoUJqZCwGWRR2mahRIqyoVieKDeklR5RAQNbx2ChsbuNBFyQOjEQLQLHYaghqG2r7zQk85bzoY6V8QarlT6AxCLdR2okuBbhO0Ag1LJf1jvQbG4l1wEJqiPSehfVp4SzoHgQRzECt32loMYukSnBJSXnBvowCyGhi5GEGZ4n5BcRAgBfd/j/m6H+7sdxuMjHh8+4d/+9Z/x0w9/xD/947/g559/wTQ7dP4Wf/O3/zvevXuHD++/A4Hw337/T/j88Rf8+MsnTOMRjli9VB0YjGmeVegtXgGJopGGmGPCNEcEEqHwlCJoBu76DTZ3b3D//gPeff87vH37Dndv3og8LYh3buQIEpt+GU+wjAkB8HrlCI7VoBeExMCcEibNdWkhxsyjSPhzXWhcLTic4/EyX4WPIOYc6ikBkk9TvYKNMrqKRlk1DFXyZ7DlcxHDSoOlmY9k1gTR2oeUQOqNXPZcBQFrMAOj9WWswMJfZS9yFhgNqDGY7SmW0E1QOMaAKKoZIDgBG5TU08nJ+icGoDlMcl6dcyVEDZ/W+XKjtgwYUFYykg957A1uG5An7+G7gKHvsNv02PYBm86h7xy64HLIV+AvU4b67bTUX2Kvft3jFR4Rzw8GX32v4dwvPFuzHANKEhO9VO2obdg6EbX9Zk1QnXNCsCEUY9wF4FpMYskBUTweQjdk1zfn63j2Ft9eYxk7r0ShKh4qpptrQqphdtsR4Lp3S373hUzE/2yMw6X2vpZp+ks9XuuFcglZrhGnGbEtlHC1Mm6eZ8wxYpzUA+J0xDiOOJyOmKYJh8Mep3HE4+MDTscTPn/6jOPxgMeHB5xOJ5xOJ6QYhej3QYF+h+2wxWazxe3tnSghtjtstgM2W1FK9P2AzWYrORx6cZvrfJ89KERAFWQvWYgOZRbMqmSeZ6QkCb6EThArF6+KCBdCjovpLHa9ll3ciAVJxiBhYebQAQC6EJBSRPAS2oZnBmDWW1KXJH0zF0VNDGxCKhNSMwniznCrIkxrBmeVyc2z+cy+rZ+9ZF+YAIiaS7l1XaB1XhRXxS3W7kIcdNEqYtHqpRLiWpvWynwNbHjuzVWLjlYevHo0LEzu4PXajOHNYu6VftSKlrpdTfsImSom0vA0SkwyG5PuwdnMl3MYcguvRObJlEOdORWaqIu7JtW0pMHyt4aSKHJ6bYSHo6R7u+BDQAR1cY6SKD4JQR7Vgo5VIM3ewxOBvbjP++SyIEW20cJKlVFZhBQBvjHAOoDA2TvnQmSwxfuup8/IZM5jepkILPFp2y18LdDHK4+z+LPVVbWHlj+57/IXNVNTuzAzm+dMqccsmagq2xQRlOfF5mmpiFBmUmV73p0rIohU4QQtr4adpuigMv8GW3NfdSxMSHV2bkBgpYzIW6jaS/U41sxRfQ2Fd8bgVtPRzAgtv4LiiwvX9reemUpbVtu/qCuPRO4foTXvr9t1ud9yi6+CsDNYvOhX3cY2AMnzR/n2JfTrkj+g/FuO0+q4VV9JH2oh9IX6FncEJKgFK1n9i69W6qby4Opxrd3nDckFl/VXr8NmXqp/rxXPZ3KcFx51nevX541fv7xQcssnrb33gkaXvtmao1xDIyRZlMcMTHPEaYp4OpzwpJ4Q+9OMmAiA5L4JPqhhTYGh7CA4mQzeAS5UtGwX4DoRsMKXGN8zqzBwduJl6CgnknZupY3ggjepUvZafojlj4q3Wa0kbjwirPP1CCoeNnrdBNScGOxUaMoawsmesYUKlL9Tqvh4ZlgQxkxaaFX1vmkEXQplSPHFWoLimPtQwwmBk7k2rajF4fKcq3E8o++bFSQNZa7uXaDnVunkqvLyt3mNXPIo4Wo/VBVXgIHziJb3hTxKADs4JMBJmB0HzQ0BgJJoLJxLuUguH+dzniul02xs2jFiRU8Fh9s8UHXfvqvpAaMFQJRzipnCwujfJtySa9eBKTyyl4QrcO18HnSsqkkkMvqwWkO07EPpb/GKMFq/mqc8LVR+kD1o4mkZdC3bUYFMTJK3xAHei7IAziN0AX1nnhATjgdRRHz+9BGfPn3C8TgiJWC7uUHXb3F3e4+b3Z0qEibs9wccDgckzQFieyEpL0x5fyyGqbms+ksEHzp0wwbDZqvygB59CHlfcs5/Y6uz8Cj1Hq3/Q/OzinUdqgFhvdbLBJbXdTllmAGgSgxd4A0bfGPbNxUXURffHFTBQS7KiMyYXeMirG7dzXz+suERW5tEKHzgCq1gxlhLb7VLR4OZdX0z27mikfL9Jd90+brsn8K5mSwl76tqYxpdZXvM2uM1DFsIXvNE+OIVQRVd+BIyMo/Ry2gG69DFObwwvs8pmp9rW/67MKOvPr6mzub6JaToV/azPl7hEbFW+EtnXzfGxQYq2Gsp11yDrmMB11y8IEzZMGn8+yY3RFZGRESOVlJGWt5CL/UbeBfQDwO8D9hsdpIDYtjA+w59v1NPCA0no2FgvBc3WlINPlAIPhO6MqDx7XXTuWqkvm5d/fX4X/RYEqFJLY+K4m0Wr4hxxDTPOJ1Okvvh8IRxGvHl8QGnccTTYY9pmvDx4884HI/4048/YL/f46c//YDT6YSnp4ecYyIEj+12i2HY4O7uHtvNFm/v77Hd7nB//wbDsMFue4OuCwidR99v0Hed5orosrIu+A45XBnUuloZICE8A8AlBqkpImIUgli2j1OPChGYCrxQS93KbTomCcfkncccZzgwpjmAiDFNE1KcEDxhPPXwjrEf90iIAEeAGTHKxrSkThbD1JFXt+OK+EytyzZVCHTNYoZRUcLg7Br90vlfWh+sC/+NbFq3mNO/LtwvZa/Bp/r756wfrJb6bitoa/9e9udSX68J8XPPKqJu2bZLVmacjKFbGYtcduVKr5XJc7EcWbY1X2sZka/hwPWjVkIY/clRmBEHWafsGExmReOzYAAQiy4CiXeDcwh9L4mBuw6+6zEMG2yGDTb9Fpt+g6HrsekGDP0A73sEP8BTgkOSsAIMsFnJkENyDB8G+C6i6zfopgkn3yHNM07HEWme1bNJ8isQIB4WzqFXF9shmGcEVEEp+6rNGXFhfCphRfMamYA92kAunlOLjCsGNTPfNbO0rPgKc/GSY7nmz9Y3LfeO3tRj6YXQeBfgPIdCSglOreYTc/4udwZl/UpOGElKXisQljDNvBWWng+s8+zq+8Zc5zZCYan0K/fbUbMHl0oIYxhbRUw1NoSzMi/BwcvwsT2auzVjZusiM7nXFiqdX1PdRjQCrNe0kVSoYe3jC+9eLlP6snaYZfKaR4jtzaXx0Ut5u7W61o7l2i/X9aiv4462nBfO95UOSNWy+dUY+KvL+pr3moY8t84vrsfrdQne5rN7Nb+3nKllXWt1F3rgUv0vhahfyZRDWi7wETAvIqr6ZUcjYCSxkH08jNgfRvzxp0/4vB/xp18ecJoZiQM63+Fms0XnA3rnc12yQcS6mzUckiPhP4P36LZbdF0Hv5Fcgxh6JB8wMiPNMx6PB/Q8Yzj26JJ4L/iAbNV9tm60OscO3ks+A+c9nNccED6oAkTzTLFcey6W/zEyiFL2FE4qmGaVLpHEq0FKs1jSp6Te2TMQCeQ9YiK45EEpgjiqN4R4Qjjl2+fkJE9bYiRNm+hx/SATailc8o5AcJLbwCfM3sP7BOci2DtREnE222/EmbWyIK8DxSeMkrBawmFq/gJOWTie9F1HRU4kRkycV1ON55+j/VoerxhUZX6vOmc+sBIFF9WEnWWsEiykjt6PEZYHgRLBQ+Lhi3NC1NBEXjwmoLjFxkjpOAeJT8/6SGg1p/k+Co4k9frOfFSlIBDaAHmPSLiwms5wkm9KFQk5rKMazdhPBJQlJ0SdI0J+lUeE1Xl5haHQQ4UusvVCKMq+FgOcz2MzZ7kMp+AgghLEcIcJzLOsPVNiqnEesY4nEsglBDUa6r0kpxbDuj2Ox0/4wx/+CX/8t3/F7//lX/DLzz8jRQ9PG/zN3/xvePP2Pf7Tf/rfsd3u8PnTT3h6esAvP3/Ew5fPIDA0HQgSIMpPQjbuy3OZhcoV9lXagb0Dhw7d7g439+9x/+Y93r59h9ubG+w2g+T2IGCeJ123pHST5qFQDwlHXnKYUABRAFyQ8XAAZa9N22xi6KQDW87ONuWCltT/nK7qRC0/ZuMt9L/tr+IR4SpOwPpvKT1M6cCRYXlzoKGrRF9S9vQaHOBcSNU/7U5B9SRrxrAokyhMchsK7EgpqrGqKXuLrMHkqMu2WNJqk3Nk3JVsZcg7RelApd0LGq3mX3IdWUFCEpKQCBaOUM7a94oHAoAQvBi9bgbcbHpshw6brsMQAjoflA9Zjtyve+Qu/4bHX4Jx+VLB9Oc6Xh2ayY6WADJku/7uc+PZlrXQrug/omiUjZPzPVgIl0U8/KiETuJK02xMi/Ma1qWDD6Hkggi9XHd9ufahCFP17IK5DorrEDkv4K2KZVgz6xmAVNdcCT5ePi5/Pf4jHybyygC12jRJkW1D2KQkiahVcD/HGVOcMU0TxmnCOI0YpwmH0xGn8YSnwwGn8YSHxweM44jPnz/jeDjgyyc5H/YHzLPkfwjOY7Pr0XUd7u/F8+H+/g22my3u7+6x3W5xe3uPoR8wDFt0XdBfjy50uneKIkJCKKmyzoRnRHBmCqGWnFFzQhCJ5ZdzC0VEJjK9Mg2aRDUTNQSQJMXzyjx475DYITgH1viCKQgRx2kW6xJO4CSOjDmGb0GjOivFC6DG0yb4yvfsBeAcHhqi/do1skbALLXRuQEaadMaefau9mnJKNUAN7+6IlRYMnGLd2qou9rOSgi7qsSonr1UgAQUJmjVo2DtfTyPbF9a1tnzpXIFhTFdfpffoZILYlG6TIP1j9TVG8L4JhRrIxFG2pqVNngqiYKdd2qRKfvDmEUjoLMSA2qFhtpazUrVHBWsPTMmSr2UiIzBQvbWQpoBaHhsInDwonRIAd5LrgjvNTGe7t8iaC6j2FwuF1p+zR4sGRUrY2kFWVjQUjRX9MP5QWd/GLNj31dwaaWNjaNyhl/lXNdtStxWAF8pYZ0ldBY2KysiVDAtl0kEYat7qoyHKSKEpKkUEZUHg7wnTF1JXm1muq1yxJJZ10mts9AHuXGFVnJ12yqlxWKsqBlbys9sfNbOpb9r9y+IbvNQ1koI+7bg7etwhlAX3tKI9Gy7S9HLa7un8BLtODV9orquuh+XAKDdX39e2vatDJPBqlLreV32Xtu30j9afXetjOVYnu/L9e/Lc84vXkEbWudzb7zuvUvfvURxVTvMXFRSkOKxK/Od5Q4Xnl+61uIv1vncaMr0vZwzPqNJmBV9VqrlqrgljmdAcpXNEdMUsT/OeDpOeDqcsD+OmOcITpSFg4E8PCykjRTg1BIbzgNOaGvvPPpOFBFD36MPneSV0MS75k0viVoTnIZedUnDIiUqgu/FaFi9jeLYvP/NG9I7uKgCdhUMJxJBrwjci+WrKPrVz4nyqBRBVlJv4hRFYeE8KCW4JHyKU2FYIzxf/J2jFVQCriUmzgtAX7TXzHsjRzgwrwhX8jTmgmuYYV4RRMj54XJV8iwBOYF1WYD6x4Kuy61lbgRzteHL2rEUCGZFw0LxkKKeeaGISK1wM//NSj9wWfflHWmv0xA3xGIsQ0mty5OG4Em+xc25DKP5bT/Z2lOcTGV86mf5uoG/FS1ABZMtDR/KD00d7Xn5XXVtnhPVs5p0ZJCmxWIVRutdqs/WD4KEpip1YdHmus9r4KplxQgWoMzZAJHXT2UTBhIFkIfwsJ1X/plH7PcPeHr6iI8ff1FPiBNiTNgMN+j7De7f3OPu/h7OeyRmHE8jDocTYgLAhUYToyltHGmkAtL2UfH/ZwZUewWYAjEEhH5Av9li2N5gGAYMfY9OlUA1nVbo0bIGbB8Kb+GaH/K4ajLmZgBNhsDtRmSGKSDPqAQyQb6BlFpBaQBUG8nFtC9xgQUlZBXKvuDldeEhsn8Clybm5lf9MdrCxqhZQgtgz/X3zd2ysuulx8wFJgA5n0t+m8qw5n1qDWGqYGnd9Mv4uPk8k5LSKecUtlgINrLQWrbm5W9TPnadKN36LqDLikflX/V1y/nBup4MVtFZq9oxkf4+Q1PY3F595cIb9Vp9CancKG5+2+NFMqY/Q7u+ShGxSmASXWzgNauAGnDXR4M0G8IlYVIBrOWCGKfiEZFD1XCq4nmrooAoKx66foPQdRiGrcTaG7bwvsPQb+C9JN51LqDrt8iJdZ0DhUpjbQk8iVQJIbunDn9gSFVbkc9XHH0ujvFfj//1jqVlRQ7DpF4Ltu6necIUZxxPJ80FccBpGvHl6QuOpyM+fZYk1B8//ozj4YCffvgRx/0BP//0E0YNxURE4k459Hj/7i222y2++/478YR4+xbDsMHt7R36XvJAhNCh6zp0oUffBbXyChKmhUIOY+aMKeB6fwCMtl/2C6HLfwMFRrgq1IdgUBKhWirafkdATEBSq+o5egAJc+dBlLAZArxLOG17eJ9w2usehsTQN8KkENissVSLJYxZ89Q0FGBWQXajVQLUfK9cVgTUV66LNeuK2mtDkLHDCnSFNT5pvFMjpIwGW9Z1Bru/ATx9LSKr23Am9JCCMwFySXGwxEWcuEDjWmhTMXbXlBByLxUBR0VEFEZE7nsjtlbKr++t4USXY38CSGK1lhUWDLWAEQtI1qRzcsiiDk72Yhc6kHfwXQ/fBfjgIEXMSDwjxgmcZiDNcL6TvA5akvfKjLAQ5cYUJ2UeyGnyeN8juRkSTxoYxxExzpinEdA4qN45DF1A8A5xCPDeoe/Eeq0PldLEVYmKmzEv854VhatrsjAVhPasT2V8ecEgZeo5NWtjdd1V39UMFlUeUC1TmlbXZXuuWwcsFRHFU6sNi2QhmYzWMAspsPijeIdMeywZaDsclTjNRObB5rKzwrKtXs3ploLppRDhvJ/npolr892Mnw6hQbXmPlGThuuyUH99LhuubHE7s11cz0ldt7z4HN12TWBMK89fImCGNi8LD59ZW+dtwkV4/pwgrXz6tXTrCo5cqWttrNeeXWvDchyETV3BEfbwWqtd2++L7/0Z6fgXrw1avA/AhNWXyr2Go6/16Wv7+xz/WF1d4Z2eOUxGw0YbXVtnpGF9GafTiONxxI+fj3h8OuKnT4/Yn2ZMpwnkOmx3g+RO8xIG1HJCSDhRBgUSD8SwQRfEuG3QhNabQUIAD30H7yT/ExEhIYEpYUozEIHTNAIEdPOMACB0Gp7J4tW3nWhoVRHOB3gfwSEizQEIESkE1DkiuhDgAMxeaQty6vnY4lhWIxehHSOSGjBJXHsH8h1iipL0WJURLY3vEGOEc4Q5JhA5dN6MJy6TlpTrR7bEF6cWSSqdkxZ7B/IOFDWXhhBNMHEoZdycMp0m8ckJRjubEYEJDlnHwITY64vLvDAZrPREqngToPBz9quvG15vnhe8Xy3M5Kasmhcw3kWMQGqBVi1D0TGDCHc5OTXgUZvvSAAnMXQh9fbNnTY+SM5OaSsZL6W/lfcAyvPCw5F+V19TDmltnwout+9q486CLwpJdY4ra48LM7gpYZwW05a7JuOb1FgD7NQgToZQPGOSKurW18GS3jGSwjxSGMaz6d/KEzCZYFY8AzhpP0lots4RggOGwHAuIbgZ03jEdHzCTz/8Hv/y+3/Gn/74J/zy88+Yxwiww7v37/Hm7Tv83X/+z7i9ewNmwmk64dOnL3j48gUxehANCK6T3BZzlMZGoa/6vst0KGk4KFMeRucwESFCcjb02y22929w9+4D3rz/Dm/u73F/c4NNH9B5lw1jJDlyRauz0LEMyQsQOSDCzgEJnawnqR7BJZ2bBJx5SADFpYGESanoKjKkrYy+tz1RrSqX11NGmllRmpV5msbDAcZeGasgyiw9194I2bMpAxRrJ7cKIJjw3Ix+FH5xqagsV87rKplCWPNS2P6o81gZv8tKLFptpUDdU44kUZvmnhCFk3nctqFcFTlcPAyi5zHSPjnfyRQZvWqhf131FYmxXd93uNlucLMtHhFDL8avQRX30LkQ3ZopNYrg/5ttZb71eEn0i6UCopJfXx3k/wDH65NVLxg/oBWgXDuWAq1LZS21+xpiWkO3sAhhq3j45gER7XmqPCEUAJkldVAviK7r4EOvZxGmet9ljwgfOvGcCB6WJNesSgpy1ERKBEXYgCEPgQLGGRZkmfu7urBqhH8+3n+u45oi6GuPNYXTS+uu77+0Hb/GOD1X17fU8eweybi0EpLm9a+5UGIVukgVEbP+xlm8IE6nE07jCYfDAYfxhMenJxxOR3x5eMDhsMenT59xOOzx8OUBp+MRk+aC6PsewQfc3d1is9ngw/sP2O62eP/uPTYbCc3U9z12u5usiPCaPKxTpsqSSDvXaQglybti3hA6ipngFESakGJEcikzJ4AIWGsiviZIRfiqhCZzxpcAwCkB5BDYiDhhUsxbU2lreCdu3Zn5ckI4RA2pppU2dZonVG4DFWuN0i+1bqmYfovZX3lRyrNkDAKqc1kM5/frZ+3+yGu3Ivzt8nwtLsvi8i7zha9Q3tWEVavPqiMZkbdY8y/ZZ89p5s8UA4txuGaBVp9ltV2GgZfwVVteWc9Uw/2qXUC1Ri+08Xn4Yh4O+j6cTpcRKtzsE6D4WWVmzuLl5uYJoRyjKCHmeUSME1Kac5JOUMpKECJToZnrMiNFCWnG1Xw78vAuINGsOFs8uDglIMacGJGDg3fCDDswkBxmsAq3WTZNJbCW+Sgjku0daXVJ5gnO7a7O9liY8oXCiVmTtOlcKXNg57oCu2oFg1TNS2FQ9ULu1m2gdv4LL9+W2TK66m2AlfBJ0miFoSJMcDDpKVd81rmywDxalkmlm9wdJrSpy1CmxKwFSz/aMCLWL6q1BlW/W0UENd+W94pQ6WzMFuPWjHWuuz7r+xdBX17xq+24dP0agW2eX21kXhNZOFb1qf1HWsh1yIjn23JJWN0cBsdqeCYPqo/OxYevo5Na5c0lhW/zRbXPLiqmXzwvtBhKeqHRPTdz0tbVXD1X0FcdZ9O3MmaZhqbFO9V0XsN7X9+21337YqvEjPe+sm1kwp0Cq9bqttUdo9Ckp9MJx5PkhHg8TjiOM6Y5gshCDJpAxBIjM5wn+EBw+huGHsMwoNeQTL3vEJxD3/Wam8lrmFHZ70kFU5kHiIwY00LwXA1KM0wGhy0cDcM5FoFsEg9l8wbmOqZ+c50Ujzu1hF5uCqNd63AgYlkvYQAX4T+qNudzqq7Xp7okil2fThgMr3MEGL9v4VVLkws+BkFCTVpfqj9feyzlFdD+1SFQ7DgLrbRUQFR5LzkrKKBCxrKXl9+vKSJK2wqfYT9A5srkn0a/mgIjCzUVBy15hjIJ5yiCiMp4UqEZzj7M58pEk5Dfpwo/t59nZlm/4+Y20LIxmVKwXFdU9bcqVxQMLGs3EZiSJpEGHBc6x9q8xHk1XsrXi2/q9V62LwEWMMg8iQEQnMIGh6FzCI7R+4gUjxjHIx6/fMSXTz/j519+wufPn3E6ncAM7HY7dKHDhw8f8Pbde2y3G/jg8PR0wOk0YpxmzJGFT/edjA2rUYuOgyOXPQZsLpxXRURSQXkAZhAcZgybDXa3d9jd3mJ3e4/NZouh70UeQFWfq7VS6AaRDzBEwWPBvxKbV4StBRav6yTzIsJynWy26Vc6rnBbOtnyt/znVDBtX3BZdwZP8iKx75SfJQDJaB7O5DTnJWheEXZD22b7VTegs/rz9swdaPgJl7tA1XqtZKSwsa0Ulfnfwr9YGxd3Lx5cn5sNbvN1mbJZbvUMb0i/JRLFlhVS4ePMzAEacYaygt68IkIQfOstxNuChmyB0TMdPWv7+gf1nD4nz7hmtHPteA3qeb3s4GuPl7fqW2TGr1JE/BrE6ZLIvTjxDXKW6ymWUDQxpcYTIqaIKcYzxO+9xMgMmpS67wd03YB+s0HX9eiHLULoMPQiWO37LZy3nBAeoS85IYSwCxWicTmm33KZZVqg3lj24PIoLUr46/G/ylEDOlu/1xJRx3nGPE1ZEXE8HXEcT9gfDziNIz4/PODpuMfHh8/YH/f46aefsH96wk8//oDj4YDHT18QpwlpnuCdw5vbd9hsNvj+++9xc7PDf/pPf4ftdot379+j6ztsNjuEELDRfbMZtlkREZzX0C9BGZ8AIknwLrEuRViWtItZuW4MTJiafjq19q6J7CIks3jjUmYAw0MEiYkZlDySJg90yWEO8t7oIdYtBHjHCB5IgbDZ9EjRI8YgioikFKwRw1XoE/HuKHFILfZvK4AEQEWZUYh7ZEWEgSeqGLTlvK+dl+8VWqdiQshATkUsr4CSuqxG6cdGmLV9auAqM2oTg/N2FcLNjrMxWtT9muMMCaPsnyX8v/r9M8icqHiMLC3b1o5GCVERimvtfi3SZlVCGPFr85vXUyaSTGhcvsz3c8gCgmWeZk6IacY0nzBOR5zGPYZxg3k8IVAAd30RhlpZFUObmDHPEfMURRmhcW+dJqlnX5Sn4ziK0nGa4BwhzR5zkDjSKXggRaTgAHRIMQLBA74ifKlVIgASvoJsASwI+Uw4L9ZewzRC+0VrnjSpXedZCVEpI4yQrpnPXLc7q3O5DxrhfFVXEfqveUIgw9SlIiEz8FrOrJaVxqyIB6fUtfotUYbf+dqsGBd5KcoYFqaSCHD+nL67JBg+hwctubTsf/29se/l3vL8srpXYVz7Rfk3F7XOlCzruHSctSkLS6i5R1QrTS6XWYezeo1Q/plGnsEza1ld1rewQM2eQcVwX3i3Pi//vnTv6nVVVb2nn+vT1877r3HQYg1ef3mt/8jCjfXy1z3X6+O5OfpLPJwajhj8urbXGQI7p2nC09MTnvYjfvy8x9PhhMf9iJQYwUk4pW3XwTvxBLYjdA59T/Adw3eM+5sd7nZvJAyT9wjk4EE5zGgyT7WKRjTr6ZTEWjmqcU4OdQiXY7sbXhRQQUBCNuYRBQQADgASQuwATojhBE4xe0QkLcwrznAuCs5IEr60Hh8wcuLsGCMYDnARpAJ0XgrcTcCbk1UnxOT0vbVY+1dgXYbX2mfNieGoWL0v4UpdrlFONZ0gMr4W+ZhSoT0YEqi9CPjyu3bN4i2a+JzmM75m+Ysqu8jnaTrjgbJQUI9LeSM4Cx+q/cg5h25L++tAmlEJcfFEZySVla7gXzAcqcKMalRBmb4w0cc6nYFMWxjSN3pn6QGReRmi3D/rM5p+t3yI9d9olpK4ul1H1iNHOkbJjFAIlMRYDkhw0WX+NaV1+invOQsRluvQVVfth6qVIARIwzqYsJmcQ9dt0Hced7sejiKCO2H/eMDT4yf86Y+/xz//09/jl4+f8Msvn8EJcM7j/fv3ePvmLf6f/6//N969/4CZgTkmPD59wePjHofTCVNM8N0WITJGteIPMBmXwA7HZRcGcuh8J2sT4pGd2GOmGRMR7u7v8e7Dd3j/4Xd4/93vcHf/Bje7HXrv4QFM2mcLd2apQSQElUNkUTwkeET2mNmLZwS8eio5pS0jPEleEzgJp3UmWLeLKm9f8Xun6n1G/bVTr19Pwu+TmjmlrIotdLRx+JQqXUj2iNAQt6nyhEjGa1nYW84ghKr25NVCGu2BJFpDpU/Q/S1rMHFCQkJk8UyJ2WNBeHSmqqdcK36fpx0kXJiWlxu5Rm/JfTuvP7cueDGEU1zj8l5VeLXwiCBH6DqPYeiwGXpshh5D16EPoYRmclURXM/tr3l8Q3nfIKD/9z5+q5a/WBFxjfhvBFnrX1frs1ot1cI1wgus1gAsyWuZGXEWIDbNtSIiYlKFRIwzIsumtKJzUmqvOSA0Zn3fbdH1PYZ+gxB69N2myQnhQtA42kGEnV4RhAkenSZVsUzvRJX70xrh0260JQFTHlH7/gsJ+pcslCUJsWzmBR7zVzxovaF06X7bpsvsQvnr19kwBSU09xpA+nWlnh0rwtSEso+YLS5oyh5AloR9mkUBMU6j5oQYcTwdcByP2B8POBxP+PL0BU/7J3z59An7wx4Pnz5hv9/j8PCI0+kITjOcA7a3O/Rdj/ffv8d2s8X77z5gt9vi/s1bbDYb3N7co+s6bLY7BN+h7wcJadYNcD4g+ADvdM+YsJOMKVBhlsW/rIIUsxLrkgjNwomwegVabEcVgiBV3ymzpkS0JM6VEcxx0QmgZO0Q6w5P5r5NSOQQggc4gPsOKfnsRcVJq8xx0TUxtjMr4aKMgHpE5a2d63ewGKOsC0dl/PpjpRMsJn9hOo2JKecqydxC0N+cjeCxccqUS7U/jPhdg9O5oWuL1epWIW1FVNfFLc+1O2QhfDLgLxKR6l9abv7VduZGwQhL2F9VI9ZKSWeNbftoTbokiFljLNvDBPZtGCbWfp0xSwv0cPEgIBLAqt3OBKUtrBwWwNpvYjVW5oIlvBOzxEcWOhUUAcyMNM2YTycc9g8IPmC72YExw4UkllOuQ3QejiIiC8N2nCdMacY0jYjTBIoMl6DCbg92HuwD4APYz5iTEM8cIzgBkSOIPSbHQPJwlADWEEMhCLNDAGKEWSqJEqUdGm5ukTLONhyyJkjHzs7iHKAjZHhIz6Lw0Hmsl6vNlzGKNcNMMM5KmRiCCQHzz9VCdbN+LWsrE+zEGW6VVto7Vmebf6ERCJOMAjOyFVtej9XWW7bNGGkiy/NhzLUyRrmvJvBC1b7ShtrjpjAoy7/r6wrvVuNR3imMSU0f2bjU5FN9b03xUxWr31XCOy5WopePxVOqR6C0Y/Hn9cPWDdpxzc8W1w25eF5Y6U9TVLVDVr9d0j6sgiWut0DZU/ZNM+7r7WpuLYdP11N5ztfLqPtlxS3W4aJpzXfNNbfrYo2RfnG/zu43LXz98cziuZzX4+zFC/2i8zFCmV6T/a01yXRTl+t82drPOH+VDzgfN1mJ515UK9VfbEzBzgSLeW2wkDWzqMiSGKc54jRGPBwjHo8T9qcRh9MEniMcEW6CxxA83nSkuXQUzpKwjV3vMGx7bG963N3c4e7mVrztnc/EoOU1nVU4ZMJ9g+tgAEl44jkmzDFKguiYFGRZPp4C8wDSUBesBjQSVjElo8nNkz+I8sAFkEt6j+GdhMQIXsqaCZl+KZNvoSIjmCVXBicPjg4pBXCSBNIpeaTo4TyBq+TUMTEoMWICPKMI7Q0nsiX4dRXOlXovKsEcZWGzJ8oeEdbsTH9ToYMFTyrtpDwFaWKIkri2Xo4Wzz8V+juvOmmfWT0bjVYbEtXKiKKUEI+XxAkxihJnZjXSSlGFnGv7oVJGmMeE0iwVmdK8X9pax043wWhCCe0odZJj2SZUjC9knlQwa8uCkB1OqJoyGyNX4WEmyu9awKxsga68U7I2qcGMgIhytnVgypWUVKhZJfe2RMPZAAxG1y1QjlrW2FA5ApITLwhZi5b/mMEqChI+krJXUXIJLLnMxfOUHRjCM5JPQBxlr1BEQix8hsSmQRQ2E2oqIl5TocPdboc+EHYDME8H7B9/wKePP+JPf/xn/PLzz9g/HjFPgAs9Nt2APvT48OFv8O7tO9zc3KDvPKb9HvM4qbEQwK4DPIPxBcAoY1xLxW2fEZkBOxJBhdxiaMIsg+u6Ab7bYHOzw83NDje7ATfbICGZQjCyKsOOTJdBJ0aPRE69IApOZwIiMWaQ8A6AWMFTgnMJyRHYhayQygsfwLmcjXWtMWbdwZnqorJ7LfcDUhLeA3pd7d/E5qchRpAExUqOpJF2XuwvoDKcYVFtOOPDWBQTlIrBmfA1hf7KBmBQWCHml41Szjw98t7X/phspaYaGny+uG/yi/qgs36Vjwo9QRlvla+5esdy9wgMILbxc9XbgoOdc+j6gKEP2A0Bm+AweEJXheHLnjS6UUnnixs6tZ2L84PyILzMQJDLv9zea19pge9zJZeqTbZi+K6UdcnQ4zkjx0v9WlPe1jjEoO1zdX7r8dXJqq8dZw0kZbEyI1mIQ66+MQvpOhk1M2OeBLGcprH1iJgnReRiuZFhECBJqUNAcD286zF0g1hyb3boh0E8IboOoRskZ0Q3wHkP3w8aZzKI8NGLR4TFPZS4iZR/q+xAvTkvHc9S6i8h5evj0qJ4vhxeufg2O7eXHAuoWFe/OqjVd1dv1Rdfs1H+3P2ujjPYJevJ1j1HWdtpnjFXuVCmaMqHE47jCcfTCYdxj+O4x9PTHvv9AR8/fcTDwwM+/vwR+6c9Pv4iuSEevnzCPE3oOvH6effuLXY3O/ztf/47bHc7fPfhe2wHCck0dBvc3b5BF3pstzfwLiCEoUni7kj2mfMhW2HXXneA8RYFAaeoCDUnB5NQS45EYOtJyQaHYkVhADP/nUBwGsqQskWo0/iGLopywZQQwQkB3BEBzmEIAYGAIW3BltTe8kCoxl4QphfK2qyEIf22xLx1eJGMJJwpIrBoM7KyQCzNIpbC6ZpxueYRkcCIqKyBVMhbu4Mvyy1wubiW5jbmd+S+xZJcUzYQC0FSyqTVswc15RbGjVtcULXF6sujV1NLun5IE0LW3zV/Vc/Wxr4+agIsf5qF++vH+XhW5VFNdmZaUN7N/O4VZnqN0MjMnjHVOq7ZEk5ZriomJkvm9UxkW4gG4qQEb5B+z0L2zccRJ9rjIfwCpIjQESLfwoUTnL+BCzeS5NJ5TAzExDiOJ0zzjNPpgHk8geYEHwHHAYkSku+QfAS6DhxnTInBcwKmGQzG5Bg8E1yaELsAxowuitWVY6DzQTI0cG19tgzdU8Y5CzUzXSmjT6iWTz3GypGacEoeVh4HZlWY/6kYFmuHKQKMHaHiNQkSYZF5U4LMe7IW+i+sDQlgYki07UroptyZWQzW4TRar4KoayvqPtN4376sOVMON0oIR42StfZ88I2Qa329rlm248I3a9/na7OQrO8BeV7tz7U6SGmKrKKoFC3nBZ57fck64Xyuj0uKyUvX+hXKhrwAUOrxQ2lHoyBZvHs2PheuL449ATVHSZktRxYylX1TY7Irx4W6ZLVfHkvzeGk+eGas6zpXZdj59XM+5Py6HfO1Olartm9eRGJW6+AFx7NeBZf698Jylpbfa+Vfa4MIl76SCT0btAqw1mWult9i68s8Ss0JLmtS+kTHIBtkG92EhJgEv+3HiMNpxi+PEx6eJnx+OmI8jUjThMF7fOgCtn3Ah14saYEEJkIkgusJfvC4f3OLdx/e4e52h9ubLUBi2DbOCVNMGKeIeY6gOYlH4TyDE8OrpwQloWKmeQYcqSKCEGMUpYG38BQVHjC4Bwdis86WMtklwU8uSjx6l0Cu01j6gpe9Fw+IqN4Wp0gi4E1GmwntTSkCjsFxEsHxLPsxTU48PNip8kEUFOycGv1IKEcgYU4MF0U5kTQOifQiVjuzzDufxdoWmsfgvA8Ofi4heOQbyiQdk0kKRIhn1u7FtJobRQRpuKlCpSpEYyqCbjjhV8hJbg9YHobi1b4WkimlJEaWSRKim2yDwZgheDxFO9c7QFpT5xzItHUDG6r1XwnaZb1X+F8pVofS12wQxMYXUbWvtD51lGFHWaAuOppakFW1RpUQ5Cw/RUWzOaFtLKytsBEyT84UXySz5qDrhVlDclf8ZK2MYEYkqYuJNLOJ5FnOAlMtM9POLHJkS4tBSZQcYMB75SO8rA+WRS6GbWoWn4gQ4QAO0h43C3Xpk8zqNCEhwpG0Iio9P/fSRjcTAgXsui12w4AP9/foQsK2O+LTpwM+//yP+OGP/4p/+Pv/hv1jxOOXiOgIodvh7Zv3eHf3Bv/pP/9vePf+A7Zbj+CBh08HTE9PmMaIaSawH4BAYJzAfAA5lfIbd8YiYmcH8TpwDnCEScO5BedyTgO/2YJ2W+zu3+Dt23u8vd/i3e2A222HzRAkJGtKCju4kgXoj2VPJe8ld0yS5QMn8zVxwkTASaYVHXkEN8MjiiKCOlUkGXPV5jDISgQAkUW+wCQqicBCcyknBMdQHgkC/xDB6l0lYaM0N14CoJnxPETp6QnZS4NsL2T4VNaWt7UNKC9b1mS1iDMNpqaauUuk+35WL4iUxCg7RskRiDV6jW1/S20RTRUNSi5qlRbOFtkGKqUoNbTCko8pHbXnKk9xDuyr2pjEY0/bN0O8boJ36IcOu02H+02Hm95j4xwG78TTRmUworiEbtg8QVXN7V/nBzeni0dGKPbZMx9cePzsZ8rrncHwFxxrioW15xevTWbyCnr11zi+ShHxHFO2+o3+U6MzO5JC+qx4UM8H21zTJMBsUnfFeZ6rBC1WmsuIjRyJEqLr0Pkend9IDPzQo+t7hK4XJUSQn/MB3kIxqSeE9x2QQ7C04QjOhQcVE4eWQD4fm+fGao1Zujaw60T3q8q4sOj+/MoIqeWrnr9gzb12E397dy9t3nWrtJpaY5g7r+6DVGKqz7MmZR9HxBQxTiPGacLhdMTxeFIviCccTk94fHjE036PTx8/4uHhCz59/Ij9fo+np0dM0wjnPXrvcHdzg2EY8N1332O3EyJms93i/u4tNsMGt7uSlLrrOmyGDZwLCF5i2vpKEWH5U/L+azIDVYgxBysuBK65CaoIHRab1KyBklkFAWWtKyENIk2aC/WAQHaFZJ4BRGRWgUSgFoIHKGFIvVhtaSYyVuDkTDAXiuUYNGY6yMNRp1ZmIXt/lGlWssLgQR4BFcTrHbPKJz5XMBQhdS3AtzixZVzFDVPGURgbdX218UzLMvV7A8S1lwmK4gFs7dW/ub1vBBVx295rio/WvVyIwWYr2B7QftujgitKW7IplTFWFYOV25jb0F4DIp6tt2lWGVSFsJl5nbVPu8/lV7+3tO61Mcwu8Up4pyhrMq8D+RjFKjPfzM8yw5kVDqz7wM5lXKwtZOuZCM6b0FnpNbWCYkQkJsQ0SXim0wHHY8B+PwCQPRT6CaGLki/Je8zap/EknlnTeBSviDgipkn2XpK9l70KGALTYgTPszC9LoJZckQQMVLnkJIDpxKCznvDtTYoRshzs4aoFtqjCp1Urw9ABd3rIcHaegpeZaB495Q/ylMLF6f7v3gSiBuys7COmpCwKBN8pleaheagaogidrCcMBYyyVe5aojMbkqSlUPDQlDdXiVuGy+I3BYqnmxNPogC013uWz1iZSxkrbnqbsF5V2Wea0J0WoxH9V5+lAX1i7pSeV+KumBBTW1ojvynwQvjznT5UnVt7y+/b/vCTfuBdeagUeRUpRaZYg0NV8YBy2u5d33sGU3eFdTKAAXuua/PMyR5ry34UAFMLUwvCkLr30IRcdaXRV2Lh0zL5/nJSrmLa6zN2/N12rfnd6+N1Vodl9fDiw66eNHeOXu03vrlq5et717ZzqaCau6bMnkx8VTRKvX71+e0WBKuPW/rKOWZwYL8YhQlwfF4wuEw4rA/4rg/Io4ncJwxhIBt6LDpOmy6III58iqwc3AhIGx6bG63uL27xe3dHXa7Dba7LaD50twU4WMCaIJzEUCEc8XwJIeCVHo2xgSaRWnhyCEltW7OtJ30r8VhyPjFOfOOEK9lpyGLXSy5ITJeoipXBDO8wuS4GGciPgcTSqNwikgxiqeFi0g+Cm6PCYkikuLEFCOSJ/Wi4JxoNOdvuAoLBC9Kl1vFck6C3M6+jBVpGCIjQxWmU02bFrIl99euEwv1bF4cFsFBDMdkriKzeI6qUeUyt0eKSen1VP1MgC7XbDSi5tIopCqX/mQ+gXMo6JosrYfgTOhERgsW+3DjYQxqm1oiP8sFa2JrAljdyMWz1MpIFY1uZSnM5RLSmkh5R1W85fpI58TogbN1UHjFpPQipSjes+xFHsmiUIyc4JIIjDlBlCEV/WhwgMjGrsXduQnOlFO65khzaMhDSNiZCB8Y3jOCZ8wzQBGg5EEpwJPPwlwGidcwZDE5xxiCw6br8eH+HTZdwHYbMI1f8Kcf/xE///QH/Mu//B6fP33B6egBeGy2AHUBCAHv37/D+/u3uL+/x263gyPJ9ca6tggGD42WW/CvOhhitNTuH0vabYaBBBLjw9CBhwGbzQbbzUby4KgsrcAiznuqkG+ka1I9YBIhJkJkpz/CzIQTixJiZGACYYYoepIxMo6AHFnBwhnofBocrPjpnLcQgNnh27KNuu4CoYQ00mWQjMdWby5HDN/wAhWd3fAnLf+RbG2Z0qFlJhf4V2cqA6Hy4wL0wYt7LU9+nkMmj8cKjVotg8vUzFfg/qWyoh45XY35vq1T5yRyRQg+J6YOwUv0jdoA64wGrOBUXffzpOz1w8b74uOX0n+X3qPm+VpxL1EwvMRI5GsMSV6q3Pia48/iEbF2FGNNQ/jIG6Mk403ZKqCcGeM0C3FYxU00JA4r0xhrL4SWD5J4uu82GLotuq7POSG6vkfXD6qIUE+I0JWzekRYSKZz5v0SoSsH87qg46/Hr3O8hHH8NTbHr3MYmF0hivNfsmbMeiAr4ioPIIuxPkcJyXQcTzicjqJk2O+x3z9if3jEly9f8Pj4iF9++glfvnzGL7/8gv1+j3kS76HNRpRy796/x267w9/+7d+JIuLdBwybDd6+eY+hH3B39wZd12G3kZBMQ7+Fc76EYQpBw3fIfjOCrBUEVECqPlEslklUKSHMSomVeOdZifh5MZ8aW1ST9YrQLVORahkwi0CUIwhJ3dOBrnMSgo16cAqggVuk5TQpfehQcsA4ELy6sIdsOUwqWMyHa4m6dUamUBVnjPiF85oFvoSkK4oMC013SSFgNE9pSzumy+8u1c3M2RpmTRGx9jtXRLSECOryamprMTYpJdQZv1cVIBfu29k3c5AraLi3M6sCLoqchm5EsW5Zs7y290xvkIgk9EKeE4vFa8zMkrBimMDVvHbMn6aYs5ibcSt8zMLwLBQ3gbMxVQy4hGTrYBZ0dzx6MVoJhHk6Yp6OGLYjhm1UxiNoaCbGNEXEOWI8HRRGnRDjCE4jmGeYzSDpYKSoYeYmYSfYRYREcMKpoYuSIDlGh+gI00QABTj2ZTxAYI3FdA5RK+bDbp0dZeW9CEevUq+UYZ3xddkCtRKC5LxS6l1Vh6pzqszMJrnatiz4V4xBKrjKdaJVGJQ+yPog3WsUZZ1LyFWBlc06oMKILmkbM7pYJsBeG8taYF4C7CH36bVCXqrGIlOMi7IufUNAE3Lret0XmLC6LMBEU9Xz9faf1bXAg/lqQZc0tGRV/1rZl8fqhW1qW5LbdqaIaIQH1+mo59og+7SeSyvers8VEa+tqzy3oioY8Jq2vuIZrQrzLzH263vnNe1YOypIdvmllUfX3n++DS+EmxePdI5/sUKzU5U3gEtPl99cK+dqOwmow1YKHSm4ZZoTxmnGYX/E09MRTw8H7PdHTKcjkBjbYcCu77EbBgyhQ+89mByS80AIwNBje7vD7ds73L+9x/2be+y2G2yGAZY/zI0RYY4AeUzTDGDCHEXUb0myhQYWa+J5jgCReE/ksxnxiQeCQV+jBQyWSzx78eBLRHDegaLX0MUeMSeplv6TWvUa/WD3UzNHmrTWKT2Dmt6L8ouz5JlwScLMesH/RE7P4tkRZyo5I5iaXURZOL62TlR4zIX3aJJW1+uF5R/jMoAqzrvBJP2DoOGDlnRkFmbmMPBISYWUGlIpqjJiVhmFRXdY0sEpQXPSpUaeEdmSVatnY05WLW2sIVumlmsei2r6dB12K+kq3yoRk2mBnBy4Uk7kmEuqbCCA2HJ+1OMH4evYfCyKdTrryIpdtvBTOXyv0UKg7EkCstCU+jOprPY7IWkoqwgXZ8zzBEQPTgE+CZ0fWcJ+xcQSyieJwQXnuQZqPswpUZmo9ZwWelmNNZg1Sjcp35uEhlP3IecY3keEIGtiZAZNDIpBX50AB4w8i/dM6ISe5RkuAdtNwM12g7/57nv0ARj8Eb+c9viXf/2v+OFPf8B/++9/jzg7xFGEs7vbgG6zQRgGfP/9d/j+3QfcvXmL7fYGx8NnTJOuv1SSzyubgBxyvN4nZPk0qlA5atUiXkyESIygnrO+7+G3W+y2O9zc3GRlhPdtqB2grcZucBWSKSZCTKqIgMOMoog4gTECmEieMQLYsSZocGoFX63Vmh/Qy1QL/rVlTl/3ZIoIUlhaDJ5kv3JRbCk8zVvE5JDMOe9j3fNGWQhGTiaRw89V+5pE2WV8n2Eog0w53+SCt84hypZ8d6rqzm3QRPQL75Gz2aFKMch8Va72EhqqoXW1w7mPFT4GkcpgRBHRhYDOlBEaOl8icjj1Sq8qY5zVhaaOi838D3H85cg9X3e8WBFxzZrrEnPVCHLqsvRftgQuC0+IaaoVEXIdY8qJF1NdGllIAREaipDUo+969MOAodui77YIQbwg+mFA6Hp0GpLJPCF8CDnJpquTUGdE3TLkzxHjv5Uy4tIc1M/+Eo/LDB7OrNyuvX/p+SUF0Z/3OAfUpIyxEcvWjoYw1fMco2jc5xlJc6CkGDFNE6Z5wvF4xDSrJ4Qmpn7a7/H49IjHhy94evyCT58+4/HxAb98/BlPjw84Hg+I84S+7+C9x9u3mpT6u99ht9vh3fvvsN1u8fbNe/TDgPvbe/R9j932Bl0QTwjvO/TdIGGOvCKAELIQC6tz04bpkX5y1c+EOYq1xhRHiGXLrJ4gkxCZ85g9IrLgwsaUZZ8mFSLb3sy5EtIIThHABGCGQwSI0Xth2oLrwczFLlQtecgSbmtINnLWTwvHFAq8sbBNpcu1NMR4n0yIFbGznVKFGLlhHmoiaI2pmGPSxNqVpUd1rtdZEZ5z1Z5YCMRMoKDA6oZwqe4DMK3GJUXFNUWE9YQX49AqWgox144DF4asIuxKH43Qa58v56C5VyZJB6kuh6v6ocQbL9paTX+FH9bGIUbDZ1Nmourvzoknswiz8a/qtvYqoV2zEyaEqBURZglVFBJBXtTwQuQ8QiAQRXAcMY0HURDwhDky5phyDiXWOL4iMGHE+SQwK45IcUKKs+5l+4l/u1lJxjSDOKrXhLjlenYy5sTiveEAojrIVR6Uat7q+yyzy67efahZyjK+tHKvPmrGqXxjnl5ruCb/UIT5JbG9MNs+wxJXeVWJEMCqqefOyspCASIQWk8IOxJHYYJIPcpMOrCY96JcMNjtztvvqtwTaNdmGRKu+q/jUy50vMr4laZewPvVc1qU394vY776N1c10LJNvDgvjsWefim90LblrNm57EXpi9daYUD+tOoDXXh+1p6195o/Ctwvtds8Zeq8LJ/6m9Xpo7VmVH3iZhyaa+j6v3K8SAFRils0cQk/1sXw+e6Fqta+orPKLq0XPi/3ytJ6Ed3O6azI19D7L313Tbn+bYfBs3oIniv00gS3sMXadg6f6+dlLgquln9EwMwYJ8kNsd+fcNifMJ5GzNOMQQUfu67DNgR0JNazBBZZqScJ2yLut3ChE4O40DV5xUAEH0SwFILmQUysOYSQPSMyPQsRTFMEpmkCETDHGUSkSoZCj1CWCpdrR9DY9qJ48M4jeQ/vAzgluPrMDOdEyOecB7N8J+dKKJ5nTumklEThkCJIc66lmJB8hEtR8X/l6ZwcEIGUupwnQax3KQvHL66Gat7YlkHFA+SfygTAUcPoELIgjwrpV3Z3RZ+yxJQ3j+uYGIlJfhA6Miq9HS20VFRFREw5cWweB1UqGX1Zkti2SauFhrdQOQVc1nRqxmIVTml2kNZxSSlXDA7MK6ENN01OwqfkH7mch+98LswIDVm4aPkjzt9z5ewkTAtTifMOFUxDaQ7JJeEyDdPAC5b1kiw8TZwBjSTgOcGnMgcxQcJ/EUGiK6nSQGc+61mEuNRkyhIqGA5IieAqmJHXXF5jAFwEkxhKEXfwlBAc4N0R3s1waYbHjBkOQJcF2gkSOu1uuMGm7/H92w8Y+h5d94Tp9IQffvon/PzTn/D7f/4DHh8eQbxD3wX4oYNXa/HtzQ7bmx1ub++w3W7hvYOFOBeZGQofoeGPmQuNKmNdTVYl3GUGUsWnZkMVAlzw2Gw22Nze4+7uDre3t9hutuj7XjxouV0HBBRPU5iQXhNUJy/JqlmSVY/scEqEQ2QcUsI+EY6JsmdEJOMXILvREnvUawTSV1K+ovCUsokmxJwHhAkIGlWFdY4tpBvQekRkuJNsTKsqra6GPqaskksKz53lguDqVw9UzaMogMv8n/6XDGcxo3hXVe1MApdjivmcuIRwKjxvyZHDrMoUcNuNZ+SeS3nnGu3MXPg5cV6RwWe9Zp0vVr7UOQkf3nUBfSc5R0IoygjnXdmPuMyTl7m5jFa+Rjb43DfXnn/Lt5eev7S+a9+Wnfl19Xzt8U0eES9pUC2gWi5UNgRcJeNdKiJiSpjGUeKizXPByYoEsnDUezhNSB1CQN8P2Gy26LqNJKRWgrDre3RdB5+TU3f5W7NSdJKNSJkWRc41M744v8gC5yuPaxZ0L7n/kuPs219/nV2ua3HfaJlLDOFz5SyP31pDeE1rvBTWFk8gy4UiHj/RPIKmEpJpmiYcjgecphFPxwNOpyP2xz0en57w+eELHj5/xsOnT/j06RO+fPmCLw+fsN8/5rJvbnbYbDZ4//49bm5u8F2liNhstnh79xZ93+Pu7g5d6LDd7hB8wNBt4J1HCH2JS55DManFVY3gUeNVqohuC9FT5YBJkypcTsKEJAvJJvfjbAqKoojIBsQsoZIMAZkFRxnbWRQRPAEc4ZR96IKJbKtQa/nagbwqJl2niodO++pB3hehovfyzZlrq1EmLWwocCsvBuTArzhfp7wY0+UxWyimtUR4i3VWaJ2abSmKiGVda0qFtm0xjztQQi+tfVOv89U6hDw7r0sJpUvlSnJxwNyOLylD1uagEejXY1wRZ2tKlloBs5ybpSLhXBGRMM2yrsfR5dCD9bfLMuxv50qUda7mu5qRhSLCBPlqWd8Ih025Id48DGQmU3iVGSmNmEYCeEKKoyoioijuQwB52XtmGThPo1hwxlGFDHOljDAhBINT1LBLoohgqCIiACF5YXio4X+VyTULT5vFMl1lnKr1lLgVmDeoYo2ZLuO4eFLNTxmjszlDrfQxbwWnHhEi8CGlU7JnhCo5W8+GYtWZGd0sqK2sFqlVQrDCEuYEIlmjJtRaCh1ahUSl4Fj8aou4AiOVbViRE10yBHiJgcBLnsnz9fdrZqPmC8/LZZyvh+pI9dp6Hd2wXJvnAtxleS2zutbyS/TmpTou3zf6dHn3cntFenFexkVB/UpbdEUv6tTQcou3LpVx7f6SVlzv93Xm9PJaednx/Pvra45zTOSX11nazQobvv54cT+Xa+4bmQOu53u5J1bZkJV22nyf7ZcrFa/szwzR2OhTxpyAaUo4nWYcDiP2+xPG04Q4zeg1PvpNCNh4j54IweolZEUEOwKceA173yH4TmC/wVwieA8wS6hQodkoKyCci5leNvo9xYQZwDyLAmKa1bOgUkQY72H40GB5cgAlziGYnPfwSfBSqhQR3nnAJ1FAOD0rbS3l6rxwwbYmyGImUUKQE+8Al5BczMoH5qR5JuRZTBEgC13k1Hq38oK5MpkFlta0kq4IIrW0d4pjHSipMDuRNNmEX9oFKuIx/ZezjE7CVpoyAhrTvwgBJZ8IVBmR1DijKB5sDutwWw2tvvCWKIlntTkaJpRQ6J01utaQstD5pZ41nFEbIzhdj+RKqBtyJVwSSPM6FMLHZsEGL9NmRNrGbEBS1b2ihLBrS1AtZbdKEatbStNYGjo5ZqQm+VImcOzBKSHUSghTRJCMCxudSyU/jNFaNoysiYS9I8kR4UhpK8p9trGCeuCIYksyWIAJHgnsAO8YzokSghFBkJBKc0yYU0SihECE+80ON9sd/u7D9/AhAfiE/eMP+Off/5/4+YeP+P0//xEcCQ479F2H3W7QHKYed/e3uH9zh7sbUUSQd0gs4yI8hsKCIpYHQMrnOjWGWSit9JqBKvKIPEtJDF0oBAybLe7v7nF3e4e7uztsthJxgXTMjPkkTRBPeYzVk8t+SX8cENkVRURi7BOwT4wjOwnPxIQEgxVcJtG8I/K+MOMhXZgafQG6jiLPppsBg2RP21wSoVb116HgBW64kkeE6pXe0hx5XMnghpThjJc0BYBs2IKmiHIxXBeNFv6Y0sG8qkT5aYoI9dJSIzDJKVH4sQrSlbrzdd4Out3O8f5S7vmc3Eu2j3quaIg0U4CJzKIoeUHiuReCKCD6EFQp0WVFhK1dsPR3rQ257jIjV9t6qe3f+s7a+9+qjFh756VlXnyvWquvacdr2rB2/NlCM50Lntp7JoBNKWGa56y9PQvNxJZOigVJolJAhCCJczXRdAi9KCK6Hn3XYxg2CN2ALvTwQYjB0PeZQBQFRChIV5GxOrdKR17JmPyHOAz6/E9+/OZKCCjiaQawZZeWAsqlRUxWwMWI03jCPM84nU4YpxFP+z2O4xFfnh5wOB7xuH/Ew+MjPn/+jIdPn/H46TO+fPmEx6dHjOMRHBM2mwFdF/Dddx9wc3OLv/3bv8XNzQ3evRUFxP39OwzDgNsbCcW03dwg+IBNt4H3Hl3Xi2Y6dIWI1R9QGDqLbV8rHuYcM1UVLXEEpyKQnecRiSPm6ahKSfWIiJNYuswTiguhJJKCtoHZgZ3XWK/i6kzKVIJV6MkMQoSnBPIQxKVxz51REM5Sl4l3g3MdiDyCFzd68iVEk3ldies3ATBlCPJYAMZs14fCvRqWMMAcr+yz1hp/eeR8EI1gvE5gZ98WZYTQF0aAmF8Zl/uLc2Zq8nfWtJTbbkJ9W9tr52WybYuTyfW57od1pmlPavpp39VjkAmm6hrNWUJYWVvacVIhC1vVrMwO28DqzF62vFgSZEm/ESuYhDlKeLRpNI+fOX9r6xowYr0VDDdjWvUp1w8UQpKsPchCcgv2UyyjilUq22fKkOYcMN5rXggAaSqJCCVQLjLVmCQnBMcZHGekeUKcZ0QNKTeNE6ZJ78UZcY4gSPxowGs9AV3fo+979MNGiM+uQ/BiWFCElyWXTE0wl3Goc9Igh8KvhbmtwofzyOmwN8x7+zcW35b7gCW6N2afQFR5RJB6QJCEfcyKCX2+nG/jcEjzT5g1rVNGvaw13RdRFBEghXvshTdzZh1qigjLV2Hl+Kq9VNpxJuQpo5S7XwkEmxHRNdZa+dt1gSSXnrfRsCqOqP6mvq6LqZme9kFT3ipZ57hVRjR/XKElmrUErBXdLsq2Le0LpX+6YishW1tg08c8qIu2XCFfbd0uaRR7ZvB5vR9NSy7ct6OGU/68zFzn+r67dBAKTj1724RGa7erAhY7+dk62zKuKQPW5nZ56yX1LefdGvAtfAm//PPVhfENVde0sUkuLf+NCRqbN5dt/cp+a2JSBjJMNeVvYhEwT5ExzQmH44TDYcTpOGEaZzg4dC6g74DOOWy7gN55UBRFeoyz8I0qmETwOdnqnBKmGOGjQ0guKyOIAO8JwUtIGkaEz4oI8UCQPEkOlCCCew3R5JzDPCc4lzBHiYserG+LXEmACmG9Cqmd5ItyyYG8g0tiWZpSEdo7IrBz8Epn+6yIsLGvfXvFClysh8VC3XFUT0inHpIenDxS8nDsBWepMDPGhOhFQBYTISXNgbRYKtafVvjOyImoq/dqZbr3WrdLMM+IklHJSinhI2vDkTomfIrlZ9bs9pvtPX2WknlQmBLCwuOY4LGmP/UMpWx0ey2jPoCXiiYboAIHa8yKZpxQvjNeoJagOhL5rSP5W8FLjnJTKQSqRgFgEWLDZUMvUMpC0PrItIWrcpS4Ythl9A2ReOo6V2hiIvHAR84noYY2eQ2YpbfQly7OoNnBz8KrdRSkb7YuSJMLWxkanycrObKAVATZkWWdFbBr9u1G8xGC74BAmFPE7CIiZsxpAoNRPE4Y03jAFCNcIvQu4M3b77EdNvh/fPiAPjggfcHTly/419//3/j06Wf849//I8ZjxG53C0cBwQ9wToS0fR/Qb3rc39/i7lYiGNTCcubY0qyKE11WBilNqe2bNXxTveUYVfJyrdcFj9B3GDYb3N7e4u2bN7i/u8ftzQ2GrpOcMpk3VGUEle1sVJJ4Zjgwe8TkMCePOZk3hMMxMfaJcUjAkYERosqRvukalAnUPWKKDw3hq/sp0/jOwWnYMOIkHhQZeNR8MtUbJ/OCJodQrKHYn/KakQ4aT2KKW+UBq/9gNLuWTWy/asfWxCeXrqVkXKgDa9YegyBZOVrlTuEUMUczAItqGBY1plxq+o9Uh2rKEOlcKG3jZPCzhkkNS9byVplvVDwE834zTzUCosIb8gTvHXr1hhg6Cc/kvcAOarx21nnydhVfp9a+9vgthPQvLetblRBFZvLyMn+t4+WhmZ4jrJuXFwg3L1x7bNYDJSllrYgwBUW2BrGFZIIaJTC6rheLk34D7wO6ThQRXT+gU0WEeEL0GtteLDpFyBIaRJiFq2TKiLJwL1pkZab3+vPf8nhOO/miMn6txrziyO2tmLwXvf+asr/xeN5i0yxYW8K4bsfaz9a5rft5njHHGafxlBUSp/GEw/GA/fGAx6dH7A97fH54wMPDAz59+oTHT5/x8PEzHp++4HB4giHCYeiw3W3x7t1b3N+/wffff4fd7hb3d+/Q9xvc3N6j73rstrcSiqnfIviAvhMPiKD7RKx5TailiACGhKy/plxhDb1kFkIWikkspqdJzqKYiJingxCTGqopxlkVExPMbdAZUeEciMWyS4gYRiO5UirFxpYgOSJIic3glRD1mt/BdUqgeRAcyPVqKbLJVsvIQkT7DiBv31QgVJHolRWSn3NF2Kwdz63ZOrkdUIoyWFmvr3rt6Sw18PyaImENyYsSIl78bq3cZn1k4sYIoevfyjmttrl4RpTra32ZNfE3wC9sN5ds01gJFaRHLehm7VOds4OZMacph2ZiFg8/+6a2QjcBSRYi00q8YmszLyFlykKuWqjuyWfhi9DwtNr/ui1EBPJOmdyIiksGyKuXA6siIsk5qjdEnBW/S/zeOE9Ic0SaxRrSIeWEcCYwCF2Q8Il9jy50GPpelCLeZ9FBSlHPluOknY/l/FC159YVCMhl1EqGohQo7y69Btr3M+kAS/RsHhJmeeioGD0I7SGwlbxv5t9VTGKpRxWhKN4QoohTi1OIVamJ20whk0M4GUOfE2Q7jf8dzus+G6u18FZlfGuxqPGHl8Yc1btr1pqFITuv+2IbGuE7X75Pa9/UVS2t9Y2n/Hb6obTkelzetbbRhbGsmb9WON3291mh/hkMkZtEL+/35ToWe5SWdZ3Xcam/ayWTFbrapmXIp/OOvtgzYFn21ZqtdXz1jZdS2l/bxssFnq/zfLxkyr+pOdXHvLjF3AgL2NbKWZu+sgFGn1f/WfGJGbMqIo6nGcfThHGcMU0JjjUkU0/oncMmBAQisWrVcINQGA6nONORWqgypjmi6wJiYvhKMS7KCElW2zEQSYTqktdB4ITEWhchN7OE+Zln4519sYxFLWhZrE3SyCVUaAITBlNyDf+bBcXJBLZ6zXWoH6M9GOKLWXtEkCghmJCSA2elRATMM0JpKiYRWOeQRk5oWsdCaZVlsQKT87neY5zHtfHenh0cJMeF0D011qpoIDb+pSgh8o+L9XHM95HnOLIpIJCfW/6HLMe4Qptmuh0txDTlQa2MqJYzJKxRGYk8L2d4Wuujc0NLNnytwnqzUmat3/JPF6+FMtZIontLSHDE4DgDLkr5jchIvi2KCF/mhypFhIYMFSt9ZPop5+ozhYK1MAtdxRgGUXhnHz3mOMNFhxSEVyTtj3jc1h4RRk8Jb+Q1Jwo8NIl0Qsq5U7jqP8QoDQwfA+AckjsBmEUJlWbte5EpzdNRwquFDTrX4cP9B9zd3OLvPnwHohEfP/937B9/wD/8j/8fPn38hH/9l39D123x7s3fIoQeQ79TBVfCsO1xe7fBzc0NdtsdnFnGg7OxlxnG5HVTjanxow6U1wsbn03yt/xpNGiZuxA69JsNtjc3WQlxsxVvDa/fpopvWsP64nkic5P0N7PHzA4TE04JOCbgxAkjCBMYiSpbESM2c9ECi0Qx0WT50PkSJSR53VJs75tilRUZaJlR254sP1/xCnMQFEqOy/o2sovrHck2qqgNqAzeLAZEyyodZFvmXNYnM8oeNZhlv9pDwjwhkil6RflAyXJUVG2w9dLAWm0/55YIbFl4H9SGcvX9apLKGJEozqWMKgeFZuwxfxUiqEeEl/wQQZJV+yB5BF0lf6r5Yqrrqtuga6WVY5/jlkvHtfe+XRlh4/n6sn9tZUQ106/u17ccr1BEyFETN82Dxbu2EUVThxy7HUDjCSGCSVNExGxFYJuLAQF+qAGhxLs3RUPfb8XbIQyqiOgRglhXOt+pN4Qw/9nSswqPQBqPzBDgN1Lafz2+5XiOd3tJEb/hBmrrNXrxvP5C4JZYoJbzZNZ9cBolxMnxdMQ8zXjYP2KeJuyPB5xOJ3x5fMD+sMenz+L18PGzhGH6/PkTDg9POD3uEdMM7z1ubrbYbAa8//AeN3c3+Lu/+Tvc3t7h3dsP2Gx3uN29QdcNuN3doet6bLc7dD5gM2zgnEPXSagyiW9bLGlrIVNBgCkTRxJSKiLGhFE9O+JkIZiOyKGYkliIM0fE+QhRRAizktKsiDIqUuJCfLLGFE1itWUuhkAl4MpCWIj1hzdLNCpJtpQAZt8JAVwpIkRQOCi86Rr44CxkG4klkGZHzTVflzu0wiITWFerpFlL16QCSS2uWF+u6QlGhXAUCdcWVpnlqQkMIF+vKi8aoomLYoCxfrZvGiJG265ED1eWIfbYCF+gVl4AOXxTbj1X7S2FW86QVUUEoO1eQcjNMNRl5wFFVpwsjrwvtO25nRYHmC32b9TEhgXP1Yg1KwHU3KuO079UCNmYErd2HjY6xUpZGXMyzx/O963etg0V46JniZVcwkpYQslxmjFzxKwxClKUPTybJ8QknhDzNGIeT4jzhDiP4gniAD8EdMOAm7t73NzscHf/FpthIwxN6DB0g1htOpcF7llZOYvXFEcNMcal3xkGG3ONQpe6LAhans+VEGVhLIjaDAfLmOWVmwUhyJ6b5hXhvYV4C3Dk4TUPTQ7bYWGTyJXcHdSGUnLKQGZaKsl4gBxcSiL8gYbqIlNq1KGZqhBNFoqSKsWTEyuxlmBfJ/JbsddyDa5Yci+IxqWFJZEyd1zXvg4D6yVc37ssPF+2aeU95/Ler8tc3rt0nOH9lbYQ6Pw95NWz0ieq0Mo5cpFxWN6/QpyXUs9fPztsni49v36ULbTOeK23DAXXP1PxdVR77anRDBfG89njmbdoveyvqenye19P4/45LANfU/vqJdtFoedWXvjmuut9JIIySQ49x4ST5oY4nCbsjxPmicER6EIHB2DTAR0RvFfhHSAx5EkEm77v4IYB/maHfhAv/ZQSxnEU2O8cOhgeEGGKDz7znM4JbeIiIUbxHPK+hEcCgJgSKEZMUwS5GZMmse40RJP3Z0FxBB8KOhGLZu/g2ZThSb18JYwgUbIXlf6VIChJUWkWShuMVjowJaFXmCOYHTh5eabxySU/1AQXnSSoNcFsjCBnoaYIQxRRlPdeIq0spv36KihIPXsB+gAXRN7glIa0jARgl5dcybNheTAKX1NCn1iIFmSvh5iFfqp4qHmizOshe4kj96ntyVL5KgYjFWGG1hOiKFnlvYQqUS6d4xgGJFwOZHrNqAvOSchZEgVatt437x6LFmGEToUKZctqKx2pDJiAZHIU6w+pANGj63t459H1JYqF0Ucgh4hKEYHitSRtqEI5Uad8GhTeRvXKjUjzjOgdOAYgRTjqEbxDFzz6ziM4D+8IzrX4jQFNUl7oYKc5FYgIKcq6kbNBEsbMQCLzxE0gF0EhgRhIMyFGh9OcMI4JQ7/Fdtji+w/fY7vd4m9/9xad93h6+Bc8PX3Gf/mv/x98/vQL/vDPf8I8J7y5/Q5dN2CzEU8IciN638EH4e83wzaHWEPSkD8kitOYlQuphFfSfeGcCeaLl1ahOSsjG5Y+Wl7I0PXoNwO2t7e4ffsGb97c4+39HW53W2z7gGDJNHIkA/NcLrk+6r0aEyQcXnKYksOJHY6JsI/AITFOMWFKFV0OJzCrOD3Umwi1MqL2jiXS5PTMoqMgQvAJxASfnCiTWCIlZC8rAlj3t0oyYcQY2/5TpYV4eFVeDaZstdB06rGcVCEbU4JjUayIcL8oThgKj3RPVxxvQZOqULQQUuJdYt+b3JVz+3OOmpTgUlKPkKhtXXhG6N+Z5+Sy4wsMqyj0C/KutYPyxLmKFy39Fjwl8CJ0HsPQYdMHbIJHH0RumxOus42dtbGiFbgqu5aFfNPx8n5eLOEVtPCfRwlR5nDljQtl/fnpxVeHZpJNUt2gFT5DNzCAkkS1yt6+9ISQUC0pJ+utY4oDyBpc82Dw2fNhI5pZTajbhSGHeAi+k7AymmDThI/FE6KyFHSF4Tci5lVj8u8k+K6Py1aCX7FZrIxvbdRa2c+1JVMFXz+m3zofL/VwWXvvmpW1IYTaA6LdDxPmecZ4OmGcJxwPB4zzhKfDE46nE572j3ja7/Hw8ICHxwd8+vQxe0RMhyPmwwk+ePjgsN3ucHd3i3fv3sv57Tvc3Nzi9vYOw7DFdnuDLvTYDFt0ocfQD+JlFDrdK2XPZIvZijg2pGgILipyjTFiijPmWZJsiyJiRIozxumAlGYNySQhmMQD4tgga/CsRIRY2Qh9oTZMKhBlJlFGWHZSruaEChHrLYyb9iP4Do6chntxgO9higjAwble4vvms8V1VwWEX8R0V01+JaV70dp6Dok8t4YtJuS5wF3a0AqtF67eNnvcouY14f2ltq0pKV7//Xm+A5nqc2t9sySpPT7Wyj7PV/K6tsk9GaNyrtqw4sVCC5xRFO7aZiVkE0el8UpumPr9M2+EmildKCLKeC0UEaswyizeCWb9s2p1TAX81s8jS6xko0mzxd9srsbIxGsN42KMiHMUBUTUsExqnWPMZ+g6bLZbbLY7bHa32PaDKEVVESExi524GasCglOUniSHaH1mCZNh4KBYgJkUt6Yn5Hrp0XBpXIwpzcqH/K3xVtXfOo4gWceixKy8I5yDI/PEVGGQhWjy4rVSG0XQUhkBua5ppKRePnWST2tunRMCFRw0Rax5utXv5ZjeV44W95VwWEsC9iWkVDPWBs6fxeG8WrZbzPV6Xbz6DjOv1r3et5Vvm/ZoHXT9vWLJJRbIl9t85VgohlrIfwEjLb65Xv76WL/gQxPXVsf62LdNW4FNX1P7xe8vt+HbvQ+UISbg2ui+YvQv1vEtLa29AdbKf273fXXdvPyyJt6yJEWfWBtrIcMLqrhAp1MWphr9IejcrEjnOWGaRSExThEpMpAglphE6BwQnMJ1a7qD2MZ4DRXciaWwDwLTEzOmaZK41qEDOcnj4xdecN7LHguK0yThrCmxXaYBWvwqseadrz0JFnhIx7PGYc45JEqV8tusziuhJMzYhspytrIrAY8Ya8i4ijDOcFOywc2KCMsXJQoKBkg8HGMk5R3kJ/SfyzHaL5LWK4u0FqKSo5zPzsJPQZMjEysO5yJwLQi+tTI2es28T5gtSWxxli33lrHbuURAWRWWXD5WjSGMt3GuQFddyBl3UbUHFoMn+QwoJ4RFDt1Yzb3xUDlcY+WFqf9w1bJchwNg4+nU+lzLCl3IBm4+BHRDn6NYOM2jBRKLeEbZFzWfBRW8WoLj4iHBOmcad1/XGziBmLOhRfBe9rJ38Jlua3rS1AkA5AlBn81ePPC9F4G0rQXHrHoYM5pLoi/xEM8oR5giY54Z237A0Af8zft3uLu5wXdvdmCe8Y8//YRPv/yAf/6Hv8eXL5/x8ecv6Loe79/9DUIX0HUWnjTChw7b7YC+l58j4QdJ4YN46xcPEKPNLfcBKU1tc23GO7A10dCRZX14ZyFUBwzbDbY3O+x2O9zudtgOvSTRdgbPNXwvVkA+l7WkqWMwM2HW3BAjE04MnBIwMYtjgrbHuBgHFmXmGVrQ9ao4nqr3iRSikOx/7yTPgwN0DrlBQbJvzbMjlfnVhrAainHeFBXNXPG4LSwUmY8z5QZX1AgXTMeo8sJwy5Nmqo7Kt8nK0TKS/V155VuYYaeh8azgKmNOw8sVMcHzPHMzvVd560zgZ1wMqFxJkSqpnMVnbwhRQgQNF+gMLzFrwAwbFCujpSOAMn5ffxR5xaX+vrikF47fa999zftXeZlmnF5P6X0NDf0KRcSSulmyPdZB2wBmBVAErWIJqhbgUWJnigWluA1F2zRavFNE48KgSEy06H0/wPuAzWaHEDoMwxbOBdGuB8kD4X0QoaP32Q1QCD9NRl1ZAFIGxrU04esH9a/HNxwGoL76828BNt96KFBdCA1rD4iicEsSskQtprInxDxjfzhgnE748vSA0zjiy8NnHA4H/PLxFzw9PeLnn3+WJNWfP+FwOGK/f4IHoesDbu/ucHOzw+9+9zu8efMGH757j9ub2+wJcXf7Fn0/YLu5RQg9tsMGwXfoO1FEhNChJFot8cuRCdFi8WOKhzmHYBEFxDiOmKcJ0zyK8HE6IcWIaT6o1fSo1kazMiXmASHIkdSKwpEQCZ4ony3sSA4RqMxVtkReWBCHHI+9gyOPENrEsex7ZcREESE5ISR5vcV1R46p2RLmBjMurbhrS3EpvJb3X4ZUsiAf54ilnBdl21kRNRt3dF560/ZzxMUqlKbFu5XgvjQ00wf1/RzffyXBVGbwWb/IBQhxlAM0ZVpD3sn90u/OlQlavjIZ1xEyZzzWjsGKIoIqkZDtkUooL8S2WQ22YVnqBIX2vQii6Xx9qPDD+tMIV9qWlyqsWUaOV3smy+fzfROmU67LiLrEwnTNiq+nada/ZeAnNyNRUUjM04hpGnE6HTGOR0zVL6oXmHMOm5tb3Nzd4e2773Bzc4u3795j0w3YDlt0vkPvO8ALU5vijMQz5umENM8g75HiBJq9Cjkk3BXVcwVkyzzU/UMrsKiGIb+TZRPV8ijCmAWNgPINqaDHZbhkwhtVMpHOrxlGOH8WJtJVsMYYRoNr2aXeCUPDEWIFp3PvLJRdAwdJrXDVA8JVHhYamolcZYXOZv2Fs362/V/uHS77dmVtrh6VoCT/yVXSvqrshjymxSLXpnuyIjIAa7fDqrU6N2SHMYJ1t67dz2VXMHKtzdZGe4+r6zOSh87+WD8uvrfWz7oR7VvnK7q88RwNzHncqrloihP4zUbYF1a6rJVlP17a/7XnLyIfqfr31zqujPkrj+tjTtVa+6rCcRbOsiq6QsAXjm+hsVf2XlVlxlWrzDB/U91ix+xFQFZbsseEqGGZxilinhPmKPU4kljuElNeI3NzkjBHwSN0PTb39xhubnD34Tv4YYNud5OFQZ4kD8I0z6BpbAS63nsRkjmXFREpSf6IEMUy3HcTmBhulsTUKTJmSHhHEGEaJxCAqROhXwgiyK2AaYFripvIYr17B5+EP6YUQC7AUQKRBzn1jCCXvT8MJmf6xrxLAbEydg6UAJdIQ/R4sIuCq2IEO/H8piT5LYgpK1bmWRLHTnEGCOg4ZPo/N34x92erhKo/SD0iiHNYH2g4V0quCKbILODT+eoyAS63hpScY8gToLRRVkhUxsWsa07apPHoc6NtwSvisT81XrrJc82KlfSbLJi3zmY+AEUIyZYBboGBLbmyVy+HTqNCdJUhBBFgISSD8oBe96TuT+aaZlRjCeuSrTlzrPCSg0TCaGsUCy/Gos4HdNkjQnKlzOgAUM7hV2MU6ZuMaUwEES87WCBKDgPQdeiGgK4PuBk6bDYdbjY9tkOPoQ/ovReSEkATkqdaU4VOlnsBSndxwOxlnOIc4acZ0wQQEigwKDEiExIHME6YEyOqAu7u9g7u1uHvPnyHm+2A97cejmb86ff/J758+Yj/4//6/+Lz5wf89ONHxDnhRnM2bjYawgpqUNdtJdzytlPv3ikru0CagUlDTEreDEkKD2f8cUX7+gDntRwSoz0ofCgeHwTHEtrVO4++67DZbrC7vcXt27e4u7/D3e0W202PLng1BIkwXp4rWke8IkwZSAA7TOwwJocjizfEEzscGHhMwCERRgaijr9j5f9X6KyaWJfukHi9kARPJkBDEjFAEWCGTxIFAU68E0xZE/NeknLTsjrdbzAvKpL3DYI4ZjBH5UOThpk2j3HhIWNMmf4zz4ccUpUFGGS6LLO/tXoFWfHZ8LBUj4rl1y18oxSkdzOg0rnKyon6WcsDf+thq4GgieOXoeU0tGHXdRi6DrthwLbrMDiPTsP0mpJyreQ/1/HvIVd8rRLiW8sD1jiW3+b4CkVE+3fF7+m5VUKYh0PUmNFCdER1h42NYDYLmQzJKsPufNAY0r3mhhhaj4h+o2GXBLmFTnNCqCeEIVj56UKukhc1ioi6fuvtBYHh/yxKiucEnmfHn2EtvnjTZC3pn6+uZxnrC99fG8eGMKyQgwkaG2umVNa9eQbNccY4jZKcejxhHEccT0ccTyc8Pj1hv9/jy5fPeHx8xKdPn7Df7/Hw5QHTNGE8jdgOPUIn+SDu7u7w5s0bvHv3Dm/u3+HmZoebmzsMwwbbzTbnTwm+Qxd6BK/5U7wJwxTxqxW1MYeMyqspiSJiThFzLKFY5nnGOJ5EETEdEZMqIpIKEdOMpJ4QjDkjQvOAEMbJ4psb8SQuso4qYgo56kojVCwKR6+eEObZ0asnhCXdFkUEgnhEODIrZHX59QHiBhqMos7wAjBLZVVEXFQYXF1mxStrZc1dU0LYmRfX7Xc6Z1kCL/+wCr44ztcbd6XspLE9L713qQ/GVJmQk1YUEWvvKxXW9PusbiXALitmhDGzNX3VamP5XVaotJbil7zQLClhSVYt35giwt47U0SgXcutVX6x3OOqjJfD9vJ+LZBfr9MspKz9QvROk3g1EEYQZgQ3I1LS/an2ecw539M8T5inCTHKb46zhF2DKCL6YcCw2WK7u8V2d4vd7g69emkFF9C5IBkFHUkC+zSDyCG6EQkR0SlMSiLsITOvAiMnQKX1eTpD9VleQOXM9fvKfC9QR/aUyNflD8qcRF1GESSYoqEoBXy24iy0SZXXgYT5BmzvJLFuTRBhS+X35CtFhHmfOEdZAVtCNgkJ2BL3jEoEtLKKbExbZcVyT72WPirWe+fPckLRS9817bO8RVyECnp/LVzSuTdDS+2eKUpX7pukzlhFgzerbda2UXW91rZX05cVDbK+KNc/ES+UNVi2KGflyC0mwzjL941Rr5thQi17fn29PCuUv9jGS54cNk7P9e41xytp1hdUfKnf3A7m6w9Cu1bWiro09b8KQ97sIr2uK2wrb5b1q5mTlm9lFaRyFUubkxjXGE1rIXcMTntHagwj8C6yGMKwI6Dz6HdbbHY73N7dwncDwuYGMUWMUehbC9szzxGzjwUmZ96z4IfiISHW1847OFbhICttod4DTo34LASU5GSw+dQ9VuE3qaNYqWcatvaMqA3z8n/LcTSBRfEsgVt4RJhVugpiTRhnVrpZJGV8UUxITgwSveY/Wxp4nC1IMhy9Em7C+HujsSvcK7QrIyf2JslxUfdM/4QpA7juKwMmJszZmJQAXT7PgJGhvEJa7YZVB4W7EuZKcWEW/AO1t0rNA3CekfKr95F0XYXAKv8g7yrFhMuhmUo+huoH6BgVWYnxWb6iT0jjtxvv5rugxqNLRYQYl+bQTFQpIog0FPeSttWI/gnqpQtwUrO1BHAI4ODRdQFBraiH4DF0Hn0XsjeEq4TZXK1DqibDaDcHiMcTCBzMA8NhNvqCk1jOe/mZERGAHBUEBGw3W/Shx3fvv8PdbouBJOzy55//BT/+/Ef80z/9Nzw+HjGdejgXcHt7I/3oCv/tXEAXBnQhoOu8zu+sJK/kQPF1aE07Z1qy3kIiC7NcZhISp9or1R4wOOHVq6TrJTzTZrfDZjtgM/ToQhBjlyzoLiuxsKS6HnUdMRMiO0Q4jMpVHM0bgqFchsyv8T5kPOSS9rKNp3DOKdx2TmMdsNK0Gf4IjVzvFisrZbBS9lTjOJNpI9th6smg453MM6fOEWgezKnyUNCxEbWAKSOSDr/le9O+KSzI8MXgUgMDWuzItr4r+JCfMDdvoR7XuhIs6NyzGsp6eskhnh6E7PEBg/N2B2WtBdm3nffozBtiES3g5R4BWsc3kC+/pWKgfvYiBcIr5UevKe+3kHO/OjRT3ahiIdD+6lj4FnImW0ynKCEdYpIET/oTuknK9p1YI3ddp4qHG/WAkHh4hsyGYQsfAvpuUO1ur1bdfSb2LMb0UtDCWbDQIh4jfnilv389foPjG5msfw/NpdVrTIVdZ6G9hmCaNWfCpCHJTidJRn04HDDHGU+HJ0zzhC+PDzidTvjll1+wP+zxw08/4OnpCT/99BMO+z0+f/qEeZowjicE7/Hm9gb393e4u7/D+/cf8ObNG3z34Xvc393jzf1bbLY73N++Qd8PuNmpJ8RmBx86DL15G4ng3oWaaBGhMasFfOKEOc3CVGk/pnnGNI0YpwmTKlKm0wHzPCJOR01aewLzjDSPwpiwxiZUxs4bqaUhIMT9Tpgx5wjBrHqzgkQIVWeCPCpEtPMalz17dIgnRPZwsDNJTFLqtq2wzxQxFrKELKm1tjJTc64i7PgCf1xRfmtMdCNAW2P0zj9ZWuRmj4CyEBXZKhyj5ff6JPhMaFyDcWsCe6FVKNddl103JsNQ+yffTzAGry47C7+a+9yKKC4g3GzbVAaiITqWCpryvCHPGqIO1Tn3o6m+HTfSjlq7TRFRiMRzwW2ttCxjsKIsyLW11tslKeF1mGlxNZcKDGtzyaVQ6rfDLEZHN2KeJxB7EE2abDthHB2SBDtF4ohxPOJ0OuBp/4DxdMR+/4jxdMQ0nUAANpsBu9tbvP/wHe7fvMXbd7/DdrfD7vYt+jBgN2zhXUDnOpAnkCfxiEgR43jAPJ8Qjh3m+YTRe6Q4Y55JBB4KayWhelHY1GvMxtYY53o86qTNmbexuajkIkt+bQ0AMIvVZ2Y1FL4V5UCtJPBwwed7JVZvey7znMCswirnIDGu1XKPJJyI5acoHm6LHBFk8Z/PWt70J6+Vs/cI6/1+Hq6sHeuKiOJf8ez3sDnhSr5qsET/XpmzOkHfWi0vJuoreELN85Z5E6aVVq6X9bzIp+Ss5URLlrR6a7H/F5/WL154cF7r1Wk2K0ajJ2xMbC8tYM16DYtmLZ5fYkq1AZdLrvb0q4/lUrqwF6614d+LVv3LOlr8xRBB7eU86esKUujXbZnLeiy8YKEvUjamSRinCcdxwjhNmCcx1CCSpNQOhKR5GCI0J8TQYbjZ4u6797i5vceHD78TAxbfYY4RpzgpvT+JchlACfcj+94slAGXQ7OlRIicQI7QzR0IhNlFRI6Y0wxmwck0J4xzBNyMcZpABKTYgQB4dQ0z2R8BWaAqhjnikZESa4x5RvQezOIhwZp4uh5KzmMWc+4EE6RRSpKkWOXsEYRIDuRmkJ+R4pzxuNDYCSCRAwDAFMXzY54jHFk8fs79eMlhbTlbBURgsswQlVUxF4G0weukip60+OU45DUtWMOuTBu4fBa+otB59qL8WQlraSFL0bYQzHil4IuSG6J0mtvSNJmHCc2R6QuvYaqC5snseokYYfkAvRlCOPESD2p9HKrwtOZNLnIZMWLL4XydLxEoVO4SQoALUod38o0YjXZqhKG5+VTBkjQfRc6TZnChGv4SFqskDE+JkSiAXYfQdfCdx83NDsNmwO12g6Hr0DmXQ/vYepZzxWPUzAaM04Pob+CQnLBO0UuotskDnSccOeIwJzHOcYzOEQbvsb17B+c83tzdYugDOuxxPP6C//I//i98/vQT/u//6//Al4cHPHyekThgsw0IQc5iNGKGdIQueAz9BsF7UPJgHJH4AOcGkB/OqAWjcb2GuSGnBhrW34rHICKNrEWiBNSxJ5KE9SEE9H2PYbPF7uYOt/f3uHv3Frf3t9jdbND1kq8jqdLRVHQZ1gIAW3JiqLcI4zQTDonwJRKOifAxAsdE+JIY+0SICGKCwhJGKaec0ELJtqTBOUYVSUG8uTwJTUTGd0Ly11AODewAYkSknAybAMwke0ny8Dl4JSppFUEZc6v8uHlQVWHpcr6IrGhVpTaAqOMFFm+WnMaZIEZHlYJg5oTZ8JYatuaIMqjxi8ISquQAWqgoMi1HRLWxwKLpwzX6ZJ2uXR4Nial/JzK857IKoryjIdSCwKah77HtB2y6HoP36LOxbGsEaQrizBMv2m1yhW+ht35tUu2lSohfu+y/1OPViojlUSsfADQKiDpWtFl9z1EVEUk0gimvINL/lTH3Ej/aOY8u9PC+Q9+JAqLvJAZnbwmPOk0wGzp4FyqrZ1fFw6MG6CagIh607lcyJS9huP89FRmXGLTntIkZUf8G6/ls05gw4jes86Vz9Ox8Z/hc9kQmbnmxJ9Iiqes8iSfENOJwPOB4POLp8ISnpyd8/vJZPCIevuB0POJwOAjCjzN812E7bHBzc4P7N/e4f3OPu/t73N7eYrfbSez1YYuh36DvN+i7ASF02asomNfQUlmnWzKLUJlUAVHCMc2zKCPGacY4amLaecI0nVQRcQLHCSmNYJ6BOCqRYiGYIEhRCXqnZ+8KAeXIwopQa+ULC3Pis8KRslCPhCEkB0eieBDFgodznfbRrH4sBJO6rDsPuJKU2lkcTackKWlOCFgM1AXlevY3Ka8hgsJmuVxZdlkhulyrS4XF2R5GQxOkC3VYLPZ8vbKmL3kNFKbgZQKWLOyWp2D21XtFYVAUESnfXwrpL8GsrDy40Iby3uXxEzqXF+9X9YMqAeL5sYSrbLH7TVlC1y3IpQ7kPVFPkPpxnPeNLE7qZQENQSw66zY2Z0JWaKwJKudZcrWYodPsEwJDYsZm2AEYpxDTjDlOqqA8FXgQZ7V0EaZmd3OD3e4Gm+0Ow2aHTuFT1+8QXEBwnShGTRGhXjzOOXCaRfCSZkQiMM9gIiHoUwKngtBNSbzWb/u7vl9f6xBXIZ6Mgbs43Hpw+dnYGJlT1VHTKct8DkWoUbwjrGzbC7XlerF4RbZSrEPsleviGUQLor708ZypBeoleVnoV+gIWnt88VhTRBRPiJcUVLc//6XjtFaGzU/mYFbfoMV1fne5CKo62rmpvufmtUphcg7bS1++koZc+WxVEbFe6bXLVzdkmZhwrU0vLu3C2vya41vpc7pyJcdlHPntvEG7By8Xt7aq9clVJc6vfywN2epVz3V/8ta5DJOWR6EjLj/n+u8sxEhqZKNCnSiCHYb5fQrBYxA9aSgTDh7Udeh2GwzbLba7LSzEp/MOmAkTTUJTUAnZmiphswiFSt+yR4Qqwr1zSIpjORX4lMOjxtR4cohFaw3zChy2mP01PskCcw2DvOQBGnhvwi0ung0WLgSorlMUz4hoiaolXjwnr0L+KHHKqzJy6BINl9XkvLg84w0tal4LQLWeCSbiyzK3WmaIxJJnzr6pFQKLH6pvyzozrxajGRa5J/LerPGCrVWhlxrBd5k0wQ3O5TpLHchlNUeF8zLNQqShH13OW+JVEdGcXZU/Sj0iQgjiRe67/Ny8GISG26ALAUMnCai95eOsBIY+BEk8G4LmGFDDsFAZegHIFK4q7LJBSManRYlYKyNi5q0TEgUkeIROomFs+h5936EPHl1wcIwz+fFiSs8fwuhu5VGdCOwdHMAe5gU8e2QLfEdAcA69Ew+QLgy4v92i7x32Dz/jcPyEP/7pn/DTj3/C7//t37DfH0H+Xj1FPEKQn/PF+8UpT2rKIbBFKJgAdDLfXPBKXkYLWhNYWsfXa042fALDGZ/jNHSczn/oOvGIGAYMmwF936PrArwnmAEEs9FsttFgbHC+TKqIkETVkg/imICD/i35IQgJJrB2GYA38yWAFABrlLOCUyivKt07TX8tx4rBZuGBiJHhQRaDOIK350BFsC3oRcNZBSit/FLGJXaW8dZZyQoH8YzIa9YAVyVbMhwg8LLksanXdbO+DV7Vl8ujapuclrujlHhJjnYRTVfjxrTYi9V6dVTyuXRBPCKCUwPUSk5VPOzOd3Etq/tzCf2/9tuv+e6lxl2XZDbf0oavlZe+5vhqRUStgMgbo/pZPHyxCBkxaSJeEWKKOxt5RZRQBtx7iQ829IJIhgHedxi6W3jfYbfdwQePvt+IRr4fRPHQDcK4e0F2kohWy17E275kCbYUPlQcJy5s2f+wB+McYf92let4/0845GJNwznUWGYQouyFcZyQUsRpkpwQ+/0R8zzh8fEJ4zTi09NHHE9H/PzxF+wPB/z44494enrCn374I06nIx6+PCixHtGFgM1uhzf39/jw7j3efniHt+/f4u3bd7i7u8fd7RtsNzvc3bzBMGxxu7tD3w3olWjsezkH36n7bS1gM2tu7Rdz3renHEZqUiXEJDHj5xnTdEKcJ4kFH09I8xFIE8AjAHHTJhUsEdSNFYyg7qGGaELw8I6EGHMlQZG3nDHqNuwqRsoIX0lOZx4NGgMdDuR7SOxbvVaGEb4DNA6qKT9ACpuM8Ccqcl4GjDRt/wKWTEe+uyAA7GA8t8kKI7N2XMMlhpqNmTsreUX4fbmkGsGdN+L81rV+FYq0MGP6JEskxO24rrMWJDbKgwuKiGVD+eyPcqMmkJeIvNY7iGXMywGTMU3GMAuVW9pqVm9LAjFf1/eprLWlIkKeu+YbG+Ys4EhGyJjSoBpLwpkiou6Dd4yYDecph5jyIcBHsYQSy78ZMcn+P50O2B8ecTodcRpPiPMosa47j/s3d3j7/i2+/93f4PbuHm/evkPXb7DZ3GLTbXGzuUVwHTrfAR4gzxLOLc7ouoBp7uEcY5oCyAHzfIJ3LJ4RE8AckaIm99SE4NY3Y9JqT4g1JQTlcS3vF2Kw7P56Ps6EFyhCDqFFZJwkQgKJt6Z5bLriDWGWh3WSSKoUEzozGVaLcs0YeOlH8LXnw6XzuUdEIerrfUlVb4GWJjrn7LOT9VWClatiKmFkBfKkHNeMcWnUOoyxWNp1f1qlUt2mtp8miHr2KACprXtRpwla2/oW3zQ05/mYX32/adICD10J87RGC68p68r71+p6hjFpur8mfC8w9SUk57nV5/Njdr1xX0loErJF5evqOGeav+4wuPJM1f/THWuNftl4PSd0AEyeI3NisuUUGXFOmMYRp9Mpe0X4OAs9b7meoAYvuw7UB9BmAG16uK4DgiSmdhABeuc8/CaAJsJESeqIInzzyhc7Ig2r5zLtzcoLB2bAJYROYuaPfhKwE13uCGsM+hgd5jkheLGKdQwYPmjHR41nnAjhnPfwidUzQkJGsbdwTYX2LW0TQZpZ+qaYNHmwzlpyYE5IjiRkY4ygeQZ5zeVEDi5EkDMvgwiKYtgzzx7MJLk0iDDHGUSMwCHTMUtK0wTTiVGMGlHh48XKEfGefpgSoPHaQWLBbW0qOS0TOLZhVmydQZUPjggecp0Ur7J6szh2KkCvKcyWLrT1npBAVBRVWVkFKDlX8SPWR1IjFCeCWhsh7z0QfA635UMQQXKnIa7NI6LrRLjddRrGtigiJIyteC/0nXpOBA2vpCGxh2EjComuF6t75+F8nz0qnIaZzJ6ZrhhZmCFE8TS3a+mnM/qMq/7KnYwmGciJwSW/qPB0pmDZ9D36rs+eEFAllxnCwYSaDKHTUjUnzIBbGEPpnAfn4TsH7zpE7xCc5DCb44R53iJRhw+37+HuPXwY4WjCTx//Kx6ffsZ//6//Jz5+/Bm//+d/w35/wowN+u0N+v4GoQu4ud3Ae4euK3kUJHRwAJAQsQcY4nlEDh3ukRV5UGxKZmgn+DGliBRnGR+i7Ak1NeZNyLxcSkneI1sHYji02eyw293g9u4Ot3d3uLu/x3a3xdB3CF7CHJn1fzIRTuaZ5Jcg0RXmecYYGU9Twp4THqaIPQOfY4eRCU9MmECIArFUbSDzQyAhdM2Cv/qJDF/gUkJRxjpAQx+pcB+SO4bZaa6bkojeQscRcc5NqZ2RtSnQAha6FnkXn2MvyfuifPiCtK7hE0O8szgb4YmcJJG2O8liJw3LF2NCnE0RrZ5BCs7OFaicKyNbI/pXo5QyuPQNwvlLR1ZsO5WvkI2NzCw5B3jBPyF4DOoRMfQdhi5gCJIjog5nXZpt/mDm6dHyY2ey3b8eF49ff+ZfdrxKEdFM5WKxL8MxRbVwiCs/0eBBYl8a05+FiIJIghfPBu87hK5H8Opy54O6EkpiXaeaeJAx8/KDCltMmywdoLYvtZCpSGGVYbJ+Lju+GJM1hvQ3XvTP1bf2vGWWy3s1EXdB1FCXsl5fI7J42dLm5dWfYUe8jIlH7via0DHjI5Q/6ktWZUSKmguCJRleqgjcWZO9TtOIaSo5IQ6HA46nIx4fH7E/HPDw8ID9XrwiRn2HmOEc0AWP7UY8Ie7u73B3J7/bm1vsdjfYbrcYhi2GYYOhH9D3g+SDCJ1aMrdJ3EHN9miEpZbPwsIxFS+OGdM8SuzbaUacJ7V8njSUygSkGUAEcQRBXAGzB4QS2F73qVetd/DlnJUM1HpE1K7C54oIDzJLYNJcEC4URQQ5APKcLfeDK6GeKMsOzBMic2KZRr2wwq4Ic84FvM8Jta/ta+FDLj9P2oUs7Nb26ddncrzLZVEDK85fW/NSuNgsfUGZ14WgLtN7KETEso2ZCVkync8JIJ5pXCYIF4qNb1VEnLetKPmWVg6tsBAAKmVENWFrlut17GAAEr/anjMkdAKQXd5tIk0Rkao667bWhKnPycIUfhiBl8sy/K8eEfOYPSGEuQGcdxJfdrvF1rwhhgGhG9DZr98guCDJqp1Q8ckRknNIHAFizHMP5oQ5dAASOAblLSVmLrEITZDaGVuO9UUlRJ6L1mK1nZ/lsWAAlFHJ65oWP2cUuZZnY5ljdRePCGCZT8YEE9ZG7YezvrQhncwgo/W6MNqolCt77DwPSlFGLDH1OUCk6o9L+6XZ+sv36CXwkc/pMqYL81IV/cwLS+hAi3vL69VmkcHnemjavb5e83Wccen+uXU9ny3QS/jIrAIv7Yvy/qVWainPgUWWQlYpKgs78kwRVW11oc16e91R1v6rD53gSzTy2dK8VMbXHNReXB/79TFf0uUtbDm/Xh7fQp4/Q/VUfxqyX+y6Sx2+oCAsz+2fFpcmFazHGBHnOfOtltw053AiAjFLqFAvHvjOh+xxL+E2FObDYlp79WYQYdfSeI/ZlVVc4QFS4WntEUEuZTrMaHNOFiKpWMWaEhxMraMkGeqXXZ/xgkUNcDUNQchrh8q45XrtTuYX9Tm1XiZGE6SU1FOx/Ci1HhGOqPHucBr6acFllcmsYGvdpvNZru6Vhgues7FCasay9Y44L8zGxWiD8rMQvQW2yHjKLJsCAcksj89Wqa5LZCEhAZU1doGV8qcTnrDeNl0nHgc6p7UiQsLwWkgmEdgH9U7wTs7BiRymD73md5BIE10/IPiAod+gCx2GzUZCM/Umh3FwNLSKiKWnfc6hYJZvRudUBjL2/mJ8mqFiGYXEQPJiwc/sAXY5NFTwDsH4Opi3c7Ggzio0gtkIyfgxVyCnmnx73faRJ4AdmD1CSPBB+FDvIJEHfAAwIvGIx4cf8fHjH/CHP/wTfvnlJ/zy8RHTyNgM7xGceBiIUmcD5wHnJYyQ2NFUeIpnmGyZ0MNRyEo4BhXDl7xWSLdK6UcdCqumsqy7rGUZfWp8degCQtehH3oJ09TXuSFs0XLmOQvvVMFvbXvSHD1zYkyJcdLfMTEmFm+ImWyW/v/s/Wmb5DaSLgq+BnBx94jIRUtVnT7nztx55pn//2dmu3OW7nP7dHeVSlJmxuLOBYDNBzMDQDo9wiMzpZK6C5Inw+kkCGIx2PpamdzMUKcpypXJX9VaQTEgVf6US1/CPNiaM4ZT7r9orGXm46o1p/+ZbFj4oXoBUm5eLdOuuDZVKZgsXkWq1IZKtmvMUMEFiox5g14hz2/k/ah+4WXJY8/GESxl02fuwGJcF29WX503He0a2+fKHpM/RNkhVSIiJDLCmzNqlX+lPGslj1zQBzyvH+CNv64vXxLh8Gvd94onnP95FTP7ZeV6Q0SKmYwBnC3RKYjRYQ4zUkyS0FJhZ2KGZpoQ4izvoAtbIFcagV5qe3jfoGk6yf2wO2hOCLO832lOCLmu63qQhhRmnEFLMOss2RLlSf+ylLQuK6Jy6apX1/v1y+e24eX7+NmvF07p+aUS4Uvn7bVhSV+jGGHLz3qJflWbr1mlDYZsnucMw5Q4SRLnEPB4esIcJtw/PGCaJ9x/updIiJ//iuPxhD//5c84nU748ccfMY4jHu7vlWlO6Hc93tzd4c2bO3z77bd49/Ytvv32W9zevcXd7Vvc3tzhsD/gsL9F3+2w3x3QNZ2Ez/pWMDq9g1cvGHinYpOEAMcUkZAwp4DEjFmt7/OcEDUfRAwzwjwghhkxTAjzCSGcRIhLAQhigHAcAI7qOchwChtizKEoNQl738rm0yjjrMyrhHs6jVJwlRLNl3VP8rHk1M5bsmk1SFADwANOjZVekqJZ7gev0VPZ4FAnqwUVBa9tqEBhIACIQcMmRC14PF++dC7XSvmt4sqFW3e/iiZebcB74TxQlszlpxeGdSvaZInxutw0N42e6/PPQDOtvxtTuLz1+n5bt69I1csdnvK82h6r9ennjFxbHsfyf4O6+fVlnM8v54XBJHhiSeAWPZA8YtOAOYF8A3YeEYQZwBAiTvOEp9MJx6cjwjggTCPmMYA5oet6HG5u8M0fvsf7b77Dm/ffYL+/w27/Dfpuj9vDW/Rti8NuJ8lBncsDHkODGAOcI4TYgsHwTYsExjy3YtyhSYTNJBBOzKK4KRqI0iXOLdeqQQEYb+JAYEVF2FbSrg0W9gwGYDlwVLhWoUOMoq3AwSnvQ/aOBv0m6qf8d23sISqY0VmoJF+UH1SUIs6bcqHkzlkaIpZzz/7OujydD5tT8gXF4KVoShuLBX+wVvBUffw8072R26KQ761Gb9S3csQAL/R2+U5a0Zlaa4FtuiPercjjr81DDr8/F6Eud9xrC4mHbPmOpTp69d3Gu+xxL9C4dbTFNRxemVTLsqCH9eXX0Fm68PfZAy7cvWrThdwam/Mwt+8Kwa36vVxCwCrCafmY7bZstvvXLPU4vkIoNiXHta2uV+Xi+NwaoVWTaD1DEjwYMyeEyJgiIwRgihFzDAjTgDAcwcMAjFE8TRnCwxKDeokCvO1atP0O7w/vcNjdYEc7eG4RQgJ7ArcehvPtvcO+7xFcQiDJWxTniJmC7BBNA8Bl+NEKKQ8+JsTGw4Ex9GKQ8HORuxMz0hyQiDDPM7wnTCGAqEELn1kdW2K2wzAxnGOwVw/hxsElDyaP5BowNYCLADmBWCJCzKF8Bj2kKkIGSvrRCCSJnhRlZ4LXSGjEGXBAnBWfnQDipJHNPkMkzXMCI6ILklGr9QzvBPZmPSMqVjF/EgiJHJJjgIrsAf0tgiAOCkngHTmCOIA4IcZZDSdV7oGsTbQIQohcwSxOTQxQI3maPAGIEUwBBOlHg6ICkJWF1lIwI5rsGKM4VmiOq2gTmQjmdMWkCQpUXvHQXXBhCCFQ02ToI3PyrH83ON5ODQhkMLTKK7TuAO8k96YkmBa9S991mldwJ/keGjFoeNdWRrdGotDVEAHrM7KoHzkWVweZNwVSp0T8SDnfkbNqlS1/RpnXiWTcRRkdwezlb+0HUFH2Jo6yLhRqLTmNvuGo88xgsYSwMJIakEaRS8nBeaCBw9x7TAwwzWi6EceHv+Dx8Ql//tf/gU8ffsQ//uP/gY8ff8aHDx8xTRN6f4f9TYv94R2apsXdYSe8mhNHkHmW+ZBCArxDImh0fwdi4Q2ZCYGFjrBjMLVgeCQQHBIIDRwIreuRHMNjkHmeeoQIJNeD3Q7kW1AMSPOECCCSgydSJz15DjUN/N0O/bsDbr69xft3N/jjzR63XYsepA5IahAhYRFNTpZcBML9EDcgJqTkEZNDmBuMqcGn5PHIHj8lj8gkwUrEgJf4lQmMEQknJMycFCbWolsKVWCQJDIn0jXEBZ6pMkARgK6CujOjhRhFNbpDq52RdK0JekPjRF/SqPHXyVtKQmwHbZPy/kmj0Lw4R7ukDn2ZfkqbosFVr2REb0uBC2ygIMtIzrzaYU90RBGUAhADmhTAMcClCI4JKbBmeFedVW1ot+/P8nI135FQ3B1rEcDGQdYzm0OUOnwm7fuc4B5iTJxjgodD5xvsmh5vu1vcNTvsnUPXOLgGcJ7gPQASnZpRA2GjlK5mef9cd7DtFE3Vv1Zew4e/jg/75Q0JX1jW8tiv9NirDRFn4YUJVVKnVT4I/WRMfL2uKDpUWNYNVpIfSdIj7xu0XqCZWjVMNHremzd30xRlo3kPurKR1htvUbIsy7Md/ILi5+zyX9Egca2X3DXXrD3pFlESawXLpkLi8rMuWSqvbdvWfeeef68rL0EK1G2m6pp8H5crtcIFUbdoX5vvshaCGiKiwpPNmGbJBTFMA6ZxxHE4YhgkEuJ0POHp8RGn0wmn4xHzNCHOgofeNBImezjsJSeEJqi+vb3FzeEG+/1NzgfRKwxT27QFn9MVKBBnyve8r4goYWHB5pk0x4gYGHMQb7E5BKQwI8wzUpwQw4SkMEwcg2xmKSgMUxSho1LEiM5NFGGWA6JpnIaArpVlyN+N+bb1nXNDkAfIjA56dBr5kA0RDlCmisgYeYU+sYiQlWKyeJi7xfnl/Cgb83PK4V+i1J4av7Wy1a7F2num2ZX8tXlhzQotjJ287UF9dv4Vhoj1dz6//dly1p5oeMDXz5ltz2R65vftBtYJvoCVDqyu/MzAJUw/OcXHNQ9Ku5aE7U6MnDcmhFk9SwNYIyAJQNM0aLsOu8Meu/1ectZ0PdqmR9vuFDqu1eSHgHequiJj7hmJGzVCNEjcaqLNCOc82KIhmUVoB0CGTcbmJQplQ9br/XxMlsbH834+M0QAMGWbJeuzbs01mlIDFpliF6yjMYpXZXaoWD8p74dmhLB2WaSYKQKEXkpbXL5u/V5l27/83oB5U28x8KWSC1wKREFXPfM5RfFn0retMdkqW/zE1hOtvRY9VL3+OX3J58+FMwCiGKMNluoLSPl1dOOZ73kOXsHrVv9K4bMzL91d37fozLPLX0VsL9RzLe++2HhyucxzrqwO6wFd31PPnUzTqnmF2uj3kkXjS0uZs2YgKEuEFt/PrqvLa8aH63G+VhinxeGl+7Z+XVMbUgWwJbqNjIyxbXmIOARwiLDIzWh43Y7hPEQ2bTvslM/2zsNBcjgkV/vwChHwzotR23E27mcUARZFmcYJy95q+5fiszvl2ykqnQdg0X4prhIrayLUWjlvnVj4cG2j7hlFFtANKRubdCfLcvQ5rVR1Ewyz3rLHJsjHoiOYLRIiIqUgEC4xLmUo8/RV/HinXr8CbULVW1RvtvoThAW8XyHBtGw0isLKnLysDWfiHgq/Y/2TdQwadVAgr1jghFTJJklo3VJ/osvLoGAWCczz39VzQRm6kQx6NkOUUInmNuW/t4jwQtOXNGwZ9ZLfl43rsATS6uRFDbxr4LxERnjXlKh042Uka1/Fs2BxXI4G5d4vtCYVPojzrEKt7ASQfSBKm+vG63hK7yJH43CCQAQhv7d5zaPav5ce/OVIoOJ7wZBcLU4+IOOJIcY7TEh8xOn0Mx4fPuCnH/8FH376Kz78+CPu7+8xjTNSInT7Dk3TS3RJ26LvJM9DslwvSZFDUgQRYNE7RcNvsVelf+qduPBoigwAMyKmvGSExrg8p+v5XnOxMsccfNei6Vt0O4HM2TVNhr1KDFVko6zBapTrRSXLnZASqfMmYUrAyMDAZV0QZEgTSzLnCIHgSqWSlbymMJ4rGSbvppURkPRqV23LdTybzDyFO6MyD0pkto4JqRnCEl8T5fUPldFZiXbN25vuvDy77v1lMQClTEvzRMSyH/In5Q9xkvwTZuDIt14bAbEu5hC11dJ8xflcskh8QGhjBTsrfc2qFxKIt843aH2TYbnJ1hg9397cN7Q+d6lscjZXldfe8yVGCOurX8uQsdotfvHnvdoQIeGkULiZhEkjISbFvZ/UCzyEkJktWTzIb+dUMG6aFr5pFHOwQ7eTJNR7jYjo+71EQPQ7iZxQXPu2ldA/8ppY1llCxoKr/FtV0v29/HZLYT+KEghQIrAyiACoErHJPJ9mgS6KyvxMYULQJNRzmHEcTpjnGY9PD5imCR8/fsAwDPjxpx9xOh7x5z+XSIhpnnA6HQEAXd9i13d4e/cGd3d3+MMf/oC7N3f47tvvcHd3i7dv32G3u8Fud4PDTqBO+u6Atu3Qtz0a32Y4M0tMZsp9Y8ZilPUa0oxoRpMUMU6ynqdJlIthHCXCaT4pBNMEjhM4TWJsjAnMAZbZlqh4sUuiLaCrQoQ9OXSNV8PEBVxzb0YENUBQlWDbN4Br4IxpzsbJRo0Ndm+jm59X5lEt8pocbWmIqJK5bil5UJi+37qB+5csL3stn18rcsnlTXVtGN36nTZ+v5be06YGfvtZ63PpBZbmpbbUiQe3rnteoZg1Q0vG4Oz7Ntuwfu/6q/GnpG1cCOPMsjYSSx1OvLMCUg51n+OMcR5xPD3h6ekB4/GE8XTCeBwQ5gnMEb5t8PbdW7x79x7ffvM93r77Fje3b7Df3eLm5k6it/Z7dIoPujREEEJQDGPHcI4QUweihHnqACTEtgVRQkqNTq8ATiSREsyaE5LAlBb8wfpv6dKitHiOl7hknMg31xLZ2c3l+qXzhNK8/JuOfPZ6qkKxy5DnCIcCWyd1LZNT1wapbTierGx/pjy77ld75ZZYVQpv/G7nz5+5VV4jQMnnGlz/CzUYDave/1JfXO4j2T3Of6+0Z59VikbuVUaI/Ozraej63nOKc23uBDts0N6Nyy+17sUZ8My9n18KF/Cqu67eM1d0/5cs6win9fezNuHC779GWSs1n2k3Lwfe9DR5S1BFpUUvj+MoDkCnE+YpwFELRwQ0omZtNSr/m2++wc3NDb7//nt0XY/94aB445JLLc0CY5gTbFIDcxOOsXjHm+MeOfN4V5hSo9XJoesEHqefAxwIczMiMiPMSYz/IYCcRUQ4hBAEsz4B5FjwzWEyzLK/Mo9tvLQq2xOLR35IksA7qRIrQ35sFqHlGSIkRd1/PWKUZwjci7yHa2bAEWKcZZt0gGOGDzMYjDDPIAAxyo+k+6WrVIVlGfHyqMoqU8p755GI4dysPIxEZUiiZDUgMASvPAFEqdwP44cI3ifNWcCIkdC2Sd6NpJ1EDEqiMMvGFOWXRC5idVCzHJoxw3RJcTnSwTEAopzvoOv6nNeBnMlEyquQXAvlGZIqa83gZXMuRtHdeC88kPep5NlzDq5p4B0D3aRw1x4NJzSxARPgY6P1B4C9eo5Dx108+Z1LIJeq5Od61HaaE0seMXv3bGGzCPSlA1g2IKwMKkXPzeqjzUASRfMIIMQZTezgfJOTb3unxhaL8NG2MYKo7l2nNg0CKMFRBKB5TUDqDOOQyIM9kBxjivc4nX7Ev/3r/8Jf//IX/J//9I/48a9/waefP2A4npBCgm86HJoDQB5dd4em6fHu3XeSX4GPSCngNJ0Q5oDj6QSA4ciB0aJNbXZurHmPqxxQ9R+qz5AYIC2XQlLlLUGhkUHgEMGtA1qHZtfh5s0t3rx9g2/fvcfd7W2mTRElP0sZEH1MHh816iahLZYvZ4qMMSUMccaJGUcESVCdLRkC33SKCWNiTDEhqjFhgbtUPzS3RdaxtS1HR2n+hUmNhU6fk+0bKnNYInliWZMNCA0RGnLw+RnL/Yiy0t0cjST3i/Hd3kteCpeEjqSk0RHJOkujdFjV+ZzU2FTlrNAnXYsYfAABAABJREFUZTtEZHFyS0mQa5LBzEXB9kq1Q6iOVTIDxucpt5/nb8t6pTUEbBXZJtCCOmok+p9d12K/63Bz6HDYCfxX1zbirHo53DnX96sXviTD/L28przKEMF6TJokywhjHQ1h32scTJBRJcrMj1MoJYt0aJom54AwA0XT6O+GS22Y9rU3QhbYrf5Vw18xR14riL3oPfbv1BjymgV/7bWXrvt1+3ApUi9EnVoxh6IQWiZrFwNcUnzUECWfwjRPmOYZwyiREKdBIyGOTxiGAU8PDzieTnh6esJwOmEcBoQoXkOG0bnrJR/E7e0tbm/vBILJoiB2e+wsF0TboWs0EsIv109OgrqSzjKslAlSHBGjJpYPZlickEKQo0ZCmCECCsGEZF4bJixwjoAgkvBq5wQuxCuGp1PYELOGnxsiCl56gWAqiV3J1YYIg2UrR2MKxFvJqedXYY6FSdNNksoGisoIsZ6DtvUw/z7W+Gs36KuY20opd20bTAAxdcFz915T9+f3/eo+GciXrrp6K7nULndBI3aNQaJuwHPXX1SaY33Pdju2POey+cVkAxVc7JiiwLaFWSKlYhScbY4SEpyZzN0e+/0eu90Bu36Htun006KxyK3G9nlWmApNVuecMPDmIUqu0AF1QkjmEcgSEsykAGq2pCvF95YSfnG0my7QgLrPtiLtCh3Boh4szi6jIM55GaravTRCLB9p9Arn9azGtRyx+r5az89M9mfX5gXG/IyG6nXn1fwSjL29Y6Usq9qUv7+ksTY6saIXW7dsRZuWi6WOr7d3rIXil2nK4jvhxXn+XFmi5Rivf929r5LjvqC/NvebszV0dvJif7wUXbsu9VwzpXCuQTfESkW82ZavV6rdYK1QOVOwrL/xZ7Ws0FXOBoPSJ1ajcQaX2/38uY3JpArd/HVBQ5cfkV0jYhLeV6CJSBOxyh7UqDFi1+/Q9704xzUC95llhJTAatCv6atzTnIlVHMhVTKEXpj3BZAprgTiKWqutKQ0iHNegyUygXnX59wrmf4bza33h9Weo1cxFJpItV3Fg/a85DVsf1R9ankrknqRJ8WvraM4SD+JKCvmYkrwGj3iiPMc2ZolVB9tu9/YCynnWTIvZVrl/ar3Sc2n5UznkUSZmKBjm3RMxbObHInBhFkdTlJuL6r2plR0KEVcqqASs5+AtMU3rRi1FnkxSSMeSt3Z36GagylpknRVTEaNNnEugcjBO3EuMUdO3wLeMxoKaFiSmDMYbYwAWQJxIEQPzwApKI20Q+J6wArX5SQyxDnN30DmVKGQNRW9k0ga47fKCFPmDyp+ahHZW+Y423qQAQNDInRlLju4ZMYpJ/BAeYsioJr1XE8oNXjJcqudE51GCTHmJHkSn46fcP/pR3z48AN+/ukv+PDhr/j48Wccj0fM04yWZPxcs4NzDbpuj6bpFAOfEOZU8keGGTHMMj+98RvWU5zbavxTHaF6iYYueU1bK/JO1ZtLF+ubZprkHVzr0fZdpn2tJiiX5W41cG7B8tmmQ9FYLC5K9JjE4DlHYEbEjAQxmxWIrpkZgXX+rvvgzJljwzhhtIOre0jiIghcutf2Nir1yfgvOPY8DyRvC9ssqdpQyQ+rj+hfGBY5ZkbPvCeQ3UkawaFvRTmPu9q0K/0FkPNHmO7F3pNhRCatzlf985ml9Ivx06Xf7GD7ymKfqYqNJhEpOoZH4z3axqNpVEeU9bznbbiEYPAi+smVOpFNHn55xVX1/NLlc3U819z3axh4rjZEBLWuiyU/YZ5mxBQxz7N6g5dIiGyIgCwaT5I8yBSiTau5ILo9mqbF7nCDpm2x2x3gmwa7fi8K2LbXzXcHcj5jG/qmKBtFYPfGOeC3MjH+Xn5/pd5KKl5kyVhXeHprA9ys0EVzFAy/4zhgnCY8Hh8xTgPuHx8wjhPuP33AOAz46w9/xel4xA9//jcMw4BPn+4xhxnjMIAI6PsOu36Hb799j9vbO/zpT3/C3e0bfP/9H3DY3+Du7h32O4Fp6vsd+n6HrhMmodUwWlkzktCdyOVdNkTZmHLy+CDGkzmMiClimE+IMWAcB4QYMU0TUgyI0yiGiHkAcwBzkGRp4GyI8Np5ElYHtI0w2m0jisOulQRXra3nSwYIXyKd6kTT3jVqwPCKt64RUkTFAKG0QWNmc06IjIeaoZeMATDi7DY3vM35cuG66/Ul128Gv6WyVl6+6l78cuqVzeetBuPMiQa4vGWslXe1Aucznu0uvPiWEuvsnAoizynEn/1ujD0tlbCkynoLR7YxFYFV8FIZUUKi1TsnpIA5zZiifE7jUaIhHu5xfLhHGCekOYDDDHBEv2txc3PAn/70n/D+/Tf49tvvcXvzRqK4+gMOuwO6rsO+36FpHPrO6XbOSExI0NB4R/AscA7et4gpirej8/CuAfuI5LzC33gkR5AQfWXIUVRw28p5OWaAAeeeSzpwft/KMcKS/BmEQQ2zscxv4zY/NhbmtVTDXBTmvzyLCBoBYfWfR5mVeXE5IbXMtMur9Nl1v9Yy/MLlc2jQ5cqe/5nJlAKVBgj19/LeF9ul/WPK6EX9n/0ea4HwBVpwRkPOx3/9/fnotbVW/XyOXWw5rXQJf9OyVEpdd/1nNn59a931vL7w7CRenKzPlr9lh19SmNn3l97r2rHZuJOLR3qMdaLP6rcgysB5DupFT5KQFS12ux6HmwPevnuL25tbHO5u0fgGzjdZqWYtXBeDIZW1zxm+NcwzmDnLtpmeK5QKsyic+7YBpYShacD2nCSRAwBjHiRHwTx2aMgjdhGeLIvAdp+Teod75xFdyk5+gET6irK8glauDOCmLJOdIiHjIanSi8GIJHAbQffvBIE58WDEWYw3vplEGUUApQSnyu9pmkUJ2fps0MnJSqnmwzgTESISGBIxOQjv71idsFKOpk40w3IwkSZNro0UIkeIfGLe1E6jTBInkOjlETmqN7Ip22SPYHKISJjVOzkxC0Z7tL40BwkHpwmi21Zlm1Uup0bzYPq21ajxJiv4zIiVkuTwS0khsdOMmAKmacY8B4RZ4bKDQWTLnPCuBZFT44ZEXTRNg9PNiLZpsN8JbNA0TWjaVr43Dfpdh8Y36DRHRGPJsMnBNy2cbys+plk6jLpCY1nXpGrFq6PJYbUBSb8nquQ6W9cyD1JyFSwZI8QIsV0M0rfa3q5RODXNK9hodAmzAxEjNbPyxZptIbayJrR5riEkmjFhwF8//Cv+7S//E//zv/13/M///o/4+acPIsePASFE+KZD0+zg0MBRg7u7d+i7HvvdDYgcTqcThnHG08MHhDDjdDplvYLzHr5tNVkvaTQJ523KoKHyet4wAdBCGYysWDfFLzvKSZcBMSL5JJE/rLyOO/Ro725w+807vP3mPb775hvc7nZouxYGgbU0udUGWNE5kNIiTo3w9EwIiXAMCY+B8WEm3HPCRzcjwUlOR50rMTHmqFFaRm+wlc9gtX8YsVLYJFQREcxAzAIZwbq19JxB5kHpRPklTwRy+kR7rirVmZGdHZ1FV7UghdHipMYWToo8ZvygJJ0nTqCohiaDeWOlLV6Mao44B/yxGoopRXCynDx6TAnMEhEh76+mHF6all/LTVzmu3XcLcemRkXliDtDmjB5hsQc1HqPvutw2Pc4HHoc9jvsdz32fYu+b+A7nyMF187A6/J706f8vbzCEFF7fhv2fVbEVsyKGCCyNKZ7hivRD75AMjVtJ56QrX70vFflqX3Iew31K97RyEJ15TmYie2CbCyI9eeUa73Evp6H29/2WZesZb+HBX6VqvBMx0f5fMFR1T6wiypjhP29NkTkT5gxR4mEGOcR4zRgGAdlOoYc+fD4+IDT8Yjj8QnjMKqyP2aF0q7fYb/f4baKhLi5ucXN/ka8irudYkz28llHQtj60fWSmWVGZh6yISLGHMURY0CYJzmGCTEEzQURkOKEFGdwEiUjOFT9WDxIQBoBQdAICFJoJskN4dUAsR0Jofimec0bVmmVAyL/3ahCz2hCHQlBAKkg5kxB6DKtyJ5neU5cVk5enEoXfr52eQqv9/LFn7P2fo31+hrL+i/17GtLEXo+r60vzITts7Ueibauoq3D9s8vzMmXjRFYNILyOli/w1JhUSvBE1KGtIhJ+IAwz5jnCWGeMKvBkpOEGDsAXdui73vs9wfs94dMsxon/IBX+ARxVjCmVTGsWb0WnR6NLqggZR/57nK4OZEy8VCfL6rf73x9156Qpb+fW8fFW2/Z50XQK59KkIZ+x/qaylutatOa6b7EfJ8/97wd5T23FX55LWM734q1o7524wJcmOibz9q8fbU+X/Jmyr8/axyxamtP7BfeZatxlUC/8EQsMm0WDuvxWyjtic7owWuiyzYaVh5uhVYjuPF98ecraUs+t/Ho0qaX50Ft13lt+WIeeGP9Ll/oGXNcfrXr2sBncw8ooSTL+VmqrDePC434nPJFe7X0y+X1b4cNGnX2PsvvL4/n9mR7zTo2BYx5xxqtzEYAMzybhzWL1zdIchw1TZPzrtXR+TIf6LkZA1OmJ1aP+coAsqbrRqWdE+VqUeySGjSkPzIOvhpYJGdEVCOL1bSiC9UeYecy017NxawoVttP9ihe9iiWHrZVPzODkyibxIAe5ZOcQjfFHBGRkiKyp+X7xJTgnBnkabU2jEcwWmRe9GVcjU9Y74XGI4BIIJlMGQgxQjiNfACnRSQLmbt0NdcSqjwPlYLdemsRwaj8ixPH/RwN7pt20ylL4CgrRZ6+u9UrxrMkBgflxUKcMccJ8yQGtXkWpbj0J4uMBIJzUR09JfoBcEiJ4TuJ+LCIiEYNMo33YE6KbCXwNl7zp4CLzGVRCfbSjj3YFOnJLbhLWYtlL2FyukVa7zmAzNC1mnfr+aZ11XWDxXgkk0Sw/T1FMAMNkypzjTeTaZXnrtbjnGkFJMF1ChPmcMQw3ePnn/+MH374X/jpx7/g44ef8PTwiOF4ArMo4AXuqoWnViIh+h5t28FppEOME0KYhH8OQaGXhB7UK7fMJuR5n/vhbC8vfF7WZtg5m+OE6u/lPu2queq8g+86NL1Ap/d9h75t0TRiIDUjrrRjxZct3iBnpgFDxiFBEksHBuaUMDNh5qR2PYbmfEZiRrD1xSxJrF+U4Tbo1NZpPbfBdurcoEzfmIv5w455LufJo31pnZP7oPqYbmIlYJD1GRfabOy6jZ9FcmFB17BMxF0bGYwfxeU+W68syg/+PLl+qVOpzpEYFc+eRkpzvRgF5UNoPMF52TOzEVrLc7LQVvlc/cSz911Z5e9Bb2rlb6XPudoQMavnxjRNiClhHEfx6NAIiJCibMbG3DWqbPRercI92rbVhJU9fKPhab7Fbi+REV23E2imrtNNWTdn9Qpw6tVNWVFZT04TC75QOPl7+XddLs0O2wRq23dlhQCzhBRz1HluURAaCTTP4iU8x4BhGDBOIx6OTzgOA+4fP+E0nPDTh59xOh7x0w8/yPHHHzEOAx4+3ss6isL03uxvsNv3+OMfv8fNzQ3++Mc/4ubmDt9/9wfs9zd4++Y9+naH3f4WfbeTBNV9j67rCrxJlVDMvEdqhWJIkhPCIprye4QTQpwxDI8SETEN8q7zpILDDKQA4hmAJKQWREkv1nwieN08Gs390DYaAeFFkDJIJu8UE7VmtrPhoYQMO9/CDBHQyAgzUjK1gGtyqCJXsG0iYWpOCDVAmMdXVgpq0th6k3vR+AAzuVzY2K9SkPx+6dSXKM2uYSH/Y5W6N+jC+fVvX//Ji/PKhNRJNcX5IGKOEVOcMcYJx/GEx9MR94/3uL//hMeHBxyfnjAPA+I0wTHgfIN379/i7dt3+P777/H27Xu8uXmL3e6Avt2ha9SQ2rUSKdUQXGsrLImAmwgueQlPdh7k1VssiREjqjGD2ZJVJyTn4CDQEiIOnK/vS0aIAl63PTYLIaE6Zwyz08TeEgEqBmGvURvklXb5VSREFiqW2MhlTEokRP1bVk45r0eHOiKiNvIu3+U/6iq0pHmpEhar8ky3rL3AFt9NEFWp1n5bC09Fsjyr/AsUxJXAv0WXc9s2npl/et2z1wb887bXSojLkRFf9Npfobwsmj9nBKCNa7bpNBFWc2dL2OPV8VKbLj/n1ym0+suoZd1+Wt2x1Vef+9yVwosueWcuS4ImPE0SkWD3dk0LAmPX9xj7CU17RAzi7c6aXN45wuFw0OjjHk3TZl6aIXnIfOvyflkbnEyJlBXLRNmAENVjPoQgRvRyg+qzFBKqaZBSQtN4pBjhnVMv9xkJCRhFITWOreSKmAMaciLhZxGZtOssOjIJ9JBGDUtcM+nRFb/jyOL5r7plMh1zZaTIXsdEUpfenBAQlR4SGMmJhBXjBCaGnxupgBzgIYpYSM4LMGOapZ+bxvJr+fNZQYBnZPgfeamI6J3gu/uEpmFV8gIxBXlLbkSZng0YpONNYgxxBJcEqpaINEErLyIRhCdS560Y1CCRMuZ+7nuFhPXeSTyCOic0KvtI/gLS5M/r/Z+BJMrFOecYgUaqzxinGUeVOYdxxDgOGMcR8xzFABFCzg8BQCIhnEfbCeJE3/dofIMUGU3jwT6haT0SgCZ4RE5oG4+YZrRNgxglMiL1EU2r89ITGueROMFHFs9t5+CSOpFaJLoTIwhWym/L/cC0VKzrCMvYmLzGgO0pXFWyNviIF7nNVeFnCYw5BPEoV16NOcERoXei4E+zROFOLPKi6wgSBjPgePoZP3/4n/jw01/wr//8T/jLn/+Cf/nnf8F4nDE+TYgRaMiBqQOoQd/foml6HA63aNtWUAAIOD09IkwTHh4+IMwzhuGkETMRBIl8cQrvxkmgkomgOdBelk9Ney12r8oIV01JQuFbvVM5mGUtOefgmhb7wwFvv3+Pt9+9x9tv3uH2zR0Oux6t5laUaKa0pMj11GejJw0YDSI3CMlhTglTIoxoJEl1mHHihCMFRGeyPomvY2KkmIlOMXy8SPIrLf7SjiMlocy1VXUyUzgbHLIjVpK54RyjVTKqmWak88wIB6dBYhIhJTB/AKgBkECUSr4TriK2NR+OzV/TNDiQCiZiLHTMSFEME9HGQSPYiKX13qBt9RiT7VfWNcUgVRsffimGzHRsACFVRiuLPuvbBvu+w6FrsOs8+s6jaz3azqNpGzHeVeX3pOD/e3m+XG2IsCQ561wQ0QwQWSBT70Tv1RDRKP5zW0U/SCRE22hERNNVkRCmZKwVkw61V+HSmlgbJKpzzxCqL/ak+oXr+9p1v+TltvYoeo2l8bdSqNpQXuyxs1eTzUqs7ZTl8twHlfVVvIFLyHJUZtQY0TlMEgkxGUM4YBgkGuJ0POLpeMTT0xNOxyOGYcA0SpJ31mSwgqXe47Df4/bmFje3NxIGfrjBfncQo0Pbo+16zQXRyfrxS+/i4qlF1XJQBrryorLIphBmpBgR5gkhzhIJETUSIkXEOGvYX4AkVIqQLVmxUnUMHJAVYt6OGgFR54KQY+0xTGfrvOSHUCg2M0RUH9ngfVaIlOiP+v1dCRWk+qhz54ISp55Ty9lSb9zLtXN276UpyNbeS79/+fq7VkD/vZZL7/ZL0uNL5cVHbk+l1c+8Ssa3vMC9QMdf+r5Ql21UVXfnwhN/Qe+iREKkiClMmOYR0zRiHkfJDzELHeEUJRrKe+x2O+z2e/S7nYb/a/SjbzR6qxgls9BkyqwsWF7utZrM1b8UmfT85ktGiKJfpYUT3tLosLy3vmbpeVknoHar37Y/W/Vu4Z7W19berdfVe64oXLwH6OznLa/jy6HZ5+evX5P8+XLQS8/Yev+VvucyPZYLagXj2XfTfBgDUalpi1HiwkP4mYe/slzs62fqf+3+la97se7n3+tLX/vr0/rVhHiJm+Tta7bW8HrtXPpuc2u7TefPeP0eX61RU9Jc4GOuqk35jBIRsO0OZl7PeS/coCnPl+3NYD2HSv+d81dKSRf8lznDePXG9Jp3KJJ4Uos863JEhFxrBs1q/6jprPUJIdOE2iBscBWWh4Erj99cK9l9svebY5/B8BFt7c8WFWFRFtYVuqfaRlnLyagVuuptv0WitriXyvPdPNAB9crltPowoJERKUVQdHqMcD6BXdL8GmqkMTmFXX6MTZ/FuFbjX0dEGArQci+0cadsfEBW9SW7QcdQFdmoHDJSWhwtB4a1zYqNdWLkiI6sHAZUz+EylKL3DrUjnL1PkiQdeTyjyaGJM2TuOE7q/DbhNJwwjhOmcSpREOplX/ajRqB0ufioixJVXdBhEQFJYXQiUpJE684RYopwqRxzlAsRSuSLjlcisJM5So7AiQBNEp0nGenja5mMVut3PR83No4yL6iQtfyAiheydeVKpIDoik0xmxN1IHLENA0IccAwfcDj48/46cd/wcef/oqf/vpX3H/4iNPjEWFKqiwXuC/vBTK46/Zo2x26dicOtTBItoB5niUnxBwkcujsNaso2I2oqXr+r/tnzenUFLnuF4JCNFGBJHV6rm1bdH2H3WGv/HuPTqGiNml2Zm/MyU/pChMSHBITYv44RDtP4tKYdAWm2s5g88i2q9x4zuO6zTBu8aEb57JWfl0UPk0Nj2QfAJGhtDp3rt5BalRYPo21Nq6+gyQSS86m6uq8OVbHVZsr1rWWewrbyXleg0q+vPz2tLre7s/785begLam2epNtd/yflP1Jpf1vOgHm4Oq72285Q+lnFO0GNFoVd/vp3y91m7N65oXtKdtX/dS+Vv169WGiNMwYBERMU95cwasIwpDZ9EPkoR6B9/06Aw+ZreTCIi2l2v7XpQSbae5IAS70KsRwvsWRVFJWOSEWOxUxnmgOv69/L28XLIXsG42S0gMifyJKWGuIclCwKSwJPM04TQNGMYRT6cnnIYT7h8fcDqd8PPHjziejvjhrz/g+PSEn/76V0lKfTwJFBOApvFo2w5d1+O7777D7e0t/uEf/jMOhxt8/+332O0OePPmPfqux+Fwh67t0fc3aNsefbeDbxyaxuX1B0tKrYQ/sTD5IcySCyLOiCnJeo4R83BCigHTfEKMM07DI1KaMc+DhHrPwio4jsLoO/UVoARHHl6FJUs45FVws1wQgh8qAlSTvXWNYa8TTJfvEgHlQV7oAWARUXJevjcASoSU8yXBNciSwFmERBnvbJC4mkj8PonJFsP4t9zEP297/Pfx/OfUWi+rnb5eG4oSyg5rxY4kUjQhdo4BUwgY5wmnecQwjximEY/HB9zff8D9pw+4//QzhqdHjKcjpnEAx4i28eh3Hd5/+x3evfsGd2/e4ebmDfb7G/T9Afud5LbZ9Z3yCh7OA86JkLqYpywMOysmbTYO208sERSkci6cCtmp8jKtFF9LBT0Wx5wjQgW0y4YHWvxdfyxKwZRWhpdskVxef8uREQY3tRDyLApiOxLCji7jsJ7D3K3ftQz8l6+CTUOn8V6fSWNeNnR8jbLVF1conZei1cb3xepaaANyX9HfmgL+AuW5V3rhfS/qEa557Fc3QqyLoUR//bVy+fta8/Z1nr9qDBZzVxjeV1TAZyslGyMurN98/oum/3PjXfeXfD+fH8ITpwr/nAgKs0TYdR3mvkPbtpgbgSolApq2Qdt1uNkfcKP5jERGVYWm0Vg1LKjrvLVClHv6LNsLYopgMFIQGKV5jgAc+jYiqdGBYLl5CV3bggD0bQeOmry6ysWIEOBmj2mOaNuAEAJC02iyZ9vhs6YQBRS9JI9NJImwmSQiAgovUyKpkf8GFwgQQgXHzKaMkygKUT4iOx+x8uFpnoDECL4R6Bzv4YjhUgeonMUEzME8wTs40uqp9K7ti5R7u+yNxJKPwzuHaNHhWRmmjAJbHij1QFa9IBNEAc+adyEEjPOYo+CDQu/GVJwybQ4SUTYYsStLS85rNLhFQLgm819Zn7KQQWedH+oopvA90zxjDhGnccQwTXg8njAMI07DIImPQzGSZNnIHMMah6bx6HvhQfpeoHPbFvANw3uJapc2y5pKUMivSIgxwDkgpSBQ9ImQSEJvUlKoXpI8XWAGkiud6gGCA6XKKAAA8JnnyuO54ssK2Sp0sl7hjSue50I1SZWimmzeN9n72jmPtm0UmkqSwHtT5jkzqUYchyf821//Kz58/AH/+E//bzzef8JPf/kB82nG9DghTjN4FKx/abU4y+33t+j6G9zdfYu+v5FuSIzT4yPmacbwJDqD8Sj5PEifT/ntZI3lpO5RDHR1yWvROWzKsca71tpquTMr0YkIjaINtKR5xsij7Toc3t7gzTfv8P2f/ohvv/sW3757h7vDDVrfgFlkg2wZyGNU72MEhkeCQ0wOkT2m5DElh4EJIzvMrsfsGDNFzNB8cBCasdLko5bYufRS4TFe2lcIWFhYLf/C6rK6TmZGVDjayAkeBA9Cp2TeqQ7SmpkIcPr+rLkwEgOBDdpWGunIQyaN0U2L8CmWF9bIB8u5k3NcWJZ7NSLSGhJLh9w1XuWfiBQBnuVNrY/PBJ/89jpf0hJe9LMKqxFG5beUOOukMnCYomd0rce+b7DvG+zaBn3r0XmHVmmpDdTvzQjxWol+JUXgXEJ/iYkqVETKy7na/tbl+mTVUaBcLCdEZoAAZehKglmJbpB8D23bwjcdfNOjafsSCaE5ISR3RKsCeZOhWRxRlXi2wrg3oroYGVoc1uVrCyx/C4/bv0V5acGvf/9cb6rXPPNLyqW6F15IUCJZGSLOPWGKV3DQSIgpzJimCcM0YtAoiOF0wul4wnA84nQ6YjwNGE+jJHoPAZwEJ9aSl3Zdj93OsNT3Al/S7zUHRIkeklwqbY6CMFgOW4P1xmKRSlHxWOekyeZDQEoRs0VChJITIsQJMUyIKWgkRKX8g3DrzFCoQ1O8uRxafJZ4NUc2KK6hM4z0mlEyL4oqKgLlPGzjzAaW6r46iV3leYwseNhv9ajThb/ribH+fSW8Y7WHv1RffcVaGYD1/FxvNktBe+v+a8qXwCp9SckWe2nEr/58bYQcPvP2r0Kbruh7xtfdY4oC1GrHhU4wZQOyd6ZEfwmURdBkiHMImMOMSWEApnHAPE2ISksMQqhpRaDZ7/bY7Xdo267QMV/TL1OmI9MEZddhwgBnI4SxsGtvS1OGiEBClVxCpu2sDAqXjBD5PCqaUSs6FmRjySA6Kh5m5m25iIowUYrOP1i0yTwLOb8/Fo9dGxhqz87tZ9Tv9lIk0Zbn6yWD5tl51n+unL/n+7/c+hydem5tbL3bNo9xyQR96ZnL+td9aVOs3G436J/5fUyA/nLe6aVyff/VytvFlS8PY7n1mQvWipDlz1/26le08TNKmUcrunn2+O2H56lQJs7y2np+q7C+pcxfCpSXmnChDbYWn2t30ZI++4zFrRdvKTyLvO5KfNafebEeqhY+197n+iD/JJUvaXR1ARnQRaEvtWd84aGX7+Ybr841Hr7RiARzgst7Vb30t4y/Vqe0L0f8k+yVstdaboeSa03axlmJ7Lx8zHs7KyPVO9+SIWcFZkqSH006vXovWhgWiuOt9dV5v29wrEXlwdW+wbL5Sv1V7kj9CHRVFIz4GAAipBghsCMlZ0TK71IjnJf2UaalpV3Zl52sn+v9cjknuZqrMgbSPpPxJF+eKP8l2j0szhusloypE26FTAkpWPaMshZqA4W38TeFrSkiLcJC+yrGGSlKUvOYohyjOJSFECW3X4y6niBGDi9ylI2tzVWLOm07iUSVoyjkxXlU5rdB63q10SzHvfAkKVk+Eo9EETGKASOlVGCFOIkajMWwJr9VI6UTiIjBrAYAox21Mrpe46CFQrmMKeff1zIjqZxoa5ec4M97p+i92hYGI6QRc5zweLzH49NH/PDnf8bHjz/hw19/xOnxhNPDiDBGhEHh2xJA1MBTA+87ON9hv7tFvzugbTo48piDjts86xhKVJApk20i5n2HlnzYK6jzqsMs18SK0UV5Z6fEplEe0nsH34iDcLfrsd/vse979F2HtjFoKCr7y4oPFppa5HfASeQDHCIcIjwigACHAIcIIJEv6zs3natxpupf/TnT9up9L213+ttiryHrnw3etraAVKrhRWQDSyOM7zO9Ua1ILvlj5Ezt6Fog7pCTN9sxG3rz1DCayoWmar2JS5vznCHknHoZsq56zYvzKW/SKEytrcXVXed8yqoPV6wf60ZRD6vdZdFhbSOfxjs0VW6cQic/Twb/XD3js46chd15oZL8z3VlKUisf6wrvfj7S7Leb61cbYgYJomICHPMGIkAZWx3MyZIPohGcTQb9R7Zo233qoho0XZqiPCtKFGbViMfxBBh0DLeN0LkvC9MfV5Y64H4BaSRv5ffXSE631a2FmNhwFcKgep8DcdkkRDTPCszOmMOAeMoSaaHYcDj8RGPxyc8Pj7ieDri08ePOD4d8eHDBxyPR9x//IhhGDAPE1IQ3FHylKOH3r19g/3+gG+++Ra3t7d48+Y9dn3JBdF1B3Rdj77bo2kkekIUehpOroIUQBlBM6qAMgWJfJimETFFzObdM4kBYh6ekGLAOD1pZMSTMJlhAsDZgUqSxkJ5PFv/hbkmywvjXdUur4mrXSWAObVyZ2kBRMrkUKMbYgMFewLBA9WHUbBGS6RU/dHcEAts9LPZcs2M2phjtk+fi2bA9ua1Xe96Yy+MhwmZ9TOtfMnm8ut4HD/z/F/9iefP/n1szV+/ZAb5Bcao5IRICDFlw4OE/gvM3PF4xMP9J3z68DMe7z/h6eEe0zAgTiM4RRAB+7sDbu/u8P6bb/Dm7XvcHO4kCqITA+uu79F1rUZCEMgVhUumvSmCc4LsiMRBDKT6SYrhXCIl9APFSiXj68q+UCsm5Hs5DywjIrYVSttr3pJl+zNjrHjemSBsURELCMoqgXUer2p/qhXgrmLQl8fz3BBb7dcW40tXwiYtyRL9L1D3dXd+7hM/876X7zcZjn6zhIdWx/X5l8pLL/YS5f2t8+62V688Up+5+tLvRYxc7v+GSH3ugejwZet0q29rvuJ1fZ/lsI0m1ca6i9USQzV3GzTiBaPLQvG0cWu+Zus++6NquyrJHDnAscivXo3fKN7kXd9it+sFmqTrKr5Wvfs5qSd9yjxnHdlWw/JIZIRD24rMGyKDkuUvkKN3BDSiMHWqlGV4MDHarkVMUfOqhayQAhEoRPRBFOZzTGijOEv5mEVnmU26RabECHp/ji6s+iWRkwgJLoowYuHITb5YjAVr5QA4MUCiKAMByRGiChGek0LRRjBJrgu4Bj4xfBtEvg/iWR+ivGtS7+LF6qKyiqwVSfd6JpFV2Ev0iIsrOJms8EtILFCzxk+M0yD58cYTQpCcfzFGjOOQ82Ky8iOAeDeL2FX6wpzWTN9eJ5921Z68VCwqVG6MmIZRHN6C5PALk+bk1Ej2oJE0KQqf03oH0rnJ7AQCqZ7mEN5KDBEtfOOw2/Xiidx16ggnuTldq5EDXuB1PUGzhwh0kxkgYpwBaDLxlAA1GjUNoKksJGeoY1CsoeeS6nRKZERiBlECJ+HLcnLwBEjkiqpYdQ5QpgX1kDLAQWQ/dWJljbQHNNJeI0KcJ7S95fPSvBtoEOKE++Of8fj4Af/4P/6f+PjhJ/y3//p/YDhOePh0AkcHjh4hMOYJKrc6dO0NuvYWd7dvcDjcot/dom17TLPw0MPphGkacXp6EGe/MCBxgPMJRIwYlvyezdEyhpT3hnIdAdnB5aw7UN2c5fX1eSJC6xySc2Ancnfbtej3O9y8fYM3797im3dv8f7tW7w93GLftmpsEoii8lgq7QBUXhcZHvCIaDCzx8gtJvYYQRhBOKLFkRjBtZrrwJLaZO26VqhRThk+THWB1oJnlLc5t7Uq90sRHabVbA8ssQm1EYLzHS5/k3nrWA0MZA5cFrGQEFjXtRo5DeapBee1D/1NiTKQEjLgBEhOm3GSk0KuSb6+YBB2nBCZETllmii6msoBajVGi/lh77jaWtmG4kVxYXUBm5wpN2eeIEUdN3MKEF1N2zbouhb7fY/9rsO+b9F3LbqmReNsLq2b/RuAnr7AC51dhs/n4uhLbv7ip/865WpDRMacVEUGZTgAC2+T6IbGjA1tj7Zt1Pgg0RBtY3BN5g3ZSPRDTlZbR0CoAtKUfaIZ0NaYFwRVa6RaLVWfXzNZX8uMv2by/62iJ2rFxTXtXV9Tf3/ut2vOX/PcVwtEV16/VuQYlNja2JDrra4TI4QYIswDJmo+iDkKxuM0z5IPYhK4ktM04KQREeMwYhzEWzjMMzhGIDE8OWWUhKFqmhZtK8a7fteh1/Bw7xuFJxIoIlfnR8g5IFDttMrQpWKJD8rkzkESqk1hlvbPapiYR6QQME8jkp5PKSCGWb2XYjY8yIaCklisEqYXXr320c2GueA+SrgfQI6FMQCypiYPg/EgupyXe6H9yEhke93GXOXCNBMRzqYmCfUwL1Ve0erslb04t55b5+fsPcr59QWrl0QtrL6uPHfPS+vjSzfwX5oBuOjNi2dVFc/WcUlX8SXeEb/EPZfKJW/vNQTG2XWX9IxWr/7DXEdCpAJBZ4YJVXJM04RpEtpm9E1yQ4iA7pxApO32e+wOB+x28rGICInmqpI1k6Es8lljhWwUjOmzTxUZkd2LlDLVsEpGAIpnpPXXcoxyhEG+9mVDRDZgVEooMUpU0V1qiKXFp4qYQGVEVb7mPCKiCPPrdp8NbtWNZ7SzEN1VX7+erznbv2tLKl5PJ2oFw6Xog9fVtXV+XV+l3HplebFtuWqqhqh44X0tOvocnbmGBvEGkaDF+UuVGzf+zAX6hAuN+xuaIa7fP7Pi54o5wllRtqiweqRJLzoHVIFJLOaIy/PzdeX5YV++x2v2qQWZPqv1koep/VHBPRgtAxbfX2zzJiNmNb3Yet0huLzHgv6uZU6JiPCtzwaI0hJGPftzdepGfr43lz3FOQfHnDGwTS6RHEym6irtyHkPNHpaIEhlvjCzRDWrXGLe+yE2CNESLUvOhKRKX5NtWPd9RmkbYFHVNbe13GvyFrLYc9UnV4eS1TCTyBTXBKKodalneowgcgLz4gJiikDyomRf8STILbL1VUcRVauKWXHvGcm837WfLc8WAxJFkiI4BTAHga1NCrkUBXbX+lQcM2JWJi75iUpQgf1Zre/cTQJxJC7oUrKcqZGkllg6hKBJimPODwCwKE2JAO+QLNrDSTLoJjGamGBQW6YKyTNU0U3aXiIguk6OBqHbVNE+wq9wXi32saiRFAlRFfghhCzLZcirzEdxhsiy/pC6lQ9zTn9XL/r1fsiMjJnFum4pIacIXsh2VVtrmsCocgRK85y3NcXq3BLx+PiEcTzhxx//GY+PH/GXf/s3PHy6x9OnAdMwYz5ptK9G6Bgf27QN+u4WfXeL3f4GbbfTOS2RK/McEIMYmIhY+pXMsFPBmm289jnPC8knkTjnVKyXZtlmeGvFLnZ3U1AbkkFSvVvTNmi6DrsbyQ2x63foW1EIG3wVTPdQSefn/KhCZakRMTIhJkJg+zhMTJgZYgjhiv9m5PwsmRZrvYXDr2nsmVS3+GaRAQBydJjpD5ZUHNX8KXOJ9BrRSpY6ipLYDGWW3rpEutl/GtOt+10q0Q9G6FgMeXVUhNEaSkbn67yklrOvGCHE/it1RE6S1NrovT6/tFX7ppIzDBKseqPcScabW1/VSzUb20uHyz15zepctnVczSPL0dQ0DbqmQds0GhXhi5MWuSK/V/zR58rXXyKXF1lncbh8PVByz2p5le6mGqyXIjvO5bK6FS/LG+f1P3v5VyvXQzOFUDqcSJSkzqNtejjvM+xS1+3QNi36fi9Gh65VQ8QuwzEIJqfLkRCibBUGCxBDBBGdQzLps43hOBMNNpTaXzJZ/z2Ua97/WkPD77GsDRA56Ze6bNTnAfUY4mVyMPNUWeKDjhinCcfhhGE44Xh8wsPpCQ/HJzzdP+D0dMTD/b3AMj0dMY0jOCR4BrqmBTsPlgzP6DoxPNy9ucF+f8DhcIPd7iBJqF0HRy2IWsmN4BqUhM2kyjvZXgr2LRA0ifwUhckaxwEhBEzTSdo/qZfPdEIKAVEjIkIYwCkixUE2VZ0/FkacQy6dYcuWcHegMBKAy8aHkMRrwKnAkCiKZxUziBw8e+VrjCHVxGZIcmT7TXBGs5jGACXDhi8eI8455AuwJq6VcAcCPOVN81yOZZB5X6CsJeN7hDFc3nRBH1fNx2X9l7axl9ZgbUDbWt+XlNbre7d+/6XLb8KT4d9JWdP3TXpfrYXnrmMWIdtwj0MQrOl5njGGOcPOPT494v7hEx7uP+Hh0ycMj48Yj0fEeUKKAb716LoWb755j7fv3uHd+29xe/cWh8Odws3t0LWdCDzewTvOMG+ZeWdh+0VJIiy0QU9EhSMQWAAVDlmuAXFOPOiyFyVQKzwLS7EUnrJBwUQ0MwxcMDzUx+ztaAlFFXLSe434cAJX6XyziBhbRHOZcGj0SAX/woTKZ8kWrSPBqAhdtMEj5Qmh77JxlrBBCn8H5W9NUp6ja3Q+CPme30LZavXmlrgqRb1xjThmtaXF2d9Puaa162surLCzLjPF3bZi6pcszxlaNwXdpUS9rg0X50JFjK4yoH/FUpx25GPqmFoBJcmgLYqNAMeAd2h7SdraKZxwrRQETLnCeU8lhSldGBttG1KDtNfrmjkgJs57bZiDKNFTK3mOdN9KDuLF3TSIbdQoQocESO66lIAJGMYB3jvsxhHeObRNV5TYaiQXmKQCu6jxgwD57DUuEcXFIbBev8aB5/0092ZRBEvQC+WcDiGoEpsZPkXl05N4rKcE+A6eCW6ewSD4pkdynKGmrK9BxRv+zBihe6eTThf5ChCoIa/5GbxTRSAjxgAOE1IYwHHGNB8lEmIaEFLEMA6IKWKaJ1EAzrPUqz1hkQ0Fv7zkrjJZqURdyDyLCJXsUORMjkGhmBRCd5oUnklhl8BwJLkEkXuZBNaGJdmv8EqEyBEJS8eNPA8BtK0gUXR9l/N5OqdROgueRvHnWSCEU5J8htGFzHN57yVSw3uEGNE0Ca0qQb2PcEnnlDqVxiQynU8aJZL5H4Ao5Qig8uGsAM6WFFjuP4giXmYDsuipimBWPHp4pa0khsamITQt4F0EKGEKDzgNT/j//bf/Fz59+oB//qf/gaeHR/zwr39FGBOmJ8mXFibhL5kmdH2P3c0NDoe3uLn5Vpxt+ps8N4fTCfM04HQ6Yp5nxDCBU0DjElwDpGie8EH+VlWcy+Mo3Z5CRFKjBjlGDAmSDJuzAWFTjjR9chZEl7RQDDKiBO6cRJA41wDeo9nvsb+7wdvvv8Hbb9/j3e0d7nY32PtWorWMGmiHL2UJk68dAK9RVQ4zO0zJYYyEMRHG5DCww1MCnpgQvJdoA+dF3lfFe8wv4nRUKVPtl3in0iLZdIyW1kK5aU8yteZC18wYQCy5GpyOksR4aJ9rnomkg0YpSutULtGVmI9J9RwpRjEASCgMENWhKkWQ6V2YF8YKgWETeWyeZ4Qwq4FUosODwd6lBNK6nB6ZY0bHKPOCMz3LSnVdMq/bi43G1JYJZOND7kuSvDtFl+tE3ds4SYredzjsd7jZ9dj3HXqFjHNeHdSx1Fv8bvQIZDOwPvVrtf153vy30odXGyKKdcyEboVcaSSyoVWopbZpi+djq+cN19438JawURk+UoiCBb49lU1DaN254F8fv7Rcsir9EnW/pvzS7/c5UQ/XPuclT8FLlr1rLX7XtKFmxLLnSWWIWHsbgBlRbkRcRUSIIUIiBuYYME6TREFo9MNpOEkUxDhhnCRSIoaoobOAg5MkzV7bRiRJsRyh7VTIUYgm3xgWrSbpydITZQaDtV3ZWUTzHpk4MMeIyAlzmBEUUirEGWP29pk0/FgiIXiewFFzQrBseABnbxVA8EdTEuY0soSNI4lvioVdI2koroZmi4k+yfuaIh9O9iBlsNk5GCwRkWKIugTyDSgRPATqBRbGS/KdmPT9C96vwbqYN0NNPxbCVCXQGOdRMzcm1JypFcgSZMk/zM8L8p9Trll7l9bupWevN5y/xeZTPAlebu/FOvD1lVfPKV6eu/bXLZfatWQ0snfe1t3VaaJagOAs/GTs0SoiIlTM7zIaYsQ0jghzQApRw4tZcIe7FvvDHvvDAV2/Q6eOChlKzitcW+Wt6NV+KLRNpsmiLakYH8rfBS+V7SXO+gN5zhWhtwi862uzr1j1+3PGiJr22MdXONCOlhBMOU9OLXDXw7kx5lvTzt5j84dFLSZl1PVyde2SLtS3XzJYXl4nWYzL10o9iwbka7luRr5/fe/2s15uw7ItZ1e9UP/n3HORPiyu3/CY/xrk+ErStG7jF6WyM5nyaqpsarxrLn1ZJb9WLNh99qSX7l6qJK4p177n5sIsMni1HpaREVR5Ef56e80WHbzkxLRYA1t9v9XurOG4fn1f3Xbrv+rfs1+VaSuOMssrSPOYuRypbB/N5+Cr3BD5PhQiTMJH2uyuZ3npw9I2JxVnaGPrh6QRzGboIEqLN7Lrc64I5Udln3aY51A+rURGeAckXyBKS/3L9VVkbou2Xu95z68SU2Atx1NVfaxRGa4oy0Rxn0Acxfkp7+fFqMFZpilt5fOn5n6QNkhbLd+GGfMzvAoLzEkIASnMiNOIFGdxzkoBo8HXKhyvGQdSXq9YzI3MczEULikiJiAmzu+U+6XyshY5riSgZYWJKgYtgjidiSnIkSYvN9kDQGAgJkuGK3A5DoSEKJ7zrO/NZZ1Z5IN3JUJk3aOlly3iFBIJQUCKLsvKXIShav4IrBYzw3sbDx0jElnY5rX44sl3OXJpBXOGvOKkR+VPUpVI19abcwlUj5LRWo1OlbGC5NeICQ/zE0IY8eHTD3g6PuBf/s9/wtPDA37+4Wecjic8fjoiBkaaCYCDV8Vo1/fod3scbm7R9Qf0ux6Nd2CIlzozI8QRMU5gjvpuAsFkCcRFlhfVNiHm6KS8anR/4GrcCPV8q2lwjU1wqVR0Svchm8dOzzuYoUYg1fc3B+wPCqHatgI5qs9kyCtQJf9ahEVprfHwshZiYswpYYqEKQJTBIaYMLLO49w+1QtkQlr4ObYckWYcvUiQrB5z1iyG4dJTqXxX/Y/1KesazRE9rM6UBE0qXkXU6b2c17VGOyz+q/hw6HixwkCZ3GJjLUJQbSsAa/9FhcsNFgmRoyEY2WWJNWJGaQpHhU1jVpuiyQM6Umy0tnqgza3cQ0WOWlB3Lu+0uN5EMQ1tkd8IirUGzVqf5aLG+/zx3uf8EBnGjhxQOWXl52zQr2v0nc/df+naS+VFnaRctDRwXXHfsobtd3hJj3rN9c/14Ra/9EuUqw0RAOvEkU3MDAvdrof3reDWe42IaDt0u11OTC0hbHI9kVMoJoLzZpSQ86Bi8RbB3rIIcbWp0OK4Ll/bSPEfoXwNI8RvpwgB34qAsGOdyK2GaoIyqKyEvTZizFEiIcZpwByCwC+NA56Ojzgej3h8fMTTMOA4jjgeJTG1JKVO8PDi3dQwkkuYnVrQNaR2dzig61rxFO57tBoh0ajhTvDDHZidYKVq8tiYAhgOIA+DIorK6EwhIGgy6pAChmmQ9ivu6TSdEOOM4XRCigEunICUENMkzHGaACjzS+ql4cTLiBPAkUBJvY0g4aaMBA8Comy9HgymhIjCuBMBLtVKOKdBCZZIzMG5qMcEch4+AqAE5xigBNKwWkesEVUrmBPSyA1yCilqxHRJG7IxoqK1hamqEl1XpXjWbde5uO5zZu8XboDPbSz15rT1nGs2yLUS8jXvmb0jrr7j65eiBrnw+29636iENPurwsmgrHFZv8NSyKmNEMYgJpj3ocHPSUSE5JGZMY4jhuGE0yC07v7hAU+Pjzg+PWEeBoRpAkfx5um6Drv9AW/ev8Pb9+9xONxiv7+REO9OhJq2adB6JxER3qlBoggt4q3pztoiSRpnDXmfsidpFvg33tU6pyiG7HNOD6R3iyFiUceq1AaI2hDRNAKp5+ujazUCQjx8crLKlWBZhmx7ltZKsq1zOe/Ooqp1XSpwrPqo9l4iukyLLtGYqkKUJIMLVRfOV9/5XH1tWbZzQ8n/q5XL1IWrny/Mpi989t+aqr6mDfW7Xr7nmtq2qN3vpWwb9FRR9CtGRmwZIS63D1f//rXve3mkr50NS95NlLGqDNGk1JIQuuQ8a7w63TnzJEJJWF3TXKWbIsbWhmy9iUWbRSQo6o33iL7IKikmRBdVYalJjE3f5gi+cfCteLE3rSR6ZpaICgCaj83j1I9w3qFrWzhiUZRWMo0oCEXekfap4tsXIwecRdZVPXcNcV3wedL+lKS/JRKdQFHaixhAkKTVrBBN5GJuYzGY6H/P6EWEvBpElCirBVpyaQxICm0yTSPmccA0PCGGCfP8KM5Z8yiRoUDuW5MPCVCIRXOiUGNQBbEUY8QcEkKUqItkEEssMhJUiWlihHSp8S7Sa94TiJosf/WNh3OEtjUZxyMyY1bF5BRiVvQyuez4Zbk8S19CnUGN/yh7vyWZzkOc5wkAdohgMHuJZtfIGueSytsaxcrlWWZUEjlO5DHPrM5iGjnkGpHlHOtRInCYk3JhlYFCtLdgJn2uxK6K0VYTYZN4XMvaRc41KjonmSSn4QnzPODPP/wjHp4+4n/89/8vHh/u8eF//SumYcLjw4R5Cnh4OInOyzt0/Q5vbw44HG7x/t0fsN/f4O72rbwnEqYQMMdTTkQ9TwJ5LHJrApMY3kKUNY7oZWnwTgwRaUDZ8WxMiv7C1qflGING28g70+K+S8WWzgIWi0puR0B0bv1+h8PtDd598w3evXuHNze32LcdOnKQyGRGMctl6WP5FEVLSEngmOaYMAXGafYYI+M0NThFxuNMeGTC6IGgi0FVgAqxptxqBfe1MEI8s42YEcL4eae5RgBohFIUkqxMGZv3k3U+GIYK4VgcLhtIUm+/1plVxkSqoGIld0OJhihtk9iO/JzKUGoOsKRGiaRGhBAlP8Qcg+aHkPx4liMi2XNTAsUo8lhK4CDRVhx1MTMW7ynGi/wi2ZjxfKmNFSKv1YPBxueyrGuu+1OhCx0VSKa269B1HfquQdc2aH2DxvkMcbtQ0rxQav7iNfzMb7e8pLX4pe//5cv1hgiNWvBtC+8atN1OIyHE4ND3e3g1RIgBQj0gm1YhCdoc9pkVjhpyQ+qFwpW1FhCMR/FMliY8553za5TPZbqvufdrWOYulbXi8Gt7Rm/WoafyElgoh3BxXXCmYOflJe8syZNGyu8LEy8KreLVUhsimMXLltWCzCiGCPOwjYojanihwzhgDjOGUaIhxmHEOE6YphlhmpHGCZgjKAoj5ZwDezEiePagRIBrweAs7OwUF69Rg51FBgnbmsAIqtYPYBZvl5gYc2Q4drIJiY1emG62nBARc5gkvHhUSKZBDBDzdEKMAWFSKKYwA+aNhaTRByztyH1cBAOBTxJFaCRGIDFCGApiYiBSgUwCIJ7PAJwvcE8AV4YIS1IPgVxypJETQZhUD6EXCUoztA/ZcNZL3oy8ebnaoHAeBZHP6XmzwBf/qnxZdZ8KbapdykJndd2zVOmi7i2jL164sK6CAeL8XvVasLGq202lccDKe+G8cXx2ptTDZUGLtvJiG8tty/ZdE82x2UW8nI+fUzbZmbP6Lilgr3/OZXVrrZg4r3PdlNw/NbQSZYTU7HUio0Znv1tbFkotlnVk85cZGXc2RaGZkRPmFDCEEac44hgHHGeheafjEcOjGCDSOCGFAI5BnuvEsHq4vcVuf4t+d4Ou3aNtdhIZ2QpUUaMJAy3E3njjZAoSLoaRpPQ4QzLFAI4zOM1AmkEcQJxAMJimMvlLHpjlOLjqCul3FVfIhJYiWGWjRRYapMVExWCRk1B7D7LcPq5TOD01QKjhuRhL5T9HTW4Va0fUSoml4dRm8PKcGWILrStNzW/Py3kp74SsvzOMepgqhy/MY7vvuWVI9h4XvudiAo1d9px0KbO8XjMLudGatjCk1ILI6slbxtiNJ176bbueF+4w3nbzOV/Ay66g117DFxvFN8Ex72X2XSpctq5oq17b0Bd+v9SXz9R21oTSm8+37jWq/q3aLvVBzT0YfbvwpMWeaPTbaLk+c2MdXsMjnD+qbq88b8EWLM/WzVvxJcvmbxp+rb5MwxYnVQ7Zah+/uM+e79b6jBf6Iju7WQ5CNUAIy8iiEGkbtJ1D2xGmIApNUANGk/keo9tIaqyA1qMGCYWjhyjF7TnFM7940xK8E2O89U9IERRJ9V/qjAcWYBKG7hdy3pHLsyvFIHx4cJjnBsM0oWlanOYI5xN8SGi8U4G/zCvrN9J9o3io214iME3OicJT1U4ABO4jRxwwckSkJe0mewYDcCo7QGQDUqgVeFNmK6yRwojkCAEY7JDOl5gypK2614tMxPZojb5gxhQJcySESOJYlmZQGhGnR4ThAePTB8zjEePwhBgnzPOAlCQXhMZrwBSMApESkVcCkThl2Z6ckij+YgKlCBcSKCQgBn0njdok3WF1/y+pZGUknNLZ1id4YvStRC70DcGTQ9s0Khc5hJQwxIQpApgIc3RIsQEwgTVRLsgJ7BYg0eqr9VOiNCjzYKz7u05RHVtxKmMQmBRqKjHggQSZh4kcItmcMc/nCGZBOZOlpwp0loS8CRHFgSyVPiaDoGJdR/UWx2rY0lwLeW/y8jHZjyPAYmhKnDBMR8xhwvF4j3Ea8Jcf/gVPTw/48V//iuPTE37++R7zNOP4FMT44kRBevfmLfa7A96+/QZ9v8fh8AZN0yGxVxhTURJHxe1PUSNIrLepcDUsiVqyQY3y0ehhMbpRtlLJGrO1xryENlTqU8aU5Dl1DpwljTeGT37y2pjkAWod+ps9djd7HA477HaS67VpvBorjHc2A9ACmNmoW9ZHJHbg5IDgwcEhcIeBHT4kxqfE+AmMRwAzE2JiUZaDJVjK6BRZzRX/abwycfVO9cTWf1idKa3dBNUTMZx66ufdUI2NZnQsklPKawNw8EnopFPDJBxKbhM1xpUBL+MjbyM9Y6vDZB2XDZ16k461GRgiJ0SIJiiixHKYvKBCHMBCf8ARSEJ7EIMmwa6Oth9lg0f9zlX/aX8v5cfqWmu3nVuxRLUEKt8dwA5MHuw8yItxvW+9fhp0jdA8gdKT/Khiti98xLJF52NPVH4vEZPXR5luOnPavwvWaylr1W9d6ioNf9GJq37eBiO01PFs/36uU6l4y3zv8vdlVbXT6hfIJK8orzBEdCDv0fZiaNj1B3jfoO9EwbDf34hhouk1D0SboRiokY+FoHqNiFgm3a0EfqCML/GCyP69bJdrw46uNTx8ifVw/VRar93zdQGsn0XrxXwu4JRzRvhLxcyEGFF5+IbsWZtSsR5HTbBqHisJdSQE59wQ4zgixIDTOApm+jhi1OiH0zBgGEZMxwFxGIE5gEKSxE7eA43iJjnApYQWEm7rvRjgdn2Ppm3RtT3atlMlIUmYLgISZkjQ6YgIxpwaJPJIQfrMOYcARgDy+wRNHjvPE2IIYngIM8ZBcFCn8SQJ7sIkXjNxPhtvQgmNS068VhwzvG5SLgtmYnSJKco1ifNaXyvRiCi/t8sYuAK15F0jhohGckeIw5lgY4oncZQICZcAyy2TzEOkYuerZ2GRGNZoS6XuYnlTIhECvEGmoN7AyhSDYpJKHgrOzPGWp/JzZdtAuRQTnq9L8E1Lbp2yZhnqxVS1y9570QY9XrPOzWhU2obzNbtRTIFbFLnY2ChLO4pQsSp271pz8spCF/4+fxNjqujs9Gc/8Kp7t29Y37omoc99N744M7ggeC6enSZ1c2TEqNFWYIxpxtN8xP38hPt4xMP4iIfjIx7v7/Hw4SOmxyfE04A0C7QBIN5jt2/f4s27d7h98w43d++w699g19+g7w/ouw5dJ4KNb10xRLBADKhfICLH/EkMaVeMiGFGmEfBdQ4DKE7y4RnEMTPjhYcu85awXGHlWBQxyzUsVztXfVUGXHiVYlC1nFfON3BNr8aInXz3nSiOmqYYJDTKzZGHV0OEJZITeIa02ONcZVClhYeQnfMo3nJbM6Z6Bftr4xITl2SqlKtzb9VGiItOA7UUUgk26+84FyC3qlySrdKmtRFC/jYjRGnLcjw3WvsMHbv0i50/3zO3vq1pfLUeq/OvpWrL/aGIZq91zjmjiWqMqH97vsbP4xO3a67n3OvufO0152PwitpWfb+1Fz5XM69ek9cafdQJi1drZNWWF/vhwv5/sW3VtVujY1j4dqYY/bYeXcEy1FAYlxuLF3rumd9eKgSQB7moOc/sIzS+bRv0uxbdwaOLHmOQXGygFow2ry+9AwavQmqQcBbRX72eJKl0gIC+aitEpiUGOudATYMTEQIx5hAkOpGBJrcPIMyq0HJw8IIw4BrprZQEg5418to7+FMLuBbUBTA1gGPsOnXuWfWkwY3kLHCZZ/YAeXjXiiKeSPNhBDH+I+S4nZzAOVX45oLjIk9KqhRPLPnxADhuQE0AJaeGB00cHb0ck0cggtd8cwJ7JNdzjkLxSAzM0SIgVLkHxhAJY/RAjBKlHScgPiGcfsT48BHHTz9gPD1hmkaB3VVYHTH7FD1EQaefAJb92YGRXDWipkRlhmdGmgMoxGyISAAiISuJYU5XIBCLmo1A8M7DE+OmTWg98OaG0DrCriE05NC5TgcMmDjiKQQcZxnEITRIcyN9rnzTzEkSAQOSl4F1KrJh44uOBWR5GABozj6oLGwwcsQRcEBMIiuxhrDGRJIcF6R6HK8PEeW6cwznGY6N9yHpE1J1NTmIOOWQeJb1QsK7MZf5SoRijFAEAOdUP0QAUQdQA1CUDyaAA45PP2EYn/DDD/+Kp6cHfPj5A4bTgL/+8BGn04iPHz5hGCf8/PAJc4gYxxlN0+H9u++wu3mH//xf/u84HG7w/t13cCTRCDEmhUCLmGfOUKExmpMj1FjlRPdL8mFHYE+ZTpDjbPwDWCC1aoWwE+NVUofImILyzAkks0dpCVVwOFI/O5HOZb7Rki4BahgidJpLLTQE2nns39/h5v0bvLm7w93NDXZdh9Y3gCM4eKF5DAAl0sP2i0QOCQ6RPRI7pOSRogeHFjw3GLjHEzv8Sxzwc2T8C4ABSieYZYug2lGDFP5JV2U2vnokElii6lIY72pHgkQxSJfb7iVzOiZawhlZO6IZHFnhEg2iW+afdxLZQ4BAUNvj1aDDUENyYoBtfS9dbCSAgBE0B4yY88xkyNlYx1kOEsNiyMtXTTOsayFFyU+RIsBBjA1xFCNEUANECCobzaW/mbfZ+AWbXnEcWYYXGUsg9rgyxPByC1djKCMC7ODRAvCI1AgiSOvhO4/DrsXNrsVt12DfNmgapzDlDVw2RIiuyBojIoj16noe1L/nmXQmb7ymkPb7JvuS33njx4rv+ppRpJeMEufXLnU3G7W/8PsvX642RLRtB+ecJJn0kgei8Y0cLfJBE1GXo4Szkvc5AfXCG7AeoPpfU9JdwTc/p9S6tvxa0Qhb32uF5KUQ6a/17F/rXqASwXn5ff17OaGLZ2W931Lu5tBnRjYaSKIfzvTVvBNinNXLJVRHMUAkTghh1lBdUcRbhISFlYYoyaSmadKIiBFzCNkQMY6DQITMcw5zBszzQ5glY+zMG4RUkWVKb8FLt4Q8piAq2OhJsQBDDAA5uGZGYmF8oILOzEmYTmWIJEQ0IEySC0IMEQHTNOaER5wiQlClV1T/Hy6bDoFK/gaUaAflFqSvwboRQo2KarBwCTkKQSs0g4CPFmoqnmDmqSCGCYcm6rX6HT6JcKT5ZJyP+j2oF1qBN1nTGBjmr1vSnDrKw4RpEUiLp1I9WYtwbsy2GisYOgbV8dli0Qn1fK4eZH1lzPWqHeVP4YqkTyNotW7Mkm3vbW1bKkAW3MblFpN4K9XKiTOfz/JPdZ+9r27hFa3j/Dvnd8zW+fPXrZrM0paLjT0/sVWPdUM23izuK8wUbXc/1oP4LIRF3Y7VmFpulJq/KUIgKqXqBQYovxTld6DSufp7keCKH77+lApMg0UdZCikEBFDUkPmKLlwjkecTkeMw0mg5zTCDMxoOvEgu7m5we3tHQ6HG+z7Pbq2Q9uU3BDizVnoXd33XNN0TdYYQ0CKM6J+ktJ0ThEGdbDYZ4iW/Vm977KPy/4ihoVCH+rIgzJP7UaZHGZQyPmyNLGavGOTQ99r3G0xXNCCJi2Gks+jlUqbyhssIyFWvNTGGpA3KHPgrPCSF+HVvWeXr+bsRSY5kxiu7n0db/EV2LDPeu5LdSzqMwHt4p2F8G727ZrWr+u/oqz5pNd4Xr3In53f9MobLpdzo3w9359rw5c9eimUvlDL5s959l/R2I1daP3eRMvfbbO+zDCs7nvm6Z8rW6wNEmz7db1XX/byK3KNEIxl03nRni04hY0ar297fgXjhRwcO+UdnSqOAIMEFjm2Q+sFFtW5qcgWiuMeucrZUNFlw7aXv6E84hJSooZGQrXfGO/GAGKKQGB1nHLw1FZ8FMve4co9cp/mvgOAmeC9JjO1pKZNI/u5d4hOcrA5qvcOw+invKcZPrcjVf0om88JGefeIEOS/Z0K9BER4BJgShCZAQmiHV3JxDaqqkzNJ5jhY4ILAWmaEJNDcA2Sc0jw4pmfgkAUBZGRUrRcEwEpSg6IeTwijCcM9z9iOj7g04//huHxE473HxGmAfNsMmBSbsJgasxBQBwcUppy5KUjoG2qvV10ibDoesNdFwhZ7QUCEpX5IHzacjcQdCxC5x26Bti1Hp33OLQCVdJRI2PugJbFsOSVSewooeGIGAkxNqrAZHXwILg6p17N+meeWsxKyWQbKu0yA0rSBNbSdF7Madb8GIzi1Oa9z2vPoKHsI31Q+CyhD3I0o1jOGwq7p3L+sHWsnSmwwjPm+YQ5DBjHB0zTCR/vf8Tp9IgPH3/CcDrh/tMDhmHETz9+wnAa8enTI0KIiAx43+H777/DfrfH99//CYf9Ld6+fYe26QBdnzHMmjctaD6Q4jhi7/iasuQpqnO0PHmpWhZRMNv8aoVozddSLeeCYHJzUki2rtXcF7e3ONzcYL/bo+87NN7nCGFT/GbSSdmsKjQvc9tiRIoQOOnADgEOgQkzA2LGrHjNvPVffEuVFIuT0dVbAQkFcplGG/CyzT81R4hCY1WvLOwsI4FEJ2MyWtWOMkp8Xk1dHZd1l9+tknnAJVqB01ab1vzAsm6jnZzfp9p3qrWP+ncAyzjdlRxClRK/MjowFVq3bNqqjas1zEgKzeTU6GByk+XZq/LqoRCi7Bz6Aq+w/r3otT6PW3xOBF+yrdfxYs85jj/n1HH+7Od5qDVPXep67v7nZMmvI0ety9WGiK7p4b1H3+7QNA12nUQ+tF1fckFo0mqv0ASNKh/gPDgzOZQ3EqgyEgCy8oDqSSdl2TWXy2vCXn6L5ffe/i8tZFw8Lc+dCdhcbYhcmF9m1mRRyJjiMRsghGEwPPGgyqxxkoiAOYzCjCoe6BrKaZ5nza0wiSFimjBNE8ZxFCPFPIlhAMj4md6bol2YZ6Be+MiQRJag2jy07Dp5vrTBuYAwC64qzRKaHYwJhsMYZ0yKRSrvMWUFYgxBvIhjwDyPwjyFSZKPGXZqCqWDqz3F6Zx0THDsQCkiaQIyxw4eACeH5CQZlymt67VexrIWdioFoCn5nNzngyrYzdBgYegkij7nG00A67OBoBbqsrcbOfUEKc/M86w8tbSvmnPqf2wnykZkggSpX9xnKn8ul7qNyAzkgjZWzyqCLC0SKZrf3rly9fMUXItP4kVfbR1x4fe6L0tLhcXcCp08709+hlndumepyKl5tswQkCpI6nrZfl8KZHUd62cuvS9Wv8Om4vIXXjSPQLVgaswChJF+cdSKdHC2aZIpP7KIZwKhKhKAnCgzRMEhFRqaNAJswOn0hMfHexyfJDfENI05woyZ0XYddvs93rx5i7dv3+Hu5g43h1v0XY+26RSmUfNCmeGVliBoa4Y8xYAYJoQwIcyjfMIkRgkTAFH2AhWbFwyUiEXLsbKj0SDrtiy46Z1s58/uNUhJl40rTdPAuQaNb+FcW8FQlshPp4qfnMuhgqZal0tGhi0jBJ3NLbpQ69cqn1f3L8HE/i3Kr/EelwSWjdb84m15vnwdnvX69/2tled2hq3LaXHp+XvXa/fL1/FnGyEu11gdr9UKrfZkbOyZv8D4r989J3p2TvVPpoh3aHyHrk1o204d707i4K8wRFEThOptqGwMWlLmCS2/BGAwS6bzKYYIAGocUeOOyTEqb3jnxBOZSn/nxLt5XxClVVQ88MQJjjwmP6JteszjJIaItkXwDq2X/T/VSjkCWHNhmNwSTRlELvMI+ZhM3korI8QyEbb1T94zq7FfKs8IMOgl9SBmZlBiNCGiIUIaRsTWYfIS8eGIEcGYOGZ+RZTCATHMSHFCOx/RhAHDw0ecnh7w8NNfcHz4iKcPP2I8PmIejnKtei9HNpWk8Pdts5NRjSIrxTjpGAc0TmCqnfeAbxRSyWnfQBWc4phFjtQQIT1gxggCsrd3HmHHcJ6wawl9Szh0LfrG427XoyGHtoIsmjmhSw69A1oCTmB0KWBkYIgtAjNCMjgddbCqlJVF56T5SBCFDycgmxsLU4RE0la5To01kJj9hkXmbYL05XoNUjKseOTPYh7oZOFUZBkClTWk2luTEbx3Oc+WGQtjnBDCjIfHj3h6esBPP/0F9w8f8fPPP+RcjvM84+lpwDTO+OmnTxjHCY8PJwDAzZu3OPR7/Jd/+L/i7u4N/st/+S9omx5tu0NKjHkOCEHQECw3WaFXxTlq6cjxTGHeoHfVOS518aLTtqoq8E2ox876X3lPh2JgBEn0U3IO5Bv0uwb7mxvcvbnD3d0dbm4O2Pc7NL7J8kKtaNeHZMNDIYgEZstpqQYIeMxwmBmYE8QYYettofA20KKaYzdxZulwtDDsbhUy8lIYeJHDSF0pqUhVqpDPhLp+MCxKG4hIMt8hTZSfq2gKXViXTBHW7rVxwGirElHkeWDGg9zdtSrdYKOqRVW/g66X9bMAg1LKg5rfsZbDln1gbEu9gNcOgdXgrARQ+yvfofU3jcDNdW2DtjFHUy86ZHMitYGs+3HBK7yS//rKhQh4LYTRFu/z0jXX1PNrlF/imVcbIvb9Hs477Pq9JKlWQ4QcJUJCIiBa5ATUiokMMmaveAJmqV/eDGfjkOfx9gBfsig9Z2m6VL6UGf4akQe1kvC5Npwrsn69SfhSmy56Cz5TNsdmqZk6awOnlScGl+gBC43MCvmoyaMUYmmep5yQLMaAcZwQY8Q0j+c5JFKBbDLDxjTJ9eOkiVLnWTHSU8WAmSJMc0QoQ1Urs4pCSRLWOUuQp2MvzL14t8xhBgNwfkBIjeDIUvG4IhDGGDAl8wZKJSJCoZnirJEhZoCIATCBIjM/1TrQmpnFeJBYmEkxsjCSCnOWeHrpYbVUkFmNdZ8UxZmixRKBSCIdnA/IkEOOQF6MNDnHjOWWUaYci+e7cgStDBF1O1YGUHvn3CY1IpmhNCv5da5T7f1xXVmviI2tJ8+PfMyK0Ype5v6sGM0q6a3cZnR3KVDUrMGi7Rdew56d2wIylLGztj5nhKgNEefP0Horel8z0streauKs2eunw+sZrc+M+8xqzrJmKksRAvTmlODVHT7WVqX+VzxIhLDw6UXqBhtWp4HIPllqvc4f6qF2ivDmytR4YQsd4q+M4pgKLAGklsmQ89NE4ZxxDieMI0nHJ8e8PjwCafjE8bhJLBucZbnOsJut8NBoyHubt/gsDuIV1XXo+s6dE2L1rfwzp8ZKjNDz+rVqFEZIcyIYUSYB4R5RAyTfOKMZBioLKipBAZbuL8Nn/yT5/q54SyTgPL3xlzIsyBP48p7VJMhOi/RoN5LFKjwQAUyyT6+zpWVmXYbi23BaknbVkbXvJ9sLq9FHdLNX4NfAer5eum6+u9rleplDVzH69Binj/X5u3O+RL+ZX3dpiCX2/Y8b7r5xGcG9LWjuDmv9Bkv7WIv98fzNTxH8156xsVx19u/iAN+cft+6YIljS1/669XvLddtzZGFNqwnJ+fa0z4OgaJ5TvazFlx6WfPyUbiLWO/feEr1sOGwH/meLDFWZHiejuGdw2aBkghgaPwSkQevunRAuh3B+zmgLZ9QogKj5HmnH8NGX9aaLDXRLjkRbZ1hAx7wiyK3YQSDZJSQkTS4ACDA5IfY5TkzjEEBO+BruzdADQ/QM3vadclTR+bCI48mmbCPE0Iszgw1XKNGTJy/9Zs4AYPrwOYFVdF5rJoCM3Fx8jPMMUWa6iAQVeJIlT3aDZM+dKQnOw4MqJjTLMYPHwTEECIo0RBRsyY44Sn4QnzPGIcnpDChBRGIE7gMMHPJ/j5hOHpEePpCU8fP2A8PmJ6ekCcJrDC2HKSNsSoSWEVWmc0NPyc20MgZBsHwDswd2DvgabNEFykKLxgTW1rvLJCykQqK0a4dS6KRkJ2RXNI4vwFic9onCTJbbxEmDAnOBZ+zjPgEqNtgSYy7pkwJQck0ZQyi9FG4GFc5q3FmFZxkykIjA9DZQeD17VP4ZPZ5p1WwfZGZ3SFlA+j5UTjMt5EBDNGOdcIp61gAk7bIkpJm6MAoLJ8mDFNk+QuOz3idHoUZ5nTIz5+/ICnpyd8uv+A03DCw/2jGB6eBomAiASiFt//4S26boc//PE/YX+4wZ/++A/odzt07QEM4HQakFLCNJkMLc6MrPMBpO1FtVddUJIvemElM3HF+2xFRCy6DtWYVOdqtVkxEaj7USWPM3Met0gOvvHob29xuLvDmzdvcXcn/Hvf9yJvMwMxliA9zY9iBi5W+uZyImk1QrBHYI8RHiMchgQMCYhcHJCIhA4ueqcO2anmn9efrO3pKp7WqHXpUgcUWS6aEKTvthgD251I4cfEGBGJFEjJZA0un8WYrcauqnt7fyu88vpjxcZUdwZtReYSlv/a3lIZR1zW9aTynmxRa6tW6WRauouV8zBHsBp/fXU/5T+U9imqoXOEvm3zp2tbNE2Dxiskk1cHLmuuPrPmgy4ZI9Y8/efyO7n+F26vdRfX6kmvkUfM2eA5Jrfuh5eecUaPXnn9+r6taz5HvrzeELHbwzmHXbeDbxp03R7ee3SatLppKwOEl+SMZBOJKvgU+7iiICsY1sgLUTYnYLmwzjvhpQ54jWHhJUPG1zRQXBrwr92G15TPrftrGmJyKSD3ZwoCMzzUxzqCof47xICYIuYwI8SIcTwhhICTJm8ehkHOT2KISCHm+lg0dJWRI2aDhEVIGISJYaOWtlp0AGWtbWEGlkpk31TJThceHhISjjCLkDFBFFnzlPvD6plixBRjhmyK2q4QFD4lBE1EG8TbWLO7lU2ubFQLZZu1OVm7JTw8pJiVYIZfbpAjdbu2lNOL90ehA0Q+15c9jlXosogIiZAwpVwRxnKo7oKBVjqzFqqUJSEiyW0GS9JnbVaBKXs0nzPYSUf00ny+VK7dhNZK/BLmbxe6s9+3FJWbfU6K9bl65jVtAaC4tudC66V7t35/6RnGNK7vc9ml64o61s8kWghLl9pcX2/rGGB4KgqDtQDwUiGSJSdM9xb9rx4pfy1/45c3fFPq5K3TWlckE5Cv2HHjnRVyIaaEOQZM85yjvUaFZBpOT9kQcTw+YhiOYhiIs/SJI+z2e9zc3uLuzRsRZPY32PcizHRdL7COjRdPtrN5UcL7WSEWYgwIQZJISjTEgBDGbABJcQZzALOlb5OorNqzp7yt0eOteVIEIqJqDAjVPCzjYu0uCaqFafYaEeH0SBopYRET3lXRIJUhRpRRJsdUAsdifZ2v72VkWVFcLuncZebzi8tKNtm85FVGCCwW1K/t6XNtea5d618uyGaL302QXAuBX2ucXrKTOt4QQL9S2eJbXxJ2XjJInNPeL+E/n9+XLp0/b2OhJdvP2eDpVzL0Nu9vs+Pys183T2jRxpfuvextanuIzeClImBLbst/ZwYzPwSZ2C5aetYYbPFcVxWl+46dQgQCiFGhZsTRpWl6MDns+gPmOaBtW4Bkj4kp5IgIzvWh0GFHcF5fjUTJkpM7O9lfHbmsEEqcFOYob+4idyhmeAgBTdNU/VXmgO0DJSoCYrxnUaQTPHwzoZtmzOOM0KtMZDCKtO7rsi+ef1BsEKg82pPmbOC0bYjQ90pIorBkl43wYFaag0odb3NbPikBKYohInGCmyNcYkyIiGnCMN9jGI/49OlHTMMTjo8/g+cBPD+BwgQKI9x0Ak0nTMMJ0zBgfHzEPAyARo94002omi1FICbOUfIhSJR4QyLbNF7gdNF6wHs1RDRgbrUeUfxTAsh1EH5E4WgBxTovylPpIzNyJJNKRB7hqPlAxPnFjBBiiDBZE2idoK63ADpOaFPClBweogMF0r7UeZHhbmvGBtpg6KCSJHM3fpEIObE7WU8VWbHwLaQykcmDq8WHIpfV53I3MABWuYSodI2T9zd0AbKk5xwxzyecnp7w9PSI+4d7fLr/CZ8+/Yin4yNOpyOeHo8YhhEPT08YpxEfP9xjGEY8Po2IkXF39x77XY8//OE/4e7uLf73//3/gf3hgLu7NyBy2fFwGI4I6qBjCec5a61lrUdmpFh4nUtKZFvPRMX4n+m+6ruKMQNZYb1dV0VHCcVGSzKPXD6qQcLohdJbG8PoCOQa9De3ONy9wZs37/Dm7g0O+wO6tpU5n1Ku3yIMnFOHPZYcLoIAK2YPZoeUHCI3CGgwwWOAw5AII0Mgm7T/qgmwfKdVcRAYMgKyUeBiMdnNOnJRj04t64o8ifOQFl0Ol7okT6dGIsGXJPA10QJn6DNajztW47vmW/IUuDB/2AwQZtbTOZRF4rofl6fLz7bfFGOxtb9m5yuxDDnrub2nXbN4EpZjthQzi9ylH9m/HLqmNkQ0aJsmI4Q4L/vqEkZuySfRoqGlEZ9rgHiWt6Lta9blpWdey3Pl6zbkrGvb8BKv+CWGmq8pn11tiNj1Yojo64gI16BpehXCZTPOkRAZesHlyccm5FfvfOlVijXodb/9Wtf+vVwuzGfr5osqy2R70whRsEHF8BCzMUKgmMQAMU2S2+E4HDHPkxxDwDAOmeFInNQ6DvXq0cXGnGGMMp7oLF4RKWqIsnrRZPZ6JVQuBAjLjZBzRDj19BclewIQOWEKE1zySEiKGRvy/TXdZQAhJcwpCq46C8ZsipqMO5bIDjYDi26yWRAqLc0WbNvKZeNXccExIhNcAiTsWBPhUHUXnR+Xv+k3kqN4DBEIQY6uMigQQBpO7pyHclSQsGdjsqpQdcrbszzFaR0ZS7Ti1iAvRgQJPyWHRo1BjeIVeqVnTuvJrDhZHZpjQHf7rHjbYDLOzl9QZtRzpsydFeHMyQTtWvVNqXJhZB4P0ARnRbh09b31WK2aszWezv7dEl4XbURuU34PGYxylTGWxpivjssxA5wmLdts+zPHfHW1H6F+bv49d+jZGCSw4owqC1ZXbW1Zdt+qPzn3mdEIAMiaDaCKZqgYPUaeX0A1x7aUW6t226uIAKLJJmE8pURBJOZCN1NESFEiI8zbbDji+PSQPQvDOIDDLBjMHOFbUbbfvnmDN2/f4XC4xW5/QNvs0DZigOjakiOijt4xJkvoecyweSFOmOcRcR4Qg3xSHBUmYRYoOTVCSJJLocPE4mPJmRbExThbss48VjZHF8NuY5OwHuR6zlv4sDdDhNdk1V4NEvq7HJ0y1mbcFCabK7rAmRaX/Dp5Zq3W2bkR4nmD32vKtkL07wV4HfO9sToBcF7b+TrCS2hzV5T1uC+ecOEa+/U8R8Sl8pKzz5agc8255+r/Gh5Xv27JlPty4fPrrn+v50Zr+7dL+8Lzda0l4Iqx5/IK582uLkJ5Q6lt63lX9Fdu8BoO4vp7jU/0HmgaUk/4BCbxOyfXoiGH/eEGiRn7wyf4aQRDcs0JvGvS5L5QvpJA3hTVur456nqmvLewk6hiTrbPiWLYoEmM8hufPs0Bzs2IKakTkMk/lRzEDNX+53pjSghu1kiIGXGexSnJDBUpSZJhrva83EVLw7dz5cjVvNFYhwLPFCUZc0q2j1dJVwFVghMSi1c+zMnI8kW5RqMkfVaaIiUkldeIgNMYEOOI0/EHDOMjPn74VwzDIx7uf0CcTgjHT/Bphg8TGkQ0HOFJnGY4RSBFhHFGChENAMeWwDar48BB4J3G4xNCmDFPAwCJWPfOoe9bNN7BoQUnD+KI5DxSaCSFuEZoEwjJRzifAOflvM4XSXPN5ouMmIIqHmdZSy7IhrBrAJDmB4wYYxLgJCe0WoxcosyVyAZJuO4lEEOczjT5NqIqRkGZVjMMFkd5GobqbArmvyiZVW5l4+3tnPBXjpEjMlxiSa6scznnDFH5iNmYPZPxamcyynNR+F+dhw5gRMxhQEoRcxgR5hnDcMLpeMTD/T2enp7w8HCPx6ePeHr8hIfHRzwdj3h8eMLpNOI0TJhDREoEoh5/+tMf0Pc7/OEP/4DD4YDvvvsDdrsdbm7v4JzH6TSqrD9lp0NBBlislrwOQ0jmh1igyS6Socv82trQwOWHxe+X+P9acqfFcfncWlYn50D7HZqGcPv+He7ev8ftneR365oWjfPIr23jJNNAvmvEl/oB5RHkJIaImT2mKiJigsAyETl4x2hVBxFiNm3p21iCXaEdjXPwcGickwTJxPBwCMQZqttydJYZqDUwF0MJkKOUzAHDcp2YTkSg4Sgnzi5bVlk3kVkTZSvfU5RUkBUk17rFEFURxJf2+twO/SR7v9yzpv4AR1ggURalsgoKZS3lHdPETYNWrp+D6jXrQrWsVFH1av+XebAQY8s8qxEqyEE8P0WX4h2hbz12XYN932FvUfOaZ9igmbb66lxGWfIpv54MQ6vjv6/ya/XjqwwRRA59t4NzDfq2E8ahaXMSWfFWLkaIYohwBdrkTACpJjVwRpixcX7927q85tr1fVvP/CUEoUuWqpfO/xqGkmvf72tOUK6IIW2ctw1laYwQI0TUBNQhBoQqaiHGiDlIkulxGjHPM06nI6Z5wuPxCXOYxRCRlNlILBCFK4WffgGrl4wweTHDN62hoqwshT5RyGYve9KQ7nwUGDNyyqiyJMp2nFQQcghhPl8fugFFTghVVEaGl4ppkQsC6RlGJs81/W6MDVPeBMXmIN4IssGIGqNWZWwLvct5m6+BZcXIP+QohnydWzJRYtCU3z35HL2wWfx5roq6sCr9urYXQ2vTwjmnuW48miZmz2drWxbAtVfMaCWeYDUzVT1nk4bUuKJnDSv9gVVfAoBrAFpGNUj3uKJo5SXdWCsy63vXz9g6b0eneUnM6GF1rcdgbUgpxgq/WTdtPGvdJq+GiEvXLY4bdYrxZtmuZXvXuUTqo6yBrbmkd569++ICJB0je+4y8afdx8i8HQCcrdet49Zaq4/OmNVU6KlhO8ckdDQko6eKuxyELk7DiNPTE4bTEePphDhPJWE0J7imRdN2Ast0d4fd/gZ9v5e8EL5D2xpzWSkbVIgRRVZN1zWiS2HlQhBjRAoCy2SREOCgnLjsA5IIMyM8V8aFIkiUNbIyRuR+K+xJ6c7lvmv3G00QKCZRpthHIrnkN4niUuNLVrwU4ZvLZoNKlNBnVZFdODdC1HvJczTutTzDb1/R+7pyia6tyy/B11VPXV5nZ6h8By/n2vXl0vVX1mOG9M8sL/Hil3jq8tvz/PWvOR+v5cMvlfKz0fTtdxGv0eqy51u1assLV79AB57jy5btLMrqrES05lYG7WXztmWv0i1UeBP9hej8vott2mzvy/fKvqqwNx7wySF5iUYDObDmXiB26PsDEjN2u73uT0kjIlKOiOCszYLy9QTvKCu9oPydycFJO0p4ecHLBzjzk8ZTGt8+hwDvPWJK8Oyygkn0RgU61hRJrN8l/1vMRogwT+IwYNej4k/5Us/Ve40pkaoruezZ5m1v897G2/DOzXvaFGny3WWdQd4Pnc8RA2DIuzAwxROYI8BPGIcH/PUv/xXHh5/x53/5bxiHezze/wUII9z4hIYjek7oCJI3od+haftsSCDNPwF7Lhc+KzEDMSDNM+bTE6Z5wjg8AWCFC/FwvAdaj8YnIHmElJDIIZLk0vAa0U1E4I4VFbY1gCcABA/zrNZxSLOO+aTzIYDhoaHaSCrjTjGBQWg8a8CCK4rbzJOoIcInpEYMEWB1fmFRihJIDATISDRw2TJuUL96ZFf4NDMgyGLKMqGr6naRQb7Sb2q/uoUC1vjdVYQnkB2vjQ8TnyFT9kfM84jj6RHjcMLjwz0eHwv80v39PQaFZrq/f8Lj0xEPD484HkdMc0KMhNu7N+j7Dt9/9ye8ffsO/9v/5f8mEbx3d/C+QQyEGBOenp4QQsAwHCt6b3tzGUswqRPkMqLVHNMu6QTWBgFbN1tyeTZSPmOMWDjVVLxtOS4NEouVTg6u7+F7j8ObN7i5e4Obm1vs9nvxTM8e6TYoWB6BBf3SrOZgFkNvYIeZHSZ4TCDMAALECOsANCSR2DHDBKEiSjK5iEo0hK9o06zvWyxqG4Yc5hx5YXPS5prLt6kTKZdEztZronSnst9BUronMCIX+d3qJH2mUfs64mBhJbhQuP6julQcrOQHyykjx/LJ/Ze7kFB15vI52h5atelsfuSaylibcaA4Y64eo4SBdJ4sDRGqIyYJvOpbj75psGs79G2HVqMiDL63VLjkjbedWcp1LzmVX+LjLuuJLvXR5T5+7bPWOt5fg+89a8P6go1+/CV01FcbIvr+AHKEruslMWOrBgivSRl9AwXGhCVjFG9kt8k8/pJd/NIk/LXr+b2VtfD4a5Z6HzJvipwozbz91fM/pqRKq5gNECEEhDhLYqkYMI0j5jDjeNJEVUdhMk/jIMmnwyQh1+qJ5BItNwBthynzwyy4ouZtYoJDipm1lPtWwt6WAqlpGtQGCXJFSVort1NK+rsRZmNGUm5k5CrZkQorzFgYSaxPYYxhteubsmsxFlU/8PoP413zBl0R6sUF5fu5wMmLO6oOk1/zM1AEWFrekqMh6t+qllBl1Fg+QtvjJNyamdH4RpP5lTHzSse815BhKmNr27+DeHuRo2X/LiYSVWNgApC2K0tp1ivVKsh8MOfOYECTD5dxTSsDk0XqhBgW41/eyyOzF6R/VUKB/UMbx3OYGFedzxXmMXELRapep2NT1+1qxsX+q/ob0BB3fY+6vUsGf+t91Gii3mlLw0g10fK5ZR4T473d6t2A8ndpJW2el/wFq7aieoYmN1xMhsVcWkbe8OI3q8umW4kAIgIaZ0YriRBIOmfmOaigGzCFGeM0YpxHTPOIcRpwGk94enrA4/0nDMcnzOOIFAKyAYAZXd9jvz/g7t07vHn3HrvdAV23R9/t0bc9Wu/Fo8nwsxfvLx6knKIoTDQ5tX3CPAo0k0ZEcByBNOfcEKKkEKgF5gIr53IUznocl8apJROO5W8rGm5HMxxLcuoWTdOJV2fTSZ6IptdIiFYjIZpsuBB4hCWtzXut0e9qjtR/r/eQxRxezKVflokt/QNcy8n9OjxFvW7Kc+vjs3f/WnyPLtdKhYCvzRG/hm9dyP6/Ytnq67+lEeLrlqJJuPSeppAvRefvb0DkeHkt2Fo7p6PLazbKZw4poeSTeF7JYA+hmoRnH9uGPFwDSYyLhJQqvG0i7Pc38N7jzd1btG2DYTjCERTyNWb665Wur5+96Rig/RkVAlHaGIXnh+ZFACFqrqZxmkFwmGeJgm4aqVvknbRwtkpRDfIpIoZZEkwHTdo8zwgGI2vXO0Ki4kCSuQ9y8CRJgJPyvFEVQslyri14EJ3l1XFz3JRH1B7Wc/JkR9CPRJuSJoNGlLx4SJL34fjwA46PP+Ov//T/wfHxZ3z4839HDCNSeIIHowHQEqGhRjydmRBGRpxHcNuCfavQrQJzJLk7nDoMeHgAOyL4tsE4j2hmD2Z1toA4eg3TiCk6hJjKHqxcoXcerRNs87ZppD2uvJdzCUQJSdxoJJKBGZwEKiqGUXrWtZCQBq/wxD0AcdAISJjmpAYHk0GAxIQIAjsCtQ57RLx1CX27wxRbReElIDpwAsYpICTGKUXEbCwisJOo8EQtiGSO5P0TlA0qDpUcSwYBpNLQhuK98P5i2BJeqHIKoQL4BLbomoQ4R4yP4kD4eHzCOA14fLjHMJzwqJEQn+4/4nQ84vHpCcenI45PJ4zjjGkKIPLY93f44x+/xf5wi+++/yNuDjf49rs/YLfb43Ar63yaJjCPmEZZS+M4gTnld5K5LWMgnV7RvqRJ79ea41cW4+fr71T/Vvcrl/OAGtFo6X2fZQMu8iRVkbhwADUeHi1uD+9wc+jw3R/+gLfv3uLuzR32u50gNQDICTCyfEXIW5dp7gtiGMAQWKbkMCWHITkcE+GYJCIikEBttQx0AJJTBygzGqy6UYwQGs2GwjsbbDRb3kCmxa0WGZFsXma5TOZrCzEWTrqzLKGeCq0q8jirEQKYUxKYKJM3oAYT275Z18xCtFdDhxoqbKsnnAMO2nowmDuu5C0xmMjHaXuMABfjRzFS56QaJuPyeR9fWzJfsNh/S7/aP6LLMgdO1RdADP4gMZo23qFrGjFGdB5d59E2BmXrMl2oR8TWyGX+hDZ+39IzncsKz743VnqZ1fN+0UJ0eXN98dbK2e2asr5U5eVfmg+/2hDRdr0yRJ0K12aAqKIfXDlCjRDk1kuslK1hvWRVebUF6xUdd0l4/5qC6Uvt/xJr0tcql6yN11rqirdXWTdf8j7F62ap9I/qiStJowpTPqsRIoQZ0zxjnmcMw4B5FkPENE/ZIDFMoyaxnjPOqWygZW8t78LZ2BBDOGsTJxZhICtSlwqQS4YI+5ghQtYM5f43A4QdLarIksFlxgjKkFYbXem/DRp2thHp1nxhqi8ZJHsaqsV7eY28pAiqlfPLGxei/Pn9lEXNlWJxWbYiJRZj4qGRD43S+wSwMGDCZJcxshBoq8OExwSBhOHEYDMO0IZSJb9Nfis9ypyTe1GdXbWd677g/NlaI5IbJGGOU4mO0XlFqAwRG/PUvpfzWF5rtH2lCL1URxZ4V9/r82cfG9tVnQ4Ex5efe+lZ9t6OvK5Pd97WvH414mPr2Tif0+u5Z5ERZ8rhVUTE8vmumsdl/eYj8eL8JQ+q8t6FZhOReAJW94pHD2MOAsc0qVF2mucCyxQmzREhWLzTMIqHZYoSWaHCU9u26Hc9Dje3ONzeout2aJsObdOjbTrJCeFM6XC24+scVkY7hRz1EMMsxogwIsYJMU6a40aiIWStqjEiI7bWBi9gDSG2HJdlS2zN2zVcXVTfWyef9t6gl1qFpdS/nVfeqI6CMOeMIkythcpFezbW5nof2Xqv9d/Xlq15dKnkn1/gCV7iKc5vwNXywUs84kvr9FKf12291vvnej5xOe71qYt3fCFP+Po2/m1KbY/TvzZ/X5evyTK/Vv4obVhfn//avP/ZaV7zWMuHbD97ffuFObtV15aIXt+X61rXwcp9UfX12km9ePlXDB7VEYTPrYsiWdYOA/ZMQ9lsPMBw4CD5GizvVtft4JzD4XAAEWOeBxBo4RRU8+/5qaaFq/5eNlG80WPlQe28KOmt+xJL0uQQAmbnEELQ/VMcCSSKsThgWX4GTdqgkRFi1DdjRLRcdmqIYO8BbzTZ1MsMR2agoAwhWEfd1d2b4U9Yx3CDF8ljpMonykfl7gh5NIX3UUMEkyROBoPDCXE6Yfj0I473f8WnP/8zjo8/4/GHfwEhovUJ5Bs0XQ9Psh+DCYmdykczXHJA4+Abi1oR3psVrcGpQ1jrGOQJfd+BCBinFjGSyJnMGEOAi5RzAdiYMkOdmFp0XYeu63FoPLookZBe308AwDyyIQKMOc1IaQbCCCABDQM+AanPcojoURMSE+YY4ZiQcuSukwgLcmDHcOTQg3DrIvpEmLnRJxPiDKQAPIIwhYgpGC+oY0ge7ByYvBhpqqVjRrzMmed8D1RdZ3xpPQ8ItCkrYGGMyDOKRQ4PccIcZjw+3WMYR3z49AHDcMKnTx8xDgMePt3jeHrC/f0nDMOA4/GIp8cRT4+DwiQRbm/eoOsP+P77/4T377/DP/zn/4zbuze4ubmDbxpEjUY5nY4IIWI8jovcILWhDtCoo7zEtQ8SASxaeEZa0IAvLdIf5zy/RVsg/36+9xicz2LTtLVn/LHSlf3tLW5udnjz9p0YIfYH9F0rzjz2nCz7Gr2qdQBsCxiyHgSGLiaHkBzm5DAmwsgSESEQY4CiiKFJImeb8Se/vD2AzNxXHDfktU1KXOooyv0MyVJjN9QzGBAkPc7ZEtNqnyDYuC4aJM6xAGbmvJfI9XKN5b/J5FGJ/YI0Zlm+No+sSuaHhKbncTdjBMrf5f0qY0Slaajbv36fraef8TPrq1d78aIipflUffI42vxzsv7bxqFtPLpGjBBN4zUfjNSdbGpVBgjr18t8X83D2zpZvqnce5n32JYN8gtefc9261YyAC3PZ2NLzbi8IDtd1K9tatk3L9SKzufFwl1qQ0b8Grrrqw0RvhVDhEAxOZBip8M3eeLJ7uIL8+HWk/QrSgxfsVyKfPiPGhHxpaUoU6+9fjn5Q5WAWryISsLoxAWKyZJRz0E8fuYQMM+TePaOI6Zpwul0wjSNGEYxSEyTQDWFOUjCOFXKCy5gCc0TJVvBfDSjR5xDbnPxSEgLxnyt5DRDg/NClMXiK943LluNSZOE6eMXAo0SVHPIWCki7XrmynbP9bXL/l7Q4FWyxjMFS3lA2VSrp26IwYsn2Roq9dbPWh5TtWEumVmc3Xv2JNM81vdcWL9E4tXsncOu36FtGxz6Pbquxe3NHdqmwb7fw3uvEWBicC3aTRnbmJP0LcNwjVlYbP0mvHEZW+MWS8LM4uF+vtfQctxUiMqGh6ie7fMEQGHK6hwoYc7XCt9oBpzKY9yEhKo/STu+PjK5guEK5Pwb+agYkE7rcLkuWpwvz1pGVGRDxfp+EiOEq40ErlLOonw3w8MiZwYBjpdK3HyfSlNkArPuY67qH31y6Yu6r2yEqO7bql4ZVe2nddsKjiagTLnNFZtPlHSFsCos0mKu1YvkfEwInZetPhnNohIREWLEGMTz7DgeMYwDjscnPD4+4P7+Ho8Pjzg9nTCPs+TQUcxhCZ8l3Nzd4c27d7h9+xa3d28VmumAXbdD3+2EwfQSEVEET5nnQs+jRkKIEXmeJ8yTRELM04A4DYhhAocZrAmqDZYJzAVNljgr/C0PT+aLbYwqugwsk1rneW7Xrcc5Q+q1OS+W8y2810gI14IsP4QzuCbNm2W42Ko8ADhHMdWeO7nNNRwdqj1kpRyqBfs17X1teUkJX19XHsGLe1/7rI1fsHyPy/ev27hliHnOCLFuw6Vr6u+X2l++13Vc2R+L5bvd3teWS/1zUYj5mxkpLr3nJQFq3c4v6adf453P53OeJ69o+nOXPvcW9vR1K57j2n7JstIHvNK4RBCl3/P9Qc/8ajwUOcA3DqAE5jrPGaHrd2jaFm/uvkHX9gIXyEnEWU4gzUXUKpQqqetBYt1RyBIgiyJFopLLeoyxJHh2misiRkv2LPvCNEcQAqZJ4FhJPeBDTAghYZ4jQogZojaXlMAxIsUJMYyI8yh76Thh7juEtkFsPFIyByjk/UP2l20jBK1k+cLfVAOmso84BQgMFRSOwzKLgSnz9iKviAKXMEuUb5L9MbJ4pYfhiDAeMTx8xPz4iC4FkHNobu9AiGg8S67KtpNnkEeKjBiSZrwGZi+KPIKHdwQ0YphwDYE8QAp31OhefXO7Rze3IC9GiGmSqHmJhmdMUcYuzpJ3I0ZG27To+4Q9Obiu16ThCZ7FcOCYFIteIiwspxVPR6QgUaAAgzsxpHhHaJsGh/1e6m46gANCOCGFhDBHjcLs4VyDtm3RKQTkLjHepySsGiB9DsI8BoSQ8HPb4DQH0DDgFCJOQWCwokHLOs1FaJH6lYJMlLUy3xy8OE8RITmAfb1ubZxlrLO87tTAxKlKtl7qf5hHhBiy4+CnTx+zIeJ0EkPE6XjCp0+fMI0TTsejOicmtM0B77/5Bm8UXuj9++9wd/sG795/i8PhBv1uB+8bjMOIxCeMs+admGeZi7KAc7QJIIaHJZ9G1cdklhIlJHuszH68giciIhEH17RKiIb0zpacuaxksSaJjBZS1WxS9CSCb1q0bYt339zi7d0e7799j9u7G+z3u6wMZi4AwmS0Lc8JlWgsIoEAyVvishHiGICHAHwIEfcx4T45jCAEcph1jhT5jEAVDN2iX1igkAKRJaPR3CPVxVwSUS/Om2ZBI1m8U4cyBiIRJi+RC8kgnjJ8bcKyh0ufR9ZcLUmTXkMovk8mo2nEAtctqWW6qHsJq95JW13LdZBG5fEuiUjkumg0rjZCF8i+Ldlwre8pSoXtPZPzZTU/ZtdzdZv+4VRmz9HfBlenBljdYzqFY9p3HXZdi74VY4TlCoJTHcOiFUCJRkJpw7Ply/joXAtlU8i1d1R/PReVsMWJUfW3XXMup1xDW5QSXVku8dzXy4afW642RLhGkieRq5JRV9BLXClScl6I8hrVHD4X9upy0bJz4bprPPFeKs8JaK8Vrl9bvoY1qb7/JcH6c+r6JSbfuq76e8wQTJUBQhmZpHAztSFimicxRMwzxlm8eodhwDRJBMQ0iVHCrrHohlQz8IylEcI2EF7CL6VUbxSQzdc2ROaKCVh6gGSm3mnS0vqcebcoscvPrhpn2O72A4NRnzJmxf6U9lwgQtbITHfozMhQe7Tw2bnSDqtue27wBgFbXVF4CJx7emxdu2YN9DW0n7m8fCHnG7RDlMyExnu0vkXftujaXgwTTYNd36NpGnRdD8vfAVReXU7wREOKmwwib/Tl+kjqtc5pe50u1vJacaHtMK84IoBixBxsbiRN1i4GiXEaJQ+ARvSQTh5R+lMFZbNUgG4dE0rywvU8f+kDSI4JUKmzjpCgje9UK12xMkTU6+iK53tlfLMhwvv8PbeFdJ+jFQSOPtveu4YEWxgh8rF+77I+lxEhxrSpUANh2mz8iyEiAoh5TtR0aIvm1/k7iEiYa9J8JgQRHhNjCgExCQ2dwyzYyNMon3HAMJzEqDtOSCGCozDqlETpD+fQ73bY3Ryw2+/R7/foWssL0aH1bRURURkBSBh9qFCaNNePfGb5BIuMmHJybEs8KUKiREHUer21cl5lr825rc3I99VlbbhYzDVfIiIs8iHnh6BGjVc2J0vE6PLZKsitjBD52Rtz9/I8t/uwKq/jKV7jeFFeo/AGz/FLLyn5q1/wmnYv61jee4mG1W299n23jBLr70AZi+d4pUvPXIz/M9e9VM+lay6+7yv64XPLpfVVG2+EjyjHjYZie258Sdu/Dk97yah2ic81xdXiaqoE/I1WPsfPXGxXXWOe9xstvVRFmdAXn1FdbE9aXL6lMMvXXMjSbjzd8qSuscXzLjTjYq36syM4ZjAcnEYoKHAifNPBg7HbCxzxaXhETFHuY1EWEdQbligPV7LJSwRTuNs9lrlI9EgJMcrHswM59bJVvZEotxMCSZ4m7yOaKK2LUXM6xSIX1XuI7CkVzGEMJSJCoyIMrrXurprH2eSdzjrVfuPSB/kSMeyQOqzA+Joqi1YxRDCk56M8g2dwcllZH+cBYRwQhhPSNMBrRErb9yBKaAgg7+F9ByZRgs6QpNMqnGUHNgYbDpQYdjS/Byl+ivcOjoC+a+G9Q2TJTQByymcPmd8OMWGag0avJMQOgHNoupQVtwbClI+MnD+Ekiohw1wcLAiwWeidQ+M9+q5XQ0SLFAkxPCElifx3nkFOPNebRmChfNOCNMFt0tpMNBzdjHmWhOaNIzyEGRGMMSoEcgJEqR4rAxspL7mWu/Q/EtsRaV8y2Tw3WrYc75QiCKKkNWcm+z2miMenB8zzhIenR4zjiI8fP+I0nDQiYsDHjx9xPJ7w6dO9JGSf5swX7foed3fv8d33f8A333yD7777I97cvcV+f0Dbdgg6duMkTomn6aTOjuLh51FyfEibjMc2KDWj2UtZlog2yBihln+vKyvepVpyWU7e4vnlBiU9G8SP7B9SvhtgAlzj0XQOh9s9bm73ONwesN/v0bYWDVHDQ6iOTyQ0eTeQ/E5U6bfF6BWZEBNhSoQhMR4j8BgZRxBmktkUqgYa3TnvjTI/GGIAgH6MZjr9TuBKDZI7bKUELm+g2kp4I1+ONDJO7yGth6r6bDwgPll122p4Msc6x1HaW8+hfF7vYzVC1HJiIesF8YBTEtndjA1JiYqtr6p/1ixGngb1Cbb9qn6z1dtWP9fjlDUsK7lF5mIdESFzr5Z9Gi/RD4toCCewgOKIZ6au0gbKDakNFMs2bOssC1++LlfLK2d1PnNP3WjIWJ/vn9V91XU1f1OqWYG4vkpuuY47Xj+7tK205FyXt+zrLymvMER0MsHMAJE9hI3ZKBMwdxsvJ8l5uSx0vmR9ec1gvFS+Zl3/kcqlTZYWFOS8rBWtlg/BNtgYSxSC4NzHRSTEHIXRnMOMWXHNp3nGNE5iiJhGjIMYHwSaaUIIAuXBsYRPOkA9VyqvByXqZgxJ0bxeQg6L5mrZmlBDaqkVAaVgYVoEBDkH39TJqSl7ymYq6QohkwiNylCSOw9AZgvlmdIWt2IWy9Zh19iY5WNN8c7l4jKeF4fzsuB8baGaROimKMlny3pc+iWsmRXKR/nbNvO6XeVvS4S03+/Qth3e3b1D33V4+/YturbD3d0d2qbFruvhfWWIcL7s5A4gcouICGMERM5Yzm/5YsyHjQYXJq8+MC+P9VtnRrDQWxEwI4ZJcqGAAU8Nwszg5OBcABEjRBGqxmkSg1qIKoCewyPZ9/pYFyYsxkcE1cKIbNVl7QcUjqCqO8MbVPUQSm4JV0UQ1ExrbShwORdIfR5YR1t4u0/3qgwtqEkZXcaw1LXq/OJ9soLb7q+E9Pw+1v6FEaOsOVq9l3NeE15aFIav5oMKfQo/ZHRKkjpb0kqTiKzvKBtvDMe3cW3pQ4IaIhKmeVZj7ohpnvB0esLpeMT9wz0+ffqI+08/4/T0hDAFpJg04aMIqYf9Dm3f4ptvvsO7b7/B7d1b7A+32B0O2HUHdO0ObdOi8ZQ9rMiyG+o7xRgRwoQYZ0zzgHkeMU8DpumEeRoQ5lGTbc4Cy8RROyVlLyKydUlOx8sV45XCYZ3N1fwv53lXL7ZMl6p5Jom2nUREWE4I16LxnSgEfKv8UadjahFvZSx0aV82INm6ITNi1M/fgmXKM2VVvpyfeZEnqp5dt9/281/kmc/ck73INuqpv9cM9XOOG1ZeMkLYvSmt67p+X6RNYek1fbF81ktC0y9Znuv7rWvXY/CSUev3Wb6MT/qSspalzsfjmnm2YhavfvY19V7m7xbnqeJ31+9AdM3DoOQegOzP7BieCeQF1xwgNF5gOm8Od+i7HkBS43iEd4RxHEHkMAwjvG/Q+EaVe1lzJNENEQCSPlBo+jRJlMM0BYQQ0bQJ5L0GO7v8mecAjoynpwFhjupAQAhzxDRNmKaAeY6qu6LMc0iuCCCFCWEaMY8njEOPpt9h17fo2gZz06DxBitFmZeT/VnyRCQ6j7wz/rfekxiC224GlIU3LzNAHkSaP9J4E4ZGPyRwDGAC4kzgNCOGAQDUiBJxfPyEeTxiGj4hzk9oPUFwpXpIbqgAYqeQmZKIvAWhBTDPwKSKRSAJDGsD+EZyNgBRYXU1UblyBZ1v0ZAH7RukmLBrO6SYMPY7zd8hTm2nRhXapwHeybhnVYhzGa6x3qspR88r2jyJY4jJiLv9DQ6HA775/n/DzeEG33z7J3GWIkaYBxAFzGEERobz4uzR9QfsD2/g2wZN28AlhlNHO5NhOSa0MzA7xugBz8B9I2M0OU2P7SQn3qGX5NxdJzDc3nmRxyMrdJHARNl2l2CwOaTvrRGhZPlPKkWqerWTykJzmJFiwjSJI8yHTx8wjiM+fPyIYRjw488/YRhH3N/fY5pnHI+D6pUcbm6+wbv/9A53d2/x7t173N6+xc3NG9ze3eFwOCif5jFMg0AyZyhngatFSkWlnvlukSFrPURKsSItVKKRE3ROOwMAWhkFny9ncoUjUFL+nItAvmV8WNSjH6dyDWs+ADP9kRN0kgRGYIlqYe/Q7lvs9g3ev3+L928OeHN7h92uV7kES+Od0TCQ0FAd8VralrY2SMlhTh5j9Pg0Az/NwJ/HgI+R8eiBQAmOPBKAAQ6BJT9ErHuNKI9LAmuSaxkvGYyEwEDSnJ5k/WVCUzUG0r7Sdx5OIKFASMToVA6bU0IEEAnlpUjlFa3XyCCjjhSRMXJIiDo3LOsJJWubfgw6Tw0JTo9ULE0yzgq3Z5C1SOW8GCM08iElcI4O148aJwo/vKTfcBJ1lXGPGFkmO9t/s2yFMgcWUQn2u16TI+g0CtxkGBiKgodvGhxu9ri52ePmsMNh36PvWnRti6bKDyHPfEYx9TfkqS6Xz5e7tmQMmUvL93xOTjmv87xN29ddx2+vjRHP1fmacrUhghTaAc4XwmQfVJ+aXzXekExtu25w6eAtK8uWV3G+80LHfa4A9jmd+1swXrxW6KvL506etVBzZhmrmP1Lz7rkRW5MS0olKbUk3K1yQqinz2zRD6PAiozjiHGaxKt3HDBPAsVkURDMVQ4FUzRZ27IyueR8EGYkZku0eBJVAEKZMYcKQkavl4YI8stQ5xLubPh55/1rVtRNI1zV+MXP1d+Z/nC1uVTKteUDGWche1cWyu99IfjMHn9pqlWPdXkuFaXMS9ZkNgbYFGF6LVebKlXfzNOoazt0XYd9v0PfSyREr9+bpsGu28F7j7atDBFATlYtiifx0MhMoiqNy3HVJ2sjQ4X7L6d585j7GcIAlo2fEFxAcCFD7jS+RYyAdw28SzK/yIEZ6uGVkGIUiDEu72J9Tpmen6/h0ucrNqRSQso4LiMe1vPNe1r8btfn+mBeK3Jdqc/lNm0ZIlDNg7Xy1wwTxmSXiAhhmCwSwpGv6nVLQ4RbCg95HWNlWLH2e/lrOyeGvU8xRJgS3fCgbd0wOIfyJ6VF5pkXjSG1vrOoEoVdsPY3FETY9i4zjSkljGqImGeLghAYu2E4STTEcMI8S74Rc9jRnkbbdNj1PfaHAw6HG3Rdj7br0LQdmraVOUhePEcNagi2Nm3dlGi3ZUSEHCUfRVSmOxaGPjP7Nl0pz4OiyEd+5tlczZRiY45aqDlW400uC9jl2IA0MkKYbjFAQCMhUN2/XEHnZbFeVlEUm/OOpDcv7/nX0fTP82yxvj/nKbbqudqLe4N3eKlcqusSb/RcRMRLffDc+20reK/jsWr68dry3G1b/NnWWHxdTnZtVKnqX51fz9+tsfmanldnLf3MOtds2fPVXDcPynu+ti0v98/5/Fyv2+37Ck2yC+WfrOo5u3Fx4VaNG9e8Yg3anNi67oqOK/PQlEoEp/wIyAFcHALarofzDod4ixBmjMMjnCOBEJwbhDCDGerBicoQIQ6rIda8t+xHMQik0jzPCHMEkxNM8RX/EqMolKZJnEuaRmi+wTIJnGFCvQVmzpcTJHCw5IiYNWF1DAFR80vk3HTV3UaHZL9b71vLrpa9CHBwyv9SxQuz8re173E19qpMBEdNb2HXqLJ6lqjIYfiEMA2I4YSUJngFYCfvgQiwRhA4iFqi8cXQkeJySkj0hnKvpIo+iEJZ+HpJhduQAzsHNIzkWZJ3xwjvJDLCOS8ypUapzNMEy3ew0GcYPnrmb61P7PmcWXlHElnZth26fo/9zVscbu6wv3krnsIc4ZxD03ZgMGIYBR7SN2iaFm23g2892raBiwnOJ1WgJ02MnZCcPLdzjJkYLTFax2i1AxsvstFt16BtPPpeDRHeIyXGOEskyMgzYgLmWhNbv3OWawv9znkOdbwSC986DBJlcjodMU0zfv4gkQ8fPnzAaTjhx59+xjiNeHh8kpx3c0Db9Njtdtjv7/DNN3/EN998iz/84Y/YH24Fgqnv0bYt5jnkxO5LPUBc0MPCv7u8dmUeFz2FlRwJwvIOxA7mQW9UkSv9wqWiLHieoEQkzoyrraJ2blusrXXhxS5rBLIsADKjASORKPl926DtW+z3O+z3O+z6Hl3bVnK4lkybXNG+w8wcdZMJzA7MDik5BHYYInAMjIeQcB8ZRyREcmic6FFmlJwLWRdvI0IShSGnk0b5pMU4wLojK/PzzmTNVHlBazZSD4IngBQGLel8IKruy/xJ3ce279hYm4pDHBLF6GA6InNstQu5wCvpuUVrSwdYc1FeEIsj23O4JLPOshGqOVtPRTKjs36IMg16thh/SISiJ1rzEqSyTnHqW0ZEqFSs9KFtxfDQdS3atoH3TiPSXMnTZ8+sjBEX9bsXfn9J53k9/3fuzLt+9oWvL7Zhqyx54Od1YM+VwoEsZZ+z6y6cr5+91s2v5akvKddHRLQtgErhYxAWKBOzKLS2G7VQXuUz2y+zJYgs6voKL//38suUik6flbXB4fwINTgw5jAJFFOwSAjxSppniYQYRoFfOg2nEv0Qgnj4ThPCPAuOaixJnU1JaBuEeRibQi9p8mqDsLEEVQxrc9bE6T/KcDlWJFSHpmkqg4NEQlhiU1FoNqJ49MVjxEIBCTa3pX5ReCdd/Ma96LNzH5+vrEx+KuaYz64txelGklMzXUEs1+XSaiR+5scrNsLL6e5rPMi6FeKrwWV3gtcNTnJCtLi7E2+3u7s77Loeb+7eoGs73B5u4L1H3/ZiiGh6iXgx77FqUy5z2V5lxbSu+nD53YSS+hRVzNVytOyZ5dnijTbPM2YfAHZwaBACA/CYQwTg0LUzwATvB/gkgiEjAexLzca0rnjcSzMgR3Twun06JrSag6v7J9L0eBX9zn9VDy3vTMrniCCTDdv5nClpUZ1fwzcZQ66baTZUKAST11B0DQ0lp4rnyiudPOUkWxYNYTkkADMRUVZw5CiAbHDYitIgeIU79N487pv8TBuPmESBkI20IShEgyjprdtMEW8GCHuvVr35m7bL3RxTwjCNGl02YZ4Fyu6kSQAfHu7x9PSEaZzECKs005jxw2GP27d3ePv2Ld68fYvdfoeu69B3YuSTvBAOzkkiTOfK3DF6b/B6ltMkhBkhzghhEs+/OMuYGxOk9+eZ5azPbZwtR5XMC5fnhfZPFjqrebbiIyrZTZQEZijyDRyJ4O98C99KRIT3LSgfDaJpCb9Xr4JawN1UCpMx9c8bIUq7X0+rv7zYXvR1n/0c7yC/X94sXssP1kr6+v6a0d5ytrjkAHP5+dv86+L+C+3/Uk8ja9vXqOdyWe7Ql4Wml/vnNX3++yr1nnjNu/wt1/YLJcOufH7k02+lOBIlPzMhRjnaHtK1O3DTofEeMU54IoV2OQ2Ic4L3Pdq2Q9rf6EZh+iVGTJI7AJq3gBGQwDieThiOA6ZRDAM9E5oO8F2r0YIiM0zziDkxHugBbdsipQDnXM7rNI5FsYpaFtaI7QDCNI/wk4f7/7P3Z02S40qaKPgpQNIW91hyOUtVt/SdRa6MyPz/fzMjcl+mW7qquk5mhC9mJAHoPKgqAG62uHvmOVWdiDCnGQlih0J37feg8x79eYehazEOHVrVPAWgB519F8GKKOw0iL4+T809qfyWwNAMT2oVrCry2SKOJf5GNuxmCI0FIMYAEDASIXmHGAcQASEM4BTRD2fE0GN8+R9I4Qwen0FhgItP4BiBMIgPdghub249GkcIDhgpgb0Dt10OV8lRYvz1KWIgwQ0chCZofKOMMJ+tI3yr2ErbwpTSYkoYVZB03O1wOp/gvdCTiRmeEtjoVDV4AHEOoWnDbRYQ3W4P1zF8s0PTtvj5T3/Fw6fP+PLn/4bD4RHd4YsIWWIPdi12Dy9oxh6+ldhUbfuIdnfE/vgpk6LBRQnUHQGODAmiHBHSiBgHcOyBGOB5RIuEx64FU4PHh6/Ytx3++csOu7bBfn9QbXqPEBNeTgPO44hvzycMIeG1D0jwSORB3gsupFYFsh4SOJhFquBtFtOkP58QwohffvkFfS8ul859j3//26/ohxHPLy8yhmGEcw0+PX7Bfn/Ejz/8CY+Pn/Hzz3/Bw/Ezvn75EY1v0TYt2CWwS3g5vSC9JPTnHqFSQjQ+rSjucKbpjI6JSW1V1CtC4il1WWIGCBLsshWMaaxX57XSvAv8IuNuDqR4MU8sZmjx3py5nJnXK/RlxikVRAu/QZm7pKDbiRCh3e+xP+7w5csXfPl0wHF/gG88oLYJmapwhZkMMBChnA5XyHd1A82JkCJhTA5DcngZGU9jwt/6gL9FxsDaX7MOVhonmleMgnRneGTzw4r3G6+kejBJRhuY+2Bk/g3JWKpzA68u9rwDEpNQxkz5eBNSUWkMdiBWyyECmMWNk9DSyEIIs8xIEKVXcxvFZuFgMR24pmNsYcpcS5lLzkZZh1qWrYfJtbaEMP5HGUhS3q0Jb5hJg2PUvFyU93XdTAimOlcF00plhf7KipOaTLB5OBxEgW1/EGXQpkVr1mO1RURmhP8D4kG/cbqG927y2RfvVHyWC/TLPTj2R+Pnt1tEZC3NJaEM27CYHraXUmn3emfe2rn3aPlvvXttwi9pmr0n3fL+R9e5UcttdVYS3rW8lywg6qshfBYLIoRREUBB8MyM03yZWzyIc39GCKJZO6pf1OKKydpZEIVJOzRInFlhmEVEdhtVj4UxbpHhrewHuOLypbJ8MPccxuCsCQ4bl0J2cga7+UolqFM9viUg1mzQafalPo/qErjUk/ct5owAO+Sql2YV2bDyyuPpatzYmzx7rQZyV6QU9RFlR21mNtcHoM5D0zRoNUhX17XYqWVE13boWrnvnVfCxGeCwWJE1Gbsa4KH2wURANH8+RSOTOGh9kiviSkTecwE7wIaz0I8xiTa6D5p8KciFIOOkcHtohd+LxOMJ+tuMvc0uTuZW0EIU6mznkCer7X6PLEvQmjP7y+vc6a/NSplRLdmXGfrpVpoALNOsCCOAPmK2T/z+1+Y3DNhQA7gVcXAoOIeymtQY68CzMa35ZzVsQgpKFxUS4gQ1YogZrgJFEsPWbdiak/k0JKsg1aFsglAignnUQQRQeNDnM9ngacq5BXNv1gkfnrWEwFt22K322HXyadpWnjfqLsKE7qaYKgsjbQC98sn5g+nEpA6I+22OKhau1TGvMwHFUKsgofGMp3iKTWiVn4TmfGnubhSs2FXW0SIFYTLZsh+2Q6UNZJ3wUIIsRSsYbVfqHCw8q6VuxAOXk2Vxtfq0/rPAqCvJlm3y72/mb8ul6/jjpcZ/tcbWONr1/ClmjF+PW3luU5IGdyoU92bLeKhzrnVxDXG/qLui627kir8X8qf/p7eX0kz/Pm+MX9LmmIMv10qe2s6fdeII5pkmx2nq+nekbpGJ9kcfowAaL11t87vLXu0Tpt0XN4jamer340xyFwr+5Ce/Q7O7ZCiw9B2Em9hTAgIKqAHfNMpXi+WEeJvnxGSWO0RiTuXxBJXoB8DhnFEDBG+i6CU1Kd4wcIsHt0wiBuZrpOzh5kwjkGfz2EswwLsiqVhsS4MwawNp3hDSqyxynh6tmb3snr2lMGuxrywmZwSEbUWJ0CZzqomRz9iCcERSOzUvaS4H0opYOhPSKFH6L8B4QyEHhQDCKMy4SIML3OOJNC0I3gSBmQiUmEKoCYSFa7BAImbTkcOqTE3SVC3q4a/TS11k/dIKcH7hMa5HDS2H7qsICdMx5jnO6YkOAML9ZD1YUhYub6VA7vpdmi7HQ6HBxwPj+gOn9DuHuCbPcz3PKUA1+wAEFpmEUR0ezTtDr5pISxMwY+TUwtWUpwbUdYDB3FxmWJmnHbegXyDT/sDDrsOPzwesG89dvuD0AzOYYwRDTm0vcM4BDhEhJERIUGHneHCMHpUGNkcdexVABGUhn99fcE49Pj1V7F8+OVv6pLp2xPGEHHuBwDGuGzwcPyEx09f8Oc//xWfP3/FX/78z9jvjzgePqsHg4Qx9QisLpuHAUMvgojidcCVNZg3jmnWF1jHqVJiy3R3TeAqLkqXzo+CiClGN6PpM5ip0owe0rZy1WRjWHNVeHk0xSkL3igVinVBwSt969G0LXaqPCQKk05w71JIwUkr/gPlqzwzVgFDYGjSz8gJfWL0iXGOSYU9AqfKGFb9qQfEzk5ClnkvQHuul+tXNg9EzruprkYsITKdUk9SRkgJxqp3ZDLXiWhk5h6qmg82iwXzqsFwqPKu9Qm1jU3V8Qw/awsIez4rs0wiKh8bMqd5DOw3T9thcH4+gBU+wys0QRmpFXzPaClvfJgGTePReK8Ka5VAbl5vPTRWEeedWJ7wRv5Zv7bSZr2FEFp/qcKBL+Hh8vw2fCifpXXdm4XLo4Lry835uX23RURVd/28bpttlffgircLIozZMnEvUSElBlWnXwugvLON1xjsH02kvIfw+b2sM36POkri2XU7FWJZ/mTDNK61BFiBMLK7o1rwUHxPJozpjKSBdmOM6PseIUac+14C7/ZnjGHESd0vnfszwigBV1NMuXxBIgozqT7kDWULacwaxokT4jiK65MqGGzNVDImogBVp1rPLvvSNMZv1nBW3+KmYZ2RA5CaEqqPVVB2r2NIeUUXKLOmHB525uUZUiR6gi/lCarZzOZ/vhxggqZWEzmf/flenOSK5WaN2EHJlOpEmsMpe2UNQM+B3lYiCEM4a+nPTnYbu9aL/8F9t8Ou7XBoOuyaDod2h13TYdc0aH2L1rdZal+70jLrFYA0NhSLxoUr7bsmeFg2Pk6QMXnJWj0fqUnJSMkhJfXHzgld68Hw2I0twIy+8eAkWmIWAMpiLhAMfpd9sXE0YjrbgviYtanxGw1lqc+GtXEQgRvN1kMxdV4broKAp3WEs16pE4QoTYZugnhZG6t9zVTdszIqpjARslabjZmbCTtySEZXYEVhLgPmyFgEEsLocE6QMu8kHomY30s8h0y1gtQiImSYGJSRIYRdEZx6L+1t2lYFoPrbW7wadUXlRX3TrCrGXizIzqcT+v6M15dnDKcTMEa4CLTwiJwQMQAdw8Fj//kBj1+/4rj/ikPzBY/uC47uEUe3Q+daNG2C8wHwHkyEqOsnsvjdHcOIEAeM4xlx7DEOLwjDCfH0Aow9fByQYo8Y+yIUzbSBBvrOBMTcRZfk9a6aT1Tm+IT5kin3YSDehEUNHDyc78SVV7NXZ9Mt4Fr57hp18+XRKLzPVqP19q7OvQwfiFRjzRgf1VpVt1YSELvsnYS6nWXV13D9bqSrtHL6bq7gRg3oOmZJLuI23OV9OM62VcJtWkDr47WmJLOVb7vOaRlZG3n6wlqh+val2bw2ZpcJJCFO10q/bf1cslh8a7p9HbxtjTPbeBQC7WPS+r4rZ0qp/1KilW/lTsac7myaUatpezFM6rwB91/soeXzUv39dNJH0jxEBGK3gJEmCHU5dlFAQhHie3cA2j0++wYxjnh+eUWICb++vsLRGe1Z3eQ0HbIrTBgYJIAGPaMTnl5PeO1P6IcRIUZ83Xc4pAYPIaIhoFFl2OcgylZDGuCdRwSjcYVRmDgI1u4AYbJHJBZFBXFjkpAiI4wRYdgh9jsMpxYn79H5RvEP8eXvKYIoAQiCN/kA5gDuACQCeacBoT2QPBgNTCMYnODUZaRp6aYYpW2cgMhqFaDnc/RwTGgGB+cJrteQyjwCHOHjGS4FdOcTYujBL/9TrNQ1oDhBvUMfGhAA78TVZ9cIw5xcA9c08O0O+zCgCwMSpH1DDHjtx6xctmtbNL7BjhmegOACnEtgz6K0RDI+3U6tSFliSsSUkGKLQ9vgtfVIccTpLPEiQoo4hQHNcEbrHWLTSUyOtoXzHl3XwDcOvhGlNMQWDELXHtF1B3z+/CMeH77i0Dxi1xzQtS3AEWN0YNcCzRcQBXh6ECGM4o4ekFiKweJoJTQpwKWAPp4Rwxmv4YTT2OOXPuI0JpxHh5gafHr8hN3ugP/6lz/jYb/Hnz4f0XpC4wIk5iGDo0foGrycWhwD4TuNSOcTzmAMDERisE9oeIRHECVrMGIQpZLXk3gt+OVvf8PpJC6XTuczXl5espAMcNh1n/D40OGf/+kH7Pd7/PTjz9jtD/j69Ufsdnt8+vQZ3ju0TYOYIk6nb2IVPgiPwJQXU+2yNBMphSZgAJHNU4LR3QFTmFfRFgyAnZ0W6iZ/Src4IGvhJxVsEBvN5aBQAUJv1BYRRlewRkA2pRsD2Sqx4yQ0htHUZtBBUqpEXYhwaOHg4VncvjmIggy4ERqhITgPHA8dHh52ODx06PYtmIQnIvQtgdhLy9lnPo4jMhYCEhIiHCKRhSUQQa52Y0iM5xTxPSUECI7ugtBa7JPOQ41wVwgjR+kYTVgLU8aEnaWaIRvqzVgBjp1gxs4jEuHkHQYADA9zowRO8Op62xFXVSktp90WKpvhmRW8JUS1YGAALiU0SQQNDoyRYxYKIzF8SnCJRfgMCWrtGPBJ6LGUxM1dTCRwMy+wCOIITgGUBiAGiY+TIlwKAAdwVO8fKvTIw2HjnAyGzvgU0+HM9LwM/jxvAtv4MJAD2qsyVhbaqGtarr0fkIPbEdqdw+O+w0PXoiNC6wi+cWgagm9VWTepYDgz1SeNmzbYfi+/3p6uoBm1UuCl9zdRofegl9fqzlVMGCBljKoxu4avTQso1/maMXdZxTvGdADvRdvuFkTY97kG6qTy+fWGdE1a9Huk97ThGpJda+Gt3b/23lva8/YyeHbdyLICCLLQASvWDyqISEkEDmkSlFqC6SY1IU2q2RBjxDCqAGIosSDGoNdR4kAEtYBIsSAg9Ro1hmBuF4zokMPHfFbWTKI5g9k0pwxAmhZ1YVj7zFyk/Hsa8C0LIWaSTlqM43S4iernU7ZE7tfs0Zp2RD1ftRaCycvrWb++ChRBqxq3sIm5sPYuwvVqv1wSShjzuC6tzmJw2GXTbSGovHPqrknnDmWOXNagKUgS5ZKyfkw+H6YanLftO5v1wguxuuz+FN5O+y9aJ6QIkq1tp2vS3FDlobEKFQkxPDZfb4UP1XRXPNTc3vm5sH3g2XjVc3X5cOTZYlzNPUFG5jmmjF+gWleKyK+NwxSGsOFZAIx5XGJYeJqOQxFkaAscK7O8uIXKggjfICaG9x5NVHN2E+yAEFkEEeL3NmAciu/nqAgoc4IFNW7GVghVFZL4xsuaUJhU3MJBXDOpq4e+7zGoUMLcPqlCIQpmD5ATYUfbdWiaDo3r0LgWDbVw5NVahNXjg646NgRWGAMxSbtTiogpSFDqGMAxKKItSLVZ0ORdM5mTAtungiPLO8XFiqChoNub8z2ZS7OWsdgPXj/FD/QqjK9hI5fzcQEnavhcrUsQshUdTZjXNZCrcIvppnpj4ik4srLfUgzNCrohvRcH3NQsmqXl2QLM19i9OOGlc+uSMk2eu/p53VZcHsKLz25o+nr/bne98/YZWx+v29Lb1vnKUN9U99JC8XqixZe6wCu4/+aoTg7f+9Ja51fLv5CH7OnScmVrv9T5fmthxGb+ytrBtKCrlusjUpcsBNM8sJhNXbdHiA2aIYJpRD+chXE3DILrR8DiiTFoglPEkBAjox9HnMeAPowYY8QxRbQsWvrs1J0HkK2yg8YGGIc92Cd47zH3B55xm/oeW1BUEkZ+GDRexJiVGcw6wGm9RkWQnTkkZw5VFrV2xtrci/yhBCJmZZZB3QGR3ncQpialJMwrUgEmC4MNqZfv8QykABpf4cIAGs6gFNS9E4F8sWB1BDQO4l+80TPZe3BU5TNlzAYmCSIbgRAtdoIKdtTCtqJahdGWcTW1LiWI8IWFmZgcgRIjxha7thVrCIg1TFAL03EcDMGGb5rcftc0aDoVRChNbBbZXdOhbTtRaCPpI7NakYIAagAncU3UsB4g0hiGCRwr09XEJSh4ihjjiCGM6EPEOTBiEoufXdvhuNvh02GP4+GA/f6IxgOezyAkOIoS1D0BsXHovEfrotAZbJEHNPw2S52xsugJIeDp6Rn9ucfffvkFLy+v+Pe//YKz4pyiQOPRNA0Oh0fsdgf88MPPOB6P+POf/or9fo9Pn37IFriAWftInMhx7DGMvcaDEOFCsagHMuGC6YmxUBzLLkCXsAugCiwK3EgzQUSuj0gFEPN6Cs65xDsnDclUJlnzL3A4GeqGSDMTVEnK0DilFVmDfFvYkrbxaBsP33jZP7PzlKp/k/u18h3EtkHEiWo4rYHMIyQGxJhLphWmwmy8FQfLx5QddfNXKno8l2E+oE3wVNO7+i0RIejYjnaf9SxgLnx3yn9yPTYSJsomltgWVPXJxtziVWTrb5aR8kIA6bzw1IqCAWKzLjFaySx2BKZjHpjaXDhluG9lzu0+pjM7pR+mPzE/p+dKKvP8NjoTvglNhk/OFRa4pbFoGu/RkPIrzCVTdmHHMAlT/ltvkkxUT3Gh+V4raaUPi3QJz7iAn1awhVaCa+cWvRGPWaMNlpkxxe1m79hyZp62Yxtfy28taGdTKC1KoVP+IWb5b0l3CyK2hBBr6feyFPgj/TZpqQlYFrJZHABlMZsmggFNY+ZHFn+LSQM+Z5dL2RIiVNeIfjwhppiRmNNJAqa+ns9qESGCiXEcsxaEIdaZZazrzgKurRFGU5cgqcSDqIQQ9VjUTMQ6ALVpzze+nfh3L/7BVzY66jN5eWDcLrlcT9fe/F325a3E+hvaUjPtBP1QYDiba3Gwo8SKIrtN08A34nrJ/PqmHPgpCUilRsomQbADV0wZLoSYmXzfnRTQLwE4TS+LsZlirJO1QwR2jOQYEQmBGWMwN2VCgFqwrMygLcMoJa52pcYe65Vb2pgZr8DmVcqfCvimQpztRBsNXBv7S/PBVRm1GaO4Dy3vre1/5lQdvvlJISyo4ANVbSV5o0tVm1/hQ9vu0PgG+32vAdK7PDmG+iaIlqEJIPphQBglyLQIYEsAPiLSeBMl4GTTVK6SnJM4Boqcc0pIZmmhsXWGfsQ4iHAXqmVpbfKNR9M47A97HA5H7Pd77HZ7NE0ncRLIi8YXNSDVA7PxEm0fYQbEOArBPvQIQ4++F8uIMPbCNIkj2LTWeLrySwDwqSCiuL1WN1h5TqaMMNINQJPtM31ehMwakNrrR+NAON+UmBB1wGrnFoIDOW+mAu5aADEVXkF9M0+F2PekvxfWRQoz8Ubc76OFEL9nqute4k43wre31v2ut4F1jGGF4lzJ8REjflFov7mWtt1NzUqYMosyrF+eZW9p49zy5ZYy6QKb4IaWIHOo/ki3p3w4V9wtlBkjqm+X9WF4ZdN0Yq3oG4QQ0DYnjCHgdD5jGEYMr2dlHinTpFJQEkttxuv5Faf+hNM4YIwBx32HhoCHB7FU9E4CJXOICMOI19iDiHBMDbhpgLYDOCGNA3gcgWEAhhE0BtAY4YIK75UJD0cY+1ewI3Q7h6YBdrsGjQeGVqwKkHZizU2NGVigYY+Rd+K6pz2CIwDfIoWAwBExDgjjq7rB7QU3ioInMEcQRNtXAgPH7BeevBd/68qUdKxszDQAHMHxDI4BPLwihVHcHyVh0Bme6UiY4d47dK24geyaFuxEOSAyISZCGj1iaEBhBGIEUQQQEIJYgXrFfTgkwCcQhHYzHK/thFZoO3M75Mt6iQmxbeA9IQSJK/j99RlDGNCfX5CGE0Lf4fHxC47HR7TNAcfDHo+fH7Hb78QywjtxVcOAc4I7PXQee8dwKYDDgAHiRmkcThInhBjkHXzbwYJ9xxRw7ksQcqIGjtqslBejBD8/n054fnnBr99e8Tok7B5+wmHf4i9/+opPj5/x8w+fsOsO2O+/an9fwTwihmeMacTTeMLLOOCX8RUvnBAbgBPBR0JMAHpx9RmGHk9PT3h5ecXf/vY3PD0949uv33E6nXHuxTqobSUmxl/+/F9V4PAX7PcH/PDDD2jbHR4fP6FpWuz3RxBIlkFKeH7+jhgDhqFHSgEhjiUot7kq28D/U4X3r9L4httXTOipMiJlOcU1mm/1/M94Z2HwGe56KRnNsqUg6Uhca3nDFasT2RjZxpsnMBrv4NoGh32Hw36HVmlhi2VGVAJC21t2ZtbKVVK2Q2KHyIzIQEgeAzuc9TPCI4KQyCERkJxT1nKJ21k1FpgJcLbOfWNQl286P1AGbAboSt8BCJxAEeDEIgRNGjid1GIKQCQgzRQRHesniRBChHsyOm7WJkcq0AAkho1khWOANLxhxhAICFHKS2qNkVQ5K2pQ9ZQioOtb4vRB+VQx06OsQosFA5x1Tafpw3p9T8Z5RiOVzDOhRfV8km/BxiBYDA2jPfe7Fsf9DsfDXj7HAw6HA3adBEr36gq54oNP6/mQ9JaybnlnQum+oY6Nmm/kBdb53vLO+nNc7ErNvymKngWXujW9SRCx9czScjAqlwE3vjt/Pic4fksLiq26ttK1Nl5659623Jr/UhnXF2jZTFOdoYqpMytnckiqxk4GrqYBq8yyHANiIoCQGBApRvGfagGnVfBg2rohyH3zyZlSynEdTMvaJLOTwx/XN93WkzmjyLSFaiFE7cpnLrSox35Z5xJ5usacvT5/9nz9/Xn59zDSr63Ce9v8Vimxfa8PrDUNQspP1ph+yEiKrd2kiEaBWrKeU5qXKhBantdrZ86UWP9VM8Snacqcnwq5jaFCmaBmFfJlbS6I4CSCs4/aHEcgJevspDX1FKxNhwnnJn2p56H6fW29E4A4Ox9uFUbckrY0NOv63lruhAgoTxbMuDmhYPmQZDLLWhTGA9gBLbJlGGUfULamJcB4ghCaIUR1yxQQRgn0PBdEcBJY6GC/ozJHDDYlQ7NLTBxdK7GyDJOW82R9ZcsbFex5b4SML23H7MMK62QxTWNCRInrk8wqoka0Nb+SPwvk1PZx/T0/y/OyRLDzdTbPU/jgVj8WrLyOKWL9puw+abkG50TtUvBR/8YEXtVtrqkOqhYj1Xdp2bd52t4LS+zzHvxDaJD7hSf31nVveddxSyCvmDfil3WZv6dQ5Per6W3pLe2zM3Ibd6rKpeXpz9UX403gSpl3t3FR1vRsxeJXneu2Nizbahv+42f9qsBsI/81GuOW8b51Tt48dwyU+GGz23X5GZ/j6kOZUde1YiURA4NoxDAYM5RVwUq4TUwSJ8r5RgQRKSGMo57b4sYnqhJBHQtJzseIFCWfI0IMIxwDDYnmMkdh/Ofgp+obhfSINa1YJBbLiCiBiiVmhNBXKUZhVjvVvjWhPjsQezj26tZF3U0p/hPVgnEMUt4wnKT9UYLcEpKqHwBsLqTgQRBrESmflCmXtK0BYh0RxEKCIyjHErO9Us5ss9KwOG7ei3UiOy9lO4fEEQ5JhgaAU2tGqmEFV7i/jpcjsYqwKpWMlHNfegF2ouDUxYBdJ9YM3nsgllheIYqrH+8oa/PvdwfsK0FESobTi4JD40iC4aYATg4pOp0/dbnESfE3tWY1RnOKSElwfoeClTKggdOjeg8QWjqEhKMndG2Dw26Hw14YgW3TANQIHcGElAhjYPQh4mUY8ToGnGJEHxNGXevjmBBYfvfnV/TnV3z79oTn52f88suveHp6xvPzC4Z+hLBuHXb7A3a7Pb5++QEPj4/46ac/Yb8/4MuXz2iaBvv9UdyGOQsUHnIfxBJizJa0QgeZEqFO6xpuk2m9onC4AiCq72sAZINsQ0WPGmM439/gLVT4hr2/lXK5SrBOlLmA5dnHDJ6ciQVJdDBLHycuWzOfYqYSV+HTq+0jApJYWpi1UASJIBDySXBiJUEsyl4T2mB5VuZ7dpmfryTvEReBi+GbptQ34UtV8ymhYYQ2ZjCC3re9n11LFaQiW4OTwlSCHiH2sfoXS4lznjmOrrXmeTSrsdoleFTFyGSLWj+lrdW9ijabjaKuVV62bzKNhAmjoX5mf2ePGGU9kNKq8/fNZVY1mmicWkL4Zko7egtgvqxrDaeY793beZqlLfeki7ltnRZG1ARGzLb53elWWmI93wQSLaZ4i19i8ACTZbHE6S7xb+5B024WRJTG3Z+KZPUN764M1O9F4P3exOQ/TP1ziAYIfOAKwNnjikGXlJFlZqLGbArK3IrJBA5mESHIxDCMagExIsWAU/+KGCPOagHx+voqlhF9r4y44gfS2qBNXDB3TCP4lpSFDDzVZBXmkzDafNPA+SkCnC0j1OdqXf/q8H7AlG4B3nz/ArJk13uFEdeavWT0XiFq37G2b393qW0MQBn24leVQsAQApgI7TgiNQzyDYgliKB0Y+oJeyIEyUO+HMPJgTc7Y3PRs/6U9nqgEkxM95p8xjBgDAFDHDDEEX0c0ceA8zjgNPR47c8492eMw4AQRiBFUOIsTLsnTZj6s7EglJAGywNpuubiVKozeTZ/Zy1f3Z6135fWsl/zzY4ynykTG8vr3K97RqdXBA/ztjAj+3/NghjnkZyHcxFETuGZg3OC+VJeXOKXE2CkWGBtFkyxrBWq2mUGPEnfi7HSQCICuQCgBG/Oa0t9WZfksruBmETERb6Bbz263Q77/U4J8Q7eN2oxIG4FWD9G0yekfEakEBDUrH4cTgjjSeJDhAExjcrACLDYINYxm2+zhHCVULgIJUrgcK7cyyyY/YAIZgBFuKbPpR9i+SAWEK1qnsmVnFg/GBJNvggqakZ8HZR7bd2tfbKbP3MfR9IjY5DlIZmjVjOC503pHS8bUfjm9/+O+NZ70xyGvzfdAg/z83fXdqnUiupeS5dwh/eOgxHJby1/TmDPfl9r3a1KSNWdeQmo2SFWZib03pQuv1uxZxaJr83lf/K01nPDW1iXmjMvJQSQnp9EnGHyzu/BzNh3BwxhRLvr0A8D/MtJXBs+vyDEgGEImWFucbVezyechx5DGBFSQuh7jG2HFEawc9kicOhP6PtXjINYRLxyg65pQOkAUyxIYQSPI5K6pIW6UcwM15gQEeCaAMQRcTijPzc4dzuxKmj3IPJwroNp1hJBAkhHAliEBjwGpHHQOE4nnM7PGIcTXp9/QRjPOJ2egCSxIhoCOhLGQkOkqsSAaz3QEIgbGRO2INPqioojwIxkFhTEiA5IzotYIxljVdwjOt/ANx5t24qbVS/WEOQaMDnAeXDrwXEPP/TwYZS4H96jV4uWhhy8kzhrYQziVkjjLjTeY982ACLa1vALD+eAnW9A1MAfCLt9g6b1SB74dnoBvzBOQw/fduiORzx8/oovX3/Czz//BZ8+fcHnT5+x3+/QthLzic1LQJDg210j7qLi8ASOjWiQc5J4Gepr3qmLSNnNoogXQqiwglSoFSL0w4Dnl1f87ds3/PL9O0Zu4H2LL1++4NPnH/Dl81c8HB/QNjsQPM6nM2KKeDl/Rx96fHv5Ff0w4PvLK85jxNNrQD9EPL8OeH094fvTd5zOL3h5ecav357w67cn2QfDgCiu8fHp8Qu+fD7gr3/5Zzw+fsLPf/oL9scHfPn0BW0nAhrBm4Q9LHHQAobhFTFa0HbDe+uPMHGFoQwAS/zffieNvRhnlqkZDjjDsNzV8/aSoHXCpyZj5tH0HDLGPy3xzmX5M9qv8jYxaxQKQ946pXVYVHlYrANg1zTZosg7v2zDHLmsmM3m+EfiLHikBMQEDNzgBI8TE06JEIiQPIvFkb2fJTNciOD3cmtlNGc0uLbVCUBMShTFFEAAgs1SFrDW5wMBcGLVALFsIAYcMzxkTYu82awRVLBQx39jBqVShxwCJnBQJV2F26xWVSlK/J8UR3CKYHVRSzGIW7sobs9iDCKANvqSkGNkcO5T5cJPm2GC6tLRmpu3Pqr1vBiVDH1rjsfkfaBEla1Rc4193HV42O/EGmfXYbfr0HUiAG28uCpmAMUd7z9WWoMLa3yHa3yI99ZZ171Vp/xGIRJvaM6yDFx8b00I8ZZ+vylGxK2pNKjyJzWXml0A6HWeLQbUWzTXbh2orcW01Yd72nRvu9/Tz3uYzfpmYa7aWNurM4ZofThOXByZdm2MovkTiyAiVIKImCKGcciumGIUC4gcpFotIIIFaE0lGHVKaZX4nzCeZwzoy3OqwaMggNP6LgKKwnRaC2bszB3H7DBfVmQjvGzD+wBXgRhvKebSGpmM343l3FvvWrpFEJfbPXuvyjB5LmewadCo8Ew/LkaEJJpdMUaQqy26qoORFOmZNW0+pwsN7vq3IQbaRsPDsrY8SGPXGuJW/E2yBiIUpq5oxIcYMMaIMQb5ZJdMIbs8yxYR70xzbYIKP72L73SP1uTk2QV4e3XNbCC8BX+yfVSudZn1m1S/W73CsCmbW7dIhvw3+6g2uFFZUE00c6xcXb2G9OraJNCszzXjqx4jnpRFEOI+l13PR/1V62KkyVibZQRVsK+0Y3ZGloJUSB0rC4iQY0VkVw7Z97ARK1MYXhNwEwa+4sWU2fbTGZvC58qCAqjaPy9/ahEBN7WEKAHbKK+v+R6xoZ2spZX2b30mszlDDqmqY9LbN+BaebY2nl09o2je8/vTRwkjtvq7fR+wgX1rGz5SAHH3WfrumrfSfB8tn15Kbx5L6FhsvH8VF8GsbStCiEtl/CaKQNYEc9/zW6WVfWhae2wNmWSni78X6crees+4/WbCSJp/LfSpolgC9xfL3Rg7lkdgsm8atETY7QKIHMYg52Pb9rp2RJCeouBuEUA0K8YQskVENPxMzz5xWyg+8EMYQQBGP4DACLGV2FRISBwVJ1TmV+5ccddhDFuo1WNUa4xxlBgG3jdo/CD9U3eOEqcplfM59uDQI0X5hHHAOPQ4n18xDGe8vryAkOA5oXPFKpAc5Kz0hEQRCV6Zmw6cKs4olfmwgL/eeYDF7UyihGS4h4bviKyun3QW661NRMKAZYmB0DQJCUDbdlmT2DunsX5rhQHFm1JCJCCmCJdmjBkUBQjvxCK0bVuJ79C1aMcOXddhtz9gf3jE4eETjg+fcDg+4nD8hP3hAbuuQ9MK/sQpqvWqMOBFsYKR4gBOAYkkZom4qVTmoiMkVw57m2ujd53GiAMRKJkiScIYWVzBNA1c08HrJzEhJOA8iPf8fhgxxoDvpxf0Y49fnl7QjyO+vZxEAHEace4DXl7OeD294unpG06nF7y+PuHl5YTzqUdMCQSP/V5cTv3w9Uc8PDzi55//jMfHT/hRg1AfDw+q0CesqJgCmFOOMTGGgBgTxtEsH6aU3DxtKQUBhbm5ZhFBNQCo7t2koDfHsy7lrbDSuXBik/c1jzfB63CWUfVVKqvqkJqJASKLI6Fx7Wocc4JXztszxe0zj5sp78FsDcESiyGR7Gc4iOVTVubKWGv5nQ9kntUzpUtqOrq0e8vnSilqjbwhteSw9q+mlQcmaDB+AtgsG6D8MIFPmSDkuqxCy8eKX5bMe4h+N/fmpGXZNVtEwLw36JzXJLKNj62X6tSv6QW7Uv6ycfZuDu6KQiPN51bPTEclNoQvsTozDVnR2DVO/lEMfWvHe/Ot8aIv8ahvTZf6eY3nvFZn/m2IcCYet/G0qZIMVaQg5/VyW533zdldFhFvTe+xiNgs87cgEv4TpY/YvPNDvb5mYQALIhWTxXvQwKkx5aBoYwxqqmp51BIi9Agx4nQ+IQS5xhBxPolFhLlgGoZBzJq1zjVGQu0Gaf5s7V7xMe4qoFf89pr2qjGffKMumNSfYtOIP1FfBU+zjbuVPlLGeyuSdGtZ87SpjXlPnVsMBL0/1zDfSle1Ei3fyjPz6p+QEDlhjAEUHIZxBBjo2wEJDD94pBThGjkgY0pKTPlJG2rhFAMXrVsuEfdm4r12kBdfncXFWBb6qfm1mPpH9KMEoHsde5zDiO+vLzgPPb4/f8fpfMLL6QVD32McBqSogYcVK+Oq7Ftg6e1rbgrv50RBvYc/EsmwNtZ1LZGk5TqpmdFqg6LakULw5zEC5fN1TfPGNHKcwZNa/EUAVIstJVaYIQTYbrdD07Ro224SSJoqK5yQxhxcMiNnyQjjyiWcIZyVayUAcK7JYyJtdTCGPQg5uBojSr8Z6i1CGR0oVm41ElNcHagjM2aBo6yEPamwA4ykzI049ghhQOhfEcYzxuGEGHrRAoojwCPEKbW4epjPrwlBhCFggb+hxBVViCzl93M/UQupK2JL6bX6uVhCtCDXAM6DfAvyrcaGEK1M0ZIUTUxHJeBavQaL9Qov+rEQpOT+VALumlCsGOUfvXc+ImVc941N+wOn+0dM2W4KaxO7thZvn8fMfVh/unhUE0TWphtroiVT8RI+c5UXn8uZWubOSsGkfzUv5937ly4N3Ur2Quj/Vml+/l56/o+SSCUPpLiBc8aTYT0bZX7DGOCcfHdKE3jv0bUtQkx4OD7i3Pc4HA44nU74/vSEcRiVfonqZvaE8+mEU3/GOI542e3RABiPR0TnEDQ2Ut+fcH59xevLk7QpJnRtB/ZJ8AYixBAw8IiRIyJFJEqAz7wuJJJz24UGTe8RXY8xOZzQII0ibOj2z9gfX9A2LfY7wT+QRBjycn7CeH7F+PQ/EE5PiM//hnB+xfnpf+Hl9QX/+m//U/r5/Vd4YnSecOg8Pu8bdJ6w9ySWhNSg27XgrgFFD24cKDpAlbqEeS5CEO87wAEt7YV2TBFxHHA+n4QhHSMa7xFSRNe1EJ/3DWILeC+uqwgqZPANnCPsfIOWE9pdp5YqvdCg6gqz9RJIezQcKzBScjidB8SOsX+QNeEcFUtMIrSN4HNx3+Fw2OPx8RHNrsPh8Ygffvorfvjxr/j5pz/h69cf8OXTD3g4PmDX7dB6D0DiaFASYVVQiweBCwHh/DeJ6zD0yvRUPE/pzxh3gh94iWXX+E6DDjdoNBgsR0aKhOgb9Mkj8B6RIrrDD2h3R7juC6I74l+/neCfRjj+DmbG69BjGEd8e/6O8zDgb09P6IcR357POPUjvn074XQ+4/v37wjjGX0vsSQ4jdh1n/H508/4/OUzHh8e8dPPf8LnT5/x5csP2O8tEHYrAd2JEIPgRedzj5QiQjypglXK/ATDJTOtVLlXU2yvoivKvjb4Y7T83DLV1HXW6LRaWURw//WTRp5rfbM88++msS5MWdW2J5L4KRfgYsGrTcB4+dwQug5ioescXHBw0ahNcZbkkdAS0JBYiZNzucHGZK97YSPO9rGxlsAP4qIJhBENenY4EeFEQHAAe4A8SXwTV9xXqeRCBxLTs9HyTGjma2k2LjybEXJVvwjJZtWsrhfnVU2nTp8kMEZY4PsEShY8WoTDjVBM0meoNYgJPRJjVGWsMQyitBsszom6YDPFwZjgUoKPDFJlyZgiYuXKL7vhqxGjNZ6NCU+qvHX/CEvG+hZvgDdmgyvaymaEADjlmR0PezwcdzjsWuy7NruDa1R4anyV4tfJ9vQ64/z3Tmuwoh6r+f3fu22LNtgMrATRvq1MIEs1N3B/SwuhxB0V3iyI2GRMzp6tp2phXiFYtpDXtffqjs8lPGvtvXdhXNOou7Yp1tp3b1mX+nVress7dWvmjMRs+VBJcM36QdxuqAVECCWYtCLiIlAQAUM/iiCi73uM2RJCArHmGBBRBBiZscZTEGhMp8J80vszZKK+X393zmXLCoIDO+mjc/auaPu6WSyImmlE5DJCtEW9skL6eirW5nR7nUzvrW76NwCaS5LReRIm08qhdAk2rNxfm5d72rp8d2qSuQYvjHnLat6bYkR0Lls+hCg+9JsgxAjD1pAKInR8GbUgQhjWW72YtLFmeuoNZ6KIST4q2kwVs5ghbbf9Z778h3HAoMGLhzCiH3r0fY9+GNAPg1pFxBwot2Yp2Zjec2jemncrz7qm0vb6meet9/W1tbtci1tI/BK5sDeMyDFme845L4aWB/GiDygMD4JqrqnJatYMMViSmUYrzCPFr+djYkx4MATJniw/mnQ1l0uUEX4TtgA17loQ10KSGCJbvhdz4EpDMzGYElh9XbBp+8SompaVRYQi4EW7s1h+zJPJGFbh++L3NM/WtX63fGaWELMrmYsEFcZMYWMlMFq0v1hcoGoHzb6X35hct9b3NXh6P952vYxFqmiht6a3EhvvFW5KtR9L6Nzal1tg4Ee8s5Xe8/YluHe9XTUH4no9Bj9L+ZfyL+nx6Rad33hLUkLPKG7c1hv+kLrvm/f7a6P1Jt7Q9vetid8qVZO0gSxn0j2fv4UhVyuDiLsPGQfnHBoQuOsAACEds9udvunhPYEGKdl7dd3HYhkYxwHjMGAYevTeYRwHDBZHIoYcN2oMI4iAMYzwPgHOS2y8CWOSYb43GGoFgYhII0Z2aBoJBhqGM4gYzgMhtuDUY2xbUNrDewdo4Onh9E0EEedfEM4vSIMEYY7DGbE/oz+d0Z/POJ16iWvQEjwajA3gmBAAeBaeUoqEFIEYxdVtIgdih9ToeeoIDI2zROK/HhCGLROJtW8I6PsA33jAe0ROaLxD26iyCCCMV3KAY41TobQaOXjfgAnwMQDM6ikzZbc0gSMsuCqArGzQth2apkHTCLPMVYofqPAL5xzatgV7h+PxEQ+PX3B8+ITj4RG7/V4CNKv7EcObnDKAvSdwIiTInIZRvAGcXl5Fu9qJi8idO1QKXIqjVG6D27aF94B3wJgIkYHIDhEeaHZwLcO1R1B7QITHEAnhPAIYM93+cn7FMI749ek7+mHAL09PGMaAp5ce/RDx9NxjGEaMYwAzoW138H6PxgPHw1ccD1/x+fNnPDw+4scff8Tj4yc8PDyq+84WRA6Rkb0mpJSE1mex8GYW9zMF94TSQVxwoC021+TsL4KJVQUosjEsu/9SymUtlGOQXa+tvrdxX5ZPQe7uhYsFT9Tf1f2Co1b4LFB9ZH+YylNWYVpp7ESRWPvJ2ZKAABZaOLGstwAg6DVZkfUxTzW80gyTTpQ5n5w1jDkjZDbfdaMr+iQXrGXlV2j6bNL/8m5l9yByFzASFauGxCzCak5ZKBB1fEsNNCnJrBrsfXO3lbI7JRjTotAR+R3DhSpazGiCtaEAqjxL+ns5dBc80Oiekt4UGrPQWSuNMPrUObStR9c0aBuPpvHw3mX4O4Wn9dRex+ev8VmvvXdr+fPvWwKba7yAu9o6nTbJuxjkzF0ovwuIw1xwdJ1nQvaizsUV3sbk+bwt19O7LCJuGeyPSGv1XJPY/ZHen2qmox3iGXGIY/H3nYrQIUYJpCrBVMdsEZFixBhHFUBI7IfT+YQQA15Pr6otdBZ/kH0p2xivRLQ0I8SMcYTVPbvoE1BcL801TjlW2m2EbDJmFhBTSwh1y3EDwOHqWt+vr79HqvfNFlP4t2zPlNH3MfuWiOAhvlQZgijMGebWrxDEBLrvPWKMYt0SWzCApmkQU1St5rkmcl2fBVUi1AzRuj1r18Vzdpv5CWriDtuHEIWLJAGszOXSEEYMMeC5P+E8Dvj29IRTf8a379/R92ecX8+IIYCiBf6jzDepx2atnx+1Di6t899ba2AtrfW/ZldkmIGpEGS+V/J5NPsNWgpvyAkMabxHm4M9K6N7Fo9E2iMWNA40sawyuOfNHB+CBpD6RTW8ftqz2bpUrM+I+TwuKQk8ZNWDUndJEoBCXT7AfPWqayV1K0EENIGAZJYdLALoIMEtQ+jlOp4RxlekOCKFXl0VhCyQqAUJNdHlaApDaIU3ZsKZ6sakrDrftA79OA84D+fV4sE3IFc+Zi0hlhHFHYKl2hKi0FO1kIMWjV60IU9gzUT7I/2RSvr9hBAGO6ZY1vys/b1STbiuP8cMPs/OGzJYdnta62XNbpim7bI/kma5v6y31y0g7DpD4x+TJqsYTotUtJ4LAa1+gCTUMUCsTCSJZ0BJcUFVIjjsGxwOO3z++gnjMODc9zifTnh5ecH3lxc8Pb8oo5wQhgFhGHB6fUEKI/aecNrvEYMIIU6nF/TnE87nExiMxhNCbNE0hMY36Npddulh8RlESYZBHMFhULedI0b0cGjkfD0eEMMzmrbB87cIIsZu16JtHH788kmCKJMEy/72y98wnl5w+pf/C2N/xngaMPYB4fkJ/fMrnn95wsv5jF+/vaJtCOPegVOLthXGLIjhU0SDBuQimBowO8TgkBqC94QUG3Fx5HcS2LsTRn3jd6AU4ccWiCOeT684nUf8+n2E88DD8QX7XYv+8RG7rsXxeEDX7XA8MHyT0CChpU7WoVMawTkAHtF5sEvwTQMwo2taEBESGEHdtJLzOD5+xvF4wI8//VmYZgYvxlFWky4lczUMAPvDAQ/7Pf70p3/Cn//0X/Hly1c8fnrEvtFA0KgZlgnOAmgBgGOho9OI55dfcD6f8a//+m9ITOh2D9gfjvi5+yd4IjTNDq5p0bY7ON+iaXdoWrGqBQYwBrz0I57PCa+pw5ke4I8dDm0C7R6BpsPz2IJjxOn8jBBGPD8/YRgH/O3XJ/RDj6enbxiGAd+fnlUxUPYBQ+o5Hj/h4fERP/zwIz49PuLL1y94PHzCw+EBbdehbQpeG9TF0ulULFtE8CAeFYIKIApKanQ6TcaajVs+YaqS7trCnGUgK7rXsSRrnJ0gZ4LTc4RWaLkCHew6hx/34WVMpEHhSbTHHWWYkLXJsUEr2f0JL55y/DCn5YiFruCt3hGSc4jOQcUFIoAgoCVG6xgeDg7upqOwEiFkIQRYBI0xEvoEvCbgJTFeIhCyl4kEUCoBeaAx6xxNpzF/Wev/jJ3KU6Hx6nsL2oeR/bcmfc8CLLAFB5qebVFfresOYERE9QiSwDEAHBEha7jJQh51f6VlRBJLiWgKvCp3MBd7umJRr3Fm8eZASeCGeXkoggqxiph7w5nQF7UgYi6Qm4zP7cl2HZRXkemqTIeW1HQe3a7Fp+Menx72eDjsJVbErsOuaxVO2IjN3/7HTTUPeo0X8Lu2pQYNvLIbLqE/W2XqO9f6MxXCWFW3V/YmQUQtPXmvVtaWdt+t786FEb8ls+s9bd0qy8qbL+YtidW1NJfKvTURKEteTRiQWHzaiQ/TmANRJ7N6COUazT+9avXEKGZoIYrAYYwB5xwDogShjuorPFUBpbI0/5ogYoW5tDU2c4GEDhjYi4ZKlum5qZuMuRVEzcxbWxVcduU6EbvBpF2u50Imrb0/K3WSj0rmzBSd1zuvb1X4Z2XM2rgKpOzZyqhsMehvSRfXtE0FVgSU9TpOCSEGgIBhDEgspoPRLCGczC/mjMyqb1lr3VX9nCHRbxNEFIS4rGnbi8iWQaP6+h3CmK2J+rFHP5zFwmgcJrEhpiwbysom1QBtDfjG7XXmw/z+NRB0CeZdS7/VYV+3Ytom2hymtXe3HhRGN6m5v8IVQ+to7aXbxmdyrqAgwOV5aUO+LoQlXE2cIblTIqBoh6ogIjPdq98pIoFKkEAzK1b/1zGOYgmhAgwTaBRNOFsXtk/Kp+6DMZFqWLN5FlzYk+sfBwmCqYJnExZlSwgVHGnD5ufvZEyxLN/atF73fHYvpIpQ4vznyiubOMYbMNY3pr8Hw/ISrnjtna10Lxyat+HWcdjCt38/YcSsPdKoK/VfWsvTk0mKWx/Lazjdom2zdi1/A/dtMqxsLppc6oz3aIS9N/1++yg7NPmd6vvIJDBY1tc6w6M+L6c9rZicnLJ7RXISyLS8L9aNaFv5bbwfyFnCzGi8+E/q2lYDxbqsFW54Wx3ji1kYtW4EwjgCidGQz2ek7SAJqqrxl8Io1hZjr4oAHk3DcBSQuEUKHowR4IDUO4zOYc/PCG0DDxFEvP7yN4z9CcPLN8RxROgj4qBBsqOc27UquJ2PzhHsWHSKQzsPOCeCEpAKeJj0zCdRZGAJKEsq9IEDyBfcCJDnHIExBHgngZgBzhYUTdOiBfScDoIjJqHmYhLL/KQKbrltStN53wCU4BqgaVscj59wfDjgeHyE9w4ExVNAmbHnYsz4SUoJlDSwLYnAqPUerXNwBBDMfQtDhBHCcBThkdG7Qv8O44jzMOI8BFlVLSMxKd7hkZwHwSOyB1gtDCIjqbuYxAEvp4Dnc8BpBIbUIBIhuYSYCGlMCOMrIic8v4gA4vn5u7hkenrFOAb0Z6HLAZ/dEXvfoG2PIvR5eMTx+IAvX77i+PCAT58+Yd/tse8OGadlBmIUF0sizAjKgJXg4KnCG2UhyVhuK5guFeVM0WOynzMdW+fZVrKbV7XgKdUoMbAK/i6dW2Y5b4w9xQaREbcr5+etyRjBtSJdjU8qNQkCw7ui0LOsQxuq5WUoo9YPNh7C2zZXrBJrZEiMkYGRxQGZRXtbGTGY1T/X1S6ECTaJOm42t/N+o9AAEvuOKlS2xm2n36wPa+2Tlps1BGcXtuqsFtltlg6I5AGYOMs5YHiGxdKoPjWqnWlyrgYkCyOqdZ0FCuW3KG1NbFcWPbEvhEI719cKM9rmXazQBrKuloII6xQRFH54tI3XwNQejXc5ToQoZlXtXd1KS3yXZ/jYNTzoXc+tTmuJDUVFQ+dUw4/S0It1XWT0X2x1Rdfb7633N2ifzX4zafdu9+5T8+FuTf8hLCL+s6c1gcpHlPWWd+WLymQViWBOCLNA0+MocRtGtXowIYJoao/6EUR6VFPjvj9jDAPOZ/GPeu57Ddg2Fu0IZnCaMiftM9eCted1vvl9QWKxer9mutvvSb1APtDrWBALSwiaAvplIoA4M8jflraOGHtcYwYbzxVgGmCsASRzZbUxE0bkdXml7cu1S4vnW4KjWxgyl9f2EjjmA5ZIgjuZu68kqJEPATExvPfoh0E0sdomA+u6jatMEOcqDY+qf4pc5uv8MLffM0GEmVxbGaSaG6S+Lev5GTXg4DCOCDHg5XxCP454ennGeehxej2pH1zV3oMXk3VrAyY40Oq6JV5HHzcW+c3w6xJz6N50D6zT0Zzu1ytpLYrJZn3X9ke1HpxzaBqvJv9N9vsMJVqkvNm7WCGoWBHflJCozKhpx8yJDLeGtNVIaUZIhViuUGZldlgdGu8hjojq11o+jVg3ICGEpD6gZf2Ku4ER43AWS4jhFTEMSOOAlEaJEcER4Ag1/xHCGwXHm54DhgRvjPeFs2Keb+09ck5c8vkG5Fo436rfabWEcBIrwjTa6mRCzznjeAH/ZrDmrUKIxYqmOxb5ann/O6YlkfWPln4bfFthxEzT/Wr+nPiG1z6+3bcQlZe01OT9aQyo7bTGhbo0XjTLt1bGe8aE74MRH5qm+2RrHn5vjcDrqYb/gk+zMXUmjKqMKWgyxo9owJp7IWZhQnsvQumUvGp2dmh9g13b4bDb4/HhAV/CiCEEnM89+n7Ar7/+iueXF7w8P2MYBoRxQD8OeH19wTgMeDm94nw+4/X0AjCj8wDaFmdShnCymFUMlxJaSADnlCLi2CO+vOB8fsHr6zMs2lJ/3uN13+G499i1BI6vQBrheYRHwnCQ+AUuiWum77/+ihhHIIlqeUweQ2CEPiAOAxAleGrXeLStx36/w27XYLdr0TWMtmXsnEfnPdrWoWkIEijX1q6MszqSArNHQAtmwJEHCGjbBm3Xomlb+JBATgQPY0gAj3B4Qd83GMcB+92AGBN2+z32idFSRKSAMY7qHjggccrxpdpOXCU1TQNyDjsSZyrdYYfd/oB//i//B47HB/z08w9wBMThjBRGjOcXEUiEAIZDexoAePRjEKtZBlKI6MihI6ADw/GoIa9U+KCBsYkUx4oJSBFxGDEOA3596fF66vHcS0yQBi0i7YD2iNTsEWiHCA9KXhiXMSGmHjGdMY49xrHHt6dXvLye8XIi9EOHPgERjKeXM/rxFX/79gtO/Qm/fPtf6Icznl+fEGLEOEgMlMPuiK7t8OXrn7HfHfDj1x9xODzgh68/Y7ff4/j4CN94NE0r+IYjIDB4ZIQxIMah8AUUt8uKjUWvW3adU2UpKoKIdYHDdZhScOPi5mb+2hYdau/bWZFp4QoS3JIWzDpUzHwbKyXJDae1WBHLd0vlmem9lahSnPQuW1x4FYY5YhAlOEpoPaH1hacBCwif4aT8KX0vfSijInkjA2MCThF4icBTBL4noGdgnIybwNJMh6yiqSsE0EqXF7h1/qGuYAmFhlkc1VTQHWPoYzrXMkGs/DB5niDCiKhuyZGqjwkMCJjbVmRwBxT6jgCLQ+TIaT1U1ms2kGAgMTiKclclXVNBsHyYK8uIVRaJPZDzby6EqCillZfrZ4UqFitwW2eFpjHeEhFAnrDb7XDY7/G43+Nx3+G4a3DoLE5EkwXJuZnVtexRqvbxGj526f782Z3J1inNsJ88pzP+2BwnMobqf9B0P0/5Plrq3cGqfy9hxDVG5UVp0oYkZyvfvem36P81rbCL0veKkfzWepkLMyUHx+USByKEgJCiCCJCzAIJ0eIZRBAxqvuYYZAg1MMZYRzRqyWExYzIDBs2Zh0tGMmEKfKQ+yudviygmI3bfAzXtCXmiEqOC6Ga8kUDvuKE8RT+cJaSKvCf7ZU5o39tvqZaqlrJYq6WzMlJGVgCksn31fqW7Vhb5XMB2mIvrMzJWlpl9M/GZnOsyomVmai8KFMRCjXTDZFE+4okToT4YSX4WIHEau1NO6/3FMmr27s2DtuMTyV4tYLCgJwxJSv2cS2IEM25UX3nntGrRl0cTcs85WZTZlbqgWltWJnvvD+0havr0pjTVTHztVA/z+/NCQJUyNp08yxRitletvHY2lPLtIFq5T7cCDepypM7cBkeEwhsQfZWGdG5B0YGTJB0Gw2DyYZ8zkioCZRYI7K2kEyb50XgsxlMFHTRrCFEu1CsGyTuQ4xBBRGM5AAwIZCHBGQcZ4ILzW9WEVz6NRHC0FToUCOm825RPZ5G99XzTlSyz/bo8lMsIIq/3SKItkbVaLwJdC8hnaU/9fwvCeMtcFnmdGUzAVVA9fvSpNw34Fm5DX9nfHuNsXBLvpqw/r3S74E735XubE59rNyU/4a5uXdMLtEEt5R1Kd8c/6rh9E2dzoyd9/dzVvAHlHFnjdoXC+78HzdJ+6+vD5p8N9cgpr3NbExTcZjITEiJEGOs/PirNigA6FnSth3AwH63w363w9D36HtRHPGNR9/3OA9nNG0jzPMY4bwHiMRtkFqiO4IqIcTspokt/lkYEYYe/fkVY0oYUwLiGaFvwYNH7Bw8DSAEcBJFsHMcMDoCRUaKEafXV9WIV6cuKSFExjgKDUjE8I7QtR67rsFeP7umQdcydg2LEMJ7NI1D44U9RxBc2xGJOybnxJ2MacVWR3vjGrRNi+PhCJBHPwgu5JzW3ajLJYbG3AiIbkT0DRiMSDELIVgZi8438E4COjcacBwkrqLgHA4HcYN0OH7C/nBE2x5kzcco89904CiWEU0T4JtO5geEMUSk1ON87nHue/R9h67zcIYuaAwKUuTOORndFAFOhDE6jMkhoEMkwHcRzjXw3QPQHjBygxQdwpAyWElgJIbE0RjVOrrv8fx6xsvpjNfTgPMQ0IeIMSa8nExp6Tv6ccA4BKQE7LoDdgDcgwhoHo+f0HU7fPn0I3bdHp8/fcGu2+PT42c0bYudxkQRJmhEigwO8jHPBqa4mGN/KTPUNMnz7nJLmrzsVaN7Cv1W7tfbeoW+rdD0FUKu1H8PHF2haS5pGE+eTQmezfbMyyFDftdSRQsYfuwMV9U6a2rKLIFkDxheq7z0CRK5dSZKJ5gJiUUIERIwRsYQgT4CfQKGZHEizAajlMtMKCKOed9mPA/j/dVCoTmPg9MEZS00bDXgFZ9AxoymVfH8DaVD6teZc6xG1B+THqjggoE63vK0rAm9KOOgohM4y5aqMnOvS31ka25Or2k5VFdxA2/U0Jlq1a7mW5yZmWchPck0jfIYTFDfti3arkXbynngvc/xktzKXuFqUtb35hQfW/LJZv27QJ/fcp/rotfeqXkq87Jsvq/gmLfSLW9KBNRWP7fhuzq3XN65BafOT++Aqe8WRPyR/vOkGgmwYFEhmiXEkIPjRnUFE2JEr7/NpHhQa4hxHBBGEUYMw6AWEX0RTGgAalSb0JmZ3gpDd35kl/vGBiJl9qkZpD43i4g5YlBbQMwZ+etMIavJ1Y2AMQvt2JtyT20XC2BeY0ivaV9szI69tZiriebGBUHCtfRWwHcLgJqM4yqD9HrZ86s0GguewNrRI1o44s+ViJBUm20cg5qTVzEhaHrw0KRU+VqYklesJlbmfNI2xRSlWgKqqwm9nGptynuyxsYoAghzh3YeBoxhxDCMiCEhhSBm4gCIXLVqy3p86zGnhqq5A1tCiK23afKrOt/rbIbM5J/rYzwXOqy14+MO9ClxlJ0y2jqpiYx5G63funay1tJkL6hbglxLwYJzoOcsuM1h4GTtuHoctzW91lKNfJrRsfky1hcFj4L47CUGkBhxDBiHHuNwFhcO3QnEjMEDqWkAbqV/QeK3hHBCjCOG4RUxyHspDoihF0I1mfWOJXN/twGTAZgeTd3nejxWhRAbe7Iu32mcGDgPsnhAroGjBmSumjRqhzVGhqnA40I0L+ueC6OWrv9uReI+EFn93z5tbOD/bZJhWRX1fdNrU1h9V420JTR+f1oruyao5/fm96+UPrsCl8dtjsG+PUlzTefy90uCA1u6Xvd1YvfvlWpYbIyxeZvq+TUFCJlf8RouwVkdedgpxAniejAEOC+a4s4JI6bzDg1aHA8eDoQfv/4gzP7TCeM44vn1GcM44PvTd/TDGQ+fjjidTjj++xFD32M4n4DECByRQnEr1DgCx1CUAEJAGAcM/SteX5/w9O1vOPU9TsOAp86hawhfHjsc9w0e9w5dA0QOcJzQ6/IVpjijP4/CaHStMBITIybGuU8YxgiHhK4lNO0Ou32Lz58OOO4dvhwbdA2wbyAa874K7qwKB94L7tN1EhtC4jGpFrce7ESEXbuDJ48///Qn9GPAw/EkinFJnL5QCiKACCNSYAynMxAlfgdDGKW2L5uugW88urZB1zTY73fiJgsOYIJrHJxv8OOPP+P48Ak//PhX7PYHHPYdOAUgMpIb4BKkH2FEYof9MaDp9mByOA89Xs5n/O3TL/jy8O8ABSSMErDcVXQptQAcPHmBuMkhMTAMHn3oMNJnpI6x//ojvG/QPX6Gazu8ph3SIAGmY2IEVQrsxxH90ON0PuPl5YyX1zPO/YB+GPH8+opzP+D59IphGHDuz6oAIrEXHx8fsesO+PLlK3b7PX768Wfsdnt8+fwjunaHx8cf4H0D7zrZByyWNyGNiGHAMPaqoDiKcnhc0qWk4I/INLdnpLLiUXGCM9k3nuC/NbPM3J2tJRN6VBhghatv02ybiT4OQzA6c47brrZpQodC+dFLfgGBMi2bPTdkejNleqIhQusc9l2LXdtWFhHT82utnzaaiTWmChPGROgDcA7Ay8j4PgJPAXiOwAAHgRRKV8gCUkY7Tc6Um8d1Kn2arYcZvm88+tqFXKUcwEhg0jh41aI0ZataCEFQYU1K0n5mZMtt++0YIBEMmmWCeKOTOljz21zkfaEVJRbYm4Ud0DqyEAIgqyuVexOBhP3Wdzh3wBgbH3/+EpW1BxIPFATAeULTNtg/HHF4eMBhtxfLua5F17VovUPjyrzl5ucZNXp4Rnu/rZVvf38GNxaPL+GQgjy8A0fG+7t9I/C6ho//Vvj6uwQR14B4rTVao7C/RbpZIv0Plu7V3rvWl/dYQUy/Txn0KQfXEW2cEAPGYBYQxbfpMI4Yw4BxHDAOI2IIGIdBEaYxu18CbH9MDyNAgjlZn7cEEfk5ikSVVAiRqvGiqpwtpvbaoT5xk5PniJCliqSHMs3bVbNWC9N3ba8U6e/b1udSiGJMy7ot2+kWJGySZ0a8z8d0nv8tvVrbD5tCCK2kHFoo3za6Zox8QcJ15FPSoGjFIiFPM1Xv5TaWwLREFbtzFanicpn3rdKQh5VC+ZtoYyuyXQ0IGBCrpGQu0VKJCREkdkvtmocU482IlHGVMZ0j60OFjRUMzDQcgFWXTWvw9y2wqoZz1w79NU2Ctfem+ZdIAlf5rmnoikChMDDsbZv5NThdW0QYo7yuv0a9mE0jh0WoWsPgiT/dCr/I645mZVVLLt9eQdpznVWTcuPFqkbMuqm491JiNMcDGoNoYbpG/FgzwxFL/iS+oEMU90sWP0hiAcUiWOHKgqcaT6XZMtM+j/NF8FURnRsZJ9MwExAgB19zZazsEKL8pSqJVIADmPbfZssMZlQwZOuznlYQ3ZXe3UNjS7vrFXAZD7lQyMXHdxH+H5TuE+qs570Gy26t41K+W3HB99R/Pc3G4FqxGcd/e/0fvSaunSG33l/Lt01nGMyd7R3agj7b7b4t/f3c4tKFfXIt3WqlsvXu+1I1F1Rg3XabqJybhMJAylMuVoExnwW1r2tCIgnIKueJMggV7jfeg1UZqmkasGN0YQfXeIxhQNM26Pszjg8HDEOP0+uLMHvHCDDgldlEKSKODmMcAWUORo4IKWAMA/rxjL4f0J8GYARiQ+gowkWPhhtwSwiQeAVmkBiCxHXq+yTMbht3lqCqIQgu4pzQSb7x2O9bPOwbHFqHnffoHKNTxrsF0yUmMIv1goOHJ4fGtRKbwQQV5It/e4jWNvkGh8MBTRsB12j8QHXfGAXvGM/nzIgTy4gRrmk1poFYPuwOO7Rdi0PXiZWGb+DIwbydBBBc06DxLRrfigtG8kgsGtycA9rab9nvrrLqAMRqpR9HvJx77PsB3TDCNwTni0W9J6Ej2DWCd7oWzAnREdhHNPuduGPRgOjs9wjs8dInhJhwHgeMQeIsDuOIc39Gr0KG19OA82nAoHFG+nFEiBFwQLNr8Gn3AAKhazr4psHnxy9oux0+PXxC13X49Pkr2qbDYf8A38gYiVLiCCgfgFNQy1ZxvczKnC0e9WWPGS6b6Y2KHKrT2t4W/HXdW8E8pcr6e60848FuQePbNH2XOGc5/i6XK+EK5vRhjUOWcraFovbukl/jiCTmHBW80vIys9ItMh9mDdSqz36zzpn2p7RSmMPmbqeaQyakBIQobpmGkMQaIgBDJAyREEhiQlvt1SwiK2etUM23J11hV88GPZdz/2Y0LFUds3y5o1ZH1cwsCIAKBvTRQgBQEdqpcpuUaVGuquccKwacisBhkZ8LzWbPWMqQaasmk0vbjF5k4wHgEs4xx2vma45yuyV3xQMho5BZXYSJO8G21Y/GiBB3YUVgxjP6tPAoijBxiw96HaeQFm2d89Pb5ceUVqfZvXlZrDBreV8m6DZcdMHXWHn1VlwoQxwCcsyUC6m0Rz9V3fN2fSRf/Q+LiD9STlMte6gAQoQQQV0yDaNYPIgGtlg5iCb2OceD6Icz+vGMMBSmkwW3hpZNQGa0TkyzAMAXrdBaoICqfUSUkfo6X9JDKb+nFhEmWKhNpudWBZbWGEEGfGtEagFAFiNaIR4XNq2Aqbdt6jUhStXCu8q6xODVG3IAzpl2WO8fTRAPLMb0LWmBqBmhT3pgUQV4UX3VV5Ie6CnoOxQnUD4jdpUwTKwpSp2mcbKoaNa++XWekjIuF2PCVzRkAPVRyYhBhIMxBHBMWQubWPW1ayGG1pqrmRdKiqxVe84EN8LwrtbUheV6ca1/3Nm1mq4z+lY0ia506TqBYtcagZkywwSZcjqO9pkSC6ahZqweRrHaysx6o5qZp2skd6DuhcFaqqd9ARaMcVLKq5FQ1jYrI4UV5WQWa5xxxND3aL0ESQcTGiLExoO5gXOk/UiIsUdKI4ZeLSHGUeNMmAG3CVioILR5P1MlB1juufxxRdhzr/JDLYSQAlQIUU+aM8GE2WKIX2lDouXMjNU6X2+DdUEIyKklxE1wsgZqH53eB6IzzfcfL/2HbfhvkH77sbhFWP17pnl77m9fvXH+cfr1kanGDP5jJmv7lNkwFcJmMjz/ZQYiQj4LAQBJAiyPCACcWss5eN8gKx+of2/ftOJDW0s0HLJpJO/+8SBx8ljchIYoZ+P55QVjGPHt+TuGYcDT92dxb/tykrP39QVjf0LCgEAD4jlh5IA+nHEaXvFyfsH5ecD5ecDoE7xjuKFF3DfgocPQedXUNwEE4TyKq5XzIIKI4RwAMDyJBm/j5YhsG4eua/DweMCha/D1cY/OA8cGaB2jpYRIHhEeThlyotxLcNzCU4OuOUhcNucU25Bz1qmlQNs4tB7w7Q6RgcdUafimCIQRw/mMl6dvGIcBp9MJHAPGlLBvJF7F58+f8PD4gE+fH3E4HtCQ2FrGMYAjo+8DUhSLEPIN2rZF07Qg1wHUIkSIMkVy8mGnMQ0Fv3K+gfMSxwL9GWNMeD6f8e9PT3D7FugatK2Db5zGl/JovQguWreHowZwYvUceQA3wLERAUhSOlyEChEvT2ec+x7fn7/jdD7h2/M3nPsznl9fMAw9hqHHOCaMY8wu5pu2gW8cjscDul2HHz59xmG3x0+ff8Z+d8SXx5/RNju0fgciD+dbgKC0f8Q5nCWAduxF+SQOIngIERwZHBlOREuATyAfheclfyomLdV80cneSmmN5rwmhDBhUFHEI2zRH7SgR3MtE2bgBr4mlU8ey3uXaRo7Q0gZ70YAmGJLTQdslrFyr7YOIRKLWnFzZrEspa8WKNo0+AmcrYIOux32XZdx2TVFrcIcVloWUz5ITMAYgfOY8DoyXgbG8wi8jA4vkTB4YCSSQOmTiHsp/30vulnaOltZFZPcYMaculFzhSmjP/FyTm3h5rgNWp4JF6w8trxmxeA0f+12tlrXzBK0XoUQSBGUIihV8SDyptH25bbY++WRCUdsvpdz+r6zu1ZUNjrV+C8idKa8TwgEr8Gpd/sO+/0Oh8MOh32HrhMBsfdiBeeoUiI2mtXqq/rwPv7R2rvzexvlL+pdL6vGJSZtpXU+3W+OA+cFT2+aenrfcrk53SyIWCXqGZlBkH/P3kIlhdwoeJ2mXqku56vPA5v08mjZlo+CdCiL6xKTcFJtBQxX0+bYTDvAyr2/rSvz1bO1uUrbTMuWFQhb0BuBuQSmRgKyuAgmRiSPgIgzJ4wx4DT0iOOI0A8aLGtADOLfNKkbJjLJLQqgIkXsp4eDCg1oGsw3m85p4Oc1po2DID8TZrl1d4ZsCIPQNpsBDx2RisFtddbWENtDP8FUqtvbACd7TqW0+rwUVSEEk0NmiUDoW7N362bOYkZMCLNq7Ob9mQuNZu/oj4y4EWb1zAQZUg7n9+ZN5ep5VjZcCEjyMZU1T1BnM8nXSuLy8qRTrBhSESaULEkw5/mIlvWi5RgTv1ynlRSXnLO9qgjuDGUq9SiRwABStPgqpM/MxFZ+z4fL1nw+l1YOzcVwUH3fni4H9D0HKtEyMDRjihDWY8Kc0Xp9pggQz8YS1RpiILsbwrLPk/0+KWU6D5NzBmvwZTquhRCxWTFmPhSvLEHQ8v4ggcnZIiIlCVbGPEU2aT4u07abpU9xD1kdoDavXK48AUGqKUIAO4ZYVhNMyzGFgDD0Enh6bBHDC4KLCIHB7EGuLWPCrIKIgBhEIMFpFJcHXO/yyeAWkMPFUdVUa2N+7huMLnNmK4VgMK3uYm35UOI/EGpXbTZj4sJhWoCckODKvV4qNYPsHCtCnsmVCAt3TDWis5qoDMwG0f2WNCfyt5GTemyXzwjb8PZauqb5eCm9V8i9NuZ2di61liz/29twlQFxB5Hynr6zEbeLQu8v6/520OrX+uYS+q4/v9aW5VnHm8+u/V5rpzyvf9flz3NfK2+9D9LqtZHYLsdwsbqExRm3iW9slbleH6+UfbWZt+IN793fnEd92YzV/a2MhZzFT/MYZhEFWUyU9PxI4OTBLIGGU/KIkACtIoAgNNRk3IwI8BBrCc8ODEbnHRK32DmPGCO63Q4hRHx6OCGGgP50QhgDzqdXjMMZL89f0Z9e8fT9Kw5PP6L5/BndT39G99NfcP7+jPP3FyAN4DTi0CV0PoE6IHmA1b3RGCNiYJx6RojA6SzM9nGIYIibT+eAw86hbcSioHEODRgNxDpDfH5r7AxAXfgofGGx5mQAvhGSStxCkTDjjC4ACf1JBHCTp8eB4XPYWAaIQQ3BNeJWCYlAXt1BNQ0ePx3x+fMXEUQ8POBw3KPrWjhtSyQn+HMCgktIkaWDLBr/Y3wBhxGeIIGk4yDCpySuVwIajMQYEOH2n/H4wz8B+6+g4wlff/gLHr7+Gd3DZ7juEU7dQpETYRW7Dok8RicumlJksUIZAkJKeB2TukKWGIync48xBLy8njGMA15eXzGMA15PrwgxgiPgXYt953HYNSA0Ys3gPbpdh7YVq5K2a/F4OKJrWzwePqFtOjRtC3IiXAEnBB7BrAF5U8IQBiSWgNNJXWjmeF6EjLgnJDDxRNWpxi1tTdT7vXyd0xWFvt1StpsyRet3ahxw9t78J5ul/QpuWLenwjdJ15+95xxlesTw0yksNVsEo1FUuY2F/uSMU05hdOFLcKYZjC9h+CKDkIgQnQMTwbMw9RwD5FiYu8yIzAAiHCIOncNxpxZBrim1ZmBnOuhcNydfzbohsVhOpRgwJMKJCd8Z+CUC3xLjOTECBSSnAhBiRKV3nA6WWEtswP/JoplNnT1bOeNLy8v6qahAeS3TggVf18YoPV113Agjc6uUTGigMC3P/GT6pEgt1tkyUmGQUg2ZBiQ2d7sWxt3aq5bi2R2UBrvnlJ8VoUftUrcIVybty2tzfczzCC325XSMLYnOlqxdCWtBAIniGQgaH8Lj0GoMIe+wcw6d82idrj9SZS6tT+UYuf1GrtbpkgLsWrquoHg977V8F3FEcrmH01Q8fVgZy/ev4FRYjseUbwdDAqsby9+SbQtP5It1FDhara8b0Trg3RYRVHVyO88a0noZnb+S1jq4slg/Ot0jhHh34pUfhrne9DLPFl9Jm7QAs8I0zpLfxCqI8C0YDuQAdoRAA3qMeEkR53HAy/mEdO7BZxFIpDBqDIgSYErZL4Xp4qrvGfrYYVgO3tLoAqTW5oCZJ4jwpM9VPvmmQaerJbw1r/lw48pErHqW86wAqukGnQLOos0snUqz8mYztKivvr+etvNMhQOWYyrcuba+FxoI0ilFliiv1YsMFT3IJpEDqOpnbt/Wpl/p2yLbGjEvCNVKZu1bKciI0hpgxxmCvDX3WQgxmzc5s2mlbct5nvqaB6gS0E3Xk1PeJKMezsmx46ZWOltzvH5k1uORS5zmuYIY1EwgQ+ClpOUpwdVfq1dwnsplETBZr5xfmZamYlYjB+atqvY1LdYa1WsCU/+2taDzWp+zgCz/k7amyCDSIIbzvWcEfAwSIDFqUEo26zKuYKf1u55x1dx3psWkgH0yEGb1AzATOMl7eUwdi/YhMaDw1ZFHHAcM51cM5yd0DWMcPAhn9DTA+wYpdWrtJkhyCiMSB4RwBnMA85CR73rdmFaMBXhE1SNbBBmuWj/ymOmHTfhiVkeaB1hsOdNTlX1lPr+Lmw3nSHxYw55bPYroqzZf9l8cdQ01BkSc7ltSwZD65KUlvCVbFPUSzOtn2uopwftxqd4Nc8bi7cKKO7DQf5i01Z9VjGnj/o013Yg73pLvVsLJ0sIiDKjj2N2fLi2DK6nGIG7DVOfw7Y4kh+NmCz4u1VjiBpuFlvq599AT00hLa/Chyjs7owzfnJc4vXlpXC61U8u+iAe8dcw/Atat9X2l31TNTiZBjFxWTWQoYz0O+qbAdU4qgI8SW8j7BkgBFCOaRtwEJWI0roH3Dt45tNToqSLnPVEHIoL3guuFpG6R1LJ8HHuEGHDqz+jHAc+vzzidT/j1+694fn7G119+wevrK55entH/8m/of/13nF+fMPQviMN3pHAC4gkpDRhfXxBTwHkcEIaI00tAGBNenhlR3a4oGoK2IXi08OTQ+RadJ3RIaDjARcB5r/EPxJp+TBEDp2wRT2A4AnzDgEsI3ICY4VndykDWp4MHsUNCA4Bg9hINR2XPCQ7jPCG2BOpINPA7h2bX4nDc46efv+KvP/0Znz99xsPDEV4tOeIoCnKxgTBoiRBCBI3qwCYFhNDj3P8KnxqxvGcGYsoWLpEJwbU4k8eJHNxDhx//+Qs+RcaPMeF4/Izj4RMOhz3abod2t0fTtJm8NVpPimOcz+JR4OUkHgZee7GEeXp6wtAP+P79CcMQcDqdEYN4JuDESAnqfqrDrjug6zo8HL7guP+Mw+GA/X6P4/GI3W6HruvQNA289xNYYwGlhyAWD2Ps1eJD3CiHECZ0yIIP4hU/huKQoEw/zQUR1Q5bnkMVvmY5axpr62p8gZpNkuHjgmG5tLC4iEYJ0bS8z7MxIBMu1PC+stgATT7KKhZ82/B0YsU5zdLCesIZbyWCWFbJF4AconNInnAAoWGHlgEPRiQgOQkmHRMDKcAj4NPe49OxQ9d0aHxr1E0F82wwpU0ZJHIC0EBFqtKPJB4vTrHFt+TxrxH475HxryniOzN8GuE4As6jIYnNCGb4KOUmQ6cXg15N5qU0EUgorWT3TViW+8cVas2gGPJzmSfjB1R4gi1kDX4iPC0RDDi2iHqzRW5oPwjRYtU5iKslayOpMqEBVo7yySUalJD7Yg2fZDKzECLmmDuUSl67D3vH7GLSZGcsh7Ia/a2Bn+5ZtcbxXtYDy7oAXB6Ttm2w71o8Hjp83rd4aDyOjce+adGaIIwo73pTpHRZwFPRgB+Iqt2LM7+rLkAWwIXFTDSlgT/USoLn2PWct0dT+CgNuKuKJa/zPqLgDkHEFeTzyt1tOL/17n0LYltD58I7H7TotiRjwNtR503y/pLUbbWQZUls729UUoHujFSI4JXUX6YyZKgRDQ/XKKOGEDKjjLNwwwjArAma/fFnDH9W+9wSQhc1TXMtGEo0Kxdrz6dVLoi0GZJVb667CMWNjXxJqpgZfyvCi0t9yohOLrMcKZl5Wx3AyzKgzMcr6UL/60Nsar2zfGe6P4xheJmxk8ejTFzJT5ff3Wy/LaIr8LIghbcfXjWDvWjPVFfI2rs/LddHXc+8PZN1qGv9GgyZDEedp0b65lT6G9Lk4FUixqRipfhqFek6YY0lMG2/vjQR0JXnzt7PXaj3nbVn2cZFPjY3S7Sax/p1aU3UvzlrwhQ3TM6V7/ZJKU3i61xes8u6KTPFpoikDcp8ndjFBC2mI1V/OLEQ9DEgjCPGoQcB8M4jJXHnYMwFcEKKI5gjYpIrG5LMFbFjoN5V+/tdqcDz+Zqpp8iEAHNBkP3NIMoEQ2xWECVouJx71TzP1sGaIsP6HpyusHtxp49DYW1e1kqUiVrSkIWw+63TRxMNazB+cWRchJ2XCI3fnvC5VsdW23ltHiVnybM1oXYWGAxdvHk5ydl6ZaUvAPQC8butsowM5RuL8+B+S4itqmZtXbx+Gae7VOZShJFf3G7PrNyMRs3aWbK8cV1OGEMXntfpVqEc6rXyhjRF9KfPblhbNe40L5gznBTGYWIAKenrERIQOUA0alM+09vGI2lAa+ecxg5YMgqyt0A4sCM416FNovV+iAGH/Q7DOOLLp88492e8/PkFfX/G6XzG6fkFp5dXnF+fMfSvGM/fEYZXhOEZaexxev6O0J/x8vSKMIx4eTphHCKen3uEEBH7F4mFEQK8Bx73Hl3rsHvYofEA+QT2hOgZwTHGzGqNGFPEGARHiDGCSNwRihY+IYQRREAimmwVYZabpbycNYkZ4xjzvDjn4doWjT/geHDYdRHHfcD+cMDDwxGff/wZux9+hj8cQPud4JjESC7kOQAzvBvBkdEEPXcPR6DbIdJngMUTgPB9Wc43Y2gmwFFC6yKwY9AhCdMXQNd26LpOlG3IYQgR/RjFxTFHDGMoro5jxPncI8aA07lHTBH9eJbr2QJBA4489vsjAMIjiX917xu0TYtut0fXtuh2HXbtEbv2iLZr0TYt2raFb7y4P2Fx28RAHoMQgggeQpRYkBxkrNKUOTZflxM6o4JIBUXVk+UGXGDrnL2W5gp5N6HHuU5bcLPrIs8afn8NFq1bV5SjstRZK6EYDlrlWNRf48pEGoNFY6uAhJUtDGoP5XiLRwpIXMSua7Dbyfps23ZxvmYLAoII9wrrHsyqnJrEaiokQmCHIRGGBAyJEVj45WKwXcpiqvqS/Qmt9E+Z9VN67kqakDX2LkoZ9rHiK5ynxtez4KEaD8rvp0k5pgh3tV0V3VmaaIp0jInwLQsnqgDVWwVbW7UdZUinm2AeGB5YwTHyYCzbeSnVEKBWCjWlq65TmKTBqZvGw/vyMWvwLHSjaZev4SP34mVrCqM3vrm4sxSkXsZ5LuN1a/Cifn29rrU2XJqzS/21ZbqyXN+Ybp+bP2JE/G+aambZ2sLNwmFdTCkBKTn5sAPIg6iB8x2cH+F9i4AeIYoUlgzIkuJubhn3QYq/DGAWyEKGrtUxVu+cG9a+6d0YY3behi3m0do4ze9fAwKXnhsDcs60XtO8n9+z2Af1nFnXjL9i6M16P6bv3ZKuAfEF3T95VrWBUU3iOjI4Z+6uwOa7U0b3rnT7XiHUop7ZfBLRVYBfr5Vr62btnUv3/hGTIXWrhE8FM0QjLWUExt4Fz5nsQA3BLA5NumMe53BgbT7W1sUlWLHoM0sMHgKD41LAZHlMo9A+dZm3MrQyA2vi1HR6NYLIORkrpybfVl4JPCmEbIwRYRwwDg2G/ixmyyB475FiFOaKFp54BHPKV9EAErhlERfmAbXqM2N9rK/BoYpdv5VvE9klCAOpeqqEjQmRhIYwS4gVuiH3Z3qefTQT/WNTvTAuEELvTP9RYNPt6T4U/h97DdyR7sS/JuldphjvTwuB/n+6NSnpmiLL79mOt9dHC0bF3z8Zo9KYdWoBnnE9yZM4qNcMh+TFXa33HtyKyx5L3jkVwttYQZn3+twLs7GFBwM4zlpjzj1iGhFTFHc+o8PL6NC/vqA/n3B+/Y6hf8X55RvG/oSnX/6G/vyK52+/Yuh7fP/1G/q+x/PTE8LYA8//Eyn0GPoTCAmNY3gH7FqIwCENYGIED9H8RRSmJ8RtbxglcHaMIZ/jvm0AR2jHsYxdRdM0XqxLHI0oNChjDII5O2rQtISmadE2e3TtZ/GP7zyOxwc8Pn7C4esP2H35IjEovFPcIyG16i5YZ8zvUg4MzSBQuwP7FoF+RkIjNpAkYRwmVGhKcEzYM7BzHkfnoRG8QRRACBiGAcMw4HQ6Y+gHnPozhnHE6+srxnHEs8YAOZ1E4GDWCQlRKxFLTWHctWJh0bY4HB70ekDX7XDYH9C2rQg/qJEYGxV+nFLSWI0Sx7GuyxRcagZ0FixXeO4lXDMrzU3mEoX4vCPVCnj35L8VMKzxH0xRZZlHx3D2zPYlK86cJq56afJMmiYwgoiKYGuG21IO3FtoxNIC44FPLS4ASHwOEqYuvEOEuNVy7CVAfEpAjCCO8JSw27XY73fY7/fouj1AI7IDn2oPGpEqdIMoDIpCakKMhJgIYwL65HBOhFNg9BEYoggjcvwHRZwZ1XGfIyuvJF58uZ4yUz5lHL0IDurnJX+2RsiDOy8P0/crIYXtlestZC1imrOMcxE45PZUAoaJAKVum91LK3lzf0taE0a8NxltLj/KR84rB+8Ju53ApsN+j/1uh7ZVwWgliKi7damV/3hn/0cmg0OF31Rgb3m+JfyY47CW3oprrfLcfsPBf5cg4hoh9Y9KaL2n3bcwEvKzG+btrZO79V5emPnv1BVLnW+N4VVuORSHOSxBquQ8k0MoOiT2ABo418J5CcKVYWDljqlq3YrsmzMA4ox4cXVOyWYQpffK/19m6PKUmL3AAMz9JQhLjiFMthUm/9rvWwjWVabz7LqVDHHZZmKW+bHflhwYaWV8AYBnjEe+wZ3RFoN1/r0Wlsz3xlr+OWKb684I6xLQrgFE+b3iRuc3gDmXpM+3pNV1AFzEzzNRgOlaLFWuI/i3tOnyGqw0RS6WgdVcpez1t6X8YoJvAkVD5utxcr64r5kQSlX5VLWlTM9yv5avyzW57NsWjDcCY13TfdLHlbK3hImsjAuQECw1DDCttBTTQkNtq93LNEdk7U85pwqIWIE9EGcJEm7OXCgI3BRNyREh9BiHM4AE74DkGwAJjiRQncCuCEYC8wAjGggMIoFdXsfA9jatuNjDxtxkfLiel4r5X9HWMyIzO96CnDXV2q4IEE4MOGGuMEclAGzOEqbbVetljzqSXOlX9bH2aQNZiQpCKeeS0Ou3S9vn6C1pC2ZeK+u98Oue/G/BvS7XvQ6Tb3//75UuHUSXc6yA1bvrng/JtbXxcQSRwKU1YYTV81ZC7JY1t4VzbdbyRjzkvufzNXzfWF+rS3DcFbh+YzIG4OU895+R792XeQ2xHKYmoyZSdpwjmH/xpDA+RXGr4aMDEiN5D248yFnQT1FOIhC88wVnzG5hZswtMkeMEuzZOw2QTA67hhCaB8Rjh/FxhxBGDMNPCOOI85+FKX46GXP8GeM44PnlBTH04Od/RwoDhvMJokAwgsBwCBIzYezhEOER4R3B575G8DgghRFhFEGEJWOo77sOjfcZF0oapKoxRZPG4kwpvs/CrPWuhW877PePcM7DNxJ017kGu90eh/0RzeGIZn+E90prsJzfLpV5YGYgMRoGPFRByDUg8iD/AIAQzb2jnuPMCTFFDBr/YghRLCG4+OOPcUAMPc7nM/q+x+n1LEKJMSCmKNYHKSHEgMQM33ZoWsLBi+VC48VliXMejpwEnHYebdfB+wadXo2p1/hWmXpOrFS5CBdqF0smkKjvzxletTvGxa4oaI/8NFyS6yyVOyUU+nptz0gZUz7E/N5amjDM70hTBl9GGi+8YBVO65brrP2T9kzPtUKvUh7ngvvNLSLs+fok1DhjxiFV4SU5iCBTY505dkjjgDCc4RzEX//hiOPxAY3zWcBZSKt5hytcWWPsJCZEFndxEQ6JPCLknurmwxHUnVoRqOQrASlzxjfGfo2hPh3Qkge8fCd/rzpX3wNnV0llDVdI/KSc6pMql7h54ObJ4FURQtTKcrYz8oW5dGNe36VUt0HjCVKup6qjvHC1LKq+r+7FmuBeq0Hrb7xH23gcdjscDzscdh32O7HAaZpm4SKurmu5r2tae7sLv3m6NB1ElxC3iy+XMbBK5vkpE+hzDl+BslfuU33/QhMr4tf4M4R1Xua1/tyTbg9W/QYi9C15PppQo9nGeUudS6bHOjPkWvo9NI9KHTXBs6x3vqBqACAHrGjeSB8TUhQpeAiEEAkhOqTkQdSCqEXTdFkQYcF85TwtnB3TA2fmsjG4tIc1P9lhPWFaolhZYDr2Ux2By9rK1QjkwyyP2AqjcH1srxM7l4QR63Vsa3uV9+bITfmeUspIxaKnVuiF5+yWFd/DqF0XQtCin4syMwBE/WVS7hqjYI2xfK3dlqZzt6zznnRLXavrAOtgqd6/l/DkrXXynjQRJgEzf6d1+Zfg2DXkScuytaEEd5qNDznKVlTWNhOSiBLFdD3IVZcT2zhOrYkAAK6pxnM692W8K+R71nhhhNSIAk3eXT6f36/vKfEdk67z0h5724QPYp4/JxyX7Zv2Z2VvLPKX+4UumI+tiiLIAU6sS5wS9hwj4jhg9IShbcAc4QlI3gMswSvr8RYHXGMmT4iER+NIyZYZ/Ji0nQrxtuwfrd43+LGWprdZxzNQAm4AAQAASURBVH86JhkxV4YFO+UwuSQ+GGAMDStGzk6pU4JbM9drq7Sp7ou1oSZQOMOAW/bdb5O2cJ+rihA3ncGXy7sVnr0V7n0srnnfOfKPJJCYiummiWdwbvnuO+v+Ow7DpOp5Q6pzuv4NzCH/erougKtGdlbu1URbTtm26ron1efZ23GjS/2fCyJupYsEN7he51voz/fQZnP8VJjcxoCSo8OBQJTUva0IIYhEWzk6EUR47xFTC+edxkcSi0RHBGKXrTonAgjiPEuUz1oCSKNBuwb7Rvt6aIU+wxckBiITUgJCFGuDIQWEFPHan8Tv+/kVMYxIr9+RxhH9+YQUA8IosQTSeBYlhP4MTgFIQ2FipQhOERR6UOwRw4gYxjxOxkBv1WWQWXrac2+IQes1LpW4anK+g3MeTdOhaTp0u0dlyO80T6PMrg5wDSSmE6t/++JvH6zBmFlzEKFVrMR894vXSEZMQ8EnkZDSiJETzmpx0vcjxiDulsYQEKIEET+fTzidyqfvh4xkmTawMeQOhwOapsHxeETbtDjujhIMvGngnEPbtjm/BDzXOFOGL3JxpTSGASGM2dphbk1r+eZKYVk7ebIVKjo7M3RXYFVFtxSrCPtzHw7wW/BJtoTLtTBiS4FoXQhhD9as0PO3yT3DA0XZCGoZMbP4zXRz/f7W+Om8QYJUgwD2AMiBnAeRWETEYUDoT/AkMOZ4VEGEd8Iz0L4U987b9TE7sXVijT0Bj0gtIhiBk7IvGUQeTrVJjSlaY9eX3THrApuvgxqRhuEtleWNMuQXwgfMLCMm+VW5NTOiqroqxj7SzGJBXeytj1Kh4ljx+KRlGRSZtqFqb+7/lBYphVeEJoBpvytlvUm51bhOWolJWVR9n+/FWrBYk8e5xLx2pQ3eO7RNg+N+j4f9Hoe9CCO6tptYRExpNp409z048r0KUNcLBHBJgUKI163G4BImzdVfUSXQdTXhtxicWiubbr+/magwT6rfhmpc4mXmEq7QhpfSH66ZrqQtQvze9HsIISb16V/d5ut5VtpkgFOAAoFJYj8wRMsnRiAGIATTAHEAFasI5xokjIiTANWKVGemkB7Ek7YibzxjyE0OaEUiS1bKiHmdtoREC0a5oZzOmMKXmVeX5m9Lm27tul2ejncpqMZcynUrXXg+EdrcyPC5VQixJR2dCyK28gFYtdDYqjcjz7CDbx0ZmPdhbY4k3a6dtwV87xFK5fvysBxCXM6yGt/iGtmaFJz/bPTr9jbO04SgzwjIsp43wTTSEWexsmIUhNy5ArGQ+62CCRK3BLqqlKCCBv+trL5mMKIWZE1RO851TAmGbfhOdq4zz8rBrNV1ugw36gCAE4YUcw5mxonVx3KYvF+IlfU+LLuyso4m7auIUxjUF4GyU5srJqrcKKl2YAxI0UswagJicCA0iI7AiQr+RlzgLs3bZ4H6pjDDGGI1wVj3cSutwSm5LuFuDafqMbH5cRas20UVQjggGpYmWpwybGLB40gCW7MRQUh5H5fyp0K/ul75ZgRSOQ9vTxtI6z3p90VX/hOk5c7/I/2DpxlNP382uZ/PY+RpvndXTlMdvPAtpfwea21rTb+91+/gLdyNx3x0kqoLm2n6vUp6NKyibNUCYmZh5pEoGDhH8DGAMqMZohHvCKlhOLL7JYi1aS2iFFs12NZoRLbMIAIxwYMKA94D7IAdHJgJR98hJY9+D1FAe3gQn/BDEMv4MAJJYz6liBTE1SJxyAxaTmIRIYFWhREuv6VRFnDXaz8lkCrAahHhyFxEqitIZXSRE/9PXt0wed/CXBcZT04UWVQJAE7q1UCzDME7AcYYRxFGJMHnguJbo8Y5jGlASgGDCl7GMORriCP6/owYE8YQkGKSQOIxSZ4hYhwSYgS87/Dw0OLhAWiaFt55tWjw6Fr5vdvp704ELa3rZL790iUSMxCCjKvhKCnFSsggH7lXx3pgVQwR2JPS3JJ9slLzGl3ug8t7kJSHQHm/3J7etbtJmOCZ0b9Bly4ElpeAUrWPp7T8kgZyzpUAxG+EkZSbUxiDsvTXLQdNUNloPJXIQOM9nG+AEJFCRH9+xvn1Gb5r0e52eDh8wsPxEa5xIAcJR6CwvoxPgf2kFABD9h7DCVabGMxOgAcSiBwaB3QNsGfOLqKStms2rOtpzkC365wBr0nstJc0aml+DaMroQOzeu1YsW6oBQ7gaeBne29KEOvV5TKtQWYNwYkBToWmqwvIQocphTobmMzrNwcgPH8nj529U8eZ2Ci3FkLkW1MFvsn4ZJrOTd7LdLaeMY336JoG+12H/X6HrmnQ+QZN47Mwdc6fKedrPbTzfXYbhPhHUvRZjnD9bMmVqJg/mSe03e1LONpH40o1r+Fj3TZ9iCDiGtPylkbeylj4iHRvXW8XRqwxfjZyvlGCtz22BuyqA2WjrBrwGCwrDXDKMBUgGgMVQQRUUEFeNVVEGAGcEWPMRRgfyjQuJu1YIANlkS8FAkUjyhGtBvu9JIgojJ+qzrzTp++ujdU1YcQaoXS7IEKFPfMDbiaMuKUNl9JlwcHy+9rv+t7WWGmuq+UIw41uBpnTMjYIwVnezXFRhO82/cLbxnerHavzRtl5zIzxmBuX9/DcqklZmYt6LrWh7sdNydb0jXlvyUeU9VhEw9/uq7ZXdQbnv9AxEcGjy7/NJY61kep3NHlf/C8L4c8zpGa57i+vB65ohFIXVfO19nbBo5cWWOaSql6v9Uc024QJMN1vU8QAKObdpX/WOtZwBWZNxJj3f9Leqr+kY5OUgM1zwYXhEENAjCMcMVL0iFA3W47EzV4FcvP3imG+RmTNv9vamQsqtpb9UgiBPEbTjGWc2Bgl9XyxMnFSFKGKROGT9Qeu/AOrho+FlbAg5LDgnTKe9Rqd7Nk8L4ueoMYlrsJ4XaNv5vrdsJE/Cl97jxbzR+W/pw0XSsGls+iW9Nb6r8Hz92p7vyXdU+e9OO5b27RQLrE5W+EaZ5o436fy5AYa77Y23taPRbs3GAv3jMtW80svp3j39PkFoDtnHK3UXMNWyfo+/Osj9u/1NZi/wU4u8/W+LEPO2tplLIHKuZLRGkbiqOUrDqCCCNMWzdrvCRONeJkCc5Oo7eK6ndZuBpH4hxdNDwcP0isKCk2AaQxw14E5ISQHZmDkI5gJMQKcGBxDYeYZgw6sTGDF3JQhHnWcamYWMeeYdmV8phgvlC7o6mxEi3Othg2JE0IUq4sYJcYCJyCFgIQAkAgjEhESJ4wpIEYgRKFtQ4qIzBiGUYQJ8QkxjTidTwhxxOv5hBgD+uGssRaGwvxPnPEhMCMGjxRkrrwvgYEPhwO6tsV+v0fTNNh3HbwrzDnBV0l87OT1xrkes26Isfw2JRV7ZjhRrehi61PWqM1Hyt8pL8zLtO+mMlmNU/MMetx4Ftyze7d4S5m+4A16cwZDbhJGVLjXJdqBFCcWeu+OzpRS8qdMR9kZW8k7h9YV6oecg3cNOJ3AocdwfsX5/ILH/U/Y7Q447h9w3B/hG6cK2AU2TdeCdVXpLhVCsNIQiYUpzUyah9E4h84DHYuFRJ/kfkQNm+ydqtuoM/DsN2rCWF4hEmsFZOy4GkY7z2ecBYUlZHCS0wQuTa/6ju7rLHyoBRQVvC+DPx06GA3HGje14rOVsmDcn9LISeK8NCgrzFf5MyxGhsuTANuo+lmPpw3XfKwn2awOay+h2mD5HDLhrzkDEtdMDXZdi13XofMerfdofDMJUl3qmLRGvi325HUc+10o/IXEvG0BUPJcel5T1NNvCxRTJzuvaV7SrAXnmZU9u3+v1cL8+XTE7XxY1vleJZE/LCL+k6YC0pf+wy6+lxdgQoLDnMFo6AuzuKRINAWfiYGofiitvHy8bjC762ColA/eghCJAKMAaLOs2LKI2Kpn8l31erkKDFfqKr9vFaZdI5KuJYHz6wj2/PeWlsrfQ1vsMnP++sEBSBY72y5moylIxAayeem9ecWX3FKslfPWMbZ38zwR5aCEltaQ/c3vmKIr9xHhlBEX63qGFxU+NsEDZyVwRpLlx0QoOIMZ8zY6SOCzpjE4ok1CQXSKiKYQF9YQhvrOdQWhiepv2Yj/xDlzjdrATPPnyABVOS6lMk7v3GsVIQhF7NkYAZUAYmtfrwmWbC+uCnCNeWKBsc3nZI2/V5+iTVOezlZrRoSF6RBVA4/UckO075gdvLoQEPpGhQcoQgRnu3DR9pX+zODyfDyW+2Btf1+bO7EEYY4guBLDwwUgpbzWdeWqpiVAxGByYNXitGpmHp8Wc1fxAKbN+42Q6j/SH+mPBBjzZH2j0QZCUp8evz++9RFJycn8vT4DBY6tE9CSc2a5979d0lEiqLuOtSzGmJsqFyCx6nVRNQc6A0nPZAaIhMFsgggiQgzyWxjWeiUH35jAQk74LJiw8xBAItGCp4xbASDBlcyyWJhR0LYSGB5OcS1SXNEp3sCu0vIl4Y4RkDXhs0Y1Oy0DVQBuYbEk88+eFI9QhJPVhRKrW6QQ5X4y7X82nEgCT0cVPCS1AohJrTZiRFRLgRgCUohISQNBpyBCi1DyMjNGtSoYxhEpJoxq6RFTQkJCSgRwg9Yf0Dpg3xkFQQWPIdJrA0CYbl4FSKKpLq6ovM6rMytQBjiw1ok8Lqz9rQUR8ru46RTrBxUG0ZQZd4lmqZ8tGeyXGW+/Ba25VaK1c35de24MUnpDGzMNcBMtZft72VZb29MxLFY9WMHRC55rWZSFviLUmfddaBqGCQocExwzTqdnDK9PGIYzUoo4PnzCp88/4Xh4wK7bq/u3ZHIIzBmezNNzIrFYTCV2SALOEBJjDAFRrWsaR9jD4ZDEMiWy7HXDwjP1tQU308azWeI8LhVyXY217QWAQCqLyyJOibiNIpSYv2/wSGBKtoTIwa/nDSy0UYG6rGOm76UEUndOaTKn2guiijqdlmbr2eiEfE7Phkqs17m0f2XMgMs+IOZKcGUsZvChWsus6xUk3vSICF3XSFD03Q6HrkPXeLTewXs3C1DNK3W+J/3jEU3bcLOe5yVOWdPB8z2xBddv5UG+V3CwVtYWfL4lvUkQsQWo773/ljruT5c0tt9W180aOCtzce8EvX2xbAOircVakJKCUNphaGUmcH5WMzE5A14x2av9mW8BvglzaUMIMT2wU7aEICKkOwQRc+Iqa42m4ppJkIi0+s5vz+RX5O9CfbdopbxHO6wQTfZ7u62K711oz5Srtik9ppoArt9bb9v0txJWNbF3RypCiNvHam1NrNV/SVper/v63QlCvfJe/ZtxV7OX7TQeuJbDyDj85LqWJkKIC23cbIchbhqkEFwbKDKczmsOvJip5+KIyzQFjVAXrbTSD50ZZJqYq+4uCBXLba1bX88GJ96rAVCNnBLf0AEvYyBmz0lxwGJCX8O3tXU3EUrkCmu0VyA1zR+Rzcu0/3UZhixn7X5tOyuCzSqIEMsNIEaCYwfvG+R9NlmzNPlXqjJCYnoG2LxN75c+bMH69RlYmzsbfSVC5ETT/ur8cEJR5qq0mwCx/gAD3BiFU9o2b0G+Ueb2H4mz99b1vXXuXNPAeU+6tYytc+Itbbh1bD4Oj72/jlvH/FJfrrX/I+q4lt56vt9Y+vptOzhWcxv8+G027HV6pbTkjTVUJ0B1dmjddq3z1+lir29a71dwws2i1/N/xB67ZW2Vai7BRsp5J14A2RjuSusAyNbARmcBgLoysSPHzr3RBBExSMyAGMVCIpWYAY4IvnJvmMfFSbvEZXttVc6KF4kmqyFPphBF3OS2w85CAqBlJHMZWAkicl4n8S80e2G4k8b5IlW2gAkW4qSqpAKIEBKQWC0dxDI0u4NMEWM4i0AiiSJKYhVCxBEhSbwGE0TEKIGiE6tlRP7IuyaIGMcRKTHGAWBIoHA4AOpGqnGNWqeI+6TWhAvew5FH4zx808BXVg5e5ycrl8SiZMLMSKEElGYWlzbmXqkWRNSul3RyytoxXIi398Yl2rFaqtjao9fKq2HH3eD6QptvFUJkoc6F/s3bC0xpg/q69lpp35R2m5a6JuRRmnOOz0qhMneZB1LuZz6L0QKo59c+Zt8nAkdixji84nz6jhAGJCTs9w94ePiMXXdA13YgCkBWJF0RQlQ0idFUYg0hZ0RkICYWl2QqlPVwaB3QgRAT4wRkuDMhODfP1gvny4IxUVGNW3iI/dUOCL1ZCRR4FiMiE2Fa9vy+vV+ZeRPX4gOa5OVkFhGlPs7fSysJKMYG1se6S0T57JA6p80seU3IkoC1kbwX9+VFBbD5I/WWkteorWlHaJsGXduiaxt0bSPWEBXNXopfCiHWeCVXYUmm6bcevw2P3cpzTcBb51/jR5bnReWSM3cD1X17b9mW9+I9H8nfXBNG3JP+sIj4IwGoF6UsyKSS2wg5bBIHMCLIJRAlkEsAR8QUEMYB/fmMc3/GeejR9z2GYZgE86FSNKY3UXOSlCUlpseODOAJoDPhgbN8dnhXwN+C3C77NQdG6uk8H/4F6Z9/v30Q606tPN7mRkniy/EKPoIQv9QnY0DP3rip3DVkrG7uJnBS2uz+8t+XclnvGNI1pHhS9kreWpBg63r+ziUhVP4+W/cXGgnLWX5XGvF2aNq+r5CBbaLFemC/5/M+R8qn74o/4BIcr0Ce+mCWzE5Qa9Ui82haCVIoAQkbBCUen/gJQ1Jf/IQsGBX6RIhoFvq4GprFhlzno3B+KsyDC4fuNQbuJlONGRZDQR4ZoSqPa03HBXGI2SjXZZNqNM5jI+Q8lPHtWgPPys1l6IdB6sMaOThmjYta/I+C7AvRLNqaHgSGp8rtBJH6vi7an/OPjZsgufM4EtNxnV6n1hWbc5IJSiHobOGwCiEykyRFEcMocp4UQU9sIjOjJJK4VnCp2gs2VvXc1RYxHwvfPiJtwbc/0lpa7MI/0n/m9N6t8K6l8t7Kafb99167W+2/DquX+T+q3bfUbXnE5R7UAtNApPAVTLiACevNvtf35J3ZWVvly7wwYjCinEl6TqQoClPOjyV2BIplRKGZlMGhgWPNIqM+i1hpoRQE30jRKU4gluhMIwB188PiAsmEBVw6UphuFpcgCY3IKcjzmmumAxRjFOsEdXMUR7FWSKrIFtQNVDJLCcUlyEHrioVhD873YozansptEgyndQDEP75zrOGsgQamfKcaLUHiTzRNU+FdBS/x3qNWoiBlznmSs5+cxsKyGF8sCnopRsSoAgWNW4Ek+KlZNsTa7WPGxQ1HrFZqmYAL6/Y6TfEexZrfK10SQtTCCGNKAjfQzOtE7yLLsiya5ZkKSYzJWNqq79gacmItJFeGdw5gD0cOcAUXrMvJyqHzdhABjtA2HZq2A4UesR/w/Ou/4fuv/wuJCN3hM778+Gf8+PNfJTB624ARMi027xdVXF3RsyckECITQiKMkTHEhNcIPEXCS2K8MjCSeHoisvh9UoLBkiIksvW8RSvDiLfteSmjsg2+a3PkTJdY3/Q9rq5WSJ3HaJkFQ37eFmR3UQXMqbWSxZlgEyTai5zHRao1Osv6v9n9We0pW66V23J/ekCZ+HullMna0nc3Ujk7NAKeAC/4tkXjPQ77HY6HPQ67Dvuuza6ZzC2T1WdXcyG3pIungvpVXwtK4y6ezOEAbfR7s5dVnlm7LilBrCmTEllkxe01VBbxW1u5UuKNcH0rH70BxXoLnfihgoi3aKh8pFRnPcP979zappsO7t/5cM9tutCFW+bJmGCJowbYSYKgIQGUQGQmoREhBozjmD8hyFUAf4U4ANNFTcbzUaBGJoZQLeeaqUTCJCKQxAklyqawdZvJuRwI7VIft1wzrTHAJuN6adwqxvL6Y7rwe3ro3iutfN8+KsjHFC8rDLppXZjdv8a0vlK1HsBW1mq2ORKK+8ZnXlap/GPStsBL0oJhbX9W1tnW+/PneUyugcAVhju75VozTfm5hsK8rK1nc+R7/tvuRTVdNo0KIwRnGQHWeAQgNOTR+ga7bof9/ohut0PbtuiHAWMYcT6dEGiw7mmIZcC0DFLKqOLFvbL9iDIKtyaEeMv+m4+h+VgmGEI7bTNt1XMJYdcNPVknVVZWpJsV8c7oXH2MrDD5awGEAXYbcdICs2WF1q1iDBFYGPyGCRaWQgjnVoQRuf6pMIJm7auafY3OrAcLzAnK5ZD5oJQZS4U+KQwLuS3+c0WDlJVPtSRcaruP+R6q4VsmWmfp5jX2bpwKZf4vnln3lPlxsPa9dc7vXzrbr2k9VTnxkefJ3zv9nvO1gIN31r0p3L3hvVu12jZKuD7lF2jOt46wMUQ/Pt0+ftfmaFsD+RKCPG3G1dZswMmVxiwFAFt12xfDt1YzGYCscZ1ScGGJyPqymA6Tz1ojGJkJVesNMDPE1TovcA+KlIX5m7SL4RVOCnaqQABtF7NYRMRRrEpjEBcsnBwIDOd6QGMEglnpQbVaQDnLLFZCTCwWBzGBeADSMNHmz4w3cI5r0PfiPiYMY4mFwIyBh6wcI32SfjW+mfSNOeaxt7oolTG1d+VqgcCdludyuQBAjkHs4FMnFg5tW54ZFkOqSMPQYL8igHEkqjNMA1jxUWZG0n6GMaggQgN4c5wxCqUPEVOLibJAkNc9gScuSG1pbu2bhTLTLGUG8JV3L937LdIanN4UQoDy7lx799azZsl4nLdpeX/7LMkocEaYiQhwsncTmWAiqTvTwoymuiJbC9WaMN4InAjGWt8g9M+IwyvOL9/x+vIdzeEzmu6A48NnPDx+QauB0mOm21doogkMLhZ0zEBM4pIpxIQhEs4ROCdgYCAs1l9ZuxIXYraWNwfrCk2DJQ49LUfrsIHn6ndN3OTn1XUyADM8flJdOSPmLp5ImfNczZl8KqEGT8u040ymRAdyMS+c85obJkZdPldnR11HRcCAc7nr41fqyGdZTUyt0LzGOxDLMKfxITp0TYPWN2i8E6uwldgQW1dwiZPAzCqQX4FbZQjLPV0/vPF7LV2DZ7fCu3UFroI7sM3Barn1mNZ3pr0sY3itNbcpuM0FqQXu2Fa87gXiPTTDf2qLCAPSv89xuZb+fjW/NWX4b25BIqvbjQBOEUg9OI2IqUcIA/rxFefTC16ev+H1+QmvL88Ip1eMfV8dnAAwlcNmqS9Q7VEzVfSFsUSUAbQJIuYId052gG0IIqb5hQ0mrlyXZa4G1p6M08r9TQKRCuFJVHW3yku0GJ9r6TJD9XK715jTa8/Xylln1vDGs/LOJnGaDUFu708GzsRYaHvLC5tlgTm/r45/3pS2hS/3aTfPhWCLAxn3rcN7106NGDAAEE8sI+bvZcRqnma3cj9mD1rfCELLysglwBPBN43ij4wYIkIIaHyDQ9fh0+Mjvn7+gh9//Ak//viTxocgPD0/43Q64b874NfvDqfzWczx1acweRE4OkXsnFpbrYzI7LryCEa4T81Ib2VegisNE6JM0Nd7z8ZXiFzOY1oEBsv61pgP9TOrek4gSN3q0iqpRqNqMmY/qhorotrhSvgAzhUNF6cCYEM0hTHiRFuTvMb18Wr50OjVK0OgFj6otQXZZ525Uu7bVl+DW/VY1N9n+2pju7CKswTJdqphCbD5q7YRcd2sXCM2XdWvqo8VN2ptj9sx9kf6I/2R/lHTFq43T1s0wD8ibfD7AJ339Pyj3r2lnAVz467aludRbfE3Z45O8LHZNQtvSFwcyRGsZwzkvEi8rb3K5MDw2QoWHCEsHnW0qz7Q06hWBEGRhexbPWg+sypAYeqwYgdJrGk5FbeSSMJQjyiMdxNGkDLSzSIiBhFApCACiJRM6CJBtUn7TBoXrG1bFcDUZ6ay5zIDUO5bTEGqzuAKZVjMmgwxg2KazGG2sGAWo8doYyFjkMoPMAcAIbfFhDQSR6vEvMgulhY4o9I1FYOUq3ysuKDE6ajWS457s8LYuyHR1sDULbujvI9MHylovr3O6dTcStfNmY9yYYkTA3FzWgQQnF1OC96IKeN0ldVQ8GXfdPDtUayRY4/XX/8Fr9/+Bc/f/g39ywu+/On/hk8//hWff/gTHj9/Qdc5eM9IqQXMWgpLxmdmA5MIJaMJLFlcpg1DwrfR41+iw7/FhH8PwItnnCnhxIyRGSMBwalBgMKJvLa1bGAWt4Bus4hYH/iqI7O0NZbvShV9RkC2vqqFDcyscSbqWBMpP7/cR6ugCDRIyyClR4gLTJ68s1KGpGsW2Fx4VXPa1qnyrnfqqi5zYkDEaBqPrmtxPB7x8HDEYbfDoWuxa1rsGg+vQvAaNs3p6Sw/mfF1hD+xHKs1xeo1vsVblSfWnm8pqqzBHDmb0iwfcGmxLsu1/Ku5L7T61gVvbZnzD+Q2mRtHMr7BWp0FY7k3/SaCiLWFMU93MXhvyLf9Hl0l6t8qybl6yPHHw73b27BuhnT9XdLFZh9jTEUwh8knpoAxDBjGHv1wRj+cMQ4D4ih+OYs0GAJAN5hl5r3CDm83Y2qX69RP+qQcA8SuCp6zUkbp5dQiwgQP8+t9DP3a9+523q021b7zLtVtz+aHyT2M61sEEWt1zOvROxOJ6bRN5Z3Vcqjmz1bE2NU9WQ7dLSn5tbcNVbwsJ79SDi8lxTchwLMGzgUDW3Nbl30rDN3Sflr9DhkbtzH3pekbVNxKvfP6nXMyayHlQNXkRJOCoPhHSogAGuewb1s8Ho/44esX/OXnn/HnP//FKsCubfHSdfj+/RcMwxlhHJTgE0TPUxE8GE23DhlvYCwJtjVBnur9Mp+XyW+eHvLLsV3uN1eNaUrrq3SLST9PU1LD9qUKHljLT5UrgAqhzgIq3efG/c/EUCbuq/oJ0+dZgLxmAYGKUVO/j/x73s+5IKKe15Kvnrhp/2u8gEy4MhksYwQUX8xgITSEiZAykUascYUmUzxtq83v3JJrCTvq9t6X8rp709tbaTpmS2R1Sr5utSnnvoGw3ELy/x7pLe3/qLpuTb9Fm27B4Sf5b3iyjanelt46PveUeavG7K3pCml7V1m/Rf+r0qvv1/HIq6W9Z99s1PnmdX6BQbGVMnZp+yAjEbdURxVjvDoDqrMNPMUZJriE/TX6kaA0EU3OudyuzKSe4bL6m0noHDYcQhlZzFGEESEALEIApASMqqWvVqRZYSSlCTM8D4cx/TXAdLLgrokRCAjEGrdBz81UqCQLHC0Kb0BS//NShVnHG21EWfmh9W1215lPfxtnHQ9DYRyZEEJcQYKK1rwpUVmXCGIoAiQw9eVZZoKxKOSBs5WtMchSRTODIzAJKD11s8QocR5qhZ0FbkooiGteK9b4ehIqHIaXuPdy2dsI1L/1G63lx6S8rUTAxIJlDbpvnu807f2lulZpXV7HkT8qLfHr+RjW+VboCYbQD5jizxmfzjipIabFMmJaQamHSIRz5FuAR3AM6E/f8fr93zGeXxHDiG7/gIdPP2B/eEC338N7hnMMsLmnjnWxMCwy49O2t9jpOharpxASzsnhORGeE+ElJZyI0RNjhAgiItS1U7V+ZT2v0eyyhg12Zlpjvg5qhrssOC1gnm+Jrd6WLqwimx+uNqB+NVhiLpIyjVUy6AfV71vap7SmXZmnY1kA5vL3vE96JqzxLHL36n7OS6nXqyvr2LJ679B4j7Zr0XUd2saj8T5bRNjruTzjEep3LJpf4aHz8+2D0z2CiLW0xfeRJcyzfJfLvpZ/VsOVtq3M42r+FV55zldov0vnQ13fPfjaf2qLiD/S7WnJvBGpbVIf7IlHpBTEEiKOGMYThqFHf34Ri4iXZ/SnE4ZhQBwHRHXNlJlaKAh2PmwnJ58i6lAt9RWmmgU6IwuOVhMYgNRHmAg2thmuegireXKNHBlTbDou0x2amYV14J0Z8nFNALEQpqy0c+3+2tVw0c1EM/KF6qtqit9Q13oqTNl1ZG3jLTuAXF3ndn3Te6qlvGERcQsBLTofU8Lud0usvhXr9tzQ5t+aEcaZYX7tYNsQUmwcxnVKKQFEaNoWDCF0ASCEAEeEhhz27Q6f9w/4+ukz/vzTz/jzn/6Ef/6nf8Lnh0d8fngUq4cUceganB4PGM7P6ByBQ4+nNCCGiMgJu6aF8w6RCYmBGNYOddr4vuic4qCXLSLs/vLm9ATPprv5gHeTcusyar+aa/evMW+JAOIcZlqJZdPUg/gsTkmEQ0kCQUbTYExRiG99J8c9IINhTq0bckQPtYIoprh1cPF5oHGzFqgFEUSo/FlXn0oLx/qVG1ONw1yoKzkuresVWGyCGGIATjU6GUkDZkIRcbgGgCsCmUrIYjA2I+CLKtbWz9vIp49Pa8QMza7zZ3+k/93StRPpt2QO/UdNf+yU/1iJwSDVNs9WASupFr4nLmeBlIEckHSBX5eKpuWBVJFazyFVnPJmXeHsUFmnT6QMpzSCKoBoEOqkjNvoNc6Cl3MttaNaRgoj3ak2c0ox03SlbD3DUNBwb9wkAA2E8ZpjNcBwFI1FZTESjDmnKUXBNfLZ6Sr6DGJBa/QiWGJI1EzcLGCoBQnmBoktNpkxDPWcV//tQdskcRGnynRgUd5IShvnOkjsS5Iq7hEDjss4JLa2WNlpMpbGYCs8dVtjFU0Ecw9aj1T5teBPLtao4UQl/6SkXPf0rb+3QsDvVf98T7Ktvwq3tE+ZmyXTUNIUTxVFooVZsswebVOgmR6j+h2a4dANQC1OL98QT9/wt3/5/+Hbv/5foPYBjw9H/PWf/hv+9F/+Txw/fYJvGyR+BccEcAfArIqKQl+hiln4Bkwg8pD1IzhwjIwxJjyNjH8bgH8bE/49RAwBGEmsPRIBI4BY98OsAmibA2+MzsvCCJT3nT23F4HarY8wzQFKxqO5krL7JLUWubT8ZgzzAsp0A2bYw5pHPuaaLvNOFkK0Zd1lb08DbJf1V18LAFjbP1t06zzN+WfkGiR1teS8g28aOO9AvgE5j67rsNvv8XA44Hg4YLfboes6dE2Ltmkq10wC3yw2RGk+5bOgbqPRyZcURa4JLtdowlvTlqBgXv8WL8CEzramt8Z+KUCW9e9umKvfM13jedwLs28XRMyZvvWj1fzTfGuk9loZPPu9lSb5aO3Hb5f+3gfzvekeLa8FzJ8E2IkaMyIgxYAYR8QwIowDwjgihJCDcZlWjAUwY5bAsxl5JEzWlDH5UEQEyMzznM+Cnl7Y8KQM3g1mf0H8p8yUOSPvFkEEEU0BKZR7VnWpZnDNry4TEdP0FkEECGrauZ62BCm0gQS9SxBBpD7u58yq2VsZCbc6NaDVBrCe3xN/7obUvHHfc0HAtlIueU40WhFvqxlGfmwx7xf3aiqD1jUaVt+b3b/G+DS0tE75Fa5zzcai2q+1tneuj6flimUEVMtcmOJEDuQJbdvg0+EBXz9/xs8//oiff/wRf/rxJzX17DCGEWMYEfcdHCU8HnboDzvsGo+zA3ol+jyp6x840ZBLM/i2mM0aWZlTDZRxXfsQzWEU5/uLMbYobkBBEskUeigTPYuzcTa383mnyeTU9fLyYn8MTzX4bC6Z9JOqoGpshD5b3AcjVOqDdw7LZwIEmhJy9sb0/nQ8l8/t3txCwlowh1U0adJ0UKcPys9aqFsTFxZcUtaVjIebsOVhozLrUxmflbmx3VatmeV8zmHpOixfpGuAaQtkzhgUlwqftoir8Xw7HvZWrfQl3LsHMl8/r6QtVtcdRd/agt8Jr/zQehbnwqyuNxT598SvrxGI9+a/uHZv2mfIi+4a3fWeUaPFl8tl3ru7rwnK7ynD0m+xTjbLrHCXOdtHG1dd9TSqz6E5rWO5lgRXZpbNYSgpU6s+P52VTQ6l1CV+75SJrd7LAYhihug9ByRWxR5OiuMkcDQXKZxpqwWHO+OkiyO19B1u8Z5ZrKKin+r3OOpzO09zcGpxl0iVKypWNyWZtrRmasNSsnmtGYK1NYrRqiKoyIGyYQGwhYFszMOCI0VdEwmJAKaU3U85pskCKZYQhR7ObcmHaBFw5WaijKtORQU2Cm5w3QJiPidr9Ma0vWvf19Laeb3+zozOWMCE6f6S7/N+bbeFq710i0LUWprzCtbxsvJsfn+CC1I9V7N67HaG7bSk3+s52OA/GL3NDIxDj/7lO04v33F6ecLjj4/YHw54fPyMT5++oG07OO+yh4tVOJWhj1pEsG4+w2VluWtAesaQgNcIvEbGKSYMjhDJZZfXkUqJyLSDfjbPRsrzV+ZRK6+Y+7nJi5G1uiqazMY6CyryQC7voSpiPh95X1bwLHeJ833ObZ3lqQvn8oDrW/UJMwcIrPYVE3hW2lbos419U3d3wk+px3M2qDWN65zGYa0FYXrPO/jGo2katI1Hl60hxIrNOz9Zr6vn6HzIl615c7pV+PKeMrPgbJLJ/szX9KI0ne6pouNi6dyZtnCvtTas8lXXDqILaS5cvyW93yLilnm9lmeLSXBHuaZpcnfd/8nS+ka7ZxkLqto40cRxYBAnFTwEhBQQwogwnhDPrwjP3xFfnsEvz+D+BI49OAYgGsOmOkx1MybTDFDNlAkCAbuWPxMcHjw9lOfEiQa02SJaihBAJbM8RfpZBQkhhEn+Ut2UwVYnl9egHPA8af+GQKJGnu39BXNzmmxsSImQ8k4tBFmpKxdZMztZey9tzj5Xy0kt54+Oy5wYM8Yd5/gdi5ZOeHqr3ZoxH9eupa75mItWmEmcVb8q+9LNvbSTL4+bVr26NXQk53M8z2tMy9lJURTG52tH7sIuuu5TrNy/oKyJnD8jSRXywgRhmrP+XxIDdZoQFsSVFQogwdGwKIdoMoMoR6IisBV+mHMRiqksK8mrAjeZIwLIAwBclEY05BA44GV4hW9bHI8d/vrzD/h//z/+n/jp8w/4p5//Cu9bNL6BY0IMCWk4A+MJdPoV7vyCn9sBx88O/KnBN+7wL+MJ54FBcQQoYXfYASD0PKiLAqfIkMxh1CEVBFqa7xigmCR+BYDogGguDhJP928GYVR58xGkxISayYUJ/m1abymlvGZsLwoOmzLSSXkT2VjWG6p+V8vWOUjq1xmk2pBJ/EAjiQ9nJHXHEIPeC+AYwTEIMyBpO7iYb5vVisV/IDiB5eQA50GqLUPea9yI+gP1E1pZQhDltWYCYqfjQBuWWjnYNVk+nTObu4x8AZgIrqsJrvdX9cTl8fR6Rok2W0pRYo8og4JI/KTKx8uLzuaJ4cnDkYcng6sJEmekLILCvyoCDEdL+Hw7Sm7CkWtn/qWy1v2NE1VjN6uBgQXM+Y+TapLoP2of/n6prIjtZ1vP/6Oke9f2dUYYza53t2jj/i2jPMszx9k2+lo0Zt++RwyTuC+/1f93XENUTiebVnH9Uxj78rz6TS7ft5PMTeD7FJcG6qNcrRWqzZW/VsoI9pcq2LXA+ZUwcZmhqDgGrB8NwEBKYpEZUyNMf2XIxzHp/QDOgaQlGLUoMXC2XpwmzmdzrbyBjM9AfI0DsCDW4u6oMPIyfp0V2qKWUdxEZWGBjYDWkTBl+qfciFSVzYoHcm6DMYMoM/sq61FAYmpIowruq+U4LjRF2f5TxtJk0quYDkIA8vZCXzAl5+Ngz67BhtzolWd1w3VsaqnIjMazsUJ5KmtLu5VWO7Kdarab4b7geiy1ng365lJtm8Lk6vlUc3oaxHw6hwoLFVwyZPoczy2uOfdJ0E3jOzAICcmrNbjbI/EI508AB3CUIO0RBHYO7AjJqUUzSQw27xo0zQ409ojjGU///f+Db//j/4unb39D3zv8H//l/4W//Lf/E3/6p7/i69cDDjuC94wxNUggOB8F143qplpdNDmWdoK9rnKFFTHCgdCwBxIwRIdzcHgdGa8x4ZUjAhyiEw8LlGm+VCHXOlAQmANXKa9NJsVDTbUNgsj/lKFwDrOwlQplEDWbK+3wjBI8u7iSKytivk/XPrU2fw3g7D3bo9WzKPw0oe9Z4oQY/4sZiGYppp+onUZUWi2AU0BEyveJxVrd6UzVTSwjAZDS3azxCmixHwx2aCxEiHCMyMnVEVLTIDUeDRo48qJcB5LYPY3H/mGHx8cdHo8NHvcen3YtHroW3W4H3zQAeT2tdD4x5Svl4a/2dxllt2IZoNTOTWDmBpxrgnBUP2gDKGemxzQt+lPT5tXTNf5TAfMF3twHRefl8cXfa8+uKY7kFs3a9lblkDssIi49uwExvZZn/vxWxL+WRm289lEE8j0TCmS08EPq3qxji1l9lRC6sNhIrd2MEawngJkYiWaouOvgEIAQlJEVM9JWgfKcDMwV/EzuCKNshWSt8K7MvINJFWeF5p9cXasDzK5UJJJSbo3AGCOJij/U2XjNtXNnUpJCEEigiovxKubXaayMa+u2FnBAWXfV0WMHXOF0VdeSLwMeY/hVLmDqsozBlpH2qg4GL9o+aSlPd8GacIevXCWjw3xVsSMQi8ZV1jiCKZ9Xh1mqTONQmfytgHgZoSKc4cUzq1zneL5/8imzfmjmPK4EPwbkmtcUGQFbFvg0n5V12yFs67/cmCNdS1iw0JbQMZb5pNkjW0cF6pVxKsh6PRacWP38CqLjidB4h/2uw6eHI/7844/4+vgFXz89IkVG0IBfnEjgTRyB0IPCGTuKoAb4vGuAfYfnxoNixAjR6m8UAU2OkWCuDkQrMFnviap1LISo8JYZXttvSFHNQLZrgTHWbflSkCeabISptg+y4BIgjVPoChIyswLbmnMbfbbgUhU8zL5FzU0C11YQsbrq94qIN5hb7/sMX2b9K/ctbxmzsqsU5TUmfS5qKrCl+lqNWxHC0mTN1XMzuVnN1WS8NmBtWfkK3wzuqWuFDNSq/mZGvfZlHjsjz920WdMxWrRwmUpTl3AUsLWxdgKX967WU8OHal3mx/adSr55v9bbvoQzH5W2jst76npvuz5S4/u96SM0yO95Z7315Zz92N59TPqthGfXtO9WNefuTfP3LzIhJxmX2a7QX7wo+61tf/s6mEO0t8CSe99ZzOGUNCl0Q77mQ9IKEFQP5RxDflzhDhUjtRynNQxemQ+yfTXF4dY7UooxBQBLTrVSzHLAJWlPcg4pMUhjIrlU4dGJNNYDgSlNzm3pB9fVVsSfKYpNcZjyu+DxABdFNmX+mqDC2lE0gyvLCpb8CXXchsoKIQeLneLUVvd0oGEYgJ7/lbaz9dRwX71dFEms47xSV749Q8VlLhc4A6+XMWlvXkNrODxm+av2Yy3V+SaEg9LNM9pglgjFjdR9G55n3+uVVJU/wYXrhWS1L62yL+55LjSt5a+xyvrZWjKlJMYUu7J9Wg+EoI7FJTSRKad4xSOlRnONlJuhdYCmcdlSOIOHHuenX/Dy7d8RQ4LzOxwff8TnH/6Cw+GArq0CBUPctEnMTWQYVcgTEjd0is/Ws2BNYTgkCJ88sKjmBDAicaGnFhNfnzsVPkm0uYoyYGClX7MQiKcEWa7uGly3MlED2qpjVRvnW2Xel/nem8Gqkg/Vp1rN9XDUfTNBhMEPg1lZ+MDTvFzVP1mfUwBbnT5YWanVMNh6sEPD2cFRPnAQ9TwA6oLQOYem9Wi7Bm3j0DUOnXdovYdzHs67yTlmdWTcYgtOTHgSS/dK96FS6/TepE2TrDcUvFbWYs2U/i2E0bO2rS6421GcldemL99LByyzV0L8SfHz37enP2JE/JEmyaSzDICJ4UiYcQ2JmZ0H4Anw5ODJofUNxqaBaxrQqO6MHIGck0OiRhDz4akrdYqVl1sLJik2fgMZ0OefVBC62eHPgPp5hUrW5+gYgyMvyyUFzloekzH/p8h3miFncwEDZ2DkMiFSX9laa0jQBehqWthlCN0CuE4YehsMt5xXz6GozPEZxadupGxYeNJW1SPK2R2m7adJUbT4PpfC1s+n7aaNPFVZ9UOWsWdc6DfNf8sNPzuwaKUvGanZSJcYEUQkGg4zpCCvPqLZGpl2LlEdYWLt4FqruwgtltYaN5/ki7ezOfos0HutuVfXIcHuJeCZ9w7tfo9jc8DPP/2Ix8MRf/3xZ/zzX/+C//bf/u9wKWIYX8BhQAoDyLUg9/9n78+2JLmRNEH4EwC6mJkvsTBIJpO51FRNVXdN96nZ+pyZ93+DmfNf9V9d3Vm5kUkyVnc3UwUgcyFYdTEz94ggg5kO0sLcVKGAAAoIZJcWsLcgdwDcLXi8AfEBhhx++cVzfP7ZUzRdgzc3t/ju7RsMbgSN70Ck0Jkengl7K473B28ln4FqBCabrUWICNpoeGYcomKysMKZMt9ZyRUnJtKGvDovRAStdZ7LyDCHxRA9t7jsGOvERJRd+GrdMjjkgPDpW+JAWzvCew9nLdg7eBusHr2FdyEOcvCaYEUpVnMce50DIno95PwPKIT0kVmbroe8hzFrk0jOkoQXK8YM+e/U5vy9VPOzgAdpci+/C4mHK1aYYhHqOXvKRSZSiHBJpEnKQGstCQQpflT1OVamb3VZab00tonnyFFq8DilmJT0QEJPQhbw7B1O25yyN39L5WMoVx7LY3ksUj6d3RXFrA95dE53reKNRGRPLkf6wQOsMh2RlRLTZriiWaZKsvh3GY42WoYzi2cfM4fcUULnxW9mDmGUMmyxzzIZczI+DufJXKBejy0qGpLCofod8lWk50vBHypFBGPeF2Z9L89/VogslAmPdKwNobuX+6wVCRH45TJVqLzvebPETZfC0vcp53gonC6B50PNX57Lq8T1eUoZsa40ntM6q/u15EEnvDOK9hMdmwzjFJRy2BoLB4sbpeCUhtUGYIZJxm7BE7nt0HQtTN+ByWG/f43DN3/A4Zs/4ps//x7ff/8SX/39P+H5l7/EL3/7D/jiF7/EdruDMVr2nQMUNSDyIAQP7eRFK8aMmXcXmD0ArwAXZECWAKsYgwKsOE7UAkiKQuYwGUuLoBKzTOZ/KlyPtGUQxicFX+wkCeeR3xcV7yG0VSsQaxjW1n3isAth6/FVzcVDZbucxiWQBKVC9Ewv93RUPETlQ9S2JHi5+s3sQZHZBIAJr7hW5nKZOqJGlJsQUXITV4HnUVnKAwBojEHbtbjcbnG12+Jiu8F206FtWjRNI7kkVORza9hOKQmXzqz7PP8xyikcNL8/PW9lnczyqzMnHpGiMeF7jq0yqeYz6ZZKBou83dL9vOd56bF7lvdSRHwIa6KHtnGf5z70Iv25MZznzlXa0IVwlyiH1dBKJQtWsWQOsd+0hjYaSgetZ9CaCmGs0upM7aFevKWlUCRflgjqs4aRpCe1QCSeUZkgmDTGue9ZKQjodLguEClTZJl+p3MjzAPELZAosg7ZXlBoUbHWPoaASo9e+e3nQtEJERavLxXFRZuTbgkE7+txRVgRGCA/e6IgzCYwlTCW7R1TpMi3mtVLcsmJ8DF2I66smQCcFpr8oCD4d8UKqQSm06cXGLoMw+mkRJVl0ZQYi0LkxbbDndU9cYwxglCWD0bfMTkgJQFluoYcgmmuiAAiE0+AuJeCoLRC27S4vrjG1W6H50+e48nlNTZdDzfcYTgMEvLN7kE6OAr7QT5uBPsR8BYEh03foQfhatcD8Lg53IBGl/aHJoIHYQxxj8Xzy0d+ITPtnOGNHj8cJ15Gszw1Bf6J625mDVwwofM1n7so5Pjr/S2+niUcFlx+Y84fn+MZe+/gvQMHxUPykmDJ9UMxRjIwRdxhmMV4y/FQZiUrvFvUKxUU5Zkz/cS6cUISTZ67Xt7fK9dm8z65R+lFyIcrQj+PP+6BYqTFmAoviUpzUs8fqL4vW7/0JCnx4LqSJZ17ibqdroPpcys4It2Z+pqU5ygSrBnopT7uXx5KE9bM4o9bPgRN+N6CpYXz57F8GD7lVNvTuf4p3sUaLB+y7Q+xtc5uYm0cH5DvfMhclWd0cbX6laiE+IeanGMTWO5vpSj4lo/QEueUch7WBD5KRfjEMCAqB5IiIgnECmGvEK2Jn8yAI0/VZMxJBle0d9531cqkzbruuZKSU4KxKIWphTC5r/uMo4I9HbD59D21No7dP7muijOznsaaTzvqCbDST4pOUEvm77V9E3d8DxlGnMApj/WwPUKZfzzaRg4bXJHAE9mB0NDRI0jmQiLX+vCRBiREtI+cNAAJraaUhiLxZmA7wroBhzevcPvDNzjc3cF5Qr+7wtXzL7C9vMZmu4UxWsLBpfkIAmeu6bv0b+J7Yuhh4WAk/6ZEG3CQsHGcpzuTsbGxmPMkTV6ciLKI4GGZR4qCeZSbKX8n7SZn+rOc79RM/LHw2mbyjlw38zt1cujZQzO+YLm9PN6az5wpR+KYk/Ji8inmp1ROMMq2TuG5vKhL3qd8suS3ogd6jBQxlYRopWC0RtsYdG2LxhgJpay1GKZRTooeX1Dir0/sy1Pyq4eefetlgWeUzutr5/bJ0zaLTXEEt1RH55nkwapC/LzHF9pbb3t6vp2C4Vh59Ih4LAAysZGEi0YDXqFjQDsH5xiaCOPYQgPw/YhGEQgWomx3MI0BaQV/eyvac+fgXIhJvrA40xmWkjZHcbZaFL4C9SJfYv54Ihw+p6QDGkXuiKLNtXJacB4Ru4xPTdBBTi+30MepvVyOPXBGvlCvrsG29js2p1Qxv8As5NKiIiFeJxmJX5mz6YG3SMRSPRu1ADMeiPOG54oITrABOfxLPvvljqYSsnDupr7mcNQxCudr7dQ8r5Wlg/bkO4uQ32e5y8YCVLA0C63Eg/acpiLBQ6TSvAIEeA8PhrXR/V7WvdYaRGJhroiwaRowgIMHjDHYdj2eXj7Bf/zN3+PZ1RP89utfoWkUNDOcPcAOr4DhFjjcwPQ7tGqLYbyFH+7g96/g9jfw4wDvHS4uNmjbHuye4PauQ9867A97DHaA9Yzbg8foGKO3UGHNCrQDPEkOA+bgBMDA6GyYLyVeATMF0mStFUuCVJ5u4TVqYjKuw+q9hq1Q0fOhDcbC2khEa36g/Jms56KCwUUPiBHeObhxgPcedhyTJwSCgiImZIzeUuwBaMFkRKoQutf7LwnzAYB45iWhgvdW/UFqp2zjFC4vieaSEYrXpzFFZ3BO5nOq5BRlsQfYIbrVxXHomLgt5IKIbSsyUGSgoxtzdEmejqe6Vr7x/DKPEeDHy0NJT4AjwxG97Mr4qCVjGYuPe2Ktwo9ZHj7ux/JYfqzyEOHzX0O574iX6v+U2GW5lOd3lB4IHpx6KZTnzznW2sfK1NCDk4Dz4YKZOV1DiJFjAPGE0EG4FOt4FZM9l5b6QXjJXH9QJH7mJWOVaKbGBQz3K1EmuT5Iaf7Y3D90f64KglaVD2sgfvxVvgjLT4yScryE7AmxtpbXlb/TPA35/odQ9h9VUmFCjkehf9gjiR4NIRkUi8GmhgPBpggUpI3wC94JI6ENYBqotgMAuLtbjLdv4N+8xOvf/f/x+nf/CvPZb/DZV3+PX/7Dv+DX/+E/4cUvvsTV9RWapoFSCsMoSem1IShoMTpihkI08NPIwm0CCpNRZgnBZAEMAAYCDgQ4DVADNKTQKQ1SCrZg0SV/Y5yNUgBbEuoTHibs/0p5GAX05W8fjYMK2jSCXhYfhfbxE5/zk+uTfkpYUN7jGpaiXmb+Clp/+kxoMcHiPSjwW6WHRAVP9JDw077DdUaRu2a+PqdnUOZA55gmvf74TQCU5AOUmCgqyWEotNe3LS76Hk92l3h6cYXLzQ67vhelRNOg0QZKK/iY0wbxDPRH9lTN+1Rs8kQO9WFoqWM4t5BDLd6N18/xOFhpgzL2qGiDGVY5v5Rz/SF5s1NK9fu+jw+qiLiPFdDa4fIxrZfet/y1Mw6ZQIYIJUmsYRQraKWC1lPBaY3GGDjv0DYNxrZF27awzqLtOzhrQeMYiG4lSc9i0tTi0KlJDvkLQJGbooSJ0+81C/p87cQaKvbl1CdhKtA+tR6XhMVz4VGAaYk4Ar33ml9CU5U2FZjhoKm2Nd5eFIzScUI60xkZCdP03pFStTkBPCFkRDnglDDllIejhruMLZqTQkVVl1jvi9KkCmNC2el+ug5i/fi7dHmPo6b8Z/17qVD6Z7Zm1g7X2dgnSpRi+JPnysdkPU7IojzPp4S/gXkkYkBFF82527gwq+L9I3RV6McYEBFMwCNd22Hb97i+uMTVhRAwRA5sB7AfQd6C/SheEc4AToe/h+QN4d0o7vrsoMijMwrcGVz0DQx5DCNjdB77g1j4K2/BkBBzAltIIKYUfHB/8CwxiSmNUcZJ9WTkbyqY4GIdpWqFEmJhUhNNXq+hguBafHASJGKRucxEryglosdDnR8iekOIJqZwE05rtISi2KPFv8sgFmt08XYgahf28SnMOMO1Cw9UyznNaRYWZZ4hW+txfBmJgZAPIcOJpHCh8CxV9+IZOgdiaSDzcZ3LgMcG6EhYh7rtcozLJd2qFiPP4UR+/1k5tk4rHVVC/0jlr5WO+7mO66H0z6nx/pg8xineZ+n+Oefsxyl51z7UcOJjlPlwlyjbxRNkod7HLrNDBUhQFAg24jtkGjI9NaH14nd674mG5NRcVR/LcfA/5juM59LUSjWwjKmsiTx4crZP+Y58LtQegbXC4PgaIJxaEfdYL1MSP19ePUCTAmeFhl+y1F+D68E4IC+Wo+2temVMyrn4LdL5RwCr1vFSKXnHpTq18m3t6fPKSf4+V0x9n1RGxLqpDUIOFY0U9pVCbP2czFmiRRBCsCSCuEtQjjJBILC1cO4A++YN3MvvMd68gx9HdP0Wu2ef4/LJc+yunqDt+hAmlAAqw5RFWKa0PKVbicvJruBpacS8ejHagETHIBhW8BS9OeJjscHY72TeEp09W/nhq/jmyXcl3D++5iqFxaSLqq/pp7xe8gMJBtT3UK/AaRcZnvIbE/H1vG8qYUjPTGGYw1IrfDJ09bIvzy+eXI/MUeZ35J2GqB7B00+8IRq0TYOuadAYDaO1RFGJH1KoAkqfdVZN6ZP5cx/szKMT8poAz3JXMTrEAgY6E7SYZW9+lucXfvI0oGN01EPmKDd2rsLnk/WI+JSVC4+lLlGY4pkAJdafGozGaBAzbNNAE4G9Q2MUlCaYxkAZhW7To910GNoWB9PAjiOstbDjCGcdnBsl7rYTc+MoyGX4WnA9k6Ln8t4WDbPf8fCtQ9UsCYancKzVmQtbKFJV8rsgsIE6dvyDx7WQI6K+f+Re/CxUISBZvHK6IGXqyVDcmP9GRmnrhPgyrFnAtfAuwjmZiNZwmPCkz6igKhUqjPm7mI59poyYCAhPKwvWCqU5OrXW1tvmletT2CaHJ9FqUvJjgsLy2pRxnMJIlF34rQ05IZyDIkKngbZp8OTyEptui1989gIvnj7Hr37xBbZtiwYHuPEOh7vXYL9HhwGD2+MwvAPxALI3sOMIP44gu4fyA/x4Bzta3N28grN30MTYtMCLqw2sbeB8j/1hxMvX38IPI9RwAIHQmhasFCwYrA24b2E9MDiGG0aMdwc0ukVDbc4fFscZ13nIHxHnyoc1mK0/pChXzFlgOsAs+DC8p6WNyIHwPbmuEqHOgVvwKTcEs3g6SJJvlz0irChwrLUQRYVLRDKxT1s5rf0CJmaJ5czsZayBCOZAbrK4T2QhDNVrfrreYj/lWkNRj6jIHzG9ThF/TxiOkvGppo8LnCwfqvzoGTmMlSTwjnhMlMcqeHboHK6w8vrILsxx3rKAiebgnCinie2cIvD8UhC5k768Z5DOSpZwZzaFAGTeKHiKgCDL+byz7Fzi9rE8lr+m8re77s/BUVNhyH2fP6fd9ynHYCho1aVqC7TtqnAznMOlYRaQzwKGCKhKL4RlGn7lbF0oXLWX4ahJ/TkdTETgeH4yF6KPeLYKZUC69pJQhYVvNF7Jfde0eh474H2mMef8ghz7xLmN+5bswRFomiWBPc7n2e6137kWCB5T6i97NbzHOv9JURIVajfgXGB4MR/exy3zuS/pJKS/0z5Q4h6tIAtTsQrrWIMVYHUHsIKhESCfQiBZY0DaQLUbUU4MB4zv3mB8+R2G7/6Mwze/B/UdNk9e4Df/4T/j6//8f+PLv/9HPP3iS3QtAA14+EAeepBiEHxIRq0DjDG3Z8wRwKIkyaJRBLCDUT7BssIIDyKFThF2DAAKB6UxkMLADMsMT1F8EGYi0tuswjIdF2Y30t+BRk+JmsPviWd5rYwomLSp8iHwo/BLnhCBZ2IfcjeGHDeV0mHym6d9B9wTmB6mnKw9G3UVY/PlJ/RbemuwQ873UH4mng8R98dcGSszmuQAFOUBma6PqLLg9qV+SEpNlOVjkZfx5KFVA2M0LjZbXO8ucbXd4XKzxbbrsO1a9MEjwihRiMUciDJXtTymLst7+v2UEMt9LM3YvM3p/l6uNweFV9DxZG2mPnj2zeXt+NQR1LgYAe0DlSWjh3OUs6fKgxQR51rRTAmVH6P8tRD3H2K+zm1jfdNxECRlQYvWGsZ7NEbDw6BxBtY3aNsWjj0se9DoQKOTJNbjCFIaSo8gS/DOwoHA5IOAPgqvkPHqBOGlWwtIawb7qfcfpdZLJdHRy8nclubs3O8KidFyG+9VFgSY09ur9ykLmGgOZuQtVh/n6Y1y7mKdJXg+dJkoH+a3hADIa41naL96hmhxPZXr4+H4hjFNMHsUmLJvEKaWJdWaZZ7MQaAwivv5uaIWBdfhYtzT+9EKb2qFX4IcCdq4Z30MacSCT5xz8FqjUQZ90+Jqd4nL3Q6bvkWjCez38PYObriF4gEKDhRiJTk7YvA2hHsTApUIElbIWQzDHgwPReLyDG+h4GGMBntGYxQaTbDwQiC7EXAEJgc2DdBoKEi8S68JjVZQJIRikZkgbQgqiN3kmxCVXGmespu50OLl/E6ZXIr/V3NYtL5cOPcdCeQ45/k7CNY5zB0Hr4jwO72jopuMF6JAYWlhZiJ5tu7O3OkVC1cqJ+J3oQipfieFRd1rdan4IylTuIYtEuZBrzQRyBRWfKFymo84J1HxkMIZLY+z9BmrToYJ0GsKwGrOqj5K6rMmmuuma1d5xvw8zOtgHfel9Tl9dvbEQtvFmKZ/f8zyMWnDD9H2X7PBzvufl/fv69T1jzHfS+t7rd6ScUtZHjpnJ5+jn3qtHR/3qTNjeVgPFUZMWjlrzk9x+hmzV+fDhN6fCmRmgpl4Jk3Oqng/CW3DOUXg2TSUZ9Ga4cgUhrpwYdSc6c6pEQEnBqHwYI6zNBPYSrtT3qAcv/wd5xBANUfLc7bObUzLnHYuwTy136JhSPk7f+b17yOkSRzM0pn8kDZXeKJFA6qFeueW+Tu4fznVfwlzXBvhV/H0+TTnrP+FvZFJpRqvzwSiQNiPBd0GyvrIuD3AItAnAjh4zRABpMAh3KmCEktzUMgtoyQgjnOgwwHu3Tu4V69gb27ghgH91RP0z17g4tnnuHr2GTa7LZq2gdIORD7zIZHPZ/kbJP4XWXI55dsF9xBTSgAv4dSihzslUbUhhZYAH8ZhQ8QBWtjn+e+4zmerM98r+JnEd014z/y9dC/+LvoK1ynt+4Le5Uk95nnfU/qYiz4K5o3yRBbC4bJuMdbpJ93m8A7qmZvt67g+w7vmqefJEt6nrGoqZQblcVOyVxR5nAQJgxRBGY2mMeIRYQxaY9DoIn9sMNASscU6b1QAdqrCByrH+pl6PtQ8Vbp6ks5b81RfwVO8UqesmmiDpUKL99d8PU6dIbXSp4Rp/fshtOVjjojHslhIEeCVJFJSBGMMAELXtCGcCUMrDRCFmKEaXduj6zYY2w2G3SWGwx7DOOKw38MOI4bDHs6OGIeDCCOtTXHJmTmHA0Eg7uSPfC5EQV4B59QzQYSeSL/L71j/WPHOV+1Gb4UlwUltzbsuWKEJDovof9r2uQz0Wlkmgk8/RxQSZmUApzWO90sluTGfb7Wi/In1HMqcAvM2jsGgkHijJPwtGe0sMPO50lRqKVzWfLK4FqxO19rSWMvvpVKNKyZ3zmTZatvTPmSMuf65B0oipP0CrIRAnCIxk9NFlfsK80UEF0L9xH2gmkZCHDkHzwxnLQCgbVsoRdgf9gAzemrwpL/EP/7qN7i+vMDVRQs/3uLuzTdwhxsMb79HowhaE8iOACscbm8xDDfouw3argsgEEZrsT8cMLoRSik0WmL2j8MAIsKzp8+gNxqfXV3gndnj+8MtxnHE/uYdrPO4tR6q7WDsNUy/weXlFaxpsWkaHPYD7m7voLSCNjoxnRQ2DhXTxwy4SAzGMEcq5LzhOPeFFR9z8Q4iflNxsoPFIwJxmd9Bzkdcvx/veZKIOuR7cL5IRh0+nO9XRP/kXa+uRwZytrqVkviIKCw5Xr3su/odPwvCu4j3KQlCMnhUZuIhyesQnyv7SrF8AQA+h59FOcVCRCuIJ4R8VMgJoaFU+CaFGOs6WX0mbhRB/xiYoTQ6gXZNGLQyS5M65e+JkhO80AoVrZcMHMRKi8pPMRGTrqLHn6eY3vDHYiQey2P5eZb7CCcfy6dSYviFM95bFPIVGB5Y5g1WBeuB8Zl6RFSloFszHl8XOhzjJUrP7NJAwkNoEEUB1wNVPojo+ZrgLzwj5kCkkZc/VvcDBYOSFMY3CYKzOKwcX76UjWVm7XKuX44z8gjvty/X6OVznsxCyBgyuITn3p4Ra/18RLzDvL7+Plwf9feHhKHeH5EengtPl/hTxpRmjp5AoQZHIzIk5VpoDKw0WDEABZAGmVb4cq1gGNjYAXj7Dvj2LxhevcTNN3+WqEm6x5Nf/wd89S//BV//87/g89/+HbaXW/SdgiYHBcZgPZxnNEq8MOAsvGeg6QFowAZaNdGkMn9COzMUe2hPUA4gT2BP8B6wLF4eBowNaRhloEnBgOBg4dnBhiVdzKj8G70TqpcYaM2St+GiDhef6nfcN/HGxDMg8v4uekIUsoBKAeGKtib9xSZjHofVvgpJSFgDTNETIcf7ly4DLCn3QwFPmps8YJoOPHhARIXKqcisyeObkNfeRIg81akUDwd+J3j7hyqmNej7Fhe7Ha4vLnC12eCy67DpevRdi7ZrYYzJsq6QI2gO2wk+MoK1sukfgtPSE9W5WMNRXq9EJWfK5HI1X11f8+ISORiDvZvhEnnuvNBw583HGp489my9Xta/71cepIiYWv2sWQGdax209Ewsa8+eW++nLefD9CnAP9P2Kzl4okBea4bWIojTWsOAYbyB9x6NaRIeVZ4lnY1SUHoAgWC1gVIEaxsoreCshRslcapyothgH2OYRxycCTBGtOxFJXgukX6So/pMnMeDPxOnSITe0tijNrFeX1zQ+0sbry4yf7OrqS5P6i3JwAvI8JCNDWR4c9tntsPl/M2fXFQSlEqE4plITC8q5It7hKkGetpP/ruGpZjV6bqohP7xjUcLq9z/EnxLM/W+e3RJuLpUIhPC4JU6ibSVX2ccOvUBVig/SoEspvuitvDK22jC5E0YpegBEb8r5SIDTYgnueu3uNhucbHZom8beDvA2QO828PZO7jxFkoRnNdg76GVxsgSyijmNxDA4gpgWDsCYDilAQaGwwEEYLvZgoNlUasIXWOgwGDnQNaCxgPcyLDvgNaNME0DrRts2x5wDqORfDmRsZBpDOMKE5NJlpiQMSpF15lKDgR0+UbLcU1pcCqeLWXDmXj24b2FBJIloV0R6xnmDHf8FWFDUi4tKiMKAUlivDiP49huma7ZaOFZ/Y59RsYyDDhjpoCnOH8n3i7hk3wOpDARAfY4CZWYJzAISdBSvJk8dEKOnZuvpTBMFGevoPnTtQhFCWvuPD8/vVeXWR2ajgvIM7XiHlysnbhOAaR8IYokpw5NdRqF1jpbrsr6m4a6+xCMw6dAG33K5T5WTT91Oc/i/H5tfUrlfKORuVflh+CfjsFytoHE0UbxUHL0o5fT1olzwPM7ACaUJR4y0AqC8uwsztC676zcmAoQ0skzYTOmltjxnI94fkmPHQ19pgr4NeVEvTbFqrM4CQPJv5ArojiL85k86SfxX8tKixmcWHoT9dWZsL6kW++jDFgQ+q8ene+Jw2oL/wk/ukb5L8g9pmtncbyJ3lxuZ63cB4c8tKS1Fn/j+NyslWQghfX3vYwjlvZlcZ2m15d+1xRv3NvZIyJuzMinyt/JqCjiCqVEYaGN0IieQc4C+zvg7Vu4V6/gb27AzsFc7GCur3Dx+S9w9fkvsbm6RtN1MEZBUenBnWaokpfUK6Lgm6sRUTCgEuKOmeCZ4BjhE3AOQtQMZNMf4ZO43pPMxSKM3c/hLBZqwXAV/Ev4HT0A1oT3+VrRLpd/89FPzM2Q+pjBMukr0MM1J5Xv5Xe/UJizHqbsiwMPxAjvNPMl0SO/mPHJTNb8DSWGROBYwnJpHaTzafIJQ2ASRZluGvGIaBs0WnJDxE8KV4us3lpnDB9G50zX7f1LPL/i3zWPG+tUe+PeNFnNRBHVPFdVGIHpiiPLZ9KxMzs9fuK+1IlwLF9feepom7nc/208ekQ8llkRy1ETFrQHeUmmJPE7CUpreDCUNfBQUMqAlEHnLPrWYuw2GO2AYRgwjuIJYe2IYTjAWQmf4qzFeDjAOwtrRzB7uJDUehxdOghKqxUfNNEctMelMDTKeTwzPPvZmKIQlEshabGxJKQGkARF4W8OB0cUuGTBC2QuVK5T91f8HW9PrIeJfJrv8vvYe7nf/YjEVsVZCcIlBDQVbJ0qExSeDqw1ojqKycyilmL6VD7AamYqIvXYmhQ1kZ45pRAphPJAXbQioKn+egraynhKBnHCWJ3bRq6w8t5Ki5EHl7i3wt/ScPiOVmGLT1U0YrSEK5lWZsbhcEjXy3uHwwGN0Xj+5CmuL6/wq6++wounz/Di+imUcrh58x3Y3cAPr2APbzDcfgcHhZE0dLtF2+0wDCrhimjJn/IFMHB3uIN1kpPGO4d3b2/ADBxGD2NaKE/YKODZ9Q7OexzciNvbO9zt3+Hm9h2++/0bbC8uwbd3uH7+Ai++eoq3BlDkxHDFi9eBj8nfwNkmJtKq3sMzg3xwT+ZoaRhxT8ZbglvyWo0xNNNbIariJpc0fP1ycptRqetjIuqQ+0H+LhgDQsqtwCriWSEZRagRPT9U+NS9EmJehKCsDqtIcdxXJaFeMyeRoOJyvGFeYp4FACFUmALIB8pXBS+UMHeBwYsJAFXAN0rrcCYUe4iDlRcJ01SuYS7CMTnH8I7lXVS4McwVNAhKZqk4H1RqN4bJEOsWlRBjjRMIhRAnzSmK82eOfqfX05k1+U6sSTyrir+LkxOpUvEunB3hRgtol96FGCbkcZZrVs7AoqOftCyLrR7LY3ksf+vlFC07xR0PEG+s0YYrLc6E+NPCAFNUMCy0Hfgg5ugxWXhrTqsuCPuXvqeQC+ksJx4TwzFLfl2loEK7JS241m6tXAhCMKrnfAkOoQ0UsMDXLY0vCgJXS1SUTPpcbDNSebP7JQ1XNY5yPEuKjTW43/fcuo/C5VMtp0/v8s3eb6zL85P3X2Vwg5rQmvLoy7x2qWyU35FHAE3XAAExNXWkGxWBmgZkDJRvAWthbm+g3r2D/9Mf4F6+xOHffw/fGlDf4fJXv8bz//y/4ut//j/x9X/8P3B1tcFm16HRDhoiU/GhTxXpTQZICX3oAu7QFHLche8wEigOkRuE6IVnhvWEg1c4eGDPjIEdBvYgKGhS4i3MSMoK76NRVBh28iwoeYNCgF5OEXN+IP6Zrtc4lYvruY2YEyK0X3phRN6mVDy48F3CFMP/hjC22ZuigK3qM8BW5L4B4nqZyFvKvpEVR1m5Ip4S5KV/qkLrIsGWYKUS/kzlxzUWFeLneEtzqkohYfpEshPuNX2HzW6L3W6Li90Wu02PbddiU+SHUEqFdSChnMrO6nnJvOFamcEZZX/nFJ6MM/Hf6/KZzD5GhVx9/+ySlPDTEdReeFGZ6n1ZX9bC2lm6BHu+T2n7VHWw9NaXrhd78yOWD6qI+BiH4LlWQR/zAL7voistPz502x+zZAFVtO4EMhJTICUaUMUMrQ08A0YbOSO8hJkRDToQBe9Eoh83IVaccw5Gy/dojOSMsOIZ4ZwIysYxxoDPQrXSwjomuo4IuRSC5MO3JgCd80HIZAVWH+/JOMV1jEJsxiwMk9h2yXa/PEuCEJyK++nWfG7j8zPxem5zthaqw23uMcBFnUW6qBY3zW8fY7qCgO9U4SjcB9UAlW1SrZWftDDve7H/5XppRqm8Ev4qhOCEen6TffQKWJPzct7vPTTS5yguzr2XPCVmippcY7m9cC+db5yvnQHPrIdibqtn43sr5qAUjrNW2G02uL64wPNnT3B9dQWtIUSVG8FuBLyDYobRBHYe4+jApAFlAO+hlSgjxmGA8yGxbhhPVEoghB06HAY45/Hy5StobSBJ6QkwGkorXF7s0BiNu9sbEBivfngJPxxw+/oV2qbFcP0U8A69kSS8jgBHJLFQw5HtA5EujhCimIiOWYGCD/iwwFcchQvZ7yUTIcXKU2oW+qAqk3OvFO7ni5gtZko4vv6kvYKinVg3NVYgQZRt5/FVxMzC1q2UEKUAYSqIqHBKwsIV0xjHE+skYXmBbyOuzwyjWJxQCDMYFdXCM+b/uCBUY58q5IFQoZ1o9VMqZVJdpdKalFjAmAj088xOx5WVDeU4C3y7+I2CM0Nao1lQhUCQ5+tgTu7mooiwsOMA9oVFEymx1lMEF95RzCeTYY5zLUxbuf/n7wmze6fqnKeIX/H++BmUj0XDLlnR/tTlY8KwNt7pOjrHcuzHKKfW+4daF1U/idYP/1Qodp1aCw9/EHimcP04QtRjdGi+n8mZo1TgcnsBz1fCzel3qloLQ6Y0ayUSWBLQo/a2XCLblzxrz1EWpKdjOKZyPiYNVvTDke9p4exCFy8cgWeRyZkVCrMSmy375pU+5LumPxLdVcxZ+i7Jm+p8EwiYJ/XPLVOW55xHinmaztla30tr62OVvKZP1MOpIdNirZL2m87DOWsw7/nJN+q1eVwZEenKTGOWJXpGpBj5VRtCC3KksZwDuRE0DqDbd+Cbt3Dv3sIe7uCJofoe288+w8Xnv8CTr77GxbPn6LcbtK2BUZCcdoEOEhvSQGPGZMZKR6hAFfTx72K/Q0TkooQARs8YPWNg4OAZB2aMEH5HsYRZdiz1fdlK2kST7ylzUrEWgTaNn/gbSNeSF1h6ZFIPy8+lv4EQ/pbrPku4eAIjynrFYFgGwBT9vYoh0aTaRNhbhdrlyTiKfH6UQkP5eiwo4C/GtogiqzN+Qi8TJR4ohheMee9KmQMpkrBhTYOma9G0DRpjkidEyguxMHPH9uCxOlxAXV45r0TfkPjM7A0tgERFzYnCYlX+stQz8n6f3VVFLelJ8NRU6f5wOlWMCxeaW0K2C9eT981ZuDT2eb/z5NEj4rHMSyG0iYSV0gSQh2FBUJ4hnhBk0FiLhgxG5zCOFoO2MN5iNGKZ7NpRFA5+hPdOQjI5B+sGUUCM2SPCe4/BjllwyQzv4reTLVEoJuRn0LgHL4doeSx42sN7CdnivccwDJXSIyJLHWLKKy2Cynh9msdhSlwmQdIEP3IUyhW7mqEW935kOtRkY58iZGsBXnWn+lrCOLPDAXpWJ8G2gnCiAE/uBkHWtN1wsM24o6ohtXj/PsjsFP2uSoFdCdux9kj01RXzdwZMcc3M2jzW3z0EIkmIvADKtJ3VdpdBXH22HHdU0sV9lIT/BRNUrhsb9rW1Fo3R+OL5c3z1xRf4p3/8n7Btexjv4IYDaDxAuQHeORhF0Jsed7d73O7fQY8jzP4A0oyu63DYj7gb9qCQp4aYYRTBGA0iDjiFcXN7i7u7A7759iWYAU2Epm3x/IvnuLy6xG+++BrOWVztenzz52/x6ttvcLd/h29++AHD7VtoYmwuLnF9fY1RA6MDnCc49ogW8dYLjhnZwwVi0DNL7gwG2LsknEh4KsyTBwBVC+PLJRYt/WtaMRM10/UY92QZFispbVELR2KisRh+b/qeq/0diP5sa1+sCwYohTIKCbA9QKyRHMC5GGNxLeZ2IEJKel8rDJE3dOThEJQBar62k3dGFJ6zhBJ0zqVGRHmgA/6Xd+e9S7QgQRQKkuPDZcVDUk5rgBR0yAlhtIE2Bk2jQcoAIXeErEX5BlFwiAt4SKmQ1L0gUP3c+CgpI4KCXMZch8Oov+Mo5b34sKC84gI/c/K88SHEmYsMjvcY97e4vb2D1gZaK2jTQCkNpbWEazKSA0Y3JoRsbJLCHsywziIKe/I4Hk5IP5bH8lg+dJkLy85idjnWux+judDIz79wFj7OlF8TEV+llCjrTZj68rs6iwuFQw0DivN9qtg/L4TDknChUs4jf08GKbSXUoCvFc9Lwopp+3GeOE6lDBwIfFn1PIVzbyI0FkJWeL6odJguz+lcUujjlOIkzjtQz+nxsrw3lpU8ay0c5xM+mGISP8VOfAgdUOOq44qz3McxwVl+boWOKq8X+3adv4r7PHs5AJGkDHSxz/wwhfUd13lDGkoBg9bw3oL270A3N8C3f4R78wb7b/8g9NqmwcWXX+L5P/8Lvvhf/jO+/t//C548eYHr6wv02qFTkpePPcM5wLOCIZW8GgQmI2PyQqfFUErRmzeOxwNwACyAgYE7B9w6xlvn8doyXjrgLTNuABhmGATlBBgDM0bmOklzMt7PvCuXsQeI6gVZCudLDwMuPRkQPAhQeBIUDSRBPmrmKj0f73Ouj3mCuNUtN+O/fOVlEVfT9HEV8auP81KMMXo6sPAfzA7eO1FQRS9375LxEE1hqKRORYk8evwZ/q2VtIFHVJIHTymN6BGflRRBXtYYbLYbXFzuxBtiu8GmbdEbI0oJYyovvawKmO7FEsRjuC/zS+WQpI3TmKz06F86z+rzJt6l4rPQ8RllSYExfTrJA7xHDNt0TAl/ip+qZINqef2ebwByHPcuyUbvy++9lyJiCsipeufU/TmXH3Ns5y+iBxaut2kWXkWPCA2A0HA4tON3MgeWDeegxIJSa3ivwezgtIF3Di7kl3CtTXGpvfdo7CgCkigssRKqyRcIvhS2ISB0Dkg8uSqzKC+89xhtA+cctNGhb0HiKiggjNaCfHXU/qqAt0tFRE2YRyVNeR/F/TqsB5IIL5+TnH6vIaeSsSivT7+nxOs5VjFlSYl0CwKtHF+Csugmvo5kBbJE8IfvtZ2Rkf05Jc5UCQMDkwNF1uOCUmTh2ZkSadLdqS29tueXrk+vTfHnvZQRK+zKOW0xJoT2AkzTe0v4hoiSAq+8FhUxcX+KsFLj4uICl7sdnj99hifX1+j7FkZruLtBiG/vRRjrAZYAlCCtoDSByIP9IKcqKYzjiMNeFBFECuNwgB1HaAKU0fBtAyJAaQ0QcNgfYJ0HiGEOe0Az7Djg7vMXMEbjcrPBcHWJLz7/DC9fv8XN3XfY72/w3Td/xvU4wGgN1g1gQrvhLci2UfBgeBVxBAHwUBQFvpD1qGg2lxTnlCPTK+1O30d5p6LVj+xzig9yfTXitxStLMYOmhBnSVGQrmcX6wo3JQZg2RvDez8JLzXHXyhxBWVlgiYFo3RSAsTEZ9oIvo4w++B+LWuF0BgjOBy6wsHRwl/Or+jJF62LqumDDmdO9nQIZ0NkOnUjighjoLQRQb2SkE0CvyhMVNQuFMqIeJamd8IAVPbqiQKQuFakiYCTIz4lJPyV93MYJwNMIYZu/K5YlBCakD08e5B3onjxHuwsnLWBoTIACKzDeUokDj4xAbtSAFRYR0EoFN5FJEjvSxet0ZVr12fCrRXa6KPTTI/lkyzn8ik/ZjkmUFxbz7G8//otzuspg3uSFpufUfcr67B/7P35/kLckhae3qmFDSjwdTIcmdBm5ftdwpWUzoG6pDFMBKs0qZPaLUFfGtUCzTgVFOWY1rOBJ5pkUaAvLaQZWsfRxVgp0Bc4tloKACDnZuJFTr7j4/fPWSOR3qkgSYLcGLJx/n6X+sjrkvIrXYhCdUxptPS9VBIE8d2cGOuH3It5+CuLMUsVFy5P1vrCnNZc9DEvnKXn5vsg0VbT60vnSKILMw0behNYwrsljnSghOKR9aokMA8D3ln44QD77jX43Tv4Ny/hb+/A7EH9Bu3VU+x++TWe/Pq3uHrxBS4urrDpWjTkodgC3oZuA70KpLwN0RCSA62vwtyS5yqCqUCdd65nCcdm2WNkYPCEAzP2HjiAMYZwwcwMC4blQF0mInXGtWR5Q/Fq04xV/EOgy+O1Qv5D0+vV9/QF8ezP3F+8uLLWl9pa6jvcqwy/Jm3ULNa04QKGctwc56T2IqeyCZZVFhUFAArlbu4hvYnqKCvxvvwu+bBaGSd9KKWhGoOmbdB2HZqQJ8KYkBtCh1Dnga0UhVTE1RFvlX2eWc7kCeaF0zgLdnOlD4ALPDL1jFqD5VhZlROVEFZ4KeKywHffg96q8SMS7plXnACx8Duf3Cf6LCF8AJ396BHxWBYLp7Wfiel4oIJE2KI1QysPox200nDawtCIkY1YOWsDZ0Sbm+PrSXgk8VRwYPhgrRoUEcw42ENSRIAZ7DyioI6Lg4iZkxY5I2jpIwpBrbXJE8I5l77j/caINWfTNGJ1qsVaIIadKK3bjxJ4REDQhsd6Lp0l9XOnCEZmnn1OXScWhLlElE7rLhXvRBgXBXppTAVM5W+P8kDMmupaOYKqnSVCfEpn3Lfkd14wAhQYgYK6Wn+PE6IIaShyCEe6gM4nytcYurV6x4R1a8qKqTfEOcRyhp+hQrz7cxUR5f340UHwGr2L4jjatoXWGnd3d/DeQ2uNpmnw61//Gs+eXOPvf/tbPHtyjc1uA/Ie797twfYg8TAdS/wjKLBqoMwI0xnAWrA9gKkFUYv93R3evH6bLDYOh1tYN+LicoOmbdA1CsPYoGsb3N1pvLu5xeEw4OAHAIxvvvkTnj25xovLSzx5co1ffv0Vtm0DrQm/+/0f8d333+Pdmx/wpz/9Cb/4xS+hRovu+gna6ycSkgciyAcpOJIQxkQM58WtUnnJM+Dg4Sxneq8g7tJc+pBgWmZ9xmBW8ZflRniLy2uSmZOHQkxyhsiShFAQooRQiBxvzGdRxmGOigiJPRW8O+Aid5LgjxZYMS+G4PY8vqQwRgidpfLaSpaPqPdMVBh0bYe+7dLvqIiI37EPay2YGeIgIwoLYcRMmr+y7bZtM2zaw45UwSQW/tk7rsyV4F3Ep+IZ0bQdtDHQTQMiBR+8BmOyNj3xiMiKitotiTnG8k38VsoLHRURKimzUH3HscU3rSl4qKmoQBDFQwxbKGKfaHnl4L2FmNB5uHGA3e/BpoE28j6V10AIa8Y0ACA0XRdCNBKU8miaBvHsLc+QqVfhY3ksj+Wx/LxKKeQ8VieaKNRSoHW6LAtnloTTOTiElGPCVSbxcCOeWysuQjsVNi3cTwoBJlHYY3J2ew9/hH69bxE6O4rkMm+3BBtwnCZfNHhANgxJ9Rb6OJfWP84TlsK203G9Z1LLtXpH+v/UlOxTEfQ59XHGXB1X4s7DbMVSCumKHpeVEOX3ZI3P3sPk+rxPBNZUhW8WLkxRyA6g4D1g93cY373B4dvfg9+8Af3xjxLmSGl0T5/h8p//V3z2D/+EX/0f/xeePfkMnz95gdYwGjUCbg92A1h38KoFkYZkbfBigU8SRnsM9kStqkWMAlO5L4TPtyze3nfe49YBbx3w1jLeOMaNItwpgoVHw4SD9zgAcJQWPqLXUpJsshjKAIA/hjYKflW+JgZD5d+rbRSfcqzVdc7f04pxGPFPmj6z0FnKJ5FDLkWafqKJKIYaPRsYSQuZZF1BrhSNbQu8FuVNVMzFXK5c4vilCS+UDPFKGY6pWPvxPDKNQdP3kh/i8gKb7RZ9v0EX8kJoraC0yvpUuh8eWCzvdcaUe3cJD0T+OvPh9xH+ny7zvBz1fFc7MeAvFHWW8fyxc5uiHCzIcWeF5YyMWCArz/JvWoI9zlk5d9Xz9y9nKyKOEQP3KdN2zm3jvgfshyKMqrVwpNKsXuh++uh0Taw4UaXaVP9MD0+Fpot48UQ5OkMxkXLqi5NCQhGgtQKnxLkMZrE+BRjkJSSGcyp4H8TEsiKQ0koHYVUQjujo8SAIXBuTBMxJUJfWfkDOxd+RWM1CaWnbe49xtOIJoQ2cszCmCXUE0RhjoEjBmCbEvTOCeJUKcsPjhJ9MUhQeRSvTCF9JUAPpbfNSW3NLYmkvh56q264tkjHxaKgUNnKhElymvuJ1HxJWFYqIApQCKaHuH9L3khIkLcrpXlyDaeF+fT2vxfyVrYonXdTbkThJ7ym1TSBWaY2XR3E+BCh1HONR5s6rjbywoQInQuXMTYAMe5p5gZnjpT2aOzqG444eVJA4lktl7WCLbVJY6wJbtvRjIAk5I8G23fQgAF3TomtbfPXiBZ49eYInz55ju9vCDnuQs1B2D3YHODfAuwF2GMAY4TGAnYMhBUuS/Iw8g9gBYCHivQOzxWgHOGcxjBoMH8LKiItoawz6tpXXOALWWdze7QG8w3/73R/w/OYOm8srKE14+vQp3r27xZPrSzj/Fj+8usGbN+/w52+/w9U44NLtBUdoA9M0AV8IDuHRwTsGsZKEzd6DPAdrJMBx+d6y1TvCrDEzFClopRG9DyJOYZTuvcX6jws9xuOMkw9OYhEGwCTz4gMFrpTseR8IEWO04AAfVkgg1iTpu4Q18o7ho30VKYCDFVcIScXgwsxKgVmBmcCeBbcqDa00GtPKOElBK0KjRVjfNFpCHLXiXaC1Rm8a9MYEV+EcHkmH0EYc8m9YHeEFSBFaLUoBBuCJAEVpfSowNAMgBWgNVgyjGpm30IfWWmqGME4x5BNQKJBCaI6maaG0Ee8gkHjepORyUYATldsAU9w5Be5iUfRI8m2frb1C2CwKbv0ElZQViblBmPOEaxnMIRRVOh+chPkKCctVPF/DuazhAIjLt+YBCgMMAYYgifJcQYuEefBuD1Yahi9BpoFjDxBwGPYAAKOb8N7EY0Icb8LaQzyrKbWX/fin2Dh1XK//dC3iumI+0j6bn9mnhEJ/7eU+tPyPMU8/pYLqfcf3U8D+IdfvlE44JcA+u9cV+OqdW/Iy0z298JOn9eo6H2Olpnko+ubqO9LtlFFZKiGU4UzIU76/jLuyQKh8Hz5VY0wswSP9yJQEnUIzFJRCoD8TqwY+ihfrUiJTTv1Uz8uFSmAVBa8JPBCiAUQl+EF+tfPgJeFq5K1i4sETL5kT4V/2NxHMxHuTcdbTkWmoBXWQ0NCJTlpvI9JR1dWpgJzLZ+t1IfWnY5yfddOyKISfNrJQf15zGQ8sraHMc80o1fq9T4Qaqa1pzyswrY07j7XmV9a+6xIobM6eqhTWdjRIAalqNqh6R0pCi7JcV5AcWjaMzwPJM5UAKNZCg8Ww0+MN3P4O7vUP8G9fAz+8Au5uAeeh+x7NZ59j98tf4fnf/QOefvUrXF8/xXa7gVHSnnDvCiADpkJwGJQLKfetXJL1E/OkqXhHDJUoJKlmz0WuTgK8gnWM/ehx5xi3LCGbmAk+RL7w8QUJMbv8ohAVEJwWQ1bEcSVLyEIUni+Q+HNKFpbf6dkCLzAH8Mo8Czz5ew0nlf1x7oSDMiBqOIIsy3MMpxRDLcWwTyEBdjAEipE8Ug4I50DeASEEk/C8DmIIFvgLFP2H86NIBBdwfkFfB+NDcFwDlJ4rz/0cMjYbTEXcHiBArxW6xmDXGFw2GptGoTMkCgijEt2vUOLk6f4uJ3Npgtevc7oS+J1p1eXjpOh7zUste5uXj6UgWw+k96hY67n5Gv9nuHKYwcxzKUSlASOxefOxxTUecdEE1+bCyKNdXueJxkjNxjXCGZcWfa6eNWeUR4+II+XUkjt2PxN+yw+c86LOWfP3feFTONbLgm8oAK0gxKHSYBcSVIcDROJJKzTMaD2nGPLxU8UtX/vAAxgBiGICjMqitRp7IfjOVi0ejNznMAyw1mIcRVAp9REUEBo6CKwkxIwIxCTm/bIV5zEG0MPDxRRNVT0OZ1z97LSOd07Qf0HkRavdpb7L+6VVTz0fU2Jxbd6XFRXxu4Rh1nY87I88v/jNCP0Gi/B4r0xGvgJDPS59ctxL65nAINbpHI+Iv57mgHxR3OCIxMOddD1+FcznhGNYYkDlYBHydfWg46JybHeh6tIaWbLSWTm+zyoh4miKLSqW5x4u5GNheBApXF9comsaPN1dYLfZ4H/57d/h+ulTfPmr38AowuH7P4CGA9rDG3g7wtpb2OGA29tbgEcAexA8DGk4eFi2UI6hIcmsG024swOGccAw7GHtCCiPpjG4vLxGaxr0bYuha3F5sUFrDNStwe1+j1dvvsfLN3d4+e4OX375ObbXT/His6f4+9/+Ct4x/vCHP2EcGb/792/x3fcv8cObPb787AJfvNuh7Xs0bYtuu0PbddDdVhSddwPsyCCzgSIDsnIOaDRgIuQc1MHSHiQEucoJyEgpNCHsHTjgK8+wTLAcyRBkwpqjckwYJUGB0QnbJ16AlIZnFcKlMpRWgqus9Nk2LbxzGMcxyhYEF8W2eYQjBceAJsGdDMkVZH0gtgOHwyQCfGYN9gTPFgSCUQ2MadB3F1Ck0JKGUYReA21jsNl0aLoG7aYTRYTRaInQludmsb8BAmnZEy4wT+JxQeibHkSAwwjnGMqQJDZ3MieaWRQMphVGE9EDQkFrCbUk4nkNrUO+ibR/srcegOAZJN4KzAxvx/AeTBBXAMmbIfRFkTGI4hiWeUJiOML4EjEp7WithNgPCchcUFaDxOvCJwhHgGIPHgpOzlM3JJgic6SYpR5beB6h+Q4N3aFTHo1mgB3YM1Th6QAGbg8WngmN+xzU9kB/AQ/g5vYGIELfX0JHzxSS81GL7icwXjHNoXhb5Ii6oYOzCJVz69Xlb10Z8Vh++vI+a/BTX7/HIStF0OW1gumd3Kn/ePi4Hz5vkaGTs9UHbzJmn5Kyqoomy3ReKSOoRAEzYXDm+dJ3PmbSM7UyIrdMk3MyjjdLLpb7rWFYkOoFoljOt+zFWLblIXHPyz6Sp3KAr1KkINwvLYeLD4X6HIQdXNLT0sHqGGq6di5wro06Yp04nvw7Ki4iLBRHSlEYFPNYRBrs9LqaCsRr0OIEnCrF2lo4+qLBRNnHjC9YgU3u8XlglO2Va3R2r+ZzJ70utDVXHJT8YXxuXShYr/Wp0HF1XtiF+Qw0SzSqKWjD1HqQNURKDkrDKQ34EeQdNBFMiBzBIHhN8GAoOBADDTQUA34EvHcY737A+O4N7De/g3v1GvT7P4uHKgHN7gq7f/pnPPu7f8Rv/s//G8+ePsfnn3+FVnm05OEpGDmRAUJEBxmryGd8BhpFoJkEm9KB96fg660U2DGsH4MiAoAnsNcYRoe3e8YbB7xiwHsFsIInhTHQnymaRfmumRIqAULOsjibJeIDA8SgGJ43Xlso03BSxZ0630L6ju+tvkeJni+6Knj9ukR6PeA1L0a0FGjjaPDoWaKAsLMh95ooFFRUSHih9cnbgAej0sGJEsJZkLfyzU7uswVDckZQijAi4YZB0Xgz4rKAA1iMl4gITDpcdcUOybhC0IaC0iYMnUWZoDLvY8E4EPCkNbjc9ni66fDZpsV1p7FrCU2roRoNFfLnsXOVeMTFLlH9Ib8qRSItvvZIIUyexGLl1avT/go5yQRXRY5EjlFafPacUiktz4KxWIwRnyOeXio1tKw8rjtapjlKeuHYuaMyCVAc0KWipJSGlV3fR770QRQRFdGzUB5qufuxyppFyPR+Wgen2jtWY0ZvnyakFuuvlQKf37ustj0lkKqHkLakUqAQ/1trnTZzDNHhPSUBjdYqCcx9DPPBy4qJMtZ0EkjzAiEPIAqFkZ538OzglIXXkmjUagtjtAihwpiNEQWE0U0QEokiIuaMUCoi6MlUHHlv0XZ5ViPBONmck98+KEqmCDKGupjTrfW8lcRafS13yJyVIqUSwp9UHPhEbMfn0/10wE+fK+vWfdd1Xa47fe9FHxHWNG9L38WYagVMIUQr5h9BEVHN2wohPus/HZh5DZZlTYmV4KIl9D3/zQt/gRjLdNqccIpMFDPSno/r7hRTXhPt8UkRzHpmsOO07hEYzHEcwN7BbbYganF5dYXryys8ffYcl1dXYmXvHWAdvLUYhwP8OGIcD7B2ECLOWzg7BqLJw3oGkexhF8LwECloFQTHwQJDQrE5dN0gSYUZUKTgrShFSTG0JrSdgXUeh8OI16/f4r/927/i9uYFri56jOOAzz9/gcPo8f3Ld7g9ONweLA77A16/ZLTdANM26O4OaLoWbX8LbRrc3Y2wzkM1G5Ay8DZ4DUALI60bQGmYpgFYhPXEAHsfLKU8FCsJURUEHUoRdGPQQBQJ0TgL3oM94zBYWJfz4hBITM+5/ORVoXSI7U8KpBxcZNSIBJ9rHdZzwNM+59lRWkEZjXbbo+sa9L1BYwiNgcxps0HXNLjsL2FMA6MMiACtneQIubxAY1ps+0topdAoDUNArwnGKHStEc+ItoUykhxZA+K9EFa295O9GZMDRquuMEFetwGHtyDFMNxDeYbzTsYeEiwr3QCkUq4RKEnQprWGC55epUVQhCSeX0BI3h7yQBAYFDz84m5xzoI8wYe4vUoHRVSxfz284MESb8LDhR0cczwQK7AP3hVhPhicEmhHwY3nUTBFEOCwt2DnYMdB9kSJX4PlG3uxwlLE0Onj03SnROTOS7gAZ+EZGA838N5KTg0A9vYtGARyDsq0kmhPiQKFtZL1j+hBKThULAZxzIhulVwphQzLzy3j4VN04NIza20+lg9X/pbm+phg/JSXysfyJv+4pYB5xgutCZ4m1x+6HtLj8zk/BxckKIIn3DL7XtBozEHOts4XC+6S1peMRqJByzmvMBvScH3tBP47p5xU4Cw0FQU7s7dJMWTEXJi8KqRf6+To9SPgxj6CouaY5XwNUxRNle9+Kghb9oSI45tcuDfsp8Y17escxdOioiL/U9U5rgA4/yyd9X1iPdbvYFkRkZtaEDJO+s7vNT6jC4Fj8vdGRaglYjrTd0TBrIQAgg57UMFT5LMYRgWaLxqn2APYWQx3P2C8u8Hh228wvn2Dw7ffwd/dwZOC2fXYvvgc2198hc/+/p/w5Je/wbOnz3Cx3cEQSXjdabLn2ZxNL5S7pd6fcwGp0IjOSeLr0QKjc+FDcJ4kxpKOewiBBi4MppYKrfyIsMUpprLOBF8DwrNQWblgFJYKT+7Hn5UMgxfqRxkURyZapg5RNB3XRaDRMa1ftAWk5NLFziqBkbkLz0ZjIWLJ4cYcPSK4Gk9ckos7iIqvtG7KPZGhUBQUzQHOGJY27hulNTQBXddh03foO4l20BiDRhsYLTn9Si8n+S7PgYnUY7JI82ufng0Z+6a2YpSLiVYqJslO/ATN2yvP1aiDWMIpYiQ6xzenzs8Kp5b4CPUMrCmnCZEhCuuN5+9sei4tKR9KWJY8wWJ7x/B67ptnfa/SF/c4lx89Ij7R8ikzX1Eo4z2nZLVxUXovQgrFOTzSXAnBs7+z4DxFGamuHSOmyjreWxGQeAfnLYyWJNU+CHnEOjPHGNfKpGtEVCSrXiN0jktKTpFhM4Kv+O1jOI1JKedpidDMMbnruTrnO70L8Oz6OW3IDyTMuNT20juu67mTz52Cf+3ZdB1uEfbkKbnS3vJcnz/H0+fL9pdKvpcPnMxc1kRbeCI/u0iITYie6mxcZkKW1lj1dyAAHfuswIr/ssdhbzECcBdXICI8e/4cnz17jhdffonddgsiBbYj2Dn4cYDb7+HGA4b9HZyz8EEJMQ4HsBelhNIGyrQY3QHjMMAFpaLSBgYIikQnz4DRtntoLYl2iTSsdbDWimDcEPq+xWEY8ebtHva7H/D//L/v8MMvv8KT6x36foNf/eprKN3idm/xzXc/4A9//g772zvYm1s0rYZpDdquRdMa9NsepjEYQz6apt0EqxKD6DXApMCNhLAxaiseZayDKzPSHiSmZAlFBDTKoG0l3itBhLmkIq7zeIs77A8Sx5Xhs1stE8AxkbAHrCwkpXUQChs4L4Lu9F6VgjZGFA/OwTpR3gzWYvQO243Bpm+xub7AxW6DTafRGCUWPMzYtBfomxZPLp6ha5pA+zF0Y2GMwdX1U7RNh4utKCJarcQjQkUCWDw1lNZQRsJfwUVllxg5ESGEjwsTFATwKU8NCYPiTZsOEgWgNaJsdT56G2Q8r5QGRWVWyOuglIJihguK9um+KPdDmfMCAEiHvBqhjrPyPuEAUhoGGloRyOR9y5Ck0WLFhuANmJXQxF6UB56gVd63EYaYrwWkwWBYGzwfdDxMHZyzGA+HwOxE2rzAAd6FfjyMAjQFz5pQ2Tof9qaVkIujKCL2d6+hhgbGDWAGxjevxa/xsIdqWow8QpkGTdujRYOOOwQ7rcDsRmCW8Nd55ei5/Fgey2N5LEV5kGeESL/kb54rIiKNVh4T6Vw4oYxYun7fEo0HSqOwD1GikGZ+fSI4Kfimk3MbhBogKujbU/PBs/mM16eil1PC90rwEwZ4WgkRngch5Bw+2VcJz4wHeM8za22uOEolC9jO7WmqNlrjheZr66Frbf7ujpXo7bH2jLzKucBwbU3JWACAoEgniJAsyVXKy5UMJ2smKhjxBD9XUkAQ5NrAdxIxWiVe0goK5Bl2vIUdb7F/9wcc3r3G3e9+h+HNW9z+4U9g56GaFs3VE1z/83/Ck69/jd/+y3/B5dPP8OLFlzBKoaFgF81CQz14+pHXBlWvghNf4pzHaBmDZQzW4mBtUERokFFQOj8SaUpCgTROLb5CbkKBhqeAa5OyoaSvEx+a/jm+lxKi5gxL+J3XxcI+Kvtaa7rQhUQFgo97m7mSjRBzbo/jc7n/YI6TnhUlBAdDNfGqYI7e86Fe4g/m+5xA1bwllolUqjnDD6XsK/KLBY+gtBbv9b7HxW6H7WaDvuvRNaUyQlemA+szfM+ydJ7V4pLpA7nC4llY3F9RHldeVPcGOLdxCsvVQn358OSpUmm69OzHKcX4E6NWn/kfou/3UkSUxMPS78eSy0Pn5FOaUwpaxnjQExGgQuLbUJRS8OzhvZIEmcoXSghBS/m79IyQ79guIwqcSgIuwlDORdTQybdzA7wiOK+gvIYiDa89KutVEoGbIoJSISdETExaKFZy2KnyHAvvo4BhbvOzXGb1uL6X33VxvZifCqkWY05xZEuhc3E/Hzrz+Yrz62JM+hPKjCzrLoEv+olnfRTqx2cjAcfTw6/0+KgJ9UXiPXUZrvu67STAY1/0FX4jEgn1nPPseWRYi+/MQKzfn91L40fqRzw+ivcc4Ek5FricUxTfk/VDdX/Ve5n8nr6/rOiY3F8p8RBK8wkfiJryoNQANFRD0Erj+uoKT66v8fT5Z3jy7Bm2OwlltN/v4QbJBeHHAX48wNtR4mmShzEaBAPvNKx3sNaBPIG8hXdxL8iejbH2tTZoGobzooQ8HAYoZUMi7eC1pRSsGwH2aIyC9xpdJ0z723cWf/nLG/zXf/1vePb0GX71q19js93gf/q732Cz3UIpjcPtHYa7OxE8A7DjCGdFMKuNgnXiqdG0gyTobltE932xtFdQaKAtA6TgELxxyjEpBWUMlNIwRmNjFLabFpok7VymU+QPxUBnLG4Gh9F7WM7rKNZjKJAu9lEmecVDgmVNElEISydMhCiQHTatxpYUnlxvcHm5xYtn17i62KBrDYwm+IO4H19uduiaFi+ud2jbRnohccPW2uBqt0XTtNhuO2hFMERiXaOCkAEBwSc4FFgp+CC0RmRuGCFUgwIZA/EEiDkdArVtmuBxIutTsZB24uYsvaX9QSTMIxFIi/cKKwVihtbFvqAYPzQLW0SQMdknugHIi4eb9/BsEXZ+CJFF0Nojh2ZSohRKuCl8lzjQh9BnBFiCKOgKYYY2RvJYKAOAYZ2V+fQhgBpLqEI7jqHHMNVhT/ugVOQwT5piAAufFfWKQvxgscxSJHFq2d7BuwEhRRR4vBUeCQ7eNnAYoUwL2+/A/RbbrociJXlVOPp9AEQhdMAnQOvEsoYX/1YUH/fxGnloOe/sOZ8Gvo+l2qe01t63nGNYsHT/Y8Jyn7qn33OQ+nygcj8mOhNr0dEwllowW66taYLK4/0uWRies/9SfYact97P2krH1MrUTgXvUeCQhR/53SzCjlpQk4X8KKckwxPO86xXOAfPUP63UkQsC2iOlWqsgRhfUjrMnyv5q5X2inGsGSQdK2t1qBrz/fbx5DWst1HwLfcpWSlTNHUmT5G3zvFxF1ewtJBr/vk0/qn3GiGG+KVwvQygGTjZ9FcJgg88HeChCxpa6CtJ2KsRBLruAG8HHN58i+H2Dd79++8wvHmN4c/fwd8N6KGht1tsv/4a28+/xIt/+k+4fPElLp59ic3uAlqpOgQcS1hcLvbnvUuc9rgXEYN3htue4TxjcB6Dk2/LOhicBoF5oLsJYfwcQs+WZ+05oEQUX73iAu9XjHOsUz4QVnqMaRfo6Pz6OLBG8X64EcGcbG75WdxH8QzJQZDmKj1btB0/PtPyUSEh9HvMJRcUDN6DQ4gmDsqHfI8Rk2Cn0FNIYoAEd/RI4fQ+479zOkDAC4OjiJMDDa5qWtwzQyvxaN70PXabLTZdjz54RBgt3uQqGM0haD5qfDI/2yqZxKm9S3k0SYm8VG3h/hIdNDW6XPN64IXnT5W6PlXDiis2dLwA/Zq34LyfGdzlcg0X1mnAeKZMr89LpAUoKLLWjAcegoMePSI+wfLTM0cl2TIlYURgwGXiMhKL5LgWvfdBCRE8IdRxq/Va4IzJd31/bW6ikNdZgnWA8lqsg5RBqeBI1q5BMCjumJnAUyFU05JHxLFNGgW0Mwr1nmXNC+NY31F4fhy2+e/yuis8BtbqHRPK3PfZSqkQYzRO6i8pImbKiHgopzohfMjKs9V1MDxsJaw/1ufyel2vu9b30jyu7wsUdE35rEB/zhwv7rFMx5z9ruK38xJvXpGGLphtIcIV2qZB0zR4ev0ET58+xfPPXuDZs2fYXool/M3btxgPB4yHA3g4iDLCjWAvHgtNY6DIwTsNZwnOejA5wEKINmQGVGLy+BBqjTCMI5xnHA5ine2sxLfXSpJAs90DLMoOBqN3CofB4+1bC2dfA/Rf8etffY3nn32O7XaHzz8XLw5NhO+/+wE/fM/ibeUshoPkndnfRZwosLWdKBFou4ExwfqEtISQ4hZqdAAp+BCGiW1I2guxzCffwLQNGuqwaQhXmwaGFHRJxGlJ4KxJ4W6w8Dd70GhhbcgFQOFFR+G5DpaHTt6hD4Sq0pKk2rMILzSR5KoJe0krQt8YbBrC5093ePbsCl++eIKnVzs0Wiz77e0BbD12/Q5d0+DzZ5foGgOJKArsAShtcHW5kxwR2x4hKwM0MQzlNZqE4cFDzSkDqAbZgj6QaRQ8IYyEu2Il3icMyZUAI94wzJk5AgAdA4mF8XkfmTgGFCVFhg9KkphsjZE6zufDyr4nDTCcrGn2sHaUsXnxWPGeYbQDcUj6TQoeHHiLcM5FBauX9cZO4sTasHFFyZFDQOkmePiF+K7ei3CfdVSZM7y1sMMgzLVSIZQAkhIiEcAcFREhh0RIDE5KSaxglgTxikSdNdpB1EhRaTPeiuLE3YGVhhtuQaZFYweAPdzlk8DkGIinmjCGyjNiqK0fs3xci6K/jvKpztGnCtfHLEtjngqv7yWkvKfS4GPN98m2k5Diw/W/xESfhKE0hw+lZuw5MOtZ+EOh7crCcoGRnwq08/eyoGRa2DOgamXE9LkpbxPvz9uv53pJ2B7bYsp/x/tKKXi3EBI1jUsEjOcsJ6kf4EQ+IQSmuRfGKWVP9bdM7hlKiNMKpCnNXf59io96SDnFo1bjxT12zqTidN6OwfDQMhPHrQq45kLVeJ0ToXYcrvy+4pOB/g6QZBOREMYSSAmfFSHRg0I5stDVzNCGoI1K6zvSrYoMCIBze7jhBvuXf8b+zQ94+9//G4bXb+H/+AbKAf1Fj/7iCs//4R9x8dWv8MU//2/YXj/F1YuvhN4modti8vj8Vtf22Prvat5mz+a9JbmTGQfrcXAeB88YmZM3N3kGi6WP7H+WsKMU6DrmrNaYrcEJSPn1UQQClUeEEORZkjs9EzjOTfnB8m/kx2ZIaLZHeeXvvBY5MepFYmpf9Ouj8kFCl8cPJwVEzCURckIkJYRLdWI7pVcEI3hEsEBB4QVSMYdrAuw8zMn5EMLNlriemWG0Qtu12G42uNjtsOnFI6IxDYw2MEpDKy19c7muTq3FMI8Juc8Bjri/+n0mvl5a+2tn4FL9ad/3L9P+uVZGzODKcpVlOmEZ7pLemEhxZn1Mn0nnK0/e2uzMjG0sw/aQ8qPkiPix2rhvXx+6vQ8B+zFB+4fq40xIjt6rNnGsHVSzSskR7INAiRPCjA8E0Y/34UyIVugIAtKI/ORC/b4KLwUuCL6IkCFaQx+Ea+J14VPOh5h4VAVkSSpYVZMINUuPCCDP9zHGr964XFw/Nr+L07rYZz4wltfAmnB7Cb7letFjoLwi/6Z+07m98DzP263Zsvz8/FEOQrM41txv8gSJ66XqIwLEFZw10Z8P2qnXDYf1wpQFk+U40v14vYAp/kbsC/nZ9HfxPc11EhVH8T2mpOyT7ygAzSEh8ztidjhHERGvxZBSKfE7q0VmqXx2+p2ExZCPClb6zkr8+UY30Frj6ZMn2G62+M1vfhsUEZ/h8uICjhl2HDEOI8aDeETwMILHEWALDqHJfKD4tdZomxbcA4N1OAweRhOMaQAnUJATi21FGlCA0QbMLGGSnId1Ei6p7TqACAe7hycR7BIzurYL1umSqO716z3+3L7Ev/7rv+HzFy/Q/qrDtu/x9VdfwmiAaYQdLay1uLs9YBgGCf0WYnnKe9cAq2D1rWG04BZ2e8APGPwegik0OCRtJqWhdANjCG3XoGmAtidsG8ZGWTTBHds5J+GCqIVSBmMj7+F2kBwEg2S/DngXsHYo9iIlN3NFBChCZySEErwoHVot4n5RRDiwd7hoCBetwhdfPMPzZ9d4/vQClxd9sORhjK2Ec2q1jLU3AxrtxZuACK1vQUqjI4aGh3KSEBvM8ETwIQmmbA8FxwqKNYgNvGrhVQhNpSgkSiewCgoHLR4RUKJ4iEmbKcTkTUrKoDgQL5qwJ5nBTpLFOW9BLAk3SYmPnwMFpjNY9QTGT1FOrAyS/A6R8mNiiYgFAsbgIgAta4MZ7AALF3QIByitYUwbmAVhf5nDIQoPkAtUJ4G9Ek8IOLjAlwizJ1UFy9Q4wXsfGGoRTjkv7z5aq7H3cF72iQpMhJyx4mFiGSDS0LqRfFBMUM0IkIIOigp/2MMzoJWc5xT3kxvBlmFv34J0Cx4PMH7E4eoauulg2q0w+qSCConhWez7yjI9Dz8GDfS3KNA+p3zKc/LTG+z8dOXU2Nfo03jvffbSKQHf+5ST8NTxQz5I38cs+tJ1Kuj5FYkuUWGc9QAYyhIFDDE+t9BG6woLoBBtFLTaw+ckwpHhmws9ivoLwsw0riPPMigJMMt5WK6/JmSpYTw9tlo4j0l7a22cun7vuaZyUX2YEhU2ZbNpTlHvnCV+YdJaJcA8vu8fBO6kt4Vri8J0Ee8nXpSLtV8Fha/X7dRTSL4R2ourSoxxogy8lD8kAW9M1KZUkjMTKZCXME6eIDnDlBJPCBB4fws/HvD2m/+O4d0rvPnv/4rh7WuM374B3w1oux5N1+PJr7/G5rMXePE//zM2zz/H5eVzdN0O2hGIhE9nicAJeAXlsThxZyshohIO5fqYrgvAsXhCiCLCYwTBsQKTT3NCFb6JntX1bq3+KgXOBXizpURFG4EeDwx0eK6QL8zk25yfjX8mOMtcC8Vn+nsR2Qe4JmGjMiMTP1EhUSS1DsmqJeywW1A+OElm7a2E6U3hmOKngGcBvOQJMXvlDGbK0SGiLCB52of5nL6L4szp2ga7bY/ddoPdZoNN16EzTVJERG8IjkoFkIQlDnxJ4MJqkCnfkT6pukcFUOfyAkv3j9VdOk/rs/X+ntpL+DS2VkjGFssSjTY772dw0/JWKGimdTon/bWqtElrgep+4l/vQ49/ch4RxwS+H6t8MI3+dOEViPZjMdFrgvKP0ce0ZCI1L04QRH6iKAX15oCQ6mcZrOJmU1Wb7DPiOTWuaZ6JuJGiAiIi3UjUp8SjKEIwkYhqiAjK1B4S58xJSahUIZvu8U5SzUmXS0RuCd+SIHkK22k4lg/b04Tq8etTWNae9d7O2poyUut9MMSqimfPl23WyolQp/hv6dljwnj5nb0vTtWXS8vMYV1v2kf8TK+LQPKYEqJsu9wniUDged+nx8GShC3QLIoJ4+EAZy0606ExDT57/hmur6/x9de/wtOnT/Hs2TN0XYfRWlgriggbPhhHwI5CfEGIbB9MbbQxIJa96m4PcG4vOWmUhNwhzsLbGMdfB0XEMIyw1sFZUUa2jVjV66B4lPibQNu2MMxQ2uJwsHj9+g7AK3TN7wAmfPn5l+i7FtsvPof1B+ztOxwOFuNghfhWCof9IMmAE8mkARahuSKFphFrqGHcgz1jjPiQjISUantoMjCK0BiFvmE0HdC3QGc8erJoFaFRhNGPcHBicUSMTSPMT2fEE8wEhSspA2YJH1UKU3TCf/J317RQBGgwjCJ0RqPRhNZoEDEUMa5bhSetxhdfPMdnz5/g6mqDzaaRkFrO4tASvLPBpV1CRWnl0TaSAJq9BkjDBCt78mO5e+FCLgvxEhEFjQuKCEcNnOkFbi1uv0w5fJKEVAo5Iih6GAgXKZgnW2Qyct5BSRLu4IklD4XP61wBkrgbmSiOZxjJCFAiagkLFS4xh04IYt2vAFaB/xFi3I0OXjG8PwRPHh1yd+gEsQTPCskz4AJ3EZJEew/LLIqIuOaCU5yvlJUMsAuKiIBrS56M5Yi2zmMcHbQGYBTEwtTAg0J+Ew0oA1IepAlatyAiNCS5K4bxAHgfPCQg2cXZg8YDYC3czS2gGjg7wChgHN7Bw8ObFo1SgXmJ7EmtEP8Y5ZhxwacseP+xys9tDs6hMT618iFhuq/x0pSh/ZDlQ7S7zgMKg7HGvpe0t9R+/zmucAXVMqCVJ4r+4yecR/eYm7lgZCLQK+7V9cIcTenJdJKdB0MeZ46dPYWp4kMWPCIEmnm4onqgKM7O+fgX56UGcHZ/qa+pYmV5zKf5jbXn76OMoBKY9zhzjvHl01tZFBXrrIyvEPjKV93QkpHctJdyvRzra62srdDZuosGi4Hy9lVMn3pvrH3nUeZelQoKGAJqj53gWUsK0BpQGhRoKM3CWzglhiislRgXkagixvEO/vYtbr75HW5f/gVvf/dvGN/ewH73DuSA5voJ+qsrXP/277D7/Es8+7t/RH/1FLuLp2hMA+UB8gzHIagZERRxcoqYvqcM8anrYQ1W8x6wVkBgzATngcF7DN7jwNEjghMRSaHyOegx8sLpQoniinpJ2D9b0PK+eW2hpDYCfBT/jMx07N7n31OlQ7pW59+UdgMDnAANsxerVV4QhfIgeDFQDL/kbFBIeNRKiIlygl2GIcLFxWdSGHm6KhwRno3hqzN9UE47ZXwcHmLE9UZomyYoIXrJD9G2EgFBGxhlED3VwRCjrPB+mZf3Wv2+1q5HSOh03cTrTvDW2nNTvLBav+b5zinr5329lqf1ZwqIEs41uIuXFkWxuf18uB7HySUNkYDK1+M+TN/AMcOQ+5RPThHxWH4uZbqQ5xsqWvMsaRuBmvDLZSHe5wqyZWYoT3CeE042ZEBeErRGAlxgichUBFYqhJRRwQI0KSh0nZj0mNCiHAcglqYx5vZDShTBVOiAw1HAyeYjIceSdo9zWd4PNxIiOwbVWY5nszYCkXYmHqoJkPJ6U7ziWmgv94/BxiiCJCIqG+Z9cDWP8VsOy6KPqp0AR1E/vw8AMTYnp1qT+/J3FP6XnhO53Qxbqpdgze81wZjaiX4JqMZUzEp1PSbQit807XvitZHmrHgH8eOIhej3DHjAB4+IznQwxuCzzz7D5eUVrq6vcXF5KckTAdwdDuIF4ZyEnkn9xXcmCgLvbCDeLDQpdF0HxwTrFQDJAUFEMMbAewmDcDjs4ZzkhHBOrE9i6BkCJOEXgMuLK7TdgCGEMRpSXQkpdXWlYLTG69c3+P0f/gT2wPXVJZ4+uYYdLHabC3SNJHHumg6Hw4C7m1sMhxHjKKF4mkZDa4W+79E0BhcXWwDA2zevYJ2FHUYopbDpOrRti+urS2hj0HYdGtOi73soraGNBjACwwgGwxLDO1GseHcA6QaeGxBr9BpAa6C1eBSQbsAAbhXBBc8zrRR2200IUyXjvNhsxBqdHYwCWg30jcGuMzBGoWk0ekXoFOHZ02tcXV1gt23RtQ0O+3dw4wFsB1g42HGA9w53t3uQUmDsoLWB9gMADcsMaA3FwQNABeUDUSBgW7DS8NQGwXcLbzp404G0lo/SQdkAWS+J4g6KAyqIayrWVljT2YAs4zKCKLXAHLyphWngsEkSricfaoecCRGOTPUHOETwhJAsPbovEIU96cWDxrlD8FhQ0E0DE4T/DMAlt2aVvSOUEONMEt5JEiGGvmNuC6r3VNhVAX8ALlgrKWiIJ4jkFbEegArhr5QoRxK/QwZMDSTqlYHyHuQMtBIGitQexBbijQKoxsh7GCU/Bo13YHUA7Rn+RmH/6s/Q3SWMc6Buh257BQR0wuktrZePKUj9Wy+fotD+sTwWKctC+fPL+6ztJeFBZtKjMVMSrBWCoPviqqX6kZeSnFdzXkugoUQnRp6rND6JxiPH+jkGU9nu7H7oO463FKacg1M4zRsVV/Lc/jR4aZn/SHzEIv+6XBb5yCDU+VDji+0oVfPQkS88pwcqBcNlLsiVvo4qjM5YA9Omj/HbaS9l6XstX0iUzjwEWjROTPNRdRwFbU6a1WbO0hIhetsKIUYQjYM8rTRBK8k5yUrDsYNnh8O7l+DDHW7+/d8wvHqJ1//1X3F4/Rr21S0wOuwuLqGbDpuvf43uyVN0f/ePaJ4+B108BdodtPMw2mPTAGgIaMVjNObXRAqNOxWwxve4tMenY4/ro+B5S7zhCc4TBg/sPePWORxAGMFQ5CV/W6CNmSjRmrkI/UoEyUWHlbXIQPJoKRMynyzLPL8Mb8FXqxLiR6KzbKP8u4S2oEsjjk8eF4lpDp8yPFP2aIjhl8i54BERwzHZ+XdUSiB7VCDy50tDju87zuGiggnzOSV5b0pRygsxPe1IEbTW2G16PL3Y4XKzwa5r0LUN2sZIjoiQpw5U6GKCURYHhc6qEqIexOpvPuv5+VrgxbaL+hMcFet/fC4jyvKOr/Pp3fQ7KiGCfmABcYXKlbTwLJjOKzHx+fudX5+8ImLNqufnUErh4IfyXPiU5mNqZZJBios+WkeUgv38jFwrEX5Zynkqhf5yT3CyhPaIGlfPLIIgpatwP0SEZCibhEiRsBEPCKWCJ4RCRcTcaz4gWuOHvONC/ju5PieGl+AqieIlJckpmCoeYBVGXv698vBq/TPqnAN3Xj/FAcLZAnp1HqJgP32Ow7n+m8P6Pq/+klC/XM+RAFyrW12PkK/M09o8xsTgFJmTCpaasVrqWxQRHo4YbL3ERnVCNLaNJK26unqCy8tL7HY7bDZbSQAMYBhH2GFIVEpJB4piXfaOtVkRoZoWTdOg9YTeKYzDHcZxgDFNSOgseOZwOMB7EdQ758IIAiHBHKxOGJvNFqZpcPPuBgcaMFix5FdQIE0w2wbOOtzc7OHc99jf3eHLz18EUprRtxtwI4xAow2GboQhwsHsMQwSOskYUQh0bYembbDdXgJg3N2+BbMDsYMC0DcK277B06stmqZB17UwpsGm6wJjLp4dh8NeLMjZie6HWSxpVAOmDkCDVrWgRsL8MDTIdGAAynk45+HAMEbj2dWVJNI2Bq3RuN5tocHQ3kITo9WMbWdwte3QtgZ910jIIgCXFzvstht0bYPGaMCOkiBbK8ADlkdRBlkJJ9S0HZgJikdEa354DR9zDkDwMoJnC5EBqwZed+HvFl538KYVJYQxUCFpcmIeKJOLiQ4r3bGjYD4qATjzD9FKlMJKYRaFHAhwCIo55LB+0Z2CYCQalLhOyLlCFC8gJT0MXikcGFhFgp/ix3oL9oAiAyYFZTgwcvLxHGONA6R1YkQYBCgPSc4dmO3gTcEBcqmX8VTEcz4Iy1xIsufC3w4xl0Z8N5B9DYBhwNDhbPRQuhV4SRQRkh9KYE15RziEaYID3EECLBPAe4Ph7Utoa+F1g0ZpEF0HmKQ3OiMh7anzsCz3ob1WrZJ+BEHYp0DTfYplOi8PFex+6kqWD/3+32fcD+UzHuKdsrbnVnpIrPus7QkdN/eQ8LM6q3Ae6b/mWaLQk9KldJemz50uS8ZaS9fjvTWl7BLtVs7HMR5H2pzDfY5HRLyfrTlFyJMO3rWJDfOWDGdDSJeHCulLRcz7lDl9zcW/94Ml/l00PhOAPbQsvZupYC3S+8faKKioLNg8s88wnDSmcl8fsw5eU3Ss94uiv9KauVZeleU0/wzEMJhKhTlgJMFnDg8TlI0hY70MV0FpQDUEkBHDDevhncdw+wr27Uu8+9P/wP6773Hz+z9ifHMDcpK3bvN8i+biAu2XX6F99hnaX3wNc/UE2FyCTAvyHpo9WgOwIXgjLuPeBvqUSip2gvM4T9ZRkWrFR0cMGZU2UbYCDB4YPOPAjCFQmmII5sU4hSl4KEt7wmvL3o+9L6KAhDCjEISLlzJ5YPZ3+QxPGi+VEPH+wmcRmGJq4vxkBmPy2Eq7zHVIJc9FrofJJ3k/+OI7yDJSOCZpkwoZRha1UYYFlPBptdQLmPN+yApk0DyXRHyFpBS0MejbNighWvRtg7aRfIhayyc2wEDyHC+NNBFhruZ4ujZX9nCxzlfLCZy1Vp8T8qrLErZcw033x+NUfcVFtYi7prRcgXPXlRC5QsQCkRNc53OOQDs5U+pn3u8M++QVET/rsrY4/spKpDOn14BILPCRBV4eFBTma6UyA1GwxAjxEoN4JW8wIRR08GwABfSVNL0R4YogLCogokdEuJ0P7hK/p8GtwRZYk+JQOBc3ySNq3jYH0qBA4lN9NRd1jz0fay4zctMDeJ2Qm/1OhzXW6yz8XivnPJfgm8RMrMdYtBGFW0mQL/9wYCJn2vATMEwZk/re5Hc5/wtIm6sXCNS5IJaVE0ILFwTJAnWX6bRcLypiKBA58pPT39OxlvfidQcPF0NSeYbkKSP0bYfGGHz+4nPsLi6w6bcwxsAGKz5SJEJKLblYtNbwSoNZ4r2K4TeDocSzYRwAJjS6gSJp37sDDoMDswaggxWGxt2d7PdhHDEMBzALkRyFvofDHp4Zm1bDaIXrqysMwwHeOYzW4vYwiFLStGAFKO0xWodXr97CDhZvXr/BZnOBvr9A02gYo0CK0WoNbBr0DeNwcLCOg/cVQ9MobrjjHkQkbqxGo2sbdG2Lzz97gYvtDl9++XlIHhwJMMBai2EYMIbkdsN4wGgHKC3j1Y2H0g5d1wCGsG03gG5hqQND8k2ACeNFB+8Zg7firfL8M1FCNAatMbjcbqA45G1gC+IBfaOx6w0ardA2WhgOMJqGAVjECL0KDoodYAdJOj4MYGcBJ3kWtGVoSK4FEEFspzS0bgFtRFlCCqw1QAake7Ay8LoFqQZQHbxpAG3AWlUhwaoFX+FsLtY+w7tgI8dhD8Z14V1iDNh7eOuCp4kkN2fvJX+M8imkX9RmK+WBkGcIpKCMKLd1fHkRB2kjMClhMnzIUyO5iyzcOIh3BHsYb+EJUMqIpwu8uOGHc0tHBYESpRkMA86lM8uTcB7exz3uEBXjsn89PAjWh/M4hHXznuFAEl5K6RDmSoonUYY4QRyZFwopHF1Q7nnJFgHrRSmjyYDIw5KEz6JOg8BQZOHtO9z+8EfxiNhbNM8dcHENTwaODIrsG2eX44KOx/JYpKwxUo/lsazS9OV9rg2rSoE7ERDiJeZ7C4KTqcfASbDK9ovfi0Y9KwwnZ8Iuwb5W5rj0PCY2C7IWwuCAc4ZfQkUgLykZRcAWGSpKAvQlPlOeOS5AOaeU7zKWD6m4/HGVoVmQl94nM5Z6nns2ROOQ9TldG0N6d6hx7dJ6z3O9LHRcajt/U7EXC+VLIe5eU14vK6ck/wJ7EdX5xGeFdRHpvJiHLMgNtDbhPkHYEQYf7oBhxPDDX3B4+xqvf/9vuPvhO9z94Y+wb25gDg6N7mAuLqDbFv2Lp9AXl6Avfwl+8hR2e4Wm3UGZFrpp0PQaqgWccSDFIA9oz9CIoUNXpLv3KjT5d8bAwoPgiGBJYaRsyBK9hkcWOQwYIFLB/j3nBph3udxPUkYk9joSnfmTRUQ1T39UFlpOT4o5Ne2cF/4+VhgzZUGlWCiUDt4hZP3O16vk1LFu4QkRn+GinwB3PFmiwVoGt+A/ijEvCYvLcwHFmi84qDQb2mj0mx677RZXmy12fYe+aSQ/hDbQRoO0AisFT0okckWfyTl9tkzV5PffIk1Weq7c53wo6ZF8tZbNkfC++YmCw5or+k/RJuvn2Pt5RnwQRcQjQX+6nGth9L6WSB+T0DmmCVy8FQSmJS1bo7f8e0m4VF/iYCQTLX189R03gdDDBQNA+VpJzFDMCaFEKSGKiDjOhfFOxie3ijlfeGZFyRpHM9uztKKRnjMzk76L52f9TITY0/7W7y33sVj/PRURx/o6WabJm1aLr6YxzQv0yb7XxnFfxco6MT6tO4nzvvQdstSegmHx+SCoXINtSrRMiXfHooiI8y7pqQh926NpGlxeXmG326FtGyit4bwIVUES+oyUEqv4EN6Gg2hbioi4PQOjddAqhFoicf2UgzKHJxAhcd7bzkkiaYQhREXEaEd49tjwBqQUtpseWhG6xmSCMAgPiERhYscR+2HAMBzw7u0bXF19hqtLjU3foOsN+k5Btwpdo8HGgEjBOZVxGUtCbLYDoBRa04Bh0FGDTd/j6ZNrXO4u8Nmzp0JQeAfvHay1OMDBDg5gCz/uMR7ucDfs0TQtmqYNQnCCIYY2hG7TQjU9nAqKCGUAKBB3YGbcWfEi+fzZFRrToAvutBebDRQ7kB3AfgTcHVpD6BuFRisYRRiJYclDEwdlhbimK/ZQCMS1s/KxFvAS6kh5AnmCV/KOPQTXah2VCy1AKgjADaAaUUSoBqQaUKgHrZLL91RRTVEJQVQfGRwsxhjpzABDFA3McKOVmjFptfdgFxUSTrw6lCgitNYiUA9zLks5WPwTS9QkBTBnIT4IIZcJyxiTlb/sb2YP9haOnSj1CCBjoDVDgxAywIinDpHkUaCQpZAkB0gSdFHIyU0MF3x3IlseFRGehSV0jECYcqGsQ+WJEfMLMkL0tfhHdWZFDxIEhlMSTRMAHcIfSlsEasSKj+DBbsDw7hX0aOG5gd3swG6A14APMZenwrBzaJuHKCPex1PiVL2fa/mYwrhz+/xY7S2tkZ/7+zqnnONx8L7v+SHzeExYeJ+251Z9K2M52swC4b0kj+c5s17xGwttRbp+Ueh+b4XEMZo8WrfW19MHWWJfC58zLFPLyKWpn8ISBd1REVEJtymEzOEidM6CDHKhE0Rbb8b6XMn1c5UIR9ZFJbup5+ChhcLZy5O2P9YZcl+4l5RG+SaSAqgs5/BwkS85V7kQnztbGZH6qJ85pog4CQ9n3ruk1KRfof1I6dCDgtYKjcnRFZz2sApgewD2N7Avv8Xh+7/g3b//Du++/wvGv7wE3w24NFs0ukW7vYDqN2gun4IuL+Cvn4Ivr+HbHr5pQcpAaQ3VKFBD8FrywilPUCH/nAfDwYNIF2Ofzu15JStNa7mM/F14z5J8xNo95D4j8SCOlCDYF5nZjvc6KyXvOX0RQF7cjPpmqbCYNjfDNzy9MG8vrgWeQ1nKmzBTRtShmJKQv1I2uHSP2IHjb5ReEpzHFN5AvDY9beJmnb+56TpYMozloq9yfAH/BgZLaY2mbdG1bUpQ3WoNEwwKKeTrQ+DThPYvjIp47pMz3f+z6yWstPAaH1DuS99+DPpwGQbKRnZnKALCr5mMcYbn5hVAgV8LF1AqkKf1K0gZeU0gz92HmKNHj4jH8uFLph6BuOSne2tC5E8JaNS3A74MwhP2YB++udTdyk6muKETYZwJpdKSiVKuCEpRNXL48Ylgawn8SHdlimUyrAXmZu0eCriXyqm9HuNmLj7IR+5liNbvT4nRe8I2beJYfQZ45bhZci+N1v4ZtuWDOHrMpOOa45xkIm7eK6e1ObuO2C2vQFbU5KURrXnLRKF/JrAqAiN+hdd9X2VI+jsJI4vx1P9Uv+u/Q4imGOMyEGv9boeu7XB5fY3tdoem66CUgrMjwD7lZ4lB00hpsRrXBvAOzruQrFgS5novoYne+XcwpoXRHbyTRMfeOzg3igU5CTFkjIEOHk7eO3gveSK0IjSaMFrg5vYtlCK0xkArh8utQWsYzrcYrMO7/Vux0icN3Wg0/Q72MOB2v8fd9y/x7cs7bDYNuq7Bbtdh0xlsNwZNQwBLbP2+M9CKwCFklXcHKFbYbXdiWdJ36Psen3/2DNvtFleXFwAkJNU4DmKZz4zDOGAcreRWUAbG9NDGQCmDzWaDvt9hd3mFtt+hv7iEaXt4NGBIqCQioGtDroiDgVIKVxugMYyuVdCa0DUhcZlisGM4AoyWxMOiPBCSVIMBN8J5xsgN2CrYYQ8/juH9axi9hSYO+R00VLODalqgu5RrWpQLensFKAOE8FEiRBchu6eolDAgY8QjAJI4jwCQz0J2EEIy8yhwF1wnVm1eFCJekjo7K7lFxuEg4bvsiKSQY2Ei2Dt4FxQRzknfCkEZEnNUKGEUotkgETyZoIQIDHBEBloOE2U0AI+BHdhb2HEP70ZYdwggKzAsPDlo08H4TSDqFbwXxR1HqzwtBL8ogJS8IQZYNAJJX4CQE8URAJbxemcxDAd5nwpBEeFkPkn0SUThWWZYLx/HFmRVcgknNwDswHYAs0txy61zchjaA5wdMVor+Zt0I0odJ/NrhxuM1kONkiz+5uUz6M0l9O4aUZgGfBwm4LF8WuXxHT+WH6+s0chLNec0WykALS9yYDqymDT3k5f3/df50t6IuSKWyvRqKWT23kt76sN5BVWKCFIocxYtCblFiCHzFW1A15TOaQyUPSKW+s/Pn6PUWRBlUZLgLSh5aqv7/I2kVFkcZ6Xk+RDis/uWmrc4ZeE6V0Jk/uZ8ZVle74z5XK6ts6kS73i9oq9CcRD7OSnYDH/HXBFVe8TQCB4PSgv/AQJIg3QHUuLFrUhyQWgiiH3FCGcthnc32N+9w/7Pf8Lw3V9w84ffY//DD9i/eg2+22OnOpiLLS53l2iaDoftJXzb4W73BNhdwFxcQG23MFqjVQqbRqFrFHTfgrTQdZQMPQhGK4zsYRdHfJ9Szn9cq3VYJqErxRvCEsEqBTGXMWASAz8X5DMqyDGDv/2sN44JoksBSgFLiReqkpIOxIYKfj7ysykpdKzHRV0IYNFOpwZqUi8KpMo+YpWiP/j8KT0hykTT3haeD1PPCAcO35K4Oj4XvCLSp5ZdHCtx78WQeIy5z8F57QTcRRItpOt7XF5f4fLiAlf9Bru+x6Zt0RrJJRj7CtxEiNZARbqKiBhCaLOzS6g7TXD0gHLsrLuPUcCHbqM8KwopzZHh1vTFUY8Gmpw/lZInyGfLCBy0QOAUcsAo0V02iDifvpqW91JE/LVaF6XDM1156Li4wIHnHczvW+5j5fchyrr1URQKxfhrswrp31LUOrfqyHMYz6IYfqJW5FLAm9n6qPwG4t9ZCUGULaApwJyVFgUTsTDEKV2Ury+vmvJcnN4ra82XxZShqVpc/bnUxvHej63HD79WT1l2HXtmXn/9d3wuXSdf1aPCI+JU28fuH9vPa9ZZ3q8wlBMia/lp3Ou1nOvVcex3/ltgs8F6PJa27dD1PdquR9f3IWZkbiseU4mkCh4RpCSHBHsvhC+CZTYDzjkM3oE9gVodkrTJ4Sm5IDSUkoNRLDOK0AcszLcKxJQih2EcQApoNEDk0TYKgEbXaHj2cG4QQbhW0EajaRtYO2J0DsPhDoMd0B8atJ3BwW6w6Rt4bLFBg4ZCEmjTwWgFqBHsPUY7AAC6rkHbtthtt8nNdbPp0XWtEPGKwAHmKNi17JOgXptGFC9Ko21abPoO202PftNjs+1g2g7MWubOeRAI200DEKFV0u62YRjN6BpRvjZaQhM5DqnPPUNRJLLFol3C23ES1Ds4kFfwboT3NhCJJngOAKRbUTKZDtAtVLsB6wZKt6KMaLeACh4RgXGIwhyGhg/zKO8yk2cUll7Cz8h2XGUYDNk+lBea55DE3GIcRhGGj4OMMVgjUVhT0SvFewfFCsqrpIxRYBBLLgZhaJzExI1JEMmHPBJhLCpAqRXghTmICjTv5SMbQs4uHlXYFxpKa5AySKEITbC6IvHcU0oF9JAZFI57tPhIiF6fxu+ceIJwOENj4vcYmtC57BIuSgiGZwd4BQrzRH4E2MGPg8xZ4NNcPJxjX0GhBqVl/CR1nR3BngCvMNy9xeH2LVqtoTc7MEnYpyUByfvSNmvPl32csq7+a6Fxzy0/h/GeC+PPYSw/1/IQvmbtmXtb857grTKtdw/YMCGvEi9wihlAosUp5hSqeJHaa2BpHFO4gZqHmdataLRJe5VHRIjXfupdCd6dDnxp2BmWaY6IqcdF8VCYQ4r/HxeUT8Y0HRslQUs9p8tjDMKe8lxJAqAlvgGVMD4pIehcJcTx8qE59Dz203R9uWemcxTFTdPxl8+twlCs1XO8IuJ7W4JtVrMUognDPu8nXa/3x/p4MxwKwq8wQkJJKKFdghEIKQMiQGtAE6DJwzsLPx4w3rzF4c0PuP32T7j7859w96c/Y3j5CnawgPNot5fomg7bzRa67TB2PVzTYmh7oN1AtR3QNtCKYBTBaMAYBWV0EjbGYUtOYUr08NHZPWtuS1lMmrWSBQUzwQHiDaEo8GkqpMzgTP8lNWMUznDVaiHTXwFDFt0MlvRnDruKqDRhFDRv+TvWO6MU8qakhJjwu2kPTWjs+WfBM2L6vXYtKmqSkiPM6cowKrlyAS3RxDtu8vwx/JQt9EMQVqUkh2Hfo2/bEJJJPOq11sI7qBimq+TWwl9RWBHf7ymcUIE2EbQ9kISLj63RCqdw1Tk0ybSNpbOvGs2k76nimleem+K3kzAclU2hvj+tz5HLRpG/6f603qny6BFxpMyI0cdSlVowWZaCQF3Z4McI8XxZiOeodPA+h5PI9RKKCUKrUjhVfAIzoEJIGF2EhsnIEyC1TJCeunZEfn7ioeP9oNA+VrTzUtMBhx07egv6rf59H6p4kfE6f6ccY4DK72N1z71ftR8Jl3wBx9jTU9HKORE685BadTtrF8sDJRA74QXWnh7TAy3TWeXFJRASg8X17+nYTikmyj0ZmVkF8WJo2wamMbi8vkLfb9B0HVgRBmuD8FWUB+M4wo+S+wDWQimCagy63QW8szgMezhn5cDzHk638FZCI9nRhZwJQ7Bo8sEK3iImKI8Ek3ONkMLOA5rgjcduu8FgDXi4BXuH4XADghitdw3h6rKDOSjsncXoCYOXOP6jA3SjcPFkh7eDw35weGcH+NsDvnu7BzHh2fUO277F1aZD3xqYry6w2/a4vFTQChjHW2it8dWXX6LrWmw2GxhjsOlaNEpJAu+I+yAr1AGw3oOVgmo79G2Ptu2TyfvV9VNcXlxiu9uhbXu0rYY2gDESwsfbAcQenREliGotmAE1vgN5DVIOIIXRinJntIOEhXIjtAaahtAqg1Y3IZeCJDoXObN4E3hP8KzgumugVdCqBUiDmk4SlLctvNJA04sHhO4A3QDdDiAteQkAUExeHkX+AZcSAYqCNwZRYHIjLhRmkShU5JiEOZ4VgaEhB5CHHQeM44B3N2/h3Qg37sES+VbUXuRF2RBD+WkSJSUbxMSEYPGGkEBk8h2toBgMVg4InhGA5FgQ5YSMx7kB1u5xd3cD5hFgee+kCM5bwFtoZ+GcFw8g08rYSMFrBU8kXhlEIdl8zt0iyhMve4M9yDlRQPjSE8TCjgcQAK+CV5G1Ms9azkRtDNhZeGen2FLmkxmKJZm8HQ9g7wOcKoS98vDjHZwbMVrJt0EwAAtsHgyvCI5HjIe3UG+/h/n297gcBxhloNotqN2EdzwXUqyVRyHzY3ksj+VjFqGVCcwqKxZ4Ge+sWWcv1VsTCuU2cm6HqSKiVkLUTMjMI0IBipd5sqkgfXp9Cu8U7mjLfHaJPMcR4czskcDkRMFsOcdxfs7p9HzL1SWPiCCrwXFlxKlSCTU/cImKp9n1hbpzeAlzk/HluZ0/d/8ybVepuf32wkMrgynbPE9wGB8kQITrTCAjns2NFqMf03RBdgDxRIXFOBxwd7jFuzev8OqH73D4w+9w+NPvcPjLGwyvbqA9oLjB5fUOptO4NL3Q09QB3GBwGntjcLPbgC42Yl3edni622C36bDrDUyjQWSgSaEFCc3JIyx7jOzhSQHURNbxPUqMHE+hl8CHcPAmdgzrHazzsMFAxcf5JgIMAc4DPpovFextYmELQX2Bp44ph2diibU9E5tMTPEa3xwqztaPr9uNSgjKbXA5jvRMVB4E5QNKjwif45oKQ5J5BfYyX1WuCE73kSzUl2fn3J22LG6aKKIpGOUqlYyRRLEc2tAKxhj0mx5XV1e4vNjhYtNj12+w7TfouxZN0wQ+JQJHGYBgqKhCDoE5ZlmF/uya55SfXJZ7pPPZ2REOmXO39Jqi+JzzKJ5nR+E+cv/8s/R4+ag5Is6xYDufgTz7tYTqEalMtD2zqkfeRFq9H4dYEPDo6O9pmdU/3suRe8W4p41wUae8/8AFd2x9zIniUjAbu00nTfp7QdkoCBVYUEaUIZrEQppScthYI/V2JsaqK51axovWTtW1+P7Xno99ruTjKMA6SY6vnG4Pt0QDwKfm43Tba4qrPPbjcJwuC+7277G1ha6qGcP7FTVZ7X6iiIh3JioHokTfTK/PYVxRLJBavl7W52x9UrbCsXMte6dpO7Rtg77foN/0UFqsxn0QPsZ965nFSjoQXyp4Q+i2A1kFFYSfylsoJVbh7FRKLuych0fObcEh1r73cf9DQjRpA08WXoVQBl6hbQ2gGAen4ODhRyvyYa0lVFNrYJmlnvUYBxHDsndQiqC1gWIG2GG0DqP1GPYWbgQYCvuDA1uC7YHDSOi9gml6NAZQmtEYhcuLHbpOwjIppWAC4ZdcxaPQAIEJYAh7oDWarsNmswvJlD26rkfbdWiaBo3RMDp4OBjBbz4Qtjq8uYZ8UgoBBuwGgLTMq/ewIYeGC1b+KrqmK1WELJXQWd55CYsHA4YCTA9JNr0Vq7GuEy8Xo8V8S4uCAqaXMFwhNwRIi3A7EPIckxPIZAjzB4CouBYVsxFfFUxn3I8lvxN3hHcidLfjHs6NcOMdosonKjwUAawArUnCiHEUr5SfatcgUWoclYgeREp4jygQCAyQZ1HcWTtAkn6PQRAT9qIlACFxNwQGIiVhjWIYtHB2TWGSvmQ/SGglH/aMTX1KaCSbSBrnHKwdZfyeJGk4WDxd3IiYLyLzXj4oIoRZGscRzD7ET87eE95ZOOfgQ2gyweska4fDrLOHteJldHfzFl23hdvfAspANX2Nj6KwiuI7LfDcPdDuKYJ5Xfh1+tkPUX4OypTTQtNPr49Thg+P5edR1j0GPn5fRacJn0nF9WdLnmOp4jFDrapeIOrLuvHZ+QxwlqERJeGTgJ4V12vC6ohrkzFABiI2P1dC0LJHQXk/QTdVeHCZCeLIHFBUNiApHbLQZpKXYkEoMxMoVlfX+qz7St8IoUdyhWJdlF4aE1inZYnmvmeZ0u2JP75HG0vwZfHJdM+lv9I7qdtCEi2cb0SQ/pr8ztemMCRDqgk9sLgtS8EeRSpS3mMeACErxmIYTBPCx2oQSaBS9h7ejxiHPQ43b3Hz+iXefvcthm//hPGPv8f4eoS7GaG6LXTbous7tJsWnWrQkAZZDceEEYQDCENroLsG2hgYrdG3Bl1jYLSEgFIhfLRG8IAFgRFz7gVjyg+EB9OcFaRlxBM+fKKsP1GeSQBNAAUP3LXVx5PvJeSSLtFMpjBvr2gwAVZ8HwNi1vSkrYQE473YR9nX9FFeqTv5+Jizrmhr+kychghu3N9rU5DGVOPSSq61MC0ESlEEgHovRkWrMUY8IroWXSPhmJrCI0JrLd70a4VmEra1aqHfCFk5Jiy8s3lbsyW1fHdO15/AVZHTO1ZWZbmT7pfUS2vKiFNljYaoz8ry+gS2yfk0k70t7ME6lDlXbZ06x9fKz8Ij4n7sx5TSOEpqzOvPnjtDQ/8BCy8goXxhsjhXpdb1nC2PcHYaHAHqVB9zBuGhR2OULTEDzokltfc2EdA1MIIekoJBRViC4kHFkCwqIVsVk0CQinTHfGD3h/oDPLHUxqlrn4bgYoXPqu+f29Z9+z2nvep00nWF96DhquV4byFJ3TGlfyOS56LK/Lgl4DShdqz34vzlcEFopNpmIdJjkQgFM6DlYa0BhsLFhYQHuthJmCERSIolNrOQKD62RgpKN7K/+QKeLZhbwI2iFLAHqL2DUYxeObihgzYthmHAYX+Q+KikhQEhhpD0gFYW1Hhc73rYxuCVs7DjiD6EJtLaYrQGprEYxgE3b/biCTAeoEihMwaqM1DXO9wdRrx+dyeuyPBiqMJAR4yrBrh1CnuIMIKVwg/7AT/cDXh3u8e2Neg3hMN+h+dPv0bf9+i7Hl3T4PPLa7Rdh3bbwzHjdr+HZYYdRsAzvBVvkf27G9j9AOWBVhk0usFu22N72YtgGhqq7TCC0ELBk4Ymg4YMcBjhmTGOB3j2OMR4p2PAlU0LaAlJysRwiuBZw5ERT2uDkCTPgLWBQyNbRgOeLBxZjOThPEsyadKgppeQS6aXd9iIIgJKkky74NquTQNWGj4k9o7xrr0TZZK1IsTXiqC1eJMQiWC+Po+DMD7uOWYAkuBAxXBALpwZ0GAHkBuB4Rbj22/h7QBv94jKa1YKrCQPhGoaEAhaZbd8Uir44qs0JoDSmRRxDFmBwVFUlgXF0niAHQ+w4x7W3sH5A9hbsB9lvNpAmzBeN4L9Dby3cGzRNB20bsF+hLUAeyMMaEgOx2G81g6ipHIjmB1gJY+DHUc4Z3HY38J7CSMgxCPnXBkBxzRNg7ZpYd0Im64jnJ0K7FxQQubwaADAykEpWRMS3gpwnnFwFuw9FPuE2ZwDDiOncLn7m1s4+3v44RZkb7B7/mtsqQW1Lahp4MODIcoJksNiQFMq5OFwHJSYPzK99lgey2P52yhZuJ+ZdoqhCyakmCghosd1/D0RfqAWAiz2GRQDyovS3tEAT8AYFA7eiXeGCGSDYj1CyybwOUKB+WDGPPVwiB8/4S3TuKYsRylwi2IjFYRaRXviDUeVgX3uO+S6iMIZLpTrjETbMgVluI+8nijLmb0wyIX1cOTVhReUMJdnCfmDIJV9ziQHopBnqw6XmSYkCF2S7UQipIHij7k8Ka6dqhZmv5aBrOsuKyHei6VJyqrFbk/Ak+4sPDNVxs2jIYQ3qOKaCCYgMRleNJwiCpbm0TomP+uIAKVAHlDMyQBeHB0ILGwDXHzWS+iZJsgQEAy7jSHJcdY2Qr9qD+9G7A+3sDdvMHz/DQ7ff4ebP/w79j/8gLtvvwHdOuhbQt9s0Vxp9Lstmq5F27fQxsBzgz0T/jBavGOLbzcE2xs8ubrC5dUTvNhe4Xqzw6aTPHtC92kY8kKrhbVOISSSRE+9tx/SrDAYTJJpgkJ+Ps8Gnh1GOAwM7JkweI2RG1goeCh4peFV2A8u7D0V13a5xgP2idszvUd5cZyScgLZ6oXFkKbi21eEs+E9xo1LgUet1zClNSWe0yF8kyRKE/dzMCRMa9Eu+QBaDN0a7rMHmEDeAC543vvA5RLLPLgYWimMK+KMuHYTwAG2yGQG7wgJgype2mkw0SIs4KtaACH4N2LReDnNISEpC6L5ow9RQYwyICJopwAWWZn4/QCbrsHFk0s8ubrA890FrrYbbDc92qYR4zwykDybsdPw1mPOuoirIs+0sl6rlUzpjc9qLd6JA6ZisCu9LF6qFE5r5fx9NhPm3+M5USrEcyzi9Tm+LPuZKyFKTz4g53xZ95DISvY5vHNJVfkOqLrzUMnv2YqIY9rtNW3K+5TcVkZqH7ycdXDfz0Vm8ugZIKxU4ryti8r1KV8I/Ku+Jw8enztOcM40eIvmDkUfmN4uhKhnlvmaKZFCtPI8YsEDDgR/SeyQENIpBn12O6v6pEkcPbl4NuxLsCy/9HyAnsSVkxsnraU+4J47VY73NSUsl9/raXjvN55zxn+0znu/7vdoYK5prNumhevpUVqm+M8stVs9kBhsP19/8TonspLkkAxMYdM0Ep7JaGitJG5qCJ9UGagEBlWF5LtOS9gbz5LwjHwDghNhNhto38o4PcM5D2AAISTqTdtcqE9SwlS0TQNDCo0xgPdoGgNSgOcG2gL7QaTqey1hdSwzmLwwIIrQNwbsPfaGYD0wBHdjzyKPb4hglChhlFYgTxit5MvowIB3uLm9Q98QrLVgZrRth75r0bcd2qaFaVtY74HDQQTV7MHOw48jxmHAOEgCPDCglHhEGK3RGknsTUqDSOcIovEf5iAslpwAnj2YhCjXPubEkfGLr4SChwErYUBEeavEAkw3gNbwymQ+wVuxeIeHJ865IJpeEjo3nSSZbjsRXJOEKeKoNNBBMFKGVQJEysyUlnzpIhwFOlWosoDns/VIAhCAEO/MLsyLFgGDl0TRftzD2wFs99JOyLkBI8mhiUvhEgV/fMoMQzxjEu8Tz8+cEDTtLC9CDB9CHXln5f1wCKPkfGheQl9JMmgPUEhy5zRgfKCVWXKohLWvorAnEKkSlkncwuNYOeSjkNwQY/BUGAGEsE7BS6T0rlREsHaEdVkRocL56a0ThaTPhC2IoL0Xb4fA4MuaRoLJew8FSRov1yl5tEv/t9jfNrh726DZPkM3DrIGTbH20ne0hSzeU8ZqCWd96PJz8FZ4KIz3scj9MebhfEva5Xrv+zxwvzl5SPkQ83hfb51j9R/qDfshykP5xzULxLV2P8S4Fw3bFnmtKR1V0FIPgCHiOVF+hDMv0IBR8FAJphgAZe+IKGKP50XJT1VWmPHRcsgoSE2e+y/IvVoJkRQv8bic9lXNU/G7vMXFbRlgfpczoWR9Pyk6ktB+dWLT/VQ7th2+V2FOsKUHC5I8zDrnMZfCHkZ5vWTt514GdYnjOfL9PnKHs8psdeQ7mbWe7b9yH86EdalO3U8UYEaePnVPFF5BCAZEmLWZIaXqsQi1Ci8i0lIIBhdKizBWEeDJiyfpeIC9e4vh7Svcfv8XHP7yLW7//CfYV6/gvv8exvVQvkPXNYnWb9oWUA0AjQNr7D3he+/whhlvlAKMwdO2hek69E2L3jQwWqzMcw7LuF5EIREpNYqDiGv+fXjB2AcRotCcUXqvinrTgeChJNcXUbbRLZZAqYQoBEnFC6HpAyVyyTCV+77kk2PVlLw64ruseMqS+PCZIqzUd/k9RTxF25Vcp8CvKWTrpL/Y56xQDXPZX8RVqa14i+vvAuFM5WyUvmk2mlmluLfC/McYIum9hS2ntEbbtejaFn3boG3Ec0drHYx6VXpuSeE6h2F5nUZ8uPa7LsX11A9VB9VayK9UOyGCjOfXYJs/fV65L21xTnSYU32Uw6Fir009ETNuRnV/qWeK9xHpg3h1Aj94dd5PlZ+FR8RjeUApBTQPev6DQXK/bhnBkloSjEYhy7SUxM1UaAXk5JtzodaHY6BWRnDk2qm+PzZsR3r+GQhaPrWShJUPfXohH0lZjjILfIphOdF7gDvurRibVWs923PR20gS3ua13Pcduq7FdrdB27VQSpLdpoTSAmiCU2stOX7bFqyV5CnwCuScMM1GcjsYswGThgHglYEhBa00GtPAWwkbg2A55WEBdtCKAMVoTS/jYoYdB+hGLHXavsU4jtiPI0gZbLYWdrQ44A7sGePoQCQ5JpgULklhGB3UwcJ6BjkPdgy2QAOHkRhtI8wLs4IL3lcOhO++f4P97S2eXHR4++wC//wf/w6mbWF2G5i2he5asLUgrUDeQXkH60fc3b3D3e0dXr96Des9Rs9oulYsq1SHDbZQpKG0klwIYHh7wMAWGhaj0sFiHaJgAQGkQdqA+ycg1cB0Eh6Juq3Ev9UtWClo0oiCd00EpSTxtygphCr1VgTpcAzyXsIwKQWYRrwHdCNKhxgzNBDEOqwXUjqs67i2s5I5rkGllHhkaAUiPWNiqcDn5fViWwS6noMCYoS1A8Zhj+Gwxzjs4e0I+BFKafGuSWs8KKyVJEyOoZGIFBQIGsHiKPIGTizJPIndD0/iG0tYWA873MGOBwx3t+IZMYyISfUYEKVOyL8hDDABHBJcewI7CKMd542iNwLBjxbeOcA6scJyLImmxz2ctxgPBzhnMRz2QUExJGbIex8UARJqa7QD9vu9KP/h09zqkJfCuRweSt5jYGB9YTFKAJEoWUbn4a2DGwYopbDpGjBILASdF68pdhgPFq/fvML+sMcNt7jzGtfPvsTl9WcgKJAheLgAU3jnJGHBklgnJFR/LI/lsTyWT7Wc8oBYKgxg0C78CDkqXC1fi4IbYlMoHRggG84uVEKI+CmFEzPBQhDOqEpAUQr8g2edzzRhNgqLJICEhDx33HOhdXW3GHH8/eFKpbCiKM5bgzvDmT0lSmFW7QEzU0ZU34WAvFBMzMsZSoiPXKaeDTP6q1x7Z7dXzH0SiIqVdfaTKYXO4dnoPRE+JGY1YArqCaWEYgswK8cht5YBE6CaUjagAbUBFMFpBrOFHV/BHe4wvP4L7JvX2P/h9zj88BJv/8fvYW/3GN7eCF/SXqLtenRdh+u2x2XTokULzRp/Oii88oT/n/P4joGXVsMqg1/0T3Gxu8KzJ9d48uQCm02Ltm/QtC0a00h4UFXLLEpx+IcqhKzsUGENu2LOPcTTxIIxeMbgJT+Fi/M6l48fLydFIQuj5MkfJ/rgKtF0USbKrlQjxT9KzEO6m5Q05+6tqFgJiq10OSbPCB9OHj2+hpW4CLVVKyHuvb/DQCNvH3l6CgJ7rUSRIO+ZoLTAzQogrdC1BtvtFk+urnF9eYWr3QU2XQ9ThGR6lBt9iiV7RJy3KbPaYVX18wC65T7lbEXE1J30vs+cW953YX/oPk+5zR6rG3RO1b0PNb5T1j/H4JqWdYuh4+M7Nf5znlmqFwWh614Qa0qI9evHhFc/XjlH6yrlFIyf+gHwMbykyrJo/fJjzwm9LytUWlDVZclqqLqPJZ30/cqxvXlsfuNeMsagbdtEmMQ2s6AZEGF0ZnoRLI6YFbwKlu5eBL8IFhakNIhNSHDMgHZgI/FZbbQEUcIEw3v4FPhJcjkQCF3XCaGlg5AyEIDaNNDWS5ggBpTSYuXvs6W51qKQ8EzQVoSyngnaK/EnIIYOOQWUQlCCiBAZIBwGcWB+8+4GbUMYrYXzHhweIBWI1MhAEcDs4ZyFtSOG8SAW5gUTTCAoVpD/NBhOPCI8w8OJhwWJkAIAmCQcEplGEkS3O1EUtCFPQ7uVsEOmDTCZAE8h6FcxaZkod5ksoBxIBddhCpZbRgfPARO+dUXtlytpySqjxBXpgxpfJ2FJhI3qNZrWW7GkGYB4Rjh45yQ0kXPw3oG8z3lSpudEKUxA5h+ysVPOByEGiBKiwbOvrEa8i8L+Ec4OSYnmnbB6FDQR2evPhxAVqAbBlbVXZpQ4rP+YHI9ijggWTwR2VvqO3hgxUV5wA48eC+LBEDxpKHg1BEVE+Q6iknGOG2yeM5LwCj6EjHLMsN5DA8mDR/Z5iCfsZfzjOMKxR3v7Du3Na2x213DjKEozHRdSZA4nAhF+b0T8V1F+DEHUp1A+ddrnb6H8FGvtvjTllK/52OtmpjSvvtfpqZNzSaKsBiSXj5A/IYZ3MvhAOB9qXJjO2Onv4rs8X7EIadEApmd4PuqXzmkGTerfJ1n0pM8CiKgI4SBUWxI8xnmvecvJYBbllbG9I0IcEuogz1uptIhjzoLPOE9ryoiyzGA8cf0h5Zx3cJxfXttL68FXpu2Wv9PK46w4AOKRv2D9HUOOUqhElOKZc+wutJOpOLmhAv2odKBTKXgEKw2AYP0B3g0Y7t7C3b3D8P23sK9fY/j2GwwvX8P+8BJudMDBQXVGLMZDGKbGNDC6gXcaziu8tYQfPPCtZfzFM26pAcgA7Qam36BvxRvChBwRWuUw0j/KKZfZkKhiRJzERHKC4SefNMfJdaEQ/vM9V+mkstDaoY9pQ2fjjYVG1x5duld0ntZeQXsjyaZyaFZEj5WoiIjrmDjwK5yiNOVOGLlzLlZp7LJWRqyV2Z7KN9L9Cr9TYF4RcbRcYxL1q1IEbTSaxqDrOrRtK9EGAq+fDXznsJwr84uQLt9efuZjnenHzuJ8Hhx/9r59xfIhPTdztTNpiyRLTcDU/HoQUBw/r97/THr0iHgs8/IT8rPHPSEi0qoFJLX3gxJr3iOKiE+3fOrwPZa6rDMpH/tdvp83xnFGpLLCKeoopYRgNhraaGy3W2y2GzSNWLBbayWvS84IIQSYz14RRAA1WkJ1sgFbwLGCBHANoVi0A0GL9RIpaGbpW2scjAaNRkIxKYYdFZyTcFBgD6PFqn17sYP3XpL0sgejgTEN+u4dwMB4GKBIwdkQnuYwIArhjdbYBCt4dh5WOzQOaEihAYF5ABhBWerhTWQcDADC3XjAaEf8/s9/wdvbt/jyq2ew1uKLFy/EC4INmBhKR8KP4AkYrMN+HHF3txflgNbw3gAQy/VhGNCoDmQ0OOS4GVmScRN6eNVCtzsoZdB0GyjdQPc7kG7gzQ4gDRW8F6jpQu6DJngBCCnAKrpXUiCsWZQaUBLg3zuQk5ipOso8SmIX2eVXePL84qeKg8hYJ/oeBa5WOXxT7GOujMhrNLKbPq7ZYG3E1oHtCD8e4McBbpT8DFpJ8kGlxDKoMUY8MYoQfiKwdyEURkgW6ArTpqAs90kxEXUFolTwXvKkjAfxiNjfvYGzA8bhVhhhJbG/JeQSA4pgjIc4jhhEFlBi1DoJP+slRwWFEGrkDlDOgpyMi5yVsE72AG8HDId3kqR7GILiJJytTlR63vvE/pSWsuVcR8bDWpsUEeX5O4TNHS2viCR802gZzjKG0YpyzzVAZGYD08aBSRvsgPFg4emP2B9uxLtjZFw9/wK9aqAMJ4ZOGDYCSIW45pGQX0Rnj+WxPJbH8nEKTYQECS/Gn+sClftY2TrjQQwYFrtlsiEUoLdyQgRii0kDKWxnLb713kuIvQKHV0qDiRCiOl8XhMdLSoVlZcR6/dUhJ6HZhA6lGAYkSqGzHPFU29NbJwXxob943kuuiExvsFCIckYHYVWGIQjB07iFVqCQF2tpVZRKnXPgS3BO5zZMyKKhxsJza20ufU9qzeozSOgMyvRQKWBd7CvBSmCYEHa2EM4yQDHOOUX5Nycak8OakJClChTC9qiwelSANHqsUtPIezDioTk4CU/Z8Dt4O+D1qz9jePcG7373r/Cv38D/jz8Atwfg9Q289zCe0DcbNM96bPoOu75H00heh9EqvHOE/2EZf7GMfx09/mIZ3995HDzQP7tEd7FF+9UX2Hz2BE8un+HpdovdZou+69A0Bk0TxpFsUnjyHef+QxE85V7joNAheCY4MEZmjCyeEDZQpGsRidPym2+203KlcpiMLPSf3j9HQDWDj9K1xaeDImEGx1TJUgFTKCaCVoyUEq/0pIyQW5SYHMnjI3kqYl4IuRc9IQSUYv9Ufdd7bhVHxHMpyMWAQJ8zgiJOgYzwfMLSKHDIt+YJMMZgu+1xdbHDs+srPLnY4XKzwbbv0PUtmlby2k3lBKUB4vIkL/29Vuc+9z5OSXiP1All0CnYJmv5RJ9LZ+r5pcbZdc6ItXO4hH/9rHiIEcE55UGKiB/LwuSc8iEm5X4avPd77pRHQ2pr4a97tSOnwUl4ltrK+P74e16be14H+2gbU0HI9P4ScTT9lO6M8081LCwjhmm95TrS/3Qs5435WPkp99SaRvY+77+uuhyLbl5P7t0HxnPg+zHK3FKH0p2lMj+4z+hjaZ4/wKE8VTiU1l1Ec9iIhJjRRgdCRHJClIwsc3LOzvRcICpThNNAIHH8JDMR8YyQBMUeIA2Qk1wDKdeLAWlRQijyUEoD7MSy2sc+WCyLiOC9ClFwRJmhtUlWHd578eRgwCmX54Mlj5lRBKMVKPjVsiewVzBKwRBBE0JwmNKCiVJc1f1hQHNHePPuBpu+w91+D60VlNHw7INFuocPOTCsl4S/ngPzRApKkYQIUpJUGdqE3Axi2eVJAgZRswM1LVRzAaVbqG4DZRrozS7klehlHrUJeSCCJ4QOYZSURtRtVSwOMZK3CmLoBQflOdUNb7lcnGkNRAK94icmC2tGEIX1Eec0WaSU+L8SnsyFLomADwoJIfp9ukZBGBD5BVXshdRAVGaE38wOEmoiMGpREVHlMQKih4P3A7x3cOMedhzg7CC5GrxF0tIpAKxAXsF7C2aFZHcW4OagQBDeXuYznU1+DPkghhA2S9rn6AHhbLhv83iixwS4SFCqwvW5IiLOc1yvKN8LkNpQxZzGdS3zI/PtwtyXeCJMvvBlzBjHPQ53Gvvbt7i7eYv+4hptPwYnm5BoEMUCDXjlR7If/KstnzItfwq2TwH2+5YluvaxfJxyzNLw7DbC91FRBJVYqBYYEc2Z+TULw2lJeXGCfFYx5Pz1HsZaeAKcAhgaPuZjSjmXCqlaQaMBc+HRIhycnztnH07HtTbuh7yT8h1kOpWK39Mx1MLabPwQWym/i/aiIiHx0DVNXNIdTOHsmczT8rgo9xcaqxUXXNc5NR/FHFZrKTaTu1l8d9N3Ov19njIijqv4q4QhjY3OOqMzFZ3ngYkn6fRYSMrk/UNB9xbpwtyWCv0meoUIFEPQQOghb4U+Goc3sIc7HH74FsPbNxi+/Qv8m3fAyzfAYKEOI0hpNE0red/6Dfq2Rd+0INWA2eDWA+8c8Bfr8WfH+G70eOmAOw9Ylhx0umvRbXr0mw26pkVrskdENKaM/HIa72y+ixe8NI+T62u/OazrPLV1PWYgmpYlUWp6ILyjyZ5KS7/cA2cs6cWRJBkMH28nrbXpdZrDclYJfZaKhkrpUMKV8ScX34tthVBMyat6ouhIYZnCuCs6YTZDXOCAesjRmIym7yqsKyLhK+V9stDg0Usfkv+wbRq0bYs+ekNolfNDlAZbEZqZYHv6u/xexyfn0EOnZFLnyqin59CqfKngP+8LU33GnH5uCS/ft88kBk7Lf1kZUfdBxWtjnLNnP1R59Ij4REtBSzywAX6/Bj7CIlzbNNHzYUkRES0lSuJ1rnzIHhFlTgipe2pAx5Dnfeq8b/k5M6Pl4UyT6yiuryHkn/PYP25ZV/a9n/Ct3F95v4lQVfaPCP28d+FMYjSmQdM26Dcdur4L4ZgYzvskjA3AyVfyhAh7OngQSBI4SSvsQLAAwOJRoIigFQcmw0piZP7/2PvzJ0mSZM8P+6iZuXtEHnV098y+XQALQCAQIX+gCP9//hcUCgUkgV0Au2/eezN9VeUREe5upvxBzdzNPSIyI6uyqrtnykqiIsMPuw9V/eohmAmFBy948TiJODFNcZWEDj1jioyHPVHMbZQTmdzViCacwvVmgxfh8LibCIwUE21oswXFaILTpHTe4TcNw2jWClHMv2uKI2kY2Kv5TDVXtS7zB4rvAp7EfhjQuwP/6T//hV9/veP9myvevrnh/fvvQBzDGEk5PsXhcGC3jwwRXNNlt1cdm27LVXdFc/0Obr7DX9/SbK9p2425VZIOJNB2N/jQ4puNxW5oW/Ae37WICE0em5T3UwsCWNxhycTbzMKUWlBmv0zGkU3bXUXIqBEt5ivaYjNAifUDCU+J3VMzDKeIxsLoiIgBJVTsWEU8rRnWJZ9a5poiajE4JEWcRnxmADwJL0pwki2UFZOGR3LMZ7yPBgAV4KHyi6tki5ikjHHMYFKOtzDFSOnRFBn6A+PY0/d3Fjh67EHIcTgczkW8jiRJIMnwNxxJPDEqKiNOA+bH2FpNdqk09ntSHOj3j6RxNPdPKTGmaC6ZxgxQaKQE87YA2oO1QUuwRzeBDQW/KX1eNGmLRUTZ7Y98z05nbs4rJnNPpRbUvR+y26gcCFsQxDsLKO8tKLiOPbsPB37U/8Lj3X6ycLn97h1d2FqsCFHM6S55nLG++Za+pW/pW/qC6VkhyVkB4My7PK2ZeCJLwCeHU6WJ4MZEczhAHND+gSgweMfoG4bmiuQ80flJIzyjvKZ5K5Cq+D/rGHp1mSUt4gKRNWpXZ3fd3sU5LQ4RXVhivESwsqRxBZWUSYhKwG1S5hPvC3VRTwMEVtY5x0Kfn84JlT8hpxNz7MgiYkW/ncxHV+3NbnaKe8hPAUhrHn05v5/OawKo3PrZWblhrqYjFVpyolZlotOcCF4FLw4ngmYXTMmb+1UVRXUg7j6ShoHh4x3D7p4P//z/Yri74/B//hV9OMDfPpKDTeB8g3t3S9d2XG+v2YaGm7ZFkoGCf9s7/nbw/GdG/qIj/9wnfh4Sh4MyRiVtG1wbuP7TNW/fv+Hfv3/Dn9+84f3VNbebLdu2pWuytXn2vX+ux4pM5LVSsSiZ3SxNJWU6LpOOGO/VOrPIHmu2fz2vV7zgOq2ND05XbJ31uZcy31EA24tTofnzn9W+ZinDL1McB129q1NDCgA4jU3hZZIpQKU0IqnQ4dmyPKWZNk/mQlaKwlQNQhztWcdC/WVn5fVbbIEyYCf5enGX58SjIniX2x7yew66Tcu7N294f3uTrSE2bJvGXJBld8yF/j+f5Mzff5w07YFHc2N1/+lc8vdXlOxXZUs2rVpY9K3OwqVSH9Ve8HXG7bOAiCNN+gtRqNfI46yA7jO0Xkq5zxKGl7ZPZxHJ0+jhp6fXtE6Z63RZXZ9CAGdE7ny9zllDFOJy3bZzQEQRnK6vzfVc1/u4/NNIaHlu2bbzSC58ysJ9ydi9xjh/ahmvNWc/ZYO7dB699N3XTs9Zk7xaH1Z7y+ckKULoSUOjHFRLQBBAnGRC2awKjPYqwbzm/GbN8DqP/J2FuCb8zoGBs4BVytrHXNuo+CwyNp/yggkrJw0F0qTvZBjArOFtoGQ+TKt2eO+zRURAVYk+4CSBCim7hJOsOS/emfCdhKqnRGhovKPxHi/JaidiYETxBeqmISKp8rjr6Zodv374QEojzoUcm8LAmnFMDKMJs0U8bXdF0zS03YbN1RWbq2uaq7c0V+8IV7eE7RWuvUKaFslARGi2eN/gcswHmgacQ4MxYZJBAlkTsVKdUdPdFdGt5lpgJr7L08wEmkieMznrafxL/ivCWiuQaq5NZjol5zeXs3jmifVc56NFoq4JobS/tE1nc+nqo5U7QBXN8UeMmJ/AFNUMRGSN/2gC+pQBCS1WDJhVQonDUIjCclbNQISb3ApMIEy1JosFQ+0XWaPFe4hjT8rgRhpHxmGwWA+aiFPZ2bJiGucjDm+xRuZLpy0Uk847j4isXCjmcVMDKEu7FYipxK+wdetcnnF5vKe5kSLD4ZFH+ZXdwwd2D7dsb69p07YKAGjrf66Jm/xJfyrt/DnnxGvs61/znPo9pkvb/4/eTyV96pz7Lfvv9WjIOa15x9fI62w6KxQ6zmPJr7y8zLo9Tk1wTFaSMHB9ROKAE9AMko8aQd0yVMSKVizHyHxG66K8WShR0Wo1L3YGhDjVHtva1+DE0iLCFBBOgDK5AtOzzHWyayesFKqyT1XvmL+vzpO1HPaSdCS8PZ+s7Iq3rWinp4Rc87jM9V1rsy7bfxl/dazMVN4rZczlfU5ag3GlzqefWdEmUoTLUl2t6IaK4ivrTDAXOVK0tp2z+GxibrTSeEDHkf7uF9LhwOHnXxge79n/9W+M9/fEXz8i+xE/REQcrg24EAhtQ9c2bNqO4ALqWoYU6WPkp1H4l0H5G4mfNHE3JnbRrEBVTcPcN4Fu07HZdmzahq4JtN7TeofPdKCr94oTXb8QjD7Z15f9rie9Hl3PI6ET04ZkwbXHZSALJivV9RxegxETk7iutZ748xhU0Cd+TW2oAYOaMT1KNY+T/9YTv8tncZ/qWl5HJ9o+WT1M/I7xImjKvEdtqV0+M69UeOhFP6zOltLmY8Cv0NNUQ1y9O/FYMx+nGI/vvCnybTqzhuiahjYEQjBvADV4vT47Tqfn5uBl1/WJZ19D7vvkfXvok96da/70c4UfPnUQvZTGWT5vvLn9LufPsjmzNV1xO3jZGfJa6ZtFxCqtiZlv6cukomkJEGMEOCHQqIRRJ8EHE+w457NLJpe/X1aXrz3ep8uriaqvm77N93+stLA4ckDR7KjOuOKGJcaYY0M42jaw2Wxou4amCVPwWq2IHAAtgWqzYL8QVUXDxDwxCT4EI2Y6hZRwKSEp4VNPGgJjUlISoozgRkQCmv1r6pAYI3gVRAWzzYBD3xOzCo/zjjTGRVDetm0RcVxtrxiGESfBtNkbEyT7w54UI3EcEGeBq/vDgXYPUT0pORNOi9BHR0qBRMKhRInWj4754Bd4uN+ThpH/9//nP3F91fHDdz/ThsCmCVgkiuwyarOl6654+/4NzeaK7voN19c33Lx5i1z9Ga7/TNNtCG1L6Lb4pgHXUDRgQCbfuSkHRovO6mH6kUzBLWe2r5hm6xwQeR7JxbwoO5TxJdkyAozRU9N6VJ2D2cWJoDECe9reU1rOwUIUeyOKXZV3TVbPAohcCZYMfP2s5KpPcS1EcaLmCam8rwniCOKyC6MELjIxIkmMga335hIQUYtrpsQY4+RqayGwj9EIO/F4J2y6a5KapYDNLQMicA7nAyE0+NAQmg7nAojLAcnTxOiUfivgx3jYkeJIv3skxpHhcLC6ZAsli5EyRYGYesg5qXkplLToYxFZrN9SNpADfic0r9/JRVVKOW+PqlmIFIo3YVZFqok02p7SiEeT5jxspjhMk3H/8At3d78QGs9+f0/XtXShw287W9fa29xyLmtw+jxGA9/S32/6Rqt8S7+3tBC8T9eO731y/ghuUs4tbvp6QjzQjjuiKF4dB4n0GohAJNg5WlytyLx/a8x7LiDM1uTT/p7Sot4FnC8asHoBGFHXvu6Hs5qYJ8AKVTVr1+r6pL1deib/Tqs8nra6KG09InjOPL+gLCiC14Xi3iREOp+H1S3HiMjtegqEOAKGnhCEHQsjX9Ku1XVXaJx84UUyvtPzQhagwel5YG+Py/cWPHE9Di7P3eyyVTzICESc+BwnMlCUnBBIQ08ae/Y//yvjwz13//v/j+HuA/f/5Z+JjzuGv97BqAT1OO/Z3Lwxgey2ofGOqyYQfEfbNjymwE9j4K875Z8fRv7TOPKfojKMA8M4Eg0RMcUJL1xdbdlcX/Gnd9/x/v07bt5ccXXT8nbjuGmFtgk0TciuWKE4VjuZXvEMFAHNtGBKtcDU+tjoOEUTeDytOLbBQVJStNEaz2d/DEKwbJVoIaltLZZZoE+uzQvX7nqNF56AyuJg8Umr35wAI0reZj1tn+zKVDXHe6gAhgIyFDPreOJb529zoZogjfN+XffXiWae2+/OKto6v5hDzhlwrQLiHe2m4frmih/ev+e7t295f33Nm6st192Grm0utIb4+04vO9frve/583ICqhfPfx7QArVlRFE0nfNdnDEXnKGvnS4GIk5VqgiJ14j9JQ04h2idQn7OGUx+qY66VKv52TZ8kdr9ftK5/l+6GTw+UGvUetaWPr9xrjVpliCEm4ictSbSc/V8DQ28T2E0Po85OTerXg7ALPP8Mu14XiOjrsPJHJ65/2wNVvvTa6fPy/Q5pPup+6+z/9VrDkp/FSErgHOSg1Sb6fBEhMicw7SmT52fpf+pmFgxhsfh8SHY4RcNiJBoWn+E1oi10CDqQUcks9kpmh/8ZOwIs3WF7QUJIwqN5JQcF6zSn/bBzLdjsrIkgTj7neNFuAxEGKGZiAliEgNkotLuE+2g7KNi8ESiaO2JzHEHNME4KncPO8Yx0vg72iYQ247gPW1ocZ2nbTrazTXXb94TNte01+/YXN/Q3b6F7XeweYNvTVjt29YCT4u5V9LsMmchCJGKBDp1JmnR2MkMCSxNpit+Vk5MtSK0Xiji1BCH+FlbqDAbRZhCFrBPEptS11P7+BKUqOtfvs+x3rMVQM570lJKVo+ULJZCShSUYmKGJgCtOLkoNTAfvlY/hzgDcXz2uerESomDz31sdfQlUHQm9MwiQgyIcH4CI0JjYNnCndXUitkyxeaZR0QRF8x3uIu5beYmaoqrMA1SXtOStdlcXu/YHDAtt9wDafa9LPkdXG1Tc+rcKBYh8/7kqj1MU44VkRIpCYgFRCzAZ4mNomkgjiO7xzt803HYPTAc9uZqzBeTo2zhkrnZ0sQvss3/nadPpUl+C0uQ1wIjviajtU5fAlC5NM/fst11eu0+uJSW+lJpmf+6rE+nr1WL7rrOkXcdqM/7cdmjBdsLJbvgw6El8O8JQX0RxK2t3tZJq7rUAsXn5tGkob7i5cqn5CGytIhYCkEq39ZVfer86vrVedTlLNozCfXtwLC8S6yyXMJJguIclXHm+kqos/w+7bP7FChzKtvSjnPppXP9VHmli54VnVWvnarSmj8/V145u3V1raJil9Sc5PhpWQFRzaclrrhkygLheLC4Wf3DR8Z+x+6v/8Zwf8f+bz8y3t8RP34k7XrCaC4kQ9MQgqfbdDTBc9W2eHEE8UQ8d6PwISp/HSN/HSL/Mio/pcT95KK2yECkMAKEJtB2DVebjpvNhk3T0Pkw+dz3vsgy5v5cRxo4kms8ce/FadH3YvRUrkGRr9dlTd5MpdCAOs33o7S6VvC3aQVWAtEZAMjXKvr5fKrfLS+vn19dO4uyaVWH6rtcn7LS6pOqb3PX+tT9hRUE1bWyB9fvT/XLE+PSM/6onTmX0vETw7dcc84JTdPQNU22iDBriMZ7QqitIequPC7j7N50qv4r3lTOXL8kPbcOzsmjnpP5Lup1YVnrNE3ps5UrD85r6TxnWx7VRV3mZpw/pwrPLtParfbjquyXghHP0V9PpRdYRDx/AJc2nE6fulGeNhL5vRDT39Ilycaq1rgp37PQs9aQndHWY/ChxIRwWethff/Lt+YpzZTfLn3uevjtGOPzdX96E3553q/dxt9uvD/XdG4+NNLqt63DGAdEBO+Ftm24urpis9mw3W5I2WWNioLHfMFnIaOqCTPdJPJVYnaNU8pIJt0kNA4UvG/s0E1q2utji4aD0fAh4LxDcpwH1ZGkgymRDBHVEdWIuAYfwMeEihDVERUs+K8Sk5CScMjuc5pmi/cJpTWXMaP55/TNxtzpjAPOmdvM2G3ZbHqG2DOMA+I9XdfRjw6NjsPwwKjR/NfndjqBpmloxIJvjxH+7ad7ghce7w9smobvr6/YbjZ89+49203g/fs/sX37Pe/+w/+A625xV+9ptjd0V2+R5grCFsS0BF3wFnRPE2D9gCqOOag0CH6aIwaTUBEXEyk+CdxXa7ai1SfhszALqiXHT8g3UyZwtAi51YMmvI4UCszcCZXAyVYf8dntlc/x0qS41nIVI3DZnJ4sITJBr9nNlnOCL0IbTWgczDohGAkkvjWXXN5ifYgzYszcYyviPE7MfZJkjaLCX7gc0Nr7gIijaQMg9HvjSAvxLxMjUZgKyJzzNGYWUN2vxqZyY5VdLUUZzV2TBtSNeAIpRZowkuLIfrgnpYgbHapm4VMAAoHsH3bF7ErFY2VcxkWmgPROPKrOLD1Ep/6Mebx1rC2fZuJWvAEyKUZidkWWMiNkdbF7KUa8C4jzaNqRxkc+/PzP3N/9wg9/+g9s2i3tZkvbbEgYSFIwUR0/bz/8rdNvSzv8dukftd3f0h8/TRq1dfoi8znHdBIleVO9SJuAjImorVGCTpAQcEEtdhZxdj1I9o1fzv0iZMjau6lS1jkZM6KKBVRA6bM1PQITjkGH8nlKCF/SZLlHlps5Zy44s/VdEeiXfl+CHqZZICX+06qOcFxX6+3L+Y6zwpoK6FiDEXbb5/eyO1Dnlv3AUsbxlFCoHtdXT7Wg8mQzjwV7Z0GNE8+tilq4NTUaqbjD9JlktHEXEbxzNC7gncN7YXSe6BqcQXCM+0ficGD/09/o7++4+5f/yuHjB+7/8i+M9w/EXz6gw4DvRzye2/bf45sGf+MIjePmKtCJ51ZaYhR2o+PnHv63XvnL2PO/HiJ3EX4dYHADg4xWZ58Jk+Jy1gnd7RXXb2/4d+/f8ud3b/lhc8WbbkPTdPimIwRPqMCIOX1J/rWMBUan5uK0gBDqSOoYVIkKUWfVk/oz120WYj5b5vRI5QWjgA4FNChy+HoDWKS8rhfgRf3cxAxkfoCJL7DvdFzXmfCuiOFVniiTNUS2bDBLhmLZkNBYLCLytThCGkHzc2mY79dWE7GAEnV5l437ek2t93tTIBS0KK+pGmYts+A2+MDt9Q1vb2757vYNb6+uue46rrqWTRtoQnZXXCbLM2DZ30v6XBCievHZ9XE0jV+cLp0zxT/Aeo/5+rL1T7aIeBlaciwgvtSqoJyAn9o1n2OdUe6dQ8uev/73uSifSzaVyyY4X18TTM9pLp0DIQoQcer+vEG+oL6fsKn8PsGIL5tOosQvRKBflv64btIurfd6DVy8p37mWVE0wkqs2uW9mSENIZhAvWmmIGqgRztyLTAtWu2SuZhzR1sR0Dote2yWTKoiGnBNg5L9IWcgIumIU480B2QYIA4W/FY8Fui3wYkzoThiwe+SgleUSBpHFIcLAZLiNZh2tou4LIHVFElxwIniUZwfcd7D6MBBGz1JE5uuZ9ONtHtHP2ayWMj5mNaQc9kyghy/YpJdCD50hHbL5votm9v3bN/+wPbt93S33yPdNbJ9R2i3SHeF+NZc0pAwLfyZGJzcK2k1lLpkHlWO996TWpD1fp0zK0xD0T6cBvX4lUkoIJqFCGmOPJEj3hnDkYUkMl2XKTdjcIrLqPWkySVO9EHVaC06XHPNShsnTaDMXKSkiDOgQl0m/otwPANJpZNdNv13PoMRzhshn10YFO9VxdVS0zYUqb6mWVAy+SwuJrKl76b652f8zBQm1cmdFqiBPAWYEIcPimbmVVPCOQMo8JGYRuLgSCkyiJjLtDTkiZoByEK0CnMZmWcr4+Oyv+XSlxakHnzhSNTccfnyTB5ml4EX55wJvbLVUWmwxYqwGWyBrRNRozG8eV4O/Z5hjOzuP/Bw9ys3738gtB3q8/jUWqy/AQFd0mucU5+axx9ds/9STao/Ki3wuekp/uQ18ntJ+i3L/twyPkW7r3rZvuYLL6/Ypyax/xTMEgIh+QAoY7sB1IDdfE55hCaDziRQZ/vzlN10hlQ0QT4XT/XRfP7kIzSDEU/xbyfzWYEFC/DhpJSbRTfXO325UuQ667yXdYHJMpBZMHfSKqGAPpp7/KycY+1Cwyo77WXopCyuFRhR0lN1WPdX/fwl805kfuq59XZODrO4f6bYJegz7+Gn81oCUucrRCZHsmWmOEya721M1Ggd78yFoxcQMcGtRIWYiEPPMPQc7n5l3N2z+9tf6e/v2P/bvzI83JM+3MH+gI+CaKBpWrwEmm2HDw1d5/FeCOKIOD6Mwi4KPw3w4wj/R5/4aVQ+jIldgkElW7mquSmVXF/xBkp4R9M1dNuWrmvYdIGuCXS+ofENwYdZ8Sb31dwZZ1Ke+OdEjqfWwanfxSJ6Ua4WGtB4loS5Xxo0MSiM6rLKVZ7bk8xlWoynv6dytCqq0OV5Hk48UqHndPpa0Hh5v1oABoW5WvCSVZvP5Vf+ngCP8lKVZ/1N/dxcpqbaPVP+FLBjsoSor9VlpxN10NOD+0Sa5abzebXYR4y5Wk4xJfNrniYEtpuOTdexaVvaxtySTTFMJg8k5eXnztV6M5oq+Vwjnm7bs2Wefuep68/SJXIMwF+6t9bvn9rnn00VePHid89mWfZiqM+taf6d6OtzygKX0u9PpU+OEfHUgbm+9kdOT5lIfkuXpVOWEPV3SaeBhectIcq7Xzq92qb2hdKnbwQvq++39fDHT6cJ0fleccW02XS0bct2u6kIZeNwZ5ppdq2mFWV8bm26onlWNDTy9ZQSqEMdiM/rvRmQ0FLMWCWNaBrQKKDe4lSMOZCveHzX4EQZMgFdtOOTHEjjSOzNfVJot4gI7cZ8o8oYM4PjUY0wDmiKkPrsumck9Pf0B48LkaZL7IYIArt+R0qCS44xE5ROTWM8OCFkN7UJ8F5oQqDrtty8+4HbN+/4/j/+T7z5/k989z/+X+hu33H9/X8DTYc216gLqGtwEnHZj3+CEr3SGFzVLNuWHNDSEaNRm9MO62bwqLZCW438pBNYRrnwCdnOIrvZKQL4WoANxeplCtqtmNAi2UOpzJVCiCfNmp65APUU10NSghRKrSUFUpuCT1WtCPoyN/OnuBgrwJhosfgZQTCrgmQaS5IBHi+O4AS8B9eY2yRxeN+YCyTfZDDCA25y/2UCe6FtO0SEpmVaFyKC88EIvBxDoQS7Ln0SU8qgRaU5uhIOqRYNyoAmJYSG4oJg6lONjGNn7ggOe+I40h92xBgZ+r3lMY7TXEBkkueXNZySot5PdZ9BKEsxxilwdGnDiDHkcRzzex7B4XyDSmLCIrIrsbEyUy9BvZFEFCVGi4tx2N3RjyM//sv/CUnY3LwFhOb2CteEeeiJL2bavqVv6Vv6ll6aagvCr1ZmcYkngjrH0HWINoztJlsB2h7cpkRQCDmOT1Rn+7I/JQTPJ2vKVhaiCGmOBVGeM7NA+1uOheqLel4AJi4tA+SksFuyNF3r96yE+X4lhj2lPFjziPP9VP0+Y5Ux+WhMZ9pq99eCJvSUhmmp4ixMqutY4ikVy4hlfsfPn0IF1n36xc7BInN+cQGXeSqYZMhgVpQ4wGJlIcGsZR14ERovOFWzRk0jGge0H6AfePz5Rx4//srdX/4Lu19+ov/bXxkf7tC7R7QfCOpp8Gw2bwhNS7e5tXh124bgPe+6DlEYBuVuTPznfeRvo/K/9Movo/LPvWZlpYQTU7hwJJwk1Lck16IpoHik9bjWcfXmijfvr3nzbsvt2y232y03my1X7RVtaLI1hLmDvbxbl3Pkk5Ma7e7UZxm68XZjSgwoB2BP4iFFHpPnMcGowuiENFX3GRCirja1rL9SQtIlrX8k+J/urdqsOltB1+tSlYVFxEQjn+B9JmBg3idml6YVUFA/P31X8SDKJ1afxb1olteFn80uYiegogYjPjNNXbzKL3tEnR9Ixqv6puF6u51iQ7y9uuFmszU3Ym2gafxkHb0spWL6cyoA8LJC8sl7028pc/rssleA7XNgxHPPvBYYUeXIgp9+IutL6v8p6bNiRNQVe+pavRed0+55UuvnMxt8Eer/gvefs4SYiCz7cTLPS+rylBHsH0UYfEoDd62NswYUXvpZp3PjcUl67tnfKxjx+YDZywCdL92+18j/twSnfu9p1jipf1sqMSGaJtC27RScquzr5Z+9Z++YAHUKBbxc5/lwWzNKMuuoADoLQzMj7HKMB5dKcLFkAASChBbXbEi+MWF9GkAcEkwYHNBiO2Auo5KAG2m6kaSK8609L878n47J3PcEs5DQ2JPiQBw8mszdTdABVfM3CyPbTcs4Jq6vNiZU7UeGlBjH4ibJfNg2jSc4aILQNIH3795yfX3Ld3/6J27efsfbP/+3XL37nvb2B/zVLdpeQWjsk4NJZhKb+nQw82kbhNnuQHLgseyrFjIiMAdoM9o5nT5dFhRq9afUsQHmGqDgcr0MU5DsHspAA6UEr15aOiwYDgqQVQj/VDH15QiV1e8q6eIr/5jnX0paPVML/2fmo/SwqGbT/tKXJSiinz4uuw9CMpNcys4WFOarWBBveU8xMSYT6KJNlqb+SSSSxhmWqzQli6am8XrZnaEawDLppcncMaIOHxpcMjdKJviPOBcRTOgfxYFWwbWrslLKa1aKNmnu/zxuxSKiTIRYBzNNCS2BT5eOhe28drYmVDLwmDAQJmaXXU5zXSKalJTMimn3eMf93S883H+k6a642W5wXlBXNqB69P/ATMsfpMwvkT6X9vgtLUNeM/2ex/Nz6/Z7HaNPbdclrXmd8cz7PJluch5VT8xgtU+KxIjX0SxIYyKqWSYmN1uhTbmtxqHQdSYHm/mmAlQzH11TbUqOy3M317SSp53ixy6RGzx3vW7TEZhwkj/MFMj03ClZxQyMSCZIn/PHIJOAY7bsEDDQBlZEcvX7XH5zxvnxJd1zTpayUC66ID3FMx5rwc61q+USNR//REmcG6tlKlbUgrhMW/lsXZrjP0gWLKeU3U2OB8b+wHDYE+/viPf3PPz8E/sPH9j97W/0Hz6Q7h+R/YhPZrEaXIN3pgwUfEvXtDjvCZnG3UWlT/BTDx9G+N8Oyq8RfhqVh6iM5PmRDTJVlOJXVLPyRbGCCUFoGs9V13Hdbdg2LZtgMSi8N16l8kSde6H0WXWt7ispv49H+jk5xFn5hZb1kjkNNf7JLCIsrlexiBiSEMWRJLsQPQU+lDFfzAud9geZ6LXVM0eAQHV9nWoWtjA7axDizGtLHqd+LvNKUx1WdTk1zevnSp0W76dFuzTzGOiSo5vbU+1HK65rLS97UsZVeIe1bHXKbf7fiaMJxu9fbbdsNxvaxuJDBO/xzuPc8Z56tDdU9arLuCRdKlt7zbzOyXSfyue5NXVWpl09/9zeu3hmZsI+Sab5VJrPlOpwl+WaPB7vZf1fg6b7ZIuIdcWeulb141dPv1fC9x8prQGItSUEzMSpfU67XZotImZU9nhBfrnxvvhQ/4S5PgvbTqevMY9/LyDEt/Rl0wwEFpJkXpMWoNmz3W6n2BBlvFNKxBhNyO2KRrflaUJGZ7RWTNkNTJoY2aLpY9O8nH4mdk2TqJqsZW3ub0Q8EoMR+Vmgm8aBJD2yGQnOEQ8P0PfEZFrYbdfhg8fn8ryYb9ng94zjSPTB6o251yG0qAqtOrx3tG2bAxgPDIdH9rs70jgQxwHnIQRw7kDwA+8SdF3LkBJt1xDuD+z7kfvHB2Ic8c4RvOfqqmHTeL6/cWw3W/78T/+R6zff8d/8j/83rt79wPf//f+VcHVL++7PaGgZ2i3izBwWNa0aJRE1GYMjAsnqn0oMhOwKSiUCSmQgSZpcMjFWBLWaBlEZi2lkZGZtzJpkSfSYlUJhVmaGyeW55CwLvFhkiiQ2svs5ZPik1UYqRWaBteg0Z+ZAbksGtq7LpfO8BEEu8Us0x43QmP35FnNqkoEoaiCEB1QcCY+TxuYiDU4CzrWIN8sIxBFVzeIa0xiNeMuriaBK7CNQ/HwbPDaDDynXMfuZrepefy8YAFWb77mfJC8bAVMiRGj8xoT5Cj5FvDcwYhwslsTQHzBftnHRVzFGYtbWqs9ZVTVGG0ghrBjjOAMmC+I0Tgw5ZKBCPRpaW8djJCUljolhGBj6A6PzBD/idMARGYeRcej59Ze/MQyRN9/9e5JCd/sW35hbEkQJGRvRdPn8+Ja+pW/pW/rUtFbmeCp9LsksZZ+3X0TXksQxSItTpRmVRnu26dHO+n4wdyqSiC5Mb55vh52NuBWvITKd1dkwYnIpfkrBVbVyHZjruhCsnQMbKiH+4vr6eVmIwSmCzHOjcAqIKG2W7Ccd4qIsycDLXPf4ZN4zWKNn2/GcpumnpLptC+Ek2Q3oiXQSdHlBOdOIH8mJz+dzSvB26m8RybSWMyUc8RmIyLQVChpJaSAOB/rdPfv7X9k93PF49yvxL/+V+K//zO6XOw4fH9GHAxxGtr6jdYFmc4trA+1miw+BTbvBu2BxJoAbGeg18X/sRn6Kwv/zUfhpVP7XAwxJGYtwW8zlqvem9JMAzQpRDmdCfRJCYtt2bK9bvr+94U9v3vD+6oa3m2tze9MGnFfEL4XLJzu46vqymRgtni9/xtwqvIArmWV5elQlYsBLr4ldjOxSYpcUXObL5kGcBX0685WnU7U/1MJBrYT2q+en+0+mGsTIjagUVLQGORZZVdYOUx1ynIa0fjY3t+Q5/UHmUXXpeqm2dlgEq67qOaG3zH9T71byacN7AiQsW1tRDStleOfYdh23V9d8/+49725vudpu2G46tm1L14QT1hCrPnnukPtGmk/pqb330n35FWvDubX6FAjxm1hEnN0EqgrJ6loFlB1ls5yz5zri+Zn7ks44p23x0vePDmad/zz+/ZK8ThFeZ95/pq5yqk+feukZQfjTGcjqz7zVFfAh5WC2CwL1RC5TX9j2aL9rYGKODbF8/vXSSzfa09dOvv3JZV9q7XBuLZyz4FleA1iXI6v759LLx+ElCPRz6bcCRmSa65+cwxGqfA5dP/EqNdFyeU2M6kyCMU7Z2sAB4h2htZgQoW3xIYc6zoxeQomFsEuQVZdLllVdTUtisZzrOq54mYm1XNDhahJrp0h2EYO4HH9BSbgMdETANL1FzLWS9w34Jmuzm2/ZsO2QGOmcBaeOMWau2qMITi0IsfjOmANSvqeM/R4BonYgERcFidC0BgzcXG8QgVETIQAaiEm43nq6xvPmZsO2a3j/9parqxu+/6f/yNWb77n5839Ld/OOcPMO320tJobzmUTM/owxDXEpgdamjrJnpoCUEzM+C0fyEC/ocs0gRLk/xfGQ4pN3pt/NF3R2KzQBwvNILpgJKkHFVHbWOkyV9n19/k+CDHMnlCJodBYvICheZGppPT3WxFERdpfsNXOK4nzWOHOo8+Bbmuv3uLFHmo25XGo7JAQkdOYqzIm5TnIBEdOcg2xVI2pWC2nEiVkClJGyeW2ap0mz8zFngaV1GKx/Rp87KMdSiIkUI+NocR1SLAIPydpos4Bh2feY2zDVHLAafMjPgAXzVAtO7cUsEEQ8yYH6YK7RgjFJCQskrilN4JMmzSb3NQNTrDCMLXKOKeaJBRQ1awdNpl0FIN5cNfXZVVOxQPFiE0AwK6cYC6iCWR/pgGJ95xAaF4iHAwe54+NPf0VwvP/hTwQPfrPBeW9WKDABcTMdVjjr0haTqi2VfoqLuOXaOZXWe+zitPwHBui/Rtv/3vr37609l6TfW5tfoz7nhKxSiKDq96cy78XuTinCT/sWSTkWQQKnpp+QMMszVZoU6aKgA0QnJBGimEsVRSbPJZL3yOLiRDAwPreIQqtKRbNOXhJXu6JMBGHun6pf6r4qZ9okt8xFCbNVwpoVLlu6vSOY5aBDSdN3edZVcY3qdsxpyaifErAYiZvporpOVWVkfY9irTqfJ2sh4/xHfcZK9egSzqj/LnzxomOYTr1creocm+pU0dqZflt7XciUHJMLzFP9X9GJJV+VNW8/W8AWfqC4xZLFmshOPzN/j2smPt/oksG08seBGAfGwyOp3zM+fGR4vOPw688cHu44fPxA/OlX0i+P6G7EjZgLzc7Tho7GBbquI4SGpu3wvrjYNNdlB4T/olseE/ylj3wYlX8dIndJ6VGSZIttkbwYLRaElnHFXEkp2SrW2xi4TUvYdHSbDdvNhi60dC7QOk8jDu8sHlnNL5V+XY7MvEBqfknKGv7Ebcxy0+JsLNOyec2kTAsWhbMkkBySiivPpVulxXctTV+0YTFL53em9VF9ks5AQJ1//XvVPTXJN5ddrUNg4a5pUY90XHbmfBd5TGNe8qstzgrQEC049fSJSxdNVTultmymrttcTr1mFs0+Iz+otelFXB5nQVTwqtO4G9MsuMazvdqw3W7Yti3b0LB1ns4FgjcLcM3Ak+hRNTg5AV8wJy+Vrb0kPW8VMe+Fx2dzzW9VgN8yo/x2nRPLcarOHlkslUut0WDyNFEBfTqXdiadmqtl56jOt2qZrpfDKqcTZ99xnXW9/i9Mn20RsaQULpk4y8N/vnbq3U8j2l6SLhXyXpbZqdn68rQgSM49c9GNS9npE5eeasepIaQ6SDOqrFkjumhGFyJt+c7S3GsmsoTilqTEhCgamq9nlnRcl5f8fi4/uwaXTIqnBNBrwdtrpeP2wakN8qlml72xJuZ/n+mSCX1hTr8HZro+S9fMzZnmzMeXMayo4sbRBJne471nc3VFaBu67Rav5DAEpj8RJTE6xSVw2ahJMhgxa5tAccnjvExrfgIlwQIrluorE4M71VOzexYHip8bmRSHw6un5yMp5ngR6YBzyYJLhwbfdEhzCxKydjo02wxm7A/EONL3j5jGeLSskzdz8LDBe0cInjA8EpqGfnfHQSMSBGKHSw6i0mGulhTl5rpFXORhD5u2I6XI7bZh0wb+6YcbrrZX/NMP/z1Xt+/5p//5/0735jtu/sP/jN9cE26/x3mHazLwQ66Tuqm/HIqriAohgor5yM3XU/7WQi2om4jeWNH3JdXBxxZzOjPVZYI5V4TZsnikjPfEnOaxLPQtiAVrTgqpzIHslgHNrpYzoZ/vRxHGMOKahlNr9mjtqWQazc6XYpUgPuAUXGNxJ9LQIK1w9f1/R4wjQ7/PTIAFWXbBzeeXN6Lb+YDzfrKqiBpxSZHYo2kkjvl8w5gEny0FtDeKLmEuujTGJZmUgzenqDl+w8EsEbIbJRHHoMKAuUjz3mNxI2z4hSk8A2MW8nddY+MJBkQMO0SUpmksiKlvSMlZzEdJBBfMJdI4gFpw9uIGLQnmfqBepFg7UjJhghdIMa9zZ2AeyVxLec2MmcAYR3a7x5m4RvDe2fx2yqiRceizn3LQeCDqAdT2BI8j+I7x8ZHxcc9fm/+Vx19/5k8/fEdLZPvDP4ELJGkzN/84U8sqiLq8PxlAIU5xUjRXJa+Z7IuakU+PNfE7OBO+pW/pW/qiSeuPzOfp5DIjPzfzM2R25tP3Bylnv0Ci0AT22xFxojin4BNjY3umjx4fB4JGwqhsY2LnHYfgOHhHFJcF7AU8tnOhVkxwBVAve+kERKx7o64reeuvqE2d+8M5N50hC6FFzlOczAoLdfalUJf7vIRxcHaWuCQkl5BUxbU4kU6LK475q8KqFkGQWQTqomw7zapYaXVv1N1SaKXlheqhY5dSxdJ1mVXppPVcqgRLCKbHHuexm/5a0m816yCF30ZRyaGIK4TItOZlGl/NE1ulWDWzDIiuFr/BHre2OlHEuRx/2oAHJyHTPGbhq6G12mTBbRr2MPaMjx/pdw/c//ojw91H9n/7F8YPHxl+/JF4f0/8eIf2DTq0uMaZW9ku4INjExoaF7hqtrS+oWm2OBfoxRGBvSZ+Vcf/Y3zDL6Pyy+MH+nHkrj9Yu5yzoNMFMQBSjg+GgiS1ANU46w8BggMP4XpD++aa69sbbm5uuWk7rkPLVjwb50yZwnMiNkT1W9Ygkpx66pOSAGHmOohk15wpITFBVGJULHyXR5LDJwM0k68YinoRFKbgaLHpJEhdiG5rcGECASay0wCRugzqb4UcrPyoYdMaWwr+F+9R1T8lU8zLVgyaLYOtZ3Ru16IueX2V5pQ4ELGHOELsDYgYDYzQWPKOyAQGcmtmAAEAAElEQVRYWKwIqN3lzv252KfEMYN7T4/+HM8vy9GytY6LxqPjEzhHah1+2/Dmuze8fXvD2+2WN13HbWjZNg1t0yIhoM5nxbd5b32RLOTMo19SnnKct5y4fqzlf1rZeT3JLrhztm2nruvRvQV4UdbOYg2tz5X131odr3pUn2Jrs5bbLVZYVYyuiqyB/iUIcb6vTqXPihFxdgJNMMt8FJ7Lb43oPZv3C9Ml9X5p2U/66dL1EDzx7OekZ7NbI+pMpOHzLz8ziY5eLxMx/9LKJUYRQOqJ108I+mvNzwIC15+n63l6Lj2XTmkznft97tpz9146/qeefwo0+xyfbWe1uZ6pTy55Ue6llhtrBPo1+ueCt07koyevf7k6PJ3XpWNXnwdHpuDnh6r62zYqC8QrNE2DbwK+CVMAPaPNsp9/1aI4PBUiuey5H+Z9oGasFvMiMzRTr8vTve8kAxf5BZ3aK5i//gYXOpxmN0auAQkkHMbxZH/9zrRCms7jkwXa1RSJsWeiNyUgwQS6PnjQFm06ixcxbiF6NHp82xPGhPqGNEY2eHzb8TYp3X7P1fUW1cTNdkPXNrz//nuutte8+fN/w/bmPVfvf6C9fkd7dYu0G1xozP8mAhQrD8lRqctIL07/isk/JgTmPXcGfxYnsRSmsvyrh69me8tefHoPTFnDvdb8k9LXWq0PEYralmShfTEKFpndTdQ0/tSuaj/Squy6vafqVurhQgcSCAguJXxn2vfjOIBmqxLJrsMyeF4AGhcCLjToOBpjnOdexJoTU+VWSZU4LN1GTPEcUmHRDUx3PltZqBnwq8tBnXPsCVt/1g/BGxBRBwAXZsZV3ICqBa12JaCpJlI0gCwVSwEnIB4nHlWzxCBFRDyav8VFcz1Fj08swMVK2sAUQDwWKxcT6kuZD1P7LQ+fwZyYra9StpBEXBZMmBBCJKEEUsyghOoEzJi7tMT9w0eGpPz447+RRPh317d0zllwS+em/jefp/N8s0mWJpB03jVtfU0WSNN+NK+VxdxarJETm9fLjt4/fPrUM/B3AeY/kS7lAV4736+Vxx+hDq+t1PJ76Len0pPKSHk/XTBBynQgaKaTnHMk75DGIS7Y0ZsSQQda9TA6VAM4Ifos+pI5K7Ig36ngcsDgaBVANLtXzP5InECJZVTqpVKUmPM+q3lf12Nhe/055+6hnPuiR1QuNQ1aaIqiBcwzNMKpvj/lemKqUybDKk4pl7wWBpV75cOJ++fLLsnoEbMotCadykMXX+VHrdgz03azP3oFO8Mn4VKGjaQIrUxzutCNswsgmd/P/7nqFDW/9zNth3jMotYgDhHwzpQ1nIRMF4Z8+uZ+PuzNheR+Rxx6+rsPxMOOwy8/M+we2f38E+PjA8Ovv5D2B9LDHnrFaYsPDcE1uDbggqdtG0Lj2bhA4zwb1+Il0KfAoJ6/Ijyq8Lck3KnwU9/zMCb2Y2LM4IKKmB8mi0pdBgwQs7hOauHMMhBhTc9j6YS2a0zLfLNh021oQpOVvo6VgI72p2f2q5OW5E89fyo/KQCSmCtXyHEvKDo+c6wTmV2AmkvVOM2QaVI8OdXLIqrrceaFTP/LNEmr79V8R5nn76nluChLj3/WQaIXNK/WD1V1AC3gRnGxlOp30+q7/F3KmdtX+m1tqX6u946uVX25lqdk0jy73DKLZZFCb5dr5o54s+m43l5xvd2ybTu6tiU0zSI+5FFvrsGYc/U6cf2lSr7r9l2aLpVJndqDl/fh4oVW5Wl1OJXXso75zpn7UPPXa8uN/BQnZQWrWp9jV+pzcyFLXLxYnqnLo+LVSt1eti/Ba1hEfOn0ysTo66eq438nqWilflb6hGaVBRKjuVUofudPDmG1IZ3/sPiATt9PV/zT0qdsjp/z/EvTKUL9S5Vz6vdz7bu0fk8xHp9Svwve4NRkng+Xr1GH31nKbnSKxvVms8EFT2jbaVySYu5UiuCuWOKe7S67eepQX5jkM+dxDuhbAJjibD/JBFtKJVaCx4WO0GxBGxMm+pYkDWZJUWJNOCTYd9c0JFV805DiSN/vTKA8JHAeF1pjFBoT/oqaxrimEWKDjgdCTEQ8jBGNEd9tSXHEdy3D0JurGVWurq5p25Y/vf+B7faG9//hf6a7fsvtn/9bwvaG5va9+cANXe6QYkU2d3QRqNaBf08BDueuL4UZ835b+nlmVDnaqBfMZ75X3B2UlwrgPOVX5e2nfIyZE01mIZEZOZxMmnZWP1mN/Ux8TfPmVDoBaLoS8Ly7RjTRthsAfL6fUtZy0nJGKSlG4tDP5TWtAVPjgI4jGodshTOiyawDUhyJh73FnFBzc1TE4YNavrFYD3mP856m3WTBfwbMfGvm0WJWFd43uKS4lI4YgRwGcWpfGPsMRJS4DdnN1TigJJLLJF62PnFlLNNogazjCDGCG80PuR/x7AgxB4SMY46rkYUUmelT1azdZXNUgamhuYyoFgMjhGDu0MaBlANQqyZTBfTBXJJlLbyooFHIoRLNzZMAEkma+PDhJ+T+jn/+r/+Z3WHP2z/9OQeDL6qFec5onjHOZfrBUTTbLMh3jl8hkn06Cxn5e3quXXD3j5i+Fm1RyvpHTP+o7f6WPjNVAqoCzgtM/skVSM7O1IjPcaEUSQ7nHWHYE4YBYsLjIZkQ9ACMQSaBI8nK8JotIH2DitQRvHAKMVqsJ3LwUtujzSVNpOz95srPScLpMc2/5vWAk/vP02vGmNT5CZnpkxKf7IL0HAgx8dMTKJLLlkIML+tYAxfLe+frs2ynzu4NU5oAqCM672S+kq0iZ2dek6B2hoemqhXyUqvy/ZhdsGC961b1E5b0ZV1zpw5Rhzpz/8UkbDeFgkDAizdLCOcYcCTMAlPTCI8fSMOeu19/Ynh84OHf/sJ4f8/+X/+V+PDI8OMvaD+Q9j0WL9JoKue3XDUNV5meIAfebULDlXhaPF4DqOMuBe7U8/+Nwk8K/0v0PCZl2O9IMXEYzR40iQWgxru1IGKaC6YplSYLERG1dZE/282G2+srrq/s02YBr/chBwB+2u/+a6WnyihOYBNp9ribp3yS2Q1cMQgxg9YimM/aaefW2tHlMwzkJOg88fo5EKLiQxZ/H31Y3TtRyTp+A2W9VI8XUGL6XUAFU+gxd0xzHpPFQxUPwvalqh15HymC5gJrnuqcU8LkxZo82kOL+yyZ16A3zyI+BBCjhsV7NtstV1dXvL295fb6huvtlqvNlrYrc9VNsYNkMc5nanuBnOglz39qOqkI+Uy9Pkc59jXTqbpcdp6dWF8XirhOyeWK0uj8zEyD1Ovh+N2X9d1nARFPWgbUz9nDi2vniI+z11dlPlenlzzzlCbKc8+ZxkYhiOZNID8x/f1cOy+d9Jcv8rXPxi+XTgnAUqpMVqt62Fk+H+alzvWn1hSoCdULanJxnV+CzF66cb50A35pOiXc/ZLp1EH3GpvzpQfDc3V66tqZt0/V5klG6NI6fKn00rpdlGdhLjCiJPhAaMJEqADT+nWp7E/55cqa9biett+dG1+7jrlzkvq9E89Vp2e9w6KzN03EI6HFtVsjCDWB61AXUNeaex1n2n/qvJlPuw4062DFaH0RI0I0ZtoH1Jm4155ymKVEm5WiBN8qPnnUDWgckRBARyQIMZo7HhHH1c1b2rbjzdsf6LY3bL//D7RXt4Sb97h2izYdiDdXQrXgfepfmXxDy9wdUx89B0Ksx7zu8/V6rt8/GhOdtRHrvJcWb3q0X2v57a3ykrJQWLNJ+zQf8ryZ6spMqC8ocDmmA06dq5rBAHG4UDQaXWaiPIXoL4xAYWRSisQmuwYQsdgR3gCrlCJp6A2MGAeLZeAcGgeGlIgixDEzIZkBMKF9brtIZpobQtMh3uN9a4bfydqm4o1BDQ1JE23SrDlXe+vOWqkZiIhji2rKVhPWnpSSBYxXxYW8pqW4OTTfFkkNSDHXTDMAppoYdg+MuwcL7h5HAxBiIqkBCP3QQ0xIdj3lvGlYhWBjGJP1sMsAVXFv1Q8jMUbGYZgYMxd64DEHFE+I7xn9gGhENOJ0BI1oVNSPDAcDhX75+W8kVT789FfQxO17wTct0jSZWrb5rim76pK5B0svTluMKFPA0rVm1/rMOLP1X0ozPvf8b5leAka85vn9WulzzvGvSUt9S183/Z7WWj1HL54TIgbiH52FywNSxZk3RvK2lhLiHYiF+pUxEWJkM+4JCF4bxujpm5bk/ESLRHEkcXi1c9E52xtdpTJguvCeaS+dKmHnk8fcRRkt4xbndM3nqSrOSVYMOO6fU99VJ0y04aK7Sv8c8Y6yWvMyCVbWAqu6rEK3opVMZyFwOWX5K/MzK6FNGbOaV18kPXHtRDr9tuLUm5OlFW2YSBNIdVKeO2VsZyS57poLm0Z/brYBVuWV6VwVcB5fa19PFsoQScT0CGPisH80V6m7R+LQM3z4N8bDnodffmbc7dn/7UezfPj1I9JHQp8Q9Uh7ZUoboUWCx4WGjfd03uNdmCxPxTkeNHCnjrvk2avjn6PnToX/NCofFe6i0iclZhdAybkZZBAQKVR4/q/0T5l9+f5EX8Pk3vV6s+XN9Q3X2yuuuo62aWi8x3mHZKuIQst9iXSZfCNTwSo2P3I8DHMzZeMpTvBeCSI0mKLIWLs8enK+Vh2zEFLmv6dFtWBwlnnX1gV1qsGJBTCxLPpk0rocFtYXReGm8AZT/abvHNshJZZgRJzcLWmqf+f7uvzWNIMfR1WV+Xvdu24lQytrdd6f5/Va5Gk+8/eS57eScN6z3W65vrridnvFzXabA6k3hDbgg8f5TEvPUudS3PR9VPUnzrbPASJecpYf53tedvSUHHaWbTz97qemc/LnNX16TlaScylXYNr7l2cunGjFdF2nvU1Xg7qw81fbDwvYPk+/zwtx8Pu3iPidp3kA1lKT3zh9Zdp7Bh+KluwzJ0FF8J0DIsr9+vs10qk8LwEXPmcDfY36fzpK+vnllu9TfXBKe/lcOkJcX7CZfzoIUQjHU3ku83quHr9HgcKl82CNdJv/9YbQBJrGtLIRMwdPyfzt5vOGYm7t0lN9tmTK6mdKsoPs6XEUMR+/okJcBQpTsgBcnAWoDZspgDUoSUJmyFsLOpxdtqRgWllIh5JN31PE4dCYEAarf9bAtlhlDpWAuoAL7SxMjg6vDcmbYNoRcUQ2V51BFy7gXeD69geabsPN7Z8Im2uu/vzfETbXhNs/IaFBm02mhTXTtmo+jqujpABG5fca7C3Xnvpe9/E5cPdJMCKnGnwwi4DZIqIwVNP7hYnxZqKvMYMVWVoiWjRs0sTkz7S3UMz8C7hwqr6l/xbgi+Tg2ojFewBjSjMxfjoZEOFr6w7f2BzSZG68hoOBEMOBFAc0eDQOaIyISLaEsbxKPSYmXQTxwYC/boPzgdB0KC5rnFnwQxdMW25yg1FrzKlO+U2A4WjggFS8rAn183h6c3/kvbkcCyFUz0ViGitmz/pwfLxneLhjHHuGcWDsewuordHeeXwkDQMOs/zx2WojhAZFGMa8frKbq+5qS0rKMIwMw8B+v5/GyjcHkMccI2ME34PvcURER3R4JI0H1Fs7h9Hq8tPf/oX9/pGf//o/ICmyaTtkc4WXawusR2GeskDI1S5E5plm3VjmX7E3+cdNX/IM/D2enSV9SVrq99zuT0l/b+35vaZJuA3MJIBWh+QsjEqYcCo6CyaLF9AcMwGL6+XTAT8e8OOIxkhIDYMPCNcMoSX6gIpnJLvD04QkaPyQC/Tmsie7+0sZmlDNoIgqSI5iUQm81WVJWprbVWJFzAGllxYM50CI5dyrxW25k4oQTmQSLM7vHAMTz5eRS9KqJFnSSEUwU1uLFjJg3lfWwqwaHF+VlQv81P3IqcPjZ9oSGwnBrFQmenrdlflaErcCW5gsJiRfFxXT26G4XbJPdGad4ySYq0kCiM+lQ2QwOqJ/II0Hdr/+G+P+kf0vPzLudtz/7Z8Zdnt2P/1K3PcMP90jY6IZIIin8x2+aWk2W0LbETabrDAS6LyndTlGCpJpeOFD8twnx/8eHb8kx/8RhY8J/jYmDsliIJiwOU9QZxYQMw1b+qj0mTBZAkjut5XgLzhH2wRurq55d/OG2ytze9M1DU3j8cFi8r123MuXppkmYop5Uywiksx0qTjFB6GJQidCrINIXzhPy9yhXiMVbTunGRBYAh2rclRXrpGoLMdP16kMl8lddX5Uq/fL70WZy+tSAxBxXAIOi8DUOWi15msaMQv7ygKjirkwV3SWKS5aUkDRdW9NqMDEMeZsZAK7vPcWU0f8FJRcgufq+pqb62veXF9zu91y1XVs2pambQjBIwWQUzVwagJwS7GrfXYtIzpq2vOyNmvq69Bjv73c7uIlcvb96fQ/wdMf99O0YVX/X1LQai4tLtbllempi7H+FJleSb8ZEHFOcHl0XZ/uzOca+9T9SzusTIRzgp2JiFnV0ja9TISs5/P6+hrZmp7//RL9tQCoFk5ZU04LGxeHbvXbPu7omdc+pC8BOC4RlD73/HPlvzR9ziJ/STrXP+sxqet1aZvOEfv170s0Sz+t/889c3pNf510fp49tdfkC3PMvOr+SYFtdb1ee6Y1lInhYtofzZ1KzEGszSzbguDadiULIq7Mi2frW64tz8ijfqjp+pN7C0Vbx6EuIL7DalVEiJ4kzlweueySKRNSihBLgDnXoOJxnUBKhNBYUDQFkglci0t8dQ4tGl50QIsPAzH25pJJIo6ESyOQCL7D+Ybrd/+Oprti+/ZPhO6KcP0O326QpjMBN6WNlU/R0q/5kybtFpaM4QXrf8101+P10lTM8VFImizYctain6ZUcdVQTNMlX/NFQOAyjeNtLhUtyLTkAZb1l5mByenJM708I5IFMHFiJwx8M+ZyynOSDwhJHDFfEucQUcRZ/AccJPWoU6JTNHk0BnNPhDct/2ZLSpESb6Ap8zYaeidNSwgNXXeFCwHftNOcVDHBjjENgaJzaoyqmzVWVqJyWy8OVxYoBu501ze5D7MlxBT7xEg+TSaUSGlc9BuixHbDuL1lHAbGcWSc3I0ZAxUeHswFWQZtmsbybpoWEUeMmTdMpnG1udqgCsMQGYaBx91uqtvQ9+x3+wyKJPa7Rw77B7wkPInD40eG/pF+d8/Q74k0HA57EkI/DPztr/9K3x9QlM3VDTff/RkfWkLbIeLN7ZWY9qE4wXky3eGnNTa7n/t6AoEvxXS9RnpKKP/S/vktBCyf2rdrmuQ16/Al0jdA4On0JdfUvB+fT68jxJBS2kx/IYvvisKyuomdJ+YiRxmSkDTQIAQBrxGfIt0w0gxmETr4lv0mEkND9B2a6SgRixOWc851UBBzbwfTCY1IoV2UGYjIAXyTWrDnlIweS0vFhZTsDFvQi5BjJLzMlWvd60tXkqf29yfccaRlXWqx5FynY5JbMFBIM0Ah1okgnrWmKpwBPupgvXPtS+H2jBZ3LrPsQYAoSiyho2WWn5hLQp1nTi1qkDl/l2NFKEzBqBEm90NGP9m3IjlQc66XKOIsplzSgRR3aIoMB1PiGB4+EvsDw4dfifs9u5/+xrjfcfjwgXjo6T/emRvMw4CLytZtcK3Qbky5p206vA+0bUcI9u2z9UOUwCCB+wR9En5VeEjwb1G4S/BvUblPiQ9ROSRlUHNFZMyN1p4Z547X0hc6C95c5rxcHvziCq30E9C0Fhvi9mrLm+srtm1D6z1hAiBkopcv2SdeKq947pn5dyXYnmI+a+a/TOhsxj2O1gkdwkaEiNInc7+ViiB9mquzbOvIonTxoK6u6dTfExBQ/y5MwslsdF6I5V2p/q6EsrIoa11mXZdVGdOzppiEjjPokAGGGVw49TtzlIXXW8SNmN3fzSJAmX+seiqpVnclr715fxCRaY27ab6ZUlLKfFgTWrpNx83NDTfXN9xstlx1G1rvabzL1hAZlMPcukadORDb+/R4bj4xV+v0SXzopXzgmXX16WfyxChenGqZXZEhX/r88np93phU4Oj5k3Lyuc61vOZ0krkwe5CS4VqWU8AIA720fnuZ4wv6+osAEa9BgB0JtkqHnp0LT9w/ohTk9PV1OjM2E8G3GJiaoJjrUgjJozm8vr56d7LDXXXlc5rna0LuNdM5IelaYHju3SNh9nTt2BXTuYP3VP6XzrenhOxPPX/p70+p0zp9CvP02sjxpf1T7l0CRjwFQpyqw6V1vCTNz67f0RPXvm46N3TPARLl77r2ukKoF4WcmLsGROSPc5MlRIyROEY7xkSyT1BnWlAyH2ovScfjdSqP+UAtTOi8r2QdDi1MuQPnIbQ5DkQmvLKW3hS8tnG56bbXxmgWD04aEHNdQ0o0TdbuH0fSKBmIkGye7MAFvJimmbgRn0ZS6kk64o1tN1cIqviwxYeW7bt/ot1cs333J3y7Ra7f4UID2f3PkoBO1WfunszbzefFJ6R6/p9kek+BV9W1EqMPnWNCFMuIkn8htgqDVYMRzhfTdhOQ+FQxctkcfslEMBPjMu8x5+o6tdMKmXkQwGXm2/JyZXYwgWLCTDhrtprBBAki5pyrdIAGh6ZAytqc09x0AR8jtAdijBRmo1GzNogZiCBbRLSbK2MOMhDhxQCnYqAtYrPYy7xOl2fr3Bc2P2a3WCWZIF5yfg6fgQiXLUJMYasERq+IZYG0icSoxGFgHEbGcTDAIjNOfntP3w9Tv7atxVXpus76b7KiV5x3bLdXKMo4JPph4GH3aOU5zziM9H0/9ef93QceHz4SnOJFebj7hf3jHbv7XxkOj+yHhPpHVJW+H/jxb//K7vEe55Sr6zfmG7rbskk3ZgXTYFpgeBwWwNWsZUokD8WCqZ6dVss5dmZfPvfcOp0Tel3y/NdMryXkfo5e/ZLpJWDtJUD6qfufk74BCZ+WLl2DXySVfViNDjo/P6a/XlzEqfZpOa8wbfTamUsJLDyRFFkrtrCQY/BEmkkQ5ocdfoiEoUdixI0jo2tQLwzSkVRIYoJdh5CSZkWUspYtRpea7URFRWflg7rNAuDAmfKCgRBGG5T2FcuIlCxvCq+QXz/FOzw19oWeOAYuZPX+kqZaP1/oiQnsWfEtRSCzWMaFjKkE/faQm87ro4dXqQiWVGfQYK7Q8m3N87AGpKIoUeLyWYUiMC8603Xe87dOORU5bBKqAMZ2bk+WmuJyjjk5BUloMreOY3xgHPYc7n5h3D1y+PFH4uMDu3/7ifjwyO7Hnxn3Bw53D+gQoQenMgV13mzMBdNmW6xIW4L3tMFcHHU+EEQI4rmnZa8dH1T5gPJfEvwUlb8k5UNUPowjh0lLvZjnVP1aCfTqdT53YPk7ZT5IygQ1OpdMvQu0TeBqu+H2asObqy3bpqHzFsvKe2+KEX6WdVyiMPspvO/zaZY7FbBlxspMASblddN4RyfCVoRBHUEdw8JXb90GzTKsY3rnJP+4eDRXoO77MtlZfdeARQ1GLOpUB40u7avyzN+2Iyicqt9UNS3mvmbpMFk+LN0yLYEIZQYj5npK/nsa+9Lkwr+cPUNOuaOr5kYFcImIuQGTGfjKDDCh9bSbjutsEXG92XLVdnTe0wQLqC7OzhGH4JRpLlhXLGU554GItezhfPdemp6TOb10rTwvd4LXlhWdEvDX6ZR8uT63nts36rX9eXU6PntnMKLkLYvSXtpTnw1EfB1i+pnN4bmNI/eM1NfWXSUnOk/rzWCdvnS7P2U4v1xaj/PaP3hxz/HUu0cggzOSyDkTlnxq4KZLBOHPCdn/iEzhU8DPS9PXav/zm+e39KWTYL5dncyESUrZEqIIBWMEMdc2ppVWGJSnDn/LfS1sWzN3euI6R0/Mh+H624gti+cgOQiyFz+1RRA0+8Z3wWXg3ghQPxSm0pgJcR5RxWkkjZFBE6IQh4g6xWL+ecAC3Yk6i4kbTLNEJREk++yMJub2/goXOpqbH8wV0/V7XNMS2gZxDidZk20SkpsY2hVBQ+6HEjBuZqzP9fu8h53XHPy0fRWMuRJYABClnAnQcvP+XXyRumziXoh8q2NWJCtCk4kZUKPVfWEAj+fGsXLC6uSX1dxRJWMgec4pTnQCN5CsHyg6zezaLZYx5YniIipNDbB2lgDOvttaUMnQzWehKiFZ/AWfUmbos0sKF1j4UsrCDFeaQPEOMPftvAZsNCYhRQU2LJiP/NvMqM0iouSXct+YMMgteHEguyMDguAka/Bpyi6TDXhpxzFbjcgUUDs0FkeFYoWiBkw1TYMCISohNkiXRSFiFlhxjFmoB911y9XjlWkPemH/8B3DYc/9h585PD4QU8v93QdyWFT6ODLef0D/kthsr4hO2GyvuX3zntC0dNe3+NAQuivAhBtUgJPtC0cz6Sg9pYRwCf1xKj333rdz8lv6lv54aSGc4XjvKM9cvr7XO3TN9lfpSICVk3MQlJGO5E24OPqWTu7xfU8TB/zYw/3AGAJtfENsWnRzA75B/QakCNZnxQHFgvqa1nw+/3E4fD6+C+MtRjsB2RTCzs5c2QV/yCz4OHHCn2hzHSeLk7TDUiBW00hPZ13ePaf8Vs7gSXCrc40NSLlkfE8Li8S7RduezEqWZ0W2sZzoSCC7xzI6RPJ5V3rbgPnybrHIZLKGmICIySy6tDIR00iK5us+xQj7B9g/0O8f6Q979ncfGHaPHD58YNztGH79SNofGD/uSP1IfBzQmPCxwyHcbFtT+Mkx65qNWUB03QbnG5qwQXxAQseAcC/CkBKHmPgxBX6Mjg9j4i4qfxsjH2PiIZkFxJiykkgqwuE4DxzMC0eXlxdyoyLIrbXZUUS8yTCsQ80a4uaGm+0V110W7joT5ofKCv33IOUpljeipkglSa2boqCpxIKBJltFbNVxkIRHsOh65ybnc6078Z6ufpR5XSwhtB6vfD9VQMMajJBVfqe+c1yMkyCEMI9zXU4NPmg6WYcp7l8d3yL/7TI4Mu1XU5Vq26Z1VbSqVPmuzgaRvDwzH+BKVB+Z5q1i69gHz83tDW/f3PLd2ze8u73lZtOx7VraJtCEMLlxFTF3wWvFx6NzbSFLO20F8BSZfEoZ5Jws4anz848oy3tJsubNwPakgFrx/kvQYnrzU0rLZR73feEvyXQB9Zi8kHX5LCDiYiHutIGfubfM9MT9ymzp6PXnCZXST6sby3qfykak2kt1qur82rKup5CtS9CuU+14rk9f+vxL0tF2dybvtRXEOW2/+vcCjJiEJ8cumeoyTqWXtPdSEOJV+/Az6/0SIcRCc+ozhBef2v5LmKpjNPX0XHlN4ctl7ak0l1bpawiCnpvvrzEnT+XhFusur+ViEVACbTmHOjtsEjqbip+o0szYnXe7Nf0u2ZzteLOGKM+X78Wccc4YErIA12VGwGoA3oGTrNVhmaakOE05b5P8ii/N8YgMxKE32jKDBbhCVAUkChId3gkERZ0Dp8Y4iQNtQAPOX+NCR7h6R9hc4be3uBAIIbdZUiZ5CyOTHTAdEXbL4/Gp/bXu6/MCzsuEH0fPaKmLHllCFN+jNRCx8HtbC2Uy4VK7jLYpo5NQ39xj6TQ/TglcJk21mllc7Sma6QZXvy4ZUJsIgqJHOOsA1jKLWjtwFjLILGTIhh3eeVMEbGzepggGQPSgM3hTGDZ1jrSgLZjmsbVFbS5PwQwzwafZ1UUGy1SzwAKO+t5LKC0CBFcFohcEXMKAtdKPlSWO2Lovz1pcjYR32brIeVJMFgi7+J4VsdgWAAzVxJVFMEYfAzTzb83u0DR3QrNp2FxtaX2gCZ7+9h1j37PZ3LB7uOfj/R51LQ4LGH539yPjYeAwPNK1Hdura7bXNwiJttsgXgnNJgftBrTL7S1CB5kHt9Luewp4qNOlIMRz6+5TzprXPCtearnwufTqS8p6aV1+T+nvnSn+LdJvZQlxUVoIvauvC+bBuT2n1tVdyNa07NHnItvkq05RJ0RpiM5BslhaYYi4CH7Y48ceF/ckb5Z4sd0QXYs2Qp9jR0AEUVRjrtNoJ6S6XBWzOEy4LJSws2zZN5moKduu2PWl4KTszS8d5+XzT/Fgl8gNinDn3Ps1GFHXoNAHyzadFDCcrLd1pZuEl6r1oK8K06PXERTPbOk4xUnCDtoyn3LX26hV89b7WVFCZVYcSZluNVmIZneKkXEciMPIOAzIh5+QDz/zeP+R/eMDjz//wuHhnsOvHxl3e9LdDu0HdK85TliD4AlNS+MDb7prgvfQeMR7/KbF+0DTdHjX0IQrkjf3Yb3ChwR3jHyIA38ZhX8ZHXdj4nFUPoyJx5QDVqHMbnAqIKK4yxFAfdWvhe4ra6zckqyZI/Z+ecEJOFPuwgld23J9dcV207FtW1rvCJkf8cUV7sQTnxjbC9K8PzzxzFzDs7+lGIdk4XkOroEmMesoNbrPO6FJQueERszNqcC8Tk6sl2KtY+08V9MT/Mbit1bfhVjM41gAgMUYV5kclXmqDkfMxPH79fcRAJLmujBbOoAun6/ACMltUGVSKl/wesAp3me6MykyrXnGWTmsyNfKvjtlL2alfrW94vr62gCzKwtSvWmM7m6Cz3R73V/nnEXNZdtX4ZnXcrWXTfSTsoML6anXorsuqfs5GW5J82W98Pnn+ilzotOym9ffaRnAy/tisbeckFXPZeTb5ayr+NqXlPoHCVb9e2Q01lv731vSaZKvBTy1QGodMPVUkmpzFDFtTUQmjcpacPXajNvXBB++ZlqDQOXat/QtPZfKmnNOzN9/TAz9gTiO9I8PJhT1Dt80hLaZVbUn3rr6e7F+MsO8Epiv5+W5WVqz3TDP51r4XQg8cc6C1BXmtgSoLXkVQr/cF8U5pWnMT++YsjbfxJgkYkrEOObPkIlayUwhCA4nDnUpU++CknDBtLVCuMa5lqZ9gwsd3c17Qtvh2g7nBIe5t9GJ4I8V06OrI0VKT0+8+3Op3tNOWURcAhYejVUlNKitIEzw7KdPDTqUv8t3AQU0RjSZ5YnGER1GNFvfmDBaZgBCZIrtcVQf+6tqGRQBTayeUYXoTROzyAMEN7u6qr41d7RW8zpldz4T7pELqglLWxZWzwKCJVFQh6bWrtRjTnEzluupcx5mxZD72FmDKn51araITEDdOrmsBTW/UywkoFh+FCZKsDk4neeZcUqF3chm5qUODgsg77MfaO9AXLYyAURTNVfzHCD7GJ9AK2hp7exKCRXzJ10EHG0TcCSCD3gf8K5BN4qXwPbqDY+7A1c3bwluJKWB9F8j+8d7+v6BQ9/z668/st8/EMcDbbdhHPe03ZaURtruiiAOCR3SeQN3SlunvW1p2flHpQ/+COlTLUm+pW/p95S+xjwuFoRFRFYEWXOqtNoLKZEvTNuxMxF1ajtGHzigxK6j9YLv97j9DjlENvEe9Xv0cSA1He6tknyDNh71jhg86jyjNCBirgrFrCI8s4DSsxTxZcoNnZzY6HR2znQFFc2Q27MSsKzT8v7lfSrlzJ/oheXLRchaC1wWQp6V8Gcaq1IX5u8yPmuh1FxSJfyUIrwVUzpYtHv9HnO/lavqcKVukvtcMv1S+kiyIpJRtXPdgSG/Z8JVNVotRdJ4QONIOhyIw4Hx8ZHhsGd/f09/2HN43CH3H+H+A8PjnmF3YHzcE/cDDAMhJnPLpS2uNSWTxlvsta4xa8XtVYvzDdJtITSkzQ3RBfayYVDPLjXsk+MuBT6kxF9j4m4Qfh2Ux6Q8RhgURoU+B7lzWdjrktjaGK2hMfeJluZrWsij8+yYemcCcop2fu5PwyYM8AkSCMFxdbXhzY1ZQ2ybwCYENt7TNp6mDYRJ0Pt0+lx5RSFxz/22izMdNM+yEuzbTfFGzF2o5Fgz9rcTBxp5Goyo2nOyhsw80Ln7Z39XlwqhvgYWpjKY709EffX3U2XL+nrJs8R6ON2OYmWhWtdJmdxFHRX8/Pgeyclk3kMpIEUGxAodPq9/kOAIbeDN7S3vbm95d3XNm+0V27ala1vapjX6O7uTS3n8aydcqwrNgNTEe5yS51V73OmWTfdPTSX7fXwuXJ5+K1qznNyvl8pZN/VBPlyeOytfvw7Gs5Yz0m7w9DCfSBcDES/ZAE9qS53rFFn9ce65kwf4C+5/Uiqby8SlLosoBMP0exaKTGlq1ok+qa4faUZPf5xuz7Oa1Odf/ayxrAXg5wi4dRkTkVltTmWzlNXnNdI5zaJLwYjn6vFbMs+fjqJ+2fQcynvpe5fm8zWYv09t02uUWdKXsBARZhBQMY3tse+Jw0D/uMM5oW0bxGdTY5GJWC8aLuu1UzS/1kNy7lBcj7cUYkapoAiO9hkthFzWGJ+E3YX40nmbnkCK0moBH0A1EUcTGydq4CNZbIgUScncJWXjdbOewCPiQeLCZzOuRXxH6G4IYUO7eYsPHe3mGtcE81UvIDpMRKsJpiuAZaJJZeFaoT46S18cazyc7vPjdJ6Rr8fk6F7u91OWEDUQoev3FhyQYkHezIRfowFgZt5c4n6U+Tm/L9WBOvdV5ed10fD52jRnxC2FMlqvsWp+rGlFkYkZy62fi1jM0MwHVG1NmLufKD6XUsbbQIgUxzyWldBbCtMrTEE/cxealuns03jd7DWxb4Hn83qs8rH2FwFQnnt5PqYU0Tw+0wvZ/Fx8zie7qHKiFqLF6ezWQazlxuNlxqiwYZoylil4zELJglmSQZs08YfBO5x6nA845y2mhTpQITQb3r77nhBamjASY89PP/0r4ziwPzyQYuTx8Z5xOACRzWZL2wTi2NN0nQkh2mvbK3ST65cFRLm+p7XQXm8f/pJn1ufU8Tl69LkyXmpR8Vx+XzLVdf0jjOvvMX1qe38LWuo1y/ytqOxapFZiQixddej01+JMA3CVEEoEDYHkPINekUIgjANOBLfPMSOGA0gPw0hqOsbmiti2KB2aglnEiQNpUDELiNmpEjg14a0TzQ708om5EJos21fziNPpWs6QEzTkNP9OCadgEsrYn+dAiqckJrIS7sz7xSzPyO+fpMdW14tkrdw91ZZp0ApNvCxztq6Ynz3Fw7qUIyAJK/dKYjEecuYFiFhrrI8TbaCmqDD06DiQ9jvScCA+3BP3O/qPHzg8PvD46wcOu0d2Dw/Iwz083hN3A+kwQp9gVHMFi5jLJedMEC/CpvV459i2wSxrtw34Fre9JoWWtHlLJPBIx+Po+Ll33Kvw0wi/pMS/DiN3Y+LXwSx9ZsvOmREQUZwqQUGK6341siIJx0AEHMt8JuG1zgTYNOEdJYCxiLmp7NrAdtvRNcGC/zpH4wq9PLsynce8mnkXyi+WDx1fqmq+JMWr30ZHz/SiXbP5nson7zROLH6HF/AUxZmahj2e5+uKHK02nf57YnOtdj+tvid6v4xL9XsyGa7z1mUeLO/VXmam5thfx3Wp50IVcHr+rp8/UW5+1np+wU0seJ5zaQlEUPFOMq3tQscr874oIjgv+OC42m643m656rLVThNovCd4W5MTXZ/PmwJEHA3vYl4eywaOwYhzKZ9qqien0vHvl8uAzj3/fD6nZRuXJM3j/hr0yPGZlgGAPDBr+cC5si7tNz0xCKfOVal9GsPTw3wifRWLiAVacv6p/L1+UJFVX9Z9eyrbV6M713vqC39/VjWe2tAvff1zyj/KbwlAPGUJsQYVJiIzmy6aBYSbNtDXZOK+NAjxe0lfmoH+2v3wKUKBzwcjnmJE/j7SSUZlcvuS3TJFZTwcGA8HDvd3BO8JukWDxwvZLLvO9GRJJw9qEZn2imnPWD3jKwG0aXDpBJDUlleT8FbK3ugyIJAFipIv18BFMa3OhFXrBBVP8pqDcyuoEMdk/upjzOVWvnPFAx51FphPVTKEYUGnfbjFtxva67c07YZue4sPLb4J1sdpXMy0NJkRF6I/1zeRCWhh9lnKTGSfGNeTI3GC4Dl3nDyXzzR/FJz3xpBkJmrtkkmPytTSYEhKHEfSGBn7g4EQ42j5ao6xUeIEVbGC1qz33A/1GGPWBjq3ZxnguRDnTMKOebJYXgtWoCp7GgWd4YfSL1qsCDJjUfhSigZRZmTKdNU8wSX795xxiEKAW1cVob0g5s9Z7J3y3MwgLS1UkMwcIhMDprl1pa42v+1bkwWlj3FkHHrrq5SmrinCiAnwW3GSPjUk53CuyeWbZ+qUIza6zE1ojOCEFOf5bG4A0vQpa9bFAUkDaDQQSQIiHu8SNMLb796yve7wbiSOPb/88ieatsU5Z27Vhkg/HnjQxHjY0zWeoX9EgGH7iODYbG8IbYv4Bu9bcoSKCZZYn0PreFh1OrV+1rTPt/T7TN8sMr6li1ORjORPiWlzXqA8C2ZeI7kSkPqIXM17l8jq1kxx1PJrcwEJOCG2HbFpAI8bR1rZ4voD4eEOiT3S75FhR5P2+BDQzTUaWtzVOzS0hO0tyQdi01qAVG8guqtpl5VwajqXpZA6aVI8mHhE5n5d9+/RenUy+WK3c0cXtNbi0RwTqQTHtv3cTeUseNpyhMrUcZR4FjMgoFQhitelAZrLTNm/0VqJZF3LQqvnn4opFeiscTqBqBMdsAQjBIHGW5wnqvO//Ct0jCqSJfLjaJapaRzRGBkPD6RxYNjtiH3P/sMH4uFA//Ej2vfE+3v0cCA9PpL6nnH3SBwGtO/RlKX7eJw4/NbmXHDm0jT4Bu8cTdjiXEOzvcaHhqa7gtDwsP2e0TU8+o6D8/zkWh5V+OsAj5L4SUf6mNjFkT5F9joyMiJeURlAR4iZkEpAMrrDlIwGGysXJ7oRBT+Ya7HEMsB3cVup03CsHYQXujKDXKo0TeD6esv1zTW3t9dsNy1dE+iahq4JeLH+kIWp6+cJCz87WRC9LGw2vmiMymGE/ZjYx8QhwpCEmIynqi1sVpU+L4BbycqmP5QMIs3C+eMXM428okEXGRY+aX78xH1rZVkZlP2wkKZF5C7nyrkwTUBephmnzbtMqjluhDCHwFi2ubxzLq2YchEK2AxMPMHEG/iA857NzTW319d8//YN393ecrvZcr3ZGGjWBnyTrXVy0Q4hic0N44dlWYNqj7db1T59LBQ435qXCMe/4PNfKn05enNi2KYz4jllxRfkvJyBJb+jMuZz9FMWzhcFIuYJ8NQzR1cWv+TE5VPZLQiWSyt4SVoLcE7+LmXL4v5LhuPkYnkCjPgai2stVHoOgCjpLBAhWQtj8l3H1L51O44Z/umv8sTq97L8U7//iGDE19AgewkY8VzfnLv/nADnOQR3nc/L63YK8Lqsb18Dyf7UdGl/PvXs0Xx31Xq03EhxJI4DY39AQkDHBmIsNEZ+n4X2VD1ecx+xOKDWDOVRvUudlq2biFJgAUZMTJnFuzVtHZkPTF/qm+ryxGjLItzFGGLjXGcBeirxCWZ5KWqmECY8lkyAJwMjyEJScRtc2OLbLX6zIWw6vG+ymxyQFFnuV5WAvBIWRArzS3bjk/tioqo/DbQtx8i5NTbPAp3o8nl4Zk1HRIzxl+MA1eXZucxFJ0J2AWYm/sb4Sj5LhNlVn5MswK4qXxhomS/lKVIJg7TcWFR+EsLMsywT5TJbnpjfX7MEKGVIvm7jvehNe27Kd3Y9Jfm2gzwnZ8ZINLNRUgljpn6SuR6Zh/ZTJpmmQKhnjIibiMGp/6v2zbVVKMCZKjHHf4nRYsHEcWAcB4b+kP0CJ5wzbdYyhi66BbAzuVJ0glOP4rJFktVCoxHFqQARKUJaCcrUmDEDIaIJk1Akxhzs2tgedYBTRBLOw2bb0bQex0gcG66ub4kpsd/tGMUTd3dETfSY/+d+/wAkDm2HAG13j/cBTSPiPM4Xzb9ar7fMu5nuqcHQMr+foh9eSlM8d/+p/f5LnEvH+/plZXyuBtZrps/pl0vf/S1pxd8Tnfp7Tq/RTwteaPnfsqz83yVFPkev1ULnfGFRh4miENAKeJ6fn6+ghaaw80tFUOdRDfQbj4sJ6ZXg97i+Nzd8wwPoiH/cIc6h4wENHeDQZouThtS05p7FWVBbkWTxhya3inNnCPW+Wc622YVRDahLPvfmPj0tWJkpKOZ889+FV536TGdlhFO/l7z3VOG5LrIGEervkyMJJDurk67eT0+8V6qgzAoIxcHTcl+e6BWZ6ZrkAuqaWYCegzJrylGqNNn5ml0vxv5gAEQ/mOXDwy8GQNzdMRwOPPz4M+N+z+GXX9FDT7q/h2GE/QHiAENvtN0YwW/AdbjgEC/4YFbI5oJJaHyDd4EmXON8i79+a64SN7ek0HHY/sBBAr/ieUT4C467lPjLGHlk5CdNxOxGdQoWTEIkIS63iay8mjD/S0lJmjAKO4JkelzziZ9sxaSK11mOQ/W9OBdk+hT6JXhH27V0XUu36WhDIDhnQaozfTuNXD15PyNVS+XEvQvokEwnTxHr1MCIISpjUsaUGJMpmMxgFpO7uHmz02mdPJky0LcAI44rxWIwMi257LJ5ZCYXSIV3XGgvF4ahvKKrz4mil+zZyXrO4O+JAZiKrHjZRZUy/Us9pSruQwQ52S/LfW7eW1e0f72PVrI35z1t19FtN1xvN1xtOrqmoQ0BH/ysXDb1d8nP6HmzdDs1p85YQshcx4kZ+4ppfWZ8Oh3+OjT2a9PxUvetcCR/eUk9zhRwPGJZoLAczVLmp43x7z5GxNefui9Nv/8afk66xBLiEgGoZCKpJjhrFySnF8ZEYq6unSrv6XE4JzT4R03f+uEfI8lqzc0fow9CE3ACbROQwdOr4mKEcTR/sOOIBm/mx8yHHBwf8ut0CoTQClw9e+RrsVaYLRQ0WZBpqfcJgaJ9PrtYKYLsTBzG2UOvqKCj7V8umPDbZV+dY5LZTltlBjIERF128WMBh50PeAJNc00IGzbXtzRdR7e9JnQNvg0mzE0joorP/PDgs7ufVAi3Qq+mSRNJKLoFQiGwzTGPaZuv97G1lva0t1aggwjZr62srAuzCT9599RqHxYyKODmGACFqF0E2tPFPFjPD00J4kgqgdBH+5tkLfLiaLy5e8B7C0DuzJ3SmCJOmCxm1nOkBo/c6vhwOY9yxrjZUhnIfn+1MKgKOY6BuAJWWd8oOUijzm7BhBLTKJeRtblKDEOzvlFc7CfGrZ6y07hnraPC2JXxB0hjhJgyUzD7Erb6y1QfT4m2bsIlE/hbnIqJaVSrY9JK+zFG4jgy9D3D0NMf9hQtLcHkSDEmVFN2vZW15hS6rjNhvhQwwiZPyhqWov2UD2BAnAhRfbZcKRYGkTFFhjhM61vH7LYrr4TQNjgfGHOQedWIiOKd4Gh4/+4H2mbDeLBYER8f77N2J2jIoMbYM+zu0ZgQLKD27dv3psHrO3smRcCbBQqV0CHP4aTFiiRN4yV5QGQemMUanOieau/81PQUIH0JgP8tfUvf0tdIFZj52rmK5PPKUjnflluDSWClCDoBNBrA63wGDPIng8PaeCSAvgcXtzRbwfUH3F2LG/Y0D3/FxwP6cWdBqz/8bMLj67fQbtCbt2Zdsb0mNg2x64gSGCRM4cUmeRZuEmRMDvw1n5c41M0AcNKEFAB7Qc/MArtaWFcsHjTv2+s908D02RqiFkSule4m4CYDGiaXyxq/WiCBZRlHdcvvgFo7F7TAE1LoQqgU2qDQHtXjJzXDs+DPaUTGES2xqcaeFMcMGIykww4dB8Zs0dDffWTsBw73D6ShJ/36E2noOTzuzV3r/SMpJvQwIEkJY6YHNVOQYYsEQTZmEYNTuuBpnKdrGpoQCO0VLrtaSs2G3eZ7+rDhrnnL4Foe3IZePD9qy17hpziw08TfUqRX5SE5kgoxm5d6NVeSpJTbGZEILnmII0YAjAgjSTIAQY7tprn/nWQWIeXxXsZsOBZ4l3GjWluKJp2UaDabDTc3NzkA8DWbrqMLDY0PNCEYnZhpiC+xT7w02ZoqrndMUaUfI4dR2Q/KY594HEZ2UTiMwoAjEgwMgoUMh3rPWadT9IlkPus50uXcUsm05Mm8nxIHLXCImd+Zx7Qqs6x3qV+i2nQzUHiKPsv7yFH9dL63trKZXSqdqHOV7Rk8ye7XU1QE7wLiLKZf0zS8++4d797c8t37d7y7vuZ607HtWtqmITQNLgSzWI6a83Ig5W9dlXkMPtSKOIv5kcGN59IpXvJT0zKP3369fdlUzpzX4wmWJ+yZNVwpLelqD700XQ5EHAmA7A9Z31vcB04dmOcffub2cx17dDI/8c6xNu9l6XIhuKAn1p3Mm1udX70JLn6f61s5ff/Ew2tB1bFW8uo1Pf5hh30p8jwBNZFhpzamxd/z6JwWaOrq71P9LosNeZ3FsTbA6edOdPrJ5p0q/zidmoN1mafzfsmecVa7/IXpUi3Mz9HWfC69ymb5bFnH62B+9/xbp54/vvZ5h9uXxIPOgxAzlVW02YLz5malMNKq2aw0YcJ5qq1KVuTT+fm7FkrP2cx7QH6SScBaBICZEZssIVI2mbUn1yVR7sxth5jUfNvnJmvSvPEUcb/MxSv2bKE3Jw7a+iRbeuPEI64hNBvacEXTbGnalhBavDeiTxzZ/cysKQ+OSoQ58UNMws/jM1ZydWvadJ4zx5oPayJu+q7Owom2rvfO6W75nYXxUr7n+YRIDoRW9/6JYyQz0FqYxTSPbamjE4fLAhIDIowQV2zcxc0jfTTiRZgwCYbns7T+u5RVhrOMqr2fZm18BFE39XfVy6jkGA91O/N5J6JoNaYmeFZTvMsTq56b63PLuqPAHOWVHG/BqQVHX8zrebRqInsiK5RJWy3mdZzSDOxpUgMiYmQchumTF8g04w0EjJOWVCkqhLbwJjg1AAW1tYYmnA65X/M6TSmb8lugeEo8Co3ZEqvPdUvoqNmFk4A4VEd8CBQbCaTMTA9O6DYbUlI2myvSGLOwLvdfro9myw+RA/1hx9DvSXFAU2uCE4HJFL8irCchUAZCNUZSzm+abzJ/U609IYNa4k6vzxXT/qnn4DmGYwYUZ5pMp//rgkuTT5/1rwVwfMn8vylVfEuvlT5vPtZrupwy1Vn0iXUoOx7k9b6mvaYy5pOydnAyu7+bXVmCVPEDLP/Rt7jkEb1CGo+LA/4gtHuHS6BjjybFpb25tYsjdBsg4rotiKK6IfpsPeoCKnOw3zWxq9U1E8CZ5dssiK8ObOuYeX+WIiIpLc9u9ZgfL3010av1/p7PUaXsH+VMrnjlqUiZvsvtVVbV2FW/F3Ph2H3Tk0o8xcKwgCqqU36Kzp5jdJ4Nk3vKNCJpzBYPEe0P6Dighz1pHIiP9+jQM97dEfuewy+/MB4O7O7uSX1P+uUndBjoDz0pRsZ9n2X4RUHDTXSbODfHc3IOcRFcZOMDnQ9smg1NaHHdG6TZ0l99x9hcMV79wCFs+ejfsJeGX7Vhn4QfR2WniZ+SsNfIz1GJagpAOTJBqcEsWio0ZSHQs+tT0QJAZBBiirO1nofWtxLn8T29ZJdn9sxU5LPNC6EJBj60LV3T0viA98587hfhbPlfK15Aj6p1tiLV0T7dPzuTlkT9yfYVujOTiqZ0kZQ+fw75e1BhRIhkpZCS3arwU/vd3GYWNNazaVpzx/yefSmn7k6NPVvMVPvj59bMUH19XdqJjp/m5KKex6+eq1zNX5TH1nNj4nimiVNo5poHynnJbA0RQuBqu+Hqast207FpWwMKS7w/54xurd3cSZXhiSafAyFq2nPZkEJfn2z+Ku/lfJ/24QvTsWzx9WjFWRkQZrp6btSlU3x53j/90tk8KyJ/Pq/Ol3WxfI6atsi8Rhnv0u6qH6oj8kXpBRYR5j9vWf2nftW/C1Fx4v4T/THfSuc3h3OFw4rnOrUpXTIYhYyaF9vFaVXe1N7FQXKmFspkbrvK4XTmR+l0PWcGNU/Ic89R3KGYP8UYCyF1+pCpN09xDiSbIWZmvFhDIEtXKi+tf0VmLr7LoTwJnObqPFHbFVN+Upz2VHodJv2iklRP/v3SdEqD5znN9i+Vvp4WZ010rNPLDrXl7yqXr9x95835SltthXkfsgsdn/m7TJ44AMkBg8E1HX4D4e07UBicQ1zLOApeLLiVTNG8avJ3YRQ7100EjSbIG/sBjYk4RDusWtN6b5ri7mWEzF6kpMTBYkMYVZwgjRgrMgIBocnsZTYVnVhRMpMkuGABlCUYwZ9S0Ww2BqYfRlL5p4mURpKa4BUg+JYyZ8R5y895xAXatqNpW7ZXN3SbLZvthtA0+MZNAASToo4QfRmaNEERCpNAszCaPvddpf+Okl3f5LfmXc/+8lnzv56Ma15DRFBXmNTCdCRmdcqs2e4yg1e9J04qd0lLRmyxZ2TAaGKOJ9SaSaDrggENEvxcLxFiZmjFOQuQHmx+iCZjDitmpIAZMdm4TURgRQzPczQLcKYzYT4bzEDEVbygZoEM08xSivC7+NBdMj11/8KsdGBWg0pS0xCxoJD5fiXkTqrZUiHOoArFiiFCGhkz3TS7wTKgxotZKQwxgkAIjf0ei9B/1nJLKTEMYxbIm8sijZF+v+P+7qMFF5UcqDqNRC3AxUBKI9GVfvMgDu8DDY62awghEONgbh/Gvbl6yFaT3hmQ6dLBenJIueyBOEaG/sAwDvSHPWMcGYcR88wkiFNwOrl4aNstPjT45hpxDQOepDZnu67j3Q/v6a4Cjx87+r25mRjTSIwJ52xdj+OAHh4Ijx0fPvzEjcD29j1eHYEGs49yJO3ROJBGE+CMhx1xtLgVUNFEmRl33ldrQxAJiDh8aBDx4Ns8v7PZe/DrpWRjldLEyMVkrrMmRnJeZqiC9/MaAsFXnKcC4zhW856Ji5vkWQvA5eufX9/St/RHTAu6S4vNHBMlgtYLe6ZQLH0avasL6qrkXGiAmvM/t4izxWF+1pQj4oy9Tu9bKUN3Bc0GNte4ccRdvcH1B+T+AzLsCXe/InFAPvyblfjjf0GaFtneELZXhJu36OYKrm6I7RWp29o+6JyB0ZhA00TDMgW8VqfEYPvgiKJOshvMWRnFCCsoVnWSYx9Nlo2TsBnUF9fzxRKXPD5GA04KNy4rjBR3hGuXTlL1jtqZNlsbmj0rWseIYlIgMcB9aVG5GKoyhNVebJXL7oOigUhF+59xBDUrU0kJYgbIx8Fim8WIDvcwPDDuDsTDQHzYk/Y9abcj9QOH3T3j0LPfPRCHgXG3NwvMg8VX0H4ANVra42l9h/hiIQsBtcDFIvgQ8K1pUfvQELorQntFaq5IYcNu+x13zQ33m+85NFf82tyy9y2/SMsex4cxckiJu76n18QHiYySGLyQ1JHwkCISzbWSuhH10awdBYxqVosLIaM9I6BlnPFMwZg1VvPH5tA0HjlA82JgagFNCYow3V5qrsumwXUNt2+u+eHtW77fXvNdu+EmtGyCxeuIqpMLHFQM1HNl1ugKZ6tnE9PcWJ7T08Q8unQy1YTrVAao9Da/hhEZFN8HxiHx0zjyrxH+9wiHJOwJU+DqfQQ/Zjc9zk2EicflQNZWTImiFvN3qutxiv+X7I6TPH6CrYUyHIm8qAu4xEwUic6bWS3iqUVeOm8jZFqYlNf/FKjBMSnenhTBVTfWD2l9rbjkTaCjuRFLtn6LcH+pJFw+hbs9nTR3gehMH6qTqoczF6eYVYNGNAib21tubq75j++/493tDW+7Ddebjs22NfdMbTsDZg40uIm3F8DDpJhW1xlm8GEBRJzovuMrl5yJdR+d7pUvLUuSyio9l1hN31neMn9fkj61zk+9Vwtoyv5QPX+y//T4uenxeR+q9ye7qUy0zXS+XlLH43QxEFFroK51rI7Sqf3lTK7l4XP3cxcwnxHnczqqQ01A1A8900fHk10W11+iIX46p7kesqpTBYIu2jBdnZ57hnPUNel6Ih8pxNXpNkwE1NGOXCZ7VYcFGlpbQBR/0kv3BEfb0Qqpe6p9p8zBqmocvft0X607+ajTPyu9lME/BThcYgGxBhjO3Tv17Kn+ecn1TzEDe+7517Co+FRw5dMOtd9OknN6TMq3rUXnZPXMbCUAkv2lB1zTUVyPqHMktUCJoqv+PFomx5p6ZZWbK5hEHEbj+5xDPKhFbpsIHZVq36mCl1l9Kqah7DEVAVTOwUmDvxBUk6/7OL1bBNmKklz2l1uYPTIROJnvMwnJnW8Q1+CbjtC2hE1Ls2kIbSAUIXvp1CLhlrldJaiiFKFgrngpp/a9udToF0xTXaf6LXt+btfUGedSRSwUbcFZhiqrvbTa059YSwurlxNla8m7xMzIfpI079Xq5hgRxYeSdaNWGeS+qoKWn7TsO9r/57ovCWQbn9qSoWhUUl2b5vVizzy12ueO1WneLip1PC5FkJHm4HnFSkPTmD+moRZCADIQgeC81cAYO8nA0mzpXoAIJQt2xgHNAcNRhWwNMez3eCc0XrKLonGynkhpsN9OcxMCiDfQIcdUcOKylUA0H+IpQfa5rN7iP6R4ABLJZQ3NOJjLh91+cgs1jgPDMBCjEKMgPiFOEQ/iBeJA03SIevCJSCCpleOyX+aUOpo2kEbPOBSeUKf5klKEcWAYe/reyjSBlAFwti5lGpM0DujYk4YDaeyRzFhqNPuMlPI+mQKCBfSzEbfYMeYGJCBqQLALJnQ7yQoUkKDQf3kMFns0RUYmiKSKSdDpvogzC5UyUWuByjT3z59Wl559fwQrhM+p49do3x+hD3/L9HXpt2czPZO/zN9KPofzlcW583p1eqmFxWL9V7zcLGKobgPqg0mdmtZiB4yKaw5IAte3+MMeejUFkRiROCI+4IYD9Dt8HJHDDoYDsu0ZxzG7XPQk14B4khTrjCzQLZLLIlScPjBZRky1PkFjnBqSMh7lLK723kJvooKQ8r6cz+C6GFn1kSiqkq0jZ5p0PVVnmajtv1qd8YJO+R67O8njk10PSXZjqeNom/8wINndIDEDE+OIDgfSaO4W9fAR7e8YHvfEXU+8P5B2PWm3J/UD/e6ecRw4HB6JcSQeBkiKH1j0t890r/feQAfnDIjIZ493DtcEXNfiQotvW3z3jrB5S99cMzYbdtsf2LVv+NB9x2Nzzc9uy04aflE4JOWj7ugZeSAyiHKPhXWgCDyLHKGMTO5YLTHCJ9rULce+XNcSuyor3qhbzq1Fv+dBr9frKdq3XCsggmAKNK2nbRu2Xcumadh4T+MdXpxVBTufnfOcmsPAGaUAeeZ+/eQFe0Ph5SbyOluLaAnw7UhJ2CXlMSl3SelVOOQ9Tsm4z5qQECbYtQitI5m2ESZ6reYTK6o5X5D5W5j7OvNRRVA/C0NruvokYW6PrZcYnNhrVvVaD5HUGdRysXlPPf1dl1EssKv6sxhhCicyAc2rNqnM5c28vy75lFI3mfnypmvpthtuuw03rcUvaYolhC8WTWUdyZEidOGtz8mT1iDE3I/nzr5PPxPXipjnLG0voyE+hc546kyvD6Dq6krY+2lkyjNlLr/Q1YZx3NLMB5/dWNbnbt3u6vmyDqf1+LI+/UoxIp6biOd2jy9Rl3/wJPbfkjadx2eOAVEsIWL9IqcGpRZYFa3NU0FMX4Px+hJ5/h7TS0CI1yzzt7SQ+JYuT6fmhUxr+/hTni1jO61PZyBDCB400G66SSjmm0Axb49ZO9dJIeSryuT8nRR/vqWSQBbqjePI4+MjmpSuP5gW8aZBgsd1jQn+vQk1E4moI8PYE2PKcf7aDKa4qf7lU/fDtC9YT1h8AclWE6KkMaFiWiIWhyKSchwKUg4OKKDOz80LAdcEQrsltBu6zYa2a9lcbWnblqZp5pgE6245sWzPCew/Jz23T6zLrPfr8nti1E/MnXXel+wTk3VaCBT2o4yOySDcURlTWSlbBWSSvJSd1KwU6vacr8MJJpLze2u9/5XXgXmOZXBMM5eyBsBjPF8vXTE6s4B8FpQXYXmMCdGYXQtYHnGMqOTAl1k7xxUhDhAjEM2dkqoFny9amyklDvuBlCLD0BszlBL9fs/h/gNOYHCFiVSGZLEbgleC0xxXJYFrERcIMtK6SMOAVyWOO3Ts2d//SooDPpl2qXegaWQ83OU4NLZ3pBjZ7Xb8+usHhmHk0PcMw0A/9JlnU3xwOG8WOTjoNo+E0NJt9/jQ4cLGwNOmARHa1iN0vHn3HYduk83MbRco/SEJUhL63Y7d/T2bqzdoHHC+o21aGAc0Hhj29xx2D4z9I2k4oPFgWplZ8JRS3jvyNpgw0HLI8TeGMSHO07QbQtOy2d4SmpbOXyM0IMFAUDXZkqpOro7HsVhdFMCtzJdCl5kwQJz5gffe9ugoo1mHbILZ8gxMPKyBSll45L2BwuM4Wcp9CkP4jUb4lv4R0+Xn9t8Hf6I+8PjmO0gJf/MWN/b0737A9Xvk7mfcYY+7+4CMPW6/wx0+En7+ZXq/udqi2y2EBlwgtVcQWmJ7jYaW1GxIzhN9g4ow5DMrqllX9tmCQrPUswDsxeuh7cgGztdKBea+KBJ0RFMGy0ubypmLGi2YhdjFRU8OIUt0RaN5ejHvx/OZfUT05RRViJObz7wRa8wusiKSNaMl9RYvK2ZLxWz54PcjxETse7N46PfoOBJ3OzunDjt0GEiHR2I/EPc74jgSh5506En7nmEYiUMiHiJpTFOMozEdiCniiQhKoxY3yQdzzOqyT/mQXbW0ocE7T9O0Rgu3W1LTMW7N4qXfvKEPG2Kz5SH8Ox6bf8e99zx6z4em4yEEHqWlx3MYE2NS9sPAmBIP0TOo8tg0pORIOuTBzYLxSUGIpQhCpFJayf3rsqB8ErKXQN9FoFt+1zKNlSQdqdyO1u+W/NcCc/t7s9lw/eaaN29uefPmhu12Q9u2hBAWH1crK/H7OEdVhZRBGlVliHAYlcfDyMMhcr8f6NVxwNymaeF1PNlllk6rz0LWW1w3W5UZL8pB6cvTBbcdCzRxaludxttyNr4suymtg+PUQtDFej1q6QwIpOrvwhdXoMIEMiwqpkwhvbUCb9bfGqe5O8ewqFyDHeVbmpF5rqeHq6qN5n3OQLYym81KC8YcWbDrNrSbDd999553b255e/uGN9dbrrdbNhujfUPwEz+26rEXpd/DfP7HS3/8/r7cIuIFk+uURvaRaekiv3NojJ4Dl16U1ujZjBp9/QFcCynO/S5VW2vXnMvnmVKrv+V0V1d5mvCiRl2XdThl1XBO+Hnu+1MEcc/lee755/L7faSlkOqp7y9S+gtAiEvm3nPPrOfBUwLUU+9dks7l+ZT1yNdOr1m+6hRT+mQbF30n1Ycs4HfmFqcwas75aV8uhNqUF3nGFgJwPSw1wa5GNMVogWiTRvCO0YNThbbJROzMRE6MXtEQEYe5PNHMg8xgZ5m39dwtBqRTmyWb/EpVv2I2X9xAqb1X/CgX4bzzZi0SmkDbtrRtQ9OYW5qiSeKcM3/89XhOQkStf372mOukcaAnrl+w9nJ/1P2z+D5BEJ8S1i+E9iXvhXA+5+mLK4QylhyDIFNBWSCg89/FvBstOog1qCJnv0u2p/r9KRBibtc8r6X+T/Xo7Fv2Q9FuL9qxy/Gv61C7eIgxTXEcJAstprM0JXMdJZaTCKjTCeyJ0So6BaMeB4rVSIqJ8dATY6QfDqCKS4nhcCCO/aRwakIZiHFkjCOuETSIWWZoMvcMmswHtUZIQ3YNYRYDY28ujFSjdZVTNI30+wdz66BNrk/ksN+z2z0yjJFDb9YQh76f1mRoTEurABEpgQ8DUT2hGQhtwodAcEyBIr13tN0GTYm+bad5bnygohJRjcRxYBh6YnZn4bxmENVcU6XxwNjvGfs9cTzg0oC5VcuzL8U8B7L7q2y1Mh56C/Y4jIi4bAk2WmBvEn400CSoBeM2LwMZhEiarV8sdkaZEyUYe2GMheySKRUaK2tbigna0pm1vzzXS57L+0+lk2Bh9c6l5/LL6NZv6TXSOd7ht0inzowvUQZ8Ho/x2nW8ZLZ/yXG6NK9jQZQQQ7DDywkpNiCK9B0ORZodPinusIMxIkOPjAdDxuOIxB76R/AB9QFptmjocN0uAxFbkg8436LZYjJh7n8SYu8h+YwyIWgydZEsFhSSFMGmhbwuAk+nEZddOLqU3SyS99wsDEzMsZ/KhiipWMaOzESc3RetaOEUja5ZbqT5O587WQOaZBYNkobscrLPlg0HE1wWiwc1N0TyOE79qeOIHnakYUR3j6RxJO0f0WEg7h9JQ0/c74mjWRqmw0g6xAw4J1KOu2RgjLmJERLeZYGxMzemXs3dowumGBRCMCCi6XA+4NsNEjrY3KDtlnj1hr69Ybd5y+A39GHLB/9nPvg/c+/hUYSPwfHoHAeEUYUYBxKRXi2mVK+JQc3papLCktT00iyHsME5/y2QaXcqedJq5dlDZxbkrA0+V6BSlJHMG6jOZYjxJiF4usZ4gzb73Z94g/yMc0WjnBedvV86FcpC85yNajEixumTGBVGTeYCSLLsrMQN0wJCrD6FRcnfhXNUUVsfzJBQqcf0VOEbjbhZjadMfX8MQtSCsyU/Nv1Z0eTrfpj/q+Zdob10/q3V9cV3AR8W83b595pzmdpbfVv2Z+QXCEiBIebkyr3Mf5jxrLkpDk3DZtOx3Wzo2pa2aWlyEHXvstVOVaeTfN2KJ7xUTlRdebJd63wvoRXP0aUvPUtf3pblu+syvxQg86TS3So9VYdL5Wpfa2v6KhYRrzcorzmwv29GSG2vfvV0bhiKJYRZQMx+kFlsT+u85s2z1lKe3DE9AxS8rN4nBGYn8366rN8zA6x6WkBWf/89pr/ntn3ptD60U471VzRgU0oL6wGXtalTobldFhIHIYjQXmUhVfFf6ooP3wxOMHs8nlImBMsoFn++Pu8BPvgpfkCMA/sPv9j+cHOL22zYNgHJ7gA0mhuncmZ473DegfOoBJyYlofLJuNln5ktuWZAYv3RpCSJmJqauZNJowXk0zHmYNjmqIWQYxYET2hbms2GzeaK7WZL0zaEpqFpG1yuw9QP1fe0dlMOPKxLjfn672k8Lx75iujm6X1CVTOTy8KFat03BRQ4WVKlUT3V8wTxVd+D2ZLASSEzKsElUvnHZWbypeofNMdQ0Cn4clX7XIb9XYNSZ9ux6vd1/x8JVjPDZS6jjImsSf+6T2YNqhzfRMmuusp0OD0uxVqofI9ZSF4CjDZNQ9OESUO+JB+MsfU5PsEwmFB9jNHcJB322QJiMACiABGHDESIzYkUE1ic8Mx8Jvqx5zD2aOvQxjEOB+I4EtoO7xuGriHogUPaIeLYPd7R9wc+/vxX0tATGM2Fg3ekFNnvHgjBo1dXmMZd4v5hx68fPhDNzTWHfmC3OzCOO+K4szgsTZORVQG5QxDa7S+EpuHmzTvaruP69r1ZG3RXNE64efOWtu3QaLEo0N7m7zCSEKIOIMJje8XVzVuGw54gDte0xP6e8eEDu48/c39/h457NA40DpyYlUe2z8maZ4ZfjoeecYzcP+6JMdGPgwkn2g0+NDzuHghtx2Z3z+bqmlu+Q1xAXENSs6RJ42garXE0i4tkQGzfD8Q4TrRY27Y45/He6CzvG5sHzqxHYoo452i7LmNmNi/NjbMyDANOJLv6YoqJ83umi76lb+l3lVZnx9/z2hEUp48AaONJjWfs3hg9cfsGGQf87pHQH2gf7vD7R9L9HXLYI/sdrn/A7R/RtDMf6TnmQeER1efYEc72eg2txbPwAcSRfBY2+mBngTc/9aMIUYRRPEmE5BxR7JO0eO0JOAnzfsqsyJAyjWx6ykVTe7YgBHCkHEcjS1ELHZcK/ZiFjtGEkFpiS6giscfFHov1lNCYg0ePZumgwwFNkdgfzOJhMLeGOo5oTAz7AylGht7O7cN+b4GjcwDpNJolbxzH7BYxznVPYu51Cr3gI7iEdxEk0YjZfISmw7lgcZekQbLFo2yvwTdod2PWK5t3DKFjv3nLELbsunfsw5a77g0P0vHBXbHD80jgR/H86LLmQDLwXpLaN5FIT5KRg+yIMtCnR2Ia0SHHvsguUyl9W2KDaMzfnBYW22StAILqu5b8KhSL0iOaTFZARMErSj7OTe5Vy3POe4L3bDdX3N7e8ubGPpvNhrZpzPVNcW/lfC5iSXP+lvuHAjGJDReOqIkhKX2Cg5oHtqjCqNBn5QXVBNndlANaDNDyQJNVJXJEGlJ2oxSLOyXrUAwEhIgjiZIkr8x6SMp4Fj5Bna210ocqOSSClKBvJyWnFsS9Agnympw7QefPQlhexZ0pcy/ZjiFEdAqCXubnADraJw0ZfMyxIWrriDNC4IUgu+qCo/ZgfFyx1ypyQp8BWotdljDNIdhcb7m9veHPP3zPd2/e8N2bt9xsN9xeX9M2DZts0e9LTA4KvqMn1N1+/2fdOQW503Km12nPOv/LFC6Oe/c102VKFXX7fzs53KsCEU83eLnDzETcqd/1c69Xv1lg9Hp5vlY6SdRWsqZzCNbTxPD6oD1f7vz3sYDmVLm1lsCx0O88UPA5WkqXgBF12ev3z/1+7vpz9SrpawjUP8dCYJ1e+u6nMF6XWjo8d/2pOry0T77EOP3emNJa6DoH+pv3W+qvTLQXf7CqRhgWLYiSjx2btilN+89UINNdVn0xuWrLJs9j1sqWJhAE0jhOgcRIM8Mxafw6h4rLjAAIaSF4rgXQa8J+IZyeHPfm+tV7XRaEgwn0RATxHgke37SELBgtJtamrX3ClDX3E9UeqmkJErw2uHguv8Xv3Ow8IvliMect9iPl0epMSMfngYjUR9N07ehvyfmfCKhdyj9uTPWp6lP4gONyTriRqoChks2pvn/qnCt1sTLVTMtX7y6IzZrBOEfwFhRIZ6GHacKXmAxmDTGO2S1TBhG9c8QUKzBCUfUGwuR6DP3B3o3mtzvtH0lxpO8PxJjMAiBGhkOPARFkRlJyfcQEHWNkjD1x7BlxuCT0vWlbahrR0BIPD4zOQjuLOPr9vQWe3t3bc2JAhAafA2T3CJ4YG1JShiEyDAeG4UBUIamnH0YO/cA4HBiH3dQXxe1GTBY8sBt6QhMyuDnSdlvbl5oORAihQdtE07akUdBhtGCf+f2Y42SMQ28BPouAKFuRjP2OcdgThz2k3mJaQDbXMjBimroKaCIO5gd96A+MYzQgIs/5mCJJhKjR3NB5xzDsca5BnJqb75gYh56Yg3fHcbRg7CnRHw6MMU5zqmlbvDMNN+/MAsQ7b6Co+gn4nYRni7VSGH1Zzt16yj9DZ55K5xi/p9IfTfng93KuX5Keq+s5LcKvlb4W3XwZI/7yd58VL/yB5sq5NPPKCcm2BCpmjaXOZ8UQjwQLhC1NS3QObVqj0/Yd0rT4x7zvDD06DhCzK6I0AmmW+RaXg6Gxv32TD6j8ycAEwYAIJ44kgncFiLDvKN4EnGoKEOIaOzsy6KBk4Sia3TzOQETKe2bMlg5hTVeV8zdmXeQUzdIuK85Qnc8yHnAxgwsa0axsQAYa0tBDjEgGInSYAXNNEc1ARBoG+86ARBzM4nGynszWvCW4rpXvLO5WpjlEnFnz+QSiE2jdNFc41+DaN+Ba1HXgAnH7xs757oYYOvrtewbfcb95S+877tu37H3HXXPDozR8pGOvjkd1/CSJn4n4fHKHpARNeBM5k3Qk6cjIQGQkacznb7YyrDXKJ7q8EuAWYfGJ72ldrpffJPyW43vHD050a7UYKpJZFtel4puaEKZPmCwhjLYuwb3rVNOQr6m0+SlJp/8kA3k6BZLPDOK08dW0vxNoyDEhEEIGIiZnaTrzE5NibUVCyVoWq/UDMj8gZfyWNP5Ee0gGIYTqu8qzzncCHFb8EoVErxpaz7t6ztV5LJ6pAYe0Kqviocr3CVnWk8pRVfVm4M0+E2+vyX47QXL8tC5bQ2w3G7PcydYQwXuc2Fy1eW99Z11a8XnT/cI1nk9P8qEvEL5+ylo4J4f5VMDvEjnTusyn6pDfLFdeXJ8TNTxb32WZfNJzz917rfQbxYiof9c7xnqinGHov6XL05numjWo0/StmiaLiKf6eRL6VILG8pl3xuNN9uIqnxBqXQJC5DdeVNa3dD6dIpTOPfc5ZXxLL08pC0MLsVunWsAax4gIBOfNd3swn+L4WYgLgDeBcZAWzVrdmXxcEt+QCZLsDskKXJRZH8ROhNBamd12Axr5uP9IGgdk7Gk3V3Td1szBQ1NagGAaHnizSlBxJAdePZ7ZEmKuktVn0sJfaciXU0acIk5L8801VDIXKIIg2SzdNQHfBELX0W42dFdbutDQZu0R5yr//LmvFu2v+qQGgur++bz0gn0uE+qFRl8QxJotIphDNZoiWnbrU3zTk+eaM027QrhS9/Hqe7KycHXZZMZZJ1dWWkCg9fwpDNGJptbjXJe5aPbU/Dnf2ff+fO0c4V+6zoT+floGEyBwAtyY+vUIDAPVsmaylliMJsDOVgvDOExBm9PQk4aBOIyMbcMYRxNqRxNEtG2D947NpsMJ3H34NedjwvXx4VfGYeDh4SEDYXkuxhKgGdomcLXZog5Scux2Ox4fH4ER1ZFIYqeJ/vDIOPR03ZamafHpwH5zTWhaQNjvHhiHnvu7D8Q40jQWyLJrO4qpOEmJY88wjtw/7rh/2JnVAZ5E4P5xz8e7B/r+jqG/x7sW7wNxzBYT+z1jHNlsA00b+Kf/8O+5vrlBcGy213gJ+NDQdFf40KLjyNgf2N8NaBzNbVRMHPoI6mi7HfGwM03U4NHQsH/4lftf/o3D7pE07PGi+VOYa81zrjCEppm6f/jIvh/4eLdnjJHDcECcY7Pd4rzHHzp803DoHzgcblAdEGlAmuyaKrJ7+MDjwx2Pj/fsDzv6g/VVjGbpYoCgzWknws31LV234U9/+jOb7RVvv/snmqZju90aqJX3wrZtbX07s2XzPq+DWDtF+Lz0W2t1fkvf0hdPRdD1D5eEoAZAxDQLExVBQ7BPtyFqok/v0LFHe4tfoH1Pt9vTPh7gsEMPe+TxI/Q7wu4jftjjD/fI2COHeyS7c1r0c9F0dlnHOiuJNDnYdYspqKg3N6Ja0zHiUHLcsWIxCxS3JinLNgt9YbSA0XOo4gYTvhY3xZOXgHL+Z2vNEmMsxThdHzURk5pSQErEMRq4nC1vY7Q9fRwGiys0jNNzmhK+7/NzcXIfVfzvZ+rIXGOBxVYTP0l2o29IvsH7YBa7bWt0bdtCaHDhCnEtrnsHfsPQviO6lge3YXAtd90PDL7lvtlycIGf2y178fzsWnpx3HtHBEZnw2OufAwU2TEy6MhoTyDa23eyINsMB4gj2vfZQma02GwKokpKI2iEOJj2eTQXk4xZ0zwWLfOUwQtzt2hxN87E7JiE124pkK4F3sAEVKxBhxrkKLcyDxBCoGkaurZh07Vsu46rrqXxfgIfnDfrX5eVGWbAaHl2/nZgRKEPba6PqkSF5BzioPNiijjOMUqil4QX8CS2IlxJmCzlA5KVW9JE45vlQ+ltndxnRQSXXTSV+Gt1X0/0dAGCivZMclnYXoESR2BE3brsVknJ+0nd7BOgRH09r+fiNm1p1ZDBBsqczNYP9UdHFjEjxPahWpi/VqQqvGypVZmS81xJOYcZCDM+zC0UzZptR7vpePf9e96/fccP797z/vaG26srtm3LJseGCNk1m0y8/gm5j8i073x6+kc8P59LnwJKXD4Gn6OM8TXTVwIinkeJlhpbc/p7ZXCeRc1e2O6j/KrXT6F6x5qhtbZlha6u0tFheWITXf++JD1ltfASMMJkY6fLfKqMT6njS+9fWsZLNo2XaOJfoqW41ix/Cox4SoD3kvQp754T+l2S39/FnnJJn2XiywjMtJhbqrOjGeNfsvaDCOZ3fIIhLBVi8EQZExl3gmC3/LOw22e/796jcSQNPYMI/f0dLgQkmDad8x7xFq9CxITNKYMaIhYAsN5jTq2BaR+q6rFoSsVzSGYYyAI75z2+afBNQ2hbc8PUGGNX3EGxKnvBWMyU9ETUnlorUirDcdc+p4Gc/zq5Pk8KxrEG27VJmjDVU/Pz03f5JF12VFX+ub1+sb5OzJlJQ2oF2FBZjhTgYumSiefLe6bvzj13qs/KnykHXy6Lpe6femzreWjzYDpIj8o1kMcAsKLdqFpiAjAFFB6z3+wxjkSNpDhkFxAJ7z0h2LoYhj5r5JvgfTjsGYeew/4RzbEmcsZT4zwN2npSZmrS2BOHAzAA42Qt0O93jOMBpwmNPf3jFtFEHBoQR79/JA4DcdibeyhxJO8IMZi2YAHtVCfhSozmhippJKq5jDr0Pf3+wOGwx0nEucA4QIrK/rBnHAfGaEDE48MjznkO+wPeN4zjCOIQn8sMDaRI8IGoKQc3LXROdssWx9zmwOD3DL19UjQhiXjbFyanc9NQLumpmF1kxOwaaxiGvN/ZXhIEVBPeBwbvOeweUDyqnr4f2R8Gdo8f2T3e8fj4wH6/Y384MA7WP9O8SBYQG4X94yNt24JGtttrEg3dZmvAbxOmgJvFNd8CkK2Wx5c6Cc9pj/3R0h+h3q9Fd8Jvw7B+6v790vw/Jd/X6pfq1J2vPUHDvnZ6aTtqGkUnsZkJJGfqo+K3soWCSj6zQ0MKLaNrcWGAfYd2PdI0cNhB05CGPWnX4IaDuQQaB6TfV0I/tSDOJLTgprHuSSNMRAQpijXMtGgSR8KEllLFPDRBm33XStaahdSSkskMMxBBMlcnUrT2M1BRrBk1xRwPKMf2SckE9EknS8Y4FovHlEGL/MzkljFNZ6OqmuWEmiJI8fUu4nBeSOKm+G3iBLxDs6s+nCM2HTFscL7B+QDtdgoMrr5h9Neoa6F9h/qOXfOG0TV8dC29NPzavqd3Dfe+4+A8Pzf/f/b+dEmSJEkTxD4W0cPM3SMiI7Iyq7q6e2axmAFAtITjGUC0RCDCW4PwBKDBLmh3Z3Z7erprqrqy8gg/zFREmPGDWQ5VUzv8ioisDs60MDczVVG5hZk/PkbsQPiJPAIB99pz4Kxelhziyjw0CjiQE03XxL3UWIzPQuZgft3sZYDDqjK4eUlbpo3zYhXod63iuv1tybeSjr8UZnSum6n8r8oondeX9x7eWbLmLGesyCtfFIBf+hDFU0irSfDk4M3bAaQh0TwBHQEDCAOheEF4AyKy9xEIxgebKJSBQjIgTVD5KzR9s6wf5ZVd9U7lJXL43noh5GE7VnZ9+uK+5oXl/JIapkva65t5W8riduuxypR/zlJ7y+x22Lxq5m6ReYnQ9wPGcYPtdovtdovNOGDsB3TmCeGNN58b7In9ewhClP3+lbjGY/q5S2Thy/TLl59/a+ty1dhtsYbX5PDzdV3jDs7W8ORvB2daeXZ+Xq3vvMxPz/8BnxCI+PXSF3JQPJGOHXQZfFDGh2eHo9LxmOH1AHYlPMnSQvmpdTy2GV0CQvzaqZ6ln08oPAVsnAIlnvKMr/R8OnaEZb1pppIzIiUQaYRLclQSvWZmOcfjJGMgOVueNIpoEUFqQeP8hymQs6K+KGyh9w7jCIJgfPsb0MMdPv7lz9jd3eLhpx/My6BHt9lg8+49hqtrbL/5Ft45dMMAyaCJUDYqmbd3MS+XbtBAboIzjwgCnEMHFeyo61SYyADEdqPvmw36occwjuhI82hkt/4l01wV0yooMVd3+dby/iX3rDWQ+dR1zrlZXYpSvClDpIYKEhE4P9/js2LzsrwMQO6hwrQv+kQsdEIOcaBAhLG7JmjnNiz3ngPG84K+aO9dghHLsUK2PJJ67uXzMmVLSK45TYiogFUpx5q2pH653BgZMSaEEKsHRC7HwJiUGNMUNUwTPYChSTcTq4Wg36llvvAVOu/wcPsRYdpj2u/BKSLtfkaMe9x9/AgRRtc5OGguAVXERzgZEPpU5Llp2iOFewjvAZ4w7R4Q9hPStNMyhwFd18GlCcNmg34YQc6V+kuMAIAderjUgXxCTw7DMMK5mpyZ04QYdpj2d9hPjIddxP1DwO39hLu7n3B39zNEPIQ9UhCkBMQ0gTlhs+0wjB36bsDD/R6bzVtMIaHzWwzjBgNp34+bDdg7IOwQJwee9hAHOARNBJ4ieHrA/u4nTLs7wP+Mu1/+jPu7n5Htaj15zXPTzC3tK1d49gJEpKQJq1lwd7+DiOBhv0PXd9heqycJhJGmHeLDA6aQsN9NeHjY4e7uASkFpDRhP02auNuAJN9pAlHmhJQYP/74E6b9hClEiADb7RbjuMX3f//v8e6bD/jv/rv/C67f3ODbb79TZZ/zgLdzm3Wtzdbs17P4K32lyyifgc8oYg3w/pJJQAjUKe9kFuNeUBXJxpnVfIYE+BHkR9AApCvBjgWSRD0JguWJ2O8tv8RHUNjD3f4Imnagu5+AOAHTHVyKGG9vgRQtNCBDJrWUp6j7uEtZSa0W8cSaHJqEEWlAQG9na1YS5nYZr2ZKmrrHi+YoA8BMZvHfnPei4IKIJvTN4ZH0bNZ3zWulz0zmnZbzVKTsDZq/z7xRY8wvAPajAg2ccy4OHeA7+HED33egzRVc18NvtvDjAL/ZwHcd/NAjje/Am7dguoJgxI6uMdEGP8sGO/S4lRETOuzcBpE8fvQ9dkT4AYwdBD8RYQLwAEIE4c45ROQcAQxJCSQMnyIoCVy0XA6RITzBp6lJjJ3zZihCJfaeVV5CDFACMNk4Br2HoyY8j+Y5UTwiQuNJYe8p6SsDFktl8CVrbbGoixyeQYj6pV5elLT66junit6hw9B7U/TWVy4ry2tf1vrP+Rl0ngdJCMwIwhAh9M6DhOCFEAnowQpCEHBNDldw8JTDMekrMpDAmEgzKbiM6VF9YhSYF8vcsAdAAyjgcPyIgJKuPvNiqbknM2f6RhkMKKCAAVm0HINmBVILLOS5VXOW5L2PMtjG9b14Q5Q5Os8NUSCVds+8gGTGt0FBSFIZPnvoIMsfncc379/j5u0b/M13v8X7d+/w4c0bvN1scTVuMHYdhn6A921+wJU5WQCKz6Wi/jLomIHwGghxiSHs0wCAS+ZJXoEt5bVSanpBOZ+WXhSIOKX0rh/WbkSz2dD6959A4Xys/p9F2W0o8rHJd4lS6xwIkRMizhUvx8uav9ZjtD8WkFi7/lLw4ZRCaq28x9Tp01Or7nhiCY+s96WK0QNL3xOb7SUM1qlrLpmH5+65tD3Pp88IgjWMWqNKbXllZJ+HzPi2SYfFQbnCBihoyyXKVhDGQLcHbmNlsgQjikIWbT/rXua9h/Q9hqsbiADO/4SYEqbdPbKlfh+vgKEHdR5baF298yq0FaBjVpPGDi5bAuT9YVFHtJgKlVBDzn5wzqEbFIjohx6+61W48wpSrI32ci6JPTB7E6zOtVagWSnz4Fq78CkWIxUsoVV2pwBFJXRBDQHTzoklCLG29y/rsg7UYDZXSl9hLoijGdk1mj2XaM5mXbiHXL4PHHq0tGBNDr2lehqqYauMwW+VT9zk3NA5vRiT3C6rI5vQVP6ze0OMIAim3iN5p94CMSJaeKYU9prnIUy2Xp3GhjYLUUlBZf3QIRtUcZoAJIAjJE7gMKmXQ5wUiIAAHBGmB5Alb3bOFwtR71SFn5p8MKVtQuCsoBEGc0KMAdM+4P5uj90+YtpFhCmYdah6oqj8l3OFaRkpMna7Cb7b4eHhAb7rNQmz7+BTssR7VEInCOs6FhGzVvQ6NJwQpx3EBQgpOCIcka0c60zUQZqvP2X4CbYmLGTZbE4YYppigkNE8gEkQCSHOEX1Atk9YP9wV8JupZQgKTUCr+JwzimQ1HuvsdiTAhMPnDDtA/y//AumfcA/ffOP+Oabb3C1vYJsthiGASLL8zoL63gxvvo1QNYvgX4N7fpr8T7JdJEc+Ynp2dy5ZG7leDteq30tv/6Us08VqMo9HOjOGhYv8wxkUC4pegFxDDFNpHgBEiC+B1KC+A4UJw19GPdww1CACI4BXbcBUkKcJvU82Ju3WphAnOBi0FwLlnuCkgESwkiiXmeqgmQwu8JvlD4QsdpWykBEYs2OkUEDBSK4frYzPJmRgP4nENJzXXNGq/KdibTtor04Gw8CiHyxbBZHQO8BR/C+AzkPN45qLLO90jBL2yu4fkC3uYIfBvjtVnnVvkca3iANb8DYgGVEkCtABoQ44IE9brnHThx26BHJ4xci7An4RRL2YNyJIEDwwIIIYAcFTGL2WoDmXSJJahWek/lC82FAlDepiltT1KasqG09HiqQVJP6LhS/2ROi9Yjgedm5PFmCEAeCSjNnj075Rohaubj8VGSJ6hHhzLCrvhqZI/OzL7TOX/ZssrlpPGlC9YwgU0V5WykdEXoi9CD0AHpS7w9n7cy8MGARgKHyY1a+CwAhgTtQcUmpR9PI+t4MZyPIoRYsM7m4bVvmRltZeSlcVFxCUIEDKeXRrC7L322+l8TWixBOpybdieFb6rjK/m03qhzbhkVXL1zXddhsNrjabnFl4MPgOw3RbJEJnHdwFuouyxZoSp/xhi8yxy47RZ8i5z7WC+EQCFh/9ql6tbQ00j1lrLvmRYGzYMShzvM0Lfv6Ug7msH8+hWH0J/GIOK9sOXLxsg//FdFLD3meRNl6M3tC5NiZLZ1S/Duz0Cgov3ueJ8RLgBBf6eVpjclZAyEutcg+ds2XZRny66G1taNdqQyFM6Y3ewaIWW4Jq4cDiSZb7rzXGLvN4di+cxOKs1UiY2Xc15S1+TYiwjBqmCP6/t9gf3+H/f0ODx9/xI9//meEaYeHhzsMV9d4yw94h4C33/0Gnq6wGbaIkRFCgiABLpUjoWEhtA35gYsdlCBFYACgru0CdJ0egY4Iru/QX2/R9T2GzQbOec1dYcL1QrU6JwN6RBoX/ZTjgS7r+sgjbfUcPF3C0rKf0bhnNswsL67LynQigJwyueqtQiU3RusRsXzm8vlaVWOy5PDayvsbGLHUdJzrqEeeA4dr5jiwWmAQ4xOXZ2gJsWBhFLJwQ8JqpeS7Wf3YLChjTMWbQrLwRBoOzTtNHhe7CfAOKUUwJzivYRg0aTbwsLtHChpKyTtC2O+RYsT+/g4pTph2HxHjhIeHW0DEwgYQaOwt9nJESBMeeF+UCESqwI9pjzTdI+7vEB52xeowhD2iI3gHxGkE4S26vofzPch5jP2oiUqds/YYeCcElhq2iFPU9X73ET/9fIs//stPSMkhRkJIETHB1pLAkca57gcN08ZISAz89PMd7ncBm6sfsNsHvHnzTpOQDl7jNg89nHcYt1t0nQcsFJT3Hl0/YOgdhCc8fPwBkYHAAkKARi5WwEZEw2dkmdW5zkAvFX6dJakcNltNxfmz5srQcBsJMTBS18E7B+4TPADuVHEWpoDpYYf93R3ub38xwzlSS0rvMPgeHTn0w4DOa5uICIMbsN9P+MuPP2G/3+Pjx4/Y3U34y8//P5Dv8J/+4/+E73/3O/z3//3/A+8/fIvtdqvz2BlAbHt9Smxr+Csf9ZW+0vPpCLhw6d0nFBeflwTOVwWcnhT53Dc+MQPFAkAcSCxOPAFCEaAE8pqvAV0PhofwBiIA37wFmOHS9+rhEHYKhIcdKEXg7k737v0ESVHzTKQIt9dcA7R/AGIA9jsNZ2QABaWonhZhX3I4pJiUN7M8S5lPo6QWzpkr4rxHOs3PkKDeDNGZ15tC8kiiCrxEgIhmbNBuEDATkmioJDgHGJ/tfAciB9f1EOfg+gHkHfyg/KbvOkjnsX97A+k6+GGE73qMVzcKPGxvQP0At7kGdQP8uFVgot9oSNGuR6IOCR2m4BGCx8PkwcHh5wfGX4Lgj/uE+ySYkka6ugVjEsaPiTEJIbDlZZoiojCihaSiAhIEC0tTQzLBQCe4PQg7uAQ4FriQ4CIjRUu6nSaIJEjam6fDpN4PYTJjmJz/YdJKFA+INqdEm0Oi8YzIoEarKDbeBmgVzSc5+XKfLJdjRRRALjMGum67zmMzDhi6TkMZOTJrc/VC9aash6CkomgNfD4rsSAnPE8imEQQyjuKAZhmaSF4EAYQNiBsibCp3VJfpHbYbEYdjpzmY4HuFY4SyJkcK4IczKnqwhfAUdHlE9SKLqHKCI2EJVJ1uiI2l5p3e9ZhEOHmucvQYGiArdlvFrrWwrPpfMweETmkWFv347Qm4i0V2mWuKMKLnJfVkwbEYhAEDuNmi2Ez4tsPH/D+/Xt89817vLu+wVU/YtP1GMcRQ+/R972VZx78JT/sOtlTTzfkV0ePUeyfAinyGZ7fZTaFL5oEq8rvx9Zxfv26bJvP75XQEp+JPlFopkunLx2MVTkMWrRy7c7PvZk/kl66vucsxVsrzqWSaq0couXnjLzSbEN8KjCw9KJYr8N5EOLw3vN1+TLnSt24jinrz7mGPfnJJywrlqDDqc/H6niqzEvvuaSu58r7FON+rn4vBryslH8wHvkaYzKKt4Jz6DpVEoqgxs5cGdt5O+b7SXvgFWt35NA6mResLJYqtQHfD+jGiPH6BsIRm+s3cF2HyAzfD/O2UQ7Tk2Nh1jNh7VShtlpZD54tEctd1brfWxJi5z3c0KHre3R9ZyFRfAFysujSWqWXPdXaKe3eyhZMSs7vb+3fpb/aYTxoZe7nlW9XQSHtmMyjA9aHDTYwK4pQQ+4VMOLQG+IYLetQp+HKum/BCpfHjyrTewqAPgGCnrKQOTXPZ3O+iYfdtkllkFz32oNi8RXYwkOAXAEPAJQQEYdnL8FiP5XyspJYrFPIZXAoR+DVK0MMSERIMUJi0qSYMSnYYYCHKhESCA5I5hHBEQJCCtnjglUR4j04BXtFiCXgI87Cm4YJEtY40Jo+EyU3ATmP0WlaZ0km0JtApvdwETohyRT2ASkRYvKzPQogBQPJaXgwR4hRvSr2U0Biwf3DDt0wYIoT+jRY3QjMTmMQW86Xru9VSEhJ8794B0cCSaEIk0QJjhTEdWRqJWHMGPuys+Vwds6AAo0L3XnC0HtwUvDFe6+gsMBCI9W55IjKukrREpUKg5KCIHUDazxQGzd85zw630GQ4BLAKeDnn/4C5wj/+R/+N+wedvjmmw/YbK9w03VaZwMeFEQ87gn71LPy2Pn3a/AsOEWvYTDxWn3xHA+JT2H99lR6bt2OAc6XkLI2LR/R/LYCIrzG0D62/S8zllVpa4GMkP1Q87ElJe5K5bXqHlmZDrIyCFxCtGSzaHIeJA7iBJAe0ntIYgQ3AikhbVQhLdMelJICDimCpr0CEdMOEhMkTpr0mhNceICEnYH+yYAItj3fEkeLKg9zsmSgysg1P48CEJLPQE7IfCSopOMpXKZ2hYODNyBC86JpLoceIA/pev1+HEDeo+s3IAMS4D3czTXEQHPXdRg2V3Bdp8CD7+GGjb2P2nfdoDys0/PGC5CNAXohdEKgTs9i9gkJUnPwFu879SSxXtBXVsofKGaAuadd83v+3lik4puQeXfJsyHPG4JjApgU1DjIB5GVuo0nBC8Vvq13hNRXqwBcXQaE5khfTnu7z+aoTfiStpdEQ8d2HfquQ9/1et5nPhk1r938iTQDOZaP/tSUe0jZIPWCKUAEA5F11eZlLqbH1BHMd2ee3XQ7Amt/lj+gBlBS94/q4b5o/XK/KuPZfkYBc0ptVmSnfH2dv3JkHqx1SpVp82QuUKNIATZqou08Bxu55kJ9JbXtgMq8ayAEEVmybweCU52cydaw0ExdP2AYR2w2W2w3W4z9gKHr0ZGHN8OyVr5D2dPXqcpDWr2nnkO1L54/24/xNI+R+xZ3nnkOHb0mP6+VJUWw4AEEYpvfmnHvorSVZ13aZ5fpPk97iJx5wpl7nsLXfsIcEU+cfGXuvtwkvpx+nUJTS2tWnPl9uUnOlT3z0BvFCtZiMM/R2cfRS4EQXxI9R8hp6Rjo8CUKhstN9KtHxCckO+myR1NleJVbJJqr6ff7fYlB75zDdT/o9UKquCMpS/n4GquKUqsECgOYGTdAY/0DJf6trnfUGJYbh94Tvvnd7xHevcMwdJge7vHx5x8gTq22u34sT1RrbVtjWN8vyt9Wj2OgXY7v7kzR6XtNKtuNvXpEXKlA6PoeBJWTJSsRs+u91Di/ApQxYFP6crGEsb03K1dP7HvHevsSWgIjS6BZTMCofZCVC1JkwWU/adJuc/PNwEBzFqzVYa0+AIoivr3uwCOCaJbXo9TTypn12yP3nCUdA1wPAZZ55+Rxzp4v4MyWNMIJgBCCtUdUuZLvTxY32iw0c74O55zKz8hKAG2i9w6+cxD0FmM6maALeN8hxYTdbg/hBJdYLe33k3pE7ANSDIh7jbksjoHkIR6AMDjsVTEw5fFiVdb3PdL0gLC/A4e9Wh6mLFxBwySlYIr2ZPXXRPTjZouu67Dxmh/j7uMOiAwmr/3DAUgBTljtt4jBHDBNO/WISA6+GzQkWnYfN77DOw+Qw/09I0XBx19uIQC2N9eIKeLu4SNcT9jEKw0eYXlgBudBHTBut+A0oOsUhOj7Dt4JOD4ALHDCmmjSeRAp+EAmQWfLs9nUEIYjh84B4zACAmwHD4cOHa7U8yWZ95nr4MiDmeBMV+KcxziOiClhEwJCfMAuBPBOk5f6zluouBEd5YTiQGJGMo8b33XYXt9gZMYQA3b7Hf7hH/8Jf/mXP+Hu4y3+zb/9b3B1dYNvf/MdrrbX8JbQNfdriAFTmODIEop/pa/0lU7SY8+bL1NaeQQRgaFnWDSFVe4BBwEclZAspBYZqGFJrAjJYS3V64xgSjyYYpoAcepRkGhUqEKuIELYv9XQcjlJLHEEicCb8tlxKrkEJOcpMuW0S/dwfK+AvAERCkBECCtIL6znJiy3g/Jv+u44oDUqKYYlpkxy5GtEgCIPm6LZdRDnQU7BCDLgQboe4jzgRwMi9N33gwEKve7tboQmp1ZDGU0q2/BgyM9EUSjm/4T3kDRhEocJhOsomDww+j06H+G8GUrAgQToIgAGxpRAAkxkBjXZgKAFDgDALMrJbLCVBVKOH0wQdgXcSDmGvzcrE7F45ck8k7kDsYNLgEgE4149JHKOiKUnRDTPiWIgoe9qMMGZ2a31WaU6g4vtB9nartr0Rpmsp2/2HhRTFDsAfd/hervB9dUVbq6usBkG9T51Hp1zxaMYBalzFfuw+fJZyZAFYc3ZEATYseCeBbeccMuEu6hgW2djSLAZkLt5RTfnbGb4RnkuBYAhqE+7Kzx+kd1mgFYjV7bgQ6vnt/KK7laaCwywEvOSoRakOotGtEBCnkutZ4TMw421Ycc4zeo8B1aOD/g5MKJeqKADwSvc6czLyneA97i6eYPrN9f49t0HfHj3HjebLa6HUfNCeDWy810Hsr1FQUOqiTxahX1T46Xs/Wujl9LRnSq7lVPnsm7eA1pQ5pg3/mP6+XKA5JBynT6/Du6TeURcSgcdRrO3s/e9pKL6c+q8lyq/p9DMirO8cmLqUyBEZXhmYEQ5VLNCaP2Zpyxmjynjjv19jI4jyp+OnlLPUxvhgZLuCSjla9I5lHntmkvL+hT0VAT3VF0/JzC2Ph5AOfAaMMIZM0iEeXJq5H3OLOYXB2hZz8g8XhY9Gs5vwbzM7oeUPUM/q8KVHNANmsB1c/MNfL8FXKfxdR0wbq5L0t+c8I6yLNO0d9b+2hGqwC4VOrxGAQkGmbLddx1cp2FgkK1FrC/JGErO4mizn7LMPxtnXpnz9tln9r3agU09TWoRavv3sGHH9o7yznL6QDMBuoAQbRgmoMyXY0r89n2l6FJbWlyn4NLKUbLSR9UyR8y66rD9y759tOKI5lYtbV+XMeb5GVoAQNQ1A1JZOVv2iwAcc1jEuVFA/jtauMQcizorN5wjpBSRmEE2D3zXoWeGpEkjGrTzEJYgu1l3KSY4YcTJqRIm7FXuyInAIWACEgQxBMQYCmBC2aW9KD5seIyfYBH1PrD6dg4gFkgM2m4L0SSosZ8JDEcVQNV+SQClqryBqBAJizmuFTXwTz0jQgiY4oQQJ8Q4IcYAAhCIwc7BZ0DRa2gjMJsXglrrStIE2872sbxOlL9xqmgCgUwAz7KaAhTQhPfOIXmP7djDO6AjBWKmKZrwbTF8pZ1TBNepB9a42WA3JXRdwJ4jEkd194dD4ojEKjCCoElAJefaSCUpKFnAlO2oirzbjx/xlx9+wH/+z/+AECO++/63GMYRo9+UfUvnrju5pi9ZL2v0Gvz4V3oaPcVD4ty4PocewxOfuv85IPRr8J8nZZJHCHSvWcflMzKdfJZF3lE4OTdESqgZWuTCzEpHfRBAZDbQtu9ZBXQjzLqvymUAZa8n3ZdJCjuVLXg1/Y6DMAFSPf2Qw48yQ3iA8FUJm+KShiJ23AIQUhSHBYgwIIWKIr5yvGJ8cj4E8zmh+3OtN5xXIIIsTKFXIF18Z6GaOu24rp+FbILxvI5MuWj8V8GJG7GbcvB+U43bcGjOCgIiALYE0eqN5wADCdQTQjIeZEWbxXc2sCgsTmMxbQdY5olFUPL66iVOZ0qWCUpfaiJxHYvYAAfK82QPjHJAWt4HKqBWHlcp41zGu43HPwPB5noOqTOr9p99V0CIPLZ5qs541VqQDbcaNQw9hqHHMAzous6MKFzDZxzqSsT6Usi8hj6jkjdnSRHR5OyBBYEFe2ZMiTCxgyOdFJkP0iTuUrwoHKGGnCqKdIAkty93p8lmkp2hjuiKWiV+Gc/6fZtnmgCTB463sH2VqVGF2sXr8HbKr/xF5qHWXuWZKJ+p+Rc4FMVmMk6+FSfyDJB53Nir7B1dh2EYMW42GMcNNv2I3nXoyJf8ELrnaoOaJb5OhT8/P0PP8wyPOAQfUf4l1572ADgs91COvLzs/N1clmzHUuyax7frGD2WVaj9UOuz9rtes953L8mnfEKPiCfS592jPx89o81rysTLPSGqwikrpYioKAUdHbecOzchH2sR/K+RngtGfEoF/ypa/5U+C5V1lXkhG5YsyHhvyfCchSFqkqoBKPvs6piKKEMi853j2FyrSnou1xMRAiV7VARI0G038P0I568AZnwTo1pIhwdj7jfw3kEkANAwLaoIPrE9Gq/TQCcNDytmqUPQjlBlou88hnEE9R7Uz+P65/aTCTnZIwKwUDvN3lrE6KwxXWG8zq2Xy1eTDtgpb4h2D0kmca6FVyrCfQtC5DniXBU+jzBg7TxYmxN1bh46AK+BG6XcMpbz34hIrR9XmKVcZvY2WH6/2pNn9tp2vNVSkGecn3MEETfPvwQgJk183HXmMRPZZOx6b0pqmRljxDQFBRxShCZ8BJzXPAQP+wfsw4Suc3AEDOOIvu/BcUJghki0uahC3tCNSAAeRD0x4rQHE+BThKSAsL9H5x3GvteQQp1HigHiCNP+HtO00/omBSJIoPkLLOaxc+oRkVKEs1BUDFXKbBwjUALv79T6Pya12HQElgiRCAKj8xrKqOscppAwTQkdq0TrIBAnEEomAW5AritxcBMLYmI87Pfodj3ud/foB4+r/YMmfY4evdW3c4S+7wHRzypMq/Ke46Thx5wCNJE1nrHPgh3MMwiAb9RwIA2T5ETQdx6EDh/e3SDGiP0uIsSEu4cdEgMxWRJvAYQJMTF816EbOmydgx8GRAGmGBDSHnEfwTHBOUKIA5wHWHQuRY5IEhFSQEgBkdWDQmKAd4Lvf/MBu33AH//lL5j2E/7f7v+Ff/fv/w/43e//Fm/fvcO42Sh4agBM13ULAforfaWvdJIW5+u6YUGjcP81k0D3fwBdA8jqS/k5ZvWYSKRwqHpQ5BAiAiIu9wAoUQiLzk0EyJ6DxocSACeCTnbGU7nCXGWvDAUFCEIdQF3Zl2F8BosHpDOPN71DlZ/KyIrVnywRUFbKMOv3c4P6tgXz7+d8RQbrNZTgUs+TxedqyFd5C+2KrLg0pS/lSpQWoyDyVPkk/VWV8hMIE5QnEfaIqvuHBAEHhxgFMSb9vjg7CpDHyTwknCXrrlStwiUDNyzla+0vX7uJFcwhTuhSBKUAjnsI53fzZBBGIs3GgRiLt8PMwjw1Ca2Xr9RcKw1vtqLrKIi+9V9WEFPb9wX1EZOJ6q2tTpUcMAwdrq+3uL6+ws31NTabDfq+R9druMbODBVode4AFYz4TEQAbL1qeEzCLjEeYsJtSLiNhLug8iMb4OYlr031oBgKlKhJ2UtbikxkYEzdAUA27xzRet8IKgDR6vYFNWk0DkZ3pRzjbZaAFZp3ymuLC2iyfECdNXmvWAO/Gm8Jqe0v4FY5L6zMFb1bHZP5nETzd8lwQep54snDUQd0A2jscXVzg5s37/D2+g3eXN1g248YfY+x7zF0HdTjzJzSrGEq4s9bT23dLunri+jlSnoZOiOPP/H8XgMhXgqQ+dT0KfSKFwMRL20V/OiGyfIPmr3lD+XQaDa9zyVkLdUuM5TpxES8tD+PXVfABjEPCLMikJx5sZZwuBnmo6Pkg6iKKxTmaf25x+pzbMM9ZkFEi2fUjbu9WjCvx2JevCKdHx86Kn8sF/VTpuap568hmZfS8Y3z+HPXnvE5vB2eTsf7sjZj7eDI951SXh6bBy/XP1ozY4xQLZeyGzmLuRV7dRMnynEhAbW+juW7LEBlTwbdQlRqnDNFshBQ0HTHibaZZ4PLVlqkysZu8Gqt1TkVajtVjJLvQdQBlnpbDe80jvCqWFj2fqvzyhxmYvUOtxwZzlvfdBZ7nSq7CWTLYTE2da6AyO3NzKb16kndg/Kk64KHGAPbMtqYredaiNj1Uvb5lmcn+z/bWokl16sCfd7Ps5V7/fvQIyLnPpjVc+W9peVZp4qBWQ3X+2cGoKARHEzUcev7G7V9daY+iweW1T07TTKY1pyZc+8XnlllWQVRzlQTfhiCkHLoLm7kIC0jxoj9NCkYEWIJwURQ7wfHGhCMOMKJ5mrQvB0EeKcJ54Sx2+/AHCFIIGL1NnIWQEEEkpJFRSAFLdKEBA/2zZpnRgpsCZcTkDLvYP1EXnM1wJJ7pgRyCV4ivDhI3IEREclrPG6x5J68B0FjKRcTTDNq6L3HdujAgRFcBAuwCwzyG1ByQE5iyHsQBXCycYkRnBLCLiD0E8L9Hvt+xMPDA2IXMfQDuPMYug7oOgyDsbpkOTIkC3QMZ6E/StgRAsTBLHthccvNO0ykmSg2lw3IGHwHJ0BwDOdymC2z9TTBj0QAJhAnCOv6GscBm80GV1db7Pd77HY725v1xUksLAQhTBH7/YQUEjiyvpgtMgAhmaXwZhhBIvjzH/8r3tzc4J//8R/A8ff4zbffopwTxt8VAfpw1Zj8LLMldWmC63V+oQz/i9FTLeo/Nx31IDtTv0sMfj43neIdn8KXvjQ91pqPyPZRtCsl83iNchM5/CNZMtZ5yMtLjHfmfOfT6TG8+fH+aFpL828t/S5K1HyhIiK2nGjxZpgXZ/dIrli5aHmu5nLmW1TmI6h8rJa71YK38D7NYyrnrhwlWSB7yeU0euh5xuKV8aBW15C/q7zUan8eyLEKOlQmZCmny/zdKrrkWQDo2SKacyGKIIGRSB1GUuZnLTxSBCNCExMnEUQQggATgECCSPp9W895U7jwBjo+XF/lelXSsjXbfJvRwlli/Kr2tbf7zFslX5fXWHGLpiqfQCy3RX72ok65/DIrlePL86S2y0IyLvsbOeQVythmY51u6LG5GrEdB1x1PUbn0BOhs4TVVOKWzXnMtidJUPPHXkCnvA3rb8tfWn3KfCFnPgjG7+4TY8eCiYHAWnkGIdhKT8zo4MDiVI5jsvwfKtMR6bxjJ1XXD+N9pO1zKUND5CAZdBM0Rm/tXNIfxfaUsnUc76mVtdY8u/ypheUcMUBrcNJcPstXoknbIStJ0ptn1TFvn2nzObdRRD3xUc+IIgOVqtdWErIMScaraujVfnTor3pcXw14czVi03uMHWHwDn3nivdx2Z8lB/zMy4tsjR4GYRIY/0q1PYdzrK6XlpaeAGj0tIej95Qz71DPMl/XS/4jf56twnOPKIfHwXxbfzgK+GTv5YyFlLOyvfzUTD5NdU+bV6Ft/1oV65yce0gctiUbdkr5G7PPM++dJzTjk3hEHIz5Y2nt3rWVkn+g9qLV4/rT0HLwWw7ryPojag/LE0UvZtaBUsg2R7E45jnGc31WTqh06JpfFJcNQwUDJGY1O+C/1jegpafFqWvq98uyVzrhyMb3+WitHoffzRnUPG4XPmGlI15S8Gzn0WO9V35dAARQhcdztFyP7cF6qs2vufcs54/Mzz/oMcGs4+iHXpMzG8OjStaEEBjZ40kVzyi/lyeJlDAv+Yk16VxuojJhWTmeLbcqEwZAku4tyeoAgXiBc73+LQKWHo7HmlDLdyB0xgeIMbtuxrcfgAMNY7L0DosctV5elYBd1+mzen13aGL6iwpu2XE8M5p1j63i1GwWrEyJw71zLr62+8HqrLEvs5zF1s+tdX3zMGNSM4Bk4l0rpDgUgap9BzAPy2QXq6ByWN+jig3UfYPtupSBqEPRfVZutg4kIgux0D5D46MeKLoWMe6zh0qpy5HfZlO4Ucbk9ZE4lT7PTChbmIBcr/JkUa8hR2ZJmJXlIVQ3bmsXc0IKASEEPDw8NACHvnJ+iCSickua0HGEgwJ5XT/COQ9stwidx8PHnxDTHqCglnrX13CTV0NFZnDSewkC4YAYdoB4JK+5DkR6pLBH2O8RY0RKJYpvnv0g7zSJO6AgRNQyu6FDxwze/4wQO4CvEVNCkogkjJgCPDy8v1IJk1VZ512H7dDj/fWIjgN4F/BLmHA7wYAAr8ALGKA9QKzWtgyksEecGLtfdvDscP/TA7x4eD+iG3psN1cYuh7eeWwGwdW4hSrOWOXJlHROI5rlbj3rxAngfTGI9SVhdX73s9njnAM6j203IsBj7xMis4a5EkaQVGRUYgdJlrDVEfphwLAZNQQWaS6fh4cH7Pd7hBARAyN5sfjMDg/3+nvYaeismCKYgYmdhktICYDH2zdv8fDwgH/8T/8LeNrjP/z2e4TdA/79v/t3AOU9rlWiAu0qaXk1WQAV2Tglr9M1OuQZfm28wV8nfW6Q4hIPtS+X6lrJoS3KLy0YkcOdla+yscLy1GnL/ZJJitV9ObnJrdZad8eGN11RbBzsBEUBiCMgBOY8V96rm2fOLi7fW4yhwlAdMf87aIivAtmTtq1WwTMHcYHqeXG8KvX+9t6q6Kl1E4KGvyGAxIGF4RLBM9kZxIgkCA6IYOUnTIG8lwkTM/bCSALsxCEAuCMgQpCoGrrUOrWMqCADDdUaPCeOTgASYF4aySor4vRwJ/OcoNQI9wSg199zuKyc4ZqchTTP9XFWDwUhKHtqlPoCc0CkfYZ+lmZeAFAPCiKQmPdNASY01FRKsNxMapDheofxesTN+xu8u7nCN8OIG99jA4eRHEbfKWivURkhzniLXJcyzAJ6DBKxQuesllt5qMwyk22SWN6ppIYNtzHhNibcR8LE6nEkAPawceYED8IVeR0f1r1OSMAkEGIkJ6rvsue6KJZDRpdkInVrd6T8bPF4Eja+M9ePoTeyTbsi3BYQ6mAttfNx7UVN+C4RgLmAEMUITAUYbR8cdC6LeeEEy12yN+8dBsQ8eVbqI3mdNN84UdWr5DnXuZV7ckXmsrgXgoMZzTmAHQM+YrzpcPVugw8frvHhmyu82Xhc94SrocN26NB5gqc65bPXrfe2llzO7dKEYkOWecpUBR1YYF1KLX9Zvzs+b597Lq7ff9mzlWaGA6sHzZk6tmBEe3v+flZeHuun9O+SFz9XxmN4kIbPkfXWZzDiMTVo6VWBiDlC8gxBpDT+wlAweaC1FmcvP6Ycf+p1tRpy/PHPWGNrCuKDkBxi8RhR99z6XDroniVYsPZaPnNZn7Xf1+49D0bIyesOn3/s79OdfKkgdPl1wPHNrx7+S7pEgf/YufcadIklxnPpGMD2kmWuXHHkezn5+1OG4KWGzcD5VaW15AtQGdSlgneWt0HW4hjOqXUdz1a+S8pxZZdxP1urNUDAZErtHDtYg7pAMiMobDHSGexQkiUiyySNINrWOVvKoF2HTdsAlHZnRbtvQhC1+48Imr3Uimt4wrNWqeWPw71x+X4Aoqz0beaZ81GaPy8FEKImhw8AMSFV8wus793H9vqD9sx54nn9Fv0xm5dW8XLktO0WmRU794gQDZuw8OSbPWttL2qraoqPpaXRspxWqdo+f+ad0VzLJRa1Kpu1fQZMORtFVi+DMAXU3Ew6TzklxDBpwuBpj9YDiYXRiweoU28IEQinIgCIACkFpKS5I5gTiHJeCLN4srAFjrSLyKSPFBM4JXueCniJBQiCFCJiTCVcFMFEcRMYcxs4JTAROCUNx5ES2DmkFBVw4gfExEhRP5N3pc3MbKGnGN45dJ3HMPQYxwFXVyOmh4QdJzgRSAoLxUwF/jRfFRBTwjQF3N7dK7g4juiHAcQE7hM2fQ8HQggRjswGlkzALdabKHNktlfk+eC9JlMt88G8zyTvQ6ZodGoJPU0B+2lCmCZEFlP+aM1d412RUkJn+5P3HsMwoO979H2HaZogLEgxIoSAnDA7GHgVc6JVm5cpJSS2PV4EkhjJhNzdfoc//OEPePf+A/7lX/4Fm6srbN+8BaBW3lqzQ16y3RPb82EJQp7i/yotv18TSuvzfy30VD7sc7Tx16f4f316qpHN5dIl0J6Gun4urd3pOnwyouXfdVee83nrdKzvyu9nvj9fvROjcOS8P0VlX7u4uy9X+pwy3GhY1sPfW553dl/LW+fP1FyUvXjqGVoURsvniGBuYWQXFUsMQQUC8vXL93z94hmzZ9HhS5GU5u/F6yStrMYsMOS1N2cKm4sE9aTPfCmXd5VlXOE8Mo/gzBt1HEZsNxuM/YCh79F7i8XvqiFn7V4BSdtOWJiydb3IS9KabJf1+AI1uEqieR8S69+5Twjq8VAZIp0mSQSRgJiHEaheY1J7t5aE4mW6J4cJyjsnMQDDhITZfG2BARs7EoAy+DH78ZK5MuuBxc6RvS2q/KdAhcnIObxTyU8iNWfJbE0sXlh0RPmiPn1m1CEqN8yvraslfyWkHs9936EbekuYfo2rcYNtP2LoOvTeo++cGjZ5ZwZb0lQv7ytWMi0+o3596fFzfgjmcu9L6enW6nDMM/MxZ6lkIOHSA+qYfuLY3r/Qey4f9JrnftZZiu2Xh109B9JXT/KCTtTPj63yl58j4ivN6NyhVcAIS3wJE4AZKNxOq6zKSsNzr1PPXNat/fx4ECLX8XTZa9//mgWtX5Pw/bnpSxhnrcPnH7NzljD5t5RSuTYr4IkIMWqs8BjjzDreNRbmLZCxVBTP6gINGeMsJuoqUAqzhnEoFtpEGYAwiEOi8X8EODGmk4pXxmynWAFQFjvMjIPyTi2xsidE13UWv75y2dm7ZKbgt3+P2NSdpVP74Hw+Z8FJDvsPjUx4Udl1DLgZt/zzKfA5P7PO88fPd5UbKoO+ZG6rYr5lsKui1ipubth5zrEKc7n+Tht0CkQDKqPfMvxtO2cg/ko7MiClinhG4qShllhDGQkzOktQOAyDMu6siv9pv7fn1jxNMUVM0w7JPCa0Pg3IIT3IicbyZy6AQu6DMGnYo2RJpSlbNrFXQSpFIKny3eebhRGmCLa4zJqgkBGjIDCDY4LEbGWvFmBE0PudK3VTq3vAdepdFGMEiOBjQHKMKQQNKxQCQID3PcD6OXEGKBK6zqHvO2y2oyWxTAiYsEsTHDTvAfIYm3WrysME7xySA6YQIET46eePCClByGEYB0hkjOOIzTAAAuzGHXrvMHSuCro215Ip74uSwUAHb79z1ykwkudH8ZBAGTdHBPYeHCIedjs87Pd42O1UTiVvg6c7nnMq+FNKZb71XY/NRrDZjBjHAQ/3DwpihQiiqczv/X6H/X4PjppINa/PEDSZOQALsRU1cbcj3D884D/9p/+EcXuFf/iHf8D3v/0dbt5+o94yUgKrrK6BNTCiBbWXa+lLp19LPb/Sl086l35d8+kcv/jXRJe08+g1slQVPr8OL2mstaZgO96WzFPN+ZgDygpXKKdbtMmtQngJQjShG+dghJQwjDPlafZwKABE9j6YhwwtXooWkjBb3SOXmNceUU2SrJru/Ie9u9nzyxu153hWdhNANVl5vpYkqSGA68r54X2HcRyx3WxxfXWN7XZrYIQCEpqw2pvBROtNXvlgQg6H+xRF63NmpsyGSJOWC4IwglioLq7QFZrwUjAAhSGIUCAiuIZHzvIT65DZ4zQ/FggJDkzAzgkmYQTWVwKrB4UjgAVzDms5xwASmuk+kf9+zKItGdntGQ0EMpssBgwwa2hU/ZznuYVqKvlSpAEnaqipgxGwdVXks9R4BhUec1FdohJeqVSNgH4zYnO1xbu3b/V1dY2bzRbbocfYd8W4xXfe8tnp3UsZF+YxfLiXZP4PeLo3xK+XiNZMAx9x78X7/hKQ+EKomZZH1QDNmjt53RF6Vo6IY0jP8vuZmmVx7VnL0lcUHI4pxRdXPecJmI/GUuF07FmPe+ZSUajvwGw3X1E+5fcsfM+VUZUxWCL7xyxrl78dU5CdByMOlUqPAUFeA2F9DXoKY/rYfnkNuhTJfgl6zjMuu/f4NV/KPFmj9oBbq+exfbYkVl4om1vPgPa6/L4oTHlDsxDhRoABUKyB6p5S6yAA2Ou+mJWPEia1rt5PSIkRwgTyHm7o0W+3IE+grofrXGH0FEQ9QkulNEH1mJRjmDbt9TmMwvzMWgIOrevhmmUR0eF5dxQ8PVZvvQll/1vr9pncdHyvLUKDMezkaBalgNx8b8/jPgeP23l0KFAfe19WOo/72vetwAfYvEvqYq9WSICTesapoEJlXhF8lWXPkAg0lFUW/kySEQAp1bmcY/4jAzkZBGrPWc7CCWPaT0gpYug7eN/WzWLqhoCYIhJHwO5PHDFNe6QUEQsQQWAxgUciwMFCQCVshh5d50sdgin72TwfiSxptiNIStjfPyBMe00KmSbkWLZJAoRjVToDlp8i2Npi84gItiQE5D0IFqoqRcsRIJZfBvpucbYhjBSTKcVF80B03vYrrStHBVe8AzpLJt11HkPfYTMwrkex3JQR3qkwL43RohDBdx5eCCEyZAr45fYeIWn+jGEYkGLCZrPB0PdIMeJqM4L7Dn032gKgMpdAmvy83RO5+ZwBGCfcKFKsMiaji2gC0Gma8NPPP+N+v8MvDw8AOXTDBtmjoeMOBAKzgL2HCwF+CmDObvJec2lY/8Y46RhAvUA4JkiqihLnvCkSuIBakscwqnA7TQE//PAD/vDPf8B//I//EYkF337/PXzfo+sH0AFEOJ/rS/7vtRWZl567x+SOS3//0ui59Xtqv31KuoRXWV57TM78vHTk7M1rhZpzYOUsn5V0Ufteru0vuQ7OyQJfypg91hsCwEEYitd87iV0oFc5Jk+jDX/Zat+btlH2nSg+FHafJiJ2kjNoSA36sQQhpPneeAeYMvrg2rZylUGGxQgFcn4AZ3mhvAPg7bPUd3KAYwMo7BrjFVUuANTgw8qX+tgZZWVs20c0+3HWVyhyjLbPETD0Pcahx3ZUj4i+Vx6tWJ8TNTki5uenlomVk7d55hF6zB56eN3sk/Kj0OTFkTVHSBL1US+yAQHsqGI8Vk6CIECwN3hFA0yZRwEyX6Q9piyLYEJCEuBOEoKoQU7JHddORKljqo2GGiCJJZxnVkOdMiZo5uOijaf6owEgcudQyQXReM3aZ2EGUlTZNSdJz8DB7AXDOaR9WP2zyR0069SVOuv0aYz8bN047+F6j/HqCjdvb/DuzRu8f/sWbzdb3AwjRt+hc17noPHsAtj4kAERDJGs67P9gHQQ1vgnavr70nNkzjsefv8Se+Q5XfSp+049/+T9JmOf8sjLa/3Y++Jqu+dklU/W89Lz+PD6/Puy4FKt2lcHRR+5+RFsxlePiJP0EgzbsTKW359/1rED6BCEyIitXeTm989BCMyUhs5lxmCd0XkpEOI4KDHvi0s2uy9dwDxFj9mEvwQQ4hid29C/TFqfy7+Wdpyq69pvea8gIkzTVNb7MkSRiJTwLNljAqjhjMgYREk1jEu2kgYA71yxBFqGPRIAKXOo0x4cA9L9HeI0YffxFjFp8l4/DBiur7Dlt+g2gyav7hyQckzYeVuPd5L+QxayRlMMVE+InCSs7aPCmFKeIefjr2YwIiMFB3VaERYPy1lhUJrnHqtBCyi0hYtxl2RyXMtDtPcs759Xdc5InwMh1kCrmXCfFfsGQiwtsMW8DMr3PE8SDVamOtfXU2OxbbWd92O1ZmFhy9VgCXdbocqUzapwdqUTiaiAIm1IphpmKGG33yGGAOYenXem41boikQ0BFOYMIV9mV8pRUxBgYjUABEqGDAkTkihU88EEfR+i74bVIHNjGm/Q2zWnCPSEEiJkJLg4e4XxGmHFHbqWcABwgkx7ZFj/isQIUicsN/vi7I7pajhk6znHDRRdQYhiADv9TMcEJN6PogwiIEYJwV0oN4UQ6cxhqcYFHA0IKJ3hOgJvfdInUcaOmyjICRgvw8InOCJ4LztHaYQYBD63oOF8DBN4MT48adb3D/sIRwxDD2m/YTtdothUCDi+moLkRFX20EFO2+gJtzCDd7mygKIUJ7K0vhJnm3N3sOCGAN2+x1++PEvuN/tcDvt4XyHq2sLJUUe3DEIBoAyg8xdXvdfQucd+gxEcMQUJjAzPOmemkNr5WdnRUFKjBAjHh4eGl5QVQPTNOHnXz5iGDf4H/+H/wHOe/zb//a/xfXNDcZxnC/xlTPjsUqRL5HWeKdfyzl/CX3J4/Al1+1pRAcHeHsGte+PkSH/2ubka9Anm0smPj/1ac8fx6oBOiVzr31H5b9GQWt8jzSNItLMBFlhSqJGHw75ldW0xWduDkII5QRgFYwoilhplLQLMEIfrveTJacmAZAKwEDOMo1ITk5tfLpjAB7wOfxTX5qockEGFxjZwntNsVtIBCXUYmWcZ32Uq5uVtRpWktRwYrTQTOOooRW7rgEjvCqPTZ9SGdTzY3nst+fN/1Yh3IbnAZgJk2hy6gAgWWOLOsjyXGR5KodmCpT7XHlmL6IZtLJu356VGIgseIB6XHzkqPmzOGRoZ1nFWjnU7iOQ8k0sKLkj6g0Lxf/i81FqQ4k1oMQShBBR8CElwDyOYcZ05dXO/yPAQn6mFKW/zC7TLq7CSWl74fc8yHm4roMbelzd3ODtN9/g22/e48O7t/jm6hrXw4hN12MwvlLZVrZdQXlYzvyvCa86xwkO/sAAMctSx9tzGWVZ+fLrHzffn3KGHrtn9uzValymm1wDH2bPfMEz/zV4iLbM1+JRngVEnPOEmF98+t5zz3jOBvzUe+ttT7y/UYI85q7Dehx+1yp+2pApRWFjm4puMG3c8Hm4pJx4kLJyx7UKrcsPwZcHI873wal6PPa316aZsu0Z4MO571+DLl2Dn1KQekr71++5bL0tSQpH/3kFx8vruv457xepCRMyU7ouFcViYd+SKmGzMra9tlV2A6i2Wab4jGb1zfsdOAbEu1ukMGG6v9cbHWEE0N3coCOH3nXwQvAZXHXzclWpWmpYNhBqvsofnF/Z5w76pVp+KNPGZhd2fKwLg0VtvZbMzHHbiYO9MI+F1SKfJktBMr+3QEI22M5etILDebJMUp1B6dr2NXBBDr6/BIhoc5O0TFmJZ88WH1Zs7qVUyiLWF5siGM6BmEo4LRK2PHZ+1mdNF65Se1ZmIC3/XcYEKp4qIJfKmqhrQ+cEp4iUAmIEhBWoc47gHZBiQIyWlPr+AYCoUCcM4QiOAdO0q/0rat3uyClQBp1boSd0JIhJwZQY9iUkEkGAFACOiHGPGPbYP9whTjtwyAn1EoQNBABDRBNJhkCacyBGEAgOqSTpzsKPrnEUICKDESIJmnxSk0U6VxXjdY4CnXdI2RsiRXCMIGH0XYfoPTqH8tr0HrIFehJMJCDnQWT3AwA5MBwG7yFdrofgfj8hMGNwhL7zCPuIh+0OwzgihoQ3b95AhDEMHp0nDE4VBN53ZWWrh5Q3wMFEXLGE9SU5OTezo74La0iqfQjY7XbY7feIidFpEGgIgBAjAIL3EU48ut4hhgTQhL7v0PddWZt5jsYYwYnRuQ7e+dlZXNZsVpAAmhida94V9Uwh9P2AGBP+/Oc/409//BP+8M//jO9/+1vtl6WixspervNLlCIvwa9fSpfwI6e+f04dj+53F9btqde+xv2vQU/hS479/tj2PdnC8YJyi6FC84jZfDo25xoV6Sl6DR76UKH0/LKO805Pq9cldK7uL9pvVPmnT02P0Tuc6pOWa8snAhl/qkbSepY7dvAQeMvZVpRC5MBoc1uhASUWDypARNFsLxSyy7tMu507Wc3uIc4AB99pR3AHtR5SpaliBllp7cyqycgrn16i2nAGGFB64KD/7Lei7m5lBeeaK0zaM/HCO49NP2DTD9iOA4bOq9FEY3il20ErZ0h1pgSKAvgY4vVUEOL0ZbMKAEIQM+wPTIhCEHQACXqX0JNDz4TkCJEAIad9rGYrGqJJBB00/JLmp5aqfhLrPU7GyyfjVydAGI5VPS7m8FKFl5WG5HlWuDM5nFbH9thlWVSLqK8mR2E7d0tOiFTfuQIU5WV5I3Kb66jXas2+g67B8gUtuUqAYHKabwyFDR3qhwHD1QY3Nzd4+/Yt3t7c4N31Dd5sttj2AzZ9b97IGv4452TM/4hkOcxgoBxCrMzdpRFZ/ms9sfrhvDvGf1mTn8ErPlXPt/bMc8Y2AObgULnx9HNPta880/aA5Rn9nLNs2bYL7zryvS5MrRPK32tlL8GWx9CzQjO1FTh3zcvr66rS6Ln0sqhzW9CFfXOqiIXQtFQKLkGI5kZU4MGtlpUVcs7CBsxjpR/W4dz3rw1GnKK1Zz6XXkPAOyfALp99DOw7d90lZS/rdOz3x9CX0PePB60u6+tMdbM9wkF+Jrq03Wv7RVbELpVP7XdZScsxIsVUQtOsvWb3clsWY5oCOEXE3Q4cJkz3v6hnxG4H33mMmw26roMHoSOPnjplyJLFVz3YE4HK6dEB09cOUQYicEJpMAcT5DB/3/xS5KfP9qAj11561ki+oWWST+y3cyXIkkPS9iz3yCWAgQaEOKxQBQr0oxzMl/a9va/9LTMr5WUu/fmagzwkzEBqvpMclktj/zpmtZTPDF2u6xlqn5eBtPzsvBY86SzgHPJmcd6qAKseBTFGeAdNahxVYT/0HjEGBSPChN3DPQCB75wpBBicAsJkXgqi5ZU+FIH3Dp13CJNDR2LJBBkh7A1UgImEapGV4lSAiDTtIXEyIVCtuDhFBUGQIHCgCYghIqakFpGAAgyNlRabp0NKOXyQ1l9KHFztC2fhvpwrkka5HkkBG7EXkQEGnavhmRxh0zt0ROiEsSfRRPVCiOzUm8WpmNt3DiwWjooTHvYBU0joE6P3Dg+7PTYPe4ybDZgF3/7mA0CCYfQY+w7dOChw4hyyDJw9w1JKZQ4xamgmGECR10871YTVI2EKEx72O+ymCQkOzhQqzECMCRCCdwEdAOc7SNQk0wSU+L25bPV+UYAodhHiTBU0W7f1HBIRhBjNg0ItSlk0YXXXD4gp4YcffsCf/uVP+MMf/oDtdlvWdbs+l+vkEt5iKXR9SkDiU9Bj+fdzAtmXwGN9DvoUCuvXppbfKCdnPotfoPyXUPJf+oynlv1ccONTj+kpXn71uoVi8Nx9n5NOjWXWpUphKA2AyO9EmgOKAW/8kyqFBCDW89cUmGyM8GrL85dZcdu8JJ8xM/2EeSvk/iZLGlc8H1pAwpTCpHmRkDJAUL219dFRwZAMcJTzcSEjrJJ1UjPg+XxtQ1NpdTVH1dgPGIceY9+j7zp4R/ZyFsu/8tmiGvoMBxV+Neet1uIfd4aufV+68+z6zqF5BMIEYUJkQhQHQQciRu8JvRB6awMTwESQ7C9DsLBOhAT1kLBmWiSgysdSzq+QNEQo4l6/h4MDWQQm5WRLQyg3aBFCK18Kmc+pGaowbytVKKnKiA1vQ+U+8xauTFGd05K9HgQVmMjeEDrXSdRw6qCq8+pkjm1VZmykMYBIw5NmcMs5CFUgYnt1heuba7x58wZvr2/w9uoaN+MWm67D2HXovFd8gRhCLndn0zQxzwiCb3Lv5RDGet28Tx+vX5nTpbzh2ty9dC1caiByqeL8Kbv9Wf1RA0KsASPLNlxy5pwFVI7sLbno9ftzHevfa9ceq/cl9CKhmc4N5mJ/f5lnNRv4XysdU9Jn4bANx5S/P3bvUmmVX3WDO7QQfkzd1g/F43X4Sl/py6C5cvZxm+gJDfUXRMt2zZXPum/EGMt+0N6zPLiyFQ85Ay7FayJXWMx80WS+ImrZLs1ntQIXjEIQ1yGCIH2Pofeq/EwJvvPYbDbYXl/j6u07jNsreG9WUUwWUpZW61jrl0eV6t/GfxbAtejts0K66Z9SmN1nrwP2lqo6gnAZo7Acl1PfS+UOFCA+wphVYKWp94lnrr3qjRcwZSsgxCoQsfLdklmpfVhBiLYPMriQn1HVrpfQfNAyH5KFUmad9ylZuJtGIcuSCvCx2+2wn6bCuLcKCg2lJGUuiTCmoGGNpr3mVWCOYIkawggCIg3N03UOMaoiXcxLqIRmKp2iVn8Pd4w07YqkWdZWVGDBWeil6f4OMexBKYAkgMTK5KRKaWjU55iiJfzT54J0/cbEIBLLu2FCNAiMynNoG0yQQp4LsO8FnVfBNKbq2l6AFtHnkPPoOofOOXhH6DxZWCtB5wGiHn1HCEld+ikkpASLuUwYOhWku04F6CkkRDDuWT0z/ETYh4DNT1sIgJ9+/gX7/Q4h7HC93YDevtG8G9uxGFg67+CcB8jV8GCo+wxn7xuT5lqlVQ5i4ZzD9fU1umFAhAIA281GQypFBsgAHQsJl/sjRk04rmGxkub/SGy5SwTedfC+Q2TOTv26JyUFMnTuSNm/c6ixECL6fsDV9Ub31e0W036P//KP/xlvbq7xd3/7e4zjFsNmM+MlMz1VsPhKlwu5X+mvi6g9i/8V0GPn+df95GXoeJ9nhe5CkWU/iSl4NVyp0xxcALzTc3yAwAvgxCEZiMBgJBKwWcRn1e2B9rQ8KauOzYfiYMwzc724P4MIzkI2Oa8/Okt46WaNmBenCS4WjyEU5bK5ShydqQ0fXP9SYxld0hoKdBh6bDcjbq6vcLXZYNN4RHiq3iaZT2hrxKV8ZXyFMAMjXp5OFSymY9ecXFNymBIMjFAP1Z4JQzbWcIQkQLT6V9knx8nXvm79UEgSCIweER4MSECUBJGAIIKd9JrAWhK4IjVW9faz8cQiJb9CI1Us3s90RbnM5mCWLRrAjExenXlA5JwQS4+IDEzk9zzfpZ33VN+KuNaOTbsQrB6koYPJefiuqmp938N1Pd68vcG799/g/bt3eP/2Ld5st7geRlxvNCxTN3TmSaEcfPVlqvJl5vmIAGbfOEUoAAkwDtfuV3oOFZ7awIhLeOxPc2Ye3yteWw54kWTVx34v1+H8XL4UHVtTPn1qeslnX4pgLWkJRrR9Uq1zjoMQLcJ6qJC6rC7Lco/9dur9UnouCvuUsi69T5aHzTPosRaFj9kcHmNZcUFpT7jnglJfYfwegxKfAtSOWax8brqkPqeB4rnXw2x/aNb2TDHulWNxzW/tnsTM4OhUsUXZ20KV6Z04iGOzwEqQjcZ5dQ7FI2Kz2WJzfYNuGKEeXWoZTTjcQ45Z5832QeNpSwi6BoTIStT6Nw5YxGNn2EyFb4zFY+gxFh7H5mZWfBx7cu4FZYBPARGHc6gd87ZtSxBiCUS0Vv1LWp7lbTktOefAaa4YzTJbBhVqmc04tRdn4aL0hQmHgprrISULu9MonVkUIGDGFCbs9rvSkznm73y8s1KaEeJk4JsmtUucSqJngoCdKryJvIFkbM/S6zhF5Miw6qUI7CUiTNDcJkTI2vMUJ8vVMkE4IewfkMIEcFArNBOmVFGdAQf1qiCBJsY2wYiFkWKA7xy8SUuaMypbRDahSagKcVmgE1MseEtcHZMBlPl3SzQvrPfn0BDeq9dE1zl4k3scAX3nsJsSKCZIIrU2MyCi85pUsbNQUTElMAMPOcy0F4SUcHV7C9953N7eIoQeMaonydU4aD2x0XBfLodV8CBiiJMGGNOx1UTmub2LMGsmgJIjbLcbuF6BVt/1GIcBgSL2LoCgIIFfxOBNnEARNQSYgRAaaonhfY+us+TkNrfF+j+DDhmI0PmbLHl1hPc9hmHAOI4YxxEhBPzpv/5X/O7773F/ewvvO2zc1YFBy7l9dm1POndGHp61crBFPJc/e8lz+bllXcrH/bXTY6z5ntrnl9z3qXi240EYz9OXwlc+hk6t8+cQaWHrvz3jGZfe85zrzsuLx+hAY3pRuWep8IiVf1GvCA195JzG+O+h+nwRp0ZGYlGXoIpWydkjzEjhgBFrw9o0ylmZ8WKZj8h1a/goahITqEVEA0jYeewXfeBFFcTZYCeHcgKjujRT0fGudk/7g7TjlNug8fn7zmuS6u0Gm81YLM+9owaMoOIVkduZOYdmOLRuTfVqN152ttYzGqvXFu5/Zc4Y5w1zOtb8EEzQ4EnmmeqA3kCfZA9icc39AMQdlgnLLQYGSYKTBC8MQkQnCSwRQQDmDgGCgGTKb+PiM9JgPEJmeopvRPa6bXlQWbyWdLCsBIejIs3Xizmc3w2EoAMQor02ewujtIfyfLfmIfNQh2icjZnmD3Peg7LhCgDfdejHAVdXV3j79g3evrnB2+trXI0bbPoeVxaWCb2DuMonan3cTEiqMnuW46pXPFFOLFj9RU7tPC+lo3sMz/RUndZj+bJLwiqeK/Ng3ea+vRCMeApdyp/nyy6pwmvw2Z8kWfVSafCVnkZZUDxITL0QEClv4gDQuFtpbEgNw5STUrtZKKaDY/LsoloqstaAhqeCD1/pU9K5sVn+PuM+X7guJ2rxdQ49m9rDKL/WFNCthW0mIio5Gsp3yEy1HtfOGDIZ7DtpXGsFcMGYH0kmZGDGnJFzIO8xOY8EqKeEJ3Teg5ygnQKX7E+5jkAFIeZMwfEDeL635utOzPemsFq3w/5erfuxtqBV/C3qSuUCU9A3TA01ChF7y+NZPV+ON+WA0cgywQoIcQBA6IfjhZcybeAdFaHMoekn71WoMRCLWgDdko277AqPhlnOSk4N9D8XPgQ1bEDSuK/WhXCk1v8sMEVuwLSfEKcpT9AC/MA8fFKKEFFFOCCWcyHg4eEjRBjeOw2xY8r72l/qeeDNaqlYfZU2qFVWioIwqUv7ZhzRdZ1Z7gMc9pp3ITwAKUGmByAFMxy0RNvZ6wGi9wFwXBXWzvIliIhZ6xOIvFpTOYfs+eC9mwGU2g5L3s0JKcSSQoGoySWRtJ+6roNw3VNinJBSsITcbHFq7X7n0YklrCQpgFTOLT96tVobe0ISAu4iUhTc2zj6jsAu4X4X4O8e8Je//IRh6HA/9Aj7Cdu+BwTYXl1ZOAWv8Y/JA17b7FmVMM5TAUAYFn7AhAjtB/X48ASMnceHb95hHyLuQgCRKijYqyVlwXFKFkh9pcRgFux3Ex4edpimgBgTphANHN7D+5yLB9D8HLreErN68IC1j0UQYkBKao+a57L3Hm/fvgUza4imP/4R//RP/4S/8x2++fBtmZc5NNkaSPmSRkB5P/tKX+lLp/k5d0JBvJB7vs7vr/Q5qOhRQcYBZDAhq3PrxLQo4CXyew9LOExAgjoiJ5iCOvM+jkw33/BvmYcz54USp8eICGpl3a6hmRK3CdrfKnMPkv+uEaEAGJZvQtEUV3/PBhQtwJB/WxZNDS9LOfeVQ9/3uNpe4frqCm+ur7AdR3Teq2en9+WVDZ7aED+Sq1ElpmfT+fO4VR/rc9vuriAEcB8F90mwT0AwVw0HQmelRGgYpizrzeeUDr1CDw6e1PuTksJWHgIShmfzPk4JQYBJ9I4JBBAjNXk5GunFgC/ryzYH+QJDWKOiRs9A2OpcWoANKy9i5XXz38VrQgWKZl6vVCSPO2VZ0M/Gh8hVgzHYMeIcYHxpQj1fhqsRN2/e4MOHd/j+w3t8++Yt3l9f42azwXYcMWwGdH2nYA0BUaLuAcXbueljkZleEXAz2VCKhnq9b3+t9FqK/+dQa9zzmuDEkad/oues04smq15Sq4g50GmcQWr+2mnZzkutJ5aKn7UyiHKs7PILymZHWZngFtbBx+u4VtcDRd+R90vKmn9er8s5WgM+XorOlTcX1tev+Ryb3uMQ6qcwR3NF63Po0vVw6e9PuefS35+yVx0b/6fO1ZeYT2teVEct25trkIURvaDOGmpsO2YAAMrCJgBkoV0FogYanSpVhbKOWJVtITPvnDD6bhFSqbbhoH5Y36NK1RfXVQV/bnMte2m9n4GACgiogFPKzD/Om320TsfAiKWAUcdnuUceKj/m9za2mVSvmddt3u6Wjgk6SxDiYD5eOD+JSBlmVgFSZdwGLPHzeagKbqfXUvOqzasNIwJKssUKRuiISVEgQwSOLGRSIzBoaJuAZDlRipCbiVNRwufyAAUmYpxw/3AHiGC72ZjngQpA+tws/isQofUkcKp1zP3InBCmPVIKam0HAXmbizGAU9B8EClC0gQkBT009HPjZk7qrSDQPtSwUVLmcTZugKDwCCqUMHKYpgxE5DFhqXktNIcMweKnlfXKUsvMwBGENVxRUoAE0K6lPMakloUhJUR28B4QJnib7r3lJu87oEsE9foQJJO7OyIgMnZTRLefcHt7pzkphg7OEe7e3mMYBw0fBa/5GcyGr/BEZNEe7JnFsiwPTZmXYnMI6JzDzfU1+hCQHnYqZrrs8dEhW5+1QAQ5grD2RwgR0z4ghIgYE6IlUp9CgEuMnO8rpYX3mVnfOafgkXqICDKyw8xwzmG73eL+/h63Hz/ip59+wl9++AG/+f63sySbeWzPeTesffcSvNdTy/yUnhCv0e7Xpi9N8F7Sa9XvGI/wGvSc0l+r/cfO71PXvpQn0JdGl9frsutOlXdMTjim+7j0WafmcDb6KXraGfjQ5pNu+SHlKUz9qImHCejsPA4NT5nj1ivLUA7syhtlcCJbf5dG57OzVdQ2n6VR5K4pg5cK3sqk16LKs7J8YvVYAg2E+n39wqqs35ezvsg0yhd45zEOAzbjiO1o3hCkeSG8naH1LM3Fal/L4nHUZK5ua7Ok8+Ne9Wun97faztLNonMisWBiwcQKQkTJCnJ1PmHRrGxOcnY2sUTmdS40U6rUi5SVViACojndJIElgVhBL7b5J2K5x3Osqjy3ZmNnH1owQjupNmqlf2YNXkylphdBDcKRzXhqucZL83xeZhmClvN0ORQ2J4nmP2YurRgQZ5nGqUeQkPLsZHx7Pw7Y3mzx5uYab29u8OZqi+txg83QY+g6dH0H33dl3cNkCmHW8lz2t9Z6VK8INvmx1pMopx4/7LCX1tFcwm8+l+YGiKf30dl9uPREeH6djr1fUs/HPGv+ef33y+59fs98Eo+Ir3Sazi3YPNDHPCHWFFa6181DMZUDsklKfaiUyuWsWEI/4v3U31/pK32lz0/H1uRSYX4ISmTmXsqnZXkirctpvVcVc/pdEnWbpsRFeLAdzfY3ICUGJGoiWXHw5OAx35vaerb1bttxjObK9Fa+OWLlv3iWLPoCzf5LjcBT63IIRqwd4xX0MXkoC3m53vm6RW6fgz4wdxMxbvQQNF0Xco55OBwDwVca0GBVKtA5qvke2jILuJDrbEnV6tnFTbGNRwJQ5hgzW84DJS3Pwis1Z2YJP4P8dxPTFcqoOwLImzV/e8Y6h9ZSLkYLp5Q0D0MwzwjNRTAhRs0JEaKzPqj9wZbgOpkVUjYSUEupZIYEJvRYQu0UAmK3h7q77wEIUtiBOSLt7xWICDuAkymi7T1FhJjUaNFp8mTK4EfU+emgwnTfqScECuhQEy92XYeu6wCQWdMJyKznAfUEScxw3QgQlWunKQBE8N4reND3CGHCfrdHtITb3hOkc0V74r0+fxg6tcpiICDBk85nFhWQr0YVcTdjD6GEX3YJwsBAAKJgtw8AgD//+S8Yhx43VyMAwWbowSzYjBpeYbvdwvtkIRbcPOGk9Q/l6McZeCpzXEEQD6B3TsM+eYcpJSRWS0Ivmpw7K4d816PvzfvCOYR9QIoJD/s9bu/usdtPCDEhGBjBEuCchi+AEKZpMgACVRFQBGcgg2rk9Jm7KWC3n7B7eMB+v0MKE37+8Uf8w//6v+L9t9/ib/7279SSs9k31xS4L+kR8ZW+0q+J5jzBZ67MV3p9+pWNcctjGzdTrNY1qTAje0docmHL6SZi54ieIdmjWUELggc00S240d2TuVJQ80LjGZFDJOnfxAlwmRcUQLIBQqq8lzDAQc3046ShluKk3ye7LmYz/gRwBFKwmP32XkLnoCqdGyLktVv569qo5YAbEOFcYxxDGPoeQ99j7Af10kZWJJsRu+EyRYcuME8QHChaSDIEYZLEhQrI55Dyn8ozJ2bsEuMhCW4T4zYxHlgwtVgAKkCjVc15w4Co6cwRLel0zUyivaKck9Q5kntLXOk3C7qFChBd1IpTDcQ8t0F7bV4ZC5nOpmVG60Sk5oEQW0kGotScZzxLXi1gkIXOpJWkgjIDIRrdGEwf1yBVRBmEcJo7A8Aw9Bg3G9y8e4cPv/mAD9+8w7dv3uDdZou3XY9t32Mce3RDD993SFY3Lx1yLjsVdcxliVx5fm4uUQUkigyG1wMGfj30mlDEmScvePG/RnpVIKJ0nrTL7sJ7FvSaws/n9MY4Zhm7Zpl8iSfE/Ls1EKL1hFgcigdgxPL3uZJv7dmn7nkKnVKWXnrtp6TXRHPX6FNaex1/zuWb9Kcco9d6Vi03M5GVPsf+1T7jMUj2sTKW1xBRYU60nPwPZs1fgg9A6wJe65W9pdm4dGJpOF4q/KgwwCQgsRj7nJokcPP2nAQhCjhwqFyf99ehkuEYGHGKKgix7M8VLw2i82cjQT0GVpYdLfpjOW7V4X55Nszbc8zaeQ2IaH87O6cMhLCLDpogzXUFePAVaKIcFqetuyIEq2dkucaU45kBV+t/Nqv9Zs6UtmRrcwNGrN9ymTmUIRwVK3QRLmFshAVJIjhFxBgQU0TxkOAc6qY2OnsQSFlXmgcFNmZiSoOMjknJG6CAQgYoJO0VDAmTAhExIOeEUEGz5hwQR+iywOsciG0uivaHI6rhl1wLRoiBGBp2IA+r9m3dE1JSAEW9NcjyFQAhqgJ9GDp4J/DeIwQocGE5acieLVmz7gjwBN859ABSxwDbbBb1iAABQ+cQmdB3mmgxIYFFozI4FkxRc2Dc3d4jjT16Bzx0Hre3dxjHEXf39xAoMNBZuCrxXuvgVbhGBtAyKli0CzXknIgmA3QEDJ1ao/W+AxFXhY53RQniOg/feR2HziOEaMnTE/bThBg1YbW+VGFDrJ47AsJkfaewWgZ9qhKKLBZwXpfRvCr204QYIoQZD/d3+MsPf8bHX37BbrfDOI7o+34GRLRKkXYN/rUKR8fadKmHxGue808t+xRP8FT6NYz963pYvFzZr92XT1mrx+TRr/R4WjNkWfv8Up4RIs0r23RL1rFK9YqAKDghMEWxXpSBiKpgpxqKcF7xGo4pLwln2njOxkWNNrusm6LxRU3uq8peEstlxdEAhnig8K0JhPV3Kn8ns1aX2uD23AJMF1UNVgzFLx9WuOA5fw2g866EYnKkJgr6v1maU/WoLKUKSjqI1QHL1y5AiDUw4tT4L39bvSbXyrxIowiCMPbMmFgQAES92frNysz8clZMQ+WzJIIEQSKCF8CX+/Tf6q+8fOX+qt+sydQopeXRkfpn4fUXLcxzTaTKqy3vlp+93jmlTCpyhFR+3ACK7AmhMVntOusvKd23KrQ1n3Lv6PecZWhbO5yLIAL5Dt0wYHO1xfWba1xfbXG12WDb9Ri9V28I7+E6D7LwosIMR8p3MnJ+MZl551hLZzKdVjHLI7XvqdS4adEL8TzH9BSv6RmR6dwe3c7LF6tPfsYF5T1mD3gJmhlJZvl6cc1ZnvgRz/vqEfGFUlb+tZvDyZwQOFQe1jBMVK3d3HwjrNcvy1uf4E8BIT4FfQkgxK+bvvbfXwMds2Rd/nbJelkDPlXJ2x7LK+U0B1f1srU9hQTMaqXszRaGQCaTWN2cPqOkRHMCpAiJFqO2ObaOMu1Eyvg37VSLr9Zaat4+KUxqbX/7vtY/bXtrnfTdueX+uPRCW/EQmBVk/+R20fK3uVLwcHxbsPmY0HpaqJnVjY+fQ8syyt8iiDkHg/WHpPl9pRyiGrKm/ni03iKCyFngqC3MSnBAIJb8Nyf9rRb4vi0MYjH64XIuBI8ctdWZ0JmTGqeU4JxDClMD6jBiCEgpmmdAxGa7ASA1P4P3yDkVBBWImDdMx41ZkDhqsCATDLwjTUwtjIeHO6QQ0DuAwODGI0KEMYlavIX9Hhwjpv1e5yMNOg4epkhwcJ0miu67EX47IonajOX568wrwvsO3ndIKRq4oSK9g1oMsgERvVN+o+t6pJRwd7+Dcx5DPyLHoBUR7Pf7BoTQXAolXJNTXmXoOzgPSAA8EpBUABRHIHbYjAQmwfV2gFAC7gKSMIIlyt7t9kiBwNMDrrcjNjmmk1kD9mOPN2/fILJg6DuMfY+u8+i8R2/xnse+0/En3UFyGIkW2BRmSEyWe0RjKw99D8cMjmyGmhFZEHVOwQPXebiuw36nHg673R63dw+43+2wm/YlxBKzAOTgve59IWrIJrJ5PsWg6yEkpCTo+x4pMaYYQaIhq25vb/HHP/6xKFLu7u7wT//0T/j9P/0zfv+HP+DDhw949+5dWT8FZGv21dl+euSc+Upf6Sspmf72K32lF6fjFvNr6vQKSrCInSlqUJEkKyEtDxebklaysrY564CqHC0W7kABJfLLFKmrqgRqS8pgRALAcAZAMEeALdQk18TAkiypQdScWUjRQItQ8n4VpTPyOZ27JPOKtFIfVF4zh9AEgyyEJrMo78VRz73Ms3inXhDr3V77n7LMNA8j2mAQn4xKbojEiIkxpYQ9C/Zg7IkQQEikIIN60zReNPZ3Vo4zk35H1c+AC7hDyFZnRB3IOYhnCOVQpgJKpWOU2rlRxhH1R5ESnelyRaesfMxzuqyKxasBLmo8s9m8ms/hBiQpr5Wa5OZKMxvMECl7qpCTUgTDPMR9h/HqCu8+fMD7bz/g2998i2/evsXbqyvcjCOuugHjMGAYB1DnIZ2GXi0ycAZsRCCWI6KIaECRhXOoVhEq9csQxONUy1/pr5lk8X7u+3N0MRDxKIvQFTRpvp3Q4hv9drWsY/WpFStlzi+oyo2Duq8p4lH3w2MtLYfHsm4r4JlgcfEzFnILRqwLf9WNqv0tgxDte4GgV+jAknil98+BEE8FI+p1SyVV/r22c+Xui57xeDpd7vqSOIMSvgK6e/jsx/b569NLo+bPuWZm2T/7wd5lvmMdL21lTS+fvVBufwo61f5Lx+HcPM0gxMHWV5hQmZ9Kswsra1P4ziLhVB+KzCgym6KPs1vsoQL8QFlm+1z7aGn/yXtpu1c3Hypfufyitn+th7JiugV22zpV6ykq5bRzpq2LNGUa3zrvRpqXf+gR0VzX3LkKsCzGqPVmlGYgz84LambGbD2hMsN5epQzrWlQQzLf/Gd/i/3OJcEcGqu9+mCxBHNsoYpSDIW9Vpdogtj8Kgy7RksqjyvnYk5A6NzcfRlZXuHqLcGCbvQABCGY1SFJ7Rex5HAHQFipufYNqtLbEQBhcALCfo8Q9oD38CTgGIAUwSFAhBFFFQ7JFNYxanizGBOc19BDeU7BjBY659B7h5AYITXhsEwYchY+Ko9NlsuylZTYF4TqicmpzR1R+zR7hGSQR6/3ZSxg/e1A6EiBI/Hm4cKaVNxD0HlC1xGGzqPv8vQQ5GhvISYICygyOkcIIZaZNm7vcXd3D9912Gy2Zb5lRU2eo96bFykAt1wLpR+ydWldI845syitnjdlLkHBiLb9IlI8F0KMBYQQFg3tQJpsEIAlqLYwGoB6vIiUpNfkCCRqYadhAxKmaY+7uztsxhH91RbTNGGaJnz8+At++flnXF9dgd/cKAhnPOOqNT3y+Wn7+GKfJZvM7f7Vfl8XVhWC2+uWdGzPeQkPga8Aypy+Wr4rPacf1nwci++UHEq+ek977eFflz0XJ2W7/PzH0FP74UXX2FE+XY5f0173JMp82qIqF/THi1irnlUXVIZQGuV6ZVdrmL4DZZFYbqd8diG/pFydlb25wFkZZFz6jMHM3Dxlpqn8Xo2DmnblnBGtQlcYTrK1uYa9VE+HBmBgBmYeE+1LQRRpFMXU8LG1pdR8rp1dVqY0PSJSFNGSvUvzGqbME1A924wX0Nup8HwCaQSeua6jWSnLQX4U5dIImc+m2bjN9piseBZBZEZsPCEYZomf62x9lZtVrMtA5kgjprrXfA+l9wSojTZPWgsVyeKNz8pzZjFLpc7IWvuVBUG0+vVBx8zWrZSmYfYUq7nYvJHK49Uy6oukXWHS1HmeVaFwP83Y11gBljja5kv2nmmK03nmHbq+x2Z7he12i6vtBptxxNj3GHyH3qvxjBpMNUnl86NzP5VukNkbqO4ZZVmWLq4FUQM+HtveXtJz87H3nHv2sb35MR6AhzOx5X4fX6dTJS/vF1uLxwyCjt17rE7z71fqKcvv29mdBfnm0tUWnKeLgQjOWRSNqmL4MF73GonF181bvpXSqmMOqVVkyMLqVaRZRM0Azjb6c3Wqi0lazUNbBYtd3QpW7f3niE59smfl+NhFEOYsVFaLtOU9zRf1nVwRdF2OcWzxDbMnxLFFodaPx3+/BHh4XaFuWfavX4D8MoS+1+/HS4GBT0/HWPWGztVN1va/Y5LTkvjI969LlwiJSwX3kZJOP4jqNe2/jgbliTiHn7FwOV1l0tp9j6DJWcPEcI7hOy773Fq9s6KvOSOtHFnkvaPKcS34VLQMKJbvStliHkvPh/k/KNpqcuWrkz0nJ353zTNwnMGofcOzz/Uczcxpc39mgNv+l+YZ5dJ8btUzo50nWdmSle7qGiwIFq+/PE6qQNTIrYXZys8qbRIU13uJFtaoGafsOq23dwAEHCcTagMkJUjca/mxnd8AJ4Hre/TegxMjRIZYGKRsBa8hjBw4hhIiCd5Boz2ZwlikJCrsmjBGKSbsdns457AZR8QYcH+nCZS3mxHTpGF5QAlwjM559L1H2N0hTQ9A2AEpgEgF9XD7F+x3O9BmgHcOadppOKYYwJzwsNP8FN57cBLspqAJmQmq4J9gQjQD5IGeLExQB09R+y4lpJgwbjeaq0EYMU4rc055jASpgoqod0PihCbKLBRIUSUCCYCkwI16IXRAB8294OtySQD6ngBxeGD1sJkSmzcMoSfB2x5wCbjuNB/DnjU/w8d9QucdMAxw0eGnu4CuSximAPGEYXBACLghh3S1wbTdYhgGDP2AfQxwRBhjQN85bEedHw6sczWDFeaxcJcSYmLsp6A/2foiYTgCxqE3edPpWIjAO4ex79F3nSYtF0aKEzhGcEy2isi2SFOykPavCCnQYsqEFhxKrKCN94SUBNO0w8M94fbnn9F98w3Gd+/x8PCAu7tb/NN/+Se8+eZ/xGYz4De/+WAhwATedeg7HQhNSqnrmNiEZ1YFQurUKtAnrW1HHgytEzIvKoBnmNKCIZ6QnCtWt186nT4Hv9KXTC/BX7aGYCyaE0iEi8xVrgOqHFY5BDRqzvXyz3x/SQtqzpp80+xA/euhS5sz1w+9Kr3K3nBE91oYNaoXCkiVuyBECQiYMCWHfXBIgYBJQxV2YLBjRAgSdxACXBKABREBQgLnektgrNcFTgh2xiQA4ryFo0GtAxPAOYNwUp6CAOT8Xt4rUJABkyR2NhovYDxBSg8AR3Daq7dD2GvIpWghmvJ7qgCF2N/ECsxLVgiXBNhNn1XOFJnRLrKJS+W7LB+4RHBThJB6BkzhAT8+/Iyb/Q1uww438QqITr21LW8Wc865AWiIRFEDBhFlZkjKfkBNnP6nT9Uc1jNByJImC5CV/8n4Pp/5ZdbXjoF7JvzEPX5kwY+ccMdAl4BRNOSSI8KEHtVzhQEncELw7OEsJGVEgsCBiRABiBB6AJ1oPgh2BCGPewgCOdyBEZjx0XtEABE5hBIwU/hTm88h52hrrhFBcTMo45w9GpK9ormAROM3zLgnKT/qOfP3OcfIBCSdk5IihCcIT2AOEInWF6kBxVLtG5s3ebcvRhpUPbAFol7+YBNd1KsERBBH8OTQKWeOBMbQ99i82eDbDzf4/fff4O/evsW/Gd7gXb/FdTdg2I7oxhFu8DrkST2FvGgIJnGWP4yMf2SB5qNjnXcGLLF1bmSCh4Pjzo4Q38xPNWqZKWdfmdrj+9w2e9xL7Jm0eG5NATLXIc39nS6kYqCnElk21KrHtywavtQjWz1O9s0cTJh/f24M8/qytdYcrG0/LOCJR9EjPCLmFnL1gfWRS5SlfEZVNrT7Rf18WPV6L+oVDRgxu64MYqPBaZgwWZQJW6CmYkDpVFoMUTuhHzO5qf1jrjg61s7ya8PwnvKCOKxbVQhlazYq73NPh/WFevr3x3hAPI8pO9fPh897fTr2jKe38zKE8jwd8yQ5fe3BLxded4wO5+e5Z1/azkvLexJd1B15b1khocPfZCH9HK1myxCfp6ej7OfLfWwfn3r0ZdVytuPz6t5WLDMKM2cxLjm7jspsP8v3rNZ52W/lTNdzo+jYT83HRpappdN8mM9YWJTrzwJbsnqSa5Xne+5TLIUP92ea9VEBEyxM1qr3RPOMfN4s75+Xr+1q8zPotcbassA5KvxY2+ElJ0hhhKxuZilegAgtsKk/W9NyPocce1hjDVvzrKtJ5eoSV1WQkhQr85KYrsRRZgupJBVbKvXO64lK6Y4cmNRLAiTlfGZOEHGl7YUbcijK/QiyfBAJxAFicZRT2Gui6g4g5xBjsHBJlqQ6BkAUBGI2S3kh+JRATLOkimWsdXCQPT2Q+TaoB0LL7M7nGAHkikeK3akeAsxoewOoob3KlcyAVF7FwSFb/hMBjmx+OAKThgeIJijr74TeEUav78ERiNWzIVidkhACA7uQ0HECg/Cw2+P+7gH7zQPCbgf2Dtx1IOfhXARz9jQFWDR8FZEmyW5mPEQEiQWBBZETphh1d3e+KEUcaUJulhz3t/GcIPVQ8d4ZG2t8H3MVYI2PzXMoy+Gq9NDxLatGqjFLrqPmR4kIYSp5OUQU/Lq7vcUPf/4z7u/ukFIsY+g96lzO/HXhmfPqgSo/ancU3HVxEkIVT9k7pM73p9KLWB4v6JRXxmOe8yV5WhyTMdZ+e+06vITC9tKyXl42AWDKr7yu2zlc9zRgtuM1fMZjdBRtVVWZdf7mNXVFuw4f63V0Kb2GIv7Srnp56ex16UA/sui7JWRFs5GcX5mvyArNfL6wJCQmRBZwchAGiKkYnmt6KNMbiEAVjPofk5VhCtIcjkfD9ORHlhkFNMYH5W9qX/mrfOLPOsOU49nrIUI4h1vKCanZklKrMrnEFmIL05TfjRekotRO874lM8pplVCAWbYLFEBBkeFInJ5nuvhADkicsIt77MKEfQyISXNXZb603VsrO0TNqWk8LIzfxQsoTts+x3y9C1GTS9z2K+unKEAQYC+Evb1PIiVxs4fqy8V4gKJyJQbEg4QKsJQ9IjJfFO1eFqe8NqkhQyCHCYI9CBM57J3yZrC5V8fCWlK6JnMUlg5bGdcqLxX+pLl31l6uL2sNsvyAGqYpAy4kDHAs+QkhqQAVBeCSOufKC00V8lgUeWA2aLk39anWDrL1UnhmEvjOYdz02G4G3Gw3uBlG3HQDNr5D5zTXmOt90fdVa7um61zDlElup8yqJaUuDCf5rDT5royh4CC02QvT4XLI+2T97dR58xww4pwnRK7H4q7mr/M6nVVdGFWj/IP6S+Xtj6qi5Phv7X15TOd1p6P9Sna2lEtRz6NcVhu2b5Xvv4AuByJStaycYUCUPR2sOmXjRfMZphRoRJgZU5gVFA5oGrk2mR79/ZH2ZO8y7cvlVa+40FaKzv2QPSCyEMlmddAyLm07yQ56onkeiAJELJR15Z5T1XsCGLH2+1frsa/0lb5MatfnqXX+Sk8HikLzWKi1eV3ynpZfx/a1al2/sM7P32N+iC5B3lOK/eX5cgmAswSLL+nX9lmX7KGrwHxDa2UcejjMv18DwdfAn/a+NVAon18xak6B/X5vDJMq33O8e71W5uGOqIYSNHjAdP3K8HPSXAI5x4L33liP3DZltGMMJdGzsLnJCyMFjanPyUIyOYdglu4hREwh4n7a4WG/h/Me3nnjvxkpRqSooABEIBwhkkDOkiQTkETw8PAAQOBJk09rckP1FJDElhfBzm7n0HUemmgaqph2Htx3QOyx233E9HCPDioMTfsdpmmPrvNg73H/8ABOsQAkWXiYpgkxRg3N5B2Avo4TCwJHOAJCsATZ0gAH5JDzNjOzWuxbX+eQQpo3Qtdl51UYEmGkqGGGIIJh6DTskvE0IWgybyrKeAV7FKgS+Cw8w4RiqLK+88qHxhBtTgGeRsA7DL1DSA5d18Ez1HISgHdqzRWCzhVJAb4jDIPmi+m9Q+86bPsNNpywIYGkBI5jaWeM1kdTQO8drjYDOu8w+A4khBCDJpne7zGFgI8fbwEA/TiCnEc3DIiJIbYO1HsBAHn4EBD6Cd57XF9fY7PZaMJooIBpICphilPhFS25ddKY1c5ryINk4ZyigSE5JETXdaUt037C/f09mBnb7RY///lH/M93/1989+13uPnmG3z47jvcvH2DJAKJEb4ISQkgAXvLFG5iVycKLDvJ8Zur5KIKraTN8ICTnAhe4GKrRPhK/xror1U2KPLWa8qOX+lfF124TIqnDgtSAmJkhAjso2AXBLvEeEhAtNCBjgWdXQuuOzkcIQHYx4QkwJ4ZSRg7TkgiCJJMwc/mDdi8lzwPS0WWaYcIyJ4AsHMiW/oWi19hIE6QFIGgVumY9go0xCknNkBNVi313YAIEa76qaIc5txR1q1ZAStNdQWIDHN7BUBw8BZ2yfhPEYRph4+//IJf3vyEn376C95vrxAlIYlBNovwjE9Ryj2VTKKbf8rscFZA25BFa+6UBHf3E24n4GECdomwNwOYCcBU3gUBjERqDw/zulBfDF+UlUkEXnX8CKJK7Q4Eb7q2ByEEJuyEEACwJURWZayoPjGDQWQISv5svGKxyuZGuVje1xRsuTuyDKH8ly9ABTdzKo9hAnHSuZiSet1kQyYDJqqXSK5f8zDrj2Kw4lRPmoEtsjBMKdfJQnh5AwYnSaDOAWOH7c0Vvv/uO/z2N9/hb779Dd7fvMV2u8Vmu8G4GdFbXrMsGx/ToTrvweRMXoECKmhCcDYydA4zWu9fm8Vtf2u7vyQDjK/0KagsrmfR43JEFHRh9oOBEzmEkaJ4xTak7MTHQIhZYavPru4ftjdJVbgcKumBjCq1pa4qbKxNZc8ryrHD4+OUsucU5X6zap1QFGXFDxcFTlXYLfrjAIg4BB9apdHa51PteQ4YcazMc3RMMXpp+Z9jA7xE6Xcpnbv3ORbxl1779D5c2xhOl3kpIPbY+55DL1H2S1r+rZX7ErRkUM5ZyT16v2vocI0UeaDs1ZeUUV/n67MEF5aAQ3vNse/bZ58CIR4FRpy4fll2+/4YgKR9ximQpVhvLopeghBLIOJYO9bKrwKyJUVMKsiqA4WDcyt1IrNyt4TGBy1vhFbhbJ0ELZQM5AKKcJFzRKi1HZu1nNR4vymByIHEq1t5VMV9CAFh2mOa9hj6Aa4nk1k0CVxOQA1ILb+YjOj3Kaky3Hm915EyAsINk1/mif7uqDr3VkCASv9BNEljyvU3j4OcC0IFJELnXaOYtuvcYsys7nV8aj28eVFiNpfEQCTXABGW+A6A806BCMD4GDUw8a4roYjKPOAqcNZ5ZsIaYSbewPizsh4MVMr8nqecbwElJGUmZ8pBZlWHT8ToRJUu0xSx2wc87CY87PagTY9umhCdh3ONK31+PoBkeTQgHTwp15tYkJg1+WNMmKZJ+8R38B2hd65EqBAY4OZsXUgdGxUoOwVTvAmVmY0uAqLY9G/WKDI/Wyus3xeuuXgtVc+IAOcc+r5HDBM+7if8/ONP+OnHn3D97h2uyfJLoMmLkRVJJcyq8skkBgLmPUDyGsgtrroD1SuogqHEWG7aCBzuLefo3Fl7qrxLn3npuf5rF8Rfu/6nAPzXBiguMTo4dc+nomPPfOzcK3P7Betw6e9PvXZO9Wx8KXot/vzFqale3aNWLsvskIg5CYidR0BMgikJJhYEJiTznoOYZ5pUoF+Bf9LwQ6YgjbAQThCkNjdbfSiywUeJqd80YB5v4kCjgqzzaMsjzgrh5Xvzd+sRwaZZN/6uGDbMFMJNiCaBKrvb4S8KbjuknTPeK2uNzQrf+MYYJwTLrxRjVKUtmvO4ea2okhp6GR1J7ssjd2GGhmT+QRQ0SCwIBlwFJkTOSalhIZNg469zh63agmzFT1AOwZ4j6m3sRT93povLgd1jeVEJX1l8Y3M9C/ign7OnbTu32r3h/Epuxt7aT22fFf4zz0kNYZU9H+aA2cILAo1A25QBrM97ab+TjKXU+/O1DPUG932HYRxwdXWFq+0WV+MG4zAon+h9A0C4uj9Y3y3lwxyOKddEJL9b/9oASJkjjexJqGFXD+TN8pd9fqmoKE8v4xxf9xL7f5mi+RlHijynE1nTZc/uo3XzhjUd7ic915YKhGc8+nIgAsmkicOY6K0QWRX6uaZUBJjzyhsTbMiOgSwItYKp1GesKYf0nlTrgnlZ+fn1eq1i/T17fjg8d0xzOKu1uGFtfdhQ2JQYNZSE1qGtc37PL6++83Bu7gmRhc4l+NDSOUDhlNLp3Dh+pc9JjxmTw3n5lT4VNXFKvxD6tOv5vLCd9zJnYUuyhXL+be2++TlQrfKzwi7vqEtvs1N0DIRY+/2Szy9JlzB9xxUb66t/DYhoaZnIdvneAg/te4yZCbaZPzMmUsV1BpucE3hvdXBq9SYicKKCiQIMEZyTKnstl1NqzlBGinsNcZOTHYq6/ac4QZImrxZSr8IYHKa9Q4gRIUQ87Cc87CfgagtHG8UARBCnPWLSpM8EQoqTWqhbeCSwggUKcgDwHkRiCaJzngVW1/cs+BDQdw7CBBcAiQFRAjgFKysghgkh7NWiiRnOOe3bpKGYUsypBgmO1ANhmqbiaZmZncI3s3ot+EgIwSME7ePNOGAcenTOwZl1fkoJ3uuN3vuiMNf1qH1drO5RPRyccxg3A4QFkwE707RHSlHnEMTKrvlTFvLUjDgmbaeop4x61Xj0Hhi6hM3QIwpAux0c1YTRkjTclirzCeI8bh8mOLoF4EHk8T5FDWlxHcExYths0PWDhhYQYO8CHAExMYbO42oYFbCxtoYQME0Tbu8ftK5EGDdb3HSDqXMmZDCGitermLeJR+d7vH37Ft9++y3CpJ480z4qwCFB35Mpk4w/dVmQt7BhRS/T9JwzHhFQD5mHhwd8/PgRb9++xZs3b/Dxlx/x8fYn/G//6X+CuIRxO+Kb9+9B/QbSdYhl7WnIAol7kCQMTkBw4DhkTRYEQHAKMpGNqfgMgDA86ZpxUIvTqjT6Sl/py6UvXnH9V0kntbj/OujUtLPf1FFAz7cYBfsguA3AjxPjpz3jL3vgYwB+SQn3SRATg1ksVBMhgRAheBDGHoyPovmXVPnMSGz8Q0kYba+0AAqEQRb60pi6AlAQ13f1TFwJrcQMSgkUEziqJTpibH5PNUQTNwrhDERArdRXAZOK0jcK5PyV8pBOTCpjVcxmPilCvQvV3VWA4JDCHtO0Q0gTElKxIM9epdVI4LSP1MvIBtqeDOzTYq/KoZbUeAGILIhJsI/AQwB+mYCfJ8HHQNgxsE+as+EBCTsBbkVDYU4sJSUiN12vSuxqaUDCiKwekhMUjHDW53sQEjlM1BmP4mobKBeIuXBCUsou34sgh9qa55E47JfiaZHHntn6qfGEEM2rIJyApLIBLEeEfp6AGBZhw1L1CMpj0M6z2RgQsnEGAfCiV6bcxpQ9JjR/FveEfjvgzft3+PCb3+Dvfvs3+O037/H++g3eXGnC6s1mg3EcC99dZlLpwiqXibQhYbNHRI0goP3kGrlv7tlT2kFVZ1R/o+Z764ejcukaiPaVTtGaHAS8BODz5dDFQITSutAwQ/xW++W8sFE7u92cDrExBSHUa6F91qGVf61Li4sQFqEvCItyUDfVtXo+cvBniOICECno/ewQyxuB1vyYV8K5V75u7X2tvLXfn+qd8JKL41KLtddckM9BVT/nRvH6nhAvW8ZaOa+rHDcm8amPOL5NXFDvzJS83to5Rk/p00vX+GVlL+7NPOySecv7mbPwczmoPeaAwBoIsWr9KPMnHFO0n7JYuHQPPLjuERYLSwayZfguefZjSI+Zlb46QsszZlnX9u8MSOgrC4NU5IM6LHVc5lY5ZrEvyqBnRXoRSNqCLHGomBdEMkBCDNzPFnPFms5yRoiogQUTmy0FIaVkCv5gr968IPR81rA4CY46gFA8JDjFAoDAwIWml5ETlGTruVYwgqh1vZlNlPwKYPXiIBM0EzM4ptJ3GVBjaawdCQbGNJZ5lNeO9SFsvZWxyt6YCanzEOnMyKH2qebyWAKEHtly3+W1yvnMrtcmYcQUtV8t2SvlqWAWhVT2gZYbrExc7TM1TpEsAAkp6GB5NYongdjaaPaW3N1JVCGzmxRwurvfYXs1YtoPxTPB+U7nFFTQJtZcD/t9ACeGF/U86Zx6D+QZmcckFc+XxhKtEQALz8eWa4QIwzAUIXM3jpbSJJa1wZKNVKpQSDb+UpQN63taXk8xRgWDOBVwlxxwf/cRP/zpT7j75ReE3QNcN8CTQ3LacRozm6GBGmDPtkG0WXoY5rSZ//nPFmmi+Z7zFOHqUt7wJT0jHlunvxaB8TXpubzep5IRLi2lKHg+EZ2aw5e2/bjRwuebv5euzc9JT7FIPWtAckRGqL+XgmaKxWj5inZJ8JAE9wm4T8CeNWdSKkpyvU8t4AWBGEHsGlgYQMk8YvuS5pU9EbLHaQYI6nXZCKINx6QHcfuO+t606/B5B61fSlDNb7Ly3dr3bT/b36L/iACc41dlA9BOw1CWUDhUy2x52vlhd5yePa9FT9+ioG8F08x62kBm3RKLARIsmBjzlwgi1DMm2HxKmV9fdC8TDrpThBA16BKCqBdF9qpUDwuUPCRZHqgqt8K4tc0rfHGWDSpQ1Dw8u/dc1GeLhpR52nhQ20skh2tqAbAsj/CiY5bhKZsKlerlzmzaW26xtnUe3dBhs93iarvF9fYK22HE0PXofYeu84V3c67ZIawuh7JtBdbyuZT7MctcmMnPdX/K8oMaDjV6TCqt0bVTlLWtnHFKY7z4pVhIrfTd4vrX9gA4VW559pmz/bF1POoZgZWeWF5z5IxcGgk+lmT96Sfvecp+9kggAijx9upjF+8t5UXB9q7WUEILnDhrA3OnEdtXeSCqolwXhcXYbVMGSlUSzaw1y+onC/FkW1q+vp3z5b7a+Xn86oAvP68v9qbQZjLkfrCaFSUAH7wDGm6gfVarAKgeEK4kqakx4qrC6Bw9FrT4Sl86Xcb8PP7ar/SvnV7u8KeihNICAWmBZQIoh35x5n7qfWH+1+qwPHCPvaP5fErofsz+dymAe0mvPZdxOFa3xwIga+WsgRCqmE9NOMGaE2KaplnSXL3PmQefO3gOwev5SbUeycLXZEGUvFerasrK+WylZwJxDEjMiJNan5Oo1VKMEwCGkwThBEpJLbwhYEmIiRE5IcQAEXUb56jWTxx2CKRhdxInq5PADT2cI4TpXkM57XdgSYUpH4cepiW2vtJwTs6AhpQiEhgxZMHGkuRBzAMiwHGAE0HvHLjziA8RcdqBCPCOSh/PPH9EEEIsfxeewVHxtsyhkgDj0kTMon+viZUd2Xrz2O8mrUsDPnRdh2EYLDyTL+U7yytBLoeM1GuZJ+x2DwhTUKCn8Dra5/3g4RzATBB2yGANR/OuiQJOAu88+qG3/JAaSqIISjXFWGkXM1eAxIALIUFIAEvEFCM4AXHS/u/AiIExTRHb64RhM8L5HuR8Kfzh/hYE4Gpw6DuP9+9uNMdHP6AXzcdQBf6677ShmJASKEY45xD8BO97wBPe3Nzgb373W4AZ4zDghx9+xN3dPaYYSpJpAMULFqwgSJyiJa1O9Zl1YYG8A8eEmCIe9jvgI7DZbpBSwPbqCuM44OeffsS//PGP+Pvf/w7fbHr87/73/0e8+813CG4Ek0eyObNngnDEpFAQnO+0b0W9Y1gEwgImjfVFTmMf99Tl6kCIEOhQd/DYvfcrfaVPRZVnaJVYZ2SlL2Aqi8iXUI0n0r9OGWUe5Oh0D+TzO3ud7ZLgYwD+MiX8yxTxL3vBL5PgAQ4TCHtRC/cIBwawF1U6f+SESRgTO3UwKEBBeciB94LG1A/IBh7C5jVnVuOSknr/JeW7JJqiN+WXlT8zas/CgYMi9GLvuSPU6MROeP09h50UoBip5pjeRTGaNeU5+e5clyVNGQIrh0Sxd+9Amx7bm2u8/80H/Pa73+C3336LtzdX6DwaXU1uQn4eN6NXR/Glz7iKQViYTDPYkfJD1TdNDOyT4H4S3E6Cj0z4RYAfE+OBgX1iBaYQEUDYC+FA6dpmLm949vIz1CvzAWpAk1kzBoMhSHlcS56HoljTK6UdmxacqErzQ8rjm42OTGYo27UZRBcQwTjIAkAkyweh3jiUAiQFSJggKQAxqDdEitWLIp8HpT6Ls6FUTWq1jU8DAPIdiuENWUim3mN4e4O3H97jb3//e/z+2+/wN+8/4O1mi+3QYxx79MOArjev5JmMJ4t3IOtJM8+vkVbYPH3rdS0Ql/cTIir591T2M0hJpOTny62mpsW1N87JnStK7qNL49i4f6VPTy87Do8AItYenBGvIwjXsTIaNyVki6q5NAIz6yvgAC3eZ0gisPJ7U3wublbz5XXzST6/9sTn2cJo+6JpUima7ZDTjYsXQIQwl98qyn54eM2VQuugwzkgov3tuWDEV2uvQzqmKH0qfUnC+WFd1hWXp+/59dDRugtVsPSFFcfn6FOvueWesKa0XttzDpTNpkBsrphvqKT/tN4QrlF0tuWfW2NrIET983T/tQqxSyzyHjvfHwMMXHrdpaBDZTxRj+QT9yxBiPacbb0e2vKXr1JW8+/sGTBFsv1cus+EiSIsiIPQcjzm3hg5VrDGes2/q3CSwyC2XgtkZ7OkiBgmm5+uCNOcIlLUJNMZhBCIKcypeEPEFCBmZU5wmhsChJQisrcjicZ+VacO8/hIEVmYyfFpIVVgIphXBAHCyUIe6ViwKfUP+BAx9/NGeHOtgYYczvH5q479fJxr38/yUjVl5PHL1lp5fBSAaHJrlGc14RSaYW8V99odAu8dOvFFd8HJuC6imSA1Lyz3Q7XqYuszYcE+aK6I3X7CtJ+w32mCctd1gCN0fR1LAEhBw0U4ceDkkRLP1ofzXuuc280NUNdUr/RrYhAxHDG6zmMzjthut7i62uP29g7TNFlS80MesPRVM0aC+ZorfxoPnBOG59fQ9dhuNri7u8PH21v8+MMP+OGP/xV/880HRO/h+q2CMZsR7LQv2PVIkq1cNV+Eb/eVMu0EYA3h5Oqvjbh+qCQ9PDMet5e+JK9xrKxj++Wx61/Sgu8lyvhc/Nglz32qBeEnozOPy3sNyr+PE9uf602zxq9cwsN86fSS6/ypc+clPB8eVe+zIFfWwRRWSfNECMwrgotnxJ5ILdJFrdTF3pNAPRbBmtCaVYldCpy9cOR7e+WzZ8a31fska/nnjWj+dvVVAIj8Dg2NxKSXiCgT4HKZggI+LN9R66ePar4vj1+cSFlW8YDrOwzbDa6utnj75g3eXN/gervFph/gLS+V8mSLoVkd0sfpV87RkRPHmqRns3Z/1jdpsuqQ1ANiz4I9C3Yi2AuwF1WIay4HmXeTjSVZjqeZbnjFG5LLvNBCmhGYU/lyhYfLnZkVeWul0GKnXa45ZC64vhPaOVD5b+XTc4itxpO68OSLPBF5b5W1emWj6/zUXD1tSz4likeBI7jOo9+M2Gw3uL66wvVmg20/YOhz/jDNzdYaHpf+Xa0D0Bp+1/MpywKyss0s5DfjPbMX8pqudd7lh+CVzP9Z1Kf9/tiMljLO52Tel5C/n0vPrdNSt9J+d+7zi1E7XoulSbYuX6IOT/CIWKOj28v6tSWDz+Ub8eHEby2nqnVlK1zr9bA9rLkPOUFO83yuXhqC5qclA3ewaFbaV66zhcO1bi3wwMXla8U6VzQBuBDPBH638H4gqr89hX7NjOmvlb4CN1/pS6Rj1qhL5dez5m9RGAI4YFWqgjMnUvXeo+97S0Z7LD/R4fsp+hzr76lPvBRUOEdr42b85UHftYwmgDIe7TVsIV5SSsUDYqnULgB7qwklAGRhlOwsJhPiclLnLK7k8D0zZsgY/wrAG7PMyay/NFaxIy3FlVsEkhI4TipIcAAR4J2WTcxIccL93a0BYA4haTI/kYgUnBrvia0HAlJkMAFx2iNMe+x392BmbDcjfNdh6DwEQNhrKCeOEd5r+J0Axi4FSBRwVtyT5kAAq7eGR/boMOtCS5Q4TQ9wrgMRYb/fIzGj934G8rH1Xde3XqMwq3qo8lis/8t6bGK9CkCk3g9Vca3rsZ0nrTAUY4BzSfNKkEPX6bNTiogxlPlSgY1owFCTxFoAwFl4rIgpRMSUwMmBmTCOGwwbQpSExIJ4G8ApwtEI72ycm/jRwgxxDp68ekYQIQojRAHAIEkgmQB2uN72uB499jFhfHjATZiw2W9xdf0Ww7gBkQcE2N3vwCkhdIKh97i+2WJE9Q4ZNxvEmMzDJuLu4QEpWfsgJbdXXkMA0CcBesLQD/BvvAIEw4AQAkDAbr9DYgY5tWQj53U8Q5itwcRpsde4skbI1nJixm63w+3tR/z444/4u+/+Hr9//3f40w8/48+3d/gP/+H/g49//gOGf/wHyG++x3ffvMd2u8Xw3/wb4O0b+O9+jzBscTt5zR8xfYRjxoYZHQQbRxAiTNCQXzFFdOTRuypuJFl3+v5KX+lLpIvlpKWY+JW+0hNIdRT57+NXAXrmi71DzGkhArvAuNszfpkEPwcgkICJEKBhcRKrUnpKjEkEQRKiCJCo5BQwlLt5z0mILLylWZGrBXvOF8GWPyIVfuwgrwOgi4TyOylP6EYIPNARQAlWUQAd4Fh5oTZETi6XGGI5IqpiGfbehItqAYk2HwEAdmYQYhYxkuvWe2yur/Hb332PD++/wb/927/Dt9+8x99+/1u8ub7G1TBgtHCOygOoAdWno9yfUj7p2drwdqJGF8lyQOyi4DYIPk6CH0PCj0HwUxDsGJhYwR9yon1QyoB5QQgcA04ICQyZJf9u+h8CS2+NeBBJpXWngHV205alsdpae8uVTVr0VlGaf7VxdMheNWxv2qCS14OThWXSvGuIQRdSsjmezCNCos1rVHlkpdazOjYIlYAKz+/JMmZ5BzgCjx7D22u8//5bfPftb/B3332P72/e4f14hXEcsdlssBlHjP2AznuofUzVbbYdkI1uWiMcEkHXeSQmbVu+U2p/1e+qHOfINWVmnj/LaYf635nMtz5sx3pq5buv+rIvg6QBcF+WLk9WfaDwWEEuj9AM8crKCszDMy3RnyXwsFSkXOwZMfuZbCPIB1DbmgWCt1gPRTEj9aqTaFzz7LxQc8zmCkTUxEbzCtkBveijx9A5BdUaY9322ymF42OQr3MM/HN/f0qdXpNOoZrt589dz8fQS1gevVb5r0mPqdeXMv8upWP1zWv/GCCxtIx/Dq2BEEvAtdZlydA0u7UJGdmbbLVW5fsXGp9F/xSlWnO+PYWO9+lhXob2nrXz8aLnyOJzc387F9pjVMwrgFMCp+oRka3S8zjkv4tBQHmO1PORUDxdlMk1R+Ws8JeaB2B5bs9ElTwHioxbBbB8reTrcggB0rwGWZhQZXgsQo1aCkLPaO8gcEC2CjIZGEDxskA2b6B2emQrqyygUY3paorylAEXR2BLmCc51JQJ+pyivfQ3RgJAWq5kS8OWX1qbB034M+uULMQJV0W1lpv7uc477aq5F0yZH440BAOgAAfVOZXSoceM9ncbnlKQEkOEIKj5OPKYq5Kd4Lse5BxECCCGowjnNO5wbRQVHUedi01/NDoJgExZzgghYT9FwE1gCPrNCN97xBjgu86iP+j1zILIDEqEECOcz3MD8L6DCBRAMRCHuU5O51wR00Vysm6bI6TJwDVXxIjNZsRmHNB3GheYS8LGqhxol3KWjdsxr/1c17WIhj2bgYikiUtvHx7wl59+wk9/+hN+jgk397fwmw26AaD7d5B+BK5u4Pu3ADmkjkAJQORm3gDe5ZwS1NRLivVfsSAsS3WFj26+/5L4hC+pLs+hL5Fvea4XymPkkkvlpJnlJ9pz5uyjijj32bq4rfsXNM7PpZfYF47OncvVG4+mS+rdaBnOlJYrWlWhZPmMYJhBEkIUQQIhCSFBNDwOZ0861UUAptPMuRoymC+C4p3ZTv7Cy2G+KFoeL99/TLdSPB4yEOH1PqegP1wHNRjQOggJwA5ADoujxpo1BFKrCK9tmNWp5T/b73KcwBL2CWqh3g/oNxvcvHmDN2/e4t2bt3hzfYWrccSm79E7h84s1NvQ2UTzUN2vdWQI5RM2/51/wKzbM//LoiBUYE1AnfOCBGgOB7YbyXjKMsVYzPskj3ljulvWy3zsy5MrwzWvWLvGVtdbMz5A8+zmuWgs+okWxbS8X76vWdzNfKgGUM1zy4tn15Z1sDKt58O8mAB5inlXgKIyV7yHGwYM44irqytcb7e4GbfY9gN679F3FqY454VoZKbcKWQ86nyfb+R50n0nG+VkXvCYPrC+2masX7tOc/lj7fcDmW2VZDZs7bXH6n9Z/R5PB2VdyAMcO1CW81VWf3meHvQcv3O0f5br+mxVZPF+GT3DI+KSiWdXHpvoYFO0zxVNS4X4+Xrkg3jl2uVYljN7ft+BEodnK+9kOw4emZXNtjGw5CSXKmwuc0LUx1QGheDUIsFdNqBLZdRaXVvL5ix8HnqQnH7esWv+WgSz16RPIwQ8Zhw+/5h9nTefnto+P3VAtftC+93zx+wQFFha37cv/d2uyyUsq5v3PV5ZY+1h+twleKLpMyEAz38UcH5PXgM2Lz47Fwzm2Wcb452iKVhzvH+zcp8l7xNVRDqpYYhyXFQ2EMBDPfq8bwGnuXegcw4kqvznlJXIhRuFI7XuU0V341rdzlkAzmTLKAqghDDBOwLBFyE8pYT9fo9oFuZwDkIO3nKU+L6H953WgQhhmiwu/wTmiM47wMMSyTnzYmADFypQ4R2pJRMzOAWkKYCcIBLAiZGihv4hSeAwgcMO+4c77O5ukcIekiJSjFUWI9LwTNq52m8WSiivnwwEZOE4g0tlTJMAcOi6ofAHWQbzLnsl6fiGEErfdp3FqXUOSQTOe5DvQOIgEiGioSKi5UPQ5NdZCZ6QklnMxYjdbg8WBxYN00WNA1RIETEKrgZNJu1Jrep3ewHAiEE7wzmCdw7ekeYpyGL1gs/Rlyv8Z0qMh13Azx93GKaA/sGBPEEooet7EAFdN4LgkYWiyAKJEb/c3WEIE95c34BIPV6cc9jtA0JIuL29BZHTXApOvSYSi1mkKj/ofQfuUglBd3W9RT943N7eAhDc3t4q4EURKYn2E4sm51ZOEzmkWOZtdfxq/9a1oNcJM/b7PabpAdN0h+QEtNngLw87hBTxv4QEbP4LyAHvPeHqf/4O/t0b8P/5/wb69ju8+T/9X4HrG+y3I5gdEAKQBBwBcoTe9yBQCe8wCVvQDaeWeUTVEPIrfaUvnppQMxef7q+o0f5Kf8WUgftF4iMAWWeRjQiqdbLx0Ax0CSB2EFGvtZAEExwSkSUQFvXoZKjnp2jISC+aG0tEgeIy32cK2eyRgEbvlBXEBgrkfJiwBNb2IiIIOcDpuUVOvQMVR2CwDAZCOMCpsQUxg1wH9cDo6vNZGm8NBiSnQm7rVJW0M+AEUoHwzFOSeh968lrzGOH6DuOba7z98AF/+/f/Br959w5//9u/wc12g/dX19huRlyNI7bDoLH7+67mzPqEsq0AljcLqLqwIi0VvVP1iABuA+MuMO4tdNcEIBIhJ1VQIxcrJ/c1C+A1LGku29m+qN268Hoxvrcwq+WzzlciV+aQXtKMV1aul+2z/b75roThWvZJnnvZZ8ioAMNVZlSPiNzGPL/Nqyd7+Sw9e1aomGw1HgRkIFsBBBzQ9Zp3QdV7BHgPNw7YvHuLdx/e4/ff/Q6/e/cNfvvmG7wZRmy6DuPQY9yOGHxnoZnOKN+x0icCkNMwmdm7uc0vhxbUse/mXu3H6JJz7qnrIc9l5fUPfr1Ab/l56VzdDpQZi8+fk0l+bL8+bRyekSPiWOes7AjPoEuV/48r9NgXh0o5cvMFVlu3jIEmh381i1gF+2pJqN9nIKJV9M3rdW6BZYu/1d8e2Xft9cesax/7/ZLaTeOYFe/y9zX0c2lVMrNYeoFN6VjbjtFLe0I83mILKGzIBWN+zOL9uXSujF8T8HAMVT51zeWF57cjDM0L9dOxco5Zgs29ENZBiCUYsdYHp4CNvOPJ4rf8ai2KVmpe71w+44hSXrfI8+N0tq8Iyw36gB7jCXGpdYLud+f3mPb7NeZsCVTbHxdUtL7Pz7Mj55PU58EU3y3Dqww5LNwWGUOt78x53gEwhaUjTR7tXH1+EZDQWvYcthMiKDkEilBA5lVAiNHE5SZEIidGCLG4S4OsDGdWTI4AoSbpsgErnSYQzoJo8RqYdSAjWeJhoIZoJFbvDOEclzY1+SmqlwTBrss9WeQ9C3Uj1SqqPUPWx6rmTBCp4a4AtfpPOfdH06bct60xRQE5mMF5LMr8QPEgaM8qkXm9cllJBIkdPGmCYxCZBwRmXhIsuc4O5ACWVMewWYVFZbMApggVjBFY3oSYsJuiSofki0dDShGcApi8Tgebnzp2hJgSXCIDFDQ5twDw3ingEBOcV/1Ku5jEPEhgz8/9qAnBCSKaEHzcjBjHDTabgMh7BGJM4TCvRmkfZSuzutZbjyV9hjZEIIgcMaUHMGtoChYgMPDAgtskeBDBFQPdzx/RhYj0X/4L6O4e/dv3cO/eY/jt7yHOI3UeIA0PpftuDo/mSserqCumP9CT4NgO9BIWz5fSMaOdl6IvVVB+zBn0UnQpb/vS5R87E9donac5+KYpp+6dKzWaXftYeu3+ekwdMn2p8/m5VNr5wnLa86kqlde+LYYFaFXQdpaL5QRAftc9PpqnXBCpdpcFUGj4hdK2eTi9w+VQ7137nHmNzIOh8PjGZ7EpbKkwe3ZokqIrAmhy4cyP62mSldooCu9awRq0Sgov2AIRBPMUhJSE146c6mqcwPkOw7jBZrPF9dU1rrdX2I4bbPoBY9dj8B0G7834ZGmtbn0mmV/QMXmN40zawW+/oNr/1ltIrAY5gTWPCKx+atQw11/pB67jSLm/pXhOtPOjXFfel79Lva4FFdrr2+sOZD2un6X5HSt/C1bqIQdzW7DwgkBTVHn22vPacbUPeYUUmbHKKGVlkhnaQDTXOjmg8+iGHtvrK1xfXeHt1RVuNltsew3D1OewX86X+dX2aQ6BheU8KE1oziqrVzbiOkctf97maTwELOb3zbfS0kmHlTtzNs725BN6i/bzpfScffvcnaVswoG2eJWWG2v5fNi3T633pf00+/3ohp/LzPfMPz+GXihHxJw+n65xOYIvcc/KgCzvO4ibZRt/s4BrDOQWgWTUDa3ZqBo6pfzL1grlzDmjSDv3vrz+3HdPeeYxwOAY6LBW5jEg4yXpEmDl0md/aUx7bc9nW6hfCcD5o+x5dGptnsq30P6+XAft91kx+Lh1aJZcBBBcw6+psrN9Pw5GHKdLlfVfGr00A3URCC31nDr1DDGFYh7vlGroHADFyr2lqvQHyOX5UcPDqLLVlfd6TriZ0tqBzGM+qW1TYkuABxW2chLD4pI/V/rkZHnOqSW785prQJXjCTHWOR9jAidBCBG73QTypB4OSYUAYQZ3HVznAXKYwlTOdCLCZrOB8w6etD/2U7D4qgRxGqOXU8T97YSUAnLopZSCuko7bzFqGRIDJAWEaY+43yFFS4TtHIauV88OACEmi/2r4+Fg3h8LECJ7o+TQS0Cz+4uARcp4AAoehBCx3+9BcBj60WIgu1Ke5pugOh8cwQGay4AIMc7niyMPgtZXsjdAEnACEhhEEZEJkR1G18N3Vh8SCCb1osihqoQNnHLwHSGmCVOMiJwQk5YLwOLoOrjcWtO4+LL/WR054X43QRLjhgds0SHEiBij5gAhgITUStPyTaSkPNxumsBgXCf1aNhebdGlhP0+YAoB97sdvABdX9eVWifGopyIMZYcEwDs7w7XN1dgYXz48I16pfiP2O8DfvzpVsN0LdZdXotLAS17IZFzcOTUW8mMbPbpDr/s/oIQ7uFSAotDcAN+8iP+1G/we+8wAMCfb9HxT5j+9AOw3cD96b9i/O3v8O7//v+Ee/MO4WpASIxf+AEQRscJjhwG14NJkIjLmnQ51viqxe9X+kq/EirLb7GnfqWv9FLUTio5AWqZEp9I+QAiQEAIAHYC3LNgEmAiQYIgmRV4NhpIxCihDNkUzQdgBFobkKZeuVpzRW2pmlZGjThYjQu0ygIIK9NCAMFrsmw2paNZoWvRqXpA5BCFTqoVOwgQX55Z/R1bpXa+H3ALNWwGDhzruc5w6McRb95+g2+++YDvvv0OH66v8f7qBldDjzfDiHEcsB1HDEOPYeiVh/KkPFjTBys61Fck4/2o1cFbSCZRI4MpAQ9RsEvaT54IvfPqIeOksfxfaBkzCGFAS9GCiZSwXgLY2S6NATtjOQx6Y0IFkUTHuAUuYKGDyufqjSDCC5Vcvp/rKxsDWe4HEstjknNC5DWQ+RGp82MOqmH+vuzxIsi6ouhXoC3ndDVAzWQiV6apgLyHv95i8+Yav/nt9/j+/Qf8/W++w4ftDT5sbzAOPbabAf04YOh7dC3IBTVkArLMVHtqndR4ByTwHXSd2/rKPGKuayt/ZyNqV7yID9s/50WXgMHcCG1x92o9/2rI5OfPpxf/FPS88boYiFj3AjrWs/PJltfzMcX37MLF70tl1FMsl1Ytmc/e1RYwv7NCEA1TQIdK9haEqB4RbczEM7U4AwiInNkdV4s8nwNiXva6wn8NFHgqvSag8Fx6TD/l69d+fy6Cef464Nh6PF3GS+yOJ5jji+rw66AD9L0oPl//Wafo3DWXAoun9tnl9y1QsKb0PrZulFcyVsZuyZbWLRDRfp8ZrGxl29IlVo+n2vmU309dewoIWe6Zl1x7adnH7jlVhgp3F4IRqGda+7ys+DxqhZoVNAZIkFiOBJrnAKlziUGk4695BzCLS8ws6vVvew4V6yN9ZUO6YpFtggW5Wl8y8ELlFC5zMnsVZMFNRAWprMQniqqwN+GhVcYTkYIQ3jd1zbkhtB+UH0iI01QTKpeaq4WSWFk1B0dEShEKplh/e4cOas0UkyCHIyBgZo0348EW45xlDDcBLQABAABJREFULbdYU0QER06/h4IInVfldY1/nAEkPwMmcz+1Ure2WQ5CpmUrNIElw/PNvmLhibQRYuOawzppv04hKDCROs2LueCzclld18GTJquGiIWwagXbOk9SYgRKSCKzPpwlMiT10AERuAiVzrw2DAzyHTzMi8QScBejEamKH+33KujN5hJp8nHvHbrOY7PZICXBbh+geTRQPFayINnufXOLpqwktbGmOj9jitjvJ9zfPYBjQk8aNsxB8JASfgkBP9OI0Tv0fsCGPBBUvRX++Y/AxHj45z/Bf5vQ/+47uN4B2w6SgBT0OZ09Ukw5I3lYCw/8urzBqX3xr4EveQq9psfDp6JzZ++pey7lET6lXHLO4OnJVp9600XPupSe0vevRS8hg74UnTKkW9Kpelcdw/IBa9/mz1LsM+DUwSAREASYBNizaFJqL5YnwoAH0xZzo/QteMep97VKC9DE0pnXMvNp1oZiqCL6+VhvtUo8oaYCuR45x4TQoi/nXiL1O7FqUPNUMuBC+4MBOPLwvsc4qEfiMIwY+xF916Pvegxdh953auyQPUYbi/E5rzyvxVPo6Pym+Yc8B9aGIdvO5/xnZq8BJ5o42ZNykxnEyIM66/YyFqXQ5p3K2S6Fma5PPwAiAOSsFA1qUi8oCmzjn9B+bvmog4qgKICN76qhxjJQkcvMdZR5GeVPmX1eSLplblYwonqeln/Jwq2T8biZB/UOru/Qb0eMV1tc31zj6voKV4N63XTeo/MervNwXvnyzBpnmWxeGxt7LPPFzXPqqsjjQFRDtKscV9tPVHn7ViYSmfcCUQ39Ot/T5hOkEQuOUHv9CmBBdUUfOxMvPSNf47yq0/yFy26Ke2y9H8szPK785bVPb/cjgIjDGVS/ananFRKisgDn988PjXK4HPz28pT31degPJjZC6J6QuSklk09VpQx1Zp05TvMJ4vun1XwXpa9Vrel8nDNem5J58o+9vkc+HSsLsd+/xT0GGbyy6PPz4x/pS+b1vaTpQJ/TdBcW9NPEY6d86b81TKXnhBtfNVj+8dSKf6aVBnM550ZS6B6+d3y2lN73nPafg7QWH6v1lRycC4sQYhluKYsaGaJyHuvCndXrYTq39nbRst0Tt2Xc5Qicg70/2fvT5okyZU1UexTAGY+RORQwxlu3+E9IZtCyttzReGaP5yrFmEvSC5aSHmU99js7ntv31OnqjIzItzNAFUuVBUGMzeP8Jgys+okUjzNw9wMBgMUgKp+OpQCKQwpUxzgCaQCAA/zpOfVsE4Vz9Hi4scYwVFjFKtHhMYFRggowgCFSTQ3qy5Xso85gyig324QUsIwDDUcT4wRXeqQuqjJiYtZvDMjhliFhjxmfPz4EZEImy4hCKqFeooaNzlLQBbGmAcMwxF5OALQfAzCGUSCEDsAhHFU/sJBDBWIgRi0P9r2+1jqXAdANHmjNOOo76KsYc4ZXewRLfRASqEmzOu6Dsn7QQQyMgoztjIlCIRoTpETGqtypllkWczhECMSJQ2LRQCCCrYxRaSiN+ZS8PHmE8acEeMVmIN6LtinlAKQ0ud2u0UkBW5KKSjHjJNZbDQ75gJmwbUAISaE4Lk+LG9HKkCIlugvKB0RkHrtBwUFBF3qEEgTTrMBMALzzmGu4EsVWIgsf9hQaVdsHUwxYbPZ4N27d9hut2AGUrrFv/zrT8jjiGFQcGw5b8WkPvL5BecMpObOyDljGAZ8+vAJcszgPOIqBnQBSMT45e4WwzDg3bsOt3GDtNviLYDrwyfEw4C7/+f/C3dX/xU3b/9HbP7pH/H3f/4eabsF7RN4KBj/egcUQSgm7AcBB0ASNJwWvpVv5Vv5Vr6VZTkLRKwVmiv4hDSfcyZggOBOGDcs+MSCowAlMJgEpnLGLNyNKemnY9MYMQa4hlFqlYXKh9Wdn7zexV5bNaWtonL53q6Qnr/TdP/y/V3rTtDcElpHqwxWrMK8MOBhmdpmETokkAgKHxWkiD223RZvrt7izdUbXO+vcbXbYb/d4qrrcLXZIG2S8UEGRsQ2JNNn1h08QCxu/FFERz6zhmkKrPnaEkWUgBpuVIEqmkCbYJ69FiYLkCmXqrj3ycRzwo2GXPG/0lCRhg+agRA8+1sMeJgNfpu3AWjyO8iUx4HV44FY5QZhBiwsKqyNkycEXLs/vV9t20VdbCCD94QZXAX3ALLQrqTeOBRI885tN9h99w5v3r/Dj3/6I368fosfrt7iqt9gkzqlr02vNAadfoGmnPKzZ7s8jikcbbD8FDOeE+61EyowIiwz3nFGO+YRQWExa+gyWVTu0Q//rkpjXPS3UV5mjbsYiJhhy7RyvlHWLL6oYNV8n9V7nwKM1pyAlr+twGbTJbNTy331dE+Tk37VPYWWrz2vrUFORTzmHINnIMSpNSnQggyOULoypbE+dBTUkUx/bLOo1A2+aZ4rG7A46jrTZKuHnz8DFsz6yTd8afp1GQGN6nVz4GPZd1O5xLPgEqDlqeU+8OExzzmn5HsuU/JwG+bz7fF1Pb8v23ofsu5aPnt++SP6+5ELIa3dc7YKOvnT59503+sym+teBW3MSW+KKX8bxvGexdOYd/cyAKhRulYhgSxeKjDF8xZj8SlAwPU4tWOxBax0jz6ajGkPCwDCmbkFPXnl8vBcus9aryrHV/qE6oOmL0u6XJL1WlvWz50+seW/10vrbtuswCsgzDnQefa7GLPZCEkC1GTStTEtXdt3ccFUAEDzHmjTpucyPD6/C6WmXAbXPQbUAhHBlLoN8I5mjFzAjGaF4xx4DJBsinUnCrs3BE0CV8oIYbd58xjIBARNpqxJpwUl5Lpv61Fj3I95sHeWyRPAP2NA4GJW/nqPMFBK1u4QS4Qo7mGhQpT3sRt1KG/A1ZLOFcchRhAEKCOEM7gU7Y4QQCHOYusTSQ3FRCBL/N0KhNaeiSiUHjBPpmjdXxM9x+j0MiXx0ycEREoWqzZCvVcCLNukCvv2IbdUPKXMWVucPoO6rSDad6JY8z7oeqFCtCr8CSxBE56DqnVfLoJcXFC2FoeALnWgnDGMHhJr8lRhKGDlY1XsnSMFdKRxeWOMEAO3ogmWUZKGtw6durObosMTcHddh1I0nBZEkIdRx7BJEqjKETaZWUNEUTGvIbHnxIS+V3q9utqDiHB1tUcpjMPxI0opcHjF5fjq88Fq5TYDdG1NEdH8FYegyceLE4IN0XEcwWPGX7cHEAjfbXcoNgc0LnYHEgH/l/8Fudzi9n/9DvTde/R/+juwROS4Q4C+E5OAiC0uMQES6jpx6W5/zmDlqXzg6X0rVnhfUXlNxdbSGOk1DX9e6j2eU89S7nzoOt9nav4ZV6bSIsSln55mIO7jEWe9fKY9SzbqIUOppxiHPLfcx3M9s+aLL/t8b/twecz7r3tGuNLcd3ppzk/URWK8uSh1slnzM0K9gyHIwiiAGWdYfa6A9T6u3xdHEsxM7JtXq3cbv0YggE0mCKg8Vagf8dPGx7J9CkQKUHKTKJhromCq4XQaBTLaj7ZGIE0zG0GtKrWxuMcLochg92rvSQBCJHR9RN8lbFPEJkX0UXM4IQIUTI4JvhTMhMPFOJ9hh/Dc9VYNDVgETC6TOfdj1vcioMKgAjATMgsOAA4ARkRkH2cVBiEkysPNtE4mKxbbu51ehE76unoqyBxQAKpkZVcvklnX6+18NX7i6ffaoZZIugIKDHI924wZMt7bw035PR7GqSak9k8GJNux6GcGqhnfspAVxeaAiirB+HmTbW2/iB6TKRg/3yWkTY+3V9d4d3WN77Z7vO232MSoPFYfkfqAlAgxApGk2Q+mdUNkapdyfzRrW/1G7W5Cxhs6rTTrTdVjTjWQyzWeb6zqfC18qvDULkEzA5zndDq/jNarfrLp55nO06+brVfn98Q1A+tLi9T/FucXm7PUhrfvSAgn4fvPVLjysGmuXdDOpf6xNmFa4y+paV7PZc++lKdaK4/IETER0FJ0OLEYbZTs7d0n15/5+9y5ZWt8s76w2Wd+puWJuYK+VnFfe5w51UVUuIClIJeCnMvsyrmHgzIVFblsQpEQBXQpYhbCwhUKKzuaGgS0DCoaXoLmx3p6YpXRKiZ80ZgavZgIUueKgkyy6B9XRvnCMC2WVBfCObN8jpG9T7n9FGDinAB7nwXy5a6/i0XA+/oRk/Nzen5oOV3YH1Nepr2X1HH//Lu0yMofZ2teLg2L/eWiBESPLJcLdLawNRsM6kx0C4xlPc4mEIgm5b+IQKJZtFusVQHVcCxtO2qEFWdSia0fpoVl1mJ/nUY4INIYmSklEFE9zm9brLgXzqG1zXC2rt1HRvcpYR54/MOA43Jc58f1OmfNqvUvgYiL5qALq02CXCH7+AhKI+S1ax4VgFhj5JviFMIVQPL2aNx+AagDUQBTAkEQZFRqTXOPl+r5QmSKeH3ZqgwDpnAuUNkAMQASwYUhxYUdTyQNdKkHQDge1Trd2Wsu1pEhgaIgpS0IEZwZzAXMo70zI5cBd8fb+l4pJcSUKiCRSwaZR0CIAcIZRQj5eACKXtcKvVyFahWSNRZvwTgMCIHMw0D7IcSoRzAw3kHGI7iM5iGSgMiABLVW8yTZAejM26SCEKIDzMKmrEBVqIUYkEKYwm3aMQRCCoQUA1Kkpm8KmANICBERXeyRUkKKPSgGCGWIKc3JszKHWPNOcjN5CI1A42Nn/A5RRCIND8CUUKiDyIjMWa3HYsAhM8YCZAkmJGl/ZRAGAQ654FhUsU9iwEnssL3aYxgG3A1HIANcivZzsMSNIshUkAAUVs+bHhH7tEHqOoQuApFQAtAlfc9E0XJUbDQ8k9FyzllzRex2AAhd/IicMw63t0hdQr/dAnUeF5tDDAoBORs/FVTYjymhByCloE8JkSIO+z3++tMHpJDwyy8fkceMAwFM7vkwAcye4FwCNFdGDNbXAVyAccgYS8Gn8YBtv0Hf93WcPh0OKDmjjxG/jAP6PuD71IO7gKvY4cdwjcQFx//HfwD/52v8fP0Jm3/4R7z7P/1fIOkNjpt3KOOAoXxQgTcyCAEkAZAAkQCCri2XlpdScE5r5ufmt76Vr6U8XnBmOOCqyoVYrU1rnRAEcoBReS7X7z2rrWeq+PzywmPLM9r3tb/aqxWC2qgLAkYzPGAAAUwBqspPmBS9DAJDwJr7AUARgojGZyosGIWRiRRsrkpZGFGZrMBYMKZzWd1+mDeT1HsPQZnJUAKCqOkJB4K7tFLJCMzYMhBlCtd4rPyF5sDCeFRFZzZAIg/6fmWK/V9lmVlb/WN7P+zZ3mIDPbTZU26BidcUcM4gCDaw0J0BSAnY73pcbzu86zu86RL2XULqApAE1AlCUpZnCmuzohA8Vdm8WKn2HqI0oApxNeoKAoSs4x1KAbIg54AhAx9F8EEIN9ThIIBgAEjAwTxlQrJ+Qx12KlRxKfYlzuikyhDVM6HJ12BSxjwA1wTw1k7ihQxSPSZ87W3uZwMLTA6gYjkgigNWba4IzS0GLkpbwhBRoxSU0X7PQBmAcrRzA4gzNM27huUUIwyiiXcFADFm2jmZkNRIJ5Lx5caDb0MCAmGEhlil7Qb9fo8//fAjfnj7Dv94/R2uN1vsU8Juk7DZdwqEbQISbO6gkcN1VBYK/oX0bMq6aa8INh4ADEgDC6LoPAAzJADFkscHqGymJCYIYAvN6jpMJ0LUOSb1P6PN2bPXyuruds+VzfUNGvBq4PtSrzFvjD37/vtPXufc9cuKToCNp5fH987jmJenghGPBCJOH3pyDenxIevoc1YblyuX26l2zyAtlE/tdJ2fhbXHJ46dFczQP1ekSzPTfKMDpvAU7gbVDkxbRws4LM/PAYlTxaRbt87O39cL9mN7x5JgiOydrO7KgtD50Entb7NxbNq3rlids9XniPc5CNu5sgyPcikYsby3bWNzxeK6dRo/Vx7bDw9ZRj3uGUvGaXnNurWgzpf5WK6V+9t3yUIrq214pW0HwJkWtTvsuWsurvxh+rhvDrS9Ngf6pnMrD23AwIk/IFJFZLv+6eI31eW1ieg4MCtDwszTajx7JNWGUlOPJnMLs3VuumOtR2W2xqr+8nGMx6wvniIRLOnu0euS7xmLalf2h/vWqHufcA4wlen3Ova2RgtRFe6EBVImCyZXZsLC/OhpNkyD4J4xZOx3DEGF5jrWBjq5VVCcAxAOHqhG3Jjddk1rvpDJICQqXKnruFjCOXO5hiBDaYg522/6LmbvjhhRwwoRBCVGAIycdc/20D6znANQa7Ou62bzwNvGYsmZLfxRSkm7LWj8GSkaoknrLRW0U/mdtN+0B5BLRh5HjMOAPI7ViodATXhMV2K7NaEJbQRM4QcW/eh8kDRj2fQyAfVcEUYok1BhVDnLwVABRWoS3y/4F6c5/6hRkDQeIKhz0XkmJkIMHgpseiZg4bsqXyb1I40gprLrJN66J2bfb5CSei7c3t1h/OWXSd6t99szrS1uWRdC0PBaQc0eHXSLRtcOdvkzvQ9ijOg6Dd0gEGBUOiql6LHxko0pIRoorEm8GQWMkvW7g37bvXrM7PdbHI5HROsTYfdHcou8KhtW2pn1HZn9rJBF0SANU2YCqhTNwyFccDeOSCHgw+GAKIzvo3rMlH6LKILURQgFfPpP/wuGn+7QvfsnhO//hPCP/3tIEBBrCLJYisYtFzGF7f1r6GspWVsQ4unPWG/7Q3LN78NK/bdRLnn/h8b/KX02yW6L84+uydrQ1HvvdQ/wkZ+zzJ/3tGc35i0rdX7ZspzPa2178nyTpscaXl2AedADEQRIVUpW+/e6d05+0jO4bNauRiPieggTAqqsPns10z5Xht4+ZvHt3rZ1BzYlMtUPzBDB+Aj2/EvKr6lHxOQZIUWVxijuuerW7F4/ZryAd+AkpjXn3VDUlbDNa5NoXiQIkLmAIiGmDl3fYbfdYrvZIIWA6JbupPtwDFH5t3acnjjsT6Vv7VNVjhtXDlf4aLcQWAhZCFk0WfXIGpopC5CZ9QhGOeHXaNGf1qW1cjSfZlyW+6M0Z2aeNfZ9lihaJo8XVvqZwjI1OSLMW2Zi5HgK1+Tf248ZBInwLGn1zBuivc9olKxtMnu/aQpMYcMmHp0MCNIZJFXPxz6dAiGmiN1uh6v9Htf7K1zt9tj2PbZ9j03fo0+Wf8TBAF8Ymq5dk/Hp7F+t6GvtNH4cQOWz26GucoHxvEF8XZh417k+k9bpfxJdTn86Ifvlvr1SX9UtLNeyMw+5sJzXtTTr5IX3zNsjz2nWk8uCXM5fd1bPdFn0heeWRwARl5V2gQdeptGX1HGpg/f563wBWSqtpjbMBRie732YgxDLSepKoDnYENB6PCwtRSvaaKVV+t/H+NTf6np/SkingILzPBPTcxZoWLRn5YcHlH3zxeM+L4Vzbb73+eeeesE7PLbORW2L56wrH+9r37lxfcp7PqauZe6SlVrxdFHqkvJQR51bUn/7wvVDgNsq7Z+5zo9rgO70u68Jgmo5A03WG+oYa7x8gOt9vi4pryYTCBGChXZaaZP95+tum+R2DYg4fbGJsXVXUcjUH5d4BtTzX1COvQ+EWBurJRixxgxcDlhIZSZdYVuV/szG6ysIwZ6Y2RpNFHwzQClSvQymEDyu6gS6aMmEAYBEBU8ipL5b3d/sRWbjcjIPLBAqmRlQMOV0MEs75hFSsoZiEhNOiFA4a34I9nBLGURUaa/fbDRMTB4U1GBBzgXjmDEaGOGgRCwF0bx2lGmfPIlcUU4Q5HFUC3Sj6RjUGkpzRhTkPCgQYeZRFFS5rvkrlJngccBwd4vj4RbH47Em03aFtwWaqm12Zf0srwomnqNaDwaalvCg672LHUE8ZIN+ilmOBSIVvH0ouCBn9bIQYgtLEDSPQh3OKYxVqfdZeCUlxSnJtSnrvK0110WMCgqxepUys0blihExCyJpQ7kIJOn76diQ9YcKDgxPNE7Y7faIMeK7777Hzz//jA8fP6IUBhffKyMgChJxMdBIJoAtdQkcouUWUd4vpTSLmeui8gRCdGBmbLdbCIDbwwEsovQgqpD3vtmEgGSSKxf1zmDWHB1cWD1QQkC/JWy2GW/eXGEYB/RdxN1BFOwStYb1qRWgIFcwBYqCE2zKKihgQ9pwAiEzo4wDeMwYU4dirvafDndgLvhLl5DzBt+/2YO6hPH6CilGbLIg39ziL//X/zvi2/8VVDbY/u/+Pd79b/8JCB0KdYhHQjcUZGKUwBZhTZOy/43px7+V33U5VQx9aR5VDQq+TbLfUqH6fxPki9pfNHyQbecefV7XdhaMvg+yb/lznYAeqfkAE8ggjQy/UPSpsGAOGub5GSyZl1Us5p3RKoRJxEIzAcGUmhAFIJhH9UgtBchHtWjPo3lEOCAxeaza5jXRtCvE67voS2uTZHZfK5u370ZE6EOEQDCWETEkbDY9ttsd3l2/wfVujz6osQAADZloeSFiiFBg/8vMMaqj716u7nGo/EQRQpGAUQIGYRwZODIwMDAUwcBFk5ijIIsaYlS9aX0lDzOqFFmV8iaPzYGENV3CJMPNznmljGlI3DNnBjA5PU3yoAIHZWJcLQ+Eez6sHxkoFgbMQy85+MV5urYJCyYV6Jjozj07vDUEM8qJ6iVH1fJfwKRGfuolbiJPVJ7y7du3ePv2Ld6/fYd3V9e42u6x32yw327R9wldiup5AJey5AW2lGmPmmQa3yd0lGpib1sPWoMi4LxMel6X4a1fRk95ZMsf0JWc65wvbYTxoEr0nnIW3Hnh8iWMZbw8AoiwxtXNaU7MzRXNeZy99tzfj71Od5zz9T9U72p9Z54/nZqEJ5+QbaLOunYaQtqCEEBjIRribCGIMdrvnkDm8vdqywkhOTRrr7dmgVs9Ik7Ov7b2rmkY1ifBucXn4UVp5WkXghHtMx5f95x5e3jhnO55DBjxOZDKtu71McCMbu4DQc6XU2XE6f1zOnmp8gV107PynHXrkjW0BSkAgMJ8TfJ16JyVQwuWagozqVgF8bSGLel0YqCszuDx36f57kztNH2coObzydfWNSDiUnqTpv61/nnw/mevN4+nuIe8P9o+X13HRCyfgSu06+nK6IvvX+y5fDwcICASjP/WZL6e10EwGS4BAIImW472HLcUoxhr0tx2v5u9A+bMbqWLqh23ZHN5BHKG5AEoI3i4Q8kjxjyogjxtQCGokppFLe3csok0JFkdBjLr92b/ZssPwEUBhlJKba+DZypUTJZBzKpyH3Oe9noDLMQSYqtiWxXdIVo4A1ELv5xV4OGccby7xd2nTxju7jCOo3kB2LVABT7ca8OPXpxv4Kz9p1b3Bk5YDpZQ22cCXgUEANh7sYUKEtLQUqUQOEZNVEhtIjwdZxAgBtDEEEGBMC5o1/t0rnxWanRvFK93JEKGhkliLhoeKwTEyIhiYFhltDw0mHL7YnsSM2MYM/pcwALsNlv88MMPoBDxl59+wt3hiNvbuyoei5IEikx5Itwq1Pm/ycbU8mnEdDI3PVawgjIJfd+jWFJzB1x86rXKEXJrS2iC7wLGcDyilILtboNEQIzJLOk2ljhzg3EccTNmFGi+kMkDghBjqn/7pCfS8FdOW/5u6g1SlH6Y67zNwjiWglsu6KTgJgX0XcLdTpO2bzkhImKXtuBhxKf/9J8wDHcI/9P/BundD+j+8E+gFCAhASggGWHIok/Ek/XgW3l+ecze+Pp8/vPLuTY+1Wvhqfeu1zXNo5ZfauXfS/n1k+sA3S+e1C7UOX+u/tcsMtdmPq3U1/h88s5LlOf0+ezNaA5GkO+pcM8CUd2vh9W3fZ9F1X6BgnqCiikY2ekyzJ/mS7HYl2Us2rppVWZhfgxhTqc0fQIsNCDYntoACsbfTVbpphRmbjwkxkbJPe371IANnpOsWjzUy3h2n7gCnHx9VN6lVHZZDUtiSuj6TkMWps7AfNckA+5i+JBe+CE6faye5UQPgOU4TTyQCExaC8gSkAUYRDCI1LxaIwtGZhRSL+MJFKDaz7OnsSqna7bk+jBMstt99N78Fhp5bn2psOd7M8R4VjjtOBABSCmalLoCCdwACguAwb1snMYckCgLMMIAs+noNDT1vYjlfRM0nkc6Jp5KyKKkgSEIBPR9h367wZs3b/DuzRu83e9xtdth03fYdJ160ibLxdbqHc/QwKWlHZYQtGGBBGK58HyKWevrgEzymeZnI/MMPtEruI7gEfkYLt0jqNFd1nunX5szk2x2eRte7trp56Z1JPdOibac6vnWzq1Xdk53+NCzzusW1s49TudySXkcEOEL/EXCg1xwzcPlope1neC5IESrgDl/7+nIrCpQxOqh+SR1ZUhrEXzqCdHs4E/g4ZZK4/Zt5MywmAz/6Oec+eFxFc3accpsXuIx8ZS6l79dCgCca9s6yHHfgrysd1LaPLYtr1kuAYL8+9cuHPzWylk6MOa/BRPae5YgQ3ve13Fq1qbq3bC8tvnuaxYsDiuC6pPUEnnxLIMf1oRzahS5RFTD2KmcMLF4057TnJdJcfmYPruv/J5ptgV6ADTjD1RhjaV+areTjaFx0cqgMpgBigQEAgvgYZkAjbcfyMIAENAntYznmIA21xGdts+VvidehYVV2MxFgYhxVDBiPELygHK4QckDhuGgSut+p3kKEPVVcpm2UArGfKtQAKCGAGq9G0pRb4OSi3pEpFT7zq35nW6ZTbEsgjEEsH0PIWiIJi4YBvOEkAIiIEZV8KuHSQGPGTyO4GHE3aePuPnwAeNwizIO6FMHsuczM4qBDzlna6t6bXRdV9voimRNfuxvH8xiy9cA9a4wlKIqznW8J6MKwEMmZbBEsDhPgzqvQ1IpS6BeC8nyXMzokKW22eRGtPufK+id9xmgoQJENF5xIEKKEV3S/BjuRIIqHPFk4U9qQcQiOB4H9P0IEWC73eEf/uEfEULEv/zLv0LwAZ9uLRcIpNKyjqkpcqx/5nSrfaq5Q4zOZC66CdTgJCXBdrsFi+YayTkj52z0OCmYlO8M9f3zmJFzweFwQM4ZqYuIMRh4EHG93yEPI95c7VDyiF9vblEYSDa+hFhpUF/KQCzziHAAKVjibRDAoonRB/Ny6zZbpBAwsOYK+cgZxBEfY0C36XBztUXoenyHPSJ12G92ON58wi//8T+i++lfgX//d9j/j/8eP/75nyAposRO54YAVIX7iFdwzP5WvpXPWqa1YclLPKSmvKzy59Ry0qIz/PzXVr54C19g6GpVj+5z25+bv+dghCpjxbWG4rwUNCdEYQ+dr/tAJEQumswXphk1fceJSoctudOq/sa0rSyA50HxBLyCSUkPTDwnFIRIYERoCKSa98IVvDUckyuD3SPC4/e7R8T0Ifb8K1U9OwEhrtw0zaqG7my8KLxvXcVCGroIUOOVgIi06dFvNhqaqe+RyEMzAQj2LDJjHX/R+0b0FeQMMgW45+GqlvjiUY0UoGECMgIGAEfzisisRhdj8RwiBY7rgKnpKzT9OYVuBQH1hgn1mB9PJtC8zln+HOvEiWrMKGqm2HW+dPJYUBBLptwQM68Gvy43wIPxHqMDEEZjeWxorxiPYt4TNd+EzN6ibZqHwww0SUXOW0uAGvWwICBgv+mw3W/x3ft3eP/2Hd6/eYM32x32mw12nYZniimYkY9n8TvpwWcWk+s1OUSVGaT2s+sDGECY6TeZ3Xh5Dka03y9f7y67Tp912Xst6/38+127fsqT9Kv3ld/KHn5puVwCoOV3OfmBCHUjmFubthU91HlzZGs+oGulUbCsXHueQTytR4llPrnWr5srTKbYyXN3JRf4vbQhlx4GItAwC48va8pJPUIZEVr+dqq49O9r50/rbSucXTH7/aHJQ83+99iN+z4F/tr36Znztn0exeR6f9Shf4FF5tz7PNqK/AX65fWsme7rp+c945L3fknLuvvKcp5VZs2nsimO6+nZ+eloU/0ErKiW3CvgxUPtOvWCoEYeoWpBXi3hpfEoM5ZNXKnYWGHo3TL9Xq0dzs/Xc9/X2n3uPU+sLlYBxvvHe23NWQu199C9tW2u6HQmHzIj/drf0tbhnhCL5wjUwoXFkrqpEOEOKNRc48pYtvoiCCmoUrTWarSn46wMeSCAkoZvCkHFz/b5ejDvQQNAxGOxMmuYKDuimPBQCiQPkHFAOd5B8hH5cIMyHpGHOxRz5Q8UQbGz/vbwUYAQI49m8T+OyHmsytliSn5mp02ycE0ZXd/P9+VmnNp9X0M0aTidQAEwkOJ4OECEEZNZoYeoFotlBOcMHg7IxyOGu1scbm9xvPtkoXamXAwsRT01Gl7DQwQBqPkAQrOv+NhVwE+gCcdxhi8ipVGNaWvCSaOIj+ZOHqMmqnMQQEMxASEmhMZDwNsZY6w5MhxEcVDCLeGc5nNhMApGIhSo1wOhyYMBX8cU0HSHmZyLhtQyjwt9D9QQSDlriKbtdof9/gpXV9e4Ox6nuWmaGKd5r0e/Fwv9lSAEpKjjGKMKiiNnpWV0lW78XhBhs9mgWIimw+GA29vbqc8tRBUI+j4MSGF8/PAJd7d3OA5HMBdstz26LlXwZ7Ptsd9vcH21QykZP+YRpbC58U/8XEhRQSCbTzmzjmNKCtawqDAOQgzQBLwx1tABIUXAwKgsooqMEHAXIw7bDbpugxvuEa8E8g9/Av3SI338V8jPf8Uv/+E/Iv96wO5/+J+QNteIm7egIgjmOcRFqvHtlynPDwu13GIe5m8/D79wafk9gPDn+NsXLTLtV1WHOeOh5h4Rl7TzXDl5nwfuf4jPdyDjvmvPlUv78v7rXofGXtdD4lSZ9ai7V/jJi8d/9s35/cVCaXsvzDhE2SPBmIGhkCqaRbMyUAhICYgZSAJkkhrmSWZj4x5qazoXmT6VB6X5hwigoLmUJABwvi8CGjQQpkKe9NUnyutG0d0qfyufytYbUxL4yUNk0V5ZfGZABFARBEu0rUYP+jclDa3YdQldDOgsvGEkDbtIIYBCND6DZoriS8tLydV1SariX1UiVKUxMzAWUtrIwLFMXjTiOiFQMw6CSZuOqXNZDMxy95tZYzDr9/ONPq0XC8rzNRUmTLC3cfGMhi6o8XgQZvOqWXg3tN4RpQW5ioUBy/NrZp4RMjW6ts/aHtxoy2Qq10eKykmFufZziAFX19d4+/YN3r99i3fX19hvemz7Dl0MSBbuNJo8NU3FyUP3OUuq050b2dT+J38e19d05X+VJ+3c8nPO+NHB0Zdamic9wCVlbQ1b1neZDH7fE9frWNnDH2r2DES94NmXdOq5ebjgCZbAxiVAx0vqSy8GIk4f5kTcnqdmEXlaA09Bi3XGfV53ZdUwH7al0G1X37tG8qpybalYugiEAFXlU2tV3FoXL2OltxbF7Sr0Esz1DK1ErfosEPHQca1eALpJEdBKmZczvnOL2cfQ0EPXfi5lcfusdcGz3V1kdryvjQ8tDufmyKXn73tue/3a3/fNl6eUxyxy59eGh9twr/h0Tz89VaFwrq5z9a1ZHCzn71TPvG3T3+3R46mHWd/69zZszjlQ7yEBMIBmbfFEq36dJ7xt37cyNSZkzN7NGWM0DPNKOSvAt9fohbPrHxLwLz3/lDrOzZsl/bc2kWt7DYHm3I5fc7In2c8GQrSeEOTXWD2e9JctHn+IwazrVBhzkXC+txkIQQCiP3NiM1xwsr8muaIBI6rC3eLjS3ZJO0PGATIewcMdeHQg4oBsceyRBlBISGmrgmK/qeMtCBhH3eNbIKIwowgrODADIjRckIgsEjDrf9P+ry/BpdR+JyKg6P3Hwx0AwTZ0ALkAy2DOyOMR492tghCfPmI4HDAc7qw/bcxJx8rDFM15jmnIqU4b0ijN4omevbtVcR9m5G7Ck38nS3ro87OhnZjizDJfkx2zAk1mQe+5H9hCRjkQ0YIQ4zjWfq3hlBqeCigopEBEFI2F7R4zll4DZGESVMgDxlwwjkX7SATJrDQ1zJJgHDWN+W63x35/hevrN/j46VNVH+gepu9aw3XZesSckYsqKxAASjR5J0SypOhOzuaNwZYgPUxAxGazmQMwIqAYLYk7NBRW1lBdnz5+wi8//4LRcph89/077HgLQNfo7aZH2W1wfbWFsCb0bD3aqrwaAgoLhjGjFMaYS81hkXPGUIoJilRBsmieHpQSKERw0XEZBRgAHELAIUYcNj1Sv8FN7jWR5z/+CbQlpP+5YPz5r/jlP/zfUI6CN//H/zO2P/4J+3c/gkaByKhJuNXQ7sWE1KeV5/KEX7Tx95ZLgPjfY3ndd1vjKloaXvIWeu4+HrLW/ESe+Vw99fwZHuA5z/way2Pe5bGg0Lm6L5EDHi0rGM3Q9AfQggbO21WDBHMeKPoZC3AsmoiYYeESQUjMiCxgYvMItfCRWikseRSEwqmSZFWTRqcfIgXXOQLCIIpQ+3Dn93UfVX23P7mRgU2pPAMgWhDC8k1UxtFuI3ar8aaNfo9/9/q96a5e8vg5ll8MiUAxoOuTAhEhINknVp2N8jzUKPSeWy6VeZcyA1e3AgdF/FVdUazdMLIBEQUYLAc4BBAyGEWa9UJkDjIYr04GRCgNTt44M9eGNTJfqubsOatkpZ1QDSrQgBG1fTaWxFLBB7I8EFL4FEioIZma0F/VA2eYhwFb3Ofhz6Znz2V2Igtx6eu8cCME6TuWUpTMYoAEwtX1Fd68fYv3b97g7ZUBEQ56RUIy/rL1ipJa27Q6PKfMgGpyQ0HlyybQ3fhUkOa2a+bqfXvaqa7KJ9tz2nt6rp0qp+1ZPu/l97rL9xx6+On3TZ8ndt1Jj6wow8/p71qZ6N5nvAAP8WSf6FNl39fA2LYdcg8R1kXxcW1urfz86GEZTkGIqfpWUdMCD66ga5PFzAilbfILMNftIsEr7cM9YMQyrvfaddNGGnTBbJVotuE/pEwnaniFR77zubrPL47rdTzm73NteNqkvv+CZb1rvy/b8ZR6nlqWSvP7rnmtNvgzLi0P9edD7/HS5T4ann/ObVgPezXcJ1Q9NH7ttSflTLefA7BOQAhxVstFrrkgXa/3NmilD7b3IfbkMeUlNt01MKcty5j/a6WdQ+eAjPl6MH92ybZvcZNIGJNcocZDqjwmMzsPXQSlCJq5bRMo9FUwAxEkmIJYCiBAdKU2W5ikKoBMAqa2RSz8k4Zh4lwgpnwHZxBncBkgZQTnAZyP4PGAMhzAw0HDIo0ZRAEcB1BMSASAAopnNhm9H1hDL3FGziOOxyOGYcAwjigmkDrw4sKnAxMpaOibtTFp9/NSFOwYhyNAQNcRIAF5YJRxRMmapFEkQzijjAPAGQEMqqGsJpqoSZ+bZ6QYVD8+owOpSbXnQMQELiHYfsQWFxgMNuUBg2v+BQKAPoGieUSkaHu08z5A7KOGTkpqIahAg+W+ANB1vSmzBaUwjsfBACBVTKhAbAua8yEhKk1lpYmcMwiCcSRotQRQAgshs+AwFhyNplshiYyhGIYRd3cHfPz4CeM4Yrfboe+7Rs0Dg0AJhWGhkTJyyeDSqXBLDBILcWVJ3MWAK4F6HRAVDOMIAdCXghgiUt9hI4z9fo9xHEFEKMwYxxEJAgrdBMSUgpIzbj59wq+//goBa+g7USBQG8yIQUNV7Tc9kLfYdZ2qImxcc1FvGhbBmDNu7g41VFdMCX3X4zgMOByOKAZiVKCxSwY0Ko2NjeAvIhiYcSiMA6sA8SkFJIpI2x5hv0P3/nvw7S3KXz/g+N/+Oz7+v/8/4GPB9se/U/AqEiBJ15GvQWz4Vr6VZ5fTsINEk/btEtnjW/lWtDzEy0rlnYQFmdUL4lAEN6PgU2Z8KozbAgyivgheLQUg2LorluZ6Ch9sMjt5G2TOPAumfdqUlCfNpgBQhFpVW8Jku7TYPSSCLIwiBvYzUF0b6zNM8exKcZF6TbXGrzpRsT/d16I9b31V+63p3qqfmCARPW2hs5swnCA17vDQj4q5vO7mtZSVW5lz9h0CzdsFDZPF/jZKI6UIcgGOI+NuZBwzY7BwRkEACgFBCFQKqteIAMEV0t5vxi9SmcJcVSBhiSicdI3RlcdE9R6f0ZHUd2kqncAiGK/YgLzGLlbFvADqRVtlGwv9VQGIJjl19YhY/q3XSclqkONA2HxwJqHKrHuEJh4phKiv63wdqZfubrfDfr/H9++/w/t37/Buf4Xr7Rb71GObOmySJqjWEKoLRftqvz6lrOkY5/oFnW6C4HIkMcjCM6nByzyUs+e31XFZ17epXP/Sc8bAni+wt/4t7Oefi295EhBxqqxqV/ep3Kese5yVwHr98wrvOU/L59zf7tUWNMqypRfEqoWqryIrIMR9nhAPvdBTNr+Te4gmXqO2N6yM66kCdK3eafHyDdBCO8zeRvtC1++HwYinrLiPtSS4tJ7HgBFrSl+q7326nz22nL9//sNjQIvnlkssOWYbUsNYLcs5pfm59eI5zODDdHh/G19rgb6vXb6WuM5urT/OARGXvOtaImEvS6BptuYZo3kB7j9ry9k2NYztGnBR19fFO7Tv3/BYzyprbXzO2Fdr6BXaPfeua0+bvesZAMKvc8ZexJTapUzXLdriVlS5MIZxRCyCyAwJHSjChETbO8msgQyIEFKLHwAopbFkEzHL8Wa/NIGhCopsVlbF80FkMApYFIQQzhAeNaSRfco4oIxH9ZLIBcAIAqGEESF26hERI7JZyhdIFSLZQI9SsoEQA8acNf5p0D3Rc0J4Ivc178fleLjyW5XKI8ZxABFQioYqyAPAWdsvFq9WTPABF1X/mtKgHZNSyuxZDpKoAjrM6D5QgBDXdlf6YNYx8r4HwDXEgwtufpwAqhqKKE7P4cIQoSk5eUwAEcaDejyUooLKZtMhRwUtSmGMY27oFRV2VIoKxotYPhprQDFvk5yDAhhmSq8JFwVDYQzZLdek5kLQpHrAOCrYdHNzg5wzNpsNuq5rlgbnBQlcBDlbrhD7qHWcCsmeCBpV2DXPicLIKDXptic6T10HFs0VcXen3i4VXAmE1DVABDNKzri7u8Onjx8RYkDqovJUlmBcbDxSDNj2HahsZkYtAmDI6pEy5BHHYdT5DrWQTSlpWw4BIWiS9TGXOr4pJQsfpvHGA9xLSI9DUUXGIMBRgLuOkEJA1/dIuy2u375DzoLy3/4N47/9Fbf/3/8f0u4KPB4gMYBDAAVCDAmMjIXp5W+qXLoPvLbS6nO34bV5oN9PmcCIZbnPUGhexf19/dBY0D3XXmqk8lB5HXpolJV4Wfq9RGb53KW25b4udKW7KXA9z/PAgmMR3GaunyNTBSJcXiDjffRJ7o5WNfN6ZeUXl2CECbAORrSNrRphgjKJeapXDGOQKW+B79uKPdiP9m6zDzc3+0lxXnaijylcUGt4gXpt6/cxveskQpCIWXxryEf1DgwNENE0i5obYbT0BDJa8txrc/M+MGJ6TTWSABGC8bfOX2v+LCAXpY9jFhwzYywT4ECW64OIQOat4p6ndfi9/6uXgNS+rlN+QUbrfeK008g5tYJ24KHRvUCYMj7D6MvOU/OnP7KlDZEmrBIvvrvXQ26AiIVHhJRZ6NqTIu6f344jJjoO+l1oCqm02W6xv9rj7VtNUv1mu8NVv8UuJWxSQp8iUooInvW66Sv1SrD+eGqRpr1Ot8362sovPj7MFn6Vpr49J7+u02q7hjyvTD0xvcL5655//mspz9mv1gwV7/vtqXv5c/b+F8wS5wu9EvEacvv5y5yRWZ7Xcqp8b/9WVFmFdRGNFzwdUUMGrNWhrnIBwQXrKmAvrZvX+ufsSv6och94oF8A0DyUyvK4ptxsfzt51qLZLYM1KeXvUwI/7b0forNL0L2HgLNLzp/Svlmwy6Q8Pm3Hc8f6vMDz3HJugboPNFi+39rf5xSxL3H+kvIQUPpSwtol7Vu2ZdmHp787X3Ya2285dx+qcw1cuA+AWTLEE99p/y+e0VpOLOue86wNE7qoY36OZvfTom2LS1bfoS1rzzr397lzl5RzoHWrLHYF+fKeSai6/x1aq3lg8mSris4aK16VpdGlU9jeDQGCChmcgSyCw+0NyqcbdJuI1BHSJiF2EcFCt2yu3iOlDZA09JAEjSufi4aVKdktszx0kQV1EqpAhI+jKnaLhvbJBUIFIBMSSoGUEerWUABoIjm/Xr0K2OTWAxDNuiglUIoQAgo83BRU4Xs44O72Fh8/fcBhGLSNpBY+m80GKali1o0Pcs5ACEhA9Yas7LHNpRgjIILM2cCGrM8eBkgAmFg9PsYRQRipS5AuYUhJrdNztrA/wfYLDeNULG+E5nCwgU8JIoIY0wyMiMG8KhBMAeDShiqx+xQhwpAi4EIoltBRXFsgrTDrAJaOYRVMgoePUk+CPGYIgOPxWPNAuKUUBQ13QGE+T5nIDfjgYb5ApHkKUl/bxKxA1piBzOq1UESt/A4D43YouMtceRlPGtilDoEIh7s7fPjlV/y3//pfEWNE33XY9D12mw1yyRg9gTQIhQuOY8HxqB4D230PkaQ5FDxclqhHA1mGQgJU4IS31YVSAiEgRlX+b7db7HY7AMBxGOAGILkUHMcjch5RSkYMhD51SJukHgoeaqpoQklmnUv7vkcCDDxQbwZAvURKybg9HNCno9IhAAkBfd9ju9thu03YbTsMY8GQXV1l1nyBkC18Up+0X/oUkYKG3RrGEXfDETFGvI+CSAFhtweNBcN334MlYP/TRwUb/vtfkP/wFxw//Qza7kFXV0jkaTU1+fi38q38Vsury7ciUxLep9yOl5Akv0z52hVEr1dk9k0qYBCghgu6v2QGjiy4ycCHkfHzyPh5LPh5LPiQCZ8K4Y6Bo5B6yVX+0/Z1oNHkLhSuVS/cKnUtZ9Osra0nAjUf/1sjJKjnnSp5lTfKkFnoHFcWN8mBvSELHnjexiYgk2qj6x+TXHGuTDIMWagq5KIhEodRQXphZGZkLsisXsKxxPqYGS7zxcqkFFe+jTQ0pwhGFgwGUn3KghsBboRQKKqyX6jeS6b4VyCiMjGYxkBlgwoeAdMCc+7o15w0WeZj3JaWfCoYEexjP1GwnGiepQNTNPCgZDR7jizprMkJUb0mGvqr6NmCPyEyLwgnS217NeJrsAI2JXzfd+j6Hn/4/nu8e/cWP7x7h/fXb/Bmu8W+32Df9+i7hL63sJiRlD/nYry+h8+6lwgeLjSp8WdhzMhG32SY4LKSj7cAIjrzA8HC0fKJnDnvJtcX6dOeW5wSz2hsHnyGrN557r7X06d9LeVr4gleFoiob3bejaxe/Whl3rnz64r2hytsv95XhzmnefgImSwHXUCvajSZLIpdoKYlCEGeI+I+EAKPngP3vffZPnI4uSrL50qCcyDE8lGnf9P6gLky3v5YV6hd/l5r5T4l3X0o7lPrvuze1iNi/oLz++9Xkt5fXh/wuw8xfQhFPafQfUgxfB+a67+fu/6hcg6YugSweu4zlr+vAQb3r5k2d42wZlS0BCIqEDhXuK+BiA+BEc3TjSnw+/SvNaCjVZI3P57WRc7rzp+/PD4Mrt7H/bZNWKfJh665tK62TS0IsfYe5+ZPBXKAe1+nAg2LsE5V4cv++5RjoCrN9WI7BBCzMtlBGc/j8YC7Dx/Q9YSUgG6ruQJSv0FICSF2QM92X4SECAEUiOACHpWxL4Un5hoe0VYZff9bFd8ajqnkAgoMBPWQUJdpFRxECjQK/7Qvq5X5CC6MUgCEAO43iF2HbreBkOdO0GTEw5BxONzhzj5jnrxEYowIBKQUNHa/TN4QXSng2Lop+xY6eT+KMFiKfliVvCVHCAmKFJBoQGcKQBcjSkyaQLioQjwQmfcBKs/BPAEfTjk+fmoRPyWDD4HMok2VAO0KEYjUk0LMwMIjHThIZEK/Jzp3HmfieSYLr7q+CGx8BeM41pwQLQ9xznCBG5oXAxI8DjOHCKECLtlCC6lHhBtKDmbhdxzVI6ICEUbSKUYEEIbjgNvbW/z1p79iv9/ju+/eo0sd+q6DCGOsIo4CEbnoe4xjrnOKoAKag2elZIAJlMwjFJOuxENOeN+FoMkv+77HZrPBmLO+owmAzAXDOFhujYJACoD1XY9u01W+ks0aUZhBYPRdhwAg9QpEbDYbAArujHk0WhEcBw3dhBjRbzbY77foUkCXQu075uZdiRCoGKiitNXFiEhUvYiOY0bfZVVahIDQbYFtRr5+Ax4K+v0VKCTIh19RPn7AeHejeUZwjWbnOL+o/Y7Kcs1/SV7tfp7yZcu5vfel+KXfarmvy9cNj9avW/3bGKOq6r1Qlq40t3buzLhdamx0rrwmPXxOOl+Wh97rJd57bmgz16fMR9GSPot6FYwM3BXBbRF8GllDM+WC2xJwsPBMo2h4PzYwwRWos+bOEvKetK75VLXoyjXrf/qe6AphzeW0BCFkUhbPklb7o2Wl8uZYFeUt3ctay07bSeblSMr3iIVILDkjC9dQUoXZDFCsHwknIOFL6Cwed38LxFDl5TTPFSOzYCyCQxHcFcEdAwcBCoWp7dJSGU39Xuudxl/s+gpkLTt3Eg6b32Q+frX+xXm/vx4JcE8VUilBQyCp9BCW99QWymLh82e2H6ezNiF148W91jZ4cwSa62St7UZH9p5C6oXa9z3evrnWvBD7K1zvdth3PXZdh21K6FJC6uLkCWz9I95PrXj7rOW1auAqYOJGhK384rK7yjl6lXpgewLr87L5bD28TBy/rNmyqOpkfM7shbWClTqd3tfOn33Ob7NQM98XX9b3fvNGus9Yc1mesge+IBBRm2HH12YSfKV7XlmroZ1cbGEKlompVWA7rxCrn7VQTL58GjPw0gzVJQrz6e9m4ZgpCjS8kr7HOQV+S3DtavO09yGaPAcee5+XNUZ7dXFcufeS+i8531xRjw5CuMXzmoL6nFL8XDl9j69jsVwque9bmC5R0j/n2U+5dq39T5mjl4IQy3PtsT0/O+eaNm3g9L2GbZqH86kKw0bRRE29597vvnenKjDNlYu+Rtb74QxJKxpgOu8MbnNPtczGgkZcy3imv2jxjOV158ol4MtzyrJfnOFrn9/+vtY27epTxYCINNb50/Pae8WUl6UUSwwtdfy1T3VvEiJNVhsIEiKYCLc//Yy72zt8/HCLUu6QOkGMgq5T6539mx/Q9Tuk7TVC7NFtt6AYoGkUBDJmQDyZM6ABYoBYBZ5i0YoVmCBBVbwTCogyeCwWJseAiKzhZoqYmz/U+ihzQWFGzgUCwnj7AbHrQN0bUAjgQDV58XE44uOnX3G4O+D29hZkSXwDWXpFUg8ST67sJfUdKIba5ylpy0vOYGfemTEcjxiPao0OiObEgyiYIgziEYgBCQmAJnUeiWqS5OX4uhJB5422xUPyKCDReNOIhl7yFJd6ndEdaVgfEUIhS/IoRXNhQAVrV6ArXerzh1Hfw63vFTGIEDZrR+Qa9qvlkxyYCCFofoLN1hKSFxWimzmhYIfNZU8KmZLSjxSopR9hLApCfLobcHssuBsYx8HCKAGIISKGiC4pUCOlYDgc8OvPP0NKwdvrPUgEm64HlwxNHUIoRGAmjMK4vTvg48cPuHrTo99EhNRp8udioaVYgY8+bkAhoOt6pZ8YNYwSqfLFaSeGhE2/xdu3bwEiHI9H5Qmhng7j8QCMAsmMzabHu3dvsdlukPpOQSoxQMmZJBZEBBBF9CkhxIht3wFGQykRAEbXBaRkbv1BheLUdegikIJgu40QichFvTFc3cDFY3gHQAghpOqlAwhyGTGMA4YyAEhAiqC+Q/jzHxE2W2w+3IFjRP70Afnjr8iffkXoeqR3AQQGQ8HEb+Vb+VLlJY1O1sqL1C3P84j4Vn5rZdr/WyldPMkza1jEnBlDLrjLgk8j8Msh4y+3I34+MH4dGR+L4IYJt8y4E0IWzQfFntdICGI25RD1OFTvhsmgwfeZekT7dwtc6G/Kv03eFiRslvVqcV49RMuoMfnLAJSMkEegZHD2MDmqHCZ2pb97SJTmeWvH6aupVnHygxdTFpN5dUaTidgyf9/d3uDmdoePtzfYdgmjFHRI+qaer4Kcw3rcPH9RnY/4GGreKmYCMzBmQc6Cm6HgZhD8dGT8dAT+mgUfGThSwJEImXUn9tH39hFhMnkhTWQsnrvDvD9hfOIJ8ED221LxWWnH215MfrV6AMxDD0lzn/3pOUSqFt3kl0AgCRAzvtE8aAq2SPDrDNgI0hytvQrvYTaWC4XU3HfEwCs0OdoczAIAEYQYEWPE9+++w/X1Ff70w4949/Yt3l+/wfV2h+t+i23fYdf3iCkiWh4wtthYL69N9UHy98AMUqxABLRrljKp6gMWOlLTZ7Ue2a5TcPnfvZ7Xc0Q8bv6c75OvQ//1OoUWx8fc90C/zJdwu8ugZl0EXp1PuhiIuGjh9IauKIEvLZdaYjyq3rX+o3ZRmV82V4jNk1PPJqZMSvdLQYgJjJie+FjF+LnykLXVWUtiF27r/e1V7Tuu1dled1r3eeKdLyctMPKULngMWPB0YOEp157S8SXK74fK6fUPexc8vpyocx84v1LDmedfYln11LZf2pf3PeMSMOW+ZzwFhGh/azfy5fPImF8yhZPP3doeAyEcjKB55Xo4035qGcJFaRXi1UCjXnp+vlcedcHQyOyKueIVHvJOJkUl6P75PL2/H9bXuzXQ4bWAiPaZl9DQfUDE8n3a/ahlCFfptrnGldm1DaaupqB7FkJAiAlFgM4A9zyOuL27wfH4ATFmxJDRpYQYA/Ixo9vs0G/vELsNNldXCCkhblRJXnLWHATFQjB5KBsHIiwvQlAeHgGev4ERkAHJmlg6Wy4Fj/EqGmO4ggZQd2IWA1wAlOEAQQGXLQjR8iOwJakecDwecByOGMcBseuQ+m6Sn4QhpLH+h2Gofbs0SvBYyw4CVNAnj8glW5xZBlcFclaPCM4IEiFRBUhX7nMjGvjYep1rNO38BRoggkyZoXOUEBsPzGAhlUQCAA3RFFlDRgaiKvO5sOJ8UMkFmVDf3QVArvNUgRluaL0FUfTZESl1JuwDQAa39Gg06qnvQiAIu4AzeR0Uj3s8FhzGjCEzxjJ5aoTmPSFQS8accXd7i+2mN5BLkGLUsEIAir8PF/W2GEYcDkcDUjJYGEHEcmqYkBWm+MoxaAglCq2HhFTPEA+dtNvuMAwDuq6r48hckFks4piCfPv9Dv1Wc1nMkgFaP5msbUCUJhJPBkwVqMBY+lQTH8KACApBAQUwhDNC6EGhx5ijJucWS1/uCismiBDYkoT78lJYk72PXIx2AkIKwNs3IAbi2zdAKSjHA8rhDny4A8ZRI79pz+C3nB+iLZfwM37d5zA8uu/8U/a457b5pWScpz7z3LN9PF5DyL60zocMklyp1crVbbmEhzj3zHNy2kPnH3rWdP+DTXlyOacr+JLlUgOs+0rd/auITFWv6/UKuzcEYyiCQwZux4JPQ8bNKLjLjAMHHFnUI4I9g4JWJGzPETeoFFUKnyj0BRWQwPzoPEYdZFEQIpj3gN9HTd4p93aVNi5/yZoouZQFCKH3kThH1Dx/3khVJEvTFv+1jsckQ8yKKY3dQIP80sIYhyOG4xF3wxHHcUSGVF4HaHgcq+ixZPgSeggAIDGuWQARMiMP7cbMmhfiLjNuPDQTE26ZkEEYjVeYerjlMM1jOTRKUDaDhlVVwIJ2VOibTkj7QTNejApogBa602nc69CLtoPq9TLxN82HKADEkKB9JPW32nFT/a0WFqK/Gb9+ojer/+ayOkhlKGn2k2jGTVf7Pd5cXdfPrt9i12+wSR362KELyaKkWDc7IEJoI41VjPDRNOLXyzQ05/Q5IQRNh0bzvVHEPICaPXPt04YD1utqx9X+m5epRbOza+vnssmVVp630Tysr/ySxYiifn/EnaakOftesjjCZ72vBMswfOfLc/ruRT0iZPbt9Rjv9onKn91Tv6wPnXl7oSYxsjh5ir67AkAVFu7SWBU5XofFYNbvp+EHZsADzRHDy8q6Iu3eO2h9iTkLQtjKN5G6jRvm8ePve9bjijSLx8vTxVOFiodAnHPXX3DlyX2+YC+F08cILuvPXxe8vs7FtS2n7bt03Tg3/y8RUh56xmP77ZwQ8hDwtNzAl2vJOhgxMdDLe9o6z837GJaC4rSzn+uSWifWmImp/mVi32XRUDWzmtuHTFYzM+W9M63zWJTn5u2Ml135vX2n9vjaxcd5bazO9dfyfleGt0reNXpv96towFXwHY8wKbDJzxEoBoTUIfU9EAMQA/bXV3jz5g1KucF4FCQqiFSQhBGZIIcPKOMBh8MRFDscbzYIMSJt1XOAkrEZZhbjgIM6TIgKokSIZFmVaFJ+hzyCLJluLqXSKwUGSHM1ZTGLriBm2SXIJrkHKeBCGIajWrMH9XZQ8jLR3DweYzsn7R8zI48jhmFA35vFe4g1b4SPZwgBw/EILpqsWLhAhjsFI/IIiCC4oM6az4LzAI4ByFmV31CaZajXRihlThs43TE9hJEz/LVNDR0QJost5VmM3k2ZEAma9yIQQgC4SA2jBVEPh1IihnFE4YKuP6pMdByQWCDmzxJSBwdIfR0AgMFyb6jCXHNvuJcEiCyBtvEgrDGoma2/oPUwebI8AoQwZsYwFtweB9weMgYmZASEqATi4bDGcQAhIFnoq42NoQJbGSWPEFmsRyp/4jgccXPDONy9wXHXI/abCjggALLsS5f12IAxAz8GTO/ddz3evH2DwgWfbm4s/NNoQERGYPWuubraI14ndJsewRKm55wRKIEAlDEjjyPKqEBXsOTeMUbbHAqAgK6LiEkTXlcgggghErbbDvurDUh6EHrcHW8xDEcMZUTmAheAAmnul3FUgKbb9ohdwsgFd3nEv+EOW+nwhwIkIsjbHYpkDO/24NtbDD9/AH34FZ/++d8Q0hXe/F1RBUFvzVxuB7/z8roy0bfyrXwrv/Wy0N1N3xkA295SFHw/ZManseDDMOKXw4hP2fNCsIIQRZBdieh1CABWBbYiw8Z3ryV7dnNmthvbBL6uVHZ1vDCCWL4uHkHscfhHgEcwj2AegHJUj4jxCJQMsSPyWMEIYVaAQiyeP9r2LTVoD/HvjTLPlHM134DnuWLV/RALJBfcfrxBv+nx84dfses7DJyRRT0iuOjeXqB5rig+T5vxvP2AFIzgAEhQfo2BITOOmXFzzPh4KPj5ruCnQfDXI+GGg/KZIIwsKK7oh9Tc0IjBFPJ6HoDRg/Vd66UwKzId/F6nE5Y57RQzRqivb/JdCBNd+X1tCK/iMo+Pq2ibgoDEpJyg3hHtESKQoP0UKECCeUuoMD3RhmvDDIyo/YxGJyaNjszvNUDLqXS72WC73eCPP/6I7969wx++/x7XV1d4s99j32tYpk2X0McIBFKwyz5EMmFAM+b/GbRCsJCr6zTn51SuWJGNRYw/nn5rc0C2Xv5T3wDEZKq/p7e9Wul7U+avhalfvnZ912+pfB4+9RVCM9FEB9S+xpI4XuoF52DEUmnXrqHrj9YZTmgR18YT4iQucq281lUXp4UCcR2cePB1Vtq4nMDzKVjrXBzPWQQv/yZ/h1O2p7luqrytZlXJilbBaZvE8u+zZX2wHrNPP35PnyszXwKMUJqc6m7BhlbBvDz/UHmsELu8/j5F57LaObmff6aS/nnF9P3PPd+ex/TJuWdfAgg8fS1a3ntaF9H6M6bz82PbxiVd1N+MrpbXPtRXy+unNt9/7QwMsMNcyX/vY1fKJLys87BnhIvlmrjaL9PFF7VLTOnc0on/f+b+qgyn03PL8217ztHp0qJE61hORlRw2BWfzgTOcm9gQZGz+tZppiZCpMlaOqao4V3A6Pse/WZrIXk0Tn4kIJAgQIAyqPV0IYAG5DyAYkBXelAKCJuNKsCtLZGaXcCEkUCAEBAoaAJt34PHETRqrN5SGG47HxIBweLgQsAEY+AxWf6RCsZqza9JptktlsilD9S+nAZvErC8j0sp9nOY5Xdq+7pYXOHj8QjhgsBZw1GZ8MWkFvVi3iF5HAEOiEDlN8TGQTCBCie8RzvWRAs6tGsXa3J1JZ/RhX5Uue4Wgf5sozFINcRQ3b6CX7longBtqyYRTJQm3qN5dkujCkYEcAm13ZUOjCoItPLOSqOqFxEUFs3jkBljYRRRAEdBLg89oYBKDGqpFg1ACiFMXi3SgHjNswRAzgXHARjHjDzmGnLKE/Up0VZbzWYMUEEhMrpoBbXNZoN+s0Hf9zV0VQUNGQhC6PoO226L2HcIMaDQxJPWPi3afjTj7fQgBjp6uK2YFkBEACRFFEkg6QHuwKwAGkNBPlhesxg6gCIEI1hEvSmi9mGWghvJqtSQoqDYpgNve5RdBx4Cch4xHg4YPn5CPhx0TpoVIzGWq/ysH+e0fu6684L111peE4x4yXp/S316SbmUV1y/+YnPxIpC52kVzUtl4Z5e70O3PsS/P8zfP6YtZ+o4x6o+6/2dCTkjcD+zrL3Ls/tKbGcS3+eVtcgsGArjWBiHzDgyIUtAFgtbKTLLw1Q3LNF9TIRQPQra3cwBiJb/b66poXmkvU7gYZTcE8K9IWAeEerRqp4Q1QPCv7MnCtbPPCwTMCl0ZP73TG7w70tdQ6MgIVR9TT3Xvgsz8jCoR8RRPSKKJX+uvHcpYMu19RzqOWtM9di118ImadeJ5YZQmrjLjNtccJsFtzngVgRCbGCEwzuTYKdhHO3PNhFDsA+TCf7L/l2ENlrKc7L8GMcuzf1E03j7mLThwRyQwHyUXW6bdHGYxth4H5EWOJj43Yk0JrlPQYjp6DISiKosM91D9Vlq7KPtS11Cv9ng+mqP6+tr7Hc77Ldb9YRICV2KSCEqKELNXgEn0ZYrxUS6z6G4RpZcL9p3blDYAi/wNspch3GuzPtuzmfLyZxtGohTfs/n2Wy8ZD76T96k2/bOntnuD7J67fn3ePny0D58rsx7Z16HtPPTj011Lo+1+qiXNtx8USDi1K7eyzkOYnH2nonx0Pllx9RO8zYZsUyuejRrmTunuWDqlqaZM6qbCqkiYnp6uwBZCCZLGqmhAWJjiQhQnYiXEg03Z9qNdyEyU11OMbl6UF20TrvL+qRZ2cTbVjdFDfVwOiZT/9GiLVORxZCfq+OS0i4yD1339PIy8pbT//m2rDEb02LvoT3ueQKd/33t/HOYG6pM3+k9tE5Y99Q1n6stA/hlPTaePvDK1LR/W40r52ZPpPnmdR8j6hYF9ep6rU/flfBLfq/9Ts3vExNw/tln19LZBiTNOzjn5svs4qXF48Xqn2qvooo1QCaBp26T7XpnaxmmmPQUp1B3cIv+2nxtzzkyd4W8J/6tyfvMKsfXdF+jFz0xb6ecWzfavpz6as1qpFq7M0PKBCgITU7StTdk8nAQZq1Tpv4EABR16iWaFL8goEQV3ii5Qtpoy4zCIhFiiuj7Ti2wCQDprph21+i+/xP6MmAjgoQbRByRkhpNFUoawog1xv94/Agwo7vV0Dhx16vy05Wj0fIUhKi0yZ7LQC35I0V9Y2b1lsjqZZBdESyCftMjpYhoAsuQGWVkzREhBWy5B0pmBGZQ6kCBavgd6hLAFpqnS0i9JpIejgcbVELOWZMKx4jtdovNZou+70EClHFECgSEhHw8grng9uYTOGclSdEY+yKE3XYPCCNYom5Pgng4HBADoQwHA38IkQS7PsHBMZ9vTu95HMHMSCmBKGDI45zm2sne0NyYB3UT7/tKR57g20EAEY0tnFlDPjhPoYmbWa2aIkFygERCHjS0TxYAFICYFEiyRN65qFAZQ4IgQ/iozytuIZkBUSW9mEAcKYFCAsCQcgDbFM8QZAYOxxGHgXE4MA4jcCwdBiYUOUIgSLbIDErtCKZMR0joNlt8/8OPCIlwV444muW/iCBhAmoKNGrUL5kwHAnvPzH6VLDrMogzJIzgJBASBCQESoghgUhAgc1bB5o4nWytAaMrHYgIqeux3e7w5s1bEEWMY0HKjDwWUyAUYCcIG0JI+v4lZ0hm+Mo0HI8YhqPm+IhACIIQGESWiyNECCK6PirWZ7QQonrQxKhAoypXAkSipnnYJOzg4bUclFLFRoGFmRKbswWQETiM6unDNnY9Nigbwfjv/ojSJeS//IJ8OyD/z/8Z4+4aw//hA2LaIqYdCBlEBdN+Mq2v38rvr/wWgQ1pAVmRKVSJxkWDcQ+o0LYra2znXhP+H1POShRnqqSTL7/dsnwFOfvHEyqVxd9fSSEocN4qbF3voPmTlB9mAUYGDkXw4RjwcUz4yAE3zLgRxh0zDiKTw5nriIuD18ZvzqzUofuyX4+JrqX+3/puKt/mlurkluoCEAcLYRjATKq8LnZNFiBzDcfElW+RSeMYCIgRQAR4Ck3oz54ACm0XLK7+NLA8G9qZvlCcNyDV2UB5YJAajDAx8niHcdjgeHeDfDwgmpemg0Dmr4mIaLzS+TCDDxk5XiKnnzNa9K7FOALjgLEIxgL8emR8HAn/5UD465Hwz5nwlwL8VYA7mcghy2gGDVzXGiFCdtdlHxcOqFZIZCue5/+oPdysVq2xi8DkLAv/ZSBYjTkmrEpl1yl5PpImeXRkQRRBYEZkRkbGKA5kFeXzm4TTBYAEAULUOswjApQAEjVGCsH4zQCKYt47efKqIKDKnpXH9vcXsLpxI0XlAdMoCEWQtz2kj9j/6Udcv3uDH/7wA3548xZ/2G9xte3xdhex6SLSNoAigTt9lko+hMBKozMplGr8lXNkdlGhOpWWhoAmwNtzUgg2pTSvDDNDqMz0ng5KFPPYdq/vGCywj9HAhGW0EWXOt3FNub/UYSwrmnvILC+R2bOfVu7r9+Wm8jWVhRdZo5+Z8yYyzcf2HE51QGtgxHMAihcGIubf6jQyRq69kuqcvmxhPve0c1YGNdQJU0MbjfITmNFMDcXgQIQrqhok/sRjoIIMVONre5iEEAyMaBSHUwt8I7l0QVlqvJaW06fHqr/D8vUXC+qicdK0bW3znI/L+uZ6ryL95MslpVF2vkJ5iNQeLzydFR1OnusKymkRldX2zC37135/LSHvqfNzvax5aHw54fQ1nisnAIWfr99Wfm/n2okXBE0zgJqJXa8505Ll/J2tIM2Scl//r21AwHyzEq9MGtZmBYyYusAT5JpgIzzV52tUA8BUJtATkhn4QA5GNAudGnct18vZG8EBYbdsgpgtvfizwsnt56o8fc15SLsqtJzZtM9avEu7Fk9trdeKVBdbe6u6z1LTjqY6AGKJ+aBQRO07MgDALKiJDBTQoDux6xC3V0jbK6TNHpELAgtCVCWoIIDJYs2yYPSEhKKuxRGjJoK2/VCSukWTCYBBA4+CwBbHtUmWmDV+sCvvi1mxd4kUrHHhqSrXpfaDQJNNKyCRNVk1ERBEkyCL2J5tNAW3Xp9yPrjbcYxRgY8Y9VmFEZPSCZeMnDPKOIJLRkiaGJpFxyWECCCoh4So94Yq6guEFUhKcN5BkGLQnAYyza9KT4Als9ahKwZI+Qir8YOO8IzOmFVYbQm3kfmdJ2JB03/6G7PSGpuruBqxkSU/J21nkDoZqM5hp/UIIvNmEUDgIMgUk9qfHUGgEE1w1fjVQqrnyCLImTGOBdnlTyEwQpV5Jz8XsnfydSMidR22ux0YBcdyrInNxcep6d8C4MiCkIHjyDgeC8rIkM7BG4b5A2HyJm2FLk3G7fGUA6viP5B6ZsSY0HU9UjoarxgQxPJTsPW+OprodJA5WFkMnNMxUQ8HXRZVmAimJA2kfRNEAAoViEixa3JeaIiGTrq61yiwqGvQOFrosuFY1xeIVF1QKYISABYFswICJHbAfgfZbcExaSiLDx/Bt7coeQCFHlGCrUNc19f7PRSX5+/nsc7ta6/hQfE5eZjXeNZz63xMX5+3OnzZck6Zt3bNJd4QSxnWDwv1W8vpYe3rQ2VNnnrS6FT91SV3n7vm/rmyHN/XGMtJHSdP64dlORWnH5QBX7JcOtfEBcTpTj1fv+ueXZgwMjBwwCCEUTRXVgZpSKZaISrooDyyezXInD5bUKLyEVrBqvWsmKKZnacQ3wq1jaIyTz0nmOr3ZxFOSZBoCtHj4F/lddoIDtLw7/MemlXnfSEASOoj3Shndj3Z27qxBkutuuqzjM8PLhM9MK4PgRHnrrvPuwZAzY1GwkDhKTdEAW4L8KkAHzNwy4Q7AY7QD4uP6NyLQQ1DYMZdVD0/K9ATZBoTMaHL9+16nJSf1I6zf5zuoGOhulJpxtevUY8JkgICEEUQwYjCKMZHuieNfjfZCP5u/l5LAnP6Mf6QpvF0Xm4KY1sFUeMnMa1EBLvPeDhmBAZCTECX0F/tsX1zhd1+i91ug13XYZsi+hiQIoHsI9VV2boZrVK35aXDY7aS1TKjvvYZ9Zz+HUhlLKGAFkASYVAjo7knx7SWNLRkI1FJZUFna2XiBdfaTssTds9DYbbP/vSIcv8eef81r1vOekpMV/iFyzvtwmZOUnvd+Y5b4+OeCka8QmimS8p9wsbiyrowPY5ZPgtw+OJS69e/ilkIuidEsfjM0yJAmBBb+xvu5h4Qo1oohmDC1SKW+WuVE2XjhX300H1r9fwWrZkeVy6ny/P3y+Lv5e/NX+cWhS9YXnuMlwvV53je65VzG9ArCGPNPG0V3eeue0w5t4mfR8GVUTu/6Uit15WgAEDs582axI6uXGsVmGQnyK1WEJr11Ri/qgKsmX6ql69wsXoqB6etDlNII3evFmGwWWbrR5mrCQyhWR+s9V97XPu9Fdjb6yevjKnPV+vmqR/1/GndTSdOIpo/lwPEVK3ety2YE2NEiOoewVCLIgZAkbDb74Dve8j4CVQOuPtwh+FYkLkgkIApqAUVGy1Z/XeHO41fP6iyv0+dekhYGKAuJn02KctPzKZUDbX9wZSld4c7DMejjk8I6PoeFCNG85QoeZ4rw0GEPI5GH6rgRlAAJAqqhwVgCdpYDRA0SdvkluzhfABYTH/tvtRFhEBGQxayBrG2oUsJIoLx7g4EIKWAGAhd3EOkYBwGIEWEvocDHwIA0cZENC9AKTZPpPVKVxHaRhk5axtiFONJWgtCu4cEuWT1RrG2qTdOsSTg0vA9U16J4EoAEziKqOcJhhEUNTxBABBjRExREzsza06DENULx/MpGPHOPIFEarilLmnOihCUiyqFUZhxczjicMi4vSs4DmKJlW0iiIriAKOYpeMmdSBEECL6boP3P/yAd+/f4vr9O9zefsKvP/0Vx9tbjIej1hEaF31raM4FRxZ8urnDNgS8e7NFTAG73CPFYIBCgEhBKYRhFESO5q1iIlgN66UeNl3X1VwOXdfVjzBACLi9u0MuGt4LBGy3W/tdhYTD8QDJjJubTxiOgwI3KSAlzYGh89nWyaDWnhXNaIRmQgCJWjRGCuiDJrrORosK/qjYOIxF+WJhDGNWTx8ALEUNfcYBWQR3dACkx0Y2aiW47UG7Lfj6Cuh7DCXjOAw43h1A2KDJ1b2yx3wr38q38q387RY1Tm1VSTL7pmuwh6Ks+kOEGBElINS8CnpPwzROz6jrrTT6X7vW+XVSEEGoqUdqrSC4MZHuxZ5kWsM+NUplfeAEMAT1VJwqIiBt9F7PP1DzUthF/jeK5UQwpXcbXsqC/lePa383t/b1NpAYr+cRh4IBDwKKAds373D17j3ev3uL66t99aCYdD7Rcqw9Y5BXykNK1eVvXKBeqYUgiPiUGbdZ8Je7jJ8PBb/cFXwYBCNbGCl7B2HnecwD2eIkLu3k7aHGbgYdgxZ88fZUJSYwdcrkT+Ntb9XUYMzJw8fJaE0MNAvi1vbm9QBG4ILImtjcmWNinsJ7lUE9HPJgmbuHKQ9JyZNnUJMUnYy2qze6z48qC1q7LZRSoAASQihALADHgJKA/s0e3dUOf/zue3z3/j2+e/ce766usN/usDOeL6X4qLyxX0L/1uob/PmtzKQrFAGs842DGobFEI00NM+Ih4ZTHfeX4u8qcf7NFAXvv/53fhYQcWINYeeXShB5wvxZo9WnWE8LNQvLEhTVK0yZw03c4Mn9brImbm+kxQQNzcdUY7SEPF6mPGaDmlqL2eJ/DoS4BIx4qA2/xfJSFnJrC+yap85D9zzm95cs9ym4f8vlc7zT4x4xAV4Xte0MCHHiOVEvv7wxa+6+y/pPrpGJVZ3W/oZOpQEhGuHH3Tj13CSkTNCGM6LNe9P03q0gQJjTqzI40zt5O1rDFbcwa4EAX+vd8t2Zq7nlBupecG7+tufXvH7OnXPvhtrIM3WfAA7NuZP1qx1/Y6zFYrrW3Yw8XKB684WgbtdiA+BjQ0SIKaHvI/q+R9f3uKNgngkFBNaEbyAN8dK0X0H9giBUFcvBcjSEoMxroKDu9yZkBLSJlad2lFI0TFIIZsWtnhEaK7/MYv23fcZFreppzBo2J2myX+IJhIDv88Ywa9aDeVikNq+A8wwgVkGiUdxzmJIehhiqIlpleQ0AFM0CntnrMaV1bf8U9lCauYSTa6Y+ammYSGVxnVPtHER9nsd/BWB92dAT0NDH9KxJT2F5M7hMEGAIVQnetllYqgxHM2FuPv/8HpjqhWxeFBYUywUx5IKxMHIRsCVb9Ho1bLGYwp0sVJICQ13ssNvvsdnukPoOdCCMx1HzPphQrXPHe0wLM1DAGHPBcRwtYbr3FWb9r8YrzRwUeO9PfGUDlDlNuUIjRYYkNtDH6H0cK3DhfVTGDM4Z4zgi54zYGbgXYw0LOq0zDkQQiOK0njqIJQzhUEPd+bi7F0f1jrG4yiklsAhGzvO1hwu4BIwlI4UINi+lECOk60CbHogRGaLrxpjBG67PWt1jvrJyDiB+7H3fymlp+Y3fa9Hl4Lnv9/XQ0u9trF5KBnyx0ujt6wk5vWSy+hbfZAE0PBSMea2x1DExtGvPXJ4/UUw7v2rHGV8qxse1fKm3e9qTKj9BBkggAsHAhxCNeRFnups2OUNvCuTACkbU0oZeoelcFTAMrKCpDbOPty0QKEb0uy22ux122y36vlNdfCOPVH6mMkpPnxNr+97aHFu7RlyXLsovDgzcFeA2C24y45AFQwa4Ag+kya3bMSHjvGYCWH3oNBb+d+XlCGjb5Ma6xv/4/2dnlWBSEPocrLwTqvzi/KAf/XuQiR/3sExSgYgy5SBhz0FioaSkyUXS1Dmjf3tvpVXU99QmU01yTUK1zZwIEgPipke/3WC/2eF6u8V2s0Hf9eiiGnw477fUuXzudfXc3tvqAtrPNCYu06Le38oi7puv+gKg1UI+Fnh5qT45t+xdXh66ef336ZmvN7b39em988+vaebrfc+4xFjoKXvoZ/SIoDPfX7eIbdBLlLdVVLBIteIrTXgHmNLAhdRWKNcwChoPOVCsgm8wy7PJcfDrYNh8EZn2Err3+K08vzwWdPiS5XOCEC9p9fjcNl96/0svvBeXxXxdliUD+xptuXQDmsSFRkAxLlkE1aKf2WOCm+KRGv618reqLNM1NVWQ4Bzjdu64dr0rDl2JLVWpTkBQKykJmMJAYb1fqyK38VS4FCh263MFCRoGrWHs2lBDMKWuX9cqAtsxqeu4tbt6WxRV0Iao/RHt/UI0r4hk4YjMRVPEmO8YELuAtA3otlt02y0EAePIGI+3KOUID2UUuk69FZICC7kUcMkgAmII6CiCiSBQJWQh3V8ldSpAlFJtBUIImsQNGspoGAYcj0dVtgZCGtRy+3g8IpvS1r0Z/VOKhq8R0XwFFCPiRuP8IqZJOUwARY0fy6ZYzSgIQZWv3o/DoMpfz6+QBg11s99tFVwwhXHh0d6BUFhwc3MDgoB2W6QYsOmiASdswqOOLQsbKARTKCsd5JxP6NfH2ufE8XicLJWIwDGBCBPY0dJhCOi63vprsISXQPRQDdb/0bxXYoqaDARTe4gImRkIhG671ZiyKSGliDJqnSUrSAUI1LEpQDioBad5TOSxIOcCFtKI06VAyohcFNw6ZMFQBJ9uM+4OBTcHxpgFGQmggK5PkEDYRI3UHLqEGCK2cYdACSlucP3uLf7u7/8dtrsN4qbDWDJ+/ukn3Nx80j6PEdQlcFHQA6SgJ4RRGLg9HtEFPfabDltmpLruEsZxBFFBMm+YnDNijECINs8ZOatXgSc9DyGg73tsNhtsNpuaW+NwPAAAjscjjsMRALDZbNxAEHc3NxiHAXd3dxAuuL7aYbPdYnd1pX1vXjUiNr9DQjDvC4FbplEV/pUnNA+cICjRAzVIE6ZLQaa+6wEQhuOAYvnTIgtCTsgCfMAdsjCu8w4p6XpB1yO6H96CC3AswLFkjLd36Ps3Sou1Dd88Ir6Vr7u0+227zbthxLfyrbx2Mb2sOgIQat6SYudgBh+qbw+YW6S75vRs7ZVfV57Rw1I3SmcIKhDQhPQRD6EDPy40LgQYE6BgQ+z0pPFbsP22xvH3F82NtbuIKpCZa34pUJPQ2kIoTZ4PBRMAM7XGeaYuapJgDbGpwRkDAlLq0O+3+OO/+3d4//17/N0f/ogfrt9gkxK6mNDHZArlgBhaIOR1yzkdjZiefRiBMQM/DYKfj4x/vmP8dMf46QjcZMIBCblRCHu0LIv9aP22AFRa8GEGRmA6UvsH7DqnEUwgh493vdQjh7Cprf2FYECDJjcnoxGqY1yAwggo6CRXWhQDHXIe9Hu+mzwiuIDGo4Zwqp4RxxrWSa1O1EOXRKb21Fdr5oBPpQAQE4IQuDBGZuTtBrJN+MN3b/Hu/Tv83fc/4g9v3+H9/g2uthtsN1tsUsSm7y1M5mQ48rXyPZOBnhqXiclMEJ3lLRhRZRAhgILlXSEQq8E2l3LmKZe143ldRFWmenx5Gghx+e9fulzWvtfi0z8TEPEybNpjleUyW/TsbztVQ3PI3FrNEeZ52+deBPoJK5+FMne2klkb0GKDi/fTBzTve9n7zxD6xbnZc2n9XS6p/5LytS6kXs6hvi9V39q5S8GI1+y7z6Wsv6S8huXRc+q65N5LrDRfDYy4B86e2qUXLUHGc2UpRLf1za+bGKTZxmNAa3sPuehhPL+xutOaK67gbs7XB600rL73KVDaKuKXbb93Hi1/q4q2Rbuqi7cyzmsg3UPPW2ubt38GIFTFxjrQMVkdy2wczj1/ta36i1ruuCVYC7Q0SekqmCRQizWt1O4JZnWtSuKcC/I4wmkvQa2gPReB9y0Z2CKizL1aTBuDKgBT0X6wEEQkAKKgps4jVI8HFgaYqlK3ekSc7OFukc+Wq0FBjtCEA6pAGeYgEMMt+VVQWAIcDkQUj+UPrIJkwXJS5JwBYYydWvt1AVa/dno7xtTM5TU6v3ec/Z2b854srrnTxlKFg3l/NXPM3ymc8hYKtthYeXiohi9Sbh+z/rVHz9YyT4DHLGbL6O1hBSaEkItosmz75MKqmzCPjxQiOAKdA4ZRjUI0eWCHTb/FbrvFbrdH6mMFQA7HI0YDeGYAoNEb1Qmh75pLsWdzBXccSPVwXoFpNU+JyCSkLUEk94jgqF4FwXKWFMsV4aCGW7ZqaLBRwyKJWO4SDcsUY4RQaQRCms1djwuuyFvD9yEAIETimrye7XkiClAIBDEGxELw/B7MRQVMZggxxpIxlIjMBSSEPkRQiqBtD4yMcjRvkmzxnB9ZTgV2p9dHV3Xxs576+2uUb0ZCzy+v2YfrVTeW4V+ovIxscX8dX7vsd2l5zfe4tO6LaJTcQ9H3GFOd2t5rK2Pl0+1PawjNwyzVBjbH2fm1djuj33hkSPOxx0lbp58lVVKShwwMqHsNQprXE8ljUerfLJajQP1WJ0FB61QFOK3ucw7E1L3X+DtXlgK6T/abDrvtDm+ur/Hm6gpX2y22fY8YzPDUvRl9P5rYhzND9Tryacu3WXoIjEWTl9/Y55aBoxAGywM1h4iW4/rIdlqejTraSyDDwYuJ8Jrz9jcRalLm9vz0iDk9VP5dQylFKL8I4xvFQ4NxnjwhioFW7TkLR0oW61QM5HBvHoI0/TS1fvnxL2x5DiUS0EX02y12ux2uNlvs+w16A7FSjDWkVyszrMlxL7EWnZNbH7pu+duJjtHHheb6kVaHqjnRULGq6dGn/XpaWpnZ237+fR4Cc87V8Zw+/hK6vHPl7Hv777isn+p9Z/QR/ttyzM/dc2n5QjkizpX7J0N7vLjGRWctFQouHJYqJNqGVF3cQ3NuskB0D4jYJKc+VQ74wjtv07mN674Nbfn+TzlK/fs0PNPKE8+c/1YuLb8X5vy1y9cuYL9m+x4COVyR3143MSmtQmZSYK6VtfNPf6+G2WxKcCa31usCyhQ/FjJZTUzMTV1hp7sWQs3a+7vCbemRcN97aahZqUnNapGm3bYNiAjI9HltaUGAJciwvK793a1KpvwUzkBbCKQYT+51y36Cyl+moa4j0IbYOWGwCFNYRHsn9YAwK3fzindFbE1O59bSBRAWlMwYiibeTalH123Rd1vcZsHxZkDmERDG9mqPmBK4s6S3pmy0x0yjywKBKfJDqO7RwmVyy+YEYbHYvapcj12nClrzgACAYRxRePKIWAMihNUqnaIglA4UTFkMU9SLewBExMga+qZkCHQ8jscjhmGowES0EDjelhQjui4hZ7WAj5Ywuu86gBk5D8jjCB6P6FJE2W6Q84DNZotAQMkCkQLmXGm/S5oc20P0uOCypDdPnu10XwVkcrlN52AIBNg7BoqgECDI6o3Q8D4xqOV8ANTiL6pnRPCEyQByyWAIQkpqGObu5mRAl3ky0UlMTgvTRJqAshRGyTaWIYFi1Dwdw4hRAjIIhzFgKITDqJ+7UYGJrgcoBux3CRsWDMOIsTCk2yDEhF1/jb7b4N37H3D19g3ev3uHYTjgp7/8d/z000/4668/a79YXgWjOggmkCyGgAAFPw7DiLthwGYYMIwZsUtIY1ZDTBRNxp7MI8asvoiM6o33WnrppJRqjggYHfZ9h81mg8PxCB5HjMcBnCdw4e7TJ5RxhBCQug776ytc7ffY7HY6xsOAwgKWjJr0naBJ6oXUqtCE/wqCFAYXTc5ol4MAxBSrlW0sAccUUUpAzqPmNxFBTB2ue/WUuOEjmAQ34xFbYvTbvYZmev8WuBvAfAcmQRkGSG7jl38r38qXL+cUQhfejFau8vL7EAF+Fy/xmywLFe6iKIDvXhGeSNeyF2vSXCxo2DWCNX9Cc36VrXce3lsjC35YMGWp8FxNGSRFv0vBlD/C9SsBoKgMbUzalqqpDFXhXHM/BQuzY14XGhOHND8Ru44GqrWmYIwy9Dp/trWTDFAPREgx2VF1OBwTur7DD3/4EW/evsH/8A//iLdvrvHju+/xZrPFfrvDdtOj79UjIlR5a9kn58slxp6XGoTO5QvCsTA+jYy/HDP+5VDwbyPhlxLwCRFHIhwycBTGgIIR4nGmpv50+qGWLurDrO+5OWJ+nawcFzki5hppMjqgKQeIsA6paOgl/Wg4JXEPa2EwF3TCSGxGTMIonMGcQeUAyiNovIW450MpgHlEaI6IAoyDhVHVOlAKBIxgfDjqODjp0vTeRWmvZAU0mAIkErZXW/Tv3uCPP/yIP33/A/747jt8t7/Cdb/FNnXYbjbG26dq5NOO53K8v7QOydvnsutk5CIK5hBBk94r5z/JrDpPBWJsKBkf2hp6C9B+f7gxz9yKnuMR8dssOjIv/74vTZvPAiJOFsrm//b3S5o71TUHDi5+9oMM46TYaY/im7iheOcVeS0qOPeAOK/8omlRX/5+of7/vg3qpUCIc313aR//LU3sS8tFFtoX/P7Y6y4pj1VAvwTi+dCzvxQY8SVBkLUxPVFyrwgHD1nY3beG3Xd+2Z5zltjOaS5BlNZiH/CmC1zFt6zN94sTdaU/V6Z4s+cQ+pYZVz36aTL0k/fCovdWutKt99GuoU09J89erKXnLNmrJYkdz/Z5A0DVa/2drF3kHHI7BnYvOdPWbD8ud6gnBCbhk4DqOj2ZhgMsFq5GFZWA1HwSIUTlRVlDKomoZ4LmSQhVET5vdPN3fU2xRLw8S8bNrPkXuKUbmnImeBhF9YhQBW/JpT53AvBQQQfvb2ks2t1yfTkGDv5AxBJGFyRz4Q/B46Vanyz4AQUDNERSaOgh5wyCoBRNPhyiWqlX/gMNSMWkeRB4YtyX5CSmHFDlfjN2mM9J7ToTFDDlo2hIq9LTVE/jCUSoQoCShUyhEmiKRy3iVmlzAXkacDHatOdhUtCTW9exhuJiCFgIhYFcUL0iWIyXCRoWIaSEKMC2T4iFUWIHigmbfoN+s8F2t8Wm70EASs64vb3F8aAJoR3cmTrT1l4Tq7zfWASZGWPRfBFKcyaQUYEYsOLVnMx969Lq1WOh6lp6cU+S6uGQc02Crt4/GVwYOY8oloshpoiUOk2mbiHLKEYE8Jw/9TFo95JKM96Otg8mAVz7WW+KFoqiUpdOqqosYABFdF4qGCIaaqPrgJGBqEntHWReszr09txXpt9PBfe2XKJUfq39/7WNF77Usx9bHtOWc3zI5ywP0dBj6pjd+5sVkZ7W8Hm/fT30+CXKY2lozlO2fSez787TwI/O60F18QTbm9tF32WKtjrb22u+p6XMYVsCiVjOzZaJk2nf8HXd+AAPcYPKYzXX1pbax+dde3SPhhWDBvHb29Lws1oagMK8cNUjOFTezHk1CgRKEanrsNvvsN/vcbXfY7/bYdv16C258BTfnya+x8KZhgv3rUuBhrXzq9fYkLIIRhEMLDgUwVFEvSFAyCAUMIoIGAVqUhLmfewDP3vGYnwXx7X921qKi9cOmsa/pT1rodWmz5QKgujzg5jsIOYtLRa6yb0fSgay5YcoY3P06+wembws5vKj88et2DZf14UF0hEkBXTGc17tdrje7rDtOmy6hC5EpCYv2EMGc85Pr/IsKz176T67lGPP7blr++BEt/ri4sKDfYQmvrn2S1SPnao2AIFMJ+r9eiLYnNNfCCY6Wcjd53RUrRxC5Drey5Xor8GTPKWq57B0E0f/vPe4lFaeUl7YI+LyydAePwej4kIyc1FLPBPyXAkwFVc2KEpMULf4QIqap+i5IeIk6H0Gxv85IIQfm3n8QJv/thnHb+Vvo3xpgf2cct2TzupFmCkJ3Sp6OY8/77vMQ8d4u+vfJJgnjjNGxeKX11po8obwOiYlHgEMcLQcEogQoimnQw2t1whGpImC275g5glQaBjecyCA7xOttcoac7MMszIpFBehl5p3VU8AUzavxO5fYzwdxxbW/oO1K7oFuiWjraD6UkDVnkTq1Co+Jgu3E7Xj3QuCAQQJSJRM+ckox4zj3YBjzhhyhpSMFIMKZEmtyUhgydoIyAUCoNSEgPP+4lxsvKcxqxbkJgwQaYzjmeUN3Dtfcy7kzOiKgAJjHNXC/HA3IOeMrtN8IsIKWhRpQDALyyMAQiko9uzqHWnWTnnMON4dMNC8/X2/Qd/36PsOMUYcj3dgLojReAYiSNBEdaEht9QlcCk43t1COIK3GwAav585I+fRIAIYYOEgiMaeFY82EABIMIW9uuMjqORNiAgkIBg9NEYQSpvmBSHq/TkOBbkU7ZmgHp7RQvx4f9Tk8GYw50JYZkaAIKADSL1rYkwoWZXl6p1iibON3rl4H0tdz6b5UocfIzTOM1MPpoDjANwOgk93BbfHjECalHm73aHrevSbDQAginou3HFCSD3e/vADNtst3rz9DiEE3Pz6K3759a/4b//5P+PDpw/IABIRkDQJuYzFrP9FDf6KAFEBgrGot8rN4YiuizgeM1LKSMcRMTEodYiq9tG55Am6F+uHh3hSjwnL3xASyDxUQEC/2SCY+35KCYfDAeM44u7u1rxq1BNo/2aH7XaL7X6HzW6H2HXKn7KgBAUFQggIKU4eH2eFEGqWRRP2tYUgELouIYpg02sul22fQMLoOgVDIgqIgTEICmeMY0GKBaOFH+Ntr545xwzECCm+dv5mtbPfyrfyrXwrr15aJZLymW0s/aoZnf0dBOgA9EQYAiGyLJbaJcBhgQgpWAJoqI7aDQcE1ehgrgw2a3JkuPdCkIJgCl5htWKXNg7/7Lvzd5Myc3rx9p1M2cwM8kTEM4/m5r7gjJIrr6NZ1IsC9BANj0OElJSHjgSEEBGv9thd7fHjH/6Ad2/f4Mf33+N6v8P73RV2fYftVkPspC6aF2ysIMRD5XJw/SnF+FYpOBTGp1zwa874lQN+BeFIwBiAO2QchcFy1L6jqH3FRg+rr2IaZBHt82J9z4sLl7RYb5fTc+1twR/qz/EfYAprqbyx/+1gGIGRRPP7sTCojEAZIeMRMg6Q4aD5IcYjUDIkHyaPCE9iLaLfRZRmgcr/hEAzxXXNqQGVd6Jg4mn3HXC9xfd/+hE//vgD/vHHH/Hnd9/h/dUVrjYb7Ded0U6HkEJ1VtWuW1fsngMNnlseo4hfPjsEgtmNAQA0TCcQAjeYQjAjHYJwgAQPXQsISjXW+ZyFTM5VYGnSVTylL57YgsXf33jftlwMRDyE3s3+xvLvqdvPo8KLex6YdGsI2NI6149OfB6P2K0gz1qt1vpcD7j0hlj3hDhpM630zZn3uu+654IQeOj3b+VZ5ZKF7KU8I34v5XOCdy913UuXNVR/qdw/d0+rPLp0Ps+tGs5fu7a2tm3yECwnVr/L9hpzWtfZGWgwv14wt1TXxRPGzCjzqaF+TnMsnGt/fQwWa+F9jLELXGf2hiXIICLVqtr3g9XxE1TroTUQ4rTQtPd4/4gqSUEW0mjlHdUKzU42dQQLrxM8f6H1rTWt+c8Ao1zA44gyHJHHjDGP4DxoPobiQJDWHQNBJEwgQ/vS2hFNf6yDWPVdGsnblZXT3n2ay6kNd1NKsfirVH9X5tcELXumGx9M3gcyeVbkjJyzhkMiqoBUm1SuxgiOcdbWibRNAS8Kbngia7egCyGAhQ0E0WTNIQCRjMmHT5XWjfk0Udsp/0LT/2QARbW+srBgGkvInj2f526sMI2eDUarDam/UeVvyMa0FE1WyU3dIFieDq4eATCerHoCWNFcEeoRUQIsRwRjtHBMpQi6TYeUOmz6Hl3fo08JAmDTdYiBIdIjdj32+x26foMYVCi6u7vD7acb3N3dYhyOVRezlL21D1zQ1bHUHCOafH20pNNsiQ2FaUHz55eXChay1DnZ9j9gSdobQGgYBgACtjBgArVyjRbWKZo3hKNeZB4LlV79syh15ptyydvHzDVZNbGo4os0i0Qwb6iUFFjrUtKEi14XJuJV3Y/ZwRJBYtCE58HbIjjt/dct56zmnlO+Rh76Nd7zc5bzVo2frzzHE6L9/nJt/1I8KvB7VJp8yTlykUWpr8vOttb937m91oeVpu+iIfai8WVJCEE0vOWkO5apmrUH0/LHSTvcejlUg5IFfx/EQhyK7udUr5msz2ui63of4IBD1XQ6cOHfZW7BPn1cDmjnn/fadFSD0jaMtnuu6hgkUxR3G+UtOovr31noyRSiegQ6P00EJlNcE3Bujj5G33LOCv6hMvnnqvFNESCLYBRgtGMRRoHnZxIFIAg2FsYM1WNtEWbjtNyzl+M3uw/r97TXVOGlObbvRZbSeqkmdPGwzoN5O6V6RlhYLwce3FuiAmFLGpLaLpdvKgjRzj8RVE+dQIibDnG3wdXVDm+vrnC93WJvNJScfmKc8vHV7pOpt9b4tNW14TSKwENluR9dqpc8+c1lN2rl70kmdl1r5f2q1LscYJct9HjxPrm47qH7prYLqmEWfGxPSe7cfveA2uAxTfYaV65bf4D36VOL6w+efP8ZXuYleZzPkyPiLI2/vkCgXhDu3q6Cf7VIXalj+QkWdsE9IFJKDwMQL1ieDUI8qazsCN/KxWWpYPtbAxm+lcvKch3xMlMwEqpFa3u9K4Xaui4pj2F0LwFGgFZMaZhBt5qxZMJiScYgYtrwlgmzPD2maBNmgIKFGVHgg6EbcuHJvXLZf22/ed6I1g2WgHos3m9t++v9KmjImbFpvSG8LNvTAhZ+zhXgHkPeS6vkxjTs0x7UJExunysi6MwSerLwUMvqEKZjCISus36wsPVu3VOc72ZAmfIRPGSUw4Dx5haHD59wOx5xOx4RSgZxxt3tDW5vb8GsoZhi16k1fiSzrlfF6FjylBiaPNzSAsRvhdjVftb7x3FEznmWE4SIMI4jjscjDodDTezr4y8ioBgst4Yr4lXIzSUjWzLgnAuGYcQwahLjm083+PThI7q+Q9d32G632Gw21RvJx6DrEkTiFCLKeAsifc7xOCKPg44RBOARfUqaA+Cu4ObmxkLuqKdJ13dOEWp8VnMNzHkNH2tmrrkyloCE5rACqDfFtAkOw5A1GXJU7xTvLxccSjNP/V3auTLxRVQ9JmCM8vF41LE6HnWadz0ImtRcvSWUHsgAxdAlhDGDKKIIwKWAWJXVmQMKBdzcDfhwM+LukDFk4Icf3uLN1RXevblC3yUNkVQYoQgKC970V0ibLd7/8Q8QEG5u73Dz6Qb//F/+Cz5+/IBffvoLspTq5aGKEsD8cIDmQ/A8moICwd1xQEoBw+GIMUWULoEgiJsOFOZzfrk+ON0W+8QFCOHrQowRfa/9tul65OGIkjWWceFSEx7ur/bY7/boNz26vkNIOo4kEYFJQxbowNf3bGaXARSTqKg8soJwbAokISBKRIjq+ZIoQGLE1W6HTVIPmgBV5ogATGpdCvPeKqac4EDgGIA+gVLEt/Kt/FbK/YZqpwZppwqepyswvpW/7SKt9wOAmaLdl3fbuaIdAaAjABEYJaAAuBPB0PBS1Vs50EJHbHtRgCmpTeFJjaLW+Cfy/A3SeDqIekREzw1hHhPFIlEIqxJ8istfFkADq/W6Z14WVot2sfiMwmrxLmL3A1Xe8PaTevHp0V9Tv8WgOa1SUo+IGAMigABBTBGb/Q7bqz22+z22ew2rs+sS9qnHJnXouw59DEhBQYkuBhQwxmfO71bGAi6X0SrPr3cp/0IAIyAL48CCu8I4FMbIwIEzRhsHwOQz0ORVa30XTLXPUP1Z9YARz9NxBowApt+5kQUh7tJs9WB+P9nf/srqnq1eB1D+PXIAQoTYuAuAKIxouSWcrtXiPkM4Q2popkHDMeXBQjaNxrAYDTmQ0r6XYFq8Zxrr5j1ZgBRAKeD6uze4+sP3+Kc//xl//+Mf8ee37/Hd9gpXG/Wg3m82SCmCkiaKZ++39YF9cOy/VAmWYF5IaUgsBwyzgzJqcMXMECJkZkQQYrBQrzVniBalLZzSxKsUF3bte7Ns1L+pufZFm/N0nepTwUl/rmC5j3x95TMlq6azc6vq216wp1rFmXpANMmpxRM7mb3fCuM4YzDdkrHGBASq0cD8FfESlLsGcDwVfJgp6eYNvaisWWyvPee3Ul6q3Uum4b7vXyMY8RRU/PdUlvR8kYXSPedfuj3tuTZWeTvP10CM12jfulfAcv2bQF23lvLvYtYpVQABTJBx1tkYSFGrX71dVAPIBCG7j2pOY4icvnc7lmuKwHotcLItt+/SWnVgZQ6v1XspoLTMTbB2rwsWznysgRuAWo9r4i+p7wVTChOg+QcMxNCcEL53uf0yVRnBGXFhDdtTxgH5eEA+3KEcb5HHAXkcQJxBXJDzWOPXgzR0T/B9ETBLOaA171/2WsuW1T6Sxv1ZJvqBaPzXCsTY+LApb3PJM6Bm+nDtewoerkg/NSSj0ZswoxT1hCgGePj4TLkE5qGc/Hc1atBwVhrWy/qBi+aCcEtyiy/sSv5xHM3SPQNICB7OqMWkaG7dXscZ3j9omKglPVFtNzD1i4cOCoFAIVr/T14icBDHvAlU0dwAEDGYQGLtZAeNfP7WgdU6S1ZFRB1mfZ4KJlQFPRGYkBY0N4QIxqwfUEBKhN12i/1+j+1mg5QC8jGjiCDFgBAJab9D3GzQx4CxMI53t7i7u8Ht7Q0OxzulW3JADM1iRnArzan3HPTRTymMccwGrJhXRJkE65klWDNXqyBRZXL1NAj2ewsoO62lFAGR6h3RJc0rUi3sUkLqks3v1rPEZiD53jHlBfExUfrwGWj8cTtv0MzHukhMQFQKEYhT6K4IaDJ5Cojkaoxm3TSaDSEqCK0Vzda3Jeh9WfH98BG3fOHyklZkfyvlNfrsNfr/Xv7Lp9wXKN9o7cuUZb+fNeRZytm+3or+t6pGEgfQRb3VTMUXjHUOACIBCRZ6iKawJHOjZDrVwcH/WCixGiCiejW4wVFznlyxK5Y/CAZczDwYmqOHHRVurNXL4u9cwz3V+1qlMcTemiEI1diBlvPO56jzUvXd7DcKyt+EUHMiRVIPE+3Dlfj+Z6b9a8mR7Xqo360v645v+76oF0xmQWb1iGDhRufuHWMeEdUdOdRanAamsW/uk+Y82t/av5uGtwp/aX9s75nu9XcJMDBJlNqVn5AZ7wiaPwraA8bjW/+4ANk+r14sJxWsqfhmr0NA6juETYer/R5v91d4s93herPFtuvQd3HKK2K05FGwHipzkr2cXl7bKJrq0dcTVD7RZbXKPxKMt9Rcf8EFGiyPzievy+XTsnl+H3twj6OVbm/O2fQ5+Xt6wEqVz+RLHnPfc/Zw4/KffP9Dz17S3FPa+pmAiGV5fcnBlRKlZDBnTbhpipb5oMyVex4uwIX/lKZNiUzpcjrX11awl9lsXsoDgmieI+LhcsKafCuL8hBj+TWCEN/K11HW5u0a2ODKZVdQRVNmOkP81LKGsl+uCBLjPyf6Vv5SqoJY3EJcisYEb5W3jYJKlZ95UoJ6W0RDfqglvYeCKsaIhkY5rMXv9dw/XmYeEa74xKQkdEVja2Xu+0BVzrEqHD2PwFJwPAcYLEEHj42ec272GvcMwOQ90IxHHSOLz+ogOoWAUAiSrC0WkoUMeIiWKyGYJ18gC2tl+0AVCljMO1lDMY3HI8bbWxw+fsDx5haHT59wGDMOuaiVERcc724wjkdrB9WIK25l7jEAHHhhE5btrVzscVKqfeZhYWIzrtoPGvZnbBIMF2FQyTgMR9wdDhhzrjRGRAoYuNBFBLJ+gAmT3tdkfVtyxngccHtzg3FQi6kQAvq+13wYIVj4J1Vil1LQdZogOLN6/IyjWq4j2VhwRuFcFcu02YIIGLngOAy4vb1V4AIT7Wv+jehdhRAiJDXKCs+rQN5nSu+ac1BzArjnBqAeDyLK93ClPUBEQ+xQF3XsyzR/4P0ChkSzLBRC7DsEU4K3+VByKcZYONAIeOg2sXBGIqUKLk7jFSQzIRMCFAQIRRxG4DgW3A0Fh5HRbzTU0o8//IDv3r9DCqrkuCs3yMLYdgkUE9796UeE1KGAMNwd8W//8s/4+PEj/vKXf8WYRxRoW1ObAwYaNkjM6o/E7ALJVDwUIBAcjiMgjLvbA/oQsd9sEImqoMuiySBLQ4NO22QCvsjc00UASzQ9eb3FGEEbTY65O+7qnMrjiGj5I/b7PTabTd0PQkza8WM2kNHWojbqQlUaTGu9z7vCBYUdXPTfUQV5XzmDaBis5LmKACRLiBJThy4kJJDmjLHHMQhEEbHrEWICO2BKrV7oc8fs/Vb+Vstz6WupiJz9/SqKoC8ph32bi1+kCCwWPkBNvMqar8GOEUCErsH+3el7EwgcCH0hdMHC+7fPqBsy0ATAryCEx/d3BSOZoQU8vI/k6vXsuR8CM4IbM7DU/BAkmmeJmwTCwsUSCTvQUIDxMM8jURMNWx6KalHftFWahpvFNiTUDUb1HqdzyPkQT3LMBIjxzqnrsEkdNrFDTxF9iGYEQIiRaoz/S2fHayiT53slIyAgISLYd9V/CUYWHJkxCqOI678E1ZUjQvtJVEvOJkug8keT0c4JGKE9OP19AlJ4CK7GE0Lsntm9y/NKfgmEIITk/JMBEQyAAivdgsxBpsn5asADubdNMZpt8pJ40uTa7AZpeEi/JpZDdvf2Gvv3b/GPf/wz/vCHH/EP73/AH6/f4c1+h91mg922R98lyysXkMn746Ih/uqKyq06JpqHT3UBXCxUL0INOeohYEUE2fUX8L3S5XCg0gH8+xr9t9c+objcfOE0/C3yoWeNL1+QfXitPrkYiFiz1r28nBKXE9VjrO0veW6r/PHQDlN86bnF133KQDKFxYkiq167BpG1X5zoLwMKHlPuAx9Wn/PQonpCXH7d/PfXRFu/ZHnJ95qDDw8vnsuu/5x9fGKJ88hF5vdBD6e0P/XLdG7t2rXuWu+SNY8wC6OD84LtEohYrkPP7f81MOLcdfPvkzJ/4k2d8URlLFs/Cbt5YoKdFzNPCVf4O4jrcWWn32lKmLcIkXO65st6/5x5V6LTMajWHTKBLu0zp3vPj4Vfv1T6+fc2t8Sy/rU5Wa2TTUY8eT4RKKoAFkiVvE4/CwfuSSfpY8cCLgVlGJCHI8bjHcpwAI9HSGZIZjCPBhrx1Gdh4t6paadSSQDIrOJmdLs6DIv3XPRBo7D0/vJwi6rY1Wtm/QxRwIJo1gYXUDWn9jxMFFiVxsksz12pP+MfRJp3bJ8594Dx4vcCAmHBMBSMOdf3iSFqMumG76iK2kAIlvzNaakF4Jw2/V5fJ1pAzZ9b8zY0xd+79fBwuqcQNCa00wpoBojW+V8BIL0mhmhABMCWM0JaXq+lE6t7EnlJ4xsXxjCqIA0Quq7HdrvDZqMJw8EjpCioEgKhSx1C12Gz3YBCws3NAePxgNtPH3F3e4PMBQy2OeHzR8zeztuk7dGYxFSV72z9nAsjZ2iYsNG9gtisPudrEcsEai7p2c+34eNq/hDS7zBlQNd1KDmjbHq1zjSa9COWfdq0oZ1o0zIy58XbcadAANt65OtGs4bp0kvoUtJ8Jg6eBUBIAaS6pq3QWQiOWNr8M4F0CUKcEwKfyqfcV9bW889Rzu0Xv/XysGzxcnU/pTxkPHTPnatnL5bBVnnAx5XfAnn81mj4a5Vt3ThYlcCtdbpf0Opjpjj6ppYFMYNCRKBQ80VU/Z+vzrOxEgBh8ff0vSp3jVes3hCtl4N7Nnh4R7dAb79beJ+aL8I9H0oTqqkCGwuPiIkRmVun+xcyvYvLGEDDo83FE2HNRQWIKqsLV29XIvOEsJwQ097c5JhwdJ/suU13LWnpnN5lKfOd+21Z5joGHx/AlfJqRqGhJpWdyxOv5Z3i8pQAQmzv0PALtT/t9EkHNuemhqER7KZPe51fA2A2gIv6qX7My0dcJkN9Ry9sfKgGkZL6b/7stq1OJ1MznP1vx+pk3Kh5aoxAiNhd7fHm3Ru8u77Gd/trXPUbbFLS8F9JvaCjeYF6myayWR/jl9KF3nffQ+v0qdw5yWFk/LFYrjuy/nXdqoKVHn55MgoXliZH2PJ5tYUr5/z8qfx9caFTnnT28wrfsuRDX4P/XCvPqf+En63/Pb+85nt/IY+IuTB0Sbl04k1KA/3kXMwrwsJ/aG2rC38LPnhOCPWEWHHHO3mfWhOwACFeozzUH89jrB4/Pr+P8lLvvGQUHr72ZZ//rTy9rI3HufmwNr7nrjunBKezIEMLRPh8dkXgS4AQbRuW39dod8kAV4tznv6GqGWwWFieuSJf3bldUQe3mK+eADy9t5AKLAwIsvPOCKlHCKm2w9vilheuHPPY921fhpU+m5RhAZ6YtTI9mNrNTJhi7J4XLtp2LT8ezqiUsnLfPPeE08UJQCHe7umamjg5mOV/IGN+G9ChavLdomgSYsCanLoMA443n3C8+YC7X39GGY4ohztwUeuXPB6Rywgwq9t6JEhp3sNAhlKUIY0h+ps1bW0UMq6B9j53pThcoJ6PkyfKDRYyqJSCYRgwjqMJE+rFQjyFcRo5qzI/af6FVnlLgRBlcsUnIsDC32z7DbqNekOICIZhqIzxHJBAVcQXt7rqkr2Svk/O2fIfaDLsw+EOw/FQ+Yy+7zVpYiBTMEeNYENi1kVunc72W5tjRUMeuWI62XsOh4PxL+YRUVqgZE67Iqg0GUKoOSJcPmUXPqx9XddVDxERQeECFDJQIKDrtA3HrKGnhnFECJ5TQ0yxP/UfzNothIACQmbg9jji003GOBIgAVdX13jz9h2ur99gv9/jcPMBRTR/DMWATbdB2mzx9t0bZBb89N//go8//4yf/uVfcDcOyGBIgOZSYAFyUcAnWGRh4jq+RBab2GhPnYYExyFDMuHu9oBNJOR8ha6kSYD265lBwMzzycFkYFqrvP+T51uoSc3NqiwKdpstEgV0Mc08Kbqu0zWONGEmm6Dd8r5Ek3VjsIEWQJOJSivU6bh6bghfI9oiIipDBsJ+u9EwbubhFYhNjZUqCKU3qTKkJrpOESFGSKTqCdOuo5eAEd/Kt/K5y7ROzcsqCPEZ2vOt/P5Lw51VkFuLK/H1R88RocmT1WacTMEfQbZ3BHQSkIg03xOh8ratvpgoAB7OEpgrh71N7gFRgQTLHVCKulzkAsnZwqwypGRIca8G9WyQMk4eEWWcfnPPh3pki+tvf1tR1QpVgKHyjpCFilpsz5v4HIGB76T9ysr8gIQRxgGbol6HqUvY9J0aOEBzcKRASC5/Qfk+BHnxSf9Y2U7aMRRo3ia4/4C9s+3tFbAQAYodkU3kCdWwhJRhgTIufh2aTmwV+7PW6Eda4GnRyPZdzWNiCRyQhe91ECI4uUkzH8QNPtQLNTMjc5nynPFU30TnJke1NEPWdw2gtAQkpr/1HeO2R9zu8N0ff8Sf/v7P+Kc//Bl/9+57/OBgxLZH2vTouw5djBAICnjGcz1EOC2P+KXKUuYnECiE2q1kYWl9fFl0bgUDtTQMqXoHS9AQqu4t/Zlf5G9yc3aS/8pw9pPyJCBiqcSaCbeYlpWp2Exf/H2COJnAXXUmTe9VOprrPWq9rVWiI9tTcupJ4KX6JPtHhiDTFJJJrdIs9m77wGYNWcAYq21u37a9d9kjS6XWdAzzv+v/tmASYf7L/LhOfY+hyPkoOkHPF9O2aqoXPneZeciy6tIF+jEo5lMna2uZsGQhl3248tTZNefa+aU3pJcqX8N7zPt46v/29GQhodcsmz0fpvZ3WwEFtd5WueLXqgVqE8cfc+UM+ZrSMEDzvmsWyhcsS/qrf1eBpAEWnJG331xpL25CLFMcW29zFRyEYBmS7T1NaBCB8jKEEFHXaH9WYHMRtyrqjLN2VrdQMgbaPm7BVB1/WyYU2kaazd85XbArI5pNvbWUgY2xC3gtA+cCn3p2YNpbaFIys/dLc49YjgH3GGGnG6jyVT8as5/ilAuivnvdD8waRXdYe8spX8fs45ZoUgDOUGsqMrlCw/tQ6jQ5Ys7qAj7eoXA2DwOY27r3qKhg1AAQSyp2fkGnWnDszSmm9qvmedAL1RNC9/iZwncSaZoxozpozMZIBBVQKQZQMS+SqKGNYo3B3yHFhONwxDiOTUi0uYDiY04BGpIGasWoc6JRIxgdZ8sNkVJATBF9F52EzOpusqqfbvV1Yc4P1L60+daGtZqBfKzKiwn0VGGCa24Ne3aIjTBq9I4wxeh1gYSoAk3qlp1h2F/NT1DXO6PxnMXq07jVEYxEghi0n1gCMgeMHDGMIw4jIyNBYkDqOmw3HbpASBAkE3RjjJAQkfodYt9DSkEZRhw+fcJwewsSFcaVdnxcPFSSe1m5taCgWnLBLSOVqFkiUAoKA4eccTdkDLmgKwoyRculoVapRtXS5MGQiU58YymsSE8075vOACzmUnO6xBQh0sEBTK9TQzQt58pE/SJTeC23lKx0Qgsh1/Y6BEKQaGt6s85B6SWmhMACKQVCjYeNefBEkC07BUDUNcQqEiKUFMBm2BNjxKZLOCJruAhfIytlS+X3nZuUZh5oXpazBnYXlTVB/7X5r3MGAJfe81rlpd77Ndr6WN7/dfpr3SPyXHkJ68kTPrWZ6J9ZjfOI8rDM89g++ZL0/zmVV/O1wbzlfO0m422IIEHBZ6EaWXPivaVo7ixSlroTYCtAIcJIGqop+14nU/4oLaX57gwJgCLTdWRHZR4aXlF5RxZVBtd8DgZaeA4I94QQT3TtuSY8v4R7SLReE2tjY3voNDzTpFBe0vemkxvhLCDbHqMGSKj8cwwa6ipY3imKMJN8v8Ms8El3qRkfRouHzpjexV5Tb5ngk2L960ZTZGPLnvPCrxRSAwoRTRTMzvsyCIxA5qFqxgi6pwdLo2HgQJhkOh3eYg3T9yT3sGijYSljPb9v1tGLoxmUTUDEFHpJ72+un42z0hizIDiNuEQhonRu4EOxqCdoPyLTc32AXJZ3uUiUb2Gx8W/XWB87Is2jZk93Oul2e+zfvMHb6zd4f/UG17s99psttn2PbZfQx4TePWqCGrm1lbeUu9wrznnKvKTu5LH7U9XVGsOp+ovJwG9uXDRpgKUBJACBBz1Y9dA/ear4ZLY/5aSPLm9/rcLPLB418Zjto6dnPDxe5//26r1Plt/n9S7L8/a/0+fMSu2Y8/c+tjzFiOjZHhGtUtqXaAFaLy8X+dq7oAqYRhCQORHoyyyeBeu3Sa9Qf/GNWBUTU8gGnxjVotiU+8HQ3gmAiCAKSCHNPCIm667pOW6pPBPkcEpIS7KallyqfGXtvRUwQuMUL+ukqSNqh0z9ez8I8ZiyRkjmJkrtNbNt+Oydn6ucm8yfw8Ku1dk2T/Zf77nzM3K738qsTMrgliGvfC4AOkNT0+bUhkrxe3Wu+N9TSJXZMc09Ic55OlSFFvncu9xC7/73Pn3O2rFyCc3frZLTvRDE428WF1QExK5QksqH1owBgaBm1xamRgDJjDwUUOf9o0p7dsGEGUEKCgSFBAUCIaCzsCBk4T84BBXaYoBYAlUApvSCCTFBmXEGCBqrP8zUXqhK8NCQR1ViohkzUyy2Fsnef/V7KQAIKfXGxKnmtjhQbtbowqJJcIsz1Bb7VM3m1Qq8T4hdh9hFhC5Ycuopae0i7xeomBAZFIxg5CocqJ0cqzs/FxAXBC4okgGM8ISELCqqUn+FbptQQgc53mH48BdwLghBrZhijBAQBpNrUoptRJa54rQCNTqfptwnykkUy8vBrhk1pnfImlj6aB4RMSYANAmZ3meiAhVZAouSzRouChAjQkwIkRFiROgS0q5D13Xo+x4xJERKuL29xc3NLfq+R9d1IKImT8I0H6IDIf4+ZpTl8yYYRzoc7wAI+k1C33XYbXutw8JJVQ8L5pm3VPR1A9OaM5owrvcCyfiWO5B5hOo4c9YcDSmlGaM8DqPySQxQjEixg1AAUzYLSyCFiC6ZpTurxV0ktRoEgGEcwAC6DogJFtbH+ZgAog7MjMOQEUmwiQGRgJ4yxsDoUkAuAWOJOJaIYYz4dAQ+Hgti3yGmhO1ug+v9DrtI2JgQGoSB1EFCRHz7FjEm8OGI8eYWH/7yb7j58BEdARwDjpbYvRQGCSFQNBHIc2wILNq25rWRgm0g9IkACRAJuMuMsTA+HgYgEr4fjoh9wPU4QmJEIkEI6nFAdV3UcdOQU83+wurS7jkf+k2PknuM44gxT7kgur5H6jp0XQIb8AYAXWchmsiULr5/ESCkgrrMeMVJsaHnfL5R1SsoQBAgWcOvKX+s62SkiK5XT5dxVJrRdZ4N5yAk2584ZDARiAcosBjBKYARUVIHCgF9l3C17cEkOHKeDHFlcWyjmpOAQtR5zrR28bfyrbx4cY+IKcQecDnP3tLpE59f/3+inPD8JjzhgfjcD31SuVcmpPrfk8rTZU6zCNeVF8rXGGcalTPiSCiZkIXMiEXAMqDIESM6DJSQAHQieAvCBgGFAkCMGxGIJkSwISpQtXbGRGdBt0MutlewmqUzK0gi6vkAcSBCAYRiecTIPEDJ8kFUTwjJEDNyUcV3m/uhqauUuVL53n6uvQY3AHG1BJlnqecDEFCj1NffgnUFpYCQArqkXiSpi4hdUDQn2p4qABvfL6120xVTi0bdL5NNGiETQzAG5U8T1NuFRD3NB87Kt0iox1EEA8TwfjKDpQKigkhscglQQkQ23wiSomNAAknWdpfXZJI3Wn2cm+NqfjmCEob+otf6AmO/+bk2p4d/r2CXj0dXab4q9sRCeoLNwElMUcnG2yvI5d4PpRT1uskFIWu+MykToOXkjBDqozVUq9O/ypAhniq3KUQgdMYpKo9MMWH37nv8+Kcf8Xd/+DP+/v0f8cPb7/D26gpvd3vsNz32XY/eQjSF6PywwVZLpfeSKl4BcGjLY9akdg2r+geCyZEBIbphosrnLofo3AhgCytXzBu7EKsO1vuE9F5uNqkTPZqIGbcJzvXMJYYUwoQpLwjNDnWTrLobl0FfqsjJ93mb5zqklyxcdVmn5SFKe6rO9LE0/DKhmZxwvIMJD+0dAFY2ahv8uQVxez2anpusjj1kRilzJdDSgmVS5Ll14eT1sExSPXvumeFq23hG/b0CRizfiVa/n9S0ct3yuHLT2Xafq/vh0niXuEJjqvgR9TyvrKHHXs6hpZdZUq1Zv5++1zml7RoY8dnd0Kw89L6f0zvhczzrKc84Z6F439xa9wg7bcsMVKQmjI4rF1sPiMX1973buec91aqxvW+VrhtlqgO+vFhf5/Rv3F6zL4gzuq1A7YnvLIY8GpAARG5ejFoxC4QYEtjigTZ7DsSEJGVkgzG1vuaziOneNG/BksNwQEXdtkOzBuiepC6m9pcz6ycAlJ4/GYXaf80GZueESK3HABO8TIHZAGOqhE6gpEltA2lM/JSSKtCrsrppcu13VE8FgQor3CjLg/UrSlELNsv/EFOAcISUiCiCCFEvdDFloIXgCWCg71FkBOSoClZSa/IU1UE80GmownZ/rknKReChXIDpt5pEFyqEEBNyzjU0EJr545bjbU4FEFn+EdJcdURKBjVUkQGFZqntH2HBmMd5HH2iqpSKmEAond8RgCBGfQM2pXGIUQUdQVUugw38cV4HCi64F+fauuSUzsJVPyvuht7wTKvrR3BPjhYsmUJ0LfkeB4N8rDysk8+RUoqGA4PLrhaCSoCcRwsr5mPQ0ORsfFw0U4+bcRSMo+aGEOu3EBNiTNpu63tVWiv/llKCxFTDFOVhQBlHdFFBnq7vkDMBPMIttWi2xzf9XDUXpWVq4AYphjNp4vQxI+eCPJrHrQFH4IJAKozLymc5pirTTR20vM7DQJAIJEy8se8jXtjXkFaDAPeEsnBnThsnz0MNceBjieb6EE5pikgtRtnjqC33ApE69m41RxQAZozHI24/fcKHX37GaOAxCSAB4KJt9rUWNHlxOa35mLTywpcqD/F2X7Jt58rnMMr5mssaL/WafaK0+sy6Wzp6LEnJZTLNmQdf9ojV+r4+2v/cZanIa8v9Y+Drs/8558enHGr2MWC7eiCTHoMIEgESCb0QNhRxzAVMFoaPtW4hQbXiqJ4S1owQMSmbBRA18EGxUE4VnGtkBWnaCt/rdM3WFd32IHdtxlTFYgubH20vqHPK+5dslzA228UINLuHV+HGISWoF1/sErp+g6v9Hle7PTZdj65LiMHCUVqejdYopK3P/RTW9sj2eF9xFWswxW2wNnJhFBFk82glZpAEBGaMEIwiKIrz4JAFQzYPCfHwTJWSUBGXkBR4Ynd1cCVsI5cJmnF1T2QbM+flSepYTy/iNu7qxTCXH9uPXz95YajljskgBkJRk4OghgLjYiG/CsiOXBScmLxoePHMZX8342fMxqnSXROf11pIvVe7zRb7/Q7vrq9xvd/jarfFdtOroVKf0HXq4aoeq27M3MiFZ3SG5+jnMeWx95zTlZ2v0/oHbjSmxjdcpvvVsAdGC805uJe3IDRv38pV59ohLr83fz+miMvA0j4Xc1KcBgjTQvJyPMFDbX5Nnsyrvp8PoNl4LctDtPIcXvcFc0TYwC2+AhcSuUw3ukA9U/Q3wqzWqddr/G4PxTSPkbt8ji8ueowWi9etlONcSXhGoG/faVIi0Omqck8vzdp12W2z91g7fv7yt8tkngch5sfl92/l6yprQNV98/7c9UuF6hJ0OPGEcKVfuGweP9Sec8DtpWX5Xqd0PP/bvRPY+UMXhqYa4KDDTOFcmcNge71aHvM4NHeSejVE+7jAYVb5CAyWYnHRp71DxSq10FELeF3rPdGcu4bCLOMrF2KnZ7HVA6BRYZvXcVGB5v3Sbs76jitMr7jAN4kF2o9Tv4m9Y/WeqGOrD01dQkjq+QAiFZSihvYJ7m7QKvq9TSZTRGunehiYC7eYfMus1m1FleMhAKnvoNbiHRJBw+FAkME1UVvcbIEuIgw7ZCoY7wZwYRAKQgA2m97e2UdKJUSG0sGakpaELQapnstFczz5XHMvx3EcNW8DoEkZbU55roMaT988BIppTNkkVCoavx5NyKIQVbHtQMQwjhiO4yx/guYeWcx10tAzFJVmUtJrxvEIIqBLCcJB4+FKh912C+aMkgejTa7eDq7Qr4JQU4imGLlisXfd83OeE2UenokAUAwWesmmkwM1mEL9LD27nJrcu6SwelVkS7StFU/gwLEMCCFjM27UO0RcAHBRXdszlgzOZjkFdX0vDAwD4zgUHEe9LnUdUuoQu97c46m2hWCJnbsNKCUgRogAd4cDhuOAzabHruyw3e2QhyP45liTGgpNbyfi9OlMqysVdM6LWB6KoEmZi+j7HwfgeByx6TrN/VLU+0QABEpqf9jsC563ZAk4BwqTxeFyLhAhhYhAqgyZeM4pWby9hNK3rSF1JRAYyItan3r6TrSha4KHNJ3yZACYJcVe21uChYPTdYZnIdIcqCYxTyH3UCsZh9sb/PrzXxECYfvuPbbv3sPDuHkeHQBmzToXftxTA3Cw+Bt/9ZTytw5GrJVvffKtfD3F1blTEJO6obJU3s35N7B6IES48lkQoNbHfVDDnD1pfp478rWeTT1q/Fh0ftgtxdWDouaECACYIIFNCR3VaxdAFQZa5MDnkm26JJrPgsXNTQQViGCto84+WdxflYP+c9UsenfNZZCqLPfeMzBe6htrm4jQbXbY7nf47u17vH/3Dle7HXb9BjGQfTRx9RL8f8kipkPqRI0YqPieWpCFMXjOA9PXh0LIEIwkOI6E4xjwaQRuMyEXHb8gggiu9CBE6h0ekyIdJev4tmCQyyqeC8T6qkJJZOMPYGbF7cPg42agAVVzsZY2/B6BhufyIwOiuUHUK5uNZ1Y6JfOYkTLWD0oGlwzOox49x4h75zcy3uy5dmoCIaz9lT9Tr1kBUFRaAgCkrsNuv8f7t+/wh+++w/fv3lZAYr/bYrvZaG6RrkNKcSnyfRXleftc5SaNB1cQk0JU8AgTH+tGgS4zq4cLq0GN0Akv7Pe+TDtXWi5zRXz79/nnPH/wLnsHlz9eq5yCSV9TeXaOCFcu2C91z5jtCScEtYCi5rUrYi5rCrZpk3MBT8Mx5UaQOhXmpmc2YVD8uFAOrglc5ywaHi5TCJXTd1iva/YMn8cnR6pxmP1Yn0hN764oTldb+USEa+ITTu//mq3Unnv/Y4CI1y5rVpavUfda/ZfMi8e26aFnvlZZghBrVnPnSrvxttaqqUlA2tbvyUvbJeCxc/Mlyn2AWf3b11I5vb6uMzNrLbfoZw0vZG60bJbbIoIYPIGZWuHLmE2hHIBg4XLM6p5FEylzUXdtSQQJvmk3tG9ueOIBTY1ZrurFoMx2ZUH9nRbhlJi5xmf1tVZ5ctYY6pjGuy1kfTUToLySepENOjWcr5jVcnOslkikoEyKEaGLFXQgVxBG27dmgdJdZBD7X5WLarBie6YJtyQCFAbnEfl4QBmP4DKCwOrNkCKkJM3JYbGHRUxZWARURoBztaya1LhAtW4iqZ4/tTu8ixZ7tQqXsOeYZyPP+9oV6O79CFBN1l1Dc1nfCVDH0q+FCZQxJXUvDiZs21go6BCQc5n6qgIQWs8wDCilIHU2HhQQo/z/2fvXJkdyJFsQPArAzEh3j4h81K2u7pmRlf3/P2pFVu7K3OnbXZWZEe5OmgGq+0FVAZiRdKc/IiKzKhHCoJO0BwxP1XP0YZb6pnRJs1AXmzvC6vkzjiNyJgjnOl8I0DpBQeEY1yRmT351f67aroLe5OtyW1eiW9bTetyyAcUeitL7IJASNT6a2MFqtPBAPj7rUGdVNuZ5VjLHtDCipCGLguca8TqYlwMRihQcc8GcBXMGGEoMiSUgX3LGvCzIZiEopKEjvM+DJdBLFoJiHEYMQ64eBWwEXDXgNwIF4tKLr/v68iSgEPUOiiGAS0IIjFIY81wwLxnLkmvMZF9L1lfEKkWDQegwf1z9TNSRB1KThUNaSL+t94O7xLjSvCJ8TS7ektNbUqFP9OiyM7NYmNL1fuSEKNASvqdKnJXmBS2u+Iu56Qcg+rMAJS94vL8HM2OZZ3wsjE8xYRgmpDgg2jrdlkcjXYB1q67fXl2ekzcuyTyXfn/u+v153xv0fkrG+RZy17X3/BpWnpeO3RoW1Lpeobx/rXpuNcffQ3nL2H1J//THv8e931qX9yzX3lv6P7q9YfXiggDBAIEEQogRY4hIIYAtpwQzMAihQPBIwEE0tGkBWl5fAsAeO583sipQAX4LgapubE2GcnK9wdd6PtXreDQKv+RmzgiuH+hiFVqpAmt8pe0ZrQ7a3qKeHiliurnBzd0tfvz4ET/cfcTttMN+nDDGhMHj/EdLCB7WeqI/87ZcsxacxZoIGkKGGVwESxYcmXFvOdFyLhojqAiYtF8POeKYI37LAfeZ8JgJCwcQsebUCoxk/SwiRihZuCoiSCjaXU7yu5BeLc3gqJx5cHub8lqHNeCvkmM11JMRXbVz23WD6Q5cCQkGSbEk1m4gIqorCkM4gyWDywLJRkjkBZw1V5fkYnJ1CxfW35P6wUUq4fZDvI4YIiCGJlPHBEoJu5s9Pv3wCZ8+flACYr/HftphNwwY04AhJTNmCuiGfH/pV42L9z6nrT395xZlZi1ZrZRYOAlIaCFiGQWCZkDm/V29lKyo7BpO9ttL8lBv6Kl3f9lecEps9Nde60+Xzz0N3f0tymv2pMvypv9+/nv/4RTV+DbP/DaPCDn9eK7ap21zJlG1TYTNuF1PMHGBsPd80GSVrihvCQ/dNNZAY01I3bHcLRHl+wngptN71Vdle5eT+1JLzCnAioyAPY+ge+/v+00oWPlG9/nWZdua3S+bResiePtn+UOVp0iIS8d72fa5W5F6wtu4Cp2zvg+76+qZe17alL9GeYqEqHLgFjAGHDmz7UoAj+fv4WK4KDhXVIh0q93oj1GKWrTMCwyJRRgsKWqKQCBIVgtxKSpYSohVDtYtw63DGIQAgVlrBXWpjSKAeUaAurx79hwe+qcP57MFvytgzqrk9d52FSB04K37jbpmqlcjNOJAYGGRNgS6CXoI6jYeU8IwJiMifL+ieh2/9inZ73qqVBKhWDD2QFAiImfwPGN+vIfkGZIXkDCGlEAoYB5A8wLmrEAzCzLrfkusRISHhQmmFBLUElrKAqIIigP6UvMmnBlTbjlTQwAxr37zfiqloGRu+7nNuZ6IgEjNZluKbsYxUfV8UBC8zSu28aB5FchCK0klFYm074/HIwBgtxuRPEm4RNPfrL7s/ak9pAROBkEwjhNCIJR8BNvY6xUDB5Cd/NDH6eQll5F6oMz714gUffwGHMfoHj5cQ5ixKQtEltfDrhECdeC41HqVokrjsmQLYRYRfTKTxV4uwPF41LwHaUAIEUMKtR3ZkizqKExanxCQRXBcMg4LY14AGgaEOEJAKCyYl4zDccZSGJnF4v2ShW+KSDFBRLBQAIeA3TRhLqV6EJVSjMAgMAUNSyGdvFkTmqvbeHLiBpp3Y0jqcZFLwTIfNefFccE0LhpKyNq+xiH2MUhbudgUOLu2trOpV+71ZS9N6XLqreJyr8vRILSE9kZCsCWkdGnmnLENsyixY3PK1zVdX3oyQmr/AeZVIZrfosrc4mGgdF0hy3MjnojU2jYvM+Z5wf3nz/h7+Dv+ykAcJ3z48AnjzQCx5zwlKBvF2bvXf0tl6Z+5/B6Ikd9jaXvy6W9nDde+hoz2DUihP8vvs7hhYS1uqd5vKmZ9HoUxkSClgCkNGENAogCyeOwRhFtRcPchAJ+ZsQA4QpMeZwFYFIDVnAMGPFfygQA2EkLYjgsaqpNYvUJXpENfNFCQemuqF6CDwJ5r4dXLT99IPfDrX+gGqFbbJsMJAMQISgN2dx9x++kD/vrTT/j08SM+7m9xOxkRESNS1NxJIdLG6Od8eR0orDu1x8qXAuQiOM6MR2b8ljPmnPFwXNTAK6teQzHiMSccGficgYcc8MABCyvGNUTBIAUJgtllUZdtguueUfPPcdcHnYzuxETTYXr2Qdr4ENqEDOsMKtyVw8Fpu1lwIyzxsEoWmgmlkhBVYpQMkQVcFjAv4DwDeVFviJwhs/6tOUkW1CTqNT+FTRqvf9DB0oZMF4El+Hg3I8NAiOOghNVffsRPP/2Anz99wqfbjowYR0zjiHFIiJFqXoNqmPIVCdWXlUvjs43DDQq7+kz+PzX9N4hYpIRen2u6rH/vMqZ7B689ub/uPneKc/hQOO2HP2Whb1teRESswRmDoKpuLFXp8u/WisxlcPecENzO1HN7hb7lhHBQollz1fNXpIIvOB6aaU1CvBSIPHmG9jCbZ3CSYE2m2O5r87u7bzXzWr/39bpYzyvq/JLJdVkxobN/fq3ynNXUOUum91rQnmJJ30pGfEuLs/eytn8KNP/aIPnXuP5L5/tZCxZb93xTJSIMw1DJiN4CtZ7fLYtnr3lC0L6uvHgd26zvPWC/He++PvTrRAPEW+IqB2bFADLYOq0g+FJDAlHQRHExJAzjAIpR0+eZBToxIzAjRLUah6+DvbAs6mYsRECqPEk9HmiCJTyuu4W2KZ3HRv+7eN4Ke/ZS+KQ/t9bIW/Jc5XTqXJxrQ0GkCWeAx9MnDaUTNSHwMPp46oBEfx4772QuN60BAg3JpKFmbDcUQDKjHI/IhwOWxwdImUHLwSyftN0PxyOO84LjnDHngpwZc1GCoBwP4DyjHO4hZUbIC4IUBfuJkEjd+YVTraq3kaOkPsy2K1EDVXsrb9QwjCKmLHjSWifkTTCmoMmIidRSnmVNWqSUIAAyWricBgq3sR1CQAxcwU8nQQCXNzwUkoBF80mwJXEM1tbSGUxEIgxDhIi6+5MIMkrtsurtUq38+7719cOUNzSZYO05sQ6x08aqgcMiNdE2s1j+iG7/PLE7amPKSS1iqWGyFIhQLwoBkEsGi4YEiFGQEleyg8CQEgEGsgEgcxYcF8HjzKpDOpcogqUUFBbc398jQHD4dIfdOCDBvVl0HgQjWnbTBBKgyG9YcsbheMS8LDUhs5NPp5aYFqYK6rkRg+Y4SZGwGxNGS8wdMuF4nFGKkiPzksHmsRVKUSBdGNLH2V71Qbufz//a+d346teUfs1t8mrn/n5iJdaF3pJGZpyiNGsSwaXkSMESr/fzFQhBPfwEqMm4iQSr0A5dfdxoKKDtj54FJhdBLgsO95/xj//9vxERMKYRMIMgV95dnw1efTkdma/dI5+Sf76FUvzcPb6FMnzpHl9T7vpW5S3W7i8hZlbGbnh5m12qZ/1+89nLtwRLfk/AzFv69Vte8/X33vQzTIpbybrtNweNIwij59yJARMRBoJZ8QMjEY4ISBzwSMBvLJg54FCC7sOs4VaPJaAIsAihBGAxT8ZV2FGiiqMQMRA0REsMBTEGCJOmmnBMyORawLcL3yeemCs9oSHSXcwBppNGwjojhO9JFvUiDQqcmvwWhwHDOOL2w0d8+PARH27u8GG3x24YMKWkCas9Z5h7JXZV6vtu+/nSGtB/v8ZvGAzlF3T/Vm+Ih0XwJTP+a17wsGT8ejhAikAWsXxxEbMIFiF8LoKHAvwKwgMIBwBMhBgiBgCxUMvtBzU4ATRsIhgWcomqR0z1FPax5y260hM9TJf+6jJHS1Ltsqq2udRrGSnBLTSTkhhGWLB5RYvniTD9jDOYNQSTJqhWjwhNhj4DZVYSolioWdYXme65GjKb9TWg4WuamFtU3IiEYRxw++EOnz59wM8//YgfPnzAx/0NbscJu5QwpYjBx8lqPjci4sn+f6J8nT3Yx6l+urj3XFiT2vnmKSSab6XJrEAvX251ZWauJMYW1zzB1LrF7pxn4vut2e06T2F/z+0Vb63PS86/9th13U1nBmo/eaHN8XrO1dV5dbmaiFg9r+CEhPA1Z20t3E556mFOhXKxPcfDNEk9Tgdxs+DS11phA5pr99oSOSJ0uSG2RMTl+jzbOjg1XQBqIkat0epwJSO8YXrVv1foLm9sryVNri0XFyBF1b46B3HNJL/UZ69fCBqw91RdLpEQX7N8TbD/peW9gPL+Gs+15dd4/muFgkvjii12pa8jMSnA2XtChA7QOSnnvnrDmLp2o+yPOX+hp6/fX0M2G4MKuWyutqWFK6nrs1TAH8tiwmQBosbk9GS+TIQsglyyhnoRQRIjoSv+SE0v4c6ttCMo6t5EndVxB75lc+ntY5PrbxoWqBSGxsIk22e49avtG/1etFqH7N9Tq6WgtQtBwXUKpKRMikhjwjANumf1a36vw9Vqd4IUOr1VoNbg0sWPZ4Hkgnw4Yjk8Yn74AuIMksUAfOA4H3E4HvB4yDgcC+ZcsGR7LwXHhy9Y5iNwvAd4wUAZkQSTEMTi6wKoyZS9jmtiy3WYjaDaHceWO8MB2hr+xtsBXXu40hl74UOV6ADUMEQpJct70BLqNjKijW/ALMSlhYPKlsC6EhEgVSRZw1bNxxkQwW7Q3/R7RlkyKAbE3QARVXKzNA8asXv6+uHz6xwo2LwZ1pbuWyLMzw8htITK8OdVMiJQUwha2DhX9juhtRtXmt9c+yN4CKag8Y1zmUFMNS+JKp1qVUgSISEZGcAoLFgyVyKC2Swm9QDMy4JlyfhynyBccDj+jHnHCCkghQCBhm+K0eS6aQcpYtfNOMxHHJdZ27A2C9XkzQCZN5VD5BaqKhFSIgxGROzGocq3RQi5aD6LebaQAP4KmqTbFe22mFL93xW1GooNug74+sGbNbPvf/VCYACx9YvN6woUieWMcMvZLrSYggV2x27dIGmJzmMISCHWNaPlQ2ljxOulZHBbl1yadWXH2zUSMMQIt4g9yIK8ZDx+/owihJvdDe5u7xDHCRRrVGtIbcK1jPzektdzBi6Xjnvv8p4y5Xtc62vKnd9Knv02IPNab7umPpe+fwkB8pLjf2/l2vp/y+dbkz9nDDyuvU73/8vvrXKFQyytRlLfCLRK3grRPGBTVEB0SAETlHxIhjXfEGEBMA0Rj4HwAYRjYTwW80hkRhbg1xnILDgGIBuhwABqnjXAZOKIQECIoph1BIJkBCGNitMgovYE9bugCbI3jUYwQyKXO6ibV9Jao7ZF18wr3qLWU38gD/kaNeSriCAOI9I0KRHx8RM+3tzhw/4G+3HENAwYLLSVhkF1Gcsv2tflOl1yi9m041RnEqhXShFBKcBcBPez4NeF8Z+PGZ+XGf/1eARngWQLH0kBJQAFAV9YcM/AQwg4hIAlBjABKQSMBAS28EqWX4womGumvqvxhH0moEsoBsCMx2pn+gzx3A4wIqGbry7cu94ngiYXmbeEhSclab+TdAZIlYjQeiv2ZyF9ywJZZkjxUE0zYF4SNYM3N6+IKta63ljHSpNbiFq4URYnIgKG3Yi7u1t8+vQJP/30I3748BEf9ze4mSYdLylhTDpeQvCQuPbcHTR4zX56ze9vwgmevrgdJOvP/nMd9y18PiAIoTOMMtlPfCxUOREQckPysHoGlylrHa94vpe2wfnjt239PLb3FEnx1Pfb/a59vnirq+//1O9bfXD9fTdXcX5sbOt7jdz20r653iOim7kV/EGnnHYVeKuAea7hegWtJyLOKWstIXX7O9A6DNOlBHz9fV9MRpwd1KfX2HZoMyZzQMV/d3f87QCg7vU1yhODyB7p/JN927Lto7ePvd/DU10uvycywst71OklrO7XJN56QvK5zb4/3oHDc54Q2+t8DaXq3Dx4qjz5bJuvL5JwT4ozBA2TdHptEUERNXvmZVaiQlSojjEhxgExDTWkk8ZFXapCIaIkgcaFB3IWzRGUGcRAiAlkylhMqa6hOS92/y42vO8pnUupg13MbJ4a0ZIhe+gaVGG1wqzM69BOYgQ6Sw1X0qHbtS08jArg4XEs3r2FpkpDQkyD5g6ojdlZ2JzpAgcZa7oJj41vAiEMfJclg5cj8vERZT6q0C4ZQTIEGsIpLzOOxyOKmWlxySg5qwdiF8aFhgHggIAAoGCxRHMhQkdBKLXvfAw9N4/FwFQP83XSvtTcepkBUECNAEuENAwql9jzN7LQiMKUVDlZuMoGMSakNKjMEIIC7Xa+gvlqzAAoKK05YCJKXqrHQykFuahytkCJiVwskZ7IyVjxweFkixJ5WD2rWw8pqal7VJV5dGLUHBkVcO6FTLRwPvOyIISAcRh0tJvy3nuMMGv4o1hze6hcQt1ngYLxYLXEVPIn2n0VSObCKNC4xiHY3AwBISSAGAtrOKbPD0fcHxY8zsXCQgElq6XccV6wLAvuHx5RSsGvX74gxQi6vYGkAOtGTbgM1rA/hyP+/suv+Pvn3/DlcMDBkms7oViBBDHiyRRwtdwviCGp8p4CpkTYjwN204g5a7sIEQqgoaSOCw6HI1IMmPaTKlSlgEHgVDQpX2hevGwAClFB4IDoRJTjTKy5daQzrulDwVWyyGlOkQ6zoZbzJncAgc2n/lr6kxFZFMDU9jOPhd3nXHN5W/eOJo8XS9LNXKoyr+CBJvUWgSafJ0Lkghhtv8wZJIyyzJgf7rEcHrAcH4EQtX9JLTnZFjWyd8c2fEz+M5XfK6D8e5Q7v29Z615OwH3Nu/0+R8Y/c3lawv3qpRtQvTGLR8LRgDWkwLV9DoGQImEIwECMiQg7AsYIpKDeERkARLAHsBsIOUYc2IiIUrCIYEfqHXEIhKUAkwCZgEMhzTfB6mWnBp2CwEEJ+Apgq0et0RfoiXmXT8W+r8mIxa3gZY3M2b5Y5wB1aNMKiCIzeIESGR5iCi7Tn87ZOCQM44j97R43t3vcjCP2w4AxJowhYjSviBhDk4W27E+9/pXdemYdVblA5UztUELOwDEL/r4U/Pcx4/93P+N+yfj7g8oGnNXboYAhNEMguMeIR2EcIrAEBoYEiqqHJRAmBAQSzND7VU+IGGxfjS4MouVNszwQQpWQaESDezaz6VaoOga5C2qV+btjOyKC3SOCq8lYvYbqih5qUr3nJZsOsmRQzqCSOw8IJx/8pcZw7g2xAl2pzasANcaJFFt/EFDAiDFh2k349PED/sfPP+MvP/yAnz58xMebPfbDYLkhNHRniqF6H9Vx7sPO1cAVhnd2hDw3grr3l69Qsnk/uazLV5eqYZ6+/RR1GVJCIxQ8F5x0fVmJRjip2WTK/lWPx2XQ+31IiO33/Owxl+bvS+55vly3hryGtL8kv1Xd4Z3La+TYF4RmOgWvuqXj2SJ1Ivrn8wPtUoOJ9KGY8gkB0dezv9ZTJETvGuRPtL7GlcD0C/DrE1apJyNo+/s2bhqdWcguTNQn6/tcj20WuRNW9Olzv6XO8hQI+zrlqXXmJRD2qbo8V76HQvfcor497rnykme49t4vLU9d7zlLq2stEi5dp38mjzffv3pC47n7vLbNz9XpJf375LHPjfNOETh3JMGDnGzqbNfmrO6yOXuiY7WiCDEqCB8TSIq54Op6H0nDFTUhRQWbli+ggAojkVr0RgOd3folG7BJSN3qLisAmLxdRAVnIbVk9zB+zHZmoBp7vgFyLZxKbT8L72QN3l5+9yqgCWDkRjQCJQ6p5ocgt0zqgHwHHvu+daJELYlQiYiVQKim7OB5Bi8zyvEIXo6gskDhVUtMzQU5KwhsuDq4ZA27Y94ARBbjPg5KzAgACciz5kJIrlyEcjJOnpsjTp6wEVIOeram1HNDSKBQ9dW6emviZwVDiR1kp0YUpghhQigMCg70R6Sk+SwohOolszZyIBANRhxpqJrFZJKcSw31BWFk1jFc8qLXYtb8BNyIHOmk/jqGgJpPxe/dcgS0vZnN04QICFFDPdXQOQT0jug+Tue8IKWEiUYbimpZX5grAKzXNpDaAd8KUlucZ4Eqid7mRBjr+aG7RktuHY3kQYwABRQWHDPj4bDg8ZhxyIIhClKEgvmlVI+IBzogl4zP9w8YhxG7cQKFpPpyEBsbhMOc8XCY8cvnz/j1y2c8zDMWZudrdM21+efWW0RmLRgEgZSA0bwQhHEImMaE/ZTwcIyYM0NAKAIcl4LDMeN4mNU1PxdIZHBhEOl7AK/mpVhfEBMCFzCntmbYvO5l296F3cegjgclBMpGVJNuzqAbO3o9ywMhlqel9u16TlbLT2A1/vV8qviCk1tO2Hlb6nGo/Z6zGgSVIdcQczEofMM5g/kRy/GAPB8Rpx2ASe/vMjq34NWu4CO8PUPZSyy73tO4yq/7VuLhvZT0a8rXkuOeupeX97rnWy1J9Rrr95Mf3qGcjJV3u/Lvszwn2/6rFQe2xYFM2NZgy7V/ySBkQKPp27o9xIghAmNgTBSwC4QpAkPQRNYZAgnADsAehMKEo+h+dgiERRiRCmYmPAhhJkIowGJEBzMh274Zg4quMQiYGBIIhTyiv8Dj/bdkxY2McHKigc9GVkinVKyGQd8q/Y9i4CgUXBb1vuz3NJdd+g1DDVkShmHAbrfDfr+rIZnGEDHGiCEkzQ9hObPqTbC2cq/cxJVrwDm9shIRBUAWlEw4ZvWG+Ptc8P88LniYC3591L2VWfvqAIH6uTAeAnAgwRKBEhljECSKiCFp2C6oeVghBllOLAkBiKRtKCY9R5wSEcyWqLr39kT7XAVwMb2nChl2XT59h2i+i17+8R6W5hXNXEBcAPM65VLAOSNYjkEP0YScLT+EERFi55lHhV676zjTvQKikhEhVJ1QySH14tzv9/hwd4effvhkCc3vcLvba06IIRlhpcZvNVqoj9MqeHaiFvlfLxsv6+/qxU/G0tPFZ9x2P1/PrqfqplFq1qA9BUKQzvjSZ6mPiXp3r+/aK2JlAEodtVd/v/Lx6mnXtcf5416G+z133POGoX7cy6//2rpd9MY4/eIEs/8a5dXJqrvocZtyZsT0Y1sI2Lrk+c8XBBInINTCqoE+/YV7JSqEAIO2jITwLPbXekQ8PxnfUlYkhClcq++3x32l8tSwevmdvz3A7uV7WGydm5Tvoej8Wb5PeYoA3R5XPSGGVMMxbb0g/Pxz97lECPg4/tqEVj9f6r1WQmM7bvtqP9aa2P9KPwQiMEpVAGBhW0TQkjkXda0tBoqFGEFDAlICgsURF9FQJ9VjwEGuAs4LYoqIpCnvRFjB3lyAoOE/HCRnE4zLkgEB0pAcpa3VJ38e33BNWaLN/qKAXgf4SrMUXluwq21+4QJhbROIIKQEDzWooKR4Z4JiVOIhak6IEIOSHVCh7bnebv3JtT+1DU2gd1fhhSGloBxnyDIjL0ZI5CMIBSxz1QUjgGlIKIWxBFZrOwkIHMAASgwQFkQyXwSeIZwx3xOEM7KQeqkUXm0PWwOABil6J0glkAoX5GVZg+owS3YiS5ZMJ3H1Pe9BFE00J4BZ7Pt47MZ0BWxp5VHgYXDI5I9kMYZb2DW1wlvygrws1VMkhAgpwOFwDy4aggbmcQABllk9JNSS3AkJgQhVzLW3JBIRhGqN3iclFvRGFf6csGclcR8RDdnUe5i0udwA7zrGO8lA4BAAQYRQWJVmIk3c7KRXCAGDqEISKakiacrjssxgHhBDQT/xmIElMx6OM45Zw0A4xFJMMWcuECiBwsz4+6+/qScGAm52e+xvCmJKuF8U+P/7//rf+O3zZ/zff/9v3B8OWAz8jzEYgSA2PaQphyZLJgKGSBiDIBJjigm7IWA/RuxHDUMBI18KCPPCOMSMh4cHpCCYljsdP1wAdo8pqVafTbE2Qo0DkoX3E7S9wT2l+pw12z3DFWpinSsxEIowlmXGMs84Hg4gqPeBBG75T2xNZBYNjSHmuZIz2Nbs6CGUxOM9S52LSsO4J5ISHsvxoPPDErc33lRzqyjs4Gud9kWwWMrzPGPJj3j88gWP918QdzdIE4O6RO2A7y9oa7TLzH/KW3+Wb1DO2cdvyXT3jDgrw20Iwz/Ln+W5ckJH6SYBEFAEyEI4MjCLeixwCCA2AxkCKBGi5TlKgSyULGMwDIagRHayPXwkDQ0UiLAw4Z6BmYCxKCExZsXJF9s3A2DXYRTSPXtBQRYlqIMR1RqitYAsXGt9cW+9vlQLdk++DQuZCIgS+ibrE7Z6Gatc5zpMEMDSYaPKUbbHBTK5idTQYIzY7UbsphHTmDQ3RIoYYkIaIlK0/FPBH3g9ja/Vwp41ujG+hhaCLMA8BzzMgv+aoa+FsOSIYw4mJxK+IONXqKENmHGMhDkY3SOChYBYGPtESCFiMDmBmZADYTGvSDb9RJUmaJJmCoBEtHAdrP1DgKU0g8vp2iCdHqnK3ppgEJP9tp4RLvDW/K6tv9RTxnI8FCUZaFkgywLkorkh8qLhmErW/BC8AJx1rHFuuSEETc5CqKoGAdXTV4z8WEpRY7MhYNrv8NNPP+EvP/2Mv/3lL/j500d8mna4G0fshoRp0DGTYjRvCJP6apMaXsAd4E4eHvP7lDfd2vpbc++5vmamhwTEkACQ5v5wysN0G9WjW9grmAHfNo9mIAL/DrC0p4D/a8nz93qGr98W31dAuT5HxEY57d9Pj90A6s7+dTjDcyt4s8LypIi6qfVKOJGpyR2rp/O8DfoQIvp47U+TED7I+s/XWTdfU1aC6wUS4qVkxGssla4Zbk9HNj9TOi1xTRJ9nfI1rNnaXJfN909/Plev5xamt46p91yYXnqtc8/wnBXbtVZul9pvq/D5+1NW/i9t4+f6zo9xwC4lA40NnDxnoX7tc/UkxLX1vuaal0r/W/27W3MvHb/+jdD7nhIFCBlg6r/jTJsYIFpElCyOEYhRwSez6Ba/l7ingoCCCrCcM+BWzqac5FJQckYaGFFj9Vg7GPiXNS4qhtZGLZplIyOk26S0L1D3FAXQ1wJnT0TAr+GW4l14lWpd3rWDWBN5KCAyS/2YoiWiI4up6XAwVZLgqW20tbPUOrArb0XDtpScwcuCsmRwzii8aI4IPtqepG7cY0w4xsVC6xCSeAxUQoma8DmZdbPwoAD7sii5URPQSR1bJ2OcAEgHfpO5/ZIpSWaAoAmRQ+03WJs5qbEG9MUA0QDhAIjmjHADhUp0df3Qz2uraLt+t970IdiIguaZyKWRCtKUjXmewXkB56yKe1S35ryYp0SXl6Q1kz6/5yPxogmiuYLULW7/OkdEVbVqzFW9MIu0sD3c7gmsyTSWtdu195HPaUEDp1soqWLnUHdvBi+L5nrJBTAypKktAAshF7GcIwFZIogN2JCCLAXFLPJKUaLh8/0DmAW76QZLERQKiCkjzAtyzvh//v53fP7yGf/48hmHZUG2sTZYIm2WComrwmsmNQSNsT1GjakdSZACYYwaomkcIoLFt2Wo3jxnUTLiOGMcAkpWiz1iruSGr1FNITMPKjKPCCMovC/bJPbX2iOnjhdTdH1sxkAaTqBkLObJRKTeYRBUEsIvzRD48CpFFUIfQ1wKOJYqBvk6U5gNp9Be9GfJy6yEaxgQRAmrSkRUCMn2OJPRg81PzkfMhyPmwyPmwwHFwmj1exLVEaNhu6RvJwdRXlku7ZGX5JfXym3fW6n+s7yxXNt9F2RT101fW743j/EtvRaukV9/96XKkq8/34FS/6j7icoQDCUiFiFkqCeCgDTcTlC50XONhaj5moIIgpB6HBoeEwEkkzuSERxEhMyEmIFZCIiEWQAEjRw0EyrwKBbGp0CQYeAxF0QjIYSdVCiWmNi9JPr3/uWCUPOCa+hO20fRYwwUUDczA9RV9LcesONLKWrobzJ3jAFDipjGhHEcLLdGRArRcompMZDKV9bqHc7hOoPvTl6e0221Sk2fcmMOYQAZkExYFsJhIfy2CH7NwG8Z4BwgHA23D3gU4FcwKGsehEUKSgoKyoNQckAUDdMVERCJkEhJCGJCrhIdXMnRygWytF6hLToCgKRL8WADgnx37uT8noyoebC46+8ml7YXTr4X2NjpDNiCJ6Eu7iFhiarzUkktWnlCcL229G1PZPbQLS+c90XhFvp1HEfc3d3h48cP+PHjJ3y6udUE1cOAcYg1LFO0sEzeVE23cwOKRlK3+fx0eYms8V5r5nP3JNn+7uOGLM9YUB6LfKD0Awi1jv7J9RjXu0JQner0edwQ8XXPJ2f+Wv+++V4235yc1mvfvT715El23BkF66rjni/PnXMRM7pwjbe0+UvKC4iI9ftpeYmURet+9GvbA7PFonOleesJsQX4dBCTAUR9TohYQzH0lszvXl54ycaanicf/KLf2sr/9eWPUs+Xl5eQEP+q5SXg+TWlgmpn2npL2L3FC+US+QdsF2NqMeY7UtM9IrbrSg+KXrr+dy3SP5+sPm8Jiir090J9FcbXz8Usnf6gYLbyrdGEsGinJY0xmxTsTfs94jAC4wiJSa2uTY4JRJY7QS14hYtaw7DHn3VlxMZNICAq+FXMWp0LgxcVzj2/hB8fzNSprPYV0twQRDX8DoCunxsJ4UUBPLdkbqA/AJCB1u4I6En/9HoByRJTqydErGGfGsgmnUjXu/y2bbSKfY7fsdS9k0XAVJq7dBe/VS32jzg+3kPKDM4H3TfTCLViUQUmBuBmGiETYbZkwIelYCmM2aNPIWli3N0d4mixW7lAykOtvbeV95nqNM2/0sFzB8WXwpiXghiBELHax9liAoPUndefnbs2RlCFgyys1pIzgrCGvBWpMoUqpgnD0EJpcSnINg964N9DsAHSkQka014gkJxr3pGq9ABIISqQXWxMduOnz+/gIW1WbQW3nCvVe8HP6y3peUXCtTEiRcNjpTQgJo+9z2a5tBVQqc5V7Q5CJYikCe3k89s8hFpR0L+wm6CoAjqHRZW+oOC3QFBEMBfGwgEFpIpjKeAKX3v/qj3bl8cDlsyg8HdM04Tb+wfEqO265AX/+Z//jYfDAV9yQRa19otwpVMQffkKDmwokJBiwH6KuNu7RwwwDkpC7IaAaVALS02UHiCIOOaCSIL7+wckKlgeHhGJIDcFCAVBPO+EIUpGKhZhkASdiqarE6nVYgBVola9V6TlmTlT+n5jZgX1j0fknKvsW18eYs7mW5WvlxnL8Vj3tWEYEEsxI0UBENVdni1B4eDeCvY8eYEwIyaytV7BsiIFkNCUDIIlK9W1zfPsUCngZcF8PKrlLKFZZQJK6jigYWsi237Uj7pvUd5b1vmz/PFLBZv+LH+WdyoB0L3WI+bYescQ9YYowFIEh8w4FsHMRkhAHQJINB/EIkC0OEIz6TGZIjiot2QIQLD9JUrU/D45YxH1ckhUUEgwkECooAT1jiUoicFQwiGHBQtmRBQEqBdgEDUoYGm7OYkmIC7crN3BrOF1eA1UK7XC9V0bxPIR9PHcXSdxQJvN2CCod6ISBgxhlRPTQIgE3EwDbvcT9jsNvTiNI8Zh0HBM7rVnmBKoM2BA036qp55T5c+QEFsyomFcATkLDkfBYRH85+OC/1oY/z0Lfs0BB9pDIoGS5nNgFswiWKSogRaz5n3goj0jGUUChAkZBYEJu6T61EiMEBizNTXJGRCVjNTiBjQDBATrI5DeK5iy5gOW2QiLHjG0eq0IJveY8BwR3n+eFNvHhxEMZQF5Loi8APkILEf723NEWGJqNi8KVyJtXFQyl/r+Q314Fg0/lcYB427C3Y8/4OeffsTf/u3f8NeffsbPHz/h0+4GH4cJd9OIm92AaRwxDMlyiKDKqb22JibTQUQ99n23+ANvGidGn/pl1Ud0XBNYmvG46m3GBEI0j5plr+9zRQRzqW0G5+9T53NS9CXJ+jmqQKQ3LFjB+Cdn6fBah7I6vdu3GQyX5Fddm0+fe2tUfq1h/EvL1UQEP3GD3iMBONO5BJwX1dagV/tbB6Ar+e4JsSUh+s5zUKe3ENx6QFxLRLwcQHyGRezu3UCYxpSeu1c77Lo6fBXQ89p7d39RBc++bXlKQXyubU7Jhqd/f+33L6nTH71c2+bnPB3872vIiHP9/px1wKV7buvW18OBQk1Qa4REDAaCna5jz3lV+DFvIbbOkWTn2uzkMxoQvT1uW//z7+faDKiEhlnEal0MdLK12ZBL3RPM7TmMI8IwADFBQkBxcA4uD5uQ54nvPGmBg/ReJwe3Qmvfki2maOHaNiYa6rVB6I08iiWoDtaWW+85qsnIZPXyRhBu+1aoz7CxhpTOCj8QQopGQMRqgb+2jjbRllzga2Ku/+98Ud8fnv+CmcHkLtD6I8H7i8Ela/icfERZDkgx6bVCAizMVQzuop4AIyCoMMAarkfDJSnhEsYJxAnIAVIyCj+clfjk7Jgzq3NTWD2kkBMzPfBOlXywi3dyiEgbq3oq1f4VCJBzd3/AwzamlGpVKYRar60HghMRfr6D9wRBRm5zAW0MaKgwA4D7BOkb+aBvD7+f97SH9zl3Ti/wt0K1nhBLiE7uOdHaPnTPSjZHNQRCu85JXNizdbB+EH1WErVsY2j4LCZCEKpAslqgAUUUYCFXTkkUtLaXa5HHnFFYEO/vMc4zllIQQ0C2EFj/+PIZh3nBbJ4L+qxtzAdbKqTKKRqmIZJ6PezGVL0UUlSCIqWAIXqSPlWkhAiZC+bMOM5HzEdCnhfwsEBMIe7Sp3e2UwYoieWnqTq7ei/4vKyh1bYTG21ceR/A2l2YNUSYeefEDXHuIQj6/aeUgmwePS35u5EgcAXF5hoLxBc19PNXx7MCEr5I6fwNPcno52jFzUMJCqJkDcHGYkBGN3qt+1bF9ZH3kjRfIodds2f/s8l17/U8J2P3Ffd6Tr57Tdne88XXfkP7XKuXXHrur9Eez5U3t9cL7vGWa7/+GutQcC8uT+gt15y7OpJ8r65bg4VmAhYWZNZQgWqa0zBdP85gYxR7MZHhy5ozwFMqRKiXIhcdziMJQIIJAJEgk6BAPScCBDEoeJsDY6GCQBkFBcXlFJZKPLDJ3VXuQNvbxOMS9eF8zjeMSzPr6N6GoHV21qjyinAVIsSEfhINszgOCdNooZiGYAmHo3nr9bIN1l54flsbI8Ha/hKWU4/vvu/lNWagZELOhMdc8LAwflsYn5eCLwV4ZEKmAUIqg7ORDkUiWCJAJh8LjAhggAPE+qsUQYHuzSEQoqHyQU1JVM6DtGu4sEW2l7tBAEGJic5RgriAzNsUNl66h9y8+v7173oiAs0CTRgEM5Rh94BQ3Y/Y80BYjghuhBb5S3odsdcFOl0OZihiOoQaDQXENGCcJtx9+IAPHz7i08dP+Hh7h7vdHjfjhH20XCLjYGGZQ13+2xj3z6jP45xMlWe/S3njutZfqR/Pm++qnFlVY++H/mhdJ9DpgCsyop7n4+Xtdd5e4rzXWpNh63FSW2713dlz6++X5fbTc6499rrf23GrT5cxte7YTU1Ovnn+ni/vqFfniPgaxR/AgRz1hJBqIdgGq788/FIjGgKFlTeEK2GX7qXXW6FEX+8B2w0bynZy/z9KuSw8f6+neQ9rtbfK099SGfhnLZeIgr5/33vOnFPuiKiuIU5ADMPQ1hQ6vcY1ivale760vufOf+qaPWC+XeYuEQ8t5ND6+x7grOu2udDWUCMwUiCqpYmkUYXGwhDzcAgpIe33mqQ6DVAFQoUTDwOioX/UukotpACxEENcFASLSdf7cb/DOI51zV8Wjd/PxwVEAWlvFuDRwWwVMFwpKMUsmatHRKyANOCK4FpZcsGpSLZQJerBN8S0IjMqcWEsC1mdh3FEiAGUIkCNGDEVuipf/bfbvnPFz8MxadJkxrIsRkTodpOgIY48HFarmyao5pLVqi6mag2VQsTNbtAcFyGiYEYRD5cESFAFFlAcMo17VSLmAMkzyhzguT68vgKAeJ3vwEki3fMZXNZhgs4B8Gxj+eR7ZrAQArkq0O4J0jAFjdhATXhdvE4iyMuCx8dHzMvSEi5baKZhGLAsC0S4eVyKQMTCNOWMMQ0QSwDpoqbLM+xJrdHqnizBdj8W3ZrdS6EMhpj7M62O92sB6Dw9dO6y/T2OY0cc6Jh0gnUrB/VKQyUVu8++FsJDlRno7xZ2bCGKxBJ0e7igEAhLLigMZBbkzFgysGSFSwgMiioj+XhwckRIlf7PD48IdMTD4QgiQikZhRkPc8bCDInJdGj1sii5mHdVRAyEOBiwXgrGmLAfRtzuR3y8GzEvGuZpNyTsxoRpiBiHCCIBi6I0RBGFMzILDocZDyR4uP8CgmD+9BGIASOzEpre953M5/NcLehQE9XXsWv9v0o273NHdO1c9fc8Y5kXzPOMvGTEEDCkAdM01b0LQA3ttVo7iiZU19ACbaz5vR0gGIZhNV59ctY5FKmSHT4GiYKO49QpdQRQTEjjhED34Jy17f7+d0w//AiME8ZJveSGEBTocYtCce+nquK/qfwxZe8/y7csvi99r3IKU/xZ/tmLpe/RImatLSpsCZS4zyyYmTGLaNJqUS+IaJsNF8vpAAEH1OOyAAz1W1MfNguPYrIwkSCQIAojCSNBwyaph6GAIyMSkEjJjpzMczVkSOAKylMIyERgCnqeUgjVCt1J7EpkV+MMz6skSmSLIbgdqX8KlsHtH9bsNWtWIwXT9bgUNMHwfjfiZj9hvxuwm0YMgwLLnl/MjSGcCFr1j93kWl+oSwZvamgDHOeIQxb853HB55nxPw8ZvxTBfQEOEiApoQQNi1UKkDNruCwJFo7LcmSUDLDpppJAQUmILEAJrOSDybrJCBZPxM3Vi8HaysB7zQPSQGUyIgNBRw9QTOaTRopsn3/VV9JIopL1PkVQ41PZGBAwIBZuiRfNAZH1RXmGlGyhv0p9VVJClJBAJcAAkHvmq6zq47/v2hgTbu7u8OGHT/j3//gP/PzjD/gfP/8FP97c4Xbc4XaYcJNGjDUvpGtpTXcRmHxWZXSq4z7avZvP87ct77GXbDGZc7/VXHO8Ps4NecjYENeHJTTdDlB5eHVtG4qvLhXycJLtmpPeSzZ8zuB0/XBfE0O8hJGKdGNje3vqj3saY31t3a8PzXSORaF+1V/Vtj9o++vFa7ulbh/PuFmdbte3ZmXr9XBiwl/nSIg1UOg1e67xLoNATx1GoFppH2r1kA2getEq5sKdL42V/vneezhfHoA2y99hgL5FMbz23Et1WbO215//VkC5L18TvP4W13qrYt/m8un127UbmENP3Lt+ro95+ryX2qBaq/chmTxmqK0tDga1NWoNTl+q00va/amx+tL+e4qI2F5zLQSsn7PTj6pCgW7NrtenABJBoKDycowGyAWABCGSEhBDUuDbJWQLHURmsRNCZ+HuQiqLJXNtSXsDNMRRHFL1ivD4/ZIzKCggSiEgSH2sZp8hblG+9aCj7nlRQQkyy4kKCMPbwMIghZY0WS2KvWma0BVCqJ4Q5AQ12l7ohVxepvVe4BbyNR+FOz6wKzlFFQxFZQ1EpTq+ewDZFQSxvgRp+5JbikXLy0DeF13FvJ1IcyEQCbgmG29W6d7O5MNQxJTQdUgzsTBfuCD49HNbgFV7wuvXwUdNwtjMUxtzSj7pvC5FrbRKKViMhHBPg61xg8olpswRAG5A8hA0hM/iO7+4FVzzbPC6rYHm9Vx0V2V9oi6gEPWeId0zgXAyl0UAS8bt47aXRdZykilPcmpU0K/DNZxU6OaI+AO1vvH7exs6ScEw3dnao4VwaPO/6/D6mQXIWb1OFOzWdxbBwmYBal5XIZDGhZaMSjxFQogBggJm9XrwWNHTmOCxhVOysGkhIIbWh7UtoIDQkjPmRXOCDMOgHgmrMKJdP/dj138hWw96wlN8fWveLD1Zt1XMPHG0e9uEzsOn5i+yee5rUK2Xz3c5VTLZiDsPt9SvXT5ONSdItwTQOgdLP9bRHaPJ4xXNmo8zwsMDHh8eMD48ABQxUEA0YKhvh20fvLZcnD8v3KO31wTeV7b6Hvf4FuUp2es1573kuBe3na9nPoyfrOLL4J5LOkDr564O6HS9doF1Pd+xPE/ANFl8feKm0m8oF3XjbzH+X3uLM0PgxeO9P7yTFRQjsdCS/oJ5OwAQ8TxYtleyQISUhICSEB4gxUFlQoWf6/ck+grCFoxQgxJKULp6JEIxDJyCAIExkOWaIFRCopDqc0EcgLUcURCc7G82yc6gSqvmcJ9OGIZDZCQHqYxU24wYEH8y84q0/A/DEDEMCUNKGo7JI2jYXrmSxXtRZFsx+yxQXad25yaefpXhpY0Fl9Vz0ZxTnwvjt1LwSy74XICZA7JQzZ2XoyYUX4KGvoSTLJ4nQy8IUFFwH56TyrxdGHAvZ5VbVc6yDCNVtly3epO1HdNSXxqxUWMe7hby1ND+tjScDHsxox1bUGtycqmeoNW3RxrJQNUzonTkQ3eNs9c5QyLX7nWJUuzpVS6cdjvsb27w8eMHfLj7gLubW9xMO4wxYYgJQ4hINdJK7VAo1YY2Ln1seufDZWf9+7n14DXr27N75xvX4yqbd3uUuG5i9a2/+cKyGu+WW8aq4UY1vb7SX7sZvHgfndZo9elkzb34IBc+v6PM8KI6ve2+Vz/3hevVuS/bmtDqYkRPXVtWby8pb/aIeBZ4FI/xxdudBOgGlsDjWatFqYdl6PQluPIdah6IRjgQBYTYhU2xZJZaBbcWxLYCVxS/uXcVnfxS67a9rm0QYoueUAN+1nU4t+2er8Wlo34XKsl3VIzey7LtD67b/aFKIx1azH77pTvINiQDT8RXy4poWCzRJv1tQDn/tvujA0XE1qEQfU2xNcZihKZuTXGgWMiDjaw34/79+ue/dqM5JQkqMOPPSW0VcrVlFV+8U47OkTfnyA0CahiTnoiocpaeCBjwXROLAQpQhgCkUW8cI1AKMitAHZLm2EiUNAnWcYYLdcTc+pUGECVAJkDUKpnzAj4S6LggLRlhmEApgseEPEZVtUoBjkfgOCMXJSJKmUFBEIZJQdAKMgetagJiGtRaNyWN0VuFWR13DvrHqHsQs1rmLMcj5lnj/wOAjCNA5rYtgoVNdDdCaxzt+aMnYe5ELRvnLqsTAZFgAq8lLTTlTmDJfJmrRX8RTQbO9opQy+IQVUPMYBQS8JCAcYe0/xGZHoHZvAKOCygUhKChXgppSBxmwW/3RzweZxxYlaI47pHSgHHcaU6NqGLFwiMYj5DwnwA3z0YSI4MoWn+q8sAQEAvAABVBLEAUUxCNdOSi+UEIsO9tf3Vl2hpwKRmAgFLzStGR7ckcsdmLNURPChHz8YgvX+5xeHjEMi8YxxE3uxt8/PABN7e3EJGanLoSB3YN1fM08XiMA7jo9ZmBxUgelUsEXKLWOwQsRTA/HGxt0nGVUtJkeDFgWTK4ZG2HlDRMloPBNZaqqlbBnlet6jX5L8Woyc9ZAe/WdnSyXjU9XMdYMY8CWB8EA81DipZXYwAIeHh4hAhjZCU7yJKZLxIQmDRPfBBQJGQWPBTGfRZ8yYxcIgZEHeOBLR9My6PioEoBg0gAC+uzmKWkx9IOvm7AcQgCEBCGsXlERMLoeWKiYDcQbibg41DwQ1hwHAvmAfh4k3C7m5BiAjhgQMAYCEFmVYJJIET4XAJ4Jnz6cgAz4ePne0gR7G9ugFIQo4EERgIFQD0lhBFFEAFIjMAwAcMIpKQrTtF8JhGurPtAI9drNbScMObjEfM8V2JgGieM46hrd9Dwd41gVEWfAjAMATININlhNKtQCtDY3kaoEVFNxhDqGgTdewMQd3ptsnxJmQsoBPNMs3xAgSqpE4Lu24KipNA04PjlMw6fPyOJYP7l7/jp//i/cPPDj8CHDwjDaLle1LuFpAFDT6TP6Mbz+f34KeOJp/bwl1iE9ce+n4x6RpF8p2v/WVrpyTYn5ZSIi/X3SlrV9XetrD+tuL+hXARSvv6tvDw54k4E73+tUkE4vALAIvVQBVT+0X0sgguhlFBDGS6IOErEAcC9CAoNyDQApHvGIwUsHbldWMdqsD2oyhomzRcU3WYywMUyMxCQpaBI0RxdElQmg2AAwBSQg8qzEgPGwNiFBYIZIjMiiXlMJiAIjssjshTMrB64xeSnAlKaI+he59b5giaLMAQFpQL6da7Z82lo0AQO6hSghRFQlGQRzQW2u9nj9sMtPv70Iz7+9CP2ux12w4CBGAMVTMOoRghVLteabE01gJZCwQF4Mb2wgdzWzl5PUtmTWZPyLpKwSMED3+O3UvC/Hgt+OQL/8zHhKIRHCWAC9hE4EuMYCnICHhBROAJlDwoPmkMvFpV8Kih/D0HUsE4S8ZkGhBCBNAAUUCiCyYyPWBcq9+pVdaeFUlIMjU3CrXGUoBLICKW4CkBsVj36G1jU8Eys9diu7ddRBbPppjWclpIQVBbNE2GeECj96wjwDCpKUpDloVAiTo3dpA4gDb9JRIjuka5uxSjmURLGEbvbO/z1r/8DP//4E/7fP/8VH29u8ddxjw/TDp92E3bjiGFKSKOSWSDzVupGBRFUn5VettZjVwnCL5RzBo2/l1K1YFdK6w/rJ2q5IjTUaeZse6fr2i7Aoeq0QAu51gzLUKNaobbztriH7yU81XvnAgB/DYhfybGXldaX2358z42xf87+PtffQ7q/ZPMDdStfe5wL15bTJ72mvHtopoub7sn3mwaTFhPa39dAWz+4zKmKooGHGj4jBLdWbBZgzqadvWdlJtsC8tRxq0Vh09o9KLk6yD9X7f7SZDk9fzus+u+9Pb/fQtVq93taKr+G29AfvbyPl8L7nHMO9EIHhp0HBYKBrz5fu3Nc0IArjusQMD09eNL7ggpi9nll1PLZPCEMXAmxJSz2a59/nvXnS8TEayww/Zg+yW0lVnrpvDt+dR9Z//bcffqVabs59Yh5dcvtX/pgXdJRAUWochODCmkxalJoKNHEpfgDdes2VcVfZewMeAK84nFBPecDQQKBQwCzkhliFjQKwKEjFbZtpJqE7iEWjsnAaz+D0KrnG65+pwCfhkPKEO7GgfctEaoY5ftVbBZYDQ9/YoO3+rtiVC2ubAysLJBXTypNOTKliSEaGiYEICaEYYeQC4ABkAUsGW63VoRQhLBkRi4F8/GIZV5QBApkQ9RVPyXEOIDCoPJlYEgoAFnIKenGl+3tsmphqUIusbR+7ZvBY9cHB9H92Vxh9XvwyRzzlsB2PlawyD1XNCyTe/fEmDCOI4ZBgdp5nldhc3RN8nuJelIhgCSAxC0T68Pb2tUlJIeGmMo51zUomOLkRhdAC6+kSaL1XHELsPYoAKmlmyq8bNfU+zRiy7yP6vU3TdKtySy+lmLVdu5V42uj+JzUDM2gECFCYOmtBFFJhYWlxrhmgbYZMShsPTx8OWgjOliHM+oDWZ2aMuOjx5/fCZpEZCF/BAEBu4EwJWAMgpEYSKpeT0PEMKj7vdjzBhgYbkqJgLAwYWbCvGQsy4JlXpCGBbws6mlSsoVOcLf02I3rjki3dceTOHtn+brTLM9Q57K3TdmE+oqWd8ZlUDKvmr6tQtD1OaUIGVINA6Zi8zqEUy+6NvnTFPqo9Q0WQkwsFJkn+7SZZWPKrydtrsSI+XjAcjzi8bdfkQJh+elnlNsblHIDJJ3jAsvxAWjoDrvy1xDrLu3br/WWeIuXxXtde2t08NwxfflXk519P3B5U2yvcovOi2Ujx+p13t52qz1Q1t9tP3+r0oneZ8pKEP0GtXnf8p5tea3BUZ174sYmKtOThWTyrU4EzZsQhAJCRtB3iigECAoKUQ1lyAb4CwMD1KMh2qrK9u45htn245Zrwgk43dojAqKodwRASKReDyEQEgERjAhGkKIkB5nHqNTsDRCTZ4KY8QYs5B583wYqeI9GnDDRag46USAwAwmKGuYloO5RarPfZPhhSBinEdNuh91uwpASYogajopEQzcGqnJ504MMyuz2QZfJqwWM/+D92REq/TqgkrUGmi0CzLLgyMUMMwI+Z8IihIWUnInVAEPAouC5ylXBcDDz0A9oXgHQEEUipISPG4hoMi4gNg/JUy2v1zMs1fg2x4P/L+YVsQJqN9pjTfi1bqN16ZQr927gdQLqPgSThmHKKo9ZGFCIdLegpqSZAFN1BWleEEJmODSOGHYTbm/vcHd7i4+7G3yYdriJCbuo4bxSiohDMMPFS49i85ZoPRYuPfYT5aWkxNX79GsXOOneunutRk4nOzWvBpsnYmMP7buar81FyqY6q2xzZvNr7Smr79s47k/S7849snGEFz+35+ue9RnZafv7+cPfZ4dZX3v1JFjP6afHxeVx85zMKCdHvma7fwMRsYUInp4E/RwS06xYuMazZmbziBAUS07tJa4sUNrg7sOmkIW46BXoS/Vs37/kc/f96qfQltwzAMe577eg6++N9fyz/FleU14zjrdC5aXr9d4Gq03OQBvfGFdgJ3wD6YQiC5/pIXPc6sU9Hmq86259eW6eXlr31u6Ip+e+RLnfekN0v6zucdZrwuq+FR6eu/456861gm3HVWEPFZgCoCSOxZC3C1ibJwWrrL45q9V2yVkBLOpuQN7uJgoYscEiWEpBYU1yC/Kk1rpHLPMCWQrynFEyI6ak+SgsVImDyDEOEAEWngFg1d9SLLZ8jIgpaU4KLnVsQPSYZV6w5KVayTsAt0107YmCvQ4pDepVEZrr+HnBou+b0z1XAFXiiFoSXPPa8OTXkVINqcRiJAQRYhqAIYOHEcgZcZzAJahHtDBK0VjEWTTnRDFrohACpjgAIWLa3SAOE4ZxUit4SmAAQy4oYJT9z5B8BNLRwOqlApGAWdOZasZZAdWCgiwzCueOLEJLpGvPloYBoctx4GNKCjfgyEISqQpMJ+hJlUEMzCWimmdkt9th2u0wjhMCEebDEV/uv+A4zy1GrNfN4t3udnuQMPjxs8X/nQFhTKNaosU4IJAqbaWUSmyUUhoROiXEYQCI1NvFFSz7b5nN48OeZ7CQUSyGJHTr17ZoguJFyY4Ae45YiTQPP1VHISlx0gRNqfKaz5l+LOZioMUYzAotgUS9FQSijkoL48v9EYfjglJUyR+ie6LF1qYWckhnA2GIHmrIcsBkTT4eQ9e/gCnnqCD8mBIgAuKCGIAxAdMw4mbcI0bCEAi7UUMxUdS8NLvdhGmazOtAqkcFujXQvfSYBXnJmOcZ9/f3EAgOhw8YRBDGAUECEDMoJlAyjxJrt5pAPRBiUtKLSlZlvBvzxNycIoL9Yfk3ssnQvo85cdaHZvK1yPOceMlpQB7m+ntmnQvK0gckIzXqer0sEKDmn/G5NwyDgkUl2zqlAEWvoLXcF7YvhYA4JBRhHI9HHB4eEFPC/HhAOc7QpN+2LsM9QWzPEAGF51WYp/WSC8n7znz/UjJhux9fKx+9VI66FqzYygh/lpeVisFtSjV6O3/WV63TH6M8N57/bKNVIYDMqxSk23khzfOliaY1V4MEQaCCSIIxABwIKQCDrfUc1OtMbdWl7s9s4HyGIAgsR4RYaL+C43JEKQWH42yygluxu/GE5vxiLhXLCRCMgHrZojeBMfMbi/+fUSDESMTgwEDUfBRwhz9WuZCiA9cOZKuBgoadDKg4TDfvUlRCoZCArV4AEBHVICRGUEz44cMdPn78iJ8+fsKPHz7iwzjhdhhMtkirnKMqQ7xgzbd9r/pR0HrRqLX1xaRkcC44ZMF9Fvw6F/xjZvx9ARZElKi6QSiChYBCmpctWshJgXnYxmRtxQBKNXoAzBhFCKBFDbdEoG6Pap/PYnibJ452j4dKPNg5br3emFn9DMaapED7feU9Yd6Y/bEeXqknHDoSopINff4HLi03RMkqSxipdXalqcm2qer+AKkxU9BIKuM04ae//AU/fvoB//G3f8ePHz7gw4db3E073N3ucTNN2O8nJSJiXPFOf6TyrVfaNo+UeCg+/oBmZCWaVB3CiKzzvEamMN24lKe8ES5hvNtj/hn3GdejgfPt8JWeu78kta9esFSuytVExNssZbqG6iqtAINuaD3AUBc6snPQg2C0GtwVPOxAw1VdCXVTOPNUz3w+85vXyd63nhAnJMiGGbxEQpySGE15W399CkQ99ftbytbq+9Lnc+Wl9XgKhH7JeW8rnWVyV661ZPlXVfC2hMF7X6snIbbHtk2uAdf9Iim0nv1+jeoBEbukxN38dFD7uXJtn19LRry4/fpnPWHiz5AXtZ3o7DEnz9N/trYUA7L7+4v/vuk/j7cqaLHuKQQPIFvv6QA5Qeo1+7/rZ/j1zINOur2lq3MpDmor2e2grAs/9awOvAZMSCUHVZtg7dZpfT+KgcLFwDUP2UT1ul1/irqF65hzbwiqgGo/cLeEQyViToiITuhfd1r9zffMUOvMVSHVpjSLqmqNHTXWq0RTBNkUT7LcHowQImIEKA1ATBjSaKRKAsUIpggSTYIMSZBhDwkJoKSWTDhAVWONWNwWXd1XNYGvq7Nrr54+ka+I6Py1GPKVhPBXb61RwaI1MK9jwTwxPbwYUBPTp+TeEIPmjMiaEPh4PGKaJgCxhasxJTpFVXzZxownbabVc3YeB53cU0PhyHpf2YJgfk5ds1Kq82w9Htp4EZtPItZ+Qb1JtR0CgFKJtH6vX81ptDXC26vW2e/DCqprCCeTz2yuKODAKIUxLwU5c61uCJrMr60ZYli8mGWlhuNyQg8AStF2iyaDi6hMpl4aek6oRARDiiXaDMCQAnbTaJaQaKRgjAjJ8ysEoFAXJmq9n9R+sX7WBPEZy5KRl4yQkpEIli/F14fuAt6/PfkNbuvN6jigEVK+TtnY8/FQw5NuiHQf13U+1MGk3kdV9vZE5w6rdKSJj1GW1vd1bbX1XXj1hOtx3M3nOrZs3jIr8VssDBkXRad87rhXBeo4flpiv0Zuu5aEeGnZXuPaa77l3s+de85Q4b3u/ZLynIxzteX4Ny+90n/F0d9IH7ikf6z3j9fWhXo1/HXnXzi31em6i//R9atrxz11GIPKaUYgkHmyApafznIeWF4GDqq3RFLvADVAdy86MRxZ80l4SwZojgmXY5kZR5Ov5mJ5h4rXK8DDNWkNpW6AZNcKorkkor3X/EAeltL8AILVLBDAJBoulcVs6ukE6LVgpLpG+TrlIp3tyamGnFSixnfqIE7MqLHqNI7YTRpmZzeMGGNUD8kVAbHBcWotameu+lX37/7Yru5UfTO7K0q14IeoMVVmYGbBkYFHESzQfZZE27MAZvRFtX+JxGTJ0CX5EFSr81pzaV7hRKgJuG2MYEU8PPXCJr/D5qUDGXWDtru3t/47P68nMnjzHZvsw5vjOsHLXtLdS+X6ri+8v+q7t4MahcSUcHNzg5ubG9zd3OBmv8c4DBg9h0hNTu16W/8s36Zs8bf3vOb15bKM8KzssTmm77Feb6vKaZX3LmMxlfCr/b5Wfzr1+0Xl6XbZgEz1nKd+3xoZvq5cbnu7M63HyGv6anPk6ZOsGhgvb9wz5QUeERvk6YVF0BZHtk3JLUj9vRRuGwxQlXVnwvvwKYGastV7RADvJ7C0zQVYbTC0/uY8qRAqMPAc+fD9BOs/y5/l+5eeUPTP534/f46uD+yJi4vG1ES3aVdLCDRwuHpApLQCWirQ0Z97YX4+pdS/9vhLhMVFkGCz5126R/3eraUvEBHb73qw09dk+7EdT01ArnVXDUnjw7qVN0xBGkdwYQslIhVMNDnZ6llQygIXkP1yACAIZj3F3ji6R1hcfMkFh8MjylHzG4AFQ4pIw6CeEVGBUSEL5QQgmzV6pBpBt7a7kxClFBwtIe2QkiWlZizHGct8VEtgZoRhMAtt1H2OKCCOeu9hUIAzpZ782goqTZFY9/1GwZA1sKeCIjWPCLOgUpndyRslZ1STiRBEsAQwEhAGxJCQxp0lISTMWRAzq5ESC8adoDAQB40BH6cdQhwgKQEUNfasCJgCShmR4wAIY0CB8IJy+A15OeDx/u8oZcYyHwAwiDS/CCNDiAHPz9EJqe49CZglP1suEKAC6CKCZVkAAgZLTk6mrPFGOfH+bUYRXD0hvE2DETSff/sN9w8PeHx8xJIzhpQwpkHXIAB5mTVJNVsOiD5xcATGcYJwwWzyjr/AqjSnlGpfsimmTpll9/wRFQyXJbewSyYL+fwiImujtpZ42B6IgIvKXClF9U5CI+Pcy6E+N1mYgo6cqKCxzd9+jSQQSmaECE02HCPSlCBFkA+MLILDDDwcCr58PuJ40KTTMQrioARBMs8OEUGGjrVk4RPGaUCMwfRQAbIO4zRYiLOka9s4TtpueUGMETe7QdeUJdcQDB92ET99vDEru4zdQIgJGHYj4jhiN+0wDgOO90eUZQHErLi6Wap7iuUCE/VeeXx8BBFweHiAQDDsdmAh0FAQEBCGNp491JmHg4sxYhxHLCXXfC8190spkBArAOO6sM6LXL0TPMRSjL6Orddxl5l7IgEx2v3aIhxiRAzqbRRirHOPs5KunpNiGIYVqUAh1j2pJ1eILFSXhVfrSd+6zjFDckY+zFgeD+B5gQwFiJaQ08Aeio66tLeXlmuMA1YE25X7/Lm9+ty9rjFMuLZcQyJcet7n7v2nfgL4/lzXnU1R8adBjW2t/HY1/Grlz+7/pkVE5S4AEBINuRQ0hE8m9ToANGfYlAg3Qvg4QvMmRUKihESCbAB3yx2m4GyRap8OAJWAmJesnhB5UaOLeda1/lhAgHoskoWM9NBLrC+3Vg+lIOaMmBekvFjuMtHfhUHlCCozSBZE3d0B0jwOQi3Zc11yDLyuBjQemnO1n1lYqJBMntGJGkgl+eLeFtOIMI748dNH/PjjD/gfHz/hx7uP+DBM2KcGOrcQhd0me6E0ucfnusrnHlzLDbbU3kjrJCDLz8WNM+AEkYADMx4E+EUYRwCZFwQBRgOjOEINgkIERdZQhRQhtAOFDIkM5Nw8C8T0imq0RRoqElA9hwhIVklP/Fz0XewzFQP/Pb+DqMFY5QGg1wecJPDG4HZNMU8Ny/2g4aO60EulexfWvBCcgbLoa5mBvGjdOQPSGTG51wl10RUAI85aHzXZTcO6ZlJDxNu7W3z48AH/8W9/w4+fPuHffv4Zd7sdPu7VE+JmP2EaB0xjND2zzdN/tbKOMNF9/4Ts0OMHXDT/W9VdYjNwKcxYSkZENGMj60MRiESgkk588X56z74+W0LxLZ32kmud2zS/zoA5bYvtvV9/35Mzt/cyvP6td3pFaKaXSSW6CKhLlqUQrMpVc9N2bwjnw9vi3gBEfykJ0VthnVjtbYTyc41jNamf1p/7bxv0I129tk2xJhWapvgs+bB9f6Y8x4peUqLeUrb3fA0z+97KzDVKnZffkyXN70mpe86S6rnz3nrOpeNO+xbYrjsurPZEJXjtKSUilWBwi1oH6tT97ykrmNNybtyfG1vnQP2njrn2t239niMRnry2CbbPERf+d79uuWVrjwNJt971okr/twNVgSIQgJJLtYlot/OVWMBsQCcaIFt3BemUkdAEHWEFs0suen2x881rzq9BZHU+KVQrXC1wTQHq9ykxQV2/M3Dc5CRXYBy0EBPKycafK07Pj7lV62G7k62sSC4UrT8MwG7hEFVnIihhHgBL9EdxAJmFeIgBMRI4MEpgtVhjQShAEiAmS0Y7jKCQIClpvFWKYAFSYSOHAkgEKaiCEURJAnqMAAdNVg1WTwz3DvC6Qk6e9eycY7bEh24h3ntadHuiPzYaeORN3F+7JyZ9DOQujJJYf6/Bp+52tS4wrwDNO8MbYqUHbIlQrRZrfaymHnLL54onIQ8CcFBlP5BYTkBX3Lv5WlG0vi3RFtIzbdwL8+fH6Wl/VCVAWtuFQDVvCbOGblqyYMka6ovILDkjkIKGSSrCYFaikKDeCynGGr5J+1iJCxZ9D4EQRdf0aVBSh6Ro6KWkiboD6/UiCYZImFLQ+cABUbNIm9dFrHmCYPIqqsx9wcdWoPlFcq6vtGRwKRqWykknm9Y+TrnKtc2DBLS2IGvtLKhePQ6SdP3V72diIBSIELq967n9rinup/tpW/dk5clT90ZvnU727SpbZX8/2tdIL5wLlnnBfDhqeKZlAeeCENJaRPZ59/sR7Wq5hsi4hjjYlqfktWuu9Zp7vnd5Sx0uPf9T5aXkjB5/eh/p/tffrq7Ci8vpteXs99c82zXHPVWarvu8vnn2fOr06At6xmtk5D9yuUZ3B1yc7EDt+k/l4UDAEIAxBuyihqCkqB4RkQhUGAT1THAvCK73an9nsZxNRcHAowiKMBY2TzsWy8opmjw2qOdDgFrq+/6osmXRvGzMEFEvQDEiQux3DRvUXppzyZ+27T3aWFpxMXN/ttwPYu1Yw6DGgCEEpKC5CkTMuxKERfT5EQPi0DwipmHANCQMIajRxApTardHbfXagWf7sXdCkPpFe4gVSA7TL+p7qHkLWAQL7CWCCIBY9HqhrxjpdypAQTN/kCaKrmOJ67JV5Yf6KPaH60Ue97HKik22qN4bfl5/jV6n3L7qsdKOlc3fImgJtp2o8FBN3UtKO67LX1XrQb105H3kXdb0qJYbQg0axmnCbr/D7c0Nbvc32I0jpnHEGBOGmJCMmAqW3Npl3O+F5bzk3idraNV1rjz+5ICXe0RUGVIablD3pv5copo3Rp9RK7yVVUVaH/T36OtBm+dsP79chujPw6rW1+FFz5XX7HPnzxHINlTFM/e45t4nx/SfKyxxep2XzI93T1Z9tgIEU0JVYd56QqwUmY3y01tUaWw2i7HsnhB1kL5sUeib7RTiWQMWPax2QQXtntvjKKJfBc+/d3X5Pkvan+XP8n2LAsmWhDU0UOri8fafgx2eGDVYvEdXdN1qugfDCB1oba8YPfH9FjTplc5TZfVaC8T3LlvlrcmA50HE7VrMbDbhGyW1J0YvKYztGJwFgCiEGhNVRGo8SBcyvKSQwEI4lKNaS0HbM6YEIlV2eGEUE0yFiztXWAihBCcDYhwQKZl1LYEtRFI+zijHBUkc5IwIMVRLjDSO4FIw2zPHmFbP6UBkpIAlZ8zLQcHFUvT7QC2vQC7VkjzGCPWpIIu5a4n+QsAUCTE1T77WN4zrhkrb55ogZy73WPd5cO+QqltYPiYPg2hWToEikEYMuztQGCCmvAUCQtT5QUVjd3I2osD0AI2nGxHSCIQEGgYgBOSgHitxHLEUxkJqOU2BQZwRqYBCwPC4t360hLNi8WJLi7ff57/rny+Zu3SydlzmuVr+wcZbdDJhpU5S23DJiYQGsvaJ4Ns80vPzspgngYZrijHWcS4ipiOSkVYFy5JRCiMNE1IMGMcRJWccfA4XnYser189u8SIGUIuUt3Ac2YseWkjgQJiCtVCsFhM4MESEC6L5pCIUQH5ZdFzPeZqb8QhECxcLESDto+YJSMRVeV3lT9FLHSPHduAYU1OLeJ5UnQsMQTLUnBcGPePBfePGffHAhZgv4tIKSANhCkljClgXhbkvICDeuvs9xOGYahhm3xsB9E+GMeIGAJSIKQYcXOzAwvj8aEgEGEaTAEKQQEVAW5Hwn6E6upF9yEQEJJ6JWi4MfXuyUuu9+wyUazkzyKCXASHwxFEhIcv9xARTLe3AAhpsuTVNkaFGRwjCqB5MYDq3QKCEXE2Fp2wCJr7wi3GUEo9xtctIsI8zwghIOeinjaEuu54KaVonoesuUF6gKd5VaRVn/scKYWR5wUCwTgmAMoI+flaHw35BrNMzMwgZAWFLLGQe+qIeVr89ssv+O0fv2KhAbe/fAbGHT4x4cMPCXGMdRkkI6Ms1crZvfb3ALxfKu8JZFx7rdfe85I88JpyCTy4dK/+uJc850vqcirP6Tp4npRthOCWhP2a5Xc6jP8sX6EQYGEeAQlUgQgCauijRAX7CPwwDdgl4CYBgRJCGODg7yNlHEtBYuAIaI4BACzqBVxEFHs2zHcpgoUFX0TJiZk1lCFnTTo9EiMSYQyCiIIBBaFkhLyg5BllOWKZD1gODzjOM+ZlRskqd3LJEGHkeQaXxT4XSNbvxeVRy68Qg4dWNIMJk3OiBJsMbDmuouVbS5rvigAS9Xi27RwkGgQ07ScMNzf4eHeLTx/ucLff42acsI8JO7tGSqkZCoUzwPslEgIV+lZ5u+HeFVD1i4j0hnEaSmonhEnUCCNGgKNUWZBZkC1HRmDNuUfRZAMCJEQI6Us3RAJC6bwLurwLEJM/fP0jjenlFZMz72dk8MvFTpDSBpaIuqUIq0eDsHk12DsX9Xpgab+750M56t95Bsps7+4V4fTauk7sfWF94DJPE+013GyYBkw3N/j3v/0HfvzhE/7jr3/Fx9tbfLq5wc004cN+j904YL+bkEwOJ4P3GH/MNVmkxzVfcf4FtPIpEgJoukNm1UtcD1ePXAv7K2z5cIDMweb32tBc92oPxXveM+J0L//+5W1ygo/xa3Du0/nwnjJKT8iS3271xevK9UREHX8dFP/Mjevgsf99UW0xnvmsMLcmIjwmm4cKaAr0OhHj+etcVc4c5o/b3rckhAoIK3DOd51rSIg3KiGXgMZzxzxXvheze8293/L771EJfU+l7r3ueW0d3qOu73Gvs785ELYRFM+RmgC6teNpq/RzpMM5gOOUIFi/X7r2pWPO1cnvu7JOlQb8n1ecz9+zB1xX93xiLV5dp12w1Q22VhoQXO8lXbRO/1tgllIepsOsgyiYsNeD7noMi8eKb8+4IpegoYPEQvxI6TzsqGoEre4+RmAER3vqen8RsbjvywkYIdWCn3Ein4mYK7TUsbkdi+smfN6zYfuz1gGb/m4KD4HMAmVrhd8s7cWka7JEfhSHtpXFAIoBIQgSC0oomgS6qJVcDAlEESEmbb+YLNC/EhFJBEwFQur1UNgt6bTtQ9AkyWRCqDfX6oXLc6G+APTelUpQeQgbav0iJkidGc+tH05LNZYAqgFEtDCQ7IoWpLY8uwLfJQx3ogyVJGp16MdDqI3vY7WNw5rglwgh6jm8qbgAIEH1ngjh3HpgSpW3gSulrtluBKKmgxuZ282bVZ/YeLOj2qXIdVE2QqUgF66xp4ekRMSQAkZ7iWbmBEPH/RCVZPE6sM0HSaqUjEk9ZUcjz6YhgplQkio0gyW/FAnQGNVKWqhnuFILvuSEDVmNbt48pdiIoHquODmZlwzOmpCyt/ITIqALJdaPg7Njs7Zx39ro+n+977nRTwg6bpOFntPD1+Oheh0BF+qyXas2FdusX7r808l48Tas3mMrcEbXlLJo8snHx0fQeI/5OGtybLPWJEIjO6jhLi8p1+63by3fUq5+b5D+a5enSKLnZK1rykvIiF6esrtiNS597sv6vPUculSHJqdc/xinB17TVtvyPfW6P8vlckl37/djEll57HYrMNTLQb0AJ98TCQgIiCaHs0A9CkXDOUkQQDRUUbatmdkt3VHlSBbLV2AvhmbrUlBfjAzQegRbs1kEuTByKVhKsXc12tGQgpoIW6RgnQ+0eRav5hehyQ8u7+ubvkN/D9TAyhQCQtB8GYH9GKkOAwRCShHDOGAcB4zDgBQjUlRPiFijbLhs1PeXdYr3Q98vLguJrxrmPQirc8WCtPJtp7Ua2m9wbWoAAQAASURBVDNa3m5EEGKT+qrM0cQP/YO6tUrIt1OV5WFGDSqQoG2ShC5UkujftT71Qdv3VQ6nzYokJ7pO67xOTqrr5ja3Q5cHYuP5QNLCN0n1jOhJjbK+VlUScFLWfdV0Idh8ScOAcZxwe3uD25sb7Hc77MYJY0oYUrTcEGrgUlP5/U6A7W150R7ZxMWX7ysdi/GSe5LNAYcYmqzIEAn1siudtuu7LfbRvr9U95fhTM9hZG+Rm16zd69/f1rveO6a54w/tsdd83xbcmejUq6nIr2szV6WI0I1gO7OgIaceLrTdePJyLmgFLW+0nwQXeVpnQNCCQe14EppWIViSlHBixWYg8sb/NcpnYJGjQUPdeNp738KhH+Wf+VCm3lwaT5cAmqfKq4k1muHUIU0Zd11Gq7Xlueu//wi/VarwC0A9ZprMLuF+jpMRl/nE9D7TIzVS+1xkYSocmonnAMtyays61PD3FiYEyoag7YsWUmKpIIIWSLaIWmy4zzPKBCgACVncFkwpAnJlHqByt0xqostQqhWRJIzpCzQWDViyowRHw5i2nOEGDHupgpmRyKkOEBE46AfHg94eHjEuJswTlMD9JjVsssE92B7Qnt23RtjGlYAtis83ooOVmxa/2y/12SFJrBxN5ZMxrbrJyP+F6tnc2fWO6oLO8MUlzSq0hJzC3EUIpA8D1NAWcwDZLZEshbWKaQBFCPSbgKCepKwCEqA5eC4x5JnHB7vEXjBwI8gXjAMCZAR0zwhZ1KrfZMJAiIG64P+5QRATwYoWVSqhyURqfV80Bj3IajV/LpJm0DmOavWY1yPpxCQ84xlXmruCO9Dj5E/jkN16xcRLMcDSsnInOv4DxQsFwqqZb+YUk7dnCEiDHGoOU9qv4tasPv6NQxqrV+y38O9Q7UB/Zmorg8WFoySafS6NjpZwkyqf1byaZ3UG0BV6iNpqsmz6waRhfTytg8AAkQK5mPG4ZDx+csRj49qLZmGhN3NiDFFTEOqoMIUGHPwnCAFUxREYpX9AiEEFV3nqH2VknrLjqO60t/sI0QCprgDQZCihmbizAgUEQOwmxLGSPrMQlXxiWlASNESyjt4b2Nkxd+aNw0LOAiKEIKY90ooODwcQCAcHh4AANN8C6KAkkfbpyzRedTcB0SnHnsOZOi9zaIRHjbJ1iBbZ3z8MTMOh4P1LTCMIygGTGjeN30JIYAiagL4nrTfKi66xCvoU/veiaaSAXibaQg+leGT5Y0gcBFwWapsXPcHFnDOOB6OWJaM8NtvKCAc7u8xPx7ASwbSUNvHvXSEWtL2c+Wc4vXcfvuS/fi1e/gfWSe4lvR4zTWeUpBfS0o8d+1TgEOBDN/HndRr+4R68fRWnWqlyZoLRnqCsZPH3hnDugbI+COPs3/VQgSgKOEQNFGW5gLoxtRODeMRQ0ARUgtiBEQAsxAWBsYAHDIwEHAowFGUXDhmRmEAVJBFEFAQ0GL4l8LIhXGwvAIZrB6+UjCIhj8UD6VZCnhZcJxnPB4O4MMB5XhUj4hZve24CKQsGp4pHyHVop0huSMjgBp1kMHoDT+l/s+VqIghYIgRKUaMMSnZEhhUBKGozMvMYArgQNjd7XHzwwfcfbzD3d0t9sOAKSaMQ0IaEmL0sKktNNMJCHgynYwWIUsgDZXR9Tipe3glDtjlds/VoeE6QxakLNiBMBFhhIYanblj2rkzPBG2/HtU66Au43AlACYgABmNDHAmn6V5KyzN07Y9bodhbfAsY3a0lL4tOtKhkgee+8E9Hfz7RX9bZn3Pml+PLM+eekhkSD7oWFncM2JR74riOSKaTOTvHXyt+Kg0ck4AIKj3/adPn/Dp0yf8x9/+hh8/fMDPnz7hdppwt5tws5twd7tToiqpF23zXKd1G/1ZLpZqYBWC6SABDF1jfO8UU+TJjmfh6imLoB5SKajncC7l0q3+BcqWkOgw6EtnvEFeeqoWfaHVl7Y2nOjbT5eXJ6vuyIjV/z3YtQHEWnztxoj3FnhrYal5QUSzJNwSFNsnbAyYVKXtvQSwSyAqYbMou1K+BVuvJCO+LYnysvKeStZ7KYGvBW+fuoZ/vEgGX8EiXpr4l+r7XJ2+Z3mPvurBqu17BftO1oDnr+9rTGXK++vW89uxAOoxK4vdK1bL5xbzl1oibsmC7kpW534tBXpl1j/34PPl6z39HA4CncyDJ67hsd63Svv2HLJj4UoGoQq+XIq5Zuv3wUOGUCdUo1nUel25MDi6JRXUNszqUwV9Zxhq+JMCJsADGPk1+/HTv/R6rX2yxXgXSyjchwP0vQ3SWyih5ScwP96eRF8rOecLkVtPbkFebe6V1ciZcdBdqCMtnLlBp0i0eKkgdY8VI4sgsIR4gwKyKYJIiQgggnJp9YtRPSpCqISQfh0RLVG4lIhsFnGFC4IIhpgQYkJMgyb9hoI5ypeQ7fXrEGvbcol469eDuiJU2WU9tnz9UaOHVMEnbycnOihoSCgKwWQtPS64bCIA0Cz+/LpEGk7H50Pfz/1Y2n53aWzoS8cSu6BPTgT2zwn1Oqp931mno+UQ0GdfXz90Y6eOuU7/vFg//4/aNz4dS2mWk9q+mhNiTBFTSpiGhGDPwiEAKSCDUaCWnJGUUPB8G9o5OjcVQFDPiRTVWhQg0KCeMZHEdPJgsbUJQ4o1ZF8gUfdwRAs5ZlGx69xxeVXfuxW6vQTwkEMQgIsqVCVnzVfTEccwchS1q3qwoxsD5F4m3RCubex9tD5/BZ6yIK6sUBvhdVZ+MRmavGKdrN92TlsLQ4TndQPEQnmphVtdZqjNNaF+3YXOb/KtQcNE5b6tfL+r+/t2Tl8nM79GH7h2T++P+1ZkxHa9+KOWlyrJz/XjNde7dMx6H/FFtD/e10F/nfNCRbc/y8m5X8OY9qln7sfJqwEJX2zeAGi8VH6+dmx/DZDlvcq5ul37nHWN9w8iVVILZogSCRhIreFZCCUohh/EQhIFILPlfuBmsEJiya5JEMFg6JpNxOpNQOa1amtuy6YMKMjsMrLK4ZobQpCZsRQFGIt5Riz9vlOKAsuWX4tYAet+b1WM3MerPbwNPW6Tq4Y1qnretu1NP2HRsJmclLWJ44hxGjGOI8YhWYjVTjZ/Qu56ri/PH+RvbQ/1OnuGjJpQXNwRweQRlzGq7kpQT/AOpJB1Pj7XH9WgwuRwlvZOofVllTlcV1o1YFd5cuva1TO1G0sdoytZqC6WzRtCw/Ru8j7U1zZZdQFxrknQa6inPkeEJ6kGAKqajLbDaumVJr4BoBgRU8Ltfo+7mxvc7nbYT5OGBY2asDzVHGFrSc/lfjkZdd92Lz5dXvrR9dRxQA13dva6r99DL5WK0bgsKAQndZhZnXj82ibt+rqwxnY2RpUbXar/nl65ZV1ao79veaIO5+q30QfWh8uTn58uF8aY/VaXBrl46MXyxhwRrp606mhFxDYpfc9lwZLnasHLxa031yCQh2lwRXCw95hSBXS2204VtDZL8nuWa0gIC1a/Og7b8/7ASsOf5fny+1i0fj/lIonXv1OzAu3Pu0YJEUO41EIy1PlmR9TjAJglfACCVKDNjzqjMpz9tr/3S8iHc+8KCDUgyi1nzq1hW8XXv+uvdTWhZTv0du19UsG3d7cIlHZzbJdd7ZP2UgDTrJhIrcDnxwdVTEgt3Pf7PdQSAhACillwu/ABkMmojFgKJJYqyJeygAgYQot/Ti7Y5oxcGIEDmIvG1k2a1yB3luQgQqx9whVcy0vGw5cHeF6NNCRM+11NyCeWk8CT0AqplXkR9RSIptxMk8a3H4a0idN+HTrhIHDfF73C5uPjXM+xqLIpbk0dIohMKWA2IV1D1jAFIKQ6J8M4IE4j0jBgSMlc6FlzH1gycC6sJAQRaEgrw4GJ1Lr85x8Fh8Mj/uvxFxTzOiEC0rjTWO8oONADDocjuCzI2VzqEU0BK9Xau7aHSLXg1mFthI8JqzFEs+JjgKnmnwEUsNfQTabIWQ6RlBICmndCEetfecBxmTVvwBgrkM523DRNGMcB8+FgoYcyuGQMadS2BlQOWmYlxkoDhb208JP6UuhhDVbUOpqHSiCyFI6CwcZVtHaKMVbLRhGpSZBrXosipgMulm8g1THl7VMJGRHLA7FdY7VQ9wIBYk42GnJLreBzZhzmjOOs1pOlFAyRsBsTPux3mIaI/ZiwlIwlZ+zHAEkj5kWN5QJpvpn9OGEYNZYzgXA4mrcPCygANwMQIzAG1vEwTVWhL5yxzKyWlENESgOGMSEQaQzgOGq+kxjVEouN/Cw+DjzRpovebOONO0orIJocW5YF+RhwfDxoro6cgZR0bQLBOq+O6VJKtdrzedTPf+qUYpdBNZQGV6BptWaYDO7gkL+kW+t8TVF7WKVrQ+914CKutOTVIRCYgP1uB/GE8iwoKKZ0EhAbWabkXaz7hIiFOBsGxGNGBnB4PODXX35ZkZDDMCCmqES1vwKpZ5sR2VRV2MvlLYD/1zj2e1zvn6W8hlR6ybXtr9We6iQD1zmlR7nVpuulMRQjn089Il5KRDwlz12rZ7xLW1VA+HXXEanT/s9ybVnJ2JrIOVRQV31ZYwCYgF30PULzR5AUHAR4BCEGxpA1PN+QgFQECwOBGQsETBmBBGwkxBJUbt4JIzCr5TIYR2IECJJ5/LXwPhlSNNLFkgsOi4YizEvBcSlYFvV6llIgeVaQuaglPEkGiWgSZmhYKTLQmEgQTZjgoPdyIw7dhxRU91BR3OtHgIUPLVjyglwyMCbQlHDz8Q4ff/wBH27vcLe/wTSqTJ6GAXGI1SCqlxWvnrQOeGu163nBXho/SSxVA2FhwVKAh1xwzIx7Bh4lIEPzdphzB1DUoCVaniV2+wtXUR2H7/XnGFSmJ5hebCf6whWKDh4bOFSMiLD2a+A+mb5o7yHqcS6HCCycUiMbhN0jonsVBvWeEZzrOEA2j4hl0ZCVedExz4t6TeSjHp+P3fixBOdV93R57Ey3iOdws0kTAtJ+j/3tLf7Pv/07fvrhE/76ww+42+/xcdxhN464nUZMw4AU3eCo2GM78fO9cZ6OGFrV5amVVur/FSj+BsVJiBA0PG8071/kDIbupQECcm9vM4RjdOQpeYQcJ+tMFn/mnq1t3v6wlwx3vm/ZPF8VX87U801NsD35inZ4YVO9mIhozFT/ea0AAS00hye2Y7ME27JYDiC0d2en23u1nHqOrXqhZcWJJfATwtaKhKDOorpj6npA72uTEV9bUXkv666Xfv/a+zy1SLxkAekP3Sr2r7nepXN+j4rme1mDnBvrZ+cG0M0hNMGnnXR6cRc2gSp4ujV66H93Yd6anUkAMlCauJIgl3ryKeb4OYvEc+TAmkQ4PxbWyubptdbnu3V/tx1dOTfaWtZudtIOROvfn5RxVFEVbt4San3lwo8yDCJiievUMt7DeKSUAJBZ2/dhnWplDHgz8khazNPCBVQIoWQFb4NaYLtwXEqGICp5IGfCCFoDbkkeEakWzQCa5VSMWj9r1z4Mkz4rXCu04WygcfS97PJ6uO7fzXGCVRxNiIMl/VixFzqlqFbKH9beiVToCw6Um43PZAcHQhwSQlKvhZBSw1QogmIBgrpJE6mAT6bISQgQIiQiUGTsygSAMY4jsjCW+WD1UwA8DTsME2OY9iAQOHsiO24K15m2qkCqz0X088dawePxI7YWcFmC3Bq+yRrJ+let+DKKsILCUfs+plQF5BAUdafQZBTAgCnR8D/kydsZluDOrPQ2odSaIUZTMBoYpmPJQ3q1HAb2LIYTKW7dr1NtHDTPIv9NwyugjqG+DdfrtkirS6tvbehGRNR13NveZUFByY38UP1YPRKGGJCi5YAI1u2KNqjCzR5wQu85xIAxRsSg/TdEDW1QdeXg3iFq3Zmiof0CEAIkqaWbh7Zy8ibGYGN9ABPAoGrJyUY0Oii3biF/+IYLuIxc86HlYl5gpZImIF4ptB5eD+JE+ZqIaLeyfoQvXW3NWBNb7dxgHjz+uZ83DcDZ7HdQazV38Ai+H5CtrxDEEIxv5u0UtbFJVYn0seH3D9KNdW7eIykOCDFhmEaM0wQKCsAUVhIFMVpzk20Bvx85+D1lut+jfPivVNq6t1IIzspl/W8kZ36DtMXhyvKcjvFNQRGi8+DGNafi1adeLL8/QOht5fLzrHUZgu5puseYTlU9GQFizeVQ7JUt4fEY3TtAj8uk1uQjKehfIAjEWCzRwUS6h0oAimgeJRJCguWmYA0oFITBUqqsTVUuvfCC6wSuH3DDkQnVqAKwMJEkq9CjEKmW7tzrgfCwaagYk7CBmSDEFBGHAeM0YdrtMA0DxjQgBYv/H/uQvb0+trYcf2pJFpvjNV/DprgY6/J5YSCzYC6MYym4Z+CeBQcWzCKV61l5ehNgyK0SCaShN2GyHLlw629VQHTDAjPmoc4CYlO/lULhHcMmWLnwxl1D9PkaXEbi/rP2eRsbvPpt6xUhUqohWfWGcBKjG2ckRhaJy0PSOsj12f4xBEBQGW+62WN/q0nLP97cYj+O2A1jzQ2h3hBUm9BlOiE6S0K8Fit7n3Vsfe/L12x6xdcul+rgOoI72JA0sqHiBsDJutHcW9x73LGky+RA88Lo67X+va/rJWz5XF+9V/9df53Tcbc+p1t0VhhC9/OVVT2ty7mxbatFpwN2b68qLyAitrHV+042lUjcUnFtgZXLsortRUZkNA8IVUpiTJZY0K3+unAP6O91rry/4H6eXAid8tN/vz7vj1zei4R4r+O/d/lnE3y/Vrnk+VAt1c/9TrCEuW2p9c9bDJLsNxEVUNkFGVFQRDoBawtSSve5hiPq7rkek6eL/rkxcG7zeoqE2BIRF8mZM9e6OAYvtPVz59UVlW3zp/XGuwLGuzptbo5+3edSoLG++1jjqJZOzJpTYVmOEBEM44gYA/b7ncbAfzyAS0E24E51FlIrdcsZpHUu1ncBy6Lx+3NhxDggDIPWKxdQKViOR1AglGVBHIcqDPmzuKV9MQt3QMfKsixqUZUzhmFQq/dhRIwRnHMXbtBCDkppDUUOtgbEFDFMo+YFiD0Rcb5frgUgFNDztve+AMSso538176EWiSrKmgyebTnT6rgAgr8czHFTq3oKWq+DM9zQYEQDFSlZUHIBR4u0fdxzxVCNr/SOOG422F5eMDh4R6/HA8QZswsiHHCfjdhmPaIacTh/jM+AyjzEXk+tufetMN2foPXztLMDBQg56zKs6Q2V9B7RARNEMiMIQ3YTVNLen08YC4ZcUyYeK8eESkpUL1o7H0RQTArH/XoIUy7CRBGNKWpjvtZwen5eDRirMlEIUSMY6pjKueMJReTk9rcjmYV7g5gZOtntWI3bdctxZkzfBAIkYXP8XGvALCDw2TAMaS1L4wQ4Y0RSa/pbcO7CaliUUqGcMCSCcfDgmVRb9iYIsYYQaNgGhJ2A7CLgj0BFKQ6lxKgnjgSawzp250mmjTVBTQESGzjIHl4CWLEQBiTkwIMCREpTUgpYRzHugcMw4BxHBHigBhHHC3B9LIsyPOMPC9KjhVlk9zKkX1G2VhnAxAceC+lIC8Zy+GAeRiwzEdQjOC8IJLvbk5KZRRrY/d8AWs+h1LUm2trFV3X3Y7UcoOecRxrv8UUa74R9Uaibm04A7jqEMK8zApkpcHIGicP9NgYIwKC5UIxrKTKzMG8GBJiSBZCRL0+lmXRHBxBx5p6SauucHf3ATe3d/jhpx/x4acfEVNC5oLH4xEFwE3YaUgNTxZfntgbv3I5J8c+JdueU2bf896X7vWSe37tttyO4d9TaXLBuXZyUFTnjSYC7kFWn5OASD+nHEjE6SbWX/3Kff+5Y5811rvyvHo+4GaoLz63tucbu/mPpi++tVRgDiqXwtd2ETgUQgAkAC7WEKlHRGBBZGBgJQ4mEkQRjCIYRLCAkAJjEdZ3MAZmZDAoMJbICBHIIMwSwFFQkCDCoFIgRfN9SikQyRBeUMqCVAoGCwWYBTW0kBNzda8LBjpDjY58eEYLmRhJCQAnt31eVZJeBNH2mMACjupBTSiQApVzLIJPEQKHgN3uBru7O3z64Qf8+MMP+Hhzhw+7PXbDqHmpUrKcUJ0cZaX9+dwg1tqe6LLaoYrbGQZfWDAX4LAwfn044stc8D9nwi8z8J8L4x9ZMDMhswDsZEQXKpQFiAAJI8QApqIGWESbnBFQoF5U1kWJcN1IZawmAzQUUQCXS/2rYBYi7gnRH2/PVImCUiyHg1RvCLCOHTAjFCUYKslQ8vo9Z5WLyxHCGSizeVDM8CTWJILg5C7cL6YjDKoeZ+OP1XAtDCPSfoef//Zv+PHTJ/y//v3f8ePdHX6+u8N+nPBhv8OYEvbDgJgI5BY+1oz6p4dgPWO892d5ppAaEEG9uQuaHluMYNOwTUH1IKBGIwjGuDq+4eqJdHpIvQs1L4xzcu25Y3/P5dndz2SWb/Ec525xDXXxXLmaiFgDZtvetAptlKP2Wlv+qZLZvCBckW3x+uLqezux3e+see4lAbI13upXV9rrD2c+d2c5A1er4c/RtcsWWHxqWHxP4eq9LN9fcvwlsuatk+ep8997Yl5zve0xz1mpv9c4+Bbj6Zr+vQSun/u+joEz5wKnC9zJZxELi2PCehdzu7ei6ad1IYJ0cUHFT3jiTk8SATjfLucUx+17v75dApku37utw9eAHxWoqk/Y/jK8v15rLZiiroer+wjgvrG1niw1eSqkrZn1Pivl3JUQX7ebMNmet8UXdyth8t9JLStKUU+7khVYTcHAVFjfc4GIJtoTIxvCChAKIOLus9a3WF4I/y6YxbsYGMH9M9exhqp9EVoIsO1e5mBGv7VtiarW1lR7qW+XNfAhVRtt358mYO77k6wtg3VjcIui0NyPlV8gC70UWvgzsjBnimiDzJI/OBFhKHIg7ZOYgIEZ+/0NwIKUJnBZsOQjBISUooLE44i4jIjDAOECyktNrn6x+PzugNieQEum1MPHou3b/fjabPWra2gC9YRh4Eby+eEhgKSFiGLWMRZiBEkAFU8C2NYg7y/xfrS+ih1J1efUcsKgf97mxWFx+okr+A33PMXpuuFymYd2EgGEqT6vz30Rqcnkzsl751ab9botgIUFYjDyogmcdT5RBZFBgpTInB/0nACo+7a1UerycQCCGHROFS6AaAgHqXMe0CTcepzyQ153zeVBluQ8peScDUJQTxeilvzcybycS7W2hAMgZHKgtCduVluoY81jaKtBTlaCy0guMpKqFAYoI0RNAg5fL2JLfr7aS3xdq4DoWrb2fqhAPaPOy6eKn9vuqSHGSi46n2OTyetavdojpMr01M2v1h5rnaAmJ4XUEHEAEI0kGscJ4zRpbprotrK+rp2XJWsbvUHuewpUfct11mv66665vd6la5y71zX3fOq89yz9evPe1+3LU2TMOTm9r1PVGc+2LxSkulhOf3sOkH/pmH1P3eY5MOZNd3ryuZ/vf5eNTi/7fK3+KATGybNIXe1anjUDX/2JAqnMLmSetwEILAgBSKLh6woJJKjnQyGF/gmCbGJQJpX/iuWFmGCfzRNiiASmABkihAkS9DpL0aTJhQVMggh9JQEyESIp4BhJ3ROJAzgECCxkUFCr5l5uFhJwNZ/wfa5qCg1srjKe/qbp56TmV4A0wxwymTsNA4ZpwjhOmMZJcwCEiBQCoslR26iT/nfrGsI1w4msXwjr3E7Oqlh3IhfBwoxDznhcCn6ZA37JwJfMeMyaVLw+E/xBTcetlTUhxLxDgVDllG2l1Io8gDwXloPsFIw88XHY9DUH+v3e6/0cbW4zoK6s/oCdl0THwFKv862O4wt/n77MacdeWg/emCw2zNDHAdRDexwx7na4+/ABHz5+xM1uh904VU+IIWpuiEBUry31eampvO9U3gsDe035HvekHkcga2EbIy5zBxsfW/zDc/b1OKuO6e1NsNpv1rjK6dTYyiFbueo9SP+3Gwdc3kPbfLru2u9Xx234q1aP14ysFxERW3Dk3C2b4mXeEDmjsCpzvbUUkQIYzcpPF4IYAmIYqlIEAhjc3YFOBtszNW8Lat/WNfPiuZHcjtE1n6wN/Dp27hkQsf/s1TwHNn7N8kdg+f4s/3zlEtHwFAkBaolRX1O4aBxSCg2cW20s7IBNs/ztQ8E5uLolQfqpegIGiay8PHoA9Nyx/TX6je5coujt5ntOYXZw8JopfnIde49EJg+uiYiajBk40yYmALADYVRVBF33s1pYcyMian8L1JqqNBduJ6mxeV6D6Q3ojRZvxcL/wCxsTHlYeEGeM3IpIFqwhyBGj8POKHnRvBMloxS1co6xecUQEZhD7cMYNQ7qsiwa9onI9qRg1u25gome8wgWuqWB11QBRQc9NfyUd4HvZy5InQLHF4Gaht81IWTT32LguOcgUe2I2zZI6q7eAl6pi7f3uzMU7mYeqom6xanVXjDlkkBJ9+2Ukl5DPJavHj8GtYr+6ae/4GHa4+G3ezw+3OPz589ISTOVxRAw7G9QuGA6PoII4LKgLKweKBcGu+ouzftjNb9iwCi7NhaD78uNgJDNxXojCkDJwmk3YRhHHROlJdINScHe4zwDIijLDAC42Y0gAPmQwcIWw99zC7R5q7HEVUbynA9uBcSlgHMGRVXzK4grhCCarDmlhAh9/miAfTEyxC3Fq9IuQBEBOGMYEoZhAnMx5XCds0L/Lh2B1prIlcC+1LXU2p8l61E5g5nw+MiYjxmlqDI7jQMkEDgp8BFFEFi9DWLU5NUe0nMcB507ppwOQ0QIwLJoeLfBwp75/JrnA4g0hJMmELfnKgUUI6ZpMrB7qkRDTAPGaYdS1MK+WE6LeV6wzIsmTxa23BlOABFK6W3xpBGmQa07tV3VA2CZFyzHI0JMyMuiyn9KKFywZMIwTiCKRqDomkE8YJ5nswb1eayrRbYwdu69U0l16w8Pd1fl1dD6qO+3nnzQtZAtaXTBw8MDlnkBbhjjMNb53a/VSvJZiI263ncKYyBQNAs3S1S+LAuGadSW24SkmsYJN7e3uPtwi9sPdxj3O8RxAKKtPZYQmwrq6nUNoPnPVp7SJbby/7V6xzmF/L3LOV3oe+sqT5E2712311zv8t739ro9T0JcljO3YM1ZMKMXLk/Of652chY8OjnqBWDR77n0ugJbWKIspQKwMCw4QD0iEaH5mCwMqCaa1j11ED1mED0uFfWmmFmPXwy/zgRECBalCZAJSCmot0VIIGaEpKR65oAlF3xBwbIQHs3iXSAYxezBECAxaAi9yMgSUQhgjopVhwJhIJMa+rjREkh0z1STmG5fRcW6K6AtFk6qEjWosmzNxwANw0MxYHd7i5sPH/Dh7gM+3H7AzaS5AMY4WPSNDhxd6Tw+rrtOujSeTJ508sPnDdUHkJo6oTBwzAWPc8ZvDwf845Dx/32I+MdC+F9HwgMDj6xyNoVoXgWl1gcUUWOWkgBD0O/IOps67wU9AXBDIsC8o7V/IQUSgp5jRE7tgBXI6e1sz2p6Yw3HZON0lUxazOCC+zCUcnrcJjwTiSY2J5Nl3duCRGofO1lARvmwyUcCVO9PMnmJoWFjbz5+wO3Hj/jb//F/4ucfPuGHD5/wYZpwO03YjSNuphEphhr2k73pXO7izjnsDyx2fDdfDsN+A9TLW9Xghh8AAAelI8mICZd9CWQRBc6FN+7mwskt15jO95Y13r908+qbD8gXAfFPlhcQET65/Rvje03RYykNjOLSvRxWshjZOqRAFGv+h0BRX8FCMdXFfEt8tL+2XMzTnUD1nMu/UkcaUPfD5nuPBb1h53rlq2u09gTvTEZcEv5eanX1Wguw1/9+vn49qPaUEvXsQvJitrG//un9e+Hw9FanIOD3Km+1MKsCU/1wOuvOgeL+fol86AkHsvnU3ttv/TW1Lt29KkDaBKAGQfThfxSA00O780WqtQZnFdIyaaLikAY4aFyXcmp1IrvntrFEdMPcWmF7O50bQ+dA/XMExvb88+d4/VDXybPdb8KbA1guVDI7KOrajSXKtWf38DquCfaQjzigyk1Y0Do7Xha6NhQLs2TvbDkF4DFcValg0fA1JWcs87G6aSMAYRjUAyEzgAwNZyKQrDZewcLs6O2MJLH4KeTRnOYjioVFCQQgatgTsf6MMSn4K5YAmd0V3upqFt5KwviQaP2noK59Z21eCYzNGrMCYbo/ulWvAeX9mIAD5d348GtZ/1aCRFDPg7Swrts9qt7TAOfWd03AEZAqRTZW9JK+j9t30NA0Aea5YlbqVTkkwribwFJw9+kOIQGH417PDwAFQkoBwzhi2u3AJWOOSV26KaJuy+6BYgqNeDJuk4mkdo6tWcUULR+cpmSIXZDZwQ6qbcnCyCU3t2BoX0S/DvrQRXoPdIYWHoNXxL2EtE6VmBqSJjovGjZJQzuRxXH2xMgNgRHxvARU84yoLic2VkJVfGt4oKDJlt3bh1lMYTPrSnO3zz6e3OLI7td7/MRo64EAMCsk7QrVTMX/ttEiFOs9SxEseTbg3JKUq/m/hkOAgicJzZPGZasQPeG7x6Noc0F1zZbcO1rMihBjm2+iHlGqyKiXhCf11nVbQ6elYUIadmDkSljm+aj9am0MCgb21PQVVe7zvtCRaKHeCBaSgDSxe8m2/hUomVrAy6IWo7GNq0ZQm/2rjydySdTbwP5ri64RtbYOUhdKlZwc8e9a/olelyCoNetcjsjzguVwxHycwdMOSE0eUIIhdOGdQsUXAB17qMCOejj72PZcEMK6gkAYnJeaNygz20tQWMNUDYOSUYPl9+i9Ms4J9QRLUm9/98KNawLt0/vI42+Vl9/rHOCyLHjt9b6Gt8KlOrz3vZ4mYHoS+JIe4muqHt/LXL4EViK7nb0Zhz6pOgvg7t7bQfueasNLrS2ftaB8AmjYQh9nr3UuyZPW4ML3Ly9PPUO/T3/rstIncNpeq2O3eqbJn9SF3xQ4OA2TrzrsoWoBUv+5ZhAAxCCIJEhBkIghJBiC5ncooWi+B8rIxJAgELMzp6C5jV2GzAKMCZgF2GXBHAUHYgxRvRvjQIiZMDAhS8BChBwIXILKAxTBDEQwmAIKdO8IpAZQyUNKOkDZbSwqcouG56UIoYBi+2MJhGA+I2Y2gzRGUArY7/e4u7nBfpywGwYMKanRa3Sdx0IyrXru3Ljqeq/Tlf1bIbKQVH3r6/dMLp+rTDRnwSELfsuEXzLhvzPhlwI8lIKjy7EMTSTNAljC5KZXlVYNFiUrgu6n2BgcrOvvcm7zaNb8D1jlnkAFdns9Wo1p3JCMfFyKGFlgyaQ9zJI07xSjOboRaa9VE7d2J5NvqNO19H+pERRETO8gVLviWLd7C/1DBIwasvfjx4/4+OkjfrzZ49O0w80wYDckyxmSai4/Cn2ndivVO67Tfbl2LW7lueOe+71be5891NvdD29eCK+y7IchwKSe3J7zRjzHiwiYGME8pgozEEmNqEQsW1wVLw0H8ZX1qb1//f0Jdudjb/2ljVfDuqn//uTokzr0csC6DnYZG1TbzydFqL91d+UOe1o1w/lde42x9vXZ4lfnnmX7+2ld3zI9rs8RYYpYE+pVkWWz+spGQGRTKlT5MmstSgg0VHArkro/BUqIISJGTRxY41BTs66r9zrb6f3HCwOvLry+RbdBRHVpNOWaNGZ0D5BKp8w15WoNsp4jGfRa369cI9xfS0K8XFF4rWKxnW7vW86TD61s19WnSIh/prJtFdq0z7VP31tYAi2eH1zII2rAQDeX+ntvO8GXnLqB2OfgYGJQYcrDopSiiW7JErGpgEmWAAvgbLEH54RAEcPuRhNidhbypJXXe3qiT9c1bX0WASQATkYA6AD580RC3yZ9O/XeGs+NuROyEwEh+LFiwp9Uq20SNJdZtMNyXuA9S0RIISGAkEJAbz0jQPPi9UtYLgHNQ7DxZCDN6UNGQogI8jJXLwIFEZMREMACILvl8HxAno843H9BGhN2tzsDzyYVLGfre2HkrHtPiAlpGNqjiYJcougmwhggwshfPoOWBeXuI4h2SEMEDMAlIozTWME3y8BaLTdIBDnPiHlwHsRit3pzFHDJ6uZNhCABUQRDiBjMitgbnnrN1PrZlcy6x6CN9ZUeL+hyP3R7ETT0DdfcTGvlWyCViHBrH/++gtyWi4lSC08DUzDEwVY7q9jfFCJCbQP9jYkRp1FBZAsPk8w6P6Y7DLsBLBn39zfImFGWI3i+R0oBu2lAJFVSRRgPhwdNwFgAoEBQIJwhnNXTUhhsbtfwZjXFLYj+XY6zTtmaVFvXDKEAYUHOlozc+k4gyFxwzEfXu0yxVYXXnDTheRyqtT0B025CjBqGAOYZ6kmKATEQNYHoBss8Y/ky69wbBlAIWArXF2AEBVxIVit8JzOkCIqw5o8gqmRfZqlzjAiVcASKrQsFEFXEZ+bm4VFYPV8i6twMbLkWYlIjESE1tksqC4qFRWMWCDEEpkzAcxsIlpxxONzrmAw2R6JgGAbsp9TGWltaQEUAG4chJl2faygHVVpCVAIymSdJSkpGcm0vU25yBpF6NY2BcDuOKALMzKA4Yhz2GPd3GG8+Yn64xzx/wTzPmO8/Q7KAikEblBADkIIn6hQQqddBKVlDIo9Fk4QKI7CGdyssCPGIYR4sz0RGlAIUgI+sIY+GARjY5qeGAgMiWJRJdU8e1YqVMKrRC4q1SUwQlV5XhEGIavCTgivYNoZCqvPfST2VyYFyLDh8fsDDr58xH474dHuHMNUFS9cJkZqvabCQELkUJbTHaP2WQDEhpkHJhazhnuZZ94MAaEL45YCcZ+ScccwZD0vBYS4Yl4KURux3N9hPltsjKWCVJa/WRe6eubdGrfsQbD0nAGCLQa7eRn+WdfmaVuQrEvyVJMSbLOBXBipoJPTZc6nKkGze8UGUgK8elTAUrJOeZbX9SjUGUODk7BM9XWe77tcsz8udZ086+eH8+dfpW5fKS8dIb/jz1rF8DUh4bvzI5h1YY0XnSt8H5LlvsntSqr5RApmxpnrPJQ8ZajQ4S1FjBEc6RBCD5oMYohpMKPEgQCzIxIiSUcBI5YgCwWjxOkPQNTOZkT0xwEHl/DkKHkTwgILPc8ZhYDzugQcQHjlgCQE5BRyXiJwFOUcwE+aistNiRHYxoxnVhZxMgHmRAosdUzQRlOo3IYBDRAkBOUb1zA02L0EYQkAkwrgfMU4Dfv7xR/zw00/44fYWH3d73IwjdsNguYZQCQmip+YAPfFJdxcRQhDdVVzHLUHJkkIEJsHCGUsWfJkFvx6B/3tO+M+Z8P85Ej4XwX2eLRSkGUEspa5TCOohIYbBieFVYIa6uAgQomH8vTEYAKmZ4Ey/gx5LBHVNtbwOgfV391SwvAxaCbZ8DYt6ObBUwgil6HE5d94NdhoAN6XRhF6wd9G1k6n2rQs2YvkxlNghlYNQqkJU/YsFqgMEYBQg1nPU2ycHQri9xXBzg//4j3/HX374Af/Xp0/4dHODH/c77IcRt7sdhiEhjYOqvbROclwJEQfhV8D69yxP3f+J9aqjLZ89vkaOeYciAExCHdKIwOq1r4ZflldSrQTBkVBsCWOGzW8yaa3luQNch2ZcJr0vf92XftveolC2o9RfL6PRlwD81/XVuTv4Z5V0uSMjXKBB3Vzl2cv3JMTpPXz2Xl3nJ7rgqfLiHBG+uvTxb5lbKCYnH1aWCBW4X+eFiHGdC8LZ/fPPR9svTo69CKCfaZhLwuc5i+5zpMNTZQWuXi0IXbkwXHu1Fwhg701IbMG2C0edOedpge+pq5y1IL90Dq2PeOk938sl+vdTTpWJ11rwXSTnzs2hc3OK3PJ6Xfo6+bwKRiC4haSGbSDD3T0EkF3fPSLct5IzJDCwzDUmN1GzOA5i3lquBFAvUHXtRrx67ufap2+na1zut+Rm/7vvOf0a44pOf/36dyVI1oC4r8G+DsvqHqZsMipo36zu5UxdXQEya7Qu7IsmxrV+IUJMSkQXZk1wXT0mfC9VS/eaOyhFSAkKVhIhQPcP6mKpOzgQgrqHp0E9HQozKGfkJYOiJ9OWBnCeJOOV2g7B28vbzAQfsdBMrb01dI5bCoUYEYPHZz/doU/6vxtCa1GmWcV5v69U2l7wqOT9+tp9clpX+vwzEXVJkMOq7wVOlPV9jO78do1QrfT6e/rEEfOQFJCFcdrt9igpgCMwpoDdlNQ1mlpS20P4ggMzypFRWKqCU5vA/ghGGLIbg7FWrvVT80xw0q+uDd4OWBsPeDgZty7fkox+bkgJgTSxcoihJmff9mRMSY3GepmClOwCUGUnAAo2oPVDbfXuPF3zbISsSFAfM6jnoztfIMies8DC4nQbMKoFTtdWpRASteevY5rsWQXVaknnVMuRoEqDkXohIKVYX35LH5fLUgAqlfjS8VUrDw0x1nl0ESkh7GtjRRdbHxBpqKIQY00mSYzqnbIOK9W14XZ6Wl2otqs2QTCCKljfMKv1osbsNs879wITJbAQBIhdKLw6b7Z7MWqbs4ekw/o4tx7URUcr6XVZSdS2X3jeGiWPtX+83TyhdE3Y7rteN899vJBdkBCAYMntQy/fW7ixzhPC9+jaX8wolgiciqA8HrGkexzvHzDfPip501iF2n/M+sw94Q10+3B/vEhVMqtCSRFY0Tbny3vJadvrfE3jlrcYIX3L8haA+fVFVn/13g1bubfKEz6PbKz5OU+90M08vQ7gZMRW73hKFvRyDhA/1w7vP66arHmuTieWpScHnso9LynXtM22vGcbvPZaAnTKaWuFS62xkrddxjir0/pYtM+2n1PVm1yKEdTQOKKhcYLJsgFmYEBqTcMkoCAYguYKk6AyQbLjEzFCEEQBJCqoPgdCKIZfD6yhFTMjJCCNCQsJSgTmAOREyFmJh6UEFGYssRERur+4TKogaWE1GJuNzF9y0X1flDCPIWo4T5NbY3B9TY2pEhGmMWEcE6Zx0FBM5g2RYjQSItQoHMHm7PmlpdtrLxASmq/Dmr0T/Wq/GjjPFp52WQqOS8FhYRwyg6XpMM0IyN79TboB5Qi/j6bVWBGYULTSDSuxsKq9HxOaYEPSfbZjTAFe38aNGIygqAmoS6u7h24yr+F6nGRAFijJ4WGn7Fqrl55PJpeucT8ln6gG8zUR0dsrRVBKuLu9w83dHX64+4hPt3e4sVBMg4XMdS/LXq7un7Hdq9O58PJ96LnjryE9u4pduIb9+swlfBw3PeWJurkgDm/f8/vw9vtT/VY7x/fSYJ65OiS53qvOmSrXdTJw1VUCAA1JWkp5uv4vKf0UW33RvpSTg9e/n17k/Kq/7auLw6PbTNp6Y20tYU1GnJz7lE/j5TZbX+r8FS7iV6/Y719MRIhVwAmIXJaaC0IJiVwVfj/PlaKalNoSBvqrJcFbC4HP1gldV296cQuYnPvtHMnw3Odz9/qzvG95jfD5Z3nfsmr/KzbQs8pY3dhPj3Uh6WTe+v1WwOq6TivgP8YKVAipsKIyjIHg6MCjKuQBLLp5ZWkhU4hCFUpCSAbWuGeEERz9GgX93Navy+vWuTXk2jG+VY6BU5fzcwpu35Q9mNW3oa/LDoj19+lB1z6+uK/923vXbrMcEpxLi3dvFuQQjVVLIWAcJ4QYUZaMslgs9sKa5M7uU4mhqAllC89quBNiBTZB6/UahLqvgCeUnHE8HtUS+ngEQsSem7DTCPU1XCXCCq5CFZUaMrAPJ2IW9URmlc4CSknDzcSINAxNyMXpWL5sjbA9Dqv+6I6ooO16rqzvkXOu9QRQkyP3/e/KWW9I0IBoXo1z7+9+X9ffG8m2ejarg1pNR8RhxN2HD5CyAy97jImwHwPKssey2yEN6iX5S4g1xv5cioYbYq7P7MnrooPRpRvDBM1Lks0rgQjgCAFBcjZBuHmAtLlp/ckF87zo2IupGycGClv7DVGV4mk3IVDAMs+1fi5Yh0AYhxElBCzLsZt/fi+uSa8bqdO8pVzYqe0N9VJh1vwF6MOjCWqC5e14cW/TeVlQcm7P4SGr7PCA1oclq5v9YOEQdEyoQkDQdRGsniS9Xqy6t3ovgAKi6LwcxwHDMGCcBgC6XldZMM6Q44zShcyiiryIXdMSg4t6+niSaZ+bKny7Z5vOWw/vI6QhAWIkxDRgGEclKMSI0tLn5Vmvl4E0dBGBTGdXxTTYvEkxIhIh5wyCIKIgiXprxBRrfx6PR4Q0aBgzkbZWrWf1ag1mZhATApN563nYMwVuKhFFjVisOrW03EhBYLkuNA+HFA3ZVcda0RwR8zxrmDqfYJBKYHiibSJpdSAyMiJqO6SElNTTJ+dcXyLcrYd6z5IzJBeEwsif7/E4Mx5/+geGYUQ5zuYmQ0AksK0vJZuXlakNvZcYoN5EBm1oThtRuEPDf9l6LlgZyP9Zvk15rXz/Vr3LCdN6vW68nKtX/7nJnKECKOde/XF+MyXvgNXNu+d53vDnPPh11vjqRWDW28r1gNnr++0ao6hrDHq+Vrk0ls/d2SXAbR9twba10dD6/OqdiV5eMZOF2k62povF3GcGcUFAQQQjkbr0MglCUBPyAgGikhIDq5w+QPNOjGBEAkYAIoQyBCxLwA4BEwBaGI9SkHJBHgkLEnIilBKwjKGTmQSzyRya40nzZ/WGDRa4UEMYCXA0smJZNM9o6eSuGAISxY38qSREIMJuN2KY1OL9dr/DfhoxjaMmJ44tOXEMUZ0DLvbcNQNBXx7hyK/E5jUAzhAu4KyegY/HBQ/HgvtjwcORIUwt7KiI2fsq8FojJDmwTwA2XvC6gTvYr3vcSQbuVRLproRYwy01wsGBYWr37Yiiegm/p4djMqMCJSVMCHRhUBjg2ciKQ0dIZGiOidIRGhrZQESqQWFraBvjRl65JzNA6mABNbDAsEOcJvz800/44dMn/NvPf8FPHz7g4+0dbqcJ4zhiSIOREbEaBK0jsPTvdNV69M9e3gOf66NmCABiW9VM1lOjm2iqo5MQdUc13QNwMqI3ljs3h7+fmFdX/a9QCycnfPy/tZzDIr5Ny72AiLABwerWXCye9toTwsMQtAZyi9XYJaY+R0L0SvlLSn/8uXMd2FSrQgWp5MyxT5EQ2+/6e309cqKBIlcd/Yr7f88F9VoLoCcuoG/vVaErymsW3/ex4nrZvbblWUG+wutnjqP2/pT14Nl7VADp0k/kJ6+/t+980z9nBVat1UKwHAF6ojADUVBQalJlYQ9ZYQJ+x7RTEQgHQAyIlwQmQoysoFVy91UHNrrkrRQ0nupZgPi0bS4pkb0Csr3WNqF1JRPELLxN6G4HGIDctyhBAXsT4l2II8KJAu1WB6WrC9FaADtHdPTfe5t74lwxQVrYgHpWQCiS7gsG7RmBbX0rBhq50OEvB+EcFCeqwgqABqxaC8SkoV2WnEEUwFmTm3OxnA4UqtJXAXhxMNqizhpIW3LGPB8VmLVW7ke3W1NTUCAuDgkxRTyniIu0GYgzbSzWgG0taURDk73WgEk/JHzf9b97QmE9ttq7g+2rpNf1+FOhijpMR62eOxAdnqxWx0MIaqE+7SZwjiiBjJwCokkkewOic9Fwjy2M0qJ1LB6jlr3xO6GVbez0QqzO/RrsiBkSFERuFjiwsbDe/53IaaHFAoY01nVTrez0OyLSZMTWjgJCjEnTRtB6LGufrL1L++/hwJn1B1z+YvPS6J6vH8OdHrteT3SqwBMSaz4ETXQdkoYpK2JxxzprtF5HBRoJ6vbyHre3mAU9GQnC7BaMNjZCS7Kdksp/IjCLTAJFqiHCALa4x6jxsPtSsoHYHnNMurq44O/tnKK63ceheURQQkgaNghEyKUYeSOIFDDEpKQZEcjDVJjFvy05dk/LC2Hrhf5mAD0pgToMA1K0RO7WfmJr42BzEi77dvMIPla7MeyEuuvMPnL92p4LIhphlPNS1zMn3UKICENn37fZd0IgxKTkTb8/sKznXLR8HIEUmIiiXmBpGHT9M5ZAw4WUel6IUcOjASisCcM5F835kwtCzODDAfn+HsvjPZbDA/Z3exBS9UykmKz9ywZY6Z6FCETRdhFrWCPi2MJovDWA6teQ687pJn35ZzDSeQ5Qv/bcFxVZTy4xZfASIVBlTNvzzuqGgVbyU68jNh3uPXSzc7LX5Ta8BHZfqs9WxmvnvB+A8lry6ZrzLpEyb5krl9r00vVXxxPahtl/h/U4W/VP9+r39f5c0MbLTc9W+F48XqgAUiwMowLgMDLCPSSCEeUkDEYGgcEoYDBi0GOisOVvKmpEQHrdgAWQBSMWFMq4CQUUBTQIFmENpxQEpQCZCcwBXBRIzEXlgjyEGpbFh5nWPNq+oPvdgTVO/LzkmmfI56IaBsT6d4gqO0RAQzNNA8bdiNudJiKexgHjoLJHitGMmZrxTMtk8HQ5uz4T3Ejb5EjrX5NjOWeUXHBcMg4z435e8OXIeMiEA7uRmzRdSFz2k6o/NUUKJp/Z3PSxVvVtgiafXhMRHmnAjfS2Ml6PAZBLMUR2bWP8zZCjuYXCPCCKCmUl6+fqAWEXN2KBihMRs47NsihJ4URGDevkxEUnj9YHaTUENVLEwepi8ui022G4ucFPHz/iRwvHdLfbYT+OmhfCPGTcCEvHVQ/p9vN/uy88O0xeXa7ZL67Fz76WrHBubd3e8+Q56lrWPAwrEdGd60YzIi3nGjNDAlf9vuawJDVE9fp0t+huKydV6L9f6dH1x6fPvdQmp8/vJ9HF89fHnbnPmS24erT08/DCtc/vUd5Az9/sqTH0XuPr+hwREIC4S0q9qEdEztUjooaqoDVYFGPSOLU26RsDeV1YpmvKJeEK0v7uXfX9/dJr+/v2vHPvl+rxrcv3r8Nb7v/HV7L+6coz3XlC1BGhIiWbY/rjVJ4g/7L+Vi1KOnDkkqLRkm7qfaMJ4yyaINMtMpo1nH6uFv2SAVJhmSiAi65VErKBlAlUrUs0d4LAwCM5DU/0XBt50VPOn7fdyPtzWz6JXknplWtU0BWAJTDT2MZSw+6QhhA10LNf43zTz5s8A2vg+rTefT95KA7mbEKv1sfj0UNUjh2CKgNEAQz3ZLFn91f3RwhBLbKDgpgUm9V2JVFcUIFu1mmcABbMxwUiQFkyQlDviygExHaevwgNZIhkXhcAlrwoOOlW6Bsd0ZMMhxSQxkEBuWFwtO9sX3ctiHMT7anxv7IU2Qoqqz4FUlLQd+2BeOZa1YBJkM16q7/epX3Wwy7qtdjOz36EWrhltWJ3a+2b/Q1KyVjmgODhA4KCw2kYMe33pmhoXY7zoon/Zs0TwsKWx0GMiJBmGV5b1YD+Umo/qp7OALXExR6GxhOB989bmOv3Wv8ET0hNBIxp0BwE4wQCcDw8AkBN4JxSMsEZda4Gs9IvRb1EfOx5/+hzOOHILeF79XzQKNCeQN21yVKKcxc27ToCq+vr4/HYLOJJI+XXtaMqfyaWCuBx0IU0T4lIFx+YtS6lshZsddH7RgOeAykpMI7NCo3teF9eEUkt/l0RJ1Q5sl8PZ3GiDNZGoteoWrs2dYwRcUgYdjvAE0CHWHMXxDSgiCCzEk1gS1BvYbSkKDAv4p4PVIkV7QPNNwLS45QULpUUSDGq5d04VDIw56zgfdRwEysZ03pP35t3Bot6RIg4WFFnLkTQ8q+5zG0u63le6jVCjBDo+CWgegSIkY6+kFDUJN7TNNUxqUQEA6XUsZcG9QDyMcKgLrn0gJRiXQcKq6GSGw5QCJqLpDCWOYOXAixKQgTKKPf3WMYR85ffMN/fQX76pPPbQAZKg/bz3DzzfO1pIJ4RR9AwAA6m1Lnxp6z5L1w28idOlfb+s06vtZx7yRuiyUjr87f7+yXA5hIJca6Oz33/knKOhNnW9VuXS8/63DH+/WsBuUvy1lNttD54A4Y9df0KBjdQydewDdTXRoI4Fsy+QbeXGKArBcwGDGcPmaP5jUQESYx8R7YMExkCRrAk1lSyhmYSzYuUKnidETCDMQNhASfGwIyBGxHBwppLTEKHKwtYgoX/SzUcqsoSsFxfCkkxBIUFh2JERM66l3Dz+qzzkDRAD6UAioRo5Ph4M2HYTfh4M+HjzQ4344T9MGBM6xBNatyk7fsc2nhxrpqeog4ELiConMmFUWb1CDwcjrifC359ZPxyBH7LwH0JcFufSkScGzUiCtZTUK+Hymyh4YdEVVarFcJ25SlVJ1uPnfpQ+h7s/BDN1SNoHgnzQAWZvMVKQEjOQJ7XZITLhJWIOJrnxBGQAiqLGmVsCQkxIkPY5A3uV8Fubpn3j8nBRTT0KUfCx5sb3H38iL/+9DP+8uOP+OnuAz7c7HE77TANA6ZpxGB4pI4lb6nfv1zwHuv9d6mD6z8AsDGQq2tep8erYZTqA8ysiayD57Bs+3Grxbo+TX/Ghe/P1b+fLScr9/XP+uR1z/126dpfo5/9mts6XX+v9xx/VxMRbtHklnt9Log1c9+ENFeqY4yIwZnHc54Qzwk8PdPVNdwl8mH1BTrASMEAwdMkxCUiov/u3P1O730ZWHovsuB5Ifa63967XLrXawfvpfPozO/fmog5xzheEpafZY1fcK9tea/nPrnDRuA+R8Sp1bgfcPm405s1iX1FUGxKv+lt21vsnhXkoFZnNuv8CmqhWTmLCITcBVWBH+Zs9RGIw9lBDMNoiX2tUvr75vm0en0rno4FBwlPv7/cv+sxfn5zrfLlpu10424W4VSvYUBXJTjYFIU1AN3fW9dutOMNqIULESZ8e7uH4DbCmoSNC8AGbvn+UEDI84ySF5T8/2fv35okyZE1QexTAGbucclLVVd3n+me5ezODrkP+0BSSFkK///PILlCOTIz53Sf011VeYlwNwNU90FVAZi5uYdHZGRVdXchxdPD7QKD4aJQ/fR2xLAbkMah0f1AmiOCE7jEOmcW/HTXh8wtFiUBiAbEK2hZUOYJELVydmZcRDDPs3rvDUMNB8WilluaED2j+jh4RwtAopbvAmDc7THudzYXG/B1fnlu739ri42eZiwt6ZZj3Zjqfk4miOBE8eQMX88ErufhGnSpVvfMi+uZ/bm9db5U5VKIvl4CJEZI0ES/gQhSMniezNvS8kBQxLC/wf279zgcDsh5xvHjJ2QAs1tPWRJmzpow2gF7MgbXx0dD2zCSC22rUkNRGRkjUq8NCGGeM2bJdd0LMQJ3luFm/e39WIq+gzosBQy7nSY8n9WbRqwPYkrVmENYAeZg3qNq/bccQ19npXDlswCjR6IUyy0J3fq9v59M0NY6miU5sVvbq4LSJkydVwKxNSAWrzlXOiEAJDhfpXSTOC/4NbVKJ8v3QkgG5vvg9HNFFSmmOCa0vAMWMk8AtewMpAmfC4NEFShB3LvAwh3FgN24wzCOGHY3EAGmYjkb0qBzhAKEC3I2bx0CyBJIcyZIpOqBNsSAHAOGFDAkAs1ifaOgC6BkNoWoQEgiDOYdEFLUxNH+CR5SwgSquh90QGYlbmtrQKAqQo2uuGIxhRZijwvjcDjUtewCd0l5Re9dAavYQzIlRElqbeYKjJIzODDY5p4qPVSRrDSqKSJCsHBX0sK8RX/3lFQZQpp0lWLS2GoxgElQpODx80dkYnz/5z8DKeD+/TsNdXdzB0TSCGwCqGdQ5yHS0y1AQTfb/D03kdJSU+f8TLGZruHVzl3zU/O3r11+NgCFFlAunuUR0fGlSxnQPKRW8mNfNxHVdXpVM08uPJXxngLo1+efM2dO+4Ev3r/Fx3ZPPmnDzw2g9eWlCopr5LjTujeeZfu2M4kqOtQdUOs40/WN97PrzXiheYIbjXeFg3kkiyuda1id0sLhcAvzSKwAsFl7IFhIJ7FQOiQaSCkQI0bBmKDezjUsJBkbERYRehiiOLPLK/YGSqN1j2fb0ydTRByzeg1URUQHQlY+PxAQzTNQgHEXMewSboeEfUoYIyEFQtTlbPcqT/pUeQpn0VrcY1AA0eTVhdUgY8oaXurjNOPDMeP7I+P7I/CxDPhsic0CSENlCcDsyabZJ8npPOrnV/939RJ1vq9vpd/vQpPxFwLlQb3z6/mTl/QOqAc8J15th4UEWyS85hkQhpQJxNk8ItQzgpghbIqIRWgmldXcuERqv0vnDNK8GtlkjbDfI+1GvH//Du+/+Ra/efsW39xrOKabYcDNoB4RVRFFTps7mepknC9gGBfLy/fqpzC0axQBJ3QKm1ToybJF576IjlPz4BVRL2TGCkcwzwi2dVWYQSj1vRdjQ+aOVNtWH1TltC0cZqNhTzUcz+9BnzvbZ1s7tq8To/Ht/+4vo4VthXhV1N+8aElX3VZrLhze3r9eNqOW5WpFRCm5CoqenLoqIpgrMSCLu9wnpE4WY3mtiFiD+sCatnqdp+2ph57D0NNyoK9XRLQn9iDP6cRZTqhLpZ98L5ErnqOAeOre1yqvXe+ThE7kFZbA9eUpRvo1GOyfk0k/wei6H2vhZLFeQlAmUE+crKGt74t1dr/XwOj6m8VicJKCYZGShVpSYC8Xdel1hoXglsyGODpTBgCWYLXAnxsBIQVbAixkyPJdHEzy2OvWBRBZvlf/ziI4ea9L5awSzoXeHrCujPCKmYqkoJI2roJb6751gLEPx9PHc2zvTS1EC7PFkQdgoLCwMtAObkmACUdFI650LpYpRswETNOMMk/I8xEgYMdigK8lIx4CpMQW/5tbXy77V9TiXVr89ZiSCTCqUHBFBA2ptlMsZI0kwTCqImIYR7XozRamyMK1JFCLf2pjrZby6hK82+/rfLGWnRndNc3cnucVNK5rYjmXlvtT21MqQJnS6vypYu+SEqLfsxdzpVNGrMl/BZdzhgP7RB6/XoAhoZSMGAPm6YhjzsgMzNksyili2N/iLhIOx4N6WBQNOZDnCZKVJwGrPR9EVBEBC6NDZucvHmO/WVX1o1Hf23uxtpEQyJUCXBMBJwo1dBUApCFVL4+miChgIcRAGMc9hAsOjw/mTaDPSCkh59lyCnioAbVmF152prdRc3WIO2d1vE2EmCcTs2AcTbDv6a4uGgvNlEFkCaSFUIogBtHnmuBH1k4xYKSwek8cZ4v3D3TGd81zCGWu4ECMsYVmAhCjKiLI6FBTYulcyUWTkouNA9yz1uZfIkIp7b2KJqhQjwFEU3aZ8UtK6p4/7rDb3yAX9YxCSKaI0PXKYt46rCErKEZgGFBml6dVGB5iQEkBwxCQMoGyWAQpViUcNORdGqKOewrqCTEkVVaZMkLfp/fy6CR86saKHSTg2p91PnDvsdbCwyRXfoqGxnt8fKzreRzH6onTr93qjWMKpSElyDgCUK+DEIPG7S6zxvKNCcGShcYYUS0kTRGh61wFSK8fMM+gmBCHoXoVqSJCP0gBQhpW8fPnD6B8wF///C8QYvz+D3/AfrfHuL9FIEKx+dFyZRjNMdCMiM3jQ2o+D1UA2iqn1xCfni6/BL78OeWXCBavy0vbRoRKiCq+u+I/+2f0e2R/7VJWrGeXz7Lrex53fdVT431OIbHmm9elb/tz59S2MiY88/rzMj1w+l5fOtdeu77XKas2OK+2Orb82fFj0p3vBDPnU6qCglEV92r00Tx71eOx2DHN4SnFFA2+t1TwlxUgdi9JEQgcBGYQeax+tVYnySBY3onASEGAQcPdpcqP6sfFERFXMCxfv3aDWOoD0dB5LNAwTyyYSjLPRXT92K9dmEGEniQA4y4hjQm3Y8LNkDDGoAm5yXJt9HvtU6PZ8d9bv0kEgQGwgIs42wkuyrMd54LjVPDhOOOHw4y/Hhh/nQg/lgGfNdGVhsuKwbwPzNCgtm89n3qPVes0mzOqTHDx1uaUj8UJOfB7vc0t/COtn0rUfdCiHtTx85c2RURxzxybY5Ih5aihwspRFVnZElaX3DwiRL15miuN1OeLiIZ1ZEIA1xxx2iXKo+7GAcPNDb759ht8991v8N07VUS82Y24GUbcjSOGIWFImhfC87HJ4mWAni9rfHQ7Jxt0f9Fdfb8tav7ykJCt6utoX5u3545f156nrrt4fgOzrIqIEEAMU3w2Azlmrik7SKjStR6L6NEd4EzOnjPN6mVnPDEqDp2s79+SKVvdJ6+9ec3F0vEtdT3XrWH5++Q6dDBX/7u1YPmXLI/LxqUnqOu5488oz1ZE5DyjJqW2jQ/ShzIIHXARNRZw5w1xTgGxLktw6fJgXipuAd0dOMNQnlNE2G0uwCyG8omO943kiYtEXqaM+Hsu1yghfi2vX04ZldNCZPE4HQhwIGpj/fTf67+3G3D9Yq/JhZfcElwZigQwj1BX1mzMlTJLITr4qGAlITj+plYyNRg1LEQmGYCUKsiFs8rUpzfraxURWyA70ADpret0czaFix6oQFZV4JQGvipYpP3C1glBu1LHmgyDhX1ELGwnV8lCuG3IbO60ZKCQBE2myrmg5AISdUV262Dvv16xzQbmUokIhRFDQkoJJU4QijXsk4OkFmbdGBRBNqv9bMywvjYhmkVYKQwKXKUi7YOCeZ5rW1wB4gxwjAGRCLCky2XOmqxaVOkVB7X2HfY7DLs9lLERNEB4zeQCT+4hOJ1PLX4mocvgVediPd/dtl6LPQC8PuYKDh/xNdDgQLvnTfDEtzXWbpd/pH9T98bQZMvQ9RM0cWwgUgUWNARWKRlzyToXY8K4v8Ht/RtMj4+Ypgny2XISsM5FB+VdSVXfiQWFWPM2GGNLpLGEG89mihQDiFUkDMhQoduVOELKqB7zpB4FaMx0CAHZEkDnXFCYEZMC0mSJ7ouFk6p9CZj3UUGKOr/7xIvuttzGXBWJdeZI41F6hRAWc671va/vpSJV/Xs8r4c+P1YvAzbrylKUT4kx4HicUbg0QdSE0xBUKgyidaWY6j6hc0OTOtc15YrKEFCYLZQTmQeVtTtFS0ivHzJaBAoWEonBULocLBQQESEOFt7r9h5pGBHHPaQwIhNCTBjGnVrtw+XnxWIBKAKU7b0iEAXjkCDC2I8R+5yQjnMNg+fC1BAjdsOoeRYsrwS699R8FaOC70nDAPYkIJB6GgDrMUVbS+KWszb+pkzyeeP3MjPmrPueezKt17nPA7LxYIFFY+jARwLUqkzpYDJaK6zJTd35pufxRQTzNKMUXXuAeoeElJCG0cLWaR6dNA4Yb/fYv7nFLg4YYgKGCKSEw6dP+BAC/vv/73/Hp7/+gO/+h/+E3f0dxvfvQSlqUhlRIUiYLYa4harqsoaKAWoOlJKo58yvXOQ/TjkVwltZ81Ob19h/rnxQo5ntGtc1nWz/T5RzSoj+3FOg009R1v122o9L2Xarzdf0/Ze079IzvuTZ635e8klAQ2g6UKfS7m3evVdCVCUuKQgnDEgwvk8AEbJwRgYAe+ikFbhUqZx/mRLClRRVWZEt5KjF949i4SpJDUOYGCQF4soIFAQwoqUHBpQH5MHDpjSArwLzfVMEaERa35ncuMkUEYUJRYCpMJiBmZ1vsts7YNhRaTGZJEVCikAizW8RzKMd0vO5DLZVTL3n4TMLscpJHipTDboCDjMwZ+DDJHg4Mv70OOGvhwn/+sj495nwQxkxAUhpVOMSAoTYFEGkoZAgAEr3rt185ZYfxA3QhAGqHSQLod49U5fF54+0ztXK7VnuzuLKge4bACiCwCCKBgi3sDmweaH3WIgwyUCZTX7sQjKJoIZkMgVGHRPvDwIgNQMcdHabRzAFIAK72zvcvn2L9+/e4dt37/Dm5gZ3uxH7ccR+GGqycjUGIZ+eWteKL+q/1zvIpf1kNUqLskYR/17Kc+mo94HyvMpE9nKbUPO+rUpWanhFjKc4bjMAbXL9uXYu6C5Ox2t53eloSU/XV1e0uqXKaefuf72yfoYT23MzTTb+Ov21PLN97ks56asVETnPnSKCNRGpbX7+mk3YVCVE7DwhPFnftYqIVq57wXNMwZcpIrD57W06/w5bgNPlsiZ+58pLmMxzQOkvwQJrXc6tzbNM91dsy7lyThB4SX++Rh3nyiVG+aQdeBr/r9ZO9qkJg4GNtbP9/VT9Dvqea/d6EzmZF+6OGjU8RowFFRBm/RtQy97q0CbdvZ1uw69oipZmnatxz0NVRqzb99R7nlNEXFJsbCkhLikjfHUQOdlr87YUqkCoSMtvALurFyUc/Kw2IA7sGKjvyui29WoIJtRwN+ppwkWTRAOEBLW07QEvt+ZyRl4VEcUUEaj7CoWgRjTcCV1CilVWtECHcy7Z+lRDdnm7az6IhTJGPSKISEPEOGhlwxEtJNWcM/I8q+BWMqrCxsC1NO6QxlGnk4iC0dYzqD3cj7me62XX/vJeYdRyOxAcBhF/Zzm/3s4xQhWErzkPuvWANo90zvncabmheoWNiK6FGJegqD+5DwtV2xPFAHdCnrMlbFZF0zQXpAjEGDDudri5u8Pnj3uExwcwUEM4qaUeAUEQuvi1INSQM3megaDxiSOa4cRyzTgQDyBEi1rAauFt93pC8lJKR/tUmTLlgnluOR8GT4IXlK60fA5tmCvYEFv+Du/3plSS+t36rhf0T8d0TYs1p40AoSmfek+uUlSZJwACXEljXq/WWhbl8eZZeUCy+MqAh8Ej2xoYQoQQPXyPv0vLYeCMPxEhQj1MnPoQoSl+LY9Mze/gbSNXZigYQzEiRI0NQUQInmdkf4uYRsRxB8kFIYvmILEk1a54rWPifVv3OZsTiBhTBCRiNyTsRkYkjaHtoFOwZNzjMFjIN8tLIgIPF1U9Bmz/ICVKyzG3Y66U3eLXxMAqIkJAqAKbP09EQ+RlU6ymlLr13pQc1uOqqLAQHr63nwfWFPNxIKdvu69xEUGeJ1Va5qLKn2TeEEPzEgmDfoabHXb3txhjUlnBcoVMD5/Bc8afx3/G5+9/xLC7wf38DXZv7pFSAsdgGBxDyBVtBko47RY2TMU3dzLTWycUP2+5lud7CoD+JZaXtPWnlkuufh45YuV0jjaZZuVjV3VLu/RaBcLy988/T4FtWXLN/55TomyfO3/8ueWSXPu1nt3fu6zHwKuOL+4B8L696/mwVkY4YyjBgTZT1MsKePO9TJr3hVUDN9hxzEa9IkwRUb8tjF6ZARGYT5vy86TAoJhxBswbIqAg2lUAQwKgSnw4vK/t9CZqT3VvG5oyT0SBaRi5FkJhxeLHElAYyG775O+2GDpTYhQGmOAiWgqCuJD3Tj8E5yNfJo+bDQZIuwYsagw1FeCQCR8nwceJ8W+HGf/+OOHfDgV/nQM+oiCHgLeDGhQEChDSsFfKfIgpeYBuRJe/2TwIxP52t5P1pYuu7/lHnzeoc6fl2tJx9bxfzQvclQU6hjWZ9UIJYXV7qKYa/itXzwdxBYSHcuo8Iaibz1pVx6eJJ8y2uecJtQnY3dzg7s093r15g2/evMHdfo9bV0IMqoTQKC1bBmLbZY39ie/FeP5+JfilUPPXKdfu8dL/ZT9cilUDss5gRkyhR1x5yzobWdDZaHXF5/QpjT1pQT2/bOH6TU7fbaPefl5u3FtxhzPl6v578rJenvV5veIpfC/2tbPeezbWwub+tNm+l/Olz1NEQN296+YlzeI2mNAYzW3brfs0P8TSE+KahdtAAnenPrmgUodL4MtaEUGkGuH+nuUHqzrPMze/lq9V/nYErb+ncokpd6HLXRn7mPHYWEv1HpzfdH1z6Z8PkbrJL45fqKPd25FeIRACQhgAZ6lDVAsLEQAGEHmaVt/lDNQNZMrUNBhgnsyCf7BQEknBjlX7tpQL55QF/WZ5XqDZFlgcwNykeYu6Vh220da1AKchYrbpqoOwfVgPMfBH6a0KDswaJsdBIGYFxUphpN0AWBLZkJJZ6hLG3YgUA2hMoNQArZqDAhqPfxh3elzE9iFPJgykpOBqSsn42RYKByATqDSmeHAf7dolLbwMlwLOFopJzLqfNaxTno7I0xHEurG7cBWoWWZTteTuGYJnMqwuQLo0iTZXHDTnagig4169hLCci72ltH8zM3JeWvb3c6IHK63Grk3OTJ6+l9MHj7+65qD8/uDIt/09jqMKJ2ZppYB3Bhe1qE7jiDSOGMYdKEVwIMDCCCQKal1uFk4eqkl8/EsB5YySM0ABcbT50M9/A2RBLle18BYxBBRTvhRTkimoHAFRIN+VM7vdCOEBkUwJUhhcROdkIHAWSMnI82RMtXpDjON40u9OEwORrhlTVrRr2nswo8bmr14mLmQb/aYoCIhIMuhgULAkkhoCIdj4EjQec/FM6GKhmSwkm4i0XCk+L3UZg1KwkGtJeT9T1FRPGLApb8z7Ig5ASBCaYdENaigmVz6wtITKLAJQQIgDgilwxt0tUgo4HhRID3FASOoJEdIAhBEUGXHUXC4hDZrHwzx7CUr3JCgQAJiwSQEhCigIpEQAETdjwrEIYpiqpxhE50iqipfmGVaTelPn6RIixPpGlQ/N68zXZ6WzneDWixkEAqmjC4ibZ2Jbz+qFQKTfw6ieCL7OvSjdDgZOQfucQqXpTnudl07JEm8bxqDKw4BhSCroWGL66TihGI0ZdtY/Fu4uxQHR5gUFQIJ6LpUgCIHbM7iApyM+/PnPOPz4ASEE3L57i8P0gP39PW7ff4do7xYCgXaj9pdigMge/5rM40d0/im4E6D7/6/lH7lcAqnr33DW8LzxWs8v/b342vTK+q0+WivHTpVlq37Z4OXPHX/N8trPvtQXWhaM5ckzmje3yS3iwBD0mxuPL4RqbBFJ+R4OpKGA6iO5Ggr5Id/TajLniuv2ud2Up2W2vdASCZOosanuYRmFBCDNCUFiBjj5CCozAs9IYFAXo52k28zQNah1lu0nYdVvSq81zbEqIpiBZDm3MqvXXu5Etta15tVHpB7aAeoFIdpmmLJFfxt/2O2t6HjnrXE7NVzpQ7cRouheydBcVHMBPh4LPk+M//5pxg+HCf//D0f8++MRfz4IPpSAORWAovJeRBZC13giKhAVprRDIFAlkP/tA2rGYK4kKMYbeq6H/rUW2KTJJlzqPKzX+B9UexlVoWBe5lQ9cNqYOn0Ux+d8gFxx4flISu9Z4X/L0hNCpA5uo6cGNJN7wwPVO3wYEYcBt/f3ePv2He73t7gZdtgNagSx22tuiBi7XGhn6LTzRF8H9bum1qeu+fvYXwDjVY3XZlMmZfYQXdTGGUvZ1HlcwDzGWQ2gPF6syFp+baWbWvobpz16qsRY721bZ9f3bntEPHfPEU+K0ikbzimyW6nS2bOetXzueSzrmuPXlusVESUDgMYZdCtY4ETwcQCiT1R9LjH1VukZmaatXLp3Aj0tXYKg67p6RcSWEqK/lwysasexePazLZeuJmPraezH2mI5x/B9SVlPnpfWedrvL25SLb8kq6+nLNEunX+2tvzKMblU72XLqqefvwVAVyDLw6l0IUScAfHrTsBwXN5WF+RePDzQdcVB2WqcYQyVA8QUorETClpDXIFqSIUrJJzUWIuJot5r4UX8m6IeR4zqLt21e+t7S9A5ZxW1pYxYh+fo51pTRHQWejj99l4W3RHrxn6+P9sG37fZi1vE9+0mB9LIel6aIqKwhj0q2UKZBFJr6pRAMWjcWiIMaYCEgICkw2KzppQCSfb+ISCNI3LJCKWgGNDEwhYLXAE0VYgL1CDYiWgd3uo9sY70SXY5FxPSiopEMUYVzIqC2WWekShqDgG7k8xbg4KG/rEYMhZrv2ekuzadKy6QCqoV/Xqcat9LX++qmo151iuTPMQQgEUoIJXP1vO23V+NBKqNxbJtThtCaOez53RYtK3N65QShEeUUT1OiAK4CDirlVxMSQHKYQBCMGu4ri0eko0AkWxG0AwiDdlCFrolyDIcVddwbbsZddXp0tGzPra+G194vxSbMykNuh6gglWej2DWEFNEADiCS6leNxq6Ui3Ei62ryilL83CI1DxKve3KhvXCsYUvspFxn5RKE0JQ+LUbR/XcgYVCaOELCgO5NIE3mFKRDOhdl2qYYu2ovJ/3q7fD6G0g82RIAwShhmMQoPKOhVFzOJTSQgt5foEYAgZTTsYQcAxHfX4cEJJ94gBQUu+bwfasEBUw78PK2f7mIbj6OREkIKYAgXlEzJpTIVj3E6DAetB8SS19nP/zeWTK+6Chpfr90teK03ZP3I1aAzrpieocdfqrc5c6njFUD4WUzCMhxRNFBCggEIwmGC9qAmFf3IPGvZwhCvgI2C6nur9wKap4ZqX/sQqOwTyFTEHloREIkABwELDlY4oxAJkhmfF4/B6HEEExYP/jPdJ+wO27d4jDDcabG4xDMrqr9LiIemuUgmo163HBBRbvvPIAr8NPL/vq9ep77bZd84wv4Xm/dnl5f5xv6zmhfsuwZKF0WP/ujkt3fY96XNv+c7LetWPylHLlUh399Vt86fVlwxDwSjnpWlno2n4694wvWV9n5TP77mWZnndyAwMHatcygfMUNfQfqcwirKFvBAxxQw7jg3o5q1dKLFq4aoMYnawfLqAyQ0zZQKKJhAMYRBqKKRggLWUGcUaEW+TzgiOsHhEbfdTvhbUPCQBCdUx3jwg1sFCjisiCIoIondG/88q26goAJgKCRY4X6by3DXR3bw8fA+t3bMxNb+8lpUSQUIdTvSFUGfEwMz4eGX85ZPzlYca/Psz4y2HGDxPwIAElan+2cTZDGDPzkMjWfwIF8+3b8SFXSBT3WuAK6It4Xo/aSZVXbpNCgDy39xbdjHXPZJtA0j2fQcXC0bInRr9EU2qn1PtPPtW7wq6pckHP84ht3tLq9R4QzWFFMSKMI/b7G9zd3moopjRgiBGD5esazFtV6Xbf7nM0bltec35xqzxJT3wMnizn6pdz0/TqveKXVtQTyDwi6lxV+c29JdpUbomsmzGWzQ//SMtN0+3Eq6f6Gu5odHf2tOtOeYO+1nOgvU7b03G4fmxaFATp+uZSHWu59uyE2bj+KeXD11BGXJ8jIisgIwb89IqFEIJ5QEQFCoKGYlIhNILoOiVEXxqhP/WIoG7CbTKBPShqrmJNEPdwK0vCs62UWBOrX8uv5R+r1PVgAEufhL4ykd1a7O+rf+PytvslhM3rDQYetXv0qYEAsViCQhEseeWCa+yrdOGIiGpIkDgM8JBMGi7EFBEIi+eda+vaa2FLCVHfpaOnfr5nePt73QNA79volxUtdKvWUjoX7E4IW4SE6erpLRD8dzEQ9RzNVG+CrHmEuBjew6aoCLi5u8Pu9hYSgAJBZlUoeNz+CFJD1RSaC6y0JFUhjCg52zuJAc4C94zwfD4KmrXwU0So81cjq4oBVrCwKhFDGqoSRuPmCmAhZXJhTFPLDxAoIJK6CDORxn8fBlVCeLuBapWOVd+eLUvZYfuSnllDDSLWzTVX0PFi/Lzt7mXSwvT03gG6dhxY9FYvQZkVEFoVAa0NOh5UQRlZ9YGIWB/PCszPE/I8IecJ8zwhTzOm4wPmw4emdAjAsN9hf38HloLpA8DTpMqgYm7sRGofKC3hXoDKU5ILOJog1e3tPYgjRSzMSwd8A1V5EJPyNGkYan4M9+oJIWIcVRFR5hlMBZIBBMK4H8ElGv1hzMY30X6PcRwwDgNmGyMWqTk4mtIjdOvZQov1grxICwUEdONOYGQbTwDiSbgZueSq6Oqt8FUJpwKyKxhFtA9jsgTUzgPWKSFVZm5zcKm0JqiSL0CVOM4bhhgxILT5bKC3wIXdDM//ABCGcYfEgpTUyp6SJp4W4zeH8QbDsEdIO1CIYCj93qXRWibIokpFN6rx/BhgTWwfBkYUQhIgMIE4IkjB7X7ELIT9cNCQVlxMTi8QDqb8Qn139Qr2vRLVGKYPjeVrUJUuudLYEJRn1V5hzW0A33KbYsfpd3G3diKEFHFzewsiwjCoEm8YhppHRfdsWxfc1n2s+Z/0SDELy0hxwevnOet4xabw0PHNprCdlcbYOocIIgVVOJOFvysFgRm7GHG322FMCSloGL1qJSlARECQgsNf/4L54wf8t3zE7v4e0+fPuLl7g2//6Z8w7HYY79+okcAwACKad6TbJ6X2O7BOCP9r+bWcLcZALCCqju85lW9/nVtfWq7FC9b89XPuP6cYee5z18Ut7Xu+oiqkbB91oO1UMeAfIIt7rAqECRHGj8YIkoDoYZDIebPmAUBi4ZOEEcA1LA7nqfHozCiz5nzK0wTmDMwHs1qftS6eVfVBBUHEFA8M4mJhkLgB3qt+WegY/De5jY4guLLA+OjqZQ7lNwJBFdPQfSSAwTCPCBEL02T9ZWAlLGpPlfCkgDnDLaSrh6KDeWDjbXq5cDnOl5QQAMzYCphFQzJ9PjI+z4K/PBT8cGD86YHxb4/Av02E73PAUTTDBqztuTA0T2HQ8FZR81+RQAF/IkDMQ0KFiiWJcYGhB/PFcn5UjY2D/N2NIkCeuntbv1TB3a0txOaWh3+yuqUmo/aQUs1bQrhr00lYJ2mfkwXkx90Ew9pW+UsCLP+ErpWgXp+3t7i7f4M392/xZn+D+3GHu/0eN/sdxr0mqU419KgrdKh+NwpPlV/7GuXn3R1+AXvTQk5wzMWibFTPJF3PzIxg6xvkWEbDH5RvDyDS8LKFeTGNrynr689vCRsRL3CpR88rja4vW09w7OU6nOzqJ1XFTGv39vLcfuZL23K1IoJL2xD1Wxdq7/HgnhDugk1wC8VmYXaOabCzpxt3BVjWV65+d4xgD6opcekyrNMpA3FeCeFturaXlnW+4vx4slyy2nnKgubXsl3OWRg99fs1y3PqPjevz/1eP+NcndUDItDC0wnApkfESR24QKg3ni3d8XOa5J4ZbKyDWsJ0PDFAQRndAKjJpRHaFY/hfweYK3OwZFZxqH2gL+Igs4FDq3ZuKR1eqg1fM7z9s5aKiO3ePbWOcGC6ebStad76fXpFhP/tYGUFF8lcK/057u5dLGwS6cMJOl/G3Q7DbmfwuWgSX7NoUGtiql4Fymq2tldmJSbEmCEcoV4Xyz5311sKAcH6C0ANheK5yBVsVkbGE8U2UN5AUwM3HRxex0Wv/Hrw5NtWB1AVBPXr3LjL6k85nT/bY9QzOr2w5Lz8UrjlleDr9ZwIW87o2Nt5XS0kkDRFxcqyuz1fVq1avbIBlCVr7pCcM3LWhM/+mY9HHB4f1YvGjAjikBR0nPcoj48Qm4+AAJZ02b1UfN5VZYoJUWtLMR9HF2iZy6JfVOj1uaUKF7cun0uuih4NC6aKiD4HCYgQ46AK0xjAxfNpRAQAQxo0Gbsp+MQt4rv2OdgLNEVEoNO13+Zeex/Jjdn3dgKaR6AfD1VGaDidOkdiMHnUhV9bn4Ru/q9GWbpzPVgHfTcEF/uWwkSvDDMbUPgcb9NTwyshAilpeKwaBs2UxjEOiGmwEAcBIjpPh2E0+tQ8unSOiNGeCIlsHiwRIQGh6ByK5sk1Dgm7AgxJYw2LCfg+nyGmCLCYzwslko8NeQLv1biJKkdVGaXgBPWdar3S055+/61rmAAKhGE3Wq4kC5cadR8X8u4KmtiytcJCrHa5e6BzIcB5faOHpqhSMmA+OGKKaE+E6nWbyyLBwpyJWLJ5BSUSEcaUqiKi2P2aAwaa10UE+fNnzESY8xHj7Q32ux2mt29xMySU2zvEmEDDoMYChnlY56JxC9SYkhfy6K/B6y2Vv0/X/ZoC5y+xXNunL+6HZ+BKa75rgYF5dd26Wxzr7idq4RJfOmPEGYJntPmnLudloy9v13PmxUvW5VeRg2UZnqvyV85z2OccX1b5rWr9LkAglAKQBDBBP0ww7N6AeOWYiTWZNImGTFJ+p6iy3HK1aSimlrutmAJZcoYnFK6KCNFwdsEV4hDdN5gdL6581kIRAQDke5ZvVf3f7lHtvEW379h6ZQYQ7du8JkEWwlE0ZBNbfiCGGk4gaP94n7T+9b7yc0Z/yfmAjaFczauteVZEAAYyMzIzjrngcWZ8nhgfJ8aPM/DjDHwsAZ84IIOq0gUQFEHz0jNCRYFASSClgMS9X005D2odJM2YDj3w7zkXfM5VbxBq5ESk5mtAPz+9J6gfEnZBTJ/p3hDV08ECanVz2wSZ0w+679MeX0Gv0r4XhLjzLIJo2N7dDrvdHjf7G+yHEXvjKcYhIQ0WDth4CkFpSo7+fTu+lNCdotMWrY9fVair+4XlKWzv7HVtyrxaeR6/IpX/9fHcwl+J1FBQlRAWipaa8Sdzo5trvLfOKnnGe56VVdf9vMGvPfHe1+5/5/tx3bJmnC+Wl+88rnDu+NalLmv1BnjncezXVEZcrYgQaVZevQJi+R0XOSGCWXzZa53Ued1ius4j4tzH44V1tXUL4bQtROvfz+9U6gjN37fo8HXK37vA9bdQfP1U4Dc1heM61Jp6c3aWsc99jnQsuyOoG2UNjjsTsljPHoeh7kb9KmSYRqI+K7hFav2t75QszE5I5iLbVcvGrG2Buev2nlNEbPYD0Vm6dFrfcnycJK77yO8vzGBhzBYeiUROntnXX7hZzrvyYQ2Kn3tft+YVT/icFCRMw4CQEvZ3N0i7HaZ5gljbPO4+uIClINGAXRpRpIUpmY4zYkqISaeIJw4nMIhStUTWNviuoxtpsXMKaAO5zGAwKCcQRYQwaBLylLRv0I0xK9MdiTDEAIlJGQC2/g4KpO72e+xubxFT0vAuBkRHuhyH3IEOlwMWSokNpsbBDfdoEJaTPa0Jey3Phn/7ed23t/dM6RhEFgZKX4cJRca4tOf2c9UtVzql0ApEL0XDdU2Pj8jzhOPjA6bjEYfHz3j8/BmfPn7E4fP3OHz+AYgKAg9DREwBt/d3GFIEHw4aYudwQC4MFM3LIFHXeZRO+LW5Ftgs/UWajEXKofvcz+weN+2cr7UUE9ySXUTDBjEzQkqV2oiF/BEAKQ4gAEOExneeE4SL5oQwIHZImiei5FxpUu+t4kByH9vZ81T0HlT9OtR1oIxlLjMohJozgEgt0ud5ru8FwHJgSJVnTbeDQIQCBrFgCJb/y4D0IAo0VNCkypnaHlegRHuGK3R0bmpfqYI32NqTqi+u8rTV5+HPUjSAPZmHk9UVonqpjPtbpN0OFJLWzUBICcNuD84Z01FB/rbWPMkxGU0BhgIEZD0HNmt6ws1uh0IDbnefkYvgyBlEGnosB40THYOFQxoShmFEGpLHruvWaFj8hjRll69ril0CdWliVl2vrIomCgrQuMeTsIW7G0cEgvLkltC7hkwzfl1mzbDpfew53vp2igiC+J6v4zhNmgMiYacKF1ObuBLCOW/zSa50NYSAeZ4xTRM+fviAv/z5z+DjBJ5mUBqAEGuOIJ9MYoqMYDRo+uEB84eAfzkeMd7c4NOf/ozx7g73v/8Ddvdv8c0f/yPS/ga7+zdmSKExg1tSzJ+fx/yVz/2ZC9ECCLkIIFzg47Z4oc06XlyWsNxPWdYGCv/I5SnA8SX9dEkRwZUPdxpoAXtEUILhw9SAa7UO93j72WhdAXjW33mGZPWIKDkjZ/VoyLN6+c7TQQ2IzNiGim7AxGrhHiSbR4TU7Dpq5hkBikCU2hyVyzpA2bBv7ULzskQXyhFu7NAlO5a2f9SjRLAdDpY6W+uxrq9mFaKYFYt7VDYDmlpIALJWypetMDeYOpaCqcz4eJjx42PGj8eAHyfgMxIOkZB395A4Q7IpFEqGMJCRQaLjCyL1iBCX60xmLYLiOY1EoEm5Gm8LfzsRbY34XucKBE9o7a9vsrYlJ697YtdNQsYA2lu6sQVVQdhuqPkeStcb3obctcO8aUxh1s+AF5UK7xHiMGDc7bHf73Gz3+Nm3OFm3KkSIgXzgGckuNeN/0+LymijLY0XWQLeLy0/DzX/eQuhW5/AAuvxYSQyY8SKJ3XKWojlrHHso2EUKmN4TVras65T/Fwznlsk3g99vTE9t/8vVn27upMDL7Wr+hpV3ubUsNaxppN7X1EJATxDEaGNbJqrPkRLHw/YY79SMLEkGNB4oX1bG3w75qDbxrnVN9VNufs0SmXX9kqGLdDvdTwiKnOweu+nrZ9ej+l7alKcWq881banyxY4+ZK2XVu2iEDT/q7G9+zdy3Kttvm1733uM55brhnftXbaPSGW6723rHUmmBo/vHzoZhtouaDbtr78Orlv+Q6dV4D9T90jG8ZU4RtUv11vcpcsrb5zDcXUQmf01k3Kg8lCOBWRreW+EC5eOm69Vd36uI7FckPq+9j/ZrMKcitUz5ux1SZnNh0Y81wJ4u+5fqai1vW+9o0Fo+HzJ40jwpCQSzHA2sBVs6wRLoii4T/0vVWYyFzgFs9eAhE4BI3Rqm9q78DoaT9b/FoVPDR8CKh5WbSxt7nQg6n2CVAwVYJA3P2bGUTq9afA41Cts+u9ymFdVkzL8nuLflg3V0FVfHxEgVIIdX3TFBE+D/o629yJi9+bTZMmyDlAunyRJbOyWKuiobOaksMAegPSc86Y57l6PkzHAx4ePuPx8QGHwwMeHx/VIyIGUCSEsEdKI8ZxRAQwjCPyNCEfSPOFcBNYXeh1utDeZSl0GR5VzysA0Cy4fe07HXSehz2MkXhuCAV5fUmwOEgcESC6ZoSrlXxMqcbJde8Ksnj9fal0mJZ9LDYhfF5Vrw+bLD5HCgty0bAKPcDcK6Y8ybUrBnyt+8iaTKDvY+ufgnmPmaBbFdHSvUC3rjx83npPYE8s2Wdr7gCZHj8gs8iPBqjHZPPbxoksYXwczCMiBIVNCCDS+1DzYPi7rdaFK0wSAxIhhdS80njKlCIGFowpYUgZs1WmCtXmxVLpXWqewesN0khDKytQyvtvIR5bCKz6W7wSOZnfMUUFi3rPDJ9n5uGBstxbdK02wc7nEYkr7vVZOWvi9jjq8/o15mvH5XfPWeLCpirwMo6PB3z+9BFhLqDMSIPmUokAQoqdgARVZNh6KcdHMAQf5xlptwPnguHuHscsuH3/iJs377Bnws3dG1WQhATmggJNqk5SPBy28Qz9HOhGZzFX153uI/h1y08BBD/3GV+jTa8hf1x+wMaoXQEuOx20KhY1nJcpuv32VbrqmkoWhGT7CrvkqeG79rrT+07l2S+fKpfW2pl162dfeU6tb98Eps688Jr/czotmx9UnstpIAUBM1koUjLlu9IzTXXXe+U1EFrMMl5DB7q3muU7M97ePSSYCzIbYGzWCGR5ogKrJ0QS9cQU29PJMBfdLjTkpSfYdj5iwf+S7blkezYAGP+67i+CHg7QLTgYr+afoHf2Il0bGGVmFvwyujGwneXMSK9bsvzZZMs2lppjq2AuBcc543HOeMwRh0KYJGAmgqTRKpgBYmAWNb4KOr6hTnWXp6O9aNCwjGyCR8W2uuvRNcqZppUCoHlMAJBQ+6glh+4soF12qUx17xGBThGBVj8WliNo+Sy4a4+Hkq2cNU5Xh/+qHdzmmN0psHE3A4+QouWR03xYQ0qWj6oZ2jSeVmq1ffddpg7bWOBarrq6nLtWnpqVXV9VQq3/fX1OoZWn6frpXrA+qwasjX+svK4rKXwamSzFpHIGQcAcQMSNxni9dDJLOhnmtNF1f1/0+xJT8esWv332ntnmLxo29P3wJGZ4fj87V7Z5jzWK1b/TOWXEJUOE5RpaH39OuVoRkdJYgYsQSHNBxGDJX9YAJdkmA6ge60LZoAC0Uh4QrVzmzJKMqsJBxRyE9u11L8QIE6wqcNp/9UoMKwLaCH1wbSefTuTLRXC6cJ/6/TrlS0DSl9R17QJ91nM3jj33jZz2/ZLLWU8eNCBqqzTeQpb3UXODIzTFgysUNR540DBFa08IrwvP7+vFxtGxI47MqNLTCaG+gTPnbmndF7d/F0OXfONqFSt4E8xDqrmfqYbdGZUaLsOCyvt1i4nRMdj95qbhO+VkHKR4YjRrjjPlhjiuE9Cu+2kLQNZXauE9eKUA0PfREDMsgnmaKnAKASQmAISS1XJVL1emWDwZtSkF2rCQAvDepZVJVACY86wWuSQIKSCFCEhAmSdrF0OQIGOEpAg8zuB5xuOHT+B5AvFBvTY4I8qAEEdECBIbiJRnmyuaQA/MGuc2z4iR1BOBNSEyhahxyM0yPZs1UDgUncfDgFgGDOO+WgYTEWYpCBTVWh3AcTpgSAk7Uo+JYX8HxoQiM3KZkZkxDCPibkQYB2WGBQiFIQy1OuoVXzoTsVWCDilURlOBk4K5pUqTIYBOeVMsjAxpkr8gPkd8vijguNtpPfNsiZ87w4HeIs/XHAVCKRqrnmyOt7wEhJS2XO2VccxzRpU4AQTMNt+TzWlr+5whc4ZMGeU4Y358xOHhEz7/+D2Ojw84fP6Ew/ERj0dG4QksBSUzbvYZd7sddrc7HN5/gzAMmKYJzGrZTSLQ2a1W3wiaCLkBsmSu+wyW7B1l8Xc1XJFwAcGt9LVbdmnELo3IlpR6nmeUkpHnCSyMGI2ShcGSPGqIMskzQiQMww4cBDkGJAyIdAvmDLZ5zZwhVMwKXm0NU0oaJkcEPGveFWYNkUBE1VKQ3QPDco+L5QE4Zp2jR0uujKgepiQFJRebTwYFuJzofJAHsu6Y+UAEGM0c4qBeDowaYksgGHcj0hCx2+2aAKiEzupQGl14VpoQNH9MoAghhkdxZgGKWLLjYYc43mB3s0dMEdnXuQnsDKWh4z4hDQPSsFPvJqOxMQApCWISo4MzBJq/JlBUgd93jOS0kyFSQEhACsgCcCjYEQAUfHu3RyTB9PiAUgp+OAgOIkjMuEHA/UgYd4TdQBgi1LK0ACim6AiMCKVHkRgRsPlSarixqsQWQtDgSFDrURMCiCEEJKgnxmyWiSWrN01KqfLTgWINH5eGoe61ZOshDcnCEUbFPihWTwuIYIhj9XTmUnA4ZuSSQXt9BoOtfWQ0dA8JATQMmtPj5gbjfo/dMOLzjx/x4V//DT/+13/B9//7f0UMmm8n39xgN44Yd6N6vzm/EaPNmab8Exbkzw8onx9x/P4DYhrw8Z//K+6++Qb06Ufcf/cbSP7PSLd3GN6+A4UBIYzqVSM7AAWMAoP2lnyMiwkCNzytCkIJjU7/Wv6WijP41A30mSs3EGeX0HzfO/G2r/YRRjPrfh3asa9anlv/08DHa5enxMzL8tfr9t+TABAtv897fJ8qEpSe2ARgi60PgXoodOEhofJPMQOPYqBc8PMmOzAxhEkVsSEgCyNEza3GRIhB6a+4wkE0t0+eC+Y5Y5ozjjljyjOOOWPOGdN0VMXDrPswi3ojS55ryCZhRpknQAooZw0jGQQpoOZ0Q9BcfCEYv+uwn3T27hUXcJ7Q5VbbmxbUd6m8qvKYmHFHldOXAjuJ5zDwfAWMIAUk2UJ2BoAi1GynPT9Ssnmp3o/wXFVedd0I1hNAPQW5CHLJyDnj8Jjx+VDwl0+CPx8I/3oAfpiBSczDLw76CPNcHIgARPXyEAbPR0ACAiVEAgYEIBAkJeQAFGI1jIAo/WHNKSGhNHrERt/cvsBfxhVMlmxabF8nKSqfupdzBQu693alQlVuCcRCfgUIxLzZkWdwyaA8A0XnjHrjTOb9oWG/eOGlwRYeSgCYB1Aorc0+X0R5Yk9mzNCcYBIiEAPSPmK8TxhvI4abCCRSzyEGUgZ2BYgEMLIFZermnDgOsZynOq/sfKX52CQGC0zkDKGrNGfz7HXlnPy4pttLtQStfp+266cweHBFm+OqRbpE7daOEAMiq4EcM0Ny0QgHScADEC2McpaiRkw5A1HDpKqhoMqsucxqgEim7lzt11XxsKH4WSsdzpeGMxF6ciRdPet6T591Dte7+OSqMMDimxeQVZ8L8dz7SP30Sojr+6Cv52XlakWExoXtQrWYZVoIfdzY7fAiwHmQtAcfF1d3v0+ATuMEqSo9PCG1W3c2RcSiczrwdVnd6vjFSfD1mDRU4tg97aStl2t4DWv5NYN27vf5uoD1pLxW+dCOL8+/5L3OtfcUjPfjz37E2bY9t71PaUufOq4a5HWlfvKJh1Nbn733Q//Z9IS4pjyp7V1uq2tPKK9CjBFgViBtySQ2ZqL+QUsiqrykVuKa3vaU8wR3qR1eHQNaImJpxHtNTxbKBHsP6V/qzDNP7u36iPyb2nVsAo7UesnC6JSaaHfx7sbYEznY4gynKTTsQ2iKDXLrYrT3sZ6ollV6vVnPMmM2q6vgSc8UddTHFUZ+PICLuo+LW5hDAIpqJRSoAu7MGv8WFvZIDIzvXTNdOCKQ5qcw92sRtsSroSYtrfFOK6Cpa4BiVKuxnJECQVhBuZgGSGBQYDBlhUxj0FAibm0sbnW7MaFozbD4mPqA1+HRNSnL/A39dw3LxAIJa6ak0bjWL6QKpnpc13NTQtRZZ3PXPSG04po4mQghNKVd33ZxIF/E9mMBscViDd0TmDV0V2FIYXAuKPOMPE2Yj4+Yjwfk6YA8Z+QimHNBKTPGYUYkwu1uj5gU4Mwl63gFajofb5f9URWBK3CBq+eMznu2ZO5S2OZQGwtN4hsgMlm/tzwouubac0VU2VmT9cFopwXnDzGAKGlOSCk2j034Mos3z1ui9/l4u5JE360m4WaLm9oJWALLN8CCbAaHxau30F42tFXfwD1N6vgnEakhdvwmbZtZzBMgZjHnbdbwTSqsVyrn/CHZs6olpFtSmsALp336uBATQtQYwClFyAwLW+HWTsoHxpgQU6rP9zEJgNmvaAcoheE61wN17ST3ZCFQJGj2SALiAOGAGARDJOzHhGmOiEFl+0NhIAuyAUohKkAUIyH2EQGdo7WOJ4u9TQZaSb8ee77M/rWsEdLkYpjRDDcFWAjRBL4mhPUJtNXVvavfaTZM+U/apyHoOHj4VbV0JZTCNZcFV3Ci0R3N4xFBux3SoIqFEFW5IDnj+PkBh4+fcfjxo1oyxoQEQmBNTohUQGboJKYwMUpuc0gBEC6MfJxUaXs8QuYjPn37DpAZt799h4FnYD8iJgENA9RDJta6dAx8T+/5ke6vblmsDHfr+/5aTss5j8ufr6w2ACvnZJ3L9fSSqRLQy7LES+fI1+ivS3X2G+WXG6mtb7/kefkay6gfg3MA25PvtJomtGLcNuUB49XZw4BWftr2GbM8F7HQNh3d6eUHY8wtkkQDiJjE0/OqPgMCNq9EVXN4/jfbN2sIR/twqV57hYuFYcyWD4vrxw2QPBecGyVRLmp8HgQUlbcWs57xPVY7KZwsgH6lVFlz8a17m/jAYTlDnRVRJcQF4NB4ChLNkVH3WZvTNRxiN/zBd1Ra5RFy2WYxF5b7MetQmbd5xpwLponxMAs+TcCnLPhUgGz8CVEEBVbsSuytiWo+C+YCKgxi3e+itVUogIPmzYMIJLhnhDSms/K73cT1d+j7pyoUtK+rsV2fzwl9HZ0nhHs8uHdEl7jc84/A+HqwJ7Y25Vv10vHxsLaYlyOq3N57UbjKKJiSy5eh2HjZu8eAOESkMWouiBSqvEGiAHgUVUoU4m6cuzmEJmstZBo4HWnjv/Zvfy6d+dI98FR+3Nq32rOrH8hX2XvP1bl6d2lHl73X/naPCJdLfazV48jmGgE6H0z+F6le1VTlpjbHGqAeTzpuC1/pz1379nVObtz31O/13LlGKXSKB2Dzu12zUV/dW7br3GrrNW16SblaEeFApIcf8G8/fim0g28wm4A/nS7WE43k1m9ywm6bixGkdTscOF3Wdfr7V0GilbWG7vkeEz0j+6IWfMG9r19+Km3x1yxO+Nfz3UGhYGvKLaVTSgYmtNwQ67X1U/ZLYxAagOpA1ZLqVpbT3nm9MUtjeGvdfk6BewUS+Wkh2hg/MbRsCyz2737DcyjJEw319LO/7tTKCifr0o+XztvBQUsAauEkcrKGS1FAOna00+v0cEzqwSAtXFEVHdrGq1bLGVlaHoka07yo4FS4ha5RsCnqvzCA+YhPP/4ILhMCjqAYEXeDgpJgTUx8e4PHB8KRZ8zCKFNRgM8SSBcuKMcMgmAcFOgKJnCMKapHCGsyPrilcWYQCuZpBhCxuxHEGHGz36snUIwowsiloMQIEU10HYYESRk8B7NUTxiHAcM41vA6Ng0bKFf/e5oqNoZXa1korLp5sU6+V8e7dHOnmy/SzQm/vp9b69wRvvYBi32fSwOXk7k7G80I5onoyqJ5ztWaHCIoMpnAs2xLzhnzdMTh80ccDwcNw3Q4YJpmHKcJj0f/HGvYgEM8QJgxpIBcZhRhxBCwv7lR3dY8g5iRzHxZk4ursMViIQiyegNQEE0YaACqh4xi83ggAUJsuSEWodq6vospIRFVDwBmAUvBcZoAZux3Qw3n1KxjDdiFAKxzzXOrcFGrMI3mY33m4dGks3Q3vkhENMk3m1KFNGkisyAX9SjQfAhk1kcqHKq3FBzCqMkee+Ko85mt/xxoTpUHI/LEx7p+CMA4ak4EpwOaA8IUKmRtILX0CyGC0oAQg2EGuuaYlb9LQ0KkhLRTD4f9zV7z9hyCeqNYUm239t/tdhp+KkQIaexqVTQ0XpBFQ1XpR/NzxJgqL5pLhnBRzwEZAWQgMHjKECYVamPA3c0OQoKbHyIgBdNRx3ue9ygD+YZb8w41xb6CDCGSLevzwtAWTws0YCyGZluqoSEEJWuy8RibYEYIlT6teWKnU7rOM2LQsHgxpZqbhEAYoo77PM+qxDFtq8NIDsAxq6CfhhGUEtJ+j2EccXt7izENAAuOhyM+/PgjPv74AZ8+fMQwaLJ2KRnzbsS02yGlAXsbT7rZIZnVGw0Rt7s9BMBcsnrwHSfjBQiHwxH//P/5/2L3pz/jLz98wNvf/g6//y//BeObd7j59jvEcYe422uCbPd4QqhhtYpAgcAgBhTpsmLrNjZtZ5BLPqi/lr/38qvI+LdRetnBf79WOcfz8yq8kQcObcydh6qRajwkQFU+VKMhdg9BDY/DDGTSXAQcCChZeWF3jQxAyepleZxmTHPGNClPNU9HzHPWUJY5o+TJwmOqR8Q8z2Z8M4NL0RxApWA6HkDMCEX5bkpKDBNFRE2Qpvxi0Hyg3tfPlg3JLN99vIAWT8NY4GZf1iJtVP6uJk8+Bfr60ISnuQ5h+6x6GhLUa0Jc8UBQA4kKkAM1hJFNpSMLPpeC76eMHw8Zf3rM+JdHxp+mgA8lACFBKCDKgJECHiMAKphzsf1n1meWBJGAHNTaf/CQjrbPR2Jw0Bwh6kIpQCFtc1VKFFNQGK/pMQilzTeXEyFSPSSqy3WfGw3AwiMC3gWmIGFWLwcuGuKRzTOCXSExg0zuqgoH86DXZ7tigtqyANCUH/asTknVxCOtJw57pLsbvLl7g2/v3uLNbo/bYcAYzEIemkx8zhqelANbfa2uNa6x/vspi/Xn/P65scZzWMILa7v+Ul+/RJVObBpaBkKQtj773ITi3jwkmpuRNNcdCVDMmMjXbAzNq8JeEr0EvvXsaxUAp8f78xf4+TN1XsJbz7Xxqe/Wrko0Nxu9gM9e0CeX2nhteYZHRFgIUz1ACZwBOL1RQNN+rwBQbC70leBFS4a/KiaqJ4T/bp/T65/+vQk84ssg9ed6E5xr47XlORPg0jO2NHTn3uX0mQ57X9++XwbQ34ABYPl+PWN1bb8968lfuDmJXJqnPr+3n6khTNr63vreXNdyqqA6pxU+be+aWdw+vm7vyTO7zaUBvzb/iJbT0A5Xi8on2nXp/VYVLkDirTpPCLW3eHV5r4zY0pyfq7teb22pApEwttZyHSe4BSidtGX18MVbN4b8NNGeg18W1WmRnJaC2/VaLg6QJsvLEyLNCBBEDADUyjYEUlBziJr02ixgXdEgNp5qTa4AdV0JZJbnovuXcFAmXVAtyD1cla4fQrKQVSEEtTKzPVysPl8nut1ojMpgoZ1Cl2/kRGF1sWv7NWV929Gb9bAs19iKCXGFhB33UInr+dQLzK4Y6JVh67a550/wRGI1PKKBnZ2dSw29ZF42YsIHu6WetcWBz3mekfOswrEpHBSUX4LzXFxxJDgcU6ubCDFpuBk2l3fNYWJ0G52w6uNt1yG08xBTRvh87S2e/L03BiSueCPmbIoN8xCwcDioc8MSMBKB7b4CF+pa2IbKIwGo1orduBIFC6dkXk+sIcnI3oe5fVokZsumwL0ljPVPx0DXce228jYvnM6iXuvKbLI1VwX8rrT9BpX3cw88XUuAW6mL0e4QIxAs3FJKiKa0iKYcJEMmNIl1rJ4TbX4aPxi6dSYeZkza2rf2UiCQulGBzBsAlccNCGRhpAJhHBLGkpDM46Fw7yHgnVbfvq6QxqpS3aNazy6VzpdIR68MIoHGDO/mb62nmy+L/VxckW/zpahyUCIhGl0FoXpWhGiZHmxeumNbWxf9HCJLjq20McXUcqhYGK9p0qSpuu7YwnsV5KAJ24VFQ3+JoAyaCF4VL80ASgKB/W9TwjAYj58/owgQ9/+OECLe/uY7CALS3Z1a8e5UHR6kWciSmGWxK2Xtv35s+t99eS5/f3Y8/wHKebnhZfU8Vc7xZNdeC6zHnFbff3vlMl/7S5HHvqwYibO/z8v4zy1bwM+Cp/bf3Dwf7M7T63s2UXqQ1etrluciMM9D92xUyFzcc8/2araQmsrrrL/NA8IMEURKC/NZc0hwNRQpRUM3kQgis9LIYOGAmGp4WcdjyATRLdnpOUX5Ngtza6Lcoh+t7yrfZhtZLwN5uxo8RJufyse6Sp0INXkQAHMCrzwU7O/eKr5AMDNwZMZjKXjIGZ8z46FEPBRBAtszLB23gaQSbJ64Z6h5KnBR2YfR8QoWmqjiXDppGh9B7iURoC7uft3GOPTruyogPPcD1yHtbmj9vq7HvRr87/pblQ+yyFPRjY+IKT36/FL2rJPwy23PkF4WNflw3O2w3+1wu9thlxIGC/UYbG8XQjXC8bnCnYv2l87X55TXftZaZrtmb3vOnujPOHfd1n3UCw7LE088q63B/sPs8hkbXuXKW+X7PJE1iftldXKq0U578Em7X0sZYZqyrt7FibNlS+Ze40xfoozo27SqpLv21DPC/76WF/gSnuFqRcQ4ao4IzwnhFnlbC2ob6O+urUDOkjmong2reqQqHLD6PuMJ0X2fIcNn2/prOS09EP8c5cXfW3mRlcfPXc4MQ8uJYCBa5/FERFXQd6voc2v9OeV834mBSk/Xf3INnc67c/N1a/5ubbALIKijUScbuQFphk9c3NieA0yfU0ScXMMtbn8TbJTRc4sqddfeeO/Gp1eLEQXofH8ywaJj5L2wudEqsKxu3563g6h5z805AyjVfTLEqFYKGQBpjPkpJDPQLmA+IoEhPCDPEx4eP+E2Btzs3mFHghIJ+eEB+eERwoxcQ5hoyCEuFkYpMSIIQaKFaQF2aUChoG7tIsZ7M6Z5BkIE5wxhS+YraplVnMf2MbOkaIwWqxYhaF6IYVC3aWpAVp03vt+10audfzKvgBNrEZHGJDShUdo4QYzHV3BfLZJVVEoWJ78+0eZBq6eFwXEwHUAN4SQiGp/T7tXk1trmCuKSWUIXi9ueS+ehI5B8BMziv05RZpR5xjxPmKYJx+MRx+MRB/OCOBwnHI5qyVdyxvFwwDxP+PhJrfc+fbzHfr/D+7tbjEPUHFYMPDweVKliFmS+PrkUs/h/RGZG3I2a1G43Wse3cajhkKyvaigbC2vgyr0ari5q3qwhadx9tSxkS6xMuLm9RQjQHCpmLQ7SWPwEguQCMFDmrH9b3paULMRByShF81E4KEyWtJ2zJpzM7nUUI4RgoawEU1avB4bOfcqWmLC0uPgiakmv3kWaT4F0iVpcfKNxwX3J2loPAeo2UgUAWHJAzTFSyQ658OBzTa9Lg4Zb8hAHMSVdYxIhiIjjDUIakcadhvWx8xQHEAI0rTEwDDvEEDCO6n0Sk+VrSYPScVNElCLImTFPBXm2cHWpU5KGAAoFKEV53WEAT5OGEdsVlEBAKKAS8Ob+BnEg3I4RZSZ8NlV4DZcmBGEgZwao6LwIEdHAGp8/3r811Jr1T88Or+kBzMMlUguZKNLWJTN3xkJKd0NnPBSCKYqlqKFiFhyPEx4fDxiGgpQSxv1ek0cHQorN2ytEQkwB+9s9SimaIycNRhcAQJ+Z9jeIQ0LaqUfEbrcDzxmHwxGHhwc8fPyA3Tjg97//fQdO69qapwnzcUKZM2KMyPOEIUaMO/WM2N/c6DjvRgxjwnB/DxHRXDGFUeaivkc//IjHzPjXueD+d79Fno64+803uI+/Q6YEpog4JISUUIIBfOYl1eSIjmQLDBD6tfw9lxNez3875ufg5d+hnPOPXiotMg3x1hD3tHiZn615EzMXy+ijYfsDFtPIawLACB6W0BQPAjfeKGAo30EQ9QiG8p8lAJKC8rwx1H0u5xmlzJinWUNbzpMZexxR5gzOli8uZ/Umzppfa55mMBfk4wGlFBweH8FFfxOAwfJWSZ/Q+LTzjHe4TlZeAI4dRqSGIFSVv8Y0OUxZwexe7nEjjqU86PepZ6J+DKReeUW0XKRNSVAXvMt2Ni+EyfKOAUBBEcIE4DMzPpSMv+YJ/zZn/HkK+JAD7oYRQ1S+ZQwRAzFAAXMsJhsYH84wXiqACciBtY1SuwBkz20eGwTE1LrJL64eEmx96N4XZHKKM+Mu6BSLM5XbMXSTdq0XIAAy6ce9IWbzjrAcEchZ8z9YqKYqVNlzgzg/afO+ePgmHTz1aKBOL2HvFBKGmx2G/R7f/vY3eP/Ne/zxt7/Hd9/8Bt/e3OPNsMduGDC4lzqR5iPQxWMKvSbn9/PxJcfOzfWX7A9fe085h1OcK/1avubeS2u/slGy/LY76/1qNBMRQjOkdLqqEX9NSUmEbIqGQIQSRUPoBkKMA4gKuDg9Xb7/c/pifbr9Xr7I9nv1b74sW3112pYlAHOtUsKfe7b+xfVNNntJ+VJc9FkeEb0nRA9QnteIeSude7NNxKTcU0XECvGyTc2zgK2vW+aCMFCn/rYJLedTu9TrajvPdOYrEIavQbCeKutnPWUFc66cA3efApaf07b+3tcqL+3T9fstmKMnFDFPPfOpPn9um+v1l6pdY/f9+rBPoKVXxFYopr5cT8AvE9nWx88jZk3pqIzq1q2t7cv5uGQozi/7fvyvsTg4d/8l7f8a0jhLH5wp767b+vQMuisMthiuSou9vspi+/nubD/FKhAmFTTSD5/Mq3afW5jbe1Smspt75N4bXIUKDTdjybJjQBoHyJTUIsuSlgpszdn7Fi6gQqBo7rfCANQyRoKGg/FwpHqPWYCZizDZuy/XE3Wf1TgRam4IEPUjdDK2l0o/7NtjS6vznVBLBJ/jvWKqzltuTd+cy9LGfZOp6dZBownUnmMd4TGJl4oxFabRHVcXWxvfznqvlM4TwpRX/vwayilPKGXGkAKYC+52I5LlbgiW0BZow+fu9p4QrZSCkDM4Z7DxB/C1Jd08Jap2Wj39ryHLRMw7JFrYJqqJkStNjRGR1FuDAGRo+JjqERQCNOeNg9Gtrz3uMxZrzBZOt45ZpPaTLysSkydFFQuqNLN+lC5JprSkkf5oV+z58q3rAcsV4G3xvvI2N6AOtvZ8fddFb32s/edAuVRFpivDTBFhygfPL0CWlB0UNH9MtJAF0UNBaQgsD6OlMZlbl/n8W+RFWRE6B0Q0iTQ02TkrIIAYEK2tw5Aw8oAhKhjkSECvPNQlIFUZKx1Q0q8np5F1nGs/nqEhUgcHTkcrENGNyQLocRqA5Tpu+4WuD1e6eW1bTVCjBcubY95gdT8zXiKmWL0inJ+ACPI8I88zOOcaVs3pl3tEcVbFoSvU54kgprjjpF4WkhKGFC3EF0GE6nxAMWVOziiHAw4//IA4Dth9/1ekIWL/5hYh7RDjDhQVYGNIDYVH3ZxfyJx1Xbwev/6PCmafkyP+dvqDzvz9t1eeluleVt9r1vncco7nv1QWskGtqP5n9W7z3r1SovJAZhIiggYc98+rPLfnmvN90u6t+7/tV+xpdtU7oYARohkZECxflPHGK08HVN5FPSFq4uHuOraQhSU7X6aGLQEwqwOpe0lT2LRuItuTrpGFTzt/OQ5uTCNdnzhBbiHglwZY7W9ZdrW1a7n3tWf5+yxb7Hto3Qn9LQ3Solqvg+VFgCyqMJq44MiCIwsGLgAVUEhV5nG5ZzkvrO3MEAoQUs9iAkE88ZyFViJIy79LhOYRYX+HTqFeP31fNP5HrC9rDgiba96WzbEiAkSNzRahmTxxtfh37zHRZNQ61/vvbtzIMD7p1x+Rer6mAeN+j/39He7v7/H2/h5vbm9xt9tjlwYMISIZf+mum3Wl+Vw5n31+OQ97WeonKC9aO8+s/0vvvYRjXq5/uc+sQXNayd7VlLxeDzAp1uC5EZ3esujaUGi694hAow0bbX+5MqKnfFi0cbu+Uz7ntYD//h1Ozy2fva2I6L+X9T63jS95pxd5RBA1S2lfNB7aAdjY9EMvpODkOqoeD8v7xASlQGqFWYtvGLTeVJYA2D9yeU2iuVZC9HX/7QgN/2DliWHpFQ4a9/3pnBBeriXo18/By4qrLaHmPJE/TXi3JsRaZ/3rSSXImjFoSpDGqCo+eD3TUgE8cgDSRQ+ty2Ol+vPVCqfbdDtgd9lWXm66GxoqIqrxE6sAlbvrQsAwDJVB9NA6YknuFkAz/FmiYHBQqyzNS20ClCUdU0UBo2QGUanJb/c3e4RQcCifFKC0OLXzwwPmYYf5eEBIETc3N0gsSCx4fPiMaToiklr955TgcW7zPGOEIMYEITGwWPMaUAkgeAgVgUwTCITp+AjAXEDrPiIdyNZyP1SA3MHmpB9n9L0nu1lbQe116ceJbdxa2Jg21i5BlOJeK6s5GQIClvPDx3qRbJ7cyswUFwID8UMHjnf9wwwE7eOUks4LK2pllyto2ABNfXbw+VcypAo3gjzNKLlgOj6i5Iz5cMBkHhH+KaXYmDXQHwCOhwmHwyPKPGMcB9yMAwjAkBJSDIjjYDyGeYTEzqtABPM8aduPU2VUCS4DMTjnLh/Ekmp4KKliuRqUB2o8h/MkHoJGmBGIMI4jmAsOj4wiGkaoGnP4fOvWZjJvjkCEPLPlfhBbmsGs3xlcLLxVYVcJVJmxMJDdQE0AREGEei8RLPE0ufLE6UybtzE0QTUY0BuIXORu7vyiXgwEDXMm/Rwsdu+QQIQqLOTMGKwPQgyIKUAyoxRRXjFo/hgKCeO4Rxx2CMMICgmzzzVqeQwCBcSgyeqLBZ/ax8HW5VCVIiJc8534/KY0ABTaumZdD0MaEEkVEQUzmIE4DPqucdbQCWNASgFv727AhfHvPz5ARFDmoh9LEipFIFEFeweBCOqp5XISRMCSIShGd0LltftyouRd7YeqLPH5lVQRAw/NVisxhQ1AxIY1LPeTtv8DxT2A2NaKhZm4ubvR42mn9MUURYkiQkrqxZI8bB1BCuP4eMCnv/4Vx0+fgbkgDQPiuzdNkWIAWrawTfmo8cofPz+CIDjEB4QQcNztkVLC3d0dYkqYbkYghGoZPNgzByLw8REP//oZhw8/4Ic//wnf/NPvcPjTH3H7+/+A29/+Ewa5xUA3kBAhzhOBQK4cs34LhpcEUwpzWzq/lr/DsgSZ/Wiv2DtV8q1LB/f9Wn6h5RK/vjba6D+uJGX/7mmo88yktu7JJ4iHVxQzCDC+iMSSWbsns+1XXMzjMc96nDMIQCFBIWj+1RBAKejWGSxfXGFwmS1+/wTiDHAGSUaQjGDJnEk0wbCUjDIrzZ0OB5Si+bvUy6CoYjkoP+WfGKPmdgpNVun7dKsPG7jfvpvxAdZiWleHn2whM73/SJSnIQex7UOWuNsBboOT6r679IZoXJgrU9q7uJjmoCirx3R9H2MUG4uLWQSTMI4l41AAoRGJC24I6qkdGUKCOdqtnpfBLbdLhhAjs+FrIUDUNwaqRCrWV9b/kVUpwSZPVqEUgCiPYxoN1DBJYL3ePLkh7rFgCoQ8WVKSuZu73SAR9Fp0uR+y54vQb/L8ETJ17bZnd0mpqwKJlZNNwcNramgdlgKkCAwjbm7v8Ob+Db75zTd4/5tv8Ntvv8X7t+/w3bt3eHN7h3f7PW5i0hBNKSCkoMnVfVQdh92YbFtYV//dl2vk/K+lvHgNZcI15Tn4z7nru7P1/DX0tuYqsfXMXDQKApvhYAJiNMmcAnIpiCLVI9vDvfoa9aTsW8/eeqc1Ddtqcq+MoI162vmlMu/aPceubgqVjfOXcbe+3avz3V52vu7TY18D832GR4QnpW6DbOgZqlVqbeQGY3aifGjXVcssagK5dNfqcTpbV19fd1FX09aAd1q2M++83pBeozw1iE+d3wJVr7lP7335hDqnhNheTLTZxutKzwy8sIYLTNHW7+fW+7U2l2vademaEwD0wrUVPOsUDpcUEOeI37m/X0vTuzXHztd9+Znr7mjjeflZW4xIbw3jdV9S2PnfauljdfjdsmSKtkbNBZ21IuL0Oiw3GFrW4W1o726bszP3BBBsA3eGlU5jj/fPbvVa3XX9d+8PjeHI3GKoszGgoQv74Rs6RCBF45aX7MmpkyaojglkSch8z/BwOi4UCjM4KBCogkdoXWHnBVBBsSQNIwOzviECTE1SLXnrGy3pXwWzezDCX9/kE7de6ucLao3LNdMzPH1/b/9ue9TSX6Y76Qx+V3yMek+ZQKF7n4py6ly2eLl178ayLEHMjnm0P9is7rTf1RuiekAYsN8s8JZKFG+rW87X3Agsll8iY84ZKSZLABzNAtBCD5HNEQkgn7O+lkzokY138oFcM6O1bVjyHG5pB6KatNkBWL9OjMfxUE6ofR7qJ1DQvBHoYiQTFuOitMXbs/SGEBPGRaiGO2JByzdYeR5CFyJ3OUWo9YeuLZ8j9jeWHhpViCfUsAEthFM/p6TRproeugd1fR5CAMUIij7u0RAEGzez/otRFRHBnqhxYgWn61It5j2c3GKOmTeD959aK8bGQdq4RwMtorDRGsLArLkiUlKwXWw9FF7QTO/gPrRV//KuwNE2ofXBBu/S7yFtPPUTSEPBVXBH/L2Ujgc5raut6zUf0JKz6zOcNglcSSti89wVS64UCrF5pdj9bOHYjo+PKNMEKqKeZKMqN92aV8OkDXqORUORcNFQhOrigxw0fEQ+TJBUVOEcA2BJ0jkCpMmBIKWAJ01sP5eCxxTxMI6Iu1uMb94hjAlhGICBrPMtJGFVQlgn+lo/TzCuLr8a8LTyWn3xdfnzp+usNK77/ZVEhV9cuTSG147vUzLHa5RzwNr28WU71ooI5zPXPLnSezZgXPkw9mc4j+ThZ2rS6s7zgV0R4fkbivG1+nflJUkQAZCo8he+z/MyLn9VcsDCMhqYT7WNFj615MqXOZ2F7YdEaKGN3Cih3z8W/Mmqb0+IZWdIuji6HgD7z2Sa+rv7eMSLyqHbdeR7lfX3OSDRn1uhpv54PSaoYoH4kRVfJwSIh7K1fS+o5wRDkM0AYZCCaHXUvgtkCoTuxd2gLGRANAyUck0FUvOGdOGr+pfpPSFcO+W/qbN+IOUBNXce2++O+RNvR/Oe0ed2cmdVaNi1JVsIpgwSS1q9yBHR2r7+OE/YeGl7hLWLUkLc77C/vcX9m7d4+/Yt3r97i7f3b/Dm7g63uxvshxFjNKMkM6Dx+VnfqU4t7ZMtTOtaZcSl8rVwoi+t+zn3rt/5KXznch8Jes/+rXsXOInTz0prNYKBr0MOEUQMNu9oYVb11iq/yKlC4Xzbz73bNYqIrTrW568tT+GslzC3LWVC96udX+EJ5+q+DvM93/5rytWKiBTVsiwGT7poxNeT7MDT9zTBD0BTUqwEaf1eeUJsTeBO2O+vWdd1uWx1yjWdCRDFK+r/KcvPx9lempDLcXgFSe3X8rLyRLdX5jG6J4RafF/jCeHlek3ul5ctUP9rlDU9ufS8E3CoO35JGeH1eoJdT/TWb77rNlTrdOZmgdV5JKzBqibIXO4vDYNtILHx+ERknjFAJGrCiUhNxFrMul24GJB6qshyUE2Mv/Z3OU5HFCLc8gQwgZkw8wwa1FNBDOFRpbftDYWRD0e12jL38mEYq4V+MOEqDQNCIEyHgsLqTo7iCXwDxqBCjyfyK3lSkHZWgGs+PoIogD2+eRyrNTsRoZQC4hYjPaSoVrMGPAe3KlpOFACoiZ7jFWvKea/eG8JzK3APbMIVPhbQH01YBJGCeEAHhLc56t99qEX3dAghYJ7nNldtvhJgXgoaX5dI49MjCLJoDH0WdeWO0a3bBFIKyjzXJNLMjDId1dr5cMA8zzg8PuB4POB4eMA8Hy3kFkAxIpQCAjAOI9wIYr+/Qc5HsGTLCSGI7+8xDhHjbo8UEx4fPqpHgo9RSiBhFGg4H09a7X2hjhOr9QioN4xIXYMOVFNKVT72e5KBrwqERpSc4ZwREEBBQzUNMSJALP+CIOUELiP2+xuUeUKGIJslpN2pfR5abh8VB9WLpljKBwFqPg9BbPK7Yx+iHhPVCcK2aX+HKkRDACoK8AcyJaADEKhWhmIJ5WH0LNh0DGaRFAIhxoBxHOvY+3yObEIgqDpXANB5GxNiGhHjiJhGUEqah4IiWDIYYjmNAna7PQIFTEcN6ZML2/yPOn+6XCHZxrGYsiuEgCGlGtbJPZHSkDBEzRvDuWCeM6Z5xt3dLYY0QMYRIow4zwiR8P7NPYQF4/AZORdM04QpEuZcMGQDqIRBoSJFaNZZSiZ0nNo+MAxDpfV+rKexBd3adEBHNMdNC5saFsrraP1IISANaLQrBASKGMYBAsHt7S3GccRuNxpdUCGsWCg8z4GThgEEQhr2en8cjZaMFQBx3l+YkY8THj58xPf/+mc8fv8R4TAjjBFhPyJPE/I865xlwrDfIQKQcQcpBfPjo+bxKS3EA88Zh+mTzrPDAMSAMCZQDMhpQAoRkrQfUQr48IDy4/f48OP3mP7bf0d+OCLGEXycwVNBuL0F7fYYBvXUcQ8IB0gc8ioWIQO/NNHg1/JF5TwA0Sng0GTZ9UfLUhnxa/n5y1NYwXn5YkPx0PHfzkPknCEiC/7c9AS6zwMAKXwb4YY2Fja11jVrXbPmkcoWEmmaJhQumCbNjVVKgVIixkBAicAYA2jQUDRDVMt5RerU8yGANdChgeHJvfLMS6LkCSXPyNOjegvmyZT9yj8m0rp3MWqenhgwxIghBgwhYAjRQN9Q96HWg6hAed/Dbq4QSPnXc8rdChgbM9OSf/Pi+HI823qt8lb1RmwGFBsTYfXgvr2VSdK6yfEv5WFEEsAjIgRDDNglwX4gxPkIcMaMgswzuBwRkBAwAhSUv2FGLvYeDqJKBiCdp4TRFXGmrQPYBWjeBTBlQgCQADaD4UAABqCQKh0YAKeWz86vs+OAANn6GRngWT0kpOjfVVBB845lgXtIUFVeGKfKM6pSoyqM1MMHkBpiqmKIoh4MWUQ9NsYB+/s3ePPtb/D733yHP/7un/Dt+7f45t1bvL29w91uj7vdiF0acLMbMaaE3aAKCVVG+PSik/nyU5a1rH/pmkvnL13z1P1bBozn7junuD33+zIee+oRsf7dR9bpaS2gYTs1NK+FcxVBShb21357PhA3Auufe86A8xzm0+8L57u0A/U3+qTRmpeD98wFdfZeGI/zConeaNTfRYAqgzytnHmqjdeeP1euVkQsNN/djiG2i5CcKhsEvsGslRBNWXGihKBKLtYNuP6tKtPYbSBfUK7t3C+x7PlSq6BzTPSlZ1xDFK953mWlxNcp1zxjy5rwS8rXBsMvlSffhRYnL1SEU0Gqsxy43EXr9+8Yzhf2jYMwF596Qlhft2yti6ut6/zWa5smqLEpL238vgmfU0Cs79kSmGrz6MzGX+tR5raCXTYnAAEKztZdGUpqnm1E0E153U6CeUSYhRcXTfgGrkliYVZE/s9uUpA7AJRVmtMwqBbaprT38lj9QZpSQOAMr4NJJhpVoVLAJYJLBgUDb0GQwOgtgkVkYXlE5Ep3Z3LJQKsteaodbX3SrCU3RWADPxbt5J6x6SaetD5fFwcpr1lDW5Yv/W+fiyBTslXrP3s2ax+x5fVgizE8TUcFEAFNUm1x4D1BnlriZbveAX+dJyW3vBHCUpUmIhpzqBQLx1UyYiQFn03wUjlJNGFkUK+IGKN507Q5oHO3Wc877+JeNktr9bZOeLXn+doplqzY14aDVzEmQBiqwmIEYcCSCEdTrAnnNg4bz+yHvl3X5osv+Mr6mgC2tD20NQBAzIjEhWvXUUBEFR9OD6h7FasX0tYS/Fht7zLfEOACUL/P+JrwhlLNt1LDY3Vg9nLf0rUZzererfVbwummoO2Beu2n5r1j22EHJppHRIhQ68MmRlTlBjQ0VmFGjAnjOGAcNVeJx+Yu3Lx7WmL5vv9tn3E64HOxm0+uUNgUHMVpGyBkRo+Ahe1qVqi6jhQkoxAWgp0/x72hYogY0tCUvOYF7dO4stVESoPNM1qFvtg8I6IaK/U5VqSwhmE7Tnj89KCKhWkGhQRJOrZ+H5gRYV5BRUzgTBozOxbDXNQaVorlPTFLYckAsXq2cWAUA3Y8kWlg1tAZmXH88QMev/8BNO5A4w5pGBFTAZLJM/bCNbGlDU4TcH9afvApfv6nLC999tfkoV+j7r6OZX2N8P58vf7LLV9jbl7Ng595Zr/HnFNGPAXo9TzY4mMelW4c4h6W7HtL5e2k7h/+2yrXXwtPiJaTQXNnNYVEM0bKVpuG2QkCBAnI5hEWIYAlviYPWySWkwnisLn9bR4S5hGhn1L5OoLSuhiAGAJiJKRohgmdccKSPznnXSInq6eDCds3na5BWY1FlTtq73p/4oRHauO4Hkt0o7Jukf3JWC126W5R6+7GQynwT1QQAmOIA8bISKEghhZ2tdhYg8Vi/bkhUUDzjgFqCK8KIkr3kwAhSE1+5Z4G69dx5q/xTxKCWoeFAPd2V0ZPLIR6rOEx9ZrKQNpzzMuhekDIhiJCoIJjC0PWvCpKHSv9NmWFr1XyYfFBVF4+jAOG/R639/eWE+IN7u/ucX97i9v9HrfjDvtxwBjVO3VIUeesh96qc0zUY1TEQr/33bVNK55SZJ4ra1zs/N5yWp6mS5fPP/fea4Hop85fwgWd96/XEZTPqvc1xVvDNFpOvuYlpvJVIDe2U0+kwoqTBOOb4fnCOn671VObtGqDt92kg0orLpdG33olaHv2enH2GNNW3y2PX/f884qI5fPr8drOresvP+sl5y6V60MzJRvcHqyof5LJkU1YtKPoJ1/7DvXsus4vKxc2ln+w8nOC5r+Wl5Ut4vSapYG1zRJaAQdCn3y+teF15tBl7b8R/Ss3vK2N7rUJ4yVA1o+9xKLBj2uoTvGH1WdWa2cTbOZ5RimlWlz1YKiPnY9Xr6zgwt21WJFae15nkQu0eKmLOqUlgM7ZPBLWjKQljtKPbsaFeQEoew61UgpgllcQRqAEkaKWuDwi7XYVzIKFSZIi4EmB65lnEJPKYBSw291gOnxGnjTef4gR4zCCY6nJo/X11XqNqFmDiyhQmM28Nc9HBRopAjGhBMKQRux2A2aziqZSQEURvwAFPB2UWgpIxviKMtNbU0XsXBVUKwPeXwMDEcWEUq7CNUlZjKcLj8K8mCeL+YHTue0gZ83rUC3DWz1uNTWXgvl4tFwBzsdo34ILhHWezlMGS8HhcECeJzx8/z245NqmFJMKrJIBmVHyEWU+Yp70k6cD5pwxTxOm44TpeKxtSkNCSmqlzayW6tM8Y78fwMy4v9khDBFhGiCZUGYN25JiRCJCHBIYQGH1nJnnGWkYMA4aZiYlt1nU+ZRS0jwYRT0EEFHXyJwtkWOf8wGafyKb5433d4wRN7d3BgRYDN55Uo8hKQaWW9zg+QjOUu9vyYObTEfJYv8jg4VRsgq7lbUSZdZjEDCaYkAxEmmKmC48E9ASCkvW90pdrgigycwN6JbuPanuJTEGxBiQYqwhfIgEFARxIE08jZZ7hWLUcY0JFAfEOCLEARQTQBrqBwZ2g1DzcHjdJWvIt3E3Ig3qFRBDVE8SbanO1axJkt0rLUQYoKLhnQJUYTSkBMlZ+y5GhGFAGEbEcUSMOvs9JMP9mzcoQri7+xH0eESeD5injDwX5ME8MEqvRNa8OSwKngcmPU9FlSCgmtOl3/d6RXQp5slGqkiLQcctpgTFzEO1qG0KREJIptSzer0Pa16TUbDb7zCMAwY75s8Xodp+AmrIrN14gxgSUhyqlyUDmK2PAR2f+eNnfPjL9/i3//rfMX/6jOnHjwh3I2LeYbfbYb/fYzDFSD4cwXPGLKpo2N/caD6g4GtM88jMx0NNuk4soEfdC2JS+niktlenGLFLA3A8gB8e8MM//zMeJsG3//MB76aCOwTsYgLSHhTbxlmIwSQaix2mmBNCRPkHljD+vku/7hwMVUyvybhLXvnX8kstzxmjXtnAFt5xoWwQgRj9bMqBpcGQiHpBRFL+jm3/DKbQJGp1FVc0GK8/Hw/IpeAxT8rzzfqMeVLjnbmoZ4RwQQqCKQI5RVAZwDGCUqwYssfpD5IRpSCCISiIovx04AzijJAzKGdIniHZEwyrZ2sMhL3l37oZFeDdDwkpBOyShphMsYURdP7B+3LNb/rvFor10sChKnv6vU/YwXrbSw3wDq7IIKrh5WE8sRsINNmsV2wsn9nNhs5To1dmGKYuUo3+RRKAiJAiht2IuynhvezwPkdMmPApC2YGihSUIsiUlB+iBEgAgudamAGIjgEKQNkEAXvfAjRX8+ADjRpaSZvavY8pISx3lCpYPDGFCUSUmiDOpkiIWfnSEuDeGZKN6y9ZP3lu7rh9Umqb9SD3iID+DWkeH16qYs3a6SoyBpgIkiLibsTu/Tu8/+47/PE//hH/9O5b/OE3v8e7+1u8u7/B7W6P/Thin8xjx+ZnGtzoqD5BeSD77ltyztDzpUqIvp7nAryXwP1Lv7/0/qfa5WXrnc4pok+uo+X1tV/ZsZFTo5veMI3zbOtNZdpouSFLHBDYPJtFEEPAMFhuMueZOVfjNpd/nGZpne3Z7bgbCK0w61Whjq704P5Lyum9BDeIvKRQPz8P2kxvSgiloR6c+Evx4ucqM9blWR4R/bc9dXG+Z8yWHdV7QPh3t0HpDeee7FdsHOu+L24ov/yyPYBb744zx163PAXG9mVNVPTn9j2vxbhfatOaCD7Xsualk+c5ffY1S8/wLfqbGiC1/DQid04J0fGXjd+pjNx5l7t2/9Pa36eObRG7LWZy656tov3UGOKtNj45X6Vjcs60wesWI/4w8NkT/PZ95/cVj6Fvn3Ub1/S2Z9IXm9JG23wse0Vxq2sFVNc6uVkfbRVqd3pS2rqJG7iEoEmHOc8oRCqiWYiUECOiAVmOpqrLswmEoh4IboijQFgf5N7a4AqdDjCo43HSfAFXCzAGiYWKYUsaGJ1R6fqjF2akt9basJxo3O8mRXErbieXrdomJFUhuHtGP35VuVX0PVxppeNsuT1c8K3jvxxjfy8i2rSYJpc/TJhjaZOeALWiE7eoY5Q8o3BRpcI8YZoOYGP+AhFgIV0CdDDddtot9iCq3NDEwrPmjzBhkrrEiGRJhiEurIp5d2l4mECaE4DQgUchgEQtF/v31/pQ14DgdI25t00Nj6MuKva7zTNXBnr/uZCuoQus4wqZYi8hxAhJESF5MmQ95mELbCR8ygFVQDalgXguiJUltzPa/m4+68Qo0Jq96K7xGepjD1la65Ofs3lcn9H1WVjRE1WqqFDsQDvZO+nYRAvBtKJJ5vUAcqv5pgxqC8eSHFZrfnfJtz5irrlJav6QjkFv8vqSh1VQO2lfOl2p4Z7U+n8cR4zjDjEmxDAjcxdazb0ixJ/l/dY8IOoQdBus07bTPanteW2ZUqUHzQjo0v5r693pJ+ncjhaG1I0U1vy8iA+W3peqJ4R5T1j/SM8sWFuEC6bjEdPjIw4PDyiPB5TjBCQCpQCmAAZp3N/AqlSAWuL6t+eJIQCcknntjTo3C5tCwlRbVaAV8xixHDEGshEYZZpwePiMPB11HxCgD3XXeqsX5VbnzvCYrwlQ/5y85GuXXxKP/LwbUIf9b0y0vKq89li8Zn3Pl9/qnSdy0CUZo+eFmiICy9/iOa82vCT6D5xe6F9iJFGos8rtwm+692i2zzRbqKbMxtdZGKiiIYaYC5gExIIkgkxAFPPhE9Ik1qzAcJ8fQvNFiHlCtDwW1BD1uo8E0pCQNUF16v4OLfxi4zHU0hx0Ob7+JTBteQC1TX3f2sVw4atHg9xswtu0rKx9bfyoR1ZSUOVRfM9lFrCEuq8zC9zXxPnPMUXcpIS7mPAmqiX3kQCD9Cv/WRNAEwBqPMkCRPRNnwFiabmeiXSsyfrCmZhF363fkLr7/MH23WJr6jjGQeuIg+6nMaoSg5qMBmEQu5Fa219B7hlRG9PepetsMu9pqW2idpm9T4wBoxkq3N7c4navuSBuhhH7NGI/jNgNA0ZTmC28IYKFtIXWt+SClrS8n49PzdVrldBb8399/tpyCdfYAqIvXXttG86de06di787WXqh0LigiJDG9Bov716wBMlQT3MiDeUpAYUIkIAYYIq61j/i9FvWioglGH+qiBAskuq11un1LsQvAP+X7YFS6/IS6rK+pBjbngPrNnU8qsuBFxUR2+9xbrx/MkXE1rGnvy9rkzaetvp7/XJGYI1o4aRt1K77otJvcT9H2Xr234JQ8nP22a8FaIQegAEbFkYh9Z4QHSBE22v8l1JOGNF6nDeJ32sJQs/pk2a1vHz20oKgAUgeN78H1F3gKaXgaFafHpvfwbdoVsYxxkX+CP27VAEHMJ6xA/VccSSGXAUb/xAdSNIwJ8tkwhZK50Q5pX3jVrytHxRELmWubQ9kYFIMKI+fwccjQAlEGqcdssPu5k4pLqlHBCxO6MwFUQIiInIpmKeiyWGjh04KENHcFdqXrb893Ec2a7UY1CKNDATnPINDUDAdUN7amJ0hpiZsBZ1reTKrMWeMSK2ZOWusSkjUsCWLfsLGHtVFde34cxd41rlBXCFR55cJGdWyzgTXeZ6bcoeChVAJyPZ+Thd83Xt9btXuyggAHVis/XU8ZsxlxnScUXKB6wTIQo2VPIFLwfHwgJxnfP78CfM84eHjR80tUrLmeNjtkULEbhxBpSAFlW+GGJBtT89zxuPjI/I0Ix8n5FKQuaBwsTBGmiMgUARMQVVYQCEhDhFv3r5FyRmPH36EVM2Vxt7XROnaD6WU6skAInXnFe+ntnaCe79Qs8YXEbAp0bzfSrG4zqXUeP3+HWOEQFDKrDHrCQYGswG/6qkx5rlOEJ8DkKwyngucZgCn3jJFFTXSJhSJjnewUGctBFMXS9jmexNFl0ynKy8qrCK6T4TaL934U/Oq0jlDCEHpVc6q5EopGXg/gIJ6OjioTSEipRESgiWfUxrgADdF9YoIFjJuGAYQEY6PB5271oe3tzcYhgGj73MhgLlgmjPyPCMfjijzjCC6/mtCTwAxhvpOIur6nVLCze1tBe6ZmqIzDhrn+c2bdxBE7HYDjtOMwwzMBORjRo4R85yRRlMQkoa8IlvslY0VAaRouAW0kFa9YlFEzLMC1auheirD61oK007vQ0jmadboCxl99FweNV+E5czwZNONDiz5+MGUZSntQBSMhlEV/Kn7l48zPvz1B/z473/FD3/6d8TjjHiYKlB2fJgwW86OFDSvSEoRw7jT/uFieRn0+cPNHiDgLtyCS8HhwydQYSRSRSPMTR+iOWFiACCMkifEEJBSxGGecPzwI97PRyBCrYmHARSjhnZzekwKlDiAmES6ZPK/lr/3osDyKT+5UJb+gnnnX8t26fn1tQLCeaJ6ndHe/vpqdLD6uCICpHmTgvOU1IwApFjoyXlCKRnTPCFn5Z3mnPF5Uo8Ini203uyKiAwGI/OMSIKZBGWIoJJQzIhhGAgpUd3rxRIIBy71E7kgMINcUSGMwIIggmjKhZ0Bu/tR99Pb3YAUA3bjoLmu7LqADvhfKK7bvtWDsc8BcYVXxlV9/rvKZ6tRi0dScnMP5WXYeH2s+HLnaxluAtPOrBuiPIKHWSysOfPmEjBnwVwYhSMEqpwZE+HtGJFFcJxHvA2Ev+aMQxH8kBlHBo48o4BQOCsIHxkIAqJlmCUBuZWJKttzqeFqtbHiAoaCrqR+ncZUKN3q5IWmCDClg8e6hZgiIgJpBNxTI466AdJgbToYaKx5/lBmQA6mgChAca/5zhvC2wlBTRrohx14ZqWhYuGqxH4TND/cu7dv8c37b/C73/wG3+7f4N3+Fu93t3i/v8X+Zo9xPyIlCx/mRigGBmcoL0DmDs+2PntY+ZLC4dLxc7+B03m/Bd5uKeO2rl1fs/X73Pe5+y5de6lsAd5XKyxo43g3LzfrceC8KgVzlXlAKiuVkpBiUnmQXaZjy3On+U9ETj3XgEarLuM258cYgCl0++MrOetMua7fVdZ9Sjm2rtOVIb2nx7LNLjXwybnu6gVr89Q4/yyKiK1zTyklNm5e/Dx9j2bVd1LExZ1twXpx8IWl106de4dfMoD7GuVai5R2fjscyXXFJ/Tz2rbVjte2Unvq/i2itUXcto4/Vc69wyULs8r42XVurdEzg08xhde807n2PFXfczaz9ebXbx61b/z6duO6cVst7p6zvIycwTtt0fI5z3iXVkNTSPj79BZYTbGwEdO7i3/uAlO9dgVYq5W/LCxsHRd3Abp6yaDVyWLWPtKs/qnSQSzas55HTjMdCNK8DxGDgccoGVwYhTNCUOsV7YNmaaxsooHMbEmHO6tzYa48LYVgHsW68VLX/7Wp4vPIhUWuOSvcQrox7gxGaVZL9s7iL+cfonrs3HhT979/Se1T/91/pPtulv5+vHsZLBQRNgeyhQuKxoDFGEHCLdLsxvoDmlDu89CfXwFndGtbLA9EMAWUMzzuMeEeJtCEzDGqcJTdO7tkFBGUHCBSEE0xMgwJuahF+zDoh1it/igGROk8BbCYhFX5VpgR2fIMxACKAShmgSaowk0PmmM1hx1gFGPiyEB2Xzjbc76BEr5GK7gbQ/X60XkbIMFimUqBxABwqKGg0pAgeQByxgxL2OfzhqwPWQDqchAw6jrVqdYRs8pwQsM1ufIAbWx76ukh1lAVE713hTWgn+Nbe8jJvuTgekQaBggC3M9L/HqjRcFC4PT1+7zrFUM9eU4pIVDr7zY++oDCBaVkCzFnyUT9zan/UF0POl1UuA1R61C6aGGcLNzBOO4wjhnDMCKlSeej0c5Ky7OFZ6r02QQX6vvewPvajjPeaj4sW30vy++mMIo1hBiZonbxVGrKj9gpIdrxuFBEEFDXIlksaTHwQYha8klbb1wY0/GoYcumCZQLEsPAFQvfF5TWZSKQAFws74TH9msbl+0pOo8DRBOiMyOqOwokN3pfk1V2m4ErcYabHYbbGwy3N4j7ETQOEA/nYP0cbM6zaDMCd8P2TJbyOTzoS4W6127HL7V8zf55qvytd99TffdSOeXnKE/JL2tAaYtXP6dY6M95iMqt+9byicA8FAmmyDS+jhQw7/O/1VCmFs4xFzfkYXDW/T3nAhZBLroHFTEP06DeEDkQsmh+4bYnNL5MjWSa14Pz5u6RChjQR9BwhmRhFgOZdTlZqMXQ8kP4Xoz2TOn6eC2bnpNdnwJdBX3/dpsfcLKHtVNnMKMrS5UFqyyD2m86dmRd6oorfVogRgiCMQI3ifB2CAiixlCHKGDKOLCAMjCLIEONYmY3iqhjYZKMb6T22mRjpsY1Pp7mByiojgou91WccSFw+H/225UBte+CPjZEEIt5RjAojtrGMtf+oByUlySXU32elcXziHzetU1T+3apiNCtXiqqp/KghsscU6reD7tkuSBCwhD1E6Jei9DkLTefEOMt4f26wcP239ceP/f7mrKlrFuXLWXGU4qKrXJJKfEcpYcdbXLv6vvJ59bL/L31OF2og7rrPRKZHnK8pICZUCgAASisijhmrjzoUn5utPvc7/Xxc31+qojw9zr17Dh373XlaY+y7bqXioh6XJzGOIE4167rFBHrc8+dn1crIrbKORCz76jzYN6aFKzPXLewBQq2kfXs+q4vs1nyFv6Nc52/ln/ookylAjRu9diHX1iXa4SULxVQtpj5c9dtXVPvZ2W0HVDsLjht9+YTto6eJ/hLIWbJFK+vuVgEK6C7eSzM84ycNX59X3zc3IJbRJBzrhbY3AFs1doLDm4t3dSrVbNbu1ZPAq4u4KUUy0UmXV1dL1Fr93IvaHFdWQQpRMRIuLm5AQE4fH5AyQWfDhkxjYgxQcDVspzCAKIIwgAOQOaCgAikoCAXA9ksxCFquc8F9v7aBz2wrtatyrznPFvYH7Xq1yTJCta71MgsyJyRyw6CUoHoYu9D0pQdBNSwScDGbJIudi10v+pnTVM8+Kf9rsLqSbJbA6KlKSDmaVrMhWgeESIKeIch1eet17w/pzW5vY8rsJy/r4oHYU027oIoBJwV7BVLWDekiEhAvL1ByTMeoZZceZrAIYBEY+KrgsqE2hjBIghRwcY8zuqFYv03Z4u5z9mEMe1bzWMCTPMEEGM3JlCMiCmiQDBPE4IEjNiBzDMiVk8FBWAFmvhRRC3efL6E4LkJ9Fm1T0yB5h9XAqUUAcT2jGEwC3MLO1SKgv1DQiABeEYgzR0hvIPILcYQwSnh8+fPeFxYbuokK7mAAUxzwTSzhumFxiAGYMoGWKgjZYxFRC3rCDW8sIeU8vUt4jkHbEy5E47JBIEqTVjoos67pio60ehmzhkpag6BNIzY3dxiLqJ5V2A5G4UAcgVShCeChIVLQxEIMUIK1YKfTNCkQLi52SOGiHE3NMt+A+EFBdN0wPF40DBhzNXTqbaZPAkxaSgMFk0qHgLGNACR8OnxM+acAYkIJBYKICK9eQtQwt39Haa54FP4AUSwROoFx8OEECOmeUIYYlMeiVQQRwlHCy2m3gvqRdIUgqe89DIEFeCeL/15ooCUhtq3FFrIO+rmsnvvUGheciEGDMPOlA6xKjEAzyvlfSZmaaYZMCgEpCEpHCRAnmd8+vEDHj5+wvTwiMiqzElZMBwZFAQUBJmPmJkxJfWE2e33iENE2g3m2WB7VozK85cZMUbs374BmDXcUyngaa5EtSoU4fRaldDj/R73f/gd3v3ht3j3h98iffsO8f4WnBlzYQSokiNC3f4LA2BBKtrf+Yukp1/L32xZKQl/Lb/ssgaSznlC9B6o/XEH7YVlUafXtVZkOP/AIrZpEtxrkI37K9lyQswzSsmqoM0Zx+MRk33nwiiTKq/zrIqI2cJgsnlESBSEEjEyg2JAiDO4qGEDjAfwnBaSi+aBKFkt6rk0bwiwKSEsNJ/xZUPUMENj0u8hBIx23veutSKCV/39XPD0tG81t0XzStoGkdeimIfqW8A4GxjRyfMBdCqV2gZN6q2yTSnqjZqzoGSpxg0xCBKAN4MgEbDnEdOQ8ImBAwvupwmfCuPfjjMOzHjIgiyi3sTiym7b7wUQROWNLCxTKFDFkliukFCAEgE2a3DNXm40qlM0eF4NTyzt+KMIkN27wp7lHRUIEiMoAUS2l8cEIEDiETIPCOUzaGaw5b0CZ1NCFBditB01ApUZs3AzJGidHhCi1OMqtalibEwJ+3GHN3e3eDve4s3uFrfjXsMzWWhMDgymtrbdaKby9i7jYtv6fTGX1nNrVa4Bg9eKtktA9rnvdaiiLaXqOUXFNWvu2QoN02o91e6t+h2nd0WEfwPLNdmD5aFeoXMixAAqBGTl4wSMnKcKtouosaOIIFJADOt1fBp6rykqTufEJWxKn9dynzgmsNUPp/ddd52WLpfeM5QRXr9IOTkGuIKnHl0c6BUZZ+ntE899Tvlij4jrj7vg2v86bXAjn7I8WjNj08kXdb+9dpJ2QOhcp1zLRCphl65NC3DynEpF+kX0PIa1dct23c/lfzfh1ouVdGNlBGN9fU9IXq8sBemnyumEX7fbjlJ/7TWsyPPLaf9c1nJvHT93bus5LuRri5ez0EEaD7FQrXL78BnUrl3XvzW2/ea2RWeWdO0S8V5ZDxlj1MD9ZTULi5hFu6wtTzxv3f7uTVGzkfn9ts6p+/bjdkf7LWY1K34fL5tPTuPaAW9rf5kwQ0gtjKqVvgGHCvb7eLlFKpkFlQLQ8zTV+qmGRoGRrTMW3G7h7X3HpTKhIgzJbmntLrbGuQqrJRAaCAYCKLZ4/dKFO6Hadxp71PtFLEyGiIDzsfZVoC7ubNAx45IBjgisCQBjCiATyCAeEkk5HLLQLcX6L3FBgIKSTGTxXdniRKriwkF20l8AOXhF3bQghGieG9njjJt7t8jF+Sc9sw3AfUuaoVJnccUC4dKs8qRj2Or0F7u2T8LXXKGDEjsI2BQDrFFwqFmxqct6c2FfjF39G2rcRNBkrSZUUNC+MAoETRgoxqRqIkUpWce3FHuWjh0HsyQTE/hrThAVgNOQMO52YFFlGHnmCOnAAtHE2IWLMVmMI6mHxTgm5JxA2FlSOlUAhDRY4jJfKr1XBXVgsHejXusxnVG9BJzJ7wRl6z8F6skUEWal72GfACUUpEoWSAAkAlEQ0ggGISRGHBkDM4IEFBDiNCFOR6RAyIE04SGrWM4O0qPR5Mo+1vwZNsc8bpORu54MGlaiZEBElSJ+DUnjT+0BPo80aXkD5aQtFgjUBV6FSl9g2qZcmnJNFQmphl4CaYgDkCWOr/RXuvnma8mVIAGJTLEugJuuCxwo8KANaOuFGeKAPznk3DxiBBqiQkNDOaJj687CI1FMSm8TIwwRN7uIwy4gJSCQIGdGjow5M8ayArXEvbJszUrjZVtfmsDga5Z0v+qMCpVeAGrxB2hyRmnJrMkTqafUFBHGCzlIE0MAJXVtj0HHgdwLwtaPKidMQeHDbI0o2fJuWOgSVViKKa0Y8zRjno4o8wSC4GbcYxSNRoEQUASIRk0jJcRotFWA4KEoRCAxWPJwRhjUgy4gKvbilExRMUSLb01FwwzypEnbmQRxv0e6u8HdH/+A+//pP+Puu99hvL1HTIO+m3vJiUBALgIaPYFrztCXKtytwIctnvBc+RXUXpatvvrafbQGUBf8Kfka7b1HUfmtNXBRedOr5cyvWxa9eUnMou7U88SxVyyVOe3a4g1bynEbIiDqicren8ocnqPNFQ8eBq8mozZLl4bJLOmx8wFwdK3yZUVDzghbbgj1EJOObrDF1WdPoGqfyjsLIwjrMWawWHhO/80ZBEFmwcyCCQCxWd8HzaVVQ2c6LetBYhQInH/SNkUP32tK+jGSxty3nBDNU44Wc566Pum7vw1btV5YHO+loDVguQi5W/ebpsiBqDTle5lxQQYze98nCNyzr+dXjQO3fZRd9jD5LfgC6PgZdHOACyOXgKkAhwI8ZmAqwFwIxWRJEkIEYYwWKooJgwi+4YgdAYUJh0IYUXBkDe+UmVGkk+Qd2DKlglhbKBACBzDEnChUASDEIAm6CVLHK7kXJnchk/qP53Xw4FZsi57F5oq3JwCUzEMCgBBkuAPGR0ieASrG186WhLrAtClat7RRr/ndau0Nj4BAQzMFgkSCDAG8SwhjxBh0Pg6RkFJAGMhYeTE+tpPlvRNt/ETQ+Ph+TLGcsyfzd/GDTv++sCep7NDWxZJyoaMj26GbAjXPEO8rr6f/uz92TinhhVe/azs3yrpd1VPF60WHi0oltrWt/Vu3tsriu1570oY1skomy0fEoF5ebLw0c1ZPCAiYCUBEKbYWYHTQ2r/cp6Xt0+vn915F9S2WNKliPqs6NpVO9Y9O3t664uRWDR8HQsW1Gy7lX208ZVUP94oIQX2n1QxYPHipiFiWn1URsVWu1R4ul8qqDjsvJ8dWtwPQpB2+qPsBka276jPXZ672klhctqRaKqJcrufLmNCnBvJyvdRtRNdNilbf9jhuHdvu91+iQNV3wU/VvC1Lej/+1Jicu7ee72afbz4e99wt3AMFhBQXccprbPVweYzJmKC1RnhL8bMmWZszZUu40wNKkNfHTytYXKdt7ITG7hlrhlgW1XTWpdTRpNpoaevbmABQ28AWTIU097/2IK71thFybb3Nw7a36bgZgMNBAVe3loIwPEa35jpQgE4QkOcj8uERh8Mjjscjxt0eaRgs5ncEGTjdlAX6qX/HqH3GlrCusL26gfWFIaVAirl1E5TZLRMKE1gC4pAUdUoBNEbzLigmNBUNp2SJzYSCJhjVAYKAMU0PiDFiPo6arDokm7PKXIYo4CmD5yNkjgiZMYSAsB+RjweUKauFFzNQiuVDUEZ9PmofxiEiwax5A3CYFaTjooJghCCSYDBAvCCZokVDsOjQeJ4ItcKWuUAkq52CkDL6zKd8FKAeHMbgV+MMAz09mpQLTmCNG8w5g7MrI+xuZxzcms/d+bOFmylah2LcqqgSAebpaNbORa2bxx00Dm1RYcUFAjJLYTYrdQJQVACuKgbWv2OyGOou0DuwSwyhonNknjAdPkG4IIkCxCmSJqUtygwfy4zAAUk0zEscBuwsH0AaEmJKeDgcgeEInifwPCNPBeAJZT5a+AIFEQ4HZdrnPGM3DpDyFkOKSDGBUsSYRkCAzGr5l1KXn4DaftnoEKoXBoOru3iwWPgiMBDB1gaRKhhANTTQkHbVe0I5nAIKQByVQZYSwBQREEBxBoK2M403yMMj5uERuzyjzAfMUwSXgOOxYMqCGUFDByOCIumcEQVblf4kI4oGgHfWnKowCRVbjwQMpvQTGIBs+qFgUXEqs83AMCQNO1W9DhovpkoHnR+FFRAZou49lIJ6p8xHsBBYIkJIiOMeIY1AGMEIYCakNCKmofa/hkKyrhZdLiDCOO4BAMnDORWz/gsBXATHaYaUUq35XYHLpSBEnWOghIxYFZJMCtMMKSxyMBArsC0okCCgYUSICgiEXcL7twkoET/sCZwZxykDIOyPGcOu1FAODnQXp5Os1pOxox8qXGnHUwhqVQtVCHaiuyXfJgtfRAhJk2jmOYOIEAf1EBl3uwrIVA8om7MhDaCBVJlDuv5AqpxQRcagHpXmuRQdqDEaNR0PGvKrtFBsIRJiIszThIfPH3H4/AHz4wMGEL599x7IBZILWIBJBKPos3cxaoxn1vjl+ZDBPIOj7o/xNoNSRLq9sXButwgiCPkIgEHEoCFguBl1vCZGOWTMB8EEwYGAu2++xf1//iN+/3//f+B3/9f/F+7u7rC/udG5y4zZ8iJJjcur9Cu4VXNYWpj9Wn755TkW2V7c29DpYgW2jcaKdB4RPYqGdd6y5z33tYs3+aQZ18pB11x38RW3Zf8nK6bVvdKfOJXqe54akBr+nlfPrmFHPQG0hesrZQnSZs4VdFMQbMMLRiz0C3RTElMwhJIROOvzSPdRCXqdiKBkV0BMKFwwZ82DxdboZAqDWWbj9bIqIsxrg/NcZT6JAcgJxxRxHBNuRa3sBwJSIEQ2gD7PqsiQGUABSwabQoKIMdhet7OQTMMQkULEfkiWpDrW/BFkRghqkND2fjc+6AcxhKXc5iPV5MalGV1vtez3BGjdbtFPHZDopgMwwyKIKnSECKAIhMG8rDu4lpQPRAAKAUSCCOXpowwQAYoY0x0IhACw8q15ZhwL8KkEfJgI3x8BygQqhBIIEoAgGVEYNymAo2AvmsdsT4JjIdyHgkMRfD9nPGTNe/cIxmeebVq5gU5qUz6Q5iRD1JxHGWakVVQ2gyMyLawiEZlSHZZQWlqYLss9gex1uBGSZU+w/VAN7sQYQvUOFSpAyJougkZgOgDzBOATQAf9lNm6W42F3FBJ67awu3WaJKOpuqbAKjvxLqDcRJS3I+hmwE2MuEkBN2PAbheQbgIoCUDFPFpboJnKKVnewwrA9kqap3A0UyTQ6mqXDWrO740i3oe1ss5buL/uDDayuKa/lk4xF0H/vtSu67+7dpwznNjeIpcH207X7YtKiYxan0eEyKjxFmq7frScHCMERKQgkAgAsylzZ7AQQNw87avHfcSQBixynVVFstEJLIF6H59KyXrl1krRsKlwkOXbrK89f++586eel5d+X3qOt23dxrbHyulAnJnhr4nzvnqOiHPXrg/1k7n//dKyrv90CSymxuLMekLU9gs2vSmaXn25mE/KM/jP5zLJzynXTpjT6xxgWB49Z+11Tbmked265mWT/fUWyLOffEbTfI2l3LoPttZVO9aRfTm9psZ79jAVi9wQ221dv8PTc9JDX1y+9hzh/dI5f/l+6omM/9e981qAXN1N23O/P7ceIyJS5lfWW+yq3XDr5QbkejtFmjVm/5HCKFCgP1PAfDhgPhxQcq7tXHs9+Pi0BzfLe7cRdoZeSq6clbbJrXbt+aIu4qo0iV778t3rfe2YK2/IJopQZ9lDS5ZM0PpEgZ+OaeCC+XAEpYQYB7D1NZOOM4tatg0pqTWSe1+IhjFyF01aPbdn/oigiow6X7lL4qz3xhhQoiG0yyHSfrKajf+zNwqnorM0r73ax9zlWOAWU56LClsBYjHm+/jFDDJLezIQ0MFkB6BFNIYmCAilqJBiCinSLK4KTlcGV+9jItVXACCYBSHUIyIaoCkq/1WmVAUWqnFdGQBnayvpuIcULaGsemWwqIAtYjGQiwYBjUGF3yENZjHYFGtukS8hdGHIqM7RwgVJCMMwInRKk2zhgNZrxS0kW0JCBpG6oZ+uq1XpgPi2FoOFDwpVgeWfxl8GBddjVACCo4ZrC9rpLkS4kmYoBWEGQEXfUaiFBVs1jU3hUieplR40MHwbIbj1unFGwdZB3ShcDt7OMRR6cCK0FIDkYYNsrrkXgvdVIN+b3AI/QETzDdTkbNaExXNDd97WFZFa0DMzCgDKoQpJtjQb/EH+/OYJo12k67yG3jIFsK9HOtlTl1agNzd7HA832I0DMhVfSbYODUwqDlK6RxW1xomPQYVWlnwsLc0P+v1nPT8bvYoniel7HiQYLQjdBBVb1FX5afdw8Zi7UWkca06WYq11JXAyBTXPGfPjEZ9//IDDpwdwVmXo/u4WyBkyayi3wsVA/oICBiQgkkUVI1X21v3NvC/mUlBCgOwyYgzYR6MLw16VIKT5Z2QuCAylA7e3SO/e4c1/+T/h/f/6f8bb/+E/4e7+voa/qi77wos+dGL+Er73Eo/yUkHuSwXAX4qh0PV85vZ9L3neOX78yXKZpXviwXiWLPhVypXgwmmhxdf5ek+tV5e3vaDzBKjueCeYiVuV+t+Vc6m/awh9GN1b8d0eikljjMuS70YH2sDsgGn9Tp1o4Tyy0RHiAiqlSmlFtzWtB87vcA2bQ6KfYHxI87Q1ILgaFFiS65JBRqtIAiYwIBFEjAGCmQCEAAm6lwS71nlNSEvRHANBExPrO3myXw2pGmqYT/eAfGr9+TprwP9KroVbeS/nzBYgW/crMVhwNY/7pUWERULqumcAda81ddIiYgbZ3s/Om4h7LFMdZBb1YigckIWROWAqhGMRHArZ/PF3JczcjELU21T5kxQYLMBtiEgAuAwYY8CHFLAnRpyLern4fEKBxcdFEPNakaBjZ/s1wzyGbdKKtR4m50hNIGbzm7O9UDEFxKzzMJsMWI1WVBaiqrhQZYVI1jlpPt0q91Zm0jZuk5FYDcDQhb7VqjtlB5xvDHWdkgoziOMO47jD7bDDPg019x2i5gNwtgWWg4Vc+NoguI32+28bXJNNiU5v8z41BgyoM7fN7MUt1N/YH1+aLW9hIScGmq9YzuFPp9hn/aueP13vXV+fqGi6uk5XuK4DnwLdfnzdO+iYB1G5kLkgEFe51A3IWJT2u7ENs5gy1NsV0NRVWBpp1Zb2zZbuT9n8Xp9/6ve20e3y2Lm/t/rtekXE+WNVVryCV1iO/ZeXf7gop89Z3pXJ+GXw7c8rjVL8TZWvqZD5JZdLhMTPL66x/6VRV2WzDCxJNf75OidE+CrT4qlN5ZzW/0s2XH3m4ilwRnDj6gVo48fO1bv4vlIjvAY2/bv/NNC0AR+5usYacGxCChkDyeaOXXKu1lzT4yOmx4OG3Iot/EagsGobdQy8gtpCLfZkANQSf56sCe4FQtWlj00AKplRsiBGVBCuzzOisVM9/nkDKGFCkedXUEulUMG8al1iGyGVUoWeGAJSiii54OHzZ+zv7rAfR3AMmp8gBghpH855Rhy0L4YhIXLU/jNLXcDi+oe2Biroz5pkLsagYFjWhMzTdNQEwinpu8YIpISSzGPEFC81MpIxQ5Uftr5v24gCWyTqIcEsZuGtyiYunriQIcW9NwRE5nFgVnstiblaGZEFxK0KGKggczwcVEmTXTh0cFyq1xS5sEQAKJhgzm2FiLuy27gZE0LUgF+VFe3dg4LnwziCc8Dj9FATPSIQUhggIggO+ucmwNcYzcyIQZUQLKTJ/JgRU0TMStccqCciFKOIer9aNHOKmjvAri2l4CiHuj6Wc7clqPT8KEpHTxUW/l2B944MVHCeLBwONYEpWCwcVayJedsGAJpzgKVoSLGidE2VCQFxGDCOo4IGk4CyAsA5e5ghja9PNh10LHowVbq/PTeEKkFisBBEUeckEauLRGjsgy1fAyVaTo21sjsls2qzu5Ln/ghaWTHFEyJAISAG9UiIoSVSZgmoiQu7e0NoiZE9j0JvMGKjg1yUlla7K/Exk8XadKXCWhkKaEgtAEiDhtbiSedFDAE0DJUWeK4eF3jevH0LYeD27gbHwwSeYCCGruM8zciDemppwuPgqojaNnPC1jBCEEv87F58ob4TzIqrzkNyKy/dZ4L10eD5SexcKU0Aq2sgqAcaGQ2Wog2J0cOIQRXhRZ8Zkt6riVYLJhGIxe+NMWLc78CFcXh8wOHDJ3z/L3/G4dNnlHlGShH7b9+qV9mk3j5lesRcNC9ShiALMNi8SBQQYaGrBMA0A6XgeDhAIEj3ewzjiJv33yKlETe3twYoqLfS9DAhhQG0v0P6D3/E8L/8X/D+//a/4rv/9/8T9zTgDgnTNNW8TMX2nkC9squnt/ib5Ku9/FKUEC8pP0Xbz/Ow/5hyyVPl6/bKChSR1XHfi139IE3JC5IWnt54D2bdFdY5IZhdIdA9qgczDUSVCob7DoeaL8yZQGEzpMjZLMItZxm1kHUEDZchIqDCCKxhmAIzQtGPywPUh7tk5Um5ZORs4DEX9aQuGoqEOSIwIUhQHtk89iLBQGQ2/tO81wIwhIAIQbEgdEOMiEQYU5MdYwgKAnfA/qXS5MElVEtdP27NnV5OakoT8SHVvXHBT2/hZh3/YDyEKtuD5bbwXbcyvSAQSkiWNsF4Qooqp4kmpy4cMDMwc8KBCQ+Z8HkGPs2CSQSTMBKT5pYSVaB7nzlfNEbNZ/iOB2SOuBXCMQjKTj0j9lPBEQWf5owi6tkCVmA1Aki+URs/EiigkCBb36nXSOmWB8GT+pILKeZtL+4JkSdVTkyzKj1yXsjlVEdLjK90YznPyWfvZx77oAjECIBBMenkdyGJIuDwtI8NEWCZ5piVQZNIiGPCcHeH29t7fLO/w5thj9HztUUzpqozwNu3OSO6a3x8m1dBpSNyfo9xQzW/Riyn2QnMdmn7WMgQF8Dh1fc50Pul5dza27yWtiGa1hd9rVvPWqoi1pjN2jjgEuBOZvw3ICFA5YkiApJicpCNMqnncCkaGi+YB2uMUteEB9x08gLIip4YN3ymPZcB/cu/Lysxturrqd3lefCUguTyd6O1ffkp+K5XDc10qbzGIjoFEk/r74VTAJddp860SZYrpRsYWq3i9e+TFp87cbYNlzRdX1rWzby25mvH7qVjfAnE/pr98XOUS5ZY57XUKyXE5r2exLNjHjtFRJ8X4qk+fNF4extX6/ASod4q67lwqZ/ssagwlGzTiP51N2nIRn8szy/PrTen/u/FfU++bwOOxBlIVu8Etc7OFvfVmXO11C6loOQMASOEZAlG1epeXNgSrv3BzoyKs4BqpS+w+LhcUPKkrDk5eBitXQYSF7f2VyDbrWwbAG1KFG7SnIPcaoyvc0O8n4JaxofgZi2tb6twaJtjINLEryUjDQPKMIBEkFLUJH5d3ytYJogxIUZgnjRHQrMQb14a/lBmQc4zIkXQoAyJ8riCUrKC9OpioOBdjMCQkK2txQVQY4a6KdmNdBPfPLqKmBVVycWSOJu7fi6m9NG/p7kgBAs7os2q6rZg/6mM4YKCg95QZt3yYkgREGUDdrkmTw4Uai6DNX1wBqUCnhCAGrDpiibqxiDEpPWIgIMqkRwchc0DFkae9f2YJ00QO88WIsHCRgFIHiaGC4IwpOws/nxAzsVyRgiy5cKIBsBWAXC1NpfWeks6tW2l0u5fM29EHjee7LXE+r53jW9CO1megx48RrB8E2AgRPVCsRXqyS6pA+r1+VCPiApY+LxujKsfrrIatS+1GmzzXK0fzfotBGPk9bUC1AovdIrDNW2t4x58vZPRiNSdr+Kn5SFIoDToNbHLSyChWr0Fd9nwvmpLVudcHUtbT2jsmK53AqHlRBAxazt4smvquwZu7eljt94z0zBA88rYPLJ7QtDQh7f7G+SbGbtxBGfB8TgBIjXmdLExY/uABR6uwGlkFak7mq8WXf2LL/ug9s96bi6ULU5bCyoN7IoAKBbCARYWmrkgFBW2QYQsxd5Z+5BNYR5JBbsY1FNiOhyRpwkfvv8enz58xOOHj8iHIyyeloYuEwFh0DB+hUEFus9ZPOsEQoxAsn6JpBalCOqlxIOijAMRkgiQZwgE8yexEBYEQUT57jvs377Hm3/6j9j/0x9w+z//F9z8hz9gTzegUjDzXJPM69wMnecPFn3q/fol5UROeUb50mf/UnnnS3zvc8pz5I+nhPk1D1qhAGcdriz12tfBkF5UntOLW/0i5P9desjyfB9I4JLMc/n5HTAj7gHR1SUtz0P1PPPkoZCOJ2q0VKR5BpSiucI8hr63Wek7ENGstgltf/Cm1bxcnu/HvDlLzpCcIWWuSFfNm0POLtheJPqJxptHO55sr/PsRUFciWDgsYNvJaMIIZsKm8BKO4UgKUJibLlOxQxKxPYtCogBSBGQIBruR0jDnxI1BUQw+usfOG9Ai/3RecBLNM55H1VGNGv9nreq66/7Rn/8pFK/r5syYnPF2hWcC7NzVD8dU2FzzBVYdd7AvWShXqgIKEKYOWLiol4RInhkQSIdwwRVHIyRkKh5MkZTJEggJFGFdwzA+xCwDwLEiKMAMahnxLF4HHzzXgGMZzA+x+Sryn/KKuySAG4lRZ7vy3KRqBd8AfGsx7Iq+THbvHV+AGiMI9TooD1ntn3dPj45qkcEWRhXcwkSa3nl54Lmt/IcHpaTatjtMd7e4f7de7y/f4P3+1vcDSMGslwlUcN/rvfo67EkNZbrS7v3CjoFQFBsDrc+ckqxvQb6PYWXRyt9a/O9b/N5TKRfE7L4fRaUXry01OGoL9Ffuzi3vnlZiBoP3i53rlbr7mUvxyOWfdTJnuvaSDoenRC5IAlrsne4h3HfduWvhXUNV5nI3L9DiNYmrrTRMQKXoZr3lr/jae6N9VhfMxeXZTU+J2NNWM6dy3W+TBkhbW0ubmuy5BNP/SIe52/GI+KSEmK7rJfEC8tCk7FeaRsrry/L+fMLLj+vgLIgTn8bHfbqZQ1o98Ts0pz3czGqtWjLBZE2lRDPKS9SLBHV0DbPrfM5CqnursX9/fdW/YvzZ/rjiwV++36695Rp8SR0KC0RnYLn5pFQqMYrnueMnEunbAoYx7FawjMXFbTsCcyhMuAqhHk8RFU05OMBzBklH0FEakEbI1IgaKxjtxQXaMgUzeUQ1SzWHgJIUYt+8VwTDqBSZxPh4UEDgWJEHAfUMEF182eUoswCc1GFQwjI84TpeEBKCUNKCJGQhohSCJJbT+c8I2fgzZs3mn9iylWx0dZSqMKmKz6macJAEdEYxBQCSBjZEqzGGBCQ0BQRAmQ2bwwG5VxDKYkphdbFjwZYbF/R8SpTRskZeZqaVb4pIqZpxvGYEQIjBjZL5xZWJgQCiQkjaIoIGAAbosoCbs3clAdN+QCL/avMmTLWwdaioDEqhGV+lV4wBVmiuBBAQ1LBI0QNaWP97JbmCgIUzIdZLZFLQc4Z8zyrMqe0+Z1iQkpqsZcDIVgs43HYqSKCFUyYpoOtlwI1mIqdd4gBsyYENsVAY4jZPAusgYvx6xUY3CnadC6HEzriiohl/gTUOV5BdVjYGWN3iQuyrReHU+DAuIUwcma+lIJcWO3IKm1vjHAjlx19rB8VJJ2pj6TCsuoELWGiqAIwElls6FiTWJKDKTUkGNXxItJZHqJ6JRFRs0Q1QIZisvwMg+YnCJ6oOoAoIohb6httCE1IXb9VG0MXILWPfb2nmOC5fDx8gntUuGLHK3MlhCt9mjIpIIQ2f8ucWx+TJlknAG/u30BYsL+5QcmM48cD3CKWgKpczHNGTApaaRiIDJIIodjotCnktM0mEHZhr1Q7qt9uGdjvnzoeoba5hh1iC81GbW24AKxrT2ps9VSyAh1FFRAzF0uQqeHqPITDQJoIfogRKIzD4yMOnz7hL//tX/Hw6RM+/eWvatUJWF8GTUodxPaOgDADx2L7IAsGCYjcQoLUEF8Wx1xsfxoDI0FAk+aROR4ewSFgHvegN28Q/vAH3P+n/xG//d/+N9x/93t888f/CSIBIoScP+M4H6tldFx4jtp670CBSgfwt1d+qUqIn6M8x9CmXmuITIWk/0H607GJa0XEL+mVUwBFUF38UL+6b2neDB66SNruKUY7mVmPuMeluJW7m9B2gBNR9cbFKvRebZLRaLjiw8LWSMngPOtnnkBlqjQygE0R4fyb7sPKjQqivWeyel0RkczNMVg8c+IMkgLiYt4Xs/LVEsAcIBxBDKAQZEiQlNTDMRqPYdSLoEpXEoCGgMo2CiE5XxAjQnDFRKhgvnPQC0VEg2BX8mvrvU0AT9CNb2+UtVRIoFuLCxvrOkEb36O6qDZuCz6sG0sS5Z0J6pXN1h7mRvPZ5kph9dQrQigImCXgyIQDCw4s+FiAzyyIIogAdkQYQ7C8IAGqPlfvkwSVLxjAyAEZGrLyGAS7lHAAMMyESQSfRb1f5xp6iSy8rf5jImQCOusmVSYUbh/hCrJW3k9E545kVUSUDMlH9YY4HjRsai4NRNZB1/QRgbyTgTzDc1T0ia3JvSNCMO/f2BZuY7hMV6TyiM6iiDSMuL2/w+27t/juN9/hN++/xW9v3+DdeIMRmjidUkuc3peF52JXelq+xJtocQ25sLxRRBqP5RJ2f6Xycv0M65/ViKg4Xeuu6b9rrWcA5eV8l5N3O6uw23wz6XDKa6h3q2EpI1n/dCfq74UygRbrmNbPpOWPfq07/0/ECIExcEFVMDOqJ2ttKbPyryYL+Fg436+GUsXkxl4R4Q0xVYhQW1+4npdaKyquuOPk/nacNsf1KWXDueOnc61euGqR7aUvxPSuLa+SI2JdngIbv7T+S9fXDdBXl3QbV9VYAQvCsGpv1WzVShe317E6p0XsGnPSrnPluYN5yeoAaMKlXbRxxdP9/XxQ+OVlybhcc93LWd5r6zg3Ly7Vd23fPPXsc6D6QkFhFqoeZ9tDI6xzQqzr6at8qXa1P78+sznb1gxo3xhphLbVe1IDANnot/P9uNXHm9p3WTLMdHLeacWqUVv1A2rhceaZW3OEFKExGUdqaBzOsx4RNGCqFHAuiOOAENTiGOIJrrNZz2h8cweoGsvUnqvAa0HOM4QzuGTdoCWY8Na5rYNAISGQqIW0hYNiaaGEKFi4GbHwR/ZiQqgAr5jbLQxYHYaxAn3aLz0DZ5bx1mzjg5GnCZ/xCfv9DrvdqMx10PZEicjzBE/kHDuwsVnM9ZuqPk+B7COEAtJuhsDi1mujISUjzwCliDAMCvCnBMQZnKGMP6SOTzTg1BsfoNZAlXkVQISsnYLZhNd5ntAGrAmMAg/LlZEGtSDnYMlTu+uIgDyrwMpFPR98TITZ5qaxXKRKJvVUUVd8bzI5qGtSnbAmrS7FQehodZtlIefFfHG3bR+4NI4qYqRY2xIja3iqqHFhY4iW36Egz3MLfWMWUiTFcmSUqs6hoMo7YkYo2brNLOw8gbhlXdYwOgXBPH389RwkFzKLcG5WN75OekXE/8HevzVJdiRpYuCndjnuEZEJFFDVl2E3R4YzMsKR5c4+cP//z1jhDIXDbVK43cWe6SogkRHhfsxMdR9U1czOcfeIyEQCheqGAZ4efq52VVP99LZdtwRXyIBGCIgxie17DocLs6ASnQjKrJOFXfCQS83WSrDLNOTQWgpKLSjFElfqJRe0Kwy5DjPWTopHbIQttdBUD5NgFkfVmHufE2FSQMx8k7d9VrZQAFJMCO5Cb/VXYEeVmCmmroxQD6zQbybSZIzBntHzS+yEO+9/P9r9tZz2iIYh0zrM6347vn68K/Zi7MKSj1MwxaKD+rWUEabIlP8SI7gecFgOWJYFa16hShrpycshZDgBd28egio5dBao9wFPIdlG3gJRcGC3l5CBZhcKsmn+OmDnf/sjhrKDwWC00iCVe9LqWsrIFUOWWJLUG0e9aJS+LjHr82pFOZ3w/e9/j6fvvsf//b/9Her5jPL0hLQkHO7vEIPAdSAC0eTtMSOEol54plhs5sGVLIN3QFB6YXNyiQSIeQs24FSqJtd+uEN6/xV+82/+B+Tf/hYP/+7f4f63v8Pdf/e3SId71LWAmoCqQGRVIVRcSbKdY3N4Oprm+tzXt/iz18p83TVLumvP/tzyJUHzL/GsW330Jfryc+6/du2WF72wzdRitHSmQ5/63l96cX72LdcBuGCRgcu+vF1k0F2T3TsfYXJ8z0c1eTdATIEpsyGGX2PvdBpo3wIxjzSjLZAuM0UHOIOB65MXhvLnlrNhCpnq4SBbq2hF+Tkpq9EWsZj+UOt4Uit4DRPkbTWLcvsOFpyPHOTlqoY+lgxbOs9VLdSqgGOESEDgAGLq4ewiIiLU+4HInCMISCAwRQQRO2i5kTCMCRTcG7KkO1d0y+T+N4YyYgJ6eeZlX5KPxcdbbBydQdM+92MbAG0GYp3PncbbXtp5WhHdW4QbpAXlU4m65T+R7QXdCsTuMyMVZlFFhAQ0gYZpEmAVoDKhNuWdIIIaBGcWMAFFBAcQEgHB8oHAeCWxvTCTav/vk4Z2WnPAmQTSNN8HwXKYwUI9glUhBQ2zpIZNNn96LggL78uMydcSIs36tFp4LwGmNntHkiVMl9YAV364aOPPamZA14rOU1NuCDd9t5cOnvlvA5VdfWUyXF6OOByO+Oabb/Du66/xl1/9Br95eI/3+Yj7lJFjRDIjC/dah3n/+5hfjv9sUNWRBPtrL5vPldwWfdREy3Y7wrVdYljUh929O1kBGGvA6d0N7OUWqHxNKXHt/o22wOnsVDO88HMIL/u68OaG23vyVI034G/XMRz3WI6IkRFNkeBh43S8uSsuBAwWAgsrbbN9O1iUAw1n7eGHfcwEGvLY33+J/1zr32vK1te+Z2zr+vnx6ls0dDO3ZR9m6vXSe/nK81/7/SXKn41HxOeXH9tpV1nQf0bln3Pbft5yi3B+TnlNKFPwdRuCycPlzPG7Z6BIn3v5nkEMr5fXBD0Hfvrzdk+7Rlg3f0+abz00E30n0sDelfKl8poSYlY2Oj+zvWXPUFzvo81mtGF03lanftz6TQUmd/EuHezdx8+HJAsvokxAq00tma0Gi1kxjU1JGUnvd+nvMDCmVQ0YqyY8aK2oZ69ox1BMiIGQAjooyRajvlvbuyKCyGKEumxhfWSMv5CCknk5qMAzWfrq68S8AmqP6RoARCKU9YzzekYMwJITALWUjUkdotfzCVwrPPGzr4lqShqIWUb3sSQIN5zPJwgIh2Mxa22z3jcr4CoNIS+IHptVA+2DSZU2wq2Dej6m7nZO5lXnQrYYGK0hfhllPatHRFnNCt1At4npb61CLHxWJGWgPHyOTysCTBhuW2YLGHFjbR43qFu3VijpO51WiFicehP2uVnoo7Emu1whWjdXRHi/d3dwAMvhCLewA2C5MNQyO9ZmuSASCAryFhuzAQxryAF12mCzeomgoCEQWmsItagsVS1HgHvxkHrmxKhzJcRkCYNHnGgSTW7d1yPMWtDadwvk7X+bwm+ex30yzw/1OeekwgQPtrXDbBbztakAT2q5zcwoteJcVqyrKyL8/dP4ixmrdSDTAVY9HwyE0H40CyB44m97FmBrmpECde+AEC893fZ7i9PpnHLfm3r/9XGIiCmDQgYmTwhQhCCowjOknih6VGprleN/uZdRs94N0ZJdG63TOnjemnn+GlDCjOBMvq/rjWCB7p2RcwYR4enxaeNhdDwctC9aw3osOBwOWPMZRAwQI0ZT5Ni6r7UhmhdQpNiBGyK31G8WxsnTQA+F2Mxj+F5PgOXfuBwXr+dQKo/eExHNyyD6aWsFl4ZDOmBJGQUFrTn4QEDUEICaTJ4Qc0KKEffLAmHB0+mM+vSMP/z//h4f/us/4R/+0/8KYsEhBIT3D1gOiwl7SgcbRL3Qoo45hQixICONRfNOEKsySlSxFEj3lxQJEEJbFVx8lqaKrvt7vPvLv8Q3/+//Ge/+1X+H3/2//qMmsD7cA6eC8vGEsBbEtUJig8RhJefKKBfm53BNsyXdlzCG+bnKL00J4c95izB7U/n7E5Y9kLMHAjZ12QFZ/xxkqWuGQrf42X7JC+DdXN5i9LTtc2OSpvGYFasDhGYFVyelhbEKm2eyWZdzf4eNX3AaoGs8uSLC9myykDKenw3mheE8NLcKrtW+C1otqOuKVs7oNtLGJjRSL0M2r9bkrzHQF1Bw2QIAadJrVqDXQzGJhVMVVuMU7yPmgNYCKEWAI5x9zKQKkADA7DJ07pIqK5Bge6bSVOfviIaVcVc60Ba+nXyE+m+PIuiyx5sQmIkfwrzkZlB5TBRnCTb3Co99nidZjAxUFPO25dYgMWgfEoAWDBfXBOCTO6r9dkWEepgzCFVUAbEKUGBKiUpoAjRhnC2fciPBQdQfZiHg0JVSJgeZY/lCjBgEnAiZCK2qIoIbsDbtgyaM4jKMMCAarhTSID5/LKG0KiHUSEf/tj6AgGFrxZNON3QvSOdLCXbePCW6ksOzgfunNfWCZ3u3lOEdMa3dPmMG4rmZNRwDkBIODw94uH/Ab3/7O3z11Vf4q998i68e3uHr5Q4P+YAcA3LyPGUO86uc5nNuQ2c6KdnzjnMjcMFbXZug8zMGt3V53f7XUEYMSfzqqujzf8IUdnXft3Gmb29SQlilejM35y+vNfRl6sehsbp8x412Xbzqbfvkfi/aG5FGM4ZMnLyjjYap8WRHPoS7ZxwIPSyr8/rRcsG4/AK7WzGZrSywr9++H64pE/zcteNjXt1WVuDKvS9hcjPNvUV/XfTvu/t04Vv5sy9ZfnZFxC3G8ksz9zvy5y+f33z7Xukj8nnv/oRBfEnb9GP7wlmt24X6dfptY/DzzsEvXAQyLagv+uSfSQC9poToY0MjJE+cElLTXvHgwDawJYjYzgmZRr9vlNcEsR/Rlpc0uNfec3m9MwufX4cX3z/VUwm/Hh20qW+911/wQh9tLYa3/avHNJeCkFqegsi8AKUDu2wW9xBLuky6ayjgXExBoe7DKS/qHWBhbYbANgBygiWiNuaSugCnQCiIwWTAT4gjZAXMCl8YAg0BpSCwunizKUkozJbKo789WbXXIyVlIMSER5EBrgEAt6qgvbU3pYi2NrRSLIl0BKWAlBNqK6A2hKn1XMBNkBZVKjBUoFCQd1jekYFibNZstZ4RCci0qAVSYxj/grAcEEpBzAeEFPSTA9pa1fquNgXCF59P2zAemnwWEPOOUEsNc7FnUzyp9sDFVwRipEgIjdBIBSOp7vnCoKhCoyoDGLWU7qECmsBxCxEj1t+tGbDJFVwjwNy9EIwlU0CaLflzLT1pOWisR5VFLLdFWU0pU/v7iCwXCKnVoY6zWXABpkRKSCI4tNYVR93KNEQDaAflijGCUkZmxmLCZz4e0GrBevqoAlFU13e29SOmBHHgljdrc8+ToLsS7Bl8X8Oz0qHT22ldjzjzZJl2fU74gtB6a3QjXRvNhWjz0vC2e/s9Ebw5Kel6NABV94gxJjE4oMBWHwdxpSfMhPeo0wcRCCYLcShDLmZxJjKePYcHU1ppYA65Ram65Lvii0g9B4LtVXBBnEhzRMQIihqqDT7+joZckO9LmhqC9lHoVzj9CtMYj9BirjD3vdXpToxxA3KxjaVPDN8n2NaLDpOGoGsxIqWI+7s7lPWMtGSkFCePkgHbdEGcMOV/QFdm+vc8t1yp4O3eKIJ8zCaFotM4O72bzxoCT0RQuaJwUfrVBBKt/Z7Dwi2Fbew8h8cSE2IIqFxQS8WHD3/E43ff4+N33+H04QPo+QSq3Nt1igEhJ4Tjon0dAmrT/EMNzyBaEegMSEUS0hjb0LwhCQEkQS3aAiGmAMSE5etvQccjlr/5a6Sv3uPh3/5b3H3zLf7q3/+PyA8PWFoAS0GpH0CVQWhIxOr9EwJivC20z6G7ZDr/56CAAH46/vfHPPtT+cmX3vOSMP4l69DrYv9MGPX+7D+LMve57I9tQL494Cebu2jHN9PmWn/w9LcA3aPRNhyx8BtOy+YE02NfFrjnRE8evYP+xjn9bOple7Mn/3XFI0OmdsnwgGhq8d1qBXNFqQW1rCjrilJWrOWMWs8oFtYTMCMAMoUAke6hgBr2QL3JmBsaq2EFV+XjVPGg73PLczX2MM+I5gYgbSRk5gRKghwIhQJajODImkzYdyCbwz3/B6knhBa9Lli/dEXElSkuJjfeAnF9p9uvuFuyZT9usgLPG5h/MOaHf5z/md84fMw9jNWK1la0ltEq0GoAEEFRACEQF32uhXYSCpowmhmFgbUSVgbOFVhZPR2KCFYIChFqjKgsaAIwCSJp7o/WVMYqosZDkQAKygFX7xvL0RUtd8Ri9hDHCERrU5OAVQStCUoTVGjdKoAKDyPlvFzTvZsEIPcAsiTVbG81LyKYIkKcuEXVjggXAKThGj0fBATo4X2lKz26J4YrITby5eTh4kPUaYTmekDOiMcD3v3mK3x1/w6//fprvH//Hr+5u8fD3R0eDgvuDgsOxwU5RzO0u6TlL2EWm/27z5cxk32a3S47wkW7o5vTQ8kixh/Pduo8Afq7Sm4Ov6RYeKsyYv/3Rg6xc3uQf1ul+XkDS7heL3v/NMb6RMc+wvV2v1Bmo6GpVlA8ROlUDNTzBTpvr5F5gxr0BAGZpz3BcxhqvVw+mPnlrjebMJtbONI15cFLSq2tEgIX11/MaZYOyr6kbLo298U/uzGEh5uSubGX7yaEnh5qXj9fWlHxRRQRb6nUj2eKP5PxBSYCSJ+4BG7U5EZbXlIq7O/9UgP50oQHnB27qEU/d+uecdX2XW8tr4G/t/twW4sfM29eExx/iYLli6A9KXAXTAnheSBiSgO0wTTHsCeU6Mf3hW68e1+nt/bVW4lVFzg+Ye3cOr9/91vX2ktabLsCvmls7ttW+OZzpwPbb3tKIAJbbHX/qBDG3drenwfopksAxLwGgIrWlAkNKVn4k4AUo4ZZEeku0jHGzryTWc2IW7oILAk2gYkRoyaTjSlhsQTRGvanwJOoimg4HY3pyiaYxNHGmRlidoOrDvw5wCYT1QkhdAWMQOWCEDTm/LqeNYzResY5BRzSHVKOCKtJeiZElbWAG+NwWBBSRO0CrRvqTEIsFEwPrahCw8K5QDwJoQq+sRSkUiF5Ubf1FEBVGSsPmcV1xEndu+4yWdeTgMkBXnMXb2pRJ0SW4E09LmIQ5ATUah4CIpDm3hcNFJUhdo+EVizxatQ+9iTdwSasK2F48nCIMXXvkZSSvpvG2GjejTLCLtkcdpLj4ECpqymjVAhxoLwdss4LY7JdKeXPCTkhKwFCiKULCiojm7V8p9VAixGULZcBlKnO5wNqLXgOgtZWANqXjRmxh6Tx0D0OCPcph61YYucnOjDThQ0ADBh4vqVPBFLl8OB4fRUYXUa32CS4hWcPKd3rMCsimBta06SJRACCgycjSbunDkg9dwV15YHPA98dZnqja9esBsWu610gY9wxgJTLfqAJ/A/eQAMzTJnpSe6D+WPYXEOIGu5MVX4XiohBR0MH9P089XfDaI/P96EMGorHLaAy8wAbJegk9IhPvOmememfPRBjTDjeHXA+H5GX1EGtTXuwmyd22BUcnjxZRIaiyTwEtn09KyIsVBSlzTxtzXNCzF5nnivC3md0z5Nb7oVajwUe3aOF1Boxx4RAhFUK1nrCDz98h8fvv8PT99/h/MMPwPMZVCukKl06A4jHBeHhiLxkhMNBgSEuYFlBVBBQEKQhiwIwGQlRAggRJAyy9sUQlW789nfI33yDr//n/4jj7/4Cv/2f/iOO9w/4zdffghtjPZ1wrgW1naDWugq3sSGDmhNnK9xtjQd8C/N8ET89v/hL5Ev35UsLol/iHW/hIX9UIaemTneug7O/tPIS//5meXR/3n9fPe5gx3W5oteAaCuMGF/qH1WGKt/WeBdKjqdY8PbO4C+EdKAdnQfXj/MgEzXve4krWN1zEx7CqfNNbN7KpjRopRtpVPeEKCtKOXeFhLc3WCimSuoREck9JBSqVK2w0mINy2qeD6aIgCkeNEyTAs1wIxb3xG22H0EBulIjcjAvEI6QqGhA3y+ncZj/U7eJcZ0P1XbwnHdxoNX6+cp66OkLdvvKLQDV7xnDe2PuoQ+3D+UVGc3GTRqYC7iewXVBC0BrxmsYr0y16gMMlBcKaAAqCyoDawtYmykhGF0BUCGopLkaalDlBfvYiqCyylrZGKtEqmQHqQ5AnM2xeSEE5KD9cQiEqJsOmgDJEpNHBgo0H0URU4QAgLVVLF/DsL43DwfmPtecP5NqlRCdPYjJFFQWiCtYn3ePCzM0Yk+gzqPzxUMy+fMxePkNsmR7nM+3nBCOB9x/9R7v79/h26++xruHB3x9d4+7wxH3hwXHQ0Y+JCwpmYfPbdzgJXqm57bW7tPZF+6Z5tWedk3X6LkwpMArWAhPBj+3nnOtTa+de0kZMe651sIrC/zKOzApIm4C4n0hjv7w0b66Rt+4iW5ldnFJQfljUk8kMSMuIl2/CACz9b/UbgDjtj+DxpFtO72mcM/dl8qLSojeHzt66+3Z3d+vn7ET6rW5GN9b796/Q3A5htrYW2tg+wSXP/dKmS/JX/0ZhWZS4vHzl18+p/maMuKXUD5t0v70Qs6fQ9kwZoG6pXvOuSsiZoDjJYWLa8Gdrm3GQ5wh2N5za+O7EGaADVCzFz5eZTzfODduzfP98Wub8OdY1m3LdYFtgFzXj9uPq3VwIJ7ZQTTf6MczAgUwTd4M/iygh21yJCuQgvXLsvREcyID8LYGaAgXNLBUlPVsgD8jUEDKI3lsiAlpOSAlBai5qcW/CmFTXgAAIIvrLYLs4B/YwDNrlytUooKQ7hopXHVfZNFEwzFqeA7SWPkOgqqXR8SSIsAN59NJrY5zVuvWlDTJNak1P8NCkxA01FIIqLVCPOYRGRAqM+CqVm76rZ4mPUZsKeBiydmgsd9TTqjnVUM01apx1RsDUTD+m8BHcr5dQMKWqNAEhqYMPkOtdREjCBZbNgo4knlQCLgW9e6AAsgOXjZWpVIOuYfmEhGw+5sbs1XWAk9EHiigmMIpL4sqn/JiQADMw2GycDIiEm0+sgsfbAKQhzkyNKADgEEVPM2Ahubz14AFBnQcc7IeI3jYHooBccmq7GENwwIixLyAQkApK2ot+PDHI8p6wvPjB4CrJitv3Pufq1uH8QZ43ohJhE/a9Slc0l6Ch80hqLi5u2ezlqmHLco5oy0HBJACnzmCWkbOOs9jPJtFHZkiwsIxmSLSmfMUhmUQYeSCANi8MNA9H5UGOYOqrsspU3dhFmY0UuVGDGQKq2jtHm2yVW7gt803B959rXneCx9hMs8+S1yteRF0LNhJG4YVVff6sz4PG9qq/YEuI27D7PR9YqKh+7CG8/jo/B8KiehgVVQ6mc0QwJ/PACgGHO/vsJYV9w/32vcpWqiphBgTUsxdYTArH6KQ0tXGcJ8hF9nF3LI8kWafc+KKBxdi6gBL+zyTnivElRte795kgSmdoyXxC/3vuCwWv3lR7zhTmpfnM1qr+P7DdzidnvHdP/0B54+PmjzzkHH3F9+ASkM8F+vjhBQyFixYaMEhHNVriQRYAiQskNAgmREtNWo+3CGmjPTVO8RlwfF33yAdD7j/5muk+3ss//rfIb9/j9/8679FOt4hv3sPooDnjz90RT7EQCAXyygAiTTp59D8bdbldj1zX1uYwedf2dR/EWWAH65w/lPX6GcsN3njgSj10EwT+OT3yv4Zm86bZPrOsxs4yh46Ub+rGYNU8wb1UIo9gTIJhIAI3zOcBlL3OBYRDafZw/RtB5IBQAjd6VPMe8LAVFeA1Ko5gkpZwU1ze5WyYj2fUMqKVlbUWruHo0BAVZ8VySx4TVkSyTxHLaSOhkpllHU1I5AVrTZTRsyhd+zvpr+51t6OFlg9IMTDZDp4GG0IaMK3qCdsDh5T3VnVHR/kv2naW/wZN0mhnzCe7xpQevHh3XX7a31uyejfcb3nRVIvBBHn6QtqOaOkhFITiCpqYQgHEDVtXDP+2BQRjTSE6VkIlQPWAqwsWJugNtjeofkXGglWQt+3Na+G8kMM9Zpoot5/kQSZbc7afh4NLG1m4BUEiAIsGHm92JQRLQZUiaokEeAQCHfMOHHDmQNODBQWDdvlCgj3VnBFRA/ZBECCdbGtmWCJprHYwli0AtI0v5IAxNpR3EOimdIB/rfY78Foki9zQT/WoDx/OBywHO/w9fuv8PXDO3z18ICHe/WEuD8ueHd3xGHJOBwXpEggfweNueRzZP5+qYgM+eQldHH2ANhO6y14P79beW0/Pt/pxy6fua/3FqO5pKWbdQB0EN7XjMz3+b2bRm4xk8FHXsNS/IjKgPt3X75v7AWCgX1co7vb7eEavrPFU7YKEfdyw2bf0L2A1Is2sMoQDEgIaIHApPLNZX9PNLvjApf9dbUB1/CsF+ahrweaL9tf7viObPvmJQXIBvcCLDclWV+ZN4yN9b6/ZaqIOM9zce7T1tlbypsVEV9S+/FzlKuywkD4Xr53f/7G9a9Z2n/quZ++7Osr079dendS+dIaelN5Sz+8pkC5dd1b7/+U8tax+TFj+NK9dOO62VrTrZZn69LX5uEgUoM32LxDLunfredcrfcE7uwnzUtKiJnJvFWB/btfI4bXFBIbrfOVZ39KuXaPt2W2RH3t2QRlwNRLwC2RZPrYc2i0yUFTBxjV0sdBvtgtcjUESrBk1YI5PvqI56sWVc0SrwrYYsFHBEtWGszbxueax9WfrXYhmlRVWfKJWSL0Dd3Nm4QNWIuxgzoAumW4F1fQwJQZcxiUGAKWlFCFUcs6QphY3cljsZuHRrMwRWFJPa8K8yykDmmrh6HxJICe8Lj5d4NUc4kH99wUHquUW+seCR7WxA2NBqvrzI71k4glABSQCQrcKigGkKhCKFJEIIADUBujcgM3s8BrFY0ZpRSwWFisQFhyUg8WAwgYtTOO3NjCKI38Hpp0N4O5IeUFiwuYjB6PWO83AF97T0F0THFq3d1bJyqAYdk/xpUNaObexx6/kwLtFKzH1O27AAEAAElEQVQqFAWOYM46V0VDkMWYsNzfI8Ro4EBBDIzT8yO4qeBZ66lbhQcngMZwbjI6iAK20mts8/MGfd2v94v8ED63bJ7JRGT18NaiP0gA2XrLywGBNW+FpAgkVcClGC0sEkwRMcItuWLBPV80MeVg+m9DBQ6Gj2tSJKTFlUHmHcDSPTxi1GSB4jmmp+4RuLX9BFYEszC1sEsyXq19FyNC0twRYokOe177DnpYQjlyL4ew6b9BI0eFBGLRCOZEzdPo0jafUp+fu3H2Y9xYDQSDgvTJFJ99PyMdk+V4wHE94nh3hBjtcvoULB9CzzcAD7lEgKgHQ2NVnupgThZoPMIzEVMHlDb7gni2jNFOT4bt7RnzeQhOBEIMSfN7WAJxp/8pZ4SYkHNWOqHx5fB0fsZ6PuG7//YHnJ6f8PH7Dyins1qCHjIO37wHlYbwtOrcFCCGiIUSDpRxFw9oxKjUbB4AEgRSRYEQCkgP7xCWAw5/8Vukh3t89a//Bsv7d/jqr/8K+f07HP/tv0e+v8fXX3+typHTGbUUPH38qG3XbkWa9iMKBImq1BHehuu6xk9tWRSBJ9r8MQzyLT7lS5TPec6fm3w3l5+y7p3HxEyPbvPcf27lGr176brdytiCLyJ9D+l84PztTzDe4kLOFAEcPO68poUtND6vKyI81CQsTKA/177mvVdzXbniVvfFWVEx2kgWOrM3wOrkf1oep1Ytp5fyHK6IKKsaQ9RS0Lh1Qwv2WPnClqdJxocUyNbEwAKY52kpZ8vhVs3LVPOeDQDZQ+IYb2qejAAGGGegoP87wlYNGuGenwTvQxtB54n303x3H4AeOrUP7W6OdDmPZfzGVjYcY7BVLGB33ufJRvaTcYx5tFtnh3uxFLS2otaMVs+oxGhVAImgwAAFcNMcTRCF0z1jxyoRlYHSAgoLqnmlOm9NpEYIxfsZKmt7ElwBo0DzSjAEQQRVbB5YeE7vomahRkltmZBJAdUQ1DBFCGAhtBQ1BFQCMjccQsDHGhFjQauCRho+V1AxklK3jSKCeqjHPNYCGeNBAkseoi+BgDiCpI1QlaLGVD3JhE6+DY/t88KGo0tATlAFyjelnJEOBzw8PODd/QMe7o54OB5wt+T+yYeMnKPlyFODq1v06/U9wWpiVuGujLgs/o4rcj+gfXUDE7j+ztEZY57eei8unn2LP92vpVvf/dleny6TvJx3AHBDVlM07d59/V3Tuu7tv9aTcx1ePz7eqTS196rRQhb3irBwwEYH9GbNo6MyxOXzfe8ZMixsLRgj+VK5ut9d+T23zU7792YMtFHzj6m+t0NBXVNGDA7G9z5cIe67sftR6+vTyp+RR8Qvo/x5MaAv1NX3Ev89L/SX73xT+XMWbP6UxTfqTlTMAjUEtZYNKXYL8Evw63oZxKrLAJebxyBPAEZoij2TuNfKApcbiwsh1xjOa5sm+Ppceend1za/W1rha8duve+1624pIvZ1dGUBMNbSBe2YNlMRDbfTauthWhQoizo2RBZLfACbDEY0MC7lZBatusH2WOOsuRycYa8GpJ9Ojyjns4K2zAhB51W0xL4pHxBjNit2i7XPDU3Gx11y1erU2RtVHgBBgVRm9RAQZcAFBOJg+7ps+lzrQeiWDsYXs/3XzN04knuhM0otoPWMFDV81DlljXHeKgSajFUgyDkCIMSYAVYPiQBB4wh4EkIH/Sa3ZepxVqGJkU8nrEsCIkFgQDAUmG9lxcqMWh4QYoC4//W0uatRurpqiyUJp1qBUjThcquQctYwTkQWRz9a/goLk9QaStFYwqWpwFtMgI2mhGrJPCqCCkO1VYtvrNfVVePhsgsjRGCuNi3ZEmWrUNLqitpG4nQJpNGjDLTjqlZRLoBRHKBwj38vA/BLlpiakyaOblBrc1isfc+voHQvg2Lu9KJ5mKycQSFhubtDTJq0jFsF0PD89BHn8xPOp4D18Wz3NTBZckYRiOhvD13lUpLYOnawe8RHvr4jXjs3jum4+9za76yer0IVjgKPYRAIWG1uVKdHIprHg1TJ4Nmloy48BVfILEKDIAXZ5HAY+Sd0WNXzyPYWFy5IrTVTilhygifQJmvDAO6pK7VlOq4eNkDhYootjTXcQzV1emjKpaheEDFlhGCJ5ymAiEduB//YGupKAxrK+Q48kefGUFrEoiHLRh0t+ba3Iw5lgtM4urI3OuDviUqJgimEtI6lFGuXh5DLWA4H3N0fwcxIFJCXBfmwKI1Nui4FwcZFwbXolma+czDU24iUJuo8Vu8xisH6OPZ5NfZUQugJ+NxCtPT+9X70koL6HywpI6WMFJLyG8tBxycfukcDEaE8n1HOK37/f/09Hn/4iL//u79DqxV50fN3778GhBHeNxADqQoiCIsMZUcMERwT0vJbHBZVvqWUke7uEJeMdP+AuByQ3r9HOByQvv4a8XjA4dtvEA8HHL96QEgZWO7RQsD3z8+ANMh6BjVGcnqDCCZC7ekeHPGp5tLvOUR0jvWQcZh4MGearDhvZJD0niT8Wv6FlP28+HMvN0GGOSY4JmCje9nufgPd20451WlNyeCP57Uj4ta8BpI6iN9076pV+c9iHhJsBhEULB54IFPKB/M4gEPCuo+LQBARMJTu0oElggj1/cvh2WBW162pwca6nlFrwfls36cTWqso5YxWC0pdVXEgzTwRYGE9NWSnetcZb8sNykEqiBtMEUHGM9f13D1yufOKDiYL0LgrFiIIoGC8IsyDWT8xBUvsG/reHcyAgTxnhJhCm9RAqNHY9+YyfrvGYdY8jH2XMGS+kY9tgHQkZrR0RUbUPvAweK+DrjNw6Lfox8FEBnNFbQWlnEAxYF0JkIQQVvWE5ARQQOMAiPaHACgIYApgWgBJiByQmcwQicABoKTvaAycms1jZvWcNH4YFMAhAtAE2SSCM1f1KmAGsSCtRUOBVR1raa6g0+eTtG44E0mQCZCo8zZzwFEYyxJxRxkHaXgOglNpKI1QmxuJ6fzTzBTuKQFIsHXrcngPAWmeESGrDUmoQBBIaJZXgwEJqtxwQJ7mHADOA8+g7gC/YfM2hIBlWXA8HPDucIeHwxHH44LD4YDj8YDjYcExW65CAiCMBlXWzFP0rUrVUYZxi/KIM2bQ/7ou88Pl3eueDTPIf3EcMvXx1bOjApt6bGvg88O9mbffL9DzK+D2RKHta5hG2kMgvS/44tmuGOie1TeKwAxlrm2bcgNfFa0XWb1kXugms5P1KRFMGSHgqkYnMShfGsAIrGMeYwCwTHv4jp4AA4gXwZDyb7TrFYD+Ndxoe43jQsA8CC8pl156PvbfL5Rt99N2uf6E5Ud5RPx5gfK3O/RmO25sxG9t90Yr9Zl9NQvDn1ZesNrpAPKW2Hl1Bxj+ia/8jHLZvpcX8k8x517bsK5Z47903VuufUshomGZHqNaX+8SU197302itOvizXVyqZ2/BsjMddtcO38b8X5JATETyXnjfamvbysj9gzJ9nuAS7fAxMs23yovbTSfPjfFYtYKwANk9U290xvzfNFQRgp/MJrFxFVmLsaIlJMBv9LBEndT9g21NQGzhmQq5YR1PQMiSGkBYlJvCFNGxBC7sMhmqcOe06BvlmqZ5UmMBwCr1gnNLHFIhrX5ZoPczdvBCIhaAVlUHQUW3RVzjFnjhlIrUtJwZTFEtBA0/qtID83kwFQIARKjAWEMqcGEp8HUuDKC+nGrQ2toq1q80boaGB5BBsq3Wm0cq1o12zm3hncBrSdvcwu31lQw5Qa0Ai5nCNSVW2x8S6umgFAPluoWgk37WHM4OGMc0VoBkSCFqNOrjYTYHhdebN7N4xFCBAWgNbWKVgFN4yD3desCgCnGurW5gegAOvDbjYexBe3FlKsA9bnjwnLyZOspIcQFMS19jiggwaCUQCGaIkIttrg1rOePCIGwHI9grlifHGBgncs6CBALzeQluGETDaDRQ0UPoH3Qw1vW0369W1/2tbBhMqmDKP35iP3aQAJez6gTLXTBOkCGR4Tz8zLWhOuPoo1FMKBmA7DCU5Cod4OuQ6uHKSdSjGhQBaOLWheeH9ZfPQ8DYOEKzGslpW1/9LcbODR5CIBG9oqZzyL79ripfe/D6P8ensna7hZMZKDVPPc8aTRoJNbu3gky6OZM52eFDrPGTEUQU5rA8vSgKzU8bGI+LODWNFRWNu8yU0J4rCTN3zPiOW+Sawt6/Xs+GfMIomm+eNeKTHviJGCP/Tt0xeA8n0MIWscYNdxUUAW0hstKptz09QrU0nA+nfHHf/ojfvjj9/hvf/+PADO+/YtvkQ8L8v29tiFofoksERmEAyIiAiJFh1cQ79/j8PAOh/t7LHd3OP7mK+R39zj85mvEuzvkr75COBwQHh5ApqCglJAWfUb9qPTwvD4BXBHqGYkFR5gnlmdFIV8v7nnWAKTNfO4r9IV1vunPWwL1C+UlHuHH8rg/J2/8Y+WZl8rnyFefW97K29+4+40y0gbS+dnLi/3Z6YX/vAQ5uvJuc5//o4AYOS+4u0yNE6T/Uv7N/RHmd+s7aOK/wGIsEptRzQjnKFCLcobSGN9TlZYpa6J43PBuDMTDw7jLDANpEWtTY+7163kh2HNlVZSiPGCxEEylrGhcUWsxbz4PDaQP5cZqYGSexyKsvJ4wgoHCrogIBmRXC50JGA/Pg4eHjPCK7sUAy30F29NiVO/fWQlBk3FFsHxqJGSkkTRZNal0MfDI6xjIwBD24z3z8UMO7HPK+mSAmtvrR4Lz11eMTM8U9mfPhmQ6P5kbqOfyWFFrRKCGWBjMmrwWRGBxxYz2ZZUAoQiJyqcGMMyERvOPUQCLoEbBD0H9ClzxEo1Xc8W/5joTNAJccSEMoKlRUqw6J6ipYoIYvT/6WvH9moxdEgKi8TEMUAxIEgGOSMQITDgz4USAZuHj/lGFhOXm24cJmhR0OiESQKyerSFCQlS5JTSYRZIyiYoCXxiO31bW+9xV46QlZRxzxsHCXuackJes324AA+0/V1zS7mVvVUbMhkK6z9++92VFxK0SXpjA4oz7RZ1mOjxf8lLdXsJXXgPIL8ugpfs7HJe4niPiCrZzveU3t8NbHhHzeZ9cG2WE4yVQoui8siqDXZYw7yQKoEYQCT0c616m8f1MTGks3fvu5fISXvZSv1yMl9EIr4/uUVs+5a3zfK+M2F93Qd+NvvX7N2t3b+x79ZWfVX71iHi1fHnm/pdeDF/4tfxJijGG5J4QwWKDRyyLxmqknRLipbJVNqDzFsCOCMn2nk/fwHbvfGFz3BQis6j4vDIeOTUMTiSlX/OW/rqtONxbI2wZhT1Tck1hOXtazB4Anni4Nsu7YL+1hA7kxhA13JLCiBBUCCzRK4WeNwRAdx8XQQ9l079XDenz8fvvLB5tRQwRx8MBeTkg5wUh5s6IaOxztb5irh00mxkVZgXIQvRYLcoQFFYXdnU/VgFpBk5hoZqiMelV3PVdlQcUgoYoaiogsRhYz62HSBHWOLrMB4ioiy9Y8GwxdiNntdIudYCYScOMNBKgBVUAFVYXbXN3dyE1GOCrIYQqShXIc0QLwAFAytTnei0VjVRIjUtCzB6KxhaeWaq4VT5qg5SCenpGOZ9QHp/Q6hnl/IzaKs5lRW0Na1MPlGpKIDbgXnkUSyxIZMB5tRjDz2gtADgARJpImhtaWZWR5OFCLmRhSsBoXEEtINbSmZBmYY9cIK7iwPcE0pH/xgCKLScA70D/aLkvJGsoKJ9JhGGpHibalw9HtWQPQRUwTSBBLQDjshhAqn2S8oKUFxBFiBBq0TWFJD381FCizGFtVDh2y39f95jaOdOIOVxYv3oD3lCnCSPRsKMfU3/NGA3Msj+MfAW1FqznE9bTGefzWRV79hgF6m0NBZtX5nKsHhKCFB1kN5f/oJ4Qh0NS4DknMBNas5wnMW3aNY9xCI4/mMViXyPK1LsQDqG+PoPlvqBAnVhTtNBGy4KQsoZ9A/V54oC+73Nz30f3lDE4K3YvGqdFbSMwuKCRcwakoeXc+8/fIaKeUzmrV8ZQrEGBHc8F0Vr3EhFRCkwAStEE64fjUed30lBTOSX1wgEhpYycF80PEZKGbSBn+m1/bBoiouf2gR7ryl+R3r4cFTjKSZWqbins4zYrV3yvUf1H7OPl52JMSKSKh2T5YWJKoJh6LhaBgSyN8d0f/4gfvvsef/df/nd8/P4Dnj98RE4JxBEpLPjq/itQipAUzPuqgkMEx4zl3QPef/MN8sM9lvfvsDx8g/zwDZbjAWlZcHy4Qz4cdF2nCHEPF1Me0bqC1oL2qP0W24pg+6i2PYOCgkS+LhkCqmwIDiAIYBuDDpwNZPLCyGMuf27GV7+WX0j50+oi3lZ2oMXFd48hAzjXC8gLOSIwZA0/RhOw2lUExj+b3EDT38wjN8McYg+A5foCQO7tFrpiOjjPJgauWMBvJSPqddeb0t/PBswrl91YlQG1aD6u0/mEWiqen59RS8Hp9Nyt7UUsd5W4YRWBWCBVIJXRSjVjkaY8dKsW1qaCTBFBYqFulNoasKYhI5V3ZrdDUmt8GJ0S85oObl2esCypA7opRqQQLUnr8GrsiggArrYFNM9SZ0teoXcyeg8AEGQPXfkU2smT14DSF9bHvI/Nv7scZXyH8ixeI5NDLTRTqSfICqxnQDgBKOq9W6MlZ1bDi2CBsxoiKCyIB0GkRS2rLTRmDQFfx4hHFnzV1IAnIOKpFJxqQ4UZErFoPyPquKGBhfDEQG2CtWmej+NaEVpDqBVBBMnmBZnCoEnr68Zss+BhckQ0mflCjBiheesC4Z0wVgp4YkEB4YyG1gRnARoLissSUnzK2ZMtl4hu+haaFhB2QNSMaCSMj4ffpWgCt83jOeGIT4iZ6U0BlCJyylhiwpEiDhZCN6aAkFXujVAeVmqFxbI1j9EtdjDz4K9jF9t7N3DI1edsOMs+9zE1Z1A6nv4evG9/lmuYdoWmfromV+zr9OUVEaN9sxfzeO/INzkUEIDzsK+9U2XWG298E0YznuT7hBtpuVjnBjtNdI+RJGb8k3Q9yciT1o2oTPktcKNKb5tGq3itZtfmy1sMk/fjqOtZ2zf1DLYK1tef91K9bl5PjmlN92xwNb9n+z1X83O5409QROw65uLY/tyPK7dBwZfLvJD7sz715Q4k7n7fetfngLVvKa55+jH3A1f6r4MIN+/c3O/l7XX5lP54aS59btltGL0fXqvDjaf9RON7q2ysPY1gzkRzbsimZhMQIdPvzhzbSbIkTbOgsLm+P+5yDV6zkLkkptc3yPmZt9bOvqc3ezxmlnd/rYWeujrIfu7KKeyabX2yrde1cE1DOWFbVu+L/bqd+2jzBHchZI9j2nooEWDEuXXALMZk79OQEwqeDK1+T35tuRGYfSMdVlWlrKjlbG7lRT0ySK3PU8oGGo6Mr2pJbta4PFmieLvtfZqnQYUjH6eePJnNak3CViCf1qV7SrhgQSEYxu7g0bAMJj/v/T0JpzFGwBQyLohC1COAAMSsLtIxRkAiWiAQ+7sHc+XjFsimRIAm0q0FrRTIGjVPQXJLLtkofZi5u2Y7w0pjsuinMaRqng4uK9gSHTaLOXw+nbCWglM5o6oIM9aD5QiIUT0DgoXBccvE1gpEAlpWIJFZk+C2prkeBpjtc14r5dZ/mjdEL+WmYaBUoDNvERGz6KduWdItTDp47MRFNuvCLdOjuRyEyJ3xDjP4TDTlKVEwmJqFKyC1kg8hKvgu0kPvUBi5CJqBlGy5QzoYAb1mJDv2ZM/cx34ul9blMz3c07JZorG5OwvoNNF4Xy2TwKbH9bcnx6xVlXqePJlsTlLvNxtHV0RAkxbHoLQvknmniCAGQjJryRQjGmliwx7ub0evaBpPctooDM/T4J8ep1q0Pe71Qfv5QDTlTFArTQ2N4WtugCr7fadbd2ptepgm07f0MHHYvI66QkS9yuy011ugAsieabfx8bo0dpDI9rcpfnkw4VnEPRbNexEwJawqDEYC88s5wsJI0PAirnjQfDXcQ1lsQwdheHS0Saimy/k7z1tfqw7wxZiQoyqEYrAcVDmbFWeYlrHuU6fnZzx+/Ijv/vhHfPz+B1BhBHNdj5RwyAdQTpAlqscWzqCYQMsR6evf4PjXf4Xjb77C/W+/QX74FunhW+QlI+aEw+GgISit/p68VXzuVwP7qibgjLRCIAjNgDWjQeKhqSwPDYmoIjgEox3xYgwA7OYrrkhb1refLlR86g0X5TV+/EvwqW99xk/JE3/usz/lvplHe/22tzz3S/THjWfI7o/PkAlntksftXvXjC7MjK2BPbYbjXrI+D0UETtgr387Dd9Vf65D57s6c9j3zc4X+t/TFR0+73tR2LyH7LoZ2HOQrQNq3j+9HfZ2C4lUW0NtFbWoN0T3iDDjDm6l0xpvQ+9vA3LdwMgNOtCq8VEFEEGQCg3VZJ6lRp68zsEVsYQevlLMKl75mtiNOHIOpnwIm33H7+t7tvNDYvxI3zDD7SnWp4b0+XEhk+1kvjHE8uL3Vrp74d3+bJHpmI+sjeXUdw4mKh+rnhGBGCWq1wCzXcxFeSlT7AhlhMgI+ai56YgRgiAB4Ei4ywGJI2JjfKwRjyWr0RULnqVZeCmvonlAQv0QVgGKCJ7dm7w2hKaeEUEYQurxHmcDGai37LZDGJ7NQr1lNexMAxBjQmFBiBGraFiaIozmiqZgocJqnZbdtLd52CW2vXOwP+gApc3JjRsE2T++sPygCRud6yWVYSgEJP8QWUJ35xHdE0I7srHme3NDnxdB7ytz8FYhr8+VZ91SRFyev4Y/eJ6QQVcg6IZJ13AClxM3I32jHT9GEfFS3zhffI3HGAqIl9fzxbt3LBXRdHC67hbOOORzABhRDDyMss9KpT+W2xHG00HAZr6ktCN2g8+5TRAfq9FGxTxIae0LyoVLLGua6/sB3d3DJlvItVBfcqUvp/vfXqeBWe3PEfVabkOlX1VGXX+Xdvbn8blvVkTspuPNMz9t8fe+9Z1+/Vti6dON708vW/eVT2NQfzaLq4tqyQtj/Odc3jJn9m39ecbAWb9uOWuvDiko47MsCOYJ0a0Ye5W7nfVFEWAKhbN752ZPlc4cCG837T1wcXtzmDhB+8zJ0t7UD90ER3q1VBmwbdO2jdPmptTTqnHNXf5GPbzDp0tEO2/Xcbfnh0x14WmzoJmMsABzP9k1Z0tG19YzpFUQVwRhjU1LBqyECPLk03EkRh1MuG6SzAXUGNUScJayght3S2Gpq4au+fhRQe7nJ0AEx7t7LPmA4/0dYl4QEkGkoa6PyiRaYqcYSBn5qoqAxIy1VrRSUKoeX+ICgFBLU1fhKggNfXNvaKAQtK6k1tfWcRBiTYJrrvUiFh+4qACYkoZxqaia6E3UIjhQAoUENHVnD0nBzXy+A0pUxU5hHCIhCpmFLSHlAygQ1rIogCZqdaabtcXk7cxHAFGCRHVlLvUEPK7IAUhgjfObCB8/nlFKxd3HR0AEXy3HHhqpD70IqBbNCVGeQOUJOH+EnE9o9QTmAkFFayvK+ojn5494/PgBpWmSPA/PFhYNl9LyokmO81Fj3i9kyWa1x8+nR+1ipjE/YZ4yznCZcKuKLUEtDKCiJ5iuBdI9Iob7vDQTDmyqp2UxYPloyjNn7lSBcT6JJTuOAyQOgphsXpsnrfRZ7YwZqxWhhWZoIn234loBAriu4FawPn9AOT3a72qhyARoDQwgCSOFgCUfEKMmPndBQeUtC6XADWQxk8Gaj+WSnulc6hjKCBLRa6+uwoBrfYgU2FYQHRO9bJqE3EKglbWAn5+xPp3w9Lji+VRxOjFQgcTAQiqkenisZom22SwpIwExCGKwsEFR50CtghiBxfJILGTxdqHJEQMzpALFSFAAkDWhhFlKqoBNHFS5IRoHW4QMC/d9Y1IoEoEoIqQFlBYgHSHxAA4LRAK4MmKIyKYEpe6CP/aXYEKrWnUOa3fPldF6nGi3tVWBNqcGEkKKgLSAmPKgwUQorSJ4GDrRyexhKmJUuhtiAkJANWUeDHZva4GwIDBpLG7KQAxY4hEtNbxb3ilwtZ50nkRCCwogBRLN78EAMQEkYNucQwiWV1I9IWAKABGYd2RQr4GUAIoQCz+kSiLqChr1LslgC/un4fvUY0gTZmvfxZRBKRs9JaSQESXCo124UuDxh484nU74wx/+iI8fPqgHiAA5EA7Lgoev3uHu7ogYtO9jTMBxwfvf/SUevvoG3/6rf42733yN93/5VwiHiHCXECQiuoIaDDo/o52fUY1gzmEFpe95fcGBkQFY3hRnBsaC1G9FKvucGVk1bBXv+Ruj05tl/s+FHf61TKXDlgC2Qw6g7z3S51uCWwvrvGpwHq3fI7oGv3z5lAl4JRjKQNp3zxT4Qu+WpSwdnAZEwXLHETGOD6bZ/7lURAjc45A2371YTHHyb4GB92zhdpQHcxrgyvtoeXqWoKHe3EcOlnXB9zSXa21XQoAlridShaSYEyx7iDxrkqhFe2uC06mi1orTuaCWFafzGbWuWM9naPx+9W4gadBE2JqMWGfQGY01DGpZC87ljGpGHQJG4AoSQSZGBHC3ZDWoACaZytpBQM7KTyY2wIyVn4hhhPBdcsSS9JNSwNH+zk6XSXvLc875mPQQjFewgf1fJNOwz7Lbbmq5XHkBpMkY6/7OIUIOWdIP8PQNf6a/Q3MlgBmBGRwIjGx7w6KyAgtSPasCYm2QFsFNFTRigKhEW+mVEEhDA8WFcG9hgg5HnXOao0uACLxrhN/UiCSCg5zxx1jxIVX8sQgeK7CKoAqj6EzBCQ0VDSdhPV40NOtHLiCpYPPwy60hAjiQIEIpT0/bBkH3OADUYCB0FwGAGDE05KjGUGDgEAmZVI+fRL05n824qWAYYSkfvuraa57cugKtQmoBuACtANIs5C47Jw7nymlMij4r3DvaQ3CKb8BZvR7uY8Z9TIiJECNhyQE5AJEbIAEFrdMCnQdk/NG81+9mreznpOzO7z0iOoHzfzAr3Ma//sdtOt9fReP2eRU5RrCni27kMAPXe/Vc98WY15SIL42ep6GD3LK/3zCfiwU7rtC6tIs2XlNCvEXp2I/TGC/t5ut9SNO/m76YPNa6sY5pyFRX5nJWgOdeQ6mKxcZq90a0MIznNkYJ9mERwwDcO3pWuvuYXtLFbWOvHJpkcMfwujzSedfd7Te2/tHHL5/3h4jM37vzcn0oSNpmCmyfIbt5fW3veFt5uyLiSiW3S3MAgG/BH69ZHL7teqdgLz9v1r7JrWsun7L9fuX61zWKnz4qNy3FJ2D4beV6P23edePAT2ntdFmuL6a3tvPt/fJ6f3xqeemdt8bxmutd1+4T+uZEE2O5sQxFv/2iNYNwyfZ7vnbaVA256PW8Nu5XN8p96QyzbJ53rf03i2/+BozKW4bLJIxtlfTGl6ZDnzOTEmKrhPHn3HjtuO3imeOB2IAfm43L+rqaRSq3BmkVMPfsmQy5t4O6FhqT0oz5mxgtEVbQtZlHhCkeEILOLgdmyzNa0b/VgtXmWU6IUS2h1KOigkStXAlRLUwNLCaz+kG3ntdE0iyalFQMuHXi2xkiQEM8yRSTk3rvWE6B7SaiCommiZeNyeiuyaL9EykADAhxt0IOOSJIRFs1nAo1i1XMtr5iBIt6E0DUaohoCNjKpE7Wy2qKpkIyVzUUMoCeTKjTfBUF5byipKxhVUUTO/elYYkGpVVIW4G6AvUMaTomwpr4mbmitYJazljPjygFKFWQctLE5JIhOSnNEFXGkK/nnvgYPUSXTACKWhe6xTWbdwUhiFiUNEGrFq8eEcLV5qcqubxPxMJYNRcmYwAQDTyc0DsTVloVE/65ey8AIwyWz/ct42NjIWSKAhc+5nnC4Lpq/ouygusKEYvHbGw8CyxhpYpLSlsDUk464iIIotdV1B5f2gmt8GXsW1+km6VPNN0n0xwf15NfNloJgSpZei4W1jnSakMpTfvO5KZICqZE8oVAox6W28TDKHkS60CkQLeYgsIUGcHeHQQ9X41G7lLPCQkBTnq2/IHH0YYpJrj3A83X+YfQYwwTKT1hs6IPdmP0cEymcO30A1Os/glkm4WHvm57H+s88jwlHhd7zo0A0rqrJSF1muLrXRWQ5iFi/ByLJwHX8AbSWPuOXX2hYfRSUC8DaYJi3h4MD6esbQvOnCqpmdjO4ek19gz9J5oXVIyaUBpkihcTYHU6hL5vBMtTA7DN+WReQ7G3L0RTRIhSe48jDjaFIANCgvP5jNPzs3pqrStyziAASyIclgMWT8ZNZIBNQMwZ+f1XeP/b3+G3f/Pf4/DVV7j/7e8U9ImCUAqoVO3bPv/faMhAgMDDsVzZg/s8AeZFOM+hcc1LDMOn8N2vlQ1H8GIdXmv/p8oEL1lu/pw8/6tGLT9xuW4duv0e9ES/lZxMRNCvuWLZ2mGUeU7+qKbduJl2c2kvQ+1BpB3QAf/tH6c3O0UEpA25xHgkB0RnXvnmLLwiQ2wNaiYDJPt7rP8hR3nNCR5+yf2whlX/UD9A98FNf2hdRjpdk7scUJHJohhAZUFjYK2MWhtKG94RrTUNYylqiNLDLBEwmSEorygVzMX4uYLSLKE1BIE1FA+58ZMkm2WX8qOOgbYoBNs7wggzEneKiGw8Tow0wjKR9lcwGj88jp0Vl83MmcegzxlM1/frtpRtEgUvZMGuUJ4W3eAWJ75xP3Z+Vvwl6Hym9OcxRDTnFFsMH/L5ww3ChFY1zBWRetY678miI8cFiIGQo96dQ0SOAYdsnrzJxiKoEn5BwFNmnPIIoXhuUM+Dpj3VIJ1/rZZsudker+EXG0RsTlnut2Tt9W/43CJGCOYdTd4Vgzb5rHYvWW0HwNaeGoDImq/C66WGOJ4IvmiuFlYvRDK5hFhzoIDVm2f2APL3+jwd/O+YvGSd5rlMiGD8pSoUs3nzhkBd4RMg6MmpRSyaAwGeXH6f32IzJ+WV35OLB7b0CUDn968/h3BDINje4+Mjl+c7TQUgxtsKXVkru7JR9Mz4jYvcE+/ktEym1TXT1Ms60fTsl9u2V0K81t96bOrzCX+6uO7qO63PteMs4sPYp6eRhMpDtrew5rxhMg86G7bGFQIgxtZ55plmDS8FC2M8RSS41b7X2nKVFr7wTJG9gfi1fnnb+dfffYU36wT3bW34XDbnC+aI+FKM+s9daPv9xQSOX8uv5XbZEk4tPVmrxaTusbK7APAj37kTRF8jYrM3xLX3v3VDekt9PrXMXkef2zMCGWFvdwJa37h3/TS/t1+9A02IxbGsDT3xza3WitqqgqbmLqzxxy3kjb5ILYN7dAxR5qtZqBk2K3Wve3DxB8qgq0mtPhuCcn5Ga6V7Shwt7v7x7g55WaAWBMC6rhZuROui9uK2wZgCRD0j1u6mzhY7fRZWx3UjnEyKKja6lRTb5j9bJZByoj2hcweoWoO0hkCEZVl6SKvQBUft/2AMXU4JEAGX2hlWYkI0AQLi8XWDMjeiAGWTBrKEhClq3g1m0fGy+L7OGqxnTfSd00HBPWOWHz/+gFoLvv72G6QcQUk9ANq5gmtFffyAtp6xfvgO5fSMx6cfUNYVz8/PmvSwFZxOJ5zOZ5zWinMBzucV67l0RUTiBZETEgQhNSAkCEgTaHOABO0PB/W45x2hEYtYDOQ33lDTD1SwxViPMYAtfNJGbiRj9XycYCHGPJHuetZQONkSXu88En2cPV69hg2Im+Rhc7ifuq4IUWPWMzfLuWBz0mKW1vNJ8ykUDWME0nA4y2IJgy0xs+crqK1CJBhoH3pOimiWMmQKE7fI3rtQv0QT2ZQ7gQLcM+BaceG4VQM2LKRXsxBtXbYMwHLMoHBELZb7xBQNKSnQnMxqtFiInmwu7SlZeCAiiwcsVi+3Bt2Cv8wMJlOKp6QKCJcbjBB0hYG1XxWeprgjMrA7oFZVgiFERIpIDu6HESIiBvVSSJYU2c+LeXZJHKGy5j532tDzWZgnQErz+XFvMABfPQRM0UoBGtrOPm696zG0DUjk1kAWZo5FsKQFgQjlZLSSWb1NzHpoWQ7g2hCXDGoVay1oBKTnZ4SckQSax6BUA9M0d8lyUOv+dV0tKX01cCmY9wOQl4PNVRWoNK9GQIoZEqEeGpYTQ/vKYTfNdbEsC5ZlwfF4VIVDiACZQsiAKiEyq2KdF+fTCaUU/Lf/+x/x/PgEWQsOlPA3f/nXCiIFDYl39/CAZVlweP8eEoBnKbg/Jnz913+Bb//yr/E3/+ZvURg4rSsYFUwVgTFouMhVJcR+7W2OfT4L8Wv5F1/2cOru7BZBuJhqP5v3+hvKXDe60S43eBo5GCzeNzczkBjGBjCwmAAgiAJlRJr+J0zrEcZH36gXkTPC0+9dvQXooJIr4dW4RRQcdhAKA0jyUEN7w4W5JwyWHq3fIed9a3P6U2v3iGQRnGwvPp2e0WrF6XRCLQXns3pf1lqH/4UISBqYBAGM0hilNZTTGfW8opzOKOuKcj6rIsNCsLoxQIpB816Zx120fd3poPsAXjPgDOZdrPxNQkqEHANyjEgxIIekYZpIPSJuz1tGV7jJeP4t+eeWPLlR6LwCuG3vQffOcVsat/Lezm/d78WEnc6X+lmbcxQ0j5jY8z2ErIZkGfKd+zzVohbggRYQpR6utu+ZB81HFlNWfiFknadR8I3oOOZYcAwVEYw7YnwEYWXBIwtWETSuCNxQWlWAv6kn7BObHCUMEkYRRhI1pYkiWOz5iVSBol7zFq7JlHE9fJLpCKSxhmy0D7EgsCBbu48hoIoAqGii+eGEWUONMauhFbN6RHNTjwhRAxkVGJr1tff+JI8TIDJyd3XBFKy1DQSKAfn+gLvjEQ/HBXeHhCUSUgBgihnmotVvpc+LPocgO2j4epH+7v3x7bELRYS/xe/vSgJv4OZudPB7/x676WL/AHp4W/JO8ztkvH9fRkgiQyrElZ6TjLZbf/OTrq3+T8Vs9mv92jMunjnNk83hHUZyu7giQvug56Sbab6MdT3q5/nDAKKAGNRostaIENj2E8XbYM/bKiLc6Gq3d+3kwhfbvjv+Elbm82Xz+xPe8dq7XlRyXewvowZvUTR9bnmzIuKWYLC95uXz187duvaahcmbygt9s5+kF8/fCzkv1unyufvf17RRrz3rtXKrDbfb9unll8Bg3+qv19p/7dxrzxzn+18vPuelcmtx3vKQmEuwUCg9DvaOabzWxmsbwmt1egsBueUJcWsj+tJKiNf6flZC3FJFvFonmTZuvdBePp4/P+MWE36x4c9zdLehiAs6jU2pwNtQViKDl+7xqvuD4cKjArKaB4IFmmetd4ODzW7lwhYbtelviAFcCSnFHqtfYIKgiDHEgEjoyXa9frpJW06L5jktpAOeva0sPcEgkdXfrGRo12dEk2Wvzzlv9gSWAmbVbKFKtuYG/iwHE8Nm3o737YHkqc5ifdAa2L0MID1MSo8XCQ1VVYuGMvG4ukSCaslr1cOBO8CpMYergsnljLLap6wotaDW1bwqqn5a0xjrFlql1qqMK0ETeDeAWoOEgMgaMotNkCHxUC3Sx0H7JgCiiggdT42pL54MAypAEJnAAIHHiffutoitFrcYLr+asmeEfSImeNLkPZPuQHhfTyQGGJMl8rX32HohYoDYlFgj0aR7PjTzznF3bX+WJsYev7sFkoU28MTfPndnRcjM1A8Bazd3bpEp8WnsSo3rNKKD/7MigM2TQ6cZKJAqtCirEFoBj8cdgln9i8ugWqGYLmNCw8ZsJq170MDBJunWbLQRoryfPFyPWpMywAMU8n7udII17vHoL5qeZfkUTCmllfM9B3Agvbdh198iw0NH+yNMfTuu28YQdwHiukJJ1/EAMMQUyzZhLXli6PuE9wPbmIcUe4JrCsE8RhpqreqBltm8DBgSos31UffWWheyfD56E3uei81+rHGhAQKDN54QHqrQwbvZctb7vRs3EkZboGG+GIJ11TAkp6cnnJ+eABakEHC3HBGCAjlE1ENYMRGqMJ7WFaGpYpNyxHJ3hKwVUsxjSTTdN+/m4Wvlp+BPvyT//HOX13jlX8sob+WF+6p+ZU7+LPPl2jtmGn798HRm7O2KK4jxX2psop5XppAQBprt9GJcne/FHQ7HJkTFRlLf15Vu1N9rKP4xvlLcctzo945v2zzPAefeR65c6JzjphrOX4oYob4yF8TytSnPpR4QralxiP89eA0N3RHc+9f2QkYzHl/zEjiffPER0fCVznspewyNuGjewVbHgMG7zH3tBh3J8vvEGJEi2cdzRATzgMCQmTZg6zSIOwxnD7bt5aCL45Ms8xpNv5TProyXbOe3Xtb9RSYeTe+acxdYQ6b3+TxTj12VS9RbQSCoBqxnQ8U8r5R/ku+Z0bwJLeE3hLEkwn0SPNeANQXcR0GNhNY0ilO1Ac7CaMKI0tDE8siJehV7eMmecwWCYvmhNM8eg00J4YoIQJAoIFFQA7hZjtx9yOQuiyqFaP1UwWaYpIoQcOv5UbD/eFLfDdPgozW63JfYdnLZOJH0pOk5JSw5mQePhr6iHqfLkgebvOtGg/1ZuBpR/6K8BRchwLwS0HNFbK+T7q2gBwnbiWlzb+KVX60DAWAzFKFtH768dw/BV0R6/jC4cs7qcEvm2NPjT8Vsen/YPL3+fatcjthMS16ti7/jhb15v92I6PWBCQg6pyBk9BtTrggPzSzb7yvKk9fq+laa91bM7lPf89K7PhWrm+fa59TxLeULekT8lOVTmb0/P2Hi1/IvtzhDmZeM4LkhzDPiSws6LxGhT7H63Ssf3goifGq59f6uIJnUEG95/+Ya2eZ1mC7C2Igu69Pf76cd6DWgrDM0xuhqPaEuuI1R1lWthdeisTdLVWDGwr9oPHQColmOEKDJ1sx6uqhHQmurbbIW01BGst9o4FWramlTV7Wk9qS+h8MRKSYsB81DwqzWy7XNzIpKRQr0ahtba5pQ+XzG+XzGatbqKvCoJZZasigg32oFaBZSbMzI+ieEsdUTNJ91HAJvKJrMr5YCrlWtk/KizLkloCZArYDA3Vo+RXVxX2NEE7UUbwIEYURY/HIRxJggwijsQylgVAjOOCLgsBw1VBXrGMHHGYS6ntFKQaQAyguWCFCOWOsZKxc8Pz4CRDjSg86DcoKsZ6xPP6CcnvH8wx+xnk94Mo+Ip9MzWmOslXFez3h+ttwAq1oIAgrsEgPMDaGpsgOB0GqBAEg1wyccEVBcGdIcuNYkjWw5H2rVsAshWuz9qB4iDEAaoTEhxIyQ8pjuBjzCBNsABVCrJ1tHQ6gBkGYKodTBjL68QCpUhQCwIEZGJIIggeK4FsyaSJkE0cNJKc9ta9SUQxbSioLO7+WQIbLgcDig1WAW8EPJ4GNdqsbi7QnaQTc9GK7zFXJxzulGnyrebzM9cMZ7ys0zM+MMlVHS8YC79w8IcgcSxvPjR5T1jPPp0Szmg5MKAMBhyVCAPYB2dQoUutJxD2rM7/dm0eaYxaCdusY9Drxd+ugRY6iUov0dExA0ORyFhuCeXwaMb3IgGU12YTaQeyn4njSFWuiClcYMn/erWjU3RmsCYRjobvMNgtbCpbISCgYk885Ry1Ue42Z9uOSMSLGHkVpSRjCvJxDhcHcEEXC4v0M19+/aGk6nExIzyHM9iWhi5mUZYRHYY9JiU7dgnjo5WW4YA2jExikl9YBoTd3Mc84QgSXSVlqerK9zzprk3gwfaimo52qKLwIlbZs0BdR++PA9nj8+4em7DyinFe+Pd8iHjK/u3yHEgMqM2ho+PD6jPD3j//zDP+KpnPEP3/8T7r/+Df76u+/x7//D/4Rv/vbfqOcTgoZBayrcX1tte2X/PI8v5uqv5dfyBYuCOjvQ6yfgbX+qcoVjtuPm+mh8DLF6i6Ku+tssoNGmfEhEIImQoIpGAiFIHOcwlN+jAs6V0XYDnGvEuo87vVNvM6A1Nn7LDDAsTCAbmORK8G3y5ZGb6XaPDMOM2UBIMU8DVy0HkHqjMZ7XFbVVnM7qEXE+PaNVzfnjXsHB0g+7IoeggG5ryrPxeYWcV/BawGtFWzU8k+4LYiFEA0JK6h1oioMlueGE7uORNAxfsL7VfAHm6RfUI6J71EfahGOK/gwoXLqdKPJShJkfX7aagtHvN69XsJy7V46D0tik7vP9U5VHMFnOjDGIlGHYGTYwMyoDsZlhkKHlbCEIK5oqdY4Zy3LE/f0d7u7ucDwekHNGzt7HNGQ9ViD4LgpSBmpj9URPgoUFBwFOAcjUcGqq3IpccUYFUMEoYKjHJTVjbEUsSprKXEEYKzfNH8hVFREegpNUEZEpmJLBcpUITzkeGqg1BPsdLVQtMyNwg3ABc0Nq+l2KJmEn84RwDwn32hdXWAhD41SlyUhHx2fIyWHS+Uk3Ask5IC0Rv3m4w/3dEV8dF7w7ZBwsf1lEVa+XdoZQQ6vbGP0+kzewv1yDi/tsuTjkCkuaV4XLKTT4K79BdvdveP4rf8j+EABMhiHaJTwpUqd7X9RDSOeBgQl/6e0a+5dM111/1CcqITooL9u+uaGE2DXLcuNclit6YVyOmyn+sG33LKP4x0PSEglqVVUjM9Tb2gztmhnttNYMaxu4l3vouSJM+/w2obxlGH1NyfpSf23P79u+u+pNYzc8O27VbdZPuWw+3/9zlM9SRGy0bNPW8JJw8OMFh+sDvdWkTUDqFauIT37jK3V+SUP02iS5JVD9FAzvTy28Xa/z9Xb8kgTI231Nm/OveVi8pU2vWVU5E+kWj3uPiEuiO+79EtrTWx4Q+78/Vwmx9ya4Ve9rfXnN8qaf64RT+vd1Ir63nulPnI5vN4tX22KXjbGxdxlTcGk5JMZkqheEcsAzw91f0EGtvpMbUyqWT4K5qsU9BsPkzMjIs4CtN4EBahrKw61iR4gPFQzN+tgt7zvgO+rt1mBs4WSCJWv0OOzNwkeJuUJHD3PCrAYgDlbODJS+BW6BB6KeUE+VGAoSStqH43JV1GSB5QD5BE5yUwZIWCDB2+iKHhdMbNR5ilfu1j8954UzZLBkVg1cC5rFmI+BVAhgoNaiCgJmCw6v4aW4FnPt1/OtaRgWtbzTpNStaZzYyiMBuVt2KPDuYYPs7/kjA0joQLeYRRHps7r3AFe41weiIHjcJfi8BiikPr/meSoT0z7WjFkVkoAlIggg7q5DY14C1PtbFRIe05P7u71e2kbazvO+pKZYtYbKqgyqArqPv7bFBQ8MZRi2tOy1sqWPMtpiEtKWWb2kRTO93NPADb0nQIgQUkJeFkRLQt3KGZCGWgKEVRxzWXvrzTEJ2yZwg2Sq/zxm/m7vnUG/HLQZeMA1AcSfwn0t6vhurSJZpIfh6e8MNO13AWqtdNnXXUi4NS5B6cAmBwTGmiZTzgQK3ftm/+nzo4/Dbu+F1yN0bzWQhjyKycE5IKSEkBJSzuolYEJnM0BgpkUelq6P1TQXtvys95eFxeIx3+ZxZ+YOYM08udfb+3kjRDObQlNDWQTWNd1aQ6sN9ax5b4Q15rp60iWEFIcXhwgen094Xk/4p+fv8bSe8E+P3+ME4PjDB3x8esRaCnIEktfNaf8VXuMarzOXvv/23vkyvOXPxSv/qdngXxKw/kuqixcHXPa87S9JfrkQcWmc2NRyItKeB8itmknasHxu1XhS3jxTBCBRy2+CeVT69neVJs/0cwN9W3W2Fru6N6B74zIPw5oZZJv3JKe9Y2+Y+0KsL66iW6OWgqluXheL2c+t82QaOlE/bPkhZo+IZtbkI3a+e0RoGBsPKyrO/3WDDVELgh67nDrfGslzM5lhEY2QkQrHDbofg1vruwxp8fVdrvR9Sy5mxoiDvxull7CM/nteF5vu38k0t76vjclFTdDnrQ+t12E7h5z7tDk3mKJer5l/ZLE53nOPofNw3bMkJcvHNMKGap97NSzMmYfXIkEmQQ6CJQiWABwsl8eZVO7IYGTSEEsN6hERIZYHwupNZLnfdFxYzLvdFAckmpQ70Hi/JknXULXBFBFka5nF5U1tKJkHlD8n2t9OB8jCR2mOCKcPk8cUe2irEQtoNrjTZSfT2uzEog9JjAEpBhxywiEnLClgiQEpaO4z9cg2Lw0mCNcxv0CqpMB23u7l+peLezzP8gt6HXU+vcDLX5zH1WsvlHzdzdmrKJ0/3Vz20p4o27pcw2T0e3j1vvnZN6+zd/Zk0/v+8PW5X7+7PoRcff+tKl3de2++a+zZyvtuOsnynakSwumo8pHqxeu881B2CByjcJxn1GXftuv1HvfwK+dvt/v2e15RWNk12PX5TL87vaY51+HLeSl+ivKjPCIut6FbhW5c8wWb2ytDb3z0rk5fkMH8JTLWP2/5l97+6+UCdIpmsWJhHA6HQ1dGzKDU/hmvgfmvvXtfnKGdn+/H53v3wNKnAHj+vGv1/xTh7rLNXkcHLf17e99InjtY5plX3l1946fdb4TblQgvbSZ7K2MR6SGZ3JU22IbA5Mm6DOjSLKgQiILU5zNaXS1OfEFtVS3ZLckXiBCCCYkWg5YtabVaIBNidG8bA5FYk+Nq4iZ1L41Rk63GEJAstIiDVaUU1HVFXVeUsqKWgiVnpBR6XU6nE6oJbxBGDAkUAkpZFSyMWS18k24/GooGPfGYiCZlzSmjWXzW9bzifD4jpQhmvc/7ye8R0fBFXYlnSbgFgrUUgBnn8xmZMw5LRowReTkos/805lUTAa8FISQsRQE4F2dkArxba+AmeOSGFBKW5YglJrBZpZf1GadnYLk/IIYAXp/B5QSu+gEXiGiSco92auw9qgCFNVHi89oQWZMitqZu5dRgcV+jhnnh1TD5CmECOCjPa9ZLXAtgjBiLoKzqEVFKAaAhX1LW5N0uwA6QgAGu8ETKvnNyjJYvQN2pFV908YCgXj4z2Bg6gDDWoCfmVgt6jtoPnjeiM4Mc0Ch060gHd92NO4CBIMgxAklDjtUYUZlRSsX5dEaMAYclg2LEknMHMGYgHIBayhMAS/7eLdN3dHEsa2cyw/aogcUzbfX53p9jNMIV0N0bgxIQFxwe3iMfj5B6BlpFXc8QbqgpdXd6ddtXkPpg+V4a63xuVd2O3fNrKBzQSWGIhESxgyE2y3tcac/H4mQvsIL5vV/EKIfELjATDfDcrTi5NUjQ0B8iGlIiBgW1e6+xeVhggOwDgJnq7j3eww2lHoZKBQr1/HFBOISAKJqcHE3DMSjgkAdwb89OKalHAQRSB32POSHaHGHm7l1y93CPECOqAflpIWRhHO7vcK4r0pJRLe8MANSkij0WXXc4ABtuWidlt/5j1kTTBKhHQYg6QgTkpOM99mxL0Nn7wgT/QMiWi8PnmberrivauiIfDojLonbTLHj88IjT0zNOPzyCzyu+fveV0mXLP/GxVdS14fsPP+Djx0f85//tv+C7jz/gf//9/4V4SPj2X32L8HCP4/sHpMOicbHNK0cVvA2CgHlQr/EeN/fXMYV/Lb+WL1ZkYBAALufkLd78ZykvvPbWKQIsD5TuF8RVwcR61njv5Qw0iwFvSggCzBglAByM9qjHYQ9LEmgAax30HR8yQHUusycEi6A6/1mdD1XgtDax/Ds08qABShctp1MkD+Vosegn0d/HcKNwvZBjLKyotN43kAZpq+byWk8orVpeB/WEaLVgXU+QViHtrMYB4ol9ywhrY5bx59OqOX/Wglqq5omo1TwiGDlZOBpTyKtSO2DJESmobEhQ7wYCdQUEMBJ2xwsDNlh/mNKC3kYnpX8bNHoNvBoHtt+vPfsN15E9T5UO5m3TQcDxrj5+bpzjH1IITWwPFBo5IjBd1zDmIGBT3vbcEBOWwxHH4xGH4xGHw6HnbJx9TEfCYAZQ0TTrEYQKAjXkwDhEzXGSCWBpWJrgOTYEqXgmRgymnIhATAs4SDccKwIImRKBvM4q36gxWkEkIJLmc1q1xSCo53AAg9oKcAOvJ0itkLpCWkOr6vEgZQW4qidEa4CFho12Hm5E1XNHVIeSr4zdljeTztuGPo4CMSUEcFwSjocFX98veLhb8NVdxsMx4ZgIhwREYhB0TQk18wifZop4aNers+2N03LmO7a/XV65eC7wIryl8iG6LH25TVhY2x1hvPXIW+tmVsz10EzApk/kRmVv5dW4er1gO94sSis7kL+950Lp4fUlV4o03GptB8Vv/tYk850n9DpMSgW90BRt5LRvhKcGoNiLJd8M5DkrWb3LoxppelLtjtfs6uLlmuHutb58TRn0OcqiW+N7eeG44bIdOl83x/4EvM1n5Ii4UslX6r237vqkm18pWq9Lq4zNQF59BV10+FuZy5cmzUuWBNfe9VNbYP1a/rTlGmEmQ2mCWVaOmM2v54bw35+ihHip7Ofda+/dKyFeeu4eiL+lhPiUuX/5THRCu+eNL6s4ANDJJOFNhfw2GBonM1MyaOPlhjRcwWcKOlv+0CS4OXDmFM03DnZPhO4R4S6DNOpHgEdJ1bi/0nNJOKPlFlQusDiD2FjjfVJQ8NfkGH22jLwRYtZczRJUO5AaTFDq4HVrvZvd+qB1ADaZVTJ6X/qAzXPLn5tSQi0Fbk2xAVV7RwOwPBYORGqfBgu7o2PhoUrcokqVGXEI0W5F0pMmNhgEOoQhglormdBQC8DUkGLW+PGkzJHXxUNuuccC5qxiNp9U8WTu1UE6oyT2XlbJCYDygqEGIACxtQ66Yv+x3plzhQDUk/aNvBs2ziFonofL3XRa99x5F7LYxrG7Gw8BgEgFSg3tNSlyRECuYLCZ2y0RRZP+euxOBBeGza2WRoIyPWpWL4TOOPb1Q8MTgq39YQI0XNlANOWO6ID3FgTfYix7AcIFgGtCx/WyoX87GtTrYCGNIjQ5dBMVSoPFe44xQjhackvngSxURdDE8z4DnNphUkLsvQv2gL8f0/rOApbvA7OQsesN+2frcTDVo/ftANDhmqU+R7agn4+Hv2eu93zdfGx62+hTCghBeh4FVSaMOgIYXgdz/UTHwZVKACxWtCmRYrQ40BhAWVZPCQ/7xY1V0cae44R6P72FDx59GRCCjm6MnhDeScqwlBXR6BR6dOSeQh/DAeYoGVJQy5XTtRSspzNaUateCqpgfT6vaJYDorSGj4+PeHx8xA9PT/jw+IjvfvgBh3bAb/gbhBjx8PCAw/E45lNfvZfjPY/fvA/c5jf++fDNP1YWuMXL/dIMo/6U9Xk732xz9EvV9U3s5isXdQK1Pzxo1LyfzLzR8IQwns2spImbhnCxj0z7P8mwDPV9uIMWzreR13q3fjtJo87r9n1j+tbk1CM3WePB47nSYu6RXjfrjr5f72WCab8aB2XwcL09LkB43wweza3BmevwZLC8D/6bbF+GqLfEiK+viohqHhSNG1iahZxqPQ+UV5CcBzTaHUkVFPvwSqOt4/js/TkCTF6dKltQ0fdcFx46L4OpT6Z792vhhsBF+0uunJcr33PZH+s834YH2X1AEPdWcOATV1K3yxao9mcGC7cYLXeSe0a4bDPdMdXQ3y1gMxqDJ5QmQdJJioX0/EKMQmK/1YMikIVMBaA+NhoqlSFoIYChHtYNlnDbvRdsnQlUCaH5JgARDeOEVoFW1QipVVM0Wt4S5u6hA5/v4l7602cjU0z8au8Ol113+8+VueChpIiAZIDvIeknW46IFEk9InzkRHMBdpmgP99ktSvkUnbz9naZaAZtfyutvbQMl+nfa8XXjo7G7pnTe+XCVeLaw/brda6ETMtqAMwT6ZvW8bU2XKv7tTM7pY6D/BiquPmC/W8t02qWl9OLv4StajayYSC3px+ybbjRSr/fZFfA8ijqPGQCQmgQyxlBJJYv0SNeDNr1KbzAq4oF2Y3sld/9z9tvuTr/92Xkc/I9cUfX9zyDYGNAcIkHfPnyaR4RF42mX4gc8JZKvE3Y+zHll8bw/1p+WUUZJHTrF88J4Z4Qbmn4qZ4Gbyl7AeyWJvel975VCfHSOz/VA+L1smcq3953t5WBZALZ7X7obRN0gK+H69jVpYO903s8TIZAgKCJAHuY+hiMkdaQRMLNYtOu4HoGl7M9W9TqHyOeuBhgrV4TDbVoHomU1AtB55gqwARQ6xjRcEAUArK5iqsnBgCxED6topWCsp6xnvUDDOvhZVl6W1XwYp3nYm0RQSlF589hsvYiQuUpwR3YlAXBnp9x9/AAFvVqEAJKLd3LwoUSMvd2T0Tn46Cx0wPWvKLVhvPpGbVGHA4LQiCkvEAEyMtB3e/L2jfrZh4DntQbza29DZlmdb1/Pj/30FfLcsByeEBMySzKtY5s4whLuuZ8r1vBCQUcQkJiIDZAYsLagFNpQDyhlGe00xlqG8U41IycLck4H5BiNivqhsAB5pDfralORa2eGquCyK1oBGqZWIomz0MgjVsfLGF0sAReZhUF0X5RsEBBfDFrdJ3bY20FEyjMKRauCCFxkDrCXX2ZG2oVs9Zuap3i3hlXAPEmtcfVh2hyZkABlwAT7mhWnsxKEuqgsr6HOiANUFfOVajVpOPEPu4zGA3Mwgl34XC+7iVgVQz82NIfIC4LKLwDNZ0zp9ZQ1wIiDRdwWI7IKaKtwcI8OChDqnAhTTQuO+v3vXfG/N5ZCb7NnTCUGgD1XKZk4bYCDYsk4Qbi1mlNjAk5ZVBM2s92PE3JnGesgnckd1ZmjPm1UxxNSoRtNFR/CHRtQFRZGCIwAQ1Oaz2pZ0wRILWOTKCOVPR1Yf15d/cAAEg56/xuBSANt0Q543B3h+V8RkwZxaxhCQAvmjslppE8OiUNBVFKsdwanlicJq+P2L3OQsjmAXMAEeF0Ohsd1HWTUrYx1ZELFJDzghBSp9HM5vGDgJg1d8SSM9rzGe1c8fzhER+/+wBeK6Qyvnv6gFIr/tf/8//Ah+dH/FBWiAB3y1E9KFpDJdLcQznj7v4Of/Hb3+H/8T/+B/zlX/0N7o93EAGqxayd8z3e4gtu8Qx9PvzKcv9aPrEM+vuyouZPI869SWNx9S4XbzvfKn1Hg4Y5Ue9LNAUmQy1Ks+qqQGVr6EoGV/7CDQl8f3P+cHrhRUVGLfzn2O9UCdtc2Wm5FEpTPqQ19VJoVey6CficPAfmvWpPNqTvWJfgjz5K4V6Npa+hbCCMBO2fIAXgAuIzqFZIeQaXiro+o5aC8+lZ80mUM7rCQqr2ZQ9fqt9lrai1Yi2qkCis+SHYQE4KpFa4KSDliLxo4t6De0SYolk9ItCVziTGx5DnysAWjhEbAZtOV2dUl2OmwZNprOzfqzR2L2fZHknsyh6rg/FdZJ6xbsmtRiGX3+O9Y96MDzov3ZoqraorsEQgRBbAsi+Eq1NUQ0Q626X8DAVCigtyPGLJByz5gJwPiDF3vq+HsbI+YpMRmDXMUoGgkSaXDoGRgvKDmQBBwwLGCRUJDZUYJ2JVSARBWDQ/VmlAY+AcIioT1iqoDTiFigLCc1HOtHIBGY8aoPk/etikVoBmnhCtAOVkeSKKhWyqgAi4aig2KQXSmubhc2M3U1iMMLB9Noy5YsYdsyHPkON8AHn6FkTS8Et3OeHukPDV3YKH+wXvjwvujxl3OSInQgqsAXJY0ITQZOa5jXG4SBjt8+fWhJ+LKvM6tbxKz0LnN99aRshYvW9/v/9m3ntb3HjelU1I2zfvX3b06reC7ZtCO/llBr2lV/5GfdRrbHSa7M5v301X++Pld+3b0Y8r9zydNwMn+1YP9BmjUmVDCL5mRx42panKLzMTalVamJIZYu7kDjeUu6yr1+FWf/mec+3krv23+n6vpLjxjrcUX8Uzhd+f35mo4ecA+T/BI8L/mA7S5mtX3lb516yAboKW8+aJ7XSd79tU940A6K3rXtJy3QJAb7Vvf/zWdV8WtP3zKZ/a7rkfby3Mz+3L1+bomwnBBNLNAEMwC8ot4bvejh9j5XZtbt2alxuw/ROfOz9nD8xf7cM9Lb5aZguA+T0vr8uX6nt7XP1FlzvMXgnR2QEX3K6MD9GWYSITqPoOaUAeengQU0IIJvfjbT6ADa+9293Vstzi0Log4Na9NKyTBWZhY4nRVNab5oS4RwV3SzDNaaAeER4/NZiHhQoJE+jpQqtsLeJm6y/0vpwEDg/aam2LMQ7LYrLnGFvijEWMxgjvxsnfFUKEREFtFcSEUoqBf2YFlTTcSas2JpDel2ajpCL5hrFwxodHIvEQgUUsgbC6em7GvVtZq1UM20dzY6iCKECTacekYWtSSpAQVHxmAUtDrQQi0fFIsXvKSKtgIkgjSAg9zqvHNm61dh5SbIx1HgtEgo6zgdfad0BfezqI084+WThOa8Tn+6Al05rq/WbCs4MGQp2R1GdEm6dq69WZJ59LNi9bn+Paz5p3o3bhydeHgxebMEs0Mcp9UAeo3s1DpvPXLPBvsYnXlJJXrQp3x7S+ERQzxkLX9eXnNFQPaxgCko1c0NfG9DynUZv3+C0TXZ77qr9ayKQZFyRMgKNuownABAHCLg+Ev9/+C9RpxqCVmwG46L/L7+vjAPgUnZnVQSiJ3OsIlrDePEuM3s6Wpb0vOg0bIbwcxIx5tF/sP5LhfRGSKg5gORnm/SbE0EMyKo2YPYM0bq3TvnneBs/zYADVJr+NwBRrqozw47ovxZE7CIMWa30CYtI6Q9Rzo9WKVjQ+ei0VXBue1jNO5zP+6x//iO+fPuKpNVAMiF8nVeDkjMwHPLx7wPHhiOPhiOPxgLvjHY7LQUMyNUGTOq2v7Z56jed4kW+jveD09vJjLNz661/hx27zjBfL8dfyM5aXZYFLEORt9734xjeMd6fYL569qBbt75ChKxCo4n+2bO4W+x77fc5/JdPeSJ2vBW0BiY6DGQ+saPUtJEAvdD5hBpd7Xojpb2GZwjENy9u39/yVPbbXxem0PtUtr4MdC6a0CdZn5Fbi0szbwUFa5YEhbMl8jf+y693b1D0i1JJ9cArB+jYE+0T3bNDf6ukw8pyFaRxoesbMr3ee1DpLgB5L/1rnETr7d9mDeyFrd9/muD9k83v3mY/v7/X3Ge/i18nFxyOMDS/XnsjcvxFGfoirM8afPbpKhEACk2PGx/fXEYzU1HE2Nzd5TcQ5AH2HW/9H414zGALGgRiNGEdTlLH6O4CMhwvEaEHU2xkAosoDjQMkEmIgMOn1ygur4ZX2i3nk1KJyQDmrN0TVEEzBPHhU8eaGUaxKC1bjMZkVacIX/a/zyuXIWRm424V3PKDPsgANJxUjIccwPomQoubfUNZTc164HlJmz+2ugCBcz7R+fVJfHorj+MT721sA8Aj7c3HvJdchFxfStM/TuMhk2Gs8+eZ5N3gKB9nnd8x71v7b5+2b3uNr8ObFPF1/rZOHnKZXzO27QsWnd2/+ktvn53ml/btt8+ifie53TMPbNxQLHrHAQwSP3Jlx28Rr40HXD+/vuXXJdoyvezjIjePX3nP11I133sIXZ0WeGzNurnnjez6lvN0j4qW5eSFI7BbfT1be+vwrm9JNAvDpdX5NCfEvr1wn3f/Si4dicmvQlLOCjTlbqJCXhdovWS4AnCtz+K2A/luu9ev3AP3FbX3z3B2+lQPiR3TVXlm5h+luWVZsLYZml2pl0PZ9MeK+23UpAaSugBKAJgmAgAKP54qAazPBRgUf9ORhFZgUAAr8KoOguRkaSlGFgdcrpYQQB+PVmoJBtTUA1MOU5OSuyIC0htI0aV+pFefTM07PTz3ebV4OON7dYTkckNKCyg211g6guUVd9VijUIErL4vOfUvUyrV2IU0EkMCQyD15VDwesJaCdFg0pIApWogAbmL1P05jOtYRhYAA4HC8Q60F67qi1orHx0fknPHu3TsEijjePaCsK1plCGnMXxAsDBUQwkjw3C2A4Jb3BCbCej6BS8Wy3CEvC47HA/LdUa8HIeZFQYGUQaWiMqFU4LSaNSAIoKiW2FlwPHpSxIonWSHlGVIYbPkUWiuqQOGmCWDrARFqoc1tUa8XU5KU05Na5p3Pyg6a4JtT7jH8wRWtqgAQSEPPxGFOMkLWWHs8Jm9nPn3lmMTSKvdrO9fo6wUCTGGeXKhzEFVSBCQBMWnC384Z6Q3KNFacTye0WnvyR6k6RuX0DC6rzreckYImx1uWpYeyYtEY+hsPBxMSVCE2mG4XtIiG54AX8z3YCmXkXhboa9HX455u8u54SgkiEUgZvJ5NUA2A6HhFYQQpaGBw1DSHYp4ltXJf84SRdg07WgfyEGQ8FHgmBYYUkfKURJkAcOw8XTBPBhdEXQCvlo8C1BCj96O+VcH3iBSTegDmBRQSAFd6bfvU1/AtwwzPo+TfvS8t9rgrRL3ORBrKLCQgICGbIN09YVwBEwm1augC9Y4IF+PqipXD4QAAeHp6UjraoMBB0LjeOR+Q8jLWjL0j54zleMDh4R55WbAcDxAA67oaXW6IKVvunbQxUshLVu+2pEqqrkS288uyIMakHmoCtDDyl6j1l1ogtzrCmC2HBYe8dAvl0/MJj4+POJ1XrKXih8dHnE5n/P6f/gkfnh7xv/zd/xc/PD+Bjgfc3d/jv/ubv8VxOeC+KY389i+/RTokfP3tV/jm629xtxxwyAcsccHKBa2Jd3mfkHsZ4tfya/nTlhnUuOSXfwmFNt9b5YMe8sXVAKmaTLlp7HfUAhQFLMlCMuleEUCk3qYI2faEQe8d4d7AK3O/ONbkNGlXZweMmRmNBY2bekVUNYhpli+s2d7h+QIuck2IdFDUAdLBkXs1ugoErpz3cwJATU809xaDkaCKhyga8T9LA0sF8apW5panCWb0UUsBt4pazuZNW+DKHha1mFcDEe4YfHDlclReeDlovrIlZ03au2QsMSAb79VDLm28MBXMdOXEhTGZ94SMobkB105/zIZekxHcFUCw/74C0rkRUTcu8jx6PPK/9XdANKE30L1t0XjDe7mHjO7rOi8ai8olLCj+XCgYb76l8FxJDmmPdpF6awv6jBCoZ3ZOC5a8IOcjUj6AYgaFBEHUWWIdq6Cl1qNVRqmCavoq75MOrBEDJIihogqjoeEOFQEFZzQ8SkEVoFEEE1DQ0ESwgNFEsCZCaQE5BJwpAi1gpWA8sHqGiGiuulZXcC2o6wlcC9rpCVxXSDlrLgix5Ng+3h6Wqa4Q86IXZnBdTZnWNvOBvfFkIK0pa4ZfwVht7pHk8x6iMkUOhCUS7paMu0PG/SHhfkk4LhHHHJCiIAYGSVHFU7M1Pk01XeqDFr21DGBenzIUVnZkAqv7cSIQwoXzRcB2Te3PjzXpSsJw/fgbthTHA6anb97eQfj+rx+3vyeXCLG6bp6/B/uvYjmmSBeT227V9YJO7H5e2RN2L58ftnv25O0EwHPA9WZOhmxzcdppGSaUtkBlTiICkxqyCTdIaqpADAmU9OHzvnGlwbdaM13i62GPmWl7Zd/uzX1+3efxHi8rs95wP66Fan6pLp8HyH26R4Rv9i5FCDr4NishhjICE6Nwvej8vmRq5uNbIrG/+6UyAVN+xC0IblkrbX7cniDz368BuLetr18un3rfePcVl9VXnvVJlmgvXvfKgL+hvFaXfVvesrA+t32fVHZNn98xgxF769xPH9/L8il94dft79krCj6lbN567d6ZOMzvnBiKHZnZPnvifeXKRW9RBH5SP88M+dVCE79idOZK+8Y7RS+xXAAULeloCNDkShaqyRleB0Jn5h767a7Zc30ddFZPCN349nPNBUEHj326kif964oNmMDYuiV9q+pm3p8dI6KFK3Hazx1sVgbVkxmKAZgeiii4EoLZhJFpbrAMTxAHgKPer9JG6/0gouECtE7xYox1D3eQcSQEHiGkmvWTWpmHGFXQwEhKGwKBeRtOhyePDQ3to4D98EJxt1AH4gEKUT+kgK8ggIVQm7p4V4YJLtzBa0/cq95TCY2jhruCeQTUihoI5XwGWJUFtRSkViz8lvZxOT+j1Ybiigjz1iAZibsQApg09XIjgrQAidGUBoIQE4LEHjqM+vzfWmyIHde5i57E2sEAneJjJTvg0/uVxAw1VWnBMtbZEHhVOecJ08t6VqVN1Ri6payWLF3HKKYp3q8B7zS9160vB88i0zj62DuwPdHNTgkuwert2rzOJ+ytj+Z7ez/OPJeFk2oOQmDis1xgm2iD5kMBXCUxYtNav4ch5M3WmTGGjjVoqCcLqwVAvVXcyl5Xt/ffto1OQ52ejvXiSUY3++MEqjhIfg0AdFo7XwN7BxuIMecSme/b544ZChXzRgpKC3yr2ozrPEb+DOrkWp/vXm3kc9bWviliNAxT6iHtYk6gGCCNuxdSjBHJrvM5C1OczBabAHV6Myu/kimTRQDiTuEHP907xeh9iKAYLfxfwcfHR3z//Qd89+EDHj8+4vvvf8DpfMZ3jx/xeDqhQWlZStny4kRVbEI0IfwxI+XUE3329T1G2WhH2Ozp87oY43x5fNR+9O8vtdzmuWePlC/TgM/hiX8tl6WDZzeE6j+NQmIPB/hqgrGVMwPtPKQ1ZBP3XePCu0eh551SUmW00ZUO/k3BCTIAi2/ubK4jNM4He22dME6V9v3OLTz7Hjv/9mrbw67FUh/XTV4W8H1wll9G/zig5NR67FnaRyQKZat3xNYjgjyXRvceGV7CrTXUOnhkrTzDd3bPc+Hj5/xHTKr0zk7rLR9EJEKyEIFh2v8u55zLG6Ptwx5fWzgPzSWYJbtvnzaXvEqPMb5h8rYhmzYKBmHl4TuP7nILhtwx9X2Xsyaey/fxzW+RC28IHX9taW+3z1Xbf2k3B8dSsRNB/9nmz3M+Uee7ey/D3uT5TJoATcwzgre8j1v1A4xo4cCW0MCh4WB8fgUjQrBCDKps6nttIVUJmjOO1eIJJQZQDOAQ0KAKEO1n93CyHIJNDXXcSxpsoUx99ohoTpOeC4U1h58ZWw3L92mNOVPks4+MB7NZ5rlg+gKe5ovNVgvPGbphkOZBIcTJE8JlBU2NMdZ33/Hd9eBiTr9cLvCBXYiiTrM2zySTy7ED8OliNV3E1d/8dr6zU0j932+61Qyj55uav0ATMaSsISvtd47tkt8ewA2+gey9IhjhkabTm1fe4jvs/jfij9d+z1jRrITordnRKL+us+R9Q/BQwW4Ipcfc2JBo5E/cj/Sns1VvUTZcf6jLVT+Wl/uivOCNuTr2mU8vn5GsGl0w3y+2QW6usUwvPHv3hP3xy2hqPw0juK/na295bRL9Wv6FlVvTwC2iDVRwT4g4Aw0YjLWXAYD9BFXdzd3PeY8DILPL8b5s1rO1xze/ITMNBrpfu3vixabUWZPLhFLXrt/X2f++dpUD5K4E6Az5rj1qKUagaAmR7bmdQfY6yBQqxUBRCgQhBrWgjKKBy0rMFUzl6gmpW98Ub7VLgfWKWtVKC6Tur8uSEUJCymo5fbawNdw8IbB76YQRqkRcAaEW9K0WrOczzucz1tPJEulG84i4R0qWr6FqfNMe2x8qlKEqgLpkne+H+zsFzKsKb2VdAUBjswuA0CA1oJUKsdBJIUUs90e00xm8bq2kBIwYE9TCeQB/2mGmNEkRKQCHw6KeAWsBM+P5dEJKCYfDAiKzhm4Vpei9zfqJCJavbRJgoe/JS0ZmwXoaygNmjQ/b3elJPWFEGJQPQGlgSigS8Lw2rGvF6bSCRQWC2ipKOaM19XwIMeBwfw86A2El1HoCN8Z6OqGtZ9RzUYvzlIeyx4QXgaCsZzRuWNfVAARVzBwOB7WgPiygoCGwJAQ0D/3iQnEISGlRcHTJoBRBlLqViU1znYt9lTBIAqRJZxqV4VPlzhAgRxI+6lYvDaAGgSZ5dG8yQEGD1gpqWfH08QNOp2d8/8fvUMzbRUSQk84HMfB2OSQV9HNWIczAamcy2cKdBaI+fjNtvK1sH4B4D5+zo+fzs66t4WsW940rpJnrvrC66icCOAAUUc+kf47IQRvZrIcqE6W5rSe1xq5u6NZc6hUVsCwJOSe4LVCIFbVxB1Wi5V1xbwFMyd8gLtCJhgAhC2ERPLk9VNiPETElgCLQoxwHeEgiTRa5VaB6X41+Hn+zecK4NwN7eK5ppwBUYTieoR3o+Rf6eKAhUNsAQQAUwBPp4TJ6WCQD1XM2pa/BD000djUDoBhxPBxwd3eHu7s7HO6OON7fAylCUkA7aU6fZclYloz7u7ued0fnn9LBJR80/0OIEACl6Hx3pcXhcNeVHd7fDkIJPBqL9kiMlsdjyUDOePrwET98/wH/5e/+D/zDP/we//W//RM+Pj7iD99/wOm8okD1wHfvvsb9VwF3d/eqbIjqASIiyEvGb3/3LWKOiMeAw90Rz2vBaS1YqyaezDHbWBM4qBL2c4qvwF/Lr+XLlgGc3uKPf25lxOXbOke5AdsBOKPiMWTUip+LhWwpmmOsWk4DUZ4zUIBQVDQwKn3Rb4Jlj91YEHe41RahK8UvKzrATL3egWXu/Bsb4KgfDyU0QOIuH4ju0xRC9yJkEd23TfHqjgMd+ISDmcaLQkAWmoYs7xWxxsonqZpjy8LXEBeEVhDaCmrFvCI0+S+Xgmr8xumkHhG1rL29c9gkIkKA8lMpJhABedG99t3xiCUn3OWMQ4o4poglRuQYNcfWrAQnmkd89O4VHYXjhmOWTCPSB293m08fbGWXTd6mSX6jaX1A7F1tDgk7jJ54ovECdCWD82HdA6KO48q36LMq696hXjSMyqxKAE9eRc43uhLCvSDJvHomm322prthIKnsk+IBKR4QQ0KkBEgEJEBYA3aBdP/zEKm16ac0gKvWvTUGmimvpCGiKDdABRwY9+GMFCtqXLFIQwwFRQTPonJjNYXEgdSQvTBQSXAIwJoIxyXijIQnXrDWgjMz1iZYpYDZEqbXFVJOmk+wFnBVj4g+Rmxhj5rLgsU8ITT+v3AxmXWSgQHMuQW2xhnccwFuCIPoOcDISgjIKWLJEXeHhLslYckjLFMMyntBuBt+tdacgkCpjOdIGSGJ9sqmfbmOddAgFttV0OcRdYI2/9bS4LKMnvO6XBhPdMMaf4Z/bz0kru4nEzaybY+3+9Zvmn9e8YC43Vm+tm+XLT0f5eUxGOX13Bg3FRLOx3YFy67fZoBG0JVawc4FN7oyTEfzvSvGotiBto0o2BoZ3tD6tplPvc4XfGrbXmxv//15/PEoPx+v8rl80aclq365Cl/kKbctiD7tfX0wQ1eDvaFcV6D0uf0CmHDr2K1rPtcz4rXyJRnkPzXzPZfXrOT+lHUbZUKCrDq9XhNT6ZbZ+xAfV5V9Dt5P7bx2z1uUFp9CNK9tkPv5P7/z5ly5YZ0n0zHfGN+iEb/4PQtgu+uutXffT5v+0wO9v/Vj4WNENvscgG6pOrdXpuf6dkkuXE110DwRUcPYBLKcCDQYOGfyxS2Jtu0SA2T9mAt2PTZ+mAC96KCbey2MZ+1jzG7aPsW6lenZ3b18H3Mfoy/GvDEwW8QUb6nXjc0Kp+cj8LFk3Xy5NSCQRlElS+ocC9oYvN5nwmLeC2bdNjGZs0V51JgxWFFM8GkGnCqTG2NSJtyYaveIgDHaFMII0URuIU7Ahg834atp+xzi5C7UKXDZY9AKobHgdF5RW8V5XdFaQSlniFgorlb7XPBucoCZm3oSKDO12reNS1QmqhZTcliOCDELMGkVKSVAmnmpZFU8xGh1dFDY42VKBwdCIhAJpHvy2Pj3rp9ph88tZeBZgCB8AcD3ERNVhinSrkA8CXXm0nOmNAuRcHp+xul0wroqGHBcjpoo+XgEkXuUmNJX3AISU/0Gg90/2BanWSMm6Zb5vuUNMZ/fPM/XYBgM76z07LE2XJZ2xRIP74UYLTCU0amAkXtoVrgStQu62JWbNm9dERncU8AFsBC2oMPGm4AsZq8oIy8y8hjQ7GEy6Na8Fyrt2Aq4sxdXmGjFrBByga4DY0YDmikimnluiSfWu7pfXReqZmVHX996Aq5o6fsyYGuFdooTz5fD/d1ueDD3sXad0itXDGQLWzfyUcBiiI/70PmDoJaEE63vYTw2WzB19sTb415WSoOA87ri4+Mj/tsf/gn/8Pvf4w8fPuDx+YQPj09YawWMdh8Pd8gp45gPyDGjriskRmiel9FGTcSqSs6YEzxR7dCaueD3Nt7trYYZt573Y/jZt/ASv5TyS6zTn1uR+V95+xz9KcuwzJxrt/tLZPBRMw/Lw/K55xmbaBMZnUcIkBB7mD6Zafgk10B2CgPs15PyZhd0dt5HNjswzWLTaJVc8s8d5PZmertpsIQ7bnwyKBreIdz7o/W8GcINHl6JZOSGQGs9Txpb+FP/OI/MLiOQj9bI8RDJLe31/JKThorMCUtKk2eEhmMKNAwcLuaAPb+T0gu4cuLnsSsuol7ITbRRRHg/2x9z54/vLqNsx2UvQ8zjth9Dv+bqvT7OnmTW+OeRF8KrM0bblWXU55PN370c2kF06rnbeu4tU/pvQGYRMKvRTQNbaCYNL+Zhmnquk15nM6IBA6gAGoj0E0JDIEYgTWqd2cBteEY6Cx0DIJgqjQCI8V5Mgz/zpwcIgkhf154PpsuJfTl4+Ku5fwev0n0QnIa4Csf36zDzYOMeuphxW96XjEeKcXwGj2ejKNJDX7mB0qjBpEyaQzQTbO6+vO9f4AIiF7cM7nsoDWa59rJt1955STP7fHQFBOI0PwnYrXOxhTqvbJ+vnY/u63Wuj/XNvGQ3j3Y+kOYj21a9wD/Mc2NDPYznfXmX9Nn9ernEi4Z8uaEjfd5ZF25I1a4dG3rqMh4B7Ok6LWQvMzh4aOgRIeIWHvUl+K3XsK6fslzsMZ/A63wpvuizFBHXGbOxYH/J5ZM67sZk+JXR/7W8XHy79DLCJnjYBbVYnqw9B1d1oQR4ab59jjB86/prBGkLZl0H8X/MahDjigdv8Dbifuv8a/dfMMP74ya4Kfg+mGQvm0itXfCgjSLDY5X608PENAAGPAqBk8Wp9I8EYyLJQhANQHSrhIDWjRiB9dMFIxOusnncpCUruG7hRjwWvxgA1PMd2DjPlkitVbPIr11IE2GLc37o1vcUItx9fzuHtH2aWBc4Hu56AldmwVpWtFJRW0MkBa1IYNY5QA1FExrnCEoBh3wHqRXl9DyEMBNUW9M8E55kzgG72lpnZEGE4/GAViLO5xVNBKfTioWB41GZxJwXEIBaV/MwqWY4E0CkYYm4VZTG3Z1+60IP62dBKRW0VoSjgq2laRgqUASFhJAWhFghklDKGd9/eMTz6Rnf//A9ajmjrM+IAUgROCwZx2VBZRfGVJButahipHkCOqMdQblCCsqlcysA1CrJhSsi9eZJKePu/gF5yTgcjyP0C+n4RcvTkJeDxq5vB6ScETJr/ga71i1IYGB4MGbbmVb3LhERA9LTpCAY8e6ZBSIa8iCILoUohIhgwgoMRNBQU+fnZ/zxj3/A48ePeH5+hojg6/df43A44DfLgoikuRViQE5J53efO9LnvaMI3YPhBRqytcSZLB+D5x3Q3BCzotMBYp4E7xC2eQ76u40kuA4sxQDKAdwIIkGTrCOBiNE4QkpR5ZD16eFw3OQcck+R2bPKw5PpOKNb0mvYCFOUwZKkU4OA1ajUQvkEG7dgCqJgSr5IYu72HkJIB81pqvdHjBHuEeFyL1FADBkpxU3i6A2AsFP4iADcGLU1nM7nTrt0fM292uZ7SmkjjIB2HnI2tiklH+xpbAQUpO/bzUIdeK6I2D0kZhrqXhSEfDjgcDiooiElU7IKKrN6otzd4e7uiMNh6W338VqWBTFZzohg8aoB5Jwh4rjh8IjalknZLENJnfOCw+FocbcZ3334Hn//+3/A/+c//Wf8L//pP+OpMVZRrw4BcLy7x5IXvH/4GneHO7zP94iB8PjdB1AgLMc7DVEXScO3BSAfF/zmt9/i7v4BtTZLfA4F/lqF+PVvLJt19ysb/mv5UWXPp+9OTeDDL1nk2wNAIgJy3lFUoU/NPCLMol9aVattSPfopZiBGCExQ0KEWP4h0NabDvOvXRduFQDj7yEreL0m72goMOY8mmPtBKfJgANYHrqx2cuaWYAwqeXrhrb7u3dKBvUEYTTLXSb23SznA7dVLcvNC4JLQSsr6umEUivWdUUp6iVc7bf2s9s9BgSKiBSQzLOvh9mL6ilxOGSkFPDuLiOniPucscSIu5yVr5zhlGtYy9RMb+kwYiDDjW9YKU+8jYxu6hDh3iNiVlrMx4fCaxzvyp0+9y49uf2475Hb35ceERoGqWmOCHieCFNI9NljYZTgVvPKc5PzMbTri0l2UwV+QsqLef1mU9Bb+EMRECvK2YRRWPNTeEjVZoZAzOaxIYwqFY0LIq8IrYFZQ4cKCkDqCZEiI6UV1AR3pKGfGpsRQ9PxKACqMLIwKoBD0FwRSwg4UcCzECCE1hVTGuqpsXplgJuFFpOxylzhYOuidYOJauda75+JEKIzpfM6szngOcp83Oe5SuRGDwE5Ryw54ZATDjkjJ+X1NHm73WuyLQujiXrCeGDQQLHPPQ/btFkZVyb8LUXEJUnfYzZhowYgmvmqaeFcPGOSg3fGLGL0LYjlUAwq0/i31g8YmMj2HbNh6twON2iZ63CzyJWQVP3dr+Mur+FHL2KsXQH48juuH/dQaWPXcOVCNybc8fJDbnCvv4FjsTSoQn3w/USAJ61WQ9OEcMWL46Zy64XyVgOZX7IS4k1j/BnlR3hETFYKYjiaC20CFW5v9OfV5ftiu64964IEXfzeP/P1zpPNl/59SezGKbn691vLT2tlM8DdW5aYn/zEV+77vPbs73npHbefP1et75FyScTfVq5vMJfPe+HuCcAIpvnfWEPuQdudNrc/a8Osj0sxE9ypQpvNCW8jmP68qz2/m+MXBH5f7dH5F+cc3JsVLwRo7E0ZG++1DfiyXnbt5qcxxTvg/+XneE8RnJGaQ7OIx8qc+I4OdJOGKOphmSYmffSRwC1+O9ClT7FEwBoexK0/CDpfVFAboZmkW6108QokDcIEbmLeCwIxwSyk3D0QQozGLDPAluNhFihojIsLEm7p1ftEPJeCzeOUumWMXzcscbZjH4PFlLdwP2IJ/NpaeqJhB75npU5tDbEFUK1mraTgZsoLam3g2tDjtAsDrEm4AUESDReCQCCe5jYFTfSdMsDqSq3uyZr4KpJaGwVSy0CPxd6agu4xRhQDCJsQhAVpYiLRGZnaPUlaraAQOjDpifaIooGHCdEEVoJAWkUrK9bnJwV4IeBjBh8WU5CoYNya9p/wUECxmwkaL6qKCKhAAoCITcDXRNIhReTMCCF2ZYZbXjsoEEwRIdyQ80EVMyJIBiAj6BxXHUcAOYaLye5GVEgHDAz1eKPTfJktW3ztMDdIhc4duPXmRPdC2MwbB7u559ewhOIWxmcGZ3ztu9Wc5vDwmSsbBnUjWpF3LraMsFsb8VAezkqHa/tR8Pjb3lPkgoxa6LHnFYmpfyANlJLG5Ac0gbspGrsiLqZuVTnT/qEMgimrTDFFarEfkuYsoDgsAimoEoi5DW8jshwn0PsIQIQmFU8mr0qMmmMkHUBp0QTVMZtAYdNLJ6VOA4aF4LJvTS4y9TkwwiIZnbA1tpZV86Wsa/dY6rTdiKZ6Nlk4webeOLrmqgtIRMPTw373vWUjsJgV8bwrU/QlgwBCWzV5ZCCd/O7RwqQCqebREUQIckjIMSPFZGM4e4wAMWo+Bu13sumn4fe0mm5hmGwdTPuPATRaxeHlRCGowrRWrKXi8fEJ33/4iKfTCedaUcViYNtTaq2qgGENv8FmQnsuFRQI+ajWjBQIacm4/+oB7959jePhHktaTIk4WVyG0Y55L+9F5KrgOrMHb+HpftmGQz+lDPDly2u82ZeUaX7suN3i/4dc9PL1AzQXW9dOLwaNdipwwXfOz+r80K2+eUWumupzeY/TOPNu4JELgtiOtwK0VT/V/6794QIzOnC6Pnn6mgb3oi20X69OHx2+dBDc54srHnrUqMmqHQTQZNmqvavnCBDzoHRqZjY6xgfYcRbNd+TvI83x4LGfZmUEW46MVi1XhhnalKoKiFqLGeCsPTRmaxb6hgu4/90mXlo64OqeiiloiCU1gIjdGjwEwjFpjPwlaCJij5fv/c1OFztbMPMgJq/s57dfLEOi2c6WwfNjmqvz/jbPM/WawZDXpvHfHGcfxwFu973Hx1icn9LbmUeehc4nsSUrFxnftv6avsZyMtCYNwDUXVbDcLYQlec3K3vtO/GtZuoFAhl/v+SDGlaFBTFk20P1OUKEZjA4NvNWPQp6/j52+Ups/Y1+sYBgfYSiAEklPizUUIl7CJ95pAQWtJIEQLPk6ppIvVBDAiOa4oEgFlLMwmSKekds+Fbna83jx4JMWS4U6XUUzyfWeQc2hm47x8aDybun8xlWo04n3OgtpYic/ROQI5ACKY/uc09UPun0dINBtO083JVrh/e4wh4jmXuo/2vyfD9P2/Vm/libe2fqNVI/kIVIc3nB+9hs+Y1OkuzB7ms4yDB0G8tQBom9uc/sNzrenNuQd2Dary7vlt2cmjfT7pVC8z20/eqedJumbqt6yQjavxpqdnN8Qwe258dw6RUhaN+3TZUmOsUMJtKwfyBIbJpHJNoKvqYE2n1bV1zrnst22us79yvjlMy9/yIf9Ab+d3rWJXt2bae4/szXlBA/hvf7BEUEbf6+7JvpQJ+U1+7dH3q98nxz1u4fOV1HY3J+cvlEBvhTGeYLEPqfXblKTT7h3j9duT3T9u25Vk/CaLtbnIdunb4sS4+NPTTm0+3BBZrxtv1mee33tVo6s3Qrt8C1ObjfYGT6m+wZ10A1dy10oAG75/RndwZu557XLgn7trL9n3FIOpzRXbT7+3YddHtbJkDqVFWLU8sa8qW3lZ3pBIIQclYLp5AyaEmDuTBQ212/vZ0SJ5BUBNmSvcYYUczSnsEojRED4W5J0GTEarml7uEax1aEzUKcEUWA2lAboTYLuRS0PvFwj7xkpKy5D8r6pNbzdVV3XQPCuvWLRIAbWuFNrHXtF0blCgRo/PjDgnw8jITTTfMtSFWgEg2b2Jj5oNeGrNuNnE9opWB9elRwXgQhKUiGaF4HIqilaBuhlr+JFixxQTgGPH78iHUtSImABAhryKF1VVA9HTIATbyLEEZ+h0QABSzHO03A/fysYNy6qmCYEhAjWspqfy8qMJwr4xiHpbRaatlqjwGRAgSa9GotJzChC6/r6QwQodYzWql4XtUTJIQFMTYcDndY14IlJ6whgFpDe37G0x//aEnCC453Cw7HrCBga2hce1grEY2hy2KhaUz4gwnGaklks57VX0dQNLHskpBzRKsNOUWU02IA+VjTIWky2rv7BxwOd5D2DrwcII0Rk4LLRBHIGRQjlPap0CQmvBAI0YEgmFBU2YzhZwt30ntFFWvgCqAAKUHYvV3UklyCKrdCzsjLgpQXjbxQFWTgWhFIkAKQzXMFokqKWkunjwogmGdCyDZvtaYe49jt+pXWBYsvPOUbcAFECK0pZWq1jZBpO5q5D2s2qKRakgdZdO4F/XA6gFhA3CCBEIVBLSHUBSKCxd/PqhQL1EAEpBS1L2PpHhBikgALUJuoEI+4UUQghD4GIal1nfCKRk0F9RAsoXtAzncIKXSFY4za3lJVeZfv3yOkBen4DmE5ogkhigqfZKEzHXSKQcNTXHiIwACeEHtYKhA0R0qteHz8AbUUrM/PGt/VQnDN+1UfK/+2MBhcE6RWxKiKWx3sca2u9a03Rwihz2duKlRyXAACMhoaVtTHR/DzMzIEiEDMEZQDatAcHiGoMilBcDwccViOpgwb7Q+WGD4vd8g5d/GX4InFbU1QNqXmAhH0+a3KBoDhcXBHwmwRwdoqHp9OeHw64R//8Q/4+7//PT48PqGwoJGOiW19OK9ntFpxXk9IMWDFPQjAD6cTQgy4//odkAjIAXcP9/jv//bf4K//+m/wm3ffIkSlx2wAjOrLLYFj35W7dD2KyFaym8qfklP88fz7rfv/OcsFv7SyFawvDGz6bz0WKCB4HhvRcDuueARgOVkGLCIYfOqPKTK/Y8MfO/SnfKF6x1agNVU0GOCO+gzUE7CeIHVFaGq8gJgUvKUFoGi8l/I/RJrjS7vGldLsDYWDO2p4qImKOkAWXFlKBnK6Fy6BWXnV2gSVBVX8qW7Trm9yK1QJ6nW22rMbMIUQIgTDiNV+wJEcUSfN1kC1gppZgJvHcC3q5cu1QKShVVVel+cntFZR1mfUVnBeH7GuBaU+odSCtT6j1IpWT2i1maJC+alg/LQbmi0p4RAjsodgSpqQOkfdN46LHr+z84ekexFI80KpBy66QnxLEgcSSdN/Y1aYvLKXm7pygLeHDM7k/fHJO2FWQPS+FpjiYZIJ3dq+y3Mmo7GOo4eFdd5VldrDYKPKeKcrIESG8qG5IsuA7tlwgGNGTVmNNFIARVJPQYiFR3JvYJ1p6nmZ8e7uPXI+IqcHpHhECEeEmDVXWgCKNJNfqTeIXcGlrhk9jC0aIzRBKOb9LOrBqkwFIUkFgXEkRqKKEM6owmBomKdgeQJj0PcJCE0EZ2Ks5KYfFRUFjIKCiigVgVv3ju8fnydkTe8J6i1sJdTLNfoY2oUe2Uc8uTWFgU+SG13pWBNN6x3QvmXqsaWc+rkB291xwf39Aff3Gfd3Cfcp4BCBTOpJ6+/sBoBWPN9gp8fBp/PL+2XHHfbfRkuuleuAq/H9VjRkFE/Xhc0avPLUbnRDgIXWeh3cvd4m5bv77xuguHtfaB/dfj7RUOBeB9Zv33sb+5zlOUzf/Wyv0rV3XffSuNEOmWCfzf3jeiIgRw1y1kjrol5Egyaqw5zhNyLgYLuQhTdW8VEu5ubMN4z3TpXrX1NfzZt6v2Ojfuj02uW1fbkCi10pgi0HQrvvuV60++3Hfnqe9DMVEdMxI1DdGwKwBT/BffudlCaeYdyy+f1p9bBnYDeBX7z6pUX005VPdYX53Of+2PJWQnS7/OnadWtct8Ti2gW7d9s/t2bJ/jV+vRPZEed6eEFs4sr7O2et3byG5MpxXJnXkyA1N+NFL4grBJ/2z5jvk1cUG/s6XnnnXonhG+Bew7yhJXCo4soo9Hv0fJcZ+640mOHeXugG3Qn/xQbsngcTcynoyYvgAG0YgscYvm1f9n4wBqjH5CTLSxADAkET60KwlrMy32ZNH4IydWNMdkKogTRO9wgar3wIRHEzdt2zY3qGjqmAiTcCuQsC7u3gFi2zsEXTtRoj1xhacqBsgGpuTQBRsNwVHd3C2ABJF77m+VZL6XkpiAgpqQAR06pJv+VyTfeQM6LCRyAdd2EA9iwASCmDSAWlBqCFkZBWgtebLNyqhkMiIuScNZl2a2gQCLmVkXll1IKynhFTRs53ynwWRisN5VxQiybpLq2BA4FywnJ/xFEqHtb3CBFgKajnFfV8Rh9Ki0lbqia09rlSTaBzSzK3ylfGd9AdOHhBDSGoB0WtAsgZOSd1SaWt90BMmgScGSiloTFhOTYwAnJmxAUIURNNq3ONOVJ7LFk2w4Qd4znc6n0+b8fQmT6wJiYUZsvhEXr6hGjzMaWMZVmQTdmbctoofN3DZ56v/rdayowExDMNmEu3Up+UEH1eE4aZpq1Vj228f84+qfVo7/weAKJAc+QEiRmUGlrL6gGRsr6b3LPDva5MQnOL1BDU2ipYmCJx1lLXRYomYIVk4QkyxNYiNxeuKxiMkGBKTOj4mvV+iKr8PBdl7Q8HS8yZs3oRpcU+WRUdnuPA+isGDaC0Tw7tfdH7BN73rtRllLWgVv9UsIEnNO0nPXn8PIb2CRY2o7WGnBfk7OtDQ0AMuoU+Xvs9zBOvi51rraKUgvN6wmoJTAMFo1sWooMG0ASMvBgeSqKHbYR5xxhdd8jJPcHIvSdsj+QOHnj9AoIJMt7WYAqY5+cTnp6e8PT4jKfHE06PT1jPCq55eMGh+ADuD0csKYNEvSM+Pn9EjBHv379HygnHO1WWqAJOcDgesSwH3QdgiWWnDWjPx0y7Ml4qe+7t5zDq+dLvePl5P217fkq551Ue+xdU9nzmfFz/6Efw2phs5KXpjvn78hH799x6OKBeq5h48s7sjlwGwmawoooI4QapFagVUpvSxjasteFgpz+X1YCAgnuAbAGjbT1pUwf3eHAsQHp9BzsuMuL8N/t7y9GS0e3+8k4Tgh3reySgFHcIO/rNBARNRIrGkNZQW0Ntzi81lPXcw44KN7ArIux4XTVXVykVxXjVZnkhuLWr9N8THruid0lJk07nhNw9Igg5qOdDst+zQUL3wrs+Sza/RCaF19RP8w37db6VB0ff+d7I7NCs8d+zImLq4z5fjCdjU8BtFRFGx+01bhzjY95DMrXJw8DmoL9ju12EgYmRN9p5F+OndvmXuseST2HrIvVC1b0w256cchp78+QRJC67eXsAS4swKyll/OcVd7lPevp1kPE6hACOEQECSQmBGpZqaoEANTjpMp+uM/d8SGAkakhoCGgIKAgyEqoHrgitIpoXPc25H6bnAuihhdlB4r4eB+UisjpY33VZzQZpI0vDQ954v5k3MkH7OkcsOWPJGo4sWZheNXzx8RxTTSax3wFj9h4RmwNv2Mo6ORd7ko3l5T74Go3fBC8bfH8fq9063Dza6ur7DZlHxE1FxK2GUX//qNe0LidMAzSrdm88utMOubh/7F20u373qCtVdblZRXmXk8alRNux070Ym3suK32lLb1P9u8e++QGa4PKGT5vdZnyhF2FTvNaa6CghkjqZXUpn35+kev9tr1iOnbtXXTj+PUy5tj1OfpWlu2tPN6n8IBfMFm1FjFwbKSVuWT4ZJx661NfueH6BP1zYIZ/ieVPoaD5pZS56Z86f3wjIkse6YyNxt02JskSW27ueqG7r4Fhn1v2m961Z22JeK/EBpx+qa6z+9r+3F4R0QFJvjy2J3YX3hv9WaOOALo7Ma7Uk4imzXXeuKcPZjdutfK3u01IG6C5Cx7O5AEwsOWyX/QafWYRrUtOmtDzeFhQArA+ax+vRYXImKIy6vpgrWuHhmaJTC3/CZrQOcSoXjgGts9JrLe7P7pFeJXahaFhOe19YhYtpFblGkPV3PmnueFhjihoP8WQNNxQUCFCLZ8ayrqaVZr2rde5M6NT4dawNk3jFlNCigtiziiloLYKNoHbwTu3WqmlgBsjpqznkoaNKWx9n7VuMGusWis4qBtyII2X7/kwuGpIrNYaSlkRY8DxeMQzq6UcV+3XZMAilxWNBc/PTxAKSMd3oBDRzg31XPD88Qm1VpxOJ7UISwHhuOD+m/eI9xnhLuL0+A737+6wPj3h/PER5/MzTudnCNQbYi0am/jswjN7rF2MtQoz7gAQO5ArBuCrEHxODTEGnE4FKSfc3TVV+oSI1hpqrVgSsGTg6emEvCx4eLfieLzHQ204HI84gBFzBiUFAUQyWAQpat+jjDFVh3AXrxjuvq21G+x1n1dVQydwrTq+i4DMKyVSQLK5fjweNETPwwNaawaCLl2hcj6fd7RjBhRU0eKhsjyM2UyDZuDaFWyb57EA4M5ACzRZ+WxlCAzLsFkRsaeXQ2FNIM4IIghLRSMgSANbyCJu1UAobYM+y8a/aogyXU4WQ5ld2ajgdqSASBp2i0y5l/MCawlqUQAGpUBQkWOGiKDWAmZBzAf1IkjqlfH49AgRQYgPSDnicLxXBdHhDiFm5OVOlRGWILk1QSIBRbL5OcJ3zX1BRIi0Vd7UdUWtBc/PTwr6W24IbtVkMOq0z9f3NUW4g/M5ZxwOBxyPR4gsJgwBDuDTpAgdCiytS0oJYkC7NMb5dMLz8zM+Pn7E+fQMiIbMOhyOSNmVEcHGx4wVonodRfNwGICIKSYsLFfqyrBo4Irz2DrOldXDT2xf8OsC0JNhu+3e6ekJ//j73+P54zNOH5/xwx//iNPTk4Jv5Ok1dYuJFPDtu69xfzgqHTyf8fH0iMPxgP/4H/6fuLs7Imbdh85rQWuC+3fvcbx/QIxRwcd6ywbx88qv/P2fovzzlg02BjFXwapr9/y0dSKMePwOQ3UeUDwWfAW1BmkF1KoqIiwfBNcVUitaaZCm+SMIADUDoRiquLQ9LAQGwUIt9hpg4s3oeqO9z0gAaTA7ZgDoYXiqaE6cZr830TyN3vr7aFZEUOz9oK/maSoKusG7EKRpHbhVkCmFa604m4LhfD5Z/q9iYUJVIbGen9Rbsuj559MZpVSczwWlqEKiVsv7Y3tpMM8u50OSfY7mEeFJqZOFZFJFBLoiIsVoeca2IQdHl14qy4Zhkv27QwOvTcetjKPzphtG8U7hYGOJ6fyM5s65Ibq3pykjfI66wqHLeFbNjTGIDNlvlucG+D/mmwPiFB0YDRaWM3TDhph0j1TPVkuM7Mp71forPxoSKEQsy7HnScr5gGXR/BAh6d4rvRtkTE2bp3xFGeEfN5LoykGwrgQCQlLvgkAZ3AISVFHGp6aOTOx0x3K+2WpgUmOnSoyKikwVCSuCnBHqGVRWhLIi1IrYCrhqfpPGtcudPWG79TP5sNI29OhG9qYt3NmNSGgjhWo/wWRcQY8GEAIhBcLxkHE8ZNzdHXF/POKwZCw5IbrBUAg9FBYg3fnEFZs+r/0zED+fI9eJsPNwY26N4+7RMAr1a53PG2tvi0uMF/iZ1q/aW+P7C3sfdmXEdTzmpT3HAX5Mdd9jDuP+S1z06rMHs3uJ21x5/1sQa5GZjo/9Y37eJV3z9t3i7XzkLxqwOT7Gzdu0vUv5Z/U+w0R7XP/ITCBqqK0AZHn8KIEQb9TrZV70p+NS38Cb+PtfVUL8aXnpT1BEXEzJaYQvtVeyuWer/eq3TqDntUn58vtx9b7Xjr+l/BRA/E810G957r6Pb7Xv1rNeu39//Eu29dOB+LcIDrKZe5fFGZ/tO69dPx9xi04PHeGKhxjdMyJMILj3Faa9dPueTxmn1zav/d+vjfUGHJNBsPeWpfN9eyXEtb/3QJA+micGYbTjpeeP59DY5I1zlP49MRJ9Y5qudyUEhuU/LK6sTLkDQCpsgGgk9vPY9MDVuvdzgDGl1k5It6oPLYFoxJWFXathodTC3n/3eLRzneF6CGOwYUnxDNgPIfQcDB4ixlm5XlVWjlQurLOvj3ewPAbqyljVrXgT59XyXHjraTCnLKIWaA7yOshodd2P7VyHlLPdgx7eLC8H1BWoIjY+I9QNN405S5a7gFitHmJQxVETTW0Qora7VYv/2q+bhzIgBGM3W7MQLhExRBQKaG3VUAcersXmxvn8DISAu7oihgRuBbWsePr4A87nMx4fP2pCNniOh4JIjMOSEPiIwO9QloRzTljXI+7Xe6zrGbUUPJ2ecV7POJ2eUWtBqWVKnMcotZrnhH63anMHuiZSCKCg1kuh6vlYGJXNyyCpIqLVijUKlrMgF0HODcIRZVVB8nxacdcYeTngKAFp0XBNUXScAmkIC2VCzW7cdYVWIzaAgQjwBPG1VgXCy4pa1j7Pl4MlyjZayk1jkqWYsOSMu/s7cGs4Ho/d+puIUKsCtGwAwqDJFmYnxa4wgzGqZMCMM7o9L4zR8j1o5ZuBW/t4yKZb1vj7tba5xk9a+B0xJYAm2vz/s/dnW44kSZYgeImZRQSAqpr5Eh4emVmZtXRWd3VX15yZ0/3/nzAvc/plpqurqnOLCA93czNTVUCEF5oHImJmEQC6mJtHRmQ524FBAcjCwivRJaJLgC8F5CThaKcNIStoQB3Pr62T5EqNUPJKp0V+UCVQ88kEMSI5sOQoLQB51vkstcpMICpwfgQFjwKniQVV0fAD3DBi3B3g/QA/7NRgMcAPA7wfYLlX0IEELehf69svSNTkRTGGqKdqzurJSdszGuDRUWP1f29lAO89YoyNMkuv531Yea42xcX11ZN9RQ2tcZ6xnGakJVbO8KFblwHS6LGNYKxjwClABfLr8VIBldZusHvrHgNYxI6rFEyV+iImyZ+SEt7/+CO+/8N3WD6esNyfMD8KrVXW9bGYYbhIf4zDgN04yjrDGY+nBTEnZJb9JbgBIEJUI7O3XDOXymcUh38OufOfo7ym/j+HjvLfY7kE9LYfnz/XdIVrpdcdznSZ/iZ8fs76yFKNEBXiYZVXuWhOCHlxyUCWhNScI0pKKDGiJPHoF3qXIjIN657MqNzyAvjbHmJeta3GqOhkA4a41oy7700Wp8qtL7kBUN+bHLBuFQOvnH7lYPYSqV+lPbVbOTSjBoTeiFMCp4glLhqhpkmml5NGOUSRq7MYJJZlFpk2zuIAsyx1nxGnl1wdC4jEmcMolEz+CEEMEpP32HmHMIiRInh14nHiZBCUosnp9xbptwXVnisrF45uKNUe6MZcNQLomGlGAYtOEP1E8w5X56U6dllHQu04Pvu91kH7AdYfdooC7dnyStR9q16yPT9BJUaRqQVqUjN6NSo0eibUhOCutWvVjSQSQQxsopcPw4BxGDEM4oBRdSfnJNLaxrU69bCBAlVnbQ0u41INEPouEQgmRHGlOiOgGjooBDgCdsEhEyMVEiOaRqkX1Rlr/oeiNL1pBtIMjkcgRfgoBscSE3yaUUoEa3RUsSTtplOasUPHD0idloCzMbhdAtcyrIkfMtclSllGI6meOGpE0H4asd/JazeNmIYBYxiqHH5JJu7fz8a9ydqbz5eP5Yufic+fD9pHsHF4dmEd009M0ban9M+j9aXOwNHLoFs86tID2TGMbk3WqnbH2+dLuSL0VmeP1C7RXWdVB4tUwOq5ru99to47vSet6n0Rf7MbEPUN1j3bWWaieq1aJ6U86jWIagiRzUgimLmK0mA2By2u8nMpEgnhHCHn1NgvIDifRXGt6tDJ4utW+InlM4m1daoCXTdrGzE297k8/3+u8hMMEcDTLcSrP9tzUxUenhQCP1f5M1dOfik/T3ly7NlC9szQOdukNUQ3BDE+GD1In6T60nn1poRuU3jZEnAN/L+knD83164aDfR1UZm6IjxsgextvfqydsS50joXjBCtbp0yVM7vQ1RTZulR7V4FTRgHa5quLFyfYogQowE5AjxEwPLGEd+UzN7Tp1/riFlzO3AVXpMmCnTZqzcswRUHIqlHWmYAEtZaSlZDhBgn6n02Qi2RVy+fEWEYKi3NUgRMziWhcO6ASYZRWomgXs6Ati1o14RFAdwyF5RixiTUBMHCTaqJZglSd0DpmHLlnjXPBAGM/Xq8GEeseuUPw6DUAQIED+OkengRj5CqzEnTi/dt1jnH0r7OYdC8FmAx5AQfkDjJqChAhhgULKeCGTJMAymFMQwO4zhiHmZQdMhzQoqLcC47J15bXHB8vEfOBbdvjuAwosQZcT7i/Y8/4PjwgHfvvgeI4acA5x3CIBRS+92A3eBx2A2Iy4Ll7oASE7JGQcQY8Xh8wDyf8Pj4gGWZMS8zUs5YloScCx5Ps7Q3nwBkzClWUJaIkHQ9irF5zTvvMMwJPngMY6jJtQNnDCgYx4RhWDCfMqbphONxxjiOuD1FTLsdGB7TbgcfJpQCkAvwXmgICCRzDaXOV6Euci1nCcvc45SRlgXLvGA+PSLOpzqfLdJhUGNEjpJHZRyFYouceP5bNETlwl+WOp689zgcDkKhMIYa4VSVQ+ckZ4pKZ5Y42ilY33P4tzXP/rO9RQwxMr/aGmmAdr/ebdeqauRgBiknlxtGBYULQB4eDi4nKE8AKiVC0dwAQb7OmoAcXr7wXJS6alTapAmAUiO5AEcegCjAVAgopMq7JYYnJHbgXODGHZz3SJrnJWoINoYd/LjD7vBWjaLyCuMOPgwIw6TPtQXUde2BAm0r+VLHjK4LS5SoKgO9xf5HyrDc1q/+tV3T7Hr23Spvx6owiAKYHUrB2bpYj2EAJWM+HXE8PuL08IiSk8ztEDANo/Cw6zlZE2aj5uSWNrComRAkcsS8PtsabPV0MEooIl0vY4YZd713klfCIr5yRkwR82nG8fER3/3ud/jHv/s75I8Lyv2CR/MIZkaUwSpeiqqc7YYJN7s9MgpiSfj+9AHIQMoRmUc4PwEA5nlBjJpzQ8cvoVfCO+9A/FJ+Kf+85RroxWjrcyeaf44bvurwanjo/q4wARc1PCQ1RCQxQhTxiOYUkaPkpCpJokeLypZwwssONuOD0SsyHHFlIc9bQ4QBsqYodbI1rF56vOD2IjflXNRZomh0LHfgc/e0RCu6IQLBka10ea2TFEYho5cxRx0BXVNckHPCaZ4x60ui504S1ZfFEFHUILHMx/Y5Z3XyMIOEeq53eYJCMEcLWWfHccQQAobgsfOESSmYnHfVO19oL9cGCaN2srxcL18Ue7CzgXSmgTA3Y0Qv07dXEgcCo0kyJ4aClb5X29su2kWwSz9s5KAVANsMDY2CSWn/7Jx6sD1HGwdQI4QZHBw5FJK2Y92fSCMjJGpQHf+8q0Z/2zN747wPAdO4wzjuME17DMOEYRzFccLuZ3IEc10LqiHCokRW7SDjs7DmYBF+MMCyaRHDkwV+e4AJngOyAyjL+1KS0KVqNG1EArggcZY8EJxBeQbSERzlRXOGmzNcFIOETzNKXACV38kcv4o5tzXnFEbLBUUKVJsuZv23GnFVL5KXW+V54o56WnSn3ThgGgPubvY47Kf6vt9NmMYBwTc6rCZT4+K9z8oLltFruIit6RcvuFrTNkf1dboEpnf33T6PybdyKnXy0CWDx8WL1rdrR2/7bbUi6/zaGn3646993tZ/9e2TuJLrxoy1Z4uUWJ1vsj+tf7fnLmc6QavrJeN9vRZ3eU2qIcLomg0Lkf3IKE9F5mekJLqcsEsMaE9wSTv50yubnfvpwt1xtPr6Zy8vNkRcHoDAdtO57mnOaD7CLfymP8c8pC+de37va0PivDzn/f3a8qnnXarLU8Dua+rykvOeq/en/v6aOvzU8pL2eu45nqznE9fbWmMNQLGF3StQJZQ9VAWhnoKj37xsDHdYxpOTvt9AtkCY/f0UkL/9uz/WBOwG0HTvveDf7QXmmXJpE9uCPtcMEbSZv22FWM/qlUCxui5gwKbsH+fP329fdWOuSdFMmZPnM6/+YjRDrD5HtZ9RAXRmBif1NDEDyLohxBChC3y1pKuxIqeEoqHapQglTiENZ2dJ5JaV+9x4Pk3RMvN2jVTouMWdE554S15sIJQ9E+y5SehoiLiOwe0YW/WXbtqllEqVU9dhhiRQTlkTOnMNCc7cvJjBrElqlY7ExiIscbDxjF6mx2GljQKR0JykoXGPrzQajcJQw0amCFcc/DhJewlqraBf83CX4yWxa9E9qs1fSe5WuKBwhvOEYRwQZw9KJDRLnDF6DxAQ4wIQ4XR8wDBI4upSIuJyxHx6wOOHdwAY4045ag+TSfcydqjAO0YYhLaKgscwOKQ8YBgdYtrhcLNDUq+/kgtilCTWx9OMlDJOJ/H+u/9wjxgjTvOsxjoZP65TuEjHJ5WWrFwSCgJsnibMIJeQMyElhg8zYgKm3SSGiP0ehR3GaYKDBw1QA54okVBvembJZwEzjuhaUHJCWQQsPT0ecXp8wOnxvnq07PZ7jNOI3W6PMARNCFgwBF/5aJm50uiY4ihKlhoWIcl8ZS4PdX7X9UXbwjkHdr0y260zm0KmfdkY7IGUbh5t18D+82reoQu5NiXaBZAf4BjgAElMX9S4qIZKK46CfK9URc5xXVec6wwRftQ1SVbJQg7FkiSSQyZJHu/cUIEECiO8Y7gg+TgyRwAOt2++gHMOu8MdxmnCMB2UilBBAT+qUWLQqDIxnjrn1UDatQGuRDhoBITkr2gGCGIvwepcqmenzOesSicrpqGGU13/at91e5YZP7d7d0qp20fX0RnyXhCXGfPxAfPxEcs8AyjYDzuhtVNPS/PqtCckXftijDIH67pHNXl1HQMaXQRySmMg9ZF9qw0+o4BcYkRcFnz8+FHaLmacjo94+PAR73/4Aaf7B+T7GenjjIKCILO2wYoK4oAJ87Lg6CQJaOaMFBeU4nE8HuGdGveGgLv9Abd3b7Df32AYJgG6sJ4DZuS7pFo+J0c+J89/Djn0koz0c5VtfV/qMPKnXOrS9SekoV8GLC4fp3987ho8e8QKOKDub8v5YzCtiTzG+657Kcz7OWdwFlCdcgSVRaIlVHYqBLjiUciJpzWXCiDaXRq/eK8bcJVDa+UInYcw17qzrrlVdO2bwFQK+6qOl6ZTOaKO3Kk73uQQFi90sroVRuYCZtkjYoyIcalGiHmZEeOCJS4ie6shIqcWAZGV7lPWY4m4y0UN82TyoHrXqxHCay4IAVa9cOETMDmJuPXe8kgo5aLKKT0T6VrXAYjW++F6jJjMrGs/A4DpRCpToOlra32sICfZEyXymiUal5shwmhgUXXAdY6IPo9D61ObM92aTt0paH3N9rkHIA3ZhiU61zFlUc5O9z2nCWT7SAineozlx3MdA0EXve7UoO+9R/CDGo/kXSi1fM3FBKyjeNj6ZQXtthniJA0XPDUDSXbUcpmR6D1e5UIb18ERiAmjVycKfS8EpTgTiieL2hGj4glxfkScj4inB5SlgGIBxQSXMyjNcEWMac6SaqOXO9eURL7O+S4PB6PKZDDkQ0WmNkddHblmJpQ+J4QguVBu9hOmMeD2IAaIw27CfpwwhoCg0StbZ8ZrWEG/FmH113qs2a+8+atCBTZA+bIsvy6XJBRbk19waj2b1sfbGnaGB722XKrE+XfdKl77dn3KOXZxftWzRlad51IdbGGz/cIMpa6T+vT77nxzdKzX7ROFdLOvv31fXeo3sG5PWs9dOc6oqzPlDhdSRxkWml1mUmdQiSa0c3tDUj2vb6tP6NPPIdc9ayjis0G4Pt+OX+E+62v/HPL3T8gR0QbHtjKXPMrk/6Z82AC8ZIx4eWmKGPB5FJBfyucp1w1Sfx7lUv3rJ2rH9F6UIQQEP8D5lj+gB7EEKHmqTdYb7WvL1hr+0jnVC7Dbz1Xn6JSJBp/I92RKRz13EyFwVbDQNoRvdSHxyFqBfj1wtzVulPa7CbYroI864QlNiamhdRaqqkI4W1Jb9RIyyhiri2JA6ikqQH99Zg2j7RoWlsAYzNXjqeixKSXx4HYSTUBG0aTtVnJUQ0Ss95Z7GRd9o0vymjTWxlzR41ISjtySsvKEdiAwCY9qBb02xqq1EcIETlH0hMKUK0UOGDWhn9TTCcBcinqSlZoTYlQaqpX3sYKM6PrQ+qg/rjADGqXiQ0AIg3rXqZGljkO9hnmEcwY7j2EYxWBDDqAC7x2YZQ6XUpCyCd+SZE6842U85qy8tiyJD513GKcB89EjRqX/4YJxnEAExEVyQBwfPyKNEwI5ZF4Ql0fMx4/4+O4PIDD2uwHTbsKO7iTaxpviBLAHBvLwxcMzkHlA5oxDnrRNY41cEM9nAfZP86x5KMQL8Ic/fI95nvH+w0eklDHPUTtWgFaJ5JG5kCmDjcqJGSkTUFwFxzMnBF/w+DiDAJyOEeM0ohSH3eEAQsBunzD6HdzOAXtUxcURw3Guda5rlb5KTEjLjOPDI473D3j48B6P9x+rMrw/7DFOE27u7jBNk0TTKBczDwHDEJriDCDH0oREhuQQQEFKvtKhETXQu187nSQLqR7qzSi1Xk9X6+vZUvu091GfsL3WRQVBqbctPl718FHGB3sB2YuMuUJiaDHV2A87OS9FgADvu7ntHEIY4ZyH90Fyu2iCYYZwpBYmZHhkKrK2ECHHqAa4EQgEN+zgvBPecWLc3d4hhAH7m1uhPNjdgMhJyL/zID+CNB+Fs9wHTnIiSJuU2hdbAzV0zbQ1RpKNKg2cARaAUr+1/B+mPACo66/oN41aS4ZBo6vIur4YtVfbx+RazoUzAwUXRoxCyXR8vMfp8R7LfBT5QKNvLIoBFXSRvZQYajxpxg9WrZ4sGbgMDk3MKWCNOAKIITHn3mgLyS9UGMu84OHhAd99950kWo0Zj/f3+PjuHd6/e4fT/T3ihyPihxPKbsIwjagjnMQgRYoqneYTXCmYJo/MYnQh5/Dw8ADvPJiB4Ae8efsl3r75Ejc3txinSdd968tLiuKfbvlzl2M/f3mJjPqn27HXuvKiM82F73/CnZ89gp54r0b1+r0K5szV0xmaoJZzFjlPqZmQZ7g8N554k0OLcrNrPgdgA6bovGc06tSXqScmT8qfJhU3J3JW4JIV0+7QQTNCON3v9DkdlOKQBBwyRIFgcrs66HCR6N+SMS9igDidTmqIOCHGBVmj6IpSnuY4o5SM03xqCanVEFFyRipZnQIIRKy50hxCF7k2hIBpEDA7BI+dY0yElX7oXHNkarRB55Q0hgM9rbb1o2AN3m7pCPvvxIkoX4wWrDoam8yMplvZAKifbSw0ueV8GFA9tl1KqYf6cWR7KRHghmbUIgLI10SxRCT7trWZ6QUWEWEGCIuG8GKcgLa5JbAOXvQGiawd1RAxKC2T5oHSZ2aL3OkmQJVMqOmEjkWO8FoXeAfHBLDs7xIJwfAgjY7Q9nGQ4zwhQ85LXJDIjEki43GJSu16qgaIeHxEOj6gzAVYClyWvnU5glKCy6LXOpPrtA+s7ob3wnRkrMdjqeNqvQ5aW5osJU5taDINEaZB5sHtfsJuN+HNrRgibvY7TOMouVOCV/rGtey9or3ajPcufLSO//rebU3t+w57NHy1PjvV8Xy5XBdS+mitM1D/mcJAneCvxzxR19Wza27+kvq1+7XT+Pz8l+xzl455cqEioCaC7u/Zrfebikj/9FHSm3te0K/0zPa3bSXtqqsjetxO8AWqBkdA3i1HJDNVamxzlNyu21vcbf08fwTWn08ufX3Xe1D9+49U9U+OiJDFuhOGsO6YcytXvVCn4KwjI67dp/vUfX4CDFid8fyzPDcJ/3QHUisvWUie8/LaCkSXvv9cdflc5fxeL7/31oInH9sGUTEgdO9VUG4JLG1R8z4g+KBy0Wax0htY7c7b9NPa+CmQ//J91vPT3rcREU9d87LS1iiYrtFgXBtTBnRUwPDCONwK1VJnpXlhAxPRNrHu4j3IZ4aBCuhrREThLAaJJMm9SkoAUQWvnGs7G/d1uySgFVXc2KIq7IDuxVD6E6iwmwX4NqG5E5JWiiexJEN3PWWMr7kroEJ0UaA3Ky+wtJXxhZqHQE+Nwt2TtfpafUxolU3bwh6hSpONoaK8ijI3ChcQZ40EaNfveSIBKPAnnrZbscK8miogmAtYKZcsyWsYBvHgB2D5OOr40fwYNk5ijNUzqjdw2DU4RgkBzcIB7J3w36MHt3NB4QRHMueHYQTngsf4UT3t5DfyHlQKTo8PSDFif7gByOFwc4uSM27u3oBLxuAdwjAiDDvAO1BQmiowkAuEwzUiKb1W0Vwhzgl1TxgcmIOMKY12OKQdLPF5Tgk3+x3mZcGb9x8QU8TpOGsfKAFDYRSWBF1s84GLCmAepUjCRUuw6BzB6RI5aoh1SRlpXjA/PAA5Y9ntQaWg3NzAgRCGIF3jPIiBxFEpG5SqDGrMimKAi3GR+VPEIMilIMeEBEIMJ1AuwDR1+R1IqJ0UtGZmofMCMA4BxRvoItRdiRKWeZZ8I0MfGWFREa4alCVPgILmdRFo+0cvw9QoHAXB+zXwEviw/a4aJ5yr3odwEspPAbCk2lRKi4QoDmwcwgBC2MvaN2SQEw81uzYpwF05llHApRkAmDJAWXJDsNFGOHCS6KZhGKVNhgFEhHEv1/rii7cIYdD6OcBJ5EMgp+N0qDRNzowQznX6SKcVQ9Y3a6WSM5hl7iVdo9HlzMlKp5EvACv9fk1EK2NDX1jz3rAjcCE4CsoDDo0iknU9eI28KeJJFRfxrI3zgmU+YTmdEJcZuZR6D2bx1nVw3frj2/go8nzOe1CManwgjJ3nZx2fJIqTLJK2J+pepEaKnAvmecF33/0BP/74I/7bf/mvGJzDfpgQT0ccP35AXmaJ3goeHByKF0qUG+/xJgx4LIylSK4H7xxySVgSwQ+yF94dbhGGAV9+9SXubm+x2+9xc3uLv/jNX+CbX3+L29s7jKMYIgwEAhkVAdA8Lts86N8/lxz5mutdkpc+hzFiK2teu9efR3l5vS832x9PP7hWnurPhjn2g7OBGJ987Sceuwc2TUIy3maJ5mt+8MwmrlFTvxmCNGqOKDPYppxAZQHySfbGzGDyYPIgn4BCcBX4K2AqtXtZ1xfF8Bqk1z9fXbfRkgeTJbSlfjnXMAAnzj2lCL1OXQO6KAjXIggIWZ6zSMJfo10y+YRLQtboYYlkVuNCTjgtC05Li4aw/Fp1r1Av8xgXlJwwz4vuIZYzQamYtH7mdEMk+R2C0gCNw4DgnRgivNOICMbgcG5w6MbRVk95yXgSscNyQjRnHUn+3EV0dzpYjWzNzdBuOoeB7U1GMYNOc95o99YBWeeHGVbacVT37qY1NzDrMi88wcaJQ/ahKRak1D/6WQwQIi9wbVONfNVoQzJDhPOatNppZAXV6EsfxPBQX97e3YretemIzWFG6iR19kRdVSUDRWZCYQdX1LCQCWAnlEoMUI1GEL2ztrlof1CRFbmIs1jMGUvKmGOU8axjeZ7FqBbjgpwkCtQMaOKcItHnxFyBckKjhpb1RvObVJ0TUguVeUzPK+CWH6PrE3Ik9eyGrs3d/S5gHAJuD0LDdNPRMU2jGuy8P5sHzfCxGiKrebAeQuc668Wvae3wjE6/vlwuz8cq69shqkc/dY3tXWyt7+f8S+WC9hztaoabNLRgfcf+G1p9e1kuuVTW2M1TR9LqffVcFfx4nezTz73rbX12kvbxec2smDOR9x7IwmYgy5vst0BzQrIoaaNZt/N7Z7pPfq5PKK8999njn/q5k0P0Yit8qpZ6DNfjXlo+yRDRBHOCebFd2mQuPrw9gL1dFfLXK4rdYzvQny7rBe6pZ3qqvNRQ8TkUp6cNMa85X2y1ehH7cXt0Pbb//eyoJ57LQGQ7rv/8KeWnPv/nKGfPsdkkmuGhectK8lrlECcIWGwC1BOgfnfXJ399TTs85YFrn7cGAtn8+eLxF2u7Eo41OdfGWLB6blsvLj5G25yu1eHSdc0QQZvNbfVuQuiZsNNHVZQqwGcFuViBKhdCBeNr/axq5injGh+hLMPyf420MN0uWMI1ebWQ57zy5q/VtlcPjgKVU9YMEcJbL8YIe77qJZ+zRkMosJwzLEQS1AwfMEPHtlfMAYU6EeBCNxpobRz8RKRCMVXFrvZJP3YqWLhO/mr3l0TCoQKIRAXUgYjOe3ig9l/1liOJrBEDD0DwKAykGOGcxzCOdS6DgJDDauzlwtrGHtXnRaud1LNwGsSjZxhGoDAe7z9UAMC7BOckr8V8fERKEcO0AzvC/uYGXApubt+IwYszwjDCDzuQd3AhVO5eS0aZOKFwS1pu4zEoH24T6F0nB3BNXv3mzR1ijLi7u5EcE4+PYLaIFlFRUoqirKeIRb0ES8lI7JEQ4CCh50IxoJEiLHk2vHPglJGxYH58FAV/fwPPEuXAzsGNwnlPFEAMLAyZe1GiMxgQHmtNppuVUszBxhJLxAQD0c9AFlCdS4AfQhtz3GgHxPtMOJxl7kq7zjEiAVhmj4FZ+fh1/upU6EP5LWHxcwJ8P4aMsqc/butRc+l8U5RsrZDx7NSNzsFRATiokiyGI2Q1RHACQGLUIok1I0cYhpaDpVf0ROjOGp9PcORRUgSY4IJ4ohp/NdOCAoIfxJNQaIMIo5Pogbdf/gohBJyO0p/kxtp+zjv4YYDl2qiGROe6+dqMIbV9utWAGUJXp0lDbd8CswJMqRldu7641u58YR2SMS9RUoJvCM1dbwAnKM2eKiFxUWqP04w4nzDPRyyzfFdMNoREEzUAwOYsGhhEpdI/uRjBDLgwCIBi3LW6OZSCCkaBmyGCvDKpF8ZpnvHdH/6A737/e/zn//M/4zDt8M0XX6AsC9LpESgFo/co3iEP0kdMwN553PkgQEfJlW4y5QwHxlBE3rnd32Da7/Dll1/gcHOD3WGHm9tbfPvtX+DrX32D25s7EDkkXYN9oPbM3Xp6rXyq7PdS5fo193hOpvqUck3WfW5t+fMur3+Gz2uYun6NNRj7fESEjeVL17+s+wIG6q+v036Wd/O6XgMprOiX7FHURDZbzxmyRyrgnIoYZl2OoHyEMoiCOYBJKHlQnDqMSEQkafxCY8TQfBK1+pvn08lcAehOcpX1u8m0DbWlFmnKrUHMkafqWARQT83BgENBQZYkwCqfSMLpJFFyKSInyYt2iguOaohYlgVpWZBSRM5RDBaas6yu38uikaUtD4WMA+lnS1bqSeh/BgVTh8Fj8B5jkO+G4DE4xujac/Xv1pqr/agbB6vRVHGW2gS17bfGhqx9LvpLb4CwiORmjOgjIfSi3f1a+HtvUGg1sH5u49T0CGkrV/WhrvNXz1BbwQwJdtw41oZoxpu+/ZpBp+6jUDleQhI63dzrfijGEHF8CM3wEEZ9DbrH+RadwZ2eqM5bAPT3NdWWczJOHQPOiyEC3snYZXUmYZnXdaJ2ZFWtjztjRGGkXBBTRkwJsyZbnzUf3BLFsJY7OVmMEQXQJNXtXjreZKJ2/SlzeyCjCVOAsVlAJTLW5CyycSuXcYDkkurGbfBA8ITdFDBNA24PI/a7CYfdiN1uxDQOGEfJo+KUAWCr97f2sO8uz42XlH7v6I0RWyzsXPOl+pdeaPX35rBLd24/1rXyct22n6/JJNccNc4x1LUxbX1OXz/g5fsx1/en++K8UWq9N9jta+W71dFEm3Xk0uJ5Pm7643qDgrRTqnsed0YIwx5yFtncd3RiT8kmq7H31IO9SK7p9sHNMz75RT/mnyzr8bP+uk+rcI7htLP0GO5OfWF5tSHibDKTRTW0Ba8//kyo7gQ8CckvFxrJOtluQa9cjAiWPb2vw39fZSPBPtl4n9o+533/UzaNf+5C1BxQcQG4MAGZqOV/6CMijK/S1mKZw08H7jGzyCQEtFDWywrqJTD9teUMhH/FNWzunwM4W0NEBxL1q5I1TVVa7BrSANs1YyucXHqZOFy3uCcAPgA1AkI1suZBrYJcBQ85w5OvnpzUUXGwRjpUWiiukhycAjbMmmQ6JuWyBbwbAIJsZA7KnWteTLl60/drZh9CaECYeVkpUqaeQE2gK+oJl1XRYmyMN2Dx1q8RFe5M4G/GZdR2M93XtGlToKpio20DgnrV6FhRENlyH7AjVZ7Vm7lkSbStg8QMEkQCcI7TJO0ACHBNJMYI7Y+eOseA6BQBRkZOoliLkM1ATCiOa0SEKJeEcRxBIE1+K7zqlFUJV8GYnBOvvKL5N7iAWMHqQTy5CjNOpyNijLi5HcWTOAkwm5cE5wO+/tVv8Pbt17i5+xJJE8i64DHudtoFJIl4TyekJSLOM2IMSMmpoSO1OdkbIfTcOt8YIBQ4xxhGhvcBb78Ack64vTtUQNWUipwTUhRKpxRjm8d+AIehGgNijBKZsCSUVGo4u6yfGQ8PH3E6PiDFBcM44ePpEeM04fbuVgxHQWiwZgVrY1wkh4R3pgECYHjvELwHewfzRhf+a6FvYgUNnNfoEyNdJpK+ARBAYEfKdkUYBwFea8QauHpSAgIsWBM61zzrXAeQtIT0OiFovU71in6/bm4Vhq1xol+rbJ1kU4Cks2QMOwdSRbYUaTNX1DChHnfkZDyTrg/DIDkjUi4VYKl6MSRqSWslFG9EELqDUGGHMGSAPMZpL4YdXQOm3R5hGDBOO1lPFlW8SaJIxnGqCZulDRvNlRkeZM24sIbXPaADTnpht4jyHZdYjU99e9pnUzr6/uj7DJBoqT78uoFSOp+oGb0B1DwqKRkItiCnBZylb0Lw8MFXebcUhit81tfMRY3ZpB5WQMoMchEZhDFlhHGU6Cvlwi4VHDCwhJBLwXx8VOo/4P37D/j7f/gnfPe73+Mf/uEf8fb2DocQ4EqByxmBCIPzSN5hccAQJMrlr77+Cnc3B/zX7/+AHx4fkFmo2sLNiHGc8PXXX2McB8ScEMYRw6DUJNMeh8MNvvrqa7x58xbOy35HXBSw6XJlMbDm//3vq7xMOfyl/HOUKrduZeOuvy71XZN5rxfaDPnVVTaABeMcwHC6GDnu1nGxQOj+nGseLYuKLTmBUkJm8dhmZ8uZefea1/T6VSCOPq6jF7XnBLq9yTlwjYSwlzwdOZEtHAsfPnuqer88ociNJj/UaAi9hFEzMRUAWUBW48ovSRwmckZKS42mlIiQjCVFzClimSU3RKzA7aKUTLEaIrIaIlZ5yXrgRd8dkVAyOYdBIyCmaoiQz8E7BJM3L4yX9ndP87MF79b9LktmowliVqpCMzakLJEhanQwg7z8psellguif2+erjYmTXiU/ZecHWGJXBujRTUeGfip/W97ensQtx7LKqcRNccDJnH8Ym1nGVquHW9tV/92sFwdNg6h8oXIa71ILDq71whqo2MawgBfX1J3MfIxanBQw2BBLAnePTGCp5rrw3tCgUPmguIJ5AmOnZj2FL+SYWX5GjRfhxqQFvW4PsWIGCMelgVLjHiYZ8wx4uE04zgveDjOOJ4WzHNEWuUwMeeMUucWoSWcb/MbSmGszl8EjGRGCtT+tTP6pPVc27JhPl4ppKRbGLtBaJfu9mJ4uD0INdN+P2KaAsYxSLJw34wQ63F+eQHlqxwxL5MfVrhlPVPz452BsP0xHahf/+5k8ut3rO8yjS5jOtvPV2UCa/f+pjY4bapivWXJ8+Ls6fq2lEus63apRetx1NbF9TnUH3n+XPX/8+fsYSL5zf5b3X0jf3f40bOd0daL7o4akUzwvjScGaYXqS6ljo1ihDAKZ3OiIpQiy07OVUno6sI4q9dZ071k/HZCw0sO582HV8uZ5/Xu5871OfrpMu2rDBFnCrVtVHWirRWsdt5mggDAReW836zRBgc/MUFX91t77YKBS+vXTzVM/BRPpecWpOe8uV58L27Lqyn0z51Zf3/xYLI+3p728lD2l/Xra45v9fqkSbE5pTdA9AYHo4UxANQrsFsn66a1L/Ur68LODNCmubaT+lOeZdt21wH9Cw/e11kqsJrEPYDTh69eM3CYsFiBp3ohC89+aV03hpC+fl1fXXoOVtBRgJuWZBrqQcTZvNAZgNBoiKBtQrXWS3MSWCg8gmhNNYwYXD3aS2qGCKcUMt5LeHpW6dRAqmwJpVmFOyeJBL33yLn3xm1J2KoioH+LgtIiIrZGoqLURSE0xeqS8UY2Zemr2u7QHA3OrZaIptQY6G9rgSqRFjmiCWJ12Ndzcyni9c7Wja0fjX93fa9cBaOaiM53SVy1PpKTRXN4EAD1AnSOUbwHvEZhEGEIA5gh9EGsCakLkDOqoiTvStXEXOtO3sGzr+Njnmc4StgfMjwHBbkJOWV4N+DNF1+DHOHtr36NlDMelwXsVAnT8RiPM073D1hOR3j3CB8YMUoCRtLk5WaEuWyo1PYhAaqHAeDA8INyXxbJOyLh5aKQlGIehQk5incIAaBpBE0jUspIKePx/hGn0wmnhxlxSbCkdRYafjqewMx4fHyADwOOccE47fDFF18ghIDdbgSYESuQG9VjvjPqQpU7TyhOkvcVBYc4ZzGUqJdKn/nRD6HS/VQF1TuU4ut4YobkZrG1hM3bRY4lyO9Cy9S892v71rWwCa5ABxBsDBGum5tbEPyS0bQvVQSlbhwSUDm9WSIdqHiYl52qiBAhWw3mgzw3O+N/VlCjQGjGynq99xoNxJ6rAcqHAQwSGrFxqADSbn/AMAwYhgkAwbmkbSz5DYZxWhkLbay251krdv0xl/aqlSyp4FvqDHS0ucY26XS/lki/rb1La56d0vLaAJIAvO8vC9dO6pEo+VqMNoo1SlKpJABZB61fFSVho1TSRbHkgpxZcrQQgXxAYWCEgw+AGwQEKca3rskAC4sy9PB4RMoZS0x49+49fvf7P+C77/6A3//+O5SY8OsvvsDkgMlJotXROZzMWOUdxhDwqzdv8PbuDh+Oj1iWGQ9xQWIxDA7jgLdv32K/2+E0z3DBKbAgBqfdbo83b77A7e0dnPerMW7TpsnqnYL1RyjPKVJ/7LKVCa99vnbeL+XTy7aN122q64z+vZVaf6oB6QyEYgMxGthgci2j6VUigmoUgb5Iz69OICq7cPddySLIFDgU+Kp/FzI5DwK6KHgJgjqdaJ36bNNVliYATkHN5riChmYqcNQS+TIAr/K+sA4WcUDgfq3ucimgM0RAqSo1L1LJcR3BqVENaYnVEBNzRsypGiEkIiJpREQWg0TOWJRazwzL1j+OLuwjWkevBodh8wreIQQHx9qWaMapS3KaPCNW4N75+DLnzSZrWwRE1qgXq7vJ/XlriMhmqLqcs8+0szrOCCo/NvyFVn2NKnuTUgyS6wxR9hz1YhbnY1+5Ok56/aN0dD1bvWT7N0DQ1NWoBgp1yrJIZ9QqCM2q814ieL1QMnkf4EKAD6HmdyiQfdlUGGrDXumVLNJWAkk9QfNbAMkRMkOcrZwY/sCafLrKG22OCgUTI5aCpAaJJSWcUsISIx6XiGWJOM4Rp3nBaY7VCJGSRbiYw4RRlnUGyqa6oq4v2ici9xOCano1s3a38jGzPt96p2ZtDHPvICdzehocpjHgMA3Y7QaNhBg6I4SXKG4FcrurXViLt/PgfF5cK5dwtTPwu75fuk/33WbeXlv/z77vlsyz3+q82J5P26+v3qPXoe1+awecDh+px9ptL9+E+RnvfVyOiOArGNK2zn3b1u97QKCddOHPDXbU//hkpdfrSN8fspaHNj4YK2OECe9G91eKB7Ovz7FVCa3dW5vweZ27lpDjzrGyvlwS966de1Z0ALxcZlzPyfbt85juGst/XXmVIaKfzAZug3pLoy0k7Zz23qYEV0UeYM6gfuO6cN/XCX4XFoOfJje+/M4/oSO25adYl/75yx+x0T9nobUnRjUwdAYI3xkiTDh9Dkx63pjCK6vwS4xVrx1n203+/P3ycVUQ3dx7/VobIp5+1vPn2D6KXeMlia6BHow3o4EpMlTBQAu3LpUfVYHzZAnr0sobKgRNdhac0OUYLYteI8UEKtBk3Sz18F48iRWULCkhRfHgAgB4AgUJF3bOgQKpsiCREIsqUVSaMGBjjNnDk4cMknXSJKAJ27mYAtIoSkTZtGTEmnBV+e+N1seKWfkNKLRE0DmnGmTm1BMJmhyXLffEBeNbpZxiMQyQJmhjqpU+6+Pe6Gevym2LolFLBVxEsTClRsKzIX1UxJO7BGsHu35BLgzWRKtZgcdhmuC9x263AwFYlgXgghQzvBmPnCbKc6R8xYSSWQxWPmAYJqQh4nh/j5Jn7Hb3yFPCMO3BIDy8/xHLOGE3TRinCXdv3gAu4E0IYtwJQdssI55OYoh4PGJ+eEBcvkRc7rEoL2wxTkstNnZzjfDRxNPqnY2StH8yhApsATgDJUqegazJq0lCVsUrTfjs3RhAY8BChIUJH2PC8eGIH959xPFxVrVM5gYXxnw6iod4lDwru3/6HYZhwJu7NxjHATeHvQDT5jlJjDAMmA4ThnHEtNuJNyYxSklIacHpdMKyzJrczmGaJoAlUTUxoWSbKwAVh0J1QUMmMZJ471HGsYLiDJFFmAvSsgBFKB98CAjDIP3ufFWk+22t7vUqsDK48oVaXxj43Uf4rNeu60Vo55oyX6MG6kvWPlbjTCkqfymoU9Tz3nkzzIihzJuyAyiNR9bhUVCUYm/FnQpNpKxJ50oumKadePqr/Deoh2GWhQNB821MOqckebutY6jXMuNRDYWA2ZQ6Y01dR7q9hiWKJqWEOB9RckJKUdvM1sbQKR6l8yRVUMa8fNE4YHPWPi6MNIihLqekSas9KBDYMVJcACLhZ9YoOqH6kLlETvaP/X7XUXt5ATssiaat3bakKwhiUXK5JBQGlmUGMyPmAucDMgPOB8Qk/OVZI0KWx6PkhPj+eywx4bREfPx4j+9+/wf8+O49liVhmSPm4xHDOGLcTwi6jnmnlBIpIuaMm7s7jLsd5r/6S3z91Vt8f3+PY4rwXii53r55i5ubW8RchL5dgZU3b+7w9u1bHG5uMU172SOI2zgqtiblStHFF6Ii/rxl31/Kn2M5192abGqinx3Xv18qn6oDdhgg6p9qcPDIujapF3sRaiJOEZwTiuY5KPqZS5T9HQx2AcXvATcALsCFCeQHhGFSupoBpFSLKAWUhV/eQF5xpBB5x/ZMS8grbaHgc3UG8W3PggjJXniWUCB7kC9ApaEBV4cYvzJEsPrRixkCnFFSRIoLjo/3mOOC+8cHpJwwx0XyX1jEXylIOSGVjLickGJEikLJlKNERCSNpqiRw6V5xpo8TUSVy955D++AQfXAcfAIzmH0Aq4Oxg7UTDho+Rxs3FwfL83wbm0n/W8OL+ZgVJiRlJ5Q9i2NytNICIvkK5po2ai6uDNeyXhbyyUVh7H/TMeouq4AcOZwJ3nzRD+i7nus5B2LupHr1XaxqAnX2hp6L7mv675vDVeP05rS9nuCyOeECp6bgWQYRoRhxG63wzjtMI4S4TcOk1AzKXVuZmmbEoQejLOr+onkjSM4xxL10kxytd2ExtJECRbaM+tHNRClLPLKMs/ijDQ/IqaIh8cHLEvE+4d7xCXi/njEsiQ8HmV/Px5PWBaNiMhJxnxpa5VFGTo0ooV+gSGgtZPNMRPDK4ZX9H/o7KN6fluY5A/vCB6Sg8x7qhEQb+722B8m3NzsME0jdtMgEUTBMJR15VZGsStr63aePFe28vb2Hiq+12fq3ERqO2FlGOi/396r/72vtCm67d7V+NE3a9XjadXOXMdV9yymi1y5RXsmbvdqX13EaAw0l2OeNvBcXsO2X7Tarr7e7KPXLnBpDNhznxt1lNJsJUd20Su2nhv+bIc4qo5HzIwQhkphJ/h2327NyczyYFo97fxrhZ8wRrys/FQ8dVu3p651+Tn4BXV43oh1vXxSREQtalBYfy8V7g9rhoimcJqaaef2lvdXlVe08ScLiM/UaW2FvLxIvgRcvlQ+FXAGuvWsW8CfuubKQilfvOrerQ7AtmM+l2K5fZYLR3zytdsmvc4DYR7nq6gI6jik69n9gv6yjZK73aN5166P6d/PPTqfPqb//LQRwrxNeXXdfnHpz+sTRleqoo3BwCiFro313hBxyRjRL/59nc6Fz5aoDAoU90qdAVlFQRsDyC0XBJdcQURmXiU9I0+VxkWeV+uTknCaF+jxtcMqeGYJxEoSRc5lD08svN/k4LxslknXvpQkJ0D1MmG5nnMOXCT8XVQ5yw/RvG1ru4HVm7/1EQDxnNVnrm1EIrCv5znVcc15ndhb2JUsGs7GawP4ap9c6EPW8QWSulBFVc/nCW3mYD/matuCwSrNkkOLiNA+cKYkey+7jlGsaD0Kp5bgGMCg43UYBs3x4FESV6FEfb46ZYeFShcA1FMu+AGDH3CfMuKyYJ4lIXQYJjAKTstDpT8KY8C028OPE/z+RpT4YYDl2kjzCbvdHvPjI+Zph7jsEZcbzIvQDKTcaLxWCo55xkUxuJGG4xOSKh0CtnOZwSUiR0bJjMwLnPLSydjwmqQ2wAUx+LArKCQGtvk04/7+AR/vjyjqfS8JNBnHxwekFDEfT+BSKofyh9tbjMOIN7c3CN5jGieJPAgO4zQipQOmvdBTUXBwwSlwLMDzPM8IXnmZg5ekwgQYIM8EoHgwcY2eAKuvZyko3st4VwoF1r4vzBIFYkqlemsZNZPNqwoMbUr1PN2sgb2w+hxwdbZGan4Z5zuF3aYMdWsfy3x0VZlQYZ1zBQ96QKA5fTgwSY6NklnXGG5AjGtAQKYMZjE+chCjUb+2B+VXLrCcIcLPPAzicSgJrNveVIrJ+AR0tHc6det9V/sE2jrDOs5TFAq1nFtuCDGkEIBGxdT2mH6t6vfRokAUaoSCrQFggHYkRghdfzIk8iKnjgajgj9F1k8vdG+2fjsz+na0YHVsoHmSZo1YE49XyTMCckjMIJdALsB5iXgwT9icEh4/POB0mvH73/8BSxQPyoeHR7x//xEPD0ckBaviElGCRGp4EuoFqa/T/CyMnX+Lu/0ekb7AbTwgTINSRBSQG3BzuMHN7S0KS30f00cwMfb7PfaHG0zTDmEcYaqfcxJFJrmY1Dj9hPOR9VkbE59HdnzN9V4sK2/Kc/L6U/LQc/f8pXz+clmuPl/mLXqrP+dyuSJ7y0VWgFd/mV5e3d6cmUGskWxGKVqyRvImNTxkdSjIwg9vRllmgDzYj4AXA4QbdnBhgOTq8QL86/5djRGs6j0YnKOCdtSMEOrwQfZgBkJ367k5K5IaMDyLt7ixdDoqEkVsYCiZ80PfP9Y+GhNRxBgxz0fMy4zj8RFR80EYemrPkUoSY0RM6xxCKju1z3mlY6DKpoDRl9YISRLP+uBde/dOwGkSqhqrfqnoILXrng0Vrg9Z728Aou5ZKwompeJJOYlBQg0QMeb6eynyjFxQDfC9LuCsb6h5GG8dm+TA1p8iE/jVu0UTN0OEr7pF7X81UDA6EFJrIUaL7p4koDa6uvS/weSe1cBo4LDJDTKOJArB+pAsulqdJoZhVHqmoPkhgtnVpEtQJELCdJ6+ScgYmC1qotEgmdThrJ2515FazraYJCn6KYpB4bTMiDHiOM+YlwXH+aSREAtiTJiXiHkR2qZolExJI/lLL9/YrrsGBdcyYGvH9jzrNakOxW4Mk+ma1HAKyT9PGIJDCB67KWC/G7DfS26I3aQ5IQaJhvAWCXFhDeW+AnWcXN4fXyoTXHP+MV20gtN8DqJec5C+du/L+wN1T6L3Xp+13gc2+jNd+F6SxHfH2W2689rffT3W+E53U43Ks7a98HBdPV5khN9WCm3fqwaYfrC9oI2Jr7cxg1C6lt0eV1c6HTt1pScH54zeOQDIrc0Uf7EqrvAMw4q6+/wUrPbS9+tnfO7aV661/g9ne9CryvPP96mS64sNEcClBaDfZNfHXX5g+Z51o21GCFOAmyL8+vJ5lZVfyn+PRcDEi4YIfykCYi1wXSuXLPn9AmmbO5e2wV/bQO16W4PEcwvhNSOE/qpUD5eva/Xs7716dbQWfenDnC8Vo73YnHZ2n96z30qlSllJhs17RxaY9jzbBG1GzSSCnCZ0FglUlI5hgAtek+AadygDECWQcwHBwZFQ3VARQbl3n7NwvrgsAr54oY4J3sEFYBp2wrlPCxwccs4gZoRAMBzVWt87BzcM4mleUt9Q8ixORcYObGtjDeqYxuopraRLVSBkjYIwjnmGhen2IGAzEDQvA1OWABG6JVLgnCPfkSXqbsa6fjNveoXRnFEFO2OMlQLFAGLjucw5AUV896qBUJUf8sAwDCjeI8UoinuSZyykSgJJXgdaZqXu8RjGAfv9Hst8wpziZl5omzE0ebAoPV6BOE/Ajz/8gJwLHj7eY5kXDNMBQwCIM8oS8f3v/wHDuMPx4Yhh2mP/xddw44Dh5iBjbgwgD+zuJoTJYboZkE+3SHNCTJZwMa/62JKsJw3Bzxr5E6Mcl+MRzBlcTkJrsNwjpxnzMYMXRj4x0hJxengQvuFZwYeC2uZzzFhixj/+9g/4w7sP+P0PH/DxcQZRADR6AhCPcYkyKiCIN2cuBcf7B0R/As+zRJ+Mo1AcjAPG/QiGUE6N04jgBCjZ7fcYyYsxYhbv8JSSKogO0zjWCA4Q4EMQsHiZFfAUmcNC13lm+OhRUhZjY5DcCaUUIKPSQg3eV4W79X0DClZrVGmh9i8VRi85L/T3EkqFhIBQk2RWL7K63TRlnIusTZoiAmZ0MMpA7tAdUuCIGcjIda5BDQk9WG7KPTOrlk1KYdAJ4Np+YRAaq9GJh+GkOSPMI76uJaSLUgUbXG1X6tvZ2iELJVhOspbGuODh/h7zacbpeC9rgBpChU6rUSZuy1WDNnS9ThkpRZicat5Pzrlq7Ov3JaHUixppJ2PMewdgwG63k2dUXuowDnAhaC6U1k/eQbyS3QjnNIKLHKhYMvaC4xyRS8Hjo0Rj3D88YkkJj49HxCXi4d095nnGH354J9RMWXKw/Pj+A5bTUYaGflemEWMI8CjwKBhDwDQOyJmRSwSVAs8Fe+8BGvD13R1udns8LAmggMP+gP3uABomkCf8+uZrHA43+Iu/+ku8efOlRI4V3d+Jq5GeIX8Hkj31OaX3X2p5DZDyS/nnKNy9dH3YgiefeNkrGvNFIAwwI0QBssgvJYuBgVNSeUYjItKpRUaUBHCGY4VmwgSMB/iwgwsj/LgDhbHmbnAlgSA0pcwZ4AgmqjROFi1ZTPbxAhs4t15LyWn0XScDO4ZaHkTO9wSwU5mCnVC6MDVDhG4tBBE+Skn63EIbucwnnI6PuP/wAY/zCe8+vhdKmyQUkZ48xGTuVFaOSjcZNTm1JqnOSQ3JzQkJkL1R5FsnlFKu5QEMymsf9O8hOAQ1UKzolSqAtQHaunFk44sBcRjp5AF99NU+k0ozNORSEHNPxVQ0Qq5UuVByhqwBNOr2W2mrdTS/OU4U6dQm51fDg+6pKmc7ci1HnSWONv2L6uzRMdJ/pto+lUbTjNYwxwtpJdLcSfV6ejpXhUH/02s49Dq6GD9kzw2YpgnDuMNut8c47jCNYjAfh1H2ZFJqR5bnGVgjC4Kv+ox3MoZrf5uulcWpzQxbOUZkldWTOtLknDEvM1LJmJcTUk54fHxESgnH+SNiiri/f5RIn4cHxJjweFwkWfWyqBEiKr1YaXhBfRH6Vq7sDr0RAs0duMp3MApRHYMdQEzVuMG1H9CB55YTZZoGjOOA2/0Oh8MOt4c99vsJh/2ohh+VyZw0XsMAuc6Gq2UFwq9B66c8zdtafQHUdu37JrL3taDN+eeRANWhzkYvob7317lSu00dny7rx17jTbWW/RoCZUIGY5sTosVJnONK/fu2umdtfaHqYqNibDnxDcsgWOKVrk4GJHQX3eLMhgvL3DyvgOEkjB6z2kR8sf1nV5UzTP+xHHY99mTn252qQ+RGj+gdJj+/I8mnGSHqr5+hPp/qePPS8ipDxLYC/aSrS2DV2fsOt5WymwYr5Vs3qn6y2fnPTNSLdp7t+rNtrAsWwSfvUYWUK8f21/tMVjH7bWU17H971V2ev1f/+7V7PtVOm2Xnwi/be68Xzet1uXKHC+c9t6bbWLs0tExwMTCzRT/4JmhVgcsWw0sb3Qv7s68XNnPnifOvbRJNSuML7+38S+/ba5/fo+VxWA91FZSZWx6A7hyZ09s5fn7P9tV5Hxv43z9T3Vg05LZqL5bLQS9l171kNEEvRKqXJhMqvRN5pf3R8SAXMkVBntdRQHEkCYvPe0WShiqgWLggpAQQ4IokOXZOPLkdNQ75lRGXgSrqKLBeTMGoz9WEulq37vvaF+D19al5Q3Utjp6ypI6depnmpSQe1G1DXq2RvG5zWk80qeOF9rKfe2OHbfzGxx6Cl2OMJkBD38mJ15W9g0QpgQKxOWWJCqn9LoIkcgYDeu0AcoNQNQ2DeP7r85RSqpd4E8nWHu/jMAKV2kZyRWStu/cexEK38vjxPXw4omRg2N0gwyPsJkyQpLSj28M7Qhg8yDH8AGQ/YgiMIYkH1SpxL8Q7m4t4zjXqMUaK4u0d53uhOVoekPMCIAHEcIsC1YWRUsY8z4inBfNxRlEOWkei2C8pY0kFP777gPc/3uP9+yPuTwucCyDyqsiQeGbqvHIkinYBI/KCQg4uF0kKnRJ88Bg5gahgmQKGaRQqCBahcBgGEBzGYYDzXimp5JklCkUobyqw7V2dB22h1zWGWegZnPgqimLUjVUipRIDHJnSTRL5Ukxh4m7uXXrZLLiwP9Xxv5l1vDZCmCFxLfCaksP1Yut9Y62sCYCgdAq2X60UOlrNZwMoZEl1NaKojXJTt6jdvAMxrD+cU9DdBwzjqMapfi2nWg8iu6LMF/ne2qDxnDequYyk+UHm04z5dMTxKNRMBmQRBgBPGcGlDpeiVSwywujNQghwRMj7/cqoWlbrnhpdOx71eu1hVKOL5hrRSBFSAysKV85xp5RNdo/MSqOl42JZFsSUAURJRP3xI5ZlwYePD1iWBfff32NZFvz44YOsOQwsMeJ0nJFiAkP2oxgjcslKLycvr4nE2UUxyupoCo4wksNB5x5TADuv3qQj/G6HMAS8/fqAm5sbvH37BQ6HW5gHrKyZ0uamAxAazaHNl58Lk3+NkvScl+OnGBifq9slB5On6vLUtV5Sp+e+e8092g7+M3Ved+Wze/9k3bfV+VLb9VtHO4N+poF67WHYhDx5lVxfbAYIjczlYrRw6gnPBkZrolk/AGFCGPbwYYSb9hKVWzRiIgFUMpiTymaS04rJgHKNFiaJyoUmYm6Sqq7iZ8mqIQ46zknkMNk+ZlJt71GKCmAboC+ypFDxsVJmpBSxxAWn+YTT8YjH4yNSKUJd5zyCC/AQg0QusRoexDEjrSLXzHnAOnsbHWA0gRYh6bt375S2sotUlG5j2+jP9Mv+HnUGWR9rKVqfol7uEqknVEzMGvFq74XV2FKQLDpPI2G4jp+185vIBRbR785zxPX7uffSs9UJL1SZSM4V2ULoXc0QQVUG70c2wy6tMqJ2ep9XkYgQ2CwQ9tI90MQme3dUP9dn0/3MZB/7XpwhQo2ICGFACKNQcGo0ZzV4QI3jpTlCmVwrfcrtCbTvLE9VyVki7GtUSksYn1MWmrCUhUpsEYPCaV4Q04LTLLlOTsuMZYlYZjFALDFKbrYsrzOHuqrrdWNN/7MRZ21S22PTvK2nuMmKMPmyxUTU0UvtJs6RGuUCxkEcGqZpwDSKYWK0SAhLTt0ZAJpc0H/X+hObX1iFhf6Xp1fkhtNcXLqJwCx9evHsetJ5ZIQA3gyY4az7/WV769MRoX3pHTbk+NoBF+tcjTwVANkc0x27ukf3/tS1+88X6wobjyYLQdtK2stq0WDGbidpD7rqd9P5z+65GidbCqSGcVD3H2mlGqxBja6XUZ2ByqotDDvk1dwzZhTSSL6skejcFLOLbfSSclk2eV6uvPi9PYUZ/n6yDPXyOr2kfJIhoheiCTCnwxqxRdxtsqZYmiLSDbDVe6eHtomin91mwtA6LwXDFsy22Ruf+YXKv+ZB29/d864O+dRrv6A8u0SdScs/n1JwrXyeO24VjWubU3/MpfOu1+byogl4TSA8BPHm8aFFRPTvIrxtm5g3708rs+t7b4F7BsPADhH2Qc0AAPD6ma8+6la5vfwOJpmvzCoW9lRLVu9Wt1IX4f5Zt0yULbaVWZJnEtmcZd30W/8auJOzJDd1HeBvilgVhlRRIUfCTetIeey1JiqIgoXj0wTxrEJiyuJFjiwgqQHzmQsyGFnXmOAH4fIOO/WSGeRaGk2Qa0RFBjwDjjESwbMDZYaLForuEDljLgvAUehwIqFwQomhtq1zhHEaUFhAdi4Z5jnqvNdErKwK0FABHv0DpWS4QlCSfBCLaAQ2mhL5zM6BFSAHGu2MU4mVO0ZQoOXQkDp6IAhffggCpjlySKUgpaJjQpItyzpO2q+yofceSuDmeVNMwFJJmsg8wDJIgWCjG4oxIS5JxOLKHwsAYkgomQAWxUm81zwIXkB7YkmuWzySAoCk3oI5pfqsJQRNMkgYh0EUQi7IMSGmiJAZHqReQgxJEiJpzRmAP+yxm0a8+ebX8PsDvvvtb1HmBXf398jTDtNOuPILF+TlhPjD7+Gcx/0P34lSNE0Iw4hpf8Cwm7A/7AWgDEFCujNXJdpEeBOwCosY5vwANwTc7G/hw4Bx3IHBeHz8iHia8fEf/4BTeo+P979DSkekeUaeF5THjPn9I9790+/x8eMjvv/hA8ASYD6NAeM44BgTTqngu/f3eP94wswZxQPwAFFRWplOuXCQhH3BVaqa4AhjgBhaAuADIYwBbhSvNWZCjLElFQwB7rDHzRdfwA0DjvcPWE4znPNgJmSlqhhHiWByThias4LKJYsHjhkcSopASeB8EpD4BFVgHfx0EB7+AjwWh8ERRh2nxoPfr9ktwbGuj8UUblmHZJ0BXLAonZq+stu65G/Jz8DNiAShyxEP007EVkJYx6L4N35YiS5j9VJ1btBIPjHcldVeg5bUELouOM214hjOC9hihkZLRun0mKZwSR2EY9ljNx7gQ8A47JXywyIhCgoYqTRKJJEDjcCg88zUdctyHxQ1sJUUUeKC4/17HB8f8PHddzidjkizJEYfNNKAmcHeIapBMAwBpkQQGaiCuu6BSEEKrZomi885I81HnHJE8EBaTpimsSa3FLCddddWY7x6dzrsQMygIkbmoED+ECZJ3h1GBYhQgS3ZS3QlKcDggiR2JQ8G4f74Aff3j/jw8QHzHPHjh4+Y5wXvfnyvBgfhnOaY4IhwGCYgMXxxSOwww+P7ecHxh+9x9IS7L97iy2nE290NqJyAzLgPHvPgkAaHODjcvz/h4XjCd/cfcUwJN998g+lmjxwyis/49us3uLm5xbf/+m+wO9zgyy+/xjiOGKagY07yKFU9X/f3fiw2cOqX8udSrrsRPFcaAPWy+5x/voIZvbLIznld0W/ytnxWYL2T2UUetR3YAMEmO2+LLNPUzq16cQNeGOKBLGKNyIykkRAUF5ENF3kvcQY4o2Q1QKRFqc80bxSxrP0hwE234N1dzQ0BP4H9oIZIoMRHcFqQTh/AOYFiguQhk3bIOYJBYD9K1AN5SB4Iyzkxite8GVKVlIjAmqRX9qlCLM4fZBRPdfNCbXYHkesh6/UAj8KMR/UK//BwxMPjEe8ejjiejvjwcBQDRU5NPjXaUs6gIs8igHFUg7HI/6P3gHMoznIAyPZqdFVjkGjXwVP77AjBKw2Ts3603BmuPhfRerRLpAmQN/pjUfmlGiD0Pau+kbIaYZLlfLDcQGKgyMVoWKXlSY1FPVphe52zXGrqnNPyMdD6ve6N/fEEp3mXKlWT6mPVOQ/q/HAJTKzKpIKTK5CnB8rkuqX7bIdxPb1TxOtnqHGIUCCyGqmeOO52GMYd9oe3GKc99vs3GMcJu90IHzy8TwrQ6xgAUBzXiNpAjEKMjFJ15lxEZzJDFqUMlxOWtCDmhOMyY04RpyViSRnHU6qGh5QluXrOEQ9HoTE9Pp6QUsTD44wYE06nLHSKS5FIxSS0TqmIHJWMqqtklU/RAGiTsfTlLcrI+qiGm2i79WPSwF6GRlxY+7eoWUbRvgbGyWHaBRxuJuz3exze3OBw2GO6OWCcJtFpQsuLJTJkh0PUAdIvnJ2jZ8/TZgPA9HugRrVjfXZ34a0RogPAqR951wqt/+plXzNCUP/9+pxrpaC166pU7LT1ZL93rKu2/rY2KcuZsmX1shbZLYB6ZZxd4TKw3PcDnX1lmE2d16biqGG2Ou7QOf3FZdiy3aNOdW6Rdl11L9Xw7Fupl2AcRt0tVWFwIYnM8w4eGm0EjTi0W+nCIE5KBO9lD3GDrH/emeGeVA7onrMbr3/M0tp8vfY+d7wVsonKrHj6pfN59Sf3+v8ryifliFhNniaLSeVXX5mwxZuD+2Wie7c1xe6xWWO2deDNItQ3gNx/03TXpMQqXNpEvXDchQWvf97td3adfoNdX+5Cp1+4xrbOT1qftn3zmcu1K5892+q3a1e7/BxbcL6Ol7PrXDr/vK2ea48a/aAeiZa8dy1omdfLNUWqfb+1Gp/f74kxtnqObmTZQtadsn2qsqlHf/5FY4S+CB23OGzd2UoJWofVdbqZrp/NyNAejbFORsndNbg+lxkk+t96UcIETdv0LZy3UuOgCV2FG9Bhxp7CJsCrV5lyhBuIJEoE0EKLfQXdesHHrmU85SLhyRVkYxPwyR63sICzHkV5+bPkBy4ZzpI7k4w9r2OPwTD3MecJGQY6k0Z+OIA8JEF0qbkulOB81dYyHqXdVp6/2mr2Xet+1j6yyAiuyolTw4jzg3iJqRLZe+SQecJtxniLllh7jxFBgQXuFzzdyJsndc5ZE+6x0uAwXB3EelZhvZi8qqcXOxBK8zZ2kmeDREOWsVIKchRamuxTSy7rxfu3FEaJQlUEo8CxZ4OkdiMAQwhACJgON0gKTscYscxC+zTsdnCgxpe+SA6J+PigHhkD/DBinA6Y9nuku1uEccQwTTquUYWcXpEjgtAokEPQ9SyMI8Zxh5vbN3LMEDCHI+ZwRMKMHCXheloW5CWCl4x0WnC8f8T9+3u8+/69zAMK2O1H7PcjHpaMY8x4nBecUkJi1jwN0n/FPPHalBVPNiGSFQOfA3wo8Dq+nSfJQeGECsmEVi5FABgiuCFg3O0ABtKSkGOGRSmxrRe+reFg8WbPmSCGKgZ5krkP1nwhSee0GvAoAH6AZe1JoJpHmGHzfpN3hTuPtNKve6jrBrr5B6LGxdqG+3ptUQXTPAv7fAJ2zeYVtZafzGALkORG0fP741q9Vci2azkn8oPNSwOLbOYSGoCh30vUiGvehmGQMRzGthagrQ9r+YxWzyH3cLU/SxGhX+a8GH5LiYjLCcvpiPn0iOV0RIkRYIYHg9gDg/RxJoCVQqO1UPWZbG1KAi557yUppXMoJHOaS0ZOjDjPwv+s3v3mIVrHnylgRABJ0nmShUHWkHFUOSPAu4DgB11CGgUkuwh2SYzGpG3LQo+SGZqwcsa7Hz/ieDzhxw/3mOcFP7z7ETEmLIKMYGDG4D0ObgQVwIhKEggpF5yOR7w5nfAQF9wNIwY3ILiI4LwAN15ovDKRJL0+nfDweMQpJdx4Bz8NSgwN3Bwm3N3d4O2Xv8Juf8D+cKOc22pwqE4NNgY7+LUOyOvy2TXZ7bXRCS8p22iE7efn5Pfn7v05vMZeG53xc5R+fX/lia28sF/OnpN7jeAl5VIfbGTr7rf+fg2suVZdGxdrGeeaXmPgmMhjTb4tgKyz/YYAiBGiJFCOoJKBlFpy6pLBadHoiEX2MM0XhVLkejWK2wHDBIw7UJgkOsKNAIVKoUScUABkkFB35gjiDO8EwC856l6g9QxqLFFZFOQ1L4QDUTNCmPmc666K1d/2vC1STp2VYB81qpUbRd8cI04x1deifPkpJXifUdjXNZU4w3GufP6W8Nr2OefEAaGQRd6yGiJkTxicUTGZwViaLGgUhOTX2Q6O5jSgbmQweZG3ez9QnRuaU4M6yGTWpNQJJReNeO2P4waId85hbV9q69bZqzNEbI0QtodJ97p2PEiNUC2acE1TLPdqusF67Wyyhvb6ptmytlozhmB1ja55z66tf8i9vVMZjcV+6AhhkOjMMIwYBnH2CYMZIXTMEgmNGBFKXeJktFpABFO3TrA4u1jfUpFIiJQzYk5YcsKSMuaUsaSMU8qIMWOOSSIcYhLa3hgRU8Sy2Pf6SmKAYEs4XiNkZFxkdYzJavwsm/WHqOnE1i+tr2x0AiCJUgTxeglSpbhhKGsHYhn/kqQ6jB7DNGDcjRgm0VekfSXqxJksuqrDZr/drJt1HKwMEU3nFNGSz8aDFNfVdnPN/p4XQPHni63hXiKCal3x8n1Na7itN9vzVPC+tfo1WWaNxW72Zl5TX75EfuDNOecH0MXnrIah/vMKMzUUo0XLvaSc92uL1D4bM09VuyljVecRJmF7XslTVJkPOvwB0KHHNgdLnZcm35LSEgv+d6l9+m5Zj/2nytUIh2dkwNVew6j90J92Hmna6WeGY4pyq/v48/c8d7B+WfmkHBFbgPclgO9PKrzlFXtZB5p89zPW7JfyRyqfOsa2k2vryTGMknhzHMeVMNYLWy8tnzoHVsC/jfPtYrYC9D+91Hvpm3lX94IwgIvz/GzTvFLWxhiFajpAoi6S6g1UQcVNYjXZMwxMEwF5m0BKNuq2aRQDl3UNzcU480WRMUXEvEBkLKAmVA1DqPziTcgFesDQwEIHGR8WyVGTxakXU3BewGkFy4rSP3kN211ilCRpQQTl3f4gnr9pAZGGBDNQ1GMHEK+fMQyinGT15NcwcwcFqVmAeO8cvJctJNqQMu8lR7UtmzKIypcrfWCKi5zsNYy5FyKdc2iGpMa32As9lgvEvu/3EWauHLx2joxFCz3PNRy90nzkLL4NZLy3EpkjQgLpvbgqJ8JZzqIzT1PtP2auyZ0l6kLyQYQQsNvt4Jyr70QEzsI1bOAjTMHKLKHdLJ50t7e3GELA+y++xPHxER8e7nGcTxjUo5pLUiFNBJqYzftNlNDCkkvEjyLQj+OEoEn2TKSqNFOaE6NAPOGGcY8QBiAX7A83uD3sMYwjbt8cME4B8/0jop8x/1eHxw8z3v3274CSEErC48NHPB4jHo4R9w8R3hf4UDBMJnCrkm5KnyP0snxVWLwAyjkmnYOE4iUfg9DAsIzjQbzLhT8/yDP7IICtgtvBe3iSJOJUGHE3gUrGEMRw5w3INQFRlRxyQICroAF5AheHxEWMgacTcoo4zUeJBggjdsOEUUPNpyEARShx2nxYg04WIt9zTLdxDgGkidY5Ehjg3AFe9m7LOwEwqp5KD7imL+jLpf0NoNVc25YmLFKdr943HmQDOoj6pN1KL+Rcpa3yXiIDxlEiIsZxEm9SLwBXjTSy/By9AE79fiwtITR2ETkvNbloXE7IacHx4R7LfMLjw6MkKNXfm/FErmmKue8Uidp2zsH5oEq5uQnKVHRO8skE9ap0zitNF2uy9Ag/BDARyEuUhSUQH8KgyrGujUobJ9PTIYSh0kOYcbPBBPJWyIFpADHBM6EUQmHCHDNKSnj3w3v87vd/wG9/9x0eHo94PJ4kF8SiHrJmOGZG8ITpMIEImA4j3PEB7+aPyMxIkfHj/QP+7ne/R/gV41e3t1icQwke434PGkaAnBg53r/Hux/fo0wTpts9DrdvcXP3Fm/ffoHb2zv86ptvcffmLfZ7WWMGTWLeJzJfrw3r8XdtTP9S/nTLSxTSP9fy1Djcgrmf4W7otdOq2YoAACpF38W4kOIRnBNSXJSSaVZgRAyvXCkiguxnvuVroPEAN90CGhEhrjG6/oFBwwBPjIXESSLNj+AS4UmvXUT2dkMABQevDgeyfJr8be5AKovZYxror0YgUo8KzgmcMkoU+ct53RPY69Ioa0TKtg9ELEvEvCxYlkWcKFJ7LctS9ypS2WQgRiCJvvSOWl1UfgkaHcfsRM62CGDv4YgwDU5pmLwaq/U83d9rerpqeOiwBjWalS5PQylmDLFYurW83b+nxFX+ZYuAYHP2QAWJGVAngjayDHS2/c1VWmHb79eGCGegr43rSueoOocZIqjlbrtk4ABaVEId5VWH6owRF6aP4c3NraybKaZL6ERZ7xsNGHVKq+vViO8HAcJ30w7TtMN+t8M47WqSapNjzJiYddMuBvirXJ4Nj6u4nDqA5UYbVpYFJUac4owlRTzOM+aUcFoiYs4aCZGxLDNKzpJHLUeVc2JLoK5UTpbDRKgUC3KXJy+l7rjO2F8jIUzv0W+fNuYQuPrn69A1ObWXLWtfyNgfBomSPtwcsL874PbmFofDHre3t9jtdtjvDxiHAcNojgnrvf4pMJYMA7FxuRkPXNHVVrMLVzk/l8zI2YydrykreaY3dujFto9i9pztfejCX0ADie35etH9pbLS8yCwzplVG9rHZtjhze+r4y7c80X9CjqDtZ4r6zZfrbAX63H1OiDgApTXr12mBwlFE1c5tl2bK+VrzuIMt6WAvTrfLlRtq7u95Dle83s97kJfPGWEWH02loNX3vO1xoifHBHRf3+tXOkHvUB3UP2iu361tNGlg+vsvVanJ++9rcoLGu81FqrXdMWZR5Z+T5vfP6V+zy1e/5yK4EsH+HNj7KWlCWMiiPXJyIh6L9DzxX97/6fa7aXHnh1nmwS1jan/9er5/AljpNv4zj3C1lFHqrOc9cOl52xrBHe7cZvLPai/3vw2FlVTlEykUsGieXX0z6R3qLyv1D1XA+iZeR3OqcqUUw/k3ot4/WB9HdvG1INqvSLBRertSTyuQGsLM9SAACqSIN15hBCQwOAcm4DfKRDWvkKbQvq8vGk39USj3jvJhHUFZbcCGrdn6/tBjlWvucqH2wS/S0r5pQ1tu0dsx9r2OrXPauh5aWu5nVuKeDypV0p/bmnaX31OE269k/D53hDSn5uSGH1MwLD1IYSAzFkjj7gKboobgIr1geQ1ADN2uz1Kznh8eKjGDukF45PnOmZzKYgpKt9vAc0OCI8IQfjYp2nCNE0rxILR+kdIXQhpTAjDiPnxQZ41RSB4hJ0kZR5uJoTHCc6P4OIwPxxBHMFO+JczCy1AlocCiiTzFl5o6/izaQEDtq2xbeZa+zBIPfwdnBeF1VvItmu5WFrYf6/syvHshXohDwrSd/MDVbXv9lFhGpJx7IQujZ2AvFmFypiShOW6UMepoy7Ef5UPoE2W1VzvxnjfMm4zd2s7XdoKavNRnVsvNUJcWoNfCpg9dax87wWI8Z0hQqnZbN8chlCpmPr62vokAMxW6N4qbuZt1LiVS1XI1XNQEzYmpWtioCncuqZ1I6B/kvq75eOpyeWotYHzAsBkzUNScqo5Q8wLyuiqJCpL137n0DyAAXDTeEgjgUgj36yNbE22+oqSpmOeNXS/AKUkpFRwOs14fDzi+HjC6XjC6ST5Z0yzc7aPQQCZMHox9k0jIpT2T4GLJSZ8fHjAw90bnHJG4oJCJLRR5AGQ5otZcJxnTDc3GPZ7TPs9drs9dvs99geJgNjtDxoF0Qxn/bh6qmz3hef2kteWp5Ti117jufI56/7a9njp8/2Udmh6yU+XwZ8rn0POv3LlTzzvp7fb5kuYXCvrhX5mqMwicjOZvFhY8huUJEbd0nJAANAFxNZUp/upRDzInjvA+QGkL+4oLhhckw7LkiPgP+cFTFllLokShi9wnUHemoY2z8W2/9t+aTJ3L6sap35Jmp9t4/hDACxytJQqB9ZX91t1ACoE50ROsdwNQk3qUEASNQelVYIYKIiaolVsLfXiXNSSU1OVu+u1O0NMFYs6Eag9ercHcnNoKLY3ZnmWS4YINkOEfQ/xfF+N4tpknd5qxgDVTdxKpjKKRWqyljOqU30SbzJ/05Wx2TsvGSHWx7cxQUAdE1an8zmh75Vr0k6n9SFd7gerY72P7uVOva59Nf4H3aNkn/J9/VdYE+re3uiOtM1Ndavjl9tY1BwQOWYsMWFJEqmzxIglJsnvkORdojxz91Ial5pgvDmXcY2i34z9sjZcWXs1naw1cx2fdf3Gqt1a87Y5y5sxRl2f2fi3PHrjOGIaRTcZx6nmjwpeo2O95Y5b96c5r7kun8xqOFS9tckTvfxdpaYnlmaqxtb1vZsOe2UsXrveRr5fG0iu1OXVW4esod2EWN37JVjeVTnBnperyar92GMi9b7XFJX+tMsOwlvjxGptf0V5us1fU/R5utNt6afNGLGcQOuxarq67RVt/q90Huu+SzW4gptd6rPPZoxoXzx7jYvX5MvnPnnPK3rpU+WTIiLsb+ZmNXp6gtDmvf9+O/g3x6mmxugNIcLT1Tx6r9f12nT6nOXnE5x/KVa2E/e1xQAAp4mpgiYiNi++oN6rrwnWe27cbxXK54Ckz2kQurYoCBje3rdg2tbw8yl1uroZ6lcGFFeQTxfvdXJWA78N8PJwPih4Q3VdEIE+11tkFj53UwyKJvZNCmqBi2xA6tHgNDQiaHi5D5qkFn17NCCSuYXFehaFxhEJF34piEkiHXIRY4IPAeR927hYwHWUgiUVBBQMAwBycGGEY0aE+pep0jCESYRTzrBk6qXI2pdKQipZvP01zFYd4QBuET3BDYCH5EDpNuQqeOfSjEOtJzU6xLygjXtXwHPrG/POOetu7pWvNl/ss0WeDIPmZdF+lYSCjJw645EKB1wYGRmOlZ6pE2SZAc4ZQEHxXnUWUzalPcw7vR9r1kZmLEgp4fHxsRogiAjTNCHqOE05ASVpHoIC1lwoYFau/BHjOOKbX3+Dx4cD/v7v/h4pRXz48R3GYcCbuzu5p2ewYzAxQiBQCEg5g6JGgiwRaT7iyIxRrxksEkAFfFZDRJJAH5zoI5wb4Bg4HG6wcw7721vc/tVfwA8BX/zlrzDejDi9+0/4YX+DD//t/8AyL3icf0DJwO2bN1hiweHwEdmUMEk8Ip76FmEAmJlBgNeuX4XoGYAaiQpDjBtMQh2lYfHTftT5LBQPNfk8ieeMEagRMkIgBAoouwkOpa4lTvNPCD9nUcODrO9gRllOougVpzKEhNoXLx6eIUkI+bi7xX5/g920hwt+BfS09ayN5/5VZ4sqtzaue338KeNbL1NZ2dIeXJpbNpf687zua2uDwLqsgAN0oLw+m3dB+baHOge8jjnSiAhXPf3tvRmPJMJOjHrMBTknuZ/rwApTNPW+FrFW0oISF/UQFM/BuJwwHx8xn45Iy4wcF9nDQ4DXCJ1pnOSZgxlHpG6W80n6wzenA9/4fb1nif4hgieJjIgxIsYFOad2jionkny9KMgi/LAEoLp7adt7XTtAXnU8QgFjTgmkdYEsKSjQKIjCyMySrDJmfP/Dj7i/f8QPf3iH+w/3mMZR1iQ4pJRrn9+9uYFzhJQjhiHg9u0e+/0e3/zqa7x7/wHZM368/4jffv89TsuM3/6YMIwDht2EnXeYgsM+CKhwOi2YlxkPc8IxM37zl3+JL7/9Fn/1b/4tbt+8xTfffIvD4RZfff0tdvs9wm5f6QW3Y/ZzGxd+Kb+Un15ephWa04sBnC817j5z0Xrt3hhRMTaLGEgiIyIJ7VLOi0QRFFlTgU7eIqNFEvo3OA9yg+jH5EBKxUQuwPlBUyYQshk99DiJPl0wnx5Q4ozgskjJbhKZIgitqYoCAuhqAloDK40SSFqYZRMvku9HPLslYe9ymrGkhBQlt01wTtbfQUF0p/J7ycjmAa75L2yPdU6iJRNDcgmxyAC2v7AHyJPsCboveOcwOlvnRYZyWO+/piOOvk/mrJEFZDYbsjR+axRDI/LMYclkBIu8FZCZKyWTRTXLe/d9WsvOJm1xlWmh4HuLcAbR2ZgFUSe7K2ZSHSQ0ikYNEfV81yhn2qtFQj71MuenusrTxgBxaf5Id4spv6Dee32MnH+mS1N7bkB0SXGU8BiGnUSa78SAPk4Cktt+3uQPeU9KtZKzOalkcQyKahTQSPeahDoJvVJKEXGR1ynOWKIY8OcYsWS5RoxiRMw5CeWjXUP/zlmuldOCHBNyXGQ+RktG3kdCWNJ1kZlqfsRqMKIauSx6cAeAygOr7bID5Dv0dG3sWuNzznmJhNDoh8PtDQ53N7i5ucFut8fhcFCnKZFThHKVGphJBoHru3uKRonqeNkaIvjCUKL1TDwbPgZE21OvRZFzQwIrOE8XfrfxXtGBy8N683W7xtqo0t8Tis/Iyb2DV32Gi8/W9hD5vL02rY7rn2WL82wdRJ76/trn/ntaNxyk7a/LgU8+J/efn67L2cmrBFNrGcDqaFggMyMEMSDaswO5RoqLTsPwuUWJuc5Iem446+78AgPAJeeylwL8Z9d/wgHjeXn88u/PPcNr5fyXR0SgdVs/4HnzDl3UZHL2M+RaWS90vXLaX0KseL0x4goQXBe810dEXK3hBaBgWy4B5Z9y7/rc9vmV5z95zZ8qRH/C9V86IC9NvGv3eIkVdnsd49x2vssJoUCqLSTA+fK3BZBeahD51Od+7vuX9OGTRgigAc58/nyXL3j92lqplTDRNiJd/BltXsoBayGbsf6MXghuUQrOkrPCLsmX62fPpp+54/RrIvJayPHOErIpEKqL3GWDitI/gTUxlNQ1c0soJ8B8ow0R6h572Pa85illa5uIaC0ODJDNsZSmtDZPcOOYlRDv3pJf71vHv1t748Ker/WHAIila3vUNrkEbF5SzKvhYCPY9MXuYcdZP7exAaXTyrWODgBIEhFzuSzoEElItfXbk+tBJ3gAzUBh1xUQVc63cM1qyOQs+1ExbymlcDHkeRzhyWHa7VBKwTAMKCUjLhGkyqfcUw3lTpQhAsGDUIoa91FUEc+IYIAzSgkIwQPswc7LySChANAEesUVLMdHOACP9x8AYhziN5Iwdz9iSgfcffEV5g/vMI0H5PgolFPsMYQBw+AxDB7IBSUVtHmgih4JyE652+1XMp7t4wpOdOuMCMG6BgehuMkq3NX8A7bfdv8cyRpugHgzIpkS3o1J61duMRJWfwLEC955OMfgQXIaDOOEMEwKHvuurr1gvR7jl/asNWB1WXC8pMBvj7sEfL1E6Dbjgs3dS6Ve+0pdSGmYzAhhCqX35hHZKKf6qI3+OZoRsrWT6/Mz1KqZt2EWj9/cvAWZVVnvIiPM8OI0sbZX79VmLFCDskZxrLw3u4i3tee+jElPgCeqXqisRmuTD+rzod9H2jWgxmHjZzfP0wrO6b6RwfAsc4l1H7KE5ykX5MJYloRliXh8OOL+/kGSW6aEcZoAEJbTUikwQgh4c3uAcw5LWuC9w7gL2B8mfPnlFwAR3tzdIuYkSfWYMceEh3nB+8cj0hhQ2CO4AaMnAQrnRagqfMDNm7d4+/XXePvVV7i5e4O7t1/gsDtg3O0xDJOCDeeGs36tfanc9C+lvERn+Lnv8efWzn+6RqrP0Y79mgtAjRB1GenfTYY1o0RhgJvnNLHp14atEIRy0/IsaX4zMsqk82I7I3OpyU0tykDW2wjH4m3tMIozgurThG6PqRvvxouaTeTnJl8WbiCurucG0DvNqMvOS04pq6PtH9xkDKKWx0HalDV3WKlrNquuIPk3CGAB2z2RUjVBaPhcI1mpUneNhLDIAqhMYc+u0g31ndbPxeZB3zss5Nw83XO5bIiwhOdVL6hzoqc2kle/r5Ezai5X69siIIRbve5hGv1iBoh+LwRo87k5RVhExNOvfkxoPfVvqt+dj8eiY7l0ctyqrCIh0GQIaiNSm0n2G4LK7Rqt5zWycyur1P9QIyCyJv/OpSg9k0VDbiIhdK7kmhsiI6aCmIv8rREQLZqHK/1w7dtOF64REqVoxNA66qdSQq3Ghoy1vl22+huU2XylLvcyrenUpjN3f/fdYPPO5MJhGJSS0V5DlRclerZjmrC5pXOm6LvbRLRbJ8p91zp6V3tsfm7noe/XtmDUsbc5evV5JWu3um51xvq3fb+p/dVdjOp/IOIVJGKa1NmfT8jwT1x+c+1t3fvfuwGw+rzWedrnl+/RZ9gApM35wm8vuk4/WT+p6CrP62c+xyIuRbNbf8kMqRhGFxXB3O7R7iXn2FbxKcaEvt1ff36/sz1/r/MfcT6Yrpz3U4wRr4iIoGqNr5suqFqyqXs/m5q6Cp5P6GuDsax/7wiUr0VGnIFOspK8/PF+QvnTFaD/5ZXe2noJpOnBSaLGtR26yIfeALH14qtC/uaeL6nTtXINrL0EPH2ucmnhqq9i9DWWI6ITwi8ACdeuaUWEdXd2zHrD0zpA+U5LQU6pCVVA3aAaKGx0Lb4KwUAT5gTPZQClJV5TCaqGruaEXATkYs6yQhFVr6BQDRAaCeGE57uUbZ93Y63/g01Ak+dLJWOeT4hxBmkEBhxJ0uQiyK1jwBX1wM8J80waem91lv5InNpqq0ugGRR8CfA5IC8LYpLoi1IKponEa96Rro1S73EYULxY8puSZIqPcdC2Zzbw3bhUnfMr5egSENvAx3J2TL/J25gT44J4NoNRAXpR0MQ7z9qelDKkFKzmJ0HyfdhzltJC2aU/z+tWz6WeU1j4HkMIlXPYvJCGYcA0icf1uJuAhYDoUHjWsaX89vkk45cchhCwv7nBOI349fFbPD484Id//CfMj0dwIQzjgJu7g1IGNQXAeY+dD8gpIXgSLmQwUllwPB4RoihXwzCokqW87BQATfYLFJwePyItR/xjjtjf3GG4+RL7N3c4/OYtbu5u8e2/+7cYR493//d/wve//b/w47u/A6hgGBi7fcDd2wNOpwWPjyeUknCaT0jkAecxDgEHJmQ+gWNB1rb10NwQRfZlrp8ZKTOWqLRXzAA5DONOnjtnuCGI1+IgOVPgqIa9l9TADx88xnGs/emGQZLsdgCz9IEHMeDVMJjUk5ThABfgxz1oBPY3bzCMe3k/3GI83CGTQyosUUluzRPaR1+dKeobJbfPt3NtzF0zQvTz5xqQe01Bqkocztdwq69zZhRo67bti+MwYRqnFZ2B5b2AniP3WRsnbV4nBfJTinUDcKSAD4mxDWqhqsq8gVJJaEFSisg5YZmPmOcTlmVGigsAiTqiaQSYEZS/exxGOO8RhlAjHc1oYgso2b6vOTisD0ymZbXm+WGoSngpTT6w6LDWX7TuR8th063TDCjwVjDHiJgSTvOseYEGGKWVzZG4RElqOQsN1W//6bf48cf3WOYZw+Dwm29+hXGa8N0UsMwLCheMw4B/9zd/DR8cPjx+BBNjHAO+/PJL/I///t/g3bsPiHHB3/3ThB/e/SBUETni/fGEv//D9ziMHofB4+ubiC92N/jw/h7H4wy/3+PLL97i3//H/4S/+du/xTe/+QvsDze4O9xhCAOmcaxRKNiM0UvGt2vj8ZfyS/lTKT3AZ8UAvS3I90ml4qWmMavcyzpn1PiAXIAsXtjIGcSs8pJo3GbAdB11JsgB3kM5K0XGQwGlBTQ/wAS/wiTylsrEJR2BvCAus0SBJeGvD6UIXZynKocTdbmZelCZGdCIBaicDy71OXJKiCljXhbMS8Tj8Yh5iTUiogwe3hECBgSvQBBIaSItEoMRfMDgA6YwoISIwTskArhIEu+ccl2TGao7QICOwROGQJh8wOAIo0ZE2GNUg7ka3EPHuCCYt+wTugOYm4H8r9HOUOOOBH23HGQxJuRURF5cycjbZNU9gKQge6evGIWlGG6a4b3KHj2tLDWnDMu1R+jlFD3GXnqOwzpHhMkKTnNHNIomG4Ok92rQrsn2Ziy4BARfnBduLd3X1rbf+32E7Jobmcd5kHcYhgnDsEcIO4QwwTnR/a0eWSYIDJxMmTSSs2heKDEGpKiyY1Z9tY9iSDLmllgwJ8acGEtiLEkiKpJGOFqeCZsqqGwvEvmU4yJ5IJYZMUkumKRJyrPOH9GXE8BZLyAXsRS+XoaJGAvIwfxzapJtmHosFcmlrLpExqMEYlmfNL0cMBrO/X6Hm5sb3N3d4XB7i/3NDfb7PabdhN1uh3EYaxStGcOq457ez3y2mlmvHwhtbK7Qdanl6i8mPjv32WLjsVyXSbZf0aYezyF+fHbUGiNlLtuDZU3nrYHi85fVOMT531K2bU7d3/15LwefCXgV48hnLWoQaOje2hjRSpPpLW8e0OQCpzK+5aKMKSomDV0f1/i2OSnWPn5CRr5a9Re28eXjFGmhlxmRzo5hXo+EKxjgT8XAXxkR0aiOnnq/VM6U5ysLRg9c1atWowKjGiUqGG2g5wVl/RljxEsa77VWwM3JL1kWL5ZeHPlTKeu+uf67HvSia33K75f6e1tMaNtGP1z04lzVdT2KL028rQHk8kZGVz/3AO1TRoxr97x83Pnvl+puxgBw972907X7tM3xKsBw4Vm4GhB7IE8EOYsc4NJd+9K9TQCgVlUT2Fk3F62idiPrZs6Vb5M78FkuRfawNQJiPQ7aGLCWNSWkPRvqPfr2A1o4ObEokPURyPbDZhBisoR0ZTUuTDiWNtbngykjpGBap3AWS5pbIIRRG+9UJ0K9c76um3aPWpfOGGVA45oPtnk4m/K0pYaxfpZ2WAOxlTu2r5f+zl1d7Nz6/GBIQkEbR+s5VLuujpEOxG21Qj+Oe0pBM47Yd7Y+9AaVUtbe0abcOXJC0wKgqCElpQgCEIKXZHn7PbgUARwTY54XFGZMhwmOHVwwcEGvTwR2Dp4c2Dmwd7VvRQASQF88JQFWMJaMzwuQCIdS8Pj4AAZhfniEHwYcyhsBag97TLc3OLz9Cvcf/wBQUHgjwXnGOA1IOQldMMRgxprc0QePEYQhejFgpaLJw4GmYzE2U6Yq3jqYpb0J8FDv+iBe9853CQ91jpXuYtZPrH+Tc0D11lcDMwk1E0IAFSfGPUuyyULN48hh8AHDuEPYHeCHSRIRsylsNm5a6cEo+3yZF/+Zvak779p+9tQ+97ThmlbHbUtbp889Gm1sr3M+rA0Oa+V1vc/Ymli6+dn75Na11xSDUmrugqKegMKL3HnO1vWx5W0hBAAsXo4kNEhGxdQcDVxbGGzdvPCspsAyuGJpMPkB3LW1jclVE28+dPshUNeOXDJiEt7oeZ7hc0ZWejvnvIIfLODckgSMSFmBwajg3ID9XviYD/sJwck6OQ4DbvZiKI35BAYwTAH73YSb/R7LHHGz3+OwmzAMklg7ZgH55pRAyODssHMnBPY4LRFLShjubjG+ucObL7/C26++wt2bLzApzUVwjWu7LcDX5bZPMUBsz3mpHP457vW5z7tkcHyuXJO1XluHT23H58ufknby08taTn5qBQde++wmOxB6ObUTaitYoXIL6yake7y69ze9uV6rN0RQW1oVdBHQMwF5AecA9g6SP43AOaJwljxSaanUM2CA2MBpMzi3faCCwLUVrI5F/7QNVEBWtmgA5cq3dXBJknSaS0GgAngn9HQQIwIA9Hz4rN86kqgG59q7I1uW9RhIFGV9OVLqPY2I8JaImgCy/GPyTEbHZNSeq97uu32773FvWGjycTbPeKXpKdz2R5O7S+n0Fu3XqnfoqzlmmQGCAOc0YtlXeiarJ9k4IYsot33QnBBUp3CdLFDH1FrWWefv6o0iG3lIh0Ndc3SsPL9GXfxWxjv1xzW5qxo5Nifbnupd88wn4a7VEYKqb8hckCiUlFENEX0ES+n0yNpn1scs0ROl/7x59eMD6vxlc8PmSaVrWuXIWt8btiZ0K1PTLZuB1K36spP3mOuztzHcrmZjb9spohc0+dqiHvoIiBACgg816mQrN7YIAKqX7j+3p+n789Kg6AfDdoUmbL/pHnN1BYYNzZeu45fk6KfPWN1Tn9d0pBV20RbtqzjLqiZXdILz+jV9fr23XZZFrgPc67+fO+9JnPAFokdtlU6fB7ZL78vqsCrE3W82Cq7Ve72uGXZwputwi3Yiaoa21ua2zjxRr+3z/4Rjztqh/fBiuW+FO+L8vGu44k8pn5Qj4hxwvPz99ULd62X3lA+21OisVrqT1WL7mctz4Psv5Z+nXO1vFbZcaNQS/bttklw3WRG6cpuxFyfedtJdyo3yEqPE1ghx7ZmeAqWugUvA9Q1qe98e+F1vmLR61xMu1ml13IV6CeZoQHtL/mleQkaBoVeqwm1Rr5XCRQXFjMIOzKR8qyrM5yJGJi8+IQSnQlZRHs2kwp0IcQ6NZsiRq39vtrgzJXQNPqtwzEBeImLJCN5jGEcR9oNDLgVLjKASQVwQnGxS5pmSUpJweK+J+nLUxhKw2wcHFG7c6sTNCKHvIQwA7arHjYBWseY0MD70muiZHMgBYRx1zTRFL2veCkHgem/tHtBz5HUYCKhmHsypC6+3OWZjxfrX+NqHYdAWxupednzKscrZfeQCgMpzaqClI2hOWK5KIxGQ6pA1AWAtRWWNlLC14CLHvv6eVXEupeB4PEoo8hDqsxgwCgCUgTkJtczHD/fw3uHu9hY+BLz98gscDgcsH094fHjEd3/4PVzwoBAwTSNu727BKMi8CPZANncgQPl+gEsLXFpUkRdvLTBVgX+cdvB+QBhGoWfIQqtwmk84Pp7w5r/8A+6+OuLw9i38bgQdAoav3+LLf/cfcWRG+D/+35iXH3F8/A7kBnzx1S28Z/ByQuKCZVngR4nGuD3sAC+RCMMp4OHhiBgznJImC82DhF8TAO8YjiSC0REDjuG8JNR13mNyHmEcsdsfMAyq4HgnCXZZxrXQRwAk1PySWNgJvZPzDvDiCR/M0x0CpmDcyRgsEYXFoEIwMMMLZ3AYMUw3IB/Abqygt+QCabzUVhqAjdVvvdEKYJnHm7JV3NvQXOdS2d7z0vm9kbAm/3PNsLo1dqwETFvHumsaN6oomMPZ2minG/1ZzvmCksNIMYqRSC5eAZXtPliU83iJUWkJEkqOYEtMnRYs84w4n1A0B00YBiD4Cg8ZvcYwiHf+OE2VcoLRaNDMYEXe1jXJa+E0Ao7ZInnk+XLWpCsViGttsF1XKm1e112lANC1ap7Fy/HxeMK8LHh8eFCaSKUAKwWLzet5QYwJ4zDB+4DRM25vRry9O8B7j6++uMEQAii/QYwLCmcMPuBmkDwUMXi44PDmy7f44u0dbqcJcZrw9nDAm8MBt4cbPBLJ/kQO8AMe5iM+Lkc8fDxi7waMww7DMOEv//pv8M1f/yv89f/wt/iLv/k3uDncIIQBAToubJxucqFsx+ul8inA/C/ln7/YmvEvtdfaOnkB9FsBs/3Yfklr0KW37r7yH1tERPfiwqCseZfUE9OpuzMZzY5GQ0pNChhKL5cZZYlAfgSXE1yeUGgA4JFTFBntdA9OC/J8AseIgQLggNGrZ2jYwYUBQxjhwtAMkFzAJYEyoZinDcSIIuBuRo4FJWaclgVzjPj4eMTjvODjwwNOy4ySssi6uwGjdwg8YfRe8jqAkFQ2zWkG5wXECQ4ZgwMmT9iHAA4ByxiQEyFTM1TsBo/dELAbPMbBYxoChuAxBi8RETUHhAoXdT1TyqINTKkS6ArMtX2712eEaklkzZwkD0CKSWl6ck2EXMfbdpxQMywZ2G8REM4LHacLFhnR5W4japETdh2gM8A3+iYiiUwkA/PRxrWNTpMdTA4Q2Z4235/rjGunhcu/MVD1IUBcpy4WuoAVGcJ+5Z5hGOHDgGnciZOJHyUyEhKNS6b3JnFMERmfcUqW22oRZ4okzj+s9FlFZUdwc4RjFsebDCDJrJPZx/Kd0TLlGNXBYpH3FMFZIoJSXLDMJ8QlYj6dJCI7zpJXJQGZVefiYrZKGJF0gdCNBWf5OZzmzWptYlhFG8GwwdeNPaMbBrBxPLFu8N7yQxyw3+8w7QbsLApibNRMpkOhu3aPPZwD6et1tP6kGN+6Hh1NjTo09fd5MaaoOvx29j11zqoOwJNnlqd+ZXPIql+YMnsV3N3Kzs9933/e6hN22DUc6qnfqiPZlXs+VV58aK3f9mu+2LsvAcr7C9pcMCO+fdfrSLa/GwYiVM0ZpRhVtqwNMZIaIQjMoeYYlXOFwQF8vV/lXpfH7NmYu/Kcz7XHpVH+qjG00R374z6X/P7yiIgrQOj2+8sVo2q53Zq7nuuElaW9/diZGK0O9vW5gv+SZ/sp5SVGilfXqy62L7/HH6s8W3frjM94zevg+/p3A7N7ILVRS5AK7mtPi0u3fm6iPTUPrtX3Wt2vfX9pIbpk1NgaIbbXuHjNJ5rbFtLVeVeOe+pZAPUe6QX1znPfALu2MDSv9yYkWQSHXcc4O/XlzCPM6qxg0YZb0+5QAbHajGuDy8WtbqWAtmcuJSPF3IwdhBVffeX21e8s5iDnDGLAaci9GOoNEBdPLo2e31ak1o/IeNwDvE8oSdtGvWgMkLX6Fh0jxmVI/WJ8dcydtVAdTz0/ajN2NIqj1kbbBOTUCcZyk/6aXHXCbd14M1G51m3VnbW+a8Hi2nq0VZr652BuBkd7TlNATLHzzqOQJltW4TblhFIIMSVAAe8QBuwOB+TCgHMozJiXBSDCPjewu1I0AE2ZJM1TwaF6arEmPBQh4WKv2gABAABJREFUqIBcEqGHHJxj4f9SEDVTxPHhHmEYMD88YuACutuBgsdwe4dhfwc37MHLPeZlgQsEP+4QvMMweJQkxj/zzApOEj3vphEAkDT3BemYZQCFCUUVW+8kH4ZXD0ZPTVFyzsEPA4Iaedp6rfO5CLUNaZd7dOu4GQe7l/PiIU91jKvKxg7MBRTCyhARwgjnB5AfJPqEuXq3mbd+L1hux8yl8jrhfOMxh35vIdja1tbD9l0FF56o03aNtmvb9QnrfaVGmJzJKzrjumcrrKtRKe34Xpi/GCmC1XG2PoM770BmFM0PYes8yAyXgEFEBEmYKmCZeONJcmpt18JgzqZVrNustq+1Kdex28T2TqaoAmx3nf5Z0MTSugJ1+099TvNwzLaGCr3Dop7CaREKhsF5OB8wTQO8JwQ/KG1WQPAO+2lA8GJIDs7DbF7BuXqcdw5R6U+E91053nVzITXMZwCJGXOMYBSM+1uMhwPefvU1fvXNt7i5ucU0TZK83Hlt+y45PbV2WMv4XXfbxxeIsc+N5Z9aPkVet/Lc3H6pHLuVy15Sr+cU03Pw6GfQGVYywXUF9jXlj2eM6gfn08XWuyqmvGTg4qmxi7pmkAg4Z2qSra8ihXK3IqETCM8lnbPnsv2kenBngBOKF6MFUwEoADmKY0eKAowWyRfhKIA8wakhwvmgL6/0ExqJa/XU9VmVcTTv8Yyi1DUpRqRF6J+WecaynLAsixgimDH4AmKPnBwSCgaI405RWZ5LrvsEsTg0eAKCJwzeYQxegF8wnAKzo/cYnNP1UQDaQCZ/UI2WWOsDbQ2nrtd743OluuFN5EOlVyo1N4BFQaTNMZZlaLPTdALtZs+q9Ermae5r3kP7Xs5peeKAZjA7ewGoholuT+vH8fnrPEdEP+atHWnTmCv5RD/zRma/WmqdNh1EOLu//WZ6v4zXoDJSM9SZMcJk+ZSkX2Iy41Gq+qaN59r3dRzY534O6/f2O9s40ZwPGu0AjfiUCKQuCqLY5y76oiq07Uatz7hLpt737bmuWscWuipqsxpofmHb7tq26W7et/xb29dlnMuiIRqDSQ9D0NmdO3209GMSMG/+JqX167nrO+Ny0bYTR0yVg85F0+un275L6ztfKms5UvvgAkYjX5jO3NfjeVniKYD7Osa0/v3yca3P+vHN3dh/6h7XsODWf0+XbdQO0Evp22tefu6nDREXxlodq2u8os2l9rsYZByMArqUgkwZjt1qzjxVx6fws62+du2ZnscR27y/Vocnr9kJQT+nMeKTIyKsbI0Q14Vf6nafzyQgWyM5yxXxmqgMvcSzHbmeVK+59svF3n9hpWnkf7Rii4UPwjG+jYTowRUDdM5ruF6IXmqMeNn4b8LrSybuUwvXtd9xxRixvTdzi4jYlq2A+dJFZrXl6j2yhpgucRGBPEYFytXTpBi3XuOwU4IMBdyVa14BV4YI9mlJVZgZg3LLa5RDhuZeSAkpRVXCpHa9wAQQ+j0xlQyAlANwI2hbuzgSPvokdV1OCzhGOPMUM68Q5+FJwGYUrgpCgQBHy2kByGFS5Q5eAeiSAc5CzUMO5M1bt6w2rZQZzglXbhkdHA0o6SNSzFiWBC6AvxmE49ZyV2jyZe9lyXeQdrWoi0vjwMYTw4RA7VeNvpjnGTHGerxFCvQRLznnGglh+Vm24cpJPaP7BNEEwAiL5FoE53IVigi0CkG2YjmLarh1avOhn3uW3NsSH1v0iHl5995epmi2NtS8M/o8KAxHCclHoBSc5lmUeiIMg3gQOefw9be/xuHuER8eP+J0OuLdu3eYphHOAdM44mZ/kD5JUca/C1Up9oEwaXJnZkLiBKSCpAntlphB5DCOs6x7oySRHacRpcx499t/wOnje+zuJuy/fIMv//1fww0e+29+g/GHP8Df/gbx8QHvvv+I3aHgzZd7jIPH3d0N+HHGnGfhli8zpv0N9tOEaRhQSsEhEE6nE5aYJBooy/wtEGPYFIDRO9wdRoxDwDQ4DJ7giDEEh5vbA8IwYtjtmrKj9AlLjpIrRClxaRTvNvFsl5wSpAYF0j4hEJxyRZEfVDnViexNxxcCB6IAibQipFIEtLUw+RxRcqr9LUaSK8k/L6ztl/YDAyq2Qug2MkeMXKGuQ6yKbTUYUFhDJaY0gARo7nKj9PXrv7Oa9R6O3vuaQLDoMayGBhmKTZmyKIWVZ2RVVEjbamOEYIB1D8hV+RYOZiiAVbglgDSw+4xS0bpT9/Zx0Bwug6xv8zwDEI5mIokyE8/RcKY027xvwHoDhIhJE13aHSXakkgMWUQkc5ABFr9gWDLvpMaGkgtQGB5AIAHIJA9NxOl4xOPjo8ytlGqPDjcH3O4HfP3FLYYQtN2Fk7aUgi/fHmp0IUG8l5mB/TTADx77MIBjxj/+/T/ixw8f8bvffY8ff3yPeBI6FBSGJ+FLhx9RQsa8ZDymiH/17bf41//63+J//d//d/ybv/1bfPPrb7Gb9vDka1Sh9Ds22OgF5a7+1it/a4Xyjysp/ssor9VzPmehDjr68yxPt1sPthiQa8DnTzWSNTyWVvnoDHDUZbx6zFdIgyGTSb2i2bL7ygLdmS0YlS6CNX9TklxlJc+gMIH8BPgATlnW4vlB5FgugHPw0x4ExuB1b93dwHnJq+R8ADnJRwVzQKlCGUtdcpJ1PSekU8IyJ5xOJzwuC+7v73F/POHj8RGnJUJytzE4TRhDwMiLyPRDgCOnshyD4wLECJcjfEkYUMAeOEweAQNc3qNoFLRTMH7wXowUQ0AYAiYvBonBETyhGiRWuBFBZG9r+81Al+hhWe+z5QZLSWSHnCoNn1ExCcCsAHfp+ljXwzqmbE9TQcVyGJFRTQaJfCDzuNU9xnsvURDVQNHrODZmu3HcjVWjarLIj0uGhacMEdtj9aLyLNd+17KVoq7qmavzpA7NmreZk0SAI4RhRBgmhDDBB6XbdA4FRmObJS9DZuTMOC0LUik4LkkNSwkEVoJbGSfbgXBWW2bVWSyhewGxyDaSb2KRCP04iwEiHcElIs4zUpyR4yKyZ4ooKamRwgyKohebCOvIIQSgsIMvSu9IJFRjdJ5o10BU2qzcNcWiMfezGTHOu8E5WlMyeZWj1GBJ1dmuVONh3+eNpneLT1yWp62/+3Y+W2NpMzxeCHI3ue/ydZ/CPM4Nag3ofeoar7mHGIrWx79k33kpMNzrHmtjQ6+7rL/f/v5cuaj7QMbHa0uLPru8cz8HzlcDw1nez7WutjWymC4aQkDhDGSAWbErdjB8qjdG2Jrcnt0BdE5fva3na4wNz/Xv+jqMypv8Kddmoy38+YwQwCsjIqxsB//LwFjavF+90+acNcDag4P1aB2hn2qEeGqQrI0QVQevn9d162smf27h7pcOqs+pYrxWYXnp4Lp23donP6EOl+p0adHtBaOLFnoDHC4oET9lDr103G/r/BLD10vu/dT3l8b1swaQTkG69nN/9lPXts8C4CrXpb3M2wNmVW6TirnUeQy0ZxCQTsJqs4JYfaUNNO+PtxdUwVvnBLGKtrFaNyvWUPf6LP04WXuZlFxQUkKKETFGuDAAYS28M5mXcTs3Z0k2lmMEc0EgS2qqSdHUeNJb1uszUlWRAc354H2Ad6GFH5s396q/tU2rkkUq7FwXeGo/ogDFwH0+e50rLLQ6fztetgauS8mtUevISsWk/bm9j3XQatkVTV4MWly/3T5Xv4asojQ2pbYJa7uSU6VbBHcxHIkiULzXemvkC4CUBMz2wSNMA/Y3BzAxHo8PQk0zz3AAyjSt69WFJZMqYY27H2CviblZ+xwZKQnNDUgB1CBGrogj3Oxw//4d2DPujt+A4RGmEdP+Brs3X2L8+AbACC6EtEiiYT8EhJDhfaqJI3POKCkhKL3UYTfBE8M7Qi4ZLgkHctHohV1wGIIAAuMg4EDwohQ5guaF2KzfFfjphX/tKy+RKNXjza8pCoRKTJUqPwBOctCTTBnrVLByZRdI+HspQqNQ1FPtWt6WrRHh2vzZltcIlFuvNuoWpaeUj60Ick3GsfXE5tjZ/O3vgZUk1l0bul6byaJeHLXW231XlZ9L64isL2W1HthDCYUSVvlDCFAOaFeppHzwYC4yd8rm2fo9YFNqO9kjOCfgH3XJvbXNjI+70XOpot/hIf0+ZEYWyRekXoxA5U8XL8kCxwzvhV5sN4zYjSP204QwDNVQkiKDShFwxItnrGPCEAKYgdEVMcwTCU3c8SM+fPiI9x8+4P7hEVGNxI5cS3KpEVvODWAG3nz9Fb78zbf44uuv8eaLLzAMY20Y3owvWXu7+XkBpFbzWDWm9WUtzf+85VNk0M+laL3kOlsd57XHv/TzS+q1rUO9RgfQy/mXj3/N8/6xSq+fbW+9rn8vF+k6edYnl2X9lzzT9k5td7F3k39bLq/6C1v0lXoX13qV+r3RIrHJRsywxNFMCSCFWEuG45ZkWdZHhnODgJ4aAeF8ABnXvvPn46nSF2rkQk5ijEgJJUWUKABsWmak5YQYT4jLqRr9wYwUCI4zUvTwXJCh0c4kjiIo4kkOzgLyguGJERyBvcMYHNh5oYNUeW7wvlI8SkSEJdmueHnb5i4iXKjPWddzdYyRfOKi0yQ1ZCczsF+IFu5zJtUb9nuuGQ5q5L6v30v+r/a5z91WqRid0tP2eq90Sn1WdCBzvS/EKcm+q++GXXTywNm7Xn/73uva1wwRLy7deSu55NI9nGtGGWfJ1YXSijc6IkgNSaxGoqwvlfFJb33F7QR1LjK3+aNUpI7UaGBzt8o1KluqwczeSx8FUYpG0nfRELXm/VYrezc710VFXJCZN7XWBtD3DdDf7d1rmQ+rft3qee0MA2bFcNFyRKKuW8QNq6tW1ytl/eRaw+3ieVaeHmf1WQAY2L9NNcFX62X3t/mBq4aIrajT6i1t8uQ2wa1u9T4XjCwiZ677oOIZVy7dX+saXnQJFP8ce3VDdV55Xh2vz/z+zOdtq7S8JT1WcV5L6uYXA2rQsHZpxggA1Rixjg66Ln/Z9V/T3s/1xeoaW0HtFedLzS9jOC+t60vLqyIiLt30pwLMV+5S32ViXfdEuXze6yMj6hVWz2dgqVwTwNng6u+5rgfhuUXxl/J5ik18773wuI+jAFPO4Zyv8EKf9JvEJ0yqLch67benDAivUT4/1bC0AmAvKGJb4eLSXL8ELjewRT6bAB5jFG+hRcBR8ygH51V9nFYmM+DgxSOFdJGHeOCXwkhRE9+lUr0zjOeb9HrmWZ+SeFI7BSWrMcCiLyDVdaXdQ8aBbCBcE7apRy6rrz2JIGHPl04z3PEoAHQImAbxYvcquDE54S8PTiIFuCAvUTxv3EeEwWO8uQHAiKeT0u1keO8wjuYBb5ua6yRS8egOYQfvBuRdAZFT3t+CGNV7fwi1zsxc+X2JWSMKAAN4+2I0STAAnCQPhYSaN+9hItp4jPtmBLow/vqx1JIQojMcyeYnWgAJUL8s4KBCfhD+YFC7NqvyAJK8IgwD9whZaQO8H1YKdEqp1tmeoR+7W0op7yX5cUlCq4XS8oUQiZfwOAh/cloWRCbheyfxogsh4O7uDuN+wm/+1V/g4f4ex+MDcor48P5HxN2Ewa8NqD449aaT5vAAhjCA4DB4MfAty1LbKJeCZT4CYCzxCOc8uBwQfAAGRjo+4h//y4zbH7/EzRd3GG/ucPfma3z17Tf4V//zfwI88Nv/8v9DSY+4//5HjIcDdre3mIrDgR3uH45YTjOOD/coOePLL99iP+6x++otSrnF/eM9Yow4xQW5MGKRtrkddxi8w+EwIgSH3TQgBA9HGUQFTqmbQhC6sRAGmAIXfAD7ANNpxnHCOI4CnPoAGgaQ99VDcFBv9QD1IBxGUcZdEY2DuDNoAksS4CBGMT7kpPlaSr4qNPfr3nZ9XK+hl9f+a/Nhe62nyrYOfeQA0JaJLahvAjJzI6GzOteoA/Ws3NbxfOvUOtQ9Sa9DBpI0T0oAXZJHM0gnMbpCaTw4V0OXvUACiNlab7zWtjYNYYTzDtO0k9+dRp3FCFKlwJ6tp2i81JZ9GwG+7h0W+eRN6Td6Em2BYqBfBUYg0QpxXkVbMGfJGaT3iqXAlwLPjEAEGgbc3Nxgv9/jV199idu7NzKencPD/T2WnME634dB6MumUQwwN7sD4BymksAggByOjyf8w9//Dt99/yP+v//5v+L+dMKPDw8I3mEaRww+wDMwDSPCOOLw9i32d7f4n/63/xf+p//5P+Jv/v3f4tfffIuUNCG907XQSR9I/g0GbRi+nwK+fym/lD/V0gMO9rn/fn3cJ95El4lrp+uyVg8w2hTnGMhCB8qQvGAAwRWT7fp1vgEldikGiYDNGUAEPIs3dWEJbghOKAoxKP2h033VwQ07NUiMEhGs3NpcZP6rBAfHWQDWuCCnBSnOiHNCnBOWxyOW+YTj/T2OpxOOxyNOcdGFnDDyAg4BMyIQAsI4SsSZC81JJydQiXAlYaAMcgwODoEdaBeA4sC57cHBC2d38L7RMxHBqyFj2wf9N6Yj1f2KWSIeWCKSJd9URi5NLo4m328coeoqWOXsPs+CRjb6Zlgg1yIinEVEeKEY6g0QRs/aDBICjK4c8AD09D2AAHDAeQ4MM0Ccgf31/dyp79L7dq5cel+1+wWdtgfAqatPa0N3fm3vQV6oPl0Y6vhlfdU5pfMkFu2/LJHFSzKDQBbjjacGwKtRRuorNSzIyCqzAAUekg+QHYs8WwgeQjPJOSLHiLgcNQ/WCSUnxPkkURA5doaJ0vQvVVStW3oDUtOfRbStcheRgKxa117msvwkDKPrlYFp+DpgkRKdw4SNJy90qOiOtTOEP19XGiL9WyvWgZnWV9t8aJfGBM5m6fm6e13GOMffXmsc2xoOibp3lrZ97hpl8/O14+15r9X5Uumdk67X+9LN1rL9U5jup4DNTxnke4PgS0szRDTc6to6cv2z7VPtc86Xjj0frz2+mDU/aXO+EmwKaA5LrPp+WwtfYTi4Uv9Lxornrtf+3jiKXTn28u+oa81rzntteXVExM9jeLhQVrdRa+qFxqxClh4H2MZmC8XZxS6WpwFjrtdpm2bdKrt70/r9HO994h7bO0r5Ka39GnD7U8qT511R9l8zfp4Cata3WnuW0EpY6z20Ud/r5Wjbh+vrPgf8v7SOzy0ibSPaPlt/TBNkAfMsbcLGpUu/pG/PBL4LR8h8Ws+R7QvcgCYJS24h4petzdYmaEK/gjiFGpid2ZKIJXnWwgC8gupuPQu5o37SdcCE1ypo2z1trnLf/gzxlO6Uue7Zrf3rZ0C8olJCyhmDhmLXtiJUEMt7LzQdJPVMcQZ4AB9EYZHcGVnpkjyYe4BnrRQQmfcKVYVkCIOAqcWoTwAffBtETZqt3XDJKFW/h9HIyHnXAPot1clTc31rFNv+femYkguKyyjFA+wE9urGXSlFdGO2/pNoCCitFxiAP39IO3ebeHib58K+46yJBtVgUoFWM0ao17b3QT2soICkGIXmZZY2Cx7jNOD29gbLPGN+fEAuGafTCSFIAmUHBpyIEAyu3tlEFlIvyce9c+BSZC5AjBbSZgLyxsWh+ACCRyoD6OgQxgGPP34AF4fpzZeYpglf/vo3ePjhO7x5+2uc7r/Dw4/vEIcE0jwX4zDC+wiiBXFJKOWEm/0OwRGGQPDBYT8OQrnkCbkwlsIgOOws+XR9kVLdmNDX5qqFwgpXLqsAGIxzqxogfRgkIiIEQD01oX3giBBI6SOcq/Nf+lPmWslFQYRS6XMkEkm91yGKWEGvxL9s72qKc5WaV8JcFXl1I9qKqtoqF4W/7Rzbzh27nwEg/XFbkEAkqgvPVNcXPv/94uEdCNGd3/9uhg+r0xo00+crm/0EEIMcoRkSaltI7YWWrxkZvLO1x632/60s0NdtBXSwRc9hbcSmtv5uN+UqYuq6yoVRstDXVQAgZ+Qk+SCKGiZIlf1Bn807h/00YT/tMA4DBjV+cm+Ysfvpuh3s3CAAYfBivCYXMM8RKWXMMeLxdNQcENI2IUgOCQfA6Zz68uuv8eWvv8E3v/kNvvr1N5j2e8nDQqWqMvLo1sbXPe/6cfHack0xvibL/BQ592lg4PXX/OcwwjwnW1+qy+eq37XnPf++rZ/rRJ1/mqU15U8wOmxLryI+cchZXWBggjhZMHeOF6W1qa2bnZhbZQXAgckp7VAl4xFMyhMcef0ecEYCo4mRzasc5MAwPjbdt7VuxAWFEzhF5LQgR3tF5CUhxxPyMiMvFhkxCwWl1jdFgueMFJ1ERBBk73Yqh0H2Z4sqI4hjhncAe1lD5ZEsN5rTyElX8wg5A2n7XW2ltpM9mrap6DSWiytrXi6RrwXAlvwPGgVhdFhnkZQwJQuV3shJH5hBoRki1ACx/azyzVq33UZGAEwWRbHOz1SjCKn5vffe/m0PxGqPW+nWF179uZcA3peAv5fWkKvXqDrQOlE2rE16Z54up0Y1XDT1uaZdMTKlXhpZSWqrKpvMuo7kNJnRrmZRNzUHic2ZYuwAQttUNEdEr0P3rx6zAHdVWckgnYqnz9iAy01di0VOdfkG9b++H5p+2Si86u+9zAabH6UaSascCAJobXCwepZideva2a5pbXUBmH9KBr8wstYSLKGC99dA/HU9zsdjG5ek/UGtAS9do6naMuyuHHtpn1zf77y0cXW93hfOQnMEBda9aVOjtRm3AzuM5ImrE52vfX3duv9fWuoY2cJHZ8ed60v9nbfSak95vT6+RW0DtmbK+pKprMZsj5MAWGEkq7HyRD2fe4ZLRoiXX4OebfMnx0u3hjxXz59S/lkiIl57jnDvUhWCtpvUatJs/npu4jw1afqR/0c3xPxSXlVMGBPeQl89nU0gaxN4ddJ6eFwYBk9Zd19aXrNo9ArQpiar9xb2eFmzeXpx2Vy5EzReqkgbiNuDSVlDS6Mmx0wpVtCFq/cwV8DHNpeiQlcqGQ4eKWdRhaLkE4gKwsQYFRzyGDFgUA90BmpisZyTvoT/FlUw7TxzIYYNAsDO6H9EyhMBSTju7RnBjFC54Y2pUwU05+R+pxOGeYYLQZODSsIzAiEoR+2ofN7BO5SU8Hh/jzAEvLk9AIBwhSqf6DAEDL4lpAMxyFGlYSrKP0uqOk7ThCF4AXC1rVJKCJq0FN6JEudMDbu8WvZ9C4jnuPDVcwXDbGyEoPkmOqCuF3r7OUnUhy/yqm3tngZ+9hUqWXj7Rbh3CE7Ax8IMx83oRYUBcnVMZjVAGJ0ThnMhirlFRlgdQwi1bnbt6g2hY6Nk8d428NPm0DgOYA6IMYKIsCzSn+l0BBHhlE4YhoA3Nzc43Ozw13/zV3j8+IB/+rv/GzlnvHv3PaZpwps3b0DFgbgDAhjwrL3tNMcHCS2BY4fgAgo7pCieHsf5KFQu6SS5E3YfEdyAFN4ixwW//z//G97++ogvvv0Gb9/c4j/8P/833I47PP7db/GP//X/g3f/9H9hZuAjM252t3jz5g5LKpiXiMfHGfP8COKE5XbC119/gf1uxHS3ByAGiFIYp5QBBiYXlMO2wClnM3kxnKBkpLjAKYAaQsB+v0eKC5ZlxjCMCE6T0DGw3+8xjqMkJfYeFAbxetN5GbxwS09+BBEhVf5sBU5KQtZIkpgLTicxbhbj4SXAo8C5AnYBhVpOgZYs+QWCl3bUSl7olM2t0nsmYNq47cZqP9fq/OiiMnqAwOZg7hKhn0cDNCOaHVO/VbmKK6fvhUe8AEgQtdwt6+awBIG82Q9a2xhVUS9ryRrDmKapRnvIc8t8HgaJCAjjJKATChxlBD9IrhyVBcxDqX/O7XM4AMU5eAWznOEWHdgBoqbAKVDQqatgyHq1KB+6JKhmpVWKdU1hzRsx+oDhcINxHDCNAw6HG+x2B+ynPQbncTqdJMro8VHWFUhCahRJlrcbd7LGjwJUeTeAnMcw7JESkAtwWiLeffyITASEAX4asb85YPIBgYBxt8d4c4P/8L/8L/gf/tf/iP/wn/4f+Mu/+dfwGYilIIAwOBK6Kyd9VcDd8HxeQe3bunX5T5Orfil/RuWymPonXXpwb7vWfXK5MlWYxHuW18tzd1oCI6EUAe9LzrDIpy2Y5yBz1ZGA3d4FcY4go4sOABzYO5G3HAEdKJOLgpTOQ3gNA0AerGA4F5b6wgz3QptERY0Q86Nw3s8nxNOCeFqwHI+YTyecHu4xn06YT7MYRmWBRSgL2AfMyBIRkQK88wANArh7LxShnEEQSqYCAopDgFBeggOIGzWGyPCoRl4PqCEDWIG6rIBhj3UxJIcGF0R1iogpo3DBktLaEJGTvluOI1YQusMpvFOw3Cuo1SIZHJHSTEoOI3IkeeNofZxgmNKvntYOQAa8A4aAN2zEaJpqFAZ4taGvxjTp+QDO9/bzZNXbeWGyjH3uDSBn97pQzDnj4jkVZHe1LvY9kxjUXfDipOKC5jPxa0oxw3mJK62O5OLbJA/XJmI9tg2UJqeZEaKsEqk3I1kgSK4zJ9IPMUtOlpSQ0oJSImJahL7M9ORcxOGpJI1cIHnXAWoSWn1u7nLqdXSLdlSrozpDMEtglI4E6Ts5utf9VyDsxghRWAxuANRhKCEXiLCR14Zbi74xw4OVbUTENWBzzUi0XiB7A5u1B9WTrud1rZ/d6zYkOc8iIlpLt3H18r3BGBeedq6w1/Pz5iU41dZIcA3LvTRX67EX6Jz78hxQ3rrvuoH/KsjNzYT8UkxtZVyg/nupA7B93l4r63BfR6tE1L0OIDiJzF/TUXpd5SX1fOr7a8aIF51reMqVxn4Jztc7jvxcBomXR0TUxc++0ckuP66fk7d/kA6CfhHZHNp+QZUU6jfNsmltev6+rQB17y98xmuLQq3FtUKb9+3fl894rst+osj7k8prvMeuXOD8uwpAv+gCsP6rAhVMWGzjyjmvAkiAHwZ4pVG4pDQ0EMnO1omNdb22YPz2Oq9ZCPrvnltI1rfZjt02prl6fttCgfr3+r6o12jHtDlTLeo637h/1k0VWY8wHm+uAF+pRgCu+SByfZkXJ9CEWTBr3j15DvMIgVanRkJQEu9SFdTyImHbfvA1cTQpTQSjCYR90tEmtIp3TPVy0mOc8mSytUEp3WanQDQxclahQ7+3qIvm9QzkFLGcjkjLCTnOcFDljjzgB9AwwTHBhQEuF1CSe8Y42x1h9DEGIjpoolQWBRAONfxPol7NY0yAafIyD6xNU1aKGTWKkAmuTpNG63g0bsNeWDEBFSwGnpIbgNjzrVdjMJ0nF3POoRceGv/ppWFm1+nmYs2twUrdQkAUhTIzUIJHKQYQG+CMdY4Mks+CVYvnmD1v73nejjdFFkrvoty73oHZoWQZ92JAK/UpzMBCqnAOIYAAZOuLOYJTxqzAvHMBYRiwO9xgnmcsjw+IOeN4OsGHgAGDJIa1HCLSjbYKyBx24j3HheEYAuiTQ1BPq6xJ4fOSAMdY0gMcAz+++ydwKPjw7i8x7G6wv32Lu6++wtd//a9xf/wB43/7FeYSsTxGTG5BHkZ4D+x2AfOSQZFxmoUGZrePYPY4HAb4QBhyRDHbAQMeuel/0lK6oHgYIOBJaJWC9/DOg31ACAzWv23u+XES44NS1jilLLCQX0v2WEgT39tc0rwpWcGDnFmTAEoxzzXJVW9h/LT5Z7JI25eq3rxRxm37Ws0j9O/tuPZ7B9ST1H29j50Lo1unDFZAv4bQ65XNu391c1uP0fYDWStR58ZWlmNLAt7NTYtKM4N2nUOkXpzaZsalbJUyJZjqviJramEzuipNBTWaDYuaIKMJUh7zMAwyp6CedM74soWiS6KmpA2aYI9ar17Fl3Gr9QCv2wdUBc9mUG3HMBcsp1mM8ctS9xsxSGTJQlsyiIAheJAmdB/HEeMwYgwDvCMwZ6E3SQtSikq5F8WgonSE3kneGe8DBicJrYt6f5oh2QeHcXA4jB6FHNw4YD+NuJkmTC4guIC7t1/g7Te/xrd/8Vf4i9/8Jd7c3mEKA0pJ66y5K9FA2sEAm1WhfpT3WoCNO9R5/5LyEmVJ2v/1EvPndjD6OY0rL3UCex6Q6EVxW0/Wv68/dyCH3XJzi94djC9+TyZKnOs+P1+TXSkNBDlvU/seIhRW4OX6+Hjama2dTWgyrv3CbTaJY4UJ6LB7O315yKTpZG/G+eTTvQhEYHXJZudQnK/zsnLpK4BbecZ1PLRYW1uvVfooWUFq3dz1Oy5J17YIjhGcIkpcUOKCFE+IcUaMR6Q4g/WFOIOUDpVI68kFOQ3IKMiOASf0S2JskZVd7lUksTZz8zh3XhduA/Bd1Smc7jG1F7m92wfi1hcmO9r6nrM5vKjsoPQc2SK+S2mJUHtZuJePfR/BsH1fUzGB1Oircro9j8kcVY9y7fcmj8v3XPcrrPZ0m9zUy9j9nBahsu7bdZ/GuSECq5eMGOpko749XmqIsMTJljMD3TOoIKPXN31MOtg5gvMBzqsRwgVlR6CumvKHBNdKMmpQgdepZp7/TT/uH0/3cWsoZtVxyyqS09rTkUTreJJcJnK+6c66aRY1TJQ2z9b/RN5iRpUxbI6TLqaWi6JKnqaDMRoNE7dZXDuagaZn6dm8ljctgkjsWlznEVcqpoRSglBKaaL6XpbtLt3WR60cd7pn/3s9UzGCValftLHUH2Pj9WmwvAPArzPWXDqrtTsBpOtylRrrLV8qRzSnSH2Y7l7oKIyo+9xfvd9Fad23q2NaMd/Vvt2B1u+X3lfnswpvq6+3wl6dITocN3Wws7r8DNvSyyXodB50cvqTZVtv/X/1PNy1fc3HYW3axqdNHIKrhn2y+VmgugbDHFSNiSJncaByzq3aywwX7frnjXD2veoqrW15c/D2/PUYuHafVp/rpa5VV47/oxsiCtaKLUHXMXXcs2m1Gni1n2UAVSEPLfiH+ovWtzU3nG5tdYPokoC/fN5vynPCo5U1j+Klm60CHDe/nRsvtsvEtRp84mN9lvKzKVMVtXnyIFirVAHA2rEI+CrjQIS7/z97//okSY7kB4I/BWDuEZFZr65+TM/0cIY7R/KWKyuU+wPu//98JydyIre3e7JcoQy5nEd3V2aEm+Gh90FVAYW5eTwys6p7yEKVp4e7mwEwQAGo/vQV04J0OmM5SW6IpO64t8rASuaD8ccoNo77WOLH/Zo1xPxiv3j3uqpx6kdrxljrb8GvL1dPB/RkocmGaUxDUwsIc8MUsMOScBlQXfLWPRgkMaYyNMGeUQWpIkxYbhuYgZDOAJFYqRNJcr1aUbcVuVSs24bz/YPEA08RtCRQBAI1lFZQau6gb7foCmIVQ5rUtGZRbpRNwlQ0jVzEaEJbdYyleBasaDUBqIgaNqaVjFaKxDhHBZGAjevlEdv6iPLhD2jrBafTCZQWIC7Aco+IBZwy0v0jGgWk+gRww4cPf0QMhOWUEMB6SItnROITlnSSXIO1QcJ0aozyKNY1XCskSikQzyfQErGtF7RSsK4biCBW5GqFTmDEuAAIsCTgpRQQiYWx0ax4AohXguXpYN2EKbmY6+6QbOb6C6j1l1n0kwD4NEJ1jX3GhC7VvrchfMUQNOwIo7WMthWUQmjLGUsqkug4SIJaoVuxbsp5EwuFJYKYUFsBscSPBSSuuyhmdDm4OOci2EUwKhpJ2KfAEZRE4CuloBYFML0QoUIpUcSyEB7uHlBrxePjI0rJuFyeAADlKWM5Lfj6q6+wnB/w7S9/hQ8ffsAPT48o24bLZcX93R2+4ndCcyFqYAaM+L+6KuMSQInARRJWpygeHXQ6odWKj4+PokR6LKicQfSENfweHz/+M7764deI357x/W//Gn/3V79D+9d/g7/b/u8odyf8x7//e/zz3/9HXP6P/y9OjXFaKk5nwnJ3j61WbLXg9x8y2u8rKq94/z7gr+/POC0JgTaAC046PjmLVX4IAYEjuJpno1iQRRBOMeL9+R7LcsYpLIgpItAJTGJ9bdZ/0Z6/WxKO2MljV2RsqH0XZGbkUjR3iib9LUKDoTMv14rrnSxljIjVKoJ591gat3WvoTrOMYDUS29UbGHPDCgQxScj59IFwui9+0xIxpwTwvfbPCC6t5IKFRK6ghwzT2Ntdrp3oEYAeHdssa7/oCBJIM3D4QAKGyjp+9I/W1JmU8wQCIIAAJUrmAsaZzSWNReizG2K4tF1XhbEEJFz6SG7KAQxQogR5zuJY86tgmOWsCKtIaZFx0VozXupSKxoFdhhvB6Jh1srGrtZ9ncQkDTslwEHNRtgJXOSgiSIlvVekC8X3ZdUCUwkis1akVLC+Sy5Tk6nBSmekNLJMCDUsqLkhssqHhHbJnUuyzvxGrq7Q0wJp7sTUky4ozsAASsaKmvumFZw9xDx1fuE33xzFk/C8z2W0z3uHr4Gs4T/++3f/B3+9f/07/E//4f/gH/7b/8d7u7usCDhwhVFE9+rWg/DJg0w3veKj90xudOq6kDrfM3P5acve4VDF9kd7+mBCb3r5Xp3n9j9PajohgD+o5YBYAFezmEnmnirUYKA7qIwNIh+WKu+oeUud0iROOzjc9A2g3mLNUBCSybZr+kOTEX5gIbaTfhlfxF8VvsVApBIY+MTOEQBZ7UPIQbVb8iZ0MRkRry0uIGwIXBDZOUqNYyL/B6EnwYDzXJCrKKQqBtaXtG2R9TtgrI+Yn16wuPlCZcnyRFRn57Alw1hzQi1ytkBSVSNElEDkFPCxuLhFtI2gHAbLBbr8sBNwWQLSYeJVqlzTQx/6nVQqp/vA4ACM2qWHG6V1SM7C1+3bXl4RFiIJmbNS6bzaN6/GgbLzhtyedSGgc7g53ruNjXcIXLXuXf/Mo/szg/Z2ab7dQeUu9fuEUKB8ez2XUidxvcW8bMSwhH2AHf0633b89qDkxmuOkR6n7YhbUb1yPOW5MI/9LCN6Q6U7iRvRogiI8YAE5fMYyRYVkIqqESg0BBYeNBKhMqSozBF9T4OPvi3KaYqSi5opQLFTPKUBsBYghgGlcDg0EAoyuMUyRnRhDduWWRckVk1JDFGLgd1qOweoB0ID8LPdJZUvzd+BgBKE3mqmkJiD0qyeP63Ns9xpzkIrxeIZRyIEagBrYBbRm0bWiW0AnCVqANQnM+iHLhM6W7e7G9gH6bPDEQ8PT5nFHus2DKcYd6nr9gOuo0TPdfWWBtH9884zs3Cu9Biwd90XfdV23hdpI4jRcBQNc9je/yc83Wzwu32dV4ZNK6zPtxWQkx9Vazqi+CRO75zosPd+3yfrgkKoJAQxHrUGbw2DWUooQvLtqFFMR5tTXLW7sdH1nq9buqmsuA5foOP+72/xqblrYoD1YR+KYXDrfKG0ExO3HBjwtPHsV1Pk76v5tnPRq2vGd7Rq1ctfrvvSAv1BQfWqjrs066d57r9uVZar7Wg+nMojnIOi8eACKTJXGMPwxSCJaLch594eW791c9C/zfqORrXl7wgXrYQ8UKh3WO95YODYS9c2UF/3a5n1pm5Mzd9gNltmFa/goo95nUzyyznAWGx1nlYhk9MdDDhlxWIDBAQX21UzLqfCU0B8laLAL/V3F8t4bK6RjJ2fTKhUriy/egOC1jZwFur0jc2C5SmjF+TxKlFDowSg7img1FbUaspFdyIVfklbddaUHLWhOkCjAtoGRFCQ1oWtCohgVgttRuCegsY806qPNKcET2BrFkPy5yYNVlgCU/DFT2HwbRP8/B6mKi809RunPzcw+ZS6SV4V/IwrGYnesSgK/ebCRaeRseWz4NmSaOA0P53pR1kcGMsp7Mkpu4JcZuOndGCCM+iEBPlknHszFB3f4BDulqLJhgGGz8wiNU6LaXhIdLbkYeRNTbsCbtSJUaIhV0FZeByuUAXAmIPSVRQ1rXnjFhiAqcRHshiy7tOav0AMLyBTABc1FK81ga0hkoiOOftAvrwA/7h7/8eRAt+/dv/irYVfPvt1/jFr77Hr//yL1Euf8Q//ecFpTKePq4Cep5OOJ8W3N81lFxRuOHp8gSg4ocfCFwTzotYmY3RlLiatTTU0NCIECMjnhYJ1XResJwWpCUgJABBV6fSd8SgN1NEBLPa8/uYmz/bh4yJKqXuaBoTLe7f2fYOo8fWBNipbFskzOJwT+PXe7/Q8Fh/14y9rU977fMbSFcGcL4HJW4bVsxM7BBw/HejnaNkzn1cdO+Y28ZVPXaNByeOGB3mEV/Y1qPMaVABWDwhkoaskGTUUfZb83yMSeNpmwWlqx9j/6pNvN+6CEYkOcmbhRpgc0YThXYdiggDs3JXGMkz2X7dFFUsgCq5Sp9D65DlmuDGCLFiWRaczmd5P50QoygjSsmoTc6Pol5oRCTJ2UNASoskz1bPoaSeEaQhBmup6lW1Yr1siAh4WO7wq69/IdMQIpbzPc7v7nG+f4e7d1/jd//qd/ir3/0OX3/9Td9jSpHQgoHokB72jNItLmZvivMasem/xfIcT/ql+PLX8vv+zHXfvlg3deK/QRM4FtvI/cu7z/Id7775vPJp43n7+Y8UD5/SBF397azwPT3sGwoBHJIAErGCqXYrbLQ9C0fKPwcQE8hCiBCpd5mAixRIQ9OEoV5UvgW6S9r52ahIAyRGIkHzNgigKny/KCIKWs0oNaOU+WXhUluVME7MxsewijQmY7QeXpQAkIaJ8kp4HTAAg0e0CZksl/UO1r1dbxz7t53B+osZyJiCQQDnEXbDckB0a1YFHcnlH+jGCRrKKigPGUNUq32viPC5IPRdz83wjCICwBV/4K/zSohJcYFbdKtqZt0XKBi9mzfBeO9r3/pCmPole4Q0RLv2B4WSHLQ8ywcyByojeD5Ex1D48ejWC/UxjFGiIlAybwiTT6yvTn7Wvhlw3oLQfVIZDiEgECMSjRBbLAYUtctfKh82UdYzmiSWn+hDxxPeK8dg4OZe7F5jlGAyKevLcLXACCriweaMLAztzFuaGYTxrFMru33NK7hI19Cez5O1IwaEFv1AwtcymGd+XNZd6G2PeXOU9xqc7+Ca5/b48dv1vs3umsELPte65/Htb1OLtqt75/3ndrFw833f6lb59o/uMH0JePlEX0YAuKIcu8kHF+i/DkXEDmNy62OuyK7x8gd0vgHeua7oEkYnTt1Y2PVXrntp7m8rIT6Jf9opvfz+f1SDdPeapwohdIOvgavoOmdCU6NREI3ICzs8ZVT78nrYj9t1H49+d2t2+pmvrz/oy1TvgWz5J1REvFB4MJrAl2Mqf+xyW4B/dQ34MZ72z1lp8NMXZSgBZdJECRGXBWmRXAEpJVFI/BkM25H2+EvWe1vxsQ/dMQBZXzzYRKTCkIFqDmQZiXlZ41zXCSyTUEimhKgTw26Ca1LAyJ9v4tJmCWEBogigaQz+2kFABqOVgm1bxSKkiStqDBFRrVsaM1DVbbpaIiFliHbMuwBfPJQRzOCq/QQBDT3Jdt42VI0PG1ks8uUAiih5A2tcXLAA3DHKQWuWU9vlAooJiqwKzaqH/enuHkTA4+MCSSVh+QhY5U5xM6/dgliA6uV0BuDivgMAMSgSxJ43Irdxn82vANG1H4ohUD8Q90LEXnvfNFRVCEMJEkLswLB1xIOpne53DJkwpqSCjj/MaHevKg/AnTbt5G6aGLBksaZbljOWtGg84wgJ7zLqoqrWhkRo1CYhjS2xYIhIsXWBR3sr466CYwe1qXVr823bUNgSz+2TXvfUkgiaSPHEZ9RasK6rJDcv4tGxLAnLcsI333yH9fKED1UUYD+sP+B8OuH+fIdF9zk/r6RAgvRzMEgyZwGsCbprKbhUURJWCEi6Pn7EJVds+f+Nx99/xDfvf4mvvv0Wf/kXv8H24a/xz//zv0fJH/Cf/vf/BblcsP7jE779/hvcnSPe3d8hxgWXpx+wXjb88MMf8fhIOKcnPD2c8JtffYWwJFCjLkU1Fm8EECHUguV8xjncI50iHt7f4/7hjNNd0rAC6m3FjEARgVwyYvMAUAXfkaKX9JkNUN3T5V5pcSQsm2cPXP227iysxQS22z2O2fT92itnffF7ql+nwLD2s7wKTfdGGwd7+b3CK5uvP8e+t5rAI8nuh2KReTeetj+oB8MMioxn2YMm4wGHUOuFmZ64sVl4AmhfgoTootDzAJlnaloknFc6LWplGqfknBZOg1kU59ViN4PRCLDkrjbuFnajh9dgHsBZyeBmeXEs/IZ6wkAsK8mdsT1snY6N5aXo3jwaN7a11hURp9NJFBFhQQwJHz78gLxe8PR0wZY3ef4YcHd3DyJSpUVEjPK+JHmnIKDZdsm4rBv++Z//iJILzljw7f3XOP/l32DLBU/rBenhHqdvvsIv/+ov8du//Vv87b/5n/Cv/u5/xP29tFFKkXxMu/PTyo8Bov9cfvryVt50v2++8i78y5EGr8vgjaYv8dZnsjsGxzNQArNgnkAPwgBgGSjxpN6krOC/Xk/CKwpno20wQRJCBA1fOvZlCRmjCtWgxisKalX/oKyeX9wUaB1PYQmUAag3dAHXDC4rSlmR8wXbdsG26ntekfOGnCV/WysVkjBVlb9QYxZSoyYAJZRuVEFEGgVhFxOeh4eWx7Q7fwdyoJjdYkCQWaZKPYzBIxSVc3KW86SoB0SuykvY6anhggiOhzDgOy5iQRuMP7tWLIRgYyl1TUqD8PxnuDavvSVmI42RG0JH5WAN9xEjAOT5WK+EMPLY8T/T7+bRoW1PAOrc4vFeMve53xuc4RMGPdjYxhgRlxNCOouygkQ5QTF2ZXrvrgGuUT2GmtDikgixBVTJwIYlaIglXYvcBNhlVUDUVlBaQbYwvWCgNemdreVp3YlXAZFdI+uA+8uhZw5PE3nVPDcbUOfxCSz9ZAvrq3grTy9Vf3glCSykraMlcooIUo+I4D1nLceXyP2lVESXZ8/q6lEgqnlUosuJby2fzm+MfZqoqx3mX2/S5zO1EqE/0MG9L9XZ91I9R/z6GgfNsSfRpIiw+p5R1Fz1oV963bf+k3pr+VqtDdv7RLdA/d36NIH7Ok48vriFpx8Ww7COv58/vzh/zLCwb76OWRkxDpFbwLvfbz2+F4Ks6wqAGiNH8Z6zHEBg3yaAHgrw9oBMfbyKU/bSWuIxB1fjcNjY4ecj+fp17b+tvEER8Uam9Y0deZ6QyL3vFyIdXDf+Zna8lRu41w2i05q+ouyB4k+ZqFub2q223lJeazHVgbcXrvvxSp+wSUdnITiixoteNCeEWAiqVYhq8OT2143Rfr7eTifztS+9e2Do6P5bn/fzcnT9eBnocxt8s3vIHzu2YQpa1MMzNQVjWm0TcNaqJazz3hNS1TUwZX4IyhiRWjuFgMaE0GxrVquTWjVMRnYH/7BCIEAVJgIStTq8IUxLb6CXgXsD7KtozIjVOC7xdjAPhJw3AZIVeJeYmJIEWYBne+4Gv0WQcFu9nWqW2BAmXdxcxWonBoltbwoIs6JdlqiAmjDIpWQF79XVtmnujCaMpwxt64xjjBqipM40MBhEAocxVkd7jqdZAyrNsj06UA06X6BrpZeBmjN9NrGScYdycIqJ2XJg0CPBbiEH/jXxPilFPAKCWLH5+7vXjFoWB6pDGmERNAnqGRMCImZlQghCo/K8DEbs9YcYkQBxfaba180I2eSFQ+oJryx+8QSOK33GGHE6n1FyRta4xJd1hYVWE8DYWYhhhDm0ubP8Fgzu87ScTpI4uwKEihgXEBPK0yM+/NM/4j/9b/8ffPfLXyJFBteMX/761/j1X/0VfvM3/xp//K//GX/4r/8F6yUjxEeE5YR3D2d8/XVGCIR1zWAWBdwlMrbtASFE3C+SMBoxyThHcWulFLGcTjid73E63WFZTggxoTbZZ6opmxojBUnOzswIQdaFuMmOg507p9t3hW6VLoqIAUBMdL7jIQYe1Aag3a7PhODAHWIV/GiviMBUt9CShgYImp/AhSiz+QWG94wB2QNYUbI9WLf7dgeD7EIZNBaptd9LHQCZkl3CrR8a1xim6AGP0Ye9ckbPFHs+6J7PTqlnRwWJpWMkVeiSGhuE0HOGkE6fycMxLT1Xgj2PgEcb8pY1gajt06yKb2h6ElVS1OG90HMZMdQTQWIgcxsJtFn3ellSoacSUSwGrDSRNH9JirHzLOT2TAawJFFEpCWp+3YQF28CqipQam1YFs0HoYqiZTnp+yJ7hX5usETstZ/JUds5M3B+aNhyxhID7r79Bu9/8yv8+ne/w1/97d/i2++/x/l8BpEotDyAZXvVc8Luc+VLCit/TuVfwnPd6qPtIfN3r+PxhR+4Lc8+c+fNXz5HXjqq53PKXu7pfLOBcziCRq77MPiPuV+0+9egFg+Kyz0KcgfInhkBJvFqZFS0IMYPcr+EKZKGtU1NExRZ7gskoSmhMhLF0BWnXYXB0j5rTBhWnt+U3J3/Uqt06XdDqxncMlpeUfKGvG2qeLD8NuLZJQph65cYtlhovxh86Fb0vZZb62Nv9uR9BPtUGQ+8+4Gtj3DyCfo+3894/a9W9YQoFbUxinpEFPP+7qKNGTqZEsFAXHX57vkKxvl9pIiwdwBX73tDg/3vHmi8UlLsFBH9Nwws5IiGCcYbhPH7QT3jrDcDsz0PMBu6kdVz1eD4bfALUqf3JhT+QL3go3wfFcg1eSdqfogYkxAYWQjT6xVr3ZXow6zeD8ASAxpBvIhYw+BCs7NwczJHVV5avA9zKRCuooG4Kk+oygj1npg9IExuHK9J9lHC9WK4GfdVJfLG1UhcPDd0PETsH+Nm5I6OpXhekvYLScfUcop4RYRdOgzOTI721uGHe7mtaXs53vKt5QoT8fLlNYGN972Mq/8MvOC5Nt19Y2EAbPsVDVLVi/w+f1UIYx+j+R1+Le2UFf59X7f1cVTzzNheDZTvv8g0U/UqX8n+NwBu/z76NOSwvh2Pf+amXzzun0FfOz2P+XuJmvYy4BEu5xucaY372RwDdeXmOBs1HwQ0p2gpYG5IMYpcoL0zBV1P1v4qZcTMcHHvzwsPTMI77K97ic+6hVu+pY63lrcpIvwiPCx0zQx8keIXHh18nvv00v723ADvW50X138/ZQ96/4Qt97+MMQdGjOUQAtKSkJYk1oEpIargPzaSL9Pvz1H2PLeYX6PBvbX4b82LMdke2Brfz8KVB7Hm+oangJpgqDAw3JMluVaVWN5qOUTGMTngzphvA1AASdqLxgpIMZgEMA0hgVisRBo3iRneKlrZ0GpBbRvkiIwwRMoYo2axNktTYceeM/TnQZNwMHZw1FoVoGyd8QKRPGfJKKXgsj6pIEhogdFqBJEeIjVrnEwDr9oQAGlY95dcAMrKRApjEYKAaK0WxJgkD0XLABghVAQinJcTaqs9bEkuBRQDTtzQWBKI5ixJ80wRsSQR5mKMwhLXojFDZD6NWbTkSS0KS0HkmZuZgbHniJoPApADvycUNlojcnRnyggF3if6lHjqgVq/1mhxXh+YaHkCRTVBWKsyT3nLKKeiFgmEXESY7Jbzem8za3YawhsY4MqozCgxq0dV0Jj/YzxiNPfiOD1j7NZWjFoJZcuTks6EVEuwFyTZhOQZaQ3btrpng+S3SQn3Dw9Yny6ouaDUinXLKKXhXFv3jJAEcqT80bD0uFIspSG81lrBK4FCBRqBK2P78AH/vGY8ffiAX//lXyKEiuW84K//9l9hvTzijx8/4n/7f/4/8E9//3/i44cV67bi13/xK3z9zTswN9zfR/zDP3zA5alhXTegFVzWjBAT3r+7k9A6EOvKkDfpYww4nU+4u3+Pu/t3OJ3vEaKEgMqlYl03lCYeUktacEqiREkpwfIaeAssYM7Dw8w9jnMpIxbnENodvWMcGTYXrc1Kor2CIfLwCOreVc15TOzW0R64tzXXmnr47MLZxZg0BE+cFH7aTc1LMXse7Pf51sy7aowPESRZ/dSnsU/bmMxJ1y0M3hBWBvAxwIL5XNEYzD1MgViRmmDBbOeMzkAIiCT7e4gR5PJeLLomWZXMs0Vp2MXWZVyeNDnqtqLWeY/ukJMK0aUU8WrS0H8q8o2zziyo1FOiK3d0H5fwGcBIWiZ9Ot/dibeCxoeV+NahJywlhBGSScNLWkBohpyTpTbkUnFPotg4nU7i9RkkRJN5Rtyd70Ah4CmvYJKzotSCoJ5673py9xPWnPHD5Yyvfv1r/Or/8j/gL/7uf8Bf//v/EUt6hyWduydEUuMOO7tLKdiXLwH6/lz+NEXAl8+5nw/uf65CvvH3n1e5pWwTkFllzrcOHI1zZvpLwUFTsA5Zx+7TED8KJDQSRT03AqOghoqGilYBaH4z26eIZQeOxOAIiI13BVpQLapEyWcizd8oucLQvZ8lAbXkQasoZRUAtnDvmwHUzHptLeIRkVfk9YJtfcK6XSRXTdbfa4V5QS8xqOJBlbdqSGaQzTAGkDPGAEPj4z3Qt5MY3YSacmYknrZwev5ct5BLpdaeL60xY1Nesu6UEB0Y1/xUcEmnLSZ+jLPXcM+nRteKgyOZzOd+OlQ2YAYxn1NEeOWFcgtXq/VIcXDUxrhe5uXq+xCv+ujr29c53ke+oVkRQf1ZLEdEz/XgFP+SI+IMistgekZyiF53f2mTPUJUAO5SQG1AZAI4IEKNuzAAdK7KO9SCXAu2krGpIoLAIJaMK7KWNGyZhfBFBUHewQXmEQGuaNXRKPNQWbDwY9WFkGRAPId1v6hEGiGgj3AfN3v2jg/Y7Ktsqz9Oc7xXRNj+Z0aePXG7eUSk2uUhq+cQoxgc1VSuwPjXlrEoB5x7WIXbfW08bDXT3IfrJm6dV9d17uu4Xee8Ux2uB9orInxdxnvfLs+1Pfp/3Afj9f087seBYb+Puo7aZPgxhx59dt3n8ZC9b9aXG32Yrv1UcF1DCYaurDVZqU3yYcdD0BBbRImW23DpbexfnXpp7r/H5caXg3ZfLNOiGPvAs7f8CZQQwFtDMxkDa/2g/nXX0pAyDU5uvVk+V5g5uv9wMexA4KP34wbszRHHK/r8qdZjr63rrfd9atu37tt//5o+vrYPdhXvv9H4mjEmJAvFlBKCxt7cE9uLSqYX+vMa+vhcWrONfoBJ0683rvft6kLDqN8DUgbmPlf674r+ekYdGMy7xFx3m24bLwt9od3uQttItCpAbmOJo7kHmm2zDOqGXktRsCir1VZTAFo9FnKWGNql9BiVtYjg1NQ7ozVzdRUrXIvV6nwu5D9Gj0srzyOu5q1mZcqiCk9uPFQJI4mVNTSVC2URAiGkiAYWUGnLKNuGtJx1fzRvBE1spwNSq2jbZTRI8k6wuorXglIyEmmoK27yXS3Sl/OCZRELrCUl1BzBQRRHnlkwj4hk1nQkTE3YAZtdY6+goXk3GOB/xGzOe44JK4OwJawMC++9A0698NLdGZWyLTmtWSHEGCX5LMRyPueMGNXjo2pIne4xIKVbPENzkmh4JeMKJVyA0EuIEYnSxMQbeGxJ3H2/Le5vq6L46QoWdXEl8ZuGWcCbVwPzglor1nUFwKhFZimQxII/n++Qcwaz5oxYV3XPZixYEJivBNY980i6X1CMCCAsUfKRUGxgYlH6hYJ1+4A//uEf8J//4/8P777+Gt98/0s8vHuHv/23/w7l4yPyDx/xxw//gMfH3yMrLT7cn3E+LaAWsK4Fy0JIKeD08BWW+zPO799jWU5I8QEMQmml00ZMCef7eyynE1qLmmy7IueC7VK6VTgnoKWmwqbu9yaohwEAmGVK35+Ixp6GsdfanmC01fcyo9E2lGQ2htf7uN9r9W+3B+9D33lrRq84sN/3794jwvpi4YuigtkM6krW0SejVbM09UytPDY3MZW1nEoyplKnF4QHPUlYuf34jQThvv8mNFmb82ne914niZGGUAhEkldEQy0ZAxnVc6yiun0gdM8IywWS1fL2crmgZAG/qno2yP4uOQ8EOGuoRZR8edu6YN1jbQN6XiRZ8zxbc1q4qKgWrz2ESJBQUafTWfaQJSGQjDVRACX1kNBQY2nRBKsg1FbQSkblCgSMkG0nfS1C/4sm7T6dznK+qvdTyQVlK0CtiAw8nBcEJpw5AI2ACNA5gd7d4xe/+Q1++7u/wdff/Qox3YMo9T3OGw/slXBGv0fhHn9WTPxLKqYE/LRyffZ7oXBc8yn1/phlv+fa33uefc+bjGtf39b1s+zBFz54Ca9gxhZg7ooICQ/a0GLTlFwiC2Td31oTwxNuopQIDUghitFIY8TK4CWBkySojy2qRT+DDRzyns0WA75V1LyqYU3VM1N5oX4miKKhlgtq3pDXi3qmbeoNUV1Y1YCUIogJic2qXnIBiSGNKKWjgc+MDk73v3dyT3/by1l6KJphgVdGyNE5QjExN5SqhlAWlhbG6ql86YFap4ig4D3fCKAwe02SD8U0lPjGI9tYjrOTNM+EKV0kD4LISLvryL8MxByhdA4VFzpo18CpvHd/iN2944z37WD3vRgHeDCzA6qOHx/1mgIiuIkWJf/47J6xGwmN8QwxiveJ8Q6mfNjxP0IWDvwzjwRVIkhSatY4R6YkZAAa1rRk1JKRs77KhlwKtlIswJkY1HEDqaKhFs011ST3U2sZrWnCan211sTTXkNvGh/XWHJbVUZPOF2bLoI64EhZv7MxktCQqPX6dX1eB4BH+3keQz5oV+ew04sIzSozy9gQ0JWEcsmtA2Z/bmh9ZPfMvNbNosv/Wgadqx5t0v5LiIe/GXfOe7bRyu1nueZ3r8+V4653spK7h3xigw8jXVszMy3vP/seuZuvv4dSureSJ+jcoj+LX8921xgP2g2j0c2+j64vbhy408dV9w97PO9Rx3iDH+ubPIQbdFbN/6sAfR5/eL5AcsdA8AxVVDcfulX70UPmYoR49vJlU2NR0Yhe939+xk9g2vxz9rdn6uF5fK5zjPSO+VtemtAXy5sUEaStHs11A8MiixEIcyKi/YG31/B9XnltXW9SQhw3dMBy/1x+1KIbZAhR80IkLKele0IMC9exID5XCWHlrfRxSwlxS7DxSojr34BZwBuHJfc1aPcG+BiTBpCZVwQw1tyhxlUBLWbuoZiYh4WGhD6ak1Q75Av75MmBBMiwpJodNVKkddqM2eK8EkIUXE08LCpK3QC2KLYaUqgV5G1FTGekU9ZE2UUZvuKe3xKKYQgCEIatjewDIpQQD6ZKFRo1b6L4SqIACcSjXvUIsRwRtRaEkiVZWhAhJCYJI1OqWN2mdUNKEqrG4n0GtY610B81N1Qayqklpj7uRcNFhUCglDR2edE4vCvA9wAEGI4xIccNrVWUOsIxAUApDSEAS+IuKBgA50NxAENQS3FYR8t0homG9q89zfVDl9VyD2P+vWXHBMY6hmUwl9S9EGIsKBTFoyTnXlc/uGPq7sry3BLfl+ucCBgQcLbkjNACGjMSJ4Q4GM2+zky4obF2KBASEhA1NwcYVMV6QpIqA1TF1dvWkwHMNn4SHka8gFJKuD/fISngSJcnBegz1rL1vBMMYNFh8cqI/bzYLkFBLMtPFWCqoFLRQgMF6ffl8gfwP21o+YLvf/0XWNKC9++/wje/+S2wFrSnjP/1f/1/4fcffi9W12XDV+/f43Q64W45Y9sqmCQ5+937B5zuTjh/8w3uznd4uPslAsWuAhRmTYc0BNQaxECMK/JWsK1FwiQ0Rk0VOQ1g3ueKCEE8SEwR4XNCLMtJEnLu9rppj8Zs0bJ/9zR5NLYCashsNDfeR4qII57HX+OBYNs7Y0w9l4i1Z2HSGGYAa3vwvP5i9DQw1lJtDZHMq8QpivWsmZ89aHLofb+De3Vo4Xq97IQZEfyGl4SNVcAi3kCBeu4PG5cUBMwHFxA1pN4fHXf1Zrg8PSHnDU9Pj92yn2tFK1mFZfVWMuWEhnSbxjYmEC2yxB2NSdzkMYeWOHoKewUgJgubdJb7uyJinAshRNmbnAKtaniHvF7Ea5AgSoxAOJ1P8koSiul8PiHGhPP5HlHzfdTaUNaCvGZwrghg3N+dEQAkZqAFtBpxSgsezg/49e9+h7/+1/8G4d1XCPGdyEDM/Zm8ImKfb8gDDZ7efy7//ZRrvvUAXPozLtf9l73vZeXa58it+/tYT3J7WZsBFBqAqBaYstdHljwKpbKEfoFYb29qiGI8RKtFwjI1whIilpSQasVSGtAWoCV5pQSKDAoRU/QGO9MstGgtKNtFeM1N98o2jw9DjIZMEVG2FTmLd0QpkocHTUCNpEBygoDJBppHVTDHSKqUHoYkE+6g8gIbzoBjud7ORbAlnHbyS5u9HkszBURVDwipo/ZBUUBQvWVDN4Iw8Dt2xT6pMoLUOM6f/c95REyUQqRY+gzA76/f12HfBz1Dj5QQvo3586BScr8fKyLs+Q7qD7OnBHWeeVhxD9BbaKDfq/MuOMv8vUyBKlj6c6rMYmGwYlIvCBoyZwfivYFOVYIXAzp7paB8iYZDk6Qpuh5qkXCpeYQd2/KGLRdstSAwEEGgVkHcIAxtUYO5jFozWttQOaPxBuaiUQUamMWgyjxvTOEgoYBFCVFVnq/MDlCEyiJXEK2MPRNCEDmvwwl93NHl7n69jbMCzke0RYC58qrMrHKzEM2zfK4AsnM/r/+8ATBeFZrB0D0welUY5nUzioWU8rjK8Z5y2L7jq4E9P3+75+z2lenk9PR+9f08rrfOoZe+Zwa4eR79uu9Hc9jHga77Zz/svTSI6GqKh0T6Uhl9HH2xsJA7ancfbysiFOjvH1+H7d26Tk8v2FO1Vp0cN8v2YjxX+/h4Wa0rIjDwmFvKvOf6fGu+3op1H11PGubdXbS/6VV1P1derYi4YsmOBPSrG24JqUdE9kzbB4fic/2Y+vSGyTyq87kcEaOqlxjY15dP0np9Zpv7Ol5myJ9v+1OfQe7Vd6kZRCThC4LEFY8pOgUEuWu9m9NuIb1AL0cKhOee57nxeG4D2Gs3j8GusenOn/ftjDpv9fnWGPjf2Q84+zjncKDcbq9huGvQk08bazMYRJk37s8+H4DWfuhj5fqloSrG7MpabK2qVcqKsD4J2FSLgqNlxO4zj4UOHkWYMj+QeBs0bpDk2ECpkBBOO+aKneWH5K0Yn6GRz7sXBSDWxiTuwlnzQ+RtxXp5wul813MNgESpYUygxR4tBbhcLt3ax4RmZrH6TSmC+YQQ5JnWVcCinDOIxJL2KI6siXQioElCUn+oe4DXW4OXUpBi6XRwxKh4OvJCvrne8454SpawWLWJFZIPq2N9gGrlQaq0UU7a54lJiwjwBiYGJwQZqQW5rVvubCz5Npgk50BaktJwkTwlOidpScOIQgXi8fyh99u8IACGxW4PDLQYsWURwmUe1cKLcQUsL8uCWgNyFuFjXbfO6KSU8PDwDk+XCxpf0BojbwVgsbY4n899/vy+0tzaIYiQxCIZS+iqlACWsEAxAPfpjECEvF3whz/8E9p/TPjq+1/iawR8+/33+L/+3/4D4j1wfn8C6geUtgpIWSvePdzh4T4i3b1DTCc8fPse6XzCu+8esCwn3C1fI1DU9cYwl3WhA8a2qbV6kxBaUeeZA0Rt6BQEZrEt9OvCqrHSVhkhyKgFyRBo+w+RJBNU+mXbdPTdKDqQ5Cno9e+KhNhx60CrvnXu7fda/74P+2RrwWL1+xikR3UR4PbjcZ6MvtseYOEa5tBWQeN9e6XFxGd5WcIEog5C7MCC0SOZzz7fw9LWLpU9SUIbScQFUUTYmht9GGPYWkPV/onivWG7XFBKwccPP6CUjO1JQLO8raKszaueGVv3fLODy/aMMV6xe4h4QD7YeNnYqVdKMIAFkJwQywkUIlJMoBhUYRE1uf2gKdIzEWC0whpOKaPUDBAjLREpSei4870ktF7SghQjTqqICFH21ctlRckF2+WCWirOSSC+Jeke2hpqYJQApPsH3H3zC9x98x3u3n8DnO4BOkME8jopVzxd7oWja3Dq88pNYe8L1P2lyufwtLfKW5/vz388SIXwY29e/367jp+uDOAAGKDSdZ8GAOu/G3+/5jkYDO4xxY/6AseshCniHAGINQCQs7oBHQgseUOpBeu2SvLcklURASwxYYkJ58RokSV+fVs6kBgSI8QKBN2fTIbSHGitipdW3lbhubcMC4UqfdbQhE3y6dQq11XNDSEh72bFRTReCsOyHTQUvSOx8DNgmBtT4vHb1RnZBi9koWS6IsKdvUWV46KA0DPIeEidgUDUQwaK8cNQMFMYvDOZMoLQQ9/YWezfj5QKvsRoPPTtME63wEPzcPT13mpnyNADaHToTF8bo/6hXOhW0DSutUTRHf/xfMKOZ5gBVn15PmUg58Y0gCh2vqR7MKpyHyF2RcgsZ8oTVpN1uEtDygc4GjJB2Bnf1VrljN0yti1j3UQJYWEQS80ITRQGZKGYmoTvlRCRswKjqEd/LQW5NJQque1KEzm0VMsRJV7y4g0xognI0/RFgOY9HPZymfK7fSj9/NuQAyAyhQxNP1sjXmFDxvNg8GUyN03mb8cy38JA9r/Z9y/tp8JzyzzNdbux8Xxrv2+HY1x5kVz363lFxL7fc12jX0d1HMgV+8PB1oe15/ajo3OEpmsOfoNKqhyufzOenGmil/EQtkcctG1jN6276+tkxq7P0ps91j2kU/c0pzdkrS7vXPd/uotf5Q8xXWdVGn2R5ooIEO/0xhaO2RQmDaUEhNDUgJJhGIAZZFmul6l+pW3f9+d6SyDsnM/H9Xvc7qWn5qs/4EM/j/7d/vwp5fWKiAPKv6mM2Mmk8qcdOuNQ6tfjZdJ86UDt7d8AZV+65rjN0XPfV1eTXfmq+o7KqzbdTyjP3fdWxcKt39+q1HldGYwrgikixBJ2OS1T7M2xYfK8wXyiYPtW7eHRfbcUEfvD+FogOx7TY2XF8325AquO1qm/htlOiZ0iwpgZEy7nlWDXVQN1iHYgjrrKsl8n1OttFnu71+f71RTsZ3WuCmBS4atk0LYC4VEFJgHia60dPOqWnMGAq5MIghCgMahEx03A0Fqb5K9oI/dFCBCrFQ5olt9CrcV6MjJVKHCtopZo1BUREnO2Ia8rKCS8e1/V0p/dOI4DQ2LMM56enpBSwvl8AmBJn1mEzmXp9BPjAI1KzgA3nE8nNBer01ozKykZF3RFhK0fr4jwNFJKQUlVgVEXC/cZeuttOyvicT3UOmisWU+nZg3uGdwRrV3rDKKMTHqfzbX36gAsRI3SVm2qsMom00gc/iUBYNRagArUKuPS6hlm6T6ewULsEMBBhBQTPDBAzQBSb5QMZhlbZk2KrWM6xohwOp2QLdRYa1hLRgyEJQiYGc93qI2RsyR9bFVCkMU65qMnwmWviLBwuaSKCAAa1qamCNHTVQQKWALQKkt8599X/OGHR/y6NpwevsJ333+Pv/yrvwAtFct9xH/+P/4X/OEf/17jPgc8PLzHcrrDw1ffI53vcffd14jnBelB9uq78LWsXx7hzEopqO0JNWdsa+57UNBRDirMbmBVKso8Wn6NsQsNWrO1YOMRAmtIA/TwZ4cKhiu6HQK9hd2aigrGHiz34Lkvfl3slQpH19j+a3UdhcHxCgzrjsMRpuewfvUx2ikhJAG4ebk5YUYXCfeRni0cTRmBHeCBaWa4C4yE4YIsUxtUIUxdERFC6IJ/B6QwxqGHQCKS8Aa1Yl0vyNuGx48/SLiE9aLAgYQTMUVEyasCBKMOe1lOhJ44Nc45EsZLvTPc8xqtUQg4ab4GCxm2LOeunGQA1fHzYoFrsckFQKzNFBFJQpSEgLv7O8kLEyVE1em8IChw2GrD0+UJ25qxrRdwA05qpJFiRGNGJjmXCoB0f4/zd7/A+ZvvcH7/DZgWMJ1Q2wbGnK/H0+StkGJeabHnjj3Jvsy6fDr//C+t/DkpE/blNgj/6hrQJW25e6qbJt5n0MVo9rV89+eP4Vt5/Am/G4wTDMw64vOnsWNoItlbsgkGGGRAn76D5fwmEAoRKkGsrlURsZUNl/VJFBJ5BUnqMCwh4RQT2kKgRAgQox+pk8XXgqNaTQcFqYQH5trQSkbLWTwiSkZet+5JIMXCt4k3Rm1q+V0zatXQeI30wUmUtSDNTWFnxxjLW0D7TZkISjE8vvf8D/PwfBBFxEi83drwYqws4a56iKp5Qvpe1xUNcfZ0o0Bd3jGewTB6/1wvKSE8vYS9R8SN1/G4vayIuAJLbRhphgrn6/deGTZG6ONEIahXo303PCcP+zbJBwQgjbps/u0n9SDvhhDdAyUC6tnJFADem4/O/BJz6HzmJIMpv0KOhsTLtiKXqooI9YQouSshhNZbz/OE1oC6gWtGLZsoIrZN5LeukBDP+60IXYryQRQSkii9aXhSU0SYEkIVhr3vJHI7jGUbY8bcdNfQ/65oBiIj6b0WbsaG260G/XsHI0sjneeWNd3c3bfLLeXEc/vy9X4w5o77HmAXzzMrdQ/Qd3//a/HEcR3v+n2z21d17c/BfZnXg58BKeGgr68/p2Ud+3Gx904fN7q2x62u29R9/qY2RPGfl3pIM/X1+g4cb2/Nz2tP91cZEehz7/cUWTMBgYSPl7OnurVFKCUjhIplWYDgvPhg93iQn65ou8t2z2CaR7+wXwh+Pt6IcfK0iua6v6RC4m05Ip4twxVufh8HDhyR7En1pUfwLO7+/friLzdAR/34ufy4xRa+hfaxpNRpWTSZpSYwM+5+5vff3Ja9HwGqr16wz9x7q47r7+mF34/b3CfLuXWdL3OMurGWDFKQsEkKhAlCBVLADUQ9aVYDayzK0JP9WogiqNLBh3RibjCNsZ153CSkTStmXeXANxaGCmSxSxmghtoyeHsCm9VWLiilYlmEZpqCPCGIdWqtGWThlSAHQiBJH8Zg1FK7gqHZvPXYsrXnGGCtF2g6XUZ/wlCK1rmBAiSsE0vi6LKtyE+PaEtCLRtayxontCmwTaiQ51/XC2pdEGMAK0gn4ZlE4bCuKyQNtLqxR7FMswSspqAwy6h+nBMJKMZAzpuss8B+a+5KDxOajL5EyUO9Pv96iVa9Z8fwsNEjTpP82oFKBIQYYRYDwceoV3rp4WnYQodoAnUNbSR0XdGapZmTMWocROEAdIt6O5G6hUIT7wI2N/1mYalIjH0oSsYSUwCE0N3+wRaWUN5TFPi/VQmHI/Uer1cDLGutmvSakblqiBhJbMvMorDIkhyv1IZ12zqgGUPErCgyQUXCRYEZGRUcGHSKiEw4VUgICG7g0ICkwnnd8MPv/xHhfw/4/tffI/zme3z/q1/hfEq4PwX8w7sHYHsCasHpdMbpfIeH91/hdP8Op3fvQEtETeKxspUVYM39wk0TYVZseZWQam3TBJtCiKaEABESAphIrqviwg5AlHxtAAvLcupKLKMlnrfTXiahfUefM2MepjBkfd5sw7T9jW3PZN2vKroKkMb6ME8Y7wF01LceFqeNvAVW9vu9Z0RFVtfQEGT77xB+BhgywACzEq1FaS3ECViQ+0lpVOoNwbxvhMYm4QR2lohQrwfAyMOjHmaWe8Iua1ynPEStVoi5q0Bw41yQEyqvF5SS8fHDH5G3DZfHD+IRsa7C4NfRFlpTxUZ0yTRHjG7zsrTvl+UkCkAF/4MCT11ZoTGwba0tp4QYItL5jOF5MhKOBgqorSLXrOeDxS2X0H6AWEyBzh2AXFLsHhBJc1EQSEM0NOQs8ac/PD0hbxmVxQX89HCPJZ1wVu+k5eEdCgFP3LA8vMO7X3yP++9+gdaTUMqE1XYNjHnPOhGqvOfZHhA4KtzXyKvl5J/Ln6R8SRnJ1YoJSOGjJNf+2j9NGSDWbaMK4Z+u5da5nmu5cwAjY5cm36gX9INlzwUMpNctVpQLBMkL1RpCqUDOaPmCuq1Yn35ALgVP20VyKTBhCQklLqAlIKSA0BpCraBWJTRTO0murIR+HoAZXCR0HZeMVjbJyVYETG1VFKdgw0e4ex+3puc7V7XNCG7s5GxnA7BJzvW9hSxBrHINeyF3fh6OtQ7QkIVmZYTPr2Rn3Qg5azIPeUiy5yEwGSZE9YrTHD8WztByEnjjq+ERwX0vl6l9WQkx/sbVtfv7Dr2ep8V14Lk2ySsHYKb9axb2Nnd6SATyHsfD+AN6NvXvXPikroToz78LG6X3cm9r/N7HAgQ7qCbPzjCUEWJxMzxAlZS7XORDcUU7v8loR3jj2kqXR4ZxW8G6bsg543G9dI+IXCwcsJzDrF5EsnYauGwazukJtWY8PV2w5hUfH59EGbFm5fWlb1ttqMzIVeW8rpBgy0E/7ZBz5oeZlvz6aMpD7mnlmnawo59RQpc2r/k8MENCy5k/Reg8Tu+Lq2sG4/fr+iUm4ej3GWMxZQ3ceDHNe/Eogw8/+v1IqbzHd/bKk6M52H9mZoep788H7XevZ2Cm/XfazQW9ThEy6nPKIq2Lbc+Z2t4VNplq/n0aNxv/XR108Bw4aqt7DXaqHn10/INs+7vxnaqcaVX+mPnWt/E88zkl7Wg+0BhALIaqzc+xw1KWuIlxUTTIXRSeI+rHeE5NToNx/vPBwKG38xzdWlv2btjL1dMdzOst/v7PRhFxW/tGx+/eMvaFQet1+wUNE26v349W4NWA3Gpj3/vXSEszb/3m8uMw/K8rb33ul8bj+DB55Ti+VAiImhfidDpp8sdloiG2f/nT2rylhLg1R88t+Fv37hftUT+nDfaN5HHU7/3no8Pxqr9klhazW3O/pjOfBEs9YYenuSZPnhAkQDEaT0zg9Y4qjAy4dVDZkv/IRix9CcRAtPsl5ndtLFZbRSxMaqkAnyS8EAsIyrGBOIoVuclayoQySMOAKqDdXLI+x8iZJVUXeLoSAp3BZ7BYkbUG0tj7pojgVlDzirxdwC2p1VjpHh+miAAsnq15aZx6bHFziS+lYts2TeIqoU1iUIWB5qsoZSSR88nwTLkn4X+aenkID59S7NcMwFKtY81KOUQclgN621tOzMyvo1UNvSNStrruq7cKUdO+xLHuuyAWkZLQcSkDoBTlA3UFEuveQBpaxYBrid0YugjK3FTx0FBrUtAUIlQQgZskYkZEHxcL4WNj0Bp3YNuUFOCIQAVMhBg0gbjSmylgDBxeFsn6UJA1dAAjRhmnlFQJ+/QEAJoXQxQTtVUQxFtgsT0SI54mASBNpNXQhNRiQGBNftgaUIrEeU1AK5LM9+Mf/4DyuOJ0F/Hu+6/wzS++w69++T3q+hGRgB/+8b9gffyAdDpjWc64e3iH88M7pLsHIBIutIG5IdcNXJsm3lbvoVrRyibvrQgAoYkehY8N6voakEg9eTCUAeZBsm0S+//urnUrduhyem4r7XS+o00T2iyskVnlyB7dumJ2WKgpn8jQCESy50lpfY+0Ofc5KcZ6QKfvYGuOxXp1SQso2bobe9KhAEcAKWhiIIIfhb4OlN6ED659j0vqLWHrbO+SCwXfQwfJhjKk1w9IfhSMHBbdi6zv7bKHy0TJOI4cG6oUhHkjVWmrubpYlLUlb3h8/Kih7x4FLMtZ91VoriHZ06PjQb1yxyxY42KWmAHpdMKynFQRkcQTQhWFHlCypPPns/Any+l8KMQxi5J9KDtNkaSKeUATbo6+nZYkyoiU1GtF5rEyABYFZM4Fj5cVpWRENIQYcLq7w+l0j4f3v8D5/gFf/fI3yET4yBXp7ozzV1/h7uE9WpDk4IFYvPh2nm574Ks/hwtt5hVqYxs8FoIGm/Eyn/ZF+McvVL4Uv/6WZ7rFV//LLB0ekE/KSn7Ks41bXsefv63uY17eA6JHAMsrKnY8AtAVDfobDALfgUCEONVhTQc9F6hWUC3gvKHmC/L6iLVkXNaLVNcIJSaUsCCWJOHeCIjcZK9oiyahBVhzNfTe1CIGPvYqBTUXVPU6lnNcz0DYfub4+34cBT3Xh2HB7AkRuuGTjY9Zb8t0MDyZ7GUX/50P32ifvaGCKLddHigWcyRThvQ5Iq+IkHwD5oEfnIecGSl4RQRF4WFCJINktcpjZcJeUfCWz/1dwatrUHluG3qt+2HQJOCATZ0/AixsFnrbPsSSVwqQ1qBKCDOcmJ7ZztwwfT8+a58oHj5nzw1hbbk5gPKN3AHooWgyY6IelosZrZKJG462NOwuNxTlzVcNL3bZVuSccdk2bDljyxIKWLyTK7iU4QGUK1oxJV5BKStazbisK9ZtxWVdxSNilftrbmp0JLSZq3hKdg8JTayu3KL934uNvX0re+u8Xo7KpOjpNLNXZo2aVdU0Q1/Tfqy8mwe5u4x33Z/jrr20tx7zVvPn3e+2h9CRt8WsGH/rmXSEe+3PkcPrGWAIX+ufaWAxY0SPyrQXAGPveqFvvfK9EmP3/ny5kddid82+jaO+Xd/rKW1e/zqFYJd/4VbZ90+gJJqI463KCG+8NSmeAiG4UG9iVDvaMEVgLVmxgIngAJ5lQbZhgDNiYPRwiH5c9s9yXJ7HI90T3rz2qsYbdfzkighgdxje2ED4xi+fChrvhaKXJmQs/NtJgW+Vcf1/C8LAv5wiYKnlhDgjpYik1q4WZgM4mJU+98cb8C1aea0S4rnyqsPHfX6Jjvf32gG3v+/WS34f9fiQFlaXzwOgP/ZrPMM69Z8mWKsDxCFJsrCgCXFVoupWqcIECvgo1icjnA3MkqpZotlhEdvlNO1OCCTHIIu1ekNFKyvqJnGyc5YEYZySun8DgFh717KB0LoVVAy69SluWIr0gTSxnexdCtBo4jkTjkAKloMBUst+lsTUrTaEKB4RIRICAsAN1Cry5Qk1BhTe1G1dXybwtWERTETIOSMtCcuSECOjtQgwROlC4klhIakAs2QvKIWwLKnPt4FGxtDHiB7Kp9aMymbtTJ1Zt1j8ZtUrHhHtkNa70K4TNeisgXnEL7SYwlfsIBtorq70dSjCJPZ6cuyJkkSQpOiSHC4Mj5ZaELgh1UXAf1U42JyJlUIDk6aJ5NEfbg1lywgUkLdNaLgfYuI9A6g3UA99FBBVuC4lj3HWnhrYjRBwWkT4v9PQROu6whIsk7ZBkGS4rTVNxNvwtK5qTSF7ocSaDkpDFbU0XLAilIz7PncuZinQHRZTCKrKM1tEEcQbRWGqQFhSQAoAakNdP+Cf/st/wlN5xK+++x7ffv0NHt59g7/47d/glBKePv4RSUFbEImi7IePYGJsLIoIqro+StFFpGGAmnqOKNAeFAypGHIziHqiaqMz84zwqT5Lq+BKuCMIzbjQOp7B3ivagvvswVhZCwqSO5DDPK2aWwe1tUlJYlTaekAxoVkD25teb6ic0UsPRxRUoO9qsrEPQvcvjaTULdo7/SjDzI31e/3ObNqIdK8YSTsnxlqFffnGQpx5D6vrs8oz6dJB9Rwz+lTFa85r94yoRKg631BGe3jLDfCue3boXJS8obWKy+NHSU79+EcJl3B56meahBhQSCtEhbzQ53kAGvJdTAkxLYhLQkwJy+mMJZ2wpBNiXLpyPaU00Un3iHB7rU2rARribSIKksvlIuPJgw5TAChFUFhc0lPSPd+FRCK19lWPvYYFCAEP778BM7CcEtJywvmrX+B0usf9N7/C/bv3+O63fwkOAV8Tg1JEOC9y9mnYQTRRqscQr/ifvcAYJyCO9Nz5ufxc3lb+/BQs17LAUbklQr4oN+g+31sijNwGwOTUbeC97X+mCw7kD4CGwBWxNaTaEHMF1gyUDe1y0cMGoJBAISPXBbklZGIkVUTAwt+x7EchRMt4pgYCqnjIWYwFqiojakVRRYQkzmX1EIY7b/rhfQWU2oYvTzMMjjoftrcg0DbsvGT9u7m5MmOlodxVEIjNU1WqaqrgljGnfsaalxx0vzXPB+j3xgPHFHv4WRB1z0MKjn8IJI4tDkybXgYm7+RS8gYY/n26ntx3Y4xNXvPXeuUEwvhtkvOwqwPuEuuD1UPCb8tFzitB332d7Iyf5hwgpjQgEImnI0LofN44l8nxM8YTjXBP9qzd83OHQUm8dglzJKFQvUeMclTsFBHGl1XhV0sR7/onzT/19PSEUuT8rrVgy5t4QVfxfoCGSy1lEy+JXFDXDa0U5HxBKRs+fHjEZXvCHz98FCOiwsLDFaH3CgvTKOGYWjNDjj4rY4/wdBEAsChhbPi6QhDjWfsmw9S9fK2eKxqdeOS+TAatduUpj41sV/ZKiNeU57AQX+fgs27hLiK08W4f2XtIS4SEN3TwoG3f59dgOeN9kmbn/pvM6c4I0FDOmicPEXTeZ6T1CnPSPc9oZp8y3Pf5Vv9n7In6lrGvS37Xe9y+Mv5gzLfQ1d+2H3RaFAHuWWK6rXjxdNt7AOC1cy/rh8MI82xYy1FbXk70Cth1W3vuS1Fem/FoHfPMgBkqzLREgyYGEDU+j8ZvPMM1zV495bN4ultnNh67Nj+Xo/siOSL2P3nB3x98RxrXfbmtLZuv2Wsf/b1Xn3dE81Ibe8L9nHK0aR593vfnpXF6jWLlS9Txpcut8fAlhNTBp6QggYHBwEz0g5dgZ4k6t/Xc4fApSgj/DEcKjX0bR/fabx68uHXfrQPueWXKcV/297gfe//YMazT4rbNULkTIha3zZgQlkWYTY0bawKCJfHpVqCdu2KYMoJ7+KORxLdbHO/PLb2Pwahc0eqGWlZNAFbUGEfM/CkENJLjstUiKTntOZOC5fro5hER2I09jX1rojll0hgsGno7fNRtPQWLcy+hPISjrKhlRatBLN41rm6zUDXdvX28aq1d+TbCEUGYYGqgygpGD7syURgEAAKOBQpgEuUKuecJCjzlIk61rQ1FBDBitouFOfU+3aIpVq8GghNITIDsdHSthJjJz4BaFT5Z6pLEynb6OQuHTovUwXXWMa2tglpAqVUSXXfB0VKuDQbNr4laC2qJKLlM5xUDQk8tdmZjnGkaJ1LnzMYgqK7KQg7FlAAClipeC92y0I25PS+VAqagHhpNktQmUkBUek8EbJvSSxZlxqKun5LUzy1bHasQg4yl7pXSxdDlFDNaCyCUy4paLvjwx3/Gh+0R5xBxfxKL6/RdRM4XhJRg1u2sdLKumwhVvKEj5kAHLolUHoW6xydz55a+aW07ehWLxJKzKgOGEokhygBQ7bRhSjSjySPGcczTSEw8nU8EtcDfhXlwiggDZK4UwTDrsHmt9D7btTwnTAb5JNO2jvQhHTvTWRt49p0GkKUXjGfyqryhgGg7Sxu/J8p313GhGe4Cd411zgAhC5fW1FqwltKToBKpYs9IkRlcm+abZA1TEkBGDVpv1nBe27oi5xXr+qQJIFcwM1JaYAomc5u2hHJeEcF9HwFCTJIv5nRCOp+wLGcsacGy3EmIJvWIMEWEAVOdNjWxqFhU2tlL6klXJD50Kcg5g1SQjGZhSyRhU+IJIZ3Hvpuc0tQmnBoaSM4MksSc5ztRAJ7fPSAuC04P32A53eP01Xc4v/8K77/7JZAiHgIk+Tuh71NCuw3RWaEe7e/22+wtdJy/5O3lZZlgX57jqd7c+o/MA/8peOzXzMm+Wz9dPz+XXp6p+ZVy3S1BfM8fH9RwIKwf98E1CsWNBhboryfAayIItj+Ne+TPAcYTs+Z7aIiNEcSSBpyzvMQUHC1U1FBR0VDQUGJACUAJopZueQFTAIegyk1pp6niWF5qQKTGQeLJaIZAbsxIzgFx5KABLvdzDP2wMr5QxkoBGRtL5fuMH0TnBWXUTIlvHs/7ELPewMqUEQbc9zoMwFHeDVHPmuSTUdO1IsJC7WmYTvPe7IrpaGcM+nPvwV0ZloN3ur721vU4+s2H0QN1y9u9PDffd62gsGkzvrb3DQb6D+Df+BTzlDbewYPbgMmKO0UE9Mzxxg27d89fw/NInrYsTCAAIyJm4W/Eo0BzMamXwciHNeKvC6m1bgwmioiCp3Wb3rds+SA0jGRjp4gQg4uq95aSUTWnRKkrntYLLpcLnp5WbHkD1wAwgThpH8Sw5lgJMf4N9m72FAGQBOsqbBhA3ZlGXVjk3jGMkJwI5cbbkUOfC4x+7BlSWDMzLveSMuLoHH8rP3F7v7a9xSrHmGt9nr7HoO9Yt9s5egpjvnm+bl/XVR87zT1z1ripM+zZ7uEpdBqP94M2r56B5pmTMR/XvKyIGHnnDmfKySZk+2yvZPd+Y8yJSB/L7SN9LRzfc01Lcr3RFAnK8eJ9t+oW44CXxxiKhZgcGgID3FCKGGbGGBA4ABiGPzMON86vSRHRV+ugRNoT32GfZsJ/7nmPf7s2HX0Nlv3W8gVzRFyXfth9QSb3JVB2/7df7J0o/wTCgS8vTdyfun9/ykJEOJ0kPrPkhhiAki0Kg6o8+CEb4POCiC9Xh+Ur5+QlhcDR9y/VqVfj1iZ7VDqj7eKF31I0GM3vmYQJnGPunA0FRoij/z42uh9jY8oRIhiExhryyPqi+ZztwLdQFE2tYs1itpQ8KStMKVBLQyBGCuMAYg0/1FSQaJoQzJKAxQAQNQQkAFEYXyY0zQ0gMeZFqGCIVWctBTlrLHFAw/IITXkrUAElMQQBna7WGKyJkGspcgAxsCxmwSSgsID1DQzxhCi1oORNLW0qct5gjAU1Cb9DIeDcIDkGlqRuu5qjAkApmjNC+3JaImog0OmMSBE1mGu6gN4Wkuj+/k68J+rWgSkAU7igrohgaCih0u+3vBWejvYCVK3cmR8bsx42hQCf/K4zSN0zRg5wtrliU3boLmBMJInnCSpEMNCcDqWI6ythgyWaZWaEFEBMXWCz8E02BjlnAITL5YIUI5aUlIZZckOwU2RrF+yZYhTra0s63crwRIohAilJXpJT6+Nn1xrdC0Hx4Lu0bYtXawhFiLFbTJcy5lGstSqYB2gKAlYCCGI9ScwgpeWisn5lEXMSJFxVQENIhHJPqKho6wX/9J//Tzz+4RHn8xlLSsgcQOd7WBLqy7qB24ayadgxzgAYFAQsFdmdNAE0RsJj2TTEQh+iYBSLOVFMUC2ai4b0dwlDI2OQOl137xInlAeXxPtqD3X7oFcI2d9VvaO8EkL2wVmZUJmv6pfnG668XjEwXzevtQF0qyeAzr0VCzFkfbH1YyBJa6KENQ+AntfAwixgCApHfRjP75KvGwiA4Z1gzyJtC8jQ52C9aIzlVT12sgLyF/GGqBKKK7DnDY3RludK4YQUA4qO/9NFciFcnh5RcgbUkwytaXJJWTuLJWt2IFFfqw74kFAaUfKvnM+4O98hnc9I5wUpSY6IJZ3FWyLKGIYQO8gCALUV1CZhkrg1cBEoj0iUxevFjUOVkA0xiOJBhH1RSgQEhOWEkO4VYCCNy40OqgS1olJyxvlOAJrz+R4xLVi++haUFoTljJhOuP/qGyynE55aQ9C8N0LTpYsVTACCqnoO9vG916T/PPNDny+I/Fx+Lj9V2QNee574UNFFZqUNh9LN5RYwAQ/aKJvNcIkoya0gq5pt/atsQwAHNaYIhCVE1BBxooCNRJCPDIQqBzo3OeNBFY0IlRglBmQCEhFCa8hqocnMoBAFCmXWcDIF20UswUupKKVO4W0IYqzQHRjsHMfYt0yiIThFAkM9UW28BNiqGHsd3LuF3NzvQd4Q4Nl3w8IJ3ao+GEhl52xMGgJV3k0RwWQKBn/O2f6IHnLKeBmXGkH5/nFW2LEf3BgNsGx8b+9euX/0vv/bf+cV73KR5OO4rkc9G0wZMTru6tO+gHrOjBFqO+i9oT+LhYWkXu+4B76vGvZq1GEKk4FiWpv2+5USAnswlBVv994xw1jFXtXkUpXzurFJFjl0U2XC42VDLhmP66oenRnQRO6kgq15FEFl26r5BMUwLmt+iQ2PTxc8XZ7w8fFJPfcTiCISLSDCCHNWzTCDYOF6bXK6p6dGvwpKN5Uld5StOxO5+ucOk/DYd/qYAsPYxFgkzQNIgzaHnGaVzfvlHmt4LTjpeY5PATQP+frpO9dfB6ky73IfvwS92Phihx/uYRv/mXfvR9/ZuB3yUDRdSzAlrUzwrbF+FtPq+/S41j/Pc/iqtGU84LF3dD+vFPwee4seFGq42fedg4GXnwmsoYPH5zEm0xR0fGl+TNtbST2vvYLorfTJwiRfjRVrjjc7F7osqfsOkfDXWQ3oJLKBGPHKeXftVTxjKvbM3uvsDeul08KrHvf69klt9fpxe2v5AjkiaP/jdM0giOdX+h5EPmIG/SJ5dgPa/8bG/R2/v7QH3WynL4r583Ob66vB6U/o10FPfc0H/POtvux30lvlBkN+4wpyHLdoKN3mofuVMHyph9YwcAYwgwfu0zd3k8dmebNnevktpvWFp+sWHq7f13U90/BheT6Z416BZpvuvk07AOx7YUj8wTtvJszjQLAabfwBtfhxVt++LhsLAUYCGgU0DMsUdm30fnRGgEfMcI0Pb8nuJFyIWdPq35LFtu8jDEnyyXpQmSeFhf+oLSNUmvoNdXtFq2hVD3G14G9mMVNbz9kw4t3qc5LERW8ahkm6EmCuqa207qpbW0VoTunDlsYLwqxKb0QR03xStIpSBXDsoJFa3kAFxRATGBU0zMfUYr5oXy35bO1MwFBADfdkIiClc/cQIGVqDGz1AKQoYCx3xVBYTHS0owtHvV3Y7DRo15ug0a+nzqtYG13gDZq8V0l8EkLdPiAxYmcLdvEYCYjRC196jpBY1hlT3b1QgggiBAF+7TmJAhrKONsYnb6YuYdgkqkWi3DS+aQglhAMIKnXguWEiDF2C2X09TKvN1EEDeB5iRFRlRmAgKKSML1KTpVAiJG7BXjVcEhBza2omkBPamUtSsSIgCBqPrCCpq00cG54/PADnh5XvH//Ne7u71GJgLTIxtwIuRa03FDXokq9LPUoUN1jJ8cA07TIPGiInsA99Ey3wOth3IRmbP5jCCCKU9JyW8vRWaRMjNsg3DHvjo4HWCL7Qe10P+JM93khB8xqe+Pstmcb66T3gUeyX5BZ7s+KCItBDYhCzcfitzHcr729UGihPXpd3hyXuNOarXNTZPi6rM8GOugic2eQB0GUblvTxOK5e69Uta6tJatiYlZE9BAXYt6HwJI+VKw6Zb/fVomv/PT4ESVnLEFhCN1fwXJWRVUYxHDAc7q2TImVTiecz3e4u3+HdBaPCEtUvSwnxLB0gMoUMcae1yzjVHqsaAmRJyC+hF+TfV0SWdreF4gUVLC/xaswxqWDWT03iYwAQvB9kMSpIUZ89f4bpOWM9PX3oJhQQ0RICad37xBCQOYmACXEu0KSgMua60wX35rzmc7m9xFO77XlSAYwAc6XH0vYOSo/VlsvyTva+tGdr+jTa/r8/DXjGP58KeOnK6+TR26N303gZPd+yNfov6Ry2WuHTbbKfSxyw2N2/eyyi1/7eo/jk/qeTQGRAFHZS1aJyEMeIPUG4FrRinl7BtQoJ3wrBdXWemg9dFFVo4dSsuzZZgHOIxmnjScB6nXsBkVZvsYjKauNqehJzOOZYSFKOm9XzSjAQLdjRcSVXD196EImOoPYeQHHE2iyaVgSalXaD0WEXG8hl4xfHkoFVUTonh3C4DUIs1fCkcJgzOf1NXv+eP8+JSCmua3g6NT2+vHso83+vb+23+NkQRIDm64UME8ITTzt7+9JvO1zF95mRUT3cEDs7amQpMcSjfr8mPWxCw7TZbuty0VGE7MiQv9T+qrqHWG5IaryWrlW5FKxZgnRtBXlX6oYq1ETjyTLhWV8yJBhm8pltXtX5CweFdsm78GeK8ElZzeaN7rdg8LUIclIAAXJQ2f3SDhOUmWDWYL7ZWHW+nbO9+m73s9sn7MaaP7N880TqO6YgmfX6K5MfR2M8/G1N+6fP19fzQef+177CWeG/X4E5h922G9L2I0bjKu86sF0syl1X1L43OQhmGXd37r2FlPn22IA1LCPdTUex48xg9jTkObXZFWJuTqm+Vda4kb9s4nbAwc7eIZOgxgEDj0H/Y7B873PzrP1l4VfN/o0PpjnyqZz0n6rzXJYJgBDBjRMZD/i3eiSGV4J8dK8HxcyRmRM0jMMzEwPet/++y9c3qCICLvPdP3emTR3MOH2M++ZwP3fs+aRby8SDIbvoJF+UEgv6fid/DeuD8dd963uyrwh8eEv9sUB8U/XzZvQ28vn3Pfck7/AhU+bsv7D/sCT31sTyxhjNNLpJFbI95JwOCRV+3ODyczBV9zNAOTN4oED5FxA5UZugwkZ63GEeWG0ebgOQAxPFcMt2R3IN8fpmtn0ZTAfzX03b47GFHamgxnNEngOTqu/SL+nvoG3fhD7rkaSsaJlkX7y2BwbaCRY7WFVLGeCxb4XxjfoGBGArMm+arHEoQ0Cfml88JoVgL8IaF4y0CQmvsT2rMpcVjAIrQXNCTBYI9Z+lW3Ftq1grghBnrNUA4sZKQYJt1Q3qUfHtW4av78xQq1gXlFbQ65FmW7SuNytg4MS5mjp1q2kSpJGK0AFlS8odQO2hBYDTnHpYBpIrNNAkERmtShdMxDFores4hHROKBxAkVGbISGB2XoRRgICV1hExVELFWEx8cLY8sXpBTAuMPpfAaQsK5PaCxeF61FSWoMwt35HrUWrNsFzIScK2LUyChqcVtLQeYMItHgi8Cl7vxtVtr4UlX5EdMIE9QYUHebEZvXYpH2i2pfq7avG91bGKpxdmhM4CZMTQhzvHYRHoEtX8AqGJN1pA2HZgMGSRpBqxmFK8BlKGjqglBOUyidcW4AFtzAXPM3jU2r4pqAlWAgREQiLA0gimhV8ycgoKk1VVMXbQEJAphrV27IsycwogKqEY0lNFNV5R4KEJokgyQioFUQQ5QH3HqcZ3n4IHleQABFVD0vGwcwTmAUABXEFcQbHj/8E54+EpZzQkwjfAxXff6kOzUvsveQrOXShCmNqGq1L8qZZCFflC+NQFdyQt3OS60KXhDAQeY7aBJvDePT2Cw7Sb08NIE4UQcJjJZqG/s9ERAswbuzFlLSBJg0cbJSi54rk4WVzj5sTcABNGHwQcx+D1ahwMKfQcL5tFxkbCgqsYZulWZrzizoohOkfLiwZTkjxADWcAqmkLI8HE09w4L+llLq9QQiUNLQRuJaAfN4E4WGPM+SFknIrgJ9zRfxfrg8SpiCvGmie9mb1vVJz6umQI0oBJLmLLD9jTRUSMkbHj98wOXyhH/+x3/C48ePUic3fP3V1xI+KZ0QKaJp4nrSHDHxpJ5crJMYz4gxYElLF+RP5zuc373H6d173L3/Bsv5PZbzOzWCkHwR0RQ5/uzR+YuqaAnrCm4FvH0Am4dfa2CyvCaaG6k1GPtj9B1DxBIjeHkPTu9kf+/gUcApRQGCguRwiWlBCBFB38/3d4gp4XT/IPuEEm5wYckAqIeYCTUimBhNdi7lQJj2yqng1sbtcnyN5/u+JPj9LwtI9+UWb/68TPF5df+3Xq6fe+bLbR37FMkClgYKII3XzMhoyOjKUZJQCtaGhWgYNE1ub39DTy22/tWNesaQrtYGUGWgCqQSSM79tESclwVcFnyXEp6q5JUpqNhaBaPKc7QElIS2BRQwKhEKE8plA0oD54IQNOQbNwl/1wrK5Uli4m9FLTdlb+I0FJQ8jaM+V4Py74yi52LVkIa1jtCGxn4wm0W45ltS2QYsiblhw8zTCIGgyoGBYs8bWozirW1gu+7lnX+LlnBaeMYReknpRJX+QwERlCcwIN8r0sdeJF0QQwk7j6fwi0qLBIB1T73iKe28MQzFKx7gFAraYNDnJuXh2HlAwtXXDyACLC9F8DkeSHjSvlfDziLqHi/iWWLCPHXZ2Hh5kChxSGncjE3seeSB7d7Q65Ah1WgHUC8LGtb5Y+5H6DL5NIy+gCZVB0JthEYin0q/GExA46JGQgJ+iydQQ1bDgTVvKLVgKxm55O7ZyTVLWDQWGqZWAYjhUqKCBQWtbWgtA/UJXMVD2DwnawO2ytgqI4YmXg1tRSBCCirPBAm1VkmMmGxuZC5MwJex67ybyvkNYjRGqpxAl250yJWOU1CDF9tj9G/zskg6tREaBq6pwUS0kMMENx1Dnurgw3xeHWIjn3Nu74Hz44uwPw8k/P7Yr8Z6+NRu8BWf9Kp75i9ucwJsFvfYtcH9908qI5/4VAyq8H3rf8K8fcUQxi3A63qmvjkFAtBlofEcNG7q/KHu7mN7cdfz1TlrGEGvi20/gu5DtjfyuH6AgO5+6QN1utD+jEtH9HeG7h4SnjyFgABCTSKRcZEQiS1LrskQRKlyYcnhSAzNJxRFnmil43h2lljeI+vOCNM4evoq+u03uLH3Z+mkUNqNL7l1NJ2/t2jPnRtvKJ+VI8IfLPt369KwIDnenI6UEVbPlZZUlRFv0QJOSogdt2ifex+llmcG8ahdtwCmv6+v7oe179/BuPpabFpfntej1m7Vqt8cjPlz19/67Wpun+2nA+76uSqjb8K/WfvBkgS7TYOgLsH7vrsx6hEQ3SFu4MG4TTWknZ4OxpiemUtlpLvmU/85op3b1jC36d++m8GBuW3/3s9dhuZhQOfdSW8+mm95hcEwMqvSmlxbe2tJC1Cp4wxMK4B5WCgzVzlYpBNgZeJqE8C01QpUSzSsnhEd3BZLssashwF1ptOUI01DBs3zYnFALRYoC7hNeqibBUo/aKqCRRW1FWXCEhgOZNcTMUQCmjCvkljVhkKetbWCRgBxFKaQ4TbzpuPTHIPB/XdJXMQAiatfbRGNFZS3rV8ZxwYCGvVEeajy3AKCaeK0FBHCHSzRe6iE2py3Acmak3kNE5hpayJpfoYaKky5Y30xQVT6Ne//nTYnxs+eV+nGhC8P/ur4AOghj4z2jQ69O+OgT50lGqCt74/lH+nWWr3SzpL2/d8UZg2th+aptSJCD20FS/eJb9FpVmozyz9UASDNClDOGwEhEQVMB8T63ZLyjiL1m9XUSGgeUEk8I4JagYegXjRsFoUNIYivUlCrflZvm1I1cXSTME8UZWdlGuIOg8CsjKcxomjImyTZBt0DvIw9zBinYDOpIbXUCqZWtUxpuvuKlmTalwgi6EQiRGUkgaAWJWMd6sGgIRUiIhYEt1/aGBDZaWAW/UKxlrTQrMRY13JgBewNIDABvGnoAIx9fJ/8rhrAYnS+ZwC9AGd7qtKPXVo1vFSkJNb9UWNS95BM5iEh9XdHB/fsRAJET7kmnPUjOh2igyTmdWTfe3d8Z/fX50DukzZaKcJI1wyuGa1kcC2icFWl3j4HkIyr1aV7IA1mW/LnMLb1CZfHj3j68AOePn4Aaw4WfngHijJGCJDQa6a9QxUrrD6u0lcKESkuCGAkAk7LCXd39zjdv8P53ddYzl9hOb3XcEzDG/OmtVTUMy6c5XmDxFdnihoWJene2GNBALonWP4KCf+2oKYHtPTQPVhESRuxnDURfIgABSwnUYTGdAKFgOV8QogBy3mZ9l7/7v/2PJGR6V4APeSjlfaPC+2uu12O5IRb17zWSvFPqYz4adp28guAG8PyZ1FuAzO3O31rDD/XAu/aItf5GRGPzaZzuwqmswCM2rn5vd/v9kN6zqt5yAdmFOT34SO5Q761cdSXHsp2/pnCNsWIJQbcxQDEgBICNq5opDkcIMp/agGoBVwILTW0IJ5rPaxMIJjCtOZV+IiShU9XnsL6KkYxrOEXqfdTB32SGSozKoDSFRF1UqTzZA3OKGbUoIoIU/8MEMXJQyTeIEOuHgoCAOAQJeySDaKOGWluHrLk1KqI8J7AcmRS57f3iggFNQ5lOwHSIrzSo58jHWvQMIekY6rhcPZ5eOy55s/zmpkVFwAjQZQRQ2EBNy7+vfep943QE0nreJvCwjwhLMRV5w18vRIvaHzu/PF1qClZQ/57wBQ0PmQTjR/HAtE/hC9WGrfvjEezsTEeX8fI5JbxhMaPiidsM0M69+KmOQThZcsCUjkwoEHUPw0EMWDilmVNoYndk6STQG1KIywyn456nyZZUqyf543Fb2n9+cAIGsapmYwM7nM/y+7Dw598HZ0uzVSB3d+kIai8h8WIPGEv1mt65/DMHt7l6uvSt5LjO0cV+wE5aO+qfR77qh+bqz7c4EFm+faav9pfd9jvl/o4/ebzGtDNfr22CMbTaz/4/tYzqVKkyzC3oWjp6TUfylBWeLqSR9s03X1Qazf3uv6FGcNM2WEOdjAzganub5pbYTvXg3ECusf5NoyE9Hc7lcgUeSSRBCDyYMfsVDFsYacFT4iS4wWOnlSR2PvXmnX/ekimuXy+GLZ3wNk/T49saMB1uabBMRbPU8d1+eQcEfPBe/z+JYrRpwnae3C2X3dzw3tlOzcZ6LdU96cTiKT8eUoonlaYuVu9IESEQDidzwgxSk6IGBHDnAzSl9veB721L9bnW+UtB8lzddl9PvTGrftYD4kOwutrXHDclwEqz+XKNcysaXkeY3P59T28VpAYECkCRikZtWZYWBX5fU5e2pol/SpgtXKVECiYDht2z2UbOOmGXorkZSg1d2Y1iD11545EuQD9HMZY1AI72FuTsE2s8cwNmSGC5kQgDdmjCUZTQMQCyffQ0C3nIIxDzhsKJARPqxXpdEYwcxJmjU1qVnkDZASP2PRgwunELmcC6WEmrxQSKAaUpUgYmZo1pJHUta4Z3AjLcodlWfDw8IB6rvjww2MH1k1AYo5TOChAYhr6BK0peU8DRmtFDhsT2Npu/1eGZa+YE0tgEWQEgB/z270r2u31ZIng9vt1p9c4wtyYhRsPIkIpGeQEO8mvMSz8zDI854wYA5gHQCteQRngIN4G+mhLWiSOMLOA8UWEFvGukLAyDO6Cb1JBzvp3UnDRAFoThKZ1S7aPynUlF7RcwDo/BMhcgab1a4kleZM1NoRADdUEUdKUS0WMUeZZw4CZEoZAU9ggAxPytmlydBtnQPYoIW27fllOgK6lxoxcssTZbbWHVuoAwI4eTAhOUazTY4gKaHDPCZJb7rSQYkKIQcKduTBjlr/D1qgps6gz1iYwj3NHhLUIyRevDK1jlltX2SgPyxZWSpPQmxdHrWBCd8cPUaxgGku84ZzLxIwyN6RTEq8lZ9gIoCtgTflMicBBwnzZ/PV5dGeojbN43shzxyBn7v6MMEWZ7WsEExQEaIjmYQFGY/GmqiVjvVxQq1gRtlqwqsKq6l6fcwZYgYKoyjMd2pYLmgru4IbL0yPWywUf//gDLk9PePz4AXlbe9slb5pvISIFUdaICqKCERA0YEkISbwOUkBMEedzRFxOON3d4+Hr7/D1L3+Lh6++w/tvfgVOCVAPmxEiy4M8RitCp63KfEsS7gbexAMw5wILL2iUIqCDhm2ota/nGCJSjECKPUSIrXOigHQ6qXeDhsOwtWbzqvlXQMc8xM/l5/Jz2Ze9VD8b9vz0fUHvDx/9QpCEymDQsoDQEM4nRK5Y7u7BzDjfPwEUUXNBKsIHWKjCBPEKpsoANdRtQ64NqBXF5ZqqanizqQJiy7KHraV28Nb62A277HPj4a3XjSVYwtyYvOJ4vGZ8gp69xvJ18xzj75wsOMB0tx/HOM4pd95ZYmQO18qA0ENF6r1dIWG5qzQnQpyVDJb/IAanQOh924Hf5n1h31udPXyTqliI+vcdjCYCqR/tjKk4Q4b+9zUOI6brPjySgdy7d6LpGtLxDZQ68cm1poDQsb/KA2Gvfb/ce+9/uOr7rFS58Uxm3W/6MCUeUUJMkKr0je1ehuWdIEDDVrn1pTwNsc5rBKhIWDNuYmDRLJSwemp749aB00lcAPNSIApgVQYNmzjPVymdK+Rv3y2gHgK4MWs+iz10O9YKWT65/kQzH7c3UDFa9aUraroBF4/qiLpuSaauw7Jznxw+Z7/+eaJRUqS/E/p99buVQ6zjRRzqdrufe+3nKOhZCVaqGDkMX8ZV/Xtz5+RzZyZP1419e98GAJgyf7zLb2OvEDXEdWMvKZM8/+66dqPL+ny6tzGpoZo8DfYVmCrC+mhyvJ03PvcmoEakrXV84qgzZgw6P99tXO8lzLrLITeuG8N3YOBN1/0bfbr6FkC4SUvPlS+QI+L4t+mag4X8UumDDJOBPzU+1udvh1ftvXKM+0F39Nv+MDi8zpE+37ruNih+BOL/FKUfZY7A7Us7YAV0Q08O1i0Q496F9W3994zMXmN9ZCk47rtu7zkliLf6eb4/83q4pcR4jUa9A6IWq3y61zFHg1gUIRvvvlZj7qd6TCDT+ghzVbIGd3Tmx8Pibu49EqAWJ+oR0fRvS/BlnhJGOIZ7jc1xft6hjBHlRmeK4b0U0MfFlCFj3qTuAUJLfxur9XqzhLAVrUX5HWMuQzSlhhN8bBw07EutBSUExLb0uDNM6O2xmyY/MZKToXVujhXEolZVBghdMLLQTJaQ1g7dWhsKFdTaECNL3PMQQeEJrY6QU/15QrgaX0+7/loG4D06CLiyDu97n2NkPJPh67xap81Csc0KTK+MYt1M/F4xAYYHlswmMA9rQ+oKGWvD6KG15mhoR98AGrk+qwWdeSLJOjLaH94YAQoiOgGMwgCJYwhoCgww82ylruOpTyqAJpv3SuuCrN0zJbG3kE5mSQ+VJTv9i4cPYG7aPoboGKu9dXhrDEa9nkvuFCB1RhmfyFHD+ECBDIunPzNeR3tfIFHEpUSQgERi9ZnN06XTAHT96vO73Af+mcRbAspswu0f7rouoFMXyuYy9iQisXgLYDRqIy6q7T0McOCpfgL1vXC/n8tcksnVE/3L+hPWnGjMzbDid+CNtdT3uTGfnvbmsVdhnkRwBsi5OGvIJiIAksen1CxJTWtWxZcAYKXn7ajdk6NvdSZs6MNwrZpbQuIxP378iMvTIx4/fsR6uSBvq1jwBrGBrU3y8UTE0Vel5WHvGBBJFalB8sTEFLCcFpwe3uH8/ms8fPMLPLz/Du++/g41EGoYHlUjTBJ1GgSZstsS3athRWMgi2JsKaJYGs/b3Jr0eXYYks8igBKBoqNDBa7SadGE6zYvuteoXBcU0OrGHW8oY997NUvby3Vbb6vhtULUz2WUn4p//xLlLfO7v/a1z/nS9Vdt97XMM8My3f4jjTEPb4g977xvmfrncbZAQwR2q/6gYRnTgpgWpHRCTRVLWgBmtJDQUCEp0XQXF+FLDB2gLCk3NE08ah6c2cKe1uZi6XPvXOfo2MITsoKmrSs/LE5+rrXXxzxyQ1iaM9JztXvd2bGpY2WhfjqAavIdxjhYiAsB9L1Xg1qnur28e7IGUeJSH885fJLnIb1yQ7okIRNFGQwMYNkpLcyzbbrfKy1mQH4kqbbnS70+44WBHU0T0EO2wl0XgoY7ne953fued9YzR/vYPSDIhco1j4lpvV0rJEAzj25t7rEiOugbQP3Msz/I8V9DzqBez1yM95p5MPub+lxClRzGwxtvpuFZAQ01ai/0td2ZtcHldJnZI/Pkf4dKUJ0HDUBghDZCKUs9Tt6g4UVknkrT4/PYZ/Z89fhsg3n75O69dLx174vbJr3c1PlM4OZO+tKZ8Opzro/7p9XJijU8V27hjZ+qiLjVl+euvQalP4cXUAKxTzTP360+6F/whPzavngZST4fXnVFQ6Ov8s7936O+Wf+e68jzP099wfCMYNf2fi5MhOlrye/z7jov6wJDMWF4k/VvPxdsh+RORvPn8Wuf6/n5fQ5Xf4kues9e35ld+WSPiOfKoTLiE8s4e573iPgpypuH+Cfr55+5gOIOMC90LMuClBbc3d11K84QgoQJIXzhDXiuZ+rewSb8HI29VQlxqw+36jlaPwJkXCsiPCNmmyWDrrzUuKNXxgjT2OCIQAosC7jPksdBrVl7Ei49uCU++wh5Ym7j3Uuj8eAXAU0YXLHlFbVk5HzpOSRalTBC3JUQGJY3fWNT4L6qmysknmfOGblsqDULoBMDiFTBJVCQClqD+avV4uAqOKyWvbVq0my1rmY0NGKUKu5zpUQAEiaDguTWaBwEfKQ4AbEGPOe8AcxIS5K4uSSzU5tYnFVNgMbaPwmTVOaE0MZs62BaUlSOATEQluWkVvwCakn+jYacK1oDtm0DkeSCoBRxf3ffk6jZGiQagKS9cpZxOJ0kBAilIfRbvN9Bw0Zog8GGfdqtASLq1trLksBKN91lX4FL4uGNIwe40H+pFdUSy6k1/l6A7NbMIYykiNrDqnRmB595RFgxiwV7GaMmVgzo1lcU1Oq+FDT15LKYz+Lxw4gK9geSdvNWAAJaTOoZIr0IEUgI4JPQFnNDjLnTZSma9BokAAQRcqt9HgEgabgBD1wDEO+LQNh0nC1OP1jCw5xPCyyEQGNGBhBVYTEcU+a91zxkqrP69qXpXtGaKEiWlkTQTxHcCKEMZYnNu81dVM+4fbHroSBxTAGBGaUBPaG0XCghK6rUGVLS+JyzVQiRufBbMADXFtA9wyo1BFhixatOTf2zPtpzlSLWdDZH3qtkv+97q01TKDAE2BY6qBNDm5aEQITzWWjv/v7OeQE5izuWfdDODGlDcsQsacGyLJMnlAyOOeeHvm+akos0QSoRo2wrai14+viDrIWaNVn1hlokKaMo7pp6CMmaTjEgpYAlBbGaXS94enzEh48fsT49Ybs89bOhlgLU1mOFcyuoIGzrBcSM0yLeSMsSRXlcRGHcEBEp4XQ6IUXC/Uk8IZaH97j75nt8/du/xfvvfoVf/MW/QoonLOmEShJV3Q3ERP9ND1VLYsp2fgZRPFHSkBW2X5PZUmkdnUZqBxlCB7iaE3l6k5I/pIfYMuxD/2NIOL+fy8/l5/LJxUC9wctIIZVBJs+oPXD6hjbkj9fJrxOuyBDvywC0SGCOoNOdxKa+z2BKuMsVMZ5ADcjrigVJvGTLhta3Iw1QqGdJ4QqqAjQzmSIC2MzjUT2+mnnvhtDZPOOnugKCm8sNVyQ/U60oqpAe44wOvMrziZLVvA1CMDRYeSdNIN3DJZkRTpBzLmkI3+GBoEoFDdHZPRKIQNHaCEN5oXXBzXM3uFDlhvEcnQ4mbwN0mrDEzF2JraGcTIFPdma474zH3YdiAmnOviv+2ajiGujv76ZI3/fRjfto60DepHHe+L6SeYz09ucQTHNXb/VvGEsRYR4P6O+Qee6m+szdEH8C5LuMxx2w24P8ALpyzORQrq2HPFHBVbxzUcBcAM5AyxrKrIBzlpwpZRNeHoQAkTNRzVvCZAxpX0IxibySS0FpIrd0boABPxld4g0iT8fAojSkOkK8YmAVlUUmCtobz2kM/Fb+6ImxbWkp72thl9BDDM/XBa0i7PdAV9jNywwkT4/3Z1deo4SQ616HN+2NeW7hlK+pb3/NZKD0hrPnuC3GAIdaPxdertvLgM8b9d7qy8BbrvvoMbgjzACAGHE+24rxwrfbcLWO/WpvRQk7L+tYpyRr+5ZiSKuU0N1ECDkoFlQnzM7jFDFFDb0bJB+iluu8m21eSxaPV3e71yOix+Nic3pUPH0c3bu7urfxVpz2k3NE3DzEjspRp251dP89jVh0n6aMeNtUvaq63rUjJuHqouere+b3o738GrQ+/v5PXfZMTwfJbe5IwhIYeOJDqezwzGef7epgPGDeXgL8X6rX3/taJcS+nomB2tXlv7t1eDFftz0zZeibk9E77dbOYBipx6GbnsI2THOvttdRm91DQA8z3lt6OasNtciutap1rMbgZ1MUtBko7F0dTBFMGQG7vqqVd52t++GXnKll/EZr1qlF49QGxYjMg8MAdnu21tuY4jUSAL4WTgX0Ngsa8aZo3BAsqTKpgyEPjxDrWwgEicl/u5hCygQCOcQSUlqQUtWQM5oEXoVEUb7IeJo7oCka7FnscPTz3A9PzEKG8rfX9KiWQq9ZV9KeCGp+P7d2Zcr1UIfF/G+dKTdLcrtvttY/XrvY0bHVaZ/9+PjSk1VTG88IaOL12uM+mmv/zEiI/N4YCspKHFfmnZWcPkNUpoRZwtY1jf/Un4xIgHHsx0ut1oMTw2Rw9W+oEszysTSNUR8QAvc5tTG1hMvjgJn3qBACWnXA6VXRsW5Bxy5M1oo+F4mfoyuQXmlzr/DY8x1eEUDMaDa23NCajbPR1DifZno0AV4OoL53gvv2Ma0R7M6m3R65PydunUFegTadg7bnuWfroaZC6Gtf7pFEpTGatb4JDJj6ZIqQGOJN4bIPvIFGGOMycn43VZJl5Jw1XNpIqN7YvHCE4m3NjP1cxqvVgrxlrOsFl8dHrE+PWJ+edB+2uMQq9JOFYuB+RgFCu1FBH65qGQsbU0kKnWJEXBak0z1O9+9x99V3uHv/Lc7vvul7DWmEZXluP69dstd5d/sLEcA+hjZUaWJ0Zrdx33+oRaOecR5jPC+rkCzVOFAIdqKN08zZYr66fJ4w+2l85q023ypcf+nyp2z7v4ey52v3gM3RtbfquHXfUd37QtPG8xwVH/8yzobXt/licecIMNaw4SI+5AyrTMQabgiW/yAtCOmEuJzAtWJZzkBjcMkSUoUlSW5l4xmtaeUjWb07SWLXM1g92Ri1DQ8GGB+tG5ru6p0fqwb2toai7x0AnsYouETGBMtd1L0PYhznMhFCWuRdPRxMcSs5f/S8u1JEWPJdyTXVFfNxVjRMigXyign5nvUzzNs0WnilOPiH/q7hWXWQ7ZyFB+KVR+v0QyMZcVe0wOhUnvvA/GF8r9f3+t271X/dT/LVTPf1w2paX/q7kxlHv0L/rT/T1Ef33us5yP3g+DCY/BOC0tvgwoxuATsHnZdo5xdDPx9NZp69503u4sFLsMk5Tc5hDQ85PCJqzx9hYKi8k6w1e7G2qW03Rl8TQ5lwm2MeY6gGIz2/2SjMLB4RDIBEzgsY+0jnTcjtKp3HdFM7kdV1j9ysdVqa+ZDxl8flXAXYb40v7Zlf+iw+amd8Z/z1p9f/2jPgdSDu8/e85d7nrzf6mq85Apt3NcHo8lOUELf687q2Rw9eV+ZzFfA7iL+GcHWhXT/Rr1zL0Dnng/ppvO/lemDIfqaMkUgM0GgeQA89ByfTu/unPYCutsWDcrSWBkMhIgb395vlFfO9X1OfUj4rNNOblBHPFQcUvXzpjyO4vKZOok8d5hv1fdbdX7Inby3P95z8ooWzlNdbz6cTYko4n+8RU+qeEGL9Asw5Aj7vOd+qMHiprueUEMpDPCt031IkvFyuQa7jPkjbnZk+APo84Nq9K/S9qBVrzSOpDjOLFQmUASTh0fq6B4lFqH4Wy19CLlWs88uKUjK2vEkCvFo0T4J6ODiFh2mKiUS7bGCSjIApNApqyfLaxdLvzBaNxNCtAZEbSDd7RusKkVatbrX84qoCTxDGlCV/RCsZLRBqtaSgBnYlsWzXRE5e8G5cUBtQcgJzw0ILoIeP5MjIw6qdGcsi8cklL4WGSmJJgBYISDEgt6w5OKQH9/d3SOmMu7s7pJTw+Bi6koEIWLcs8fRZ4ufHmBBC7B4hMn+YYvV7S/uccw8BZc/l17VZUjMzUgJCGJb0RnceaPU0uKdPb02unLbOZ9DvuSfbbq2htCpxgI2pxFAumFBgFvfVEqKzul2q11XV6/O6IsbYPUT8c9q6IIiyKFFAiGL5X2rWZOnUc9xY+0a3Fr+/C+e1gCpJngQT8Nz6nHJGGB008QiyfqW0iAdMkUTApiioWwGcp0JRUDuS5XmIqMxYS0aospBTSri7u5McGNwgochY9uZlUSHL1l4TGopRQIo2FFZ+frsiCw1rzggt4KTjeTqdZExVgWPvrIBGqRWJzGJr7GvNhEFHh6clYUkRl3XtuTWsDyEGaCRdlRxNUSOARqDQQX/LDeLn3mjI0/K0/3pkR/saoKA4xEulqfdI79POI8LGbU9z5pnmlVoAsKSEFFPPBWFeFja30jdgeLCZ2754D93d3YlHRJIk4znnPldyrybHjhG8S0QaSF4lr2i14OPHPyJvGx4fP6DWgiXJ/FuCx2IhyfS+lASA5yq5fdaPH3G5POHDDx/EI+KHDyAFAc7LSZ9VLFtLDV2xIQAOA1xAxAgBOJ3Fu2qBeYcRQmQssWJZIk7v3uP0/lu8+/Xf4N13v8F3f/FvcHq4R7p7h219xHb5oPknonHp473DAbP3AfvrCACJErhjIlf8okEkjmZ0jkThEDvAYmDJFM7KTcYRnvDjc4R/Sp7z5/Jzeb7cAjRe4u07IKql7/MdXKD91VN5TiZ4rvjdwLzyHDwC2xoA9YggoIUAjhF8OoMpAA8VISYsYNDpDo0iwvqEkBJq3lDyBaUwch0hUxkFDbUriJnVg1cB01y5KyKYGQ2aV8iMl2jE6xYeqEoYJvMA1JB13BoaBbAmjBYcOopXp3o+2Pkbono+2Gdl5Ml5RMxKBFFEhJ5XZ4QrnZT1RCP/grbZczV1zwe1UNU+2PVsnhI0lCBQZccMtFsipzBAWwfcHwH0pmjp/4UBGMtlkqdhKA6GgdJol8Y1nhUhclR6rahwl2G+0f0wddn6ZCGYlDNz6Jv1yXi24ekwK9K77KRth13fWjD51XWgy6dOBu2hviBHsIhfKn9wz1W45YI1byilopSsPKR4+VvAQ3BV/noDapEQuK0IL9KqrKNSsF4uvW8E4anNUI3bBrSMvBXUXJFzRd4K1i3jsm3Ysng2VwkYAGqMQMoDgtEazKFaxjFYCNexD3UjBOXtqAntBjDMDO8Ioxq0NTgZ6DQSoefTCDpbV6RATplHgPDUxi/aFM1gM9+goT9FOcZMuPO3f4q+fO41n9EDHJ1hr777M/HXo7nYGyfc/Dzth8+VnWcEqSmq5Ypxcr3/PPWzaYO+DyLUz9f3vtlZIWslRdkjCvEI5aZFwh5mMBqiek74HIbXndnNmcmet+bydkXj3csuz64Da+s1ZSgk3krDb1BE7LUeRwNxm8hvdmxSQlxtof333vpbF8EB8d6q46XvBQB5/X3a/PPlhQm7GhGax/vH2LO+xKHhx3y/sQRVPsSk1p+BRqIkna+XAPvbc3U9Zi8tiucUB/7vF/vh1uyRtvxIkfHsZjhdd72J78fVvvOKQQ8E+7/37XkguHtEuP4Kw6TMEKPnOgCAgD1IrYyLDsoUeoe7LYsNmQpDXvgb+4hZctjze6WJ5GIYNqLj2dx4w1u8X8+fhRhC783YrEdSMrWaaX7unCBhwo9twL6vZrnfKhhJ18WYP7PGgQGSzrtjphfjuAGYd4VjyKPE98GyLDqXrGMv4UZKEbA67BIkybhgogsDfQ1QZA3DNdwqZyXCcV+dq/BEG0MY8bS3V0iMOSAQZlDWaLExuufHno4Gg+8SJPJEdX0aAQHAgZFA+ihxsq/X00tTa6i9lX/3ZtBnN0HWPGs6EL2jyW61HiOaJnQefceuTnFhN+swuDGcFEFJQi/Ma2Moifv6bjLmrUk4nCG7HuQYoOt962gfa9wADaEUHB2YZ4RXXNjdYx53e6oqRbr1OYmVYVRlDlc3TtNyZriHOezzc89ytffCKHwvZA9FRIypW6vZ8/axQ1eRdAtRAyd8m0PZC4BmL8J9MmV7TP++7595QlgZIZ/Gc/PBfTQIR0MmZZScUcrWQx60JmMy7QV93LVK21dKQd42XJ6e1BPiCWVdEYMkjSRoSAB9xRA0/4bu9Y7WwYyYBFaoRR4ghNaTLIYYke7usdy/w937b3F69zWW8wNSOnXBvnFBQAKaS4rpB7ITpn+T69yMTfdcc8P7kUVno1n/7iTrc4z0eZDPbmbGesZ1+RIC477vP0b5cQXvn8tR+amBoS85x3ueec/7PtfWtTyF4fD0TOnjdTVs17z8S60eXTdJ131PkY7ZbsJEmthBcgAgRiAlCS2znAXcPJ8R0dDqBgRCI90Ls+xxkgdNeXgA5p0LUyyockGgxmHcAQDU1NhG+9SMv3K81Th2SEEbzWdh4L/lMNLwSLHneEjdw2HiRdPS+bHxPkJvdkUErr0dLDxTP7/05Q1juiEIac4IGkoBBEsY7QwFLDeF4/9lEw7uszz/SO7s6Eg/BzIPCOUJJo8Iy/0z7p0hYq9cuMG7zI32eg+/35fgLnB1E2kOj6uE07t3m3+SyuY2Ha/jPvd/9t/D6JSU9oYs2L0M2uCjWUMWNc3FVGpBKeMl8m3p56i8TJkgxnGCQjZtyBKvm5GL8PXCdwYMRYQYrFUNR9Y9hKq8zLBkkunt4FcZhP1G5EjHzxArQyxgP7rXFNv8TPzJPHdKltjvR3aD7Tm9vZlUeh1DIWKy8UF95HlQ69vx/vgaYPhTy23MxMaadt+/rrx0zjzXlx+zfGobL983MJbXtrG/7pbywcqzSggIZfIR7d4sDZ6ej3nkmU7dL7JHuD4w88Aads9B5GQBh0OR3992zy971ZC/bf+jvh/cGAf9fGs8PMZ0VOa1QGMfOiyvYI5u1P+W8gmKiNu/yR5JN99frvuW8LPfjl9f9pPyOZvcc0Lff1/lWsQ+uobV1dcIczktiDGJFfeyIC4nBIqD8euy9/NKiDf19EY9txi4TymjLhyf8dq2DwPzXD37awwoMgbsNXVMyYV5Vk7sFRGtNWzbJjFdcwY3Ri21Az0TsOuYBRFf5L/gmHXLu8Dgbl1fSumKg4AAJqBRxlVxj2UxVu2HEe5Iw36YVZdj3jo4qrkAKkR4EkPXwUDHKHtKKcJckmmtSUxTxC1W3HVNmWAW7SJc2d5CSsOSXA5gNLaQURLBs2jy0jPuphBCkiOioDWNIU+xx+MMJHHta63q4SBCG7O69FXJkbCFFWiMuCzdo+L+/h7ruooFTq2oNYNCQKkRFZa/g7UPVVzYU+geAQYKl1Lw9PQklt1pQUqpewwYfZkFuj8sLdG2JXbuguEufJK1YzTSFR88M7dENFyf1WO6mfe0A96JCLkWNDBCS4jgLnyMWI2aXLm1npemQIXuVoFtQwgBy7Io7zXyC7TaJGZrqGgkAZJSiMial6NV8aKBUk5VrxJ9CNydz2AeHgC1KgDQruO8xxhwOi0SViYlrOuKbR0eHsaAUJQkvCaMVTBabX0813WV+oLOAwJikNj5cHuJn0fJuS1ruYYRUmnMnYXZ2Qm/NAvGY25EGZG3LAoWi6WPoCGGRizmUZcp45oq1STEjig1GFwKGjRXQgg4n8/i2aIW/j0EW7X9YE6MPbwIQt8f9wqoPV13utwJzUd7LgCcbbTcujBabdyAUrtQ2Yu6E4UQEVLs3kgGkKSYDpVk155hI8SY0bOFcGJdF6WUnkPGYm7LOuV+n/wmlovcCmpreHp8RN5WPD1+lCTVeQV3jzN05Z+AHyzKmMYoraLkDU8ffsB6WfH44QO2dcXl8cnICqfljPu7s1jnkYAExMASAhDVK4I1WXVm1JIRY8DD+R0CBeS6SvxnVIQEnM4nnN9/ha/+4m/w8O2v8f1f/zukuwec7+/ArWD78Hu0lhFJaabtx/FAjDmSuxmQeOcGMHDfN1xlA6jq8y13WNA2B7soS2TwACZBhvw7/cyT/lx+Lm8u9FMsnFeCNvrqFuUTIMiC/Tbu+WL4fAKShqFLJ1CIiOc7pCWB1gtwdwcqGyivwFbR1gqqGa0VcF3BLYN5BXNB09w+rRRRQliYVR0fbmHaE1WKkd2KqFuJigcChqU5AE4LoF64XdHgzl45+8V7UTwijN8Yiguru5/PU2imAGhYJAOBLCm11DEUGx1474mh5btg1qzR+BwzFVd5YcoJYUZW/jrIE/NQJlDAaOcI/Dc5hQx8OrrG32n9H/3o71dlxkv2Z87VGbS/2wyJMfMzTOq5s+N7fN/3YLZXOPRn3t0z9azPVQcDesVs4cIaoxXhoVodBjdB5bbSJATw4+WCy7ricnlSL/KqCguRBBvZSDWgNbS8iSzWMqgVBC6gVsAlo+aM7XJRIwHu/KPxp62uaEVyIJZS8bSuWLcN67ZhWzNKaT3puxn9mJzADLQGyQGjHp8EMcSIMQDUUBnD+4Ml9OgVbGb7xH5UnRLC+PYOknpGwr6He+3nY1e64sODtSqveTrxGMR1HT9ueMZjzOQ1GNbP5UuXZ40EnlFCyO8O6wEwPLZfM4+679te3dtwv0/0sMe0VYZjzV3Jcs/eYM4wK7GLo/5OaixomD+rnGfyakppijwhZXi1z9igGefS4bLcf3/k+TPWhJ3m+i+PcfgpjVU+ITSTLeD9u/7qtEj795frfb4cDczLgzWxdM/ec6uvNO3WN/fkT+jb7XKrD0MD9+l1vPa+zyJEObHHIUNimRiXJAlEryw6fftzP46BgVt9RyfH14L2+7G9VgJc338EwtkzH/eLD9+PnudIk+wVEf7l23/LfO3BtQ7w9+RbbQAqLBsWs4AsnbecnpbdJ/l7AMXWnmeeCT3gpjE6h/NMo769YmQ3DqSHzASC6gnR1JpLBAhL2qoHhA1uB4Hm50Bvg12fgqNT+86q8XPj+mjMn13rfvNj6a3G4YDGqkmQxVNDYpeapU6IEdxG6BdRsNDOkl/qITf/TTngqGM+x6jX8EtECJoYej8/+z3T5tsYZk/Jexr1SoSrdbajB6MDxvy1XxfjeVyuAwN+d230cScn/PDs1dCADvAf9dmPwzTP1teJNjXxIuY8CPu9zo9VCGJPH5lHAuM+XhKfeVrxxmTRECV6O5pAPsYAU9KNfgO1tiGcQOLTmmdUoKO9xeyi5uLX3nS1CVCtIbRrsJ8UPPBjwW4/tbVtEz72JMsjMJRd3Np079H4doXARC+iQA2hNzjV4Tp8RctHil6/Rjx9EtEUym4PQgDoyS5jiD0fhNGEZ6B7W/ofKz/WxwuDlrqnVeOuqOqKVUKff+yewajJwhqYN0SrFVxrn4eR20X6FmwJ6/lSy4ZtW7GuF2zrhryuvZ6RuyIg0oiXauMnvxOg1rrQ88nOLRPce0gDqGL1LDkhzu++xenhayz37xDTIiPFFVxFDSlzgpmmSc+7aWJm75HeRx19vclRzjgzdhxDv/PoDKXpnvHdoGvCyOB5zMf8OZXP4Sl/SoHo5/LTlS9Fp6+tZyiRv2ybR60fgV57Mj7qN+vZTcCImGCW0uSsKy2co4a7o2WR93qW/ZorQoloMSKEgkAVqEkT8BLQovLnCqY34QtJE+A2BkJT46M6QkcC42i0oJhgHn/rBfIYBMQE1lCOgaKEXfWKCBoKcCICmYc8DeWGP/dCVEUEaT3BPBFGuKRxfwC8IgKuX9N5bZ4beg4GCz1kIZlivxYYoZrEC8INCIc+P+Llb5N1zCfAgWP9dPBvfr77FeNs73VcFe2b+zT9+tx+OoYGe0VE79uOb5kVEbtzzj9Dr4fgHsydhI7tMoGIxm/CSljYsNZzk8DkDI3PVKvmKilmBCd5rFqtYDCSew7lkgHWUMHNckOwb1XlrWu52z5XNQwrRUOVVcmV0kxxYjxrf7jxYD3vhJeX+pI3Psx1x4lGxnUYnzKLUJ6vdHM4RQYY/F3v1UR347apOJn4EOuj12OAe0XFlzgXjvj9+ftn+PtX1Adc81u3ZOKfory1rXH5a+9z+Mgb5+lTxuH4Ho/B+GtfUeHbpnvc1teaKRuM/6e+BmTVNmCfJ9WvXV2/tsI9jtDl0ABYgCZr95juoH05fvb997fG5xgfHetD6Fif9eq6W/V92hr+pBwRry37jejTyw2h/bk77HrpyIvXf7m+/tjlz0/IvCpKkJboLJ3Emvru/h7JWW735KU0ACh5Pe858LouHAP2wNgg3lLH/v7jzzNI4UEuq8+/H7V39HmA+caItaPbX/UM9m7WIT2et3pE1FKUearT/R3IpyEk2CZL/XyQDdlcUCUER9N4exZ/m7pnBBqBmiWXU0c6Mgb4GLS2MBq1KZBWG1AYWDDdY8Bz0ZjyIQQFdMX9elkWBdZyZxbFvbYJM97UWrk1F+NPBZEQEdOCWipyLiBUgCsseWpz401EXeEQKIoLOiUQ3AHUGhiERnN4oJ5Yet0klEneBJBOCZJjoiBnsQBu3JBKwulOrOLu70Onk1IKolp75bzp2PP0W0r3ICKcz2LH7T0jZFoFDEwpdTrwc+MBaK+02jPGnokx2ss5T8oCExDYgaGsFoE1N7EeJmh+CE2YWMy7QEDFlBK4sXhI1IZShzt2IEKxfAshICbxEBCrQFkXpRQQDSN9r5wxLwtghFGyvtda+1jbmEhdQ5hOMYqCQRULfi36EmOUhNLJ3hOenp40/m1BaVVD1ABmp2i+EiFY0mJZ009PF4AZ0fKtsCgYUqQO5pqQG2PC6QQUFR6Tm7spbFgTZZjc5z19jq3Kq465LxRoonc/DntFjn1n/Wdm1JzRFLAnAlKIYFJPJ9s0YdsT92SRvu4QIlpDt3KjIDlAoILhUJTMMait7PfjnlhTFU7+efyY2PreKy/6HqtKCK8AHMoT24sSYgjiKUFhhJpzZyqR5C8BoImlCy6XS38GC1+RdB0gJJDm+YlEsie2hrxduifEtokFYOMG0nBZtWniaEo9p01rjJIr8rbihz/+M9bLBR//+EfJOaRrLSXxTJKXsOI9kbyGakopIsWIjRuguUyYG8omOWxaLQgAwqIWslhwun+H737zd7j/9lf4xV//OywP75HevZe9unxEqxkom4YFOYOJ+x7s2az9ac3h4EswGtoQNpzQ0WshslzpU93MgKlPPA2Rjv3UVKfnofqQ+d735+fyc/m5PFuUpxsC/87ApV94W/ZkXcC3ZZV5I3HY6rNXj31iANUEBkcCN1U4W39iEEbltACniJAz4noP6P6GrYJylXxStaDmC1rNKGVFqxm1rGIJXsQzIrSqYyJ8XFSDItvT9nBQ74uFQQqWLFryWbQYnKJZvCN6SCbLtxDGOzk+PpqS3IXMFJnRQjqZrOCAd+0Lc4TlbegKdrlgBsIth8SUC4LQvSncHPjfebgOwFuSAnqm7kIcuQ6q4sTT1ACg5I/hoTrg/Wu59ViOJXhFxNWvL8i+s2JhdJ/c77f78Vz/uDPUU8LyqS0nV2i4E0mKDlQGcm2opWBTmaHW2u+JIEQGci3IpWBdV1wuFzw+PmHbVkAtqk9R8ztYEnIA4AYqkrtQ3K0rAg/vCclzxT2nnJfDmRlZQ02WnFFzwWXLWLeCXCpK9+LXRBDEnVwaM6gBNUA9TkyhJ7yU8dtR72uoQxT1Wwspr2df01VQLJiSiWgO9BWI9FoLZWP0PijvVtnz6C8pI75keQkduoV9zHd/Xp+ew3L2MvKfT+Hd+xvu5GNlwPPXX//9ZYqv7/l5ZOaO7Rhlz3vkrXk0upb7fBJpw3asfieG99JzPLoFyzwbXzIrthIjwmk57vvu817R9Ryt3eRbcEtZNuZYvClunyXXfTPZ9G3lzYqI1ygEbm5MB/d9KeK81R96oa/7vhxN8NhU3rp5vWXB3r5dmvZ9Ylf1rb4MRvpzD4DrOdoxTVfXkYJ+cpr5uNZXsa07U4jursQKat9aaMd9mpqeBYobtPecZvdW/a+nJemMbULjMLyua1KaYTy//duFAMaUp8AYt32Pbo3V0aFsOSFMmJosxzuYvBfJMM+dAil2v2fUbE7JCQuVNIksG3NtcVIHo3SthHBz2o77SjsXNFMIGKgl4B8PYcIx9nKQHBzQDszsFirqUl4t/Eur4FZGrD/rj4GKcLRuoG0wIceaG+0Ep6DbK1agjGpzzG0LYo1TQfLuXM+Duq9f0YQ+mylPamsdkBz5CYx59vMwa8n9HE1eArOsd0B3prCYLdOFDiz12hjD1kYuC2tjAMJChAznCdEaWrCQWiPkU1IvA08XxggwAITjQ986NARxz2ChP9Muss9MX24f8kLXfh/o680LvyEixjb20BgRmoYpMuBT6W4+TEj3CNmDLBwUc5MEmBycXG7KE0KMDRR0DPW1Zyptb7A53Oc2gXtG/3y9DjDAorAGM4KbDz8OYoVyvFczsyTxtjXGlldEnn0Sj92+cmsfF2Fu3if3NDe8EnZ8zngwwI3NNB4YNL2ve1b2jM9Xz8uMHrrCwluYctgQrF291i92ln2mDAm7vBOW1HOcRxKyqGo4JwspJ/Rmex4Gr23HQmvg2lCyWCSaoF5KATEQg4KA0KSinRVw60Q7Yd4Otk5Th+IhZ1djcGTEJQEUEOIJy/1XuPvqO9y9/xbnu3cIy1lpTuOiM4/9yb2OC89/HZAPsQIM7t1NOmyzl3jXdr6PcycctM7uXOhtG58Krcbq+jKs9I3i+d+j315XbvFi//2V58bz5/Ka8imy41jyM19uv001Xh9hRzW+sj9jv9pftV8TV0pGYDg/AWN/JxbwnyVfBBEj8IIGQmCAawSHiEAVMVQgJlAtQAygmsE5gloBShLDm7JJWLvubab8nIXLN97tiG6JuiLCe+9xDOAwFBEhiMI8xDD4W1IZgMgpBWSszBvTFBWTIsLOShpAPYAe6pcRAPX4mM7Bzovbxz1/Tr0NY2KpvzulxkQYBB8Cg4Lb4yb6sbrmnBDDqw3jHuL+XF1G8pXR1Tf+5us5cnP1LEnvCf6qyWMe6pYyAh070X7RrbHxHzvE12XTzmsy9zC51UIZkZy/xBpCVfl+n+sOaCCWsEZEhKbZDSWIZOt8gb2gygDJW2UGIUNW6aAse3nCwkeNvBBmd+effzymyi0sy3nsIfMaE5lhyP2s8iWYhqGc8r9s9ESulonXHINtlLIjZeWnd/10MrLJUDz1efDCoGslxJEy4iU+4FV7PO0A1YN7vjQI/pr6nlNSWPkUPPRPrdT4sdu/Xf+c49CXMYy36GnIyaO8HjSfmzN6vu6LKOVHV0gXl2EXR5EZbI8KBLTmPfgwrZ1b5aXfX3qmZ+/l/s+NOvby+KfxtW9SRLxGCTF36l+Kl8Eo+77OhECvpVtf46ddy8ZiEAzoHchA50G+SKtvL8ZU3PpZfjeL3ru7O5zOJyynE2JKLhY4dYFabvMW1deH20saZgMsPXh+vWG9XWh+7t4rQebwPPQMmozNYGz1HTrHfXfQutkxYs19RwAogDAsyI/6eKR4sHcBJmsHtack1fXa6yJ04CpIKCCYUCIMicSYHUxYycUBlAkRllC26RGgVsxJ3MoFRDYLXRsKrVuZu1oaam6opaJmtWDRwSZgxMqvrbvw2mZvdBSgluxkGuuGkqsk/RvwlgJcFaDY1yMhIoYF6XRGzmrRv60o+QnbtvV2mVv3IBBrrghx3Y5I6QxA4r2jNRQqfd4DEWISr41k7uJRrMm3LSPkMEBzmBAlt9cmSWNDiDjd3UmS1pQktr4qHFISDX3ZZG62bROPiCV2i2jLFdEtjhidBmutCIgIcYCy+xA3KY2kf8I0N7Q2LOKNxnIeeSE6AE3DHd9bglvSN6sjpTStPZEzmiZkHlboOUts2MvlAmbGw8O9WLK1BqjVVPf0YJZQAmyeIDNoq8tSWZoBGlRuKJUlSSQHhMiIJPGNmRlBn83i8ffxcefp0RnJ7l8LadCY1e2fUGLs3hktM5iHcqqy5XMRgfp0ukOtBZenR7RWkfMGguZKkQUmfYoBp9MZzMBSzZsJXXj0TA/3edz0Oe6dBUjfgPq9U94a2H7f0MpQHqF/r5YikRCj7utm7E8+/8S8voVmXFsdHNkBFwY2uHjUJrjtTzevnDtURABDQaxrBQzkkieF1aw8Oz5PxhgP8OdIOWOKg/OyqDeI1GXPZ2dsB4RUSM5ZFAhC8wvO57ueK8XWfWWgWntoyGVFzRmXyyO29YK8XVBzhuXhGOOgIBHEkyyvG3Le8PHDH7FtKz5++CgeLLlgSQnnuzOgcZ7F5LGiEaE6z5Ogj2J97HNv5KX5RbhWICWc33+LuJyRHr7D/Vff4hf/6t/h/P5rvPvmOzRmrOtFLR6L5KGIZzQmtAo0s1S8KnsU0ASfvcWhnB/+2J+n2Ksdxjc2doP6RgXNwo9pRebxEmgGNXlPtD+Xn8vP5bDY6W0yne2zonD1imPu+/Bnt2m8LMauQcBuN7gBPDCP+PDWfwIQCIEDGmmY0RZBMQkQmwpCawi1ItSi3s5VFcpZP6uHRMvDO5gbaud76vTwTTuhtkXXMozjEeSlSbUpjHNY/+5eB1P4n1FX/1tf3jgHZMmexSNwFLuPRqJoFsv30QYU1Ke+nQ8LcA+Sjz722vtzXp/fDExnB5mIdgN4HVFpTdbYtUM+LwWwO0hG6a4zfuzczzfk5DeX/T0zSj3q7JO2K+HY+GYOE6TKeFaQr8u9ytPWhlIacqlYc5GcEdX44SDGVI3FUEKNj+Q9o9QNFnIpQNYM1PsmEUDcQE1D3ZqHMDMCEc7LCYSAVhm5ZJisuufLGgOlWkgoy8+n8iBoeHhjPFvlKt+zKLICF5DS3uD/1QgreIXZdWENW0lqXMQ63F1eIe51dLyBuK8HoK8g5eOM13Z4ZJ8uk/4bmG/kVXNyzVuwwDeDqldg6JBPjn7/ufy3Vjoa8vJlhH62X19/bPm/x/jsbPNeeB1f46pypK7bQIigjjPtjdOM75D8dEvH2Dy+cRQB5S0KvaNr5zUWbq45WfcvR2AZ99/Y/18or1ZEHB2+rznQjjai1957VM9Rn579ru+gz9ft778NguuG/onP8Hw57uNkF8NX53+/bwBlX27Tfe2BcOs6A/hiij3kxa2D1IMLR795DeFRuxNAxnB/8/T7Xtv40jM8p4w46te+mv3no/VjtGUD4AEGq3sISwqMTkqNPaM9x2k/UspMQF7bSVtsrIsDs8g8AUZIrd4GsyYSqyLIVE3wbCCKbsQBBLAlMdX6GquL8xhLsyq3JxxC4WyBbcwi7frtxwv+2ScgiWBu23o69aNpxo6u599cwjs4VBuyKl08c0r6jKNGeY8hgmNSr4ORZE9vknExgYoEmLfDyBI7hxgRoxxuouwR1U4pBUAFxYjIrXffxjDEAGJGlOzdHaDcKwk8UCvzO9fjx8PPSVf2hNCfWu6RBOMi+M9zOI0ZfJJcf9BDvSJuCIKsyRNdQitrYyT8HnTAYDSWpM4xBJCCnCHS8MzSBNl2H6v1FTRRebO62nj2EMxyaIyP5C3g7kGzX4fek6Sfk9hfp6tdlYAxJrDm06aq7uRgtEDdM2jQnwgxoYn1vAEwAIPrEPaIAGJGDVXpSIv6pg+rxtDrJh5AuTBaYz+cz/oBOOz3Oz8We5qScdPLdf36uju9AkCQ/BBDCruxf9NstTn6RLvFj85wmvXmUFKij6GBAKMpG3/omb0Xvh2A7f+2z/odO/qeFA0AUpLwFsEpIfzz9XlXptkANrt2hEJK07y6bsCAuZFMfuSV4DYSK9tYj3BCQhPruiJvG7Z1RSlZDXglwbiFYWqV+roy4RUkscBjiAIQgPvY9z7qdQ2yJpblhNNyxnL3Dul8j9NX3+L8/hukh3dIZ0sbblnuGeZ/0Nhy/Vi8c9woNM5nL+X3X3m+xn7Qr/0se5Z0WMRK/9hf5ftiIJOtjV0jR2zu5/Cn+3vfDA78XF4sR3zon6o8x+e+5vtPbedL3nurb53/BfqamfgiHt8x3Jnv/n22XwfXzH0dsoGd7Z7H76fxgYw71WNnjD9ryDwHggDuTOjexq2BKQrgGgooRAm9FJIYrMRF3tWbt7YC5oZgnqqqiCDsDAR60wNcJv+dnqWyRYeezJpAAwglCxyzq6PXZR6qwtdaEtDhPS11SAhKHRx772eoO9NdnywluGH/pHvrOJ6tBztZ1dgD11f306Eiwtc3fiT/5uZxbmvu2wFtuzPoSpYEJhlubh/H39td/pybunj02ajXaHs3Zrt2+32zSOSaN8l2L7N62c+9WEIbEXH3KOhin2NPuizoaLg1llxoJv91+RF9gREUGGTGsogfZioFBXPI5cGbOk/8dqDINNrpcoiGoWQGMYkhE5T34/H8SsmqoCDAKQ9MnlEpudPMGFNAXSdHXSQeFlfD369iN49DZrJngM3RTp4RGtjVyc9jgG/BY/z1z113hf9c/f76/f1Ll2sgeC63zuI/Bz5hLp/Sn+ee+/iasR8x9kMw05TsHDfHa4ok42ndigfcd+ewfdvbYvjKelu6Jc40PrCcq+v1+QQHqROGYte9hu95iZ6eWzO8UzRMuOazLc/3aG/ecNcon+QR8day34g+oQZcbyU/TjmatD2h3zxov3xvDr57qW1bIPSKa3+cYi2flgWnuzNOpzPSkiSWqQIInXNjF3ZGGYDXbLjXi2m4Sx2B8MDLgsqtz7fu328Ar9k09vX0w/hgAR9tSP7zVI9jBl96NmbugJK975P6TuBSCD1hakixM3bMcj9XiSG+adgNryQAJAa72D6JgsLA0BgXcAigoCyU37xZvBHM6tqDneIZIeBytDjmWlob3hOW38AYr86Ac4DEaB0hTmxcjIcTZrHzrtPYBoqIcUGMAuKVKjHXxSNC4osCrLFwEyp7C2eS9dASTucTgIYtrL1tidsv44UmSovzcgIYyCQhTi6XC+7u7xDjnQiLlSUJMQKeLk8ouWIrGTEl3N+blbp4CMS4gIiQQkLJRXIOtIpt27r3itHWSP4rsUllfBuCxg2UpUydnmyMlkXiHEb13LB8I+bx0tSzpxQXO1WLtzw3q4DB6I8cCj7EGwCXfLd2WmqtSUiYnPHx40cAwLt3DwghoDKjFqDkR6SU8O7hQazMl0WA1FpR6wiBxSzW0iFEJEiIgVaKWmkJLRqzYc9jHh0xJnDQEF48x5ZlE0LoWNjsgLtdp6ArUcDSKvKW0GrBFkjyuzADVBF0XEMUIIJrAyXCaTmjhqhgchUvptbQatX5ZIA3sJuLc7nDuRYsi+T6OZ/PCCFgIVGmPT099X1EhDF5rpyz1NO4W3l0TwVo3g9c79E+mXepDahtfN/kbgu11cfSQlXFOTkl16aKw9bXuiXLHMouAyzm8ZecLnGEkTARre13apfkGmOfiGBJQOZyQdh8g53i82DuKUaAQn9Gn0cjhIDzchZlohYbD7lOlFWmMGWWPA3WB/N8CCFiWU59nvfnl4ScE4+vbV2xbeLh0DSW8gD4RLm8LAsIhPIkyah///vfI68XXC4fhR9IEZQi4t0ZMQYsKaHkjFVDgYBlzwxpwXJacEoJrWQJvaUKoRTFiy6mBSBC0bH55qtvcH54j9Mvfot4/x7vfv07nB7e4+4Xv0AMAbWtaLWBagEjALT02NOBGiiwRGVjGsqBvgj3YVKMf7Hf4RQBQ9g/5BMZMKWFBRET4b2goQxaNDHZwi4p3ySgybDyHe3+FNzepwkZP5efy59jsbUzQEMLJeq82w5uuhLUeT7DDlrpPGSXUw6v2m07XrbAuIBBduTIbsHeQxYIzKiBEZq8mLO8lO/iCqCxxK7nAegWrmhwoVXlQoDFCpz8MxJUmSCN0o3xChQkAE4H7/svtvtNDz1ZmQJoVJUXsX3R7jFDGTkDJ6W99sksugeYL3y/eSO4Rnd9UBVGc3svAAnio8+7FxR2hVSWvQJb6RjNoANr3FkJMcJezg96DehK43ImD3lxX+8NGIOP+dAhpxrPsuuEv84Dgfu2bKwP2hZPAHuEAfQN5YLQbGkVpY5E0JZjEM2wRoPY97KwWB43TUbYVFukIwVw67KjjVsMhLvzInnaQkBao/ARyFe50KA9ro1R6kiobXnbbLRkz9D8YRaTqTIkJGro9Ga992C6KCICmtGDa7crb3ZPrqQ4xrkbiV1jBTJqrfO6ffw7jzzaGDO0q+OGHHOEAT4n87xUPL/6GuXEQQ34UlzT52Kj9vefb9kxvL18Tp9vnYLH190aHq+sPMLkeh1XC+Ol9p3Rkyn6+ny1vj/b3gQczycRifEpH2OGtQrvQQBqqkNObNeGi/vnekkJ4cvLa232jOiK5aM9/vB+4C3hrnx5s0fEn3s52pj2vz1XjjS23bKAjZJZiHNfX29zUPw4TF5o193pP7/0DC9uYoS53zcuon5dr3jfsrZjP9kCIQdcK2sZFUxcIkJKYoVtISOeISOCMH1Xw6qi+3gO+dZbItnTeUvityo0bv0NHDB77poZLN3f58dMn2YaA888jM2u1wvPYLAjPxlLC9NCxifceMbbL+vCAS0boKVu0GNuhrWyxAEv4FLQckYtpbu2GvAX0yKgngJrFJP0M2gC4ZCUg9SXzKJ6VLSujDAvi6aeF105qGPBELC3FHGR63PoFA1ieWJSof3jGEWlUwYAmq1M7BNILGlIX60VFHVzb7Vo7kDqzxNDAoWo/ZT1YQmvY60IKWmc+zG2RCTrJ0ZR4EXrF/cxqK0igoAoTLYcZg2ghloymBtKEs+JVtVlsCUFYhMYQFwSuDUUVSRUx4QP4sXsBdNHbQiHRttg8RAhGrkpLJGaWRvZwW2uipPCbUe3vphVnF1lAK7JPgNYHgvOFGmlFDAkyTNIlD22pTdmfX6C5OIWsLaxWCg3qLJU6b/WqB4owwrcKyBSlITJPrGV9VeeqznmhfV/c5G2cWR0SwWG9IK5P6sJ5jFKuC8BuxmxyHuIEsKgVUvurZtDEGE8xohGBElaDZh7NUPCv9RSwOphEFNETCq8MEtSLR8eTJ+NG4NpJKvvCqbAPRE8Axo2QYUqHtbctVZEC53EAlVYsDSjK2ZbV7JlkNKVJDEHkFJXnBIpYMsBiG5/YVM6HgjcCCAml2vBkzb39pld0rKpAgv/hM4G+JwnIAKp14YZqRkY498p+FBcQb0fCCktojhIlpya+wEjSpY4JQC3OeoKFwt7FCVpqEvMo7Rp5+dQVNVaehiPpn9XTeZORIiLjLnMecXl8oT1ckHNm1zHEuJAXuj7Y1AaiMH6GZAC4USEaNRIJHSIgMaEJUTEqHRPQfbQtOB09xWWu6+wvP8W6f49zvfvsJzvNBeQz7FDfQ9xp72j5N1X859Xl9navfVzr4COf7cnF3LZAQOdgGY+5xDE2Xdy4uc+n3e3bexWDNhPFab3gs9z1/w4MsjRwF3//laM4OWuej53z/1/bnmO1/+8e24BTV+y/KiATKffwW9Ya8brdd6S0MF2MxSisRBe7PfN55i+nsd9zwUdyRTWad5vKsr2yBkL2+7RmIAW+lZiQxAbaVx9UcKKQmOEM2VYcoik+xRPW+V0bnX5Zy6S48HlN/BykD9c7S8vX4FBFFW07KZWctbZd3auzYewigTjXf4f1+7P7KOPA9jvT3P929z9uR7f1sQHzlf1a68rGJXvu7L78vpccASx+8krBaadx/MjR8+zX/dHl/lh6YOl565dwHruEeDDofiV0GUMwxaUzyG9I5JjW0jqk+Yi0GUzCRMZ9J7GEm61D4J6EDVr0RmwVYuFpmMr4SGF70gxoFRHp/oo5Dtuf9I04JP8A5NHIecqM6E1eajgh26ag8FO2JwZB2GtmMlMAFkaGUn7pfcRj1j7rmd9vcxlMC/eW8zusKnxHZTpph1bZR2nvp5lPHZ739G+6qvH/PxXit0D7Ge3K7vPrzvHjnbxl+58FV+DeZh0Gx3vsOe8OhVurdAXenXUt1fdotfNF0s1L/MN85S+jsd46zUyxrfue/2Mj3rtvMeYFNtnDfds7G/s913JAwQxCuPuo7frFmvo6tYjN3gjy7lfO6VmD813+9nG9XT8Qy8WQWOssL0ignbPN/DDZyt+sbw5WfWfplxr6a80N1+IQZ7rGczXmBAeIIU0bl1094yvaP7qxfL5TzBqmdv2TOSOOTlYwxZfPMYxFgacCe5hoGLoxNitTU8npLsTlvMZ6XRCSAOokKrGbjswz7HQufkOkVsW/unGb31x8rzpeXqYw7zcnpCjDe6WEmL/ujXRNlaDicVVPdp9sP3n6wbEMnJwDRIexpQQwW9wNsYjcbLXrvbcEN3qybWrwDsU0AohIi4n6ygARlPtLaOh1QLUgrY9oa4XsT4vGVmVEel0hxgXnJazAEYKXiauQCnIrYI5iPUvIAnzuKG1DK4S65ObtCPgbUWrBaXmbl1uZ6HYugCtbN1w3iymAknM8goIIM8SQkcOALWGM6YzChvXjM2iJtcGAMRgriAURDQEKgBVlLpi3R5R8gUtr1jOJywxCUjaGs53C0JaZA0EQlgWgBOW0zswIpbTJiCfxtqvtYCWBcv9We7RXBIhRWADGheUEhDWgHAmGT9uaK2AQkOKjFKegMyIVMTauQkdJyIgJdx9fY/ICff1Htu24cMff+geAUbzrP0nklApRl1iLxMGSAwCHJCdc0VrwPJwUoBcLPWLWVH3PB5VjjpNWtuqJJNjR7NWBIQN2Dax1BYLJcsnQmgtKDg8rMQZwHI6gQGs24ZSCp4uK86NkR4eQESoEK+bdd3QFkZaFqQYkU6LAPg5oNaGrVRENESXQNzi9NurVknomxQErm1Y8sv10sd13XbnV9B9T0WKEERg8i6T+jlA1n5kYQooRXAQ9qBW8XSgGgAWYL9xBoTkJUnfEhEaYSHx+qAoa8KYelYFF2+1952J0SBhrHqcfkDBcAG2I3FXEE6KCGZEkvBerRQ5H5Ja9wex/qqqCMs5i2fDIvtZIgGfK5PzuJASe/4R6fN6WcGt9RwnpOA4gniEIGooMhJ3hgZoYnIR/IggCoggFpxRrUxtXwSpy716y4B5UkLZWBERkq6hNtnC2R6qojeZSD3zHD1klCkK9PfuCXE+IcbUd/uWJb43JWHlQkqIIeCcFjCAbRMre1MWxHQShpRCF+I56FpWxRRzBdeCumXUklHWC8p2QdmeUPOG9fKIkjcsy4IYIx7ev0OMEZd1RV5X/OGf/gHr5YLt6SO4NSQERApYVJEYCIimbCCgRQJF2VPuQsSZguzV3NAooIWAggDmgIdlwSlFLFGZ+/M3iKcH3H/9lzi9/xZ3v/lbLHcPeP/VVzJmTeawVQdAyMjBZngI+9MJ6ubOKa1oFmWncijE3yomxnve5jhGba+YrwXQm/ziXnr/ouWLV/gvoLxVuPpTj9GntP8yqPAvuVwFIzFWGWK13Lihce3JbmnR/EHdel/hNx+D54YscSVHvLaTfF3lTXFFkawOVGnoCYJ45xnoiUZoLc5yEwPEsxecve9jUpMHXDAMrvYA02E/CYchBm8WnnfXK09BJ4sJNna77ltepq8uykr6GkyJPZeDNujG1zsFxm0FxL4VHr/tbtnrRDqWBDdGrxkGf9nuEa/wFzrs+XWV5DvMHSewEEy+UQIUuDeDKKAbWDVGYEZS1L/FIF7GldXLhMXYC7GD+JECEgUsTD1/A7eCYDlKlO+pmjuiaWiyvFVooFdAwcgYGEsk8ELIp4TSij6Rrr8hIop8ozV08YgJrN76lmhbRCHZT1JLYATUIsYzcbCmut8or0Doxjesa4vYxpP6cxMBSb9JkqYFkayPDd0nggaKsieTbugHU2ZKN4LuO0QRVlPfH63f7DyRoBPrFDLW6j4szEQ7B98JbQ+DzWtMyPNv1ytV5FffixfKK7ePNxtgKHA+76wYC5iO+z+6dPTkr279qraXy24dH/ToJd5hj5F9eYOGL8m7qPTXhzloJAijwTZvvL0Qet4eJxumwBoSWyZ2ihKl2EdRw16LLhFTREpiWChKyxFJ4arVA4xSru09xmQI0IkNHeu5GgE7cvoebgbh7hq3ybG/6Y3lJ1FEPEdwb7Wk2rukHL3fuuetxSnC3Jd66AHDuMba7BOH6TNwe7l/eesfcv8+d8Xtz3z17WzJbLulaPElHqlZQMeY9CXW3HvNnm9k6CXmOT3qFbuxvTpc/Io+et6bi/TlsX/p3lkRcb03XX8/DvcjD4xr5YbvzOjT/jXGU4UJ5g4IHr/a8GjgAZgFS+wGUgWKWIqbIsI8FKp6AeSyoW4rmgK9VcFmopFwlPQFdQkNMSECSMtJgf086gYNd/HmE2iPnBP7sZlzVsizjHkLB8CRPcucp0DGP4xDxE2cbbXmCWLhhszqH3Chra4SHppCaRwIwpd5e51BE2KRIwdSJEuUK1bQpMl4mUc4lkkXqmu0KXDbY/0rh7+uK2KtWHIGSJM+N+4As4Vnem5fZrZtj/rcWtJqr0CwvBPWObMqtDBgfVy040dC8f599MGvuQEEHykSezJq7VOpIxZjfydHA+Nm9HA+usYsnJkHnn1yqaZW/425W/wbY2HJfa1f7ml0TpVuHYPdrwe6dff0zCQW42YBLyF3Qg9nZM8Uwghr1cA990fQXCEh6lrTuENiqcXgWhFKQc4CkrbWBGjXsQ4hdCVB0LA5/Ti0utpIZP7/Z+/PtiTJkSxB8BIAFlHb3SM8IjKjsqqrZ87peZn//5s5M/3SU5WVGYu7mamKMADqByICCLyIiKqpbREGdzVRZQFjX4gubQHipt+7YLB+dC0pMe/sS4dW61GztHVg7qW6iyJCcAAyF7GYCFyFEwkSABtkPrADyKjD1YVv5964Dm0ObOzXP2OcFLZD2jREHVBCbq2Ftqe6SycTREQVUPh15IOAxxi7pQQgFlW6lq3eTiCjTZYx/TaOnMXyYZ7P3Y2fufJTS6GYEqaUxEtIrfjw2284nR5wOp2Qc5a+heDGVOq0O6baetP1GEMUMMGdKWaNN4WIFEIz4EBMoJgwvXyD6e4Vjm/e4vDqDY7HF0jHYxsv69z6HBupHC9o8OusTza20yN5qUu81xadtHr0BObtedi9DlxczPVIev5rpFHRaPmdfrNBmz0mbZ/zQw5cp8Sflp7C31OTxj03OLCs53ZXApfK+NQ0MtkbNI7VdW08bu7KbRzZgsq58g6v/9RPP0ReCQsAWEHCLRprk4cO7O4xaZfnNfzzZeIVA315/rbPXU/3jGUsz+1hvog29sKlebg2mTK4vUlPKWvZJtdi93zrdBjeunRXeEziQv6xFe73C5UPynhXyl1/t/M3Dx9ozKzd246XavS8upKszmpdsjDMBRMa7Nx09wFmdc008hpC12exNM+qlRyXY6j0VqQmzKhwvB0Lj9jyDfHH0Orqa9wOIR75d4ajXMfxpPbZBTl2dA+8FlH7HN5ze2LkzW5IC564veyoKOmjZRmfr9P6HPHt2ttBK57Q8Uu95J17m1cn51DnRnbNsPfFE9LWhvdldiJk+73h+ZLOuDyTS/5lfHedZ+v7JS24h9kt23i5zM+T9qq5RoOsFQn6pUo7edC+bQhxyzdiFABRbeda52HlecMYAkHdXcDuHWb7XPSR9dBuhE3/qP7ZVpPbNtqep/G8Wq6VsdCnknbfiUXEp6RPZIi89YN/bBNPxtCuD4JrxMS3nOweqWaiCL/IRAhhwZgMREppwuFwRDxMiFNa+XHfSlvg42OYlWubZwDrH1nWLUKIIb9kvti25fPl73tCiGVbNokciM9rQHxPsoJHPvZD+yy5HXh20AGMmELfMgxw7UFrpU0VuWTM8xmn8wmn0z3K6YR6Ojf9X3E9pEF10yQCqWjAGmGaVGs5EJgzagZYfX8yqzuZqqCiAWOqrbb0y+mDrDKzgsylg4RBXBst96KMBWsAVokvQBBNGxlbHpkbo2m1PTlngE0rXjRQDPgvU0Ks3c99KQVMAamKVjuRmhgH53veBfnN6us/pIQDEY7qimWaJqSYQOriqgsi+hq3OZ41XocB5Obs5HQ6Sb2HA6Zpwt3hiBQizqdTe9fGFW6d+3r6mlTf8jE2KwdbUxbgFgCgViZ2qDTzZwPoQ3dTYWWYX/3lvrA94PN5IcTSr6J9d3d31+JFMDPu7sRtS84ZgQgFNPjJ9+NgFg9cBKzPOYOZm3DDNMNt7ux9iqKFaM/gmBQ/lt4nrYH74+XOfU7QCRsAYqnCGGJ7lJwRIJ9Wnmnyl1Kkv+paiECoJGu/lAxwPytYLRrq+Yy5isWCxXngWjGp9YH1b5om0R0N1N2qMaNmAgKjRBUAqXVOKHJGTNMExIBYZc4LyzgFkKPNnZUOa5wFOAuvklGyCQcjYiIEDohMCKzWH8woQWLSUGYVpkBBb6g7C9V0IaAxhSpccnHQ27oyIdRKMEzickhnEMzQ9d7vUx8kWs4cd1+KlGCIl+LPOttDXgghd/BB19wMAjBNB9lzytyyyFyEkTaXfsbAFxXmzDNKPuH0cI95lrgQOWfkecZ5nsX1HhjH4xHHwwGBgHk+4z/+/X/i/uM9QhbBcoxJ1lO2+BR93GwfmZZPCBGHw0GELCQxWEAR05QknkQEAjFigGj+TkeEwwvc/fxHHF+9w+s//gsOL1/j+OY1Qpra3ty6T5f3+Zdiij5r2mMyfqRPSt+yQOVrpU2w+ntMJHTdljDCgLuvycCtwLIr+ff4JhNQA7ae19bh1xQ/hnbt5Hn2vTLi1P3xE8/v6/n2+c4R6OvKP48ta7MNW0IF3AIIPn9q+PEnTuVT2mqKGswsjKz+cDXhAhqvRUobmnKa8BOMUirARfhWzgAXNAefjXasg6KPKVc8nM9C61VRojgcJrH4lWAjSrsQkmoqpySx93Lu7oNBQkc2mi50RTXjOb3Ck5F6wrabYpbFgfCCAqPVhC5kJkSl61o2J2CwcsXTqQlOhM71Ysl2xF3CaHoVDowdQdnVO1fuCOOHPgfRsoWf+PQPcHN9Uhp5+I2zZ4GfbT3/hNpvODu/vdTX67WzTYQQwzgxxF0ujFcsLT6mYThWfq2EUjJyEaUr5tS2SdMVWU4Br37pv7qmrvck2/8X+y3zvmFHxA4HdxU+ZYl8kiDi2qJ8Cvj7lDbYBllKnls7bqxrqc3V/26lDs9t0XVwAmN+Eu3Tz5WILi+i7Zeu/O0LB9CFEI6hHyTp4rYlpYQ0JUyHCWFK4rZjQwixd0Hdytzcul72Dthby9gTQlx5aaHHMAZvXWTVdWKbmBaben1ZkPnabGBmD7QqOLkAXj7wdA8+zQDXFgBaBBEikDBBxNBTCyTOXZPXrBJynnE+n+Tn9ADOWfy/ExrBRg7AFTAtIkQ5biImUA1gVNRKoHpuUlux0ujm8RIsWAURNcOCBwMGjHcQDjBhQFGQX4RlITCWp6MJVdo4FQukXNuY27jZJaEG/BqHYkbl2uqPWt84x07jGRjGEZBA1DGJYIHICMwqxDRV5DlLQG+WfWaWRimOxza7AydogFrrlwkDpkldTnEBV8bp4YRSKlIUQYUH4Ym6pj3cWmrBq7mqe5refwM1KZjwUl2rcJU4FtRd6VibG8AOB7wTVLup5/PBnf1+MGuGJUC7BB2JegBtn2yfwMU70BFdlWNgPru6/bgYs7/FpBsjYubYSw1F36f2Lq3Pq7Xg0zSUxnJEACjAQzpMCFmCVVcTZBCBWQQ4be/XgMABpYHgaJ8G9JOC8+fzWc8vsYKoap5QagZRQgPxbb1DrAlqqbJOEIHmOsKtg0D9/NB2UO39impxYS6fvLpSE1TArFbU3yVn1KpxJ4K4sQohiLtAQIQSjsi09VdRBz7JAnEDZpkyarxtuv7zdKEnCmCCALNy0ADTXrhsggi1jGhrvLVHGHQzyxShUlhU212ntdr1nAoUNMAot/gdtRQRss5n5PnUYkH04KVyS8R0QAI3cOvDh/c4PTzg44f3OJ9OOEZx2ZVSAFfSYNO2T/V8cvNO6HuYYhC3gCSWH5MKemOowkTHhBAj0os3SMdXOLz5GYdX7zC9eYN091JdWoXNc2Yr/UMAqgYKfAddeQqI+LnmSJbFLczlj/Rc6TnA6utg8fU0cjeu7FU+x3jfkHb7d0MRTx2bS3zNLeC75dvlpZe/mRYku1E0VHWz9KenHT3AJ+3Xa+9c40E93//cbbiVT/5c52V7Z4Fl3FrHY9u61d/WAOU5e5hnCz/NEusgCK0jNIlZthrfIAprxFVcEGk8v9BJKqUJuhCjlIJSK07q5hIsscoiRwh3MvLiMQSkILEiSiG0IOaOP2l8KRw97QjKRp8oAS8UpwgghrFw+xOw2IOQfIC2jRc8gPIBjjc2q2JyefoLW3tMMQmrk5Yv2VTtK3ksz5OGHW1gIUOxN5yDnXZsD1qrweMYL9vV3/tKd77SHY0m390Lz59u2adbZ88WHrbGSW/BV9dz8hiB65aA5DnTo9bectwuvGN8uvHlMS6VDYW/FEGluCJOKQnGAY8KkqHOm23aWlND3q1GMi9zjW3D/rj0/fZp8/EPYRExHHRYLJAdEOd56gXkEuhSIFrM+mc7UshfU7e/c/HvC8+7IALScZLgqmTa2ocDDscjDscjwhRBqQMr/v2t9BgtnNbEGw8iDwY/Nj32vTXT0g+by+uvkQfoGkvb/V1fCPJZhX5DsYBbalXADmhiruAs8RWqAkwlZ1eHI55YgdpmjWBWCmoNcXrAeRZhRGRC5ACELoQQMDSJgCpNoqmrAZspEpiLgJE1o9QH0dBm6UjJ4ms/5yxCiTorGCb1M0ubWns9YJoL8pwbsDVNFnjPTGgtcQP9Sy4tmHOt0Y0vgVDBoTYN71oLcplBuYPOgcytyJLYW1jjqBCiVNFKT9MBXEVjvYHEbL79gUpnUEyoRdZEShOmdEBKk8ytd2+kHQshIkY0qwiziJimSS1QpP4PH95jmg44qD/7aZqahN4CyzIAinG9d1kFWNbPIGbMoaqGDkxLKaNWIJK67HGCGBMwtPEiNM8xAvh7k8UuHOpN6Ge9AaJmhbEliLi7u0OMESdn+UHUXRdJQGdjyLugwZeBEJrlR2NglGAwzXhgIQyhbo4pQiFegdabgtmlaMT1iRWEH3gJLcMsRNIklkgIpFZPGh8FEmODqbb4HyWogAqs8SkYzck0WPxmZxEIdmFAxjxLv23fT5N816xpLNA8WHz9lwiwWAEJzl9bUG+QCLRHIF77WzroXSqBqrWnCwfERZgB5ow8F4TAqKR9LEXOJAXQJ4jbIg4BbMEKKEAC1Dv1AecPnIwJptDcznVrhp6vC3/h+tHvBhMim2DRWw4O5zqrsDJGOV+I+vmevaBMGHMZV1t34pjKgpkxpO1mhRWVXhLhQwWX0qzD5tMD5vNHse5S4YS4URJfwYfjCyR1wwhU/PWvf8GH9+/x69/+gpILprc/6dk/yZmdZ4QA7acEfLQYRsLfxu7GT93PpTAhIeGQAlKECJMDgw4TKB0xvf0F04t3ePH7P+P4+i0OP/8e6XBAwrgHPydT9yN97+nH2viRemoKOwCaIkADMK86afom0jVQaMk3LL/bokeEClBgks0awCuWUDvLV2Xi6eM2Orj4dPDp2vseQ7j8bufPtmjSx9R3S1v+0YSku8ArM4CqChLetVJ1QghVjgpGgwNF3fEyi2VD4IxaZwRU+SFWywCjZzv9LnxSRi4VH08nBf5YglJPCYhAhHORGQIOKSJPEYdDQi4zRFumKk3u3HKaQAJaNzk+dLFWqkbeq0ozyn6ifg5JCwBAYx4KPSku2v1agVpxkNJ7hEihuZKSohbrtBft5kPcTplyXbNov7IWV0LMpXDThBFYt+PWdJGmUx7/W6b7+HPiglfSrYLMzzd+ozDi0W9/1rZ9StJ7d/8r5ZFFSWvO80Lg2HGcUgDK5LxZdL7xKX2/OON7xfEgNt3OsmrL0+f2ZkHEJljyiEH5VKnfnvTtarkmfbxQ316ZF+top/e+NLEJKj4hXT04nkKjLN7hDaLK1y/9cGOi4FoMESkdME0Jh+MBSS0hJIDytp95f2FeS1vv9TY9nkjbKu8p63CLkJBL9nK94zvb7d5jBrYk0r09UPAUsODLojHbtYdrFauFnGdx2aTaH7XksdlKLBhTJn7j5f1SCuZZ/H/P80lcIEHd11ASQFLdiMQ0iT/zBrJpnAiCBt8SoohbH8ylj7hYKQaQsbNaUMsIZrOIwIJQG8fbxmstmHTHqxNSEEhc2KA6QYS3yDAA3dwiiYUJUBFiEO3l6MxxVShjAoom/MgzKqlmsgJ6XAsKAgi1EbFgaU/OpRGXIURM00H8mZbcBBceyDRg3AIo25jYd5XFhRXjhI8f3re8IHEnY5rLxmAyB0gxSsgrcLwl5NvUrnDzYOX6FELQOejMvxfgmdDA5/dz28vuAL/1277zwoqlcHT5A4gQrpj7mOpA0xjggzHnnFu95kJnns9tTQPCEBD3MbU9vhR02PPts6ULm6h/0dvrXK9tuadKUwJH2X8yfxB3aHpHlRARQ0XRdQB12UaQ/SrB52xNADmXVq+ZoOdZhFNJ45iQ9p0LwFxxPj2AQkDlScdqkiDaRdGesI7P0jTiyCwQgBoIc+Wm0Q9mtSwyKyYZpOqApVIrqBRMROAUW+yEEKPUEAjepRtUwaAJRUgsKogk0DKZWyOs7xUTeBIFDYBtlGhoYyJ+jlOzHLP+9rm1YAjyU4oJVEZLt1EQu1gzUBdcTHI2Q5lRqIBZBctcqp67M3Ke1SLi7NZUGdygHZIEhPzw4QPyfMKvf/0r7u8/IhAQUmgMv+3hELrFQ7caM4sQkuDwSSwgAnVBibUVTKB4QEgBh1c/I929xKuf/4jp5TvcvX2Hw4tXCIcJFCNqZr3vtq2olvO1TP9ooM+3kr6XcX1uJvdrgol7dX6bjPynt+um1x85DYMLkp13n9ruR/Mei99WbyvOx+7vjuKvKpevVmtklVGfbnsdIFKFFQMZN0t77Nq3TpD9P5b5CXvp2p64Ljxov91c9mPbtNeWr3mG7tV9y/NHtdvT4cyqYQchxwxPIREFSRyz2plfriDOEoSM9QdV6BKlJ4K6gZWfzivXKqKAKgQyiLrAovPeQtOBGClFTEmsNc3yoOchiPtd2ztuXAAEAspqq3hQkswhAVqX/bpjVRRzz8fx7p/jj51mnjewVtk3/XQh64FU2QQZT12HrctD3bw6Np6CFS4V5W5NT95T/mx9bGK3Jlw5BGm6fS4rcCqON1e+h+ntNu0R9Mo13HS7PmXObijvWr2PTRaXcOse227b5XaYwG6cTOx1T9tgmE8EV+h5ZD+GediRprEiVBHN6vTYgS932bfL4+TautVNu8+JVqtwyLP1/AnpO7GI2F+8m7kHYUA/Wp+zNYA16ZLOx7dJ8N+WbMwNJBMwiWGARkRKE47HI6ZpwnQUTe0YIxD75twD7j0xcLEVGyD+EoDZS3sX2lMPuq2+7B2ey7xb3y/f90KI5ffXCGgTQgzAfRHirLtiUpdCpaCcVRBRc9M7sSZKu0vjariWFpz6dHpolhGAECcCZKcGwqfpgJgmpEncdVGMGjdC1hOTEnx6Clpbc87IuSCXLBrPpcC0XAwMK7UH1t5iUraEECYkEoCwdj0rdvMkL6tGTVABjmQLMaGUihBkXKkW9befUcsMZnE5E9V3aAgddKfQCWCoIGI+nxFCwEFjZUjA6CLgIwIC+YDUjPN5xpS6u5LD4Yg8E8wmQUBKCSpu8QqmaWoazT6uxjRNqMw4fbxHzozfNI7EmzdvmkCiafKQaPZY/+QMMMHNZfC8rSOZiJXQwK/rJlhQwtfgZ+/+aMi3Uc7SyqAHLR6DOPfA0eMelXr6XmXwMHb+zAlqrVFqBc9zE0CYZnsuswrwCgiEKU0ACLHEYZx8v+zT2n4xLYZ67MNaEBGIEA4HgFlcKdUijFYpIGVmSslgMGKtoFpbMGrU2gQRNvYyTlKHB5ln9bELtb6RsQrgLG06n88qiDg27XgxRZdYFwEAyAVXlh0DsdRQi4kgsR/Mry8p+jJNE1gFb52RrcLw6VwJaMJIZUJMk4yHqOp3YUFbS6xMpwlH5Neg2mUxhrauvaBsHHeNX4LRhZMPPL28x9g4EXW7R9QFX8s5trYSjTFWjNhlAFkFGImStsXcv+XREiLPyLMIIebzA/J8gp2uVp/FqUiBAFT85//6FR/e/4b//I//wHx+wN1RhM+dpQUAJ4RQQZJMr/Q/xaBxIGJTboghIhIhhbYMEOIRaTri5bs/4vDqHd7+8d8wvXyLFz/9HvF4RDgchWiezyJMdoT65hj/SF8sfS9CiB/pRxpSx+fag29BuLNXk4GGABRIkKeb+RsAseCt7dd2fI+A8pK+NgUNy7s5Dk8Zmm/6yBjRm+W4/LOkxwonriXjwboSXBdG2IiTorTywd16Qnx/gjQ2BJdZeVjhNCPJD5M5UjJXqcJTFhbXk1XbUE1IEYx+MP6EESIhl4LDYcJ0jkiRUBZdVk4XppOhBhFqS8Pj9tO8fRRU/YYcPci0Kh/Q8oKvcyF4IFUCpNFfQ6ttY9lW8OCOqgLoEfs+cWM+Dsp7fPFfYB8Skbpz/YQy7Bc/Hk4I0YURvt5PqlLLeP7Bf9z59zQJzqeesaaYtVVW/3vZNv/3ZVD/BlGZ7knBdlKU2A8xBpGh8ugOuhbBxEopSGoNb21dKmau+3nLPBtAu921hkNeKEfOw+dZT88iiLgsAXvetEkI7S4sBbWutO+aFPCxy38s76mb58aF9Ijv193bK2PNtLNKxwxImSYJdns4HJsbBnMfAbql1/uE3BaIvwX+r/u3fVgthQF7B9qecONSW3x7mLG+PS7Ue+lwvaZRshqjphhiIKS6YlIXPjln8f99nlGLBB41sBQAKoIC893MFa3siqLxGTy4GdX9UgwTYpicIEKAvqjg7FIoWGsRdy+1qNa508TNs1gMlG6JIP3gFizYa+T78fCEl7k9CSE2l1CWr9aKgtIIUVQ5VK24Nn4AmIO6QPI/Ao7aOFqcDSL0AGXOEqKvK25zUsEoOauAQ/zAe6ASpAApUXOXNKWudW8Eq41BVtBcrE7E8uF4POL+4UFAYA3SfDgetaypafQzMx4eHhCjBYwNLQCvzV+PIaGCnD5Yw5onQIVXPXAzH4+AllkrY55LAwo9yB9MI97WPKEJBOwCBtBcIAFOa8ABvSZwMC1uH8PBB200QUllaWuOuVk4hDCCsHL+idWL35NVhVdiGUC6BtQlDrpQhOQlZRT8fhg/fbuWZtyE7TPEPn2sDG8JA2OASFxoEckerRpLBCSa86KRTsKYqUWErX07J6D3gNYq06+fc84oakEVQmj+MBHkQrB4JQzGlCZMSSymDGzXkkAk5qtmhr8865Z97euOEaKcUaVKLBQUnTvT7i8FhQhlFgEiiBB0rYQYEJOcYyFGFSBEx9R1oZe0RQ9dCm1crH1LAdP42YWVlsZ5VrpB1/xSYLZM8p2MrO0hmyHT1rN1m9U1X57PcmYxo+QZ8/msQoizCCmqCnlIaKhAaBqA9x8/Yj6f8Ne//AUf3v8G5ooUI6Y0tXoELFCrNd2DOvlgEXvLGEcvmBEBRISABoEYcToipgkv3v2C44s3ePvLf8Xx9Tu8/On3SHcvMR0PoBQRinL61uad+3P/7v7nA5I+Z3oKD/DlBRb79Pm3vB5uoRl9vuXz5wBOn3N8Hl/W864To0th9y36OUye1tl8b//vW7+7mhxdetPzIQ9to43u/SFt4C5LZamW9crf60JvTeT+/bR065ly+9lzGSt4Wpla8hfEUZ4j7c33/jqQtHXnmvChKu9Qqrr1NCUqtexv7l3Bpn2n8SBEIGHx68ziU1w8VZUEtNoAjDQ2mNX1KmBKINJWNEvOoMxNBWNKCZNZRTh+AfACAXJ19TPGMjVhAll+ox3HI0eap+8SwSQPJpsgpqE833Y0KQg1YYQokek8+Uqov2vlE0GUdBa87LW16e+eth6YoYPo3t84G66dlX7dXM65qGuBDd66vzbOQji84FPThZHYzr+YJ1/SVp+27n9Lt2Kj19t067iOyLc/K669/5zn4R7dv35+qU7Z6W0Xba4TS9Jv29+Gp0zTQb0uiFKfuRs25TKu5inCuf9dCg88FuP/9s3cbLuWtchgglITjG0W0LpM/Uj7hPm5WRDxXITr4y/n9tvq/WtCCHtttSSutGXr+435Wpe7eG7WA5+Wrr1//cK/WsPmplkQCvopPuiTWEFMB0yHYwugaxcUD2+sU5c+rttwTQhxex/2GYVrh+8WULhs0/JyIwXwlkDRNebk0iVxKQ2gJbP6DjfXTKo1y0UDPxeUWfx/5/NZNL3zWduqQV0pKsGjGsXwmuPdIqEJIoJo8gtwPYFoQoiiKRwPIogwLXHQqDXfLBxUGJHnGVmBsJxnlFliQzQ3TFWBxGqCCO4E0salJkBfVGGEBi/VPH1+1OVONSDcn98K+skLrr1dGCEAeMZ8PvXAzXBBVwOh+wmlNgYE8dFPXJFVyDG4LVHAnkldwYCQc0ZU8DOEgMPhACNqbU4sqGxSzf80TQARTjrf57PM9+F4RAgBU0oopeD08NCA/D3hg31nFhbiYma9rrtHFiHsiwkiqjAKMSXUYFoAY8DmJogYV3kDX23teGGCzbnFafD++n2MDFmvMn4WAMqDusyjICKliBin9l2zyghmntw14VnnoFJt8251WfkiiOjuhpb72NwbjWfddVDDaHsbO1sfq/yOCIoxoBKQkFACIan1QwWjxoIYQ7ME6eOUAe6xQoaz0KabgPM8g0j2d4wRx3CUuAVBfNrOOYtQsxTwoeJ4OABsrrlIrJGMCEoJsZXfx8iD/F6o1PrPKiTIdubkYf2ULJZDJc+6l6X+nLMITmuVT66IlBRM1zl3a6vFwSAlxGjNqPn2euHJMh7Eckz9MjFBm42BFzyNd0W/U7sAQd1IUUAKEbVWnPK5nVsERoQIJ+b5hPl8xnw6g3kGNH6H0E9dEJFixN9PD3j//j3+8pf/xMf3v+HlISHFiIPuwVyNmNXzWM8VW4tcVUsxBCQXI0Nc/BES0Pw6p8MB6fgCL979ES/e/B5vf/lvuHvzDod3bxAPByAqU67nOGgU9gG33anPAc5+L2mrn18a9PoaINua1gKeB+68vc6vkS7N95de89/EHuP17WpY5Kp5BvDRNif3OfuzV/Zj67xlDa4xDDuvx3KafQUv/t6rhzf46C+6BjYmFGvsZpve+vp716fHzPtznzvXhAuPyb+7rqH3eDXXkVV5KxEyNC10BeVN0ECsoZtZLf9LFt6jiKDCeKVFTcCwejtN5RWtjKeLJG5rDXcrpeIwdWHEmQCLZUGLulgtNsRVq9WF4XciURYyN1K+pWj0obVIPi0Ct+eCraxOJ/YfX1+TOwDNKlrK7+7WGELXb9G2yzHbSx6j87SrT1dX1RPOi36MjXU+dh23sr4BeuUxeZ6KK31Kul7HthBiibc+Be+7+WxcH/ybz6/3xc4JrHHhzXU+7hnjXVMSwYO53F3u1VLEM0dwgggmHvK0eravXzQp54W+DO2Dwxi4nzirt25ce7ekL+Ka6Smb/6llP2ddW8IHSXb47ly0u998b8mAd7uAAqbpoNrWd4gpISTRaOU2HJ/O9OwJDG5u9cYauLXMrfe2gKLt/DzU/TmYFN+WQVtWY0KIBURpoH0pBVzE3ZEFgPbxF0i1SA28gkr6K48XRFTN5aB+0gMEnE7TBKIIUGzBscwlibVXQ2oJQQVGzXMLiprnE+bzvQoiTto+DUhdnWuppplu4x6akMGDrwJQYnCVExSEE+36jFq1bQ3k60Fv3UBDboD+yM5zdSiDRsyqUMXWvoGkA5HGFRJAlhH1UmnuURx93QDHFmdinHcDkyWQUW19l7gdMx4eHhRM7wGURVBVgMzIJSMhYUoJMUSUo2ixn04nzBo3JKXUgjubS6MYowjaWkOr+nDv486xtwWklysz5nmWPCk1Itk0iDzAuiJqyS7F0UWTCUjsfeuvCUxszcoYC4h7OBwGcLiByW4d5JJxzjNAaPkpBJCtPxAK0OpqwgMwSs2gGlsshZQiaqUmKJF9QG2shOAHAHaWPwsN/8Xc48I5pEblnanReBARUcouKnRxbxAgmk4s1gs2h7FUcY+mAonAQQSBiuCYBYicd2hBxptbpApQyOIDU9cqmHG8OzRzeyLTzhdBXwgBQddq0H6YBpqtiWUsFG9t1c9CYaIk7grjXO+BArHOYDk3SAk/A56KznMpBamdMwmVGDF0EkmsoIQwZLdHSeM5RI7DM6JxXXdBadGzdC00amtSLa9MINRn7pJWmglol6eZnntFLCFEED2LNQRXzPMZ59O9nEUojT2X805jzoQIrhXnnPHb3/+O3379FVwyUgg4Hg6YNM6FCYViDJimqe1BAtz+FYuXqblj0mCKQVxHEYAQDwjThOObn3F8/RPe/uG/4OW7P+DFT79gunsJSlGEtcrc18Ir0Kv1foMeeDIj8yP9SP+QibANxv6DJQ88K4PHBmzqXb4pkPinTUsAd++7S4kelfv50laNn9qKW/fJPj7w6WV/nfTcOM6gnGZKLywWB0Ut4Esp4ppJaSCljuAVwjrPW9TKuzQ+l50SCrsfAH16VKFN3BEFIAbEIFakMYgSRwyEFIV/E0Wb0K04o9B9gPE2nZ4ZFI+hoo/2WPMSMAWxuIhmNeteFP7NlKbMYkLo9hHIlTJNR/vSXNlKayuOF1glYWXRT2GhWPOUtcAyBl9SQL8UnDyK1ttr5mfYqp5H2GujFzBdKufbTNuDtuzvtTna6t+1PneOpuO6vAnUXtozDme2vBsCAc+b9XbpfUAEYoCTMGppkn2dcwFI+C/SvWciTbXpkqDzMYBJMQmunechJzxQbJrVLR0ajuTbstPndhjIn2EfBH/SPOylZxFEPPfltCgdHtpffn9tEd/imulqWmRvB/6FchgQCf43dCg8rt8G9NnvAuhO0wFpmjAdjuJWQ13B2FUvVoLXF+7WOePn6bHCCJ+/t9nqW5T1BEmRJ5q2JJ693nU/Bg3imyWu6/q32tM1thm1cLMy4FrElVGpTcPZ/7ADt0gRdvkIeoCNVAkRIEJcJdcoNNdMoiru/Pc7tyPC4/W6mCtqVvdQ55MKIk4tQKoISfLAHHoA1o+fWT54bXIB8kZf7IHE152MVXcv1f2t98DX0shhpBe/M0gl0s0cGBpIGy6OgLlnIjm/BMQVMNoIOBMIeRK5g85tYoaxCFp2rQHMaRiXUgpOJxHmvHr1qgkjaq0St0AtOziIQBEM1HLEeZ5xf3/f2mTCBwP1p0msW8g0ghbax971DBjavopcC1BFMEFEOLZ523ZLs61tAwX6S9Nat++WwjgDTVtb4MBxXRtLy4MYIwqAOs8SjD3npq1g5ZS2lnmjrWY9wygFg2CMyAQlswDwMHAX7nsDncVSZtSYV0txAhhj3IdhhQ57Q12ERZVIUBBrhFraUu6MGLX5SDGBAwMQSxkqETnPwqTVvgcBoNSC4IQRbQwskLLGJQCbsEC0vKbjQSyM1CphnjMs7kpMERFAYA0iTYSqLp3E1VWvf+nqyOZKhI09cDjXiqyBw0OMnQJtcRc0LghJcMCYxv0UI9BlQ3p+VdmDYHaB6VXggL4fLIaGzc+4pqkJIpbEq/1UdXHlBXDrMuCeyU/bW9yfA+JGrpTSXDOxusUTd31nnM8nCKNPMKGW1TVN4kbr/sNHzKcTPr5/j/e//h0oBTEQjtNBBG9ZXNSFSZh470KNXT9CiOrKyWJoKBNOhMByw4SQEKcjDq/e4cW7X/Dqd3/C65/+iOnVO4TDAZVmAKWteVZBhFlI+HH3DN7evfvcIMuP9OXS51T8uLXu7zV9zbH7Wonh+I92RrsvR7jyy7Xryhx8yvd+mfps2/w2sKJ722NeZLsyTp6w5uFSup6eYU1eq+p6U5YZLgOE43uPOxsMV3jq+nsqb/ml0jUe1ujoyuaaySwjWIQR+n0fnzpYzpv1qNA5ufHC1dWzQIIaiIdGk1WAR+tVU5YwQURRmrR95xRigJE+a08ZjVYBGATBTYw/jWI43JTU/C5kof6Vl1Yhg/GR3BWaLAIFKT1F6KDkVmptXuAhrOUbUdnoJlcUuZ9baSfDiAhjbJnlrOy+fwM4vdcOf8+NeS7ff4Rt//+Ex7tmumV/elp173v53G6t9ee5zoCn0Af7dcvKWo7Dsr9bfy/Lfkr//KnKbc0vytkplrh7t7Eylk3Y4uVgXOFwDRIiAUBRnhPiUhiltcswOVOsqyw8FYWEgIJK1K3/F+3p+9pvVm3bsHM3xsjmxo/TjYKIT1lz30mw6qcn5t219cS01mL8x0tGDBmwHCQGREo4HI+iCZ+mdnlb4vZmv2yAxx1it142ewek4tatMbb9BAgeLyA5h/bEJr09ewDgMs+SeNwivD4lrYUP3cWMWEQYYVaan8yipqoGEhpIb8s4mnlnSHLw1QJGRfPMxOa2iEDwga+CukYyQZTMvGiOiwZLKEpwQX1usoB/5/M9Sj5jfvigfslPKPmMXHpsCKHcTOvamaWSmMlOacI0HTGloNrn3bQtBCClCSkmteCIMHDNu5zhNoZSDwECupKAwxR7oOkQqbndaWNgWi/sDnBy65NUww5CRIu7qz5mlsTtlbqqYgkMHgiIDRAMCpKfRTPHNHhCd1GU0oSUciPCzQURBUKaItTRlBDrtWvoW0yI8+mEXApmjSURgmg0C/HOoBhUYEOoqLAAulJ3apo83oqCT6I9ZLEBzhqkm3TdRQOYa0WltUBZPgMiBVQlumvpgKYXRpi2vAmfjscjALQ4FU1AtLCmsOd5nuUzZ+QY23tNsLBx3nTNA9Va17ZMU1JAOLTxqbWi5O5iZ2tP72mCEGnQZ+pWDZZr5WbKhF7uXTJBg5ZtY01QoZGuStJ1HEiOSlHaUEKKe1tDzcP5Y/u0lAoU098AzvMZlKXdU0p4+fIlCECZ5TyS4NZSbkwJx7s7pMOEiQ7IemaHIHEE+jhRi0EB6lYRZoVj42Brdz4f5AyIURlbs2jQdQ27Fqi7BagVsRSkVFFjj+8hwqLaBAUxiSC+BYwGQJXa+SB5w3BHDutaA3ablZmspYpaIXE63Dpp6yCYRpz/xgRQfY2ynqG2T81toAjFirhyKxl5Pom1FKr6QRaHTQwWt0nqloCY8fDxAz68/w3z6R5cM17cHWUvq0DBhNFmiTUdDiAGznwWioAlePzxcGiunLTBzQdzjAkxJBze/oTDqzd49cu/4uXPf8Tx3c9Ir1+DUpRzVe8p4Y+pjb/f235PXVQa+ScCYX+k7z/t3RP/HOkZuLmBVh8BD7P6k686+GB3wHZxl/mDbyldb+ZGBtftLcU/KXf9TL54Xu7766fOG/9IT08D77r4FGUWodVyVqU5tao0150UoNYOXbluzgXnXHDOs7gB5QwLRu0VO5b71YQGQSM/B0qYQsAURWEiKs8ZKIgWspK43ULfWQmootOgqASv9Ecar60r00QipMBCZ5m7YaM3UTVuhrSV27/mFs2AQxHMdBSzQezSBu6A/96O9Lyrta27Gh5dil6jpza/597uRi9/gb10Afb/7HVfS8txukWoY+vq1jK/ZLpct7R76w65dKcsafhb+7fKp/f5JV57vwySWCzWiwtCCPkMA7a4diMufAsngBBQimBT8zy7fWr4AunWCU35O7izDCZg1c+gJvFcRWzrlYSl8is7YjEsW8PUShjOmqenJ8WI+JSF/rml9svF9ZSDrm2EneerYf+Evnyucbh2WdxWBmDAtQkfpmlqQYC7CA7oV+S2EGJf86YfNFsE/S1St6GOtmlJd/v2nBl4sS7zcetlBD72nj+eUdkXtGxokdQeP6GbqKplhAXuYgu4a30X8MsAZMQkJEsQia1p8AMKUlJQ//hRgTUD10ZGrnIFqeujWkw0ZYIIcbWUzw8oZVaLiDNKPqOUGbUFxDbBAC9OQdVaiQkxThIcNYmrot4GydfiQ1B0UmCoLz4dj8pq3uYItMU8gjrw59eL12Y2YYlcsuPeY+rWEMwQrXPqQguQuroZgmHrTxsDIUZzZgn82rS+uyDCAPhZNfsN/JeY13EIXmygOYXuPsVcOD2cOgBvnxQIsRQFhgNKrj0AM7PEr7D9RGjg8DzP4MKtbot1QQp4BhLSeWuPtLGGasA3MFzqtv76Pvng1IfDQQDY0i1gQGigtp9k66esj87Y2LiaRcdWaswGM4oSOEkJ7uCAWQJQUYRdqNW9uz4rZEX18lmBWqilCRZ52vgNrIk716gHx2rCiBqjwEgAAQAASURBVBBA7IKEazkE8grxjXgL1AMnl0II3GMXQIV5IUSpv8o82biFGW2NkZaXMbdg7XkuLbYJCGr1IkA6Hez8UIbKBIbav8Yg1So/uvdijAAz0jShhCAWUbUCnLvQlkX7zqiEYHuUFcCvDE61CT1sPFsQdgAhOkusUpTgLDpvdlasySxzzwVEzRtAZPUXGRfnisrM/bsQYs1IexEV1zLsi1kFsHYvlFpQyow5n2XCtNwQAXM8F6PEfgjEIK44n+7x8cN7lPkM1ILDYWoBpn1bogoEzSVXyCqo5oAYIiYtd1JBRBOKESGmA+J0wOHlGxzf/A53b3+Hu7e/x/TqNcLdUc4AcDsjSc+efg2NZ8kPIcQ6fWuM6uduzy3l79Fbn1LmlRKeXMYtYMVzp2vj8iXbswXe3Jrs3N7P4OoZ/9ms++Z6H/Httd58yTNr2VthrWiNTiz5NJe/Z3msW5TLIMctZY3cw6XC1vmHpiz/ovGF1Xt8qbS9SrbH8Fr6EuvhOff3Fg/rLZe7pXpFLj1odWChTEIQy0kfu1BcqxbMpSBnsWwGhN+8JIQAjB9WjpYICeqayStikNclXpw/+swswbWYRY5eF4yXNLqOgKSumUAdJ2TINvOihlaa8ZWoje9ybO7AP+mgY3zg/lzBWaN1rqd9V2evln2LwocfLaP5DKrZzLmxrgcesTd4t7YOvm7jjo/dOr28G/K0Oi5jnp72uG2f7eXrC2CvnGv42l7+x+z//bxu7l2eW2j0NdB/W3vGfNTvL+zfR9uYo9tcWG2Zddt8cGmMmJCMAQAwYhW8LSUZG1Mckz73uvVUER67zYmca2wKa7xwyRZM2borUl4dN170rh9Au+k57obvwCLCwMyv8TawOuGXG/0rMnWfM7ECNNMk7l0OhyOiCiOaixM02GOxdvvFtCWI6BLdAKFp94QVY7p0CI0Exij1vMT8PnYTDRf0qu7nIQiXB9ie1ogn6Ew7xAC2USChoDaJ4AGQgMEG2BERWIFniQ3WD0po/AQRPhCAABcQBAxCyQWFSwfPyeaTAIb4Hq/QsipKPqHWjDKfUcs8WgSIce5qz8qYi3Z0UK37w+GIEIEQ/NqSdiYPVMPcsPhYEzZOXYDA8GuQYT77G7jm/JkL7aflsoy9g4bRzYVVmEAqAKhAnrO6dBFhkFmvLJk2czPFkCC7eT5jihE8iaVHjP34nqYE4EUj6E0gcTgexPWOChpyzqiVMceMFLv28ps3b/BwOuE0nwGgxXWIMbZ9HtyYAmguvggEjtwCRptLlpyz+DpURmOeZ9QYcVThR4xRg4HbmI1Mgq1NbwINCJBvdXlw2OI+mFXG8nmggKJ+FT2B1dqiZeeccTqdmv/XVncdBRiWmMd1kzUOSW+/rF2zXDIhh5/n9VnJW1W176sCKnYOGMAPEiGiD8Tt+2p5zTLFvg/uPPGBve0eIGhMk1oRYlBrGxfHhRmsZ5UJJu7v71tbTcM/EDVTeWlfxTyfwGCkcxIXSm1Q0a2WFneM9c1rbS0FOkSEw/Eo62UWa6GTuq/LpbR5M2arlipWIdo3OyvMxZkJsMyCh1Q7zs5oEECVmoVFgbkL23ILxEObl+d5LgW5FrUQsKAPIqxoh5Vbv/qXWKWAUc6zW0e67+0MLAXn8wlcM2oVV2SHaZK+sVhxBIpIU8IUIx4+/IbTwz0+fvgNp4cPCMQ4JmHSg+5Tqb5bAKUkcWgIAJvLrpDb/SNrdBTcEoDjq1e4e/cT3vzyX/Dy5z/hxS9/xuHNz8BhQqECcNZ4Jba+pepZuo+0ggmWY9TXzvIM+J7T9936r5WMDv2R/rmTo6O/0nr4plfhsnGfAHw/WhhxubD1M1/2kl74hKp4+O2WkrzKxPX0z3J+L2m0kaf1lpuqMFFUuS5n8ZMeAK4EOHed3h3TPGec5hmn8xmkwaOr8sWN/+M6uGsiMAJxszQ/hoAUAqZkihjqPhLCAhgdX4sqrABiHR8JVJ1iD9CUg0DqLlS526UAIAQNUq00lHJVPcOIp7byfVpiEx2D58YXDEWSKuBoXns3OAEEaC2MWEyolP0oYURv/2PW/ea50SGfz5c+Q9mfQm92/Ox7S9Lu5R3w2DthVyi2I2Qx3qJS53n36t7HBReCiE1hBRoP7u+mcU+aUi4JL8dysnAVSwauophaSnbvqQBFLftb/JhaQJVRyXhHsYAwBdUWQ8JhNg2/dv+uuunGkyhcWWqXhE63z+mjLCLWWkPLyRgb2ISwhOH3p6S9RXaLxG4A+NAPwL0zbFGTyzEu0j1hRG+qA9ZoMfVPHIhlm1eX0WMKW24mK9MBOSEI8JvSpMGBo2p92gsjiQbDSdpFv27lpctq70C6JoSABxaG3vj69+bP933d3uGdpTaE62cTHn4ioe7bOrSFfX1de3cURphlRNf6bUISkkOJINquApKpSyYA4odetHPH92wPyAEq2q19vCQeQIatdwHLoFrF6oqlsgYWZXA9j1YbCtq3QVTibRxram5MBCAWoRiFCgpeiqyuk5yv/k5/dYGEtMOsFTzRNrrN6bWbZnjohNpC4NDnrwOAjRRVYhukPvbBIogARFunLR67uKwscwmTMc9nYEqiQZNoEMCEEJESNw1+c0E1HRKAHkejKABbSmlrzVwZMXOznvD+VkFC+E/oxLRnAmIIKOi++33gaGbGrDE/ilppQAURRvQa8++ZFE8gDCbCGH1M2o8XMpngwPoD17Y96tfqa9pV2lb/frMqQt+nXgBpoH0tVbQRtG0pifCuhCA+bheCiD2Cil0e41yaEEIFEUN7CMIwoLutYltXuiz9nFegu6py+UeBCDD4mqwFOtn6VYBZMDHp/jH3WUH3OaABCKurB+33UgtCyeIuyLsjYm6ukqD9k+3V76flOljMKlKawJWbj8+Zwsq1GDPLnca6tpgA3atWvsQ/GZloriwWT6zaXXqesDtL2nkRlhoy2BzvpgmoTLj2QmJysJ6JytkS93lYjlvOs7bXBIHZre8sf6vVRNC9aow/2TmrZ+2cMx4e7nFWC7YAcdUW3LgbUwvS+EHqekruGmHmC1jfscVdAehZLT1CurvD3Zu3ePnuZ7x+9wum1++QXr4CB0aFWLSQEtiexqy2PmHWIfvJj3mfjyVt+2XSkj4cv3zmOjbSlxbAbNPrz9PRfoeval3mXP2+fOfW9dDz7dX1/OkaA35L+tzr/HOW/9Sy7X6WP/zzIdOTZ3C8tX26vMfWb3y5M+jR595evsVzxv7ZQm6jXqq10dI7mTb59sceZ1e7vdffTyx2Iz+tDqHFn4+Yq1vPraemW95vZOdybQw8rLOA4C6IKLU0N6xm7d9qDEEtIvq7XRihFhGlIKggAi6GhNXj6XagW2QSSVDqpMKIaPS00V1Dux39pnRPIOoGxUZ7Mzdeloi6LwGHOzTcHwCTt+FHo+uHPWZ7Y4FlLHnHxkM3OmOclxXeoA1ZAa2t2n36ag/X2cXAGt801nH1+vbDsN2U1taNxtzwZn+/4RC7jbtSn3v+KRjmmK5bRLScG+fAuJSunROrqld1XBvK3tbOj/j234oHjoD++Hm5bkKbQuq88bp949/j8/XYbr/XFQJHMtP4cvXuQAGoDA4EjoQYhSeOUeJqMjsrfBLeVP7u7tEYUI8bUF5ZW2mumJqnNref3fxdxMxtTvgpSlq37zFLNwsiBAvQbenK779f6pS9s2YA1umGHY/Li3fIB/TDpBW/OGzbHK3LCwoiku3exkUvDvALPXjylb/PWV2WJj+JyBgnldIRIQak4wvRCD1M6mu7u2CBv8xZ/1EcZ7xy1qcZKxDBQieAIQFZAAnatCUlHTaTB+TMFxpUgqf7vAMeaH/0i3rgPoZJMwIHQPPNaJLM1gR1P1JtCBpNw+7XkeCyZMGKVwedHZp9lMCM5iNSCB+rmxSkE1+aXMQNU1ELCCHipN0WwNR0dMyMVJ75ORItffEXnlUyO+shZ6AYgRU2agSZxqGQMWWD4RXQLsizAoxtzM2ffgbXDC4ZKBWJImoIKHCCEN2vMQTElMQqZzpIHIJpssEAxYhI3M4Z66+OomjEaEBTYh1LBcbkkhLhzTmfQUSYJrFWmGJEChEE0RIOIYEoQU8GMMxVDqEyyTxBdHFyLUCekaKsy2DjnAs4VHAUn6Mh2L1k2jUKzqmicWCg5oo6n1FqRS4MOkrANLQLCUAMCCki1iQBgZmBwsP6LpVBJMGrAUap3cIpHcQyYp5nnE4nJ8jhFmS4ErW1YFpG5/ms+7UipYiYxH3W4TghpoByL9rwuRbUAszq1ilOk5hbV4tS0PeMtxowgYYB0hRkbkvNAEnQ4FpESHB/fz9YSpgrOfs7qWkjB6eBXuuwPxmMrK5+vBulZgjUaHYTgoxtJ7c2QgiIrO51oiw+0k3dBC0xQXzZilVMUauDpmkOaP4KtrMjhH5k2V7hfoQEChJDXvdpcyfkziID2E240Y+ifnpT30Hua/FRGeLUygGASYHt8/kM5IKQZ6BWTEGA+A8fHwRs1r3w4sUrxDghF5n/U54xcRWrCII4smJGrHpPgEEJ4CBB/QJ14VGIERQDivVRz/kgg9Diu5zOAqRzFMIwkp41MKFHAbG4I+M6WllIKOyKigDUilCrMJ0M1NWVK2crEaGq0I+CBiZMqrcfi7g5y7P2Q2PI6BkWIAx3YKCes3oalhM7piR90/bZ2aEbE7Wc29hY2ZW5WQixtimlA2LoUblNKDFNCTVnnB5OeLj/iPuPH1FyBSEipaOsYT3Pu/soaXqqFbFU1bQjxBSav+cQIo6HqHtH3CoVEI6vXuPVm3d4/ef/Ha//5b/j1Zt3OL58g3g8IoA1voqeExZBnAkWvlLiWNj+3U+7NMXGd186bVFtn7tFt9LR/1jJj+q1vl/6/nsdt+Wq+l778djkCXUft0f4AeaMylmP1ABCkh8D5ywCLIxf4VaiCOG3d6vBWXupsVLLpm714BFn1OcR9t2uvcoLmmJ9RdK644t8o6ji0/qwNwN7pW5wrY+u69obz7HzHjMn1wtzbNpT2gFgr9cjPSI/uTBqBXIW5ZBzndVyszSrflQVFACIELdMgPBwOVec54zTecb96YSH070qPgFZlfLAwguVqtEa2Jad0IimtGQxslJUy3eCKLlRQQGjFMacM+7PJ9yfTjifH3A+n3A+n8GlIoJQKYCjWc8rDQrhL4mqBqmFwZUgVNVwVv48yG8SiBqYQGKFodibAYNEHfAMGquwsyc04DGj4qjgKzJfmocgfAmJh4oQ5KxrMcyG+IhtNjEUujXfbjWQchLD7h6u4UU5vDwzCTSUaJ29voO2aTyjpPfz08aZtdfrL0lD2Tx9ypb3zb1VKKFvXvjrWgnbeKDH4tjWreaTtd751fUw92erJdTmcREjYfk+xv0Bcvtn2XaH0dFQqZWjfPm4yYRXQ8dtxcW4uPaNRWMJRvHYQJnExTlZXBZ9t4oe4OEwIaWETMLLEQTzMw/lZi2eomKhcDjCou/rZPyuz3J9bT9dfUPSo1wz9UViEwzF5sl939NaotTzdyHpclH6ui4TXrcxUVov+kXZpEx7K7jX0EtYCSHcTO1KOnsp1L9cNO+GA2z71Ngmb6/2yaXWp3U9FCIoRISU5Mfcsug+ZL3AuPKiSI0Rga3GtdIHgMcIAzfaAC7M7QJAHAlePyqeqvJCiFbQXgNbu6wjS41b0Y7u/W/EjW6KPSHEaiSor09jWVw3YQNuQolWD+s4mCCidksIA2VNA0yUeWOvhdb90V7KM9ub5nKoVlTTZrf2KIAnoJYIE1gFAdbfmsXtUpmFuMRiaTZLiCpgfqAgPdX1VdDdQoUYEacJaZowHY4CLscoZrpVwF+KOs82omSa4wLiukXmwFgbbABsQY/VZzsU0G1CKEcAqtspM4drawDUqhGAV4jqQBVmAQGual6s/ad+Svl2mbzPmDOuFRUFhQNi0vk2YYRKxkldV7Gtgcpgqk1KboCuuEqpzXwv6KV3PB5BRM2//1L4x1WJWxOAsAQpJgKKEqoMdQOWolgGPIg//GoCjVoHENzuA38mABjy+aDRQlizExKgHclmyWABs71QYtRIp1bHSA+7eV2A9iKMcISIMgG2NqztlRmkSvxiKaPvUAAFIfg5MFiFLfJuAJmJpdunltgT3W5efL1di6GTSuYayzOrvtzm19aPDbaSWA2QrntZA2PwOuak2vwiMAkpSdB6FZqc56yCPwkCeJwOqFUCrZdaMZcsYxfMQstZHjhhgXGi1qfKLIIIgsQM0DllN06N2VQhHynj1gQxtcoeqgyggjis1qOt4dDOFFY3QX2/u5U01E9E8p6tezJBbtfUs4DrRIQYkjCluu9aYDKbNwpApFb/+D2D1VVeHWJFMGqZhz08nG/QAOAhIEZCmQvm+aw/swrllcGGEbwuEHwQYUAoImwTYQVgxiREDAqMGG0PyZ5giojHF3jx9me8ePcL7n7+E6a7OyQ9iwhSVqM1GlHvhHmLde3Tlkba1lnwJdOKJlgx3pK+fMu+//Rp07nNj1zPvwdRfL70WK3n/fxGa9Nu3lv3yOcX5m3vk8ekxp9gpAM7nQjIidLPxv7yyKAaH3SJD3cUwPb3PH63N4SfNrbLdfq4Mv0Z+iTge8lrLsrdrQu3gxw3rYqNosax9zQS7+a7tZqnrdTH7+vnusNM+/uxpXU6Rzmw1fW2tICwv5VmrqKAU3h0nWvMbrMoaPCLKiwpvTkXiQsx57nR9NWsaVWTzzyrtmKHdjs6jXq8BkDoHFPmmKvUkfOMXDJyyeqi1qwq0AQaDchufbA6TTghIKux3EZVQWmeQAArTUUqVIDyn8GBq9bmNn+W3/APpfX8GTTCRI4u0n+E//Qa2H6u+w88X+LmuvFRWh67OWx7DK7f7MrZoYXcCLXGGn+zl/b2hVTR61njkNvPh7HaeWdd15rvekpa4qlbxd1+nlt+DJjNTe+u/qbxvBsyLMvdFiZIWww/8m1cKgzstGnrCwVQVnf44h2zUWqC1IvjQTDBwFCOaSk2iwer29aRxgQ0fkXjKUYCLNZDZYlxKbiH8wJBpvhr8xXUMwgUM+hjCAicJvy61R/a3ruWlrjYgDvsvtT+eXJ6lhgRj70I/zm1sL5+asAK/CaUNIBTRAiqSdyDU3dAb2+TLoG7vftkDfBgaMulthsYugvyqwnTEBn+CUvNCFFfvCfCfd23MIT2bgezt5IM2CikMW3nLeBibNt+m6j1pwtjFiZq1MuoVTRQxZpBYzioqw8jIQhdk5qL+Bo3ArKPm29/b5PqETezW4QIT2hOUUZi0kPQ4iGkwxExxRZgmYgkGDdcQGIl+MzFUlUCspQ6BO1ezaPF0lDiuINr5lpFGwcjqtB8rpsroyH2hBLcBKCw+AWNAW7+acjn436MGhkqiFGrlpwLzmUGByAksYAguZFAUMA1sfhUraRa1tx8ncpl2zXkz+ezi4VAOB6PDZz269WD+o14betNxqXUCiqyZoiBOKXm2i2wmTJ390lWdnOVdWUfjYIItDGy7xg96J0JUmxMvXWB9af1cVFOCEH1GrqwowlNeAReQ7Bg6WPgvaHNWr4PGM3MKEp19fMh9nVDo+CACCCNv+HXjC/f1qIfR6urWUC588Hy23j45L9vmLHrg/XN3vV3QwihBRS34NpcK/L5jDzP+Nvf/45DmpB+SqAY8PL1K5xOJ5w/6FlTisSBiSLYmOfZ1TG2HyRkJCXZAylF1OqEC4GGuT3eHRFiRKmljb2tPdG67/vP7j+LRyL1ShBpQl3tkRXz4lzErQRq6EGvfaBGG78QpB3mcsC+89Y9/ryf57m9CxioxjjPeuaZ26jGNIz3xBBbhcVS7f79B/z266/48Nt7nB4ekFLElF6KliJX1CLu+FoQcpKbYWIRlDycz4AJfcKEV68msRWqFUAEh4Djq5/w8nd/wtvf/xE//enfcHz3OxxfvlyM+UhX+H38+YHPH+lH+pH+sdNIxzz67S0+5Ef6rtMPjOJpyfSCjdqwbbEMSt1iQpSsn0VpxSIKcLV2F4yMxntWAlArShXrBIsH8XA+4awKE7VofETj9RrXiiZoEUUQam1r7SdShSmx3C5VLN0tdtz5fMbH+wc8nE74cP+Ah7MqabQ6CySANCtvIBahIWNQ2jTrgqBAfxdMKG3nkOJGW5IoAnUejIZ3elLYn/VzF7yVMTHe0tOnjd8TycqKzrX8fXStuWOsCEYXhCz3lIeHBp638YR77ba8/e9LmNQSt+p5w+Y7l/b9PwbNSavfG0+PNdQ0vDlIgm4VrqzP0qXig9S7h6dZXh7mfFmercXO7+mOb3kN8xyxQTsT0Nq0xv56dQseD0us0blUcv00wWFlif7ieRu/pgQ7kKDVfa/1ddrHhtRVPjR/dznu51LaELEtANpOvd+KdF14j1Wg96k35ScJIkbQeS0pvPT9cgIem5YM6V7dy++v9ePxaU96a8v5edJzHH7tksWS0Bo3F5FpRcZBCDFcIhfaM4LbvW7/Xf/0TegjtjWPxivYo/0myOZnnRpaTNF227fmcOzvJSHELcKIQQhh/WsV2Md22WyfnulhBwaz+x5767lbhDTCxrWhaSBz1+S3YGGl5IUgomux15LRAk7X0kqzS6C3txOorb06FtTUZtEk1EIAqTVEmpCmQ4sPYV0TBelxXOy68ePl/fv7NOaxMkaiaLykWZRMWC4qH2yt5XFli3a8XJGkrnqYWRdln0fWuQSrv/p+4/a5IkLhojEg1CyP40hWtH2qBHc1+NGVxXohVmpAtKzvgBh7oOJlmZ0g7utnaxxrqSihINEEA+yJaNDe3gRu3ehtMfdW91by363ns+fZ3Ke0nO8uLNp8TsvXx++NiDZB1LAujYBnAec7ZSdrfSlE8Gc0URdsVO4uo3wbePUehnygfihTCKA6ljO+1Foy1uHAaxNO+PPagGkbg2pMpgo2zhoIXeJIiKuiYBZXrAybBu+rzKv1MqQFSC1Cuy4Ust1s70cV5KSY3D4cBTZ+zEYhi/7DVYhe7nGU/Hj0Atxl5dpg9ZkgtglrNuah5dMz0wKf95mROkwISnqPWlN9EGyb1HY8uLVjQeanaUKeC+pccD6dcf/xHvP5jJIL0nRAihEiwyGY7+VurSRjHVjmoVQ78yICBaQUBGTIGkMlRCS1hLh7+3vcvfs9phevhkD03tLjGji0eV5sPL/23udI3z/z+iN9K+nWtfQl19yP9f350ucY28eWeQt/s/MNLiIZT6jrc6Q93uA5hBF7/dm66+X59nt7+W+p7zn68ejU2Js1j1Urq6DAgkcv4gSyp506DyOPhJ8rVVwRZ1XWGBTCaoW5zTVhBMEwQ9Ph3g6ubHRjKQAHBhDEYncuOM8Fp/OM85xxnnN3dVl7+9n4WDKaT2lZTxrad0GtJ+B2iePLBwCfR5rN+HACRhpVf7FYExdTYwvWgob2vHdmlefSVh1xoJ295LCZJY53bR17BOVWuvDantp6tsS9Ln3v/17iireeA5+S9ureyKnfj8+kfxcq4OU7VsjWXPk/HK7SvlyM226lPS9trJX+xcbabesXtvm354t8m7bHYXxP+ShTfG6PtwQRaPvXHHR7bxD29/gTxz4Ma9DaIwqqgjfIHHA7I2z/dDzo1nVGhPZuH9u9tABXn5iezSLC0vIAGQ5Sl3/r+VPSY99/dH7/Hm1tt+8r+YPKz9OgtRkjDsdj05C0zXEJ4FumfgndckHQ8K+/PsmAeQWoBvrEvbX8u1/edHGf7BGgl/IOAoIFEObzLp/vgmn2zuK9Vr66XNr8zgg7FT+w3QmBxoHyByJ1MEppJo23AQ0WVpDnM0qZMc8n1JJR5pMSWaal4oB+iw1hRB+ZxoQdamHRZpkTMlBe3Yh0ybICenogp8MRKSUcDncqlIg9PgZOqGBHyEr/revNYqF0Iclynsxnutcyt58YY3dLBkBcnhDEIqS/I5JsdsRn91/PXGS8EhBqaFYWrbE+EZQ4HS8h25f1fMb5/IDpnJDOEw6BQDHAfMALWNkB0TnPIBDS8YBIYvHAYNRZgN95FlNmsXxKOBzE7//hcGhaQH0Jqd/QSKjJj60Q45ULSmXkfAaj4qDWFcfDESFEfPz4cdDwPhwOrW+2bmrt7mSsbn9XMEZguu9VAZW9qxsADRRvAL6zOiEj1JmbW5wYZX681U17n7vkn1mtbGoXPHirAxu7QoR0PkvZTXNciY8YYcHlSRkk39/BcsS0kuxYraUJdmx/UwwILG5/jJOpJcuYsc8rey9CtP4r1xYoOpcCExhSCEiH0LTLPEg/7vPxfkgpIcaIw+GggicZ31NIqCwAdCkVv314jxgDpiRWFi9evECMAef5hAMx0hRUGLpttQHbPcwIqnVC04TKjNPp1BhCVv+2MYbmuiyXAq7CzNo6KMFMeGWkogrjbC4IAFWJS+AJOw+cj4IJXXukFjbM4FJRGP1cN42xoH6FKYiQBIxczrpfarNmqkx6XhcQxC2aWGmIRQSZhkyz1hLT3RjHdVxLRUoJx+MR0zTh7u6uff/h1wf8+pf/xH/+x//C3/76l3Yjv7g74nBIKFn3vgIEIcbmLg1MKOrSZEoJIRCmSfofCWAE1HjEdPcad29/wds//hl//O//Bw5vfsLhp18QCYihr39vKebX3Q/g80f6kX6kT0l7tLSlAcS48P6P9CM9ZxIw6TtdW7anag8KzTxaKnvL3blZRIh1KGoGcQXVoi4kNdYdxLVSUQFGKRnn+YyHh3s8nM94uL/H6XzC+XyCMYAWqa1FQlQwMFIUyoUc/+fOgjk7SwxNpWScNCbEhw8fMM9nnE4n5CJumqgyYK6gWJTVAkShMwWJM4ioeABUeSeItT8BCLVbUcOq1jYYReqFEUQkDleUnxe+n93L69SEIk3PT1BlbxFhFrzG+3reA/YDx5u6au25jeOtWJvPu3x/C2dq5X7KHtnAYpaCkO3XRuzge0jX5mFvzjbncKeoPZFXe13d7Upct502tWcj4N/4Yl5UT1isR21JW5sGwOtzA6T0Xa9oOFZLygMv1seyx2R5FFPzuexvbcdyjPvfIlAwV5CHgyiEmlu5jnWIVYNfc6YoTiQKpTlLnE47AFpMPYTN8b62LgTbu57nOdLNgoiLYLPLsyeEuOX5Xj1Pad+lgb+9Dsvv/n5M82hve96enjzRzMN9tHXQazb44Qgt0FJYuWS6FQAYhBDXLiSPjrkP/9ykc+ZuZynAWL22EHQt+7hs536fej3LPEumxZ5ZvUvgZFuyOWqqLiX3AtKvmaQl42SCmp6UdNnaE9aGfl4OYC5zt4bwQFB3a7QWRCxvCLsUtiS541oggOygDTBTWfNVTiEixIQYE2KckNLUAXmBOMEhgCqZK8ze98U48oI6M1B7OcZjH5Zz1svy1iPynn933GesPkq5BonpoM/JvdfvQjcx6MPq21EVQB19rZrmtMsPQlGf99bPmETSPhcLGF6bm6IQunZ8s9wANsZFfA6GIMCuKB6Z1YlZW1hwWbksPfHRAsFruR7AF5+k3cpkeeYwr/frte+vCQDbPDG3/B5Y9udfJ3jW+3BZh60Lc9UUVu0CwIQeqru3d+t8kS97Hvg15jWDWtAqOQPY3QVLop8CARWoQYNsmSsmx/BUqFWP1cn9d1qNLyEEHQ/leCRAesAcZzEnjRFgMa2vVUzUCSo0CqFbVrm9OQ7s1gwqXRrCMM7sngPqdpDFxVHVM0CEBTJOIXaGkMKCgGxnibjishgQW3Plz0C7gLjqObnhwisu1lg/h1VrUMUBssfkU4xMzG1TdeuwDV27+2zf2r6OoGYBMU2pudyqtWJWxv788IDz6SSCpaah4/ZBCABL/BkhyiVVlvGM5rrMrRNQQAgJ8fgSh9fvcHz9E45v3iG9fA2ajiAuAj5g3F/D9C/Opb29fe37L5Gek1m9VtY15vm5aO0f6XnScwMZe/P8OdNT6nrquns6K7T/4hbtMNzlV5p6e//5ye3/EunznQ1P7fTnPZtunbevc2Zyu7cvtWX11ldYYFtnDmHcS0JXdFefA1/Z3NkagG8Bpmujt4CRxxEln4KcJS5EnmfMOasyTTFVRLN50HFc0gIjn2h9aHwUA7VwUw4UQcTcfnLOmGf1BFCqxsTqfBC03Z4+Ds7FSlP8NIzITzaj0fNwrL3Rso5ZFLprWCcd11EGA20vOb6UDD/1k6YfAz1v77RnIy9lwojHpPb+hfXq8ZvNd5+YHiN8uFTXLW1b7o1bhBuX0mP297W2+OdbY73822MgG7VdaEj/RXiEEd+4+IoTQqz/gotfQLZwh/XrYz9ABREEavvlMh6s/JZVzMtedgGHtcH4eesfbXz2fWX4jhQeAlThNSGErvRn2Gfj9eH5OmqCQ0C9D1SgCejMuxmFzRm6tu4EI3v6Df6Y9CwWEZYuCRu2FvnWZv7W0jfevN1k189yTnrqwTKJCDFFhBhwcH74g3O5AewfhLvzuEVNXShnu4g16N4O9q2XuBMP40Hjj7ERqN5qk9Sz2czLF4K1bxec2h5PX58niMC8jonhtPDHIKXm2d7Jcmk8Spbgao+lUJsblFpEk7aUjFpmsYgoGeDuRsTaVQ2IUu0O85sfogXI6f2NsQPOArSphUtI6KSXAd0BpLEhTAiR0qSgVwCHClTAgmk1JMzN5xaQ1cBw1bRhVPmvuVYy7ZCk/Rn931cu4KqOlhqgLu92TZIR2KvqC17GoCKVhOhGxkzxli5eusBI1rIBgiEEcGXM8ywBvB2Bbv0NgcAxoJ6EsJ/PZwDAy5cvpI0kwgeziDifz6i1IqXDICgwsNT2U0oJaUqIaZI1gYr7kpFZtLPh3pEyGXfHIxgTzucTZjVntv6ZRD+E0KwwAPGf38ye3V62MTXtHT+/bHOhAhGi7mJuKdDwa8EYDSCCWdx+mUWE359woCp4GSAYrR+hAfBZ5imfUau6rvGBrqg2a4U1odP7unVX2njZ/PlYGEQ0xBXwgiWLS2DPTdg8TdMglPI+WhtTREo4qdb9AEgTAdYPHaNghAwBjIKQJkx3d/jp979gPp9w/9tvmFWz7e7uiHdv36KyrEUi0eIvC1exFry5jYSe9zZOIaWmxdEEMERI06QyACkwTgkoFVW7E60PRK3MQQgxzIGyuFWi3XhC0DO64nmrW+/4fd33aRcO+Dm34GXrdVra5948+3vveHcHAlqMlForYiRMMeJ4OOD1q1copWCeT/j48SPe//YbfvvLf+K3v/wFp/t7UAUiAqYQUXPBGWd3lllAV6kvkKxxJrEQOaaESAwqM0ABHA9Id69x99Of8fKnX/DTf/l/4OXbn/Di5z/KnHEWN4CDu7v1nviRfqQf6Ud6rtRoiOXZQgZH/Eiflp5yZv8457/H1LwrVeEPs1rTCmhfMc/npuTGyn+1vccMqhmkFupcu/tK43XnnNW95xnn8wn3D/d4OJ3wcHqQd0pRS/yuCGLKGS0tYIDC0m6LV9HamjsdknPGw8MD5vmMh/sHlDKj5JO6ZCqgWkG1ikcBrjjPJ8zzrJYeBRaU2qwPUjAg02hri6dASs8aXWt8DTfyNFRRwGMHqlpJ7IpkdSGqxcM8/sZG6nY6Ueh6l0kzeppSLPnXc74FWLfPQJvPW6PAuyfskmd7LiFEo6dxoW03lPW906IeB9rDZ6+X0X6Td5dDaCB4y7jNg/f6t+N2tFe7NE7Xord4kHVL7fseO1M+g3uvt7mth8VzXLj7W5k8toEDFhYf1Nu2t85ZgldHiphYsKVUhFcvLAwqA6giVkXROIUTCKCIOEVEZlQmoCmAMmAufJeT4sZku187nd5KG7jpU9Kzu2YCtoUQl4QUy+fP3aY9QGEpqdyTXPaDawf8/gzpOcZhC1xftV9/JQusGQUUpYW/6632XJL0sgoh9kaqlae4jsE7nkowIGkLUMaiH3IBcwOSVmuQaXfa9vtGu99v5W998OAo916NAoBlmV2ToX1nQL3v/+KzP9dKtvo53P1L7XB3QQxlqjuo5vvSCMa6aIdSSqol3A9lX2ev2zeG3PrRN9EEERQa2Dxop5twww+fEnQybtyoseEMUKnyIPzByIDa8vHCmuXa7mOw9L3e3wtKtHkQ3wuXlvPp3+fFLrB2tvKdlnbzHT8MRs9rAdEqXOBhAywVsDb3R+aayGtp+z4v3aQ0wjQuBDVVBEyhgaVd8yfFJMyJC9ILoJsAkwknQtOU71th3E/DfPQ/3Fyu9+yKYF7mMUAX4/w3c2t5EeTWyf7ZYMKRUSuMQm1aEMDiXBu6Mq6ZpTBib33675b5lwKd5TveRZYHy2UOO8O0rL+3w86AVqjuO277OcaEw/EIMOM+BAc8Q+6c4gSilZtgw4+JzVs/N5wgAp189HPc3DopuE0hgJgROLSzeRAK6Pm/FAABKz52dT91gcT2+1tBmFt7N577+TJw3vKaIGLltqrdvXIet6DmWv+k7rMIQC0F54cTHu7vcf/xo7gcyDO4VkQS4VsIZoXh99BII1ifiYJYQ5Dde8qQTkdMx5d48eYn3L35CXevf8Lh5SuENEnZJhzeuuvxdPpwa61/a+lLtOlb7PfXTf9Y4/EtAyNfcu09dRx4k2a03z+1TdfL+Jbm79qZuUkXf8PpWvv2vv+UdfupY3KtTY8p/1as47Fp4KccHev5haK8R4/jUJziF3fendUigqt+couhVYrQiTln5JJxzjPOOWOe1Toh5yYMqBC3wOKUycAFa2ff00bmMYtr4mLWFlrXnE3po7Y65pyR1dVvLlWBv7UgoqhVr49NaDxDIGctqw2pyrsLK9+V9JQEhuELAaLoTMxgMpXDTqsOvMQmb4Ch7o6XLpn2/nyg8Y2FN1psgwdZgcuLv3u/1/WZHYvHcVYdaGlNO19Lvk2dPl7SsNfTFl1/tc5PTLeUcy3PVl/3hBD7Z/44cT0bbWDe6zrW7zrrgiu3JG+806fUlP2UDxmCVXdBxNgU9/eNbRjaq9vPCzOMn5RkVhkXBCxaZrOK0B/xQiDnZOM1geFckPd0jJWndTk30KRrc7J8/mXu9We1iLDkQaPHLPbHbO5PadveRvtHTg3IWIC0sugDpsPUXDU0l0xhDJ5qyQMCm4RIe4AbKHgaLirbaExQn/cjeOvbsOojMACRl+Z5j4hbAZsbHdh717d3AIz0wt5LzCZwGEEts4TwWq9wxNnoP1uB0kDrs8MH1HHNYKD58ex/F1QWC4hSZtHqHtwylQb0d4f1bQSknCptYPM9SR1oBkTbo4OwgAGWXeAQBeQKPT5DO+jV1ZBYbRSAR61ZE5yYyyK7FARI60D70oJA5goNMLWOLQFhlAJiMzXO7l2xAonRhHniYoZIXawUA5MVTCQSNzgAAst1JWvFDav1GX1KQwiI0wQQVNumyhYK4jM0F7HaiFH8kpZpQibCPJ+Ra8HhfETiCcd4ABM1yw0ZF0IIp0Hwk1LS4NgF8yx+6CsIiBEgYEoJKSWUlDDPJ5yL1B2I8PDwgBBmHA4HTNOEV69eikm1MiRnjZ0glhip+dq32BG1FjXBzmhA/gB8Y9jj/rlYOAClSFkm7LD+smoVSXBuCdQrbns6IWHgNJjhxTMhikWJCW+Wa6lqzBNbT53QEbc61a23tq7Qz6xIZulhzJusRVubNkam5R5CwMPDQyvHnz1eE97y+vW8ZfHSdrN9r+6aumCiW7OsAjTbPuS+vwMFIAZMd2JtR8RIU8R5PolZ/cMDKkGYN3O/1zRJAhKNsTeA5m63AddmPRNjagEAK9CEYlHdQWW795yWF8H2XEGM4u7IzlxLa4ELGtHnx9KvS9PMszFrwpKFZcSw120vGtOnyTQCvQWRPQfQ4nI06x8VCslZK+XGGHA83iGliLvDhHme8fe//RW//fYr/vKf/4n5fMb5fAbPZxCA42HCQd02iRVWxawWFaQulrw1h63NF9NRRqiexX3VdId09wpv//Bf8OLtL/jpv/6/cHj5Bnfv/gDSYGvEGQkZ6mp5Ne7LtXXp738muu5H+pF+pMelJe8y0NzuPJYfZ3H7I/1IXyx924KdZWp8qMoXzKL5NM+Yc8Gczy1WHzMjQPiWGAz6E9eXoZZmAcEqeCil4nyeMZeMh9MJc854OJ8kTsPDA+Y8Cy8BiQsROYjCRKDmPlN+pK2iO8coRfb7nCUO1/l0RqkVp9PcrCBqlTgWJRfM5zNKnsXSIc8oWa07ShGXkrUHzD7PM3LJjXcCoO4qQ1NUIxJ3nSZoqCy0Z2VG1thehbugRhRthJetyrsEB7A2ftrJXjpnjzYGWwCz53k87xPCaBFBnVjeTEu8z8Dh7czoAoGt89UAVic8QhsP9+6NaWwbKaj9tHP9qUox30raA6M9v7KNt3lwH51P0b873L7IZ0+bhQwwCiCsuCuAvWJZtmb6614wYUKzMDw3C4m9sZCF5TAXl5V4rLPFYRz6C8RW5qJfCMDeam1DGbT/Zk0/AzC+uNjRisIsAlfd3yEKHzZVRigFOZ8Vi6xDn/pQrffcsr0+/4L7Ag/82fLv7S5eS08SRGyBz5cA60ubfU9Sv5f2yrr03lYdWxvuatlE7VK4lP9LpGttXX1rkvVBYxUNNDWwwQQQW8z/LYD+UmCwdagN7W+PyUn93JpiXpFky0N0az1andvrguCFMXttX15ze+t+YGIcAEcqg1Bjg93Ey9/aOyNzNJa/YyGykHmwylKGuWuXeh8LkwA1kHZh+cBK1SwJG6CbjI5jI1Yovr7lmBl94TWYmyUECSFpRJLvvxBdzqTXaZZ3rTY/j3pxtPEax5B17JbE2HLMq2rqiD8WrzG+pR2+Tr4ssGi96Eq8ukYadUlmgjiuR2u79c0AcAPeZw1ubOA5xz6HfV56EDkPcnvQdNRowhDcjBkjIO8C1AlwnYBESFGCxXV/r7kBtT5QuPzUto+kX2tixZ8Ho8DLhFK1B63WM7y2tdtBdbOEsLkaBEHMWAYQ9PMs41PbHA6nlu7B/oeN93pPtPWwWKNeoLG8s2ysvEBjK7C0Pfdnx9K9lO+PZ0hsvrbGeSsNZ77u8xACECNiSkglIU0TAEbJCnRr5r5LMdSzd56bIKCtEe7nhm8ruzKszBCC8lXsxpB296InyNu628hnZ1BbD63O/nxr+JbEv18DPnj5sj3t7ra+VqdpSOqiLER17yZrNc8Z9x8/ys+HD7DYM8Qs+4SCjosyv9Wvu6HRrS0BJG7nSPYYxYh4fIXp5WvcvflZLCFevUE6vkRMSc++HpBSHb+28rbW2CU65HsTQnxv7f3U9C3RzFdYjR/pM6VbeT1L63yP5wH38vZ3jAYbz9/lcn06+MQ3r7cvAXA9Fki7dr4+hS+/VtfnTM9dx61r9JY29Mfb9Oa1tm8DiLcmz+fd9v6Kr6vQ4KlZf0pzqQSjNwMjCIEn9UCsIch4OjbaXYQEuXSlJF9uceC/8aK1Vo01BqAJOiB0nvESQLPe7vEruuWG/d1dIJemANiU3dz3qPJT1cJXyqnNskEHc+QTG7VPjXY1RQxpm1izNzJaeWY1idDxCmh2EVqX/A4wm4a6Z0CMturPaYEPGE++ydeS0rEbS3AthKA19rCR/9I682WxEc0eO3jk+u7lbbfj1vf3cK3HlPEl0sW6OkPpHopHAMbCZRbJP+TebbjK6p5sO27N45A9H9fK5fa6tevqGoUj1g2zECAsBREUdoQcbS/uVKt10UIIsn/Eb1hdXHI5ZbkCQGwuySNKrQghdqECbF+rRYTjZc29NwCUGsS9Hfe+j93dGvuNudpIUibv/v3U9EkWEWti7vtJS2HEfr5twOB7SL5fDfxU/9NpkqChx+MRKSUc7u5EGBHVLdMCyLLPZZlb4HxPBhpfsz5Zb+oBgHEGRnvgxJZQYavNDevndb7HMkb+UwgUVh+ZTtOfdLMyyVligWSZ1OdbsyPojBB3wHoQOmxYQnQGwUzAfEf33YLYQBg2ZrEhqhFQFn+iGOHVAVQKY/Cb5iN+GGQLwasALbobERvmoD79UpBjSMBvagdqZwQF/Oecm6TarDMsMNhyHgf/4n7NQk1nSxmAVYlfIeOTklhkMAMlqyVIKBqMTPvP3upFgcAr4KwJM6oSkGTa6GU042UGyOJpyItCQBM0FocGy3X9Ns3uWeuhKJr1d3d3qLXiw/1HFBbNoloZU5jaBQZ0C5Hz+YQQNEaMxg7w38/zDDqdwRQQk2jlpGMCwhEPp/vGgJhgASD8Sn/HNB3wu9/9Hocp4dWbV8h5xof3H5BLwel0agKSaZpwd3cHInKWERXMEo+CKCJGW1fjuiaiJnA4n8WXfc5F+0kqcA2olZHzjFrR6jTLB6jVRdOIZwar+bVplwcQENdEsv3X164T3jAjocedWO7tJhhgBqhbBnRBjWhLmMXC+XxuY2aWbETkLAN6XAx7buNkyVtQmNVJzrkJpm08AzMix1VMGi/M8H1eE5dyD0zTBI4RgQTcfjXPyPOMNE2IIYBDVOZL/PZmBiZArE/U5L1r4I/7vbg1R6Sux5jFqiok3c+1jU8TVIDExF3XQoxxPDtcvzrYr75GnSurbSKh+yaW9/uZ1p9bX8TXcHtT74vm3kAZZLMaMsUBa6s9X8YCIQKmmPDy5QukGHGcJFbL3//2N7z/7Tf85//8X3h4uMeH979hmhIOhwNCACJFsVxiJ6xLCSA0l0tt/G28WPpB+QQKETy9QHjxCm//7X/Hy7c/44//9f+Jw4uXePH6J8j+PcMEhUyMcoFE+B5pzB/pR/qRvv3ECkYuzxg598LmnfaPcB49FUj7ka4nGddPAQ6+j3nx/JbQkSIweHg44XyecTqdcJ7nRju2EAQxqJvZojyo0A4BBRUFrBYUp4cz5lJwb5+nh2ZNLQGjhV813oobvVJQY0CowpeN9JnwVeI+ibWMgoez8CHn09zodq7CC3OtQJmBmgEuqEWCZIvVg8RR5EYfV2Rz09TMO9UdJ4LGMIv6t4giiuIyucg7c2a16F20WmnnCEZFgDh6FQt7UglLo2vBLV7aBmIiwh8wiKaBvg1OKdVbRHQ6t64KfIpA4No7nr/y/BQAN8+X69kSypGB4dij229Pjz1Db1WsWaZPEy4OlQ1z110dtQxN6LAJfi5A7KB86QrwJsLWqutzYEKC2wQRxq2tm0IGDHaBw04dm8IAkl2ARfuXtUn9vZ9NBGL8/M6UdH5/BXCu6gws+zu1wjU4xAzUubS8XBlMXYAaQkSME45HUuEpo1BWfIylnEWb+liNbXDDos8vWzw8F/1wsyDicxMsT9Vou7Vd/sC4vQ479OwdFaV/AcnEJ48DETa1400CHrolhAXXDSHApIjWhj0N1MsCiCttG9p5pWPLPpHf3NuWAdc1TdCmUj55dcHt9WEJeK9/tB49xL3Aw+obyvWfSkhYe4b+7dQnw2KX6mrA1hXC5rXXzgCg8SCgPyb42HgZ6wtk/Nv6TMwCrstSHNydSPYxNkDXwtAyrXUadKvW0sbU4la0mBVtThZztBjo5XrxF2oIIpAQQYiB3dwEBKgVTBIomuCFM1vWEOwrbX/3X7ll6wC2z7Nl8YK2/tv88ajh3daC8kEUAgLEBZs6IhVhSPWgbm8mK0PgY0UYkdrHVQKZhzi1sYtOI7sJ5rSz85wBJuRckBIhxQAgIaao92xuwiEPrrb+rIhW6yuG+fZt7e+s57sDwr3cGKPsAfR4DHv7zfvKNwGE38lLgsj21RjMeH1+GXDMbk3YCrbzwQvZmLkJJrxQaY/Y3Tor94QH45jJHC/PwK20eX4ylOERFDvGiJoSpumgxCI3s3UQUDkCFHowexsnJ3xdNmE5lqERmKHtl3Wz+51u4xMoKHHtCMSFlc6STO2E7liytWuIcbM53mvhqRwBJMy1CcDMrN9ZjfnYD34cwKIll1JEivITiDCfxZ3Bxw8f8HB/L8HOS0Y7S2rp9bu9QwS1UOu9ZzeoovOj/o9DQogJh7tXmF6+bZYQ06s3SNMRFJXAVgCB9MzbWlVba25kKD8/bfop6ZOYxs9Y1nOnb3kuvuVx+17T55znL72GOinWaSlbMk9dOqt79oYuXeNjnmMdL/epV1bYqnOvjZ9jT32Oeb+VN/wc6VpdjxVuXRv7PV790jtPTXt8sI/nUNQ6wOJ9MXP3oQ6hCaH3v4DoVS0PirgGzgU5z8ilYNZPb7Hg6Q9pzDgGtTJAWmfbgNSo6mKWEJXb7z2QdhVaSNsFtlCx1l44elzfVYUje9b40SUfzoCZZ7Rxs5+KZhXh2UQA0o9GD4vSEjF3alRfaHPdpnykNcfUgVz5c3nw7QDDjeBc08F76Skg/FIIMeSny+fzMv+KbryxDXvtMt79Me9v4zSX27DFU33KfuZlG7bmBbpMN+v1QLbntf2663/3ZdjXVMes3PzstoXQTJsWbWwMydCm3rahzRvCDG5YE7l2r9NSEGENoOGXbazNtbbXu/pe5oXAqqgXEWNFTAmhZlAJHfuCbXUezggKUWL6xQiAUYOej4OPqW7RYV0h159lj0VQtXMvyQLZ7Pdj02eJEfEl09bluwckP2XzKp6n9WwfIt9k8hiofVIPbHI8HBBTwt3dnbhrcKCQB9EuEaiPIepuIYja5toA//pl+bQJWBLbS+bDt/ExwojBQqFwV2EwRNFfoPp3q9eXK5SFPGWsyjcgfIwLYcc9qbueLaKgg6Rb/WIjAPMsP7N+5uIsIfph3n4nGg/lxWHEzKqFLdoerBoiDA/MifZtUo2MLpCwEQKgBBqRacWblYmMWa2jq6DeV6fRziJM2A24TITjdBg0wa0dFs9BQGSAUQAqQCUwizZPjPpeA+LFLK6vX/mplRFChdj4hC6fdwS1vWMEfB9r+zGQVNawBXCLTiM6RAGNSylIIQAhNcuIDAE253lu/bex8OutlNLixQBogLcQzRXn+QQKYtUi7t0OOGoQ4sqM8/ncLFxO9w+Y4xl37+9wOB5w9+ol0jSBmTXYnFhpWJwDs2pYCkL7GGCVzD+/t4zwa9HKWcZMYCXkp5jAobu/kS8tz2iBZDRHP6OK280YhDa1VuQqcVX4JPE30jSNrMFijbQ2S6db3BebU7//LVZEFyrHlbWUjR2AZhlhz2zN2Hv27iAMUs2opYBmWY+tIy9wIYKYrYMQoFpwaoUXNG/JL9tenecZDw/3IAZKYWQuCBGNAW17zNXtY/KY0DBSUNX9KEIUtewCk7ZEzqKs64aoC0JM6NGeu5hJFLpQYzXG/tOtXRtnv679erZ14sezHQl6DlkMiClpDCdjAPQ+BwOsrgBs3GOMePPqNaaUcHc44PTwgH//n/8DHz98wF/+498bcx0D8PLFATUXideh51kLuAhRUIhR+lGLCtZ0LZmQYzKlhuMbTHcv8eZf/xuOb9/hd//b/4HDi5c4vPsJBI3fUiuoFrEuooDCAgx4nrjvjev0ww+w+Uf6kX6kW9ISRIXxAI10N7Clf24BSFtC0u8xLemsH+nLp3H8v5+5WPIM85xxOmfMc8ZcCnKtYvGvgJfESABCAALUvVBloRG5IucH5JJxf/+Ac854//EBcxaLiFIZ5yJxG5qVAkuMPYaFpzDiTDSMCXWgt6TNYhGRVUByzuIN4JwLai4oWaypSV1GRuUlNeqYxDPTOTIrhFIq5pKF34TGXgR3DFCBa0DbWpXvVr4414JSubUpqx5YA0oV72OS+kgqAaiIEggFg0obPkhk8Sj0Z4QIBDcgNDqyKbo46/4VWcW8ALGlXbt0Gcaxt9+3FHKWSlrLeVsKI5b9sfe2ylv//WkWEZ3W90Dy/r6l5eUhDbrQPi1zgdk8Fcf0ddKSyN6oe+/vtZWB3pFBxzN0RWb5fnSPtKTjR8ESYctqoeFMBHiJPtGirmWZZHvBsKt12aFVQAvAfjyFSaOx+LIxZtfU8TbflqVFhJwnCzxTeU9RNOs4VEVBVuxLTiARhhYGcmUIhyZebiQ/UHJGPZ2aKzlrs/GmvUpqZ/PmEl0/Gr/nS6v+9vQsFhGXNsZjN82tEvw9TYctosoD0P4w++RNLaXfluvGevbafmv+S8/l/BEwJcYeHFZc7QwwysX6tkCu5bjz+E/Ltzm/i6Yuyx/qgWyaTWHFRj1LoGysp71hqM+6MRv9X34O7eC10KHlGysdy3W/bPZ/2Q8779plvn+p+35tCZaYgVrUDdMQG8LeFrDIl9EA8lbW2Fdg9NFvwgBl+5qw4dJ4UxsuE9sY6EYNEB+1pLmPX3vLfjMitY8Ps/k/765OPODeQEl2YPGwxrvbkhbIazEG1svt/qkPT7LLQH6q6weImmnxGK/BBB5q3aDrziydUMxnPkTKbu6zVNVmqZ0PjLSJdwfTv1cgEj3IuRDs8n2M4oPeglpbmQwGV8Z5PgMEHF7cNYC3A/+qWcRdALOMZzC21YiOZUDeHszXfrf+eP/64z5YEsmww7LlGdrB47PK63U8rgt1C1SKuDkyIcnq/FqfWYAKNqpfhz3Pcn4a8eLcJd2SrK1W9soFk9s3y/N1D8iw+duy1CAi1fYQc/1WJ4CDEk9GQHU/vX2/V+YVeK9DunmvN+GjbrRAoZn0AxpQGzLlPpjgclyvjqPv57AG1szXksHyyc4dAkC6lk0w6MvbigUCEsFaihGTCj9Opwd8/PgRv/76K04P98jzjBgI05TE9WGFjmkGUWoKC63Nwe0Fp40YdOySCkmm6YAXb37G9OI13vz0Cw6v3+Dw4iXi4YhtzUAbtaH3V8fZ2vKY9CWEFU+l175EWrbtEtP+uev+FhJtrr3vLz2WZ/ia6XOA3o8p75LwYAQe9PPKUN5at6f9L+3Dx5RpaYumf+w7K/7tM6ypvfZ9zfX6VFxj7/3+95ofWpZ9fd4vr5enzPvnSAMPDOWzyGjKqKx1UKUHAcQDVVXoMR6CNUh1Rsni7mieM+YW7Hpulgu9PvQ95TjKDvhz+xTMAC0PA836gBnd+hbcfLJbvAqNLoagJQZ4HNIriFkObrNvsfOMmDOsxb631vd2jFwxmwlJ+2R1Taz5FrQuA41fpMbD6I/DT3ztAzDpadeNeZavO8/kwfzN/UIOL/CPd7CKWwBxT+fa17fghqt9tAFi35x4vBs6sHxj3bT9/JLQwf/9KWcmN7zoUhtHRVP7vWFNHsCGrn+3zvr68NblXrt+acFgdfl33WMQQNzXNQATLKyFGWhtGOvQslcXfV/z69TX+SCICFt5x3d824h0LwMA/FrZXt8AHD4S3TnS85oStVlfWXzVGCI4AiEoDuNdCC/G69LeuyWN6MnT02e1iPgaBMY14YIHTr5lgv25UgMLFbSYpgkxRRzvRCtVNKmjv1l3qe8tcF+y9w16iSjaHnOCh6Z9+cs6zA/+4DhxlewAEuB7q+6xbDuYpB1S14XisR6HppG7AOxWdTNfLnwA1NaWIVugZZ+yEeRaAlRA3S27VglcWvKMrEHFuPUjACQxDaxecq5LJFttBKEvX/yxd6AUgRXog7q/M7C8B88w4LKPn7bdgq9qksO3aswFV/cwnKKt3gBMtTix+SAi1TQOOB4nBA3myiwa2B1w1rEj1bqunYjxWuhoRNpaWxyLdgHcYm1IJAWJ6QACCkzAkBEoAehuYWI0P/DSlpwLqFkfqOZ0CDjfP6AWiWsRiJDUDVLOPdaDtd/GQfYYNR+sJhAwAYPNy7nkJqQopTSf8cfjASlG/Pr3v2POuVtU6Bh8+PABp/MJh7sj0jS12AzH4xE5Z5xOJ7ATRMg8dysWn0bA3SwFuI2TtdfmwXzmW9wJ/z5BA+s20FW1v6kTHwOTjr5vBBSvw8rzVhnMDNZgex9PD+15O8sWK9f31caeiMRM3dzmuHU1zzPmeW6WEfae9dfmdW/8ls8suLmNnZwFFSVzW+teGLEEL/y4+Dns676fh4fDQUaTJ9RSUXLG4XDAy5cvMc8zzqcTysMDzqrZUWtFSGJ5VHNGBaFY/BldM0trMduLZgliZqvCmObGQJAbEy+MtLEIZi2x6OtWsnKirm8vHPP9t7z2Od6PPMSEePHiBe7u7lZj7GNFtHs+Brx5/Ubit8SA8+mEf/8f/wO//vp3/J//3/8fAgHHw4TD3QGvX70QIcV8Qi0ZZT4LE04TLACa1WFCiDnPqKWKBUkIOEwTDtMBb1+9xvHFG/zuv/+/cffmJ/z+3/4N4XBAvTugAjiXLGBEW+6kgcXl94CgZyxvjssWY+bH/Ef6kX6kH+kxqQGay0R2pvw4V36kxye5m67jEDvfYuRkvv205E9DjEgASON+2U6KXEDMCHUWRqpCXN6WjFoyTqcHzPOMj/cfcJozPny4x5wr7uesQH3oyh7chRmSCMJHCqov8dZYQWNS9Jc0ADSJOyZmZA0M7WkrqhVAAakAAmB7XdyfqJVBjFGtHyaAoIpUml8FG34qWyBdpaWEpSyo1VxF2Xuewx8B4iZIYXPmYl91QFUsGnych07jboXNbfiK+7Tyqgpjgo6EKQ41YQDWvISVad8tAU+PT7S8N9JwjTZ8xB5Zg7CGBd1cxNXybxa0DmD6Pu16SShxrS0XvoQIzLbfufq5WI9tHoO3lFDLBuoKXktrBF9uFxK0b/ue9UkNIK4JqywmwhicWvotZW+MD+2duGN/bxUE+T05lMAdg1z3273vMKpcMwpnZI2HY6kpi+aCEhLCMSLFBJ6AEMWtHRENyoqP7cctWPpzpNstIh5R6KWmjQDjpRK2qcN9oNsDIiPe61/xeHB/bozu+Jzc4uzAa9+QKxnoAM7eli5rM6xH0rd54+Hwrl1YDDTLh6iBTSUuRJLNGvqFUqH+GsnXYprl9tsIAHiSi1179no2gAqMdmG3kn3DYT4Q3VjrJHnip19k/YJZCkeuaaB486TWH0egbP/0fO1ccT8U7KBdjAYRyMB1obBajmbWuVi4S/LU6hPwlFrQ6HYZtMvRFjSjU4U+wG6V/5z7oqbVEggwIQTZq+Q2B0OMbJeukbo1Atyh19pqc9/mQcF5jC6Nmo6NI3JtThqpRh4YVANdrsN7VhJBzFhZxy1F0zJW10YUNTh60cvJzYVQf1Cv5jrGUa0QIsQdFFALQwRh8k4gQiW1SLB55D5WFhyeg16SLo8FJuoS7yhujSDumwDNY3WBwOrnngM3gtUWatALmamDw9TmoH8KwcwoJev4RrD6qyctBywm0i1YOQVQZIQUEaqOY62dIFDiO+csxLI+N8A+6KXdrCS47/2g2kYroteIZCIgQILLMasJOEkAXB1M5opaJKix+VaNzu2R9dt818pWkecG0HsC3MZ2ec7ZuWBa5bYnSdtbcgYHiath+6LzUlZjPxtlfTBEpiPrcXm2NUED9buToQC922O1si7DpUa9P/tItzchMLUjw9dnyRPge8DwFrFi5574K1VLntjJkVAZIRbUGJXzIY1RoOdaHd1HxUV8ki6UaQ1XptD2HNw4LNrmCSw7Tx0t0AQdC3DcC7gMxJf70V8KbjzaAe7+BImQtgIxVEwpYpqSi01hZ3kAkQmFA0KU9dWEBhAh5cPHjzg93OO3X3/Fx/fvwfkMxICJJkSC7AM7H4i1nzLngTTot42fCXMZYCKEJO4dp1dvcTje4e6n3+Hu5Ru8+OlnHF69QZgOoBT7nLb14Wi1gf/o4+rnon39TETvU9LWur8l37X8W3ku04TfdnpKH24d2ye05pnKef50aXzW3V8+uDa2y++vj8Ot8/Wpa/PS+48t+rFtkewEkNE8fr1C6BsuaIiHA1TkbBKr10HYvQciKY14idt9rn3+KeUs9+tS8HutzufYq5/zvLvWj2vv3pqWChmfe889uV+d0ETbBPrnJt6wQjl4+DD+PBCBSWLspSrulyKhAfwtkHJVV0zGd9aCWgrKPKOUGQ/nM87zGfcPDzidM04PJ+QiQbAbN0CkAGcvR1wwsYVegAH0Dbewvd8Yc9hRIPRu2/9VecfqeNqqfDaDAhAjkCphmqLGm4uIgZGiKhIxO6U3G3Y37tAzhAjIpfGFoCC8HrjfAWQ8CDVeXyx2ld5EBzrNnVJodHK35pCyegDrjlUs5tzRsP1rqb+fC7Y3+ny0ro3dHJbUpf10KzA6vANrm3+vzzct1rTvi33uCVD2Uj/30PaFcVtdKORo1kbce/zKGrNs236djxqXi3mpzz/6OujYlxMMtOfdymApiOj8EfXv9T0CNd5/Jf5yZY5tHj9p8Y6N3cA2bKzhAQez7qggwlsmXD+nF+0axsIeb5ShuMDAB7v+4tr9yYwQIyIDKU1I5YBaZ9SaYXvRsIBqsXW0lhgTiAJimAAODi/rwzP00M3BCDmOczDcNn2DjWVt9+Zq+iwWEeNWv5bzUgm35re0R/Z5IqEPeB/4fqB64lSugOAO7r59fR99zV8scftnJ0mf7BoidcV0vHuBw+GAdJgU/Il6JmoPFBCvnogmu9Jt8WPV4dqg3g4yVfDQxHFTUtsgVmY1oIjRAZL2LoaAb3s993vDb6otIcQS5PCCjJ5vdP3jtSaa9kK3s5OYOotAop7+GcZB+yi+vRUYBqPUMtTViE6isVM2b4GEOopRDlv1F9nRbBldhU7lkKQCJpgIAoVnzDxjLrMcanrABhINYtQlcGljWCGMnbgKsoC/DHkOk3MRDdrUgDYFAAfNq8QsGqPXNcO9FrBpzItQQzQ+5LuCiiz1s/oS1fgRlauCukmCqgYB64/HO9FanqIGzCWQHextDsQ6ASx1yW5Qv5yBEEMFx25tUHLWiySov7+EENB8pVYGCkvbiESDuSKCY5RZ4gCmoG5TK7jmRnxPum9xTyilgpggzgIZCFVjVRBqmkAUmmY8ZakrhQSAUVQbHLqnS8nogDzhMCWxnDifQGBMKQnDUDKIIo4UgSKuXJCiBMMOhBAT4vGAFAh5zgAqXtwdEVtbCu4fHjCV0sDi4/EogXQfTiBmlHkGYhSNchAiqTsapiassLOBdH2kKGsq5xmVGS/u7hBjxDxnNPdgpeJ8fy8C2RAQwTim1DXmKYBClOXu3PbEGJvVRs65CV64VhVa+U0u/mLBLJwYgBBSWy/MFWeNFXE8Hoc9JdYZctCZuWUK8l5MATGys0LRwM4qOJxLBgp6HIIgzNXpfAKYNUB4jxFh9U7T1AlJ64m6KxNTHW7R85jFssQ0pmw/L7XhlmnJZFje7JgzClGsdnR/BwQEJlAtQDlLm6rsFamzoubS9n9Sy75aCmbuVlVBD0KueThPAWGWU4jYPGt1HPzY9LMfOq/bQaijnsMxHgCys0kI4Xb+Edr55gaquVYLICQC7u6Osj+iWGpVlnsz2Fmqn9Mk7728OwIgfLg/4eHhAf/+f/1fePj4AX/7j/+JMp8R5jMOYcLLiTARA3kG1FKBACDIGVwgZ0VMqd1RZZ5lvYUEpoT08i0Ody/w6l//N7x49QY//8ufcffyDd79639DnA7txoFaC4olhBPcNfNmHi73pwAs34rA4ntMX3e8Ph8I+e2nXSr2i7binzKRnfX2A1QuKHVWRp5ASOgsMmNvmwx3hn/ugCpTXfmW01IIcQvY/ViQ7Gukp4D2T+3T8whVPLJwez0X27zMrpYCIzrK/dfhVads0cqS9Ryg9CJ14cOBOq2kLCBq0RgQ5wyGxOaqXHCaz8h5xv3HD5jzjL99fI/T+YS//vXvmOcZ9x9Pwi9VAGQgfACMzo0E422byyTlESSUlYkDCTBFPVGjkjYSw1TPas0odUZl4VsYVeJYECBKH0AIjKQ8fggJpQSUQmAWvsro9qI8fTWeIOtzBQ9ns0xX/gxhEr5VsRYKVflmFQSxtUMt451XgghGQEUK3QKCCIjBucCC0LwgaviN0bamxOhxC5lTO7mwAPUI3bcQloeeLUYYGOx/lmnvu2sCArbxGARNPu/272ydoX4+Pymt2kf2P3bvb4cfNgE3lluTV0/663v45uWxWraBdB1YvtEDRS+yA+kLl8aeV1zGjGifosDUBBEN8/LvOtysYZBb9jrWpCsxIbae2zxTb0s7O9mdDa7kBVemaa+f2+NMTgjZNg/1WoYts1UGM2KIoFhxBAGYgPoBtTwI3w9VH+aCUjNyDSIAJcI03QEMlBOQKQN4EGysFsjZYlWslejAwq5trYnhzqGNO+gT9tRnc820B9R7ieItF+5ja/1cRNG2aISG7y9JuZ6qQfJUusak8bbAUoyIGvAyDIDwWuehpb1zr33XARrL04QV6qqmzf9wG+h55Ms1UBQQ4GPZcff3rcTeEvhatuMSgeqJcV+nB8R9ByzQdyOELly+m4nHdvqx2WyjK9/8/5M3j+PFBaxzzCREjQmBqpqn9nlyBArUtI5ZCb7u951bI8nNDYnWMgdVYhZpbJOj0yjIEEDPtO694MbYtj5npmVuYy35pZ19eKgJCeWCqf05BSAAkaKChUndpiQl3FyMBydsYtaryly/2MCSldsvZmY0wNtcJzF5H/l93hZT76b12tnR59zctmzl80GZ1+unt8HWuF3WXTgx1s/O/RBzRamMgChWCPq9rbsYAmqIqCTCnFqqRpST90ueQYQGqJOC9GJ10ONXmHbReOkZA+XOLB61D8j9HgKJYEcFcsXiaQDDuPiL1+bej49omouLK2tHHxfoWas0OvdxMkI/Qtxq1dqtF5ZxKwT8F5+QQB3zOSZsiwhauQKjvudY+y1Ehu2rvmbR2o32HSu3Ym7AiLBaR1sgxN55unp3+KsD8FamBS1HmkDHYxMMxZg0qLScdSH2YNsUQqNzfZwRP6c55+FcpiDmB00IZGNHes6YKT2g5vqMfkyNhGkXNAS9DyTZXhwFF9LvZm3lyiMSwQwS1D9oHPrALNoyIQRMyWJGiPbbfD6hlIrf/vpXPNzf48Ovf8H54QH5fALXipCSCDUQkCtQzxlzrsgVYIoI8aBlyzgTSITkXIEQQSHi7u4V4nTA29/9AceXr/Dud3/A3avXePnmJ0x3L0Ex6rnc70ygU3ttxewQ4Lem5d18Ld/XTLfQLJ8KYj22n0ta6CnpmvDx20ifvy3X+vspc9t4+N2xvlbCSPs+B1Z6q9B5O127M7bfHWiAC+9fm4tdrrPdnZ3Waq3ZPKr2he9b9d26J55773yKkPaW/LcKI26lFb5kurpWvuA5dut99ix1LR84urE/Gs8N+4YsnxK9Rq8J/SpAV9sbSmsbz0kUUKmqcKHilCUOxMfTCef5jA8fP+J0OuHj/b0Evj6dhSdwfE80pacQYNb6A+1vwCMJfUcanLopllhPKlADa8wKFZiwUGXKIGMIjqufEoMhgGNXXrM2VLWEKGo9WnVoSxRepqgr4UDiZmVWfiIWqYALGRQy0K9kf5PySk2oAhBxC0otlsFCHoujC4dDdLa198aPhxvHca0sBArjStjEeC4JHrb+fsrZSE0B0guJ9+tc5dutcv/+Gdq52Be3pO0xaTVoPRvv2JzRsCQvtpkWcztUuOJd/HoY22q8DC3ek7TkRztvM2Jg+xYEbIzzBtC/7GOzrGh12HOMz7UvNOR1OIzho/2lto63RSFdCLInjBjPbU9lXF/jvizPA3f3uFUsJGJssVFN6Ln8aZhvSgAR5noW92p6nrVmmAU6bA0EPSd17Jo1y3rtX7rzn3JnftYYEbelXbLwy9S+c2B+H8navR4/A26DWj1Mh0OzhDA/2x1Dvo2gHutcJw88NOCY1guTQe0wbXlNY8htqGXyvuOXG+EWRnCZ/xoBbWvDg5I+QKrmcmuoA7LjIbxeZ3v98+NxoWEDsE92aPj6gGFZNGZI3zcQVUxjzS83moUMqyVEgABc5IR8YnpaXfF2AAKggEgEcEWo4jPTrqG1NUVvA4BFX8Z56JeU+bwUALJUA/3tojGTXYtzYaCiag6rAOJ4uEMHDvuAcZVYAxYctzbXQgSKIsgAuL+3mD/x2TfrRVFHgcFiXWwx0H5OLyULXrteGv0S8pr24uufu2AlhEHgZyDwODf9b3sfEGuBUqroC4YEE2iZRlKKCQRCyRm1KPiLTrCfzyeUWnA8itXCISZA41AIWFyHNsMYA+iH27fLs2Lpe9RcKlkg5DzPbU/7vWlgMYAhSLfNBzPDYnTI92q+rWvYvu/qQz1uweFwAGLEoRyQc8bDwwOYxbrAz5OdR6x1WhtKKaL5rmtpSfj4tbRiHrW8POc2Dv0dICUWd12hBwwn8kJAtZhDWZ/jG+f03t+X8vX4J114Zm1M9AJ1cm6xdP5tPcQkQZnjNIECNXdlYm3UXRWZEMIEETbmMUWUAhR9Hsk0w8y1UnDtXAuoLAmTqJYQFnNJn0ssjJ5vvAcqSh2tVIgIlBIICXE6gGISgXEpyLonDgeJx3J3d0SKAfl8RikZH95/xOnhI/7//+f/Bw/3Epy6liqunmLC9OIFQppQaMJcaosFUysBNCFMBxxiwBSpxbApLEEi43REjBPe/fInvHj9Bn/883/Di9dv8bs//BmHuxc4vnyDECMKhd15v5q+Pjb1I/1IP9I/ceoCaXvgwbfLaRC0/kjfbfr6mMDXxUW20nJE/BgZjSW0v1PkQlfWqZXAIYAr4cwVcyl4/3DC6fyAv71/j9PpAX/9619xPp/w22+/IeeCeVbeLvS4azElHElovynQQGsN7QtQ10uqtNIU9YSmC6mi1gBWo3/jHomhVsAa98/ceMLOBuVBQYCyDaYYog6BG/5RWow64StzLeDKOJ9zswqZ54y5nsVLUw0DnxZjaPCr5w+9RQSRAIyRxB2tkaxeeSkEan/LO65PC6zCUoX1eWMt7ICSS+xjiYEsP7e+9+Xu1dkFIvtxw7becd8A2IoycR0s3sKNLp0XS55Mn+7mX5VJmrsjyLvaBONYbkDqRACF3TkCqcv5nf6ZMMLKHvltD/YvBVcb40NeQL+tYDeOw7ZVwiqf1bZcLxSH/FvKcf3+Xp12w7OtNmzx5bekrX0hSnfC98ZUEYso5pWScJ7nptBoOFXDJksFTQGRIg7HI2IpONcH3cx2p2j7uHac0TypEBRf6Z5VDPv7FIWGa+mrCSLW++hxk9dTP1iv1SN53GZ2i6uDncs8j0+XJuyx2ju777T3GGDVIB+yUQPYLDCsBIeNIyCs7221Y19TaQ0yjFI51ebdOTAkfy+nF9mFEXtpC9jYO5Bu0ZS8lmcLnHU4WCtHyrKre3nJbgN4W4BvK3yvWUTitoo6GD9aRIwHaQNy0Ulbq1PALXNDBIDVfUyA2skIuAziwYsGc9GCrETVyFW/lRLNWdZkaHZufX97ME/akbV1UZk+c1HjxzKgW0JYvyMYDJFjWK/tP7HKQAjtYCUipOmAGCKmw7HFHQAzKheARZOl1NJA8BbMuFYQ1W4yK/AtTCDh15xcCGV4JoTlSAAs19Y4zWtiwOezvb1cP1sA+2rMsSTB1pe7geB9jrqGedGA5mSxZaquwWQa5FJO0FgU1QIssVx0tofm8wkcE9KxA/3SlT72TfjBJtjpWhHLfd6EAW68hn2ofWcHdHvi3gtlfP9LKSo06IHJzQ+rBPf2AtV+qyzvAXODdD6fpU8muNK1QkRACEjK1BHRIEDy/bFk/fUBi42IMcatW+mMa4W1DSCIdYsbN6vfr7et83Jr3T7mjO77Oa4sB3TJgKMKFxkSpFqoMDl5klgMdG233i4TjvozY9kGP+/6sD3f2oO2Rh2PYC+iBwfU8zglDXw+CliWbWSWclOzVFTz+hCAICa3pY7zejhMmNIELgVzzvj4/jfM8xn3H97j/PCA0/1HzKcHsCxOmDsCQNqfc0VhEWyIkDg1l1w+vg0CiQCCAl68fovD3Uv8/k9/xsvXb/Hu93/C3cvXmF6+FldMQZwELO/2Rwsjdt7bo5Wu0VCPZQwupecmwH+kf85E+1jCZ0tP3YfPW5fRjM9d7jrPJt/hfutU8TY9T1jwlbdIGRbNu9TeW/mUW9NTxua5637M+fjcbXiOOj/H+f7YOkkBo885LKxrednbLZBVvvCAoOcxWQDFCrWGh7iGVSUsoXnMDbMEZM6Vcc4F5znj4/mMh9MZ7+8fcDo/4OF0wjyfcJ5nlFwxZzUVoNBoL6H7EpgqQuQOpsMHx5VGi2sl5dWC8oaK8ch/jECSrwkiVNsYpWrMBhJWN1ig7KA8seMfYkRMUQNaE0x3qqoFhAgiqggfKiOGGblklDIjhoBzKYgZCGwaz90Sm0CIri4iUZiReSD02Foau8/F2pIxke8aqtVobyi/7VLLaDz3yCetgOvFCtrLt/W5Xd7+Olz9vQG0C+26fLZup33he8+2KW7A/a617db3NvM4K+z24cdPQBz/xmYdTSgwlCV7iYhaPUHn3LCq5iHFtXWon3r7iEalyUEQYbhCW2PNAeyq2UNbN9aDlHO7IOLS31vnsf22XGHj72H8xspzuRjDsDXMoT26wsPY/DJ1Pj0GRkqMlCZ1j21KmhaDR5SDm+Kszm2axI13PE9ab0EXRHiLEMHwPG9ra6H/K3vrc6VvwCKiA6X76dLmveUA8EtBh3Z1mK4X/21lf+1k7h0WT3XjpmnC8XjE4XDA4XhAiAI4CBA1ggXDBeWSlG0P13O1BNXNZMjasUvc+He1NQ2M9/1w+S4RdVsX2rW0BZztAcAdHO1N9Be1rSMDowxU8utoW7DhBBJGaV2iQom6L3EDvtQdhh2VrQhyjfW/co9nUHO3HpCgyyRaIOz8bppfuSratXLgAcwdjDfflOqvBwCjMCDBvtaXvrVhzmdtngC1VG08uxWBYHkCwoUgWsdB/bsTVTdcpAKVBA5VgzP3n+PhDjEl3N1JbIiaZ21DRVXN6FzEXLitYWaYpQfVDCLxB9rm3gl9ZEwllgKAZhHh14o/VsZ1NYLNm4y0y2Og+JYgwn4sELRdUhIjYLwcZe66Jo5J2S0ZYN4C4WoeM0G2NVhZiHFrWyQhPE7qB5UVkGUAJWQ8xIhpOmBKYtkh45Qxz7Y20FpZa0GpBaCIsCBAl4D/Uqhgn0X3l7Uf6BrzWwC/jW3P2zX3u+CER6GVK8cLhSwmREoJp9OpzQeAFnchpCSm3lq+1evbsbSW8YImv47s+TRN8jz3Oe1trsi1IBIQBkuJvibtmSeUlgKNS2mXOCSvrRVWLoi64GACjHxlxvl0Qp7PTZgUp4Oaqffyh/MUa0GTXyc21ss+7jFRckaPQb3sOxtzcxMVDgd1nyR70OK1WB/b3mWxpkjp0OqKKSEm2d+5qrC4Ml68eIFpmvDixR2mFPHw4QPOpxP++h//S1wx/fYb5vMJD7/+iloykFXQEJMy6eI+4DTPTeiaUsJhmnR9E1AyuMo5AYqY7l5hOt7h93/6M16/eYc//df/jldv3uHVT78gTUfUGMEgzFkJ55Hd+JF+pB/pR/qGEht5OtLf9nWj00ZQaq3stVf698E5/kifM32/K2BL2cTA3EYLDWAlgwMDVXlA/c4sglldI1VmzLXiXAo+zjMeTmf8en+P+/t7/OX9e5xPokCR5zPuH05qTa18CJHEEYsVEzM4RHGjFCJCtBgVSscDKh8hjXVAjTf1XGjVn0xAJZbg2oBYQpSCmjOYxKts9zigfKAyxMY/xENCnGKjAYUHVl/uSvsJ/yV0+MPhJApIqKLhzKLsdKYC5oBaexw2c8dkR9IA4EOoY1blD1OG9DStWUTIMI4YTxuj0MeOiUYwfCcZL8vo9LT/HPJhm67es/6/BZdRzmrj3RuUWHbr7CX7tOQdniqIuOkdN64+n+edfPeGsdbvG4S8wcM064NAq7kx/GRVtrZpXd5aOLCs2/fL3P/49q5w2CbA6GvL6vKCj6fMwXpd6t9scW533kPEIIjYqWv19IZlsZ7f/h0zg5OcoYdJ3CvPOSMUERrUKu7eQq3IJYtSHuRcSimi1oLDfEDOAQTjP62n3sU8jWugNZ9u6cInpycJIq4eEMtJ4vUEj3nkOLWytyf52nDsfb8UQlxqx/Ona1oQn6qt5wEjK6cBgUmsIGJK6nInXBzG9dj3ebn0zvBTPVgqZQwHjV6Ydllulqn/9IvBj1dvW5dgo323f7bvd3zr0rS+De6SNtb95bU/fre2BHAunpRwkl+X40ONAIEKnuSBuhEJsTFOVqMdMIOAA10AUUsFO/dDYH0/JBBqc51F6h+erF3UtVusbSEQYuwxMpjNbRONbV6Ma6kGjtp3y/XA/VIyQFEJTptoe1ZqcX7zrF1pRRylaUIMsQUk5FBBzOqOSTRWlkA8cW9zqBpQLLh9u1gHDN5cM229cM9j62Ll4x8dRF8SZe3y4PWYbhF9JpDopnwMXrjDWr4zzILrCymRGmJA5YoyGzgecKAJYG7uvbywzLSBfJki7BFXTbbX/bgbcW3JtKyYuzCwx2iwvSR21nY2mKCsC45srOTvWq0OHzfH1jM6YJ8rcg4toLJ3JWTrxQh5P3peoGBulQ6Hgwi/5hkgEkFEjEhOaLJkJMAi9CEbQz9Hbg0yc9OOMG18AjAdJvTg7WwUa1s3WzEVrG9b1gQ2H37d2O/2/hbBOKyvHcZllVfnT9ZWQtDJJ7AEUw4EVt+8rP0yIUetBSA0f5kxpjZeLVAZUTtDheHsPxb7x2NQ7Ihz7aGud2FKgwkilHk18/xSF0JDZzVl4+C/L218A6ZJGNK74xGHKYGKEJ6//e3veLj/iN/+/jcV0ohbOIQJrGe6MRAEgOss/VIbGDVkQgqQDVVZ3IClhMPdS0zHI169/Rl3L1/jd3/6VxVA/B53L16B0hEcEipUiyoAsvfy6ij/3HTWLekptNa30O5vOX3q+FwTZP5I/2hj9JVheva/djq7M+RoNOfANZI834cqvl56yvrYApu/Vlu26M3PnW49t/bujGt8veR5Wp17+Z93XIzO2K5raMeqXVAAsX9X2faH7CuJO2h8nihAzSXjPJ9xPp9xOp1xOp9wPs+Y5xk5i6av7MXeQlOyZHYuZWtAcsLD4Uf5K3I0j8V385YBxIwqnC5yEH4uxoBalBalLnis7IQuhGZiQESgKHEGU0pqMZ2Ud9D4WlCLCFUqKTmrgEYUkPJ8RIyEeT4jR0Jk48mL4jiqnGQWENYvR3uaVrTwQNTGxdpsQojVvLYJ1HkjR9uuZn/kJxvfq4KeLd5x6/dlvi1+E9jGAVd/b/aq572IU16sc73vrrbliXt7tceBtrloLz9Tmydy/1DPrI+614ahLhMeBOqCAOrCNT/nWhz0AhxwF/k0QQQWn4rZLGdJ29T/to9F24xvWdRFxq8N/SRflB+08W/mdo8Pj+193iijNdPiEi4afiVZE/bvEazGzn0LMCEEbm6ZmMUyIpfS5CIdT+QmmIi1qgcGYJoOII3XyizxecjOCOrre8BpZWC2tslN/X1s+gYsIiwRroHen63mb5bZ3LF0sG8XYPYAPE6TaBsfD5gOB4kLEUeQ6ba02BiXWsv9Z10KaR773I5NL19aHqw3R6vLrlre/B7ol9FyzB5ziXigTursgPv1dSOH8VLwsPkDbq6CfGDg3j4hKDwgrOjXAHr1sWEwJMioaQ/3vhRwyagli6lXNcFBQIhCPgklpgKKRhkuQWKgCb1UENE0MsBy0bG72Hkcz1KyBEKFaXH4WA/6AhZr2wJLNzJMfGEWZpTc/eVFDexjPvjtZ0oHdYOSQKRgKlfUIoKIc9ZxWWiIN1c5uSBQHAUMG2tmT0C4JVQw9zzFAfXeqsaX2d6rfaP5NhpIbnWZOyDTjD+dTq1ODzxbMg3xvo76nDXXOTEgpoByFsuR3jcGp4RkQH0IoJTUCgOtbgNcTyfRCkrqXscsXPrcd1dnfe8Yse0DL5t7sVEjiBlKhMuFGgi6JgHm4gQZERLbpQdBl6DUUoaZQs5zaBpQJoggokFwNZyWOmemCW9r8e7ubohBcs5ZLBKI4C00bB3EGFv+XErTEhl+VFhRIZpnuVZEIkzm7gfj3sOpC8DMUsb2jK0n0+KyNeb75e+dLZdHe4zGwIgMliikRNGYL8TxXAuJRSMNMp8WnK/kLHtCCViL72AmrDElIATEaZJ5hwgZKgigKJaCjsESilWITzuf2wSzVu4stohILFrMskXdKgFQc/w67G+4M2VpkeOFEFFdNh0PB0wp4eXx6CwhHvC3//gPvH//G37921+Q84zjdJD2hwOABJST4x8YnM8aH6av4RgIkZRIrYww3SEe7vDy3c949eYtfv7Dv+D125/x8x//BS/fvMXh5RvEdEBmoIjsQuYv6Mmf0cbrU2irLWbyR/qR/lHSj/X9ZRMvFBuMHu3KOvLY30n6QAEQ4WN+zNn3l77GXvvm9/eNMkGCgHQdNASIuNGVYHH82AQQDAnKXMXitpSC0zxjzjMeHh5wOp1wf3+P0+kep5P87QURTuVDy1PFIa4CDURRPCvqxgiIuj8FxPTKKDEQUoxIMbSA1GYLwQSxgo8MqsAUAzh2WqyyKisxIXCnCVnpbSJSy9WEaZqQksTt8zS8jUlxNGCtFVMMwheUGYcUALXCn0iUhUrJjbfuFhFrmlrGBigVEEuKOq458lw0ht8M8GXli4x23loBq7pJeSpHu+6B61tCiJVQY1njxt55jCBiWcaqjt065fdhCC/QsHvtv9au7TZtt21LkEA81rvMI5/ruTFMChtzIvzM5TaAqPOfJhTYqXvVb4zPN+dkw+KhfTqXzKR7fG/sN59vZdWyGGLzsHtcLzyb3JKG+dnLs5O/fcui2AkQpukgn4ejWLNzgXmOKMV4ecWSYsXRFEQPh9HLQgGYWMdzb48RuKIplz22v49NXzFGxPKA8Lei14R/XHlPbcvnEEYstaG3vvMXik8rSeJG2SPQGVpU9WguT46HBn5tEkU7VWwN5RY4aWAfs2LWvOwHuR+09bwEVV0tfRm4vFsCBd8We7czD/vv+Pf82C/zDQFgau+nf29Zhl+/y/r2f9bjPTBHG/Ut3e+Q03gY5qcqYOhAXCGEygCEGjgMAIFE2MKCz6Nk8StHXNGsKSqLVJUkJoBpAptWuvF7BNXybZolXTO4WiBiFmDbAOAOjhs4qRoXGM8KW2ullBbTobs6ESDSLB9iCGIVRB1INuK2lKxEsMWFUN/zzhpBDqEeyLdyHcbag5EXgdeN9bsEdf07S0GE97vKpMKIxbwvNdqtHAuYaxdSXqzD1ZrSepcCGWbxjTpNU4udYO/nnOXidASEnUfWNhMY1FqQs1y05/NZQdGkAoZRO1+HWIdvGXB5Hbh6KejxhZB7bu/6vm2lxphUCe4rsXb6+jD3W23vVTkM7W/vgsnyMxQcrxU0zwDM+mKcN2uj//1SO/va7gK5JojbyGPxKgwk94yFt/rw7dq6Cy6N2+37Ybwb+nne11OIEaAeiC9qMTY20l5uLtlYxao9xkInecSaTMZlOgiRZ0SufIrlQK2i1cYmsHWMrrUp6P1r1loMoJbSrFOYhSHt/YL2v+8zL6iIMSKoy6QpJaQoAQrz+YR8qnj/97/j9HCPh/uPyOeTuNdKEQe1/GAEUCko81nHQwR2xAxUAiMCIQEhIaSE6e4lYpoQD0e8ePMOL968w+u37/Dy1Ru8/ul3uHv1Bnev3yEe7sCIyBVOgA20Q/9Tk7v7h7G6kK4xrLemLXptl5H9kX6kZ0iXzvNvOe3xLc+RnqvMdTmOF1nk63n9/XQ7/+mreKwr5c85ltfSt7T2PmdbrpV9mbfcf/9SuV9zbFf31ZWmDHefqSK7vxvd1p5pFmVguVagWkBmbtbuuYi1w3w+YZ5nzKcT5vMJ5XxGnWdQqYgMHJXWzGlCAZCnjBJI+Ua1Blb+bYpBrQ9E2Sm02FxCs1nA6RQDYiAcUkCMAUn3MzGULqyoBORIAAdMhwQGYzpOoEwaN1D0SSgGCbQdVBudCIgBiISQAkIMahWRVLHK3NWKGCBn4Y9zDjpWoig0Hw6IBORDEqvUmlFrQCmdfzLr3oYKkfxmVvWlAKGKN4pKofHZlkytsRrYQH4GtwHt9VqywXPgM3V+Yvn+1ucWf7kC2TfSLti8+8YNZezgQsJL3K4J/pj2D7Qk9T3WrQHaG2N5tu/a/lOLG5e/17MQGsHNlc4hW7w46nXZd2gCd7Qx4vZrL4fcu8s6NYfvUGsmuViEvX6fIYx9dWdOt5YYx6jzU4uiVyuEx/7pLw1y5Evz2BXiHpNGjHHdpsvYs7QsBAaYEKPs68M0gbnidD6pALIrGAqmVZrrbFDAlI4gyohRYrF2LyT6M8gtqc+LdflCt1c49RPZpC8miGjnH7DTWBrzujy8YHKfkylcAlmfi+HcE0rsPm9IfPtyyL8EzuRCiEhpQkoJ0/GAw/E4aO5u1sW9rluJMQ+iwwkhvNIo7BBEgAQutvbXzbKtq7L11q58ttq2BBOXyR9U14DGrbL95t4SGGxfQrZzR0B4CTr351h87gPT1o9BC6FpMvQ2NOFDlaBXpVZwc12UB8lpByxVw0NddFQwClu8j25ZwVwF1IMCdc2/e1A3NxqoWm+vLgU3ME6EEL6Ptj5HIsV9Li5mEwSARds45xnZAihru0TokJBiUssIC9Tex8jAc/tpmu3MAlLa2oHtHfXTH9MoBFzOk2dm/XeLtTIKu+qwlrcEEfZOCEGCD2+s2eUaIqJBGLmMK2H5zQXPKDRYWy1ZrIgYRKNHzKpzMzuGgt8AxBpDQXo/r1DXSrmKG5l4OkndSQPTwffdziY0d0nWPz+2fgw8wbcl1LBxtHd8fAyflnNh7pT8OAEYwPo2n24uTMAwzzNijCIUItGmggpzbGxtLXjrBN+GZf+Wf1seExA1yyC1jLHvg86ft8bxYL5fM15AsjzH/NrcFThgPCuXQog+7qMFIJGZIKt/XFaAXkF58UcsB3OsLDFhlvsFos1WJVhNswxiJUgoEGJICHFNChHJ3QUSN3Zs1GrPoO6v0nDPQrPNKnTzAgbS9W/vW95a+/qwsg6HA+6ORxynSQQIXPHw4R7z+YRf//5X3H/8iIePH0QQEQgBCcdJBBGFAFAB0T3ABaTCZHBWZkQsi0CEkCZMdy9V2PAWP/3hT/jplz/h1es3ePHyNQ4vX2O6uwNoAigg14pSbA8yIvUYHkbU7xHte7SP/U1LScRnSLfQecs8n5M2fGr61trz/aVPXWfPM/5PmcdvRUC2CxJd4SWW6VbQ9lJ/r4PNbsYXWZkdx0FGr13hwrfa5VGNR7b3sWN2a3pKOV9KOPI1hQ+35H1q+/Zeey6h+XOX4RMDXZi2LNqDfWz0YAWz8JelVsxqQVxKQVb+4Hw+Yz6fcT4/YD6JIKKcZ4RaEZlxDAFTjDhPCYVEaaeYlW9l5Kp8XYzNwiGp4ocJI2JQhRAIx5liQAoBU4qYkggigm5QZkahjFIIOckb02ECEzCdJlAgiUkHjZMYSAQRJBYEHAIQg7ixjAExCc08TbEpKvk9FJV/SMp/ETNKCMjTJLEpjhPmCBBbQNpOzy95wTZPSsdmqsiFwUSoBBQOo7KcCnOoeTRY0OLYptXHeXc4gx6Lni/ZSr68S5YTe/Xu/d3uvr22Yv9+bGVs5B/xos1id/u3VdfFthhusyivP3HzvapH3ayv2qJ424W2Ce+1BNXtrtvoC5FTvsLG/G2sH/Tn6+TqdmWOfdhuC1vbr/VvKy3x52XZDYBrGRavr+fr1vTY89nz1TbEITBilP0+TRMYLJb2DQshxR362VuZESGWFCFEcQUNQs7zKKihBQ5teJvb48/Zv630RQQRyvMLT3/zW51JX5f36Uzh3kH1JRjOvTpWzwewcMwH2KEiZntiHnjANFlciEk1zcXcavNcdUIIM1M27fqlL1QP8jVQfgOc14apZG0dVHYJ+LGTQnY46nLyoKyBcZc2zJ5ARZo6alV7cNj39RbBh5W3BR77MrtLmcW8Llw3+fKIqAUZN//2RN01iBVUiwWhLg0clmdmxqVCAG1DUK2T7keTWr52uNWCWvOwXoiCCr4SYhRrhlqd65E2IBD/7dwBdzvgLIhzD3KtL8ho6Npg/V2EKYX7nLOCd3Oe2zhKP0TwIP46u2smIlJTX9EEL7VgPp/boc2AaEyz6VGjvVOrAIEsE9XbxN18uM2Xs+zY838/7qdxXXmf/FtgbwOUHRi/XNO21gwENfA5xgh2+8YuMSIe9tNmnAJrt86SWVpY+80HvgHzMSYQM8TlEeuFmHE+PQztLSWDOarPSjk3xFORI4aYzYEXuHYLnmF/LMbZx8zQJSU+TTm0MWout5y//mH5OiLatNa9G63leDEzqtv/wxkgTRhiBRCthUOreA2669q6d/msHmu7t/hp7SkFxYHkRKLFn4gwab/neW4CBxMceXC9LtZas8xxdW8x7WsCf51HvmeY2z7LLxplykQ1YtcEZer7VsubLHiglnU+z2A2oSg3F2JJY0qYBpAEyNazX88UbQRgxCd3wSQW80ZBLSGCxc7p+6Dq9Uch6H0pM1kri5uAGBFAwkiHoKb9BxyPRxwPE47HgzDiecbDR3HF9PD+PebzCaf7j6h5xhSBeEhQUlkFDBBLm5pF8MBV5eIEUATFhHT3AtPdK7x4+zu8fPMT3vzuj3j99me8/d0vePnmLV6+fovD8SgCrDShQEAB8TGqd4fjJwgMVg1COCGdn8/lutj++/MCX76+a3Te9yCM+JG+Zmpity9b60A/f/9r8nOD3bfUz46paVCIx4G+7yH+JtPXnvdr6dPatz4brtFHz5W2gWQsLHWEWrhQSvu30deQMoTE4qaRX4vEHBS6OKPkIj+lIM9nlDmj5BNKnoEyg2pGQgET4xgJiQPSMaFUQgpHlBRBqvR1TuJ+qVS1DI4JaTrgcHdEShOmNAkdFQMCRVCIiJA2TjEgEeGQIqZAiKTW2lXqDhwQwShJANzjYUIIhPzyZXNVys61sWJzCKRuh4N4BIgpduvakMQaX2lCSzEEcGXkkkUpcIoIxDgcJhAx8iEhBIBrRi0BRTRJmoKg+fO3xBC8oHK3mBY+nxFqRWW1emaAi0TxWs9vB5HbfC/4KcOYjGf3oPMeb7tXzhaf5nmDS/tgkzfDPjZ8mde4lm7bj7eC4CuMUR4OjV8LAHqshD42gpOwKneSltM/1ZNEw1m99YDlkXeHuu0FV4c9Z1+WlW2vWn59OLTH2rIaix0BigVTb+6hrB/LMQr9+fITY5U0/tHBtsV8kB2OXYvKUC6X/WlndJtPXrdv9/htbZFP6zaYgQRMtQBEGuS+x8is6gEl14KgSo0hMGKYAIQWK6Ko63HvHp/IcAWLKdPXztWuP8P99SRBxGMZuP4FWqP35vbWS/kSkfCUi32rzXtKAbe04Zb6gI1DalnmkmH3f5AG741JLmUVQhwOB1CK6ltM8q3A94XFQZMYeiZnd6fwvhACcBK1EZRf/lhuXf9Xx3togQNox0N834XT8rO11+Vfx3FYC1CWY7n8XIIXoxCitjK3+rQlrGmDYgQAresH0KwgqgNLay7qIqS7VmL9Hayuzsn7pocAgjmAQf1w24hf0DSnCSpkd3ONcR0N4wAAQQJwkb7bZp/9nKoQQoNn11LaOrGyLPhZEzrEiEmtgroVhAjkGphcGef5jFIy5vMMZh0fQIFJ1czVOQiuJWhj193v9Pnqe3rp990NxmqtLWM7LAm85VoPIYCpDoDzcj1YuaYZb3mMuPZ5+rtdAOLd96zaMpTFyPOMousvOyC7ltouNRMOEQgnPAz1mh//1m9ihCAmx7pA2zqCAbob5/USEF8K9GTZBQk27vrvLRF8Wf5nuYdzzqt58gybH68mqICA3XUxZzbmSysD20fMjdwbkl97fk/amLb2QoQf3f0aNQGDtxDw6yWE0Pzd+nXs6/QCii1geW+OWl42Kgs6x515b/uHufVb2mGM2Uj/pDipT2CpO5cKk4syc5uvaZr0HAWgwtR2V1VGgbMWMgaNSOJZtNbpHje3V8os1mJ1qQXJ5MomYQiFORTnm4lM6CgWRjEmHA4HvHz5EneHCccp4XR6wPl0wsf3v+LDb7/h/sNvyKcT5HRmpEggteawfnJlUJ2BWkBc+rgSgUJCSAeku1c4vn6HVz//Ea9/+gU//+m/4N3v/oDf//FfMR3EraO0HcjFhCtAj18kgggZEzkTuBYdn7gm9m+lyb4gNvUUEOgS7fAj/UhfI+3xEp8jXRI6b6W9fJ8DhH5s23xbPL2vhfmSN27fp9d36/tXecPvIH2rbX5qu25/7/a1sZ/ntnVxUx4jAdqfj+vHUEZj1bi5IW1KOjmj5FmFERllPiPP8qyWGSgZVDOixgbkANREmCihVkKgCaUEBBVEpGSAutCKIUbEJHEvY0yY0tSeiyV8FCWPQJgCIQXCIcpnBIlFhOhUiPIcCFnjGx5ZlNayClVM2aa57FW+j8BNmaV5BDBhiAavjjEMFtyRSBWoGLWK0h4RMKUIQkJOSeJ0lQklFHFLBUcHK73r6WcppyKAEQkopBbzhVCqBhBniR+Byo3CNnq0Y+HUyvbrpwsiljiH0eH7lhBLYYXnIbZ4gmuCiM33cBkDffp9eNt7twoilvlN3I2N8e75jG8wTCC27wSu2xpTWs3Jdhvj+j4jGga05bffBbSRZg1V7NW5J6Ra36Xj/KtrWxrb39+9bBGxqs3fsZfWyhbg3sZ06/Z/TKLhs6+DnTPY2qqfJvzlEMEAkp55KSXkJlRQbyO1SkzLWJqLNuNTpyTuh2NIICrwDi+6UML1ebEmrqZPuOo/m0XERSav4w1ftG577r+/hYhfvvc5tBiuJwa7hWz+EkM0d0yTxISI4vMZThq/JHRWmsK+FgPClnTMglivdRvU1wZu1u0BL80IW71yuCrwa37iWnHjXHnAbvuS2wb5t9qz/L26WBd7wpPl4dg37/jddhkjQDrkXfSrfe4sNSJq4Kb5nTR3K6bhXLOYzHbqUUAjAyW7VULsgJlrm9IwGriGVBPZBTpNCeq8SG8o0f7lKgIEgFEL93gV3LXsowaMNsTQLEVGX+oVJl0PlNvMWp9LzmCuICjAurBCaMCfLrk5Z0h8gtw0wBmqfW7zokIaP0P98vDlMgJ3YN4O8BAC4Hzz+/ykrqukv/XiWr62Bv0a2buY7Tvv8gcQYYF3GSPF8hDHoH83CkJyLTCLETuDYozIcwYqo+aCwsBMM0Ko7SyiGBCQMMWIAgkwjDpaYrA2RhgFyFgpQyBEt1nt8NBG32cbW/9pfUihzwszq7kicD6fwcwtuPcy1oKvozMnvDsHgwWJ9mtLqGNl+zg+YjVETeDGbBYBuu4V+CU4v69M4OoEPzGqBVWvywtSrB1B9/DhcBANtPO5uaCSPdoJ4K0x9pYRvj9b55svozNEfq31s9vKBkbdGiOMLT6DAf0HdSUVdQxzYWWGz+JWyc2D0JcqnDTfu3rWVLM/adg96boFhIAHuFPJqPYry9uVGVmJOrML8GubKCAlcStwdzyoz+PUhLoS9DCh5Bn3p4+4//gBD/f3eP/Xv+LDh/fgfAbXgpjEDYEJBljrSSmpgHYGhYC7l69BMeBwvENICfHuBY4vXuHdL3/Ci9dv8faXf8GLV2/x+t3vcffqNaYXrxADAUzdvVitjZElq83OVRbmmgChOyDusJ6aPjNpuK7vq9ByP9KP9M+bvgVw2rAeS7cDs+6dDTr+R/qRLH3a2vh668pgN6LO0xKAwaSCGeJuV63t9Qe1ikZ+KQi1IpSCUDJizQAXZFQwKhIVEFUgMCoxOJBq8UeUAASeUDniUMXakw30jxYc+k4FAKZsFpWmFKvYQIQIRiDGpM+iUibCm7IoJAVV5qCAggNiEFq71IrjNDXlHFHIK2AW7wA2LkkVWSSOodGU5BTgZDxNYEMFqFUsRoiBaUoAKtIUIVbjCTEFlKKKLw3I7/MBGAYjfEgMDM5AJnEnRUSgWpFVGmFsVJu9gcc09qwLFzwfavR1Xw+jotyW8AIYYyxeEkTs8a17Ch/Du7gdI12mJUpkNLrHci7t38cC4cu/K3Wex+YZ5KwL7KcFnLbvoe5qR8xJhAXjpUY6rw1jt7ZQbO8CkPd0ni1fK4UwlhnGtdPqcO3p/NR6TEyQ4PM2QVfrP8DO4qO/u79+ttIy3/58Op586Pai7kt17YJ0GLCkW3iNFdYc5OiNwbzbiFX/dDigcsXpfBYsrBTM1N0tz3MGUcCBje8U5bI8zSi1IGeJHyh1BfW0shQIbs/jc6cvGCNiyfBR/3ejn3sH0mPqW5a13Y7by1sukFvStbp2BSFLIKf92y+DoACGuGJKSJNcyhQitiKm7YHwfhM1yeECiN1q29YYGNHSgdtergfDxlcVfJLGiNbCzgF/y7jvrZ0lSLZcF76dDd/bAIGX9Wz9vQci75W1BXpqoStLkVU9ELCIzS+ni3uABv7ruywT2wkKs5rpwY9sPQgQarMjlIxZu3gAWoDj6lrY/YczNM5E7XPeCBrVJIZq25KNO5YWM+o+ZzG2TYudJYh0VNdSPdh1z19qDxg8xMewWlQQQcxq7DC6mepj7tbWznwGCkDggWDr7daR5dH6xo/LmH8bQN7K798Z29yfy9jI3PWy3TipJtDyjPPnHlcRqiTzydqIJl3HRTSjRQudEVMEnFAmhghURtGxGMZQ13MIKpiiLhAopSCS+Gk1d0ZtLjDu++W85JxlXqJog3gA3Vs4eEGZ/SzHVN5R10zq2ozIrGnQAiAPbXBuoJbn0wDQc9ttbR/IHh8PZOYusNNR1E95M8QAVrdEzZDEtaFZOqhAcZqmoQ1mmu7Xwxbxbe3dPLvcGGzenWQxIIRQMsLUlxkk7DTafqZO5JoFDxEhTQLqBwijmVIGIYPL3OpgsCM4OmHZCf3uPktZ30Yge8FHrXACMzF/hwpQRfwq7Y+LsTLOyYQOh4MoDhzUp7AFOxSh3gPy/Uc8vH+P+48fcf/hPR4+fEAK6taJImJQwbmOEAOI0TMFhMMLEUAcX75GPBxxeP0WL968w+//5d/w4vVbvPvlTzjevcTdi9dIhwPS4SjncS2N2ZU1JMEi/XprQdmtX7r+63oZ7N7bl+7za/fttee3pks04V779vbwp7Rhr45bn/9I/9zpudbiLXU8Nd+Nr99U5q37Y+R15F92tKr/+NS2LVu0x4c+JV0D6b4locintOU5+/Ec+MHT3r+9zOfar48pp6Ev+sr+3qLhw1OaqgUH5i6QoFoQ1D0QF/mbakHQPBFV3CKpQCIGRmTBNZgJJQWUChBXMIeGCZBatYvL6YQ0HUFkgghxiWRqJAGESATiggBGAiNAAHmjVxholtEpCF87RYkhKCwpI2kswBYDrxThHetZJ1gtkckJIVS5pcdO7CCmYCsVtRJKtHh6InwR64mAWAICm3sUxys3S/U+V0KbkwhyIDxwcFrOtZqCCo+gPRnt3p8teZ5LwoPlGvGf1362ytoUMuzUN/K8qgD5hCQrbl1+3wZr3nqrPVttvfY3iARmNz4GBATrmylGqSWE/u0FO96aYhgTxqpXW3V7c/LOW3k+pWN4yyJtLa7PsqVwinbA+UVdrU3o42HjszEH1/5etqqtlAs0vm/T8NKQY98CaK8tvU3GVV7OtyyrYRFybIBJVOEY4t5clEmTKNcyo3AFakGpRawimgtpWU/iqUItKgqpYJVBZB45tuhHAnC532M/n5a+mCBiM22dBl+q6h2w7ttm8kYQ2LQnD4eDgsLpIkPtwfbVJTJkxsoion3lLAYem5Yg//LYqErcsDNL9G30wKFPW4DspTbc+mwJAvu2kDs0r42577evbzknvo71pbtop69T363qozPnWdzl5NLAspi6ZJ3IADlWsFL91lcAzVdcACGoH3YBf80KwtaamHhFMEoHOwHneobb4dSA6vUgwYJBM6P5hJe/vTsQAAbPsgfWowZPVl/2XMUPJ9AsAIhISFRm5DyDmZslSNNsh4BtpVQw7VjdQOwALgHeIQQJZIZRusz/N3t/1uDGjXSLoiuATJJVkuyvew8P+77d///X7r6nP9sqMhNAnIeIAALITBarVJLtbsGmWMwB8xCxYmIWzWygLi4/9uMY+7mXnUZ3nXvD/mWArBHNds+CFVt+UU2Y51lc2azrqvtBM0O2d40Itz40SwLx2VpECBGgGkBqZeDrTCKICFNUF/Xy3Pl8RlaQ28/7EFIlRpgt1oTAuibhLyr4sPvWRz5Q8F4SwLjUgObWJ94ygrQ/LFCzfzerW7AQdexkhgEIKEVijEyxCLCvvspI11jOq85txjTPeHp6AlHTXrdg1SEE5JLV7yOB8mPgpI0VgGrRsnGplAUwz1kEEcuSEKPOgzDhcn5CDJMwg2piv64Z4EUD8TXLCB/7xMr2xOkocBj38Zo2rsh6KxJ5Sfz6skRGVMFE7x7OgnFHjbnAhXG5MHJOCKTaeerPVwQuyoTVdgQRlGHCBGXgSgHFJkALVVsMSBp/J6kwsxc2aBBySP4msABQBRCfnp4xTxOeLmeJ7xSbBeDtdsNvv/2G9PV35K+/I68LcloRiXGeRfgQCJhq3ZWMqn0o/Xj+/F8I04znX/+B6XTG5Zd/Ip7OmD7/gtPTM3755//CPJ9weXqSesUA4oyyfJX9VaauzHQ9sLnCdzoWxrQoI7EzXf826a8E4v1MP9PP9ONTBQwaPtv+PgBst3lgTwfsZ/oT0p+7p/954MYuHbzLfO2+XXk1oe98fk5ox1Bav3SxDQmAUFgGtoaq7R0ISGAUFHEZyQlgieUVla6+zDMKM05RaSeLt1fjcc1qFTGDQkQIk7ibjJMICbggQinJnAFWywwDLkjdDSuITdA4iUQ4hxkMYI5RLFszKz+Zq8ax8NeTxCtMCTGYRjuJ5WyMoiRifLJZRbDwl0gMotzRr6VksaxgRp6mXSzA4ih6OtsUhZgKmIqUk7PQr8ziqkn5VhFGOOD3YL40noGaV40d0Lt9evxltITwaRd3Gr4PZ+VOfhUsf2Wd79YD+8uh0dD7acQE9sp49W8iIJhVguJItd/0Gx6vaRYRch4RwL7/mxLXfvs9kExg+03VxmCoH2Dg9ZhtCDT0OXXfrf5H47rvxcAwP0KzDNnOjSYY2Qo5ePunly0Yo7SbWrvvzYtDqwfstXOo3Q7evDd39+6THiXisA6IUQQR83QCM7CkLLhZAYBSFXRFuTLWGIshTsKfzjOYoBYRALvgzd08Esby1bbda8+j6U2CiLcu+N080Abbf7+1rI9Ou0KICoYcXD9KHjx2/3aPDK0+zNJXoR5KAbEGCo7qG/94woxgqV27K8Fj7LT7oHLWpmHXsrt7gPxeexvQ4fPcHiJtUffljYLNvbI3ZQ6g2dG7e8nGxMq2LrPgzPtt317ftqsHto42QA9yGfFSY0Pk0oBv106hL+wgAswFR85Fx70JD+pDjvAwM9joYi/UIM4wIYKf973wxLeFdfGzni42L7ygofnub4IcPz5VOFI17kWAUXJRd4NS71wDSwtBaoKINrZiCUGlafb7cQ9GTA/ze2+OUCCYMxcviCjs1pZbX3sAbvcxU2Jz2WOHE7eYEZ07qkH67vMEzIVVBCJXENw/Z+CqF8KNwZmLxclADybXgOrMQLbg3jaNlJieJiXeVXBRhDkxl0RAr3VhQqWiLsbMlRYRVWHGvpYG+v6EBXrnTnhia8bcdVEgzJi7eVbU7RE5jSRpVvPNWAIhMEBhUgJRnqoCpbWNuXfbNdS4rmsD+DcEuNuvRqFYE+q0cQFEAAFtv9RcxnOaJI9pEvYxJREqJpYg9yvb/Oj3pZGpGM+T8Xfby7bj4wltdur0zAoKuaDU/Tstto0IRsV1EgIw63hxmpFVIGDPA1TNUG1dQ61YIiKIihjxhyDMZZiqoBMgUJFNyuJ9QPhbMZ0FamwmPzZW9jRNuFwumKcJ59NZ+jXomVEK0rrijz9+R/5DBBHiyk20+eYpqDWEuKCjKiQGQpzQNPImnD79A9P5gl/+5//GfHnC5b/+J8J8wfTpC+bzBU+//BdiILEiA0C6nkvOlUUnm+QVgGg7C9mkcN/eEuIx0tUGev/ytxC270nj/H1LOtIGasx/fbDfn98BVh3TI2/P67U8H03fUPQmvbcux+238/X43tvz/Jn+Lqntw/eeYjcVqJ/Q9vcj05L36dS37GV3+Q1fnQ/YGj9qf30kn7+jsPdbavzou6+N9whDHIGh3bv3gLqdy5tzikxX2mg8n4VTNFM+xH4HCH5tiowKp1evMYHMnW0BOOt3qQDkPEUwA9ni7oaoAaGFvgnTSQJST9MgiJiRS0IuuVo/8CoVIEAt3cXqAvrbmkskQpKZxIo4BFFSEmP/glVjRORcUHLESoScVgRWXsJ4myB0rNH2ITYlFjFdJcQgMbsoOJ6aROGPi9B1FoC6jXEDgD3PYDwZs3R4Ua8DMWQUdnPDsCMp2S7086WbS9TPA/fxz46CiL3n6ozZwZveIozYe6a24oEjmnQCMytd+eprr9zdWXtH7eiv63vB4qg1YUK9p2I8wAQ7LUYEQgOa9vocRDsHg8cGWll79ePadLPOGPpc52IviPDtJbdn7PXHdu4xsGk3hVDXZle3HQEHcxtNHWVXXCO8+z1sZ3yJuqk/3NzsqW+hDTe8MO6vie63YmKiQMwIJYADY4oRpQhvmkOBeGdXvEgt1HLO6kIcNWZNVEsvcaVurs/FMqL2gztzHm3nPUz5tfRdLSL8ZCU9nAjuuz53nIfbDz8k7QHbdr0DE/cKZH64ItbOPRb1oRzYzMQaUBOnCXGKOJ8viFPEfJIo6BQjKhAOdJvsqxo8Cvb4WjEgoCdQJbUmQCgWrPKoEcQA60bHrL4VbWH02uwjQRXssNQoS1UPnnogVa61j/SxLag9Imxvgfsmm9angY7ehVQP+NVNP4hbES9srlYkOggjmF5KI9ikTxXo1WC9VjGDOYsRdg7YaqBwv6HnVJBSQU4ZJSWgJAClcynCIAlsSkEDXjNKWgHOIAXwcykoXLCULFoj84zIEdMcEQJhCkIAUpxRKIKLuGYiJJTMKEksK0ioyDo21r9g0kOGgCJB01NJYBaTMubmRqn2vQYX88RvIHHtNM0Rp9Ok2rl2v6AggUtAZtGAJwUSYzzV9QQAp3mGWEKsKAQkJhQm5NLmaNBD0QJhiyBGfJeWsqKUhFIkVoVNACYLce3mnAyrgP8s1hx28AUKmGJQolRdnKQk88IsgFgCdhsobvEAANHqCTFg4iiWl5C1GqIAloyCwtJHrHNPQOn+gPSEroGnpRQsy6La80HWZ2GUIAIEA4FzzkiljWPQQOYpLQglYD7NotV0uQA5Y85qQpiS1FfdROVSMKlG/zRL7JsQV4CAvOZqvSBzSE7ptK5ogb2CTTXRZgKDojxfnGYQB0KYJ3AkEBiZGH9cX3AuJ2V8CNNpRsoJS1oxx4hJHO7I+LAIrzIrw1UkBggFNQ+fTwBFMCRw96oCj5eXlxoPYCRoA5GahGcVDopwxgIa2/OJ275aGVVZNGBmrLcFFIJYy6nbH78fLcsCE+TEGGUdBMLpckGYIiiGGnAwJdFjMysLc2s2Wsp4CxdbN4D0DaERl26CyR0KlSawIICg9l1AoCgPSFkGxAfEIMJ4Uj24YsGZJ+mzmZ4RM4OmBJCYszIkLE1lAIw2YQZNGrg8F4CEyTWBf1GhGUOIuzidELmdQ6Ui8cLuXUgCEkLjcJyfvqhFzCeAGcsqwaSJE8q6IN2+4uX333D9738JF11WJX8JgQuICYQJhIA4PSNOM+ZPnxCmGdNn/X66IM4nPP/6vzDNJ1yeP2nZz6A4Ic6n5jKAuDLk9fyrZ+hm5zpO3Mj0twI3xPff+bOA4L1y3wOk3TVXHov403C6by34zxmj96W/Chj6/j4zUMWnHwfy+nr/VfryLclonihAKAoYC5hugDHiEv5VDyRRNAhMja6qvMFosTuU5MZEmPQHasfjuMr3I/ugf+TvgvmP7f3Y/f5b8lIXGO8s59u7f3s4vAF+eH9JDAQS35NBfZIH3W9MKYJY/mbOCBBBwsQSN46QgZAQsKBgQaQFFBKArwi84JZ+R05XUPoDSKu4BwEjFRU0QHig+XxW2jKq4GFGjBOmk9Ivk/ISauEtSk1zdVFcSgaTxickiUWXkNV6OanlsZzOIWjA6yociMojiZJeSkmsqVNGzoSFMtaQsdR1zzhRxikUzLFgCowpBEwhYgqTuurVvgMjZkJWRZKIgoKm5CWubg1qagpXVSEpBAcSFoRYAEoAZQARpEIIICEFoAThbWh3LiumwUr7stGDDtgd6hBIlPFsrIh61KXhdT1essFPhueOrKbvCilMCcgQE3LX98BoV0Gyf7uFSt23dxvbnnACrL6iDkfr86l5OJ6GyGJyks69Jojw/I8B9MEOH6JWd+sXsjbq8yb1o4bDVJ4X0OCLrvaWJ3U1dn3e86dioY4qtCBjoIZnW3+4PqoD4OaD70erd+0HuG9gfHovjQp+XlCx93rL0/fl9pmjso8wZfu7YhJ3zrpNHvWnGxS2PSQiFsJpOiNgQpozIkdclxtKYdzSDRkZ8TKhMGNdbwAY8+kJMcjeikBY0qI4Q9K2BeFXBMDbPWvutfVbzu4f55qJhonwYJ1fl1y+pQrHm9pdjU6vkuC1Ag86/lVSnYVB3Vvo/j3WDUUAS4sJMWGeT4iTHM62kfn32n7M3fdRasIId81Alc7OuG3wu+eC/UFQQUoDc4sDdve0yAGoIML6WAI8eQHRKBSwUmmcW0OyPNp7XNe3gf4yIk2baSv4GDdU1A1ztw9cHu3TA+ydFrNQRFonHUVmEXbsLX5mv1uh5FKloQbOEsR9BqnQRA5LNXElhoRXtcOBK4hZShELAqAKDewACiGCSIhDRkRBAFWnm1znjQkLbEx6qXU7MBmMwqJxUrh0/bRNbkyUcOyDU3PbSK0fdQ1FA6mVcLW6REB956duJhQ/RwuDNYhZoIhICryzCFBKyb27MCK42tQ1STbmNW5HIzaIUIVG5nrIr5naqfY+RNjBVgo1opFZYgQohq3blu/XXmtv70Acv7vA2gZaFgaHpn1vJtgMDaJM2pdFxndmtYSIGltingHKNc5HFdrljEyESftomiY1kY4iaCtqDu7cZ5VcQOQCX+uUNJdcwdXN9l4mgGIQ4jLIvSWtCDFUoN3eK6WIy622+es+bh9126XLD6QxI6LGxAABCtSbFcrpdNolvAM1H9YilIW69XRMQQlg4qpJ384q+RQuqgWmgoxo86K56aqriln9R5LE86DmHi2tAsRQaeVbHze/tUOgbaC7f1+Dz51fw5yTAPLmE1W1woIzU6+MW6zEMFt5BFAkBMxAAKJq3MUoTGYrUvYgEXYWySerlAITiOYq7ACS+OFEO5dl/WrHs1mgkfgmVrdSpGf15XJBjDPm6YScE5a8qk/lBfn2gvXrH1i//o709b8RIoMCC8OicTKIAgKJO7w4XTCdzjg//xem8xnzr78inE44ff6EeDrjyz/+twgqVHho3+OYbL5r6+6fqUfp0ce7s/W1PF8hcI8I/NfonsfAvZbX3vP1fkUHXsuw/+l74Rvo+D85bbXA/wpp25/vECTt0pxw7X1/w9/PuMkq/Sgm8P3pPWX+Gf01lk31T+nDDCChzWOj1uwZ3Jnfjd7tL79/rh39Hvt72x1+r7pfnW+1OvoIwddeHt+iVbnNtx/HN6VH/Wt1TO/ujXenvnuUo+B93htw64Nb+R3GQMfj1iEItYzmoaD/bvwlWN0e6TVxZi4CCeKEgAQgIfAK5gVUbkC+gcsCLsnxMmq6EGTuTmrhGaPwmtN0FoWZ08VZRIjFaqUrle/N64qcgcxB6PIifEBQxR7hNb2ioyqpBaiCl9KzUD6AWOI6EJCoiLlGAUq1jmZEcp8ARAIiBcSqWCb8fFGrVeFdAdFCLrV/QyVMpQ5e2cf498YDC42PIrRvLJJTjIIFBApQNZ46csKDNppbONAjO4k2r7wrVgOP2zdqXkCj8bvnd2n/lv/4/N69MXG17nb36ED1o2cx+oub32oxocyzCQP6JwfvHbUj9FPPEbvfu8pVO2RXhvVvb01tZY/WCR1WWcu2OWL8gj3b8A4ChI/d6eNNl/n21GaaUmvPQ42Bsndy09tu7j04J+7V8ejdt5xTTcDQXFbt1N49t1/XMdlZ9siZ1o1nVwUSvW4orFVszUXEwEAkzHEGR8ZCKwoncU0eGCuvCByRS0IsUfM05dJJsADo/mF14ALvuMwfg+NYfMRZbenPjRHxF01vmUD3M3JrrzvqjeCVTVT2Ik/46sGgrm/m04wQI87nswSlNs1iAxVckfcWhf/2AP9rbTAC5mHik9vz3iLgSADhwc52PKJu7vcAgNc2Kj+OnkCt46GCJQnAiwoAj3EodjLeXZgGXOOgnX4cGrBrtKPc64gPYNN3VXDBVPu2BV9mmTccpB56mEzTJBqxQfzElbKqdq/UZV0XfV+0QGKIYFKP7EpYitmtP0hYDv6SUbIEgYYSeszmtqQJJyxZm5P6B81q+jqO7Z7gyg4Zc3PSLHYMIGQ55EkP+0r4qU/O6mtRiQXViitcUFikwzmnWncDgYP6YZTu5LommrXLngVNbxUxaoyPYK1cUwuSof3d/IJYDeSSO8B8BIbHA5mZqznv6NPf/vZ5HK0BCqH6qLe2jlr3RE1znvXZ2h6dv/M0owQDkYWBqe+Ugtv1CgYQZ9Eq+vz8Cb9nYL0utR+9i6ZSRGuJwcqoEEgP2erWilrfBFcv3x85F1yv185q4XK5SIDtnKs//qBa+UyoQeGtj9nWujETjvizMViWpa73UThg/ZlSwrLI2rR4QBYXgYiwLEu3LsbYJxYzhJWAjJMQJFOaZM/TvcOCdVu+0zTpHgaIiKXft4hoE49inEM6Oaolx1brSYnXsL9327PNByp3YydEPGq9xD+m7CWsWmYREYGAOEcdC5mjSQ9n0+6R2DhiHk/MSKUgUEGkBCoJvBA4Z6AUnAJjmpuWkVnyWH1mFeqAnhFixKdPn9TqZBL3S1//hbQuWP/4HVxWIN2QlxvWl69Iy00CNeYA5glxPmOaZpy+PGGazzg/fxYBxOdfMZ3PePpFvk+ff0GcZ0znCyhGTNOlztPxLGn91aePAJd+pp/pZ/qZ/g6J2ZSPPJ21FapVclF5tpEm7TP9lhr5c3AA2N4EqDcgYf/3z/QzHSfDI+4BhVXwwFxpd6h1hLghSgBncF7BeUVar0jLDcvtBbfbFcv1K9aUkFiUDsMsMR9oarSiKV2GaHTQJBa7apFOgYAYan05i8VqIELMAZkYJYhb3pIhmr+sSjQEmBlujEJjzrMoqbV4c2L9HZUXWtMCQkFOAVOMSEq3M5fKh7Y+FMsBs+AleD7Dg9s9UB+r94NYf4uV/CR0suPnRAEuo5QALuoKii1uIqvlq/BIQWn5ogMs7m33QXbfhg48Jxo+PRhN7sIRPjPOJ89vjvffCkILS39HoUN5CPfjTl6qqKZA1H4dGn7XgHblS7h/zzwymAW2CQ0afd5iRjRhBTWcST8ED7TbNVc22r1qyVHLtFq3EN9juxpuse2PWifQ9gmzZN/0kE2Q/X58BL+7d//oHf/efSyPaptanXfKH28M98drexjyPcy14jR0JO6QOJ7QgNIoLS6mKTTe0gJOrJiaeM/IKSHlLO7aFC8RLwmEdb1gTWt129xojtB+61z+KIHDUfqugoh7lX+bttqxxtVbJE1j2XuSnXECjfceKXMoDDXoC/q5bNoNu/mRLhE1P5ym5iLCADCtzO7E3euuURjxUPUVJa+vcKtbDwLZbSV6B2FEB7xbE3cIncJiHsi2cQ316TeZdq3eu9O0w3Gz9vl24m391L/TMjoCfHYZGZ0QY7/YRtqB3YwOSGyxFKAALFxezSc9qTufuvVU8FTAeH+IEcQSAExqjjt0GoxxK1UI4hk761S7BrQxY5hlgLWp5Sw6Gr11iuueDlwj+M1dhBCMAmJxz9PMbVtf1IZU/oyd8CQ3IYQBn/osVTC0jbEXRIzjTa4Q3lkP9rwf63Z/u179/iNl5s17teydtTUKSsZ9za4fvV/r6wBO/565r/FCB8Ctadc2ANXlFZvmO/f7by4FUQ/TaZ51/zPt+/21VbgAhdSBEtW86poJ/Tsjse2FCZ4xmKYJeU3IbD5u+7UaSIJ4d/PflRHQBA62F1oZR2PkwWMv7NoH9bF5x/IrpWjAKtSzQyx6clcf/37QcydOGsTeCQrruKpAYm8udHWjcQ3as3qGhX7+d+NjBHX1xWv5al6egNQ9kVlchgESt8HmAREhkhqqB99eFouYwigBCKp1Ir6GhbkVLk400MQKo/ldzdDYI9qOqQqeTqBpwnR6whRIAmdzQV5fkJcb8vJVGPW0SFDq9YZSsrhcowkIJ8TprAKIL5ifnvD05VfMlwvOn3/BdLrg8uWLCCY+fUGYJkzzSRiPgbge59hHp7295C1l3nt/MycOmJlH8/w+RPX3JdS/Z2I9A78lfW9G5T3pI+f5Nq+/Xnv/3dPbeMajPMYL9zLc/PFAnlzzHGmAt03HLaBm7x+1s++fnn/+qPTomnrtPPDP/Kg6fWj6hiK/7TzqBVS7+IT79+19c1yXxjbVCa74wI5QotjfGVwSiip45bQip0W/hZ4WiwggRAZH4UyJSKxf1QvENE2ihFld4yqNFajyZqx8I2KROpYIgihCcfEAryqg6C+hp8Xa3WLHVQowMCILDxApSBy4ABfjAWAecAqGA4zVE47FpjBcZ2d9t3nQFG2iWvBHiykQvJtq/YQA9konRmeboEEqUylChvGydDjcx7jLvjCi3qea+YYPOAKV7/Gce+/0WIK7Xq/1a6TdbXVzSPxu67mWSYf1dpVE26974U7tJ1VEa8rDfQwIExr0fJ0JGajySD0PFYa6hSa8AFBdMtm41Gb387VvlxNgbJpJuGf5sI9j9s8/Mr5vuX/0TtsTX3u3F0S0OTTUgQ+myk7dbPaNs3DEesY82pzrk8x31w8a49Kue9wlhCBW+8UpgDv8wJRIWfdV4+EPUxdrpvWR/13xXru8uf96+mkRoWlPyHBv4jyYafv2QI2dIXqPzXzObZJEhPl0QohRXTrIt5kjdsXslg2AtoTIo8IIk3kK/sR9U0C6ycmTok3awGChRdrk90C5aQXsAVgVPFNNfgsMuy8tR71GRA9P+n3QtwlJTLv1kTSCyV3f7oDOI9hZgUXrx4PU181AQxLzUO8yRzuGoAG3iDSIeRCt8jipuxPxkS7ubhJKljgHzAxS35tTmKUNJcvDmSAaL1nnbEIxUC+tmocB4wygVEkrZxE4GOEkuAdXS4hWd6C59HKgIrtdjoVgDCEiqBmjaZhL8xkWhEfCNLAuuObPt6411hgPOSOlFSmvSCmDS5Y12RF0dTRQCgHIEhzNze1xryhGLKrb+nE+jC5u/Pw5FFZZN5QWQNqAc7+u6nNDWeu6aj/15rZ77nb2hBaAxeeINX87AM39S0qp1sncLoFFOz8CiDNq/IKSs84PrvseIHE0rrebWA0EwhNQ4x3M84xSCpZ1wYxTjSdh7ShcEKdYXb0RkcblADCJhlHTPGpCLetrIlQhwbqu1VKgpFyFd7I2GEzmsgvGDTUCWfsv6/O+jqz94a0y9sZSzNFPopGlsTHMOsKsJoiaRUgF3LV90FVn1gtmtRKn6IgZsc4wQYmfGzFGoT3ZE3f7wrToxsHvy+z6WT7OR6muLxuL7XxvlgcwgpFk/pD6Dw5hgsVVyVn2x5STrv0scTdmCcZtsY+CaphYgGkmoAQGFVTzeV04tSZRY1kEZYCNYS2YO5Bomi2OzkWEFlyQ1xXXl99Q1hvWr7+hpBXp9gJmiUfBIGC64Pw0Yz6dcX76BeenX3F6OmM+n3H55Recnp9x+vwZ0/kMms+gGGW/pogQZxWGoc7BSk4c7CFj8mfYz/S2ZIzHz/Qz/Ux/9dSggnu0VhNgQ58vO88flLDDd/0VhXU/07ekP2c8Pb/pvz8ukYL6Pl6U0uds+tQiaAhF+CDhEROQViAtQLoBaUFZbsirWHsutxdc//gN1+sLvv7xh2jjKi82nc6IccYUzuIPH2KFPs8z4jTjdHmq3yEEdd2EinEws7h3UtdOGSRxEjmLC5IyCd9IBZE0Np/S7FWpRHkQc4dqcRQJRaxUS1brf+UR2WsSa08Jg6A/RWlNyGeGufMJ5Cx79WMKMwyjv8U1lbmoahbAJDQjZ4BFoTAQgdXav1BGCEAM5kpZ4w6S2NkTq76zQ0u9oiCAWo7njTZCDmp7o3yU3g+NT/B844jhjN9HilV719rvgeqqj23jM27W6g42ZuA/V+8H8nvfLZLOjXpNeRpqQgAAItwi6qzoAaCwiwlBBILj3StPZEpYQBengmioixNYgFoMTs9j6bus2F0vhxlxNaqfDpu6S+Sq0t/m8tHY3b+2f69XPLPE7t/2jvUP6z52VHGHlZC2uptflicqZvQQna99XjGUzR7dt8PKPqohs7laIyAqpEUBoTBOZ4nHeU4LaAl4Wa4omZHWDELGbV0BRCwp4xQCntT67KJ76bKsiptIrNgGUPOrRxy7ra9ew/0x3UtvEkR4IOKR59yVw4q9qu32lgoe5P/WTtkTSrzn/eNrJkk3dF8OA1v0thiiBrmUb3HH4REGrwHhc2cDX3eAzb36jQBEt9h14bGbccyiaW7vVgUJ0/zeIfBHrfFREDHWjZTI3yO02ibs27Dp8s3ze2mPsdgbv43Uc4cY1O5q/XEHANrMB6DOAC9K3ROWGGjb5WN94k4Y0oOMgvpS37gzgVgAVEGGCoDMr6WVRRAiz/qnug4SU88WI8F80/r+FA2ZOifh52FvITP2W/2U7Rq2ObqZN0QgKhLTwdpUx8EEImrtwVxdMpWSOwuNWo471FrdC3iIgeLnRKuP3odVo58P9+aGraO953wZo7XMHhHo+9RSQNh9zl8bCZ76HPWxAkYw3wcv9mWXUkDe/RCRxEVRwq66D4oRuc71gpSawIecBkAuBdFiN2gdC5e+r0nmSptLouU0jvHe+t4ImKzf5YGap71pWla68rrxs+d8f9U+GfbfJhDp+9VbUVQLJzcWfozH9lgg5WY1FYQ4MksArYdpVozzAY4Q1o25gvrV2sLKDs3sWHNAn2jz18iY+Ge788gI9coYjcI3HSNby2C1uOFKSLpsGoFPQEBB0f2PKNRAzpUY163ThLu1/9Frs5hf4xCjwFdpQUkLlutXsX5YbmBlkmXLNaGKMNrn52c8ffoHnj79A/PTGfP5JIKIpydMn54RTicgTDrvhaEJEBdnNia9coAN27fRNXvptby+h2Djre147bk9uvaY+T3K5KGq3KnDQHf9TH/xtMOB/aiSX1lSR2vuLev+9XX749f9a+mxMuWE9kKEPSFE3z4VRnxQkx4VCn/L++Nzj/LuR8+/tuc+MrfeWoej9BFz6+E8xmZtkbb91+hxof5R327p/v7eHv/Z6vS+s97AxAO0xgoX2sjoVLOCULBe/SABJYNzAqeEYpYQ64K8LEjrDWtK6iooKHjqeUmtjyp8hDgpFiIKOFFdkFpcuMZnFQQipeMM5HXfaIC6hVjszl5jbAGIW4HGxzKXgUd0zH7t9/6XcQxq449qh0GNT7D/AkFdsxj4L3y4B7AtY2Jpu9+WjLU/BjTp4VNrjy5vwPwdQYTD+va+j+6N9zf12b2+M1Pp4Pr4Ju9gCiSiIq8YddQe41nbtSaIaL+VticnzNF5Do5dGUHfD+Z+ywkixn7Z9lNv+UBVsNYmuOeO2Org8hv7wVs+dDiC+7d/yeowXH6Q9n7svghstmkYb9derrP+lfmAtr8e8a3390ZfS81zxC13n+rLPspPbjelPNI9AEHiPkZIXJ0cRUlZ8IKGYZgb71JY9xX18pBzdQvG2RQrX3FLX9sHrcS28nddpO2knxYRQ3qP4OIoHTG4ctlNRD3Qo0q/zQXT5elJfOGfZtXCbL7eHgO4t4TkI8QRV40H0+ru39uTbu8BaXtug1of9ICcf48UZ6/fwwEwHoCPpD1Q1urHzEipbPrmOG/PzDgGpr7eb2RKsznixe7JtmIaINpKJXaMcFBCq5h/f7EQIAoIaLEPlGRCSYySi7okEuFViLEertD+FmFCxrquKDlpnwb1vSlaxmCxbimUGjCbzS9lRoG4JQGn6nqn6yVupmFgdWlEcHNhJOQaAMzMnaWDjccIwo/uvoIGTw4lgwNr3NlQ13UpuQOKs1py5JJQSoL6oelAXiLdmrmAVYtd5k6q82dvvtR5Js1uIDBRN2/2GOFOkLG3Zl1f2Dy2uoxAsn/fLCJO0wlAi0eyB8z7uBPStz1R5BkhEyAQNa37Ufi4LAtCzpjOF7GMiNMGfKMQME8Sx8QsK9KyYgk3fFVNj8vlgpRSDfpcSsb5dFarBXFDlNcEzgVhapYbpRQseelAfN/OKhgAqjDDW4oQoQlBssSioBJ285N6becpEdW4E9Y3ZgFh8R0A1NgOFqeia8OydHXr5umwHqwsA6atz2wMp2lCLgVlkTqmlKo1RRPEDKSGAvsUQl3BzOJKi4iEmSLqBERi6WRr160DoApPe6KNgKol1DRaLDh9jfkyRcQ4V8uGlAJKgWqtFZTJ7cV2npHsjeJzM9pdQANfT1Czf6ZdV38hOBN+aqxgXe+5ACmD81eUlPDy+7+Q04r1+hWBgNM8I84XXD79ijDNCPMF0+kJ89MXnJ8/4fLpC86fPuH8/AlhiqAYEc8nxGkGJondY4ZGgVUUwUKiB4mgiFXCtG8rfyd9BMDzFgDmZ/qZfqb3pp9r7K2p54EaDVa4nc9yRt8HBlryMODH1/UjBcbfkv4z9/N7bf5rjIul7Vx5BC5raXxyHxA2jX6zcBbuz2JBUE6Aupnk2xV5uYrQ4foVabliuf6B28tX3L7+juv1K66//zeWNUkkLyKU9Iw8nzGfPiEQkNOiipcRFCdM8xnTLNaizZLVqE+J7VdXIzPAvRcG66MWB23cD3I1fjWaN+gzWRWh8qoupZQHhmkMkyhmRnXZKX3aBDUAnADDrL+dCyoVODAXtJiGU0djehqYla/gXICcmqVGUVerxRTgJDi3p08lOYvkO2kToHpHkDDOGVIgfXxujAXhy/DP7fHQjwoniCqXoFe2mM7euxVTCBIT08f7IOUVNnU1sLv7HgURvt9EidhibIriEOoz0LiW8P2IUAUUhhnWNjqw3MptILViS+r2yYJZWz3DBsxv4LYvq2JUO90v3er61g7NHeGHTyPEPWKhm1ptCt8+e28md2KMI8z0oK5dPgdYJ7DFd+3aZt6yu2/tHt26DS+YkCKY4IHdXAgEFMYUCSEUnM9PIAq4rYt4OkkFmTOWdQVRRMoJoUTkXBSHOIOZcD6vSGlV7IPBTG3fIKCvIQ9j/zFn4Q+PEfF3JGq+hyah5df6o23gFox0mmJ1p0M7QghWUGWsp/xAvecJ73qvVmL4PSZuFhGvtt/Adu7BVU8IWLv3iB1mO7xb3buNZHMYDuD0zvPHzWp9WIppPPTPjHWs72i/bDcl2vQlD31h1yx/1tf8Yrc+hBJCprHMxeIwKKHj/QbaC1ZfItc/dtne1r+YqwstqodgqNYT1UUWXD1yVsYtK5ljGjHW8GEOYvjZEX9mQbFvXTCmcfy9QKk9MwD4hcWaAyqAYK6gI5hRg9tWArEdgP3calYKhYuat+7Pb319d12Nbby3RzL70dJ80dbFODdH7foj4RuAajmwl/aEEt0H+2trBParyyHNrxQJGF1yVmuIZiUgh19fXoxRhFHchIZTnFrwZ80z09alTxX6cGx7nK51u9+A5H0CePw0orHtG4TW5zWPuhFxXXF+fHz+9vdYj1GQY33i6+PbMBJK3VwY1swwaBth0O5a3NtK3d5gzfZl9POo/tWVI++P96j+Pe7BVdunzpNtIGzq9uGRsEaXbz/ujuhWKTiPlDOAEKP6FJYzmSsDqK7zchIplDKu63JFScIwIk6I8wnzfML5+TPCfMZ0ecZ0fsbp+Recnz7h8vwF8/MF89MZFIPGiZqAEMHB2qL7JwCL4QM4wcnBmP1VwK2j9CMFGXvM9HvzqEv+IIu/Mt17jxn8O6T3zul7Y/Ij1slHz4lvye9b6/JXnt8+VRZo4JW29Sd/aH2nutyff+P91+bkvfzeOj5Hz79nnN87N/7MObl5c3Ph/WNxRIu9Vt/GN/bPj3Nlj2c9nDvGLt5pj7kUUpLWWZoX990CVXMxN0ZJXa8mlGRxIlYB81f5JIhSXZ7UtWReUfLUFNisdoqBmIUAmSCCmzJO4//ZGG/loXo61OhFrxDXwDeS94x+Z+6V7zqXTH2eezR8/ebS6mP9B4ZpnldwcdSgp2AFGAPt8jQe3vMp3muCL6fHfu65gqmNqn96nMH/bvhCfW6nH46+ff579/b4oi5xv0U72Ejff0wrW+aOCXv2+Y3xg65e5L4BdHnpbxUKVJdLGAUMMs7s5pK4awqVz2rf9Z+hvl4oYc+Ts66AK3vTC64ulr9/by+5/YrI1WtPkGmlvO1M295//5m896ZhDo+8TTRgNooHbXjIsbAG3rR5Ux8feO/hx5Ztdnw+DNsT0ZIEqRc3xaEUcd1OahGhsU/FSoKFfw0Se2aaWqyItodqrFXXPw0DUfbyA8mjv4lFhDHePz49BMC/NU/0E1HAX4kJEUPA+XJBjBPm81kAlp2DrQkV7swIBqqEsgIUQ18enEgGGptFhJX7KnDKAtR6IG0E07wGMdDcyvhypV1bv3jt0w7Ct6QG4slHfIpnpJQ35dhv3/ZRSDCmPYJuT3O/A8+MwDTAdgBATTva3LIYOOX7MpciQWqoH8+CBshTYFARt0olN+sGLrkSEB2IDJbwBkU0zHNekFb1a86l6lsQFZimTLclU9C2KSCrMSQsdgIN69oDrHtM2CiEMAsArxkONNM0uSca4JlVE1zNEiuQzaJ1zzkDXKpp5DitmKUvCgpCIZQAZE/0YVwfAlQymRmzy8dZLowudbaJu289CgDq4xr4+TH2G9DWWLXgKMC4Fu1+0xqizmIiDHPO191bDlisCEC0/dO6tv2AGbeXK/I0IT478DgQSm4MD2k+dR0CyOsqgoh5xqyflBJut1vn65+I2r7jxpNAWNNa22XxF4De0qEUrrEBvAAABIQpIqkQDmpdwFMRIsCsEkIzCIW2jRDA1foqbcbJM4wWZ2NZls6SwmI42POWj2+P1dXvGSEEnC9PYLd2OusccBczY6zPuCb9Pr4HmHh3YUSEeY6H+3Q7C43R8gStfEtZAv7XvS8GmEm/13KbwgRExhQjmAnTfFKBQdQ8LfbFrO9O2l45boRRmAHIWsipadapfhHOc0SMQZhsLvh6/QM5JaR1VQZa95L1JusGQDyfcf71nzidL/j8X//EfL7g6cuviKcLTk+/iHDi6VmsO6YTaCLQ1Pq69v8qAbMjaxBuY07r+SmBvWUDeyfR/w2k1t8FkPyZfqa/b/q5xj4qjXyKsFPiIsOY8B6Ygfu+l/zzwFvH7Hvwne9J/ykCqsfSnz0eH9yXO6x/B8ICzQUQc6M1NGYCWPhJ74oJahmBtILXFSUtSGlBSjek9Yq0vGBdX7AsX7EsC1JWjqYUlHXB6fIFYGBdrggxSCwEYoRJ3DHFyeg2UsGH+DUnJo17qPVQV7sSNFvaIzxJRIziWhdAR9tmE1qwdz2lcRSLeA8QTeO1o5+FNo2IJHEaggozupiKanVVckbJSeLNqZKV+Y9vNHVAqPStQnTmHqK071IKSkrIKSOnhHVdsaaENWWkrLHHclFBBRRXQRPMFKV3uY52xaMIO+A7PB9u8wUH93v85F6MCP/8OBfv7YNG4nrBSOWWWQRc+gt+G6o8jmXbWUIMbTHhUFBhmAK/LR8TTATtk+Cut9/1mvVzMH6kPUteUGECiLHfNsIBEV4oZ+bukcbQ9HE9jEc+6s8RUN8PWm0l7V53njewwxvGnXe+d6rtKoPgdxf6JDcxfB5yj6hZBMjO1dudG/5nOdS7d48OW3s7l92fdfu1uRBsfRSAJc4OYsB5uSGEiGW9gTnjmm7gSFiLWEQs64p5mnE+XYA54OnCCBTFOwq7WBFsKMYOzrkztt+SPkQQ0UsQ94Bq4NFD1AO+r+X71vSqdsAPSFULVCoi9TFpv7rRqaCSuWOSF3uw3n1jmBAbCGLzwgiC6dUKRMjkM6FAFejtgGceuDIte9MwGgHWvYPtqI9A93Q0pA19FtQfsnCbwgCuWRNbHV+fG5uFV8vyhNt4pW/TWEYrS4mL+sV1vL37qFIKKBAiLIDRdqeS/ZLafGHu/7a6GFBb2+QOMQNf7T+zgCgJWYPAMhc5AAlCEFpMEjeXjLCqQZsxWJ1onR/RHjqaO/cAfK99wkXzMaJPO4srwLodf9+9gkOrdjsRcKfOPgMj5v289GtDsuo3+81c8wuafU5Di4c1N+6f/v4YnNrn0TdhnKuo88OD9H4v8LEimMWFT7V7ZtEwytQCZBPpRNJ+KlyqpkIntLRuIlRXRimr27BckEMWoNrqhBa/wAhrS3uxGY76cuzTKtzRdWR1I207cU+e1Hd03oyxNcYy/XUbq3GcxvEax8C+cxZNiHkQLHTv7xD79owInHpCfjzPW1376/75fvq0thH83PLEtvXb+N2IeuWbuutBhfoxRBTWGBJVmN8YC2P46imjQcfJuBt1yyQMqTLelYHLMpTKoOZ1EdPWVYV8GpgwRCGvYhQG+unTL5jPT3j68ium8xMun39BnC+YL58Q51mCUNOk1g/NlZ0IHEgI6WYxO5x/Ot/Ju717e2rtf+z5e+vnvWnvvH40PXKWfEs6Wift0P/zaMuf6bH0yLw6Ogc/sBYfnN8DJX4A49iyeF9e33t9vi0ZP+X5FKPgqT+XqHvl1TSeaejKGGpxMNdG3umt4/dIX/97CQoktTa9Pp/utn/DSD+W56Ppo8ZgpPc9HXa8po7bQd2HW4BqVmGE4yvrB+1j8fcYXlHJLAqKKOTopyS1kk4rCgWxlIgrchZrCrMksLhdFlOuuioy2hBAtcpQC/cam3B3fY0YhLMmKCo8UHdKOSdR9NM6sfMAMPKl9aMDYeWzWo1InIlmyWA8c0/zUmsvmScM4Z+h9Jnn4a1f7W82q5TBU4HJMu7PBdpecvWq/U1eGOHbvRVCjDz83r3xb+m+xy0ihAWjyk/3fNUB/yFgiZsPo5WCtanNudZW9O+Eozy2wg1lYLWTLV6D9WsTaMD1KajOEPe3Ncj+GAUkLu5E/e2fbxnQ5roJTd6War9XfnV3E/2hqfF4mxvbxDQyVu55auSB+6bxGf+Tcdf6yJ3wh/WqP7nNWd8kC8YdQkTgghjVwmFt+EEuuX5kv2ixZ6Y4IcUoGENh2cEZfRmbNfWxihIfahHxURXzwojNovsbpREcslRYAN6gfqrneUaIEsU8xkl/h7ZxYLuUGy7JPaCzA2zZ3w/XG2huJgYAywOPvox6ENa4AO2ZMYit16TdaCQVOWDrIghtE+9dqdytPRopNdxlwUR9mU2zW94nasG4+0PM70BoOwy3kutBuNM39jvaorc6lUasgVV7HSaEKLgtt5rPNEvQrhHINPdNgB1tSqykDFABUZQgXlqXdbkhpxVELG5ytFMFpCOhf5jBnJB5wZpekNcb1uWl0TZB5kUhnc+65RMFxBgQgoxFCVkJOghxpJpnGObQCMSOBMzohsbPx01/KHBoQhyrswXmCRx0rEpX9mYqtWp6YbTmJfWxeAUjWE3qRoUCgZjrM027XOZSKQlEsXv/KLGJqgafMXt9uJeXEcArrzXQrz3nBRReUMHMnbWFvw60tWSWEBbjxmJ8lJw1qLnGREgyz01b31yMmbso8VVIQAyIviwl6FNKmE4znmNAyhlpTbgtC9Z1xeVyQVRTQwYj576NFr/CLAb83Kr9RdrLrt0552pxYB+z9rBnTqeTutSburlq72EWgcmyLCAinM/neh+Q+B2+PvM817qOa8D2EJtLy7IAAM5qRXc+n1FKwb/+9S89R0N9x1vS+Lxtpvh9SqxOSOepj/mBuk/6fdneb+ugXRvXr1n7SbyGnjE8YmI2v2No7osATFMEYQafL1JmjLopt36LIWKeZp1zup6grsoS6jwryw35dlOmWp8BY1kjVhCW2xUpr3j5+oJcMk6nE6YY8fT0jDjNOD2LpcP5+TOm+SwWENMJ09NnTPOM8+VJtaxU08q0iXgFZwCJmzaTno0GBpB6HCtBq61jlnXTCkyNJngwWZ96IOPvlP5UUM2RBT/Tz/Qz/XUTO7rO6CEPXss5+97FvM93fGv6aMb/Z3ogveq/5ihVSuoDK2P5fvwZZ7U1GlCjqiHA4kKohYBGBTRAvQLtsLPXPpIpQ2h6iV+XkJK5ZUoSdyGJyyYwsAIoKePr7/9CSiueP38Sq9YsdFkgsToIMSJQQFT/6FChQeEClATkRT5lkd+cwKzCAyGIEKK2jJTXKGJ5UTRe4KqWyCWt4g1Awf2cs0ZWNFAggEgCaMcw9bHiTPGuZBQ0AUFJGSUlpFV4xqyujoMCjPJ+xBQnEbpUi12ueTEzOK/I66J8vFhFmEVESoIbFLXm5WoVUqFspVe2sSIEQmog9Chg6RXee558T9Awxoa4J6TYzEvaKiR390Nf+4rOHACmozCgCQ+sbc0q3AQPIOq8T7Q2Us+7KDg8ulxizcNiQ9h1wtQ9174r8NXqSoTOOsECWrt2S2OtPU44Qs0y4rAfd68fP6+FdfK9Vu9hz9Q6fYTCkvXRWPZu3YBuDgMAwuBnt5mSuEK2j7QbGm+DuX6/dj50aqO2NdZ2DPcPaIdekOLns15WheJJrcXO5yexiFgW5JKx5gVYgdtyBQDcpgXgAH4ihDDhchY37PN0RSqrCofd2HBbi7VOD9AibxnbhwURb5swDSh0Vx9+/6+Q3rZo91M9pDGQJnXNqsZvjIjTVC0iqAI78uaRMKEDUIkEpJCMd4iE+2M4TjQBX3A4+TbPGlgzgLpHQPFeO0RDXxZn1Sp+ZdrVuTbkJ6TANo7DcRccE3n+Hd6RiI5twU5/j/3iD0jrN3MJk51rk6LBvsdxGAH5XqvLCtWNjlV7ghqYWEpWjRNthiM+JM8C5iwEmlpD2N81FQLUhRPQ6PYe0IIaS5AShEDhgI11hEv3BBH22/frHiHU9bm6o5JrjpBwgifmvbXtN3xfjghr9tZj/7aWtbMWW/3g5oUenwPhdHfd7/THph5DPzKxKA/tzJl7+9ves7a+joQg4zj69jJzDR7cwIHGyFTizvoQUJdqsj7iNCHGUO8X3UNCcYF6a37bPvWCF79PmYOxUdBShYfDPBPBiQhcCACbCyVHnAmhG+DpyXGsxvEcx9/Xd8+SZe++tcuEQkcMQ8toGAdgU964j+3m48raS56g31u7tX6v0Q2OUfCpukWzta7/mnulqrWXks6VZklg+2O63ZCWG4xRsDmV1fWWaJewBJMOAefLM+Z5xvPnz5jmE6bn/0KYT7g8f8I0n3D59AtomhBPonAQ51NrhjLxcn4z6tHXo2Z1z7J/u3OPAIzX7jByjwg+x2fvpaP96r3ptXq/tZyxvW9p/1Eej6ZXn/94fOkNqQkM35o+Yqz/DgDrW87Jn+l96b1r6/1lbc9eKR94M786srp/4nq+tyZ/lLB2j66x9Nq+/i1lfdQ7vPnj8IJLj7XrvbP7I5dFzatiXAPYVZ80uoMbH2OCux2eVgn2Spuw8qDmCrkqs5g1QFHqK2UQEtKyIMRZLA+K+ShvgCwq4Gu10//U0kJiTKzi/qgkcE7oYgBWfsLRtYGUR1W6LyewBqcWHrxU3kK8AJC8E8xiuyn4BMuTtEe5gAtVK4VqGZKzuoEt4IG/F0LVglaH2rfCy4c6dsbben6+uVxmdbPixg5UicQ9GZunlY/nTKMVdvk86q/vPXd0b0x7QoSuPuBuTSj3vPt+q7evZ3R8pvD1da6BQMEpnmlMuNbO0N6BxfGw8p1gogoFQsXmSDmRxv/Ydamf/BH6+nqQmsbBc9ehQgsre+Cztmmf9nttLoyHXH2+e+1+Hnz37l6RbiyPsDoA1aWQ9Wn9bgHfKxB7pwIV4jN6oHPZ5Pj7VzPQYvzje+9yj8H1iSDxT7fjaL/Nnfo0RTBPiCEqZiIWESklxLAil1SFqz4mbIwRjIJE1rvU8MGDKh+127DXR9PfJEbEj0v3wJN3J+bql032GNmE5vmEECJOlwviFDHPp+qmSQ5xd/hvsuTNdwemHYBcx1XsnzXw2ywi9rReR4CsWkSof0JLYZAoj+/YgVz9obt+2wM6H0ly7Pb9IVmWniACAPQa3kfl1Gu8vwnV9/Qz+v/3YKEH9krWflBNjFU156X/C5JqXAuh0zTOfZ1dJbqtzAjBtCYgKfGTM9bbgpITogaoCHGqgB6zEDM5rVhX8emZ0ouYz+YFlRgMESbxlv97bW1ZS0BJEYULKFEVZJSSkcpWs98TNdMk29OeJYTvRy+MsFS18VMSjRDLf9J+rPE03CbeMaO99vse0cUs8zZZrACtV5vn2/q2OSd9wEyO2NSg4ej99e+12+bWXt8YGA1g4/vftPOzjkP2c2t0qTTMcb8vWJ5m+WBgt42J5RlDQKI+noUoU6k2vvr7r2bb3IQZMcYKxFrZyAllgWifTxNOp5NoAy0LcsrV6qS6aCqsNETbx6yutQ5Ew9ijq28dYyIgbud4MesKAEUFyaJ5P1UiFhQwQQSBNibNuoBrnXyfW0wIb/lgfeyfISLRftA5H2PE8/MzYow4n89I6j/W2mpWK5Z37d8O9O7ns8XQsP26WRq1PMb5atd9O/39cT2Nv41hZDYAHjKeqshV+zlG2XtKOzNDDPX80BdBIEwUhDlcrxKH4/oCOMFE4VzjPSzLgmW5YT6dMM2zFkogknHlMAHzCZ+//BPzfMI//+f/xuXyhC+//oI4nZDnZyBEzKcTKAZM0wmggAKqliSy1yYVvsv6DySikuL2DxsbrkG0Na6PaUcFIWJNS4wy17XzWvLziaixUm9NPwrk+pl+pp/pZ/rWxO6M82dTp9n8Jl7wg/nGf4P080z4C6eKGw7AFkShhpiqJQQXRsmpxYEoGZSyxCDwPC6AAkIh5TtRkErBmjOWlLCuQosyF5N5AMzIWTRxc/wdhRlpFf5UvDERQtS4LRXIbe9ySsjLDen2Fen2B5bbDcu6Iq0KuJkKib3vAkKXIvUT0H5FyiuW21fklLDcXsTlq8aPBKnQYZbA2jFOmKcTzucL5jhhjlPlzaExE83iNudVraFvSOuK2+0qFgxmfYGsvNCESEAIopg6qeUuMyTYNxg5mM1KQS5iabIuK5Z1xbquyBnIFv+SRQDklyFrhkIrD/S3nxsdLa6Xqe2Ru4IF9LS/PbOnRHhPGLHHf473pVI7YPjwfnNR1LsusjgN3mqDOgC/xwCqO1cnhDDhg1k+tO7rXTJVTwyhB+drvIlOsYzgvaFQJ5AIGwUkqTRQV7OVOVhCtNgWrZwxEe1fP0pSF9601zVFnqv8S6s74YHzoRPQOQue7rqVyU366a/XuVls8t8B1nu3RH1DSEF5rt+vJXMBbtD+KNRoNd/Jy8bVBBkwBVhpYptLavEFma/n8wVTjFhvz1jTgt/yC/Ka8fXld+SUcJmfAAZutydMccZ5Fizl+fkZ1+UFqSwaAwggs8J31fJ13fKJZo3ytvQui4jXiLMfQXx8uLDglTKO/n6tLm3DRJ1YQYUNAqJMXUwIL1m8p/l3dK0C9zvPPDwu7Kaaq/9efUYhgf+MoNJI2I/P+wBQwDvJeg9aYRRC7Jl0qbYr98/6emzaflC/URAx9tX4rJVnvubNrZWPCaH7ZgVHKWz7UoQ3tknKJxhoBmlzdYujgggRGjECs+YpB6yVV1Q7JKsfdC622ekDm9ZLHqYR0g5tiL9zJpQgEulKTLJ/twcqPaHj/z4an9YfOsZ1TrESvTuSZH1vO0KtzKoFEWgoR7TzTZN6rFcD9Lbz3M8BDPflfamD7489IZm/vyeoGfvL920JpYG8ri+PGPC98u05A8B9ua7AnbyKWFUreB+o7z+zhLL7poFl40nBCSwUVM8poVCp66a6Vqj1RiWufXstdfEqXJ93+xM3QZIJWUoIKHU+9EGao+0VNhccEe/3O7/v7ZXr7/l3vBBpvG9ur0SYR0hlAdz9vbnlBk1GgZuwz69FL+jy88PPP/89/r2X9hgPq4tfu8ZE2XXT5qCidS7K/BUlkc2FQJE90nawXApyWrFcX0AERGWcmTPyKpp5JjStfRwm2eOmE0KcEE5nhDjhrBYPT7/8U5jS508a5+EkgfDmSeoZJ9k59XzoNfWkTbajGIFvvcZEADGY9bvvPRhJSEaDS8Uf6mObAz+CpvoeaW+P+955bmgreQrjYfL37NG/d3ptrD4ise1B7xxgNkLrG9K4337PtH9GfMv7b09H6/oteQud+epTMq7vGlwHirjEvHddzqzDc+/dm4dxAsfptT4b6aRH+/iR5/YUEt6T3jOnHqFDuvRwHWn43lFmM7roKIcfsJ6PgELy87buTcZIc6NThk9Pq3ZvVQzCrAmKWvtbDDgrnhlqFUCAWjMoE+cC7Q7rgT3f1HjVXN0/Ler6qABBXKqY650QY+X9qOMtxQtAzmIVsa4SlDqvSZU8IjgCiJPArvq+uYwyHEfoe4DRYjWIsqHWMefqlqlaRVBRqwzueBXRpDe8gcHslPwc6N67mhb30xKPwuhaNOKQoR4QbJR0BhjweTh3Wr1sLm2EETv3/dw7ws4exdQ8rUqbvVN4rZGWNUytr6cJEgz7AKqAyu6HFmNhTxABizFHACF0QaBHF01jrIi+z6nW0de3PdPaVldql41vH9V3qFpdQHlQq6vrr/1OfjPdWtWX7uyXbM0Y3rx3Vm2oDuNXd+aLXWZ3rftWM6Cd11t5jHbTf3E/twxzu5c6SL57lGoZsv9xHRsMj9W6cFs/rf79fLE5GkMEImOaJnFZl2X9p5QQKdU9KOcsXho0D3NbHEKo/LKraju3/Qza0NrvI5t+WkRo2tsk/T3//YZMO+LCNrRZfYmfzk+I04R5PlfhhG0kkjL8QW/5jPXyf+8BnuN7R6kDG007WS7sAhX+AKx/sxIa3AQRoyWEFzyMHzBqDIRvoMS7OnpwzwhEo6Usjdq7e2Nd+/DOarO+Ax9bRFidKqioJpVZLRZu12sl4CgETOoXc5omTLFZQ1g9DfTkEpBJwCwKhIAoLj25YM0JpTDWlKpZKHNGBiNwQDyLD04GiRVGSmoRcUNab8h5VS1cKHFoMUyoBlWfQkRQ/5YdOIoA89NZiJBz6ubjqCVggoxJ54HX6mfutcI3DJNQqCjVr6eUJXkQNAKtfiSQLHQsZGzanBWtl1kChMfteC/LTeNe9GuuCmJUqcEI8VGbvRQJSDtayDjaAcCeVc9Wg+8eCGzPAKplXxiIqJr+o5/P3Tmt+fm1avPQ2nWkJW/le8sJFMa6rggxINIs4xZI/TVrmdK5LUAeREDGGYg51UP3fD5L3hDropwzZhJfsJbkPlcLglFDxwsYmgZC3/6cJPDzaZrlkD/NdR0XZS6ICGRxIqZYY1xo5UAksSRSSrher13/WEwI68t1XetcMiYHkFgSq2rsPz09YZ7nGpfier02QUiMuFwuYIasOzdG3mrFC0WkU6S7CxhLWjFPc62Hn1ujRYeV6+/fJUzZiLDW9/tzJyoTxQ2cJ9nj4iR9zWtBASOpJRdpUMFSFqCwus0ilCjWWWlZsK4Lvv7xO+YYcJlPAMQX8rLecFuuiOdnnM5PuFyecDpfEE8XhOmEy+dfMZ8veP7ln5jOF5yeviDMM05Pn9Snb1BhcAKB1aWrri0uQF7BAFJ2bVFGNzMjmwDOiGoGaFJmRteC7FdQP86EYAKIrIHeozPpfwB06ta+IQo/09tS12d7DMjDL//HpL+r8Otn+vsmoiYI2uOXyPbj71P6K7/vPf/ePeI/c2/5cenfZw8T0M1UIRxvo+g2K62LIi5QjddnpRkMMyisn9Lo2ZQS1iRxDKQIpe+IkZKA8WW5Ic4TuGQQGFOMmKaoMQfNHz+0fupKKSWkdcFyu2J5+QPX2w3LbcGaE1Iu1dr/dD4jTrFhLdomo4XFfcmKZb1iXVa8vHwVXnkV69MQJkzzCec4IRazFJ4QpxNOpxmXudHJeV2RMyNV7wISE+N2vWFdV1yv10rDFy5q+RERpzOaCxbjgUXBr+SAQAWcZ6zThClGRBKaOaVVYnDkDGWvUDKLB6wCSADaAov6UQep8vJbgcEG5EcDIQ+FESPMPDx3dO+huemeb2C029uof84ueguYWg8SeltUNnv+t7rWCnsWEfp+iGIF4cvpXPcMsTFClHOls3Sgof96HMR+N2zDsh4FPENA7CoECfX5tydC74rIV4nrfdkvXgkqDjiPMOP9186mtg+9VsZmfsD1cW3TNuiya5htgDuZowoDRjzmtUREeF1sYYW0r4YxWltMENawWXLXpToFp/mEEiLS5SIKtIvgHy/XK3JmPF9vAAfcbjeAgfPs4kpyxnWJYAJyKod1fm0MgLcJ1N8giPDSkEGK+tqbVcLeA+Z76XAi+2dw5CGsbZfoxpA3T0DzEIaf3O/xu+HO7ftIi2Vg4IlgUtMQVBIfA+I0yyESNS5EGPuxgeXAcV/5xfbaM/fycbWvYH3tQ7ZD0W+UDix02Hx9tYkkmwZ/aH7gK6johBiAzi0TNpMtsqE7q3xC6lXbVJ+z2BJ+g+mFDwb+WGaeMbF8TOfUlvtGCOPaYf0mfiB5+5w7/KwuFfirAplcCQlx2QM9cFCDsVIwDQ6ZU12dtHHSLKfdUMQFkQg2xIemlJHApSAEOySo72y2wOGmDQ5Uv4UVHGw+CM2slMIExAkIUQFGrpt4Ww/2oa4fDXzriAWS4F2tP9sEIwUn/Y5UQVHT4EGbSE2bITTrIwtYFYK6ZlfBTpByxVLJTCrdvIcGFFc/nNUXJ7zASr4681jrB6131YLxQiudk7BYGmjCjMI98zwKHMbro/uq1tHtnVrnnT1t3D9aXUudD2YF4wWSXd128iVoPrrHELha8fiVK2vPrTHL3wSXBBmfGBBK0HGAjA/7+kvnF7UiqMItvVsDtnOp40ZkhKQItggyXUrJKEacxiDClCnWANjiqosx51lBaNHAYmrAvxcmjuNpY2X3R/dZ0zQ1bS29NxK0ORcAJuwkRAWmzVTcEzft77ZtjgSFtxjxAgwv+Do8h6gRoFJy24T7LcznYQSfMJx1X9AMA0ToGfS/lFdwSkCSb86rxNtJi+SjeabC4JKxLjdx41VEOMrgek5NmAEixE+/YPr0qwoizpjOT4jzCU/PXzCfLzh//kViQZwvID3L7Zzz9GwlRbgM89H9qeugMvQ6HmRdNZyd0nd75C21sqldYd1v/NGO8V33zqu0wgPCjfekndPz9ed6kvQua6O7uP5tc9L16Rvqej/t76evvPFN6Vvq/hrPcNSUQ3r9DUzIxya/b/V3vk+VbP9733t/RvqYsXltf9g+/9gc27Pi3Dw53L/PU/p89h5h9OfuThH6XE+HdLRR/aO5MXitl9+yPTgK+c5Dvj7js+4wssOFR8s6/0hPw74ljeOwXwbtjAWhq9GrZdPuQ32+O/e3Dw3vOwLwVZzC5t6d8uolre8eiUS0fe5NSfmYg7uVxECbRTS8Re5hhioAgYGcQVzA5popJcBcSppLVbVElXXR6PMuNoIqFvmyWXkjcaFEoCzKPjRF0DSBotB5kQMCk2KgDCC34NTphrK+IK9XrMsVt+sLbrebulxiBD6pEGFGKOLGU4JfBxQqEhS7REQShT+w0IglreLudRFBRIwAhaieCri61wxhQgwzYpyr14JSitCcOYFZ3S9roOqcVqR1UUW/q/IDAYiMzEXUWIT5QIjiBmoKqmTIWQQrMQLB3AEpP6p8aGaVsVSWtMeWwFCPysojGs3JADvwmbr/XD51AlGlyyuN7/n3+tj+3+33wV7VPde+hVUVqtbzFR3N69ZnxV7MtU+N9WCCLQsobd4P2rddr++7vASHsYncu2bSjqjvNrdIUh+2/q04h1W8F26MlDpb27o+PRJEuL4d8MX9NIzDMdHXPVvH3X9vSrETqY9t+Po+Z6eu5koHe+NwXO0J0Vrd9dkO89jOw+4Xk+JkFn/2larwgBHTHmbtGL0x0fiD9+/5IgJJPbPMtxBnTFPBFGcAqVpkpbwg5YhUFkw5oKj3hBgnTGHCPJ1R0gKmDJC5Cx94TfLj4ZvE++1/Jb1JEEH1229IH8e6HZfcT/v+d7u+m3Y3Op83tYm1+e75f0+XBOz4sLPaVgJvAigiTjNijJhOM+I0Ve1V0/gWULcR0+bq5JE0akcDDVSz+u8R6Hua0wyDPSXYp99ObNO2g80D+2oAYBlIyQGilana8pXw5eaKyMeGAIDJtJWnftMksg/qorA6+MpXYUc9gK2NpG50gGwaHAQVetg70h6JzyFaqWAZ5xiCLubW3wY8V4KLuSqSyLkghARKkXoRISCgMMTnpAG6hZHXjJITri9fRRM6ib/IeT5LINSTEDiIsRJmVUO51qUAZa0ga2XOYkEhFv+bnLCsL0oI3QBmCZgaglZa/aoXBjIDuYAzgzOQSwQRi+mWgq+WaqCu+QKaLyKMCBGcr0BZdU6wzKFAAE2Q7g9K0ErHUTShBqpffYQICicdU2mnTEER7kmnZxELsNPYzxoMm2xTVisNIxajCXbswNbDe4hzMU1T3XCb1n8W7fL6yU7wAUx1bel6TmaBomuj7iE6dVMWv6q5iNZP1NgYVES7JWdkLkhFfbI6oH9c+zZHvYb7VjtAGD4Gqm/Kwj3rakxC3VPUoiHnLBrouugJqCB3VmDXgq1XbRBfNom/VwDIOUkvZI2ZE4L6xbfNBNUlVhNyCKOSY5ByCaAomvEFBQQThBTkXCSYdQgI4Op7logQz+dm/UBAiCLEMH+wDLEeMdD/dlsQYwEhIkEYlRACpjniVGaEQFjSgjWtyJwR14h5CiCeccIs/RxbzJMQQo1nYeNlsUasn+Z5rtYP9l6MEfM8d1YTKSWcz2edsxOYM1LKyDqfQgg4zRPKxFhuZsWggaqC7I9tH+9d6tmz61qq/1sviPBWMFuBiM5LXWNFaQiT1Zqijs0Pn6RPAISk/M4EICLQBFBApDMinTDRCRMiltsNabmCb1+BdUFZF5Sccb0uAIB5mmGMU84J1+tLFXgAAQVRlAPmCWc9o+M//w/if/0fXJ4uOJ/POF/OmOYZl/MF0zwjTtIXpbbfCV41Z9u3xDx/exZXWqoARS1DGh3h+qa0NQHUKDJ9Hm69SB82yucuxN6BKOSL+dPTw1V5kAytjMqQ96NU7BYkPWDwvj9Z/G+R9mjTtwmx/syO9pzIX2jR/CXSlr94PR1w9t9xjIkgIKq3COzKbXSu8VJ5EEK4u/rXCLb099+Wmtj0tX64m3uHZNk1x9D2rNTh64+mTtN0Zz0f13WvpHstO6rZvpDlMNc9ocyrYModXOGwcMdVV1De3G3cw1UaIHdcD3L/boVq7O4TiQsam1UWC8J4dLBYH1MpoLSIAGJdRBixLjB3SEb7ZVXI4lzAa0JeVuRlQVr1o3+jFATjv4lQMiOtBbcloUC8IUyZQc9PCM/PoPmCEE+YiwgRUBhEGcAKpBfQ7V/A9b9R/vi/uP3+G37//Tf89sfv+PryVWIAUMQ8XxCnE2I8gWhGoBlznBGD8J9UGBMRvs4XlFxAnIG8Yr39gbRmLNcMUUoTev10PgF8FguGeMI8PeM0n3Cez0BgYaMBcX+kbS7WH9cXpOWK5foblnXB1+UPgBnn6UlwoqcnEM8ocQJp3nOMOM8TUlrxEgJyKQi3r4C6+lQbFGQuWAsjFRNECFRvFhCmRV0MPyHh6VMpiEQoA73ohRB1phhPYH8qTQ1P7w/fuzxB/Xb7a7do2t9NCKHonP1WjXyP9VSgjlpcBlGKJFhsN1IexniZ9rHnmpJi54rJacmO7TJhACpIbXyzxWlw8Q2g2IY2jnS92/fRXl+v7vbjtn/hFDi7vqwYmu93G+W2Z+ydiH3d2F2qg3TnLX23O2vu79K9QvDr7x2hw7JOXLBqrev+brrlRdslsv9rORtaoBNw7KQ9xuOAGSHrLiKNc2lKefqSb04gECIyi1rndHoCwoTn0wuW9Yrfv/4GcMHL8hsQEp7TCQEZ63LCab7gMj+DZyBdCPkm1mABGcQJrtFyLtaYhG0+VDxqBMsfSA8LIvaWRZu0P4IZGMs4KPOVuuxLZI+/bQp3Ul27wztxBbQOBIg5losB4X0Idn7v9b09DVO4ssa00Tyx+rg6gnuiecxzq73SFv498KIJItj9dhsTxn5sz+xp/wJw/hr3D7K9tnfX3Vl01D/cr91tIig42W/y9bZdZ+60082tlN9yu/oLFCp7R5GA2aYtkqtJZQv2G6KAjsEOS+d+xycT6rAiqubfcEx1g/B9pfUm54arbdWtM9uwtrHx/RNMO6C6JDLTVz2Y/XhXNQ32dM3+UOyNPbX+3bKC20NmnEedv8e6DgEjiJqZppnBUZd/80faPlvtuMbYmtCqCq7qfNd2cettNvGAbuSPADKjtskogNjdN1xP+fVX15TWx+9tPTAtALQFU9677799/eqep3Ngo4mIntga8x5H3jNbmxOirr3G+HXrtT7TC0z29rTOeqEIZFzz1/XqA35nNRkniIA1gECx7cxGCPu6HPWbnRV+HZlAwiexWujbUK1GuA/ePK4ts/wYzzrbM8fzaXtO9ntyO4vaOdKXuSXmW37UlV0Ki5aYBS4MIoSaAoFLQk6MtN7EymFZRJsjLfKexV7gYiMMUEA8iSAqzifM8wnnpydxA6BB0Of5hOm//gemX3/F6Xyq7q+maUKsApmwM++OEZ1+XPfX9u5ZvXfW7fw+Luv1592LbwQPH0vj3nD/4VqVLr327lsAbH/GNcWTfn2+K3WvvcKQfFRSombsnXe34Zuq8u1z576w5zhtn7N8Rm5vj/t7X3pve49o8r10RPt+j3X6V0zbffP+fvj2fnltX3n0Sf/U+9fefv23BM7D7fTv0cHm+kp1v22u3c/81X19Dxh6Z5lH7763dferclCHCuBRdds/VsYU0+t9OrYo2ts+Gl3c6OPDOlWGWf4xipkqjV4AEzyoayaxetBYhuwsoVMC54ysPFJzA7zjwslo6VLEXRPEEj1EVd6cJvVZboAx2vLnAuQMNrdMyw232wuu16+4vvyBl69fgTABIYCZMLHSgAyIq6MogggIn12K/DYlTkZzqbSuCYSMEhlhimoJUmDCnBhVm3iaRAhBjFImgAtWzc/ct+aUNAbZipQWpGUFgxHRuwgWPlSsLUKImKK4r52K0aEzYnAKhx78UMUiccc07JE6N9imht9WBqzDv9TtaOOEG+baHm/QHh2fkQL2sLT+OalBBwUAslAGMKCHC6yBW35DeB7vcsk8TZhrJuX/Kda+MUyg4VTmJaIJGqropt4nACOWQAf9Zc/c2TM374Xht1/zO2Pg/jY+32NXOkkOakCN1tzh2X2Rflhqz9h4PZD8nGjzXP6lYV7LT5ul27q3+jbab68a435s66RFYd2vo/0txbzCl417cXfN1aVbVq1TCe7c6daDBdqWuWd4xBwnlDLB4mamlKort0SzKneqlZe5gM/qDWTAZqRP/Mbh5sDmucfTN8SIONi0/mLpiODf+/toA7WWjvNrBPrsYLINTA7TU9UkjfNcAeYKvhAJILwDft0juF4jxo7y2BUc+PYcSSD3AE0H6o390DZ6SV0siCwEjT1r33GKCqT7RbgfY+JosY/t9oBcBXt5/zPW3/+9AUsdgVEDv2hcAYXz2vshKFEnoFrKReNCSD8stxtyTljWBBDUl+WE8+mkLo8ifFAta5f1pQlBKMQab6GC2rZrqdNOCY0gPsWZVYsdhJP1AbW2MRqA3g7e1id1nCmCSALdUBAXJaAApqDEkPoJLUnnSgajHNI90nFWjhEDAAqJaxxyfi4rAda/bgIZmztNABirGRoFUksXc+dlBERzg2OiGbZA4iXVQGb2MWGEjTcXRkEjzlv8k5H560mCOheB1ziczRj45Nekny8docftWa7j2+fVCQnddR9bwog5v+ZN09/X1cck2BOWHO1nfh8xxmUrKFR7Fu7f8+WalZmVbfU3F017MRNM4AKgWiH4ulc3SyEgzHMVDCyLaeNfkQ28jpAgUq5+FhPCB6fvXNVpG8xyzru8mue5xprYq1cXtwPsFHCoPjPGBomxWUXU4IIaWyFo+X5PH2NG+DGte+ZAqPgxGX2zeiGF5VNU6BOYEVEwz4R5nnCeI+YpgtOCNWfcvv5WfQRzWoG8AgRMk4xJ5ixMGUXQFHF5/oT5dMHzL//A6XLB0+cvCNOMaRZrh/l0xunTJ5w/fe4ETMwtvsZd8seI9T8BLPxPASh/pp/pW0Hfn+nvlj5uvNkAUXdtn6+4p5L1M/m0PXt+9txRqjjODvjl2RoyYuIbu3LzutGZtUApJ1QajGFullhjr5WcUNIqoL65ZVJr7VwKeF3Aa0JaBehqPFKjXQs3q3ULDH29LuAQcJlOCOcLTucLTqcL5nnCPE0IU6jW2wyWstOKdLvh9vKCr1//wG+//Qv/+n/+L/77t9/xx9evYHUf/MsvjMuloHz6L9BZ6HARHAg9Ps9noeMpIJKoJXApGsNhxfXlBiAgxAQOwHm94JzFejnGgHmKOM0zTqcLQAwmiXuWibGEgESEUhLWJHEsbtcXXF9ecFtveLl9lTE4A7kwppQQS1HlpgnTdMIcRTGGYpQ4GnnFeT7jNs3Nc4Xy6W3eVNSq8Xhuqo34hhcMdHsgNTC2m0sjRraT39Gnf6e9J3zDdrbac1TB5noDm72ZIJhBcOVVvkP5yShCnhgn9IIFe94HpVZXzvW+xcaUVONbVktkwyW8QmPDFeyZPUHEEaa6OZOG93x9+n7dugPqy2r92YQXrW672w1L4Pc9ASp1+bZrHWY+7Hd75+2eMKpiUzAhzualTdnb+rl+ussjbc+wnW26r9uD6a3PW/mP5y/ebDhwxTfOpxOIGF+vErz6druBALzcbiBMWEtCKAmFMyhIDMtzWXFZTxKzMK9d/akO5H77RsHMI+lxi4huwrztRNyr+D2p0WuCgdfr97ZnR8lbB8DtPQc4oMEy1UFQCX6IIlmK89xbQ8QGANnr7PL3APregB79vXnW8sGdhb1zD0qY87hBDf0w+oPvAbTeX15Xpw0W24OY8ndf9h5A6tvhhQL1PNbBqcxGbWd/IKPvrs1BfAQ4eSGMAXYgtAPJgaXi65/Fe1JRf5G5IGvg6JSWChgGSHDqOE2I06wuilTreljkna98kAZfQn/GdA01YlO1WFRbGjlo/2hfsvaDdYzNbeqGtY1DMKB/QpgmmAumvJIqr/SAvAmDzPiPaDMtdg4rgsRqZVAx4kocYTKXZhpcx7pZRLS5FcQiIrRvUrPNJqkO9b02rzWGR16rKxyRKCfknJqQQSdW0XpZTAdrczvrlcj3E8vN01Hoxd2k7u+Pe8beZ5zPe8LIbk3puO8Rm1b3Dqh2hNqovT/m7b/HehBRFdjtlRuCuE/q9oX6vRXIHBHHfu0awGzJx7rwz5j1wnjQ+nftmZQSMvdB+gBCmHSuD+My9pcf971ro5Bpu0e3/q7+bGM/B3x+7e92rxMyuCoUtgDUjXCth+FI41J/2Y/FMcHdxkguaj0IVVgvTxUEDTpdsmjF5XWR2DdclNQPCPMJFCKmOAljd35CmGbMTyKIuHz+FfF0wnx5khg38SR773zCVN1dhdqXvt/kmNpuXnW+c/97L/1IocG4Du/VYY9muPf7I9N7++S1947q3N5rlMH3at9Rv37EPNjyZh/XFqOnHn/+fWPx9ryaluSjZf4Za+4tzzyyPr+1zH+HdNRvR+PseQK9Ur96Oql9f8dt7uFxatV9fZ/26YjuO3rmLfPm4bX2cI67hXxzHt9rLXxLto0vtN+Plnl/nxif3d534CKzK7itAxs1QmU3Kq/FysDWb7OQKEkV4kQ4wDmpcl5BUvq3Wo+rO+KiLm1TEReqqyr80DwL7TWdMMUZMUzqqx9CUBGLm6icUHJCTgvWdcFtuYoiyvUFN7WKYHXte7l8wjSdFdNovAKFoCx7U1DrQFyltVPOEBdOwJzmGsfR8AzLK4RQNaJKjuAQq6DA4mSIW+QVq7mtWhIY4vKYSRWIsrpNJaFb4zRjmk7C9yIjzQvmeVa3s0q1FOMVdH/bCTTcaGrDtqjV/w5d3s+3fT5i7/f9fLQGda8ubh0c8QZd9RtzwdyvIWoPMlBjD5ITMHiPB/XbWUbI82pxQt6FU+j6oQKzBpg0n1XavhZH07e3emDY8HD7fVhXLuk/ZP3X96PPY9+nSXtHhFNWvsu3CjaO6zIqKvdtqBmOKEeNc32U9jBY36yj1187x/w7rHtf2wuHMnjnvYM6H9X3Hp0/Pvet+PZ2Hcq3YBsRp2kGuGCeZiTdm1MSt85rXJFKwqRWEYgBUxCX1PM0g0oCVyzAzZNX6vFouyy9wyLi/mb1rWlcmB/FED5CcPkJ1Zi4/hlm79bEvQvduOJcXTdMpxOm+VTBDB+gtNZD87sHDu6lV+9ZHqVstow9gKtrG6MTRIx9N4LwG4uIg/fA7AJKNLDLLESmyaZjA3xGANHyqv7nN6Anum+LDdG3twffjOCqlR/qP27nvv3ZEVoIBMTgsmkHEpiRCyFnRkpF4gYsC3JOuN2u4lYFIsmf5xnTPON8OgFELW5HCAjABiiV/pDYEdIQ6z8/p6ytBqwXcM4oKAisQY1t86BWc+sWIdLagd+NN5FomMwzwjSLb06QWC4wVzNdHxOEayDr0q9xI3zRxtSAZiEsiobeMCuFDC4ZSWMH2DtindHc5YiJq7eIiKAQVUt9IAKMYQU7F0yi4bOsNx3vFeu6IK1rV3eQ+KDP6K2AAFRBUiUeCm0FhXwEDEIDW7f+H0F1A0v9mvSBqvfWpL23d3Ds7UPybLOKAIBo8Teot14a/S57kHss2z/jtc+9EIJZfRNyvzYDtm0bhRB+vwBQLZj8fjb2ka1vc8vjY6/YfWau4zrPEn9kXdcaA8c0qxjAdDoDaBYhYx37Pj62FLG+k76PXZ+bdYXlkVJSIru5Jdsbfy25q48nnsQdlUzAujd4Kq0S40aIt1t7gOhIGLa+6PvAAsQxGGbTFggIXECcsF7/wLosWK5fNQBgAjgLPxgI4ekzpvmkFhBnfP71n5jPFzz98ium+Yz56QuYIkqMKCBkVgu0OGGKjCncAX8KAOpJ8jpmfEw0/9XTfwqQ+W+Tfshw/ZwTP9PfPXm63ykpDXNbSOD7mn8/Pm1Pk0f3aTlb912fjM/93Pvfkv4aJ/yWdu958e1fCg52jC9398GlMcesVuxZeC0oz8UmDKifFWVNKCk3a4hlwbIsVYErJ4lzl5OCYblgyQVXo1PPT5gun3A+P+N8fhIXRHGSoFgESByLBE43lOWK9XbF7foH/nj5DV//+G9c//hvfP3tX/jj999REMAUcbl8rlYPQengQFQtlEOYECkpb6guN0FVWLKsC5gJgTLiMmFZFqRVXFAZCB6Np4xCC3ORgN5BFQhNCLHcbmoV8RW3RSwkGAAKIxfgvCyYzwkBhBgmzNNFrC3mCwrPCFNAKQnLTaxFRO9RlBwtYHgb614RkzGe4lur5Nem8wYb3sHnfH5Hn82cHADg4zJa2+o3OWLb+GtrCxEQzFOJjK0pJVLohRHNBRihWUKMQgvSMg5wShcrAt2zYXi24YCvY5xUBUa1C9zZtO2fbaQE6dt9Hrmvv/Rf5fLGMRn5s702uHlUlTx9le8cMWO+He/44FZ77xwb98qxTv5+n8e+wsuREKLHkLe8/SN1fSTt4eQt7qOM4uV0QSTCZT5jAeG35QaAcL1dEcKEW1oQphkrZ8wUMJ9mnMsJazrhVhLyusCEnEcYUSvbea94Q7veKIgYKtFqI3dfXVDvT2/Ne0/wcCSMeCTvDlSTna5uYEQkfg1jRFTBQ/XjN8SE8KkJNHj3+yiNz+1OZkE4oZhIl443fWoA0879zu+904j2QF4roweXlRTuQEV7zrsIkfy3Bw9zq7eBoVaXbXukNH8It2frbuI6aqcn/GGjG7LPZy9GAIN7l4XMABNyUnA4ZZTU3DL5PMBAnMWiIEzi3sg0QZoZXAOBbTxqnWqZOlYqcOAi2vmov50LGPUpL+OZUUqED7RnpAsBLbCZEj7msoaIwBMQaNLgXRJMltFA9lKaZcHexycGRCu+NkYBYshaK9yvYROqlCJWHm38e0ub0RVNJViYNnOVuZkPp5TEHdN6U5dMi7iY0jEcQWU/3zZB570Z57guPZExJDsEvADK37NyRmB971OFOl3ew8ExrJl7gLiU3e8/YyDjMf89AH7vcB7LJRKhQyCq+5sMJW322L0DkgD1B1s2QpK9ugFNmDTe7/YV3YCsPTV2RpHQ29V9W8qg0PfD7viQt8Zp8Th82V6oV4OqE6mpcJsHNjdEkNC7y9uOTb9ugGblUcaz0xGkdm1PgOE3Zi/08HNwPDeIeisVkXOIYa3tQ1wyMjOWVRjdAgLFCfPThECE02kWAcT//D+YThc8Pz9jmk94+vwL4jzhdH4CxQhMU2UWgoi0xGpxIokDNMyTTbJzVuvZzXO3xv24Ppr26Ja9+3+lNNbpaD0evvcdacjXU2Pf9tb7u3J8tN3/JunR9rwGiH5EmUf5tDEF7nLFH5Je4bx30t9p3b+nLkfM7GN5bftzXKP35k9fhlLN7M8vLWMvjweqx/0/m5pv6/BaHS3f43l0tOf6kk2LtX1va8YeaGCj//UH2bX2yr1mkP9+ZQ/9VjDmPWfqXyJ1vN1QNwc0HqXj+b6zRuSNwzztfhVS1MeU/4MollW+CTpfwKCSQSVLzIai7pvUaiC7T42jaMuOWYURGUWt6ufzE+bLM07zGXNU10Nkc1GA/5ITyrogp0VigyWJD7bcXnB7+Yrby1dcX76ikASrTqso/DF7a3zUvgsUquUCWTcZflBUmZGBDKPjm/ClcIIIR4TWJ/Z8SmjxE2XAwJxRSnLxM4TGX0MCwlqVGo2eDDEihgkxziAmcChiJWFKrc3sttKiUH7RcJQtvqRt94u5m1c2vvtrfKTzD3GfO2kfn9vWZf8da4CrYAMn0LiLhtGZUKEKIXaEDKb0ZK6YapDrsCOMcPUhxQPrwmHABBINa3AxJOrvbdtqd1fGwX5TW5e13LG/aPje9KC+Fw5uU81fMC86yGrnbBvxi4EvbDU4yhONj0Lbwd6HKZsgYMx+sJxpj9e5dFge+Xr7Z+rL1gSHU3YZdHWzZ/3vt6S9NVfzrcNIQJAYNqVMOE0nFGZVWCasKWNNCUtaEfOKVFYEJsyYhYeOM3KcMMW57d/YkkZvpb/30hsEEX8mg/jt6UgI8Wjq3mGoDzrx41ddL5lLh6ld2wCgLr8RJH+kbnvP+cVerxe758EQvTW4qx8lqlvPcn19DSQzMMyDaGNbZYmyxCfQSoxA5FZIE4b2te8OM+a24dDOJuHr2vefUVJNWDEmD9jJs+05HxfCg63uUfkuAJeClASETKt855SrJYX43MwAEeI0YTqdEKcZwVvPWKAy1uDUPADc2jfFEXniEihXgYMPOObjdIQgMS3kegJYrCqsPGuNAYBSVg/O8km1SsKsQbXInC5VV1QtYFn7FM4yGet4oJbN7E3oe+LHz/VmASAWEYT+uXEdVs19O2z9gLk5ImOURPslr1jXK3IWl0wm5BmB9rFOdq3GUiCqfk5BAFIDMIX3pVp/XxeZS70FjAfKrX/2BA9eeFifA2/zP9iP9u5Z6uYAx2492/090H8Euce6jO6SDMCu+UNAYiP69wQRY5sDEZjE6srvW74MX67FWfDjuQcmM7O6OGvzzYQCeV0BbsKa1cXVIOpjPozMka+Dle33pJzFtNLP7WYd0cbG+j6X3FmStL3TzysAoC4/E9z4Z/37Vt+j9em/O+sbEdHAiHWrQ7O86jWnAgFRxzGStKdwwvV2w3K7aTDwE87PokX3+fNnzJdnfPr//H8xn5/w/PwscXfOFxs4FLD4NdauN8uWaSLESChquebHxKdu7QDowBu+x/b/TD/TXyN9Kwj456dvXWXfukIf6buxjL9zf//Z6dt3VU9fst+zAQD+DBsAuofHba+O7x9zPszz4Pk98AfG2fFQle1zUloTWnTAXy0DHn/Zy26b/5295nvsQ993lX37PKw44g/dDnZARLSWyN865hJQUKzwQYhEKApUFgICRBEscEYoCaEIz1RyUrA9iaAhOV5ZwQcuAGdgSRlLzsiBEKaI06fPuHz6jMvpCef5jEktCpjUgr5kcFpQlhvScsW6XrHeXrAsLxKk+o/f8PX33/D1999RaAJClBiMaVW+WfKpvAGASAHZgg4DykxDlduUPlfmWoJXizuoNYlbUHCGEXzWl0FdK5lFhFwXLwQ5J+SUkNaEvAqPkQujsFhTpzVVGrm6ZopnFEQQQ9xWTXOl9YV21jY5Q5ael3Yrmfu5S+To2/qeU668sy5HHsD/PfIDj87Hx5IsnAaA7wgHavlh8I5gvGr/bVYQvTWEVzgOmzY1IUQV4WnXjs/2FhAU9i0iFA/fbi3u954AyK/c/vG9vt+55ngtm62Pbm+jEIL37h3Wpa8DAYrL1UncP/JYjSy7ga/ezbJ1OlGt/HiGyvi2fIaXAbQYJzWr3antXz46Q+6vtz2sYDOHYDiKYHOYGOfTRa+LgG1NK5a04JoWhDRhyQtCCSglI1DAaTohTyvStAKJxMpLd5EN3vxKPV9L31kQ8f3Z8EekLveeub9hNjC0gVqyqYk7kijuaELQWBAiiKhmes4VBmse5PLaANgH18d6jc/5Qe8FJjQQ2vsgXV10HsxXl04j+OQBrlFDexRAuG7s2uGBNjswnMCwrmAPRneH5dAXXvpZjdKk4Tv9QiBy+Q75jfOB2Qj3XgDj/V56wKw2gqFaD4zlJqacaVmrJgSbv0xmWHClOE8SsDsGhOg0l4vUt5Qm7PH9WPuqiAhAgm1JOWldkZN+clIfnU2QIbEnAgpnlBKQi/jDLCWJH8yycyAwat2ZWWJemPuhECW4rPUHC7G6B2TbcJuPF4YTStS/qM1NO+i0rdUSwgvDnIsgAWZjJTz8PMi5gEikw8aAtfldsK5CSK+qTbOuq2j4qEDFYmzUoOsgFVBIfzAbVboVztWyjHi1faJbg46ALM6dlhHFTk7mgeq9PcXatQcS+7/rtWHN92C11573fdbWs61Jq9MI+o/7xVhHDPWsYzus/9FSwfezCQe4FHAIdV5EXTvmVsqD9ZYPgAHYp+rKafeAHepVBR9iI1nLsQDZFtR6L4318WXaXmMWEBYYPOeMZVlUCHLq9q9pmnSu5d2x7vuUkXOzshj7duOCb6fd95IfRyKzcZDUhBRiWlrHUZlPIgICIa0rbsyYbDxPF5ziCU9Pz5imGc+fv2A+nfD5yy+IpwvmX/+JMJ0wn0/SJh0Tbz0lWy0ZPwHiDGQR3Da04H6bWifc7YJXCbijMvy8O6IHjso6+r1Xznvu/aj0LfX/mVp6ZF4c9eWP6OO3lWFs13D1QUboEf5hL3l68n7+e+/t1/m4DMvrW+v67Xndy/N759Ee7/fBcV98PV+u356+kDza57XK7PJvO77ZrcgjQcar9TUW5IMQa88v+Wu+Pp6O056xmy4PPp7+lt+dcnwaz7iaxwedSY8++63r4m3JM73vzGEXt3gF8+g+pDwjGhBYINr3Bkp6nnjEEOr68bS6KiBxFp5OTUN9uVC2MmWxiIjzjPlyweXpMy5PnzDPZ0xx1nLlBeYCpBUlLSKEWG643W7iIndZkFeNv7AuWJcFHBmILPVwlvfdzs2uHcXHvTCFPVOmAphJreJXie+QFgnk2ln3h22f1TagAvuWb8rCw1JhICSkNSM5RSmy/yhA7Sx2LPytIa19DCBrH6tBxx4bD8O42P/HbkYO+Ne3zLujRK/Q2Dtv6L9kZLv2t96zuAwhqkvaAKIoXiY6l0yxPiffajVhAgpTHtxxz7QBgN3akCO+KRVW3t7Vm7zgC25+8Hj2bM+0VuSIO43fr+TZXaJaD3J1vZ9o+yfRm0ZyTPf4y29N237w17fnX5c++FjYK+NxmvLe/bYmbP8AiWB0nmbkUjBPJxRVpF3XFbf1immesOYVU4rIOYFAmKcJ6zRhnueKS/h9SbY5iX9bdxPm7dp4IL0jRsSj6T0b0o8hAkawzIO7lgyA3kiEdWMyS4hpkiCYVRChkmqTVssJ3AisMp4GQ9oFa+9O2oO/ix0u23fG5/2GNoahGQHJPUFE6xqqIFwXqNM902mlq+shm8bMfY3Heu4B8Ns+IyEMClewfOteo23udojB+oGaRrCVxaXVaxREGGhXx7vyOFy1Hm7XK9ZlFYC6FJScKsHDRf1Wxohp1jgLsYHnAjxruU6jeE/7mzkjkPSmWT0IYSYaISYAgQHKaFrAArITco4AFw3CnAX03mG4uGznAiCHt21N1h1Fgb9D7QqG38oasesIuPpg3fCaJUQu2UmrmxDCCyLqWGr5OSeAAibK3XywQGTrunaCiJSSEqdq2QEG52ZaVLh0a4KZQXEbxLmNVeuLUE1BqQU7b50tAbmL08wxStHvKxurn/a3t0poREYP8B/tMaMAQvLuDx3Jm7u1APRWRXt7z0YwU0oNyu6veyGAH0ef1yg4KJ5JKgVhngFSt0mu7LH/yK1/A/x9H/g6e0GK7y8jYkMniChVEDHGChoFRP2e0oQA3kWTCTNsL7I9QQTkUxUkxCgWTksqXd4evKG6BzgLCmftYxZ+vr+OGJFxvPeuSR8FEEyDxBMvfftrPoEADljXRfZQdXsYz0+YQ8Qv//gfOF+e8OXXf2A+X/D5l38gzDPy/ARon4NZ/BqXggI33iT7YONM9fwwhlKebLCBm3sbBu1jsKLdvvuxIElLj4K6f+Xy/qy+eyR9z/59qzDq75eM0hiufuf18t4x+9Fr6WdqqYGlPQ3W0xIdXLqTR9MuHq/rX4fvfmPtv1O++3tERxc6rnAUiO/N5S4/Imw666AOu8KIH5j+7L2xF+7sg7xvAeruAUIEjatsH2O5HJ1DBI29e6ys2QDrBubXwNVFBRHGt3ED1g0WWHPBmgvC5YL58oSnT59xef6Ceb6oUo0q4oABzkAWQUTW+BDLchWLh9UFgV5EEIFJCqk8m/WdEz6Q1t34hFp/teI3lyRZPRyvSazkl1XcQpW8Ci+vQhdzh0To8RDpTwajKK/IyEniRRYu4nUqRKyrWJG04NM2JgEBAexcDFUeAaTuEABmQmHRoykw3ntvPXmsxbAu+2x5Pcl7uwd57OwtAORHnM808IT6B2DCBhM4aPxMCmahonFALB5InduxPl/newiAXR8EEdv6NzDf6tI/1+q6K8xAD5TLsFG93vZdoI5L5ec9lzKC6ndA7q4O+3UaE/uifZavjKc/N47ujzz+W/M4eq6dLdtnu6wIIKYN5oVuXAae78G6jO/s5fNemrL7DVSMQ6aQrFFzzXSaZqw54ZZuCFEEEfM6Yc0LphyR0oo5zvKZZqzqRcKUN8Gm7m2nBbt9/n3pAwURdPD38NQAAPn0ns3prRNzrMfefU+Ykm5sBgpF1USd55P4xJ9nhKg+unfcg4z59WDMDuio3x20PgBvRyBId52p0q67x9BATPabJVcgz5e9T7j3G+sIPnaAaxgkyvZBbymy1x6/QW0B+MFUiL2gREAlI+76Tbm1uB0aY7wKPZq5WUOMgZfbs3AEDSuhtOB2fUFaVh1eVt9YHvjUmBAUYSaBgBAUpYgmddHyY9BgqgZQsggoLLYYgmB2JScJjqWaIzkt6lddQHuKYuZJcQLFqAIJViFJQUqruiFKMg8UfCdSYtN9UhLg/pRVcBGaZJ2oI22HWaj6OH6+E4YxaOPQxiBpAOxUtVYwWELYZ5qaIKID1qFjQRJs2qwrJE+ugphRuFC0o2sMjtwI3NENUVQfoR6ct+eMqCPSdVH3DS8syV0/l5xljCtBjzqHxnXir/u21zW180yb7+3v0cWPv2aguMx7uZ9Sqq6J2vxurpqsXds1plrx6A9kv76P9ge/99gnufVa6wIhXgO3IN7jXmrP+rxGIUAncDBi1aVuL/R7kxPgjFYYdT278fZ1YW4CmVJK7WMvkMi5qACt1LranArBxqmVPQpcLZh1v9ZyN0735tiYeuagEXftDDDtMVRGSJB8c+1mgcChzKuYsAOM6Twjns749PkXnM4X/PLP/4XT5YLT02fEOAPnJ3AICKR7rbnZUqFN9ekbXB1tXsHWB7XfXNqKG+bNjwYw3gvU3HvvvfceLfMe3efvG9FynxF6W30eHZ96PuP1+n5U+qi501HfB3l+S1m+b/4u6fW59v3H96j895T7kXX9s8Det5R9/Fy/Nh9fq9x91/N/w88cYCo++4OyuP9np9Y/ru9fo5vG5/aSgBmkGvKuv1nomV51jaosXx9sil5vqOufsT5f2zN/ZD0c/qiKDWR/vHkP93z9YNvSIEtyv7nAXDMxsxozyAOF3adA3AkVRsqMzOLmsqhVgVnU+1h6pZiCoCmysfKiAc+fP+PTL7/g+dMXPF2eManHCal+AeUM5ISy3FCWG5Z1wbrecFuuIny4LeL6uAApM1IuiJO64QmmDT/wOoVRSBQGc1qFlytbhTLjb4QvzGINoVYYaV1EyS8lIKeqMCNerditBVa4Tr4zyycVERoEMEJWS4ksbkfNlZS4KnVrzMUfaDyjYAUicFFcgIWOrvucYSAQRaC60RG1OXBnetX+CyTwUmPPO37v8TSuqdffbeXsxGvQdrSYEBacWgQRoQoUnCAC5LwomCWE+4b9Vh7daFPDN6Rwrf3o1NzGqFZ+aEez4vBYRz1bbHHyztrfdJXlN4Lt1H3tbWNeCEHWf3B7kbxZv7r9eVBcflTIcO/+mNeINb6Wjs6zN/FqOrY9XnK8B4/n19F55tuzdzYf5X1czfF5BX1bM8TFAMQV9lxmnKYzwMC1vCCnhNvtijlOWJYrIgWs8xmRJoRJYr5OpxPWnBFyRmag5FzDnWop9fu9p+SHWkTU9XNnrD+KiX5tQj1Szgiw7L6rZlohmgBirt8UogQWNgGEAp57dRmBwENmZOfaXt32hBE9oBc6gnCvPmM/+IOBS9nkvQEzPRhHPXjgwSxfRgfeBbeBHxH2D86XCuwpULt1HdWEEEcbotRrX+tjBOfG+Bj2IBchJnLKWJYbbtcrlusL0rrCQPmRIYlRBBHVN6HqqhQj9Aw8AyQwrutHsAL5CooTApiaIGJdFtxuV5SSBpdMaiUQowoiZDsxbZakAblKkQBhQqQqMTVoyJvLos5sS07qoS+H/ob47WfNFwo4mgaIHYx+vkksCNW44SLWEEowUwiIIXaCiBCa9rmBuQJoyoAxRBAhFg8t7kMZCFJ72o7e+owPVu6AWiL1Zx9CtXjo1gSzHvo0fDD0rQkhSrOKYEagoMHGqc7/0arL972k//n0AAEAAElEQVQXJBDhEFPaW2/jXiMuwtiVx13fAtjE5bA6HO0Jdj0AKMNBbvfuETLVCkP7fQ9IN7CfmSug7/tmr998cOtdq7mdPrOxR/BC2X4f8eeAtyDxc8i+LVaEL4uoxaMATGglAsEQLNbCVsNl3LP6PTwghF749Cbi7aAvaj90hHToNJoqIARZYQGMwhBrsW4eAwCD4oR4uuDzf/0Tnz59xpf/8b9xOl+AeAYH0RwDGKEsEAsHVG03V7nKWLjTEAx0TuLqmBlLzm+nY/4M4O97lvla3u8FvQXDu0/r3SPs/y7pQ+taec37YNpfM/2V6/Yz/ZVS2xbuCyCO9gdm28tHfmYsyejXoXynKdyqsrcPNjCg7k0byOb7Jk9D7N6voDR1vzeIJLPwFOBuf/FCiKN9x3DYcfvZG58jIcR7hXbvTT92r9xvF/m/yCiS7Xzcf9fAxOEqNV1p+bR5SQZOV5GDUGHENr3ljgkhTOteNO9ZleQYRS33TfhQFcY8L1W4xV8oypeHiMunz3j+8gVPT59wUUFEVI8JBAaVBM4JWBcUFQQs+lnXBXlJEocxi7JKLixOkmiqwogtDiLBs8V1caoWETzUV9Y9qiBiTStWs75YV6S0gI2/LhEgC9Qgfe24RqGrmZFZXCcl0ZFBVEFE9ZTABYwseanrLFa+GDCFycZbmSKijAvX72x7nQ4rkffqG+RDcLz6KzQE1QgibQfZ4ctGPGgvsVbKwPgRRN2UXf/eKoxWQUQwmt6sISxWxyiIIKDmYUpbqgQ6CDI8r9Ke6wH8Wr+DPtvcdPflO7R9tDEe/fuvJqvP/j0Ppm/rCtem7XcnbLDq6XiNxfWCCijWMY5hS2/lMfuXx5/387p/bts8ag+2P4/PuUeFECOfcnR/t04PXOsbqM8wFGcVbwlTEYuIUjI4MzKpIGKasKxXTHHCmhJOUbGHGDHxCXFKoDUBlOse0Aqq/3RVeMuYfkfXTH/t9JqUyTa2aT6BgvjXCtEsIQgxikYqDWCbC1lTB4SHDx2VfwcEvFdnDyo1kKmgiaz3g4uMfxthORLqYxnjuwaWjYIdDyAa+FcPDNrP8zUgdKyzB8wqmOUA2wbs6YE7ur7RZG6ixn4qSpjkQTve2t3Vswgxl26r+K/8+hXX64sIItKqWh6qpVEPDHWnMkU1AwQyM4hVU0P9uBnw6L+7vi4FXBJSYYALltsL1uWGZG6ZylrHoAZSCuZiLFSt7mwEZDbXU5Kf+REl8GY8uAbBlo+c8UHpG9nMYp7EJBVFVojFL1EXYp4GaYcBq8VFquOc0iI+OlXwIcQeIarWiw9ObcB+qytUG8dcz0jwMOaCZAIKZ+GAyrQKMQgM86oSrZ5B5W6cYpSYH0RUwWRtJCKJ4CvoM5ZsjpmWu1n2jFYJNmYeZB6FgnuHvrRvO4eP1p9fD/J8G//i2u8DKzOzCGuJuv1hFI74+lYhxc4Btgfg27cXLuxZn1i9MLwDtFgRo9BjdDs3CiP2hCRdX+8Q5QTRQhqFAN0zrm6+fGsjEdU1YfWZ59m1E1VQ6vMPFKo7Isvbu7yS9mBTB2t7l9dg2ebH75Fk6/JojnoQJ+fck7uzWB7OpwsuT8/4/OVXfPryC87nC+I8IwFANcNnQAWpAqg0JqxasehZZ4HuG1HVQAA/5yqByVTPmzGNZ+NR+jOEE3/5tM+L/j3S37XeP9OfkBy3+zP9oMTd9x6fc/wmb4dreIfZntmhX3av/pjEzHdCV+yDSTX9nKbfLTHwuCvHVyaP0JevzTA/mKa/TbC4gkYnMQuibesiq/BB1EMCGBFMBQUBBaFq9a9qHZ+TxENcbwuW2w3LcqvxCQsXVZyTWsznM8IU8es//4lf/vE/8Pn5M57OTzUGp7DErEGqV+TbDWmRuBDLuuC2LlgXccu0LCuutxXLmpESY9YYntN8wjSfNG5nUGVD4etYecq03pDSirymGsexxofQ75wLQhE+LqvHgLQuKBqDUYQRAUykynIaJ4NFGJNZP/p34oJcCIUJ0bn/CUSgwBDFdOU7TTjkpkITjCq2VHlxydPcSRXFdATjIFgMBQThP3tepedF4Pka1Vbs77f5dzQv791v6b4QovFXXhigc97qGay+JqSZQCEixpN4JjDMDj42hHO55Fw59S6azAOFCgx2eB8vAGCPZfiOhe23bcdt7euV3Ia3d/pqL/UxDFkFTxWR5F6wuyd06PhY6neLbdmkyqno8tk2o5UZdp4ZMbfj3wfN7nPDXv+I0qspK1vH9M/1/Ltkww+cf/eEECMveO/3R6ZeGETiKUW9hZznM5gLTvMMRtG984Y/Xv4AIeAyP2GJ4r4JIMRpxjTNOM2jpRijFbM3Px5PHySI+PM5sCNw+C3v+vdtY4rTrP771RLidOqAtf4d228ESC5QEzb3Xx2oo/F6BQi8BxR6oFKR/t11eQ/wlxpugfx7Ze/m40C6PZdMvPPsEbCzl+94rbrF4V4QIakXxoypA9PQbxCSN3cxEewd/z4zgwyQXVchwG5XLNcr1uWKnBMCF1CMMg/IfA9SiwkRrG+krHWVuA7etzwR1bgOnSCmZP0klJyxLjes6w0pr8h5FYsIZgAzQuBq+RFCO4jBjFRdTzUAHFygs1nlA70GuYF+FsQ5cKhzz8oIIaqgxg7kxgh2UlyfLwAURtK6m5AkpWbuaxrNNLhkaoB0n6NNsZKFSEzrDczNEiLnPRCxX7MegLfA1NXdkyPM2pg1IdcILlMIEktiR5BXXYsNa1ACMQ9uf3aIjHF/6vMZ29jadm8HNcDahDK1H5wWkdfeH8F2X47dG6+PrpssjYC/v28WDj62gn+nvothve+ACb4O4z2/n9m7hWW/Hy0mfJ+BmiBiLMue8TEh9vrOx2mwvcjiN1i9bre17YXWflvrFDpCAmhusvxaGd1WjQIj+z0KZaxufmxkquytqS0R7B/1fStzUvouQBip6TTjdDnj6dMnPH/6jHg6g0IQQaJnqkvzXUm8RwibJp/sYWLJosyaP6+H8WSwepHazpF7v4/S3nN7828vPUrz/JmCj28p+4i2+ysJch4lw19j2N+VXin0LfPmR/VpX/Zfd1w/Kj2yvr8lr3tpZOz/XdJb9wWjNyvdOfA5d0rS/+/zJvpkK2zM4welDd0E3lane9aDgEOfDnTiPf7zXh0eSUdlvPX6e8p8b93eku/mXe57vqOZtjmOpMbeIw/VS2BTKZmYmxBCS/f0va2XUpkbsTY1oYSpqCUGUgZyLtXVUXLBo3POlZYDN7oqzjPi6YTnX77g0y+/4HJ+wmU+Kw9nbWYxhU0JZVmQ1wUpiyBgTRK/L68Sj3FZVqxJYjoQRYRpRphmxGmuMQIMp7Hg1FkFCab4Z7EcexfEyu/k5hFBeOuk1hTyKUX4PR+f0vi4bLwSN9dMJuQx/kAAcBIBDFk/aZ+RWv67+QMbK/uPG2bhY0XYS0LVOl6EbG7tW0R4IJ31u7/f82N7fNsev9YaMP62Me/xlWYB0azHzfIBSrPXskMTRASKiMHcppsCp3qdqBYPOiGqJURzj93HhdBrocdhNjwMjtPeEj3un6M3tnyJjR1z49GJsCuEGLGr3bLr9bFk9y729y9fSymau4y+hdbljUR9OHdrzYakLn9bx7CuueExv89rA8dzfxczoWNhxPjc3nt7+frnjsp+NdncLk0QcZpn5JIwx4hUGGuSWKjX2xVzPImi75SQcgYiYQoTpjgjxaxrKG3q1WbD+9J/rEWET35wDcSUINQR8+UCCrG6ZJriVMfWpy5gjztsGX18B6BitO63TsSD+t0TBHhQagToyS+8ob17YD4AEZwc3BvT3qEjQKmB0vtg45j3WP/A27Z6hmGsXweAavmtv2SBxBilLkxdRx+BpF3ePLp5am33m4uBXuuyYlGXTMv1qwgCOIMDgYmrqxIicYnk4xqQ80l/vd3ASvTM89yB7Kzl1b5gIapMALEuV6S0gnMCwUsxC0oBJBwFVSDc7jVriFTdDgHusJGKd33QWcOUgkIZRj8KXSD1LmBQEZqy5Abib+aVlla0P83qQLTAzWXU6E6nnydi2SDEnIGnzIx1EQHGklZ1ZfMV5v/T6OOe8JH5460SWp8PAjtq71fhmxK+vs+aKx4htkdrIj+fN/5Ka7Dqfh76ZKA0cwPHR+D53rr2xIWV4csyQtH39VhP+71HlI7XrI6j+6G9YNdjHvVvt8+Ma7mry7hmd4gAm1tjDAWzTjqfz3U9AqhCMV+mjFWp9QIAU3oZ9xzfT75u3oWVv7+3P7eA0qEbi2maVBtE2Q/nJqurKxsTsC9M8cm/c7R/dnUcnpE6NHDkHihpc100ywDEBKYI2Rqo7i22T5gFRKismW9PC9xXDZVtzaugOhBgmnII7TzcmzP+ekdQ1tJ+pp/pZ/qZfqaPSMZafVRq59TjmdZ37lXkb7TxH4Emr6URcPmZvk+i+u97+rgHlm145Sp1NBBB6R4uIKcABU/LURDe1T4qkChMYolbgGVdsd6uuKklhHwWoFi8r4BCrKA7cD6dQJcLPn35gk9fvuD58oTL6Yw5TuJBgAIAFUKoRURexB3TkhZc1wXLuiIvCesqrpkE2A+Y5zMul+f6OZ1OQicbv+WU93JOWNdV6q+flES4kZIo5qVSQAEVE5CkOI8q7Ensx8arMXON41hKQSpZPrkgqxspcMMApiliihExECIBRAWgAlCWfNG7TTUlSSlHhI6ZRfhg34XbuFdIJDQ+N5DnpwaBQv18G4B8DLLvCyP8e41n7q0QxOWSuviuPHsLUh3DLBjLNIEoIqoFBCAuoW0OG69vSplhsJRoypo+sPWWr608/p1+GPnNe8IH47NfTw2dqWucnPBw2OMZ3jWyKnn5NtCQ7b2S7+z/4+gS7s+hI9C+5d9jd2AcWvrt1obNEuqvdV59/Bnq55bsC6K/RwisHhQ443I645YIy+2GtK64Xl9wimcs64p5WrAsC+bzCdMsLqDneca6RuQY1UsJ4Ef4G7aHxwURu1IZw+MGLYq22OxdbN99R7l92cPAjdfdIq4L4mhC6zUiiHuXEDBNsx4MJ7GI0OCgEvRIWj3WoW9bk073ZdeG6VP+jZ3n6uP7QohOiODHqOZ932CzIyZ3zoURfJeu29mEXfnM6tNeZwb3E6D2/ShcEMLnmOTaA8DsehNEYHdc7hHa9bq13/WDJyh8O7yrFCuTGUARl0rrahohC5izEhDqLouLHmgK1BOpFoQcfOZnM61rs/Lg5trKb1ym/Sv1zBoX4ibBtNIqfisH4FKRNzkYQtuwwKw+PdW1i4Gr+k475EZgmqqrEwHwVCNEOzUQSeDYEkQQo+uiMFcqqTvCh/mRE5o7GlZrCGeVIfXpiQML3GVBvoxwSykhFzFHyyVjXRclugFzZUZEEIy5J+St63bnLdrc8cRTMPB7mIcE8X/vfU9aGd4KolShmu2zbZ3YuO6B1HvzfVNf965/xl/r6lzrSbUe3hJiBGjHvaO927oL6NfS3vq25SjjGTbEnP4Q7a6DNldXVkN9xr3TvseYFCaISGuqAaIrqD8IUGpfOLDf5revn7W7s144qJcfC7vuLResLvMs+8ftduuEI8J2ciegGsfLzsA61iAU1n5glnk8lG/1HoVGjejFZg5YO3MemJ4hMZsYQawWMjMoF1BogkNbZxLwnjtmUOZNdNufEeEmdOzPy2oTUufu8cnJVp77/Zb0kYTnRxPWe/m9iW6jvTP8iFnRvWvDsjxWr3v3v4Vx3t1jHkj77fEZH5a4m9tj6a3jPzJ495ih78G0DWcq3tfXLbsDnuCgaLdqd+u0vTdk8DdLfv/TK39STb4PCPDaut/SO/3z763RwIe7fjYmon/4+/d6oyHf8squMGKHD9y8erBnvLaO3zsHNnymz1NujG+4YdhhbsdnN7+Pz/d+rN+adurpy6D++mtbTr3N7oJOQWY090YwawhgVDcRnkJ4zWIBB4ynrQWp/3wTQpAJI5oroJTFkn9N9hGLgchcS/f82jSdEE9nXC5PuFwuOM8nnBR7CepGCRrfi3NG0fxyTkhZtHZTtmsFKTMKCygdpxmn0xmn0wnz6YQ4WbwIVTipAgO1jKj55P6T1J1SKYijYph1vNHQjUms1yyGo+eVil4vxo4rAB7VaiNSaBYhZFa9DBMWNVLXcCZpT9Gg8ub+Sn5blVj47wo498C+H5cOXyHIszYNBhDddrvxezNP6f5vNxu3daGgPLNaRttHBRHkhAXmWkksIsxFU0CgSXlxa78JFpq1RQt0bf3fu24CegW5XljToRiuNe2PnmWtPTp0DLBdofdSz1fXQsnK9EKI3uNBg76Gum/+YPd8v1/tCmXu3H+oRXv8IAAveRAs6Yim6a+z1v3+0TMwLkck/IPn10iWHvXLHp7pq9D1xWtk6TCeAGkX2XoBphiRVbCQWd2e54xlWbCeVtlX1dJsOs1VIXOMuWpt8ySDH7W3nPOPCyJ2CqBhZXH38/HJ9+hEtY3eFoMBelZDDyvo3inPwxzLdKVqHlEPxBkhREynE2IUQUSIAZP6pI7RpKP7RG4HuACorlPqwaQ1HMZmb9Ma8zwaUA8EMrv3mCvA+ch2NgKYcsjZodeDStXNjFUQCqA5Gkok/lk0Dwa/7aIlTO1vaB/xDkHllA6kLRrQR+tX1KVOSklc7WTnukUnQDBTx3qY9IdoE0LId6iLiis9YffZgDU3Rq0TgZIXlJSQ1q/I6xUlrTWgcCAxb5qmCQgzTJuEEQBd4HMQPd7b7SbmnmkFAZimGfMUQJFEI0NNNikAlIUi4ZxQkmqKLIvWT4nFAIQigqGIIqXmFUABlwkFjICAooKMkhOIMxji3xJG/JAEX67mmLWvRCsGXBA418DRAMAUwfEJjBnEVwSsut+blrOGhSVCVOLWQNzMK7iwuGIqYvJbtXb0QDWTS4vD0NbFCmYXC0IJMxGwMG7rIsIes6KBTZne5Vq36SqAmVPBmlYgl1b/YDEfQiWi/dwQby86HhrTXuoMGNFRSptwEtRNzEdMA6eCn8ZYCKUJkBd26lqKtkalZVUwZAwBtRgejVBqe0Dx+wH6uABt7vcEkBHY9p6tFSNOLbDd9rquEbVaggrfssZv8JumAVeNaTP3dwATQWdtpU+8AIoBxFksBAyIj2pd1LXGGIg6Jwin00nmIiekNYOwNiulMIGIm4WSVqhAzoCUZf+M1Ls4MmuZSFNtY22pzRdlKmxszcrM9v4adFvzDBOBOGIqEYUZa1r1fIu1fZV45jan677PKnhF2+eMIK+CSb3nBSejRQi0nI7otQFUZgnIEnmGdvZjI3YJIGKJLVMK8gpwWfH7//P/A9aE//mP/4WZJpw/fUGcJqycJaCi7fNVmGoUwjFxVPQs6tdDZZ+tQywzXUfbfB4nv/r+6tv/75cOqBiMnfhRPfBn9uubSzvio75L2hb2PQDiH5I2G8zjye/79+6/M/sPfPmRzP6m4/enJAMGE3IR16UprbicLxr7L4LQ4rjVc0P5OaNbXMglmOW7bWdbvq6+9Z3SvQl2RxmN23dVqhpvD65Yu/uvCIG+Zd89FI4OiJJ/Yrtm37JB7N/fCiFcp6GrSlfFx9PQFp+fjok1uRek8dBgnXguNiRIFCoYwnZ43QoRIYhLYeEloIp0SqYhgglIYZJvAIUyUrkg84o1nbGGr7gFxg2MF77hayb8kQhf14zrsmBdEzhlpCWBsirmhIA0AakQnr98xvnzF/zy9E98Of8D5/mMeT5VV9hcAFaXT4kLUijInFDWG7CsCEtCWhJ+X1d8vS24LjekUsAh4nx5xqfPv+Lp6QvO50+YpifE6QIKJ+W/MzIYN7WseLkVXG8Z6bYg3RI4ATkTbmVCKgVrTuBCeBLKHucYMdOEQCcQncB0AsIMCjNAwokUiBJiRkGmgiUnXNcVaZXg2hMLNnE5RzydZ/zy6TO+PH/BaXrGHJ5A4QSiCZnEeqOUBSXfxD1VSlgzYykBC2YkBCmpZI0qjsaLk/h6DyEgqvX0PAvuECcDGhtWUz8kQpFovL/+rnhMFUYJLqdepjwzNa6Mw1VgwoCGy0H/boG5KcQqgCBqlgt2z4JTC281CQ4X5ZvDJPmZiybSPV4xjRAV2whj2e4b0m5WgYaBvNYuAvWLv/49rFXHZ2zpELdr7QWR4QfiSRCcNyJnuQ61Eqedd+9uWvc3tKN9/i3ilNfSWIIp11lykECXmHU3VJ5tfG83OUZcI+diGMDjevbHU1dvRt9XTQmgPfl67fbuHo9P5EkLFit/miImzHh+/gQKEdfbIljB14RbvOHl+oeEITjPiClgXmZMISKen1QZWBRk15Ta/FTlPyjPP3oseS19k2umBn5JGg/L9vdxep1Q6QffDmrSheY1iSVDe4faT8jgbrkWA4OixoKYMM1nccE0zxpI1rSbDUBCl+NrNYYRrnzf9/omDwPsBkDQp2aeZxq1QyXUtYT5xfYax76cPtMm2ffCjZoEyaqbnAUM9u2z4E5VIxx+nLgNlq+L2yw7gY0BPjZ8lSfgKnwoudfI7qTpztJgBLv8t20Q3aZRwTm03W13vhowmJHzgpJX+ag1grhgItXGUPNAkqDRdtghiASeC4NTQkkJXLIQArUN0gfmXap+mKuZaSnOTQyRHNTcglyJV08S6k41TWy6mGYIlwygVCEaK+NWxVqkG7ojHIqBdJx1q7d+VQKACQhJiF4rUYUKTKEd4NT63oDdnEWgU/Ja79l4Bg24NW7uJqBb1arEryMRaqgv/dzPG6JyOE/qvCsFOZmlCVerBxO61e96+KPOxyrHJOoCp7NfQ7UvUderB/btEfLrs363B+q6gRM0mtzHNtFaP3T7TadNvzPnN3I4D5DX/YNdvv6zz9iJ30/pm+pPdrPLtkO6atzbh1AFHXV/du2hUmCGLm3+tLgJfm17t0ghBI3jonM9FyQkTHFSE+cAYWusD1pbbW0QGGGgThqxq/X1eyOJ0JHdejFNqLHPfa/YGRViAEpBShJkPlbzZVudqPsp+X5z4+PnDAe3J7t16p871JBsD2rZ7KYr6552sObIxlfi1JSSAC64vbwgIuL28hXL9TPOT59ruxhA0dejltvK3z9L677j24OBotwIKbbpLdq5e7/37v0oEP1DwWi3j98tU//tVEq+Ayg+ah2N94CRYrxfl13tJltA92vyYIWP+cLD/vmu0+Sjx8SfOsOdV+b7RnPY0eRvSu7I3GNe9x9/75ocC3jj6z6nTV2NOD5KH7+e/qw0Mvn30vE+0jSLmZv7S5C4+6BqG9dRRrXgdrU7BAfibLf2j1X83elww2hP3Ju3/qh745zZy/dNCobHGe+9sDsRDnbqu3cbuUXD7/263ePH9/I9qk337N18GlDV01fGK3h6GBVsG8/fpg3dz95glWVYXGQYmcmkYaxDULc/QQD1MCFTRA6MFDISnZBwxVqAGxNeCnDLBUvSeAtZ/DaVLPHKOBBKkPznyxnnyxPO8xPO00UALweIsypZWmyFYkopOQM5g1JBSQW3lLHkjDUljYlAmOYZ5/MF83zGPJ0Q4yza8QpgF+0fU5xMalGRawxCsTBIHLAyYy0Bs24FRBBwnkzTPqLUuI/VjhdQ/rnoR8pQvKIUBEREAuYYcJonXE5nnOczJjohqGshENVcShFcoajr5JQZmQkZZhXcFG+UtG44QAigGIWXsTiKkdQ9cPv0WInthArCU1PqDDW+gs5sshcaQNF20Z1NsbvUEI0uLoPGsiC1wglm7RAVP3FBviUGSKzPqP9pwCwhVOmYwgSzsjC+3AsbRNnYW4iY4MV4KBHhweFGDFt3lbFri9I30dab48l9d8DnUwdwTP5s2k+VJBjo3roDHL3+wJ59xJe8ZgnxKC19dN9vlLYXNkzT85l+/7Zu6HmMR1NdP8gPtMOVuUun9H3f7e2e/0Flzft6wM7lnbP2oG1N8AKxIIHiVDFink9IKWMKJ9k3kwhI13XBmhesZUHSmLNxmkQxX13mrSEiBNvZWp2OUfH76bvEiPBM3+tE8uOpB/Z6IKbbEH1d/KJ1G6aZmUzzCSFOmOezDs4MomYBMbrMvgviD9cfJ1r2n3/texsb4rif/eFy1BbRRm7atp2NiYGtDqyv1hgK6FpPs4F3AyDrwUpfPg2bNas0f5Sq7QHKPj9fHjng7ag/atslQyHq1H3LKAjq3qFei9zav64r1tsNaxKtXAoSLEv8UkaEOEsMCCaAVcgVI+bTjDhNLTaALm8iJRw0XonFc6huVZR5AgRITEU0yEMMSluKzQXAQKRm4grRegZlwGkR2IZuh20TqQvI0nkqIdPob8KmrO6TpqjrJwTEeVL3LgBKRIEEvAlkmuhuE9ODnxXQ8bESLHDYa8yNvSPxJGRMxuDJzIx1XSFCjlzLJqIWEHwQXu3PubZCAkHGJqp1RoxKyDd5g2FVdT1Uz1el9gUBYhni1sbe2vUElD3nD2arr+8XL8CJ0fd565u9WCj+26faBz6gtoK9WyKlhkbZ1HEsy6xJUkowgs3qPb63V28vwLDnxSKCMZ9Plcjz4z0KrKwsAygiJKaHuWWyuePnyq7rNG6CYrtvcRv6fkT3jO8Xm6M67N3eaHWI4Go+Oc4Z1vb79to97xaqMQLU1YFZLEq8ZZuv+zhX/fnkk5hVQ/Y1bu8XGy83h+t8LSpYoYA4WdAGwrJcwQz83////0UBIZzOuPAzwhwxU8B1FauwwKETPrwF5D4Cr78HUP4z/Uw/0xvTx7EW/2FpZHP/s5IX3nf0PbyiGbrrveZlE6T/+6f3N/Se8Pcj0x7t+1dNH7lldeAbHLBlIofxgZ0MmNUjQWFwLm5uUw36S6o5HorGOMwA8wReI5hEtS2BsBZgSSIMWNaMZc0oqYCLBVluWIz465cYEZfzCU+nEy6nGfM8YYoWVFikIpwNeBdXTN5tUkpJXECt6lKkFMRJwLLL5QlPT8/q9ukZp9MZ8+kkrpABjb+YJOi1xlVclyuW5SqxLdYVy5KxVNdMGazBqINq4YfoXChVcUOpe4tYtmuQ66Rx/zT2IgGY5wlznPD8/Izn5yc8PT3h6XLB5XTCeTqJYIaieiwASsrIy4r1ttR4kCkZ72L0tvJ4QQBzihMQWtzTSQURZrnfu14JHQ9srlhGPKcTVHR/K69Htp8KbV/jEMjEg+c1UPddwx3sQ4B5tAiTlj9VYYhgFxOaxUSsVhGEAAqTvh/rfdRvU6L01v5j20JXR5hHDmx5+Tftc4pS7+1XHa9PqjRG1mf1qVfPHwPCR/yCgE4B0q4/ml4VFgC77fqQpFvCiHncq8vH1ekbaCaCxKbFgKH9sNTWF9CwimmacDqdcLlcQMsNS1qRc8LXr18R44Tz+YJLXFHmjMCyJud5QuEz1iyWETmzO4ia9OWt5/6HCiJGEMdvUEcn4t5C7O/b9eE+jzobbbOzh7U2dd+r1XBA+RQnhGnCNLXNuYFKVqn9uh5dq9d3QPejdE/o8Nq9lvV9MudoMY6gHvzfRDVLPzSdMKSoD3YtnaLzq+cBsYM2eWGFNWOv30YBzJ7Wto2djfM+iNu/o5mLVq7vn3ubnPUli5mSAebZNCmA6jYoxqlqyouas+Vhh6z4huwAXUBdSlENKt1O+tpNrssUjCUpl0tph5j1AaH6qxRaU9zfUIhAtObaGoZqKbuP7TmVaEC1RhCiq/efaX0fSGJDUCBQMRNH52dxHAv080SsbvrA1m1OQdjEDoSGWqcUpJw6qwcDqfcCvN87wHbXYd8AIYDqh7TLlClwhEvdlyBrt8aBQJF4GoMAcKsxQJUANAFhHRgehcDo+tLGJYT7MSTGGAn+GaB9bP955JA/Eqp0DCs5na2dPcD4E1+XcXzGVNtTwkbbYL9/27jX2BKQmB4xxi4mxhgfwffXKFDYi6Vwr586IYudY+7d+j6hrqttXqhzjIg3dW1lcD+ngK5fHlkrY98dPe819gCIOyTbe4YyTQAqlomt7iKAkQBbX7/+gXVdMOcT4qzaUAzAzjLXVv/9SFvunu8/KL2lvt+S7156c1l3aKUPyf87pv78u18vT+vu/f6Y+vyVQLVvYMTu5fpAf/21+uGj0o8Ds/fO23t8wv30547FI312PF8GGq4eDP6ZnX5RUG3Mq/77N5qeR/vU62vs486gR3nh15Lfe0fMQZ94c522CjRb2vCRfI7SW3bR18aI4NeDj/XYRGfUXkZjQsY6o2EVlbdxfJ/yaxJjrWiMCLnOJG5qCovr1cwsoH0WkIoLyytK81UgNwjIGmNAnMQKQoBw08q39jEs7heb0mMplec2q/YWe6FgIhJhxDSpW2NVBjTgXXkMZstP4iKWnJDzWuMkptxiQ1R+sQ2O42cAcYHlLa0GjMaCSmsbbHxjkPZP84RpnrXOk7p8Dc2ltI5KrW+WOBklJ5SSOz6MOuxDx80LEgaFTaLtpxc6bD1K1I8T3lpfkI5zs/63L2o/K+visBoABv5bRqRuYc0VU+0PE5BVYVlzzUTV8qFdl7zcddAm5oN9N+HI8NvhKUDfH3vrFUfXdS1u96ttXlUg18NjO+fRG9Owd47pLTTXa8KY12jjV/dMe8/tXQPkgYOsW7+98Yze0PVaqO+vt9ebDPXZVpHaXl7zr0DHTp5vaox9Sen9Gpf4xymLomIpoqSbXKycpqDJVYBhsWyajqTZXbyvnt/FIuLjk5reeEDM3W2S9rbzVQKxrmHZ2MwkbZ5FC/10OsuhpT4JQ5XGu+x8TR5YoDwc6vee2/u2v0c/7R7Qsu+xmM1eiH6TOBIKVGAt5VZ/AGHyGrRu8wJ6QiDnOgJTDJ203Zfjy3ptIx/7enzf3vHgWhVq1ANj6I+9slgNGodNZu/T1adIu7MGlr4tK5bbIj7vETBNZ0wTu76IzQUTielonGZ1CxaRWJxzxqgaKJD5eqqBttQ1jAl/NFDXuq7IagFAQNfnsBgRWXwaFt1YclkBEtPbECJSnBpBAdGiIMooWcDbos4f5W8xsAA5AQmAVBIoLUAKakTBbQ6wWpuYlkUMICaw+A4bxlmIRBPuFEeAWvsM1K2bn2peFJa+qRoy2i8jA1pNWI1oclrtphWyN/ds7gggnVG439hrkDUijOs2ur1FwOFGUNe5TQDFNlfvAex1jttJ5mB2D74yJAh5t2aKWMBYO/3eMrbV94H+VX+XShi3/EHUrSPfF9ZPfh135en7vs9LyV3f+XucC0AufkYRn7ekhGKtcRETcS5FRr6UutaAFjja/vaBoG0eEkmsiGVZ6iHN3Fsi+D6Tg710+Vgfm/9V3x4rw+dpf2fTVqtxBPt+yyHXvvbli3m7MUjNgmLc58y4ylyTjcS5/V0J+R2tGhNejVZw1k9SvwCKYn3RCyf6VPu/MJAZrHFQjNFhTkgJ+P33f6GA8cvv/wQC8BQDwhRVoCeWYZWhfWf69wRCv1/6T+qtI0bu3zPZGfOtefxMP9OflyqtwwYwltdYtaOc9Puvr4n/ntRotn+/tv1ZyXj6cRd8TRliHyzs8/H0+YZuJ6rsgRm6Gz7CDKA0pUL1N4rqOjhoLENMAGeUWFBiRIkTOEQURGQmLJmxJsaSgSWLqySwOTAjEBOyAloMcRk9TxGnOWKeA+aJEIkRUMTVMFBdDqe0quXCWoNhL8uK63LDy+2Kry9XXG8Sk+J8ecbpfMbl6RnPz59wvjzjfHrCeT7jNJ0QUJS/XJHyDWu6IaUbbrc/sNy+Sp7LgmtKuKaMNZdqtctAjb8pfSxBLLgkgCWGRMnc3DPngpIYJTFy4upKfQoEioTzKWKeJ1wuZzxdzriczzifTpink8QpJYmMiSLYTFoW3K5XvHz9o36WZcGaC1LJyFw07hqBouANcZpAMVaMqwo61Hp/iuJ2xa5N01R5XB87wtP2jVd2whgTPlQ5QkOOyYD8mjTotFrGcBVsGI9hsVnF4iFGCzztLL7jLJ/qUinWPM01kwgiJI/gBBE2r6kTgvQCCMMUPfY1KlEdJ4eYY1jfRE1RtK1Sd3sPF/MBsrfKVV3Jtb4H+3bYF0LcO8P8vY5vO8DuRp7/Q85H6iG9KmwNqtQx4BOu9i2Dd5fdQPwPP+ttb/4eyQlA5IeziIgzeAaen58BAr5er+BSxCJimjCfzjiFE87zWTDESIiqsH9bFqWfMlKqiHuddm+lGb4tRsQwIPcZskcq1sC0w8HuUPf+j1a+micOQgg4sLD7VBM72Vgt3yrMqEXvg4K7AJk9twOm7/3eE0aM10dBxViVblOg7fUxHYHttawDQQxt3h3jM6AdFgPo5bWJN5YQB3XsfqPvhyNJvYG0Y5/554eCNP++b8Z67H0X1ZrIuShgCJ1rcviGGNWyIdZ5aAdnCC3gEzgAVPTQlLrEOAY/7vu8CoO8xgbtb/7VcsB84gKgnCtRSFpnEMQUlAQ4RDAXKXYSNJ+lmjEAIbJzyV196v1hPrS8dke9G4P6Ue10D27bf2AFK1mEEcZkmhCDdYztu/XJ8XzdEyZ0zwaq/bL37tF7Uv9WjXHP6No3rknL20D2tuU1OUQ9ott6Kf59NDD8aH/xde5Gxh32HmD3ZsH7z9/P82i/3+yn7cZw7yAP62hu74wb5x4xtQXqS9XGsWRr6KiOnnC/O5bogXwAW8LfykETRHR9VGT+by00SOkc2u0js8axfPzf47xun+2Zt/f3/tzZtn2XyfZ9I5LDum6kPQxwxrouWJarMKqqHYZiJtTCKB6drXt1fuT6W9L3yPttdNfHlPnRaY9xAT6mjj+6P46Aom/J75H0kWUe97+t0X1m7m19+Lb6vpZ3vfuB6/SHCZX+xKW4D2r+mAq9pX+3VbrPS93jcyy/kd6pNHMHBAEPzdWK9Wz77nueHfsV2a/Ht5dpfOaWXnlffo/d8/cfnTOP1O3o3pZWsesPFX037dKuQ9l7dJOvwxFdxYMmaruOSjPuKXyQsvcETx4bNyVW+2yFw/iNZgFRP1AFNyj/xxrPoYhlhLlkIgj+WV0+MwTcCoRIFntAAS21KpC6lfrximklm9VCRkoZa2reCEBiEVGtIuKEGCbxPEABPQ9tcWISShErg5SzuBkuRSw8lG6t+G4wPAlKlxblLTS/Gq/RW3CgCiHAiguo9UeMVJU3o3pHIEf3S3dxVXwsKalgJiGnhJxFoa1jbRzOQD4I9eCOKahXhn0hQ9hYTNj885/QXbcpM867URDR5hURwSQYm8DU6m7J3Dl3gogw1XgPRM3iIajgwVw8mWum2qchSunBXMV6PkSEIb6e3hK7XbPJcJxqe3cwgV6gURn3w5z691EX7v7eqP3qrjCGOGwuv1qnHczokX3+CPPo2nvAL74l+aYyc9u85ErXhfu4w9tJxVZv2Vf6fqoEwO47r7Wz3+eptq/hNB93rjeBBLd5Ts0iIkYRTiZ1dyexIlasyZR5s+zJIYICVVxS1qtiibuS7sfSX8wiYmzAAUBRf+n25jZFk78r5AEz4TJJzjzPmMwvf5Qg1eJKCAAxmEZJ5T7R7hfbuIjr/TugjD0H9IDW3v29su3W+Ejri9A2+YMyG4jYtFaLagpLXr1JngGaYKg7DU/I92V70NXK9JqxR20DVFOJhZCx3AnUzPTcxjf6Lff88t4y2CNuWcsCswaWBRCo6x//d7MEcX4q11UWcQEIocYLiHYIElVzVAtYPc8zQogSZBesMRcmTPNJFj3LtWmeqxRbiBu1akgJy3LD9XpFyatqQyhYaYGyWDQ2SkniEzOJNnfRzQ/pBmLRCqcQhGCDCVEAzDNKCSgWt4Bz7S9ms95APSWYWf3xi+VED5oqYVBNKS1g9/447QG3BtZ6oLRugQywxpPglIFc2nzovpXUIICVAPKWEDSsm7EORrAVDlVb/8gawt7fW4ejEMkmLpcmYBnN48Z8Rj/8e324dz3lhFCaUKdbQwcAcdvf+nVg5XhCdATffX7e2mADqKMxUHvjv9eWUnTeCzfVtSPUQ1fKzjmDCtdZ54Vy9R0dS982iX0yI4Zt2V0MB6Aj6AHgdDqhlFItKQCJr2LWZtM0VcsdK/N0OtW5OM9zM7/W7bkbI5Iz06wdmjBCCAYwI1A/H1qde4La5zFNU7e/+nH27ezODrRzQCyWJL6DnB3CqK0l1Xbbc+3MlHpEdVlXALWuyioMsvYW2b7ygnW9IacFZV2xLitiAabTSe7fWR8/08/0M/2I9AFo3s/0N01vY0i/b2r8mX2X6g7Vzn6jFxrwwQpE7tMhhhaj0pY/Pr0GZH1E/j82/SjB2J+ROiHE3n32bqYfzXWLWXBFQ7ZPEkiEBGPgP4glqXzHJnwwYQPE5VJWQUNWTKCoK6aSxS1TKkDKQOCAgChgFTPWnMWCGhmBJFeiAuIVKAs434AAcJrE5VPJyHnFutywLFfclitutyuWZcXttuB6W/ByW/ByveK2ZCkzzjidn3A+XXA6XZRunxCg/GZJQBb+Oa0L8npDTjfk9Yq8XiXGRUq4pYIlKyZAhClC3SiJNw0Kak2eWqwJcEEOAevthrQuWF6uWK5XpGVFXpMqyTTFwhCBqPnKRwJIExhQHp/VXVFaE5ZlFQuI2xVpvTVXUlxqkO6q9RyjWEIY0OgsIoK6hOp+D3xsjAY6buMm7ionoe2Zqjql89gJMaqVjW6wQQJJh6BeIJwFhASldgGoayBqzS/OoDA3fsMsICpAarEiGuYAsiDbTvBgIC3ZGjCXTHsL0NbW0cJ8fcESkXjndjz/m/Zw5fc6ZH6v7HaAyb1OMvFt++uIEbxFwWBP4PHXT62dre7jmI1tqouhxUT8jjV8JFXhMlPdI06nC1IuOJ+fgNsVt+WG2+2GP/74DefphNN8QpgCaCLZT8OEeZ7BhZHWVXBT53HDlfRwelgQ8edMnqE8XVA2/IcaMAD8xDG3ONUCQjfmGgDYbaTy/igQ2CmDjyWIHcF657l73+Nz+6kn8rv+sI2W2vW9sjZg3wA2de2C6xsPMLpaWF/6Ptorc9MSD/wa0e81eAmdK5NOIu+BrB2+x5d32C5rdzHvmAFV097JlPy3gG/t0+pqdet9GAY9fM100CxwrGdJT3IKBGJxO2TBsNiAXTAKxCSqaYg090NsuVUBgGpqlPZOKRlifSGgMgpVorXrndq/4iKGuICLA5hd347AvdSnuUiz9do0lanmP4yW6+Nj8LkbP1aN8LA/n618mx5dfR1QfSQsHOdsfbawBnRrApFeiLmfXgPZa/uxfW6vnq/ty74MYXJUyEalB5nR9vlazrh+0ebWUf1rLzyw1v3+IHUbl+9YjoEFe2Pjxqiv0NBXrIQgNn071pOIpB047mcTjo173Z57I/+8XztecFO1vpyrozCsL08AilBM2u8tIuo+jH7O+L6050ZB+tgP3btD/x4J3lr70IaGBfzx1jibdcfCwIgQg1BU8FCLcBoXhUu1wuJSqsstffC7UX5Hc+E1gvx70FDfI8+3MBb++ZF2ejTfvTY82q631vV7po8ci3vrcHhSn9+/+7b+aVTwY9cfzPUNdXhTH34wBvto2R8xzn+dWbvlEe482f16fY4qz3aHBj/Ka3v//nOPvN+dcYxG0DjltzfvJx3R4s6eN6Zvm1MfuxC249pff8+e+/5xe+y9bzlDdmmWLu0wljupp5UAYI//7zjmOq/J3e5G89UpNQKQ96tbORVlippNBbUnyP3tGtTzVQNtbnEQlB8zpb7KMwDVUoJJ6bmaVxY3TJzBnMTVERE4F43d4D9qDWEWETkjpWYVYC59Ymy+zKlN4FpHzw+XnMFqUStxIdS6w82HQBrTIcSKHYFk/Mz9ac4AqwAh6SenhJIySm68rQfwrbu7OWfWFbmIZwLQ0A9Z3D6p0mbjGRtfbdiDWXIHagp3FiuCdoQL9wUOBx/DL2BrwDTwrWEO8AfVOA2sClPBB5yugaclOLXF2iT7kCradr8Vb/EWEBS6skwQIcqQba1uwfTxd7cE7t7frJl7T3iaucYNbasR7hn/TXf3+p06u6vj/v0tZ86jQog9vGLkf+/VxT/33rPi0ecP27JzeVvvET+wQuyW7bL9e7osDun3j0gtb3Jzr613w8cNOyhF3M2v6hIv5WYVAULzLBQiMmUw8jex2n8xi4jjtJ0H/ZVSgZXeZ/s8nTDNZw0CFDHNJ5FqT7ECwwK4cQWeu+Q2nhH4uqeNrC/U90Yw5963FTuCO9u2b4n7DZg2MAGmvTpaJzTioQCMqs3a1Q+i/eDWVC3TwDLTxLX3vLa3lbl3kPk+SKnVEejdlPgyj4DjOoyEbryO+tysCwozkLiWaZuDgfuCc3EleAqLlojxMSbJtySHpwZCV8EDiNQCx7ttKULEaYGkh3dUE6gQIhiMxEI4pZJVmyNhXRes64JSFnBegO4Y42omuq4LsroxKbkgTBMIATMmBJKYD4EkoK0RDNLPUQQiMynhQygkGi1gsR6KgTDNAXEWU1jpq1ItImIVxphVS+sfgKt7GAFetd48aNxvhIPtGYsZYXPGf45SE0T0Y7FXxhHoHmJEpKkeLFUIMWoZsXxKlv6V+V3EcmRcD67sXJrFzWsgeNemIY0HPzO32BY5d3E+4NbVHqQAqMXSYKWxR8AKc1KUeGp72h7wX4F4LXePycw5Q0I6mHXOKKDpLRH2TnZmBkiAbkZvleLftd/TNAnjlDOAZnVg8Rv8Xurf9/uV9cs0TVV4mEvBuq5gZkyT7BmWZ0qpHvTzPON8PiPPM04lY11acDqrRwgByWkk1Pgpfj7oGFg/2x7m6+rPM6unZ1waw1k0kH1PHPq/fZ9GCuDIQJY5YMH/1nXdxNbw61r2i4g5ThKjBgGik6fWXoBooq0Ja1qx5oRPqgGG6vf7O1J3P9PP9J3S9xAu3U8dCvLG9/ae/yvB7D/Tz9SSnQs1RoRel3PwvfN2jz/7d0jC3DC/T/jwau4PgE/fuyx/fwQjt8n2u3v12s4FIh7okUeAxOGZ14odc9KqmlyivkrmupKByKAiroOLMrOBIgBC6choBnIG5YSg1qdYE0i/eU3AuoJTlk8uQBa+VkI+CPC/rCtyWkGxICKi5AROK/JyQ56vSLevoJIgnDUhlYJ1WfDyx++4Xb/i5eUrbtcX3G6itXu9XnG93XBdFmQuoDnidL7g+fkTTqczpumk2vdCwzMlpLQg5wW32xW32wuuN7OyuGFZbritGbdUsBax7CCSmA5PpwnPpxOenz7hcn7GfLogxhlAQClASgUEiZV5vX7Fcrvh6x+/4Y8/fsf15YrlekNJovhHCgJaLMXCrHHsssSCWFcQAq70B2y0brevuF6/4nq74rqsWFJGUosNUHPVS/8ve3+65kiOs4mCL0gzyT0is6q+7umzPDPP3P/FnTnTXZkR7pIZifMDAAnSaJLJ3WPJrGCmQi5buBMEX2wai1KUbSeESZRuLc5knCfFxmZQIMXC2rie3jvASDBRXcaauMErPw0mqiD/CGQWEMLPU5iLwCGYJUQICFEtHbwgorhXsnibk8SyRHXnFMqzVbqzscqg9nett13zQard8uMqbLFWugYeWpPjx2n7u1bKfdf7LTZ3XxDwCJj/V0l/l3aA6JsdU2XOdjg1RZglWlDh3Ol0wqdPn8DMuFwkVsTLywvOpy+YTzOmOWKalKaEiClGhHPAsiwAgJeXpK7Tt9j0kfSQIKKXAI2YhKNSsofKlQwdAN5u1hV01nLV712ggBBrYB7zg2XS1tJptmNrJga7y+9SaJNGwoNh4pFGxDFhRK1L+antvV923SLaMm9+wDfnjwDuXLqkApxG87fClk07OrpJtgiprV8PcvaCh5EgwoQQUiEVItwRRDTulgw4bStYBBFjySc56WIbpBWl3rHEICEiQIUctlGWupk2CeptK83aImawBp4aGKxxEBxAWIVB1RoiqVQz5ywWF1Q3wND1pwG9qiavbbP11T5nAKflUYfBmG8q7zYWEeXTj88A+Od2Tu0JoUYBkPeStWVvLu3NHXu3jxlA5Nn9vfy2AaE3bdIFdksI0uf9CLNRKJwt904wsOmLriwbC1+nfo0290Z5dOVYnb3Aom+j9Z+tLbg6mBBnMy8qsWoEE7tCzK7uvZulUR/bvBsFKfflVG2DGrTaC2p9WVXwogGrVeiwhipcG62Hdr72/XB7f94Khbd7hi/DC8F8Hs18ZIAjysGrVIS3ViZ9GwrjT3bQMUqse7zeZFRXAZZP5nb+vCWN9rO3Mr9H3xs99y0AoFtl97TkkXe358/vU/ePSLIdvq2+7wXOvuWhai/vdn4fza1vH3e3+vvUP7Wb2x6PvHnnLzSn/irp0fn3kfP1RwAKymZWPhfYmb+38ujq3TM63XO3FEW+d3pLmZ6feU+dj67zjynnbfX1Z9t6zf6qylR7Zeqxx71IxrKO322Olm4X0vNX81BPcu3vwtvZ9VrPTZElS6rn0EDqqilUUNv4agaIGZSzfhIoJSAlIK2gnFRTT7VmLW5CrmdTJC7ujAMxQiZ1pZuQVxFQpHVBIMIaBSxOibGu16KZWywizC2y/a0KTzFqXIhpVtAslN5kNusHZ1lQ4iysolyl8RayWnQAAktHIswxYJ4iZo09EeOMQFMBugU+qcpJKYlG8bIsah3hlD91EJQM6RmCtQ4r8roiUUSKC5L2vwXqXtdVLUFcbAjUsS8AfDlPdLEf9Js0RoW/vyd4GOEw8nedrSbcaumcPw/X87a5aIa3gGgsIaK7b3UUN+vSrqgurqN6ygiu3oZtaHkwfKb93ixEd53Kb1snR+KA7Zyb3Xmolr33Vl8l6r59lY4ITt1z7M/+Y1zjXhphcbdwCV/396ZbON6tZ4HjfP0uz1n+uf/sfrIV0vbLho2w657Qd88cwrb8s36dkoQwKHMKgj1MMRahZFYatqZKc4SmmYKhBLGPzl3aLgN0IH2oRcRbhRA3F6JkWMlZA/ZJEqaSFJ8IsglNEXGeMU8nzPOpBKU2qTCFPpugwJZuJhkQolrL3QPHmvp2xMueG6V+MW2++zaiBYf6vFpi178nGqKyydoGZtroBvD554Vj2uSn/zRdt0UaVcO/02M3wuTFJCx1A7ZxKwDUzVMl9HZtHyR2YCK2fW+/TVvetM2XZZG+WOQ6xU6qHlv3Kk3dYkSYJwCMoEGuxL5BFvt0mjFNs4stYH2uwJlUFCsn2bSy+u1nkrgHWU0w1xUpJyzrIgzcsgBpBZSBSctSuFDbLNK6IKcF18srlusr1uUK5owwma9GIEQq68L6SGKFoGyi4quRgJnBKxCyA+G1PNPgXpShs7lq/ZRJLCK49OtoTBg+BkFl3G4TOA+O+pgKNk79uBWmK1btiB5EH4Htftz7DfneQXNdVwAomvBe677kpeshpYx1SUVw1Oc1KuMI3TVw+NH3fNkWg4PVDQ4FUnNo25BYmX45gDWMrb0PNP1XN19sd2ZXfmm/o5Wj8bG1b3U0M+vAjAgVCjAjK03xFg5eCGBjDUBNq7mMmW3OPjaCH1cbb3t/mqaGTq9Kgy6Xi2gozTOASpNeXl7AXOOwzPOsfni3lhyBgm5hrcCg9FeWvcyskEL3rNXfrDakTYxlSYiREaPPExCrhPqe9aEf05xzFTdSdaFnZUtsDyBHb17dCmJEewOgSABFgOWexdcJ0wkIEy6XBS8vr2Veccp3acavNE6P0IRf6e+aDh4qygntbWutQoW/0q90P320AKRaRBDMfeoYaDmmFKJv6PdfS/t0v65vX99/5fQuwUsnOyiXBzhC8/yhTAcZ33i6AY7lD5gLHwBADCKEgJ0PxCIiGI+XMygzeEnAdUG8XpCvF9DlK+jyFbh8BV1fQMsFWC/AcgVWOZvmRYQHYimRcX1dkNYrwimDOeJ6ecHlZcLLn38gMON1OmOdZ1yXMwBSy+ErXl6+yLOXCy7XC16vF7y8XvDl5YLXiwgq5vMnnM/P+PzbP/Hb7//A09OzxFoLhMCMtF7BacHl8gXrcsXr1y94ffmC15cXXF5ecb2uWJaEZWWsCWAW5ZdTAJ6mCb89PeO350/4/bff8PnTb3g6f8Z8+oQwPSGEE4AJnBcwiweCy+UVL1+/4MuXP/H161e8vr5KUO0MMKLGcwxgJqzXBdd4wcvLV4ACvr78G/NyQkqrnAmzaCr/+ccf+OPPL/jzy1d8fb3gdclYkh9Pqi6XgsWqVIxC46SGGDXYrNC7GCu+Utw2NcKKfYsIlI/OyS6wM2nMHYSowpE2oLRYPgSx2ghBLViC9GfJuxdYWD2nElOiPZNbPAhZBS1Y784nznMBFwFJt84qALg9lx4hCcrg1HOfWcMMYmMSAOTt5R1cdZeWDN4vQlkmMK+1eu/cn/bOCt9DseZ77q2sor7vWeZH7LqsJ3ViCTNbhREqzAMDlDHFCU/nM3JKuDw/4/VywfX1itfXV8T4B06nGXGOiNMJMU44T2f5Pp0RQLi+voIpFcHqo7V/U4yIW4fUPWDu6GHjkHTQPVXmBVEhVEGtH6ZpEoGEEmMfD+JmYgPTAGDr1sR/b17dEKtjAOoIPKoDWrPqgSZLvRCCy4zgzbs9Mz2qIjNAClryRsrdTjFjbnz9b0oWuUpo4eCiETC2J4nHzjuW40gI4d+xbwPdUs7gzGoR4co2d1Bu7ntQrdmcSfyZKxar+2hQyxwXoIoNbNfaqkCCs1wLRTAkkiEx2+TiB52TfrhKjkpQZtiYSZ0rMN+C8/qk7vNUDmDN3FJBBFy/S/An20h3xtrVpd5zGglFAqHV9XXaO/Q5oYal0YFxb/6N6VKvJeGaMJg79kzPmI3q07epX997dMTA83Ega1e3MvSOJtuAWtvgV5d7vzxxPPl6b4JUmyDH9ZEB1mKS7gQEvK3RqO9rH/VjsxVA3qI1VpoEOkaJJaIFS+wFZb4rAL8dFxlbbgQoHjQf1cWEBD7WA4DGDZL1J4DmIOADQFvdQ6h+Xv37zCoMol5wbMyn9VVtlx+n7RwOZRr5MW/zrZYdvh/uC+aE1ogCmxw09t5r90GUeQY9yETTfJtmzQeFTvodarh+vlP6iLJu0bKPzPdbpD2e8c0AzwNl9uleHTb09ECee3l/j9TWaX+/uv9+zxO/4Qi0KetG2RsW+cetz79j+pH9d+SMeK9+R+t/dJ1vn7N9xZ81bMb2wNWDqWyR/dp8O3243x87qLd/4kF6du/9e/m0fPnmLur5evS7KcF13V4f8uCvt6XRmXp0r0/Ds2mpO7lpcVzI32vx9vzXrTftVa8Fq3/U87HRfbsXBKgU10GaD7PgADmLG9ecEJJ8KK36WcRlEydQrtYQxBoMPou7IYn3oBb5Wc85SeIzpHURn+TLVcAzkvrlzFjWq1hDqOKPxV4wa4isZ9QYJ5w0QPXp9CRBpZ1yVM4rGIR1XbCs12phsCxYTOM3ZxdmTBUJAzDHiFOMOE0TTvOMeZoxTSexighTiV8g8S303J0T1rRKQGm15GCzYChndOFbs/bFsiyIiwTmzjkDFOXZxOpKSgQx13XFmrIKNaB6uKQ4GCmY7ywgqHosCMW9kbOSCGEocChnux0cpggjdLr486f9Jj1jWb28iyUK5rbazj6xCFGgbmO85YQ8b8+IUGJbv9DUayOIgFksjdfXdn06QMdS//MAPWWuZ9LxOWmwT1D/TEuXDtFlncu8d/9G/e/lf1QYcivvw1jq4N6RsksbHqjm5syFyi/8DPzVQ89VCEBnmLSGSKONaODqqHEipmlCXBcQobhQLrRSLck4nkGQmDlZBZspB3Ht70o6mr6JRcTm+gfkbc1ythHyK0CJacQUZ8R5wnw+YVJLCJEGe2lpZUPHE9MWx/YwNhIa3K70YxN3A1I2QogWCCwAVAGBBKiSawDBaaOiWht4gKvP15ed1UURaRyAArYbQWsmOjW/b4KDjvj0QVsLsAU0QZT6TdKX82jyZdki8/7aw4rKx5FoUnig3vte74HnzBnIK4KathbNg6kGghFgMilotoJzxsormIHEtVxAfKmTMiiJM5b1KszNchVGLzOIRaFFxJ1qUgVhHDMzlusV63LBuq7K2DiiSow4BflEmSnChNkck2GNYCBKeyeNgZFidfc0JYl3EKcJUYU6Faz2jFIQ/6PGJCgTZnOyphakZasIWkbez4XGxVZutbX7ceuvY2ed+TRkwLp7e/TPrG+sXr69Pmivaden64KkTGld53D+92piOVHIuAZjs1zdCj0TjpWdwkWv7bKX+r41c2ar90Qk3saUAfTxZ4gI0yT3fB/3fevLyt18uHWI9mB/k6e8CEBisJjrtZhWgIAcqzXKKI6NtbeNM0I6dbcM+Qiw7+dLM+eIENTy53q9qjm5WMacz2dcr9difv76+op5njBPsamzp+mTxjvy86npDG77zj/n613pbdTyVzBn1ZyKbr3U9vpxEa2mya0tFJdz1hei1cTlsGD5jGIBFQ0rtp9imTWfnzHPZzw9/475dMY8P4FCxHVZxDpnnvpt6d3pF0D6K/2c6VvNy6PA11vytKx/CSF+pWPp/XPD9jvNi7HhM7xFhO312zwYx9aE8Nj10Y84Ce+U883y/og0oiO+vqas0tECd+VW626NxHt65cNokWv+e4C7j0rMRd4gnFwwV0wKjiQRIpilPtSiISxXhOuCcHlFvLwivr7I5/KCaXnFvF4wpxVTZkyZsTKLFf91wXqRgM3LdUHOK8JEQAbSsmC9XHF5+YoAwldVLKFpAkBIANK64uXrFyzXC15fX/D6+oKXlxe8vr7ier0iMxCnEz59/gf++a//Df/1r/8X/vXP/yZWC09PiBFgSHwKzowvX/7E9fqKP/74N15fvuCPP77g9eUrXl8vuFwWXBNjyQTChBiA5xjw+Tzjn5+e8c/Pn/CPT7/j98//wKdP/8Dz+Xecnz6rUsyEJctZfk0rluWCy+UVr68iQLheryo8qQKElAHKwHJdEED4849/47pegShKNqfzV+Hxl4zL9YI//vwDX75+wb+/vODrZcU1B6ym6KUKgjFGkAKKIU4lJkScpgo0xlDcsEwWO2IQE6KlhyNlUMXhlF7Cx10FnPBDzwTxJHVUYUOczk5RUyycTeAgLtbN4qG6Y7IzRDAXTRtBxPb8JSnUcwTMikR/le89irGlT83dW+ua7f0WzB6Xtd1vjgou98quQq/b2Nybsr9xTv9W6U1CiHfuj8x+N/o+fOpHlFA4A2oFUSgxF6VdgUR5f55PeHp6Qs4Jy/WClFZ8efkTp9MJIUScpjMiBczxhElDHQhm8YQQAl6Xl4JvPpLeFCPi4eeo1Qh4KN0oU4AMqPQ31DgQ01w2BnUftyFS22q0jNH22v36e1C6PPegMKKW4wQmruyR0EDK7spw4G1fp/sLuTLsbfsAI+EmxyFDe2ycuryPSGw39dkBfO2ZEQDY1BM01ATvy/LgaolJAQHIm3Y4E749cLEFGmWR72oZUBWpMVzgcA0SBr3O6qSSVXiRclaXR3VsiRRUtE/OThOl+uQ0QipLxjRhUJiG8Tg5ywzYswMBzEaDX0BfEc6gqS+sWNR1WIKklz7ezk/WHdXGvK9DL6Dz828kKLAx6M9wozWxS/eoWgEYLSoMi236qO1v1q7rg74Nw2DbJEJA60EG9KDg18RtgcheOiLg26wXFWyUPLQ15J5tx0I+t6jgqJ+sfjdeGtNEG3P92/LPWfzcGvCNbg714HxW37OjdW+/9+hq36+9VYH93ccM8WbSdj+nhKSv9rEkgC0UIdfdGsG4br4OPvXzIWeuAgLazl2fRwlSrW6v2vUFWEDQIqjo8rHrRNTEvGFA4rKoNhUQMM8nnE7PmE+ifMAsQd4jKi3t67mXjuzRt4Rob8n7Lcz7oXXxhrp8SFl64ikc1J33Rvf7Mj+y746mx/m1cSywj0gfNc6P5XNUCPHY+LI7lFv+fT1/xHj/HdJ3ORwbovEN6nL0nbe2s/Kytmf6fCpffiOH44X55bOT5ceO142CbpT1reZMzdfXaUzP68/BfTtWun83dGDvuM7vmSvH3uvr0vJbtfJyVpY/7u1rmtNuGU09MRp1Aw9oc1PZwlaUZvkrv8xeeMassR/UIqJYQ6hFRJb4EJQzAjMC5ENgCfkrBzywfsAi4CjnJj3XWaDmlNZSLpO4z0nrinVZigKUWUTYudaUc06nM85PTzidxSJinmfEGEo5OSekVRT5lusVy3VptX3XhHVNsLgLILEimEIQi4hpYBExzYjRLC80yDd7F8GpKJiZS+ys/DRDYpuFxCKcSAL+IRBeX18wTStSZnAG1jXhcrng5eUFL5cLrotYRDCTG+vqkim47+I+2v++ZQXhzwZ715t56eaPewegYqlNQT1DmCVE3LGEKPEqzL1StZwwS4pQBBN72Aq236WOdd3UxdG3Z2+N7lsi7AkWemSquW64WTmz9s/VmIktx3SUhrjydx77qH3a875HML9H8t/DI26lR7Hqu/sjtRjWkdTgs+7f7f07df2QLZrBtgrq4axuCJC+MIVD+6xZaKKPdZPWVOLUyjsSXyLniLASsivxaPpQi4hvmbohLFcCheKi4XQWc7zT+blIfpkyGKkQL0tVC7YlDhkQHDoICRh4cju+eDtg6v7jHlBrmRkPtHoNXmZW7VYgBPaZFVCwz/tWndp8K4G1BRsKE9Mz8XeXU1OGFyJsgMdiTtn2SwEPb9S71mh//TJz1T5XwHdZxRdjQJT1qQBkRpXq26JjZmSw9IX2fyimhOIGjAPUNdiE3h+g+KcHVn3/ermAmTGdnoAQkBmikQID8yUQ67JKfIfMqYD5FpA9cELEimUFsBqgvRYCwlniL8QQ1ae/jJkxLPUg1s6XrL7lmRkBpi0tpVs/ruuKsCwSZyJGCWjDjDVnZAZSTkoAnRVP0e7XsXCCiIJ3+s3EHSp6IUTL6LWujGzMeosImyVZTqdDEKkvZzTPTJhTvlEP69nNWx4ALtKHtVxjrq+XS+lXA3QDQjWdtv4Y5DkSuuwxScB+MOY++bFOSeKO6Ays4wKUmCbJjYOA6ub17PZhOXMrUBK+dsT8lm4ofWx5MLsA6rpe7dAiBx3GoppD8XQq98tcLpZLYilVGPluD/F9PaJjPZN/vV5LnUg3/IYGLUuJswJUq62UEsCynmf10WjxJkp5HZ233qlxaeoYWh2sDXa9mmy3h5TkDohEBIqt5YLFtPAWbrb/Cl2U+kjZdVysj6V927gcIQRkVMYGLHtDiFNZN5+ef8Pn3/6JT7//E9M8y7xbrpjPdjD8lb5n4ofYz79XukVnf6Vf6edK75mnf+0VztyeKeCA0TZGxK+1/CPT320nUWz70PK5P/NuCIo7fGvDM+9kTmYlmwkcAKzqoyitwLoC1wV0vSLYZ7kgLAvCuiLmFRMSIhiRxEp6hbghFkGGBKUOUhAm9RQga02e4ZywXF+RQkQOwrslBtIqVsHrcsXl9RWXV7EyuC5XJGaEGPH8/IzPv/2Of/zzv+H3f/xLYkQ8P4tv80gAMtblguV6xcvXP/H6+oKvX/7Ey8tXid/w8hUvrxdcLhJUOieJpxYD4Xya8HQ+4dPzGZ+fn/H502d8+vQZz8+f8HT+hPP5c+1bDsiJBbxTV1PLenHupHL5ZGZkEsHHMomviT//+DemyyuuKYtS7ekk968J1+uCLy+vuCxXfL2Ie6aUpT8DSRxHcpYPcZoRYpT4lDGoJUR03y2fP4wFMThPNnOqyEFMFS0UXIJIYzASaWDvgBhnjSc4lW8RSEySh51BNPYDzP1SmGrcCwoQ7woj5cJbieuaKAvBCyNurKk7aV8JZSycYFYFN4X4OnFJ8ywcX3l8V+qljd+Wlv7ted+xxPeD8v6mmbu/qVFwrjxOXePi3u6EdV1xPl+xvnzB9fqK19eviCHi0/NnnOYzlmXBFGe1ugo4nU+gQLgsL6BMSA9Ot4diRBx+Vl5ofttCLQvWbZaFFBTiNihLJa214yxYTcQ0SzDgaT4VMDTEqAGYhDgO89Tk6Qd1A2evjTTe7vWJEZEi/Ry0yYQF3L+Haq66B9j7OlUQ2fpXtMwraR1ZUrSCC6kjl3XhXUMRUV2LTjjI2QJ6G1AYUIT0MDlc6U0FCVuLhV7q7OdD1ZxvhRGlLXD01gGi2pSWkFNtpoHsOevCZB0rJ8yxeVs/sgkysrahPie+5gmIUQQJ2heevlRgNFlxxW1JcV+Sc8k365iJ78qEnFaUFheNAQaYxJQxzkAGKGieaQXnBOak7TffiiSbO4XaeTmr9rFckPEmUGDJOwRwifBOZWxkPmRwXpDThJwCsmsTGFIHAsBSl5zFL2jRDLFnYUIPsxZp56XryG7MGUXjxnQdOuB6KFQoQH7d5P1Y6UMAuJujpRrSn45OWP7StlTie/SHKlsynr7Y/E5q/ZJ0rodOAGPrh7nm4/kOW6so/dP2A7v1YO2wxtr8ss0KVAPcM2uMEtXSabVffPutPTfJ7jht6Bx1eVTXcAyo9Y9oYeWOjtozRfgFNMwZswj4crmvfZtZhH1BArqxjiUTg4hlrevGVeiumx9B+60G5daxC3X92Lxy4iJkBeo5yyEsUBDttNKnNeA2SAQda1qLoJJRhR+9kN060WZ+Upd7QYVb9s66rogRCsgAcYpgZGSuAbajlu3L6uOG+E+/v2ctO1IVOtg4WVvteTnUWB0BKgediKhxIuI0YZojpnkS2qzPe+HlSJD4rRnnPaHekWfu1+0YPzN+5R4a0u5tPVckhdyqVxlApQFUx9Rd1z9dxWz/7t0/2hrzxdD29+2KPTQeb50be+/fK3tU3tE63GuVdfH+tDgiPurv0/DPzVubdpNj0N6WuJlMg6qNj/OD9CMPzrd6/I31GiyTD0/3SMeNerQ0xV1/x1y4lbb5ej7OlAdEUY1h1qdujx6dypoj06P13vKAR8D2I13e5n9//ry1z9/y3ngc6t/yzOYtdwaoV6mn+/AnxrY/bynXvGdv9vn3Z/Dh2brJtH1/t36FN9xa9/vWDi4OyuK6X+oZeLQfcDu5NWainl8y19iEKQE5iZUEJwRmRAATCDMR5kBYAyGHiERiH5FVgU502AjTfMLpNIvlwukJIU6igabPy5kJGkdiFRdP9kmqkasxJwII8yQA2vnpjNNZ8pymM2I4I5gteZb8UlqRVmcJcU1YF8aSGAvXuRkJmAIwRcI0BbG6PZ0RZwlQTeEM0BkUZj1rMBgBmSW2hbhg4moFId0p9/VvzgxQxjUxQAxaM1ZKyK8XhLiCllXjZCQsy4qX60X+TiLAkEDOik2UwNSqOBWpuiYvcVLJfYL0uVmGE0ksBxNIqJul+oGe9/T5IIpodrYJXpCgCo/1W10shUkVsczl0gwfjJq84KGxhDChVRVEVEzQneA9z2SYFbX8q9CVAf/iz/Dtw/3LJX//Ri9G6GnXbkZ2SCwH5pa/GVSvvN2wQDy+zwUjYXf+bdf6MG0bcCMRTOfe6FXl9X1ZXSMA946NjI1Xx//vlezo6J5CKVgdfhf61z1H225gX7SfG2/mVyolb8+jLSNbyXYt55aC6M1Usm7nar1pE6KurUARU5wwxRNiuIBASGvC9XrBslxxXa5Y1gVTWhBiQIRYTzBzoR3+jHckPeaaqf998KDUg4DtwlKgwfJTYrdlXWzWkhKziOn0hGma8XR+QpxnnJ/OQhCjaLVbP5PzOrEFJgZR6lGqsQHwikZ8p3ndv28H6XxrNBxQNvoYSNtr+w7LLENR2yVCApFOq062ulQZM+gWJFcWoIBDk/aGEH+Ay3+5MihQdxsGthHAVAUFBCBwJVRijkmFGarVoUI0CCJb98TetHmL4IaogI+evqqCRQFES/8QNJAUI63KKKxiLmlUSvRvRVPdu1eqQa+CmpYmOWwpkQ8EQF2RiMAFYt1QRqQGo01JAmLlNSOlbLG9wEliOKwqQAokY7JcJTbEslxES2OaQZEA1RoBAzwFcDgB/ALwKzKvWNdX5HQB8iLvFJ+LAucFEJAAcEbOS2EuhG9VxmKKiCEA02wzBYC0I4aAiQKIV/CSkGLGSquAliBhYpnBE4MRgSxCiOvlBcv1FeuyIq3C3IJTyZ3YmAypmwU2KGBuIDHbBRfLEfFLJ2Mh/FQrQOpTksErc82YGh8zglkZYRYLGKuDAbAxVPc58ryu1yRChHVZqmsfoH0WQIiSp/f1n1ISTRf9e2Lpfy8Qs/cZVeMdWm/BX7muBVt/zs2PaGNoH2lz2RvU8RZUboOeM3IGYom9owI6XQ8m4LM1bR8bB1sfObfa+dau5GLFSPlGe80lldaWGQgyj0WY0NVXtazAwBwnZTZk3K0fX5dV1jNFkSMiIqcVy3rFNE+Ywqm02dbHRBExRIAYIQJplXUaYFoFQgOvl4vS0wyigPnpDInjAhACog5SULPPdb2CeZIYM8yy7pjL2Ih1UQYoAUSI84QlrUg5gRdpk/hqjM2+xgDIBCpJ+0AtP87zGYEIMU9Y1gWvry9ikRGeEGPEaZ7LHBFrnQUnPqkpvHxfr1fknMu3ny/MjOhMqBkSfDBQACYZ+9P5jJwlzgxAzvJN50YgREi/SEUCTk8nnOZniQ9xmnE6nzDNM0zQjRxUeNLGsPhe6WPKGlv/HSrf/euOaS4d4d32n+HBX5v3lJNvWW2qtSEUPqAvz3iNklHvQ7x5r6vGMbZ0kL7f/Pieqe+qzX0wgJYP3gP36v3+j8O1QdvP7+jzvVf7Ot2Yom9NR4q49V7fC7fyfii1Z9ob6R39fqCCo+X68ywvUcDJOWFNV6R8ReYrwAGEGeAIUQmXswBgZwnjR+qZZQh6DFLl2kbX5d6t7vGKT+PU0vqfJ7Uzve+v2/ukagx7RI4dbRo0dQsGPuYyb6Sw0OTvxvduW96s6GBnbKC2aKstXZ6m0jWuq+zAW3mBEtC4VrjUkeuEluDUeh7BmoEVyKtYJqRlRbpekZcrwnpFSCsiJ8wAnsKET3FCihKv8xxnTHHCJUYACeCrWDqEiE+f/4mnz5/w+7/+B56enzE9P4sGfzgDILBa/ycNUr1eX9Wl0gXrdUFaM9KSkC4LptMJT+cn/PbbJ/z+X7/j8+//wPOnf+Lp/E+c52c5W3IG+E9wykjrBcvyItYQX77i9WvC6yXjzxW4Jj2bgfEcGKcY8GkmfHo64fn33/H023/h/Nv/wHT+J3L4Jyh+QoifkVmEM8wzUo64Lhmv1wXLmiSodGKkBKRESImwZkKGKB+tTPhjSZgy4TwlxBWIyxcwgJUFy1kVm1nXVaxEWBSiKAbQFMBq8RCmqO6iIqbZYkCoq5UpikBiUoHENCleoziLYhw0TRU/I3WPSqoI5J8nCVYbyblLihLbIcRZzlQxqmBiVldRs4tNGIHpCSaIABGC4hTVMtrhLnYGhp11W2EE6zm7X3dbtEvXDLl7VLGqTaLuB43uueuODhD5tVWvoZSmyKYqWpVvt1KbPYXcdVvbI1LFJsg1JU0ue1e7Md+hi4f3bNb/nWWECVXsdyFQ216uogejeii/61mg7iW3FHeG9J5cX5Vxd0Je3j5TXhyM66OJcWu/2OOJP2BPZ1FoBLbul7c8f0CkCXM4gycCnwOW5YrX8EVc2S0rnp4/I8QJ8+mMTIwYxUOKYQHT1xmr4X4PMHzHLSL8390keNhawhZgB65VAkLt3JUrMJ9wIaolhMaBMFM0czNDSjRtd7bJZR1zi9m4d8DywoDRI+U+t8NwT6Ll8+2vPcIclXy14Qb+lGuDfAzAtbwIAMw9hx8fyWRTr43WOUHA4pwFPXP10SyGG4bVZSS0GvUlu99F+1YDIPd1tBeKBr6r+0ZbXu3lmmbnDKYAIoavje7Vm6b4fK0PS51M04RbrXHZMABwVhKpcR5UC51ATb6lzrZxsauzHpbqO6GYbhIFAfBLnapQTXxXUpk7xU0LiemoaJCJeMUzr1n7NiUV5IBK+3LO4t8+iVWH+c1ck1lGmHBsO/a2dv182dM29UKnRntidHgo67SOVz9fisAR3Qbb1aH2nQvqrO6imnZ0yZe151oKdIy+yrzVee824nKMIae1tUPcPLMyEoyC23XTu/CpHFLbR3589toyErIWVq3MVWUdhvQOpX4tXaLC+xCoMKsmtS/7wqC9zcfnoWPc8CokWlDgDAvEbB9ZU9vYLqN2D+nW4J71Y+9yzMbOJ5t/IiSJDvSXQICAWD5kziWuw7Iscl0PBPaetMeEUq2fyG1duMzLMh5c56SvpxfwtesMgAkyoAcSiMZV2fOdphcyCmhDb+cbN+ne/n1Lu9Hfv5dfvT/cHjfP3E59BjS+fKuMzR/3ytjJpJujVCblrbz7snfas33wbcmzCt24PpzVOw4tt2jk+IW25aPX790f5XmvzHelkv/g1psBvCbrkoYtUMbio6yiPiaX92XW9OWHVqhPB4Fd6uZPt9bv08DbtPTNa6w55zt+fthnLb//aCrzi0fzcrtPD2tQyPbRPcSuj89Xx/Jw9SI+sNfs1KTjbR4tu6lH1559aF7zR+8xoJbbg1WPCipKHUagF4zXGfBwD+WtreDCqg63y0aDmAGiqky1Lb+qAhjP3JRvPHbh980K2n24jQNY8tCzblQlNTs3Chh+Ej8C8xlhmvH59//C+fMnnD/9F05PT5ifPqvLoDPAYp/EKSEjiQKOi5tXzlbOxYgFY54m844xa6zQEziZa2K1zjCXp8XCQj5iYSFKVtbZRAL2B3MjFCcB2eMsWv5hQggTOAOZWIQEWd0vacyJVS0jkllGaP+W70xImUGUsa4ZOULOzwDWLM8ljaOYuPLyZIpwIYJiqNbB5ppJcTLv811iRUw1LgNVSwlz2xxiFNxAHTp4pb4+roQJIcwVE2msB3GtFEFRFB+jWTgUwYTFfpjq71KnquBmCklmAWFnOtJzXTkL7n3vpHom6leHvd4dZoe/2mfZrQN0a2v4cvO8W+eF9x8xctxe39m69unM+GzZpxHudjQ19JX2qXSlQ5Wy2biWfLC1tGjy2DlXba+3tLO1wQCs0M6ew+dwu9EfkG4p/Lyn9BF+vCfI8Ws8RrGMmOdZrbsS1mXB9XoVS7J5EXocc4MTTDFiSQEZveBjP32XGBENOKQArwccDMRi+dG8WwgPmSVEwDyfEWLE6fxUfFoZwUUg3UC07K6/33NAfG/aEyh8tBBir8wRyFVBRvlt2skS26CCQx5s3fPFXz5BfEwSAxlJ0TH7kuUvIThoh9a6OgPwqFIzZwbtM6Brr/96Te+yoappEecFYEKYWuHEmhJCEK1rO8AWl/0kdhQFoNTNNKp1Toyh9GsBqUsA6crMstPqZ87qWkm0JuS5iECxFRAZIIkaPLj0GyDMCjNCEdbJuEJjRnAW5iaQWmPAshGroilOxfqBORWrGQtYzMwa04JECKHa2kRB7gNIaQVnAqcVOa1YVwl6c71ekddVBFYwF191XOr8ctuFG3/P7G/XBzlGZju/ONX565kPLzU265lClwa0pAQ0BooG+LquzRqxuvoDUS/4KNouXoDh15Sbi0PB4wC87tdK2WjEkdHw/X7NjNaQrPFt0LMMrm6OBuu0pRcyRj7f0j43Jq6G9mbD5FgePlCygeNWTy/I2ghW0Y6jBHevsRlSSmWN22kwgwHOJa9AAQjAdTWLAPXZqrRzWa5giPuk2I2llW19xW4++Xu2ppsx8HSrp4PuGZ+maUJKEvgurSs4JczzjE+fPqm1lsTJ+Pr1K56fnzHPcxnfpp+ci7xJ9wrf/2VMGOAQnfBHaAUg5vqU6zqvVmc1L6FZNRBgVBo4z5MeNuWwRSZkRd3LHtHI+Dulv1Krb9Ez//13Th8Fhv9Kv9KvtJ/Y7Quyn7ZnH+Mtti/a+38FWuR55o/JrwJjf63UKN90Z9XR9Y9Me/vawbd38+tgyJtlsX5MLMHuOrl3+7fEijiDeYW40pVzW0orUl7VQlhcLVlsPyuLQsAUJwHBgwD3FGacnn9HZODp939iOj/hv/6P/zeePn3Gb//tv2E+nfH8+RNiDJgY4JyQXv4Er1fk64I1A8uySnBpBcHSspZzcSCxBjjNZzydP+Hp6RPOT59wOn/CdH5GXoLEtKMIRlAhwYrlehHLfLW2SGsSSwtF+0UnhwTgn2fM0xnzfEKcTuK2JIqgI0xPyOsVnBlrZlyWFS+XBV9fFrxcFrxeFg0uLS53c85InIu7Kg4krpYYwLIipIBVvSYnPUNnFUywnq2D8v4hRoR5QlB+OEyTBumOwhurECjGiDirYCLMBWgMIWA6zeU85zEfQNZ9IGzOekUYgSAKkOoRI2psB7GICCW2Q1AvJuZqqQgippP7TZ0lhLlhIpnFJozrhAT9WfOvnHq6NBKkPpLXCPP7Hul99E/SR9PnAEcDnWCiAftvFPdX2P1H6ZHxt/U/TRNyzjifz3hKT3h5vWBZr3i9XEDhCz59+ox5mrCua8EIiQin+QQGcF0XPBIo4l0xIt400ajIM7cExDZaBakqQBgKcarBdpzkd1JwNnjzVdsaaxqBNUfTcEH37e8X/o5wwV/r74+e3wMYb1dY60MASLXwuzptwcE6Hn3gInvHA9D+Pf9hFTT5RS99oz+CuTCSf8vBQPM08Nj6cGNS6vvCP5erW6WbQpeu3k3MCVZ/kqxutVISU1UNriyBr3ybu25n1WUgE1Z01hbwYF1h3xyoXsepCE20PBNsiGVDLL7Va18KQFrycWMZQ9UiJiKRVrL4aw+AMpTm9ooAkkDtIdQAfmAxCe3BTuuELKor4homVBdgOSXR0k+LMLTqoimlFTmvap0xsJBqBtoEAc4yKtg4Gzjdz4w6zn78+7nRg/x1/eqYUc2zXw/+40HaNuDydkPt17p/3tepB/V93+xt1Mwax0B32VuHrns0Z/SbgEYQYWPjvdyNwP5SPm3HptShp5FljRlD1r5na7XSmkqbAhFY3Rt5MIFsXMrA2rw3oVN9NqVUuHHr0khVOydQAOuBxfo46XwvNFTdnXHOyDugq42RuLgaj0kGi5u9lJ3Gkrre42pxwVncWKlcD0Wzy83bGGMReligbAP+veXD5XIploeeQbGPBff2h5iG5hbQp9J1eaZtv73rwaBWoALVrouIJAH45mlCVLPzYnVGZaBtaDdz7R7I/Rbmt1+3f+U04gk+Ks/R2H7UOLD9+44TwwjkAd7eD3tteOTw/Div2pbx6P1vkfbb8Phg9XNor6yRMPx4vR6ry6PpVqlH+f3vDS68p8wyJgDuZfEt27U9g23F1b672b13NP9RctzK4dTuo2P1jDs5uLzaa+Pfe7Tq/pjt1uANa66uV1/Hvv3b34Pj+BDIu1X+6Fx+q57fdq5aOYDwqNtWy53aQ8akctc3fiZBLVxq9zbMmCpzdGclZHG3TEC2DwiZCJkAJvkbptUeVPs9zohzRqAIDhGf//U/cHr+jH/81/+B8+fP+PSPfyGeTjg/PclZM63IaQGlDCAg4U8kDlhWsRZIa0LWj8UgFFc+UxEMyOeMMJ0Q4knPVkCmiKyuUVO285oE0Ua2oPUEaIxCBalQzn3mTogklgVRBHMAM2kMCMaaMq5rxnVNuK4Z68pYE6sgQbUzA0AsLp5FuZEkzyD5ygMCm5p1S7BzdvAayyrwmaO4UJ6nYhVScTENVq0uneW9GSGQCouCum12FhFFyFCVhodCCFJBBKi4bApRlSVjG+OhCiaqoAEUtEx/fqiCCpDEgtOBqLO5DA7K2NR74783a2v3ji2DMd93K8893vZRfqV/Z0vDymrfzevRe3tpdI6/lx8ZHgCHz+EGhjeg0aP8i3XEA2PQ3dW9zPVpQc7Y0c/BnjWo79H01j1iuw8eT7fKvIXl+7UeNdD9+XTG9Spuk9d1xeXyiuvlgst8llgRig8QiTLhzNMGB7iXvotFhJ9oZETd3VOkpE4EA5vsN8RsywQQp9MT4jThdD5rsOrJAS0GJ+mn64wGEDuY9kDEvefq5r1zvfvdPyPf9nnjQdbeYxbztWJW2QYWtWTxGMxEbipufOrC9n6/sy5cG8keMPVtZ2aNzKTcjzhlL9uLmXh6bfSGOCmjswGpayeVT2YGuGq274F6pd2hBf4yKvgvQN0C0hgbxRWIq8uIwWVl5oQvq+6Bctf/IFaeRjg7VisFqEDB3KcUYcJsgdjnGnQaqP74WSwpcl7L+MuGDmXSpiKISGzmrQmJMgJPABMSy/YRYlDCYgyCCDjZzSMiMVut7c9I5mPTAmEDYvUARk5XJLOISItooaSEOdpMGJsU+40NSkOqRUjQ9W4+fbE7Pn78e3951p4+Hot0I9n/m1SAZ/3uhRE+734t+zXYW1D4cS99sJOGjA+r7ExOY92h4jY9KoD2Dt0yOl4FETBnXZt+9e0ulgqdC59mXJqyZC4yb/tgI4hgCxBeLSJQNORdTJ8MOVTlLFZbFKrVXMff5SxxPhACwhRlTTOL++hYhQwRwvBfLhcwM9acQQTMc/WHmm2euPkwmgcAIce8Yagk6HlGRqpsuVpeIAQVwsr6lAfUusCYrRiaPjvPM1JKeH19LWUY82FzOaWEr1+/4tOnT5jnuVhHXK9Xaee6ljlqVhHUzTWrE7vDDSKptVHdV2I0DaitIMLG28qZ4yyaGk9POJ1OpV7GS4jwI9uL+Gumv2q9f6Vf6YH07XC8X+knTMw/krJVPrny4lyuG+i2+94PSlz+faTnKj9Rf/ft4J2/u6f4Nv85fucj+qyvH+38HsPzhim9RWBw5PkReDbK4+0C3+17XP7xI0vaA/rdnVWaNVf6BCXOmvHQ8nAG5QzmVD6ZE7L9Rxk5qCAiiPAhhSBBqS3ocFQgOkZMp2cwzZiePmM6nfFf/+f/F0+//wv/+t//Pzh/+ozp029irT9NABi8vCCtF1xyAPAFK/0bC19wXTLW64rlsmC5LkjLgrwmgKmA7NN8xjw/Y54/YZ6fEedPoPlZGk0BHGdkmrAyiZXFKmdRzgs4r2Kpa8IIku8aTVG1+YMGUg4TgBnMESkDa2IsKeOyJLxcVrxcEr5eVrwuIpDILDENOMi8JR0tCnqWnaaSNyiIAhVplDAVUgQ9h0gcCFXGjbPEfIhU8IEpiuAhTBYjwn7P8C5Np0l47qjnlKjeEgwjMMWoqvgXVCkxNPfhBBHFIqIIHCYNgD3DWz7Y+WRSIUgVRKh1dTkHGCZAdTLbVL4hJDiy5kZU46PTW4WV76Ud9zDK75LoPo0sjw76yeMZrERsT5hxtD7gQb4H6tJf/9ZC6G+d9sbE1rXhAE/nM4BPeH1dQHTF5XLBsqz48vk3xDjh9Vk8KZxmsYA7nWaEGDC9fH2of95lEXHk3vAZKv/YzfJdoBJ7hghEYt5lYKoF5RF/d50mhLrOMSDriHuGvfobvi1gGG9+N82Buy44chWJMNz7/rsHxw34PFbfo9JKA44N9Bk+pxsJ6WbjO9W/5z8FVOyBRYnGKqCYdgCrpiK5PHthhZl5IlfgiWHAZwsw93UrwK+zhhj1BVw+/re0B+AsgLaAy8LchdCHDeXuG2WDZFaw0gkdyPzJcy6xIWCamw709S6KmKFB3EUoIJ+qPWAbtcS8yGphsFR/l8Xdi9NUUG0Dv/5svopgJNR+UD+gnFNxb8PFiiEXH/nmUx6s5qNNW0ing/TFuizIaVG/nEnBQmXMCjPi57VbvdQLGNQdEEODh9smZVy6mrIqwzeaD3ubZCuEqGWP3m+f78B6t1n16wbYugnrmY89YYr1t/VOM5dRBXxb+qJloloW7Akh0NGoJun8MZdFcjhqaURPo5p8ujz7PjBrIZ9PH3/A8mb241vHrJRL7QFW5q0IBshOaP7M3tU3JXGnBGbkxEDOCHOwQtQdkK5XtVZaVVtrTSsCK1MOxtq0r64dq2tKCYGq26Nm7N04FUGL64d+rvl+JSIEbinYNE2lDsyM6/UqDMXpVO6v64p1WbAuK9Z5K3TwLphSSpsxGgkmyuElcIlT08+Pdv5bEHTVCDSfw/OE+XRSNwCxjpvNKVsb2K7bvfQjGcuxYO7t+flX9/mbY2DLrTweTf04j/bmt+TVZvKmqh0q62hfPtpf7+rfHqP7julHrJmjZX703D1S1r30lrp8dB//lQ/Q70vdHuH4vO/RJe/ff/r7R+cSD9799nPqe82z8ZKq5woe8BkfBSTdy+NWOfu0oOcFxk94tlV4I/1Gc3ISKwZIiF9TBBxWyfh+hcmZglg7mPvPaQJnBk+znDnXWc6d64w8MdKkMQCnCTydgDkh8gRMGU+//QPz0yd8/td/x/Nv/8Knf/wXTk+fEZ+eJY5AlLPnSgFEEzC9ADGBaUJGFEUei5eY5GPxJ4UfnDGdnjCfPiHOzwjzM2g6A/EksSYCI4cZOUxICFhZ4i+smauOpJ3L5bAuZXLGmhYs6xXX9YplvervBUtaIIHvCZflFZf1BV9fX/F6ueJyXXBdEpYErExIqBYjgFiIBAoQAwvCPM0IUVxABfV8IMpUCvzr2T8q7hXnCTGoJnIQhcBg1sHqBimo8tE0zarIq9/zVNxZUQgSIFotWcRSQq0SiuV3jddQMB+YImAVTCCYhYMpbIrViLwjApZ6rqmCipKny9viwtW1oB4PmqXRYn/b9VTvy3xvMbsS3LpM/8fowR7+Njzzds8/UpbRr0f5mR+1z7MxpB2+YtcNywPavhr1Z0+/qzzqPt31z3lcefTuaH9o6oF9a4z39vNHjtNH5GXn9qDreZ5ECXGeJol1kxKu1yteLy+4XsVjQspnhKxxXpgRw4Qcj5f53SwifKobqALeRI7AUP0YkYtCWOOskblPJ4QoRLnKMIzZqh8DWYEboNqBVLA5lvpxRxE9YytAuAY0ZRNEeKBtC7zt1W006feEELWuLRjlwaK+rKZMggYq2gYdtWc3lhSkEn0XzMieFTC6AvISbLn2HxEVQY1pMierq7rpiSRzJMJL6EeADbdldmBk3389UNowqiFJ8KgiiAAYEdGDaVJw5RD9NevXDHGhQhmUVoCr+ycYyGSMH4swoQgiFNy0AFAGcIYpuqBQum5gLlLEwmBZLliWaxVEGHOhGhR9ylqfbJrU0PnMqhWTLZh0KH5Cs8ayCEHcRaEECLexzmDnkS9nEV6s14vWUzRaRBCRgcKU+Hnn5ila4mjf5pvfmG+N1OEA5XZzubfe+nklHThec/066i0B+uelH1oA2SxemvLghDuo7mz8+xKPoS2jrA+odVNXT2+NA0AscTowudShErSmnXX9UbUicECztwLxz3uGggGEnUNrGwxvLNAYpbKmcnUHZu9woTO1jgQGq39ZM4Eu/a3vANB5zAg5gzgW364xTKBJ8g8UgEgAy7jlacKyXJBTwrqI26L5NAFEWK/XxqrMxtliM+SckUjuA1VY0LfVzyNPE6WP7UDqaBEBIcciTSWgWBGs64plWfD169dyLcaI8/mMnDLWZcUyXRGvEfM8i0WCfi/L0sQ0MU0ra5OVlZnF9F2vBIpC+UO7J1XLCEfrm8CLuu7VGvL8dMZ8krqQzaFO+eAH4bM/NP1VYMZ7h4835PgxFfsPSN8DnP+VfqU+kUdQf2Dq+SKYYtCBd35Meo8Q4vunHy3skj2kPeO1975P/UZ73Ifkq9+jnD3mStSw86q0U1/sl6Pwa2KFnCmCA4HjDAYBc5In1lXOxRrXIKeMxAE5MVJekfIVeX4CEjDNhAmEz//673j6/Bv+9T/+Tzz//i/89t/+d8znT6D5BFAQN0+cwWFGDhdgfgWWjBxOyDQhJbH8L26ZVnGnJLESJkynM+bzM+an3zCdf0M8/QaaPgHTGZwA5oAUzljDCddMuCZgSRlLyk0AaRkv6RMRQqy4LBdclgteL684LRdclysoXBGvFyTKWMOKl+UrXpdX/Pn1K/74+hVfXq94uay4JsaSCStIAnAH4WkjqceBOaoC0BkxREznU3GfZGd/MkuIoEKIYhHh46JS4b9rLAbjl80SQvj76TQXSwmiAMST4C36fhFEaB4oVhH+o2vLXCgpvx8VqyONZVkFCk7Q0Agith4m7Pl2Vg6SW1fy5711Rs2fm7l/hy585Do+SoOGYPwD+XxPOtyUdIDu9UprdwU3ndDp+wm66/mz1AXb+fAt6/NR7T1SZ78Op2kGkHGezzifrvj6Khje6+UFIRJeXr8gRsK6PIv792kGYkSMEx6p7rsEEX2j9htpoIh7rhFwmfZyyUgkruo/bp4l2M7pdBK/eJNJXEtJBazsEw8YzHsLxA9ONq3u0ob2uwHftbwKfKFo+Y8ED01Qzy71wP69OjdBdh2gyNnKy9r/44m3DUKkWeQWZOwZOnPlJCZ69o4+2/i9r0IYA0BlHrSa1L5Pe+FD6QN2Ap2ckZNp72dUzdkxkbvFkIplgW+nmn2GiClEdTekZZt7FwU/BQwVCwI2V0ycQNliGXjXTF3QZ7UOMHcitj6iajvYd103JhAh5LRiWa5Ylyuu14uA/BosmZkxqQbFFGeEEtjWuYhKAoanNIkFqGoXG7C3rkvxtZ/WRQNPiwVGDMIcFYY/AeBU5qONe04Lck5Sz3XBqlolQBtHo53zQLsqes0M+4ifzTqeufRNIRCEZi6ODpS9kMDmaZ170u/ybCuE6OdUU+tu7okAZz8OgH/Pf/z9nDOYpI8K8OvXrKdf2m4Dv+1e8HTL0SITtPVWJG379F2gWJzcSyUn114SxLwbE78ed5ivG+0sh4mdehAAUhqhRKSu364/mBmZUyMMkmeqBUCi6tc0TqK5Zess5YTMjIklWLNZeBX3dp1lxLIsZax62hRC2ND4XlBTyH4/pxhY0wrKVMqyexYTYp7l4LMuS7FkI4JaSBCWZWn2CLOk8PXaFRrp3phzBgVsBMtS3S2TF2MUc3a3DlUyqAcrC4AXmkPJe9Ot9fyWPHy6J1ir7729PXtY348Gh0ZpdPgY7dX9Mz97OtrXtw6afR63DmpyDj/WLx/Rfx82l74DMH2rH9/bF4/2Q/P8N57GP9N6r7x7+ecH1AHt2absj6oYVMbDNGmrjW17Tni8/sz7w30vv52d4u4Toyffmh6hZ29NR8/le3Sy31uVvTyc7u07jyRfpz26fXfc38t7dLRVLCNYXBBhHHWEAXH1CYBDFMuIiUWhZ87SqSmJZj+zAM2AuCsiOaciEAJmxHgqZ7Xnf/4Xnj//hvNvv+P86TfM5ydRKJ0FBF9zRs7AEmZQSKAQpR4U1DqDKunQj8QemDDNJ5yfnjGfnhHNEiLMKtSYkemKhIiFgWtmXFLG65pESJAYiQkZAQipLlRmMERIsSTCZb3i5fIV88sXfPn6B9ZMYDoh0oSJJrxcX/D18oIvX/7Ay8tXXC4XXNcVa8oirAGkryIQAbFWCITpNCFEFUTEgPl0gsV1ILWMMJdM8luVciexeLC4DjBBgllPkGonkwkiQhVEzOo+Jc6CscWz9mUsfHdrzaDuqYLx7Wa1IGMAp4jqhRDmtgnUCSIAGV+g/nb8vTqtcge9siDQ07p+ieytmdHlrQuzY67WrJyjdGKIS94p62h6lFYdLfMW732Lto22Iv/8LazgHl23/Pf2gZv17+aS57mP84P74zjK68OS0iMiq77DtOnOb6DBZn297xZL5nkkYp5PeHp6xnVdsaiF2Osr4XJ5xTxNWNZFwiXECQTCPE0FYzqSvotFhIHQkvykEgIlswtFk7FIYVUCbAIIIdYR0zyXfH1bG01I2+zfwYYZ0FbhsS2j0v/t9klkbv3E958egLd63xLw7BG1DROlQBvnrQDBOm0E+AswHIZ5+HwazXSnyV7aZpqyBagv3Vdcj5g/8wKKa1/tS8lde01AknLTRp1Bmz7qx2orhJA8UxEMyNwyrYPJTCWziZlaIUQZT7Ms0PYxJeRk7kXMaqONJWC/4TanQAFh1v6d22XKGmiaGRJzYbnien3F9fKC9XpFWhYASftSTKumWbQiUkrIyaxQxNWSSPESAovwAyrw4JyxLlcdZ9J3q9CEOZS1CkBcrZg1UNFsz8jpCs4Jy/WCZVlwvV6Q01pYjhB6awjovPBASxVE2EcOjPXdXARRblzdd7/++rkx2gjL3CvnaLV0yuN8bG75OdY/19OE0dwczfsSY4FUa59cHYVV3OS/J4gwRnBYF/SuyGq9qhClXY+jNhTivNOvMHrZjMtYeNP3TXl+876n1IM2eMDbf7p2sK4Po+HsaF9xRRSjuF2jKAD7NAEEXC4RKSesKYGQwVy1m/qxIKJi+WDtWtYFQHWbVGhCJ8Da9otda+NyAEBeuaHVdn2aJjAz5nlGTgnLdUGONXDf6XRCyhLMutBC1cay/Nd13V8H3bwPADj44NT1EZvfzFyFHRTBGhDP5hIhOEFEKAIez4uZ2fVHMfy/0vdJ/wnjtbfP/Iiy/w7pmx0Af6Vvku6N17cfzyoUER7Cdg/juYAqjGjTR4LV708tH3YrjQCXtwJrf+f00X3wrWl7g9H211lvGH8FRiBC5srf23u13XquCGZBS5DwgeqeN0RxhRsnAFS8VYTpijCdJWZgCAjhjHi6YooTphjx+b/+Oz59/h3Pv/8L5+ffcHp+xjSfynmTlgVrgroVmoFgvJ8JIdTCJbPGmxSAbYoB8+mM89MnzKdPmOZPCNMTaDqD4wmZZqQwY6WEKxMuifGyJLwsCZc145oYKwIyMiyWNJmHaM5IDI398Iqvr18Qvv6B5z//F5Y1I3PERBNiiPjy8oIvry/4449/488//8DL6wWv1wVLyliTqGshUFEoNGHAfJbA0uenuSjbirDgXAQQxUrB3B7FUFw0Nx8FDaWcUAQCRXihgog4T8UiIlAETc8KOE6VLy8Bub3yXyxCiHLGDUGt652lgxdClElW3UmTChSIunOmCZtUMblDwcp3XU+e638w0UZOd1NgcAQv2BRxg6Ye2QM/OvVChL10REDaCCMc6ta/Oeqno23zmGJTzjv3ql5wcCg/qtiBpVEe32Yfdfu0/SLtC779+9HUj63gwRGn0xmJGV8vLwgLqdeVhJfXF8QYsSxXzNMMzCcEMkHECEUapw8VROwNAJddUb5L8FGBc+WqMn8AFcI5n08IMWI+nVQAMXWgt2j5Z2RHHIXoVQuA0fKQNDoQ9oym160tLbAseyDbAeoj7dWRT3hf5satRQe+23c/6X3+pW1a4b4MUoDG/qHQCiN0hBpAORerg6rRvbGgGNSlKZsZ7FTcDej3mtdBwctR3tKeClYaoOeBMMkzFJC1AaS7frDUuKZxgKNtyAa8WVBeqFCNGCUAbVpXLNdLiX0QIorWiZQtwJ4HhU0A4QFOc6NUzDGdX0gDRi0eBDMAzkjrFWm9Iq+r+OdU8DTogSpG8SUZggSySqpN731ugoEA0XoJsRUq5WwWDtB6J62vajmzBNwOFJEzg8iEQto+FquLnBLWdUFaF3CSdtfgV50AQpo2JIiBRAukbAwEYWByBgWq7q1Ga34jGKgC0io8qO3vhSMMJwDLeajcd2QT8vn7Obhpr/rL7CXLZT1Zh5ED5TvBQmN15ZkHbg8hDY2ww8hgvVQae4OhoO39mne5UIQIjXsEVOGPCVhIJhoQqtCgaeNgbZeyvcDD7pUM6hfbs/qxdrKukXVdZS/SA1hKCWTB5EOUXosBgSZMswTeS7pHFMuHaQID1Q1TSgXcZzbrBEZaExKFEgx63MX7Amujj15wlJt+bi3oYow4zSeskHgQPubDNE1AIoi5E0oQayvPCyT65Om6zTkZxoyiIeXa0bdJDlURIDXz1M9WAGPaclz+pm6e3ErfCoAZzsfvXIe/Ynq0L5rnya3vb5BuHeSOjvcj8+Ij0iNlfH9BxRbwfcta+FmA1FvAQ/ck9qr71jH4GdrfJ89Ljq6P7h25/76ke2BznmhKb59m/1oFdoUP657ttBHLOWvAj35MuzaFDR4Zq+N9pDDivcDQoee2hfpMyu9upn3T/f/Iu/2esbcWuGsPc2vZu99PDGbSeGgtBsXM9fygPJiJ3uR+zaP+JbM1k1jCC1yjSjDazxQiAjRuZ5wxzwv4tCDPM3A+YblcMF0vmCcRRDz94194+vQZ8/MzpvO5aPTLUZ1BWBE4iWJPzuWMWGAWMqtXggHkgcQ18DTPOJ3PRdmuxELUZPzscl2xXBcsS8KyJEiYiQCoJUeIEqMtsLinCswIQc63zIzL5YLw9U/8z//5f+F8fsXlsmCKM+Y44evrBV8vF/z55X/i68ufeL2+YFmv5bxtsRrNFdN8fhK++3xCnAJOTyfEEMQ9ahQvIHL2nwoOgWLtoJYHwWElJnQIoXgSMWvhGCQQdoxTzZOqayaanlBdMVlZIlSQ79adEnkfr2QYkj3TfrsH5f8yhnXf92IFu9JjApWOenBzQPs2S8TOFu3VzVlwkO4JG47SjWEeLm/eAAl1jyGFkey7vN5RuR7r2qsfNZ0+4r1cuaO6dXgJw3a37nyPtt23+nHvXiPsYPO8oPibq0/XE209+zwfrEN9oNbpo4UPe/uCv98o2cPRbbrz26XjvGnt8wARQM5xQj6dcZpPuM5XrKu4aX+9iCDi9fKKGCPm+YwYSZUEj7UfeKcg4tah7M6bqAwCywbKtsGIICLGSRo1iQVEjOIXr4IV7DbVOvla4odmRI7WswohUMop9zqCYM/fEzR4H+17oLjVsQdo+uf2hBCb/LgCfZsyjNh3ZZX3jFnPW43gvXpa3YoghrlziVP7jogQcvXHDtusga2fcD8urk0Givm+jZEaIt+PT9+fbf9lZBcAy4C46vuc3UGDSl1SUkFEygrGUwnwLGVokGrtF6tz36/FDNMzDMqEZLMuyCY0EUZNhBBXpLSIMCInABWELJrDqlGBQOBMNS6HgopRm2R9b31StZ0ZJgRpxpoZEQacE3Km8qxYemiAaxXYpHVBzuLeiWL1N1nGS7vXfHbaXJFNszJL7UaozGLO0u/mKsYvBQOku493AEXKHFnf1eulanXOoBWsNXP0YDIAesQ4VOFLa864oRvMcvDgFtj39MDP/SrUqAK9vmy+A5JQYWLaerXM4w5zAcd4NnOwjnXVlK9tA7Og2LG+2wPsfr4UcFvrojN4y5hY+43383RN+zenjJVWnNUyKmWJZ2NrJ0xzDSanhwkCJKieE0rPbryFbiS3ToPGXViRUgYgQggvqBjNj70x6p9b16VhmHy8kRgiwskd5JmxrmvRzopAEVjbeFndvNC8n3OlDirQM/qfsx7wbIxGdL6s9wkUZ7V8q3k3Y63j3BwuBszhW5jFWwDakef37n9LwPftLPE2fX9g+n7a78OPbPlb6/B4PvcOIpa+xVj8aACfCGV/++h63MrP88/vSUfHrt8fbz19lOb8iHH76Dl6K79v1T7jk9pz0y1oSs8dDiBqNBv6zPd+P7h8jwNdlrnnrvar1L77GO35yDG5N1d27zbnc82HeTCCFcD5KGHEW/J5SACBijuU5zr62PdbeZ7rG3aJ3JS1c71MXa913pVv/LJZ4MYAJhUKUIS46UmINIGnFdN0AtZVYkecZtByRry8Ii1XnGLEFAOefv8Hzs+fMD89YzqdEOeIGAOigvyEFcQJIQOUVNkupzLWUAVTsGEXyjNHjV12mhE14LOB8IYxZcUJ1mXF9bpiua5YlyRnaRBAk1hxTAtCJlCGWvdDBRHioul6vYLDV/D/+r9xPr/i9XLBPM04TSe8XBZ8vVzx5cuf+Pr1C66XFyzLFcxJ+lljb07zCWGKOD0/YZomnM/qkunphBhDUXq0eG3mVqm4wA71HAzSmJ4U1UVTKL9DiKAYi2AmaKzVIpiwYNWNIELO4zFOig218R3QCBgMtyGJUaFCgubsVc7t7XyVvNw8bWdt+5yfnf5Mp3N4m6j5cpndLKtPPcD8kfSvbQWwR7ftFpXDzXH3naNzWFMBcuPXFVjOajt1o+6OnKvHYPat30eSB/vBXghhc0NdzG2wT+4zulnOUZD+I4UQ/Zy6xeftPXuv3qw0v2KR93nLps+JAIqY4wwQ4aRxmiUW7SICiBBxuYqLpvS0Co1RF01H03dyzdSnFkQMJNLeqEF1TucnxChEOqgAIoQgQgBSKwpmZIErJS9Gs4AMu2ohiv302GQSWw6AGxctI0GDBwZHMRaaXHfAfV/H0SLwQHx51wF4DUhzI/9SBgYWEQbuKjDqrRaG7XQge9HKTlIfVgCLODYa8UwOgO3dPQEC5ruyxFVQdaXEzMhIZQH494eCGten5i7F1k4J+tSBqwTRPBHmRgQQy/WKZVlgL5fg3b5tg7lBEIBvVtdLcaouXAJViwjjJuW9LGB+SkgaoDqlK8AJIQBTDGBlTIIRhBBhLtCYa17aJADmcz2WfuecFGyvLrYYdf6RjruAsQFAMPzfWEasqtkiAogVOa/ILNZLKIHRhdgV5hdopb9UGStj0kKM8hQzAgedr1JuZvHLT+V9cmBHP/d7YYfSXerXyXidunjczbja7x4Q7t/flm3zp7o9MxavpylWhvnot3cbIZeb7+WdQTv2aJ+nKfa8tGsbzN7nuUdJPQju+6y6ZHN5MoCcC7NZ6q/XmsDofk11/ez7iplFU974YN1HCm1Uk2bECJ7EqsEEe2lNyLNNcNXNyBkrM2JaAaIixAtRgtvPcxJhBJv1jJTkrQi8sG+apiLIBFAFHTrGfpw83fWgGjdru3X7ZMKCpj+ZCz3wz9u9dV2L5pXV2erln/PrxbtYEuua6kaN3Du1LXWN9cHw4PYDBm8FkYN5/TOmfm7+Sr+SpXsHke9R9n9a+lEg/i8aUNMPm3sdT3B39+gO8z9nqrDQwxKPv3jq11WdV5V/7J//nmlv3d+qhxdDMHFxu3qoPP1HADr5Uc4KOj0YkudotnBXNyZWqwjogTHq2RaIMQAxIKQZMWXE04xlfUZ6uiIvC+ZImIhw/vQ7TucnTKezBDRVPEf42iRxBFMCXxfwcgFfL+BVXPoC1QuDWMgmFaQQMoDE8mHOoJxAKYlgJDOYVqyXr1hfvuD6+ieW1y/I6xWcVgCEADkvE6lbKGLEmRC136YAnOaMOEWAJJ7a5fJalJGmEDHHiMuScFkSlusrcr6AAmOa1MURIO6QYsCs1iDn50/iU/0sQapPZ7kfiyBCXDNZfMgSFzE4V0l6XolhkjNyCVYtAoYQ7bsGn4a7PqlyYggnva4WEcFbREgvlYNxfxZWfKLFXLyyGtp3Cl9vXy1c2cvS+tTAMTw6aw6A1d21c58OfA9FjXtl7AHRw/P9Zm97W10aMHrv2Rv13wiR0O5Mj/BB32IMbgkS+v4ueOqgyn8J/nlHCLH7uJtjYsnFyCEiEuN8PuE5P2NZL1jziuv1AgLw9etXBAQ8nT+DGZhP8aExPiyIGDXiqESnewv9Y6TmH1OcEaYJs0pdZtXIhIHS5DfJKoSodWxz3ZMi9m3qv2/WngimMWxP7wkhPDA/FBagBSEPCQmG4NNWq9prEpfcuvxvMUcC8rVtqPXDpp5NH+QqHGj6RH072gSI8BNe0cFOCNHUa9ivNb5CzhkixW+Dp95K/Xhpz6j2QRiMhxMspIRVAzCntKr2gYudsdc/2hbbwGUvJ9Gstj4210wOkJN8xNIgrQuWq1lCLEBOoj0fCAhR3THFYp5ZmAgL1AsD/CvQV91hSfWyCiK4Ax/JaaynlACaUNwDuSVkFhTVbZQG5FbBgMSGIA1GWwPCl3IKcEnq/zKoYDJWV0P2sZ3C5r2izbX7zLWWH5PRmufBmLd1AhQIzrxl2gcMwEgI4degF/L174ysIXq3b/7bW9xs6g6lWdTmOxJImNDJ512fHb9jQoh7q87na3NiJPCBHi4YDnjPFvytdcl0q8+tLGad8Wz0Ud0z+LbFCDCrFUJGjrG6JNM5R/ps1rmXUgaF3Kx9xAjECZky1nVpBB4j4S1g8WhyuW+umUYWH/53Ox/aeT01VoRbF0r9+FnMCPus66oWiTUodRUcbTWgRkxssb4bzIN6cPFCPy+YqHuDCXYb/7PYruHNin6QWez5mvfk1b97K++PSn6/b67/hUDQW/zmrWe+d+rXz5HnfBoBaD1/drid/WNk+TY/u/tW1rEi3ps2fTRo2vdYIx+VHq3jRwgjfuZ+6efwiL+6V/1v1T7bFyvPpnvoHabFgF3PE72vHrfzeHsZ+w157Iy+n96zNh8uu/APuFvm+F7r0uL+8/tp7/lHwR3gwD5GdoShom080jreL1sV5qA9IEdNpT02n521CPysKaeEWk5RuFJ1rimCsrqMTap5nxkxM2KaMaUz0iIueCdiRAJOT580OLVYLdjYZjar4YScF/B6EUHEegWvC5jVwt/iHlj8Aj3rGb+bDOtgc+20QkzWV+TLiwgjri9Yry8as3DV7U/wAnPpHJhFuALhM6fAmCRkBaA8/7JcJJYkJ0wUsBJJ4GtTKsoJRBlxqhhCVJdLp6cz4jTh/CzKtrMGqT6dNDj1JGf2+XQu3hAsHgRI3BOTuW8u5/apPe9bsOhQrUMsZgQRARoLIqpFRKCTnn1qjAgqMSKUFyc7TG95yj4Y7i6+VA7jzVQv87rMww0+2MzG5k7rqqm9c+t3yadnRwb7lz/nfgj9q/DEsIzRWbbnG/awy1t5WNG36jY6v7UP3mmbS5uyejJ3Zz/Y1ul+/98bl71x7d/vz9oSfOFj9pJbdXrrs7fzuM1z3TxrkeCBIWQEFkutcz4jvkTQQhLPkhmX1xfMYcJ1uQr9mlhcaR9M38Uiwpg+aVzd9oISMQE6JpyfnhCnCfOTWkIYEBuNAHLzGQHEtcy31PH2ZNhMXEaj9d8LBvqPPePBTP99RADhr/nJZ59KcAb+JW8ArJsFmarVQQ+C1c2qlp9zxpokQKu5TCqgqXD+5SAQVCN4k1cXL8CPCTMXi4heuOO1or3rIO9e5whQKZRO7lk8gi0oLQKI6/VaPmldAe3vQBU0N9B2S9wgFgEUEAiIJvSIJxjzLGVacFptM4ubmGURS4jr5UUFBSuIGCESKM5KOKZSDwACmpNZN9SxjJH0257VfmSxvjDXStfrUsaKERFDKMIJ5gAJEt3GvSiuqEyQkTOIs1iMGDhJW8GkHyPT/jCmrNKFIC5sKAvDmW0uSj9VH/Gh0bT3ZXnwuw++Lv1iDJk4cCK0644C1cMtcxOrxJ7rgVr/u6cbo+TB5j1hZv+cr4PFXYGOaVCXYaO6WT5+OLxFhD3XHmxcHcbDuKljGghSfB0kJkQVfkmZYoEmIDgXV0r3AD57xgSkERZsrd4rOTAQIH5naZZ1BG3j9XpF0rUXJglQx5x0bq9FWFLaxCjxViRGTB03A/uXZUHOGdfrVf0rzuLzdprElHyt8Rp8m6yMfl8QoYXcKy7XYvUd66/LPLBdgsucEKuM7Na20tTU0jG/N0QnMLU5NRqXssbKoQaAE0L49ejbmctaQsMXEFUrqsxio6gL8q2xun6lnyD9zEDrz5u2a6c9sw82Wbv/nYQQv5IkVj7zV/pBSed92c8A04HSZcJF2UyZPvz8FhHfLv2VBNg+cRnZnfs/6z7DUBfQ3PCxwFGysW13OR+wWKCqnKOCofKQ/EU+H8hZSh6Qd4LwycwCBCeoC6MMdcsxA/EEzgkRDCLGdHpS10kCuDMkaDanhJxXrGsSq+PrK/j6KsKIdAUhIyioz9HcFotFRGJgTRnXdcV1ueL19Stev/yJKU6oixf48sf/H19f/sTlz/+F69c/kK8XcFrlLKq4BAEa94IwR4mdME0TpkD4dBK9omkCQAEcq2W+xDtL2ieMeSbEEDFjBoOqq6hZrA/mp5MKIj5pbA3BuoorplmECafTSeIhxqkKYYiqUCFGwRpCAJEKISyGgwaVrpYQUxXgqGVEIIk9KWdcU4BUzEIt8bkQxKC4SIdTqdRgZHHQ0wz/Ti9K8HPtXuqfOrIexvSL8J5Dwt4Z5/D7b3inFxIcFULs1qE7+9vfe8KXR/IGsB1Zwk+zh3okum7zhTHQhwgV7EAzaPcEGE1Z75wr703vKbqcuxEQSAQRT5RxOp2wrOIO/poTXl5fEcOE6+sFARGnOd3P3KUPEETUEWqAVgDcB/LyIJ4DHyz+wzzPiNMkLljM/zRV0AgmAnebZV0khMIr9pNkVOVRSxxj6lNtTz+ptpPvliBi1A+9Vmlzn42ZaiqpTETrjmOUd3m3F0LoAtswN+7aBuz3gCFoU+fiZiQl5C5ugwkiSmnu714Q4dsx6lO4ungBj4CU5jaGNwCqTyPCy3rYIFhfBfSSfjuQWJDqNa1VA0K7NVD14zgWqtRyo7Z7moQx4Ch+LXMhiNq3XK0oMiu4v65Y1ys0qjNirFYYNXhVhAX5snliLm1sHIUxqYyOANFWFqsgQoQRMuYTRPDg+17MZaFxLMDd3DetbwWTg+OAqdZkQ6wLjXBBuWLx/6mB6pX8EBlwCrVUaIMb1XGvc3ePHjUfY9rduqvzRq4b+NvP1X6e9eD/nrswnw+ANkC2fhtt9GW19CYrL06bNUNMMIHbiBlBOXjUulRBxVgIcTTJPB4E17B+cs95SxHmAEaGaHLJOBoI7Qngpk0GVls/ocXkqiCiwBFlTwJnsALzJlBY1xUnPQTIMuEiECs0pxzaAihwY80BFTR464JVg16fThqgTmNC+H4gUpbdmCO0c63+ltsmSMhFIDGV8pq+cn1c2t31P7MIQG3OeKGXvTvaxzZja/fLAWd0gEFz3eYLBTtUVbN0/0x2/UC2b3Kf11697Dm2oftmaUTjhs/5ZwbXbqU+x/cASXuv1mbc4bX6/I6UWfLpe2EPjul5pAOFfOP0EQePR/Jgpk23kP+L0cfVbR5/a3371/bmSz8HKw9ya10+Nm+9MP17p9Gh/fYLOIxG7LbnPc3cXdcHAaGd50Zj0Dx7K/t7y/hge9vz0KaGAEbWnlQ+XBgL1DPlkcLu1cv9K39tTpqD5/fu3i+p/vz26+FbCiv62j9EF+/d/0Z9c2t93OL55SEIsfZ8KtytG/O7YBVVxQTQv415ly+PG/i91ZQ4nHtby09Z20ASWyFwQEYW90YMcABCjirtiBJnARkERoxiCRHcuTpzrufZnNXN8rVYLCAnfR9qPV9jBNrZJ2XGmhKWdcVyFeW86+tJ3Avphnd5+YLLy59YXl+wXl6Rk57Z9azLet4xt0cxzAgUMZ9OmCPhfKIiiGCSAN6Fl80MyoxAEM8GIHAggGYQRdAkrpFpFgGCBeo+nUTpdpqfRIN4njUuZCxKSUGFOkRUlJrMQ0horBciAk0FcxAPIz5otfQ7W8DsziKCMLmzcT03yXgLRgAMFGaDTIiRIKJ5rpuc5XKBOWQz3KUgzXPleGWoo8zQzctc2lMm8baG2KUQ3Z5ValewQL71tj66xwy5Kh5Inrc4KoRoaMmNvu3P/72wo7z9BvK+4dY3+/udDugwiOaydX7/fbhWO696HLCCHTCPH01Od377dEQYscsjV6KOulpaFnLLK41OkG/jqSkAlGWtxxgxk2D0U5xwWRZwYqG9UVzUT1Fi1T5S1mFBBFmUUGKb2wCsswRg9MxcSQyAoi4Fm/QiZDidRDo8n58RpwlRY0LQJD7qOMiGCYg7dgskLMWTA32sLgZPuclVgChfoXbgWBea+B7vgQJ5ol3gYgIok0I3aPNZrmBs/Xur9Vxd4LREYDRwxFANduWIbTLmqrXjRQoeZAWq5nAB+g0EBdqgviGDyDQdROu/d31im5V8JHAUmBQL56LFi7QCnMBJgk0ZOGZmPqzueGTXCwVkQpCy1yTmPtbeMiYswoasrp/SulY3UPJgycu77/Dd6sGyrbBDGI1e0FLHMCPlFev1inVZAPURyUFmG9EEohkoQL1hbuqCiHVjpBkAxHRTmQwQgXPQskxrWZi1db0irytW1eQIZa6YoCQBmACagKiuzEKsLs1sNbDGeUAWLYmJxFSWCHE6QawM5H5OGeuaSwBuZBYfliFqAGUTjiTkdAF4rXOJs5ZV40pUQRKK5UthfnIC/NojGTQKESGKxVSYJ4RpKgITm4digkxKU1DG3QJ6A5Mwsca9GH1QJo5Ny8M0TixAuPOtnzMjs3NNZe/mLHFPtE9BLERbwXKzqPFBfQEgsVlGaY2yczNnhF9mnqzBlIRhT0pHlNZGWX7iCVfXZwGEAxWiRwBSMqGHWnFkLmVWoY1dR1m3Uu8ts+L7rE8joQzgYkMoLeNGIFHZSuuH3oVRSsJ9Ur8LS6uUzplVkjzYWJIwY8GKkANCFvNw4iqcEDNlVrdPGZkAjgGYJtF8ohrknVkOWAEA0orECZjUXJoADgFrWsDMCDqXkhM+MHMROGRmpJw1zgwwz1H2vaxBqtcFFCdRy2JpZ07JMfa1I8QlXgZyAhhiIp+Tkn7CaYrSD6sKKizon9aRlWiZoJSzdwmg6872Ngh9ikUooJZuEDqfyn4n69SsiqIFt1PNuFUFa4ECIslBDCEgMSNwRmQVZhIwnWY8ffqMeD6D5xlLSkjLImvMCWmyHS6VTvq5vp2wxmjXfrx7ODqUDp40vkE6ygTuns/894iB9i9+AzBnUy/y83B/LMn9+5+VbHWNEt+49wFpc+I8/qKBvt8SyPwW6UcIO3x6EMv40PSYgGz07P5Y39Nib1t8e86IItz2ednhV6S0IKVFLIlDBIUTQjiDKKLwzFTLrORQDzQH+6FuLZ5i8X5LGtp6qIibL1DfDYNUSP4AMPnRc90n7r7rjTt71M4jm1cOAEbvSYfyNnrIyoE4+njv7SqQrivJhl+5/+qa1AHDlf5S5f9hCIdlQkWAQeBiGVHLBjgwclNv5ctCAAeAyfhmqYQoRjEkDoEExUZgTDEgTxOe5meEDKxPv4NoxpIYYT4BzAgpYVpWUAbSHy94Of8v/Pv0f4HXC9Llz1K3r//z/4evX//E5Y//ifXrF+RVLOh5moSHVb4+EOtZWCzvz08zpinifJ4kkPQsfCnUfbGwm3KuntUSn63dIUibwgRQ0LNrRDQLiPMzQpwQ5xNCiDhbTIg4qWBCLSmiuVaNRWEwhFhcM8mZZdK4EFSehYu1Rhbrsvttymyg6qHCJoSBz1UxUyZB3abHZ8Jyt9vPbyncHNn5y3Nc5zOB7xA3O9kOSjHGwxcwKtSlvp5bZ2k7Gd1p5G2a02JU1npThCw8VPl25++Sf22B/K2xJ0d4o1WUMCSYXon0Fi0rSn99PUqRR2iswyKsTu5VrhOhltSB9n1+JenaZRIcwn+X8hSTYoLiK9s2+98fsXcM14meZUs/6t/2XTfFruyP3MaIECACzwDG0+kTwCRCCF7w5fUFa0r47fNvAGd8/nxGUJzzSDouiCBzFCibkWfQ2PUGFcLgtclDIXbyjGhrx+mEaZ4wqUAizFPRdiSd8CUn9i5DaIdwdMQQQiyKoMGAuO7kZFs260SukqhNAfJxdbHJWYnB/sf6Z6Qd3WuTbia0I8DmWqcCeyibRZVs+0A+uqnoPbb8SxkMdd2v/QXxie6FCE2vUlkYJggpgGFKoCxBo8AWsFqJtu3eJRurayigFEOEDXuCCBF4iHsh8y3ptfybOnap7+Mqaewn01ZYwSoESUncsbBaehSglhhArIcYnQ9FAEfCnBhTWbQcAoFiLYtLe2UTZc4SX0E/nFJpXd2MlMnQIFVFCNG4z0qwEWZwifNgLpnEyoCQOYGzaJpk/bATAAZjSpQBY3UZxSoBFY0MLmNl5TUE2/6jAn/DJlp5St1WIRAoqm9Q5x+USh+7OURcBBHN2suFUvUTQqegMlvWZ13fgVP3mjBxNSh2174g7TLXc941DoDiYkynRaVHhaYa7RPAN+laTNnXQ2kVyjKRMkMQIFqFhHUc4ObYdm0R3Cbq1nxvjst+jLQP67gqA0Lb+DUbjQ1wsfyp88BlRO3GLtONRf5pxZY6qpaXtqNZ5wpiG70Tj7O5Bk0v1gY6bzV4hIjRIOsoBgSeJHi2bw+zCsjN6ksEcFa2CXInPTSYIMILcthi6qirIzH5DogckGMQc/WcgZBRIwZ65q7bM9hok9SJcyqxXuxgg8zgvEiVqXRc0/eWdxNA3O8dOjeJK8hvhxWYhK2ea8p8tjnr9wKbC3Y4FjNyEbAFaUR5NkwTptMssTxUWMEpqaZcmYVlAnu9vj2Qy9gXcvVpK/+G1B903pEezmUgoDr2mrWZS/ONTm2exc79e4z4vTrxrUe2/N1j7/88aXgIPCo86p6rFHm7v/mnBhkdKu89aU/Lq16o198rjPiZANPvlUY9dg8UGh+djvXd+/t4y5tveffd0u/cP/o8gznpRyx6iSIIE0SY7s4oD1Lfe7XX0nfujdbofhUeWS/3nm1G4NY59E6+R4QYb13nO1Ruv46bPZjubk9Ay3ceeHqnVjvVacq59bD2k/u2UnowePsqN3ebYg29U/DdCyC64uu3HCMU67DK6RtkSnYC1GXAWVSYVbmdkfWcrMqlZOPDKOc6ObaIm+GYA6Y4I08J0/wkhhZPVxAD4XJBWFZxtMqEfF2wXC54ffmCORAiEjRHXL/+G9evX5Aur0jLUs3oQwCmiKLECDm7TbNaJZyiaP4+nVUQMatbJHVVBCesMW8AzXkUAE0AlO8OEXE6I8QJ0+kJFGMRRJTg1HFGUHflphgn/ajWDVGtNmIVPASaG0EETLETxmdXV6b1vsdj9PzrJ2SHTfnv+sjtdXzveS7c+T3apNYHjtWsZHG87rh/brSeeee63e5A5ibjMVsM+HN0PaB2TxxPWzrU7mmbc7WjE22hfgwVP8FgDCtjPyRQ5M4GI4ysPtfiAqN0j8buKo/RTjsdjrA5623YTm0H3/iGUDG2rG7sbbZnvEUYcXddcbtWqnitflvd/PDV/Pydx+pScmWbNyJgnacTcs6I8RVryFiWKzhnXJYL5mWSeD/7ji826UHXTARziVJH1qTDPoCkailD6w/RhoxqKjbNM+IUMZ3PmKe5uGQKMerGpoCLafUOAq/26VscQurma8BaB4xp1UZ/Wz8AralTL3wY1b8AVYwG+GrcHUEBMMtLMoQRKpOWS33IzcOyquS/LBoJTOZjWxqXYcIVKnkLMCUP+XpZcNzq9qNbsL47tN1EJjhRUM8AbQemmcAhp7zZTAq4WFBLrVfpP7kXXNyJHhT1ICVpvSxegz1jbUpqdZETABatgqh+GLXTIJYQAUWJXNtiTFZQTWCLcUCT1U3rYJYELHEW1quYOKX1CvORL0SYSz+GOIm0NpjF0hjgqBtPRKCMKU7gkDGbBUCcwGBcr+K3XgJhr9Luxn2LG9cOYLZxNSDUXHQB6pc0BOFDiVzgWeFei7BCuEHVTJkQ46QWBTpnOSMzIWUJIGxuq6R/pI9ss5XxS2oV5PS6bf5BQkuYYKHEoegEB3bfr9HGrVKZTu3GZEG/mnWuhwCCWHj5zaunD9mB1D5gfJu/P27YPRXisAn1urnwAOB169nR+Pt+uCWE2BxYO9ZBLKRkHnCugaAZ2372dfXWZs1atx5iKcfcIdm74pIow9wJ+jxKvxMN22sHEnGHVPcvP46WJyABpBkQgS1RibWwrmuZg37dmACiiQ3SzZWmD8gM2rXulneMmILsCTHGYoXh841qdZG7PIkIiY3Gq69gWxeZkZB0vxRtNoSg/nMdI+TWAlFr6i1WFG7+cCucCkprJ40RcTqdcD6f5aBW+hkwV3Xerd7Hcwa/0q/0K70v/VqVv9KPSRsFieY84vfVX3P0PzFVntFzILfmQwd63c59kPf9+rxXSLupgc57Zi4qoz2/6su3780ZepCUg/Y/av2JCpDIBHAI4MiC9UwR4dNnhHmWoNPXE8AZ4XTGFAKwXpGfPyNeLqDP/xR3IK+vYs07z1jjhNfrBRQIa16KQOTL6wuuyxULgBQCaD4hhoBzBCbOYqEOAOrCaJrNIuKMGCPOZwk0HVVR1pReiDxEKsBPsSAwXCIYpmWWEWdQiCKICFHiZoSIeRIXTZPGn5jM+r8IDdSKITq3S+XMI1YUxYrBB5n2QgZ1zWQ4BOwZ5c/3ANE9QcTo2aPX7d63Vh4YnUtLysfL/ihFCTvDWniKrSBhiwPeyq/97h7Yqe7IjuM/Md2jYz9r6oUeu/P7QwsFwHJmnzDhNIlV2jzNyKvFs1zw59cvyMz4/eV3LOl0OPsHBRF+4AzwhiN6vtZK4LgliCXIj4KMQQPQVpci2w2sB6FLbW5IqMq1G9KgIwPXCxWgEjLvxslnY+C4BzHteySEuCeM6Ou7Af9K9Wr9DLAuBKchegboGuBTtXuLZI1FG9UNQgHqrSt8HcxdSZHCNAKUWn/LQ3E0lFmj4GBxUVN84ifVFC4q7RXs9n1lC7F8rO+3z7Nrr+/nBgzu+7z+KC2RecoIxT6MwVl82YtmPlDWi9ZP9n8HUAeq2aogQtyqCAC9LosA7yk1ratDbpr3FktlCwS3m2cVUJEKBYpQJIQ6dgZ8p1zGtQW8/Zxn5Wkd8OstJcoctfqZEKAKR5pUuti0aUgtC9p5K8G7vWCO3ViWWV7mYB/vozAEjs6M1mi/jv28KOsKvOnzPbDYn2X8WvbCIv/siPH3/dines1bRO3TOr+hjfLp6VMZz8Fc6/MdCiF26BrZ6cTRGCo+SEPpz3YPwma8RsITv+ZtL/GHrSpkog6Y0IOaCSXctVIHorIYJEZN3tSjGWP7SME1H1enhtHYG2ds52Spz2BP4czIGscCus+SKzOl5IJObw8kRLQ5h5f2odJ8e8jPEbswrq4Jbur89zSj7FNGN8NWaEhBXMqV/cf3BUqVdhm2vQPYRzCq35Pl/4iDkuTzeJl7dPJHpPeM2Y+s/716H+3re234GcZolD5qDn2Pw+UP7cOd5t3a45v0hrof7dO74Al4t/6Hy9q5vzcme0Bq5ebh+Ivj6a1A2ncBDg6mw3Pmwff3nrnFa/6IdB9D8Oee8Vl9fP3Is+M6jej8EcCJHL/DVLXImzyxc/1GP2x4+K7+5Xdfj20FBTvwfJkcYKvLo3mW9TifAQBheRJeL2cgnXCKEZjPSGFCuFyA6VSEAxwnJGYsaQWtVPjBJa1YOSMTAVHcJMVAmILEsAhgMBFCOIECIc5RAk6fTmIJcfKCCBK3SAD8kdJbgcj/qo1YcC09Z8ezumg6qYulWQQT07kKIChgmqt3A3M1XXhlO7+TCSJi8WjQYB5eEAGtsDubwgkhRuP2iCDiVrpFl2/R0FtzEFrte2toLx934VbVm/yO4I3jpHuerWPoWilHvw6beqCM7fm61lf/GL5368wzut+05WDdvkU6WuaWru2/dyzP4+0eYkWD67feaW+iORv37/U437119Vj55IzoSPDOoHGd84QpRqwxikIjZ1yWK0KMuCwLEMJOntt0WBBxubxYvRxQU0FQAw16wFg0v0XgMM8zpmnC+XzGNE8SIyJGxCkK6ESoGTAUOPIumfbTo4zT0QXuf1cGtgIePXPbv2ubh58sewGq+7JKvAZnCeG/fRmy6ZIGirKZY3k1y0i/cgGPBKRLmof5oa91BULRuDdAyiwJkrpHSrlqvxdmB2iXv22cRIiOUFhMhFWB73W9lCCunDOS+ikPqgUQo1jWMEHUYHMqbWTTraZ2/Ezr2L6t5wv4J90FcWEUUGKi2HNaf9nXI+Zw1vlZBTDiLgpyTS2HDOAEqAB9UbUezA3MdZU+zMsrckq4XF6RUsL1cgEAxFj7DRqPQ8w5TzCAtTC4Ctr1xMmA/1A0JMSP5KRaICha2GrlsqxIaYX4wi98Yp2fMFNUz6BLe3JOGnhM5gXrvAkUTIxR1hFxD+zWZycVVk5qhmrzLqVc4pGYSWzdeNkMUMCM0ibAtNrrmiFA43vUuC1+bfaMQQ9QsrPcsXll/W7rPvQBz10+0h+tiyJLZd0WQxizPBONlhjixkqjyV+toOoctHlT27cH2h9NPQO1KwBonmcnIKr3MjJyrv1m65xZrLUokEbJq2U283tATzeMHVHR/mrKLhYBXATXNm4NraYq3PFWBDZXbA709bHrU4ga/0PGZgriq3O1WBEaWLrQ8xvJlzsaC5mbtS5hiqAMLMtSY6AEKrEhlmUBZ5Z2s8avUGGk9YOB/uYOr8S6CNUqwfqBiEEWM0P73g6gfn3YOIOr2wSb+7ZYbd5oy5s8bC8o+1buxvyHpZ+hDr/Sr/Qr/Uq/kk/1zGN7hQJ42OeLfqWPSSM+8WdJPwff8HGJ2Ys9ttetvaaSY7xxznmoxNR8l/O2PkMYsjzk7mf9mOwBRGAD0NUCAGDQdMIJhJBW8OkZa1oRX1+RcsJ5vSKtCz5drliur7i8fC1lTcyYIFbEOZC6PWXw0xk0i2XDnBPmJKDZqoqP2WJn0gxxeyQKcPM0I0ThkUOQmI6B5OxFVAUREseUQOyUoso529xSqZLPJEGs4zQDZDEgIubpGYEipliDVhdBBEg9CGjsy0KfKi4g91GuFUzO+h/Qd33d/Ai5MbsjkPgYgPN42sPsPOzxpnzeYRExwgU272wzkTPboOxHhBB7z+0Ni8cdgQpqj+r/VuH6j0gP19POl7Tfhz8ivXeN3BRwAMj89vwtxjAr/hZDQABwnmZEIlzOTwAzLq8XrGnFH1/+wHW94vev/8QpLYfLOSyIKK4sQsusidcIIXoGJhQhhRL4QAFhiuJqZZ4R50lBxqhAAjmC0myB5ecjkvs2GSA3FhTcSqO86yY8Atm6kjsCvnetL7MwyYPrI3CvbCgKQhtFYqdBLr99hqiMuP9W4DZzBbpsO/M1Zq6WENmBUj57dAtgw+iXtlQBiwWitm+LBcE++FIB2oP6OKdSqCyc2nd+3EqeflPh6hKGS3/W9rrtRsdNWxKcjzazBoFoWORs+4yyatzmYoByHSNWYE/iQKTlijUlrOsCIiDG2VXEgYshogZHx81kbSH3GyaaKExN6bT6UYGWWRSwm1slb2qmnbw6AJthALkTNjK187zvo+18MTdFqQQNNkFEZQJrsr4lCiBIMDLrP2Ufi/DjkQ2hXY/eLZk1tbVwaAQtVRoi3dsX6zl8fanIWcgY0nFdq0DG8mnH4VY7e/rYun7q6EhHg0b0b8hclX/aPP3ByNdVKoLCfLOnb+57WM+dRTFqPyvtFHrX5tn0GVUBlZ+XQpMkoPaeQEvmaih0owirQihCiJL3po9kQHfrbt/s1la/Tyh9z5CNn0hc0Xk6zt08bt5XKy7xra11BYrItm4/RgsrnSkHpMFYBHUXZSfi8bA5SxIdB/v48eGGjo37aS/9VRhwS/fp1aPtMR7rLe9+fDo6Hj8jsLXHr+4d8o+kDV2suXjFxofTkUP1/ju3n3/LmvqrrcMfkTwv93h/8Q6NdU988BiU/AaH4qN0+S61O5CPCbm3vInbN4Yvjy8fBef29rQjY7HD6ZX3HiF/j+6BD8+s/v1vsJb7Pr9Hs/Z403vP3Lr+1uduPXuvXUff4xLF1PNk7nlU+mF7PaHGzmTs94+tH6DmWd8b1E8Pc/UJ49NK5cEkbnsBAFFiIoTTGTFNmEGgNSFjQswJIS0SS226Ip6eEKZTWcsxrQh51b2QwSkDlEEQi4aJJ+Fj8yrPq0smDgTRENK4DAHiQlxdAk+TKBDFqEqUGsPMezgitvOeFwgAEh+VAIiLJooWhFoEEaSCiCmeECiWGBFhUpdOZN/G61YXzF6goDIGxxcb6Oz3itZ6/C7NK89tMaxb8/2R9ejn3Ija9HPrrdSkPxNyP4nvpFGb7Qx4c+27tbd59kGa4+nCPv2quJJDGjbjuCeMuN+mFhV7TzpK30bprWc5b5H56N507/m99hzhqUf4hR+TSi+hC3oLGhGorHXuf79xyBhcLdionOQRg7hwnryiMIBlXYBAeF2vRcn3SDosiPhf//43QCha3dM0F1BM3BSpzrUG0pnnE6C+5+PphNPzGfN8wjxPYhkRJ4QYqvZ+k3pE4r6Jx0cxDLc3YA/Y37aEAOpE6v3N703YJvYDoMGc0Ghb13xQJobMDgmUJAF0SbVh2Vxm6+a0LZ9UCMCq/W7aEOyl+wRMQfNTxMgCGSf3XgVjCbIB52YFeGAu5wykFZSpLLRVA7Mu19eiaS4dRLLRTtU3eek3sk6wlMFIyBlIhe0BlmVF6lwNibauHzuGzbUQtL4hwjCyBqBhETqA9V7OqAIMBkxAANZxJCQFK2OeYcGVmVmED+uC5fUF63LFlz/+lHdJtDGmWIUAZbsh0QbOLBrKBXjcA5l1TC2O7aquTAJfhTE6OW3uQAhRmBnOsTJbvt+7g1y9T+BgFipcCwcK47RhZPs5oq6rAmmMjyDl5SwC0eWyyPe6wAIMi5sWidchdIiVAbfYCgwT3viyTLDaz9HSb5sDa72W1oS0riVGSiM0KQ3vNnwTfICAEMHEGltgh9agjTngLTdKG9y3H/CeZjT12Gmndw/kv/foomdaRt8e0Lf2Z6M57jkhV6kRfrRCxzGAkTV+hKehzQbu6S7sXETtM1BakfPmvu+veqDaJqmL3LWxkbgTtY/WZRUgX9eutXWaJqEN6GeLrKGkVkmEsOkL325mLpZqe3uSXVvXFUSE+TSVeoMZl8sFMUY1EadCT5h53Hc5g3NUt1U1f+YMTgmZCLNqkFXrSQCweSOHLTkQepCo9Dwkro2apsdQ41ikhEQRHFy9VChbLKGa2FX/KenNxzX9/k/rr1/p7WlEtX6lX+nj08fNtMoXiavCur8bDzt44wPKHdSe/fcIyL3X4l9r7166Cxb+5GmP/929z/39A2WgzqQjfdWf3Xbf0YztbtIjaokmSQAHQo4EpoCYBZg/U0TOjHn+hJQzTqcFKSesaREPDEks9tdlgXhzyEC+gtKi2Ewu57JkCmuQdWyWEGvOyGAJPg0C0VxxfOVXiUqYB0Syb7XccBhMUTuzsx0Z1Ktn4mLJIJ4IKErMCIn9EDHHM4iiBqG2oNRmUYEC+JCvoObPclT3qoHtGPjzAoBqpeHPqd92fezNk3yz3Jsirl3Sd0jRTgCR4f29d28pgW2uW/0M++hoEB3q7p287woL0Czon1FR50cmGfo7dOs7pkfHZ8/6zGnplS8CHJz+9nMhk5zJjc5FtdZ6Oj0hUMCXr1/BYFzSivV6wZ9f/8RlvR4u4bAg4rpcQUQF+EHx220DquBh0IDGZL8lBkScJsTJ4kFEdU2jgIZkAGDLd/VDNAKZbhIQbDVg9gQG5Z0d4LHc4zqZ98q+p/m2ByhtiOVu3lz6qm4nqvUK76/fac7IywIil4L1zcbfPmAhrASA0o3KIcjS/rwBvkpJTvDRpwKQqtAjw4A8C3qdNN8mx3EfMDYbrYBRIhwz/t4EJVbfoDERahxvB1jaR/2Rt4QLpe+Z+3J17ylAfa4SWBLLiayuT4rgo4DFWQUSqwanBsI8aVkODOz6VMDB0NS/T0TURLCvgGVGAktQ2TTpdi+AYwgqXFSA0YOMuqpgB7pimlomZAfIU7Mno/nlx9iYrdqwts4MjV+RkNOKvK5F4WQrYPOZc5OPAcW3U1tjP789Pektgdq21PfKb8uZWo37sRDCrVnUNo5cuzX9j5aFe8sGtDePrAO4q7ct1tLjfTuUMe9rUugptXS6MNwbBpDKPuTzqOWMNQxpT4jgx0kW72bsyvv9HCvgN2lVqzs22yerBgokZkquwa/Z9WMZ06ZffR+2v43G9H1dPoNxt7IKjSJo/BU1Z08S3L0If3iPSSK0c9Zok/a9rfecAbVaI24PT2227e/2kGuHL+0nCi3vwCIACkWg2K9bYDvr2rQnZAN+HBO/x2sOnx3M1/cld4r5YXX4Mem99b/H9+2V98g82xxEHz3IfOQYPZhVW7btce9bY7tgwJ12/tgD+n1N+L3UczkPl3xjeX/0+t3uQfvnmiN1eJwybfMu+4tesz13L9+39MnmndFcs4FgX5P+me2f27PkG+pz53qf+V7Zh/P5gLTLUx8q+1EauXf9WDtHT214X/d34ckAwPNo2IKYfdq7v+X+ygvtdVYcpz/PDv/y1g1o/hJWqyuVSM7FOs1ZeWyrQyblbMkA9YAARuACIYByRsoBISdQiMicEFNCzgnTtII5AZyANAN5AeckPKEKIqLGKzSBSGT5HcyTgPKOgSYAqvgG5Y0BhCC8rTjuIJgnJzkrU+F37azWfGuMVC4CBHXRZBYRFEAwF032TYXHrevNnRWJ0AaowGB6dxe6M9SIHt3ie4fza4d3uUdrhnvCjVTuDpbwHj0aYWs7ud6sm8/vMI2jzR9t31rpg+y29XikL+up4Sgf+uj14bnyg2j/I/R8l+bdq9tDVSX3df9E1s+5vfYc5TvLGLuq7LMKFWcwawj/fIvf7Ze1qRuhoH2FiOufRIQpRuSsHo7SBE4LOGdc12Vk/LqbDgsiXl5eQCFgnicJrpOMCIuEF0SIccY5zqBpxnR+wmmecT6fMT/NmE8SH8JcMpk/QO2Gru1qKKib2K10n5FqF08Pjt3Kd+8DBwI19d4BFvtF09fZW0L4+rHzh85ggNjtH1Q3asvT/GSzuAbKzqrBAoJWJNQBqTlV7YG06vMyrgxhFlKQTTusScslfT5Zo7RWWgwBRAEcvP9++U4p1ffqMFWhRh4d0noLFP04M1QAooWbMhAicojlMbGGqO8XDeeyz0tnFpdhGiwqUFTXJUnrkGvZqnXB5vJJP5lXHcuEzBkmtAsgBAbStMr7ATDXQjlnXK8XLNcLlkWsFM7xhHmKmKbgwD6q/aW/p2nabExb0FrLUhB/XdTqRJ8Naa7mnaha3Rxjaa8xX14I4T9WXowRgai15AFgVjtQze4RgRYBUChgMxFprBDRgF6uK67XK9ZlwbosGjug9EgBJCuQfyPGjILI1mpWa5FiTVsc5Ok9PURLPzrhlk7AXkDg+O1aJPZJ2qhP7IVGQObKKL+tC1xeXkgyetfTphFN7OnjRuiiDezbZAJGW89k1hsaE4Ht9AGlIxavpsRLd6Cybn6b45Crt6+nBIyufbBpC9exYmsThOaINR827xBR1cJXAYN3vxQCqSs2WWeentu7mUi0tzKwXq/InTC+HD5syImVhpvgQtpexoqouBnz47FHP3POCESYtYHrupZTIIWA8zxjpYRLSkhrAq8Js+7f1o+JM9K6ljEIbp1mzogREH+3clBa0wogQXZ6BnGEXxu6mJr2y3hC1jUqw2MWEdM043R6UnPQ4GLAQOtibbe+Yff33yf9WBD1V/rRqad7f730MYfX/8T096Ro3zN1Zwly/AbqngO0PMRblTreX9v3jfd76/xrpb4t8c7fd38zFxD8UDndXjAa7937pNy7V7N1BfdtKIiNe+3W9LJ7mQGQ8KZQ/KDcZ4jFQKjx/SQ+puQfOeAUJI7alBiMLJ8sVrclXmFeAHW7xMzFA0IyrENbkdQSImVdW8prRgpFgY0AEPXfhrc4rMPOwkSobkGr9bV1GBNUkUldNGnQ6UASIyMEcUlFGgczUCjYhJVGOl6mmNOM7SFeoNK4bpSGAG5RSLojtLiV9oDh8n2g2ntz15/PHnm/KKU9QBdvCWma53y5N54ZjsJBIcR+OrZTvFfx43slP//2aNrhvU0As+M9atjzG7uqwaAeqecHpBbfQUMb7Lz+eJ7tciEWGn2aTggh4vOn3xDiJBYROeHL16/iwu5gOiyIgCOKpKCoDZYnkCGaBYSAuXFWS4jOb7btf9vFVj1bjXRYR4D+TUlu99wRKdq9NHp6SOweKKsF2d1zbvGMQM1SIfe+gGuhmThlQ+F2danurAI4FoAYEM/fpuHqGPecy448rG+pGYngRP+2vdITWc4tYTABg23mNj3skOBrPehBQBkSzkldvdSPAVRboLcDvELQwE9VS1cYCge4G/OhFhZiyZHAOYHzKr85l6CuolocQDkXpok5ALlqLm+AY5i2chHLtXPbgbA9uOyvN+PMdYxZ64ws6zhGArH4v2SgtL/mwSUfP1b9vIW9YwBtplbhppmTzRBsGCrrEyJxNZZUC6Zazsi9wBqYLJD0a5f8shnRB1sTTVNLPWkzz20etfx875bpVmL3b1fXAd3YCB10/TXCBUdL+7r1794TjPoya36jdY4tM+fp1h26avPaX2F/1+ppwog3Mr8AHO1DNyEgByGusWHK8/7vrv+aMeG6VkZ7jQQt1yOMBpFmqvOXvOu+vi1dm0bCv0Y4CV2j7r6+CDBXoZFnVho6YuuuXddkjNmwf21NyKFNtgxu6l7zquuMuWPcjc7TPsha26sfrrSt1m1/j+3zunX/Z01HD2Aj4eLRtNcXjxz6juT3d0tv7bd3lmqlvD+nO3PmPTT4o9MtXvro++8dl7e2U2jwu4o+3P4jbfzo8doDoG4hT9+6DvW63tM9Ss7qNN58BzzhLi90o0x/jntLaqryhvGt1XhfH997/9b9vp7vqfd729ELmsbn9ZFC3O161TfHf49+72Tc8Gi30qjuPSYyzMN44grG7NaybU97Fuz/7rg6+W3rntCcGRqMAjYuUicGRMmMxYVyZiAQA/JLz3yhnKkpE5BFYMFgkCofBtZ4lsIsglRhMxr/qXxvdItdaILFOWOYThRB3remGGHIpCpvpIgHd6TDfphFRLGAjsrThu675k6utEKnuvPJTXB8h04JIF+Z8NGcuQWi3ru/V36hn20Dm7Qn/NijIffa37dnNOOPpr4eb8rHz/vBWdzjZJa+p+LJj+TXWyD9/jy0Z2/9difpzZl6VHadl44m7NDjW2fV7536vlOi+lBf7ucNNx1l7wghIILFyCBPGnNSFBbzA+0/LIh4/vQJZJJbMl/rQQhrjJimGfN8wvPzM85PT/j0+TPmecbpfBK/zlPVIjVpf98VRNQQ3Vsr/BYzeOv5e88c+fTcyVGJcQ/a2nt9bIjmnX7w9YeA4xLvwLRmTQNd8lH3WSEUjeQmX9UqMDc3KS+qYSCCBg6yEhksgHkScD9RKnVnZiBlVSrv+0Cl//BgmW7aakVg9TVwyjThQ5wlB679a4BdCJUwaKcCZtWRV807ITuzR4BUu9ht2ppfjCJ4iOqTMcapCACsv5lZ+oUzwEnMPNV6ZLleJLi2+qzMazLRjgPFRPsBEI3rtK4VtNO82QkhTidZM9PppHEg6pSz+ZNyxrquOJ1OmOe51LcGcLbOM0GT+tRMV6zpiiVdq3sjIkSIpvf5fIZyawoLV43jsiz92ivuaOrcDCTBx6JaU6xMyN7st7wvv0OgZlzAXOZHmddqEbEuK9KySN3ziqDjy5mApLFRiICcC8AK2rozKmvvAbDO1lZdY/JuDBEItBG27qVsdKCzMChWKMyuDAI4b+pNjjH1IHsTKwDVdLhq7wddu+K+bHQg68F2q4tZMlk+G4asqfd+6jfLHvTvf7d0c5/2cuFsx+XVkwRJICU264EtXfZ19NcttkMjVA+0cWPk3zPLh0gBmcwKAyVOg/UlK1gRmvZbH6Dp23CP+ddvE3YYzVrXVeleLPW0FAJhniexOlqu5f48zzVmROmrXOYrQnUlkHNGWlPtF9T2hpw19o4zO9H8pE/FFV0IUBpa8/TrrlghkfEM2/VW+Mkfx0//wESoXph/pb992jnMf79kIO5/5GL7lf5iqVghK58EVNagec4J9Hsxwn+KYPVnSB8thDhe7ncpZly2VuAettCDSntCiVvAbgWlNY/Nk/5Ki7tsyhoKNOS8QXBuoqluWsqaAgASCeaR2NACFQtwAIFBWS3cs9rZlrWZQfkkCjAMPfOK0k9SHj9xVfxzVSv1oGzYRtvycmww/IU07qPzd5yJGuCtt8SvEE7QMxkp/yoWEfKz8rHmO6CZhOWdItUAUM92w/FogEduRshBBJvUz43Rff/c0XRk7b5F2HDrfUs+lqDgDK3HgA+hK+Wo+ThDdksI8Ujh5ObJcOwMF3hDep84/WPTe8bre+/fHza/Hi+4YOojvKZP2/WstBVGKpVAQ3DiQOLd6Pn8BAoBX89fEK7A5fVVvcEcS4cFEQZ2Vj96EUQBCBLzYZ7PInhQYHSao8aECIgqfAhuYRQ4metyMwGOYgy6AVln1E47IoRoJFvde/73owTDpKm+nFvEelcafIS50s2pLP6uLeSAPx8DIakrjwJQdvUowhQ2Dfn+GUbb56oZYoz7BhyECd62TWhAzQpieXBJqkmIBNTYI+LGqGzSDVF1BwRnkWBWCTkliDZD1o0+FLagB1pNuEEeQHYT0cfb8OAx54S8CpCf0irAeEpIyUCyzo2NIHUOyKvAKneLwKyKSJ1RVmuGth7GSdT2CHOWcw+iCohf+2ktFhFZma+QJTi2VbWbbgdSgQ5HUPBuhmWeNjnJP6x1CiQuV8wighsGoimhHB51whbiuS8cGKM4IwFk/5GsnWCrB/H3OlCX1t7tlvHi3fpvgG/n2s0z3L1gQZ63itT3h1UdtHtvU23owUGGsz9EbYQglq/Ls+4dbf2N3PV9U/P3bx+b34US9uM9KGMzj5t9wQ4b5aas4RCKcMH2lrZe1TLE931fp/o0CvPhn/H0Hhkb4bTPy3zgZhVcBCe4GAlbQoib61rzsld4utcmL3SRg2rdtnJzzwL3lXy4rg33oOMZ3p/ewzzqjqfVepzxf/SdyvOMeYuj+fGYJL4pr03dunz+U1Lf3tu04i+U+v33G4zr0TzfUvb3AzW7crq96LHMDpaxW/bbQZKaxTiPQ+ead6a9PO/VqfIwxh56AQN1330m76zjHQDgTmZNFT6Sln7U+HzkOO/xlu8vb6x443/f4k8eK2k7XntlWur528I7DdKID38L2NXn46dWn9Vu3tx+b54anhm2nC779/u1TACYJH4DQ0MkCChWPGiQCCoK30skseeoP7exO/ZVSLYYbXT8tPHtXhABVmFEeVCZZuP3wC3/VyaDBcbW3NVltgF9BCpxK40XbvuhP3vU356HOLwXAIMBa/N7dA7ulbWHcY3evXe2upd8P7Tz+/ZavNV/e3XQqdk8c7e+D67T3bKb6wfLbqqxT2t31/sHs6lv2c/26vix/EdlbslW/w0+/ShPtJdu8jVGshw4V7mCzpsHKlXjLp8j87xpo9HLPk89pNtzMUZMOWKKE1JMuFwvD83xw4KIf/7znyqxFc1u0CQg7jQhxgmn+YxpnnA66/dpLi6aAhEiavCfCsbYl5Bsk4r3PLp/pwcC35sacOfAR95xbKsCIUf8bvWL5+jhs04aF0OC1T8is2qMJwHEVXM5xBNCACK1sk/WypsVRU5V89zAvAroVUbdAKxMuYKDVhciUDQQiTYguWsJgCo4WVfx5xiDugShqEY2AURRrW4EGLN+Z+YazFrbvK5XpKy+zfMKTgnm6J9okrziVAKnhxAwz7MAbLMA/mFSYG6VclJZwqqVr+B9WhXET1es1yuul1cVQKxgJrW6EGbFAEMB6lqQ1oQxzNIPOSVArTHifJK1pZYhSS0mUkpY1xXLsjRMKwHiQ935WM/Z5oLUd7lckNKC5fqCdbliXbTeZhFxfgYpX0QgZASQaeLrXHATcjh3yxro1gcUFM8a3NySaHJUSwArxfrHcsmooGi2+CIsPj1jCAgTqdDGymGknGofUXsAacFcKdWeadc5N1ZGW9qjfv0Vud0wIdp3vuwyfxmlL25tQNZ/tzY5ZlZBWBXQcKcRTVQtNnyZt4BFb6nlBYf92O/RyVHfj2h3z4D27yTI3MmcESA0raehtW/lutcSGvWr7xOzGtirY2mz+90z/neTMTOkLA1p/1peLt8YYz3EBpL51bfXzNJ9XYAiYGDVBivu3nRNLcsVIUScpqnpC7N0iTGCZ8astO7yelGhZcZ8OmGaJ6VZNc7PSV0vajFIGvB6niZQIPAq8XVsPolMo5qlS/+ijJvV35OcaZpxPj8BkJgx07pKrKrp5JmDZq8sHf9DEqsY+1f6lX6lX+ljU8HRfqXDqe7tys8wF/ewcu5xACGMN2oVOz7q3Pkr3U8PgakfXvY3L2K/bNxe2yMQ7mF+dJCf5nS4zPYBA+E9/I7K3w7ODP5v+yTWOli8QuVrcxEAyDVk4SCDSgkIBHAGSOI/MDOICQgsSnZcFTeL2ySHjTCAzBFNT5AIOYL77SrdqNxFMverXhBhfC1v5hOXvPQsUs4XDq+hdh4StefM5jpaoLEpa4A79anXkO8B/L00moN794+mw2D+G/Jt5uFBYHZYF5135Wf33AZc7/PTELn9WXK7FvmB/nh/v91d5z9B2qvjzTo/2hzDvTbDvh+v4tslQfkaHPfm2ZIHf25xnltrvKyTvX4jxb20HqdpRiDC56dnTBSwXF6xpm8giJjnGQp5giiAggStjiaIOJ0QpwnTPGOaDPA14KVKcopMpUQ7kt9VuoMWwCPZdDzR39uIb6V7EqDdZMISbn/3eW41Kx5jZkbSKl8J5lo0GwPNahHAFqugfkiiiey2qQB3LsC1gdgjZoRLP1SNgwpKyn3fhjFYx+WLa4bl3Vq9quFP1jeAMBowk8usWv7iosc0/lndPkmFRUBCBIQoUz1QEPdLISCoWyYKVBZ2a4VjfV8DSpdy1RIipVXLTMqymH6G62yYgKdnIjrwViUB/XM2Nu34bje6JufyfCqCknVdxb1OibGQkDlBwmij9jmxxF1Qf5XclCLJj60sV5mgOeeizeHXgm+HB5t70NnmuswpE0Z4wY2BwtUtjgk0RoIEn/9mjdbWoE/eFcwIaC/ANPVGuJajbB6j3UJbqdNsa0Vwi9Es7XLjLPVtXSL5Fu5Rxr0Nde+QsJduCSH2yju0mdsW0a2RWwzIHpMi7QJszd2it/38aObNA4za9uAynnMjmtm87wQV9pz/7QpU5oERKCBTdvnpBkJC60Y0xMosAhp9t9AdzojuuVKXMu5GC7RdZX8f9Y3lcYOd0jxDCIhTxDzPiDE2ghsbk9JnzfttV39bZvGD087Y+LR7aNrJcp+/2H/2Xh1+pbelEX26l249Y3vJW9PPOK5HD8M/46H5Z6zTKD0CNP0dkp119AeAAt/oxeO08ZHzZ2FqPyA9Qsf7d/Z+f3Qa9c1R0G8vnyPXj6YjdbhVRJ0t4zHgAeNTy5Qn2vPyqPzjbbzH0x7Js76/xR/23/Vnez2rDd6mO2UX6KfJ1/hw4fEablGPVsQeLCMB+MtS2/aFQUqkvHBT2ub4QWV8DRcprSUuchF7wDwSQIUQvVVEywxT23U79KcZRrL6aD3ewtf6w7irSz9qR4QQR5/f43XqWB7D7r5F2qMDe2ej+gM3efSbgghGM37l8mbt1rV4TBjh5zmNj142/DeQ+ZvndNpiD98r9djOrTo8WrdNv5aut36/dZbdGfM38lb3sJEWU+2rLRXfm889Lrs31g1u0OW9fUb+DkSYYkSKUWLN5m8QrPrp/Ekqo5rXUzwhxIjT+YwQJ8ynM0IQjUoDd0k13S2QKiE7oNc13CsvbsBrgvd33IAxrhNuDY5P9wjsFnBUml0wqLpBeiKx1cAcT6Z+IuzVvwVoE6wi1Wd+BqdVgyKLNnRaq0UEhRnR5dNPZA9q5yTBlQ0sA8Qt0pZYGijPGreggsJB3WaAxB85AyBmiRdgbTMGoGSXIQGmJahxCKEIAxjUajWzarqnhGW5IueEtFwl9sF6bfoFKYGZACaEiUGRMc1nxBhxOp0xTTPieVJtY3GllCFa9pSDGzq5k1OWuARaZkor1ssr1vWK5fKikyODwiwCOtuklHiZJnqMYroUg0SuSMx1LJjFPZQB7JB+NNYnZcZ1WYpVRIyxuEvLOSMggKkC0ubPf7lekdKCy+UFaV1wXV6R1gUpXSXuR17FUiSIgGaehSRk5ZNSCM7lTzuXS7wBJVHFqgbCKpmww4RkcOvVrFLq2jFQUXqdWX3F6zsp1VgRlkfUGB8W36Of3zbvemFHIa86wYNvi19jOt98vv67Tw2gHCoTW8q1T9FSRynD0zPTCveWIrcOFpZHdnWl8L6Dqs/bC2PuvdOnflzu9WF5Vr9Nu6l8JNNNHar1Rs3Xx17Ye97qZxr9WV3P5cHcsfc83Q4h6HxtGUn/qfWv66NnZPf6pdK/rmw/1q6saIJMdvFCnCuzQELfLpcLiKjEfjDXS9YXp9MJYMa6yJ5yuVwQYsQ0c2l3WSOrfE/TDAu2B5DMRyIJAkgW5wKFvm37xzHibDSAMM8zPn36hH/84x+Yzk+I0yxcge11XIVw0zTpoffnA1Z/pV/pV/qVfqUfk/we2/M0Jhi373vg2N9NQLOXfqZWfqs+H/G2cmPnhUOshccJ+pdagLEHfNonjqejGIjl3zePhDlDGOTz1r5vkZLBDTZBg5wZo2lP2rlGY/GZdX4gO106sYTACMgRYI3XJudEGQOJK0kFh1Itlk1d2B/9IfhBVQYatMJ4TO034WulZwnquom076haUJRzjC9r3EvN9SqEGD23Pz4FX3K5ue7HaLb1c+kIqPqwwOAHs+g9FjgSSvRt8spho/rvgdImopJ0R9scbX+O8hz3d19X+2eT++ZZn+/Pno5iCH/X9KiQcC8PS/fyGs0UL1RnxXkRIp5PJ0QwXqcZ6wP1OSyIYPVtJ77rA6bZXC9NiDEiRvG1r3E5tfatFEnpcpVze2ATQDVOQ7NRsG0gpeG+Zp681r/rM9Xvdv1uhQXsM2a3UfHeIFF5b0vU202+ASOxbwqzT8S7DmQW7Xt1TeRd/ChLraCqBqkeCCEKGNpEQdZ/XF83RMz2fBNYsJorgwEOEse5A5ZMKktartTfginnAjhT8ZsoQZ19jxW+wYHa5TNiIJtrslmEQAgxqJVOBIUIMFl1altdVvWgYrEn2H2k/tI4CaIFA7NjLH1DFAFihChWQyFO6naKrFMakFL623NoBEauZaqLJmPamsDIhJKPxYEQdz1XpHVBXhcR2KRVrSRkHAMFcVsVJei8uXahrOCh1ADeXzu6jbGsT5ufylyWeapzRgZWywsBFFVok0nng7n9qqCyrU1j1okgwXEpaJwaZcxsGpcxpDp/MoND6fLm9ojh9gfVjcs1csPUMKee/hTedJh3HyC531hLgOGcC+MNyDyufLTRAm/V5GmFvkNmkUZN3vf2sSJwLP2wT7P6PrN7ewJWL4xtwOe2BtLuQou5uiMCbdvbHfz6sat1ledG49OcOboHiESMbloBWTffInSlLYPg2wmlcxRUGO/KbgRYtrZchZprcPQnkwovtb/KdssaQJrKHDVwpcwxrb/FqWjmoB2s1GqM2awoxLIKMOFqDXidUkYIjBCyBLAq7bNx5PZDtT1+vLxwEzrvROABgAJinDGdTkCYAIqlH0t5Wnd3lNg973wLRtbnGfYKPpZRHf+dR9oZ/0jWd95y07NfYW5Dv/9yLXCnIvculxl/o6pbWnb0PPwYH/bt064Qcic1B+f3TOV+It0cXwzKMn6Rd+4fS29dj0cPZh853ndLq+zH3Qzu1kAfaACSnbyPtXHw8k5Fh1PhoflBt599JPm9tfu9Nwda3ooqb6r8JijLvizOg3W3EKU5wByzrIX/3Cvv0Nz94P3mTbT/jXl85F55PKshYXog/+3EpcFaupnXqFaMjfb8OI0fGgGem+fLeR6jg8Ruvg3P2V0vrzdZeUJElX+6sZbG7w4yd88xUR099s8aDlQYi9LGduTtHCQf9lOhPXqVNrtDmiuwtnHUjoZbVIanWEX07SSIuycy/l9phDXBVUFPOVJWD0JbxnaQ0J+ezBr/vgd0+6xqT3J3pVYd5f62l0b9ciTtn+Vc/Zp7txfRaC7v5Xfrmd17ZPzjDVe7dn7q3sGOsJr886MjrT3EUH6pncjiwtvmUlsHLu2t3hjaIroxHnQvt/9odX4czws8OM/K5OVNO3afHaTjYD67M+bb3d+VAWG/6vTW0Xo44jOqgtSt/danxzm69XqLtrdlOdrJbr6TeVKIiHHCNJkHpWPpsCAiYQYFEtdLMeL09IQYA+aTaDWLVrKvNEunM4sQg0LBlEaJbFH5swwb0F3fa0Bm3CfMUmium4nnwdnyc+BgzoqVKMx+Z54z7FkUUGqPvRB5+XYCjjSgK5DmclPXQ3m5gjmpOyLRGrCNzmIgxGkuAZh9fsXn/SpueayBVDpZ+6Pd97W9jCJIwFoYCOYAThEEie2QqTJqwfWUxS1YU3URJJL6CUAEwgyiCGKIVoa9pzEs0nIRMMxZQEglrN8YQKoEnoA4R0zzjNPTGfPpCfF0AoUomha5aimYRrD5Q1/XVctaAZZnc85Ia0bK4suSiRDiXLTPpxARQ8SyJqScEUjcl53Oz4jzjPkkVkQyHq4/Nf4ERT34pFz7NmfwKvVYr1eYZoNp8ZuAQ203sOYF63rFurwgr1csl69IyxXL6wtSWpCuF7FUWAWkPZ+fMM0nxPOzxKaYTtKPKuBa2YDuVda5Wb44ImP8a2lXSvJ+WsH2nTNAYhkynZ5EiDmr9vKqfZ4yEiesaXWrq64iChbwPirYORXmrwX5jYkToFj6EYWRM20EIlKhRsvMCLCa6hyD0qcglj/yGiGxArrOkkUyqMyk5efzzKsIaNYskUj24jaEEGSOBfU/KiYigI4JLRKYvropq4KACI19EmPTPmtPjFNDO3thpY/jUsfZ4kyMLQWsfUU7X8vu3QDtbXykbWN7ngDSdYqUy7rIzlLG5yn7QW7a6YV1o3GuAg1qni+TmciTQLHN0/2Es1gxmbAoBEKvie8FImGOIMRmnPxz8J9uP1OlrmI9FYLVFyByggS5Cg3KBJalCCKhOyk5N3Na98CM3B1yiAgUI8I8IyfZd9b1CrxmnNQqAQjFWiLlBGIS94wncctofCKr1ZtZcXASkCdMbJMHmYGFUSy9REgOrMsCzoxlXZEATE9P+PTb71gTIN0qfRn8/AVUcWLECj12uPrZU3/M7v96U9ID8eB8f5f3hzuIvz31pfrT/6A+N978T0n+OPvwuz0S8XBG3Hz9iPQRWmIfnjzANEp2OL05aQcvc3ssLZePtv+RbuLB3Dr8Pu0KTN6S+nzaOu1rcfcKCzmvWNMFjAUUEgJNiPSMSJPylQmgDIgtH5hf5cxj42U5/Yxz7ka62X/fLI12kUeSd+/w4MQdXhvPkWEOrRqz5rAVi++rOhxP/Vzy6k+j3PeA4xFY5n+P8An/HIBiDTy6t5+M/xwrF7V51j5se7PWznAVOVxWGrmJxGkBH0KtQy227YMiYHEKXWAGuxhs7Zs2X7ZQXrnvCBw7Ssntg/WNIuyBK1PXyGBQiQYY1wDzqrU3gY/Dc9jaV/EnPwLfjRK8AcA9Itw48v5OhaTbVdHKhnK4Z3V9TuqGu96+Xb+GCuqULvNPvzH6hp9LVrbOu+56/95+aungLXB9fP377nmFprnimz57Z77jm/XL98Db9vwCoKJyU4/tZbZe63hQN+xbIYTH5Wr59Xn/vS2Sm6r7mlR66GmT4EJTPAMc8XT+HWlKOJoOCyLiFEEUMBULCLOC2Pq09ziO1v7hQ3Iz6bpO6xfOTSkr53qMdX3bDAD3AzI21Ww0gEue3NwvvwvguZ0Je3n3QJlpLpsFQHWnlGodyL8bKlhIBtpCz0KqtWzxJDiXQG3ltFEkdt3RgwELfsvqTil7DfmysPSzQ7xME8lsKRtpmiFtWrQAeJJfiWfg+qACiA44K2CtWleoO6RYwNhKBMiVAzBy0jLXFZwZ67oUKwywbFIFmCQBpLkAspo1ggLLEVBLAwpRYlG4RcFlKtRFTRBmDa5d8re63tJ4DtpjAoYHjXFBAT6ORdIg1GldsC5XdSe1lLbZoY1IBFZxmhHjhBhkjcMOXVYXdguYap/VtSb14SJq6yw9lHxZQO3gPgQgUS6zSNaen1O2PnT92TiTmdFbV7XCiJy7NXxro+2Y9v5TnrV6OcZ4w6B0eQE12HMJCm/CQM9s9GXt1Lf0io8R49bE/vve8sJ+j8vxgohbeY40Vvy1XuJ+XFMGDeOxaclOX+0JG/r89zTHhvXp3m/a4b6NVhsT0NcRQD1cdfnttatvm7magqMTdqap7wOgzqx3cJb3dcw5A05Y5IUxvRDHdUl7H+rWTOe45dNormHbN+VA5+oyisuSinC4zlsR/ADiv9MEhrZGhD6RK+V7M9A9s/j42119K2vhf5ab7yhqUPZOsnXVPz+gezfz36VvjvXvGbe7LdSRL/30kT3yMelb1uk9OR99d0SLgf2Vtd/e47U9Coo9Dp59QNptRr9I99u7P1/vHBY/IO3VarMPPZhfs0d40ONwzR5Ph0Er4/sLHzt4wEGR/SNHwIhbc/HRdbpXSxycF0Rbf+HfemV4wOQ9lMn4KXflwFs2fttWjsbtJigzXpLdpVFv0sP0aMQT7iV/+urL6OfnUPFnp15yJL8fa2L07oh/3XtW6mCEr3/O/6L9IR93QPtIx+sbn14EAYbR0J44yfMePBx/4zmx055CS/q9smPkSkm7dbmR9rr97lQyd1IflPqKU3dx+Pt+und+PPJ+Uy3PrxbkolKNUUn9GX9jj3Cvfn64qS1r9D3Ooz3R+LKL4G6n/rfS4fXeYDI7K+aD+JUtPXS0wK/h+kK5SYMqsM49f14+PqcG5/+d9D34zltV2KP1dGufG73PY8uLbc6+XqYgHQfP76fDgojz+VT8uouv/RMoiCVErcSNKh88PNx7f08Y8ZY0Ah1zzmVu3yMKRw/cJjQYAWg2cKO2EIk2cVKN52UVdztFSxuACIecWyOXZyhCWzVFZpbgyurqBznDAkBbO7m4SVLzZG7ddjCSQs2tbkLQQE0Vm6sxH0RrNau1gWjJy7Ohuk0iKROWN1NxA5JSjX1hH+tL29caQQQmxGlCCBHzfBLrEK0fq7sbe8+A3DUtyJyR1Ce6aYJbGcXFTSBEmsoxRfpB650ZOQNhipiiCiIoFHdmUOC4zB3tf1KtDk6SH0GIBmug6WW9aLuvCBSLayP5nmAa0Rmi8byuK67XC9brKy4vX7EulyJYsbGM04yg1hrT6ST9FKXPxJOSzlVz36WurHKnq0PUrn87uOWckVTYlWWCyDgH785NiFVeV7SWDdUSqC4LEwD1wh+U/vRgv48BYEKozcEArPmJn3+rdy/wqmVoOWBQg+5u166nKavGbrler8XFFqAbo67xMidKX1ampwfYTQDB3sKpa6+tP6t4EUSWsrz7nJr22j5KlV62bpn6w5Cn1Uc28eo+qm2XtxzZY5x8Ob78I1YZ9myfV73XPuv72uakzRGgxqHoLV76/PvDnHdRVMoJARxbUMLWCnPbVnC7t1R/uf49LnSOQhD9HpKYEb5twVnhlHboXOrnqK09Y0RKDBgt14/r6FBqtNHWi6/nsiy4XC5YlqvEyJkk5k8294TJaIZqhKm1W6DwHhzkzen9ePMeQAa0Dfr2TO9fKe0dIn+lX+lX+vumR9Z9OYuhB2AGOXwPYdav9N3Thv/4ycb5iLBrL/XYiP/dC7VGoNVbsJWfrf+AVgjR/q7LeiS4+THpcc5lr+6PtKXC1m9s/xYRP/DM24r6VmksrBqf1faEEA+XCR3xwXn14bw+II+/RLrZ5V5gORZeitzitoD2bhV+YB+/He9m+78Qvr02eCFE/9yt8u2eYXrzPDcefu6lw4IIAxWsANMyNxcRtcKDBczjho8W/h4403/vAVD9O+3ftwFDd7XynyG0x/6dgRwRg1InBYxyB4j1QNamhwxoh9NMB2BxFIg8QEcS+8DVRzZcBR6TlG/+xaWO1arCg1vynpVXQVKGAYNZtPMNnCeANbq1APdUJbOlD7Z9bUGkgm8/W52paL/mAi6nUnerP9y7BrpxAGKYECYRSIhQwoA9Ro13YBq8CYtZQKyrA8NV2GP/kY1vRuCoAhOtNBgiwyGEyawgIoBq1WLCD+tPs3RgEwgVIqBjlFYJjL0uCvKtoKjWIyEoyEYQledULDhSWsWV07LI3+YaiTMsHofFrYjzSUE9EULU2Bns3JUZiGjuUDzAb0Nt87eakTFzYzlTwE2bHhW5LYCjrBHtT/UZIWOnc6lZwlqWf38HRCdsLQAa5yMmZLgBwhcmHWri6oUig2T5eOFILsI/NEKcUeqZn0ZYqnE+WuECj10Ryc0Njevp4agPjdb2Bxvm6oJpFMy6FxbcO9yMDk/93z2I7elJX8dRPnvljsrwdfL0pq9nQ7+55cP3BDNHGIqN8MaEEa69fj64N5stWISzAHG75zR11H0BIQwFNn7+1bnXCr19e60+87z1E9mPnxcQbtsijM00zZjnGZMKl/f6j1nl0NiarTb984a0X+aYD4ATyj+S35H0PRjhR8t4FLy4mf8Ob/fR7b7Fax5991umPZ74W/THt5pTR/Ld68ujfbzXH3v99i3Ttr0/Geqyk947/uN2HwPX3kJrHk3NO5sz3IhvAFA4WrvwfUCIjy7jW9Z5f//z1/p3gLfuw4+lLcD6Flp/K+3l4cHuo+9s87i9dvbLfrtFBADnPuj+fPeoj2AEb099UW9tv707OlPs8elHAcbdZ26M93vTvXPT8Kw6WJe+ne05uKXT9/qh6VM0rx7eyz96L+73+kfX9q3+6cu4J4y4d1YgoMRM8ffqOfKOtT7aHcu3/RhveHs+3UwHhu1b8KejNgItHdvDgHffffDM0r+zoZs3f799vvfn8b0y7vc3A1Q9jhScrqXi9fedPWSvrt/YIuJcLCJCEBdNpm0vdfYA77F0b+HbM3vfxybRmEh70M0DWvI5VndLI+Cm3Ccgg4sQwq437mkcYGgAJxjQeGkiQCgbDmmQUIbg0ZaHWEQAChpLJQEWHfbiQ95rLtcSq3aQ65uqpV7bLBrY4i6otgMgqNa/Asw2IW2KMAso3QaQrX0AUosBZOTcgZ7FX//aabtXQDsA4uc8TmBmxPmMaZoxzeeigS+BmMXSwHyLr+sVKa24Xi7qhslceakIIlR3V6Q7gARvJWQmFFkEMmKU2AVxigoaSsDlpEAfcVagTPs4LSqIWIFcfeSDEzgnpPUi1g2Xr8UyxlxOiVsm8TnPJrRRQcp6vWK5XnC9vGC5SoBqcFKLjggKE6aT+Hk/nT9jmmfM0wliWZHAWSwrUuKab9HuRhn3CrZV4M+7iPJzTdaFjTeVOAM277LG4MgpIa0JEFlLKa8S8gEh5hZA79fZiPmsk9DGo7UG6BOz+pBkAhsxNxDaZky3yfk4CyklrKsJhKQuJsy9x1D3eaaU1G9/v56kPlHjxGyFB37Tknb3IHAfG2OvHqVPVBDh69EzUiNa3d/33x4MH9HZLb3ePtMLLUbtGPWNle1jXfTljPeeugbsncZF0c5+MUo+//IdQhH1WT1t3QSqa6yvo1g0oHxGggWjO0ZDTbDQCy2sT9K6ipVYFOWEaZqK1ULdI0xgUg/lVl8rV+raAvb2vu0L83zC8/Mznp+f8fT0jGkSCzCg5iEHYGuk7j2RXLs9o/Urfav0PUC6X+lX+kslbkGe/5z087Xb7+OiELJvWenfkXPJj0t/bap6pPZvA83ek/YAy48CSHfPG4fTVohyvOy3W0QALp7DAYylhbB+fNpT+OmFED2PvQfoH00/gsy/B2x3maCfazdB8M05Do1m/+iZe9ffmr5FfvdwxXrvHWUTbVZ333+3hBG9IKJ/7375+DkW68H0yHy8de+IgPY9ddlN36Gv9wVwjkITdL1vhRBs91Wxt5udLb0clG/3DDuYVPn7aHowRoQCiMFrHLYBmEeVE2auvbaXRhKe/U4e57kFqkwTfD+vdoIafR5pAh/bsAoQY6CzavczV0sAUldKBeGGBcxRrWvnqx+AWGcoYARIzCUKKpjQPGr7BFDmTgiyaScgcy9XAJkApGQgqwZXBtT1ULVOKIuSgkRHUMGI7zdhaEiJb6+1XBcFIYOhoJkCeBbHwqwGvN9/IhQwWywhsgoatG0G1AfrZ5SxkPHQgMHLFSknpHWRecKsAYJjydsAdMlY6s2mZUxU8g4hIlIUYQVIBC9cAflMBCRd9JydNYQJIGSszUpjXRekVawaKuAmLkgyc7FwyXCxITSWhFmPiMjEiIgGEA7iFinECaS/y1o1ML64wTK3WlnXhRe01Tnud7fSFDW1IXLBnJUZzMwgE2qptUdOquWf1RpC545B/QSonzsCOMvMUUuS3mVXvxa9RQQzl3nq6cG9dS0lM9iCW9n8ltXclGeA6jimiTwvMTNacB0uz74N/hDNuV/LBC/cNEFEAaztQM1bIYF92xwqdMAELR14ParXsL922jOi1/f2hVtaFvcOk0eEAP2+c2/v6fcYorrG9srphQujvCvNGT0jayLGqPRY3OSZOyR9sLIeNta6n1j+fjybMUZ1QbfXX34OUkjFF+dIaFMFDeIGLBcaUvMwi8oRe1OEv/r3PE8al4rUY1wu/S5WeFpH/YcZxS+mdo3dHY7LKL19Xlr/3nz9p0xvOZA3fNI7yn5vdz3y/i0esOR3h148ehjeo1W3yu7LemvZR+v0PdOtg93R/aO//kgf7+WxVxd3BTvk5M1pWL9hddj+f3u+b0zfM6+3lrW3l5dr+i9jex56Sxkf8dyjzz6Sz3voxBEaObp/e0/t3zlWl0fWcf+OvEeF/9ijO/XaHtx3NN1TaNzSE0seW2nr9EDpHU85XgO33nc4iKvTqCp2fB1dv/furev30h6f32M2+nSpix//BnymDTxc83GX2vr2/OXx+j6aSvY3Crq39236RttsXL/Rxv26tmCkhUt8dI++lR7lB96a3nMO9dPkaH28MBDdOeuRNKJMR2lEJS37Z+SbyaCeI2UdpNd7c9a/PxLOHBEc9eWMhJNH01v3/D0+8a372JF3ex4IwCZGxOi7/m3/eCVjwxPGU8BjCXvhBvbSYUHEZIIIC7zb48m30hs2mntA0K332k8u3+ZLfwPqDUAE2Zdos2D3yhxtfrWMWg/Lv4CFxe82VAghIKUxyfLR6yECzNVvN9Dk4cvOScF77fzcMEZkxhPKRDiN8rRqbcxULJdNKmcWoNsJIojEJRSrJcGwz2gkhEApByaEUBMQ8xWe1E2SAcz2DlErhCC5AMpZTd4ICJMC7NFJ5qp2f1rEGuF6eRV3RutVxtH6NEaEULXWDegqm0iJwlpdlER1l1SCE2e1HNEB5ASJsGFWA+YyKct90vGTOCALrpdXpLRgWS7ajQTwVN5PKem1jLSK8CGrKyYRGInlh7hCknrGOIlbpmlGnCbQNIHipBwakJMIBtZ11Y8IaMCpAK1VY9rN/yJJhQq/zFQklLKhQszMGSEDbAKU9Yq0rsirafonRet1fjlhhMzeSjBTrrESPOjvwdZ+TVbhga5RoAR/rlOWyvoq1xkqJEE3x9tyyvi7mCbVYkCFKiFIfJ0dUHqv7lWw4Fx5aT3Fjc3kgrO7+hQf+ts87VOFOVUQMTKx425nHR32+3J8v/YWAn0eI6b2Vv63Nrx7+0eftx+/oK6Kms15UGf7eAZqxDTZt/3d7z0jwU+puwqli2BU15gve4/JCs4FmLd2GPXF6FDRpyYeCQAfm8j3odXN4kj1c86sbkyQHqhaSHlhGjMjBolLFeMk13KGeJNye3XpK3UoaAfhm635NumDzkp/ufRmKI02f7wjozfX4lf6zunRw+B/VlKe6lf3vCntnhntTJb3eY6/U/rrrrH31ZkaYNmEELf5yb709+0kR9/+tvuVH387cR977z4f8wCW9tOkoRACAAXabw+7L+p+f+P0rcqoNGFfADN8b5jHceHDo6Dqt0h7558HMviwgbklEPG06kf00zZ9+zo8sl/1Qgufx63r/b1v37cPSHA+stSCXZnizG1hxJH8jgjrJH7jcQ9JhwUR3ve4VchXbuSWqTyjdO6I1HQkyRl10giwsWe37pZMCNG6DxkBaAa2NtJL9/wo3QQNi7uXujBG9d70ARtgndpyHShefjd5sbj1Ufct8KBp+dv1cbE20IDQeQHAoFX6LARdQCbEUcsJ0cwPjaYtPCDk2loLr8yhFwSJxjy7urFaQliQau9+pgWJB6MBkBfMGKgqNbBAqMv1KgKItDSAIKlgxwNhNifgulF+KliuADuyWSrkMoZaCQHerO8URM4alFmUghk5ZSSzhEiLfq/FGgEUdQzEgiPFBaSWGZyrFYSUa2svAMRqGUKgGECxCsGKgCUnqVNamw+7OlssksrMO5AUrVCPiMCBQBnany3tSClpHIpUXBcZYC/5jwneSJBYNfnHoLCn/w1NaW+5Odau54aOtX/YU9ovrSVEbY9f+wIMB6puv3r3Sr5cA8Q3oLcKK4sQTN0xefC2CiFsbnArlGNs+nEUG2JE93tS2DP1ewD7Xrr1zK1NcgTwj97dYzz7jbWfW15o0mfRP3uPKfdtHLXplhZBZganKhwygU4ZL/gjN5oxZHARRpBa1ZETZo/6zvIAOxdPwGaMU0pOqN3u19Z/pJ1X6GjXd66DNoySuTQzATiKttb+nGCnMSztqHe+VdqOm+5jvHd/nD4CGPtIpvoIz9M853mND04j2rJ95n7h/fu38vvWQOWRsq38vi7/CSAqcHwO7l1/9FDqf9+dK3+zrn8v7ajvW8ds89vF+u6UfWssGsj5znooe3az/2zry/wYcHurrm9J27n28XvCIwDEkffeQptun4WpafaIX9vPr3+2tYi42Zb96XszHeFV35pHP98fSXtzaVyWrKa2j46UMq5V/+6j63xTyg06Pnr3VnYNz46gLXcvsP+tHGWTof62fLj80xdUj+SN9cH99Oj+9/izobTx0XnVs1uPCiNGZ8ajgsJ+He+Vd/S5h5IAXIfyfHQv2OM9Sr62MbV3m2s0JGDUfd8v8yNSj2mM0ogXO1qXR4RKb+ENf6Z0ax/uz9+Dl4fPPUKPm3NIg+lu0yNr62FBxKiC8n1jAx4gfkeYRf99JPVgnQFEQBVG+OduaaTCbRaPTsotCOg0SH0Zg/4s7VbtfR9cuvRZA3iNylZt7HVVkFwBdRuH8k4VdphrnJRUEJETiALYAOGg7kDYgu3WMbcsLeg0QijAN8oT/ZhX8I6IEYK64wEATtqGq1hhpEosRsF4rd2lLA3IXPojV5B6WSTw87JcFChOtR1ULVWiBpsu4Lvv5G4cKUp707oiLQreJxEImKstcMa6ihVGDVZsH6mruIhasSwihLheFzAn6Q8QwOKCKq0LQAHLckWMQIhUrCG8hYWUESRYbbD2RYQwbeOTKJBvga4bYUQB1bI7GPj+NbdeTghj4x3FisqXVbT611R8y3vXStJj27GVb9lwfSDoPZdMdZ1V6tQ8w8qkYJs8mL8h/mQQp7vm1ry3hPCxFqwPIkRwJcHGWzB9tLF44YAXWlh+Zg3hY0P0VhkSF6W2TVyPVe32Nj7Glia2bR102KD+/vqtZ97KDPp+u5XuHQ4LYO/mmcUp6J4e7oHVeuJ+gOJbAplb9zhzs49shFNAMZMG2jgbsgZ0rul8D+vaADdN2cxCu1Bp+6ivrQwn9m3qXOZTl7+fy411Vdf2PsaKCSm11ih7kC1Hs1Jjz6u/Hbx5b9pSiV/pViJ3WL/33M96UPhW6dZh+lf6/uk/a/a9JfUAf3v1W5R2b3X050JTEiOSs4s80+X6H0Znfq5UrRjKlY72H98L9i0i/pP2k4NiJ/xdOJfjZ5VqkUtwZ05Upa8qhDDes34J77mX6H6X0rayb5mRR85g4/r1Ze8IPzZA3vbMc49PuXcevHX9Xto7X/5069sLrx5+d/BeEXLtzZufdz2PhYf7iqhAe2736dZYv2ce/HTzp0uPChXuPm8Y3wBfpoKHjoU4e9dupcOCCMm3BcmOSLes4o8KHvz3nrCgB6JHWr0GbO6BfD5f/z1q5x7YuVcHAwKtro07JmN8B31R69+7jaIC6sC9LW4oLNCvANlZ3TIFv3W4MSxa+ebKZ12Q8wrWeAQpRJlwgQEK1b+Y/hsgTTCf3V54I3NYx8j1G/N2XJgJIQiIbYeB3GiUM1ISt08hqOQ+kr7bgrM5ZxEK+LHLGUkB9pwSluuilhCrWnW0c0qAenXNRDJW7AZKnoPbRNTdE7eAMStwD87FqmFdlwIIi7xG+iypBYgA8msB3op1A1XXRKz5CbB4BbMs4pwXsYBhtf4IATFOEkiEczMHKVCZCzmrsAOQOl4vWNerWI6kpEIUB/h58JNV41eDa7P2uWkL2JwIMaK4Z4K4f7J22FhYe21zqS2mUrRWsj1MurXZa6XXaV9dnfk1RiFg63hoTEsAVKsSUBsLRXmKnu70AkjTZI+OHvp2bK0ntrSotEnXVi9Qsj4olj9KC0z4BWyDJ/v21vJvA+OjOlm9Rsny6tvQf/dgtS/jIzY8/47NtZGrqFESOhd3Gad+n9jb7EfMU5+Xvx5CQCKJolMEDiEgAEicGwlEvx+VNsZ6n4iqRcQNgLOfyyMhcHOogJCbzPX9fk73wpzSNd1Bzb9rgrUyl2HCGBRaazSKqO6t1A0Te0Lu+v7W/PqodK+MW/PvKBP8kfV/F+N9Rxj3Eamf57Xg73tgeO8B5dZhq3+mF5j663t5/aj0yJy9dXA8UsatffLR9NF9yO0/byp7t3/eXKv3z9uPPJgfPTy/5fnRHlz2NLdH171pN9OiHHP00N8/873X51vG6NGxeEuej/bDHp07RvfG+32/f2xpyGM7ya052te3v/5o3vfyvTlGCrbj4DiO+ube8x/x3Fv5Ie6+7Vd9xfMKxioSDNwlavfZvW//vhzR/Vjs9Rft/CrgwqDuj6dHz0mjMd4IHHYLA4DxHPmIdf4WejPiB74n7T1Cl2wN7gHqPo3Xef98ndeKjg2fe3QebPv/5+Gxe4HW6O8+n3t7ya2yj/y9/67vNy7j8xH76WFa2vEtt/iYiqHKD48liEKjHtl3+voopmLpsCDCT773bjZHNplHmb29D9yA35t0tVO3YE5fp70DZA/e2LO9IMILI8ZtUA1z53pDEXARDABgVJBHfJ5mrBuf9K5JZHiN02JXrfeUrhoseAUgvveJSIIKU0DIUr6A2NYeQojb4KoF8C4LAE27rG+sz3NOOnG9dnZSgYQEb5b8TfouC7kHcJnVssIK1bwIwHK9Yl0XrNcF/w97/7ogOYqrDaMPOLK6Z951/3e6vzVdaaP9QxIIIbAdEZlVPavVnRURNgchhNCBw6G7IJK5AyIl6KXUHIzY5CJhNyV3Oz1YwdGgD9W+IumbwkcmHeJs3z/FoacOwXYR+CGBCr6XoR2lA8gBWOJ4BhEHNJBA4kZnJ/gn714Qns85g7YH1A2vtE55k50rXHM5dukDxv/z8696QfZRdmgwRMgPKiScx3dA8P0nO4h2QC4bp8qqyutbDTJBAzelSB2HBCQK2tFpJrBFjWdrfsjOC/TBLct/tb2hw0q+lwJgkzGFfiVMNIYJNW1ffrNafD7mSd1lI8cnSRs1OGL52MJsslNeSEAba2b8DfdTyBFtCeiP8zFtbbshfNtGUOU9nMAuKKS27vh4tV4eRmVcUTxi3GP8dOJUGtj6I6e7L6/JtnNnxaq8yFjVyZ/A9hIBIocyUslmbLQ8ff8C2FijaOXFpoanu3/mA182Td03Ju/02D3ejbh1PNWMDKmrData3nEceDxaIEKDa0S8grUgsewpBYDZZdZQcLIjbq+fu/x7T9tLUKe+Z5wncd1nesszSu27YGjPNxp+3XyM1xy087LXcMVYupMvSnPFaP1d4Q5vXtfT75X9DK3vwtxwf2OfWbmO13n0XtXvkTFXbMCrZdTWT/jC63ReP2vzYleaLag6jqpJE8zvK10z4qeZTvMr5fg74d1y6i59xv60x8r2/RaX2fT68dXkRfB8Nud/ZT9P9QzlW/l5xTF5F89X23XH99NBau0adKehI3UgqyVliknrIMQsiPU0v3fK6pXkyf64NLNccc4+B1Txv1rOmTN4pY9fLbtiNynjl8tY4+B9h1531744o9OUPr9I9fS2+KuwmkvOnl353ucF1FfYPV8EI67MFau6p78DnegMvD+Ap8V2wX0EK/9RBDcCEQ2pV+AqwVaKXuRgjBx6zLgY8qhjI8JBnSM64qjwdc99mb0TzNZtL83V9+q8qUGIEybj8nonHJsz5s4CVYoJ7LSujvtSHUDseNbLxZNMuursP9pdA8cn74iQXQMAgMyr2HlDBO8Q4J0tfKRL3tpdCu0YJuPEMsr7eKGwrPZHc1iR7k8gwrH/rI5qayyo81Yd8hqM2Pe99QeZ9+WoF9JxIEKCAVTk0nUJCGVtVwIhcw0pgc80MgIrcFaXcnR3QhCxc5/0iKNyyG4TdbQXEGUAhF3uvqiOeaFDygkZGenxAVAxgQTIroMiAYSfOFJBSqXe9aG7H/K2Sa7eUUmJrwZPx45U2pE9JP3CF2Tv2Pe/pDx1MBIAiXKKM1D5tBQNRCQkpVlKSBsqTUgVWiLsclSQHo1lnf0AQsd6xR/Neel3HESTqe4QOMxuC/1MSlAzHK2xagUwf6oTNnc7ImZ5bHtqICLxSaQEYC96HNbRtcevPPeOZQt+QtWyuuOudDV77p3AHvdGy/VRfGq4R8a2gg0w2Db05fRtiOi/AivTBz5xbbLtWcn/u0EN264iQTrfJ1fabXGxuw803bZt9ZgvfZ9zNseZtT6w5eqOPD02St/XFQtKowCPTs4dBxKHV5HSR3fptecltfF441UfkJu138pPSyuV75+fn/j582fbKZa2tmNKx7HiLS1yQxtzr0Lf7vc5UObj4y4eq7HwXpz/gX/g++B35d23OSpolELvKff9RX4XvNsJdIfCRO340G7HeYLYN00HOkMzsttmOtPvyudfBe9p6xeNnTvVO7D2n/2d5ln+gRfgipOupW3OvbMyZGVnWzT3JHi789kAtmQ+FTrsywHquNA4d5TuUpUvHluUJgg8Uff1AGF7v/p9pYy/JTxP8nmRE9p/B/1+ZR+t2nmG0/M437NDvT/prO7OL6O/30pfqsEIhStjcQWXAxGjs/48alPfR/PAxDkzc96cNWzu9LHKZR9p9WXbPIq0bt/1jrEo4mMDIeGxLNs2OHAs/vqnTmv9XSe56iBHDSwU6uskGwDZHiGeRLIq/ThQjk/zd/DRTJDmJ3GMAqDcLpW2zqyeruIkU2eQ1qN1aTBCL2xOsoKeCqjIJExUHfi8Il+7Qh1ntWt4Xb5byb2RC0Qc4uTfd+yfcvwUiAMRAAchcr1EQXYamCBEpffIr9oe3r1yNGVUghBHvWxad6gonrqT4qg0U5oQ5Ez1zHdUJNJAAoGDGNI2OlCOn0iJsCcRNDZ4VVfem0vayWwJ037GJwBgl6O9fn7+R474+pSyDMFNoEl342hg6Tg+kTnyIEGqjYMYdmwVDdSYwEspKNYh6pzvdmzIIKj4kDPyrTLY8boanXAC3rTLQzTetaosvA89tqurZ5QRNhCpOyKIAOgxaOaOCy+Xrgj0zmEsPGnP1QdQz/GfOf09DWd1cJreCR/Jfd8XUSDirmPW4xi1xf/2wa3ZZH7W7pmSq885CNGCq1EZM2dEhJN13te7RbZtwMnu5LDP+3IgMqAFAuwdEwjoVmlDAOSIOSqoct22389lW7WRqBrqczqanRFm7lKoRxzuh+yI6O864boBnbNLIbSVcdc09gi3V5XjmtP1yUq5nOE1+32G6yvOoFEnWqf7LaCy7EQPdb+fkUO3UVr02bvK/q364CJEsupqO67aH1fgql3xHTDYI0/mm71/Badflf+dZY02VlulmOqWPKXhc2Pqne0944OrMvqdcKXO31Ee3SeR6i7jm1kwQr9DfldvwjfON7Ye/70+YyQm71W3nue/Wvfq2atlhumAYdiOOlT/Pk12ds8gmnMi/eIZfYyI2Pa3v8P8IqusvnqzLlvnK/xIZkdEtcZvlOdtn9Xvs/zRb29Tz2h6Vdc2OaczxJm++Sw0f+rXyN6I9p5+Nt272nOZB1Oqba+y1b7jwuL3iGkza+eMX67ItzO63NXrgOv26JDG2Pj3OEP1IbokI+ey6ho8FYi4BwnKDrNOnk2cVwnvlcsBA+cwmTkFTKnivOnL1rIiiI4JSpK+HskiOyJW7Wr1kTOom1O8iGOpyGrnUo56MDefxw92BOfN5GNnj/rCa4BAgwS6el+OZiLiMthhlZt7PpudEBNHaaVbaU76ekxMPYu+yHE9BI0jaNDn2D8lUKIX52akpAEQGZRg/5i/h0MVSJDe27CL43tHPSff8ENOsjMiydFM2leyY4KLkguzqe7bELx1dwe1/pA7N/jeDQ5CJOmCTXZd6Er4/fPgNgvNUgYyZeTHgzuARPCWAyCmU3V9C32PHSh0cDv0uJ8EEB8kjyIBnyLO7iRHLVHqd5Z8HgeOcuDnz/8IT3xyfwvySZ17pE79VPm0HAVlP+Q+Ed6JkYhXROuYySnLLhyqOyFIHeXUnK52rKLWYZ2PCG1E70S0Y1t3zhRqq7J5fLZLyBLFwtQ6sjfZ1aC7jDS1HqHWLtTtDY6+TarCNLnSyQxxLvt8swmwdzhTDUDYi7K5zNQ5tX2+Ht9xV0o/ztf3V8xkw5XJ7Ew2WjwVhmPogrR+h8dM0VjjNyoHetRVStS9XzmF/N8qvb7btq2bi+ycouXq7p+O12SuOA4+Ek6PohsCEREd5FlOudZfd9yZXRu2DbYdlebB2DKV1LrIBLlt2wHwLrHcZDLvGDzqPAuRefV4rLyxnBhZ4/vgJUV9ldfpBWHa388Z9D3wfU6574ZId/27w39TW/6Bc/gdRmebewFAdgrq/V9dMKLpj6yjfr/j/+8EM3vw9wHW9S87tv8Pd/OvlsvP2AH3KpDPL2riqwtZovJquUPUAU8L1tfxVBv6OtSARS1hUvJN3CJ+eHc/NPCtuA4vdNfbSjit4cvo9hqMntp1OttLrw71Z+jR8vja7/sfngaip7lVOa3jBxsQMn6r6PdVeCoQ0So9y3U9CPGcY+g8baqOVCPIaYzy+fJ8IMKmCR1s1anTT5RZHd7GgT8ETAIaaFm1DQLsmueL1nQHBOdTJ06WMzEyKLU7BDhJc3qr85x0VXrRwMYuIQu5h4Ie1dmjQYDeoWrpQuIQMrs6Sjt+p+Jc2647J3il/y55yi5HMqmDMRcNL7T6xYiwdEtJD+to/XaUIkcH6W4DXUygZ6WLc0v5JOtuhOZk46CHBBv0YmfZwaBOcg6g7Dg+f+IoHIiggwMI25YrD+SUcBQOQBzHgaMObjTH/7bx/RoabQGqsxPgYAIRUOTYpiSOt5y3phQof6fEARniNqAUOb5KgzziwD74+KjPz0/wvRA7EviIp4og1OmbUIhXItdAxHHwppHUUqeS6pFMBbpjh9pxTHKUlB/GGoTQodE5bLNdMdL60o5L73C2gb1QZhDglSlbZh3HuqPBRkOMc3gIREaKkR0zHX6jx7Qba17mVOO4lxk24OdpYoMc3qnusbT0Y1rUOGiH3wy8URoFeWbvbJohOJH6lSg+GDPHJVf8Pc284/tK0CduY5/+DCKaeJra/tPjmSyvzC6FqjLSzEk+WNTNb25Oqt91DOQElHFOnPVrF0Sr0ntBB52kHL/bcvrgmMqNpuhxMEj6NG9upK3hsto069eLilevlqYBs3P7eMxB5qLF7s0JD66CZXfznIIv8ht9HNPWjASb5onNiFXhK0gdG90h6SoY8UsNxzopT37HP0O4yrfva2+v91/DiZWdKQonqJ3NebagKGXEMr+i//s6F1IrYPh34zubt/1n/wc0O9XodWi7JVBNsfaslvcExJ3oewABAABJREFUfmsZSpPvFvrB1fSaK2Vy/jHP2Zjr049NaHqZi+VcwGf2um9nnGs+Onr9gJ/f9zP06fpss9nb/v66iW7gFPK4Bm08nWyaAL+qB6z8KMuaTtLdfh/4Z8NpiNobla7XbloYIR7LJKrsvTL9vBbZAjVNMs8C22yNn8FU9Yn24AqitoRuzidAD4+YK00pHhmRPnOVht4nNdfkHEovTUG9bGmozub2KxjZ9PN58hndfVXHKv9KV7lb5yxYFEEkVyrfzPJMnr1HCrOAaWj1AseToc01MZKDZreY7u/2a2fLCxLhTHmjDzv/hMEpPTWv9nDjjojeOThP45UWEVSBk0M//eWpXYnGAWHPmPZOk7mji4VsobZC26bxONTy5Bz8IndEdOUS8SEXml5XQx8Hr+In7hy+g4CduXosk12N2q2eBrAldg9nIWJJub4TSgJFVp+Lk7/ilDZuKZGkzHLJMeeUq32Bwqv29/0Tx/6TLyc++J6IdoQQsOXCjmgCshTLRYtTEnyRNQ4+XojkEusND8brs4DAjvhj/+RdDscnQAc70sFOUxDVsoscc3Tsf6FQwX7wcVCPjz8AbNgeP5DyBkKW3Q58Cerj8SHH5fBA4Ta0XRm66j4B9Wx/3gkh54xTwvb44IEmK4bV4a47M46ffLcElV3oyytyC+0oxMGW4/MT5XNHoSJBAj7yift+Q5H+3QvVM9u31M7TJ2wqNfiPEjgQIUEeCdQcumsFQCqJjwhKCUUui04A6GgXZVMhJBJayy6VT72wm5gv9v0/7MT+/AmqdeZ6ybQGB1T0cteXeoRWIa6DAyPCszLwDtIdHXIXAnFg6IDcaaEXoOsKa81cAL+kmcdL6pQaP5bVscnsmsBBHv7PHnPDxyTxez59puD4lCDYITwjbck5Y0uZj59Sxa0SooCOdkF05+BOqJfTEwgHCg65GLzsO+goMk6bbPgQfskiW+ql9Ye5TFo+dRW8v6NGaVFXwD82bLLTB0iy2wgDvqNSYI3z2gud/Jo75s8np1kgYLoiQydUDUiYibTZnanSPucNGowmGBlj7luwc0t1noe49+1WPmptKI0/YWnRlJdVcCmin6etxa/KanN/RF8gkB+MH0h2zx2mHBL6E+/0auULzho8RuFxtCUkYhmJxEFGG6zNqQUeUUjkMcu4SG8sABLpxfck8phln8qbj48P/PHnv/D4+AByqn2n40X5gcDzLvejOAiJcGVLxIDaRGm7AwkApeyerGoNrGhG5mI6k6MNhJbr2QDCW+EKDq/iyfcvPVfWOW0jqLvqbueU/MRBtL8rzDDvnjvfRfs9o9rVOeNVfjmn+8zRNjHPX8PmkiH3HJ/+t8GpS9Xac+avlE/s5X8BFNEPNt5BLjpDo+0BXvS1gUrmOca4D76qB1LneKhLsGzLxjxou5aVOyqXDMnJ5Bvrtimi9zGPNjvW4rQaKZqGU8zKzP1v8u8jMK13+tuV8dnat9Id1nP1Sjqdj94Lc/zkt11AMiv5DErMNINuOtXRn4BWTs9BJsWFQjBtYALEb4FmX3ZZie31Cdi2zoIPY4XnKPcZ5nTt7YY23sW47Sl10zFc7GhPBvGomMEUTMOYPwVT7mt6j0rGyWjrfAWp/a7vfFl0bYBoKV3ae+1Iac5rY1rHD188/ft5810w4+uo7tXvlBzPGYczGZtQn5mEl3Cyz5ujXsvryyXri6rPtUxT31CF+lWuyLVrfBktutCangVC3wdR2YRG2pRlgTLWiw89XA5E2IEzczANnaZpyD3EyOwrpj9bXTuDLGe4n6kf4yoZdkSqg2WIzPqOIQlcFBJZJv+pc9UdZTRzsKXEUyE7iUho3hGTf8pK8qr81QlK7wMgZOILjyHTTAbvooDuojh2lEOPcdnrCvUiK/A3FCTKjEdVbiQIUfU77bMEwoGUN2ziEOJi2MHFFxOzw55kRwFIj9aQs8cJoHrfgl5WzStbN/oDQDuag1eAaq8mbNsDKbVAkwYiFD/uR5J5tt/xoGVkubhaneLar8dR6op/PbqKyV3AgYhPHLTjKJ98vNXOxgsB1bHOASnercD49AJ148gTDnqIUiH4k6x21eBNAvQIqMoS5ngU7ovGI3QU0M4OSL39groLktsF7PVejv2zlp1zc9TalRNtnJTGO9VI4FCa1sdny6sBKP0tgSj9NGc4VYextG4cK4uhX9NaZUr0j2iFdbfCBNIv6sQ3f9pPdUzXQATxvRc6ptx9JdA8mf80j94HUoqUb/DKEiTLalUS6rFaZMsOHNZ2V4Ztqz0WLmkw9+jz6vfeweOVBPs9Dh4/I6sH+TrJa53eZ27b2r/ZjnPq8J63PcYhpYaDvZsmCpBr2hGzsT3Rcy3L4qi76fSdXlo9wwFgGQQi0N4upYfQBWDJXVeFqR2icsqMUUpAgvBPS1jn11qAqZ9kHgxjWanODihUJDCsMpsDzBro+fj4qAE1Fm0F25bMMJexCw5mMA6N5lcVot6uiPnW8lf/IuhHpG6c9i/d2Aq1FP+s1h7jdiIbr6x+mkEUNIsTnpYklV+vS+EU34vO6XU51/qrGSJ9Hz2zSkyLezZWdGbcfSWE9hUML6bghbHidV6dlDavtxp67zlCZFAzzgzi+u1e3fcN+5nT6z3eiHc6GhjOZcyzdQ6UuDnWqp5EO0r5KWVurJ9D9ISq4wJU9XDdddhcdpdbkPyAiJL0/M+y2rfrjM+bnmq545RLbopxxe0Mj/p9lVTS+Pr6oISzfzGXd55ecXVrb8DMt3HOYx6n5x1A6mC+zNfmc906U8esrNp+j9N4TnxEq2ecl2N6Px9cl3XzdvkxEcgl0Vi78gxv+QVTY8UG3zrPXQAyOFpbe2EbzHCZ2TFTnSrUX/Q0hXPUbRxhCEKcdhnXPapWao+cy/caPKLuo76tekL3ye9WyF7RKV5RO5L59+y58qX6WNIFmr0KU19sMBav1jnjzbP6IzlTNX1bXtJxZ/sZhjfW9VsahmOQpGbhJfK81D039YS0TENfz5e/jbQ4a0Pn14DvsQCbwXaPZXuEmbqqpKBa251Z4MaOiHO46nS6OlF5Z+Gd+jqBnUYhGTnvqhOPqDpPyQl8fy52vWfBHW1RL6bdxvsU7Gd1eqLfGRIpQtEdGGO5HLxgpTTX8oscibPvn90fX1K9i5P44DsNwDsBKBd1FfF5/gTsOSGVhFQOueh5A1HCBtk5kA45jsoFUWwbZAWspzU7wwt+fn6y0Ng+kNOGbXtgy7JbIFkaS3trUEYvi9Wzwgm7XBxdL6LQFeJyobIGN6qjlj1kclQRYf+580r5/VNwlWAJHShl590k5cBRPqu/LeeHnKv+4Do2Pa+cy667YyQQkNUwTx/8G7p7AaCyYz/4/gy+AHvHfuzGySqVEgGl4JALuvf9k4MN+y4ObOVv2Y1w8I4IDY7snz8756qCX2ltgx7an5Fz3ytHGojwdyJ4/uieFQlqOQU4gn7CaCvQPe52V5INDGpgxTqZLT4pMc+XstXfTHMyMmDimEdPi3qkmjs+yR49Y3HY9agyJ18s7v5IKHXcPh6P7m4IL2O8Quvv6Zg5558xOCzuWo4v0z6P+v3MmcoyIQ0yl9PGuM/a4vGwgR2bXseMPw4rKs//6fNZ+2Yw8Oakr+oRTHltWM+MF+4rDmLzDqk8pPVBPqrjT3CU793RShjpnrqy+XneNvz48Qf++OMP/Pnnn203IcnZ3oNryCqB73HW/QM34Kon5B94Gu4YdP/d8D3M9uw897XwO+L0e4Ofd+0ijaYv1NRdXu/b+DuAdai8A3xZV3SIN9SK947xtvDiV05Uv7NmEvF51PczZ/m9us7yv5dKc7qnwUf0Uj13aJMAUKrBx2jcRv6jf+DvCdPeozi4kZoJ9W1wFhB7pcwZrOz/d8HZHPbfAF9Jv6+CGzsi7t+c3eVH7Gy6U/9ZXZGDhIIghC1j9gcSdYVi6WDbUXGhVi87imOH2AyX+Ln7bddiBYENedNWopZUHXClOk0l8HBw4IH0PgfTbnXMNmdSASjxnQiJ47OJ2HGfc+JgQhJHds7IGjCwTmGlr6x61XPJyX7KxdZISVa9qvOrRb6bIRHQkAi6ZUPLK+VgIa+0UYeideDpdzRncTl4xX+9EJxaIOIoO0rZse+80+MofPn2ljSwIcfryDEmKbW1x7wCi4SOEFolUGYndwaE9gn2grxSCg51wgHIHXOII12CEdWRbfoXaDshqkMaeqSP4QEBDTLEfOmdiPNAhE0fOWE1/zAGyuiotfV1/Q43huqumT79TKFT5+lMHvAFvbmnSTG8Gxi5jbdM4MLSAmMwwLfHBods0CdypNudEDbg4i+evmtARnmj9nr8ozZ55XoVgIiU8WqWqnx2ZUc8qOl5jMwn6gjH/n2TOVfmo7iMOPjm27nCK8I/GnPd7xN8bdk2Hzv+CwdZF+PbP1N2T6nNWWNgyLRjkOUAQPWi7MfjgcfjUXlAVwfV5atAHe6UesfRWb8+A6f9bXlvkX/Ka4u8z8Kqzz1c1VcGXm0JfImdNXWnL55VqL9DEb8qB67I3Lt8Ou2DL+D3u3BVhl2BM9q94hBtWcn9jsuO2Hpd/tfw4BX58I66Z2U8y1srjK7iW0PVT/AQ2wixzoBubjL1JVQ9/B1gHTxWl/MkvUrj2bwf6ZbPQuTAmS1e8PneUffV938n58tIK/18vg1qZ9zt9yt1en3zWV+OL6/lV7vMy/P27qTE6Zu2AEbG2qS8aMGqzT8tvyF6f/4VYc76chw8vDLWllWs+ihyft8Yx+/WM57REb4L3tnWsCRjY3bjzSYxtu+07IXfZvVb8/o5qr283idnPLTyE8w+bbrZWBkRQbMV0xqP6DvrDPM6vppP2Wy6Pgfa36/o3ZrvmTx34faOiCuTz8pAihxhM1g5NaO0lin7PFRtYOu083/WmccX9oLPpyEaAgq+HHWmWOdfPYfeOQI93roG3Tv2+kHhFYFcgw3ZXH7RKQit5XLU0Y798yf2z5/4/PmX3BOxoxyfoGOXNuuZ8weAhFIIOcslzQfJ0R4AcmJHe3mAtg+khxx3VHYAesExmT8DhYMQ1cl/7KAiOyJIAhwp48f2gbx9YMsbUgKO4xNM5Aw9JgdJt/9qHaWWte8Ht3c/5LzyjA+hXeuXzH0s9C96KfXOAQwqPwXHTz66SHDlY6aUX5gWj+2BR37wUTwp8X0TEpBgB9qBJG3XvsoJ7GDLGY/8ARBQ9k8OchDvhNj3A/txYFdeRTs5leml/aL3cez8efB9IBpI4UCU4K9n84gz/Dj2cFxZ57blX6+Uese3hWjMRYZN952IHf3OYLS4rEAvs/UBCIurbw/vdImDEDr5UzI7FyQQse+73M1wDMGblBJk4z8fjUYkvCW7UhyOSnNPMwuRHFJ66p/Knm3b+LgxTt1klTv+duVkHmk7l+Or+cEbyL6cKK/nk9YSqFDsDK96mXhyil4VQz3f2rbbZ3dhxl9Av2PCHq9k2zgcgdbx5ahs+fSzfmMZk0Db8GoKfsxtcneD3qmzopHmsWOPSqn3HXVtIKqykICAZjynbh8P/PHHn/j3v/4fkB8A8W4xux2eat/q3wbz4vuBjEXxD0g//EOPd8E7nYz/AIMXFeMc1s0+/8A3Qp2TgNtytc2lepyqvePJ2AKLMlKKd9k+C7ccKb8BeHv0qoPiGUfGCq74Hf474J7Db+CnJ2lxNdeM1lf7IE5ndYSv60v1S/qn79wR8U74O8iH5yDuiS+p6c1y6P8KfBfdrgYg9NkyWDJkuFbvNAgB9aOOwdd/eOo9tsjlQITvJK+UzNLxpDhnsGci9z7vGVMSUC/mPPuruFGtMFR8vZPS0sI7Zq85Ti8GacjSzHrbyCer6KuTlfGVI4WKOk7bZbWsvJD831Zsa37IER26lZAJm5FSaXWUAkp6dIkNhVSMURQn3YlxHNVZzvnY4ZVTrheegmAceFyiOhyz3LGQNNpJqTqG9RJxpI13HsjCpxbIUH+WOJr98VjVeNlrMKe2tXW6GDMb8vaoZaYkl1UnOUaJ+PLt6qiDOvH5+BzKfLFsvQRW+KIoXUlpKUJR+qdUnhFnut0NUe8jkECE3jcg15crk5TCfbVyyJ45mSOHbi8PRtnhywZMPzuHra3L5x3kE9oYuO5YR6jA1/JTQpJ+yDmHOyLO8O3kRpnLUCtbvGPYyz373cqfGjwVhY/gaEXX6dPT6bwPr9LBl+/LWeEWzUNGMqIaNp2TOi53Fuzuy4+dVZ7no0DRqlz/LgqSrcbjrA0epwEHTaP/1GmP+nlGghksM/u7KGa4JZGzjfzXHQg6Fi09tu2Bx+MDhx7GRLY37TzD8j+yKc90jhn9I7iqt1ytM3hzqfxVGVfH9Z06ZuOkey7DLihl9uIl/J41Bu7077P66g1shrpm8P24vQ5+TFVcu6b2TiiiIUFQxshTV8fDis7rPljPSf8NcNaOV9+/gsMzcmtm68HskK4Tlue56NGFOeIOjmoT2LJnbfE4zOCd8sDP87N5/yvh7nww80sA2p2v47+WIX1tFSexJZ7lnRXv3Q1CDGUE+u1dXF6dtz3d7vBZXKYZwFUfjvOrBfHcnHotz935/ZlyLs+BcKNgls+kP1NNL+ujK9/xzbExk43vktNfIetmOK/G0sp+tOXcmZ+ncgSB3L+op65wWNnDK18AccEdXvYzrGuK4bqu4TmdByH+W3S/Mzgb38+MlVs7ItQ59ix4JfDKykrPbCuBEzElFcKhR0tQW23sV2cPCqp6Z4xjb9UWAPXCY7sS+ZJziNaOx47mJ7Lct4VX9R/Yy479+MRxyN0Q+0+U/RNEBwiltZe6wuROAZ2uklzXlvhqhrwBYNrStqGkhJQ2IBW+RFluoe7akzPSIY7wwkGCff9ZnfxAwuPjB7LcC5GQ+AgnFAlgyEpaEKjwOeE588qmx2Pj9wX4/ORjk3a5hPmRm3NfIhHVQUZU6l0gfOG43GOh92PQwXdBHAf24yc75PLGR4ZsH/xdj2LKWwtO6cWueQNyxkZ8aThlDvLkLLjLjoiCXI+rOo6Cz89PHPsnPj8/6yp6It2RQny5hJ5YJYGmo+z12CiSeyyI+I6Lox5TVZomVruc/1U+jyaimQM8undhxvOWT/3zbkzpn8PB4rcOlkjbzPj0MgVo8uA4ji6oEJVZSgGOo8kizUvFhnWmOHFwrAhPlrpDwt6ZYOu3494GFmz6mRN8cGajdHXojojIeW7xnvaPgbM0M6f/cxP5uSLWvzcXuy9wsfc++F0os8CXPSpL09lx4BUuvyNiRs+oHZr3TBmagtk1x0pVa1/dUyY2rEjX+l+ubdqQJcgc4T7yRa6GsW1/pZdr50gvwnEQygHkvOGPP/7AXzvvDNMZiSr2rTWAsLfYn7+ve/Yf+AeeBy+f/4Gvgn9o/HcGO1eqTcS2htgPSXYtI0NdkTXG9Y04/jOW3wszmrZuVR3oK+neu3o7H8Wb+vvdDrBXWP8qLvN0z/uXFrXhy2X4bzR0b/PDjeRvbeakW77KofvO4PGLmIRPvc28cnif2eBX4VlaXLW/7y4+XNmTUR1XAx6zdzP7+7Z9/RuB9929sw1fRY+nd0QAz0U+bAffIdLZ4NPfHs8uH42O+plTxW7Tm0V6BicnmjNq5hC82kZLn5nzrDYqaC8Rr5TXo2Z0hbw6s9sfO0M1DmFXkxKAeleBOH9I0lHhIE2WHQNaDhE7r0DuL24wO/3rXQYHkDL0iCtFCXJMlu6k4DZxvpSS+NU3yLUT8tec8WRw8Gum66LpyiO6Mt7TSS7zpgKkzDGAnLE9NuT0qLsaeMWwBI9San/ab4kDVpSL7PbgVcapqn9tB4reU8FO63FHhOU5zdN/UsW/yEXkSo9Kh5QqDfSZDwB6nvPPvTNW03h4Ru+OHJSziaObPCpDn5d9xSEMsNPTOpMv53OTHhFJwOt8Uo4c3TO5YNPY/JZveCws0R1wPwsYR+20n5Fj3r6Pfq+CTHaczNOswZZv6WuDBLP0s7q83L+Ln6e1nwM8XX1w/srKkFQ9LD6iLVEIY4X6si0J7tADhh+7NlpZ4eqymLdxwLvvGiJNZgMwEvQ3AXqfswG4b0jd1dNecYRVnGoRbyjr4vO75dzJu9L5fhX48T7rtysy7Ktwew3c+J7WVb/1uS/S4+q7GU7UI/EPXIGqi1xfkEBOvp+NyZVTxurE/E7npyw1JPTnYN/Tl14BHstznevK+P0d5NPvBEP/D+9Xb6+XO0mFaB4k0QvGMpL7fm8OsuPkTFeYj7l7c8RVv8YzZfk2ND19lv9SJWLv94+T0ynvTpW2uKvzT0dzitNEOD5L86l9ELuTJkhcq+sKTkqmV+y4O/ZeJFe7/G9Sj87kNBkj5ayf/Kd+97byO3RdLWuGF79A23v+ZJ2Dryb4XOVl187FsTCMub6sVd3j8/fLxmdhJhsjvoj446os8b6rWZ5VXVfgViDCD4AzJ1VNJ6sWZ442BduYM4fOStjbP77ct7BuaZ6vHIl2IkdwtFIkCPiMUb2oWM7Jv8i3io8/P18deO2c/izUPFwBPMAIrW1F21g+QceBY//ELivsj30HHQUoxEdW1fYmYJNAQE5IieSuiCKrf4U6CUg58y6FxPcjoOyglIHMRy1x4ECOBirqDFeHU6lHMfHq/c+2Uh8E2ncUAsqWQSnzvQ3gledE4M/Cq9gTCDkB5XiAPj7kHgR+xzsAEnNfUsdYRsobkDYOerROgN65ARCOnXcT8G6NXe6nIGwbt/fj4wcejw98/PhTVlR9MM4E5I2QW6fIEUOslKYE/PjxMNUyrkBbif35+ReO/Sd2ucfj8/MnyrHj2GUVV7YCiHmNDtl9IkdvFel3vhPiwHH8rCvyAXPnSWEDLMvq5W1rh8n78aj4+ueze1Ci8RUFLWxdM/CryP1dFNE4tvVpeo+n3SE12xFRy8JIg5ngT0gsc4rs/gHavSPHUS/itvgrH/jJJcI9ieM4pbbLJzJAmGea0nfNxfMceNlrQfsAaLtQovya1vKJLYNEi5vln0240Y42+97yn+5aUdi2rRsXNr+9Q2U2Xvy8d9hdNQt+i+rx86+nje9/f8fLDDebZvbb57f96D+7+oR3dZxVnjXt0IB5G6/tqD3eQaTyczPB5M78A6ABVtm5R2+zLf6BqxD7Xv6BL4SrevjfE0xk9JfU/Q/8LnBXtMSOBar3c1U9Axrk1tu8AL0wt+kbX+tYsDiughFnef+Bu2C8gu8s9YqDZ+jf32Hy/B1w+FqgaRMXfZbqP5NCX0PoytB9dXzPZQrVT+p+9xDdoSHa/pP4AMko6TNHcK3/RR0n8uNVuy99r55xxebzv88c5hGcB0Veb/OdtthnZ+2alombHCfF2vumbwch/qZTqw8QvBq0msHKj3AFvmRHhH1PRPV+Bl+OhbPVXWf1eodP/V0/0QUiZk5Sg1EXeZvh3jsf5060VRnWabRypqnzkYJyNAjR/qSsoo5/XRE/Olz7C0hZKI/R6gNEJh0BSY74sDsr+I8DBjUQIc8U99oXKF2faLkkWxuoFD4Cqhx1NTqB5LJoCY7IRFYO4Mh8uTaV5lhG3W5tgluI+shPUuaOhaLGATvIrGO43g2RMuMuaZFSPWZJ+6Y6gyXoQ8QBuqL00ns7jh3l0Pst9noJcg0GkcHZCdeBB9wOGNi7LSDKQA3S9PxmRb6wnvlMJt94b0E0xizLevpfEY5WkPpxMoybGxNwKy9+7wMmKxnVv2tjgsci8xKVtQPay8EwcIPRDTtro5WbCamqm1dhJrP8pBb1edTHVJrx5x3S5+qgpdu8Dgt3JsYZb/mybIB4Vu9KYVz1/1mZlu4RrWdzbcRTUdkzXLhvxoUCHt9GI36u90t06ZIJJ8j8XOdRy++LgF9VMIE6V1/h7Kv6SwTPGkNndQY1Lcap9sTsd3tq667PLwScZnBW1jthJR+/snxgHEtnoFSY5Ts3CIFInq3zxON+wO1JnF6BM1zuwT0nwXsNrXisPFvHqwbbHXhGvvm8d9t5OqfdxOOZulZzcWcTAk1XH1aj27zAy56IFLnxBiwrjrOFBVzU6FCLvvfVv5fXrvLHFdzeXaepHbOkV0p4t9PG2yfzvrpf3krXvIwTXubyddlvm7f5M6LTjEd62td/fMknxL+2+/DqvGxqxYpX3wURP7fmXFjxHO0OoxfGSOJ6bZlRv830VaJ5X81saC9bWzqxIiZBkWUzbsvW0R9ymmPRN1fyvSs94cTvcrOe2aeFd8xdPIVTqH88Kyu/C7wfunvn7O+ZHz3ie5t/1bYr7Z7pKlfh9h0RdyrpGr3I652Y1hmxmmy9Q8Y68utKZ7uNKMAhFM5IchFyChlgdLikmg/WqT8ZPx5nXaGjK9b96t2OPjNHLPRS4mJWqhZ2ZMtuiP3zLxyfO8p+AMSO8ZR5pa9e/EwQZ1PmIMFBhz7sHVAk55XnBDo2lLIjpYxED44KEHhHwlFkviFAHOF6kbQeO1TbIRNTOT4BKtgPrgcloRBhrxct6+TFguUgQikZ+/5TaKGF6WrchO3Bq5pz/eMAgtKW8QAgOwr2z79wyGXXIMLj8QGgBSG27SF/fD/Etn3gIAm6aQCD18GjBgAoSXxC6pT2cLvkUuzjwOfP/8W+/8TnX/8f74j46y8p70AGr9rS9jFbUz26SWlMNXjBxzGBWtAmYks9JsqxnvCdfrKyVB2Msmp5E1paniSiys+NT+NxsxrzHuxZ+b6+hu8YOIgCCJ2cKGXQDIYyDd76F+JK4rQtBMptp4PSw+560jbZ+vR5tBNirKqtMrd5LW3GvP0xO7asK5O+L1u/azv8KnybTxL4AjtFQeVcpbnuLkuiCCHqJ8Whf2fv07jarrnDrvWLn9hT4t1E/p4Uy58pMYvZ/pop3oN8v9g3UZt8GfbP8l4U8OrmKioy3jeRFf0OF03b7R5JCXnbxjKJYIVN51YXWqaU8fH4wLZ9gFLCZzl4z0M37sj8a3/xkYJ/b1jhX8MM5l8Lv0Zp/r8KYsb+uvoX8uFZ2fF7wb1gxOt1/QO/GzzbK3YOIyIcYm/pPMUqhg9GADyHiEX0ohPiRqi34nrXEf6rHCW/NzTdsNpMp+lHeHdQokwdblTtxKvwf6fffTvfJ6e/a46cOT9XXfgup/i0jdRsqtuO61c0HxptuQiHlYN1Xfyd9N+pX/T9fer8/w3G9ztxuBOEiOA2tyXw/cALHP4bIAo0zN49O59d4dVn5OhTOyKA2FkRIVSdDpOJ9+rqvFkd+un/uveqjEyYb+gU0UlTSxDiPhLdtcWsaoyEa/0L2qBpziaW+h3SPGqOOS7L3sGgTnGePHg7sukHcZSlROx0BgAN5Ui5qrBzFfZuAj56KZXCoz4R6NBdCQJmdX7RVeH6H3EebkxB0d0WheQSVXXokrH662E5fNSTevoAIG+1bVmCETlnpJzq5at9wCdBgwb2joXEnlHe8ZD0yBDvrY9XV1RHtwQmKr6S/DjECX7scjTJzkcwHXx81iG7IXRHCMA0quuLTX8TNR4CUdcvJHdsWH6uZleyOxv8uO5XTPSfQv9JoC7iZ93uHo35aNwm825Wvn9uncZnY2cYb4h7suIcBCOiMqNxT6Q7ItruITL5ovpmARTFFeidwF4mt2d9yzSZVtv6Jw2/vSN7rkg/ObGbvrb0qFjbMS0t907rvt62ssgHZVZzy4ynIue8/rYBo1WwS8cn52vPIzzsWLBpZuPA5puB71/fDk+fOb8F87hv7xQLtwNC6wrwVBx0t5kGPqjOWxJEUZpqrfpRcXq/krmi5XthUX4jJFBlTUfJZcmr8X4XBj7u5uUb+Z5IO3s+DYDegBmNZqBz6au4RnXPyvCB/DMd/R10CcEqNXezLuz/Ne3vOSQuYhPlvlzPa3W/D94xtn4neIVve70k0kkBNfiG3hfDx+obT9NLdG6vT02wnjoKZs9X+te7neh34dm6Z9nuyMV+/PpdhGfQnwyw0sGegVi/mwchrtal+vOr+DUDwTyrfpFqeQ8i8u8gU+7CO3SjuzbSNVlxD7dBr7H/Bvid+uNe2RFh6p6Wj5mvTfOu2z4bt7ZsLmmuO83gKt2v6oRndLxC53fZJau56Q4+b8XF8uyNumc25tXxxXWe89pVW+EVuOofj+bIdwUjZuDLvMOLt3ZEKFwlRl35SxiUsCtw1XnUrWp273VdOtS5FXSY75yUxNVrHI8RnAVjZqD4HschdyX091VE7W548RjUexD0eZtEFKECEB/ts+8/ZUfEDhyc4PHYkNKGbXt0A/woAB+ZVMDHMamznOmXSB09GzIIdGSUtOHYP1Eoo1AGkt4rQaBC7PhPCcexg6jImd+6OlzOB5d7KAA+pTWXA/snM04B3/uwH22ldc4b8tbYtxgHbyLC9gGk7YHHI2N7fODx8QOPjw88Pj6wPR74+PjoVvFzG4G9/Kz9AiK+hDrxjopKX+JNHwnAsROwFaRUOU3ulNhxfP5E2XcJNBy1c7SvdBH+IYGKUv5CKQd+/ud/cey8K4PveJBz/jO7nbL0A4hkV4lxSBcCFcgOm0+Ugy/sVuOmOU35guwiwahtG7dCRI7tGXj+1fGofwCwbe2+hqjMzkh0MmPmFJ/JB308cw5bmWFxjEprgbokgZsTmYRervi6QDSdTPs+mtelR4/pLgvvFLc4AUkCiDHO9rv2TTRZeSN+BhaXqB7rfLoV0AZEno8KRMOtL1dpE+1CsG3xq/ptH8zuItHnmtYGN21/e9msvOZ3vkVtt7ByWkbPLa62nbqjI0pr21TfASzzZKdBJnthWAsUFzn2jdKGlHW8NIeADeCqrNZ22ftX9Nnj8cCff/6J//mf/8Fje3AfZp63UFc6LjyZ/2fhF9LkXF//r4SqY355gGpS/y+s+zVIGINoZ7z769v5j8T5/cHPfbqrmOiotgbqvX6psVVK0IVYnLe0hV4vwtr4b7wfpfFG/lVH1t9XNgDvn1B+zwnK9xHR0vVwucz7mfgf9TN4FJIjn94x2eq8X+W74FcH3L4KvrRNhNCeup793njqy78y1/d550GJ83wxDha+Xm9W38Z/C7zCm3fHK4lQXOWJbWTAE93rBv/NEC1Y8rS/Gpw4e/+srnE7EGEriSJAkUPSD7zZyswIbMNmjqrIQVa/i6CN7qmYBSHk5bAjwuYLcXTorbadWaflbPZuTrWo3Mgh6IQtkdy1QHxpruIPXdmf6vFE7ExCveSzQ6ujXXMQtz9xtpUCSgVAAdIh10IQwFc3swPW5kFT9jk7yfFBBYTEF1gnvkOhUHMqppS5Tyt9U5tCpGx2CqhjN3U7IlKWi+m8o11pSqWVmiC8kEw6Br0QPKUDx5EgLRfnY6lBpv34RJEjngiWn5O0mwMf+/HJRyrJ0VV6h4bygGw0aZ1jOoiI6t0DWn/FQx2HaE71LE7ByVqwAaKx07+Ld0FQh+P8SKBIZtTenSgfdsx6oYrFbg1N32hlGX4W2FgHJrv2TpQe6jMMZdngwyyAYr/7v2iSaLzWqrNJImP2LAhxRxGIFMA0WfXl5xbbtw0XCuVqO2IorjcKZK0+4z4gLJrewYpOnpdnfe15etYGm+aKYjWjQzTOeF7jYIPOA/a/Wg4C/bqbNwuQtvbbz7mm+bYPtm3Dx8cHUs517rH1eRdm/+XrYDbOfgWMdV8zdrwsH2Xo8xDqJsYguFL+avw8k+9OfTOdc1Z2C8zdw+HueL2SzuO+0q1fBm746LA66d/63t47Vp2wy8ouw3N8woLu/fz/Rqimzet8/mzaZ+mzcvV8Kc2kXrU1/DzfAmLvdUYpnZJ75vXQEdOxHG+31tQLnSBK/6vgDIe7cmqma462RyDH1cyf6vv129tot/Jj9LCWg++cMxbVz6Wtmcc1nbXznoV36lDW7uHf/PlqT6547O8Md2y6ru03d0TEaa/pKYMteHJHhMV/Jgu8fXcH7uhXI7/0PquTiqblWljZ/zNY+RjCut4wRK/LwRGI4gXlWm74/MQwvIRHkOSMdl8JMxqucIr8OlGQYlXnO3THCJ7aEXFWsXfyJQD5RQ6OnGL6/dC7AxaCQfGYlWvP/a53RHCC8/VZJx00o4v/rmXpCls5zUf9N1wGIJcxj6tYuQBNRKCDndokfzjaStyH3JOwPR5IOeEo3M6yy4qhXRgU7NgvZRc1XVb/psShADk+qZSCRAev3k87gB2q2FMmJGRY53wpfJQTO/M5CLHvsvJ/YzqwM54DEQB4J4YckcTH/DRXVEoJWcqjIkc4CS23bcPjsWF7yJ0O21bvNbC80/5652CC3MWgl2ADQMogOkAEwfsn+1oSIJTBvvMRS//5X77zQXdZ6G4MJA7Q6A6Rn3/9/+qF1USF25iBvEmUqPZrQckAUuGACsBBoOPAsfO9Fvu+Y99lNwQVPLKu/JJPDUQQEI+Mnn8tv3a0ScwDQD8mI/6vLBoIUTsWjuMQ/8ZcaliHqXdY87PzduhnvQjcZdSy6i6DiSzw45v8siHXRnuHQvQX3TPgaRvtiIic572BME5SHpfI2I3kbgQ+v8dDaZzM3SyD0xt93/p2RDsibDtaOSJ7qO1K8eX5P4t3RM8z/o5461SxexJWY8q3aYarfeZ3aXQ7azQYYdrn72mJacjZeedeht10RdR60fOKpduPHx/497//jcfjAQ6ECDpgXshOevGsEI+//ztw32H71kCKdpJ/BuC/tV/+z3Lc/9mG/2r473CAfSfU+YuKmatYF855a07pOpd9HY1jm7GvczXHz2zcd8Ndx9bfAajSeb0j1dqWwJvp+wV99Q88D7+ar0XF/nZ4NZh9R9cO5R3Rbf3hrr76nQ7iVf0VD4POO8Peb9fjvwHuyNbOZnR5/HzaFroofZ/j9N8liP/d8N3tvr8jwvxrI+dE1BQ44tXZnV7lxsez0aTB6WecKPxOh7YpX+1iUmHfr8CyOFUnljrmMDL9NehXz3pnoj0v3jpkOjzqnQmprtaveCQIjqiNYzzVUWPoQ4QCvQD2gZSA9Hggbxlpy7LyX1bfJ+1H6L3HQzu4ugIidUbxpdhZdhsQCnQzgaGG+dECEqR3IMgfQCg5SeAq104jbTSJo5/0eBBDXwgtUkbKmxzftMllqQ/ktAHglbXk+rT2CYmjU/iFu0S4ILV28OXcCQTjmE9CYwlE8O6GHaXsckQSD4hCWQILHIgoZa/BB3Xqc3P1Do92FAlJAAjgAE0Cd1kNYOhdIKXtkKgMow7CekyPaj9VWjcQb1/bJUK1TN6akerF6RbOHKEwPNrYQQYmd0rjm8ih5erSZiAx7wnBANzbVYBKYUsD/ofcI+WdhjdVmtff6HcphLRISbrFjfsTUF61x5FF2ty67a8oaCrHxjcx/mr0A8qHbgqRzNoUu9fJlaLjU0Wj/Layr3Wk8OnEIb/iURsUankGjIcybYC45WGkorES9ZHHK1KwonxXAuJV8VOsbH2pP8Kq1kNM4Tq0oIEw4XGAA9NG+RNhbHAi6D05gOtXmVNULjUfUAbShrQ9TPBKJyaRE5HoAlaLpbp6r8LZuLRBmGkZl2tDPLgulqfG4S3Ve5Ah83FxDqmNzx6xyj93aL8KqK1wvFrHO423vs478vVeG2fvo9VOq/RX+PYckmHXq06JmnNsecWFjKCyxfcy5JVgb5Ryqe83Bn6i5PtJ+rpvpvfVdX001818paMzeqTPO8bQ0M0etxjB9v7sndhCVYdQXUR3QlRdX3XiBF7x+5y76CpF2pj19fS/++b18nre9BSq0Su9ZwV3+/11OR/b6o0vI120yTTV2dr3vqy+TuWF9dyifXU2z5qb+BxmMagedJffamptyxWaL5Kc5a5q2M186zJVrwUWoz9Ib8dAdORITw6rGz4js66Mm9V8NDil9bl1mFTbBWLUIOzTZGVWmo2TENvGszr/+ypS3wttrjVVWDsrqGModNKOWv7wLnUf6o+wxfjR69x+E9w0/XVn66B+mAeDXKExn9qBVd/q7ENJGaIS80to9PjndZ62p7sMX54AJUDqSNEjMD9nwy8kjD6n0JG44dG3O/VsRy2tkQytriUTqaJqbJoljuO4nQ6Ry/Cc/nEVPO39ol6f7urC+ztwORCxXDtAqE4J6pxjbWoHmrCenR0+LT4Q7EVWA9tABJ9BPRIwCxZtJYQty/6Ss/ONA8o6a06hNpSPFlIy+NWqRe+GOA5Zwc808+dzqxO8SD5d/UwyWLJc4qnpqBRuJaH2xVEKDiooOaPkBx4fP7DlDY8fPzgQoZEG+v9AOID0CUo7jp3AmygIKHy+dxL6cTsAkLSDPgEipG0HHjuwbdBtHAlAu6RY7lKQnRPl53/4LoX9J0o5cBx/AQC2zA73nGUrSPXNE5A3ICXeNQEJLKAdi5RyRto2bB9/4PHjX/j48S98fPyJ7fEnUv4AYUOhhKPIynXpoyK0It6ewTti9HITSN0SmSnHgWP/bPyVeYcFIYOUB0H4/PyL7844foLKJwjMp8dBoHrRN4SPC4h2zpuYa3POUr+sA6d2/Aw7Yw/+A1COnyj7T67r2PmvrgIXh17O7NTr+FHKPIR11duozGv/ZNcFJd0xlCAXV0CdmABOVoQnU6TQQMZD0ns5dE5O1I2fyMEkp/cibXqHSrvjYLaq3f55HIvKj2Qu102QnqOqvHDeg3en6LiUS8EJhJLKUKcg1qbq3KTjbDeDbbvFuRwHyn7UtEnwzs6B3jvE9XcfJI2UaO+MjuXfMINrE8M0tY1bfEdIn8uqDKn3ExRUWluoOjkAFDIPUlMIRJ9YGdRKv7ozzeBZhB87JV12F5VCSOkw/G8VLv3s25wSHz9k30XjxoPdwad57W4bC0Rm3ZLwtj4TCvFf0SPtvCKiQYiMnHmuLzsfNWc4WGS+Om8sT3MpdWeE3O2TwCKWSgFywra1vEQZoAxKD9DjB9LHB7aPB46joJRPvidH+oODJBUL/iSg66QArqhLr6jrr5Uz6ir3a7ymwJKzgZIbs7eBvFHdvngFd+ZMX71/RtH9amBKl6Cf7zgIXofIgFilfRkSj1lT6tWMIotFoCM2XatPLvKK3KluhkMAqyL7HKOsvQd3kZ8R4W6d1iqb4WD1hl6OEPk5/n2wLPYFfiXS3dd6J91R77pD2pCwIaUDKe9yvKzq6FsVkMl4wM4wuUoeO9fyeMyudHGgXGr6F3XKLwIbaAjeXpJfqpupk9/kXuWalNX0GtYhyzy90fNBQW3eQ16TtjY/s6jhHbNMWIab0odYiXVw3hynfRDCPncIuPTzcvrd3EpqDXIYn+JlmM2rZ4seVkGIS4sWUvNcJRg5ZGRyL5FSl7em64oP6qJeyqv+nHxStQ9pnJZ7vJu9VUslk3HEdmZO9joktfbq4lrA9H2kQ0T4EdVggLdzQiD+h+p3GRBOBVixfp1LiaovaIXpZec8pFxfRkfPZNLdnycan2vBhmYu7Vq2zvX58/amoLagLTT72QZ+DSYP/D3WqW2ctyuYp2RBd686vWd+/oqFU3cWbZ3ZGF8aiOgvkxwHjAYfOidLVE7QAO+Y8c/sO+9IjB1KZtJSgyeYEGzrIpye257SlEaWO72iOThpg7Y3h6QJKgTtVSdPW7Wq6UuQFkg5110LOWdseQNKAqnTVPMWLQe1q4fJT5RzPqbDOOtsm1Lv1GhCjKCKpDrDa95kJ/1+oiUCkqMD6YQptNAjl7bHg4+fqndBKG6FDYwixxvZo6LKwRdq22Necmt/xVdxb42CzuR6NBOZ9vWCiGD7tXEK1TboXQrqqE/FTiKNz+rEjohH7OQ6TrCenzqnt0tT+9t0JFUeoL6XgnIbTCYNx6trCeLHCercWh2fgdL61Hi2DjF2d7bf0q+9vGsrTZZGRErQlR0pxcqTracri0ywt9aLzjm+UtQbb0z63gVD9P0of7zDum+3Ve6aETgGWmyZM7yp8npqY87Q3st8Lbu+C/p8lKNznml4GDD07ucWuABEXLc3lvz3MwUhyuth4PcXFBgim73thLB1+YsLTW75P1DY0Ct40msSDNrkXh97n08v35ZjWh/P2n1DFqxovIILavO0njNZNa2764crfT6vx4/N2VhtuCanfPfz3BUZ/Iwi+0r+M/ljYZ5mxh9axy2U3gqzPlyluV44HIutHTP9XNZlmRt603nhBLUTHFTW3IHB3pikm3JJqOecwziPXXcorHWw0Y3QP5/99nVcx2GK9YlT7xnoF4Oo6tB6vtcX1/pm03Wvc02U7lz+nZfSbKmF3lTH9HWavkt2XpnHnp1Tn4Fh/lI5NfDzyXyu9pkKviuourHb1JLnVpamaFKhxtP3ejAY/3O1oq87kPvw9gquzT9jTSNuvtwzX5KmUfuj1p9WFtcCK2cnreqdPetxmvR/6j6a7u108H4e6/MaLCbPY+iSVVOxq7jyWJqU69VubWIdBo5vajsTEAi/NeqeNhHJL8xN1l717ywmVqb2Tu243K+AWGJR+I7fq78hyRzGyF9xKsfvUvs3mluo+zB8et22CWGR5TVKn8uRW8U82e9L/8dF+Aqe8/LqLAjxjN/8qTsivJPkzHnSVkaeC+9VnbM/X8cVg0vzeDyjdFcN5yGdczbZ8+hXuOtq5qJHFZVxlaydEDNQ1+LpJcX+LHotc9syto3viNjyBuSEQgn7zoZNOXinyWGPjUp6VBLPIqoD8zE9vPsDstuhlMJH5ICMuGILgHHTwEPhS6hLqe1DbZOncFF/NR9HVGxdnDhnIOWMHx8/8OPjBz4+/sD2+Ggrw8sBQkI5EjIBB4CUUz0S6Sif2I9P/PzJdznYvmAlpgkEIuI9CnI8Ca/0TUjbA3n7kLabAIsqFgFvWgfOVg9RbyusSyEgixElq6VomHQI7XJqqnV6vgoDeY6vurPhtXSDa+ikFhxs/d5BuhRetqxAdng8Wr/IMVPmN999MY7/6Hskk85Ax/EMV8VN/6L3ACsHfCharNhG9cLIEK/cdzQJyrLp7srdcYV+zw+eL1Zy1dYfyUFg5MGOn24Yr3edaxGvrfpZEoRprswZ/hikq/nsp5XxUxDDa6lwavmmntq/k7pb8c1yauds2/RtZ1YGOX5p9OM7RHhXRd4e+Pj4wOPxmMqkZuC833Hxq+F1hXKw+L4JqDNcv8oY+wd+F+j7+7ur/nXwvZWfGYC/Hn6VvDmHYS43njLdAc9/zcF0x/j/3UEdsb+q7r8HJFyMKggtU927cuZw9t9naZ6Fvw+Nfw10cjNFx8l8P5wGIyZ5nnVy/i5wOofZNp4lJfOZEO+CpmeCc+fw+nz8PqzOStEgRFtMKX68i87l98L5Irt/YA3v6i/rizyTQ1fl1bPz2fUdEcaJCcyDEFE+7xzzTsHZZB05d7wjcOVsipxZ+t0S9mxFSVReVKYvWzJ1eEdOTE+jEZ+YJp3qRBTSJyU9+oOQs6wyrZcA26CAOLPl/gatISV2lrJPVZw/GhXQ9pJrv+JFPAuoH4rqnRDF3JHR34vgm26NB6K+neqYzJkz5qQO4K3u+khaRikoOJBKhhychVQSjvKJUgr2/SeOfcdR+Pgldpmh7sDgY4I8r6c6G+ocSHLUFUHaJu3KEpzRAEHUl3yEEv+qjjbjbON8EpQpeoRJC3h0DmqY48VS45TRCVyq09Arzpb+0fiu76TdKye9rdvWRcInkfSYjekuYCfBiOqIBxuX6uTtHKpGgEfttHjOaOFp4tPYgMAM/LE6pw5i4XM7vvWZDXzMZFkkx1by2uazO7j6gIKmabpjr+/rj17h4mqZsSPesg7qNg5a+mGrsAGla9Tm2u5UkQjbPZurbD/XNJX3o8uy5477mSIRjZtVf8540JcfcZe+V16a8Xptp8WLEPRZb+ClNO4Y0Z1iJqM4gwy9obIrcRBi27rx1Nr8XkXMQsMXU4f6TI7chVeU8XXe+/g0nSWw5xbyskun/1p2MXmfodcrNLoDs3H5DPyOTuMrdLwif7r0LeNzOOgW9qDOK3PUrOxVWzv97ZvgGj4xxPRou1y/cnyMdd9zoLwDt1do59OWosec6o5UOwe9nx/egfsVO/Qd+KzqWOWf6ZOzefUM3snPV8eWeRLma+NA0iSbel5XRJsrNsgSZnPvN8iBryyrqh9Orj2ja4U2tj4zummMx3voeNbPKydwaBOJkRVx7CsYWz13Blfn1rD8Rfu8nULOkLxkGyfZoaSfLpHKesDRqdNzVXM90Wu7Z6u0NsWIUzv4XVLelZWBn2ya1DqRQdBz1WbO5ZUNvaozKuMZx/RUPtR/ruN0Vu7K5/w+OXBZPY7rvSl6n6F3xAf2nX82q+9Zmj29I8I6QGaMGzl3PNL+98o5YB1x1vnzzCSpdUXOu7vEnLVDn9mz8/U8eeVMi8MqKAKMTip5zMIWLtghdeqK/m3LICrspBeHN6+iP1CILzouR0HZZSeFVLVtGxIgq/WpBhAK9OJRwko6EKGuuj8OvrT52Hcc+8G0OLh+Foyx07zRGHyU0n4gIaFsOzah1ybO2EfmS6lz2hotpZ18JiDfxaFnCx7lE0cp+PzrPziOA/u+SxrtQ3UwFsfnOosJj2tnSF2A3CFQ9tou37eH0k2cainrpdRCN7Ir34GcE/hOjIKSEuhIdTeJ3h9SCjv7UlKHXrtvxI4hvV8Fx3hW4cwZG/ev7NZIGMbl1Fll8OA2coPXnNTjl3PmAFvmuje9LwXtnpVZwNLKGHVe+1X//ru/18aXq3WejeMaQIFTwmbj3vVDrdMY0n3wo9+FFdW/cvDMAhH6F8tLRTN1fzYY0eqUcRHQUM/zrUKtcoRNFxsRlvZR++ouM0XzQvuVBrN0JI33/OMd51F50Vzn+ckrCKs/X9fMwPFlA/GYm841s3cAdEdErTexs0yPqkoiV2162xelFN7RJOP54+MDH49HHdvjmPv9nL2/A3ydO+Ja5VMDzfH87+is/weeAZXX35t1WuSbDMh/4C58QWe+Eaq+qfOR6E05mPf/gesQyfLfYQwuVJiXIQHIqXd7flebv1r7edWx/Sthpv/3OumccjOH3FfBzEn/nTjcgcs4nTDnzNaaOYtDXOriVWsvat0t9KC+D6nkHqKmtntAUz34rN5393vHTwTIbaodvSNb9G4ds++t/34/fgZimfE7jr3vgFVQ4gye5R3gRiDCOxfPnF32MwLvdLHPo++rPF8Bq3Z5x9HMgUQRzsZZFtFp6SRUYcseME6vTrridxbwXRDiswRRMY6+glJYFLIDWwICRS9Ntg5H/uSLRAHCgZIS9Bh0qk7H2jzBsTkeqRwoVOTi5p0vqC57rU+B73MYV3ZXWqIAJAER3XlAerGcBH2o1MBKLhmEHYQMPUIql61zBrcdEZ/C4+o0Q6Uzoe060DZpW5WmFVsheKGj7v5gT61xYEp7UONRuvvBOyQJ/RJwqs4+/ik08EfccGX1fgymZe/QtQ5ty2Or4IGmsc/48nR1gJeKdyzYdTNzG0ckgZNBPQgmyOrkz5l3Qchl3u0eD6VLP0btan7fxkgZ8u9nE1XvRJ8HFD3tVvKxkwvBOw82CFGd40E7onpsfRF9lHYAgmOErKJ3TZmzvBH1QRSwPpP3PpjjJ9GuL1Lj0at94SqrzxNrt0O6Fd1Xst3i6/tGy4wuou7wwZzXbM1XjYAmT7qHACRoIOWm1I4rMJXAZzPDs8rDPmDV8Ms5dzsiRrySryIEMjjb8q/CHXn4jvLeB6+5KSJ0mBev5o1p/t+s4K8o/h3tf8UZODX2L5ShZw4/BcmpON2axjQyouPBtMBvJW+vwqr93Orr89OdsqN0V/v3mXZfnWfbHL4u8x1y7h1jZbRXm83EOnKqE9Mwh4VlzdoF826cm9457D1drvDzK46lZ9O/a677FXPHVBcSHmk93d6fOW/+HnOgHQuvwbvaeUfXOhsbqb1Y5n1nYHKmm0dg+eiqM/AlXC/6iG/pEvXLOV7evp/RaN7G0W7xduqKlsP8fdZMtWF4Iolxu0Irk6XOSR1GxqYcMtO0ipmPoHv+wo6IlZ18Lu+bP+uqfd/VPe53CepYP58FXq7A8/PWrWxBxej57gJer8yxZ/Jn9eyZfgVuBCKsg+WssjMhcuYki8q+Oiii9M8K6mfL6BxIGNurztT6/YIzFMQrMApJOKIKL3aeF2pBBADtngaStASo8x6Euir52HeUsmP/lICEOLVzeohDiOvdcpJ6MnAcyGSEsejyclIO/wEVn3J84jh27J9/4dh3PgbpOHCUHSS7B5CATY6NiicwMYAguxvkfoeUM1AOMVCzXDjNTvgi9CJkHIX7Qi8+rYEIodvn50/pt63SW49j0rssrDLK7RUHsIaIiOSIqwPl2FEODkakmsefLY96MThAHFeAHVv8x4uEqV9vRsRGeNGAx9EZShzQ8WexC456f4gyhuM9y8NnwDzOmNnjmTrerWkPSWfymr8V1AmEGRLCmBBfpvRn7/z3R6FZAatl6rPhEnkB7wT1NNLy9C+638C24YrhbpWx5J5Z5/AQ+DCTle8D3+5Zff69758znogCMX07EfLHLHgzlE3ut6tv1seR4hHlXQJRlU1Wttffwbw4KzOaIz3d7WcpZdiVo59XDZao/qTtcmX5+jg91f4joronrt0LlNCEXc3Zj3dAN4DVpF2b5Pe2bfjx4wcej8cwRiU1gJP++lvD7+asSJb9p3CHDa/OMX8feMEh/zeFZjQ/2Y+Ekak6Eq7e/Uop8Kv7+b9d/p3D1TnPzpX+fq2Us6HiWXA7XgggtbjvUUG/qr++n1evOob+fmD0Jqj4uhYg/Af+gTPwTsArwa1XuO1LJNLFQu248XZblO6KrjjL/7uNyX620IW2VH9fzXupLktX0n8avZ+5q/Bqve6J2ND9+yt1cR++D5/vtjtSeiUg8Xqg4emaA3/E2dz+DG4vBSI8zATGFaUkckLN6jsLQNyJEK0cbCsB5p2ovi2D41DKzzkPDmDf9vpXRDwVe4xNWy1vnTJJxjev8Mk1OMBXHpj8eiZ4UaegBh9kpTCXgpR4y3LOvGoo16OZOAiRkuxEgF1RLY5wIkDufqBSeAfELjshxEFfd1/Ierp6cW/ST0MLNR6KNDI1+pTjQEm7kJSAjYOuh9yDcUg794PvwUhyzMfj8eAdI2j0bH+o9OOvqfaZOstSZrpyGYyv3q9BNjhgLuHW/vVO79qPQsJC7cixJFEnrv6o28pJA0+VZ6T9ExvIOgMrj8K0sXMgrsZ5GsrXur2M8OMncoCfje06iSa+CyLnXINJFtqdEELD4EghW/6VgMDMOR45+iOn+FJOGjKSePhI+bvHCPqwK0/GiQ9+dAqOU+w8XjPZ53nzVPYHNNVU1jUX8Yfmi+g2VRyC/rS496g52hFLLXWyR4GmGZDUXfGbBNw8eB66o1BbmimP26DFrP2z9xrcqtI66A+tswXywDmsmKoyK2qLKLparr27Ayw3kXWnh8ufgJQztu2Bj48f2PJWleW+b6/1+3fAK3V9hUJpnSS38l1ox7PormTNM3g8U/eVel7pD56m/m87h58BT/LLNFQ9uHt0bgz5eXT67hyBCyh+vcF4tY5ncDnL096vpc6duq/Yi/7Zyn60zzudUPN1PNAUM5f7RVzXNusrcCX/s2LpHfz7He17T9k3AsnVsRfPXzM/xDU8XoczG+Td8F31RHXeaWtNMdHDr5b1THuv6VdjEKLazSl1OwAj2+4KroNNEPgMXuvPGJczel+xoZ4JRnhaznaWn+H6Toj8ILN5a8DFvH5q7p/siLjKQ6vFdas5mhNRxd/T4Bz/1/sk8kt9F5zZPpd11qDMZ+XVlfwRX57pPXfp+1QgYgZXnHtniNr3szqtUOrL1jWa9/GPnHZXnEYzPCNmr842oqrAzAYuSZr66ZzW/JgNMXUsZf2WExLxzgICAeK0PsoOFC6L4xGEUnZTNpBkx0VOG1JO2DbZQSAXXvM5OAnpOFo7sjUCChIVvky5cMDh2D+xf8rfsaPs9lgmkiCEoU/qiME7Hrip/Egugi7HAQDYCcib0IIS0pZQ0o6DCPtR+G/feZXvJgGIHz+Qtw1pE0ckFfHBMw+l1K+wTxqzFud/KXxnQynKIwml7HIPCLex7VLg8qxDkf+OqscyX9h+5fKTnF3AOz0OaASpXbrXjkyrihkXGPKV/UwAH3FUMyl9V+Ncg1V9FxEwOAv9+PHOTntXitIgkhXV+SpBCO94T7U8EhqSofF4j0yk1ETjeOao0nYmoF4Ubf/OyqwBJmu7E/F9F9Wutwa+9rPweOKx3i5nN870hdz07Zg9179IYVOF2D1stEqpi4WR+ax/M7kY4DGkMfX7fjzrP6K2ATYKfpwqgAKllGGnyir9Feerb6d3mkRlrZwvs7krmXy+DVqXnfuO44AeP2fnpdWsSJy48Yowu9QixwI2gZ7lCEHFMKXEgYgff2B7NBWlyZfvDTL8CqX1Nfh1zvC/G6X+gf8eeNYIero+vDbS/p6yZYav1Ve+sPaF3nLFVvM6qgbm+btTbcjqQy8i/g/8DWDs55Gn3q9/fKUM+HvKmC8G0UuvyIzvgMjvBGDQxavt4/E+acMqAFDhF/DIrN2zdNGiKgXrK4jyewf0VVvvK+GKr/P9leo/cbDrGTpYuq7ljfhnfIj/Rrtn5d+Rc+9o5+8Cd4IZ76rv3UEI4GYgwsPVCG/nJH0iWLFy9syclyvcnxU6Fp/ZUS4en1CIlraSfeoIM2XrxcK1Lj7DpwYgUJfvs4NTHbPQv5okiRNfgxHULs8ufNRPXSmcdFeEnse/iWOJgLTx0TiFkFCqY7rhuEs9Eog4dtl5cch9ERyE0Oh+yv2RRdqqIjsKirSDkyckvhkZBUdHu1IK6CG7A1BQyob9KDiOgn1vOzAyNoAeACXoxd3WOcc0bK5TPtJKdzvITpAEoLTASQIfFXXY+zZkp0nOGVQIR5HAySFOcuIVwXr8CKNA2HeqQQYW2kxL6I6Ywjsj9PLzY2/BJF3vbNmN+Spw6gIwbnNDy7kwCSd1c7xUGrJp0KN3NidD4ZUSNA1A1PHCA6EzFqkPioQObUObmWP8NG1q7Vo5tr180sBVzsrnZmV9MElHgYGUUg1CpL6z63vflkiu+kuep7t1TL0RTe2nf+8aVJXpWdqlUmbGW7dy0ToNdJdWi1mIPOzb4Z3+FhevXCnuhsW6NqjcXNHMtzeqcwanAYZJUKILOgT8GdK5jusCOuQyIQmkkqGBqbw3hgigNLZLhysRAQUYlw2kiqNeVh3R9VWb4Qq9O6wWym/0ParrK2HgL34aBppW+b8D1zMcvqMu//49dSuN8XSZdwKWIQY301+RN5fqvbOS+ARCuevr63Czc8m5I7qvDG9zwDzL13cNaFvmXSP0Xf19B27x0c322DQzOlrZ5/9Yh5ofI/leWLXFv/P6w+tsetUGvmI/R/Du8qIyn+PR6/4G/t7XP9aZpD9o2FH6O8J9vKj5Kg18p47g4SvHp5UfzzgaV+nP5oSrc8PMp1R/88NrCAd4VJsswPmZOYUmutDZvL6iR6RrL2lyhV8rfu77sNRylL/W/lzhfCb/vB0WtemdeiqZf54JPpz5hVbpyfy7KusMZn6GCIfIH3NlnM/mnlXedZnP61727bvk7+82X10ORERwNti9E21muEdKgVcgz/C4IkDfNaFFSm1UTzIOmq7unHlJfYCndfZ4p2ALRLQVqa1cdUAnXUPdn4cq74o4gviC6sJBDlmZngzONRAhR2NA7xzAhkSElDewN4k6Zx//8XEeRLzqv+zinJc/kt0QyeA19o2WU9rRTJIeJYOyHIEEAigjl4KU2NFfCCi04cgZx86BiEqLBLBj/wcSMrJ4K3OSM7CFkm3mKfxXgxHtLgZKvWNbAxFUCsrRLg+nQvV0WSKSQIRWpHTO2Dbm4+PgugrpSvhDztiiGtwoEhThuyg40GP5T+ZTM47GCS2lhE2DSBgdz9Ek5RWjmocmotZM8Nrf0rsctOCssZNAA2y5Hctk8Sh64zrcqjWK5UYULPAO98iBr2m79koauytBnforeWbLDdtjaGbr83dd2MCMxVGVKt+OoVsuyGw/ya8UyCtBCJVrqvfNjMFZXpVNXpEnkntc7B05EJ6jsXzftxEOIe8j6E9gwMdDpCTbcqIzOi2eER+vFEhvwHTBCNO+pRJM/E/BAbs5bEZHriOBkOrY7uoWZ0pHwwNIqc13HEaVsSGBiG3bOpxb++a219V5/qoyttIlrhro32FMm8qeKqczTK/Ug6Bd1H08i8pLcFfJvmuMzcuZt/cZxf9Z58+zuu8zODbj8jn6RYbk5XbX91cDEAGvvtjtr/SNlSF3yvFJ78ix+3XN0q6dI88Z6/dwuao/eDu0pk2y89nMX9N6F3Vfxz2mWXJz6yBSq1xZO+ZXfTWW+fzc913wuty7LvP4o9kQs3GSrE21wPHOOLviR+nS6/OTcpdjoiWaIHW9rL8DVBpP3s98ONfH2Btwm8yFnX5yk6dO03Hi27w6Azs2vM3wrI51NXBzBp3t3r1oMlf9E0EoYvGrh94ev3a8u/4OK7nX9ReAFZ936b3Ar5EPz9b5rH7s014eM/0/l3wdYwEX0l2Ar9DLPDzDU7cDEVcNGu+4ixRwfe+/R3nO6uNPTPPNHD3+cyY89HcUHFDwjsGoDi3LO6P0sxQJDlBhpzaVdseDOyol64XUCSilMXnd7VBK52DmP+PIFgVbJyN2iuukoW3RFdepOouQct1JUFJh55OWD2InfGkr+kvZa716rBKp800cyZU2AHTlvx6tcxxt5wO3+ZBgCEBUgLSBUuHgyOcncimgY0POmZ35pfVFlr8EqvUAqLsukvBRIbl3AtyWsu8oVHDsfLk2odFNnZ6F+Hggkns3AN5lQnZVL1D7M6cNOSc8Hhty3vB4bNzvx4HjIBz7Ab4XgumHojtjDtkJcWDf97pjRtvIjmr+3o4mUoOmd1DrVX0l4MUzWI3RyCF/12hFagEI6+S3RqX2Ra0D187894bpQD/n4PeXHPq0qzr0z8qHQU4AVQWyE4+VMSsce7KN8sfLL/s+aucsXc55UMKiQEQk76dHPU1wj9vaByIi3rG8tlIaZnOPLdt+agDFZEIx/RrV94qiF42vaB45q8ePPc+Xml9FsQZXlA8SeBxqmweNuJbdeLe6XajtslNnyhJX813p6u/xIOM0iPjlnfC3NMCJXnawjkXecF7Wb1eR+AXRCgfvNMp+Rzhr3+/A56HjZZEW+B0453W4T3t2JHxPXbP6f2+I7LV651GxOyKy21nKinLdkfwbjAuG/wZO//vATAZV3QPNZvod4RLf/r7oXwZv6/w+43UOM96KbI5f6eC9W/fvSvszvCI/oH56e/B9OAG8bdzgaO/Ls/wRVfsF+v2z+u/fKQjx3wLf1f5nF0PdhcuBiJVzSyH6fTWgMAtC3A1GRL9nzorIibMKQljn5WwldVdHSkMdZ0GIVv4hDnziBfneATS0ob0muQfiOA7osnMbiCji0KZSzFH0cpwP6fn1xvmnuNd6OUBBROiP7DA7LXZdoU/gI5r6IASoACnXNI1+xP9T6Y2HwSHHTn72uPOFqOokK3SAZCeH3vWgAZUMPY6o0UU6oLaBDRETwCkWlz1wtDb6k+BO5WgBHmrbeIlIVm6jGkJb3pC3DY/HB99jkX+ilITjKBLU2CVIUmr/HceBz/0TRXZ7WGdtzrn2u59MFapTXEiRcP38xMGBS6NsuAKrcV6DVBOHe+UL6K4RWcWQClKaByN8PZ63mtN07TDNOfPdJhNHcOTstW2z5aek9yr0QYgZ3hFukSzyzmfb3pWstndraFvPAh9RMMJ/H2RYkNaW6b/7QMQM/wiuOOE8zjOnWK3H5LvrEJ+1YTa3nvGjLTNqh4co0FS/m9+lFN4dZ+TkgBd/0QcT+1aPi2vjq+LoUhJFO/7WENLzUs6Tsp7UP3xZdwNT6vA4xW9VwE0e7PjhvIYuz4hTcp9xneO784sEz3B5Jf+7ghF3+/uddZ69fwdOrS7VDe/y9zg/zBwwU2OI6KkxXsuxSrOr6+kyXyznRo3wY+uVue9evWP+dxqs7xjH/lP1muM46s7JBNHjqv6i+SF65XuccXfnsJGX6rdpHc/gtarzbv5XcLgL130CwPNawLV6rvgZruLr05/5V74C2qKuGLevrt3WfVXf9b6VV+Cqb8s/fxd97gQhonnstr580q4h/QXwPDTLe8bNPldN7+R6l3bSrpGWCdbcXgUjNP+rwYgubzUfk7qiXGJYwe9eBTa0+31GD4/Xq7JrlvadARwW518jA1/VY17B6hXd6dl5+UyevVL3M+24vSPCntk8c6jr55lzSGFVBjB32ozPeuEUOXYiQWO/+9XH9rcqs/bTllGdwFr+DaPMOgD1YuV6HI8RVB5flWJEBHuhdfvjXRX7/olyfOL4/ORLnvlcITwem/TjDkDvo1BBluTuZgJlxrPIkUH19oJSZHcB59VARDmKkYFCJyJkEAr4GJVEfR9w+lQNhVkggvEtcsa+nHFUdIeEOuwTeOcGr+jNSQ0OAqjwvQpE9YLvQ1ZJlUPvt+A2lXo5tPwuR3suQRM+QSiJ0zzXzrKCM3Ks6kqsTXZE8Dug7ULhFdf7zn2TJKBz7J+8a0KCPSnB8J+hZUp1N8lXwMpZqmPpqjI/jvV+tZoF60wnE0wiELbUjnLxk6CXDSuj0TvVvWM+5+w383TpZ2BlRVL2kfFNJo2W49vQdvSMdTI90PgxeB/JLQt2zNn3tg86x3MAq2AHaDwmYAWRbL1jkGveWX9rv/r7N+7CygiaKbF364mCPat5bOXMU7mgF29nFwTraBbOtdSl4aBwL+N6fIlrST0v5SozBb9CbTcftZ1EY/1c5jsU6GfgHUbvP9DAyv3X1Pp/4Huh7g19Lrebn60j5kq+l0agk1n/wH8XePtzZbe5nGxLvkkOvWcu+nV8+h0O8K8BMc6Cp2HqS83kMgmxszqSW3edcVH67+yD37m3I/vMvot07Gdp97vw/WkbfsN57CrlXqEw+8XMGJ+pjurPIpOv5Rps3Mh2vhMguteGZ8pqDdXcFL5dZv12kHNIXoBYnv96+MdmeRWe2hGhv6PJchZM8DCbaO/ku1PGbOKKFdG+Pd552Y41QpOBqX5h17Y6T6pjBBgkYVBPPZqpFCS5lFoKCp3ZtZ3UHH1deXUF/c4ObLnYOKeNnfPbxvcjFA5a1H0MDlUqulugtUN/EwiHCaLwjgyqDnKQHp8jTi3SyArVdnF7Ui23tqFQ6FRLKcsdARkpczAim9AyQQIdgkNOeryI7twokpLPiC16/NXxyfjKeyql4k4ceZF+kiOaZHJKKcmlyjHvdviL06852nlHhA1aWIda0R0kcvn3LoEIXa2cU+4mVZ5QFe8RKr41V+ysDyFi4cRt8mPp6qoOqvyRxFGtx13FO4q6v5MJYBbE9GPbph3GlisvJb5MF4X5wqc/C3J0dS2x73Hm9Ambddxa+XSS3wZUVrKkCwwFxw4h6OcooBG3gWXG2tGU3KetI11aGeFle6RcRt9PCpWj287rXs1Ns7nIwyjz4jRnY87z45T3CaAaj5goVynVIwJt3V4Rbt9T11VNTsgv+c7TRAssFqIhONTqo6AmGHlWG9rhdj7WRnnYihrlgD53nNWVZZ1eUTkrIFfWHLtZATHO1+q+9vw2Tlfqvon3XWNull51lVtwQtJ7/b1+MC2Jlm+fghjvtmq8x8kownfoN9GTfDBi6pSj667iiX+iw+GOk+HaSOqDa/OS14bsHKWzURrLoFbufZ6Zjv8zXvXvL9R913Y8K8sHIqoe4wP8+i+dl/0UDZ/Ic1Li5Lutbz5/LUt+Addf5cht9c71+OfLBhotyQw13V1OUq3TRqodbB8FUiSQaQO/a/7L+IZvurJ84X6H21fwwTMLcaLPszLvyPV38Mk7ndaXyyCqPAarx8xofBuvYEyp/0bfvtkfqxav1jvomqTjj0Ap1Xvt+jSCFvW/FWY81en3tT97sjWb3OF11q7pXGj0KPs+KqO1wPjlOHvrFZuwt9NmI2/puxLeavPnpJBhrnEqqsPJCJ243CHfWMcgMwOqXfVHXX03yMZJ1mmJOjaNzI+a2tvj/tNlCNXw+7pW50M33R3y4oxmN2TM9R0RKVUmt3XI4Sj1P5gG6N8VBdiv5tRPzsD/FHH8+fPsmcFa2TMH4wxsWr/jIRUAlPiiZSK+t0FxSglb3pByxrZtzFcpG9mZOubXM0f1cuh6B4LsgPj83M1xSakK9yyrvGdCgujAUXbs+08cZeegwycHHviIp0Mc1wDSA9iAlB9IKfPF2UxV6J0OXM/BGMiKWagDiOTi5H0HHQfKzvcXFL2kWfoICUg5oR75I/caaJ9mZKS0MQ5pA8E4V/UC7aNUx79tL8cfCFkcWCkn5ATwEU3NaUcguZy7gLAj4wCKHDNTDiAlHOkv7neSoMfxKe1pvNWc++A0RDiOvQqStrW7Fxm67Vvx3z+Zh1Lm+yseP/7Etj2Q8gNAQgHTZz8+se8/sf/8D459x/HzLxAVgORYKAmCMD2AoxBSKnzx9pblxKuMBOt4ztXh1/FP5XuqfzrhcMDEDHqbSZiTgzzNWe15NOdcn4W7i5jzKq2REvKml3dvNVij6fn+jKMf48koKTI4rTzRwIHFUcuo/Ch1+MtxO1lg+jmlBDth2rI0SGTlUw2GVYOlgHT3TE6Vntb47QIC2p4tIymOJPK3XoISyzrbJ9kESCtfi6wtxLxNUl+uco37xesJPoChbR76Rz4Poc/HY+vy9yyTZKdTy8pluTbJX4d35dsG1pm9cuzP5gg/rm0wIgpm+ACIL8vi5NP4MXTFgRS987jwC54jD9I+akdTaF+3MaltzUhbRj1CzwQdiAg5Zdlvxv+1sbQhIUEOL+uUQl4/zddSq/zmu3q433PO2D5YHn7uB37+/In8n7/w+fkJOkobJspaRfuG5912vJnSUtvTP/eqniVj72yQ7+4ZyfxfZZZT9HlG7eeDVtuIQS00KZWoSxsr/dHDe8b9HbiuVv5NQY34eYILhTxL/xTmpTYaT+C7eieZT3re93DBSDk1Gp+p96S+q86xJg56eliDv18BGKdD937VIm8oRkeYRYpaP0f3uDwDPZ+O7ZuBmQXe4Oy761DgefETwH9A9BOlfCLTA1v6NzY8RH6bXc6UgFTQtq0GevC3guz8jr0yi+cx3OH1Z+BXBSG+B+yiPAa7IzRZXUF0jioJTsiiIzYBIA1e3HRos352LV2Yt9NzvnPnZy8DfVD6Gi4p/ln7pvXTSKP38eyZz2sIppijpaNAhmqSVr/0bdW21c8IsaWjVecUL0tS/aCAj8l0G51NYwNc7c/knmk/9hQJYWIvmZPBbWLTN1xX33fWpr3WUNuCQlTHdkXf2PyzIkNWrSLG8QHWvBdpAafyxfgwlfap0wOC+aevIHioz1+RLzMpFjx9cnhfCWCc7fbo3nlbM4l+Iimjvk42Y0fq1DcsQkKzOb/CFei6ECxjrI8hLuv62FC4HojonEOkPjOWnWjfJcGQ/c5k1nW8ndQrEUp1hvSO/obfzImjzyJnkQ1i8Cp08Kp6cVLz81Yur+7kFens4EsdnaQ2LR1EqEcuWcddKUWOMzo6x1l1nNhJa6Btu1PiOHbzyUcxtXNRCfW4opRaIEL7MSUQ2S2nBKCw0z8lZJ1hSPCXIEHRi7WPvdJQgwNKI1JnKXEQRp1CrQ/Y2aUDEYW4Dvkbgdsip0uJ45KQktmFUduBqjRSaeIiOwGofLXvn6afzfFA6VHLqvxFBMjlvboDJikN5LvFpRBf5L1tD3HyPrA9Pmrb1SlfA0fHzn14yGXVEohQMulaBJK+0Z0bja0tHdrKY9vm+l12sZDyd20MJs4ZoWPqL5JutOwnfzu2eie1mRiVb3JGMhcI+vzDDhmY8WHaZYNIthxgPD5oFjCN2lLTOaXLBku889+u/FYl0q860uCZVUyiulNOInd73L1Mm+HflWeOvenkpvTBzKnuy6tyzB2lZoMR5TikDzQoZBW+rlTTLg6SpUSDzlLHlPYl+AYCi3MULJi1I6LTECwIyhqMhoBmkSG1MqxsX0T863FbjT1Wpvl33flVVJGXo5HqkXIyPgxPDYJDxyNEAfO0HnTSBHWw6wVttliVl4rvtm2gBBzlwL4f2OU4wXCXTc2nMi5VmgGo8kz1tRqX6WgkCZye0cYqmiLeWuRoTN1zUr0lyf0vJmPHhbZcGggnO1Qs45vPgZ2TeV+111uKp4fIoQeYcd9eOPyuQ8THqzp/HQR67ZsCP1bN9TVczP0ePJa80uRIkyv3Dmb6LRyUTQg8XUTsWHL6AwL+qLLGp4ye9yX1dc/HSY/TrI2v8O3Y1hmMwY+v7f/ZHMnz4gGiT4AOtmOwIeMD7SjUYlii4ctl+va8DlfLam3w899oC87KjWToFcfubIHRrPw7cLf97ypvXg/Q20xhLVrZOAIielqdQ+sZ6g3qVFs/tPln+HM5upgoxLuhOtYZpm+rwa/DG8+Fp3kQYuTpUUd2otPosdVqlGS9TH2FN21/rgIog40R5GsYsm3YntvFM9YW7j9nvDNrX3tu3ysRzXwyMLFVAS9qRYOsHcvUtrMqbnssgZLv3GUlri8inm7luS4BgOr7A9wcfKJPWF051U9d8BdWH4O+Kwu9M0AhBeOx4mLG0GqMterZz9SjTd3nCrHOYe8N+kUb4hfNxmmKaf971D9Gu7xPh/B9iE2XZ9Vx0Zjqn/IfndsASjP/Oa1Zy+zpcT7+0ev2hEZjIqiNPKu165sLcPuOiBlEyvHMmXOrXIgDitpKW15ZS0Y+jorxrM4rjh/rwN4PVk71gmEtQx2c9Qx7uxPClal/eoeC7Uh2aLdydWUqN6mtHE4Q3dngx7sQeOfDvn9i32U3ROEdEWVvFyuzjqVOWT4OKCXZSSBpChXe8VEK+NLqfvU3014uSv78KccE8f0FRMx4TAYnXRVfVZCq8OMgQt7EuSqXcrMzt9TVzpbmKWVsmzhJzYp5SyceBxxI0nuUS6E2bmUGqHgmRZPw8/On4MBC+fH4MH2cDN4a0OkdtkzTNit3Du8EJFntn+pl2m1yP44d+/6Jz0/+O/bR+VYnjJqrZzrvCNfV+Wooe0dcXcUuQR+7Q0Dr8/VHnyvwAYSZc19X3+tnb0SOAQjF0wYqNH10rrwtq44L044zmTE4zJwxcm6sATpWCIRMlqfaZ1WwiAY6mNJO6hqDPp1ClNIQQLJ1rZyDHh8r36L+9XfXaJ5ZH/l2zBzuIUz60O7GsU59y+dXjO0ZH/qyuv48w3kBVq5Edc7GJzneQdBnvpyofFtmhBcnBMs247Dp6hADP6W2Q4LIlWnqajI9Yd93/O9//oP92FEO74ixwTwuW50JvBuv6Wk2+F1RgtKW86vhU/U2mUy6+cw2WXQtKm581XbnOo+2XGObu+9et21ae6v8N4AVL6e0njvOnv2+YJfQ3R/LvwtccUBOcuJ34sF/4B+wsLLt9LPTh2qe5u5KaZRtVCeEvye8yyk8K/vvJcN/LdyIKzxfB65ya+wgG9Pc69+v4jdvM56laX6cKM+6XVfsgVehGzuB7h3ZXTNd/W690e+ZndIWI/W+ndfp43Tr8TXUPRJ3N+P11fKtt1u/rCp0Bssb4V30WUqJrxZqL8NzdH3L/DZzVWj54svWzZfvh/v+h+/uz8uBiJnwit55Z4h/dhuMMCi6Ur4a+wlIVBVKyzTeuXjF6ejx0yM/2PQ0TCnCOdVPfqaOdrty3uJe5Fgm0Mgco+HenCPcNolF1vJLvQOi7nyoxzA1p3Jdu9oFUPRADUBvyyVCvSwUVGpagHjTMlFQh7kwGWnob63dT3JqBCQNXog9QKRBn1Jpr2XZY0SQ+hXzrQOlTp08yGJhHdaxw3U3wZucM0rRy7xllwOfAVUvhdYARQvY8AXZjQ90MkNzOmc5fsbVXY/qMv3X71Bwq73QQ+Twt8cKeWFcedMEIWw/zcaOhdVY6uoI/qQAwwsp7NOVU13zXNnhMIOZ0z2SH51so1guzuttPKgrA2zKqmCm9jaib+Wnk3ZEyixgDfA5RM7vSK57PrMO/wgXq0x7nGfQtSWladuS4SWf339GOJzhYttp6wxp7PhmpuTbsmdzZBTUiPLN6kd1sLQ8UX7b57avVvTyOHtUhtZWMaRjoSlgWoaVAQcVFLkTRy/YbgXZIJoePZe63xEN7acGj3Lu5YpFvk35aQgU6LygGFWattnVpO81zYEXqK0pStUoUanht/6eG+WhkLgJkQxY63ABHYPfK5iNp1m9V3XL6H33zAySK/Jx9XtV55Xy3wkzebJKc7fMd6Zf2ROr9DO5H8Gr9L+af0p7M9bP8lwte/b+v9FRfJf+4fx7mSyjvvWUHftk3mjOv1LeSt6N8/Y9+TVLc0UWv1t2eH3mHfCSv+Ji2bN3d+c/hf79Gd7kPs/SXh1vM3yitBHv2ZX+8zw2X2TfDuN+KCmZf82vKp7HXc5nbZr165nefs5jghedByE83h6vmR1yZp/UEhzNe/Vpbb/MYH6oTa9BD+lSh9lbx+pKdn6BSDC2v1YQ0OyJepe8EtRyRWeY9fOZHnYV/ctzh7GRzvLq41l7r+FzuQVD6oiaajvWboc2KeC9SU1+rE/bPwlGnNlEitsK3qFnPrUjwjonOgegQ/pZZd07jOjYUQphP5rD3ZafsqyGFOeudUrYvwinoa6ubVR3QgyCPWdgk7/knMr65+jjd0RYsHhyXcRn/kuJTF7Ox3cYFJSy4zg+sX/KjgjZpXAcO6gctZzE3jlAroTgrxKNJj5aiY9a0hXNvCMhAcibOGrA9Nh3Pv7p8/MvTgt7WXNzJAOoAaNChANKS3tGXqr3KCABBQVEB46D6/d06VbM5wzkwEkLQruoWQM2ciRJkV0kpCty7Xn0LAqOY4fumGD6FdSVkMmcsY8WFFH8ClU3DDupmLGYJ0HY8gYg1aOZiAqOsoOId8Hsnz+xf/7E58+/sH+y861ug0kJCRu3jSqHwQPvijkGXkbtp038LZYn2wXpunui5TM8b/pDFZGVMuXHlg8WJHH86M4W7V/LQwDCI388b0QQjWmPh94JsXJirOq4ApVGXLCtBETU3aNhgxGqeOp7q7yegafVsPvB0diXb3cr2Hf1yBtTdhc4CxTsEsg7S5eIh+4qldGE7B3pEQ1XOHiYjQmPh+cXf+/QLK+t36az/BHVdxX/K+81TYTnlP9S/0PTFD7Xrx7Tx8HvYBdM1x8ZOT+wbR/Ijw8UZBxHwb7znKCyjHEUtiKz06uWY4Ps7Zn/jPSD6L2nRZTf7yLLXj6n1txmQ/lwBU8iPD1ZmdCRqc9B1hA35bwJVoatx0PnUcY3NhItr478OOe9Vd1RPbffr4jcgab5Aov0G+G6jP19HdnPOh/e6bT4B35vsHof77JWO8Tq76ifXlfhn78nv/zDxw3+7rSweoa1w64EISz83elwBjNdwuvA7ROoi0aSnbvP57W7tL9bzkrXaZlhvJTndXk9feVfi557vL8WJg0SnwkGvTZKOrfda/6oCCKriNe8q8DNO4ZW73S+1q1f3gs3fAuz/NH3MeHTVcRlLVAe+fwVKsb+tg4C3cFYpC/Wv6h2KaNoGoQIUy/Kse9nMqQhdVpVB2/ZEXGl/rP8U0YmEidy7IwEwBdoAHyfA5otqSv0I+eQry/6U4O6qytpsGPSzur87ndFdCuGxYNSFQ9btq1LSyQgQS+SlRXsZieEXkitf3optiOSif7rO6rBDVCp92DwX+HdF/U4KK5T76EoejxWda6Y3Qq1bDg6uGGpfZLU79oCQJEjuN8R0XahDD2gg8TQn+plzEe9/4HbletuAwDDMRt9fyh/qfGS686IlHLbTdJlSu3yqJRQ7+hICQQ+Pkov1C4SqNJP5cHc8UlGSuYCXv2HmsDpHf5tAk31HHjnJHW7jFZOT6scX4F+PMVKlh+jfpyGY/7ESRjhMGvbSvGInI/6/so21YZfjFcXHLC0NU4x7zhXp6Ov0ss0NWbOAjYznG2ZFtcogDHbKUAi6yzuUSBg1o4hzULhWSmkKx5YGgEnECkBdpxE+FzhWV/WCj/fLyPvEu6d5N7qsv3oedUGHfr6jJwAoLv4vHagZXLQwJQDla2b7MSbz9F8WbXKe/SKYAJSivta5/Hs+oIXNdh5XvGbywKdl2xQc9zBoHmaw6sGD8L+tTMlmfLOjDJfzhPwpEESjb8r47t/tsY7KvNqW68p4k0XsTDWqc/731ctrdn88l1w1r4R4vfT1kZ9fBEXj9NV2+MdcLlf7uLgGGWQVV8Gz/HXnMbVKumfTvpqLPhKHVdxuZ6300OdX6K3wiaOoS/sqjP+n6X7ynHwLKxw+pX4zh0m6/Fxma8xn//6vIFducj3rCP8qny/2r57OLx3Tova4m0NTgc0ezfWlqp893Ksqspz/bqv6zo/zPJ6u2+Z3wmlq3wxS3Nm69v67+ooZ7zmMAnHYHs09zVYuT31SZB+TPSRqnbO+yLum1b3HeDyUVe+h3NNj+GwVAkX+n7ahlpUrJef+wmMvXV7PtK8PV89Ny8QAHqJv5el+7YZX+ciU5/Gy6A3zn9ntAvxX7yf5Wc+bTb4DQxvmZG3AxH6aY/geHYS82VGSiOVwsfl1IuRqVmLgQOzOffFebAIRth2+PPr+a+tDC5cqJSHbkUxgdfg8//GMWcCJ/q79iqM8JRjkrLDCSiABACoEF9eXORCZaHLcex8n4C8UxpmcajogNW/JLfec/tSDSrwTgfeYcHBDcVRnNf12KCdVxShHd2kq9n5M1Xa8WXXpR6rQQA74rPSUBxWhVBQcByfspq/3VPg66iBCAgZ5S6ICin1SoX+Ff0sfZ6sXLIBCXhsGzuopM6PD70johWdUNnPOJQaTzdnU2o4kYiCRNKvQNn5gu9CCYUKfv78Xxz7T5T9L9BxsBMtJWQJIBAOvqjIOWYJ/VFMlpezWY3snbF2p8Fs1XoEd4IQ+mmdmQq1fxc7IXybtH7LB7YuqzxZJ6pX+mZ3YNiybHttufU9rfP5OqxrkpWgtiMipKkoO3ZHRP8yUK4CJdfS1ivonj42j31ngxqzOn1+y/++nTMeumOUV7nq+n6Vf6qwmjItHh5f73gfHNCm3XautGVHd2PMnNy2TKWhvzfG0sy+s20osl3LjkM/5qKxos8PuWg8nEd1PkabHzsctLyisrFvf71jCfxJiXfifXx8ICPhAM+3+ThqkLp9NtomoLZT8eI7hlpArKrBE+Nf39VPJ9stnbJMADovPfRuG5l7M7ahT7X9OScTxB7rqChqP+mFqhU3pTZkjjBzDaCHA05hxm9KN0xwugbvdUR8NdS2i5pECG3jEJhUf6/2XgfVdp6D95ldvyv4O2tmEMzVpM+fg+GOnWXd7wQ1aX9/nvfy2t6fpjI152062FXPNyV25f5K+B1w+AcarHTKZ+cHH4x4Nihxp66/A0S0YBqzdne9Hc0pyhP5r2n/GY/Utpo24gl+uOOcHeydLxL3Ubtf1ac6fVropY7/HtSO9/6bV3Tfe3iy3cL9miCHeqv3l1O9t1LD8ndw/MrK/06y52n4Zc1rC5Sfyk3aY6OP551z0tOBiKjylKppXNPY9Csnlk/bOxnWl9yu/wLH2KTuWR3WMPUCWh0g1Tdpy9EdBuosM06ZgXZCQLIR4GLxM05j3QnhjkTRktSh0uvQ6ohRRMUZbgImeidB21GRwMYWtYAIUceT1qGljpUWkLH0YFGr2j23MVUnJYFq/VHZUwcYPC+a1bXSZh1ISYMxgKGDEkomhHoHRK7HRvV1Anq+ecvsFSCaOijI9kM5ACQcwuvl+OwCPUIeDiIAPGE668jzrQ9E+LPSZzyPwAE5A/8+DuLN5YXmH+7XCGjlx6Pmjxy+kZM4llPz9kV1RZ+2TptnmZ87URMCOh7M4/Zd851rDjWrOFpnMkadmNYp63GeOfyjtkV9MwPvWA/b4esxDuGaBiPv3jH2rgRSfH/aSdeXFfGcL2vGwzPcLG+t+NiWa9P48aAy2xZhcb1CuxWP9I1weZLsCJuUmWp5bSww+0sALiUgZQko8HjgYvsdXB0fpK4SsNOOeskfyqcWRBnHOwY9RGmoQbpSWuCXFxb0jko/n21b6oMI2hYlYwIHoVNCzqV+TwF+cEHPy37KCFIaZMjdcX4HxrIbzVNqv1v6aUkv4GYEsVFxtPp4/Ho8/w+Cjp/b2c5zhHLswvuZnq8QORrO8szgWrc3hjJSdJ76Yt2Xa6/T6et1zlLN8of616Wazsvy/XimQw7zcALr9z6PRZTc84ku5GHGs6v2XH1/nT9GfM7q+h2Dqldo+VWw0u3P8lndsUHPVCsbxeuecXkBrhfwHPpZJzFjF3w1xLxGFf0zeXVG2ztgTbMOx/qpXgSjHFg9Ic3H0JX5S3Vhl7Ero+rTxt/Az0fkZ3XNbASP6wjPy4WzOt4hc2ayPzme7u2kmrArZ2UPmhpr99yVSy2f7Xvx/clnz8qjfvysTFyl9raslq80BGK7YuYLGdP1X3x9q7yj/EsvOdjvQhL79AxHYJYmsN/DX+2T5okvQ0Xl6SFGmDV55hd5Bm4HIqLLSKvDBJhe4Orz6O9ISfRnaqtDvxnZ3qDns/et46b9BRcaY9wJ4Xd4VFztUQ0OusFaUMspVHCUAhx67I2WOTomus8M8ABrDn8iqgGHdj+D7Fo49nqMD2BXeW/iOTHBAzBr0/HJApDYMap3A3CZO/ZjFzxTc4IaxUAdPZn63QqN1hm6cr8cijMPqpw3Xim68Q4D5GQCEAWH7PRQfP2OCHs+fccfxinkV5e3waLd2ZwH/D6jTiri+Ek54/Hgexwej4e0mWeGUnaWxiXXlepcN9MsZ9TVujmJuBRFoZRSHanWkfFz5z7863//P+7PYweBsG2y4jpvqJd3J0JJAEoBHSMd+jtU1KU1Gt5dAKsqOD10zr0TiMbxTOnRPqq0zXlwYPqy7Ji2fKEr3Cz48W7L0dXr27ZN8fUwdZ57Q3VSTsvr30vQTANMgMz0XrludakiPExbomxVPlC6aTBNd0RIer9yfjDSb4DtGyBe8a/Pq6yQIJTFv3i6ceG1nYT+vhC/M0BxWT17xTFgy7IyZ3Rax/OYprFybBYMiJ6vxlZ/kXOTe6UUXmlT0KVftc0rhTPe8KRWmdbhZmRdKUX6v/UnD/9cw8SFCMfBKnl+PHjF6rZh2za5i4Tlqd8tpfX5I8JaXxw1HzqZTPK7V7h6uhdJCzneT+9CAYCE49D7U0p9ZnR3Lk8IlpD4LqWUkDf5rVOsjO8qk6HzUT8HppTqboz6aYP1NsAZ9K3/HHjtpqE4OgR13ul5PIJRJ7TlAmTu//DvA0wi9J8DkvKSVHqpzO8zjEZ43gkzL+8a/IpW+zF+xxg6c+hdLOWFvP/AO8D344wP7Ht7j1XOGXnLohupLDR5qo0ADmL7Y1f/gf8z8Kys8H4StGUG9f1XBH8iDXyw795e6/dKxUiOT+2008KCTFE+tc/qJ2dWXfYZUEe0r37AKLVgBECqIE3wv1H3F/Df7wBNnx3fqf5vF2hFvDS36b8AYS0btjsDX8DLFSRde2sexXaozXOifNf8S1n5BJ96u/SO7mYDFy9BNY3u642sP9Ck7c5IZOdsMwjri/v4M57vkci+yeu+uG+L3AhEAHXgKlFTcz4ktaZFfqvDYOXkmwUiomc6ENQp7AMO80DEOLiieiIcKxssDHPbGfXP3LUAe+9CQNdukDVCVwHJzhOqDpBSHM3QmM0eBUOy2l5Bj95RRz8V7i8q6tzxZ7xbJFEnSg04FROV9UAVd6Wt7R+zc0KcT+qEHPpb6wv6L+QR807z2e9cXi+UGu8Acx7qHabaQUwzT4PmgCFxYDT+KtK9Bxs2wtPl4AumiwSatE9b4EccVqYPKHBQ1jqpBV46+okS09I5rAO+jmB0Hp0HIfwE343d1JS+lbyY9k1Qtn73zmr//qpjNnzu+C7CeyZ7kmkzADRVNJg0rf1i7k8ZeRJdHxgkLvXlqTISvFvlmRoJFxyTM4fCbNzXAKQqWYh56DWoJRvDIf6M8PSy7K6DNxpjKx6ugZEaAIvH9Uz5voqbB9UVyMihRpd5mZHalDIHrVrQl8vImXcgqEPJyn3fNkunSpPaJ21Bgj4fy9BdD+szVNtc1+s+rTE8jyZKKCkhKxdJo3oZzhRpxzi1QESuxxv2wVlgPA7Ofp8FIaJAxFU+9XRtNJxmmdDNPoCQMbXP+gIjk1Rkhi/X6jP1juH4a3A2ZGJ6pD7fzaorD5+ku+Jo6NWuc8Onw1ttgi+CSN+I0txxqJyVebWs+0ZpP06egbN8s7a8ZT6sQ3A+T6/rur7gYZbOzqezuTD69DqD2iMi/V7C6dl0V/J+p6NwpX/9KrhKy3He/gpsrkOsV/VOmjN964rs83BFfyfSkxwMLjBT79PEO1+p/E7Z2ut2Y58vbQ6no/kT+1N91mdqO2vbZ3fs7s25yAYzOlyDsVj5RRubYo3lTv/FenFQqnnU3s9XTN+Fs3lrZbdE+VZl1TLqv9d2HjX9SLtgTHvPnnJttk8G1ht9A3fn9jT5Pk3vfEeRprfyh461B/6NRXnPwlDGTR4deG1RwKn9Xf01sd7aZ4IRwrXyafpnaXU2lizu/G7k6cj2GxC+CJcDEdYx3p6ZHQdIkO0QNQ2RNchj5bGla39+l0K9QNIZ2dX5ZC4MHh2csWMi2gkRt1uj3fFgs85Ou1L3OA7QwccntckwNtAjpihEOPZDyuLjmA45lklXaCoNcv6o5VQGKlkc3Oz8LuXAse8oUmYyK2SZDgeIjipoBwcH3BnlB+/CiM4kL+WQnRDqqE/IiVe15k3PxgbUKDkOuaBZVreTdlvOoJxAclwSz9d8bFEhQqFDeE1HbhoUBz9Y7GrkPh0Xkbcszh/9aw60ttsgIaUDMDtxeFUvF0TlAB273BvS6ika7Dn0bghu/18/P1GOAz9//gegAiRe6bolPXM8gSgDpXArdbyZ/qNy8PtSkEDi5ErYwA6vrGhofxXi9DoG1UnmBJCOEbv7w0Nk5M3A8pWerV6SotaPRauA2Hx29W+0Kl7z6GdUjsXd5rFt7JT2hcD3cszmXeVhGcU8LsPh3DAB881sItFP5XO9u0XT+/sKZpNJZLRbuq/yXvl9dwJVfI6DZYvlS7tDJpn0Pq/+vaToEFCDj6SyRFfAy2dJ9TmLar7jJWd2IF+BTpZTf761TaPHAp3zXTx/2bEd1XsR2VYuNOhta85GaZc+0ECsBqNtfbnhkHPG9njU702n0HnN3mcUO5uA8+Pjorb690d4FOIIJDpDERyJSl3goippIsJxpNr6ojqJ3tdzEOhoPLPlLLubZPVunUN7uTboRo4O/nO4x8boTr5cn9fXrb0NpLE8zHmzK0/+1fUC/mS61LOWI3yf9ipU3jf/mhrNs14hHyEF7183qs6AXSHv8AbcxJUgNV+9K+F1eN5B9ntA77j4et74CqBnB9o76j6Ruyv7UufQIjvTU8rYtvF+rjo/1N+/lu9e1ln+gV8OjX/Oz6AfHFg37Cub/z5uc5xulIbnZcNz9Ub63jM1671axtc8ppMpvm5cn6WjuJ/9p60/tcSNFHl+/Mm5k/s6rOzgNUQ6z3vgCg6RA3XIx8ZHl4bzjuWoj2tet+qyfX3PtSHGvdXiUthiflM1aEmPE53nLj+nC0HPWi7w29Hsq3SKrymXx3nkV3tHfbePZuLvo0FbkQ0Fbr8qcXw/1tFBMlFfcZiqoYzZ3xT3+ertReM7Hk4wY0o4nDQd9TsimoPHNudcuHaO4Op8afQANDAjRmiyZ03z5cfsBBD8ZNdDKRwgIbPKsMmHJE4j57iVN/pMgxHVyVIIRU3SZHdtcE49PiJluw0aIOILrEtxbaz9GPQDNZ5q+NsZpb1JOgGlpjVMp02hVbLt1gnL9YmWVQohZV2JwfWQNII/W8CIHZjqSOSVkEWOW9JLyPneDqo0l660SHbY13aTlt8msdCBBJPdTsz2XzcZ2HEbTfIvC6PUppNZWWfjJQo2rPJFjtYz57l39DJvAdW1GBgKY0BjQKTvX+neCO9ITs5wtPVfcfpPDfGgzdFEtCr/TLm4qnxYZ4L91HcdHi8YbLbM4b3KJwJax7W+7cQNdJ6qlQ3ybGVg2M8zQzQar8M7GvtYab9qsz6LndItbZOV1Oik9En2U8pV+riHNaBUy09GnnE5HMxIMhdwYJvx5DjrzAFf52a0T/7/WiAC4DPFiwnc9Bn4Hw0wpyrnU62nTU5N7hIKEsnwTwnJ6BsE6PoOgNhY5rRmUYOZ+2dBpFUQoepXydDa3csUyVUvF1rZOXx3JRChZ7Zb9aqzv1Zje9L2qJ4ISPrPj58q6y2rTsbKvK6TuhsCT8GV/HN8bfCxK3FW0nW8Tps0p9l3GmrP1H2ZL109qgO+G67MDxaPr6xzlu79rW7lr+zLbg4VlHlKToO9OK3D1RfBjK5r2RCXeUbbMwfYnbI8bnf7dVXeHb68AjNd/UzPDHGYpD/zS5zJizkubezPyo3qviSPAr0nxGCh65zBKU8uHdOi9CzLOJ/fDTLLuistjT3dz+0T/qwKfEDDQTExfenskBlPRH0aLrAQg2JJ0cn4ujuOPZ5XbUab9tnxPBtr3t8Q0XOWvm/DPbz8XGIhmT7Xcn29V8ofy2zsnLx8qOyoCVsmb/vOfte6tc5TLGegi+7W+u8k692uWJeFeXkDPaDy4R50bQrs99XvK2VembNYtNybQ5uMwVLmXtdXep01Gmev6OuXAxFXzuNWYewvzFVuORPMfiB3xixSXU3aGcLq4KnfhSh2UjZ1XN4JAUG7vm/pCtrzztHBh0iDjoP/urKTnNUeVBPgVkrBQbJwXR36unoxc/26OVAdGtaxRFR45b20gcqOsn/yrojjQEob6gr4BGwpA3LHAxA4Iavy3q/CpQIc4PswSs7IR5bLrwkJGVvO2B5bO4s1Jx1Z7IjXVUp1pwfgd7YoDxXCPAJKpsuqcWH4QXqOZHInfajGSE5Aynxud+oFGe9O4bsuPve94rU9CJkSiDauRgIJvDvhkP4s0B0s1hgiIuzy/ti53xkFdqwhJaTc8wW0bYZnVFGpzXEOoIjPqP7HZ5oTekeW9vEZdMbdRfDjO0GuQ3e0mbUhKkfT2jzeATlzhoWOuUk7B0V/MrHOHHh1K69TjvU3Zw4UkaDdEU4Wul0CRi5EOyI03Uwu6nt/T0vUbotn7YPJnRF+jGsey3v+7h67M0DT670fK1B8/a4O+97zX6zUWpmEgZa+XVonAgen/kV3ati0fhX+wFd+TIXv7HFSfbtn921EOIVjyJWrQWrfriwymURm6byuAWsgYdse+Ne//oXHxw9YyZaT7kxsrSEuVOgohmVWA5Mxy6nxRg1AEIFyWzwgjbNEqbTpZGawwMDT0n4WDbDq3UDB2OLpWXdCHBzUp4JycH0I5IjJ2Whu5gMAfEcV4nE6yE7XfisTIjlm0wGtn/kzuU//Ppa5tU7V9ayOF4B/r8qyb+6ZQR3B1Bgm6oyRdynhfzsYPSZ3M/wXQNO//4Hvg8jZE83X/jkAozuUWlbeVMapLCaRxaonmXngF47xla4Xpf0H3gPfRcuVQ+kuDs/MeW8D6h1WCtV/O3Mc1n/GJKvWdGnVroeft+NCOA3q3G4XDkX6h7cH3sYbhGEhQdU39F3u8fou6HWfr637TK4D6/ZP7bbSzwMKM53R13kF3soPAzLo+Xcxjq6V1zSXuz1ah9NT7V3X9qWyVvwtX9ZFi4JXsv0rcai+d2e3PAc9063loMrR6+17akfE1MnpnDn9JLrujEhIdM8k2KBGc2c8OyGl49YL98jRdKHlU0EVPasKa6S4pnFim5Xh6Q0JxBAysjBYdUwZoVLzWQeKLVPyJlN2ShBHPJ9Jbcs2qNdJm//azglOGlz8KY6FnDe+qDqrwl8EL13VKnmg7qh4wln3F1UWI6WJcxL4sx0bEQwdKm8348U6QTUIk1JCLrkzUFq/9b85Tan3dFQjR4/hELea0kd3kPh2N1r1z/28NHMc9XSy/GV46MIE452wUfqZwRjiFMgM7+Cxv60APHMC23crmCme0fe7Ckqlhe8o5flObjUhbgMSnp5X8LmLZ5THOwpneNj8iu+srFXdUd/78TeT40SjYyiaV84CET6fb5Nvnx8DseIsMjzFCvZqDM3eXTaKqlzs+8riEI0z+3v2qU3raNHh2Vpv21/pZ3ifx0LG4/Fgp3WVw71cnUGjx+jsrpXYbqdmXHU0cWXW50kdU3rXjweVzUyDLLK2ZA5Ql5xF/JrMRCiUQbnwcYpZ5oUs82lquxR6Q7C/dHsanx/mpl42k9IgkNWadj6X8HsNYrVAw3kgwvJRd9Qext0dZzKjG4tpnm6mb7UfY95ufDhLZiUL/fiZQa/jxmmv6Kk9W48y76yca7qwGUc+/2Xs5jnPaDZrV2iL3ISr/XWG06zuK31wFd5Z1lXo63rZqn0Jrjqj9HP8k3IG746U0f1zPu/chdlc69/P8l19fvW9whXd/9XxcQefO2VGoHbzs3V+VZ5Vf8/ezXRA+9m/m9Xd3vc6rsdj0YDleBh1iaZ/TZ67Yqcs5scN3Lwn+pCft71dUfHskakIRLrurLwVf18fK01/C/lH9LOoHdZ+jHBoRZyfamDT6vOm+zQcZnhebW9ou1IlQBCISuK10c9Wzspuav2zom8trcPP9+1oy7a875uH9XSNEbuubl2EBQz9cUnXA2wJcZon9aFzOC/vDj3P8LO2H4n9ebcOzk5TobiS0aaA3nzwn1fxeNNcfx2UZk3anum454J8hNuBiNDAl/dUSj3n35+jfIefdXWuXVGZUmJnuYladwUvjBHr0PEOJw+rgRzlt0az0iAS7GpwtzsHRoW5O3aksGOa7wkAgNwcBqRnZff3M5DcB8F3Sgie9uJsIug9FTlxMCHLOf3IPFK2jfE5DsVLnS598CJnnfQVZwIg53XLoNs2XkH98fGB7fEBSjwpHMcnqMjp2IIWFQCFHQk5xee2NvXD0Fa8u707K+xZKWcso7WJd3CIyKgXrpdS6p0Xn5+8I0LvN3iUBygp8tT+TJ+WYwfMzghd0X3IpJvThpQzfjw21uNSBkHODSeqfVn5pYBXy0r7I2fR1OGq/7kxYNOvxkdX1km62bjTYE4pBSmnepSJX/1uzzn3yvqoWPb96POscPTfB7lm/qJVvb69drx3DjP+0sqGTk5GttbX0fr1EbeVg9DKT78TzKbTtIpHlMbexWDpEuGmn7XMQBZHdVv+sLjUceSOY7I4+E9/d43ipLsnPB2jI59mc92KT6I62o6IPq3FeVR0U5jW73Sx+FuajuPGm21924c+CyDktZRGTqVmEIqEAlLq7tvRurLKiMTzwfZ44F9//j/8+PGH8Aq6uxlGPKjSttXZOyE8/ip7Zu1SHs1Z7wBCV9YlxVNwY/Y/hn5U2oFIlFzhdZAcdQgcBCQ9s2mA8WgyO850co1kb6THRG3y/OnHpE1jeU51B8ur+tt/Wl5OSRYupPHeCgv2ud/hpIEIPw5WTptarguC+HZb2427bm6YvN+AWwF1BvoXVnPn8T/wXwh/h76OZFqkQ9QFSJMy2hGzmDoh/pvg++XWP7DSIa7rGQy9I2hll/ULO/zvVsaz8CwPvWeM2Xk7pebEXoFqqrMdEbMghHdYv4q3/56aYhu06x7McPY22RmOb5URRMYpG+ixiX0x6pPpeGumjwR6W2D5gHV7fRkfSf1bwLvRIMidoL8AtBu/vd5+R8Q7x+1lUFYTll/ed/dKNYFv5nW42XHpXvrrl1VDhfUIg7FrDVyMIoR9wRL5rIJe5C0AcgJHHXhJnQLeMPW4SYVNvjWc9Dus4DXKKInQt20TdBkzao5cQM5slkhtxwAJSEkv2TZGcUrMkBZZPwGJUlAjwLJLgQsrQAFSKnLvMDfUOpwYj3axNb9LqEcvZcgZ0O24pKT+93o/xCFOFM9Q4vhPtg1GibEOqCyBDgnAaClF1QIyin7f2w2ET3TQ2rd1YrWDRI2GTgkxxSljUEVWak1dxF3xoiLBHLlINJE4FKWPmL4t8p5MPUTqPKvuf8A4g/RyLGQONqVta0Ql4iOeBAftV37eFEeqfNErTVEQAor2As6cy36yrn/Cr6OjXDvFlqnPmpFXFWHqumXAbVCmlN8kj7pFq2Jl26EyBM65lNDRy7dhVndC7PBqv5v0G8hu2lfzjk0e8ND00UQzc5yvnI1RPV4pnfHScqrpZGEv47wDsaP7xBFqK4qcnxVvm3+CWhRAiBzF41iI+XJm+Alb2ie94l2RNAmT9q/iYPEQuVqd7G3uTHomkW24jAcW4aYv0SfTtkYGStdHiYPXjQg9B/ROdq6B8ykteDxQkj+VX/wUOclRfnLBOrq+7Qo+lWMWvCF6bnQ1udUb90oXK9tWYGSAfO3nMWUoG7ghUOZjCHNNMjaWqN+5OIxp0Q34LgzAXu4NowPpxa02mFHZR3klWZq3+hjnsW9aGhgcNfiTQHTIbxJZYHYZpowtG5qh57I6WzNi9RhDPfbLKoID/8LKtIGkMlbMPCG6pk+aErqdF7NA1h1nBTWCheOz65dVGTWFHZcN70npJu3Z2LB50/BkLHdWXzKP4zqVbuu5Lg2yYETd47CYuZ404GbzhteburlnUpZHn9y7iB7PGp538nXzkJNJ58WInNBhTVc4xaxote+oT9Vl6mSVlfl6TOohyTISNiSwzk2+Zi/3hWVOx/FT9OzhqpPka5wNUT3y1uglnf0KOun/9+DZt/d08g3rXeHpeYCGL+bBWozexG02EuTXRX7oSp/YcWNd75Abo27Vvwvkt9jawQtbiXuXBvlHJi25MtWc8A6/qmfZqkyVdt6GyzcLRgCpHgGk7Ri7TB+2z+qbQWkypurELbmyXPvZ60gziOx2/3zlgK+/jezvKDd09zzkY3Uck6HDz3/2bXbc5OaGoS6twfV/s0vtiB/LYl7wWMzrCVl9sAHlmeGVma5V+8hpdiMudpFbWJTBddAmnE7cv291xzrYSi5d8VPcA0+H9mWGhq3KnDGxrmHQL940z5rh75T784xVGAg/nM23yY75Mb3ydd8/UV85PGB3JqU2JokGzro2RzNcDkTY054TW7SswJnVrIVklbczmkiEk5i8Vqax3agrd60zyThsMpwzRLJ3A1RmHJ4SmoAuRDjQnKWlHgskZUt5FgcQNUdJOcxQbEEIrdv2NeSsa0oJyBuyHLVTB554+9VHqc6ZQjuXeRzV4a0E4nZrGZtUJPdPpL0p16Ikk1x6XI5PHPtfdTUpUkLaHtgyr7bXXQd5e9Tjk5ASauDi+Ck9psqnFdQU/lXTMG9I2wP58UDeNjweD2ybWZ2970zm40DZd6TqWOe+yOA5IhUlUj/Bax+rI79NWZqEkKh0+iL0t15SWlfXyt9GfEko7azQKD13Prebdr5vg3FLzJM4QDjQNAVGjg4OAh1lRykHlPOVv7VPKEGCNOCzan/8yWXpheLl4FVZ+yF8dwCkbRO6JwkC5P48dC/su90GICUH2hLSppR4Q9qf9U7kVpcJDbljzMrnSnYeeRA+5sAXX6iufMvtEudW5YQRvALIo0LHuwa4UJXCLONRHd+b0KU64kRI6w4X67TyK/NT4p0wtW5xgFkngwaGquOVSnP26fgROlnQAEpyE5WOabvbzPev7a9hhbDKZukvvxJc/3zfW8ed7X+fxt9uEDn1PS8+xNHs73bgLkxV8bVtZ7Jm6Opyu5pa8Tu95yBQgOp9PMcxzdaUcytQAF6VDtSbhqs84vGqgWgk5fMEUOLP2mJ+5nGrdwXIfQspZVktbvKAnwPAJrvNKg10rKnqpXKzKrc6ZzZNjsz7bsxLlXnbsG2PSpOKqyol2uc6D2cgJarn/h8iz2nb6qXMGxVsVJBTxmNL+OOx4Y8//sD2+ADyJrJK67I75dqc4fGxeNXGg8I0LZ3bBVQHIbl0E/CaseTgJzoO5BdRN74iha3OuQvDjtNR91mfF0sXavOZ/ZN2D3m9cWpwYtXP37NVavkMyrP9bhKLg+LUZBCnezwaj1lconmp+xQCt7IIVr6xvND5vs+r9egOHR/A8IHYMagxfnrZ6vsLGO9QMRXYzhjyRXJs5LveQc8i1bYjmbQjbjFeJr3wJ9/DnjoemWHUPRd5xKwQHWW3QGNoQ1SjB3Lvx/F9D+K80ViK2vRKrQq1B8/67Q3Q11Ew0jqWQ0M5ZdZHaWAYDXZyufI8W761fZBlftV5liqPsrp/oJRPHOUnkIAt/0DOP5DTDxA2KYlAcjxtk9Xg+f0baGzhGefzorSbz21z9Uuq8noO30ujM2AWsDpo032ikaTP65uUTRl92+JZ+zJmrZzU5rVmZwNwmvWlYHbnjLgPr/BcHafjmwk2zS1YNZzkU4yVdPO9ScfTiN0F3eZhFJmH5UQNxjXVzNWXI6dO+MUDS56v4shxxJSMKqOkXr/Q0039CdSXRWrv2/Je40YPcx5IIz7d69RsihUfOdvB1xvrS6nLesqrgf7avZZOqHWqbUdDKm21+0zgw1clv+bNqVeYw7rXELi8enuNZnrLmgeMJO/NlWp+RqPqDNfY/rL6nNX5X+PTM5zmNEm1jc0OGbpbU5t0KVEXNHoFVOyo2WrUkys56zxk5dwIyegrneDoS6SJGaGl+CFsGSah2vtdVWYSuEuxy4GIqTLtjdvAiFUjEUaxrC2bEKM6GzUvguSeUDPqVsO3Fz498cyne5aA5vQO2qj4Kmfr9z6IYJQhQbO7GJasAmTwMUqS+sIM8ob+pXOqlaE/3I6MbIz2lFpfFgR9aQNEbSDbqHWy3WQGvfezDGXXMlJ4kXc1xKE8oaw0crs6pk2iod7aAHlW+brqBNpeGFq0i+tMBwGWDiRBm9SCGK4ho0IbOC6QUnPeS9nssJejnUx/WMd2otSxfuSoHvg2kBYU0WZSXgRr4RavrO/SONxmjvcW3DOKrEWgzt7o2kn20+Sd4TVzfvkJuPYh6XgV/jByozWwTY5d3dTyRfVXPHxbA9w8fl65i469ipx93kFUx25wfJNV4Gd85NAewMroQX4pHkrKizxZ6zVpPZ5ROZEyZS+67GlLYVv7woMx6JMvmqHzRw0unCgTtg3w9LFzXOpXNnT5FEkvyNe1mk+TL/Wv2tyoK+OzBDu2uiuCShx8O22vg04l62jhFbb2vAYWV00c6u/rUHZNQaaV81Wnr1N5OTEE7D5AP767eT1oSKTD2fmvlDyU1ekDEhTrx08bJ53egxaEsLrSCH0/aV59prZCp3egybB2pF7s9CYiWZAxXtDt58GrAQgfaLB9Fc2t3gHStd6MAZv/quNoJita9nM5CD+X6aMqk6l9Al5hbXpXYocFRTYFjfX1k3hybYnLuPIszv0c+PmvrzvurwilpLq4g8HecPmv8oHWcRVGuVJfXC5jLDPGo2OrTl+5WLAhSjUtqNelichMRwmyzA3wgZBfAJFOaX+/WPqlVDM1oc6HlZftGLXK9lDiE7hGeFnZc7Ety2fnekIPpr2hHA309AvjTOUd07Wn/4wfZnX36Xv57fX/KH8s8+M8S7g5jmqw6ELGKmOx0G1d+oqWygQ3L1WeYgVYbAzRi0/b7cfBOXDxbWVxWJQvlVrKml/wbNbRvG9X38/A1xW3qdFM7bezMms+xDwY4uDyz9Jf4V/lutr/QfusZFM6+xm8BbIGJELcehfQTA+0uBvO8vKv4xmlf6CPpLEFI3qLPntyboz8TX1w+CZMs9yTv2rbTa2NxspWNKxRW8kLr7CdPR/SsExfLoYDOM1g305SLuasK76FKTyR8aVABICq3A3nb74A2qFZLndMQf2X6yExjorMQvoJVJdOAqpjrSqrcoSBdziNRrc3UiWqnrQ/7Mo8Of/I4FDPbJZnZBnOCJ2kkS7wfQREBwrx0UsafNj3Hce+830Gx+HwhJTFl0yPK6d1J0TrT91tUcsRWtpzprXwGtSoGCuu/dnzXPbRzv0mqrTxCwRDgw5AyW2yO5u4fN2rCYyIQIeECwiVD+o9G9yb6DUFDVQUyacr/a3Ka/HVFcu9w4KdcEnK4PKOcqAcB47js/EueJIqGtYwfLgaJ55vw7ZfUCAseMG7cmxHzp1TQ8tIQ6+ImEpjwwB69Au/10UjNaAo4yE7XCzelmdmQYh6V4dxPKnTzu4Cieln7pCA6hJOtjjazGge4efbE/WvHSe+XG3T2Ob+vP6ZQ9XyQSuPO4Kb1lZWeiXZ0l+e8pgBhiDKGc/OFFjf3ivKc3RPwUyudGkAYHrJcYyz7ZvIKar1Rc6rK2OMiOQEH7ObLVCM27l9MZ5alvK9zqq8X6aZl7qSKBEho/EWT3MJ+fGBj48f+PPPP/Hx8YGcM8pFml3pvxEI51rg6xCN2dmYiXg1SndSo1k53JfV9Iv5qho/Nqg+419VFXAyxc61Y1uajhHNxb38gssHlJLglWxfxkoWtPJ7vW3oF/RjJ+qr6PJt/9zOB/6Sbitbe9xinrDgZYKnw9VyfNufTcfsVIZh1HRAwYWMCVX1Rn3QyxdbXTsa1POzFLFoYjTXdTg+a2i1EmAbPhj/T8DlPoHxQXxxXd8NKx19CkmPVB2P6qr6hMgeNtGaPtJkjsgY0FDGP7DQwb+hXvvZxtz7cFl19zier3iPrkGk572b9yKZNJu778P388NV8O2mQ48KTYHwJ9GDk7E7+fMr+P4d/X0Hr5Xd/w4Yefi+bvGd8xHXZY/Gks9hmKfJJ15j/XQl7BZlO+MX4V3qeazytgYjUivvHRDJkVi2vEq4a3AahHhRTzsr+1fB6/L8ej3P+AxncCsQESn248r7MV/k6Durp30Cdxg3ND4Uv+r0L9V5E6WvbSG0aKdr52g8i2KbMg+1zIO+Mz5tPbVuxauI06XU51bhIRD79UmPaOHPUki2HcuOiKGc1sYO346qGghBDUCUogEIdirUIz8KQYMfSlvUfjKtowJQZid+KjggjohigxzNII2c6LM+1eWPti+qE1gVCuNcrYbIIlBWaSVl1C5QSO2jKjMuP0GO/DFxS9ZnRgM4kfJNbsVbp0opcsRTwXFIUKz2Iw1nVNeg2oVx5vmha/+JUIkmmlXf2XoiR+odiBQvLTPEa+GEVfCOdk0fybQBf4qcG8Y5xF/mTkdUN40WNhgHNkfXztT3d+Q4s23xEDmpbdrIWdaNkUD+eYjK8o5GVMfmXA7r+E4JQMrIkYyfwOC0A1Pb3hPUqUlihCT/zHw/a2uctjlwLW4zh6j/9H3raav8VvsmKM/j6/vRgq2Pg3mt3vk4toqubYOdbZpgzTYQlzK2xwe2xwceHx98t5Crc2a0TBVLarOnHmkejwXG3cozTmt+OJiNe/874gufxr67IkevQZyW+3O+EgiYjEXzvE37/Zwxm0P8XDxbFBDRQ9+Nx0GNMisq07VsOT9S4TB1NP7OPlUnSOa33nOSXbqkgYogn6XZ6rv/9PLAjgU/jt4OlOqirVp6Au8OnFTH+g5EGZJianf4vruG832D6Fr6WbkqN7QsTcafXj+Map/LhhOEJP85jrb80Da6C0Qh1Wb8uC7qifpn0EwlLV30eJU1atcUbLr1Oqkuzz9Sy8r5+8m668Q5T5zbMJftnBehlTfXV+6UM5Odkcy1es+7YSYnQvy+Qt5xwSEOYcqT/n7V5+HL89/t/PsuaOMcAHqd/motZ3baFd14lTb63SHpSKz7E1Id602fjaWeLWI+161A+7tf4KjfyeiwnuYWOwz4nY3PZ/D04PvA6+DP1HelnmfLmfHGKY+En887nJOZS2Y0tHiN7SfDv/JOP6imqHmrzSaaf7znstU/xfkkT0TP8VmbZ1e2UYjLYojNylg9j2g9479Zv3id+grf3YV36wV36zrrJ5/vmfF667JqXzHROhAROcb0+VmHt8FjjJYTfJZ4Fr8aT3VLGtLWtpBMBO65ZVrbRru6mlTJNcavsLEoyLwqsdBhAgl6ubS5I0LygKg68Y+D7x4oxw57JFMpBUfhMjGcI5agxxJYtxBUUT+4PfvO91UcZa949PRodfnjWQzVBd8CSgU7sSOxlB0kuzeOowVcEvodFb4vXMnVaW/fl1JkBw11/ar9fQw7RHpjXXEplpeMXpByuww2yQWZokHUdMpXTLcCDhiMPASA74Ww4yOlGmApBweZ9uOTP/dPgNqpoTmD02fj8LOGlO+NxRiN0imsJojBSDPp/ZjzjtSZEvkMRM5ZfR45XuyzlFK9G0LBOsl8eR5/r/yNE1IvJ2yalFIziPkJDuqdbew0XNNH3/nVtb7PfRDO4+rbrI606H4QuHS+XlumpZ29h6OnE4BAwPs7H1R2kTOsznha21INsqBsmHd1coAxCaTdCesdGbPf3AeuLQsFxr6Pxs2MJ3Q+ThJs93wBaY+Vc3aM+vr42Up1Vfy54IRcHTyNTt2MAxAhA3hsHwCILy3OH/jx40/8+PNP/PjzX3xHRFf+GgOvO5icALWjB6/DVzkwpHRHa//8NeUzDY65K7xzBnUcoK3KOlO8Ix6fBRVmuEVybKaPrZ6ZVoS8UkRnuQsVZycLox0Tdlx0fxj7yI/72fhcj10MeS1uQxvugiGrLWHURnqGtO9f4fRojn8Vro49m8xnOS+izTHPwmz+O6PHa7LleaOTx9tLVcvcfJpIPgoIbdGT2i154wVAbez5xRE3p4r/YvC6jH5GevX3QrUEOxxmvoW3QXIT69uKfd+OiMFmDvrwPfC1OtJQm5vD7HPLk6HfoLNFcu9Y1jQaDtCy9DOJDplafSNyxltzgca9XgTnHp77smo+Us8JlvPIFRvpWfA2oK9vVue7ZMedfBE/vJMmt8tKsb/mivy6X1ULQVSr9k1tP7O9z9LcrO2FvCO13zFXfPl884thZt+d+RTv6uSXAxGRc0UNN8KI8Mzp2CGa5h3Y5St93dH3Fd4+CMEXz7ZjVPxnJS437JTorT0mCBG0Qx37R7E7A8bySS9WTjr0NFjAivR+7CA53gjUVvvw1KT4eSNU2yevqBnkRIITUQ2GFHM2d+d8tM7SWjfQCQkpm9u3I4ljqu78MA5q1QhIswEG11GQpVpF78ioBjYSO/8d2PS2X6xzBGlc+aCONZuHL1u2hgwqHe3k3CsW+if92vnKCJBAVCHCcex8dJX8UdGDhtBolpzTgXravGsSWDms9S8R2mXvizJm8uCqUvCsw2HmkPHPV3Q7k2c+D6drwauOR7udAePOnalzxTDOysnkcZpNJnYS9UbmSunXP+9QmzlE6tFjwTFPnm4ex6i8qG0z5XbWX9H7kH4YaXhm6ERpeDrhOWVFhwgfG/iY1efHaT30ilrwpEPGwMqRmXJCt/0qgCK76aLyPCSwrNDdEHz0SkHOGz5+/IGPx48asOLj7p43GNpw6fFrPyb89UR1szG7khcr3nvZuTptA0U+nPZ2JnsULxeUCtvsvlU+l6B8ErGYUwbrIH1mW6K+o6pTtIUcTTdr73WMEUm6QT+VfFK4/dTFFTMd86ru2ekUBooEB8Pxht6oGcaho3N0DNRKbvsy/XFRNk30ffUM1OvSnWOIJuMqKuZE3nt5Oct35gCp71UmvxWqFva+In37zDM/h3oesu/0+xXj+V3OoqiMV4qi/p8mL5p6HeaqNmspAMmCCOgioAjPXpeLeHOmV5224SIBrupFd96/WvcrcLXMV+a+c5rdKTuJDtHvbFWeS2yQncqbaekTeVbFJbV0V+eeGVyVkWf5GsznmftlBaWfzEkr/VJnXa+DNzpSW0xONifPB3b+Ihrvcoj0nxTyyhx8uk6kVb21Q7Dma3U3/XYm61f133l+F0LfzYTfV/X6vngXXu+Eu2V67vB0OWuzcQPEhdMoQ7xecnd+X/Xj5fZXtWuun9yFq/JnpMfz4G3tWf89C8/qFe+qS+HOeL3qT5nB04EIPd9fV2DayiMDamjMOBPcgqudFQUhOF27v8AOqG7yombUDvciYCR6tu1NQLIOcWqBm3o/guKk9erRSuUAAGwVjaNdQl0OfO4/Oe2hK6cBWcvf5E1qePV0IbnzQIMC3D7dMVB2/tzL3uGuBnwfPOnvQqj1FAIyoWgZgcBqAziLg4JQCMbNMQn8iBAmQ7++/tQ5xWd95wX9cRyDkhM55/gBH7nQDbQOzchh2uPAeYUPCwdzjvSJQoR9/4ld7vqgIu+l2CTjJsHhZuisMFvdP4OZQ1nb0LfH/AXK/UomtPZfh5VD+fpkdNKviPll5uzlroi3Pauhy+6w3iHFTiPhUWrleVnUyc9WMEB9UMN+2rKu3tszUyhmDuWU+XikaLW9z6+45ZzxeDxQHcwTnmwKwxqX28qfyzuT4zbNrL6rRp0+LzK+m6Ex0tXzm/3jIKkaK9f6sgh/6jGEedtaPSb9UnFIyXTInE6ltPcpYQxQwU5LvBOoBlcSkLDh8fiBP//1P/jx57/weDxQCBwMf2KF+jX4GsXuKpw5jF9XPC3V9YnqPQibfzYmxowB7py5m5+6twkgGnn/Dnh51caO6j/xDoqoLruYQeWlLTP6m+HANWPI7+udOdhTkM7PmZGMyDnj4+PjVEZq2pR4dxowBkVn8/SMX5MuJPFqmh3/wRzd9C8IT3z/eIw1l++Fp+qf8J5+X+lKZ2nOq36xn97SzeQ++buMjDG12HB61xsg/Kn3Q0zy/AP/AODm4zpuyDj9XneouRrXOPxy+FqpeWYjznQm+/SY2LAdHTudVvWHNMjJKi8J0v9k+GDE46qtbeVwn6V3Gl+FlY3yleDt5JmuNcs3++0d8s/OWVfq/nY4cX36tt8uG+vyfx2Mdsmz8E5+uFJX7K/on7/Ub78ZRD5T+/zqOL8CtwMR3adDyDs1ZhOGlKgPunLt9yRON3uet69nhat+H49l0sGguyMaDn370LVx1tZaF3SItVV6PG8Zh1TpjzZiBbndx9Cc++yY51V9BwoVHDtfUK2r5EtR53lk2KY6qQoZ1ZPVVgoSBzOIqF5urUcmHeWofaQ1KA2BptSTOQJKnQEpyQp+pZlcstx0uVR9XEmWR3IwQhzu7l4KS3Mi9GV37wiFSncsyRiAGvvO83ZviMuzvKHuQhDaWqdpIll5nICS0DvxhhlBV2LyLw6CFBQkUCEc+w465HgtbrCsarYOShuOmLfFwxVn7sqQDfOY4Vl5jX/JsywrPnOPbx1ijv7IlX4rR8joiIrbHzlbZ/IpKjOqt+G6oIvmI3U09f2nQ2cW5JzxKZItJ3ZU+TKiyZIdMapYN6cS7/hJ1ntcy0ipd2h52nh6aVq7C0SDn1cnsK59DZ0hjW1vv+uqpVkFmU7xoXj9rFU+1g7csd+sHKvHywXligRd4+fyWLpchiaYDaGbrOta1M2R8TjTlgOQFYRyJJ3IOqSMvG3YPn5IEOIHRMJzX/n6LjXB8Dxp/d55ZcbDE4rxil/OHBMrmRZ9f0rRq4YzoEQ4sX06mBmX8mNWaacD8b800Nfy0tQZnPifiblfdTjeAeF3MrYxlXMOdUv9HinXkaI9U767NK5cfRcdQRXC5L2tw+/qjIIGA15Or7HyONoZMSs3vly7aSHa10lkR07j/Utdv+rz5Pljrn+8AqOecT4i5pyu/0zez+ZuXwa/XOIwy381z0rPGXC6gLekdJ/R+zFAda3sBTh5npLq0qt5lxeDEMTu0rm4w+UanldlctjfN+zWXwUzWWnbfcfJQtbQeQKHV+FOWR0LOdNt8FsE3r6rdDnXG7h8a1++C57VWUxK93k3/xynmZ0WYhErpDzfECGnJPc19tznbYL6XP8N7CTWv60eo/tCzfyh+tYFXGMaRf29np98OV8hP+7o3Ku0K9n3Ct5XZeozjuGZnq722LM4Ac0WivJ5nEfc08BuI4/VpPWHl1x3YEVHj6dNs6L5Sj85gzP5EI+N+/PvO/h2xnsrep2NpWfn37u69TN6ztW8Fm4FIrxx43dDKFwVvKujmbo63arIldMnYkA14PrVwbwjIkpb05iP4V2QR1Rv4zSStMYZ3nY2SCCitHNMSw1EHOBm646JnfPte83PdTaHe2frJXueoWXGAnZul3YvxX50ZR4Ht+Wgz6686s9QGtC42r4eD5X4DHB7d4WdXNkQtscJcDCipKLEDunN/S5JJkcoUOFyrJPPOh9nPOP7ta0cFKdcFwQQIagRAq1f6JRTQkne0JEAEMQQIuEVEqGSgOOABJw+2eEgx1/l2peGZp1axJ3jHSbDOfg3wQvI2RiQ6iUdf6eC6pSIHBLquJkJXvZxXHOiLvFy7dHPSH54fpnlt22O8Pfp6oXkKaPvuZiuHj/fNvven/V91vaGuow1LQtgkYwWMOCxVgy+zKcpoe46msl6j2N/vNCsz3tDJDRMoGj3q209LSLHmtY545VnFCJfX8jnJN6TNKb1OEV9rWnGSue4RPVca4j5W5StUKig6Jg3fdHRIKnDko9x2/S+jgKkLSNvH/j48Sf+/Pf/4PHjD50CmBZuhfoVnCw0FdzMx1fhhGxWPkY4zJT26HNWxqycc7STqDdUH/I00/PmXejzXFSGz4I+0SORM/2z3lN0ZlysdDb/PZrnZu+n+RCP5Whn4oDXYn6NyrI0sXJwlt7yac65Hn8WBRe87LT5vJyb8XGU3r5reRIQBSwuwN30Mb+flEH+S+o+bsuUG7Di218H3hG5ol9zpFmb6tlZdmy9BMD17RCMUJkvi6fMXJxU4UGz1QZpYseivjRI3JXLfydYtWtmRym8okf9Kqgm8t8P9QC+iifn+smX1LbQh6bP6TwYEYIaru5RSup0TmLft/8sw9h/n4FU/TStLSyRcojbiP6vlUMrmfDd/PHOslf6uk17y57USetCl1ndrulwypurIrSO63VdgVk/R3j+fvCagF/a4hfyznjE0+13ol+EyxU8z3QED0/tiGgK3TWCzZmzjZBZR/i6Zg6qyLjs8g9tGUdn6BSEOEXs2cSTPAUFGYnX3sjkoav3QdQ55kspIA0oQO9jKLrGDwm8up8K71YopMECvb8BaFr9uFY2IbEDyNq6jHA1UNvF16XuhCgHBziKHOGQpBVJyKXHqnA5biW3tJlSbIi3PgNKsY5DcXxSlqDMyihHo2kARHzMVHc5rflbTSiVn/VdSnwXhF3RndWpJtShzrUjPWcdX1K3rrag1getOqZDScSrhIl3WFg8E3QlsRsDan85cswcYP7dypE2G1Oz8Tyjb+R41U+lTe0fE9xZ9VUro3dYebTU2TEqFP1RRhYf395o9b81ahkHPe98rpA0p5FBNuBzS69ZeUl4c/DWVaSTiAfGSwNftc3uvHLfX7bN/rgS26YI9N3sDolobPe84XjflqF0C2gV8ZiHSKas2nCF1zVd5HirZYCQ6NzZFvFfSkbG+Oziy/Pj39czo31tB4uyiZrWFLje4QmRf9QFh3ocUs1bHUCG77eU8eef/8Yff/4LP/74E9vjQ8ptc/5MDq3a2+FueOoceE7lNRJTglRcWrVKl7nc5d+mHmPMpqTP7PtrSunYdtveft4FUjCGaWhLj1Pv7GY5HVGUxm+jYnKC+3WI223nNK7Qy4SzuXA2D3Q1Be9LMMZU//HlDmVPdB79Hu/qbW3ZzNFrNr0+m91XcYe//DGAURDcyj+fLg5GZNhARCTLI32/lsPfDO9qnvF319TU3vlygajfI33RlG8ftX/6/LbMN/pQzvrxSh+f5aGReB6LIZ0fI1Vu3EBnwGOoWrWaaqCg6t1QO6e3vQCnN9T5yepJTVuytuAMtys0vtsPX53+FbhqN5ylXZV9J09YzgQfW27Xh2ZSCwPm9TWp2b2u/2J/xOleERDx7HwVhzU+cX+/yyns5+Yrdsa7+D6ymflZ8tNFw63mmeNyFb9Rx5J+rDbj+8b3TAd6J8zmba3zqv7h097htUj3u1P33XpWz2t9KXX33s7yRDjzc9Fn1ubJBF5v82vy+Xy+WOc98eGdguoi/W//3taZzOC/wzuDryh4fhnrN8u4Ge1W8uvZ8XoFXgpEdAMrSMuvZsKozxs5SOrzycruFSN6I2xWfvS9piPFVIICAWGtYssr4dvliERyvI4pdwhGlAJdscNacGEhA9RjnHQHxXHsg1HJ9z+2VcvVYdd8P67tvYF8FD7qSXdC0MEr9msggtSRpuUJHcw9E5UuHT9YmsuFpqbfmnEKNGNRHPI05wfFIpmy7GehAlA/2UQKxhKs4SHH1LDjVwITxrGGlOrGHqU1iCnYDBpz5BZRPdaqQHlMnAeSWs7k6scORkdfRVeCF/Dj8gbMBNRMOYucCrNyZk7i2sfGgU+1b/t+jfLyZxM/EW1SGoMI6iBteuQo28ZyRidr6z/rCBnln/8jIhm3NUPjucARE5aXM9IWBFNqa6Stm1GWA9mqMDtqyY9Bxr1pQCsc/QXVvhwLK2PR087mjxxf2p7ZpLoaH9F8pWUX2aHk6efT+fZKaR2f+nrODMGcUx0Z3fvUjm2KxmqMy0gLNrdGUENsfMaZyPC/51tBz2nMHJyHzOspcyDizz/+jT/++Bcejw8UaizrcfV9fw5tRJxBLU6anJIRLr5UouBVH4xgWpzhxp+z9q7xHQ0WeQOef5fZXVnut/tC1Pi0Gco6fbmx7PDr3k367kraa/Oa7e940YotX+cCzRvrGyOekfwi8zzSl1flWtkSlTELRIQUkHb5I6EGOR7Q48ocGI3zSB5Haf3vnDeey0wwItp5YWnfydtwkcH42UnilOoYJzS+ntHS04CfD9Rx+aLSevvnjMc8XjN5F/XlLN1ZWWf5Zlw3m88Hvg/k3GUc6lwi8pK/OqhX1dbxxPfu9TuzIx7mXGTmte7Ft8IzOvyvgDOeivSaFe+9u919/W2eG/gVBO/ZY1vE4Uomvfxe6XIrfK7ifSfNnXEdlWP1QVMqYu3QzJxvZlerZ9S6gvlq+B3MXV2uybj3ZXZ2bpVhthjfz2v9fQkJvHDU6lZVj+zt7WfhrL0+3V3da0XTqGxLv6tzV2zfjzrIqv6RxvfA5pvRZlZuJBtWNPD0MrmaveYU9TkN3jdA/RiZpRneWfvqAgy8aJ5FvgqPW/TcPBl+m6FucBhxujO+z+z6d8KVeefqeI7slatz0l0aATcCEbai+odmiM4G0lJQnMgBnlgk3YV2rbbAh5MtjUc8adoaYCB0v6N29eUSDio4SjsGyePR7ofgY5n4yCQyn+qs1gulD5R60Zo4QJI9Pqg54OqdF/JnWsb1i5enHAfo4CBEVdCJQGYnRNW1FCcAdRfEobQ++tGrvGAHNdkVlJ7WLeLoDeHYeKeqUYaONmIctf3Kp7XvfB+qdmq1VAht3U6IlqenKZCET1iXtUEHKA87HlADie2rVHU9e3ZgTnoGtqKmE9B84JwpxTFNz8uy+d+tFPnx6NOtHCbMN2vlUssYy5G+coEIm946R/R5TDuLay8rou8qN7v6gHnPat6UeLeDNZgmBolXvDRtSgByrhP7KmAwW817hQe1XLs7SQW67QrfL4xTAuoxUa0cH5SOnFcRvr4uK/sjZ5dN09o8TkP2vcehh96svcrrHldNM2tfhFeUrhtDDo/1/KZ9r308tmFQBpnReEdXTnyPj/Ttx+OB//f//gf/+ve/8fHxAzlvda4jkY8rZXfp1Ji+adBoeiFxkE/x+BXgjfRR1rd3i1KwolQ1h+sU6WTKifJ7Z67wsseWcx18e8yEOsVNJu4XIBy/qntom8zzCJ9oro702Fg3anpJ0y2oHeMpO3r5f6OTANBFI2f1zIzA4zhaO1XnNLrnwAM2jTuWaXb806zurMcdBumiPP67l3VX+HUlq2dpn4FfJVfehUM47wDdHHirHMnMl92XOmybraL6oCz40s/jwL5/4iiH8GrTQVr/p1rEbAx8VzDid+j3Z+BV22DV7lDe3SobgAT8p04qY3xVXkBrU7OD+x0RV+eq6/w+z3tmv1X9/iKM5ejClufgnZx7Rq9BB5O/Ydy2DJfrszpOSnIjhCmOhpa+3nJbX4zf++q6C3O79/vK9H3i331l3UNdT8i5mS9Gv8/63ePa/FYQH9eYNvpMNHLtK214Rz/cgsTWyEr/mvVrRMM78mX27qq8v0OXZ3hzVddVPvuV8NqOCH25ct44wTEqEmujrLpvJrSLJmj754MTPGE1BWNm/Nm0oH5SmzmtWNEp9RilWSCC1PmvK+VNAAK1nHglj5I75dTds+BxMy53qd/gUApfgK33RHQrfZuzW3tYQ04tv6Wtcbob/JhwZus+CS5BP1Y93xkBtl/7ckZISS+ibf3hy6j9Zv6Mh2UoL6uhmjOSPQXHeCS5/xL4wkzUi9WJiHc2lPa7CO3b3R9iTKkhLeRKcqxOJp5kaj8Qdf0SOXBn4y+i5UzYzZxsZwb72RiJ0o/jFx2PnOUHmD5b2ipr+BzV2Eyt49rKtxLS58wJEgcmlf651jNzdlg+1995NUGo0qF4LOg/6/+WcHTO+D/fNxbXFdj3490QbagRzfkpJSvXklzSzmUdwaXzinN0R8QVHvfPryoQUb9aHIZ5BBBHynqO9HXruL/ShrtONamgo+mSdrYpri5PD/NSaCPlFkLauL3b4wP/+vf/wx9//huPjx8yttpcaqeW0LhEe3dFOYxAUebPZBp5vsrrbEy8ZOy8nL6nx4in6BxBLtOz02DEBJOu7rH8KzxJ7rPPOx/TPo8tp+lB9a3SxTqfzjBzdXdjYPL8Cvj5ROuK58hgzlT9yuSzuuNMnvPvdpGvxcV/RlD1GqvETdJ56GWGaJ2T+SiSayklZGyneWZznQ8cnxm4qzRnv4fnRq/z7870tCsy6d0w2G0n9th765TfQ8VurLtgoh0Hhyy6anoM6ryETp2aBSE0qBjjOpu7/67gefGsPXfmXj8frfJc1cUmmadlDu2LU0J1el9ktcEuBkTu8wMN6M/kPzDabGfTz1zGpGCcrbAcy7s59Q24PwOkiiLF47fWcTZOZZxbnZz170m9wbe7skD1Thv0ugOvypqI/lEbVrjZefSOrDjzI3gev2KDvlL3DNRubQWt0s707f79Wb4ZrvV3anp5j2ccjEBK9cjvM1xm+owfUyu7dSgT/Ri8yreVHkEQ4iqfzmh4plu1dl9CNYTZHDrTM2e4xXhd68+7aa7AK+PQw60dEVa4l9JWnUforBwTVwlR07k6ZuVG29fVCdSrr/xMHTyUWrBDdwyQOLX5MulmjNmV0R4Pxbcc6tyXOx8MzYio3g1hQ+ys5BL0EmheyVO63QpIVA0oe+GgMm0zGNkyjWlfxBkeX8qbknU8yOpV9csA9ZLoFsQ4ZHWIV0Q8DqkKIk+7SrfCd2As+UORA4YyOF9sjJwN7A73Ce+SWiKEQeFJxEf18Dmj/fEJyoMwv0vNW4/zR5ZIhCo+EbZVWfFdKxlmwu3qxdVnTrU7k+tVQdXnJffZpxucKBKqrKuUAOcRMpO10MiOuogu3knh22GPY/P90NJrD/aTkC3zcM6n1aSiAaho4vUT3Uw+1jSp8Vq0AnWQ8zA7rYDuczVxzuinhtKZs6bljy891XojZ5L9HhokDr9LypTIxtkYm/VNnYPsijuDu8fL1t9kY5P/9rmVrxqsUhxt+R3P2nqMk9bTpKODOHm84rumX+fh4R1m4GkvgS+t/vh44N///jf++ONPpPwAoAFaDY5z264q7/fBluuV0PPcV+eVu3BVuY+BoIsA5mNspVyvDM6rSvlsrrDyvT+GgMjy4eiI0eJmONjnM0X9EuYTQ7jVs2aM2ZhegR4lF+mUVn55vPrxmYY8/nimqMy2MzeeT1afRIQP4llY9Rkyi2/U4U5E5p41wTQBIJ29AZgymjizNkZLKcmRKAOI76OIDPuzvyi9wiy9TxuVN8xLqekGHl+Lw1VHwffBqGOHqd4sE5steD19203uFl0B/S4aF3ptc7Zrw/vF/D/wDdB4cc08aoOvbRy1OFBl29lYfG4OOns/zgfPyoTR/vpVsmWElfzzc9oVrOu8E72zfg5j04R0pf7Hs0GEJYhCs7Kx3g3fUcffAYcIiIxN8OoweaF9K/qoDux5JiUOQlAagxHPwmqMzPvv+2VLpEtF9HmG52Z62tnvO/CdY+E7ZY2Fp3dEyA/+wNr4ipRsvxpoBSlhufLAG0+dEWYcwNUvaGwAVSqovu9X/c8MwcgpBoAvlybeDgx1kRp8dPeB7pRI3X4/E7Cwd0iQTnRMi23bJBDxkGfJBBX4L6lunXoaEakTfLzbofadGH46uVvagNAdG6WrVtH1L9AcEfyX1EGm/02cdm017MTBVP1bztt8wk9+cK0GWcUvVEDE2LarBQm8qSVDcFd6BGOl8lepY8DPaTw+AkdqpaGx1M36FUWX0I+XyAmxAu8I0U/fF5Gw8ulm8iAqvyvjwlEZVJ1XRppYQgAqPOozNTaswulxs3/RCvdWVUK7C5p64zYl6DntUR3+92oyV3nZ3DF1UHfOHg8RnSvmae5E9hA5SGo+kc0rg2F0nltlyaeP66m/0dMrciABPW+uePBK+3vcbaAJEkC0ZVhN1c+X/E80RmZOyPYpQcvc7zKr/W6ctBj4cATlKarCfdV476jp+0lx8rJCcVH8dA6o843MYX/88Sc+fnwg5Vx3AYJILnRrsr3x2MyxcKb8XVWOVbbO+cLy9Expe0WRuyJrZ/WsdDF+bj+DsYH4+R3odYAG/XRIVRZ43CSVeZ7cb4Tje063iHZmTghgRe/VuIo+Ld5cRo9FkXd6T9as3BA/0lJa2Sp3tm2bGkVVF6l3lLlyZ+ntH9rdVlbPjdKG91uYoCOgF37rnMZfZzKRCMBh9Esn887m9tpHmXVSf6l29Fv7yM87V/5sWTyFjPPq7LeH+n4QcW2ATaVdKEtSN6Yuj38avrh3gVx06c9swatydCRF47ujHkFbmg3R8U0/cytvj1PICS5VDQgGeoDjZbgyT4d5cLkrl0UNY6l+C9/bRFern+mC83QnfINuOHRlhroBBZVSz61N5KrdtV5AdOX5FP/T5H0He/36Wh03+TOQG0PuIclzDBj5mVZ4kX6avxjT+VxqtQyv262cjimbBY8TTP3zNNE/kpUdKXKYzmXmzIacQTQXRPPtNRvp7P2YYKbXrPTdszKvvb9u8wKROJ/r+1dodQXq6E6OT4wBFokrnceT4x0kCULcERC13Gsy7Yp/6WlQ+3GVZFgZqll7fUkDh55OHVRVlHDGLxE8z5tfUPaNYVAXvUJ3x6nOLe+HPN7nsUQthBuBiMCpxlr5YAhecnAZYaorpeo9CGJYpY7xks9eBXINGhRdkWUMFaIuqKC51RBun2Ta18h/oKj3S5tb6QE5m57qnQ+Qs0kLUI0ucTgLLgkSuU9t+yR3OuGwBlspnC5nbGh0Tjnj8fhASgnbtolCXYB0iOGZQZT4L1VK8VFMx4Hjczd3TgidcxYJ5oVeQhba6TnAhXjXQr3nohyVzkrPlBLjnfgSwrbqWu60eChv9AaqshRyRqJxtbrHDULNqu6mxHxleNQ7EGcTNX8mpG0DUgbyxhdVpw0ZQBY+KXLcEre751ccJDsipF3HITSyvMW45JybHZrMs9RWpB86LuT4p6TOvJzdeIgEpRpSVPsGSYxuYoO/9+3MnVf3FehYsdHnfudSadq9GOiSsZD3gXYtrqOUUqVldQprt6gMgGuvKqvQ8ddwtX0ROVlbwxQX6n8nas9FdvA447KLaaytd0XlXFVk6Sdtb33aJg+pTb611nWqdsqgJJeFpoS8GZ6i0vxDRZum4zc7x7vIYBCQgUQtQIEEvvReZYLyLz1ARNiPej27waxjSmNItme1f6DlGge3nYvQeE/pGx3fZGHtAFY+bvRMBFDWiYFpqA5+vn6E6WY7146DFS4QhVKPewMBR2m7SexKTu9s9caEV7pUbiUk5JSFDzJ0JT1XGc/f3qk2KOA6ZqRfMgiZeEwWJBRkPPIHHn/8iY8//sCPPz7weGSgfDLRyiHjVvl3NjLaavoeP0/rOP9UPXmPHTHAFTm6Mnbv1JNSgb1/6Wq9XIDmuevM5Hx8b0iq9A2dPhVXi+MYNLByd6ZPzub7MV1fd5On/fgeDLgFjPOBSDDVDRd4Wz2z/ktHgDO/j1HRhyaAoXjocBx05yRzorYvXo0fthEjvYuR0Sz3StXnYT5Zz7c4A3qUKXQuNgtbdH7Whut3+8k7mEdqQNtVrKYguHYsoDtMrR7Zzx31maaRzyYHbYACfJSnvk/miE+rgwbldZ9mPtBn9TsSNrDslpdVt+lHbBuDls+JkUQHCWoCtOQdUeWBMegHtja6Vfdpihs5HsP3AVIrKqlCMstBwocoosccKGVHOT5B+AtI/0HaMrb8P0D+QMlASYQCPdY1oaCgpIKi87xpT10EFOJg+yhAbZyqpu2N2rVqdmWFIMuzoLJ4tpuyq9zV1/Sx9n6Wr5fBve7n55CmMrnWDU4k1XubjqRlhvm1CNJE1OVLIn91YWErZU7leO54pVfihSNDidHYHGjtP6O00a+49rMenrd6XtfAFRfm4mZKpm68qa7OfMmneVifEJHXM9le46+imwDGmtI6uXTVuVDtLodbQAEyyK2HVtBXF9moHRI8h9X7a/4An6afPKJuW7kGV3V7HN7l9F+B8slgGyK1OVc/0+jcTmr/a75EKLnE/DzYgJ0xwx8X5pHIyZ6JQCkN9yxGeaNg1JkeeKYvM51ekH9GTR8WZfp6fB6TtjrZyXgPo/ai1y0jIfeKnfYumNtXE1nhFa9B12vArNYzXGfyvGn4XQ5EWKeJjR43hHwAou9Yz7TdBKB/pXFaMuVGYMuojpquPNQyKVqJxanr8/EeBtbsrA7eqG7Kkrr1/NHDnEOqOwY0mRahfw6Tmq7I8VDVEBEnYd42pLQh5wcfz7Rt4CAEHx9F+UApGTkn6EJ9xlV2WMiqoHK0s7erE0AR6j+qYFUsYftLd1VQHzQg5LrNMflLn+ufpb8JRBhcwr5PZqJXp41+J3UCxsIgMrAtX3ARuXZQdySMKByJGj2Vb7py7U6a4Yxm5QNLgwZ2BR4ffSYkl1aq4Tk4GZUKTWuvdPB8n5KVPcnpoWupMpuQ7fsIPL7R0WltIusKtIX0ZQV16XRfDXTL5EZJ5fxoygMaCXKaH8s0yJBA/2rl9bKkBZAc+qZdCfGk3wKyEd3bSkY7Obf7JgwTEVw5RhipY4J04vF1JKjTmpO73UWqHCSjyGhXKS1qGnUQlYkzYq78ElF17HS7A1rCVsKgOKKndyAP1oEIACk3PGUg8UcLJCnbkXxPyF2TvHN1GiSVPz0erxaujqycGiPZsRnUpW3pQWUpzy8ptSBET7WWzwchPN1S5adU585MbTgCHIyglJEfH8gfH9g+No5d0C536rATnW8iVSrMdAF7tI/HEbICKMh2AQZF1JR9y0G9eH7m9H0WuE+U5p5+I4/b78q3q3EY5W3Pckenfgx5zbfXjaI6fN1XaLY0iIaJ4Jw2M4Oj5evnEZXlPhhhiyEqo5On05OnTeih6lIW77ENXXLEQYhZnhkQD9dYn6dYB7FQ6KgXa4f55WhUPy82x2SZ/JZ/cmurx2UtG+Pn0e/Zn38/u4jblnvlPcA0Txh3bXR8WXX6NjsREZBzXSxR01LjX/t7aHvH4JoDXd1n9G2S4ITBrapXs7s8jLB74P6ogOgA0Q5KuwTefyDlTeapupQCIF4oUkAgUn2UXFvHMar2DFNaF0YE+Hf69k1Zv0re0aiO8Gdq4Ty1D1sJvX7k5d6ouwDojruxMOj6nbO1ldLXb591hQ382uavQcJiShHHzz5dlenyeZ+ui7ptqhl63o6zc0lU1RQsrcf5uKVpBdlfT6pTzp1lS22l+5EcYjjRQdq+Pt2V4HRhW4SbN4YwRGpfqmyt49vP08R+GNGhvR3RfDtxp+hYmOqWSf8R3o/mKp+HaKDuK+D1uVm1QU5EzKhmjC/b/tbvV3S5r9Sjo+/qyLbPtZ+9zlcNIZs7LeRHYAd2zxc2TZckjcEI3JBbkXN+BdG83yfQf57jyMbPqf4byXdri0dI2CCEVWdaRVYfohDlmR45+33Gx1fhrC7zpn4kMwZb8tXkYZ/5ucK+VLnly14VHMONQMREiAbKtfYa0VpQ+Y70nRUZBysGiNIRESuVOtU4hZII6BTRWrn5UKHZMWTbIUKl4Nh5pwBvASaMAtI7ns3UbpZ9NwdbqkZUdYjnBx9nkR9yWXUGcIiunVAq/XmHA5WjOcwvGoYVJ0XNGojGyV6dyUGQRy8l1bsschCImILh91n/R++6ixklOOAntKicbqKBuOQCA1DTaj0lCkQYY9jSKAxyOVzsZOGPMLCGrP75dmg6a5hbPKP21N8JdeV7RKMzmDmCvIIRORuiNqz4o9IEvNLzimpfShkMdi0ku5WBOfX8auv1f5dxjZxyqom5vvHKg81vn111ooR9mNIgt7lQMD5Bf/R/ffkzZ82KNrbeFZ+t2nZlfLtMTZkJyo36U8cdj6u+n87kmQZmIuXB9u22bfV7dagRIU3u8Lnc3kU+m9/vcBnzjUdoRWVHz9UhlnJC2jISMlLa8PHxA//617/w5x9/4PF4IItTqN4N8B474hIMyvobyrvz/KvAy4gr7eQ812gQyZczWTSTSe3Z99LI1v+Ovp+VO+UJGE3wm/lDYSYLz9IAouM7X8Nqfh/yg6D3U1QjmdousM7hZ94rWH2HgD5wYcrxn6S4W/1PbIP+U9NQl4a/9wGUtQzt543Ze5tuBRsyh5Hrzk0xzmWOS/I7i37XGd0ik8/w8zpTna+Fa/lIK8DaMto/rZ+0fsXhNR5vqxp73PtEjs5Wj5NdijklbCljS5ssrtC1w7KrlLLs/hZdD8Q7i2x9jUFEnUs8GLokMjhO/AUXG39aRGhi3qkimCfi4+JS9+lEwCnclXWqMofZVJc2P98J150/V8DY/cs6X6jiBK7I5XeDZcUrtT5lE1wse1JqZ9cAo/yb4ej9V3d1yWgOifT7O/1lVejmXYrT/Spww/ZvDVZ/JTjdOAHrnXS/P6x02O9Dgv90inVTbU2zRFPfu3Q+SzsMIKpkhNkc8ctpFsJVnCj47p954jzX3tt3RAAIFbxIaKvSXv1czpFny505mKP6bVndu6DMaGW4N3qrsRPptGhJk/0hRRTZ9aCXoemOCHZQZ9TVgR0/69TQnJEtGNHuVmjGhDhptocYHVs1PrgtpeWpxgL6IEFA+3Mw9KHAhAjKiowa6zw/c06aGIjjpTl/RA7uXpGOV7eflX3mZA7pSX2gJgoq+HIivCLnvHWOzxQWbbfWbQMRkaFrjcszB9rKcRzxwSzdVSfFrHxLs7P8Z/UkMzATRiczgL4PXX/PHMJntPSGtHeqR0qp5xMimo6rq04RW15v4sfpVZZpuiv1PAsDj05kjf9+6hxd4DYbTypfq7Mn+IvqnuEW8bPlN50WWiHNCXPG+3f7HhPazeg7K9OWN+RVh0bKyClj2zZ8fHxIEIJ3zbVpnLTJy7o9zhFdIjk0k1U27VU9ZPb+rix9ZZzM6lCIDORIhp7Nd6vfM7B1+L6I+8ma0H0ZZ3w/G/fPGAN2Hr0CVZ6T+51OnCo1raWLK/tEnp2heLf9V8a9fe8dQNxmfqo2gHnbp6vLP3pco0u2o9+zHRGzeyp6XRHdsVLtuU9n9Uo/xmN+jn5bPo7k7GrOVDpyPtmZCN0lLUcsQuywpAGItjPS92k0z/m/SG8E2j7GjFj38PRJVsG6QKcZpM6CmjkIUqtTaNAqQu2uJP/llEd6G/NQ21BnpOqhIPlNpmGCE9kVmfq+2Yyp0sGPnGXjMWlwJwC8LFGb6o4M6OcHxj/Ofz5n0aVUpxiZ0oK2JNcPaONljdl1eJZnLTQ+e1fdz+koV8o0HN/9npS2eNdGLakcmeWnkX+Bc93zTl+czcXeNoh0D6/jzXSrq3qKbc8s71IHIOrlXJ+RP+K3T0Ovx/XvrurOV/vvim58Vye8Us4KL9tPHT8Yw621r+Za1v0eOJcxK95cpW/52rxg57Ueh/F5I8M926H7Xo3C/rNrz6KLFX03XZj3thyjS0TvV3lP0l55f6fsZVmdmvHMPEbu0787mZ8vwOVARFc10cAkzVEzW60dl7MCL6giY8MUBlDvAI6cwa3OXljMwJ+vCxT+nwhEBce+4ygH74goB45yAGq0bB/Ime9z4M0Nme8dyC36TmZApwRejZzlXHUJOGx5A7Kc4y2roHiAEFASqMidEAUoB9VjmA75K6XgKAeK2SEBKujUZddMT0fNq3dg8D6TcaV/SvOdEB78HRAN+t0jVyb22t9mFfGs7sjBcC6cydGj0ceWC8NnfieErcu2y1QRBgTsfQXe8WlxJ1d3FIiwq6+1bG9Q17ZchDPh7Cf3yDFg26mOS38/hJcDz+DX0a0G+/QdqmHqeabIXR8o9uTZOLh1aQIKknhHhZazcsRFslg/U0p1x44/55edws2RpEePUbCbK+K5CO9ZW686WaNxETlMiGjYGaT5PF8NdS+cPVF7rFPGPpsdiXGljTM+aTsvwP2wuMzUy8QZr8zOd+Z2AUQJ0Q6gszZEn8g5djwIj/FRNAlp27B9fOBf//5/+OPPf/FuCNgjgaSNUVkLuMNrUT6b/5myZv0a8cazuL4CM4P5lfLeiZt8m9rUvz2IWL9q7Or4UzvhHjW/jkj3+KLtJTazUnttiulsyfq9n+SncnuBa/TbfkbOI0BOgaN1nmhO8XZIM8D4e/vUP0eTWofPC/e95W82jNxFRxLCMbuPq62Q2k6I6ghMqdK9t9LaO720u17eveVOx1G9rDuydKJf66dPE81Dq++dfmVsJQLxme/V7tRxpJ+yYx28C6ZQqRehV3qp/kAACkBZ6dsWndRz5VPPp+zN4Fp7fUxtl9Qzej04xvP1uePo2vtYz/X27hWI+HV8P6aJcjTafQ1QReiWpnAt1cLevJLu6+f3u+2+UmIfcrhfg6dFGn6dWEe3ansFhjnB6PQrmRXlPdOtznjJznszmfgsvJ9L3gO/Qge+Cs/6GLxtnsVXp4+bQ/37+Py9UB2X/aeHu89XNXaK43vgajDmbAxfnQu+ByKnUvz4d4OnAhEz8M5j/32l1I9lxVzny3Ivw3qiv5QQThi2niTKvInpNwNCnPPHsctOiB1EBeXYO3zqJNAp8TBnrCcg6YWufHYr33nEq52QMtKmOyC2LjqnChgZg4qI6r0Y3hndLs52Zm9q6r2nZ9t+blQU/R3xfeqDETMH5rL/06jgh32Dvq/90Uwep1lgy6abwSXjdPJuVseVSXilDM2eD/SY8Hho7Llxu+q7Faz6bkWfitui3Dt4eUURcH2AXm55frVGKQzO6shNbfCwcQxrHEGM/GgMzOXeqq+iNsVO5nFloy0nJcXN4GNkSFRvfVYLMK2Z0P4Oj/vf9jPCaUaTKV+d8LutKwrCWGXS4/ZuBYREvs74weLuaXNProiMxrw//Tub3zzoP2te42rRyVDmh8fHBx6Pj5qK71O64zCJ+84/uxIsigzIpXxaON+ivKu55juNsZXB3OMY02D2e0aPCHw/9fxrHV3tt3/O+aZVLN/751fIP+u/oZ0pVXxn+RvtgSTjXDWsK/BmUbOUgVfl2oD7xHY8o/WZvnMJl8lY9G1pgQig6bPXghCr5/59ND90zwkcdCbnBKw/+qBGIcJeDmmD6NvaX5Ijuj9JacoHv8bzqf3LZdTfWbfnndn1Um75VL2nfVLVfXwds7rtsxCSoQeALany5eWPoTP6o2mT1teKg42CW52vHqlB/cxU85lPQi+v+iGRzERodDDJSPDp3YOBJNc8DHfGMHCu21u6uoou13Edl8W7S/kjPXZul1x9fuVZpLO2ufIcX8l1CcdrZT0PqrZZmLchyi15ABMotHnIvA8LkTp7+TDI1BilCZ7xnDCzRWDxqp+m4oQqW0jzaR0TBCMcZjyzAlvXDPTts6N0Pj58LaNPzaNndcaVrXlm99x915ddv93Kt6qLfH93aWjo/9GEuopLJPu/Qv6OfUN1nkztc8y4eH4POv0A96eZld5u+e+Z/p+Nz/M5NOab6NlMf7xT1kv5Uvi1fzKr8gZJLwciVkKCiFAKM0m6EelbMYFlFL8Dwh93o0ojKF4NvjIIqnKecytL3yGJoouqYLOT/8C+7yjlwH588h0Rx6GjlHMmWeG9bd2FzbwSR1bNKN566SglVnzzg98/ZDeFrogXtVhXZ9O+oxw7jv0njv0Tnz9/Yt9/Yv/8if3zk3dDHAfoOEBHEcurtc5q0AV2izuh7HyJ4KGfxwFQAeGoRmdKZtIVGm7bhrxtyxW2850Qje5qbNg+mRl5tr8R9LHt5xkOVUCBhgFHmAV2aMRpcqTAMzAzECOwdJjx+ayc1fh4BWb952nvd3xgi86k7XHVNvnn9j4IC2f0m9VVd9nojgiLN3inU1U/iYcYX2jeBLfc+FIdurqacYajfp/JxYrXQp5VZ4LseKlGuL73XE7v4wOvWJ8dHzUbr95h4RWj24EIInEUjor/M45hi7/nSxtItbsSVsGV3mkOI2etO983KR4Pvn363bczJZmP8jiWzmhR3/HEX1eYdgZjSkBOoJRQCiEnwo8t4+PjA//v3/+DHz/+5MtuQTgOG9zWufS/G74zCDEDzxerdPZz9m51DOOZk9s+YgNWd+5cacmsDdHzibH0AhAAVFom/4a/BTQcXTMr+Hp+mfXPM46BVdqv4v2rwQyihNIdtaPPeznE3///7P3bkuS40i6IfSAj67T6X9qy0ZhJV3r/x9NINru7MgjXBeBHOEAyMqu6154f3VkRQQIOh8PhJ5zs+14P1ST4zp+9nPnOtnWma6nn06B0L9d3KB5Hs8NZ7/+shxu31obitp/p8Zk9Nps0kPf7A6XwQqNel2k/+2OV1JYWe6Rs2BLeijZgXMQ06qOq+VC6Jdb0Ge/gfj4PPN8r3n8+8fPnE89n2yFO7CcYe761QXd52/5QF9DwAKDHsCU61tlaYnMZGo5UhWp8k/jB4p6GwkHQwosXAPZB2+fa38pwH+vhhQIrWVzCp23Ax5Ln5Y/KjWvydqXnrpSN9qkfS6Pc+c9LV3C3ecqSM9qY+r30EH5nliBq9jCPI2uP9vd20lIuY68NBnWTdxU15dCP/awnMsTieyd56q/fv5ayXsxqZLsnnCABlZFX7dB/cqLg24vv1/9tbVQZ/btwAtD9LCvH17ZB5l//HUn9zL8NhdQWzvTlbKLjbh1XymmeX9g3V4c3Rrl2J314IoKFyYpw7EiygW8NffnMCiYdE+txBkpm3Ie/WdtmAtCZC+xYEIGoGsegdlzZWNYgjAv+yrFMvMK2mk8AHNa0gZ3CK4/MhAjX349bqnIEU/te+y4NH6zUz9EGYgdIVwJV4mOOjhaA5Z0RwSmbBctnzuBsQGdpFsiOQUfXvyHPLGAZ8+jDDJGJ42h46ozHZslOgNxJM+FnP62wnPWNH5OUwr1t/CwM+FUwSwKX7ceiAvlnWccsaXtGeiVAG13qyLfy3WJjDdVSjGsW5KddIXeKJ4Net++sv4b3BkwmV1M8uqF1FpSa0jTxASN8JO24MrbO5MiVtG5XmeaL7SXkffWKgdLgQugWZVg0GrMJnty56fIAns4jvhjgx0mI2GeOPt0z66EdlLJh33Y8Hm9yVFwmf64aw5Gmrzgzr8q6V9IsQA/8XoM/6omIS5Z3ZYdZWCvH8mwyQmGq7difpPnOaJe/t3xl8yLJm+H2Oq95+BqAXNsAc9nzu1LWnx/h11cDD6/1d0a3Te5QiHitfgu84NBfsVPj75l/wt/t0ZpEpEejVnsZptnFYBdhEF/ODV1gUwoKJYttkrrT76VgKxUoTZqXYqbRqD2rNbcl20REuyQ6vpejpWT397WJiH3vx9XKArDmG7VFWObz2T6p+t0RbWEZgbaON4Lf5GykSLSRRpn8Yx3q/K1SHGx+XSLNzfvzVODZuUyej8nKWpW5FNo8Tm5ZW3JmF87G4SXZ0XlXaO0hnZe/me7Ks7X+mvHFGcyrdcu304DzPyFFt4OD+F5+nOM/pbnT49d1hPKwGZeK1FCvwLSfk3Gf13ketMtgrOy0q2Nq9vaMTlm+cz+b8/naV7ai7Y/Bp7qol2fvPP2GINhLadDhyOy4sa5sl3kG20FxfXF1lHf7kkE1BP2iB1dHZnczPhdrvMqLF3mOnxXMw0KzGNjVOq+8P+f3+fG+WdlsLGX4R52bw8jHxh1ZetuWH8anl2t30u2jmXJDo+I4vDPvVuZwPglG6CeM6iHzb6+tw887whnw/W+2Ujhrx8zg5b+GXTs2iY8oapdRV1mh1CYhGN7mzmzFtoNKu1S6Pfd18SevWraxnRbc6SuOGmLNgK4Vx8+fOI53PN//RH0eeL7/xPH8iefPP3G8v+P5/o5KP3HU97YbgidLYBlEQmW9vW2F1dFXWh3Pd7SjptpxTrW3k0ttAKgUUF8V1dq4y44Ivt8i66+sL/i94Ca01jJZHxHldzGcObhZ/uIJZOqosnrKXkY+OJgGj7sOdkFpx3JhDKitgnErAQZAAn3RwZs5xZdwPQkgZbhN+6dAVkzTNh4RM9TNn0H+8qo2AOnl6PNVumu5Qoe/d4RhZH0SPzlfrHNmpF7hmRkd7WdWb8w3U4IpH9h2LfDkcuN9FD5IwhJ/paTvjp8zHs765tW6zvAAIOOYZQWgPJhdOp/1q3OSJvWs5F40iDJjP8K8Y4wQ80LC3/q3YSvtDognHShlw9vXb/jy7Tu+f/uBty9fm+quLxhC8HR4tR8zOfur0u+o66p8/qw0M2bPeNjmuQL7dwfgb40Fk19cXcF37vS6Mv/UCNL/IumqjMj0dZY25LI71pPZQfFZvGss6oV4311NeLOJYg10Kly/Up7Az65NhkTc+xNs1KMa6EHF7iNVYyM7/ACUsuE96EYiEp34eDycnTrisvV2kPgdTc+0CYmt7OLP/Hz/E3/++Sf+559/4q+//sKff/6JP/9q33/+/Im/fv7EXz//avYnKireUXHg/f29Leh6Hh23hn3DxzoI+tNarqndtfX+6QtQinaIS8Yriy9uy/W57LwfhBt5HBLIErIUb2twHXfE9mh7Wpr3oNoSwj9TiJ7ZXi3pauU77Yj04NjFr0kftStigEy0ZbMnT2yBz7YBzuzr+GwmI6/a2HdSZkutcD6FF35/BLvPsC9nNPsV/Wzr67/wa2TFyA+sfzk1ebmhFEJ2esPnpAKZdKg93loZt8xuKSxe+yyEaQ3p5+9In93/q3ET+S6WuZrO+PeKj3P2mZeb+xTAdS7/nf5ill7aEWFnQBR/vzLTd26x4wKWfKMStZVew02ImHScVRyxDbNAoeSVBk6MddWhKNi6san3I9BWJHDX/kYcZoPEBWSJukDhXRDPvgvCfPZjmmSXBB3wF685ioXPVgcR9RVDbeKCJzDa7KmayIUbzW0v3O5iHIOiBqrpB4bCMJjM/CnNDY4KMB6flQXOsoBsTPNBN8lr8Jk5btTpE4VQdKamzkF3UqyZfVeYRcE1C1Lzd80/jpPpmAhtXAvJ0Xg7DQCvxjyFLCxbJnVGJZ87tt4fdEZ80s+z8XumNCK9Zoo2o7Ft06rMmUyL6a5Tu+Lrq04yy7XI51J2wR8zGmQOwqwNTr0s2nM1TR2ZiYFwNlHAz1fG2F1ey+r2uMLpzgHHkvQFjN2KFT8DdoyWUrDvj/6398CRN3SjAX9HDg5tS/KejY2VbPvoZMcsfWZds76+7nRfdwTOdNKKl2dOwFldZ/wQ8505GKuxf0WmrN9LLcg9OTJqbOIgBjxnNs9VnK4G2rOUw37dibk6vud9pEY4Z8nftzzx3ZWVidPUuzSSjwPWats2u65QMSsRvV0Zx0Dsa16sxMH9K7Lf5hcjG+iLwPJja2f2TGYHuT7pmmADsAql2rbayRWGeRzHcLyU1g/w0b+ltAB3rWzvNLibWVj1fD7xfD5x9M/nwZ9H+3s+8f58Yn+2e/0qnqjox+4eFcfzCRA1vw5owaPYqm63t7q9vW37RI566bq0TUh4+5UpaRd8WRhXbJwstbL63SFv6zUa3fpj8m6oW+MAzFkwdX005XBmctSUuzHR8go9ryQL1sqlK7rO0/20Jqydps9K1+iUqxKPo/ZOX+zJoQQCAuONkG7aSa/YMbN+OrO7VzCv2jhXYDE8915fGL/Y+ukuVyh4j96zOMOVslmeLIg7izF8dLxetSHP0pXy+qzLrMEWPG/nrN+XtF+YaE7HW7jhG4Uyszb+6uTiGebY/xn94zi76gPbvJ/V3rMY2ZW61/7IBXvgg12W2aSrPK+mD19WzQIuE7rKQOgGyrqDM6I3A7Bv/w0KwhnH/e9KkIaD5u3TBytdeSIctRmjvN241hbgZ1j79oZSgK2ftb31yYiybaDyAMp+GhycOSEwuxGIKurziaMe+PnXn6jHs+2AON7xfP+rvXv/C/Wo7X4HHKjQY6MazrozgutjZ+A42pbvZ790m57vjbZVz8FlgxsgPQsRbdXrvvs7MLCJFOPbJ2yL27+y0oiJ39vbd3E8n0/nqPDq/swot/1YgOmKqqtCwdGnVrlvg3FaOW1DP54kEVifaDjb4HSGi3VUZw7OVX6d4ThzmiNOvLL6TLn2UgOdLPx4RwTDmo1zPVc31GkufL8a+MnyZeM+GlpnQcNMsUbY8beVlVcMHIczkK64jO3K2jMz4q2spcP38xXeW+mMme6xSXjxpB4LY5ZWsnyVVobQEOhJcOV89vMqTpFXOjTRc+GuT+mvMeAE522WUCb+AcBRj6bDy459f8OPH//C9+8/8Hj7gm3fWXUbaGT+2vO/ywj+O+r9p6arOjQ6BasxZnlypodewZG/zwPYednP6HOxl4Z2Xw+Q/eckO05fLZ+GrP2vaRWzY2cW3ngo/0rSwOvkfQ8ybz34DJ6EkODtBp6IaL/XCw0y/RDz2M8VzDYNUV2ezKY9c44zX2x1j1rL17CPu4utnTboHLITMPyUfTASmPJHBKoH3t//wv/883+2v/+pf//n//l/4v/3//s/8X/8H/9ffP36/8GfP3/i7fHAQT9R6cDPn392e59xb/28leJ039bx3PtO933bNZ/2TMeT3WC7E9+0tcQ+tfYVULf8nofMtoy/zwIwsyS+HvFl5BWgAlCOSyhtvl+XD2kA+HI9Y5n12/D0l+h6L/PPg2Ezy+/3pHXtow9/nu88vwl9Tku/kjI6n8nYWbobnFzZHqk9lPi1Z7DlE5nsiE/H32TeXE136RDLzd7NJiGuwribWh3Aq/o/pjX/EDtOUnfMmuntzK+9iM0AR2I9AGqc5EYT6+4TnUOIxJ5lDto+iWZT7CdxkXIinWZp5Y+c2TizcXuHF2dxmRme52Ps5tjDZ3H5hbpeHKMvTURwXQQdUIPxsCD07P0sRfZLjWcOqCQGdAyanU0MSFkHsxvWqJB1/QU9OL+h7P0Ypc0Ylt1wDfarrSSlBSlRmwChowfD3+UOiON47zsieCdE2w0h9zrA7GQg6n1lnQbABnyId0EQyQV5pnMZM0NH7hmEXRDeomZ15wc0D45EsFihaRyblSB2Qbbk2Yy+s4A3A3H0WlxSndUxS5lyiRMRFuYrwi/yO3+ugqBZ/rM6PiJMHT4nzlSHDJBOTEreCUkuj3EkRs8kQJAFc5mXZzR0Qd+kjZFPY10rxRXxibhd6Z8MH0LevzPZyThGZfvRFHHIxvHMaJsZG9y2V3DhQMdH2na1PQDLR35nXNqFflvjP35SB8yoZPna6k2Tqb04rZPpxaqmbBu2fcfb2xc8Hm8Cu7Iamhiarzo/V9Od/rxK89UYPJdJr/HoZyUJvl1IK718JgdmzuddPZfJ6hlumZyOjsodHAJwHSepQ+2DUtfTiKevdm1rC5Sb9F1i9Av48zW8yJE9gzXFVWzgV2oFysz4sInt5CDa1OnXAFQm/UQH9Lzmp/nkyRj9bDhS2ry2Enm0OXjR0RWnXHyX/p3LUa04wjFSvl/binleMBLzzI7K1Wq55RvYd+G+H/ym4EPUfj/E0e+OeH8+8f7+ju3xAIFwHO8gOvDz5ztqPXCEiYimr9RFKKXfebHt2EpB3Wv39yK/9UVcKDJ5IYu2Jnaq+12AjQpM18qLyIPO9kcxAaZ+7KvZhaG8Qv3/mR8qZHWfYxplXeRBP04ndj7jdFlccl3z7KNsydv6Udmo5dletLbVDJcIY8Rvnq7J4dfbdbecPxaKkm+cnL8AdDt03Nk281UEcpAvNs+rwcPP0JEzHZzCZvl+se7Bboq6vaj3kMcR8pjDlXSW1+om1g8wn5me+4gd+Bqur9pin5SsmNDuGGQs+30Epo8WzidtGNCsXoKV9OLvGzRsUWsP3E2Zfb36bZ/NbLardmdu+8s3WLmZ0Tx+Nr019yWuppW/tE5Xy5zxe1JiEZNY1rTw++6ml3dEUAUqoa/WJxkQzCjunPBmtbnyGUPNhbTuiLAGprtDoCuzKwHQ/s23p+ePZ7HScUgQn4gvf+OA1oay79g2vWRN4FPHW6ohgA40QzwwdO2vGQeu43gCteKoT1Q68Hz+RD0OvD//RK1PPN9/tkmJ95+g40A93jstOs49eAtUA5t3SDSB1I5yUmOdDj6WqQushZCIQdDMQBgdkbnSafRtW6KzFVOcN654d3/mme3XmWM6BIs77bnO2o/Datu126dNkWdXwe9IB1sHgL6DZVzB/orwyoPhI59n93CsDL2zIFr8izixEyawjGxIaUcA4lnDLo93dGJdGb7MU1yeiHS3TdO8Ic8EZvc1mtwBytbGMjt42875pWIjdnK8svqy4NqsbbO+43IrPhKeAVAnRkLcaWRhz3C8Gii/Y7hnfGbrck5OaUc+2HLzO0Pmjk/7PM9/luJOoRSHizCiLMtS7IOZDoz55T4ZdlpMFGHZo3Igth6lt20FX799w4/vP/Bf//Vv/PjxL1DZ2mnlNF8L9hnOyKvpV9T9KwK4vyvZcZ2N91UaHaYc9hUc7OedOmd2yOz9nSQ8nMAccT1zgj/GI6+244pumLxFbMvv5vNX2qz28Us1mrJj270Tm9GCjYdmv5TC/ONtDqkh8i5POhQNUPMnp81MXMS6d2zpeGAedgGkUP/MxsjsvyjbW9ZiJgeqKx9tHtZzqr+57uY0qb/GNhvbtocL7jTY/YgrAM964Of7T/zPv/4CbQWP44H34y/U+sTPv/7E0f2ihobfPSL0LW3n+2PfsZUN276JDxL7bUM7uqlsRfLKLvoOJ6Ntg1ew7+1YKLYty1a8FCGTv7BtHRdomXcYbaVZsrvo1+MsgROy20DzGoalY6xz4YOsQE9y/R4b428OfH4ovY5zkBTTN/zMmJgfTnd00B0eWAVQr8A9szleD1YyADhSv2KvzdLgG2HSk03xoXCsLH4yvJew+IzECxg+x05Ruoy2UJYqNdXP0+lbKSLIidDvzGNMe0yhQGVnObeprQ4WXcvYFc1zxQf+HemObX8XLknDc/lCVHrcp/UfUVwECUCOhbyH3++n5XV9+ek1J/HWK+mFiYgCDZrPg46AFXh+cGbBtLnAJsNAYZuR+V3Ce8nfvohhRgy3SFMEO87fW6b/JUEv8SNK3xFhttkK0xbTbtI6YntZ6LT6244EUAU92zFJx/EE0dGPZjJ3QRxH3wVxgPqdEBActRUwfcV95/GIuyX8s5QLFsFjEoE6D0hnz9uz3KHh91mQM5uMyOqJ5bPUaBTo0Y/piTgPCh5zYZr1eyyfrU6weeLzM4PiLBAs9K1zGFnfzfKs+myGW//hYHtD7d5F5FkweiZjmM8FnvXoErgWPvOZ8hMHHVyT1krLWmQOp3mbIg5ZmYzvz1LmANuyWfstzhGf7P2KF+TdAtesnpl8mdXvOmlSh/2M9Dgb12e8mbUnGz+qm5S/mFnO+nP2PvJQ/2bWx+T4NxvZM/iZESyMLXTb8Hg88Pb2hi9fvuDx9gZWomLCG761TTgb/1edwFfLfSTN6ljZPZ+NwwzmmRMT+SXqn5h3NgZW4z+TGWf8az9j3bZ8ph9X+neVXnGOMtza86sQ1vx5posFykSWfw6PFeitAK8lh8dCB0/rn0U1+BXp7zSfx+ZG3Xn++zxG4XMOTwF34yHYG77B9sVYXarDYcySiax3fEdoq+ztJ6nfFPEnNP/I3nmR6XAux/mUZ7luPxFxHLWrJ9aVu0ykyxFK+47H2xsej73dT7T1PPxXe6SH/wyxRC9B/c2KglKBuqmf2mIVRdvfddnWg6xbbXVttLU79ao9nqn4EV+a/kcp2A+zewJ+MRZxUI3LlDbZkdmN7ZPftQL6fOgC1xexLy1cEmZQrDo6EVL69JVEoS6C4/yZ9Oxl53rhNVzOy/ss9224UXdmcM9wOLcNPyvJmL2YD/hYWyiZeM1030reZDjN4J35TDO4g61SgIJNcJ/ZDbeSRY3WOv+VapwtMbMr+fns84b9+dE0tpsnvc79thVMx0usi4dFzllhlttdDhvSEGXy1sAc2VzqTKvyzhRQbBd8/rifpXt+aVL2LD6gQByPCS3z3PKrR5FNDDjkuDkuf4UPxzr7LuywHMR80vBWdLTwJevsUGdBs28c2B7DvWlH35iI2Mxg4dXrNKxoYcOxfRrBG2aTzgaADZRY4yGulLdMtlnc2MCFktFCrPK7GU+8U+DoFzQftf1uJhYfWxSVCht0G8r20LaB8/VONvTJAoRUm4FrV6dTrSg/3xsuxztqrXgeP0F0tN/0xPF8R61PHMdfbdX4cfTxZ4SX1MV95y+Ia6t+zKQOKq46lkPAASSD2U54ZIo5U8jc7tlqqajQS0m2OId6ONnV7VNh1wlF5szaRqujnRnbeQ9AuqI6Gv4ZHtlzcXCCkTwLtNiUvVsJdjs+7FgqmG8Tv5JsX8edBIxH/Osv1INK8LWwLZxZsnyxgsXj041Fg0dWV9xKr03w/bRabZ/hk7XzboqG2xVHJj5np/1srGXG/lnwRWCKjltPQmftO2tLyl8h8W6zWPesH1Z9eHZx6CzZcWJ51eMA8KoXoBlJ1nC+Wk+WvG5tfUFmQu7q+L/qLOz7jre3N/zrXz/wrz/+hT/++ANfvn4f8ICTf9fa+TsN6f9OefqdfTCbjOAUv69k4mc7u7EeqxdmOPyK9DvquILDJf1X6bVISE+xCrb1XZ6sXn6+JS8RUaJRHBVu4xq/K8EtB/bEntOH3adix4ajGTbmEAIWZPyCGCxZ1WdxKohBj37ME9tOJZQLONVeIrPrs3Fsdaz6MFy7tzlr1WOXjuMdQMVx/MSXL1/w5csXfP/xL/wb/wN//Ne/8a8//sCPP/7Aj3/9gW/fv+LxeOCv9w3P+g5saDvNn21neK0HgCq7/xtOPMZbX1BvK9NY/Je+iAl9ZUHZNtkBwZ/F0G02drfuS+/73vrA3nnWfXHJa3yibdsA0v629oa1k2a6v5RkjAVbvJTd8KCHpfspLcw8gJv+Htg0RFiRBY3+s9N1+W3iDZ9V9yfB+TvTys/5LN14x0a2yd6Ho5kw1UOfkk4Z5HWaXNbziYy/hNovS33y9nfZrqV43RxjgAlfzuIBIUwR33BpB0Pje+pbxnr/bl/qEh/hOr+QxJ6bbl6st9XYWw+ZktEtgJpZZ/y+smXOUowjfY68mlCscCyG7W8a3zt7boIHwxF6RcpdS7d2RBC6EUbd0MI8cCaBPernUp50YOa0GWDpwLV/Be04EUtSomYgunpaZWbhEAkdKfz2hj2LzOICaT4AThLUYYDtgi9e6a8XP2eB22omWNrZV89+N8SzGcH9omySfVvqxNluEGFjJgSYRfibGPHdNWCG20p3FMrEVeHAcVFnTj6FsSH1asBXiNqFcp+0YIEIP3nUss0NirOA9JmjE/mNeUg/uwMUdkNEAZEGuxWJFPeoYDTYSOq4cZA7BAv5e1HChUpNXdl6JKLmXB3qWGXe+yyYXMMkTfZn2zROVsG0kbmHrTAbmNSV0fHiZILhgUrYtur4y9epvEeEgfaeXgYng4qlo+M90U7sdAOlbACS7edDlQnRcSIHh7YFiBeCXuOkgf8UvisanB7aa/LM6pnjSihkVsEvyjNs2y7vPAe5R3R6xnSEo7JbYYD/QvtM0xUmCQvwi6FnhzEwMTqjbGhwysAmU50LMmw2l0/g1ogxOuLqAr1G3jhabkOIAZ5KDHND2XZ8+fodX79+w/54w7a34AWLn5ZPGijQVJfxe2VU/9vQwehsluOZzJ79Pkuf6dD+iuR0rUlX+FDz8hCYBYlGAef76fckOw6HZxfLZ/2fBguQUVVKOEbVPrAWEtc5RcbBG532Yn+EcavtOUt36DOTH55uQKTM2RhZ6rGruMk/F17a34WamapOwAkGNK3nVZmh7Y8GHJm+PIW6nFAAwd0JoNXQBdgeUG7PzOnC5I74Gekt9oVc0Etq48pQwgZeOerrZhSavjzKE0UWuxGABx573/mwF5TSjt98PL7i69cf+P79v/Dt63d8+fq17dB77KDyxHaUthjq2HFsR78vry9So75QrKofJ8H+0hdx9Oe1EI5ygAr1PoDYiX4ywFKFfLsMISq/YN/T+nTkF1ptpegxUduGQuys6S5eb9cV7xdzH/V37cJ1FTjMUQJjq62fN+5ZZQBvDdhdGKaOwb5OBJuB0cjCNNXFhvra0nM1vim8jnmvKLLJ0aEpvAkeNDyRL9r8md6F9pvxnWc2ZoaV2OAieBYoL4WuQBvARGk3/sodJgKscusfEf4IJ9Pp12R14261DT1uM7Wl8spCsmus+X0RueEwZ/pz/AHBr7CZLTGD3k9tYgF2Pbh514biyqO1Y6E4iMbxzDXEqP+u2pWv2H9DGaEjOTEx+H82P9koTcC72xvOb5z46lmMYqiPiuePgVlyOsRsLpbUCgl+3PBhZFpchxpcTv/Nmsjyj8+d8a+OBT/+bZqagRxPEYsjEil8Yd+fn7G9xP60wUeJyQ3rWFoQULAuH1k5Y8aN+F36aUfUbb8zBkn0BfwikY6B0Tdnor6Fepu+JirQY0YnVS7S5YmI2leEvD/fk4HSjAnZLlpUjRAOx6128K1WY7jAJmnAnj/tivlaa8PArBLhdf2bYGcx1ZvfeYUs+g4IVGpGXl/10vhwEyG4taUpKGXvhtomkmaTeioIbeJAg73KnVRrvzTt6S5Blm3G9dl+P/tERD0AEEo3hIE2UcGrTZqxbocL9Xr7pAW/KdSW1lRCLW1So5rD6Eoh7NsOEMkkk+vrHoy0kztkPwkoFSjUaWj6rs1IkoyuAgCPtoWY+7u+1z4J06Dyuf02YDRb0RMTBZ7JBLtVQOJYiwOwO757Pp+OHlw3f9+2Te/2CPgKf5u2AP4+kpiagd/oreUTyd3/bBu9YtFPIsLxPPo9HJ2XRO94IR9pO/CCSZHG00BpH3wHNce2sBCuEKenCeeW/zia03cY5bXxmOvb6fetolTFcd/ZyeEdTDmNo4Ev9TevSwx7yVZJVprp2fltpGNrVkY7F7PJARDakWtO+HljKgvyxcCYlY282yyb7Mn4eaC/hV2PXnZjsntDj78bAcr8aHebWL6wO5hsm3jhZjsYU1W5OO6TFOFZ5z0Oe+5f2z8WP8Zl7zqCj2sQMAldJeDgiMjtMCQqGwpIzuBE/4zjP/Jg3LUzjDGCnCkd28KJ+ZbjNEc9XL3bY+8EMkYhEQrDROBRKK95ucPGEkm54trYzryGa08zVAg79v0r/m//43/Dv/74L3z5/gPb/uirSIEDTX/vArmZST6Vyec8WVKldJuWG8dQ7KfMZvnc1KyUCYYXyt+0BCdlhQRm0PFkq81PBL4SBAW6YjjqV0u7tOYwXrP3IucIRl973Wvzz2DdTx0GyT+L95Z2E1guSJzhnRX0591yWSof6e/XktL6A3VPu6XMwbKHZPwMh1fRLHldXQcRL8T5/YknSJM3ybORSP3GgWCAn4ErbITi+nFase7Emc+qtX1gOqMw75bQHUGuUx9jtEVbpxemB9AdeUJFraXviHii1h2PjbpOfsfjbQe2Jx6PN3z78m/83//9/8T/63//f+N/+7//7/jj3//G168PPB4Ff/31huM48Hz7BqoHnsdfICJs5QEQ8H50H6DbdXKkKbNTd+ybX0U4zE5zHrRxUYto4N6+eHdbZd+JgwTV1Ee8o7m6O7C2rU9AlC6rKeDHOlZsoO5nxM/Cuyp2CeNI1xcM9rCfVOC8O9qxM+MkCErBxvZ2l8/Db/K/S1nzbXFsVEHlmOTz+itPVv9mgsoOvuR9gacZRlvLPTV9s/H4vmDnWOzYRlO5posxGot549mqkmL+PGSrozL764IsGXzgSAce59nTYr7PSp5YTBf807yGAl9DnjabzeYu2ibWVaUhYfwPc2wsIGPF1ug4Terh/iCDWs6H8iVp+0cW1kT+MRi192yX+cgqV5zje5r82F0F9E/xz3wqkUFcl3aggS7jVZ71/IPG7HEBEOT4QgYR7z+1eGe2rMSbwAsfYYbouJjNtav0YxGtDkptCBr5hHECUEMDV4shKH4XXRlhYGAF3dHZ9aYZI05+W1yzsdP1bNk6iF6GW6S+hI6PEmnIWVoVSntBoU9zVNaT425QwYqAdsKQIGOwVT+bP2H8qWtpJj3GxvhuDnxxp6bCfH4Msagr6fpExCJo2hDxiMdOiBMQs0mIPICWCwzOTyzgJg23gWAXfFLgU6KxUSYytKhh5AVId8aFsXtQKdDNTqSwEamB3Phpwj6Co3kuAkuxzYwiEWyh3XYtidjEDCELAgzf1Uzgs+5kUFcToGRj2lywSgC2WtGOZZ2fP+36opTp39BWE9TLgiGrIC6Avp3abLE2sGb4zhRI5P1ZsORO0IS52F4Wvxr4jh51pM1ZnWcB7rPgXQoTczOEx3y17eKgayg3BvS1hiu4pf3Dz3ogHWWUW5miSY0Qg5c0RZw9zzsWfuTtGa/GNpzxQZakvNFhJZVzk3KTd9HA0ABbbuis8NRJiHNePcsza9cwGWE/C18t5vvJGyx3DIbruK7G6n1TPo4Xv1vA06V/isGU1xmbwGTYSsHj8cDj7Q1vb+1uiHYut+E3o3eaMW0AVVsbj5Uwlqb0W4+DzObI+j2T9/H5FTsmS3fz3zNIP56ktgWfjvaHLxthRJ639sxV5zFWflZupZcu1clahxayaVp3g+ALBN0x5Lk5qlfK9Eaa9/Fc37ySHLxEnjU1sdYtHZIvaJ4WzZwBwHwyYILnFIePpZeDQDyORjMk5gQAyZvVeVuGXmg6wQbes/E35zWNW1l5sRofbWVeG4cUxmPzc7Ztw+PR9NDbl6/t8/GGt8eO/VFwHL1crah1QyltQdmGtwZm0wlQCnJAJyHU59mMbV6C1+/5d5yIsHdoAG0hoJYzd1BIoFl3YZWCdpk128vV2MDw8siWYZryd75vo1aux9uyPFGx77wL2PYJ+8MbUPj4qdIXEukikHY0FQTXzenRgg3+mFPryw9yo5TQjgokExebhSFUESi2Ba69th7vZw5VdFWRDMx0OBXPG9NxofWH0g5J3T2k9Ej9trSWNs78vDaZV6RqvoT38qtkj43NNvdf2upaRcXunvYYfn7K7Dn//qx8+5zHknxycs3qu6y86QLJ0wkq5BJZmdVmgKS4e3vsLJB4xW4d4k4pTe/o0Ot5z/TbSuVGU8qZt/ysQmifLeSyOGhMAaYf1zboHXv2zjslQy5DOMZogHnYKdAZHhH4Iv8sxiCihI/Jt3gm4Gzsxry3YyQbOw5BGuNpebwQw3sG4/tgGPlpI5VMerJOwSj/RjzmdQ2aTmQ3yxx+mFXS/zmJGZ3GlC6kyxMR9l4GrkSVh89LoYOjEXH2PCYbmJ9NhJwFQDPns8Hzgf8BNzGE+J9tyGPhiVFJ1O8VOIYdHHYVi6+332rPuxTYWCsa9Gy0rbArvbMgNBtybKA2e9MEoPvvQa1Lnbr62rUtpT2P6z4wKp+t2tsbVqXbYFdbTRN3PmzdIPHBN1/G7MBh6pndFPH89llgiWekSRvh8s/uq8j6PtbFeEv+4ge15elYhh2RrL47qZoJFeY9e9eFQWYKI2tXfJ6OHft5Ef9Id3HkJuUbT+iKcXeJn+mXeEdIhBknGTi1M3bbcUKW70rpExTJiGCbIzwF6cU06PMQaf38O7YltnuVloZkkC1Z3ZYWd4L62XgtwKCcrRKb8c+VpHbF2rCLsLN2W3wsDObDUnQnRYQVHZisDXFMp85h0s/3g9Wr1HVCMLcdXxdl0sL6IxqoSfvkLRkabQXfv3/Hv378wPcf3/H161ds+970C1R33F3Q/RGZuII5+5w5ap+Ng8EGH70E+LOTNcDnTnfnVS5jy5sc1vKgFM4aj/7F+0zGgP9ImvYpTYJOr6To7f5N6SzgcJ4+iyA+RUePn/2T0q8d/5xy+JkTeu5Hfda5w9fTL6FRt7uI4u8YVvALb/b9gW/7hm8/vre/79/w7ds3fPlasO9NLx5HxbMAVA8cteG/lwcIBY/jcLJlDD4Ymx66iIaoBVEmPelwjwv+2m/gOPwirga74qhPd9cb2ymQIHSz+Q/wbnqtz6E/sUdayn0pb0u1OmO+aGfxDlz+zTZuvFet2Y0F2+ZDFM6uTOzU0Y41/np7iA18gbni3F9J7KXFZ+Iu6tG2m9vYSEVjOslAcIGnq6tRB9jOHrW7bQkOIavADWZCC9cmW04fkdRH3nhzuyXtWEH47sKDUkZ5SeNIouatnW1qCBGMaVrJPh0z92kvwc0XkuCzqHfuxs3s0gRcJ2Lefk/BaNte0Rcv0+0T0qfrGPqoBTmmgUfKRBbgnN6zuBj/PvMxF5Dxq+y5WZr54Vm+q7jN+GHts+X6MIvlZXW8TvPXk23Pss6huf2BrKs08r0k+X5Dur0jIg+4+GAJr7XP0hXG8wYeK6N1YGkoZ+qa5dUg5bzc5vAsgDFsrCVcCSh9Sy4RAcQB7APHYYPZFcfRPjUAzcoo4AE/9DjvOEh0G08kq3XaXTkRtiG4RGT4T2dy1XjIUjOKtUybEGj3WvS2m7rt5axtIDFPxdYzWqOxGQOfQ9sCjV4RDuwQ8K4W6e8ybprN6joLVlHA0xrug1M1EYgRTjQesjoGmpTVas757HD2PgtgC04B9ixoq+NyLnMG2KbtV4ySDFb2Xn/P8zrckY8SIkDP0Iuw8/pnsmtWJoNhFZULmCd5FdcxuJEFxGc4DGUcLwJ9bmdIrypwp3sCv5zBvGq4iexNVr9c3SU4u9w64+UVvDipNkte9oxjsITy7LirM8z4MCzJ2L7H8Vbkdf/csJUdX758w5evX/H2pe2IUEeTixXVfWZ1RuGfosI8382MsNMxGsZEfBc/Yx3LcbWQaavf8dkV3rV5/W/AjvCZDpzhmNbtaJ4H5BVcMQZuCe8LONrj7ToOaqx10fg94jk6eDPaz2Rq7mBMkJrUMUuuztTwt7QN/B5/f9DfuaJD1vIw2myfg4OaJWv90nPjzGH6XY5hli77OWlZznde/q6uu4vL56XXGYac06zjktel+rzN1oo2wVbaUUL7vsuxQqzqCtv1pbQ78qwdg4K6eclCVjmBj0zrdji1yQfRnWCJN7RKYLBvlNnqxwHH6uxPHbQ3/+qozTqp6r+x1Dj2tiCOfV0P29DRyFTPDkVpicB38VszdJX+MvHB+arTE7ldrZMEW3l3QqY9Lnq0ppvYiDbzBjcRIT791o7SCby4mf5HKYA/aVJgrMa08AwK4krTsRg/YPqojcZoZ7a4TZkNM42xSH+0/rTca9HJvbUMdYokDO3Kn6lLkPs3yotKH8ndCwcVadjv98u31JazP4wPNLzzgMKD3CdTsFaeF6mmfRq+EHqNdqCz2cy7zK/O8Jjx5FmeO+9nieXXHR8gk3GprXvKL6so54iDxHZ6yULrvl3WPPEdsrjQBLMJzCt4KN2u9tuqfXdiNuDY4irHRR96fG9l8bkPGFPmY32ezFFJ7W1/Mu+8LTIjJ/MfTB8SA3QqmGWHr9+mvH3F5L7e/ts7IvIB7wcVH8Wj7+8bwWIsAcNlwdFh5s9VMCAL9sSV7qVoB7YVGoStGDilgHdEtPraXQ2CV+Xf7fM4nm01ilmFzvXyZ4Pbt9NGAVEQniR06HdFYAgOmB/UDFSeGOAdC5mwVfm4gc+kIUI/0mzVf8agrRUw7X0eFbVqe9kB4DsgtG+04SK4LxhZlqaNJvMJiOx3GoDo74Tvw2VwAYh8WkO91iqORRb0sTwYg4s2v70g2uZZtSeDz+0ZdmAYOFfpZtvA9dhVTUPfzQRj0sf+6LLuQG75TqT4LPJFJrNi3TPD3TmitDDwTX2z5034B9m55au4LG4WLj/LjMUMb/4+61PNlJebwYw4ZfliwI15r6XdBFmyidW8zrPEbbXjLuK7KjdLArMU0DbqmQh/JqNW+Mz67CxlsmV8XqKdMtRdSul3XbDzvqB9U1a+jS4Q0D73bcfj8YYff/yBf/3Xv/Hjxw+8ffmCtttOaWD3tbXYDmvCcxqcOeorI8raDxnMbNxEm2MG425a6aXfnc7qJsqCKjYZvkvsQAMJOZ+t7cTPM/DHtKQ5zfD9VAxO3k8G8f9lUz6+V+lX8s/fla7IC81z3Q+bpTuy6aN6PQEIvgOs/eYzlL37K7apsQnKtmHfH3h7e+uTET2Ap555P/C9XfKsflnbNTGSSGWdugHtnrBq5BUHuZPGKN4mf6RZPbYud3sogdrEwzM5+teTikB0oNLh/M7M7prZYrxBv+3CX+82b4vW2uXVunO/5nkzalzildL7LdvFaXM9wLvtGdbKht8L78Jok1Pb2+b0HJfJdm/Ez412bBT922grpyQAwH74SKPM5szskJRujdH9o6zykscGBOcSfvsIFvK9P8V9ZnTVlNhdUGtBx7f5pD6Gy++xnVL+XdWZvTuRt6uxktmdbJc5fgA4mDHH+29Lr/WRtsHz/0dgObrIXYY+pX7WBG7mF3N/iCb4QFfMfMmZL6M4pNA+hsyLKcY6ZrLtV9ZtKnSxu+wz+uVncZhZ+rw2RalYwjtXq74JdL6G/zU7u91XbO+3uJYuT0S4yhKFzoEFvrCzUsVSKWLsbEuQmZGU4ZL9ls/+L/VntQuD2hmPV5aocdFXyHCQhFdqiga2ncZ1E3gCguoh39skxBNH3xkhhiB1RW9WSJcSGLqUdmGKwGd68Ar9qpM96GxYAjMZGtrdCaujqHz/nOhKsQTkn46q7iLIjjaykzkxsbBcB0K8MHATO4FnIuwIZxZQijwY3wksImMYeWEWg8Bc+8wR4DKzwKKnkadB9nv2F2kyM85nZWb1WHjWWCdDI342a6vwa5icOcM15ovwo4xZ4TDACjJe+AWzPmzGhlNepG6yBm/z+i1uDMM5OeFIshUNstSGq+Xhc1iZkZApsMEopJGPZrx7Rb6TlTXy2+M1M0yXeCZti+PM4nRW1n5GHWbLnvGfhTNrAxHpkY+JgyI60Di3peszuZCytO92hahUJTYI74SAM9RL6aZ1sb83bNuOfd/bWdxvX7DvD3fUAp9t7ehE1jmYamUAAQAASURBVCjmin0fnDlm/v2cuWP+zMi8YzTO+GWF95V3d+pc8cqqnM2XwrR5+6KHM7k5G2MmF0ZDWp1AqfJiv8zk1Ay/+D0rr+0AaHaW6o0kOPEuUMViqWctnncM/Cx9ZpBGmvMiyLkjdA6wGKEzki7j7fF7xPuuUznH7TqcWZ6VHnmlLj+ur7Xvik6+UneOwxxeXrb3G9tky3qb3uAFIGyDbqLzdMKdqHb9aXUN0xqQaN6gmyzt1f9yn90pZ5vwWjsTWUA++M2XY6Jszg4dqEAEoh3tAu2qC9ISu4sqCSweIAT0iYi5LxHtG/eHCl5AB+jpA1qeF9C1T8ufNPSJJtn4QRV6FKSHVeAXcKnNA3jfvX1rk0VFFghtx0Plg9g44z0X8t7mob3fb2F9e13oqHhZ20n9gk3UITnYpddtE9fpfpvUaA13V4jDYSjADyPd53UoNXk3LXO+a2X7NKSXT3GnFzo7eUYEM3bPj2XMZI0+uyPzI30M3DN7Hr2dqW9jf+f2m7d1JcdgAxeY1c4GxlpWW5ysbm6/76RYDY+7V2yFtS0LR4esbov7ks6zTFKXsRFZ1kxwzmxJGRl6E/Nl3bnyU7i+uT3FeQaoPW9eV8z32SnGc5ZxC8Pbrt2toOTJ6viMlNH/zOf7tDon78/8LH2cj+NrfhrjIt8GHNK6b0w03pqIWAVNiMgF2iVIfsJYs0Fl4UVDx+Kz7gSOqEAEMhk4fGQQ0HXhtqHwKv3+t8EcOTTAJrFN2y3rbSJCj2B64nm8DzshHI6bru6wAoSNtEKEQvYop1ZHC+L0lUAxUADIjgfqkyBUnzjqIWUpHEflBRjMJyu7yVDgtpuCdPgV7TwJo3VVZE59rN8+s3jagJ7tS+rtveLo+CDDGMSaGdxRyMc+o1kdnYKO906C7bYem3iHxCqYFOvI7hLhoDYbtxkPzhycWFeG/6wNWR4LL9JmFihS2OeyZhV4ekVRZfLJ1DbUY/FkIzGrOypk28dZkC2jbZyoKCU/Pkhwv0i3WfmZbKOuB+ykZIM5TqRE2T9rtzqbtiwcfC6T84rH/Sxd5Q8Lz42r8D5v00KZJ/xg2yJtIN6aPdGH4nP6cdBOTNZJiCYLuqwyvlYpwCYXTLfJCkcbcbQ7zNJ2vD0eD3z99h1fv33D40ubjGhnb9cepCjgIAucrO0o3zDS7xhVsdzs3ZVnGawV792Bt0pZe7P2zNoxy3cKswcO5rRrjPOakT7ru/WE5a0aJn0UdVZ0+BMz6/XUafgxAP+E9HfiUeSTZZ9/l+FG8EfqmBKf5LD+89Pf12d35bNPRcaigzm0h/pTQrt3j49WBYANW2m7Itp4byUq8SKmuFCLP0vXV7aOLfzOPqG68saA9zTiS5zts1b3o9tYswMrbBvWNqu3YTJbycIAxp0R8T46qTvs5Lfvs0VZ9u9Z3xOZS2JDU+0ymzDAZD6IdB3aKL6wThqUsmF/fEF6tFO410J6xO4IRzuWUn4nPs/KD+GYQFY+w8XZy/C79qn20TDz+bvNxyU0hJ35zcVMJiQy1Mhkfc97iiZ2lv/ngn5neHyrZtfLRXG+EgMYn9+RS1cU+NqvUhzHfrGfQ83OJumTL8avkLFhns/qWuMa9aRyyGuphM9rKdIjxhtOXNheZv3bv4TYtzEpv6juuOpHtlJS/NPVcPSbT3K/UkP//DV20srXXrXtbCRe9YkiLlneLMaxKvsZ6crk6j2fyMeW9JPHhYH1m0zFyxMR8YiZ2FF89iTviKCFI2obH51f+1wNi2YgDkcaGTwsUb3S5gmENkMfhZlV6PznlDpp2YJolFlDTycLWuC974Y4ntOLd5uRo3gMDEy6QkUN5NpXlbChHf5I8zMecoaoTLxQggu3mVW8FfbdADHC2YcGYerVrdDSv0FxsANQxJgh7auF8rWf/H32Z/s2frflV4JvZrBfheHyAXK8UzYxsApMRsUbn0Wc7feZ4zFcEheM6ln7s/EZ09XgLfd5VmfkT9v2kTYjf8Uymvc8DflIR0SkL4/P2K5i6tYL0TVAB+OY3lFcNm82uTALsq3gnZrTsT97c6lbgG2Mw3ZDE0XwtOrQpvXEsWDleDREIrzYL7NdIzFf9nzFQ6u00ndAJ08BytbdstIejHxVzfuWn8iY8UF3gqETHK0UMaCtBYX2UfH0bTshGl+ShVkMiFZ5w8vSSHjZj+eybdj2HfvjgW1/Q4GuQGWd0TJavcV6bKTfKmU8cqVMhH9F5l/F6UqZV+AA8/beaf/MqD6HSbIKKdVfzNdWPpSJ71U0n3qA8srD+ETv7UxOjuPIuzuv9ttH0lmd00BP6KOZzfFa+gUe9YtpHM+xfZaHoo072l8f6eMzO/YO7TM9tarrDDZFZ/OF9Fm0uULnkW8BO5kkK385/1Bhl+u9cOHjfLYN7TB+XtDV9V3XcWRZBRhIpv5LQu+gN9WDPG/ngD4BuuUxoGNka3TKusfb8eihZXMHBTdC4E10Xzs1QG1t8T+JhJfUZrc+McMytjLHCVrGvjsD4GOf3DHMIDyPp3xXYijewhsdfx8j6MckD/T0tkaz4bk/0XiiFNRKKMUf3Qyo3T3z2dSvMb9L64OzCQXuq23bpH2xDJfj4435O7e7IExEiEnV+6sojAIeB8YXrJSPqCLDY+C5YrKWWA7sHoxjQHiEP0pul9sUNbL9nMlCaytFn/COrf+K/J7ZmfHZWZ2Wn4gMDmw2MW4oKi+GurL6jCwd2uWFH9d9Lf16HbPKM7Nvs9/ue2LSjGMdaDausVPTfOF3+DLzWa7GLV7Tw1fhhe+/0dQbg+T52OW8NmW0XPrl3TZIZc2kH2Z0f8VufKUPr9ry93xOlaYuz2/wdS5PRNiAkE1N+YWgp3kXg0qcskkFLsOf/KcXbc2DqkTkVyQIvtICYyhZe6bl48vL+N4CwaVx6DAJ0XMoruhbX3kC4Hji+XzH83hPg85twiObOIHCJp6AaLsY5I4HOROVcbB//aJomQzpd1Qc7Tdk0kRxlz5KDGWr9FreKvQA/PE02Rmk2ar2TXaBWGO+YzARKjPFbfvEGrgzvruSbBtinVedPluv4JccV3VWLsON80W8/Jip03rSACRGoRvHWtY3Fp+Ml2fCXfNwPiDyEZdfGYpsXK36YZUif6R9Tc1VReAHPRwtwmsX4tlnrR0A8zjnu6NAzoKtZ8E1A73jwQVPsk8gQBxHdOe0B6TJvCcyW8KvVRT7HFgpeHV+Ld/ImdABjr2nJvL3yiA442mbL2sPEYnnNkz6Gaed8zKv9EuKmqSla/wSx0uT671OU5wdY7srygczmmEiDmcx+Fj5iq3Db+OZe5onIfa3fkn1xhMR1HfstdbHu4/Aj/XjNM2M1TvpFYPwdxidMzhxTGS/X8EpM/gHWNx3WR0FEvRrfF+aLRPyGES7bO2GMNlXdhJCKv6UFOVltHH99/XE5n+nj6exr//XTSs9virzT0gfkbGfBUv0I6xNDNVjtg7Wr6Wg7HxPRPP3ym7kigmwkthHo43X6rIh0ET2KlT5wpC0vYRb8qzEvAQnlkr4zrZE1/NS26k97Z9XqL8c9TTb32yDWRiZHol/8Xm0/d+P96kPmMH2pw8cqPQcyg7+aveZPcy2YCJx0VJ6xTTzDfjT2pOZ///APkxcRLvu8Wh3nfACSvG3iQYJqpw21mnv2bBLSma4j21pcEvnOUYzsxnsZMToX5MbJ3nyMZIrNrnkntiInynPrqRZLONaynpnlAt82afn+zkz32n/K8HWX51m+JzRerB9+Z+L5GDTdfC5wni179oXj0O0O19NnwGjQ4I3xD8ILqth0CO9qkUs56P+TZQX6m9ei7ec8f7vliV30z9t3HK6NRGRBW2a8tOzH1ve9o/dYRDLAXELp87IR0PhqPZ+gzUjzhR3HKDtwkyeCIDD0wYO9aKucYW5XlZd5bfdDcETCBL4F9QLA2XsWkWsoGv7zUcp6S4Lvmi6TSiIacl41bZbgmpF7fdTVDMJ4ScwNMlgMwqs7LwDpPenG69FjFw1RPskTG8XPy+FQ1nULkNN+EL7ZhzsMViYJds3MPlXAey0/YmxenXgsqGfCbQIN7skfVYmqyfi7No/wX/kf2MItwfL+mfjyQreVSCciGSlwaD8CVN6z5R6JossPWZ4rNKIFztyMPxv+pKDswj0nAS4rBNgt15n9c9kZtZ/Z8pvHEsFHAsX52NhNNkAncqxbHfCWC+Rdyuu4vy702qcC63LmD/j+czY4buJkPCz7pjJZYfVHRnfA1ifOVpk782AswRuevsIUYTpxMLKPpci3K/dUX483vB4vGHfHy4ok8Kw41/ZLG1vTNFoXDmod5zXDMcZrMxwvQtvlVbyIst7RW9m3zODX/i9c4L+agYCyxWHI4VPV7kfTyJHiSTgxjaEBzeE+Jb680yPndFU+7fV3RzPzzLmyYy1rh/EE8ap8+f76EJt0kdjebE9L+pOff8xPo/1KL0XTvzk+wz3f4LzNZPt52Xu68hzOuR21u9IdkzP+o3sGDCpSCA+rMoV/8Q4Kg1S153NP2nm2tb9kM3oRdZ7uhJfdkn0l7KaHNR9x9FGc3YWmohTkq9kdUajmPIjgiVvKbmCLoCGl325aLtEm8z5By0HVAaqRaDocvt9fitbolxe+VxEhEd9nPox/CzuNJejjGHKUp80AeE47JHHhqql9E2ajVe1bgCGD/hTd4hYslccdITOsG31b8axykeH+XZyH5VuXxGRLKA8Dj794HC+oG0Xwdj86YXfBTv3OPNOtw25HIzPYG1jjqUUHlfm07bTvrN2Y6cqsuR5ca4bbPmZbpnJul8hA6/APNMDre+vlGUa6L+cR3mOQm6I/ebsvAntGJ6VGVPsY9tL/6d/2rczW/SODbt6v8r3mn3AchCnNuHUPnmR3TLb/hU/Yg7D2N0DjnNb+xW/6kr/zPST+iRj3TO/L+Mt0ddB/9i6bZmX2mm/d8HHVJ6cFKrvx5bYRgX8FE/JO9kVeAfzYC3qv8W8Y3vH2j0X00t3RAxGV1CsHIjg/Bx4tvn5u12tnQZS+a6ByQryiF/yFAMZu8K1q/KtQuY8RKOBFI2ctgNB7yeodKDWp0xItMur2wpQXWtA3UqVhgN9RUMnQDOQzF0LeudCBajBLH0SAoAevdT/ns8njudTJ0X6NtXRgTSD3IabWFl4awHNEPb9zcY79QkJ3hnC4IsxaLayOX7wg9rvnpgdxSXGj1GCwlcTARRTDBy5tiRGcYQTy8X6MsEYd0Twu3iMTDQKYv2ZsLV0inVkcOJf5tzcMQJ47Ni2pHQcaJYZTGu6jzIjV1CvGRi5c1QMqk7IG9lhcbVmljXyARjD39Mqw2GGm6vLjokJrBkPcDMsvNV3kfWBRst6jaGSjblXkqVnqsUnaWbMZN9tvq2v5s8cesZnxoMy1o0+jMbVqr9rrWGr/XyCNOLNzqHFPeMbcv0xjr/mwGJ4FmqHjIltw9vbW//7gv3xBvTJK7IwkvGutLtuq0d5fnXsnxnAd43qz+LvwWm5WcbicGY457KHAwbB+IbpE7Y6+2SEPjY4k8nak7QpQSe3ycnnKO7XtC12DH48IFBmyF0o2yFEHCwxCbCtIZmJm/EBhe8L5EK5EdV2ROhMLsb02QGbsX9UZp3V+1m4vGor/GpYYnNftA+AawGBKF+yvCvazuyz83SO07yesUzzA4oE0/IauztfCrayo5S9fQ66XP0QCV73F0QFOkGq/mEWqOA6iSDjmsxYXrUnTwS+BcKuV3e06faFmqZG9ovpndt09lmmd4r7p+sGMz7XfGJlSmhTsKczHq/1OX0f6433TbSTGhRWtFWPcH/eiPwzLefrSHZzAnjWd7AdlcFYtRsEVFSdBHD0UB/57e0NRIR937Hvu8QI3t/f8f7+7mEX9VW4vI3PsD1dSsFetjSf2rjbUFZ/azwl2sQjnGuJebiVsTsu4HibMB79FOv5HL9D0yt22t26SMyrPI7R3gS8kPFYaoxJBc7OW7TL2cWTZqf6IX4qsqmtfcePv2LbjjqvVw5DEjZN2feYtI8fK/ku9H8pGkcIdrXH63q7Z2lWNtJ5oHkMfw9gRhtxFXdY4WdxeaWts7F4Vlda5iLuV3zCzN9wLhH3P/qfc6pM/ZyHypBhxnPObpHKMLTvagpuiU9SP7nxk7XnLF2eiLCKNz5rBhxEMaGUfgmzn4DI4GXO4qDkxaCwhg8rM8bJClL9a0pxmx5Pw3HTiKfgEHDhY6jAuPeLn6keqHJHRGagkITx0e+GcEbRoasneJLjebyD6tF3Rugl1e0cSOqXWPcJgFpRnx2How73U9htvX4wRa5hh5sdfn6vApsqAdK+TpeDL9IORzGhCDM3o2XDtrfL18o24Vamr6nDwRQLxOZrE0LSBtPWEbznuSiYM+MxBrlisOeK0zeDbeFcNWhi+bilORrGlh5D0DTBddWO2Z0ns/a2e2OUzywcHqeZoZ4ZriP9+tjq9cS7bGbtigZ+ll/qEG3h39sVRe6M14yERY1FeylwSYIMMVk63uGP7DM6GPH7gHbiCLEMyAJXKyPnrH1Z3bHfr6Y4LjOHM/Jphrcfl7oS7Eo7Ha9yYPHEEcv6pJUfnY1V+dV71yZzNBvgL5zkvOn4MJ/NASS0eyg22Qnx/dsP/Pj+rzYRsT9k16QfVxD57uxf83nXx8vwneX7nSkbL2eG7dW2XClzxYjuANB6dev3P3Ynv+vd9LRz8Vu0w2ZOxlmbvI4FWuDDrvA09ghymzeTfx8LFtBglc/aN4VwmS+5HjKOsS1L4ZO/v9q+bpneGDeaz0SDXqk5saVeKb9KM9vtCuxX8PnslI2f7PuVIJLaTPp7Rr/X+OHz0tjutS4o4q+IMPK2E/QuQNWDBSh8lA3bklK8yz7+pXf6TTBQHusLthQ3LzNVB+d2z8hHzcMnzGjQohZF8B13b131UQbf5kLZef+rXNIs5PpSg3nezG4wd7B9n7ba1LuZxXzNvjATM9TvujC8cVS9c5HMO/Vdj84/tcPhWIf6HNb3an8NfKUDlQ6x3dqJBWwH2riJ+u+tigaAL7pm+crwW5yg+x37jm3fmh+9FVFRlU9TIN8ujqxqOzfwzgiV4wV759Xoe+l3fwS2HU/7vmHf/USG6KXC48D6da43JfzA/NsLyUIcW9aoR/1i1GBB6WEM42sh51UqBGz58YsOwxfl3Gr8nOkjpuGZHlB7Kas7GNbtR+PFsg/+7ZW4xizN7L1R96pMzOy16JedxRmu4qQ2ZMPBlTVmHqGI/dveKX0rSEbMq2kVo5j577bsHVsmqyN/R5MAhuRCtDPv8shZrGDuv9jvax+c369s9JHX1ryU2akr39+14YZ5ftWvmNEpli+/wCb19Y11302XJyLibgX7nB2nqLDSoKcRMBFWZAwb/G+J4dsVpe05C5dIhwwHr0CtAaT16yRIx4FxYpzNH5HPq/c5xIAp+mjiwd5wjpM7PBFxPNvxTlUmIvTC6oaD7saQS6l5B0WfiGB8pGooGgPPGAXuRk2/+Mg2W9rNE0HUJ4w4QOno3f6xF4LzCmMEJuZQRzO+qtLa9h3nByDHTZ0q8rngy4T5TBHOleq8LoEH7d+z3T1ncLNxNHtnYQyByFagfYS6zxS/hZ/ldePI1MBlNLCe7wyYyRAfLG1wY3/MhHSkaezPPJHTI9JmeJ62vDr0H//bjfF2Gd11ozZTTplM4zyZErZtzB0MOHgZDuxQ1UrpsXuDIprwR2zX1cRyegZvhvfMwJgZsxmdC/qRDj1Fuc15s3HSAUie2HdZG16l2VmQ18E3snpm/F53vpre2Pd2dvG3b9/w7dt3vL29yTECAlfGEOuUjxtLWR9cwX9V95Xg3pU6Zn060yP9Lbz16u2gPP/q/bnT68DIpALbVpNxZ/ObgBlgeClgNsNAAgwl9kvDY6ar02Ysxvt9R9vryrO6ZynKAoWXGWRYODDGpnQAF3VO05y2vyLAHFPOV3MHS3JM+nA1xuLnZ8idDIcr6YwHT4fpxNY4L6O8M5MHM7l31gefwS9Xx7ciAbOgQ9tGiPq3YNt2fzSsuDrWJ+tlmDZkKhpw1XfsUwmPoQgOMYjS0QGPvaFJIWAXJ0FzfFh29j4B+3KWhpG2CO9HndQpMqFAwhc2U0nax/LdTAowfVzshoB93077f+anFNo6XzAvaJ1EYQeFmzbqZlE/nmtmSwPjLgx973fz27srQBpHGPwkbqtZpGfzQHin9EmITS5fZxapxCcz8B0YXh8rPfNjs3fo8U+j3dIGzCzWw7bezN5ZxYbyOk1ejkxMcIselSwOM8y1kne0CMCey+pzGXxXR5zpxHP57+Whh2RGNVGS41qysmF4F+zxM9tz5jed6adMj1/VQ9QHzViHEUicB2iHdhSVX7H9y3qtPC9A5v9nPuiMZpaeV+3Z0/f+n+R9GZTACr+ruNiFb2v/LTyfjeVAxzO+uzoCMtxm/rK1O353krpfGNvRUojtmsclblZk0u2JiCxozgoD6Kt9tyLKMQtUzY6MsXXZfJwYnj0GJR7TkgXVOG+E0b4zbto+W7c3Vnqn9D8i6vc52IkLcy8E7P0R7WxRxqEZugSiAxxHlzsx2Gg5nuAjmsSwoTbp0HAwZ1xWPcpJAt2Cqzf02AAupZ0K5egzCEdyhpMcSSUB5vnxP/K9X3Bqg7ZNiJTuf1tGJ9BRBwMv46Xs6KZVyoRGhq+tY6ZMU6Va8tCyFQrZ87tOHOPFfJK1x8Ijyi9yH2AGOBk+lr9WTql19IWO3biOSmfb9Bi0rA2Zsez7xtMlKuhMgM7kxJ1kd30JrFJAx7hrTIyPgiGAz/ic0X71PtJuNSabDDB0uTAhEp0mnhyOxwylfXgK/VpqsL1MOEszXXI3WWdIcfGfVjbYdwOMRCdmfTvLb8sp391vT2YgWT2fyQylw2iq8sTc29sbvnz5ih8//oUfP37g8fYF27b7thJJ8Mi13cD7gF3zW9MZH87kzxXnTKlwp4NpyJ/J5vO6L9QkPKh1VjftnGB24qt9hrzI2hVlRiZD5nqU1CH9IM16RXArz2jss9+XWt1XZeovwSDYgC2dO7J/F75/d8rsvjP+/hS+/c1p7uSvCrGf5n1OKV8KyPJWH3qDvQrj50GDdyo31Z6yOGU2avQjOH8rO9+Rqw+MA5fSybffK+j4MoWQFO60Xmpin68wrsW+n9W2gMsgyDd5cLk6nAJbZ+l6psvsQm0tXfFtKZu6yFau8yp63pWwilVE+836eoXGExXY9qHetsZb4fQHEGiD+GP2z56csO87vnz5IjbZ8/nE8/lE2YDHl935aVX8O7SFjYZ/qSMjNjLfq7EVmcySiRz5I6W/sQuP+sTb8ZbSyfVbsHFdpxR+X9B2baCdoFB0NwXfsWd3SGwwOyeCvRqfRTxQSrvIPhlf0X7LfLdZmVn7r8viIp+lrMtd0YfDW4IE1F+xB7tHts4TfCSHT/CVYpxxZo/93bpM9MNN84Pl3ob17ptVXCemGO94nTYct7gm7z8rzeyU3I9+3eZzNkCo/y7JZj4+P/un2KV3mkWTz9+RPrwjgp+VcPTP1hWKzWMV8krQnE1EyAQCRYZQh6oX6IpS8zYltsmEiRitBken+JMAFrlvJIzcDAl/eTV/an52+CDP+UJsDiw/n20CAt1gqBRh8qXM5l6IY/yuAR+lH4QerFSNQW1mgQuMYd2Io3SR46kqeMVP7EuntEsZgrY8KbPq/5kBmBl+3AdqV+SB5ggzwznDaxXA4f4s2OZmvhiCeXts/fF3luxWXzIrZWxbLJyZYSY4THAb2jDpk7NJCOYh2z6FO9Iia3+keSVq6pzbyjgkE1P5JERxZLuqwDPDNvZdPiYSY5bOjQd9xw7xeYBm1kdxMuJOsjK81murk19RyPMysV05zeLEyIpvL2DTeYSdonHHg2AzkQ0GsSmvxDHfdKifLFgZPQV3aV2gjmjOs9ag2oyDOKuH3z32HW9vD3z99hVfv33Dvj9Qth1Un55ms/74qAVk9L/DL1nNk9ab5Lk62eDgIBnvAvxs/PhJ1WYvFASWCGWXKAoeGZ/OaD4jCTufBTGAfWLUF3vUiVoea6Q5u4uuXU6ZPk1pgHGMxaDjXIed4FWSn478NMu6qENlOSy8+HuW7HvfPLGbY5Ul5IuVxPdnIqnlG49syGBHymhgxtPhjpx/1WmfOaJ3bIhZXk+Ha3YB52dZkf/mvOc4zmzSV/Ot8V+/z/XpFdlF7j1PlJe+IsRZEt1XUnuVdKz3SUgCCc95WWJqJP8ZEbQ+iv295CORffwz2sWBEFkXlzP7J9pVlvcM/vlSK8kzEQt5XbM8xoeL+UqZSQVzYGCxEqS6aRXn8Yh8MycqGKCrYOHM3pf31CY/bGA1s0GtTW157ygQ39r+2UV3vOiD8RH/egf2Y2sLE81l3EdtI4LjDIyLLFrsTn+th9CnUUrxIiIch7enrY3DsQnbPm1/p3ugoXkAFD0qtNm1/e5B/m1jOD3OJM9Km4yQfFufqOifwz1+IUax0R7QGX3l6URG+D2LPVxJvmyE07h5Zqs7fxMEWexA+cgFWE5eC2BH/U7CI/qvARzKBluqeFtx7odYgK39McYwtOlFvT5LRBTu6TPv+ifbTGPcwubCKF4XdcZUShF95F8o7Ct2rfwemMLTPvV7ZkJ+MN+SfhmhpfjNU5CzF+HbOqL+zmvxNF7mT/oy+kQ5tjl+vyRZ0IsuHTR+4g+1z7R7e5H77bg8EWFn4rky/tOLau12wWBtEfXjgo6+SgDooxb9m/HO2h9PbpTHLkaETEKg5+0Be1agpRC2bUcLdJcuKAnYjSFaGo4oBaiGaFTaSv9KID7W6NDdB7YtbTdCOwKp1gPH8x3H8cTz2S+WrkC74GwTXDYRUgSdTCBQV+y9ELb+rha+DLsZBtS3ihbq9D/0SCiGJcZzKe0C0q0HqbYSlChvOwVYsTXFX1EYb/AkCOF49vspOl1aQSvMSp/Y0aOZGrwiOyKYDvbmlpYXHX+zeqPaI7k8K/EnX0Zmmt3wKP7P8mz2HeBtnZ3CpDzohYjXICLLe5AIwUxPjcygOGd4To0dIqBS30Wuu15Yv1tYfFxQpuD3fTcgdcswN2gzwU1inBJKwNQXBf0woVjaKC576/Nt71Q/8knJWX+Jo4jG563ngvFGtt+gY3DTSQhuK9D4LatrGnQ133mHhxjdYpYZBinou8Ta74p+rGvRC7drP6t4K8pjtVI/a1YNRpjJwwzPzBDxhrRXKK7NgnJfkiUyosnPAh7H3pmxdWYOCozhyJVsfMzRBhQqcqybvficiCc+/eTSGAwYHT1rrM4cCYZlx6qdqGq8JDn79u1crmRwhZYA9m1vfct0El1TVcoUoOxmqomNWFKYqaInNLmwtXsa2qWc3ZEzvCJ6zzkQSq/IR/LXnqA5LO07rzXomrZJz7Lh+7/+C//6r//CH//jf8e37z86LxHaUQAazGm76XS8dDUAM3KE586MOC+r+SfJYgNultKCwM6X1mtrUduk9fdJ9Rk6vasbH1r+4PYMZl/7tdBT44SGVjjCD3xs66mMIPjkxaQBs8R3+2hPtfbVrgd9AKfYAA+RQb24D65Vx0LQOEXlB8lCCi7fS3pjwLeIwq4lM661JfkYNhpP7JdBr/pWdZ13zrm+9TnenEZ9ZOznAXuH9UltZowRLxzAgD8lAKN5MufRGRZx8spWksOSMeuOMFmy1uU0c6TuTfSe1/FK8N7LjFjOSfPkvb672pQrTvvvTwSA/dGGW6UCIj6Kpb0nHKj1Jyo9+x0RBXvZsZUHNuzdv3yCZCVo008kzMVnp1exrUc81CdQX6p9WqlbXBngFmcWQC99zpahUPgeB+l88dVZEm5LiuhYMy31ZqTPt3iSVUrme8QnPmtdRmPeRVN9dj9eCnksW9cXbxbwC2p+iCvPunVvnxuZ+ysMnfg3mfuzAONDsK9j7D+turg4y9v+QH2rOI6vclSzm3DofqIeN23v4DS+fn06PKnXyyczPNluHWxRwmN/YN/5GE67mJSPplrv4qdy9PrYJ+QXHJ9oHcB+3MY+Jfusxoad2bPgGJLxcYGCfX8LZfno7uLyWv+A+WLrfR5jDwJP7FjFhTmlUY55q1tL8jlOINiJ0fZ/ixPxQhUr3x2r9tJ5sjKD+9XYWAM0LTNcxDurIcC0+prL1Wp/x0VdxcRaPprmllGm74p5x7YjyZ/af23CDM0PG2Qh6wS2ZxU2HzHOY9DGvjKftUsN0xb/xn4Oz9kvHWzd/GQR69sPWFBCxZV6WXTdGP+J9/rCjc+sqqgJOe6AlIYetvQiyx7bc9JONYhZ5PNuO/GjhLXmWvAzJh1OJ1NiDEzfpLCcf8Q2TdBr1n6RMVzQ+fX1BZ+3LquOv33g0QjsGKRp2q8fH3SgcocVEyQR48/+tUa2VSyNCJ79mGk0iC3EAAwxSZW2nYTgejtkMQjkPgaSI4hAbUJC26yB+VoPPJ/98zDKHQV8DmP7IxE69nijdgcEteAAUb8SjVBQuyIyNDGBk0bWroysgdL/pU437ps40z4YBB22GzOV5H6KaunCUKTf0UYjabByUMpBGVt8qShPyY6LkJjps4C+g5cYArOJAGm/jDflvVA7NNOosIshnKWrOyrL4MF4WnwjTulECkE6X4zXSj32o/Bi8DVOEgytMyttWlOK/x0owJaDTFj0Z2o3+kkYVqyloI3HvkqFab4SXlZAuqTWQVc49vFogrFx6QpLv+WTRArfIgQxKIZgFPMYHDIiG1HapEkxBhyxUZHqlYiXHvG2VPhJ0jEBMXqlllp7B5tRWribWTHxuL52pImp2LamIW5kVpvsIp0s5cmiwln9RFXGD01Uq2yyl4eP7Q9jakUzeNzHUZEbBCMfqaPk7MfAcyKCpCyEVjLGVrLP/LeJfu118qWGUoU3VGJbWl9sRmo3fcZO8oa++CC0+cu3r/j6/Qe+/usPfPn6PbSRx2DtdoAZN9MW+ZVsMbHej/KXmygGoxvGamA5uVGKfDbn0DqrF5JxShilprfiZERvW6I3oBAc2GJgjSn2of5NA8PE55gbGW9xKFkRleMOzcJ6tLSFDEFgOnOW4DvFtImK2m4CD/DjwhjHAkrkyiE0yG2IZKWS5Z8S+2GSpKgfScLRqgh7YNOgDke2YRiual9NSmQau8i/WT5bsd2havKTx0edcKPPTe9GPld0Z0cP5pPZ3s5iwlh9IZW75FgLo0yZBWSv9PlnB+VPdU+Z5Wv8ukbF60YP94b+m4yjCCvm+Qid5vVZZrTWaOcDYl1RYCcjbEBjK1v/2ztX9UVewvfGbmB/plSpJ2/XuNhHcgXT0bVl8gbQcWRRsePBavEEm/m7hc80KeBRhv9ZnPw2I464hTO9fs4jdwIaWU6H+gSWfzyE5ozloxbQkKSPS/JcAztzHKjdyR1wvdp+yb+1z3ZEc74ADRh3abhPULvouucn4k+SRaR8EXac6CCifln1Lu9K4R0ZXK/eu5GlyotT6uFw9D6zOZop+NCyuKnT3ybJu9njn7Tsvn2BnUzwl9p7/yE+36gv+dkaDnoHTelSZRPYFhfRu904ZfzV9azCR2mfd9uFUEVm8FHHztdouQ3Dd9uQn3sLTf0+Z3PqApD2HU3OWqPGgxn8Ga6aCGJ7OniA+yRfzNnB5inupqEE0zuxkdsLHeFsU8nYsCD6sXROHoh92Z84o89mYxv2rD0kPrEx3OWN+wywvK9JY3tNir4guH0Gzh0tL7wgvD2WHm0yvwOs0U+Y0vV+g0/6vagPMY0hmVTEh4HrM4d/oBkPMWOJjD7TpL47+u1jyXoGbMeMuPi4IQFU+nGGC8gyFl+fhABuTERoxSNzllJagMMMKG6U3lXAQSJDhIkhEoNF27YDoL5yujeWSILjrCDbudbeaYFTGptxoLuZxMTrF0LXo18MbXZEtDz8qXdB1H6hdK0HjuNdjlBiJi6mfq6ToPcs8E6GenRj+VD6AQTa7Kyn0kYGXofnlPTWpjG2TqPS6T0LHLoAKgDZ+WEEWWZ0KEIetx6eSvt1lmQlRtgyauGyYWDxjwaK/PWJJjamENrK+aNQJvCqkfFoqBjcn6XMuV0Zlp7P58dVyfOkP4io72IJY/IDuMXfs+PSmCbWIY3noup2Ys3jn/c6MD7PJmkU1oiHvOviKDrdsQ+ZppG/eTV+VrfI6S6DVnTjNtjPnnNib8xlIn9GJ5XrXfGmb7MqXRkHTXNfMkwyI51xsH+868bhRWokWZ7JjH1XxsopGu8mypyiTFdZvM/Gcvr2BT1r8RQwQb5EPLNqndEb2mOxbjJQBoAa/in/542SSYgy8kRJwgsFwJcvb3h8+Yrv33/gx/cfeDwe2Pcdx/OZtDtt5piEdCWQsHjPBLqDx+drx+W1lYNFbA4i6pPfkEAxnw3NnzP75CraV5r4it12RQ99PI08u8xL+BC9FFJOOZV7noe1RnbMuq3YHQqiY+qAqE8U9MEsXe2rmM84X0PWyK4vpaLV2D7I2h10kC3/SmrDb9TDqZ515YzDM4cevg7eU8JzpPotlPh9jt+vS5/Rhs+UH79aFkX71FfVhTa1AJnVqXx0qbULRr3fOURoyl5ApDHLwpVfc1XiZ+VW6e/nWW69C/j8d/plKfoLZzZiHCPbtksnpXov2Onx70A1MMcYgO6cyBYIwenpamI03n+MNmB7dpCNkVCfUKk4kl3zhe1Cbaz4x9a2rhTjKGpLSowGBaU8U/pHekffofSAqN2R0U7l0N972dxzOeq025lRNs3uZ7P4KN2bsivd1m9HVo1xH3tuAPvGvSdaUDqNGWj/jH4D+ryS6RNwd5QIQHMYmLWMJ3P4qIzBhSEQQ2LfZws5riWS1mtZt2jDtasvHmS/kzrtxAdRaNXs7o84uZNiQhL6ljFQrCh9nvS9Gi/4lTis0xDk4MBFoxF/JqVKx9Py+7WbZNfpdVtnLGftZBeLuZju2F6l8LiZ+1dpHaDTYWXl09X7emO6PBFhhWAe5PGBAqcMKKykZwHsnH1+p66hF7wFKFUUI4hk8kHr8UYkKwiZ5eY6jSBUPCvk8mfiC6c5KF3l3MSjH59U67MryGebkKg2iG52Ftg2EBCD3FTbOY6yIpkEs7QPBkYNfNImI4BS2wx91nfTIHSnaQOYHZcTnVpTJ1g+RBrPUxZcnAXGM6dWPqH8MjgbSXtTXGZtNHWeD3p1fWc0ngWqp4LA5GcepxDgV56LY3KEMYUb3p2Vyeqx+eKF1jFmkNcx75/RKGy0TulWION+hiPn4/ETjdcYHB/QDG2Z4TvDn/w/6QSAiMsLvHFFiVna8VjVMiPvZDwSx1isN/brFUXpdco6v21ixrer3xb/7LnHV3HxwT2CTEKdtNXCOhuPWXnOa+V2pnv9n7zp1ge3hbyRHeqI8IQCYuhZXW3Vtg7sfd/xeDzw5csXvH35Ik5XntbyJQZUfaWaR4ciT45kq3zU1iAtbCxWASJ1yKNQ53nfMc2vGpTjpEzrb/+u2d/eWPW0fdVAzsa7P0opq7P9dhqnPw/23FjZ6aMyeZHp4CLY6uQsMZ6dN2e6zo3JgNPYz8VkvOOIqR0Sz0Tmt6TMNqk7lMnkBMx4sH00lUm28HUHKNPZZGiS+QeZ7aMybQY74RPpZzcoBnyk63Gvp+6kfDzcL5+lGcwrduyr9c/s7Su8mI2pj9LHlvHjF9BebR1td+SoH9g0Xgts0YAPQ+HAl/BihibrCii7jeMoGIWhDQIngkbCwiHHZU2ykE1n9F/yI87HU2prTd7NeGQG62P8fk1/D2k0i/Xxgs5X7LxVmY/kV7utOJ6NyY+rHuwHyZ2Dux1LaH1v/XP+O2iciOg1SB67GC1bLGSwAkB4hrp4QlHiKx1HjZNwfehHdFdUOTqyyi6PupCdSs/8MttVUr+B/+xEhC562ku702Lf2/O4kGv83T1Ygdd+63Md70Q7QO2ouVLQj+XeBCfBtUtKDpDz5pF6ScKMdp3Gjeb5/U6g4vMXgFB1KiDAG2JgsTo+E8fUeU9WxAkqhZ7JoGL+s/5hO66XOry2gHErehSbui+RhjM/lFi1DTY/dTty7A/ryIw00OYov3ocdHe0wSaU5fqujY+hL4wpfDUN+pNtS7Ztre1hsGv9ZT4FxLkPPEtDDGdSZmz3uLxqNglxJY4T6zrTB2ovjz13Jut4gfMZ/Mzuv5NuTET0U/BKwbbZ/m8M0WZwdUW3U1x9t4HSQ6Q2rPAoPXCyb7uN4aP0Qd2ua2Dl1I954tl2sGEpCPOXJqxqr69/ctCCdyMcxxP1OPA8fja4/cJovhOBdzHUPnHAdVd6NuVYD1WQvept29slnWRnfQFW1JXpwtsYgxggq+iJwPLOrjiHMbyZhu2P0O4wjoOG0M4TDKv+5Z6JGkEKvlHAzZj6bBxFY82umoCpu/R+ZAdbsDdlBObWjtyyK4SFD3uDeKBYgRKNorjyP5a5kixMa3jFlB0fE8tbPMUQM8c9cZ5ty9eynwWVz2YwY/lVe0wFAw2bEQVwoMruOGBnMK5cUSNsXH1/hm+2ldW2m1frs5PKPKIr7T28szqjMx6V1oA/LZQf29mEbmgl3lC00WgMUNtnfsxxfvJbmS8m7pMB7YTf0wBAZYtElZxOGgFFVrefKfsQgDD42UkSi+9szLn2IaE58kdZ3fZTv3uZZ+XeWcodN99OuX+n61V/J1DpjlgekBmayTBZlorw9etF2zE6fN9JwZevbTfEH//6L/zxrz+whXFhjwRgXM5kSUbP7LnyOq+IX4KVsleMp7umFUugbDFBnmZ0GPn7XD6N2KZt7E7zmRxqDtGKRvH5KJz0PgfjQHwglWKku8iB7pfwfTPUgxGV+XciR/q/9m1ODxbKH8N9gErXIEZbIH7GizhtXvvbprtOzwwnu9aMcckc+dXvk5rCb+PRSpssDjN3vJf+AP99xNn6SJrpgM+A+VEY0Z7/DPqk7XWePLqdCQknsV0TfYp6+CMb1UaUygycz6Ova8/N5/+kFAOJv5P7P5Pfb9fdEPB2AgEo/6xeG+R48Z/FPkMPLgHghSll87ah3pNofXly4ws9TxwxftzyjgZr6/mJa1Oy1V35yBt7nBP7knHnM8Pt5anFNvSc/S4D7MI9Um0feeuZTJTY337hny9fcaBdjF56wK9onAsFe5c7+7a345v6kaccHOQDUL3+bh3XTPrxmCil+Q5Ch1v6camFL/L2vlX77M839U0KiuwadvaVlDG+holoFqCfzhRtUnvHh9powlB9LFWnKzLJMh9rOR/Z96O/dAUu513LHtE67qnlkVIYzuh3Rtwtr/VQxFznk/mw6rFv7SZ3fJKNOXjax8ceP78rw3bjy/Kf4OeNzrInMQ6eUMzHwet9ejYRMPNDY9139NVHJyFs3We2feCEK9gBWO9qjvVl8dSr6eZEhN0yZhi9qACLQpxntNVh1LxcVuE0UFthY5FXN3kSMkO6WXZGiokinwXtnM82+DSwwitlzP0HfedDrc9+qVLb6YC+NZBk4oLwlAmKfndEPVwQ1AZRRbgUoK0+s4Knzwj3Nmi/kypN9oFJBZ/QGby6OSqDDTHmRirhguAj8MXHURia0lL3lTRzgLOBTNXXyzSMg4fgBXYlM0nggnKGD02746BnfGbGR3xm80/bMjFiZkpx5bRF4WSNrxjEtHVdTXeExgzPGGAvpbh+ijhmExv9i0wKnNXZ304FazYJkcIj83mRfkRmXbnhtUiDbCIixaFjbCqAkoSkPVGpxP7O4K7rZOc7b2P8PqPhjN/52WlQQmyj+VjyeoOgLDXiadOKZ+33KA/kYMSo3AHQhLfWdatRl9HWlrG8E8dLlEPiRNjPYpyEMDavJKu3YurSR9rkBHQJOyLevpzIx2u4ZJ/xfeQz1odncE/509LvBGE7Vq+kO0ZzHOej0erpIzq0jDrEAHKOBflCC8QdkCmhPW6tIuodMylhyqaVCTT7iVIkHxHrH2ZMw6CJJb4ai/736MzdHVfiyMF94XiqwXeGgz7LHJgZTqtnCmNdZyzj20WucSunKpfRKxcpWn/FfO/vidLiai/P22BZ/Y5Dm9kxV8teSaM8u2anverE2jRrV3w/gxF58g5OM1qqbI1DiPS7eSHlqi4gi3rT0Zf/JYXlJavNeW/c/5I0pek1+zVLZwEWyRdrsnpjmrxsu1QkqfuVNIMx4/tZXpFnKrDT8jOZfSddHedrHWRgxHzFfUiMheXhBvRLSqMe16arf72aiIDsYBhl2KRfarM7/aIVPwGR/bVUUdCOjCLoUc/xWKhMnhIRytEWk7q6SY+OdmXExOBJUOo7MboNKDKp0a32iYi613ZahT1SldrymZllZGMcm41bCCV3AH0Hxlawb7wLw09u8Oe2dVjdxN9Kq33rd2fEezZsPCvKzw1wExGllL5DQJCD/9HzSRj/bGxEf8u/IXibcpBLrqzRSwF+pHxbYlXUvik+F3mDzpXkuqJdPkvjeF9TxWfPbKTU2NVnlGGe4TjavRKTfCFRXvGyhG2s8LuRf7/C/roSN8jSWaxkBjOzl2c23yzOceoj8keQ/VN6Cb/P+yy2M/NJrqbLExFtS1k0y3owOCDWhD0H9hszubDMVpxAkNWqe2uUTkToLHitFc/nIRdDy30OrFhMAGXrq+NtqrVNasiMZd8V0C52OnA833EcTzzf/2o7I57v/X3f7kdmYqWX0yObrFK3eOz94qa+0hqbG8QtftSCSO3Wdd+xrABJ7pTQHSASiKbcam54bANDVzfxYpQ4tX7SHQHt8YUFxONgqX5F6syximdOKi5NAbCytncn2PavnItYF3WDwfLriFN2r8ELQYdgIF0VjmR4DNBdA3aFIa/w4P7ndtuyq1XfFnYMyDIOZ4L4TNhYeWANz1oLSvH4lVLMjiYvTG+d5z/IJh9gi4Jajbsclv2LfSkrTIyRl/XxldX3WbrLN6sUjVDut8r30WzzfrR8zKImcUUv470KWEzzDrDGgB3D40/HO3x+KCvgbSznFbm/h+bu2M+SwrD6MZ9YGPj4Eg7NsWgfo7NgoAUjbsTT8f1QD8lETLNTeBdGK/vl7Q1fv37Ft2/f8O3rt7aybuJA3rRIP5xmwdrV+H2l5zUIfjH/TTI4OVQK4sqlmHc5zkqB3qRs/4B1/9yhjIXXt9JyxGOir9nJi/LCfq6SM8Rl6JXUP+M6LzXhI8nCCP6dWsKjjbQEafr3jvPz+Sl3oH4NLr2ukuuBZUlquwDP+DdzcHNYv47WvxL+Z9gVGZxXndDL9QG6GF2OSFQXiGVHs1cO89dWVZdSnB8r2HM5P6OB+9L896R/Ik7naTZeZwEwG1T7nPQpfK8Ce4D9u2VvFsBqz6tTrZmdp88pfAJWI52lEsLn1G0K4vG5tQGqATCV364cV/7oNmXwJcg0hH15DD42oR3HRDKhQDXEF0jvIuQ2i+/f6cAxK7tLnn3rSj0eA2/PHnTgoKdaO9UeI86TDH2ncm8/d0K75sbYydwe89v3jNKjo9wsc7mHQnc1TO2m0ndaoKCUNxQUH28pkJ6NfoG8L+34741MPZvumJAeLtp+ngTRXRWPwQ6Mvlx8LjwDYrdnnbK2o4heSA1oe3GcfKL5P0YAR/xsvEMaDz8G0+qcf2SK30grXzrzK8/gZDGhD8nQy0UJwtheSOjYwNiuK7id2XaZDXNHtlvYzj5/oUPvxA0v6x4ixCNi07If6OYr9nNMlyciNKhmRGEyhlUh5AEHFpBgwRwGcin6qVuNqgbjOTAWAjla3gRKoAKgwbNMwmcHmiOX5O+QY5P4bgjdclWFsVhZQIRqx2EIoM6Dnoxs8WDaZxt1vf3h3ESjoAWsU+7qmDplTV7oqTIzis/RaVQI3jjQumzNV4KRVvBq4NGQJak3tp/z2c8BTyPArBEwGnApyo4mVwf93WBypIuty7WD4IJ7nFKjbtKGmO/KJMSrCkjLFQkCpPXIQA3jeBKs0vG2DXk5XCosNRisFoaXUTMjyPUPSC4by3DLcD4zBAb6fkThL+rOHZdRVvBzFnFKt7yOK4Eb/pz2KUZ5Rcm7rA1jv7Gx2773WnoeX05hsutLQz15YN7j/6ojejYJkY3d9l7xas1cTUIAWaAzgnXliRcaLBxTo8+3bcO+t8n3bd/cFv9X0rwdkyRV2QAGB+r1U/gARl6c0GuoatKuoURqH9nvs75dPdNJpN5Ng33T3uXjRcdHw88tE0n0eZ7uGuaN7sUgXDSTVK2yZkIXrtnJ5gQ7brPkszyxGK+Rh9zvsV33xnyEGaq+aSsMThNZXk5WCUr5/PtnpZmMtqlM+mWZHKnJ8UCWhZJvPpo9ty8yXejqCbT/iJyb6bIPOf0L+PbZzC55xQ68aj++3D7i8U/TYcQuP/WxcL5gyfMGWbjeNJy25+9ITUzP+fM2vJvlo2xZ2SeqmyKvqf7Ka/hom+x3b/+PeW/I87EpA+xXgjGvpFfqmPma+sxkHugRbeho4DB5CnRVeY/2ODts5nduku/M1xg//ZGffNE1+zEAL0bU43OavTGeLGD/suOa49+Tnjjo0XAhu4i0+xKwOllHD8spqmiTN5XkOUrSRqExDe1mmrYFf3P/2aYWjztg763IJyL4c3P3V2xoS704vtXgjfXze10gVrq/YunhbXWuT3HwA6+U1r/btnUfKNcrUdr7WMlc0tijjsRsBZSruW0SuNN8EY6307XGq37z7Plq0sD+PoPD6QrfzMpcwb2cvHfvbBAHo6656jdZPDP6xHLRb8pocsXGVbgcVVD4n52u6AFn14T48Edwirz4CrwbRzPtWjE3qaALzhwxUxo+COJnhdk43OQcPBWwtVa8vz/bSvBnOw6p3SWQT0KoT8ZWJaHN0MM5IERtouF5vKPWA+/Pn6jPd7y//0Q9njj6jghixWDaJoTvuy9Q2pa5dvbf3ttS5D3R1i65njrv1HCr1ddT2/0T9Xj2XRXmTgzb/j7LDCMQAX/UUrvT4mh3YZgdEQWEQpQMSBk2E5w1C5l/GskbvLjqXmlP0o+tndUFg3RmXyd02BA4jqP1f0/Z/QHRYLDtmjlE8e9K+ugAjnBmONv227+ZMoqw7eeVtAqMXoGV05xSBSxtTuqP932s8E1xIAw0tW0rVFB2iIVQQt2r+qJSyvpjxR9TJTZpZ6Y87fMzPow8Fp+vy+pOmv7E4cGfegzdSIeId9aW+Ds1ZBK62f6wumSUXd7kFD5AQaUe4IDKljPa3BkPzQAdt5k7PBbjd3xunEGCWNj5uIWc/4o+1hodNU+Ut648ANlZAsK27X3HH9Ovr0za9qb/9rYjkcjvALyTbgd4YzVsotgtMK3hWLsmCZCLieUY72wErw6b5G2f12HzZ3GBnXHC7Fq6kO8Dqm0cp07Cq8x1jBzldSIvQh3Zm3TMiF10tU8jn3xWymC+NkakNLFu7QEgKn28W/CZ7GVHW+G8lu7Q9Qqsz84JOPzi/vQINziiKbRPsv3upM8Kbn4GjCt1/HL6UPxJaH6PLi47jkMCj6X4HREqmwvM1ikDsdsvqCGAeD+Vsl7I8JH0O/rzbooozXj37xhH//Q0s/Xvlf84T8ReuQMxt43PfaHiJonZNMjsYvud2/uABP0Izobw+dsPvTcN7RPVvc98pVlMge8OHWIJfDR5upCh776AHiel8ZrqJlJd3dR8CW5jxROVjgB7/IynPTR4QCnvAOyF2JsQOfY5x7Zg+qWYd/bTfreTHPbzUb462uikR9jdUfziXq1r7j/Fuu3zRjsIDI+/NF8+rZna7O9NW1+K+ha2kIFR+a5HttO2PA5yJX1U3p/543Y8rvzzz04DbKJUZGS22WfZRhHeLFA/q2+q527WHWG92rYcn3+eHr48EcGpqwsJMFxB3upFIhK3xQqAOJHQ8kKONRrO93Pw7TY0mYnokxGc2TvFfOG1/h36jPTOCBuPV8HV6im9cS0Is/WLgnYTzAwBsow2YBS9AOvaBjqj74PPnr7rQBYJnFGpFYyKdZXOBNSgiG1dpeTvDA4s17M2rXZCrCYVfBDn3Mk8o68N+tgBvAJ3Vt/ZuzOa8iqEzIi92r+vCKJsooAu1jkIvyAPsvwuc0E6pthYQ+j/IR/LB6464bnIQ97Yyvs98oS1TzwMb4CwbIwp4jMzuLLAf+T3OzzIBlgsx+OT38GsBDljIWv8nfGjvA/jzb6PBuZsDLyqZF27ASCsypnyljxX2tCgh9Z4j7BtsKTxH3VjzbZulFVjQDyOpcyJ4Hw2iKK4xok6rqOAUPTEnxeCN75PLU8xr6mOjzjwv6F1pkFjmRmGrJdWLZjpwTW9fS2z91H2XMUh60N9XtQWa4hyISekBMLVccP8w+3JMRV8ihUYDv98EsL2AyHXp1E2jPid5dcVi3a3zCqZYa5fzHiM8ofrMRDM7w84UqrKpKmOqhPQKmJzPpzpGs57m08GWJn9NK9z9TsfJ5SQ1XRaCELcdfg+0/mNMDOddcduvWPPf6YTemZf35Vn5k1/n+U1fMkeFcvOLk+GQJYds7A62tdYTJ0zMs1wFr7CfRpP6TCRc9G++DsCC4NMhtGFiVySWIAr432JpWN1mn4/DT4zvdaH9+k182GjHpMa5GfuM2Rlxp6O9RNQrL3FujTYFASUQlaKB4y9XvH4KSxeMML2BsHrgKl9QSQhJfYhs0kIUF/AFRbrSryD9GSPg/QibSJqd5IS9btKAY5FVVNOymNDpUPGSiWFT0Bf6Nlo03Ar/V3tso3gzTE7URF9v+IumNa4je6wtRY47xbYSj4RUQs5oVqQTURscpy7+8M4ORH9QRRgI7sLQzoBRKPfk8V51M9s9GsTNl7uNvh2UQeSpAtGmIFWeuMV2yKLFWT+/8reW9nVWfqIzbSsyyreBY53AvbiOjpdmdMgxvfOaBvza16u41yWT2EaCNd0YrlSXcBzPRnxKk9eSZcnImqCAMEPSGlE2UB0oGx91WVfTKtKoAJU+kL+8Tb52i9Ofn9/10mI5DgalwIBa59hFqAG6ybg+86AZ9sR8Xx/otYnjnqADg3aFwO7CZu99XEXbCwgt32XXRBN/jFt+Iz/OjBGQZFLoSye3E6+C8F+WjoKTlkgq6K306wMqsdwv0KlmvLrbPCdfUZhZ//4ToNsx4LUB7OrxNwNweX5O7c3rpqPuwXip/CxuV/BphSnSXCT38UBHOuMQiXS+Cx5Oo4Xbs0MrpXiWQmdjJ/i+wx/oX/gMVtOL7vPA+OxboYZ358L9rViamPbrMQx+M14Qtvd82wb0C+FP45uHBPQr/CCbsm0E6xsKCuOFk8ixSXSecVDmfGUtf+M//S9TjTE+0i4DaVUqPGql5/F8aPGmeqLlUJzPDrBMybhK+hOCDsGlK9CPcYwXPEKG+tl4yac49Tg2T6uQ55Z28axwTQP8qawltEjlLh8wXx7e8Qh433Hk+ploCs4g9mmTgEK6nHgeB586dM5AgGXMcVGlMn3MzivJTEAT4xdSy+E/vi8VMzfKMcznaMv+SOMg9KZSJkbMCvsxrpPknrpw6SQQwTXtwWLxEwN/nwxRaSF0Awa3Ihl7lnvJXzGdD74lEc+ZuA32TLHPePZq07F2hHjal/F/1eMEZtWeF1zDv87XU8rh/xzKpg/EpsSLchWqe8Ap3a87rZteDzesG0PwOzwU10bbCU7cdpq+Pz2fCCN4/fXBAmupFzOt+S875CRSl6WIwWXDJj/Tr8tGQs+PF2lWR+O5bzIyMrRyfvradBrapZMkCKfj7+yH+Hu22of1S5mBWTiAsQ7IJoP9bStIp3Y4AuzWT4RMYz+nXd/oYJPaKr9JI8Yf3nWA5UIR6V+1Hc/kQLvgJm4ifEWu4MifhKAA6aN1eCF1k6lI+RIY56YeCvFx5v5S/c32GfzOyJ6nGj/gm37IvdSxPsp+Pe2b8lRygWovVyIocU7LPnT31nK/cz4sW+8DeXsJ6cNYzyQ85UCUB1jEFneDHZ8z+VjjOBKyuzqz9Lrq9hEf+BoJDG8cA/qdVsjkx05LVpMw3/69zwpNd7jOsa0gELXd0RmkxAA+Fos+WRRMpTnf6wfWqgfCFSGuP2d9KsmIy5PREwrl9iEHRQ6u8y/4AIrxmE3tgYTndzZfrxqPqnWcIflk5a/E8wI8JZ0pjkec+NtUT/Dy4GYQXCxcNr5SCY945C3CV8OOHfOigokCygzradBaOQwBJYQXQ1uCzeDefYZ8czwH94NE1llGPQzOLOAcVZfpN1ZgCxOQmR1jXjYGXEfBJk5Z2fKYaTnhAcmNIswZm3w7chxiHmyCZpsrJoaHIys/tXE0Ahr0R6a09Rn6qAutN3WLAF54dkiCkuD9ZBPsa8WbGeVDsMERh66mlZ5533ty68NEe6D9nkFZn+yxG/Gr7N3XvcUp6C5DXbyKqs2wvV8zRVZwBjy5fDsM1Mw4J0Fk2f4nBmgUpZrS9vE/WZ5dsTf/S4Ar+ghfSFHEPLKpUH+LrHUNAt4xjz+WVjphJHOMz47bTMsd1vYtl+7hbO2az+UfJutbJmnTOcwWZpxzdY1G3AAvPRJmnJeN/G/JFIhKaFjbehP4vZqPlt7bKN+b/ln/OImI5yOCjpDymn5WJdPESu1BWa4BgTHylepGHp61J1uOXXyzvAaqs11UbM9VJbcdVIynRZle5SBs/dj/eTsXPPBpcF66xXnyo2tk/KvOO+rdv+TUzauVz7FCo773f/NJIq3BlVIy/nphfWcCWgtbJYI6iqOV/Ke6u2TsVrM9yt89yv5RqTXMAZNG0uofyIyfwd/f0oQ7RNAfEZ6XS6ozhmDletSE85ERhQO4s3yjrqa33s87biO8JxLn2F2hzYlkywWcvE/AZQe6yqloMRZNgAbeX+j4UOAHIvYjy8l0w9Qv4UvVFb7UqZHTUygTbz29buyaLftmuBJDWC3ExFkjjhHD6xz7K6OExE2XtOa0L63nRxFEBe8qbQjvxtE1zahEmn8J4vbaLd4X5i/bxXYd5bp7ZPz2LxbNTsibKrNnm1HTfXj1ItfLAmeaJATT9qxsyWZiGj8sw34ymcpoB4PJCnv26l0hKPHzBeexZUY3h3+/6hsfFV+T+23Yuw38z6zLWZ84+HO8Rtjjiq/7pJl9CvhhOcqrpHCosS/7J9T1MhkKIDM+LvI/BxnzRF969ft5VW6viOiAjCDR425vQ9UQAJ6BOCopmxFfZpVzVsTGtQFJTuRRy9DfbfCs98JIUTaNj1/mQhkZ2qNUmbhWQlo9zzwTgKA6Ojvj75tzty3QP0S2uRsZ4cDIBMQ+/ZogvBhBVD/q++g+q5AnLPclYfMjDecQHrJkt0JMRPSkTFEoMsRU0e78yLcDYFaUZyKCO1M6hkCTLHOkzw8o+yESKu0k3YD74iw5ZkOs6OpVGGP569neEhXQMdYVsZNOAWjL7bRBooyOBGPK0H/2D45LizBMZbP7iyIMLNA3CrIGetKJyGCgsgmLrIJB+aDSGsxmHriC3Fnxm+GM/MelxfcjeFbEnynxlG0SxP+uJNiPTawGgNAsYzNM4OZ0XuOh/xysjSra7brhXH190q4mqS+CNOWY9yz2zpGZejvhJjhvhezEhJdP0zGvtHiXaYS+MK0gu20r0dZsTaWsrL2txtLm1/hE8cML5CmGmjs6svHUBzDJq7TYBIr7fbi8faGL29v+PrtK758/Qqgb0nfSB2Oibyx9byax6cwODHjwVwG5vmMUQaIEymRfXl+Cup20jY3/l7J55gGR6V3oLWXMijWaSOdqb2O9GU6VLTdYuMIFydgVsUwtvyqvah3LC0seq+5XkmpdCgx3eY8OOZlYJMkDkXyamI72M87zmbqTGcw+k6az3BS1nJvdCaJMu3Q8xGtSWloc2dc/Xf6GxM1mTTYW7bfTBDH2jRtR8RD7oloMAx/8apm+ft9zbqTiMhNRvyedFEHOFvntR3gvtpiYP4DUjERpX9suqqvY4yjjZVSvL5qz7xtPZfz0Y4eJw9m+YkgGzFXrDKDR2B28T7+9d66ZgtO0wbhj9JtF6Lgt7m6ijyLc3VqN/tSHpeuc/t/LOvYPq/ou9q7rcq7LI5+VBPVPrHQd0RwxXwiyVH9rgx+zsdCERGeteKQ3Q82/tImPypp7IokCMq2HWHDs8GcXAgO+PsJnTzZCGU7Uv+WTVyxZa166O1mNpcJi00nNGI8Yuv3v27hHljltDYhoffsbb1e/7zFH/g+Dk0+LqL+5Up+xgmXWWwmK8O0PLPtos/1K3VOHrPLbdoY81zhPYOzSmP5z0+zGOVnp8L/3AA/U3O/ii4v7YiwfV4KzwiCo3miuLwxSBYYYGdWOcLRnYdax3LWFbFBlVnwgviz8jFLrXSVAL0e9wQaA232WCCUIoJJGsrCpvQZ0mKNW1YwCV4mqCMDhPRPhbhOjqz6YxagPPsrCH1i6QoOfHiYtt6z+gDdQpXxgH7XHRA2ADKDndEh4ifBhrQ+/b0yjDMhPxMcWr8fvatAf5ZmA3usJ8EROR+sBEb2PB1LC/rP8FvRbfY8g5vxTVSMA5xJfbGNBdCFKCftPuu7DPfYRo+DounHlhpNq76w5VZ5s4BcLJOPy3Hcn+WfTYiM9QE4CVy5usM7W8b2pciOEmk6Jkv7jIfsRITKTHRjOpvCHdub1VkmfXslsYQppXQVNItIQtUpt+cEduxbp/cYpgOvD/Ye4Hk8HtgfehnojBKl6CoxW+/MkGZckI0pkF1MBjt+bPuniWk1NrPrkIkBLj85iKWATCvG6k5knk3eCVC74uXJCMPBbJ3Yc3LRg3KF2M6hvspvDGxc5V9rt53hGPPz5EmsKZc/zLd5EGOUMw32IFsWeDL88MQU1CDEfRO9b8mnwJCTvBkWTEGpmzSQoeaJge8/8ppOHFWhO0an1eW6YIPM9JrysK9zkBEJXoDhqZinML+cO1czR/zqeI76apVnVecVOFfh/13pLg1P35t8jlZclqj9KpGPVWZofi49Sq7ifzoE5rqOS9o+tO8wPJ/9DlWafJFvRpv3I8mr18ROMPn8EKV0jCmoizrkxXb8CnaXOIDUMZdrr8qMK+3N6PjR8a02McC2QDSQ2BJILHaDj4c5NuccT3+cra3dls/1DHHFk5qmY3WhCee0tbYu6RNLJGdEj3CMZeehio84s/PHiYhm07T8lbqVRxwP68fImIuuG1aen/lvTy7Kjn87VRzu8ut+R0W/hLvWo0129OC/pydho7aoUCY9DjMh0WNjRJDJFNcPZUfpF2xbG3bwYVFEHrV293hg323CEwYbH/HE/hXUz9r6ru9Ndn+3+F+jOcTtkBNS2mprgTFc1l3y4590EkPjjysbzMZZrvoF0eeN9s9deXvXBrqbj+y4YkIbnxA2HgCMz8XOv1Z/Zg96mXgP//bwmi64ohtm8ZeYr2UAmP0LjyF5MeoObV8RUkf8fsVkxI0dEdUgGoLHW0HZFVERziyY+u4Gzr+hDXoWmXz+eFvt3Vbxk1kBv219UPcdETJDOgli+LoP1Pp0uNhPFkboWG+84wEbCOiXAXEqjaFK/9s2YH+g9FXaTYA1wUoE0KF3XNTaBPZxHH2HQwXMrgWqtQtwc1TUZAdA1s7hd9+SbOvPVjDH31sXwCwn7QJ8a3zGOjP4fiC3z+H8vQK51Fvedd/B3m8R67QDyL4n9DFP5FYZTA1G80khn1UcK2PPB0M+b0Vg1q9ODxsFSYDjF+6LMwUV+ycL8HP/ZmXTPi5F7j4ppUj/WLxX9GSYXO9x6KoHqxjOdEKmsOOOiML8ntAnKmyRMx1lNpbiLpwzpb6uh0CY31Mxu1/F1jmjaVZ3rGP1PJMdkUctDjNcrLG4MnzEiJic2emN0olTcoJ7hqPelaDBL+6b1v358RDz5AOCK2f8VHYI32argAhE7QxIro+vqdsu4DvnVTVOVLv3lT6l4MvXr/j27Tu+f/+O79++N124zbfLtj7v8M70G5uhMvaqGOmlWHy0hHVY1+dhxvaOTuXdJJQqmSP9Ajzh87kz8moaZagxQtm5vQMPwHAIeJbpTG6DgwLeyXBg7LgWewdA2dT/v0KiCHpa5gQY8T8ZT8YAyjy9Ztx3vo3yAM3GtuaJ2O0phDlO9vOVdNaulZz2MiPCoCCjOU9wXtM626szff0r06zdq7z/l00T27g/Gb+JT9B1N4LeLFpC5EgaKGRtb3ffMNN1OZV1Tenvi/w4aeBH09/PH2PgAm6MSb7fPM7+V0oz2q0nZtfJy6FMJgV/7SL813Aq4dNhGp7r7+i/n4EXlb2o7Wpqd9JUCWSzDVMLH39k/F8U+Eu5gY1t2oDobMFTe821UNofhE1kDwHmqKbN+SPAV1cL80CtEaYP5POCWYYrkwUiTwE+gcS+a/9XwFw43mI9em+FTEgkl4AL7q1VDm8iKIw+GSK+kPxu5d7rXz4uMdBXv25lw7a3hcdtcW2rWuNO6ou3/t+cAbr3+/J2e5KK8X9sfKKdCvKQ5zYGlcUxZn/2fZZizCeeGvFPTRLXYwcmxgHsc1G7Pc/FmNHMXo16zMrNWbyDZEyMZSLsZXtfSAToeBE6eDvqii7O6BLjfx9Jlyci4AYa5JLmHrmWjmchDOoE7BfjUDVMsZGCNIaK7ASovlMLX6JIKpibwPFCiCczml9q4Jg7J3gnBG8v8wYqT0IockUc3U4BHthuN0T7QynK911Qcp316DswKh/k1wCmqpbbztnEOPBCk+sRm9gJ6wOg6ic2iPOOhrMa58UJ0FEJjAOudmXEbeUglX4yLM/4bvbNtGxW3ypoJ3Vb+UN53qtG8EqIx6TBolHIyJhJBu0qyBInBaxTBQ50FXZ0SKRO6+JgnPTxOZiW/RkRyW/FgaTP8qCi5U9tK1PiVdcr47PY114ZQPhNnonzGRRygTwzVAifsb3cEoahAbqzQMIdvmvtsMaEXh5rjTD7PerdOeyRZvF97EuRl4Ef2/dZoE9lFZGdmORdZZ5mMQA00JGfG6QLSh8CuoKFZbillW1H/D4zHHwf+TGtiDB/aZmZbFLlP47rWGfkJYdbsX9ZeZW10q6inM66ovTnLK9iH9rdHkUqRB83BhWD2rY98Hi84e3LN7x9/Yay7eAAjJUFjIenaPs1HRtks7XSxPlF0JsKQtGVkdR2UxSDTJTN7VmUKiNy2VjQlmZjLcPGw9vAjlvUk+dyxJwDWsw4E7TI0YzsuBqbdi2R74Qp3QOvl/7MyolZGa5HZC+jWQC7LYYlBsvTdVo7aXneGXF6H47m1TxxPTp45TPCYFoZhWfw6fq9FDM2WQea7rbd5MRapt/NbrATOrLcmE3Q6phN3pH/XNViAfj8FD593e4719fBxYn8FP/M/knxmGSCoX/ESgigGaNVInXwOItkNqJQASdGAY26q4G9Nwkz1deCJl3Kdy+xbup6yxn45kviO7QyO0p56/o6HV3JoyLjeTb6Kfmmyo8wTs5SYGWR1o4/bRhS+SAOFv+ZdWHWx+QZZZGs9oOjOSXPlxCDqJtaWoFUn8I5J8G4lUy3rnHkgjOfdPZu9vx3TYheH4/WevtYut+k0bBboj28vFBhZMITbMQHcbyQZWQ5a7Uvr76P1ZWXqCw8wnIGHicrYgr6AkEQNhSdPxUb3dpuHaciDTFN64udqBWuRG3JroglknxNFPMdGOToR3yUZq9XFwjzJIJdMAyQ28XBNnX1up2Pg5IFvj1v341hJzfa4ufcTyQry4wea0uoe09RhxmO9tXYlmemVh9wdJ912w5LbLCcaRdsb7KjYittobfdhbFxrJInELozLpMU4ffon1q+6X1fzI6QbVN+iL6mPDOC+Sz4AMuLOiquc3yw++zTiewkgzrB86TN72pZCqg4Pswzsu+jvcU85X1B5eOoI85qNw/E//WFSvH0ssDd0+Klk1N0lk4X++kjNt6tiYgCyGDBo83w4WGZujFkAWQSAs8DeB6g40AzrQq2DSi7Oow8s1j7ZTq1r6DmuyS2/YEC4MA7qKLfHVFR+y4LmcnjYJq594HqAdQDVe5baHclsN/aVm9u2PcHeGKFgH7/BGGrT6ASjoOtqA3YNuyPRz+vvhu2GwcNCWTqOo4Dz/cn3n/+xPF8ykSEbJOhfqERtiac+2CqtaIWXnHdhFaxLBF4jSc5ZPcDPVH7XRs6QYDEgIUTVvZ+BhAGxdBA6MCuaGcHVqo4atvtsXVBuu+M6AZg60qiCWkOzDfB2WfuzfYl3kVj6213A+gOGpt45TzXCOkTCMw4CVJE+1NnWBUMcSdEhBPpZmnKQsYnPhewGOWaK8HZ7gNLi60Apd3U5HywfjEKeIWoOLQcvOBtlIwhKxEi94zvYqkgh5OlH6+Y0FjKqF68Mxj4Z3CSGw5uhwvFADpPqHWjTkDYM/ObtOg9qvTalCcaDEFJtniyEdaOh3MUbMFBbF0G7J7OLkg/Ot/5yqANbUUHyw6exNub3NuU31sfoK8aUWOYtzDrEStBaU8dI7van/+0X7jP7f0cKiN4Ys3bKWx86dF3fidM7QXWwX99xuOdkWxyufWbTBxLm0d5wH82MW/F57oLItKqMYkaNbrd0479uRIe65pNSPRmSj8TwdSRO7wqQ3fY4/S4TqYh9XNhncEBAsxZpM0g5b0Tai4yb3YTGRs1PVRr69PH4we+fPu/4Y9//z/wrz/+jbK/oUJXXcktetxAk1rbzJgMtJNPis+gcioE6n1KzuenyXeQX/RqHairyaCgR0KuV42kE96kE7oqmderStM6OhCWvwUb9HJBAkqzy/icfzug75uV5Po3HedEDnALUIsC6fpsviKLOgxiOcJGs5y5y8cEeMeE63cB55nBvmqf+4yvZ7DmhryyNR+VNdGNgOrq1PHLn7PN7uu71uYsOD84b05GWHczoO4xFd1J2FqfVtMXTqcU9wlshoe63VYc5LEd8knuUz5MO+85px2Fk/YukeL85CXuMCnI9lNvN9Uw6VO4FEtvc0SYyOGcxlJN0v6PphXv3E6lAP1OEBJZ5bZsg+Wk9SGI0M/3/o5t+6/mT+7vaEdrFLF/mm9LfTO5BqAr8Wpl7SHPU10Xw5KVwr/G2IT/agcoX/Aqv237qeEw0yUaR8jp3NprEYhjKyRizU/2UcySPnf1ugKikAzCI/9L1t+StP842ZiM/bwHk1t0cdUo8XgpwPb7d2dpWtlTAye/APdOmtsTWZ4rdfZr3jQYeoZWonMbLur7tV5Ob7MDsHupkdmyabUX9fSlXIqNmsvtSzv1w9vVHo8USl52hqOjXceaGBa/AKhfElLlHovxtAG2H9pnn64l6GfXA+w3Hwd/+vsqjvpE0xVw8ZWj+61HqJtpU1BQt3fU+sS2bemJI9wObi/Ru9YBgH1+QlXc0fBiH41jZHI/RY9pbdibv2fytbhB+xyPgWp2tUxQ4AE7xrdi82/9Dgw+bp5hF1OHJQfHwHo+WB6zeq23rl/lyK95DM73XltZ5G2XaNexT751fKxuijE5tWuziRrLr4zhjna0WTu1Z6AFAewjW6zlPpWwc4c/Y2wgj0EwhU6MRv5a9CFTjcjrcbEVS7cpugzjTzbHZaRH5ZzgaBpxW9RfnohozFX8b4tQw0qcKRsYl8GcObkEEQzUKebIX4JcZEHiBn1jjPaceiy2fx/wUPxhAslykXKnYd02NZq4sQRABnNx+LXXjFdtkwD9GCa+GNsJNWmkBQ4nKH0QV3F2VO/t5OCfvdQ4lofAmTsH4pSFezpikJIVAhX4OgTR9EeHz8JZYfKgyOq0uFpnKQ5onqDQlQLKS1lQmwXnRbvA1WlxSnKlDpj/5Dbm9WQCaVCI/Y/QZU/W3yF4Eem6WhFnedDislo56Mqzh3eWR77D5Y+XFue0NpLIVJXVGnmAQBeOrLErovwKgyuBmgwHS/NInsHRo3wcMm7+c9HWAddxDGX1nbdrxCfCcjAm/JDxU6qUKb43wZerPBm+5xMCQ0/ox0XL/6ojcSUV50HY58VkOMGF5U8Kv4hMEV7R0vLRJsvbhFzbFblj39tfC/ZsatT0emVhVZRjiVHr8O1QppzXdYnIt5m1NJbk/0P98Pw50UEZ7kkN9xRLB8pgo8lo67wSHOUvPvbIfap8LzLC0dAY8ZNxGfXF1bE3G2uMA6GASk5z5ZuW108oNKx1TqMMMKwMtGWdfbXA/fXE7V7LmVTPOyjw9kpIEfpMW6awJ3ye0izByRjI4lSfJc41EQeD3ZS35sS+OMXixeTExFhLcxVKgoCXLzYVmyVrGoXvgwNmYekOFXIAPeCVDvzsdCYz7o0x4yl3M3PpO4l+4yMtEvzEB5vgb/5N0cnakugAX/fIIyLNpuTwfTjAGz5HvXivv8sVpEYU5WPiY4rc57xql/9daW1r5GNnlsgbAZfLzfJFPTjrw1d01ViXfFvCjP7EK6kY/b3C6RIshnKiGtwOAFPW42Ps5gUuTq6ZYc8TFJAFWhGpj8nc3Becp4bLOBbH4T3ywqwvYsD5ShJyFj6SSvufq5G7Rbd4aTMJjiQLV31Z/s4xt31v8bDj4GPT+3t6iK4A7II/PUqdfRjBvTeg1kdf7JtMciR6LR4JX2WFfItx1H6UOv/uzWgfFSBU1FJkopqGHTAq43nBq7t8Wz4LCt61XAH4fls7EbHxRERvrwatfRzGxkOAtjujYPRLOTbeQ7Xqu/f8eqAqDTzoWloIG22O5SK9Yxwws6sb2/c2ifvDfcJ52P/kuDDp+96gwj4Wx2JDEIrIW18I34cU/HRDlbStg8wEyzbLs1ELc18q5EJ9MsL6gQWyzueWJO6w7qTrExEuCNcRLGhHL1kEiNxdCEffHWAA6YI8/o+PTYKdETQys8/88CBvdyocslMARpjpgCdQRdsBcTyVGTsOpQ/SFkDZsO9+ReyBNqmAo20to94jwuCyGpekQ9EnII7nO47nO95//oWfP//C+8/3vhuiHZdUCm+Xj7NcymxUabgbQRjZBjL7ymNevSwTEWDBFpUKpVxlhbHANoLT4UE6s8sTEYzXtm3Y+ha2cZKj9kHv38XAZVvFlO8MiOXsPRLP57P1p1lJnQkhN4vbhat1YGZpFii4E3z2z8e8TMNIk4wWsQ6ecOtPXN1Zf3J9s+DQjCaz9sQ8VxMLa578iuWj4mufS4hTfDJDIdJg1r9R6WYBuSVWPW+2o8eizn3IuxFm97vM6pjlVRoAQBX+y8Z3RqcrddvvTW23ZFsbFduVemYTPtcmEfzz2LYhYHER3qrfbV0W92Ug1pQbg365ASjfT/DoP2ILjAE68jUbXQy78gowAPtW8NjfsO0PvH35gre3L20lzbb1XUcFRx/P1e6IYFQcOvlYz+mg7coD6f9ZSdvblZFLpt03m+ZIW+KbjzvAd2XfZ6e0fkJ3mv5z05kk/HjvXU+xn2d6q5Md7KohWLXz9IGW/AM6ufnL5/bi3Qk7zjdMwF3DCP8I4kzSR2RGo0NWlswfuj95yBEcJLuD89WPYx2/Mp21fda+K+XLhTwX0y8mwz9Bh9xNr43Jl2qSgB1w7l9+dt2vl/tn9KPMbZlJrnlm/fIfwob/kSmz6wHgYU/gAECU7Y7OYxASSm2KeKiTj2Zif9rGtviTQ8dDvIVjLsFXZLyPfgKIjUFld0Xyn92J32JcPbbHx0a5k0eqxDbZDwP1GGiPGVZoXVmMjnG1ExHM42Wzefi57qrftnaiSdl0RwSnlmd38AA97WPvxzupT+nzUdkkv/ieKNjZ99ySiYjeJrkPlcjdkZHtKoixmpE+/UQFALL7cWvfIZNcymMF1K4UIDI2HwF9RwsKx2p1RzbzjkCJY4Cf2TyLlI+B83ylx9JL2LDVduMktkXZZNKl0chOWZwnsYtvCNRbExF5jSFAW/3KfL7QVZwVvluiaDf37tR6hLlNIIL0bLdKB3gHgMHQD8x+hAkf98TYb1vrlTbg/NlrMiMGoPCxM4yo1KIrcJUMBHThUY8njuOJ5/Mdz340E++IYEBt1lAZXc7rI8tEJIxN5M8WZFqTEVqNLvpnDXMw7S1Lhb6LAR87cKNwlX4tox9WShloZAeoo1uoz8K/Eiy2/S1lJjBjfR0qtMfl0dC/MVkDehXIz/Lz754rVXIz/DM8+JMVk83P4AYla494Cpce2bqtgp7hYZXNCteeO32qda2Fnaf3HNbquaN3A3qab6x7xGtV553g9jDGF4bGqk7+no/rcdxGHsnwXq0wuJyYZ0NdY7b15JDF55VAz9U0jqnVNs68bMQx46X52OI2jjAyuCt87viJPCYB6H2b+rbx1rZh33c8Hg883h79MjfWMFCjLegafq+n14+462+Wn1xv+1SZ2svwZMT99Ru2Van+iHSx+E1hLcqO5Y2NYXTDUMekyqs8ryb4tXyzOqw+u2ocx/dz+pFHQPo1wdtNQpDr+juTwxbEy7yT6IvV+xSGFv4UHGbpCm1s/2aftj4dn73ssnKGr3mJeCc1gEHWZDyjY2TVrit66vUgn+fTlR7LxsjVPoiw7PPZWJrZ1bM8s37O6szatNLNMc+ZzLhuP462/fAnfgHjNF7EueyHBSpXdP4M97smSp7/Ct+O4+RK3+lLDkxcqOqFNNMhnwGX0ytyeAXrer9T/7s5zoXmTb5cHZPn+Hws369MHofX8ZFgJ3+nK9CK6JwhrnODNpmsvs1rF5+5em7VcB+LWROkbQsEzvxi/q5xihyHFSygoN31YP0g/eRFr6pzx9iX+DmdYeSuCbLHJnlcar+Dgu9G5Xtnqfs8DIuP5rGTFtSPem96yl7K3e+SJY5x6mJQ55f0z1p9fEDjOn0BWVF8mVat9NPQv7ec+qr/UkFU2u6LusvYUN+BjwA2o6VoTHMrOsFg6+aYTZyI2Pe2G2OXXRuMj6V4+80TETKBMZGD9tJt52NXjWmVzjeWNzayR7nDp9InpfhlKWqzxoUCpNRyIMTm5Z0t/rMTyjKkoQBGebaQb2X6AzIOpD3ioHP9rLv6xgAXpxjrGuWc33l/Jd24IyJR6qA+IaSDkZLdEJX1MQf924Ht0gjZCVE6e++dSTeup99BIEH+dtcCHXbWsKUWlB5Xfg/npoUdEXI0Ex2N2tSFUi3dx7WDOQSQCCAcOJ7veL7/hff3n303xE+8v7+3HRm17QYoMhGCxoSEtk2r6HAvnUlq9Ts5St/5QVSgF1EfOPpdEPFc9CFIVQiFAu7hO3/OdkKwwLM7ImxddiJCBUU1imIWlFc8nk8VlNnsZsSF+cwGz0xG1wYHr58rXWAMvhcmIfiP68kcxpXDswrOxD6wbXBlCEM+m+K2w4jb29vbtO4ZzoOSmTg4zT5ct7/N8o+GP//xGPUz7R6G+eXeWbq6VZ1lPRYyPGKdMTgj7XnBwC9FuS+OtTg5NwvC2zIRR24/i7dZ+YjTnTRru1PNZnzM6HS13gz/lSP6SvqIQxLTjJeyfPEzllm9s/hIvotuy9AGygwSwr7v+PLlC758/Yov375ifzxQ9r7JliqKHA9o5U0vz+atQSlrQ+PdrdtHbCAlY89a3rN2nDYcvzTokqdi/hbpU/C62kBvC0TcZ3Iv5rmFmeNTg8ViLHtjuwfDP2G8/3dqKfbzLHA42jymB8+6o+enC1n/E1NmG2TPf1Xd9lOeT3C8Mq4zeHdx+hSZYQJEtp3WXjqMbwAApYQgxontcA2n12nxO1PpQbnLiQNUHx6V6/K/Yxys08dsu0/F3Qa1uhi9Oib/10gfHUtsD9+DpDELg0nix99Jd/srq+FWG27k/czk1P0LqVJFeaHbPW19PGCmb/nT9mtzG3K/geNJ+eLIAnc/RVKP/Ww7HvSUA77wW//6vRRHX2RN9nQTX0eligoaYjpx10WOC+F56C5BfVcBHAltPU3aJQ96YgcnucY7+Lfxs2J3Ovjx1u6+eGx7EuNDo77Ex7bpZITDJbyX+JRck+tjwjwZYicwWhYTN8IBMnfCbP2P8RRykPpyAkJfwr0ggtx5Bp+lwS3+gaziYbrE9yaPIUvjefS/SK9o83Sc5Hnjfr5fgp/JRfDk0ee6jat+Kd2aiFCn3zcEzPy1tkuhj3gnQpGdEEUuFVQjh3HmNzqbht7oKhMPbfX/UyY9wGvaO052EqJ2fDn4tW0bNmG60udGLDP3I53kslWe8eyvCyPlA2m8Ffg43ttOiOc73t/bcUzHYS6oZoXHdVITMKXycVXK2I6+5jtxwIXrBdffhYvhDA4eOeFQ2zN7Ca0P3GmNmfM5CulJkAzKtEC7/DcaVP4sN2bqcfIoC97NglbjMMsT9wWKn32dCdBVgJy/zy6Ztn8rJyylcXCOZvSIOM5SrGNGUxv0myUrvO2YSDJ2/j833O37fPLQ74ggIrh9zO1p+5NLe7jNnadBTYlcMKKygL9t54rmGY3P2lww8tzMSY6rDmzeNW65AbbCy/4msOgqElD2IUT7qcIz5nIYXaRVxMfKp2ttz+FkYyqjeax7lrIxa3/bT49zbsTNJhuuBnU48OLzB1oRLceD6C5sXZ/u2PcHHm9veHv7InqNV+qIGW/A6yfXNWuT2TVoHHLGtwwBfNXhsX1XE1kkb6aMF1a8AwB8uWE2QZT2K9uhF8Z3mPmboT1NM4eKcZsFpdd4jXkyp9HMxrYP2PE2TkJr1thuiNEu38n4BjS+v9r7azmlOwR8toxH76dXZGVW/mres/5eysLQHzZfkxG8AETFD9utGc/Bg5vifPb9anqlTAbjVlDqZp2aPxlLl1IJ9kBxz/U7y3PfLw5SYi/fTanuSrFm+w/iSxFRWxxXyfiI1C/6tPbqCQ+FMTprD8ud10bi9bSi+bUyYoY7eynmk/w3W3Sl31eyI9UDN9Pduj8jRbj6m1I9tSwr/wCzHRGZrH3FDzzBrPN1Fuhal7tia6zxm78753tbf+n/j3zl7OuieWP1d3wJzaJ1XO2HF9W41PZK8c8bD9ZoMpiIkTUv5r8ubNkY15G+Wrd8ZcNyeetBMBZZLGtMrSQx79BkEWz/WmsLOO/73p5T6SqLj3/aQUQy8aBHNR3il/BnP3QdRHzyS5WjpKifjEIEkHwa35gIz+MB3mUh70GQSD10goVlgeTvNoHCa3niZFJO89IC2qVgJ14M0GMxm188TVK3jZ3xHRbsD/uJCP46xotkRbvx8UwMb29w963de7gVPeqfmEaFJJ5USml52S9HkWPFazztiH/047BUzKiemIpZd4y+GNAO7Hz0jwLN83W09fS5pflWjB+P+ZhysjUbCyfp8kREDFaw89CYuU8SHAeOp05ESGCWraCtM0Up0ijeTcGN2IruVmgk6itcjqPtiHg+8f7+3gZNPz6p1k1Qc6v10WDt/dzq0u8PaGegQbYRcZKjnGrt9xTo2NTANaT9ALWtVPUA1SeeshOi/R3PJ46nzjKWYnZfbKXxYL9XQhiytcQIAoAN3UpH72imXZsAiRMRBUxXQFcBFRn4qHnwrtVkYhfGEEp5wRUwCl4sqvaSAwjRoLLBNQ1ajbsX4sznKiCXzZJmhpsL7BX/zubJyvH3OFGybZtbcW/puwpqZkJ7ZrRnQcmVgWZh89/q7g3vEEzBOnxi3qytGe4zmsR+9zshLM/AK0PLq8VOc/pjXIrIonX7Im1s++xnfLfq6yy/oz2jP+GhM3xkEtU8s3RhxZrWHeDNxpmoJvFuxwCGfmbfr9HjagAnG2dnwRL7jPnrapo5zVdwnU0qRDhDvyxk3pXxv7VzDof3LK9qrd0AWziC24at7AB2oGx4PN7w9uUrvn77jq/ffzQjG+g8SLK92Dt3U/C+TSiCr5hUzJedl5x7YnSnqW1d2ZA+7pydjXvXvtiGZcEPIvZCmsm5qMezMh+seW1zwPO92qYOxPidfMBbYX8CyolBfz0vMOivf1Ba9bd9P6YkumPK6KfuiODlSVlw8u7Eyy+n5cyB/NtSdFJnadZXUV8byOyQU5PvUmqiz35LYheDdQw134YnIKgvWgNVbAXYE1/CgbO2Q4d92Y7rn38DFT6U/m55cyZb/q+ZSPzqzH6/Yvd9Gh6/laM/mxdHu99+L+y/LJp4ZzIilvtd/PyRWj5M8dEsuwH4LJMIeCNfz+0s6//NYitqeZep8Oag6lRfFoONiT9NW2N98CraGtbe5U8+yt3fFdE/O89GfzeeYhKPbOK/46kTFEC70xfU/LWIg8aLOkyqOEh3Xoi+TXzv4ROQWwYrL1qjJ7ZScPB9DcC0PWyfzOJg3GcxfpTFnaR/YXZnPB4oZcPjofeWSBxb7szoExF8t3BpF3srzui0gmPv/a3fjwuVQ2QnIVwzyPPkL1PRzd8XNod+8mJCFELZyO2IiPGV+D00/VK6NxHBA4+NtM5aVGubgKiH3IlAMhnQksyUlMZg7ZbuPilBSnWdmOhuCZHA5aOZ6OAAB+8yaAOLL8eU8gV+AmLfse39IpbQPmb648l3PRx9sDaRxZMHbrdGH7y1HqiyE+Jn3xXxE/VobfXCqa0q3bbSadSNf7KdbAjX5tt8P0hes+uECOAjMFhYIQnm97sdTM/CC3qu2g/aaYC1JIGzLJ8twn3eaahxgt5whjnsomGac9urYF620raHbUHgBDyGwIlpoza7QLuFhSj/Z3DbeHdLb1O9F7QuXNeQ8rz654PochmfE7Q8EZUHMNlQmjmRCoOmeRRWjjO/5/DmqQNoeCkqEoTyPNEWpZ7SWZVNdHa4vjNDcVr3iVE6E9RXAk3NxsiCADS0I+a5gttY3zjOs/euLoTe7oqsAAmvnNM4OluMR0qviWKOky8Rf8Yr9n02BqayLuBmf9u6bLtWZeyl9Fkeu+OFad5EhqdvU3cawLOT+zbvPCyozwUGdyjQJyAAXkTQZN6OL9++4duPH/jy9SveHm8NF76bSXbndRmaVerGlv75SYhi7LQC9BUaEsifyq5fm7I6Vvw3pMzpuVr2Ai4Taa3uVypT57AjXnF8fp7T7SdKL5diPD6562fycN7uc0d5UpPA+yz+vQPnrP/O+nt87qVNpg/FTpdXHt+M5+S3CKcl2gOcz0u+fdn4tc+vpJlzN8Vg6IPLVeE6X0Z9OF8QEcvM8fyAzBC4ycWjyR8vuuHFBhxASEHaZyeu9NA/jEfIN+OLu8mWJqLEDuj1JThY/Gb9Pow1EOTizheCIdrHvs5fMRYjzM/XSR8b13dhr97P/JnPxuETm/fL9NnMN0G3h2f24byCtTxxdQ84Wb3X6o5+8dz/5ffXUfXImEjiB9No36D/zvNx3jt0vpyzjIJHbX8M72JR9mFEb0lki32Kc0hz+Z3Y3AVoemkd02F3R0Wj7jxUXmhHsCv9Na7BuzDOeJV1H59+0i7fBuqjSF2uXN9rAeJFB3qyDLUHqDjaArPu41E/OUbyVm8rVIFFvgckxtP6gTWy1dullGQygv3SHvDuF9Wqj9gIXIAWnxM7MfZ190kl74bH/sC2tTsPOddxHHg+jx6Y0XhUsyN27Dw5wfFS2RGhcqEA2J8Nb43dsf8lSCc8w+83ZLt/rukkjhxoPSwulOeKkINpKUeHAbKw3/JcrN99B6Ts1XR9IoKRtCOmM1c9aj+GqE0YtKOIzKrr4mG0GaYWVLBXeZMNwvWBUWtFfR44nu0C6LbL4OlB9zO9ZBYHaAxW2vER2/7Atu/YH3u/FMXWQYJTrRXP92c/X/ToGO/tUs4tbu3l7VB8N0TbDfH+1194f/8Lz+dfvYP1lvcYXCVpO9/9oEITInB5iFm6o9NXmYyEs8xwL5sZNHwHBoCiRjwLCOkDyh2HqIw1kJEHNWzZLElQMHFUG510F4cFy5MQVSYhCGUDVLBtAhtKtYBzFxpjSFUkg7g7YYBpvKwH5MzERyl+8FlFkQeQW78qvrly27bWb/7IMsWSy2ZGaSasGI/szyk3ePxH3LjtRtkkPKJKIDcMRdBx3uJ3QThY0q7ef9U+U2U9a/NVZz8GqmPKnJ2Z4Rr5YFW3VWpZWhl98WzIVYoOosXf4rJKzdDrWm3jgWHrmB3dAlh+PZuMWNZv8M52+jAes5UqcSJi1S+x7qu0jm2z7RpppHzl8er/FHu0hAbxuiYecSIAOhU4xa8FN7wu4CJb139EGwgF+7Zjf7zh+49/4Y//+je+f/uBr1+/AShyNKLyIuJw7Mj7cc0TC5D7khD0X5eVdqrcyJfb6YXgyirZvv381HX73WaW/GcmU4uy0qkOmeuzjyeLw1Vaqk3qufyzcftd6TMnIz4jfay//UB7dZwMwTj8+uNw/q70sb6fy/lVmgfJvJ5TH+X6+Lqb/wSa/EVeivYX6yIAciwvnwftcZnImkvd4P2DX8GTmVM/qyt7Xm4qumYLdLuebYwXG6Ym4nphh8P3P1Rufzhd6KaVvfx54+t/lTRn3JlPN5Ml15K1V/9z0kdN4c8arwMcDsIu4xAxfhPehZgYwFKtANjxesocm+s2UnPjrP0dy/IiNd5l7vXMoA8mNjv7xcLHBABvUjfHjqxe56AK607/eYDg76KI99PacXOQXuI9ynmhWm/UCIvp0mJEehk36+yzMbp6bsu1o5ke2Pfd3Zf67CfwcLSRj4fSu4XbjoittIXQJEFC286C/eF9+uyP88bPUvZ+EsE6TccHkbjVHK7RMkWGifjrgLTDjp6Z7Z7ZYXkkZp5uH80UA5V8FAhfCtaOItKDskoxhgy1/EKsbQdKlRvX0Q0uud28tt0G7+/vciwTX8jSjCW040H6Bay1MoE4kN0Mz8fbQ1fC8BwET1rUtrL+eD5dO8SAfXBgVIOjlg4ygdEnSJ7P97Yj5KhA8RezbBK45skI0jZ7YvcH/lR1nfdTZecNb10VHAPzEmi2Axj6yUmMm/7IXnqbGozbOJAYrss3ctQIq6d4FA+nuNVsdoGvg8vUSgZ9k39zQRaDovyZCQ5pUheoEpbt8aNC/UIfU00xn0w3bUvMldNKcCzj7PlMKcYgexYAln4vVwLS4zPPDy1tW3QA4XgR8FIybacpU0EAFRTK2rE2ra4YDAO/BDzOnPdYZibAPXyojAqKdoVzDBTMJnBM69J22Yvu7W6uyOfONVaLQn6fcMyIzYVAV8sTIAWDIvbPIJuCA5f1b+y/2SRF9vvK5M0sgJK1V3AkMtogjiEgGmceBpk8Jbxb8HgTTO1L2UG1beP98vWBty/f8O37v/Djxx94vH1F2fY2aSvGzDyYOk4gqDy2y1Zmayp8AJ11o8d9PU5NJZ+Qrjuqpn7yYybKiyEY3e2ny3UWA9w902T5tckd1ft325TJu1cc1ML9TrbJcZyNBjVgcMc8mH825rL2zJ6PdeTBDc57Ds9AmuB/BfZ9fjxLeoeA/TQ1Ch7z9l4Jd/jdv3eT4mRtZC/zXG3J41u0I0QmPOGPe3Wl9vZpvgtBEJz3xBq3OYRMDgylE306s5H4Geux9hsQfRcnJfg/Ut+0bOxTzHcAr+peJSuf/inhx9yWmL9LYVgfU/4Z4TEvjGBtf5EBMOZV3DK5/poeOUvj2PocuIrrC3IsDqsMRBnp1FS9ibNYEGc2WJrUhht0r4H5ynj5zDTW1Xmxo1360prMXjRAtIXBNk99Ac5q/pVvA+MqTgj5PTRv3sWxNU+/TuJEGZ3FI+b+zmiv2XfOrLVuZYQnKrzRgRdeLSnCfJuRjn/3fmENou99DMa3xOoeoJRxIYSUPbu7Qv6JOi3WNW+pjWG137EO9i/MpDLZcW3alhyt3GzwretSPnpoA2gHYE4l4bsRzPf2u+nho/uE4htGXcl34XA5PpkmuXi7RXyqjNk46RF9a/kuC127bSDx5V6Gj1Nv93D7+AsIFS2++zye4jPbE3J4IsIuDGQ6cj/FeKaNCXN/xricfMc2TkR0HmYRU4wfX0qxBG48EOr2PMSTPUo7yU8VlRdYFz+oMp59Se/h5mXVjCRgzjAjMwnR74lgI1GJCdjAgg6wtqq8dZgadXzUTDvu6Yn3958yEVEPnSQgNAZuNepsVClAu9Rkx/5ol2kyszB8YfJ+jNSzw372CQnq2n4HhGF4ay+XLb0tbVfEszPrO+qzXVAt91HwluC9X5bN53WXdvZYb7XQrbdGaMRELFTbpSmsYlnuJQOxIEyAmICDDGq57JqVjd7ngMkA53wA0M/rmAbzXF6b5BLh5FUpw6olDooy3ePMK+eZBdTiJIS0M8ZpQqDSOpKrQKGrr9bWvKoX+JRuOBbbaupkoDZBwYZ/FnyLgdQryfLGDOeMVq7PFdXBSLCGilUYKd7txzLoS0R98cO8fRZ+7TPthQqAuNqdlV7eRot75pieB/HHfBn9bL2rII2n7TiuZzSIz7zDN+FPsNEynxTi7/bOE4vjjEdfUUHr4NW8jMU3o3lWxo79VV1TeYe1E7aq+2rQJdZ5hmf/JkbeDKbqhQjb8sFM/jQLrdKBehC27Q1vX77hx48/8K8//o3Hl68o2wNHv2ANWtMwnrNJiOIl47R/Ih1n/P33OsPzZOk803+2DS6oYfTVZ7av1cM/ygytW/Bimk3kZfmIumOCzjppmSYjV+Ii45PP5o8zOfLRdEfff7AmnHf8OBmhKePZCH+UA9K2ojZSdHbO8c6StS/bgp9IxobmB2jb+VR/5nr5V/LHZ6VrOsbmB8745Q49roxLInskBz8DOLjA3zTgYhZvAG3l4qY7Ilp+OD/nDId/UvooX91q59xdY2yggyF+h/k9C1Z429c37X47f4XcfMVOfQX2SLOQSP14NSeK9pFG4T8hJR3/jx4nfbEOhzB68Holh9XEIJEFQO7HcX4jPYZ3NsUTLWZc7+HGlOlD64enhW6n2ZjJeXNdZkwxj/WF/IkXQ19J1uxZkthGrv0Hu8S2TAsMSMwlx4v8E4ZrZNhMTM0WUClsiEm/zpdncPQR9oh9oxm23evYECUAEMdHrqPbX+m4z8cKUZ8ySN9nnUEyEG1sb5hoKLorYrYDw/4NcMJODqr9XmDxSdsfSeCufScQ3o+f+Pnzz6EfbHyVJyJKzIOCtrNF/e7shJw4ESF/2Pr9jR5uzDuDBf6b1N36CP1YKQr5CEV8zzNhY+z50Mtn6f5l1e67uan9qCCZJGjMpcfk8Kr6Jni4PVvZZFSKUSjKhHC8v+OoB+rzQD3kdhdsHPQyArKgEbsU3oL7wOPxGI54UXwPMxFBOA7zrBuvpQDbvmHfLQw2dnsgv7edJ2NQu+FbCvattLL7JmeKbdsudx4QwWxbgpyvTbKluAn6je9IEHpV1C4MOlElwGRnvbIdHLxKKA5gr1RITtbKlLHUU0o/kkWVEnEf0hi49oFpfR4/44VyVyYhYoqKJA5WfhmDdxbPnOdHvOVdEMgzwaK0sTC9Qp6lmUFVSrNBXR/SOtBuv0+dsWRnyhiY9Qontlv7YBto6+id4Bpxk2fgu2aarOCLcm2O2JZM2Gd15W3U77Efo0LO4ES6ZHA95teM/XHsjm21sBSvvN1Z3giXx41ti8V9jbXqgwEucr7w+U4rSGHP6MHf+b6GswDKWbAkk3tZvjms+YrNVZ3AOKnMn7wyjF0jfR/qCjIZBW3SvOvtfX9g24DvP37gjz/+C1+/fcfbl28oZQcvBKDEKM7SLMdIG8ZznhcYx4ylQ8rH5lEmW4b8F/p/VgaAGKnqxs6PikvHdN89OePh0AD9YpQt25Nx7Cqpic2xoR1Rjsb2zVIcC5ecq0XdNmUydlY+8sUZzNnviK/nUwAzuXiDb2I9Z2WvyqeTmgaYHg9fV5RzGU5ZHdH2I0ILFxV+25h0phulbhRdyLcYy1JviuqrtELwP/K6r/Td35PmtuYZvqw3YpkzfnilriE/CLPVpuwL+UAE39HX/aFg/5+71bktkKWRKr8u3ZUtpWRy6iRNdIjWOSk2vNCAHZtugz6J+F7DcJlmvJjh155zM+e1R12yqrdlmfunFp5+d2+ndQjmQRZrnffkUqYTbw5lwX3qM/yCNNXhxkfgEzhWeqtRrBuviS/3KfiVpEcT/dXKzTKGp2UEMItTLLDkEaADNNSZ+zD8LoF4WTbM8lnYGf4kGA7uYP9h76Wc+aRtuW+IjcgX1hFeC4gvZXxgW+/nppkMw5zIaX7rJ/HEvdcHRJ7eM3uy0bsHqAvLICND2NMk6utKo2yJvn9/3gKa7W5B8Op8a7ej+ScFcidFJdLdDqz30d+D+j2/fKxTu8+X45863KnfoaHxQY4lERHe3p54e3vH4/HAX29vph4bX2uUKeB7OFoM19KR62Qi1n73cIujWs+8vWe/HQV9sa1P8s7A2EoBONZh3sPesVva0crbtuHxeJOTfmqldqdxp2nh+DE6XzCeSSzFtpPxp5sy/6WjmUopepM6T0KYIDGgzNnK9eAT6SDuGWRxfMurRzqBqO9SOPrOCD0yRIJGANS57wTa+7ld/TxQezmZGqgVR5+MoDgx0fPwmV82oN9oSwB4Zq5q+f4J6pMC24Z92/DouyA2gwt1OMzMrP/c/QfEq7isYCit7hgoEJJq3jgBw+1n45wnO2aOOQ/SVYCz9B0RLLQlb8TPMK+gY5zRmMee5277zDsZdaiD6xbVGhzYuD3KCpQBjqPFfHKBv2d42nqzuodkBFJ8HyeUIr4swBXfBHwxu0GSNg5t3fyl7jMHaMYnUmf7gqVBFQJWswA/v2+OZ7/Do9LANx3Dod8s/LvBmxXdLJ5X4eUOQb4qPZbLcODyfryVId8sXQ3CrfCTMZXkuhK4mik460iftetsIsDh6vTZHKfYtzEYG/txpahnMtfJx4jLtBVWjo0ykY2Ubh2G9wG3rouH8j2I3u5ZeuDb9+/48eNffSLiK0q/owl9tYyUZ/2VOStjIyatE+TnEHoWfnLWF2KCnOHk0JuMhVPHrxjYTJ988pDhUcxT0OyKMsfD4qLOGfcr82wbuzMdw3hme5uWhuc/OK0CLmd6/wpcXy7jqhswg3M4vs9TQd7OId+0D89xjrLQ8a8Z4mvdZSdCOX93pmBhjLrR4uHaYUj+qYGjTyibyp4b5T9rjJ3ZOat2Z3rO2c8TWbvSj/H3VbuDJdtAFXUZnZ7moANRP4pgcuTrNNE5T3AQwmK4gvda8hN4Au4qPLKjci0bfHtJqH2u52KVLb8EMlohkVWr8vKmXNtl+yt00auyIGvbymZ0kxH9nztVDzAmdnGU3xmc/q3/Rs9/HZcVjja92l+X+4T0w/LboLdM9mwiYgU+a8FczpL7iPoq7vT6/Wnw1E5LiP7+mMpd1jeHXVwpPR0kLAI7qZOc1cGPFTZ1JNSeBrT3756Cr0lgaSXoVZkXi/Im1qPJWk8j7ayt1uKXFpvC4VjRZ2n8qNPM5mn07uOK8w284XVK0iCgcsRgPFlDEWhxotqP4rf+bowVEZE7xp+IUOkdNkbH+RkexxZsHOnZT7p5PB54e3vTo6Pqc/C3uc52Wo7HjU/hmZHAtqE1VXUF2UkMAZDbWemnLHxv5fgujK9fv7pTfo6j9r9D7KS9Hz3FMC4dKdVjDndEw0s7IsxDd0u6BnZ8NrmMlnTgEwhbIZAMitLvayDw1ePH89l2RPTZsW1rBNtKkV0MrLjbxcF9N8TjS5+EeGtBEsafiV0PNwkBw5g8q7RvWz9KaUPZS9uu00crEckRUcdx4KhtN0gbmFs3uKjvgIjGbxHDsE0KHDjqIRd91+chAwidLqVvyykcJuh0NHoTuiOkB773cRKiDcY2gVIpH/A6QP1zhuUmN0oZFihpUCwLxkEDYwZuhC3B9ckWLYtP/M6BljzINwr4WTtnAcoY5HUBc8DhOCsz4rAOQGT4Dc/MFjNWDhYNi+sq8LrCPdafGdy2f1x7TdAj1iHHnZW8nzJHlQidzwCqyc4Pvn8lcQJWQXqmTzRY7ft4IfrMsF46WxOHIfZbVE5nTnR0jDP8Wz4yhoSHv0reoPm16YrDMrbrWl9Y/uc+tb+zAMss6MLwZTddMlay37PATRYs8cZw3v6ZIXNmnKv86kedFSOL+ehEFHz79h3fvv/Af/3xb/zxx7/x9val6ybW61vnKyvPFuYIzelhnoJlxpQfyDiTH0qEe+bTWVJ9f6l2mox9YjDXApszR/m8/hcL/kPSLMgCeAdl9v5jAa2PEW9pAZyw0O/sthjUaYmd0DmSbPWzk9IeFhNEKJKxhHp+R/pd9fwT6i7GSbxTt9rGKtfV5xvtQl4wxs+irr5bf8bp4m+gL4wj1gR2QZCuXLT6kKGJmA368+P65J+Rugbtv+5Lio9Q4T9cpbyU/m5ZUsp8jGV6LvMNWvrP7TmxaM3YziaCOG+zfX9Vv1k6/q8hU1Yp83vm+twuHszjUQou8C0/aYEXAG1hIq8GVxgQH8FCsWZH3pAhN2Ra4uQeiDFN7E7xnc4sqCWYZYFGGutL5HGwgk0WhrRU9I9lg8EzypkrrSjhiCEtz5Qtpn74/iktxluk0/PEMela/UQEyheA2j2HPAHEMTtQ25QhOwx63UdfCP/lyzc839/lLox2DHGcENKJiPo8hPEIBKrPjlN/Rv5PY50sg5lepV95UAc5LnEwQ8NMhLEt9DwOFPCujweez+/Yt3Y591Ernu9PPI8D7z/fhffbRMTe7wJuR1zaGEU7rSc5Fmor67EV0usTETy6U+EBcZz576iEYm4CaTM91PJx5/SLo9s2HT7uSIPyvCuhoLQLNIgFXDcw90bg/bG3WZ/HDpSiF6XUiko90M8XSjOOHfFS2jDY+10O2176yv/WpYSGL+8EqTIJwQzUVpFvBTIRITNIzF0Nnb6Tok9qHP6i7DZweNCZoSnEBVRQdP+uH33DuJcQXKvVT0Jol/o+XE1G+ODyWJoHdVqmFDmWKns/CxDPgghiWPBvaY0Xjkx3xcMi7R2pWXD6LEWBwkpyFhBktO7aPrOJiFWQOk4kqFEwKpNVQHcWYJ21Qfq8/UDbEWXLaV3SL5OU4kVwFyTFgH4WV4q0mk02RMMp4z1iuWLKZ/mGYPAVXkvG3vg7c/NGhzvW0b57e2QMLo0pCzjIULrJyLH+mFJjtiarIZGMTxFPGc0w8Mss4GUN16F/LF9zgwI+Vuav8B54w/QfB1r4XdY/1iixKMV2w0xW+1b6vhee5cs9u97++uUr/vXjX/jx41/4/uMHHo838ERE609dSUNdT1nzXakJYxcHQ3/CR3kfUfg2DJoUpurSKbjZgwxKKGK5xmomtpVynLRsyinsKbR+EhRmOIRqPYmVn2I59rGSd1rmrgN2Lf2K4M1q0sEmH5gIxLpaF8OS3/HJNQgj7UlNvYm9JuUGfvYCYaXbtUiwBcN7loUyHkVm+CqH0qbOzcmhKnAt5a9NQuR26tROHOSBJaoj8Gk6w83TOLFtjN0wMwQz2kv+5P1ZeQxy/3oaaejtnRjEd/mpcbHTQy5IeBGJk/wkY4hlrfp2hf+L9qPJNzYa8GPufCzPm3Jtdf/V5PHN8Zq16Z4EjwrhGu+t0jgO51W3j/PjLl0x43/dTXfH1Gdqw9EcmdgtauC6fCXpGxts5yKprRuCWScktgUXr3I5fB3kTH/n5Qb4lOs85wcx9U54RuAsMDMScMyVmRbBED0bDh9bKLFOo2k9t8NXv3PYsx0pVutLbiNyI10IHCB1moy6HyG8boidxLLEnlqlEj4ZfgHaXWr5gtcVQPUdGQ87Xg1/zqQQZblnadTL/k1eokiMpoS/nqP0E294vBQLL473/tSZoYlfjyqAdBLJ9CF/bDs0Jsp2Rstg6xpicdR0fOmXss4W4cbHMgnwVvGl7xaIl2nrzpgGW+5Lfj57w3v99BO6Q9PfXyH3K8uJQh6HAuBp/HuqAIqfxAAwfHK7jj4J8v7+LjAfjzcUtCPNa/2C4zjw/v6O9/cn/vrrp8D21wno/b2yY6L/ts9bADyeTrJOr11WLZqKj/qxQZA+SDsztcA/6blc4FmVFuSv0FWYVS4TaZc9v/ftL7WwMmnwt9LOqi6bmJHgiYht21EeG7ADtHdcK8lOg+P5DjqOfpkwiWNfSgGZuyC2x6PvhnhrnbC1QBgd7ziOJ55//Ynn8x3H+584jicIB1Aqyl7a/RB7wf74grJ/kUurmVnr8Y6jPvF8/xMHw3i+ox7P9tfPSyu7bXcbpFTapaEoPONXmfAoxe4qaJ/C8P14q3aMFqnM6J8ynHrgi2UGi4Oytd0PtHV6J6JQAmIsyjpj8l0dLDTaJdlaf1NmukGfg8tt1wrJRE/b3gTVRyalQZWOdyml9eVmBBZ4e5cPSMpF6MHBYucq7nCRYKG0HZB5Uu64bQMV3azF94IcTASZnGmfikPtde7C+5ynfeW6uf/t3w6IAW9WgVFcMdMCjhxUGIKRZjJsQmkleXBWe4XgoC3zEvevGMU9+96Dmpuhg50UGOpDn5HttHHOcK+6EW7rUAt4V1Y7KU4nK6IjrbQaFae0s+WSiVTw0WwdFk+7btB1DwUAqp5J2EHoH/QzTmwMAWRjmLCyzdqQwcoMFNu22Xv+3AIqrYz2L4hlSCYnGjfo6gg1dFiuFEMLAhsz3pmwY9JOACpabfecGkskm/KE5KTmoO1Vaw4wKWolWXHT7FGzeqPrPW6P7Y1mbHlaARDlzoZf6by67w/TrrYjUMgxj8Io/dHGLW+7bMGgLQkKZbsvGhAxKIC+umHH1x8/8Me//we+/+vf+Pb9D+yPL0DZlbbgszhZSPf+tfJeW5/+Hp3QdpIrkS9yyRCPhVzB8Nw5R4QE4QEGay2f1Y5LPU7SvUd3NtI6SD9KgcsU8xvZOcIqloRGlzuvINSpuM2cIbYNzEiVvOqs+wUQdyY3PztFPb4OwmR4rHBLZNvFkimsFc+tKhoeWN5a036FTgaa7RoqCHrQfstpXIqEg2HtvebUj/Wt+KL5DUj1y71UwveZvo30CmPT5k2N0XlYUcuvuWfaW9IPCS3u8FSS7LjhiWa5sLK23dksE9Q+3UFm9/uIUCKXL4ycJlaZtxu9Kp8XbS6gbLvlf+Kof4HwF4DvKOULSvmKgi8o5QHbf+xbuDZTU+e2585IObbA2CsQYGvVMmHny8H7E7wsfsOkI9mgCudSvjrX4Rpo3AZ+TnAoZ4E88UQljcevmtwXaDPWafsI6fMRp6uy/a5sMvb5QLsyeedt4rORZd9HcrGNvS3QLqWgmIBypjk/KHISnO7lFdt7aF+3T8Iga5GZUfbfCeJeT7a/GCbhStgu4m9l8h1OG2wihHZlJmKSri0WAFTW2oV9CsO+t9gQbJvbe+Fd013EsoYdPafS+VmX5CfozmQD+yDFvLnS9nzBER+OdDZaQ5qbV6HOrNCVOjj2x8TdTF4Dx4x7zzsrhsknOFnXDu5OGfHUHQhdL5l4mE0cdmv8xjskCtDLb4Pd2nho5yOMAIkN2gD74wHwEUv2JCBLBV7kLRMVXRCVfsqPTha0MnZio1a+r8LHao6jXVFA/LzH/CqfHMQwnnwHRvffCCBU1Np2cjzfezydKFw5oHdjtDu1Sp90aRsB0G39Ugqez7iolick/JFNd+3y1y6rBoTbO13EQFUk+1Azuwek4x7AtgMVtcuPJiwqtUDGUZ9tloj6xETv5I2dn7K3AOTOQweNWFsPNu/93UYoB7WJiOOJ4711aD0O2BAYB0MLCsreZn+2t0eDt+8arCxtYqUezzZx0CcPqD4BVAkOl61ge+wo+wPb40u7EKQUEF+WQk/U4x31+NkmJZ4/+yQEX6DdhS/8lmKmfumD1J47VhDO7zJ8IJc898C+TByxICceSjqwqNigPbrjqWZYDCDYYLx1JJnZ7QUwRMXQ3TulhaA4xNXuXUKMYgTCR9wOO3gaDhq05oF+FpyNv22gP+YjagE4vapdyzT+1IAVoU9GKPdOYLraJXArAQAJwPqAl376/N6ZVPxQujKPQSH57j9n+jeuhLPBYi7NAh6GT1jD84o1yWcEsuLe6dXlzVZ0l43vS1VUwlvmGBkJ2k6suFifpaPJ1TubJ8h0EqJM/kAMmwDsoxkiY3LkvTzxWGYe4Np9W7IgSuzHbCJi5KlxxxL3l9DTMtgUf+6T4p+Z7mA5KLgLy+R9MzevVG7Z33b8qSxSveZg9PFNxnb0RhiaM2NpY4Ntttn2R1GcekOa/uAj8IjbOfK4/c3ynHP2G47ahIRYZtbgb4/iPUK9FSIXKo/hfcPjy1d8+/4DX7+2S6q3/dHkGjEdmaLMizwRcWd1RKS/VVSWdOeGTjo5ZyxeGvJKTmPjJPKZfPWOenb8FjNhH50I4wTeTTT8iMyajAVS/V26rKeYAUxt3XKcyR3mINuCWYA/c1aHcXvJmR1TOjm9qO9ePdcMaQFZQj/D02cmvwc574CQ/zXDn+2llJuS/lvQwU2OR/XPGBWVt6lODEGdtB4Gy8pjlXcShOUxenciS+HZZxazvG7PW0EIhPwxDU1Ms91rx1DHHZDW/rOPF30hNmm3vcjoJubUUjbAHB2b0qPYelQnXRqfJos9Iqr9bs9qbT4Wof219EDBA1t5QBalyJhhG9roGbNYy2rNEcNJf9scln9Pujgdwc7xX+/SncMNkiWFYQeELWW/Ddi5Dx2PXfct7OfTSWr5d7RBp2XUEIUl9mpx0apZI/yGE82zJP2SP5+lXI57eUPuG9uQue2aQBqfDQ/nNNoWOpvyQXIxeb13VV372NRVuzCpOfo1p7ZJ8F1mEuKCjL1iK8Ty4mNHG/dCWes3zGhGnuVcin5+LJeUQGbba90rvNnvarxuwxI8zJ06QaCDkwcX7e7Eri7D+0nRE8aNy+WGCs7sM9LMzh7xOXv+Vd0jZpqnAGZyviSyR70+W6ffnaAl5nYoN2fkt8hX1dUhdz+VnGTWpuPIoLBOIMwW2lfFxvH6Iu46sONJrHAi7PY9ARs1gthYjI1B2p0R/FvrfLYTfCblucz786n3FUs+agsyqOK5P6UOjovygkUAZnKi9DW1LR5PtQ6xT4bPv3nCJouPXkmXJyIqHe0LeYNGL/7gALmukNOLPcxxQ/05SsFWq9yuHQOgtkF7aYbjXnYNapd+ZIQZlwUANh2sVCuO9wP1/cDz/R1P3i5D1I5dssE1tOD7vvNdE1s3qvvsUz8m6vjZJh8OvrVdhMImjtW2b9i2h3Rq6UYdr9w5nk88n+94//kTx/Nn21nxfDpadkI45pNVCJ2O27YJrXm1v15q3BhJtgpVcyeG7T83kJR5t83QZghQtsFFk3Py7ARAZEz+nQ1GnkCh5E4IWz6rTz+90BvOLjtJcWIiCqJZQHZGhxnOWb1ZcDXScQarBQboNI/kdbSNk12a315KE/G1n1k9/L4J1SJjaShTcnouA0hGGZ+1NcP/U5KgZflu5HV/jn4ryA4NMKfh0qBxdQNI19RYvFhm8DgO4Bbj7IyGUTlmMK+MYzGwMcqHLO/Ar8Dy6M5sUskaAjZAtSR9wG0mk87GbFzdF+XsyoGJRoyFqXKDdWSfEClFdl812BGvvl6ZZbRxjB6PB75+/YYfP/7At+/f8fXr12aooS05sHpL5YtespWu1r2YXFdYPrs5pqOMFeeT1ub5Hfj2E/C4s30wOE8ZrDL2zrLu4Vc+vsR5/WR5KHQl7+zEui4FwZHT8k4anePP6OF/csod0Q9BzNmov3uNhyiMNbY5f4l+/u/0y5OVJ3H8Xp18e6FWNJuVMIt88k5963cyOroT54NoXEwfba+l5Wuwchr905NYKN10yUyWMej1i3Fifh9R6Xh8HJHzAPivS8IpC1thZpNfTb9K3l/B6NW6r/XJLCi8Sq9fevxPSJcn16b5rJHhw9orWK0/fpsI/8cklj2/vqJ5/dcKXcPSxzv566pjKXy/4s9wzLJPsSRxNuEprDmQ6+H7r6KM5J0I1dyPBSJsVdsbfZvoyw+TDagAmRMf+if1QIWNs7frBzSA0fBpCy2efcKi7brQWMG+7y1Wfhx4Pp/4/uMdtd99XOt7X2jv8ee6nD1PUuNt/XBjRwQHE71Z4ychIHk4wF2ZOGaGqGxM+DwAa1MpkBUsW2mTA0WCLW2VfQuuWBZS2PXgwH/745AgiWUDCdS0R+Zoo63PcvTObnc59IuuiecDu1HcDdt2LPgmdzTwJAeQzX49+98hK9uHgQlPI0umUko//WLrdYcAsGVua5QnTjoZ/Bz8xMEAAKp5HKi1V+VIDGKeBRW537KJiBhIz59D6BcnDS4b8wl9ssBszGM/XwmAz9pkn2WTBU2Angc+Y/sd7PYgzX9miKbwBp5pTqPKZhMMTFYuxbpGGdHGPD+a0SaDKbC1kmndMQ08RMyzDScLgmUJkKz8D/DPAnT5uDHgyizU2+ik9TNNRp7N+C/DxeIcx2k2bm3+GWxHT8zxWuEnz16w1CLOba78nB9muMWxeIWeM94n19HjO0tXXy+Prv7b6DvzofXLv2NAiY/Ye/vyBY/HA4/HA09zzJ/iqLjK2EzodDbJYt4MZa2Bd0e+DuOo6GzA1P64CHvKq6Xxc7MCup2i1Y4VJWhcNek8TBoKOoN7pQOL/CN+4ly6GANccNW6Y11zO+/6ToarevyuMXxF/i1Kdxh5+Uu4iAiMeXO6nGN4xxkMfTCjMY8ZGwFMZBjbYRF2CbxPyfiOeEXYH013+OJVHprZIq/A/UjZLH20PKdVoHI6RoeLTG4kgrNz2g58IOdzrx+dHi6TIrM6Z1VgLc+mID9Y5my8jDYH+6lIFA9Mnl+bVvbfKhWELkv9TluRfT73ea7gmsEZ/KYk/xVYMc3GzHxCT74t67uSipXnnV1mtsIS/sWqP0sGXU2pjsM5P8R+n+PNY+yaj6BlfOl1fo/Tqo7rY2xtt1yBN5dH63zk/zF1+Xqj7BO9k9RxhtOvTLfGSbmYL6unFXoJJwfj5Alg7Pul/lGLtdl3a9tnxNG7PxKpyPic6yONYVgeyevS3cLRF818IvFkxc309kNm8wg8tAV8GwqoCIDWphN52o5F0gkMxafC2tLx0+7SIMruwPCTB8ehp2dI/JDaBMXjOLA/+hFOlVDrT9T6DlCfYOj3Gh/HgeqOxKzyngiwR11eSdd3RHDjpJcsg3ohT8QrUvq9DP0yZk6l74hogfdxRc1WCmoPfhARNmqwt56Hb/FuOwK6YYm2RU0mDGo74+rnnz/x/tdP2XGwb+1Ypwefnd0NUz7ztvBdAnxRZyVUqjje31Fr28kg22QasijYsOEhR2rs+47H44FSdmwo/dyw2nZS1GfbBfHzL7z/9ReO9594Pn+2nQpBKMfgnu0ADg6h09/EnXoZcwlK381hJyIUdtt+Az7n3jCn1GHwkb8K12cW39KdhWgQW6aPToKDE2YFLQzA7voYhQ8LmrMA4DQ5Mne6cHvQ9r3w2bEwl62TOVIrw9lVcdMJzXaWjPnYT/M7TjJ41riKwjfm+6jz7xVYqygL1kUjnEBu8jIGW88M3jP8qRvcZfPPzhSNzbeqO/t0dSNpc9Jnp0FDzodrPkA0rOMWw48kO6av4DENsFD4fSHFSYiBXy4mVerz/rP4xomETPZE+bfE38Dmz2Z0j8ZdJv/s5VHDsUtEcgTbtu0AvBxoxzjBPWswH/j65Ru+ffuOb9++4e3trcE+2oBuhtLnrOw66/PVWAHWYy0zQM9TCZ/Zd0o++7smlPWTZyEo5FOM9SP0XZYSP65nnxvmp464vO62Vbo9Iz4okK3cBp8r/bnqi+z5mfyNeX+LU8pd+nEwgbJz51bz2jyvI3GJrla+LWrsYsbDJqAWQI8cLeDA9J0+/V8hXZc//8TERyPk9tKv7McRsrd8eLxXPhLYOOViE14dIzFg8BLGitdnpDP9dwkGxoDMtXS9Xz+bA6LM+Z0jJ7XxfmOdvz9xoC8/gvm/0yxdoY3Gy/4p6beYR5MgKoHvS7S5E9uyFQJPkOmbj4yT/1R742Mddq30RZuS+8L53XHhY+6DtL9+JOILTdKjmtTPtfJqsP05ZhvwGORcGRfMzu6Ojd8lFWOZlHV0ZiZnFZ+dn6rDR+oelh7L2qzvGHxLKUaEox4mH2RMyd28tceECSB6tmMue9y4UotzHn3hvN51we+p09kvmj9Lt++IEKLX6DwHg7CSrsLvBqESmmEpBGeYm4CN7FRo0Ur5K+ZTHLLeIXzBcT2Othvi/V12IWylANSCMEUmIbogLNkRNQRUapMPfXJDnHyGsW0SeOdbxm2gh+lG1GlxHKi1XUx9HE+h0TYZ8J7RxyBC6TtC7EpiEqZR+lc+KsMGuWSmTdvEsF3Qmu9r6DNfPCYGlWH67SxNlZMNkCdBk1WAsO8NSPNFgZEGfmH40srYaD/0xsvEjrnPwtJtVvcq3TVC2xjIHUGL06wONglWwSsLz36e4W4nnppg83CmSqojNlsx2UqNR9vY7zEAHPsijcElgbGxXJHAyqrd2fOZAjvjj6FP7KRXGIgZvhm8WV9mPLsKxse/K+2ZJtG1oyyIeEzbd2P4ZPBGHs3zr+DNJiGujG3Lg9L+4uXajE+bDtqGSQjqRnwMcNv+4sdSb8+zbRv2xxsee9sJYWGz/Oslg/HxuYb+zAicGXCz8TUb32NS2yKese3bJoSVT5ZfxU5CUJafERzhRlrOg/UT9JHT4yyw4OnBZcN7a/PavC+M+yuTFRGvVf/dlaUZP8U6T+WZ9LMAWucPyWrDsWhut6zdG8Vlxt3eRwsOGcuLWKcKCfd7SScjV0ecm2H1mYH5O/bTVTvmbprp1OzZK/y/qmtWz+pdtG1msHnnN9HoQH/WZMQ57Ww9iosv73d5W3/xVC2R5VEr6MZAxtU23ElX+eHeeyMvTZ4x78JmRBy7q3Qvd4bLymcRMTspO2Bzc+zM6nbyka7zw5U6s7o+E26WZxj/MJaM04XeVnFQ4u8A+wy/X9neWZkrPtKVOizdRodyNg5nMO/JTGcDLd69AvNMfq/gx1fTOI/9l874wN7b5qCnOJz6aaH0VXp91C6wdV7OPxD0PpRBn10stcoteNEMeqRyxKj/URAgExKz3LV91sadLV+WWGfyz8k5FxfRMhLnM82JJzd4PPn7FJW0falfj9LXgvXj19kvZft+NNcjZNi+2MxxlZw01mAaCIDoCYLeT2F3XWSxHxc7uMFqNyYi2ixKu8SCeiCsNbDbeE7Q8Gr8tiK/zZzE4IjsOohBmz7pIDsialvFslG/CK2gBwY4ENlXwBwV9fnE82e7d+H58x0/f/7Ez79+apCmtB0L+2PHtm9yhJQipcKQagWez34kU9uuIpea7DtqKQCqXui5bdi3rU1ClB2gikpHu9j6eOL5/AvH8x3v73/h+c53Q7y3m8mJ2rlOYfLCfloGV3S988+0n/2VMLj4lnehT7+sey8bSmk7AAiEg2q/9JtXPfbJG3MclLB7GBHZQI1Kx+WZBBliMC8NSibBEOeMBDyGbUxJ3Rzcszjbcs/ns18Y42GNF8Gu08xwy3CfJR4zNRE2XIcNcrptXRhpmtUrgjnBmXHIAt2DQQv/0+azvGn50zRkOdl1KUCS8MorhsYsIBxxngcSx+dzRzFPGWlXdd0xVM8mVawCimVW8D6SZrypcd88oMLj4pVg1d1JhVhuNi5mZd04JgLKfLeFPe8x7qBy43WfyyQy1gx/L6Xgy5ev+Ne//sDbt3ZBdaV2MVblC9K3piVqfULd2OIm1q+67J8ZkPysNAytOA4mn5+KQ6LT7pT9jDF3Bu8z+u0jwYX4LMqkO/BeptdHSJA6FAsZgbuhi1BZh2IdLj8ZITm0zolNMeBmsznTzsMqm/oOn8mjvzrdlVP/ae27m2Y2wtV01S4hp1O8zCUUVCqoBDwPwvMgHEfnXqevWS/CmYCU8LtC13L/eWnUHRML4AaUe3W+kuKYOdM7v8puiD7oP80++Uga7AqY5V1JvMFlnP3+DxgmK3n8+f2bwJu4o5egDbjfHJnWb7tV8temUx35AZr9r5D+Hrljtax9GuIqQUW25+OR0DzVKfcHulNEWhmz5G6oN5H+QN8ZUfh4C2MUlI4+Ub5nP8YsdDKiPXP+N1mreZ58LHOG99yni3EVlE3uUvb5F0iYWnURXV+wXApK8YsGt4Lu13Ld7R/C5iYitjSmx7hymft8enkiQitrFVINnT/kCYEUWEGjW2RtUCd1ckIXlmCIykoV6jsw+mTE8f7E8d4ugT6Ow93qLYGabQPqkeuJznztmCDtiBZo5+BPAdGGjdrhFA3+ppMZAIiPZar9iKSj3YBej6N99i0u0j6ZZKGBbt6A5CNqvGO3+gMrHgqOejfIC9rkUDsCy9CaZZEZkKZSg7vJ7wTSPNlgnRMKJs8s+JYqLUoChCKYKJ+iJP0SnfuziY+BxhOcryqRWf7BKDf5Iw3jZIMtGwOocZY5pswZsDCzIG3ajlCBwvSKiJg3W+GBFgPuSToLnAturKESeFcMVZZfMe/VQLWFNQumTZPqDDMzP3eUVoHMGV/fwXuWP58sWNPFNG1Zbgic3awn5ok8vSoT+/hOXRbnVV+5z9J4tZQiAkp25CU4zXi//fA4ZbzQ8OuTG3w3xP5A2doGUNkBJtoqazDARxCd9rmr1+K0PgbktyeuO8g3Y/t+KK1476oOifl+B92ujJks3xVZdTVgcCqvAw7jGPFlbgWdJjCvp6b7SsCD381LcZo7baPes+Xz0Tu2m9y3lXxxOp/G9xnYO7T+HeN/xiN3+DiW+6wxeNem5LTKfxVmfHunPQPPyL/s7ySVlDAeErYcHol/wyzI/uboo3DAxH9iGIQr+zhLr0zU3uWpe/m8pFiNbw875LH0Y2Dy28oA8Brmqfy9g78bO1bWTPJf5cszvp/5M7H5H0lndd/hm8/T86WNrQWs6DUacT/FL4Uz8EPH4BeLeU8r9aHs7/H77HcRfp/lnY+5ha2epFxXnst2CzvKOaX5NRvqSjod10nzbZ+kNkVc3DSxAe/pMVU8U3kiQd3R4rqrh7nKswUeLvsH319G67K9G6hG7pVLrU/Il7Pt53hPaS+6xNXyAbdMf9npC1vuKlXICB0KY4KI+nHs0Qbuek5slHgigMf/1eSjknehZTFDoN2v5Q0tjs23PNSPp27LCakSqISFXaYPr8aNZunWRASgM0Q6EdGOXLIrseUvIMX3J/DfbOUmb6l1DGyTdHqbWaN6yE6I4+dP/PzzTzzf3/H8+ReOLqvsZZtfvn7px1cUHGRWjlPbVYGi28Ce7+9yAQdQsO0PtJWprXNKKf3YqQN93wYKFTnOqdan3APx/vPPthPir79wPP9CfT5Bx7OdU180mMSB2Ni5PtjpZXAlv23m6PdzULX3QkAKHYdOrqAAW3kIjUopKGamMvYrUHRniO2WF51xxoPvfijyjzcEV8E/973v2iH043McG7HRoLOuMofX6UOTNtj+sGfGKS1HXGblbT7+be++uOqYvxq04fEqdZcNBO2DDBb3v20/w7J9M+x8KmZL2dCkcYwzXlZ+xEDk3bMhUwOHAGzaF2fBzuFZMQZK0ldXnIKrEwdJSSAoxrM6Rb6SylcZc04Br3e8WBgrXC0vOcwXQSwW+bMAeYaLzUNWZyc4xzOjI5w7ivTqZFOUW1fG90jjKkH/DZvebVI2gJDqUqGHa68eP6j5eZJ7HLf7/obv337g3//+H/j+/Qfe3r7iOAjV2J5lK31sM5xeT199wUbanZT1/x25+Jnp7mTTZ+D3u9v4Gekjbc/G3yt2hP1uxw8/u+tI/+5Jr26O2ScfgJXhb2QeqxAjc6dIRZyoly9dKsWi3eZMPTOLW6//Dq3/jn75aDqzLf5J6XQc0335pG1mZ9fYYABAG1x0w9TVAYR6NTBE1O4ktGOe7wk8jrbb3Nukxs4BXW7Lf55EzlPT0TfLuGBIe3IlKPIr9Rj7yfP0sXE20/u0kGt/Z7I69CMyhqCBttl7DUF9blKyXsH/TqjxUu2Bxe1vCiyf/B7Gx0ld7vtH7JJ1XdFuHoK4v4GVY93ZxMJZ2c9PZo18i25zjSMOtyMO19PvmmT43MTBLquzi+5wKHBBfUly1zD5T/5efHxmiAGv+BjjotlWpMO4QMYWDx3viBCp2IOT7H7XvrNAdxiw9LR4AaBrMatUbk92RATExzrDt7lxNQDr7e70ww5eCAmNlvZ3/IXpW1+SyDcmIkj/aDTeYpCrP+xI6moU/zch/LIlwdmsBOoXMh/PZzsm5/nE8Wy7IahsQF/Zue3tOCaehADPANmZIWvcMHzD0O04KYD3/JTagkKFL07pzEgEcz/DIbsg9H6IA7zTgsM2btJrGAh2UJbeB9wl2iezP8kX+opJyv3DF4KzQMiCk8qocyH5iiHUFCYTYJ1mQUD33MhE7tfSiRtNmMykifCzYK2nQ6LAknGSPc/qiUHFAEgmq2LQOKszm7SxE182qL4KFNu2R5zXgdkJbDee7fOx7pWBndUdaTPi3HWfCYScGfGOjpjv5JoFTc8C/Kvf3jFKVhAWLXdlMsLCnfFOhk8q60M6C95m9XFgivsjgzXjPYFVPB9l9cz6y/zCjF+vtu9Oiv01kzENr00m9ViHMh7jhIe2p8n0fMurTBuEsjxR9Xi84cvbF+x7m6w+aruwijGy0EopRp0yjfT7mVE9n0jhmu442aNUXwVmJwiln94UI33P/Gsg+yCcjtsZKc7ez1A0TwyGZfI5lvmc+OhM7uTf7W/76WWzfq5h52M86oCVTFCTdS4/s3RFfq4Sm/jOH3Zv53Uu4Up7S+DZDrcA+WXkWt5+ttJFcEX/nqIYbNgo0wU3GdrXaXeHyld1wN10d+Ltqo3xO9MdeWxKDeVnNmNmd7b3/I8Z2ATMGdHC1oeqhfyuhhp0J+s/jx9PRIT2ZU0tvb6L3f0R/rpa9nodwd5blBU1Rrbhqs3kuWaUOuzvzJ+6GnBbjY0rbfbl78nxFayZj5flvwL/Kj2SF8Y/8nlnfscd/Ahqw8zaOzw1ZH5ZBwa7MeriHO7nylHH/0Ytsqia/S6w7wbOP/mdl5v5OXkd82T9qeu2ZW4P3fFf4/N57MPbqpflRAyK3tHHKduQ+/D5e/xoacfekMe3y7w2rnIeKsYCZNtt0bAIM31iaB8Md+0vhZ/yQrcB1UZqoEUOlXESwuopCjakb7v316/FOezv9ldyzWY+k/hEjwtnO2Au6yH5EhiXdUGMVZLaRiMVPN6UPqf0jSkW8OO7ORaO2iLdO5oJEOOu1sYoUThG42/r9x4UlGE3BAxT2CATmbPhQWhBjwIQVRTasPFqdLRV/+/vf+F4f8fPP//E8f6O9z//bDsRjif2t694vL3h8eUNb1/esD8e2B4PkShlKyh88XavD4xDZcNzw+NRsG0F+74xJVCp4lkA9GOWmgF8ALXhXOmJWp94Hu94yt0Qf+L9rz/xfL6jPt+BerTJkm0DqKYzX0OQ1zIZX0hNulK91tp2dhxVmOL/3967bcuO4giAwo59Mqu6H+b/f3PWrK7cYaN5AAlJSIAjYp+s6rYy94kIG4QAoRs3Yg17yQjjrxecbnXSBlNp4/M8eWVRy+MHLayS8pyTKJjY8icIFlK77eLhXxU21jHtHJdJWW0s5O7dKAjt0WXpTol22gSGNIAqv2wd8+vpgZqM2DbYchFZrzjIlj9DHM26bY9IgUDcNh60QMgknWlz66Sw+BQBglnAYDRBRWVZPFdh1m+zdJZ2yStX6bH1kDLEo8HywRXnjIwPS/uMLxuNMAyqRUEpO/4l3bN6xXWJjx605UU8MzPit5SYf2N62s4XNPXHQYNt2w5fX1/w648/4I9//BP2X18AG5WDSqfQNs8Eqd4ZUfriBdYP69A+Y9OqAXbv5YRIjL9/hKman0mvabFmXG/WJVMmAtZl6Ii2HjXF5P2c7naUlZ+uT+/DtY6bybneaZt/UtuV+mibI8JHdffGy3yMlfJegRUZNcHANHjOwvswoE05fNPUvV6r9nki5xMBrFM2lf2Xq1nGGUmhK23/ij6+gcDXF6/y/xWHXNraRT5mgER+T1k0dp60c/tk3wUAis/ZthFyTVqQAdjfFAVers+/I/Sy8sqOCKvfVnNd23Xx6pjs9fHPgA1O/TtA05W9jfjvMtH5HwWiyWY+XvcbYJEBP8dAuvy4vzuJjU3hR9Q0++tV2hYTquNhEMQNJfMywIz/K3zf0TdoDDf9G4DSe/q9gIhCDwIkTICQRf0m7dDFwcnrIb1cE7Ff2RgJsQbIO53fdDA9TzSxkQwxgW9ciiiLwYttENv+Bc34xAVftjrxAfEeu/RUOyz3G3vt5gyUPh4xHoxu3A+kp5xbSvapxA4OZCtapGuOmFevT9vQ6xMRwi8m1iuBhpjAlBJsUCcikribofnlvVMDwHibYUhCszaaOBYHz3Is03kckM+jXip9MnOmLZVdEPteL2LeuDOog7l8wVh09gQJ+G0rlzhvfDlz5qOZJOF8FFIukxKZ7oGQuyIyTVxkQMg8yyZXmck2tEABntJGPeN6fxKXfab+dFer9KvMNwpKr+KJVlKNnr2SZiYQPDxWwNGnRDEKEK86XV45/N30bwIyHmY7E3qg4TAyZqJA0yg4q+ugzQbmRZC7U8btMpp4shM5kcLRuNBQpeXRq471KNi1ElCfQScvL+C6qkA8+byCx+MHr3/sO9K5Xvtb3noHZnWK5Jc3ubI6MdHKoS8ATdrS1s06mYLSGPJplDQtjXszRqJwIxmTKZWj+vb9AfvjAXQflLRZyYhkuliO+MGqGfhphMGgflO1PPkcr/CP2qjDI4tieQV9Go3EPjDf5zsiJE+UdH7C1pc9/X4d/cmIPu1YbqzIR4/kaLxFgZSWniYjYlytTK0nI7r9sv3J6HdgNb8376R1Z6D/yosB5joWm5IXbwR/mSE2pVuIDwSsDq1lbN+2akOqBURE0VMoDiDlQOWcdunehFW9PZpsH+kx+/tTDt6rdkZkx9FYWLVxRzJ2JgdmQD6PzF8CAU0XtaOaAMj/lD5OhE/usQD5LdCXs3a8AldtrFn+RoPqtCh3UGbSaYSdplYjGxy+thzTa59H9r6lrrMKjF5cKXM0fm1eKS4j+ITuCMtfSmvpsc9NvwZljWRTbKtpO6dLYRpvqmo+3I6FBt8+ioat5b2OF4XtEfPSQj1snip2kvdOoIwC26Qru7dSRYd1lnyzpgclmbN+62nW9oDGqUc5jUF+2vH3CrgFXcgx8p/mRUeLKJZsL5ceD+I2tUj8ci0/ChvS2tA2W6d++p0gzfZsNPKugxS3pecrEC4aiiNb7NX4jkeDdei6cmtf22O8R3aPju8gANG7ylzqUz5voyZCR8+Vmc3vYr02i7mN4OIdEQhl5qusxC8dGc9gbtteA/f6/HiSGhkzpKxXjGazuh8AAJNgOszAM145l+OY/vVX2XHw/RfgeQIAwr4nSF9f8PXHH/D44x/w6+sLHl9fkLZUzdWCO6VUL60unV1uc0eAnCFhgn3/BWlL8PjaISWAfU+VvqPSUvLQRMj5fJb7IRDhyAeceMJZd2w8n99wPL/hPL4hH09ALLSm+idHrzSc7Zn7wMZ2PfrpPCHThdjiLgfthGumI3xb3Qmx10+rbO3qZ8IlQeKSOOUf4aPPUbDYC6isGKWyDA9kmcRb9jMK5nnl2XpYGmyQ0hM8o0Ct3BEh29GmKU5YCyxI6ILWNZ+8G6C86LJ2YPPYfrcGmKSRCvFoRKAJNdFHgVN1VXnIfp1BxGPzoJvmqVk+b7LG46MRbX2C8esIPmHkz4L1r5Rvg4HeuJTt23hQs3JEm4e7pfXpJ1nsycm1ujZrWa8XbJMQSRjagAiYRYWmRVAddB25bvRnaRKGKN0BlFKCX7++4L/+67/gzz//hF9fvyDBBudRVp2edRK99B/9aRmEwor5CWfy74ZZnYar1P6D22NVLlJa+WmfR+lkGfJ3lL8+7XTPCi36/XxHXASfcG4+D00evKojwqxVRnEC6SAj6gcxVS8DhZ4haPdX+/EdWJ3kHOV/VzZ8uq4dTegHGWnM2TZfsZ2mQStlJxHbFV+UJh1ypr/MvlHxUwG27dH09qR5sAvc8BQHvM+1r8GVQOAbpaiy6FlKW61/4rFm24IXFHHeeX8uUWT8FYCfboNxGSTX/j5OeAVmlNr32l8cTR7G+KRCQPMugv8cm6jnj2jiZaFOCJB47IkyJihe5T9lI0Gnun8E4uArCp9E2gxbl7f9LhSLaNmP0DyCd1Q00i6El8HU10aLJ+n9wPcqFyAADtpbOOA0v9DWvyTI4k5eFchXxWc2LUcxvthXKDs8UNBZ0MggfFAHvLZXRcXyYK0FG03xsd4aNwJADttjQJ2L28Ycra0m4/EJ2okLlF/GHT8FyxMRKphp5wUF4fZZSi1oIwM4iKjvOQHZAQNHkgLqiHwHg/wrZQNs+wb7vsH+qEdB7TsHabgcCgelBHSrMRu5GQAS1jshNkhpa0cG1bqimBDIdULgPI7KNxkynnDiwRenySOUEIsRrStIzlWqMSN/lSsbQzj/a30DCif3QVCGLKsPnJsVRsbhiN5JXLZvo4Ch907SZgfIDHekEG2wMzK+7KSKxWuDgPJTjaEFJ9kGVfQYtAZF7GBdEV6RcPQCwxK3nYSQdHN9AZhGWxdpyJGBZPGr7+DzmYRIUCreCtph1j+tvrosGmfys+VRGC4LcqUkRH42xlqcG2LDuKjLWK5cg1ngJSrD8onMR9sy44kCv/yUUnfceTTx4NHUyujDZDT2raKW78dytGGU9lcjVLQZWEe/Geq9LGvhbjK2bLuBxGJ+k/Hktfe27fB4PODxeMC2PZQca20WGeXSsbrOV718EMTy7zHvRaUqSS2E0ojKaGwMZYwWeGw3yVW3sgYo/lXfar0Nuwg7jNcQ9YuQQJOhP4N6V/vC43Gqmxeg8HSg93kVrgVD3inzukPb20Yj2kaIfJyKH0T7vwOernYJ0bnEv06uxfHR0Y6+P7EEpOeC15HN8hKdgzJWYZb21f6d6eB39Posr9duK7pWfrefkS0psLR/pf1FflF9q+RjcX6U/zJWS6g+utjPYru8MlZHci6SN69CXw8rN41GYTmc1MiT+qjljfvTL5uK0OkTkA4ov8K2J51mDatBWVHZMxpnNK/km/l93m/Gz79dzNDbr1NyLBVMYzwOV8HW0/4OBplNteDPRWkjf6T9rrLDFBHl68tr5uirdg5g43UPhjGaIP3LetlMjKzyqsxr03SfLYGmpbNm+2TsTxk//KrOW+2z/v3cf495xm+fGY/JmENf9Gf1jElpyon4E7xum1JW9DjyxAVxxwr/hvE15WMJ23XGxzW2NOrbYbs58j9Bcu3cZWBDp7X92ErXtJT0pEtlgKTGgjrnUBYQdCj7pNjSKlPhWm2v3RFBnS1KiIJDKbU7IWxayn7WiQMK8LTV93pFf9o3MztcJiHOZ7kHIh9H2QmREbYNYP96lAs2f33B/vUP2H/9Wc6t3qSQKpIsbUkzCiIATWqkVHcK7PVuCABMbbfGeZ5wHE84nt/w/f0vOJ8HHN/fZXdFRjix7IjI57PcFXEccJ65Hd8E0GYNsdw5Ue5jL51Id2koB5dX/7TJjZwznPksbVF/276xAV36/Xg8ShuYFfddn5u+TWIyQq7Wl7jtjgiJz+L1+GcFpECidlkRIjK9/L3zhFWvyFeUsRecHAVSIiPKo822oy3PA6/flwK6Dl7rXFp8tp4rs6bFiMqsXLUAB1YcHe2LTr1VWPp9KhfNL+AapcmZaK/uGNJRInqrb3lfJjZrzulYmINUIk0ToFJe9B6BzlFsR8y1Ol6lYTROV8fwSAZEPEjvaMcQyaCSIFbSUYBEluVNRMh3Uj6M6JdAdJZD+MaGcix7oPJqVysAJYtFoAWgl+miX3gXRtL9T+35xx+/4L//+7/hH//8J/z68w8A3PjcbQoMUHtpuVd2Lb7M0l2jqKr670YQ0DG4o3cJprINBOk1PoLGQLMYQt419n/nGqTYReB35tOZBdH5jDz3jP/V4Orr8k3juZLu3TL/z8LVZpNRmJeRvAZUygov/h3w70jTT4Jn83qyYj0I0tvsLRCDAKnZTxnprogMdie3tEeWu4T8xP8T0OqqbcGqxVLioENKchKCfHq9I8Lu+exKW5XN+SwlpaZNh/E99VLbce+AppfWif5eWJuEuI5PQuKAREvzicm0/wjw7Mu3kP298Dt1Ym8jRs9Nu7zQ5p/hrU/Yo/+Buh39APHaJMQC8OryeazMIU0tjerT6njGOLYDwLtO0lwPeP42Yv88qg/HvJy0MmZ+JXagys5VP+uAksnA/6j3rNmr/7nV/kkbAO9uEeoeQdgA4vLZMolBdWknI4m3orxrO37Wd0SIOxOqaQde51rDTwnC2lCYkYP+hWhkL7qFSPSKi4K8/NMM0rrDoHbQtm1lJ8Rjg8fXA/bHV7kbgu6FqB2hhR8ZWRQooMc1YEjRn9Q8fUSEfJ71foon5OMon+cB5/mEVCciEM7yR3dC1EvUyJimoADUsjdFUgLYtnJBJgV6c6krZv0nJyRoooLab6iIuI/s0U/WGJVZ6iREvbSUPxMFXf3dEpI3FF76zsGxvjwPPFxeUNdb0SEnLCJhVh6ClsPEIGjSyHqIGiR6TjSY9kxN2pWxYBwuj2bZJjIoK9POhGcEkeHirTLw+MX/LvEgC3eJJ2GqDqUXFK6fxE/8n6GdHaHyy9IR1o/EgeoK7OiwNBE+WV6tEcRATnQ9DgxZ+gn5pIF1Sx8fNz/6PvLiQ7YuK31rYTapFYGeZGryiekZlOdg40C4fS8Vokje4RNDr04OIWwb9Wm0wy9pnI49WvpM8zgYnpVB46gtufxmoWl8CQDqHUyU3pKjVV3Jh0QNlVfRkxOaUqp3Kj3g8fUL9v0LtrRDZrmEovEof2POznwMZNFIhsiG4rYKec1/XvKN5SCNff7hJVDFBAM1pAfdrxGzJ5rMVCiUceSW5KIzrJqcz/beKDWMJyEIgw0wdqLQgVf1kgRXHsgBNX64XGZXvwUZuToRksTYY1L9lDBknIiOmlblNnXqbDPs02oy0KUEa/r2jEqV8iv13wOY9bdrlwoaaiYr4EU+U9cJDeGk+LAWrSiSYfZxh2/Yl4o4EoidTdkISyIjpQvSL0DjG+A6FT+jl7Gy2cvvHLah52eMZQTqbzlBO14QoTnIQlclgLTtkNIGW9LWI8o/zR6qTLIJ2siaNGXSPLna6qvyseN3kDwmxhojlu/Q+U0yXPDWkEarNEW7kC1Ov6f9q6UK85lbt9HAVVaVg3umt3tQ3FZ5zJuEWJX7K+CNlWEgl/IF+NDUm3vMkbM+6dZa6Hlf9xeaT5UybJ9PBJgjn8/T5116MahX9PsoXXlnVZKtu9GmVH4nXBwF0kkop3yQsrkfD23VeKwXoup5/B51X8S7TJ+qamJR7k/2jXjL6f8+gShK74CZ8R+aPul5AZz3UaOY37bPsU/US9oZjT1YD60lX9ZQHWvqL75sHMYJUOiKER3cJkaHsbpD95MmzhGgzmd78SNJL0BbTEq092PEKy+qg9/MKPo0Gn+JF66P9AIAcEzFFqX7OHELWtXYPpD/AwBeA4Dc99KmSTYzU3NF2a7viHhW9Fiuny7/eA5CmwmhFaT1NOnCO1ivY8gAud7LAHVVMi3e3KAE4OmopTIb1JxBrHchHOd3CSgnhLQn+PX1J+yPB/z6+oLtscP+9YAtPWDbdjjPzGeJEm0pJcC6MtiupHk89jIRsG2Q9w3SvpeGPQ6A44Tjf/4Fx/MveP5//y8cz284/vofOM8DzuMJ5Rb6JoR4kuL5Xd7TSndyFKvuKTsTUr1QOwHsG2BtC0AExBPyiXAcdeLhKBMb53GUHRHH0RizHinFDFz/y1CCHFuquyB2f9eC3VkhdzzIc9LlBeS8KrceZWUd+NJ3YkeIGkSNZ2ZgJxBswHhkFFL/+ndfJNigBMZlUC9h4cHi79RdPIQfAFKdECr10E4+lkJBFCIrUuqdy5l4x3EM6X4+n9zm+77DY98hpwRnpdG2iefkRe3nGQt90N3HKe+y0HlKi0g5Ra8lT4HBnaqi4AkIgVcGkWkaExJw+zfaNujVTQ8ZQS62aqbZ5h8rgIjM/zlngNwUVR/0F+pVtXFRBhka35a6qoYT9JTPjdoQAOrmis5SDB0Wpqmn009DcjG7Y9LbPRWB5Rva38a7A6Rdwf3aaKF8OWeAJJxU1qbCwTCKvuEVVovgwfLJyFhmnufJ70nG7dtWFwRUpKY+ul6J40Ft91g71k2wHCTxJ9sMhIwsshNYR+7bDttWdGvTumU88MQGPUkAjzqhnmtJWCVYoRFhJx2cAPZ9g8evP+DXP/4L/vyv/we+/vgn7PsX5PwsE+l1CxCe5Ygw6OrnHDso62W+r8j8eYoobTOIOoqwSzwGs5VAB7QMdlL/Yky3/k5dHt4+LHZt8lhmS2FE27wukVMux1cxprHJmkAHkLxrul8a2+sGqIVL/SxpAyh3iSFRbjF6zyT0DTjTiT0GzyBfAzX2wzfyd1Jyy6NG/VuR2kUAFVOVSdjZZT1O8Y4nF85GWwJQ98YRLpT09CheAzQ31IkysPWF4uOuwDV7M+z3aV8PBubLdVfGilNk8hkK7QODddIZbddhkf+5LowCJM4XVjF3e9URKUGqk/zyWMkrAdyUEttMAACQAc5jhzIRcdQ+PwDxgJzLJ6Sj2st/wGN/wF4XpSFAXSaW61/l/Qw0l8HczhYl6r4ctpZXFWX6rwsJaxv0No1IK3e6YsR9hjl4u12CNgMu7SU39K7SdDTa1NP6aial5Gz7I0cAgOWMp9AR2nsrr6bFO2mj5xGaN3SfhFnQCQAgYWd1UEJw+RTFwk9KxnZvvMOR+6LTN9il4cGjKXXyzDgmbstYFvvtFdk7GlfVe2/po4rH0Ioo9JQo39WICRod3FTUn4FNnXyVHVk8zaqkB44c6fxK6CZWynO/rymIOwWbhOJmqS2wapjJb9KW8wyl/25k50hyIhvQky1OK2PzzHpTNNnkEbFEjFPOK4DBdw9KXYcmYZfeSRb4etyuKHo1DWqYTaHBpKL8nmt8jfW4iCuhSY+mbzgWgsCLvHV6M96DjmyTfv5b/buVr54P7FCEurDVeZ3lfchC7KKiK+rgar/VdufuysJ3cPKuxN4kLE9EZDUIijgIZ5YBOIjYnPZ6zTXS6u7m9MgAXQnekTAqZdnVY8jGQVndsqVy7BIFaLfHo+6E2FuDIELZQSHoI7rJizaKPQGUSQ520OhC6LPcB3GWT/WXT6af68UTHPKoGqprLYmCRynVgbKBPPcfsW49xlwufBGXUsudEBZ4wkUIAqoz95ETRPZArtzVkxDOquQoQGp+y7Q2SDpbCecFxqPgu5dHBUc5KA7FHpc4tMQSyIRuEUJCtrk1H9wWJh6cgDf5QuU1I7xvF0nbLFCtceqyVwMyVKXakLNqTWmIy9LKQ9U3EK1d/cnGsz1lx4sAvnwbRXAxijWMjDeOjRhZCtC1dRLjlNWHaJ9ufA+hjTPLFz39a7LB4himT01Rlb6quyOi5F6dWDQOykHb38mdQPfKsPVWR+QJvMmmN1R5CtnTlXHA16mWQ2cb45P+suOa2p1lb9Oj+16OOPSOhHMQd79HzkjEr1f4bQWUP+cmSCbxRAfyoG3PiIfX6EmsX2Z5RsEBKlfjrs/BflG5mlCSwknKQ2h8oVwWjB0SRNN0b8j9IHq2kImgOcOFFB+hln1rBXrBDFt6TejmHwa0Q5ncjy0qwrOXcNCAw6A6kGNBBMk2rJhdh7xVgo4nHE7YdPIveq7bwcfptLOxNdU4QsMnyWZ9hYYJCL9CBr6sL/IaxPykx674HNjYM3vgIhUg60nyw/oAo4Br1DaVy1Se9iePvJR45AQ9in8BBFV+xbTJdhmsHL0G2qbwZLMsSLrL1kbqyuafuqJ218iYOq07Wvv6eaPxHyCHVpOqZETlfZ9XFJxsC4xp8fAN/ckR6S+O6xX+oCrOSuhxaZ/JYonkn84jqfDyWV3s1Sfk4MtgYws9PfO8RJJsz+v9J3Wms4s+sNfAf206F+OBgjhhBOsNj0YnFVz4osnPpttN4dUOsQT06WySYRchgOfBW74P/YsBapXGlR/GR1qUCf6zWlLlCVN4T88CzmHtEgwaVvCBGa+de23pDdJp3Ot0RnJJ/up4io4nEmU2PvXscuy/projALEs8C7EmM/G51IrrvCFwhPAlHdwiuJ96JzFQZqaEGlMYu2HysMuqouic30iwlDsBZ/L803YNpvKhXVXAp0zDViPYMIipHLGKvBy6/jUVk7jSes/SyNsaQfcNkhph21P5WLqxw7711cNHO31vgaaQCjno7cz2itdiHybO02O8M6OOnlxngCQTzi+v+E8vuF5fMPx/Ibn8wnH8YTn88n3NFDMEOsEwXEcZecCrziEmqYm3DaAbYO0Peol2ztASpBr+5VJhgzncUA+TziO73JHRsWbzxPaWV3c+N2kAa1ulnc3yN0NfV+2PqY+oPR0VvpqgFL9OWWsBqCs82ID7lF6+i53RIxojXGMabR1cQPKHm4TIBi1iWxL6k8+tmtiWNNvdf8EIAfIPBgFRV8BNTmWykpyhDbZafnDxWF+2/6MVhHb3Rv2OwdXMpQVtoYOlQfALWNGe6GPbJOkxt/VtrY8Qu0a4SnjuBnMEa8SLVF9fAdwjgNg3GYRRBMsSbyPoOVDAPCPobMg+4R5g1C8CCv9GveddgKskd52qBX9thrAIWwyxbbt8PX1C/749Sf8+ec/Yd8fUzk7ej6aHJsFRiWO1fKWoZOvmr9XHVFvXLwTWpzhfhkXgPKJaKFdqiYPH/9J5cFaPYocT5+KK1wGnpglgn+YjpA3/ob6R7SMmkE6bb7dZx0h6wAWKLq0ww5XuP+TdsVKWZ+a4PxPgk5uX+sii4y/joOUPQ3kf4HQB9GnzLfiE+R88OIw+ivlka0jbG+esKv4ffa+AWAe8e7a7YN+AuFLALQTPUG7c3Jsh1Sd9CKj/0659L8LvACj1wfvCKGfgNf6W/sW/67g0Tai1xpScdRSym3fVh0L197WIGhnz1/lk3d74lN2Asuht/KHb+NX1pBXeSJ+1T5g/2xcj9HilzCPsiV6n3YBQymzxpFm/Vb8H3J2dDraXZZqPKyQsqm8HnVrCz8D6qNYCTK1H4H3eJlicoV32g6f0Lt4qZT1OyIWglLKBafJJkpfx4C826AFeoDz8DZexLL4QQTLiuFYApY8pJK8G2KHjS7IrsEYvkMBETDnOlGCotxKYQ32A7YALVDwJedSZp1oOI/6d7aJgDOfkM9iDKuJCKwTK3ScBQ+WWs8E5SLtuquD7qXQq2/7HRD51L8BxPhKOrAqnU45MREFxkcBJXsBteUDrP3mgQrSmKC7xRXiHkxEiJzAA4gjFE0G0Z90UiifP7Mq69DT5tEs29xOhthVZxTISfWT28m0i5w82LZN9SmIGWkvmLkaOI7aPMr/KnA7VMHfJqmwm32Og6rtSAnCqd5B39Y2UG+PGCp0QRlD4AfWaVKPtvgpmgYBU4UrAY9zOw6tcWfH8azP5sFLuRurh4hfV+s5+l6LFxPQ8zHXlUnjpTzkiQ3b17JAmvRa4dhooqpFO9fBaz9tgMXjjf5SqtFiiQeF3FA8pMeNliWp3DkEWgYmINRNN+x7mdR/PB6w1eOqLO3SURnxyayfPZnojf+of0fjAaBfiRVxAQXoi3nr66QIPLrBmRj2aRy/n9W3yzt8y6S51jUZ68NVt0FgQdl6i7R275Wf5PPJSF7YCfVX238GLl7jv63YzGyCOg55JDcsr7ntMbDBurReVQbt08qX9lCUZjZm1+2KHmdAfJCvL6hv81mZ7cW1Mjubj/+N9m4afdfBBu31a86fByuyxusd0h9rOHzbNLJtOpum+1ZX62HxtXiXuOi7LTn+DnJuIqQrISHMNsktw+v9hPR/h8uzJVb6cFUuSp/CTS8SoXnwDl+yzlcKoWikTmUMy7kuH3xbZ0znCt6fhlZeL9j6cdXlbnkH+T4LtkyvrN6WX+lTt1sksy7C8pjCRburI2idnlf7QrWusDsibLYeyQofh67Irl+hrtgRvT4Y80VAy4WyUyCnZr7olXqyjULxne7dGIZ2ZphpinSM35Gxa+/A0ObYu4k4rw4YxOYwTOW6c2oCEp5F517gdnFpqtW3KObxymREpGPK715+t6KtkwBzRvJsdM/+d+3pGnvANkHTdkVEZV2XU+s7ImoQ1B7ToAJ8lW6fOCiVoTsCcm73IWyWicpvOkWDgq70d9LdEqkcY8RBk19f9UiJneZv4IS6QuY4ygquvRRXCtyAIjI0oZDr+dZ8zPV2AkI5TzTnA57f/4Lz+Q3fz7/gfNadEfUvnyecxxNSAti2dsnIWXcstNmkUu+0bWUF67bXtnjUZ49CXy4TI3jSTgjxmTPk4wCe5IDKaDShsekAJ33KnQ02CCrbmHvCBOX2evn3vu+cR35K3rC8I59bvLPAgA3OWXy+k9o7OXZHhJyEsHR7gjDnDUzsOgQbNImCkkg8uG1qGNhJDZn+PE/eleIF0+3YtO9oTJVaxTDCdQW8YDnjBmeXSh2eM6BJjH6Hy9g4kncAyH4q36EGZ9tEheWLrY5f2WGRonLHlQn6EqidKiMFY/WRqcsobws6x+iJhldh5OjKIK/khTWFTtGXBDShEZVfh1WVBSlk9D5gH8klbwurnQjwoeTLXX5JL0B/h40oCVLqeSyl1CayHTqU/KdJCFEfmU7udvv6+oJfv37Br1+/YNu3AU/5Dqyl0dbTq//qhNc6IPSdHgQUe+/rt8BK2/wUzMZcNYkFaL5y+wa9fO+D1H82OPluq73iSMxgFPzTfS58iTcarRs/WCcKJrS9Pr6QTHDCpN6tVKbQ8Qla1qHrlzfKfKvLmA4xYH5D/d+HnqPIZtK/ff4vfmrvD0T6xZdR5N0BIN3nhhky1oVi58E+UqGn+FSb3QlPEyIIbIPX84NLPqoPO+OTpvlBkLx2JVDu4vqgrCNU9mCOtTJiG7HgpH+lxYLQrttcCZqP/ZbIP/jduvijYJSJ8l38DPXzd8qfqEw7zi+Ca0MKXBFKV4/9Z0A/Evxqrmjoae0H9jvjeMGe8vP8JF+SLop1Dn2/jFnqdoKMy/p9WmbUua+L3A+AtOU0R8r24CXkPAkBIU9p3JPXL7DIvJ/XfNtZf818/i5/5wx4fqwkIrZNqIkp/pH4ofHsCEWHp9pHFJcKTpKxWa7CpYmIKNBWyq6NZ4IliFBmArHthGBDL1H6dmQICQesuOniYDABPebhREdRlL82CJAJaBcTZ0hYJh/YqOPAT50syBnoPouUMsBZg42YyyXZ4i4IOu6JJhkynm27ujRuORpWaCM6SyBz40kJ2g2BlWnoUu7TlIn1uCk+CxUasyUoq3+25O9akH3m9qMTOJXBLO8op+7i59o5Nnhry7WTJA2nLtejLaJdBlhlWluvEEdgUJPQ2rYMiPHRJzqgXb73QUWH7pRKn06CcRSk5FX5g0mIK0Femu30cHk0e6DL6APjXtANUR6LlquMlI5IzwflWf2SAcpOplILDtgqKnq6uzIaYTVYTqOJH7e89EA+G8hGCy0oTLKKGbbqHPE7yTTJyJW4bFlWHwArio3a2o4Trw5RGaNAqjVOVwNNIzlBY7y+GdBGOqB80hjjLZiTNvMmaeOyxnWwk6OzPN6xcUX2ODzjGElqrJXKmnTGCElth9xW9dBmdGokN1shPi1SFjeDivhP4ir9lJhWFJ8Sh/7ePoHz90GrGFJqZXkrky2F/E2pKm/XBXDbj3SffTY3av1x6uVdDb44hDCzyqRTf6GkAkeVzMu0OAblefqMRKadmPTay9obK/pxneoB4eD0m8i34sz7fJ7UbzX26xfFx9YmwNZuJessrMEUKx3SauTRaOvRcHg0RXm7fn+vy6CvW1+eSk1tXLOuFj+y/4Axjvtf9fdiuRLaxN06f3rPvNOgm5xvZbnyOsA9k2ux3hW6JLDxE5TjBqMjC3lHrcCnCUX+GLXdEESxQ7sweJ8G+WZ4vTSztNJWVNpUyij5nP5dbh4a9365zT6X9p6hxymrr9d6m8Q45nl/xySqHVPjRQSNZ0lOt4z8T0uPnPgDdKqCFuCqbRD4Is4P7eXhcHcTyXRhEhoDyDwybYYjxpTlvBHkXoWRtBy9bwnXaPNSXZNTfYwnLiWmWumaxbL1bVjyefMFpFyb1GrKxr2N1NM0ehbHQVLzQzj/mJY5jfH7cZJ22oL3r4yzDD91qfxh3yZlePQ+nI0pWlrD+o6yge6L5Rjb8rhIph0QYPkEC5faUaHd95nN/hNy69LRTIjYnWfOQZOUIG3SodGBszIZkbmyqabfdn1GepkEwNYoQLso6G4JhPMUOCABbDukbefgSclX6Tsz4HkC5pONVQ4kUpC/HrmE+QTaCnFmabgDABYc5/MJRz2W6cx09wNNEJyAeALSgKF6A4WOymr6VCcJ0lZ2F2yPnX/TvRqIWI5+Ok84vp+lnONZgtqnnABBbv/SB3TM0/jeBy/IZo14a/TQbhMKWEUBTNbT9Vk3UWHoaPwyhlEwzDMmvT+7bZsC+TTRhlsfWG3GJgAt018JXMg08jNq+3yepQ8n7VJ441S7W6I+HOGQwXhLn1d/r43tDilZlnatdT5J61nHphzX27Y1o9BpT4GsXmJUgHY72dArCFpo/Ech3QSllxP48t/m8+qn+tULLBdqATBBs47FJ7b3SEcr1w1cLB6xd9C98TEyfN1gwSCd6l9TtpzUCJ3taixcCaWMjLIxGA5ELAtTBjiuOpRWjr0Clle8/ttoh9u2tWMmtq2Kff+IvQIbJCy61uNYxrltsG1tt1tZQbpznlGf1hIH73HwJ/OX/rJ3OHn1agZxL5Nk3ewzADnZUQ1IOfHRNVGv12CVfyMBeAGsrJTPbLpXeNDLV0SosH3AN3BfLXOJrtl7qafonwRKtlwJun3MuF7AY2kvbKLHg9bDAB6fq2DhYHFEVD7L9PZmKf+MFqhYV/lD6hbr2EW0t3zzQRZ3SS8rfhe4doyIno3bDi/rUAky0HKZTsq5wOfeZERkDw5tBsLjyWaE4gdBPT6X/upRuE2/7WXhFzQflXzTlr7WS5oMIvoheug6vJP5gmga2fwfBTRfXiiOSPTsyIYy9CKgNWpk++hFaSvwE0GWT0AU7BrrLtJ/9kmcNmrTn4PPt3fzomwd5roiVZJSAn8VO7Y0jlqe4o+p/b8KLbDt87Hy2hewXSg3yKdsSA6hTzB76ulFWJNBsl1G7fYTMOgTsmPExUuq7aSZ2zre4DXvl8nSNtRChsWE1ldtsDoJocmc8ZKmC0U8PPLzYwrXYBTjW6L5Tbg0ETGeyS2Np46IgLplNzfDEEAEQPkThMEAbBCWS5hLgAIR6tFJbXU1B2ASzW2mGtikrbq5XiBdJyFqh2LOkGveLCcRcoa6xFoMHqpzBsSaFg+Aep8EIgqiC91k3DLLVBpLbLWtzKHjXTY+momC4iUgRZdTl7soyqQJZm1wUzvSREHaNtj2HbatBK9mjBQNImvseEc5UTrrRNigSVd2YHhGz2xwfVyXNog9OuykCH3Smf8ZrgUVvUDuKC0F7ztH03HSIkdc1kVOQnhpZnVpM8qx0PH6gp57RnFEt4UsLthG7J3rFjD0aVHPzfs4MAs82ePhbTxuAry2TSarM2xb2rFa5KPvrMd4ZW3XFIOduW8XOF4LItpxb9v5kqJC37Abje9eZ3g8xqkhNBxq+Sm1Tym+ActD+V+T8fPjrKgelu6Z0ePJJmpzJXurkyj5h/JrXirP6dTDZq7oPtw2K9NTnTC39xTNDRJeCYMNP1ZvzRsTTisAh2Vr3+Tspx3hmvGkK7MoOKeyzHfPjMDmmgVcvTpFcsTnMb88mcaT7V26wB+I5L7UtyrDgJ4YWh+MnL9ObtJ4vhhk/VjAzsYrhuPETgLQVMRI9o/6LVU5NnKIhq0JLCG4j2XZhCEGK3dIv6zYRBLzlYkL+301zwpE9oOe/LrunFlbSj1HrF2RFD/19U3MMV6aORG9/bLcpsj/GFkU23zKdg/1YOGDpqcI6g52lkuiTGzpS1mZvyO/KzvE920DOg6T7Ex28NGWa/SAiDxe7/GKkeyMURrHjmcScJ5mmZZJX3eylVuysicCyF0xvd7UuPRv/gbSBnXHPceU1vR5/362eOJz0MmHHyjX869cmU+dBLVvlDm8Mu7X/QtJW8PD3y7h+ARIKxag74+rk7fD8bak23ra+LfvWi7z0O/i7U9BzGvLGGre9kSLjb49en0SgRDQ7LdAMyzreyn1TG7giJ/ql95uEwauyIv9b4Fb0efo/YhnRrEc+n2Fj9Z1RwJaUNEyeHjaZ+cvOeXM7LJmQ0Htx5m+jOyRHqJ20rKv2eKyDC9r1PbWtrSLlEZ0BRQKWePsJh/4ltI+R2F/tTrN22QFliciPOgbsQQxKIDD6egooVyNaA7ybWJFta48ZoTzeJbPXJ6dZzm6paQUl4+ViAzkkhkAkXcpnMepVyTX92X1OcB5PsuEx1knF4CCvGdJf2Q2RBFPOPM35HwAyIkLQNigdRrmE/DMXRDJXk67bQ/Y9jJxIHcw5Pws55w+vyGfBxzPMhFxHIc6lglAB6u2OgmR9g22NGY+rx+9QCDhprsh7FFAAULwAmuNS3RAtoc4sOLRJ+vggTx3XV7uLXGklMoxX9jT1spoNHj3XoxA5uHdF8aozJU3oyO1bDvI1dMyoC93fUTBlqj9bfvaY7issPKMYo9e+SnbA5GOZgKgALVqe7cFetD1ob++PqM2UJMESddNBY8MX8h3lj8iZV3kQc+7tg1HgQtKa9NER/u0thDKf0FhfCxYV8vUhuQ8iGrTzuipw8iVF3YSgvw0jjXQ7yS5qD73fOXAMLLPZmPZfpf4U0r1fOumM/mOEsPrImfRwVQRY281HSwnI8oOHKm3mF8G46jVJYtCpL6JJ+aiNvG+j9ItgXEkSv1kPTVkEfSK+u+VseGNY/vO+1ytr8dDI93f16EFW2Pj1CKSBvTFfjF4yoc/FlwaKEiZgIOMIZ3i+VUn7FMg25yMeQ4YmXQrOGh8eTaFxhMtdiiN5zlpqv+XeJDeOxNcb8KrfTV3Rhus0kntcTXfiKYk+HicB5f4/BVYsmVLwo6mApqmrp7Kqa4hFzkGOnrOqniTfNjkIVIZ8njPauMjlF1+dFStlR/1qOAispAEnhJfv186OIC6zfnxsnxYy+Pl5T6R4lYSdgGInEbWmj33KhBfvQI/RdO7EE1CvDsBovMNhNAc05t5/j3b/YoOuWEMr/FaZ7k4z7w+GfWT1CkCZ5cltWesqxruMrnt1SL2BZN43/La36v1eA9et4O9+lUZ5eKzAXlrO3wIUHxZii+0Fp/FI2btFFY9TB/JbdlWzTcIfRpYb8UoRuG9Q74sGaCNOWGHDuI0V2T5xYkIIkIE3lrx7mwz0YmVKVKxDgFSgm0vFytzI1Pw9Dwgn2VHAOYM55GBgkQACUAcSQE0qJGMSjJETzjOA3L9o0mAdpRU+aO7F8qxTHQRFt0ZUfCVeE75znc1YLsbgv+g7JKg+yRg2yEDwJ7EkUlQdz6kxJMGfBRFNa7pHopTfuYM+STcOtCoJiE2f3Kn7xftREUMrs8O10cKjYIj8v0ooNA/a8I9nDF0AgntU8seei4D81EgAhHhBHTrK2m0daO/KADgBZq79MkbPT54AXQWDaasEX2yTmU3SCyQhoY5taeIeEqfOol6t7Q1n1OOMrYB6mow66amLp+lU6KWfd6nGwcahzycEmQQK+ygTCihpZgnNlJZZJESbKZIL3DjTRbxu+D4tagOrRzpFPaOzHh8xjRHssD2JzWLVNotq4yaS5Ms8V8/zvT3kVyKJt/k92gCyqtPhMNL5xkpUaBZT4r5vJAqUoS+7TfRv2X8ZQBsR8+VXXmNJ+V4SmmDfX/wudqVUhBKeAhMC9GKmQMpTCvq8cx1MZ35kos60EkNGfE9tbsf5EbQ/cZVQv+5Ko9WUQ30oNQHVHakN7o6BDi8dBH4wWsECvCxyxXSX20jYRN6Z8hfAmzGbqSrw/pAChnFjsuu7S+S2Ze1jkHzOZCS1GlGZXfM56+6kmXZ9XxjnmmOvs4f68KRzJ313RVHeEXPeOn63wAA62f8driu8uagveU7toRJN5p+KD+L1XEV5GRH1D5TZ9t53x719qf+bvMaA6DDrQNOpD+w6hTWK4jQdkRk9t8AANKW+EjZYiAUvIyHF8KI9he6h6XDW2ItuW0+A64D9s+i3wCGn5zxeW08OnVP6KQjH4BogKoo2/Mk0yWTr5Olb+qRgUwcgdd2yyW+oIMDTMHzNh4S81Pj1HkgDNku8WmelW+ocWX/K/V+rb07LPiaPLf1WBlj/vtX+3z9GLFP6sqrPPqJ/tHlavm+knf2DEDbOgp0mMl5ENWPjTSIaEZA/yh/o+ejseelj6HZfhxLAWs7oKodpxscfTukC1osZ0QX+UZtN4mg6VLdqt7hm5TnvGdtWH0PyMjGKS0UxT9WbCPyh/znhgccXGG8syQOyzVI3MeRrWnfR/zYFiw1mhqv9fxt089geSKiBC0ag/O/XO8UlltUZQJMZRCkva7o3GsgDcXK6JwhH+Xuhfz8hpwzfH8ftYR6hvX2BSmJmcWqi8tRTsWwPM5yj0M+6t0PCcvEAB1NUjPmfMB5ngD5BB64iIxLXIEBABkyHqqccqMFHTHTJgrKTNLGmUtQp+58qMcwpToRw7xTd1nQ5Mn5LHU46oQM8hFTbSKCJwp20a6pDkC27f3AnMeMXtBTTkZEYPPJXQhdOifAJlKIANlY8flCQe8MsJ/03QaisTooNMAej4eqs1c/mdcGTOzAts+6dnbK8IxaLzg5ag9Jn9e3Mqi9oV7JLw06nrCol2R3QpQVX+G9VOUBOew0rhQNxjGVwXEum+rFLzkz5/OODUPD+55j4QfhLkBK7V5pwXf0n6SX+L79qcp0/WTbXdJLOVMwOahJHAdnvDSj96GyDJRqnxeA9Ud3cxz93kCrOnoX7aAq/e2NuaguK3JlNBk0yxtBZAR47ad4WpTPu5QW+o15I1eeRC1/SdYiNpZMKYmJiDrRUSfq5/UXsgHl80nfOB50V5ojM20ar0W69i4P67sT7GRM3z+y6Gba+891SXJcW7xyZ5yk1aYd8ZSVFxLHKrj5K7/kwVii+hfVyaZ+N3JtWUPAJj1tG8RjX9C2ME6tnBWZV3wdTlvqKTOst7nMUnwt7Mue9SFHLmT7O0VEdlJ9tzltpldCNT1OO3Ej/FK+FxJnOyN8h0jCu8GPGURjyKOhyTZ/fK7aqyPbm2xRXqBlJ4SQ/pnrMo+GlMZ0TBAMxnd7M5NpLT1IYy3EiXV8NLlQ24jdnOqDVX+sTETkquPq/UfVL0qYyvnvPAkh7EO0petg9qucaPEs5RF6dCRTR3lfDThKPH0IYg7kl7OpSz4BWJnZ/6Zy1uqMviFgHq3YZTLtpwKuL+aGuJ1lq2BTATjKA6aN/HHql3EVRvVesR8/0/ZXfLvrMYYw9YW0svwl0/p/Deg29Sq+0v+fbbArk1YhTOQ0xUDgTZmcoLfB+jRIJLWymU7luLxQ/qz1A103k1EGR5Pt5TMhiKmFFRRaVkqfYiT3PLmx7teX1rk6CarSY50sdmoa2qXDEjRXenZoaAcidnxLv8knYFooPQm0Czy2PBHxeOxcHCLCWYORZz6BTYmNLv81gZuUALbE95dsKXEAPqVyDnSZgDjbRMR51jsScjk2CUBc1loaIFWDHbFc3psq0+Z8lkD++QTMZVfBtlWna9sgY+I5AszVwcp1N0OiRq5GKp1RTTsi8Gj3StSdD5jbCpzMg41mMLayA4Tvbtgh1dU5tBuELsmmY6TOehk25hOA6Kp4eRgmOrJD3jWxseVH7WQDIaOAl33ufUo80dFL5Rl075JkZPHbK1eWZY8aondePQCas4JQVqdngYPu19gkLanulEGswq4FiXT9W70sjfa3pHMWuI3aPoLo/SxQY50TCTTBICdS/GBNzzNLZoMj3Bk3ApR/+sC6QNAipYNSrxqyUZtEimgF99oYI0WTOp6x5YS0QM+LES22PykAfdVRtRNVI/CD/tJIicu0kzEycA5gx5zA7ow7r+9G9b0yeTMybPr26WWp/Uwp+bvQHB7yTRU9PqivyUaqHKcmIVJqxzhRuXQUX5s8AuAjL5wA2CzItsqnEYwCmgr3AEdXhuqHBJGxJnlx5bkFeSSfpV/mv6IzIhxe2oi2KD/bRBDrW+I+fi55nXbABGWNgAJYdoxHE3hcdnVUkByXBbAyjCfqHLp/GkqVg/oNgOwSSbc3KdGNHda5lffU5IHApIRrvwChLwcAoF/dafu//SY6dH94Y2vWF6s67BUcLg0vyLFZGqUzaewBmLEIxOhT2WN5PKW6c3NSzxGtyRnfJa3WSDPfw5YxbTuk4/IIH5VW/aOcAc/yJxfLkD5LG/kH5OYLeVtuhzPFccuXehsdcQkQWpmymgmCcqs8E+lnnDXSD7O2nxFva+3yhUnb7DUfugkIkgUcOxpNr4JK9y5cbZ/fpRc8GrQIGutInTHGqe0F37Ls0Hm+IXgjBNtLF8yACGiMynQxBvaa/JTfZ/brFVhNL/tRiPtlvKMYwlxPX3s/tN9eHAvr7XQF/4W+E3zeBYMHtLC+Ap+lpcx2w+bYL7RxyRu+NydMRP3j9lf//ELEROgnlBFJx0Z6oX95JUCxUdU4Tg6tE79C+4bazrgyrmf+fXsfjcnV/FCFwXW6MOSHtUUQnnxR/Bu0W2gbXGjf5YmIfd+L4VeZI6M4b184E+UC3Rq8qIEOpEAHVJ+RdgQkaqSK65QTEQfkejcCnk8oQ7ocbdQIKZVtDj4CrXLJ5wFYjzZCLJMT27aVlX4pAV0IV+5cqCu9sNWFJiIgFxpznVxAuti6bv+FnMtOBjoySRp9qazGKTshdtj2B+z7A1K9TJoGdTnuCfkYprPWnyYoQFz0TcHYBMCTENtWzkBN1SFHYgIcB/Gls2d3O0il7Rm0Ht5uIsAxgKMJjva+8RgYPCODuuEix7ryaaXzNPdDsIMmByyWlaCJ+Xjr2mzVMPXol+86pZcST4pYfLJ9vaD2yCCxZfrEA2ywAWy9QqbJCYl/iKuVqMqO8vCRRq6+NryFUHYVtiiHG4xlJxV127lUOmOCknp5xgb8fKJPBtRRyE2PjhENyiAaKGHPwHb7IVKK5tmUjwP8ET6PDo/HSEbJFfdW30VjblQfr3wvzczot+9j+eYbTut84++SEDn7wAbrtPrDwSl/t4mIZlDSWLK6I2qr2biY8cyMV0eOYwShkZ5IiiT12Mtv+WPFefH0l2z7K3zr1SeUyYRngqOrQ9WD1Tob0mBpkeW+DNjKXWljaW9J/l4qSrabKHc2cXI1EBXiqeXSj9k4obL186YPVd4BLXIyQmEa6iVc7Nv55MFML8l+/6mgXzEX5zp+CC/InhFPRfye7URElfNe+0Q8xPg3gIg7oryMA4AD+YZ60DJ0YbwGZYygTcgIndKMvbJz3Ox8Jp2WWM4T16PmaxTyn8qg1XO1jpd4w4Gu3cRYs2kQ/cO3rtBwpW3d/C3MFCVokBrtiQXbaBcrirQeQp2Oi/HwdbEvBKe1Q3i3XxUpCzbBGsx1gS2zfPZ5BZLRT5F3zYbv7NulnIxBfWdOuyA7VumzsnXVH7wCH2ShF2BNnhP09Ze6ZQ1PqrGoVRtxHYRBpMrTuiX0e6G3W/u0RRekBX1ly04puRrQ2m/tCEPfDu/lGj0fpwOgI2VHQf/od1IFXInjtF8y7tKC3KttGL+3XxrelFLZyah8No++MQ2Wd7o+MFj93Xoal/3t2WOjunfvhfhlG8DRKer3wPfx/O8RLbPnfdv1Y+uq/FyeiNj2DRABjrOG5KuxdxxHMYmrUNo2s/U3QVOOko8Aud1yxnYZ83nAeTx5RwRtEa8hZiCjEcnohGb0JKjP8BQTBshBZbnKPXGQJQOdQVboQcZF9Jdi65ZfrH80GUF/ZyuTVpxCSgBpa/dDbDuk7QH7Y6/0lIkGwnccRz0q6skTKDZwUdquBeZoJ0SqF46yoV7bR04YcJ8IRrLC3Qb/omCJvXhZ4QsG+1wQiT4RZdkAjZev0anrKOts23NEkxcUkgaezU9t1OdZWw0GADyjOTKW7CQE9y2u1ck1khEg7Qk27HckeMeHvBogIBzyuCtErJN9oISvRzdPRshVMyKN5mffqLLBV1teeT4+iof7VxgyHniBXvlpJ2DsGLXtrPgpLHVAr6ondH1t03i0RLg/DbL95c6AfnyP6Z8GVhZ42PLWKJ3EuTo+LI3eUWMk89Vf01KzEoBGTWcyCH4vOqVMmu972dmIpLgVLoSyas4fQ1beeb91+THfWRg5+a84sLp2VK8YLB+s8sWoDWQa+30FPFnBaxZaKlFumwhtwblmgreiXxvb3tha1Rco6PbslFm5diLhVXhFv0lYDUZ59YXgd0wbgtrJYX6u4fDTKDqs2eDSN14FHZVhf//0JEQB32mLfvdj7JocGulY+dzTy1mMX6w2EDp2ykjOspzIuNRHnjxCAN4RofWc1RNjnF4ZK3mkf9Oeka0qdj4Lu3irdx4lczZ2LOcCWn7G1PkoXLFrLmCdphDzDh8tpx0Ft4JY+xF8tPgrlAS2h3w/C2Z/Eka2w8/KyN8BPzewrG30U/3W8v4dQmJU5ooNEeUfD+jONRhSIdonWfs2QvK2QBlSBFjiZa+MH15AKTGqOvFSmmAyeX68EtPpPpP85pbg/i4klrL78WB5OCpbf98YY33q+HcRsA0xuLai2dICr6g3AkBzbuOx0HY0Yv9J2VJ9hjqm7/nOEkayo9lHL4KT/6p/+B40fiD7U/qJtotfKW/9joh9K9x2lrM4s1ph3k5/zLlMRJQJidSoZM8XFA8gtoD5SXcjHCdgrrsCEMUq6MKMxRgux+5AlhMVdFF1mcAojUYXmKHmJjbGUf1x41K9q8BB6C+nzmInBOa6ihBRTES0SYhtK8cybXvZGbFtGwDWo0oR6qr9drk2HRVUmq4MRHmWLweOnMAqYD02ydkFEIFS1KJH5Xv6tIEVa/yiSb8CnkPllSVy1HzlO/OaE9CJAjw2SDwKDuljNbQib7QXBvNo79oINS6JPDKWIkMq58zDaiW44BnUXZBc1Dul5O6MYBz1nxbcKp/lb9z/Tca2sT3inaS2DfeGVAlG6TaWNHdjxbQD0+SA2+dIH+Qg17GTev5S+aqyIyJRllGJ6Pqa+KgqA+2K+33vjR0aM2PQyi/ux8bz8ftGY0efk4opS7RLyDqB+tPSOAr0RDLLfvdwvOLEjAJF9rfHL/zdTEKw/ANoQSGHhMZPLnkVP8mOqqvqJ8kbYlPNSwgJNsW3qk6Cr1U+W/+YrMLnso4L6V3cZoz12SwXxrRFesJLJ997fGfHptU1VwIOWn/7k06y70hOV8ycWulKgWNqbDoTSsx79f2KLZAAjGzT9fPLBhoEy/aGxQ3glflKkCe1SkDHkn2fUprBuf0joP7W2sDIggtVQKGLFS2o7eP2Xueny997uWdoQf1O2g5cLwdHErqgG4ezyhl8RYw2PU6WAzeBxGiCWX3FNET6w/sUhaj6y3xkHZGNgbAN7RQPR7Mfoa70p6oJXUPpZdmOnEoib3k31vOy3WZjoq8PfysWIvOkeC70E+3WL7uby39b2llvIrQd5qGt4NQDAf3LSBdglO3VQPK83Vqfs4TrWU5+9HSi/RKllPYKfZJfFiFN4pfQNmjSGiW0LB6FWPTsdReZfc9F+4uxuiKVve5h0uStvMCO3006+byWaX0xrR96XJENdBU0u1DjcyGjHH3RL+jyDtJ4EqLrw9nvUfMI+8p9zSRd4+ORvcnyPEQWF6L4OciGwX0EMtYzU7xN+qAweAS/RbQ3ZegRL+gU7THjIStbYDI5FdEEzc5uNFSBg+IZiy+LqQ/k+qzX6/JEbSgco66Jhvyg6+3zjugzj/xCCU/HKAtUVEy1LdHMsTsdb+mOsRJ2XvFvJS86Hs7A7iZv2XjN/GnrqeNSoAZI8+H0i6ndbjt8AWgSQ8qOJf9glGaVTgBRvTgWG6Nbl9/LExFPOAAB4cx1tf73dzmK6FnviNgfAJAAH/VM/tTuggBMZeMBXfKQM+R6zBHkDPn5DXieAMc3wHkA5nI580bB5a+vuvK/XCCc9gRlVvVZBnquTMDGpRWebaWciNgOGy/xqm0AxFQuis50b8QJUC+4xrPcF5HxBLq0mvAk2CDBA7btF+z7L9gfX7A/yoXVkBJkyHBihme9kPo46CLsiiK16YCU2hwgT0LsG8AmHF+6zBrLfRvneUI+y44LHohbdVurccpBqGq8CKlQhi01ay0j5zYRBYI23YRt14TahZJa2bRLBaCtkCcGP882eRQxv+ytJlzajpCz1p/v+MCtXoFbBzJWvjS2A7UvAdG/CX7Ild+2TV9mzY5O5cOc22fz5ynwz01Vj0DRAUbA0rUAhRdtAKs1tWyb1DiQxk7FTVWlIhDKKrstbeW32TWjHcdyB8tWJ9Qo0M5lV4Et7TCOi1a+FVe3l6PaEkBKO0BOsJ25OUt1HKOMSgiwR2ZR3EdDb6QkssgLUZAqNTmfNWmVETtR2ZSgy8e1IUkVJ2zfuQ1qQ1OQOG1le2Ey1lIUHKfxwu9YxjnVBAC6nFEC0aqDm20HW0PHkobz2PEXTeI03tWOjx94SGyQ2qowauaPyqyp9g8bddIDQ4Nf82400cDlBkaoCsg6joDnmKp+c9tJ9jPJBeS6UvBfBtoYJ/+bBA7g8Z5Y17alJUwnYL0MN/EkQ9l1Qeq4jdDH1waPrwf8+eef8HjsQIEdrPc4AZ6qPuwESaNNjjukwLojv5tNDM2DIH1Gv4Sl7dieU7Dpm6hcyFD3YIp+GDktCouR0fZd5BR7+m7qPIvn27YJG6TUodSKxkprAGpbGVyT3SidhkvgkcdOyPWs65mwd364+Jcwz4t2neRBWtQJUNL+Wu1NoS/0l4fN0QvaWBIOGEvl5krSBAmnJHvS5qoLCxBpl06ToYitfL3YAzjAiUoewcUmTIYmEAoMdVch6Sxk+6c5vX67cD2xH9tldb6ftshVRzao+qFuaxPNUDaFsLuB9ZZYQFZtxd6xzoX2bO6EQNLXqGj1xOLIdi/vV/lV6AGiAdsCsTMDZCy7RDJmOPP/QMYnJEiwpwc80i/Y00P4ftQvAIAbJMh8hyFg1VvV+cEN67NXxlhsWwA0W8XTKdYGj3DYPB50gfX61KfR4Ba2dpQMARX/NDpGA1KOF7+ezZ5JA1TOZBiR7FSRTQ45bCekjiYh1Ljx9Bx2X2DIQwgAKbsp7TiU3U07QEhS0/Et2tDS+BKACTUjNE/tOlBxmk7RVubTdkw8bbNcegPuZGk/FlmHpI+STl6woGnzpt9GZbu00/hVj7zx7o/vlfFPPsQo/8geGtdrAqvd5Y01BDP6bR5n555gMP8VtkGPYkwyNB9K6zojH0XB3p4GXuwo8QrboQzGxhPYCRtVzTFndTIRG283h9sFKztahKL+UnIzKJ+prgO7u0et0LKRL8i2U+0/bLYFLZqh1mPec6qQRD8jF+QQB5SG2rrH149Cot0L7GPXLsj2n0iFZANJ+6f5iSoh2y3Y+s0D936e2mYjn0biN+loATvLBL/kUhIaKaZkubUN7W6apmyvuo7LExEHHACAfFkznk/AAwGeGcqWhQyw1aNc9g0ytAALiMBW+ayr9Y9nCfA/y6XSKC5oLhMRUBp1/wLYaHdBDVIBAmI7egmgvwxSrxIVs0qm2UB8Z7ZKW/ncq02QEyAxbbHOC53iImlAbHoPEuwpQYIdtvSAbf9qOyEqWRkBMOdyL0Q+xe4FVHR2xioFmBPxnCgbS8AIz3b5NQVvE1kdKQm+FSNdCrcqsNmQMeNIAgVAZFvKHTM79ZvJEwdj5DnwzZFJSQZOsX1sqX4kJhAzQj7lStwEAJsSgCVQbEwiqYBq2RT4pvLpeWG3DPu+M32Uj4KMNrA0CuR2BoGQKaMgJzuYlcczYK1uYicTa9Wo+TKUG1fYvg/obHXNfOG8DZCXLI2mjLUvqmLqVHCCOhlR67Rt4h6UMiZYwTrtpca5CH7IoG0JGKhGAp6MABDGSitTKmjZtpGR0nioI5ErzJMQqU5CiE5QKkcOrNQ2Ecp3VKcWlEj8GsRZxpJXqA69U0tH77SWLHn0RExrA133EZBCluNYKWjqhp7dhehJqu+LaMvgyaFVp3w04SDbLDL+R6AnqKJ2QoVbTpjLyU56r+S+mqBouLC2FZdd+UuWw+IdezqbPMuwbWW8bfsOX19fsG1FrvGZ2/WPad6AOqaNI6/NbLBQvkLSLUUWa51dn0sD8xLI9rIFu9SY7AlozzDzCZg6TsaDz0MtOGknveUnIPIk9GgC2uVdft6kL0kIchaStawNlIUUqBXHBIatsYBDqpIVWWMzI/hH2q2AWxoLPp2q1+eoP7gilnfRaQfkPlmi0+p/Zdn2NEeyWzcLDt5xyUD6UbcpWVXsgjSMKDRqau9RpWrjVKlopjfVd0U5KD1vbcIxS5vaOPafdFmtfqk0IPdh67M+0ND4ooz1dp9a06f+vWwaHwTPmi3gO9NNRnR2Bog/0ZYgwhQAwDu8o8kE6hMvEBbRLvW2IglG473xXOL0VCs6Mrf6U9XuOPN30WmwFR8M6tFMqWEkWipXQXPKgPtX93VPs4VRsACdZ5RnZTLCwzmigftOUS/aMDWetxh1oLJVgEiMSaBJNpGpJ9B93wfcKrVL41m2k/yupRJJG+r3lsy3MaK+klWRbgqxiupLVzbgWFkqE6P1UpfFlF1koi3T1MEv5iVw5UL0S6glpT2Unn6Hohb4tbEftmGqT8qLxhzZY208pdEi8qy/CX7beO8iO2U2GTHCGaX1xpg3/jvfzNg7nv6flS1M0S7WEQ4Fz44T41xo2YZc9EVnvnGqRbs9kZC0DSJ+0/t2jju0wxQ928DgqzKarR1rU74BKgbQYYz7UKYof/14IHuM9T+dPiNbl+QTiqZkPPXFqJrC77L2iaSHRn4TIR5PjheR9XyrdbfP18nF2/liNr9WwPVZkqlDfKNnjFvZdZP0MitEnEALhSJbJIt8pfwrE5zLExF4lB0Bz+8n5OcJz++jBHszQtoQEHYAQFqAHXd4LhdHn+cJ+SgXSp91B8SJ9d4FUtL1WKP9a1fGTZmAAKAVO/qyamaN2hhl5XpZEY7t3EgWanWXA2hhQLNIGwDglnh3Bm4JMgUAgY5UynAe5GiUAUbBnm0HSDsCpFzLAsCjBH6O77/gOJ5wPJ/1gmq9Kh22ra7CQZAzZRwArQ5aic+V/8ql3xmOs01CUCA5pcRBc4IWVG7BRgQAWlfpKkPRv57hbc9ppWftwjhQeaUzNQq2UJpy/Jc23mVQOxnlhYhwnpknB8rzTZVV7JSk8ko6JJ3W+bJG71XwBjfTQPN8TroIJI3ymS1DrvKX5dr8FCS1M6sAoIKn8oJASYe9OJAmFLEKTMkjitY0F2V9QEjXd2SQybpL3tTB4nmbzwR8JAtt4HFkcHbvsD0vRgYq1vN4wNLiOb8rkxiXA4RBXSzYIPlKntUxQWlntF/BF/V7FFBadSg8XKRTOrwLfcFSqcrtLSW9Cw3L5DUdaSHHId2t5AWk5P0xnuwO6XGNp/7diuE0rPcbeQvsfvMqe1I6QPSKZNKcLrJHyYqm/igvE5/nTrZleSVXOpKTkcpxKzx+G5qao9Any4beISxORDXiMOtKTHgt1TRoC78AxbfxbYuWJuYLT4bM5CBAxCv0LJlnU63kfA7ao/c7lqCXZ6h3r5PZOEjf6rIwdqst2r13+ykx7kim+0WgK+dimWrLdF/4ZcGYpWeTf0kFKPxOROVcBrQuQGQTjMbCqs4e2Ymz9CMbYkS3/T4Kxku8OWt8nu1cZGiVbQn4+FqRSvwrbKj2oC8jXe0xDdKX8uh/dfL0JVrIVMT31p970Pffi8KNsq4epS5A+2MB6qGKGtvhmr97OVFe+7KVfr9rQ1+Bd+2o/xQY1XDmx3iy56pc/CS4cZeF9J8jAMSGgrG8v0qHjS2M8nt23Jif35A3IfT1dWlIzZ5G3gXQ0kqbvYu5jEqfOSFvgbbTLNj7H6JiV/p9ZcyNcK7z+Bin1bFLR9e7UyCmVMfuIVskwqqDNpzZpft3wGosC92dG6/D8kRErsfc5POsfzXAjVCC5Shn3NogbI2a2NGWgWr1R0YkGfhbOa5ir0cZkQNOK3XKHQ12hXQhojQo1Euc6W2lJUM7lYcCMbJNOWoD1TjVR7Iww4kADMUPuLYpAaQEG5dfV/rnFrA9j3YxN09CkHGYWh2gc2aofPqo/9VA0pnPdk4qGdlOsLnVVw/MxEXqFbyteWj1LahjcqhvUZQryxwp9hXml+TKOillxW3f8DYeixzYljfyTNeEZuM1VLzR7/6YO9jYiPKeO9BNyiw6iLZf7EQC53WUiHxvg5G2bG8MUdCqM3ZKprCuI3g16GHbx6uLHkev47bfo/6wOO1vplM4ylHgxzMCRnX0nlF6e5zaCq32t22fmUxgvpiURfhmQRDv+cz5QNS7vyKw7TVyLKxsts9JntkxVvRFcvnQC7yQbFTjj/Vt5SdzNxGl48s/nfawf/a9B+5z8cg6jX8HlKMk/XdRPVUQJGCTrj5onwtDApvmRy9doZQnEEguoXrv08irArs0dedgPUnTWh+S4bzxyPaDISFagagRxU6RSu6M71W5P0wXGQZofjg2U0XQfSo7qMONNe180nsuv5uNLEmVKWL5NhljuEbjiGZb/ivQ509OlxkHL0RWeHIWOJfP+/a2tHgyUr7zy1oJFnr8vtqe2t40ttbANpnJOc+uj2xlqyOu8LtHQ/9b+GJ1YcYmdtG39CSLpO9GwlUkAuiCA/YoKWvHR/2Pzjubx5v4GtV72c4dPB3Z6+0HiACbT1NsM67bYD60MXNddmD3bT7RM+fN0bgl31TFQN4M2MzafMQzOngrcISk+X22Tqv7lDHLNLO+eKm/hS0ry7D4IrkVYh7w+ev0+vk8Gbnqp73Slp62xPqPF36N5NVKWQRRO44mKTxAj3ggur32aSnav+v0xeDFqOSXlk6H3vR7rTv9saistkFbh/69gzWub0nNuBZ0gYWZrTCC1TIcksP0nrz0bB2VJs15JbSVrI/lLnASukM4e91+xos2wFzf6bSe7ebLnkJ/iUHoel4pk2B9IuKvstL+/OuAfNQgNwDAtpW/fYO0J9ge9ZMOuId21FDZQVGODDrOA3K9EyFj3S1Qa7g9yl0Q+15XTtPMATlZ9VikXO9tOOs57xQg53P7IUE7vqTcXVEaTKxmSrXMvQQdEj+q5eUDAHNZKY+laKpHrjtCcqYTj8qq8W3fYd932L8e5T4LmiQ4EfAskzo5Zzi/n3CeB8BZOnPbEiBudVUbQqpLdLaN+hrbAKM5umrl0s4MPM9y2bdRZmNFhnBm7STTMR7KieYgFtQJHh3QsuXwHRC1T+R9Ch5dEY19gLjNYNrAWs4ZjuPgOyLOU7cFpds2uWIcy0QQIOwl4tfR4QGiTVr4064gtnWcOb4qTQaAbX1AywCxvGB6E7sQZsYN/ck2szTLuzNGAfzIQWGhBwAecznhAAAYrklEQVTbXi4SPM9TJgoFom1DL6D9ilGIItASHffm5nP62aPb++7lswphpS6UxhtjK/lk2e9CZGx4fCd5axZ4YH5cXJs44gNrHEVGfSTjRrgVf5v6W1nU/jbVDnJs2fGnJ94DS1xTBI+d8Fc9WMcaj8Ftg33bYX88hAzJ4QSEbJ+of0dyRuZvD/Q77/vvhRPs7aTFbIjlkvwUxzwPZX486dKMULHZ3KFTOlUl4LBNaKTvvuzOZZIil7GGdMQfO1biO7UH4UKELGw+SR2q/m1toimlI+PiMRlBpB8kjJznJKhVbYpSprKHo/PzI8u3KD6hH62OjTaSg55NpqgQd8QAAuCSqHx9fJUqa1lqaaZ38pPeJZgf6+PhaeCNi9UAbemQRvPY6bNyfKYr7ZiTK+/sHREr+CL8ABeC0hi3dyTPpb6x5Y79ijEdXtmzPKpsAHUEas7Ix9yeZ7ljcON7l7YOf2d/maogj1mEuo5O6ds1u8x+GdfvlXd/F8x8F0QEOit9ln8cCHuLSmgda49Ck3RoOR2Xb2WET2Nkv9tno0C5fW/TrPiShMN9x2xvbY53IdBf9R+W2C/IvE+BJ3+8xVVX5OpojF7VFTOfUvep5snfBaX89/ov0rHeOzcvJ2khW/7W4YaaovazU44cn/zdtK2NoxQody6RkUeyBLp+zcr2NcS5eHve8XX4qq/vpQrtbWj1L/ba5/p7dfxf1n0f4EtbNqG0cnutzRHK0SbyN1Qa5Uk//E39+X7F63XxILLP47QiJgJkF62V5cH6RMRB9zpkcYRQKufQb6lewLx1OxBQtGnGGsDHtkI9q4FXZgHo6JbtsZcqZtkxADS5gbneEXGerQE3WsVYaSNjEpHPgUcQATAyVMVMJdMvGCMB8OI1uhy70E4CsTrr2w7btsNe74MgfwOxnGOaAEpw/Dwhn0c58qqefV7ogeb0Q4KUyGmh7m4DQxpQud41gWfmy56Zesdx0gwHjIffiX6RDopkQglKgZoyvGCjNY5mjEs4ZHC9vugGj3cslDQYqQ5NmBDduDQJoQ0AWR961hsSK0EGty1SIXBmsEqwwUs7uTAT/pERLA3IOBii6zoXSDQOzeSHSTUWiu27x19R23vtMSunTzs2GC3Yfh45cxFPpETu8NqOhlGakZO0Wg/v+ey9R48fFLU4RTBQ5L3ihL1iDI3y2zpEMi6Ckqd9l58iFZc3kyV9sK/p1CKi0MhR5PFHY7Em6yYiOj50+yj+lNA9C5rqlbElaXwZci7HHQGYCYhmjrMmKEqE2xfLR8uHKNrVb0Own1wxWdIAKB3rIvmOaArKpjRIO1vrDgsObmOrB9RFGyA0oBqWgl8g7n9BiKnE+05E6FgN9BUAHYMl2ghkHSSpMQ5Ky/YvaDlPltwrMNZX1D/+T34sxjfV2cfn60wvXU8bW4Hq3Txfb2/GeZMYf309ZyD7ttE8RjS2ffSO2NnnTE+PZJc3jteDZgCynl4bz/T4Cj2vgKzHFEcnF+Xin3oLmlgwRUc1Ee4mD4VO7WbutEyOjiQY0Yo4l95XbK4rwRtkJVSBZbhfj64snp7tbahovM94cUUGKJTvgELpru9Wf5087ertEYcieRLfvXo2mmwSXlEKpGvmC5L8tl5pOKmn/JZ5DezYbzK1+Y81ZSAnrgT/TdGh3ziTKVb22fRXfKOI1hkOWf7Mp4zaWNIap2/wbmBZ4n53UunVtiVD2x/b0tZpzxH8vuj7G3qmcumtsgIpE3bpQr9T+A09/Wvta8sIba3wSbAa3trvThddtRE8W+9K/hDYEbnGS5F/q54ZW9pr52h8N3VrdIyrI2p7Swer00vz+sW0xDwV2eB+mUI3Vv61tu8VWJ6IeP7PX4CIcDyPOjGQALYNtscXpMcD9j++4PH1BfvXo67Gw3rJZQmOY929kPNZV9rR5dP1O9TVUVShBJDqhRMblEB9RgTAernzmeE4nnVFTL3/YNuhZoWUkpj3LCveT3EEFK3C3r9+FSN1k4EwZAbZUrm/jI48ej6fcB5P+P4+4DgOeD7L3Q45I2x7udMC0gaw7WWya8uAcNZVqBkgIxzf33AeJ/z117/gOA7IeAImgK+vvU5eFMf/PM7a1xuULQoICRPwJaeVzJzFHyKcAHzhtw3wEdAzXqVVJ3uI+XJdMStXWKekV+la6AIqlI8mloK8vQMGIAWjPArFBvtEBnYuyrOOPMbntseWWI+AIxz9fH3QEBHVJIhXvwgondxtIHdErAhsKzxkYFOu+JAKwFNaHh46O1y2Re+Q9GB5KInnZbdTmzDiskF3oWckyk+Pp2Rf2DawbVGOGAMhVOOjP1YV5yh9ZGi6/O3Qk2htnqMsPCU5M2ZeNgIdHCu4ZD2jMenhfIXO1cDIq8ZLxIfSoUBEtTurl4d9wE63iXZSbJn829BUvs9Cu5WbhKdIARpb50hO2D/bRlHbcV0Ci39mgE35Ir3O1yltkGCTjQqet4uI1T7p73pJUGwLGqtOIfqnrEvIj5MORcIkHznyRpaN1fjNWDc8tF2jieyC+qxO2ZP2qwc5+TTNgqTd84lsfSfIuQq9rKXnpdbCfzQjxB5ovk4ntfWrwOMOhc5pP192/q6AxtlkWv+uB9unp1hcFH0CewwxnjG9YCaE2qSMp3/JLms7BHx7sH3H7jMlu+L674coUGLlvW1/790KeLbaGn/4OrHhLBOwtGN928su7H3f4SF2+gmk8qPhKgi74YtI/KLrPw4QDau1DFGAZOSHRWOh6dvXafHK+LhMSQkWt3QtgrVpfPu81SlqI++5zRPRbd9bXLQE4HP1jm2mVuJnywps+fpPEml/Qg+9AlbWWb4e0fpp3+ldfP9O7fqTQJq1KG3sNK6U4Vrkpck0rCijopi3p+X7WkKNd9CdEUiD4AfA4981PvhZXnlXR6zGMYroIftK27sj2mZjj58Funas/3s/WhGc6k4asHVsduKnZEJk5630iY0ruXoLX7cBLt8RgSdtLSpB97TvxeCjzzq5QEofa0C87KIwxzyo4Ga5IJnyskMAZBhCcZKRgovmDgTGBCrYCYjVCSc66qQABSUr01IwhxQpBReoKlQuHYHEq+6zY6xTYCil6rSXiRSskzLlboj2Vy6ZrN2REsh+JoHKyrs6wyVYVJ1hFQSSTmk/aMOgrZh8oWfgKOCUkhqPXhBKmXo2UBYafWDe+zs4XGY3wbDWcLIc6ECXvWb6WSfMOkbvBk47oZig7xcnjzu5EgRIe7r1c8I3CorLAKSHVwZMezrab4yipJN282iMJiNW+qDgE4bMYr95Rv5qUN3CqI8Ir5fXKoZRWo++FV6dGQMRjpjeGMZjqClo2eejcmSdozqu9PeIbo8HLf9dNSgUToxotLJVO7FKFwL09jJQQM6pmzGEvMCUJ/8pj/xUaB0cpNM8GPHUnHdfuO3SAE/6AXCYQJUm9G3n0AIC5NSNx+EYmNZpvkXaW8E6TM9lkmEsXLpcZDQ5UpjU2k3ARGdHftahedehjm0L6J6XIHOIiVKCahc3WLnAm6TXnaDYCnh8RPYq4SLbgewlb8ylRGktLQMdEv1+sZ/Qw+nQ4H0qHCLPCxQAAPF3X4ZPA5UHnMZWxaapKbnMVX17FVbtC5l+pLeidKs2hrWzpW1v23lUn/IxCyGRv6cdZ3uEqMaNY5QqPXTlr/XTa+N79H7EI1r2ODZ2c7Nm1ICtsi/X4oU7q+DKe6e7Xx0Xq+C161qZ2GkKFz9bEjEeKtPSEsp+8R4d7MwHBg9Kgrv0r4Atg/7aWykzZ/VRmIP3PB7Ab/PX+7OX/R7M5HiUbmQrrPpkNv8svtJDwACL01MrzTiTCzMfwcKrNmHR776PHZenLW1fzzebMKKMbGf6lGVGeUjXxHrLy+PZeU4dJ7pWPXtJ363TeAWGY5Hb9vp4j3xzLSf796vj28UrmUHluTYePHpGbT9q/8gOpD9XllLeF2kGuDARcT6fgEhHOmywPXbYHg/49ccfsD8e8Pjzj3I3wuNRGlcE/um8/ur3dM1MsUiaxCjOcBPEdAHycRyQc4bn88mTECmlch/DtsFjb9VpFxSfgPmE4zjVUVBfFOTZ5MpU4LLOo94NkQ/AfML39zecx1E+z7IbIp8ZQBi52/7g1Tf7vvNgP44TMB9wfj8hHycc39/l8zggY4btUe9PIL+fJmwSzaY2QdfapKywtRd+07OEtLuk7WSQxjgxCa3SBWztSVEHKlsa8kkEjgmHPQqp9WstO3AErLK1K5aiALN8D7VViE+O5xO+v7/heJZdM20QeQaSdKpAGdyuUSzK9APful5R3gh852/swkR0XgHqX/ouA4yaX8oYkWnkuceWfmkcaQGXgQKoKdFOpn5rbBK7Fi4F8sDvA0mf/UzJEUwD3BS8ot7paE9tBaVXpkwnYcbzTIONKCdthq+21TtOneW9K7hkPUeGljcewOH5sqPFz/MqjRHNkZyT/Y7YdkB4gRYpU8vYq3LXwUf57O4e0lkRrfqzPC/XDyHvlqOyUwKlIxARMjZ94rWd5G8rCzzw+kfxkJPNG7MRvr5chLd2REBZwQygZdhIj0l6vUCmzBM9l7hcupx8Ixj1hyef5M608kmyptgF1dbvbIlV2TWmzW+nWV1Wy5q1ufcZ9jfYM6XngQUAEDZdw0/6deTMeH0+lu1QnbO1VVtR2W18aieJ0xuHKlVdJNFFchAG9Z0DAoi7Fq7yRjmqVeYp9Yv42I5vG9SwaWUe+3xKW8B7vxNmNpetI+lgOcZi2eyXYcGTD60fsuv/nHWneoLEdxlKv2UGKP5VNCAFmv6+PpEQ9U0ne7zVB6tlgFahQ10bLWZQw33M/1pWIZCyeUfur4LUZzO+nMFVv6yXvVoH23RDPQbgtrnVMYgk8coXq89/AnDgz15tM5sXwJeX7+L15OBIT688t+9nNu4Yd1u4exVelwyvg2xTr37LOrJlUHFF9VxNjMm3q7X2W6inncYWWyNjrHIcT6jpdCmgWgo107Hd87S+34rso6YD7dTMIp6Axt5PXbOp/HEObO/qfr9iX7wGL8kYRBG3+VkdZ23XKyDvCJv5Y6/qzvUdEXQ5NQA7oeWCyw22vWx/TXSsUK67JxDaBdXnWYIcaiaiOLeJcTb2Qaok0kQEXQzdX6BZnAYdZKf7KM56F8N5Zjhzwce4OX8L1FBn5Vwu0E75LJMp9WgmFXSnGdBEwf4SdFd2FNF8IhvJx3GWi7qpHqbP6FkiE1L7eUARc9ph0j5r/VBPQqwEUADlIKe+icFToI3RTRDNKX/FQfHLpD//fUY9QSPeAg32MlD8ekmsnnEj21K2rQwsjOphg1Ne+r9LOEratm3rAo2Q0N0t4Ak5+Vv1e+0HRZXn+Ke2fXI18Pau4wCmn6P6tLJiRzsSyK8qg55gyZ9MtKIlCqa8VFxgBFzF9xOBFRv4sA7lFRxXyrS/Zbmyn72AgT9RkDpcBAhtt5vGJdIaG7uX++R2+qsXE2h5LcuL6uLVdWYQh+3sPI7aMaKrq9f2zlgruhVSKhP7tV+s9inqmHYDmh2BIPyhLiN2yl3hGuiHNX6NnDBGJvR+06zlt2QmelN2PmDN5l3uWJ5PyBpSrFvwitM/xR20XdNvoOwgXVbfgZJO36HW78guU/whHKeRLonKMDVk25B/Yqw/G0+MdRLRDU59iV89WjxZ4fLtq/2bTH2v5GUqOecUjyd/CEucPp7gmdI2mQi4Cp29YN5dtRWsTeB9voJvJSAq9Y7ng6h3Eo+VwRYv+XRd0Wi+v2/HXKnvKq6V9179Qj8MqLbz+sr6MD7nsuoRrZpv2Cmf5nPxJ7FC2dZ3kF9PoC0V2ZB2hoFFHuPUz1EtzurTrtkAth59vV6XnT8Bkc1j38105Sjv1bI9PbaKc4ZfPn9dXl4iwyChj4C2SUCdfJD+Wc2/oAtmutbi5XckWqTdxlTXF1250hcyUh093zbR/xO6i6QUpPBvgI4MXab5LX65z62N3Ofz6+Ontxapk9ZMRlydiIjabMVmWC6D8ftlz2yJURr2DX5iym7RlFhtm3dtihUZ1D970X4XsDwRcfAqufK3PzbY9w0eXztsj71NREC5U+E8EY4jw/E84fv7Cd/Pv8rOhX2v91vTitANNiBhWi+hPss9DuUYpQzP77YboxiXRFU76gUB4ESs91DU45POE57f33A8v3k3RKqrPjO2I54Qczl+AIDvVoC6m+L7r3/BeZ7w/OtfcJ4HPJ/Pekl2oXXbTWAaABIiAGbIB8CJZUdEwfEXHM8nHM+jXrANAAngVzmUGeiui61KvubslRlQNqrZuKY/gHKpdQ0CZCg7PdL4XgZpxFvYtjK5I1fIUj5AgHIagx7AodOECCCETbRydiY421+vfAlX2xWiV/TTyl+5+0XhznViKW0d3pyz2tGRuF1dUp0JCt0mUR3thEdKSV22twKRIOnPN9Zp3LIp8Ia0Ewpcq0eOzYgmLgMBAHI5kqm85OCnXFFHgoYmPmZOecQ7UbvJy3pbXXXdZfvJelAeMlQiPp7R5L0bjYEVGJUp6YrachSMeNdRkX3oTWZ4ynamgGVbenxypT3fMYSoLO+77W+i6Qq/yoknjbNPKKvgBR+lGdvafuPdgRvRhm0y35vc9SZeImdxzkcJAGM9ZZ95ZXi4+8tH1wFTrSvp9dQmalJ97uejwjfODxCY+zIgUPuGbAEVkCdvSDhhqnRDi9JjCByvZbvX8z+wPZJFZaQ6tbupAGybJ9hSu0/DaxpvzFuQq71G4zF6PhrrkdOjP/1didKnpfaLabOfgl9B91vkONnfkY2l5BvqsQ+132K9KfWfW5U5YBzCANhEsiggURb8XAGuN8CSQx7i6QbRjFbbF/6q5fIOoPES8m9Z+o84tgtQZGqzwSOd7+liL53EM7N9PFqu014Xi8nvjv2Jddc4/ZV78GqZbr9LudcmlpVMw7+v3z4FXM9JAAqgl1cEkWzubFtcK6fRpgVYuenxU+1tncYZLVHewH5ZoTMss8nwlnS+k+2KrxANtXko8nOQPlBYJJ9+Aka2p/x9xUf/Kfhk+Z9q2dnEtNeHyzYfAjT/G0U0rAg4FCcWaDxMXIfXtREdf7mnESstVKJvK7BeMTbhllI8QN2SPgVjbN2OiHdLM77+KzbDFDjOpCGKfY3kiRev+BwkkHpDxpS8Crw1UTMYU17bz8pBZbO/L9SXJyKYgFquDVZ6zgxWxyijPCKnNnT1qzl4n4gZyGmu6bM2NFsDUXm68UgY0feyQj7zbxDvbb2aAGm7JtouDBtsabshCFS4AREQE+ejyRF5YTaxYJV1TIVmuH4Vne0RkmE0/pJoWwDdV7pvjMesIAiyMOOGBOmgjZNffnKeicG1DCgcCIN7WIZDy6hc3ynre8qmG9HgC+PrAvCKgo+Ev9t/SJM1cb96uLtPIL6vQr4UyOUqHBC1y2dg1NaR8TSahHgHfqqOI/AmIVb4f4br1UChTdspSGdc/yeAnYSwz2dwVZ6tYGT+JXxOFFnqvFFgrjOuzTv7vCcH5YfLg/PA4Lp8W4Em0lG1SVO2BrfnS5C8m9BgVXHv5mC3Ekml6QzJRjKC82mq1N7rSiD0tLQypFwH44T5OuITY3Ykl2ZlRE5xfTvALWUQBI3Sr6T10LXWiQO78veqHGYnXFqipit0+0hbetIvCzT0To0u3O2bqcMTO6ldfT+oiz06vE9Jo8kx+f0+Le/kj+hflaVX7D2dZr0eUztk0gzIQR9gn0AGVtzsVlg2aipNRPuYZkb3cyw5BW4/WRnWL68RFvdJ4C++yfe+JnkHJh3opVUw4dl3qMW+tqv6bL0Iv98+ZUpL9A2nNkRsWa/6Gz2O6/k/UfanwNJyhbbIJ1jB8e4Yi/jvd7QpRfyanartr54mSlMMVtcKlDaiDK6J927d0HzpdOmgPS611Zvtav2ZH5CyEiJf7pXJiJmss5btKrzCq+/4MhQHc95A648+xU/Iq9W2l+nlp83xSrsk/HeQwDfccMMNN9xwww033HDDDTfccMMNN9xwww033HDD/0p44zTfG2644YYbbrjhhhtuuOGGG2644YYbbrjhhhtuuOGGMdwTETfccMMNN9xwww033HDDDTfccMMNN9xwww033HDDj8E9EXHDDTfccMMNN9xwww033HDDDTfccMMNN9xwww03/BjcExE33HDDDTfccMMNN9xwww033HDDDTfccMMNN9xww4/BPRFxww033HDDDTfccMMNN9xwww033HDDDTfccMMNN/wY3BMRN9xwww033HDDDTfccMMNN9xwww033HDDDTfccMOPwT0RccMNN9xwww033HDDDTfccMMNN9xwww033HDDDTf8GNwTETfccMMNN9xwww033HDDDTfccMMNN9xwww033HDDj8E9EXHDDTfccMMNN9xwww033HDDDTfccMMNN9xwww03/Bj8/5JqWn2VjIgCAAAAAElFTkSuQmCC\n",
+ "text/plain": [
+ ""
+ ]
+ },
+ "metadata": {},
+ "output_type": "display_data"
+ }
+ ],
+ "source": [
+ "plt.figure(figsize=(20,20))\n",
+ "plt.imshow(image)\n",
+ "plt.axis('off')\n",
+ "plt.show()"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "b8c2824a",
+ "metadata": {},
+ "source": [
+ "## Automatic mask generation"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "d9ef74c5",
+ "metadata": {},
+ "source": [
+ "To run automatic mask generation, provide a SAM model to the `SamAutomaticMaskGenerator` class. Set the path below to the SAM checkpoint. Running on CUDA and with the default model is recommended."
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 9,
+ "id": "17ade22d",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "sam_checkpoint = \"sam_vit_h_4b8939.pth\"\n",
+ "\n",
+ "device = \"cuda\"\n",
+ "model_type = \"default\""
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 10,
+ "id": "1848a108",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "import sys\n",
+ "sys.path.append(\"..\")\n",
+ "from segment_anything import sam_model_registry, SamAutomaticMaskGenerator, SamPredictor\n",
+ "\n",
+ "sam = sam_model_registry[model_type](checkpoint=sam_checkpoint)\n",
+ "sam.to(device=device)\n",
+ "\n",
+ "mask_generator = SamAutomaticMaskGenerator(sam)"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "d6b1ea21",
+ "metadata": {},
+ "source": [
+ "To generate masks, just run `generate` on an image."
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 11,
+ "id": "391771c1",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "masks = mask_generator.generate(image)"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "e36a1a39",
+ "metadata": {},
+ "source": [
+ "Mask generation returns a list over masks, where each mask is a dictionary containing various data about the mask. These keys are:\n",
+ "* `segmentation` : the mask\n",
+ "* `area` : the area of the mask in pixels\n",
+ "* `bbox` : the boundary box of the mask in XYWH format\n",
+ "* `predicted_iou` : the model's own prediction for the quality of the mask\n",
+ "* `point_coords` : the sampled input point that generated this mask\n",
+ "* `stability_score` : an additional measure of mask quality\n",
+ "* `crop_box` : the crop of the image used to generate this mask in XYWH format"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 13,
+ "id": "4fae8d66",
+ "metadata": {},
+ "outputs": [
+ {
+ "name": "stdout",
+ "output_type": "stream",
+ "text": [
+ "dict_keys(['segmentation', 'area', 'bbox', 'predicted_iou', 'point_coords', 'stability_score', 'crop_box'])\n"
+ ]
+ }
+ ],
+ "source": [
+ "print(len(masks))\n",
+ "print(masks[0].keys())"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "53009a1f",
+ "metadata": {},
+ "source": [
+ "Show all the masks overlayed on the image."
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 28,
+ "id": "77ac29c5",
+ "metadata": {
+ "scrolled": false
+ },
+ "outputs": [
+ {
+ "data": {
+ "image/png": "iVBORw0KGgoAAAANSUhEUgAABiIAAAQeCAYAAABVBSJEAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjcuMSwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/bCgiHAAAACXBIWXMAAA9hAAAPYQGoP6dpAAEAAElEQVR4nOz9eZNkSZIfiP3U7B1+xJVHVdbV3dPdg8FggIFgQYJLQoQU4VfhP/wA+/lIkaVQlksuuQBkd4C50D0z3V1nV+UZEX68Z8o/zNRMzd57Hu6REZmRVa5Vke7+nt2mpqaHqRoxM+MIRzjCEY5whCMc4QhHOMIRjnCEIxzhCEc4whGOcIQjHOEewLzvBhzhCEc4whGOcIQjHOEIRzjCEY5whCMc4QhHOMIRjnCEHy8cDRFHOMIRjnCEIxzhCEc4whGOcIQjHOEIRzjCEY5whCMc4d7gaIg4whGOcIQjHOEIRzjCEY5whCMc4QhHOMIRjnCEIxzhCPcGR0PEEY5whCMc4QhHOMIRjnCEIxzhCEc4whGOcIQjHOEIR7g3OBoijnCEIxzhCEc4whGOcIQjHOEIRzjCEY5whCMc4QhHOMK9wdEQcYQjHOEIRzjCEY5whCMc4QhHOMIRjnCEIxzhCEc4whHuDY6GiCMc4QhHOMIRjnCEIxzhCEc4whGOcIQjHOEIRzjCEY5wb3A0RBzhCEc4whGOcIQjHOEIRzjCEY5whCMc4QhHOMIRjnCEe4Nq34T/3f/1/zJ8yPtXxCExpwf5ewY2WKBnCyLyD+nGQiNY2qLmFWiQZ0cjqUxSZj6gg6Mg+QlggEP5eiQo/sNgVR0z4apzcOzHxm0drl93uH7zHF/901/BVBb17BR1u0B7coF2scTi7AKn5x/h9OxjtHWLtmpxcX2G09UctqpgrEF1/Qq2W4MIIBDIEACCiWNOO8Z914TosRoM7O7v/n8wu6xExw5wDIce4PAbfkCY2eOUY4D9OAEO7Dil0SMtg8sBFzm8Df9ISubQnvDesZPiIHMk73xan9OpsvJhYVy/uMRqvcF/nf89XlQv4Poezjms12s459BttnDO4XrD6FyP1XqF3vVYbzfoe4fNZouud9hse7DzVVpDqCtC09Ro2grLeYvFvEHbGLSNxbwCGuPHBo7Rd4BzwJYrMFnUi1PYusHi7AJNO8ejx5+jaVosl0vUVYX5bIG6qrCYzWFthaZuYYwBWQNrLYwxAJHvrTNgZ9C5Dl3foeMevevRh88u9Lfv+zA/BALBGL/WK6pgjEHTNDDGoG1btJc1nvzTEtXVNaoXX4EAXz9R+BNUM/47EbLFz2qOJ2DyHZcJxlMmDEOGX/pLwj2O/8UXEac4lsFwYOfAcHCuBzsHxw7M4Tc7OBeQIOKmWgsQbE64yQovnfNrzAlN4rKzYW0JogFYVQ2u5wv88eQ7fHv2Fcg5EDMqA1SW8Ok3C5y/XsASYIhgDWAIMJZgQCDr6YyfJoKFgRHCR4H2xDn18+sTG4RcsR8MF5vLLP0Mo6vWYwZEweJOIGPg6V0sNlGrkfKYAed69L1DF/869H2PzvXonYNjod0GIAS8NqhsBUMGdVPDGIPK1jCGYG0FIoKxBt2yw/Uvr7C8eISPfvXPUFUtqmoOa1tU1QxkKoAsXNWAbQ379wTzewp9kdb7dcjOYfOH38BdvUmkiDmhGjQ+6LmXccjpdnrL2a+IXpLOyT7VgR1HfO37HswM128i3vrfnR9fF94HfBa88/jv53LdzrCqZ3DMcNzjq7Pf44fZ99hsNui6DpvVGn3XYbVaoes6rNfX6KkDPnHgBgB6AB4fiYDKGhgQKo+A8Tmp3vfOt6N3/s+3kcNc+/f60/llCMeUoZ+NOJbvmxGv4twkPiGStbAeiAjGGFhjYIwJ7RVshrAWQ5yFb+t224Fd6NPrHt1/vca6Y7whg0ePHuHnP/sZzk4v8OTJx3j6F7/CyZ/9Ceq6QlXVsNb6v8A7GGthyMAY8m2ghBV+6QXaEsesD2RKaBin54InzuOFvHcy9y6lZ+cge7vQRGa/7uA6P45lnewST1GShLBPEFE2PSR7icwFSZrEJ8leQyj4pILxTCuJ414kAxV5CGbQ869gvv8nfPf7l/jj71/GMeh7T1v6vkcf9k8C40//mz+DeTLDu4YhX63exX/Kp5SnGStnPPPOyuiQ9GN1Dlp1SGFv9foWaadSDfn0A8Sl8ek6uJR90h8OO0skRFlKS1MA0L5cAd/8Dovzczz57FN88skv8Se/+jdgtmC2+MPv/hZ/+P3fYrvpsN12ftfkHtXffY36q0t8/b/5HG+ezYou8n108VbwfpoxVesuzvpDgjFZ9W3L0nv6rlTvYkbvZp6mSpnSmFD2doxmMEwHNC8cuJmjqz6FowW29UdYmzm+nX2E9upL/Iu/+n+g7rZ5ycRZScK9EXiE1hMaMrCUztw6kceUXMSihBjrj8gFAHrnsIVDBYMKiQ+LvApc3N8R8rL+07y0qk+fCHYEdL5QmD7xQbFHIteFf7RMpMt0gR/rmcGOwU0FJp0mZHCprfmnU78HQrFSeuR6mwH9LL/fgJLf2xr/LzqFC3N2uX2NHzZ/xPq7F7j8p29TQqoAqnB2coKT5RL//tm/wSftF+gDf7nZbNBzj8UZwza+4lLmiUURRXnNVBZg4U/ZyzFFoykpICI/LPwjGRO4H6WTYIYDw/UuyD4uDrPk8WPqccQ5P67MUDwPK3zMYaJbGZgo85hQFYd+jmUWWXGs36ot4EQDtIg4wg/3HePVtxs4foN+9ld4yYS/aX8NLJ+g/eTPQAQYt0FvVuDZNXoYbNlgebLB2fkGxL3/k/5klXKQETl+j/qRIF+6bKA4PofL8ZeCPjbJuCLwal6ewzqUNaTWYDmSnK8RiumSXKCHeYxfncJblWKy/qkyy3oBgC9fAc+/v7Gqhf3fo3af4JL+P+j4y8mk//P/7YayAuxtiLgdHLAJhgU3DRkFvbs6b5t3L5hqM2ffqEjDTHBZKoJjh+32Gp3boGoamKpGM5ujbueYzeeYzZdYzE/QtjNUVY0GDRrXoCYbFBgMy32ueIlGiLzJfks/ROAo045sPqlz8XlSYpT9D4vWiTIh/pM25ahoFobChX2zfJ4WaFRWqt+R4LC0iWN9DhwU58JoIFNucGy75BmbbdltGFVXoeE2KF96bHijlBKJGcoU1gEyOTFbK5pB4OlZCgoUQwZMBtZYWFuhqqqgcArPjIGJn35zNWS8IpmSwYrECKGVUXGs801MFNBE5HW1bKKCjUJbjAkGDkdoXm/RrBjUNSDukswtSiFFVbP+3khDkOPErsScfxmb14wpGEvPOq1mggTnNI4GZhFBGRuVay4pZ4NCVJRSJGVEPC2NGgrXi/XDMKGNahNWeZxTRg7TgzcbuO0G266DcQxiFzStiAwbG4ULsh6EiZK5YSpwl4rv6hlLa3I6mo9tAUTjuzpp5jBVkanLSE+ZpoLj+CYzzZqZC4uCCHDkAAP0zivDHfUADMg4EAySUjLx9MzSIgJgwAhK3w35RF2opt+Ct71qEfk5K5iqEnbzMzzybSSNLHwg9N0X7MliUoZ7epaMx4lmwzPcQtcjbU7GL3lOzsG4PmAFoXI12m7mjZzUR7oU/wJNYXihdIKKDn6Rwpv4lUp0Gt/PbxxSGj4afSDLZIJr1HSWBlzDeIbY4rCWe8dwCAbsukYtf1XtDQ1h/KDorKwbrQDmop74Ncwv63mVlaIE2gGelOWM1zRe6Y7+66808Us/9uOv0jADRN5oQH59EnHER9XxjNufbl2BQ7YG13OQvfJ7KnMwxKrxLz4fJOyxpQJpLT2MruzBMPzkYHJjVZ97rL37ggOq9jqGHiALkEn8o/znmcp8Hcd1H34+IPQou/5umvYe5/qdwI+9fx8GBPHUf3MOs8vXaK+vDsfxAUn3e7VWtkYZRyvQJ5iyXIegdBaqHF+WlDn2PjM/jO4641hIYBCYgiAlbVLKbc6T5wUSIeozzMRIvjP0378iC+CcHFbMuILXP9RUoyOriuMoJpE6oKjro4phHQ4ilPlM7UqnJFcW/UTiGZkCh54YysEOWoqq+XxOyBn7MP3veNNi+K7fxBkQgKoGNj3h9ZZxTQRjKsDaMJUMWIa1DNQMgtdBWMvZ2OWfIqWH2vOPmJZlsAeDPtLIlCt7EfUB2QSm95m2QKs1DoD3zhcbA9R1arfrvU7BGMBYkGtA3IBQ+/eVBbgG+u4m5cJOuGdDxJ5wY/sfCBN8SxhjIFm90Yp4ZsKqDwf92YS5Nej7K3z//T8AAE4//hTtbInTi6eYzRY4Ob3AfH6O+ckTVLZGVTc4XS1xspqjIgu7sLCrNzDra7/gbZUaUih2k4IuKDr4BsKWWctTn1z2s2ACokU/bNdOfgXCzWI1TopZcGAc4ukAB7hUXjp5CPhTCcWJh0zhpdJJ3eGdnCIQA4QLaYWRSac0VVlqDplZESIv4phZhXlj8emLT/F4+xSGCB06/HX119jgEp3zlvKuCyesnQsWcU+YjDFwDBgTlJ5gUNj0tGGG4PkNOzJjFE5p13YGsjXmJ2eo2xlOzs7RNDMsFyeo6waL+RJVVWHWtqhshbaZwVqLuq5zZZ+x3lATNk+HHo5dOInrwNzHsSdjYDw3BACoQlusrWGNQVO3sMbXUb9Y4cn/8gJ2C1i88RucsfAeFLmCZkqZ5D8VE5ajYJGYAu/AWTJSczrJpAq+Fs9SnaKEE6VrwC12QUhOJ30jHjODISeGewDhJHn481Z/B2IHghgBPC77qpQiMLZLGdeCwUI8IuLpoOhNkU4R+OXj4NZr1HSJfvscL/gVDBwMM5rKoLKE9brGtm/A7A1dYMRTIt7Wyd4ARZ7hQFBeG0N+rZPxRpU4bC5Mi4ntl0nxSnvWh6KyCRLvCsENEW7kNIg/tTJUqQpNlrqZ/XT5U1aU5YnoF4xCXdeFk/PC63hPH2u9p0/d1zBkUNXeM6JxtTf2cY2u79H1QNcDvbOAsyCuAK5gUINgAdSgby3MHwxM7xvQPf8O7vVzRBZNUDUYPRIczhGNo3vC64gXocOu74NXSB+U3d79qg+ePdwnT57oESGGNuSfASllN0C1WcNs1li3c2zqFk8uP8L55WN8ufwnvGxegB2DjEXDDGstQIweBn29havS3mLiPCdvqoQl5cR6pTNFrhMAcTJWjG2HDKWE90n6wPfmRCXD6IyRvWlOKPsMZ4KzOSG1D+nCPc3Y9g4/bHrMZwt88uxjXFw8wtOnT3G6PMfj88dYLpao6wa2EkO1/zPWeBpO4fACFTgXvA/E2yoaTWUu1R7lmCMeSLroKcHi0ag8ZIReiaF1hJvKucKCu9J0pRjlqPSfGP8otwCBPiVjhLQlGmhIZSja5z9ICEqQV33BfPIIbnEK++a/wvz+OYi8QdGGeTThpBwzw8TePizIxjX+yEd7OPYPQOj6icKHOux65Y/3IXhekgHBoO97rK6v0bQGbTsPa4lgrEUNb1AEW8DYfJt8C4H6CEfYBR/q2jscdvV0an35fbRZrfCnv/l71NvXsCj5WZ9dzjPlUttIrQxsuSxD80jq92hFeZOTEYOxVTnUcYuYyrOPQZ5wninMjgqqCvN2pxfOAGADZ0daGDugDqWo9qYDHiKYDDo4rLMsaGqqDn1+AJy6Dv+OX+E70+A/YoHWzvB09gwvZg6v8FXstzEEU1domhqz2QxkbGQqGMBsSbC1CXL0zWSdwxgNVFpjasfIwIhOxk+1MQbMBkQMJ17NUXwlxT/6vEnkEFwTnRLHR94OxYEnDmVR3hTEXu/qn8+XHGBuMVlar3AjMSO1rzoYAywfNaBuhf/yO2BdzXDy7BzVfBn02Q60cKibHovl1nuQOAAm8MHMMGGMhMWU2Y5HgwTviRD9jAyCoSToNAhBQRnapwRC+clqzvxiyi1aCctkNJKcODkWxfxwKbk8gM2BZgugTR7X/Ool8OYVcHIGOjnF7OUXqK+egFzldXGnF6DGgX/4I7BZ37retzNE7Knj4MkfbwkP2S5RSl6TD0VBovYQFmJIYNdjs7nGZn0NU1nYqsHs5BztfIn56TkW9Qke1R+hNS3avoZlC+uA+ZZRdwxr/Olp41xQxghxKC3Iw6YRECyJUx1Mn5ktd4QwJoNBeK5PQ0bCG94GhVRyHXPqfVJOaAOET5o/54y4S11ICpJYVnJjTCfG4RWNLO/ZK0yrOrRxjJkpFaR+/CTAzHzjYDcdsN2i4w0ebWeoeIvLzmLb97ju32RKm3Iu0snIgVjvn7M/aU2UWKLYHgqK4aqCsTXqpkXdtGibGep2Fk/F1lXlPSVsFRWpeUgkpb5TzJkOvZH64FtOoX4bTtBbW8MwML/sUbkedW1gTI/K9mjedKg2gOkZZIIbngq/VG4FxRConyxTMpqAy3R5h0aYFjXfpNLBpecxaTKqaUOZ4LUOUeJRMRkoEr5LKKag4HUcDRGi8EU53kgGB/8h6yFs1QxAjCAyPE7hPXhQru63XTFmLwiWvBdVN+uwaYErWqOtKiy4ReMAJoCdAZukmBWjIRFlQkS+hSRa6A1JruC44nKOn3qSNW4mR4jgPh08IgSXhqSZI56KMbF0Lx1qrlP14q0ibZO2sHMwRGBjAGNgweidhbMEnDD4xKCaLWDrGRg2/rnrHv33lyBTeUPcHy3Mqwou0G7ebsBdh0wIiSMx/TvrjjDtzHnaEvkFnySVGGHFjVjhrYTagRge4ADu4UK4IwnJE2krh+dItD3tCb5uA8D0PazZghzDMuHE1uC+wbWr0bkeznRgG4wRzODOgcjBWQaMN64ZYTQj04iwHY5xgBRopqe3BgYOLggWwUyfZdM0wTffqKIAny+Oo97/JmDILYQnQaKIxoixvFzMfZhDqirUswbL5RKLxRyz2Qyz0yVmT89QLWbBezLQ/Gj4NcrAN2ylxp7UH06h4hRNivSIVfpIJPL0utdpYPUzDYSdx7LimAF6+xyMcVy/+n0Y6TBfQiek/bnHl6p81CjBSdIhBCWogV0uMf/oCTav36C7XsGxd/32gi0nQyipch4QRDZDfoygSvn4YGPELQW1qZHKhck9Cy8LewDC477wUJt69+3yNMsxo+s72L6Dc10IASe8gkHlHKwj9PA8y+6GTSD1e4QDMfcI7xA0hR7Oz8Obsfeym5A/OOS6DmwcYD3Pzdyj3r5G1V2B7SEcLfL9vZTrBr92c1+Rk8nKKfmcYQ0sKhPOuCEF43zUeFmiCJV8+q2WonhYNCt+Y6QV48AjX8d7cV9YY5lhmbGkHo+pQx8Etmo5w+rzx7h6dYXrV9egEEXh0ckCzx5dYDmrUQUe0HBkrUAOA5FmDBgMSpOXvRuPEqLycuAUHUCGIQch/V60x96h2GDF5nocoiQ7qMejvNPwua6bIR692euDoZQP5cuYcEyJJzQOtlnBujXqiwXQLrB8XMHOALNYgytG33aoagdbebnPOc9hix4N8GMB6H5ywHVKiz9ZEhAGUBkVCMoWFAvKxk2fjJSC4jMq3gt2TPipk/oygluDuosR9O9zWf3OwBnYbjrUKzMBVAPuFNQtYdwChtvQNobpF7B9DyYH0MY/J4az137h7QkPwyPiRtixkB+eTBYhs0gDKHYJSMPHdVsEZotus8H3X/4OAOHio5+hni2wfPQU7WyO07NHeLR9hKebZ2iu16hfXsEQwRDDmBWItsjC6RibNSOLc5zRpqkB5WwhJUXKyKbMuYIi3ePAEEuLKD614to/60MyUXBJHTr+Ykg/9j2W6+tzWdn+u+NUVvqDUo4lQ4XfIBhmvsTs409BIOUhkfV6wCbEcQbQPvPjsP76S7jrS5x9/TP0mzW+dgaveIVX/f+CFW/geg4KZ1aoQ/FErkFQqplwKoAAAxdi6BkkFRj5k+/wxMSYCs18iaqe4eTsDM1sgbOLR6jrGZbzE1S2xmw2R2Usmrrxd4pUYozwFtCowAmKV8fw8fJVLGvnxDtCCLyFMQix8Q2aqkW17vHx371AfcWwdgPv8eBPxlsYwPpxEwPEKC6qkS7Xmsx9YianNs/yMav3rJ4KDum8gscqf2b8EgNZMCg4H2syGticj5UvYZCSh0SKkx4ND6LIjUYOrfxVOByaJXebZEYJwW/4EC2ytjgqg+ENbKyMI0jGtbPVDP/y5Sce3wzwm5Mv8fuzl+jrFb45rfHrNx/jfHsCwMAYB+p8GDA/hX4VOBCEDMGFyySKu2E4ekLIR8YhTO4GWbgFuZMixOuUuJiIhomQR/AlHhNxQWEZTkAERlBqyCGMjfOKde483nNYc6bvQRQUicbCMryi3FTgBaP6i1NUyyVOL56gbmZgswSbFmwWcL9/Cf5PL72LbwiV07O6xUHaOcFTKrJ4GDiNz4GWhu8uKpZTPH+w8zFZ2aEPng59cNPsw3vuO3D07GFlYHPJ8CX7Qmh8pKbsR73erFBtVnEdz68WcJjhVTPHyhB+u/g7vGlf+RM/vUP32sJVPfonazjrPYj8DDJiLGESnCGoEMIwzsAZB+MMmFwYf/aoGgQLnz3EJZaRilubb3cMnOWvUxicYhrumtPCSixbylHGiJg9ljR8Bvh7hc5Pl7h4dIFnz57h7PQMj88f4+QXn2P2pz+HrarsPoh4L4X1xom8E4neJM/F8CceLpA9PPyOhii1X4d9We5Z8YYr5W0T92NEmhdp7IApH45flmRSekOQEUrDjrzg8J7U6bS0rztyHheEUKRFmrdKjJNwRT3A/GefY/bZM7z8z3+Dl3/z25Cc8k+Wc1cPmOm9AXZj+c1wK4+Qt630vcFUo993Z94v/u3qPQcCaW0NMGN9fe0PRTiL9WqNzXrrvbzI4nTjsLh2eLUGVkQILkcj3fsw19oR3jXkePK+V+m7gLchrc4Srh8Z2C3DbDYxHHVv16DqBcAb7OL3p1rkZaAhjRroZ5XicNcKTyUdotC/sZnZj0GJ4cFAH5q9L7UNWvYdqWaQdEomVrz4tKB873Dhtvh3yiPmmycLPPr1v8M3v/89/sv/8L+iqiq0bYt//cWv8cuzn8PAwjDQO4AdYduH+8r2rVDYyvLOC2B0y8vPnHi+1AGgXjzwCYSkBxkWp+Ys/JsfHtTtiikiD1Sys7kuSjdY8CKEFY1i1tjI7DlapGoIMjcrRXsyBqqwSnaL6snv0NoNfvXFR+jmJ7DPmrDvvgQD2IpXPCwAhoGaPyKAbZTZIziEhUIhh4ttBCOEJWPAeb5bPF+80KfmeoT1z0YlnqDkNAAIvw2BHCO/7UWkoF38UpzNwZt3wXVUmxPMn/8iyS6DRgR8vCTgyo+/ADFh9voziAe7tNjRFlcXv4GrV/u34/ZdUHAH9HmXtfGtC78z2LOjev0P5jdtacNtMj1hdthuV9huV+Gy4AU+bj5BY+c4wxnqrsFs1WLpKtS9g3WAZeOV1DDeGGU4XeiSNC+hNhq0rdyS/eIrlRqiMJCHeS+yk44hf1KQpnAvolgQRQaQLphJdzA4pZzgVLZ4RAjBDouAhSBppUh4L3m1ocGFPDEtAWhmiLH9ZENm3w/TtCCy6ZQCkBPFEbSg+A8AMiB2MIsFiAjV44/g1hssr9cwXY2f8Se46lb4YfsaG97gOT9PBpFkkUjKsxAqQzwWkhylEc/Ps7EWZPwlpHXdoK5b1HWDqm6iN0QlnhAmXUyaLmGiqIhipcCWOwui8UEMPBHHKMZwbDcNqt6i6TvU6w711qDqGTY017jYAZ87U3wpcj3YQAvqwbIFqN18gpsbf6zXgMury97p9ZrWiYReQgwRpi5nVQrYnnuA5SR9OEkOpciLxoewJjKFn7o3IpYp9SslYabIQzQ49M4BxLCNBRmKF+7K2iK2g3G2sKjZ6/KJgGU/x8mrK/TLDpfNClsXDFFB++q8lh4u0KU8bAz5teoQTl7rOdJukAWlJGHgkJ1s1iFWor0sekHERMixSRVLib/IOED1TY9GVAiWGmYopjHQEMcMIxf5GmCz7EGnNaq2hZ3NYJs5bFeBvl6DrANVDPNiA2xDjcT+iA/lbUg7yRCTb9xNx5hQMQgM1hMjD03nIm4iKJ6dwsf0KZ47fQzJE9MHxlAbh2OrCyHILyW1bzKHvc6g7TwNPOmXIABvzEt01IGpDt4323ACyBsTZN5IlMcUn4Q6yZ/uCHhkiADDcI4AY/xF7eRPTolBYjiOaetnRB45m5RDuBkvcKRCoyiSzeGEgj1sYR17EaaZzzCfzTCfzTE/WWL29Bz16RxU2xQCLxxeiHcVKDzXJ8OEFid8L3kHp77LVqr250ijVUMjr5DVMhg3/XnIWCbpTe+RGPk9kT0m9fMRTyqpVgwMEgPwtE/wguDDxbA1aC7OsfjkKa5fvIJ7c5V5Iu5uXdmXdw+Ufbl5LN+pK/qN07vf/O+CQ3Nrju7gGu5q7G5dzts34LYl7Jop4S38wQMDxz50ImiNru8iX2qMgWEH63rEU4zjm/wRftQwiUl7pt9Fa981Ah2OvHexU9yecjLYEJwFKuf5wdnLV+DtNeLdYgPqGOSGiTaktkz3jKD5sV1KwsncB78ah7HEh8/IdI73wwfcVf2GgUYpipc94/HWYdXWOP/ZOR6153g6u8BZu4RFHcIAe07fGwSKAtX8DDR5kbd24YCczmYwapxQJUSZFgjK/hCGCbmcOg3KCHED7ma5RmTVVJ7KRyk9Daxbd4snUUYoLCUOwBU6XFuCOVmims9BVQinRSFcc+i/K+0Dem0FYT3OoSzowfqTZ2ECQr5MFiuNEVC8POl5LeUQ7f0Q3o/Vn0np+XMaeSOl3zs4A7tdwG4WIFdNGyJuaBY5ffDZg2ED252BeNrTooT37xHBauJ/jMA5FfIoWCKnVo/5P+47vH79O7BjPHr8GS7qj/AX+Es0ZFBtGdQZ0MafVLTmDQwI1uax9BEVCamKbFuP/HdixLl8GR7mxof0mRNCpUQoFRRRUaoU60qJCnA4jR3iijMgl1anUEWc/U7KX45lO3BWv/aGAIurF7xiONQpSl9UFeZPPgZVVVQipnK90iGVPzLVIw+yU5bswATUj54Cjxj06RfgbotHX/4OZ5s1PsIzbFZr/P4fv8b33Q/4/7n/GR1vYxgdAFE578Nn+DmvqgqVNco7AohX8watsa1bWNtiPj9BM1tgsTxFO5tjPl+irlss2gWsqVCHOPZV5b0XjLHR0OFP4PoTnb3zJ55757DtO3T9NsWAD3XLxadVVcHC4unXZ2gvLZofvobZrr3BzJJXbCPhKk1crDW2dyYsywZ9iNuDwkYxPb1TylDB+wzXsz1IK/2B5AHhFa3xBLh4RMTnW//Zi0dEuFcj4qScGHfKSOfr61mHbgLy0FgIimJEXI33rAS87noH2xLOP1vCVja9l+6NIbjqMgj4+VeMx9+f4q9X/4ivTp7jut9g03cgVLCBUTCGQH0HjqfKw8kJIj//RGAX5j7TZA1mBVETT8rUpskrpfUhnhAkoZiCITYaLDK9nTBMHKfWKTRItkg/B9Ikz8J4pa0FwQX3USfeJsYru10IdMlk0TeE6z9tUJ8vsTy9gG0XsM0pqu/XaP/jaxAbGBsYAxImbXIqBsySzF9cBtETQHd3OLeJpooROF8fYoBw0QAhnhAM12+9EbIPxsjgGeF67/HDXR/wuYeD91gA0vqArilbeyOdzRuNxXaNGYCf82e4qhx+e/L3uLZvQL2fD9iND4MVL8KOPmKiW/d/Jomvhr3BOJ5kYgLg4G84Cfc2GQcj7tKGIy+r6RGnZiLaQvLeqp7dxAjmfMTYe0X2IG48zIzOOVz2Do2t8ezxBR5fPMKj83Oc/uwTzP7iV7BVA0PW31tiE82X8EwxRBNSmQxEOiV7d6IxTuFf2ufVQkJca3HPRnyW9ZkDVuvwXYInUAZXqPLfEnI6VLRHja1fe+qEGjiQqHB3RBCOJmeOxFmcvdeNc1j+/AssvvgMP/yn/xUv/+4f41o1xvgTV6M0clDwjnf3A/mQEXbjqtBp3JiuhIyfekBw/y16eH1+nzCUoRJpISJUVRPuq2Ks1ytcXa+xXvkTehLSo+IO1m1Ars83+yQsHeEIR7h38JuB3XR48pvfwnRrbGzvdYta26g2mdEQKAfsebL1CKs5uWOOvvCyzBgN2gsO2ZoJOhJw8WXHPr8XK6TyZ2z4Hg2cdNW4P7hYbXC23qA9q7H6P/0K//zyGT5dfY6mqtNd3FpZIjoQLWVMDJnopGKQHUf+lDuJ4n4sNNPYb4fo0e8QT+NTkUWiW0S2V+sQYlrN0VPxqZ/nEseY8lzbBJjLMt4WEr+X1ivHT1klPQP/4Gp0dQvz9BNQVYVQ5wwOhzJ9q8LYOzcU+agch9RTkXURDEeJXIS2Be5R7moLLu5APK7NoXaK8yL6HRRlIRzsknIzniH2Q9KH97HQ8Jyh1pHQN5/2zkMwFWC3Cyy+/yWwrxHiACBXYf7iZwcRxrsxREyO2V0j/IcMY7MiYqiH3hF6x9is36DrNrBoUNUzfDT/OS7sOea9DRf9clDcGfhr2YIy14RT8YEucGaE0Io+qI1KEy/1stigMvVKtgdx/j4SVU4LUhQTWSx8UVhwfjIW6mLKaEQQLQ8r4q0MES44Y7FSTHBuzHBBQ+dE+REMEqZpQdbAOfZEUQILBqLFYROi0XGawOwyDRd0h7yCVAhZdXIKs535dM0a56eXwJbx8/7XuO5WuHrzGits8ANeQOZRTusaoqg08qE0KMbzJjK+L2RhqxpV1cS7Ieq6RVU3qKo6hF9Kyqd0J0SBDcEg0zuHru/hXI/O9TE0Uxyf0D8pc/Fii3qzRfOmQb0ysL0/USyXn8ZwOkCOo+WgFseKkwJqOPY7jZvMY1myjT/9KwYIVmWnTStbFhHPxYgQQiuJ4YH7gO4pBJM3hkmom3CEIztpzgmvlVLPBaWwU3iuw57IxbGC99W8grFSNHvDZe2NVKzuFBEkTZRbbbIaCKjbBrOFw7PmMRrUuOY1vjev8IRP0brK4yETegKYJByOx0uCNwoSsT9pzhxPB6cwOVPIEDbrsRSR6ZC6kClRpyCpVFUV8qYwWunf/qSyARmGYX+Sw18qj+hNZIwFVwbrUwafWNj5EvXsBLaaodpWqL5cofqhBzoh3KwuNAgMz0TzB3jMw+dZ+gmCFb3KFHOsR0bwVodkkguo490Q3KtL1V00uOm7T3w1Tq0h/zu1b7zlo7unOhnTOAb3hPPuFDUqvDYv4YhhNxa9BbY1gw0CLYcPYadxUo8Gwc9pCMtk4ABDcOwNvY4kvzc0GSA4kEfONZEG2iUu5nilMDdPxZ726fC1JZ3UuMsFnSQH2GtCjQqLswVOLs6x+OwpmkfnMFW4gyR6QeT3AVFsVdkuTmvGJZxJ9JjVfs0qfaJlaf7FWArFB+RjNFyX2QCNjukojAgyw/JGXutiZYpz2WE878iEEYWQasGzRnpIhMh/zJ48Rr/e4s0338G9voweiUSSfoy3vnt++yCvhftW3IaxzXbvQbzgI/xY4SbstobQLmaYNU3cp7pui20HbDtEHrXugZlzqMK2sz6Z4U1r0bV2ouQdUDbmPeChNOG4BN4GprDqplF9n6O+i87f3R6wC+6y9/5AVQfjtiCbFH13UVHOWx02NtMc6YRHbJ7kbRIM6mKxTExkKx/vLP1GZecuGfqGrAD2799+RRj2lxUbAmztw4hWpgocODK5nqYKCTDKRsaUwmGJDKZKGcmolfxjpSbVthIGJoYmK4b2UUhPSno35LtbCOysGqtct0lEgLGgxRJYLmBsBdgqKcZCrrLd/nXi2WMEEiUSp3svVP7M00Ez7BpD9G+pjJAupi556+hrgxxbwvzGx3reNA0LbSjnhsof03N3010R2vNFw+C3I/gwV/ezfxGbg1DwnXpE3MvS2KvQd8yq7cCl4UYRLrBkYNUbbPst3rz+A5zrcXb6z3DRPMOv5n+JliyabuP1U1R5RXQ47Z6Uz0GRR4AEph4LwZTawQpBlQIhPsnfZ2n1vywfydAgIWC8PiJ5PMST3mAVakaHrIG3jgKimYjkTBS9qSxAK2l1GKNkePAaDonmJMowxw5MBvPHT2HbWeybA0R7m/U5m7exuZ2cc8qyCMFm5mhQap5+HBIQmvUK3G1wsn2Mef9zbC6v8er6D/im/xYv6GUke4bEG8YGrwiDuiJUVgwK1p8Kt+FuiNkSdTPH/OQM7XyB2eIETTtD2858uKaqgiFfVn4xtYyxC0YIoOs6bLqtN0C43ntEuC60ycIG5WtV1bAwePxPV5h938OaTfTkEOUX4O80mVYQ5bimDV6+aVMLbfhcz8GY8irNNasfwxO3KadT6UNbRDHLrDwgwslx1yVcd4yetx43dUgbAPH+B7k7gl14lEKU9RIGKxgf0j0TvnW9S++MAc4/XqKe17E/MQwUHLpOjaf0KFvrI1pPENrzBu15g8f2DCDG//DNf8R/6f4O/1v6Z3jSn4FrhjUEhg1XM/hLVy38SX9DDmRk05a4mv5iYID8pV9jKlBG2PgTbdOp8pAyKrTMTloITcoCTVaX1SPDvthm3+501N2Fk8ueH6kAY1BVLfqW8OqXS9iLEzy5+AhtO0fbPELzQ4f5f7iCceQvpgbF2FdsNPVQHLHgHDSapgkczGGGs6qELK+EW9LvQt/VnRDeyNDFcGzs+nhHBDtviOhc5/E73BURL2lXocV80WmPQLa+coEimoFlrvW8E8EysOg2mHUEwue4rnv80/nfY22A9s0avTV4/hjoTbiMDuzvjAinVbQQIaPswv5K5GmeYf8HdmG+HQwbgF30uNEuz9EPRXhPAMZpOpdmZJcSVWY+rkKOxWZidbF1ZyWYLTB/2eJseYonj57g6S++wMlf/hlsVcOaGtZWsMbGuyGMoWAIU59INJCLuSw/5X6Z6BkR6F28EwSIRtVkhBKPFaQ6xFiREW6oMobrVBVRDMg+So2pF/lzWfrk2J/QojTJ0bGqCNvl9/ucRkmsWgP/3R8c8YUvf/4F5p9/Bvx//yNeXP5jwLlAD0lvX+9TEaZaQNmv3WnfBnZs929vjBjZ6x4E0M6fPykIdz9JqL54FNYxZk2FTz95CqrncI6x2W5AV2+w3jis1z026xUIBsu1w+mGYTtPOV99foavTglsQpk/5fE9whHeAzADPQNbbMHoB4FwxqXCmxTON/vO+b10TFGtlZqD1wFMTD25MU01LXuB4UudXliMXcWkhscvjPz7DS2cSMHDdzcXdLdQdJrgPe29nsEo5SygQykTFJ+1VyVJls/ZxVyHoyHxosVB30FqSmXp0E1l2zSPyIUxDih4v8Mg8aC3K4BU5VyMEVg0UzJeGv8IxtawtYF98gncSQNqWoBMxMwY6lZ7ioS8qcWh9Cjz+xdELnxSHC9vsBAdKJB5tJT8s5bJRHcaO1nKEMoYoSYi+umOGgmVBBezcfb2pw5vZ4jg8Z8HDezt18WBldwFHNDQ2C+90Yy3o3febQlkYQyjaloQCCcXT3FiL9D2QMPsDQ6AP+QewpqE87ihSopKikI6HOnF2OSVijaVWgT8LB97/UGmOhKjQHjP6YRjDC8DBlxSWEQjgkv16XwpNBOiEgRRGZIrPMDq4sv4PcXPp9kcZG0kXDAVkueD6hmPjtI0TCWkYRo5gS6nc+XEs48VXaE+vQD1PS4csKkvUb96g8YRKv6X+OH6OX5z+WVGP+Xy6uTJEF4Sea8EW6FqGtRti7pp/N0QVeUv7QteC6LUZY0dQUHpQIADeufDfHRdh/V2g7536JwP0dJzD2sIMIzFizVmK6CuO1gY1CuOnjuyUSVlMSY0CKkdWsnqP3IcZB5i+tR0cPFtaDkOiMKKeeP0W/A7laEUui4ZCpI3g9zxkAxwEis/Gi2iB1DyHPJZOaV3yYNIDA+9KI9duKsDwWDhGPWygq28hxUZAllhDgrjGqvxjEsgrYXxVUBB9xa8c8LrZ/UTwDFe99foTIen7gytC0ZTDh5cYR/3nhDkw42YEPDLKcaeGCb8FhftzCGb0pzH08KRZZyi90ManCv0OdER1evEN6TTyBJqCjCegTIUHTyjcsRUYGOwOSO4hUVzdoZmcYK6WaDhBrMvV6hfO5ALYVxAMa/0JdtCiq7k+Jnj9jjzXcxznHtOSl2F+4l+C555rwdvhHDxDggxPKcQZHJfhIv5/VbBcS3Fkc/GXepXLdYCgcLJjGQEHDQEtM6BOsbZ5hwbW2NjN/7yQ+oh90LEDOC4d5aQWEcOrKfxBlND/v4lwUYSTy6O+coRl8M64rVHqo7UH4YcsU9K1Zx3SMpqjAgC5XdPuxHGata0mM/m3vBcN94QLMbq4JnmDckeB42s7bHBEdooeCf0kdXcDfBPG8ZKoquLFnxMCL6Tlg/6rdbFCGRoU3qMjqQcV2WEPScKTUGI0vmGpCYKgrlgxZF2RQMHGGz8bjn/+AkYjNd/+Brbyytsn1+h2vSgRy24tqqndyvO3F6pP9LxDwr2bP/76OINdd4KE+4Hfe4P3MjK5jRrVWVAVQVHFuyA7XaDbuvQbR36rgtGcQPxR2YAbPyfbA263Agfyvgc4Qa4r4kc23HeZV23A81h7Hp/dzBV43D31RyVjseeVJ5DjwRSJ6ynxcpS6cTDJOOvRlo6Vt4NsDN5+XIs8VQB4flNTZns+jtRxu2HVNPTA/Rz1NcLUD8Ph9aQDq2U9QyYRBzQzfFE+xoCpGoiwVi/S8VgUbodQSTRXGSpk7oPGB7YGYd0F5rOjDCXQ55J2/YcgJUDOhC4boCqEiWm6n+pJ80Zk1i6Ep6yGouhitFgpCQ57MpA7tkwaHqSqSV9iUfkD6CNeziIbEkFotywZu8YpjwjpjNMPH8H5AC4J4+IIVruHuyHGPP15i163zKmkc8L84R1T+iZYOsG1ljMlxeoqhoXT3+GU5xg9u0GlTOwNij1KHlCABQVcWPDmNEZtaASgnJSLGQZOMs7MEAAIVx6fo9DOjkuYTmAZBzog3JVKWxZTsz6snx6B218cJCbdEOqIIxkcfHFICJGiFCPvhOCAczOLlAtTmJxvpr8QuJJRuSu0DQYXJgCwWR1/qKuMP/4UzA7nADYXl3hkrd45j7Gr/Fr/O75b/Gb3/4hrhkTFCDxclH/yxNLY2HqBrZq0M4WaGdLzGcLNLMFmjZcVm0trLH+9Dn5efJ7SzqT4hyjZ3jvh67DZrvFarP2z2V8CaitD0Vz/uUG598B1vQxZJRVIZ9EwzWu6OL4bwrNJUiozV3DXFMyZHqYcg/mOyjA5A4FlHVDKXe1UQIMcbeJl06XitkQsiadLO9DermsOoVikqbEkE6cPCa050TvxEMlKX59HgYT4/zxEvOzxl9CHRiaruvTuGTK5pEx28kD+bxBl4suhLj59cXP8Ev+HP/3r/8n/KfNt/g/mD/DI3cKZsBaH8rGMIG596Fg2J9scU5OlXuFvg/h6E8oikLWMIoLxASH0h0QHrdMiGo0DEUXv+hdWs1xNKjKOLJ4QijyA4AlPo+x/vJ5H+XHh2ACByMFgaoGriG8+bM5zPkSZxefoW5nWCzPMHvZYfmfr2E6f1rEx+KXvoTL0uLpFY3d4+vjxlM/nKfRZ6S0R5nHCxfpqeRzzqF3wROi7xR+ew8Jjh4SDNcHvO/7dDdARKrCAAF4Ixt0unzekjEiCKBR+avwwXjj2GK79p4R5nOs6i1+f3aFbU2A7aLRLPLOcXYxqFsU1J6hNTDOgYnA5D1gGA7kgiFDLq+OTGjolhi0iOJjzRFETwlZawR/kmdSCxzGL9BNlkzpbRQs4p5GBGMJy5M5Tk5PsDg5Q9POgwHa035jquhBZwLeZQZtUMQ3BhSNVDiCsOfL/h2SxEMBupHZaoL6rvFDCZbKE0xR4zxvNo0utm8cDt/IM+NkQA4nhoXQRwoxZ+O+tmMufRFhbJnj3MdDCYHeLf/kF1j87Av0m/8Jr65W+PLL71AZi8//1c9AjfXpb1j6DwnKffphwofRyp8ajKK5NkwQobYNYGv0pvZhbq+use0ctluHvtui5z4ceCgu7Iny09i8H3HhCEfYB26rVhtbelJWpook0RcJYzhIsXu5Fg0s5UktHwHDvtwfJSiVr5y/i/xBmSSqtTPQ/NZ4T26AncnfIcMxUhVtzrF88YWXFytkeijhvwYHdQ6oj4NwS5O81fBhzuY5IIR+lfJIov4JGrOXZuSZ3CeW1gED7MPDen7+5qbv7/2xuy831DKeT6Gs6BsYXvbpmfA9G2ypQl8bmJrUgAl2Ul5QhuhFfZEGSPK0Aqa7T9knKW+M9DggTlChwYU5dAyQyBRSL2EQm1Vkr1EriTAYRbioEfiA2Pk7gzsxRPy4Bu7utpqh25+mjoTeAU4uJQXQbV8BzHhkv8DcLvHkaoYZmeSCZghympyiESIUWcaXiDDcdVk/iKcb80RR55rl5+K5pBUllyizFPFkjie5xTiQlF7h5HcoK50M9+2SE6SZwoNzD4h44XQwdkSlVriM2jQzmBAz1isHa28AiAqRWEUOY0h9G0Qf2xCF6I0pKUK7xAJt6xrNxePYyKemw7+//Df4fvUD/nH9hzTuQXHKHGLvw5/aNqaCrRpUtb8foqobVLbyOEXipcBpPMh5wh7GxCsgGV0Iw7TebrHtOqw3m3Chb7ho0xjMn29wutqguSJ/6a76D0qpFYcgH5A4ABzKjUorzrBtwFxJiZ4vU0rmiQlJOJz+SbHxFb5JO9TCibjKgBhrogEsGtiCAUx7NCAZFsQzQkLWpHIQ1kswrAXjghP8jsYGPyeO/UXXjhnN3MK2BnKfqamNTwukMGYZQ6P7lA2P+pA3YzRRUYYwRN6BgfCz9hMs0OJ6/RIOV3jcP0XjGhAZWOsvAjZhnhx7w6rcSWKYvR2NDMiFE+zBY4fEuwOyrAoPG0wtKX2hLDLcSPMsYeHEHOHnMeKD5DH+UlkK91oYUqwFhdKsBRvC9oLg5jVm52eo5ws8+oFQk0P7co1m5S9FNkrp65eHKVZIvjYig3eTEaKY1PKeC/lX38eTQjSF8Qh0xYWwSy6EXpK7Ifyl7A7cq2fRG0JfUMyqHaoFjNiHKPgVXaGkcQ8XlYWZHzFGCGIQgLbbgmnrw9RRhfmmQW96bOtNmHPPbZIozSNDqYrTayGQLm3zz1GtHN/0XUXuiTVHRTUohS6l9D5uG0VeyTZ9Yl3VTgxjCcZazGZztLMZ6qqGrSoQ2fhnDCnvAMHDnF7n5Wt6JziY9tFItuWXMmoPRmcMdWPYJyTaGOm07P3yu1zLHPFKtUYGZPg97MVTh2GmBbswd5yHXPL1K6FyJw0NbyiVQzG/n3gKYd+Wnz1DNW/x4h9+j/7NNdwfX6K6noGfLOGqfeKxTgs+9wMRg98J7OXBcfNU3Dbxhw+T3b2//r/NCI+qQ8gAzQy2nqNqZ9hsO3T92u9FvexPjG1tsGprNFcrVDEKbFCFaGJdVrarIUf4QGEXTTyEqBzyble5U/vV/cLd1DS1x+x6HpSKMYnel/erLvLLNPSQyAvL28ATn1rPcaewawuOilDsSHRzMfcOJUt1aF7g1sh2Vdd4PW9wxQZ208HUYkz2dD0eyC344yTv3LRWFZ7IhWw7skyFSRJDhmbsOTDtOSaOZL5hbHgP/MjbeD80hAos1GtIO3IQ+fsTcXIFPqmAagkm47U17LU2XkWq5XdKoZUkfC8oFjwmIefdzCQoJDkj3PsXDjvGNacnWnlUpS4meTGevgQhGUJjmAefTWQfkVeVDpjzgsdhj+m96a6Im4DtBpvFH2G7GarV2a3KuEt4p3dE3AvcKVW++0U71TwGsHGEjg1MVcOyw2r1EhUqfDH7P+KEzrB4fQ3D7C+oNkFhZ7TCQDZt0ZJMt4NHvmQhlORpPAmgWp2dakyLVisDkleBaAmSIkqH6OAYizy8ywwT/i+qLULMfDkpngwQ/jS4NkBk3xmxb9XJGeqzC7W/J4+KbExkQd8H4R7I5Gmuyo2pUDvCNA0Wzz6Nja0WS/y3rsY/PP87/Pb3v499Dofx0TsOofGMVzJVDep6hqZdoG0X6aLqYIwgIN5ZAQByWt0rE4Ft7y+m3mw32HYdVtsNtl2Pddf5bhgDa3xZ53/c4um3BrWp8ouvTVC4QoxoyHpdxmDURoik3MpPxMaRVHiplZaj06BROmxO2hAGwZv4Qp3KLdolZTA4ebgoz4UYugYuejyIB4TcHYFwebXcleKNZ8jDLXFSBnthmqNxqA9lOcdoz+c4eTpPuM3BW4VV33IMzJ7lo1aO4WDU46OMWji/Qf6zRz/Hn/IX+A//9N/jq9V3qJo5TowBDME6CxgfZs4G5swaROWnCZ4SEi/SGAPq4U+iWwPjEPAnLSAyN4f6ispntRZ1aBmhat6Q52mNk9/KUOT5GQOwXLRNPtADJ0aYbA1uCN2vF6gen2B28hGajcXTv2VUG0ZVbUBE3sPNkgqpZgbt9/tHGm8nk8ZpTUzvf3n/stGINDKsrkjDhWaL4SvhcroTIhghXO+NFL0YJLqUPtLzpKzWg5hMY4gLc8hkF/MYjA8ITN6Y94D3jGDMNmsQb0AgVGaO077B1q3wsukREEomE4RgfE0tystUaJMxv/CM9LiqHl6hDOTeu4J74YEJcyGVTG0/DCXbyO+CbqZ17sO0AYA1FlVdYTE7wWK5RNvOUFcNDFkYsiBrYnimGFIM3rMt35wCtXPJaBVxRYxZiaAiGhKQz3G+6Y6NNwPKMxJAKD+EupN6BPeh8NtxTANVvy6bOYVjKoc6jv1NPECkIf6L/NQxeKMxokib9XismhArVwKCEQAYg9Nf/RLLrsP61RtcXq/w5usv0VQGi+U/B500xSjuVvzsIBh3BIrITqWIuH5z2iMcIYGExMMIW2Jg52eo2wWaegmia6w3awAOfd/5O7rgsJoZVIsGtjOo1kDEwbjBK5w8ouYR7hzum/6+D7hpoRyiqCnVnMPS4wrNeOWbct3QlD0MEIftVqmwgd/Cri1aMYzTo5YUs4e1ZNfbfQrbkWZX9jtA+dfzBr95+gj0ymC+2sBWnu9xQZYxFJTUhMiVl3LuTghMSTy4puWWWFrgvEPBk/x65EOD0j3woyk5I0O2KVSlxCsdaoS4PxDGVj8pGOrwmoyBqXrg2SVw3gLNKZgsiHtoHHcIXuYi8cayTJgHl9V7E4s+erCIvDHBextzfj5KGyQyKxan1wDSIQWZFB/pIV6YHj1ztMC335y9y5l19Rqri9+juj6HXZ+Oj9c7hIdhiLgDYwKzQYcahntY6u+kWW/VnvBPoSYBAHTOX8zkwoZz/eY54BiPm5/hxJ5gwQY1d15RHJS9fg0VRogbcYcxpF2F8F78O1ALaKW9nB6VJ0KotYI2Gi0YKVSDKJGTAiwZIdJvRIWCGB64yOt/63BLDip0DTNMM4edzaMhgpp20LeR4RgZuuLF9I6j0mQZinTDrKN6iInmSGLbtGifPMHp9lt8Wjl0cF4hzf4CY2ITvNU9jtiqQlXXqOsKVe3vhbA2hbMRA1Hv+thP2cIdM7Zdh67rsdoEQ8Rmja3rsen6cLmpwXw9w2l3gmZzDUIHUFJuEUid+h4fxjQv+jQrIh5FY8TI4GTk/hCmTOoQ7BBjglJu6c+UXp/QVWUIjsYySsWdS55BHJRqLqyhkDfieziRri9WlxN9PhyWeEQ41AuLel6hmpmwDmSs0kCmtmpGm/L+ZfMyNZCSyA1xPeAcM3wIGwaenfwCJ80jwG5w7V6i685Qo4KpLawjMKp4aADGhxeLpwpgvMEhXAZsjPHr3e/74SLrQcPDE3WqO3sabUb53GlaJv0XulWMRRxVMXwYYSj96XMYg+4xwCcWzdkJ6maJ8+8MmhWhZn/6XC6aNyEOfDSilIsjKseh8ApFW3XLykeczX3+XJjj9KlptTZCiAHCObnvJFyEnnlHuJQn0m2n9oXUhGxUo+J6qg8YwU3a8R6Ra7fO4pNXZ1g1a/xweomuskDlw9mYbhuJBgcGN5frxpkSMUDIF8pOuyT6pfea4dJKa07eZ+mUgSW+52irCKeFwr1GyHE8w4wOcGsGqMLscYvF+Snmf/IMzcU5yHojhPdGSncLUYjqNzoKmg7vmDeOLwT/kpGCIfu60D2oPT6hSaw34mdqgKo+oZU2tsmShKJvwMTpsMIbojAC7gYl7Mbm6QsBD2HuRfHJEEUEBTrqT41R2rMNYc0VHCwWB9Rwb3BbGebQITrC28FBdqgx1d/Uu7eDsjlTpecrc9gJBmOz3cLWDlVV+cM2waPIqf3LF2EAWwG2AahPxg0AuUeEquv+huBeYIxD2nesP7Cu3gL2WgQPDN5nm/fFgkkt/w25CBaEChYVDLqh6v7uYLTQ29U0ybfuU95Neq999GKF4SLluSnzA8P/aXEugkOPjb3ERbXEk7bBzJhwL6PcR2fjifrIXJR7nrBZtzxRPrjsmRUbM6rQ4eDJPfpqHO5xam59gp73mKA8R5BpDcgybNPA1A06Y9SaSQxgaRNIHuIm7Nl+3A2ED063+/XiPYwkI2W8ZfjuQ+BSXDNyr9+YiDxklTR/Lo1EmESNE4S9DYQhG++10O8HXLXG5uQb2G4x7hnxjjb/d2+ImBrzt+ywg4WDhcUGVsd+fivYXcbNNYxvpJ0jbBwA8vHSV69/QI0Zfrb8l5jbEyxch4rXsFUTTgVT8IgQhRWGGl0lfBOpLZzTS60c0VQwN0mo9FkROoySSh0VCj5PMCFEb4aoZIh/4bSseEZIw5mDE1ZQSKg8sW5RkkVlWVDgyslxdqjmCzSPP/JN00q22LVCqCD1qZQdA8gMDjR8JmVqrURWwdgv5HXtsQbsfIb5/FOcr7/Fz2vge8P4nsUrwp+Sp9BGY0wwRPgLquWSalNZr4AC4E+fEnruUgNCm3rnsNlusd12uF6tse06XG/X6FyPzjnYyqLiGvPLFk9fn2O2JhC9Dp47Jp1o14pW4Q1IdV0U8qFyUTrJ6e/MiJVtDcrVkW4evnzDibuAMhzIlOp7T3T+4i6RgMe+DBV+jJPnQjRChJA1YH+/A0KMeVmX0cim8JtdboTotSEieEecnMxx9vEihXDSYziiSJeRi5u1DMhNDPHoaI4r8Fy44+Gzx78EU48f6n/A9eYKL35zicbN0KCGNQYVPE1jCx+C0RiwSSeMiSUmf6rGwITQjYHBK5mHzEtMnpf2/pyGCUuUFPT7iBYUmB4vMBEBxhqgIuAXDapnJ2iXj1FvG5x/CVRXBFt55W9lbbwTAvBrJB9nGtQXaaVu9xgHJU+iojhD2CxfVBJHOiv0VRshBP96ZYRQF1Znd0XoC9rVhuRSOwZ0WD3LSezu1SynzwssVPmBqrf45PkFVu0ar05X2FQWaBqQ2wKu8xWGuyVEYNA8ZMSLQeH5i1HcYgzCMd0Iwdownj48zT+y0rPtiAHuGHhZo14usFicYPn0EZpffArTtN6IbEy4K4KU15p0Kve30N4zQl+i4UXqjoaF9E72+2S8EFqb8G0X6cl5kIBHap/m2B6Oz/IxuwH0YEcj6P6g8ZTVP2JE0EKVjNsYbifBJ0cu0TMEKgMiA0MWG2qDgEsDfPypwX04sR7hgUNYXEld6Xmv9XaDxjHqusG261BVFQgb9H0fPVSjUqVqgYYBswZMOqHpywdKfvhDhb33n3vK/2HCT6/HdwW3PV1ryKBGDYMeHTahrAn+Lmx6B+/YPP4zyX77FTGhWh5WcBOMdw7DS3APK5NLUnZvsJN7u9OaOtpiVfc4aWd41rVJ1lZym5yioRGp71DIOFOld47eCRm7yWnOMp7QH3CCgz+FH/eUibERmQwYMRo8wI1ImkT6kWqnMTCGUDUz9E2LlXgOhAMBfiwp013KnakuU84FrYUYIZSlwBDyswMhS85TQ82hhFiSNUbT8wFCutxaHiXdEcLBSOHQEfmRQ9fv+2HiXb3C6vxLNNePUK1O8b72vTsxRAytRyPE+h2McTRO3bqyw/KNTVkSRssUnH0AwNXrH9BtO3w6++c4ax5jQRYt96gI4dQs4glF73KmF2ZRu8JjHmgk1BaZNzAK9tkTtZ/65MXJ2qgQUOollrAIEN1sDDmTGRWcTxCVyoyojIjeF3JprxgznA89JKGZXLyIGqCmQbU4iWFtaLZIysRSqTjGJxxE60vBpMSAm/FnZ4p8DxtNL6/rs0f45F/8n7H94St8/f0f0Dn2Xg2OgJ7QMABYVLZBUzewVeUvDIbfvHvXgWHAnY2GKz89fp56AH3fY7VdY7Pt8GZ1FT0iwm6AxhhURGi3a8yuXqLut+Hy03D/hEkx3KcMMHrD1cqmPOxGUj6RSh+2ebUv7GeKSMotVuVLG+Ri9HT/Q7EY1KesBQnJxPFC6nRhqjfKhUsfPI67ZOjw/Q/rIcbrFwVvMExIKCbHqOYV5ksbDB2MelFF44Veu4kZKDa4Yv1Pj9LwQY6bu8Y6bMXsmYx59xgVn8KeGPS9w/eLVzBssLxeoqYabbjwmRkgF0I1maDMIwMGwcHBgIKROcSODIpjOPZGAN0qDkyLj1M2qrTXunJWMx3/wlRxwC3vfimhIdhfps0yMART1UBtUc3OUFWnOP2qQnNNqHvvOWRtFU4020DCA7NM5eCW6yFfJ+XcDE5UsO6voHNO87V3meAcWO6DcOkEqQuXUXMPx+Ey6nBXhA81FkKQsdyFkvDYySAW7S7nQvYYxLHM205lt7WCnxUNyNKIGGL8vLGF7SucXLfoGFiReESId4+Ja77YEBHtjczxXpxgQ/RrT8ZYu+2GdrN6Eu3Xu0QkMUYEZpxoKFRxHAKZd//EM/W+YQbesDJrZ5i3SzT1EpVtQWTDqaJ0L4uvhzxHb0JYplBTpE+xj4pWhvmVqeP0MMyni8JbNhJjNEiVSxnKyA91j07EV6lf4RvSb6GvsX8TeKI+opEnG+wsff6S1QvhyjLjRGhAohOIRjRpHMUGkF9P5CmN03nBIGtx/qufY/70Aj/87W/QvbnG1ZcvUM9b2E9OwFVxAe9oo3fTfhp82zUASqjee28YA71X7Q+DcAB3Wt0NBXOe5LY9eHAQ+1X26KG0tWyX7H4E2zksn1+B+hrXJ0/AZLBcnmO9diC8geMefb+Gcxs43uD61Wtsv32Dzcc1sBy5vFoImymqfqCwCwcPbfpDme27h31Holjgg7w3rYvbIMtDHvWb+lPuF7Ibar5z92g5MDpsYdHFIsZwekyyGS+35DHkQ/EvkfM/DIZyITJePZWv0h9UzUjiFJ9nZ44sxah+U3i0MrVSzGZ35Ug/x/pQjMHgx0ieA4f7sqnxw2KGF+0azeoKldyBiSCTBBmeA19INMEHKQVyOef62A0x4OBgw92tiVfTYYLy/Blu5yeqYtsy72kuZivDldSqVLL+BCYmdgBST7pD8TYXWucgngS5sYzLRHDkcHnyHNsFcLl4jK5pQRQOu5G/YzHqXwDIgT4WY5Kw/hTmNZOCTJQ1XJDNpJRyBDWl5vhFDjFggNe5vMnw96aqgqQQAsDGu1qEBF53WayfWDFnOJi3Va2xkXndKYbsSLcv9PU11mdfxZKnUKRencNu794P++0MEQWdKreifAvaH5TMtl/ihwI8Rh7UE71YGLi6fIO+J3x89iuc1o8w5y0q3sJWNchQukQyCtFpWaVSR0Y9SL/piSZ2elbKTYJjiJqUPBGK3HAgC0ZOPnLEXgaiMUJOQ3ojRCDJUgerMXGyBv1zp07VSqz7FJLJReVrVc/QPHoa6/J5C6rO+schcChjeEB6vZ+o3wMCUBQp7+vzR/j4/L/F69/+J2y+/QNa59A58hfHkgthv7whQu6EMMbEzTopFUXR5cd2y70PyQR/N8TlZoX1ZoNXqzfoug7r9QbGWFRVDVvXIDJotiu0Vw51VcEGd3hjKGt/zranTV+H5EgKLvkUrxr/D4V3paqyVABODzmXD5BuJEnKWcH5LKwHVBtUWsFtH5YmMEUsd0CkS6qDewPgOOxralUJ3oO9J5E+jc7IDBGzmcXpJydBEezHR0LhuKhIzVsdqUW23A9fCzIcQ9o8XpZXDBos+icAAY8+MVhjg7+ZXWG97rD5hx4zJpzXFtYQYIPXFzPI+VPazogq2aBnB4mdDrKA4+SWyapdOmQNIWJ3TurUYLD6A6mZkaRBSc1iOPCG0KhpJt9WqhpQVaGenaNpznDy9RbVG+8JYSoDYy0AAplAx0l/FmOn2ihGwl38Y86/pIQOFGksq4TphDsgylwdQszfASHeDh0cq9BM+g4UFXIsluMy7M72nXwvCp8ZP8aD8ShJ5VjnNVXI7PXwBiSChXXA8tpgTYTVfK14QZlLYS5ltBJdEQOtcy547qV/M4OWnO7RNCs0Rutr9QXVw3EIP1SbtJDDkRdIkBfjR9kQoW0WyhAxQ7ygmsgfdIC/AN7H1/XjFHXi2f4cOsVpJiMuqd+ajkuL0upTk67nO3te7N1SQ+QNlBGNxWgrtCaddtaeFnqYs8HKnpWKJZ5Om0Hqf4oTqzugPCP0m9BOo18QQOG+Gf1YzocZY7H4+c8w22zw5g/foLtc4dtvn6O1Fs+eLkC1UcOna7t5f4wi3tBSM5G++HXjIp2AW+S7q3i2A7xQNbxlAXvAe4jKK+0dq5hH0mUv3nlrDwICYHvG8s0KPSqsVis0zQzzxQmaN9cAGM516PsNXL+Bc1tcv3oJ89UP2F58DHCD2MdoeCj6/rCHYABjq/5hd6Fs3RS9elfKgXKDPgTuY6Tvosy3HZNd5U63b1etwgH0cNhSuMOr2H9ZJ4zPoipxd+2aj8iecfl1D+D8U/ExI+y3vDoMiioAJN4wM0aEh0GxKj1MfG3gBEf0naN9iHXRHoOi+LaxMoFbdHwcruoKvzs/geMe880atTrgIvcyMnte3ITnevsqeZWBEUIfEIHgkrorIsiQnhd3Qd8wbr4SXk8jA0Ep/1XDyi33Jkhhp6SurKKdEA+/7AnTaWXOFSNBI7jgT0/j+fkbXD9q0S3nQGVh3RYmjLAjxENrso4pHCBjCbs1KFfkOf/IsZfFRecnslb6FwXv7WWqGJYpLg8hKvlCiSOsv5BqU1wrBA4hq1nGRrMNFPQ8GWNf0hItCx0KE/NFxfhNgKtXWNdfx99TS9f09QM0RBwI+y+b913o/UDnCB0DjirYirA4OYd1FqcELNChNgQLA2tMNEQAyInhAN/SghIB3+uvykFh9Y2He0hcyPmLaHwIG092bjgUk5+S5BCWSZQEHJVXDI6nwznU6cIzvwa94lXyOwldw977wann1MzQnJyC2lnWhgEzMMUdfCgw2mxGjRZLPMJjLPE5bbHpCBtDaGBC/HzKTgZERaPzF5n6S6kdgD5Mot8ettyhZ8bGddhsO7y6usRqs8GrN68RphZtY1A1NZ68Nvj8j4zzVYp7T3KhuoRlEqWZKLd0L0TRykmZI78BjjgdlXxjTGAZs3HPMc1OBcjYpCZkStpUo8LxmCcpxARXdQgxqJA28fS5YuJ0WBwnJ48dB0cKX0bnHKqZxfJshnpeZUYIHVZK9y9+ua0cNTZoWioYDLvUNZwP8TJxzitHP1ldoO962BOLVbfC33dfYY4Gn2+fwpJBZb1HjbUc4uEDYAYZhiP2vhHkDRLGGE8PfGwn70EGChfvUmyuHpLkgZNoRn5KpNDWiMaY4E+1kPMhpcKaMdYCxqL/tII5XeCkf4L592eo+CWs6WCN9YaKEIpJQuuZUXqejBAJ/3dPXgohNpJOFMgJsRW9TLjswm33nkaIN44Yw4IRWF3GLvgs90Xkxjl1ep3D/OvmTW9N+0EwVnD4JHkGhOe5PrXqLT7/4ymu6w2+ffwalbE4Xc/Q0RbX1SowoXqhJMEE8OtRbZlR8Z3ucOH4TKZi2FX5Nj7ne+sYJDRjOSThX1HMW2tAzqJtZ/6C6qb2xmNDISyY8opAMI5RPm77T4vee8NsixE2o6uJ/mVjFHkHXWJa92lv18ay8Ew8fTIj7LiQ6KEQUu4YhK9Jgpyim3uCnFobv+CSYpp0r4dRKpkPEB6cdvTwOftgYJ+ufYBd97jvec6eCNvtBtbWIALatsX5+TkuLxlXlxu0a4f58xXWV30IkzlS2Ac4Bkc4wvuBu1gsnv8wdgPqu5xfL2tggCmoDiPfO9z/0g5cyCOsnkbe+SbIpIib8yShdb/0O2pNX8q2cv5urP6pNpTizqDct+UmeD/d3B5peuqwrl7Drizaqz8BzCMwIZO106EZ7z+P4AmfDvLu5gpvBFIKa86NFwLRcFGOc7QdMUpRKBYfkTUX2BmF7WmQh9Q7Hm3XnYISYzL8K0iAsRaoDGh5AXPSwNjUl2HYMS0TiXGNAGOAvo+vKOhD5W48ORxWonLWlp2yJkWWmiKhCfVzEY4JUBOhLAylMUG49qyLVMippSFLEt+ZsubeYDt/Dlev0Vw9htnO76zctzNElLRv8Esrc4bpf+yQkT8GOga2PcHWPnzNfLZAa+aYw6F1W1jbpEtMjdIKBMVVJIay2koBPlOa5t9US1B8+Ddjm1nc+Dh9149iPqleFA1IiliWE7IIJ8NTXenSSkkPeCOFKL78xiIeEVHB65y/gPnisdqQVJ8GG+9uxJtiYG4F5QZwkxX64DXhM1Rco6YG53SCj2mL79ng+dbAWoZlQBsi9Nixc+GUdN5kdv5y6g5eOFv1W6w3G1y+eYPr9Rqv37zxd07YGk3VwMLi4rrCsz/WqCsLW8kFvEpBAlGUlGOQY2jEWs5xSOPX8DSL+tx3wqSsUhEdlWVJSaaahMB+pLzKCMHxngdObRflmXPq1G56J2Ou113go6InkFw8LUrgamZx+tE8hmry6V1almoBDHjKqXHYc9gSCg/nYDgFI+1QXywbPKULkAWqjyx+uHqB/+e33+DUzfCEL1DDwLGFDZdaWSnOMCwFPAXDGAfAh6giI7TCgU0FMSREl1rVjnEjxGivo2gTGdDiLUKsSjIVUFnQswWqT57g5NsnaF43qNw1yDKMtSG9KBFNYphGtcocaGLiWrNulA1WOCTF6uc6YcRvKZ/TnSTy3QnN1sYIp0I3ifFBBAEEI0U0SKR6We0beSvVOI71H0B5KmdsuWfGiJA3GiNCYttbPHl5iqv2Gn+8eANrKpz0S6xwhet6PYUAsTgXRw4RX5IxIt1RNMg7VuDgguk8x66wTfKGxJg1Ulu0xxgDaw2aqkbdNqjr2sdLD6GXjDZoRM8cMzDsaiOA3vsz+qyFgbCHy74uvUq0d3x0opFCvS+9Gjy7kAudQLxiKBR+s+Eujf9daxvD3HLCc7nckFlCuuVtYNyAEgVEm77aZ02oI17wx6n8QeapZh8Ih269o2UwQkjn/Up5Dz4EPx0YDO2HN9Z+L/ZGue1mi6ruQACausbJyQn67hrrlUGzZcyuO3SrHluh6mMs6gcyBNO7yY8V7rJn+07yB4IM7xzeflzSbswwtoOhLRwq5GVrSUzxImqhlqYIVv8CI7wH8wTrpxjWqdfZb8WlDHjurOJbQuBrsupVv0b7eMgq2VM5t7cOb8+aNRuWdy4DR/6S6gVfoL76FGhqcB0O/yhDsvDlKuql1z3EoAfjHdibXyQCsYMhCQO6H3gZxQHhboLMWKH4wajWk7bueenxmKFizKPhLowTw1tZxtZcOBxTE2i+AGa1HzsDoM/nYPwcqYQ5VYaVcI+ivvg7rlKdX8uCsq/H5S7CEZAO9LC2DWCI5EEuikgUBnuftVDaFQZ2BlHo+gZQFg4NgPLaeCjQzV6jx2vY7fwBGSImoRy5n5YVohDl00MQYAzW6+cAb/FZ8y/xpP4UbV/BMAVPCDnVm4iJKJS1a1ak21EzoJVqUU2AAfbnHxjdPFmVpzLo3040DSFvVLTGC4RcVHSxXEzNQjrECJEUqv6nV/mkUExBKcsOqBpUjy4AAJYZpm6iISO2fnQz+5HhXcZoMOrlGR5/8a9x+eIbdK//COcIgIUxFSoriieK49n1W5DrU4zzeMrZK3h7DiGZ1itcbzb44fkLbLYdrq5XaJoWJ8sZTvoen65f4rQ3qOxZDPtkrIlhmayctlVePcm8AMTTrVAbRFQkqZ/IGa0BAmeK/SHEuOxlWTFfeCJKVFlLRSPkuX+kPBfgovHA31tSXFAtp3ddiqEvd0SkcC8J3526iLrru3gxdd9b9DJXsY2aueC0lAs8GYO3WRXZvq2faXIzlo/TSQFioAOjtXP8+9O/RMdAzzN0mx7uaou2sphVXplac4UQ1QgIH72jrDIiz3Aa5+CMgRkL1zWyDeX0EombHQFRAqZ/LWAMmsUpbDuHOzmFnS1RX71BdWlgwCBTxZPnuNEAIa6mUEYmRakj51VkQsYmJVqYGadUHwON9nRYvCB8ODG5G8JxH40QLGGY5A4UuTtCvNtC2LFIx/XpdFZ7hR5I1dZJRQqPuxN7XJN9NXlGSJnRGCG/hfEk/YDg44ym3yyMPxOiu3ekj8FDSX/Kc1Z/xRQNeFBGirGq37O/3scHz0sXn6UOj45CLDP/Am80rirM6hbLR2c4+fPPUZ+egGy4w8ckw7EhyhTbClOy2vT+nZ8EiwkQPW3Cm4SzBX2Cor2SV/KokjOvOY1nEEOZ8CHKAFyMxdhaK8943BdMu8QXkzo2xwFvRUDxmOGVrY+eLbFsO3z/5SvwdY/mr36AXTS4/tMzoDHDfWCijxJq7sfGJh3hxwkJnUf2d/i79QiAcz26bYf1egUiYD6fYbOeYb2Zwa4NuHN4/dES338yw/V5PabzvF/CcIQjfPBwl+tjhLmNQoUW7ZW8oxIm1n6kjOK58Pk5m6/qHzBtO9o8JnBlTdxXEMv7nxlNFPuc9bHk6wvZdqSSPX/fFg4sZxfzr4CIYCqLi7rGJ7MGZmNwec0g60AV4jSYIEOTsd5DngjEns91EF3UUCewT/tiNBJDYEeTXd11lIjhQBzCYweJTcJ5Rt0ei1x02Fh6Y8S71rOKDJZXy+Tw/MkbrE8NtstTwDahfUE6Iv3h7y1V9hgF2gDEmTgksoGsGjeSLRobyrWv0mU4EL0hVIeUgWI4L9KREUtQ6JfkKDHig2a3CdgsvkffXKK5fHonBol7Ds00nIIbafuHDKpzyVwgY0A+XIgz6PtrgNc4s2c4sY9hsYZ1fYjVXF5gStFwVo5lqfAo3cSmNsJsWY5ucgUZLBUdSlmXFLScTsTKhQ9KORBJBitPiFBWUl4lTwgHjpdTs2OQrVCfnvvYcUphzbpdyZw86PPt4AYpfjL9jkeH8m6Tu6XvvJ0tcfr056hX1+hefBsuuDQwZGGMzVz1vEKtB+DQ9f533/t7Dfowjb3rse17XF9f42q1xuXlG2w7h82mg6UKxAZzdjhbX2PWn6IyFSwFA0Tw5tFGiHJTjtgVmKiEUiUjqvCrfFYyfwX/OKhQf80MF5xwsGDp8oLTWxRGCI+3oswVnJfQSer0uJyr1pcGs/ylS6nFMCFGCVH4ynuxoGcK37L/E+NxW7GhRMHM0aBcIirtaH3OMw1EADuHxjb4k4vP0RHh0li8/OEVXr38Dh07GKpQMwJTCX9vBBwcEYwjOPiQYHKZlYORw9iBl/CEuNQnjK+oIRM3YDkoMDUhBiQZb4ioZwvUJ2dw8xOgbmHX1zBXDKqrqPBNR5mnZyGeqs8uSpe1kWjbqBihjLLpeVpnMaEyXGWeUuDo1QDm3OOBk0E4hhnT9D16rAHxsne9mpTQR5TaIJdMjzFqkD5PDFfMI0aHUuGrjBO+Yv8PBe4znazR7CXBh6hzcajE6yGuS/nO6pI05miISKM7Skn0ARhVe/rurzoTlfM0lAaNDAjB68Ggrhu0ywWqjx/BNG0Iy4TcKBO91xJPnZHjrCOsp1clSUJBnHlOnwMFQkFAcsE74VYsmYWzcAk/VXsyF+0bJUwZp/etaAzrIrpt63ceM5I3eBJ2yADLRws0doOX317CwYF+9xJm0cL86gw9FF6VS2AUr6bX2buBQ/msIust2z6e7XaFvW9MOgjeYszuEu6lCYGuef6pQ9dtYQiomxp1U6NtapitN6Cvzmq8OKsfxFjcBg5p9ofRxbegA5PwYfT83cFDHY/de7bIaxGiMtkTM80xjWlJNG9QsgciR5UizCh7NcJbZPx1xvkNefKRphV5igSKd8p6MmJsYC6eZzzR4MtEOyaacl+wR10Efx/w3Fpc1BVWG8bllYNtHWqjPCLCBcYiC8RDFrog/XNMf1w0TSvIA0cGOa8/1XhRPVP+MCq+db3xQIw6GRPPccWpfpcTktc5fogm9X0g9ofJenm+weunDdq29oYhlJKrMhIM6khlkzH+4KY+OcRJ7kq6RSRngoEe1mdKmBLwglWB2df0nvWzvKdFa/OeCa4cvJhEJsOQTj0k6Gev0fMbVKtTmO0Mb7uvvP1l1TsH6x1seg94sqRpHfv7IWBq1FUN1Bc+TjW1mHUbVMRRYRVjNQd0jtZbKspNWvhcsS8pJsalTJNClezqhFrwmVI2aSySYpa9MjCL38eA+h0pbXyfFLDxZDj7k6eoKtSPPwLVDVhOv0blg7TxoTBXd9yOXUaIAKadozWf4lHH+Lw5xWb1HL27BsiCbAXAX2DZdVv4rcBb4LvOKxP73o99F5Rr267HttvixZs3WK03uLy8AmBgbYOmbnGyOMGTbo5P3zRY8AkqW6GyFtb4T690TbHHdYvjnzgGhAcDhXrESd1/wVedUO8lU0zB2JAKLiPic3wu5UeDhWxfTuGbGNuSwc2f+04x9iEnx5VnkL8jIoVTEsODzEH0hHAOrnfonUM9szh9soRtqqR4kzEbW+Y7eN87I5UZh6bqVbxC/iWHyMhxugSYQWgcYzbbonr6Et9vVvjr6ys8tY/wufsYra3Q9g5tnbYs73EAoLcAAdZQivlMCOFnKDY5G4FsnKh4kNgI/zP8ZvjYtEQAvAcQmQr9MwP7aYvq0RKmbmGqLYzt/VowJl1+uSM0iot4mIQP+Z4GPa2hPL/C10HRiWanMgUXxWjG6tI35cnjRmi40/dJ9MnTTfBe9qOiebH98ZQKAgpwPIWfjw4NngyBsu+57YIGeNpsG/zJl49x1a7x1dMXqFDh/HqJtdngql2lfQUcDRC+zYw+/LneoYv3t8AbcNXAy1ToqofrLjFOUTCBEl1U5vhVcE+Ebs4wNLYdAKgj4BXBNC3a0znqpgYZdYcP1HcSA4Qf7zEaMWailbbrdVMKTAlXefT9FAg9TvQu0Ot4V4c2Pqg1wmLojSMxXHIaP+Kzu9q3b1/OGEn1JVJCAHgjGRkLfvwFqL2A+c0ltlcdvj4HZjNgXhge7ozm3xdMdXw0qe/NQwnRFKflhuaMvz6g40fYAQWWO88X1bW/S+vq8g2MBSpLmK07zNY1qm6FijuQM2CYg0KjHeEIR9gFh+w65cIb5W7Vu/LnkN/wu4TsEJrfF97hhnJ3NreQR3XuQm7UXclHhHe0ffhlIAtz9muyB9nBurLwbJjHc4+1cZBm5++7A17PcPrVI9T2BESEqmbMTl3GI4PhD+0ZgGCinDHexN04qg/FZIfPMpZR7qJLF1FPe79KA72Cm0tl3mhTCx2Xatt7PT+j5OmxZhhbgyvAtga2rcHGejklXDA+shri0/SFMnkG6l0mT8RvoUx1J2pMzxw9ivMb16QdlP+OXhHylMK03YTfQ5waPFHk4eEz5nsAMdan32I7f4n29TOYbnbrot7eI2J0Td/jSvlAJlAvGMeEngmWLMhY1NUSi+YM886g4q2PIR7uhYjqW1IEJ1rJFNENr5zafmPNar8pt3md5ma9gF/q5WkEsbzHM5BKISAhauIp2xiHHEjahfA1EvBQTPCo0KdOjalgT85A1iKdkLxhHz0QbsbWqUpKVdMeeH9TUTHd7o7JW1PVqKszLE83uHAWz3/Y4Prq2jNj5OPZMAOu79HD46ID0HXBEyJ4RnRB8bjuemy2W1xfr7DebLDd+Ev/mtqirirMqgYn3QKnm1PUtoK13vPCh/gI8cdBUbEV9hREDM35KQy3mxKf01hwkTcvLGcgorop19UhbvGCc4phK70y9JrKjBAZU5sUsVC4n4xsUGvFpTYE/I8x+TmFeWHnwz05MExrsbiYAZQuxc0uA9Yj945oo6Yruko5fFLwbDkoAxUzBeU1QMSowZg3wPIjwvfPV/j7519jVTFOzTmWjQNQwxhCZQh9iP3p74hwsCz0IU4FHBg2NkYZUH2NIz2Q58KFUDzBz+GURGSmCCBr/N9ZBfp4BjNrYV0NQ9YzP4YwuB5lZDC1wjvipKaVZUvHuNOJshOqc4gbxPFFCmWjFLuZ4QHp7ofoLSH3/HBuhAjl6HB5qXmcNSoaHgJXPW2MwATjPaJd3vnbQ9VbnF8uYXvCN84ApsbMkT9lDwJDhWSKe1DAJ2WUcZw8IGQfzSnHWGuKNkmoHUp9zPs6vnNnq0+Nq8wfAN+wVYWKWtR1A2sryB0lVNDm5HVJitGPJU7j3CTswMWbcgq9lPqiMCLGiJRG6GrOEOVtJnihb0pwi93XD8Z/pA7cSum8GzT+jxaYyJHvqjHgxQVgWpiqAiqDNzNC3wKlk/SPWr/6UDqnluS9NukANvPgMgXoxhcPENIicb03olfGoOt7dNsNrCVwBcw2PWYbwG17OO4L5vD9tPwI9w37ClwfEvwY+ySQcyD7rcuScyylyqmzycJIjNY8KHP8+3hZ+6UJT6f6eIMRYthe9Tk1eJpnSkLsjnYrznaiS2/D8+0CBsEZgF2N+s0ZzGwGzAFTAQ2Avgf6INNEEdwx2Cjd1K2bI30eV7x73jEZIfYpzeMgDzA1O1jBZS71S+Y/3m+wV9XvFgwBlkB1A1PVwfNcJCC1ruQ+BO2ZMMJ7xG+BPx4xT4TsUdGUQBk1skcoR1YbJZQXcvxdylu7DVmlMWOsxkGWnW8fLvTtG/T1FeqrRzB9e+ty7jk0008bOkfoHIONj9m/vnoFMPCL5b/GI/MxagsY570hfCgFAJCQNoK6w2iookh1EgZDL0Au0xYQhf3hZj26I+q0LKddtTI3nZaNF/M6ieGcLjgFi1ECSWnl5FNOjCvPCFuhffIYVDdBWeXyPXS0c+8byu3qlll3bm75uxYLWK5g5jXmzQzd66/wfLPFpuvR9T22XQe73YbYiQZd78exT04p3iAR5mG13gRDxDW63sEYi7ZpcXF+jl/SBf7Vd6c4w8wbIUwNaytYk+438bgMEEmcarV9hLqi4jU0IFdeJgROm3yePn3kjF9WBLHOmo8eJ8VWxG9R7sfyZYBUmJxs7UjMSf/dyb0ozgHcK4VuimcuYy35Ir733ujQux7Oec8IO7c4e3oCW5mwzB6GEWIXxG1aTaeyoeYMMAAxuzqFHxXPccE/B9pT9J84zE0DQy/xu6trfL/Z4J9Xn+Dz9RO0XKOqLdATGAbUEyyHuxgMgxwAY0LJFOdP2KF8PodgiGIIKRBgnDdsEMgzW2SBLxqYZydoPn2EZjbH7G9fw75g2CsGWR9/P2ew8sHSMS7jBb8Q45WwrfnYJi3scMzz4jmWFzj0UGeisYDy2lFhwJj76BURjSJhjWQ0PhokUlg938QxdnECGIG+YzpM04GgmXs9v8ION/0Sn7z4Ba6bK3y/+ANEAx9GBGJv8V55Dn3vQ9eJ4ONcuMfIBS+JtBVqSgXZu6fHYqqn+XNmgMmBYtzRYT6hC4Y8fs7mc8wXSzSzOaqqCWH6PE7GS469yRjlCfM7JSWCg0V/doKy8CSjmDIUs5+pmEb+c4mO4I5w6W1h+oScQKBJnJ+mkxN3gLqwL46b3CGSVQRHBh0MAAMD9977foS7gnLB3OPMPoRFcwOMUSsCsFp3+O4fv8fs8SnObI2+c+i6DnKPUQW/j39bAd8uW7yqiwB4PFrBEY5whLeE8jxyDpHzOqTAvRiV7OAQ59yZfs5FriEJ2LPCfZs7Kp6qXyLvxYR5G8ueKOZzGgp5OhOYtWy2Vzd1j95ubKbg5Zzwm8cEtwLaq8rzQSPViDwn4Xkt88Q5kiR77gvC11PpNhe6rENfyydRMjlo3br2aM5qYDFoiByS9AwYmfU4+4NDNvevBNB6Sc3bkzFgAl4+u8TVmcX1+SmomvlDMxD5VHJz0c9U9hjsvPqCCBQuk85ucZCCCcguCZcyFS2Q/uRH4Qy8EiEkIJ6QW/LGUYqlGvsZm1Ouv9SFPTr6gIEc1mdfYeO+u3URd2qImESku6xkEoILzhSlug3c6nhbqs6B0DFAjkHGx+evqMWpOcecljC0BqHzIRKMr5AkXrCOiVb2hfOK9H6CAaHLMw+NEIxyhe0eLl1pUq6m8BzhfdDOxLBRUYfAeTvCAs1ibwMw1sIuTkBVlRshANXeMZFkGF37/sS4sZF6i9ri5rM/WFhYmmNRb8F1j0UzBzlC3/mLjl3fx3sgAMK278EMOM7d2BzgL0buOnTbDn3XwTHDGoPKVli0Lc67Bo+uW7S2gmn8padkKBrS/CmBnI3TpLc8GV3iUnqlif7wVG7EIYfojZdtPrqowQUBsgmmejUTkRs4Uhuj10NWRngW/1IZrniWN0+dPJd7VZw6YW4A21jMzho/N0qJPDFc7xx21Rm3c89jDWOtaoIVTmmHGYVFhTmfoq96fHb+CMYAlTX4qlvht6++xxMzx9PqFKb3oZEcOTgC2Dg4R5GG+DD4iiGAjB2NoElBMRU/4BkLAht1hXDw/MFZjfqLMzTzBSzXqF5cwX7Xg2wVT537y9o5tmZ8GDj2X78YsC3RiDU+5jlSCH4q2iveOtJndUE7s4+/L3eaSGgxKPyEMFOK5ifPt8QAjp4SopwJHPOAGBojhuNWnlEb0HqFfIKDRUNg2WJ5PfMGsHkw9AkOhr6JQUL2o7TPIXpJRG8JqbeYA1KfY3NWtl2E5uGutsceIhWEe6aqqkHdNDBVA6pqX0YwjHmPtUCr5b4I0dwj68y7hwz3078Jt1K6+DbyHaz6gP22XoqqigN33kMhCKaj7Qp4PmqMKFqVyImfv3APjfTCOYA6bye9D4Xqg9LRytAc2Kg0xu8Rz9837Or6FMG9hyYcWvyu9B0Yl29WsFWN+nIF2zNM3wPOe0BYawFrcNkafHNKGQu6F9v+jsalrOIusXSfbr5/+Amvyx8xTIfU41FkH1V1k3qaKf3G6pt4MMLs77UObrpU4CaYVDQOn/GO1yVvNAgbUwqIN7Zr7DtjouIAO7XDiHP6FsO1NsB3yx5zAItrz9cO5BzVNp7otzboiIxxE6SyXBBi1Xl+QjACGKTQzaOlhDz6DrCJBtxynN49q64V+mpBBVni+gR4+dTANjXI2nhIq5TbBqXSrjSZ+WO4hxkAbEDhqGBmCIiZKI17eD0cu9HSU/4bJylapzAlp+/Ot0cVDxEI6NvLtyribgwR72oAd9Rh0KPCGnSIVX20CtY/9jjRNoSOga5HOJNGeP3ye2xWl/jo0z/D+fmnWKyB2eYa1iAoc/N45gj5dDy2KIhLKyeVUlODJEL6DUaIqAiQ8jmm06FDAFFkpVOzSUEsz1xsq4Ro4vgewRMC6IMiwTGDjUX7+GNQXfkTzfFkAKC+4G1Y6IfLjO+ziErFif93RktUaPHfPP7f4V/ZP8M/dL/FD5vXWK3XmaJ92/n7N4z1ccOtrRAvy3Qy/wRrLSqyqGdzPGkb/Cmt8JE5QVPXqGwNa61PYysflsmQj5kvlgFF6PUZ/uhRw8jwOX2MGMsyRX7AScniAO39ELf+GIexxO+yLt+eaDiA4HgIeuYkcVoPHF5wuJDaSSgl18dT5fpOFF90CleW7kIJf733GuqcQzWzOP/4BKY2ACPcoYBkhAh9HDvxnff3YWJ1ppyNCmOhc2nO5jjBM/4TkPNz6RZLzD6t8ceXz/HfX/8Rf2l/jc/WHwOtL4z6HtYCxlmAyM+nA8gwjEPwYgh4EXBTTLbeOOFKVMkUVoYJTMazOsaAjIWpWzT1AvM/nqN6s4BdrwFz7T3aSIwQutdpPISyCl0NyyGj0SX+TzI3QhMV/svzaMSCxkdNowPtdeLFo7x74lrz3x3kDoiirIjj42LCEBPHx0W6umvLzbCbFPbQMJ1Oq/S3MK7H/PoKa1rBnTJ6WPS2gusY3psJ6sJ4DgZdh94x+uAV4kJ/hY6B/VUgLlRI0GRJhfQa6ZFvX54i7fxlzpExQ8IYgjcOt7MW7ck57Bd/AlycgqxNIfMomCNiqCYTDED3SzPi1n1QprR3CQ0W3ARr7zo+rOx35NdeGhcYyA2zlL0ZpE+KEgoZA5YxQHWDp//2L7G9vMRX/+N/wPZqjVd/8yXmixnqX12AqyJm7lvCw9lRfuKwrzblA4Dbc/LDxX59VuOrf/sFeAN87PzBNGsIPQjoZW9jOFcoKcaLO8IRjvAOIZdpA2UgeacjQxTGCECt3x03CGXChzrUQMHTdMzoLxDTUkYr0rFPiuWmdhU8yahCc4Tw7KBFY+Ie609dVZZhF4Hjic8bKs7grgipmmXXw7x8iQss8fmsQR0u2xvIvFE84mx6snCXanp3HqIb2VoZHMPIhoJHCkntHvJwxS43UkkmOWlcpiRXjbR2uiP3Cqk/0gJb1aC6Qr1o0C5a9FUDJhP0sQmvJJR8xM+4vjUUtzmQD5tLXtkT8rKahyTTgBkD1Y8IgGHfF5XOTaM6zptoSXKIA0nWi40fx5WJiB2DgfmJMCZ35xHx3q05DIN+P2vnIQ09gFOOCMzeGCEroO826DZbtHaJWXMGuyFY3oJgY0z9qHAg7L57OSg+xnuwY2lx1JeoZ1ymGv2lRP3UQa3QFYNFVKpxamPSrkGUuPG5KHNcipUPAsxsBlPXsazpvXRqMzgMDt1Sy1pG9QqTpU+VNrG7TpQqT4Ups+G/WfsY5nSOP774Bi+2L8Frr1Ts0AOUDBEVDAwzyFRKERY2CQKssTDWom0aLKsKZ85h1nsPifyiU/UnG+dIPzTuZWiX0ePEVfEgoaTixKcWG3du1gh9GVlMERu1gWNg7IgvVFplJOGAzy7c+5COTad00XiXwu7ENcJyildf8M4gQ2hOapAB+l4MedoIoYZpomcPHaZWqQ44YlFhjtM416f1Cs/aM7x8c4V/ePUdft5+go9qh8o5GEewhmHEo8QxYIRR8fyHGat58oSTGC08HkSmUhTMBoAFDFlY18BeWlQvCegNhoLQBP5FPFMUruRNCs55dHYVQpRGCC4QhmPFYlDj6IWTjBDK4KyMDJlCeMQIkRo/gYPyeFQXzxlj7nlLDozlRB5tfbiB7OsiGAAcYLmH7Xs4JgAGYPGhkf76drg4RnGry7ZO6bpQT4PA78aOTFN4UhppUn+Dru61rYW6DGDYwBoLW7egkyUwX0DugCApMIyfvqxa77ODWTyAv9P70uj7qWW3s2sZJ4BMkXBQYeOQX2p/txA9gBJJKu0PtwIyFvXFBaiuYSqLjhhXV1ew3GPJF3fS9v0b8zb59st895dUaxx914r9t6xvhzHiffXovuGmfrmacPWoxvoV0F91/nCXMSBmuM7BVZ5C6+0qwhRTP1XZOxjkt6VFY3rUqTp+bLjy44aHPlt30b5kNch2ZlIhVPS+r5kKVT2prKw4k+Gp5R3KwUHTdN05n5PZGUZjxd8F3AuXcrti701fSoBzMNsOsxqYGwOCDvcs1eYV77IlvU0jmTH07L9NORjfahJO+yfvXZ26D1D6whagCjB1DVvX6EWeUMsqY9+LDpL+IoOkLQoir4hMDoBJ0YbIW2s6oJVRKaJBxJoS5aXuXGz2UqF0BkCMPZ3h/g4DBY08JkrGLZ7I9xOCd3tHxD2ONd3nPO4pLDoGNj3FU3peY1WhqpeoTuf4GJ/g4vojzLiDNb2Pqy8KAlIKr5J8FkpSV/YzCupTjU9lxGelcivuwaySpNPnTurIvBzS/Q8xhIdSYsHJSV+OigNRdkFOg8f4+t4zAq44bSsdH1CMITx09mx/GM5kRsMGbxPy+5P2Dl+szvHsqseqXaKrG/yu/T3eVJde+U0GZGoQWVjbeK8c14McoaYKxhpgbmHrBifnF/iom+Pz12eYoQ0XUxtY6/+MCXeaGIIOsyMU3UHPP8fvKUnCMYV6GUeRjAMc80hKlS37InZpptxCnXS7Ml7quveAn/mgK6MCUvsZISZ+VODqmPkcPCPkd5gXWTMh9E0fcL3vHXr57P1zAqnLqfO2T8OHsQIG5CsKBP5fCnFjNB6c4ByNm8Ocz/B4MQO9MPhutcJTmgMgGApj5hgdvFFCajNMnhZThmZgJJ+IkikKLYl8gtx7QkRYP95ie97hCZ9i+Q9PYH94A1z+ADgHGCOJMyGf1Z8Od6Rp5ugYFXRa8JaKhFN0O3niCH46j4/Ka82xvieij5elawNF6S0R80SOLSmGh2iqVYgS1/QmteK7wWXnGHZlcLqusaIOVy3iRdS9Y38/RPCK6J2LF8oDSVwg4xFLxCS5yQFmhyv5ABKdGrXVxOdjzEiiWcZ4g3TbzLA4abF8XKGee281f4m6P/jglXRprWUwcYpnV9BHnU4YdZEliNNJoSiAUMAA3l0qF/2LewCQ2rNDBtgH7lJtsiereKsK4jgSxX2N4afLGHUwQCxOP23Z5gj3AmMI9W75jqk1JrT2cr3Ft7/5HsvzJc6enWL1+hovv3mOV59d4NVnJ7iukbrxYbBMRzjCjxoocOMUfuktnaB1I0BSCIafcS2PS8aZNSIqe+HDwAOR/2YYlSkvw+tEdcx4rTT2+7FXlIbvWhkKzQ9RYIqCVyNoSFGJVTmk9nFtSuEBixaT7dr3kyCR/74p38EQCju4TI7zSIZQNQ2MtUBfplL6gKwCPS4Uw48SCOT2v1waKORu2of39XVKnjGUldZG1GX4A0lKM89ZJjnE8hYM7p1DkqKJLMgQXl28wOqxweb8Y7CtkDlCSHoVl9QMBihK3J63ZQOWOxqUrEjkDVS6DBf4XXLOz3dcO8gXhQnjLDrMVK2CcoyLA1AE+INrReQduYNCGUMJlOFiIDapmKhcGLZjf7nxxwF3a4goNwb1uLTx3c+Smii1wPebROo8xr0g2ER5CrwyHZGoeGVPB2srVHWDFi3aroJxDiAfuClEDFFlTxTOQDyOOUDTG3ad7CNtklwkG8s6tlq5eJI2hfSX1cBFCeG9gyhpEU4NGsBWcUB2tu8eYd/q7qZZZSm7SJCnrImcD/Gdw87bugbz7QKW5lhzBTaMrdvCb86CA/5+B2Ms4DwbZnycMNRkUNsaJ9TgFDPMu6U3UtT+QmpIKDHxhIjKj0KJlU988T0R+dQzYKgEY50lW7s5eoaymNUyGmH0xkZ38KjEcPma1x6XZEynmCNltJD1IYYMF4wTouQFO5Alr7yMxjzAe0wMm/vQIeJoQTfjc0VSx+cnN2pZ1JhzjdPmFNys8Pwl8KZf4cw1mDkbjRk6ZF0yNtHolN8IlPFO/gSGMcDMwJwBtqtQvSLQdQferLK7IdLfOO2LxgKVYGo8NO6NvRgaIdQ7RqrPo1nEx3gniRjINKHmNH6xjoDsgvPlfnIrKF3r5WcY9916IjU5t6naEZrOYutNV/7cQIM0R/KfOgiQwlBJc5XARbrxujuan8BwP0RaEwShXSP9YqGSHA8wlLTW9J6GW1uhqiyqisKWGph11U6C0O/UhrsiNVqRwLFvOWO+n2FjZLBuAdFdfifKjI3A+JoblqF7XLyR8S70J+Pl7AvD+kYPstzVpJbtvCtEYSAdmbtptXNIla+n21OAm+t8PyU9ADioM283C6O08MbU06l6MC4dg5zDjBkrx7hmxuvK4sVcfCP1pqvX0EibduH6fqh7J3DbKm6zVA+bk4cMH27Lf1IgJOTG6ZJNlBGVtwRoRe5gfw1rPEoTmimBGPYBGpzwLIuRIyasHhacjjwjjgenJz0jdJaxFwfozIZnR+5Hw3Yz6Hpv0QYCegK2hrA1FjOao0YdebfdbAh7WS/MkVfg66Be+0BJ0DnxjjfMxbSn71j9es9MByd1FhpBmbeBLETo28hsKqu/Y86gaxnrMwNuQkh1pywRKioFlV/knX7ByeDmP9O6TiM2xLSsGA3Feh/Ons5187gU5KZo/hgSjLVqYp1E+ft9rN33B+/WI2If2BWH4C5oayT++4nBgJCJwxma1ep7rNYvcXH+Szx5/GssNoTZ5hJViKkvl0fGTSqGBwiCKwdliNckqZPDSaGBqV6wUqConkRF6kC+zjVXUXmaJ/IQw3n4U7GZggrewAAJZ1HcE6HjicsdEz0zQAbtR89AdQuyNirIpgnGjxHK+Rq+G3JsxQa5WABti/777+C2W6x5hVVf4dpd48pewZoa1lZg9idk66qBNRaA8THR4fGvtQaP+xn+8rsLzNGitlUM12TC/RDG2HCyNmq4YrOYc5xieaa0mOki89BvrfiMuM1Z1yNWxqTDvPI7Kp6y5yN3yHDGXo6MedYo/9ypO0+G7FBSAEfcl9j6CJ4S3vuB2aF3PWxrcfH50nujhBMQ6cR5CR/GOhhsx2pMwIWCjvMpleurNXYzgFM8wgKnuH7yDb52r3C2Icy252iqGpXz00IA2BHYUHBScHBsswb5+XFDEiNtlceUGFkyFmQqnJ5foP3FU8z/2gLffwOAQGQ9VyZ3pEDhntD1cDeO3EeRTmKNjNeE0aFkTkc9IeIYc1xvKQSexzkXjvY7l35H7wjtEeGS94OPrx3Shuf5AE6xgwfsoJo/35WMd7MKw2LDHKrRW65m+PMvP8YPs9f47dm3QO1b6oBw70u4K0L6zay8IaCU+4o9ZsVbM8W0Y7SFi2CmFP4x8UdSujLg3ZK1S28BxhEWPxi0qND+skXVNjCVARkTDM4ppJ7sIboFZRtHhRVK7tGToNyIvL6AIi9jCD4cFg1P9KVByH9y+YS0oOLHkShfS7IVHYIjdwaqzvKOsbtpTug3CY4VIRJJ0ggNwxgC3h0c0KnRpHuu+Sk4lBYc4ccIaQ+6etTgD//2ExgyqC2hPz1F//Mlusak9ZgRnyECRmXDEY5whPcGmq7LwYn0QDNb8R8FrN4hpiXJG55FNbChEXlAydbhX45ypYuEItMmCfEg5HQm04NGRdT43kyqiTIQueCrDlQLN5S3eFC05GfOf49VfiPDUNZ2V/kJr1uD//wx4cQt8eerf4GaGhBM5N0zrlXrxCIfwPE7GTkmGW9w2xP8RPlykvyUDvJQeB5kgMiHpvqHd0VonjrwrLGOiSG6T77tDsCYCqauYE4fwZ036I3N5AYSBlR0ndkiAeQmXb1242pSulrAj5HhlMPzvwy5iSJ6jhTGAA555X7IVAtll2QndVGQccp1GuSYG40Ecom5nGKcTO/L1mqlD2DK7wXesSGipK4PC+42Bi3BuR6u79FUM8yqU1RbC+N6wFgQTKZwGIPc7FAqPPcbwFK5Ve49nP9QH+XzUXWZFJsUz4xBOr3Q/DoOYWpkwzAWVNUw9QzU1sFAURazz9yMj8m+s7ovSu5Kdz9oPVZqKTwFEmYIMBVQV3CV9Rendz22tMWWt0BQTBF8OAcb/hAuLDXGX/ZLVYW5q7Hc1mjIwrQEE8J6ZAoPYwatinikUahAghiOhod4lfgkSZN+5/gryqeJUWe+YfIncHqwJAbcabES4wLI3yZrRGo3e1WnrJcYrgpA3VYgSyFk08373YcGeXe0Zw8GO3CJ3YBnFCzX/v6IdoYZXaFbS0ghF2eJ4RXGkdVhz8DoAod0cAxEYSv1e0WuRY22a2G6LdBtAFMHmo6oBMwKzTqicHZAYks85EE++V62VxupS3qdjL6cDMcsF4eJsS95R8S6o9EwMdZSNut+ZO3VDGXR90EIoKIPw0d7wT6KyLJshr9LYdbN0FbXYT9CsQemle/SUGRbEunE0HfkJK+sSD2KSRsTi6bU1sPujdB/BszWoKoqVLMFbDsPdN0L8ATlxRaP548NHKf+FeORNYjz7xn/nwndUpg8UwnDEqOiPG9XyNffIUDFF33PS/Ze5RgXAm4WDXKfEvk63u44a4PXIzO85wZARKgai7426Pse7BjVVQduLfrW3I9C9Q7KHA7RbSnAAXXea+nvEu64JzcWtwsX77YtYzUdUkNfE1zj+dJrAN60q2jJjq5Mr88d8ONBqlH4kXfvCA8AvINnsd+Pf0X2NLkdYLiwJReP/FQKRnUg5DDPgvEy9LvE/pQFq/SjfNZUvaKmPVBleS+y5D5tUJ0rYWK6nAHezAyWG4vWLUNIUcQxjP7Ko8WKXKIKNNNNGC0hyhNDfmT45JAjzVP1vA/Yb+4GImwh/LjagVuHvq3gbA2mcMC00Jloz3EtC8XDiEq+TUupwJ3R5pL6N+3y+UoTpp+RMcNSPKW1Ol6NKjEwBz5MqqS+jdRQ1sWjv28N96g82rfkQ1D7Xg0RaWgLgfkmwW5XDyays14gI604GCLuUlZkvrR02aqfVMFfRH0CWy/xzPwSH60/xtxtYU0HS5RfnhosrBoJM6UI50Q3KYEOAHW6mvXiKQopvSjihdEcyigVWk42Ba+lcUhBtDNvCKSLUB2HWNuO4UBoP/oYtp2DgydE0k2PkZUjAEOy5SG5jtaPn4KbOfrf/wFvXr/G68r/nZ4YmMqiri2aukJTeU8HMKN3BGcAGItmvsDcNqirBhUqVKaCMT6tLVQv8YAtlLdLpvzUHjEIJ6mVokUxhhmOxjAykiYixojVHeOUryDIcftQCtd00oLT/S5Sc1Twciir9/gd+gPX+3tNnINzPUSBm9ZNKCd4ETnHcL1fA71j9Mzoel9Ozw6GTSjikNMbHxokhcDYyubic5CVCZ/SU3yMC/xx9T02rkNf92DTo4ODswSiDhww1RiDzgnTk7gdlsuQ49wiIFNiLAkI9z74e1VgWphvAfvNFUxvvQFCHCGirjUJR55symXjLixPVV+oe9INl/P2jAIj4qraNNSaS54QHO4lca6Pz+EcGC7sEcrrgRnMvf/dO+UNoTx+9LAJ8x4f6rBtJI8kYd6nMDV6u007an7HxFAYQJ6xLFcNZayTA+tJhB4GW2Zs2XuEOcDPuWMARtEk8RcreBRKdDD1L+Gai/uhqjy0WVGX0bb7UE2kfiP9w8jDaRGhm82A0yeY/epfwT4+h7ENDFXeiEzBOyIYJ8hQiJOcxi633eYnk3TDIs2PJwrJrxEE+k8MIuffkI6b7Nvrn/WQk24cQ/0pWSEMKhnjwyZkJw/z24j0gtXZU1tFzZGMMMkWc5g0KB4lQzxN44PyHSX+bmy72r8FMhmhfmLY2uDjX5xh89riy//6HLi8xsX/+I9wT07w/N88A1dvKe3eg7CceAYUuDW6uneXc1OawROpg3emurmc9wGUfbx/eHcNyVUOw7dJWVJupjs5igESZfRkv0b9aOF9d29qGkZZ/T3SHOEdwCEie9yDLQxZCO80mDsa/oyPyJ+IHsRLwTjN4CAwZnKj8IMAyGh+LaclkeMY2T5I6StY9piYLuzZKnY9a2an5J1DCZwd2pDvwvtQzCchiTgWphWrjMzSQcWn3ohH92QM+1vCCI84rFBD8TujwQZVVaNif3+lDTwcRw9uLnj5vKwk94g3u4mGrv1MBsq7IfLFDCaX9IEEEBvP444UmR1IA6sppCyNb5eJQzS6bd0bpPbR4LHWR1KULyOGGwKMwfOPN3jxKaM/PwHbFiI/e6kq4CUT2FpfEvehrrT4SC0T5hSQyfuwJNxhAF0mLyVmnwCQC/lEzg7p0oEwdUcIAcZPYsY3UFi78XaKJOgEGVlkFMrwTmiFhNp30gvOLsuIY+7xsHi3Y40J3jAPgng9UDislQcYIg7ZXcZz461KuLOmxPyThGlvCXG6IUQGhmpUtcWMGzQ9wbAQH3UiMVK18JMxOMGWGxDGqrxhMBSBG5QxmjWlSen1bsxhz0zK1nSidlBh+owKakCUXiCAqhqoa5AORTO6qR3Q5w8S7pDENA1owajnMzSra3+Jb9d7xWPAQWMIEiGMKdwXAYYhwsnWYN7bpMAi48MwhV1jsqVh6vWphSzGuqQZmb7MLjGGe4nzyJ5HtcyA3k8oNW6QS3WVg3R6LWba2LQmynI59kmNiYrVbxoL21hV1o/ZCHE3UMOihgU5Que8B4QDB+YnbPPsDZ1gB8N2wHMn7k/tA/p7EBY8w0Lg1oJmNSwszBVANmc4B2642Q9Oa6MkcpN4eNN7Qam0sDRzHtehv53a/9K0OrwTZbZetwjtzAyLE8tQlkK50g6mZpFhLMSYYhknxnG6kjy66A0VQroydp9MLhSPyJ/+U/Z1XVpwFRanMefyXCm0jr6EsKhdsQnxlFZprdHprYVtW1TLOex85u80QfJgi4p44wuPRiLPk2fL4mamTbe9fJwY+Pi7EIApxRYAsfZIGKYd1jrdonLwaPTleOZSBTLulTDECV1niZZTaDqGR9N1oui4+mEM6tNTOMcgeg4HRrfZwG1aiOLitvBOTuwdWEc0fL0VHMY/7lPbYSN9SOoPQ/R8WLDn/BaeUjdm/wCmomz6bZo8lecuyt4Xds3g21G1I9wvTGzckyAK4/G1mHNpFHPcVL4qMSthLN1oScWLPM3b6x+G9Y61ZDfzo3++fYseBjAT7LqG6f0BmpIRFbl5VIkAzfWL50iC/bEy4dperPBbKyURefDd9bxrGKeyPQM9COvGYH1iYaoqhF/yLY8BiimIAklSgu5d4i9HwqtCZChkeaakOlLfRIoXuSzqX5RYclOvo9mFkPhofWIwlnPDStY8eyxrFxRl3QETfvhhq9AS3dZD23FA+gM9Iu5gsT0UiDLy7Sc5kTmlvEG6ALhpGsyaORa8Qbt6DWttVAyM7pIQxVH4HpU/42EjBqsWGsc5Lr4sjIaUVyzuYf0hHra20DvOlFPp1G0qPyliXRoZTt99OjkZrxRc2sr9I0Gx9wrLBWgxxxMCzp88wt//9m/wzWoLwBMla/0fGfZ/lQExUDnCybrCv/hqhhkaVNb68E3BEOENF0FxNRXWg3VooRKHkzeD9kpQuSGZWb+LHy7mYeiNm3M+lgdfBs0cPuBdCQJ+I+G7rKnIFInHT2i/rJdwJ4TEnJe7VZxzsI3BxRcnsLW/LFfG7ca96qcOgVZse4NV73Aqp/YNAybdP9L3DEcEQ+qC35AfSDiaMRfhNbE/Ne7gA+mZz+eo/+IL1H99BbruQWQBY/zJcgjjopsoeJ48gFIIJaGfujmsM2dllN8jkywGhRBoKdJu6ZyTOw+Uh068q0fuPnBg8ZBwHL17/P0lDtzn90KweMFBPDyG05PCAd0BcFA9ThSmT/RnNdIufkW9I8C7tRRCSzDWSmgvJoCn4ikS4mmY+G+owhvDgOB4hmy2Ix0pldeacR/ydI5dOCDnwnvf/qquMV/McPq0Qb20gRcRA3LyhKAsZJOvh6ekIGUwyN+Fk2riQj2SL4Vi5ugZndyak1KBByMQjCfsx8LHc6VYbkzOfm07ymnmIXg3Fsu36Agm95Hbwi2Lk/HW4RnI1ug//jVo9gr4L9/iutriP59bnM8JS6nrNvBONX2HVRbPfjLekbXkgcEdo+Pt4d005MF09whHOMIdgzoYE2EfU0PMjUN0U6Mpp7LfiRw2XUh+sFrx+jx4tAeETtyH7Hif8qhSRoMAbFqc/uEZmnoGmlM8rKM3gPyuhfy3l58dHBMMSqZwjzvODmw6w3tG+HbtTs+csysclBjRECcsLvOYg8+dw6gGJ1uGnE0PAu/+kglvuELfVKjrBmxNysvC3ZOXjxGl0yif+RWbd+6mrt6oFzEAOQNjgqytZEKGjz6RdUX136OGeH4EcdApdYHISex7MyIKFVGk9DrkPE1c83Gy95pnHa3mx8YL7W2ISAN/6OpIiPfgYGo2BwK1PKTRxxLcxYVTgP12g95tUVGNU3OBmhsYTm5NpJQZsURGUASk8c1PiJfEMyFvvjhLlRaH/9POlhshis5mZY6UBXE7VMYRKV+XG75LvTEsk2qPqRqgskGRd3ebw08Thko0EMG0LSp2MJX1F9SCQSTxyxl+i6C4QRARKiI0zqJiA6p8OaXhbErFGNlJVt4yggfMw1ku8XrECMEa0XQeTiyof+4pPUv74stshxhp8S4o32vsd1GxrPZfNQ5prSAwR77Z+qQ5UNUGpjJhjUxdUH2EMdhggze0xlNq4bjyl1a5YAZlT3fk0vIszA04MTYZr6ooJXkFdAzqwhY1lrDoQLRCPFE+sCrrPVIZ4rR0oZiqkl/JfkYyP0L/ldWEdQYAybCrK1KGZCSDBJzgYsLsaFBzytCsBkzbEN8VUyT9v7E+NceDzBP8C4FgeoLZBIV3iBJA5A2vTFIs5eUp3biBqlfSE8GEC0si78mqjEz+SO1yga/Y1d8Mb0IZ1lrYuoKxBGPVfT6Cqfq7lK36FRXck8zxyPi9jcA0OJGch+HygiZn00csoZ6gJPnCvzUay4viJyHuGvGXL0bcudP+eBuQtZ/lzzavA0GPORmgqoGqDiGvCJ0lbO9AQV9O652u9bfp/wOFvWnULeGQpXavczeo6f4n8l7HdmpQHwh+7tOM+2Ab9+WOy/aN5dsnzVi6u3h3hHcFU3xDeFfO0i2R1oWS9tThRcjp565fu9p2QI0H9e/wwdAs/90B599L4XaQZp9yRmBiwRoiLFyLFk2eSIlPu4qWw38gpDBclHOIe++jmQ5hrMEZI6bS8cDoMGznrve5HpBvnGhd0M09y+rNwnpNlcrqAYGrHv2sA7UtoL1W9HqkYSlTT+KsEACWUK88JCc3KUfCsJV8usg8WUjv+CaFg0oihfbR8t9dkOumN67yJQ/bWybZExGnvKR1yKYPGd7xZdW74K7YiPuckNIl3GNRz4x1nxbT6s0PWL16jT/76N/jM/PPMAfDum04mWiQTnAWy3xAbESZm6WKX8cMEOW3MklSfhXjpOvg9D4q0cJlsMmLofiDVlglhWvaPMIF1SGMCgNon34E087B4dQpdPojW3kweGwUlVb4drIEzVvU9QzOdfCx+xwIHQx1YN4GImZ8eCYiGAMftgkEa8QTwsDHMlTaHY8R/kQsBH2150zhIVD8RXDKewYAWJ8uCE8FD6UOyat4gOzCI7VpULbOhvQhO0kbFU+6/GI3FDwW74YYN9+p/gWvECcXs7uE/85/73sXrpxgfwLiaIQ4DBj43j7H3+MP+IhaLPoW5PxJCOoBYxlwBMMcTrIDFB1qKMxjeC5lKrJDBB8Lkw0MLMzlAou/Owe96gDqEC8C1hpPCMaSn09wvBNFXrqxSZ4QqCbRQSwtCeEhzC+XnyNrz8k9Jy7c2cMal11k5jneC9HHdSyXkZXXmNzEeN8GNIt/M5DSroffo0JUYni1gtluKtSXLWixAZ9xuHLH41B+smesNawMEf53pDsmu80gfWPZ2yVfciEmIvQ8zsLHUhzCPTyAJYCsQVPP0DQzGOs9dYzxYfW8w4TJ/4ILR4pRW4aqnOCSB3aK4LGAPhoK5HhQPLUv6SnQ2PAsDL73PiIEDxSKMVijx4UBjPPPWZXnmx1i9aZqQ7+Stweyz8PgLlyj7xvE6EXZ/vxwYUgrptbVNDyoXh7e/INBY/GRTTjCTw0e1Ho/woHAxec+OZJcWYbnBETvUJaf1zilOi5zjJskytJLfnu81TdCQcBzrwhV0qTyv+Qmx+o+ZJco5F3Ovow0biR08KCq2+xQDMBiXlf4+ayFtTUMGTAckvN10jcNBlF0UOAoUxsJ+Ukm8oRx9A4Znini41lTOA6hhQBlOBgvLN4/IU84HZCLHgOkeOayr2ONgOanSNW/Jz6KrDQoNZQh76wBqEL99DWaT7dwT2ZwVQ1n1D0SDISrIWJYWilGeunTjuPoQFcfdDJj61aDgT+g5MN5ZUev4xCGmyHLDsaCDXn5I/fZ9l8MUYwwUDZEt03mLIU/HvbwVhfO/4jhPRgiHtDAT2k5DsSPhHxinQKsrdBWDaypQdwhnUMcb8Lw+QgSj37PS8i2TjEMxHKK2vbqY7EhxWYJtWVVfl6/fHfhctOULPwmA1Q2Xm69f3vuFh4QRt4ZiIXXe5sYtBY4NQwLDhumEEoHoA9TQICponI1GszU6dK42ZHGjLBTc/IW0EpQcPoNQH0WBgmNR4oZyk4DZEYIVXvY17I1Js2axPuJdTGRNLY51i29TXWUxkFJK3cW6ZPnzaKGbU0sPhZ5hGmI4+Px24GxcVv04XvyNoG/GsEEttkhhlACErOYGaGKbyYwaNwQ+KwCVQZ4swJte9H8IZ0GKS+jVXRRvRgauRBT75r7HK3Gy8gfhHXHxfpRZXAwkKXBQERCWbdO4zWnNeyZunJtkVIw+sUXluAEjL+J9xbcBCNJxuujIkX+XM6+GFOhoh49b+NTE06Yx8+xdnAqa7Q1YvcQxoKF908CCcexD8854d9olWFOEy3yLbbWwtpwn08YR0/PTURZXWrJk+QeAIlVLj/HYfptYr0VCy5tCR4nKeSS7DshEXEI58RRZpIvmUEDKbwUqR7G8qZarQdG9eRgeGsDwBA3R6vBrjm4Q4Xd7sX73urIcZazdfNe4aC+3EFbBQnuott3WdYdQ4nvd9rUXSc/dAi4I+yEfeZkX9b2AaPiEd4pFIsv/tzNK+8o4R0BD7/dm1zHiW0/POvUj30z3U2/QhmdJVzODFxjsDAGFZnIAib5Wvi7Me4UKo1SJMTXN6mydzVQyzYlDMudMi7dF+z2rChh2LDySeSzCwG5s2ts62tcW8aGz2DQIDcRjCkxxMOheCWVlEK4yAAsecO/xFE24jFXqKz81KbUjbKehEXyTOZY0EZC14puadR8oMoaNie0+5a4MDgYuyMdoPQL75sXPhAekEfEO4ab5vYW8+iLNLBVhXpxiqaZobYVLDsQa0VAWbjaLlksblrpcygiFxq2kVZOlidVKY1TPFUr/7GyUMsC19o/hAXBgNwaH0/jOhfilVOkWXl9R7gtJAY+aZtEyfZRRegbxivTA+TA7L0hCB0ARuccgHDpUIgjDqhY4hoyRWNgDBjZiWkdi96BA74IXnIME5UarvA9IEY0ZGhkjcaHxJDE1oSQHQNjRNbu9IIHCSYg8jQhj1N9DKfGo+eH4Loq2YW140+e+9PnVBGe/PwUtrE+7v7RG+JwIG/D7B2jdz0cnI8DyQ59mIAePrwSmLxFwh+WiOTK9XmR+gSHgYElAj9p0Pybz1D9A+D+8Q+AMTDGAGTAMEmJGhoVjW4MRTM5w6MBsMbp8mS6AheTp4xSvsLp/C4Ip+wM6p3j5LHjvFFCPCMQcBKBZudWMsVwjzRRr+O3PaHthzYpkjXT6D+UkrmohnnkYWQjpZHe04vIwJCFMRWsqUDUg8h4fLEc+mJG5y6e0AqvXKRR/t9B81STEq1mSPxVwCveM7IX/tHKfEFkfyG2gWGDuq5RN030ejBE2ae/rBqRwYYev1FIDLY+mZQY7PA+8tvBcBAFt9CvPDgqxCFaj4N+FsxAADlVLikBxSSxQAQUGbeRcf7wQPGECvxdGbLn0lD+MezH/wMTRI5whDF4r1gctRLvuyEPoglHOMI7gTJ6YQaK/6KYYvrAC2dp96gbiYt+a23y4GTZdFm5Yn1MRpiUCKYqH5Q+fFWUKEzmiLydEtyfkHrZEP7j5wYXPfAXlxI5JF2cyBJKA0i8oJ6jrGmprZ7nZX/aXfCFBxkmQDjucRB+rNTZSxMny4xeEcIXAyNuP7eCMZTN1xRlCblMFLTwmR93UF6+nL3A148vscGfAld/jmX/EhWu42FiJS3EvFF8kx9cKNiLdSbe0DHUUUgfQ28TgRyUMUJ1WOwdnEbSSfQA9l4ykpAo0Y5YjxoKR3IYzM+zgza5BPyKhpMgs3CS4mOnpZuqjYC6q2TcsvGT4uH3NkTcHflJgmuahXcMd05LQ2ecrDULW1lUcDD9FhQuNwF2E6fJDWISeOQXDwlM+MV7lq9Pd7N8iR8cU0EUMEHJHN8Up3DTc/9p2hnIVuCqPF+6ixDf3aTd31b6PsGPnSZ2osAjIsyXj3Cy/QRvwkW+zvXxjxjoHWDAaLY9ajeDiaqhoAwURRBkhsJGEzYMjviAqBzzpJqjAk1OVOtY+Tmvlj8fnGxAjlFxS4l7OY8bI8riNa7mLyaszxzbH/si/UwZc0ZOG0wYIXQTYr9I/BYNeW35EW4FDTFO0MeQTHHo9SfpcDbJUMAcQu1ofIwMFcG1QH9uUZ02QNuAaFtweQMHTikGgjOs8UXejaCYTjPmwTOg6Dx4GdP4fqfPlC7HW28ck3Ub7ouIHhJShqo5o//TsB//dICCZ2h9CB9DJfoU86afKlYUDEbjKnx8vcQbs8JL04XLnJPS219abeCcGy1Hypf7j5Q4OVL7iGmEAHASaCBhiggRT0OSnMaon/aKURHBnlgYY5HChoUDEJGKB4qeCPvO8eKYr8DKAfO86/HIU8X/DQNC6WvsSl/SzLk+tnQw5orhynatEl+GXXgreDvZoRynfTiV4djGrm+2aL+9Bs8rbC6adNn3AMbx9K7hrkrfrRq4oc6bH7wjKKnHGDwA2WjvJrwbHDrC/cKHKRul3eoIHwJMMA8Bds1iYhl5b/Yxz3cgluxu6mg9Y98PrW6y2vLhmGwwSJrL0DsLHSl/8GNnx27ba5+ztwiaaxP5YGJCOM4aksu9Z3q85FBGkHuS5jsq0SHK7D3bqEMmabwTV950cn7HwbHp0sG6HAxxOe6odJPhJJWV5xQYyh85buzDFPvDqaaqYBdzYLsA2xkcXudjg0wLlZdAapxY5J6bWk0pTFUQggisjBXDzFrPGeVX9Z6yb5z9OzYO8sZgNChZQgSU46rr2Fsy8tXeUpD4UO+MuB+PiBvX+uTUf1geJYVk7hzBdRUMLdDOasxdh3b1BqaygA23XwITCz0vMjPy7lBcTW02Kf8hCMlF/ewvK5UFHU7Rxkt6oxJLlF4uWJylDeG9iqfvmNFePIVdLv1dEUk7q/rxISHBQ4I0dunAgFd4n3/6S5jHDX74+m9x1a/RbdfYWsK29qeAu75BzQ4X129w2i1g6BMfa0+dpNXGiVwj57kh7xWAwiMCOa6ovxy5C7wNWuSkCB3HYymnVErmyoo8b75m9l0fyrCiSwn3YQijxDHSDccT5+Ul1XGNRINNORY34f9xjUj3Lwzjc+5g+x7OcrhrRhgGiQiZ4u0Lq+TC6Zo+GohCjlCuMcD2xID/4gLLkzM4M/P3TFAHhoFEmtRKTiDgQMBbjvc4hHelIWsfKNAt0XXlGqHwSOh2XIPqQnW/nrxXDuJdEC7eWwJONFp/ildbMfRFL3JF7+7THNPvdp092gkxBNGeELhgIuBss8Cfr1t8vXiON+drWGM97TO6z54OxosxOFGPZC8Ns1IIO/Fwz0iPopdkYLZFztF2glhHyJTxmJ6goHkOtGzQfNTChkuL5R6IdC8EQa758WWNBpoabWfGrQXGO/eQSM/znL5v4HCPAzgKVmN4JGaGoRs0QbAjpic5VUSI4ZtopP5Be4rPu4A7K+swzUeQzaJgJzhEDOD1FS7+37/B9tPH+OHffeYvYN8J725fUQ5kt6pTnTs7oNKDqznCe4YPS5w+whGOsBv2IMJ6GwrfeeK1/+2fTO1e8rxgpaebpkK25OrE/WAfHaA67F00YL9aMqlYVxjlSM7LnyyWJwaGU8jsA1q0/3MBJbeTgbUWBhWsNbAu3boWD/KFeYn8LQGIh6ig5jDVa+IBSh9itWdJeHP/Ep/KEc8oMluBS2VhfQukvbH8HGO9AaVEiiSn8E4jyp5zpVWQzBMtTU8i/huCqRrU8xPMLwy214+wdgswWTgGDMmRJckgCig/gDKTLBe5xbisg0VQtDeEYhJ9TqwgrHk1z0n+Db8D/orOktTBOm1gigIW5wcLTcS1He2T1ITsgG3obNIPvEV4pp8CHGCIuO0oTm0P71EquKeq5eQkUY2qbmBgZR0OFFYZqCFKSklZJMNxz40QPEgjyqhsE9p7+vRiGtnQyvL1xpd99b+dakRUqKhQCjzZtrtftT8ZOkAJ3ygQQdMuUJlzGGPhuh5dv0XXGWy3Fcj06GBQ9QaL1SnmbgEKCtwUOkR/Slz8AAE/HJAbHORdpMtK8Z79yfuUDhgxQoxxeDsmdbfCt2TeRt7Fdqi2FxdxJ08JVuk5Gdmy/KFN8dA5jzThqC05BDw2BhoV5yG990wix++exwo4qhiXSNOCgtUxwREBVQ30Hfj1C2BDkC1TM3A5bR/S46H2OCW9CTIjQpFxnHbqhyP7QqTdibZn6RnRuJYZiFkXUvStfJJrGW9MP1JASJlf6rbPyshEAVJzLg+R1NksbXUGhhkVfMgtMuEiZxeMDwTAuGCUD8yvMhZkHuOAdx0u13dox7APxXhKuazU7pnQmjrEIT0D2DpCVdWgi0egszOQsWEog8AUT5HJb7NjPA9Thg+zTuRn/27ytE6+pYy8ywcw6rAZGISKUoaLTPh6j/R1f0NZgbAHlL88n2FNHd68vA54pN3RHxjc0ggxLOf+51Sv7/cO77IRD6rj7xje86m4Q2u/TWvvmjK8H0rzU0bSDwX24SmUUhaich6DoQL1EC+5t4axbnD5Yow5vy1fpXnwnQJvrDdLxWW75FnZxj3l5YPe7ZFN8QFEBtaksEwpvKzIbAmiowM8/7db1+tP9LMTrn3fNntMG/6bGuH1WBTkjayFk/Vobwstd+5lxXprSDyy+CiMsu1xfghbELZMeNM3uF6foucFHBE2XYN+M0dbr2FNF+WuxKuXsuB+4xMPO02n2Fu/LyJ/dohWDBGuOFrKZU7/mW64S0/yxhUDlz0XwZNuXsOxHcfQTHcIN6CInsi3kH0fBoRYzFUNQwbNfIFqW4E6CfMgqVL6DDjdxi5qorG9bB8jBA8Wwj7AqrikpEq1DX0wVEtVY7VSy/92CCfGQ9tEV8jFxnKE2wOpL9oT0RNeg2p5jtZ5q3a/7rBeX4O5A8jBmBpcVVi4BZ6+/gwzNLCtjYSwCNDkQe3GcS51nHlwULhzwO3ASGgjwwB3sy0hfFOMU7lJ35pQcyxSoyxn+JvWUTzhPjCQ6P7Ln8TcD/dGhI0u8xQBB+YlrTNf2E9n47krYMjpf2SkiZRhCCBEVwljCtJIac7Y4y8ZA8vwXhRUga4ugTc/AJcfAfQYSRGcB43RxaY7dZAhSsSpPRnOKZrLPJJCLZVBzkiLXVyr0mePuN7zwYmXhB9ZaDqenT4ZaX70wPK/iuV517itlNLKVVvXFpniKV5XhArDMSCotRYmhGYiY0BysYiMrYvXd0McXiLfHS9WRnAdLvf4tMy1ujy2Rugp+xNQhpHCjQWmOxbkE0rFWBuLarZE/bNfAU+fAFXt740gggneEBJyyht4RgSDG3mwPI8ILwTxjNBBk3wM1t2nuHbBeB5fhwGoz5OExmTGBtm2CubrfVDZOxEqbhhGWxs8/dkZVi8Mrl6vfL3vs9P3DD/CLh3hocBPSAlwhCO8GxhZU2F/9gclwjNhjBT/k9Iq3mO8xFHgkW93BkPm++ZqeJhknFPiwfeMDSyMDElmlUp0u4o2ZrJnJs0WDcmE5B3tuw0Ic+tJrrXeG9kYA3IhJBH7+xXTzCMeEDJBtCO4xCNTarHn7wPP26eIDjkW3dTCEEqZEm8e3ZZ9Y+KYJh5+oqyRF3JYjnWZsWhKdU6Uu0uWpCAApTsp4htEPh1els34+yir+Im5gsELavC6X+L16udANQcZ4Hp1CuormJMXME2X6lCe15EnZ0SFfrIg7DEHuhyFmnI/hxCJfCnoHynawWh4Up6eLz0fYr9gkimXfuj14sbpwUEQVu9PyBjxzi6rHhF7IzhYOBXuYu8C72FPeRvouxW6zQoX84/x2D1DxfPsJOI0Tg07QhjDYc7/HVUMcbEQJurZZ/wmqenIq7IeRjwFjkHbxuCnseDeD8gmabBYPsGaAOeusd1uYY2BsQyiDj07ULi8FYExJAqeEfFUbXF5dWAURPHqTwdzCFEUlPABYfJ4fZy1LX+2qxcJ9MVDKU1iGnaVUuJvZhLL1hWrz/xCarDycoB6rjaSaMRQ78VgIesoWyJH2A8U+pDCHfmXWeEHI3GoUKRPOAvPIUXy1NkOl8sNaF5jbirYTYPm5RK0qhELkKzx9wChEhnmOPv+VTTA7jHrGRkvjRCShlMdEb/y0jUtTvtHepfVFQwVuu6Is1MNBLCbhvMN7wNLnHlDjGxSVHzuA5RNv+Zk/U/2RgcRgESBDwAwPvyPCelddOklGHbhovLAlGaFly3n7CvDu4w7FjRUJwCDUUML4aP8U0RbgjEVqrqGrSyMtUFQI0Dc18UbQhshaKxkMSDsHtDbRMUtgUPbswcjaXbDRHsp/xINVffB2N9Q5u2FiSH+M/K1qlPKFwo37G0t4+W8B9VjkW3f344Tw5G9TRlvU0C2/oc8xN5ZHzh8CG18G7iTudh3bb6HiZ8kabfI/6BwYYr0FI08vP9jBT+onh/hQBioLyZFu7eb51vvhrfMOKWWmUw/onAp5UYuPhVDP1IX59/LhtzYwLviH9K8GWfxyasTnJil10EASZYRPlgUwYD3PIaJHu9g5BcdZyJHOlwEh8Mi5YRycoNBCKUa5ZWUVHhS3/5DFJWMFLKofDdezk0H2pIyWzpxw1YmikctJBMB7QY4B9A+AlVzwDLYXgO2y8aY4wgoPcwUr6qqGKCqOuxZ7mMy7Ky/ZBPAWdo4H8U9Gi7WKXM1NibjfYh2m6nh33PKVXPH39/KkPHhwTszROyCDg16frumjJ98vEtrhZQ1pVAhbDevcfX6Fb5of4FH7lNU1IFoA7HDRpelEdi1J4w+yJS6KU1U6B7a7XJHi4Y9FX5GFGGqkTG8km56TIvixK1P5ABYUcaVlOgIbwXK+QYDXCWD88c/Q3XyGN9981dYby7BvYOpetTmFD31UQlmYGL4jngx1ITQJhHkU/gi+R6wwCWciRfihvZNEdoxxmuQBtkeuAeUa6ZU8kz8knBMPt5S6qdC6MxjQodvcsUnw8foZxPx/yey19w9sGd4gMQXJIOXQ+Qew3O9ScipFkPCkPiFww64brZ4/ugSi/MF5rZGfUWYfduitlWMsx69hQo9qijso0eQ0GJF13OPtX26qempPBT6yYnci7EBDmIChM4j683pfcKltQtGug/CIRkvxtbpGFM8odeZ2jInQdOsMU52lF3cXVpWTCov0UvvMWAr4z0iDAHOe0SwMZ6mEUDkfAbHYDI+7ijBG73KplIKQySkQjPSDul0FSOEGJPGEsNwoq3DLZJj54iAurFo2xbW1rCmioZjQ/CemoZSZyk3RnAUgA4hRG+5Z0/s+2Nsz03Mui+pvB/igGbok0f7usfvqcB8+xNNI2O0o3m6vk0FfHvWYzHrDzni8+DhnYXgOMIRjnCEI7wT4JFvY4kmdbW3rPEgrmE08S3KGSlv6pDBqB1htKBCiZM9KhU8+zZsrPKp/G8nyDZo8NnLT9BUM5jGgOHvrnMhPFO6oJrgQJ4XNxw8JwxALpP34n0A8PyvMeb/z96fNUmSK+mC2KeAmbvHlplVdarO6dOn1ztNyh0ZmZehkK/8ufwJfOMDhU8jFIqMkFfmysxduu/ps3XtuUSEuxmUD4ACisXMzZeIjMxyrYp0W2BYFQrdoABc2OFM4cyAA+rnXYVSgCZmdV6ELwj+gO3pncAlP5jLTFJCys5fGMgZhmcDLgOfiZBWjDsBZCzM7QfQ3+1Awzcg3IC7n4D+PrbHo1oITwXJmxEOVoy5aqOIOI1Wo3CoQiT0e6yzEpRFb8VMPryuUgdofZB2DWzHOYgJ82Kb9Z5LdIEWHKX9p4hm8z3cGs7ccvgUoEs4dyklVqkeCAK+tR066lI4BCee5bpuOZynpvWCESd/lXZqdhQas4I1YDUR9RbApGRWnwSlrbxlBuz1Naj3h2k2SHTdjjPBL4YOlAPNAEuokEB4NyEEy+31V9gON3i4/xZ2cHjTvccNdTAcFgsj8cTFs1ZYAMoKitgSUaOYH8qQVYY0asEyC3Cm7Wsoe2bYtQlmKtZMK66RZkFE7WIxSrsdPKa3qp8dSE3A9RdX6NYWxtIvBzefDNpGsuTBHzpd84rlhTEg2fpLBNgOdP0GZn0LMhYUQxSR+rhBV+OWA87wSe844BJ/mpSQ8vcsYYBUamGewrxmpw0J8ky+UYYxocfxN2YW+yyGbAIDKr/8t+YXvQ638MBZDImuxPFUVsYyp9aMp+J+tqiMhHjlsyG/S2E1GuCdxdAzdr0Bk0PaIRa+DXvCWSmuZadL/AtlOFbjJPVkKRdid8DURq6c26KigRRQ2O+EkB0d2sAixg0xTpT991Q0SDP77XIUfzCZqkWnFwI1LydAYdC+/fUNI2Sr8Nn3x2hR9gk1tge/+gZwG4D+ghGEe7boYLHJEpZzOV/Tz1nlp8gxF9cP+vBskHMgxQvKe3Ya9rVhWS6/dJga1kW9pl1t597PpXkhcAx6P5nUNTlBTs/yZY/CBQ4H5VTTeLd0bXp2vFD8TZIAJ2B27S7X46eUChfkfVTxJ9RZDZ7s5CVD4DEIJerQbAqhdQ0c3EjIdxGnmmQ9GXRz8ic8/DFRQxkIsqKJTLteFnQopWPCkoqakPSDM6FDW/cxRVW1DEeANaC+B1MHGB/SW8LWUtzi6geBQFFWzeUQbpaQasG6ku1mi6ykTEKgUJaIWRoR5BsAzCYYiRggUgegl0VUAmJVG2lTMufMDNIZx3AffKo7KJ5uR8RzdH5RxvPyiS0FkkHX9SHOtAE5CYswVzluXp6/dod9myms4q4GiLZKJ0SyQCSy4sJ3znGMl7+6ewN7e6e8x0+s6AUWgYsKSsaVG9AzY3z9W9wPO/z89t9g3Qe86dd4ba0/hpqKHRGZEquhLRMP9Go3BOL4JszQuKOVmlNM6JHQ4F9rp+7WglxfaUOK3hGk8ZjZW9v1t2VbHTuQJbz+zQ36TYcxzIsLHAOilqVIW30sUCQaJX+kvT+UEssAxnmtkSPv/U4goFuB7u5gb16lEDcojEZUzINC0R8NECzXvux6HtTjz+BMGZq+lR0KE+Wy4FMyTLhIr6UuUNcJP6OxQu4zGu10l1djEDpEVYkVQ37oolynz5jyBSrI/TMqcrOITAT5nK212Dz2uHoY8O7WYViN3uagwxzBe1O5SR6n4G6lf4NAJahjnGpczCtt606PNY+gx1HSEExnYXsLazzvAZkXlBuPtTFiqt+egyQ1ZaL4iPNfZeA7DFKb1e0Bn9NkmSfxmk/Ep3LXg7/8HUA/gOz/CjcYfOAVNlwaIj59yM1y0x3aYAOeoC5tY8QFLnCBC1xgAciO0qOgsb6fhYeZyaRS2yieb+qz2XhAPBM2n9W/e+oVk+yrzNy3jZvZbE7t7MQEG0LGryaZhNNZD2AwDIhc5GerrlUyjz4XzYRrFieghSDe+yHDhK4E1DyiT7d/c+3zMAmlc9gkHrWaIbpLY0H9GjAdYB9AbkjnLsrnImvIYLCSz6MidFT5qw6a0xcXnRgDwyqZqfmxfk+I4ZmSA5+IwYqX1MJmSU+yXSlhjGeqvb9hFxBYbIg42ANpkhjPvDsR0pagpwRREMV/4Ce3wQrX+PX4G7zebbDaPcCSEACTvs2xPXw7OQMbV/Vd/pSzr/KS2unlq6SbmlCOKRWBeNrG9xlNEsVd/l68dbU+7Cnh05r+x9Z2AuM9zY0M3oqvYdDBrR7gug/YPnzA427A1XaHqxH4qv8Gr+xrmLUFyKjcDbKtapFnCBM50HQVUj5hlCxUWik80c6cLBQzIijf8jSF4rNpIMl+1EOt0G1qwsK6wwiWlSytD7WUnnP2XrzPfb1LL2lRLMc0R8FFyyHYcPP6Gl/efA27s56G0ejj+1MXyJABAg57ENwW5oMBYpjAOJI1WFmD9WqD1Tig//7PMPdrANcAGc9sxSXARD40s9MCieFRuBzHPyJmQT81iIFL02dWzwXvIk7KtmSZk2nOxfNbEA6iDkZJj4MOgAv47NJONj11G4u2Yt2qahsTzJcNNA3OKAVQNn/z3RDI10xC+QJAONRualo051lgmNV7Ow64uX+PLYDtagPYEZBwdcbBMIENgZ0+lFlnIYMvzLgcVs9ZHZgBFmGGAUNeyDLSzaqPJLuEH9I3frwpCAp9b7BeG6zvCN0VwjkX1mO+3s0h3RZvxLdIBOEw2mrIq+4rnu81InP9nJDwMp630ypNl8VJxilPqchYjwWgbRPJowtxnSkXvKT41gMzX14b11UZB9Q3Sx5laG4MjuwQ844E0lvNSlT3T7uu5CWcqawFFqGnb9l0ofNlH1azqXkYoUUizwUL8D0l/Az4kynmrPX4M2juBOt8HtizPMQKKByjiWTAAah4gQNB9/bcCJRpjsm3XEcZINcoTdeD4pPmOiJJFiOv5NfkPOB52LbXtC6ymS3XPEp80VizAW566GsypF8n/h+NPEvGrZY3qgxzKWUqURv2kfzW8MesGY+W8MfXHUxn8VfUwRgbuS5/SLULm9H9GQ/MnleNbCwljx7NB4rOiR2DbeBztUNl+H6JHB65wDBIRGFXhMg5XOIpq/xbfaj1F0hp1ddU9l3qtHQnoZFEmT5xnyA54vn6c3ya5CFVf6mYtRg6A9AIA+flF1j0/Rad3aGzOxA7L2fI1m4SvpmL/tG1SRecEX6pl/91DBBz5H8Nwvl6YYeD1JOkrDhvCzmEdQ+qByqlC4KG4Xw8qjHIDGDSzpREzq5stlgbP7L6FECkzkKdoUMlEhf3zUO6DwVmiDNedE7PiXE2AQ/Rb524I2JisZqqwEF9sWQhXFDGKRxVxvGUGY8qGcHBYI0b/Pbxb/D6cYNudQ/TWZC1KZOYDxWDlxB4ZnNfqlLTi1bnkyP5FITlL+x8099qr96Ub/IMn8otpC0CW0uOXNb/lLH5hcHeqZMplwJwwoQ1brCia+yuBgy8we7DAx63DtfDgDcj4avtb3BjX8GubfRKIM4VWH795qqcqIh1SqnEDB9nHsq7mmdX/SbLw/k3pP6d74yiI9R1xcRVIB7lSPWWusf2uYTRLApeVl4CrNBcl0nJyyM0bykzdAFkQ0sE3L2+gzXfwP3Fwo0e54ABRCvvASGe7D7AP1hhEAVNMDEDBnAB33trserXWA+P6N9+C3P/NYhu4Q9xl5iXwQihxrMVxSgnrYq6K4OCTzLPSMgz7VkvhgdW7+J5LBmdVkbB+M4bIMAuM6p52YDLYmPfp0OZi2HJHidhs6AUQBTO9LumWBnypcZ0p2ZqzdDrIltdmRh0YTWB3o24u3+P95trDNe3IPsIwmPI0IAsA84bTZzzGOCg+hXpByA4JyG99FhQCLPl70yotwGHcHiseLtcuEpLqlBKjrsrVj3h6qrD6sZgdeXj4VLc1UYZDY/dI/xItOIUbVGlV+z07Brepqlp5OsxkVIC0U2Mrjxzqcx47lzoB1Y8z4FMZvqGit7mJKj6FBP5xmILQVhaxLUwmPPuLVzetxjk4ySb1KUa/k+EZFOxBdONaMGyFXcpSI1PyfOY79IsPw8syisUOo+ZR9RM6NwZsjoYFpXxHBVJ8GwlTTXreZs7CVNc70epmlpeC91SG7RYsbDiH7V9nx0cI4Dob05VvIQThGd1F4qgKj4mrSZ8WLFR4JQcFH8SXxZSqbrl4kGr6Ozrkk1ssfjy2xSGp2RkZDWucqvZuXRRVbB8Fm5az+Inh/AuNews4z9/bXBHFn/9toOBj8zgJRTnIzro3b1ht7V42adnBkkvR1HvII5AZAjGGR+K16ld27FZgYcrCFXOP3ljhMjsRNr9WXeSUdcF/jS7SfJ14TfxdCnc7vT5ExWPOcv0ecNNlDSKpHE2sG8HEYGsxdD5MMXkRt/fZLFaPWKz+qDkg3xWOtUHFEqtQbVHCypBLvWiq0vLbNGHWYmx3wjgMefHM3LF4BDSyWXjJOYlwBG8MUI+5XS6aVawZM8c2sf5WhZlpQY+hHx01CrW/YAq6fNCoZyiOABFW3R9j1hKTjJEpOpME+snhycvy0u9efzmosARcANgeQVjbRD+ZJI3PEOriR8OWlRju6RJWtF0NMgaU04EdReXWVb3zSIzc0PMNIUoKQq6wIlQTn6uLJ8EQBSgDH/wEwB8dXWHW2Pw+Oq3sMMIsAGZFIYmfVwe3aNmAYf450vhCYb+3AdX+n4KyCqMDBc4LYa5aHiZyS/ifAjdFA8DvsyDkyB03xW/Qs8r/Iv9Ft/3D/gtvsGNu0I2XnLAMExC7cjVAIA3upmA78ZarFYrXD8YvP7xa2zGG7/LwqT0s9VS46wNXomOCl3M36RMasFGh1zyD3LvMWG2Wf6T64iuHPHVIe0IikaUgOcu3p9CqrPObcDCOdtgxhpHudWl874UIkTkz1bDLd68/xswDXh3PVbfaEaXgveNASJuOHHMCh2oLn2Z8V+KJIADufWG3FBQkGEIiUkOkd8UPZGsfI90pkPXrWCoA0UjhOc/pKHzwsl56VFqqxIF4pQULE33iPgJxfk38hVWQltzFoPe2bekT5Zm+zFUYVQzbsj7OD77+QNe//++xe7NBh9+dxud0/Snk00IE2XfjH7p8BLq/ix9+KkP1EuGS79e4AJPB9lSNq2Ia0ujp5Y3zU2wvuLGsyVFzCY7hffa9+2e9xN6nMVQGjJYPd8HqhhDFMKKWr/zGGFzdpBZYkjR4IXuLRXUrKrwnt7JlsHOwYUKyfKo5Yi02/VAiGoSAhsOymQxUsS9xYFNCx21qGvbzr7J+KHyOxqWMApBbyHcOjO67hHX9mc8PqywdV3MI5fKCA2ptiqxMvhAoxK3nyPdyPMYDiqOsfRzlMDaTWvkH+kLK6MJx1xRPKpJVlZueKwNZyw7UmoZvwnMi0bqSaHylJXdRaiMQj49cGiNjzusWgkyk9PhI/RcVuR55eqoNGg3i+EGgkXvt5V5l/I4KZNX5wGd0lBGnQ48czf/TU5W5r7kRLo4EZuKsFYr9IXLb0FLFTcJkWCKkiUfqaiQBHB3dYebfo2fXv0aZrsFPnTB5CBhbFIe/ndSUyHasVQF5ArY/Le8Ph4o1jFNzCxE0zHFZAuNUqdxcS8t1bsbdB6q/eHMYCTW5Mi6XaCiGxu+g3G3eMBf8Af7Lb7iN7h2PiK6Zio8OFD0d0j/MnGG59YY9H2HzdDj5ucNrO1ANheCqtkgylSlZE3jzOo3p4ezRohsDUhGiBjirrAex106nBjHyEhKvZR7h5wfIbt/pNJ6F9BT2Y0XU3tqGRsp+4lQduW+cor0q+EGq+Ea9+vvAfy0t06kvebFSwpQ9FBxqgoFsiqE8XAhLhMRgZwXzCSp4zCK4bB0nQ/B46yxHaxZhcPVrWzcySvdvJ6A1rhrg+wimBIA6p1Bie5G0wsalDW7znNfLpjRBPocBHuND7Qs2RNANWc/POL6j3/Ew9/+Ch/++rbZ8Nowp/iyltXu5Eri4AFIdOAwolQV0yz3ifjQ2WyX4VDdXsqePiuKfWy57tkKbVjrgE9KTPmEqnoSXCTIzwP2RYPQI/wpjHVbFTsj/y1d1nK2PypMP5pcKUJWyaa1BqnBo3uG2sAQwVgCORPkF5fkFZEDhHfLdmZPYEMm5zgQ+YOuJ5NPCDv6udaD5FIkSUQgX11vfQjVOMZo0O7AUw/DPqz88sqh73ZYr95hHO6w3XUe96JuM4xmqbcu82opAxeEhWhJgayvFG7M0RL9Rsv0rTIQ9DYZek/scEj4oO8FH4SPFptJ2o3D+Weq7I8xmWuIhhQgGgVlPtb9XPboMni6w6o/Jpxr/JrzPGGkA7BzhA/37/DTD3/Gm+t/At7cwK1siAhCGbECFCHTg1tUuyV+z0F7cs8v7LpsjWRQf8mYIN7cEsZJ8k7KgspQESYwM8Pe3qFfX8FsNkW7XsZEexlQI9upbBcXnIkDgsdzOnz2FX+N3o1YYQVrwjY848M5GNFmlcpABuI22jjOiRFiXT7HilTtOxXKQ0ib50QUMEnb1a4Rdkk560LcfFHyumxuhOvopis/fp44VocFE3D39Q26jYXtjJp3T6fs/aWAY8Z2N+DebeHsCOjzEuASfhh9PoT8If7uVgPevXoEvXmNVd+hsw7GoDDN+c2/Y/zMe9zIeIrBihmgRCwRCKi/FeZGQHsvh/t8ZYAKFSaHoitmiAPeBhotux8AB+cSjop3UdzlI/WF4LuPxyq0/nTwpreMjlVcHykb/RIN8blEUD3+Kuuq2ZqxDGcpyJPQHDIGFgznDEzoRZAYE/z4OILa11uv++Q48nAEgiMf+kmTUO0bI98aMrBk0Hcr2G7td2MaCcuj/xCfBetFVpeyZ9pvihRcPtU4zvnzxh+zCwaWuI/H416JpzEPmR8upd0nvBBlqLUfNK+29JvlWROQbcM+OctoJzCI29eLej/2jD/fDbAr2aouRpJy7RH8eroFKQkxB35XEY5f8qKZ6MAFLnCBC7xMOIBOs16ZWjmUmpTDizgXpDXzHJoMxYce1F2JB6urM5FJ+X4qfcUTtOD0jt9agz/d3eC9tVh/+xrr/ha06gEAbnQYnPPhTYlgyHh9mjE+uAA5GEd+p0Pgmb0jUIrbL33kQ6QCxor8Z0AGIJdj06kyD4Hirnl2iMYCIuFdG0rqRUU+BZK3+QeRczPZhMvSCevVPQy26Lqdeuy/zmtb4hbrn3YHiM6k8XkJKQBWEQqLEAxDedjSTCcm045CjctzLLK0XN1HHVBWG5dlgSDFcaiTbk92O/X8pYByzGDmpEsR8mUo3ROivLkUnt8Q8cQ9XDb95OJmpFFmYHDAdveAh/f/Blz/O+B6HXZOjIiCPwolafwlhdzl9F8K3LycSlI2IC1oWoFQeM9mAn9aOHMHSe1tmxdpNzfoXr1OSllV3i8Vlk/RAwXOSHX1fRo7htaHEa75FTbMsOT8AafReJYOrG4Ww0KbdTgNQRYpU3m1TjI9x+FBaXRYYoRIRZY4qOqo8F/iobjivTQvLUTyLJsQsU84GCKuv1ijv+7gRhdCWl2MEKeCjOU4DtgOjxg3o2c8M2OEitlY0dhEk8ZuxIdXD1jf3uLKWvhIZaPygklKYKe8hDVPFUoDILEmFX7EEgscUXkkwSLtgJD3pRFCx9EX2qt3Qshh1HJ2SXznXGZ81nFUc3pR9tn5oRI8K4+jVqoAk9VKRHBfzam485FTPSdFsn5zvn1bj69DYD8NwRiCc54nc6yZMa5aoLvZsf9mBMIhfOJ1ksz9GUFXZMYbGQyM6fzOHVjEuK7VX93iku09x/Jcf5r4ginUisbfaJSomqp4EfnlZpbHQyuM5mHr72RqUhdH65BnWkq5CKjHfWcJP9043PTszyJhxBCObWPEdOnHVr19Iszh3x723UuGJbWbw+w0GiXLd1Y4woD3SQJHgpo//yhh1y5wgc8dWjwaF++T8SFbeyj7eVJYwlvsTaNFjerFxNeLmZpSvt5XiUNh7rs5zep+GInwb7dXeOAemx9eY7W6gVkZEDkM8GfXRQ/sqEszgGGQM4BxMCz6jJqTl9prxysJZZpXel875yF3txLHFwaHcwnFEdEr9A/kJ6PD8nOop/UsS+VJjBP9urNbmI2PRZu1iPJvY7YxL/1qnteshJCJ5BSLC2NehgLR6Zr5pDHL0TkJQy2nbi33i+yov071r1zYMrTLqkUAON9rsARjykPKz823iLFm2pFXlceAt/Qtz/+j7YjQqNphC0sDdrwCc9mAAyfgE83VdpWEQFp0/Qqd7YPlFiDnUrj9SghtjdAJQnU259urXrXYa6WpVkRBdkF4wp0O5QUgcc/VocQ+vf5WedlWC++EnusCE3C4yH5wCcHLwBryYcXiAaf780s7IXLcrfX7MwxXlp/OJWR0Vk19IqTx4FMofBX8DWXnnuP+fI1koGCoKROVZ17PK96+HM+u1gaZC/qfAHHVloUXABjXo8MXwyPYbjFixOiGwAMafxi1KI/JG9i0NwOFgaOuR//mG3S3b9B1PYz1ijopMxzvnCAzRmgsV1R4ZrDrA38L3CvLEjxiNe8UDU7G42DoUp7lTjH2qQx1joXC90le40yIK0tg3GcSHlCWhlA/PRRaFZ7Oz1eDIHGN1uMG3TvGh/4BD52b/o4IhjkcEM1g5zzjJjtliLyxASlMG4Ds0GqhE2IIoRDzlMV9ngohSoRx43dedF2Pruu9Z7zE082Zj9gj2RPO9ys0++2EgW/JEslwjYh36T1nuBk/EBzOztgpV54zwCeqeBRzl66+GCJGsnjrevTff8Bf/b//hO03d3j/t7fBGMFRVp6FQOsq/NlTpyXPjodPc6wucIELXOACCTI9g4JohJhTAx2kIiqUgYr3lp9Cml2a8R5oakL2PppKNNvk2Xz28HbnFk7n5B8CPth3ILPC765/i2vTez6PGeMwYHTpgGJrQugmCryynBEhfK7ukFIPHnnMkFs0bHgves9zHmuQYMARvNpScUfB8BCkTlDcmV/KfG0gMuqaMh45PT+WNZ/hm4KsnAfdSQeCT+fHMWUU6Vq6Dj3ftKyp5NLMgTPWaUGTGlOWpE5q3uh3EFlL75zAhLmoMemmZWXfHh2DIdMZKSfDqUymxv25QUKBAYh9wBzCXGsDBCF65lnrnZqXwlGGiJP6ppjvRIDFCOYRAzrwHk/sY4trlX2CeJ1lShSUuOGw30rRkhU+MTicXx9Xt/biGRfWbNEVJanqDGVESERCCIMTR9ssD+W/mJXsnFYqtGt0gRJmJu5UzNomhIWV4t1ked7oQEGhJYes58WKqlVfuTCuLuBV9MiOitH5khs13lPXrNaF5zSp+QZMq1Ib5Ub0VzgvbVDPwwvEA31FWRa/yVuS5kpaUCue7zINjgfFFDCADRg34wgMI5zxW3rZhJ0RAJhcYO78SklBAZeFmiMDc3WHbnMNQ8aHZFI72pgILt6H7xT9FNzRNHRyscm+y4k/Z3iYypkyQkDfyyHWyjDBEl5M3wt2Z/VqIOQBvOBRUJI8SvNZ8fStKjWg6uQD6iBcveyEMFi5FeCAR7edFfxkp4EhwBmE7eMOBgYODnKw9VR1dd/6GkTRJRTg6XmmZA5pZcu6tRaWbBaKSHZBUNWRRY9ydYGIV0K7oMjgETBFk3kmjZSsjd3Z81adARyroD6HDaJsZZ1l0YmZm9b+CojxvwlxmAnGGDh4HHBE2KLDeL/F1V++AzqD9393qz7iZW0/whhRVO3Abya+ovjPgRkupyT7YP84L8nhBRtSDq7a6T3yLHAQH32Bc8Clqy+wDHJEiUYI+Q0XLcoiZ2pxub42oeTmZniTc+Fus7gJ2UCBb7Ovb50sKUwrDcw+gfqp+Xkl+kwBk8Ngt+hth9d9hxV5ucw59kYIpawlcRDSvHpStKlMdT2SviJnuSjw04GX4dL/fF/nCJcuqTmw6PvdprSKf5ouvqy1M4kNIpQpHFMyBSlbRfP8gKnbQgBK2hdVfjHvtfYnpi2GLr+VinGWVzRUEKfzrrn+spY+ajiEA1o6/eLZEh8LpGwdBp29PJrNmUI2tdZkxrR98ILPiHjJjHpCTf+vQdetcAWH9fYDrLWgzmSTtG6KINg0krXEpkmSuYR2qkT5WQ9ICqyorCr+QtrkdauIaUlglCXTX4lKRe6XEPsLHAMyUp5416T7Dq8x4Abv8BNGbL0hwhCskbMhvOdB+qIxUmKxLpRVojSaWXEm6tx6eB78KJW82ZIi1oKgZWNwiJUfznZwLnqVO3bZTqA6Bjogu4EkHI4ojViVx7FpF/w/DnJlo9y9/tUXsBhA31kMuwGD3QHMMMaig4UxBrDwjAjSYc9+TBFDw/g5Y2BtB2MciEYYeFpukKJA5oeUc5wTYIZhF+LAa6FAM1uCBxXhzIwQOY4BsZgSZ/W34ZlzY2iXg0PYzROMEDlt1/d5F6fiD6PXyYOiWMEmFYjBZP+s3ugzggcB0aoA9UcMYn+QXhnSRphww2KQ8MYIMQYYACMJH+ydAOKY6ioR4nga4cAlfyRZwIS+tNagMx36VYe+74Ix2fhfMaTF2K2myVNkhWe/h3appm/CG2gC6P8RnHWRHicjW2agi3NADi3Ua05eboTYZ6mlz8VJfiyKHmWVUAHTG3zzd6/w8PYe3//h7cep00cp9eWUf4ELXOBEeMkqgAs8EYhyvdBsFdf5o/RF1COiwRbEEooXSvGYqRk55/Hyb/Y2ZBk08uFzljGnJMqZqChTNCu3ty7HVZg6H1LUdh0Md9HRzzkfUcAYA2ssTHCyyeLwa3XyDJ0I/lkxvSGCMwaGLeCcP7+NXFAFTOkuyjwZ5GsYPNeDaSIaustPkzYlBupROmbv41Hy4PNwXv00x2qmEFIc5TJxzpKUtdxQA6mmiHMZt+ZUpmxnqcYkNk32TIW6PnyXlj90Kengby90JTKQ6pDKDJrXeJ5Eo1JKXiZR2Cv7R8pZ1UK2wk/pCl4iUOtGGuoPR1mvV7DWLs5ysSEit1C1lQkvvgOfrHp+R4QF0I07GAIoRAifSt+qWqWYaEHjpe55wf88uQj7yBFdErrS31Akfa6STlWFC0KST6z6A13fzwnO3p5FHlz7lEfCqBF6bGDh8AFvvWKMCEY8Z+NhvnWsbIbEQVSkVBRDsXpeaZTqhIRHeybfIbsY8pYlJmQ+D1aLvlLyFsyXV3SpnQ4xkSRVCmg9V1U79VRInut5uouX2IlQkJerm2uA3uD+e4cdD1i5EWYkr4gngoODcQBMTp8YEgEzKVEj0xU9QDyIfhoIh1VPVIoKnFrWFmXwlV0cRaJkpJCas2pFSeP9hYM3pgk3Ho3IXMyHMqcG+W4/eXoKPt2TE2+m+r6iaelxNJwww8DAOAuGCeFrKAmsIUTS5DocMiNhQsNhdRx/s+Gp+joyrOQV9UZIuy5H+PbA4Bsyfuu6NYBJ1F6IeNu+85T8WgNrZopK2Cs0Na0XzMppopkJ17fKGKEFjX2oylz3Va7AOASmOZysKlmhR4xHQIY4e9l7I12/2QA8Tg1+mUmj3nNpDqjeR+DwPh2e8lAu+Alb9oI77XOVFX4RcMISc2GRP2XQCqoTRrJheFhasi669X1Vq9lq8nySBU0s+flDs0iq4fzf/Xns0x0srMCZgEFwBDgiWBh0FEKaR9Gb47mM6ZBqWsbLFIYlKVG4Lr+zPYVJ9XKeCw5GI7TBYFlbAAiPGZ88hX40fXu2kD1S1bLKhVLdh8sQZyyKMyFjXSeGpnyszxqoelorVopqpGIm+jfKUA35VClFW70mol/2UsmDZUVne15kv3BdltTYJ1K1AchlnY/L91B1V00vytMRAV1v0XXL9zm84B0RLxMEnaOwD4Ihi67boDPe83a/ZyfniwgXvyfVb07iV29F+SRxrIOCVA6UFgVqVMwiKbC8gks0Ku2FTJI65sqDuK7i5yJinFeIP6VMvca00wfPWQOQIRgdmkkr37KvfFgbjy/O6zdllwA4R2Oe7o2UqVam5s9PhlI/xe1ss7orZW3lMR4OQNbPdSHyuRMPe0ZU+rowT5IS8hMw2n5SYHDnvsYtvcb/h/4jfu7+jH/P/4Db3Q2GbgewA1kCG+8pDtkyKDp6J5tf2IdfwmSUyDY4HfufI3VPkCtWOXskeJEmTzTqZaRVbhS9VuVF45rsgHAJbzl4GKUzT1wIL+Yi/oPzPPPiufg9EApGRRTozxOPX7Gyer3KihZp11PNq+0b/PX3X+Kn9b/h5/VfIOfm+G8NDDEcJ8+sNO7+puTNfeg7BlwwRgRbrXR3KTJlVTMAyB+ETfIb/oNj2J8IK9th89UVus745CYdTp3O4ZA20rMqhxOFT7tuUriwgHMyeeIUSDuG/O4fDjvVUAgDXNxnNgg0evMkOIZql4YQLdeoRIvngmwjT8buemeOpDTBsUDOijAJG7IcQ0YzZV7gAofCeefeBS5wgaeClyiLHEI/Sq1YkrJaUDnUNRZ2kefU3d6ST4HEYTeYwgK07pinQrcsYlYUX1/qctC6Pw8MhvDPX9xh26/wj9u/wmZ7hY57WDJwQTaRcNEEE/iY8nw00ixtvCD2hoVy9GNLguMlw8A4r+8yYZezKJGXtDrqmrGcd8vrEjSIpOTCMAba0PCc5wR43lBk31Bm1wPrDbineAg0qYgP6RjmwhAjGuvcDqDah/gi4rPwx9HRS+aopJiXQ12IFBB1SlprTgi6zfR5dcDzEmjOtVjxFN4JGgNZTdgss/Rgpgofl5MKfQSGmKDEmJeEGkCEWtMRus5is1mj73+xhgjxgHua3DmbDFKiJ4jWWBhjZTZjDnVY/8sN3Dw3lLieecCWibRvLNTE43RdVTovRHqJiQBjkCk+mgve5wHzI34kUi7xAp0td3/+hv2CH89aiDYIXedEdOrdL2VVUwgNjef1vOTm5SE4wmAQt/uWFU7qeuQFabxPxoKE+8kTPYasnFy4FDvJiVoQEdDRx1xNPntY8QbgFR7J4Tv+CTveeQX8GHZEjH4PgwthkyQ+KOI4URgzz1TQ4wgMnHgISnixR04IUOBbREXOf1njqfINz+aZ+raYf0lw8c+igVgYMpVejMuubEhjGtYzPG/POdfYyawmyWbR+wsYSS1ekDBPrbwJ6IcVru83+GB/BjZFiEXoDkgMshYkdF7xgnP/tTk88sZgVgKXJ8ppizT5rTkMmJ1BhxU623snCKMptzb+7DH8FHTxqVZoTZOzucCMYJHwzzhPl9K05kV+fZQNggGJHzvXT/vV9nvKKC6faklIQnoQL3WbmGAHgjMh+thcPmer0L6HC3p0T2UmXz9ryLdj4Kmx4YAqLIWX3qVT8ExKnaeA58SSqTIO7r0ZheiLn5YXwOHYtjR9CzGmsOsYF4BDYX8Z07Wt+VGeeHUqTNYy6VsjV5XX6YRCD/22TF9U2hHh500Ht1rhN7s7bNwaZL2xQWQy4V+jUw0yU4TKO1ohfApiMIvT0ETyuGM55CthVA9saq6AxyLUj/nPFOar5hnYJ12uFogDjggw1v9SMFKwkmMYKgxRzR0rG1Foi294bH7E23KvQNBFBc8dJQ40uUZdnzn8bzl/6bpydqE/1Q8a8lEQ2XReVCY455x8LihUt1Q8riUxCzChI4Pe7BEuFJzFEEHqqokEzwCOOzziChYDemyftrCseQSQRdcbf2A1CsX7nnymJkQ7fe0/vmezT6xstAaKUO9EgRKmpfICT9eIlk/O0qd8NcRDfIP3ePfqDbqbV0DYojNdy0O1Bp8anLNtU73o+1CwgeJ9+WVYCAyBnIP96WesHi3MzavoNSnWiJKYpnxlnJF7/0tYplhFlynnWBiMsCpl557H36ll4jAo50RmJFEKLWF8ole54Ho8G0LNC4lVXhfmay1KM5k3oXNe//YG/VUHszbpTIJPYRF6yVAyt+xx0zkH5/yOLedGDMPgxxAMYy08c2tgyAIMjAwwU8RlkMHmuwFf/IfvsBo6MNvIXzn1JxB8thEPxeaE5068WgpDgOCQY5UT5/jHMU/RKIYcWOchHuNIz51/5s+EcHA8+rnmvJLXrwP+HbPL8DXNU2lb+FcxcYcN0AGpz6SV4MkbKaghQBTQDVtcDzus1o8ALEAdIDsi4k4IWbOUx5LaJeaksFgJin09VzcTzugx4dBrKzsh4m6IcM5D2JG17jbYrK7QdytY28ddExABzsjOCFUMlXVr3VdVywSCeeCAk+kslgxH2c9PfaaJ9I3syJT0avmIeWVGifRCNy6vDfNh+NW2mr8A2CcqB2MTIe6CANK1bIu//RZ49b9c48dfD/jhr5+YV25UcVmyl9j/F1gOl/G7wGnwHOrnC7wMYAaYijU9vY1X56MqCrv2IlnNhxSvw6+WOmsVXes7zm6FP1yG9UkZWGiBCKjjp5SFauGpVeaZZl6D12TDuF+9A7od+scRPSOeXiYHVBvjHYAs5bshXJMBTbuE/YHRDC6cEzl8S45hrOeTjDFw4Rw3GAN/WATyXRFlN0Y+M/6jtM5KYxLPEgga6qLaqVuCpqayZ2jtCxVfuljEcTLZVGWCVBN5a8J7x/jBEXZkwRJJIJyX6ZhhY1sR+HoflL4qg6UrD8MrMXJUXxVNyVE61QdIuk+ndJj5romioo1ZPCW2RbmCTbBEeLkw9uZnsIBRDGSW6xYBpO4yADvC4zsLB4vNusPt1XpxGecxREidIrI9PwvhN45YmExNVEChVW1Z1g6H5KFIZKLFdS9wfpGXf57+4/wflFc5fc2VsvKd3gVSLZJcXjD0hKWuh726imFAFtT2M4KnEMT29REXJTOm6iHmMjPsYAfxtEX+feNT7emfxlsr94ESp8UGJlhN3MChE4b/HP67scYstJWRbkQBLCm1Ihi5cjjjDBhMQL8xWN10XkF+sUKcDyJC+VsZCwk/BAQFPBFG55dP4wYYWMU8EUZiDJ3BaHymdgv0PzMMOcDabFbNUbHca1seTmBnwdxqE3Okw4y4dRdcfyYPWOFtwlmHTAEc68bKaySV3cw7q0/xjKeXuVONCvsMBVklsu/Ki2bmwRgR5AMKO6pUccY5fzy1c2AygWElTAt3UmtduKaS6f1c1SRoEpE3QhhrkhGC0jXF7BnWduhMF3ZDyLlUOT3/qJANivrT/EVETVYpNe1FTNMc8Wegp0dt416e+cSL48qSXRByTcEw4YzBzozodoz1Tw79a6dYTRGcdUYHzMX8s/CrvuPi5ez3VD5YBAcUoVIe/lWZw/NBiQ8vYYL/wmBqSv5ChqJs5hIKtXgdOrIPfyFd/5nDYWvdtGR7GEyoZvcWzvpmTx6FSLgk03lQlfbKd/3tPI+6/NmRfE71WWuUGGwGsO1gCDDpcfyGTHCJJHG8CVp3qhIj8TpTrKD0Se3Ga8j4kD6ZhgJo9SOFAmrcm8HEffauwk5B+T+NzKQu0tbz61rj6BNhIIf7zgGGkrFIBELmZGehpHw/bm6WfV0+UjdF5tEPbAbtowxWyNqSX0sllbp2ymiBBtIRqIlDe8aoyPvYkFxPJqfEJs3kSwQavJPnGitcYbM4+7OGZiJFK07qhnOtMpjJpxz4maokG2W9+0AONjXWxu1l54Eje7FB9CLdUNK8fyYTMwWtjl674V4UATHefVQQ6Pzz0qKuNXzHhQZhulWnCYWfNxw7o1j9q7Vt3vvWWgtrQ+x8JEVWBGootDiqkCahxeClpb5cOZ5wvCcqGXEyeuC6DM/B4vfsYhYRp/V9sdDIs3SWRD4X4jy8wPmAkbyvR/bnPcAbfWgc/TkJcCHOv1fyWjvCn3di8LBhfPsbANcdrhneK0dvC5hEz4THakOBes3FLSPR1AnuSXASHC/z+ccKxxIuOaR8vWeK0F5lkAAUMkqcz9SOp3cfeDo/Zy4uOLZJWihruEpDiR61t33780SI1LpOyYFM95VzxTqXhhrMDi56nXHMB4pXMmH3gjUWZAy6zqKzNuzeQXRyMAgGER4BYvSrNVbrK3R2jc7KGVUi2gVaLsIc0gh4Xu3pR1xAaKumh2AOO89Q8SQVk5F1LA5itA82jJHClWO+PwtMtI8A4sSHMuvk+mwaeZ9ozY8rwn94TfjV9nv8zU9vsXv4GuA3Z6313p6apKfPh4sXOAPMrosXuMAFLvCRYc9yUsmoE0tQJubFS0b20xQAirQzTxM7oxnL6QYs0olOfpDzqVP121OF5RUr34Ngug6m72BtB3Imq7ghQM7xM2QSLy28n3hnVx3QLtvvUKe4G5w4hXpi8mX4cykQldKLuZHKe3O63Zpv0+4a4f8ZeCYeHQyonSQEgrl+i+3fvoN9dQdrXit5hmN6BgdjRF5j358UDC2sS4n/6vTVgO7Z8qFF9Gr2KaORFzVUdAtdauk4mteozNXLf9K4OJRSTzFCaC48ydaZ/nTvJPlUeGGvoOg6C2Kgd8Bdt8Kbu2tcP8WOiDl9vu771IXP2JnHFtVQsLaznuG6KRgjwiGSe90/puVL/yprS3O5mc6kWVgRDkImQVyLlGCvDA/ZLI/pJyZRkX/Lw3bB2no2eLlTeN9qdXjN5/iOdmq1AILgD62myuBQf6+/04zMsoUi/VviTqpTS0F/kqybMYl7kxXXkftBje85o8bFI9k+KsyTLLz1rLjAOYHZM0QmhGbyW50dwAZudCDDGEcDYgaRgSPG2DEeO4cPK4N+5YBhGyxQfZH3VKFTj1vMfTtxtgNNjBAK72qPqmILtybwkV6rb5MlLMfnrDoTjNdedA3zd2aJPA32d3y+tpRmcX2lfVUKhjHztkpAAIwD7ACMINm9nY2mLj+Z9dW8V2toUR1VkJwFARjjt40bY+Mh1dmBw0xwAwDnYKgDBeMFkYSGRFNAainUS26i5t3EWlOPw3GUTDySXDE2ij5GVNXUsznijdYsqkKdlCYSFOnmZKMpzmw2NFR21si5oC6LGRiIsOsNbncD3LgDu132BWcXp9ZgyVjkA3EOM+U03zP19jxEq+yy59HR5+1i7Bc/ng6eruB9YtpZS64t//vhF2qQWUQmlGLv4/TT3Ny/wMcDLi6XjU9r6fbPZOFq8baLa3IUTH4/zfIf/nxJgnOLlsfmV1l4wi0Bj5Zw3wEr7rByG5jAsbrSkGNMtVNCc4mVV2AseIaBiV4wIXWpTF7ABFVPw3oxj70hvyrb56dJeidFNLxM1YfgNcRXI0yvDtHWMmSckZxnFnGAVXLdB3qeTkyUBqNdL80TcqvUoSAzWsaYR/B0DPdkOjlrRJdFqDcNMPImLhQglrDiT3aQuXISjtKXaliuE2fwzvfple1xu1pj3XXorV1c3FE7IprT50nkqCmWcwrpGqbF1sp1AJTCb5y8AZeZALZA13lvRMOJHOpcPL2i7FlWdSBt/ZoyRgSC10I+ZZQLFfPII/HRfCxxUc4Fks75X5Y+esymXRN16BnEexfimvvvKaoZMjIR52x7iml/vk+TbZzVbhzxPc+8m0onT/LFsbTFe+MZYIlgye+IoLj0eyT26KonkJwQIakYgItMRIZLnHbXFFRYnfosT8uAN1Pzvnxf4lFLAVPv3SD1PM5jRqyvjq3P8fAAh3I/VCJTYe7I+QThb4xnFUi/uGr6XOA8wM6P3ys34vFhi23n8MEAV4AP1+c8w+gGBzIWw4rwuHb4w1cDtiuLARu8efyAq2//Gd3Dl3B8A0PeUCd4luiTnxOZkj+vDTKcj8xYOsFFKq3psT/HQZ8dUXNRek5lMfadxHCU+ScHuPjzegSPhY47V9c7KX49KN5qotNDOq3sDv+S+reEkm333ci+v4Wf5bCmlTlwXWddl5Ky5E3kQiMia1RRo2xbLOPqvcF6Z/D2boeHjT8lhCLtc2DnaaD/g6cDDAw8ghkYw1CMTOC4NgomyPkPBtZ2sNaisx0628HaPpwVETzDCH5nBAP0k4H7QMDdDZxdg7oeZLqweyKcNWFs2ElBkXcgYiWB6c5J94nTKfA65OFU3+gujqkFzwOp53jejsdFOX+H4eACPnJ458LzZDTTo5yX56FYO8QtSyNvRCZWyKqZJYWTivdMeJFjIefok55jGnTRHMqZmh95A8qM/D8U/vVHl2j6kuYgIDxnXkZ0mCmanMnhrYKr5wfwN1T85g2qaMKh2S6D1gh9mpxmE6hu4VlbRxOI/4SwpP6za9Q54TNClVPhIAxo4OWnB0tlsU8Rnqo9yzRrstOTnUXFh3h1wvTyEcAV76fwramBUbFxItuQsR+B/z8EiSNvzIFvz2uaydCc2jqVT3arWTfmQi7lRqIio4J/S1Ce8ThRiQjC5ZcydlvPNRjgP/wa+NBb/Pfv/hFXuMXabEAgDM6fVSU7ejsSXHBgk+QXOdvUMeDGwFMiOHqwx6MUaClw2IEFYiCdawDy4dSZATeGb0Ngd/JyejorwacXBX7eRi+PsfO8WNwlEPHJl+9iv8tB2sKfhVxmcesc81OF3hZZQuaZc6GmBuIkRGRA1sLaHqtVB9OtYn8xu8i5+uOrGd6cpGRHV4paLuNdha+WXdJ5uO40YVjuQxvEqaucRfKXd6OEJfXn+qUpkySclDKNiteDhfMZicEsGksfxjcayDI5KlxnYoULfQtQkOnJ5bJMmyi6+OgslPkktk3OqSz4dNEfGANmxv3vH9Dvevzmd1/gq9e3eGVW6PkJDRGHCQzPz7jm5R5X9vwXaVCydEobMydetvIpH1NA5jQ3ReycqJt6ocNH6e1Q+S8yI4NWbCF+GSaV9qxtQr3AJQ/fLItZ+JQZ1fZYn05C5sTmkuAugVIFk2KSU5VwyilM8T/pnjUe+afxuaRiedrmtjSO5EpBXWNdB6UWjh6nXH5dLU3TLYqNyb+NbZv7vMZ38flN/13gKUGG4aa/wba/w6PbwfAjVm4NIhNwhDHCbxWFA7bMeEsDHPmD25kNVgNghyWS88IR5QKfoGivxpv4q2h1k3AmL/GyCmmupXIKjq4myHuJ8wzuF0CYX/vyeV2u0aTmsX/GYayYOJEBFHOas5/mw8h4RstGSSe00lmztf4fAsE6A0r8YVo7ETbQcFC6izEiMNhO5CedN6e8o0447nqQnRAhzJJJYZuIKJxZQSBYGBiQ7QFjgWiomOj78kU57g3mQlPrg8/94vwiF5XLQWshcotm7qOj8pZi32av9Foi9yrdrCN0a+FV6etpVGeW2UGOgqUT0QCrK6Db6Yfxe2eBXccYMYDdI0AWRG1RYJ7fr9fb9IYXfP/E8BEU5x8HFN433pxHmC3F9qeDF6XmfUGVeUFVucAFDoBMQTFJjs8hMR8g7c1DVs+pSnPxm99R+aqdvA2cf7hcHGkyxAs+nGvfgiwWDB4D+NARdmuD1eMGq3EDWgUzhjhfsQET4M0QFLmIrDc0cx41/oQsNlCQk4K6P4xF4EVdZJfVWFFQzntld9K4LW2+yFZtXKHwyteD0kOdoJXxxMNzODRG5XrzZQo5b0wXzuygVPWymSL4hbGJeSpFEasRje+iPDohz3JtAJTnUkg9+5bI7zVQ/Dcw6qpgynpLCQ+TLOahE1916EdkV9vNma6Qt/EQyBn0vMbVZoP1aoWODOwBFP0gQ8RHFSqequwWki/8hsI/ROTDKRQC8JIa12QrWCKORMbJJStY4vRuCBT3zBziqUv65K2bef5WCueyZCkr3eufzx9OxdXTFdf5gTn1W0FeCf1hVPiPfaY0Hd++JLfaS1uepnPKy1btX1ST8qbN7Wg8zpRtUwsD588yTNYGB7U2zrNqHKaH7K7IDXz6EO9zMA+/eCjROhBQBgNk8E+//h+wc/9H/L/+8L/gvwx/wf/o/gG3uEp4ZACQgSOHd+Tw9v0jeByxMh268QZf/PQNNrQBWc0yRSScrE72jNl7eGiPGoVEpYFLvHpkR0SiuXm+GTMd0ZlTni7Qb4V3Mkdd8EhJ+KgCCDFXdcwKOQKEjvgfRU8myUpg58t5rKqSrZXVdN6/kM+GyJEyitcOwGjXGNfAQFs4HoNxgTE4v/thHLwn/xjOOxiDx/8Y1tBojAge66zwwhshLIy1sN0KnbXouh7GdOG8CN+Hxnorw2jXYNPBrghmJNh+BWO7nHZXhmXV988YuyWhkccxQo6X0VKDtGbos3W8p1nBcxQC+lNC7KqXdEbEHiAQeHUF/OafQP13oP/4F9DoIm4wA29XjN+vdoD9DuP9e/SrL9H1Xx5V2rkgNwUe8t1FQftLh7OP/+kWwwt8tnDBi+OgqTWEUHACA6YM10j6y1ZuRT71ZS4wTKypDQFvqSKuLdHOVGNP2Vylrfna3MG02A0xVUiTf1pSwX1Qe6FPZksAdR2MXcHaDgY27B52GIadT9AFj/O+B8GBnQh4yqmPWe0aL4CQDnGT2mW6LsDvCjdRFjBk4IwDRgNgXNgbIncBgINDCiWVsDbHuXiweFDxHQe1XDgN0zJrOtOBYj9o3CMysF0P2zH69QroepAJZ3kETz4vv3h3Vr+rKeWf7VSOcqd2dtbPoGTlXLDLHPPiVSkflzhYKgk8GKLg3y+7Uoq+zLan1AYHGb8Y0YV1Gl2dQjjNvXaBfQM4Q6pOgpPzJUU+vA7Rdh0sGdy9ucYrusPdq1tc3WxgbHcQD3XAGRHHLMBPKyguggWWxvlaFqJOlZhg2GKz3cB2ja0opf7liZDsEJ1RW6ZPypE4sbNVMRHzYtoVmac89BajSoNUwIW9A3TPHQOH9GGHHgajD8lUxFZJuFoyFTmbxeEZZ+8KVqxcLI5Qbk4ZI7SS3xuwkwcEZ2VnuTV44bLOauFoNSvmU7KAmukB7Mqis+SViBd4OlD8QNetYLjDm80rPN7v8G64hwOwdisAwI4e4chgJIMHMB6HHcyOcbV7RDeOsGMHY6y45EAOOtPbeyMswOUpwUIbsJrMZfVh7RmSIacy/nm+TpS7oZ6KCeKCUdJU59Dl6aCDfPcoduPsjvwfg8NhZ7GG2Tqlrqr+q1lTKu9Dt+ioPdpg6HuL4IjgYMGBERO+WRTmsgNCzjh36rmQhDQE5f4oEzj4EB7P+D9jjN8KTSH8TmD4LXfAuAYRgwyHbdYSPkz9NbtY03lKtHsGYlzYpVAy4dkr7QyhEsU+TXiqx5erMUf+/YFQ4oKuekLNUglSCCanVeFpgQzQrQDrz7nRc5SIMIJwbwyutg7rH3egVw7opzKLXyJv7DOsac+ybJYDeFyhn/8KPzVrnh+etRbnQY+zgFTlJYyC1OEpyN/SvPf3wzl76iX0+qcCE7RiL7Icj01tnNHrNNdVqpnzhTDN42TPp97vZbKnMuCqyu1spmTwPUlPgkajGo8MyJ9pRiaw+H43xOicV/Q6jjsHlMq32Y6SG2mIWeml8JHC40sCdTYEGQTDR92MVrZyT4pn9ZuuJcNSYEx61MxnUvHX86jBe4ezrHVeTvaqkX3Sn4xmwLh5xG4NkLGAMTG/ODZhp3oyQngLS5Th4i/HB7kswUpcqOdU4vt1ZhT6oEQGEbaqRmGyxwQFpGGRRpQyT+L9s3MjWoPF1UW7HhXtOW4iRiPSXhlt2aq6uBYGABN4O8IxY9Nf4bpbo1t1MNaCoUP47oejzoj4tGDv1F4AepNXTeOu3AZ/9/PvcHdzC9wQAAOJp5xSqW8Czvt5G7Y7NQat2B10IMjE1pZkUQbItcTeQ7wXT93k0Y2YXiZTKY6L4kV71rJL3zDa7buAhtN3QcxDwkFDhDv+AuAdVvwOxrh0KKpKSfWnoaZyUbB9WsEk60JUvHFK31AS6mLivVpFc2OEzoKye4YPwZPe63kgdy5b+MSb3Amz4hEYfrktdwWpChaLaFQ4sgPI4c1f3WFz18NJLKALPCF4YukCM/U//frfYzs+4v/+L/8zvn/4gH8a/h7EhP+8+S/Ydg49vgBzDzzc4NVo8avxA25NB8LfIjN2RWrXhkD2Io7r1JrXSIaH+IFSzCLR3JCozWgpvFdzSe9mc2pHhNBwJ/mx986fhpJrVszZAj4nMnTqc/8qvpw0QkxXyRsjar4vn4slI6bHIOeJg3hDMlYtGpPuRwZGRxgdwpkv/pljYHDAODIG5+Bc2gkhOyacU3QBarxVHf1uys6fD9FZWNODTO+lIrLpiJLQd9cf7tCNd3hw7+G6AWT92RCOOjhY1QCKY6Jpet7iedjPfygxUQ1HZnAIgmaG/wg8haSPDIjiNdjl46bS5KPaqtOSZ5iZ2ZQnYIW/2dcnQMh7+U6A+fKStxYAJnA4d0QfdE5k4BxjoA4/OYPbf3P47T/v8P7fG7y9m889tX8/Pbyo7D5X0Dh4GeULXOACp0PkUY5cUkuZlUu+pZDX6hf7gBckbcmG5UetTApOv5RbdSqVp1xyK03r5WT5zwkGtluBuxXIGsAZuHGLcRyw221hyMAaG3QRXjem9m0nGV7Ys2I5IgoOiIW8woGX9OeQEJwbAWOR3HcMjCE452AIYH2mQDWOmntH0h/IU737WD/X6yWl115fkSPstLilXc00tLSS06JWpWeJ2Ye+M4TH2wf86z9+gL29wapfwRkDJ2dDmOAcxr4QCrxhPOMWqgDOBqKemJyPbUw3CwWeq8dUpBN5O6MPIn2wyGDykmKehHA6QjUY3gDD0VhBqj6ZgKPkFYSd3Vqub8zPp5qeJzDlCZ8pZgUgnBcCbH//gPVDh1/9/St8+eYVNtdr2L7Dbtgd5MD2YgwR+wXecxQye7uo/JoEeAGv4w6GTV5TfbNHAVPZq5Yof1o1Uvhd9ymnF2rCaCVa7i1b+nxzmVNB8MP3toNdWVC3183uFwxTg5svKPNYMycYziGQP5jIQA6o5vhFpjRslF6Nuyib1PNogCoNE8VlnWuxjOjFmVLsxjxZTWWrta6sOLd+Ee9TmCV5xGrKNPp0opuNAUxnYricCzwl+P517A1tnTVY0xq/3nwJOIuft+/BAN65LQbHWPEO5AzsyOAOsOzDKUX8b028gBCTI8kAFcdoIbtrsZHKAAHJn/PPIiOOiNy1YTmyV4kOF0xahr9Szh601GcOAblxsJV6Ns2x4S647Le8f1oe89V6mmeoUjGYPXMJUNZH3dhj83CFezdix2HHg5yjzFA7IHzoq/Qs7Y5Q1W/UJfQXkqI4br0pY7L7GE4gNjDcgajzdY47InSr0cbfud7h1B/NLxbujGjjNhCNawFBU/gl/VHiQ+SbOtP9o1yvCOodK+GCGs+b62j95OAzM1p1ASP5WO0zchxeHhHh+m6Nxw+A++DXIFlHQQZwjG4AzEE28kPnMCdc3vPpcqPMPvR+QUryg6rS5oNO+XxxTh+xy17QaF3gQNg3dlOUbGnex31/waiPB3zMUpW+az2PfBKyX1TLyvFrcsVblnD6cn9AHZYUpZSaimed/a7ko7j54gAI35UDkkHouMB32Ic1CBsQW4AQHFY94+yMi04srQ5v1XIZR0pR3iEEpb843Ybz19gBcogzgk6PeUz2hinZX+GnyGFyFl1jQ4T3UZb2EQPuGRBrEtQEisy4gYEFG8K4MaBVl+SLINukGifH1UJaqVpUPZuSJfbIGPqg6UwuBZeRkmrxRjn7VdHv4zdF+ZJflFM4S55q0Zi9kn4Wcc8z9qXMPeWYV/LGkzJdFiWlIQMZr+temQ7X3RrXmxXWqw7GeMd6Lf8ugScxRBw6tc6io3uyuayl1ca7EDLBGKtiNCObnbN0ehEc3zjv7a2VImmXA6KnIodtNBzTAC4R31Kp1SolzjdGd/cK/Zuvgs5hYiL+omFC2ZOR1ul0R0GMfxcL87gbzjcBQogmCoqxmEzfSbWm6lU/18rOtJg3iD2QPDpjBXWRHBf25DkjE4yzKlVHRbBScCkFmFbWOlUvVhVO+XLxp4HyPmECSzz4UPzFDnFu0BwH4qIjIXJADgSD//Nv/3vcbx/wf/tf/5/40+OPsAQY12PsR1iM6BxjdAQY47cMc/DsiJ4emJyGGrfADMPO09T4TH0c8C3ioMLHmFnBy2QMTjyzR6dRuyFY+GtPu1OeYVePxm/O708lM7KTCmZiF2BTwVvlkt9y/ah6j8RIlU2Y0q1q8ufXLTXORaG392/wu+3X+MPVv+DD6l2MZzs6DjsgHJxjjGN6JkYIj4tFZQjJuT7wCf5wahO81/2WdVYMRNqJ6f23mCwc9YBZ+TSmB0wXvLgQDRYVSCzXyU49VSBKRodSaMsMZEg8B+KOTLmXz5JTxLJt6zOIwn5dAag+ozym4QOV1x9TeFwO3cbim398g/ffv8cf/9P3B1f5LGfCEQDwQhrgR/7jnkX36cMknl/gAp8YfBqU9gLTsGwEs5CIQY9CQHWub0nWZlTfGSzBoSxNxmjPcx7tN1xc5gx+9l1e8N661qJCkG+FyYpvCxkEyNv11EJpJqcTwB02334D6l+BrlcAAaMbMY4DnBtBIH/2g+Ns7A+tq9Z1xYoQIKHCmV3k1SN3bQDAwhFg2Xrvf55zINSLbJLLGAghi7SSHwGtS/6bAHKZDDJf3mlQOLdXufu6E0zXoevX6NYGplv70LTMcDzGJsWwtqFt/lp4+KLfq8lY6llQ46mu98Sb5CTHMV2mrtWeTmLwAkd5LD9HlfVowkWlaV5yrIs2yDin2h1kGZeiECgJKLU3uyhb93JWPRnjfCob2K5DZw1u36zwhbvBm1fXuL1Zg6w/MWVgHEReTjNEzMaQn4Dn7t9TiO3cpwy4cYuH3XvY4QZRbMu6pLVszmu3jkLBvW3UEz8hf5r79WSN/+7JOo/3HAgCEfweN123i3TkYb5Dl/bQsnRNrQsyFUNA2lKBePJINYltwMPwqFoQZXEj/V2+2IdjzWKaev2ifDqUikqF7xXLp/g2bYxotwszk5WLy5exqHxWELkgBRkT4t9bsuhsh//u5jVed4w/P/6IwQ0YA9PUsT/j53p3h7W9jsxiYUv2GRKHIrXJMNWBwdW80cMvDExCwdKbIiUssDa1SUoq3O39AWyMDInVfBPlcMacRTxPdD6zG2sv9inYa2VfQkkaNOdYI0Q5XxcpmBtrEwN2ZKzdCLvyCnO7JfQMuM6r06X/oh49GPSbhseATJFkBMEkIZk6bDoYIKKYRASzM+hGA4xG5R3SkhjPjGSc3tOBal3WFPcIbmQPz6R5goj1mlmf+l6TVHVdD+8BfIZ4xOnv9hklonwZdoiELko9NdUAqm5jvOAn4os8SpjgaFC+q+sDbtXknHW78IDnhFm8uXT1Zwef4nCeo86fYrsvILCPf1Da0bizU78tFLrlZ9mDlMAQ4LhanE+sa1FWI99TVYj7vo38eeH0wYqvWpTRQaWeBo4IP19ZPNgOV7bHyqxgZFuqOKPAAZzGP+4qMAQaU6jzMrxpSJ0/Ucr/SrSKLF4yHsTQQiB/cDWZoGA3ILg61j2p7HUeQeb0smeSIVl4fV0/qRMRiEVynBu/eozyai3UCGV2EH/4NKtGjHbA482AhxsCdWvA2Fq+4rxbszMyJvQdOXom+VkbcKYrnfpah7XXskqrvFyezuXlMnVqA0fnaS7nUzggXdVe5ZfyTxha/EnfZH1UdoBCqBN01wed3bgH4k4ThiesBPD9AAeDtbnG9XqDvvMh1aI8HD9cBufdEVF13sux7JwbGMD28Uf88P2/oLN/B+oBED1Ba4/JMVexyqTJFrFIzcPOB6cmhp5fe8rXBCYpZE6p+wXODjMGw+hAq7WuJxExbtymlasi7q0cMl1QmcivQiWZaXkSeOojz11ckBgcmQuWRUreqYVl+pBUnX+qc9UI9fVTO5/8IkH6tIGuo2PP7BpGD8L/9ct/wHZ3j//HX/5nfDvu8IcQkolhcD3e4Dfv/gG33RXoVphePyF01gYMA8IAxphVQNdJzhXRzI//hxWB1CGVNNOTtiZnhDTDY1F6g4NCPOyDjHgciLJXjLtYvnPhOVQaxRAx9DwSQWGm/0nYd4rMoijTc+8b2ktTEulZRnsWGSHSIleUVJeR0xzf9tWww4ofsVk/gtlh9ZaxGYDhDWN3xcFLiDEy+90SLu2GiPlE2qpEZi2TKJuB3s0g2QgDvn7XY3O/xnbVY+wJjg0cp90T/kA5q3C33V5G3c7sZXwOtAc/ilcRl/JvpD/THIhnRURGPxxkFnEw4aNm6MuK1YLXNHIyglBEDLUNRd7Evk1PlkMq+VBFRyuv8wkMMczTQhnmJUUwOhQOG7PPTw657Bq5wAUu8LkAw8Kro3R4yjwNRa1u+iq8meVYypKaT0s2SN3HsMCFa3DiQGdK36cLyUWELB3VyWayyPU3RaYFKzyT2xMsk46A//R1h5+vOvyfPmxwPazQEcCOMY6jP7MhOHUYIJ6LRuSdxJgBMiYc2+jPbqyr6c910FCu+n4HhAsykYFzDmQIliyIAGMNHJPf2U4I/DVyvrTIL4egcYi4QmGXuHZSzkeVALAhkAt7QZu6jOMGJTe05LJVPOSYCBxlRML9Zov/9vdb0M0VVqsNYCwGp3BSyapR3ym3ADgbgzQC82FdD+OhY9IwH0tOiMHBuIPgXC3nfTqUcyBJR0oeYQbUuXYEeLzj1DaK8nZIq6IhyPexc1z420MDPgbsDblbRFLxTuYG2z9t0d9bfPF3r/Hlmzts1it01uDRudDUw/jT84dmClJQJawVsOTJOeDoXIuFacg0AwR2jMH52NAAQOlUyQDtgZDeqBBgQnqcRxQu7pK3bVJ6tT5RVjvOv0+UpfHtDMSDOYtl8ZcJ82Ky7pvpVK03x/ZqXh8GY/jwHma3BdwIgkHmnNuowdIY4Yvq23rcUs5NfKrNfSXTiJl3mXJYvysYttwzl9Pi1Kx6u7J+TbvMhrNDtjDO9asXHtaPBOt69LjFIxv8yr0G8Xs8wMHxgCu3xTWPsCgVuDkwoxHyIqd5uZdSnk4YWsGLeWBBu7qkiJ+NPKOyV20VDWtBVSY3rifm0VPjb2WEmOVhuHGF1PeK61gGjLg1Oq7v4bJYRx0MRhi4ojuSnSGognPrQrTDRHGVVJer8WFmmB2jGwiG/GHDbDvAGIzjGjv0GJjA44hhGOF4xOisDxO1vsJ4dZ1CNLVAy/AttkwE/ZPHOyFUaqfmKTTTX6WUTsnTN3gdX2WhB8IpL6gdpzi+Ua/BrA5F571a+jZ/y9lPlhgpDID8+3yq5HZJHyzh+zWD7SF5SeM+F0X48e14uh5Y2MefyRDsb+1yNeOLhSZNWAafyTA/A5yjp5ZJZxeYgqX8g+L1yIDJgo3FITSPGquwPtPMPyvrk78HGvx65mCRymLPHFQoou0Te8WSvKCJ62WYF7mi7OJjwrTpxBkA1sKSCbshPA/H7Pw5ERAjRFDcx1CjgGGGMRYODAMGO0qhgbSyW9UiboZpqdW8JwyccTDOgI1nBCkIAURBH0KELDbYgu71dWIIh5pkRkryhdQhZJydb7AH6vZMLSwzdIx87dJ5GeG5sTCdBdY9TL8BGRt6PLRpon6lTiXaW7I21eM01dyq5oXc3ZobmXZLe0ZLjqGd0eigfimMTdT7iFzC4ryq6hFbLLK1i3lHB0G5iXXguk1FY1s80LNx2nF3ki6wxhkwsHu3hdsyNmOP26srbNYr9H0f56s/8wW5kLsAnvSw6uUi7ccmoAUU1WEGHsf8IEvngO1IQDhgkoyONV2ImUkfcRg0O7AUyNVVmERZGr1AyYSR5PGxDovgVBYc3+sqleUmb97kda6Ka6wEv1RoWfIPgSmBrIFZMwHu2TnsvvsW9PgAjKM/VVnlkdGhpRxRURRrZo6F6ZhezKpqLyiumbTJVMoCKAsGx+dRqavnjvbe1VkWxgjO2s1Kqbi/DRc4EbTieCqJA17dd9jsCEQrbN01/sH9Gm/4LQjvwHjE2r3Hl+4GxlA4gKlljmhjXKSTkQFpfKLpaPavPjCLGx8iptP5pN07vkwnuBx/g8cQu5gmzjtlvMhp0YkIWy53wrsvmMyHGSEQ+1rPybyPqsuiXjI/qaI1TXRSy+oOFlsYjIo4UvDE8tu6PXvPoTD/rmhoyDMyxOzi2RPOjejfW1z9ZAEyMMbiodtg6K/wgTo8GOM9InaP2A1bMA/YDBYjgPHNl9i++QKOLGwYEGrR8GysikFrES7FI+wHmZSKn5D5AeEHZDeaU+OW6HIdOiz3YiqNyRz7cp7bDGJhM35+fFS820NeKuN8dQCeyiiuqey7+tQ4/jXdKOoW/s3mIqXBZ2Z8vzb4rgf+ulsqCCyjEyc27QIX+Ozhco7HBS4AICg62fRgY4MTh1ELpof2lV+PEuuYlF/5zsBkLZjmtNN3TVaHAFKhnoTvaK+Ie9bJFp+wRzTOy5ppBU88L5+dXUhtMFWaEzAWZC3IWBgywQDh/PkQ4xBlEnHAISNnVhqADDpmjOQwwhss2DkQBQNHlN1LhrehrQp8pgODnIMjwDgTdmF4nt0Y/4UxBg5+3LXubxoCjpHf8Rt5MGH6irrovstlExyiPF0EabO1DouUdteTMTBdB9tv0F8BtL4C2V7pSrTI3VJmaqciLWYQuDjDE4SsnZydMt2Wf0l72IuzeyWzuMhrJx2mi3lSzFHfI+XBXh7LnaBENpB8wkMnOyaCIS0LMSbfF/JM0bKG2PpxYVbY8fX88K/v8PinLX717/4GX3/xCq9ur3F1tQEZ76DHY9gRlM3H/fCkhoiP1cGHqHtHhlcezHiMRjon9wpvxy1ApoPsiGh3fYoGfDYCI3lExWdqtYvziOPCmp/lEFuFtL0oTVEt5LYUEO21Tr7iPYvcHEG+gIfSGqm1I4dKMDXC+Sdc7eEplXNUva+yiglLpaosEmm98YkYUKH9hdKT/lkMGWOm0C7X+Sm8jInUCpDVW7zLFQqr9Ky/b/TDBaOfETQZq/BGCSuMaFwwxuD25haAwa8BbB3wAOFBqY3vjYJ99H6CRUkzW3UsjVnFr0qsFerpQGn1not3mRFC46z8TmNkxPlFSLt00Wr1Xv2spjmHGCHKRzk3p/hblE+Ya1KayQehmYlmeHAwfqeBtTBYwWwHMAjmkT1/ugXcSHCDCxuTg3NCOLRO08Ao6LI/EM0YAvUM1xN408FtLR6pgzEdiDqw6YNQJny1P9xuHEcwj3DBA6VbE7o1Kweuok+JtB5aHlX9edjOt1I8bn2nerOFq02aWuc0VaUSl6auJnc7BSRIZIRRHh5Yh4SYhvPoFs/LI7UMgnGciWB+/IC7/9rh8YsNtq/6s5R5FtjD6tRz/VB4Bk3w6ZV8nrz3odpHVZp/HpzVxe5wgV8GLMR0AsaeMJIBPnTg0QIczQvL8plMonmTGfpxCGnZxwYvyUvJqFlycU44pMiPThbnasd5MjKRjwW8ot45pxS4qmPIywTiPGGIg5MYg1w4y8EQnAMMS0CmUsdhwOSq6mm5QJxcHIedEcIykzorwjDIeWcj5jRIXqdfI1/SbwRdB7H6jppjnNcsCSKJBz1EaTjFFDQMRZx0NaMd8eH1e2xfG1B/C7IrgCx874bx4aTHqfNWbYylMbgKjaq+YfJjkNkh9J6mlDa/D0aeTJej5BCWBrrim1yezqUCCb3k86QYhinJ2UkxFHRF8V76CEX++i/11BREHfFHmNhmWMM+3qKs4dh/gOsfAOPn4WrVY3Vj8ep6g7urDbq+AxGw+v5ndNsdVk7ku8O4nSc1RCyBZTLvHonkhKQ7RxgdgAb6J+UG6duYzo2M4Z5gunVW5JQx4izQFNa16oSLt/pN7QGewp4JAiWFQG28KKrSUAzl9fzoK+ULgiP6oqWZr4wSM98J/edkC86S6EVfKwSBuLZUNhG0GSbJM69SIKqRtop3AFJ3UPr2OJBFIX9SppALWX/19j09J9ilxSh6XkfL9kS+QMwj06fFVB9ncfksodWNGS4VOKzAWIMvv/oC18M1+h/XeDdu8c/0wXvhIGwHLvJoLSfEQAcOXuycp1NGXcEtjs/nCKbPhfPbdCl5Cb46H41TPMTlXSwz8kycZ3UQXSZQ6c1S1u/EZa3ptT9RVmacifNWtya/oupCCgpeG5SMEwyE4wTyxrpgdnJkQLaHAaEf7mB2Drzdwowjhvt7YBzBO4Zhb/ACBT4eALtASJ0fKzeO4LADgo2F6yxo3YOvN9iZHoPpYbs1yKxhO4KJ9WeMjj3fsdvB8Qg3ekZ+fQusrh3IKMZXHdThrxqHQRLFfqzo1CyaeMGj3AWQG1qErrqIpyWhLlkM7UDktDBwDBS49eSKwEWHM4hgCu81VNKsme9k7h7izChruh/ndjn2z9/jzX/+Hj/9j3+L7avXyzNfAKXxbx9UBqMz0JjPEfzeq0vHXOACTwOXufXUwER4+dMiQAABAABJREFU3Fhg7MDfXcHsDLxyUgue00b5g5aGyKdUAlqW3zykupD698BMJnKmpLSNJXG8bpY1B5HPZ3X9McCPkiEDY/0ZZiAvZzs3gJ33KBc+iKITjwGZxCcZYzz/T+ytD7AAOzgSJbk+r0D1WNSBhOdRue8NIUSAcQ5+U4TfEW9CHHxrLMgBbBzYAS7IBhz5tlZzlQxHsjOCw9aNUCuKqpcCqLqaxv790N6ZnhhuDk6tZAjjZoff/90OuL3B+uoWMDY4YAFgl3iNVuRXlpYVOiQAcAGv42wN200o8PYctrSUeqbYj42O5vK3NDhlgnMmzUdZHMG8IfJelM9lV0PIJzNCpF3c7ORMCH0uBKe6BD0AVZWtYQqVjguHfhzY7Q2ufvi7qi4Pr/6Ix/7BG+eswc31Gteuw1ev7/DVq1us1ysYMrj7w3fYvL2P9phkDFoGH90Q0YQnFD5GBpyyMLLzhZWelboqwvanNawQOElf5BWnBnHhPAHqgHbtRYfLizhZWQnvSHVzUO/TAtzCbVb/TpSaVzm7iMVPCskXedLDwX0wueAhrTStTqcCLVldAwBM9AKPz2eUIsmztyyrtGDnMQ8rlKb8W6hmlDOktXwex08ljVdpvktKuNSNrd0Q0AqguPAuZV4/FhP4CwUGrncWvTPoWA6/CwxJ9LQJaSmIPXFHxLx6p/bVCIwy0MAxjVAc6bVs10yKWpUMErqGoec1A4iHE0SU5XjDrNKxehc/UDvnWGdS18t/soxSMThtm11I3JYeSJ3KOCAVF0+iprwRiokLGlkBAWRA1qLr1zC2Q8cOLuzsWg8DRjdivb7COI4YBt+3Jnh+GcuxHO844/HQe4IxBh6DYGbQ9RusN1cA+Z0QZFcgs4K13vtLhot2wEgMGgjk4LdUKw8yEWPjmT9VX7eoqqJR4fIUisWt62xc9C7N5bsfSjiKn2h8pLm2uEQt1KCfR1hYwB01iygX2QK6Ffj1r0HbHwB8Nx1964UsT9O7VjDbPb9U3jIaIyre7inh/IW8uLErHXI+YfhlzI1ztvDz763nAR29H/4q6jqgtKQAjYxXP/+Mbksw5QFcM5Dj9pLvpiRYebogDy3HtjPKn7eUJZNZEnLPjnk19EHL9pOt8dPtYgA/3Fzhw6rDdtXFcEsEQIcFynjPIsdaI6B43bBjYjIkJgzIB2FqT2sWXjQw6DKu5L/zuzAcaDRg4ui4JDJU7hMaakgJm0j428iXF7JVizVnfSvpZnQUB0KSD0PW5OUV23Xorwi8WsPYHg7kw1KFNPo4eL3LW+qX3lM2aBTO35DGseC4M6FdehZLODWRYhj522ZrVF9oISNPTYQwDpx3QiYDh3dOPcsMDGnXAze+L/E4e3+QHmh+3j8pVHK/159sf36Aux/xelzj1d0Nbq43uOo73Hz/E/rtALsdvOwb8XMhPQ3wMg0RTwiD838JzVEhbav7MnGZ89+ov62IHeVXzfet45SKtagQ4luVrZZY7TEaJ0v+EdcZHARTLFtmDXshQu6nAVoASgS9uYZmmpM6xZQ5wf8rSrkUrmOS/WalzJqlpfWLlFwpgvXiOlnjaqmbAS6uqXibCGKLNsY5oF5GRZm8gsbpBh24wIsCIoPXjx02g1FkuYXh1LxdOpsAjwImHliVm7laaeNVQipAmGGoHWpc0HqXjAV+Z4A6j0fjJnPwJG8xZWpnj1rDord6NZdC6ycUmHMwZWw4XsxXvVHthuCqv+pyODG4FL6BsNUTYAhwgLU97GqNjgJZtiF+LbxBYbcd4EaHcfR5JkPEGMoN/RfPmfJ1Hd0AB/ZbzG0P060BeE8kMmuAethQlvfgCmHByAUPMeOFCLJ+Vw+ZsK08NFKFG1tk/CnlYOTXy2H52l+i4wSBziCJPOfGMV3oAiMEnnsJyPGbiyt9S0TgfgP31d8Cux5k/jPYcRKUX4r14aPB56FwvOyMuMAFLvBioMFS88x7wBsffvXdd+gfHe5XA5xWakYF5sR6z0A8cKXUbwS+mBVvmPwxT1n/Dlv5tXJVM1gxXHHZQbGZ3C7mpKVbZI9T8iihvf4wEf58e40fbjbYrh1WVg6qDvxsKacA8GfeRq4V2XlwQNRbGDJh7fM8PGdjLhqEgBcTlgofEsr40Eyc0htDgDMwYeeFMc7vQKexkoNKPioaJEL7Adk1zMnQFFKUxgzBKmljyrTZvYtA8/01r+3BWou+77G62oA31yC7gmMHHkeAEA8X19K0zKvIK5PWK4UUXkTyu+ohh3k4/yKMiTdUhPYG71UK89k7ik1PAF98vms6hUuqeiLqYLO32ulP5Gp1740RzodqEnoSvpMzIdilPD6iCeHpgAzu/+0B93/c4jd//wpfvrnDq5tr3Gw2uPvnv2D944eMpoSZe1AfHGeI2CfUijCExoBUD8uJDHFgLejbRLMKfcuUI6ffCaGdSvNZOdVpaiNBAgIYBmwsYHpQd4Vx02PsLWwVK6xhIGtClCBRWgkbtVI/KsxSbBnHd/Ln/w1biQBADjMN12lPjeRZr1Zl18ZDqpHm7X74HKZotjQ21BYTC/NMjqRTqPk1NdNIXXDr+dQHYVwJXs+W7YqISZV9W/FFdfS+aUUQxws94eeuJyvc7rfJHUmttMgZGtaLDTJ+Lx3smx86pPOSspLyVo3bZ7kSvSCI3ITMurT6EQM3O+N3QrjizAeRA6LnuAm6WgJM8iYvecDmTCzXsArPPSR8U3skAl5l+CapC5qdg9B1bWBW32TfyqO8XM5zAmJ+RcOa6J5RqGJN43yXCerluyF/Nt/kvkOsa5V/zLoNUGueqnfG9ys6VxPs4sNUM/EWWq/WMNaCyMBamw7TAzBeee8uNzpVFoNsiF4ru1EiLytnRfitvo4BIn+Qn6crBjAdiHq/RZ0M3OgPtX6wO+x2Axyv4UaL9WqDfrUGyEJOL8lxlSDW5iTgpDlTCVZZ63UIgqJz9DcaF5kVCrVodEijDnWLc4Jr3qmsmdSHIq7Xk5WhhDkRkOL7xvZxXYbs5Q9Zt1El9YfuJf+qwe1lmaTdKsvjkuly0yGc9WqaLWQx1763+PI3t3h494B3P3yIuRkiOGbcrxjf0QhnHfJcVeWLNuyrZQXx++nJlzbjL+2PVuF7Oabjsm1lU06H1jQ5rdiZ+jxRxnthjngeDh+rFYthjkU9BDSfHrrwxbf9k4GnnHBTk/wCTUiLb7z1UPCWYS1mu8K4XuGHL27QbQes7/8AM47eGFF0tSieqyK5VZ6+Vutwg4epnHNauVUKZ+TtketZJUjog2yJ1Uxqs3rxOy1Xz+taatmhUfm5AvP6Np8vLduHWfrt4xvcbNewY4ckgei0Jv55GQ0xnZNDrR3D8Ri7iwyB2ICIYQyB2R907RzA5JLDfdXnngAzEM4CMJ7/dAwyyTBEIUSUMV6J7pwBkVNDPTsICteD8xixlzsnFhWWwS3wdb6YiTEqxIBsOrnYQIzdgIc377F7swZWX4K7FURSzHU/RX7FuQ85P+vr7cON+TsTPoErTAscwiEzQxsUWa5jPyDrN475myA3KKY9TjMGiIKXvr92FQ0QSSXIYyHecQoDLO+T9kuHr5e2Z0MXmpLGTdVNA+lxPh7mZmhBtbKfGLYVQR+SIU3CAWMZV5sVrl6v8erVa9zcvsbt2wfc/PAe/f0OhhPnLl/ygd6Lyw0Ri8MppAao2ykRdnHxe0vNEKzOd3SEXYxfVYnJkzVrpfFIR174tyuY1Qbj9RojAXAuRzexAGthTuPlBBYlI+5UIj1Rwl+0BjDSafHiPStpADCH3UfBohdyjCFB9vaOqgVD71iqp7iyED8XTPXY04AmMGdsZSOrJbk3GbWZe4pqmhSiRnvS6hyTME5xbY+HMU2U2vb6mKl/EW5qXwAkPe2TElPNb1YeMYyo7Cp916MxL27Dg/rT86oo/xfvWfrcEDCz8HLxTwm3W4vrrc10fBkGh1A4wmQSmYg3Gec1VXQFwvwwWuQzPtJ4FV8KTXb5ffgyLqF6R0Og8xx3YUh+aVeGKOnlMxfxv7WTQjUuGHcW+TJkTK5ezIo+XEgSy8OVI0VSxkIBPXPj4cfFm1gtxZhmfC3XzHXZamM8jnRdj/UasN0KxnZ+h4SxYeeDAQxFBjUzLJEy+Qg9y5jTmn7E+2iYMAAbjKPDODoYc4+tJQArjK7Der1B328QeQzpTWV40XRbFPRluTnfSGlMFdMtbWyD4GW6jgOXyVYc+z/xLIiG4vYh7aoCuj0x/2mEK40QEzVvfAmIV4w/sLpeB+U7o67zPJXiYRLCKqvxsGKiyvSlMYKA4EdaOpAQgG5l8eVf3eHtt4T3wRDhz4wAyBh8WAO8GXHb5WXklTiOx6nsMlTmty+Dg4o7GU4tbgbNzlv6U/fLM/T7Mw9tGw4ME3ieMv3PoZzjVE2n8tFqhV8OtHrjmF6YWedm4ZfX4zlQttZnUDmlEdBt4OwtvvvmG5j7AX/1xz/DBE/sLKSO8KY0YYxQq7JEVol8MLJ/YrqSr0wwodBQn2Wti+x8GzdmMSZne2v/Or3Ox+5TfEXrIOMmM9Jq7GQH1BWchRmGhbyx4Ff3b3Czuw1e9ckJJzF1BB8GRowRIbcQxnR03hGHx9Hv+g31MsGRzDk5YNpn4XXT+hyC/OBiGUgO4ZaYSlwh7xxEgLEdGByMHC6GWhIZilrMm2ZxGEFe9XxaDENRdaOaG8rhbN8YkcYH6LmQsiPpYlZ4agzGbsS33zwAX26AzS1AFi5w6aYol0nC8PqwSqULbsl5+5/QbgKIxTDB4Xy0RCvifGcXdpIkzrbqH2lHlOtyeYaQyiOwRMQFQ4J1FSAyiIMvX8sg2tlaXWj52UteerA5zll5QsYg08Hq1pXRQZQcRtErv6zyPE5kb1vEBSLeaFzU10GCIcBY4Opqhes313j96jVub1/h9e//hNsf3iN618XOUXkdwFudOTRT3dD66ZI8ziEOtAtnNB8306S89PAwht093r//Cx4fHottVMf4KbWEvon6KUQSgT/qSPU38bwURczihBKsCZMvXDpOGRyvW+WJj4/O8NhaPCOcxzeND8mpsDa2SRUm38uilIVcQk7nddpKcCoXx5IhIsAwxcOd1BoZM4vbJrNmqfu4tk6oRUMfxLUoq7NYzKHiAoZnNIXfBWNZKQ6LPlB3z4tvv3Qoe5s8UxSMCBQ5LuQMGGR+pXBkhnt89fhb3LjXMBvaM5AcmZ6ldfTTRBgTzt5G41i819+4xDCGdNGQpvJKxvdE2zkroO1lnqUJGWU7BM8sS1dddkr+B/AUkcdl/w9zQWEj3eOijuK1bkDGoOt7rNYdun6FzvbouhWs7WBtiHsbDqeO4yVCVpNulnWkNNZIinymcLYJGwCEYTdiHEcAhK7rAEMYxxGbzQarzRrW2mg4SexIOjNiFhpEMW3MLBaHvPKt2dhIF3BR32d0fRkFzVFTfSNCzUcDCv11/Eow2YQ9i3t7Bco/Sp5PbdjBgHmFq5k0bc75Gfr8CejRBS7wKcLUVNjH/1/gQkReHLCXEb/4t1sAr3A/GgCjZk5DOqq+a44m5Xyy5ILqXj2rJo0ud7LaKo3iu88xAblsV8mXZQGHpqtZ8nORQDQ1AcijYRwDUxSI8dg94L5j2K1Dx16Z3zrvWLIhkDoQ2efp2GEcR7jw11kLMp3fqRDQJiYnghxu4EYZz5xRlUOaVTUDi+p3RbBJimXv0COHZxu/A6PEs8JRRRWUdzsxwD6klCFRxhtJ2ugOfYA5ly8VqvoLCu0vtZHR2VQ7qRDBdCvYNUCverjNTaiL4hWjnpzC/Ar9y4KJaYxipYKhsGoPp7Sil0EcB8/8EnOx0YJCOS6NLXPRFRTl/HJYxQiSDCYGDIcUKs0/TzJ1kknymaYL5IU8uVxTzPfFrECzFckbNmwJj28tbs0Kb16/wjeuw69/3GG1c01dGpf4sBDOZIjIa/MinIS5Qp9Jw8hcdXP64tFqHB/w80//DewsOvNVCkuhZ+8i8Eg6v4tFL5+i6CgnI2eLYvaNtuhFBVahGIjfnGlBxQvBgZOhJeBPwf5xP6vAUCiIlmFduWggbYPkxvsy1wzHEj7qKuX8jzIjFJbd/UaXlH6y30KelH2DGvkIysG3yC1rd8md5ktt+s24mvz6s8D7FwwlngrNJTkoyehHFYOYNj0QenT4cvsbrPgKWE+yx/Aj3grBNvNFZTSeoIkKuUohShsaord9TJc+dGpxSzNTaL1+qssTowVL4YkJa5I91jf5671KYDXb96VtdHIKq1Z05N41U5hASsaI+NynizVT5QrekPFeVp3tsFpbrPo1uq5H36/R2R6m62GsDVu3Q1nMYB5TOY32VnFbmeL4Zus1AS5sbNx1A8ZhhGPAWAsGwkHZa6xXvRfwjDr7pyqz3VN1uL1lUPIZsZAC7/O1QtHzeNsoW3gclHNnhs1VmvxjGP4ovB3w8bK+O1b8UOvUrNah+Cp6hxXrrex0DA3UvOAAix0bcPQzXArTNOGscEgxTYl+GW92MJyt2UdkNCu0HF2Rmcx+oYzNR9QetHp+igd5MUqOFwuHyHJzcOnpeajXnikwDnj10xUM3WGLEaPiKTjj10TGq7E/cheFHKcdNcNV+m1GgFT8zFTVNS+tdSmn0sZaXC3uFJchCttmH8/1+1m1D4uAAQzmEY89YB4ZFum8geYmVs94Z+33xgGHYfTnsPE4hl0QCIdJKxHGeJxi8icSuPZAp3EUXkikO2bEne3hAGa/gd7vwHBOHH1EMd6W97Ws4usXFPRM4VsTcJtSmKQSRD+PmVGjvArZkdEqJEC2NzqkJwJM18GuCHxNcKt14v6YgaCw92Bii6KKkxt4SiJ5zOAZAaXTqs6QgqHGt0H60I+m6G70jMvmhX7Cqk5swDJmQa9FYZy96CwnQ3DMyzu5hh0ccY7Pz5/ybSlrLoZyiWmytDkfv79iiXYuWsHII5cbCO5hhY3d4NXtLb4YDL58v4XZynilfnPLc6/g7IdVn0MBfah4E/FLYefIhEHdD5pmNNabdJB9qbgiDMMj3r/9PZwbvAJg2AIUrLvGoOcB/fYe1ljAyoQ8rEVZ9XVF9ULK6ZlY4QURnXwY3yXv2LhY+lmn1tMyz7K+85ClLzv3FwFPxZTStMTRqsIhtCh+RJHAx0dZkY3CG2VVrJAoQlTsCOLcuixrz37jG2d386DqS6QOiIL6t9gVUc4BVV7qLxXKBhlLOAPRN8fffR5WuZcHYcgNAXePHdaDwXr0xNc0lE+WLG74DVa8gxuu8ECEt502QOTjdLRaM6OFrBA94JCajBwOPEag50KfWTE/chiWNkYIgjoHIGymBbM/1DoW61K+GreVEYKLuvmrYhXMaNFSwnQYMNpGgTodYlvTLhF5o38l1wCZgKPXYylZfResVQ+bn/F49QG7m1v0/RusVhv0/Qqr1Qa269H1a1jThQOlTYhrCr+dHPCMc7X0E6qahDVa72B0cHDsfFxcBxizw2AGjI6DIYKjIWK1WqUwUaJsDr/JSSJh8zmp0Txt4wL9UxsT/mlcPx0OwsxK8C2+XmqVKIWruaQLskz2nOk8U7e7mETzg0vqUocLexmQ0YKzZMjLx/ICF7jABS7wRJAr5sgxQAOAHeAG6JDS1ZqqxOL0q5+oNU3pJPbLbEo/okrMeeDGDs6Cb38K4EbtPbshBgmpaJK3fZdQwQKoVkXlqoAEl5xqw1zb9qyrIQyuMYAZKeoHcl7Fp/NFaUk78dNudGFHhIM1nHRsZECGQxge0WsQ2JHP0hHAIaRXMb7MQRfBXsZyxgGOQCaoVCkEJwpho8hYEDPIec96jZ96V0TNtXGsg6+fA7Oph6jsVznQucovEyeCfiUVFVEhKvmDeSA4qJAxcN2An7/6HttXK9D6K5iu98E9mQF2wQhQCGJyyHSjJpPsFRcXnOQ39SC+r7BdZGI1x6LMJLJNVlU9D3RecqqcmgfBG8ppuTlmM6ugKtoXdm1k7W3Dft3X1Fen0hetzWhSOMV3M4bNO7jbn0EPb3H3OODNF69xd3eN9TvAPIYtSGHnf9Sdy5gcAScaIorpxq2nTwQy4YqqCPkaGdiOjW/UZbqlLD/pSk8oCM4N+PD+T3BuBwDhcElP4IgMejC64RFke8CumtU9FpV07GSZRskmqP/SBE/eAJmEqghAboyIiqr48LQRPMbD8jmhnCrLayvYMauuPxKmiEPOusnCmSh/WrCqSjUbtly9msePm6qzXlTqkupWCQeRh0OZIszl/M4Sqy6o0pS1KLcCTllVmsybMBut7M+t2rvAIpDFL/xudga3j7YwQlCGvgTCGtfonMPoNrBweJe7XO8rbvpt4YXMVZ4Fo8VAOhtCY1qi08zJCOa0EjcKQJw+FoZN/8dC+jl7Hw0Q+vusOaUqcK5vllHAjA4U/G1KUxgjJphSfa96u/zx5VF6Uhkcsqwp+8YQYdvf4/72R4xX1+i73hsh+jX6YIhY9ZsQoinsiiCpogv8fN7I5KWUjF/as07viBh5gOMR4yjGJh87t+99jNnBDbBuRN/36Ps+GCLI436pTy+uhNE+2EAakfSwFT7bwVnQ1yyniJPCy+yryAScuCgT6j58GpgW4mpjRFO8nYD8TQrBmBQBZfrqrJKQx7RB4MAOOjD5IcaIU4bq1GF+FjT5qNDmS192zgXMhZd7wfBp1fZTg4rp+Si1+DxhKeYyvCF9hI+vM4RPwwHCADLVWaGjYfU26Z4SE5jxhvvqWi+JE7fKwSx+e6aZujib1HoVhHjBN6EQAmrHCVHqHtqWUkNRl0mGIu9RfZp9RnGcBQ2EdXSjPyPCOTnBIJgcgtMNjIFhxhiV/RLWR3je8pwIXQ8OHvPsz4pwzp/7FtkmUgdj+3MsUrjnoiFFV2Rhm+SZ6mrShzI3oaHfaSWZ6M8oDijFOhmC6x1+/mIL92YNrDbhDAPhu0LHkyogqyPHp/piCQVtOx2171s9IynleOrYNkUDooUn67dAKbT4Lfmxkjck0ymRRbWhNposmTvn0Rcd49y6X2vJEEMTbz5gfPMd7PcDXg0bvNqscH21QfewA9EYW5/Vgg5AhALOviPiYJgZF61vZfa7HICEL1YtIkQjnNti4BEOIaRBkVd2P1sh/zOOO7z96V+wG+7h4snsSkFr/EGVmvCVutEsS5outzbAqYmVWQI5vou7IRhRiNemCihk0RM4aEuUF2a+0Ooyl3uS8afG50fIlVOzWu1mynMxsSx1KYmnmt+ROGcLxf58Eb8piEXL2NB4JPmcnflqlgJEZZfgdivdvjU8QE5iSg9xhp4n4hGQe+si8Bgc9c06T6EAatUvKnaexecCgO51IuDu0eJqtNgMNoUZAxA9nRs6iCZJy+aBnCOhPMoxpZRrj608zQUkzdrknj8shgfAe2coPE1GA8TDfOKzaFxw+ToQ04XD2SWdS97oAEI63Q3H0LJ81csY7GKOTsZTLaBWdXP2vF6vYk9mbyGeR6FOzEn5m8hhwcTGS4IxFl3Xg9feANH1a/SdN0T0/Qa269B3YUdCiNDkD9gDHGucSqpdzenKWMTxDnTPuRHOjRjGEePggs3KYHTO8yZuwOgG9H2PrkuGCG+MMF5wCjidn72juezT6FIckRZ91vMNrfE8DPx46RWQ6wQghWuE5nRVdToHxPBMFK6XrotLwgXtNRYtKyt6/h0BhxgE2mUfwELOwcl5LGQWLnCBFw4XTH4OuPDs54fUpwTAGca3v/4BoEfQ2yvY7eBj6yAkq7yvE4isrOP910aIVg3KcIqNca4+5pyHyRn7/cDFBde8k5Ylo5SgvtNZJCeNsvCW7oKQbwUIaQz73QJl+qPQvlX7dipm53c4sANX0RiSvKXlF44HmFLks6IBggAiA2OA0TkQ+eOIGXKuAwNsfD6NGjEDDiOMM3DGwW+KIBhHcKLID4KkIQM2FsZ65yDhqzhjckp5qtU/FPQIyQN9Vjm8dDyyKnDonrxeo9ni+1ffYnsD7L74K+D6BmS6cGh3mpst9JrSbdY1LzQuItdIppw/T4XVMl86d0/PlUaHBIFOytCkw8HjnXNyEHXKjznsiJA8VNmV7N0CLn73wstcU4bVe9y/+WeIGsvcDlitV9jcrPHV+hZ3N9e4Wvcw2x+B+/fg4RFQ50/GVs2rTyfh4xsi9kHUZ3jCIO2LJ7pHpHZwbgAgCgBluZ7tlGIaMUdjsXMDPtx/i3Hcevt83Hrlw9owCG0pSxHJWMYRrGPpHchct4XVTCi8RasFU3VINn+0x2KRLeFwSTJfWvdhZJn3c0/UmvjNQZvong+EwfJIH/o+zoFCAd7gn7J1T19yPR5x615UwpbK8/l65leF4n4vlBQr/66xJLVziP9k2s79xXPKk7N/cuxNidMiDTUsVX3UdVy4aVmVflFQcjpzNCYRo8S0hjHYDBa3j9oIkRTNLSD1b3lZVoUaDxfFha/48RYLHH6LfoiqdAbAEuInMU+Q38wrQxsXSgYQ6j2y/Jr1UoYC/fYYKpdo2f5U6a6YeWppYv0JauGM0036Xg4sk8Oqg4Gk9EZiYV6Z4/ZSL8hYmK4Dug626/2f7WFN+LX+EGtj/GHRCB5VDIbjdPibb0uk3PlYNn69IcIBGEAYMY7euGFtB+ccrLUgA3RdB2tsEMyM4jtyQ5xvT7xKWDxBnDIniOy9GL6qT9qgEa9+MXNfQ5q7RVoxuBQpl8Cxq/c+J2uqLqbLLGmKXhmnRXuefHM4hMO2HcdwD0SkZlTjHKYZ4NlUR/T42VisNP8+fo6n1aFpIDonK1o17Px99/Q5SwENGWafTPMUlTljQ+fn2AXOD0vl1MuotKFeQZgYH17dA8bhbmuUU0xY2/KTa9MrdZm4t1aS49bHmvttZd6WW+fTc+P7nIeYlYK5bmWz9KjbFt7O86X5Lgh5Vn44meuJkNofHaIUP9zWaHveM+ONGnTb87kUDpNmvwMjtD+eDyAKlKoL/drgxS0fnomYw54cCb8U+CPj9X6GbZQTWPA0qw23l5dsLfXfMaYcs6Svapxoj1LNKSbViMcBB2Akhx9v3sG9vkJ3fQXq+0rek71IHHNpyNQzMrLWW2Z2hqqJ6iWXkp8ySCojhOPcw1x4Z5bs2FU9kYoQ40N6mM0icV5sUZNG/VM5Ok2roUXKfdNrRlY6dCfE0tXIdY9wNw9+GhqD9bpHZzfYrAxuVte4Wq+w6joYtwO2H9TY1eWl7l1e149siJjX0AkdHZ2JiCbgAOw4nqkeDlpJIt3cgLdRhcBuwE8//jOG4T4kNLizfwNrOxABA9/j7fD7KAQQy+E1RuU5QSjV9f6FsqXqSgtfVPhyOhtC2pzFmo7f6Qk3rYTSEyrjmTkR60+bzZqbGE/ZskMX9pZSPZBItV7PjOD0i5hAFlh9wJF/nkUx190SrMfxv2ka3X4+oVXJD/bVkzwtaFP5nzxqLMrSxCQl67vE3s/rMOkhqjV/n/ZEeTlQculByXq7M7jZdViPuRGiNCJks6caE2EalecLFfQ5zDe9YcIfYqUZUA5MTFL4F41Qz7ha88QYkXYsJMZMnxsQGTLWeXJksmRtAJInR7kjQp89MTtxZ/FXlPqtd/XDpbsgZqGsa0HPuHiee/eUaruEFdEbRhsgAp173Fzh/de36G9eY9Wt0Hc9um6Frl+j61bo+3VmiPBnRQRmmYGWH7o2PLGqa+bxE8bNOYa1A4bBx5gkIow8gAxjRI9xJFhrYcP5EOIBFQ+dS9uDcBxB4tnbVuMi75XhVxqFmE9rPI8xYkcDYfGOZCXLXjZ2hyztmSWrTRBY53ja8n4qy9hV5cK9n1+eBJkTwftN/xIRVr//AV/+6QPe/uOXePh6o7jp0HrB3Vz6nCnweDjrGRGXtfiM8IlKARdPkAvMwieK1y8Slval8KEM8AByDvrI01zi4jY/1co2fjwhcFbPA5M/QyPy1VfpSRaRlZzfnhEF1It0rcvOHG4OhUazj81qeZFpZy6ALMSsbrzXQ/gzVw2lQ6hdiE4AwDv6wHqnHygnH/JnQhoTDlVWigk2AGDhXDgbkoJMVOkcHJhHsDMgGoJeL+gVQ74ECmWEjmQH5wiOJAb8no6MynZxiPIV9MaI1GOlbJf3534IVfdoLYdiwxtozKpH//VvMdxtQP0asJ3CMBdkXQtBTpa5gaAnCfXK+DOlQ2K55zYOy/e5HKpxvBAOlHOdyFWpI5TZwIXdM+ETUmXBuYB3UM6ynKLDSP+oPox6oKxny3bkfZKljHNNyZeYGr8pOnU66DLZccCJUhJOfWyMQdcb4P0I8/OAm+s3ePPmDlebNTqr55d0AOmMQmsI7R1I03AWQ0TbojstxB7a5f74olKFr6yRzBjBsFn+lb2qqLPL60T+LIiH+x+w270FYNGZDb64+nt0ZgMCsOW3eD/+BSPvEEYUpOI9J42u+imeTUE1AWPdWePycqi0xBPjwa2HqnxROD0Zn3beCXhcbtS8nHhw6ECof5d/UZWqvWlP1HVXdSHNLOSZt+qSM0b5VV3fsqzJWkzUUy8Gh3lmLsg8XnM1HzSjMp1NS2FyEWfOBGXHEwAmGALWo8X1ttgJQemngtZDMT7E+4T0HBG/VKLn7MqCRsw/b9HhzKjg7zNjhdRR1obA9KXkwtylGSRGjhZzuwgyBvAjgfa0CVdyr27zpS8MJIGDEEJIs1ZPfJ/WC0CeCR2Nxe76Dv164wUkY2GNhbGd/zNd2AlhYayF7aynpWVcSN2E0P/aCAFVZtoR4WCMjDthGDp03Qg7Wjg2sMbAH3hHyA1xNL+cLYCDdjxk36WLeo2pUjUz8OjcTlOtRZmhRb18ZhytdjRQvWtqvwlDta9agwohZ+nYMIBC6M7qmBkIGebtB2w+vMf9r2+Br6/qcpvteDLG8FngXGTtOcnjpJHmKSrRzPMTHfNTjOHlFHoBzZ8iAy+gap8hnFdO/eVCoXRj9hZudkDh7TyvQGlNyFPGaN/3B+Rd6VSUDkf+5XaePPGutedjUvY+BKpmE/aeSXBA1oaAjvIVa0rllMlxBsDoeUGNFcYQTAw7OqHLCDsXyDjAGRB5XtoxpaZlIUoT/+0Pkg4BkxzBGRNin4QyOdglnAEbA3HSTQLjHnkPPo94TgSQIltkzF+u92hBVpq6odA8vdwxGLAEtgRc3YI3K5DtwMqJOmqASEJH5c5beY+H9mpH1qnaFg8ydpRzKTWb51rhLXITGjtBRW4A/K7eVLuixkpujFm3+rbNd6dnmYCZ8ivk0Pl8yvpN4U6SD08CqV8Y17xWSnZhHxmAdozVwwo3t1fYbNbojIVxDqQNDFRdFNfL4aw7IvZNnCp96RkKNTGXtodGWN5CJkpusGgNricab3/6b3i4/x5Je+WFx93uAYQeb9b/gN5cw9AqftbjCl+s/glb9w4/7n4PUQo/OAfsLCxZcL+vvkK09gPDKQUUID2ULHqMqHBq5Kn3RQChv51+71QqdXBqmVdrPBpN+DQZYFFikP5pQrIFZBR+Bp6AeU0a0nxHYIA5Nen0tCo1V3OdoDJmjz+nNJMj6irqkR5WzNbREaujYramUnEh5HzxZ+bAGy9pIOUMgOd21N8T4MKnDMGo0IQWfQxJ73YGd1uL3lkfyzAqYNtzt1wN4r+E6IXj44rK2ylP/9OBkTdNe4WknTeIDJffkVMyboAP2cRx8kS8dhzCAiG+jzslZNu75pn2GgvLB21Gqb07QvD+NEgHg6kqqInrIlOZdmrl3k7hNyPzgeU1BFJnZET+gRhEDuPoMLgdHI9+tQ0TPCr/rQV1YpQwMNYbxtjIoXsuyzsL7yX1UgaIGMOUGYABM8Na/dvBDhaO/eHYJhoiJG8lEpwBifexKawGpZQZUqNFUT9fnyQXqB1Amu4rHj/PSRshKCuzTEekKUDItNFPTWFnCUSadhytny1RZakFP8eYLm77Aeb73wO7h6PrtB8+Ptd3iLhwgQtc4AIX+FigmQQdZUF24ufhLLMNjNA8R83ZKw5O1DxFupDKAOD585daB0BXqamsU53L3LqbyZpSXlOPI1kV/G0SFvLysvtD4Qx8ghqW3133+N11j+v3BmYwIbSOksSDPkzOfCAiGJjAM4amxh0RxocktRZkQkgehuKZvZMajPVe/eLRD3jHY396LDgYOCi4zssZDxzOgXWOACPHlaiIK3IOW7hmtpHvdd5qksZKs6URciU7AyAKil02WYpJnKr0h4mnTboSaTMAYrCxcHbAT1/9BQ83Fu7mr2FWK4AMyBgwxkLuTUaXhMNeHg3bSirjg64NhZ4uzzjTuxGU4ifJu5nySuFx1hehfUqOk3NH2OV737WM7J3MvGwn/SIZU2aUSvKkr5I2XhRySXmv515pVP3YQABgYh83u9QQtj894v7bAb+6e40vv3mF25srrPoetz884vqnR9h3o86wUUzq00N48mcLzTRBXvPbQovqh1Z6rj0zCQyiUaiayihRQy+wObBLW6i2jz8HQ4QJeN1BdjhYs8bavEJvrjMBn0yPNd4AMLBmBec88XAEMHqAZE+GalJDStonqhYyeNb+2TVvzzOfZe1POleZ2IuiAJ/Errl3HxsmqXr8KUO6tL7OaLPOopn9nvFq1o2qp80ujVb4IhGjrdvlEpmOgVpJryuaLTJH5J3fFt4Aeu6TLDUBH+MkA6YQsDGN1DhynWhvbcuOvhgajoJJXG2kY4CY0I8Gm12HzPF7j86bkCckfbiK0PcDF85DiF2iBPtwRFHoyOMkbowLfI1Gas0TZd/o8qEMbctwtU17pl7s/fJ4iE3OjQ16R0jaFRFamKzGaK5xRGDHMCajNCG0kjc8jLwDDzs4NyKGthKGORokvOAsIRo9KilPqaxHhNk30TNLwkDBOR/b1vl2anmDCNELLHqDTe7SKZt52Fi0fBAO8sbRzPwhZVYLq6LVavxbramFoQVtLhhyindT356JOhxjIOLyIvXT7Moz7oAPP2VeTHoHTvQqlGfEcMTZ0lYedvgc0PJ4yy5ONrLV/MI8B/GyQGjdWcNXvQCYnH3PiYJP2aUn5v38M/GXBhoDL7385MBB2csM7EYY5RQi/Pj+UWipQitmb1FOy0HjyFze3Pgp1/D8t52TyAWoBNhY+iIe7RlwuijitjPoOwNrKOksmkoUFRK6VEjHZBRCN1FScitnrpiPMYBjEBmwAQh+Z4Qhf24biQNuptRPO9CJg0OX8dmSM+F8CKmGyJGJF/fORaque+SkqMLh1C062u/ekQrCStVfjfKJDGAIH25G7N50wHoNsp2XV0J7U0bz84lwtCtoykfxc6WTnewmjrOBRbmdJxQNEJDk2igXRt1AMcdCyKiqb9MkUrlCckS+v1kLJRzr2CquumnIVtXdU07RGdzy9kEHd++Anxn97QpXmzVWtkPHhP5+h9XPD8BuxF6EQ3AQPaAtH+2MiNwzVJBIPQMwMlVpcwgWdAqb4xlI2+Tznnj/9l/x/t2f4/0w3Ic9VgYEgzerf8DK3gUFl0FnNoihlwq5f2Vv8BX9H/A43uO9e4Dp19jerWEJ2GCYHgCSlulWirDf6KPwT3ZafHqIahbvAVGGNKZizMItWND2pfiUxCMy0ivyoBSCG4cD7Z1kc0zFYTC5nmktVUmnyxwKWukVnSnsR1xY9g2cYiDqmPO6Wgpfq+/L5+rbENIkvnd1ar9eJrt3XEO5XaZWWmZeyNITnNogDF2Kw7+3MyYgMVWJeVnIK14gh9CBNzuLV48dVmzi7gfZLrtYL5WFsPEMqT4fQittZadFa1JMTv+K52DouRANB4p+x7kIjutg9Bfi5PETJ7HGXbh4pgSLp1HAX3Y6D8HptGboMxSWw/7Uml5NMsk0eTOZp5x1kUgDq7Ynw6iLYZFkPgf6ngg85AERUtxMUKzwh/57vN38BRhWWP/xCm7c4bHrYcwahA7GDGBY2G4EyMe1ZQCmE8NECygy/rFanP+m8ffrsDeAODC7YBwZ/SHWPIJ5TH2im0ZtnF0Ee+jT3Ovk4+YxgIhDTM3Ciw8J93SmyZDULm2SZ5mAfLgJTYPMQsKxxJgT+c5IHE5TfuT9mb3ILrL1llGnB7L5X55FouHHa4dhPaCPUoFuQ3k9DW1+RV5McjR74CkWz2Pr0oZPie99qXDeEbnABZ4bLhi8r/1Cyc3IeP2HR9Do8OV/+4Du0fM2eT6F1qIQxturrH9K6mWVhoCp3YvtlaZIS0lxHNf+1lI5kWdzqeY6ALkkrJ1BOOq8tDI94w9iIRx/5it2Ti9uP3Ym8Mcm7CZw0hbneXoG/CHT4S8IXt67nTmlh38Vz5AQZ5/w3jmH6BwEr9dha0VLABd2lxt20YGYYnvTybLM3hGJwkHShjkYMwwYNraHDMGgizy7GzicG7iET9H8WqhBsTNiGQTXHDUXshJCP9l+A7Neof/6rzHc9XCdOE37MDyGxBgh8y1gIfk+0sp7yktQ5E6VLq+4bqfoeJCFxpddTDndCBKdLyK2Uc7CS3xtHH/O5wlpfKcUMcfrYigaMwguytapZJGPOfa0lsuzvyCL5vOnmJOzO6WniNR5YG+2BGx/eMDb//oer9bX+M03X+NXX7zB3c0NvrwHvvruLezPPwEfPgBuaJchfS27ZQ5cAo80RGihsnpSp+aZFA3iKHdeDznXIo8EcjiGc7vkGZohFTDs3mO3/TkgsgVAsLQGABA6rOwdNvZV+IaC8SFTqUQgdFiZO4wMwD2AyMB1xtc3brrwKL6MLdmPgdP0bY74cfF7DCSlb+nlmUBW5XD9QmGxvjL8+uaEu9IgsUcbOT0fDu8fnUP1deb5i5wPbuJFXZ+Da1TyPYogV+2eoQ/lIdW6ZpMGjYzQhTmmma+ymlGZK89yxiyWkC1EM20OZbcpVgEvdyp8UkBE6JmwGUxUGLexdm6xT+krpXRRVraQUvqJnuhNq7EovhHfz66JzTomvESJs3qdbL6T+ZT+ckNhPdfm0DProoXLx+TyMF9CuAsCSFVY1tjU3nAdjYaMZIwBUiiqkLskc4bUodRhPOHgaIxGqnf0iLf2HlfO4erewT0+YhwGjOOAYRzQuRHGOTj5YwaysEpc9Yf0d0bjoI1QHMdFM9j5nzdKcCgrQxbVXU9DdxbwKOFX2rkX/xt0u/X8UCNEhAZHPNU1U922rysVe1B8xe2Ei2F/q2eXK07CWhTakNbc/Ndfby3woSPcEasmNDQ/B0DW7NjJ50fSc+VYcFOL4bD052l7iSFPskOiyvL0Mk4z0S0p4NNkvIqZVsFS3Gx9/2n2yKcKT7UIny5LPidMz3P/lBjo7ncgWKw/PKB7HPGwYTBJeCZN0WpDQC6TlXx5nqA8x+n09qjZOtlQ/6J6VbBs8Vn5gPUvivbNZVDIC1Npmr8t2KeDm/qEAWeAXQflph6aH5S2gVYbyh33gNDcgo8Xr7HScUzay5DnwfnEEIgJhgq/+hhRQg0eI+qxOCjnHRiGHcgBPl4TxyGXMryz8hieJzwre61NvxmcOUstw1Geuwtyh8jK3DN4bcHrDbjvAGOz+ZJE3XT+qG9Lwo1Y5wqvAq4dtOZy1UwK49MQkuJPjFpS6reclxFTlI72TC/XVxEPch02TzPWlaFCf9iaR/X1hCR0Nih3OS/8Cjwy3E+M/lc9bq6vcN2vsSGD9W7E+v0ObrsDxu1MDsmYFxVkB6DESTsilhgh2h+2Hwn6DAzdpCYYOBg8QqIPPzz8gJ9+/C9BWE/nJ0jmbnwEEeGu/x2uul9BTz+A/A4IkHJaDBdZDGZV+SaNPxdSTS84hywfzRSEaO1trZ9LmeHqo0xo/RRAFJpyK4tBzvpMEbU2TBGb84Gea5NM2uIKSGzGkMes0W8qe1WjyDiVKRS2cnEPxLj2cu/cNHYns5hQh3x5j1+wlBXK48D8OI5liaeuNs5nIxjn9IEjWnJUFzgcItMh9NcbITxvSfk7/UEBGjs8miecyXmnwOACwSuHVPinpYOZ/CYSrgNJ15c/SLskUKBYyiUxbSUeskJTUVQjM7rFuca66Hz2zbbsUK3tAjg0VFC7eI7rPDv2YRcZUVkPCFOqJiIDD90Kf7j9GiPZQPv9GN/bd3jb/0UqCDZ3YHuNr/knfL17h+HxAebhAxg9hhFg7jEMDMCg6x1G53zsWsPB+0vkJZvV2rk8vqZ3nkgePfqMCDeOwfgxYhxHDMMOu90Ou2Hrf3c7jOOAvh9AtkM/Msj5nRQkVpez0yBFHbnEx5RGr1ERL9VTEc/jTokG07yXjyb1I//ImJZJS5w7uF/yD86p5zzMeJd/lxnrOQkf8ZoRjRCY+PUhmnyej+jx6Cyudec2x6HkTw/x4vsI8CRz4Vh4uopE3uhFtbcN00rKC1zgc4BPYBI+IdQtn5rtBo4MHg3gTKvP5N4FmqEoR1CmRiXm3jrlxgjxjM6lBM6+KOue2TsyXQoFj/iJrCQfvWbL04LZae90KGVSKFmiqqa8bKeT567xrMrnQNB6fSaM//YF6Mc36Ls1LCi2Kx0OHUKOWgvTWb9TPYRdSru7tZNPrY/z70WIJzhrvZd/CElkHMOZEJbHIYRu8udByJj58QsRGUIdHTFADmAbVCOJfzeGYCyBYUMdLUDsz4qADhyElCemmD3hx3TY4IkVUsYxvC7xWcs7xlhwR/j+bx5w/9pid3UD060wGq/2NWFHdZRxjeeenTx0DAlj5dskB1urfgppiSWaRWFmEVm3xFsFwrFXdqUCWl3HzvndLg15JDrjiJ5HGSuSBomzPkyXqa4etzhlmiXWf6qulTNiS7P68TkgIgNjDVb9Cl99ucbXv/oC33z9NX7rLH77xwd0cYPa1FoWxs6wd+wT9DxQJDjAEMHNO554Xz0Na0yZqi3Kzg0Rw407EEYQ7gH4aTEOD9ht3wVGvMvQixgg6tCZDr29wcrcyZuUbbb7QSmloxmuUEpxmkDtlohAcCBDUnds80W55vh5nhOpkpgt8QpYLCBMaQqoVAU8LTO2bCrXC4N/ehzUfTQ3Cw4RuQ7DleWpp8o//Ouq3XGyKo/wVpHMFcpUhkyeqKn+kCgtMFn1pTdSnfR2OqUezuupvtf1acwydU/5LYSBIGj6cYEDoDnwBMOAZYINPFxGW/Z08/Ssa3yY0ffGYVwVXdtXcETC2Zroj6JiVj8tJl/yOghp4yXHXIqKVKApUklDSqVtnGcLmnBuR9R69nGa3qH5EkowCz0DxpZsEDLT+n1vLd52hJFM5l3zYAg/Wwn5RSCyIFrhAfd4GA3cMMDudrDdDmR26MYdyHQYxsEfYBcOzhsGC2v9CBjy8Wy97BTY4YzQcTRCJIOE313BzmF0YzBOjOmPB7hxzJ85H6YJCncy2ZS5GtMMSxrfzI7JMuag4aSi3zZeKBwun9do9TLp6zR/pRjfJVUP861i4zRdUcBl37EDDVtg3EYhasoYocGBwMVhoWcFqi4mYCm/VH91rprrGlRsBqZeHlPKufv6yDz3frJH1jlXMeeApcTskAXrZZKcC5wdjqM903m9NMSZpGxnL2VR7uTDY49kYKdsEEqHp9V5Wu+6hEXdP7LLGN1kjNBGEUSjxHR+jfwni1M6hSm5eM93+bNCMOfy/b485xSR09/zrodzaz/OtrFuBKOCP6RadhikspIEn0orr/KWpUOohZ9nQyCXGH55Bjc1Pr69PhupgYNjA7CDgZwLJ9U38QB0fZBzq1+metE7pDDSzpGZPp3KXQ2TF30MYAmPV4yH2w6m77y8or6en6P1eBHVepw8JSt+NCFuCp3fwKYFhKKVJHfiC+0p8JrrhOpaTyzO/7KxLwuG+rYxOeeEnylofJJrUVOQqBbEw8U5pZccqy/iK/K2yIFgyGJ91eNmvcZd1+P6kbF+HELzuDBazkE4e+TApWWxIWI+ely7krnAKSFU8rQaMUsVSE50/N04vMe77/+/cOMjooWSgdENIGOxsV/hVfc3k7yooR5ywCSXQy0rm9ACSrGF45pIxltWDcOwjxeXE0UhW8lPrO2ppCapIGEc9Px9NlfUb/R2ncR4HQeNYzxDrcmVY1/ybKqZFfwRSt83H6fQBC/bbAwn16dJUqw+OIVByvNoLVwA4tkQaWC5+qIFWbOqNk4Ja3N5HtvW05hIOWiJwX5nWzkBY9gSTZ5zpsAvuqJAVRSitE5XC0EgqTHuu8djF/A5KknyVSWtz/FUJ10GsvtYU+exN7fIh7essE4vKlKHdrVVZah8EKlWqfxbKht/9pC5UbQSpFlIBFxvO3xx38HCxHMb8nUu0ThViMopy1aRX4+3hhjWMDqCjz0KC2KTaBm54Nmu4vvHfwVZHBA9RxgMUf55L514MDEUXopyMHpqIB5UXFZbM1MxDGmcOn5XQDT0hfcaf9N8bR/2W3RR3o2kUb3JDhZjoeepf2YOUPjEsVT9knZ8yO4H2UXgD3qWHQUMv+tgRxb/evsrbO0qq/OjecRf7O/h4HxN5ZwI8uGO9OFzAPC9fY33eIWrDw7XP7/FMBJWmwEjCP24w2Ac+nGF1biCtR1G3sEag76zfmeE7XyexuNOHO8QkzR6eiGFXBrdGHZBMIbRwY07ODdgu7sPuyLusdtuMe4e/E6JLWC6AcQDCP7AR2Okz2QYPMJEb8KIGgph9JgXC5vQyrZgXWBDoKPc4BjZpXGMBmK1/kbsV/R2kmwq/AID/iiv/Wt3VdmpUJPtwiY+k7izMmFkfdoPxSqRngc2TcRGF/tTC3r1t84xaPsB+NN/AoYt4IZElXhsG3tOgoVzm6qLI4tbIDpPLS1HQj767ZdlmulZklaCBbkfBIlEL+U9D8p5BmqcWsJLH1zSpExxIpwTWc4MSZ1wgU8TWiP3sRCutWY8XV24onMeNG1gs8ZIN3BmC0cjmIKeIoZqyeUFCgQ+cfyq/mq7gm5pKRXGh1ymLOt8+LwThWAqyZ9FV3L1UwaL+FyLn1mVOL5Mu5sLRknL3+KxE9OVTJVKOwtzuCIVLPhIIjiQV9szw3Bao7yzD4NNBzIG1nYw8UyHlIVjRPlGSio0OQB0FAV4HGLAGgtjKIZpNcb6DA0A5+AMg5wD0xBVYrpPvF6DwDzG3RIECyeGB1iQJVhjAKwAGoFhF2SUMeKXyLJ1f6b6e75OeMdaf5CaSxD9hdfeBeZXSmL4My0MYFYr0NrAbhhm1cF1HQADg9HLgoFPYokEwA6gkFtEE8orz/UyXKGTF24AMIzIOgEnR3b5V1T2QxpjQrAVycM0NYJ84x24Kpwuz86T3hFBpvijIHfHqoTzFVmlJw5nZQT5Mwnbugf0XKvLr2EprZniAkTXNPlh/rWRO1GGGAyPhOFth9txhd/99hp/22/w333/iA4WQAfs3oF37wE3NvPO6kQGdv07kLmar1ADlu+ImOyl9gvW//D01jk/nN4yk1T4Nr4lOIzjAJH+3HgPDNuwrYhiERY9jOnR0w06c6WqVZMuKTdDfVFykbqXWHMKYWTiRokH8AqnwfmQHidxjOdhN2NtMzzXyHwM81F/NycXpDqc2ifHQ93K6XYfzY41Cc9HavChsLjRAc8n32u2qmRsJuiD6rdoJMiYrYlPyS/YKsLOJEZXhs+sCMWoQSmDy0KzdGHBAuXzivKZ8ILl2hcEatQa6ys5oIfByhF6J+c26HBJOnEjjzrL+edqR1yVluYyn3nHaWZoUaP+mcC5Kr9WOu210fiOVVq1KByGo9S89LcUf1t5Liknfhk6qSV35byeKLOTUWJrLEYGRmMxkMGDXeHR9hhpF/tnRw5bfgxChS/TgAAmGFYsfShrZyyYLczuAfbDFtY8AMaiW23977D16GcIjhnWEthYHz7MOVh4I0R0SIhMbAor5T2tgiGCXQzFNI4O48hw4wDnfBim0e0wuqHYJTHCuQHMDqQ7y7NdsQuFgvNCBXkF5Ti03i94lvB9CmvLjzhbK8R4PmV0oOKidCSpP/O9M9Urh3FLJSHSX/J0Rly+SzTjEIjd5BywewC50XPUo8PuccC4qwU0orLOS2F/7c69Q+o5YErkOwVqHHoi/rDZ38fy++eAdtltcXphNkejK6G5rn6ErtlX5LHraJn2E5FCfoEgI3Mo8h0rtz9FXc4BBKYOIAvRUi/H2ZoQiIwwZWwvxctzwannT8zN10PYrVzALRO1ZOo5hu40eOys35XcqkqQFoi8kSb1gEmOQFko9DnNw/R13PVsfFgh7zTswBx2K48IujypRyt/4cUo8OgmOA0RYBQfGpyYfJvgeXzCtCw3VRpTXKr28k+zCjjCuBqAjQVbC4jDtAFo9H3alKMxnWdzNa/E7zYWk+Lj0+HX+YiRQlGdp9bgRmyIaUuZeKLmQW7URjopI+WtsbWFd+H7CcfaFuxnV/alKHu8HLVy0CbyoviPekAgB5gtYW0MXtsed7DYjMHwAvaOTOOgM5mpL4FoBTLrmfa04aQzIibJYUHx26lSpzyOwOgA0A6MATBXIBB67DCOH/Duu/8t7IAwsFjji/7fgUhVXWYsA97iZ6NVNB4+2hAFGstYskRGAVYpqBqEwTmHYXuP7ucP6Nc9sFnKKR/AUUeFE8Kc4v2fTjDeBCgLe0F8PJ1GRj9L3FX5xzMNS4IbkH758vwcLHOqvIq21XyfPw6xBVvDVVW7tZjtW00OFsvODi28Tn2UcKRW1+xjZNTypBYAfSYEZ/i8AF/CyiHKKL2kZd4UynAQHvg2ZOtI6V2qjBGNuZPllZ0lIrQjT5/13YQc/IsHzVWE/jIEXDmLr973sgkWFX9aUPVpakqJHukzJSiE05JtwcJIZrmqOlKW437xruALWD1LDhxaOPAGheq7vcaH+rXsyHAsO38OQ7wpfFalZKmbecxy0Y1+XqhoEnRx7Pz5EM5HZf3D9Zd43298uwEMZLHjLb7F7zHQNtrD2Y0KJQShCH7xY7+NWyoyeFr1His8DAaPj++wGbYYGFhvtnDs0K9WGFZX6KwF+Aqd6TAOHYwx6FYORAY2xBxItEUMEQ4MORvCPxtHfy7EsBswDiNGt4NzO2x3D2FHxBbDOGAYdnBuxDgYjKMJu0U4hKryB+yBTdqhIFvGZ4YlkcWAY9U4cJ4wpD1Q1kpTPkwKPTdUJdqfswo1JfOSRLQNUF80byf7IobZ87/t8FaNzwIzNL+KnaJMkvVqf2pfe5/w/u0j/vJff8Cwm/JqWlp+C56ZX9kjoXslQPngCaHJSx7C3T8/v/dJQrEGHwSfokXsAhf4rKBUVwYmzFjAWpDdgewWQA9g2ZkPe7j+ack6k8VSymK//zJoFDSbQ2koEUeAMo8ZgTGvJWv2oE6Z7Xbl/N3Z9S6BzyXgX1/f4fvNGn87ELoxSCzB4cKQOOgw2BkYExT4kY9rSmEFz75cc2LIwAQe3DjPkzOPgOuiExDIeNlAc05RLBUlug+VGkWGATCGADLorAGHnc/kRrjgYJSQbSnzKaCdhhp6vCbq+wfGGLAF/vzrH/HhCwt7/RXIdBnek8qoydtmqMIx7dQynNc04JZGvXDvq92IwjKlfmu9cuFMQMfxoGqfd6l/40zGQBhD7XwaIxnEOeSy78ApckEh+ExX+MhpdeinUeKJYhnHfLJcG/IQEWCthcWA7nHA363W+PfvO1yvLLq+B3YP4Ee/E+LcVKIFR58RUYITTS0XuBUkA+bkrycdqGVOjs8c3PAhTMIH8PgAcg7k/ITpTIfObHJDRCSAHPOjePCLlhTSwFVTPCihiArUbwgagjCGLFZ2jREjHrsHrAnosKrpPWUXB8ApdvZ9ICQhjclBpaUP82cHw/lbWFdjfjzn4bAxqIhAM5fzCUZ76HgDJhSHU0rB7CJXiAAt3iZXVvlHrNJyNu/zxarMUJepF0G1jRFJNzGnnK3zS/fJGMLQbWulrkDIRYxtpSdFi2pcIELLUOqAHoTVaNCx0GQgX1BD2sYzeRP7msp0fl2II9TKQq8Vx0BTMJli/JMQlOOvEiIm5oRm5KoUmXDyxHi3tKtqS111O1VTYWQlrI/whhwMDztjsDUWW2zhMAAOGLDDFo9wPET0SbuZ/IrnEDYysg/NJLIDyBs74AzGEWAYPO5G4P0Duu4eZAy6fgWAYckA3GO0PWA9bhljQOFPAuxEQTcYHeRwan/OQziwehwwjGM0SIyjN0S4cYAbB7Ab4+F87LywI3+22N1FGgcYKfzsPtAyRH2xGDJ8buaTb39O68OhZS1olZ7wxWPKLhpZ7s1e0/ypuk9zJVOcYdZli7skCU8U5opzjK3Ee50QoJL/DcFuCau3BtuNw9ipfI8Bmrx5HjiG7T7ukwPz+Ah98QLgpJVo38fRQDmlJNCamKft/1/m6D43LKG5L5nnnpPenrveTyGfTshjAHx8VQJgwcaG9Zf3r7vls0YRVCj7ExaoK6rJREsHUnMLiveehCrj2Q/2j/QSPC5lh8YnxzEUC0HLXITBGmw7Cx4p8u46KcWLWgjwtoY2s0rq3wwM5XHsOekF/Fj7XRAO8IdXIzmeJXwJXHqr30SXGHYyMzk4IsBZGJNwypABSIK/luHfD4W9C16lbdB4PnTAbmNgOqv6WdGc1lwTWSEKlrpP5+ZGq7Zahk0pFlFlTmmzzCuPpYnSK9HD76CP9RBZQ+SP1PBGfvJOpZsoVkPc2TKfLCT2iZrYItNqBpcmuPriNz1nJowDYBzhqutw3ffYwKB37HdSu8HvhljqZUZrEPU4+JTqACfuiPAwOmCrTsyW89M7IvRg7BgYBhlC3TmiVkSYFwbsdnj73X/EuHsPMgRrVvii+3ew/QYQ4kF1tRkphJK3FkoctaKcbLTroY1Gkol5KqUBhJW9xtf9DVw34r+++T3+gb/BavhqecdlOZ5nOVIzdjofLXSrsFlpGQ6H0uwtK89TaDWJ9nAvEj8Hs1WwEtWgljtdcsl1ku61MtULrMovhN5T2ZTLx1NCq+KpzBQXPd2nuekHs413ebxNT9e5/R6iOJyIcy0W69lOVim4Zhlr5qFcQFk9ZohSJlrF2ceY51Dzuj0KSqVV9o6ydBQfTW8ZvgBiX12NBl+/X8V4oiZwkuItU/JP5fdT84ri2oG086EwPmcGCz3GRyktOP43xfjIzojKAFH9cP5W8uACnwGIx4c2rJ0NKplhKiBTeE/qfUkjVVfnFHcCGOo8CIYbw24IN8LBXw9uwLf0ezzSfZAZHBzLOVKU1clQCvDjmINHlpdcUthSwgAH4xyMGTC6Dg9bi3H8EbvxHqPbYrXawI13WHU9DDt0tsdoVzDGYHSD3xnRWdVeOaQ67YTwB1D7urpxxDCOcIM3PIxui3HcYRy2GIcB486HbXLDDqNzGAeDYTBw7EAqfmky1PjOZQCkD67KOnwZZ6HHYq/3oBIcYiit6G2kzW4FhgfcjsLDQpo5hz+J3StpwjmhqGfZpbW8PZ9bXBobtGHPd0GcjvQhHcW0rC9f/zeDr/54jT//0wN+/tWwqFyBGWqwOI8LvDRIEsIFLvDy4MD16wJ7YBFHdiSEfG0PRx24vwabHkwEzpiTko/nKhfh4RNw1EWLLNDyEi6pWb5Mk3doXYpOkSEPt401tnoi23ObWp+Ey3WLZ7iuoh7zNZhIVz0+ZU5FDi57IjKDNwowjPNhk0qIIZq0boDgwyxF1UQSsAnwOBT5TL9L2G92CN+4cF6bZWCEdxRynvcH4EO2zoj8YIZDcACCg2EHaxmAjXoUQwQYC2McnJMxE13Ysv7cs+mz7KiQbdB9IpxKQgTbdzC2B0wHIov67AQ1xzJ+MwqW7frtbYBqSMxT4UJA8SmqTdEIUZw0FwVm2aXgwp+clZGXG38lAofe4QAOoXFF/4NgyHIxTVaGc6ktB0yLgyJhnLyMJRqR6TOKHeRkCMOWsH1LuOY1fvX1Hd7QFdaPK3TDI/jDD/H8wmVgYPu/grG3SMcqHAbLD6uelTmTRTESDfZH9Dj4McyPKMln2W73Hs4NAAwcD5440QYEA4sVDG1gaaU0GKQzy4wGcmCLECf/RTqwOdaRG0ttFm5FHqnlivVbhoEBkcVIjMGMGN2opP/JzjoADtunkOZ/e7IkC12+9TGbLOGmufxP8CdU/Ev5i2KRfC5hpqhsoWOc/5QnKQjrNEChYGup5QhyroEsFJIT6zRPBq2DseRngvIVusME7TAckcgnDMxwsVqDi/v0ffl1zCRVTdPUVrxz9Ygn6lvUMBYxO88mF4mCol1k9aOAHGHjCOvBwIadEHLIcbSTkaYygkT7O1zW4lz3qkLVUDknoMI0xeQAqEEWFgw41/jWShPXs8kE/rdtwJgp/CTQiN/eND1njKiyir/1WtsC1n+ZQttzFw+mx6MhfKAtHjBgwBYjJ+VprHnk7jnwnOS3hgtSsYhJBY0nDjwow40GDIft4wB662BMB2bGyvYg57DrVt5byvmD8YwB2Bi/2grbwnLAtgvnPHhDRLwf5c/vfnDjDux2Po3zf3BeGOJ4VkS4B8OBIZF5k7GXokEi9jVnKFdTbmb9MzM604/nhPKS5kvJeqxzngvLaOsUIW7wdjMfNyCnNQc5Vms2pGCs9pWYFdZKk8lfnH7D2ItBsm3Y0HVSbRseQdu3wEj59D8JltHqs8NskZ/GYt0OiYkF1f847fsopXpN0UQFhJ9HTgCfoKYvEaNeYp3moSl9Lvxm3/OzELMzw3PLxkug7Kfz1m312MO4tTdGkFX5LyunncrzdE4SNMX4pP2owi2Teji37rG+mGXapz+t8s8ftDgnnkxRXEd9y8fEdZGpDNiUR4u3pAg0q8sTLzL9XDO0kDi7BH1WdDbzX3vjRAoJJY7MHPQ40cELOvvAVyGE63bO74yAN6zEQ9ng8/WbNIzX/4AbCNeChetShreZUgQwBEOAP3vF74bIS63zz8/snO7v/Q9z+aFd4fI5gSaarR8lpzsOIZkmslNjF684hWTy54SoxOV1lD3CN9l8b33XqrSMyZI5qNa7rMH7v6x1ANS81A8NCMYBdsdYdYTNpkc/AuZ+ALkB7MQx14cHEB14wotyfWaAd2D3GA6qPnytWGyI2DqNzHlBmRFC0eXBAYPyuM9RIw3Uzz/+Mx7uvweRhaEeX63/Cav+VlkZe8geK6838t+KcUMz6sKPll2Wuo5T8a2BzjVeec4qc38AOcU8x3FE2vpzODRNDlLHaPV0SKg3NeEn8pcFOV1AEJ9YvAD8tjKA4pzI+q2hFZBtb/4D8So1keAfuK/igLRLIRC6cjyVkjN7U1pTw3WNw+orav2q+cJ+ffA0riagKVTZUzEOpRJG5lI5O5b0f94v8VnrMvalapsoE2NWJXtV9EGB316fyEVaH989yqKkPGGiMkbhMMs4uLx4Rno2CxP9RFJBRWMitA/D+sWBZhqjNg9YD4SvP6xg2S+Ucb4ayufW3uynRBQKaK8IgfCw4bliI8O1nFCxEErGJKJb8lD3jzl6Luv5AvV5hYLCICl8lrzKIp8Kyn7Iz0Ch+EuhYZEfI6MJbzOvEjJeQRkgHDs4x343gHP48+2v8NP6Cn+if8E9PnhnAFI5sC+tJXQ6RmWMyHgt6VoaMY7+PChvXejxuDMYxx+w3b4HxgHr1QaOHTq7wqpbwxoL51Yw1qLv+qxf5GDqYfCHTI/j6Bm/YFQYxxFw/m8ct3Bum3ZNjM7vBhl3cG7AMAAYCI6HcDixA8PAOeeryqGFDCBce0FM90egp4uFh/A20FFWfV1yCZrhz2g+N74PmSRPpRryXTZ5TatV7onCr6S9NG2IvNxZi9c0RMYrvXUuH0N2yYvLcejT0Enl4d+Sv8D94x9x//BnjOPfArhRPGNqoa7XbEOz13pyteGULqu+fZrhPxPs6bcXCftXl4/Son2FynpQpZtrz6c2Nhf4fOApubinhv003jjCqx+/guU3+OGVxUgDHHwIy8joU7nGJKhzzhV5WvwK4mDDeYhTZAgXv46yO5jzszRbY1LJpnv4JZ0uY9t9/kkMLcpjrX3RfG3ON7UFgXAx50m8GPaPbZ6MwKsVeFj5My/k06LaHManlnm8jJ68030GaXd7Xg8xPTjnx5wcA8b5wKhC/sk7uDkQrLG+OqYDscPIPpyl14Bxpmsox8M5BpELS4sDuAMRZ7siWHZawFX82f4OXCAhZaFNEBtoyADGeLHL9GAvUSNqpSgfSamTnC9Xetksl39FAHApjyLPJJppYcG3RRsjMvQu9EyaBzaBXviiJcOybNnloH71e7hg2BDDQ7iG7KQIetcWksbdU/NzY4KCPB2ouZFQzsCA0HUWnRlws93ii/UKX7y5xs3bLbrHn2KfZLRmAS6Ouz8C1KFb/z2Irg+u7mJDhBycUnZmQq9EXP245MRWf7fbvsc4PHoFBTPG4RHMDr25RW+uYM0ahnqlNDKQcD9+riU1UapHXr90l0RGBnLL22z/JsIZVcqBEMbDmdWC2Rbin5iZbSJNDcnIkU8HHxtPPZZF/IBZEyPhEQWv0+Oaciy0mRLO70u9xUICG/F4snCVTzSSlehFcORHiZj84lxskeMnwpW9Q6j6hdS9Vha2UCEd3qNLESxsUwihDNx616xoizOR8lUTCEjB4BITOQes6tLe7MpFHvnCPJfzBY4DQwTD/i+S/cp6qG88TdOv0nc6HcfPYtgxSuNU435eVNwJoejI8VDjlDbWpVf5nJHrUmG73NviRLyklMd+s0xNy9JINL4t55Q2+qr1TXZWseN0zYADYQTBq+DHyBjGFvP8tE3GiFRZYZYjTxEYTec8Qzo6Ax4IH3Ydtg+EfrUDAei7Ndh6Ou+shdkB1tm4PhoRAIJBZRx2/oDpsCMC7I0rLhgiiH2sTic7H0YXFMou/nF47pzfKs7OwZELBwH6vooeXuSCUMLQvDhrNGvS6fSmCZERn8LVyY9yHn7fNycukydN34Uf57tOOT6bzfJEusIFvRDBPXp+ioGtcAzQsZE17STyuEXZQjtfh9Zr3jP3luTxtN/WCLVU9GrldPh3lVR7YKknQFnUgVXZX9P9AvnZW3vWDJ+sls8GL7/mx9bw5bfsAiVtzXlXxzuAtujfAcbtYMbTIgTkHKpIBlrXUbLL+/niQoIoYErOnU/Hs1ctVkhJqKXIPVlsKdM+r1zKYIzYYTAGGEcQuyRngaJyf1LuShmFs4gnuMmUqd/ZABf4HnnulVkMZIo/Iu/sJodLG+O8HOAMHFzQgaU4KrEy8TdV2ol3Pjm/C4FN3KVBBBgmODYgeCdfXqhcK2wBk1AGziYCdqsPGDeA665B2Y6IutxS1hLZiaQS0dlayis+Jv19WYa+no/uEvNVBovMyU70ydFQEGZ4aD6FCZ7PqpQ2fafL4WKqJH45ZaGtlMeBOGvnPZmgpntFmixUnOQyRX8oR5roxE5x58+4NTCDxc2VxavVGq+2hM0AJQwubllePo/g8QMg4ZAPgOWGiOya64dQ4ZfUGMc6qnRvf/pXvHv/B/jYbMbbwanDq/7vsLavYakLEpG35BnxqFRel2Xx0SMzViAMvrKcagUqy31JCZsTX4XxkIliDHRkGBH+vKi/cDArmqS2DcpLAiZD11VznuuEEyGGUol+M6MJQqn0CDe+q7omSd2qfw5R2J1BSTabN+K8TEJ/bsyaghY5bclqkpdf3NIL3TITUjqZIaGv89Yf3w/LujutbF4fa6JyLA2e/1s6fG0lfgsUMS8U/JNfL+yO0ihReavGTmb1QU6/4iK8aNSXgDp3JF0cmddnDKFrkr8GIhomD3L/cB9OisFAwjmVWr7oSR2Y0Hw/UP6NGL3LemZw0IKtv9NZCK3X+FfiXV6OKMWrqVTVSeZ7wcecE5QgAJQkVRiitDgcIl5qh5q4G8I5r7h3Lv6N7EMdubD2tmi0KOOjlZ2CYjYIG94YMdHjRPDbVIExxJjc+thL+KF7BTIbdO/egncPgCN03QrjeoS1Fs5tYYxB369gDNCZxIf4nQ/JEOHHlOOOCGIHAwc3buHcgHHwh1S7wXu/cwjdNA4E7Hb+m3EIIS7Jbxk3fheH8D/GkL8H4LdEJG+zuGuswpVyF6b/S6jGxb+1ESLmqWSDesBbjzSLXvNpFHHsZYE2RigJayLxcWWk+ZGPiQtefT50VxgVF4xonC9HzBKyIPC0ZV+W83miAR97BD52+Re4wAUucIESGvqV8PTRfA9nRnz5zw/o7h+w7Qdwtl5OwyHqBeKGQ0DB49SSmQjwfDz/3BIl1Q0378IzJaPW0QPkVwsSU2WHi8zvcWJn/pkFhEfzAe/sPfDwDWgY4aNvidZaeI1pfYOcw+DcWHiia57QHw5tyGHUCumg4/GOSg6Gva5O9EASkgldB5Jdo85hAEDOYQxMalu5Hu5jlcawk8ArfP256yaebQhY79DBHPSRw2JjBJD4vBabm6TmxL+xYXz36lu8ezXC3P0TyK6AlkaSNTbVCN6euaJfSdXXfZScXbwTjMiqdbmMushMMA55yAcyB2rcjTqD8F12xkWQ21IkDHkvoZkkIka560Z2T8h7XZ+ibzj7qSEYAlqBIM4HFfWKBXK8DueyDAaP73tcocc3X93gN1jhb78d0G3HgEmn6Kkcxt0fjvryAENEmxpHkqgVB5GIyrUfjN32HXbDB2x378GO0dkb9GYTiIkNOyFs7DitTEZUJCWl09SSJNvAMgU0wkQVxOAkoM+fbM+xCpKpHKKiIs558buFYWXW2ThPDLp+3CDA+2AKlfREOuS7Y8o4OuOzgNIoniSlcn2VjV26ivJ9o8j0iWgo6GzUqG5eGuXU7ZzeyYL98Ai724FMH7+ZzmsfLGzLgmTRwh+9NafyUu8aWzSnyuTwbQoJsqdSjTow1cyTsFR699Tjuy2cc+g2FqbLYqFcIIBx/oDq9aiNA0l5HRWOBcz2JCmlGlfZxTSyrkTj5MyasqTsBrVoJJpYRNU7rYRvQ2AZKGcEp8o7HutksW2EolG3R+uCF34ovKDMXceMD3aFh97irX3Ae2wxYphgbKfL4ECLCcGpqaLdiedh9Y9zDIKDHQfQ9hGjecRgCMNuCzAw2h7gDoMFrPGxYtkQYAQn2e+IGH08ztGJsp/jzgcKMTqdG4NS2UVlcmKO4c+NGAdsHwa43qHvGUT+GwBgIxvNCRJZym+Ddll/aWOE9iJSRe0dJC7u9SjoF9k8EZlBLoB6fWSASXZ28CRNCB+HLOo1bR9G0MTLyfQz6Fu/K/zBmt8eM1MVrz0OoPc/gh/fQ7aT+xR5aINUR1m1OHvmnX8Yqx/ucW0Jj282GDf6ELr9c8vn1UpyPJeRMt3z7Uk834LPT8z/dHh2hvoMkHBmSg756N16gSeCoxmEE8v9VOfIS4R9NP+wujPYO0vQI0Bbvzqe4FTQoiWy3GljRBMoxPyfyb+kWUspcJXrPnFTXzc9vMs8Cv5fK+OWQjP5GXCRkvwmjmXEKbSSMQRy6p0af4YK0amch1Xm8LsMQjQO4x2axdEm+p8z4MgBHJwuMxkzfCc7I5yBMwA5A6/E3jPK0uXkgqNUaLNxXo8J72btiIMTUAg9Bs5Y3UbHLejb1jMDMgzqe5jNGqO7gRuv0fWal+b4cezViDPtOa5xsDTK5XqxHBeT5Mgllk73qhJ+JctG1nk1y8w0vugdEaVQoqZUuleHNItcUvDtNF15NAcmCha+sFK82aeXbZXSvjOqrJQ3I0xF493OV7sRV90KV+s11gPB7rYwTuTnssNVPUs921KPsgWw2BChxzA72ARA3P7EatgyhPUD9PbtH/D2p3+NCqDb7re46b7226qI4jYihNhqhCC8h9BMcrp91DPrGwXS+ZxyKd4xQDZOj2nEyvOnmGvY2gWEwyjVorFge0uGl0IcmauQSCUZPEl3rVdmsI+K5fysigs1EcDeU7LpXVvlyQfg3TOLGUoRQerZlLJBg97xs6h5maKTVNku5SEETBTshqLH4nlgH4NI2W/383v02y3M6zfRW0EWcIJnEqKituoIju1Z3ILafXtvW3JF63LIlU+c/m3WgcGC70uNEyj2XUQk06p0ws9//gCGw1f/8Brr29XB7fi8wfdx5wy+et/DslfYRqYU9cKXfRk5OUQ8lXiR2Xdxbir2lJLRIymfp1YTNPkLzv+JT0XfN8Xbx7VRMUaazlffFQ/UJjT1zbQQFdOcgdRUsfkJoKJjonKzZPoPhsAWqXnplfb+fIhv797gh9UN/kz/Fe/cz/59o40m8GYxRFFkJH0n6p0R0q+qMaom/srvZhgBJlw9PqAbHuHcWzywhaUOfT/AEKGzHQg9RmPAzoeZtNaG3pBdHUPcHeFHMO30gBOPHL9bwhskQkglx2EHB2McB7gd4933W/TjDuuNPyPD0gCCxegUTaJw5onaJSptyvpc7kqLGCPsOuHs8cTQZfcTsgIiDdZ8j2bU1S+ThDdENifjHI73Bb5RKPAIRceUJ9oxOpP5zenHgxN2bfcA/vP/Dt5toyEKQOHtFepCBNkb5idEcsyRxt3+b3/C9X8mfP9/+Ud82Oi4r1RdVf2xsH+qZAd07OkcJf3/2fuzZklyJE0U+xQwc/ezRURutfQ23ZwRDu8VGd4HCl8owkf+Yr7zP1A45My9d3q6p5fqrKpcIiPiLO5uBuUDoIACBpiZ+/ETEVmVmnnC3c2wQ6HQFZj5dfHKPm/4U+/fL/AL/AKfCCp7HgFsDY79HubwCIcOipn/uM3TOpjyecl/h3/kqJXyQKk5lqjkq3LPcK0/0vqkmCn/1O+0cq5sweXZDVXozDwFNYjX6wm/6e8QJUMwNh2LhMCLSHnsQxkCb5z0JyyRnibJfhYWMCEa1AAWahg45y0Z1rfLyBkVwZBhLYwhGDhgJDgzhuLFM77stxqJMF+OBojeEmwA66MiyBhYhLZQcCxS+rU1bOn8+4SBxhiQNeh3d9hcb/D2+A1GusH15kcYe5jw65nzj64PlZnl/PjrLIo/CbXI7odA7gybpIuGtBvnKzx3qfwodYSIBt9OJZlFvavkkblTcxhxIh+FVLdqayX6otrm2LM1C01kF85lnDVQTggXLxTvzlnyJLN3nQENDjeDw+tthy/u7nDz4Qnd/m0Y65rJ6OPACXdEQCFCgUqZ51zqymF/j/3+p1iGOzKu7NeRKHW0Q0T7ifsUAUYf2ZEGNA95T3k4zx0/MwGQRVBlpAPGpsOexHT9W/s8e8FNE0mNWTIW85tqWctKaCSf2wgRBc7wi/VJijTVcOnfUWPTqFF9AIB7esLx/VuYfgfabKp3TtRHZsUGN9e/rIyiGKo8Wwn1MVU9CF8zPI2VcZbjEgt82oVWp+qbjP/ij7HRoYwNF0bMY1aKVFob7FFbp6006wj20jrL0+YM3tK6UQ3BVFkpFIEVD22IMNIzEO5PGvKRJo4Y1FZqlbm1d4MQ76rCEPUX8jgwyqDklfNcqDpetJAr30TzF9EoNlfAHKzC6nZuNRaky5qgdRr8tZcDT10DdFnpM/IT7L2jPI8Rdt/Aj8gFa0mZXt9VdJ2xxeGLOAkRyjv9OO9nxm9yuI+BMBwGkB2x2RwAAH3Xg9nBWsAYGwQS8ky6bBns4MYh9G2Me4MYIjjc9+Cv1QvGCsfBo8wXY0AYmcHjCPfTj2CM4K93cHaDkcL1j44AYyDh4M5Z7zWlD6MSQ09g+BEiNhDGe7rmZPAi2454D0HxbA6Wonm84YhPIu9rcLCFKQzkd4gh7WlFwxollDVMn0f2arGVp0BaL/4OET/2w3HEw09PeHx/yJweiBLNLL0RkyHYt9SMjN0f72EPDsbeAl2H+y9GjL0uT7602reCY6F6uvUlLr2oJzilnMvO2Tm08pSsM4nO7ojsqHPrulX4dD/ST1Y3aa74TwyfQRN+AQAfW4ny5wUtTcna9ALhcuose62sNXPZ2lFLCnOKBL6oTYlOLcJfxmNrgPo9m0pHJKxSnQPioqWlHMCqgIIvmzT5nLVw5vrRwjohyFUmOr6Q8XonciZcqAxQiEagZIdIfVfCttbucPxHVBbhSF723HJSkydZnwBMHKhVuz1fHQwlZADDgPPtZx5Rx4eiPHZwPAIOIOPAzgQjDEBkYBDuigtREms4wVl2Vo0BE/C0ucewG/DAt9gPX4E3OwA2w6VpjfVd2KfjKiqUIlJqS5GYUhubpVA+t3F9OJnBJJNkTn4ilyj5LMofIjuLTFI0oUkFJgZCnrZfyTjVgs9gApZXWy41eNpT4wsbjn/GH8vUdRamJ9zstrjebdB3Paw9xNKn8toSbvr35zgLl3CCIULZfgUhZLKQE1ZBiA/3f8SP3/9vEK3Pl9v/A95s/10kUJIvH7yC8hAFgwQFpKX66iRVDifU1h7KkSJJveHM6LiBTNZj8hJXAwF/+aQ/d83Ex5yPRQ0rVRfVcdVVRKxvg3oBnD/5mWFGxo09chtmOB8usbioCAAbAjnWXcNw/wHj+3fYfPUrbDZbpJ0g78WLAgnWYYJSzY5pIsOVUW42PHnI65Kz9SkU8ZmdXyHSo10JQZSu1hAs2XgUg3iJe4QWrFcrM2z4p0Grv+tIr6ScVFvju4IGabmFsrWVUT+thugSw4KtjIN4yQpjJMwX14r5BRJk67QY6yq0aF/YH0jj7MJGijRPXvlWCkZY9liZEAhN5DSiKs+anDBMK6xVw7OvY93ZvjEvS50Oje0MyMeIsjltlFEd07LBHA0ODH83guMUNeCCwtUp3oQostCTyhgUFc2Jl0nGeFb55V1twKMX1Ojn9Gl4wpEZXddjHAfP9I0dDBjWpsuqnU2RCByEFnYOcOlyr3T3he+fgTco8DgGK4kFMcGS9+o6OgceBwzf/hPMhzuMf/kFYAmGLJitZ584RZgaE4wZcmEgaUZSmHjkjLiMMxhwucFhOjiTwYrlVl/XS5GGhe/yQQ28QRXZlkjuWrlBp6OZJqyFev7TF2oy/gByl4cuZv9wxL/9/ffxaF25nDo3OiRDhBxRII30ERMOr/7bt2BYXN3+T+DrHf75Pz3isQ9egyXTs9DLyRuqPl3Od8aLxRomfOIl4fRS57mZGnF/iZbXyjy3nnXc68mJPgPe6jNowi/wC/x8gAzSCReFTucCi6nUVcWfGclMNJTDz6o+Zo6pJnWaBTDJ3Dw1QPFcsQVc8GLxOWfpM2VbXmj+/XlqomcDQaIh5D5KrzOz1nm+mADL1quHyKT7/TgpoCnINBROReHgde95dc+z+/sYjHdaMRQc5kMZSqEt0bSRByLAH9lEcMaESAn2xhEHkAl1RV50RqCKDlHeOco48oeLwADkT5hgtjDW+uOjoqPPmYMbUILAkSl9e/s93r7Zw9n/ABr+A5yxYDPoLEgjM1s0NPI0lyPrI4/8Jd+Y4G+eXhbEnIOplOnRvCI3x2AFWTNy8ggrPWz6HiMWdIWtIYh9anZafa4o72LQ4GUzuYey33KMLYwBdQb9tkNHjNevr/Fqd42rfoeejijxmpfm/QVgtSEirO30u2LZPR7u8fDwPWRBDu/3uDr+tScAMCC+xXHwGYgkJMuhv6JwLMdUOEzq0CSIprEulYShLVpwzYDUN58w3q3clEor2pd0VXv2Kl/gdcyMERWEZeIm6WKS+bQyI7WFVBVbCGhdnOPnQgZUPaw2MV8AyaMO4kieofm0ZbXn50JLU7CwrAIiz+lYqmkptZ9ZlFlSZaC2L0KvWv3hIk1eo14BJDdVR2NEQLeMyi3gp6QkudPBK7nWbLBlSyddUuGvs1gS8bNcxCrQTJnGz5mDFAmVfvu+hnesngnux9b8IqZWQeSPCaNfh3x7VMpn+c1qfyj3BtQVO3JAiTBz0ZCk6dfi9HHxUTA9Wbrp86k8URMy2vlrsG7VrofJsUyT2ubbgmp7aOG9Yp0DU3nf7fCw6XDsNon5nJRZYkCgC2JVKiryR/74HFMKwRlOaXMzg+GYcLCvAAK2A2DMgHE8gogxjh0AxjiaKJDFUpnBPITjlpQhgh3c6PwdEoFxZ/8CGBlWCLTssezDiIfjADocMI4DMI6wVi7hMwEVR+hjs4zcHaE2vCgAKKtXhnGTL+WMcT1ZAxK/EqubQPI0rPBhDTif2gqehD1nzgK5sP3qkZgYUFps4mzD5wczk7Ea3zVMIiCK36kt4Qs7HLo/wNFbXP3RoXun3h9txqfP9UWnmr8cuwUFLT+1CJVg/2aLp9cbNIp6JpxbWmWXaha1UMezO1TbLy8Mawu8WMWfxyx/TFhNYp4FE+b9AmV+nJb/As+BnAsXvpzUb52WyYDIArT+VPBajdPttHAmreWbMtrT5ycwzmVSOeZQ9H8tCaD6O9MRcD2xfhb5tpm07douBC2lWeB7DFIkhAkKefJ3JRiigAuKl600NR7txLkMLsYEX47wV5SPu2P9K8hlwQk3KGpEz5Ukd2F+5KwD5VA40deVsxx4Z3Jwzn8adoBLl0UTGRgDsAtHoMd8Rcdj+TXgYuS9/tR2HeyW4DZbYAcf1aFLC2NUrysvHzJGureUv+ciSwsbVInT9jDSfMj4xZ/6oCBZ5ek+vbz8ogZV7smK9Zp4U0bTnGBBmhuXWTg1ExWfjOhgRI6An47o0OF6t8Nut0VnO9h4b6GfDJEBT9FbXSIy4oQ7IrSnXHgkv8O7p6ef8P0f/2uMlLgd/xbXh79BFOCPwB5igODokWU7A2MnYiz0yFL8SXFBZQOlJoGQ8ISLJGmODMTiKtaIAtWyHKJ6kDAGIV6aMIquw4/JqlFVjZPMvvzUmMuqlOZKI/juGUa4jDukrW0URXkEBKuv8dZeYphawk8ElP/Thrl9fZJWiF845iIuSE20W5W8xGDoldkOoBfvhEikoke4VqJTtmDm71GRcnO8zyJvUNs+UBkGvWCFpU0Few+AQCpVZbF9arPUlw7Ntjvb0ikcs5TWYyQtkdkJjAplhRRlkffOYGT5LxDF9icDdcNAHXLeqUJMIo8YFt9kPopypJjgjRUjg/IZVGllvhNOZQrUSLLl35JR0qtzutPVmB/NqsY6Q4WLaBSG6KXIbpu8yV69kompfM8ZPWFOGXCMt9d3+H73Cm4MxxdN0ECZCkg/F/SoKLWFWZUogViCiwPIEM+r1FjP5xA+dF+DrcXN8C06OmAYegAOg+3A7Pz5s4bgz8gNe0SIhPDHMAXsIBUR4cTQ7TkVjBy8tMK1WYE+y7m5x+MeGLpgiBgwugEOFhg9rQcQwuB9mDmz3BcRukPBuSTzKJJ5CBFkesg4/8yfZxw8pqBWQ/m6UrBWOqd1WoezGP5J255fSr3fc4tyfpU2gnMK77GyLlVnrTUxIoLV70YDDLDf/QFuB2zeAXLjEQ1A/y1Ao+IfwvKZnaeKEULvwrN5Jjx9+TzP3+rTD//xt3h6vbnIbOctOiV50VbgfIJ90Y5ouefixU6/fxT46BX+AheDU+jyJxY2f4EGEGA7MFmgC/eBPpMgaL5adDT1mc95kmoaqiSdLSfPqk76XrW9l46r0f+oKhjo73MNbL1r6BwuuUwmFh3P9yZdA8Ex+XvbjIFhf69BtNyU+zZCBDGlSGIt+0TnSZKoCwdi8veYhbEsnTIIzreB4Pligr9cAs4bPBAchsIxUnCknHVbdCWvhAF/RNPoTxfxrH8YjxAVwoYANnAQh6B6ucwlTzbFXWO8scb2G2yuDIbdBuNmhFzbndgj0VOxklcboN7XVuUERaeIu5BruliSEUJ9ZrmV3Bz/CU5qXJWq49G9p+P5TIZMr7TAt59a7cmQBLgoWxYpbNeBBgb9QLja7fD6r26x2+6w6TcwpkNphEglzx/CeUlYHxFRyIcMxnB8xIf3v8d4ZIxPBnwccX3424iXnbvL5iw5jzNAFHVGDv7PBMrBUauolBGFurCQXNTzkGsqsyAfZP9vOsyiXCTTPOlVqVFksDti6DoMm6ugdAjhY1GpUVe66ZA+rwRlRKttSfcmdDBNSvLC5Xbyovb8WIa0rqrb3RwfWG7gpHmMJaaQK9+eLzKU+dNctNvRbOWEF6i0meHP/WNXjQLJsyXsW7PQ58diboYBLsc/zI0xBBsubTIFfhKRP3JLZdJW5UwhUPSpul7C4qciikqSUv5PtvFG9Gxo8adjUyKqrCNFiIoQvXRchd5gEGiU8j7IvoTa1X7qf/uLiAwhXp6cMVK/QID6eMyRGZ0qrbuwl8QFl/Aw0tOyXtlnMhykOLcMJGOUPrw0pFTBnrHNGdWVdlSizVLasoSijaqPtRWuBZ+ybT7TIvtYKbS2p1YT5l8LIYL1o0nIPcXPGo3WexCHtemPBQoXJbM/nukDfsIejzjyId83lJNAiUzys4ylmbZDaB1Nn7JKH+gKs4NzgMMIN4wYj0cQA2Pnw6KHYfC0lsTTxO/VPA5wzP6IJsEK0Tgr5ppJU3JJ69+TMyBngaPD+GGPp3/6N/SvbmH+8rewfe/HzFjAAGY0kRbHUTJIYxXZCY4P4jwEniftAgo7c+vzLOg9RaOD2hnSMi4ZggLP/GRQSjDBNZ2/xdNNEtbbXPCstdR5qXPMEld+5vtbYzetw4RVzGmL3t9SBAQASumMMbg9EK6PhG1HGF8VhicCuMvbBnjyyK/I36luPAWq9dNPnR64hEnq4cI+OZ03UmVl6WZJmX+z/ek9vvr7Wqpn7NWNrCU+mO4aZG9PKtpZxk/fHDD0fFYTpQ0tnLoIh7Jm26lWdGrtp0sLf64c2Mfp9ypK9cyyLlnHL3BZmO5dtfdDT4DpMDztwMcN4E/OTxlXyEmJj8sxwh9lqWXyipyOChbpzVbvpVwm0jXXetfGTx0lnY6MUW9FfJFzFEtGOMo36jN+l+dzEkO1UWfCEm9DwPEIfjwkkUKmOEQkExl/V5nzF0abcDST8CoMF/l9MIMdwxk1TsZ75HhDRbEfMgNBDe9/yjFIBEfkL4+W/lNwoHUGzsg9DjI2gekkylQIaexYdY7zd+x74B2CDIxcIkm+7wadL9D56GciV8E5Th9K6CA1z+yVOUBnwVd3GK472N0Bxr5HFwREw0dQOGKKwzh4nBO5gvK6Mhm6siQn/GZsmXpaS2EifrPCaY33uTnBl+GAdCRPlE1cXEfpUmuXOU/5dpbSnpSuysqMGHPtV62qzVMFqEwTaUAzCwpkrr7PRtqUOorwJjjA7TrAEuHN9Q1e726w2ezQ2Q1G+BtEOCtV07l18HHviPA1Zvq8w+EB33//9+AnC9zfYWNe4VX/F9DiSGxikLOUYdMbCQM+yIWUovyThA6oHMtekzLqA1cKOpVeQS+8ViFxamThROWAXwDOHXC0BsPmCh07YHiK5VLxWa1AhCl9gXZ1Iwx1a6VuXEBTG2J925xCSkPTcvRktoae01f/J5tE3oDTUPwcmJKdNTVqPK0OWGuxsR8tiSSR6ZteJpMWjmADIyeUp8FcLpkFnU6NS1BEGGMSbnLyPkhFTOfPGxRC2hhJ5PGxjICQgoRsxjtRwo6r9tbYXonMUNX58eX4w+cN7RMreh4SUd9ASkPddOdP6zSeCynzKZtQcZab3jBl1CXs1ATFlZH+xXVbw9E/F0jzQ+pfDYz6LKa3nP320yTGW73RyIKUqoUeiuE20ar6mtHPOeA5sjTSk4ijnPeppMeRTiuhZAIkjGJ1AFTb1Ce3vGrOgwmdjsNTRCfKSyrTqaZNHoVRVxXEu3TVp5yBz04MEBw9w9/jJ7zHDzKTsVQvyKSaEiuR1mtOd4o5ilusqOpTy1lllvNQmcjfXUEO7AY4HjEcjoADhn7w698YMDt/abUU5xzYjXA8YuRxMndRAEMIDw/tZai0zCA2IMdwg4M77vH+v/x3bN7cof/qNUBX4WLqDuQIjhyMA4gIDhYGFC+/VsMBbWaLnvglCWXS6BwTTHBGBlUvQ6GXaqlG9kenL5dhgTP5Fp+Y8yl/0qaz2sUlj7VQ1GmJadFkg4DMu0TeL23XqKQ5cT3LXlmz2adzkTn9wUe6GDIwhvDqQPjqA8F8QRjvyp3R/zIowALjG0mzsJ9VwyrVqMfBbmSffIm9q75Y2l237z/g7g8P1WEuUaY1FYldovzBAnTbv0K3vVqVVnpy3DrcvxkwbJx6ejqclK+amOrTRNWv2Q/O5rjFAaxr2JTT/JxBt+5y+/TnD5/3rPwCLwkFnhMwbAzGTYf+3RZ07JEoWQtP6ptnYSaPSVz+NHym92UUQqu5S1t2yqOdospMxTskfp/zh4GF0kxQOBt/zgih2tCUeZvtnn/dBmr/VLIPH48Y9weYXeDviGOIt8juiPdChMhMg6Rcho/0jUYIuHCGSWAYDXkFPAji9DvtX3rq4E1e4QscJdnP1+1g2cCBYa3BCAZG+HseHIUvY1FBixlFNH6Mg+dlLXcgAjrb+TP7YeBvXRtgnMFIQzhJJIxflF0Dh6plj6wVDNgO6Hq4K4PjdY9+c4AxP4Gc7JJBaU9Jr8EiL0Mffap0MpDokGK9RDyU42wz6auYg8TYxrdxUWqcT99jCYGHlXXCoQ/+zoggG7n0LK2nUF4x/0BSCZRvKDh9UbhrwugMHEtMucJRvlwrTOmuJ/qwhhFiMnIl81Smp8Rv+hn060DaKbgHSyBL2PUGvSF8dXuN2+0ttptrGONx3IU1lVFgvxA/Kpey2hDxwx//14SDA2F4tMDAuDn+HcCE0Vh0ZqumSy9UtREwRcIkFrnjg4M7MvqbDp31ZxqT85ERQpxAUErAovgGiPW1RnU9zRRJWJCjUqAKW494mG8j6M0WFhbOiZLAJeQN9EQLydMly7EqvXGt2wznEab6NpNU67Ws3ohDat8vmafkZX9aOS8EQhxaOKM9CZr7+VxP/CQzvFfG1AaRE6DEGIV5Vw2r4UWq/1KQPA/lOIXs1IPVVaXNK2GTNrBQ/EyDf1lsIEob6umZ/T+xBAphmOUNY0J7Yh79KinAqTJ4VEv75wyyCBq6jPm89UcZK8XhUDmHxHnI1EXGbqZmUn/NBuSfmeI2MGlyeawY2WPqmkZLDPwnDci6DFz5Ng+JLuShSem1kK6krJ9ff7Iskrfz9PgmUoyPE4+xqIwP8xoYxsh8yruM+iApXaHQTSnAhOp64+l0dFI7g5FL/Zau+no9Pt26Icz7gBFytNKIYfCGCBuEphEmMJEeP4Rf8J+Cu/k2RWQC/5CUdtkdDmEcxjFcHnw4Avs9huMR3HcA+QuqfaHGX1ZNBGvD3JHNlMuGEGwMqQ5BacFtZuFvFBZGgWJhbc3gSWTBWP0OX3xWhg5VZ42DQdDKefgWLdYRfjR5+2yoFXXu1jehF1x8Z/B4BN5+C356ANyAw37Aj9++x/7hAOdcWKvB21CPAsnRjOHBluF6Bu3CMWRZ3TpntqjOgsm4L/Hyky/Vt4sl6CaPW8aBppdGlsaFpT07crk0P8m6lYP5DmQf8woXgAm4/dbhuhOZpCjfGdCxA82Nx0mvaGngF4HMNYy9y/IzgPdfHnH/6visVXdJjvjjwjkt/3PiGz8LqfEXeBa05i8w1/7iAFRM2xeqZw08D8+ynGoD4fyfqBSt8uJceVb5ueJF/v5keeJMyFh/wvfXO7zvO9xvfoLFCAPjj2ZS8+xlbUCOVAIQj4j2DCjDBeejMUQMiDOSVGZqcnZwpBQHWM8reh5eYxmDc11iyOsNEr69bBjGWpAjjATPexKQO3xVjnmVGjjI++G4KM/bm3CRtfN8PYf7UoyL9+j6dElGhnIUmsxnuFj34eonHF4xHq9f+6OuYtIxfIbLnNl5/UZsfupHLsGp+mVcJ0x5wujcIFFva5uLFSNEzoNFg1SUPZDkQZEPdTlKgPZfXZQdfVc4dUF5V2XypLwLhaRhSuN0Cpyi64kj3JIdst9aktGzls9b11kYR6AfBmzQY3d7hc1mA2MMusdHXP3+B/QPT4CTy74vy1OdcgrIakPEjz/8Q/zORwt+/xo93eLV5q9AsECvxdDCIhWjB0J+GfFwDNHw5OAOhG7LcFZubxDBd9oZ7cW2CBXhN7dKCwLUCUpelhaeXGxbR1sYugE7pfzId6lJG1pVXYIFa+1tU1ACVOPS6tRurjybe6JfBqH2E/OXVbzhhLMlrZ3Sn9pYyM9EGAk6fE7XntK3iNTqpau1MSeAVmglhes6ZYAkYTSmUj/UQ9XKtHoJE+QSMB0VEd9TY15my9TTSrmFO1aj5rHS1owclKRC/l1zucafJTSxKE+ytiR2EA92taL9PHBQxOm5mJBkanyfb5RcnqVxksP+l1rB03U6oS2nMjmYrINmK9fSiBfQyabyZEVMFYLyO40ZINxEPP/TKeZUM69qbLXCPiup4PCmRokCOKz9kE45ucS6Bc8MA1c8wIwOxANG8kYBIsIweANDZwlgA0s2M0RwMFqw43hXhD+GimFFIEIyqhAom0uJIpV7JZgZOB5AwwbDOIDHAWJ88P0xYLk4EF7wMpQU+ATykSlaVtG4zTIHMi6V0ePye51XmO6O6c3HMNhmfAC1mWbK/5llE2nyqERyzK9FLe8teCRlYz8OwI/fgo6PYHYY9iN++N17jMOYpRdjRFYliWMQwewY3CcmqDoiJT8dWYcFotEurElvJo+p+WahqvrcuS3D7Vp82CnM6nQvm+uuhw8AfZhLUM2+u2+nt3vC7gc7OxdJ4JUxocn7S4LtvoHd/WpS8tgzHl4dL1zbnwcsrbVP4uzSUjqc3ZRPLCz+AheEUigkL3PRc40Qa+pcgqSbKnPUIguz0jnxoWWVPGWEMj1BJjMw8u+tftSZppkGrk08Byt2BFX026stfn9zjcfxAQYDSC7KDXxDGhcDMi4cYy58SJDfwhHXLnq9u8iHJrlavidOS5xfOURbUFTEFw2NcoTqIlNwviAYY8EAjGE4EAz7iOdZhKgNS8Gr+8gE44MyCPHuCHYGThwqCxTIyCpnHyD4tt5f3ePtlw50/QZkbNZHEmUkSdS5ZvAZLbzIj9hMe06UBzKcryyAmHpaPjfTTxJKV5LxIRojwrNgcKA8sVpSXBQn8qIyQhTrE5mMUzRmRbOfDeWSU1OR4odLpysE3AkxZkSwxsI4hv3R4Gq3w9VX3hBBROj2R9z+7jvQmIwQUtVUd7nQ3Gc4JAmsNkTcHv5jGn9HcNbAUI9oNlB4MAGt+Je9R+afGN5SCDh2MEzxrD//Gax4DmCjNgzC1KqplBDVwRG5R5SZzClagWtJdflleSFsSQvb44jufo+uo3h/MXQaHV81HaS0bE9EhKKY8otuMryFlZt2B1Z/1fwzQERq3HKh7KOylCXfo19Fr0DOkpZEfplWlqRal8EVxjz9jvZnaYYI9xlRb3TgGcDMOLz9AXQ44HoYQOKhq/UBBIDmRR0JDZOwvWj9R13ZkRpwwc7UWcdGJe3n5ZvZ9q9oUuP0icJo8WcsZNXosto7xPmC43n6NUycjl9iMpAYxkjfSW01yUiQSHdekw59rIL2JGH5XTI2iWmKWZjhIlOF8/FsDjSDeUL5Sdn9aUCPI4KCnZ0cxxQU9Mx4h+/xHd5j7x58V8OlzpkzMgU6T0X5/ls0TOjLebWxYbpLF8aIuK+Hi+3ZX0r3ZL8BLMMOHwAMsMMBYIvRADAGA1y4OyYIVgjRBY4B8fpCYqJZzsCNkGJPxPDgQkTE4EY4xzi6EccfHbr/3/+OzetXuPnbv4Lpe1jnQMbAmtELWuxAZMPdFYAJl0Vo/kp1X42j9lTi2AYEY1FMnxFVA2KnlpoQRBMMvgxD7CPgoxcbgQyfisYXxd81zi4tjk6jytraztoTIu3kVdkFn4wx0Qux2zL6HYOODBqzxHkltSZjxThNXpPOvJylwYOvm2uqbjnzdVP75WxNM+VS68VCWTNPyseuZxxeu5laqPp1oYazwXum/ghjDrFwIRH9O4evhhPxnQl2v1nENzLXMN2bJiv47ssDPry+gBHkVAH8nO1elknpkDdTtaRdZZCobZIXUCyk8vEMVvcSfPJcX/5MefCPDoG3dIzb70eMhvH6n39C/8jo9kc8m/Lw7M+iJVMnh7ZGpvE08NhKCiiOlkzp4vGipWw/q19QAlH8ydP3S/kiuEnKdXDavDAYB3rCQzcA7LChHtZY74AT91QvJJMBwAbGWjCHCMzAjzPDR0Q4b4xwTvM24UbZKGuFZ56dhIE406SypHVerhT94gjmcEaT5kXIK/dFhjBEGIRXdw5M4wyCaW5Q5kKO7fV6TMIICpEMBH80lTOAYQN2wKjman4fZ5CxMLaDvbqDuSNw14PCqf/MIygc+RplI6aihRxKq/MFsovU+8lJxkZyMq9xjFP+PSm+osq/dLDKnktEh5I9orytdomoZ2YEQVvJakjlVOR2H2EfTjGIdVe63RqSlTDrh0SoX+3o32bNIDXq8Y0YZQwBjrH/9gkbZ/H69jVeXd9iu92gNwzz8D3o6T7OH4qS5Vtburk8rDZEbI7fxO8ccmZrfOVmQHIPhL4TQc7cEmRz7BenY7AJhD4OUPCYCxg4YUr1s1VjGBZ161VTJFBnkgNeGYER3eEIyxa8BZJlba4pbQFSNq+EFPXsrWJ4puyZ1tRBURivJCzHneIi8EcQp3PH9Ob8cmi9sGiUJmnirfBMfrTMTgGPq0dDhM0uMf3xn/x7i2I9R0hgxvHDO9D+CeQcyNpUX5gtbXGdl3YQOj6d5ZkGrGvmEp7E8VtTLxVjqU9DlF2M1GYlafwznuTX7aypRmp3X1CRApOcf45QbKNpgw3hqMkYkaebgObv4yUkgdljoYOMdPahMBs+TcZ86bDHginL5YLkLeH5mESIk5OFGBzim0l7TwFelX26X6xX5C6sdz1Us0mT0HEylnNkc6MhJ4XPMu7xDu9gMJLzgoHKV1aWk+DK7sge1/JOIjoYpKiImbYSR8Hnsf8CMIzb8R52HDAOA8CM0RqADaxBOPZIwq8DIxzPOtVMMGX16IZEA4COonDOh7E7h+NwxPi//iO2X7xG/5uvYeF5VDIG6L3DByBHNtlwp01+twaKr3qgWfqu5kUMcP5YrSlPle0SROGeIf8gHYlnQOEsWDEeAnIfUNmgGZiyhGuThocK0aXeZihEeTBZLopNcoXy5oyQMRoiE85SmfV2TKEZ5aG84Y0xsBuH/tqBHhDOQ6ai4RTp2clQaUOLKtTHavqmxZGva898G5bKa76J+LK+LYu1nIruFhhuGkqnzFLbbkR55MXzgAE8hr/0hAGYAbh6P9uUCdBAuP6hhxnnU1IHdNvf5HtDqIAQ7tp4PazswwzMKRXWJ12so9rbFQVWDlNbKKcmH6Xn9TrmgecSrRoURYvWMDKZYWVF2bPwTMHwzxZachlh9+4ItiPufthje7/HfjvAZXet6t10/fhz+W2GV16znuZq5vJHoULQJ27ob1zLu6qSmbTK8andwArMDvHaPUCPuueDBjrgiQ7YGYeN7WHJeMVohRsk4hSRGZxSREaTi6qd031jNd6cfrKU6h2DDBk448LpuGns5Qghdg7OeA7TsNdZSzSGb4KBcYC1gMMIExTVLjCicTuZ4QnL3/7Ibi8rkDMwBv7YJvIXZDtKHPOqaEwikLEg0wG7HdzWfycyMfJBjno1xVqY0vc4gIr3y/swWV+Awr2U/XnAk19iS3Ay37FvyWVLcIEkU7zY2n9GVTMnnEmIJMaHVG7sWrmmWlMyF009k62dJy8vNoV8S0nhYEqUZDBDBDcC4w8jjNng7le3uLm5xmbTo+MBePgJOOwxc6NO8ezldVWrDREZexsRIgdufPcPgrc04EM/mMBhhZAD2ACHDyPGJ4ftK0JHFg4Mw/6SSAfnFdzBc08VW8eDRa42LHgRnCvnwi/lR8if2uIC4Qw34uQDUBHwJinO5n24+GyCCP+TtAvEj4tkrTFnRccIRX1LBPa5CF8ll6nkGrLwNF3Z1XqJLVAKlJK5aXWvJrVc0iupqIygN1FSipdM+zLNqRUDhKBAQjtisUTKM3H7NJgh/5WGnnQMSEmXxRw/qT/z/0Ay7vwCGrj4l4AMnyRwDdDDXJmvsFAz+hkMEpFUkfFMBxMGYnzfDxgNwWA7aVcmEyUOtt4DLXRE40RijrTXCOI7yXvKkphLWXBJkfFsbNQ10ORAaMIpmbJP/XXKVC2WHCfSj5U4RDnm6OjSYgxlusr7glH8rOkNm7wEZoZDzbFz3p18dAMGHtBbC2KH0RBgDUa5LD1cFBxxVM2RCbRYvNWjeCR9Csy0c8EAErK6YIw4Ho9w7HAY9hi3hOP+Cc4QnHUwxsA5B2M7oGeQMehM549mMgbiRbaGYvkuh/P1Q0OceNgohj8y/3re0qgCMIAIpCyRmhJtSvFyWzljOEbvKSaDwoN8C1sWDmjy9OcBSRgrWNbWPowgaJuEVxG/sujHmhikXwlBXiugPOPojYkwXE2wXIxOJrgzUYqsrKEkc417o1olnIRlS0WXiU9F4cr4ri7iGctlnsOcz8kW2L8a5Z71mTb9CDL/Jf4qsXXzk8M3T7yuIUzo9hsAhGG7L3gBAjkDu++n9LLG06+GduK0rc4Jknl+FvyYHTP/fuyA7/9iwGEn7y3IvgaRXdPwdnsbL08aFprJ0JJH52CVsHwufBRh5zOGHOGOuw6uM+ifephjh70ZvGK2wSeuBq784MqrrDltPUQm72dya3IS8XuvcPHlWpP38qCUclqNb3yf9K/WuefC2v28Dd/eEv54xfjHt/f4/f844D/95lf47es7vP7VB9x0DsefvoI7biB9SDKe8HWel/NOMYHfrXTScYqWjmMbLhn25ejUJXOPVK4j8DjAhXtKvE7Ef/o7IghiGLDMgPMRxN7BtBZ12JrLJJwykh7TuQFERkk5XkQl13BSKYsMkRum62Gtg+k6gGxoswvdFXyhyLb55y4fnuhMTYh60EyIUgK2yLPiPCWjRCVPneQA7bTXhMD3x3Umdal1WCzHOJfRwMSARMywzLNKHNesC45gzqXn4Sgwn4B1r1NlClbrjDBHbVSaoCyadcENOKy0GlAjFn4TbGfREXB9u8Vdd43r62vsdjtYa0HjGOcjn69PC6sNEdxwtKmS1oVRjwMQDBA+D2PcO/BA6G/g74pgBksiUHB09QgeL9+rCSyLgkFLWlt60O6Y9EG82ZLNqlyez5j+FeMav82kzZZZuUrib/VCpwnN11EqyLJ7YhYvsNHS8poVuQBl9pNHcoViTtHE2Tbn2DSd1+r2vmb69ftWc9e7OadiCdl6IXkGmTdVfWVJMQC5HJpYjmJCdECvjVfJgK0l4Fz5lh5x+90poPq7tiTpe6ydKu3ImOv0Th8D8wskyLEjHqSUrZUpagknWy0oG2Nv/w3GYfbeFR/MALYWtzNrkUJBabUIb5Q8wacVoyC/s5gcny6hRGRYIz2tMXetstYhXGsohB5QhUCQTlUIlTU6InMMntelpK4KE+nyvi/1SqFQtWwEvQbrYxxDNM6EqZaOcKPNSQnPzmEcGaPxl1ETAaMbATg4o/osDBDyNvh7G5SyGMkoEI/f4RRpI+MgURHDMMC5Ee44AE8bHI9HcNeBmX3IOQBmBxMEGdcBTAYEhgH546AgDLGe72Js43gFRpgRDRPR8BbTtvgR4RW80Od5OgOiIEhFYUhHplA2hrKH5cWWuDntBlUezqHjp2TYl49wy40J0cCQRXele0C0ISK9M6BCyVqdtGJRt8dFEe6FxFO2u56wGUlx0uRUsaCdqoFb03etNtceqrGtTe1k2S10cEX/M+/4Snq12lfC+Svi7JxEGHY1yl+WuA9/AjkSmhHYPqyr0jjC1Q8diAkPXx7hbF53dzS4+rGf3YzibDfW8dJ+TcXn1Lq2Zn+veFGqMuXd0DF+/BJALwk6GHOH518q3GjVpFGV9bWme43OVeUNiYw/BxFX8+7LzkenKLPOhTwqZm19l9rtEm4OG4Nxt8W46UGDxUCMkVxixM6quyYblm9afZ6um/boqJFTrMzUsQLFGq/z4/PHKCYed03Latk/JoQT6fHDFvinW4c//I9H/PA/jrj5Zotf9Ve4vjni6uY9xodXGA9dPAmFRHiW39Epolw38j799oYEkQFcZII1nayIHXCBf5egeWecj4gAwoXaDCbyZgnyThsMCzIOMMYbCrgs/bS5EUOGc85HRXDitqX1csF2E4jgz6EyIGtgbA9jLZwxmVwgLXVRGBJ8ZKW2oDh4DDUvQDqRQMlcuWOdXgCU5C1phKSH/p664Hl8Od2GUHY6GRM4qwYicygZWF+Yzam1mCiuWeTJkDIzdsSVndoZs2h1/zzMyhHTbs7mnK8zRZ9HMB6XrQWudxvc9DtsNxv0fe95fkcAae30RyYYDVhviFj5rN2v5D3tkwVFtmOwKRQT4egAxwxDWhBjf8SARRTeZcGdBmnxZVERq/KpThZ9FWGcnVcgZLidFV9pNU++xEWwltWck22qQEDuOqrbpBbwZCcNH7UjmhQM737C8HAP++oN7NXN2lZdDhjpDpDi1SqckU1rYd/JsaLOiExUI4X0XGuP3icuAoHp85s+19tQ7LP1iAEq3illWaWx5zdfsZOTQpZLze97SAMZvWqBaHCi8KK5SXDqW/RgkHZla1e4Iv85ZYouOaF/qiC4BIjROdt0MysDGos5T8NMgHEgNhkTU873Ml2YEv10jmX4jMxTSQtS+OR8FYpRqtSewpK1ZxYg7Fnir1Z4ogDRGwkI++FKzV5k/GuKrVJJJ3ttI30TXOqDeLwwm6j0znZLzj5mhznurZR4iWbaTKlbzmmK8rwbj2ADPHa/woFGdMfv0LsRBAdn/eV5hgjWTDcUUQ776yRMEIxMZX+tbPLBCDGOIw6HI4ZxwDA+YW8Nfv8vP2J3d8Drr25hOwvHDnb0BgljDJh7X7e1MARQOCch4UEZQZd49oSHTs1N4IGU15REieZnvCIK5JzPomxTkPsi9KxFQ7rQcEXLszlDA6q4Wk9NKUGrtPm6PiaE4w/UUs7AR0T4Px0NUUmp/oDz9qoyL03e1NOf+u5UWC5rtqUlTTu1FmUgi/JG41KpxZZWE0wfTtbFKQvjxLrWwbm8DzW+V5LNaZhPjDRm46MwAB+RUeYfO8bj6+H00VA84zzHXMEFFcW0ZpUqbnVFsxhffg+4t/LEgczv8RxDxJyMzsWP7mkD42p1zbW9Lj399A3jp6+nHpTUvQbRDnXTzALQcmuyFs3yIOfTtiUFUtNJ8IyyLgHe25wAY8DGgLoBZAewMToRErYstYkr3+q/U/mNlxOWXM6kLxJxkknqrckLysTCxflqcfvNRlbb8bz9+hTw9fyzBf4bD/jjvz3gx3/co3+9w2//b7fY/PsewxuHd18/4nHDGHf/COeM90YfLLb/8Fegx13iEIoF4+DvTKNSJg/HLSXZR81L9l16FvgiAx9JwXKcKwEjwMSwgL+M2nR+JIzPZ0Ce7Fmfz42d1z/SCNnBmdfRVc0LidOQY4dO4bvvL5QzTmt+fbs+XP+Iw5eEx7s3MHYHB3/269P+DqMzuN6+Q2ePSukueg7tXMdKe6MGWTtbyr/MPopAjBGcq8HTFHLsDwf5wK+nJLtwTBq+xajqdtr2yMqMhk/2fxLhEGVjJ5eei/FKjFpKZi9GuqokuDC0WJIWXU66tpAqLAORK48PFuw6vLq+wZura2w2G1gbnNBMB775Gnx4D2DOG+OcPhuY/tcg2pyc8zxDxGRinisseCWTF14RFuoYBOWElNGQkVk01PeVTLYIuf5HUKbPIFtO2MK/E+udR5sxXkSZKxv8k6kCYhWcihOT9O0C5i10y3VwVZAK7w57jE+PoKvrRUPEuUt9KurW0zTUORmUog6HL9pK7BVdKjfrPKVBq2hdgyNvCRW6DZfiFSn+sypl0RDE8ci2oBXtm75uMMWr+rkmUaNR4bE2UngP6JU0QKVhOU5kpkmeXHE4ijAxHb/ACgjDlUh8gytp8QqsmJRA84VvFEZ2zjuJUTAJkk9RgJrin1X+mOYcYP2l3G9SAmHIn41VLdqk5cNGnkjDqPxRvqfJO+2pI596DOOFf1DGIz3n2Rx5ZGmORbDsM/Lz0LUxQrMU0wpyELQkYmx5ALPFo7nDQCPG4TuYcYQxBImIAFV8vpiDctgL5YYIRN4YIe/TYNRxXS72HsYRwzDgMBxhnvZ4//17HEfG9esNQD0wULhQ24bjorxiGgDY+H4YEJh89JA/d5cKfamf5ChghEY5ThEe+i8xy7I4dCfa668c6YkRIp+FSo4znoYQwamqby0sd6a+zSShiduJZiHf0yqKKBUpkb1nP5tTRVWFa6qsuZw0nDhejJkTjqhMWm+VsCGzVaf5rJGyRaUgTb7MJyuflnRyIceKQudqq/8O62c9D7iqEWeUcypur6w7DPPEDqEQ7Jxuj9u0/07yG2DcnX4Z7JRnbI2JrlfLrKqBS+MZJnyWQ1Cv+gFAvEJjBHA/X/6FgBxw9WMPe6yv+2a+4rekf9wyzJtpeoMrwJyuLDkdnsORzWDqKvFHqNy0HDacrRF9EfrKrXi+TSJjIchV5OfWN8l43sI6f1EMekydQOfXwhzMy5kr5LvKm4Lzbuea82JDvn+1WYAVM7CKbpxSxungiOAI+B4j/uvjHk8/PuL4MOC3f32H27/cgL5iDDcjHq9GHHsG7/YAvAKe9h02m1+BDkENzwZENrIX3p9L0dy4YeX8+oR1LHhUIjn2M8lLSnqPvJKPTlAnrMg+SQA5X078M/AkUdHi08bSr0txpHLhsuySL+DwNLY4yq0yEoSnzRPevyLQzgBydB4D49jj6Do4WIAGxXenJpfqnXIAGfnR4ponncrN6qgteRIiVrRM4Me8Qo+yOsL3KCdM2zZ5MrMk48PoBCV4k2TNafKpE3Y93URQfCZUagnLoM6bczYvIAKxgTtYEHpc3e2w227QdTbKeDAW2FwD/QFTSvTM/YosjLkDmeuTc682RKwXjFriAqICIC22OMsRkZ0DDu9GmJ6AVwZdb5GUPYmgUwsJJo/Csi2eazuGZlAnHrLhnQuLTBRiwh7qYp+6J/zL3bf4bf/XeNW9hhmPwHDIh2XSxpWMJDdCts7g60XxGpWo8kzqAMEfh7WSwa7Un07JD8dL0AkodAkoeYRy/meyTITFSd4aFaecKGRtUJvJCnFfT2n8PpnntczbNItvxgUI6CLucfEZer8UeljkSY/ORCCCMp7orV5eIhB7jk45kQ3itGVN6meO51mWTY66Q8d4+7sPMD3h7tfX6HadSnzJTexPAALz4SB0l+Izobfp3+WyEisb8qTtJtmEwkvBDB191/RGl1+Zx4W0Ukc9hL9CkSx5S2zWz/IyFerF8ZjiomavBJLR/fS1M+39fAScSijstmeOhO7M0BzhO+MRRxBFNuLez+G9ntdYX7yRjAJvgPg764xi2iLju6igml+r4mYQPZ2c1+QcjkewGQA4uNFfSmeM8RGT5L208gEQP6w8EiJnF0yYUxf4EsbADsdhwPF4xPF4xDAccRgG8LsPGP7z/xt3v/kKX/32/xL4LwZLRIQz6Jy/O8J2Bgb+YkEvwKj7A0jfyxXjWhT/liJ4koAi8+eyTxf+ZDFE4WABP0mt1eJNI2GrgDWVzIMX0iilL7eUubwR6SaFxhHJ05e/58uvRyeludRGCPm82QOvGOiq7F5DkVOw334FVO5F+2R7XBNhAOiWLbSPsRovnuPhXCvtZfKfsxdceg5fBidkPv1nuRN+LExciyvlSl+al0RrqPi9vs6ZdJ75qb76WGIbE7C/G6Z36y3ka3FpuwPw63+uZfgeRG/PauPadtFSgrm8jtA/bjIDwTlg7FdA9zp7xgT84a8f8XCrLmuviLMrMHH+oUZPBl7/4QDeEOBu4MzG8xQIR25n9PUEufZCiDnlw8vnPEk0qboQ+0XGqPGqADI5c7F11UQXXJWNLX4O/nBt8E9vCN9+t4d9IPyf/9Ov8Ku/6LF9vUV33eOr2y2uNj22/Qjbp+hl5xxgCMN//CdgNDiODma/xe6//x1w2PjIXjfAhWjaSOuoIHWRb6cooyfWKqQnAoz18oCSxZLc5jzuhWMvCAQHA0vsoyLIJCcddHBuBINhHAM8It1NMTeAmQQan0mTnLdqoLz7NnZb41W5RZAJd7sZtX0wdrsP2DJgzRDtObm6VO7EkHLyPTNn2zgicjRAhKgI3RR/T5z6LYp/LcdB87OK22UOl1GHHJzyyXNIallY8HM/cQqu4W8SSVK7mBEjI1QdpdGm6GWdWBTzxjiPF4w6icU1WMc321lYGGwHxg0ZfHF1jZvrHTprY0QEhgP4wx+B+0e0B+xUIJj+N94AcaaB/1lHM/kmtN4WQsjcvHg6EDYtxnh0YEfhtIu0inJ7pk+75nimuYCJFCItH/WeUvFL+h1JJRGcGXG/e8ShBxgbTC/W+JiC2bQfUxzXS9m/JRhwNECsWBXqtaTWuS5qMLwglL1a1cyakC9lCT3KhHOaMvcrl8TsyPMz8IiQGvqMuYmGJa2IV5D0UUuEbgUhVBsRFY/n8KtWdcT4MMDVca49LJTOse01RqTIe3g4AsS4+eaq3dg/Y3DBw88geV5P5lah/Bp71CRJZcm0PAT1c1JP87lVTJswW7riCv6sjVloKh+5aEPJR7BKcxEGQ5SVzy+LJl8SlIKfZhr9V8YIwkBeaE1jzdLI6fzGMsMLvU/JO1K/J+06hZVMHWCEEGB2GBigkWGN30/H0QWm2xv8vTCgFMOBOBOl8/ulLdJNgBTdTQYbfzSTP55pDN+ZRwzff4fNluCGEa53GJ1vixkHgC0cEQALGhlMzhsjwCAyPhICcoyftEP+lNFM3Q3hPwRHQ3i5hFvHsVL+SMWSmtDXYk6qUGwC7XmbOqQ8Fy5SnOBN+F4SuOU7IlK6ceDIdpYGBx2uJOuaDGEzAruhwqsswpLaqjU6dZoSl+ECexN5y9k6a4QmvVo/b2tSLtOKOobO9yTCymTrWzGn7PtMGfZVUKGZ5eNPCLkzVm3ttBRaLbp3qZZJebJPFkLdS0GFvI+by/AtgFdzb3R0RRz8fS35y8IJ3TIjcPXjAWZ83uCb/jVMH4zDoShHjB+/Ydjd1Ot3NczRZgM4dfSkGRnkgP7RAdxh6E24ILgsJPA+SLvD2maVMvgp3Wmx6/WnnHgU1cCqrNF8lL/MdCUz6ZYet99fbj1peNgQvrsF9m8Nbjcdvv7mCl/8hrDd9Oj6DrveYtMZWMswaroJnu92rx7BjjE4B/t4hOsPoNEfx+4wRr52SW8IEwqcjKs/htIfpVTf78QZF+QdjY1zQKlPJPjjLNnAyLGWhrwzUTzmKa9Z1zHfeCFJhGgMyQQl3ZIKsWQDOFukZ3T2AI2gtZ1EO/ZMhlgbCzLm3P+lCO2iZBLOnuFiksJJqTUULGm5+K5kiqxJenykXbVx0t0q5Mai/nrDpumj2KmboSGOQ50nK9ExFj9DvDjDBdU6vVUTwTDhigxubYfdpsOm61I0BDtgPIIeH0DHQ6OuJCPUf9eyWJC5gTG38+lmYL0homj0hJU+Yc+s8tXsvYsZiJfJeC868kRChUCxc94SuAKSV1+9gYZC3VHAb5Sj2ilPfLmMZFH0Fl83jnCF13er6Az35nfFVovaMCknETy/a5MnfuH8PIJX8hgijLJjnLiRRXaCuCCqUieKlfdSoLmEmXooJdM4nW1E8VORlYryQ4hcnEaW6JLT2YHl9AvSehMIfvd28delgCcd5Qpya1rS4uQqedSmmqHQ2eC9jzlcmJahO6e+lHM6bZ7mSPXGX27/XPz8TKTjTwgM4GAZf7w9YDcYfPHYA8IcwmMoQTGS50z6LKlRR5REOlDiLMl1H6rMwPgI25UxSeqdMFIcLgwL7yVsNWegVNm64RWeSbU0+/fjQT5mUemjmdtS/m8p/yJzmN+tkY5j9OPz9uoVfuhv8GR+B+CnjLSkvRkASdxGbmDXSrglyklUso/LtNZ77/g7SF4NBzgDfOj+AgZHvDl+i96MMBRC2keJQrCwhmA7C2M6f0+DtT58VreBNEObt8M59gYI56IXmT+myQtXzjkcw/0RNAwAO7Cxng2wI8AOxhrwaEHGxGOhojEk/vZ1+5GV+aYwOpFQ+japOZS7IvxvhxQhkSIj9JqJ1LPEewbi5dUtHq01RRe2PjzH830SGTqzcFmtg3z/DAacYpCO+wF/+Me3ODwd4/nKvk4dEZHmrdsBm+sRtAcwAAYu/LWkoaLxasGvGhGGX5tRglNdywqgE9gbta553VRfLnKBshZM2/SZQXOAPtP2/glAiev6mJDwBHUikPZYkuR6HyjXS6t++Myr+YNybc60cD18XO6kCSfvA03ma111lR9rinAWeHo9nCTi6WSxDvpXEP1eYx8A4O4PjJsf6i157kx9+PoaH77cxMLuvnvC9dtH7K+/xHB9CzIbAFvflqigTgxjZMc5l8dzXm4e8lRT4bssIdfTlPyHlgOn5bXKqq24bDqLvbuqbsnkjuJFRkNy+bPdugsAef1BB4M7x/i7f/8V3vxfd7h63aG/ouB9TdhYC0OEjkYQib6OANOFplrvRT8MYDPi8D/9PY77Dh/+eAv70GP3uysYQ5lepdWlUjyLUQyOYQyD2QLOgQyFI59Mpk9wQWs++lsWMJoRhgnGeuIrUczW+jsinHVwOMI5A8qOYtet0Nhbgaw7vgeJt1arWQsBJeP47guAr+C2HfhqVK+0ZCjOfVy55acgLpzyZniXPddOR6nnDqzkZIWP8WvoaRDqIymOsrJLsjT7Y15FB1yWpbDC87LhyOV0Z4g0JNQZkpM4b7WOZ4n91H1IXydTIO9LGq3pA/HkWQvm9M9ZGaSwlwCyPor+eL8Bux531zc+GmK3wWZj/ViPR/D7P8A+POHV7x5gjg7kpo0icwfT/0o1ZHkD8nf/bJc7OAPrj2YqoByzqvHyZKHAlxqPYXCACRfMgA2WL5XUG1bxotEsDu/FMprOMCsmKR6CpglO7mGXFpKLiysu1rBY6t6XnxY86dMRJ3qpr8jMk69xXqme9EVhuh0IEasoMebmQ5KTqGAQcSk5fZhYTwz1yzop879c3elwTmnNQz8uArKR6DMcs71JM08zDN3cm5NxqJVBNihMA+Wb+aqKmPWNu5CD+Z8GsGcSDj3DBJovw5ME6PPVRs8a5snSKpG1YFigmb88qWZ65yssS1T5dPWRz+L0u97S5hMPbQ9xzf/Wsk9oSPxYM1unz+jB9HjYXGF0PTAuzeycGJh3KNe7kNatzjaz9sqzBw49AOcM7jfXYLcPRgF/PBNMqts4E+yRQVFsPIeeebBzZayzOnn6B8/HRIW1S4Yx/zfCsQE5hvMeB35/YwZMiNYgHxXh2xNWYYiQkEGa8IBhDPQeEL+HAUp8vjyXFaKx/SUI5IX3ukVml6eDMwNl33MjREgjY6tpzngEOX8OsBsZjx/2GA7jhE+ORiXhy4hgDMNuABoZGPwu2DRCxEZOx/HUka3qwyMyrS+t5DXzckqYL7fW62oOzl+2RmONznOt4aRVd1lv63X2PIxPy7Gs/eAXWA+tfbXF/C1usjNrY37HTdR9yl/MtWiuKadAVR5fXShnHydDRdw7uYDYEj6psNbViWuKYMojQ87vwyH86QYQDAPmqCss9plVjaw8I8AeLeyY+Jbu+IRueMJoHAaSY2SkAq+cznn+VJbsN7l0plLNns9fx51yFawx0bW4dy6+1MVFzhIwarixzM8uQ5lmgY+aDHarjDyNM4TBGrAl3HQ9Xr3e4vZLg37bYbPpYQxgDKEjr/iWyF8AwSEilMXkL4p2BiMchrtHDL3B8cGAsQHvOvDegY4pApr1QGcIwwmHNXpAOR2R/PZKuOxeFPbt5KD8duwAMoEXUrw4+WiIeHyqqHpUs07njmRDDtKu3qQXSuKhBx53oCNHR7dUZmobQ6+yvDRN4WI/IqlTfCY4LbeMB9XZ1bPMKbPe5Tp4B6VohHBFO1jpCEJ0fJjSiZx8adBGxkSzSn2fgmLI5/woS1oyV9QkiTN+jz9aGPTYXm+x3W7QO4duGAHnrwhwj4/oHvfYPI6e55/UYEBmC2NuC0xZ5/T/HDjDEJHY2ll8OgcUlWZHOLwbMXQO11+aqPhNFuuADIX3Ys5yVRh9yr9oz8mk/AJy83QiRibmcjGfbr9zDiMzuHq/QiI6Is9nVrALLKKTi/CDCECOuZIVLat7Batap3F+42FeJWytZYhPhRxHK4yLOtZD0mY8f/Qk9A8MIWxS/p3JEwNAxAzvCOq8FZ044mzWuLWdiN+fN0rqdIZi7XK76BVVqsM2EsGMOyHHoef4z1yxTZK7GmqepBEKi7g+FoPDhiptT17tlfHRuB3Wzgvug3+aUBnTGB4b3jko796Vxc6R1Bo90gpWn0/YjTWV6rBQBuQS31Ihi6QoFmSLDHZJmpr4eyKGCQM+RzdaeoJMIZ5MQil5/jsdLSQVU8ze1qP4PaLlpXLqekpMt/ye4s3ccVMUjyPSdyTlDW+hQ7r8jkHk8HrYA+4JbjjgYPx8GwMfBWFsUAbLfRHe48pamymRp02lNJ6hTqeiIcj4o5UwmIiD0RjBDDeOYGcAHMEhrWMDZufbQ+TP1SW524miQcLEOZV5VfgRx5sBifiJBogQCeGC15Nz3uMJEr0hm8Ppl77KfKziMS7KrK6p7IzdIAqDed7MQzO8p3EA/fEfgP0DMCTNUstZJy1LMXx5fuZjDsuCFPpCJVYJD5bnZ6bUZ3YjCrXZcQznwJrMJaf35wwfF9vLek9i3zPZsORFZF9bVliR8n6LcrNK91Ky18VgbQOp/Hm5uW46KzUzVOpeOfkVzcPzYInAzDhqtvPUH1//+IDt+3183TkC9Vcgu4EhAzLWK7YoV26ZWplxIBoIwJWkjfe1kS/1PJEbF9ocmfL8M/H6jcrkp5JzE89fLOuTF55qy8VAlGsT5ciknu9ue/zTX1zj5gb4i6+ucHvV43prsd1t0G06dJZgDOBwD9DenzgA8Xh3IOoAYhh/CQO6roNhB0MOdgfQrz+AB8bxq2+B77fAf/4twIBzIwzZcMdYMRycD6rnXQE2/lgwieIQfttFPlPJWCw6bwfjRjgAI/lLrIm8V7kx/qJ1HyERIoUZ4VSFlfMRF3a+wmNux0HnxNnUpClJdNyFSGc3ulC9Ccp5qYsiroic6cu1sbiJmBlxluPJBPF9vFNBNWehu8l/O8igpU5by32O4ZzIyy7KLFoMj7teQE0pt0qbQwaKzZY5c0Hf52W8nLXWu2NNHk1rmmScMnkz1pTh5CojxAyQxhMGxKOdQXh4Z8BHi29g8Wbb44vrW7zuDb7+x39Dvx/gQP5ulnHwURDVSIhb2P63AJ0dm/AsOLHW9pBN5K5V3HU7DQNwQ5hJraTJvtR2rkrVk2oo+xSEUj+S1NbockQMRVAIBB4ZzozgDrnhkDRyz4/N2VvM/BoqktYZq/xQi/w8/XV1hy8fmbOdq252xMUtrZqowqCJ4ctQNEakD//dxFgw9gcdkAuXW7aYmPV9WZ96paQshHJd6no1k80s/eDsk7NsaP1aMF610LFU1hQf9YJmS6yVrUtUx0FEpVurxkuKRX86EMkVMQbj/Noh7zhuORE0Zk5r71mQaP+6stgzdMIwZcxZDfnlV/mu4J4rX+vCTPqSSpvnas5RLKSlQPnvIkF5lBVla+i82fFDK/lTOYtbziyPoff2vC75okj2vPJ2oQ7tQeQVi37/69kB7I9GYjBGAy/AgBIDzZwUw9nZyRX8jNJrwAhl4NL9SwYEXQIHGhW4Hcdw5IUZf8xuuDRSrzFDEM81IoIDBQWCrNEcF0ItygDtPx2ny+0kOiPD7ZXImmitrlP3sTJb2f78wnBqHXF/Kvar1UItA4dH8NMD3GHAcGxEQoTPEifIsT/D+8RmfzTIFu4lC9b8PxfPWm0p1tICRAfN2WIV/VjbP020WnUr2pc/T190d6pSyVwXTxmKiyPXjMy4aswvC8t1nTKxlcFccE9vvqXyRy7T5RjycsLa82pQuedwrujrS03/s0s+wTixjFYzKSLPSC+w/ubBjgw7DomDs1tQbwHbBf7GK3MzOFvwPC/lEv+8XFaNf098TFUiqLD2qypc27ZSxHgOZItW0SUyGCzh/sbidmvR7Qi2hz/O0xAMGVhD/mRRMJgYzqmiAHgnLROfEAEGBo4Y1jI2W4ehH3HEE/DEcNePwJMFHy3YiMJfzaBWnKPY1AK1E8W+3CdrYMDEwe8lGZ4I/pnniQls2N9Vq9GVEv9eyhjnL7Uit2YI9CtC9Pxn+OhVG2SMIbSzvvNX+Jwqctbl0klEvxfY0bpPt6RpS/JobdyinBArnhnhSQWV2qhAa7Q0oOsh6i4qpcQ99hJHcDsDckFVT1IzwN0IELxjmbPYdR1ubIcrZuxGh/7hgO7pmN3XkbdeAXUgc4XGbNRypKwnPG3BiYYIqnzLhfu59jRUHGltBGSJoVL+KeJxR0wAvEXTExN4b8qwbtNSqx0MlN75pooQIMI0B34nrPbYpbilFgssr4MBdLiCGQyOtIczAxgOjv2dC5KmZPaFnJXKkqhgkAszUPurDyVnJZZEIbQlhqcZIFh+5aw8So1QrStZykARqwxRTvgIYRzF25l1OfVc50Ndep2SMU34Me1m+GrCA2900JEQ4plKyFxUAW+FBwDjfEQITLBg+3EXA/5cy+PvtTqJomf+t8ufRs9TwX0ft2MkCikkcext5tI/JsmjN94ccxleYZW3N5z7LmmU+T1fO4ot4/wz8BPTrbV40NbdtLaK/D3iv7ImAoNSiQjSTKScwUiTt2mdJvJI0es4RV38eYOM7t4y/nB3jE+vjxZfPoTtKQwUMcNJhNKckMUa6+q1pvPvQyuCkcEIvUKgu+FIPUDPrMKXgOIkSuForPCfTiIikEdG+G6JUjbsYYzgsZg8ygH4BRn2wHwv8K0QDM+MH7yGyeLEKKnhnLKxYcSFuS+MESCT1rM2ZIQNvbnvt1uluqn3P6mPMFk8JFjhibiWdRXvFvuRFLRhDw7PyHcHgMvS6P0sa2vRLIS9O/ImzuF4PPq9ANZ7oFsDIobjDoC/TMwYAyuCupOyKPP2itSSgNENGMYBzg1gHmENwVkDGzq0IWAM7SPhazjsvcZ7HhEYjnxfwfBHQ4EAwyC4EIYu+1vid3zUBYW82Sjnm7gIibIG5NxX5xeN00aJ8KkpcQ7TTTo+Kecgg/V4J8lJ90W/Ukr9atMmD2vPNBXR0VEIdEBoREgVxzAvk1ICDIcB3/73H7F/PGI4jFl+bYDQa4KZcbMHvmDArt2HFA+nW7NuhHN6PeXS1pSSeJAyB9UeVvOjmK8V9er0BOg81ak/A3imoLzKS9RW1H1yyZLyBAZmsZLL9WueHpze28vklZxzvF+93BZqtOhUq+a8DafA8xnVNU2c59HzJbC+Rc/Bq9WE8YS0ZdbLr+eSRi0kvHzVIETZMxxFaWFheQvwFo43cMZ78zqNwg1En46sEg6zl1NZb1YOKDyDKfDMUkpO5Sr8tBL1SqkvsuG6/mIPD4KDyhz4+1ajNftTvp+kp7mXBaT7IivDWcyLw+a4h7U7mOOIwQCPxsEdHEYcYczGRzlYC0YHF3hNx+HTOQBjpF2iR7BEYEN+PIYR1jIOtx/w/v/4/0H33R36//3vABcMGFrWIkS+MvLwkadncDgN1YFgjPX5A985YvCGhxAhIVKMG0eAw/wbE/CCw5AYGNvBMftTxkCAG0EYAx7k2DJxCmjs41OWklUqxXzIRQzMeE3AG3J46wb86DowwkXxkT46+GOoQhbYMJUcR7+sVVeV6WICLkSdkObb9QKo9S7IRLpOfe9jlpXV/AKIUdITXlyS52knOib2mT1J5DivcpdelB+K9peOhNMkpaTSMlPnPENtVS7tHpvHL7H58HXIJHcZMw5f/R7jzXvcXm3QbTf49fYK3/Qb/M2//QFX+wE0DEkD+Kwt/JzMp+U5Kw7jRL5nZaHLGVJoUb5RlBXHKaf8yaRxWjbipEhthrtqBUj4npDInx1nuPOX5DhORxRA7x/BcnvSPD2fESwhtpsAUUYJoZC7LFgnap3HWAh1JIRPnhDA4wB32PtLOBcuGX8BtmxdLaofS8JlLeImIzDhVI+ouEM4eoS4OYxlU+ov1uFBSSJjI3UrYycTkV3HulKj/PqjaZrTRaDn3qvi0bhkUitc3Wwd0+2iZHhns2ZI8wzB5U8RAq05Wo4Mw9ERDjbReMOAdeoYn8D8lErBlpGzhIQT0oRWnvoRhNHWIB3IuxP+NFOq/3RenSvrxAos0cxgvagl8CG4QsDaC6BlhJgejJi+r4cz1kNFaipZvZzpC2+Vx7+OYiudKWI3m91ovZAd3gtfxIChHo6P/sJoa3KDlB5H0n2gjMcvqVe8+BmJESek9RD8tmIVrMthhY0cvL4sA87LesY577XoEIiv8cIBieDl/bGSYltNhpJl5FgooDTCBYOEdC7zctN9XMUWLkJZxuzeXhEYVtURPttYXO4WUyPEPFSkpVAKM3B4GjAcxuydjoBIl1WnntkR6IvTsGqCUvajNEKugcVJXMd51IS5k4sRyOXDZxd1Eb712QWty1zFNC6qX1PUKn6v8vsjhiwwV7ryUar/eH08B3J6Rep3bVLn+nI5PrZFQ2u1v9zo6lZ83nM4hbld6LS+nNvz6dyR+mZA+wHdCJiBM2fhi492U87m7KOEFic6h+WTNSOOR7MlTPOcB3P5TuerK2x1ZVIJDiMODnCDgyMDGAcYg6EHOuejGyh4B5MBaPRcsQvKYhMYRRd4S3++hNfvebUEw5kBw/YJuLKw1+8xMgPYBqfOYAiojVtkHJVjEgFsCIYpRFZMx5ADvxwdZ5zzjppGHd8THAkNGTjyd0Uw/J0SgIsXQ19qVnzr9epIuTsCLBjW+WOMdORGdMyOsl34fgo+lA5fNQcwaaTOtrb8SVFaXkZeF2NWEVSVwLn1uwEvqJaZ6A9OyEmugzlegdibykY6wtljMLwZdPCOZ9veYtdb9McB3f6IcFVPRoGnmGkA6kHUZa18Di0+Zwg/8oFQNPNrHlh/MpoRL6TXq1acTN5rgUqMAwR/I7lG2mJz1+VFYwRl7ePxgN39AX3nvEUY4cb6SBQaC6pYCDUd02KmE8HnDv+GoyPA0jU/HqcQMI30cl7d4ccfwG/fYvPNr9Hf3J5MDz8aiHKEKHTbRwwQgkXdb0uFgmQ6j6l74RtRuCtDXShYWIIXh+OZ7vMEWTOpvUoHVFYW/9XLhRqLjiefdYVJ+f2SjGdrj0SsSc+I/K4sOOXNfh6SllovfQTMz02weXmIOBa+CL/x1I/4/Z1XrBEZ3D1ZvH7swnue4NwilAaLxdxzcXV18PQ6CTplHZmnMxJ+zS7t8iVP86QLgRMjF+vmvN4qXETZW9/P0kpTm/YKy2KMfG4orfKVWxoX8n1IBJGsXSqyRiIeqEx3IkSlFzE4hC6z3WJz/beAe8Bh/08YMcJSPicSnbOGRoiQpO+FmELO20SDgF43jsFwcOqeCHFIk7NykyJ7DHMZ9i8igBzIpVGuNjuLiAAk8sIpGlsaDsvzXv2Y1ucl9wgOaTiXvXz/F+b1HOX6mRDHv7EkWY1ZPSeUUWmaNr9fhPJn2ihBU7/o1UePUPXrcuKfO5zRlZONaYE0TrIkxvG8hlwSJntS8f5zn3Ju0KtF+HQdi9zqqfj04lAl/DPpVnJsEd9Pb9EvIPDpB8/jLQFk4ZzB6//xR3Tvn3AwTy+gAlgqMfHm80k5/1YqnyZJG5K86BOqVeTPI9czp/RpCT3P1A2IBrt+r2lRlbV42u7ww/YR9+YB2weH68Hh9k2HgQjorjCYDXamR2cN5L4Ga/3Z/Dx6HnBwQ+BHTeQtwQw3OozjgOE4wA0DMI443r7D8X/+L7h++2ts//V/hnMjHA+gcMypv24iCgxBjPdMEkFOIEgRoc4RmB1I/DbIJF4VjHH03vJsGMaGW2HJgIyBMQSmLtyywBjAAFw8TSTy8DNTMuG6FpZpjeYTAHYj3DjAuSPcwDCWYKkPjnrwzkQEH4EcZSmvzcpCMCP+iCUjx4MTKXcbPWWe9Tu5E0IdxSStREOnI++TfM0AK+cml+Yy6nJYdLBK8ib95ZQe6jy1X7qf0zLbnH1RWqFj7N0Glrf48MU/4OHuW/RXhG1nsR1H3I6EV7sdtpsOZGRNNStINZkb2M1fQd8b8ing2YaIOYXs9M0cE63eUeXZcktUflEgkf45aWZCZi+Be0bP52Jh+DPlScygcJiy12CGs4yhO8I+e4M4EVobVYTQamql8S/k3xnf9xkIuf0ggsgTBh6PiAcGviiDtKZs3aNK+uB1LdbtFAcmMozgxjR7dWgJIMGrFYRp8uJj45Guf+1Ucb4+RFniFUG6yHpflrqoA5FaoKL9XgD05lY+p8aSkvXWXHC/ABSaqWUFAGPYGwmMo2UcrINlgnVC35FzOeqjWcdnAG3DgF4oMyHmkWm+eMuwPEplmqgiCb+n+S8x7p0bsTs+wZoBLatj5LOhldSJdie+QBjdwkiYNZTUJ6un8wxoGp0QGcEEmB5wFmPY/xh20v6p4rEMBw5zHowQMcJAoiEIyI6SioQyZwokAsabIQjGeWOEYTmWIPEIHNpRpW/K6yyGf6ue66pZwqtZcN+3OzdCcLZn6JGJUaRr8PMUZMucSlakv5gWUM1JGIM01tMqa9+llKqg1jBGkHwawBTnMcUjuFpE5axul2tlvpDm289L8wrgtOE4mR9ZEpPKBBOJk7Jfi3Wd8nwhKVUffGr4GI24JF04obxTq23oRzhL8FzO4ryxaBpnFx4+nzzUCjh1HGqcwEtDq+MnDEglaXmiQQ1OpWleq2BgjgP6/QHD1t+Zdbm12ZAr1yWrvOZ62kLHMpEGuZa4XW9LqpyHhUa8IDAAR8Do/B2uPIxwPGJ0wOgMBjfAOIPOWcAQuszJI1wWDYZhixjNywxmF06gdV5xHo6pImKwZbjtiHF7wH6zB8PAch8uvIaK6C5YtKCDgqFwabVRUbkVjjLqMDhGasCxP7pa7l8IRz8ZY8DBMOHYgHhcWBN1wruedrX0JgwMR3/XF29827kDw8KYARSO5tB2B6/HSj9K7t6f2jGlf+leu7VtrnShsf+Uz6oiXpmfy+96zXLxe2GVKWSY9k/pG5pltbjb9HTdsOV6DCKCYQvLHQjW47xx4G4AowePBhvT4dr02PQdbGdVlbXOEEDb9MtcgWiL+YkpgAHmA/zxxZvpnT9nwPMMETT5Uv05yVa+j2MfCERtcwTgLXYU/k+Khkh3MmHcxGdK26DS5r+ZEe4kDW2Qc/RjC1R5qk1eyM7b9Njv8W+/+g6/+fEa28crRR3nBWlJMRXGnwNzzIqMt+98XFxEECOCND1b3yVIt0SHETz/JX+48zJHl4+4ec5DSaHDt+yRt6Y6EAz7qAjnnL/7g9h7hs6sRQKlS82joQt1xcPky7mwYpBX8DElwT1t6s5js14C5iMm5mB5462RM7Uc4tNEcT79eHy2IMwAkkDExLjfDHjoB7x+7PH6sYtJJ0qYWV5jVrvzLJgXlpUnOhdKx9WC0ecAYXJyXimn6xQYW8rTTr4v1VTIWl88vMX1+x/w3d0H0E4xyhQOISJEXkAEhvRBGZ8AQri3SZSzqUlaiEmt9HUtGSGkvYnpZ4CCg45zGIcBbIF+NHDWBqEmRB1keFw/DgxAjISIERHSFjIwhr2g51zkhdJdWCESgRlMDON8SDkbE4RAG/Y4F+kUxftR5F6ngkkOox35g1hXee6rfLrYFuF00jIoJjzLXMcXrsyJat56ODGDXDB+FkyWvRhgwnjIvwUj4FyRSxmhNIiwKN/1p8xPt2Xs7kaYIwFP53VjGbIFNEN7U/Jn1HT5Qj8xLNu85mWJs+o8ocTPa1/6mUNFV1CbjfSEindUTTVfyRyU+T/hbD+r6nKc/lxgZZ9bepYV5wevk6e0JGTA4WhmLqM/m9YOqF2xLJfLpOlzrVdbrQQu60samXLzjlGe8W16kZVR7OXlEZupGl0XsAr5L7I0Re+zXD47h2E4ontgmLcddq8O2L4+golxOBqQsRgcwI6w6Xts+h6d8QUbIhjbgzpEPvX+8RHjOOB43MfrANwwwI3eEGENRTnw6eqI+9/8Aa/ev0Z/34NNB2uit5qw20H3lPhqwwYwiHyxCydU5HhEQDjq1I0OZByYDZi9BcKCYUwPIgNrDUbAn1gKB8cOowtuuwX+kPo3h9OirzNHTNFNOgfQEePDe9h3DHQd2BjsD19gcFe4vv4JXbcHO5ctNzmCSvYKomIsJJpbD2xq9Un6HE6DEh/ocrMjWwX9J8XnaynG+wdjFbt0TK1HIikv8M6hfMPpfoiszNjFQJe01YbiiGVkY3X08EmQ6tTyRe922I13KZUl2M5geOzAY4+77Q2+urnFze01tiKDxX8KWkk7dNt/hxgBQQZ1/JwDhht+Dze+Q7f5G5C9W86yACcbIpIw32g8tX/GxdBMo74Ve5X2ZoxoEPcxyuSe9DktORMg1RzJZcrx3PBA/agREZE1FAD0sTXkMNoRjlxjYb0cyFZ3cp16MWaZp5v+pMIWQwOlrAjKIJA65/0je/pX+f3qGyBGRYTXfmgYjv0RTQQDR4BhjogaR6rcvLMvBTPTTHcalKLIUiqufMvhDEG31pm54qvPGy9e3CvyjEGPPIwSEUuCl9Djz1MmWgGTYQnDqYeXAbABDtbhsRdmI+XejATbOq8vFOoAuMOIo5z9ebEezEGdtqRX6zeIRKI97TyRUj8DprSA9JeXxOtQvmFGzyOIRxCs2v+1MBui+Egz+cUtFsbE38lxgVMRociySy0jRBmFJftvTM/ym7F1zrPxxSWJumgRpJMxXxhLz1iniAgfFRHFfKJwkbsYH1Kh4/6Ahz9+h/7mGtvXrxKvwxRC0IX3SR2SPdqTtnJDo7A+heEPThpRQCgGT+G4NkLkm2UubOTjUh6vVNub8me1b0vwMsJFgvziaURZSeY8GiQUI1CPnmLQ/h4Y9uHi7xxaRpJ8HSRjShQuVV2n05H22J09rpV+TNdl80s1JU0fFanWcVJncEcvB5X1Ujxo51n3+BeYhQtjQkSuc7BsHv+TwIvIm77EnLdFu1zGz9r0bPhsViQuP7JzfZsRwM8plQtS0txP1qgktVbGYADQVXKdjunz43v6yE/5kCobk311C2nr/YyyfyYvV/ifWWVCJV8VLoiH7PVZ7LwDC8hgM17j6mkLGg3oYMFscRgNOgMYM8IYA8DEiMyuszBEsNbAMaM7HgEAw3AAQ44cTfyiMQQ4giP2XuC7B/DjFm4cvQ4Gxl876pUxoccVRx5CPHpcj4gcwCs1Rh7MATDBUcYxmACHdN0zkY/uIAr3RcAfQ8UYccmzxzPld1CZkXrJzgHhKKuOBwAO7AjMctQOZR96PKZNlE0hyJeRFa0l5jTGmvcqPcgmOdT30mBX9ruUj9V6SDyzLyOVl+SQlEnVu0rnWPQ3eFpRKQdVG7661Mrb8FE6ydsj3EY8hhiwI4w1MKN3atsFg5/tTNRpyNyU3SUw4I5gOZeMyzatGR8GeA/CAOZHhNC2Z8FJhoimEFB5QJN/A4JP0qh0mQeXnGNLIbpBLJwUPNEpErdJY4rnpMpOSfIFKt51cfIF903RSyq88NRpQ1KkY8Y4jmqRLEP94J56zhyhL0HwZNwZhrwHp6dFBqBxfRVxATHABAOCk3Ghlxbznw+J6AbdC3Nof1LUGHhjBJODGFdMDE3KmX05pzARzPR2StZrDXrO3E4oUL5pBM/Y/HiMORCsU9g3277lMqNle0XtHwvSBre+XbL5pRGiSEsSGy40DfHJ59XzTwNNmlDhywHgw2bEfV9cygrg6/se1webSiTZiD3nRkxwo8P993s8uRF8xQiRrKmOlVEKzSZreh84qcSXMWpIdfISFyaRirzRLT2F2uamisR6L/YjpsrZ+TKKUAhKxPGcK9WNU8Ls6eImQDCGQM7vKSSVcZ7SSHsIkTZTbKPiLQgwCk8CgqiW5ZPSavGcbVR7zTOAnh1+7Q44MvA978AcBBnj28lITDKBql733ggxYhwHjOMI50YQAGsMrL+5D50xAFsVGUF4+P4n/Of/5/8LX/673+Lf/z/+7+iohyMOR0f6OXYczlB1wjABJOa6CVeb41J+tnBB1zh9yfYaBsqzaEMni7J0QeUeRL4MDmPIDEtTXCvnKWJ1w+18wpfGnzmf+jxIQlRphPDfladkmW84gv74j+D9B/AwIB5x8DlAyS6fy/VNxnimpLoQ0E62vhH5z5wclj9/gV/gcpCIFF4My1azoH/OvGq5B/05wDzdi88KeTfPq3CGDBgWI1kcyMHQiCkHP1PXRfBvLn/FYTTI7Tm/or5yaYRQsn61bi0zK14oq5fz76vavgZmxk/zZJM59s8NSDlMjBjdiHGzxfHqBtc/vMI3334JJoAN4e3XP+L+7gPoq3uMOGAcGdZa9J2F7Sy2XY/OWmx6r3okY3A8HuHcgIFGHJ8e4dwAx/5eg67rvUf7yBjNHtz9DnhkHA9fw3WMrgOYDcj6KF8DBJ469T35GvljbUTB7p13Ek/LrPnRMDHs4BwBZvRRxMbrerw8YuBs5yOKnYWD88ozLvnaFk+7BlLeyV1nPswZ4+ERh8cHmOOXQL8FnPN3ksp/gTfW2pYoQyHo+yB6u7z2MjgqRSOU7VTyVKEeUqaCKAOzlMVJbi7XmjYuyJN4XDpCpIM6xiuuV1a1xmIdJvKLOLCHQ21i0QZeptDzWJNtSytRJUm5putLLM9bphmuf8JhIyU44PYB297iCoxXzuCr62u8utmh7y0oRMlzMCRNVj7vMR7+ETUqlbV5EfzAuuO3F/EnX22ImIoF7QdUS6GMEFORgtLr8I8hgtkQbEcgk4wOpbECZCDHM6SjGdKM6jzTZuUiJ6uoh5inseDiBGczncpzzuWI+plJLb7tlNroB2BCecS6nNIsFEwIRzpwsRlwmI/TQrteEuZbkXCBPUIkz2yI0sZvvg7Oh/+hWPnsreiyCTALw6O3hJfsw4k5n0NRKEeOVklx/k/hLV8gGmIakDNt0Dnsb62pMWKrIEOfxyr4NNDcP4pBYf1alqTJ544APFkH6qdFbgYDIx7cBByvCMMoHsCqkikP9gzg6a+FwleQ1fXtm028sBEF5WxKlafPDfgvt6FFJwSQ4vGSM0JJqya6yBglGfgE4TEKhjFFRGgETANY03ESpj3X3ko6ZzQHUY9h8xoDD17FXApKCMxjoI+JZ2HVXw6REC4ITckgJcOij2PSfM94OOJ4OCpm3R+75Bg+TJ0Dmxzue2C1j1Pg0idrsfAQ4gr/EPugF0FrQczsP2u2gFOwsbUKqni0UHbdMKHmL+MDOXZfBLOpEYLzoVICTBRc3AhyuTpnrm35Z2nkYhgtCF4IqqaDNZNUMVqeQ2maearNOo+WZWui8eSjwaTql2vLYonNDf5PDC46xAUTxMgI32TPOaviBqO1Ol8LnkM7clp0ft5Lw3PLfkkuf6FtZbWN5LXWVZPWtuu1bYHfwRgGbBzYxFuC63mrQzY/lqtGupWAi9cNGWSuyPWicy1hZe8tk3GZ7tx1ch4+HqzBfd/jvvcuPDfDBl8/XOFqvIblrW/ZSOgfd9gahrs6eqPTFQMYw2XV8HoUI8fBMKyx4I7RbzYgOmJ/MDDGwshF18Z4o4RxoNGXxVd7HL/4I3B8DXPoPN/ryJ+dT/7IUWITTrTIBUV/wokI49Tg3coRYx8V4ZyPZrZeQU2GAGOCQ5GF4dFHKyunsOfAHE5JzxgMR4wBwOgcLDt09ghDB5COEGket1bBp0nFS3lbY8j5MEyMEKIX01W4+C5vXTJCxDfqqNcUnS1rRMscrr24kfZRrecDBS2fNkZOMq5iZrXAlL/Sw5rJo3lKZ0Yc7WMkl9QxbNdhuzG4sVvs+g5dZz0+xvszKfaFy0gOdrMU+zQjhauJ4yfDeXdElBMw06s8afRLzN7pEHH/28BYwtXrHmZj/CDDEzAi9UlmGh0RboovJzb+rtz1EBOoY5hEGEz61elWR6GgKJOLQgE+ImKMxojKJtMas2xWizplw9TFnYwAoUwpuvgpSXQAm+/fsgFhstUp7125rLmsd34wPh2kGRAFAUe5gIgwBo9V5nAHBiP1LyJCIrSOXSSY+fELjT3r0h6O2QRzUcUMsS3LmHt9JkGaZSIvZIRY2y4CPAMT++KNaFwJt9TKx5hXviTiFvOR+vsUR5P9nIGbP/zPn3Yj3tOYkU7rgG/ebbB1waOnJwx/12MYO+BfSk/i9lxk5KpoRDXijYulFhmlEyDSTopRHc/ka9uQeYYLLUjhlq2z5lvPKhUgEs8Zep85E8iebryQQRLdEJ6bcExeyhtLiCRY9meJkNC/U+rQLpKJ8m30Q3Ka8JboAWVdZAaO3Q4/3P5HYPwAjL8DKIV2exojNRURl4GJZWaMowt/IdpSIihknNgLR+Tm1aqcioUowh0TCA6WjTJCCHuu54zy/Nn4aL4l9T29Y5xK85pskuIlE++Hy+wXsauKW21EQ6yNjtACFdRfNRIi8Bs6X/pB4SsFoTrhwKQbVSOEfKaSDTtYDKv6UYdK3SfydHOp2zhwTmm/wC9wSTgH19buKxSJdSJJWoL+U4SyZ+UYvXDPdXU1HUE14RwUhVSFvaWsH3G2F5p2OgvqY8UZFg4G1u5BZg+veqKMYyg5wyk3sbItLV55cewTN5/tviLEx0cuPYZ6Vylba02mZVcEmTl4aXFxws+lXz/ttvj7L1/jaXeEMUf8+vEWf3v/l+hsj67feP0GHF69/wI371/hrbN4uPsAfPUe7moAdX2YYAsyNtax6Xp01h/WdTgccBgGDN2AjVxkTj6ydxhH/zeMGO097u/+N1z9/q9g/+UGBBvmwMIYwDkDMk4ZHYRfTISUIEcqeZqqZTxjhCcPvBY7L2u4EeQMxtHrHckQrDFAt0HnHIA+GCwAwGVRLzL3mk/LWeEanWtPuDdEeGek0XY4brbYMMM4h6vdPag7Qrov0pxrGhhYF1zopjhDVVZ9kZykf4XyWK0XBvsjYMNYZv3X6aJMIzoyWWdJbtCRHT4IIhzT7EJeVhI5M1IkRG1t+n+9DzH7yB+I61gw9RCmAS7NsuZS6YEl9ZFSZSf8pIfYm0c80SOs9Th3t9tht93gzd0OX9Er3FzvsNv04f4dBxjlnB9rLuZ4BojzBLnuot7T56qznndZdQU0myRBCwAgl/Tqd4kw5NEO/rQCb2iwIRQK8Vke/RCFeFFSxCrUpFL6NSc3ZspHIB31FhEmagtUfzku9lRIWDB2A9fvYALBYBai2Bg4zr/Ok6LnwFzJUybZp27FMpTsQ700ABifnsAwoO0W6C6Oei8CE+YoEFoxQvh7QAwoHINRGnA8jXSJINdo4uR3fZRPa/UUqoROZym5wDkNACMumCU8bWGOtGaNkvYU/ZK+sHNFamQLb84QiFzBwoEAl6WlL1Q8DD9ebmH//GBmXk8aIkLhaQ6MBDxuRgwjw1qGMwTuLLRX8rSyVq0fccLK9UUUwnLDkT3Pak1brKudw58daaRLOUnhSyct4KQwldwU9375LcW2BoKyP22EqPABGaPAnlch9W6WuKmCgtG9mpwJjryXV+qjFnaQjB/xT2aB4QKT7sLdEOmvmBepDsK056ay4JQU7oDw71zgzcjz88EElWigHzvNkVC1j8ImNYeLJVXOW2Sv/eBU+lTfuzJHkwmOhbYKeVevBR8SKpV5Nbe6HnLuqfiX08upEBb2QX1KRLaHBVrw9A447sHjAHaMh3d7HJ7899oa1X+Jhy47Ng0ZX9PH1sNTjBDTlIL08+NfNL+Y+xxHl1tz6ixPYX1dy3Ah34sXhUl/P4M2nxvV8snrmohcJaH6OUCdrs/yKZdiqZrltJjzS0Btr2nA5NUnmNQTx3ou+XxRwmAAwn35/cxHRGSM2YpytRhalRcj2l1aqKqXNZUb9Kaud/xK/ow3msOXqmBSh48gSzK8nuOx24Odxe79DXq+gqUOlmycIPGXMkzYPu1ABGw6g+5wBLoBzjBG5zA6B2PCUapBJ2GNhbUdrLUgInQ2OB/DYnAjzPEAGgYv5PWBYbp9wvGb3+MwXgHDBtvhCv3Yw9ou3BnhT6mggHcEeBlH+PzgtBM1FESeLwYipsmH3M3m3AhmCyYT5RJjvK6SjAllllMi/FWN221N4Ip5FzhcwTzswK863zcTRMdCFiHRTc5dRq8QPLevqQxKfhb9Z/5ar4Lpd1226NOyI580b6yqTjod0adJREQwRmTKNQbDFWXVO62bX9NV5cYjTZHaEA1P2bMzpAlVHVl/twodGZ1jbE2P3WaDzoajeOGdk0R+G/oxXN9X9IiXNW5mMLDh7ofSMJEVFRs41YWdYpj4SNrgPATKiFAE9QmKcqEsajLkw7SCYC7GCRgChQtw/KITeyeFd7mASrr+BVwg/Y3Th3/CGWIAQtjkWRJ+nHMYNlcYu1cwh0e44SmEv1dFrxwxCMguvDlhQi+xL3n9V/IKJ5LQrkjNFwsgSChVmBkCjm9/hMMP2P3mL2G728am/Kk577JvOWGS7ovlVizTHjfVhpPhSCC1KjStVlNMfHHIDSQTMYGnGwXyFLqo2hCdh3QfgYmKVQVcFh6E1XOZrxTBRiqDbutU2Ko13ztYB3pVKJMo/vuROv4zhfNHR1EVAt5eDQDCBm4MejJBgQuIF7zysZjQ98u2zdMItKLLxFNZ45ngp0bYJRpRYQqXOuW7vY7J0koYCm2SdaRzRz2vUviuou86aoGMv1h39GvSGO8VQmyQh9wW7ZGWitY1OjHk5eve6zHP+M217h6FYVYcaQzS+DIQjQ3G2GiYkDnmyRCFaIggwI3jiGEYwoXVhcCQZSt878XSEbrr7/bznkpknD9m1RgQc7gZIo2HhJrLPTjqH+gJSKx3az+vCWLpjXimTXIXxgbhJxBnGWnOs+geqWce5+aUiln950Cx2StKk3mXaa8xsUplSx4M8AB8/6/A4zsQOxwHh+/++T2e7g/wgkDeztIQYQLe+2R8FqtV517PA6p8az3N81XeTJBmad6X6/kU8HMwQvwCHwmauHAhJOGSCj8Xyna11uAptV5wQaxjb85P/ycCtW6vnjG930W21V/mO8LCIW5AVcVclZXBdIc4DW9nJO7Mc1u+ph+lw4AuMf7Mohdri4rzHK1OTt7p9CVn9IIgm5Cqd6Aj7jfvcPPhK3xx/9fYXt+iv+oh97dC2MvAVty9fw368Ab0nQH3A/b/y3/DoX/C4XgEwOi2GzAIlggOBGM7WGb02x0IwK7vQGRBtsPhcMD94yPsfg/wA6wxGOEwfvMex6/e4fDhNcaHV3j9+y9w83QLZvZ6Q7CPOo6dEf6HAJROQQYklwVAH13jnYBoZBB7l+KRCOj6KFsYsjDWwrCDVwMH2QSJf2zP3Po5rfEGzAC9/wrb4xXMqwPolYWRqBMehdMMegdvkHE8Lt+nzRpn1X1lrHhU4V51OezUe8TvZSREWmPaqcrF31m/VUsQ7kAQhItyTWGEiB5X5drTTW10PRf3lGKIgalRYgp1OaiWcHnudTOMNf6ulZ8I1+MGX/7mFW6vr7HpexhjwKBkaDPA090BrnNlSct1MmPz0KP7sK3IozlQJPI1A87qKi9kiKjsXMnrirKXuWCpPS6D0oGAbmdhewMbjmRCeC4CaB5JoYVUKbYcgVLFMjdCelMpU1Mla0A7RjzZyfERh+MeR35AP3jrVRSQGeHcZV1yQtoq+p648xIoEJp2JgKato68uqLyif5BeqL6QhyOYuIQHqZWdsUax1lJnzf3l7cVSWElhDcoE0mt4BhONkv45cvpbNY8FMrBi5WEKaVZU3hNwQ81hBVv2GWC1hgzeRw+JYpFNuYpzs+pPkobN8fn1RyU2k7wnuyPP+1x3B/R3/Yw9vPF8ZeGZs9fgs+m/FMLD+m7bsJ8I57dRE7N4cpnfBuZnyk1TsUErKUiUuIsErKO7q46GqJJJhKFX5dV1RUUqde4wx02+IAPYOz9ZXOFgEgTZXTRmMk2TtkGzkGaIjXa2ilk1htWv9IIpsatNtLJOFa+iC0AQxsfFE4QksJZWkeVVrKUw/G83ox9D++j4juckRpHIaQ34vpWBcUIqXGezjmlMYlCCzfH5yRqWQuBWAEvTZEzry/FeNWUHZylZ5in98DhCRj2aS8KglgW6bHQZyJCPzKuD8CmchpTUzibe7o0cJX3tXV+WWjQKZp5t6o5bYz+uPCnzj+sk9Y+OZzYuFms+RgdbciEL4PVrZ2y1dFza3+hgTup2KXEp/VNbxF1kv6ycvKq1i4o0jI9IOReAPk8te0rWnQu3xtZyOkePJ9V5/U5sr29VkapCFjb3ksJHifm2XcW77ZbvOsNrt5v8Zpf4avNDje2887CIZ3wIwKGDEwwUrixw/Fhg6E7Yt8d4ZxDby26ziKWEPJa44896npv5LDGH+k0jCPgHIajxcgAOgacP4mi2x4A/oDxqwFP1z9h++Er2MMtYDp/EbHNcc4QJTNBcGSO/C6l0ysotIsdAMOAIzhycKMDmTH0PwmYFO6rjeEIF6SmJV8nl3kDAO2ewK9GmF0PshZyPH3UdUT9h/80UQ8CaK9MYY3SHXHreqAp0TR9o4RAFxhFJUVy7+YrRCTcH6H44mm5UrD6DOvUBQNTfVeSY1IhDUsN4jLltKGtfrfGb6ITzJqUVpWX571s5x5HuJGx5S1utjv08W4IA2age/8O9LSH2xKYOsAmGeIkIILrGcerYbKum1AmOZG8n2eI4BDGVDakzvXrpZqE5YD1YoAA/GIzlrB7tUG/C4SM5CxlwMjZV/In617E74mCQdeOtNLmgFrjPiPYyMINwzC6Aw7Htzi4r7A9/CWAEWPMWBmoKH0rD2qieBqCyP2n0Lbl9HMv07tMyRXaly7jUclruaPyhaNhKsOaQik9U+RnB4mOBwJGcrxFIECkUlUYG03nptNwqU0s9wxedI6OG3BlFTXXxfmtWlXHIiKQ+kyZy+OZsrdxY55exK6rE5yVS1g9Y1ItMWsL+YMq4yIkAOyAt//2AWSBb/7DG5irn8fRZD97YACkIiBYjrkJG73mBtYKIGe3JdDUonmCS2obCDRfeRmUNFdggoaXZYDPh0R7kH3OtZAm35MDgv97ja8w8CsM9E844nB6bzWPUDJ/gfOu0r8l5WWlJzosOXOFUDwM4EmFMfAeQfEIy5AreApxDAt3cC55FyWfDuGJKHmBqcZyZMwR+RXHDKN4dQrSSqJxrIiy/yQCXOADSDdAZVk3Onoewm8lAObvwqRpQ0vkJYt+Yv0crYY5w9bJZaUyJ0dmcXqeKzQc8OO3wP2PoQhJrKGM8kHTKHF9AL54dpco+1CtqCZbLKd4dInRrosjC+v4EzKefxbREA0Z8dO24SPDsxlpoZKfvit/snDxgZ1yfWfDM5U+F4FFIwQnfSDCsUzFvRA+Xc4Xrqr6pHQzTD3nLcnTCa9U6ifyA+O1s4CuJDunPitHpcv2+Hrr668/An8fmnm/2eC/ffUF+KnH6x/f4JubW/zNzQ5d18OS8bwpO++pHsbAn1cihggAIDz9eIWng4Pt77F1B2w2PRyArvfxwuIN33UdOmux21xFY4Y11l8KTYRhOGKgAYYByw6ODYx5gtl8wOHW4WlkvPrvjM2HLQyA0XYwpogWpXB8DRHAQcfI/nz95BQSVN7h7gEeEXhQBkb48+ONDW0kb5Rw4YLtzBgBJNnulOMidXPz1NqRiIhg3rwHfguYu195ww1Zv95oDPKMV2wY9npUB/i7BFzZioCrxht4mDjw5FrKquOeR2WF8zKCVf3WJKNvJ2sdzVQZFHniLNpCRVFwKi+ldaoOMWNUGlTSs9gVkb/ln8XONF4VvP4k/RQjIq4YgCzBfT/AvQVe/+UN3tze4Gq3Qdd33vg0juh++g44POBwC4AJ7kAluVrVVAAYNiOGzTibZv3x58uwWht2zgLSEI9H0loAAqaXYqqweyWsE3IjBKJIutwiEU69PHmuqDodAVbILUoDgGHcFnR8BSYbFJK5R+VqiMrRMy6KRsi31qypK3wOFASk1PVMi/9cFGdAjS1atiiSZAWrn7M0afJlGSpbRvFmnqjFp5dmWsOGG1vxzOlcK4znm/Mpd0KkiuJ5kIRwGTuqG6CqJhcnsglXbQ8kRo7rKsv4s4eGrqrE4JNmVFvZsvIVA8WRvQybwSk1nNCixaS1ngqxn+KfeLLEC86VgRcsrD8yY3gq7oy1UWsxq8iLszRmad+da43e1dOxSuE3COJRl0XgPWv/yKOaZIwvskwbJDniuxjEgmf7yOyPS6oIrZHXEL64mAsipKN35EHRi2SLYGRskGonAyk4RAwQ5N8kHkqNWHWs0txMGe45UHhNlD2bJZyqL4m9XJFvBZTc4iz+y/PJelNziOloJB6Ds6eaLDC7cMRXLtCEiiultuGc1VLlmgvmbsLrtX+eBKsikAr2nMr36scMd5QKWqRxz+dbdQkkVZ8yUC/IS7SKXtfjSu5qgfMdaL69WL9bzHopBWjFwTMqbw1eu/rLQcPhq4QV4ss6WC+WpCWX8QdawvmITPNLVDUZi6VKGqP/McTkS9TRWCZTTiHbWSvPXhpO4E64nVIbIU7jd9pt+qTAwL6zeLvd4N2GsHdvcde9wq9urnG32fhjiGTzEv418KdkFM8e92LC1cM1utHgsDvgsD+i756w3Xbo4Dn6YTjGy5QNCFYU/OQvj+6txdB16PveO3s6A+NMzmsNA4AR+zc/YrQD6P1v0B3vwMZ6vp6Sk2UeUUxgw/Fuh8hjyTFAnI5sYkZwCnIwowN38cBSGGP8ETnGYHSU5DY9sCfjd3UhxZLIEGzXod8ZdJ1XSnMaeD8P7B2T0lHpAIXoD+agI5T3QS/iCNOICAr/RM/oU7oxlWsn0RAJdVC+mlUOsCov/mZEI0QWJdEGdjU+XD06QZea8fqxDZMmAyhnuJhvBo57YGCDa+5xe73D1XaD7ab396gQ4PgJTAP4pgNtNugfB9DArRKTfqDd+GWwHYgMeDyicpv3yXv2+W65tagILCw1CioEZVzQHn3+E8m7Tyx+ZEL0A2XKiUnhkIl/jrKk+JUwaSotZOE16dzf3l3BDndgs/Hny+mV1eTRi7sICGBlUc3S6zX9fHkoFBPqF0VMrJ8n1RAQbppfXXgYvtwi/BlsuSfCdPL8lFL8scrgVCGiLwFR7I5rzP++JGP/KeaxNEI8s7T6o0mnIhIvSHIEwxwupnUpa2DMpLaPyW5/jlDrf8mrLOIWT7600wUFfvQ8LtSCcwbHvK1rsH3ZdFzv50yPKTGKnidSR4UlzbEqYo35GpCeE9MiUiYlbL6RJboij3NngmQ7SZ6c1S6S70a6sFnVQj4Bxfr0dlxn1tcYmmqi8YWjqmdrFSOEYwY5B5AJd0nl7yWNFqBE8AEAn4uDdxYUzaG8HIX1KQJBjmhK3ws2Jx9i5wVOzbZX6Zp+URvP2vvCgJBwSu1cqpIqS7XCCCFrCKBwVOZ6iny+MU5qbshE7IPPhV7JPFD8LYLW+cjJIkQKs1KM5XnwHI7iGTthkw2g4hlNk2SId0l+Yh00MXRWgLpMvS/Lr9Hsz88DalT/nHyn1NcY9edOxonRWh9d5job4X6eEuKl4Gfb+4wpCEwIAL/PaqrXkqU/LtQiolsjT5jfeoWHwqRM0Q1xpa7PE546i3/44hX2uMfx+Du8urrGX9odertB13UwcoxpiIaIyl54ntSQHFvEsCC8evcGAx3xO3rE8foRdvuAq2uDjTEwBBzGg+d1AvPamXSHQ2cA7jqM/Qabzc5zqM7f/ScyhiGCC9HCT199B379R9h/3AGPO3RdB7CBRcUhOOIoRTrquxIiPFhxzMxwI0AYQeOI0YwgR2BL4bJgf44/cwd2A5xLAu250530own3ouQXIjG6TY/ttofdbGC7DQZDmSO8F6UoRqhwkBVEdvQXdss+4ss2CJHPAGA4TW+UK1dSqBb/z/lX0TfKsfISQZ6OHGaVZyrZ5s48QchnxDn0z53OUG1+rUfT+uchN4hUCi1+yzFYE+EmJNw/EfaHDnfo8fruGrfX17jZ7dB3/ng0h3uMeAS/6UDDDbrje5ixHc0wR2NZEiz1tdsApgexA49y0Nn51PtkQ0S2WUShZrkBNcFNGyGq7+VLDJoIojJxUshAxsz5CyxJIXD0IJWPiN6z/QOXiB2ET6b8yJ0yX/yX/YUwboQbBxj4MCcH9gQ8Ip70IPSJpd/FQouLOTu1Wr3MRyLvSwurps9ItDBhTtP5wyYsFgbHi3hyCpPwQhFJiAenPz+PMMZ3Onual88LltaiUielX1xNcEIFLdxaU0j6HkVvtc/m4m/4Y0Cf6d1stGauVCmuTBLfzayy5OJdyVkk1SVW2hd7RMkzAeBcWaR0LjkjyWrZyKKU1kv7w/PKptKm12lN+v8MTLgIK0WG0Wzwxc8OVuC9TF9NZyRl5AzXhYCoQF9Vgf6LH/mLkrblOEARbShGB80bAOrB3aHgjEGacktz5ZLCu2UThKYVtb037FPRQaC+R1fbUc6pj4NutiiL2FCkSNaKF2oYpC6Ry+whxeYhLKfJ9rCcWsc+xtqKwvI44exDyEYqr8Vxpqc6AkHaI1dHeYcSBtmAS2F7ZeIkvGbCnisGIFRA/rglxxwpj+fH/egx1XjiUKYotCashB/JDAiAC4NQ4ITmSiI+F+Mke1NlS5lUU/+x+DhPU0lE8oLq+F/2RI91dCwpd4CSviwBy5RqI1Fj/2f4MQfAjvH++0ccn444HtO5uYqbnKxbIgJZYHPFOBLjvSVsBmA3rGtxddflmbFdhMiUnJP5RKgZmgq+qSRa5YCsaBdVvi237NQcM4VUq1/fqlVrCRNyW8+4qkN5SauyPGeg4mAvj/pl0TDny1k/K5nIlYOQJZtjIttM6seDEwfznHVUg5OH9aUhm4vlSYltniRd6M2ajs9WfxrCTNm3xCD5LvujmRzCkTFZHVR8tlrU4GkXUX+6AOJ+uiRnnCCIOEnIKNZjfU9fV7DUr8uoEHta0041Dmv6Qw5P/SO2sPhr/J/wJX2Fzvb+DodQiOPRK/959DssJSOEI/KXOsNzJo4BhsHu/R26wwb73YDjzsG9H2E6BrZPMBbYbLYAWX/6ERD0YgyGA8jBWgPYHtSH45yYgQ37o00x+kiNg4+uOH71R2D3hO7dX6Mb7jy7ZwjOTR162HnFO1jkcgLkdoJwHwNJTKob4dwIcgPYkT9XNZRjjT+b341dmLr8mM3SFTfugBU6HQ8ilYiFkEOcsQ+7Rxxujzjc3QL9FWC6iIfGj5iU4GsO6lGRP9hR8GELrcjwVjdIxiTpA31L1EXg0dEvL0NK8VpDQvKelxUtvGvxGfhhBhdlAhKFLcMaRyeuExGsOBydri7bLvm+VOQ829dgV5vkvHxRW3NhHggEMmmmpBcEA7LAtrfoyeKWelxfbdFvNjDdBiOOAD/BYYhO4xxob85xNKrWYCxgeoBH8HiY4qPtfJpYgPWlmA2ILNCIjFgLZ0VEZEtJ8/CKr6w5ami5Vb/TQlPxIhAAqJFLlQhD5+VCf60JsQEbn4bZewiWwmLplZlH1GvPM53N/0c8VcjkkQwe8dkxRhowugFsxnAeM0O8V5MVTAZKl0kKD+Rd2tz9Cz9W0TNWBikaXpY50Mo950jWToIhwMkZ95Te+nCIdAY+pF+amBHCWAEG7E0QBLlHJ/Up1pz+/XSc85wCr2SPG0SbMUX81TCte/1I1EiPx610pInLekEIcxRxbNoz/2C6HnJ1a1KhRJzVXto1Cg/KnLjnQUdRTV5NvwarQzxOJqxbv4nrtUFx8/RrKKwpIHhjuHQvSj4gqUL5qokbZDRDeeTH35CLG45PHjaPCQPwMwe1D2QbOYrelV1V07IK8avpVOX6qZDZ6CmRJ6spAYU1kv0leSUrfI7EtzTQFn3kVF5ZR16hZjqhDDPal31KpeJQSERbLK42kLqvxV4mBjwSCoHMCEGUGCafu1yAep1KHcLA1PCc80eh03LfATlvhEjUS9WfzR+UHt1/cfBHufp2c3oHzwNQ/NRIp2lD2WYpq97sDDip7x1coDkUczC8Xtkx4BzDBpJJjHAGLQcBIfET3vPEhUSC0C61lRLz7vE11BnGgotZCWgVDBTsw7TDiGR9JOf3fI3Lwr/EdhSdL/FKjRCrfxe9aEqcCv/kZ/7OF1EvMsfxOgQsIfV7Zm8vLxBPK0ztlXrpBTqU1reDTjYpO/D548j44dt7HB6OPqUSVHXryrZ2PbC58WH37wDc7oHtULQprpdmN3WyMNVpvtdPRXv+Ps0OeCLP2dyy17V+Mr+rc54CJc9ae7OiCJ4+WvFjJbxMz9dVuZ7vysjhuXU2yltqQqu+Ve1YU+8KqFH41XUvNfTcRv3s4BKdfOm1clobJzpCxK01gGwoFo66SumnrP8SUc4UFBgQJfMU0gY8LX2+vsxeUMp1k2gIztJW28EoC52CMEWRda3tLAuQhIXwm+CI8Xh1wOvhNX779B+wxQbddhOOSyKMPAZDhDdGGGWEMMbiQEA8OSnou5gtbj68wfH+gB/tI8btAU+9hdkM6L58RLch3FAHGIcRABOjI4YjhsMIIsBaA9NvYLkD8xGOjzDG30dNGGCJwW7AEYz9l9/h8PpH7J7ewDxdgToAo0QD+D+Cj+51IEQlFVpOU/4ON8cEcgPcYMLJBwbWdt4A0/UAGX+5NhjsHBhj4pXVoCtff+U0mfhigvBhks7jlDEEkMHj3RM+/AUDX17DbG7AtgOLwAN//5vMpzjjMQUDDyOPUKroIPIjWKEFLPgRS232R8C7LH/i8f1IG+JwUn0uw6ZfIu+kvsoaYpkV+c2c+4ohK0yNJXuv/Vzqiem0VN0CP3UVGrW4tFIDZS6cXJNulHOXAUg5e8VpMwTqDDZ9h952uLMb3N1cYbvbgfoNmO5xdPcpnzbQkKZWK+irscDmGjQ8AeMAMWhEWmU3oG6btw8A+m2IOnHA+JENEacBNb7P5FDKjhmxL5XJCBerEJhCZEQYSBfkNFFI5nkxXYOCp1lIFac1ZioWuiIfkZcZn/onfHfzFq/4Dh2uwG7wno0yyUUP48IvBdpABDKFqFrrmaCb6VMWNs7aw5Lj5qzAarJFMARyCbGP737C8fER/d0rUL+pbJ5tyEncS8CpItunEZvXguxjspoIBFjCeHuNI/ym2shVh08oMKwTgHmC+9oY4VMkhguBNsTgKUUPRLGjTpYM5CYvu4a/lI94zmwUpf/JwZolcallExnxGk3m9FnRrFWZmBPno9SHioJWs2Cz+attURwWA0ueBiWFznB44qUy35BTj5yJ66p69xJVnmXVTUYnbYtp/8+8uo1nqm/4DTre4Cf+EQccQmGcrzXmOCHM+RqXujOR45TNZUkzMzP1onxm5ngZnnMMIs/ckyGwP6VJMeQueYBBz1NqdCyz/MPCvGpco1CWFx3EryEIGmEMwdHOTNETpyxyeRAjXdaDKYI3oXyDGoZVCpUvi/XHLM3np62FmuMNI/CSmYAEsYcC4jG3JAlxbsyIQhqFKBo54Dht9smoGIupV5IrTHAGbb4MMT+plGbiE9ty7l71Elv3C7GScxztqipPTfQCU3BRqFT48ViWCtJ85AE4FXXXSwjLtOakSpaKWNiDs35+FmLauURjofGLWrSPCTzhsRIfWNkgn1lXC/KRnnIn+rvoeJabo0pUUYy5kwWXSXO5YiJj1L6fMWmEGDE5fbHAYCh9z1Nn8K+vCfemw/X3X2DXvcGm69GZLkYms/eegXPeQSYKHfC8uWdBapyb/zTc4ebdG7hugCUCbw545AccdwOMeQKDcX/YYWM72N6CHGCcdMMbDrpNB3aebxae1XU9iIyPCDYGw+DgGHh/+wEGHe7uX8G6Tc47K7knOuDE1oY2p2SBX2U45wAaMI7eEGHI+COaiPzF2sagY4sjhSOkqjoCPURJ5iMZThBS9AEA49XVh90jHndPOHy5AV5fg/sdyNSijaZYIK+F90x1c3YsaPrzvyOKRN7SJJ4z6ibzFRT1khWyV0YqyTGxZaq4XhzHsY9LSUc6MCN66ujICEWBqmtzJXCodz6ytsT51q+IdEiOwimdSL7GWn/vBzO2TyOu7zpsNhvY/gg278B0jPI9MbD5cIA5jjBCB8I6nKVrxoZjlvw1CWw60GYHjIM3SIjch1zPkPWGCOg2YNMBwwHnREY8yxARyQvPe4rFNQX9Ze0uVEmndjqOiJaEWhZ3V0b0hORWaRWklI0pITzAguSTm+bLvEnofLJ7fP/6LTbDG1wfb8CHB8Dt49pqDllco2mxJsIIINxmj2Khi/KFs5zNVjYTTPJ6TQSU9gE1I8cUSSWt/PKzdPzwDg4Me7WD3Wxw3k3enxoabV5S5DV5jfM4xnUClNpJjQ+hHK53MDDAwzAp7UVng5srsQFzzGtbQ+BpTlLCakOk51sUvQgEKvaeJH14QrIf6lWoVJjFnKeLZIU/U+uY0t+fFHzq/pwzoE3vIc6SpGP0WnVjsnxPVmIWRSyRh8gUCI9bFiA4x2lq1lKYU9se6X74klGRRlFziopEqsiHSxcyLIFww69whVs80AMOvPdlhj3R7/nJeChGCGFQ4/GOs/diTAZU9XZtnmnqiQEinGtLRHAuRUv5s2Z9a5NRwRVTTFm5yNJyc4yrW5DevCWqMvJTiY8SpjRdjM5ZQesiHKQaFbHWRpR52pKktkklz6KxK/LWgjKmI97GB8HGer4KRH7UC4nJSESTcWrx5Hlc0ExVwrOtHMPTh3ppYmdaObtmL7QV0Yr1/oyKcpnomXBGOZfbruf4s+njnKI28pZD/oLjdOpe92yYE7yeU2QBtV6dUmudop5Y1sfmCSc6Bv3tsmN+FkSZPnvQgFMGb2nBvFzfC0fuKiS9ReK3zm/RvGYjSWgFlzNbYVMoXwZOX5JBX2mc9HqffP9YsLZOwlNH+Ps3DDpu8Pq7X2G3u0X/aoPOGG80CHyoc0EZL44UPntg1fUJBlMu1LDB1cMbgB3M8Yhjt8dP9ga4foK5eQcm4H5/gNswrjqvojTKGGGMgbUWbuSgdGUADhv0GK3FyA5EBuwOYAt8uLkHLGP7uMX2GO5VM/4ybPEadgR/WseYyy2iKyhlQrDDODoY4+DcCMddvMPPH9FkgdAOKF48bnGaVqWwWBmheIqC58ODABTKfrp9i7e/OsB89Qa4uQNten+sjkm3y00jMBJkamLtcM1IbYnPp2WQNjwQF2s/HyuqYkCebrKiYzvyNsqyyjS6HCKJoxwiiVg9K8rWnwswzT6XkZs/s9EM+qUWE0ggwBCsMeg7C8sjXg2E226D7XYL0+0Bs48yGBEBzmFzf4B9GtIxAGv2EGNA3S4ScjIdYDoAPjJCiqF8WUxaDLsFGxeOaFqutoSPEBERRI4gd2hjAWXMfmvQQg5GiHrwghc5FmNhxFtTRj1QwmEKxxQEWlGvKUMcfa7YEgLmrZVvwzhgv3/EwMdoPXbMAU/q9yKkRY7kzSqSP+RoGbXADaVTkqREUf5nVK9cgWv6k5l3zto7DSgEQSZMpvD843Oqz4PF1n5kI0RRORK50wKWR5jD2x/BxyPM8aDOo6O4hsShoakP4vPmv8YTph9LIyoKpZq4SLO/5AJSwdyo9JLPuA9Q6L+sIIr8MgsF5sBQJYtEVmd9XPK2C3NGsglJKgLWHKP2c4SKXPhZgkxp9om0V2l4nuKiEAjUhqN5US3QCAt7EnaETYLCOhAaMGX9Ah2gGaXQyaBp/fwKKauLTFoswa8ZA/E6YrzZf0B/3OOH7Q0eug0Mey8kVuuS1XqN3vvKeYHC92x+qdqalVDfHye/GdiA8Wp4AizDjddwZLxAV6YlwBg5Nk4iIhImxOOyQt8kqoKdj94sDQQtYOZwF0XClcSvKbV1/M0ATBYWrbe9WaNCo/5atCoJ36Nw9XOFFpqvCUSaBWbg3R/Bjx+ApwfE0GtlbIrpRMET97N2sZuBcX30d0RUceSU4a6lO2OqVmf56Gjwc92bP9/1Apyw33ze3fgokJajKKROyZN+XxJqq2L9bv+MSlZlulhhfwLwafrMxp8pfrjbYri6wuFqC1Gops9lmJ+18q36HdQgWKu5qPDk0zRanZj+FOuZlxFftHixMl357AS41DQ7B/7wgGvq8ZdXO9z1PTprwxHnvh43BuX7KHcniISbjpcxDGw43Z3h72XwynsHhlyQRjDYuA2+/PFL8P0A8/gK5s0BH7p7HLcdcPT3PlgGmB2sMVGOtobgYGGMg2EHZ7zHfGf9UbD92AHksLl5D9c/4cO+x+PTFV69fwPrOq87Y8UrR9TxyENsAk/sj2SSozN9egYwwDmDYQCMsTFim8grkYEOnR0wwjsciWMRgMjLQfHxfqQEp4KuIFzaTcZiv7vHw90DDl9cw3zzFWh3DWx2gN2Eeyr82jLh+FbSeoXSSKbqS4EPOq3vIxdoGcmrCTpVBoj8HSA6Eh8xWxKscx1SuSpjI1QbOZwg459TiHogGX6JEI/Cs3zXDVYTO1liJy6aZ4shlAwQFKVvyCG+0lIyXvYbjgbu2OMVNri52eL6mtBvH0Am3BHIDo4Zm/cH2OMAc5QLqk+gIc6Bjw95x5gBHqXFHkeGo1+zpgfZDnH0xoOaI4dz74l4tiFC5iZdDo22MhNyjEP4LcjbzhLkXxcT+rXlM5ILOQkAeSW/Pz6gVaIQgbV9K61965BX0rhhxOG4h6MheDPKgqn3NipKIQKlXv2p3qhgYtkEOKaPygmI4mm6lU82zlnQ+YO3KSNRnawrRd9CVgrJk0I2da3RulWtOqkbLw0tk+FiA+cTtPo5t150KsGP8eEe4+MDNpstyFrIhUeANJ1mlRfnQD63p86ytK2t6Zi8ydxzEvIJzdHGiJSFsvwkSs1gEEwe5xQVmNIBjp0seiNVyxIRZo1SAvpZRgGdAY1lsQQvv66F4VOMj3o18SiebdCyuCS63FTeUg8VczzxmDmlJSKRlVzidEaSF9PcbJ3Gjfki5/NMjo8KTG403BlCuOsdt8cn7Nw97u0GD90mtjXtdaqVrHdBbjRDPwxpNRk5SSM7naPySQfGFxhwGA1+CuHt4zjm/YdnRplNjJqIiucsmeqv4tu90Ldu65H7IWQc0oV09fSI85naoJtOJLzHehwRZ4uc06hUWRT5IhT0ooW2xa7V+e/fgt99F38mcpCMEfWAkPyhxq9uBG6ezpWqqpW1Xy/VQbUSG3meMTdVnKyyFs9FgGVO7eV3/gZ/tD7rxfJR8YvaL5/fho8BL9G2Fmk4sa4W7eRKmhYsrO6Mxy7nNv92ruvax4KTBbXzYVL0per6PMfXs00W6LY4Xu+wv9viSD2iZ3dMSBGf5najee56GWo6Bu24kje8BQU2Z4tKMVtzRgiurMTq4pxryMxoVJUFnL+vZuXwL3kG8uEeu6tX+HrT+eORjIEBRYcediEigp0/VSFEFiTS4O88A+DvRQUwcnCQceHM/jBmZAwIFq/vN3D3wPHHEePDWzx+/QPGwYCY0RmLre1gjHdg9X8AE8EYHyVg2HjHHRCs9Xyz/3Rwuwc4S3h8tQP1A64/3MCO3shAekwUASW5TMEB4rQUp5ITzzyOIwCCcyOMMyDqvNxiDSyAwRgYtmDn73fLHKaQ7pGrHfHsl4fx+hrbY7wFPvwG4Ne3wPUN0G9gbA9HBkxmqtdTfGCsUeFidvy8oGMRfZDlyUAGLulZ/Ic4NOVtSQ5V05IytI8Mbp5A7pXwli1OAk+yooQ/FR3BqXBG3qZyb1rcDeJYJIZ1aXtuiGrxp5+eXIaTMTWGMBwIbtzAwuL6audtTv0jjOngb94F4Bjd4wH943Gm8TPgRv83CwS4AXAjaOMNbHHChyN4PC7kX4ZnGCJKtke/CUy/8mpjdkjHoASElYsWvcExXaLCPtyGWVjXoKgI3tsw/vJHigtNtDy+1EhdMj1SReJZ6lpl4dRCEVuyyzgc4fYjhm6Ao9FHRcBf/MhQhpvQZkHMeIEmAf4oBL1sgmKJQ8WhIc/drEuIZEaqCG1p7HYLhaW+RVUXJcXXzwFy/42Sqpzbj5dkJClRu6jUE28CzzgYSAhlWkspZGymzXEjnq/62R6hM9AUkAB/jnwwSgLIoiPksiBjZA/zmE7GeOtwZiWjtPEILWOpPdG/msiVxpNjfgLAg8Pbf30PuzW4+WYH0xm8LB58htDCL8XoXbzKuToVok4umNP81pkgfFKknEX/EgOiGEP9q7IfrRoiHUK7dlCb/dSDIJdyl3sBFemxkGa+HXGPCAy5MQ7GkT+rNngeEQDDPupOCxWRNQjNlj2M2Bvt17SisbIxP5b19/LkaK/x/dXfgemI0Y0wwRgBINLmeEyTARyPYA68A0+PW/K4JSHzAYcUY87O3y1RvSfkFJZIsVUSOZGOLKMiHTeWzHxtheyRDL9z6y8az9ZBZP5JeMsVoOpfOoY0ZpF1WghVmq/SHpsZ1igCUHqkiRFCDE6RlzJ+TYoTXGqjugTvRG+lVjdpKcG60vOyyrKfW97Ph7VcCSdh+EeCP7lBfnEolvMZvM4yM6JT/Hlxlkv4eGkp+XOFKLB/wjZQ/p0MGFbrBidQw+wmJ1UICqV0zsX3mrf2NLPeZMvStYwgnyXHUukdF5lavb/IVJVzXmlPFS0ITx3wD68J94Yxug5dt4E13ghBgOclAbjgGOPUBcDRs5s9jxEV0SCI8t072zjPz7rkVCPSr1yybAHQ+yvs/utvwW/u8dNfvEXXG2w3G2y6DlebDToysKacz6ChCUc1EQBLAFsDOziwdeiv3wL2ETBv4JxXpooTlHYUzpwGDcCuNmgeW32Ux4hx8HdBdCDfCfjoCGs6P+RuDI7jI/QJCLkvb+BhjIHpOuxhcG974G4E/foRx5sd6M0r8Gbj71Y1Fkw+EsKrC8N8iPBTPVIKqe4oT2qZt/jdhJIxTV9JI1ngV5PRQ2QUP/8ufE/tcPE9Rd45jRXg0rPM+BC88TNjxBz+L+0VtTFo772lLOFpTqG3lW9yOTUh8tD6ehcy3phmRsbmYcSr2y2udlforYPBAf37PTYH79xOjmH2Q5JLmMHD3hsOzoxOqIMfOB4O6cgmIBgxnr/XXOBopuRrVE6TliMlbTSWiSAYE7GsJ2S7ALMYJYP+gwEOl+bAf6a8IcQlKpD0El8nQGY9mwj+2vtPL/CEhrqvIw3gAzCaI0YaIURZswmUFZcmNK2XNIDlZhrTGALc8gFKz/VQaTK3at/J+iRCMeS5/0ZU9PNT80wLMIs1LZxaZHou2IZQcFl0GaRBCEdiiYIPiomY1LFS2aIQcnka9Xq64KRLX0g/UndCyEWfSkmToiPyPLEgNT4czyEJDEpgylKFdUalYkKEY+Dxpz1MT7j6aqvURCnfn4KAf3IPPvL6r7GVdWEhMJyKeXsOLGF91gSuv5u7fHqpdSXT+zyY7PiV32VdshNQ+FVrMWXpiOS+lXBBGnlPK4N0X0t2VlBWTigp/hNawVPS7fl3dccUsc5SKVlVmTWhPcuj2eC+/xXM+AHG/ZDO2gUyQ4Q/lgleeAvGBH9BXtHuCo5oXBUSnR3lg3xG1mKCNkYgEzZzHkkalvb8RmMzaLVimR7W96/LwKnRHasg05SEH4r/m5CAuO7TD+ZCiGQoXrg9IqwM9HPtW8sqt5MV3MRMgeePboNj+RjbZ4W01VZBE1a1sUagltOXyUpaRbVEa9tQE+x/hnDxNb0GqkzHqQWUQtZsyrNhkneyWRa/X4J/exGesDUqTen2E8FzZ/Dj9iM5aBb8QNjXvMLU5I/1j0sLDGesrWoW2WNZpdKOS2GXzuSHuC/rjbsckwU4VTyupl+QxiUahRkHQ/iXO4cDMczDBqbrYWH9fQpSeFDyukIJRYYQuA8/EoFPRdDvJT42XC4dFP9gUcASgh+F11E8bWD/+Wscn4DH19/CbIyPqGBG3/nICLAFs1cJRiVuJssDMP5eCTL+qCi7eQD4AKIjnBu9PBGmNt7blg2o71UcWmGmw/cUSTz66BA3gp3193CGnMYQwOFeCgDjKLdu53MkckM8MpsMBjK473q4V4TjXzjYfgfb7wBjw1n+FCMh/EkqeZSavjM2tTn0jGutKPBDj2X1TflL1z/VRXIwEiXnHE5jGvlZnUEi2WXMXRotFmwLRoh4VwirzhUcWdDdrFtbrf1gSqwmx/uqKlJVoX7NmleFMI8DxhgYMG5GwrXtsd30sN0RBoRuf0T/4RDWEKe7TqTPw9EbIp4J0+kgYBwBTO+VPZ1g5XDZOyLE25ARvZDZcXQslgtizWSvciACHBtYRogc8GcnEwhkOMhXviATEJKM+JIFIJd+K27bV3eCdKX7k9AIOebkSJ4fpeRzWb6GMRu8u3oHe2OwOX4JM17DDAeQO/rxoNyME62xSmrwSlVdZW74iOLr83Ah7/rcs0k9lBa4ehbP1YdX6Iil1hiCYwpKcS2Ify5MYILpSZYa307Hp0kZFwSNo97q6qMgAE5KLmO8RzHkvVBEyb0mKmKpDfVNbrp9LVeSzhCfrr6l3PqOFTFG5EaIsObIJC9eknS+Ek/P9BY/xdGqxzkRYBjk/NmZREHZqDakyHQUW9Yv8BJAxWdBcoTPjowSz6zvGnNyCijWLTQi82iPaZbLnbFJeCBA7mWOdLp4X1tIiTbMF15LsaS8XasEIrVODBk48kyXJYOvnt7h+ukD3PUtrrvX+AG/xwH76TIqCMU6uqGHqbbuW7SgqFzxvj51mGfn6do4jj4E1zlYYm9jCUKTY4Cc54VcCIWf1hXKZXU/RNhLI5/PCbe0yCMl+KiSBhLMQLLVlOuEgzJCeOMCF1oTMLPefJZAn2cvGL8snGyEyCJc07w7tZanq5uLvMLNJSNSnM8A3iuRMToX9imChb9wUdsYtLGdqha1U+kWVb/OPjsZnlnIx8CNZ2zTsXnr2J9f4HOCjz1fHxlHfkHHX+AyIHs0wY43MO5rwF5jqirN1BzxdxsPhZFqGQ1mCPOUNavyQ9NiXOLflD5o6gxU+V3qNBb3jQrPf6pYmKUtou1Vm4/W4F9f3eLRMJ4ev8UBA44PhFt7i/9g/xfc4g5dt4EhG/hhHwkxOh8N4eD5NTllwfN9PnLXlWPDjMGNgGOMwwCGC0ppAKN0MzjghPsd2DHM2xvc/Je/gfvyA/Z//RY8ek7qquthuh7O+PFy7CNEvfwWmKDINzkQnMc8Arhj/PT1O5jrEa9+fAM7dnFemUctmeUzwq1p8CecODdgALxRZvAphbc24Y4HA8A5Oe8pFer5Wvi5NhYHY/BgeoyvGfTvRtC1RX91G4wPvR9zQ2GZsRrvsLpY2MnkEc/6j6XdqRd+jn0Uto4AoUUE5MSkptJ8W4hC9AuSbOJkXEXgFu7Y/+YsqgGp7Pgpx9QC8U4CpyIg4ljMRwNoUaNGNvQI+A+GNqR6fC0yFN/l+G0C4EIUfnbySDlq5PHHHQmPjx1ujwavbq5wewtsrx5w9bDHdjig2w/RkJdURwwengAe8XKWEkcAAQAASURBVNxIiKqk0ESBZzDDCi5miIgbiAqDiMYIVvceQAQkhDSiJAwTFspyznkrYmUdyOXHJpwXFusOMx0F1ijCAvHylnKXK3fC8nWmPNZkqtzAZLeSRQUYs4Udr/CEPT5cvcVr8zXcsAO7wRPgUiqZ9DX5VOtXWbJFPWZlc3sm7sxWVd7PERRhQLi4mjyB9ltkSTwWp+MjQGp/3oaiRWcbIcoyL7OQpxiSlEvp+CX1x+l4LK8cp9P7VKwBrr3SO+BMKdOaU18yY4TCMZ2veYxEYYyQxsbLomTTRLLgx+PgdN9q4UjQj1pzqTasir4vGrMvhQY/N/iY/RYUr+oyNf1u4aROFtinBdw+DQrPKlVf5cdMMTPpFpCN6oPTSqlwej7TbMvV0il3PM+cAXBItAvA9fEJG+fwdvsbcHeFn/ADgH0qT9d6hvJaFLwg2afq61sL0LUy/FCXcQGB4QYHwc2BnIGj0RsfDHkDZgwbb4xetnUmI8R0v+f5cnTrJojP0/dFlpwuKr4rsoJ6n6AWmUy841p4BpOQDom8MCxs6Vyk0dtkls65cKxWnX9j9gYJEW4Ez7TSJBndkeZ/iYSsGZCSb12bb7GKj8z11Yj8Z7ERl0zCiekbT9eN7qfjvC8LK02ILXmw9f5FYIYuNxmR5abyzLtKTfV0fyro8LOAUwd7Lv1aQn95ehd3ViIQ9zB0A2CD2eOxZ/C8TLb0Yn3UcmX3bfLb2slD7clL/H9rg8/SXFSIKCDNs4vKT8YA4IfdBvedw/vHezg+wgxXuKItvsDX2OAKtrcwpKJYwtHiTuTpMJ/JEAFvpHBKESrDFO5Bc270IykK6aBQ9QYNKIcpgJ626B9+hSMB469/wJEG2O6IDoTBWM/XUnLMmILiO0kcohlP108whnDz0y1o8HW5iSNYqzi1bqJ44YKi3QXn6REmRCoQETjw88E71JfAJXYFUcoQHBEeuw64deBfMagzMN0WPgbc+mIiGy06CynNxfJT2aRS1voYGFLtDENBzbICLyNfmSUNOJGtleRgk8u4Sm4RmYaBeMSSPMz41xAJUb4H+3xKLsq7WhAZ0UVP+lSIOIppj0aImKClfNJfg/KhQgKjSEX+OK9xNMCThTUb7DY9tj1guz26hwM29/sioyrNDc1IiFOoi0zN2XqpQrZZAxcwRNRVOnGxRWMEQF6bAM4iIwhy5jTDgRwFAYyCMSJdZEnBIiXWJDfx3Kb8m9KU5LqS9X5uUTk5pT/xOesSCSnEi/b+bLinAf3jDQZ3RO/8GXkOHC7yUQJxQO4YAZFVRongK2Io52MryuTzxXWzRjLOf9dT18rR1t12wf54G0meWn/8/o84dh26L76B2Ww+CyEwkWyaPPVfP3fOXPCJkJZHwB3jGQsDYHv/iB17DwSyXbJD0PzqaNF3qTmh61ThVGd9l+bcz8X0bO6VnGulkXIRLjNgiOHCpWk6coFl/Ijgj4AbC/RcrptkN1d1GgIM+dC7ZBgKPfr06H8RWNqfW7CS7zkLkue34HcLyz+HSVBtWCDftSwa5GgxfWF75DAqA1AzRCQvjuzBmROtOyQhzDxhelKdfk1K1JIhAhsD40xcS2lGpQwODg6qrfCe+pFhV7REKEmLomgWNLH1ZV/qubSSWPZW5xhwDOeGkIbAVq7g8/fXxLYFZrw0IsQzV8UbzJH/izx58BwKHmqshQAZsQn/FGitjANLs1NkQM7bpZ6qhqFmjEg1vMBRR2UbVqaZ5Cnxfm074zgB0VszTIQWFjPjZaOF0Tnj7bfg9z+Cn+6Dg1PKJNEQMWKYOAinXoj1e4r16yXgUu4BliSFWlPWsjif5HibBnw+LfkZwLMGa+2G9FLwpzbT68ay3JvO5H5/gV/gZSGSB4l/ELmKkiNYC5MZQLxfKsfuJHdWpMfsWdrU9N47t8w83ygJVC71LEZJh+dhJ08cFet6QhuKMiu9uRwpzeorwWEkg395c4v7vse+v8eAAW/3/wb3yLh6+ve4sjv8jX2DK3uFnb1GZ3tYa+M8OGaM7DCE45WM9Z7+hpTDjHNw4xgucM77N4wDwBzuihBHHOFvCSaEA/M4Blnc12zJov/pC9z91x7jNz/h6S9+AA8jeBhhO4suXEgNZjhHYDZBvyhygVEaNgaMw+bue2C3xbuRYB92uPnjLcgZ1O7Q8tOudYChv6Lwj+lGjI5BA+BohLWdl/FlBRgDB/jIbgDgETragAF/pJPtYW5HDH/7CLzawG6vALJgI3daWIgCXnKbiIcZxuedaP9UUnHLhFfuNCmVdoTKB0R57HMy4lHIJEaf6GzDCi8cQ6Idouc//LvoxCUyjROBJ7SBMRmA2SXWsEJUH2sZuKUfbIEptQ5hrqR74QQ0awyMG7G9P+KLux1eXW2x7UdYowxMmaIkSr662KxZa0lMiRdTcrJQUkOeWAMXiYiYTANzuhCSURgj1PFNspiI4qWaHJ6L4tE5VsoDF5QpJtWZ9Zyzb6QF4qAMjG9XSlspvKk+q2qrgpJGvYKABxhmjO6I47DBiDGekyabbjZ6nOsGMpUNAawuzo0KDpUorZFkvJmWVGn8ybBeGIkpw5e4xRBj2D+B9wT7+stm05ZmKV/W6/KsAxlcVdoMziyOCNXx5/lQGQFptopy0PcfEBH6wxEdEYztQpZG30omT39mg07wF6v7kVgvXq1NR5WfQa11qietgOBkMI5GFRyl8cqUjhSUSJFerSg+lGUM/NkZlC6pd47hxkgFT2//ZwirlX01OvpSQ0DZLH62UA7NFCtEua2ifFDIQGsqKZZTNVlBN0rbAxXp1lRbfcDpQeINcoZaDIRGFK1+gWaRRvFO+JIHaDUooxmyHxc7r9q8omc/L8/SpKthvXPc8wN/40bwCDjrw98dwR9b6AhEDi6GSJd0l8IvUWoXgkboXjyOKUZEtBo4JZ+nkNTJOJ9qjCjqOXuNLjaYJlv64jooElCGIx6SLDaDB6xeL3D8DICfHsAfftS6D4AZo2OMx+CB55LwpyMh0mfOB0ZjFIXIVEB5va0gCqvSJFhHG1akmeBHI8/adJ8QThvBEuZzriqXJl/OqHI570uO/EXKbhXyEVCGK99OL+G8hq7O9fktnTOhwXBOYOVclMnOGqdPObgfoe5saw+8mmNYOJjqMCt8VmoUmqSZ5lprhNB7b3adWKY7qdRR8NbZEZdaAVpm0hVkr19AyBGGr/FyJIPBEH7abvDuqseh33vnlMcnmNFix1/g2t3hzt1hO/boNt4IYYwRRhKAP5rJK4MdgC4oV30kgwsKVed8Os2y+uZ5nsU5MULIfakucP42yDIyXhQ9/81+B/puB7c5wH3FOI4OT27EhhmgDsRJgk7DoBg9MvBHkHi9me33cGbE4fYBhhi773cwo015c68NNZZGyUGFEy4zwA4OI8hwiogwJuj0vEmEjAGpuyi0LAd5vxngvmaYDYGoA5swEJBjsCjOieBfcl0uZIRSNqygSZS5klAHMba15adybKAWrd7huIH+Ca9EHmKFazkfq9Z1PLqJg8FCrcFKm85abRW+tS4y0PQllw90krIULdsFgxV5p9crR7gyFtvOojMO1kGtxRYHQHHuUlsmX8+EGuIsplgNzzRErN/UorqNvZDtjQ5B+RcU6ya81xc4+lpkt5DIhnCzzVz9elGB0ule1BJPWmVxyCYLW/0mIFdMKBsnh1AtOIz7J9ADYdgc/RMXoiHU8VHaKBFD3jgYUChYa4MBR0ZTn3fv1yFHRIyepmggSOPhIjIpPC+Lk9anpZVArhdHuLuAHcIlR2JVB4QWvsBWfQaUUm0b106V7V4OKI6vbH5RkWgMYEy6IyJY69OaytOXMD1rHGqy5mdNTqq8xLxme13BL5xqi/C2E0qMDAWcdL6w6D0eN8JcqKkpASd1QNpFsERw4ax7Hhk//NM7dFuLN39xC9N52ve5YP85UA7/ZDoa87NiGC8C6T4U/XDy5YyCgXxRzBeneQWiioK4DA9oVplJfEnA0vtEjASRMzd9wmrxYXimO2TJRq0bq+l4L+zX2cbhW2EIcCR33PgyyQDG+Yva5Iza6HkHl6ESA95oGPZTv39xGqOL0GwxoiDeRTPtVGqLc4wrN+CLwwc82R7vALjOAM6A2QKwYHYwxkKipjIvdhKeieAvAUS8R0JodLpbwoGbuFQOwIU2sEJZP0uXG+8++VaqQZZ0xQjhn/vPePKvCFPyneMv/z4TrFI6Zj+PcA7j6I9mci7xnOMw4vf/4y0e3h2wfzjAOR89E+9OI2BkDs9cxB1ps6DBU8f47ga4PgC3++lIn7yXVgh9i4947rx+jsaFnw180qG7ROV/vnNf6/nFtq+zaq8k+fmyrr/AhaCymwDs8OUff4/ufsD+8bGRUynYwj+noFO2p6YvuXARdSeFoq7qyRNf+mN/mBUfxVonCHCSSbOLeJtlLj1b824NeJPB7758jZ+uNthvH3Fl9viP+7/CdtyBtyO4J9D2CoY63Gy2sNaGC6GN55sZIap2jMcqERl/aS7Z4PXvlfKe3xzhhhHqXIGo76mJOYY6X57xZRnjozDkiKIh3BkBAszbX+H6/7vD4e6At28ecf1qj6vXB3SGgtHE65NE40BkYNTdWNEZhwCiAf3NH+D6LX4aR9iHDW6+vQWxMkgEbiMdbV3OjUm8ntx14DiduCBHKYG84Ud0icIfKZ2d57kMyHYwHWD7Duh3YLuRBgfNWoiQBoBM1lDj6yQFyU8ZACTlfxVdwh9nP8PwY9J9pOiEfC3lhoUymkgul2Yw2IVIiHDsF8u9D/quCOVQJZWnaKTwJ2nLJmatzvudorzXrLOC80xKs3JkymzhMwtzz5pCwWHYWIO+79BtO7x6dYubmytcbTe4uX/E5t0HmMEVbZX59c9MtwPggMMjsrs3LsZ71Wha89FJ8AxDxELnWEVFyCPAL6Z4boI8C5EQsvmMDuwII4/hngglhANNBUKmABBhKiwYFzSC1Tv75rpTaMezoy2UwBbP4hW9pSxCRxjGEcNwxNiPcGYMC25m7FR9BAqKh/y9fpT0wSs8tfUmeTEoELTUFIcGJuWZV6LInRHsRn+GIJmLLJnnQaUFa4wQnxwo0kXfpmA9D7c4+cvCCYb99khpCUKMdb6UE3sUNtSPAZOLq+eIAZICpw2l9NTqe1LEKt4zfE7r8G1jhfeC+RSYL8LoGIf7AcNRFIVirvl8MOo5EKPRlraJl21E5Vkrrbw7VQN3mR4QMI0GEKNy2G6SfUJT0nqLpraMQtOvNsKmaV4pMik9zNKsWT2TBrZeST+hjmuKBgifwLfJADR64QQOnRshZ8BOGlVAvsKEF1nT8FZHaus/FxCyeQr7LwHYMuEoR+w4b3DxemjvrAEEAavVFxGsJlQJSgCotFAMM9W9rlndiRDwhvQTqiXJEmUCjwiAl2pSE8oaltd08oxbgrCetRyGIEppry8vxQJu8McTxKO1/JFbw3HEeHT48OMBD+/3CS+Ug4yTT0Y49lPTC5FDGaPx0TebQQQxtS5WbkGXm5UZCjL5Of/+5wIZm3xWToGCNq+uZ4Xg/AxYLOLMOp7dtE+BLy/MG5+8/xZw0SFZ4UDxceAjTvT5i/mFYW2DWnzMCmZqNr3+zeieHnH14RHjOGCcZl4Gnv1Z15FNdB2t75XHkbfKk3L+D+LumTN46+prdaKEs8SMkMEYPPRbPOyuse0G3HTAq/0r9OM1ODj7Uk+Aof8/e3/WJEuupAlinwJm7h7LOSfzZt6tqnqZoYywZ1o4D+QjhY8U4f9/YVMoHHZPV926mTeXs0WEu5sBygdAAcVi5uYRcTKzioXME24LDKtCdygwWAtjbQ4pxCLfcgglKk64QOTFDdI8i9GCQ9jxpAMzFY5K2YU/DAcvm+ggKYYIRIcjjocyMwBzPoAeB0z+AX5guJ3DfHMCRoOBoo4jcZCZQetSSWJgOAHscb45YXDRgbb2qCcxRpTDmi/V5ETnYyA7CAVZJRoqVNndQEgE8OCBHYHMCDYWINvOKetjqKu0ZJwIE7Jt3dT3hWeKwHpP8yGcJFA44KTH6j3yLu1gUvDxSAjJH/Iy67EVuELhmCX59Az3l0ufa10LSpXfo9UnVLIx65uqhLZhGWek9QQDsIE1hP1uh904wFpgnD2G81yinV49ZgDS8Qf9GeqnXr5OBQuwsqm4C+nVDqvupd5YpcUeNfZBj8lp8LwDjh8dzMDYv7WgMQOjnnAiLgCjNGpz1LVEEKKA+ChKWjlUoQaQXuziaE/iXK6EZzCC4ZRgWdAkltjNHhOfgSPjw9efwHcH2B897BR6FOS+GlApK15kgZEBsS+8LgWAS2QTyyMFiCs0kKpvm1TVtw3GVK6o8AjTHfoT4uQxjLGBEPzwHdiO2P/+j6Dxt3FWxKX0m+Q7Cdl6Hx9O73/C/PgQPBhAOHx+xI6BYRiDF0JU7hlC3KGCpnPcI2CIdYmLwZVNBZ6Fr56fFFG8hKCpty6BvAK6TGd+1jgdJKV8ZmrIUGTANOP024f7LWlruJ5fMhUK0Y5nc6EAvbbclZ0s2uAnB57rw90SGyRF1L+d8kqjhFxXqyri3cR8JoOhxvyKMV7RrAotSvcLYxFoZUmXVSkLX7W5GLpPshKjUSTIKPEQPcYfP/+ItwR8/+YRTyPirodyx0fuMRdMdZ+RvhYK8jj2QUE/CFSUGTjZN/ju/j/Bz58wzT+CxZOLEM/FAoIzGAccQWXLhA8RJrz+l3ZEyHb6Hk1l9avXxzNGIN/kldQ1QtSFV8z8bwJzxPW5bKBb+Az9pZuCOTDSXIgwpb3GPDP8T3+F//A93PEJfmb4h3vweY8f//IRT5/P4OM3OHiGibBi2QKYcfZ/A8jBE8N4hLBNhsFcnqsWGxQHOlw4GDAMLDzsi2nQl5nB36QR4rfQht9Y+rch+bf0b+lfYnrtlau1EownmuHpCK9VqNTSyqxzUfzCBZJUilvxyvf4HSX5cSy6Vjwj0OiyDzoSgHhnxz+sv6vq5IXrxV5sTdtkxRAWyGJ//gpfP36Ff3/397iDhR33gDWp1iTtmmBYMDF+CEcvc+/ibgh2ACSqAsFGHiScUkCR7wz/pHCK5y+aqFsIuuYQ4YMo6iHIYBh2QWlvLJiA2YRdBORd1msMFjxYHE4Dbv75Fk/nn/Fpsji8PeLmzQwb8wU5Pe+MABmEgBCm2jnsIWcThJGQXePi5BF4bIre7IG/F35NZkD2fqi/DDg3BxmFRbcZ6vA+erVrr/ioDzjvnvDDnz7Af/0W2L0D7ACfzriIcOdnMEnfJDJMKETOU0hHiqUlFNtctLXS/akrRquCayWjdt0UOxZEFvF5J0haPymkUjbQyLO0w0LGKH3tk+4mrT9lnNBt5E4PXz0luWVdm5V2XaQlW869IQOYcFarny2eng7YY8D93R3uboHx5iP8+QicOU/OUrcUWigxxNJ4rOEQ/U4pG75Q+nKGiBVllB5LcRwWIZ3A8LMgBRO9oAsSgLDoKANdb9FEOV0U9ykERtQWkFSe2qvLb8tL2iQfr2Vrld6toa5z58K2IzfPONMJ03AGIiLhXMxlRRgl+TgotOSrwkiz4om53LOFu2tSqWzpvcu6rGjUkAVDAE8TePYJGMTwUypeLrdA8vVa8Gppa2GLg19A/2u0qKgSyCFMAIafzuDzGWYcAwPhGKNnmCHGHbxGadhpbj1HdbeTtXkLQ6mX44Vx1qg1rPdoKusxt9xf2yWBzC3ua8Vk8ekGdDrUAKA2a+SxEO8NAuBnHzy6Db0yRPwyidKfteWhYL7uJHcvXyEJIlkBpovrOTMcJW7dJgzkgVnZrZaKygrQAjKr97kF2YCRs6wzDXnXgWqbKlEU/q0x6bIi8Ll4Nq8LaVwgikScYSsuyxDiL4/pwc0gnrFjgwEWE6Y45SUd7LaQhT9Qr9J1PbCqiA3TvoTh5d7RgLPdAf6UldDs4TkISyEcY97VIP0tyqeyXGHbcwi97HUU+N+Ftad4kOWeXOowrd2u561rWqNJF/FMvwhtCGl5LUVNqM0fyusShSuSEpjSXOR58vGZn07gp8+YnzzmmYEnAp8MpkeL6cmCOKyAEBwhKAOYLUhYeQ6mBA+G4RzSi5mDV6MDjM3NEcrkAYnSfF23enjgMqq4sopXLlCnWkbrdf/Z9b0q5/lKZX/JNm2scxHZ9Dj+V9h782t0uZeuXl41cF5f3dXvXr5YFdtS8TGvmTa38xfiqLfgkV+yEb3xeVabnosYy3eOHTy7K0pRjMli/Qs6h4WsDeuzIofkR9zJ0HumK9ky0JeE4e1Zl+ZmsgZusBjNAXvc48btsAOFeI56o208MLo8jLd2bkGBt3vOZktTZcIHSWYKTsRBwS7hmGwMQwprwmkOBCVxCTxH54sZGGaD89MB/HAGHxzm8wwMwGCTtin9oxhmSnZUMyTcT/iPzAyYGW50CJfx26BYkBZU+LsGKM4/UYHFFPh6AqeoQUvgQcaALePpjkG3BEsWYuAJPZIdKZzmoef/JkaIZX6+bbLcpN0vPTjXykrFx4bf/FCMLHpHBOtOy3U0cpX35T+9GyJ/rNun26jqf8WUXHoJUe+q33VSLSv2nheFiCNwPBtwIgzDgN04wIwBLtn4opjnk+hnjo3IEIvl9YnNNbW92BDREx6bZnVGr26kKAPSlhKPaC3r1Sbbn6ryGiCg6M0f7rOOhvMz5Hhtq6lCQD5adDOb3JZBkneeMPEjHh9+wM3eANNX8LyDYaMO0M7FGALSGRABo6GcdIacGxH6lM+EWE8t5uLmaY1gpT7ZukYwiEcMKeNOIkwrTZDQNGCGNzEMCSN4h8f5kbZQO5nqd6mSlyzT6zjITTXVw10g1F5ddRiOjf2M4x/G1+TdNBS9a22wuBoyGKyBNYA1BoMxkP9IQ7IqPilMNHTJYvM+KlfjPFYtlp0wnDwCShUQ9cYhKU5y1nzoPKC9TuSQ6exyzi34okSJ2q9FK+1C4/OaC14QPo1KJoFCIHvEMM9H8VjKNgjeqpGxsobgJ8YP/9t7jLcDfvfv3sJYpC2wbYG/nUQL1yH1V4ewVOV8P6PyJWK/khLkUd32wARIJqL1Iin9reafFnJFQiOMTHjWg52M+UD5QD1RSBvykakN+RJJ4AyZqErKOwOyQj/xkzG7PpS6Fi5yWKbcn3pwOt3OK4YR16ZRLzoFdGAgjYYJ/Go4GyL+Q95J5Jlg2eL39EfsaIfvzT9hwhHOq34DMBwMr3JOhAx1htQV3Jv6VcPuAvCqbHHpK1hA9LgzwfjgPWbvQB5gb+EdwxEjHM49x+22NhguOeDzgFdDo1ysyrGH8w5z/OfYx/IB7xh+9sCcBcpiqhVaTo4dYgxCuC74A4GHhNJL+nzJS0gNabvWavAQPo4yFKbzuWSHGQAdg7XciYG0qDWN6y7y2KGUbwNuKflOTaNYwQAp2oEY9lYObpQz98LuFe89nPf4239jPPxgwO4z2D9gOrvsaYhAR4gIlgOOGOgPIEL0Ujxhph9grAcZCxMbMp0Y/CMw3AKHt/21Xo9fNUAVz9vLoeDj8vAVX/YvvwDtu47V255vK9C8cq7eF/0mK9z3RdPGhbMyXl9k3n/lxNVNj8vrc37ipFc+XS1/Mdc1UHXdHLy2Eqhb/SbBa70dpRSiZYKFYn4NULwWR11T5rPK3ToImrIH5bb3DDp54HFGIFgN85Uu9Hmgua3Lje3OWSsAIoQsQVx33GburEdA+HBW09F+G/564cyrwuR6SV6k8nEjWjwDAEwY9798u8Px6z3+R3eH2/MB+3GEJaOONU1cSbnjw/vIl4QzH5x3Qd8V9QRh3wQHJgQU+84whBheyeSzySi0RwwNTEg6BUMGw7iHIQM7DnnnAXuwc/DgGJqp0E7EMy49bj69wf7xBo/nPT4+fcLdVw/A3aSUBxYggiXAWBsiX8LBTXPYKQwCG4fx/nvwYY+PBNiHPd7+81sQy+6QMLdpCpPMFZ7LOEqc/zyVPugwSWPu6qB0kqVAMHYHuzdw7+5hbu7SeFHi8MO6YcjuDF/QA62DEae3ZAZWDnDBAVLzqSoJ6FbwSvHWs4ME48qONPEsAtHbeDnUnNM5EBGqErwRAmyxD7ttEA8vB/sw94VBIo9xaITL9+JYVZ0NUXaoTpfw2BLvusCR8MJYpl330SzGghnC2SdSiaGgB9pZA8sOb08Tvt7f4P5uh2HHmIlgETd4saqSIXa5+I/K9920lUNov1nHQtxcXou1XmSIeBl9LpFxQZM4C20AI8eT04PCQKXE56rMcEhlVNGnUFAt4k8HPm9ub3wS26cVpb1M3nvM84zZneHcBPAMYNfN3lsASyyr/F0yQsjz4rDLTnHcXK2BUcSeGps2RLYa45SVEpEgqNjnCAjbz1O01sc4gYuLoKzz5XziSgkbd/b8OikjTS3TSWguAIAJxgljKB0KbjgqXxuNTT8FMK8wjGa0ns0tX5CKL6zPxOiszgJ318ZSa8IXelwyzNZtLaAzUXqU9/Fh8u5Os5X9NtzZww8+f//c4fwV0qKwuzAvueeSvlRnO1iDhJ3Iu4Z67aTqm6VOylQF/LWUI+e8NLUB1FSuCHsRW7ZYvoOKZSdguT7bRlO19rPnRzUWJIJAzHeBTm7Ch8+A8TRXFEShbDgJgsmIPXbYBbzGqTdAwbDHVJGr/jER3YW8vfF1NgUkAZ1kDyTtddYLs1TivyyU6SkuDz2WaxTllxxqj7FWCi+xWFXv8+8rUz5qLnILZX7i/LffVvk219Xe17T0clHVqlSGwQ7HmBxtPOf5kc+YgfnkcfrMmB4J7mQwzw6OOW5x183NAg4xMJgx0nYTYzQPgHNB8QNKc+9mwDrNh21P3aVf073+7W8zvZTWdpfBFWtjMesaD93PXb968fhfqHM55cwXpIir0chzxOhfPcVG1uxzL/XerQ3REoVaKve68XrB6H5J9u6Fk95j5wo+rvdRby0s9WtLf69Culfk/ZJyw9Z2LLUh6hphWJW1DN1bYXs56dlsNRxt2qL7CK/rIztXMzcZr+nRFbxmVTQTwHaH3eEe++MeO0MQrUrOr/RuBIC5Gikdymdpt3Q5bmQI5LNcZaK3N5mwA4IMxWKjXEEmhpAyio0jGB9PW4j+JaaujgDrLaw3ME97mN0Ef3PGvJuDs47JGcXAYYjymXOxLCIGhhmAgbs5ghxCGc5imCv1qPDTWqdwyVDECMaIpWyxz8YYWGtAwxC2rNb6GSzrB4SNLNDUtXiyV0j9ungQGVYu83j1uoQNzuWzfuXj8/JdsXu7yatq7Dr15XRpGDYbz1ey6UPsi1oL9BZuUs5C5gasNRiNx42xOFgbYIFIHTReX1BRbrj0aYy4GbylTl0GlM0YawOPs5S+6BkRz0oFp8CVx3Pxs5rkUGmKlk/RJ3bl614zusi2V0+oS2LgFe+iV6Z3M87zCefTCcfTMXrChVhxOfTUQqNE+cIAw4BIWWc1VpJLQ9HFbrV3rVJrLTepcWPE8eQWB0dlSjiXY2WQdbOjpys84/TdX4FxwM0f/w4YdlAdXSxkial8fioa96KS2qKzQqCpq+mJxta997nIBCNkkoHBxPiIWWlnYKyBoQEhFGTcEmaCB0PyPK2bVbRkK5VaS31Yf47jx+VSO5mgCYcwYVQRzgupBrJFEKWIuqJBlAhsAPJhfoxB8BqwHA1FiAyZv649v1J6jdVRGEm/RCJZHhUjTYH5lXWg3yfF++Y6ogcKBQ8aLwx1RJg9wSX3OwJTgimND9RXkQzKroqAh6OCmgHZOhBKDJmZCSaGKV3HparKL5UEsZC6L7pXGc210Zri2BoLQ5zWkOCvcN5QvIfscIn0zev6tWdpvN7Giz2/z4pONxg+8g7OuehNFkYhXAc4CmGaCGRtIZto/kT4CDkXQuKs5sPgwi6r7DdE5a/iq7RSZq1jxXvNHMg8bhyi1RoiXSufy4Uw8ZEAUtvmxTYsdHBp1S+FZVJ7NArWv60uSVfIglTI7cXIEOfqw3/3eP9fLKYTY3Yes/Nw0R0qr+PgryFQHuDdgzwBA2BowM7/GUxHuPl7sAXIhMBLhvqcn8bBjB7rs21GGYgOQMvjufxlW1cLS19gsTZFNtj68nflgtj2vWS9dpiePQTP/PiKzwTDXqLoqcgFgayu8rfNCf3S6XnzuB2///9X2qKy+ZeRXi79frG0gccPlLyH7VuaRbHIpsfdIUiKi6IkuZLIDPI0/eh/vT5UqpfFThW6mhUuRRj7osBe6Z3aqm8IBn9yf8b40++xGw4h9E/8tnQgrxTrRZkGhjwGY8PZU4rJIqK0Q7PwaSIDGw+8BhjW2iBnRf2Y8RR2OYCi8t2m0ExA8JRH1I0ZyKYL4XEyz6zl47sP97j9fIeHecSnp8+4efcR481JtUn0HwNABDsMIO/hZ5d5ZHPC8Oav4P0NPg6E3acD3vzz2zw7LHy23JT8UroVtjW9lbMN8jkTmq31jBAy2w6wQwjLw4MtBnXpjE49h9uSCJGZ38vd4NTHgkdNXdX5gyyhxUqWl4rNlbbr+ih9pRdW+FZ2TejdE/m+LBcJBl47iQyzTiNb40NVRuPd1i/NWoPBDtiNI/YHwhu8we3tLcZhBMyU1iyU9JZkn9hKkWcxPYL9HOS/3yodWEivZ4hQDKVak+q9ut7KBSUoj+X2JHlAKS10HZQWiIjGJMoIVdCSrjktnI3SbF+ZFp4ZGmDYBu82N2fEkjy6F1LEG5qE6V+dL0mPi6tzxfhQP4yKtZYW5haIsBGq5DKjICGSxVKXo6tS4TLcDJql4706L6VXYq+XJv2LcO+9QpsJ6dyT+qkkYqKwu8S7ED6JCMZ7WGaYeL5JcThtUupUVWgvWm5bBZSEbJGhWUy8WG5bj6zHBglk2F9I0pVe9Veneo2t8ogtOZPhZhRDn97+SxAQS0arerc4D0vPyx1blJ6u1J+m4BK7EEoMCtzSk0c87CkxiDXjsFqiWjO0EY7WEX3CzQpHtiiwj5ezzl7aEvElcUFius2kft/rsEwvS+0aCP2iTAO7ZKJDMAyBPOf5oyDc7OYJBwJ2ZoQjjzMmEIITQlNGATaBN2BwpkNr6cJc67YTEA+3Wy6MmLHnuI2bbdq94Du7IqIFuUQafZ5e8esMYw3e/PF3uP367doyzIiyEoI2HT5fGyPKYvLg9BKVFzU85vttsFii1AvfJDLYh/d2hxC6+eqkp7z1hq6FGAZPJ/B0xnSc4M4W3jlIaNIseCs66H0wSnpO2/+JEMIqGAPiAcAA9jswHNhmTpg9wc0EuLIPSQi9xJRueCS9exb20PSVaqFwe6lcrMSF75uiLjAKG51TShmobfO2XqzlKmtYw/F0KcNrJNUcfv7Md4vcUOW/qqTF2tV8C89/kfGQxlVOPR1R8gspjJ6XasisMfGmAn7TaSMf2xGjVtNz+s3IzAgxCM9XkK2ir5aF7DSkvl3A81xkWiiq/66VfYVBl0/qVq5MVJF1vXd1Oo0G02ixoz0GtwsHU1NsocbTLK3m3P6aDycTQwozvKnbILxeljOIkJwhg2NRMEIoEQbM4nRDiY/PRZYK5iBrBucivatXj7XxFsQEe9zDDg58eMJsHaw5R0dNinISxdBRVgSmJHcRADIOfpjgDk/wMzDf3MDOFna2CZRDE6NzRHS4SEOxmhaoFQFkGMPhDLcDyOygw4xWrH36vnUCrm+3uAOUH4elqoWHXrkpY/onS6LrPMntNcfB1Lp8KbcwQghssvC9uoCFjr9i4vquqarl6HsreqmFRvQSDJgJGNhiN44YrI0OQ3EEOgXUvlFhnDzCgfIb0iU816nrS9Lx190RseDd0uZDR/ERf+uM1Y4IQUPhx+R6UQseXAq4LPHsgoKmbHLplVt4G652KXdkjXm8332De/MN+Ozw+PgI51wyRsgCY6bm26TsD1gUbBjwIXZ9yNASDukjIEPHVaiOiqgtcrNa6SUjmsNQMcLBoZ7zeRVF0Z2BIyCcEO+Dt6eBAfus6DAmEi1C9CzWXGwHaFR1W3UenY5uzvnlU28yFtoX9VGiFA27IQxgwl6I88f3mD9/grVhx8Ph4Ql7xxjHPcxgsxc4mewNDkihqTWJ8IAVMShWYZVZE6Twj9Tfop9C+K4ZoVoxpqlg13OV0xPpCwFgibdN5TLqEtO8pJ5B9ziNLZMByMP44C3iDWDYh7NijM1e3ZGJ81fX9Sula5fQdXz1QhmKA1opMHgOh7UhayQcDB6v47kDSVujYD91q496CjkjfVtx0Q1e0kaXFSG9fhfgJ3eb4gOWWEwUFOmi+C7WnBoeQs7T8sTrE7lJIV0WqH6pGI/EJtfGiIWppFiGoeBRFXZEGBjDADz+9PADfkcG/s23+DwYfId/xIRz5OlLfJCCpHHcqRTrF5Fkk0EiN6qZRCquw9ww1x0Lz27Y4U/+CZ8x4KfotW4NwbugJ5Yda+krkiGjqKTWDCun2LxyDgEz4+4Pv8N/+n/83zDe3ASvMOEqerBetFDk13W+rsiXBmDJGLFUjqwiDSRhh0saSSINSvm7Aq46dV1gDhojhPxca4ToLeaIo+ImlWzbFwNT3A3hPnyP+W//iPNPE5yzmJ2Dm8P5Id6zihEboNTF8fAiFBtKu3ItRyHHjNjRn+HxCDf/EMMVGJwfAT8R3hgD7BbaXA7kVv3766etMsV6IdvK/AKSlpIQ0ALipS8lXcDL1zbqS6aMDPAba9lvJK3D2G9Jaf+c9Bqs3ZdOmyDzt96Jf1HJA+MRNBxhYOHjbv3y3JNGkVHer8xH/3XJa2XaWcqwtUK0/eWqDKTvVtPFhbABNy7KnFXhujtE+O/f7vC3bw/4Xx8s7qbAQXkwvJ+VvIKFcLKxBu24xQZsPLwnyNlWWR8g9YdVZY0Bm+z9n3lB4VLDGaMkoaJja+QgZif8K0sbIh8Web+gA2Pkc0Zynvv373D38Q0+zAYP959wePcB4/4U+GdiWAxgExwyQQaDP8N7gJ3sJAfMMGH/7jv4wy0+jMD+ww3uv3sTVQxR76GcwVpQ1cxpR+chPVYWITOecP8PP8Pc3WDYvYOzIxhGwWpZQgmXWIGzdaWF1nW0jtTc/4wlrGhgZD20s0yECRYute49KzhgyM6XsAYzg8xpVwwAr86I4CDrVcqaS4Pwyqmspz7PM8jmWXPb+54QdKdkCONgQU/A+J3B3d0t3vz+HvvdiIEMZmbAhbM0dGn1Du08HP9yidYVhohSmF9MryA4mAEwllKd9QB3lmZxz0A8BDoK3KjPcajbVwJNreys57fsXv1tkTPmD4f8zH6Gc1Ox6IICpNeXrHwSo8ASWunqcNLDoOgJCrA4Gi/kFkVs73l7UoV7uzodIhhBVgYgpz7yBD6e4EYP2u2qXimxzntgnoP336APGtXMzS8rCG0b1msGv9aYUPUqaqWEoFPuO/tAsMnE8EsgDJwPOy12RUh5DVwLj8PFDNToP+/wKYnl8jpdeqb7yP1s1K7PVCLX63xblc/OF9uz+r0I5WJoFE1izBRUbR7kGefHGXYkmJ2pwGSJqP2WU42tqkFJ/XsOMuKyitU2yOHtAY7PTzPcyYedZtFThxLwPxNzbOjCYpaKLBFfEzSvLTnRjJUikjEiXjce6Hq3R8nzbG5H+bz8XLNpAQQijVK0mjn/LnmERLseCMDADPYOAwbYEKAplddNmk8RpEbhOcd5KPt8aZLXmf6iaogcxWAa4e1dOJgvegTpMx4Sc198T+WqqpCy7EwTgYEMYby5wXDYL/BmnHmFK1PNd1DzZnuqjRBanuvv4OvMUSsZ5rLLBsbstPy+V1B9u3Gp6i3vNUZkZvAZ4CMF/icaKNJh42oNJF+AeMZIgH8K4eA8YKIgx2wCDLMFeAD8HoADGwdmgneEMzNOjjAQw0aDnQehE2X0mek3TLcuCG0NCV/7LnpcLnVVca2oV4i+WHd4Ui1ZEmM6qcMlPffD7SlVsXX+F0f7Zem3AHoFs3wB5l5Zj3BVcdeO1Upja0opuPu3pCj57bTkN5KaSYu/LxooxZhQvNblLtDqpQYsLaWC/anbu9T+7nMhzhc63aljuxTzDHnn4ichw9PO4DQa8HjAW7rHaPZhR0KSQRH429hobti+ckI0zxV2LwQnWCocazLxSlw9t7SsGFb1jjl4pYbiROm6zmdn8ZmiOB2dV9mAHWF42mMgBxyeMJPHMHoY6wGK51RQ0ImQiWdqkY9tjk7K5EHjDNw8wU+M6WYPMxmYs2158aavGrAzv5fzVL2j4Fv8OAJPOxOdFdu9DLUE0BmWFRh5joxdJ8W7JmNCfJzkFLkvBRKui1k0eig+N9WjfhXzXNax3LdqNlbz9r+qn3dq3Mi+aPCXnUPGGAwEjNhhZ3cY7BAcitMH3G1yFpOEtl5oywumfzPZfgGY/fbOiDCE3RsDO3SEyiaV1Cg55BFHRYvBsmVqS9lbv+vnlW1hjGBFnucJxyPDWRcVBQxiD9HWN1ua47adwv5qgvCZ7sWrE2qBxxjaBcp7DpCobygYlYujP4kBQyYGwJBdESIscRqW3CuKBCuGFWBNtEyI/80znr7/C8xuj8Of/j4c3lPFNAQIfD6B338A3dyA3r25smO/dlqCq4UJqjw7k+pEdjRAiGhWKsohUNZa2Bi30QIhzrohlV/KpE67RKmBZOmWZmqClNveMnKsGJ+mf8+BSYGpi8aI+rn0RxHUDZUH9ipBb6z+WmUxIB4chGAMAhtYzzG+vcF8cvjb//Yeh/sBv/uPXwUv/RdsZf410haP+ZoJE4aSqMegbChDQXDZlkjso+GNjIU/e/z03x/gJmCMcUxlRwQZUcBRy0U3BL0Dyyvz1BPME5xyNgx3l8Patgn1uoRJXVJ/kV0TculyTlLCysL3CXfVa6k3n+sHe5MhGDbBOcZ4AAbGe8jGloQTNfNc9CPSECUlMKAO+s7zS1R+qdu4dKuTxhN6KqWK0/gOP47/GfP5R/jTX8GewGwS+UzYtfL+YUbwpve+DOMEAjNh9h7Oe8zehzOpUmk5Smt9PkYtVD2H+xG6QNLh56TKCKG4h/ROBGzFjXR2X6Q3+ratriSs3RxbU4sVglFBPC9bT7H45HEEPn4L6z7C+QfM3mN2eTdEghvvy/JNxHXxzCHjCGDCTA6WZbfjATv6Mxx/gsPfwDbgnp+Y8Gmy+JP1eGcYDgYeBgN52JLpqkdqMT1zxr9oulYCuJriysJZqSi/em5rXiBV/hYnZTE9R0j5t/Rv6bnpak7+X296DX1lSty/rXmOJFEt6dDKaBUlF1TX0tPG6duqHC0Lcva0TrKiUipl8ZdLiKnk3Tb1mPtrcNaGSYky1D/9bof//ocd/k9Pf8a3P32L3bDHYNMR1UmWp3hIhEt9URERAEDrBqJOISj8s6K42bFNgGyxEMcvEHLkgSh7i4rdxGfzPMnbitQJPTWFbsKQdDfzdCZGdeCoT7v7+R1u37/Bzx443T3i9usPGA/nKJ8aGGsBEAY7wMOHcynUeJMhmPEM8+57uP0dPoyE/fsD7v75Lg+3/BG6H79Nzr4ymqwhHMl5l334luyAyQL/5WYEH25g4zkWejA4OhFLnQ30pOwGelX05Ko8X/2zGYsd890U+tMLHSu7JNJcKgdVuRedBvvgjE1JNpFz7eKp9s1OCKTyWyzwy6VGHttYfQFhRPFsCIPDbsDoCG/f3OHu5ga7cYQVmGKBzWf28VpW81dMVxoi+mh/U1+vGBAigNSOiEVFjKYHSsjL3sdSxHNnpK5XEHpuZ5l3vQ7vHeYZcKOFI4tB77pY+5BWxqHAWVGJo7xqibLCpUA+QjiKMB0XxlvVldRFpA9j7RDdWHb4qRBcrJPiNxJvnbwDu8LkUTUklpPjFXQa+orpGthF1aIlDmsrblkxQhR5il0R8XBXIpjZYYCHVVsY5VDr2hM6UYwY7iNPV+LWFLPWsoSsfzdarBs9awf2CmVeBqZVY0SbrkDmC/MtGElgfflY1v46TYpOKYsyiyX9Evqb63pV6eD1U5crWs/+8t6slxLGFogbIEGKmWUX8JUJARrjoe6a6Ua6Thx1OfEITPVLOqTWBakiNB5XOwQ2V7SGWwhxl+DCu868FXvL0jrrl7E86wm6cy754byCONEuNDs6wnDE9xR203kSD62S5txOR3gecDPsYMjghCeUbGBBkIqnuh/yuvV4WunmM+CAieAwgGE6jH0oc81AF+Am76TI11DGiSU6qcpQ1wn+i0z8Zchq4gGoBo8MNUkoXi5pCTxbI4SCl7W2Vf3PZLhDbzpjm+dO86XypzMXnmLYTZKPcsmNMkTXE2bMew+CgfeZpqYQBwywN4AZQXwDxAPN2Rg4AEdPODhgNITBMjwI+ewcNPOSbri8bQbrS6UC+daVL3yyLdsXpbS5Df3W9OWKuoS1cvusZreIpTouvV9qxlVTnrjKzM89q5xQSm7yl4a76v7SGKbb50PVF+7RL5ped2fE5ZHR62iDCqFf/KWmXivPfcmiXgNY6jKubZScY1Vsq8vXDa+R/xQvM6vKzXcoaGq92BoK2d4qJWKgr169ZvWiW3v1pEfPF5jBF8kKl5MnABYY7IiBdhgoOB2yopOJG6q2lCTzSpRTwRxCLDGHOWUuP6lxNuvykS50NkNI4Ya9KJXFu76i6SlUMVPeoZz4Qd2AmuEjGG/ClDoL9oT5HMKR2nECGS1gG5AJjoAF3SMKIV2ZwcME3DzAnz3OdyPs2cBMS2rTMAhBZighJ8g5VMAuk8O0P+O8A+bhFmQGWAL0jueSVi6nBkoUrOU2UPrbZI/yV57XCliLS8WPcpY1ZNn02loYJ7ru+6qi9FrgQ9PQGoN8idQf6dysamCvLJkQd0MwQA8egxsxjgPGIZwNUcD3AuHays++dIi2fV4SieeQod/MjohW4Keqe8vfhTx66eaDJ3O5W5ayIphNe7akTh2cF+DsZ0w04/HNHrvxHuN8hvEz2AfP3N6BvBQJA8ebRum/krKqtPTg1ipUMSYsliAW3Hhv4rY8OYg6jJMOpRHHQQ9epD5sqECxFOsmE/tFMRYhB29+iQ0II/RquZ1xsFfH45dKGgKEuG9rmsrYcU3Vipnwa/LOBhmr+C6ct2FxeDjiMDvsdvuwK8LYFHechGms2xv/egDJwl2tMMW6qCf5RpRh4EtzlxUnvVQLcVqpU3iWL6alevvPs9JTHoTlEQx6efwDYTUFPKfW1fMt82cCQ8UGAFM8K8KH81IMYDiG0Yqu3RQdHF5FbvvNpOW5qg+tvoTdNNujGeBA7MPaMMYGw5ux8AbRkzo8t8aGsyKMOiclrinEUoO38Tp85dBkZYt1HzILyO3LDb28mK9eQ4LWBZ41jq95eIFPyvDdhr25LlE04iiUVNYZJ2oxFJUYYyjkLWgjEaxhMDy8ibPtDUZm/PnhR5zIwL/9Ez6PhL/iv2LuendXqc89x/G7hGM20p9oJC6YepaudryL0OI//SFHDyLPnM4a8N6HcyLkV94h4HOzxucssEibD6xuv0Tv7KstSe/siw/CulXGwbRKKzguykAJcuFXVuMLALyTtNCZfyMtXRNeSP5QylIYk5DPiKjPDQpzw5BI0JY94A0McwjV5B1kJAxuMNANPD7B+58Da2WAn4nwyRv8GYw3liH7IRIKiIaggR0IvsUbRV9ed0zX02Zx7DeYOgzChvwF6k54vX8sZRoduXgNPuLqMup+tvxcsQ7XprSuuxa1rinr2rQ6wMv5lvD3ZuNEwg3/lv4t/cYTIcTVHnbqoYmCT6RtpGRFRmFwqPllAIoPKu/jTfEOXK0U5QxXeNznJ/lrRjDO6zpU+UkGZrVyCwNGnwtcRg9LCGUpLSDwVDFhZOAdDO73B+zdHkOUawLvF9vuY7uZYjQOpD7pfodzPwPfR3FsAITdtdH5oQxfrnhExesUOij1mt0MZo/ZzbFdga8wFOBlGCzYDIAFiC2slWEQuaLUA+gQNWQoOF4A8Gxw/HgPsh43X/+IYczK9nDenMVgS70CgLArwAMYT9i9+Q7zcI8PO8bNj3e4+35YoaeRHncMJcUYEzDZM/7yzd/Ab+9hb74FjftwLmoi2tqFSuvsOlXqJF7Ykrn4lTNmuXDwku8KOfUizyA8qo+GJRRrAkCO6CJww4y0+4hjD8WBKoWsl10AiRPulr01vZTt2cw6EbLT1ALNJgS4G4cB9sgYfzC43R/w5k832O92QRchrV44JPT58tgvkJ7JZ15hiHjhdLbr8sWFicKwsY5Tft4ypll5Hj4RpJoy5OzxtkQlklrmv+maIoQAYHkPOAKfHQw7EGVRVUd95iI+dZ7ZglAnxVM98wqJtE1G1KxkYZwhZCJnJwoHeKZ7IMcPIXWIdSY0WXFUbfnS9ReMR4UfKZtLiAjwDvPjA2gYYA43ysixll4IXJcEoGcpVPQY9l7U9TfalKLqHLdRPLmp+IZPJ3g3A09HDMczrGdY2R1BWjEoIS4WusXpT/W4tE3r8yEAVHP0fJxRsZhrmVKLXoycNf1Nf8LzoDClDOd1nlREZBea7Y1SFkNibUoINTEwEhF48nj6cIIdDYYbi3zQ7W87LY/9hbZXC2Rpy+h6AdIGuchGTKIYeokQjQwxpEvcEQFSaygtJTHu6UIlZVx8fdrQr1oa4+pZJ7PQgrgXqoLBwLQzV+XpIvRt7QleEsBNXoaXU0kE5DwnLt7Xg6BalA7mzvNEFFCi5cDUGLULZs3QqVNkD1Lz9FDVMLk8/2V7S6P/WgGtISJ7G5UfSpkB/wJQ+ZNRIr2vVV79ltdg0bxnCbcU/qSxis8aNmO5pH6uTOCaLyg+Xy03GQ/7xZblZ77w2WGZVuBpyZmJgWa3TwDOao3FdsmhdzUpLoTcuMx95OXE05CZwRTvPYlTI8AmOJIo+AIIMAZH9hicAe0Asql4gML+CJoJ8KbAEUzAPFZYUfXFemCYe6PUn+eGJWomsFdMi6OpFoj7X29qw+WPLsFQ/bqupSN3dIpv0xJxoCZHk6XXyZSRLgxCp76LwtBSpTXmX6878XqSj/rvU3m8YW42TniLSftt7RoZNDu4gB9eK60VW0MM1S/+FaVXGd/EALxSvpX0hcDhl0nUuUnCJvUyddbu2jByNZ+lhCg8VlNiIp46p77lmE0/z4uVIQrUUvbVjeHqvmzH1lm9kI/QYR5CehoGPA0DrLnDH91bjH6fdnxruQpMiNuJ43jFQ9ZAxTiE7oRzppg58g7KOaZwEKraHvlN7fdEzRVHJxkP71ysK9BrjjLaDMBGxzFjQrhSqbMZFzWCngiAARvGeDrghoDT7giPM7zzmI1DUMTHcyGAeFZgpicshpooW5Fh0DCBDg/gO+D8ZoQ9GdizVTMXxm/1jEpN54wJYcfv74E3tyA7goyFBK0KuVl9VwqDvfWhRbU67O9SKh0vQ8YU4GlBcCpboAhbwXNxzsc6r+TXIYdK+Cl+UWf55bDkVeTwIpsR5Q0K0RisIVgD7O0QDqe2BtaUwLylp79po8QV6TezI6L0mqTqXaucEgSoCYNmrgpPv07qHUjdM0aslLAph+ABJuAGX8HyAfx4xECPMLcGsBnBRBTerZ3U8iedl0oCLWK2VoQ24ZmgQmBggWiohZXtFrGcSL9YCIMoZitk2QxRPSkkYTagFEAGTB7eO5y++wvocIubv/uH0O6EGDVj8eulPpS0rFSiBY0SYlvhEYUpj+VArIxWtkYqND98wvzhPW4/PWJ/dtgf9rDDkHdCUPxnlPc3UdaFcGBMZDeE+snDzpk5K7pa0ybF2HyJlITSyiCZ13WNM+rBX26bjKchgocBkwMhelEQ4j5Y1b80wQSKp6ZowV4zY8YghsoIHjjeB8bJguHOHj/+t484vN3hm//wNsK9/2JC64vSM+lfM/JpujKxZu4obxcaQFC6IJKdEIGhNdYGeLcDjPEwJjLXZGDj7hMyeQ3ViveUFMpZalch4EdPpGTpS2ixv3uiLKe3S+ASNxnyBM8jrtpa7hjpKlQ2pZour3Zj9dvmFUOITBIQwiMRpDT5CPNlYog5kIExjHDYXXyHqDwV4Cga2qG0mjZpFmArOwCoecj1xNbmsyeo3BUYqubIo6sdDdoQob4Q3/bo4xa/YXj28VsH51046Jg9PLg47DgPeAZpbVCoW9/vevXmmjHamqi9Tqud8nXfWFgVUV1kv6++9HANY58Fd3mgBSk17oSWESDBXUJrcrkGIbCc14ZvBuoFxxx3unjAGYb1DMDDuxBuwESDt/dhJ57E5C2MXXEA3hPhAxvs94zxJgrhpNbTJ4P9FIcrttUZws9vCM7Gh9XQHc7Au08+n2vWTkoJP40htM1evlWUNa1ZB+vOzwbJq757lhGily4voi6qZfXdS9cgs+JZrvqwrfyZOGErv6j5rgKPN80oecQNTMXmdlzD2/ZEoV8rLU7Nl8Djv1Ja403+FXXzt5uiEpwo7MxXCL76DakRiytFf77NBgOuvkzOEr3EIv9xlF8B8czm9Kyi2che3Jyec5aLUx7dmxWgAyrO/gIS2IIjCPjpsMM/3d3h/zD8Ed++/z0OuwPMYJIsk2QasqFQE8Nee0bYIxvkS8cOYKQzE7wvf8u2Cb/sC2fEQheVNsKQhFcILzzDuTmEKp/O8XuXukwwsMMAb4aArod4gK84lQEtz8fAbAg+HfTLePPxd+CPE77/9i+Ybx3meQKR8AUMA4YBYO2QnjEznMsmJ+EYzXjEODxhGt7heEO4/dsd7v5228pyQo81kyQ95yzm0LCD3VuY3+3h7g+g3QGgIYaoRZiT/GUsU5yAW3lGjbpyyNPtkcpz9hxRQp6FfBqeC0MGYxEms3Oyzgy1ptqdD8kNm9U/XUnipes+fslE6u+mrOGSSh1PrwBDiAYIwm6wGHfA27sD7g577McRg82GrZWhVulfDyX7zRgigL482TBwWwqqFd5crDMUbo/9AtAFyE1zriXP2oLu4THhI33EYW/xe3oDw9EKmizSyIgh8c5ZuRSuNSKqGGylQJGlITtDijJ0CwVpXuKOFcLK+EkQdieeeUSEERWF8AG6jVQUCpkg0d0RGcBPmD59hBlH2Jvb1HeyFrg5ADu9DfSZC3PLJ7WyYvMHXN7pD5eGu5Gr1DbISGgpD5IizFFNZQhkDazhuAuCIlMQiVliEktBPjcrw6ImL+Jnq2OPpxjkiog82/hQMHhLeYqBye0FGoNE+1GdaqmU0ngmz/KkCApjlY5ViUyBckdXJekdRaUSODxUIX8ozFeI7R3nyRHcyeHhpyPs3mC8Ha5U+n6Z1CzbVygLUONWM0lQCri1cghAfWh79Kwx8dD25GEc14CEY5KDzrRCc2FFbIPP9IliptZlk6verCUFigrr6N07MR9aQ0d3J4QqNz8vW9h7t9zApmTF8FdtqpemMNiJRsZ1GeO8kicQm0zbCcFgLhh0bf0oBr1yTk88cA3z+QD7qtCm3ZdSqHy2NzjvvgVwwsjHUlEsBolo/BdDHYuxIW6N9tEoUXqvXdOW2EXF+HPBYNftluYr5FeMXz2S/ZIqFh69GhefLCmumwf1G2oeLxkgluwSpRGC1bOtg65hKOKliJNAXum41doQHjYSnKINTPCczwjTRizmsEaYGIQR5O4A8vB+huyQoBiukR3DnTmfoxPnd1K4WZIngnPRMzI5SmS+wjmPM7gcwwYs1HdEzVTpKeTRB6/O9Kw3OQTj8nhtSc2yrdkCBnYTZ4NKt4wWpnrFXZOS2ZJdB2v3v2ivFrLVhVHv4QvSLyQnFzsq6i3XVZ7FUIBfpmHtDWNz/cvOdC8fVEXyylJZX1xXb+8LjRt/ybRO9zbMQLM2Ft4v5fuVefVXT5tBLuL9nYUfLdxuWDfsL+DK1WHsAlr7bXrG3GbqFqh5dW6/S3KusEhZOq7hjRq4r2WHCwBSV724JgE3MOjGY7AWdhpS+EoGssNpxwmP5NCGuENfy6EXU+QJsg65LJ+B4mg2LsYWiaeV3Nr4Awo7JQiA8wPgCN64YITwwXgAk3mMwLczjKfgkYFAN8MuB4PD4wHGMabhBn4HDLsnkPHByZAIEvVJZH8T+699J8RJhIcz+PAJ/p5xnAyGxwH2lErIfUjYtaRHRKGNp9vPmO4I2N+Dhh1AA2AMsvsdl2URUrh5En1Dyha/obpGSrLCUiL97QVhQfQ/F1OdRTlaFeHMWP5I6b1C1M6K56RmYV6G7b5EodysqQ2jv1hqnj4QCNYYECz8yQLOYDeM2A0DbIzawAA8T/B4gpmOsPMEO60wnQywnwF21wt7v6H0RQ0RV/GhaULzFzXq/mXT9Vx0+UWBdcOvcQB5fD884Hj/gHfn/wF7fxsUCgi26UAzqu02iWOMYSli8dlLlBJRzMxlRjBIeeKC1p6nlHdL9LU15a6LJBTLrr7QMTB5CL2rGdwSpbbI2TDBx7MijAeYTPbkcw7nv/0V9uYW9nATz9Ig0G4E7d51avkCaUkwbl71YvWWLFUxNgvgVaO2eidEULICoHDUbrbcIMS8txbWWgwjgWzeCUHGJMNE6cknqD48S8xFb0yLiRVKqNgr5XXynHQVo0b1ozjG1VbD3jg3Qph4ByAoa0z0IiWOuyIokKKg7PSQSItijEjNiR4I+fDdtg0EgInillOCZUYKtsIM4xnTKeyMuPl6j2/+49vwFfsvCeVfNFFxodaJ8mJi9V6hLqSDvwSPFWsj/MruIIMA3+H8h3hGhMmwb8iCDYczIuwAY+MZEZAQP9X6UKsg+XA0QsaFPkvvXn3yOgUG4MoMaCIDVDCb/V0X6+miPFnjSa3EJqm1/k4bI+IaS7goty+RJtIsfjboEQWDnvERBoyYDoXG1QJPLr7nLFu3U6Z8i4zWYpeqrx2F37R7h+P+G9Dprzic/7EQCiS2L8ct8mHnQ/h1zmOOuyjCrggH5+JhxFcaI7pdY07GiI5/R8Z59cAkmlWWlSZwvdb4bTayh9+8PV8bDhdLoupi2+QVBVz1ifLgkl0oRWisuDZ7sCHnJeYdiwaeGYYBZp9WiayRqmfi55Lq9IGhhJcdEgSQAZgNjD9gR3fw7gPYvgd7n4wRAODPAzAT2ASDradAzz5YA7JZUE/prNcpgZHDN00Aft6X7/VvwvUZkTdjk74xAN08Adb1x78AznFBoVK3pcLSac2UgqZhwtufJ4zTwmKiBYlhTVBtHBikqJw74aP5hGCMuJwu5lFDv4jw/oUmcbqKN4s84itU9OzPrmGNA2q9Xhbd2hbq3ffaR70vfs303Lb8S+Wg/wUlAqa7Eae3exDtIWGEM+2/bt56PNvifXxEXHqU612ngZfTuyHU+/hNimcvJeiFW9GIXnuSNK2MFcsdXHi41m8ASVOw8xi+ZuzdiPHzGM6HTJ/lfmU+JMtXiOd2ypkK6SQx5cxS1EhUcfEcz7/ShKQK9q3HIOaV+8TPpLp81j0wg+gM9iGMVHCuDGf9GScyWqav4ZzF7FjGRGBYvPn5Hc444Ht+wnQ7wr95hBlm0GCjrBjC9RqRE8iA4AvHriRb7k8wuyMmM+N4A9z99Q1uTzpEUz8JtjLGwO8cfvzTB8zv7mDu7kDDHrBjbK8YUnpjD3V4N4AqGkoaiLXUlV0VI7C0vuQ7NdchEDCnOvMrveYEjkMoJll7YX7jrm7oNaK/yZWTasyXwuBbIgNknUTLgy8mRoy6YDDYAeQs/PEAywNuDzc47EfYEIcMnj1mPMGbn3E4P+H2w9PlGqYj4KeLbf8tpy9jiEjKt0btvMr4NlO7wLHxwpp5CZ+0KnAuvevRIZWXVDbPDOODQMjThOP5COddQvhEQdPAamFneSEuwyLuvC5d7ktRldX3SdmjkGsmA1SVvd5JrQgqvJEU8SEKW/5AlA+rRqjbiOJCjVVA/RwIY9wySMYHQZwMeJ5x/vgeZtzB3NyBih7+cszlJfCqGfvyDVdXS9+rldAAZvLxVXkJ/niCP5/A5zNMJK7GBK9GYySUidoNob7NcQ0ZdbzAZFdIT9VuCNTP1waGgIJheX5qDQ5SR/k+PboSLxDywdRaaSg8tJzhIsaIsGRbnMeRWejXEf9SPBBMzosAokGOg/IIav1v78Krposwf0FbR82FWgNd4yfSYKdxRCuQl7a0qHimuBvC6F9hnqMXkBwKTgYG0TgX80uhslYMcjx+AMgHaaFpd4+HE6PF0tzxIjFbyL85g8q5gHC6nueLc0nN3TXwSN0bNfeafCFcZ8+TOHfaE0XqNxR2Q5CBxJk1zHj39AmDNXg4vMUREx74Y8czrEpaoS44jxYONdbTRpfXyKU0gnEPj0EZEOq2aeFQQjGl0AHCvwu8cYCthfPOOp3RHnScxn85d6wHEY56xojuNxtSL+MzcMzF/BofacX4C9KiAV+V3rwlAt7sQb+fwT8FY4uJgrHgtLwu8s6gQn5PDVBtSDARdiwEwwane/gdaL4HzAzmObZfcY1yDlXaNRZ3ncUD9e4O+xjX1ud+ANlhQsU7LrtLOjsSJioQuh4xJG8xHi2Y/IIcUUxoU+/sHM7zXOQhIozWYLRWyb+BTzlOM5zLeGc2A3joe6eVfJvuX93XkLx1YDuHOSzK6ZTBDDhGEYOZMo9RjKOq086MoWM4eSmuSjz+hZJ6qyDNswbc7tqrv6b2OTPg3UJNKvs1Hb6CqF1t1IiyDEwntrrQOO9xVSNemNoWtIl0xgtj2Tuk9ddNC2O5BF5XFvPsfC9NixP18rS2Cjd9TQbkR1i+A5tdhScKpr1bS92NBJeLTHT9QDlscUY1Pf68XxiX91Xl7drlbuGruyO5yfy8RAQyFsNuhDnZsItRjWsjfwi9obxrP70AIq3XfY38dtIdaL4cgR8xUjCrrrDiQyKPijy6EdthGeswmD2ccwAI5AwMm7Ab0gAegUkyMOlYBeODzigGZc01EcF6g/2nA+zZw914sHXwPuhE2PuAk2UkDIEkQkGHpTAg2PEM3HyEe0d4YmB8GDGch0X5QhymBjvAWcbu9g7m9hazHQFjA11oZkOjXbVuMqOOHIL9EmLOcFvg8zZbB5a1Ax4KI53wZUEHkmWHrDhiKSLCgU+yjO4gQ5UNkUaKVsWrpYWyInvET6jj5JK/7uCoTv2XU78OAoE94fxkMHiDt45xawn7YcAQw0d7muFwBHAKjmR1vX4G2IPsANCQ7outR79K4ubyWnT264Vm0gxi+q090Ja7U6/3gvC8gmIgpWsL6jG+sbGOPdgD8/kE+8Rwg4NH8G4M3/iAWCMS7++KkPvKDMAVgYjf9LYiB4QRvy9jdpQD2UvhY/WNlFPnyRc5txJhuAMAJB7oJkbZD6peMgiGiL99D3N7h5ubW0T3vqpS/fvlE3Wu6vedkS++aNl25XFQ4EbZDRH/iHI1rhn39BnT+/cYxwF2sGFXhOegcI0e4YWSFqJkCOVkQ0KPKRJiomZRe4zwZbAJjX8Bw9VJDVx3DiZMUNZbl72U4DsogzxHCJYDpmV2InHOhLgDDVStL5SXsj6TB0Y0QAQSHpXlRjOABr+JXREFc7Y+qNRc9N6JElRjibIO5nICk85KDAYRjvPOBwPITiAJzxQNcyyGCPWPSL7LfZJdBBqHpiWSmDJpEavfvLsFxevmo2enVX16DWTq/vrDwJfTouKiMjIvf42E88WTdVWJG9cmq8UscfRFADNEGJjxh8f3OJkBx/Hv8HlwONIjZrSn5ia40waIdFni6jYpruuFZGcP4AYOHg5nlIKftEV2QxBROkvCcz5PIoOXhG3avJm6m9LOzMbIUJaYvJBljRqd7yUDQ/J/uIvKi0QDcy71fiUtGEu2GiGWFa+CG5TQ1f16eS7s79/CfHMP89dPoH9CxEcxXBJHhw5WvFTTFMptYIr0SQA5CPXg7OnIzLB8C+PvwO49mD8WeCHh1YQfqfhnjcE3b+6wG2zMXzQDeT9S1UplbNDjWcK6PCv7FtJ9U2bO3+GbVPr0dMYPTw/pXjxH3+5u8O5mj+wtGwx4350+42maUp8fb/rl6rrbHR9t/wCA7RN4fKoLkYvyFgCwK/pqugQ17xADgN2jw/D+XNh6QxmlG89KE9rESPz+Kl4hgceq3LIoVVWvwpY7Lmr1HvDVGP5C6TlYlQGwsWAzoj96HHa+bLMev3pawtbPw+Ly1a/JrS7U/asz0C9MS+2/YqIaFcULmtNL1h3g6St42i+oyYQ+rMPJ9RDEwoIj8eHCizdMe1/e0N9rnkpZqtXn3H5bFlK9W5AFe/1IaXm2TKTR426PYbIQR8O8E5MzPjFUwUiphRAjBMOAFK+Z6lI7LYQHJRPdDaKczBTCFzLL+Yc+KPplPHzkFxWtypEYNKESQ8QE9oHeGGPhrE+hmYLy1saw0wawAPkg54lyNjh1EJgs7n98g3kEPnzr4QYHi2AU9j4YLyiGxzFEQXY0DMDBecXPBIEBw+EJ9vCEyQDHW+DtX95gPI/VhlfF60Tdix0GmD3h7s2A6f4Wn8cdvLFgE4+I9gYUz8vQ8nHSYcgLju+pD4Yyr+mMhmIddLMWv0siYj/iRSknSV15KcR7+bT+Xl6oyjOYbl39ryCEbUzr2AotsxPnnx1h+jzCeoPf7QzeDCNuxhHDMMIaA8YET+/ho4N6k/wEuDNANyAzhOvf0k4ILn6uSlcYIpaHfxEElGKpq7CKHxZvCBCFX11bjZpbMsJ50epWEZA8kxtvrF4P1Hd1I6pu9BhSUhOSsidrMWM6nwEz4/zVgJ3dhxh1EnshfmhIL+yACLMoSxClriBIPRZpZwLFemP2pDUVBSkhHTKT6kreSqqjXUyX25DqpHAOhI91lJ+URC9k4WIiwsHAnK7hOJpmHDzFXfvzhPPPP8Hs9rB392quNUOzASFtwVktPlHX25BeK0LR4vv+w9ITIRkfJF/CfcGr254njKcJg2MYsrBkc7gHiKdinPsYDoK1137Bx6k5ZAm9JWGEJHOHQYvflmtjgQB2ut4V8tKaKt+Vtqi88LQxJ0HEUv1UfCoFxDWkWCUiBEUoQJB49HE86m2SrL6RXtXrIrlYBOYtMEAEzyFuJTPBnTw+fveA8TDg8HbX9vkLpe0kXUa3pxhZeFDTAq1gW2pP8U1WXeTwP1lxRomRNAAZeA8c358xnwN2CTYKC2PFQGeRvH6RlW2lQlWzSopxYoGB3shkhkwYVA2/pVdIVoI1I1ExidL37niVaHkpVzc1hu/0WyPCfE/PAEaNO9fnHIVBvhRUciaK++kIBkQecdNLgg39r0fm5beggwnhUORGcnvKvsRsFbvRKanuXdX7UAAjbM523sN5Hz3YW5hJ50ZwoLfec/iGAccE5+N5ET7CU60Yjf9KP6zAFyQ2oWldYFPS+xroSQ9k7I8YM4q6+9Qz2a905ZmBynaEvDe9qnoFa1GeFZ21bNsl3iE1oAO4ypAvT6IHe8kGqbYrvEcUwh/d3I/w39zh04cnPD3EEIAUxizuMa3An3KxyPQz+LYw2FMIZcBBH2ESfY/HIQqYewA2GmSVcTYpDAh4e3vAOFgQDKwhjEPAoUX3YmMy7eul9n1vWULlubw7p/NtlQ6jxe/ubtR8hEE7jEPmrRDNagS8vTngZjcu9mPpXJ2lbpdnaxh4k40LPaMLAzhOc3RUquqq+OabcWjgmocZbnfWvc1lF3xT+36tH4tKCl1G9a0fHLydq5edRiykkgYooG1ty+qbsmi5HU4Me97uRchLdwX69oB3aSeT57ADCcYAZDHtCNNAYGPAZsB4dFXs59g/YwHKoc0yq2hyp4jKEWQfvSM55wEio1PHL89fkncJR+k33TGg1MJuzl+AJe2kV6z1l+zA1rrqYd7y3SUStqGozUORgBMIMe4tYG0kjyNmvsfk3+HMe+xh4RW3sXRoc5cvkBzxItFMtLhoqe0lC91+tNrnHsKraH2+XOLflxq6dVL7+RkAn29g338N9ofgeJXeBRpf2ud73LcIDWFOQogiCuEiOeBcHY5R78wVvRQiz83egynuxGUPN59jeMiQP5cT+UIhWpp31Hw+MxhzQG/GgX0IFUmG4M0AYzyIA9/PGGAsQF4ck4T3jfyTtSDswKev4egR8+EJFiEUsomhmCSsq0EI7wsAVkKiJjIcOC1DAO9OIP6I+Wvg0XqMH3ewJ9tyuGTBA+Pzu89wNxaf8e/g3S0Yp9jVaHwgCRmmPo2Mr+Bf4Z0YHM+NKJ1IhZ8Es0yrTFwa4uKUWI5Sio+hkgpjg0TA8HHOUgGpkSmaCSFGYOLUzvKcOxfK0eXrf74nR19anJdTgvKaPspzXWuDc9vK9QrvoloRVIhioDOCtQA5Bp0n3Jg99vsDxoMF75/gzQkznoDzEw6nxyTbjccTaDpL44PjBRB2gc5HpB2yr0C7lng6PVRL3Brrh7yJ/DTp1XZEbBDhlt/XTA4vD0wC8IYKyQgopt1zkLRFIZGY9Fxv77dk2DNSXFQ+V0QlEU3ELfGxnIArGOfpiLNnnL4ZsN8dMM4nkA9hiEDcbGgnXUW8y8SZUJlhlb0hWqiT8pTV4bu5lGS4KPLUHcx1sKooHYYU+1Y2NhIr0l64ui75Jk+AidiMWYiWIGGCI4CnCdNPf4O9f4Ph/r7CU5e3ixepu5q2LKRAiK5acWloSsAu2II6jE9iKkShRijPhYirJl5bYzA+nXA4z9iNO9hoabVkYZFDLAAULV3ZsNUTDRMDJYaGaIyQ6oWAsc4DBA8GsJrzDnPWSyUYFw3a4oFWGyWWt9vVKJWrSwXvcR1TODQiwWJoj08KyDJmI5efS+HpJjMM6VsTvFAMh22k3ngMILjTjI9/OeP2dwcc3o1t8/sPOn2u8z5znTznmwrhNrQ+a5wTbgI6vYqIPxnSEBlhkgNeka71TiB2Hp9/nDCfPAbLMNZgiPFG026IwC5k5TVlJW1vU4tHnuu8VwaJj87hyy5A7qKQI5clzi3JniyOig72Um9tLaRiR0jxrFNAV1uVsFUB81SsAcm5Pj6aNgGMuClIKWCDJ1HY9ZI9tMK2awRvqS6u1lCm2fJqzapcaa03X/duyu9ljmr6pHvvI06YPcMyw7GH9W2opuBlpnh4DzjP8V+I4jI7hnOs6s11S29lfijyTZy2etc7U3NLQ1YSNq07rBEVQmh35qFa6iwH7yWBVp5TboOwddn4UNV8CT8pg5TOv36GQOcd5ffyt/6tl6SeOjmPKwmJkPuc7+7tAfs/eUyTw/FpBhHns8MU5TGpTLngon3wHM8UCa988RsOOU+dYg6xlRHO1Ann59ho2A0KCWMJX9/f4Ha/A2ASnizHJl8sGQ5Wp2pB2U76fY0/NuI0ALjZ7XCz263UX+KKr24P6VVdTb1rddFQIuuvxql0myFtYVCcZ3x/fsQ5eqYWdagG7QeL3x9uQqxrlR7MjJ/MsW2bhOZK7eemDes7HbnBSUvfyb0zj/D2ASBzkQxdWs6Jq2QG0G5T6cKN3DPj8P6MgaeirLWWyHdlG6ovnQP8EYaAwRg49iFqFA3AsMd0Z/H4ZkhKHvKAbcJmUQhlo3ErhZjgRhB1x6DMfg6GCNU6AICxoGHfcLspTcew2+pSoqJUYLnEKl2xOF8z9ZrHy1mW0nPY3l89/RqNZgRt7RDwJTPgeMTE7/Dkv8aRDxgwIgUdi20Uw3ouJLxspozCGT0NL91zYOrclDx0K/tlKbXKxyK5CjEPf/IOXmR5T5dd8+d14xaB78r1IgN1fgv7w+/hbw4wA6r+cDrjS/7V0oLMSZJz4llc7JFkoVSf3oELBpFN57EBwfga90LAe4d5nuGdS3wz7ABKDaHg/JCccEVJHRuSFOGAgwd5goPs0rQg6+HtEHe/EwbB85bKKSECDMFaC4c9/NPv4HCA2f0FIAfrHcK5VqHvEoVgGCiegxqcfLzLfLPsnKfDCcP+hCMT5hvgzdmEw6sVixqKtfCDx4/fepzu7jGZ/wzDFnv6fwE0QwwRnHjxFPg5zhtXkycOQ6z9WnKGSveSP2UUEMIAQ+QJCXmZBQtt4CjALgN/nvv0l9U3wbjh2SGHEQrlh3PswiHLlMLMokzNkrgWwVEaNx/xhSahfX1huw7rIPTyk2Wi8rtw3kcYeSZgNIAxHvt5xt24x+H2gPGGwbvHuA8e2M1n3Lx/EiAAzSfQfMxtknXspored5vcDMNL01IRtRzwHEfZKwwRaxDypahfp0c9WFU9LxjhpElCGqBl/pqRBex61fWbxKkxXDwjgdCEFMRyFRD47GZ4zPg4fgIdDtg/EqwLCMF7E4VPpPbUsjeBos4/E9LCdsDqjQi9BKQwMYUxIndzHX4uQ1crWOdSF/hB/bGqikAUCKgBQvw88mm3BXkCn884/fg32P0Bw92bqnTGJpjU2WRoeu2pGkmL71dSKr+W+PSlvjFF04L3QD6sUz70pyPc0yNwPgWjgxEFq82hfYKbVpRjKDMFkrhk8ASuNU3KREu22HF+mZ5ny7ku+2oGq5PqwBbPQXa6tPC3ZE1THTEMU7iX0BgIcSSdAhQVr7s4QKpBNpoBrQCNI0PDHImXgTcctphSULAaA0zHGe//6TP29yMOb3YoafY2YFTQu21GlkE13HcWi/CX4Vp/sdzGMCJR5UylobJRYla/lBhHA9kRgbgDSMyaur1JyZbClZlibRU7InLj2pTWQGbwllXqkaHOmfs567XC7QwnXL+GSEWZvHG9NGFDOHuxl0qdy1Si255OfZpW9Rk/vVzK97r/2VYdfMaNMfDwMIYwwOObx/cYB4fvblwMtVbBf4chyMrDTnf0JFJ+RMX7Tk9Who4jAtH9Yg52zxRmyTPYsHof8a2P71mFavLaC4k7cFSvzEBPMm3Zlq4hgVpxvf6deit828I3z+c6L30psK+eZJJbrmHlYFKmjetkCS4Sje6vDZmrWjeZcBeJwVYOYjR9eAbB8A3IjYCfgmCYygrlvb09YD8O2I1DVDpEeKl62iiApZC6xo4ytcqwmv8SXVph8osspZGovS/r6EPgYlUrNFCmPK2HBRxkDOHtzR6z6xgiVEOtUTsBVZb9aPG1MqZIXZk3l7QQPGXVULeeqFo8DhaOZAfIVn6lzOfZ4zi5eDjqSmIFi0owGg1hN1gMdxMGM+M0ObjV/pQe3PuhDYjl4TANZ7CfwW6Ei3yijzgbZoCxIzAg8HOx//ONBdu6tEqOja8NAzdPwXM3tKUcXyYD2GxgE/zAZBN9LMqVZMe4Y2PLfFzDY6oeaT51K+tQIJZXjH/t5xgmRqelRi3PzZb0conn+kKS3uH5hHG53s5wcPE6ZPDDDabxFuf9W8ywGH/4GYfHCbvHYyokSekFuqqcBVCRxoQ0Kesu1njz+oWwxas8rHoXFw5FXFnInquVq0bouXiuwLo2n+pdcuPQMieXGXMfMm4kFlVxnAHhaUVEVfeIPOY8y7k8DGMAS0PBC6fqOfOmMvZEvmCJQxSMIK8xECILpArLzopI7dkDcoYDHMIxEQZsGCF0sakM5YTgPGFgecDdhzeYjgNO9gnzeIK5fYSFD8Y0/ZUJTp92GEDeQ+J1iF4q0OTovX57BFmH+VuG399h9+EQzoyIIxuMJcBu2MHv9vDDEAwmJI6N0tJoOGKG7DVIzOBFENLyaAU2SXBAARoMjue268PbS5mhNMQVI1Q8DKSWUgWF/CGibSp6qTOV/JuqZvX+GQgurv+LqVizVaviO1kXqy3iLDMYMrDWwg6M/bjHfrfDMAywJjj2mtlj93CGPQejDJwDeI7nX33ZdJGVkn68UnlL6dc7I+JiWgfUSx3OgydIeCP4rmRcXpBl8rWXCcvXYSV67zHxGR+Hj6D9Hl8/3YHZFpPeb0benhXoI2WKIYQDre2uRsmsn29CcLofdYt0efqvCD18XR2IoQyjMBGYFQbYwBgP0XLydMb08w/gt19huH+TP66I71VpQVBvrq5ZmRfLr993PENF8FdIULK44xHz+58xDAPIxrMhTOdsCOTdEGap/dogwQreM/UI18K6CHGpuVLo9fkC4JK+xtelMaJLbldK12uiJ9CjWBgE8URj+Hh4FZhy+LBoeRCI12dHZSok9WbmWSor2lMpfUOIJoDZwMZYGvPR4/j5Efd/uMHN230e/y+Q6tGhzk1+ZspXVOcvS+usJmTkRelSWKo6JFNWwIV1EQxt8cBpfR5EPAslrJU8vrY4G0J2U9RGuqaTRVNrrqpyPoGshwbXrkzY+nLZRnekyWWd16UilI78NBrZ9fpBK+NXtTPPOythscmFXm8S+SPkA96R7wfP+PbpI6w9wx4YswkG7VBy2zgG1PbdsHbbfGpnwEKqMVOiihfPyBHeRoy9IhMoo0IsMT/3+bwIH86b0udGFP+aAcwX9RSHZfNMOreWNhaZz6fY/k1b17UfarpbPe3iAla/enTr+35dRAp3lG8Sn9e8S0BlIGfvaaNEuJfdQJRCxSx3ArB8g8EPgH8PxlOiTaL8fnN7wJvDPsZQ7hh4Ow28aGxQ+Rf5kcXn5XVLrzbMO1VGBG53Bay24cK7S+dVVFSteCe7ZgjA/WHX5FsyzNTv94PBfihFvNYQsQVWO+2/MMQt7tgDuO/WtnWVzt7jh+mUwreu7spQZEPa8mYY8GY3AnuAvwbOxzPO55XYTorRtgR8fbeDrfo18RGMnwuqIFejymfOE8x5CvSJGdPNgClu5mjO9dP9IMA6xs1pSjxFbXAyxpYhmBI8sLrtwOMwQFQAm9ZMkdbzJxwCcYpT7xbnrS47QMtm5UaXiVK1Twxgq3LnCzHXXzClMedr57JfWnOrpmUpGOk83uDhm7/DTF9hJov79z/hzd9+wrQ7wtsa2xSQCeqMuYYdDRUX25vauV4e934JCkeyYjSBywaIy826Oq3wQKn4jbyO8LSNjNPATC17cTiSJ51LFrzlBwRHuTr5yMOWvCeDQpzJHCaaAjfBxkR+16dw4d3WRwW9hwP57BLhARjv4Y0JZ1RUbQqyosHgB9x/fIfJHnC8OcPfPMIfHkFGh15CiFBASLKi04YICB5GPjrycIIZn3ByA9yBMDyNoPOQ85uw29TuCbv9iNnYQuYEZC7FIU9anp1Pw6/Qvu4ANePVuy90B8zpvkSf8UEh3Kav9cCqi/ymzJ0L14aJopzlm/I5L7xf4RXTsHV4RU2nlqove0wq95JcTvkkAEMgg2CIYGC332E/7jAOA6x1ICIMk8fhYzgbKogSM8x8jCOXuLp+/7r1r2RtAOf1ZLyXOAdvNkS8RvPXZEoiwnBjYEeSc3mfnbTXd9dLq8ibrtYL7TI5+nVc5J2DxkqlLXC/eweHWzx+/AkHMsC0A6t99OIhmaqj0M4Uiy0y1xqhBAGDkM6OIMpr1jDgK8E3Zg3kP1QSrLEo9SXJ42+t97pMStvLoIg5yUFJi0QmlyHeoQSJgWcQfO0NDBgwJpwZ4QA+HnH64TvYm9tokKBOIyvIuxJ4M4i83qLtV1J7cIsgFACg9ikVJarsfpAdEWSzkjXFzY+hmORQV1kfCSw1FlFzLkyE7IbQtIDlPxYEVzIdUs6lUStj5a+MTxfT9WtgBkACPxcaUFSTz1cJDJEcmR65FEJ4wvkcG1J7I5lIWd5z2LNiTaQ8eXyYxMgBEBkY9mCKke/DOVxgw7BRwW48wW3ZVl+N1OX+X/OSyiuNS9WD+rNW8aJ3cOmScwgJjafLsxxMvG6NEOyBx59PmI7BO5EIsIPFMAwYhrAzwiaDndoJQUstL5mqnHyCf701tQDrxHzlNbNEuTO7yGkN6roLDNpjmnpN3JgWlc8b1tA6jc0w0RPl6h1PjQxIEUJYwUI0DAZPK07nghDLjsFwYHMI1RXOjgDJltlOI3RSdLKXgkIp9+9C9m4FXWymcIfeDeE5nBlBcaecj2dAODFAOJ8OBmQf+r27O+B/+r/8n3H/zVcYxjEvyUQCai/rFQ/vq/omH2Q6pe+L8hKNa9MW2nF1o55Dwy9+sqAsk2fMxe1iNWqY8q4G9aVizMQIYQyV39aCi3qOsrSimWG9qPkiirvGKNIcGwy2wowCDa5oyUM/X/0NmfZ9oxhV7PBavu3TW5ffw0pFK5tHOY4/V69quI8vesV32ps8mzv52v5edx+e6bbQhkGL8NvQ4qWk+IKl/jUNupwGInx1swsh7DZIvXXfdzafvUAA7scBO2tb/rdqLRDWmzGmoV0WOxzwrnpKTXnWeuzHWbWbiz4UcplmWYlgLHB4N4OcXu+kvs3lEBFm5zF5n+BSG56W1mwGh85cLE18b8k0/Egh+qana9OX2xgymcnj8OEENgZP73bgCl8Mxxn7j/ksFKls3k2Yxxmpl3YAKeXCBUn0X17yLuz6QM+B4nKKe7n7iQzYjvXD/BsNYQwbwjLRgIkHHMEYaU40JsEMhQfihZ9XZTsn6SlRipfPrEIbdmaSO1eLXSMATGncRKaT9iY9CYXyUjhqFcry+Rx3t6fXJS6dT6RTqS8o5ZmWVzWRf47F+WyEEO/14KjtAt/pSrlTn9sTdunKi1BLseZExIu8ODjv/A/8fgzYVY9pcRvHnBmIRpFwXKOP5xz4aDKooTngf2s8GDvc//AG7g6Y7wBvggOxYQCwsXkm6UsMeRgTeWu1TgwjhMCEBYjgbh9A4wnzv/sZfDQY/vpnDKdbjO9+AN0x7OFb+GGEIQsYhwRGeshUh0V2EsrTsAUNqal4zaj4TzsdgKSj1HnEYBDe+cwUynciMOkpUXWzkoGFnpYOVOpalavf53riXNY9FjB7Bgsv8s5S6uHMZfpAqTwJwbzk3Bp4BoP5cYTxBre7G9weRtj9EyxPOPz8CDPNaQ40ikyI8YuSqesl124pL2zjC0IzvX6yB8KwF2Xs9vr6go4I2XmVZ5k3ClqVnJDSYtW1QKkXSQ22pQJfgRZux7cgQ5ieHnAcDcj/IX8ji5E6SlwB/kiQExsQvZy0ByHz8ibEQukjsL5huLtZFEHWWx+T0aTTik1yDMfDgATpE4kza6SXYasbz2fM78OBP+PdG7Sjlhn/PpO91iD14qKCLsf0K6pdTaUQWM51AFbpu5pslTcgwHSwpAlbHK3EyFfGC1HaApTjpveSeDIUz/S7krAVTEgkVALDV2GMRNDWJBRcdireVNVyCaQqYRIoFsaM09rjeB+IkXRAjHkK5oXxAjXGCA2SBAYMIWz6oeDZwWFHBhsDG39NPEjLxcO1XkoAyr7XF72XC6/0x+qBFqjLYirWiyu8VH7W3IvRIBsjTGS+TYJzZsbjhwnzMRiNyIQtkoPEQY/rJZwRIWsxs+06cfEf0jQmWE/3+Qv9r+DlyowXksTUzO2omcIMf7rBzweMLWGZllFmPc8L2VRp5TWl85/WeDCBAxEdTTQw+HiWizHiJWVgbfAKN0TBUyrR2DyUYuFI5EDKL/i0UlBP1G2BtORcba/XZicZqqSpEaeyCF7CAHsEwSh6qYXfLJTubw/4h//1P2F3ewtEnJ8MeFcznlRcPlvh+wXSFljbmqOna1tLF1jFNkfng2L9lsOs6H6GWUFTxU6uos3yvCyrxxXVKRsh5DcceGvSwdULeH0BIOp8cql1m1R5HrVFZUY9rLcaD/XbsA1GS+zTQ6Vl2apQOT+454FMSGtNP1sMI9tr1qWWXxr7rhFC7VLelALQ1Tju0tjWBk59VQ/vNTuv7na1MvT56TAOOCBT6SKt0E/dWkMDBtw3OerP9+Rxb32qRx8SzRWJKFn9AEP2Lqzg5EhUNrYo4HGa8HSeFKz1eZpQR71mOrzPKszSYl5pGXferxmS6jrs04TdD5/gRoP53RvwUOIL+/MR+x8ekmNAqsMA807tgLBD8OiJDbuKMr2U0b6msktVLZU1n3M4jyvJrhirWnFYIWo7IHmJpjYqfp9CaFmHATMPmGjAiTxuyCGEui15vvQb5SGSgpVo0OMRL/Rk9bbpllTfZNUOM6zwJsUm8hX2h1cU0pqiGeE8hrhTISrRAYQx5T6np5Wn6W8kzIlDpSiRccBXPvKagruITKVszqy1lBMcxBQWEH6W8m4GRgzRZCjSUr2XS+1UpDwfQaaiuMMibIEIPLEHwyG67hW4JMiIHmQsrAduP91hnmd8+nvEkKYWXuogpJ32xhh4H+oKB3H71AogOLzxwIADxv0ZZnzCNM44z4T7918D5z12bz7AvGXY3e/hrA1nnpCExetAn2L+NLa7BuSyLK1lxWwokHeFXJqHt/hOdbhpQf4uO9g1oWGTnkgZRZIeqQ7n3esP5z4pfivbrKuPruApcrV5TZQGEBZGNZZdVITOw5QMGRAb8GmEwYDb/QGHg4Edn2DPE3afT2knf5Moocbr+3V191vMv7W619BB/bqhmQgJGck8r7OsdaqF/HjVHbxrZ2ah7iSpZMS7/E1N2qIiy4dtbdP5iKdjOMRGW8NyNUIM8mHTTT8oxLBPBx2rKjORrXY9yFt1kPVSf9felfXE2lKlkWBTIBjyTowl64xoKJQ9JZggAOKI7ikcXkUIhy8CHv7xCcfv/4rh7h72/s2CdLGQumuQmr/djhdMvoLZVfAVhLZQuhDpxOAhH1Adf9zxCe7zZ5CbYUyIE5zCzkiM/OTpLUoE3WYkxqMYCs4gzopQJEYDylM3WcADM8Q1sdk6AQl0n4PR1tc14/pdEbI2cnMoDlVciynCS/bMkfKZ8zoVhkZWR3J94LwaUxcUx00mHs4WPbvZBwWrMYzzpxk//++fsHu7w+HdThF8YImYXOjp5fc1yln8mooPshFsrabI8MdxSTtSejlFWEnnOiiikYzOej0iGaOtMfGQ6gF2GNI5KtTZESHXmi8rmbLE1QUoV8wWg8uwxsF9M+H+xSQMXLxJa6/IoFsj9KcqU9CPCE4VItLreEkZnZgxrrdnf8F0lVUtr5sUEk3OdTEEwMAwAybEsB3pBl/zWzzxjPf4WxA2kqZ/Y5VxKNUy1Y8Tr8rNR/q2V1m5+Kfd1ziONyD3ESM/JDzrOYCSieWmsyHqHRGCqxvHCNLDlmjMl02vU0MXVhlg4V966P2CQSyD9TrfyEDe4dZ5X/A+cZ7SLsJ2BlJ/whpHH/5KFJYb0pTFSYlvNN4tjLS6LE0fFLBWPK3kyLsqkcuVHEV9K+NPaOeOFJZX5eue5axUNDU9q3IWNGkz2EW6noh3pNo9XpCqOlQ7FNZWNK/8bUqk5Xe9dq6+LYw8l8u8DqdHCL+WfyrqK29K7qDJnlO9NoqCNE3rZY51bGh3rTxr61pvZrfMxNSEtjEInkxwYmGG3vafq2L1TK1l+Y2LWcOO0HhtKNoPA74ylPrURyjto55BE8ihhpfeN1LvJTqelGGddxTo3MM0IwUX2A14/Ls7eEMwtj3Twt/t8PnvS5oMZnjag81dy7aherAxrfWr+061czg+gNwxPT/dDXBjDE/DwP7zBDNHxrHHCi0AX8HdmQEYqh1xqx/ox0t9k+emX2bE7zzewO3vMe2/ArAHYwfGCBomGHuCJ69ODwxOi8HppJCEVpM0vaSjuqndji3T2JqmktD78DL4V8Y2SnuFPrBQfnm/VNFaIzamtcFhwO8+4fzNP8Pgj+BpTHgCNS3T9D6xAZQNeEkqFffPwKN45ewS8Ew+jy/wH7ngrAMI8qq1NuSNOVw6ALnF29lwb0DidSqybckmpwcMF+XkGd4h8L/eg4yDnLMZnDTzQIazHxjGDhjmO9z+7/8e7u4J89/9CFBw5iGmZLMkqN1wyeE2vvGIxs1gAPJxJ5oxBt54HP/+nzD9/gfc73bw7oAP79/gfPgdcGdhqzBxuYvl1XJagKmlZVEgQrV6KuNEmhfhh3rImpH4V5FDWIXsCgdfR544nVkHJSv7VE7b+MxP6Q48fwUVlOG61BjzV/CqriLyzuNgYBzh7dnjzhBu7vbYDfHQbBkfLueDzQAMNwDPgJtT2VexYM9KGjH8sulVDREr8tpKWst9PQJPzJp83xEgJJVePm09DIQTIxdSy9C0i7X3QJC1m2ZM5yPY+nRIT73kNBspcaZz2KVwL0SyhthUVuxnQOg9LkfSSwhmHGsORIiTxzapKkuic7FEE76X0DjECAvcA0Qhdr+JwQD9fML88QgaLIa7EIu2oxna3hcoaFlsao2YegivHlNKQLck6uS/VAhugHxK4GmC+/wpHoITthwTouevKBDkv0CNk1KBcnEFAeonhSAry3ZiPBQh89qSEZ9tmYKWqSyGBGsTKWv4NSyzqtRQp+yKiIXn3UecYRuREY1jK7BeKtU5z2PMVDSXMgNoyIRtohS9umXOjYE7O0zHGWY0oLe79K3e8p/bf7mHa1l7j2tcqmFJhBKdpb/O62dy+JwqkzNMiKEn1FXCc3gruyFqZiGvGTKIBjsTDXZhnYhXMdI6KXj0DN8KrBOjBUbesZCxd+xSBsgF8lCPyCr4xso1fWiNENfh9TVjRFvCQgtfYKhIJV5Bdmq5igLgJIHWgOANQD7QDWOAETu89e9gaMJH+gnMcxK3Lta0MKaJZSMlvnE5HMVKXGWmA9AxgHm8w2TeYXfy4OkhY9rIxGdQqgwRLIYIhY8vzVczda/PiK6Bx2JtzSQv5y2fl3dU/T6njUWpF8ClDEkQL1+VJpX1lfd5l0vXoJKcWvTHij8qTvLLhgw5BDmFT6qQZMK2tZIyvaeMs3Xj63ugVXQqRLwJKi8Yn/qf5LJ5EcqoaVtdRszVlt30ScHnxoYu193hIBcNH+3zdYVxzcNen5a857Vha72AhZZxb56W+r1ehf7aX4Azjcf7dWU+jCJx4vSlT3umiSifRdTUwAVjlnn2yOuQjJteM9pQRBgtY2wOwl6/Xx8n2zxZmrusZORu3i0htZxnnJzHLJaI0eL8u3CgRi9qMx8I50NWZTS7Mi7cb0nPKVP3e5jPIH+SN3A3A6abeD6HZ+yeHMiVcn9b4IVGWhv+bchap8UhqZRk+SIx5AAB3u4wf/U7zPwGwAjGCI8BsDPIzJHUUIj6YnJhKZz00vqtqq3VF+U9K7lhZZ2ixm59R00S3i7yl4RQWdoNz8oI0TNG1F3aBHYXytBlCVNinzDd/wRMXwFTeE6EZFDpfRrK1jSd1SCj8MNrnFsiP2CLw53LXbxRoEuRGaQuP89hXD1DzB3SGaIYCJl81HEJ88dlN1L5Uq+PBy670M6465nIB2dMIMgDsoMRlMK4wh+w++7vMb99j+kPP8LZYIgwWu0XQZ2MCXKfV/2J7TFGHEIcrPFwIMAA01ef4fgR/uEbwAGPDwec/R1u7kwXHPKM1XMnMl+6ymO9lpTjmZTq9UfN96Ww2l2ZIu6C41kgcYdIkpNLh7pUe2x8VlVU89oTlHljP1fSNbhwm0yYL0vet5w9oqBzGEC488AbY7EfRwyDT3DPjOZMFCYDtgbkGCQLernBl5/TpX7VH2p6vcwbvKZs80qGiC0CbN1qYa0YQOnlUCoW+8i0Lqv+dr05eQEwIynAyixLxIybfF2EUhTZQSje4zydQEePH/484X7n8dUnDzMTvGcYk+3Sa52R0QlMMIEMQ+36RVaGcv9DtMS9V0vfO7cpqiBqFVnP7Wi4i5WaKcyPYYI3MRagWLeFmKWwEwz/8IDjNGN88xbD/X1gdKQ6Daad4dBXma/fLgTm51RloRZ5dfuq6o7EO4ofZQujMGKthbUm/TNyWLXl5OWdDuaNzEPy3o/taZBg+lVb6BCJDPJuCGa9hoQYyZrxiUnYhBrq1DAdLXBqoe/laQOOIaRzB0JuA4PoPZE4N+2dS2D2BTSJZ02eV0mRdSaTDsc2MAAxyMcx9YjhVYKZ7/jhjPNxxu3vDrh5uwPiut86ItdOSf5G/hIK+CaB09y/nIHkcVN7z2s/FalcnbVCSzxnKIYgC4oyo56n0kEIxoZhGOI6GWBt2A1hyKYyTNw5lJhmqnBeZYCDanFivpKhThsnUHxTfFikMq8wbqKApk7eBm9rpRrz5jXS2/mQvZNQzrNu/NVGiI5iDpVcsYXcd0vO5RtGOEconqmw5xl/9/lv+DQYuJs/4tFMeE9/S99urq6iV5k+qz7o4ZF35WLvVpgYPu7w50DCuRLcIxsgxBgRfp33cClMU8bb230Oe483znOXOX9JiqNa0ZBAEoSAbWpSvKkzb2tjnau7pNKcrRiBVHnrb1fa0pMKKTsciEOCNTkePgJpgt5R24MHj+Dw4ZOAWddNVQPUhJcDrfJn3C2vQv+pYAXbfmVa0huSet0VbdycKlxUfNtnXC7tdFjK3z7f2qbV0i/Ws9SWy7vdlt+93ICyfRxr+lXuBJB+bGvLEi1MoNnBu1VrsAYTZfviveDruLvVCNFeak8aF7nNDka6/LUdEW0by1BRmw1Bz0i67J4SQ56LEqaXjCG83Y9oDIMrvEzjk1HN5CIfdKUMUerwlut4mhxOKpb+fPcWZn+T7o0ZMPqoGfUMf3OHeZ8ph/c13HcaQ8tjk/Hq8hzrcDoLGWAnh9ufjum8PCn9fBhw/GofeXIDv9sDACxZjDxipgGeBkVnIryCwZ4A4hSeR/rc9FMRynRZ3D+TWSxSLCmuSzlvTHRPcp3507x+1SIvm0FAd4fEBR6wbtPW5GNopswDiCNiKT7zGoKLIkqK9S/8pvfxbIgg+NokdwXdQhJ5UA6NIQNvAEsGGhEQgiLcwYU6vIqPn5TWrMZQYLiC1dgxZoC8g6d4VgQZeO8iXMYDoc0AIsAaq3iYcHYcDMDWAn6P6eFbkDthGB7AA2CdSefRpM8IYVeWmif2ET9bg2EwIGfhbIDOmX04y5QZ7GZMPGGe53DeG3PXsErFVS2DqsnqfJfXhH7Pcf1yKxc2oJagJn6nqqzyMCNEa+AQrko8+5HgJ/bbx7M7UmQNraiodkZwW+ESfvoC5Gt7algBKh5TjFIyDhajNzgcDjjYPUZrMc4ONz89gdwczzTJRX65xj4n/y83wK+4I6LPpGVouTwYhBK4ugpyJZd0BaVURkZ8QOmRFVk39aBuuxIltRKIyvflVZly20qkEJcwGAw/T5gc8HBwoBvGu8+aueEGHnI7lJDG+dAmQd6h+xUBfWZa9RzVzC0yEpQxZ4pnRQg1VFuVL8N4hY6JY1y9aPBG8HYNG1bCYaQA4OcJ7nyC3R9iNawIZUYW/fo1zCxkEmq02mLkeqqXa1+W8yvbGWN9xTIK3hgh7rlR/ygf1hvfCeGVHRJQa6NeQCXp4uoNx/+j0jwSNnj1TnMlyhKfHV6qRdhL8nm8oE7eRCprpeYaTC2gp9VULJ4SjwWYpBD/j/LhWvoTYaAyA02AMkbohomHHMs8GYLxHt6EA7ESJ2QMPDzc2eN0nDHeDLh5s1NxqvPMXcS8tHqbHpayQYOMijxLa2fNU1OE6XL/SC5CmzVkbAJ8I8N3qiM0plDgE8XD3G3aTpxinhsSzgE95VxqjYbt3MIkVOvnUrfO1+LK3mD0XuR1tyIxLhZxyRjRVVIrFNc3RhQVLJa9mkRQUnQy7wmKK+maA2FIvqKi7USAZcbb8xOsG/Hz4RuAj/hofgznrCQ81UmLygtAOHShsaBq3FGrUSrap2mhYvy1vUvjWkBwbkheCYrilaSNxJnpvzhwq7dagNySVvOJ0oy2l7cVbRf5Wu3X4m2TtUvzuZi+6uLKxEDatp4PBZTbFxWN0Ew5G0rzwRUbqj5QPBGQ4afIIni1NxMEVLspUrlSvzZISHlx4XRLJB3WsAeSaxya1LGCLpG7srxTgKr361B4bXgk3Ya1srbUrb+5XHXEk4VR4nKbnpO2GhuuUYgLPdNlX/JGv1RPfeaIh77PC5+WALYHhYk+ZPxppC6SA3F7ham6Sa3hgsdp+1Q+brHmNTtltqT6u55SO2TpzQ2AhJ/66ca0uzCWUmOE2GhcuMaR6VLe+uwLx4yzMibw7W0RiMVA7e4wAN8jvWdmuMYABxTcxCLeKti3i4aIpX6l548TBgfQrGV2wny7w/TmHiADE+fKUHAYtGRgKTr6xMZrbjjwspHbi/3KOxJell5AOuMaq/UmDUed7xcZ+U7eHp91pRFsOSkdBzTtL1kXQLGd/VLUtQrJ5MuIANpxK9St6KWUQkBwqwv4Lu2ohE3h6XxUwgYFeXs4cUnDO3xoMlzkL4nFYy8egm0ojIE4qhk5+BmRdYm6ER7hn+5BZODcA4ycBeFDOQZ5LckZpSw8DYWQsIaRjDPGODAbGB8mYGIHsINzDs47pbgv0yX4T319JdApOL2kT1zOq4/70AakHB66bierOa7lZ07l1AxqpUZqUmbLXpFhqVNP+Qxx7IJqbru2hVZbYzCQwTgO4WxKS7ATY/c0AeywxPJT96lu29UvnpFK3FXO3+uO+5c9I2IRSBRSMeLlmp/XRZTwcAn7L5VUpraEmpvJF+uy52VlRWqZEmYJgPMOfJpxevwRtwSQ+xbMu7KI1IJIXNLhQxy3+lI8J1ksnbFeHTYm1P6KhG9DqoTNEMYmtCufJ3GhPVq4YwKb6GGeQ2kCJh7cGcs37OGtAT98wvl8jESUsPv6a9jbu2YM2jtSI1Yx9CtGiG7zN+TIXYxlJ8FDlaBkYXd8gv/4AfAcPbt1mBkDd3vA4w1wd54xOgQCKUrsqkEFTYEourhQhIHz8+wt4SEeE9kTPJ8RIdsum8oapoyhnya6VDFEvXG8yANuTFrM1FcFE5qUnChxGiNYCbxBoZgk3d2oYK950krZUzABZFLDDDPAId4lgLDO1Xlxx/cnnD9PuP/2Jp4Z4RNdf83xERa31Qpl8SELS3JP6tu20JrJXKpXE3bZ1RNCKoWddIb0jjoPPwOffzhhPnrwDAzWYBws7GAxWBt2EpmwmyjtqAAQLRsKKKJnsMAzy0FlshVVrYO0fRko4bozC5EB1kZnzagl40Z3CVWxU9HJo+8v4Pyu6KcWXUlN9XpYK1PDwjPT0gKv5UCZrmJtyQFzDAMGyMMYBAMtKMIMAQhxXAHIYUPPSsr0rp5d6L1CgUJ1OG71Z2RDQ9oJ4eNhj3E+vXNw8VyIsBOC4XzeKRHOkFgOK6mboRVDrY9ipx9pbgVLhjHNpIxSea+d1jy59Zi/StWNsJPxeKKdnGO8xgamDL2lR0+fgJ//AnIecDP49ivg7R+Azwb82QBPOwCPhbAXmpANtSSzpFkTxN1fkZ82hsp8inXJz8pRMu4edLqDt0f4YYZjX+GpcmCW1EZagVrsikCmCfl5W05v7VzCJyUfpduwtK7XytL0bHv+pfvl5wvjWmXrKx1R5e1/2yubuW5vva4u0IwrF/Zi/g1GzsJ5CJkPkJRgpbvYNrSTs4eoZDcoFaeh3ktK0t5bRc85yCGJxi83KDa95KnMgiEid6NUEpCWrbhuX157a4mbq2vXzPI3240ALUzWzh8ZN5RjV+Z/WdoaXkry3e1G7Ifnq1d8RbuvXnNdSlhJu5XxpE7MAO1HmP2Iefb4NGVTihvC+Woa3wKBhR4AWGLYSJOE9OhaWMoPTE1UkHN+1ml3jyW8ale8FKB0E+k+0e/oIKNDLZUC3VKhqoFa3lvDqb0e6Xf6u145mVLmoxqiopQJIrtnRy7BpZGH5HQSRMgbnQrzTogZ3jnMbgYQvf4jb6HnJxk9iOAFe4rTO2U4JgDGWHhmWBPwrY+bx31oEHIIqCjnRRAzJHqeIHexNvIlhkxMyIHnJzKARzgvwhlgsOHAaWNBauyJCMO0w7vvvoa7OeCRgPlwBOgRgzXYsQUTwdtgZMMg4c8IFOX/YGfxYB5AFM5sIzgwe0zG47/sP+OIMz4/PmIwJ9z4wuSyAgflbK+9bfB1RxEQfLsCfSgNIYzsJImSCeOcJ8CTdlYRQ0PdSk1/4q6IAGRIzLH8S+2t2/4a6ZmSQNcIofFEpuNBZguAKnztEKMuzI87WB6wtyN2OwOz+wDQGdrJrsLKqc3lKoMirs/s0284vaIh4vLgFKycIjaiJ10qovSUjE/SIcgq35b52QzfCxkbAF0pUC9mJTBQJA4ct73N0xPc9KQWpv60hxlUIqDmOctdDKt7Gr5AikxutJInj1uZr3TYD9VfYXUsCSCYgAij3jfYvhkelIkaGRgG2E3w8xSVMh58/wbkfYrpJwrH7cJFANDXQwGlESIvB2qrRWQomMHTDPf0hMEakB3VgZJBSeuNwUwGzjEQQ5OUCGwLwcvIlqE8vBUOFmFAFLSJKDXFczHX9TzX+VNJ8bnwgL1xr0t9SWpHRphQ+aEENkh5A7OaDWzZGJi9fYB00TC3XFYlnkOEEJLJUGSkDMhHrwsA3huQibuNTh7Tk8PhzQh2I0ARN0p1qT+dUax53NXxofpB8ZTUX0AEE9JZq8o4D0HNtNdkQsqTMinnK3A+MbwH2AHnhxnzk8e4G9LZEIOxyWCXDqdGXj+6Qm0kEAasfFLni/esc7C6L7H48ips3xBiXM/kNbSQ/6JgqVnfC5hPj3GBk7autRoi+lkICgckY5zeT8Bq3NTOP0lqCQGk4vfG5RPbTwhrx4JhYx0pJi378B23Y7mYuISXxO+3IFxmWi808uh88V8+AC7AWDjMmhNuZvRw8XKq+a+kWOrlUyxy8/5SRVHpsIWSXg4fs5620/aV16RhUCCxEuDS5K/xgj78m47A5/fBc2+eAbsDuxl8suBPBphJzeFCo9LcLPC/wg80vVxksMMP70DOAm4C8yTUvYIjKmY+6XBKJF/V12mvWpclTb2emq973l/Cc+tlbi9nrQ1tXu1FWrdlWxnX11t+WyLR8vuX8VOZdmyCvrbtnb6kMxX0O1GkZe3l5bJVanYnVPSxnaElb9EO0o/EQAwcJPu4FSu4VlSxvtCGZqr7sTr/1MO2G+BGlEQvgI3lcFhXr3JdatOOHPJJ1y3vmlZtakPJDijY2ND20RqM2zd1dOqtg7Y8b01uMaCsPh8tcBjhZof5NEUFcCgzqJyV/EkC5eJBzqgPwc68b+bvGOJAKfVSuQyKMEetPkNfp5yNXKlHcIUDj6/WtSYdTn6lyLYP9UvdykspNTA/ibyoZ5YIvgsyQmvyl7FSfuvBgSUePOzj4c8AwEYf35zhRtMTMXQnuOMKj1Lgy9kQyNcwrtudaYiceykOYZ4N4ikMxUdczEVkokjCKQfZUJyR2FAxZcYbHB72OHsCPx5DeMq7z/AU5G02DOsN2KpxNHHsjTRC5HJEB1Gf6MtHO+FpBEATjD/DN9BF7RJfWpfdPPVvHBG9GCo+LvOt1eNuRW0xhajbzVgxsht1pwXerZr2mhq4xdQd997ARMhOy4uTTsEYE3beTAaGxhgamsDmBLZTyTKzKpeBHEKENvBQVwh5uoArPnu9EOjL6ZUMEZeAo+qIZDcCWJdBTDOGPQKxzhtoS3v57FKqCWkHfWwoI/8SEA9ZZrCb4fwZx+MjTvYG7F1ZA3NUkJRtD48CkBqO1mQKChVBwln5n4lqSc43wCL3x3qtnym3MM5y0BNLu2X5Mtp9gpHACaPYq4MIEovfSEiciBFJeaUzDNgzPBmw9XAff4Z7+Bh0eUTYf/t7mP2hwAGdpuiKN4/D5aQ8Bhfqq2vzpyPm9z+D/ByMEMbA2ojwrA7PFEI0nW/2cDcAGQsD4O40Y0yHoZXGAQDJw0AMDj5asNlHksnR6ztu02REBoUz8xLkFrWrIjFMmRXpMYmpDVBtkGeMpKB/dRK0QPA62CX8JRk5Kp4DCKHDfAibRPIuGR0431M5Nnl3UEXT45ZSRONDwB0e6QjsuK49ESx7PP10wunjGW/+dIvDm12MD+/TFIhy8ppRpBo4Vbf1GGRYpuJD0t+0CwphzaKWEqo2UPoN/0w0XJuyTjDYEz5/f8T5cQZmwjBY7MYdhsFiHEcM1mKwYzJKkMk7LAo+MM5P2A0ha0Jg3CfPIaSfrBQu418+J4ptD1tf8zUC85uEhMvnRLSKIP2c1ET28XKDOrWiVOG5tPOEOkx3Wgat00GqgaivwKEkc6St1p4QGEMTdskZQzjwhH//6Xv8MJ7wt7c+hlbjWC63xoirk8IHAGTnzCalu+ppxIIKpqAMEOUuCDESczRMeG7j+yvf+NV2Z691eZy/CYZALvOlSVPrZ0khmAtS35dtXEu5ScuMebeEFeV0C/YKzxXKu3JmACQhKzt01fdQFwQcH0A//SN4OmU66j344w/wjx/hP96BP9/DT6c8n16cbeRfmYIC0mR5KOJ6A5kS4Zqr73rjpN4yOO2q8T57vGU0HdrT0If0RoJK1nRS0Yz202clOSTymlSGUdr0xabytoYgyoobLp5fU4fG71tTEWZKf9YcslqVWeHEmp4sGRKW1uwlHNHt08qzrYJy0eW6naK04hLK2xIWxr0wkJQfZy/S3NZ1uUpLaUj8ztJM17tGQtKeyL1vt8NcS3QVndvAWyzmuDRvC3BY8zS99dcaZ3RdOt+26ptQm23uVFbPyHhNCvW+Dh9Slls+v8Qj6h1S+5HwrbVV3wyOs8fjrNeEB2gCaIYlHzYZg9UuI8qK8tQccZySsI26DqpYwFpvU+GuKjVynWSvfxNNynzgesmqiawKI3Wv1w3pD3TdPbjsw+pSsm7E8HCHn0HwbPEVgJtYTuoD5x1fBTcTeQ0IzY8yv/ceczwbwrk5ylu5TDLCA2Q+QOQFYaMDv0pJRkqcLSPwV4ZgzBBCG3uP4KQa9Qteh72glF/y1aNUpAijciYGsQOD4B1D9GRho4ZV8x94qeE04N0/fg3/rcf0zoEjHrXGAEPcARH7T9GYEVm/MHYm6KTS2ZzGBOcnyxhh8Pb3nzAMP4LtHM6f6LN2ZXfkdwEgWV+xgJQvYSstKULeldCWIInUAklzVywmbh7JJzm8p/znU/4kH6ud/bm8ksd+CQZ8VkqyVn50ib0qViwjRlUwGEaLAQZvnxxuyeNwu8Ow48SnAz39swxgvDQDmAzIz4CfdEOhAPdfRXoFQwR1rtZytV8ZA1DjPcCdnHroCdTVSpRMgL67KiZkXv4X8pWJFm/irSHAz2A4MDs4DlvfZjfBGYbhEE4iiWo1TyM0rhYx03ONsLJ39LJF/gVJCVTlri71V/5Eolt4u9bzd7F5mTEOxYUQNoa8Etizp3U4aMjDswG7CTxPUbAm8DwDgxywrKDN2JfwkBtSZ71UFwX7zAB4Bk8z/PEJ1hrADjnGPQVYIAlxRgCIQngq8fwG4M+zKjT9KZIYELRBQCtZhUyIYSLlYV0Cp6vETzeMdcHhF/ao3hIVoaJYCj2erU4vmMcGVyQlpcBYPBxetSOcY2LgySvGLx/OlxaE3hmx1hmlICVDoHjIGxmC8cH72yBsh3WTx3xycGcP77ICSXTJUCtParpqeLqZW5VioZxqAbxTaIcJqr8TxXV6XhohEmPNjOnJ4fzosRsHGDnI3YR/Rs6IMCbytkoxLikxCQLpXsE9ynyKidJYZBOWzShR9VkZECCgIsJZFnSV2LNAA56/B66vBOrQ70ro7xe2gTuQ5aBbvUaqKuVCfYxEEWaDoX4JAxh30xGfzDm3TQ1m90iKUhvRvr+gEOyus+Yhpcc6SzGsrPBw8w8JTwugDocddjf71H6hCxda1k15N1Ld4qrMjGy2pV7+1c+3wea1qfbUL40QVerBSJ2hfsIMchPw+BHsPNwkR0IDPJ/BpyfgyMDJwM8ScivT3NzKUkgr21g+yUalmrawEgrR5Nd5k1zI+SnVcNuj7R3YzpfthDU89MpaeklaD6G0iHA2lbk1/FBW2rRlbzVkLOXdbJSgcr6ZWmgqoKbCgZcMC7mvtPq+aZY2lFyRrjLGIK5HAMWcC395saxlikYUdmwX7C3kINxEnEPehWDtQfHVzrPp4OD8UeYZpJTao54aD3spv19k2abmq/T84nilsZbbcsyvSsqosWaQbtrFdY7clstNyPSdF8opy3rZLr5c3vr95Sr6/S3LKOGsNm4mHpgJlghGtEWpGAMP4ORCpIH0HXkQeYB8ge4JgZcVXqtp3ypPoplCkoWcxbKlVIudr6ECKZoSbzRDnt6vVLjalisaygzrDMYTcLYeJ+vhbFCYk2PArzgiKQIv/wX2QDtd+aTYDrpiCiGdfDijk7mGIylazTpxYjmSLAzxHKewwz/CRdDjV+Eu66EB+u/KziWcK+fNMfvE4zOFdpPMUyzXeIvdk8F8HHCaQ+gNb3zUP2i+KTrFRauaTzxVLIuQz+1E2JFvYXAYHYbhjKMFkoehjEgpDCIJgVqak2f6rElxAk05VTs7vN7ieOnhVSlDY6dsgRv9SH49ktyiW5eweGPcFV3lFdLr9Yhx8fs8hv1xUNinepoXPhFiZG0DA4MdCLdkMFgDQ7qf7W6x1AWpg8J5lmGRzVWuPCM9LrbhTar37YOXpJcX8kJDxEsIbt6WPdwThp1B/3yqknERuacVXuqv4kRvXYcLVbN4AV4D4BX/nQArKos/z/+EJ/ceT9MZzBbHpyd8Gp/ww58ZN2Tw9U8MmjluAwNUgKNUAckWAyAxe0U/e7RMPdtKu7d3WIfQiHekkKswIRDvCPH247IYlEKSfpmnQG1z5nCfhiL98fA+xDMU63z+Zbj3P2Gm9yEWJ4e1bsYR+9//EfSC2J5bU4swSNOw+IjApyPOP/4AsIMdbPDmjr/WmhDvPsa6NxFxpXBNJpRLkTnWDEHZkMSGhN8U9iMyo2KQ8GLZVsovMOR8CC6okEKSGlvKBNX07Lmr9LWYy9CSyCxtK9BQYLj04auMqBxVHDLFfClck4QoSytB8FVkOtSaQTwEC2xBQ9ieSj5u9zcE9mGfRHAWITx8f8TDj0c45wEDfPUP99jfxrMjQJrmPzvJLjaKTZRnWblC6C7hC9Svp5yBNrbFPKSe63UDAsgaDANjtxthrcVuDL+DDYYJ7amSPHhUq7Tnoih2OcS9QQZaxbjLM/HoEAZarYVGwS0GJv2MF4cljZwww4n5F4MWZxZPJLx0UFzInI15aW0K40mxSRFnpJFeakUraFciYrqgOlPufuryeo954U5XwmnnEMCyPRDx4CRYY+BBCEdBeHhtsIXMwwISuUjzty6iTr4lbvdCCVkYVKGYYgbBI4e3t/if/+//V9x89Q7jzUGt0Ut11FxGnZbGSfKqb1dAqLfMr05ELYxJEmXp1YouZB5zIXGzaNEdFo44Ic1NxCePH4/47r99wO27Hd7+4ZB3GMbdLZ9+PuLjz494ejqn3ViiEKqrBUEZ6RkSrDLhozQGCm9FXOGjUB68AinxprlDVX/U00xCwlN5ThSM4wILSemESA+h7lXZW2fpVUn9aySlGO0tZ31f52vydgwa14aD2ZqElkgdpEb24viutEPDgc671vKlEFitrSO217PKtd6e8EHFi6r17Ts0ptcWVdiFtlKlxM2rw0Ov0xqP6AeVASENJS3DANXKxrpfPYjTn6+PYTrjDEh4JDzdApOloupaOG5GfNHpoUO3tOeGLvOC80BZd2ZWeo6PIrvURrTXDmdxvc2mVUBn2AT6K73FQVByt3b8l7G5GQfsLPDkPB4nHxXKrP7l9ps8lJke1FAUWdpYc9m0IsRtftR1IFno4RYi0uc8Ky6XgGRkEzogNDdl71HNujIZlGvgpWzhN58+4d3jIx7+4Qz8xxn+7T38/gb2n0bgg4Wbg+NDqeCN1zrEZ+RFfNwJEXYlxMgITPG8TWmCgU0hmMI/2a2eYYaS/iXpqGrvBlgYw+nAc8DCe8aMczjQeZ4DrHgBusjnpCHIOzXqcc4jH3Q83gcZ3HsfWaMwXybu9kj6EkPw0x3On/4Is38E3X8AiDDCqpZHSclQaIN3KYoEOIRnYgKsNRgN4WANDPa4H25h7C3OgwXESZjiPEi7BY6uTFnk5NSOphTNDsp4LeDJ1bqqi+ywmiNmQM4UjY3TvLDIyQ2u7rC5L0t6DS4vfq7GpJSEeq0RSFD8GgEgA2KD0+cBzCNuhhvc7A4YhgHGellN8J630zI7AnYA3LnYGbHGe/aevW563RqepXHdXn3JjHW/J4STxMce275e4XMEE65X0GolnKOqcKuAyeUohlsxjvIwh1IJQDjjhIkf4DkoEud5wuwcTjuEOGKky4amzOmnII0X3QK2pgWK3qQOcY2NaeckcwqUmFevhB9SJS1VnhFJHuNM8Fm/5cAAMZtw0FE0SAhjFhAOwbs5tCkSYRIE6WZVNIGsfUXhV8MEyr6okfAuHApGROB5gjsfQ5zEYcgKQxLCT2lcsrCS1LYlA9dNas4TgRA2Rc1KzJa9NCtY4bY4eUz6fV0l6pfFVxuTYhDVz8Xsxf3GWdagT5TWdrE7V7wYkhIoG4GKmU6eiJwOBS12DEmVokhGNHoYgHxcC8bAsAeTgTEcttNOjHl2AAHu5OFHBxri9vy4FlNvl3Ar5QyNQIACbLFshGjxfm+UFxVgWikYiXzxgcrOHmAXcHTaEmtt2BVhsqHO6HXTUVYmA5v81gyuGCcKb45l2NGQWeRaGIzycYVUk5AjE5jfi4clV19fqG5zIkqN6L/f8GS5bCiZTdGySDoSWu982xtfKS8ZVmSq0+ozsDyEOLAplJr6uHfLFc0talW7tfQgv4hPSxQipbT7jBFjzIohmDNzz4C1A+7/8A32b96gOldwk3zTyEHt8n9eWlSkbS1gAf40kpB1stiE+l2Lo+qniyxj3bqGriGEEvAO7GaAGdPk8PT5DBqAm9MI7zzcDODkgcnhfJpxepqi8uASP1ZNbodtjtQlvdS20uUyN6YG4HMzXqI3rxWF/dAzVya6tAieiSHXOtqhU6vZGtxzDQ7dWEnVoFoPtrQ6tkhLvR0QVL/rN265qdW3JatwYXwTzcwKw6JtyQi9NS23c2k3RxH+Bsie4JVSW9rReElS5u3XAKkcsxZPrptXL4AoUScD1V3oJn/BsLueWvzHHThaLJ+a0VzP31SvviZ0YSWxRemTEne9droYFm3leS+mf5VDvZc85RjIhbCgloLO4uxFJkVU8IZQyXn9N1JakrHrFiSeb6GVnd7iEu5ezdF7qXUqmvXVghMh4xYgO5+lfGVPc6rK3diHxeY7B+tnGDoC+yfQ/Q34jmE+MHhiYA48iJk94AnOmYoHUG5VzIm3VDWEXCzDEkPNRcbce4q7I4IjBBU77Cj+r1zuQkVFDTnEIgHwwTjAMTCS8L2o8OPK+HXhhrmaRuGMfOwY5ba7AXi6AcjBOQtrKJxBanM12ehS1aYEEWMMDDOsGTHQiMGOgLUIu4U4Zd+MLVbBJI+TFlfXytbrbZmM9nk81ndcvRU+UxqRPiobKI6by60DruJJNyfV+gUGP0/jAhdEqEkEJNoWJoKBxbgb4sHVyqALwNmwR9H4xc6rgk1cFqZL/1LLFnTAzdOL411Ufrl9r5A2GyJWul/cbWU7hCdUu5NWas3AW1jzCwYgZNf0o2ldsQa4AvOKgejwla2Hkt7iS3V2GHmgFcHRaBpwmAfjjM+ffwaD8afzEfO4A/MuImtRvJV9zAqp+oVk3kLUBBH4NB6pb3IXCe3FooSxkQ+r1UnRZTx7iwdvVdIjX3zS5QxaISlNlUnzFqqW+HOAh4ElPXeRHHrx8o+j4BmAx/TDd0nxa3YH7H//R8Aa9b3CJhWKblvc6YF+GIULo+55mnH+23dg71KfxsGCYmgZ2Qlh0q9NilZEBashEzwcQR2o1DsjOI5Rbc3myFREahK3aepfxPGCeAGUi6uAgewlWczABbAqyXMTnunSYHfL2/Z0mSDnVZ490KU9FJgLEOIWBpAPuxA4eq5nWTViSlbbPRPIMyxM273o6CrnYpGxMD7G9eSgXGfPIBNgNTBOjE9/fcDDYPD1v3uD8WZI+NNH/NXQLiov0tIWpquGJQ1jShgnhfdYl4OMNUu8VTWC8gGNIBMJvMlINfGtAZk+/njC9OBgecC4H7Hf7zBYi/24C14pwxiYwsHGw6pNwpQAUpzUzDspPCFMc4rD72MMd1kPAv/5X0YX5RgQBBeF8Uo7MIgQD7CJOLNdH3LiQOo3Z3ol8VDVCenliC4Yq1sFhkfYsybbTPWc91dGNlLkbOkMIKFXahR6jmIEFMtA2fCQ4amFV0rrS1WOuGVfr09COsD6hu/wB/cNHugJP5vv4OBhpK41pFRaTIr6cu/0WApNonKcuwhssVIAQQjyBLgUtzeeE+FceOYc/DzDO5fi6wZPVmWMQZ6O0u+2MyHpaexz0+ZcSO6aT+8KXrCAAR1iL9NUJu2ZHTEK6dzyW4YuqWFyKYTJqmKIFJwUz/MP62bUScik0FPO8IDzE9x3/x9gPoPdjGl2mGaH9z884v1PjzDuDnZ+C+8nsP8Z59OM2cdzPmLlBAq77xT/K7tJTbQ0GTZ6iBEiTFLAcxwOeAxDGGlRXOO9lGxaHMIPgozKX65l/QQc8BaFrYIR5yDhs+IeRTGbU511aRUV+VYMGfV+uNW6k2FkqTVAYTyPWdZK7ejur05bQyWVaSv+ubINV3fkcv7CCew541STLz2PaT31cERJb67pWjaGp6Lieo5ro+5IUkqZSNelyS3t7RlASrpYIqpLOyLatq/hSp2vfNWDKHPlAi93f1Hyotd1UN2QzFhKIbk9naoXFU8LSv7cmoWCqA1r9JIU0PTz12evLb0dEpe/kzMY8/kOEtUgwKuDMAHWEKwZAGIYTHDk4MjHg3vjodYIBw8X48npT8FBG3A1z5wIsUa/zAQyIseLXgHlAiwUoerjimfNBDfz1olXN0Jzc3tjfJ84Zpw92aOBkwuHoeq7sjFILvQKpvTYdFN89Y93jP+6P+HPbz3+OEzY3RmMbyz4/+jB7ozTNME5hz+8f8TNacZP//gNzk+ySx5IMr53hZ6DjAXYwBonT1Rjg+gfmh3hBAQiV/F94cdYgL0BTNC1OBcPw/bidAkQGQx2DOcseIZDOJQa4MjTZmNJ5hV9Z4RWzqUJXFTkidXR3sLvIMz78Nni69NXOL/d47O34LsnDMMjvDimEgEiJ0HjpAiDFIx0ZhxgANwOd5jsHQy9BeMNZv8AmFl6lHzsEgutdY1pqsNVXjdxzRZnFvrslNR2HZ4ZLjGsSm5Ki4+L6ss9NKF+D0S5OMwhMacNUD4VHS6y3mgKJbDssInlpp0gqUPdOZORWMTFRVrieNZ0TvpNwzB0as+0IdEkAgZjYIlwd5zwFgPevhlxOwbdA1Mw8fnB4OGbGwwnh7v3x3IeEMcu4hWvauNhBPHY7x4DmJ+AuJ6KHjWdfl3e7zXS9h0RW/mJS/wi5Ukr+EL9wVL8TEVPoOYuKQUj0Si2UHL5W4J9/ivHeUmMT1GeL6U2vmR/gEi3WzFKIY57UCJO0xnn8wnzfASbA+CHdgxi8ZQKzReUXpPqYUNq04NaJ8Wdq8tpIW9TKTJMMNRWSgNQPkxXmIqc/TKwFV7/0Ey/ScMjKl1fj5kJIycQIMp57+eEXdiEcyXIK2JVd0+t9hKVUcMIl6QlEDwClJWT4Ocz/DQB7IISgQjGWointygGw7cGILmmFI8w1aLq9oYwgxSDp1ute6WMfWKU0L1LTH5egBmPtpBEMUMJEgsEQSv5ErUl9TobI4qRTFmWyNQ2uL6cKzOUWbErSrQAT6JADgpSSgJFCskkxcQx1ms2kTvlSZTxFmI8SlHNhYUcYmwSCIErlLMjPIfgPG52cPMMd/YwxodQZADMLgSpJPJVx2nxmorH6l2FwLVCLK3vqtRLY53Zu5V6AXA8D8NNHn4Cxn0MV2Z02LK8fkxaL0Dm/sqUIJxL6C8Je2bYWF80CKLT8cLbSjwLw3xK/OqQTcclzYNJrHCLCI8r1ebqc2iIFrtuJPBrhD2Vo8os6OilOtIqQrk7SF6XhGutz7XgrfNaWIy8xxDjblLM3+Cpqqklrn5uytS6/O2sE61kinOdD6Ou/0kM320tyCliE5b+LbPxxfcVn1ei64ShVmdblkK3jUto6FK6an46/NqzprdDz9gB0wQ+P4FPD0A89wHEGPYW56PD+ZExOAJ4gHMezs9wcmAko6M4aiFeKztJ/ZO+lBwiSr6SQwEiSMrDFj5yWfpZPX5LM35pxW9N11B1wZ9lAb3a4ghtnPituxa2FPdSI8RzlZ69z+qyGqXslvq14nMtXw03G7qRjBFXWQPqiyVOhBaKbZ9fa4yQOi8pgTPNy83MCj1q6l6Hw3YdXrsvYXNuqZdrvJFL2i5VcjFma+2i9DdfgYRVUudELdQTmrwRDhfmTvMCS44eTWqsN+03BH3U+PUpsAqCtzMMJQ5toZ29kJthTOO3LFJt5kUTJSCA4o7jQFY8Jp5hVWn6a0mc5rt16rzMkWreqVb86/MjWl7rEsecvlBlBNsAF0UIuyPnEMhH2RFH8Qb6nBhpF+nCeK1J/cSMyXh8HhzcjsLO98EAlkDxuEuaCfAGcAzsGP5uhieDmT1oZpgjw3gEBbXqf7blaBgq8UyQeeMVISrzcx/FmSw4RTDYEQwxsvuirMWgjVEYGeJU6cUgJnxRb6KqVC7HMlODK/VucukqGwxng+k8gecRfj6BmZOTSZLzwmILdSU+KupmjI/nERJGcwDoAPANPB0AcmA4MFVOQUv96T2uRa0kg9ZO1pKFVV55r/oj+aI8KjZh6RsQbR4iDytjRtM+lrXC6o0UKPn187pD1/GGWxJ36mhTj/vt8bbViW0UdzgYwIKwY8KeCKPRODHKagT4wYBcPM8FlM7ulpKN07ouwcAm2z5rOuIZSDpVDZzrfd48Go2SXuj+SyhVTteFZrpAGS4yO4mLEEWQYPIKvRVQrbzApA0sC6FqHOXwO0271YX2iBCk5Els9qnW0FShRp2UFLYQ5Jat5oR47JhTn8d3p0ePx8cJ08xgIjw+PcHD4OOHf8buZgLP/xA92IJ3qjDhQvSE/zIQxKC6KLSOsldiUDIkNjdmK5VS9VXq4DNoIyUFLCV8LcULyg/420RmhmOXLtSUYCVx6opxV8x6qic+z/SlYcI8RXKYxlHgjAHvMP/4HcAZAcurAlmrsnsEIMN7Bekknqpy6HZo62AIREPc5UCwxoIMhVAzZNKvxLwn8fCOXt4mHsYLNU6P+xEYGW8ezxhcpcRCvg7GdR8t1VnJlSzt4Py7MF8XPW/6H6m3pHDNBaTz0rRK3cvUENuKocwHC6sMkSNS0YHBBYDKWRGAHGBKGgGm9UFIZ0sQAKYQNpMNyPhggEDYJpucDcjHcyQYn/7yEAig97Cjwdf/4R3szgBsIr5t+12urZoIiZDeLLisHFM4AKoE1uVUUyt0gfqvUzIgkAEefjjj/NlhgMFuZ7Ebd7CDDWdEmAGDDd4IwzBEw1405lVGiEwSAmz7uNOBfTxUVmK5J08PFDgDak1wZMKEgUsM0BIuJSTjghhEQWLUEmNlZuBk/nvrr1HeN08WON2yOc1V7/ZS0juhSOG+pLtQZSpwCX8qQ02iVfFVLpcS06t7mphy9HrbEWheO9HSOPeZ7vxd8ZOSj7scvM87ITwzfNwZkYxmCkabatW4Pwer1vlp4bkQYeq+rFJEFovt6fBeFBHDVuXaRYXts0lMO8cicOD0CP7r/xd+OoKn4GnovMfhbsTf/U9f4cM/Md7/9wFgA+8dnGfMLsRlDnPs4oHVZT9KfgMx3jGBo6ee4DYyYa+xjkvfdlvDooeoiggexB7EDsQUvNjYozbcGuWvlfB1caYaRwZadmvIvYKcL0jaL6WrlbMbjRDbyip/X3UgtHXqC6VtRp7LY/SFm7maXjuO/5dMa0aITm6UeOlXHOSrUsshmqW+JgVn5UzSKODbT+t5XwaD7fINNzTkggyk+Jte7qbfV8Aqx3J7dDmwlgtjWhsfRZj2wuMLXAWcnnYxMsEail6/I2D2+PAAfDg94vdTGBhSIh1rXjDV2WuTYtIakFY8YnwpskPg74TXzDKIOG/JOTPppOFqLpK3JAJfLs5aMnakDQaxUxTHRERXZkTvb0phn4sNFV32sKaHa3OeCzAAdha4/+oNxt+9g9mP2A1D7o41cJ7x4SuDn73H8Z7h3AmTdzAnxtf/zwPo0SI4unjMM8MbBlyUNU0YG6PWlE+yTdbekJKDIE98dJI0IjOGAo0xKToIM2P2c9RbRDnHBBnPjgMM+7DjlwlgF7/JB6Fng4mMS55ObYyQ98Yo3EGxLOSm6z23cl6G9x6zm2GdwezC2IaIOcHo4Dk4xIXRYFgbIlTAWhCN+Hb+I87+W3yY/xec8Qa0+4ywe0TKaOf8sswmkqV2mKtdrQUIlI4rX0R9AxfPudL1cNpxwQD7qKXIO1QKmYMzDOhl8mtTID0mkki6dWVJ4TNffBuikhAGO2A0BrvdiBG7yIeHnewMF4xqFPQK02Dw4XeHPDaxsP3R4fbjebkFLPhGdwbAeAh8+nQEeMYLBJuitwQCm104q6JO8xHw9UHa16cveCrvygBohLFpnJRGgTMpXDuga6mIcFlJc4hIM4VMycUFmlRIg/3iWYwaspjz5rGZz/A8J2Ls3ATnJMQHMM8zpmnC+XTCZE6IpxTCM9TW1CWgKjhUxRF1ALU7PBfGbXOqyhE5VOVI9u7ElUSiI8tKhNXF5hB0iVT+ic86KF3R92RljC9NDKOTQrWx3toZFUDJ0i3fKeaFMxzKeQG5PiVwm8TbREUKpTZQCukTiKMhiodHhh0RolwQb26TnpF6H3te72WuRk8anQwQcp2ISL3VUfKWZE4PQTadt1O3ClldiyF1bvPz2tNHwKjq4Eqd64/qvneL7Xo/CYNKSbGfznaguDVZQu+UHHUeU6r2RyjcBCAx/rLEDYUDxAgG3vhwhpcxgOccc9MDbDgrK31kNo8O7AAPD0MEu8vhzVLXFfiq5pZ9bpjnxcxt6pGAJaNd9Z2fY18mBmYGjTbuhND/lIEunhHRevVIf/MCL/guIBojGJnxlpwl3DeG8QspySVaaa0M2QwkGEKUjTIeQ4S1vOhasNyO2y+GY2gXwULZCZsvFNS7BuTQaU7fq74Rchiz5G1Wtv0apZJhxt6dccIZ8RTr9abK/YvJ5IUCCCA/weAM4jnjOMHP6loOF8w7JFDwRsv1r6/JLdSj+3QNfC4qzuJ8Q7bMS5GKiqYyXkek6cX1vbAJtpMWRpoBdh58fgTmGeJJx54BNiFmLAHEBjnUm0/X6RByJTwutoCF72CogavGrG6zCi1YVOAA48Ar/rhdDpTq3xqx13CnedS2xM27E1BR0gtKy6JJxX0u6VrjwjXZa0/ML2KESMXzdY2r0qZxqA0zi2Us4I4aXr54avnISzH3y3C8wBeZKym/V7aG3aJta+2o+nQh93KDrgLu/uNnEU1V1mK59V8kfgnqvvttU2Q/Z71jYq1Jgfeq+PqVrjdlXED01+zEpFhed12t1FPXkeAxxAVEXjtAcoiSnBSde4wFaACmGcPjDDsHJZWWxa+BxkIE7KSEuRM5odh3PX+a3pSXmVjKs8hkJ2ZAGAM5x0/3o9/glItiSOdCoQRVPgMFjFWdlHwrfIbkGweLcTdiGMcUSUHmx5oQLsiNI+A9CA7kPaxnkPXwbz1oAObzBGaPeZ7BHPRSxgM7F/gyYwjeDfBz2OdSaAricPlCJmKY6ITAXmQW/Qkl3j2EaZIDpVWZJoaqYw/yFTZR7MM23Kx5S9MwEIx8n6bFE+zRgkYLNw1whsA7D+8N5EwMJKkw/iMJEQrADjAYMNIBDjfwvIczY2gHKfm5M8/tE65+62vBQQrOmhLaMhhZv5Vljbj7I5XHSLoheVyUWJXbE0Tqsd6YSqwq7Yz3xZRfQa+W2lcVUXED8bNO62UuZw9iChEZyOT2eg+fDJqccBbblqbP1mMeQ3mEsAY0mjCOswd63VqykFCq2ijYzyucwdpsxDUXQ7+3yYQ6X5i+iCFiDRyk67JOW0UW1Lgoz1NWS90L6AszGe5qRk4zBiUC47RIjR5ckc3idWJzNF9Ue1NU9eWFkcH1w/kveJi/S8Lh59MR59nBeRf69/SE2TE+fPqAvd/BGQeDgJzZRwaBpERK4yexp8XzNHtZ1B1eT1mnrpDIVUkLHDJwgmBzTLvwNhsdEu1IDaD0okVuPQyR6yVZV/rZxtYzS+x9BqfNpAH2LAex3BZKgbxFj71GS4ozUC0giWtPtf8OqZ/oLaANDSb4ypu4I8IYtROCTNopYYxsBVReC2n8w93t8Yzd5FJMvtp7Np0PkUJ8+Ah/MXc0yMhazGPUI231eHQGfPG9rPIIC52pf9WUxqg3j/luHacpJaliWBlRMIprgE1UtjUCTrlgpbwMbpyeQ8qUJxKn3RPYMAxz+PUEhk0GCOeCB4OPhogP//gARggXMt4M+P1//AoUDlMpiW3Ps0oEjx7ulu6od5mxjO2vp72TTysk06cU6SERHn484fRhhjUj9vsDduMIO8iZEBbjOMIYi8EOYa2QDWsrrpVCyRv7m2GbuwpCWS/acOfjmkGBD2QNJe4u/BR9zp0jZjBRPqcgQhyrd8SUBUKhd5GB5STQBCRLlYEijW4K+ZWNWWVTti60Ct/Xb2SeVVeTF7vC0YlJi3cUaUHars/htAofxyQZI5aaxEIXM/1ochNwmE/4jx/+gr/sT/jnt1yExls9gVORtwU2sJsY5VzkMdBrPvzdn3/EzdM/Y2cNMNgAe94nWMreWfGsCO/iP4ZLimyPYvFUrVnUuFfwsAgNkR/pg03i6tZTjVQ34nm9G6Ig90I/L33/EqWnksIEVVTkMBl72TP87OCFz/MM5xl8vIF/eAc6HeHmhzS/Lu10kR0ROXRnaHfR2U7TqgFMhnoGEM+ySf3XAkr+xtmP4N0jBmtAZJOjw5bU4JD08yWJ93WpR8eKn6v6SstLrMhb02ydvjRz80ppy7pqPqHijdzWCoS+seJqAeSq9C9mJ4Sio9uNEC2sURaorqr3ddIStVzPv7YWl97UNfVQJnP9cLmuxlbNLc7MZXbGffU078x/6m+XQPOqGSFODlBlO9fHdYmnkdPUmOMOgsgEccphYZhg/QBHB4Du8NX7v+APf/kewCnyVxXdjt+KKCQ8Us9ItIolE98XGhTkMBVwXxsUGnlS+DJNByIDmXa4R2lMnIGEp1RqjqIxpMoNDDwk3GpQ0+fyi4+FIdffy33XGCGyhcdoLX731R5f39/i3c0N9nE3BEU+bfAIMpEJuyb31oE58Bxu73H+zzOcO+F0PsF5j6fTGd47nM9nvJlm/P3jEZYIxhocP7zFp++/jXIkB/1UPR2MpMT2Cb1T2XQKoYvC7gSDaZoBeHg/w4iuI+5kZ2Y4Y0DRqYO9y91PMLO2hsM7qctGZ00X4+mLw0ex9uJ0jJ9GvH18i+l3OzxhB37zhGF3TGUbEwDBR2c1onB4e9DNGGDYgTCC6R6W3+DkTzjBg8AhlE/RckryR4kH+kiB9QUjhl3mpB/VMq7wpilzEpI43QY+keHZRV9oOWuV078ohYS6vNeHQiT5WM4N5bzlJa9vAHGL0AaycCXtWICDKNGvf5sRUc0WLn+i9K3WECwI/i8T6My4/d0Oh0OIwsCIchv5cP6JHpOqpQTCdLD4tL+BrP90BmxMt++P2D1Oyw0bD2D2oOlxhaBY8HhzoYdly7pp2OlCc/4reaxXM0Qk8rJCNSi9ykqsfla9GDk94fwwKY7yZF7wiiwWUqYDHhxieCUrumKaQTnmexLsdJEMdoDjM2Z/xBJTczw/4Dgfk0LGzVMUNEPZzjnMbsZ0nnDazzi/CcLjoJF8Imz5Pq07onhQUn5exAX+ImkjO0hC/BUiiqkMFYW4IwVVH8q6pM8a56waIRaJVEbSYhQrHCiSkScod4GsEAPnM0W88XXrchuSEjfCepcJzIYlUPYsCUQuhlcw5U6IFOdeFLYI4WZ0/63ncD5GXEPWc1B0Iq+ZpIItDBKytnxaf4mQhQGLX+a50r95DVbvO5nXoPNyhPFOSp9knHApe6skXmhV/biBa+VlmrYshw+bU1wqJXEoitRWRukI5wydJGHjmMMBocRxW2mhhMqeG8KIEBPYBSMoHMAT4/w4gWxQUBtLGA5ikOso/ORv06w1bL48p92v1EMiwM2AO8/xzAcGTwjeKoMJ3gcmGOaEgTUUtkrKL9R66bYx0Rq1HtIYynOdWXvByJrpwc5lWJfuZiepQIgS1JDs4hLYApgzTJXwvhHnU3MRb3u4qr3O3k1LIaLyFVVv1KcK1yOiyRxKEIjnpXCZP1XOZanFuhLeoKL7QGD+B+9g0pZSjfjbPhRPSVHX3lAvoJxihhSPUSfjHSzPMBgL4bq3I8L7IBAkYxov851rqbsqtyqjOvmWQOvC44V2XN+k4vMLH9V8q7BR/YZc4i/Dr3gFitGXPcPNAM8DpieD+bPH+Rj5P9aGBzW3mv4C6B5wiXJMSlIbOpLgInUp06EWh3uAXNpOPlqD/TikUAa90Vu7bwznVD6/lK4xGuk41teUm7DRmuKzUTAWdyvf9b+vv7u0c2BTWuIRmjrW8y8Wv6kJfXioHQpaxe0aHL2uDPNljRA9msn59sVVr8Fhm5d0E66Z7z4CXGlJTm0XOwdzr6Zlvn8d27TPuuRZ0H162af93fo7Y7h0FkVr8Fgqs/ny4jeXkjgoXgcvUIOS1yWpD/NfkXMoP6UQ9hRkwTTAOGCcJ3jrszK6bE1RU3sTm4Ry6bTL6MLCKl4Lg112o/1c+qUDt4suSMlDSWaoK6rXnvCiMYa7EGbN/NbtLJnblS4SzG7A/v4WwzBiiLu/k1JDFYGojxgshYOjCSAD+IMB/AA7eMA57AbG7A14AMxMmK2DB2CswcSAm2YwOzgfHDStZrsjL0MPAzDb3Oxazo7NC7vUXaQLwtfGcfIEE8VQAwNOOz1MPCCbU9GXYDs5D8TKs/6idDCtRix4t88W7jjCfj6AdufkDCQ7XUNEiyhbR17JmOAYOsX1MJHFGQy2TyBMMMbDmHOn3fVkc/lbt1WMC8nYUH1K5Tc6u+ykTTPD5W+xuyJPcLFTIs+qypvaBVWmKqRkVLvPt5LLGhfUwxn4335J3WlfrSev7+yoKXBMsGQwMGOkAbthiOG54vcyzomnX2oTA2Tgo87CEMAUYF/KmUcDs9MuzVRc2dlHG+wAijiMCXADkHSqZgDGofi2PxjlWRh25nDWTEr9czav5S+3GyJWyr3IaGg5xIjntwhC5belEij8Sd7nEWmI5a/cQV6CSm+aC4CMNClsWhNjRIsEPFGKJVb0hQhuZpweJ3w6fo/vP/2/gViOvJfP5IBYSV6AI7bH8QTHwOeHTxjGA77/Hz3eWIP9Xz3IIXoiKOQRtI3B8O/joo3tZHnYLD4RuNrB0cJBwZeJ0oX747mcKnYwNLCEA2SeIJ/hWzGFPQSSJav6QfrNINXx6CuYKrUwK7wpdwkGESzYULtxmAErB2PnGjMjn7pMCfZ7yUjG+J3EU5QzIoyEZTIWJt7rWPdihDCK+bydZhzOc2x/9NIUK6xniCuDPIfaCYGoPCnijmsqx33kvmyE0AuoerWahJJekdY+qSt9lhFCLSDNRCLOsnSd5EDrwNCmWP8c8gWY92VRxbLhtP4WB4vymhFG00SYNSZszXMmzqOEcfGhTmNiWBAbGMeP//g5vgdu3u7w9X94u6II2j4nBTYV/HXx+4yMxEB3/HjCp+9PGIcBwzDA0oD9fo/dboch7oCwNr4zBoMN3gjGmmTEgxgiqKop7WhQOx7AaReQV3DNomgUBXD0HEk7JCDeNRVjtiUJbuICXYb1J8bmCoEXuPuaqtA2LTHrF+a9Rr1atlOPk+AjsXMbhZRqSGpPsaZC52TOUpgzzgb/wqOQUe4Oie3KYkJIefeLjF1J85fhU/eQm7Gvv6xJ6pbSIyZXRmwkowOQd0Skfy6eFxHXt3jj5y5pmM81i5eejte82DiqLlNxbeZG6VwrcTtlfql0Kab/ZQWZjAunH2bKhnlGpK0BppJzmJoXdh7z7MGnPdznr/H4/oy//dN7uNlhnnLYprSjxXtImIIUyxrQOh8AKWxzepl3zSpY5xKfyRgEVEhpTdY6fKLAe3zz9h5f3d1iN5axYWs8oZVei2Pe8HhfIF2lbI0tWVmQ6wYILH+Iciz7ZfKz8PZCQ1Zb9UuEPloyKvSqTvDXyd/JjWuljy+RLg/hlx7jF5RfD+EvgHv/LfXTGg4JLH/GD1tSTw7rGSHqutpyenjCgCC8llZIxZ0RJJUF5be1FsAOjm/gaQBgwXAomL/M1Mad4aVEkKXr+lkJxtw8aW9B4ZxNXRLrUuuxriuiGBaIvLQY6azNaOjPvFOnzQWzE85eYhk7eS6eDzVrr3fTMBTDrBoqdPjre9z9wx9gbg/Y2SEfjgsARs7EyAfBj5bARuRRgyHKgoe4+2ByDo4dpvMMeIcfnAtcpDHgbwH/H8J774EbN2E3h3CODMB5D/Iew399A3y/h/Mx/Lh3SX8HyDmWBma08J7imVghLJSHg2cPa3KIYWMNgAFsGcAcZK4oh+WZ7cO85nlCn33i05IsIANag2mcot2nEbuHEYwHnL8+h/MrYGACmINi3FxjTTy0eADI4PNwgyMOOE8WMyYM++9hiTAYOdMkh2sWh5E8yx19Sk/vovIWoQS10JP6mYSeLDtxLsUzspFFYhTLN8LvRn0Ril/1XMKZJ92StIM77W+k0OrZFmJ1BUG7gpXoyW91tSbqFsbBYDQWd7cG9+4Gh/2I3ThGeIu7TNihlESXywU0f1++Pt3vcLrblQ9jHuOB+x8fYc8MjDcJLtxg8PmbG3irCu1a0Nu2aJR08/6I3cPKbozFgtbTM3dELIsTC04xhQBbyVQpNaGUioWnPU456vCSeFUXlMvQj5ViiBCE8BTeiDOiZga8C4g1HAjtcXYPCFr/7CUwTx7n44yn8ydM7hwEuPgulE9l+wSfkLQmPPDeA+QxTWdM0wkTTpgxAnzYNp9JIxJCwyzZIC4x9dmru/1ebVa4MgkArJRbh9yI/al3oRR0XV3UCi55V0CFUuygyqOHJu0sKdoOGFFuGXWSPTPkLJCyWwLo+U0yNnSS9uYLBDPuiIhaguJsiOgRYBkYJw4HFYuSNS4sYoL1PrA8kRB4GeFMT7KSQhiEpIyVtSgEKD8vyKNScDSzqwngGtT0YLV4Scuv18qkbqtylq1GiKJIPdd6p0PVwHQ+DKv7yKiKIhUoDQ9NEzRQt20THFoLELKLK9hAKIQWiwpyqytUPLBBZCARDiB1jnF+yGfa2MFiPAwro1SHqVAM3cL81tlTOUA08nrMxzntBnJnhmGCgYGFwWBDrHUbBSATd0UYORNCjHVpUZgKdjLMc7pvjW/FO7Ue8jZXn/Bt2iFxhYZJaEnBQMa/SbSJeDJvgpDt4iLgZPyZ5JUNTaD0R429eqf8pnOryo9i6m/clL5VT9SPhDQL7VViXuoVUJ4VIdl1ORrX5N+8XyVsF46YiAFHBp+HEU+DBwc/pchnczF4TOWKL9pcrP18XZAPac0y6lfdyDkSzFZ0sVA6sDhlZAU4EfC7//An3H3zFexgc9uLOVvHoDXGbfm5PoPXVThWBZbt0fBBGmU0dW3C+VemYl7VJffed1INaZqeJhwhOyHOI7wbAWfgHTCf5xBCS8IbqOsU7qCHQypGKKKC8EgsCvIuIaWWHxTjrvAaTDPYTAA5GCLsxwH73Q77od0NUc9z1wixYcJ6yvHXUpivrjVleSkNdJzfF/l7JbN6t0zELxrC+oOpiuLFd5dG6todENeM/KVpWq+6pQdL5RUKovz0YvvW26Z4JSVjbMm/kivmzU/atrftztJrWsTdkhPmXmhK28a+rHXhwXVp6fOm6mvqWZNNq/tEI68ofjVpev4Kpa10e+kckhJ+tozbZfjdknQ0iNw+RWwiU6mk5cDTJAOF2snPBkwWIIfg6d6X/mossGXka65rSfZaLI1Q8tFNaxbWTUF3o0OQHjAg0FPm9qPEqyN/U49vV17QZaDTecaTBY4Dwd8M2O33QQ6C5lk19pAydJlhQIJTGmBB4BjW03oDsyN4b+G9g5xdKTKR4RD218wAe4rRPTy8IzhHwFsG3DkYItiD3AzyWWfipgPIGYznINM5a+EoGiSSGBUcM4yhJGEQBYOI8QM8ZkBc7/gyny15wnDXZ2FeWLNMgPTTa4cRQvD5iyNvGDDATAbeDCC+geVbeDLBHdF4VKzaArRmDjOKqR04YWFAw10lHxRTX+hwegODxLfm+jMPKXJR+M+n+/yr/kH91mWhfFTLGyGVC3QThnsl3rFoQ8Jx7bt0ol3U1eEUDGI72uGwG8M5cEbwI3J33IDFMxXIg8jF6/7IAEhOR8Wn8RkTY95bcMW3O2vgBxtiW6+kroNxkikANxr8/8j7sy5JcmRNEPsEUDUzdw+PyMisvHW3vt3TbHafOXwgDx/4yGf++yHPkL1Mc/rO3WrLNRZfzEwVwgdABIJF1dTcI6tq2MgMNzNVLAJAIDuAae9RzmeJyS/hoi9yRCxNeTlnHZXOKipdIT4rc9Y7mHdCROwNonmj7fSlbTh2yCJTKhkCUVTsnx4nhDl6K0/TA/7lw/+MiU96JI9EHMfFLYw87qCwRnTbRyV96sWN/+ZEfJ+eHzA8jHj4/Dvc7r4Gwq9RGjuN31cYGkHPMrSGmprZKg8EUp2kz3LezKSy7UfudGCtux73bWrCkhRtiLKle1Rk6RRLjMmZJ2S/Uy5rFq5l0rLUizxZGst0tuoVK5DCJpb7aZXz0tTX7ZRxRIjjIRlXEwOWY5h2pxnvnifzXjuS2s1RvxqlDbmAKGRGqkYTuUMgn4UPiToAa1RF5DFyduByV+Lr5UsvF0esob9WAruC2SwhKDKNeDnZTOsHob1ETgWAtEMJEsWtKJXBYbN1D0iXWRuBSkGjlMcydpnnMk9NVhnp3giK+O5COjgkzXvwPuJFkB0xQDgxPv7zg9Lg268POPztHjr/KBuxDt5yjKCCr4EYcQt3O5uWZJ4eZ/z8z49wjuKZ5c5ht99hN4wYhxHDOMAPQ94hYS6qds7D+bx7KDrzBCbrUJOLqdNOB+NkUGeE3p2SfiM9A+v9EbI+2Hxqp1+YIg1P1DcS4Ei3lTCXCkytFy3X2zqbu0dqdEhVQVNT4qrxPIdU0j7D+u237IygzH5SfRqtn9ZU2z82jhfZGpjmI+0KDCkiKyDv8nr0O/zj/a/xiT4j8D/FuU+dacgGtQMhMFejiMUJZ1RKUkvHpBW9aFDWfMJV2RGR5f2Ih3O6eyBwwHC7x//p//F/x+37d/DjYHjOVZRzU7L1XdQBDNHr9rxHCxa4/mvSFsNjrxlRXoWSJSlU5VGhHSzOhHTM0jwzwslj/vQNEFw8UndmTPOMeY73QQgPjvMoEmIGwBk8KAxVZPgJIcsLaTBnTkdG2jusVFZw6a6dZFzwnzGPnzAOA4g8vr6/w9f3b+I9OyTHIayP2x9154NtNza+Le+VRuc1A3rfCbHcxmW8W5MLa/pzoaYrnRDXpMtOiKQ1XGzypTCt0NlNZc0vqgIAVoBePtKplsOgv7tF2FKRjdDSlvGsS75C+PgzSoRL+Lw8MEnau7K1P49x2yrPfZm28tHU8juOhT2aKH2a4Bdh7OkqY8QLgAcAO2A4Av4JSPK3qaCq0LaJJGPX+k7Wh/KTHGhSAOkY8Swo244VQIwwJjaPqm+2WPxw0CNOIrBl3VpPNvJl+0nqj7P1MSCXydqLrG2qHVEq26YUgB/uGH9/f8S//fYW7+/ucTseMMj9d+QUrKw1chEYJnexSbBB3HUA1Q/DnCK4085MOcJc7AhR5pk0Aj4wpzN0GafbGWE+4zzN4BBwe37GkO40C7PH84970JPDzffx+CcHwhRmEMeguPM0xTuzpgnBxTsXAIDckHYieMyBEOZz6qPRTTvyZOxXNKAH2TFMVmepS5T2hjiWDA4zpnmGnyZMzmEgIMyAmwcQdnBDALmAD36PE+1xc/w1fLjHI40RLhdXi6yIxC1fZovQ7HlHPhKc8XUK5+KsO9R5SCvKz3XHSBqvGDiZxpflXgjZZx5P0ECyF8G8j3MSTN0W9txmOdLXdF94b1/HETy+mCxp2iy3RJubHxwGOOB3E4bjgK9+fYv7m1vsdyN8uh8ij7sHzved+hL8/giMH7WFFV9EWYOxb7IjPL67UYySVNKtKxPnL89vdniud2PU+V7AuDY7IpYUi9W+mZeqaBeKcR5peyST7bgo3foiTSqbfD1ho3BOA5inqPiRCMmJs53CZwQ+F0ocM+P5aQKHuJBP0zOm+YzAZpuhGl5axloITpm/GsFXuFxyCaQ9VPM0YTqfcD4dcfJHnO8APxMGOcq6s1IoDTMJBbZjQUARnb2QSrZtDUPxU+7JsE13I525hO46dMyLSS/8rdBBFyhVDzpjkn/0ENQqD1Tlo/xhx9UYr0nGp8vApHgrLDdwdzomgnd2PJD+dnBwzBjPAWPCZUf5lLYiXt+uDbN8wNkQKxmzt5zzbxajSOlF1xjx4mFn/XVH5culSkRYz1Vk4ebvde3leWRuZ58NbYhrB/GYJuSz7zlZkHI9skMiR9UUR6akUZdLrotNqFR8aK/I9J2IEBxi3d4l2dIIY5zjz5kZziFulyVE4+2Zcfp4NqJ4Oa5qlF0YzgLNqb5QnYo+yJKan2d4vechHrfkxekwiNMhGtbkTgh1yunxf+0azSKarAuD+6idEKYQC4/Kjhz9ZFtf1emXJKWldleEjHmm1plEX7gfabUhaF12LpRmoWy+eG3xf4OQk2s0NNfgXm+92K142vP2iyYrZ7N+ZidECMDZT3hwn/FMz9kJsSCFZr5Zv0uz04LQwEKS5yJzjGNj7wDK9JfUKSbFS6dEJChu8HBpS3AHZP3sR9GKLNZO58sMy9T7yLXV697iBuoyV7S6VeBeyCZ4VzqD0juU8ijrrgbr8I/KLp/24MkBwWE6BTw9nPD8dMq7H0JIu1nkfoiSLxHynT8EMy8Gl1SWJSVT5W5hzpmdmf+6LDmYu6jijjNX0IMNA6fzKfJOPf/Vcyn2KkN5LVT186isV+GiGtREmaWyXB9O7uRdaZ3sgOfyGwouQLJxzK50YGyvu4T/8hFWTQtNvvqovaV6hBa+NF3jfKjLtfNW9qPdbWFph8GzDbxa8dPiwIvXSUtXX1TLFShnu7hWrhyKzhg3a6duUP/0am/4Vm/3QQnH1nGSevr5a3nsJXPXG8vXpx7fv7Y4wVrJrAxoQiiKpppWrmx26xgQRES2dN0eL20Z6OVKaz1xW6m6/JbUg6tqrWIf7AmHuwNuDgfshyHeDyFzwEkGEINvOqJKdEO268Y6iijlYsDBp4EPuXlhoUkAZTgwRf8PwPAEwAWQj7sHMAA8E5g8ZnaYJwJ7At1MoIFxJgbNAefzjDAHuNMJOALzjz7ZgDheF4Fo74DaRjw4GcFDmI3+WY94msGKb2R3V/m8V9amgHhCSgweCXAc78iIt1gQ5BjaIdxgphuceIeJPGYCAsWjk4EFeZpkTKuW6we934oUK/1n+6y8gbUtJeVi3toGZHEgfk1OCxh8YaM9NR2yPzeskgvk8/XczVSyatszAiQh3UHpMPoBh3GPwzBiN3gMjkCOMOsWHNFy6x0JZhbYA/PeXF8Qj0ilQHpvWxciplK/7IiZVP2OP9txz0UngCa1TUlxwgjAN/WzO0HmvQnO3ZC+0GXVtmGrfbdZ8tnHlLMnDUwUp5A+WRQ7QfAQlT2JXrSpZPyWA8bhfn6acHyeEI23lM7VD/iXD/8VD8cf4Jwo/73JTsyMonEu0YvsiTOfNnosM7G+MClxlRGnA06nJzw/ezw+fMSn3QEf/maHm2nE7p9nON2xIww+qVDGYeAQid2accQKwgXbM8xbNx6J0C4GoqIe82CBotVgbEFPFRbIyKAbymUQcsGC19arlMqotixMQd9biNjWWTC0Gr4SJ/rAVhKm1i39zgaBSI9kRwRhf5rx5ukc3zkqdIyCsMgcJyMJh3gziUZ4BznPXv6lOwSSB7vcCYHMIM0668WkGACW+38ptYN66UV8WwkifWXjuhiptURkzjc1TH7RGUEECa8td/zklRKdEcHs1pKII9NIapQ6fQRKHFXalI55kSPGhKYWdyIYWivzHkIAH4GPv3lEJMEJJrP8CwcWctfru1+UuSbBV3iBXPBV4/9+v4tHLnkP7326/2HAMHgMPl4GNQxjyjNEh0Q6psk6I8zoFgJTBNv8TgY82HUQOK+ZtEa0jOQx/W8cEq9NlKgxZzzZVj1BlUUG4g6p+EwdWpcI69L7WuCBwXckOW7VcABD3GPZHBVUgi8iXH6e+2EQMMvELBf9yrzFY29mPfc04JEf8Qd8xCR5FTBDXzJbLZ+joDDoTbbIMfqbM9tth6XkkPkOoFaqFKeD7PJgzndGzCHAz3PDk2tjn2EXDTB9+KrUlY+K1xUA8rHAzLW+lajfohOdOgDI+Hyp431Sjfk7Z1opa17u22HZTSb3dDCDj4T503tgjjTk6eGE3/7DTzEgJgRMc8CU5hFAvB+CM39NFBIS6FJzPmJDK82gBI7Ra7JBKP5jQHahiaFC5PD0THZdZtopuzJdd0wXI/9r+afHA75YqpGhIUypzfLLEo62dS/BezlC/fpdCcvvmyXzRcfwdfXVOtC1bfV+rznVN9rxF8tuaWOlhtU6y+c5yrzXlOpYa/NueOSXnvOt6aXNbi1n82VjYaKBl5wQmzTDP036U83XqxNRLUJcKoBofE2XVSd5sy8v2R89mWpZn6yf9iWv8l2bZ6WU1R3Z/lyAiatP2D5cSgkOFQo3FqsyDn7E+/d3eHd7h/vxgL0f4MWpkGRhufPROhOYPOQ4LSako7RQTDgBwDxH+FySzsVOx0Y+8XK3KsED8I6SzB1lojB7MAdMQzzKCWEGAmN3M4H5jAeeEZgxzYALM26PR/iPBPf/usd0QrozAkCY4053R7qrE3MiDTOB5ynrXoxiB3JN662eumWdWn4R0rFM0xzg3AwKA5xnxJMqdmCKOwEO0zdgvMd3tMeJYQ8/UMq/cZpX0EN0zh6PYcXjInBGdNRLjbKp06yNHAiVdklIxnRXIsydoxBZFGU9dp0Uo7C2oAnYdlxdVVXBYNpqmzJUlRFbRcqhQ0ExCNinI6Jvb0a8293g7maHm/2YLqom8AwExF1HahdZkj3CDggj0nblGIgsR0/DdcsV8tcGGtI9eqn3zH1GoI+VrESgcAcKtymTfMxg+gnA6TIAC+kLOCLsdLZkXz8XcUgWTGe5sf1YN8CEmTFN1VEwDDxNn/E8fcbxecJ0Cojb0ZEcD8A0PyfDCUCyQ6GAN3miSD6p+CfRvXqpjsv51JxrCJ4gNCDGSEY0GDlwmDHPZ5yOzzgenzGHgLna2lQQWKCkQIKM5KICy3ZECbU3IXrGY6XNgR31dJARmTkR0q6OVgoYub/FoC6m2Gwx8at58xdRrM04rzoDluqpX9bKa12N7VtWbNcjSGsFWIhJ/K5bY/W3zWqjTjopgRNkXSXjRnTeiYEujbEaT9M594KsXBKn0jueGmGDk/U7XKswljizJW9JPLmTA7BHcawrnmscsPno5eisF/NbHXmccYNzn9n0P0ZZx328Sh5SHruTIuLEyriJo43zeJDBqcDRIB1ItutmoQYMBIo4QekIOhXEkGSMQoHM75U2FOOW+pbOTBSHr7whJzlc2t2cDLKy22Hw8T4I7zF4F49f8i4KplTfC0EqPNTUx/5g8aSw+W7WhBXa4n/5GLOYLW3zlbz9WcjT0YJwMRUoJGUT/oiDWBYZJfoe7zyqaX8fmIZemrlpDYc1nlU9WqG1lnbZOgthUfDc9omqfsqAmIFh+2nwV8/dT4qDKkY6pzNCWgcFrJWwku86DKaPAr/hxD0kW0n1yh3CM3bTA47TQz6KrzOmstZ0azzn/gVewcPKMLyWJTXU9Pei8XWhLeVXlh4UWdqIdWF69ucfM1m0KI5mS3il9EH4a3JqhdMZ0/efED4dwSFgPjEePj3j6eGEaQqYWY7S4uSEMJdc2zblL2eDpqS4XJpY36ioJRmxlgu9dUC4+J3dGexPcP6stFYdG4QG/5Yi37NsW9GMmv5fqO/S8967goY0edsfGZ9KmMuQvRLe7UZVqh+0ea6Qha+te7V8U99Vxft1XnBC9B1YNTR1nvXj0+q1cE0SuXrzEW1t6yv1AjVPtM4IArL6lfiZDZpaARol5m5LUu3L+2rr+uWJb57XbTTC5LiqnYZ+qKzRg+madnuZe7C1+X5J59tleDIMkl7alF7iDGOzKN5bCCpYFjrI+qfzvJtIIFnV6pbelc/bo4UjPNY+kXXjpJk29Yiu3bRS1LOUFjQHB9BhwO7dPWg36u5xFqcBCMk6DE7zEekPZV6XFUnDGE1T+p2NfG2M2TLdhXACRHtSmgcHUIgGW+cI6QRo1aXibgfABwZPwBw8wj7g+O0D3POM/dMZ4Txier4tR4WQjpRyYHbg4BEwpyFllYN6V6GXv7YlWaPDyYM+O9AtMA+M6RzvyyDv4TDAzTs4cnjkWzxiwEQSvKwEOcpuVOKJBsYVgGUdtYsFXZJDsEe/W1Trawd5TJq3qtuKopw+mLM9g4F4ekZ2eDW0rF7EGwa+0sryR1U2B7a3ZbvN1GJUrKR5pjuGSiFSv8lu4flhhueAHcfjmAbvMXiSe+7jfSbM2Hu/SH3FAT+FgNMMY1tOJz2kli/JWZd4Zd/xVjvF4qgFjHB8k9TubKFyGNJasMPhQWEPufuiVj+2pFc5Iso+dVFHfxTKaFWOkRmxELz4RjCPNedSmqaAh0/tbd6/+fDP+N2H/1UdD/FID0rHekQPbjzaA2bCTQdNRFi98yFGL8bf1nhgDS2yWOMdQIYEEqe98pEYA8AcJpxPRzw8fMJuvMXpfMLIkXi74NKRFYjGJrDySUqKvD3aJToZHIgkahf5pEPHoJDHPC68HKOThWSDbdbIIYu/50nrLrfOs1XDVeJwG2RMzbKiqDWkarXehAUVb13LX8JwjWBcEjmJDHcpetGJ8ysRxKzQl921qq0eqJTOhpZz7NkKEcU/2SFh7g5IglN2QECZm/4uWmbzvezdinhZ/CrjoS+N4TIdsBDFtXKJIi7dY/Fy5Uv7bQeg54wAhDugiI7TZ2kNyno0a4IWYaTEPyWjiXw1RcT54JTumrkGjIG2fB53BZSzJbsnFHeqNUTGOWsZqjVkxWeyA4gyTXXJ8eAchsHDu7grwg0OnqJzgtKl1ZSMaUqzI5Gq8DhRZXUoZGexFbLFwAizVqRcSFFGQQR9I6RvEbKW1oUKQCbiv3YR17si2l1rivmmYtKddHLBddtyxiYy3+zvLSuCqJPPIl7d3+qHtCQ91P7r++qyaB33NG8hpIuAxRExZ2eEOCfmGWFmMHG6GweQiHEZ+xwDY+FiRdpVZeBCEtHPynK708/4+vP/ip/9AU/7N12DiTgbZukLpzN3046IeQmWgmaU375UaviwflA1/SUUNSSKaR08oroHfxTvRF7/ij8h7jwJc+SZc4gK8DQHzJ+PmP6/P4JP8Riw5+cjfvtPP2OaZ0yCi3Pa3i94W7DPtL7TWlZ5TuTMlNUjOR5SCoHhiBHSll0HTvdIOHgCyMWoLNkpRo7A/hHB/4hh2MO5MTt+9ai7Wq6N8NXf84Sg/a0ySzlXX8IJYRpdLGPfK1VrnBBtnS92QnSU2pw6MlLHiL14rMsL8b0ZtaYa7uRaK2PW4cZ5XJy7tmTnmeF/r1rzLS5ee4RONly389a2ZXaVy2+IbLiC51K/kZfspfHX7Oa4bj0tQfOl09o6uIyLf6z0OgfAFvwu8fp6Z8SSJNl7t3VMe1w5zUm3CtEX5YORdSpOPC7KVFZPLWvIMnq3+i0g1121to1OtqJII7ZzMdhq3EZbwEaIF5/clhX9ot+v6sHa1KYM/OYW/tv3oJsdRooR1CoSiF6PGRI0JZIrczq7XvW0RGtIIBF5uhyPfDRoOWN2xUa6lXQNxCObmADvKX0hFao5MDzHi7IDM8Lg8UzAaZjw8d99xuHxEd/++DPOH9/h4+/l3PsEOSHJKWLCJGBizDRr/XmasgxVfEk63jW7+fYPI4bfE56/JTweAsIEhNMA3O1Bwx58/iuc+Q7fO49nijY4Jj3MJrYHBsPBzAjYfC62r3XkZ+ok6CXBzVDiHOl3lqnq1pDnV3RRGEhDlE05ziNCOiIrpF0R4IR3jHTUADKdWF/UuV0r79eaL7pOiLqOIlFNAerXVMiKXOXW8acsR8/fnzB98njzNzd4c3PAYecxehdPpoE4E4BvDg5+8Z7ouCYeTgHfP54bO3K/R1Y+FRxe551bRSdmwPEBzPFeUGvvUzen4UcEguP7giYaErwpbb8jQtYul7+vSxcKXQE4h4DTKWiZh+cH/PD5e3P5dEzP50/qaHDqgHDpuzgSMlILsVNB0GVHhAfwztkznBG3whH0WbEjIiFJjCAukSTa3aJaGdIF2R94RggzTucjTqdHhOk5Eu8wpBPyJEqak+OgJLQyxNEJgXwyBydHRcorx7TkZ9Ct/oLMKjyby1H1/PqiE2VaVyOuEDFfgGBawijDF9Sr8me1jnu9a5+x5XCpeSrh7y2aWiCxTgzKLUldPjB284T9HJI3lkzxFLZrrrdn86liQ+g5IrLRw54HWBpVrVBWCynry7Yn0m5KCzS1T477764gJytA1K2s5Cw4evqxxOWr59bAKkReojkkwpV6vaUKK8nUWIBNZj0IPbC7IaTWJISrwdribKQlLlOi+NiJ8K09yG2R9A7qkLBKNQCDz5kB624z5+L9EHIZtY/025NXR4VLdFrrEfkaVu4xYjNLX/I6aShpoWCIsyILV4FRzN+1uLaEUZF2cx76mnhubYgSTVfRzbo0Mp3J+akpL6nAAotqhfHgCyRFOTJ3RchayLFmvWGQec5OJPs9GpGfMOE3hyM+jIyQlLEAcfIFEDvVnAoKRyKCbe2tgVDpdOt8yHmBMxN+woBn8pXht+pnh37rcUChH4m4BOGlJ69NraG3rzhko3bxoPq+Hb6ro4AvkXnjkBT6Eaqxn09nzL/7gPOHZ3z6/hHhHHHu+DxhnuP5x/Mc7yqRHREhIy2C4HflGLZgMXNxgbvSNiO32UJCQ+3Rjk7opdDYIR13QITb/Q63+z32u1FlYiDLxgJLnqYOHTHyUG86tb4eQVlJS1FftbKa85dfWpgL4rfQ1hKM3IWlbutSascvzmsXd6+su9uOppZGbFkuW9aUzdPPnzFoS5usgtUvk651bNAC3tTVZLjjfBKbHRKSB5d7lnWJXKrnSGmNFnXNS3NxOb1M119Ol4/Y6OHnOvx9o8daOwtr2Obga3bfXDdIPbzOxqTtsKyPZV1/3X6bZ1uqhVJSXhTF71YOyXJn/XxZXtlqyOrKZWnNiT7CNrBHhEopTfYOiaYm/a1/RVfSOoyuYHUCLt+VjqbQb2pDetgRPoyM8x3hMA7pyKIYSMOiW1mdRoJ1EG8yYEI6hz4dAQOZwaQvcJSMxYgcgxrlUmIg15b7pCMRWO/N0uAgAby4KRuAY/gQ54YCAAcMQ9zhsN+NID7gx7tbsCOw+ww/A7szwNMtwile+kspapyJEZyDQz62tME1LtfAdbS/lDPGI3D7yeHpNOCZ7uDDN3B37/C0f4MzxZ0QepmyIcdyoJHq3WlJqEMhLSQdtayQ5k6geraWalztLqplulPUYWFSmONaDyxBeeJ87OP32pouX/Xn5vW78xb4iJF3tyzJKDN7uGGHm5sd9vsddrsxBbYD+8HBweEMH+3ELtk5lmonwm4g3O8Hlb2dy+uztpmUclb/+ZY0BcLzVAYZZ7FUKEOmlTtPGJTE5Laepnzfnd0JujVdvSOiMW4tpDUhy4gPauABiwtgm5o/BcbTw1nx/efHH/HPP//HPGSVQOyc090P0ahF8ITsiCj6mJUe570+vyXC33pgSIoUGSQhVfgqBYMoEed2BOQYEgbjzMDTOeA4TzgeH/H49Bnn4wcwz0B4m4iaT4pnYpwd2VOMT5HJRPNHBCcxIk67IpIXghD3zomgIERTl0y0AhlBIv3lLTNle1s/XFasNvNmI9T3DGkvV936gjxpdUtEEjKpZQ5qD9FhiyMmX0SZ6P9VAwABYwh4+3SK82qjo5KxTcFiibCU4x/imYVy1r0KCPaYpiRsIOUDLMPg0jjCnflZnLAlwnuB8TX1czu/XyStwWAE1RenrojczcWI825M+VnJRHZqFqW6RDYyj8KQJJkSoRNHgYCWBQzW325BYoj0h1BfumQF0sKAk9qTtWGZaqJOhha4lC/hvyM9esl5l5zIInjHY5m888kJIbsgnF0eBi7W/oHzkUoGvY00vTRf2fio60yF8bqS1P8XJALKe0Z6eUh2QmABvaoXid47E5nG5tWWlNGtjta4tJ6XI1c6WZv7iGQ8iLPgXsDFQpusgT7E3REpCp0D4+Mw4T/fAxO5RBtZlbSIOwEI0RlBCb9VaZC7KSxQlzqykuql+wSP7zBi50bs1pwQegxTvuuH9eipStHbBOcvm6j5dgmgzLW1hC1KV2HTK1MaX+R7R2RXSjBjPs8z5qczzn//M44fTvjunz9gOsddNyEwznPctTJNITsvQrkXL+Lh8ppXFpgQJ/4WXg/A5XWgu8HU+SDH3HkNwnGO4nECycHriPDV7Q1+9e4e4zikSK606xexLpdoNSVhoxWFLIWIqWer/1JOCKmhHrGtTohe65edEPFZA8pSW2Ky4Tq7lf8Mtvfo/gudEMtK6WX567UK/3rbeXy3GIK3GiR/+WTH7YW8Xfj2Sg12N4TmU5GNzHgsOVzr+bXU9Fp4O7BdSJd2bKxXsfxyqW2hjQvLpsl7qZ2yvZch38vHoJzfEpa27q3r4xdRn8oW0qc5O16fJGNFyzBMnqqWi32q1+LKcUyUA1ugunLSQSqHf1neCKJcv8l9TJqz6sd1z7jWsaxBt1P3amLgp5Hxn998xr/+6i/xbrfDMPh4moIjBAdQiGENAmNAvCuN4BAoyJUegHfIQTi5V+p8CLEc0j+RhSSn6m9J7ojy0azyt44vczFeUceLTo0Yi0sgF+IjH/XA28MOJ+/wPXkM9xPuv33G8PSM208POH78FsfTXdIrHRx5xHu1k0xM8wU5St7VIepL89Di7P7J4XYa8MPHHX7kX+Ht/H/EAX+J8+EnzPSIAAc4B4cZBDZBvGVd2WGSg+J0pFhaFxlCShuldQl39LVxFrG5dHxjauxAelQ8AyH+43S2qBwXi3RXREziFeL8+UKauhnmDXmKMXBGo6Ac4J1pUV7ngBwbHY+L3t2MuPe3uL25weGwwzAQBge82w8YnMcs15PrbiJanLL94LAffJavndgBa4CzDrQkh9b5JNVW2+eJcZwzjvR25lne82bncTuSVAYgHm88PwLPUzBOiOsYzguPZqob6Yys5T1SqtLj3Y5AI+RoKfNGpjwPWwjA6TjjND/j49N3mKYJzw+TNvZ0+ohB6AqZyFpEwhORh/DV4HA3OP1NDex5QkA5WpcA7AkYXLyUR5BD6tFIMzHSyFxRmvyCCWdyLt+JgF+PHkdy4OdnnMcHPD/9jLMHmCPRZQ4AubijgdAx2OQjXliXUkJkTo4JCnBIpwZKFnbIBEI0BFZE01mhurV+ysS1WhTNoun/aOek10hVYReYZvUWFWj37Uvx5Cn+2jnr9dnCEL+L4p7lDdkEScXvRoEuulSOHyOdpZgEG8UnwygkIiMaTiJDEAFJzolUJ4Q8T9+1vLYGzd/rcYEJXWGYuvpuc0YyoSrcoy1XEDXLwW0b3bwLois1X3LVvWzmu8xs/t2rnPNXdQhCF6TQC8UX7p0nzClivF1UZBCpiEqmzlBYHFdYek5G2yNCT4jTCBD7p6jf6VF2BtpyvAlq8JIL2eWoEHVA6G+5UDUPTbzY2YyxOEyNM01pL2fhzOK+UmV11MHIT5zoZ76Ii3Stc3Yw5mHZkJYzRbpLif6nfqUFF5l+VCo4cOJTpi6idGmtEaQ4YyCZNqLjJ/M9Oy36SZaKdSEtenOZdpb4yPULofEF4JaKmlIiCKd7IeYQZYbAjEdM+MebR3wcAiZQkp8lukvWXiIHiDsjFB/EmV8w3Gq+Ns1x21NpQ5ZKxOe6wtrRFdceh3hkIzPgvMe/+b/+j7j7+h3GmwMURyz50+89IpCr1rybSG7Jn6hGmCZ3jx/XyNaH75LzgRToTEMNNeokK9+UGKuzo1vMY9583Fe6AJ0Z4Tzh/C8/4vzxCT///gGnhzPOpxnzzJjndJTWDJ0rZoqOMUD9orG53qBzMeuZBCU6w+mfrBF7OT0cHNKuX0fwPkZqxWOVjwj+CO+OiM7ftKPMx38kx5SRjlTmKUrXy8kmfa5PSjpP8gxFOam/O1NiLOrMXo/39vCvpF02k7zvrxNbenFHQVNX1ZY+7Zx/X/DAotam3uW6L6UFSr20Pl9orby8CyI/b18vyXc5oq4YupeQ3hISRJp6RYmi7Rqn22R71DoXuZSPFhoU6crqnzbSkHml/GIHNpco816JFw0OSMDERSgWKcGF9tCNVfoyxve2ks2G/zW1ppeSbJFVx9polZ5WTs51h8sKfAv5VqiPeWQKMiCR0YR46AzCDjyPUU2Qs6cTHnBVV7k68JJFrUiQqC0kUlN1GaLqeNLYkMjQsE4K5LszY4U1QJzFh/S7ENFMniyfyp8sr17dT7M8/O0O4zjg4BwGl4MfHRvdjSVIkQDy8e5BIhB5JC2r4PEKczIsi82AzU6IKAjlvqjNQQzUnI5G0mN5Yr484rU+Rkl2z8dKE5BOMAEGD3AgfD4HPMLhp3HAfiDcwGigFPtIFIOMwYzgckBmdxxXnIzl3ucST/l8h/PnX4Nuj/C7MwLtEOgOs7vBRAfoEa+OAblXEBIN3wLCReXmR728Kt2q/kFp0CIau9h2SINj8LWQTCq+1BuJfruik+RdEKxznXAmdYjS/GcnXdsOV59F83VeYzBfSi3pXcpLijup0qYOe3QVI5EzAgYCRgfc7QhvnMNu5zGMAw57j513IO8hDlDtHIksuAY7FXD1s5ayVK6vT7ktra/HYnTA/c4VuGfRIs9+hGnnyYxX/HAg3O0cdoNxYlxJ2155WfXG1ihHT2Umy3A3DsOeAEs8F1IIjOPTjM/Pn/H33/0nzOEc6xTmjYgcsu1bdinEHWukR3r85W7At96eIQ5dpGoYUCOeIINBDKDoi94x4XMEWTaVpDq9Q3OwSgjN6fR/5YCJgH85PuHoCA+fv8fdCHD4VSQuIYAd0jFNAqHlT4TshiDImeuMgLRBAiBCEGmgUWDLJUe6p0wYmgwX93Bek4Vt4aWBeCVvJ2UDUb/awuNMzZel2kzJaPDTC1+r6roGNUMIiv0QaTjrhStHY9l6SwNRNtypLJSIueBMJJAMMQ4ojQ/RSNrcAWF/I0c3cNdjHetuPaMRWK4Rt2LdLYeEEQg6c0GmRJVNMVwJeT+Vxrr6ZVmuWIcF2+rVX66xquKmhOLQKmOvWKWijzGnqVMi0SNjSJdCNSZSUw9BKyx6J4xFcxWwtMNMF8c/t2AdsaVTxKX2HOW83VpInMhyETUVzgenxzIlZ7LsQlKGkJmp3ZZcCKayHoTeWUFb62DYC96zoqOVWaBjfzV6oqJTiwyuflHXyXEXG5E6oMUJoYqdHL3HaSecPme9IBwhXrYsioOu88QvyVX8rZwQEJWKy7ZEZf5kLViKmNCxJagAV6/qauVIxVGRkWNvzOXNc2A8+jP+6xvG0TmNYmclYsIzI3zRwBujxyIQ0Ulv2WRssob/siyUV35ez7LesswiCmCCjevdDmmnBlN0RjDgxgH/9v/2f8bdX/yqGU+VYezD8kuTqljc9j0ZLDFZLYlYFP7NY0sJVQ6wJKsWsMn0pVAaqOSfehGgjrYAjlK07mOT8MLCWc9c7D6JDoaA+fmM0z99xPHnE77/zSecnidMU74zQvQzZgKzS04Ilx2ibGHtjVumSoSo5jlh1YhmH5EP7PqNa1p2Asf70OI/BvsjePgR8AMAD6LkgHCZ3kaaSrkyHd/MIKTtEh1SP6j/WafeDU1LmMnVd4Gif0SUcs+uE0JHu3lX6gD9RJ22pBrzYkVBXKgVlsTkapon2+rbkG3RcXChnEohC/O79LtgB51vfRgNVIZ05vq266G5lJEJum3JbzufW5pqZcJMcVjL98a3N2b2qF/5rI896PchZ9g4Ol0Yrk09J4Swyq01XwNvbvfL5FO2vCLsiKxl8zd5OjSiaWtJRyChXdJWH8YWLtL37TRkulbvqChhqmDRcvlM+7wQQuL5Ib6nFP0NAGEP5j2YzwBCwZOFXxVtcfFRpVJXXkxqXBL9hlE4I5KBlur8uq6t04KMHLYETVrVVq+APkhfjQTbWPgqybZ4xhW9Se9DlPHpdofdfsCN8xjSKQmE6IiQ3b5yfizJDQUuOiPIeaSoo6JqORUhWCcC25nKdYI5HX0lv0M2Rgc25fUi0yIFOYFB5Vk50ifivqds7D15xsOZMQ2E880N3j863KZK5arVwOkeneAQnIu+L54rLDPcggEqAms7QBppTOWv41vw8R5++A479yPgDwj0FpN/A+/u0n2GceLiTpTUX87rumEjzQJPU7+JEGaLFFE6pJtlXGczc1bu7XGH5cZY6B0JLqf5DvmfOicUJ+bYKuf8LeQLLS8s8ku7zGzBTKnKytq2RLaNsqDVjzN6mD1eFKnI4IH9ANztHN6NHofDgHE/4u5mxMEnPTMkOdzwwIKGKq+pZKOCKBNQB4CT5bPUFilzl12txnDnCLu9R50iSYtzzvbhQnqzs4Gp67yxl17oiHiJqJBTMYTpT75kGWARtgBM4Yw/fPhnHE8nHB/POE3PIGJ474oFdUPA14PPdzWAAEfwid5GIxbh7eDVgywUoVyiJaRq0hNCL4ICiaCIdESIQ3H+LsQ3mNuQ/jIDcIQcd5naTWPwNRg8T3h+/IyPd7f49NWEXfC4ew5wAWDvUp2scFrQZVw4nrqk9UvwXIzuTEyZhZRxsYNFFF2SIyn0LCi74+LCBF/I0KomnQosJ4AsrOW25e2lCMoOf6oUo2ycinlsfRWuGMmvh0U6y0z6uxb4yt1DNfurK8yR16SeZmERnJkCrANCDK/JOCJMwshJL03rMyKZSBls0RWzAoTQX5O4U2cPvutybAPiEi72miHlSBVi66+EeyIjJoMV18xqa7vUWQti+YQ4BcqaYxaLjUI4ikpzngoUfe5cgdNCQ8VdV1/AGJeR9D0Zvyk7IcRApheu1iJVPSS6BjKQsj4y/eQkX5uFoO9rmtB+L2i6HYNiPLm0W69OXQenMlFLzghhKCLMNBMAcVawoV+CS4qHmQGXZYXnpTmvxKJOF3rbOXPGCOoCLVtLqd+WpjNsRGjeDiyXN1snRJjThc7MGoUegmwZl0ZyBKIcaygNyPFYqjqTRNVd0Y9Wx4hdS1/OIDwjnifqjeyQACoMHqVTzUYhFcMFFVblIXRG9W8uc+WcrPSTdPgW6qwQSeDLMnVb7kpb7nJam7PeKy7/6VeZh3SsV5gCPnz/gOefTzgf430Q8xx3GYbAQkqSfm6CBACdu778WVIf8SfqbkvKcl58JE6BfDxo/hd328CdMPknkDthSPKq9x5vbm/w7s0N7g57vRNNWYThRb1B6sla1xgzDWnrl11wWBZt1Qbcbs5++eZd0/5K5rXXizBtr6/dWbHaxHKdTcZlWlzy/eXGlpresjuirmP5yJ0eoyzxUQI2rk3LOzQWS3TZpU0FLEZ+E8MmJWbGSiPX5+DS7pL8+zL0Atk1I0Xmbysib61paS/kxRaXa7zGwnFlun5N9WEperIArw1YtNnjM8PXKWconVCX8SOLf0vrsoVNHfgiYxZ1d0qyCf7kJNvQEUQnkB77vNaiilydtCBAAXl489cNWhGhOEpCfxIKGRklb3oJxhmNI3eulte5+dL9aR86R3hzuMF+2GHwHvX58Uh6vr2pgzpnkLNmz0JKDlyU4AvrlChh0f5xyHKRyKimDtvvLAuJYTp+5jsG4uXarBcfx+2kxPG4KWLG0+0R3/3697ifgK8C4fzwBuH5BgQCOQfPUYYJiA4A2dERB8J8qIeUi3dsHmX5ptL5Ul93NxNudj+D3AMCT+oICiI7Sa8VQVlxqk1ipymfqQAKs551/EXoLj7iG8pFa5tdAUOBg1ZmZf00wm8JkzoaONfxUvrciH4vEfqXuU1BOqyCVK0Lyczlzzi+Dim4x2PwA3a7HQ7Y491hh7v9gFHkZziQRAwRITB1xrsGveT7maaV8FknhNqJmrHaJscpSLX+LvYDi1FdOTI/1qW+lH0lvXJHRJsyEBnVCTLXbawd2QypvAhvDCCEM37z/d/j+fSo547F28dzpAgBuPeEv915eFHInOxQiJFgUbnKRiyQXX/J2N5N6Rw9StvFkuIjR4zE+p3+88lY5oigh96EFvNKY3QEJoQAh+iImMKE4+MDPu0f8PN7xu2ZcfMcSzoOkO1XlvTU0V2RqRrBnQGGA1GA43RBIuVJK4/Nyd+t51iiOV9vwFgScBIUneqz2LZ8ztpC0fVUE34CINHHUl/yavaEM6T3grNRiBNoa/Lf0qH6CDPhEsoQLQWT9o0zQus0zgewucS0+Ad9fx3P2JZxTSC09L5sNwm+F0How/BCtmeIzxXZX9SOkbKbSqp1YOU2ggrKGmlv6GS351Tuhsi7cVpGVbK7nrLSet/7SnK9lhNzN/kFFjKfS/dMZEbs9J4ISheqiqMXJMJ107xUVo6TCBZyB4oRpnLMsRG+KgEw1ytZF7CuFiKUtubipVybcL9g5n1XbyJLekyQOOHaOpufymMp5Ah/AbfBBCv0vIrOZ0ImMF7vj8hzUz7N8xskUl2Vn3yPQgghRSaxBmpJuQZO4rzrBCyDbZQRk12FsyWouf/arG8CcALhZzgcyOMtaWx/gtHgZEW/i9+WV6dG67W9BmtPhL121mXIlNxsK2F+LZfovrvWIbQxGXKRmkljbC5hDCE7wKY54MfvH3D6+YjTaU6OsLkMCgT0cupMPmpZYOkoqSzVixNCnVWKY/Gd3lWWgmMclfQ70AnB/YhxGODcqDLr/e0Bv/7qrQmkcdALrpV9GFmDZReClRdfnpS7VPJr/R51PhmPpXpXwCoNiYvC5nL5NZg2VrNd0RaeeyHXxfosf7+ujiW57tJOiE4DHRFo49hx+/MaY8WL5USTllpbgiXK8Kx8tt7N0NRPtDim1zlsahzPsuWW1Bz3sI2VNHWsnNy/ObVy0Jen+8upbGvt/Oylkpc0G6rqFHmjF+x3Lc24NPa13YPsty5trXslQXQJbyXa0R9B7oh8IYE2uErfV7FlpSu1jt19V7EsezIBUeamKlgD5i5OUp69Gohp5Dtrm83Zucm71JNuomhvutsfcBijI4LSpbZRzshyh0iGpI4KyvOUxkIDs1A6H6wTojBEV/K42qGRj3sWR0j+nmGR3zEgiCE7jqF3Wea73ThEeQphhuxkITCeDyc87c/wz0f8ejohnP8K09Mh2uMYgPPR9sXpEmxxjhQyuT3Eto2bZ6IqH5X9T3Lh7mbC3f1HnPGIwDNm67Ch2D0ya0ykjaWpv+yEyG33KGPzbAP5tWtHplnxx+50kdFgzldFyO84qxZQI0Svt7+FpsUleAXd74jRrbRKYqa4zFPSvMru4WHw8MOA/W7EnvZ4ux9xvx9F3Y0kj6GEJW6SsQNBWDI562NrS6DmbWObKeqoyP/FkaN6BeRy9S66GtLW8XA9f77CEdFXkLo4ZkeuM1DDnuB2FHeGS20c8OOn3+J4foKeYR8Y03wG8wTv4lEJOwC/GggeZcTXjSPszI4E6zDIjojoMXUGCfKCqz2RAnaK3k198ukcZ5cuEnGOzNEh8j79FuWTZKHaMWyXxTzL1qB4p8Xx+Aw8fsTT4x+wn98gTF8j3hJAIATAeT1PHdwyRwLJbkQ1dseNECRfkFeohbAjAAH5XgprWH1RqqVa0jUrbF4S10Wkn7+kLJrmLDZjYBNnQ6NMpFEL6bIW6gsqF0dMJ6DGFSiTYhPNYU/Cjnkyu814LYwlc4XMK9fVhEUC1ON3FUr0pqcQOCnClKt6rcLSY8pfTmlRKmYnvicMWGJcDEgPDm5/koWbEy7mem3whp37bPhMPTbCZybFRiCVtVY4H6TmuNMrvxcDpxFi4TojS9oOKbExsEOidZ0FaxFvcmSBtBv/FebaJEzXUSvWiKvjY7+nsbU7IYoo87SIrKBeAFjdL7JEEuMaSoAqlLwd3VPFkf6miK0k3FASmB2iAiI0ilM5OZokApAaVEJuhDsVaPI8u+I5FA8tN18DP+ubAoOMHZv3W9YmJVbFHZ6dtwbHXQ/R8TCHuBviic74LzcP+OQZZ5b5zTDA4BDMzj9xNsdIKpf1aBl7W7pLqitBHDZPOWr+/Bn7888Y+ZiOx5Ep6dQBJCdLNILPyenC7HLdlNe2rJW8ZkSwTCCZH0RNN9r0YlJq3SuAGDi+OAvvzMXmNozQL3exSHSfXmqeaENgxnyaMP3j95h+ekJ4njBPAXO6GD0kj4PG/ElAXodAyDrKcpfNwzpf+cz49Ikkd1KWb2Wt6BF2SS5lOuPsfoJzEwbv4dNOiPvbG7y/v8Pbm4PKxlF2NTjUmSnrXF4fUio+u+8TvVpyQizVWShpa/nyA80vvETOLy4ruYwxl9fJF8fsi+k6J8R1shbV3691PixWfBGB8vfC655heY3EuAUEaTrnpfpB/LqgD2X9hYQ8y4Ou4l4Hg+TdSbQIrKyj6mH5s2npQiLavrZW66BXTlLbFl/jUXl16o+jpEUnkP1r5J5+5jKwTuW2qrV+W71nUvbypaGihxW1VaJuWW+vtURPk/NaSarlqatQWFg6+bn8utijTqFL7UZxmIyMneU6RjpSIh3VnIdpQedLcmThgSjkzaojxReq3tUyasCHg8dv3hDmb3a4f/8V/GGvOxvteo87AUR6SESHKO+K0GYirNnhkHYSh3g5tToLguiWojdZOTrfPak6U5LLAagMJe3pkdDB6FacoE6wROdDKHZExE/kS5AZ+JkC/gsB/PYDwu0J35yBd8Hh9Pk9puMBcrfirBdnIyOYGVs7Ikuph3PMAfN8wvn4hCMewPiM/XSGGwLYOcUHUjxYaiWPXf5d5rL2HL13oamLm7+2A9l0lOYQcvxQrDeigcxx0CO+iuOV2Nz7kOqhVF7RIQOc+/aKtF262KLEpAqr+zVLe1313ZBj51zchfTA2D8Qbg83uDkcUnCP09JEbE4uECecaU/oXGdslgIa4rtePiszVO82Et9GfqFyVaztALTiR9b7r0uv2BGx4BU2Y6PeVxilBIDfOww39VYhxs+ff49Pjz+p0peVv6DHKR0I+MvRYaSocIHs2eOkipQYU0gUNVjHBaU2U9vSTpXyQo9HPcW6chs2Sjfvisi/AwtfCl2EK3iPTiSroft8OoKfHvD08B1u+YwQ3oGZ4DBHph8YgRhi4MtcNBmnDPGR+wQondcUlVvCnOk6VILgErkEWD2+KWKm4aV15zZgYp2lwF6zsGpSS+X7qxwiF7KWrJ9THxMVkjFBOpqKc26FkeRIMbMakxGw9n4uivmMwuDHUgcDUKMTxwtqO5ct23P6VFhQo2zIz5r+Cp7UF573UxJzLXfrKlYGsKajJDqKvlqjmtdwM6E1VhHo17iFTpPU1eBsbitW2BLzZaFZWi/rK8dcWg7yMsulsg4lp+VUZPArwUgNLC3zkvasE4LEiJksYE7PDl/qWVaei3NIkXmAc64UAqygmGuJ4ycK+IoiHmWFTLtiXSYCp1C0RKiqxDZxQHTEu24fUc9VAq8rWMhazaWXnBGW7uprohy9pRlMYfkqcy00R/4KYImw1Duwlpbta514pYOIiicFMvcSURaSUfOjJDgzJA4rn9/P+ZimJ0z451vgybl4XE6zM1EwIFae58kSNO44Tez4Lna++Z3xJTuWhukR4+NvMI4jaDdkNGcYfMxVcpIngiiNRjFoxi9/TUu7pgAd6BsDbv3Trb3u1HddBgH1WmnWYlbbxOW6qPjGBSmQcS92GE4z5t8/Inw4IZwZcwgRx9KcAJlt2++Z1WX5oCcK5d1hhm4muk6EfCdiei9ybpQ9UeweYzdhdh9A3sf7dZLB6O6wx7dfvYX3OXhHzgLPRzzl+nsDtjTmS06I2tBarCGjI6zVWedbNLZ1ULncTSFfLtCiztvlNvt9WDcIXofry3Ut19Ms643ra3GMt5bvGcQvzHOdhAdaHhdfbNhFW9ejcPXha8pw5yicAoel7oV1IO0W/KVc15fnjQp6nt+Rwrg+HzbQa1tSOlzIkQ1gF+to9LWrU4fCXKMKfOHEPXxeSKWMu15vrNbIIxfqznUu0d9S5lyppVwDKqq1On0hASWhwtIHuxO6DxdtRgXJdsluUuJCpQt3a+7ZKjijufBsBcAhnm1BBV+uSjctFAEvpZJrvi68731n4GFP+G/fAN98s8f7u1tgN8CT02MbZSdv/g9CaKA7HKMxLNkHRM6Juk8Qh0SId1zpfRCQeoWSaC8LGGU3cuuEyG0Fufi6uHsv1StOEdkRwTPA8pmM4Ajis8CDBz46B+xOAJ/x5nTGPgB8vgFPtwjsAVCqK+hkCUxEroC//q67Igq9VD4Z4ACez5imZ5zDI2Y8YpiT40R0Zk42s0avX2pX9NDlFMx81DpoOVumOasqCt+sdBIRdiM6GCdERIZYjjVDhrPWrxU1uOhW0fVfItVkpxnGDUB0ht6GaMf7gD2GTx630x5vbm+x3+1jgA/Fw/YDOPFrQnRCUHESgMgUDORrN5q+1HJzr7Pt+1qm2Mx+rSxRFSnYQ2982La/oa1OerEjYslIKYImAXoBplzJ4EYAPl7iF56Bj8ff4nn6lCpkHKdHOEcFjjsm/KX38SJqACMRDt7BA5GoIgt1USlzyhQJKLanF1G1aYbk/DhdQEXPSEdWFEDxPnvjiNiPA97e2qiymC9WLYs5C6Txg/H5eMZ5jmQlGxWjIjsS4av5CfzMePz0M9yBcP/mJ+ynPXbP93BwgOPcP9mWn7ho0QsHIDgwQloASUG1xKmaRGv0KUal/FhIlxW7orErlLR2PVIDWwPdJsGVi29UDIJEIYsJkQ1e2GY5j2stIDUgpTooCz+qdEAIQnYHSLSCE6N0SPWSCEjSZmmAVQOIMY5sHZOekPXiVFoSqza+WCsptRHyPXzMJDvnbUtk4blVD0o8V7l/i4JcC/8F3OYxAVwZ/2K+6olVji2YlcKgeKufklkYbfytDoiCBjqtXCNwOwyycB4g005p0Gk9klxkZl084DzMDLO7DKqA95UWI1TZejmvp1yG9Xku07+oTjCFCAC7Cnd586JZc0ZsTkTm+D2OiqdOZTpmSOAy9/vYnVSNocPlowjLXtu/XH1bTq0zony7lU8oFxKaZo9gChyPwwnRIBzmED8pIMwcjyBcBNSsNxUQS8FRho86ZVaARRl5XPKAIxMe2IHg4Z3P8slC3TLigv0SuRYdEVA676ys3amqFFgpy2uNgTav2Zc4pHT4rhEFuunyWDOtOCG21LQgf2R6kKO/REELc8BP33/G8/dHnI5nzPMcnRB1S5xYNaHkC+nwBZxQAAEAAElEQVSLXksCHXYAKbgmyRNEgE/01MldZenIOudj8IvKo7I71xHgzjj7j3EnxODx5u6Av3z/Dt4PGIcBd4e9OYopy8WN4XVhBDXQiMrfl3ZC2HfL2777+S86IRaaJJh+NXBdhrcLS/tiU/mXpK2G87WyV5d7WbFfOL20M/ZOPnm0gWbUchWynFGQTOo/F2GBbKi11ttvvwneE7a+AO9FZwqy4Wnr6ElkewGA/LyqDr2o8AUpj9G6JN9Pl+jKi9ZSXS/1pdZ2dre0le/GVP5g2mrhvdS/rsrVgdS2ASPvWNwnq+BAZMYIbdpJJ/9Eb4DIucuyIlWfdWwdLRU0kNhvFkLzJ8LQuTC3W7nw3g48BeC10cTePbFU/5KNos5QyZ9AAOYz/PMJt3SPN/s9Dn7UwFc1JAIqI8r2SZLLrKudExqAG8wxSnJ+JKwRQz5D9dvArGdCRS9BDsbITomIWEHl9/QTIteDGXOYMc9zkufn7ETgGeqoiApcFnrTYH3nCJ8dsLv5Awb6iDcPv8Iw3QDBIxBhDrOOT08XsVHhuecsoltVgoF5xjQ94zkA7uZ3GEaGwxtwoBQdT6YWwc9al39ZKhxdYB2SGJolrgqbp0RZDZgFgLTLOt8NEvJ8yZylnS/MwTgjQiYw6awmMn2Na+6LdLeB/6rEQMH5la8lPFBBv3ydg3ljNnKE09GBjwPeY4fb2wO+vtvj69sR+yRzB442a3aCpqHAmygOGPqS6i5ZSssrlvpdyiCZmorNG0D3aoClVAfpr7Vn27Lwv+QOp82OiEvGwka0NxxGlQDHgE9K9Jnx8fOP+Hz6LuWP0yL3EYigNjLjG0fYU9qOropTvq9BBj0fx5SeIz8nQB0XSqBButMrI2HdTyMUkt0RkZnvfjfi/vZGHRNARFroHTliEJZG4u9jMpgAkeG5RBocExwz7qYzZgKOxydgGPHDrz7i7cMd3j/dRXN0AEJSToX4RS9uT2zTK6iyiEB5MfQXeTM4+WMR2XpEvpf6YhpVry7x9Zg9LR5CyUw2r4dOzy3jSZwoM7A8xqXnOQvv9o6UTMuqcWER6AwYciiltJlwN0BgsDCTMkn7tI50UPFkYTy6jxNCZCLzYjZwMXVrroG9QmmQUe9FMS/lFiiWcvSVllgm87WMh1YILouohtGC0FsTzBnbCAUOWi7fPRqgMDZ26tdnZH6b1qnMR6KcKJOjdlwoCltqoDLOiLouOwxEKvI1Y2FkTajQKvjJ1SiT+a0GRFMPakbJZi4YZW3179iBuERFuRds681nW7wEtd7lUCbbj7JcW7VEX8TuysSxKpCMgKzVWceU+TCO/fxUcG25H0tJIiXEGRF/s0hjavhfq9xGVOUnJjKd4w4I/Ux3Q0xhxkwiWKfRalGrAzMrjgvO2ewv42zl/DGAM4BPIIxwuEce82zzMU4khU0puek/NNBhhZFfhLD83nlyseN2vWaaZVfHZocGVW0qCr4ACa9ISUpEzWVrJYWZEWbG55+e8fTzM+bzrJeh17SmqL+2qlQ4ppTYOiHSEaBEyfmQZFc5ItQeFZp3QTDIEYKbEegjyDs4P+Bmv8M37+4xeI/RD3DeRzlWglgUxmWMr3c0ZPqxnO9iupD3ohOiYUFtfb0mbG3LdS3AstDAev5L/YyfS6LPlgh6m38ZjusV05ekq8suDYC+T58b6HhTUOSO6yDq11bLSQmokm+apsXBzdTPU9Rdy1RGznrhXBgyc0X/yQ5bF87LVQgXeJ3xrTYC1rsSFpvflOn6MRVD0mo73TW8vu6ifFQeTGzH+Zr7KST/pe5l3a6EtSlWqE/WxpB5tey0I4Np/eZ7C9jkL45BIixZM2tJPXPXmn+336l4YuBJR3PWxzUV/a+PZS0ebRLAWoB6kBqdB4GBmeHCGTfe4zCMGL0zOyJJAyY4wRPHMjohYmBCnpcsP+bLqPW4pAKcFs9ljKO8I7JRqoPzcbf5pJEsp1rbhNqyRXjVnRAxwCjeVRGgBu8QoNshUrt60TgID97hyTmM4yeM4Sccjvc4hBvQQHDB2vpSYJLiVdYB83KwMp9amLJUnmCc5xPOM+P2/iN2+wGgAYxDNc8X8GE7O4bRAHQMRCaVcYboBCmV+Fk1q84Egws2h9qPJC+K8YfOse3n0j6NMr2GF3ckPOVX9bLKq0IkgLiwIgp0ZH35rf2CyuLh2WEOA/xuh/1uhzeHAfc7D+8p2W+5XChZWIW8kgBKTo9tkdydliYXMDXZs2xonRAAzB0xVySLP1SeANOCQAV/e4nM+IqjmTJgpVyWo+w4xEtpaO8w7oGH6Xs8Hn/UrBN/xuBF0WJ8A8JBOp2qdyDcAPkyPhCclyOZzP0N6oBwOhGqwIlwR9BnMrMsUaPGyFt4wSx2kxwrAjjvsR8HvLvN54NJ9JpOhBOWLURTlkTs79ubPW73Iz49PuM8h+woSbDI2ddPTw+YifD50wf4MOBut4cLgD+fEJ0pnMbCg+AKhlOmeFG1zloaL7gAzLUDoyQq3AxOLy2xfUkGJrFSfaFkRQrCEpjtw7UnLS8WRBBTSwU/sxooIxzVZbzW6oA0B2muicwmB2lJOsKEyRM+3R0wnGfcHM8Kjyg3pTOiNFKpMTZzKYiXTIWAptdXcccLab2u5m1v8jbiy3KOJcXPNmnZmAjYvah/W6dxSqX5EpqhW6PLj7LhInWEQLIGvYwzUqHyyppxFc0YplQY+aj6bfuUvltHgsVbqcvUn9sUGtsxbBM6MyEdDtUzwW+zJgMQKIBCEr4v4ZYVlEzV1rAd/7KRR0XYhRlgU14Wp6x1NnT+imQd0xnepgNl3gIMivSGBRzzOwOa+RgvQUjqhJBjDvvGvIyF9ardGtncJovdC7DJGIQUeJXO4Q+z7IZIOyDSjohnnvD/vn/Egws4Ox/baLTJooX+A5UXOvCtglyqbDadGPgQHKYowMTVlmQViSTMo6ucQKuKd0Pky5K3RH3aFZ3BN2tX1jXl/LmTnY5emrIvmH5p58NaahQaYZWi3BSXpC87+q1LiYrnmW4TZXNd3o0Gs6tYjvyUQJiIMX6IvwfvwJhwcj8AFBCch/OMcRzgB4dxHLEbBww+3g8hOynIweyKkGOZap5ghoGzcUycdm0E98vnrC75WifEtVHEq7BVsFwyMLzECfFLpNfMx59fmz2tfUMZAF+eaDWruWlDZfP8ReGp5fb4rJXVEpN4BZQLuy8vWqkX6tvohIifbiVIxrbVb4yrrLpjYB3E3IatdwHuF40s0UVKUsDJl5hmdhpY/l9OV4swa/x/246fto5WF0KWIRXaLKGASIOwrN2laqkjNWrV1feck6vfuf38p9b95ceiPL44ZPlFLc0T0MjiBVTNFzHa1g129In6QZ1dBI/bHb76V1/h9v073O522I8jnPOQI4aSVp91QZcuChc7T5qDoI4H2QkRYCNys0rX4XNihBaBKNUT9H4sc7cETKCM/q4CiZB0tDAjcIi7IeYZ8zxhSpdVB47OiRiVH5KjjDPOGWN5mAPmmwE4DPj+/mcM/AD8/BnuPOMrEDw7nH76NcI8FoMdZuDxc0gqt1O4hj1hf5dlZXfzAf72e/wYPuD7D5/wMO4wDYwTAeyBEQE+1ax2ADig2I1jMafWTS/IFFoi/9WaxLHU0SvzEe1GpTUOHt3pi+T8SfhLEJor+nCaB8lj+1GSixLq7m6h16ZCUSvWfmyrOvKZ8tpljmbSWsYHoqpobdBAzOudA00Tbp4nvLkZcNjv4m72ZG8td0PbWbL6VqbjMrblCXpX6poLycrpr0m9ncslG1qSca+b7Fc4ImyDWUC3MlM8PgDwmEHe4XT6hKfpB1MuwCdvzUAO78C4FauKrV8IjosKkyhlQoA1aqz6TLp+vngTOfIrgku6hSywWVA2GSIPZKeGd4TdOODu5lA5OlAybeMJC0DaDRTH7LAbwcx4fD5hmgO0AilDcaFP5yP46HE8PuLo3uHsPTziFikCx52v6VKIeASgqrSoCYR2i5AMpZTblUsaO8MQB6H7cOVX1WajELTCWbf8BZzOMgDbjybH5aXRERjqHElIs1vQNOkYSp8kClley3zEZ3qkBItzSlqOeXSUCJiJEHYDmBn753yJZclYpGwlnnEWANTJZQWcF4zHUqn1y9s25F9jxBeUCruu11rv2hUpz+1SnrYX1bm/cdFmP0ERydODIb9X0ZZt2+YQHRWCS+Cy8tIbN5uvNya2r5mp97qebdBks2p+W0c0aLqyoH5cZo7Z55SEV2SJodTne0ey5N8i8BYpqChS/lWiJ4spv42/l48X6BkULqU28sjWUQmSxTKsG6Iig/zSp/aL0osSL4vpNF90Tq2Q12mvBnExiTDcoADndgy7skKj0rQgBmCOd0Qwp6CeuCNi4oAjzfh+T3jwI8IcDHBFR8o+y2+Dr4rXVOW1uK5934YAAYSHRC9cCOVxASo/JXy3DiqgdC5z5j9Lx9NYTlRUtLDAbf7XROBuTp2la8nMMtd4XaNU/uyCIsnuqMrP8rtIJpadELZuqp7Y4XXIF1GL8yE6IOIzn3YueDLBLpSO5nQxSCdQwEyfQY4RvE87IUZ47+MFe86D9BLrfIxTPpbJAFTNfUQbS1ksHWidEbmaDp+meiSW31tYGv7ez1bOcHdiW7gbGJZgWhmjNn+v7wmCFVHm2mXXl2fWZKBlZL2ovG4ybvZx4WLayERfShXWdZOLhKBfzjjl8ro2MogIMwzkC2/bqMVFuC6slS0pQiYBglX9G+tYWpMXy/XKNq1zt75WjWt3CKxBUcvKtsUGkhfwulaWKl9ua7nEnSJ3T16jy86Jst7LqRxTdJ0TbWgKZYM3pffihOjIWTnftnCdtlul3NkRn/VFX63l5oN62Tamtiw3MtuK4NB/330UDZXBEcJ+wP7tG/jDDvthxOC8Hs3dlE/OBxInhLF7FZYLdSyY8lRLSZxVJP0tz9Ku4+SEyEf7ADawrLBLiAyLHMAR5JjVOd1/FuboKIEcEyRH/6hGCEKUm3RY0z0QPA4IzuFhmOBoBk0fQE/PeOc9/LwDPn4DhEHrBBNCYJyeZ4Cj/ZCR7JfOYUdpURDA4zPc3c/4/PkJvz+eQfAgN4Odw+QchgSU1eGzFm8DWDccV1eRR6v3ylSpTYf1QcxvdacCMQzuJnzNO2nEMZXrKPRU44Aq5WKD2NaOWq/fV57TxAq9+ezhviEArL+BZqFUxyXKt0LfVL4Zbb6eA24CcOPi8aae7FHGFXFZoy7ijJCJ7bIHMt1aH7syQKhPw2OzG/n2hXzl60pXuOh0b9PVjoglscjK6WGOnskjPuAB32M4BwwPwDk8Fvm+gcNtxHg4Ihw4RYUVuJYj+uIl1C7vjJCjJNKR45TOtyY55xxUbF0DgPvbAw7jaJwl0gOZ7ryAAzM+PDzr8Umjd3j35jaex0vp9nSXd2BIv4oxImHMnNcpZ+RreC2kLoZzDjsA7x4+I5xP+LQ/YNoF+LsBN3yPN8Ov4EPAMJ3BwYE9EhNIZ07LJdYFRCmCnhwcAhwRQhrhuAgXEL5isBeWxaanpFGqyv3iJ28QVpSSrjVb1bMimPUIdiscCym09RpuoY4cGWNS2ht1EdtPwJxSosw51hgvt5b8Ln2yRB/wDMdxDiV/Ta7yVr1kvJIdEDUzkc7rmLMp3+JD9hRnhlMQ+3IEizy0lK/XRicVxDFbqy+kPp3qEcoeca3z13msQ8FeRLgJnvqrDFKaTqF7DCgTJ2WQVeJKQSnqbw0umQ6XjJ1ECE00s3ZSlG1muFpmFJIzInVKefQCdiielgKUUCa5o0XjhkMEViP9BArrsAGM48G03uCXGAgEjrx2inUiBPxF8pQV/nttd/I1edHT0LYlAmB36HTXT+ZXakhL5Ko0UqY/Bo7OI2MYzHy67orwaVAGL0uD8gPZ+M75MmpO27flnogTJvzHt8/42Qc8S1RTAWDzNTvMzEt7BGTm37I+qMmft4df4J3KCwh0/ozx6V8w4gzvXTzvv1YqTRnBQka6pDrh/b/+D9/i7qtb7G/GwljakCBdwgS0b9uBeVmGlItybjvHqX1neaChN79kEoh6reRnad0L5pjospKvyncYfbKhvg2tUxiMj5YA3RnjAKW5IrOK/Or1KFAACHjm7xBwgscAB2CmAUSMcSCQcxgHD+8dhsHj7d0N/uqbr3CzH+Gd08AZ3dEmCkyCMwbMMEIHj1SuSXD3eMtaWjT8Lxj4qX6/hLpUfr4ovRIFS1jXK7uWjNd8elveGjL729DulzoOVtr9U+zCuJSuh8jgP7Vyad3ffhRiHGsZ8Xre19ZDZsEFRa3S9bLAVePwxadxnQIXeNlkMzJuxymxpaWyugs56vfXGHYq/XQxG/fr4M761N+o+NAlmrqR0NijnCI+W6wraVqWCZ3mt/9twxvVCrVOO/tkolK4k2OpxtUsVGZSXX5V6F5sCaXkV0O5Bu+FNhQoxoeDx99/40Df7PH+zT3eHG6xGwYM3gMu2wqCYo3QjihXCT8q9I9gz/fPzUqgrjVAx2/5mCROl1gHZvA8g+d0QbUcqcSh0nWM4drI8OBURwjx/oYQMIcp7nDmuLs5GskDCkmsFsEpNxZVt7iDIkqaDvz2Dfj2Fv80T6BzQNj/VwyDw9/ejXAz4fMHh88O+Hu/Q8AANx4QwJjChNvbgG++mcGjB+8PCJ6B3Td43AeMXwXQbgcaRtDtPYZhl+6INYpMEVQtI8toAgcvIm7RY1ObPEk6ga2PbRCj6FHifInyreyEYLDOqz3+Ku9mY30meFk869EYq8+VP75Mqslz7KC2EYytioF8VZHIvdyvp2nCEQYXdx3vd4Q3vMfNfsR+5+EGApy2EPHZFM4krKR1RRv0stME2iKx77G+3LFfRhT7spVudkTQ0kB2aK2cn3bCEx7pDxjmeBYyEWvUlyPCDRhvKUfUZuKdqjZ5QSl6C8kBQeloJsp4lc/TzYJ1VN6y4rUfR9ze7Np+NDSZMU0BD88nhWgYBtztd3FbO4kShrJNOyCq7MWxI6u0EuklIqoQyvf06ZJh+zCdcQbj89MjGMDPb36LQAF79yswMxzmWIZDdEhIexXTzRMmgxsvEouXmppVs4VHXkqdJsuXlD8Z0PNF1BBwZRudF1ZoLd5uXfNLkSYA8jgaxKH8hlm6xAm5c/5su039lYtk1SCQmAAcQAx714xEEcwAXHIhcV48Re/FacDKoPNWtdIJYUZMHRD1ULRCS863NGMlMl0a90vEuFH0jDFVxeSC6lYCPPWfLzOI9nePqBeCB2w/14n1WiSz5duCTwDMLpqyfr2zoKjOVtg0YwzF1ZgJPSV5u6RY1DyhXNf57fK8coG33DyMPtt00WQaCNJ1k+q3ddjzEAshIONqvVhynkx77LZhFO87dXQ7dvl5c1dFflE8+mKiWyQW+ftClvq3NYKpbrtQmqqolxYHl9fEktpmRd+gl91BZG0wgBkzzjzhxx3h4zBiPk8qHEbWlnnyWodF8BSc7xnXbJ+sLNsdE0NPI/xpTMMJw+kneO+iImPaiqJFpm1iEBA6rp8E3L+/wVff3sOPXulf39y+PPJ1CbsbYhul3N7Wi5LBuVfVW5Lp9MzIQ5XzS75amRBA3Moe5qrqRQwwTWX80WYdVPl3RpYk4iibiWPCscq4AGMOD2A6wbkB7Bw4bRF3zpsLq11SnuIRot77fGFlYpgKS4+v1gNO5rcwqSsm5KITYgnnKicE1RNJVT4L4hqA1MK/2Hb9fLHKJZmj3/y2vMWgL+a7pq1WNtrWzyUM/1LOjC+eCrxey5h0plywKN4zGLdLpp0fXUrpvRh715xV5S6IbEis298eeciqC2bZr1+ujL7v1H5hfvv8Yhuure0MkPdKZatBfjHebexP0+bFJPrsep5elYV+2S3W0YPWWtkCN1sDlsDWo6cGRtU7jR3EShOVXlqvv64uVWS7xFO/mGS8LRGl47XbpouTZ3gJ8g1KQSedBuAP7whf34847HbYjwOGtLOxFsizWpjkCNcJbtH2Wj0mc5rYg6KvbOVPzkf6MJvjKXNQV1GzlJPqJK8ebRlygBHL8UAMLuqpBx2dIPuQlEZAFcT9DrwDjqczZppw3v+A3fkMvjmAZsL0cYdnePy422H2Hn6/j46I2eH45ojh7QnhsMd8w2CMYB5BzHAhAOMI8gNo2MVPV1CM3mjmt6X40vSt6OQiTi2MTT349lMD7fL3QuesEFyOlG/rt5rZAkyd4bi0ahs6szVZh4v5U0v1VAXhcQc2fUQinzs4EEYasB8GDfQpNCexGSysqUUC2DjVF/LXXS171aHdrM+tHNMDoZ8WqFjz6PV0+ModEblHFv7AjOkYj6FxRDjSR3zCbxDoGCfMxePqvibCW2OsPRDp3Q9av0nWsUDGEUFytnL6hDgz0v0NetcCoOcuv7nd42a/wzjIWbiRPCjiGbh0cAbCN2/fQCbUOYrKnCj7zgifariwtQhTFgE1Go7VH+EILjDev7nFeQ74+HjENAclvhH9o1fSnyfc/vg95t0ePzLjcXjC0/iIcbzD7u4e98cd3j3uEZyHR7wzgmXrnl0uFBeKoJgjQnAUdyeEaPiWDWR94/MawVt43pWX03KlfJHpQsYuMVtOFdFUGtsvXL663ICMjTI52dWhoOfFq5GDclxTyi/yqVMKkQgGrDGZoMfBmCE5ecL85oDxNOHwfIqviQxDju3Yi6viuX6cxiLBJhcPpee9o8nqc/Kk//rN8rUi0wpz6gjNSw6IXoRZcQlT1vD6bZnUN7oDrfm+W3rhd0WvKkX04vntS21bpVHWq6EznKyZ5b6c5X5oPB0VD1FqmjYP5XNCgLyDsUjclJXn+V6HgHz8mynXerkUT+PPul+5Tlk7ch0u1/wolLHpGomjTTXIClkDOW8Jj67nnLUGv62yaIsXnpcFajJb9OELptpZrvzTKDCgxEs7ToiMoFR0XvAsx2W1OyGEX1cAVQjGSfjmPObMcXcLQ3dAyHm0Uzjjt+7v8QGfcOK/AfMtiBwcM9ilesi0j0yuWyMnQOT03M9mx1B/QONHhRvSV2bGBMJPHO+GoCRHjMOAwcdod2ci3tVGJUKwvSOFy38VCNXvJJPoL+lTW4bsoCzUtYVSfqlUsNPqOdDOG5DolMHRAteolIFsX7tkrBFg0u8wI/zhHzD99DP4dFIZkMicOStLy9DX+D6ttfQ43//g9FovCZp5mn/AiT/BU4zrGyD4EfsxjAC5Ue8n894n+TTi0rjzuDvs8K/+4j1245je590QnUWXUz22JGTC8AgSPNqGFS81FK6XI2jwR7VOX9TWZWBeXPfrkiBrQ13yrwZ3ybxbWNj6vv+u99RC8RqnwzUlizavaqTDZ1az23Eqj33sdpW6X4sfziXnM4mouh792HXoUH+su5H0vbqtF+KCKGHhy3TxNXj/yjVjh0EcOeZ11CFX2lgcj6ua7g5dXUuxOrc4ehbGxkpRfXlj+/FMqdHld1WdZDvawCqCHBsZhRCPEaZSJViAveCqHdWNuznNsyt09aW0OvutGtx5WT/m1devSgGgwLgPE97vRry7vcPtbq87JKUzwejjIrfm6HzKCGx0eqVvzky6nNYBzjYEcQ4EBvOsux7Ack9bjqxf0lZEggohOR30Trd0OfWc7oEwO5zjhdVsTsUtV74jIHhTOaLs7uRoy+QskbXoHeBGB/frr4EQ8I8jgZ+BjzhgOrzD3bf/FjzcIhzeIu7DOOH2/gOGv/gZAVklZkY6UpWj88EPGPYH0LgD0xiDRGUcXZa+478ZXSXSpjVes4KXeXePxUerSJr7AwsbjVUqzOXgJk88JT47m6RMOdvlbgC1jRXEs+xIj6ZGupdvVrtMMctxqHdCZOHBUFQjUqm+WgQAJAnAOTjvMB8HTM877LHD/d0Bh90OwzAAPq6tkOpjjjeZuIZ4X+Iea3nL/H1HhdURc8BDpNWuG0hxDW/ewrdek77AHRERb0NcfWAXcOZnPONHDM5hdAMcMTwBBwLepDKi2GQ9kZr+ydFLLp1154yjQXgg0u+YL2pMzghzLmlR4zDgsBu17VTS6lqxL1a5dx6HXd56aEvJ8U8W9loxqyOJBbn1XDtmkIuweR/weDxh1kvsDSAMOA4YT0cwB5wfH8D7GRgYA32Fw7jDMDHuMMADcCE6F7wY+BrJLc9B6k3M5DheWk0JNtjT7aq0REjF0L0hfxSgYJxAsaWcVQz5C211XnD1o8cWOb80zxIMhobH4aHifV1nu7UzU6A0jCKrKWFWXEsCJJlyqgJQAVxqjBCIEIYBNM0paiDWy9omm66ZCO9QkXUh1JWxtHY+laNniV05buULK06aserMY/fop873JaWr74wo8+Y13lPmWpjW0yX1xNb9MoJdkREV8oE4nuSy0L9Rx6i+dFtc5S+Wr6ozzrwp5wqQS9QLKdGUKAGvDM4ocYCIjEzD1QXNKZ92wTiXdSEIbi/0jMtPPZopQ2shXRifqg2Lx3U/y9bNj3rtcX5uGFQj42xNSkf0j+JEobA09RsnRC0Qk3nAmtsW7QCxDXrhg4IR8SfLl+iUQFTCPtNnfKJHTIj3MKQ9gon/2Yu2hNux4X+5QxIhThU9ySJDORAylIvOVESKP4HwnA7Z8whw4OSAkAuIcyu1IwLCJ2UsbFPOg/xQjGlNP+rUfXVxWr688LnYjGmqC1aNi6j36y7Amierg+eZlvftOpku8dMD+OEB4JBkPNI50zvAuKRJRDngRqZUHAsxsjGqvvHCB4DDCYxnsHfRNpB2AXOSdaPDwasDwiVckt+jj5fp3d/exMit6i6ISxHsbfS3GXTKMmOPp157Ud4SH798dEotY5v1U2Rb6mP7bplFmvXefd3KH4Utual4A+Ou8pd1rI9xMwbF7+1z0wSCVKWvlXFKMDaWrYzP1wpt12RvenuhsLzmzjNgQf5PxMLqob067TrtZGsTL80H6zGxrS2ieqBrcT3fJVBqfbmbJ4PdlLHP7ZMycvT6OyLqti8l3aW+0Nba+37Tl1uuHUG9YKySEiw2ludzQ5vKAQVXF+e8uukhFSTF8dfKCuu0ce0tLb0X2XSxcPtC6qrrzL/rMuXv5fswtihtki0Gou79gJtduhsiBcOKINEEDAqfh8iPVcsGvwgSGCuTWIGoBmpAjmXidBl1dCow1ECdq256mVWsvIMCCOYeiFy31QGbERQZC1QEyEVdUHi0JcoMEREIAJyDO+wBME6OMINxPrzBTO+we/sXmMcbTId7AAxHZ/g7B7o5w3G8k1V2J0ctg0FuBDkPN+xAbkgXhPfk0W38vg76owbbOmurmH42n9yZEM4FOjIum7xkdOGyMVa9LFe7pX8WuZZWBxW96I1dbVe1Bdj8YfPcNHs5GTmUKJ28MxNo8hh3I/bDoAE/ANUjXtZTwWe6aH4Lvpb9LEBfCl6sni/thJDfZb7laSvLscn7WtreT1c6IqzhnhBCwPkUI6udA070GR/DPyC4M8bR42vn8K3Pl0XvSM5fjnXkOx5cUv6yIijvrTOhcDQYXKwdEQTg9rDDm8M+1eUwmLPb8hhfHtT+TgejxKgTgvoLpKhLLrOQ5ZWi0l0AgsP7N7eY5oAfPz9hmmeEMCOogMCYpxkuzLj74Tucd3t8PM/w4xMeHh9w3n2D5/e/xvvjHu8eKXrkGOk+DRPdmvohBhLpl3MOzIRAgEbQ62hVZK5ZE3223E2GGOh8J+rLlhGmzCXxrVpYaVAhUgJlqXVJcJeq7BHY2rCeZycW0OOYUJ0Zy4BEXBVtW8Fae8vNO5h24g6SGDkgb0qWZT+TMyI5IoJlUJZgh7Lc8uCanRA2TyE8pL/VIC8RvS3OCBnLxUgj/FIkMtf+Qr/CC1JqSI5bYhhDvL0XoQNTPchrQAsN0+9VVci4aI9uI1DE8YB0sVeAEfUAlku8O212nkkEA9c7IoROprWjqpIYEtlgvCVXxXDUQkz93n5mgXojNesnpYdc/u7SGu4KLHnpmAeVQlGLbDGlnSNs3MjE+RhAne/4KU574Zt2Hpu1tor/gh9mTqhEPzLtKqw14pkpjt1PCo9cZBfi+bKzREzNAVNg/Hj/N/hhYPwWd3ieHcJMGX9tYmAPxjcumE0/Vp7gMpJMBpqqwa97L8oHFxwCM4Dv2WFKO+H89IT94z9iwBmDdyrQOnLFHQFRrmB1nAh1tXdlgAh3f/fvcPPXfwF3uG3mww5rkgDWadjidK8Uqgnvpd8vTuuVUIG/vffmXW30tkZ2O7lUyyOJnjy8gXv08PQR5CadM+8osVWWDT1JkYkLwacAGoC1jHME5x2e559wDD/BOx83ge/OOLh9PIKBKN1LlvFj8FEO9sMQA3V8xNlh9Ljdj/i7X3+D3Rgv1CPndDeEExGU0hGnssuYJIqylPHzuBaDoAqzyCNLaatT4hrnRd6Vihyk24Xhj8awmza/tKyw7Bh6Xd6r4cCrOOMXAOCXm9Nr93yVjqaSpNgXmYwIMbQjWM/VK+Bamhw1SmJZCN9a1x8xtSCUTy7tLnl1+78Ari3KxXW7XOlXa/nx5aZKeWhjsbdO5xykiM1tLwgCadFQka/8uqRPLqXL49HHKuq8tXXZPhdV8XKdrUC/Aks3DyHc7nD4619heHeP290Oex9PumDnzLHMckNAdkDY+woKWIiK42kcVcZGo9/bXRF550M+kkmOVoo6nL2loBxNCSfiUF1sHWboPQWm/hDkDjgYR4vgoBBU1oGOppUoXzlykLNQwFDbh08ifUjbT50fsPcOX/2He5z4Hn9wf4N5OGC6mZLsPSKMJ+DwCCe7BOIZLtDLs51PDoh4ebvu0NdAZWk0AUlpgNO8UTFMLW+INNupjp1DTquscokG2+dW/0x2IHEsIepGeb7lWdaFtQq5O6KDnzmv4JbJ98fiIamNoAD1goOh+NHSIYP7JhFBZefdNOOrx4Cv9jvc7m+wG4aITyiHnVUQSO38gvypl7IcLX0SefQ1ipjg8S/Xl+2OiDSzugwoEpPzdEoKjsOMJ8z4GYNzGNyIgwPuKCtdVhkUpQpJObJKstfLqEURSvmsIyJVZaNL7PfRe+zHIRsUoEUiIa4VzAUFgopVhaLtDMNlYVGMdyV/TwY9jmPgnAeRw+AIIRBmm5cTQZ6BkY+YQDgen+Fmhp8Zzu3g3FvcOMKbRBiJCczxHgiAivWhlVpoSOgjlTJzT3aW35ucEBUR0yEVJsmJKFPbTq/2urGqDFftNZHRlwHu9wFQgx4QiU40+qEYB5KjaZTBZ+OgYpphQJkFSL3ypRy0HBkfgDltj1wxzMcqIuNRh4R0XgxmCnclhtXjQyWx5iZfjawrdXWg3UKvbVSzeWjwqF2v+blQL6qe/vmmwkmQjD9R9mrEXFPoBX1aKaJjakI1Io5D+SyJUJjyKTOuGtCZMQ5nWTtdhdIavORoplQRJSE07wSyEG9NXH1eTlkZMQJx/jA1l7i/7ITYAp/kXVtzVAiB9RSUDiwtYd6aT+qghH1QDFtefxmcVtwTvttUSdXYFcRZlKCoqOg5tCG+CQycccaZjnjyN3gaPJ4nhyNbtawdYCLGTIwgckMFlQfBE+UjFLtrKtOZwOLYz1ADUV2ZQDjBIYDhwgQXnjGERwzEetcU2X86Mty2a5SICBbB376Bv33bXcJUf+lkoqV3DXk0/M3KBwtttlS4zbTFz1Xg0BWkrcG9JkOnca4fdIRvBsLRIRxHEOcAGCWPBLntWXHbyr9JQtW7IeJOiBlMJ8Adwc4DlB1U3nl4J/ecZRltvxvgyaV7H5LRwRGGweOw2+HusMc4eN09LLJzlEVMRaarZOBV2VqG4ZpBv5S/R0u6aZlHl7y8pTeGe6LAxnpJFfUsyBgXUoNKtPzOwneJ7zS7sjaBlMfkl5JuerT8F00vaGtrkWaUFgou1SflGeai34LJJtmWLE+2+mq/1t7XTamztooqLg2M8vIO37wGBKPjXUMObOqt/novQL1DYku9a60vzvOFcbM7I3KtPabaZ+s9sJZ3cpXPe7sxsii2YRSME7iQKJuLdsvvBBP5Telya5Ot7dYSvbuki/HC9zKt99TKL+2rizhKC/N0EaqNqVPB7AiTA+bRwx/2cLsxBSa4Zl6LeaN+wB7X+YAcN1R3kJGOQo1OCE7BqZzuaIM8V72kdZsVHE7UQ4aR6WW9mDYkDxsjeVMx5Z2nlKuPoopDNDi3/ZchER+B8x6Dc9jtHBgDmEdgdODdjHifbQANBPhBZW9SRwQj3uEV5TWNaiJd5W37osPbAVpM5W5T+dboSd1BKgdM7T6F/sjl+6JczqftSjumCnVCdPXRL5UW6lzQTxScSzCtjH2uWuzQDgMxbuBwSPdDDM4luXy5iV4vqPmxnn85lQ0X+Y1NjBq82MYVG/MNo27yi6bNjojj0yx6TJweAk7TEz48/RbsTqD9E+78hH+/A5wnDANjAHIkl0aDQe9+kEunyQwaEfCrt/fYjb50MsC2nQBxGV2kXvntHJnLrPsCfU2sIoHMvwADG5Vt6UeH4C89KaM/WS/FJAQwCCEwBg98fX+L8zTjuw+fMc1ThITi+b+BGdM843h8xk8//whyA7wb8fDpAx4+fY/p3V/j+eu/wfvHG7x9PCCwT7sioiTsEqVUWBKxceIEIIdAwXIoeSxcxLD0mv3U2AvF6C7+Vkpfw+h7gnQ/S/WgJJgo5vViDcU7vUqhl1/4QCcHc+KTDtD7GMiV/D7fWp0KGq6aflqBlsEYjmccPj+CUhSCzKOwoq5AypbhR+BYZk55T3/wael1kTXYwag4QTERbVEIbL2X5rkR9Mt1ZPBMcbjToFz4WjGv7Ci+RKC5iHjbTtLX6yxTVmtbEaT+eUEy7ta/oFA1y5bzuZyEpEwGcCCVwQQ3dbuqMimJlrJ9skqObOctG9e/FbrIDiOJMIaLW2IDKDn8SlzYHoBgdvZUZZZkc2pzQA0QnL/zUsWNwGeqavLx4vse3sVshNIZIR2gLH0nuEneGxrT7Bjs0joLHWdih0IWr+oxDDyVowoWAInWBoSkoHAA5hQ5NYcZ8xzyvylgmif8hv4eP+IDfsP/B3wIN5gR4lmwJAjsm7GawfgDewOjOGDiGNxTwFeYdcjMbJRjTrEnP/GAI7u0zTzS+8hTI3MlR9hNzzg8/Df4MGF0cbenpxglL//s7jlGDFIIiDuG5D6MMAeEaQals2+JTVA48u5TgZ20j0LPF+hJJZqU2dJss9APGVtXZnVp3XeMubXBV8qXZNxijMgs+XWf3ooTp4Q1CX46r1tTYGgUkUx8nn+HAMJP3z3i6fdPOJ3SQWCO4JF4E8PcrxNHx7kUn5ecD7ozwRFO/AFP/CP8EHDrB4h8Owwezqe7H0z/4n0QDv/DX32L2/0u3TOB6JAA4o4KT9gNQ2pLt0DofWGQ+tI9PhFbEu1IY66yPtl5LMcx4gOrfBrJoKGLOn8ibeislkSCUc0fle9NaqeSFr530kJUWLmHqVeupos9eFL/FiPPGiaLcuWup3oOWjnP0mrzNvGmOKRk8l5mlHrXHnOTe+uKyutb1tRmBr1c58bG22wvk9i2tEcW5xfroVI+WKvPlfVYufOPkoxctdb9l43ohoqEnuhOzl628hhOG6CjuRcA/CMHql6ftqwXa5sQPfslHRO9SQXHeLAlQlr/xRhSoi8hqgJSFISJRswYAR4QTUtk6q7qqPRLeR7fcFGmntVtydLDcrt/lhBqHTE953bYxTguurSVgUNH981tpB4JHV6aHysypAY/7R3+4689xvcj/vL2DjfjHp48nPcIQwow4HQ/BIRHKNPuD4kEJlqazi71OfWDZcdDAMKEME0IPCPM6Q6H9D5oUKYqHGhmSnS9dBG1HO+EwOmy6/gvhHj3xDxPusOCIaxMAjrjPxlKn5rWnQgJGQkBRC5uEjAkwHGe83iXxADCDtPhG5yGN+DDv2Agwj1CupgYIMxgv9P2KWTZmslnvmqEGsFhe2A2XKnT68hptJPIuCm4xTwrHQn5tBLFwtSv8hglTlJ6PuqKdfz0XAzF6SDTGOR+iADiucBXqZ6iUgK5J0TtP2ANMizo0CLKtzuM2A6IyKJmLMrM9kvGi7JKq0AkQZNJT2HJ5S2tSnkoHoG62zkcDsA9HG5vBxxuR3z1Zof73QC5v6+YI87cKFR9N9pJgtnKakYYLmyt1bhVZKTOw+SKsYqwbQ1kqSoUNiTjSgv5Xpk2OyKm+RjhSkTOOWDmZ8z8CMYRAz5j5xxuXLyc2kOUGYqOB0I8E1l+I935UCzgeAHNfvRRkZKjmwSXJK8aUFz5HJYolM8hbynnbJQcywitwG/r0bqXRKP2m+0DIEhkVgyZNcLA4BwwAKN3COwwzUHbVCYZAuh8RqAZs5uVyBwOdxj5HW5BmMlhSIJBcacyJaG5p11QvGgnUDLqEafICE7bzvL57CUidrDSOiFqJC5Kxpf1yXorNa8mruG6qgIhpHXbvUrWK2YwEKIBIvYsXt5LOheilC/Uw/nCHk1zAJ2niD0us7zLEOUdEMqALnfhYg+t4JQLGIbI5etNqeO8iltJARFKrJEjk/VlRVDfWW9CVdq0tgJaWX4130Jajq6q8F/HcmPqtVmNUVm3+UJytIwtA4iBPSqG4nRIjK2gCUaoSMZv2SKYm+KiT+2umho01rONmfL8MWURhhKMBczdVLlDloQjyruYCqEA0CG0R7IpJDIsKxB0Oyv11vNhHwsopq3qBXqPpT+56Uwrase6dbiXjr4IE6e2sxPVDIt9uLg0DD8tvsSxlkgpwY94jmx04AazGyKkSKkzn3DCCZ/phM8u4BkOZzgIg8w7IWs+HdubGzglSjVeKD0VlD/RM64LxTVz5ngHBKdLwSJvZAzhBEKIDofwjDE8wyHAuWhcbnZD2LlKO+g0eiyNfb4srhrGZqTXUxWbcVUqaeaVhbV929cSjBpHsivzZW1VtW56LKlYrQm9p3PA+TRpgAEBekaxzH2WNVPwh6NkXAwImGOfyIH5DLgznHcYvId3DsPgMQxDdCrIruAk9rr0/vaww+1hFzGcogNCjluKz/KYFauA+hyyFmfL0vlFbx4MtSzwQnhuyaHLWou2zTgXsFTvL0YnNz3k6vsVeFQ5IXLbLR23Tol1GOMFgtenChYDyaIBvJ2ckt0stVSsz6QXdRyM65C+LG13NLyglY2VNzhXYXDRfpIRqIewHUFj626bXv+2zF2R+ZWpoclXNtZ9utT/zuPiUV2O2aB2IRGawgtwFVPUk/3rUV4agTKfDSZ4TcqyHLU41Bs/wUEyJx9sTGyY2PK9BlCd39bNTGCHuCuUHJhdugGr6gyg8vHLpYZcXQ/GLtyNnntpYi5qvEXdW/XazetWMzJmAj7vGG/3DrthwDDke550vhs0LXkEF4Pd6tVFEkszp++6Q0EcD9HgXFxYXIAu2FO3kOoMUi8XbVm5Xnc9iz4gtXV4GFgOSTKOCNumPqI0TqwqXRwqDyKP4EaEwcP5U5LxGA5kbJhyFBM0EE+FKiOsLuF0vvlz/Uiz7rrg/Mn2t9WdzZDnNcZ5KquWYj1BC8muFi4gK+cp+4Gq+WWbX54t3CvbeVZQnF7gHuNqZUXk8SUSTtVctVnTGqJoYfZgjI4wDA670WE3OOy8w+BJd+ejGJ9+X8ue2Tt4O9BkI6HComU5H30tttzlwbggK7cstQOrhc08XROzr0ybHRHfP/wDCGkbupsRDp/AmIFDwP0A/N1uxM6nSC6J8EsX6ImC9O7uBvc3e4CycuZ04KHj773TeyEKeVgv+7P+wkQCyA5qR4Cj6g2Vcko50R3UrDS1pbZa50dLXuQ4nxqZ1MBF0Wnzzf0tjtOEP/z8GfM8F3UcQsBfT8/4BIffssPxdMLj0xOOxyM+ffwBD+9+jQ/33+Jvn7/Fzfw2RQ/HIyKI41LMTsFKEIsTDQ0qBQPkMpFL58PLmEdaFMesvvy4+LokgTAAykSwVJ03ph4Rq7vWey/JHrlUfFb5ePFNkUkMYdEZIeMkeBUHwsgcuT6Lp1TNCwPM8e4QgkSEm0KryTB3lt/LPbgsdlugBXdLhpRlwAsUquSwBU/LNVinjS6cblXXYM5VArvyh37bOd96f+u7cIp3EKP+BeAadF9oU7WSODIZtlJgVeePLmjJlncjRHqRjW+BHIhK4SqDlpwWpo2y5c766XLBbLwSWMAhXkoEUT05O/iUsDcVLTZT63qF70HWrZXoZUy0QNuZzYpHnWoHgQBs6II4iONHGge9v0N4SEv/rBGy3umX37fjl7dnL0yRVXQ4blft1WN5psW7WgmReyBihFTAHALmec47IcKM39H/hh/dD/jd7a/xefxbzHyTa6ZSRqAO3tfJjsMjHI68K7Iu84K4hT63BIAdaD7i5tN/g+NjvP/BMXZDvGA4ntefdosmw7InwuB9rJQY08wIs9mOp5dAbqFYWXbSfpEpuyInrSUnYyrOR4urhSxtcLeHz12IafX3Uuob1o0wWMmQVycrDHCi3Rr1BVWiwazjwwkfXFqQWQYmnMITnvkPcEzYwcONwK0/wPt4D8Rff/MVvv3qHs47EEU8sTt9KdW13w15pwTFnQ/WEaH3pdn+L8ms+m3BOF5EjxFkdl5kCJYqF1hopksvrvqq1GvmJWfD/xLnyS+la2Wca9NSX151Jv/GAI4/h7QGZmM8sPR1rY89g/JSC4kP28//btOGcRNZa+k4mstNVPf5FbW+ML2meN2NzbjzouxZfif5ZXhnylPfQR3fOMwgPLPHiUYwD5jhccYgV/kioJeyyyiJssWdQ5vUxaU3WypoKrM6cVm8tWfUn5260DfEElBcWn8JLgoz9qcz7v073N8ccLPbm+CEmC2EUBwhSmSOD5eKGj1cTM5JvpS7+RCSPB4AjjsUAs9RFp/jrgUbCJPJXWfdcf4SA2nSBdfq4Ih3S8xhinL+lNqb5wSSNYznASyOC1sji0aBoxQAp3AjybLDHqA9pmHA7J1es6D7FdJdEvFqVweSky2MbqhjXMHULGH9aw3Qy6hQzJQ6bUIhf9YpVyX6qdUfRIkH1MEkY8zmvbSX9LE8lmk2UjbBOXnWG4o+cCt4fy3hKiq3a7Vqs6uHFqNV1RfvCfTeYx8mfDVNuHV3uL29xddvbvDt3Q5juiCCzXj1u3S9zJTpcQrjqQLg6mBJlzF2g2y4nmPtqMMayvU2rkubHRFnPEKjuzAh8CO8I9x4h1vvcHDxXOV8KV665GOM9x4QAbtxwG6MTcqzKHhFwMuTaowAlvTKUqWVF+lbRRCXIlqKD6uor5Ttv1tSmPokqMm1Yc35wWNkxm7wOBNwOkcjBTnAB2BPwJEZOw6YzhPOM+PZPUVF9XCL8f4OT3jGDntgGNM2/gAKgOchR/ABEOQRuBzixdUqJDBr3rytKRkAwYbB5rqKIbiEm836sAUuCeK1mYhRPVioVx7V5Tu5uPzCvYwGTPFaQoiK3BsBiVhJTLYwpAhBq/aGkDRERd3COwon24pgkJ0QHSJT/+wNebfTiTkJhzZ88rIDos+Bm3nU7xTfa3Q8ShtJXe+SAle/L+hO3S6Kl6UzQp63kTFbeM8S6VDTe3cSMoxLTfRwlyocKhwPFoTCIg/IrhxKhICRoq4AEMcdPj0widCzheffKwSw7pnuZEF2njIHaPQXyRyQwtmv91LKhErqBrhwRlAGpZQihVZq2aoPl+j90lQzBOGUNhSXUSc44kcEzAovvLTbCqXQsWjsYEC3oovRVTokZXWeDY2DNdYsdNV0S+iHtGF3QISQHRQnPOOIIz67Mz4T8OAPeHI3mIOD7kwxDfr52dCnheQ8mPaGXiPtmKACRr0nx/aFGTSf4mV2ZtAoHOH5iIHPyTgsMlG6tJgQj5aViHc5mknlGUMFL8ju/Rc2z5KsUo6VLUvV1LX4cYkn5wa7kcLrBTfme105Ely5AFfNz0qFvtN6mkZxklCKqAt8BtMRjHO85NAD4zDi5rCLu4U94fZmj5vDXp1V6lBKlcpRS86ldzDGB5ElpFzqYyHn6m+ZF9J64mud8fx+fRSvni0x+i0ZMmoZOz9fbknhXzQEl1/ycCzlv9zvHkfZepZ8TyG8vDz6wuZqMepn2g7ndeVW04KhfnnKrmyrrqiRV7c7Jft0MeEOV79VJqh+m3JyOeyXuFzZYlDv+ZdOFzDlF2zxghyv8ntrSpLSvaK9Kejj9TKu5jpWaJJ5lQ1HLZRdGFGNQi2nV3lL4K5gtQm2Mpio5AVk5R5CMYCMePJCYA8GIbDDzA5cOLUTraxIZj0ijPZ97/lyRzbmS5nL9nmhrNHtrly6pEpBvZP5MmxIczK6eNfpmO4z0CCfCiS7AzIz/rbaDJtMozlWWZwM6mzg6KvQuyLyrtxcC1WV2vby2GX7A+vhQrlOc3k152OZLMxRTEj0U+VK7YTJlItx/R6V7BEIGBwC+eQ46yVWSUimU/Ux5JVStN/ltbUyvIAMCSl1xamRm/Urm7rqWtpac3mtB/KZF0ycDwtmifSqn0mZyiGyRN3WuvrFU68dWudQRXYW91CSj4lAgeAmwkA7DENah54Sjy/n9KK9awv8qT7rjIjP1rm+wKMouOCUL6TPBTlbBBi185hsq/KLjv/1MsH2o5kOP0GUaSJgHDzeOId/PTrsHPK28nR5nvceb28PeH9/BxDg4NKFzPE8Wpno3IPM8PS3EwJQRWC5uqMGeRTzFhi3trukBPSpyeKkdfMsZNW121kxBeXNCDV4j2+/eoPTacIfPnxGYAIo3idB84w3gfGvw4wfwozfnM6Yzmc8PT4iwOEcAsL9Ce/ffcTh7lsMuzfYP37CcDrhzeN7DOdDC6ohbo7iRgHdPcFxS3n8LscM5SiCaCAGCiOY1LcFNxcFqLUFzhdzbEmtDNORiOq26kYrahx5ZnwYd0YkQx3ls7Sjg8d2OnI7O45Fg6FiApQuCQMZu+jKaFTnZbYMst/ntSRHVGwmxJXjp48algHmR/ZSNTJCyYtScq4ti/gtPPabNP9S5TJw1ZpOqVk/L061ACZ1izST2kgvMr+rpDmZhzjgyXlZRfzUSpIa8dukhj8u53W1JyT3MEAmXl4AiMfIRR4hCzAvxEVHMXefqngpdZn9GLluZdQJBzRftTek6Kfkj3X0BMhu0hcOrWdH2ktm/3R2r9ICcNeZ1RzDhHadAYiRUUh3FOj27BI20vooRQ4laCsebGzs1aSw3q0wz/nsWQ4B0zxjCgHTHDCfZ0zzhN+6f8D37nf47vBX+Dz+e/yeD3gI8ex+HRMRIucj9p//G9x8VDwXg4AYQImAef81zvf/BrU5I8JsOlWqAQkVZ+we/wHD9BlqNKYYozIOBIcdnI+R7L5yRLh0Z4D38QJC72SOGfE0xqAwZQVQ1iu1yJ2mQcb6El2rnQ3N++58radKoivkrurJdanTV6sgLsPQr+qSAyIqxJkE5iMDrOIsfLjACDUWRMcTQM7hHJ7wFH4H5wL2Y7x0chw9fv31W/yrv/gGzqdL8dIOGemXRkXLPV965QPpeznmC0A+msnl3StSl0uXOArukKlf86EzR3buCsdIf/z/eKnEskb5WqD914oMOi6vkTW6qa9Ubsu7khR56rKbOM7//6SKyb7K4WELm+9KQyv6RiScwkX5OAFzKULSruvmEy+XNV9a/k+OJbWg9CWqNJ16qV/o2jqW5703wqV8WEpLG+bkyjHTHSE19yY5h4YNOWEjzBHiLroRjAGBR0wYccKoOyJsfdkEav+S6SdXb8tvtYYpOnTZVyvHpvoaXTbL0WIc76bO4/bRSnlJhByklH6XjqyqvNED79/d4u2bO9zvD9j5vAsySvpxpzLUniVyABW1tpe4yzimHRCy00GcAWECh3gvm+xckB3KEpwFxB2eAPJGSrb/5HJrLuoOzODAuttimuMuiHlOOyNEwegcXRjlGsVCGaSIZxsMTHJ3G5wHgTCeHBgjHv0ekxurVZeM7nLHFqduOmnP3i9p7nQwsjdB7J0KAVDof6TYX9yNUKMwgjkWS9A6rxyBWqdGHEDqUArJ7MP6TB0L6a4HGwgmDiFdG+kuiMIJAbOTwsC8uBKME78XaPhqI36uDHaBxfmuNILInCttTlLWr8bBgz85TB/vsf/qHnd3dxjGUQPLAOiuktzNLxNsEKHtHDdo30s3tVsr+gxlPMkrSIJMY2uleCiyNVb71+ygeCG/3uyIiPeyMJxjDORw5xzuPGHvkC5dJI3uG7zHfhyxGwcMaYt5LccZ/61tRT/qPOpgMAqTnv+mpS2DrOouJqtqlcpM/flcRobydy02VL96fEcNs/UCBeAIAxzmZMTgkJiNA8AOAweAgAMBNwiYQryM83Q64vnpEQ83DxjDCOAZe4zwQxSKTxMDLsCfkY+C6cCcYcnnHysRlchcgnrj1JCplk+IHHMRP7+4nndlqhddmS6vLmEEGQVl2cuij4zIXmhoyEGuxUahK2TprXMIgweHAC9OCWmLTd56LJVLVaJeI6RJ2jJjrNU2ImKvul4zC/WuvkvG8Lz2y/FTkbpxVFTj3CldUePqGTVZuNfXzX1ZiMJQJloTl6Um2H5sarnCAhXkuhAZgqsXR1tlnMsxa7dIWuLfOdf0UtKjqgztSTinzgBCFhBNc1wJqKWzYi21zoiLSRQO4V3MxjmYIKcMUzvWawTQiK2UoBISS6YtaYfTeCSarS30jHVc4prtb2l8NTsiIE4pgBCP6GI43S0ngrEaPm2TlOvWdoIRkkXxScpPCAHPeMKRnvCRzvhMHp/dHg9uj9PsMDOB5mc4nrRPngjEZ/hwAvGU14gImnKBKxMQjgjTg46/rOl4DI697NoK4kJSZwx8hMcZ8UBJAlEAIe4QlSN5sgOCsjJJZkeEOtOQ5R81Hi2ghMyfkW16RrVaDupJXssltsk9khidA3628nXq96EpvlLfpaYU7gtOiPQNERvsekBnQjI9EVk1zjuMowAgN8Ut347gkvNpHHw6ZikdY2ruhIhgkn5a35MYKO1OCKo+VZkQepR+CIwAqQ2DTJ12Z07u4frIlsOZYW7f1TSopQ+XEzXfijpWEKbM1mm3plVN/VcJMlela+5giARq20JYXekX2rrWgK319fIv4IO+Xl3YnXovwd79ttT45TG/Fm4xJFAiD0win1yL7xaGLF/1aukdrbBp5+NaugLVv6yzrsSXRRxcaLOI8e/kuRzHtBXnyzpj2y2luDQ2RaR5S4LLBmz7dZbew9WGLWxcycwZFrZnKCHzECYCswMj3hMRyBkAylW4OKJdNco+5PoN1p0Qbfk6K7XVVm3UbVY6UxeqyzhzSV2cHOFxdHi4IYy3Nxj3O3hy1ZFLaMeMio8oTzdtlk/0rxqgywup8wXWFZxmeqmojfN/WieSE0JgYoBDvPA45HbWR67Hl9syDXfu4Q85AA5MAwLtcCbCbPKULbGuZYu/ssuBTIFW7GhhZvOttx5adJYdIpzmO1S5RCdZqUzXgl0feT+EfV1Ju1pJ/bQDrfl1iS/XIywWm0iQs7OrW7hNXLfdO2avhZSrQRN9FUAKmo862+B2GP0I79OxaFJfBWLm99W8X8sTZU2JXl6IPrl/ejKK7eIqPZPS9d1tSwiMRCeNTNHrn+n3S50Rmx0RuzF6EQfvcUuEfzM4jEQYfVS04k4IBz94vLk54Ffv7s0OiL4yVHuqsgKbUEKySx2SsyvQ5roK4tAoEApClWydl4Tz+vdS/mpG9KfxbMafiXDrjzzhDIAcKBkzQPHIqxAYM83qIX4/B9wGxg8c8Ns54OnhI+b5BMdn8PSEMJ1we3uPcPsXGHZvcX4zwDHj/W8Z47Ptc726SAGNi4KTAFeSZueQgwNJUD2WLc8vvzSmX1KQNfV3vhWePtiFWhfm/jSamuxnHAJKRJWVaWkO3RkRa4trt2oAiE4eaT+leTfg6euvMD49w338nMBjM4Apbx3q31ipL1GK5fdcnfzZiDsbiVB3pi8QsdhVTv2rGbJcB5XnslND+Z0R5wkoIhwWWt/0aGsNy5tB02cdydKcFdiZ1nXR5mLwT/e9old2BNiMGvm0JNmzwEuZuWr+nJbpaBa0GA7k7P6DNI4hlXWkDDsa5MpJrcW/Yol058PSuWqdLxokI27G4ch4Gset5R+bbDxmyEQ0lt0tsvxFqGCWnT4JZpVWTHXW4FutObt7QJ0CgfWuBhFixYDuHavxMxCB2OX6hVfHRhu/oESXB2ZMHMDSzhR3QExTwHma8Qf3T/gD/RO+2/01Pu3+A77jHT7PPq3bGbvP/wh3+mQM/NE5MmBOgkVPDojw+PkTdp/+l2pO4u4/6pybL8qArgliOO/hvex08PFThdr4fHD5HP84NJwdFURZHuIaZ/NcLPNPGe+yj9YY3PDAL81qLR8iqkG5LimI/QoI1H+3xaC4xBmKJR4XVlbEc3RZYOiOCI0kNfKtvReNiDA4ByaHHYa462GMu19G7zG6eD+IHtMlx3YV6wZxVw3yJMqOI5fOMZaLz9XRoOcby+80ZukHqWGjogPFUAoMZk6ln6syb4l316RaDszo1Fak0G1s5IvaSJfk5T+H9GU7+mXSa2AqvEcdoee16RdwQnQyqqz5WviXoi57BpAvFZ35i6dfBGXXlYnLU3FBGfml0spY9BxNa8U3QV91M6qrRmCwuqXmTTyAPIAhfTrMGDDRDrM4I4SBSRmUkd9yzG6589jqFm2KZpJSJy/KRyV7qWT+SAxf1chGfc2uh3wMC6fnrOXleburOMHUdQgsJGY87h3+p7/2GN7u8Xd//WsMb97o0UzlrmiRwyNeuFLIM1XK2GQ5hjToJ4DDHCO7wwTmKOMzGEi7GFQFMonqL0ZG0l3NbI5bSs6NwDOC3PsWZsxhTjshRNeI1TkzozpmHUeM1fRV3tRAIckfEtoymAjOjyAaMQ13OI+3eHLA5EKS96GXVEfdIvaLIBdj5zm0w20/CQDJTgp9LjDaGHcu6U+BHMlMbhxCctcGMWTjdB57M7fxa0Cwz7StkPNoNL84i6ysK/dhxPdZOK4wWflaDX8nXRSZUiWX6qp1yDo/tZkjbrhcpuiLyevi/bxDChDaHzzu/Q1uDnvsdjt451MVXJX88gxM+BPJD53D+P26XXYvBQIlbwAVfc94/TpnxGZHxFujVB0I2MudECQX5Ul01w6H3Qjvs4KQI7QSyHGlwk4fdRetQSLYCUEX2UwT2m4nc9fZsGQIXxRAuy/qZ4tstPjkpayaj+GIsN+NapghF4+7YkbcpcIAO8aBGfeUjEfzhPP5iOPxGcfjI7x3GHeP0bFDBA+P0xgjIIazgwtlu8rwF/vy5fSCbMMojTDbCr+oxfy1on/dNbS4sFRUWWmKYYU5YbBZ6CpN0qTUJzVs5ZvE/YJ3mHYj3Bzg5rlzTBEvjosVjK5LdgdE+85+LKarpeSy9UwRkrOLs34n4yz57GbjDqQNOPqSejn74L6I5G/tdyN3lQxAZeOmwku/r09FlFRnS0NcuuujoZ54NdJrSX3f1pulPVkpHORZtYWdgLhTmRAdpilKvxi3CqbagSff2Ypdl8ZvmUZG+lgpcrnxlGe5fpljHQe2BwiZsVR8EKdAHG0tL2PI8n5Bs+CcT5WtAFUmrFBMjkAc63KVvZ5NtcK3y6g7Nu1kITiEFJElOyH4EY/0iEf+jBMfMQGYyGNmYOYANz2DwgkUjnCYtBsu7c7IF/12EtlRmEv4Sahyby1FTUDkCDE8e3MpsR6pA+ixOk4dESqgZKOzjI+h4znyZh3/7HxupUe/iK3yQqVXN3lVAVr5tTVlxiY6mNg7mAOOHz7g+PEB0+msyhwgvCfvZCh2L9CMCUcEOkVZ2ccoq3gnhAOlY7uyc8rMZ1o8IilTcqiJ+CoOgehgkO+2PCl8Zd5Wpq6dDo1zYmVu6zd9J4TRBWrS01Rdll+S49uGL9Xbe/GFBNiNacuuhxy8cmWqDdEb832pVO5KadvYbMy/BF9jcF/IV4vExfeNdRTFRWK/Dl9q5f3lKfPPdfzo5XvNnBv56Us5lPoZLhS/IF9ucM7Ugk6Wi+py22Cq2+6Jk5dqyPIrNc/WSmwZj61t9/TNjqjayOzdOsnmybT8UhDU8jNuv1mdeEnf4eZJlSdL902P+JJd5lJSQXpDFVaLiTFVkw/Y7aI9bRxGpCuhDH6tarEGDGNnqgzNUbaXcRDZPo1n1X+RK2I9nfY0f+mAKO6cYJj73kJx90Q92GKubw2+BTUy7ffeV4kQnQ3kAPJgN4LdgFKjKjG3Zh/5mQS5XRRDNlCQFn9Z/oogCrsrwugmRb9NvsW6UeJkYd9jrSO321bRjnF6sjj4FVEsCEvNV9O4dmUZ6g8u9+BZAAHSyxrQPKtyjK730aa9Y4/BuySjGxqtDr7LM7wkO6wGU7HspkwaAKUa1pb+lXxL6X0jawsItc1iub9dZ8TGtNkR8e/3A0BllJcj44zwcSfEt1/d5y3mijjGEWGUobqHVOVT24YZHFuOy1dFWmLSWbnRJwvvW4S7VPdaYiAePwHZDWEIMOfLOcEZWbOuyxgGh1/d3+F4PuP7j48RIZyLBhdyCD6AvMOvQsD7wPgOjB/CGc/PD4hnvAWcjs8I0xmHww32b/4K3t/hh68d/Ez41e8cxqmN/uxHFtheleMiZ3AjMTObrSdEFASCzcxuHeMtDGhLBek4TFJBjM3b9doXRY00FJlxUPtyqZiWrczpqalpt8O8GzE+PGL/+QGs8bfb0qUeLYlu9vPVCvwCEGuRXCLs6HE0qNejHW3h2q9RwlbSK7tfVtVW1pzvXzHTbUAZ4c68aofkUmeEJsn6sJNnXD/VehbAE0nX6IU8b7UY2GnXgBY3GmWBjDle4KZLllLDalgLGVwgOR7MilJhoulpHuOacFVD1RNp4rFIrKSMlYEbuqLy2RJ+msuxtXJhUBF2Yom8YUs0Eg3Ztk3U0heNUNPImujUnuUs1zCrMkFpp15s3cGFbFBVWElkgTxWqpRo9FTQ3RbzHDBNc7wf4nzGd+5f8C/89zhPJ5znM6ZxwjzMmEK8w2L89I8Yzh9iRLjTJuHkX+pzcfTRhVTy/s5opffpuqu0EyIet0OQc/rzuf26c8THnRL2+FtrvJYxyzzUnEUKq7DVs7dMJ1b7WahcG8s3WUnlNX2d1liR90vRYJIe0yLYWbRr22z89fYd8jgbqhlxdA74w//z/4M//C//AHr4Go4PmT7I/IrTyxEc4u8JJzzxb+EcYxzjPWq7YYD3DsPoMY4DhsFLx/TYTd3EU+BaximRo/VOCCQckvEx5zfLb/0kp+thaYztWDcOjaX89tGLpzu3BenTUiOvTNnZUhPZrekLCgB1zS91RvyJ0uUjnv5IgNRt/gLy35dzLLQ15zVXff4C+L8drJeujz8p1P+7Tuv62fpbzbWiR10oGD+bUONOniax+Zeyyi8ht40Yk0PMGnm/Ebbrwj19Z1kHUkXB2iYKw6ypwyq8G4exNm209WJ5LSVYaA44zDPejR5f393jZrdXQ2g8HUTgY924koNW8pgp2OmMf3EIcJij7D3PQDqKSesTBwXLrl+Cg0OgGPAaQozK1+kKEQaR6/UuiVA6I+S4pzDPCLITYpaAo1hnkEHTkRJFxryQUe2oYoQyS2FkJ0a0KBLgdyC/RxhuMA834GRgFn3BmWrkt9fnZBoQylzievyyFAZZzne7wvJ5E3J/AxDHXWTRbq1JV8vOpmjzU12WAd35AJFzg2aN2Uz5om5uOJ4DIdiL2HVx2w518Lzu8DZStjH1Kq9IlVkfGcLMX50jjN5jNw447Ea8mUfcD3scdjvV39aatLJBb/4vvd/UrdXXX1ZWaOzg1Vi2sGSd9xoZabMjYhCFJyldA+Xov8F73Ox3OOzi1nOnClTpWBBAxZmQldaoHeYj8e0700lbrqrXPuqopFVq3y8rPlsUgvX3anxB3m4lL/reOVsSOh5ESGM9YpoDjucZcAwvRmhGcg4x3hAwgZKhZ8Y0nXE6PeN42oGI4cbP4DGA/Q0CPJ73DsE5jKdoUCral1+NAMCdZ2W57FSpyW2ayZrmJcb6x4hSi5hnlrFVwNXgmslGI0EJ6lZkmqovryUL/brTpUmU4Gylu7bxWh6rWlluP3+JQ7Ii6K2meiS6nBg9PGpyFIo6Z8RRYkk2c0EnmibTe2WnbDJehKQPeZ36FGl9HBuW2t6sfaH1bVBvXWokdRaDZNuSi9NbuJT12vmRqHg1ENd1tnfXZDQXPhIQOIqYVm9SzKhIGaW1UohzBP1NCq1ZT4XQW9Kz7KyoITW/O4JZAdaiTpcoVJItGgMImQ6zGKRZnQm2xbyjuxzjLcJy3trLSaeRHQ0BCA7sKuNtOpZOuta0YOhI3mGRd0HMaSfEg/uAx/ARE58xhXiZ3en4GWf+Ecwejgk0P4F4hk8X0El7zvBM+yl/FnudxlmIRNcXmLoXjbpxK68cnSjykTUSi6Fa31f+fuuIaPjkKoIsduGqTL38rbxNzbvCkLvYbqZZalhrZMMLYFrn29bUyGxJ4lhca63yxSrfxHfzM4POexBc4RRSmZbyXDLiToiZn0EupHtCnP7b7wa8uTvgZjdmMVZxR76nTqdPJ+MnmG5wuth9rI63XI84FHKwj6yPhVnryN71fFclLj4j26duO9KH+l35vNvCVtzo6Au8VLlJ5RGb163HXyKt7T5o1m71/iWSdQ9PukbOFbpyrQH/pf4DWgcipQv04Jo2LqQysnW10s2tX5cvyTMrZVfHgZczbOM1f6r1Yvu8hAhJmmwIyXWrpObfBZ27MO+90VkT9bfJBALHhcvRu6VUOwcKGTyVoHpEM34RGI7nSm7vyQeE7mVxXXtC04w+qLNXkn1TvtBfK10hy/l9PWwzaK1KUJUjtPiVx4OIsNvtcLPbY+fjPas5yibltQGfUjWXgUs6l5zfixwvjgarz+iRo3YEUpOO4l0g5BiUPAZWT6oDa+2OZ3A+3lUcD3pUU6h1h9xuQ7aqLnfUKvOaUdxWJmUdAeTB8GAXjxSzoTzyWTojIucSnLdqV8ZsLsovpbo7S+/t5dV6BFgPEeVdNZfdOssGjGwrcyDlkfHD1CV3QTZw17QuC1WdHpp1v0iW+lSp+LqBpVTS43qTkoVSMB07YBrgeIjHonkXHRFC/+QuRGucN/rAWlfW3hN1jiLTe3hFXsm7kl4ikaqWvFKw+3jNKVGnup8X0nZHhETzpYunvfMxCswTbg87/MX7t8kJkSMG86rNRoHYHyo+raJByBlr+cVGZ6kSVifj8JBk7ZBLyo0ox69LNZpbYozkjTRb2CC7I8qyIrBngpfh2g0DfvX2Dk+nM3749AiA0r0/DoPPEaY7ML4G4wcX8HM44/j8iHk6g4hxPh9xns4Yxz1u7v4afrjB9195jLPDX/x+xMjetLnUp/a7fkI+LZNr6+LeSrBZKuNxLy0SluZFP2dPRAIgu6Ei3rIQd1LDlBJlwTc7h1R8rKRamOgR4I04yZwucK7q6RCEci4649KfciOerJLzNiVG1fakVkzNGqCKp3USp4VdCJKpABUP23ZLgUUaa/etvCz122zzXBpHLr4t3SlxLcSb9cJiLVbPhQmv1ltWEOmA8IKsMigz1cFfoj0JB4u1FqllSI5DiiHAmbZIBIl1WtVYZdaIdWa0RpMe/TKPLZ1TQbxftk69KSmN4Jmvtc4IEY7T+GYilXOn98SXIzKiYTUrsJz6EYzDQM/GdwwXUk0hd8RBjLMxAhsEcIjwBED5VGh2QgScpwk/4ff4R/4vOE0nnOYZ0xSjqH5+/hd8F34H5zy8i/cyRLkjXvbrINHpEr/ESW6xvH5hDipjLlDieLETAshHLaUdEd4lIVUdD66oT/KbGS7at221usbVknf+SteIhLZ4K4fJ8lRnDalYiyZzt85LbS48UJ5q1UYD0DXpEgHUqDJxksU7IYbjW9yAcMIZM+fTgq0TAoj4MfMZz/xbkAsYhkHPnfXeYRgcvrq/w9/9+r3eH1LgKJndNHIckzoUalyWe0ZyPhDMedGExhmxYLju73YwZTeM3dIOrNrQt/y8rme5vat3DBTyZOb0Xdrbe1Y4I/506bU7JZTfvraeFSNnu3xfL1W9JmW+aWXkLXLa2tPt6U+LMX/m6U+LGn9+idb1nquru+CM6JdhyDEBoi2JbG3lb0IAIcAhgMDwmDDghIAZhLhPPyCH++UgD/21mAqIQw1/z6WZZe5GyuJsd9GH1rCqlQVTSDOWZW3NnPNcl5Z6HuXlr97c493dG7zZ7zF4D+cQA1+8i7sQ0t1zcm6IgNEzEBYOCKR7H5Izwh7XZNX7gjNSlPOJuQj4UvsVWHdAyH1vLLscQmwrzNHxMIcp7qyeJ5X/g4xjd3gZUANsLSOnQlzhUeVoykObHDrDCLg9wrBH8CNkzsXZYJ0QZP4DBd0VwYQGH1RiqcVT7UxpPyHpA1c3FxrZs5yjqlPGQZFtbWkHBUvQM2e8COlZMHAErtqLOAJbjgVGzm2aHpbhgqknqwRsWQdaz09LgtliXRrsrHrCcnsxeIwwjh40D8DzLUYacbMfsB9HDMOAeEVEqRMu0lYqZawl431PHi9GWOVvTs4IivYTlt85r4CyLNu9gNmqTT03UjhMvkAzmx0RrtjaLTshHG72exz2Q+uEcLKMoYzVAtnzCq0clV3k63aydkAU1Vslh4oir9363T/GIXckyIJO/+VFb2vJCm0Wk6lwoBRtgrAbBrzZ75WIn6cZz+cpjaGL28mIcUfxHHEfZviZgemEyTtMZw/mAD9+hA9HjH4HBOBIO8x+AO/3ycgePeBuPuvdAuqEMIRRGFL0fsdF4qcdfBghxsPyyAMZ8VYgYeEELAR7HemVzpialyKvukonMabhGYHsMVS5X2U/s/Diw4Bh3puauxyohYGW5vVyonmGP53z79OUiY8+zFjUVF7wCLYIV+Zthm+joEX1T1p6pTO/OFeJyF8cF2YTQWSBL0tmPGlxrl/vwvPVglcKpBW5WtMXajnksh2hZPhb7Q4GVcrGC4bXAhrp1ZX9r5pAUceawJIveWcSChHN3MwiOnKWXZLiIx6umh9lx0WnU80jKwxKnnbD5xbdr5mSap0KLSuXZ28lASDSHSexz7kGeZ9dQQvwcOQXdgkRki5CFC+jFkZFJd7mCPL8nWAipRAvo5NL0oLhFRzi9uMjHvGRfsRn/hlTOONzAD5OwDwDcyA8J4HYE8NTgHM+RZvLfVVJPkmG2KwcZNmkDYRA87w1OGbHitNP42AwOyKkDp/ObhK5wyXCvyYOM2f8EiN4MccduKtOGD5Q57ORX7SQp1rqPS/EStsmo37muio4Esss49HypBWBJ+l3T77LoFWRbfUizy2XNK4zGaWcI5f5VXl1HdgVNePED2AcQZ7hXIyk8j6eOWt3z8QIq9RlwTn9TM8g3yWPbd46Faj8TWb8zHf7advJ6EBmjOpBruazHtvKubDmhKif9crl/DUYtbDSBXPxQXGUQpW3kaWaVCKLheWPfpTSS9ujZmavLJ8+ueqzXbdV1vx7hQct9EeDBC7IVm2dS/i6PHR/5BlMjS6PV5uWhdKlPuWgsQWetgbSy8W5K9LLRv0iiFptXx9Yb3uNS1+ZXrJOqYWsuYdCny9UEN+mMusw5PPOi6ed+uw6C8k4HZ0QjgI8BQyYMWn5mvbmc8Qt4DYXV3lbiBYYdiWBC9UoDZXc5M1fufmds34JXCAsnlwA4EyEHw/A0x1hfHOL8XBIATau4JkajNXhoXUqna+xXCXel2Oc5JmoO4SiCbVPkVQlkfT27rh0JBNCNHwHu9t5zs6H9K8J5jJwFLMWJKAozWqak9Y3VDuSzPgkYWuYAHjCM4Ap3fUmR2GWBw1RWZZQ4kPF+pr12sH//HIZDwo8Ns4GgE2wXpu78b9o0fglAJCdDvGS8qS3irDLlc5hjvRq9dsebWCDJL3OvZypNK01VfTrVFmjGW47kGm2Zdeydxhm4GZiHHYeo/fYe4ebgTCs2Tcsy+iKN8vrdFUnT9gldsN8dG8ebg0uJCBHSy/hXoZnXRI0+kHZkWyXu9LBvZS2OyI06i/dLO89DrsRf/H+Pj6TUSKASCIBa/grBaeWYavxK4rrw+rYiYU6C9GuMyGZqK0z6NcoF6rHsux+iIs6GxoSAhkELhUb04dcIwBg7wbs3g5KkD89HXGa0033CMk4AnwdGO+ZweEEZsJPpwFHxwBm+LPHPB/h/ID9bg/nPJ7vBzi/w/72r0AU0cNNZxw+/wwKIfep4BTiaY3vZfvdbfgat/M7Pd+ulgGssFCgc3pBnX6vjjUyjjRFLCMxNRMR2M14PPyE2Z/qChUyNn2V54fzPXbPBxjOHB1P2mQrhHU5lgC4AdX86Yz9Tx+KbinIZrtWoRTaTIvydSUKFvmuIza1sWc5X/7C5ZPULBvBo4Qh0wjBovSZvHfNGcvyXFtZ4Rj/naZ6JCpdYUOqBcO+opu99nE26rkq35fPBC6ZbzV2mw4QJFKHDOomrHSyfg19NdK1XbOtrJPXPgBz0ZsVzUSga/v90lSZV9PXVhDMf60In+J8koB+USE1dF14unME5ng+reMAMCEoW01jrPd25Chy5QuW3+l27KBnxM5TwBTijogP9D3+gf4TTvMZp/OE786EfzxFRwSzXPRLGBzF6PJ0+e/g064IdQ50Ir8XHBHLnwxQ0N+yw8F+2p0OtSNjMGcwWQOxPUWuGHvzwDoj7CXhi+SqQ+ZTw1Cm00Gjq5NUQ7FuZWe18bgC5KLps5LbChGZ5HdXMKzab9dL3e1FdijLGllmC4F1JxCHUOlgBHImSIcCAs545t8BLmA/7uGdwzgOGUd92kHj81GnEPgpObkAdVo5gzdWES9322Rc1LFS5wLleUrHO5DQZcpjp7BUg9TI8Kh+N2umzLnshKjXJv5IychnX7DNl+gJL4lUfnV6baeXFs/Wdb6U54+AAGoj+bNOpAYCsmu1gPzaXnD1Ke1YY8wqSP97GLj/btP1cvrl+gCYSmt9juDUccEgCnA0w1PA6Cbsw4QzzWm9ya4IkdMtH8+I1UqzWQ5tDYjbUuO4NDKVraqQ+E0RTmU4F0WOwq/b2rpIlvM9D4T/+f6I3dcD/t23X8Pd3mJwXoMXov6ad113debip1FENIpCDIj14xzs5CAnP4j8GuUeIgKlIK+AWZ0QUZ6fwYHjTtGQ74mY5xnMAfN0whwY03SOv8Ns9IR6LFtsiLCy4ZdZeVOtnsWxkeUgTtDGIvEQ8/EUEEaPkwcmmqXHOj5CFa0M2p+xvKe/oaJqb1i+02ERXwThujtW0uyLApGeZWcz69+Mq2J/TI6F5ADKTo40bratkMtmZwQgu0fyHLXrd90ZUafrmYvlWrnHVTWJ9mRnplAVOxv5OTkH5wcMw4BxHHA7EX51dvjKD9iPA+72Hu9GKgLFFrsjXy/ING2gT/er6ZuVtbmQH9UmLkuhqKdt56IDopbP6xzJloYvJMNudkS8u7vJCj6i8r1LW85zJJdVrMouiD5slUlqkKJKXS2Ilt8XLVZ5zaNcTU3UVitrQVynUrrQl3dCVHU1xy+UylyL2Om4EyYcdiPe3jBO0xTvjkiKq2zZFzBvecJwAvwcQM5hJsLMjLOjdNxWuqDn/AlwMWLPTRMcnkGULityA+BuCg0+Ku3Z0DSHgLCbcKJHuHmCS4ynGqBqIKWvlQHTOJuE6AxhxBgyDJM7YfLHhcE1qJKMQ2EYEUDw52cAE454QsAML8eIqNEx9U9pfiLQATjSI7z7WfsSEC6coJGNB4qHkHXAGKYzXJcJ50pdSJfELuGsLq/y0lghLYyIZqSETch0RuZ6e53dmbBGcgoHhKUDq3Qqevl7vWFLaKWebkYFoPPiyyi4RTcaAfaFNXa86zJsv7x9wghyVD/LALzGPqAktibjnfZ6R+AsjoFwW3M5sz6Xn0SgAjFYBZNcjaU7HYGq86BwwPbyf6lUj7tpSA15S9EZnChl0lAja6FNSKWGTnIICOlsWBfPuQ8OTA5MgHOhId9WaI5yNAMOyRFt+KHZwi2G3hMe8dPwPX7ij/h+Jpxmh+fZ4XNIOyvIAQjw6Yx9jTJ3rt0RAdm1IBdHG5RJAGc+U8otZYR5ANLFvoQorMonQIWxOBqMJG+i740jJNUr01kst3xmrw1YyI5w0rJLOzpyG/ZLlr2uSXG4Eq7bdhZpMLdEWj8sLMsicCs79jKt/jSNZl6UyU3+1URbWiOFjH8oX7OpR7ZHRzaZ5ts5EDwceZCnfGyYd9iPA756c5twl/DmZge4LOc0sjOVO2hEnpNxKvLD7G4w36WQ4oy+L3EoGztNXbbBchTz+8VUvzNtkf1d5SqFvibPKr53wTAwd173IvOv4Xev3QGRZZsX1POFy/ScIkvrsdihQO3zTpGNMCy+aurfmqrZXWxjq6O01QGV+V0N2/YU6ep6U9fJupbuXFXgzyi1U0Gd91aONQaphekqWF1pXdsEhcLwanSw7a3TifpugOV6llJp1EK6hDbzUqv7iXk2m/TI7IhwYAwUlGPkcimvWUc9jDVagBbO5txtg9qO3BWpaSavPWaRGxDHJCnScjwKy5lF1sGnMrIxlvbmUXSXwcHvPfZ+xOAHSFCL8O+Q6uD0SUlWICA6K0zvg9A77kWz94xZqR8iPnDSmlQkygG1YgvR5+nuOKSdzSx3P7Dc+5YDauReiEIoZ7FEbE+6vrl4oN2xASlR7EhBShjA5NMl20Y/SuuABP9lGinNs45caQDQEa/AL/28/b7pgYFc5tGf3HnAS7W1SWFmI9sCeiSTahji5FFgktMizXfsRjBwKNBXzFo/Z7HmizFo82fZo62kkKc6xCUPpYxKKdM654Azgz4GDBixGz3GIf7zRm+5xHeWUj8Ao19Xicq9+uXEHEo9EuqspMSUXhR6LsNs11HRT87H0Rt7zUvFhM2OiF+/fwtQNFAQUTyiCQDBGf2OCkhqQVYNldQTCKs4toUe1arK8iLoC9HyLD+uqJf99VrZSxlGS2xqoUGV2QKyUgCxTEcfJCZw2I3YjwM+PZ0wh2cwopfTe3vfA/B2nsDTBOAIJocfHWEKAcwznPdgMJw7Yw6/U4WTCHhyLhIzitg2jHutN/aNwcm4NM/xwtHgZvDuE+6eH7Cfjtp/68HMfanGQsdD5qEUa/bTPd5NO819pM/4NP5QLpxygJGVdIfPt/eY3YBw+g6EM4YhMv1xzFGsvQhVSSEEPOOEj/xd7H/yMocKI8tiTuetJl5+nvD+59/Dz1MJdiEZE5je447+ru2fjERhYEDGF2OYAWcjpTDgDDYVQohdu9kZ0V95Cqmj8jf1GYfW3KlOBAQltGwEpHpcFlPP1PD69EXqU5x+mcZiDUfb8hq60gja+bulLXmd9kWFzeNgeH6ev5XszCvzaySz7FHLNevrLMZYe1rJLFXSNF28oPCrcGiEONvw4nS+fK4Xq+vSOYEjqUyU4oUKuasuV9I5UXocXLz42jl4AOwZzB5A3KEg8l5ZVXQsOAZiFLnEwyV6wpE3cEg7ItK/B/cB/+z+M/4wE/63yeP5HPB8cggcldxoPI0OiGEYMAzxArHBeTjnMMhFwCj55eBbel7vXCiUPTuUFM9IrndCqMPBlImCrEe7G9RqE/k5AUl9F3kgC/3M+cgqVRDSnMrckaXnTbJ5qHp6Pf1SnOgI99JD4Sv1wqZ64dfArCXtY3bulK+pylcui/w797wwbKPvjMiqitmJoj2t2qeMR95H3BjdGO+GGIe4e8c7vLk94O9+/Q18cpjJ3ZORPyfnABCfiwSkBojEdU1bztmOZNnROhysLFC0U9Rr+IPKlgoBdAYtES0GAd20tBvJgrycaEOe7alXzWudCK8p/9q2v3SyNKxxjjTTTcX3rAD/efWpTmJg+9MDcVFjTVkzbfnyYPypB+KPk/oS1wIT++M0vrHsH3t+hL+Q0fla5VxujMiclRGdEA5yV8SAgJHi0ZlJslYdrIhGFn5XKYfZsAazVghwDJa7yHomSjIg69g3HH7TONS/6qmkDDzkCCNRR6D9ScDomhf5qWdv4kycRg837nAz7nAYxnxcjPMx0FEvEc5FHCgFNWR5lAE4BISwgIhmvDSunwjMBEdJ7hGZLxl51Y6dIuvj0apBNSErt7JcRi27nvVYphkhbjlFaId8NXGBJ1auNoNhdLr4v+AmIQYVOcAPgPNZbkqOBjhxM1FmGJRrDaZ+I1E2Y2p/ZviQ8aI/Fbmhbsc5D0CnwNoQijNJdAkKMpdywgkrbGxhlXlHzCt3aChIF9r9pZP23AwNsGY/kIGz8nyiQkQYBg96YPjPI27f3uDwZox21WGA93IXS2rvS/Rc1Zca1nVpyuq3bGkLEsoW+GEQ2Py8Dsi8DizmczIqZBPMy8dk+9FMKVJcPkXRsUqMgB0z1oBLvg2NiVZmCXUqz7A6UVaXmvLLP0t4YOBeg63HP+xrQxis97gpJ7Skmdi2YukdSXA7lQq5slkHOI5no+9Hj/ubPY7TGcdpKtoCAMekDJPBuD2dEOYJdHKA8zjfzKBhQPCjUXgjCRIPN3DGNHEk7KlLHJLzIQRMc8A0BcxzZGjH4xPG6WwMKpnw2W6r4wPCw9PcmGMIZC72FHAebrTwkT/i4fGnPJskyr0w6DgQnhzYEc4ugIcBxHGMQuDYVwrR2eYI6mTT+c0CklyOmwmTKyJYY27JI3ihHY39NEhHnnC+exu3NtYIa4nsYQfaPaNNCV4VSKKxbDw9w/OEJK5kWMBAcDg83cOHQRmVUPVASJfeBu1nqZuatdzR8FrSWnWnIAVREFiLQIrbQmGXbNN7XcSUYaScAcCKW8JOjU1Gb6E6c0+oWNN2W0KFzsgYONjgz1KFlu6WqaCVtlTFm9ofUjvpXEmeVcPDKp0tM/S859sUZGv8QCmD9kChYgqVccuncyKYGAZbCIx28eWf5XBtYMA9vLoibTceUB4YwY2kAHEHg+tfURkB4EIq50EhYAbgGYAHZiTcSPROghOk1Rj1BMzEII67CpSucIqMCtFh/eiO+N3Nz/h5/ozvJo8PgTHPM4AAl45hlF0NBMSt6kQYnIOntCOC4nFNBHtMjqH71RguOSIsTZb1J4738n0a5rRdXlZgxMNMv6WMHKlEKU+kw5kXFmxRlb2s/ImgrSQawF/+j/8Dbr9+h92buzzTSgLlSY3baNYDqhwWz9JKQUn469K5baFHFpbiUmA7GWzydOniUpK61vJS9X2NG+XZiApb0KOYkmAD/vwTwudPCKeTVV0U/ig3zJjwAMYZ3sWjTD0RDuOIb96+wd1hl3fvUMK9AlcFnCRfi9CnMpBxCFDiZMqzCIDNL7CR5s9OipLRKZ+snBbFGOv0k1ZvUw7EtOsqj28RSNPh6+2clDixrFRiQcHqGQqM8ECdIt1k6WL/XZ8sL9ec+7LEAPqKRtFO15jVB0OpsmqnFQ8o1nR1j1R3nOo6FuazibRaG0vb5OVZ2ZwqcvOq+q/h10tjIO9Ki9pCY+U4i98xynTl7hWlC/Y3bH4Hm66ycwvavDhdKKywrFlKXo8T7fERZcdWacxqWhogegHYVua8XHjtSIytTbejQkBwxVtWeuMiKYl/EAPjUpAGZgx0wsQjPM6IwSeGriBrX82IUY0GOUcRKKcnBdUYLtWYo4S0ilQ5R3sFWGgcd6oQ/pBMzrLjIQKSaaVRimJdyTYmegNl3T8+4Vx9R4E4O4ff3TEe9w5339zg3VdvsR8H7AaXYSUgXp6ZNXgr40a+zGXVoWqoSQloNmNMRs2RHQ36by6OqoxCaTyKie0/njGnoyzVATGnuyOSEyLOFps7yCvYUdLqEtepJa3CzNgZ2SmNSRqHaEfycTeEG7StoJdVA4JFUaKKl3PrlBFF/V6C3ESGJYFW5kl6xPmUcP3Tzod9YnebpNscIHp3I3p1dVHV2jWQKXYvX8gtjiS5fFouxdY7ITBDgsbkgvMMvaVRC7jFZc5yjbZlWgrKi8+bOllwo0+Ds9Zr4LZ2OJG3HTB4wjgQ3ux2uEuOwMPO42ZPGFyeg0gWShdnT65Y5XwKwrIsVeZfp+il3EWlTWQbO9G1H4vI3RqMvPtr4agx6csr5ITNjgiYy6oBykf+tNakRPtbibbxL1Tvyi9tnuIrmRaoL0hE/b830ZXw3GkxV7L2ss0TEtFTW3uH1Re/CN0+k8mgSi9R289AKtsyMw67EbthwMcn4DTPnfaMasbAm9OT/p6dww+YMQ8jxuEAonimMSiSIrlgKKYPkPlnjob8eZ4xzzNO5xnnmTFNU/o3q1OCA8dLjKwgndAoGpxKR4RsmaojUHeHE97c7HXsnh++x+Pn7xBn2cERonHKlI+RszGCdocjvPfY7XYg2e3BDCKG8xy9o6mMTjNnAm//2dRjmIx8d4SSWKpx0GM6/ApqMKjqlHrPRHgQxsC5GooxyxiGAc4NGp17++PP2D1/AgplJO7dcLPHzR/ewJ+98pUQZjAAHwKYsqDQWyNKkpaU6768qAy/hIewrGBbQ03BtmM+E7nQG79FmGrWvkp6qNMdYZW2Du7TjC2MoMlEiQn0K6TOSK61tTQsXH9phoQK/r2EDZuAaMpcmK/FRBW45Twwyv7avDbCOQShM1zlRCvsct1C9XIDzMtpYfxWh6YWXewiK/ljCA49IbDXCFE8/g0MOGbMaZ0oXQYQiKJiwcJ78ywEtts2GS6NrWzJntMW7SkEfBie8D8dfoun0xGfjwNO8wkhTAAHNdiCSe9/kEt/B+fj7gjZCUHQ+yGUbqvAIf2ihU/7z0SVJSXY8oDCkNvcQ8FpjXCu0JQRDK330gCCazKOLiqAQfW8uNVdeC8R/vb/8h/w1d/9bVQKIWeh9qZUtla7RCYFFito1kjGsjKNvFXXa6hn+mON85Rohq0i196p1jzI2Fa0gsu0wuRlFP3VtrW7mXZKb/U+jmAuUg+M8PP34B9+h/kIMA8J3rQeCPAOCJgx048gN2M37OBcdJbd7Xf4V796j8F7EySA7IRwVr4z+GccCtBn8lMG1TgzkrMuD6YpK/xTYS75hm2zrCMvoZ4DQuswa8Y6IKTu8nm3ho3G0U5eQ7YbXKpliA11L/9+fbmyjxHzylQp1Eo+enXajncWZwOSrOgOkwcgckvT1FJ3tiqdGyb2izofqrRVB7+cXlBL7XSwzxdTDbEQUbNmuTofuldfatvS5z9J2tRsLdNfXcFCrUtI2nveMZAt2BTaVK/lLzHW11t1ltSw65o1hJ5mREN8vOFB9CxthlzK79KF1UcMGOAxwqUIagOd+bu1Q2lkpV1OemKyM8fLdrNEk5NEwYYsV6XyYkzLcgJ3gHJp2cX70LIjRsYg3w0g0deUho619kjL8/GOFQMVmsyMk3f4r1/NmN84/PWvf4U3dzc47MURkQJbJJgnpJpJdv9KIIR0J9JxtTaYyBaSn0SpfwywAyjuGBB/hNYV4qXTQY5Sned8X5YauZPzYZ6LPGGe0v1vcwpQnYu7zmJTWVbrTX7WS/sIrfc6WH5P0Y1AhGSzRJ4v8gCNYDemo5niXXe1Qdkj6j3qhKCEgyLTGqAFv8qAnfxOnBGxRG4nu/pq2pF2lqiWkGWCgnOz5I0NcdI9ZFoVjORkoHSJOELlRGIAYY68Ijkj5H12QnCGoGv05+LDIGAsWc1fl11V42OfF1Vbuadjf7NlZPJyjjmNi8xT3N0fjxp2GAaH/Uh4f3PA/X6Pm2GHu/2IuwPBdkN2jq0Gna6lVbnu+rosBlG1pl7GCmTc2FasdihekjdfwX+u2BEhhFQ0kzrKQka3I1hSA3I/9ZwaAGzPFuVibrfjZDtEqZBg8ZeU244g/QsmgSXBpojmrRRC23+r1MsXVyBAeuMQCUcyXsQdDAE3+x3IEY6nKTkkWrilOu3DPOPm+Rlnd8bzDuB0SRIjb7kTR0Q2VEQjfpgZc4hM5+aG8NWtwzw7hNljmoEwUzqWjoE5MWlhkLowozJtDUpAPuebjEHI+2fsDn/Q3wf/jLsD4cPHCR8/hngEgiM9U3zw0QFBQxy6EIIR5hnOIR+bkJi7nEVO04Th4XMxdsXuDjuulSKRI1mFpRDON3cIydFhZtso0iX+rUa+qKI/gMjD+wHeDyA3gMjBf/0XwPkd4IbkRBS4AzDNOM7POB+fVbCY5ynCOkchZJ5nDNMON09vUa+jVoE0vy3D6oJfs5aO0FpZp4z9xbRBXbqxtIKpqKD6LNbYSqp5a0GmqMNoucpoYcl1lbsNDKUgNHjWG/2G7C52paQ7EsmhUNblWOXvppEaqjrHIgxpHpp+XBp+NgJsUX9/bLfW2eTjksEvpZyHikIX0ah6n516S9kq4My4FQZjoCu4k1sAiBfGMG6JilFA4LSTzsUABOFzQWJlpCpRvIKI5nAQp0V23M4h4Nkd8Zvbn/ETPeB4OmKazpjnrKwAiQaTQ3Qsx/4Og1e6HM/f99FBQVCekR0RFVWx/LUwnlLzLw9HpMytEbH8bt9bx0ybp08TMy9q5ylHveVxlPKESqZYgHLbC9uRy9Jkn6pler7KH7pwSP+LwazgqqpoaH/+bNZFJ39WsUpl0H77/NMTPv3TR0zHOzgMCFEqj0udGCf8jEBnOA+4FOiwH0d8+/4et4ed4uKSE0IdC2n3jdJGQuZlxvGR+0bmM49R6XjoOCEMf6SV8e1x0WZGr3JClL/r95edTJff9uposXCVKeVfG0SBa1Lt81uOwu4zkC44BU1bz7/GZ6nzrLcMl4WEZbi6wGwpuyL3dttYyn+VgHEhvRAperJEd/avqL+lfRd+X2wdeKnp4s8zLUtwW4dZgxLU6VO+zyj3hYlFCUX1+8vNUV++jOO23srSW8NzoNITYijE5dK2FjUjpmms7zmj4nfkySWI0ZBvnRHROWf6Z+ooSFyqTqKfoyxZSTxcrkFSHV/+UQy4Tg+MRgwAmMnh+zd3+LwjYP8Rt/sd3t3d4u7mgP0wYNDggrxDU/ZEaMAL52AqY6IFkIIfxRZlbFISK9ebZZJyIR27lO52CLpTlDWgNNjjluzOCSmTyjHLxdalLaMQh1Wk7WOGlY1LeaLVi/NpLOmPkXHiTlQHtV8yrAK+xGS7LSnEXN7RQjbzar9WDg6ziFQVF9+Z2BnV3lijfzu4Wmm06QHFXRAIKG1NK7DVP7j7sl9cdZcW1jVdpql5CdQlQ3kLCUDJRuijjXAYHIZ5wO1uxFc3Iw7e4EmjtK3Ao68rwakD0msCMXJoialf76y54madBRCKXT2VXW2x+y/ozmZHhJ59LMpTfqENLw7o4gLvtNP9Td3yOaovZrHOiEqlWG9rFbbeS+7+yg4ILr4XtRXOBn2I0vGQ3lLMb5/ZyDhpk9JZ3kjHAznncNjFY5o+4Ijzs0TQl0y8caIw4/b5GWcifGLC5Fymh8YRkXl/9D6Lc1WOZvr6/R5/85djYkYe8xxSNGxkbJF/yjixwpN6CCfnJGtfKTEROysM4GM1LyNO5zP+8N1zOlfRYUgRtMxjckbEOkOYE8OIUQ/eEbyPgoNz+aJJ7x2GKeDw+Bka3qD0vcYDI6hUeXQcyeHx7g7zOJb9FkOBmZ9uG413OV0gTyPIjYUjwjkP9+YtnBtAfjDGyORxPx8xhf8Men7EPEVP+Pl8BnMwEQ0Tds9vcHN8B+LS+SjQNquBYZgB2zcL/DgzdCQhVkeDBBdQ4AAVf66kfIUBpCKuhp61nVOxEI6EnVPuQkcWVuKUJ7YPDleGu2QAZjlI84tYRZbqkPFYYFndfuWSVnTYRkpJc/ecHqvg1jSyX323DiuelCoFi2S/DHLzPONCOQa8gj/LDSz1aa1tqgurBFyJQNw8adqvYeC045E47o4gApzKZJwcDIDTS+kSeSROl1PHrdcWq2VbdwgzHvwR/+nwHZ7nE06PZ5zP2RERu0LR2UAOjrzueBAHhH4Wd0OgdEQAxZ091zsiDL1ZNBr2v9e7LspU03AgXngYL+SWMa5312lpGW+VPc07bMGghVTITkJzr6zD6iW6pdc00XypC4tR3UIi4FXrfYkmLj2+QENzdFn58PNPz/junz9inA7wUg8n8QczjvgZRGccfDx+yXuPw37EX33zDqPsrFxxQvz/2PuzJlly5UwQ/BQwd4+Is+TJvFuyyCqSVV3T0iIjLSPzNg/z/3/BjFRXd9fWJIu8Wy5ni3A3QOcBqoBiMzePE5n3klPIjONmMCwKQKErluKIUIeTGCCM84CAzL/zN2p+Mx2v32dh3n8GfzWddWTkSqos+lSVvccJ0cMxocVXhnvLqTIPs3Y0Zf6cYZN2YND3Ez6Y37tGzYoapN2E9Gb60FDJ2zJfLfwLytvr1Pg5AjW91A3olXktvy/Sgta40tS9tUjqS8Ne/NiWOXeW8aeY5124DYatsZiV9LKjVayk6aAXQj6Hv5K2e2isDF7Fk5HNuTgj8p5PsfhyLsSW1JRKgDojslxS2V9qLUCbRNIikBO9TvOT/t9Xx1yOkVKY80I5IJIx6EkI3uO/v/sKH04Ojh7xcHfEV69e4eHuiJP38K7sYmY5Itn2ZoQ4KIC8Yp9zl5iaRPFupclWb6eSNDsbgt7lxmU3g9qB8k4J/QvlOcTixCiLZ65h3/j7di7Ly/QoKxLBoiNe5W+0MCsbKIwcYWXXDpDyMdqxuXWSSTF998wLqm2OsANXrI7M+Xt+r0plc/80m7J63YPkUvaRTbO8cvPeA51718xzRTyuIevrsIwt6z7XwoAbUolJcnXaWb/4dDH1MSx4dTrgq7sFfnGmb69WtguUq7ym/bxj50WxRyD3Z7LxWhbIG1PQ5DdPt0nSWsbtHbX/aCadwy0l1s7dDTLdqC3PE9IkzbbfZuMTjSLHQdmDDmzkslNgyGDzwwBW7Ub5Vu18aI2vAOxulAyy7IaIHKstePenAxbn8Pl8wXkNGc7cAi6/UbfZAbgPH3Emhx8WnzZnKQMShhIZePXqgF9+c5foGTNiTLsj7u8izudzurBImVlUZ0QhfpQpU030XOVsaVfc9c82PNwz/uJbByKfd0R473A8pAtNf/wx4LLK0UtghHBJBlj2AHsQCC4EnN7/AA/ALwt8CPAkQhYIjhgHV85rtKHdEZHpFzPOkbEy8OrpE3g95/EuhsWBYGTGCgDWwxHrw6uML06MbuQOIHfEshzglwXOHeDcAr8cjSPCZaNH2vVwj/CbvwGvZ8RLAC5POPzhH8DritU5uBjBIMRTwPu3v02iSkKsYbt1pe7941uc1lco80MnSemfSAEf7n6P4FbU7NEepZWOl3J6pIVzWB88Lm9P3YzXcPzxjMOjnnFYeo+apNrjIIKLC159+gaO610qCfRYDXPhuVpqK+y0PUMjNK2SJuYxTkTUK3u7KNRmohsYBTe/V0pqhd1OgJDI3Hu8wZhnfMKU09TW52OIg4Wqz+XZcItrfGnwTR3htXqj3KHN0/bWnpEc04TRau+crokn0YDq1Xu3CAtiOA1Ki2U+ct6ALr8x10OgdI+OkV0jRzy6M/7+/jv84B7xeH7COVywXoI4QtNoeFe2V+uOCD1mz/s0Rxdfjs6zzsN2R0Plxh84IuyuO5vGGoev9s5eA7kEXaHXrj6qj/4r/arf9Vt50/qKbGYkh/JvC1+D52T+bJkqXNQOr9Hl51WlRkkgU7BdvIJK5qmM1SOj6qA/xyvfa3l0OvaaztI2OVIz/XA5y5gBd77DHX4J4JhhYjCe+HtEnOEWhvNL3nWZjg/zhY+RkwUO/T1ruksi94ko0wq9HrmUj16SZriMp6WthXWZ98aBkH8V321cHg/No/Ng7oSop0ipo5fVRmM3midzPjiK0O3ie50QW3NznxOiQfLht+thDMYGbNNydtZp8KVauVnVsRf+/e0clXtb7j+jsKev/ywM2v+Swpf05768/2PITJiKhuNOSqpgOqKJ5VR9Tu76cZFKpid2vSqONF0xhFpnRK7/qjNCC9JFDizwappeUcxnwBOQjy/aNuwYmUvtGlTaJEJTJXYQ4zM+4uII3/ziNb56c483D3e4PxxwcGn3cXLMpKOPwCS2HQY4CPMVZ0S2CWkbVX9l6UcDi0rtshhUNRaV4VnugwhhReCIEFex+cgl1dmeE9JRTGFNNh6Wo5my84JR7txq9FhqVnJr4AJjliGe5ezsFVdSB4RzgFlkm7+jkWuHQu4AZhNr9zhskZWCskbmH5XcoHKVR5UtuXQ6t1iOYJKXviwtQx16+Tf9Y3e55wyzIaja0H+s78goWbrNS5tyVfupGbVd+GFmnlFnHBEO3sGthOU7wp074O50xGHxcN6PHVY3hxsWdX1hdbmVpo2VDW5K3+chjZfQCyf37ADDo2+fG248mqkw7c4h8dJhS2HYeLv+bqK6T4MPNg1XPyaaq9+cr7UWWGWxKj71ZeljVyFSyW9ytN4JTgjiouyOiIk03R0WnBaPNUac14B6J0Qhguq5DuKMuOMVRA6XcMAKNY6U7XXMjLdvHH7zywWgXF1mUpfzxXjMOf9xHHWiZRZNzzR4N1NuNTw8EB4eTmJYIiyys+F4SEcVffx8xuNTYrIERow+3evBi5ScLmc9fviAhSOWZUFWzkUpPzjgYbkB54VfYI2gCByeRpdN7wvrwys8vXmdYcrHR7kDnD/BiyPCu6M4Ik7wfoHzCyidHZGBYmZcjvdpFfL5DP78Afzhe7B7BF/SWHowomd8PHwvggjknMG+geloFsYSDjhe7uVLuexakwKMQCt+PP4Ol+XRcFhtkwc5h8UvsrPF5x0ul69f4dNvjqjIjyn74befcPrxsZynfi04wrLe4dXTN6BYLt1VEsuxVKTb1NJaFII5ABQM2RF6ky5fRNcsWLeJSJkJl7S7yr6e+hr/zrkndK8qq4PcXFNr5TkjpeXdBDyaz9Slr947aa8VTtoyFYiJQlXBOus3HmenNgnlpAXMXqgd9eewj7PkpjR/H5KVuhWPrMDYSyQjsbskJdGKkvMzqoFSnRzgvKIcmlwEWBbmEGPEJ3rC/3b8HR6x4nw+p/uDzB1CAOCdcTKgOFvtXT+eqHIeVMb4Zg6Xbmt5yo5fVSYHO9G23nP/ZUNplTqvlhvteGPWrdNmKzyXstr7lbTM/qkO3VzcCtJxlYF7o+RKIKU+5abtuS1DB42MY6VxIrU5bdnZCUHj9G1g/U8VMdZt6kmucesJB7xDoKRsJ0M948I/IronHP0R3nv5c7KbkowToux6GDkh8k7FjMdmtwSQFxBUIp+m1X6i0skzJwQsXks51tFgnRAweYZlzMZi4oSo09VldPFTNGvHvcA3gq3PPkfCMZx9Wv3Msx10+fs4vtQx56ZTCCY0Z47dI9iFZucUtJXlOnDd51m/7ONZu8LOsnY5WmZlzQbyC2C62rU1kuwWJdvQSjo32h0aoPTneeNq5cJrPLJLV9uNXiTM4R1KPl2+HlZJ/UWdfC20hT9/ZPf2ZW3zo+rLSEdJskxyRET2AJzgDOUk1TWngx0CM4hVbiVCWtwC3R/BKpLKBdZWKbC2GCoytLaHzBKkRpfImpjWRQCz20ARznKw8vZ8T7S0XR0qVoFhYjzFT1idw+t3v8T9wx1e351w5z0OssVXy0n6rLRDLoJmp1FGNjJNTk2gMXLaKN2tIH8suxmC2emQ7AVRFqOWXQ/qiCg7IUKx9YgTIsbY2Mb2YWFlQN0Rem7Y2ONE1mFy6c+kS6diCkYYhXQ20xptM8fWqi4P0sg3UzB35ReFmwbR+SWWGnTHSX0X6QBmLZoLWrD5Z0jH8jxVHKkBqsqRp0raG9gPRiaBbt4OG9C8zEhj2+PNHNe574iwLB7+M+H04YRXr17h+Pogd62WY5m0/ay5DQ5v7wq0snlLOceyVxt/bQYYcVv9jjmCqdhY2rS2Ujt2oxp0vNorEGocfz6nvuFoJkvslLoC/RT7icJIgW4UqzE0N2ne887MeF8uCs4GGLRbmSx8BraKuJU+1LVp2WBklcAOHGqeG0TQ0x1kwT4hXbb0cDrguPjMFD48PmEV4w8ZaYpjlLscIlyMeBdWPILwHfSsb+DhYcG3v7rH/f2CS7gkmhj1eA4WL3rIxhN1QERzjMewNWYyjQg9dQ+jQDkJEeEiRyDEeID3Hr/4xuOrt4Qff4wIITkiECJOHx5xJMLh8YiFCI7LRd8LGKdDuTA7HRMyqLYDupZS7+FkTWUPLwO4rONNTRa/fVix/PhDiX/9Gu7+K5A/gZYj/HKU45lO8G7Bstyly6uXdCk3iZFPjV3LckGIEeQeEZzD+S/+LeJ6RjifEWIyFsYQsK5n2Xq5Yvn8EYdPPxYOVrghAODj6Ts8uo/JmGPOfGdlnJzm0Tk+IoZ0IVpwCz4/vAX8AcvhiMNCuHvtQM4lR4qc68inBd57xOM94ulV7mL39Anu/Bnh3Rs8PqgTZDswOVzevIMPhPU3T6DwBCKCP0fcf3fB4emIu49fFUmBk/CYJEDj6JDvKjQOcaOrHLALxudA2kKubHrj5ndjmlSMaavaZwazmVqEO1OZKTz3QVdhc+ePzcOGBJi2pipGLdqm/5nJXk25P/SCaw/ZWMhtcrY3yEEEn5GhYtKALGiOBLkJ3IVOGwe0fI25TLuKp2y/joYmrLTiv939EWdaESPjM634fLkgICKsUY5xEoHQ+Sygq9NBHRHqgMjOCDR8P/NMV9HehgUPnQ3TIw64TvcSx1BU9ywZ3qu8spzBKwsDOJq/omjYkE34pDLFADdmiK159PlqhushL6ioZKod5dHttVZOCNK+KAVRA0tpK0SvKvtO+p5VrK8FlqfwR6z8BLdEeLfgsCx55+Xp4PGbX7zD/fGAxRcnBFFxQjg95pRKl6ujIu/U0V7THRHZQYCSN2XIY2+dRtOdDxLvSsKSvy3LmXwm7dwpYd/a8a9D/8XM11EYfpgt7LktzMXJ+kNjJ765zD3G+DqNUeg7J8y8b9H2KjW08sW43L7QO6vK87YO//PC+WcRBn11zXE1CrUo8KfrRzUY/0nqpi+RY2/v839Joe47Q+etHCloVXZCJCdEZFdkRMNwLXtgK3RfhwZak0JS9AsxtOlZoRVwrUI+e29lbN6GrSJaRXZoKbQIGJWMnAuNEYiEIwGnxeObVw94dXeHo0/HxGR5RsZBF/OQnCpQjn0iOE2YfwvNIKg9haGr56GXTcfawcCcnAhBHQuh3AGR9QBzHFNYA2JcZUdE+pYWFMV8cgbMgsDady8vztoPxiM1d8qqnEe5/OpUiaz4pHciB3JLuqza+Vxp4aV2DG/VBmsZss3Z2bysw0DVjXyMVZOh093qgq2eBi64wl0BpSAV+4fFNguV8/NAf6xtddx+vsLgu4pviu5CMRA2v01ZgjN6L8TpsOAQHN68usfrhxNOp4PcRUhQ++5Pzgq2UO1mVlTLemycrrc692xgIN+DI97ZrC98adjviLA9Rd3D1aDGI2UgzwoVbbAE90tFrQ2hvppbZfJl4gHGYC9TXbpVhpVfNHUSICvjjELWKHYW1g527VumygkRKYKYcHc8mJ0PEY/nC9Yw3ISVGZVj4HVY4UH4IxGCAHVcFnz7mzsAEGbFCKGs2oycvOWpKLMbonFCdH2kfcr1MRVVH+5AekNrysXXDjhExtu3Bzjn8fHjGZcLwMJkT5dHHJlxWM/J6H08AnJGo3MOJ09GKRg1YOs9vRwWwmGSMV0NTcOVdrZOF2O5OJsIOJ3gDgfQsoCWQ9oR4eXPHbAsx3RM03JMOw18Ou5I+5jcIa1iYAY5j/WX/woxrOCnR3AIiE9PCGHFen5KAsd6AcPh8PlD6WmO6UcEns+H9+AlrR6FMFe9wAoyXzIapCs6sDrgw/EV6HDC8XQHPgLua4JbCCEf0ZTOHyUi4PQAvPkG6qyj94ALF4TXCwIK3mwF9gvO734FICI8/BZO4Ds+riD+AP54j9Pnd3CRxAFRmpy29lIlCOgoRa4pyXAaA1lIvQpnsYveFvb0wTO/Xa+zMMA8H3v5XR55YGjRMRx2XJ4nrUPCHkmfeE4nEg7Ka/YrZC+NyStLDfbKVW2yPXIGV2/mx0i3tpxhv44q3BBki7zI3Yes8Ogz+iHMvFBeIvSOiLSi/Mmd8V+XP+CDXxFiqidkBSc5qNX46r0oB7qaXI2wMO/ym4Ug0+BsaK0shgXi2c6HrVDdO9UZiXonxrycvlz7q4pEOX+3HJVYLgs05+1Cm6kyhVkhPw3Xv5U5ALRzcn+5xeigxvLrJVBXzLVc15wQw3SjglnHwRIlVeYs/gCIESt9xIpPOLjkFF+cl7tKCMuy4BdvX+Mol6pTU6mFJdvzYXYwWEeEGv5HOyIEoJStdkKgxXN9tgq9lZtHTgita+SEMOV0+G/aVLUX6N7V+dKANMWXDXNE/b6Jbw3fmObZm+6WMOZFV3dXtWMhkdf0qOnOoaQc3Bjm47in7nqqkkDBs6F+sTCFcyBv2MA703XpnxH6cSpz9vn4ZgUhLXVnvhcO19rwortlUoGjxzbRZlbu+mx7hPc04fZ1DFPrY1Pu7dg3y5F4wDWB0paQ9KDsiIDDGnW1ueIgDZ1CRtK9GjRtztM8EAA0zoj5Va1NvAorQwBHZbD5d7stXP+TY9UWcnTAsix4e7rHw+mIo9x7RsRm1bzIyVAx2yiipDKPUA3X8Hhrp4LK8uW9OCHq+x6SjJ7sAnokEyIjQo9kimA5mimYfHq3RNIFYtkZUjp62MUkYznSiEez0MpOnNtvtLhKMZFSKJ11xc4lR4SVPZq/tkaDZQ0ko1DvjGhX1pp9DMkcoouP9Osevb0Z11KFOpfa9hs5NrdFXXlcYOS2gmKI18uPM/7nOrmpon3/gtCBPynUyp2E6i6YUZlEyLuXD37B3dHjAUfcHQ84LGlns5l+sKM2DVd4wFwW2f6ucnnVhAmOlGSU06kzQmPrrFyl3xUEV7sFfF8w4DfdEZF+iwJza7XVSlZT6O1iyC05aPy4s4jKn20malRrKvcDMBKsWieEviddzGX4yDz0KzW3YVW+k0/xYMAhedcjojDrdPnK24d7vIrJOx6Y8f2Hz1jXNTUpRnC+oMjhxIxvmfEI4A8gvP9wwf/nP/wRb18f8e1v7qF3R2SnQzaalMmgxHLUjuRcK5FR7qmovHdVphlDYOilWXk7Zx67iNUHOTZhweP5jMcLcDx6eDjEGAyTl/rMCtUMqKl+ZuDoCIpexox5cHB4ZbwUkYFzTHUSmfMeObGarIYuDv7gQIcD3OGExR/FGZEcEIs/5SOayPl0VwQZIuVXhBAQYkiOiBBBbkXgdFdGZIJbL2mFAzmECFzu3+L918gXjydvgggoMZUX1xV3n77Dsj5m51cMMeNXgMMPh9cIzqUjRv0CRMB7QvzVK5yPHu4hOY2W5QByHt4lLzU5DzqesCzH0vcP78DHVyiXd+0gi87Bn05pDr/7NQKnOXcOwA9fRbhPT/jx1x9w+HTB6bsn2S0Ucfj8gLsPbyxlKHSAMRS6R8B0RrNNhsfDQjNedIXfSlsrrbVh/KNSrvWu6RPStmrZprz5lohpPYmMcl2UtrdhkmyYzohnVYKVyVdgMrl2XBo1C2zoX6lymy6wfWJO/r6s2PEooTHmDQsqxdWlm/7vV9hEFXRjlOd0R5CVERmJLq0c8J/vfocP9ATmiDMH/BjOCDHKqqlyDGB7MXU2+gvvU6cjoeyQ8PLbXn63x7mg5c9++wypH6ffrwSW3fQla81PrJO93g2RaGvmq80f0LGcKrQyhDVZqr6qMc7Gj9og/+xv/o6ERRTq8hSe2vxmOKlJh9weS09Hiz9uDj/+Du7H73C5/BOe6D0uvCIiAO4MD5e2dHuPZVlwWDz+8pdvcac7IaiR8fLOCP0zcOc5bR0QxgkB5HnQiRzqGGjbLTsh2p0PlSOh7WMBivSieru1L8uj1LzbJM0cbMUgO84vYHwcDeu8XIVt8OXZTohZXSOKbts+Z3ets2EWblnM1YM94oTDSq7CMa7vy8f2S8NeB8RtZW5/49GzjvWky0dOiP5NMX2vxv2n7/8XCbc0+X+EFwm9tN+uF1ddGADp6liHdCyTx/fxgt+FH3GIjFNX+nxAh7Yx87J7VTIBY+fBdqglcakry2n6jWHBsPYJNpFs4I1NmcwRqyP8l18f8eGO8PBX7/Dm7QPe3N3hdFzgFtn5L4tJkz5rjg4iB3IMJjm/PgkJSPdXmk4gAnE6/aKW9DkJpnofKCeHAkdGWFfEGBDWizgj1iSDhjXlznd+rojBOCtCkOOajM4wu1txEHS0LF+sWU+NlZZk5uGuczWYlvoHbgG7BR8Xh5Ugx8umtI6SLExSPgnUtuaWxo9D3dvUMfrKapBHR+X6aHWvPTgseJr1IVWLspeg1edNyA2SBnO5L2Q8Vzk7I0qzbPk75+gwDFZzc/Nr+g5t/Shj1o2OYcY5tTgAD4cFp+OCO1rwig64Oy44HBd470wB2/Rka7f8z8KJu0pqOTs7I8QW8yU8NXel2tdk0lb6xDPCs45mynH4ojblMl4+Y6cBpZ8rlZUpSHVsMyEyU2wMOmNIjFKmimdWUOvnNl8NxViBqVdw5MxmZ0T64JTYRAaTw92RMgELkfHRPyFGB6eGPAYoAkSMBRFvOcIz4XtHOJ8D/um3Z6yXiF/98iQ0j82KzSjH8BQmPZqnWT5vvikxTnkbRo/yrS2NGeL5U8ws40RIR4Nc1gOcY6zxghAo7QZwCf6RwUf7sw153Ca4Vr9S9Yknyb1yQQCBgdVwwFxCaiQAucjVE7xP28zcsmBZFjmaaYFzi9yzsMAti1xanXYXpD5NuzCIHBZ/ADPg/QIGwft0vpf3yTnlworIALmAeLjH0yufzq2U1c+EiDVc0gVXlwuCu8B9fg8SY1pyUHFaVcGMQBE/kseFFpADPHncM6ftcK+PiMcD1uN9uv8i7+ZYALk7QldGJ2LIwN1DbpMy4T20xenKk4McmkUu9f1rBj5/wNPyAYcfL4jrBzkPM+B+JRzpNXQlAVM5fgokcw1Avhytm8n6mcYS+MxK0aXlPjp/vpUyb9Q5XCE1K8bOG+2HNL8y/lfG1LnwMpOdUHWb9HCTmLNvVxglZZltUGBdZ5Z9WyioatLtoXWOXRkj+7XQo57rlpUqyL08OpdzVHi1Ih+AblfKZ40yZ8G2bLcewM4Ac0RAxH8/vMcf/WNybKtwHAtdVUeEhnwWp7awMtiWP+dc2uGm4E+M1BYoO0MI206IKb6N4icrVIpQanG/L922X/tYnRAx1nworzRrHBhDuDah3p96y/lyixF0s25qX63KZxTAmZOJ2nwYp8vJmzGbzI6c/fN78I+/Qww/4IIPWLHmlUVOnGdeVjAeDwe8e/0Kd4elXKCeYbSrFLX8euUiaTtURiQkowNMflNkbifV5VT9ZctvG0cqQ1DWRQFUToiqzuI5aTppPFYF1tLns1Xys3AVzwZ1zApuHTXTwq6mH6fTwNynGaUd6lNTvN0XhvmnfbQ3NHNvQnpuHdvnwNQt+NrK/6V9OS12/MXyYBJFrXBsqnZqXoO13glRnIyze0muFDfB0Z1lzMZ743Mt7fbySrVIZAuGvaM1m9OWgD2ziD7dPtj31PGMIv4kwY7DaDx1RTqzw6dwwQ/rI95xKBpKw+82m81XU2SoCjQGplxJNr1thrYl4/iYI1Obil2hokqsb2b5qsjMJU2So3/7Gvj0xuFvv7rD3as7HA8LTssh736EExoSUqOE+yY9RhfjOOSLCbsFHF27RHYHm6N70k4HjozIIe1wsLsbVE7XBTEaH3TRYSi7da3MGo3Ey9gchWIgTe0doFeT/npM1WZJQmY3xArCSvpdZS/biz0ANr7diz0NPFKfzX4ILmlKhEnZoPS0GqPYqnOsmkZXJkHb5Q5kHGg9bPqYW1IGuqRpyr/SgnHG6r3trDpxtyi4V0/rQCQ7ItIC14P3OLHHUXZDFJ1Ue2cbMUfOiE4Of8GwpbOO0lpnxNhxUnTk3UFtxUMjNPYzVdyyI6JrMu3qhF2hFZYnsv+tAzpbmdUHO4khgyXPjaMuVkxposhWCluJVQNlVvaywFmIYV2QXpZStkR1tktNSklQJTHEKxOsV/iSbohIzIKSAYSI8fXrV1hjwPcfP2MNAVgDOEZcCODoECjiFRh/BcYnR/hHR/jw8YL/73/4I75+d8JffPsA5xwiIjhsiwDWoTIW6Grl1RrLRqGUpUmsE0SY48rpWKPHJyyLx69+uYCjw48/XPD0FLBixcIEzxEUy4rb+4WQnaPM25MrC77FKFW3pm1dP6e0eE/APSWmZ/MHdjjHBAcBcJ8+wv33v4f7xb/C8vA1vD9g8bIjwi9Y/EF2RBxkR4QczSTNWQTOw/EEcg6XNQBuxSVGMBFcOKSVAs6DyC7x1T/DlpkAJoTIWJnxw+EBxB6XkFZYrOtFVl4EBGZ8fnoC0wW0OPhlweF0D8cMkB7BlP4c6WXVwiT8ki+wZUCOTVJCWlZlzDBwOII6dkRiDIyIxwes775FPHwAA/AfPuPw3Ud8vnuP87vHJICFUAQ0qZQIcOzw5uOvcFrvBwrRFQmjMtTbHNzFWEat7LKWArYEtbYDNgQCk2oWOhipYWvP4cgDMCl330ABURobFYQtAX0wNzueYVPsvAB9GuZIWQmOaJOJ4sDI/KL9psGYL+Rh0umSRXf21StzitMhr9SJhcim3UbmuL0YsVLEf3r4Pf7oPuG9O1d0XY+JHd0fb40u9leb6SjxzbJTIlFE7YdtgwCBjUitB3DZ33w8zKi7noGvNa9Sjl/3be9QoOxwqP6a7fKdg7yq2JKZwqda4/6Njdnkd1OlkFm229fnk2o/50URGBS/F8xGZuxwSBO4Ot0wcP2gXfz+D4/47v/4Dp9/PBc8Zc53lSze43BY8K9//TXujwecxAmRL6QmJw4FwWlX7jsBkI392aEg91nl366DFHdr2aKbQ9Tvfmh3QliDakcjR4ZRM2auSefavp2MzShNqaN92A6FTLvthDlt2XlSB+7irjstbg/jojRyw+m3uz9mY3AF97dL7csmoN0Z+HPtgNjVjp8Qlq12bu6su7UOqxOSLXue7xajttW/Zt/LC/ZZO0zyrq792V84/Dx4+S8zWLmSclTS7I0gJ0ia7oVwOPzD7/Gbv/snLJ9/hB7/0tFX+Sev12AYSthCUes51XeT156CoFWmE4P33lFS0qj+KC/5c7YqZP3S7nJm8675VVY2ZcUAMHB/Bu7CCd++eY2HVw84Lovs+PeAOBk4quwqvMtRWrxGBFq87Z05qhv4s9IP0Zf1QumY7oRY5W4IvSOCrQwqJxrEGPJOiBA0jdpZYlddtoVMe9uOUVn8sG/MSmHJZmfxlYqkLztG2Kf7IS7OI1DqSzI6RtoRYd0MufcNrNsksRuGSrZkRPuecUj0AiAhrY5T7svBoVDS39U8tWPbKpTmc0mj9TKsoZNtmX1DBtFzvXaSoY/bLMdOfvNM9kH0DEa+K6Ry3FP9QERYDgscDsDnB3hacHdY8Prk8Yt7B09yEkDOc72BWzsj5pn056flVZUzQo/M/gJPeJ5pSt++0OlygyNiX9jvFJmsuMpf29SzL5PSN5wQ0/7neZqKMG4JcaqwNYgPiU92D1VUU0I3VJBsoTXXHqXknEzStGWqtxlyvraTkmJKe3c6IASPT09ngBnRJXFjcQ6R5BRIJngpZ3EO6yXiu4+POCzOHEPhAIr91JVumdtRChMp7cgta37rZtnfrlyZKFEY5mVdQQS8eX0CkcePP6zp0iWXTFYcGUzJEEdgLI7gnNS7uazJ9LcxwBb8r9eVVOknJXkhtJVywxBDLCdDx+UMvA+gN+dkqBdhRg33zmuck8uqk3E/X6zsHBicj0Zx3sMxw5FP4y558vZPgUVX/nUChgglkRkXd0BcCGcmRARcCIgIWMWgFsMKEMFhScIsOAkHKkhYA4i5IyJfZOtc7h9LVHUXxqx3R/FEKsY6wIkIvRwQ8AocI85v7nBYAxZ8QlhWPN0/5h0SqzheVBBzAMCEw+MbuHCylcgQCntrlvG7ARITKBn0ZLwqwcP2u3mg8ZdZjj4+C6wDaLaU4abMIl5qgueyKUt7afRoOaNCKq881LwzdWmNbt3U3GLWz2Xk43yjLufmY2vsqIUJc/FaewxWO3C5PLN5nFUo1dVNKI5cY2CPkKOVIH8UsWLFHw6f8NvlE9Y15lVRbdvyKp+BIVRXoSRjTOJLDlQuP66a0iu4VX9JZdx9a/lJCWo0ucWYNN+SK3M9s6zaiVD6lPK3ahcEt8cyzetK9bH59/lhM//g41QW2QFIEdEaIbZ1YLb5ivRev/cJt7+3gQE2Ctn5ccWH7x6xrrEUR+WuEu89jsuCtw93uD8d4KtLJtWQWH6Lg6KAl50IlbG/nrPV9xINmLw53bXQKgxmUiXZVL9beZUMSAPY2irQfJsOj0yORlhqx2tLhxjGjmCaFtL0aZf+ttm0NQRjGEZ0aPt9Wq5JNppTts7dNK6hvQXcHYQA/Vg+K9xAj2c9fL2KZ8Kp+Rq+3O+K6GWNrqgBTNPdYCaMnBRbOzcs2FNYspw/lptm733hX+Bkm+HaRnjOzpxxOQJCbr6dANdh32PkmRXR1zmtpYLlSwxLN4WG3LCacJng3n/E69/9AdFdsug5FgVIcpK4NTZ0mmuwZBZSj1GVhLroYWiTdAbxyglRJMpKbm4NqsZAHJgRCDjFgIMjvD2dcDoesdidEJSMhUym71yRJxPP17ObdqB4hxcKHxc5vlv0Ek2bzF1lMZadEJIOWT5NRce2mi7Upn02jSABt3Yg0XyyWKsK22QW65x8kL4F6UHlFTSUn3fM3WHsoJ/NMzefrM5uFPyMYzZRIYVcj6fiW1e+xHH7pdHvG9xgm1pgqHuEc7oWxlmYzey25qoPhlmaTtO4gQ7f10D5L5myRI6PDi4csLgDDt7h6Aknn5K2XdT2QbvoSXcb7A4Z5ydyMreJ+77ZSdZS2hd2RtiQTxiAacYNZX+BI2KfyptW6ctLKzArbSgPVbKKvYyqGg66IkUhahXIMzjtBBsnmJbR7oAw69mEcSi45bxfyC8JcbyKv1nYsBJSAcYqqZnOVBd1ylYIYpmolH5dYZKOCF+/eYV1DfjuwyPWGLDKxaAhBKRjnCIcA/+WAqIjBEf4/DHif/vf3+OXvzji2988gBxwpiBb/jivWFfY42RFQdurzw+WnSSGrd0RQsSF1uSQAOPpcgFWYPWEILCRMOUQHWKMIDhd7J9ELkY52n4ErSCfZXW7oR5I+pZtLwDufDoMKUB31QAkqzT1z/slOSEWLzsJPIg8nE9Gf5dhZ1AgLD6t1Dj4BWDA+RUODCIPUEz4A5LVD0J4VNGSuCDnRl4uK86XM87nJ4R1xeWcLry+XC7pPorLmgUZEOF0/wB3OoL+4i3w6j55YISocZowyZDjXHKU2EtrjXE/74QgzkeMdbxtMBSJvsgKCpGJohp/HMDHV3j66jfA+Xvc0XvoyZ+RgcCMv3/4Cr8/vTJCAUBM+O1XRzzEtauTM2aW1ZzL5RGvv/tHOFllrpTv7vIa7z7/GoptbBvUcaExo9ps/DB0nPe27FM49s6DfR/HSnBTlxo1B1NLv2/CeQsZ2i0RXMs/4UWb5dcfCwulNkaSW4FSV+qo0Vv2/cVaKNUZ9f3pH/HRf4fvl3t8Ji/OuIA/4hEh6E4Jw6tQLqROVTsBqwhujsThQGU+KtTXVqKmMgfISrom6mWELRvsUUxtHCBCKUj6TVcuyRfj2NHnEEL+S7wnll+UYw8jN5umVd6oRagOti49buVPswl0LQv179Qk2gsCeqG9UmmtYlDJljeEpnPJ8B72HmCWeyE8/vWvv8br+zucDgfojoc0Fk7uRdQdDjpGZZUzgHL/g24DJ5ERyeQ17SbhhVV3kdnx0L4PntGkze95bIos2pKOUb4K30BNur57u/GgGh/2j9cNKaeG0GvpnieD3mbUtmkLPbx5J8RoPpREgzwjHt12CPouIEJxbu8C8WcLM3C0tS8Oru1XcTz0dXfLMcZFmXLKNB8NQBv6hQl7+OVzwq6cL+QIyHlvWLzyc+3M+ZcfWpnJMoKRUqAXVhOie4JzjyrEbdaihitZTpYdaox+Ltl1idbqkQyRA7BQT8mcpEmbi7Xpmu9De5pRkWodk40BxgAb090Q/8evj3j/QPjFX7/DV1+9wcPdEaeDB7wDO+N4VEU7b/9WfTjFlTswKaUZ9EGW3nMjpEzdCaG7+eVuiPyX73xIjgbd+aA7JdLOCHFWqBMCSd7vF6M11LdBCZY0Tgw0MXOh9GVLch9hV8ll7wNI+x0OT4wQHdbFI8AnY2wRFU29tvCan7JNcw2mFmcNsrD5kHuIR7hW6xRaRkaxQQ9klJNELGMul8/lcYPuYNGjtGQsi21x1k4ePs7TDvRY0zcZLzFpFNtxHX2PyDOiQ4pavoLKuC4dq3pk4OvHiHcnwt3icfBJds87mb7gXkhUEjy3n3KKjezlYUS8ngNR64xQgzFm+LQdEt5yok8jZ8TO8IU7ImyVE+GWmgcrNEEHgiYzWAkthi2jQeoWuvqhhd4aY7bTtnkybKbqSnWsmlWUUP1AA8VvT8grNWZIyYY52dXDQvGKCUImtVgwXIwAAafDks499peEmF6O6SBKdwIQgWKEi2n7YOB0gfHvP6x4vPd5Jaz3HgERLkZxRCQYMt1BY1S1DZhOOCWYTSzbwStYoSISRBlINFfuK4gRRIQQ5Uz06BCdHJHBSohqJkDmSefvgF/l8dkzrC0OXSNQRMBCwBqRHRGl/mI0yR5forwLQuMNEqU7GdhlQ2A5DskZA4Zl1VRW56ozIv/VKyZCCFhDwBpWhHXFuq7JaLmueasniHCIMTl2Hg7A3WE433XqFIOOWQ0qEieBZeVLYViknoXpANRUhCjtzMh1gBD9gnh6QDg8gv2SLjYnxoXS0WUfjgt+PCwoKxlSaceDw1O7jRkFX8nsHFrWFeHTByAE5G2q7PCKPRa/ojCjMTN23ByRMZg+hDRe6oRqWXSXbzQ1Nypw7Aq9HgZp9xzE6vuuby2etPOnNdzJS4kddpRkperzLjK9wT9YcfEKwR+vUuDNstuPNRXs61RBqxwXBADprNeIiIAAFRCj7ODTfB/dB/y4/IjfHwI+uGM2nkfZCZFXRwGySqmuWw1htUNed0To3GjTt4G6+FEP2H+rXVMbBr/KybDFjsjyopo3pSxGvrC8xDgh9DcfzaQKoDnuzd7XQd5jOS7ZeD1dTXM1bM1TFNq6r6S+rBH9nsU0MmIm/6b+apy6Ob4TRglb06j6Rqh4jd6nsHiP4+GAN/d3eHV/kntLdFEJsmynzgPlWbbM3E415hu6oDtli2xhnRD1WfQE0zeNY2DW/vF3yvXos81Hk/cqfwXLXIZBM5Yd6kyBvYJkVRn7vvXJWlo1LWajvtsmY8paOPLuHRBNdRWeTespaceJ2udBuj3lzGC4KfEN9CdnGdPzHseu4OZMK+/wXpK331Qp12W6G0RnNKe2cdSCWFO28U6eCfMal7qdaseYVI6Raf07wxYdmWcpDztxaLqz8Qo6/DmF0u/XZMVb5qHBJ0JvmBNmrY4IpgCmAIDAG8fmVSIVQeztxpA9cez1OxskYiajbQWT5znZC1DyD9t+5/qbvLy/J/zw1uHbNw9YXp3gvcMhnzpQ0w/Ny0Ug6sDPOuW2siZFqhwqx/rIwha1iXCMsnhUdzmoPF/fGRHFNlKcEGxQzuBg7tRaTrM0k/KvHqMk7Y0as9WieTCSPlQac8xAJAAekSjVVaUa5Z2Hmw6n75Jen6Pb5dWUNe9e6dJY25ixHjDXMW3eqhijr1yxATQ5+zRZMRzEjbgFVy0sY2Tmme4+LHy20JDRIoBsi3UEFxj3EbgDwTvKp+FrjSRK3sgf0Tr9r/KpjnTSMN7CmSpKtLfn9wnKrbwjvlY5I+w8HcGxA0cZGDojbgn7L6seQCn0AsKJoC0qYzMSiq7Ukw2f82x9qZq+IeQS8hrCCa2eT8EdQSiYrm4uiCwfSMEqSkZWGAZKWF/4CPUGRy+Zb+lLy7RqBsGK3GCAI1gNGxzBTDguBzjnEYNLKzZ1RaYYSNYl7XgIMeIXDLwKER8/ctoZ8at7/OrX91jXFSFE0BoQVjGwRi67CQbdno3cTavQpG+PJJn2YFbuvUTIeYG5P/RCyL4kboh9ZmqNcNyNhSlrPL7bJGuP4E2t5NTIQbVyQ8kB4YzTS/AyshixnYdzev51Sk8xOSUSojiAyTgdBG9ikNW6EeuanAyXNe1+OJ/PuFwuWM/nvCMixph/4xrgnMfxXtcMq1BlhSYRI0gu53aUVjiQ/Erb1JOfHVz22TD98Vyn3E9KnsscTR1E0SHevcH7X/9b4ON/gnv67/j94YQ/+juc6Ue8pveVY40ArAx8GI6lOics14v48d8cM5Kv6wmPj1+BeIHnpzzGsG0yY/9VdHilUvqgiUQEF1a8+cPfw63nIlQ0eNQz+ibkuvsEv3j6Szysb01BEzxuCt+ivqMShqVOmHyZ/813ha+XPkdTubyP0acvo39FEaYKf6PN9CM4eD42TSmZe7RjYYTO+uilpGR8WP6APx7/Lq+o+XC4x4fDfaaHT3TGhe5wWRkB51wOIHjmXOYV7bf6N8U3V1Vf6QnkMuwui7RzDbLlugwICUPOAtJOZ4RkF+F2zKiZKy6Qd/pl/4XwVz3up3aYl75Xx7iuNrO7I3Qnoub99//v/ye++et/hfuvvyrzV/lRRqtW8C6/VLBi0t4+em7c7Cadcsj0S66kmspyJPLTQIYb1W3aWLU5G8r7ivZLn1XFGZe983nRIRHhr7/9JV4/3OHh7gSvzn6pKOGk7GowOyFaOVDLrwYHegxk7YSo25LmR3ZENU6I2c6IUVlXu+DKew2TrXtDhpkYcm8NRUnr4/fvJuhirny/AstGa0Zlqe5s8944RPV8uDnzpKxs3PoJwqwjrqSbsNgmyxe2/1q4BXcnhtQuWU5e6LKVWbaa1Ku7yjt/4n7YCL2D8kvwiOZ05M88tLLGz1w7Xmb2WllKg5X9qUrLrUC7kXoEZbYnQuUnGi9W7IjBvL32S3meGIL0sSrOgSgKXGlC5p0bnFoNEnvKUAEwticG7mKAY4dfffUOr17f4+TFcuRcPn5J7ylgpB0C6TfdgZDuakwF6q2jUY0Bw24oiwTB6Z42vdstLyAKK0KMWEOAHsNUnA+cdkjo3RDMiDEkHUIcEbEao0YOI66AskNHaEVrKt0lC2nb9PUwUZY55VKyLgUAWXzpAHcAlgOic2BKh4LVOMkoVogUHHq83R90QAa2qo3pOdauuxKgYztKUPQ75MVh6mCC3D2icysvHNMHs4qM7e+LhImSXDkotnuALYxII5amQFrYmkcwo4B0CFOy5ZidR/o9mZOsDKX9Una2fxEr6tSYGwrT6T0RKZ5D7a38rPbkL2FXDHTOiFvC/h0RM70CtfdjWH8VZwhEOzg2ouZxVRR1H+aNzlOowe3R1JqviujLr41JFkBDiKmJUwEzM5xBXai3t1H7wHXqMaxcPnNruGr6njkT5TQyDs5FLIsDArDCCZEqCJaNP46BQDjFiIUJ5wCcLxHnp4g1AGAn/DUiOgJF2WXQzJxrhjWlTRWry2XUmVV0zXI5UeJPckG47grwMjzLtB/NpYwboUsymycT1N6T1+bPAlGOs8JiI2apE0L7IU+gZgsVlTQKSP1qiLNMJHVE6Fa/qH+6tdP8hqDPamTTS66kjNx4kjZyO6xVJ1V0wJIAsQASkqmfzFPGnREftAVpHXrQoLEqsvcIhxPYAziuuCwHXJYVQMQSc2mm7EboMGNoa9TP0Ze8Fw98jgdhquYU1WaFgLaXOB0tNp1MBLg14PLxEX59BAy89t98tcCwGK4xrJGvHH/ExR2B6PYxWhHkfexZKXG6XD7jb84z48QqlLbcoaa1lp4SO/i4dIw852ibwCq3WCHIMvUbBLYJ35iHopzY7o+0oro8EPUaENK+acR4xSW7fZcBBAAf8Bnf04860/GDW/GDi7nSlFKO+mNb945mV44hquE0I8E2/cjo2PRZoWdtWwudG8uSBTM6pVfpyQ5Jz2ZN8pgxREifzRwR7d0Q1jnRfn/1zVd485tf1S2wRviMtlfwKdNN07cW5WlWSiOMdSloA53b8dY6qUpBVYJBbiptrdpgQRrx5WoMx8qOhY8A2SWItMNQoHu4O+D1/RHeFydEdkaYf3t4S9vaX0vnCu81ZVKRbNrdCTWpov59I6iTX2WADOeIyWZYm5Lb8Zikr+q1Sa6C2tRJ1CelOd6YjPP3CbhbClVNT6gvfgYjkI1ZfR1G9t8jfyqGVIr1FTjGBTV1NvM40/263ltgndd9DUfHz9P6rbBsvg31u2fCXWbgmIZw87ZVi3UetjVU3yfBGkbrfPrdQtSOm6bp6y3MbwLvRihoQ7u6uIyNSX+F5+6H4nqYtelP50xIYdtvN6N1E5h5+FhnrZ4aAb/jKpzj05MzX/b1/XgGPS/V/mztB0I+WJ6AfttFscooTSwOk9pio7JiObEifV094ewY3ju8ujvi/nTE6XCUkwcAdpJZF7NwqQMEcUToHY07zZidGq0Sve500N0Oqs9ztaN5JJfqx6L/D+gDDN5Wd32ORkBpnxwZTlQMmqYBLYe0EpAdrZmMn+4u9YgkFwBQm3NfKDkK7u/NSN14jMrdkYCLHWYrlBT2yerubHCkLavYF/YBNap98DqxK4ygHiXRnR89rGMMmcZRKbTQWCp/Vse/YZjnoZmzUzGV0CZUuba9C8ry+45P7ERr3fX/Yq6mZzojnnE0E3VvBLProPqopoF+BX8hp5S/VSUzTO/25oUalHpCKIHjKo5hJ6HdlLVLSESNJN0KPIJR5GqBXrNVymhTXt0slQ5HAPUQ9+PtigBFVi4ZoFtU3kvS5wzvHN69cQgh4ofP58SExIuqW/T0DOt8BM8a8E2MeB0ifvj+gv/z/Qf8+jcH/PIXB5zZJVFFV4ZGmIs41SZKuSFUQVv617IuAoG8wQzpF0JaXZlXJsqORzUs+MXDe8K3xwVLJDDOWCNwPBzhfDq+6OAd3t6dsFhDg9ZkuGxNwGCMEVV0N15WoNkXDMaQCAHkVHrJsIFCHuwoAgsnK0q+4wIUpKyS14ElHeRy6pSPQWmlBgFMERF67FIAcwDHAMQVa1yxxoDz+ojLesZlfcLl/IiwnsGXC8LlCWFNOBJjxHpZwQy4xcMtC46HOxz9Hbxb4MiLfGNUOacSmV4zZS7lVRakNERJgfIrLqSE60HL+fPKgDw6KIRN3iMD/vEDHv7xP+Pvj2d8//BVuqAaMcGLOOGhvfS/h+Qv/hGvH/6xTl9l7KWaT7lNs8D49PoE8HEMX5N2APo4nYTfxU8gPOLzx6+xrndzWPMEZxwYeHfpL+pePv6Au9/9ncH8UteMaeY52tFpQ3OdVs048QO+ffpbeF7QVFTNWaVTSkOKn+y6MChAlGcj3Vmj376VvJQrF2qM3x7/Gz74P5b5MBNwqN53kHdA5F0LER/ogN/jiJVWnNeT1ojwRIjnJ2OwlH7WHUm6XFzL1rnmkhOYRBmp70bQOalz1soBuktNeULh5XnHXyx8tYx8ExgAu3ZoiyTAdiylezUdJZwkRANH08ENztbyS4E4GmeN3easK85CSKvRzpeI9RJxWVmOtJO/dcUqDtzixTRyiSFweiGya/A43V+AIn+MjF6ZkI6RqGJ3RtZprNaV1EWg7AdzXSfZwnczQymZE14RygKJXInBCwua8IZaIWTZ8YbM/xwHBC5ZnD74xA79QvCe4LzwH5nDLt/vkP6cyiXafukrRzrvy1zK6Uy/pWRJBsnDLsA4vRg7N013SOhv6dfrPZtzV12l2FNoqKFbJu8XHUtUSum+7CrJ1M2krpqrqCzpO7J/c0hTr50/1wudG/ILlareG9m4lT1H9fc9qhl5Z4MNFpi++lMbZ224RdnNd7EAA2PG1dzIPcBc+FaROJrUQv8JIHb5nrwp3FmncCbK3da+q0lvnJtf4ly6sd6b6tqb9KXAB4aOnt3WnmfU1QN/Y1272t7rEIl2esCsxS/WFw+QSzIdRRAidO1UpAMuuAPD15WT1aqMI7ZtFaGCpaLjJqbqfYKRs/oyZPKJ/JkWXCbBk1Hdc1NZGjnLuRyVTuocj1mZJILofSm7JwDsUo9pmwVpIhz+4zvgu7uAv/p33+LNu9d4dXeHu+UItxySnGz2BTOlk0Y493vS0R3SXQdq1Cg3RZTjdnMZClgm9SVtksMDQkxHJUe91y0i9wszwHIXxKp3ScSED3p9RTpNgeEYcvwzsqxX/Iry0K5X0vuxDCIwcZZDkowu8h2Mzsci59l8+iBCVNR90ZyOCIM7gv0dzv4NLv5VPknBwUGPZ4oAgvS4ys5O+992Lre7KKSZUNmjXgimd1ym9ZBlvhHZTkJuqxJxnS+oUtQInslRSxokTp1JwfyWtFEvkcgLP/POdVv3lvdkI+Txiq2OpONYtWKbH1cLuGqqUH3vZN3a6KDOmxjS/bZkFUDjdEs5RwdYm9JG/GqUVEGzkibNSp2FZvcziv6cqpj33Qg9xukIjuqx+TmlvBscEa3gnH7NQgaJqN/N3NoobjIsvCGgZMHNTtyy+r9Mqb47a2/ivss1rMOhepe4LDw07ap1FPu+AxuvfJ/1jS07n0uuX3L/WINGYtbZFwHAeQ+Cw3EJCJHBLl1UvEIYrNRvlZMjGJ4dPkUgrgHrk8flkrzp3hGCc8LAYlbW2Q7FqB1NfyTWkJR/vdw0xSeF2EHvOkh/MTCsVYG0rS6tuL5DapMjykZ4IofFy5lx0743QNm+6DJs428/cWahTd+8ZRxk1CtiqKQSplsbPDbQrPuQVlDk1b1mdUTkUO2KSOdNpq2e0PMn2TA96YN0d0W6gNqpxWbK+2axbHBefoOsSSHKl2q300UVC7JDwKiog9kDAg4r3Pkz1iPjiRyS80FS5LyNoNBXWISNlvlaACnCu6dhe0txlegJaT3qgavxi30bb3ZbDIHW6D1sKQAc8RgDzmso0SNBCUIzGDgcjJgsaZe44nx/bvL0HDIbpk3Llda2gkk1P5mxMOHgP8MZRwQBoJWxXMjkYyxROH8W8lSIG3RDnn9KG1CzIrawyEprptpQ0hapkIhTJIARwPgxfsCP7gMyHo8QHc39IVIgM4Nl2zkj4j0W/I5P6WMo/MURgxCK4ZSU1nI9LhoaJaESp80q1eyMYM2Uyi0jqtRe2i5pMk/LCmSRyto5NV4c2F+qJ5nlMsBCg6pVwI3yMGh5963eCVHgsyvN0u6HwZ8RjvNf1YotEeE2UbdmJHvSNukmz2N0nFeQaTkK/rU7Za+ZqC0tGMI2kzeknrgGxKdH8GWtHAveexwPvjqOKX0r8zzJJSj8WBJl+c/8kn0fdXsuoJY3xulQp82Ga50fpY0FBq2XqvQ2p/13VHcBa/qlB7NLOSu9wDwKXBKMCp3A0NPBrbpHBVcoVHU9VY/XZPz5OKLG0c4JQX36SZlTg/ccrKa8HX24tyx65nE1TX2b/bYn/tq3re9sIZj3JVe4wODsaJ/XYcf3NgdEnXbcxy0d2QSlg6kNs1EcNrEyoDT8dFZ+pbcO6nkxJ8l2sLtpqulZ4cEo3H48xaD2XFaWe3AddadTjAaJpgOcqJw97yLLch3/TzwikgfbFfJN2VkqboWY5nsPNA+e5Y0gtlIeJRm8U2O0MkKoFqgSp0mboh1AUeoTe4mu/DX4ms6XUFxP/fT5AHy6dzg83OFwd4JzHovcC5Gdj0bvbVqZ+XC2IVm8bDuw6sjRbaLpqCfVXYu+WyN43glhnBA8qCPLDGS6m4Bh4iboCR4MFJs3oSwysfGQdhuxv4ykXRWvb2oXcIBzWJ1HIC/HQKsuSSLz97pKwXEqSDs6gqvLlztx2u5hAWwfFDdLMVVvclv6CPGNDtJCqvm5YEBWw4Bq3t8W2Bbef2ObDr0+NSNena1j0uM8o7t2/CJsb1oqy7aqqkv7Kwem8qqNN3JhKy/cxh8slIUHJLLTl9ONeEuL7fyl8Z0Ro3wGhBcN+++IGAiwhRdzNnTkMdwSIroYZbTXmewVKJFWjNuBSp4tdRSUbazXK8qr7BRoUqJb4rTcvGrIKIWOqkQZpv1KTw9P09oCW5u2mSzditJqUpBZIFBm4cEx3nk9G5xxXiPeP57TTgjv04rOZUEMAd77dBFxCPhlYLxdI/7w3Rn/4fsL/uLbA755dwRc2mVBlyBnEsbE2GNLQLj0NVFezenUiy5dmo5ZAnTlEBHgycE7JysGCT/+1x9x/t1neNn6GDzBk8M/HRYs5OD9gtPdguPxAO8cFufhZWdEfdkz5dWIlXcTiid2HL4Iib8wsPnrA9WAXilKhZCIEOodMCEEIKa/yCGdOxhWxPWCqGeb69IJII+P9qdHuvTTLwsOhwOWw0HGM62syCt6jeFzRBxmLInIZdGksPVtCkpUzrtMQlhpcz4vUxwq0j2yyUculO2YqkLYQDyjPVPwWiaMgSBSvlZCxHSb9nZf8OCpjuLJZ8bD3Xe4Zzf5bkFI42OPlNLk4W3E07e/GEM2qxoNLoxlxqqo3+P3XfTlfcDlv33OZbz6/IivPn4S4bwIcHm7sgpyaijmmn7B4K+lHI5kZY6cYZqOqGrRvDZgMNJxSr+lI75nj6enR4QnIC3pLoJ9eU6/3lMXl2AX57AYvvXOhyqvc/BU6KHO0zxmXNpf3s2vws51mtYw1Rqetwwy7b0Ts++O+3jGbAcn8nwpBoiGBt0QQnYgaG0GT1gvp2aENfHCy+WSntfV3BERq36r4a0VQG1DtTNvB70vONnLeNvBaoTFmN4fFbVD4rki/NVlUQVkltNop2w1oQsK9ef/9nf4/j/+Jzz++DHdEeEdnGP81a++wZuHO9wdj1k+KP1NZkdE2RnRzv3aEVC+t+NonRsdjMN+6nu5lUlLvabsrT7vDOBVR1X0re7DUVnTap4dCMiLYmzdqV227qZfGjltP2jZHCR199/m79eKbge6Le1KeqDDnVkdjStlkOzlB6vnO//8gs4nq6tc66lpTw/Gt5KRX3AMKtvrswqYxPd2r3Hl1eu+8c/GkRcz5rfhzx0HfwKCubPeclefJaQOgOpUNo4k3lV5NQy0nzqeW0PpaGTGsyiXVRHj2bhSbhGXV/OZRJwxipUyZU4tS4+6Zj/mnuBKdkmTTRckcIwAMY6nA14/eLx99Qqv7h9wPBzglwXOe8krfSDHV9tz8Iu80zA2lSqtfEgEQHfOclGXTFZNH+SiakI6Hx/eIcQAvshOiHVFiAFrWJO8GpKOEZnhdAFh1bNJrlZd2DpJSvVJXsjHXtudKST7QljuxDCtdKCie+nYbchxCSsTzqaLwB0eF4eLi+m+U7EPzAM1l9dJZRNiqvOCzbv5WGKuEmPVPwCwGobHeerNCvZmETunUnw0EBUMKnaMYjKK+Q4JyttYOC/mTAjFJpMUUIFn4i28AEZH+fIg7Sh/C/0sFKexSWsITjlk1ex6Iap0QiLITvNtveR6aITmnz1oQ66kmjgjfq5ww2XV+mAFf0XkAvX1MdsSDPrdCboK0tKeKldFgPWRmzRKRBTM4rDooBtqfun3mhPCZsoTgWpD0pbz4CoszygjJxWiZo39yWFv2QgqxpCNZFDCRjgsHiEQ1hBA3lfMJuSyAygSDpFAMYKfGOtTBMkZiUG2PCYm6BKRNPNd26eKvhrAvCOsK+PpKcIRcHBBDAJpJatzybvNxGDHyRG+AocAOGmXj2XFYnSUVziqYWHxPh3JJF1Dzva1HWfKY1TTPEL12g7HM4har0jTmD62KxAyA1QDmCo6dfIxvSkrJTJja1bnKkMq503KnxrrhUGVIyiE+FOa5857eO/h7o/wd4fKSNMKXemtUdDMihNg0OfKwElXSBgWvCUMDKTlts1boXyOVedy89TDO2LGm6/j+m3ZNzCTuaiPqi/0Z1a0o4ByBNigvGGfpKDUZl7+Noe8lXcG9HCul4jPr804Owa8wXUg40JkRrykuaXfsZ5BMWLhUNFQPapFjZBeHahwYCIEkhtrlK+Q0kKLt0mk/GO84Hteyj0CiOO8wn9cPmGI8vdSpigNDCDvVqvpm3OEGGO+iLo2jit9KYqR/d2Kq7ebFufEXkPENUdEHZlF7zGeMFfKh+7Mz3+tsfwKHah2NFhKKg6t5Pwpxxzm45q43w1xenWPw/0J/nRoO8A8Y/y8GU2jnxcIg5K0jp1GvC5vxunnQlRkmWkKAuLTEy7vP4FX2QXkAETC8bDg/niA8y6zqMoJ4koZ+s3O92y0t86JmROCDLe6ZpS23xoZSh2Tuewcr3BRW3xdB9Xl5DHIcaifTdf2ovTLYNcWTWgV0JlDp5LfdjKNzoExm2Nkk80S2Ur3zYeZalKnyZNsXEab7gXDHlo9o+l7VsrbFcrPhrGtd2c6jWMYnLpWVza6N/rmZv4vH5fRDokOdxq+e62MLjB3oO7FqZdOt1HCBq5dK7sxokk57a6EOTreVv6ecJOss7Ms5i1YMsaX5nC5lJrJpV0QwvA4K5fyx6aYDGxdW7UgZCDzG6pQYKk0qfq9/d6/z9po303Npt25NgLSscixmuOgXkZkaVRa8HjAYVlwXJZs00jCNer0o44QOaQzsFYM18RWaipX6Tq7ce4C0btYF+HVun0rObVULC2SqnfvEqAntGsz6pmh7bE4TGQM37BqfOmaBh1UT8ruAC55ASeOh7IWno3NqYBnIKuY+AiHBnSlNRzsUta5GZ26eCsm2DRlapUjt/Tfud48f61Aaj/nZilumlom9hBq9L2WdI1p1pfx9rakWRNJBj2uBI6iH1M6Xs1ZFLDlbQrd16DpZez9vK1NV9OnSuyuppDQdzR8mmt4Wrmrc0ZU+X66cMNl1f0IsRCQRCg2OtYK8Ix8NuuYrVijoaRg7s9/bY0CVWUlnkjPwJZ7CuTor5S9JhiVYqWMJQuN8qvKZvNdBzcTNCqDfZPjoIHDwtJ+nxXXTkIlvLUiSKX9FQfrozRODfWXNeD90yUzHN0dEWNEWBas6wrvV/x6Dfg6AJffPeLzbz/h9DdvcP/NEX5ZEUKEuzg5h7C4m4iQj+lxsjp+cUu6YNo7/OG7J/yX//oBrxHxFxTBzoGdS4Yy8TBEIN33QISHSKA3D/nIJU+UypI8h0Na3bgsHov3+OrhhINP77rKMY2ly8a9ouv1RKJnsv243RJ257FMghMDy/NE/OGjkiKNiSxLXpY7QdJZkmVngK70Rd4tEMEhgCUdh2KE9+RBjhCdjg4B5PBwusPx1QMe/vZXONzfgQ4ioOX5k/6c3ZFiCCzVk6Lqr7SLlsvlV6CKzuzqTmXuKiwoc22Fv5GM0sTtYrs3EvuaibRF7cGbiZRjozqBYQLkjvZW368qTztH69Y+6w4r7cvy98Crvy53XBDu8MRvy5yQtCy4/P0Pr/H0dErxMYB++1/hPn/E2+/+gOVyyef2q0CuNGUxOwzew+P/YgBQ2gcQFQcpkHBbDdXnEBBY72spq+YV/10+S77ww6Qnljq1TCUYSjOqOadaQGQ45xBjhBcHdIyxMWjIpudmbPW93EfBpu46tLsiZuHa99mqVTbf+0KR+iG3GwBzdab/oKJx/UB12XQCorSfGeKA4Lzz4XJZEdaAy0V3QzBiTM//t//X/4pf/8//DstdubvDSB4qcpj2Gge5lUtM35FJU8koXTO3xPpcQPVu6+7Sbrzm6J148NJBnd1pJ4SMeUjGFrtgIa141Ps47G9Z6KDxUPxJDYI6H9rdEUT2uZYZ81g3mnx2hFSNGMiuZoxv7VJr3B7B1nRgIifdMA9g1CI2HI6jRRhtdSPdxKYtnydlteg7CS096di+wfe93LeM644MpuBqHHpAR1leNDyXPs9WxO8uT/nRM8KNXdzElbG/Rg1tuv7DFp43i9YsQn2BJaDt89Gc2ntk0pfkeanwfCNOyf+n35UzxRD0cI8kmI2SiQb2mC0NxKYtjoZ84H+2lBeYAzlcyOOCIxgLInlE+J16hxiCDRiNCbd6GVCLWge71iVtV5Oe/64VK9OSaJ13iiNZmSZJpvaKdDyvc660Jwo/1ryBwXHF8Rff4PCbN7h/uMOr0wmL9yByYNFpyejvlWlaebkzl122jc7CQ92XuXvELBDk9ILIUe6/UFmHkhwaI0JccVkvCGHFGs75FIBKcyICXJmHDGANaadBCFF2RKR40eaTruPkLg0Lf+bRrgAL5DskosjgbO9XQBk2UsVKdRdbhlxQDefB7oBADoEIARHMTpbAJjnN4l+h75b+Kv+xSFkQa8oTuOC6dQAR61iXQaqXfqL+HbKBATeSC/rU4RJhnxMueSDjUm5GU3YebU5HXOWd/7G4cipQ28kqOx/q4U6w/mS0t+qKsVBHIJBz4ODw9MMBBxzg7xfcnzy+vvPwC+Uxy8GNjjd7friZf42Sj4AZFtsMrpUpzIK/FjYy43TTDolnygE3OCK2K756phjJhXvNvG5DXg0JLgRdhE91RpjEOxpeDO7M4swgcXgYPlzAspJ+/U6kKYQ5mEEt+qEwFhqUtwXlyCjT5O0NKxNBqxIw9DLfgpAF7wrsAKrxsZ5By1cXB0TvcVhiZl7ZcKM1cNle6JiBQLisAM4R4fOK9RIQI+NuIdBhwZMYtsk5cGQ8PkaAI+48J2Ocl1W6HnAX4J4c7hk4MOCiHIkQZcOVjENaAUxyAbUYDYB0vjOSU4OIcDp4cbAs8N5hkWOZlGDZsURWFKgei4wX/ZCMnBXjYIQhmLG/JeSBLUKNMgyqmMak7qqswme02LI5T3cHlHqtMdR6ybMzgYph0+V7OBYsywJ/PMCdFvluoDJzTA0u2sej/qkMJo3zUudBs/ACexgjRYK7AC7UgnuZUUpXIIwbMmdcFlyomncvEa4VNhWN6vyTYvqVUuOEXbIdYa8T4mqx3D/S+LNWfK3EVIYDvLnPW0eQonF/qXOLCXSXnGRrcODgQfevQCA8ngOW9Qx6eoSLEUu4JD+4SzjzSVZjeM/4wIzPnGipl0uendMN8QWSolRwdgawrF7SMU/skjqFNM2vfrdB+pHt5LmrSl9xBKI49NUZUcqzdH/uiEhwy/q3rCiMeB5yG0bCJM1euB7vzM8n8sE+R0QqlNV43JS1hcc6NlU6ahwRQXdBlIuro46rOvnlfTmdcHz9agyzBb/lS1MSUMs56XEsvM+E+jZyxP82gxVvKqN5W+7zhNs2zHdCpK8KDOU/M+5EcmygcdBR6bPsPNcyKqGyd0LUaWHKq/mYbb3CMQpFRJn13Q1E2vLRroL6nQZIVvHwCkEH+IKJ7GuQaVNxo+bXlFnjY+n3Kuuz5K0kVcxEO9oBd/ZNWpB2gNA5k67hQ062yRn7/DsVyp90cc28gHH0DXVnZ/iVdF3gJs803Yi/1HLj1bpeMHypY/9L8vwU7fuSMpPZYD8vH9U7W+l7Cwy3McsMAdr5O2qLjdqqq4U/S97GGCDUDor8haMQQOlYpsunRzx9eAR9ftrFaazeUGmtO8aBpy+Dd2lAr6eU9lwH2PBQAtKFySz3UzjYxU1JbiTRnRmPR4/PAPzdEf50gF/SKQCZ3xNlvXGoTBkhocP5tq9y/tpwn+O47FSoNTsWHSIteolRFhPGximCxH9UJ9fq0k6I5IRYdaGifqN0DFNkhosEONFSGBUuKZTU/Jb+TvWoWN510mBbo8JKUeEsF3y3zoH0twsZ+ro7fXWjnGxMMfsnuIYFTWkmc6PnUo4lKjna3w4scgBHsNpkczl12fa0k1kY6d0z2OffejD3pUQrbA6gacaCinPMnRmLTwsCnXPwTo/TN7Ca7KXPn0f06/l7o7xZGWkxlKWHCzwm9bGWMXBGWHiHxzXN0DvbE27vnxsuqx7UOwBiC3mm8DUWhOKMkDoaZ0RX91UoxUBtHBIs8OjUpjy+dfl6NE/tfLCKjq4s3Q1QD6FVwm3l5nuGalc9irTluZoCk/lg413ToMLTGHcOOC4e5xDw8Rzkws2YjVTOOXhODHcNK9zicFgD1t+e8fjbJ6xyke1f/k9vcP/miD/A4SLtfHwM+M//+QfwU8BfIuJIhIv36Tgf5/AKwP9yd4AjYHH1ivl8ZjMgxm79VnYz6OpWJTzvHu5xEGcFiGSlAuCdz+kAyD0VikszJbeM13A8rgUiXHXozUImJGoMTL5wdQz05FPnRJoXKVlft3UqaZr6SBYgWSrLjgmIQVLvSHHegx2wxgAg3dHhvMfd/T2O9/dYliX1u64OyXTXOC7yReLikCDpL2fnh+l7S7iN8pDIiBprS54tAXhZCYfvCe4jizEqahdCpVxyDIoJcL3+uWcVbWhW5zeC+XaonTa3h6FEl+ofCMS3OFG20w5wTGmwMrwrZY6FUU23X+C5Cp0pqhLcdfWK9NPrh/d4df8R3/34FZ7CEfHdt8A7xvtvAVovwD/9F/jPH/HV734HHwNcjPjIhP9zJUQQDosDOQZ8hCMG2Gea1hqz8y60WIzYzDCOCHtXBDL90qDv1Y4H6BxigBIs9njDkAXlQufz1vKmX9Jv7ZDQq2JGxzPNQuUkMbC0Du+t/EKth98zLMpSM003q7NFO7AGaUsrrrWn+m7aoWMYQvkNIWJdkzJX7ocI1Z00dQP79lZ8yE2T1h+sSOEGnwcGcsr/lTLysWO2trGWUkXVhuoZoF8YsiBp3ncEEnkvrXhMMhE5K0NIP8hvEj9aJ0XhR5UTYiAilP7uOyI7Q5om9I6QuYyoblTDEhsQtgdgE4+uhZkRdpxslzJDBYl62UYS2FpHfd7uE96urxGcLV3KdewrrcgpLUh72q0Td5y279PbJtbPubr9n0/4H33yc4efCg+35McbSnkBGJ4LBOEW+Xbe3r6cvHSLalpEgJzbr3JmEjI43faHz3/393D/4T/hFM8llehoOVRVpXq4iS4m3Y3+bRe6DN663MMus5H1YrIUNYFdrejWm6xHN1FaZBdDQATw337zgD+8CfjrX77F69cPeDgccFwcyKcLlCudPxunOdunKO9c1h0RgBr/U99FGS4qekm2nCZ9gPNdhyEvXNK6IgCOyfnw9PSEdV3xdD7nuyGTk0FGm0QHz8ezQnZRRJxX2c0bIkLkfPb+QU6moIUAl3QBB6TFwFn4NqNBZvEgt9gxCkUmrTRuRupfOBzOjBgJ4eRlR0Sae445wyRqfKWDqh7vMkSqyNia66c6lPFgRsEr2MvCKeuSurizVMG2qJQ9xqZLDA6nM0QBcTCw6irZ/pH6m50DWJwQThaHyV0milupZANfrqe01erq1fQYvD8nVNNvhAatrSdHG5kYMo6imxA5HLyHi8BXjwHv7gin0wGHwwLIAtkvCb38NrLT/FR8bWbHqulcFWOcERq2dkjUDs6XC1/kiBiFW/U9i8xUqMHcGbFR0vUBTsQxFROFjxSFgNoSsoInr1TyZ8WvIqS3IxjVBXTfKmI3nnfDwE135Me9wl07uQ1zJtHBFvY4LpDzBNPRSDEGXAjp0qXoAPhsTEMAnBjMGBHrY8TZrQjkZdsYAWfGA3mQJ5xiSGKOXOrqIQ4HOaNZj26yRjXv0q4GMkYDIpfHMRsRTFqvzJLKUSZKzMo4qIF8rxPi2eR3V04iglOBRFc9Z/f+YOYpU2+Y/0sENVJa42PqkzK30msy4jvv4bzPDghnHQySL69mUAaCpmfyfNV5SLm+4slFPpqJbTxZcrLlhJDymAAmc/EtdanS6qDU//Y6M8sEKAuRGlrLXxEAcsfiJ6H7yAANPeEoOJVhr9v8U2yv3F6xbOveinxhuK6UywAcMZgiDssFkQmX1YPZF2Xs4XVS5Oj36aoJAgIDT4EB58AxYcJCDHYiRKpgqgJA44ho/ypQDazt8Un6Hs1ONp0XaeVShAMhUvme3gGYslTA7fg9qxOUDTmqHZ0t7rQClIU3KWObIzQM7YKCKtg5WNHtspIwrWxDEdKavqrawQPMzQK9qSzdxJf7wjqT9OLqKBcItmPe419PC9svHZWiRoYxwvrILlr3oZWT2pInDGWPOGYr35Hl5jDWoebwiNKdeT0R7o6LyAo+yxF1fxc+VTVCZQjFHegzqnIqnKNJb0p8nn8tPjSDvi1Xourz7lub3xSyW3ys8LOei1XZKi9UyXsMntW7JW9V2NuDU4w9t7CMKn0zDzb6fLvIjXI24LhW1faCmJ4G3wzDDaFdSf5i5W7UtQeeHQnTLzfvTVmz1Yi1+r8HhhengC8Sbh2/W/DnetqX7JOa3tjFSOl9a8T6/M+CoKlzf75r5r25rD6qKhU3LiezM67jWJ4479VNOyJ4PYPOn5PWM23WgGeNBKdRWlAn+LNNx3Uey+6nGDvRf8ZpRwWJzAgHUMw6EwP4fPT45AmX1wecvr7Hw/0Rd4fDYAEPj58rwcD1CKftzSKoGL2j6T9RJJg5XZqtMrjaDZBk9bQIRha/xCB3PFa3d4gcXvR0zR+iHMcUGSsnJ0SMnM0ModJhWkHEFJ4aMen8+RiZPepw7OAiIVCyL4nACxCBaUl3mqC40tRUwlKKrYmlf4sawLnPCTtESqM3tk6IfGqEwF9sNsaRVIn8BWLpzStqrnFuibyfF1jpnBf8Yj2rPttPKB2HEgGWnRPFOUNZ/qlIR4UopS9LG0tiRetdfMSUX9C/7MTpBHHYuHo8ASRHg0sLixZHODmHoxzJXt3ZYulCrmww0h060zAeGNP6veS/asMsU5aj2+9jfqY+VG7LvOaUYCRnhBb9QnLibY6IVlgd9HhWkLgwrnloGYvmJYP8pd58AYpVbNSieEXR7IV9n3hbNU1seggdS5NTcRRmdf0u+WgDrsrgkhUms4rLKhujCbdRqRo9O6a3YwwrpVrjqiP8Up85DxwP3hiakhf90+WCj+c04cMaQd5jkXOwIzOOciTFj78LiYFDu4ngGfhbv4A8sIjSrkcrOTk3kPLRScY5IAP06nTE6+MRqvCnUo2hQOitgzgxvEvPThR9l9KklcNUjDEW53K5ZSi61XK3hhuzeDA8MVYmrID0oOxGGNitEnuIkBMCm2/IAss+UJUVF4aThB3OhEzHCpxEAmaGcx4gB384YFkW3N3d4XB3h2U5gNQhIfeDZKGHXHZU1P2sRJ+yE6l2RowE9/YyXC1CmJY6KUBoL7yfrVStyifpTcnqSJwRVgCjzErHZVRtk9fpsOwUoodZa9raif25LVQlz2LFhFmZIpt8+WtXG1U9cmObXtAB0etEPIwf1URgvH31AYEd/vjDO5wvPqV0C/CLvwRefwb+8R+BNWSfYJStz2kXBCMKzjnKOgSAtJqHxcA/MuYXo7U6Acr3jn7Jb31HRPqNIHgixAg4pjyPI9Ic02u958ZKhScOHQ9bjogRzACGOthWaNt5q+FEj64q9KE2IAMDR0QTSny94yn1eXFEhJB2E4bIiIHz6rIQy06Irq8UFnkpZIkLfdw0QNo8RbapZQ1qsmqahi5ZPmhkpY2qu/ClYmy1svxLCyuF5kvZiRm/fvcGb+/vZMFCvZgBwqsc9F3BqResWL5kRJE8Xg3lt6Agc1zTVl1xqP2ejCF1n1xzGPUy8RiGLwpWbjKw2e+E0R0Rpb9K0hlk43bM3m0urh4m6TLwbGTJFLKad6NC9pxFSyYzXniU/lmGn78H+hotv6lotRozslHjCpI1eDWu+8tlnP8R/v8vzA1LI/kcSJKgxfb0FAFEIjylZTMALQAWMI5gdwboEdlJMcHlTjUlYHORrdE7qjTV4o8+dzVb4ixVnfKm2SX8W6e2cGBR/yL+4Zev8HevgG/+6i2+fnuHt1+9wZu7E46HdAQxHJk+KnJ7WYym57L6bOOQlKYnWCusFiWRFBM5AJx22HJYwRygOySYI8IaEOKKx8fPWMOK8/lJduKuXQ+BXLaJgBw4FgfGZV1xDgHrGhCj7HoQO5kDAxQRnUM6eYFyf+VOzBWVRYNbQ1XjrY4d4W494RiO+Lx8wOrOcratR6QjojsiwEF6AKB0vC0AeGZQZESnXFmwmJ2xd+k+H7WllPGnAkZmzSlf0YMqWV7fO4eCKn1sGsg5SnF+unBC+wcAk0s3mFBM920wUv8TI3ICkB2lnRBpi4oAHtN8cZyeoXZYsStRFLhNg3MHlPYV3BwYozDgl1UvWOmIDY7oEk90eFOAKb8VihBA5EDe43g84EiEVw93eHV/wvF0wHL0IO9yzXluG+tkXcee8DISipq3n5kbW7m7r43xpuUd2Zn1RTD14YY7IgwSdN/kl9sUNai7nc9UD331JsJd9Z3NW6uEVPFz8Z9aAA1yW4WyPGuycYlsJyq2086g6pMPBOFBXO4NKqkK8Z8rZl3d1iBk4vWS8uzoID3TOqnHB7/gtHC+lyCq8ZtI7m5IWwP1aArFEwe99JHML00cEciOCICwyGXWp2WB916qK8K9dSgBwiiRiFO5jBRyFJe8my6w4950ax2x1Z9fGoZTy8yLyiirzLMN9czSqG5qbsFLggcVbeZsZFEDZvbSOgZHcS5EwHsPvyxwPh3fZR0JqT+T8yg7IFBWYsAIZTq+1glRSFEZq8S8VXywzoiWJhmy3AgIzIxzDHgCcNm68Lju1nkH3kDGqRl3o0rsLqNNnZy5BWdGJeVL6yo8EiafmXRN17acElW53MV0UFa75WZ9YIUQA1NOeENoQU2CWsvDNkaVGB4Rx8MZhIjzehClLAnEALCC8TEQPkbIpW5pNxkc0i/SzjKV/ZLhK720zocWniLnzmFUYcLe85B+C49zQuMrp13FyMxPTQClDrP6CsgCd/VrCqvEh6ZI4hkO1YH034ZO33wMlPaF0B1mVPSmtLHv/wq+RgBPtEb7A9lpn441NLsi1AEhNOfNr7/B/VevcXrzuhRUwW2J8GgWl8Ei+y7pqUnZOiEyD8zFXKc5LTsczW0NA2700wWuHyuFygTSlVMRgEs7J3XXpDoVnOE3GV9tH2V+RXnMCn8zfZ3ljDpdAabwv9FEsHzR5m1XZ1WyH9nFGeW9JNgf9oxfqaavg7LaWZdCTXv60ppYat+pix8VpWxws9kt7g/k4hloW/Nl/6r8m6J399ko7U+1E+InDRnnX7a8Oq7Qz87JD5kHEzko8c9bDgGbgfO8/LPdhu23cd1j/LDyn/k67rovwoGtCbw/d7/TQcewVfuv9Y+O9i2159JynW3YYxvZB9tWGBmWhsnSP1z4Qm3akWOFkC6oTn/p6uYahp4OFWNuDzk3T9stuf6dTMIXMZpl0EbQpicGJ/utYxzuDni4P+HudMJxWXBYFtFpbXlFTqw0MZf+UftG3waxvzDy5dBqk8meF5UlY0SU45gQ7VFNK8K6Yg0BYQ35KKbcXHPseHpOfJo5HdcUQ5JZdUdEsTqU/o8oZ8yzNRhkcabBsVy/nZRd44dYEilgdSui7Moh3bHjnNkNUfclI6l4RAlWu/laW1TdT62tM/YXzv9a0GsdyChnyK6kRgceImll1C/5p7xf5Xq9YF1/1FaCchQViNI8zrZKBlRfVWBIj4LSON1B0fSDnReZIRaoSnvq+1RykzV/17Arghk1aZrkFp+d0yPZ00kox8Xj4D28L3amurwGB2ey56T+gbS+0ZZBucprB5JDhypT3siD10KD1HE5zGXLZGs3mx/vWoG0/bkKux0RtPFWRVvDiBJntvGtxjAqyMz8LChoywkU0zlokUYqjBZbI1VL9KofnewDoasyZmcCSuW9g7wWUrdCB0s2pA4m2N5AFq6Cwq0wa5XQJrt5Me1sJ1geoqTME5AuKSKHe+dwWhw+OI9PdAY5j+BjtcozHUmhYDJsj6ozwMn9HI6Sg8KbiyIr4wgR7haPV8cFSal2ZcyMQaCMn3V6lDsg0q/S6GIUtwbuEtf32UzY+cl1sTwg6V6ItA3Pnuc5DyzHDvVFGuxWb37jqMuGFGVy8ue97IbQo0eUoTsPR4zD4YDleMTheIfleIJbPMh7GXuXz6DX+z30/o5sLAXKmJIrjqnKSGeIh46XOCyLcbF2RpQVCjqLBU9FgHsfVvyeuDgiOkGiFiZ+iuOL7FTc8L+OM1ZvkjlzpFEeLpW0FWT6VEv6dqfJDPc062wbfI6dTqiaeRqZsMHlAX2uYNseHwJke4LhQYM0bLqBiPH21XtEdvjD91/jslZXTeMpMP7jZ+AsAhuJguDSzXdwHAGK6YJ0xWsUR10ftB1j59i1XQhahtI9Z+qyf7pCvK+753WzOtv4azxy6/usPfWvbtHuy2pxy9IwfecsXNflXt8JUb/r7iq9a0CdDEkZNI4IuStC7/0AgH/9//if8a/+1/8l00fl73ovQaaJhicW9lSIQ+ZpuY0ND7V9ZOWd5r3igyO6kAublFEJt+jzz4Y8t9NENfLJXkNft+auZmtp14MD4GX2Cf7nYx5N34NQ7oow46BjpANSxg6Fb9r+aPC3679RfxiZpuuPqgxTBVnYe4dEXU4N66w3d3Gfpp2lGTSKNniyp+w2z95g6p7yGv1pxmeSbnfNXyQUPj+vlXf+RxiEybhYelrJmebXdmuttPMgxRYItd755xv2APinwfObarl5Tuwfy1tg0LB/web23XaDHOZ5fgQHSI2vLQ1WXcqlo25wROQjAtJq82KsxmAe1XNGxXTiIj+r2HC1RTubnHY0avJBpslq7TaG2pdKbaGs9xGnXc6RI44O+PrhgF++eYW7N/d4fX+P+2WpyskLIfQYJGXl0sdWIO0h5QJ/pZ+XndNR7n7gsOZ7INJOhuSAyHdCPD5W95G5YgQROqSnQ/h0dKjcY3ZZV1zWgMuqx4lq2wzMDERERHYgLqb+LLsM8MJgW2cLznijw2fCk3/Ck39Cxm1HgFvSbgi/IMIh6ACyaAYMBEQgEkTCzjvS1Uxen2BQnontN92J0qRlHZ+kh0Q9saIaypk8GnM9bD6y+Tf3VcV8pAwiELt0dDAjLXBDwZnkU1D9XTqeI4Al/TIB7AQAljhB9Ayo4H62A3COT+On7eUCW37lsgPGyvVN99S2S+vKbIVG24WNXQIEWjyWxeN0WHDnPF7HEx5OBxwOaUEsE8RiWl9AvzvMRMM/KSPfpqgzHpJRSN5ZmGSWazZLvT3ccDRTo0BUgz5Lf5sANgwdvs2010zFjXJuvum/RsnK5WWiOGhFq+RNlL2cPp8T2BhKJunrMpHbYY2um2FTL6JqEncK52Z5vdNmlK4wk2TMSju9CJDz1yKOeLqsoBARKWZCzMxgx0LwS5FpjNQ5UO+AsPc3eEqXvGo4LuUC1fqYgrKqwAr36oggsdrUCvlovE3fUdslJU2tjAw7dhJunCNtcU9PiN9/B35LwHIqxXErZJZ2zYyr08qsYVKFJXUY6GXSjkDRgZzM1BizPKWGOL8s8AcP/+YO7tWdbIkrwgmRlKNOCBSnh4KT5AzKf52BQySVckcEicJhnQ8VV2zGr98iupLD0+Ee0TE8Hqfp6l6d929L/6l7mBb6wmrQoE5Oc6LdOdEnJyNIcPetLTP9SLqWQTPX1N0ItLmAVmqp3rj6NNLR6rG3I27L5PqXijBIUsBW/xNxI5DW5aZ1R4Sylia9c4xg2RlhDRk6N1zTX2X+FuWD5cOodmrzGtrGUb+Xo4kg9ZKj5IzbjXXc9/0uh8j+MBSehsbciSNC/rWxSkasEbQ4La/DOtqxkjIKzcn+y+KIKMcalu3a+h1A2jV2OBTZpuLppi3CkzoDbhVfGJe+akprKLaKF9l6TbGbwcgGJc/MkQZUy2sMAWiN8s8KU1ra44+7fAbOn4DLkzEGqkOQsixRH8Fk62kcQ8qo5HvuZzOnpaE1mFoGSv93MlvbN6bPR+9ERc5NY9/IvLPynxEKDO18bOqQlxpvzYcbwBg5LppqR4COn7tkPV2pZYU+7Ry+SZ1tYcPk251xbSdEq8tUJX/JHOshmZZ3C72/amTtCOHLNWJUksZ1EoPidbUID1nYKPnmWHMdmudLfKM+t/LFjhIG+Z8Nzk317KpoSuNtMSLddItfVBY12Qb5qmLtCqCbwp48ukthizgoHBa+/fhR6z5apy1HVz8T8r0HRFgJiOTBzoPhEdgjYMGKBeXIX0LfzhmMCa/tV8shuMmTZwGhMc7O59W2pL4vKBzj0dPyk3D36f6Az0dC/OqIhzd3OB0POPolywy5jGwANhBaXm//YPA2G7ZT3XocMluDb3ZExHLfQ4zpAu0YZBdEckaEELJeo7aQYu23zgLKToiUNyBWOyEM3zXPWWvQRXqc9B/fXlRNBfw+UPU01a2ptTgmZ07aEbGYHREFs1hBozLKapNq8a/Sbw3+Zfy1+iurM8+Mb7VQkfu2lhWR5ruNU7g4f+fm/dl8gpoHI0+VWWQFH2kpE4iiKYChTg3Kcn3aDVPOsTE9VzqvibOjnCWwZs4XMGxonRAgAA7wzoGY4D4xFjgclgXLokeCb3RKPi6tlzGHuajG1+eGcqrOgP/eUk6XsZELJ3Xn1qrNw9oLgImN43nhWZdVjxThfSANMg5Cwl+zmVVxXj0yMJ3QKGTFiKJKsHYeleRkkYptdljCUfhCQ2S3sIBMulmSTiGjzH8KK76Cam1XDg0thrW7ts6csaNBPaKO22yVXuZ0/pyTcwApEu6PDqfDgo/O43EN5SLOKERUjC/qYHUyOKzKuvSH7owoRiLCyRNeHRco77SKaPboA6gdEaVpmcVSjScqlOU4yywHTzB1K33+SYT0K2Xyjz8gfvqM+K896OErhUZNnLB4nucHEcrJ79t1Vyuj5S8Vw4js4ThdQE3OpVNoRCiIkHMiwfBLGtvldMTx4Q7+L97CPZxSPuk03T5X/soRTQQyq1HLheTtanFVFLKTH0W0LjHFWDpdtdYQtcvhhI8PX2NZGB7vm+RFsIhXhIL8yX6muqjdQXnuFbLUc+wrVNvwYC7EyX6SUq3RnboEPRNEtxrdMty+DXZrLLWVVw+tqlBANkJNNz9HvabzmZAu6wJYjhWzRyzUAmAlcpZqd4xl3j6d4abqF0A5m35WBvSCaBVQ+4p7x0+igyz8cHqEA5EsEZ/BX2+37etAFjS3jokYl93nuxZqRwpXQ1z1rfmkOyissc4q7NecEXZlSe2EALSiJLCXdiVHROoa3QXBnEeyrQHZkU5KD42MUqes4nrBuJYF+tXqKjOkN9fM6yymUCsbKEytTLHhhPhzCEIK/efvQd//PdzHD4nXkRNdVpwRTu8jMlnJ8CRof5RxKv0k/azjNrCSZ0NA9300XnVasr0u49I6cq4asgsgFbzbeWj83sq4NGqDFbFmtHuj7i5RKXNP3hlFGfVT64TQ2p6tio1Aby0bP2nYW8mtwFxL/3LK688ZqJ2HIyOBKOyaZiBRDmM0q9J3amnCCwfLy67z1T8h3f7Ctj83txnGyfd5v/V6yM21Y04cGkyq4KQqfguGvn2D+oiQtKZkvA3k8OTThb/sFgQ+YA1HnHHEE064wMPBTS6qHsCQY61sIsI5l3cmMYNyk094VO1Y+qloi9UJG/3Q/DEY3//qDn/8zQHvvn2Hw6s7nO4PeHU6wJs7IRL9iFZ1KN3g7AkNKU9RJYvdBGJHYdmBwVyuYeYgzgdxPCQHxIr1ckl3QchOiMv5jBCLTOq9L/YYKvoUI8mnIaY7Ic7nC9YQ5TgnNqft1LKRamXgdHwUcXJmENe6RCWmmLml8hTLDvj5dBJ9Pz9JbucA78FuQXSHdPmyGU21TzCn38AMDwjOodvdoHBaC2GuT9NGvT+iOIZY4stRoNfwVNJ1BgHu8K1aTKo7a1hsPiw7wuWzA+T2Fz2CSydVKreSORlgpHs9wHK/R74AXHZL5D6RVafMqI91kg4mknK0nwjFk2jrzBgDo91UPVDJSNrsjtGOdKfkePCBcPr9Aa+Pd3j97RGno08neDiX67TYV3ru9tC24c82ZMSudXO7UIHs+Cjt1cQv4JDYfzRT159txIjZKJLxhlBRmrThANoHY6UMFghGK9OKQmEZoSVkPSxXnRDX4GuVMymv1NGsUqsT7yyzzlzD32U2imL9kP/N3TYBRDpNDTs5vXOJKBPjdFjSpadyJvY5RMQIsDDBoxiTxd+ASMl0fRFDkT0KwYFw9AQvd0IobKSDChXoC4Ej89viFplIyqUBcNUbWsyYG6S6Dr0tXBvvLBzU802NmfZM+5c9Gsg4hkgcEcwAzDFK4kSIzHBwCJGzcSXZdBKye+fgXLocCK5MgFrZ0zEsl4Zr/VlhyytV604jUuFFiCeVM3qtw+GawlEJjkQgOuOwvId3jyaBA1EEs4Oep+iQjLs8ZYx1+bPom0aPsdMZceUTjaPbuNSDvNmB0y9Uf6xX0PRCRBaU2jJzRynOGNzvKkyxYm/e1beCJebfDiQT6jQE4P70iMWveDyfTKGclAxhidnWR6WcYtiXua4d3tEc294iWO49OijNTS5CJcpwVqv77UShnhOUuklWwSj0Cr9RoPSdkHcPbgcezqO2iRXdZetQQDWPW4dCpjaq/OjqFzKXVVvlaED3W8NEm7Y9H9weT6iOiNw6Kg/WwTMMLe+iEp8fjXOh8Eiq+qQtEqXYArelLYNhowFe5KzXBLrchjpdeznaLCRnqKH5mMC6OekJ61PA5bsnXJ5Czls5tdD25bw5NEozkxmgc7Hpg/Z9T2j7/EZ5ZGusDCrJzwgRSoI5btnJOSh/Byx9qX0Zs+zDObxDtqurGrcxx+0oo5PlBt/2hOcYq2/Pc3sd83IGfMiEvUf3zfJfq3132gl+Jn5M2/G6aE7kT6r42BYUP8dY9nlnOxU7krlDdqp4Uf9lN0y5/pdCPVt2bseYQaRkfUvt4qV5Hap2fAHgw5MVRrLH9mjM51ZTncVNvaNMZIWk2zgwebBziOQR2SPA41Nk/DE+InCESrlDiFp5TXj6KG0RNxOtoCzZlxFjmzgPZkNbCNsXYV8LV/VnHZ2I96c7vD+e8PjVA17/8oj7V3c43h1xWHy2a+giKAaLnq6rjMsiycw7RB7guroaNmbk43K4yOG6EyKGgMhpB0SMK9b1ghBWrOuKGJOM4yj9w+SLfJ5tCEkGTUeHBqznFRfdESH3Q6TRUcDt7QVGH8nj0utnOylCnStPQlSL2iyOFNmYkIwPgsuD0iNgFrv1YXwnwxzyJI+auWudD3xljw4PAGHkMS41lF3T+r1GD67xIv82f7M4aG9d0SmRh378UR8q+JupxU0BkrSlbep0SXadZrdTBoTqwsnaiwgODofF43Q4YPE+7ZKQ6caKT1y0CKaq8C8Mt2F9ne8FmeCgtEQ+TaxxQuQ86pzIEF3ZcXYD/7txR8QG8xWgrPKdv2WkoS5PSpv+reEe11XtirCpheYUPVuJu2vS1Qpao1vB+no6tHkmLlzbAfEcB8fcAVEallcYDNP1WSrlihqnyKAAa6SwxhYVHLxPo37vGHesx1EwPpxXnEME2IOY8fa0pBUDEtgR1gh8XIUgytFMIMKBgFdLvQo+M+/yU9piu5aKs6NEke0y829r4H5ZQvCTh2dLX31Qnp5WhhIiU3IkSHzkJJh65/Ml1ZFjmaeUVtU4DxC5dDTTspTjnGDwmeQicRnfvCNCJkw5drtcWA6Tv2OYRM1F1UVJ2HbUFLjSqlcH7z/jwf1TWm1iLwYQ5sck5ynqqggiuR/DSpRcK2obvMky+L3DaXn6Jt2aCei7KipHAG3CMY1sGk/2cZu52ab0xZWC2u5tC7miv+W8lRHakdxBtgM+F/Hm1UeE6HD5bslKAoQmV06IzPsSXskVSADMKnsQ7FVqum5eAX3OFnQ9pkyN7nnHBZfvCSqUbZlUaG+ZP9wha3EcQraHNwKtZpkoylrXXqeK1llPGBk3pe+Urq+zzohC7VN6m7Yow0ZuMLBZGC39yfjii+wxuj9CHRFSszgvLV3RyloeJvijexVGtCMLRDnbVRaWZSB5cIpvIk/VglSWXHJdY1h28s1rya7J4iM62qYfdK0Njx9W/Pj3nxBCqDLkXQ/VnC1JynKX9qNJdk0Oy+UUmaTcdTWYBxt9YeWyrdA6yDZAK83KReeJMs2TPo/nTSuXfonNrpR9Y3r06HDNCdF0w08SbnY+3Vr+S3T2v/DQ9VHjeBgtmrPxWe40kdX3puhMQ6vp0RKzFxTqbwi31mrT/2kxbbv21KPXoL2t9Xb8vmgdmAx3kYdn4//CeEFAvjAs+PyenBBL2g0Pj0gLVhzwY4j475fv8SqseIX5LrM6WBmQqthOZzEXSJTLjq0xLCXmgceBurfn9NMkD9d/v334Cv/h+O/x7//yCXe/esLruyMejgtOfsFinAppxwGDY0j44dIxxkknSAZzlbU6W61WZhayqPGYgLRDguVuiLAihAvCuuJyOSOEFeenR4Q1YL2cEaPeJUlY3JJKDrJD15WduiEAIQSslxWPT08IIeKyBtN0ayfpZ1QF90CZ7VmRHdkd40UAWPVsLgZVghwV7RBdOk6s5t6KU8j5OFuiVRvYwCH7oQWTWRZj1u2d31cyK4yrbqudFEX3qvQwbQ8j4wai3tMpqaLcJWq+l3I0XazK6+HLSmKypxjc1D/OjjKbvn0etbtuLppkTA0MVRFjBkvOwS8eh+hxf3fE3fGQL5AfH8skWccl/rMKtU3lGRy5kmF0cQVetGP2OyKuCOiZaTYCmhKG7DrIwFs2YplMX3Qtj1H/TD3RyMKdUfD0Q1UTzYcmwcU7FDZqfmqG2X0fNmxPaMniPD+Ziur2atxYWdV8s5V5czQYCSEFW9P3CHKE0+KxyH0BBMAtrtr8xEQ4eOA+WZeKwYgICxG8Mu4GIJXdbUztiDAt7wR+honOBsJbxmjQ29X8uJ57O9FILSEbbxiSeszLf0VwyPkr2S2VFBnFxEnJOEkAHAOO04VOjhyi9wIAgdiD4pIuo/YeHOWILhEG1DAfRWhZvMfi00oRi2l6FIQafvRIJpgLQgE1xIkRFSLA6Xiq05MA3QeR4recEUpk5R8G7OW/tK64e/9HLOsTsLTYkkaBSFdBEFh3JzJ3x5qkMyitJLY55PK9WZFxDS33oCzloq+GXmwSQU2RaG9oGzHIOjao93OjS7W50oS7x5Ytz/JWK92HKXrBWYXax6c7rKtPK8rqmQohbQCXOVZ95EHX2pVAaNGg7qMtUbeNy7J3WtI5Nf5X4rIVfgcVZmGlLYOscwVdI7kVeIApPG1oV9KSzMsR/AVGGnS0LWtctk1XYLU8MhmirMFWR0jPkrUcJ2FHopsg4PW7Ozy8OeL+9RHWKV4wyThlob/U4EOuuuKLhSdaw5eB3eIj1WXZsqn5fn1HVlPkFlLuijezmGxcyyn1k6U5onwZzmjByqOVnT5U94VxYuX6Kyti0+ml9zu5NONL6+Gwb50Bvy67zspAg6d27HsZsFkMgEnIrKxO4Qxc+d2mz7Ja1YQaJtvGVtndwKoWPYfomuPbhDbpZNXjpOqsE9xo1O/ofBdnYKmUqK2CZv2ksklffkPNr0K6R1DY7+BoaejW95/PDLDlfOjTbscXUlMr7dtd1HD0Dr1uw7VbwnSH99WInx6GGQpcX8A3+6iyCW+uhO7LaBdLXskznKMbkHH9Ul3iLIStTsJTCjIO/SrXTDkqNpkWjqXjWBwCpT8CIcYFl3jEOZ7wKTzgiVesSCvjRxtcDeoPwnwP8zA11bTClk1thAbRP2f1pz+7A7mVFzWu5k2a6uPDAT++OiC+O+Lf/eKMX37jsTzc4f50xGlJTogsl7Urzo2YkJ0/oIkcpYhqV8NzMcDHtJM6cgTHFTFesK5PyRGxnpMDYg0IsoshLdBNiiohiQyB0nIn5iTPriHdA7Ge5U6J5k4InuC3nlOhDpJk+0ljnQz0WdXIv7korvvfjlAeHaq6UdIavYUIgAPTAXBHBPK4wCE4a5AXqKjAmPu/qRvVs5HjBCJW5DNA6XHU2UnUOQswGmT5rAv9gHzulR6hxWYBmoy71qN5NC5KSVG/K3xaRoy5DmJ5BwMxSHqtk9E5JhiAOX6qjJveAWvz2vlnygCab+Z10jcpf7E28ixtLoRkwavD4giLIxwOC5bjAjoke9X94rFU3oiWXrSYMKkKKhtftcwmdGlKfAlJp+OhXGxgtjbF8WmdVvZsOjnDa3agj+n4/hbd4Ii4ck6WUTLs7odyYYnCJgjUcK1eVub6gy0CnFdCM2zxhmEQssKHnKZRHoeVm4tXdLJtBktF6wHPoLeaWZtqiLXXhIv2e2s8GCDBUIk1Oe1kar73K3TGxWtZSvATssuxCezADNwfBuDlcSoDfvAWbJL/qY5Dna8IbQP4CpC2ygqA60pb+23QiD1hc8z7sRslpy6+JfpFIdJ7N2rBNbVNWTGDEJHkNhU2HAGeCI7TdWQLObCDnKPoEDiA+ACEFeQXkFvgKCIiwjsH3Q6Y7opIDga9JIhkza3WDnJIF1Snv3TsUWIi+QJzNeKQERYMbdKVMQQUQ7lpbm00FCFOSFRKWrvUiAjL+hmvvvs7LMcn0IJyRh4bHM/4l44JAUkfNQZb4gGz2AjViFacayeRH9De+vuOIiZVEeh2Z8QG3Nur+gvbrFjdZt288bYjrj0aJxYI1amVeTTXeZkJ7z8+4LImQ7LDaoGW8pAd5pXoUuFn/WihtLu7rJDMg57sRZGuuJy3De1xRqN8BXQrkgjON9lGOx1G79vHHzSUr8mvxk8rJo1KK3dqSDezbW/JuxUKrLJ63ghxZNuhdFVWEVmnMJG5x4aAb379Cn/xt1/j+O6+tEWdtJScV/X4U/XU2rR7PmFlI9NeajMZzBRhyxrmW+O10sZZuIFDlnlxNZPOk5qv9TVat7zipxlfVt7RLnKgeuce1c/QMbdjD+S7V0yLMjzZuTQ0/pPqW8KzkOvUdtp6alg1e6xwIicxtKZ1CHTt6uBq29O2qqlr4/e2UKtsdRmGVw+e+jebv2gqdvHQPOdPE+a1NDrQs+CZtee5au+YsxRauUWzbxQVTPnbMDw/tA6+LyioieAse6e3faE7l1mLr0qegLBV7pXvL53vpcI2N8Fmx26Lvs3cmn1voLkOyIjvbJV5JTTsr6fHfak8xeXNDslpYjopH6AVkRirF74eF8RwwNPlAY98hw/8Gp9xxoUCAtnLqoEiIY9g3B7Tsfbb0kJkPW8778aXDGBeOQZr5KRkzGpKKO1jAN+/PeEf/uYtvv3miN98/QH3796B7h5wWg44OpcMsszgdU2Kte4O1jESBZjMEcWgGpvyEjrdCaHOAJXZo9QRV3BcEcITQjjjsj5ivVxwfroghIh1TUdjp4uvyqKWpIgwIlMuN3JMl1pfAs5P6S6JuEYEJN0mG9+F7uejTWG05yyDl3KTvVv4rsg49WYWo1ObX9mMXgTknCMCcUG5AaH0HNMRTHc444BHSo4IRix3ksqNCY5cXhTZShFVTB42XQyZxrdMJZUn046DfMdEtnmiBJU17Ukg1QOXfNYJYRmK2XlQ8taOqmR/kcvL5VcGGHqsF0W5xlscEVEdEvnYL9lBoQoMEiPPuyDUGSJtZ4ucbcNautP2iVWkK5mWoE6O2j5jizSjReWdnAf5BYfF4QiH42nB8XQAHQ84HDxeLz6Vk9X9Ri9AzYtnoWD7gEqPsndxVKrfTjgNc/rXl7HFjVpu1paVuxdcdL4rCxm3wrMuq74WqoGYrDIpDgtk/KZBOg322CfdxupcQTw16KAtB42iUWvbQ7WqOlaqQuwRfNRF1QSttGwoVFVdtR/hqHnpDqtqcX+g1Nv3sYL5TBGU5JgPLuIIab8ah0SXjUwBDVwjx0MdVca+WjfS4Z9NOerzBrDNMaGesO6QAbfDXEAcsKya7lafLHNAZliU04gUoHHZyJUYrP46V5wD7Byc9wCTrJpxABN89PA+Hc3kvQe8B+Ri8rT9k7NDUo85ygY7qwiKkQsEqZOyMapKihJXGWjQC76JUQkODoar68gs3RJKpXsGr5OopP6aTiRHSZ9uC6oxDbL7PerAVSr9N/W/YkRZCbYFiK13nC6vCq3kjjh1XthGcFMuQWnGRGnIApAdX+nX4cBaGowOT7Yg5ObpecHUKGiV5xioOoKsxNczveJpbPBJImbOgQR5aYVNNV39eC1+xF+1/+vq6/w2E9e83L5ztYOgq6KBydTHnFFQodHPVkaYtZHy9KA+vpM7ZmWUb60Biao+0i3LmKIWEXB4+zVO3/4NlldflfLJ0INJn1g5qO5Kw0ftOJKNBzJ11eeG72oKi6U5ScZf23r0b0rjQabeMn4znE6LGUrb2zUut4RbZOX5cT3GQWSj+2RQ+cv2/wym57ZpmM+OicVLqh+GOD0rd2IgfU64pa3jtI2UuqM8KylbDkEbBX1pO+tCJnxl0r69UFzryy/v6wRDfXze8+t4bnipo6VGToirJb903ZP4TSf89dKbdysn7oV/rwT0Mwz4C9RhxI06TGhutfJ+Yyzqy5KvQnHlc11WL1m16amoKy1c1xF5CpGXVbSBFkTh0+n4m/QX5G8FwdERD8s7LHcn8IMDLkiXO6LYUSqbpLFlts3LaumoPd3DrFWlReNjt+oKefRMVM74J5jOVMMu48PDEd+/PeDyzT2+eXOHd1+9xsO7exwf7uGXIw4+nfoQYwAjHdUTQYj5MuP0D3ldZNfTIqDYZtPxplEcG1GOdopp9TsHcAwIId0FcT4/Yb2ccT6no5nCGhBCOcrJifE7Shu17LCGBOcakuPivKZdEWrAFlxwGXiBkUQTrQZWe10bMJZZMdJi81gYHDKllXd5kxORy+JmlcGTQJxOIZAGky0ti627aOpVPST3iZH1ZF2zzojcD5UsIAXlRZNpviXfit6TpsJuYyzV7JXBg/K8dbBLq+3uDO1krv7y4hxu/gAzkVMc2/w2nS07p2mD6kAbE7r23ORibPNtH9Q0zTrEUrc4Ini4fDeEIzdgDAMddAdPHodWOLqWjq6ke0bItpmGT1Xk8EtsHG1d9THFe8MNOyKqny8Ouvo4FTqe5JJS6q0FcjUwtApzZ0zQOLLv+tFSETNQlgmNQmOcLPJsjVBkf68qCXPBYDuj/bVHSNVttgXbiVY7jWaw3RZvKG9Jx8grxJPh6VqZtn/tasD6IfPEnHF0jFaDE532NE87jtGasNUJzwj9xE1t2acK9JAM8lVoXhhHZxAlJ4bSskOBXTpSieXsocgRBIcQzimN99lhwc7BOZYVGDEzA3VyuHxJUDVLGkOeNdCmAvSsbjTxqRn2gsC6+aNV2OUbyiJ0ZeCOwNGsEN0dCPZy5f4rIRJhaqmfaUpDu8WIqczwtcwXyq+zI+f2xJn1xFw3ltiZ94HoWMEpTIvKhwomLnWlj2lgW59PFtbQZG1hb8ZmNrOuzbptB844h51fDu18GzsjMl9QOdRCPROQCFUZ2i+F7W3Twy1D++y93hY9F0K6Yw4FGatVYqZ8tkekTeocT0/95q63t8LEuoyZE+KqIUkGoeNbRlgnfR2UT40CkgABAABJREFUefz6Fzj95b81WYvjvTV850mdaWdT9waHqJMMnBBDuSQjWKElGW/rqjq5prdqz2H6qcOIPTKjNrQauklU2qljYH6r8BNbZK/tGKphmcVP5rnBLyvSWl77ks3r22Hfd9BZI/ttfy/JdEVnbUiAGcvreNopxNvJmw+WBv60uHLTAqcrdG2Gd3vrUNryvPA8hXm2s8AANBjthtcMM/d1zGXMvXLWgJR8MY18Tv6mz9opNJ1q87pu65v9YZZ9Y9F//9yk3dYRYUSwceXPc3SrzLNVcVPJhuwzrCvL23P9w3Fa5brSArhkzAxwYFlDvlJyQqwEOHfCg7vD4eEeeEXARwYuBD3Q2sJSrb/iutLKbtkk6ftyNGh0ZcDbY6y4gcXCSnk3YsnCuQ5m4OODx2//zT2+enWPX7y5x9uvXsE93OFwPOHucISXRXSBHTgyLiEmPTMmZ4RTWc35alV83zWcnQ+6Oj2KQ4Kj/gXZCXFBWC84P57xdE67IUIM4MDp1B0jnJEjIKxgZoQQwMxY14AYI8Llko5kulzShdRis0m4YHE1HbcdjbBZ8USrf0+4ZTnoqaTnnIPzsDIMPpgxLYKm2VGMZL9QPh6hqCG2CM4iKwjmuNNaBUE2XI0IBqllhlDplEb+J0Y605opz6mcvMKt+i5NsvYLMocQscpmMRssin/Hyqy5WkRGdkbo73AScrPLRv/JDoZyKXoZqPZoJv3enCRQTeo4mL1VZ1hzzriMurXNrz4b/iV2Iif4650smqV0JseEC0PHnibGnN18eRc/72OfJ+0MKt+SufRbQztL6utQVOM50OH3hJt3RExvS9jV2a2C1xiOzCywYpA6Oku7yjEtVrDNSniuzaKrFfxbsCyzvNLxnVHDtqcvvHMCULuiaCwIjwEdR2cYqknJTVyT5gqOXDfmtw8m1PwBYCWYCXtmh131Rov6oY2f9flWuFXo3UrdY/BPEbj5rYMDY0FEOgkwseL60iF9tPEMrlZ5NOUbLp0Np84DPgJBL96NIE4+d+8X+fNYlgM4BCAyVspnz0A9+uQJeHcPvL4zl7la5k7Z8ZG3qwo8JOeU5h0bctFXcT6Yevh2U/HQMIVinOpWC7QpG2l6Xn+bYMplbwstQm6T4EmC/ZVlatsUE4dAtHSu4GjRp9JYVwIKAWm7tAkqk1VlldLrN5uvCG8tdFqOlbNUMMx7NhW/oOJJq2rtDNqmxgGRjiNDFo0qozez8V2JNKs0fmDI89VrwdeZUX7PSsxhU0y+rYumZ3cstOUMvkzTzHjpVn2Vo6B6n8FUH7e0t59a50YarWjoiRH6jXFPHQFeaF0uQ/Bdb1NqHR2VQzfHN3OPTDmVUT3XPHFC9I6Pau7bPhwIooVvK8yjPqcMkw16eA5178q1LGyt0mgL4uFEZf3WyKZEhNd3R9wfDrg7HmpIOyPVGCfI9GP9fPs8m9U1or9a94uFgmT2p/pUJe/ks58u1HXY5ytUeYoq1DKXFwstzXnOFnYtaV/cLO9t9VIzp0fH4P25htoJMeE9N/Xd9fqeP66ljj+rPv2TgvITVD414L9gtd00KxF7qi6rxLdwqb2XsUi+04O0swxLCG5BulK31hWd0zsiUvpIDswegT0ieUS9hpcZxBHEAetXf43v/h3j8ukR69M5Gc/B2VbZGx3LG4FwoAMIcpSRdsK15pteUMnfnmcRZR7qUUBRhK50dn5EDEkmCDEAAC5Bj5VJQMeQdgjkuxdCBDgA4QK8dXj34PHu3Wu8+eY17l7d4e7uDge/wJtjlgiUrMKe0v2FugAP9UI8zi3Rdou8okc7yR0QHAMQAzgEuZQ6IIYLQrhgPZ9xWVecz2esl3SsUozG2iJFruGCfFIsAX45JJoVgZVXXEJECCtCWPNCfJfhJFlin/TwyDBjJjtWpT167FIxyxX7AyKDHXL6FjvyPWraDVw/l/TmiKCM/qnC5RxAEcAR+Z6EGm/KPMkgbsmQGk82nTlglWyccJW8A8Icq2SKspJ6hPSHAxCz20BKFDcLcz7yk6EnjzTtRxoThgeJC8JFRogJw9jJmFWypIMu+uIWzjwoMPU0ToicKdZdaMtiNn08Clt9r/DI93ZnSR4ayvYCNskdGHeXM14RcCSPxXk4cvBZH6mtxbnpZI4e2hUsUDW423n+uYYy0DdI3124wRFhtY+ZQLe/DOtAAEQ2KBb1abmlamsc0FRNxgFe2/xtKJdojtlmm3fLCUGou6kV5nsoJr03i+7i2xlpJo+dpKP3rqS6fdO6Z0YcM7Z5Sx+nOCbATcq1wHWw73Q6dKtF94TGctk7b+bZ9k6+61DNiPBEeJX+SDcpMALS+Y0ZCjWmyl92snM9rtbwWsrtV2U751NmH4RhEYgdCAzn5WgmvyC4Fd4tYBfT3Q5Rr9OSMXQO9NUd8OYeWNKqBc5wUmaKyE4Han7LvRHpbggx25Ie7WJ7bA857Dht1/eAbEPsnBss/1urYpdzXG2T/ouCRZ1raDYSEG4NHdLXlY7nt9BWRl6NWs91o65k2Hp+kFbJUL2hhGswqCtHiyMTP7wNQXCJczK9gBzg/Si1I7S8oTZw18bK5Iiw/GZQSNWKUi6gNNiIWTc6I7YMK1tGqucYZdq6VZm0fWQvsbYwz1bt9ny7p2+juoF6F8t22i5r95Lk9ZbWWAmAEq8EAWTvgNB4FMGCUGaPfc4/Zn5RVYypTx+kNySflc3c4G4wogJrXWVfJ9WZSp/XJQ6M+/VrUfHS/B7pOmOyM8C/KUmul0i8Pp3w7tWdgJ/GpG7PAC9sE2SsioNnO1R9sCHH9HV1vWkA2FnvFbmplQmvyTO3LBK55qS8NbS6xXblaObPOF9ZTzumjTPdJcPU0Jr2eU8o9K2UmuLH6UZQpDDnBXtg+7MykuM6PPn7QFYpWHqljFLYLnj0uECAzHht88JWn6zh3h9ecnxaUawsaGg/tEC0BdwA1zYr+MIw6cyuzm06sClHC6Mq7eWMA7vaQs3LjF912ojwbNQ8v3owCmB0B7Dc7WB5aHnWJUWyG4IcguyKYPlOHOEQEN78G5zf/S0+nr/Dx8t3edFbHBhJbdMIadHFV4dvcXQHHLAaMYK69hOlRWZOyiRpb16z5kq6KPraKs6HNSSHwiUEBI64XC4IUe5CCBE/PkWEEHG5nBFCxNPjBWsI+Hw+I4QVT+fP8HzBIT7hr7664G8ePuL1m3v4hxOW0xH3p1PmIEabgco37AkUnOjixRExGdykbzLLpcLpl2NyiMSwIoZ0HFNYnxDWJzydV6yXCy7nCy5yJBNHlkV9peBwWRE55gV/y+GYvriY7neM6WimEJI85Bano52G0iWcINHd0wlCoiVRWuRYDaFFw7pjqm9ZMtZFfwO0KWnKO2X92966BiwXTjsDDk6uMWDk0xnSqICQ7r9Mw5CU0+LYQjV/envPTIe3i4E0QbJTRH2vhFbpR2bE1IkpDSVnRLad5LsiKJ/cVPUiIc9vhgOcLk71GVaOjOCQHDSk/SELhaNozlaWGc3bLCdLv7OJlzk5dvYOBn9UvGlSFZEvdEddtvRhq1vor6O0I+UhXPDgPA5yObXPd4MYHV/6Ue2VMKNWqhvN2SI7dlN6IluPFhACRqasmj8bjDrvs0MLyw69nSoILbaPjwzfCjc7Isby9qDaDUjaSV4pal37uc+gb1bxreLaEooS0RITzSyLBAb9bxB01Ba9RHf8VdLo25Xh6SZeW9f1rEqP6g+25rq/BiX8NMHiDbcrORoINO0NyuxLhb1OCP3GG++zMveVdi1+EpgROciaFb2aU1antHvdOBl0W5quBhSIoEREcD4xNPAi5abLmChGLP6AuBwQlhVxSas1dMsnOQZIll8QZeErVVE7y7Re54Sp6B0RYsxRWm/fs7FHGTCb45l2B9PHKjeb5RfCwutRICoCgxUCqh6eCODT+NtCRfCvHwo7hqMKO8t4FuxKCwcCpkqs+S4P6fFBPXktdGl4YfQNeoOQx65WZqoCqjzWxEkwq090NYcjpMUkei7qvs4ovErX4YhDjQjVcWVQelEbL/Wy3EJHx0LdzMnQGllHBvUR79S5NJpPW+nLO7JRJscO+Btp4iY4TqvkRs6A1ukx3BHR9JEqCES1wb2qmm2ZtuzWWF9BnzNyRiGzqkt3VeU/C5N1tkq7FbZMK21aw8XJjEP50LXLLtqwfU26C2fn1B8l62QLauKdQtvIHoXZbJSOolyxzDsmmX97eet2cI/v4T59B/r4Q2mJ0SSnhnrhDaOdH0O4rhj7R+lmddu6Xj5wqftPHn4GGNIg3pjpRrnsxcOX9Ms27H8e474v3ATrNCn9LGjW1WnfqP7tkv6JUO0Kpvx8gPwM4Vm8ZJJFjbS5ZCr61p4Ch+JFk04XqKiMm1QQNkw+heAWRLVEq5rDSHH5oubyWRfLg7xcfO1BvGChA5gOeMCCIxYceEFwHqtzYJ+O410PD1gD4dMHh6fPxXCYpV+VqRzl1fKeHO75Dgs7LAiZHltJpyoD0kQqzw4E5wleje5UzMlB+HSMSe5akXY6rOuKGDndgxAZHy4RTBGHu4+IHPD58YzzGvD+8QnnyxkfH+9AYYVbz/jmFePdAXh9cuDDBYtzBcjcz7KLgTk7ENI41XpwpV/K2Tkslwnbi6jTTgg5gulywSpHMV0uT1jXMy7nC9ZLxGVdEVfh4S4t24gx5h0eIAfnFtzd32PxC+7vHkAA1vsLLpcLHBHOlzPw8SOi7siA7LKWfi07IVI9DsltlWRLtl0wpG1JdqsdB4Si01a7Hqy9W3cTG5zVu5JFK0g2OfIIWMDkEUBqAamGiASGcuSKhayddiVeYaJqJ22jYFYrPpN9Iu0Q4YK8bSCCi5Bj02ReRicyLwMuHfNVAJAdE1qWAO0UqyJJWQR2DIT0SyEA5MBOdDsXkpNLDPYBAHRstW+YABeTM8RJ+3K/8ZaJdBgarax5bPrHKgytrI3e9JEX3VZZNZ/LF407sgeNFdxQEPaHQqfaYc266q4yrn37EwgCiss/cdjtiKjxouvtPv2ViF6xarXXKSRVncrc9uUdp1HDVjYg7DFaDYqshQdFzIFgMSyknXjcRW/XLwQ4R1gGToP0PVS1h6v8WAJ9a5g5hjanXWWc2FPHzWBtl7e3Aq7bsWUYuQbiaKoPZxXNX6ErCSojZXoeOah1HCydV8NQ+TfFkXNwzIBfcpkxBhBR2g0RF9kZsSD4BS7Ijgh1JFAxQzlTdjU7TBpyclSHNpJ643U23lnj542Ec5R8cFhVm6t8HfAG3ni7xkfaz7N1+z2Mz1AXmyzUaUkvPLGkzKEzIldHaB0SGsaryspbOffWUDgRovumcK8U5vrTd7Y9TQ66EuRmccCSVWE2Rcmq/7Jjoi2ik83inNYMHQSjle01jxrl3XJEzIKdj0mnLJSRG0J0zRGSlBBXfc9CZpO3vApHZAZk231KU36LIjjCjSJX3LYjoqyEzWckm37Y3lki26xzva7QTNG4KT8WeWcs+1Aus/02hvp6sF1b1d98L+DUcA2dEHXKTm6pQqXYcbez70uCO3+Cf/970NOn7lvrCLhq+LzJMNrgfiMrDndhDPK/hDOmyHeNnLeXeVyBwa4Krx2GkpvK/Jj1sU27p659QzGYJAnMYTJu0g7YyuRDH1pysLdds/S3GOWfsxPiTx8auqaxu2He4DU/S7tb3tqCMIOh0P+batvIMGNFbZ5eRrsRii/t1pGceAsoV4hBpxur4WjSQXtpbZZP2BCEnvlNQ73QpJE5uEqYD3DJUhbVSQJ5BFcfL8iV9a7ITgwxRAKyEMwBtIB4gacFyTmRjmk6QO4D9C6l9Q4HOsHTgt9+dvjj2YuMUo72cbK4zMvRpI7EIREAEGORQ0UdXBF4LKRUFmaQ9IwTXdFxckSozpkyuLyvI0ZpH8vl0RzSocbECBThHeNwjPjNb44gt+Lj4xMe1xU/fHrC4/mMHz4twLqCzxe8vTvilw93ON59wGf/XTpWVQGyY6ROiMgZF1S2TPJer8elRXAh74bQOyKiXlIdAkI4JyfE+ZycEJcnXM4BlzUgBoAjy+IlSu3k5KBgZiyHI5xzOB3vcDgc8eruFZwjrFGOdVovcE8eT+cnxBCwrmvW2RmU7voEI4pR3JHeRUByVoJZzjWgJ2KRGHRWSUU2VvUxBvKRTXlFv/5EUycJnjoE5xHJOiLKsUkuP8uRUhmcWkcpx382djEdLxPZSQak36ic3NR3i/ifGEwuHXem/kHX0GoHcNo2AT1YqqMmLpXlHYkjSaCU/iOobgQ5egxgIsQgxw2T6rwyWo6Lt8cR5CbscX8QrvMWNomrR8KUqGdbkEO/jLmvsDpoSXVD+S2LvvSXa9wBzIhv6L2kKcc8xCacqzamzRP5l6smXuMd+/jThkmzTjAyik/r1DlwO9Pf74iokKZVHvdWTiZ9HTfMvSVDVDg8SNBF0fSj+qXzKgZr2Bz0vxoxNKdF4GeFxrjBk8Gf9rG1sCg8U6F3e9KM8rYhrUhEo7NuCNEduFuIPYPbfuNBnL7tMJgN0WVPy68Vu6v2Sd56A9hoVHLkFEhG/P6PuFxW0K//DdzXJ2NE1G16Wkt1iryQUxHonB59RHDk4R1j8QuYXPqDlMcekSMCXxDjisNyBB/Sygtmhg+XJPiFJNqSd3CeMmPIxJmBJMYY4RSoGAd0zlkhs+obuvFeiFFKAohrONo/yCoDrnIhu6SoPcufshBQwN2gLd3783FKwzD/QFqoVmmP6E8lnJXfHh3n2uO0LRW3NWL5lcbv6ZsxtdmgQdf47m3JTIaCv3oJfN4JIb+OaHocTl1bklQ7fJkayosz4Zrjoa/bXlI3aleuovyQrvqvVCyIlb7OJy8jFtpiRJZXbb4RSCJ4MhonhvmlXCe1oPRpDd2Z7zqpd2NVv82OCFvRqPxCH5tnzWfk1/Rjzxw2fUmldXMJaGeg8auFM70bwCb1VyWYNC8WWl7JRQkG1Yamp88BT//wCU8fL3UR1+ZGy4saOcwOkOq5rNGTwchgK61omzVV1PSnkQXzXKH8vS9iOCFvCjddnj3MLxDQtbJaGXDMgV4+vGwd1/26P2Wb9pQ9pKry+6USyS1wNDlegnD9j7A73Czj/HMIm/rnC1UBACN9xMo/XQYbJoZN88jkEfxSVowLUdF191pOZI9yVYDlxr1MBJAcc0Rw3ss9fEc8Ph7w3XevEOOCiCMYHqBFLlv2+ajc1RGi8zhFwtf3RXbJsglROUZJv6EkcliMLDRijOnPCR9zRGnRmqN8r6DKI3VPAnoSgxqOoyyzV2PsV5HhPOMVPwAx4uBWBM948xCxfB1w//aMy+WCx4+fweEHIPwel+WMzxFAjIgxpsXiIHlnxHVF5ADIvYmUO0PkkSyXiIyoOyCCOCBikN0UK2JYsa7ieHh6xGW94HJJMK3rBSFIPumnEBMmrGvIRzF55/Hm9Vc4Hk948+YdDssBp8MRROmujOPpAnIO5/MTnF9wfnrExw8fs0NCcZiQ+l7707nUh+mYJmPcVfla7WV53A3+oZ0SJkYM4Lr5gGMZwVaNJsF7Igd2aUdEwAG//fBr/EAPeP3V/4XFX0AkCzD1GKY0WUFiYGcqToPkkxjdE2B2NVPDz1t1X9tDFpHrkDZMERwiQHpXivYDo+w30SOvh8U0vRflDgm1QdgTI5DuK2HOF6iD0p0iqTsEj8RhkXZDSAWO8z0hNSDiNbEel6pbKoVlDPlAxu4bp9qoLryV8rWLq3sqMlZ8oRRQ5Gcbd90JUWXfEzlM9afjwZbwmrn3wmH/0UzWeCH/WGJyrU87hloRpKuZNsdxbqDfzI16iBXRGmMN1Upr+TZ3QtRb7praqaFaA+PG2FAvtU2bOpoUNm8Lf13yzcH6SqzVY3fYTtvCXoO8lff6tJ3hS6nyCj7xJB3v6IGdXZS6d0CEt4pgBn/6iPh0Ab/91aC8uQFcBcG0Ejetti4rcx2c89D9EywXIEWOIET4kC6rdi7tiHDew0UnvwHOpcvOdIdEkUwbEIiQzwEUg9oQt4RufOnqvf6iW1kDr5Kc1OG0L4bzS1YRJD4/cS6QWa0vZd+ywnx3ykH1z9xWxwPqlbc89mh/JWKzIvPA9eu1LFsVZtqEPC9vcUawTdM4nvaXUpMIMnibUHzg6BIHxQiiauePGPULJ7L11Dzl2sXNV+Mm8aOEZcWNbXtyXlYG6lH2QR0sZ7ruPRoqxZtn05d2h4Eqv+3F4KM6tpwQbbp6AYN1woxDKc/W4YQWGjJp6Y8hi/lbJqdjoYnQd/tsrFXOoEFZ7RgW+YeG3zuorqAR1f/sDoUWD8QSW5wZCH1czxGffjgjhoAumLlqKmqSmJ6ipv3UbPMnE0clv+3tazshZj0zckLYHLWDqsMWVDTl2nw3/bnXFbCHhMx2TtSV1uln5U4XQ98sNtBA5qtn9N57LlonZP1Nq/higG8Ot9X5svDcKsZ9idy3hwe+XBjjymaOHfA8D+QalutllPTbSW8H5tpyIaVjbP59Xp3zeq4ZkK7bFPaCMJFNbZLhx4ET2vBWBsBi9GdQPradmRGYEJpqkwHXLsqgJMiTWg6MvqX8xx1EHj2CccSHj/cI0QM4ACj39Dnykt7BOaQFNQAejoWVu1QxHBUnAqjuisT3fJF/JIFeR5wFeZJdEKBcH8mRTG6K2EYCsklUXMsOgQg+L/lyakIykn11R/ibvyKcz2e8f/8R7z884oePHxCI03E7zEi7FgiO0lFIzCwXSkcg74goi1+Y7G5jlp0PulhFdkHEdGxODCtClGOZ1uR4WLMTYsUq90FELg2MnJwZIaaFgctywLIccHf3gNPpDvf3r3FYFiyLBwGIMWCJBzABy9MB67rCO4enxyesDDCvSAv1WFCEcpuSEFB2qhY7cOlzbXc7Klshn/GgfZw/KOMXaa8SqORoJvJYyePH8xt8x69x/+YfsPiLijkVDqR3XUSYIlIVIqs1uySQh7OGK+vIbRv3iFMydmlXQn1kmrh4EjVmaWMFklYs85xkxwSz7K4wv3L8E0cPpogInzS0iHxkGkeStoVcVykz5pOjEsgkDiPTyKt2h4k8beRStun0Ub8PVXLdTYTaPmm/D/JsaGemoJr+AkUf2y07ZUSYfbf9NynymfacvUFBGJioyy46tWV1oDxflrrhaKbCIPO/eUBmmcyDYTqVQl0nnNR9DVE2AKiKdqAOEQZ1V4NOmRjZTxnuDdA76CbKLNGoFxo4qU7b12VXuo3b1+rIozTlcd7nt6LbttA7/zhuz7XAuyDsUsw7Z0fmqvrn5cOgZ7dfq+DBcKQXSUfki4iQhBFiTsxCN0Jw6qe0RbVs/1TFg1wSLOFUwFwAiiCnG12TsBQREULaEbGsK2KM8IcVzBHrckGMDPKrnKdo+ojZxDnYGZCE22L8z04AFZJ39OUsjFYrZ9uhJb576rjCEzIZQT22mXlPDdzbhm9gPgvr2A0rDUp7Z4qhrcPORaMWDNwVmDpkegDqUriK38jSxkzT8/hzrndQJrf90RfAzS8AIfZlJdAoqBy1vSNC741ox02O/Kmsa1wdc5bryUbMIjjs3Ss0dUQM6qigM4a4emcApXtiTJpb6tZdFe28bfuoNQTOnCxZpCRpEynvHM0TziSHZPBa1E50wswThqwuQlphlb+P2l5g1SLuf/UbPPyrv8TpF79OSrUdyxGINBqdvv2U82/RhAlNySTXyG0Kl8qAZOsoGSsppjLi2rb9TGFA528KVk7L/GmAAy3ftriWyxjj6a2GUYvDIxgMxmcczm3Q+khp01jgKLBO2rcHzi5Ro7i2X2XeX98Z8fzwc2Jf5Yi9lvYLd5f8Sw4v6YT4acNeIWh/aX9+4aeGatZ/23LtTxv21lvLQ30pJKkGMg8BwR1zVayRKNIyczpqqBi85T5AZgR2iFwvZlE7beIDDsyEP/zwGk+XBYQifwKA9w4EB794EJLutwYHsFzuSmmFdmIaEUSx6GhysbW2UncCRuGXTJQu5EWRHwr/JBAWkaMtP0tH64CKATwA6Yx7+fMu3YoYK0dv6fdKLGmOpSr9zgB7caQwvE+67gEALsDv/t7j9asj/vUv7/EH/wNiOCFcnsDnFZEYawwqLKdF2eLMQOTMX8mndkU59kZPF0DUexyDDGy6v4LXC2IMWC9PiOuK8+WM9XKRI5RWrJekc3P2dXDW6Vc5meBwOGLxC95+9TWOpxNev/4Kiz/ieLqDc+n4LN2t7Mjh7nCPxR1AcDid7gHy+Pz4GeGHH+Ri75CuQCYnxx6p/ib6z0jAyvZhRmTKl0eXte3pHx2/GNMF41HuzNBjoIr+o+VWh/AILnnAp90QT7QgHM7weA8goFy0XOS3DABZG7ZGGFrTmDC0rSObsd696WZyO4pawJIpH66WddCSlw2A5egkA1O+4Dr9Zvqieoi21S5kkwWlDoL7kpaZ4QgIrPdUaLny7jzyzoc06crN2br1Sr1RVceV+dz2yWiRWmceUcKXHzM1NB2J+pfUxpNwKYqTMMaIaJKO2LWOn/pkLPy3Sun/XEMPudXhXi7cfll1fh0rUjMEo+77zpVXmmkj2c4Setg262a5qAkAj8SFMUxt1NX+mqQbDXTrDOqyGOV25NG6tiJ1AtH256swbZd3ffivA1uVwcVQelvGUtVzycau+4I3Gjyf9KjaNCKDukkyWMYoRDhdyKQ4bLmpepBZGHojuKkhTLa9psvWCsWOIjB679PuB+/hZGdE2tbrQS6IU6MapHHrK9lTBFNSya6dI036K2HkcNDtzEPDlDYzGwn7ivaS4pbHVaM6dLIO+upZdH+bvlm60PbB9vzV8RgL+p2QtCN0MssXB65kk7qiIsz0WZ4DQN3Yayg52gnhnDgmUBTCVolVJSyFmHCTBzwnG0i7GX+9Jc90RMwU7pL2ecY1XRnU3lMxdtbU30bfyw4IoNAXjOc4lT6vHBzdTqrSfov7ZRU9poNQO0cIy6sHPHz7F/CvHnJWVDBW4Em+XFhFKa9IGtNyq7a1skOG2XyzIsC8sDEMVdl78r5EGA9GLTMZRwMVRqPjYXfXZH5kQR4wp5kTonNKbOD1MD7D1NRvymp72NaVh41SvuG4z3BlgB893LM2bDsjgJ/eKH+97FvqvtKWG0obt7tV6H/K8LJ1GVWqr+mq7KHxt8Eyc0bfEvpj9G7K/qyQ+U1LP16m9JcpZaL3be1czIsFboFhmnTHbBrK7TcKpnONfogLVfPFklbaPypeZTT7MZ1tDyNTsRwrFKFn5avuEpPhWY8CiozA45NblGc5l8p7/+mIT49Hgc/l+xsWlUP9IgvCfIY1sYZY8Zuy50/b4szoVMIByu4G6yLXX0qrbolAqB0p0aRk4VFRYGC5dLvFPV093lHRbFs2mKi4Qsj3BSQjsvR/IPz4A+Hu4PH2/ojPn444eA+6IN3jsCIb5OV8oqRTy68uNgJRuf8XyCu4VUdHjOVOiRjAMSCGFXFdsYY17YYIF4SwIsSQx11tsqmIhBMsxny/HHA4HnH/8Aqn0z3uTvdwywHOHQQmYx9wgF8OIOeEBzmcLxdEZvjDxwTvug4FgTSzdMFUi30yjtL3yWlGZUMFl3FWh0SUtgAY0pVK2M4I56SPHSIcAjmwW+EbPVsXQQ7FkUzyLXAZ2U3dZdaqRkkCa140LuX1dlLO5RWDe04sVTPysUq7QkvbFGa5d0JpTS4/4Xp0Dogx6VqU0kMXk+m8roV8+ZPjoxwAlmOZ1M6jJ0t1dHogK1PTtyZbfdy2eVI9nuv4qvmseCP3tLADx4jo5AL5hK3GXkYGp9pupGzg62ToOmEftyW3D8LmaP8cAoithgdx0Hn7JbapOjxrRwQpVNSjWBvZr8yzD1SnmTUoZ2KUKdtOjPJtHJxs23O5vvGYamSspjWbf8oqtCvg5oimnW1aEz8T8Nr81ZQwP1peZgYbcG6FTLS6PtXKNkrdWaFF7DqMlaB9Csot6l6f9EtWybVjeWuY9HR+20AN6BzItFQKzPREVs04hqz84EyoIzPSXgqREogAl5iXcwuYCeTTfCgMPOVjRISYdkSEJSAGRjysADMOywVgxnpZEuGPUc6/pyxIkzIyFQyJEjMzba2MtuPOuTGU8+szQ1MhV2mrOmdilO2uetVVbRRVQVLP+JzxxLr2Kym+lLC30+FqojSe19KMvo9SuCxQ1fH2AuNSPA3KacQ7ywybuspF1G3HK43W8WnqNM5l+y0pQ7cNQEsj512uOCzGP70TQpwQuiPCN44IvQC5YvxE2noBvV593vVod/F3D+WmoZOvp2u/Z8ODnMh264XXAmlaWdY4ImZwtDsiKqc0lX7JfNJ+a8BTWtQ6Iq7BoY6XNswu/SbI3TwgfPXNK3z71+9wOPqMK722ZIVhZFzSiGqlvmmfprcw9/LbywUrj9Q1cM8np8LUBCetjNkW0xjl9wblnd0YU4Mz1oivYwR0CxFsX9t0lXw8aXhbV8FTfZc2DmRZizOKH1qTGkMK/hRabZ0QbRl1HZ1kUrW50hVeGqmeFTpK/4JlmpirjX2pzrhRxv0XEv60O0V+2j7/57kD5qeFOS0pe8k5ezsE9SuNHqdZCf19chqitOwil+omYzJnFeLyFLOhWnW3yIwQiyzEXFbBc2T8+PGE79+/RiQHVIZ8peO62zbJFuc1HceTFr7EvBs3+pTWxYDUCt39kMoiueSBnPInuZuBHEARLEf7qgye6waSF4RE5k8RyDoeCF53V8hFy8hyjfAnJ8c7EYM4LY7T/m2HZDxEYidqbGjMJP2W5HliTlUzifNHMJEJh+WAz3zBP66f8RgvAId0N0NMJwiozAhKd1dkR4RDWiho9EWSy4QhRzBxSDsc4noBy50QcV1xOT9iXQMul+SEWFdxQnCCHRD8CBFrDIjMON3dYzkc8fW7X+B0d4/Xr97icDxg8cckL3JpOyA7swGAIlw6pwfklnRU0/EIEOHzp4/48P49wroihgvUnlbjOXWdr5ofCw5TcOleCZIdGbLjIYreHeRicd0RoUGP+CpSkY4/5wTsdEfEggsdEJ2XsU045VSfQn2UFINq34MYWzVtqau2NuZnY/jWDz63XPtWeohZ5MVeth95cdT5qLibNtRwk88kVspZLTJV3I8FXsVDyaquBy2PtCQdX5nv6d3uZ+GEA1GotrNtsLp5r3dUybjNN6CfbL7ZSNX7m8QxMIJjXNYVZ3/BIy5Y/AVrDFjYiWcWhcY0uq69Evw2Nv1M/vinZHk7Q9KRVHcY87hbwu07IlrlpFOuRt/VKDVWUCb6zQSGPiNR+VbOaOYqD1H5vbYTIgW9DFQuqmGdlVatk+LtCsmJ8DJ3yIy/10UM6hx+H1a9EbER2jpnyZ5Z/twJ0ce1xpPN9NNjvDZg6d6fR0CeMxetityNYuV4YpThH8Gna2AK/rcsLq+6UIZpGKfdYqi+CLsyi5xLq6+FKRMlZhpB8M7nXRDee7krwue7IkjO8MzNY3ssk0ZSNY/tnLVAzXB9b+h5/GjUePJlyBFL7BV63ClV08R70w3CTBrnyfs044312NAJBKmy4nCe9a9m03SJd4ycJDqOpTmmYVXVSSimrs46Z4WNA2Pz1bA7ecFnQpljpA4J6ndEMAuzF4k5C8amX/IRTab5ll5aR8SWQWcYf4PTwmTKbbX05JaQ2h/lVxWmbZjJ4g/KAp0Z3K1zv+NnVMsMN7WhgUWD9kxlqJbfw0I4nQjOS16q6X01ElSXrmXMqq5Ar+iodcj0daZ626NlUis6OdA2fRRjABuSKjKlDYzstqzn8oB5oDznqB13AcS+t47xYZ8P5dWm1+04Eg3r0m+aT50QlRNgIDdR21ctHjftyWN/xQkxlWctNLbpz5INvyC0g5Hfa0a4h2xbXJym6TtqGPayCYV0k80qD3yB/prfcfGlWvHLz9KrNb5Ah8z4/54+v1V02Fp8trOEFoJnljMue8LG6qpzv8zb0C5Q2JPuyxaG0Qt0aU9Tq/IlbB3Imb9RthEmMxoh3ecAkguTKZ/zf5HV7BzTbofLWgzNxRGRjrlhSff+s8P3Hw55h0ALaXFEpKOX0gKRCMepzyP0iCUH5yJiHlszyA7J2Kg6IVFatBbVsJzkUnVEqCpAagjWJfGq25HKEWkxRtoQQSB2KYnyYpcMnI5dWjAXxUHiPGxw2t9DFYqrpy5FPv6KSxTqPyDdQ7HGgI9hReAAygnTUTcq3GU+bXhhPndAHE+k+XQHRb6gek33S6zpkuqwhnRHRFwRdPeLte9CVfuCictykLsgXuV7IZxf4L0HIBcUi5E6DYc6i9KYe7+AARzjHWKMeLq/R4wBT4+fwRyhV2qRsY8RRH6yfUzacrnLxMlOnugAx9U1C3qVRhBjc1m8JkdJE4xhuKWbNg6I5BGdQySXbHhZXuKauebnEllFyUt3YkSFF+ZkBVN8Xgxc0KtAyPkf897iZvOWCUjpF0Go2vQlcZomuyLUKVE5TNIzcSwOjqraSjuuxxbJ+ZjyF3pLeS7lrREpfpNVNfPT8gnz3M9vM0gZypJEjwO7rBGXyFgpInDMzl/NkOEfnC1teeCcx1kYivz+IhJUU+U1GaMxtXThFtlxpAvWeZsFA89o8P4dEY5sF+feaRvSKzG1stYrBz05qROMWtXEUUnXKlylHDKMmExaK6zU1ImVqDJksjVF5ibZ8jSehHgBM4WyvNLw2ZRkK1NbQQdM56h4phBms23h1DXZdJqvEfLaJreT5BZBnfQcu1LaTVB+iRLz/JyK6fV21BqU2uQwK8EjwsczHFYASrRrBkoSb3cFJGEiXQIWWVZnM+C9XFKd5Es4lHPTmeUcR76AsSKENW0ljQeAIg7hCBDjcDmDCAjrCgLg//CI5VME/eYt6NjODZVTKQs2jUVjuyN3a4HKhAblMcqOCGC6kpltOuWNusLlZw2WCVzrn58QjHaaZkmgpii9M0mEj1YQy/xizBlUAKlGsVuWnNLpMXutT4NtMgFCaTZXUmRKlRyCcpGZqduIhdOQeE+6XA9mF4T3aYVa2RnhRZdpHRGpogRrrLpFbz8q37vOugJdgbELsl08fZd+GE2bSoAzl/RSK8rsC0k5LvTJkse8pV361C40AJR7QxTg7fZJzvyc60BCp7ytHhYv0NGE6t6ZjXYlVFJFtSj1zjn84X//v/D5Dz/gN//3/wlf//u/6eFXrKuEjRr6keBqd5g8l8epMsiyjOwa/y+y0Wz+9rLAnzKocR+ox7bA2uPIsBzhWSoD2t0Q80UlE3lEACv5FRZX3jshXGXEUkeBSXlraUsxopt0A5bb4mLOn9OVkf8yW/ANmak+iHNIl0wfV8ZDlWOAmwTdlkYUOf8KqNufq2DXKI5K+NPPlpcNV/vuRbxTP30oZONWQcuM7Z9bW4fg/JnB+DOHqxJNlHP6nccFvhiJA4uhNRmS1/gIBrCuUZwOASECn0NMaSLj6ezxuz9+hTVSPis/6S96IG8KIXis4ZLoNLnCfxRitX+IsdzJzghkIy0SLaOyEAZqmATAMe2KhwMciZyaL4r2cOTTJdJ5p4TSMfkjAtwCqVzinchvaVeF93JfhXdwcCIrS32U7oJwjrB4l46UYcA7BmLE4sqq9ySKtnai9h0ZjQmA57WWVyV5up9CTtQgIMgF0CGsQIzwAr9zPt1ZQVTv6s+r31Es7TEZfV1MF1RHDogcEdd0FNN6kR0Rl0eEELCuZ4QQxCERC3Uhh8jp2KYYGSEGnE53WA5HvHv3Szw8vMLD669wPNzB+wNALusBnG7aSHjCchY+AOcXqJy4iKMn7dgFjssBBManT5/w8SPn48DUBZRFC6NYWdM1I+0cCWAQxWr5ZMZsLrZwO4SEtK8goiwwcoqzoHyv5fEc4Dni850H+wXwHulEFJd3HjsU/T7juQy6rjnOfB1U4iYhw28WvCnojgGQHtdU7k3pCmijpANG+ka+iyM7FMzxXFqYOB3Y3B+jJ1MwkO8lge6y0mPBQhCHmNwdmoHRA9J0buu/rsBEAJigiweJXS2fQeFjU+5An7KOklFgY49tVIz8qPM3Mi4h4p/+CXizRHz9Fxec/QWBgzhyjYzOBh9+fkPOi4dkp5t+fYkaoLTi5sWbJux2ROgmHJ2hQyPpyAFBNl8rVmcNJ/22fELKYW6dACOFUCbHSEsAMhMusLeCfmXOMk0tW/LGVp5RFDV9UYSBesI07zTsna691MFeCKcmbyf/TcGMR3vfQme4mwjN27K0FbrTu0WBfIrkDQ6IptQvS/1F8/O5mbdE260ySYiNUGMGiGJmLpQJqh1HzhNFBeS6vLJCxVG6DAzkQJQEgeyIEGbuZEeE3Rnhok/CZJQ4F8AiONIlXXqd6YORU7W1DW+Z9kKRH0orbjsCZotQ7wtsn66UxdXv8yu2/VOPXk/H6lTttxkMO/B4VuSsqEyP2zqVVrJJd6V3ROApubmDpYwrDb8DyHee2KRlF2pZ3QMgKRgqkXKTeEcgKdPOr/Jcjmay8dYRocb1FNL22Kxs8mTOqEJIxoi8BWNn1ASy5GwM3mP6XuNept7PNKyQKD/5fGBTTFThnuo+1XzaTN1dslkPjHwz+ti0oW1Pf1TTFZpiysw4IXT3/PEz1s+P+OZv/5VpT6uQzWGtRJsK3oS0vTv7i5hdM+S38dSRTHQ9PM/IXcbIKnPmTcmDaUvlBG9lzhEQg37Qkka/LR7kL5VhqHFCmAGeOSFamMjEN+J4SU7I7a2cGG0Tp6hnCqrS7x+sa025XoD8M8xH/SONP08itj+PJt5WviF96PPPuPkoXD+6bi/DfvlQ8ddJmi81wL+sAX8kpwxGY0PR6nltI6mx0nbdgWU/3+K83yOAjGWuZ4ch/u8DJY/TLC1vvk5B6fnyDlgwgGVE2hvazrYuFsnM6FJqb75E4EJULpUOSZ5bZUV7EKPf01M6hiaEgMCMT6ve/QA8nQk/fnQI0ZXFTxnkmq4xgp4OJHDLCn3h/UlekpXSDlBHgPZfMjeGYixl5HsOOIaMp0SygMb5vHjGkRdHgXaY+XNJyoJP9w4glvPnCcmADEdg+Cz3OUq3TRAn4y3n7a3psmogHaBN0s6ImJwBsGNvjZvNGFP9yTU9KldymxhCiAEfHj/j6fJUlafyfDT6bBbcqNZT9Y+iIooYfDnKQr50RFMIK2KI5XLdKDsm1KhsYNd3IsKyHHA8nnC6u8PpdI/j4QTvFzmVwAEI2c7aUjSG9DND0nPaGbFEHI8nrOuK0+kO63rB49MCrAExhmxzSnrIiMjLvGGASFflIy1woupAIGOtMCutZbNJ0fHNnMxmuYQLLgI+OrBzspAowqOfw6VCJcSq6kiv5J9+Z1YrTbJ9Qd2vatPSNlHb6aOSp0vZ9Rs3acvCUgVGj7lS3EhH3AKMmPrTOhk0neBXiosFXwdUODmcLJ+UZVJZfjT9WIAvfWE6rT7JxnZkNcmqLpp2UGsARXKWff7IOB6BIE5iTZogr2WUrp4NmbgPdB3MwfdWJufSrd0cvQpJl6jPsUtcIqDFxalUqc6IZ4gW+49mcmk7VyXryz92flP9MQNe25Trb4PoKuTLkroPgyhLEQjIyyiFURQ4qwpyK4r3UZM6IZz196kg1kRaolz6icx3C0+ddrQCDUBz8e+oNzW/nfC3Bar/GdQwzTWokMbP7bkZucpRnaVs7uJGYY/S1SHCGKcGlGDepTfMQtp8HadnhYgqcJMQngQN3RgZ+YKFFzgmEIfEJjgiRiDCIQK4xJBWUoQgjCuVeZDVLewXRASsLhn91DnhnAOznFO5nBAZOESAIVtnyWFdAxgEf7wgUlrPkPqOEJngaQFIzwhNFbtM8Anp4nGAmGQulPmg7KqaU5VwVolpxpmpFxUlUbbQWDkfVBhyliVBpm+b1TbCiEcn2fIgrgL+OZOyKWJUglVRhqHlaNO0o/iCc/U20GsCwlZbzW6SvaFKrEx/u5BqJSzQNEDEprwDQgRHVuYq6ZvyiwNw/B0ZiwouORAOlC5RW1xS3Lxb4L1LyoI4JLKDLsMdE85mee3/x96f98iSI3mC4E9IVXP3d0RERh51dg1mu6YXvcB+/4+xwGIxwE4DM9Vd1ZlVecTxDnc3UyVl/xARUkil2uHvvYjM2mKEPzNT5SG85RZdAcqwKBYRrqfSz+yQV6mujBWhXQ9uhIrWCgOI1bWaDUU/DlI1l9IGI8GEAbSLXI9cbxlojEn/PLIMxGgWGlQ+e2EBAZhCbEZkFMQRwMaQBtCzqAg1KoxVSFTPC0CsyQxqYgA5awBDNV1W+CI7v8hqbSGahDKWAajMBBvbM1uMSOvW/M1tS7bydFSrf7060IPvrkTz2+A2YJhMiOMVPJym2c6dqhVtX3fXdq2zzWBaneTbKVnqPi5reCCIKJA4lI61TSKU2CbtGKLshWa9ASDERlgQSv+C62d3d+s/tR175HJLJ/V7BbYZFc0fRnNrfekfl+mRDtd9TOVcsWk6l/aEEJdKfWrat8DYr7s9I+3fvYuDBt/2cu2Th9T9sh3Cu3l86onAl4zbzl3+Z5SuFSJc697n86Sd+dw8dvc8tdaz2bROS2rPIWZbu1m/mxV+e07/ec3W7amH/5rZI9Dgvr5+3odLitBe9sPqdhEjMAWcpoMIFTIEJ6Gq41sDRmesmbGmjMQr1lWCC69J3q+rxAJY0op1Zfzbd9/gdDpIAGKG+MhXiwhmYFmfO8UaPQnUUwU5hYsQklgnkCqrkGKeRXFFKlrXBGC1QSk4pUXHzFm0qVNOVbJCQAxBBREa0yyqElqMqkgjVgti9Ss0XpwmUEBRsql0irJ5mYEUkLPQejRBNPQnmYdMGUwEDoxEQIgBMRGWmBByQMwBUwiYKYtFhvfg4e7aMqtKh0pXFUdQX1RZY2BkslOdJM+64Pc//gv+6b/9v/B8egJlUZEJ0wSmiEQWK8PwI8d/MTwxJfmektwBKQPIwHpCzgnrckJOCadlEUsIXS9LFpp5tYC7Wl/OGSlnpAzc3T9gPtzh7dtvcHf/Gq/fvMXd3QPifEAIsdB75pLJ6OsGbwwAWMQ7FJSXEIEJGo9DFXqnMAFMeHp6xFN+lLWCyoSughKpvNx2blNWOkHnAgCFqHwGiCa/9jOxCBgQgEjmO8LwPAY0pgUTkOmAJbzCU4w4xRXfvvk9EsTiRURbCb3go9gWGbrook2buy/T+y/3PVmRLTVuv3zMZiKAND5DZsNduwINLM7qIWeJJwL3zAQQnjYCi9svVMsHsYjQAOjQsQLEIoKh+TJySiIYyqsqsq5oBBI6UrnBnkZHqHfIxO6Jtmm5euFDc02OlM8ln2LCddT9pvaQ2TbMss/CygiRkbIIQ7+5n3A3BURSN/ycay1GAHT92k0tg/uzpIbma9bH+dSTOjts5DbTHgy+wSuu3pcqg9wQrDq47/qpP8YS0A64hj5qF8pF0G+lbzyiYQRc83u/beq2T3m6yXhpVnohRN+gF0IYEmtt7SHALRl1pmlHcPEL98bLFpRnRmzrGfdtjC92T92upNHzPu1OT7cWd7tJ3XvqX31y2vbx3JqqGpItGHudYYCTIhVcju0+YLCwyeqFX6syxocihqYJo0HJQghyVxBXjZgwIcRJPsMqiGmKxWIihwzTHjIkpUjOya8dj2q3/fW7eY/09yS+p1e9b9Wajwal2hYrJAGZZwArCoPXso2+76afgojea/pT2q6IWrs/epbKpTba+bkJor3MV1Zy+drl3Z+XE7mVvT1bympSYV6kGpzaPouJN1D85RbYGQCZgISLJqW1bHXX9hR9Joan6IvorN1eXeJSgzEmDQjqh6kgBFuE0pjtALAnBRidwX6shI5zwhGwYle1/yPLB4IKaIx5hTaEo+/paBwqc1jHQvfOSOjRzIUfoM1+oyYflfr879L5YZ/2HhAuTOlOnaN6SmI/v/VeGBe+/mIcM/PGebxbqT67h2VTw2bvcvmos1rLcmmznm0FJ+uAquWqAMYLDDyglUbpcIoOn9u20QshNBfVvbHp/ABtIrTwliYIZW9fFkKcm9seV7K299ZJC981z84lG6PzLXUwuXnkM32rU9XnGa3FczBe3svX9buu2hfSfDemT2+EyJ2xg/v0Er0zgmf3GBu8qHjtp5xPZ3N3329BUuxu6do80/e+vmtQlJtncXTmfmpydRaf6U31PR45+knNnbq/P0ftu896FTQvu5O4wG1YXQYhsVBUibPQMozCFDZBxJIZa85YU0JOGc+nFcuiFg+Z5XnOOK0r1oXw4ZFwPBFyDkVZuVo/iMumCqneARRUuzqoWpnLEcRtbtHu9l1ipXZc/QBEYxrc9IcV1qLFTyR+/SkDHMHq418Y2IqXUQCHKCjalH286e4usqlklToonhq4znHW/REkX2bFR1UIAJJ1ZAzwEAT+YHwCUtc4Om69xwyPnpnXq5wBJhF4CL7DmIhxmBjP+Rk/Ht8ha4CEcveUi1bu0qqdXv9EI939hj0T5m/Owgw2KwjO1fVRZvnjzLXKxsc9IcYZ8+Ee83yHw+EO03RADJPjv/m223XffC1XjK2zCAosMSDzhHk6YD4cMM8zTqdYeLacFWeBCRDd2msGXlaB3AtUc1IVIAUCMvlYE84e3CFuMsyVki+0CkWY7v0cTuI+S92iwe6jc0cbo1hHiPxj62tg46nlzPG1ewP1MDRc5P6vL8DNq7KnjZ+j9ZkQwgQWlfFv351FDuTTlKfA9hvtoNkY9vDYB1V4Sl25wlSLuLrPTsqWjtrPIwD4tQNUJVqQKH3NAZhCi61vWnd076btXfT2J0HMxolva/3i7e7v6B0U+GXKMW263jVTbOWBlqpZuT3wuTyyvo9A+qjkw7SHdO5kb+QQhXBzV+AZwsGYHaHrwX4wt7YdK9FovfXoTRmzmkeqdX5/B4BuGdc7z0sd/dH58jTiX57H/ba7lM6sgc+edombzZOdfHtADlFVV/n5zjXXcX9ZlTW2D9e2lhEYAVNeMC0fwGEGcDib39r2xj4ifKgMvpgjAolvTvPVyTmDOSBxRswJMU6YphlTnME5YZ7uAACHdRFNGGbklN161Sve+S41jZJGuNmfMRiMc3O5eQS7Ch/6Z2DTWKPNmAvyVi0jQACl1/h4+hpT+AGH6U8w7SLmoIi5IbpiTkweILjz3DFX/1KT12bp37y80hGy5Z7cUDX33/rL1B7ztkTpHdd+Ninv9X0EhSJFbrmGEEAxYppnxBBwOBwQQsA0TboXxEg8dzCVdcTOhNa61SEgZt1RttCkSP0G6G6kDIFsTyoQgtNgGZ9AZtU0chFCniLctL+9W23flR3Lvu8yOuX+6wQDTdtNhLgdlKm/Vr2gwL2rlg+hCB8AYS7494CeK0k1kgbmFr0lx97vS8kLjDcMZd/j7sgkYNCGO3MrJbZpq2Zty2+FMbQZ2+s6Vf7BtgJq3yjy1K/WFrALzV2AsbTXWUKE0tdqddsy+v14eWFCbbRVQmmfb4UQcJ+0rYe2c2oxbWqddU58214A4es+NzYl2xA3HKytK9Klcn3/bd2fa2lTpxNC2OdoidQpGZ52Tcc/BzF2S7qdUf7T4hrbITdfzADcObFffjzmlS8wOlP369ow+j93Otv2/tjXWC9yXu6f/ZeenZvfKzu+2+6nr52NX/RRU1xbqraLsr9DzbKF8MzENnR7h15u9CL6a4MZmQJOmEUbXxnBKS1i1aDChJSEgbymFSllrOuKNTMW9+4PP3yF9x9fqeV5xlLKikX6sp6Q8+KYiQqQWiGw3QM2HkQA5fLJak5JZDESGertaHf225hWVfCQcpK+JxFM5FQdFBEFBPUtw+oqKDOEyZire9FpkvyBudCLMU7F6lepMGWQeqCyCCVygjlLkrWj+4QDmDRQM8v9Zi6VUs5AYLEu5upsM5O74wbznRXZN+FPdgxd68ObN8B//qsVv31+wr++z06Zzeo03DjXeVNt8iJsYBYBBmcRLGlMkJwTeJXg1CmJQCKtKzLrZ85Iq64XmxsTVHDGFA64m2e8eniLh4fXePXwVqwjphkUgwr81P8/GKKg6MchFjxKMYZKARDEIhoBcZ6UqX3A3XqH+7sHLMsRx+dJrDn82Gapq+xiq0z5B6SxJ7KKy4wHUOLjgQHi4oLL4GGomy4KTthjCmBydgaS2CVR/9agij5ZvEJk1enPxCLz0sWQ0akkqNIkkQj1QhFHdOkFx2OHjpdK7F9HaqGoYBUB0paGq7IFE25BY3fIWpF3Qo+QCaOy0lHZ3MDZWjWrmQ48rrNQAeT62yl5kuO1WNsVdFfePxv2rV5LhRtDe7S3VzOzMRSFP0TG/d2E+7sDDtOMOc7FGl1b6Trr2kc/V6P00+J/V6c/U7D6dL1FBKptd0sIksvj39o73mWsOproTLuDsh0cozIt32kL+15pskVujtx0k2xMgjf9drBS+7vk7Aggy+rHZ8TLviiAGCJiPTPp1tQzk15eU0Wyd3O0y6Y/ZHzBQSW3E2Vn3m4oqP7LhfIXXlL/oGn7bNVd/m48DZmCidzUSRLVq4t85iJ40O/63AKgVaJITXqL2an/BDIr8qBWEqRIgP222BFZzXbVw5EgkSuDIgMHxlBXebAOisaD9YaNceqZlPqq3JXuWVOx/9wn9OqbgMwHMO+4irPcXayDWo9nXPjXGwroTP3/TtM5/O6G4eDRrx6hgh/ibeX7eFFja3M7cECzhs3FWROkWpFxQ4qL79dCHtg6b9c1lWBo9ttr8NtdcT6oFAGFYSCGyHYSqFsyMs3/cbdHdxfgrBWGFhEEIA8YqJfO0tYiYl/jmJp+7dfnvu4IIvx73564qeM+07iZ5q6XdWDPGiHEJyGQbvTKtdWeQUMEvG+Tzn0fwNgx18eQXegY+TyfC4t2p/7OdjUcpbd6qQLx9i6o95CVx+Z7j5/tCSG2czQQQvRtdbgk922WzCj9GAkhHGdfcVFq4D2Pk3T92nnfwD3KdaXwYZx3VGKEx40xr3KmjUGr9eyeL30T163Z9nwe9X+0UPtx+Vz74/OmOmQNxlnujWssIM73TZhD5963id30fcqYeaqS69cKlWDgBBWUtPnbu5eG4+ShbJ+fgbswiM6ka9fKMNsNY3YOzCHSADdMdBH33dsZw7bLFFHzbFxeGWYg89ADZgkqvahP++IOJ2UsK+PpqG6Ykggc1iUjZXPDBHHLlDNyynh8BB6fCTkF5AysOSNzQFpV2z2nDqfrzp3QCiLqXxDrBwaCWb9ekWyt9tbjRTjglbcange35JKNCRiBszDzSRUxdD4tbgDZXWTPQVXrXa0QbJVI7ABpmlgteEMNGiwCDGNKs9Sj9ChlwXPqNUk6w9yukconBRhIOv7mohhQF2k5g5hxCCtmAiLEKj6TKcO4u9h4R8qINYU3ZkaRnkC+V4FCVoGEiweh7zLnkqcGGzaavVpFxzBhivIXg9HihncbI9v7/B+vCj82TG45afBzESJI/TGSWnITmAlVBFaXSoDiJoaDON6AURcMgMloHw16rbyIQmtwrVuGksszPV2dQrPuC4/3ALCIc3X5auDofs85fJHKQNgKavO0aVxPO6bGnxknbv6pczU8O5tydc15wrmuP1VrK3wfQCwhlJ7UoOlsAwz3WXrV12+d4nIO1FmyJtj1Cdi4XCpt7NCkFeGun3XS5ePc9ceMoIK3eYqYpgkxSvzSvZkoz43n696MgRy/fymmscEH+NLsX2p0H5JrFGg8OA2d25+ln5CuFkTEULW+fNolLvaIlJ4Zf6aOWtfO0zPlWhSOtg8t2Z6rX2AaNJXRsUV/GvcLGEyoA2/TrCf6XI6iWFc2Qg//dux2E32ajtZI42i/rfHPSwTq7rzsCgP2a7o1jeZk1DYNvlnizatNR3ba2oHp4phv13xBtMwtiq4dCkEXlDtQTUMDVCTfrOZ45ovULhqC+EYM5mM9ih/zSf2CTjGW8ilnzIpAMTPWdABzQsoHgAjpsCAEQl5XpHVVcDLm754Q7mYsv35V5BBsvlE5o0HK+71ybiBh/XBumNzlyv5zMwfnavSX7LmTl9qKtgtFflGL05fslw5EvXkHIVb2i/SgXCywk3NALO6dNDdcn3rE9idmHgPsjt5xC/Xpphu8zdO83gitADNX37a5W3kDbN2j+kSReUOK6uehIOPZVltZr84/qIOzfsr7sDMbFaUalx/CXghDOVOqtguaspVZ1yGhVk3PiN28H7tVsmnOG1i3be0xruJmz7mzUJMQQluYewSsaMJ3FhH23n5nJVwLmtsJSI0YF+GTtCMxIszaDAhUg0ju040to1yhU9yi5gHqeLaTsJ0XT7hZFof311K+TT2IQj8HL0BAdvHG5u1L0u2YcrESoNCMXeg+LwkQynegmbOthYlHQ0IjcPDxzdxHqTNU5FEfuRuSqGurjrHNdyOAsPJdXeMxwvjouDBRY020c2fEeB97PPcW4UNfV78/LwFFo3w3rs7zmu/jus4xrz+t3c+T9uCz86Mjm9zdcC1M58fnfJlPTf3ZeY4DormozddbZ4ws4VpB95ebq58lXTiGq2Dw+n77u7mvK5j2veOG9da8xndmFl3pJ4pITMgraxyHj8isFhDMSGvG+8cDfvfHrzTeQ7VuSNlc61ShRQYjrUDKj8UiYk1JrQ9yYX5zAaqebRZfKwRRADMGawZAgZAREKLoaoPY0QTk4jWEuq5AhTFoY13x26rgYsxJw0HtvLP7wiL2ESrumRMBlJF1zCMDOWYE9W9vOIi/S03IYIzUKsDQfqcICkqHhlBDfgb1BcQAsyqCRIMF8HhQHxujXYNUcO3EAcxUmLLBGP5pRXpKWD4eMS33+Ap/jSO9xyO+k9VEkFE1PDWT88uf1d++urhh9dXPEqQ8pwWcM5ZlBedUYocktZjJ9skJTbgZW9SZQRQR4wExzkJLhIhIBE5J2i6OklxwYkBjiFBhDrObFwCF/KrCCFJcQ3gBMRLiFBCniEJvK/8gK5fYhEUhTEAImOYDTJmRQbL+ZUIVJyYV/iQQr0hwrqMB2U9knrlkNQWY2pT8lvXp4LQAWSYVKQGZyxIoY1ofdQdVGYgOG+bBmrKl1h1JUoWukRF/rgiJ2vPJ16uDVeAg6qwn7CzLZm1kPB7IWgRkDWoDFj+BzWLGuw+zNZ2Bshg8IWwD5gUQJpQo77ntSC+IOJM2V6DDUaHrq9kPZMNY+QYExv3xiIkj3r76Fd4+vMH9wx0O86w0V8WLuYnzeAmBvfjgzyN9ZlxvV5Gxw+tuTdcHqy6E+QXEyxNd9WFPbliVg6eX4HDld9/vPXaL2L7Zna9fbAOZKWdlpo1gpuHXXXA6ArCpU/vVXNI94bhb8bjdT1mDt64pujwU5e1WE7B93+e/XCdGU9u0uH14qUabC992t4rjBBzm3fdb+Kj/2ma5OOik/9fCvK7g5eTqJjEjXlbw8zN4WkC8AjwBiHpeG0vdXRSNpJzKhVe1dqkEGmsCckE1uTUOhHyG8juELLEi8lTiRBSENLOooeiTcqeUi9VJ2TtOYcELzk5jP6A8eHYuv3/qEY9LE8XDr32e0aur9931h6V+4/LkqhE4x3wiairZZR51QPp5PQtuQSJCDRpmFdhhOYhH0FbEW9hsGX3ChXk+XVe531PktJdCCAjzjHh/j7QuyKeTE0TIP/uCCHkf/BnTQWbrX4axalN5LG7LkLOzgiqTQIvU3915Purvzuv9tbNzPWD8cFertNyxtMlfBCkocQr1t52z+tJxjkjLkhIS7PIDkrdl7G5nomE4ld9S73QIuL+fMM2tFeeuMGJvbLoxr9D6TNufvRBiL/um3JkDqX+35bG164cK/PqgP+fPXrPdy51xYzAor6D1CKxLYRBu6ivrgNq6h4zwDgaH79W8urZ8fdTha4ZrD/FAdu1t55A2ZaAY1xYmE7Q0z63eDvZz6NLu0rgCxxrVfalcLzRpyvT7fA8mn2/EyLxQzw5kV+W6WMu5sX4Rg9qYFqN6boRpgNpcNX/liOzpwwG9ePa5VjZI510gnXeRtFema6G0P6yKhIlWx6W9H1vXq1fM5d4AcJ+tzXdTPz/Pkr2igT1cbVDi5rVJbT/6hTngmzE0/jKoKDqYL/5nJUvyKspV67JiSYzHI5CTCA8+PmY8Pkng05TMMkICWOdUyYTMwTH5UAQRaVVGtPf/X852KviW9Y+ZxBulxkAQJ/oAguP1ufvUPFhUXKO6wEWxPqj3hMfJe0xhm7QxxafFAIABYmQEEGdkyiBKRbu/CDZC1v5ZTcoMVbdBWeuUfaOChyRBk03jnog0UHSNf0YkfcrBQkwIzsassgtlMvZ9MyGMrQdAFF+sT6TM/jWt+Lg+48QrAiYEbxVf9hs5ZK1aH7DPw4aDq4CiWEMksFlFsLeMyGV9tluJiwArc0ZClv9Y/1ISHL/MV2f/ovgFESTmR8G1WuqsjJe3pnCKNWorLStOx5uJS4BnkAoFovAGYowgijI3kP0ncyrrVRSeM8BJhGrk1qj12y1BQwXMnRYc5WDfiGwN6D/eXSu7L/a4W/xlazVf9lOhtTfZuPa70B4GhGfeO7puULu5jJZ7iJtaXBVd0119hd9jgorOeoe5qZB85Z4XwpVC9O00h+1gGIb3Dg3ebe7I7qCvw9fsDwBifcMJOAEBEXcHdWE2T7ifzWKoaWwA05n7a4t+76abVKg2Q3YOF7qyuksVnMOdujtidD/LeftSCG+JERFadyT7OGK9Si1ni/sPJn4zodtLkrGdzN2x3Tzvrh87iLiGyjEGFZFpDMihYe/PVN4+pVHz7SYqw2D194wa08Dr6/SNnJ117j5vTbTVbrw5ecSmm/PBmeJHgLun9esZmJqldAXsozPHwcp0JqOm+PXXmP/mb9uHjmG+ZX5dBoqGGXeABWH90x+x/Ovv4A9lArD+4Y9I3/+Au/+UMX2bke4DOExOA8YQiqRaG0kRSxsFH7nFuZAhcbFEIco+5Sy+P6cDQk6InBHjAVPMyFMCAcjTHQIClsNJLuK0VmaC3y/uYjTrCvtO0RBfVi0aOScUHe1Wut/rhqVnh0s55M5qcrhkc5nC/W4uZ31fYLZXdgH7XFskYAfa84no7IVxofDg27lco3b8ftzDJs7UXfZohzF0yaNlQ+ZfgaVDStzn0KKL2nvJELEWRleOhTSUrabfHYFDDs6Lyc77QIgxgmMETVGEdEEsImKMOHz7C7z6x3/E6Y9/xPN//+9OELFvEdEyHkTjZGMZ0eRRQsjVU5934wFB8rN7brj41h1Rt/CHQ7A9H0duNkhhLnfxJsO4raZ+QLShuudSZTuOwbdB1O6DzTku9zPrfjQmNpOtCImDQ6ha7fVeUqFuccel32NAiMC3f/UGf/u/foPpV6/LGWxUwC6DyW1F49+3O6VBwHZTryBQrukLB8ae8skwe3evXnHN7jV7uRA3H5sX4ekd5h/+Bad3jx2MdbxMUNTisT4mBMr7ImiAXW3k5r8OahFCEJr8tta8gGBkdQFwx3yjTb02OuU3Ofjh++f2YR0A/3Fh2byUSGrbqE1fWKOfWwgx+n2pfJO2xNlLruhLY9i2feuAK2J4ZVvn2mnP7xvB0ELnZulTLT1GZ2TL0L08OfswtH33OIYTR0JuX2Hu7KFsvSVItYLQ9f3J9NefURJOyKcUbtK+4oPHCR1Orp85iwshCQIMPFHEkgmr+to/qZ/+47KIwGERl0un0wlPx4jfffdrpAR1t8RY1vdFqABjCqvaeokRV/hxKojIPli1xAwwQYR2Tu4Ni803xcIwM01v6yuTj+us647UHW4MiIpXWtwGW1+Fn6I4XMpZnNZQxW/7mGMypEJHmSAjU27nA4Dhn5EZmRMoRPHIH4LQhjlr36R/WbWXLfZBSnqeFve/sfSJQhBGtnNnSjkgxipUihSK8x0Nm4HMehcDKuTQ9eG65YOOC2qsn/r7kZ/xfxz/FTV2ieKfTay2Sh8WV0xKdJIKJoSK4CKAWNcTclqxLIsIvdYVqVhG2HqCzq3RkSoAWxPWtCBTxEqEeIzFOpXTggCzlHFTqOsGJIG9KQTEWeecLAC48cDsnpV+cE7IaUVKKzityOsKMCMGmV9ov1hjJTKgAoiAON9LsOv5AISoxiwS0L2ue6vGrDgyJgrIlMEkAsOs66MEEg/SlnAj7NzUugiIBMywkBUCYw4RQC5xDKoQRvvqmM/XUrnU5G1vgzryaC6Deiw6Lw3+fY+/FnqjeQhvFVFLVCujXSpb1zYDulZtTbs8FivC0cqkZ2iDYLP7Dcbw0vN1bwQM259lPO0fO7/MwqnEBtE+5ma05OzMAfj4gGl6jV98+zW+efMaf/fNA+7nGZNaRAzhvJRKsYFL8U1Wfy9dWf9fWHqJoodP18eIuBIx2hAH+nRX0277Ez2q2j+pa/gKhNF9Y/u3SIrtVtKd3X6cgRAux1Yjzu2eTQ1GmJaSdk+4wn3xnnivx9041aP1p0Zm6wHeMhDrF7KLsH/VpD5oN4AYEe7utiV0sNzdMd7nG+Jz3HZF1jagb6F8eEA4+EDQ/Zxv1/G5KaHButkrYHWH+wfEN2/ApxN4OcKYpGE+gA4SrIqKCSvay4YdIlWwdkVkfDt66YNMu8bvZ3KIYXSf8sdBma2c5VkUjY2+V+z/HDJnMHPOgqUwVBjBKHoXdgh6SX6/Bgz59Iclcz0T7FsvhLAD4cxcbBoq93OHBHzCQb0pz4ztKPbL3Pu+Ho346B1v3tYc7qxsfn/eREoxXMPk92djJcggSDVv+1H2oCF0HlV0yJavvzIcuFRRh6K/Lba3h6VAJCxqooaYCiEgHg6Yv/oK09u3iHf3iPMsAgtdo8XnNKMgmAAKodL6FmZ0omznB9X6KvnaPm8FEYAy6TtXYzIufd6s58+4/x43qAyY+qwDEKTEx1AofkHoUdrpcY8r0kVmqOUxot3yu9/9n63Ntu8VPvuMU8B0iHJuG3oCQo1ZZWtwH8aeGHIPz/K3PHN7jEFVxnpfF3v6bTRdA2DKv6XN80Dugt40bs9GP9uHeU1YPhyRTqs2SxUqmyff13NMWHe1W17a9KvOufxf27JN5YU6/Xj4/VObPYMfOK3XUZ1lHTvmcC+U2OKe49Y+JV1NW/j5OFN2MzUN7UHDPNfB1Z2pO8L4l/KQz49D3/antnG5gg3K3Ky768npotxV9kjfFz8/FyrbIObtu6sEWZfSlWheryRBpBiXaikomgEbrb31VM8d2uztXiFDqtsZ+XI1nDvkr+jbpybPQXI42UsqouaXptHF5jI1SgYMZIgro8xAEkV0cGYcc8LCwJIlyPT7R8a6Ek6LWD6sJxEQnI6M4wI8PWWkTFVbPQktk1J1Z2KKXhLelwpQPr6ExQYwRnOxGIDOuZ3NEBc/UEYsQgBnFhdNTar57b/iI18D9lIjiFDf8CTa56P950+JMu7saCQGOPQ0E+TQIACcwBlIeQXlgDVHIFlMQXMbbL7+uSieGWOaOIAoQ5pwLkep7ooMdb1JrHEyRJAiFg1c8XbdiExUwze4C7swbHXtsDJg6/oRZZzEGaCESLa2zH1wSzOydAwlJoMnRGydqPUCJ3HllXINRm1ro7qZqnu60smyblLKQEzI64LTesK0TlhiRIAo4ZiLz8p3kfVlTN3AGRxUgKFWCczGXKWyldniVGQG51TcV9mZS4HEq0gI5jcJBFLBkbifpRg1WDkh6Rg2dIoWRxahWOCAiScRaGnYaj+M5PgA1XKe7ChtlnTZMnZOswiLZfnIORXKmaUCGRij+7pUmmzuqFp+hC20/AZPh/XP0H33dZz/vS3Q/Wj4CtvsLcy8BYl7OK3U4JmjMdrKt+c47D7dvvWNj1sLAXEKCJlwONzjYXrA3UFcMh1iwBSd4B/cjfSoNUKrMLd/p+3ev+ML7Ip0eQ3u0QFXX797NJc/2nfb0Dk4Q/tfSje4ZvIa0h64/oFDmajmoGGevUq6KgfEtztXzlfgyxQEhYq5nknISTe+8GcMqUSzBtqmXL3lvhsQC82BWC9Gqasd0+oqe4xo7HRrk2zEx8KA69KL1tPeODTfBsuZ+p9buMPDK8x//5+AKJY5Gy0+X6A5L3Y22B4B6+a3rC3qLxGdWCLAtF61reFmvWLsCwK5cwjuPZp/8S3mb77F8q+/xfL7fy3wTr/5K0zf/kotmay8IEAVmzGkwhBloLkMbSUpUyYQATEUJqpdStMUkTEjcwLASMtSND6EmZhAIeBwOollRLm8TJMY5YJibTmxIGVEJPWAkbP4UJctKgiDzKP3fVn/aje5/AGdNB82t+y+VQFIHWpZDxTqGh5uEa6jx8BmI42Y3buVlETdp5IsA4J0g5S4b8aQsjGRKnd60sNNte12le715arbb7c86Tnc/IYpPZwpU1Jw1bv5to/N/udNm/6d2aCzmp7bOtnvgSurYxFUo2uaJ2CaMU0HTDFimmfcffMNvvqv/xU0TYjzhDzNOBwOThBhd5d1wH6nZn0PNUIBBPTr0NfTW0h0mjngRpDR4dduLYVNWf+e2J3bhUkvlW2sxxS2gBojwsqVygZttXUQ4s75v42RMSg/KMrMNfj2oB7/3gLyiQUEHIHn+q9u7oplhGovojCIWflaijQ4ZK+Bj7BlnF+bdvOS+6hCCOqem93QSB4wFMYP2qxM+etgLaoORrCUxq/3L748rfj4zx+FmHfJ5q8stYJrOBiHjPxujLzQoaujdEfvvb7/F/vgytS1UhlSJVNDXnlYIabrPSxwt43DhfbBuGWhvTxdK4S4UElTftjG+M1OVX58B/P6WdJe2y+o6SKT/roy49U1zt9Yiujvl+LIF/NdvoxfXvcmb4uTjc69lkXSA9eXt7ND4wPVE6XN5/69jHeMvn/pVA7oYRopFRR8+1x9FyaHwUXLGmr5kJNYLjxjwjGTBojOWNeElBJO64KUM07LitPC+O3vv8XzacayHFQ7PennnQgx0ke1YjBhggSYzjk7/pqcU5HavpqwISVh5ia1iDBLgOz6TxABgsRBYP0EKDAwEUIGiILwjpUuI4jffTK3uCQWEVOYMMUoLm/07DfhRyAg5wBA4hIEImTWRYiKz5TYV4C4OlH+SO7mjBgiLAlAYLGyZyKsnLGCEdcJFBY9y0PdNEUQIcHByyhQQAiL0JtxRggR6zQp/ZkRQ0SIYn1hsQRmZwvMut5Ix6lYM9dFI/NnvJ/iK1+FRpmL1rzw6c0V1CpukJLQu2Q++N0WLwIN643zP88s1gwpLViWE9a04nQ6lTVnMICgngcEJ8kyQEhISCtjXVcsy4pjegYvK8BAWlespxX3hwPmMGGioMGrK2bAintyFEVB8KxrR+e+3G0ylhJWIYPzipwW5HWVvmdRhQtEItQKMmYcAASJ7THP94jTjOlwQIgRCDMAQlCeA9JamKUEsWAAASkTCBMOyx0eccRHOgHc0X8SoV0EEghFWIdgwjzpb9QiQfcTmxDMjDFMoGKLRhBK1B29f37eerKaiGOLNVRBWK25pVnPNcZ1cTWZ/VpvoGZfxspxk/HSiSvNtWXawnaWWH6qPy8hMd3rHnz7Ilu3u1f1HLy7u8dMEb/KX+Ob+S2+/uoN3jzc4TDNmGPshHtcijuSfQewWxGwnwZHHrZ8/jq+ooLbCr9UGHG9RYT71q4har91xIs9+yS8vBNAnNf46BBh/WzIsSYoCVRCarn1ROIqeW+7NEY8qwzBvaBuCRIKMehhq0TlPtIvVW+w3TNpVNd1kyAEQ3eQXdWK9utwAN0d3NMemWwR6W7JbGslgB4eQPNcTFZrrd0gbwCm9m7dwHQuf81lRMWGOPdrwoDd1HjFuBNQmKeWuHk5AFMQOgIQXr1C/Orr8jLcPyBOEzbSMPRni2Bj5Zkt+G5YgyIqFvgsBNXypQDK9V0IARSrZQRzFtczISPECSFnhBRLIDRiRjiqtsV9FJNfziAOxVcmZ9EI4pyRQyiBYEEV5p6xWhCLvvcXz8juYNhNNkjalsddLrZxLlN7NlXsyJcxJGC7T86lIcF37aXRMKYNosFaJ5/r5Yk9ogRgLCB4edrOgD/7ryjV5euLFdyuKS5nf2sRIURiYAY/PgIxIj9H0OmoFhE2b1u3TI0WlwvuPnKv1J64qIKFIngg/VTzcVeHEK1+Ltq1VttrLSIqw5wGeKgXRGzvNrvne4uIesaq4MTq3rLEypj3K8ff6bfgJd7ftyFc3sKh6a89JyGomXPT1/IHavLbcW1zZu6fmp7t4gG0ewddSu427dqyt+37Fs0Z40QtrjTCi+yu3SsvM7VHF5TnXQYTjNj3mrul05jRelYAmvltoCYHY5enywIT+O4KIcjy+P5z7T/tjcf22XYtUPNZ8Zh+/pwgZVC+0cy+Yj1t9tjOGXoR/ivf7VVKzWMa5jlf/7jNPVAuWU3s1Xdtur7dc6nfQX5ub6+z7C0a924ovLhw4H4OgRZ7pO+F6RY4qqKOK0sMqGuSPWvJfjbaHHbeyeCaD/BeDbCqCXXVw9Oy/t1t+Nj2/By/75PRScMyN8xNvXdqvQTHL4OMfzZ3K6qwUYJEM8SNUmI85xXHBKxpRTL3Nynh3SOwLMBpBdaV8PEp47QkLOsKzox1EWHBmkT7O+ckeJ2zagBMEFHvbxPNe/F2CfxsSl+5Ux5p0SvR9Fa6BwUnk5febXARPSvioCKJEqQ6qvJLpJonKF6VWGDNXBUnpNZUlMP2ZrnnP9pKl9gHhBxkBFJO4ETAmkq/CAEIxpJFGUNGFW4EskDadoeppUR2UdCIhBkeSOJSMBUBgujJOc8XVhNz63bZKd6Y+6wyJ+auhhnIE17FV0h8xJFXyJLQCAdl+owxqt88g0NfsFnTZGHmr0nWolnXVPqiKqgQSJirxfWMHrwkliUxJ+CYEMOEgACOM04hAgHIIWBCRGRqzilbpzknUASQSRVg6tiaC0oOJPsqJ1n7ahGRdeysPuj6Zwpi+RACpnlGiBNiVN6NunjPyHUJ+HUUAM46t5SxhhWJkyf0izIfGfLHdQ8UIVeoqoVWtBcokO6tUi7ncn6DqgKQ1D44BxsaytVb3vsfXVF0SmyehnGbq+yp0heGGnK4gs3q20LK7oPbMu3369KIV1pxettn+q3pvxfOo8GNt2fKDkxGW8Isp/wpawpEIniLkwji7g8z7uZZBRCT0NsOPy4wGV94hKsUPL32srzawyP95eW6Xfsy7uK2pk/HjV5aA5V/BsmOqg5XeIkSzg2umcIGqmbh+Wd0HTDtfF87K3UBvTx5tx+2ofRQMkj8od21ba8rj9fDVMdjrB3UEQFN+UHfevPvKzu+J9i4prxkUYb/WY3RcWXTN98i/uY37knnR60vRsOeox+rKoRoy46KbDUPd/IDXdtjAUe79Mfza5fhHmjnEw3r88kzWPo2pm9/hekXvyw5icS3JhfAjfHl6jNEGKzIHArSW/dZ7WtxIxMCgqouSECvCGIJSh2zmGHmPGNisWjgnEAgHOYFBDFtTknCa9HKmL47AXcJ629Em0YsKYCcIhKAlILASEKmBZILLZQxCcpRMsJNxgCZETirz9DbEnUIUigP+/mlgguZmSgoi7kneMNIrPX2qM3exWtN9u/9ra0nT+Oz2Hdmt5vjJgegjNbyiEh9gTD8qrRHEO/mL9nz1VeLR0su5lOElTxsg+JeS5wg2u4hzqA4YZ5nTPoZjkekf/onhBiAScyX58Oh0EFCJNU1XglYE1Dk+mw4Hv1zdeyllF+xhDBftu559SpslWFnouu9uhFGWDnL6RnvGFtEEHSP8/Z90yfa/i6MnAJwV3fZK9dtDoNhTxjhf6ck551pK4Zg2jfVp3JvGVKEuBRUw+wyTB7X8rEE+lvSM8BHXa6EZFNzsdD0hCaavI7BvXvg+EvU3z+ju260/yphU15Tfd4ej3Wz+fXa0zb9WTKax/pJZT0VYtveuf7U326sdG5sLdqI1fxWr9Xi7t0OX6HmWV+uHcUWR27H39q20fYj3vTb7aF2rDZNjq+nnyHtbpmrEbEbL8ovnPbAvp3Qa/fVOauFyzXVs2S0dnbr3KHbtvjsZVj2Xf9d585xL91G8FMzP7JXqPCx7H7s0D/UqIQ6fs0+s/MmVItNouHe8rBuzzPX3hlm2OdN5xvZm9bKvLBaaFhAzpiqAZsBJCIccSfukYrP/YScoZYOCadF/O+vq/jdFy1y+f27736Fx+OD+uPPWE7PSBnqt1+01ls//YIjlXXfmDGYkpYobWWYspbkKRYR6nZHXPAYLrcdl5xEqYN0TQUKyCGrNYQflfpXcI4gLnDmyf5miRmh7pmyuthZgvSbVkLKEkNvRQKFVZjB2tOyJ5U2LLidg6JQXZk0kLZaSdIK4owEgJLGetDA2aBKs7S4nDLFA4lb0BzEpSlHTFBcaaJCk+XEhR5cSV2gJhHJiCVAwzZ0e6L2x3BsZHV3xMC6VtrhVbrD38x/jffr9/iX9BFrljUXURnizT6vXF8xolBcfdUYC8vphGVdsJyesa4JpzUVzi2FgCmKxUiMk44TLBx1ca0kMRdmHD4+Y/54xP0zcDisWNUCaJmE6XqYAkIQawOLzhEA8KrrIa0i6CA7h4JTOhR6nzUA9rqesC6LxIlQa54GeQziFmo+3CHGGYf7B3HLNE3Cj1BeL5IENEdaUE5Dj+uAkEPGx8OTxG5JYvGUSwUynpQBioaHRok/QRNSmJBIg1hrzDZk7bceqSacqyey8BFyAJDFNVhdNVQVIC/eMWfek/Is2J3bzbrp6ayW5jOXX97Dg60tlDq5xDexsaqCMWP4W12Xe1GuJvZfKq7IZQ+U3AU/2HZ/P6aCLCOuMHZjU/ujArtsdGnbUogRcYo4HA64jzNe4wFvD/d4/XCPh8OEOE0q4PMwd/Vc4MX1p8q5vD93+vOCZpxucM20R9z4LGNk0xVvn535tZf50qCOGRaA+ZJvd55fgFyQviZCQI9PWxvULmNpewChEe99ng6Jbfexvd9usv0R7lM9KHwKD69A87xbqjl8dFz2NlzJ03f51SvQNLl828OnPeRGJEBf77jP2/OPumFrD8bh+PV5FaZSXwf35tAtYz1ef9fM13Ac3GnHDSzb9UJg5ZazLuVQYGEQAq9AOgJ0L+a7zLBl7HSwYAz/0diHQO5PtSWY2+cxFBc0OUQgZKQQESMjxgnMGes6ASBkXms3C3PTLiLREAnZzGXFRZMEVRMNJLGOAERVpDI+xUxbPrPV6y7rMqBn9jkYoLQiHD8iLE+3HeZ2nNiI9udOd5a1GmxULuM21zWNdt8+4w3UgP9z32w8/DrOxOfyXNXEZ0vlRHGM5xqoOJbfk7qfAwnRJFp+pH9unZvWHGDcDzdPbQ9a4lEPSAYk0Jlqdrny7FwfeeKzFB9gsFIrD5n2ADZKmSOLCI9D1P2xFUSwwu77NrQUcHeyF4rIEXdmIffENtF+O10KSrjZASv5a7DBXgjh/5Zjwrs/PeP+bcLhDLpb8Ql3J3THWNO/MtDbc6UygWo9TS0XcK8mP9H5cb2UaL/P22Qrbh+2Mos7+6I2SzvfUWsfrNH6uxVCGFPoKiGEa6Ofs808bzZR96XHwfWOt7r6+iqO4J67CR8v9dHDFq5Ld8RNlhBDXPuG8l3ZcZ6Kw51LjdDofM6u3IXsF9u73MZ+Ggh698boKkDd+jhXx6ZNOLxop71LzfMFGD/x4r5JyOOF2aR3BPRE4npn2HMpcw6Rage0CFb8GbSB4YIrup04JtemS2e5Z+MB50Hd0lI8fufGJatr2awMuaT4SM4ZK4BjPiFDrR1StXZIKeHDI/DhKWBZItY1Y10JKQWsa0RKhI+PGcdlKYIIcYvDWJdVAuOuqVguCFyjsTacglAUGTNA5irfbqDsmd5Vd7ngW12dpR2WdplRgktXhqC27HAoU2SIIcpflL8pRhVEAJkCOAgMKWRMuoZSFD/8q94BmQSSCojQULm0jC2G4r1NECSWAAicUqFzgrrE9oWLTEcZhEwMygQ2D06ZAWSBW5BiCH4sSl9m0QAOyBnIgcXKmP3KlL3UkH7dPBb+rXiWUrKR8fQM/OFPQA4TXod7fMwRj8oyIpvPZu/WsaskpwU0F6t/sSoosyjbP0Slo0V5hSwItAmsiERIME0IvGDOGXGdEJYZAXdAPoA+RMSVEB8y4pyRKSIjCJ/dTxUSiAl5XaReW0fqoilGDZQ+xWLJkZIE087OArumUOJ/hDAhTBOmST5DiLKmlE6h7NX6q5VD1glIOYl7NQkvD1t/9XwxJR8R0gUKiClhXjLoPiBRRCYRCBqdo1EhKrQOpap4mrje5QDoP7ZsHAqtENn67ej70Ylbn7H+X/eJPffnQkNj2Z7nvsYqjOitqpqN6XHfZvFvXQtXqqcBzp057OpucUif3x5tycTByOzd2ZuN6gdhp1AIEl8vBsxg3IFxmOT8m2JAjBYzxXXjaubGBZyux3fqzF5T3SfjLsO0Jfc+X+pQ4Yv9PZNeFKy6J1S332rGQvycw5UAXDsLQyT30kIaCB8qY6HbXEQOFGoOIId/wwjJ9vkF5L4nYD3MNKrh8urZ3zdl5N1PQvz1bxC+/npcpCBcXdlLMPRQm3S9pKJa2YCz90tAuIAAbxdbhWXUTkd4n6/8DFzWhlAeVwTebsdnt/m9F2dgacqRkS2K0FDwkCKsj0B+Ro4zQDMs0BNBBBIBGvyYjL7ihoFhSEYIJNo1yixlZkROCFmeM8QcU5ikSe/ojBAI6+EOFEJBaJZFEWtSJJMFYc9ZEOKUVgCMkAgRWRBTxwwMLDAE8tdTi/hniUyn8CiGaTnLHWgXXHuW0fKM+Yd/w/T+iLPnk2DOMJdvMgeGwOi8eIZPd8GO1/LldfqzCQduuWc+82W7Qz+guOr5hNpG2iGmc1GR4UuttO/as74K8YrJ/BRLYOrpIJ/zPOuEBpgLAOasPol5+LftQIWXmcs5tXHfJJh/FUaMrC7AbTmPJMPVq5ymkWUGuaHx74TmrfeFfQaqp+YlK49dn5S6jbjLT0ATr2KncjiQS/leKNLPgb03bTIiE0y0Y2Iu7opLOx2DD98f8fTjCX/9i7/D4e/LMTJYcQ5nKIts0J+NFKE74+wq8+8KLuIvt9FduG17q+F8Brbd1GG4N5RpabXL+xvYroO6FoULEpQxQ/au+26t1/uSKn5I7ZiMhRAOe3HjRQ6Weg/7PG3fdx6j/1mboAu/B5V06ae8dno4X1zPT3pZvjx9LjjJJADl9+X2Xtr2Hq1juLLdAzcLIHy+c6iY4VnnVD0/JfnNVWhFp1mrz5iUycP92DsBvTsHCDWYcP13e55u4aH9g83Kf6IwAnj5eJ6D/1LfGIRTvAcDYkHNjEWFBqdVLSA00O9pXbGuCctpQVpXLOuKP/zwFf707k0RTqwpIaeEnMXSYVkW5CyCCFbBQ2ZoDIisTHToegUsLgNcbJ1yhHOW+8JwnCyFCprVuP3JNRgyzO99NzZlaBhFycT+6xACEz4IE9usIWbM0wHzNOFungS/VJyEc5ZAzzEgqVspCbgNrGHFaY2lXglmjY4Xmpsbuq5VVCf4BHAAOOfq8SSLhQEHVZxzuEnFYYVhzSAwZQQmUAZM/FFcXIWsijmxjKkIDzKYVHGNWOhct+IaJpnhxGr4UIJSZwlWviys8TwYp2fGD98zfvH2Dv/w66/B+A7fMQPB6OQWs6pHrrRopGdKEtx8TRmrBuhmQOhpIsQwgdStjO2BzAyJsiFLgULEfCA8ZMbruGClr4H8NfIxgo8B/FEsGubfPGJ6c8QT3WFFxAGiEjrDXF/p8lqTDoTR4jL3cZJYI0bPC92+YFlPSOsqrpNt8LTPFCIoToiHOxwOd5gOd2rVIRYwFhsiU9Y5lTFISn8wCd8gpRVLWsVlldsrhpKIsE1w5zlGRJpwt2S85oTnhxmnOGGlgNWOP5a4JVRGFeXMLoGsi0soXe/mKotldVAJKOvO3J37qHAWGahuzrnm5ZqTbezbF+V7+VclZBYEvVjymGVVqX8LVCXZdgkK+BXcQsF1fTPqoeczFXzV10XwcSyt/W3TBrcC1sTw9GPGRSAJhakBVuPghGnGNEW8QcJbmvFqOuBumnGYJsxxamjLa9Mm/18GCvkXk26wiLAPjyDx2RlqF+a5NEaUDIHeaCJukNgLxJIeunLQoVzsFUEnDWRk+7jtQ1+XIZw0z6DXr9s8Q4a3fA92ivZIus9nG56270dnx7DnBAjznzaPw/2dSNu7d80hqblHdXN5u4W7/uzfUi1BO/2wTkPmadRKV2K8DDaVV4TfP9r5sXlOwyx+Dm2+z9W21TLdbXLvVblgMBhf1469NoaIJrvsCgFEKAxAKvvY0Mot0Wo8F7JlpXG7hOkmQojMARFRvqtFBIessSIYkyJXaZpRTITVdzoxMD0nwZJiRHE7U5iwkh+Biz/LghO4gSh3LZtlhGhUiECCS+DbgtgaElWueyrly+2tzNkDEb4KM1LoJqlcomdpZPfuZURdn74UP8Xq3aU9fbvX5Omf723vvq4dJG+cR8/0K4r4xnb7+FJGRscY8DebMS5DCC5GRLUgsk9B3OUwEIsj0bBnDoqUVx/FlwQRBfkre0NFKrq/KjJnVIlpAW0FEU07tkdKcSNiOqGF9XunHCD4o+UbCSKaNga/zzFJ2GKWewECO22o0SbSg6XHSnpBhH03H9EGR7GI0FSwDM+Esv6Cyrow3MIT9ob3b65nV3f7xX62991oO47upPOolWn8DxrUxGhjegxhvRqL38l3DXpQ1qpBVeFrWhjAejdF3M0TDlMYj1stXH5XAYXdr3XQe42xrRBCzy5q63VAYvNqB53ZwKZavJdGfMNA7nGMvQq4LX+JYTka712m96UL7lPf/wyp8C9+AtCGe7d839mjVwBWroy9smfrGAnSypuz7Xo8rz4Yr7emHw3D5GwTV+Xr6ZkCOQkdWdyhsj13uCH3Y9zvM3dKtqjEGYC+5GLq7vDx6/Nzt3lFyCFuXO0yQ90gyT2bQViWVdwwrStSZpxOC1LKOC0nHE+EHz9MSJmwrAFrylhOASlFrCvj3VPG01GYpmtKImjISd0Q5RowejUFj6y8LufO041/8FNexsRl0ADDYGExcDPvXqsd5R5gYgR3VW05IXau1gyNQMJyqTJDY2lLhKi4ZnTPskQSQDbmt7oiCiEgcCyKEyGIdUG573kfv25htg5ZblUCC0pL5aDfa/ZaL9exDMaXYTSZy1iwWkYAyAQOBHNhyhzqmFvtBOeSs4FUUVMuVUpQctb1odr/OeE9JfwbAfzwCt/ef40Fz3gKjwgIlYehRGnDEyBCtjiLUa2emcGHWeNDaKxHDfJMIUgXS5wKqzpgoowpMe54xiHNOMRX4NcPSByQmRAyITEhHxcsALAGhBnIbzPyRKK4x268U91zhvtTCOAcJcA0ADaBQU4a7DwXWtqvAKJKz1Cof2UdIwut3dBI3lIoqyAiI6+5uDKzVN2fBURd3zFMiBSF9xAmrGHCEoK2FAqtn9E6CXenOIpSDTPENR6rezKo2+WAImVj3dtN97eHtUxZpcEsm+3hOmomjHAj6fBX4k3V7nX3wpY6QZUfz10ghcLA2Y296ad755/7z8F9IMPL7V4vC1HpJRNCNIIZLmcE4JrX/cYdfKRWOevzjDTdId5FTBRwFwn3UUOwE2/GdO8e3b3ZdvPv3+nAGRz5Jdf4NfjBDekaWDe4/h5CeEO6IVg1NYQXum8CYF9mr65B7f3DK5DmS6kueCrnRBFGeCiclHPUkvXdFyMA9PCA+Ld/hxBDtyeplnNHX+gQr7MaSOXnzglUC+7UKX5G62XY1z9Ad7g7YQYL6yyJ4erk7rddxjvVwq6FSp9fQID3IKO+BT9v5w+I2mw/NrXu9swzjPKG9blDrLUjN3hDIyR1tG7kd88MIujFVG5fd8M0Y8btO1gwJ0AVRKswguSSDDEgIoARAYjAgTODk7gAy2pGO+cDYhQ/jEULKWcA4qJper8iHxjL/aRBqxOQRRtKtugC5giwmBcHdWIeaDt6VVM5OySHAWecyayum0BKZTgqwdVmu/ktRfz14RV+yDMeXR21vh6K+usz3xcvSr0FF+DgGl44V1X6EkCuf34JlyrlSAmf3FSzV/QaAr/Pwn4ieZznbCLZrxZIsAoe1Hx+mjCpJps7CIuPYlvP2YgBL4hwgoINwx5czLIbDX4VspkrCSvrLSM8Y6CWqwPYtOkIxtbqwToyglHKFKGo/p0TRDSWjJvn7Xj7M7sKUlRMf04I4RBmj3iNLCK8EMLOtMzmXqHiDqP7vukvOcsQfeeJmD5VoXLDGvMZYDSGsy9pM46Y3IN6CqHmv+NSwWFlN+R9YbWNEMKPXv/ARq0VLr29v8M3r+/hBQZl/myO+jmlVghxrUZzVWTQ1dbNf9POHk5odXW4RWGM4IuN+n+kv8D0KXxrj0MMq7m28hfA0K/kip1dcwt/HgysP2nrePizHaoFXr74Chzvx87UUPa6VXBWprPTlf0e3q4B2gKcL+baS9yfQfbP4R5ZFZIAiKUCs3OTJPTBspyQU8ayLEg543g8YU0Jx+MRP368w2//+AYpcXHNtKypuGZa04o1fygWEXnNxcUMQxjNYindxxHj7TVpM+8CndbxqbhMccek6KgnCQTTUdYhGXeAShUFe+oYvAyLxScufYgDPDNTkgkaFKdUF58xREzqomnSwMdBhQAZQkelKLjKNAlT31yD1mDcyoQltbnnqrjVCtUrA7GsOFaaK6vzT2JQsHwtvUVQIRAIiEHd9wRnMsLCqIxG14ngQUBRq1MLBm70HrO24t2cdXOi/yStPuWMnBjrIoKI9ZSLlv7pecW7HwN+8/W3+C9/c4/fT/8D7/ERUxDxTl3itoGVRoXEBZjihARIEOcgcyHuv5SorqiyCuNWN88iaHrFjK8DYcJbTOFr4PUEfhWwJmDNwLMGYD9+JKw/ruB8Aigh/ZeE/ApAFMse8eScEdYFQBZrEsgeIRLrjDAF5HwQmKBWETkV10llzSrOI4Gp9W+aEOKkggjtAbOOBtc4dOBi7Q0L4r0sSGuSOC3GpgiE6IOwh4CJRBAxhYiJZ4TpDqdpwnMQA4eskSQBNj36OkeK44cGx3J0hcJZaCG3UQ3XE1KkO+P9Aut5Aeyec90BNb+SIKPqrIzW0dSF8U1IgMXeHr4DlZAul5NV5qEr95SekBZKuOmVNa5xYzbENzv6tebdCiMqn9V6HEjmuQp4zcI84vjhAWt8i+n+gMMU8XYGDhMXhXB2NV3u+n9g0F8yXW8RAfJ0kn9aF+NeyQtzSJsvO+930t5S6glQrxHZHEmFCNxqGdDbr0BTtSCoxDhA9/dy0JaDrIWWKLQLeCPMsHeecOw6TCgbkg3cLhP1A0hWO+0Obg9rEcZY2dy9RpvGc1LLjwkVeVjEMTvSJ2paPDP7tPujfdqM57jN7U8aVr8Za/g5peFi3BMyDVhttsD62epB2/ShfUeDjgOEAIQIhAmkbpPMfQgoae6KEFH3F4CCwETtFxGQmcAhipZAYKQwgycJIgZIIDQAQngkwjSv6kN1Vg0lQxZFUWZ6ysBM4Cj3nrwXp53BEEsS885A5neyHUcLamXmlRbQKTskAKh3XRFIkPnkVG10Q2A44ykn/LAecSSLelVmrb002X90DX2J1NItZ7I5gNsb/c87+SN0D+cr+bywlxXxHZxftB2AjWZFaYsr4okBAAVB277rj3IQEKJYEJW4EIq4T9OsCLxoqrUa9GqGy2KB5IUQvcDNI6mlTzostg8qU97cDxgSLJZDYEHCY4j6rLoWwEDwUZBIadXh81yCHkte64tl8EwXFXi6e7Iwfux+KrDWge41rEpbBRopU2K1aL2+3VqmClvI7lBrZ6NFYxtJXABUzS0lykgCBHoCqAgHSM5S7Z2WwuabT2VINx01HIbqeHlUoMML+joN4gKfPjccoX135oDx9Qyf+o184VoeJCM2zmYdCVRx/pirQgiAKOodEBxQ5P5QP2s078uAuSmwYaxj7Opw+RsitbxvSVdATqeN4oEDpxd69d973KbvBgFnB/DS1J1TJtlTpNhr45zWfbmBue1/fU/NWriFuNz2YbSqtjv5JenlbpGued7CeF1TA0Ux7CyWzSMq50jf3icT94Tr8KriG+ZMPecflOeCe9o9pNW6DcLur9ZlDBTNM4w14E8ZOyCo9s/ffXvzvAN1S9Tas528w/d+zXCbYWfsmhJuL3KcwCEga9/E5RJEAMFZLCByFhdMKeN0SjgtjO9/nLGshNMxYs2E45FxPEV8fFxUECGCiiJ0SAmJkzKVlcmazc2LsFBF29wNcXf+gjWOns2FP6xLVkdLdB1vbstynotgIYR2nZhif1WyOHMOKv7lb6Xg31t7JFeUWN9GcSlFth1YaThGnETIEFcRBoU4IUKsUHrSqi7J8T0PhU9wLhUkMIOiDoDikULq9ouNyjhlsJBYip8SAsgNNAHiWthvOJsKUuGN26917Afw6lNpoeK0K4vCz5LWgmNnZgRifHgC/vmPAcc3r4BXb5CmBRknsWwua8baIHCYpN8TQGHCxEDOCRQmdUdslsrV+iKzxEQJOeNwWmTNgnBYJ4TjKyzHX+C0/BpME5gi1iSWCktasaSElE5Yc0JeFzAvuP/uR0zHhLtXK2gCTnMUKwHD54swIMkYMiOwClfUtZJZQzQ8Y4eWEGxOWOY6M7Kq9DOgAoesLmETKGdx15TN9ZMICtdFxj4BYCJEioovBcQIRHX/HQHMacUhJYTDPfLhAac440h6xhCKxVHWxRLtNGYgU8WZ69ZVgVvx+RzETVhWAUrIbvOaxU2/qmRA7N+6wv1h4fZKtyJrsoG2g8pTE+NDXKaDarsMjYOhtGFTd9tWpXH8DVaFOd0F3kBs53y9CV0fdcEQZ6HJ2SDxfXOH8c69LpZmZp1ijRouIpYQFMQ12UQRcxCrHoqxcxlPZXbszGm61c8EDZ51IF6Lt13K99ndSl6NZrm5fAkIOvnUrPjr0g2CCLsEUeDdvy5dfsIY2WWfaaesfjvXxlUd7hDxIRMexvRxOec7TH/9Nwh3B1fWmCTt91Kjx/lcwOBNT2wMS9nBwrcKqR53vfCibJsBIdoP7sZVxqaAe965nykIUK18P5XDva9gO5cvJbpGC4cAxcguwXep6g2Uw3Jj4vS6PONu+/Vxvu4t/U6DvN3aoAAKExAmZLtbFMEgJDuT3dqstZgQIkKYa2ZsSUTgIMgmQgRlIE8EQgRnAtGElBkgYennEABKyEksI1JecTqZJgxAGYjvGfmecXpQxmmWkFV5VXNhZmXgRmRu15oRGWCzdnBmzFwFEmWjZitvbqvMR6n2iQEzqX7MGb9fnzCHFffRH9bu6tUyJWJBd6K3l/z+QqTNl+3lMCw9Og7Pnb9fMtEZ4Ed5RmnQ6Uvbtw6xXj7s17UiY6Vadz7re3bTQ2yICqOamjtEqGJePZhb3IVku01TRJjUEkKtIOI0YZoP5ZkxClmJ9Yr51ngD9icafmaS3lkvDIe0X5OtMAPgGgQbUFv11OU14qV1D2WWBKW/BJRg8oWK9fGZbOzduajzULVPSe+UAvBgrN2e7vrJyrxpPq0tbduIVZl/OXO8IoHBW/lBBr/Xpk9NfebiIFJLEEt3nG6tEgrmjgBkuHntk5Oh1E4DkNg0cG7AqzCnz9r/or4yg4nQ/LY+je7vivs4HKhpba/1/vf5M7F0j3ey7D0vdbL7HEFg+xogih3uRqgDUxZ1GROgHbNtT3QObf101Y26zb7OcCajfzQ4S01AsSuEcHkMsBEm8dJ0FX53QfiwqeuKOvUaroxEe+7WvF/rL6P9/Ho6Mz8/e9rfddeXva7MZr87JPLzjMwNSNB5Ds/Ocxo9dK/de8MXmpaLqov8eWarkU89Xm716h/5hXmloO5i4p5dVqCqXRm9Y4PYw1PP0p7+bu8LAMSFSc4AOEbwdBAmYEo4LWLJcFpFkLAoA/L5dERKGc/HBU/PAf/8r29wWgJOR3Flc1pEyLCsJxE6pBUprWoZkVw8rWrt0OIqHW7u8YtyNiizqhz5Nkd+wMiNSU2t74N2gNytDiVLVKvXFKAA9jV0d7liGxrjz1TH2Dlj1lkJJMIHFUQEZdAJvsGIiKCYMTGBQsK0JjABc5wUZz4VQ3HrPjOpEhaXtdHOvK6KwlAUpa2gbsqYU2FEQqFnX07HV8IUk7jhDVC3V6wMVcF3NLSgMBht1ro7usanJFzaO4FtFBMYwJLVDVhadf8wCBnEGT88Bnx4OuBufYU4fQ3wOzCeMYeAGRJwmhqByKT3UURkRggzkDNSPII5Y10WEX6khMxJBROipBdTwuvTUXCSMIGOd6APv8aSfoP3p78SIQdN4LyC04q0HpHXVWI5pIR1XQFOuPvdgml+xOFvj8CrLLEjAiHkDMoJWJPMVxIPBVmttjNnseKOUWKocFaBBMl6ALm50UkpwbhTie2YmZHTos9XMGexesnigmnNGcdFLCLyoh4TxJEOIk2IAZjVimQqRhaEV+sJ9wD4cI/17i2epwOew4Skl05UC55FbTgCRxBVV01eLEzlT883IvEsAmGuWtwYW+Nc/CaNEFCldcqO5PJEro4e6SgXhPxjCH8vgOh5GF2y09r5fpD1y1zgaAtwdU2vbflTXuiLOkKNR5kSFqf+K29qfB1PL1IWWrYKIyp8m/GoF5Dg1dYucWnYxJQgEiXbaIKIiEOYcBcnxHlCmGMJmF7mm+q5MaSVt8f6X17aOfK2LphGmfdopgvt8RYPvJRucM2EBs7ChB8Aubmjdys894j2sm0W/nCchu12g0qE8PYr4HAYZRYp2jyhBP5VJNFrHW7MNN3PoG3U5voe+gEdgFoOJJeXfDlDaPcq6J7sCUU2xfTdhmbv4N+ZXO6FGmfg2IfhQpbdPHRl+VGmvTVH7bi3H1e03Y/bORjOl6m/x/PdMpf82kNFxhyjzBj7Y81EJ2zrWmrcqARCQEDIEpQ6BgLHUINXpwgxz52QCQDPSESYpoSQxQ+paZsUwicBhw8ZfADSAwkyA9GUURQB7qoUwIyJCoCLBrcShup7MJdASEoKsCH8QceFdYwiKAvSudFZ0D1SzBEZav7YkWX9vbrBOzoy0A00N1+4f+rp2nHyDMK9jO443GbZbP69JvbTNdydzyz9H9Z2053otD/Zm3UrSqnCgXrhXndNm4Y8Udi4YpqmCfM8q0VExKQuC0QQkQtDG2gZ/iKESPIeQnCbf+Oy7o3pXnZNLe8/xQw/VmFGcL3KCZxVy0ERyyKEKLABnnHeJhcMz7VZx8Z931wd/oFrvx9f6trWuenbHJkFe5PswuwPAb1FxKUkPpXrfIVAYA41WLWDz3CJElfjwg7c3SYdw6rFDLY/tjgI7EAv57q9IF+mEUr0X4Y/h2lErl37tuTinba649QvG59oeUZ8/hHp8V2bYQePqoKdkWZ4Ox6VyViGteAORDWPZzZSV1Hj/qvZHIP+7MzFFkYqnyMXYVvcRy+YGxmf11g/nNv/t9a5W/rsRN306kIaF9yr7+Xt7Ld7GTe8BpbL83Yh29UwfLIlxA4omzP0hmaugYmHfRrgzdz50rdn15S/EaarEg1acTjOWMDHlRFmdzApDlRz1PNuc1AZTi54Q6aIRIR1JXWbJNYJx9OCNWUclxOWJeNPP8w4LRNOCyOlFU+njOVEeP/hiHWFWEwkxrIKs3ZNqjmdVrGuTmuJPSddcjNBDg9yZhoew6hnNBAhDC87/wMFUKguliueuB1X6sbc4/Om1FIoEbbhVvqEUPzT13kwuD0O19dtDE5XzuaGSOITUKiAhSzxBCYGEjDNE0AQ17pgCaAMw2NUS7y0a7Ydrm2qDptaXIwaEiYzixY+ANOgaFYVAxKhWgIRWp8rftnuc1M066ehzutWffMcSSQM/yx0bFDcUmN5iBZ+0B4GpOd74Pu3ePUq4OHVhBMdceRF3GJFkhgJCglB6mPOQJgAJFCcROklZhGo5YQ1J5yWBZRWHJ6fEY/A8v4OgWaEeMB6+hqn4y+w8gOSrR2CzAYFgCIoMMI0g0ncJmdOWMOvwfyM6f0fEJdnzFgQImOhhCQ+kAENpA4AAVmYv0mtAMylUiE+PXNcafgklg7rukACjgfpm7plzWkFcwJrIGpovJacJI7LsoigwmCwNRtDQCQUd1agrKF3GBRnBDrgFF9jme6RwwQO1eooBIDYbGqcJrxfc/rbVmNzl/gjRMeZGGLZxjbuCkuPRzG7Nn2TA5q+W6P1tV+9+9Sm30NGVdS7qO6b+ru2WHXYqeRo9k5zjPa4qa8rl+MH7NaKo0vL8qlfxoKADYQOPvLu9OR8ExaOnnNB+E/mwiv2cT11yvaa9fh3gW10HXOX/wulreDgDExXlN++t3qbpyj08S0wvSDdHKzaAKDmBbdZRnjNbrVXIPJN/84z+0Yt7P4mAv3iWxFGDHKCqAaYhq31PUJuQBDgDCPjIvEwRv6pH2QHW5uC2yRjEPZTRTwvZhs9pl19kP1CXdP9xF6NlHfr9HzWS4TBYGzJl7t+YPeFD1es/+b5uO3KLBnV6fqhTCVjjplAwrSvffHd6lCFEKTjETQIV8gZIcqlHydBivIaVQI+i79RTgiZwHNCShJ0euPzPgPTh4z1HlgPGugrMwKCmKtyEIuLBh2uzMbmL3OxuKha35JCWXBB97si/UFMYiOzc6DYobVEICbVitBzUIlOD4+024/hwESS2zXJ/bl6SzLG6+UD0oN03Us9E8dSdJftC93NF3t0RZfP4BQuU72d7ZYjYOBz8wyCaIVIzsUQoFYPEfM8Y54n/ZQ/E1BUhmG1emhjRbAyu2tg5N4SYsx8r4K1Xqix+zuT+j5GEUIg81AIMURGeKtxUgUkngQYnI/kaFilNqlvo9wX/Z1hj8+NhweCxPWb/hFffesU2E24K3MTwYwq7PXMAYfEswbBay1cajqH3zn0pH06ALxaX/rCAgz59/6ucmVewpBsk5F5KBYcPUn40mRMkmtSWJ4w//g7LI8nbNYMkdt7VQjhGfn2vCsI6p6TcqNuEUIAKLGPYG1vkMW+aRo9vpj28YXPn/Zw5msFKNfm93m+HG24d97f1mCDc7ln4zp7Npvl39Z5qc3t+j13h1+/57/8Kvo504bFdLmE4oJn0ZEryKxPTXJHdK3YPWRM9a4MdwLLek7Xtd8LHzbnlKEKICw0YeGIZZXYDRbL4fm0YE0Jz8cFp4Xx2397jcfjrDEhEo6nKNrSy5MIHpZVXNaswtxMLl5W5gTOqVg9hxgRTSJgzHxmYTS7wLPN8FCNH+V9x5vCld3xQL/X2ooaI7Yy5IZ/1CIlFjF7HEpwTGZXL8xaQjJv8KmGhtBGHEpUhCkuTqXRLpPSgSmJi6YpTgAzTjGANXi1hArjonBVEA9PMhp+1o6IdR4iVJAYFxK82p7XsbdpkecadNozLOHoOgCm126kiN2XXhBk63/ElWhPVaEmgwqbhOktyml2ZUcS7XxgBXLA8vE1ju/v8PrrN/g6fYPv8Tu8P3wPoyctSLhX22UO4CAYSwgZGUm45Zyx5IS0rDieFkzLgtcfHsHPBxy//wox3mGaH/CUfoF3p18h0CRMdhsv6y1FUAAkFnkAUwQy45gPoLzg7sMz+Ikwxz9hOix4PkSxyFlXncMkdxMFddGdQM5SBIBaF+maAMPoiqyW02mVIPMZIozJurZFEJHBaUGxwjaXamvCcjrJHs1J3etMwkiOouAYiUCUBR5SbDIcQNNbpPk1TtMr6S+F1lJIBUjGkC/CCF1/ntL22HdzwhEBCAickcjzBLisntFZTtzl7S+E8dXelBnhCtvEpXp23zcEhN+j+l3c1sr3YG0ROUvrPYS9NIIiUdXntj6AaknS0GOlip1+CWCVHgG5EBUBRRhhdAoFCXBPQRViA6YYMGucHGAfP/Lju1HWIrPGGMP42RQGBrCM4Pn3mK63iPCERPNC/inyqs2g2SY9V/foYVdF+eqIAPvoJ61SdzDorCH66iuEV6/K+/DwGiFMtbKeGEe9xH2tRcpNTbEOcN+d7fMRMXs+Q33ukWIa5r80qJfSDQj36Mm5zXNpY9HmtLuqHHWf2zd7P/fH7ZI08KWHxLjc6PDZXzfUz3e/Mfs9S6TmuiQHPAIoqp5ACEVLxXsfbRC7wZ8w3QR0DgxMse54zoL7z7Mg9UEQFaKMnMT8N6cEgIpWU3VFI/s6LBmH9xl5DljuqymoaCdVOAvBp/8I4lOFG2YJ4Zm2Mi7OHUcIitgFNfsVKw0u+T2CohpCBDVbVIRGudSBoX5wdUR1KlrmfU/QUfOKXJ4vknaqvtQisc81yF36SmgXJbcZfJEz2+hFgvbdvl1fmTG+z1TXJMWbHDJYn4OgJuSEECJisKBucw3uFicRRMRZzvhgCEkWIZz5ZkVdzz6YdIF58+k16cZ5vcuCXhAhgoTYEsEq4JPy1Vy5G0BpUU2960C2+Taee6nLDgcvc7ceWqKB+8CaLgpbg/5yBy+148AsekwB+0IU/9w/q4KI+omckbs13qAqgGN4VJLZtzzaPYzuumy2nMdlnGZTfVizF6a55iWc35RX4gdGJ2ye99dVecGDAtLBTf95p57NZm0fpFPG+98fsT6vzXNp1rT8LIA6ymfJZ0qlBDempjlEzfM9IYR8bJDHDpaWtO0wkwbnbKfcYtq0OEorUNlt2sHwMtxmU74n7G4pWx9c2+h1+dAeRdePw17Gz4kHjurr8dJb6mrft9muw3f3unf1zO5f/X/2yTMRv0TtXz5V+rz0YY+e93nsTgvWf94Mgt0d5jInh4hMk9yhGVg5Y0kZp9MJxwycTguWZcWffjzg8TliWSTmw7IAS2K8+7hiWTVGhLlqybkKHpLgQDmLE6xcoUCgAA4uXoIKD2rHsoYsYFRFPXOeUztkopkpqJqSuv4JQRhdgaqVxHYAuTuL3aiqFYTx7BgQLzZgBPFmUxheRIZPYDPmVbvZV2RfKx5ns2Z4JynNVNez4FJRBRF5Eu/50zQByIgqkFhILBMSGe5f6Z32DiKI8KCCZxo7oqylVg4sAg9k0pB8VPsadC2pNIaC9UMkFMU1E7m1V377yBA11bzumZsW/4xImN0cCNMUQcTgJGyyoIpEcyRwnsF5RU4L0hoQpowcgdf8Sxz4FR7ogDlEfM/f4zk9V9xAme8pZ+QsFgA5rXg6PgFLQvjDivy8Ak8r1jXjw/EOeX2D5fg3CPEOU7pDwgMyB3EbVIgtO6dE+Q+kLpMpI1KGxAdPIESc8Gus+Q3u3p2A+QPuXn/ASoxHW1s5CSPX5puyMvXryMr+NsVBsXIRax6hmfNCCElcSxFVi2BhSIurV6H1ZRySi+0CFmZ4IBMGiSVEhAXYFjw/xEl4d/E18vwNTvNbPE1vkCJAlEp+m2uLMmKjVjHgjjZodtrootXVzmWAZPy740DGy+iRUOgh2z59W1Zm76axN/JJY8hZFZuy0UumeFldVkvuDDv7LJ9vucDR7fnNHeAOqIZHYt9z+1kU2bp+7ybynyIcrneYU9gpAfeqEMIsIioPq86lB+Eapv9VOOtOrpuUQS/A8WXSp7X1KZYQlm5zzbTzkGh/EuqbHZSVNq8GVfTMh5q2mgH92vULMCC+/Qbxl79UuDvISn/qc2O4dlCXfB786xbPeYKimK/3GeqD3bZaDRbajOvtkjtDEHYOxrNE1HVEUZ/Yn+g3tanF+IrldJHBcp442xa/PK77ddgXv3K3+c6NNZHhctQ93yyu5o/UfyjxvvlVAXEwpcagsbAcMYr+wcQmLoxSJk0qiBDLBwIjxxXEjBREyyIlCZ5tWt8mQAiJMX/ION0l8GHCaq75ycbEA1aRd7F8GAgikOtZYkgtxHyUckCclP0YoKaqGFyedVgaxIJI3DORIJwiwW8vbn2Fdje2e9WmkhXB6bklBCrM358jVWToTAYIwgfTHOEuQ7eWeFfloKsU5Kbiy7AGWqFWi0icb/HsqEgOCoghIgQneJj0e5j0XSx7kw1h7GIx2G8KVcBQwefNJ3M6K6ww7SRDFltBhKDwfm9Kk1UbajuEru6tZMFNv8K+O/0VgWWgata4Ntr6qHnPVPOYG8WtIKEfB7U2gRBDuWvTNFZaxLbW0QsizFyYRkvjrAQO5dzhnfuhMO4HDPwNo1oRmg63Lz/kdYPwbHGbM/AOZQi0d7O158iZWrvc3S/X6OVdKs/XJePjd4sQpO5+LWe5cjuIUJhQLa6L8r50Ux86WQTOWUL4gtTU0TXmej2YlfZ5N0WX8aBz727DFfcZ2B2MXf6zROAFAcYGRx7/vCoZGHv4+DZ9pvE5U/elIi8hVvctavfm7+zPzwLTT5mupYG2VkjXrTHma7CA0kg5c89B9eljOsLBCgijnO7e8c/HOHC5NxgARaRwEKEBMp7TiudTwnFZcFoWHI8nHI8LfvfHb/Hu4wEpTRqcWiwZ1jUhZ2HC5pxxXFcROqgrp2oVWvFoQb3V27tzmxSoHbvq51xx8hIIuTKv/dk5hVjPc6qW40HvyODO83YcFS+i+tsz2012wLpYMqslpoalK/HlGpzOPVPYvfKIIawFX9Q6Sn+CWnhQqHgQVBARRbAyTeKKaZoimCf9FHe7jKAKyHqPNed27ap0ya0WBsy9koyTCiOy9bf2k1Q4UYPLs6KG7Iajp6fqRTyiy3seT7UyrvNs7GahZdWtCzPmKSBgAs8iOAkhYAoBU4wy/nnFuor2PU0AR8IrfoVDjnjDBxw44In/d3zkx1YgBkZiWeendcG6Lnh8fgaeE/I/HbE+Jjw9HsEUEOY7ZHqLI/4aIU2I+aCxPoLSlxXBMvySVDPcmN9BLU+YExgZx+WXCHzE9PQnhOcFM/4IxIR1PojQMSUElg0k8TmUdiioFmnA6srEhgomknoUyAtAlBBSBkyhioFKK8g6lRARSd2qJaSUde+KEDBQENdMBaeq1BhRQIgTiF4hz1/jNL/FcXqNHJ8BqCDCC+oMaWMVhhh/oswKnPWCDaZbbzbGJF4dhA4AyCH2dh4CKjQzvNIju2Xh6cpTYUaD33kvC5vknntwmyH2CmoaL7McmpV+cwdpi4sXuOuFVrd8PaEkS3sG1TpZ9jkAc800ohUvJj2Eg0Ou2c5UWSSSTy2Ygp5xRksHMgup7T16CxO9z9mf/C8ROLT1je/5Klx+QZ2fAR/rmy4s6T2QXtDkTcGqfSMbItdNQjuguskaqm1YZVOiz0Du8mjfuYOYam2kCza+/Qb01dflaXzzFkSTI0BLA2UDUld902/ufg97sNMb1+iWHKCmmi0i7Fq7imCjzfOzoI4GXV8UJHMHnusb0bdnypK/UTflztVbkZGXbz3awDZCbq6HadBCk71Zac2F1ta9M1bU5btAuDusuvNnXv2bmyYwuyLG9K9bnkUrlOqfWQBYfAi5yFRuP2dFnpwgIk0AE2JKyrRLIJggYkUIEmTLEJVwyph+SFhnwnof6qHvGNimnSE/EoqbE2WyVmZriw+AAqY8SSBvRXwIAdNpxf0fP2I6rvAbYEmvkPk3mMJ7TPF9g2QIT5DUclD6X929tsROr23RzxeVzNv5Jwrbi290QBZE/NIpa6d4JWI22UZHknvP42yfIXlYeozuM7fEg35z98DhprzJPEiGSAUNVBej+pDVGBFR/6ZZ3AlMkzBAg8RWYWbE2Foy9MICiwlhCGB5rs9MM6etAyVv/WuDUpe6WdyUNe0qkVj3orZdxkgQUo4RXrizda20P35eOFLgaiYga7u26lq3Rsa42Kz+0ndDjP14oAoQoJqQDuai3eWIHLknoS4HRJgZYwSRWHtRJnEd4QU81n1dH2JAJLgS//g9+N/+Cfz6G/Crt4rfZxVOKZ2C6pe5jgC15wb5c6Q/x1sYRncZ6zvG+X3NaFCxL5SkdoYLBrqBebyWirCu7OVKEHlN8UqSuUQuT4OneZyD1FKCXBn54gNG9+0Nu9DgliMchFs8tZlHg9HN9xdmDvfCqxfX0T6oX/fKdPnGefcx9C81Kp82FO3a+Fzpp1gH//+SrhpGQQTPvL9Q/CaILie2SjdIWj3PGh6cMmzLqddZqTMF5Dhj1X6KtQJjPWUc149Y14RlWfF8OuFpOeH7dzM+PM1YlhnrGvDhKeO0HJHUd/ya5e5MOYubeiifiSJCYDAHBGIQGb7hxlfvVCIutIoIC7zms+RzkRkKw6w+q1gwANGmtTuUqnW4uOsRHLykDhmuggMbY8f8JhE+mFV1ADR2nk2HV3IwuCr+A1S3OASHD/q7r/B7Xf/smFbGnBgZqDU81B1RnCRGBDNiiMghqbW8BI8m4oJhlfup5WIUKEIZ6W0wXIAk0LS5woUydYOahRRayc1X+ctdf/buyB4zavdVszsJMMYvQZRW4hS03gnQNRVCwBQnwRtzACiAKeCZI/74fkYgRkDGHFcJrvzNG/zmnhAmnfdFgrK/f5dxOmZ8/P4Zy/GIj+/eY3kCPvzhF8hZdPkpRMR8AIVX4DCDaQJCBIeAqHEQZCEGHW21GrFPnQCz4AkaRFpkPQFL+jsQf4Xp3Ufk6SPwrcyVBKMOIpAAY1KLGCpMeaOns3OLphr32YRw4jKLcmq2qs1T0H28rIwliwXUmmxnq5IkUbWIsD1gyC8FzJlwl2asd2/wePcWH2LEIxYRnumxZqNSyUa3OgsORdVyoixgwoYucT9NyZB03dr+Nw8LwdZfDrqGc8WR2TafwdPiKLobYEIKZkJjat/sBffb6BIVNJjFSlYaKWeGWD7Y2SdnbflenlvNXKqvwgaxQ3Nkj/xTLM9dv6xcL9y5Ip2zQpWtSt1cBZjFVwgmNASmsnaMBvAW7nam1nVZ16m762yOujOmjBEP8Ne/iPRSmPtT9NP7fr1FRONgb4TcUzNXWyZql7tBdGqq50W3aEmv7YJRlYwdUlX98RERwus3mH711+V3ZTRXpKVH/ttF5eofrkdqL8G+bLf5PGzb8RjVM55kf7VuCVk7ysapb4ubMRy3tPeetgPisN79dF6mcO3C3vZ9xNO69pC4VegwqnZ3zHfqrIxivYJpL5/72BDpgzUwwM4Kw0CR6tafuWxw80/ujDAdLH7f60XrL3NiMKEEBooaLYrjhIQEkGo0ZQleB2YkSkhpASUCZwaZaWcGQqjxHGhlxNOKdE/Ih1iCX8k9QPUSLhejXKycrb6sl6g7W2xMQ0UeQo4ATQiUgSVj/v4JoidUtToy7pHWe9C0YIofsN3jClNgQbZhehzU5CXaFL0pXdLaGxTY+yGJa53cLLi9ZOcGX8569V3lD1v32X58mTQQQvj2hpoJ1wCk2y6EgJBlX4QojOoQYuOaKcQIilGDbcXCiK8gyvc2XgQcw766b/Jww8F+ziKiuGBq2krwsVWKhQD7+5sbYYgXcoBrLAkw78gdxgPJhvjuwK7Oi61qOBZ1RSA1eS1sKgX2XS/t/ZazxCPYKL8pQK3MRNMQqMEtg45DY9lCdZ/5VvLje+TvWIIaPrxt+k3l4PCfPlWT5UpdwSE4NWfPHHfc+AauvZZcRe79J+5SKz5szEExQD0ANy3NSx6C5fvP6HBAcvhadx56YYIx/rdDTa4cNfU2d/b4qj+LAo6mdZhnk15GOJy3mLze1vYs3rsjVLiIv53DTa8pf1PqNkffZrc+zqcd3P6mOq5o5YwQ4npLiP5evlDP5xzyK1PFXV5+/tyMU52tjMo900BUjpJL9MWVbV/Mphk8nWd3YXMZ9PXJl570ZwAcAvJ0Bwaw5oTEjFNasSwLnp6OWJYVp+MJT8sRT6dn/PHHX+DH96+xpgkpC1Ms82I8MImVAPtkbUc0+OVczopHGa6pN1I51k2TGs5tq7rqKYNv977iDMwg1O+Wx/KRamXLcJH7c3vKCwzcuHFu8bac63lvjC+l+Aq9xcrj6O+SCjs53MH+FO+zgWBtoOlThatY5kmn1PiPAKUFI1BwzxgCUgjmybfFAWwNN5bMXN8xijV4WWlOwFDiYun8kAqOPMrmazZUhpu9tEd3uH6T/W7PQHK5qma7fyh0LFEA0VTyWeBkQBT3Iok9zWkN+LhOQF7AeQVxAnHC34cHvGXCFKW3x+MjltMJy7+d8PjxEd/99js8Pj7hjz+8w5LukcP/AoQ7TNMdAiKmLJ9BleSITEghfK5U2KyEuppC+RUCAWrxEnU/ZCTkTFjSL0F8j3j6LXhhgJ/lLQOEDMoW40HWU3DM5mz0gsZf5NwrKTEycnd4QGM8ELLq9ixJXLdJ8HploCtOVRjLUHhsSZPszcgR9/SAd/NbPM4PeCbCiRdEdQltIxNY+eTdUWdrlcoTe3n+/mhH2wsNqfmXmAAVrBVXSrrOsiKb/dqVemUQTPAzgobKVnK0FlAOUjbBgp4Dlb6TdQBmF7ehVVLTh+XDny2twJO1qDtvPE1YzqJLVhA0+mi+nS2jWrGkQjk7nwPJ2glULd5GQgj/2bjE82OxuySoq/f2VL3gjOtoFd6urdSV3Xu5l871hah7TefzX5lucM0U+gcG1+CxW0oEmNbylrDqCrNdEP7U6MjgclnoJeQECQAhvH6L+O23MG2F8OoNQogOXiUOFYcgA6y7+WuNToOaBmfULsK+zbBlMo+I0V6/oEcUPZIyXlBD4UCBYfvCXE2MelFxuI4AGyALJeuFdU5nYD9b7oonZ7ru2r6udslP3e9z5fY3pCGdLXZF7n1Brbfr5Nx4Ne96BGyQ3QkiAGwEEZXh5deeR3pDcxF5UsYIAVbkgZURx+rqiFZCDiqIUEQ9BDHLDDEBFJByAoORclAhu5qBQm5vOmbE7xaELGac6T4g3Qvz1Ey3q7YGg3MSpEiD2LWa4wCrQCbdMaY4gWhGTIz5mRE/HMXclAXxyXYhDM+xHj2ul0fV4O7yXHl+j6dy59JqkPMO0A4Z+/S0GYid1J0dfS3D4rXuMXFiZ9anX4KbNofupM4U8fM8eE+GtpIgl0QSe4AgJEPV/AmqcSWumUQQEdCsG104QZ2ltlYLjAYxbRaZrcq6FgVPdIgqWkFG/dS91Lhu0jrrBeEQVhsQFQZ6uIyBb88uDK+Zkxdmjn6SCSEL0Y0Cv+9nXSMFM2vGsfZHLSeaqa/vW5gYZm1lv4FqVQZAzjkEhJj1PMvgxc6o1LTJvk7OCEx496dnPD0u+Obur/D626ZxaU+FHSDDTWQ1QRklxRWAEjuFMe4Y6JpBf7vnt5wR55jQ1J5C/Sa+rpn2bO1LtUda1Tptc4xX2dBCwZhNzVj1OECPz1Ipa8/J/rM6rZyiAH6cdxmSVyAy1Ndh9/qgbxf5+aWKz3pJXE47AohPgeV60cjnSz/1sF2TflpLiD/DAbgibcbnopvIM3WBxreacY5o+9h/qev2846lCUu5UBqSzt2/VQjLACLydAATkBQnPh5PWFPG00ncLj0+HXE6LXh6PuHdxxk/vL9HyhMyP+B4useaCAwNpKtMbz0Ni2VESna3qsZ0yPWuLUc5V6Zxud+zMp9QggyLlr/rpN23Ja6WBWawuut9TsaMsHuzjKG7S4OfJcusOENoIk8I1VSYXaI/YUtCLCJI8qgbGzHCJGSLK+GTw6O8axzrCzOLZaZjDDfCCxJtc3kvY8YslroAMM8SMzNOERNPolDBATmIsljRh97ggJB5gKdDqnBBAlVLv8j8+TKqAIaNgCSwatRLPAlrx/UBde4FIllbBQXNkIDQotEGJnFPQw7sflArv69aRciVHWoZUm/76nJG+L7qIimQWAWlhLQekdOCf/qfR/xLWJDTETmt+PjhHU6nE77/4T2OxxM+fLxHSgck/hYIB8zzA4hm0HwAUQSHCRwiKE6ioBRnUZyzKNXmmkCpCY+5ggIyQflfMqYEBnIUbzbTBOQHrPjPWNcfcfiX/w+W+Yj1WyBHERJEACHLns0mSGIgQ+NccHV9bLRDBsOU/sTUp+Jw2VyUstD3p5SxZhFGZBZhXET18T/ZPvYTFmeE6YBMr3Gcf4Uf5gf8GDLWslczYoFF1pvMlZ2/wYlvnLKIrtjzp2KbjfRMHRaxqgjlTrG9Ydwe77a2HDfsywvNyGifocwydZ8NSdbsf9ZzLts+tPgNzfkAsLdqAKq1Q2M1wbWRXMs2CDjb3eFed3THlkbYT5lFaMmBXGw4KsgtqeBh/VPCgYD5YcJ8ILyZCa8mW0OV19kKJfp7l52wB2hcdA3Si/FN8nDclno8o4Fhn2S6UOkWlgZn8JfYTv6XpBssIvZ707zpNxaVb/Bc/H7iRAvCJtsfBm6j2eZ3bwsBDj2T7x8Qv/11QcCDmuyUrNQSiB7kcQ9DafNMprqMqX/KXY4uX7cRt252+kPS/d5jAtAumLtpTKxUjZ4hlbVD4FzV9h5xZOv8xmJtnkuZzr/fCNc22d0ab4QJ5xNfgM3en83X7a/2R7/GRnXIJeKZLP1fx91x0NllZhrOdX0XTaFAEliXCJlINBpYhZgRoExgdVlidcRpBlJAUuw8xSSfSS4+ykFNewNCYkynjJQSOK1YMSHPVExExbQ7I3MSJEldP+UksSiyCjpssgxRC0FcRU1TAi0MfADwLIHyAhThtGLlPLDg2e0o2Tefv33jfo6x4mYCNgF429fbxHbhezdLdnHsHHY33Cd+WV13D+2cfZ/YnqzVcUdeqhUpK9ohI7hpaHYz23Ujf1TuIdhvVIEEqUCCiIq1Tj/QLTLFRWAxthxoFltTR+uCSYm6QR3mtqnPP4LJ3AF4d1CsfWAWxLWa6J9PzGEIk7TRwWjn02AcSvfd71aIk9t7HrbvtoKI4u5JF2Zv4WBWC5xlTlOcAEpISYIfWpu5C6TNSjjkzHj6cMLH98Cr5xWv9kcHjNDAbCwToGpuljcF/8EO3jHGVVDybxd3n7MSB/17Gn28KJWyenae3597BES9/8qnjQ+RG5jzUBguWbXvL0PfCw/2tMn3NLz7tnohRMVVrx/lPSHEOZdJPu2tnCEOckbwcEube+mSJUTv9uR8ngttbUAd74ifIu0pGQ1ynsEvPxWITyz/GdI1TIHzFj7ln/3Hu/SL0kojxKjfrxWY8trTpXvlb02+ynKmnD002zNK3JUHcDyAQUi8YuWE03LEaVnx4fGI4+mE94+POJ1WPD2f8P2Hr/D9u/tydgW9E8RawTS6HW2eVJFBgx2HbIzEBM6MEIw5ZrdbZY5BGZ+hxEEwX+Gi1e6tMSsNw2BegUzihsYCvJYxkLw7q2Bz5ldcwOUkpz3qLq26ROoJb9errbFAJOx1ExiU4orPlb44XMoEEEUZi60bBU6Q+7Q5yVQUspgZMQTkGBFjRE5JgoCrdcjGbX2DX1pXrT8GN1cSRJnBxSpV1dzZziQNwgztE7MqXHT9toEtQiMvmCmzx3WlcOtyeJhcO0Qi0MosPH82eo6hDFyosMx6LwObmIWxvqxYlwXPjwzOhOXEWNeMj+8TTsuKd+8DlnXCsr4GQJjmVwiYMIeDWkXPAAUgRPmz72TfqxZ4aZ9lkgtpbu8pFFc2jCx7jhgUIhgzFvo1KNxh/tMBKT6Bv2Ywqecp3ROZDc8FwFndN+UqlHFCCI8P23yXIc4Cj9QBpAysGWIlxawu1eRckIDVIgYiN86BIsI0A/SA0/wWz3HCkwbUNmsQj/axw6AcJWyjJp8O5RMLhrJga17304SeWd0vjxjV/Voz4YPtu25oOrzN6iubtUWyuPnSJS5/ZX3anDT7xM4Hbsuyq8O+symaMYrAFlCLdLh8fc9H+PcOvjroRVOK/VxSPTPsU2mb9B5gTJhfRcyR8DABh6KLXs+NDZzdULR3JO0Ayvr/7bgk2Z69Iu3V39CdQ/rsXBs7dXYLTc6T7oznUf6XpxtiRBTM5AI+ZBpl7knB4MhXUxKXS8I2KuuB2naw/CLALDTo4RXCr34DiZYeQIc7CfZJFlgqVAarXr6Nid5F5K5enN1IXIcXFkJ386IcSGNY/Hi5Fgf1DBrdvLl2sfQlWediP//23X5b+ySCPT+njHQNbfhCXL0k4/tdU/OY6Lz9QOrfX0MEvygHZ+D5RyB+BN19DaZYmJ3eNVM5fLSeajqm1RQkkZp2gvlvo4wcGJFJ9yGQc0AmQWAIB/GbTgExig/JlFT4kBMYhJwTQBFpXcEcEMIKUERIK2iNoLACtGJ6XsHHI3hNQF6RHwjpLiAlESKkddVAWKsKK2oAarvLg7rIyccFhx8ZmWcseIVJtTSO8z0+vv4lHjtm3Gl9i3WdMMcfEYO6aGoOaPm37IeCm10TsOnCfr20nTfvee/F+Tpp8+UiEbtfaUus3SqQuKo5O8EarZEKyzWgNyU7ZESvZpjmo91YPqO/xv0zzhk5y1oPSdZkTNFZ8WyZ3rugbs4Kj2DVNTY0t4XNQS3jCVp7V1aM+X3lCfamR+RKGY/YeusEsFoUcZHqVTJ1fz8UIYFviCsi2X6ijuO2IvlstHdQkPJqCeKLJDBSO4YMBI3XEbr5KjF2QtRYOAkpi8YXEiHGrK7vGCbAtHErXmqrqk+Fcfu13NOGz3jCjZSpAKBoHpZ73a9xj6d1eMZoa14jlmMMtuQV+Yw58+lpvN63zyoErTDCfID3mnKS3VvgmpbxRjBQFF/kQXA4oGcC7Vk+NIIFbjWYe3xyJITwRJnPe2v67Jr0FwQQn6PN2zTTLq/ns6X7efsMQog9gdDlctfgp20b/5H20s4AXbGhjIfaW5nvWkr8zGkkFMnzPdg8IDCwZnG9cnw6Yc0Zj8dnnJYF7x8/4scPAb/70x2WZcZxeQ1mIIGwpjsgzJhCFMZhMHeTU/lOZLHkSINRZ6zrqrEi5E6OKQFOUcD2qwWYrmxY0cQP6kpI/PnrHnCWECLoF1eTORGYRakJLIpTYMVTHGa3TS4INLX7rPI6ALFQtBcuJhHU5Q2M3iUQiRsbU3oCqXEA2yxxKawYj2MsyrDkooxhTHPFawqzrADc3BGGEUlMDCDFCZwZc4zgGBFDBEeJ82dxJcAZhfzr0DdC3QdV0ACFIavLGstpYy36yqHEdYDet244WetWv/ZlDRTrEpm7lDMCZeQUoOpnotBTrCsMUOfGE6Tl/d6l2g+ueDBDmO85S3B1+VuxrAtOy4plyTidEtZlRVoW5HXB6XREWhc8HROWBcg8ASFgvnsAUcTh7gExRhwO9xpPUcZEAjJHxHmWfROnSq8Hr88vTpfk8MlFezxD1n0gsYgwpj6BVBg4IcyEMN1j/uor0POKj//H75DfEPjvXyGpkh8FwFj97P/UC0HWsffvdAfAVnBZuyaEYMYpA2uyPaeWUpFwmAKiChODLaMwATRhohn3+Q7P01f4EN7giYCFGBMYEaKIyEGFIiiiCfWI0MECRTwd/sm2L9w54Ptg6xBQflF2dbm+92dHi5nK4i6M5GFOozbhNlWJelFrUuGTnSekrqBAVANmN3cWNx/lh1mx2Aw25wu3tBNQaapL99rmEPXjeisyIvsCECVXgu4VEiuaEALmKeKOAqYYQFHiuFhsvUo77qU9mHinm5fh32vvap5sh2+M6jvfRuhQlv12uV8T+nBzEw5dWL08XW8R4ZGwQeOFmNsU0J+7E9Zu9mbjuwvBVVS/UAAO9wjf/EKjowtiI0S4aZPagqWCJJj2H/m6donWgYY6X7t9+jZcN3YJjo7o3CMwuOa9irC4wdy4HMh8bt7avNe2tQsrNR9fJl0SBAy+XSzf788X9uCSG4gzBfUL73avebw+AykCh7egMBWGS2vCv99m1Tyul5LT63H+RBkUGIEBbzKKDLGMoKo5HFkwyZgzkALilEEpqLBdAlqDCFHPArkfNYjVkhGXFXlJyGtCDoQ8AXkR101rXpFZNFSYM/Iqrl6KVguAGCPu5kXafApi+neXkJMQQGuY8HT/BktagfRchijzAZknBHpCpICeOdsOHDbvLzKdB3fiCJ8YJuqzdKv7ygukam1cUaBUfAlIKnUDV55fruRVoPtzl/3Da4RAXWv99QRATGa3wvJzKRfmtZk0V82i1oS21Sg6h671e9YIsvrZjrVW2ox52+ZAAYC8ppkhqR0iZb/dp1Fw9h8ZYrup7wZBRDYEyMq3Vgu9uyRvtWBtO4CB0Zi7poygb2Fq27JEZPMo33PUMzFEfaYu6hDEoqMJpmgHp1hZjeAZrn2qNEphihS3TEAhwzp8gzYVtO0M11vBObh91MF4Nrl9tDkpuGZo770rDghdd8Wlxgg4Jbbg9kXrZskFltZxKQIJG1uPc1HVHIYvV382+PBWeND9dnntY6iTu6mnn9Nt2p4T27u+Zai1dW/q08+906+ZP1/vXp628Nk2L725bAnhm7kVX7vUlh/DG6verfO6/FcpsNgavvIivYz/XwfrS/HinzrtwVlRiOv7QUDD1Lp2DF5MQ5yhsXtca7z2VVs5zOISRu+gnBckzjguC5Z1xfsPTziuC969f8IPH2Z898MbLImxrpNqasei3BPCjCnMwkyNEXGaJTYWeUEExPo5MygsYoW8CnMzhFVwBLNkzhrbUQUP8qcMaUK1ioCCYv0HF0FEWoV+SBBtdTCrqyRj29RxuzDg7kuLJ5plogkQMgUQuMTCsKxVcOWqJdW2ZttfVXGh+jrXChwOU/Ayhmgqb3BTKvdQ2besA8XinlfGrTL1yl8OykeBaMmT9m2InBLAwrZOhYHH9ZU1bPwFqrBXGmIH62X33g8Cq3AgcHHLJNc9i9urnKtbIJsh9W1ZhBB9L2QDV9iBgt9lDaxeLPGTCCPSmpDWjDUx1gQsKyOtGcuS5XMFRO4VQYgI0wEhRMyHO4QwYZoPqBaZSpurBZEJKEitpj0+Ah1HBmus7yr8IRalQQryPmp3grpMRgAiz5gPr5FPT6A/JODEwN9Kz4tLHI8627ozisDOih6R7L7bjCXOSFksIkyARop/BbJ1124xAoFpQsABM73Gx/gKx3DAQisSVol9YG2I7o/+5obyK0tsD/2wGd/sZ1kUhBL+UbKUH87tj/7bNsHbXx1fsSU0nRCC3e8bUovmnamDux9sd5a9NDrNLYKupu1wnoN2fwL2SjG5bujarzxdVTwHMAXCpIpZomh7Sys7sI3AvXUyXpiGM3ZT2wNBwjCbr7TmF9q9r9Gv208fiOstIkrgJip4bPte/hl116Tv5bIBynfbaOz2X9EWBDc7qblEHh4Qf/M3YgExHeTALlYQ2h6ZdoSWobpw6yL2G78fUznch33l9ucwbajRQQmPEFL7nnwd6JD+ISLZJa+R8wLcluj8GjtLR/5cdMeNxK1PghheyNfdG5/SzZuFDhfruu1AMOFD0QAlUj/nhmn0e6Re5czeIiKK10VD5K0fQeIqEInP06xm0BIsS/ZqzgwOASGJJUTMGWQmwXFFSisoTEgpYVlOSDkhrgvCuoCWBeI6zXypEuKHI9K7E5bnJ6xpwfo2gu8ilmVRhHEtQZryknD81x8wIeLwywSa70FvHnBIJ3zzww+YchZkTbE1GyN248cgHNPXOKV7HOL3mMNHRUaCaOWw6sLZ1PL+LA33miInNDyfDI69ct0D8q+uX2tXryrefNnJ4M4llKXWwUQ7ZcghZdt2tjfQl8IW9idyA4FZPKQkBMy6gtKKNa0IKWBNC8JKWNcTMk/FTF6shkxzSeu+ksl2Po0XjAhWQrPnZb3lkseXbzW1oe7TpJDw1E3MoK6alIizO9XM6r2godRoCL3CVJIRmAZPIbjkoWnUGWFu+9UEEaxIhMdNy7vOKiUwgREKg7x+mrChRcZDsDxBrbEA5oRAEUxADBNIha4cNFgjC4PEGBcV97G/LbJf9q/iOhTsDG+JVXvfDGw7hW4u2zZaJEdbvIAPWM7KoOgDWH8epKDQa1R/FAKwM5H3LcblI+Z3/wZ+96i0jPZU0cU39we8uT/gIJElh0II4RG4sfUCBguUp61etITA4Lzywg1sz/Ze+ND3s1j+kmG5/mygruinz4dfJcPaPst5dQM8X6TeHk/ba4s2eW5u6YVCiJvy+uVwDr//2ZD4P790O3Z9bcW2J2n8+zOkyhQ7T7Dx/IBMEWsGclqwLAtSSvj49IxlTXh8esLHR+Cf/23GabnD84mwrBHPSwYhIMQZMc6Y5wPiJEzVKR4Qw6yWEAFhqkKI4A7GzCJ4WBezZBbXqjkt6spRLRPNFZNZQBSBhAoi9M4XphSjauRr/LicsQaxuCZicBYlqcLwByv9k1GZ0H7cuI6Z4azls7mUKnPDPd3QacyinJB1hhS/IZL7gzuzg6IBT4BgVlmCAhteUoJvaxcyV4tWm+5C15Fjy0jbopg1AcyYpgk5ZcQYwDkgUhCcJ5j/f+40rRVfYddfPxTMTudEIdJgvgit8owvW7ChEs8jCB7FotBhga9zyOCUQSEBSUoGDpgAiVvo2UnQ4NlGzwmSWKgKbyFh7jKzxTHhLPEJkwogFJc3q3tZBREUZlBYxZPSlEE04wEHMEtMBCETxSvBPM0lSLgbHVnjxZ2Zw/MszgfZGNQZNuGIKQ2mTGUFEQEHzuq2bNLVuYLzA47z/wZ+9S3efP0nPL96xpMq8qYkQd1zsDUosczMLVNmiRnjA80b7JkaNUTZrcxICVjNokQZ3pEIcwyYY8AUdK0hAQhgipgz4bBOWPnX+C79P/DdXcJxOiIFEzSwwKH9zIV2RuM5SYxxqC6t7muL1W/xb8MHA/Q4AqH4sNI1bLkNH66zyYNaK67fBlVW6ok9zeMh6evS9UAM4VeogKdY6GYwNEo4uMDWVmd15i6PpwXaESrj4r9w8zFOKoG9ljKw9U7qaswE2aS86ah08xQjDiFimtQqQoOelykv5/LnuNE/H13zRZu4UliwzWXroXtzpr6XyCWuFkQUVsgOAWS/em0v+y7TTs1C7U2ZyvciWWwJqPIRJoT5DvHtV6BpksWJKoiAScJKBHUPuiMEN5O74xNytAhGuElf27nFQ+PxrK/PIaRunHdSK8S5lHZWzjVV/IS0Crl/z7b7CUg831jc5zf4zmlJv1T48JIebcq4tjgnIK0FafcWEURovvtk1hDCPAww7WuQrkiu38VwzokvKCAEFmai+v8EMQJHMAhxSqCcVRMoSHAsIsTMAK2CWGQ1tmUSNzdRBBYhR4ScQUcCnTL444J0OiIdDkBgpNOKlJO6epKLNJ1WnH58REZEvjuBH2aEt4SQEw7Hj2IAGGYUAWZ3joBNm+aAlCdM9AHZgn7rngrIxeR7dPldPrNHF0HVtAKAPk5FybU5kEpxm6iLrX/p1NAazfm7hwpukaD27Q6C9MI0bImtpTEcnIVwM7yOlQoQolBjmOSkf/I96R+IJP6JImmG8MoWq1ZEF+G+Hm/YSR6jvGz5IVuCCnJZBJlwq55MKEcOoJbxWumYaglSkHP3b63TtDU0vyHfXIWmhGqVoSZazQ1aBREmYK3EANt79ykCIrRjwiiWIzFE7ZcQA/4zQPLlDGE6NBEUDR6rcjzmLV/ZTlmH+8AJrzo8oq9xDxWS/m0PkPq8J60GaUNo9GfOS8+gqu1X6uGWkCtv7KwGwOsCfHyH8LyU956pfJgCXh9mGKF5TghR7rwyfv69VY5SzvLU5/53HQMvyNhNNqebxyN8uX3WCyE+B7+zQfV3pCi7zZwB4DJot+FSvZXULWuvr3qvjv18L0+X6vikNnaK7q/Bl62bnhH6JdJnYd73e1PT5tzc6YNp9m7wEH/ldY2Rz4TPsycvJ2q/EyFrcNy0npBSwtPzgnVNePd4xGld8fTxGe8fA75794B1BZY1KDZGQCDEMCFOM6b5gHlWgUQ4IEbxex+i07CHuMwIytDPLIKCQCLEX6O4aMqrDFzOKwAugaZJ3dC0gghlOpK5ic0gC63MjAS7DxhZhRBJg1yLwocEYybrk7+fLk2KnbUmjGgRW9R7oGH/CbNVGWPmnFqnQ6/PDo7yzeEmhR7j8rsw1Xm7Dq21ZvqBwi8JISAXawjTUHd0ohF1Ht8r3RV8hpsL2u5n16TlK7QMV9S+KHi0SBHbsLLldX3lrIIRFRpQFlpMhQgBAIcWhlBAq9gJu+qNad6gebpOy2exZu5icpCsb4nxkBHCDDaltsxANIFH9eJhlgCAxDIsyLCjp2UdGa1OZfKo4KgGggZ/Nvpccwdo7AeGunbSkaAJib4GxYTD3T2WuCocQAiidJhZg67bKDbTwIVmKSQAehREHmZIXRIjQt2Z6utYhC3ONZnhYxwx4x4n/gWe6O/wjD9hoRMYxZEczLYCrHGyAQS2AOqh4qte89klRtlZBa69VHA9NoGc0SKllVKnf3aOkuqw17qDduivxl1q+apfiMq6kPd1QD31uu0jt983TfPO99IQxOp9CHJXVaURNnVsgKOyiKtye9DHaqkCQgyEqbMgas7PDX/5hamd5p8mcf/zPADU32O3NvcSqcILytwQrDq2v3uEe9hRv5h0U/MGRaunzXA5eg0yAt0/YPrrvwcOM4KZsSmrJuiCs8PcLvce59osbr8lN924YlBp+HW3dOsGpyLQ1yHShOZm2cvFt7kN2WuqpC0m/sXSZopuLv0paf947lCpfQg8w9/NwZfSAhzCsAMfEYHTiuf/67+BGTj8wz+CDneNMKKgylcS9tZiIawIgPkCBYq7JimDJhAHsbpvIkLmGZQZoCAB6qL40SeKWPMKihIzgkIAaCmXMAUGQgCFWJi40zwj54TnP3zAkhY8PT0hratonRdiBpg4Yj4cME/2d4c5L4hxQgSrebnEnAndvq3u3GVPPi/f4LS+Vl/4wMPhj5jiEaRBuIEsyKkh0ETN6WNITT+TzZiXf+jS9IwT1S/dybdt52dIN7fbEzgX6tuGjuD2N7WPKhNanrSmt9tWmAk/fnyD02nGmmJBejPEGienFcvxGTlELMsJIMK8nIp2VAwrppTElcE6laDVgfy95vq7uTs6Aq6k3eA32q/aj5ELsdFdUq8hZ5XgazXGvd/79nxzdnjoK+JERZ+qmydfwOrQc0eSUp1BJlQYGIJrGBO51M6QAI8UUANy25g6t1nWYEFkHaQF92cleKlot8Uo6yBEEa6KMUQQwppYlfekzaRrhc3M3sbJGBIu/oAIHKDMAyqMA6KgwhCUM6YMV1kmFS8qZ1hHYFCZt3ZXEdX5Afo9NyJcuveG8xFgjLuXJ9b/2a3TeneRG77lOeHDP38EJy7P/Ofm9CBbAwNLiKZ8GxOCHOPA+AVDS4iunnZLOFh6YnILaa27m2+f2wtd+iakmeuEnHvpkjunL5m+JG7Vj9u/93RpP46H4d/32Iyp009N/p7bybERnt2erIV676G5TtcwgyngdDwh5SM+fPiAx6eE//7bGY/HgPfHiDUBx+MBayI8H48QC4gJMU6Y53vEacLd4Q7TdMDhcFcsI0Kc5M8xtuFw6RDMf7ec3esqWuXLIpbLeU2quLEKHpVWABmcE9Spk/hBBxf/99ZnYc6ncieIJjeV8zSqhrcpD2UWuDIlFKymZ7QbndP7qtgdeTtrW0y7RMSUSMiisJSpKDRnAgKz4/cPEFRLeuVZlhJIuCi9mCtaxfM6/gGxMPMCCX0yxQgwY4oRaZowTRGcJ8U/MzIHsYpIY/bhlptjd7RPgo+FXO9B1d8HZYIxGEPIQCZ1f5M19haQc5S7Lueq7EZiVR+IkIhAKSOyweKD2ypUZIMnK8notqxjlZPhw+YOWMaPM4p1BAgIkRATAZFEQz5LLApxpxSByYQeZtHBCFmUUZIgQWptUserzrf0m3Ou1idk1pYVLjBqUG8VipiVUXFnKqMqRiiBMAfBQQNJcJL5cECI95hevcWSMp5//wx6yMAvKoyqfihWEFksvDOz2OYwAIcbWncyV2+hXMZaXT5B+hKj4KxmDTEpvpuZhZkcJ/DyBuvyf8fp8A94uv8VPtCMj+kB9/gOh/gOiYFV2xAmfAJBcGqj9wMqTsdMqjykVsqOOKzYfV3Q/l60ECdZ6Q4JAaNCEGKYNRWp8KW31D17oagQUWStjMIztedubH1lLfml9L0XWik+WxwskeH2ozrhntnhUl0ztafZoAs7z8eZ+zO2VlxWUrm76pm6yU9yx80xYooTpkn+QgwIMXjixwkjrkx7HTWJ27+L9Ak4XOGLsP95dbo9RkR90j3fR6jOwbT3jvrLnwgUI8LhDuHNG7WEKOSewtEJLcriddSor5c2X7bQXTugwwXJ7jWd/X4W0eze1fvIXaoDQEeE5ovTjWt0rz/XwHAeNbc8O/XfAOcWxtvG5xra4MUWEJfyDd93I7c3BwDy4weJq3B6LkJGKv/VSvbvS72iWp5UxdGp9sGyiMYSCQM/iM/UkElcmkCQNtF0isjEMNFnjBIYTTRRgJAZITBCyEIM5UkDwbISR0n80MaI8MjAcUX+eEJaF6zLSVyhEINCQHx1J2bjSlSFEEGchWBiQooROUjQswHe3fQ544A1zTAT6cwHMK+CfDHAHCqCYSNDotXF/owazphmx21rvJuuzc/d+/VMVX829y5vz70eQdogTD3w3D3m0UuHfDHgJnBY3bLOWNbDpqoUAkImcFrA6+KCVieAVoR1Bcdqog5IkPcQCJkCgo9JQHW317tvBJED4Bzy63MWpNP/HuVD26bLVxHnOm5e06jP7+scgr1TZPN78wVQjr9bKx6ZNf1V6t7lLp9e8YbBewAaIZDDSeoMoWjSsz2xehTHMIISTgBxjtlRQPC+grWNwjynBlQAxXpkiPgPA7zXrK1A4sxhOHh3iXC5Lg0WRzN29TwoGoKG/7EERD1+XBHVBzaAImDwVm9FyKMQeyFERS/93NaOFUsKONzOwO3wNo/HiQl9bceys8/YVrMdaSeEoC73l2Sm71lBtHDs5N/J8+L2r8x7bZHtuI0LtkPwecb4c1pCXIR/8O3WNq5PL8Ug2n31k6arm9SgsSWVG7DC7ZXxHP5cTo4ep/Z5z8B07kRuhBCKgxsTM7E4QDmtK9Z1xfuPz3h8zPj+3YzHI+HjEsTf/aK4bRZ3QuIWMGKaZkzTjMPhHlOccZjvMU0RUzyApih0uwkiqFofEALiFAw4gFliI5jFYWYkCspMV2tFApgzMgGEXO6zoHeB160l0/41rykUhOEfCKGc+eq6gxiEAK6Rj7WSPYWf7T3XPmnLeSYn9Jz3GteEojOhfUONL7I/5QVOsrp1HLIyMLPDKZqa/F3kgLB57RUbRLMYIHPdqdbqnjnqgNoMSMvUFXrPekfWD6vP1StTmGHulwpOyWpRr2uYdF2CuInFJsNQ4wp6WH0skIqj6mhlferxfBlS3d1c5hJMiqMbPuGGNIgbKTJGKGs8DpIA0OZpLPh5MOqQ1XWpNaxtCr5B+pNLmWoNg6o8Y+WYTR4hsTJKgGWZqGBBsRERD3eYjjPS82N1qUyhCA4sBkWdCz9AHc7ZnWWWv1go6zoJagkRipUUl/o4A5QjwPfg8Buk6WukeI8UjlhwwgFTaYIZDX3sz9kAiWHBDV5dAz3b4cuuZNFrKbDu42Kguqe70CKFDdlYMHgYda5RxmabuPvOg+d9otIxuV1GvAObooKj+0GzeR0VKkTZGQBekhxurV88IjYq4LKpIpauo1DOdz0h6zHTCiXLl0FnnABwk/bu6lvSLeNX1lH3oKuKut+XG/VjcS1A3H30lurXpxsEEXXL3YQHFsi4G8Cmcmw5mnVzEwLo7g7z3/0nYL5DmOdKbGtGu1DNCqfQ4ISSF+fWMuoi9RDYZtgwvAZaaqB6sMtZ6onUrlGH4GyY6juCBw/Vn1P6nITBz9sz+qx9+XnS9fDzesLx//z/Itw9gP7+H0FxRgyswa1MTxeFqbOtWfaVeItcYD77DBkiDTZFijBSEFdOHOWyC/YbQKaMCZNocYSAzBkrERIFEBNimgCOIKxgjiDMIBxANIFpwoQjQCcwB0zTHQDCPB3AKWOKE9KScAKpy1jG4U781r568wscDvd49epr3N0/SJwICuAw4zTd4d1Xf413YPx+fcQ64HpWBFYPHTN75YCn07d4wtfFnNyIghLkloEQVry5/w4hrONLUMeZ3QS01+dPv16vafFz4ybDpGesRxyH7ft7p0eSxz90KqqlAJeH2bXHzUe5kLt7jhlIccLT3/xvOJwe8e33v0XOT3i+O2Bd70HEulYT4jQhHySAXZhmIdyjCzhcNCRD0YqS3/JpFhR90GYm9Xs/wrOkAofMt5lEmy87YYBHg2v5oWDBRm/zirsxHicRTJ4XilQk08Fl2TRoY9Es9Yg+c9nTRhSz1iOP9Rx0VE7pj4OlxJwxQjCLm4CcGDkp+BlAEsuMnExjUVxzpbwKcyXnQoiARThpbgCaPe+UF4oQKoRiFSa4RVRrCWeOrgQpak/7wdb5IGwpFrbBw/YE6OvZElubRMaEGOA6hWrzOFbfrrzL7Mes9jNr2WqVHVQzdAWrWxBiQkRU4UEo2J7qTjZMBY9Ckqr3Bb3gzALC4qj1yiWWv0A/wP1snjbD1H2ef8+uPq+gM8bRenx3k+dz4nVfjKFN7nOv7fLtbJcuC2vO4+Xny37udKmddg3++0g/Pb4zOCUHaUT2M86V3uxrvW/A6vdau+pF1v5c6xkzzbXoaF+rgQrjkLDGA1KYcTotWNcVj4+POKWEj0+PeHxe8X/9jzt8fJzw7sOT+HJPqmdMUZR34j3CNGE+vMI8zzjcv8ZhnnH/8IB5mnF3OEhg6liFD0F9dQdlaAueYhYSFY9JaQJn1nhwGaeglhEpyiepQGK18bKYCPXT8Ao74zmIi6YAYaoG5TXEKJrrmSMoyX1OGeK2NkA18/2MjnCPdt6p+1J4ECZ8Us1p436Kq0bJZEabYHGfExiFiV4Yz9C7OQlOpplkfhT3YNW6zzkjp4ScRKPeUIdm6VBlyGfIFZ+jxMea5wk5J8QYkJMwqUFARESJTUES38NGqA/4LP0xfohozldkOZeRM6ER5UmEQkGUxThLHEDWy5ghbn3WHBCwSjw1jnp7s8QIS6IIZmz8TIavZYdfmFCizp259GGN85At9kKWsknjIdg+QvG3n5ERwDSBAmOaAnJO4JxkRIjAcUZlQjNoTUDOiKwWPqrcZMITcUWmN7q67yQoY5UhEa9tkTm83OJZFG36bFYYMjsJwApxvfXMERMRHoJYmURMmOgO92/eIvERd//jfyJ9A6RfvgaFhBUB0ejcMoaCpzInFB4eQ6xBYHiNjZUG+WbGmjNWzkAUnCWGiClMmKcJkRjgRc7BEBAfZ9y9+1vkV/+A47f/gOXwGusdYQLjIWdMgdUnilnxZkeD1bPFrDkSCyHE5usr6AywiZjYDysI6k2LpJ1ApGIxmxd18qCxTpBrHbbRmBkIVEkZhaFmc7RFQ8ZU0SqrKMXDWBYAobhMK+5I2fLbHWKCEslclJ247avsR1uq1h9zPcYVqrKPB2lzHw3uqXJRwSFTxjQqjuoafLmU4wBSt2Z6EiJGiQnxMBFeRWAOARPJWWb8YTK3uNTDYs3fiF8Msg9lGTfW0Y9fP2xnK+DRTXUp7ZToq+6ycvft9nYlXR+sWhNRC9ulht0+c99b3US2ihuCW58FAsVZglI/vAEVIYRbux3RFcr6JX8O7TL+ixbd5j07mrp23AdUqqCOqJLyT9umh6kHDtufQ8EDFWC27xT2W9OnEi0tQ+iFbVzkX3w6IfJSK4VBTTe3dWv+7Znzctg3eRnAuoLjUtwjFaYMOQbYDhOjgY7kUpNtzK6InqKeuDL7Y73sgiIcAMTEkRnEQfy4BrGYCCym1DmwBH8NhCkCKc+InJCjmB9PkwhQ5vkA5IzDfADnjHmekV0w2nk+YJpm3B0eRJNrukMME6acEErwsxnLdIcTL3heTs1euyj9JSDnGcyT005SAqFc6EDkgMyxRV6GFxlLELa+kRemEdj9XX8+nctgwYhvBOolqcfndvI4bO5i37ibWN78u/28lJgC1ofXCARMOSFBiG0OAetyAhiIYS53S4hcEPnAdt9Vpr1pe5T7RQmDGKsgojLUUYIj02BS/N05SoJwV2Z+76rpWt/se8/P3hedIKLP37e9EaIY4u5xC64If+a8uV+rKyYhEL3wRoi7qm1W1grXZ9BYIFkDRZoZugWPrG4TuAQyL8+kEZhVSloW8OkIjhMQo2h+GsQdEl+PXEW6YcIqmUMxRRd4jeXeCHnGE1DxHwB1MDx2fPE02UmX1o3LSdYOte91Lpu5cJScKEkyAi+gtJS8hmua27MYo7hHcKBV4oVggrrGysGjl/bdc3r0d6PZhfra434OJbw6ncMVaJhvfI8TbevatHUZmDOv6Kp8w/wujc8JWxPbg31frkJn8uyP1fn8n54+T13t2use/ezpzwiUJt2ER+/vNOwgb8YrssY2r0vyy5iH2UdVNwU8fPKeCuOFmZCYsKaA45qxLAnvPi44nlZ8eDzi6ZTx7uMdHp8Cjsui91QCgRAnAGq5HIK5XJoRpxlhkk+zjgjqYiWoj26ziCD1791YR3imE6B+/kWgHqLXkIe4MsoQzl/puLIFi2RV70ijN0BgrgFbrU2hdyy+JDXPN1Ja8GDttqO/VSis86dyh4b/6J8ThG9h1hD+ThlWa5xWxxz0TEy754rbnOzpFS68EV9/gY9Q5qlYjQgyqrBRZXaS0GaNhnvBSSu6sN0ZFYNmj5cWZF6FcmzxCTJC+czKsJeYHhabi+xuh1hDmKBAmPOidc8wwQs710z64ZQvBP/zMNa8JRZE0xWCWaf62KR1HpVVbmeBxSojmz7DYVQQYfgJRmmrM1/wfHaQKi0tfctlzWUYPVq8NiksBEIExdeI4QOmVVyjCZNe8CsJPu0Xdjs6lSumQcXNTRHZctX5cHNllhCx7D+pjVR5J5wmhPWXYPol0vwKaZqRAkA5Y8IiLsVkVeo683FeSu8AlFDuHZZoXzrRlM6VrlAZSkcMbDAOUjmE7fHalSZ/Axe17/eSh6uJX+POE5sSgp6XtqFLQz3A43bI/+ja3uYevGsetKL00t0NLubgI7fye3za5/V0mT4OZDEiLNZI1y7cnuvTJ6JLZZx2KrhWgdxcvvl6rwbKNvnwxf5PAGgI3bP53JdysY3eX59uFETYwVPOoPLbw3BuQ0kmd9GzM1baIGgEmu4w/8P/inC4Aw5zuRytHlm37e9m8b50VWk6x0yr89HDvf02ytALIcayjOs6IMfwxZH/j/QfqSSaZzz8439FeHiDhSoTlLj6ih4x/cqF2L0rgsBADWJE5gc1CDLDwYI8KxI9RTAzAktsiDUE1egOCCnDfHt6H9YpJaQYxP/mSohTwLpMmOYJaV0QAmG5vwMC4e70DIoRp+WI0/EEZsZ0kMB6X739FvN8wMPDK9wj45vvf4uJLQBeP2CG13FFcAsBYAwuRx9sR7z+q/1JPOH946/dWcrDQ+d+/ohX9z+OL4vPnT7xzPSEyCh9cuyaQXNFo32vaoe7bZ5tIbz8yAgKYKvcMkgZwA9zwCFPuDstWFPGj/gR090RKYlgbF2T+Fw+3CHE6tKAQkQIQDAtHlTLBwPG9p/EM6l+bj1CV8emYphUym9hbu4xckTOSJhxlluyg8Ya8p8dEW2Umybx+9wTXefXT/s+l/1UcANtXI6frO10RCgzmLK4ajDFiax7037bfrdxSTWIYc4Zp3VFSgmnRYJ/HpcTcspY1lPNxxmZkwot7DQxu3nG0+/+Gc+Hj4i/+QfEb34FhCjEXVH1d2vAfrMQw+W9jqkwBmRdlH+pjddT+C/dPhH3B3b+63iWPEGHeKMPuTdDdQlSi+EIXpv397EWzDoXyazNynq3NZoVxoBw+oDw/b+Af3xETgkhtmv11WHG16/uMU2eQYUWn0Rd4w3OqQ+MmYU+T4eHjoQQ7vXVaatMUWu5lZ/d4NQvSZ+RGf8f6Zq0Jzj+9zAPP30ftgK9joKjclx19Njo0rTMt/fD123ML0CvLzuUyd1lXG+AJpaEx9+RkeKMJcxYTgkpZzw+PuG0fMC7D+/x9PyM//7be7x7mvF8nLCmjOfjCSkvMMPdGCfRTJ7EUnM6HCQGxDRjmmdMccI8zTjMB8zzhMPhINqpkwt4HMxFhgAcQmjOVsCC3GYJNJxFYJAnIKeMxCqQyBFMqomtjGioy1Mqvm4IQC5zQXonBmJkmCVGtcgWBnUo52Agkjayxyf3kEV5PqIVytULSCBshlDpjELPaDxlxSO5aFuHAGk/kLgaoupOyyQsRj4xs+AeQXEJTqrckOQvrch5BSexJgecK94iXNBYXixMYQ6MEAJijJjUIiIQiSDINkVBfvXTj88ubl0WOMp9zYwcglqNZJC64yJURQKzhIgQy5GoOAdRFGVVDhqU2izOqcSTMCU3VqUTdvukZfg5ZZKC6zp6DzrWQFFqM1xP9hwAi1ihdz/bmqTQ3rOckSF4GgeAV7X8MfwyJ4EzBAROosCi1i8iDGjhBkxxRj+5fhqPzUjLpGttXTMQCCnIXgtxAucHvMf/Daf4AIr/Oxhiwcsxyl4isR3NBW8jQNVjQLm6reK6XoUeEZxuTRkrm2CMMEMC199NEVMIII2YBoqgjxnzv94j3P0V8Ku/w/L6F3i+v8NzjDhGYJ5/wH38HTJWDVkva6XEDOG6vmyUZKkanizjUG0G3JpE/bB8AKl8xawKqNTp02ZpGf7teJ71FO82yc6eKfcQk+D/1kutU2oSC4jAhBxE8UmsRKS/RITAQeZbg89wGRQPQn3AGyjY5bm0ydHihh6nbrrb8nQ3yPJmlFvrEaF0zL1YULeAE6YYEWNUN+AELvGC2urLtGA7l11nzve1GbnrS/0s6VqgBse6JTtH2a1rP2O3pBsEEYbYtC3V31w2Zvl9rrZBBzbIHhEQCeHuDnR3X6V9bjF7bbXNb1Ik4cKg7zP7HVR+P11DeHkkqHvcVOgYuGeFDnttut3UCiOuOCQ+U/qs5t+7O7lbf9tXl6veEO8vg/vP3dy9HKi2BweCMppn0Wx69Rrh/hXCKRXk3+cf9tUz39i8fVJpyiPaVE74ut/7Ko0gMNPdoHWL4CIgBJZgVimAI2PKUc8CICOCMSmSKRdvIEJOK4iA9f4eFAin5SQubkJEZsY0R8Rpwnx3h3k6IE4TYlowpRMiZ1A8iGk4J6yFyYXyWf41hmYzPuN9V5Z2s8YJieeKLwGVEenSmmakPPmCt11weiaGkLBlGAbRQNsUYXEZNezJy5NHAD5vMiRtp+4rwG7KFWJp3JZ8yOQzCIkDcgo7bQuBuVDA89090vEEPj0L4TBNwqgOEdPkCJAploB3gZQ4HQoiUIh8CShYgykXt4S+J9wiXYqmbsaooprk6MytsMeYoPa5sUoI4zE0wV0xieb+qKImAKW2fvZa2wopaoA1f8NaPZY/lB7DCSLUtL7Aan8VdgNcfGcrcZqEoExJGD9J44CklMsnswkhVNvMiFCLF8MMZCCfTkhPj6D1pH6PWWmoLfNjMyyG+Nt+c7Ne/Gc3WKZO8iXaoi93Q/Kl7I5i8jMz3rsOVVRa0bQCvRZkS3RKyshrxvL+I/LTqUxhHRuxIjpMsfL6FB7JQhVWYB8P6/vl81L/s33Q4K6lv55gGrc5er7BL4flrn14fbpY+jPgTNfiXV8CPfs5Ub5rXUVdzv8F05VNtvv/p4d/bx9v29zizOOibb7i+qI7IT1PZbS3Kx9m2/ezGIgFRbVKCrO/wpCYsGbg8cR4emQ8Pq84Hle8+3DC03HF+0fGxyfgtASkTEirutAxWrv42ZbA0uZzm5yQwQKCmkumOMn3YgmhDP7ieSOEZuTEtSlAbAGsq2U2mWYriXWFqByHcpCzxp6rCIQpbLAiMIQaRJcL08nGuzDjqbZjmsT17rw9eVYtW7tc58a0rF2m0qaBXeuxOS5XV8EDijWgY6J7pnphmLu7UqZWx9zGzo8JvJVIcHmbDlbaziGV+0o57VMvVCETNCmOSWzzamgXA2oJAQS1hLD+V3yW0eIDDIhbqmCYpI2793Zh0HVQ7+H/XkhRUcIu2frRtRpsTAOEwpMYiWUxFuKPa3BxUgzNcJ1CH/s4B27su/7XKeGGMe6FKYlFsMMCIpgiMu7B4V4XouHErle6T5s+k9EmBblSeMhQ2WoZzHWk5VwQa4gARkhJlmcm0Ckgrl8hvPoauHsNPtwhxYiVGCuOiHRCCEvBxf3aFDZ9jwu2U7u7pz1x5DMS16kiEyyUnemHYiOX26ZtBt/kqD6yveYR5AbfsxicXNzCs52bJjCktmV3soxAaqGwM9SNxzDoBA2+lnutv3dH/dhkK4Bx85Kb/MwAJ0KAcwtYBN6SvfKlbL2i8AwqTLXxOtaVxzVKxWpmBPonpotL6Zo6XghUva+2L+rx760Rtb0bmTs3u2YqcLh/yzm4afw8MK0UrGavi1OleKYZqi+CSrh7Qq78Jr9kXjiNzeBfWX6E3HLbH4FIH1g3ekq1NPupy+8vNJ3bNP0QfVFA/nLTuQORYsDD3/wKQAQdDsrAJJhpabjy1OqZfiaQEI2lKmAATNtJbotQiCRDbmOpzywoTCgSIgORkBIhREJKGfM0Ian/0znNOKUF63pAWlektCDlFXcPM9K64O7+gGU5YX64x7IuOB6PUncMiHHCw91XiCFijjOmRcYAEMbgIyf8y/EDkjue2MGZYUzZqtFt7DHtUGWcYW+t2g3pJm5wZp2WB5zSXfP8lrtFNAYSvnr9R/GN69KaJrx7/BWYW9ckd9Mj3rz6fhfyl6cWAfi8x9wN5z1vvlxde/spB/m7D29xPB2QUhiWZQDr4Q5/+M//T8yPH/Htf/t/4+4EPKzv8TTd4U9Pv0CcZ8yHGRQi4hRBFNTdErzyOop/Zbs9nIuBBt5iJt7C5DUoK9lQ7+QGGQOVPvaj4YUQtKFUrXTG1qpB3jGPSQVfV1NloblGBOIQxPEjzVuEr67N6popocTKcYRiQzjqs0LwMoogYk1CVJ4W8cX9fDwipYR1XcHISBoHwnwSF+a6MRMy47SsSGlF0LgSACEgqOKnsyRBKdYwoxstfjemTFmJ/LpfBJms2oN7id0MEOpc2m4oROt44vwTJZK0Ts+tQ1nZBbZ6lrJqJKIQ7dXtnpXnwkhZn0748H9+DyTGFGftP1X8UoU15o4CjjEFdx+WsVT8M/hYEdYXtHVAvjY4Hrm69tItwgetdvP+S/Ojr2EY/7krbfxH+o90KTWMm4Zhsl3bPfZxjdCWjMnhGH8908MEA9aqz1X22DQD84MKtxPWlLDmFY/PRzydHvFP/zPi93+a8fgYcDoRno/3WNOEZclI+VgYdwgREYQYZtF+KEKICUQTQBGgSSw1Y0ScA6Zpwt1hxuEw4f5+xqT4i8TR6bTBzarDMdW4MDYJnDWuGzIk5FECpySay0FphRJEgZQZpgc4szJpqyVk4TizHfIRACGEXOCgwl+gZo5b3eV93LIqYrlP6t6zWm2YI3f/npQRDKgZgOLsQawDOJgFOexCUZyqwmNuIU1LXywtxSpT7kkXK4KhQqG69sgQI2MOxyi++2NEDsKDyZnLnQ1Q44umokT9SHVEkCofAEAJjCFccInnwXUeZM65WDcAWVzUBnHZmXIGiBGyRmogAitzPecqTAlZApyLVYe61laUozDGmRrhzVnCpNB63CqVeBYvBVAkxAC1ZDUrVUbMouKSdD1wsnhhSfAaTjD8zVxPZRVSIKC4a5V5Fxei2SmYGVwWv6yuQ7EmFXdLK6ZASDFgUiFjIGC+m8HpgDjNIFqRYDY02i2i6sKLCC2DuuI5ZnnAEEuIzMBiLkt13c1RLCHmGDCtC+5++CPSc8Dxh68w3/0Gh7/6L8CbvwJ//TfA4RWW+Q5P6Ts8pT8B9LHMKwcAWa2ZdP6iChSTmxVZQVAeugSvDrosTRmJwOh1AX0X5auu24I/t2ulCB0N77U1Rl5sUa2k6lnT1QOgqhjL5/DWIUbWM4XIzo8AKH3DgUA5iIU3BVDIEoiGssTCITlTiUxxSyx1iFnc+hbzFu760NJvZ5Wp3fvtnTimmSWzneN+VKztDFAEUcTxwwzEe0z3d7ibZ9wdJsxzRIihnKeFD4X+Lq8j38x7mUjXr8Gx4BX5hmTopzA5/hxRaB0XW/3+Lvfvr01XCyK4YWRIQFsAzeXzqalZGI6wqgdetXRo11BliNR/B1+uBZH6oi9fCXtCiH4ToNscu5KoPrnJbrUbsenvyN3OS9JLieifKv3c7f8lpBAjBMvXB4qsewT63Dh6hK0gbX6Psl6dHuGD30nlCNss88JgDYIkhEyi0RKFgGAGKBEyAZkkGBkBiERYAxAzgZAk6HVOCDFgyQlhmQBSIUcgUIiYZjEOndOCKS0ABDnkeMApTjhx1dhtL0+HqHr8YXSbbXt8kTjt9y8jCPHVXPq3JEEM13yABWWzStZ0QE4TGK0gIuUZazoMOnNLy6OyvnNGBIxLB8o7VhkvTJt2+pm4dDYSUpK4HobkmxZSclYrRuD0ZUGEPB+Q7lbwm6+QlyPCegJlgPCItE5I6U4EZdPkNArRCCJMMG/aa8W5kJ3xQGFSeK2/0kPN4G8lL1Qo8AIABZwTRIyEFz4FMQZvx6EwrLcWFrUb4/oaJP9s2gpmyhsjJB3Rb31oBRGCmNfmKmGB8lOfZfPva2boYh2xrsoUSqv8TmJpUQUR7NrQw0SZCsfnBe/fHfHmNwmBWd0nGQEsWbPWQfGKQ8iNjTAd3PdGjas9gFpEc4BcXHw2eg9lStid0cLs/fHauzIFDIA1zoaNiQbVKykn0HoEPz/idFwRIXGFTAARAzBPETF4QdpAmCADUMbBeiOf7r7s8hbc1D0nV4e/+MiXvyHtEVUjwcR+2dtb7i0nry53qc6rc+/Vca6+2/N+SVTy0/BUt3Yu1eO34OdOV9a5z4D46ZJilVtGwzVlr12abeVKrNPg5bZi6j5H7TEpI57avsjpGgEEZGQsmfF0zPj4DDw+ZXw8rvjxPfDhQ8TTMeN0ylgWwpqo3KXlzCMNmG0uLYogIaAgIhr7QRQiRFkixurKJwTSczUUxEXq6Jg6jj5oriMdmkBAsrOG7JRUONjYctQSGOwq6pAd0ypuzm13zle8w/L3c9fPTu3P3nlabj63Hrg3G3D9r+4KldFjoFLVuG3RIy5/xUowt3ej+fjnmnVz57TnIUpg3hLLw99lrl+GNoyphO6pU+goI2f4nI4PD/ZEXxN7PEjxb/L1u3yddsYQnG0Lo8f9+5YGLFYLxnQGlfkLwfaBrgEKA0vhlqYuNAT7+YXOo+Gtjvz0k9t86/us77PQzswaeUzrCyEAISLTmxLoW7rTn1AtTke0pWsLJqowmxtWsXYSJQ6jbyTeSALnAE73oPga4eEtcPcamO8RwgwJULyA8BHAWsNgEJo9ZDR2H6ehG+3Sj9GObXb+cNtz92Avbd+NboRmNLl/Tl3uK3D7wWPi+nZzstWDCiB23SsHZ1nXHlffjt2o6ZcgH9x81OoZxl+ys5wIoFVibs4hIoaAQyAczA2rbkRv/cCdNUdZ3v0ZUs5jKvtuN9H4NfF+oX7P9PdHd2OerYfcpO7dWOfnooWmgaUnx1z9PYyMC+PUpasFEaf4qnwPnDCtjwWcfUbCtckucF/Ypt58OipiAFK8pi6OUYf9hPTp0hZuvu9eYJ8Bob52hV1V1c+H4P9H+stPYjZtFhGhWDOcW+eNIKJJleEiFg5yRgTooV5ww3aTmlaUIRUxBxBUG4gCIkG0N2IUs9KUMaWIwzohzQk5JaS0IOeE9XBAyisOhwPWtGK+u8eyrjgej2JNoZo4MRwwLSe8/e53CGkFMeM03+P7b/4W78FAPuq95xBBVGsI5lw1yfaSxwuMGKm3/laDuNhku/dUT0Q3AV0j5xMj4v3jt0Pw4AO1ajqtd1g+/GanQ9em0biUcHHt+0HW+8NHvHn4fqeeUWsDiuj/x96f/kiybPmB2O+YmXtEZGbV3d7SC4fkdHNmKEIQ9EmA9D8I+ixAf6wEQYCgAaWZ4QzJHnaT3a9fv+Vudatyiwh3s6MP5xyzYx4emZFVdZfX/ezerIhwNzczt+Xsy+qjC7USn61YmUOb78fDNe4fr6WN0hihXNqeNvuV2pfDy8yMedzim3/1v8Xm7h3or/8nRD7g59MjvkPEb8MWMSaklCruE6s9NKXCItmjkd/FC6mBSuSHjhBaWq3T4nPxnSLWFBHN28Lw9/q+CItQYM8pxH176yFq1t+l1Wv1iZq31WrYC9++X7HK5JY2N/qvJRRcfja+UsZ0nMXK7Xg8Ys4Zh/0BuYhHhFitagzfSnCXNniFq3//t9/iH371Bv/m83+O8RcN+lQXdgoIUcNbFVKhA6EUgbsopXmQthdtX/zxq67WLpk1gCrcN2J+wca4o1Hnve/MzuQZBqlai+GUmFzMqZ3vokqIXNonuAliiAh0uAN99V/A7x6Q8wQKQzfGq3GDn72+0tjEVOd+qWyoCgTzhFCOXax93c5wwnnBf42GJNevten7eCkZuO750NPR35dBxvsqIb7v8hMc0geX9TX8R/iiP0hp5+NpauKHmt9mWPdkLT1uHAi8uYIJ7w1oGsgsBchzwX464uHxEf/wVcCvf7/B477g8bHg8fGI/fERh8OEec76HCGNavk+JBU4u/xCIGRK0qdanhJFBJKE1TENGMYR42bEZrvBOCQMw6Ahm9DaqSDDhSPyRnQG221eqMHThnmpTgZREHxFBEtK3OaL6rt1TLYK/xsslrCvLVeEhNWUPA3ST6UnqacN/Br6Rtfhu7ccbdi1hgcynAWI8RVLImFoeJXABOYAFEZwgrTmEWGKeGGsSsnIZUYuCaEEyQ9Rsv5pomdY0u9+o/nk0oGExrQ8H6R/7f08jWCTY5+lu9D4ROObKoEqVYLOc4wVd4JQk2SDCCccCkPfweinlU8nnF/qwFo71I2r42m5znBtp06Q+2QGSgZy0VRiNkcURaETxbuIat0sYUdVOeE9VqT/jKqJs/3NLIe8bneNPsDiHcLLP11v1Bj5Mq6sXjGggsRqJqR0vHiMADNv8Zj+Dab4GwD/ADhlpJ1GH/Q0aBstzE/bF6y0brZccBC+JAaSXI0B2loBUgRtt4i/+HPEmz9D/OzPEcZPEcfXOCKIoJne4dX4OzAYs1MyVXrL0agyTQIrimXmtvwVbvz2Dm1NXf6E9jq6E5S7W+UZufsw2rarpe2DxfRPnA3OM63sHmvnzDZ/q2EhuIRAtjrdEejmqQT5h8ybyWCpeXso/0BK94McT+vYbH+s1uSu3ZuUpqRrd09mCDhRALf3EGVUm+cQgBQIu6ngk5lwEwds04BPNgHbEUimjFCvKysn8qd2oxuKA9FP0tRPymAD96/o+aVn6I3nqBEbfVNf2+/11p7v7SnqqF8939+5+5eUF+eIAIACQkFEBdF0WvMkbppnnNiDMHcuKQIUEHZXoJAEEY2DMIDG8FXCBJdzHot5fe6pS1pdCknOC2xVoKMAszpYGfy0L3b/qT3wA5c/BM+C97bm+577+tC5+z5m3odjkQsA5iM4MICxv3dhW8tPLxNxuKIyf37L+3utYXSEKKiNiUjdKCOAYhY6EZa7tZAmpCskllRFXBNjCJhzQQwzAKqx2wWxDIh5RuSMwBnikhhQVNmhWa9g+J1hMd2NYNUXsk+Pobui2nheQj7uYQnZHDWE4Oen54FWEOYzRZLV+ceXQXN8iU/Ao+cQlh/Rsp4hTF697/ucS8I0b57pp7VhbXbj5rV6y0uLMWgjbd0BY67mnFA41t4sfq2sJYNrfM7KkTRYD/nNRMgpYN5ssb/5FGnaY7u/A3MRgjtKosFO6RCEOaRAmpSaak4IOyM1BqudR2V+aPHCS0WE7Tu/i9q9dY8I81Zsz6/vwOB3vNVfjGN5v9XjqrTsn+3f57SYMCMu6jQFy1L5dE4RYc9UQk+ZwmJKKPVo6Az4mTFlcUOfZgmvNOdZ3O9z7hQRzcrGkuDJ4JgZyPJ5vLvHfPcWaXcNGjYaIoGFCS3Oi6NIQsYSJFyBeGc3ZUQlqhfMT9vnS5vh50trZv05B9qepG+sX08bNXmAfWlCF5t7e28obDbhDs8F89t7TA+HkzNuir1UrfEWu9/hHILDQefGbvjKraEzlaltdW37Zy+Y8l75cIbNWL38NGao1qTnG+j79eN4qt6F5YfzhDi9/jH6/r7K+feQA/xiGrOBwA8vz7RxDhc8xQZ/MM383N71/z47fiknx/IDxmiW8M+JAoxO9jRyFQ65MZhnKwOSf6gUHKcZ7x4mvHlb8OYdcHs/Y7/P2O9nHI8zpmnGnEUoWC1J0cIvBXJKCIYYDhGhE0QG+bMcEDEmyWNluR0CLfZHLyJZf+OueoXJ7ZN0LKhh9argjBahjrx5dGVECGIRK/uE4eG+9wLR/iDeFsK3eAS23Geermg4o9YHNJ4+t/1ndCEZPjT7betC+JcC84hQnGy5uLuumyGM4D/vCVHES9OFazJBd0fY9hvtDPuy9Ieo1K+j4pXmrHRzqTyTfHE8kz3DUL7I1qmNoPXG7s892LWrewCNPnuqrK3g+ps3hq3RzATipYSrjcfmtwqybY8ZTWo8X/3t5t/Gbg8zGo2owue6kxzd1XmH+MHa/CgdU0dpibsdTxKCJaKWPZgxoHCybBbuTbkf0xNz3fN45r+kfZHsc5kR2dghJgAjhs0Nht010rhDGEZRiul8UCgIlDWttdsljMWaVEgmbVM/VNu9XOs4QoxMSdy3ucwnUBs6c41P7ju4dObhjhys53Qp5l5synrf71ev/GMsW/Dwox+K4wHI8MDiOWoPVH1wHT0ajFuU5Tt4uYf7OKnZz1lf7FxFAAMFRIoIJB7P0dHc1MEY17LLB8Qn51rrPIf22fD7+u2lEvRJpcULSw2T1w3mCTrrCfqjN6A8eXAhf9Kuzt1/QXlZjggDdgU40Pik8N3i5wIN+dvvVPaIZTp5JscdMG4R/uLfANc3InwBg/ItSDXErZnnmCv78v2zFst58ELZGlpNV0kIKd20tl8Wyog/lj+WH6RwBh6+AUIC7X4BIgEHzcpaq50559XttxSE4IkagbqefGFt13tIAEoohOYeLsSKhCAJeng5KAmjyCRwAYcAZgKHCA4JpWSJ05mTfJYZpWQchwE5F4zDBlOecTgckUvGcRJhYC4CU2JMGvbE0+UqilTCUkKgSDiVUsz0pcWf5P6fWgwOVEYIjki1OtSEiZUR4+AatnptbOsUkGe3l1jjtN5Z4HgRQjmPsPq762youSsuGQEPAqd5h7fZKSLOjMsLlYVQXqu/hv5NmbRS70QR0fBf9x4AmIJa/osQGCCN9esIxMpwNMLvuL3CN//t/w6b777FJ//h/4OHTLjLk4Q4SKny24EComf+06DJIp2AgICccxNKL4nXhdLw4qKDWAruL3oU4mH1Uqx2Et5gyeRf2HsIzSNirR1/3Zgke8+isXdNYGPFnilmvea8YnwpGnPYYjRP04RSiuSIULhZ2yNUoQ8RVQGC2bHd/vq/4Ca+w+5f/HcYPv8FkMVyMpDm49Fk86Wo2qdojN7cz1l1jqhn71QZdJbkd4xKZeMcx9R9b5N1+vji+unzHX/VYB3b3HOd+1yyeETkudYVBR1hepzw1d98B8wZm00Cx4bbqhKPUD0dqrLL9oK7bm/tnwc1JsgYs6qEWNCpq0oIX+9kgvry/kqIDy/tVZYD/ghtf4T2/jGSzH8IRkB/LC8vpoyovx3MAbDKAwotqIYzyFU4zZA8RPNcsD9MOByPuH14xG+/CvjVbzd4PEx4fHjA4XDA8XAUxXlhDbOsuadCkFwPISJQqrnibCwFTfkgHhARwzAgpQHjOGKz2WAcN3otIYZgA0az+McKQlkTNNmjCp8JqhxRT0EByqBQwBxEGKxeDPK8GYM04ZJvnygIfggQHiImFMoIiodjzf0zgwtVmr0TIJ0I2Kj2uVacFOSU+jRBTu1H7gedCMERon1gjcpqwlSjN0QHI9bvRY3oc4gIJaPkGTkQcp6R50n+UkTJo/BPJEojM7aoMmVGVWagjkXqmheux89QQwBmVotnTxP5+1CFQZuAauhhV9iFB7aL1oYQAKDCQBDlg4QXKporIKiRq+OlTtbjCbhKfZ1OjrNMmXXC4xg9pDyxzaVD9DXJOwGBIhBaHqsAllCdapxSmCXIGhcElhDDJRC4SHhiyZViHdRF080hn8Rur5IqMBjVi5TI9q2MLcUgKT+01cIQYb+6DzArzYughjQ9R9Vxc2w8b7tJJIYfgITEDIEwqCGI0cDp6grAa1xd/SnG3S9x8+oTMLbIYES18i8Qo0Pm5hOgqQt0Rvy6u6BGdpS9hWSbvTrQ5hlRTWNOaLU1fcRpYfevexZqlEjquczoPO7b42qwXXlZrmdBfnJdbwKEZ9DrTenolY/NaIdRKk5pDPDKSynNR9Zf90aLQ7DCH+qp6B9DG0s/VW03kSpAugeJ0eIT694nBmkYwJQChkAYIiEFUapXr7pKo/fnv5f3PEFb234+V3QPBzqdxUrxuxs+csIHlwVvehbGXdAVraxpd8aX80OuT4YqWF/+TpfniLCcEA7B2Kavr+DeQXMaGZqugxQwEWqsS307ITCuXgHbG9Bmh5A2Yl3BGcwjCjJiEYvmEkfdU34FMigvlRu1g0tf86LSH6DTw+QPlTPG0DpKktAaUjwd53Ldz8mQ1q0VztT9A2ZynrV6+ojv9pPytjgjmLuoOIJSfhrRT4KMSgbmA0D5REDSMRNuKP6+J8BaCBTHWAD1WBjR0R1deETn7TrYbXj/jLPuUJ/QoMxHIUlSVgJQVJCfg8RjDyECLB4RwIxcCiiz5soQpFVY3D3vy4yDEoRQchmK2Isicy+o7qH8qXDv0rL0tNLXPS28XoE8BukePEUgTw/kmfuXPLrsckmPGL44UUj0xXtx9BwKuv3RCcpPhPBa56SXpxQR+o3b1aooQgFrzEm9pAw+170sPKSxoO5MdO9PKCGhjBuUm88wHA54df+IqTDm3JT4ZMo4F57JlBOkRJcRXEKIun3LgHFS1VoL7tO/vvvSpoTdXu+udnt/rQ2AEDWR9vl6Jz/8BKFCCGOaVmqea6FXRBiNQj1807bJj5IbHFr2573Aln9+LEL7N2vEnGdJFKiMQVErfjYit1NEcLXyJzDu3z7gm98Sfv7LI2IpKKGAWDxgqDIcVJM6UikINXyFsvsKG2GM0ILI1JdqJIy+yami4pSx6JReC3h44i3n57CfMf1O/Z16y4QRqIy+Jaoubv4ZDGJhluepINraQ+Y2xYDdkDDE0PBonfuGW7t1vwDf2s58LyUEnd/Xrcr5Gh2T3Dd8QZ0zbV7Qt8cyp0zKgmY52977I5un3+kMU3lBd6ev8kPRzHTR+D6oLEmDH7m8dG5/cP7le+quCTzXYEb7zYCErKGooViELs254HiY8bAv+Oa7jMMh4/Yh4813jIfHGYfDjONxQp41RAsTgIAASdhs+RtMBX86QA2HEwKgoVQiBYQgoZzECEKVuSoY7KlgpdYunL8e6lODkUYDGY1jygFxg0ZXkW1mzTpVkGvjO3wd+deHpZVmg+adk+SuZKF7tD6fSCHb/Fkb9cWrEECf1Z+mdzDFhrFMJ2Q9udbJPGoaPdPRKlUwqUJ687gsuSWwVgFlKYwQ2NE/TWlQw3tCky973N4tpqd90BJKe09RI4SAqoSwsQtPR4t1qU3XZ8iSkENzZJG8B1HohLFAAXOsfGTXUDet9XDVOk0Ax3DD0y+lro9/aun5sl4I8HtX34UCgapXv47KCydZKU+lcaoQWelB1JBLjoKvc9tenfyGczS87WabDzPMCI62FYUFqsC/sB45Nj54EVrUTxvcEWAL/dze03KPhMqHAOAAngbEeIXdZotx3GCMERkacpYLMrOsB9q5kL3vvI66dWoj6uGLa8AvVX1+QQPWpXZrvk6unpRl1XP3zha3ro32bvRzgwd23SLO+HClRfeVU24s6HTr7JxH9FI20b3LaTNu8P6zdO9Try8mZumZwArHARYYyNCwZdCwcWKUF5QvDicKiAvLE3WfUj4xdH7ONsHrKPZZV4vLixlhPXX/0uJh0bNjpL59U0q8pFysiChlYWlpCM+NRc5v055bLLbAllwKALG4fFm8XkXcFBPin/0FwiefIqShIjRQxDy+RuAZ4fgdECLm8VONVdiOcZj3iOW7ekC7GfqQ8hTRbgx2PVjcntEvFeArsVEtoyv1gTpnyxG/cC3/yZc/ZAXLj1rKDDx+DVACbT7XuKCqrad2pNp2tUNhws11C5RKZAIVyVf0w74eDJsq8SxJYtksnNwDlfBSKqdZp2qonCKa/qxE0jElzKUgJfGMOKQj5pIxHA6Yc8H+OKFMR0S1EGIwHgD8ZnrATKgENcOsDHJlBKtg/exBbUSd/w0bP3dfFt9Pf3ZzuyAXLlFqXnLryfKhx2uFhutvr3WwQGonVZzVSq1vsNXBY7IeeAGmVZngm8DCfk2bqsJwhiRwhCohgjJVLASxVSsMUGAJ/e+G1mnnANn32yvkv/jf4+rb3+Ivf/Xv8XUu+PVMlbDi1EIyxThgSANijBqPOSLGCApBLZYkSbKRn2AG56aI8HvaPjP3e7X/NM+AttcF3ZkFTnniWUhsadD5+4tPK6Y0AT9NYNXxuI3CugdILWi8IqIKC/T6mrcFL/o8N8blPQ8Ha+im+rspIOonzCndW8yRwLHCsGTZf/fXX+JX/5nwf/gX/xqbn2WZz8gIIYMBhJwRhfYGFRUuBWGgCQRz0oHRTavTyY3BKcv3XCj6lJOpCgh3r11rigNtdK3H1iez8u2OvT4Zhu5X9UbLnFGKeJ14KBrU+pV13IEiKERQDNhtR/zy9bWcGcMhyiBTcGIKH84K0Hsr3hBWyBvjLBlZ95scCOhrnS2XKiEWdy5qa1VRcmHfZ+s8oYS4ZIz/+Ms6vr6MhP2nOmd/yOWMGMBoFcNXQBVaWgkhgLbXYCLMqsg+TBOOxxm37+7x1ZuA//T3VzgeAx4fI47HjMPhFtOcMc1TTVAqVtgBFAYxXAiSdFpCLwodZcJGQkuwG0JCCAFpGBFjwkY9IqLSIKHi2AIU81BoSv/l664VU2RUxUMhNYAVK+0QNaFu0E+OygMobUFqx12FJvZpMc/bNPt5DgEoIUgcf80VYbkjOIj1Nxfj4s3o5PT8db0+IfwS9r8Zp4gegitKblSr4FczGAhEaiVPTRAnjJHScUVlzQTmDCCpsDhjzjPCNGGaJglTO24ktJbxPNqpeX5LKCfGnAtKLnq9tPfWjyog78I+ocmFvLyoWg5oH/bOkpxAQkoGjT1VAFCpSatF8VMg1jgEFEZMklUghCiPaBhe85YxOleGsc5t+L1nTAIxoQQf6svG21gKxtnldW0CUOGofVaDIbb8Uo3ea0o1W3qlDFkMnkouIJL1qCFmCoOi7SG0Z/vI50asq/GGKhiYq5EOKCBQxJAiUBiFJcfIcZoxDzM2MOf/gsJAoYKZ5e/cgTaRrMm8Ask5NiVESkJLxVIaXVoi+PELbK5/iS+uP8OwucIwBuwZmPKMwhkHngHk7hx42RsvRgA0rwndchUeej1So9PW6B1q9R2dS265/Dy7RdTzvrJfai42aSiweZ81mYnjZvyDJ5iE3XUzQqueD4UBlVmgeE8Zo811zN3nsk83E7wY10k1rnNksECKroJ6bdR/uo2LDu+dx5fuBCrNHkPAQAFjiEgURGEOMyw7IbhPm33y7vNlwdGvVCCsnpVzw+KVOs8AnQ4v1b7aJr3EC+MEt9HT9f0z3bMXPOfL5R4RN5/IZ8ngeQbf3yqzqq5wNhQLGFYAbHag3RUEfQZw8IIAN7sEIETQMEhbxbliMoEioXBACaMSTewIDilyiMe2PzmDeJYxA2BK4Bp6BqAyAWxR5s4RS8sDT+A4yhhZDngoR0W4C4DYbSS10AhUNdQSB1Le45yHhIN5P2j5IQX635sHwQeUH/P9fzQWkwvMVbMKZaqArlUzr6aKhBfCt87bYqX0hHa7umZd3KxsDbpwQ+rGTLAJhwANog9x21aFAcxiGCASBQVlwjxnABkxFlBU99AYsY8bHOOguZ6aFUopRhQ6JewzZ7MJ4dguKI3ZExbr309/+t9rxAjh9P7zdrYvKJdQ4Bc205XnsPhTfZIRR6pQMI6BLdo9L9pvDEYjqtaUEZ7wbJfNIq5at8HWmVDpHeNjuHVZFWlr9AgRSog4DgPSMGADlRerGbtY7UXEkDDEAUMaayiEYRThQBqGLilx0T1flDhlC9kEw1VtLxf9q8yb4rL6HRlYUTY89efrBoSzzy6vn3wyr+6LVaWF2yj1frd31uJ/ciP8DbjU/qWBk7FSf6qq11Tx47ccEm08a8paK6QdVpGH9af/FmZgLvj2179DGBI++7M/webmWi0DlVGN4vFAwVzoCaT37TyYFd5SXtN4LM+MLOeaF/Crh29eAdHe2e6vMB3+me651tcJDVbnuFRGi4250bnL04zjN99gevtO3js0KzwiQlRFewjNKtbqCMPphBT22+HFxgP1gpn2DPWXF0qIZe2unxeWPmTTSrvLsV2ohFgqWC4awzO0zCWeGpcWv0Xf1xPiEq+Mj00LPtVnu/WjUYHvXT4qnfFUPx9yRt6Dl6pw8WPsg4VsoO/IzqvBmvaIgGQRwE/HGftjxtdvCg6Hgtvbgrd3wP5xxjQXzJOg6gANexKG2h6rR4Qy4ToUb8XZYAap5wMRAVHCN6Ug4ZwseXENkmE0RGGUUMAlVnhq99srruMBNxH1euNFWh4sIg05qPR+tYo3iac+bxb2XEMS2DQLrWbJeS1OP8jaD2r1Ta0NNMHgU9ugwn1yRkKL/AdiLapjMoloreaIQ0d7KpJS2UGvsGkz2XCnrIcLy1KyhKqdZ+SUkHNGyDNyNPGPzK/PLVFO/pwAVDel0QL2jDccafRS6WkAX/x1i9fLMhmSwyA4mYrMbg0DXMMz2X2jT3HSz5KPbZ+eXjT8zE3QXxUhckpI942XxnbQnPwfqXeBX6h1euGpUmlg2ByLoqUKZOucY3WK614zmqryAG1eoylKlF/K84R5njGXjDJl4GEPwgikJCZJXMy+vr5OnfYKaqnr3var0WC2ngyACiOVGbFEbIYttpsttkNEioREYmwi3hMFEQwuIya6AnAE0VRJdv/qyynmNqJKa7VRrJUzd1zC+/YGOJkLD39Owvqs7FF59hnRbfeCVM9K/5DfK8uNYXS4/3Tterp+tWM3QifrPO3f0emmgDBE1vXjHubWh/84V+pWM7o+BqQUkCgixCAJ0B2QbOu/MoTnOrLyLA1wptGKey47+FyBke+7+3h+BL4vdy5l714wjoqX6PlOsTLmS/vRcrEiIv/pfwUTyPH9Hfj2LTDPaERDg/JCIwTQ1TXoT/4rIRbIJdckWsTfVSA4JEBjvXdWiiya42O4kbYzgzVVjX+VHF/XZ+J8j5SPdfvNwxY5Xdf76fgdQp51zHWn6CSub6hCEdPwGjW5yfSIYdpXZFEqwuifq+9SQmN4KaCgiAuRpQP6AQXgfyx/LMtSzyeCeDGhEZp9vRA4dfcAAQAASURBVP45s+7tkqLSSogh4JQWZUBcatG7D3ukSIY4G0FjTElg1YirdWsbsxBtFKOEYApRPDxi0GTVjJAzcgFySqAYcQwB31z9AreckadHF/KjgHNzR+2Fdc+f2V4gt/b+XOudmydjiM6TW+tEjL/6UYQFF7y2f9VTgvCJZ186vCeICRO+do06SwpWZqMm1oMp11j/75mXis2N0myUECplajE3zQivs9yAC2gq7XnSKMeAu+2IzXaHAdo/ixA/hYghDRiHLbabHTabDTYbicu82W1FebHbIqWkVk7tHGRjLOcJamNVz6sXjlcr/TWlAmcQtzO5ZuEPALlkQM+xr3fOI+ASpQaYO+v8SxUYHfxAUxL0ZUGQ10vWDgCmk/HKvmj0jsAJwHuG9ML0uuhdMWYl6BhM8VN0X1WBhm0jBv7q//lv8Tf//b/D/+n/+n/GF7sdcsgANFcEi0AhFGW2isFi1DAakhaB2samxlRVUcOSpjxhUBpzwWjjNgsrY4Aqc+gZELtmDJO/73pY0v9tCG0PSY6fFj7A5ml+eMA//L/+LfjxgOubHWJKEr88mueQ84Sw5O/1N+rcBE+DAur5BCy9ImyQtPjdPbu+BfxbPnVz/Ymz9OISdq3Xf84TYq2RE/7omTbOKQk+lNT9I6n8h1fO0oQveP77L8tDc2G9j9ArBWchbTi8ejgGZGbc3x/w3buCf/83G+wPhPuHDaY543h4UKWskB9bjSpAg8R5LwTkWXJKFFALblIgSZAVLtd8EBQkR1UICFGMHIZxRAgRKUVRSBBAzChzQaGCac7CW0fzJnTxvI2mOqGDT+lZ72kWKICD5yskEWkhsRAXOQIDHNzeosrTV+GxIVBmkFq8E5FaVksopqD5JiiEhj9JPQFYacYTAphhUN8EY643xbVWkyvOYMAZqjCqhTS1dtXESvkdlulkIDChOFrSiy1EyKy8SikoJWOeM4gmTNNRcicdBs3BF1BiQihiwFWKPp/nmstqmmfll5S21XBLzOhj0OdSQ0k2+qenHTyvU2eJS/u0fBU67wADWXMbBFUGBBLjshCq97t5SdSwMx2fpNRNVTbpVffdfst4NVwQWML7Kk9rORvMOKglcdd9inqU9FMMT+HkPZLz1O8hm8/lmB3JZ0qlIh4inC2+P6NuAqeMqIqL4rwVlMepicyLeI9KbhjJ1zDEiBiAORccDnvJK3OcwHPG7pvvEMo1ym4LAmPmAg2E1aBgHTp1P+uS6zxEVXhEY6UKEErBzbRH4h0+/eQVrq+v8XozIMQAwgSmgpGAkQo2gXGfr3GYf46UvsMmfSeva7QzWsLtRl8WnU+uaxXAIIo9FLfpcixb2x+NTrY8BaRTTxADTmEx+vVthmu+sX4LnC/rFRtM8fS0vYCdAw3LxG6vONkFVX7DfXfteHq7zY3jl9j3icVe0/aKu18Hyq3uWmE1Qmfq2Os6tX4eAlT2I/lNhjRiE0eMSXCUnfETlPOHVj6U1Lh4v31AFyfMhof9z5fLFREqZMlFEsXi5jWQMxh9/GaQqhUCAeMWxAVRmVzSwbVBt8EzsXpCADCCQLX/JlBqAv3FC3aAQ70yEAHaap4dQoEKJJWrJUooQZKgrk1i+976KhSRs7gIihUlATQ25A8B9lRmBPXGkPEo4gsAFWF6mUTIVAIQFKTbZxMYXraQqyLI99h4PwSh/1P0gPgh+/hRiwEGJ7Dv7xfQ/AhCBFFanQ/PJFkby791htP9PhEcWjsFjYi23/Zsj9yJ1IWcSEgPtdKyUopYO0XhrhDVeyuGCGYVzBVHIFDDrwUtDq95Qlg8zDqmC4BsPcVrx3OByJ9UQpwtl1Y8s6+Xjz+1/Z8Y3oWPfdxyScNETtEAnGJkYVg7oxJShrBeawyiZ21Ej+Hcg117YCGQLD8EjJENWBBxi9chIG93OPz5XyLd3eJn336HiRhzCIghiudDGjAMA4Zh1GSRWwzjiN3uSoStaejOba6CjLkpGmD7uikeThURpZ5L4iKKiEr4KtFf65yGHGr12J2dvq+ll8DqdVa6wKbO9SnXPOO79unHxB3XzkDL9eKF4Z0iwo2rXuy3UlbmtXmqe2tB6g8IOy8Vez927+F3qCpamYNyt8Jo58MR3/7dr1GmI774l/8cm6srMYJQmFmgnhEEUMlOqGMBtkTgVLe77PA67mUxA4v6At1cAaZIBvr1tNZqRCbH1PSsj2uTetxCDi5LE0pn6b6We7qX5wkPv/8Kx3d3KMdJLf2iWvAGDCnh9W6DqzHVRHYt3FKAR20eL8iwGl22poSQqovfq/hzZYKBJ2Foe3a91tplL3C5pC1au36pcmFR7zkPBT+2NWbl/emw9X4+/jNPtHZxA/Tivl48Lz8AOXupccOTSrMFSl7+ON2Fl1EV7+U9ccGV9y4VtpyesWVFjoPAOSrIBdg/7rE/MH79VcbtHeP+4YjjxJgmjfdPESEJTxktdxTEa2FiyXt2pAxQwZwNPy748CVdq/R11BjcRCL88Z4QzQgpax4k+ZNXa8pdkZutr5vA+FPBMEMEz6Fo/8ZbqGBXrNNLuxaE5jdiSvjzIloYU0wQBJ9ChNkS8afhgBBKN26w8yBcSMOWHh/1nbXqEsJWDGtkIhn9qTILpSehZIp1R2zeetTiT5gHbycrMHqiGYa1tQnIJSPPGfM8ixA6zggAIkWgUF1+7p51f53A0nC7o52MjunOp9E36K/5eWGu80vMaAS10Wss4wuoCZjbzu3H08/4JaWHK0ZvGIEXNNwpAaqka0qs+gcIr+GaY5gBTQAHoaELm3ewvl+nOOn/Xb4PeyJILgCGP1n2jnuNVodFQmfeE9zRaDKREnotylrmgmmaME9HlZf5EE5oa1zBNnX3HLsDVloXgBej9e8VCaUElP2IELfYjVtsxwFjAigwCgoiAgYAWyJcEeGRRjyWKxDumzyPTe5te4naNFtnks6mk7D5KTO+hshOal9vAS3PlLV9+LIEvh5+yFbUTWlgrG3SOsZOR1qHYcoGywvRvtu7Wq06WY1qN82Kuwada1eHW1/d3u28w92c8TLs1FqpZoC1YoVyDkmYwlrgtnhExBDE4CgEjULbDKyeWrc6hy8pJy9hQOyFzVwgS1p2+QQ1tVr/bIULyksNWCtmegH9dbkiYprAbLF4CfzFL08QsH1Wy+oQEKZJiIFQaqw8SSikgyYlFkwARCSCDxP8sEtNo8D+nGWX/8yIyOFGNbeQXZazu78BxTOKiFr6UyC4g8EsQh0RPOxgWmtD2CkXbMok4zXNOQghsLgVhqDKEnUDVGvFEgzQGALuUfbLyvs+98fyT67YVikz6PENKI6g7WcV0ANPA8tzyoi1jup/nQARLpmrfJ5TZJASCmL7C2WQIkKKiE4REWqc0IBQJM5mCEUtowkhRoRyiiRZBZ9CeJeaG6fUOIu5PmNPnwPUS7rx9OrKvP4Uj21HsOiFOk6qxBKtPINWrb9HZ+qt1T8zHmDJ4Ky1I4zOsqsmjxaga7kjKuEHC9fTBtPyk3jCkBZjJZhgVqzUFb8ZUSUcOZp1XTcqzNc3ePeX/wZXX/0Wf3H7Lb7miC+JEFNS5cMG47jFdiueEVfX1xg3G9zcvMI4bmqIJrMgnItYUFliZPNWaL9lz+eFMqEJxRmB5e+cB8Jq7oPaBqNk8cbIOdf7bQyn8KPzQDBrsCfqnPOSqPSKq0+L+0uvjuXzz7W/9t5Wsts7vhhzZgob89YoKmTnUtQFXuJVs+41NgsjZvzV/+O/x7Db4P/4f/u/IP2zDUIWKVHRMHMZQA21RwA4oECVtUQI1LnnaE4ve7fliO389HMAY2aNlamMS6ltsG+Q5bspqJYiixPG66So1ykzcsnKZ5fa77w/4B/+3/8DptsH3NxcIQ0JKUUk9Yi42W3wy9c3GFILHUJQZQT147AvjdlZeEFUWtOq2hdatPEelP9HKhcpIc5qRvr3OKd8qD/P9rmk1ft6H2ol/77lxzY6+ZG7/xHLM+IAE7T8WEP4GM2vgq913tXqV4EmhCcuaQOmgGmaMOUZ3357h7e3BX/1t1vsj4yHh8dqKBMoYEwJKUZsxxEDJYwpqlKC8JgzHnJG3B8QDhNAGTwrrrFxmR24DdyNKUbSnAJU8QkBmkNOLOcBIIQJYEjuAbYICFRxjnG0y1lpaJLsi/YhkQLEmjxoVCkJ01IgdJt4R1CjtWD0mDLTJQDB0auM+g6wdy6ksglR+hvtVLxcgXsDK29MKWO9DIaZULK1qZSmF9jp0OV7aGQiQ4wNFvuokdIstJ4kTUAoGaEQcskIM2GeJhAIaRqljRAQSkbiAWblLfORUXLBnGf9K+p56ATYVQCuMhHLFwF0m/8c39NGrLOiAnPJI8Co8U1hsiHxRuCo0SPQaPaldM4rkoKlWyFTTPnzt46rgnoIBV3vEIImfFOeQHUJRZVg2nzP4rC8A2vOi1xKVeAJHdMUO9VQx+gov1kX7YnQqVTjHAlV7qoXdC3UeWbUMFtcWjSRQIQUBXYwi5Lq8PiIw/6AeZ4RAyPECIriac3Q/I2S+EFZGr8DdYhKq1kIJ4nZb+BdIQERSgjgTCj3NxiuPsHrqyvsrjbYbqTtOWcMOWAH4IYCPgsELlc48oiZ3gJkCbTNKAUAk9sWqhS1nUaWJNvxq0Zf60/LjalNyfp6nvW5sgoK6NyNrkb3OMkARPG4wCl6D3pPX7y9D9un8SnmJVFaXUe/y7WWx0E5tA5uwl1rNJt/Hq3Nuhal1iJ73r7Xx87Qzs+VQJXXjTEgDQljHDCmhCENojiE3wtPFHpuhRpuOi3s/n26znuVl+y9j1me37IfrVyerHqe9Iu598jhbjypHV5dMIZ4LpBosgUe2+YXBrJ6UtipV9fUE6GWtmntd/1UxrD/JFJAhx4si3WDs3KglQ3mJr/hLQVrerjNXa7kDC4FuZgQtaCUSbzmlAAbqCCigDmiMCFwS/AVTOFSIR21RN/wW/z0kFYNnvMlq5c8YHqifCzrM3/l/ZUnrq0fgVM7JTL/sMoSkS1X4exb+QdVQRaUaKsWPrzcg26zqda5cMGcMzRtdFXAtT3ZBFYMZzntY31X+LLYRdz6MgFSoGalJUK3BdRQRsjOFDlLlkCEUDLi7TeYH+9xN2xxF4C3ZcKDJsuuOSFMwFjYaBZPIp5o0pcswqmywSOulXdc1NNelrVfUGTtqo1HAzULAuapFs7dbMTPMgJ/B8VPiCh3a9E0XYoAV+qcCAHOzXW92N+pXTtlRJueyja3igRwzfNjnYuFGxuuKmqKw9nNkVmG9HNmgoHp6gZ3/+wvkR7u8fPbWxTSWPchIMSIOAyIw4g0bDAMG6Rhi5hGDONGvCdSFNxTEyYL87EmwDemoQnTZSR2XomL4nrF98Y0KdHZCeQBlJwX12d0OSmc94URyrJUK0oG84xaJNc2OOE9OIS8sGRoUm9W/NwrN7h5c5T+jNs7mhLEv8fyfoVj2Ski4N+n31312WWbyuAX97vG4q1KDoHHNo/BGGAok8UMJhVMBUlMSGCU4vAZMVAE/mWjsYz4z+5IYDHwen0Rh5n9E+29uzPnmB57dw8zOkhq4ywLeOPaqx4xPipBzrj9zW9x+O4WmCeMQ8CQAoYhYkwJu3HAZzc73Ow2YinswiQs5RJCEno6ciFh8NUr2dXTrEaerio3uFVo9an2vejhTJ+X0Cfn6zC7dhyTU594iiFcE6TWW+vMWv/I2v21nt6PBnuOdDvtqxIWq/Wfowk/jFb8nujMFza7pFfar3Mb/8J2Xzw3vNL2Ej8+ze5/aGE7EAu+73RuVp412rAjwD1xrfizAQ4gRHCIGiaFAA2tOM0ZuWQ8PDziYT/j776ccfsAPB4mTLPA3kQBaRiQQsB2GDFYIukYMMQkxjosiZ5jJoRSQIWRFd/PNk7Jm4tAUEtSFfxXIEaVDhLYKwJvooISTIAtOKcUCZdn4WzAaNbQDj4swG5HT/uLpEYiyhLDvB/kvnpAVCaAVYrswokQmhUxSm1X1krhdggIBbAk1UEl0eIxURouMHzBbqwNaPqUD+1VOzxqiWhbnjHSYD7VClvxtpGSoqgwoxjZQw3v271S11rk9kUt95WfKhkcAkrOyCFjOh6l7ZAQE2vYbFSlhyWrLtmJexhKk0AFzLqjLWwunIHBGrHd0QyefLazQHUfAeSE9rbwGtLb1l4vVxmOyyMin8F9twE4S+sFHFlhGRZr5+kWt6IEkdcUgxlGl+mkqeCeMiShtr4YlwmF52oQ1BnxAZ0yZQmKbCRVQuTgTAhAVmWEUqN1/bowUATECMRE2CRgCEAuE47zhPvDEY/TjFIIcSCEV9egTQJXIXK3OnU0UMUNQ8M3Gb1HLTJBABC4YNwfgFLwcEigHDEONxi31xjGKwxpg0FDl5dwwICMLRg3iPgcA8AiZ7tFxqQ8yuwPm51/B2TakWVV0Cr4BTpvDZ8mzieFl1Nmdf3Blu+lro0CHA/n/RwZPeHWsW63On9oXh3gM94O2jtZSFY7gQXKrbUzqs8IO9PgTN+eAXc9J44v6yqv0fCN0LcKMPPxE+y5gA3nydklUWrbXFctCLymQBhRsCsFWwoYQgAiARHQSLVOD92/eze2GsLPOuvfeTmWtbH6d+xfcy034QvLk2NY7rMV0PXU7+f6fGF5qQcF8JJk1fPUCdRk8TyCtBvU4jYCAhkBiZdXGIUKmHOXWFMec3H31oq3TqifveJizTOiP+qyJci0yOQIGVi1RiwBcCC3j5HNnFFKRs6zuDzmSX9nHEyoQQEIEddhwi5kUUCUAEQlmBAr8ic7MEQgxDacfsZ7ItYTRMZUrqLW80UUSOc2zvr18xutB85/LH9AxYg6dVU2AX605PCEiiTbGTEqSa5n574boRZRdtZOhHlNgIdZE+kW+2Qja/sBVsJd3fEgiAiBQYHVkqadfbFm0feI+lwIoFIQSVyV07f/gOlwxJvNp7gtBV/tbyVJV41/amNqCliGhy3okVa9uoA9i+PA57+strm89XL5hyEoJf+XDTzV3wv7aL/aenT3Oji10opHJ77eKb5d7XepjFgdf0csnHtDJSp1KS0pdiUsOmZRPS8qQ0VCujI0tq8oKkgJuSZGlj2ypAun69d4e/0Kr7/6Lf50/x3exILbSAgpIA6SpHrcbrHZXkl4ps0VhmGDzWaHGBOGzdgsj5QwFCLsVNgvd/VzNb8DwysS2nNm79QrE0Tx4Opp4ngrTbguVu3W5+l9jf9fTmEHWTieEy+Mvq+pTK4tsezzeWhMGYoVrw5CqbkxunmrYVfPe4J0W21lzmvf9X379kwRkbNYqbGGCDClSwCQQqh5DICigqAZjJanJ5OdIcHzhUJjmMmdrxMi/PR0sGdY7PoK3Cje6gq6u7ntJWv1BAK4jiqIMMbM+lx40QBAPh7x23/7P+Pw7Vtc7xLSGLHdJAxDwmYc8Opqiz/97JXGQQ4uT1k/AhM0Vfqxhuxo0gAPj7wCwq5W8mwNQBt46OD384D8pbD+EgGwxyF1/NRo4Zd1eZ5ufzo81QezZ2faPXf/4/b3o5UeQeLl83iegu/n6Bz9f0EPZ+faw4tFnVVpRaMh1q9eUL5nVsTzwur7WIVcfggVagoBCYBQxgQMmwqTGBFg4HB7wPE449s37/Ddfcb/+psNDseAfNiDGBgRMYSI19srjDHhatxgiBGbNIh1aIrVsGdTMnY5IrJghhkFMwqChrwXrwXBJzWsU4gARUCtSlWEAwKQc6nhhCgXlMigwphLQSgF8yyC8NhIp8XSUpsCN4dGCVXaP7DwI8Yug5rcoE4yqdeDxntXj2fm3I4GmSdDS/JL0BDLAIiiKGKiyC1MEREpoJDkLWASq+5G9/RUW1NqW8jmBlxrPW58SVVGMGSONSeCd94gxX9EarRBqpCBGBsY/jPhLoFBpWgYqwIqBUwzuERwIcx5AgjYHwNiKWAKiLlgQEIIQEgiQ+AsvFkurIoIAiMgF5wqIpb/NfLAbX5u+97JCOr5qMou3QWaqFrW0c+lejmQTaaOQdeYoIZpmsTcQrYYvHM6DKecWIcivcU32nc9QwXshkWSa7s0+oEAEeYWyaNaeJa1DzKInCfxPEFWepSrVwkge43cfwZAmhCVNReF21u230jE0VJHDVsq/SkKKiJgGALGIWA3EDaRcZwOeJz2ePOwx+3DETkTxmFA/OITIIg3hexPC91RhD1iMTYGZG9kFMws+elk7hmRqQr8Q2Fs796BHmc8/m6DMN7g6i8/xfbmE2w2r7AZdxgDiSKCHnUdjxjCBpvA2BXGODF+xxl3XDAzcICRizZJBRKeva2vrWSEhDwNKG0NLYE9Gi+Eer7krMYqqW48bd3S3Z43erGtTWMijTml9jxEjyXCcA3PVkh5xmXbWLQJyOYDalhWACdKCBY4yTUc2KIxVS4bHiMWBbB4a3NXtR48vd6UboD3hjZlRN8VtylcNQpZIAVfNH8pNPcKYkBIETsu+AwF1zFhjBGUAkoKYohOkIA7sJDb3Yv0387O8+XF75Dvl+x4hvpZA18/4XKxIuJ6/F374ZnMBdYxxUBL/qeKCYqY8ivM5UoAcvEbzikS6JRIbmeutemZn/VPOt3nUPRHCtzJ2OE14luJ3wpLWkxiwOIuZsx5Rs4z5lli6uV5riFdQFEsXCJhjsA2ZgxBBCUxRJ39AoSoNBdVGFZDU8Hehet4hJhZDFsP8VJ8+zHKObal6m+41YSO4j0kpX8w5WMwtD9FplhwIYE4g6Y7BCQEjArQ1YtIa1YhJzw40D2qrn0hSBK4htd7gZyFTeE818Sj8plV+KTj8uedoInKGKyMStCwIk1NQt3zdoY8k2Nuo6VkZJ6rtY8lpO4Er45ArM09W5bI+/sojSB68TNPYN+PO9wPa61j9pzJwimca/DxZaPhJ5aK1y7aaAA4yzVAPSLklsS91dR1SuESafJDtZ5iltB8zeLNvZ2dt901pp/9c5TjrMwoVFEY6h/VHBJRvCViRIpJXVZTZYYFf9mebmGAKkPJMqZEGZvowgxxs5A5UVDIaXLnjZsHEVufua0YN6/CJpSvpL/yrO46QxURaGfSCN96zd0rue4NZmXIlsoCZfxQ++DTPooy9lxcG+0+WMPJFcY3tw84TrkpCkrvldE8wKTP5lXZ1qIyioW1XUkQmfOMlFKL05yNmRQhxpf/8T/j8c1b/OK/+a8xXF/J9lvZr431KfUc2QqS7du6BgrV3WFqW9Ndq0fHKZLYVrqH+/7TsIj/d9FAY6AAgBtzY3v23d/9Csfbe1Ag5GkCHWdshgHjZsCQEsZxxHYz4uef3OB6u0GKLVeEhQ4VGtVyQ5DJQxoduQD03nqzE6LV+jLLZBIB/2z9eeY+TsspifA04rmMpuhpZVB//cn2FkqK5oj7/LPfB83UvBVe2s/74M2PU9YVM+tjXvJWZ1q8kB5ZPnLpQ+fqrY/tJet8cdVn6r1ob73vNuzov/eYcAAgbs2QekLwAJSAXESAN01H5Fzw9t0DHh9n/MPvGPf7iHIEaGaMISFSwC5tMKaE6+01kiogUo2PTaAodEEponCIBMSUkGaWUCxV8IQqoO3lQB7OC64KLLA3qAaDS0QJJALKQp3nYVGlf+PXvdL83DIs9xRJXqNAlWYyz+ZgoYxNMa2Neh7ltE19UW4vbZ7fhVXw28kiYMx4NSBZjq+XFgCdl51XOng6tipGTlurhkI4FUISKSmpeJGING9GP4WdoQOhrkXMBZkyQpa8URJSKyCkWbrJ2rMaXVX6TGk6oR7U+KQaRTg87pG0H9CyqPCC9Z3qeqwU8msAWxeCyXDMO77BwVNZzvujHq7z6a8t94FsFVEm+TCOpO9a54+Aan5h3ipn+LA2p1gJLevmuW7zRjObNki5ZvVa0fBFRbxpQwjYDgO24yjKLS44HifsDxMOhyOm6Q6Yfo3IE5wbR+V1Tsk2WUOl/ISetb3JJLJjNGWTKXLSZsSw2WLcbjFuNkjjgKCJhgHZJRSAUAgxAiMIYwI2A2MAIZGG84I3bOF+btz1AmrjojPV1goLlxNgDJ8xfetULGzuoTybAqhOEM7t6/LJy2gTpeC5eWIbD1b3qco5dFXcmF2d2lqDnGd77573T6095/Mqnmt1AUHtDOuZ9/QpgWqUGZDwvCFE5MOIeb5C3G2QUsRVJFzFRo/bjKz3+9SLrj/5bBPMi9trZ/v50gwJHe44wzfwuSs67T8exXtZuVgR8cn2t+5Xz1guizF3VYCo7vDv9n+KaRrWt+MZpQLXgwSYB0Qjbs4/1yksOtsUZ73VsNzKiAIIaO5lMCGIxtorsygiZomjOE2Har1oSgpQBIWEKUY8xIhPRwIlY9IlEZDErRKhVdBxF3sPqmnB3PubMMi/Axb1/rDLT1FI/4dULkVjXVGqkMBAyQiHdyhxRBy/UCMjS5QGoEMarUdDgi3kElcLphOrYmax9GVG0c/ZFBRO8NSIST23lnBKZLqi0JPj1Nwq3d/ybOtJRmYI88dZw6w1oWQnCC0LwrMjdi+Y6e/hSL78eKwjrz80eCECe8/UeWZ57YEz73eGAFySC3ymXiuy/r0yAn1CMa+MCAwUs37Tps365WQwoowou1eY/vQVyte/B9+9E+Y5koRbUMVD6BQQTRERY8JmsxVhLbV9vHYW7ToAbOmIV3Ff5yCwG1MlvP3k+Ou+bvWzOOnDj8Nf95/No0JF2zXMlOubpa8q3FerntZWrwyoIeBq+1goM6TdUhhBbYvkHq/8SeJP/O473O2nFY+HvKh/2k7nBeGUDXOeMc8zchYvS0sGWuaMknN16f/1/++vMOw2+OTPfonh+urJ7doLRQw6OuaoUqt+vSq1V9f1tA+3Jp7RqvcW+8Ixjask+nIv+Fi1kDChX/8v/yve/fp3cgZCwDiOSOOA7WYrnhCbDW52W/zJZ68waAxkU9p1SojQBByVZiUTKJFDdY3eIr1/ajRz6hlwiUD+Y5A7Z3QGy1r9GJZo3NV6Tgmx8sVVff6dP0bpvBK/x35+rOIFlqeeCo4HuLxF9+8FVVeyNzbW6VSY+n3M/w+/piv9KS631718SI7SCmhQjwmFRslRSAFUCHOZkbng9v4Bh+OEN29ucX+f8esvP8PhOGCeJbHwZhgwxAE3u2tshgE3uyukIN4R4oEMVbSq1XaRsEMRQEoJMRWklDAUCeEB9a6r8FjfkxQPdgItLiCWkCkSNr8AhcSYhyT0k4QnzggxCM4iDTn1LMm83EtyiaklqRZDWAnLYXH7S4XZznqeNY8ANZzU9qvx+wxCAKvwOAS08K01MTbqn3i8CnFn3q9mzOhXm7pfi3NyCWOmyoVGW1KV0zOLBTwHQiiKH6sgvp9LMwYjAkrJCJqsGpkQsuT0KGlGJkLMgwqrFH+xGUmU9gez2jc6DDCBd0cXFlRiuNGbblwdUX3BQbL3I7S8Tl4GRGg42eQ95M+oXXu6r7WlYZP9eJ5w9Vnz1Ago6t1COnZpRxUEgITYRPN+XeVRHI0lIVGpq2d0JAA9k9oPNBdcaTSw51ct5FZMASkk7MYtdsMICnKG98cj9oc99vsDpsM7hOlvEWmDEH7h5E5urrjf8ZbrjFkt8u0IEkCQcG+2W4tKR4dxi3G7w3a3w2a3Q9oMiClV3QcZ/0FAKuIxsCnAbiCMWWKHBIKeGYNXfi7bAhcGoiZ5Z+YqL7BXObdD2nuTwFRof+f4S1c6ftV4RJ2BMw/A2W72Nxw93Ix9FgpDU0Tp/eIebxPiaXibszae5ciW7EGDq+4sk+vWrnaGg0Yzn7QG7maeKjyv9HWV6UoMQdY8uzEGpBBRHrYo+ATpeoshDdglwlVg8RZiumSZLiyXNvR0vcvQwMvonmWbHe34wr5/jHJ5jogyvaBZEVmyEQBFwE+ib7CLDwDcIWC4jWaEco/d2Tm8EkiEkJUIIN2gntZRxAUCOjLLmvFadE8h+WoKvBUqsEJVs7IsEAFmxIxEMyIdkSljphklFCFwhGLCYX6Fw/QKD7xBLhE3lEFgzXur8RlZlBEE/a7zY8Nji5vjucdKLNo8vHDzPln/+2UA/rExjd97WXBB6wxqK0/O7hpk7pRzgi+iCx0mQiz3KKEhdIeUmSUcEqGo9amhtYY0TeA2z2LlPc+TxpbVUC2WDKsOjVDDPIUiwS1DBEVIVlYIkSquznKuNZWZuBczY84FcynyeZyQv/x78P1b5OMB+7ng6/CIRwZyyUJwWzIxH2+2judCIvoSiF/P8QJFtIN/QSPPdXAKUzuqoXJbC0LzI/T7sdHemhLi/BDo6flbDLF/b1LiG5U4bFV9TcNdbPxX9YyQJTSxqxBFCCzWfcaIcatD3mISAJgxEeE2AvH1J/h8MyJFcU01i0fY2ahJuyJiTIhx0CR0IygGpBTq+/pz64XnATM2mJBowGhzzagWWU1ObNiJ/UVHcBuTpERuhQ3tLPkWPOwwZs+8DqoZgjLWnumVh0rry5hna9P6B1evpspgn+Sc0PFUZQdApohYeo+4z4EZf/6LiOMsCR7tPb0iAtqeeETAXZO/XAruHo94c/vYYGP1tJxVOSHKhzxNFXYag0sI+Orf/w0efv81fvGv/xWG3a7uN+anQi+2/dutb9t+lRFfP0Vt3U4ruD3eToAdkI4V6veVP+GMx3d7HB4nTN9+CX68E8auZMz390hDlNABMWKzGTEOCX/+888wDgO22w22o3hHVIWd9yJSJURwDI/ZpXglhFdA2Idda4zZ4ne93NO1y+v9tdUJdnP5xF3q65y21eNSf6kXYi0edA11tU6E4mvXP5zGu+T59TqX4p6fPg26+n56hi5uwzP9T83p+eW/fGzPjeUFz/wQPELto4KiJ86AAgmz7G9osd9nHn55yMBglDBA1AIBnCGKZS54OOxxmCf8/e8ZD3vC48MG8wTkkhBCxKtxUCvmETFGXG+2SDFJLogQEDS3hNmusXkJhwJmDV2koWpC1DxTLOjTqOUlHLF3EbisoX4CIImtTehl3skiqC7Ou68URgml5SkqDFP4nl0P/dfmjmziFR5LQmlqeRwoCN2va8PavmVgqHjIyRmE7iJwYBBbNmMRlJpiQoTexr8obQY0ZYRTgoYV2UGV0bJZhTv8Zx8NPeqYHdZUmtNx/CCQ5ApjqvV78tbRWWwyGDFsKJSRgyYVnyOYGXGewSD5jBAFDACz1m9/7Ay1mtenrLM3srBdvqQHnqfZK/7t6hiPa2/feMHeYMDjWlRB5lK0s7zu4aLpNFZJmXNj5rZeBheEnggoIYhiTrv3iiHob/O6tbG086eTSR3lpJ9caVsGoSYnQH0EgEi9Sq3eG4OMMWEcBlyPG+zGEUSMucy4vb/H3cMjpimjMHC122IzJLTQO7qnuhH1coFi9LtXlFGTxNlks+a7G6+usbt6he31DTa7HeIwgGKsnjfiw0AIVJA078kYGdvEGBkYQIi8EgLIpquSAnpu0c5UL1WE2xf2uJ97VCUE11lYdGa8omujb89+66wR13HZJ3HbEdDQbewbMsByoq1o+8gPW9KXKLAIahRXJASdXA4axUpgYt0opGse6sHuZkI6U8NV2xDE0DjEuvbdQ0qy9CH5W1EZrp1ry/HSyaWakoIAUCDEILztiIQhRvEKrLmGFwvxPuV7okH81DyrJF3jF55psz63Iv9Y1nvv8vE0PC/IEcHzs+PwWmg2ZMmyqRiEMXyHMXwnz1ak2T97qt1fFHIWafU3db+lHWvPKSI8tHG7lLprp6UiWBPeMKPQjELi6phzxowJOUgyqKoB10Mz3c94PEbcATjyiDECCUXC3ej5pwpYqGMybJ5O5ZJ20BsCNsXPc+VShvG5tTi7D91jf1Q4fL/FC5peChbOATMAQBBiIagiolioEjS8Y/17K2MAGiuTUIp3G24ElIVkyvOMXAoO01FCMlmoJvZwQRoIGr8WIYIKg5LoIMSDqCCwRcsUCxJTRJiLaFVC5IJ5OoK//jVw/w5lOuJYCN/ORxwAZNYksfZeNo5u0s9M3vuWRs3i/VDEktTpr5OHf7Ws9OOAzFOv93HQTyPLPrilZwZ0MqvdBSXqdEh9XWpwmdp9LNurdfWO1mddU+EvCF0SNSZAmVwOBDIrs0U5BsIUCJ/evMbrTz7HfPdG86IEUUbU80FVIGGKiBgTUhoQYgRtxpOY+FUpqGdk5D2ueQI4AohNwMLcJ3RzSixTLsivZrne8DvrlOhZWiyWtxbqvAVgz3m3414J0cZhMEMZNFYLH7sv2k30igdTeJQ6rqrMqGPNIJSaPBrF1VE4AQZ+OW4ERlrCbCPEeW7jghiqeaULgOqN9dW7RxxycEraCbmoIiKLkqPkjDml6nmZnWfE7/7d32D76gpf/Mv/CsNut2CWGiPRM0gnnFf9LI7m8eM9LY0hqrSKo74qw1PPljFK7pBUXobbPGqLd7cH3L25x+1/+GtMX/5WhGiBMAwRKQVsxgEpRWy2A3bbDf7k88+wGxOGYUCIQT6Jam6IFs5soYQIjW7slBBOwNHPWU87LqHYc0qID6GLzj36lAKi69O9Szd+cvWWdPRJ471AsSpnvkfh9Gm9J/akjur5Nl/a56In5ovqPXX/0jaeK5fzTpe3sWZtfVHpOOLLHjnp8wL+4oUNrxd+rgLcefBnoxfw+aebkkL+NQvcEiIQNqAsAqBpmjHPGe/uH3C/P+Iffn+N+8cR8zQAYCRIKKbrYYsUIjabDWKI2I0bhKAhGJ1nl/GcTEChgsJBBU+SEyFoMmoJa2FWozbntBg/Q7zjhIcucElMlU638IJNCRGUnhAjIJNjLS2QT9bkhHT1sErUCoHUM0JpHS4MS/ZsigciQgkBVBw/DWvDtx1U/ldMWidTp15zophpQm5mE9zpXHH91vaFe6dKSldc50fiOCidk2rbxO0aA5oTQioyJNGuaShKveqLIdMCLio0LhklE0LIKCBkErokzzMAQs5izVVMQW+KCO8RUemv0vijGhJm0f/Jdz6544sJqlHnpU1EPW+EKpw88YpwfE6LgkF1/dqat/Pb8NXyfp/Qms8E6T/FhvIegQgIVBO+EwHELexvbalYaKamBOxhbaOLLCwYM4RuJTlPZp/PHnmziHqz0bSl7TbDMykmbNKAq3GL3TgANCHzjLv7B9zfP2KeM8DAbrfFOMjJNzq67bag4WN9+6hnn8HqgWBKCJsP2dAlEEIkbNM1dlc32F5dY9xdIQwCz4rR1ygAsuZzKAhUsAkQRUQGYjFTY3em6nou+R1LvcCa+6VO2WItHXy3fVDrGrx0TyqslLVuSY9r78sOVvCNlxlbaHM24TwXbZNRkyqzb0z+bBsQSPNaOKWGuZXA5e8FCTzXHIb13JEyAC4RfT/4UOtUet7mhYDOSMLvzXMQwCsbjCYPoa5hU9Dpn8KDQBIZYIgJI4lXYIqhgwvn1vinUJ6ZlReVl7Zxcd8XKBvO84aXl4sVEZ1W7EzHspdJgStVOoDrDrVKjoDzbTnmp5uoRkHUg9Z+Ok8A8yioBE9DSnBNeERkG3uBArp3qsJWLs7iY0YpLJaLlhuiFGRN1Alm3B12uD9uMBeg4BExBgQqKOMGhQI4BiEWSJP9MJn+VzGQhPQgaiCxvcTqCix+vy/F/oHFYNofyw9Snrd6vbghR5kZDulJxEbYOOGgi23uhYWVkNdmTFlhVr4ibCvYq0dES15r6LMRmyGoG16MAA+OMIbGUFeGQV9DZH5U804cVelxnGdM84y5ZBy54JvxNd4CyHNB4bywAPJIeDG/P/k9/tzgjOhYqXeq9fwJFsdguld4XinRqDh2Vyt1efI8uanker+R4Cs9OPfTDkkbkVYJN3Xj1mRvqpfo8CLrZt5Twbc8g/KM4Thjs9lhGEbx4OFSLdNMMS9EfwSRxNEMMdbcElVxqYoIOdeizJs5IfERA++FkQE0Id0JuwvAKQa4MditansHE2ycMK71cTlzANfzb/WLMkEm/OjPpVccGPPCVfFgFjumJFh+miuzz9tgjAVcWIL+WRuLKTXMQ0LHb+MrQ/vNfeI3/x6lFHz2OiANA24fj/ju/iD0RM7IWcMzqeJhnifknDFNUw3bZO2EQvjy3/0nXH3+CX7+r/8C2Gw6eY6TL8NMZ6t172I3i0WdMgELvOC3M9BiEFsDwe0vOQNA5zFkK1eVELa+wP3dAQ93e8xvvsJ8+6Z6RPDDLeIQ1cNBkyjGgO12xJgS/vRnn+Jqu8F2TIjqBRGjJV4VC2CLjWyWi03Q5OjFOkcLQUYVXDTK0m56Sz8/S9+HEuJ9y1NKiLPPLJ9d3rGPF1jn/5RKY3DPIY1z7/UxWcgfpphy7fybXrqGfr7Wnlnp4Syt9Nz8XtD2h5ba5GXvz2hK+bLE7doeKy3RBEsAhwgOGloCjOM8YZ4K/uH3jHd3hLvHiOOUcLgHOBdsgnhwbdMGQ0x4lXZIISINURUJCURBeEYSQZ8YtFEVWpkyYNYcAdnweRXmEyJCjf9v8E/oiOLgt+AX8ni34kjBk94StnpE2GcAqGhYYdAaKulOVP1ucidFPwz1VEAAhaJeC9A5pZq4OrAoYSQ5dW4AvpEM8B4ObDIACgjE1ao9BAIQEIJ4aFcew/ityucs3oUabdhkFUvaUQZidKQJ8KxZA6ldX4tJEmEjKu5sxdl8K41TWMNFQxQOAJDnST+PACfBk6TrWPN9GE9XWj81vxbc5yW0tx/mggj0xIkxcSYIZZtk7p/t+ls7v72RapP4rCkotEmiphSSUyXzpflOrG5r01/TtrXfGAKyeuwEKihVgtx4S0I/8kCaK7R7N3/OVAGk+9bCjtuZD3pOjAYj7vM1EBF2mw2ut1vshgFjCHg8PODh4R5v393i4XGPOIwIux12X3yO8OoIVoMc28PsZrLyAWgJkou9GUF5jiihzwqj/P0d+DCjMCHFDa5+9ho316+w3eywGUdVXDBY96qCUvPBApgRCRiIkegk3slKMcF7o2HNsyGzmimTyel9S3Z+oVxEj/NqhAhfl2VGLDQv67WuXMRTW6/aMtk8tKgPzbMxNBo/AFQIRZUOBBaFbALAQaeiCB5ydDdxUQcI81hX7Q63Oa9nUlfYcBwcv9WMqbmDd22KqE3I4txJvD00ZWMw4N9R1O1fPV8xEFIkDESaHykq3+ta9+D/D4dk+ydVLldEdBabC0TgmTVugsp61e2lKpDwTKgrZMh17WH3e41B7LTjtgepB1W9JlwJEHjg2sYkQgaocNQn2C0awqVgtpAJpojgWYhDLri93+KbuwHjyBiGI/I8IAdCKRHMUd31JISNEXCBjPhoE8xoip3l8T0t55mEiy3PLmZKni/Pact+ih4Tz1mofQwLto9lBbds773bPCNsAonW3KvsZf9bzEsT3LcY56YksD0c7Izp9Wk6opQiwrSScdAQTT5euuC5llg0hgCOCWBeuELLmQ+KxIROZlVEsIRmKox5ztUrYlKlxMTA7eYGd4VR5nf1DPpcET3hoEQIKQnWES8vw3AvfWrlNLfxnDnzT55jj6jP9dbRZZ7kuqR4lvLjFureuyceT3Qo3tTEtdDcXo1EqdTemRidWDBDxsSu1WyrS9pgL7OguodYlRFgoRVJuVBvScfMOARgImAsBeV4xKQW85bjxJKtG9lewzBoiIGooZxijA5XYqE8HAFcIeR7DJpAPqDxg6fFQhEZ/HHvudgv1Ypy0UKDW83NP4RWSxLENSb41EK/9SvnN0vd4IhiLBUNvWcDMyMq3Im+bc5g9YgAmqV+sQSZ9fk+N0Q02OAtBpnBnJWeb3DFLEpfp4Sbqw2Gd3vsS0CZM3jOmPOEUpriYZqixOAOoXpGeOXvt3/193j87Ft8/pf/HHEz1mMupFElilQ2Q+6oC4VRGN2JQN2rdcVOdgEp43wq7DZmx2iupfWkLRFXT5X9/R5vv7nD3d/8Hfa/+XuNC06IKSCkiDQkpBgwjqKIGMcB282An3/6ClebEWkQgUpMLjm1ywlhCgij+0KdEmWcHT158tu/80Kp8JyS4RIlxPLekna6HK+vj7Vba3eN/BNubvo+l3S4++Lm6X3Kx6aFluV8syb4u6Tfnxid+hRqf0LSuxTKnX3mBGUuaa7nBraCcy8sT3AwK+1+WNGdd350vBiNJyc6pN5sck/RpQrPYwJYeL3jPGN/mPH7bwd883bAYT9inoOexYJhM2CICdebLYaYcDPsEEiUqwJupSYz1XAeRv8CakfMQC7yN+dS6WI7r4HMCI4AphpqBgqzuTAoGC3PFSnYb8mTYIYAzRjCDI7MOroURvSepTZKv6eo+WSIgl/WmoBOIREULkuYVq6KFxHWE6DXQwlNkWIdk9JX2qgZLpF5RNQcESZMXuS6VCVE24aNK/fyCKrXrRp1UjBPtdp3e6YJGLn1p02YgJyJYBYiRoOy244yxZY0j+t3Llk8ZYpYmeeSQTmoZwQQc1IhJou8Rw0vK42FRmc0/mjlKLid350D7u8JXcLrMMneddneCf3n+qnrhG496r90XgHRhWjTfVL0WoAobwJ07sjjK25bmhsuNYv0QKIwCI0akvPjlUfGX+tfcH33b6i5y1SpQc66vRrdoI3B8rw0flzyrGzHEdvNiE0aEANwezzgcf+Au/t7HI9ZcslcDxh+8Qo8PIDxTt/TzpOfVW77D54XsHnV3KcIoALkXz+A7zPo8x3S1RWuttfYba8wjhsk9V61UFDcvYv0QFwQobkh0BQR5PeWnjd3ktxWsP0DsEYlCd3b+X3j95j7rV+rf8uymnZgT9Q2ua3V8rHl80sedJWNrZUJpHlxWGFjCUBQr/ZQoCHmGUBQ12zBM4CCBxRRWujZV2ZL3qMCF1vrUteDxcUEVEM4scKlhWlTnXt32ju6NOirNE8IubQSyklhMpFElEqRkEBI1dDOPVeHcBnd4I303rucCCE+fjnX8rlxr0GTpzs4X+NcHx/ytpcrIuCP4uJUnIxgBUkAAlzcxuA1wQSaRpHsmcUoKl73A4M51TlXHtIDtiB4+hF2WKv2Z5Od1X3OYsdLOAQWz4fCTSFRJH4dA7h7HPH2/hpTHpXhl7+rBFwPos1t3XcjOUXWdVjnrN6XqPqP5Y/lPUt3PqnGBzQ8VArECrdkzNnyOYj1AhdNqpqbQsJBCwASC5254Hg8SqL3o3hEPC4UETaIABf3PgQMacCcBuSxIOUZKSWkUpBiAYWoLp1CVJgVyKTjOcwT5umI/W/+M+aHd/i6JNwNr/Hb4x6PzJgtGWwpDRGfThAaIr2gLGmZj1X3yWYuHd1ZdmFRh5+steDF37Ofj1UchvK0gCnTPvYICE8oIypaEmGBxs80kt1ceJvzqFOIq+t9c8E1z4WCOGywo4jpcMRDvMdm3GJICTlPyCUh5xkhxOY+7xjwALEmIgJiMI9FIVa9dWeiiMBiDWZ898qbwYi9PmSS91roSw25c0I6sNK/zuOgYxi6Lx1+hhG8VcGgyethhHL7ZP9pbvKl9NeLjYrBJYIxK01uz0HwvHtH88Iwj4fmAZLruLm25xQTta6NnfH564jNdoPb+wNuH47Ieeg8II7HI3LO6gWWMR0ntT7NlREo+xlf/4//EbvPX+Nn/5v/BnEc3H5swhULiVBXjt3iOKa9t+qivt5yS6DB+8YAMroQB+7dbb/c/e73+Pav/w77xwMeH/bId7dIKWJIAvvTkMQDYhyQYsRmMyDFgM1mxGYYMI4jhkESHRKFmpw6xlQ9gcSVOwoD68KU1Xiy/jee/31piMtL7n9wWJ6F4OWk3fpB3ft2/sKERnd3Y1q2KZ8tiMUfNv25zuT/gRS3js/V+SfPJ3wMVknb8JStP7sML0EicEiYg8RZpwwcj0fspxnf3j7g7n6P7+5vcL/fgbII2K4Gye10vd1hiAnbzRYpJAzDCKKIEM3YRvsnACR5o7jytqoAYNI/QLISNgOFGBlJrWlLXuBYg+8WtlBhPnPRCE+NOKnRAoLUL8WFZcoFRROLFqU/2OGF55eCRFhmLHqgmrjaLN3ts65Hjbfe8jt0wiiDbwSJ06L1ubYXav6JEEREGQKhFKe8dZbtvfjAQ9NKzcmWUaVHFVCaQrwUZ4VPgIZ0Dqq0D9qA50hk/FRD9vR9yTqIN0hp68YAcwAXoGQxXgjzBBRGSAkMVsv1oPDQPNQLWtjdni9qosYlv/TU9yU+cjyV7j8iMT8RIah8N8v+wGrlHYzu8/RLoydW+1yUUzy3Usfo97rDdM8FAhVa7A3PDBk67b0vO2G0MdVs797b3rdXYFj4s8CWcyUIf+6SSEs+BTfnOgZbv3FIGGPEzfUO19stwBnH44Svvvkat7e3eNwfwHmP19t7UJogSWyyGiG3sLIGJkwFJgYsllENFWYQgOkdI88EGgqGwiCOiGPAzevPsLt5hVevPsX19StshxEpDjJn+nzQ8yihYhOYA7JNmcK1pibTt64Hrq1wPW911Bq2GUBgriGMTndKU/K5WW3LsrjIYARVCmuAk9ae41fkg+vZVC6i7YMFX2BbpS+mPtHvgdXhoTScoPDQPCCskRKKa4+BqONwcF+W28bUcuqR8qFWn4LxOKV9gtVDAm3foO0J+24bVM6JyxEB0nwW/VpUrKthzwJJvqMhRAwhIcWIFKOGdfLw8g+VuPunUy5WRFQXQjRAc7acnFiHsCry9Ae5f8Af/NNeVDjSKQ9QWzRwY0SZ7eta9QTprPTgBCvC5JcaAkHCymhiXXV5rUJUff7xEPHd3RYxRaREatUHbCLhKjEaD9yImSfLyUQosbU+/GfL+zK95wRu65UNaDzd10s1jz+kB8VzFolrY3/p+JbWgMsWT1qzPr+HefBntKfwZCTmrZCzJUtVL90yo5QZec4aTiTrefDnXZV4XDAdD2LNezwi54JHtdayWKViaUU1lEbSUBsWtxREKJyaxRUDgQosF00lUphxzC0PxXzcY37ze8wPt3i3+Qx3RHh73ONYsihJtDHPTPaiOpsXWlmY5YWPhPzOrXNH8y7qfNStUdkb6faJ1xK4vHy6Mcc4mcu13j508Gf6+EBpU23VMxz6Sj40yYkVCPds4olVHREkRFOboUrJajxYIUQZnIE4bjFsE8rDdzjs95jzpMpw+cucEUtWJQR3QxFlhHw3120j2D25GIt6IK1qIXrhizFUjZDVq9zPAwOgssJmVfpclTM6xmb5BtQkam5+TyzzIGMIHNx1oJBIWVgtO1mVq0UJZ9ZQGXYfwTEKIVcmwJQVck8ZfJ21oLGYA3kBOyp6rwoHm1MHE6snRRFBzXWIuNoOIARMhTDP4gFBRPoJ9YiQ3wEk659lbs2b7Lu/+Q2mt/f44r/9rwEeuoNpDHITaLRVEeahKe7qRTf3z4mR2n21xHTmXRWOLPIKPXz7Br//n/8aCAUUiiifqwdExDgKDtioImK7GRE1R8Rm0KTUKbUQTNF7RKyHZPKvcOL5QE3o0L3bGSXE8v5zZa3eEkQ9r9g4ubL+HJ2+3+lv9POxUEKcks3nbOv/cMr7kFAfxWLufYuNl/ufT637s02em4S6IZaimadLnZXvk05vEoZFpxc+W4fW3u/yJrxYoz8jDYMbDCGUEJHTiJglrOJ0nPB4OOL2/h5v7x/xcEjYHyO2akizTRJq7nqUkEzjMEreJ1WwUogdWW6iKHZwSwR0ovytNLqNm8SSOlCRMDxkzzjMXOn/hpsQBL8a+cMqACWXw6kK9jSPQC4FqQQRHEbpw6QIz0C205kmoy/FqIOINL9pr1ht60v6kLOCX8oaCErLN6VGCACyXKs5hKjhASL1QKGekunex/9YknqQF2nX7MUU9lNTttjLMHhhDAClqUyAL/9YbcO9jZ5UxREXoBCYhM/KeQYDiHkGiOQ3S7gTkSkuaJnle/obgBFK/bX6BqcPe6oZq++se4y47ppqEGKPtcffqzyphIDOsbqiBJIwaFUJFgjImkC99CDPIILRWD4yP2Akq75Anbf2sL0r7DlH79YwOmwKLO6uL8GjTFBBiiOGccB2s8FmM4A5Y54OuH33Drd3dzhMMyIfsNvcAiPjwAlQZZSFVfOl0eKoa2J/5hc07wnlSJiTwJEBASkRNlfXuLp+hd3uCtvNTui3YB5hNnoC1PeBOQpfX6gpWbXvmg6mwl2bNLLJrLDEgwLmxlrUUGjd+9kKtndbvn2dEeNB9JrpOPtH+ORrXeHagVOkLTZMt+f1bQgEmEe9KpYpAKEUIIjMhMjtPn1xtoFW/qmFnJXQTPrJDJSo/JFEcAEXmNrJ7VDXh4Z2AoPKEkk3nFn5Dxic1fuLXIb+GZa31ETVhEgBKQYk9foP0fABtzP2HuUpOu+5SCmuot14ui97/kUjPNPnSYUnf/qGXtz+x6SAX+gRoaCZnp5bPqnQEEz/q2dt1/sDKpg5Y6H1bFliAOpvetzpY0iLx0NTRFgoJmYRxgItZj4APOxHfHd/jSkPGIYBwyBWep9cbXE9DrgeReubYkKISS0QNNlY/TMATGgCT2qUzJPlp8IUfswt+k+jnPd4+R777Pq3C1wvcMlAzshMLYlqnjHNGcdp1muMnCeUPGkCVVFIWAgz0Z4LoZTzrIqII0rOOB4OmEvG41TUhVsEf+aCLVatEcOQkFLCPIxI84BZLYJTSghxAMWEGJJaMMmfhWQ65Bl5npB//7fIj7f4JgOPww3+YTrgoRQc1cOjZEvCZsLHRoaczJs7ls+WShRdWi58gOiEeP3eSgfLO/JrteraNqaOmCinFT5aeWLuFkLXnmDl9umISP+2JytDOJkOUlhdSVLq2W4558EheMOnRpjpcwbvjUjW+vcBmJDx6vEWrx/e4TGI1944bgEi/QRS3qNQQZwHSXg5A6zCDomtvGCwF68FaKJEdlO0uE/GMAGo+ZkYur79JmjkfPu0KTKFhykihAl1nEFBt6kaY9ZyOkgeh4CaPFuJanLfGdB8Dmy0u4yGm/VRbxkk62LKllKVGPo2Nl6yTxW8G71SxNLQYEnvMdFYm6ogqfeAz18B19uE7+6OePd4RAiEeZ4RQkApGSlFlJwxxSA0SrZcITVCL/gw4+t/+x+w++ITfPav/xJIac3RGXUV3Xnoo9WwHot2Pjyq8ItMK9eXZ4nBOHz7Bl/+L38FznJn/+YthjEixoiQqCqfx8ErIFJNTj2OCSlF/PLTV9gOCbudJHMNUeioGAUfxBRBQJeg2vbtySw4gdalSoilkOpcuVSp8Bzv8hLlg3ws7vtz/KwyxZ5dv//jU3nfL730A5NjfywXFbcoT5Mi58tFvNSiT1W8kQI5EV4ZX9ro54rjQkKOQ7VRPhxnzI8HfHt7h+8e7vF3Xwa8ub1BmUcECrjebLFLIz69usYmJWyHDUIQ5SoooKQEpgBETc3KJhhsMKtG1EBpQjZiyU+hgikCEGMGI1QvSLGwFuERcxOeAlwV0oazSmH1iJCJNGGPhWQqgUV+VVg8qEtBKIRQLASxXzfHizsiQ+VIkJwQWo2CC9kowmGhZTSxdA6NrqweC1RpK3nM0Vbakb6lhmSSBOIhyKqVYN5zWYerIZQJoJrUa7EFl3SSkXIG0MnmU3EhOR7DvbclqbbY/oUsj0Sbr7rvyNozWYZkmqRKA6kiooiHSlCjScrC6+R5AnOpicyhXjdcspqfi+Cxp8CMPtK90d3zc9ALbJ3JA/qKdULktyUnk0lATY6rAkYWcm+1nOKr9XonFXhNtrUkZhTnaxivoJbbJYinhoV97J9v0QGqUYr9xza/DMv6AKP3qVdGsFmmkySQJ6fQqjQxtx6NZ49ESCnik5sb7HYbbLcDYgTefPsNHu5v8fXX32B/OCCGhBQ2iCki8xHT4QE8ThgsBUw3G0U8QbT3zNan7Acz+IgEUdgEAkLAuNtiGwd8+snPcPPqNV5dXWOz3SCqoYgAMQIhQoKcJmSOmHnAXCIOOeK+AO8y46EAewCz7s5uD/pj7v+M9pNDWcEOu3dbcqfrdI7RQMu7bE2D27StNMiVr8DyU2EpdE0bvyR1GnRbjKcmN5G5JhaYb29gY2m8j41W6XsLMavhlsSbXvkJBqpSl/v+5XUccPKAqe5lX1ngG9xZqUoIq9MdoaY4Ya0cibApR3zCwBURNqPIiYY0wJRgpyv5x/JTLZd7RFSgqKh7QQ92dReEnhA3ipIU2dTD9AySIPuX+ivnCoNVA+gGt3yEu4/uoFviSWHsuQlbZxGsFg3RVONEy2MoIBzmAXf7K8QYJayAKiN2w4CbjTDQYqUXK9IPRuR6BcQqZUNuwk6ZSuY+3EDXwgs5qiWpcApsX9AWG7H+cbi694+b/MP0/SHj62MrrjP71CovbpwKTs6Nab3SolnDicUStTUrp1wK5llzo+RcFRESPmTGNE8aommGWekKEyPKi0nDi+z3j8gl43HidqZY4z4SYYjqCcFj9ZYoLKHWLEkvcgHFjBAyYhDrCaKAOYuQ8jgdMU8T6O1XKPe3uL/+Ancx4d3xLfZqRc6lWUi3CV+bMzrzfa04zOsZiPO1XL0lIXvmqe9z66+M+T2NC1p7wMr72e0zL7MKu0+Jv7PdLmBka7IlCeRu8vXTfSyHw35yzuCWtdcQ8G0eEaYUIQX5DNRYz8Z8KKHPrc8JQA7ATckYHu9weLjDtL3C6+mAYRwx5xkhR0x5BkLAXGagADlHAEAuQVLwLeGyX1zq14NoqQtQ2ERG3DeqX94oLOZBf5hQAc0rxCzdPH3QhbtiSEgG35pjfANDLe4DQIr7Telg1oX6Hcyg0Fyz5a+I1Q4VNRxssaWFANZQRLZRjAuGwEQi/wmASmN0AlXBggA2ZTJQlN82nA5V2jZ2KISE3RBxmBiPM1cFCwAUS/wZZUJjKcg5qLJXPDcDGMiM+7//CmV/xKf/6l+AQqghIWTvr+1u2X+9lw8a08btBDwJfzz+sPBX4BqP9nh7i2//6u9azwSkFJBSQEyhejiMQ0JMEZth1JBMo+SG2CSMKeL1bofdJiHFBJAkRiQiyYnickJYyAnzBDkXR/9EcF/Hd3qdVnDuJfi+tbUygFrnKWB7pk9a1qKTe+ueH568dvSm+3lur3yM8v3TcOfoIv9+L3u2Y5wvKB+bDv7ey5IOunDcP/jbXcJErpaXPGMUQ48TO22tp92IRPifxgr/jseMw+OEu/s93t3t8e72Fd7d7bBNCUMExjRiO25wNWyxMYEKBbFqDYQcgoSrCD7nIaGGR4QJsFTsqaiFLTyRwUEyuCheEYVU6G04vAMGUkw50VunS6+mhKgGHqyJcdnCyATNHQH1rEClf84ZrdirVRCoYzLLWVCpSmMJkSMLImNstFmD80ZLyPe6bBWXUQuVRGb5Lvm1Ctp1jwM6L4UTHOB3jXwWTy5WkmtFqGgKIAeXOtLMPbCEXz19a4JtrkKKuk6WnLYUER4bb5UzEEydY0YZpTZMrm1fzHCDz9zv8mU8RzR4RsGEK8tJ4sUjNi9+8xJ113q8fab7Uy3EGXpe6NWgiairUY/uxc7w6FwzdV7bn4l2JFoYtdyMQDVQKfWsOfq4zq9StKY01HuRRMm23Yy42myRYgCh4OHhHnd3t3h4uMdxyhjGGzEEASFzwTwfQdEMe+qr12URulf6aEqIWq0LT2R0Vxo3GIcRu901rrY32GhIzWCJ56sAOwAcUDiiIGIuEVOJOJaIx5LxWBhHBmYYvAtujpvix/NxxmXYUvvaEViBRw52+Jdfrqj/6rcrtdXtqSq9amvHaOvpSw1z1OiHauS0wpvKfdvvgMhCzBvKjaHKCb2XkRubB7wcqgeVwcCnKNNWlnPXLlO9f6640TiZTKm55uQdBga2pWATA1IgJPOApjYTl431ibd4AW1xNmLKuTaWskK7fHGPl5dT+LPeyyWywkvbekl5kUdEp+l6wXRVSzP1g6qWJBcSgz2S9tdXnie/xVcASS0GyPWAqzbQQrRkTdaZNZ5i1ljzs1ocsvZPRHg8bvDt/Q1y2WC7u8LNNuH1dkRKI4Y4YKOx+VIaEWJETIMoI2JCoIhAcUHsGMHlk2XZ+BXIOIDwUqbo+dKRRn8sP0L53jwkTEi3AB4ihIvgzWshX1VIWvYTCoBJE6NO04TjccJ+f6i/5/mAeT5imo+Y5xmzxjPPZUZhCdfErN5EpeB42ItnxSGjMGHKpTEqgHO9CwgEDKN4GI2bESnJ95BEQEVhBMUBUb0iiCJAQQSIhYGvfgV+eIu3iDhuP8NjIUw8Yc5ZvDdy1pBMpRED7Kx/7GwtwzF95KWpkOoERH1gR889vtaHBzffA1a8FO6fL+83KCEMjZg0TwVP0Rnx4697gr/VemoE5xS3Jmw3d/wat9SSU6v3BBcCUWlRQEmsrazVUhjfffpzPNx8irC7EuHCt1/jk8MBTBHbcgWOCbMqI1KWHAExRAyZEaIo6kIgxBj71yOAOOEQXkOHpm9kBDzVdxnLPRIfYTjpWXrEcWXCc/Rz6wmx7jywf5TdeDwt0Xdhv6pFHjfGwHdAgLodo1pf+qfFqV5DMOntoMqKEKh+ttK8MqpSRBmNYPFbNYmcwWJttTH0rH1QwRevNrjZDfj6NuBuf0DOSRTAUxRrtxjUWCJXOgWq9K0z9nDEN//ff48QJRFcvHqF9Cd/jmE34PqToQ2dXOhN6i6fiBaeO4N5znj79SOmu3scf/1fgDyjqHdcQcF0/4jNJikDL0KfEAlDjKqQMI+IQRUSA2KM+JPPXuFqI9diCLjaStLqGMwTooVmIqgnhAkKyAlu4JRdaDBpqWhYXlu7folHxGnbfi5Xa+snd7+f83w46cuvo2/DPbfEdeeVD32n3Xn6Y/nhCjlZwfda/qnzAcqLAYuN7oQkyteWEFE2o8BmxdWlFBwOBzw+PuJX/8D47Zcjbh9u8LCP2B8HYAY244ircYPX22tcbTbYbLYYYgSFCBCQSZTHJciZFRhungAEkOBvMSDXOPKloMwFoBk8A4jsBIMZkQMYAdHCGGoYjYKiFvjs3t4EUwLzRQAvuEuQpuIxbh4RhYVeySwhQmIhMUyioMLLUJX73ojX8CD0XeSKQGrzEAjKF4cAyWMVAjgGUAnKPxR15ST5LIQTMFaX0foT4wkOMkshyJyGEDRpcUAhaKx1pTvMShfnTkiPI9cNOU0ZY+YYgElDg4XCITPQcMDWNe2NFyRJ7PJdGZIrgoSvYTTeCBOII+Z5QmBGjEcgRmQdjeX0q3lA7D+lZ3xYTE8m9/PhcWzFHM+AFTXBJ7i9t15qmEWY0X0Lw0jV+xey1y6CZVTXo0qm+fQdagJ1bZesPwqg4BRJ3YNc17D54ui+Vm+hyGjKH24Gr75IE7YazSun0sishnWqJNltNxiGATdXO2w3Ax4e73A8PuK3X/4Wd/e3yJkRKGK7uUIKwP74gCM94EhHtTyPQGihkCzxcXF7LTOQ5aZQzTEgQUNZoSDdHjEi4JMvfomb69f44rNf4Nq8IYYk8A0S7EeUmAGFA46cMJWIx5LEGyIn3OIt7uNXeOQ77GdgAiG79++XWb0zIApXo+hl71goKKrzWtx2o0VjVaHWnbFT4FJP+clZbLxhze/C8ta1sjd2YtQcd3JP8zLAKRjho7hkXXt3Jh3eCuZkUd9Do7oYTFMPGvPSsdwQ4JYrBqWIp5Ttv9LqAty/h4dNdS5s3/owXMZz6MwxYN5m3bOkzxEhhoj5YcB0uMHweify1SB/0HlgQHGMqVb/MGiZ57mrf3zlYkWE83aESQjOWsqvrLcXLHhruwt7d8zeuU6eY+hWm9XPJhTgYl4QLfeD/6y5IzQhVkDAnAc8Hq8Q04hxGLAdB1xvhhqGKapld0hRvSFitUxBcEiskn6G3IwZ9EwoVZrkUga4zsQLBdsn6/ucpOn7EJz/hMslVm4fYgl3iYdEvc9nT6NvUPZ4Vb452yYVjBYMQIjViyFryKI5ZxXey6cpIQ7HI+bpgGk+4DgdMc2z5IDQME0Sxkw+53lW67C9MGwYwRQwI9pLAIBaIQGFAmiekXlflRsxTUjDAIoadiOOoDCqYCqCQlIBYAAKY7h9A3p8h/3Nz/EYNzjmCXOxpHrGUJQ2Lyd7/FSgc1lZtHOOGVpUeZLGeeb5i577kLofo3xof26S3hthLx48EfkRnGWdW/+OIXkC/53rT3Gft0aX8ydW9JWxDQwulmxRCEo263qtdNxsMW22SOOIFAIeDgeEh3vsrh8RUsI4TQAIaZ7AAKY4S2ghIoQiVpUhBBQXQ9nws/wz1uGzEZkwol2FA2weB08zebRgVu0LL37XeTWGXT0P+nluv8yDoloy1QU8aba7Serebzwm1VblT643b5nmxdK2gVwjWPxgUxw3BTIbkoYpm6o0xY3TJ9Dz45JIUwHbERhTwMMx4TCL5xdzwEwAlwzmrPSKKEdizBpSUgbKytTsf/etdEmE8MmM7c3PZWavqWO2278MkCguzh40y7NReHGZMR8z9rd7HL+7x/2vfg/kCazxxIsyzzGFmschRvWECJqg2hQRoyggBk3ierPb4GY7Vq/SmELNJWTKa9I2zRsCaLnvwtJb1pbiGWXDuetP02C9EKwerf7KSb1uLtfGuKi76sVB/b2T8S+eWZLVz4ZB9UP5njinl9JMH2a48ROmXdfW+2S4K+Pv4KFfT7Nq//7e+ax14Mq9Zfkx8m+sogw/zwbOgf5QKmgHBXBIEjqGlH/MGYfjhIeHA767Tfj67YjHw4j9AdWidaCIMQwY04BNGjVsb6gWvhJYR/ADSK5TIFCMAEhzRmgM+sLVy0FeJKqZcgDpXwBXxS8FQihqyQ0AHBBqUtrm9WY4gbygyeFLlUzrL6OpVXgdUD0iahhFNhzq6KvFvBNQwxaxNwJq7LDy0CYANmMOQ9oSmqTRcoAJupoQTwEXGU0WwEGeCSTJcospsQMhaFz65kVqY6J+T5zZVUtlRFfTmiChqcxIhew5rPDjHd3krzSPldoTq1FGMUWTelkW8+gUI7GiShB1mah5Ijx95LsWvgl1XZ/mUmWkdXu6d+/f6aVwSelPw/dOTlKVBL4zOoV8df6o/nMKE3TgVULj8HEzdjBaeIF3u/dz13S4FAioNL94LMh8VoSsj7czZMJgC5nTVkhDqGn7w5CwHUeMQ0JKAXcPBzw+PuD2QbwhuAAhRKQ0IFLEPE2YMWEeJoSSINmMUc9JM0vierZMAG5vHyDkbmQGZ0acMoZI2F1d4+rmBlfba+w2V4iDwLtie8LB2QLCzISJCccScOCAQ4nY0xFTeIuCjInFK6LCCI/r7Lxzu6U7Q+e/0fRCw9clrueG3Lq3dRPsaYZD9XpN6Nfqtrb6dT85T3Vt12As3LXSbqEpA2voPAst68fGotwp7PYhtzFYGChTQnCZ0RSYqpgoTRFRBf3M1YCTnOfU6TjRgEM97KYclQlhajixMln+1Bi8VthMgcAlgcoWEYMYrQYg1vZfRkNc5Mn8zH1efPNH9kynZxrqVSY/BDX0Xp4QH7G8wCOCF5+XF88/nTz91Ix3e4pXblw8gpMOmuJOiSQVTJrnQ85FXRfNiq8RE/vjgK/fvQYoIQ4RzAN2u2vcbAd8erXBmCLGISKGASmItXaIATEMmkQxgiioR4Qwzeb9oCdNEZ0IjOx6s1QLi2kwUOrR3QLI/bH8QZf39pDoBEyoCMSUEPP4CoyIec6CK6YZjLklZ59UEaH5UaZ5wuFwxH6/x/5wwON+j8PxHofDA95hwD1tEO7eIj3eS0J3ZnX91bAhpWBSxURRt/FS/cg9AFfLFkikyBAC9lOuiUehrtOUBoQwVMGUWaUYuRiwAbaf48AB83TEl9Mj9mXCPk9V4YiiRDlb5x5Srcz5x+DfV4Hh2csfrTyHpp+6b0zdswj2ByznluKEZbtgrCvsYX9l8eLPKiPWOiV0ygghhoMSwaURXIEBBAvg3CwEjRlQq8s8TShEeJcSDgDi2280CWHAOG5QAiGlETkHxBCR0oQQIsZxrongO+bQKTSrlx6KJlBs14kIE0YEGkQgYAxf5a6MPSzYlbewdNieePdWhW7SlBavrE5jrrlZ/5hHQXvKnpVvpVr0+PqtjoVCYvNwXLRrcwH3nKFU0jaCHxuERqhMhm0dhbUNqhgbg27s9rt66UgQVYFhzPji1RavrwbxLiusHmcZv/2W8HicJb8OuIZoKjl28+EV4nzYY/7bv0YOwDQGZV7aut98OuD60xH8yc/BN5+1Hd4xNwX45tfg+3t885t7TIfc3ierNfDDhHKckAhAGpTTYElIrcxEjAEpaWLqlPDF9RW+uL7SxHNRw1lq7gj1gEh6T2goVURE2YMpeg8IqoxNs4JrM7/8bnjxpWGYzgntG8N7eu/S0iu3WjPPeUA8dX9VcbFW99nB6edPAA9cUj5IT/GTKysvU+mXC6//COVDlEXfN23U93RhiRFl3AFKc4LFaO14POLh4QF//5sjfvUbwldvZ3x7e4t8nJDnjN0wYBMTtmHEddpiN2ywGUaEJHBtVow5k4QNCklz3oyjKBKGAQCB1ZLajOW4FFBhhBBR5kmEggQY8iICEkcQNORwJCQGchVKERgZSqjIOzJqUlfDlcSEwoxQ4/YXyT2gwqzCAVQkjnwhzRXBwSWsNvMLP9vNoEFC05xS4dWzTb0TxJKca364UgrIvBIrrGutsMe2ZlzACmdV+cAkYR5Fea38RoHeh9BrVFAsLJa3aji3o/R2U0a097F59cqIYPNeEyEbnYILDwFbh4KrAYn9ThCahyArQEAoMwrQwt+qLOJECeGFitx4SZM2GLX21OnxiZ9l8m0HVOKyjd/vDN8oQW0k9Hn9M4OE5V8LnRTUKl6bUesEv7dQ14Kql1FTPLkQ4ycvBjlotj+p98YEzNi0KA1kYFleJoaAQgwgyfnKQAmly8whzTgZTzeMUOc/F0ZmrgmgX93cYLfZIgYgHyd8/fXvcXv7Ft/dvsE0zbjeXiNFiTYAjnh8fMBEDygbYT/AA5yEuL29GtYI/NHtpoa1MYhHBH/7BnhzxPZnn+Hq9Q0+//nP8fr1Z/jkk8+xGTZII8AB6pXMdTEKB2QQjkw4lIB9CXgoAbdM+LYccVcOuC2MAyTc7JOFbHmaGRXphC73ajHSW6eaCRo+nVsGagacim9lIzgealGLoLIcx98Yj2AKg6pcKHbezVCyVN7EeBA2uM8Fs8oxGnzRT+WBqBhvI+9QtO9K/5u8pmQA5unANU+MbAa7jjpOuD7d7uw+7Lt5EoHsJBlfZYp3rvdPp5aq/CfFiCElbMIo+zwGXCfGVZgAiNKl2bv/cJTDavnA7n/k0f8g5WWhmSq6ef9C8BukZ5gszMKy/uoP6r+cQ37rtIEXhJgm0QkouFSLcA9UCgilEOacsJ+2oDAgkiZRHAZshwE7jWmcYtQEupaYOlQlRFVEBBPgmOUhKW52Gv4q1HFvSWsAztdDRzd8eLmgpUrs6s8fiPH5KcTefUqbWC2fz9R5ybg7gYTDdNRXOn3O9W/CP1aCu1BCQcJsArKchZjJGSVzzQUxl4xcCqZ5wnGe8DhNqoh4wOHwgP3+HvfxCvfDgGEixBJqPPACAIWRWcR1WfsqcwZYiS1FbLbPQwBiKSghACmKezSCJJVjdesrBMqA3hGXToJyFmYCmwAkzCVjQsFjnrBXK+KK8FcPC518WyU7HE9zvtZpq0/Vugjx9PzVRX1e0uT6GNovv11/NAR51pLAVVlnF55vGsYg2Jo+/Zberffi2SC4PAi644nBrLH/2VnXh4DOlIUrGSpnSGKqYRo3QAg4ThMeH+4xbq8AAobpCGYgYkIO4tUXQhYCO2jCSnLsehVIO0tAsIpFbKzCbM0WDkdDC1J1t5XzTEQImDGwMNY1mKARsSvzJUeyKS2qIkLPaWN+rfSu68XIWcu5wHa25boY/zQGu9XhChutbltSI5bZBr9yfaV0fdeldztz+VzdfagWqbrDtkPAGIX+EI8HQs4B23HAXBhzbu01ONrDfbhrfH+HwoxHzf1ThQ7MGPIG27gFj9fA5qa+Sz/tGbi7Q7m7xf6rdzg8zPWVxJ1bYD8AVRIAsJAFapGbUkSMhEFpppgSbq42eH291dCVojwLUTwmxHMiahinCJB5QLRwDM1K1ughZT5rYtnz0PApJcWlHhO2juTvne2yNx15dlzk2l4i/hWa+ikPie793Jc2ouX79mPybCe56rzY788V6ubg/Wm45ZNPt3QJFj5TKs49xQvP4cOORF7QywCtw5EqHMPZl3p+/pZI+wLM/ZGRe78Xn8Lf5w1uKo79GOMyIa1re7Hjfad9Pbd9GAQKSXIs1FxoBfvjjNv7CW9vGW9uI+4ej3g8TMBcwLmAIwRuUUSkqDkbmgFNUYxbVFBJIYBMARtCDbPHGuaPS5HcTzowCgCFCApFniXJL0EQGFm0vxbjXvGzBXY/mWTu5sxoZgvTYnjQZFOGK0XA1XjtApZUScBJ1J31VXdjqWdB8WPll+1hqvecxKvR6Dq7bP1WTwmlV2C5IuAb7RTbqN0vrOwX+6nh4tM3OfkkwDxwPVhZKmMWs7E4oi7UqGsf3ZVG65CF1AK3BMjFvGnEWrkaZ3kai0++9L+7wfYL3HvfmfHLClyoqG2h1FigPFv7tlwELzPxSgGrZ334sfS4vm1/80SxRaxbxhaJfTt0Mo72stTWdYFja5shiCIvQATesH1nYHF5Omy+ub3cAvfGILm2xmHAOCZwycjzEY+Pj3h4fMA0iwFLiglDSpITJTOmPGMKGaWGC3UTjpXcLg5eqK913TJ0mECHCeMwYtxssd1dYbe7xjhK9BCKWRUw/S6vMJAJmZtnxIEJR2YckDFz6EMydeNcv1qX5+TueulUpQZX9FCe9GKLSTjLE/hz3xR6z4/D50qwh7wSQ3QFBYxSc4PUPWr5bO3TFBpV9mnhXM0DwjwiGECRJNbmDQHzrAJqSCl7gVOg0383mseDClMGsc+bp4Z3burrFHfKiIBETeGYCIhUOu+aZ4mnl5QzR3B5e6mk8qjmqWb53FC5v+Rfi1yvLyS9Lyrnd/Ha1ffv/IWKiPcsddL6vWqlB8snj1WCY/U9L9kcVegAPWiQpNPgahGd1cUoz5IEt5jFpDUUCNNxwO/fvEYuI4bhGjENGDdbXI0Jn1+PGGLEmJJY8sUosevD0CeoDkEJRNOQUyUQyatiVcN/lmg/mYdTqu5U3/uSsjLZH+Es/7F8vGJw3a+L7HG56JdLrKUAVoFiHj5BQcL0mFF4xlQkOfusCaXnaUYu4gEhn5L/4TBNeDMBX80RfHsLvP1a8kRMRxz5Acxf4y5vMZcrVe6Vmgy6xhm15HWGSI3erfQjgeYDNvlbRJI49qa4q54QpsiLEZQiolrNGtPlib3CjG/KEXvOOBaJd4il9cAaAu0m2s23QXxqN41wXpY1eGf1PybOeGr4L2uIakNVmN+k8mf7Xf7o5mMJw56B2RcM8pn7ZpfliIHlKzwxYRVPnXvtZ/ZKVTL0Eovup987co1QYwWTMcsyAAp6bgujxgEOqGcJYEzHIwoRJoo4lj1u33yNaXeNMh2R0ohpc0CICWkchWgbRMCbBrF2sm3dbPeBGCTcWQxADAAsXnUVSku9FAICCClEVHUEQZPHMx5pg4iIa74TpeGaVJNVZVkVpXLDlKbVqs8IX7L77BoBOsG7WfPAFA+oxLVXQvpYxzW+KqAwAlUxUtupQhbnRbG450a0INCWv5f7x28SS0yoYShUkM+BQUUYzT/9/BrHeYPfvXnAYc5VgVWot7y0seWaYFC6CLK5kJErnP7u60e8e7MHpXtg+NuVMUp7dDwAXDAfSs01In1NAFC9FJoVK0lekiQ5tH7x2TXMeo5ImIvtMGKj1r+kzEZVQFBASGLVKB4RJIkYiRTu6zx18+gFEOtwozuWjo6i7n6DJ6tKCDIP1mWfTxTqz/95QOi9Yan77Rp4op/ayum4awVawKWnqceKC9HPqryFQf/zY+rm9AW84rkqF9G6J8i43xM2pgVr90xfvLh3YTkh189QCl7q4wURteqCOHlqzzn2QvDNc/uzH/CJEcx7ledm6On75+is9yqdlNjtyLDynqSyNYKEJASq2B9ZjG3mMmN/OOLN7QN+9buCv/n7AW9vZ7x5e8TxMOF4OGJICWkYEYcRcRwkETUK5lwwzeKJQAHIAEoAKG0QYsSw2wpfOQwV3hmfKKFVxBsgZEJWQVlEdPHCGTxLu5LsmRGijD8WMQ0qFvubDHM5OMgEiqS0t/KuncKX1eGN1awYNR9BhggTqQBRogGJMbUmru5C59RJl0/L4NDok2p4rsoW0r0sRhxKLIEhnhHtqQIz36hKafV4EOlve7aQ5CcIMQFECBp6ULxFmmdoidTTK26/cN1CjteBnfN2r+IYq88AKv2n9J7Opd0ngqMzZHYIrQ/rqXWkd4p5iZj3dxavzjJrOLEIoCBTwxGFGTwLz0Qs6rEoUy77nxgta2YL4dnmXcbiFQFeEEx+nmzcLAssCgWjVwrMaFNwvPtTWgF6JqoOqvYh+QGipZ0I5PpucND4USKWNoquwZJv0LHZf5bPS/wdZB8SRYQguRdENm1qQt3LGg6Nhijh0UoW76Zc9FwE5U+DGOPblJo3C4e2t0IGaK45HBISEiW82l1jt91gt01IKeOrr36D+/s7fPXNl3h8fESkLcYx4vr6NVIImPMRMx6w/yQhhx0yMiKC7HMCgAxilkDK3OYCUdYlFUaMhEgF++8mPDwwdmXE9uYKn/3sX+L151/g9ad/gutXN9i+GjBEQpmkzZQZjACmEQUBUxlwzBHTMeGIAY/Y4JYDvikRt0g4UMIewIEAjm6r1S+hfuW6R9uaSQ0P/7FIA6keNuhLAZyiSn50vF5VVuiOYju77YDb0dafbdiWjLmO1XalVzE6HKiKXZFXCj9SmKtRkYXELaweDiXXEEsMBrLxQaZQyAq/Vb3jcpXUsHwK6KiOvQ/B9KRShd1716gujX6h5nYnFyzXjwKMxhMkjClhG0eMGDAOI4ZxgLk72fHvMcll5Sz1UeniS1tbtnSa6+Wk3nmysn+C12+fu/7BxWhLh8es2Na+mO49U34YRYQrzzEM3nVxSWufPkon/4JMONPXYiVOvAdEMc8HE5Sy+9QYZnNOtZG5DJjmLUCDJlEcsBlHbMeI7aCuszG1PBAhVQUEqTKCgjHNRsQZEaWzY4hUJmN1jljn6fRuA4gfpoT48PKhHgDPeRL8oZTnPDZe6tFx6gJHHVNb6VPqgRJzUFc8sW/OiGBESdhcMuYiCrgpz+L5cDxWBUSejjgeHnDIMw7HGfcl4YG34GlGmAlzDpg5YJoy8jzhSFtMLC6mrO7SzLEK7orXoAPOE6qd5MAFuZDey0AQ125QQChiScbRxKYMJGkucuXPapuFGccy4+BiGxZ2ULuZSJ2ZdWuMz1dbIirun3xpcT2er7PS+CX9nR/+Ail207Ly4pf0T+v1Tuosif21wS7bOTM5L4MY6wtaX58APhESOqJTO+xqKFHVIe0VQqZ7HWpXquyJIZaWKNqewHUmDWrgCAOJ80uY04iJAsLhAABIgZDjASEDMQ5gXIFiQEFEyAGZZ4Cg0fsJQIu7XAKDI9drrEkEM1veJBl6zkK0Fyo1MRwBKFGYpokIkYGRxH4z2vitKEFbnLLBWGph/tEAm4MdpgBoRBLQ3JiNcOb6rGfeLS8MVJFjTB1g4bFMQQFw9zzQeVvop9EXNn7/2d7TAjx2L77cBO1bJyhTuFYINZxXKNgOESkQNmNSRrRXrFgTpQohFoghaJvUhNt5LpgODGBqAhE/SqU9JGFqy7tAumlFmQZRDENiFAMtkeQwDLjajbjZbWseB1FEEFJI6kkqHg7mCSF01JoHBKkCQibonPHGsyCoah3p9LprodFp6+1fZPm9NiYCzplNNV6Nur69yPwsN7Cou+rZcdKvU+NfhMB6gN1Qx/MP9yz2+VbXR/cepZHI8Pa2lWr2y3eJ58AHjOXSJ5+tt+CPetqh3xer+/RD+l7Wv6jdM3VO8PspH6ednOv8gr5P210O4tyqd4IqAkRMFSrfOE0zHh4nvL094rtbwne3I+4fgf2RUeaiuvRQ+UFJACthVGYNBxyC2AKXoGH5AoknhIaoI4V7FrqPiERwWSA4gVRQrpL6jtcMktTZPivcJVMOWJz3xfvXM9P6PIUYrW5Fxo4ULopHi9L/Hkr04OtU/beAch3/W5XcittEfuAPhCdkOzKrwT23qJV6MTgPMXwCJF+EDVRCJlKlnRQr95OGRRhGj2KYT7ar2VcYuW1o196ib3lBnqPf/o21UQWiTbUqFACA2DQczQOifto8MKvcxES5aLTIYoxGLzcmtI2re87NR3vYnzvq18nNgYfYbZ1cJ+QHh7qvlgr8hg97PNpR+bZe9beFSXTrWPsgVUBIngdyY1l6NPYbnmoobrCuSTUWUQ9pQIXKFXGh0p160Io7S0IbBfGEGAaYkvFx/4D7h1sc9gdMxxlD2mCIA8aUQAGYpjsw71EGiZbAWfaBp4pO5kQXNSoMoSI7vhwK8rGAQkJKW2x219juXmHcbDEMo+YHA3hGjdgpDQYAEYVJlTES72BGxJEz9nzETBkFhFwpbpvWJxhCciCpR5CrheDCeeq/7US7ZYQ7d+6cLWn3FzKl/blevEr9zkC14lQepMbI8kZR1eNBFM3Qz1LM8Et+k37W5NP2fHE9+7P9wnfqisSbc797OF1xyAJIBgKoACHLuYrKN4hivh/S2rRfHnb0XL1zq7Fe43wtf9fhJqt/bs84eNtdXlx/dmkqEawQ95y8lVprvaL7dFgX971SXqaIUCi0BEYfWs65vTdr5fVNsXp1MS4LwSLW2EUTZzGyWoDbfflE84RgYJoDfv/dZ8hFEk4zIra7DUIYMGx22A4RX1yNSFGY6xijKiLEkjSEBKqKCKox7DvlQ0WQ1AO0P5Z/UuWS8E5dfdj+l+eKIiN5oNXgLLkfpniNiYb2ez+h8BH7/QG5ZBymI0rJOE4Tcp5xOOwx5xmH4x64e4v4u7/DXdzgm81nOKqX3sM04HG+QZ5nzPOMokqMuRAKHoGiBFJxBN7Ka1bhjlqJMBMKDdgPf4JYHsD5W1AByAlJKWREDgicEBSMcSiSbC6I/YkRehIzMyOzhYKCxrI9M6Bz62AQxxPQixoVg9R7fL6Ll2Gsj1ZkWjwR4AgLPyYiTZyn7265DZ4bqGPYan+urD69pEOeu/5B5Ryr29fpmCs7bd2jttaKzFVZ0P9eEhp0Ivc7eWVt1oIhse1lMuIwCMFfLReFOMzM+CYf8ZYDfpkTGBNCOGDkR+x++7fgYcC7X/xz0LBBHFJNeskAMpPE4k8JKQ0Yhi2GgRBCAigiplEEIiFg0oT107SXBPRZCNhBrdViMAt4Y9ACCIx9IAwgfBL2Xaze3pSjqRcAcwF2ng/1w1iQ0iXxrvZ5lQZX4b8y300J2rwczEpJ2nBwwQh8f4YZTRGhf53iohukI9rr72Xxdc5t8vachOWV0HWscVWHQPizz68xzQW/ffuIKWcRfHHz+irqjRY1FJPlx8k5O0WA2p9SqHFybVbN6tIYa6rwmqqgRm6zeHwSkFLCdkj4089vkIwG0rwOKZIwwKZIsKTVZEYcLedDH/NZJoGqEkKtk43pX8zcRYwH2dhPJA+LVbHfPcndQoRQ9+xFIMv6YPtncbsCUfIf6FsndBKhk/v92E7o7YXZnyi6Lpk3/fyB8NbHLie83nL+zwoQPvyFn9+XT92n/r4hqRXG3T/Tdu8l+G+lfHQ8/CMVO+erc9V7+8F9bUdMcDCPVygMHOaC+/0Bv//uHX7zdcF/+lXE/UPG29s7zFMWq1+KGLYJKUVQjCiBMDGwn2dQOCIdDjiWgg0YMSZgM4BiwLjZgFJCGoZq6NbDGqpCUckjgG4fc4lAjAAXSUTNAbFEMewJkh8qlIyIGYWCeNtV3Kdz1dFxziPQ8IJtx5ptFOgQpuFYxdP1b7mP/RLByabqNbOmZ0SChvgTYWUIOvYMNaKllWPq++P+fFeBMdXEwSFo3HKJnaN5KWRg9igzKU527TEACmC14q82zSzjMnpiqXKxe9Y6Q8NoQfOEQQyzzEuym6uTGfRXhJJk659b4moZt1rzKx2XLSE6zOpex2uW1m4WjTQ+scal9VF1g4bJPMidRQvj6HBt3V+90YL/LaOl1qajDdqzfp39GWr0l9NfVAWTeUnau/vZ7w0VWF9FDU9ZcrWYx5Lww7lyFt6okGgEwBqqqIAwo5S2T0r14rHz2M6XpADQEK4AdrsRm2HE1dWAcSDc33+Hw/EBX375Je7u7rA/TAATbq5eYTNusN1uQPket9/9WzyUtzi+noXW9101Yr15NMtCybwFyany+O2M490k3tTjiJtPdvh08wqff/4FPvnsU7y+ES+NoN7ShaK8m3onsQaCBUVwCCgxYuaAYwl4oN9iHv4WuUwig1jdVH6w/f6rFLsq53qvg+VOYHff1lqaDmy+VQEne5zs9BIsjFMXktY+jWQjiMGDwk+yPC4uBJS9l5zdfu39q5+euAZ7zcDacj20XBCsOSDsbFsIJtT9hApv2n79OEXP1WqbDibYuQ2SCy5/xyhzwvh6i/TKvPbD5UqGH6U8Aw//iZeLFRGGUL0y4uLyFD46QQrrvT939WwsZDYLaK9w4JqcuphFpFprTHNQbSwwl4Apjyg8AhpiKaVRQlykEeMQMaaIaLGM9S8GS6JoboNNCWGCVDlczZLQC7u8pv+lHgQ/9XKpB8BLPSG+D8+Jn8qcdrkh/PX6j3wpbPFeSfEPS5xHALNaFmSz3spZFA/zhLlkHKcjcs44Ho+Y5yMOd28x5RkPxyP4/hbx8Yj7FHFPwJwL5nzElCOOLLHK5xJQilgyFI1VaITrKQCgiuLNIsWYABAj8CT3A0k+CDsOVoXMPbsRjna7w/KVYCgIzEgAJrCGNjznKre6Al0P/j3WiyeEziOgkzsvwFUfd2eS+9a+83L8RjQ9DdDRGIz3HsZl19fq8flpbHLG/p1Oiif+Fm2d6m/6GtQ/3vDmmeEur1QbOlIrOyOaWQTEbIL3AKA0azezjZogwudDDJo3BSiFcZyOiHnGdPcWGLeg7VaYmhjBIBQOiClhYIAoIiVgZhFk5JJQckKkgICAYwEyB2RI/glLQm/JHmOgmqtFBMYSticHQkHGnCQkgDCKK5aBfsaK++Ws/E0RQOy9GYCmiBAivno+6bM1fmrFF821uFcwoD5XiXALIWcKC7TxuAcqw0ELGHPCJPDyKq9sihX4WenzppAYk3gcbMeEMBNKkFBLx9nwh84JMVBC3VfmxWDw15QKp/m6yNj8WieEppCotAsxxjFISL2UsBsTrjdj9WSooZgqTYQqWBDaKSJQrEoGo6MaPYXajvAnDTnU392wL6SfbJaXQnq9RicX3XVycLNTXtDKep72a0IbWvOIcMyYow5P38t5Fa6OeTmepxQlbTmfREfkv9hedjB47fnVPs+s0Tms210/QckXKoAc/XF2gOsc8gVNv2wMTzTz5IUTZRRQyZ/lM57eWvO8ufg1VzfEOXz//P73Y2tdGG5eIoZVrP7ea+Ra0H7dl5M22/yZoAwk9PRxnnC/n/DN7Yxv3wHv7gccjxnzrF6DRC5HoPCEJp6aGZgKY8pZ7uWCREV9LTTcjPGOJmyhNt8dhWLwUdwjKl0dSBMxU0AxAa3m6ZGwRgZHNZnu0rwSS7jKiz9099Zq2q8ufGHnubCkooAacsjgu66L8cdEJhRv72oCe7m/MrxGBNafvk71BDDcGAjIpqAnSdLtlAzyTroearRjdByqclD500Vfa/veR4Tw9WweRIC6AFMr1tfUbtqk1bqW6FbyRPh48UWVRUXjgnml0bn1RrdGtb8LgOcazOhwl1tPj1+bd4OdSa9kaPNl9ED9bd8dveDnZiH3ha1jWxNb7zWsxm2s9TzZWbM65Paf3wx+ItTjiRggzZHIDArqxaLjlfUoygjIAggtBqQUMY4RFMTa/XB4xMPjPfb7PQ6HA8DixToMGwxplJHwjOP+DaZyh3KzBQWpw4WRjwUhEULysHaxd9WIPk8FeRLdZwjAOG6w3e2w3YzYbEaMKSJFTfIOg6XWXHsXQ+5M4uGUGdAsj2Cl8jvqui7JAvrQCYXtaHg6WQHSShYlqN+jUtsvofBogIV7q6DYXmOFR1wOuZ0UQq/RWwCxBXvQ7SBC23eLriqb0dgTx1/pXDje6nl0eoIx3684EOFb6uCiu2+4DJkQ54QhSDJ2Cxf4UcuKEfxZA/kLZI/rO+BHLIsxL2Ha07TQmSY/YDgv8ojolBGXljUEvCSoz7T3vpuLHWIVyz9RQNRQTMzILka8JdHKOeB3bz7B4TgooxwR4hWGkDAMGqtzs5Hk1JsdtkPAZiPa7mRhmDQhtcW1hyoeak4IQ6QmeK3v6YnLn9im/WP5yZXlyaiCONvPGv/vSFeYeMA8F2SIl0MuBfujKB4eDwfMecbj4z1ynvG436PcvUP49X/CHgFfXf0M+zLgdvjvkAsw3Ut+lXkeUQpj5gfJt2KxBxkwq+IqQ1HvH7G4bYRkFWgpESkxGY/Y5jdNiJcYYdhUhkOYulhDnYUYK4MXatJ3VCqlsKhiPmVgYsLXhXGsrsbAaRTIlWJzS0sbiUtW6TlI/nFO+sWkAXmYs2CQFsOsClHGQjBpsQCe7OLHKY6pANb5ULnRz9hzArdVEYgjyv08VjsbzcpoAsazQQc8FcxUaVGPD9qUNmUEQlBvgIbHuDBmYnxDR0QEpEPBQITD7lPs8oRXv/qPmFPCd5/9KThGIIrXHsURm+0ONzcRMW0Q0oBbeo03x9cIc0DcS04J0ljUYMYvBsL1cI/D4YB5mpDnI8AFUdLPS8heiFeFudFuiHG1PSIQ11wSAWh4UbFfw4FFGSVdp/qp8Ygr3CuLT22nGPOI7vkTylw/eWlnpfe4+yztGa1E3fq6Ma4d/5NtwCf3njvHRj4Edl4MgfBnn+2EryiM45zxu7cPyJX+YYRCGsbLQmtpHGJj/CCML1cDDdR7tkYxhrqeBrtljYAUA/7Zz15hTJYTizCkWJkIolCfr4oI5ykRSENYmiJChW9RLSCDwvcmeFLm0E7dcq5XgNFJFa0n544W15dPN8RWj+1S2Gu/fN+00pRvlZYV+t9naeF6PS5vdB9PStyN+3ZjuQSEt619Efe6Xj74ubBy7cKHVzxQ1vvAGQTw3ENrt939p0iDF5EZT++NTgnxgV2t176khY9FFHwfxIXxYnx6GQvBCAJ43IIBTPOMx+OEL7+7x2++Kvif/ssOD/uCt3eTWpsnxEjYJIhyNUQRSgYIHiXgWBjIBfE44VAKrkJEArDhDRIIHCIoJoSYqoEb4OUIDFCQUxBYxsdAjALXgwmVYwQXyeVTShADnyCeiiEnMAMhZKBIglg4gavhZQZXekOE8nxuytqMaRvCe5PGMwdKIbRcWP1R6CBwA/HevqjihhgF/xX95BxRCpArfm9+pXU9ya23N/JSK3YgqIe5WLNHtQ7nEpVsDBXHGrNhyghi8XhtyjS5Zt4OlxrMkb64vTOpRb1Nhm+GYXNIvbzF5rYqprSUAjGgl5wkKJK/IM8AhyazCCRGbCWbcUepdJXQHOh0SeGCV2u40T51LapRpvGIysvpeIIq5HrvSKp8n6cvavhr4zdD+xN6JXQn2nhA8USAOB7XvUa6R9xcu2/L5RTRTtDcEKq80vGCNc8FVABubqelTSRpcpWU5KwQyWcuWfaPGuaUUtRfBSBKIEh48GGIuN4N2IwR0+EB+2mPL7/6Ld69e4c3377B8TjhZvcKm3GHVzefYEgR0/0bHB9v8earr3EMj6BPfo5IAygA857x9h+O2Nwk3PxyXF1TBnB4V3C8KyhZ6LnhbsKOGZ/9xWf4/Iuf4bPPX+PVqytcbwakFDUXK0Ah6ZZV/yo9PwWqhKCAmQh7ZjwWxgGMQwEO3Az2z2+2Sp3A0/CFmqLK7pozV4ddWKBHVPqowwKBhA0g1vC5+kBFI7pvFnilcpuef3DH1q72fuH+nXSsdkYBiQRRguRtCXpOCcL7aFcBpnMQmAd2Y2jDOD+Vy3F8rHKq7UFVyBpcIFQYMCTZ57swYjuO2GwGDCkJT7Hgwn4q5Xubu39E5XKPiHpKLicEmwfFKRH8PkqGKhgD0CwV14QUpoTgXgnRJXPRRJMsAOo4J0w5YsoJmUdJ0oOIMY0IQcJVmCdE1KTUYwqi+aWg+SCoIklTOoCaJaBXQjQNv74Ztbd8jmm9ZP48wfNTsez/Qysfmudira2zz54Ipxb7/YlnzGKF0RCNpGYjzGZNULLkflBFxHE6Yp4zDscj5umAw+13mKYJb/YF/LBH2BccKeJhCDhwxCMnFGbkeUa2vEfMYD1bNQQKIHueGIFnSKiOTSPG4BUQcgoCzfIZAgIyNvbuDFApCPmgDTePolgiAiIiJRBJYrqAgJIGlBArMqciZGas58rZkDFwkuT9yUVEr4xYo0LPrNG5BruxrJQXsfgXvkZPhJty+ekHTq2F1uq9n0hjZetfhrjPVqS6rks39vqYJxj9OjwzViu8uFtJoGVDtP5Qd7bptL6FdarhYszSRTNVV88IjUurppe1kxmsuRyESX4MESUHbJhR5hnz/hE5JlBKQBxBmw0CInIYMNGIPW9x5BHHEhEgFu4BBCqSkI+ZsceARCP2GMUTIz+CyozAkvzSEgnHIOF/MgIQCh5DQQqMIdRQ1z1OrNAMbm0cjvcWekpQN+8ETwuYIgKNXugUEcYAufteEdEtcvOyWB+fb7uvf7J3uNX5OIUkkTUTBmXoWTOrbscBc84oRQQ1cyb9Le8poS24wkYQ1LvFv5/QLEsvhVhDb8kbDpEwpojdOGJIAbEKERTeh+b5UJUMQE1ibbkgTHEtypVmBeyVHjXhpIk26lnqZ/sUItGiSn8OO68Esn/8nmm7tOJy1yDVGst+/JPrpev6ufdYCJnP3IZprJa1TvUS70GPV+nMEg+ufn3/sqZMerLh53s1y2KvjKCVb8v+LjuxF07AGvy/6MFuF64/Qv39k/PRrZmegRVc2fVZjRf6zgw19V2fG//p9dM+z1AG1Ib9dB/nyhNvd6a9/uQobiFCLsBhmnD3OOObtxlv7oCHfcDhKGEOSeFdNIWthpprejOdSxAKA5kZoQCZITQLG2YhV/f0Ddg3p0SNgMtmmS1CbGqwE+6e8aPU4KzfD2fnbIU3ajPFfR2Pcx3atv32LAXut4OSdqobkfwW0BxV/r3cnPXHQsXAXC/UcXl4HjRJalFenok1ZFM7T2xtGYWiltzVkKSOwWgNC61kVMfKeTtHz+q6Ggl4Uq2jE/26+fNeYAJ/E8pKUQMy7xHBqMb2gIV1sXYX1G+bwjaUpyhqd9bWjVKp5U3Q9TT6w8IFdfs3wO1j3d9uLFT/Q6Mj1oZlZ07XsJ2B9i49juDT77S47t+v7i+bJG6/uyoE9YdC0agAgYoqCC3XDLumlB6LQQxACABnHI57HPYPeHh4wMPDI3IWDUsaRozjqEpNxnT4DofH73A8PmKOGYOORbYMYz4CYSqYDwUhASGFyrMa3ZvngjJxXYMUEjYk3hCb3Q7jOGAYknpLSwJ7kw8SFwTV/hSEOk/sxpFZvMcKCYVeapjg07JAT/WaZLjz1/i0kn0hd7JZvYfQVtrAbW/L0Nb+PExj9++yzho8cFdqfw4eGH+h+7ro2YEqSU1eYcoSo+XBhi6ovUxHU7h9X1/LY0OnwOXVkV9W6rg8tCCn3LG7ilMVlya2SDRNvvpU4f6f5+nr+uDKua5fT8/vUwNY4oN26yk4CazdPvfMsuVnB/VBz3+88uJk1R5+Plt3SQS/Z/FHxF81C4NeAcHIymjLn3zPJdf8EC0Zpkx15oAv336Cx8MGIYwYxigJdWLEuHmFEBKGQTwexs0WYwr4dARiCBiH1KyzjaBbU0SAagiDZpGBxfxQowE/bMr+WP5gC7l/z5dGa/bus7bvj+EaEwYhEMqE4zwh54z7/SOmecbt4wOmecb9/gHl8QHxV/8B9zPhV7t/jYk/xby5QuaC6VEUevN8L2er+JBLOmICKBCiWrFE9f7ZlG8w8CPy5k9QwrXG9TTXUxVSUsYrfINAc016GvBK37FgeHyLm7e/7wRTFgYtxQSKCTEOlSD9Lv0SD+N19YSai4SNARici5xNzmrZpUTG2mnzlKxfDUW6jZb29/i9gN0T+ObiZ19cOvrm6Va8pW8Vti8Di7+gLHvz778khS5q7AnmTQjddaZ5qYz40LJsrhIezmq7VsQT805oCi9tpyk5NC4pabxitc43wWxlGNVaZ54mFCL8PswYAcyv/xSRCByTEnUDpmGHx5ufY97dIL76Ag/xFb7JrxB4QAhDFUAbJjblwbfHHb7BiH3ZIOOAm/KIeLxHPj6CuGCsHhGDsFZECMR4eIjYReAXO0YMzXOiCZdR583OZvVIAFeGWWtVZsg4o0rqm+JgbWmrmaV92o2miPCMkDXkYUXLSyH/dsStmEx2Xfji26xD8vfPUD3dK3QMrHAp9ayqteg/G65lO3CGhai8O0z47Xf3yLkgJqrGGJWvUO82+x3U8sqUAqF6NKhiQvOC/PL1TlzvQ+/x0BQRoTISCC7HA5kSAkIvqRWUKTlEga14RmHuiTDBhGwn0v8lw7FGd/kVoDMAag2G9Oe5WoSSs/g8eerMuByje2ZwXZ/9bbdXqL8q9Oa5QXQVX4RLOkEw4XKm4OL2z7z/yXt/QNtL3H6u/nth6HNY7sOLt+fs2z63kIt9vaBb6lst4deiCe7W219fGcrTl15c2hgXvy8sp1S1g+NPjNDLG9RuGoeZsZ8Kvnz7gN9/k/E//vWI+z3j3f0RzAEUN0ghYkwDIiDeXDmDSqmx3kOwcxnApGFTQZKriQlgUfpTFryYazx/ew1ejFJ5R+VBAzFCkD+EAA4RIWSUkEBhRuAg1u9ghCi21ZTFMj4UUY6cnEFTHBSWBNlcJLkutxxC/a6qRLbExycxDMyBkaCC+zb6xYJR7bNdIgQVoNlcmEK8xIDIDM6arFoSN5jYCZJfTtbPKCooXRUaZattEjQZEagAiGJYVYrmTAhBBYClWcwvViPUnk5WqfusZt3uTHpFRlNeQBQfzFVmaGDXQgf5sE51Zt3BEY+WrEGlChAiANJwXYLvJYG1Kl9sfZQ+EKOWlsSWbK7IBKCsZtc4xX8O5tLir+5dy8PheEQZo3oCkQoeY6ghsGMN3RgrfWIeEYEspJnSDkHzHlh+zsXYWNcX6hGhh0DMfjS3rqy0re5KWRij2NyThUELsqfIPEDMa1oBafX0JeknUJL+WTyRSy4gKhKeJgQxjo0JKQ642g7YbQdMhzvc7/f48ve/wbt3b/H7L7/C4+Me47DDdrvDp59+jt1mB4AxHe/w5a/+77h/9zvc3b5FuNlgE2XOinm9U8DhPmM6HLF5FXD98wSwz7cGzHPGlBnDKPlUr15f4/XmNT752S/w+vMvcHV9jd12QApAIMZEpmgqCIGxmR9REHBPrxAdzZLBmJlxyBlTyZioYGZgfgFWWSosirFSdf1ZM11AV1cVwZqPxZaVHNzxpeEWzw/U3hyZ73gS+wlbfz3zzsiqyikX0QeIxBOaCZUNN8WuhFOjCtu5BJRAYpCldHThIs8VMQzjIvCtGuGQwHQEzS2j+Qh9rovlJKxRuqfC8p7Xqd0J0BVYV9Cs0zzM0LOeYsA4RGxSxGYYMKYBqZ79c8ze91DWSYnvuVza0VP1ztyr23f9/vcR+t6XFygi2kE7y9h8zwviCaNzSgiffLomZOTcckRwC9MAIhznAVOOmPMIxoiQBsQQkdKAGBPSMCKGiM0g4ZaGIWKMhBTUZVOVDiFEmDBFbUfRMaSrn93bvWguTuJIPsFtvqTuH8vz5dI8Fx/l2XNnSoFGCy0m8V8zhNCcWa0ISkHJkoRakk8fMU1HHG/f4Hg84P4wIx8eEY8z9nnAcSRMCJg4oBTJB8EutAerJa3Qn4IwQpR9H1EQKCtxWHBdJFHuzA/IDEiWBnFbtRiUkTJ2VBDJwxUhmksGhhQRt1fqoRuqAkLCn4nLegiDJvEiDOOAMQRkMAoK0nREyTOYIkoI2LAIcA8e4cOfPsfpKqVvNcxCx01/FSC1G9z9vLgQzoYTWlR78kJHYHXXLxzQspqDlcJwOabtmSYW0Y+eqLje9fLxs82dG/PZ2Vg8+x54a41xFua0MbTtvZTR6axvV9Zj8Ywneo1R6SbBkkVQqaQ2QV2Fa1eSF2FWZucxRCQiDCSW6aAApggOCYgDEEcwCDwXlDAjStykJnikdgYKBCZkJhQk7GkL4hE0P1RvKElsJy7mkmeYwCEDCXiIkmh5kwQeWqK2HjQ24rIS28trOprGdzeaYH1tuQoPTukvx2gsLYQrLFgMT5nS7l5lPNb6d/dMmgAsrICe25S63vYI2fo7SEaSn4NhggRGKYRNKrjejMhlRp5NodhOmcD4FpM4kFn4miICTtHQFAzbccAQY8UN5HNAUPtdwyk4Aw0TIJhwmFSxYEqIEPx7dS/u/tVvDo+cwJTuQl+3PnNyNHsM4R/velnQdutjcmNz12oPyzbPjX/x/ueeenoMvt4pXfISj9BqLe8vPsm8EHAyT6dVLrzYXV/ii9V3p+dA/4oQrQoMuKt3djznF+PJQk/80mHoXnH3FpvuWXz/1G1etH3J82t7uWvupQRRa7Ttw/dpw4/JUy9+7rC6GSreDlG3slglH6eMh33GN28Z394CD3vgMImVLiGIYNAMZhQWigS9WbWrFLfmf0D904StLCeS1avfhEGWMLefCgcDiYQm9YJeJ5wl9U6E+6sKX9IEriTUB9nEuRm0770p3ymes6gEhKDolutzJtg2dM5tQ6+sWlsLT1f5s2kC8UJo7w2shLuzpSYlZ13oFEdXmbeU8fDtKb8rdE87YwTbQhZyysZAQFu3DoK4TfeEEMhvzVXavg1Dx7RS350hUkWSDZJKEeWKhmyqn+y8J0wB4cbpMCYCMWqkquXgK65bO7+9TMQ8eUwwaUJKkBo+BDgDhp7+aOGZzCihR5PtfLRx2fgbcJc+RBBLSga11bV2V9+lM3Bt3j5oT8LTz7JwVC93u11/S8J08ZayiLhCQ+H/z95/dUmyJGmC2CeqambuHhGZeUlV9fRgd3YPDs6SF/z/nwE8YA+wO4vGTHcXuSwzg7i7makKHkREiZm5B8m8t6p7SvNEursR5SqcgEgEsEHlUhI+TPI8nk9HHJ+OeHo6Yp4jUgK6bsBu2KHvdwhdwDxNmM4nPD1+xPH0AOw7uH0P8gKHTNFAlJCSQ5oSQtStAG7o62SyuCnBR0J36LE7HNDvdhiGASGI4ihvKCKAE1yaQYjwqrYTX+9yRgFC5BERnwAcwTBdV7XDud5H5fLmElWfdnKJxdNC02RL+8pfcfVmhlN8ofLFXrjYeN3/DHoqzoXr11dIaRVRkuyifvDiYWKD88ZjVPiiOsX5kCzr12sZgtGCNtyaCq7w5xbUoqr9+ixW35dY33iH4AiexfhJvA6BjoAtI7GL/Vt3d9m9KxfWa3K1srcWXv+4WHXGX5ee2O5z8/jG2sszz7RdHnzuiYvl1R4Rv3VZHptSKktwJXqyFfQ8iwIiRiSOiJxybD3WAyUI2+Gn+/d4Ou1BfsAwBPTDHj54DMMA7zvsdncIzuFDHzUBo7nBCRLwIYCgYWcEg2pYM1fOdkXMLMvX2rN/L/9tFNm/nCn4pGHGprDDye0wpxmRZ8Q5IaYzplEUEI9PTxjHEY+nR4znI/if/jfM5yM+7X6H0QWM3Tc4O8Lj6YSZHeZxyjlVoGfMLEm88yBN0O4tCZ93ONA9dnRECAGeCN/cP+L2dA83nkA+4OHdf0Tc3YoVNDmEDnDUofO/L7w+M1KMiClinicw3oG+/0e1ppa2fKgUESR/xmi9TwnvGBjHEdM8ITz878DxHj/c/h6nbo/fAzjTjD+liLEipmqCAygEfT6zJPCjEAEL6nEjuatWdGUxS3vNK21XFhefKy9WObyiTnu+Zj2W411DsozXNgjEupdca2CWz76hm28t63aqPlb/X3zf4LwJy6ld4ovKh+Xv5fN2NtTinZhQlPAMZJu+uoq2r8wSrulnYvQAvp2TMnsAEiT8oO/Q9zvQKWJ++qQErlmRrXvvND7qPNxiDh0+0TdIYYd9+owwnjFzBLHlIoAqGwmdIzwS4eHe425w+Id36k1YpXjJDKx9rZm8PO71NK7vXVgzs0xdEXt5g14VDrREm+3fxbNX8qhkQrlh7Ov1fmbXm7ApE/CFkRBmufJYYgazMLQxJtx6h10fGkOO1Vi51F+YfG2iCp1UWzb6yqPFFBcgy+tgyoha4EC531YfSBlBfcbZzFDNqJT5WV8v9OKKblxMKVXwrLqodbXAd0VjU1sdLWDaNs26brusX3tmi9X+hfexGDe77QevvFt+82Y7W0qJbY+TxbUiFXtBZ14H3VsUUfb8a+rMfkML5nWjc5v1mlJ4M0rtxbZfOM63ILtnlBCvVgJcYEj/zReDjZWgo6VPlufCCX4Le8Hl04QpJvzyeMJfPib8P/+PHR6OEb88npASAQgIIWDod2qp79R7GJLCpSLsxKqb4EIP5z0odCDvIbFPJEdBjIw4RRAIsQ/SV6dmbos49wCyQNq81cAO7BlgL/S7izmvGjOLQQC4CDu95JlJgBgFZGNeI5BFGsrMIsxOCaI0KZbynFIJE6nCbXbmra0KFcca957EM2KDt8+S/MVpt6fL+TVcgRzej1PBXVwl4FbVtvyGKmyqDUC02Pgaisk5mReZJ6jQHmDSMTcHZk2XsOE5Liqw2nsBm28iw9Ei/1/wClcVxbrHK2GxCZCtu6KwUgzLSWeFAZrV08Xnfra5ueQ5FXeIfwCbl6IKsBd4uXzS4g+A0RMoxg05V4QKxcl5kPPwLsjZ8U5Ds3gE5xG8GIo6O1eqtKCcR0K/U/GwXMxa/hCvGxIvCCc+M5YHJHtGMEr/dYLVl0EMPpQ3Xxq+ylhkbvMbCh+IWSzXlbaTE+6Fz3cMSglAhNOz55xDCAH7fY/9bkCcTjidnvDLLz/i/tNH/PjjT7i/f5Bz5nZ4/+E73Nzc4O5GIg786ad/xvHhR/z4yyfMNOLmf/pHhH0PCh6AhHYlhljOIyJRQkhB5Gk6PuMNEjPmmDA8zOg54MP37/HN736PDx++wd379yJPCwJ3IkeQZMBBH58ggZokN4RX633vCI5FSTu6nzGG/xOIEWm2ENCkwGnBuW/A8kscca3MsNwzmRwmCW9tvi/PU1f6oimuuPpkNGc9y28WvUBiDctncKURTGwWMeBhibqmMKFAoxay2mgkjJ3lYYB66+isWpgAgioiK9qQS31b8KvtGFZ9zwo/VEDB6R318C85Z1wB8hrWO3tEBI8dHPrOoQuE245x6+fLCsK/cvlyb4J/j8RYW16eI+IFk/Hy6drg6uzb1j6qXDjli6aUNGtwjVGf80HYnyIETpKMGgycJ8kF4b24/M08AH5AUIIwdB2899j1PTrvJdSAJwQvdEnQJEiScLEOwaTIv7LyywCzGRhlGNrORi0QqGbmhUzEr+0687XL18y/8G+xrLxULiHLpWxLkRjDIZEHO1W+scaaTZKIfY4Rc4wYJxHIn84nnM9n3D/cI55OSHNCjA7jHHEmwnEOGJPDVOVT4ew2XAg45xw8MTo/wzuG9x6BR3QxYedPGAIjeAlbNhxu0A0ewXUgH4C7d0jDQRQIaslBzsGTz0wGc1EkTvOoiFzOk7fk1CHkpKaOvHpYaFJT9YiCJj/F7gacIoY0ARMjkUcihwGSqG8ECizRlbCZ1qFXPxudO7L1uR7oBg++6Dz+Gme2FdV8cVUvLttt1leNCVoLwhS+VyGMGhfYTMijoYsudpPqZVgIqqp1ybSScIulto2hlES2z0+KEGnWRqnvmmHnYpttNtPMS95v2pa674M0f8SGMIqhCeCsNmWkPAH7NKFLE7rpBI4SIiL3H1iHtzK0xoCLEyg5uBgl/FnqENOAiQjgCJru4Tghks6gJhpk79GTQ5x7sIOEpECxfl9a98n8rBl+YyLK5eUzG32vmPzlelgMad56t3TkwlG/FujjleVKRbWgmnTD17Gxa8WR7CkCOAkzzk4IPwaWybnNSpSquusQSnZtqUwoForIIMg1Covqs47/DGr6b1E1yhiLpVtli7oQcFTXl1NXBrJ4on2wKIFo9Ryb0IXb99bLs6h9+QDV98scl9v1j83eVm1T81wLw9Z9WMODZYWXlWbgrb4tfxZ40Xr2XC/l3ZcgG1r32z4Xk3mtBwY3dWDX21tcyQJBsjq2dsGl6p6flxcz00tc0uyX9d6qH36udoEXr6VNLmD1l2yF54QtWslVeIzFHr3SVJnjMonrHUiAD2p6LALoKSY8jQk/fkz4+RPwdGKcJqgSQhQPQh9r7htAz4JiLWeW2pST6ZL3zZ9KTEWgCWCOEfCEqFbqjh0SqKSmr8fMnMeW4+o70vQQFqbG4LQpMwwnqEdEFuBbbiBe4TcRGFX+xFxod0B4boJ5RPjGaCLzL4qny/WNvZmXh/L4qtXJt/J8ppRxkXhIGCajUocSC3Vuh7qpsh+kT0YjWb3LFEJZ4EcFLBi+JRg+ra7xGj6208vtVzOssDmsP/PbjPUGNt9c23+1mjvBQnwSJDQLNNSWhEZJkgRXjRcKGbVBe2ktpLDUQkQVPFrDSlu4dl7znFfrldFafr6K2ILKAMIUDhbOkdr9bU6WRemBiyUriyrUUJajpQ+MyMkKmbxFy0yXs9E0As22rvvQiULLSg7fnWdFd2ISgWxiwDOQBbMlJ8SoOSGOj494enrCOM5gBvpugA899sMeu34vsMU8J8azhO0Eg4IYGBZOuEyW84QwOPhue+8qmw5HHn0YsNvtsdvt0Pc9+hCygskUswY9CEkSxNdrT0YVKiyCKGBW4bAawFRN9IpYq6a/Xsrl2uR+2UNc3ypfLu2hLeXBS9EoX3+ccOn+ujPFF8f+Xl5yyojla5kXa+FZ1ei6rXx+Cv7epkBoMUBakbREDjwBRAzPPnvYePWIcK/J9QlcNqy5/MLl9MiXWMSVovmFa1E91hqKvaW87MW1PPYVDS7H+QZZ9G/kEbFGYOv7tLkpapqxuHXKX1Rlg+WEiJoPIuXfpoxIubaf7w/49HRA1w3wPsB3ewxDh36Q37vdASF4fLd36JxDCELkBI2p7X2AxapXrrpimKki9IQYTTCCTsbx5v309/LfdKkJeAYj+h4x3CHGiKhKhzlOmMYR0zzjfD5jnmc8HR8xTiM+P9zjeDrh/v4RUwLG8AEzRTyeThjnCZ/TN4jsEOMk6CuxCv9d9vzxziH4Djv3hPfhCc4HdD7g7ulHvD/+hOnb/4D07T+g63qE0KEL/1EsVnwHIoeDCwCZEk+tVkAgCgBzzudSezQBRkg6TZJqSkQjNEkFXnL+YorgxPDOY44dTn/4HzBPJ3zzL/8fpONP+NPtH4Cux/dpxhgJf44SxKkQGhZmxShLu+Ea5lyIVDvQnM92QbQVIY6qqpqReQ0weBWevfDwRaS7vL6k0NrXt2iOl5RLyrat+0tBYOE8121fq3Up2CliYjlP+U6hrpr3Cx9ioQq27m+Qh7XiuXn6jRggE8+ZRdZrlkvCmGQW5n8Rc54y8ydMeiD1aAoBPQG78RG9i7hxCSPdYKZ3gCbBq2fNtlY9Cn96AFLC7nyUcD/0Hql/jwfXIcUJw6f/B9z8BEknKVZP3jn03sHNHc67PbzXRIRKXAKEOhzPtWnZJG5zvFCLc0vtGFAJn2oBB5UT21hMbbT9JbjcLIry/qwYT/3S1L/cx5lZq5Q2tSLCLc56Ys57lxk5H08ZSdnJlGGrNOkWORusG04ZRcsFYYqGbLVae0SgFTyQDmo1Lkft78yIVO9xy0Cs52Y9V02p62oub++3RuhfWXvmFcrk3VVItPGzYsCofW7L02Oznvws5f5xc3353EbPCLhk82eJzLd3u65pu1NfwQ62dV3iX1bdzutbr+M27li/V9d7yc7x8gik6e252Hz+hZPxJq8F/VILrV7Sp5dUvYR4GxTC1ftv2wUvgagbBMArW2Age1rJ/4vzDIFDPBwA34HnCXGe8XAc8fOnhP/X/9nj/sj4eH/ClIAEscoeegnjGzIOUVhBZlkqyYKJSDx7nZPQv8HDdZ3AyxDAzmNm8Qw+TRMCEro+ILEa4HiAVcJ6CTwYfc0Wl96x5kdTox3vJAcFKy/Lct8DSEnDeTBUqTDnygUcKC+SoliOc4JLTjwskoReTBYHPyU4JzmdUiIxFrRcEaTx2lMtZL5eTEliUn/zshNLBofonFiPq9KFNd+GZZat68/h5Jb4n6F4S6kr0hjqpEmDKxxoAvIiLzIlh+JSw/N4wa6t+DtUcg6G4W/On3a9FXsvqVFp1aQf+X6SNw1tiO+BKL/IJSCpcJwM1Lk8QA0YBgJbGo4KxpEo7tJSsF5wVOHVkD8FlLcGCTBa1Wgc+6386PLPe6VDLHmtM88IVzwiyIwqLk5/VkZkXI92bxCXZPA1DlrXtYjYkWdI5ohY7ewVNLDGXGq8RHQxxSshwRHDd5qsVw35vPNgPmOaHvHx44/4+MvP+Pmnn/Fwfw9mB0cd3r//DofDDb755nv0fY+np3uczyc83D/i6fEJBIay1CLyj7H0QXFtf+Px7g99pv+KoZXuLCLABXT7HW527/Hu/bf48OEb3N7c4LAbEIKswTxPYjwMAkHjPIHz3DjySOxBFEQu4AIIYQORsk3c4joVAN9uznzfsH7Ka1zGks+pVW+/G9i0XnOuu2M/1JCTjZ1uctutR7O5kxYwMXssQGFhrhztp3niGTypikk71gJjqTtzjibcbxh+WtWXX12MILPTXK6UPFO0OENbtLAURwQfPNJnBh099t/tsNt3GILIn9a+gf8+yt+Ccflv1YM3KyKW57vhz7C+90xtF+8woAlc9EBnDwiLW580gW5aeUMwGOfJ4TRKbHoAmGIPRz2cGyTRT+jhfcC+79StNqDzHp2nKhmSWGNnK5YqoSKcWb8oUkFBtNJ3yojWRvpSzdh/K94Bfy+2JyqWqNoi5g6bsidEh4SAOao3REyYY8QUZ0zThHGaME4jxmnC8XzCeTzj/v4e4/mM0zhjjoTH2WOOhOPcIUZonHfKfXDBwSGhdyO8JwSXNEcKcOAR79MR5HdA12F/c8CwI3TvvwHd3umZkvNUQihp8jeqQ3YYopNRxzhni5qUGM4tFBGZ8PRKtGoSVSNgFXkml8Qtnh18F5C4A/Y3YEhSLIojIjzYEXYzIaq7OSBxThMB42XS4Arz97Ln3ly26Yb2ESoPF4hjlwox0fbJxvoKtJO1Er8BqlrTkpcfzQzhhfu521QxG5frLVYzOj/LNa6oredmwgiva9YHtgoXcak9o/8Z/ZdJvEyo2uorXLEKnXhGnDyhA7AnsSYhJHH95pIfoO3RmtbMu4kBsEIPBkBiBenU1dj5PZgdjuTg0gx//hkdETh4HCnil0eHXedwM3g4S4BZEantXLTCF646sUEGl09bx3xWOfObqK4vrT+vnYzlu4uvWHERy/cboXw9v/Xa2cM5SFGp2pQRRtQrnKT6ORsDqyyGHNamYEqv6HxITggLMUlVLgfrgfaPkAUFJcxS2bt1/wp8tuvVbC0UA9QooFr2r54jonY+tub2WaXDUliPy4UXzxdVFlX92i5LkSE1NCHl+peKF1RzvXq/6bXVQYt52ujH4iZd1IgXOMIb5mCli1+K2KxvL7u53BHbePZSfzcnZePn5d40KPOZ8nIa/m1zuFJCrJRP5Xu9ytcUBVvBcup3nrtfXXhZyQD2+guyfC+c+K3quAgbK9lIBYYqi26ouJUZ8xxxPkf85ReHj/fA0zniNLLynQSvsdrlHwmZoPDUZOQCrIKEHCEnRnAaWsXCygSlb8mJUUECa3hUp2FSUhZEe96mEwpOIizxg3gNCLx2iZBIFRQClIsXgSNQqnB+gwGFTjbL7zo0MqcEkIZBJmTL/doDQmhss9Cv66nx/BLjVlJPrvslX4rnghkm6RhyVmf7rEaUJamk37eDjTbbsm704rm2TSbPPRdfW6aleJ2wCStZxIUS/ko/We/nd9aC7lyXCSBzvaja0JZJPCNEtsJimZ40R5Rz2geCpqJu361GVa8bV/NapqycqQpV5R+GsUy/I6ixoh20ukw3GO7MNEWlxGhqLM+hyiNxjbY2Ej/PJ1Hb/+qyeMgUeshom/LMNRjbVmYQtRiQuFIHsfLPCQ4ql3KS0wA843w+4Xx+xOPjA54enzBNIuzvQocQeuwPe+z2e5BzSACmacY4TionJ4T3B6ATY8Fsv2PnSPvnHMF7kXkZXLO8BABA0ww8Mrqbdxj2NxiGAUPfo/NiWET6otN8rZ5YlTF5EnReNEdO9QcL06UKwVYwvpzYagENCNsyVvSaLcIGlVBuLMAQVz9psU9WPF1z7us3L/Q8v9/yglvfr9Zz5c7SL2oFZuvf+cBXN/QstMZ4l3uxRuuUp59yeLRyfuXZGiHrOdNQa8F5DKFDHwJCcBgCYR/UgA1lrtleXCgS24Fp7/P+eIamuDzMVV1XX35BPb+JTOVy489f+RX69yZFxNaaVWd+454hqOXOB1Ahm7rUi5q4/K4VD+YJMZsHRIwZMVtYpo8PO/zwcQ8iDxCh7weErkPX7xC6DsOwRxc8vr3pMXiHLggx2IUgMQlDl3NCmKYdxqgTlf5nBNcy5eUAIyMsOXTXN+3flRB/L4CA1doaJroeo38neRTiKN4Q84xpnjDFGafzWXNBHHGeRnx+/Izj6Yj7zw+YEuE8njDNjI/Te0ypwzyPOaQZIPFinXfouoAOZ3zonhC8w9CbIiLh7nzEH073SIcbxH/4A7rQY+gCfBBPCOckb4N89zmhO5QxMAtaxjqxfEoJIXT5O4B8npzzRZEBApjg2GJnSnEExAQkDZ02Rw+gw/H7f0Q8H/H+n/838HjGePsfgNDhu2mSBPfKDDEzzgB+IhQxJBmbQhWOLN8rvImG0t5gEhs8vwUOX7wvLrxbNWCIeS10WDxEeu2ZvjTw/QvA05br70tKDTe33y3U4XNTa7CajbJ+CUG11abNnfXoCpLOs76C7UqEV0z2+pnSx6z0JwCaDLImw9qeVgybYC0kInxyhB0BeztKAmnAHLUBzsnb2qoKEW9tpXyTAFXSO0Ts5jM4RaTDf0QEcHQ9+PQZ/qd/QccRQxdwfnJ4fHzCt3cD/tP3t/CewHp22ZIbL+aiDm2Qv12kjwtjXB9XE6zaYxYWKmuyyA5QUp5mcdiXv1ZHnvLcA8v1XHNAS4H6WsDU1mceDcuwR5YvpOYjmBOSWpE6t3H+qO1fCX1QkkubEKAVoGtfjKnI1ysaRvdMI4iox7MoFsd5faP9WtNS9Y361UvKiMu01TV4dCnkFlVNbNOym2+tBBstRCsCmAutLq9z4b03lR7Nl0VdNS5blaWwaev96rk3IYZ2b2zRxst1bk7aqsnrc0a5nUYs8czbiyeuTVnT5gseemN5ifKhvV6dg62B1/VeQZ5X1/it472GsL/WHNayHtoyCGjhvHjUE87nEZ/vZ/y//+se948Jnx8+4zwlxCkC5NEPAd4FdE5DjFbCDfFEIMkl6CTGtXMenVozd12AJ48ueLXg1rj8SGACIicgzZhn8UrwwcMD8F5FxJXMrJkvQ2OOQCxKZecS4DzYOcB7uKTCTc0R4b30PzoS2poohzS2SqVvGnopKc2QotAAlo/BiUGD0xCvFvc8sRgYEQnNLx7M8pvd1S2XF07lsmjDl4tAOCsgHGl+B8VbFgpHKUh5x6K/y16olRHZK6LeNhUMvSzrqHwP1HN1Kw8Em6Gk5t+z8NGoeT31BjceKOn9hlLl2kNC72alRt1JfbcytgJIYtKTKNOyDAOsUfpcyW3RIFbb29xe0kmRtBrleaMXSH8UL0tdBZNHZu94nWa9BqVDavmKlXJSF7QAoTKOQElmrdcuOtomwzxOkiZbdZIEI9dn67+pwFdaqqZ3bM0syXKTuB1KWeQEaYW3Na7CESQ/qQM6xyDHcBQR5wlxOuP+80/46eef8OnjJzw83CPNQgzf3N7icLjBh2++wW5/ADNhnic8Ph1xOh6RkoPrehz+x38Aukn3Gkm+ARCCDzrnjI7E60u2FWuOgTIed5zgf064++4d3n/7Pd6/e4d3NzfY9QGdGvOCGSGNIJ4X9K6MmckhIsgfy2dCByYvsIW4KEeW9H1TDGZVsjcLx1YdXodynspeWtMapsSr9/sm+uTyt/RG4FoZWx/L1VgKb162O6HON5fbzZpFofFNOVk/t4I+iza5ejhv5zxH1UV2EMCwrPU6cq7v5ipVfqrbHA091TBxAq298+hCwNB53FCP/dBh6APeDR4fOkbntOKkENhwiXa13S9/pfIS4f1yTzeGo78iIfk3UF6tiGiJ3CVyuvrmhjJizUyY14PVm40qALUK4O18EEk9JRjgxDhNHsdzwGnqQC5kS+oQOoTQ4TB06LsewxAkPIX3CN7l+PXOe41Db1YqNXNuSNuQJCDW3vVg7BQskGQe+dZk8WoS/70rJJ5jtF/qnvQ15um5tn6LtbCwK00oJk20nlJCQhW6aBYGZZ5njLN4QZzPZ5zHMz6dJjzMCU/3T5iPjziNE2YmPI4OUyRMMxBZXKglkZ0QXx0d4eEwuB69S9gNPQZE3MYneDj0bsCud+hu/wP47lvQ4RZd6ND5oOGbPJzrNIRSl89RCf1QCESx5NFQak4UiRKORRQiqVIw1GdPXMmVqOTiIgxArbIcgjIf3hGSatSTd4j7G8zeAzwB0wSMT3BxRjeP6s7IcKHD7eEOKVshQwnh1vIGlpDenqq/v7QomIhgnGjhXH1VGIDmGd68ud0Trr6thQ5XJBT1M5t9W5A9azDfPMYXLHEvCTq46flSwcJbH8+Wgo0udJLar+s+LSu8yKU+35cXwJeWDKTVxSWz1hC2hpbqdoxgzl6FchblZAK+qBnaNhdE7VKXk4XPpFZNDIQYkeAwH/6AND2Bzz9jCA7eMZ6OwM/3AYch4HbfKYMqjEeqOEfamN+8Y7emPU+R7h5j8Ki5nZO3CeEqbdT7s1gBL8/HBmOcmffF/ZV2gcp7tGaAGqE6Sp0ZDgGglUJiwUolCwdisNShzltCF+qs6yt/ZRy18HqpaGi2GAE55XR1Td/CspQxtLO6nro1XZWnezFvqyNhZwHU1nv12G4bj1w7s6+/VwQ2bZ9bIcx6PMiGgO3U1XOzpCtXTa9LJWBanzh7acPz7lV0UrsGzOu+rt5o8Ow2ktmyYK3brN9YzvXLkAdfHCZd+fXVyjYoWTyiEIsWz1Qg7KIR2Bd0+7V0crGifq7it/Wnfp+4peOK8r/Ar+QCQF7yrbGEOT2dI45nj9MIjHNCjBJKRcKkFGMbwxFmxek8QJ4QQkDXhfxscOIdEYzfrMLHwFAcF2FlYjTJnoWV3jIyWcD0zKcq3ax8MHPSkHsu54hIZIJaJ7hPhfguw74lsCxeDSYEo8VvGD+v44F92G/GJrlUb9WLy0lGwXJWQJDiOqd5NvJezJIpW2duwpzkY/8W0q22fi4SSB1iCzvNw8FgalEktB4QWSGhPFAWZNpw9H3jDYsCgpv55DzZVVdtoEuvUOuz9U9vEq4npi2Cea2/JVwyTlu8VX0ulfDIOJAWT2+Xjb6t2BgRfuYQYITVvpO9wnDEqpyRioq3abm2Kg391OLC5dC3DbpUAaEGe2w91lClnZfcjN4lcJoQ5wmn4yOOT/d4eLjH09MT5nkCGOj7HsF73N7e4ubmFn3fwznC+TxhmmbMUcMex8/g9FHOgvHXQFHiAGqgrjDEwmwBwn87oZsZSWDb7SDKj9t32O32OVSdI9u/onSkDLsAM06Emj2JAo+Q4DCmhIf4hDNPCtPkuWIsZMze5oRW+7y6x2vO0eim+rGWQmi48ubbcjtsGhhXMC5pn5z1rT6eG2iw9MkOWTUuFChsbZffi57kPrwBwOU29cub5GC1V1HZS4Z966bqQ2/6OQvP1CEUL0Iq4b1X6/4ywLEqlx4vsH1N37w0F8RzXXnNyqxyzP4NyIm/JJTUqxQRXzJWY6S4xqa4NoGcrQBMHhlTFE+HKJ+1J4R4ShRt8+enHf78840IR4NXgs+j7wd03YAPNwNuB9nUznt0oRcCMfRqueJBJLHxQRJvUIC1rxAlqYvR4iDkEWxM3DPM7gsf/Hv591i4IBQAJdF6SmJRlBLmNGOiSTwhpikrIk7nE07jGU+nI87jiD+NDh/Zg84Md044nkdMc8Tn+QMmDIjTXKyfQeiCh8eM9+4BXXC4vTkg+IDd7g6H6RH/8PQzAhw634G++Q/w//3/DK9KveC8uqcrU0UBRKL0I/IgJbKSDtGsYMylO4WpnOOkFlps4zYCRs6GI9ecuwCGB6kbO4OSz8kDXXKYgzw3eiAFh8f332Oaz4j3nxCnEeP0AD+d8d39j/AGV/bv0d9+ADufCWKL7VsYOyArVzIPWzj+fHprWomq7/mnjG8E48+Ym6A460RFLUFUaANeQY4Fat/Ya/ZREWq5XxXsWUqJ8vWG+mq7icXv+rXNBxbvPZc8g9vnlozUi8smI6K36s5TO9xnyxcoIy6XBfGbd8+q8er/6pvhLIuLri6w4nGVkHhGTB4xzkiIYBKLRfYlAmc9z1bEW1HPad5ABDiCi04tKsVraZ8iJvI4ffs/g0+/IP2XPyF5BqWIj9OEp9OI37/fY9/dqdWm0zC6RZCdrf1yV8wyC9X+RekHV4IdJaSN4ZRXjIylzHizPcPcLLwxh/JWNSnGtBG15wWVgB5mTdfOZhHuoynZviErGlomtwj3aVF3S5ZHQOZfGWLOsAuFuQY133PoyarepVKi7ks1GmVkq3FcGCAt7wPIOTOofq71tij1AmW0bZ1LeLyWgdDm/Q32bdHnNX32Yo+FZ0rehbS8Wq/X5TqbOcd6rq5fuNgpsRTOB6y6kav6MgaoVrCU35fWYL3vtvDbukvL+Siw81K6h+dGdVFZ8hswhKWJF+CYJUjSayJPuLx3n2N0LzGdfwsM8aVSPNerA78oDELq9mAXMI8jpmnC4+Mj7h8iPj05PB2B01mSwHry8I7Qew9HHuRyCml4T/CB4DzDecZ+12PfHzSuu4NQxULHEkitrw3/ADHTjcoDRMlNUOhiieVv4JFRz33BR6TCGscOYAcEB5c8AEbyE1DliDDPNkpJDXySGAEwbZ4TZgCJkSgJnKYEkIRkZLdQUsCMCsWqVmh1ox0MH18/1/UtagwKxGo8wXIAFHy2/TqtaVwjgyvSbSl+LFdLXHtU61Q/klhzM1TXi/IgZd5Okvcm9cpWDwiVcbR5BtbT0uSLMIVHfnZJB6oQtKaRGSCy9akEmhaaCQnMZsSwxt9GI2n6DeVHSHFGtaKZbyrfgUJXGNKX49nyWWUQ8gxDBNkWqsr4J9trS/Rh9bic1Lo2qFiMyNscKS2rSh52spakyglR1KXc5ywLIlHiRcRiwBqbGWuURS1F77VDXuGz5CTxvkPwDrshwFGCownjacTp9IhPH3/Cjz/+BQ+Pj3h8eFJlkMPt7S0OhwN+97vf4+bmVtI8J8bp/ITTSUI2xzQB6U+g+RdwmoFE8DDjE10HkzmzeGQEJTISkhr/eYhpJHA4HNB/9w2+/e73+Pb73+Pu3XvcHA7ovXhwTQq3zA/Jl00EwCGxhGRK8IjsMbPHYxrxl/kTHvkJ4m2l3iDVWbVN1qCjJShh2dtMJYMLNQ+zngX1AF5sjjbvS+E5WSbDlgvK6qAsLpffQD6nW11cXSOjTUqPGzNFbcIUmEnvNnCIyti4aiPv72eL9YarAT/39CW4nf2kGz6p4BU7lPUs2Nl1cMGh6zrsfI+hk/BMzotctrJxfb0M4MXlC2r9dTr0m5TfqusvVkSsgDa2fl9nIJpNtjiJ5ezWoWgUKavV9mwhmdQLIqrgMKWE0+Tw+SnkjXgcO1FC+A7eBwSNWd93e3R9j74TrbGFj7E49mTWLeoiCxVGiirdFSlqPkxblH417pXafWOqtl5/IUH/GnDyt1eWDG51uaXrth5pvn2dA7MFbanZsm+t9SUlIwvFNCkxoLFXIxwm6jCxx6Su2uM0ak6IEafzEafxhPvPn/B4POMcHRJ7TMeINPU4TwlTTJgjKekgQh/nPRwYO39C5yL23YCeEj7Mj+jYYzdHDB7ofv/fIbiAruvh3n+LbriVHCte3NK9ej5YDhXxJvLIbniowp/oGJMl7GILJ2KuvZYg1yihVL2nRK4SnUyc3ftySA8CKFk/NCYviWW19w4piUs8gYGhBzwhpvdgjgKHugFdOkvfTBDovFrTaYg2zYZVPKKUqJeRlrWszjvbGhvVzgx2DuPwDo4j3k9PKwuqlpFpd0omJ1qeqN1Ni3g1DGFgTsSN0sPm7VIxJqO0Up3dDYXAF5WXvr8Y90vO2XIO67ayJSgvbtSVr+DSMzhv+VRu9nWTlJnkVTd4s79LQpeI4BnYR9nSlAgdEZzymMIUJ3H35gnRTYBjVQRYQAMCVYndk8asLrGgSzfkbAIVZ5MVkfLHiNOIOTEmx0DycJQwzwFzjOik0xDrqJTrE3iyudPzTOWxVxR7LXxvrWBZQz3pNbZ2taZqIldUjwm27GYjoF8w2zAroIXlHAG0bEAZppV3A4CVB4Tip5UFOMyG1eWwE8tBNMoLZ8IrgXmuUoA0yggsxty0qdfdhoWjNb56x/6vlBALQXOeliX8qe9v1NuuA1YPNIyTClCuBc28VK6Sxi+qYL3Odb+WDWyN9/n7FcW0+e6S9jEL3K35W0NcWn25UJZgdbneXHyPlr2rO7IGx/S6dTDlyuI8LF988bhW72wgjK9Y6KW5EmrAt3F5WUNe2Y1NUo/oOYXDi3Dxlba25m1tlf+Stpe/FvPRwDLD1QmRE85zxPEU8cefe3y8jziNCePMQBQl/RAcOu9w8AYjtX8kbKMPhNB36IeA/bDDbtipoU6lPeCWJklJdr8zulLpxJwrQrJAIyWG9wlgC0vUzqXlTRDBr4NzDGaSME3kBC/AA5QgYYs1wTOxsroivEWifFQyfqfSXxFWJxBHSHylGYklFwU0gXVK8puJwOw0moHMV2INksSQHAWGE7kS+eU2dUIuHSkzFnTqxUFUphDVdBq9mjUOKQ+HgOwp0YSjz22KwLSm6wr1K9/M6hlK52ThY60sMCF3juIgAt6UEpAY0ZQL5kGRts6D1VkrK0q/dBTt89X7tPxuhgD2LstoZU2KHTmbgYYqIcBCm1nz5Nr5hq0rZH8aWpF3yJYOSsjAUnuzXrdbXN0hG3u1hNkDB5wVQbLeNnapewXmbSx2fBnF2Z0h+jWq/pyQxqw/uAotJnMmg8v5DRwDaQYogUnClVk7rB4ByexZtX/OeQQXsB96BEcYAhDjiPH0GY+Pn/Hp0094eLjHeBqRIkA+oPcdgg+4vX2P2xvJ0xCCw3weEeeIGJMY9ZIHXABjAjCiEMg1oSyHwaKaTRPj6VNE6AndvpzDODmcJ8Ledbi5OeDmMOBmHyQkU5DQTkU4L+/kodbyAJIclcnOHAGJzkjuIzidNK+MzA6R5DNJNv8Lg6GmLC4zsfIUZeevSBvd/DXrnPcxizTC5R1VvV9/WWlGjINaNGX8kvEk9RkmOX/GltqZlCeKMkHCMiG3kfFqhVtKSLr2bNafzxUxUCj9a+5lqoc2wDRX9wpfU2jwFi9nyO8A5yURfecceg8MROic5ElxlHcS7EAZ9rvUz+1rZAf3ZdRapUy6WO+yoitoa6s/dfSgeiyX6C5e7bfNLl95b7Faub+Xe/01k2m/OVn1tbLqH9lGMyiPvH+4esmQalLha9IDFqMg7kmT2cbsETHDrKrvjwH/8uMNrCUf1IXH9fCux9AN6Loeu90B/dBj6Dv0HeB8J54QvpPwNBrL0wSqcEEOoDGESiCSEjqbh7hG5peO+EtO/m9ULhzNX7lcOFD238UObNz4qp39DRdmBbuk7ZSioC5VvHGKmODwiB1iSpjiqMqHM07jGafzGcfxCafxCZ8fPuM4EebTGZgmHKc7nNMtpthrPpUZzJMK6aFnJOFDf48+APvdAft4xj+ePmIHh12MoNvfIfxf/++aA2IQxZ4monbk4UOA8yHr6LKuTseVBVgAwISkjhhC/7Mkp2VJXs0geAIYSVw/jaCsgL98FyusRMjxP6VtYZ5c9GKBoUqI4OS8dkSAcxhCQCBgSHswD+DbG7GYICA4QueNkVNiUr08CDJusr/KFDUjCddG1+e6/5lAFkvwmQKm29+hiwn/4f4nkK49Fu+0G6XUYQ/LfmG7uvFeIdonZvwFE+ZaybGBSOtrVH8zjsYodRTRcPaw4MVJehUiflvh1ZcFMn0J4nzxIxcGRMtnK9Iwd4NxuaFt+JaJA6PStf1CpGwQH1VtBIInxvvICOzUepNAnoDISBQRMWGkE1LYYQ4jOCSEmCRGq/NFSK9DT2rZZxaaxMqgKRPG5ISYd+pyzcjMdZojeDwDFOHShNgFMGaMY8A8z3AAvHMtA64M8UqSyuW2Ubf1uhcCnvO+5GxPIHRJvdMLVlfieoGPyLqSOdOKvgEETpgClUqOBVR5pUCqOKUFI6TMn4mK2jHa85RDRVod5bmU4SNgsFgsybiaJ4vRmpkDDWvhNFSHtKEw9YLiwWYrzyOtrz9nULG8XSsPFg01dFV5tlRi4Khum+rn6rqq07HyyoDdR3X9er+36YbrzEH9Xi0Ep6rvm42ulE7bz12f+ro/9ZwXSJ4FkF9YXP2Dlnhlsd55bbB4ZqNQhoSr65eeb39XZ/bCK9cmcaOrF5563Sw+c2Rsg7yqzvb1C2fshX0o8PRNjePifDxbadvv185A+6bCYP0pAh+hqmJKmCniaYz4fEz4//35gM+PwOPxScKixojOOdx5hz543AZTNjNAjAQCBbHi3O93uLm7wX7XYxh6mOVzTGJYN8+aL0GFhIwITlwUwUonSyiomHMr2KeFVEXOESQDIsW7pCFURHDqlMY1AamagFNUMjeCYJ4RDG8HN8kezgr8zMJbTPlY5YkCKM5ZyCx434GFUNecES5HO4gMUGI1TIIksZVG9eQsIg5s7RGlSwiA85KImyr4ySqJNhQqXIYJ8hRXFgmfjlGVGEn3xmLvmDCTcx+VH0FETWtbvsomJBMD5kWaErJxZf4EI8EUFJq/LpXW7f9itFR5ROQ9sFDoVgZOVkfBOVxGVdPtlQS0wYmk/JstSb02jjLNtsQweYO6vHNKsmelY3JPMnpOij+sY1yNVxUORQ6LvJGcPJNsHypV18yBdkfym1R8SxVx1+TnIIBdzVhoHzWkmSepg63H7GXNyIstm2MAUTxdYB5EJFsP4tzEJLyxJ4/eS97F2/0B3iX0YcLT44inhx/w+eMv+OHPf8T5lHA+MpIDvB9wc7jFzW6Pb779Dje3t+h7JznBHkfE8xlxZsREYNcBfgLjDOaj8rHVvmGozEs/HWEaGZ/+MuLwPqDbB5iKbzo7PD0F3LlbfHj3Dh/e7fHN7YDbfYfdEJCi7W2ZyBXGtXPiJIRrjBbnn5D8ESn8GRwZcZL1c4a9HMvckYZqKgdusfNKM/ZIpAQCZcPI4mVcoydVFlKriM1brDozzrav7os2k3ULVxzV3ob12Vs8T+UMLVGmnfXElSLTktyjatq+Z8Orat7rphb1r2lBNLil7X81fzVCbsieBY2bJ4sKbFk8m8DwGho/eI8+OOyCx252GLwTL0QneKzAOWr3QjvaK6Vdo4tlxXc+88IbaaSGx381lcNVHVt1L2/w6tcaev/65Y2KiGUnn5+s9ugt7uUQTIqE1S3RQrPEWRP15usxJ7A+jx73Tzs8nbssALDkYKHr0Pkend9J3LzQ4zAE7AbZ2M6TJqH2cEFDMTkv1iDkARMgULG2zkLVelMuaKTmPL6dX2grv1hesmHeWscXd/4F5UVc1+tfe0v51YdbN7AGfmbZYvteiBaHEQOmRBjnEZETxkncK4/nE04nCcf0cP8Rp9MRn58cjtzjPDLm2eE8ARNP+ezIdpbk656AG39G8AlD32EgxjfTAwZPCL/7v8D1PfxwgL99h2G3h/Mdgu/l3UoR4bxXwZggpTaJV0UO1wlh1YohW/TAEkan/CfnPGXFTH3AjJBLSneKB4TG0WUG8wwJTKJJuAkSkzeIFdiQenCShLjQPoBMqeFACg/EWsznT0eqsHShKCvz8hrV3pDtOi5kdiZlhi4hkkPnGaCErhezGhOa1hZUkx9w7vbVtArM7MYjwnTCqdtj9kNmr7LWngFwQj+dQCkCDHhmfMMu27Y3c1tvyarPTakeqAW8zU7m9s08pnVtG/VeuaFI+oyEs5qsrVApLb+qoJmWtvRbR37DmmLBUZU629oaZotQCTVL2J9c4arf9ipv0B/tfqopyGL5vkRCImTZszo2MCQchKvqIMD8YpgpexlGNyGmCMyyx4gYlFjztxRrohI6LZXwcRV7voZxwg72nJB8wPj7/xvm02e4x38R68jO4fF0xg8fH/HusMeHW03gaceKF3PQoOBG3FnKYh8WL4R1KbNcE+KqlsgEzIIIV/ZIpxxACT0ghDKVTzOzq8LLyc8F4a/wzVoQZsLoD5frNmUBVXtRrF6L7bDpcUoO7tK/8t3qMSUEcr0wmN4wE9uT54rIoJmPa2U7lv+aEVoL1xfKEZv7nH/U1vkS/VCH1yrPlJbtPOkuaLilBUtnR74Zy5qJuJ4ct601X14pHS6sA20+dWH6l3CrnB02RlofexVJtCKJt6j96ggBBWc21VxudXmPl0OsYewz75YpfmaUG/fXvX5L2UB4r2IYFohpWdXFW5dnuJ3LC0/xK7vZ1FnORXNaeFEpr75cgNmL/bDa24szudqjpZXkeyQQ5gRMHHE6nXE6zjifPcYzIc0TOCV03qN3Hp0PmnSakL3liUDOw/cB3a7Dbr/DbrdDP3To+x6WjHaOCS4xgDmHErU8PolSgRVJ6OSUGBQlN4VYpoqHhGcVOCutVrzGCpwoIfUcnEtqaEf5z5TZCZJsOivIle8V2fKC3rH14sUZZKHlxZOb1WM5gZ0kRYYluNbwq5wkKTcnqY+t6hecrgxd9EuN1xwBcVFFxuNkc4UKpJM1vMWa5V81ZWMGGY0wMMlaSahY6DoZTyJvioKheESk/In8XP2v8ATrvmRa25acS99gY8xL054lw2tF+U8NPG7tvanMkVGcVPdLhLZyy1XPtXNp3gI5BJMJ5JUmymLZ3B1td7Udypwa/UnMQBIhv7GYKQHJmZGMy3xAjZ6XeHfllZ6HX5Q3clY5X2fz4qck4dgcwztGmiHKLBblhEPMYdiY7T2ritF5h84H3O1vBM70DnE+49PnH/Bw/xE//fQznh6PmCYHwKHrAXgPeI+b2xvc7g/Y7/eSF4KihNmChi1uxqr0Hq3p5hKGvEy68TLTOeHpY8rLkR5muGPC7puA/W6HYRjQd12OhpBPC5WParoBFkFyYvOIcDilhB+ne3xOZ8wsYeqMk08wpVK9IXR/LHHIxkEu25KzMsGUaq7ZEOXdGr7aWZNtkIFJWxZntf6ZuO0MNS8scVf7uaq1qcsGUitY2xp51Zt1my8rr0f+tFr47Rrzscw8FCFwxC7N6HlACF6ib2Tjru3KWhpTP94y1Lrwek43bl8oG/vyZc0trl1s/YX9eF0fXtL2l04r8Ct5RGyVgt8rtrmxDjAh4sI6IFkuiKKIqJH1afT408+3gIZhIS/eDD50CF2Pvtth6Pbouh5d1+NmF3DTS+IT77xacmsYGU1STUpMgkjDDBhhhvw9j2vjLKzg4d/LVy3P8o1YCwn/uqVx4AOwRhNi9SJKCNv/Kc6YqcMjBswxYpxGzFFCMp3GM47nE56envD49ITH+yecInAfBzzNB4xzp/kjJsQ45jNjsSu7rkMgxrvhCbuO0Q977NKE358/ot/doPtP/xO63R673QHBdxj6vYQwszBMIUhcXA3H1BJq1QizpUL1QVFdJIXJykoIId/BHNXaetZE9PMCCKrbOBzMAIaMIGBW64tZlBEchblyQq91nSakpx6cAmhoEToZHAidjk3HCA9yQRPfeyW0fLsZXUvU1aR4jg9bER0tIx6A29/ncTbu3Mx4cANiuMv4LCnDczN+xmF6xC/dHZ7CPjMupU0GYkL36Qf4ecx7bb/mblCWqiKM8mNlx7Y5wirmqnmO8wQwUtXUhZPJy3tL6jE/AjDwM2ZMJhJvCISKMFxYlSxsxBZtWylCvHx5GWtTb2yHiqlqWt2vLOXqW4tur4UlF+bFGKG20fzbE+FuBvoK/pAykIUrUfs7BigBMRIizYgYwV6TWroE5zskTfRZaF4uClPWUGuqnCgUfwl7wMxwKWHPCXMYMP7+f0W6/yOmj/8EooQuetwfTxjnhH/8jnG37wDyFQPJtRxrUcoq5wcubzSZiRch6a1KqOXZjS5oYuyqAgKVIkIzrxFMyKPxgHM/ONeVV6xqpCgEKCuFyhg02SWLgIeSrKynUketuDBB0xZtk40uXN3uhWJEfp6DxZPPzPE6pFRd8kFrqlr1xu4DOcTy821foA/quvS5itp7wfOX2zYhR3ttUXt7mJuq1vv1AlP3DNNXU+Pyq1q3WtG20d91W9cZy2Zvb7R/UYH4irZyjxva4xI83qz4cpsXr+eDv+jJBXjxgvIS4euytWff29qyVzvxXB+WY35LWc/RKi9FlnJexrFb465p/2fnpSExCNEPSM5jOk8YpxnHpxMeH0ecjgPGE2kyWEYfJEb10AUEFxDUmpc1GTS6gG43YHfYYX/YY3+QxK1dF2B0hZvFIwJwmGMEEBGTnvdEGhVAKWPNEQECYkqgSOohUc5ngh1dLjSAKh8k7JIJpU0BId5v7ByScyBOagleEFtRYBT80FAiiTWmTmVvboJhTqAUQeSF1te8EZJ8meBUAZFSEqt1tpDM1NJCuT/b69ZgfMW7Itde8FyZvpQ5NZU5NZXIniOINXgd9siqMEGkRo2WkEomw1CanLmEVrJ1NP7O6GLLRSAW/ZXSQukmM8o0GYl1YEGxZ1osd5Cq39iG32xjhsHElh6QGagCr3NZA860hM4fmSGL5ghh2w0GC2savNRNsFwQmixd86u0IKAisBZnOYFBzMofavJl78Ds4BKDvIXQMV1eMY4S+cwaL+X90lq8FD0IEUAMcdSVc1TmxkL4SqYD5xk+sXidR8ldSAlwmjQickSiBHgvyn+OcCD0wWHoO7y/e4fggeBGPE4jfvr5j/j86SP+9Kc/IyVCmsWYsN95hK6D6wLe3d3h3c0tdocD+n7ANB6R0pzzjsgQRNkoU+pWPKtshVbIyxa+lRnTMSGeZw29TKDHGcPkcPv9gJubm6yM8L4ybsh0HBbFooqId0lkQkwOxxglN0R6QtQQwgksyggSWJ2TVpOuoWlDM86wFeW8nmnBwHlQPgvEul8qtCMf5Qza3kmsXhBLMsN4ngskUxMGpzDMC2pF+wyDqwuAt6irKC2ruebyTB2urBxHXvxdKNtNbz96DdVeoUebW9lQVebAaXjAjiNu04Qb5yQUuPcIIaB4hFcVbpMKLZz/d1xepoT42ysvVkRsDXApdFxeL+duYR2r/5sSIiVTREjIpTiLwsEUD7FSRAACUKbJ4+PjgNPUqTJBPBtESOrRdz36YcDQ7dF3e+y7gF3vses9fFBhZK2I8B6wGPcwAq5G0jWR9jy9/lspIwpJsEHcfznH8KuVS32r4VFz/ZmhrK3d1i/8FsqJ5TkhKi03a5UJ76JYi3YOYkQC4YQdonpCTHHG6XTCNKsnhCamvv/8GU+PT3gcPU7c42kCxjhimkexbk7mCSHW0Dt3QqCIwe/QO8a382fsAITbG4TuFv23t+j3B+wPd+j6AbthB+879N0gYY7svIRQCJbNxSlx7rLiUIl0SzIvYaIk1JTAgTnHqU+cEOcxe0RkQsrmlCUnRVJEawyTtZHSCE4RwARghkMEiNF7h+SA4HoRjOaF03NuCbd9r5ZjNk4Lx2SKCPOWaLKEFpiBgvNt36VyVT9SBTpbS3z7boxPD4dd1VSMQmAPfod+8PAUcNb3inW0vk9A2PWgueqXupDbBWZgcgGn/qAMGRDmM4bxEatQQlxeKkrhPAqlx3SPg3Ac3iG50BBebSnj9PMZw+lzOw9Unumms3h37G7Qhz2MmOK2uvL+gjBc4SFeXG0er0ZV4bJ1TVaW54BzfYbrZNlbd3t7desYFThWzXFFUIanj3DTqWndmCZHDv3Nt3ChK7VVwgg0+IxUEMFwfMLAn+CTgyOPmA6IOEi9rjComSm3cECcU6ahxC1t51K6bRaEUEZ9hrd9SwxXxdxe+bBQmYkmXzrl25vtNhNUr9Mm7NqiZik3uCk8J2QaobZAtQSGUMFPbQVoLvG0gCG1UL8R8CvDKzxkE7gJDLH6k9AXrCEPCotTh1uyPi4FTtI8ISsjKF9px7yY5OrNdj6pvnu9NMzKehFL/fn5ZTv6letlpsUD187uRmF+vuNNOxuP56aVBrhEM2/syWr62ieeU+5s1dN80X3B67eaN3ijv5tN0+b17V4a8Cpr87xC8PL9jHIvPnp9H62uvoJkvlTThYevd6t+9CV9YF63/wqG46VPLtfmazK6Szx7MVcELxZ4uaEXx3s9L/X96kwvGNXEQEyMcZLcEH/6IeDzvcN4ToiR0SlM771H7x08IIpeCBloYQgVqEv+NR/gfUUrq7La+QQPh+gdPJQXsPOaGJghCZ9V0CRKfiDGCEJRSCQvglFkmL8YOgnGSCQ4Q5JQiwLCORHcknPiUey8eE9qLKecvFVxATugJAOo1wfZ+yFxgkuuUj5oYu0sFCuKCmhYInaSvNqxWYk/sz+paVp+c8G9+k0HL2GTxFNQBeEtSYilsE/oNTFbyXSKKR6YVDAqdEiChV5C8YZIElrJ8mflhNQmzYSEE5JPRvECN9qpdDDTeoWZaPu5nJv8Hl+Eq4bvzVCieB3o3KnhhHn4gEqi2bYh5bkUnBO7Etc+96WmK1yRq5ghmbZp9WdFB0Hm32ilZnisXp9mRBPhUkRMXnk6zSGgiiBRRBA4w5GC5UzpVJMdRpZLAnSdLx0QEZVQTrrHZEyS/wGJQOzhSEKbOTfBUQIhQtJYEwCvfVOlGAG7bkAXAt4dbtGFAO9PmOczPt3/iIf7T/j5p484HU8gDAjewQWvyXod+t2AfujF86rv4RxlJZjJzAqiNGVMQBj+IxD3SPSv7U6istSyx1KzH1ncB6TtfsBu2OPu7g63t7fY78wbg5TmkQPk4wjiGXV2BumLeGIldnK22CMyY06EmQkzgJkZExMiC4y285cXjXU9Wtcs2ym697hoa3UsEm8COU9N5tNUx1H2pfRUxl6dwawsX5QlgMnz2O7ffGfzINtCLLBkVXXmCKsqrI81j5jA2RPNwt03pLD1peFt12OwIW9B56W8c5tOsHoNaRY+q5F9gDIedc4hTg7jdAANO4Qh4NB73HZA59uubHocL/p6iUR6S76D51+5/MBz7z7fn/X9a68sw3RfepcX9y8qsr9y+SKPiJesnQkjNwdvoR001nSMgpBzEupoiolZAJDFzgdwmgL+8vEGREESTnsvoWM0N0TfD9jt9ui6Hfpuh0MH3HRcufao8sK3yalzfGc9CKTAbksJsVQC/BqKh6Xw/LIA/+2N/5YKi4v9rxDfBVj3onqW5bdQPtTlEm5q+mICPLWQMYuFOiRZhMcxdcoYSVLq4+mI8zTi8XTE+XzC0+kJT4+POEbCY+rxOB8wTzPmOGKeZ1XkifCz8wHOEQ7+hJ2P2O8cBiT8/vSEHXVw332H7uYON3d36EKH/f6A4AOGbgfvPELoszdFCcUkiMLcDYuW3uZACSKLAavhW2KK6vkxIaWIaT5LP9V6I0a5HmdTUBRFhPF5YAmVZIS7UwFpttJOsygieIJYmwj50gWLOVslY82/Hchr8nrXqeKh07EarJCxe+9RJ7NuNkBFyTXWVEDZ16JxKntjsWmWnhEA8F11f05mTSUg/LZSCtTrkYXFu99VdTGEDGvbOMLjp+5dDueyjyd8mO5XG5rZ4uDKdQvR07YpvyMDcfgGowul6WZeConGDPTTE26PEEKNsar38OmIw/EzOtrjZr8vRFepuiKAm243hGAzt6vzyvmMlj5ifbDr31vAv+oHQ/EXs4Q9YgnBIK9WOKYu+tNRlfy8SazIuDnfo3/4seYdYIpzDh3u332L2HVNnTUu4/YGgITAJ7g0g+Dg4XBywJg66Weiao/bVFVeECpoYOtrvq7zYX+AnvUExBkhSVJqKP/r6tDQxievV6meJkAZm0zkU/1U++TGNG/UbvjeGi8r1NAFKNaEbRgMlz9hv+Ey7AR59WxAEaDQRnt1gurM/FajFmQiwgfziOCY6y1KETSfZXIrOEjlnTw/FwRc1343c3f1ufU7F++u2lw/35yDVb3c/lyW+jwzP0uDbDax/XNDuLbkPtc9r8+z/H7hXK5u8KJPlPu07m8FF5pqrtNRl9ZiVZjRaBDrcV8Yz3OeEJefW87x4rlNRvt1tPCFFVv3g1ZX8vMvbrEWnNehxd5QXjzOZ/b1awvXcHWFnxcXajzzkk4817nNsVAWMqXEmAmYpoTTKeLHXwZ8vgfG6REpRgS1Ah68R+8cAlHOYMAAyEk8dVYhLqnnbDFcKcZtEhGU4b3A6+CpogdKqJ8crlgk160igswYgLLguQigueB5J/jXQi4VBYQHMYs1umO45JAcC35i/QSr8lq87EAFnRehknlnJBH4qvcDW2x4p4YJyYGdJNjOigjjD/S5jHev7c/Nc1u+WM44C51KEMVIka9RPj8C5hf4wahSFsv3LPzUT6PrRCZhf5zXq4SsNBq9VjQYLSvtWK6MxlirEjA2rrMLcnXpJQ7Se1U7a/xbGx64JgwXAE347co1O4NF6FHaY4bwQCmTWly105xnbQ9V2+U8WJz3mtijCjWYSUWFm6B0Z0pIlBAR4TTRd60Isvl3cBIizHKpWPV5aGV8pOEJzTOUc5cW8fGd7n+HnO9QU83DQQzAHDGIRAmRc0NAFJ6RVXlBDvtuwND3+HD7Ds4zgEeM58/46ef/gvtPj/j5x0+ar6SXmPmDeexLHpr9YYfdsEfXiwEdo+xF6NyVNOAA4OH6f0RIe0zuLwBNmfwxWjTT6QshJpm1h3fohgHvhne4u73D3d0ddntRhpCjhv4PfIZLlVJE5YKqNgInU0gEyf8Kh0kVEROLMsLUGGkxkix0IVTnZXmm19eZJaOLh3nPuOb1hhw0Pi4zhdbmirCr2qzbLXs2kwMVP26zsS7r85/lR9ofC1NfPLj0t+a+sTwz5m1lfFjTz+vk3WaxuTDYcVHuVS1TbiwPSQ2mlOCUDz3tyjOlKSCOt/D9AV3X4dB53AZGcAXOcM5L03Yiy2bzFevrywb8ssdeN3l5Cz1b+fP1rkUSL6vz4mN6jup6Xr01Xji3dfnVQjO1Qq8ljyc/DEHPUTR1WfFgCgmLlQ9gioSfPt0gsTD1cwzougHedwjdAOdFWLrvA253HbrQoesH+NCh8w69J3hPcD6AfBWKSUMwZaSYkdJ15ujv5W+//OZKCP2fjCqrruZiSMT+KRGeAIzugMTAnGbMiXEeR8wx4nw+Y5xGPD494X6a8cOUMD+ckT5/xHmaMSXCeSSM3EkopqSxITmp8oCwd0f0IeFm6DCEHvuOMIQe4cP/AL8bcLj7Ft1uj/3uBsEH7LodvPfouh7OeXShy4oHS+YOIAupzGqiVjzMMTUh1eY4glPCNIuiYZ5HJI6Yp5MQlOYRESckjhKTV0yNAAhRVzNS7Ly46JJYGJEST4J81RMEEZ4SyEvy29bKiyRhHwgE8W5wTnLNBD8AJIoJC9GUFZbOQqOYMgR5LmTltwQiUGufcok5XoHyhVnZgutGZNdCf2GcCjHSMDiZCVPGp84Qodd3TOjJ5f3ZpQG7gar3rGsp951Rt7/+ZAAdHGJF2NUEkfXR6gouoO++KYqI3D/BBX7oQO++wcH3CL6vvIqqqbQ5sEmprsWKmKtWRvGv9VuZKCXypNPyUZIctkWYmpbIYSOurG3Fa3OKYEooKR5VOEFtjZlhrBJwWb+EV2Lw+28w39xUGIsLh+UIoXMIbsoMUGEoNyRj2pZ3rAyUxL/27gEDJQAeiTzOvMOEviGM671mVLLtjWL1Z/fQrJfTnDNd36Pve/TDDl0voRR99lasifayd5ZL0RDzjAJ+sxHBgvFuHip8d/ndkrC0wXgYvM/8M5lCQT0gTAFBJewjgZQGqRh/rYyqNTKm0BnzXnPQOvdm/UbVp5h1FWvW3BeyfBVWT51rYtF+Ne76c3nBVLnNG0sQSLbPy+lZv9UybTrAjWfatreep/ohoNk/y1vNq7xxn9f9aDu1ZHo3Hlk1tBzrapYX1RPaZblEmLZ9aYQsV/q0sVwZhzRPbFRFW+vdlOU4t+epPWvPE95Z7rDVLbo8n3UF2zv9mXZXB2Gr1PttY01f3N7WWbo8hy8r/Ha+5ov5oarv9tXy32AZUvXKWX1Tu+V7bT0/uwERDiMTpjnheJpwPI6YxoB5dnBwCASETsId9t4hOCcSaJAYyhDALsjaeEEEDCCyeDq7RPAsNGMWAjsxoAkBgOVmAJBIaC6Jb08AO7VklRBNiUiSwJJD1BwSLp+Y2jCGyxUnAnUR0EOTWBNcktA4qOLC29xkxQWpgI5StkSX2gkmwpPQNwmJCR4JSFHCriTJgeHYKS2vtscpAU5kAM5ZzgsIXW9HZrXNC75voHkhj3R5qzGY0oVF4FvOo4OIjRkmPgYXsxjDq1nQl7h4PbCGRtV7ReBtYZqQhYM5d5YpXjKNWeg5m1E7CszI1HnZu8L7gLdzG20KZhfTR9quCO+oAZHFmwdZ8F4cCAwGUVuZfsl42yX1RCBZ3xqeZ8VCWRcTpNee9az8lHns5hCUavhFjnJdlPeEhPSNHJE4indPJDjvgETwJGuNan87UoePah5tLzk9u0kcg+TcWGgzsicLfpXxeI0DJYqRBOkLg4tCh4A4jaJEZCCQx+HmPfrQ4bu7OwRHAB9xPh7xy8//gsfHB/zw5x8wTwn9MIhZkOuk35rvMHQB+/0Ou2FA0FCqoswCmFNF7lOmgRw5JKeBqyJh/tNnwJ3gvn8H6vyKOtEVUC8IkvDnpxnd/YzbD7f48P493t29w+3NDYaug1f4xZzg5hMotp4Q9dkVD6OAJ7rDyD2mFHBOR0z4CZFOmFRZMKPkiFjsaP2afRp0Q2sLhisZohzmJf3ZMI5l0zPUTaIGOLU3h75vjEyGV1zarkZbcaQwXon0uuh1FvRpPVsVfDOecvVMbiMHac38Vq2oyBoMVP3c6O92X+zVggHkWuudyc23qq96jgCdZi4Y377lrIpEGjlMjD6HLqALHt472X9LWcoz9NA2FfY1yuvosDfI6F9c15cqIbYMM79id6+Wl4dm2mSaLj1cADXzeoKK1bJqbWNUNzJLUls+bdNP0eHj4wFzLCGYsiKi38H7IDkgBo8P+yCCjRDEfc1LPGaz5nZeBYvUIkERrrpqeIVAvjYnz93/TUsloPi3VHJ3XwgtXjO3X2sqlrK7jSfyXthsslJCZIEc1H0UHqMbEEEYecScZpynJ8QYcR7POI9nHE9HfJqBXzAAySEkhzEC4/mMMQbMmpQ6pll7A3jv1BNiwr6fcbO/URfQHXaHG/TvvkHX9Tgc3qMLHXb9HsEH9J14QAQNYSbu5VQEayo1FcLW5rgIHiX0kpzpmEMxjeIBMcmnKCYi5ukI5oikoZpinFUxMUGUEJwtTISYcJrsTqzJ2hgtNs+G7CVHhBG2wQuD5b3lgOl0YT3EWrlXj4hdDs0kCgoZv7wHkLd3KhBKz20SKkQvM9rYPMutcn3TJi6u30CpKgfHWSkpqu8NUYTmmXeL38zDBvyOAMeLCohlvbemCLH9YUQSUjkH+d0AYLdRt47s7h0AoNfrYjFYnjMLoE2lCDNmTk1frvU7z5lxl9gIFaQlh7YxqynWsEPVOsxpQkoJ0zTJ73nO7xRXeauLmqRxW+spX94tQGbKTCMRELRfnnxmzoWWpc3x130hEqajJwLTCB4jZgqI0WNKnc6hzGUhZsuYwUUBkfeqEcX2OAqxGbqA0ElSz67rJfatemHpwZakhAAY8cJKLK+WM7c6mfkCl3k3xs0YdSqP1p4rxYOAqvvWnHog5OcsRFMxejAm3MI21V4IlkvC+i6XbR5qHGNzKoIuSb4nDKftU6kLQKWIIP0t3mW+aXv5uZzTNXgzNdriyUtzXl9bKjyMV26WcL3Kqz5cUAS0j3ErR9mC0ymtOiz79OvRUpWo62K5pAhaz1fFNDdPKttF7dXXFrqckGX97MXnFmOla8+WZ6T968+V3m0/t9nO4tLzNN2lcq3lKw1qec2O2p6HL2GrFzTT4tZvW7jZtmuBxlaHvmTslP9ZPcl3mClgPk+Y5ojTecbpPGOeCTECxCLM7AMhEEmCahCcwl5OqYQsVEt8EHLYnhgTvPewlAoM23cF53sPJGJ4AGQhRyFxss3KmwFwYkSlr52FeGRkqLIU0wEo3lhEGY8ZHQ+XKoGwXSc4NmW14a5Ch5Q1YZhiQXga84iI4hnCEQwPmDGR0eSZDkDDLyQiy82NRrS1pM8Wn+3qGrozzwgRShMoC7+yFa4JIrGg+VIVVom5KB9M4WB8XDL+DfmP83du5BibtFstI7mEGayLxmQ1ytp6lat3mVujp7oaLOaWdH9kYfmCwqU6VBZVm2oJl0TRI+Fwld9q1s1oGd1TlUe9KbukrdobA5nGasIAUztqBosyMIkCzCePqLkWSUN/meA3CzhJTXNqGk/XQeTo0khKBOc0rXFq2y31iTcRHIHdnNc7ZQ8Ao+eAGMW4kFwH7wNu93fYDwM+3N6BKOLx6U8YT5/wl7/8C54eHvHzT78g+B43hw9wPqDzvY6XEbqA3b7DMIg3BRltzZX1e17baiMoTSrDIPCPj0j+CfTtLRhe+YPqcdicK63qHPw4o39i3Hy/y0qIm/0BfdfBk56LlNDFES5NK0TL2jZAYHic6AYTeswImDEj0UckRPGo5yocE6EYh+WO2gUdJ7e0HowmZoN9BnuqhYfRZtXgrSGdy3wMtddojiNlIFz3qOooCs9p3lgLk8VF8/Wl8l3hRNOIwSqYuKTIXY0HQzEEs7wXhW+z2nnZ8XytgS0bkPeyPI7bb1kGUQ9V1RFUqyWQcU7whA4BwXv44EtUDNQ80KLZ5cRy1U5958X0zuUHX8serGU7b6/7NXXV9V2WL9Xqst+uvN0jYpv3y6U6epmAslJ7QjAnxLlSRIAbxD1Hhx/vbzDNAeR26DQEk/cew7DD0Hf4sN+JVaXvMQSHXhPS+hByCCaz5G4+q5iFZEx+xk5/L3+VsqSm31LFb85MLdrfOhRGwJp1MAgj7ZCcFwElM07jhJgSTucT5mnG/dMD5mnC0+mIp8cHfL5/xDEyODmk8xHT8QlPk8cp3WBOAXOahZCCgw9VUmpPOHR77LsZt73HMPS4u3uPYXfA7eEOXddjvz+g8wG7YZffE2utTpMG+ULQVML0EodTzm9KCfMUEWPCqOGh4mQhmE4lFFNKmOME5og4n1QREQHNFSFUfgTBXEGVeGZRFnIiUUakQr4XWssskkUQZwnsiQhBYYH3koSafSeEcaWIEO+HQRm0riRTI7WyMYYNG4rLa3u3lmxuItAKaXP7e1nEIitl5F4QjJIUldIB3FpYZZaHF3vVGKIt5UV9qDJxU9Wx/LR36jb0w4jkxkoe5ehny2lG9ak4Ifeeq/6Wyi0O7yXvjBI2aDGuZhrquvOEIitOFmUpwM79tHwlWRhfhxzU+K0VRZaVAGTW7C4zY/ValDUUIUm95Wx2ipUy6Tkwzx/O163dtg+lH7bPEwiJHc6PTzhFhmcRxHAS4Qnb/DDncAtZwKB7pQgiSogCcg4+BBzu3uH2Zoe7dx+wG3a42R9wuNljtztkjwHbb2zMfRRXd05GeSOPm8jmoVqXxWc9/K01vOQxkV+qGVgqF4s3BNTLoHhFOI2LbFaATvPP1GE75N1KeaCLUlunAmUbJo5gdkiU4DkJXLTeVAKGNjRTpVAmlwl+sXpbChBsDurxZ7FE81meLszE1bJgFkn3Ym21dvXVjWW5KGBd9WnjOefz2V+18wKaYt3rDVixwQxZExdnLG/N9X3p3/L6M8T5iwksPadvpMfyuXgtQXZlvIvHrrR97a7RDG8lNJ97z+q+Mu4XT+ql595O5L5kbn+9spj31Va9JFH4GkQ9NWNPvge7IPHIU8J5ijidI/74Y4/P9x3GUayLvfcgSEzqQGogYCMhiVboHMGFANcF0KBKdHLZ4MCMCnxw6m2oeNnC9IFAZMIuFs9/MCg6EANOwzYlZkCNfEAa2hAEzyyCNb8etXWWRLoDSiIAFstowzsaZjTHvi/CUzvGBOR4+mU5UhHosYZjARXlTEolTJOLgp+IkIhAqYSYmtWCvtME3haycLnsL9oFGZcprvUSggpJjJkcM3JUeJK4OqJkqbO48ULxwJnEsYgzxTNCFRcpYempXN7jBRhc73Mi81bQiV4YWDUeY1VI2EzpK2m3JWRiaQKMKrxtrRQANd4Gdi/vDZ3Xgh4512n9L4oSyo/bHrL9JjIZ+STn4CsaCCAk+Ny+fGh9FkrS+gWvebdsdEpjJgnlmyKBkwdSgnj2OnjvELyDN8WaY9RDYOsvlymQkauyzTEixMufQJiFsZI5yThLziW8CL45EVIiTDFhnhO60KMPwLu7d+j7Hu/fHeCdw/n0M86nJ/zrn/6/OD4+4OOPnxBjwmF3B+87dJ0aAroZzgV0rkPfB3RBDOcKnyIKIadnzFYq74lM+zEsPCdV9Ge+r4c+9IT9e484Ms4PgPdiLDTsPW77Du/fv8OHd3e4Peyx74N4dQDw8xEuTSCeq71e4xydLRZFwwSHkR3O7HBm0nBM4lGWmhiSBGebcBPF2kLoouRLyvvkaSCJsABkHiq3YtUb6WK8Y7vQ7cIvjQqNJ615XaM7ar7aVigVpUQ5V1ylm6j/l86ZuRG3vQfnf8hKTuPLDIgRuNLolHC/uYXVd6v5hWXrwXxW7YwZvFjTBOK5J14/XQjYkUcfPLwZkFftFBlCNYOLn5e69KXleS+Etz//3LNva3uJhy4828zWr08rvk0RsYQnG7RjrXnJ2jmdhKUnxJyiWh0kDeNgITEIMTrcPx0wpy7H2/RdjxACun6H/RBwt5d7wYkHhCkggg+ZEHFkYWV8Zr4zwsuhE7Tzr+S8XnE8f72y7HP9+68tma/KC0UMXwY1vnS8F9Z/We3WY0Xo2j4sBGwloAMwhR6JAiZyiClijifM8yweDvOE09MTxnnCw/ERx6cnHOeEeZ5B5zPSNOE0nnBOtzjhBpxEkO/UGsuTQ/ACxEMg9H2PXe9wc7PH4e4dDvt36EIvcSVDj6EfxMsodCqoD5XAvliuZCGz/qWkSggNpRZjxBRnzHPENKmHxjQixRnjdERKs4ZkkhBM4gFxEkStOS3As8Z5T8q0QRgoAMROBZOkTA03MCgL3lQo6I0A1nEELwxiCOLpAN/DFBHCAPWA89VnRSgTZbfAzDzCrQnyq1tLicPV/rj+e1lSWnhE5E/pQyu0Xrp6VwTRRpsv8XTYUlK8/v20ui9LvbbWZzX1qD0+tupe5yt5Xd/kmsxR+az6sOHFUluU13WKkIBLnGeOigtFGG+J5LJg3hQRCwv52iNi1fZCfLl8pnhXWDTrKi9F9amVVQL7cl+SxBF4nDFzhHcElwg5w0lukzPTk4nDVBQxWZkAUZcSCW4e9nvs9nvsDrfY9wP2+wOGYUDfD5k5yp4VavkWAVjiSDYlUTUX+VtWMFR7zIh8VOtGy/eaaWkUFTWV2yg2FnQRQXl5VyxwTbFSvDGr/FQmEDAFVK1EAPJ9O9/MrCyyxuimagRU+l0US6b0UAEYKgVrxYQKXLjsrdXMU56Pdr5eU9qQPNb3t+HwIpi42BgK9lqUjEo27tEztAtvzQmtJkOs4NawolV+bXT5ankDo7BQJl2t9835CHSuVwO4vrZZXPyl/M/VCi7M9Rc2mWuxjXzpiS8myV+g6HtzeTGV/oayZBhrQNtKDGyEXMHbF5ULhHpWzqtwhskjuQEpzeqpm3AeGR8feny+J8zzCeAoNCQIgTR/EarlzX+k3vdelBBeBKWG52P0cJ5BKWWBr3kaJCAL3r3iNEdiaCOJpVm0Hayh9xJlHjomBrlKSF7PVCWIUfAucjMNUZJxiybble/yyRDhPKmgzZamkjM39CNXAraUGM5Zh4rxgCgnCl1gCopEJDwRybuikGFDaJdJ6y0wbULULHA1QwAbvOLhDIc547zlFsrKg6VSARruxLqgzxgtYvSpzUWWk726FPhbDRBmnKCi1ay4J21X5C9roQzp+ybELJJ2yqG5sgJK1zl7IdR0EddTX0xfmvlY0JcWhtJpnj0XxEA0+FoR4RBz7j77tEbLX05iXW8IXQPk9TJa3ZR+ygs6U8JpvTnsKS9gMuX8x+pMj+QkbJhzrAHJbPwMivU+1ZBIDhKejICouUR63yEEh/e3N9gNA+4OA8ARP9zf4/HxE376y59xPD7h8eEoHhM3tyLTyuFJE5wD+l5yo4bQgUj4HmdCZouxb/Nv5zAvjaxz4ZWrJc5LrfCod9h/CJgeGdNjyrKBfkfYY4fD4YDbwwH7oUffBXhHEA/dCS6em21c1srgeqHhZybMLMqImZ3kg9AzmKpKyrKxeP1snivbvNzsGkCUfeZOQI4KXINmKqlQkPF/KW9q/bT9TfXvjW6wqQP0uRyiVpShORRweUL6UrXHy5v5K+k5b6nZGnPLu6nguzw7XBmGb9B29Xi51PliOae9uuRFofIa63/uZA3nKiM4J7mUgiP05BGc0/Dauqpc+rj4svnzObrz2WFdiGDxeth+/YVGdvNs3Uu89Vzdz/fhi5UQbyDcX6GIWFZeUTlVMUQt504/LYFTSuKuGo2IkmsxJRXOMmIEfvx0g3H2GqvPg90OwUtOiC54fHuzk4Q9/YAuBAy9Ck9dEKWDad1zHogSGz4noyZqPmsk3Y7y1yP3/162yiuZjtXrX8zhfUHRvhsBa1fVCnvye0QEzJoLZZwjIkeM44gYo3hCzDOejkdMj58x/fP/gVNkfMSAMSYc54TjRJKUeo6Y5gEze0SeVajkNBm7wyGccQgz3k2POEwzdocP6G/u8O79t9jvD9jvbiWnyrBD8B36ThQRQtgUjwETVNm5ECJcGCJTPMwxIsYZ8ywKiHEcMU8TpnlEjDPidEaKEdN8FOVjHNWKSDwfOHtAKOGoZiZO6WRPlD8zGZp5fcoEM5F6QGRhrsuErvcdHHmEYL/lk32vsEFjkHrJEeE0N4TT0EyULccKEWfCo0s77tpWXAqv5fmXIZXMFFXPrD8XddunEk+ctq37lwTQWmAvFipc+YauBPeloxVNU5Fk5j+alnVXNHCFRzKpxUURUegkeSaPy4iuZZ+M4FQi5poiItezpQxZEiNU4YhaycSmgEBJFmbW+1qKC3fK78s5pvX+UBxl48mKAizXmUsTmXc0wrycmSJXpzwGqhjPwotwTtjYux635xP85xOG6Qn3Y4dzDIUhyHMtBHeN9/OfMUvOSf6m3Q4f/He4u7nBh2++xa4bsB/2OOwChsFn8z1J9K3KyyjWlpwikGaxumTLCYOyVnm9dRaonZNWuYCKISsWr1tlS2BM1ZyWfAvVMhiMggn9K7rEVYoJ1zKIyMoJyu8DktibWOJSg0kVEpoMFNCwGpUnRd5T5trs8u/SN50AZmX0F2NcfVmW+rxefXCz0vz10pnceq2+ZkKDugrmtjc53NAS9pZLZAzmRlebXiw71BD5q6e17gV9aYf64lQ9M4dXb1+4WV3eno361wvosY2N0X5bMNWrOxu8y/Ob7QvKVj+/Rvl6tOdzYam+iM5dwL31wcoI+FLjb297LZWS2rTJAgUunfa3ty07WYTswpcyIsR7d54Zf/5pwMd74HSeJKY/BI4G58X31QntmbQm8g7kA/r9HmHYYX93BwodwrDL6FDCxjPmGAENxYig9zQsk6sAF7MoA1JSBXGYwdHBRfFM5AREqBEDEeIsyatnnxAAeHat0a5NrZEAWdlAmptBcY59JvWMyIYLSudaPTawmgbNwizpH0jCM4EkQTCRSGGZIpjVelvpePMYTWpcEJMaUrErND5ggLJZz+WVok/Q3pATfkE9C0UorMZDXNeRqnfXuyYbV9gvpoagzlSdkDaNUqhsbFdNHpXr4EJ4MLIQ2Xmn9elea+Bh9Vtp36w4gYaI2oLbppBRBY1mexWPEUvuDaFNoJ7klpehmXUm7ELAh90e59jjad6VrtXLhUJPeklsoDIZ/Z3pHsBceTgrImjVfaCsb8rrXOg7BiN0Hj44hOAwdAF9J/Hl+xAQguR2KSoMWagwjWr41kyWDBVAz8BMBKgShZxDikn5XqUzPav1PsDwGDFnPpmZsd/tQCB8uH2HoQ+43TkQRXz6+b/g+PSIf/qv/4SnpxPuPz8ipYRh2Gu48UL3OZKw4qHz6Huv8zYLTBA7HKEDNb6ZCL01npQz+l73AUEN7bzknKCilMyC3rLbpArn4E8z+vuIw9173H77AXfv7nB3u8d+16MLHl06w6cISlOe33pds2cLRLb36O5wSj2OHHBmh0d2eAJhSqQeEQIpQKoUbfDSNi6wHZHzo9kYkr2jJ5PNA6xSQJCaNLEa7y3Q4BI7tV2pM7VUOTE0b0eWC+XwwGY+xfopdUhVlYKgaqwZ8YV54MU3br6hJo5Rr9H6evXKV6RtSm82zJmUz3Gahyk4j857DEk+vffFW+43LK/1Pvg6bT77xFeu72uv88vLG0MzLTgZVHtZN3BJImpCiZgFL1GT2Jo1dcqKCCFE7o89TmOnm87Bd73GkO4xdB63g2iVO7U86UKnCgd19/MhA+3C3CMjWaoIv9a6mVbD04ean0Wo9bbZ+83LsqN/DWH9S9u8TBG+vKlnDtOzyqVL7V/YB80tLsJQ+23WMzN1iNRjYokjOSfxGJjnGXOcMU4j5nnG+XxEfHoEf/oREQGn/e8xJeB8PuMcB5zSDpEjZgR1DxYrZQHghOA99j7irpvw/fwJH/gMvvkH+PcfcHtzi67rMagCogs9gg8SyiwTWmq128Qkp0KQM+cYnHOKmFUJMU2TeHSMZ1FETCfEpIqINGPWz6SeEIxZKeiUPSAAsegQwseUC+JG6bKyIdNWOveVhVmOPerVE8I8O3r1hLCk26KIQBCPiBy/3XUSmskHEEwRQZLUuoYVVYiTywqD69usuOWvEd01JYR98uJ3+56uWc1xweLkMjjO1zt3pe7EZpG0/dylMWSvOLNx2VBEbD3fELTcnu7ctjIN1z0fimfAVY+I5XtZoZJQW0WshYq6lkmY16Rhw0zRYIoIe26liEC7l1tXfLNWlxnc9Gi4MB6toaoHm3U3uJCQiXRLwhhchziPGM9/REojjhQwYiG0V4Kcc1gmWe86X4b0huEdIYSAfXeD/eEWh8Md+tBjN+zQ9w4h6GF3pFarIkBJNEudDuCZIYoKiz1te8bGm79WM1EY+Ya/zy9ALSilqpopXqLSVf1VPY3io/ld1kCsYpXxz9abJXl1YRDtZe0fU4ntDICdCl1yMAFh3pwKH8wL1KlAwAQEFuqpDvVQ55hYljJfSzEQYAJ1O6GvNuIw3L9JWL3OKj8rE6juRdkXbc280WT1VqMovdILazN/XH66Oac2l1t761VlySYvr2+8QXrMF8+0gq/LJbeUGf5Lz3FbZz1cema/XO3C9VavzuF6yr+gbO+ti+Ulj14e1pcxH82rFyZhKc3O178G77ASPyyut3NZrr6l7RY4swpSi2eyCIkiM+6fAj49BMxz1PjuBiNRJYOW3E8k1QDewQ89uqHHsNtJ2OB+UPpefAZzYmOLBJCcCJy5HXvByw7kEhxT672guJg0cgAlCc1ETkIXJh1Xxu06jVRaENhuEkmq8ZAJnV0jfCxc8YLOgNFynGVWBAcmGatLLEpxNd6ovWiZU8ZTrLQCpyRCQBbLbuZqC1IZQbNfqp+rneFI82iXsRoC5mp0OexOM7bqiy6T0YSZvKj3k+6pVmBYI38UvMZ1CxWNwmrhrbiAFAMv0WyRVdjllt+supDryU3p3mKq8oSR/M4GOpWnpoSdpTL/5qFChD50uB32CHGH5A6L/pVXTNbSGIiBikzGwgMZHVPxFUvwY2jKjAZY+2RjjpQQNIyuc5LjxBHQOWpDMkFpRQjv6VOEi9w2WjUuuQnEwNX2RKr3DstXNoG+vlyzYl0nfPbd7R32Q4cAMc57uv8J9w8f8cOPf8L5NGGeAxw5DLsdguY3zSdRDeqChpmy3tmWyl4udiALAVto3goH6wxlryzJq1ItHurtqrkV54j+zNi9D9gdDtjtB+yGHl0Iko9yjvDxrHS/8VDWZLvvGYQTdji7ASM7jEw4JuDMEKUkVPm6Wpbn8UDZtqSKJ9bl0qgOTKXmWgth4y4xkZr2S8vXrhYvhKx8sKcWOQztHBs0NYiS93dTc/uzGNxlSLwqsn4N0Nqur4EcLVD9dYTTKwi1oAQEJnhSZQRc9miq+bc1v3upr4sz+ZYeP/vu6yq/ptxobz1f71rWcvHJZ+tqH7vEj33d8npFRN2pWuhafc9x8JX4kmS1UT0fzEpSiTPIJCYm/PDpBsdzQMQOoQ/ouk6TUt/A+4Ddbo8heOz2EvOv6/rs3mdhVCQhdagYcGXsYQRXAYLIhB/y4V8dit9gEf5eqnJREPHC138VoPmCdrXbmUCszsPsD6KASEBME6Z5RkwR5/MZMUYcj0fMccbj8RHz8QHTP/9nnM9n/OTf4QyHh+MTzjHgfrrDnBymOMIsiRwcfPAY8ITBnTD4AV3f4fvpF3zzdET/4Tvw+29w+PYf0B9ucXNQT4jdAT50GPpBc0KI4N4FE0gCIBEislrASxi1WRQQMWKaZ/mbRozThEkVKdP5iHkeEacTUpwR4xnMM9I8AimCOeosCVL2RmppGCavrrOWaDuogM5nBYkRmVSsiVXp6Lz8dtmjo1OlpHo42Cd5gByo28M8PwRWqCJGk3ObggJOe5mpOVcRdnwBvleUX8OA2O2a2d5i9NavLC1ya0bQNiIbxY6GtsrVEQAEn7HVNevLLYG9yHspt13XXXemITsbplEJtUXdlIno+npr23VJ2WHRfcvtpVdS3Ruq7rdEJOuz+QzbgFGWupR23ozwtX6bIqJY07XeFDVzXuowpqNdl7KTuAGRJSnhdZhpcTWXCgzrc62Yt/atSMJ5xvjxn5B+/hP6CeJhpIQhszBhFqspJQm5mOKsIRiThI5TJY53DhSf0N//K253Ht/+7vfYHw443H7AXd/hu31A7x16jRMKhxzeYZ5HxDjBTR4pzpjpDPGU0BjP2evCvKvyrOksGWxTmOPa+XOunR+jCVbeExV/riuxmnPx0KjZDOR1zYrM2ivCFWVEYR5tPVrFVErSf4sD7MziUpkqc2G2JJCNAAAo1o9u7flQz0f9bb3DVlISnYky168qpohoSsu8PlvFogctMKJFNfrUMyTDpXHw8sVCNBaBSXujtLlg9rO136Llt5WtutC02+zdzWZeMd/XHmV7zoijfKF6/1oFWzB2+US76u27lxf3Wa+DV5VrbV24/tchVf/GygbdQ9fO5EvW7NIzIt1JfgA7L55+2ZgmYZ4dphmY41wsnQkSxoeQLY0tlFLqArqhw/7uFsOwx93tO6UffTbSsfrN+yGhErbD5OSkprEmLElIrDRvkvwUyZnXgFjTpsSgyJJbQb2SCQB7TTZreIyRBfrkpAMmEHY51Ix4KTjnkEwZwakwNHlt5PgmNciw9GzFqjfBpULZp0gg8iCXNIG14nFSC2EkyXfnNDwzSs4I1uTc2droBYU5h+xfLztlEZ9iY/GNsfCGdiMp7cCN8iQZ0bui/9bkl0wymabKUlFkgFerDFrcScyCzxUPEqnTMBl+WMCsmiava3MAuPAnplj4/vY9DsMOJ36PGX1ltFXnvQMsN5WFlHSlovzbe48nBLD3GFzIfcv4xdV0bDHaynnPqMhkVoRVO6Gr0gh2TeYEyd9CowNmGU88O4zBoXcR7zzBzxbkR+VVUMEvVzxGzWxU0xmQcDNP+QxMRDh1HkGbGzkBkeFdRHKMQBJard/dgJzDYbcTjwycMY4P+Ne//Fc8PX3Gv/6Xf8LxdMTpKYHh0XUSjaDvjSe10MiiTAmhE9qOHRgTmEeQC2JAt5ozmVvnLLdhOQFGi9p8N962uvcIhHgGHv4cAZZwxn3vcPA9bt+9w903H3D77haHmx26XjwrzOjITlvm8QCUBDPi6TAzMDLhiQmfI+FhnvGv40ec+RMmx5DsEq6lJjfSGeQLFU2hVLEoIXQsUO8Q0jNaiDSncH1BK4J1z8tOoYrvuly44m05f2pm+zz7Ri2YFzfnO/JJFZ1EhYWAzLAadyt8yuHfKgqopoVWpKXCk8KPcjuhaV3HxbFeKVs0ZqHmF+der1noQO8d+AiEB49dv8Nw4/Gu9/jQA0OVB8l4+IYnXvAQJlf4Eq+Gr2J/0dR3ucIvbetr9/W3KG9PVq3FlBA5NncyD4iiiLAwTFkZEdWqmlVBSITEhKdzh+N5h9B36gEhuR+60MNr+JgheARPknhIw8g4DbciuSB8Ti5G5FSpX+V/QIXMFwfltXxJhhVX3ns1M/4VSzmYL7tRs+964Vcv6779+g0vAeyL1+i5Ba8ED6zIiAFEdIiuR5zHrJiLST0h1JNgmiecxzPm0xF8/zPmmfBw+D3GyDiPTzgzYeQBiRkxRQBqpuxZtMYUsQ8Tdh1hCMBdHHGXJuDde/hv/oDhcIe+36HvBoTQoesGhBAQNIxZHZc+C93I5koUhVGT5Fk4JgkPNWOcZozjpB4RE6bprIqIMzhOSGkE8wzEEZwSzJnZhBAmHHT6ad4d3jslepUpq6xqTBGRE9F7E+apNYzFHqVOYUMAkYdzHSwkSU5GbWFSLCl1JtyKII800SzICCNz+15SrsvvpIyIunTX2+UFcGMrzmK7JRdneMHfpAttWGqN/HtjT1/2dEDe31tlTQhIz/UumH31HFfHSikmFSIv29jyPll6iFzqw8WQVQtmzojRrbETKDOEW2Xp3WLxQLOyhNaKiHUbyGeiXqBs1bMcG6mXy0YonbrffqWAqD6VUd+6DwDzLLlaeBoxP3yE87dwQZK5K6JVq80yrhxygU0JUTHx3sHPMw7pI96F99jtDxh2e/T9gMMQcNOr9Qt5OE+Ak1APnKpwS5wQSZM1q3JTBBEMSi2hK8T+Ynz5P52hxffaqrRm2NB+vVIKS5BxmpEdRPlMEKAGE8hKAgunZGta+lPOUJbZK6NknKWtZ22BiErx4SpFxHKdF9uqLfW85fFtcO1ABmztHD9firC6qurlr1dP11BSYca1flA1r5s1bvSCN+iGasDFA6Cdo7WehavXtjv5ehpS29x4rd7nV8tiA3yZzF73KPHGDL++7vW8635bLdOF/dlW9rZS5ARvqozxzJ58TSdqCcyrS9n7v0Wpu9gImFDT5TUcaPHvtcLbi7J4BqKEcD04zqLETglzZMxVnsKk+YzMbh/MWaDDTgXezgEhwPcdur5HP4h3LUAS4iiRGOEpEsnelTXerxTfxZvBwTkxAnJUWakDSjtXODZVf67BOnkaDLSQ4ghQJSDOwjZnMvSWB2hnDoU+A8Apn2cRBCW7DIBE4cDVX3LVbxNUJoCdKh5EQcFUQpU8e4LZaN7WaKQFtFS2UkUfi97eBNKo1qfQt8xrOnRdFDdnBQIBrGGguNzObVpf6te5eEQQkPdaQ6MvhRQr/h3QSPcCa00Z4CTM9X444G5/Ax/vMGJowjZmuid3liqjjOK1UCsWZlT8mdFQpsTQ/VNCYrt83wGVgmlBt2Y6o6U38r5eLEOq1x6ksmbta5T1dTEhpASXUoXqK4t9bJfiqCxPeIgXeQIQneYUJCA4h+iAaEnoITScJ4cudPC+w37XIwTC+fiAaXrEp08/4P7+E376+AvG8wRyew2trMZ0zqE2inGaa8x4YNsgjAiChmmqSbJMaxa6qhjhLvkz85CRv+IxAKTImI8M7wmud/CB0Pke/TBg2A3o+x5dF+A9KS/M1SJd4A8BMUQGY07AxMA5AccU8RAfMOMkRwk1RUYX62tI7Yofb+BfM2AAcCCODXZhkhBNqQI8tPjcrvCZknkfmx+tvlbSNJC7KMYqx4z8LriEXyvnIjV60grMrcrVYXB7Kq74WawbeM38LJczkzBmlErABPjzgF3oEZxD5wk7D3jdy8XQb92ZWlT36wn93/byWxQirbHmtefyt6/Xh+WzX8YMbJa3KyIMQWsYisYLglkTUZtHxJyFrzkMUwJ+vL/B46kXq2MQpjjA9wHd0MOHgN0wwPsOQ3eLzgd8d9Oh84Sh05BNIajioRMErgjXeanPgG9h/IHmlNRfl4xXGSheD3n+bRcBkn/FxoF/k1OeGKAkYYuYGZM/YKIecwTSPGIcJ6QUcZ4kJ8TT0wnzPOHh4RHjNOLj4y84PT3iRO9wCh1+Ot9hiozz3IsFQZo1NmbK3gs9HXHjTtgNDvvdLT6M9/hw/oTwze9AH77H4cPvMdy8w+3hDn03oO96eOfR9/IZvIQ1yznKlEpOiatxsSofEs45jNSkSogJ02QKlTPiPGEaT4jxjDSfgDQBPAKIQDJnS1lecbNjhBw2pMpz4Qgh6Dl3LhN2ZG6+dVx1zWkh3lC1R4OGa4MD+V6UD/Zbc0LAd0Ic+6L8AAHkjTjXSTF6WSm2sk3X2HQFS5QTXG7p5y0OKopyo1zDJUaION5GSXVMVCqdvFBTQVxbgrT1pWeYtoZXrPqRmQQPITBKm7Uyo/XOKP1rWt1k0rAxGbUVSVsfgEZZREwbq3i5ZFd+I5aUqqzDapVhVTXb7/o6lb22VETIfde8Y9Nse9ElI2SMIazmkrBSRNRj8I4RPZC6HvCdhj5UjySqXCE4iTCBWY0OYkmqrnkyIjmMYUDnb/HfH/6Ad3d3eP/hG9zuenx36LAPHYa+hycP74Lq/lgVERHeO8QY4IgxRxlLjDOIWHNQAewSshHjIuyVybhqTwgbchu2yhjr+nxcoLyNKeAi0Mh2VKVyASMaIle8IUjhGMHCJblMryhArmBKWRuSEB0kymhGuWf9l5jMtSCALvy1ggALYdaeyzXkugibMjOI7ftNHWUeG4EDlWeKtfu19+tbWA0pAAEAAElEQVSaFk9x2/92KO04l0rc65VuNp+7Zut/lYGuO7SEhRcauMSItDDXOOd1M/n+oq46pMtX5TMaoLYdAuvyGl+pbuvCZsefwUVvJTQJYjX+0odf3KeXFuO0v0JVf9PlmfPTPGln7nIRobKsO6tA588/7vDzvcfj0xnTNGOcZ8m9wBFIQNQcb6zx8ikEUHCgLsifF+lIYjUYYDGmcb7D5AiRkoQ31CgATvlisfxHS3snEWB7JXq8DwAinJvB7IohRK3sT9SEOiYWQ53N+VFcwNm7WDwh2AlPAVcZF0A7VfEFRi+x8vGFzoDkRSUGNDwTpQSKCeQiKGoIoJQEV2u/pR3NFwlIOCsCuhRBGo7DYPhybbOyAOYJcU14hvycEgYSPopZjCxQvB/qqA3Iwq5CSBePRZnTbF9NlCNCMdRUSZUT1gNSCStTrWrRe4I8i1FndTfTJNVYQAXHEAjD7nvs93/IawYqRgdEAPoOJ3gkHxBynruSA6LAf8tdInuh/ST1tnSVsYPRL5DZqOin3GNX5qsieiuYXRNb1eUtMMflw9k85SUvtI1T7/mPD8DTKeL7O8Kuo7ZSRZXcLgXGifHDfZLcC7VUU+dpZsbMEcPB4+5dUGPbGSH1YPLod7dqGDeDKOL+8Y84ne/x5z/+Fzw+PuDnH3/BeZyR0CH0A0IY4LzHbtfBOSqhl9jCdApPlHCWMbOsb8Be4FjiiuIwvlirYMvPpuuoZyou8a6dp7LpdH09QvDougE753EbbnF7d4e7d++wP+wx9B2C15VIbfhaoOwBCzzEDPUYS3iMCY+ccD9F3PMDEv0RTGdEThqWqfJWyeeFqu/1pqgs49Xin0jlMigkkRjhcYZxxfjMqZer/mldxBIauh1PzTXWY8Xqd6OXqR63n+3eLg+Xx7l4RWQ4xRr1Tvkre5UrOrb+vu7V8mJ5/qvQJ1ttZtCQL2V8pngJKgPy3kn+X+4wdAFD8Oh8u69ztxfhkmthPCtD8SvIzv9dll9j5V9SvkARocy37t5GCaGHo8TErHNBJMyREBPwdPJ4PPWSZNoUC/oZfFBtsoRoGkLAEDTWn9f47/peHfc4xzdUZFcEC2gYlRoXlouFyKvHeY3Y39rgr7dg+8LyzCnbus1GPTYCyULs1cN+7easm3vpu6vnfoUTcWmaLhGuF9eRV1/yTyGMhZic2SG6DjHOIpiL8jdPs4Q2mkZM04zjOGIcRzw9PeF0POPJDTinHqfYITJjgp2rmNuUGOtA7xL2IWIXCIMnHDzjlhm4ewf3ze8wHO4w9IMmdu/VtdPDOw+nwvtivVINpRKWJg3FZOGYihfHjGkeMc8ypjhPOXSKhGWZJJkshKkjSP/NesYpoeqV4LEYgMGXz6xkoNYjInsxbCoivCRgIwdHmgvCiUcEWW4IyH223A+uhHoqyJKyizGI8qG4LGevBYLt3tkS8D4HJ65pv5cCtmXJbA7XNqjlRC8VjZfrKpZ68rl9f9m3q0XjuhK3wNX4JwCZ2Fr20S6tFAbPNFqO7GUmdVkfA1+siFj3rSj5llYOa4FppYyoFmwdysmYx7L/uGYuGSAVyBtTaQtpiogSGaKF3lxxed45xDrcIS2fRkMLSEL0lI0VpCREYvTeY7+/FW+IYcCuDzgEhy6IctQ5j+C8cQ1gIiQieHWvjinAg5FSkH4mr0nmNMkjQViMmhlG/b0ijPM8UvVpAzLY2BK428dFbSsZWSAjk7+gNwy+WLIbg722LuaF1eyLmoLnqqLFvnE6RmWyzOU+Wz8uPhthtNXFJXVe+TBWsD2zXP1fLlbMxdY0AWg8k5rnSGHsAjZsndtl5RveSrSyqFju2PbMrb0lF33darfpA2AKR0Ktpm7P+uaLi3YuPrsa9/JZ3ujjdt22zddKiOXzueYNGPoCRk/Xc2OFLvTwWmnPwYUuv6DGl7e4Kko/X6KRN5aofjELFd5U6OKP5x9f9Wf5lO1T/XWhi19Cnj9D9VRfDdlnYKzXL9SwgBkXHmrqYmYczw6PTwHTdM6edymJoDqp4MdCP5qSgZzTJL8u5/QpyugK9mZvBlWSMyrBkYRjaU6GwUJHoCTGOpy0HheBKHNhtDlSAjunfWQ0EqklACZFp0Q53FQJX0x5XmnzTFaQvjL6aI0iTGhYCcsU/ycneSNMgcJJvYlZ4B6rVsieTXq/6MWXO26Jc7hZWV4/sXq9Dp9S+lzRnvlz/brhc5MvmCV89mQgzUVRKXh1ZoQmSbWiej0eabaGGmppr0Jk1nhbOd8aMUJ3wG64zftObyi+l+9T3pftnzxah7BGRStYeEelJRb8V6ElAIvIj2pOcj9szlabsqUFmie2jnNFmhQdgeHPqi+6/adZLO/HWSLS2u4IrjyUQQ3ESHaKjKezfG/4faq+A0i9g3cE76CeDELWBTWSBWYwZpyOn/H4+BEfP/6Ih4d7PDyeEGeg627gXEAIHZx3GvIUILUgS2yzYQ0Xy3dTOFi/LRBoM3d6EMrpoEV9rVgdMJ5AJ69adw8JydUPPfq+x9CX3BDEDKSYz8wlOsJo6sSiuI2JMSXGOYlih+kRQESJm9DWUXE+NrDVnex3qfPnqru0+N4c2jzDpeiJkHB8eXYVBm/Rt1fIVFo8mEUKW2NgbFCPnOFWrYAtwM6eKlBwubbXSrMHrr71mlqXtPNiNvIiUEZXBGTD1OAlDL+Fml0pIZZjaLQ+9fVrffwSamaBA1/8zm/X1ptLc1A2rn/F8nJFRHbHlE2YjIaIKVtMs4ZukfjQsVJGzBpORt755fMen54GzDxIwtxugPcBIfTwPmDYHRC8x/e3Pfrg0XU9vHPZEyLk5NRiwZGJvRznXeMfZ3j7WoajRoyX3/2b0LK9sROFsVwwnLz8AntwVS7txyU78MX7dmGR8GuWPPxLHObqBc6InjVa0kQ7nH2HcWbE8SiWwZwkifM84+H4iGke8fn+Hqdpwh9Hj/M0gz8/Yh4TPqb3mJPDeRpFoTHPuSPOOQTv0dMJd+EJQ+9x2N3g/fiAb0+fEb79A/x3v8fu7lsMhzvsdwf0ocfQSXizruuF4Ok6ITC9uPI6iAAvpoiEhCnNSMyYoiTEm6aEqPkg4jxhnk6I84Q4j5inI+b5iDjPSGkGZlFAOJ4Bjmo5KJZHRJCEYkSqPCDsvViBhCBMnSEdcffUxFyZ8CVNqF3H0PQ5ObXzlmxaFRIUAHjABUBDNAEl94MPkow6KxxMgJvdlauE3YY7qSJ2zC1W7uj9FwgHvnAvt4LRdXHlwa23X3WWXmaF+/x1oPDJl1vPHEFDiNkbDuXdhlhaMG4Xr18JzbT8bUx3++rL523Zv8xBLDB8KwxfljXxdU3Jta7DCLzQoML6Mc7X231h3oueGImA2Xsk7+CpWPEbo8AQ2BeZNadERAnRKMyTcw40P2F4+Ge8v9vjw7f/Cfv9HXb7b7HvPQ57oPMOQ9dr7GyXN7Ikq1aPx+TBYDgXwABm5+EYQJylPynCYQazCtybOZdibu95Xy08JMSaUXHZQlFUCxaW8l9k9qBm9lhBiwNIFKJwHo3RBBHK7nb5fVMkWHWc2nEU4YH9LooiERoUq8faO3TL+j0z9lXXX7bb20o2lQbWmM7RczL2HC5Ay7rGjQoK+N4ovAEv10rULUti3lzjpuZ1R6iGc4Wdbv2v1q99lULVAuaqF2tU/W7W4iUwbult8eI+XSIit/bLS2pddXyjXMZF20rl9fObeCXP0wLGP9OV8sh6jZa76jrx+VdiPuq99Qqm2EQkL+31xfN+rYLlFlsx0AmOgJkTppgwRsY0A1PUfA7zhDiN4GkCJuFriYFJRXzUMZzz8MHDdx1u+hsM3YAOHRx7xMhgx+LQSZzhb98FRGL4KG56PCdERHDw4siIkoTT6LYACTOYXAQFhusIHAluRhbkM4AUExyJgZNzpB4FXu2nqynRebHUzEQMNtTjSRT45JCcB5OHxDd0YFXmJyo4CarIKOtJurcTCKThQCUht4MmrFZPhzRLLqOs9DUL1yRzN0cGI2HqpMveAY64ws/VshZSsRG9MZzKpFNzN0GTDDMDnMQ4KntxipxC8ARnRYD0kaCuJIqqZWxEXi57X4T3KQEUpQ+QsaYsO6l7S3rPFDOp0EtA9oqAGRQ4Qh96/OH9N5h4wON8W06TwnPnAoJFh1jRKjZxkl/PBMxGY+R6SETO5u1KhEbhkPNZWRtZWWF7o6JJKp7J5m5dbD7snWph29Vu3qi/5D2e2yqKOmZZF2bgp3vGx0dZU++A370DhoBMbjEcxhn44VPEONdKiIK5JURPstFhTxG38wg4h7kXxYMPE87HTziNZ3z85c94erzHD3/5Ix6fHvD4+IR5nhHcHv3g0Q83cN5j33cyh046O8dZYEVkJEfgAAkFhyBW5KT8OifJoQYG1MvfxM/iRUHwbkIghsOkey6IhxZ1YNeDfAeC170oZ0S2hgaEZQKdIrrjEYcPA26+u8U3H27wh5s9bvsOAwg0nyT0Ms8GDnTea58GkTQkdnjiGxxTwHnqcU4Bn5LHIxxOTmEOK92ldGACEMGYsczlsES66ulWAYliVlP2FQFwNf5i24mUE7MwxNfbwj05+yMgwqm9SUkw3fLcKTdEjjQnA+yIZP62cAiV+qMaV4HflceWhrfT+EzteeAkMI01zwQngcGJswi3WPPJf5w/n8PnK4S6cctmmvN3M4wCWbaNyiBOq0mmwCcnETt8j53z2DuHPji4ADhPmtJO4GRu0VV92aQnX06n/Nrlt9QjvKn8lfr3YkUEN7tdPjilfDhql8aSE6J4Sch9h8gOpzHgNPaiNfYO3gfxfFAPiN536LuAXQjoPCF4C9viSzz7nNixSu5Ya/gVgTcI6qVl8fxzMrvXWMl+cbnQmZfIFZf9FIK0+l2wB9pJ4O05vLJpV7eeO4GXBtAgC37ZQC/1adGFa9pVqh+6ZI1TCRYl5qEEHprhEREQ0yiJ71JE4ohplhwK43TGOI04Hp9wHCc8YY8pMhwTZnaYUsCcCDFNcsaSIiyztnCM3iXsOsYuADtH2HvCgTzo5hbh3XcYdjfoux5d6BBCUC+IKv6kCd9toGqhk/S8Rj3DU4yIM2Oaoygi5hlpnjBPE1IcJe+FhmHiOIsVdJo1DFMUxFghVYei7bYcECGIm28ItceDxsWkKs65qwhhyw1BHiBTOvicLFASeJkiwgFOk1OTeUCoF5V5hGy6JxfLopXwN/+/QfBv/P7aRY7CX0kY8UzZ6ldrOXf53VbnuH6wFt/U8OySh8nq+isUEcvfvH79aln1J6bMDAIv2zPrZ8r7L60DQE6WmZ/bSilhxGIzBamEj1AFYs4Ap+8YK5npALaE0ayMj66bIzhE7OkJt90gOWv6HkMQfB98EgsYL8o9Z2MlZBENeweGnH02LyhVUICcCEyIJa62CkaEmq+SqzdrkAe/+N0y0utpbQX6pRisa6Pb1u8YbZI3szLxVD+DynKNmkpKS421Jar+qPKhQhpNTojNftfjzOzPxsBbfLhZyzW4tDzXV+iCppavAOuW3hErGHqBvMj8kmoWeKGZWAr57dnl3gKgMnzGSiRr3Olbymafn4ELq2XdhknbTS1ow/Vorr7dFr4MVF+z5hcffa6OvLrbbV7AK2sByJJG3oAL1bGSY03aBG++8Xzf31p4OepFm0W6cfk5vG59Gp7ipfucmo+3nY/2bBotKkZykjS15FuQfEaIUWjuLJxKJoeGRC/ywqeGDp0POWdZFhahhOYDScpUCRdIRUAKzuEK7QQJaCxW9I40KTaLoiIlyvq8bLGfShSCOoFpxsnV4Gs6HMb7kShfExmuW2Mtw/HL9S7bWQV3xp8xNM9D5bkB7S8nJI5wmrTarlstpgRISYwfmFnDG5V217xl9UGoc+I2uHf9vPSLKx6lDk3T8INZ0K7n2BGgniqglBN8s5MOmDdASkKDyPbnpq/MpT1bM2dhkSB4RhRAYmTpw4Au7OGxw+wOeopbuoWQCadqyEZL1OMp9xpIlnFgTY+oet48I/JclGeqmldXLsGxWqREZCnP11KK+v2lGKqZUFo+r+sLmfpxLrU6xxhnDblTJeedEnAaxYNi5blRteW8KMlEwM8quBdxeeIR4/iA0/ERD/e/4PH+Mx7v73E8HjHPEZwIoQ9qfKv5UIPQvHaekZIa+2oOFchnBkS5N0sxez12gnLcqnxiEFmYORjBCFvLdqz1H0CJEZjQh4B+12PoO5HPOc35YXy/nSqjg/JCGYwgJDjMHDBxh5QIMTLOfMJEE6olykMoSsHyWejG+pQWpmYpwuLm0QoqVmi51GhXyrzmZwhIpNxIY7WjPnOmpM3bpT2LhhdcTQs8U0jHbfilLQbD6nHZaDQXJ68eXzX+cgF5JnCBxUndfM7ONFF7ndrvdXQAAuBmwLPPYbktj14ZxnaHr3tyfN3y2pa+RAmRIx38FTQZv4V8+xWKiBZRsyb1mpMQbfM8awiXucRYzFo82R4/fd7h48MOkfsChEPA0O8QQo9+t0MIHt/fDOi9w9B32QPCURu6iUwqa4JKmIbfYur9+pP39/Lvq7SgsqZmqYUi9VnQGKIpMc60w4kHzAlImDDOI2ZNQj3NE55OR0zThIfHe5xOJ3z65ROmyODxFyBGHB/uMUWHMx2Q2GUvIktcFULAQCe8C/foe4/D/hYfpgf8/vQR9M3v4X73v2B/8w7DzS2G/oCu6zF05nXUqTVXSU6dhY7MiHEGM2NOE6IpTVLEeZwQY8Q4TojzjPl8RoziBSEhmEZwHMFJEnEjJrGKUC+ILLcEELyHc0DfSR+6roMnhz54VUz4hSJCP70pEVQBQVWCbR8AJ26wROoJQU4VEQ4ge1cT2qsiwpn3lJfEya0iosCUTeEwCtH3N6/h/hWLhWt6zbPGbAPbSLUJFXPhPm3cf6lSZhkT/1pby2vphWTORSGvcw318jpFhL5IC8Jg9Xsb8y3HXf802pS0jw0zzqxMtwq9s+KhEL0MM0CI2TNSvpd4sUSQkIu0w3eH7/D+m29xc/sO73Y7/MOB0QdG3/cI3qHzYinqSJkCAlIkuBRBmhAwcQARI84SminFABDDsVpDIgLscjJDGIur1k1Fj3KBmbe5rQnmi2uTp35NcF+hQ6j6r/ZYAEoohfx2xUS1TIeUOrGhKFoBgnmRaZiFjT4vr2Vh0rWyxIdfVLba2jj3F95+eS9ahvEtpQ5PV4a/zVFeho3y/Pqtit54Uyms9KuVELi8N54vW7T2K+aYtudvo5mL5UUw+aX9eXF5hSShfuvFOHMB93/LsgyF9DdZNuZnqdBayEqSH8ChQ5wJHJHDBUvIVBIjoXFUWjdCvG0JQQ1ivNKsN7e3GIYBd+/eIYSAvu9BpHgzJXBECRNKqgRmkjwSmTdG/g6ypNQlR5DT4QQOIJcwxQ4EwuyFTo+cRFgZI4iAGCLm2aFLEYkk9wS7MgFyzNbralbYlAr8MfweuRgmgY0eurQvTNBogrEEMIGThFkhVcIgiqdechFw0NCKwi44ZkTnwGB0MSICSB4QQbx0z+W26q4shJJUhFrFmh9wFJEk3hWQOAv9zeZa4J94O2Qlv3MiXwZrAnHbTITgGYmElkhJkwZXFvgpsRh7sdPY+cgKL/MYrUOQevL4w/sP6EMHZmBmj8f0AYlMIOdwhFi9e+9bYd5GySJnU3zZ9BAkxBdRFW4GMlYw4ERgLb8he9o5OKXfE7jKUyCC19oH1MITw7HGgC9KvUu0RVHU0IUd9jx+NDkTVA6cnBrxsYV1MY8WUer98FmT0WufEmZZN64ULGQBj7RiEMCEm53D9+8cuO9wHDqcTg8Ypwd8/OUnfP70GT/98Bfc33/C08MjpnFEigznAwbfA3AIYQ/vAw6HO8nnhTNSShjnMfPbwj8TPAI4eVVmJiRHcMnCd16dkjxzSkaXK8o3EEmOhKSTRtDQcyBwTOBAgHfwvcPNcIt379/huw/f4O72Fn3fw3mPCPNDqhejbZNZBNJH2mNChylJWKYxMp7SA6L/38GYqnw8pZ7saa3K46xmXW2UBcDnlK9qJ/JzRglW3GT1YYR/am455RvEM6KpGTVdJwAgMxgovAeEzgfUqSarPwVGwG5YvxTuVnDNMTRMlPafId4O2fBL4EwOWWOfqP+Qr3Fd/2vKMyTCcq+Zp3Fq9is3y2i5IfgJSH8h9IcBw7e9GKmFksvmUvlrCOn/5smkfyPlFTkiane3Ng8EW6Ks2gsiMWIE5mgIxOE8BYyzJrt0Hk49IbxabfddQBcC+uDRe4sZr1aPFprF1VbKZvVXGPgVrnoFB/JaPuxZZcebGLu//fKq8/7Shy899xvPIW18b3qWlRCCXpJC5ARGZMKUlMFhUcrN84xxGjFOE54eH3GeRvk8jxinGTMTeDwjzTNG8QgXAgoEo6q8m+DIIziHzjOGHugDoXeEIXjsQgfc3MLffUA/7NEH9YSw8+V95UHg2lHm81ySUieOOcH8PE/6OSLNs3yqJ4QpIqAhmIRKKIjPiBOnBJN36gmhCCd4PdfeklUvPSIs5Jp5PlkIptozqlZEWHi28qmm3BqqRJEZKRyxE1zBjiKYvODejELurCxq/0bLaxH0S0NLLS2yn+uDhVsxGubauy+p++1zvxRYbAtf34pKLnolbOGnjecvjou2718PzWSvLt/Z7kf7vjIq8xnpNAKx2CsV+yQ78oLzOZkQAhUs0AadByGg3x2wG3boQo8+dOg90HmIh5QzjyeNYa1soPRNGUrzjIIlXKQcS9uRxJ4lchBvLG2brdfLM10JaupJxqX765ldiZSzgGBZ17JmysxgPd/Fo7N9tY1hvVUj9D2rt+rQCpZx87s9z9eVEVeVFRdgzZY35rLrm+N5plwMA3X5DZSxa19yV55rV8dtFm/58tZ7LfxirscrdXx9zHEFDqx+UnvP9sFX7sfz5fpe+1plE9+sztDGXnrhPn9u72TvB9sXtRylyBx+o9L4Era3mk7Vb7QPvPrU5f3FMIH4mr5+RrqxOcfNQVzfVmGpPOrA5FUoK2GZziMhJio8bRKL/ZSKcoAtbJLyoF0I6LsOXRfEsMdLCJQi4zHhciUYo4Jfs3UjNAY8SyLZMkfSLkGE5ayhiZJaH0eFQTU/nsN2JAZ7tRvmQtMWJbyhQ1KYb8e/4JwssmK2XM24Kq6q5X8mUNY5FqG10AZiz8Bwyh9RciLkJgfS3BDZI4KTGBUYvgNlYfYluoygQ85C0ELHL+UEvNo7uYY8R44oJ6EG1DslWVgmnS+iAj/VSwJKewBlR5a5c/BEiBDrcIMjRFDL+D26IHGpPAKmtIckSRe+LcGSQl8uMvtpsR8BEzzWZzFqmCmAgJTEOwYsih/mLPB0iQEvq0nqrZJj7+uc1/kxANbk5WW/aWdMNvsM+F3go5ytd9uQaDkD3Ey60qHOeF8Z7zTVdZfHt2CjRAG3MRBCIPS9wzkAI884jUccn+7x+PgZDw+f8Pj4GY+PDxhHyaEYNCeh870a1UpuVK8yrTQXBVVKUcOEEbzTIGvWdJ5JGQPl0TanYGNOCq2ZKdMKDuV6yZ7UeiMDcwQ5h27oJZ/bsJNw6ZqgmlPModq2SnWqkMgjcQAjglmUEZFnRByRMEvYKOuhDilBFaLap8bLYtVkdWGNYPKPUkPtV6TXyqYDLeg4hSjyJmW/t5J0OY+0rMyS4hfjKjufrHC3yJXIAFn1tuWjyPANBYdK+zV8Lmths7akV3jj26vLS8i2irY0XNT2gzNtRtAzFgE3BXQIkhPYOXjaDru6km0YzFuM6yL/8Wz3a2iwfa7+Fspr2aDXeFj8FgqeFysioloFiCafMc8S9z7OotmfY1RAajGhGb/c7/CXj3tVOkh8u77vEDrNBdHvEUKH3eEGoQv47tBjCA5D14EcSdJKi/uuCWlFQCnI3uIrZ+HqMxqzv5e/l2uFtr4bsshCoKQ/E6Lb4ewPSDEiImKcE6Z4xhRnxDjj6XzCeRzx8PSA0/kJv/z0EePMOJ+PmOcZx9OIOEc8PT1hjsCj+w7JdRKbEgnOOwQ+4wY/o3Meh+EGfedx2N9h74D3797hMPwDusMe/eEWw+EWfS9EQuc7eBck/Jm6kotwTkY2R0FQQvgw0izMwTSfEVPEaToixhnn8wlzjBjHESnOiONZFBHTCcwzmGcQC7NhigivkydWPEAX5Mx2QRQIfScJrjrzcLqkgLCE0xqCyRJNexcULniQ60C+r4SUqoDQJNRQ12bLCUHe3ItbjwfOSNKBXghGLsqLXwyGXo4M/pbKUnj5qnfxWwpc1oRPeg0tsRT4Pytuut62uzDwl4RkkoYvK2eeU2bk6NOVtaB8CileC+hNqWCM9/TDv2D85/+M+fgECd8msCJyQmJSi9Io8GGeVSGhsaFZFJAcPOLNO3T+Bt98e8KH21vsdjcYhg5DB4Tg0WvCvi6Y5RpDXLmVCk8EpySLc2Ih5pwTaz1SizGn7HFyYCcMNIMz/1qzFEvlQ2HQK+HMVZqCmk8zjDDBh1nDksKbrEzJCU5LaEkRchVBlSlKLZxUY2laMRo2DqOFnOaGaHJEUAmncEkBtdwz1wj1q+feBPW/Vfma7T1zuMU4wDjFcrVheHNXLkA648mycqyq6YvGUTGur1FCVA+shl/Xs9W3pSZn1eC/Lbz2m/Z7uT0WW2p949Icv6X8NdflmsBsS8y8Vd7W/2KNnhAj4y8/DfjpU8DTaQJ4bqzVY0xIxKKMcB5whK4PGIYBh5sDhmGHfreD13xl4EJbbPVOjOkY8yxPJPWeSFESvHrns0AGRHBJPtkLfOm8ByXG5H0+bsziyQwwaNLY5XNAJAcOhgsvC24N1zjnVFFASM5oUvszfG/iSn0XtbDNBIIm0C5x3UmF+XlejI5xorxxXvI6iYCteETMcwAYiN6BLdQRoeCxRuBoOMDEfGLpnxR/W04HRw4JHowI89MmaGgllk/jCViFwLkdVcoQJU34DTA7sSRPVG1nWbcEyUUi78nmSInx3eEG+27A5+kWU+ry+jgNPTK6gInLCMUb3ATI1Aj1ZOKKQkpENOplgdowxLxaaqxe6jMBtXnJey/eIV75MJ8k9JRnB6KUvSyZXOkbCY3ZGlGQ5jOozvoSXXM1loYeo7JnQCqvJdSx95s6YPi5wEvJ8cXIVubJ6LNi016UVPV2MpwunWIQdh3hdx8sHyAh9cDjjvD58Wf88vkn/PinP+OHP/+Ax4dHPD0dEWeBIc6JzMupImK3u1FF5gCQwzSOmKaI8/ERKSmfrZ5azjm4oHnRMk1ZpohsI1YruizFIIXqi7puSstRNVIGHKec0yCdz+DTCf133+Lu2w94/+03+P7bb3G726HrO/h4gpvOFe0icKLQ0sVomNmBOSCxR2LCnAhPc8JjmnFGxEgJJ/OtMe9xR2IkCdvjbTttWeAPXn6xjVLCKMnVLfqnNRShjW8g26cF8Ns8yn3NI2HeRebKwAxWuCMuAgxzUaf8PgNc4Jz1kHWL2+jrP3BlCMrIOSSWT9aqnLeXC/Rtc7+FW6t9iLJiBn9C8PCDx2G/w343YD90eH8I+PbGofP2jrTLNs5F+S3DM/29fJ3yitBMqSA8Db2Qk1HXsSk5YU6EaRQPiCkGeAQRiqp1toVkCl2PoPGh+148ITpPxSqyYtoNwWXhYgbKCgwaOLsAG19Csy/qu/7gFzb0ivKrNnWBwfy3IC990bRcZcy5uVbjsuLeSkgUEOEQmeQvkWj3Y0ScJ0xRPCHO0xnH4wNOxxPGacaYgCkypsgYJ2COjDESIjskdGIZlUYQSYy8QBN6z+gDYegIfXAYvMPQBRwOt9jt9giHAzq1MG48IZzXEEQONRVjChVGpYiIMXtxxDhjnkb5nEfEedZcEDNSHJHiBE4TwBHgYiVt4kzDz94JcyQeEKShmSQ3hFcFxLYnhNfzbudfwy7VOSDyd0n+Spkorj0hCJLAyxgSygK7mgAve2LtBfG8Vf7rri/LS70q3iKk+i0UHK/RrP9abb+0WIz3twoyntkJ21drORJtPUVbH9u3n9mTzysj0HSC8jlYjqElMnk8Ix0fMc0RJ/I4JocJhKQUcckRpYkZl9bCymR7zALH+h36rsfgCJ0zIY15QtSMLTTmKjL8sjEYg2XW/zZe+yW8b+uB07ATDdNbn/d6vjenOb+3LdS3e1XPaoY99x+FabfB2piqda4ZvFoAtdGdzL5nqzcqbbTjfF7gd+luFkRdOnv8MmHiJZpqi4lYPrl64qJA/NL9+lC+gpayfag18GqsnNfB6ITSxgIQYPnqy73Ltju2qHADkDSXagEGbV9vX9+AXERXQOlFgNc+lRnl15e3z5dVkP+re/SKd19RshyuoitpsW42F782G/FFqFr29MWp5+Zj9eb2leUZuVQ29jkqePhCOso8ImIkTHMAc2xz6FhbXAszIfS0F4M4y29mwnwmqIz0unBG5GtUEo1ySVi8Bb9qLwrDo2WYpQ6LSlCSHksM+9V8Gc5phHQ1jqC6anD5cnloWcBd0Q2sIW3UEEDCRJmRooQqgrOkqtJvye2cwFx5qHACQcJeUQNPdB/aCIgy7jGsn5PMksr7TBhGyIlwAWg4JYYlNgaR5vWQUChMVCLxZ0F3mVPjC5PKhQN51LJsTgkTa2hYt4fzPUIawNQXekMND5LhbtiymIDyEr5s91CTJ0TpMbY1SDX2kVakXTO+SiBySE4My1g3dWICJVFOkHnyOUKStMbaEUKRtOpc6/lpUMGG92BNlrN+aekzFe/WOHKxF3njYsm9YzBXjG4kHNOlfVXJbmUY6AMhdA6+I0gi7IjIEY+nCfePn/Hp088ShunxHqfTGdM46tyRyrGKx37ohDcnTRKQ0iwGPJZLUs/venyLC5dAXb15KnhJzXVq98Bi/E73LI8RmBgeAV3Xod/tMAw9hq6TaAaa7J2S+Sosu1JwHcMhkYfFSUgsiroRD5jpiIhUvB5IEy3rmU4oXl9laZ5DYhfuX3mtBr8E3dKgDN9M7m2KgMVg5b8aRTX0Zrse5VDoZ+UZlRUQLXpEgWnIIJsreGHzQlypGupmX1io+v8tQv0MqxZop8Evdb1EOQycTwmeHYLlBtbPoLIkK6aEeGn/3qqcuPreC6v8tyA3tfIcK/VrlZd7RERxpZrnWQSW05w1tyaASHpg758G/PmXGwAew9DBhx4hDOg6CcHU9QN8COj7PYIP+O6mw+Apx4x3IUhyajJ3thJrU5CmywRD2dh2fH5tKv7v5d9yubY7aqEWgIonZDCSENUpIfodRn+DGBOmSWI6TtOMKYkC4nQ64Tyecf/0iMfjEZ9++QWniXE8nxFjxOl4xDRF3KcPmBEwu6jKAQdKE/rpT+g8sOt3onDY36HrOux2B+wD4dtvPmDXHXC4fYeh32E37DEMg8RYDwE+ePEasFBMSszWLtxzEguwaZqQUsI0SQimaT5ijhNOpwfxiBhP4vExjRLvNU1AmkE8AZCE1JIKy2vKFoLX5PJBcz90QT0gvOa60JBM5pbqvVchZK14cFmJIh5RXr0aRPngVMnC1AEuKEImsHMZVgiC05wQpryscj/IP1NqlnV/VvkAU7lsQ+uXCUj+7cKp14RkWr2LL5SD/Lsr9WzQhevLe1+/5ea6UiGpsqbjlPCj2+GHMOCPjx73Y8BJw7bFOEsYujgjaY4I8YgQC8YudPA44/f8L3jf3+Lb2/8Od/sB33UTBgcEf0AIXuCCEp8mZHCQeL5OOfukSSHJOTgWmJEs5w30Oxw4aVABPabtdlVaYaF8sNLakK6FX1l4sHxPY4mXT4FljjQEHXnAQuRlTwmqPqu+bQjbzCuiPnvF40Gt/RqPiCLIco1nxxu4k383JUtEUDOAL3pz8fjKM8SUPFw/uzzTF+aevmRNlmt75faqzbpvr2hxqbG76BVxve7lnP5tlA1mefOZrecuTHYjmHjuBL5MjP/XK8/1ZUOg/qI5fUm728L6F4UYACOCxWAoldxFwUv4k67rMM8zvHdIUen9LKcn9EOP3bATQzoXiqBe++aCg1nANwJTFRqZx60JVSMkVBHFiKiC3kxb6cEwWtZ7D2aWGNrqrSjjiGIlPMsrU5gFJ4aoHgGolqsSgNlPB7UMJhTPSO2jzXZCsa5lVDmXuSwH201AkuqKGTO7iJQAikI1M6mldXLgyHCzB0LJ15CShKWd5wh4xhwl5rl3TsMBrfee9djq1kyySJDwRxLGFfA+ARyQvKy9U8to842AlzkPui4SOSlpmCggRt1FWeCfEJP8JY6IKeK2G/Bhf8i0EzMDKeF+usExDpiIcB8l3JenwntkIwW6LsGwnFtgmXKTv8QqNPZ2js5qrTT5NDkHig7O2d7zIMfgyGBXQmJ62HaUfcdgOFaawzEsB4fsa+RwYrXguygZ1oJvoN5GBU5sKSOa/Vu9V35Uwnf91egpWXZGXZfpD701pXcSCPuO8IfvArgjPO4cxukRD48/4fHxE37+6Qd8+vgJv/z0M6YxYjrPkusEBFAAyCN0A7zr0A87McL1HgRgPJ+Q5hnH0yNSjJimMSveANIQxE7XWQx/iSCJ6y/kuSuzVc2TrYPtMxRLfxOhWYQRmzkHgI8T+L/+guHuBu//x9/h/fff4P23H3D77g6H3YAdIrr5CcwRTLxah4paBuAw+htM2GGaB8zJY0oJT3zCx+E/45jOSHPEDCCSKr7Mc0AdnFvr99fikEKXrV6/qNiSd3LuE9acK9oXgkb6+v+z919rkiNJuiD4iyoAM3MSEZlZ1WT27A7Z79u92bt9/9fYuZg+09PnNKmqZMHczQCoquyFiCgBYMQ9Ikn1Kc30MDMQ5SqcYAFeAay0b0zVdwfJO1L7dNW06BrHZUqDAMCBKQmI1bMib2keFgPBYJjThVViRh9N7WpMQsQvn9ZXlKKcMhyURApDhC5F3J8CunjAYfDYDR5D70UJ6Nc5Iv7m+fCfp9ysiFgm2CpKiIQ5Ek6T+M0wA+PcIWFQS2hJSp3/+j57QuzUG6L3Hp2HugL6bBlNFstdCaWsua8RHIBs6WAUn5Uz+/SrKyu+1DLrF6763HhrS4G6La6x919JqQ2Zrk7ZamgiOdBIpNUznL8XIK7xCpOET4xJwpKZMG4Ok3hCTCOen55wOh4xzREhiTJvCjPGwJiTFy8I7lCFCgWRxEvvPbDvHbreo+979N5j5wn7rsdhd1flghjQdUPOBeG9z+7ixYtIxwBenV1LLh/CjBQjwjwhxFk8IaJ6QqSIGGdwikAKkESwERI0RYhYB+RP50hDLlFOQORdmwvCUQkbUsIqmZJxEcbE8j+YIqL6s7i/BhOK90c9fkNiFSypFQ8VHGn31HkihfLz3D67fPfcFmTr77n7X37+bmXQ/1rLubF9saXsK8rVJre30uI2Z3fhrQfcmXtXPSGoEKzl2rqeejqz9VG2tmQEB8wQD7CZqRggJAZHTZ5plp3MWfjivLj1H3rC3SAekZ3v0LmSN8YRFVxf86kXty/lsVycfyW2t+Zk+V6Rr1JjvEfN9/ONNfWaspPqcVGuv/GIqGHSkkmvvCKqlspnTQrBGE6UdhvWc1nP5ijWSDRbF1aXzr17Rlh4U+EvYC+utVETCdiY66sNF+FIwddU/a6Yz6oyQoH3ZwmUfP8rlHPVXJqfF+KvVVNnn79MkGUr5FeWrw/rX7Qhzq7bslsiY6DmQk2Xc95bdLOXyOu9EeszuoAJr5hOFTEvrpxrlpDN8fni0xtle5wmMM2/q7O4Wgf9t9Bfcl4t51jOR0hOEhuTKQNIPYztueV50fqJsjUvZwGPwQRTCgOUhN7NiX0ri1+bqsyTSHXFe9jlKOrqUVCSSif1LkhVfbb3Gv/AhQaQm72IzbQ3m5C5EhCySZvJkhMXIXjOU6BCfOYESiSC10QgpwkFlHZgDfuYWPIWMFB5caDZp/UU29IXb8SyD2oBeEa1eYNQyXOg+JPrCrOHQfE+6EhyWcF7pETwIDjqkXiQuVDJIDvAuQEdOqASQEooJLT92yxLa3CZxxyRYpGjs1FEAOCc6MNoD86W1A0ubJusvidI3otqDfPc5pUHzLME5m2AZg2yvHUFe9Y9+DKwvlFvXV/N+9VkgEMOJcwgjAygIyQXEJjx6fmEcXzCp08/4fnzR3z++BHHpydM44QYkkT8YaX51FtfePNewox7D/EKkggEIUYx8gvxDAw3TykUpdaNoH5J6bS4pn3KKQw0/xbSterhMHQ99ncH7A8H7PY7DH0vcjqO6zi3GbSUFi1cVmSPRL6KIuFEfoKIRDFHKEpYD9F0nGcHunnv7I1F5ZdultCoNnsJooRjYoXvbVXLeW+OEdq5b+/XZ6JhxLa6VfpEq8vy3dAsCU6Ss1hB8I3pqb3Ktvxbbi1suLe+tpirZd3Gs3TE8CQeEcYbFkXtYrL/hyzn+Cv55EsLfEP5rcRFNysipnmG5IYISMwIMSjNkPD5OODff3hEYguv4LHb7dB1EqO+6/fw3Q5Dv5PwMfs9uq7D28Fh71nj2Dv4TtwXnfcglFAt5LwCdwVwmzkhjDQrH1+Lr/tb+R+gmBWwkuTlQJobt4QiiykicMCYxBp4mmfM84R5mnCcTjiNI56OTziejnj/8weMATiOM0IMOB6PmEPAp/AOkQbERAAH2bkOIHLw7LHv9hh6h/v7B3Rdj8N+j50n/OGbb7Hb7fDw8BZDv8Nud4++32E37OE7h65zWRkBOyNK/xmDEsIsuSDijJgSpkk9Ok5HpBgwzUfEOON4+oyUZszzScKwzaJ4cBxBxMI4gAFKcOQ1mZBqtjtxXe+6kgvCk4PvRJHYOV8YMrJQTOYJUX47r2GXNEcMYO7Ncl1+dwAslJMIPU2BATJLYPOQKMtdiKVbgcRfJzDZEtT8lsqJ16HH/xztn2H58j0rv+ROa9jZjC7bFi15vcTSjggpIKSIwBEBEZFJlJcpIoSAEOasyGTNFSWKCBHY9H2PgYD7xx73D29wONxjv+sx9MDQdeh783ASy0WnEgHeIONNqNEw50rhZ2svAuAYlLgo4yrBi4V+yoz5UjiR/6jKHbMuSy+qOqSSeSmY0Equ+VbglQ0uqhwO6tEgJZXBLXaPCcLIlDhKH2VPCGe2o+1Yywi//BRs1mJtvRLGULVOv9w5bVg2/bx0Ouv3rKzY5fW3qurC4/3WEPAXKJeGdGW89Pqt8isonC0d61c4K8txLi60wvyKl/lK7bedyf+Usplw/VxZJ1rP/T93RGqe7NXDuaWPZQ7X+0MT/nJtoCEeuY4IQ9chqkdx1JxpRJBcbV2H3bDDbhC+Vrz0c0vSlhNiux0eZVwiJKpTC38JdRxjUn5abG85yfUMx7Xbne9EUOM7sbp2LgvEkyBrRHIIMSFEyT2RnJMISNkrIksKkSVZFnQcKrDSVhku3+P830Igyjbf1R41QbWjnKyYTRimn0RAikG6EGax8tdE3Cl1cCReBkwyPwSAU5et9JWtqcYDVXzIXDunCZYBcCI4l5CSW0jCCCZcR8bbUMtnG0ZCQsreBnOccw6RnhzeDgcAjJRinpvjvMP78VD2Yp6qIlSTtuxz4X+p8ycjMzpH+gLGIuwSZ6OyoCF2Y9JQTHltFkMGGpoje0uS8aAqVlmCB+uP9kGWl+ESQF7otZz0mQEJ8wTdR8hSUROOrnURVPb7uWOerxdc3TxqRhdUjTw/KvyhKXyakGdU2u57wj9+5+F6h6e+xzif8Kfn7/F0/Ig/f/+vGI/P+PThI+IUEU4BKURwSJXzrfCfw7BH1++w3z+i73e6hozpdEIMEdMo+dTmMSJxLDCknnF9J3GSXGfUrmehhc/kNdSxrm9ydY4IHamSQPeEIwfX99i9ucebb9/hj//w9/juD9/hu3fv8Hh3j953cm5TymueeQlqYSvgwHCI7BDYY0oeU3I4MWHiQZNXezA0p4u+d8Y5oMKKFb1Wo8pLZVlfVhCfeRYQWAbxpCOGJm/n7EWz3G+G1nNTTPo8ozaysbCWpXmjeatYCxUcIADI3lBc8QUbQ9CjSI4AdjmRdfbuyLi6pkHK+c2/mdHSJa8reUwVHLDrAFQB6OApoe8ceuexdx12vcfgXZYX2UD/MxtXAlvbeMmh30JE1fzM73++XpCsOgoSUmsLQXqE09jjOPWISYWD5OF8B695IPpeQjP5boeu36knRCd5ITzgPVQIYZbRrUW0IZAayQBYYqCNa/Xdr8yw/OIM0O+jXAVAS4DwmnnZNB37Zcq5qrkC6HbEayFXibsJBOowMyFyFEGcekJMYcY0TThNI07jCafTSRJRsccUgSl4TLFHSJIwLbEviEX3uAmuJMm0Uy8HEdJ1zqEfBgln1vVyvtQLYnl+6jlNOg6LPzkn8YCYQ0BKEbN5QoSSEyLECTFMiCmoJ4TFrVR2xKwBXEXUmpcDuZWwLed6MeLXwocQsgIBJkxDBQNQrhc4sIAJVFtSV94V1bPlXr3qdOZ7szEW96vnMuG19eL1c9BaKmtzvCAENjl5Pvv+LeVLwip9SWms8n8rQsKYv1e+/lUIoBvmXuSVX2+NsiA+144zk8CZxi1CDpYoC8xISDkRdbHGSzkUU2oIZNZzyfDpGX2XMHQH9OoNKaHjUhbGWyQ15ZSlDi6CwCwKqeov4hEj9fWegKiGOdBJLb9Rf99alhZm2M5pZRkL8tBgWKZVKrhGtYLB2IECP+u6hZlLlTBhIdqi0hfK42jhWam73LNHzm3jckY3Htjaj7wWSF58fvO5ZZ2k/NH5ui/VvDW0NRu+vMobT10uS2v0tUB9gSu4DTWxmuNfACSfVaCdmZHV/sYLunXxwcsr9lvgo9vLFWbuAunQYhve2HJUvqMw/Zuw6FIPz8zfpjCyvFQ/9KL9R9zCk9JgoVlMRtO8p3e4ltY079/U+oV7Kuw8N39Z0N6eWzBlATlp2Jq6GefVmzfTs4WmlDoXPaPt+aHqNjmCY8qWwCLgFfxKrn6WMuygSrFtJLFZvYMFA6ZUe0coDoeFNFrAVGF0VKCJdtEqWLX+VirIqJUXeIMBsJh1JYjXhjMhOieQhZtJURKCJxH6Gw1B6jFhnhSrrUHtyVyOK58JxxIWKi9XewgLdjUFSxHwt+GOono8CC538Aip07nrsnFEQg/OwR25itJSFFLI/djCqSmPyfrELGEy8++khmUqqF550jgCrdIMkEXozfkospGW7S2jd2ryZd3DZp6FF+S8Htnmw7AM23kHSEP4UBYAtyuXf70cHS9rKNxTdZiLEkLnwdZEu7MfCH1PgAciRYzTCafpGR8+/oinp894+vgJ02nCdAxIISHOovRBAog8CCL7IudVETGIApGc5FfUXIxRoxBImK2FL1IGJtzcefl0lNNRqM22IpsalyehKKacd+h2Owz7HQ6HAw67HXbDgEFzQ5RATtXaW72kfDxM+Kx5IeDEIwIeEUCEk/BpIP3cKA0P3u5zXl5vH7lQ1/ZMrR9bv8DL74u92ighgKyAKEvL5UE0y50rZYZ41dXgtHm+glvVYzU0s5EJeltPzNn9lHkve6oe4Mt2oSmT2rfacTcdig7x5DC4Dl3v0NXGWoV6eFEfSvXLXtxWz5bsOL97bb+VSvCiubtJznCuviU18rr5+rXLzYqIOcyCEGNx+zyeOvzrD2/B6OC7Ac57zQfRZY8IiVt/QN+LEKLvezwOjEPH8OSFIHNeLCI0NIurQrUgCy6RKTvOzHtdXoW5/lb+k5VNpmzjYJtQq74lcLNyI87fxRNipgGfcVBr4BFzCBjHURQQpxM+P3/G5+cnfP78Gc/HZ4xPJwS3w6f5ESP2CAhIiIhG9BqJoN4QXdehI2Df77HrHYZhh857dN2ArnMYhjsMwwG74YCuG/R+r+GYXFZGABr3Eho7lBOmIJ4P0zTKWGbJVzFPooCYT09IMWCcntQz4kk8IcIEgEuoSVesWuyMmjWz19jnlsyv9Mtr4uraEljjuhNZcHUQdcrgdXrWO2iwJ0ik0vLH8MiKisqyuPxpbgjXWhwtdsstO2p9hYy32GYmbhOsrN8lKvvRhHF1m1a+RCDehjD49ZHUbwml/7pQ89cvmQS8QhiZ1Z9ZV+YE9tSJV0QEOBJiUMVlEGUsJ80PoUJk7z0cT7jj7/G4v8ObN/+Aw/4eu+FO439O6HyJ/0nE2auKQcKMxSq0g4WVUyGGtZeUoWu9B+SvZkhrts4EE3XJAnsUBlWeXZ7TrVkT1ouo+qRK8Wo5HIgaGFjDrCXZmwVEQAMXcshKUPk0JjInxi7tba/1rVT0hdICpa9c9W8Lp15ezg8677/f7TDOwYJbofW1gf21Q147Q+nag025Ptq1CGRtgfilGHPr/ZqueFn9GXVsDM7g5SUlYp5HI6LO9Ot842fKpVep/lK1SwSxJmaB2TnkEqNe667zGPoOXd9l7/2ijBDxM9jlbMXZytyEJ6aENFgPgkcHooSYRAxnuRFSSnBJpIOkHhbk1EOBAN95sZB2DpTzAAhfDpfQK+6OGq4ncoJLTjgC6xJDhdlAzIL+SoylOCMR1dGSMiAry78x6VlgxjInHGWOCEg5JJeTUOkk+yAmCf3jPJC8PE9R5j8mGasJK5ewxHB1Ds3E0ITPrPMmHhGUmmQZyvtpYlcWQwYTDs9h0nC1lv9vhgfhXT+AQEg+YYweP53uNsU+zqlVOFM5L2Rbzq2ez/2xVVAjD5lz8ZDhvNayEKKXMCWUnGPvIHwPsEx0lTspPJxTuYsIjLPHptISWShdtgJadZsJVlXJlRgo21+fSkh6togZUNG1KSPM4KARyFIJj0x1cH5rl004v6VstKJuOJXwMisG7V3Y+dImiNF3wN9/6+E64COOeD494/vv/zuenj7jz3/6d0xjwOl5BicCkkNMhBi0VnLwboeu2+OwO2DY7dH3e3jfIURRDs7TjBBnTONJFBFRPIHIaWi1CORcHgBIw/80a0e2r6qNcyVfRL3wK6Gq1tk5ByZJJg3nRQ7BHvdvD3jz7i2+ffcW37x9i7d3D3jwjF16ljOT19pmt67f+iX8ekSHmT1G7jGxxwjCiBkzPAJJ+zKsosSra2+Al7VHBQoUF4oLZQWuio/AYlo2hPrrHkkNEqoJYJh+XfABqlpUKZwF/GxpbGB8i517OSup1dPrWZNqxRuKzfupghuGtaj6K3v/QilH+vqU3VwWNAwDtXVYccBUfOgd4kg4vn/A4fEeh7cDdkOPoZNQYFsjWNNKv0H5CrzOLU18eQ2/b9r7ZkVEnfQoMuH51OM0DwANcCR5IJzv0Kmyoe936PtOlQ/iDbHrPIaOMHhJPlmS02pIJ0usm6UE5nJGi9Uo0S5z/+orNfym69qvLa3Xlcm4/dkXEvpfqzQCzRs24XJI9Tur4Z4b/2sEBnVHX1BuftwInSzQSfn3ljLCCK6UhOiJ1IOJEclhZqfJySLmGDDPM6Z5xjiNGKcRn+eADwl4HoHx5DCnPSL3ovlndfmliikAKzFQ5U5QQX72JCBCT0DnOjjSUEVU54CAEmuy/xMzKKmNMDOCuu7OQYSJU5hF8aBJtqd5RAoB8zQi6fWUAqK6XqYUK286cZm0OPZc0B2aeOf5/GoCPNZwkgwgqXWXU8Sr02B1I/9GtiaiPLpqXzIjGVjgeq/afbEDSzkJ4HoDEcwak2tjvjweoxOqV1Zba70PaXF9+cBikBWz+tJy6Z1rAoYvFe790sLB89a8tyPmZR1bhCRw+1heY7n71T0bNupvFVYbeUFo8bmsV/+Rc2qeECkrJKLmiDglwrNzmKPAmRRLviiTVgizKY1Zboj9bsDd3Z3SAgN816vuUQU61rWtswQh7AuT1hLerOGLjEG3v3ycCWrB2zIw9bIsQyyVrpiAf92v5RrY5zLsgSSGNKWAeqxlZtoUBoVBbvaLjqnOEVH3r+3XmslcFm7uLRgF3EYnLMec+2adyb+Xjd5acfWy1rVq6yVVXbjOF67c3MbNfaNm3rOF11eCo5fgzEvo26UV5iWRcnnuS8bw29DHUl6zOW95Z2tMLbdi5x1AETiZQOMV53GzF2endj2OF/NAZx/nzbpya1wpW1ZTcq0PC9jSvHuxU1UxnFJJXgz+Lj6ttB4RtjYbY9O3LKnmCheTzrMp26ngF+YEJKdKdlE81IJU0j1C5vnsjDdWXJggudxSRExe8LZX+hfCd0hnKXtJl/jzZRoyv92Ks1ZzSJVQrcW5nNeSVcEgOEzGZaIyB0m4iiSR6ZNktNacEU69J6D9KziwYEpte8EjCL6H5pUw/qp4XFZvKt2QQCmCkcRqnS3MUYRLMqo5DEhwGDUELCMhRA+uktCuT+qKoYatVuYtUPhRm8s6J4DRU1s4wpHwYY4hSh3l/dwNIMPCOWajhSp/HhmeUt6yrH7hwCTcDOBIFHCJWJURriEyTEwo/GJSnYLsB9nzizaUcTJZTsXWLrYhg895ZVlfq7wsqPkxQpaRk3aHegI64JROSFPET88/4zg+48PP73E8HjE+zwhzRJxEKYQkPczhRDuPvtuj8zv0gySzJ9IcaikihKiGM2L374jVE0oMaLbgPAOaYoTzEeNqP4hys4RfzrNupNMZzN1id/kzL5+o4dTc8wQPj/39A/aHA/a7PXZ9j855eMQql4rVw8Bma7K/hK+Q3HIxEaaU8MTvcaSjyFMYWRFRY0AuM1FVv8Rd59pf4zdWQbjVfj4aoQLFTK8Z7KkkHvX+47qnqdSBgsMLBW+AgMtjtsb2HCOfnfyixoKytbcIHSbnMd7Num6tWgLrpv5F3XXKpgLXz9Mf56nljXWoj6Ltm+Y5Qlbek0PvOvS+R99JYncz2KoPOhmMyGv58vLa97bevYHyX+d+fInsplqsa9Wc50du43Fe0M2vWm4PzRRjHsIUOvzp53dI3GMY9nDe57BLw7BH3/XY7Q6iWR16VUTsce8i9i6q5XTrCQE4jZPsSpBC+6yJTGpSbi3wU0VRVZd+I13A76LcMv6bFQ1/hWWpgDDX35RMISEPJE28pGQzmBkRHY7dAZGBkIJYx4RJQjHNI8ZpwvPpiNPpiOfnJ3yfPH7CPQI6ROcQfARHIWwtxiexxvdmKgSRKhW6zqN3yLkVyHl0AO5299jt93C+B7kOJWGzMShCIOXYtwSEJDktphgQU8Q4nhBCwDQdpf/TCTFGjNMRKQRE9YgI4QROESmehFBihlnxCpmqDJIjMKuiAS2SMGrPlA8hCYHsWAjQRBHEpL8lL4bQvZoYEGbNlOST7Z5YuzgjVRkSB14TZhvj54wgNuatOQAFphAI8Mp9bdJSDEvfZXslKzXICML2pZU87iJgryiEZctXzmDDnG0c8HNC6+W7W/d/6bIpLP9beVVZhtraDL1VnYVLz1kIupiieESEUP5iwIfY48d0wDjPGpJuRpiDxKOOUZMiJpjFftf16Inw+PYd3rx9i7u7R+z3d9jt9hg8w7sgOSEcxDLMGAQ2Rt0+xfbOQkXV4aDEmpEBrkIzZfKBwKlibHWcNuziidCWnF0hKyGWZ3zJBFOBkWQKZQ/nNPeFd5D8EF6tbkWglT3CkPl+GGFewELFCFm/qzBWoryw30rUazWMtcFGqdN6vr7610ou/dYQ5RJcOzenv5ewRFtrf8t85j37gqd/+5V6bbllrW58ZjVlL535r1e2LGXPduWyvEceOOf6UzFuK2vGW7fQK0smS/VPoGpLf7kKhosSmQHNXej7TnKfOY+sCM9SI/UCWeAVOxtGk0sjMnbnxWPX+1iU+ix4NBmNiWIoA4LgVO+RfIL3DiE4JAjvEiGeBNM8wznCHDo4R/C+A3vFH44ktr9aBmWBFqDeBkXoUyvM2z9TJBVhYVnJaj4Tl3nWsWRjRsXVxML3C3Pg4ZhAMQIgJN8Jr8Bi/V/PteFkU8SUPSXXs+WtBHQXi/9keDlloZgIhwM4zuAUEeKkguMZAONdNyClHs+8R0zAz7HaoGxtndlvi/1d0HlqeIDGcIpLKF3Js1W/aeG5bB1KvU199WrUEsjqm1NXgHqvm3dlnsU8tCw9zLWwtpISiTIimbdKyp5F2X+FHZq48CRGeC7n32lplHxmzHMCBDKDtQ3YUvNfLamme6DRQBSjF5kCmdM3f2SQm/Df/vxveH5+wo/f/xnjacTHnz8izowwakjyIH1nCkLb7nbY7e6w2z2o4e0u93OeJ4QwSwSCGJFiAHOCczKW5CwMmdHN5ilDuesAxBhQlRogRooy987JrJlidFMsXG+OagmzIk/P0uA0pDp5YE7wPzzj8PCAd/+Pb/H2u2/w7uERj/t7HHwvAsM0V+C63Y/5d47MIErVORGm5DBGwnOc8AP+K57phBmEAELKOiyXzydVxke1i8829Xq+FLq/QKxmnjI0K/NFaM+VRYQwqOhyvwpcLMdNv+T+26kpsErgH7KMJT/LKYOvPH5TdCRT6IqCyxLSJ81lY++bgiuxQYNU9aBWQhSonefCuvhS/rwylipw0WAHF+PVGhfac6R5mHqHu8Me9/sdDrsBu95Cj5/xwvuFaYavVojWXRVN7K/R+LLl9u7vRBZzsyLi/eedfCFgDj1AHt51QqR5yQXR+R5912fLx7532PeWRBfoNTyLucCWkAUWD96CY1K2XmgEAQsBwJdoteqy1Px9rXql8i9Y5K/EpK61ZhvXFw+9ptv1PF6z6lrN8W2S26tzUruFswJ8KMHdfJrrqyKQ4PpCcOlzEQ5zEBAfNLbjPE+YY8A4TRg1H8THjyd8fI54BiFQQAySEM8sRwQWiwg/GS1FhU4q8TkdQEmOgbrLOk7ojx/RxxEOEXT3CN7fZwRErHR3MvpbZnyOEZET5jAjpIRpFtfQcZZQTJN+jqN4QvA8gaPmhGAhnABxFTRhiSMnMWxJvKKccDDwAKJh6sQiVFTCSRiSJMnqTJAPB3KqmACDnbjwitIsSXI9l0C+AyUSKwwCkGROEslvYtLxcyaonXOK7IQYyAI63XWF0K5giy07kMdqlmvL3ZatmfRd6TOtnvmScgtiqJ9ZWsRvlSXC+U3CMm0AnteEhviK0HnVh2vz8tsJDs/1qyU0CrG98XZNw1Xn0WAgo84BlRCfPmF+/yOenz7jEw0YmRCTxbJOSJErhYARzShOjV2E6xjDbo9BDRUslJzzScMWGdNL2aBOhDwWH1rzVBjBzZqPIodpYiHQsb122cJvobQrTH07J9VbDe1xPjxTsWotMEj/MpOv8F2tWeuwHq3QCovNzRvt1WM7gw6XCiarh8uVppJaWMGL17fOw0XidcEYn+eT2+uXxnGmresQ7HLj17r2mnIWPjRj+KoU5svLksT6KnXdOqK1IOD8ozf27BrNeP7F+qVXvPP60opulFY+4xnx9cvGGtSCqk2hwY33C3G0vrFATV/N86Nu+tz9zF5sUxDmnSb5FyjTjUTISmO3tMyUF3XINpYyTKrqXvaQYIJgJxbS6tln+QmgRi45lE3pqEYSoBJKB4qvE6kBgYRU7KJ4NErOUhKPC6cCLROcLeouORqxOlfXZCeGZrMIOcduUazO5ZMTA07GTbCcSCkbQ9h8ZQVEjaNQr6DONlW/FIexhTJBa3lutEJMCRwjUgjgJGEmk/JMzMBzOgDwmTZamlC3cohKTKYJx+WdqtW643bUc55Am7eaTikvEAgxMo7PCZ13uBs84BjRG+1T6lWKTnkVqq5b3cg0xybaXV2xfiRwzttlV1RErHwtV7SWXBSvCQJXHu7CFwsPx+UM5be4zHUzX3YmtjvOKPU1c5dpLa1yEFozpgAg4v37T4jpiJ9++B7j6YjPH58wjxNOz6OETIoA4OA6ORtdLzKuYSeRPvq+h1fDOcvlEdOMlALAmgVBTdOL4YwNwsNC8dRzUMsmalLKkZ15Ks/RbX6LhWBULyyZHDEAtr1Ckhx4Nww43N/hcHfAfrfD0Pfw5CRklJ2kTXi+8I9UEUBKQEyMOSXMMSGwhI2L7BAhz3ADW8t+qRe7jPTc7q3Gi415afZGlaNT5UJVt2Fwh3jZ8rJurt4w2Ffg9hZ+E5zEq7nKYrAKXJhCKen3zPdkfJGbL7te32HmhTdFGV1bSuO1B/aix6urTQ1csF/r2W20Tb1h7GyKXEmSVTt03sN7zYnqCXvH6JzsS1SwcqNbTXubz2x1/NwWegFJcjX6xLlu3CxLqODhomPnSN/rnhGl7kuGrOfopa9dblZE/Ov39wBBrfwc+n4H7zsM+x287yVuvVePiH7AsN/jrgMefBKhg5vFIhA+xyi0cEzkPDKmEOpO/qvjuxsSaZD/RlkoK/5WbihLJcRXZc1//SI4Ze0BwYwcBzRbAyUGk8MROyR2WagWFYgzJF7oHMUKeJxOmEPAcTzhNJ7w9PwZP3wCfg7vEFRAFiKKgC6Jk7UQXiZwTxlhEKnbN1FlLau5FYjQxYC7n/6EwXn0uzvQt3+P9PbvEH1CTAESO9YSXztEHdsUAoImow4p4DSdpP/jMXtGxDjjdDwixQAXjkBKiGmSuUsTAHFKcqQhmRxL2NcEcCRQArwXDwVHQvB7EKBx3T0YTAkRxugp4kl1bHSnTgnGYDk4F/UzgZyHjwBIrElACZL+Qdok59Ti2JioIvwjckrvGTCtCNOqTzVNUxQRVaLrqhhRe67O5rlX7d3bz945BHLt+jmPiEseFnWbtyg+tkqbcOu3KQvaeX3/d404liSNnIOaqFuy6fZevdy1EsKIxwTOyRljFI+I+cf/QPjn/x/ec48/DW/xNHcS/kG9Jew5TsWqB4DidwbdJ3R3A+7fPOBwuBcX70GYmp4k+aN3UCEPsqCjENmuJIuMMSeNjPYXxRsjpqjJG1uXY5sq4ooLhTHi7Xw0n2VGm+vrQgXeZCWEeUOoJ4R+OupKXoiNHBG3EntZadEOANDrbrOuM4wHUBh7FDIgW/eeg0UrbcWql1UflnVcJ4xfXHi54C+v4pcu2yzdf5ZyidP7WzlXtgW79e74leZzAxba92vhH19j0PB6K7xrJ+fWOlvazTzgcjJqCxescDVf8+a9L02RSWAXfGo2hqICW8leYsCQHeU2C6/C6vEnsceFV8jDNgW3F8+I0IlXBUO8GBGA4AIcOcxzB0cE78Xb2Lti3AcVSGWFgM2GSIWywhwk4aOa/XHLLBudRxBmQQ2YnJPwTM4REkvoIyQJ1ZRDM6UEUMHlJjwTWRuXMB/nG899NIMKsxyGGkuI0iYhhBlxnhBmMcaK8YSkYXdj6jC7Hg6WkLpex4UcgvJgixJC+y1KldoLgpuPctxa2ph0ve27I8I4Jvz8H4yHHeHbPwxIA2MeQh6rCSvrGotwsC6u7IVF+2dnVeshMmVEIQOSiW7UuYVdkrj55vlPKasu8vzBlDUOYIarumjJdfNepeLVau06LMaltG82hjHlg05y9k8iYLhPGIaI95++x2l8xvf//O84HY94+ulnhDngdBTa9nic9XiLd+9hd4/dbo/7uzcYhj32+4MsORKC8s5Gp4Ywg6PsZSLzTeUc3x/JaazmHoSExPNy9csZBctY7GxqzPxiQZ8HenEN81Qp6DPa0zsJHyqgyWF32OPu4R7vvv0W7969w5v7Bxz6AQO5HC6KmxVZtq3rDjHITAzMMWGKAcfZY4wBgRmRE6YEzCx7iI0wNwW30qFrwa26OlUC+M1xCvGfe2feJtVOQf6VAVt9PotA3nE5h1sZCxgozjoq3zFFQD1feRimYaqVrtW37Auu/UgMNcAqXuGpqtuekXdYDEK5yoFTgGg7Z0s8vIRTZ0s7T63ywrwA63NsE8SZRZXltug4Dl3nsRs6DH2H3ne46zzedAyfJ/sm7NM+Rmeu/1WVv9qO31xuVkTAdSI07Ht416Ef9uoJscfQ93iz38H5HkM/wHcd+s5h7yUJiYQk8DkUgSMJv5QtTNQC42wiIkP6W3D2VxQcvUZAf6vVzznFyqvo9UuV0CJe/ldo4NLYlvBdu3ChskuYZf1iPb+1wpRNc6/WtAE9IkkKrYSUCcSIBE7AlIK4RKdKScEmnIvqURBwGk/49Dzi50+z5IiYgFPo1H1Y2iNFBKyCKgbgnLiyNqyPEoNmLWteEWaNzwCC83ja3SMyY0AATU/g9/+G5D3mTtzWknPqAknisscJ0+4esdthDhNiiphGDcl0EgXEPB0lAe2koZjCDLAlzUvqfcCFGUFFGLEGZHIAESMSI5AoIRiadI+BSCVkEoDsYud8CfcEcKWI8JrsGhJySROKOQ6iePCKuBJAzus1B2JXKR+EKHPmWu5qhcLaCyJf0+vFinmL0C0EnyUSzDswCwj1H2akDz+Ap5O+7+Df/RHUD9tUjDaywY5sFgIDxKiFmK1lf9tvKp1DSzisa14ivXpclBNOcSEaLxSbm7p/t3hzbE4Rt/vxNaXMVn3x7IK0V18AKpePLke2FP6e60qJwV8D0OKqztXvbKNT3be+NDCa5RzZ/mVGZpAk74MwCXMKmOOEz7HDe+pwSiIwiEFdzVPMRC5rKAYAqkhN2KcZD85j6PYSQ7cb0HceO5wwkCRsy3tC/0lAhqUpxUxoi8xC4VOKQIpgFnM14gjiBGH4E+rzQ+BmwWn1WYgLqq60Ajl7Y3EuFBzUSghRwggcQ87pY/QOiaAHqP4EbunMFQamOqONImSpaCCrQ9e0gW2LstqU1FwvIyznensfG2Nxpp2tBsnGdeaZqg/niW7pYXO3fV3eZ+viBhzb7t0XldcIVc/O6+t7sVXhTcXWXeaO0QKh+iy9rv7LHbs0dzc2sqri1s79GsxdwbmbLTd4gKpr1QHjrZ5epxFWPVkx9HV7pVZq3rlyIpckwGp5DaJUbWUl+LIybemVy3LVg8RyELoqF6HCS4Lwql3n0XUE3wEumtBPEq4akiKDuMlleA64KjcEKhBp8FqFTiqUFPsBqsJBSRcjJ1AiWP7rktxYFBMJxYCHsgpFhVQExEiI0WMKQUImxwTnxIjHOxnJNo1HK3yWr8OpoRFyX2Ach/JK0gcTNNnI9Y2kIW0SZd7AQcKxuORlLUxRkBiSnIEzvjCMLixbKsZFOUM1mdGvepNoIu5ECImQkvB9zBGUAlIYkeYjwukJIUwIsyggYpgQUsLnscfMHbyP6Ah46MVYqhFdboDJEmZJ9zCnquOXJQBLusSRhI6aT6OsPRFoBA4e6ChhPDE4JQSe4ahH3+0QicEeyJbeKsRfttKckowra0hF+Rg2eqh8TT0TUITRDKjzAxXPiATVTCgcqYSTnBN5s+6oRXgcqq+tiQ0TupY8fzayJTBL2PmI3jOeYsSUEsLHJ4AmfPjwE8bxhE8/f8Q4jnj6fESIEdMpygySQ9d12B/uMAwD7g4P6PoBu+EA5zswW06XQpuaoLiAsTKBDBRhu4Eeg5+6j2Wf6DkiG7ueheqvXlGjI/Ow9Xw007JVtBveztX7J6DrsLt7xP7+gLu7PfZ7zfXqCZ5FRuAkw4v2sa3eZHhJvwcMmNEjxR5xJnzCT/hMRxxTwAnACGDSrcKa9ByAynIot2FrvTUY8eTgdpsYQ8FZn6f7ze5lVNTUlN+rrjVKFzavFOuazgGXKmr6uUx1DXPbc5PhBYxvK3CkKGJtV9R+U3W/GXWYJ0Eg5n1j91p41Iz5Kg3bzkl5ndtHMg6X0a29AcuOZRIDNAfGLs7YscOu7zB0Dt4ZP+Uzrqv8r7DyFFx2tcFXNqt8/iwsy9nnlvTJ1oO0/lXJPr6MOt2izau7i613NkJCvrTVm9po9dWE/ovKCxQRA8h79DtJxrPf3cH7Drthj7uhw3d3PbzzOdGudyIk9K4D+U5iQCpEMEUEwT4pA+WGYNXPX2cq/srLFiDZEtjdyDTfIGM8/+7yN7dgaBOfNKdno5bFWFpCkCoEUkB5MuEaM0Y3YEKPwCGH9WBOiBq7McaTCL9QkH1KjBDFOmIcR4QYcBxH/PQh4j9OD0hpjxjuEDmKm28QDwhDLBkAKUHonJBWrtrjBGNE1BqLEswMgMGYux4/7f6A+/mIN9NPwPFn4N+ewc4hOY8EqIKFxcVRFSmnv/ufMb/5TpJShyCKhzBjPD1LaKbxiBSjuCOnBMR5JVDJIUWIkJzEpXTMQrjAEqNpjgYQYoryTOJsOdZ6H6gFhvcquLOcEBJqybtOFBGd5I4Qw7Ek1tXOw/koHhIuSW4Z34GSKDprIrRuC7S0PAZMyVNoDhUkmnUIGftYkQW2xZQxlDwUnAmQpk0AnBLm//5fkd5/L/e7Af3/+/8L9/C2mZd2zltC+rJ1foRY29j4AbM0ZFSE+mLc7fpiow/bxZRGpW+4CUAYA5IZkUV7y7BITZiauti7W7DhBWXNlmn16wa34dBLYeLlRm5+YfnqEoRe+s22d42hAcELx6qAUv44MmIU5WsEY04BY5jwc3zEj7xHUO+qGAPCLPGsEY3gTdp7ktxQLuIdHfGu3+N+94j97h673R32HXCHz/AMuK5K/mn0sHaqKIzNk02tgGJACgEpzkCcgBRAKYDY8vBwsy+JFvsW691T2cshe0lVT7cCB+llkWFVHhFqcEG+U8OLQRUT6g3hlahWQZh5bTnyOmpWuJ/WjIzBU9QeFKV/JaSGKTXObza2sS1Bz2JueJHkWye0nYvtw7r9fWNrL9mJrSpbsFX1qf3I9dHy4jXF5RcoEtY481qpWc12AV4O1c4Al1eAx+aViriirfur8kpC8WzNX1LfS9t+bVsrAvbFNaz42eaCq87GSuzQtH91uc/g/1v6tYaV9kTF5l/iFZqbZx9afL80l1+418iDXMw5z8woiAgSEqL36AaHLjmEaAoLD1YRvvWwCE0JlFwJk7RAMKa22MJBxECnfPBEAIE1FyOryMXllNWMqDhdFQNm2AehNSUGvcTjp+DgJg9QB/IRTBLGpwc3UQZsfzmdgPo/qLID5OBcJytOpPSXGAGQmHFleMtgsyIAVfujxOQhMXgwXMYecAlOhWSCv6MoLDiC2SGS8EuG1iXhL0mia4iiSJQOUJ7NZeOFOQFzUhfuBHAKQDohzZ8wH58wHj8iTCNCmCU3RGKE6PDn5zeYYgfGiH3v8L+924tHSZOI1nC1rInh7kw2msC4Uqjodjl7Hg3iOojhGkJE+vkjEGXdehD+eNcBBKQApJkRPkd0/QOGuzuEHSN11jfOngXnaNiWW94W8xpd5gAwcTZqBsw7xQm6MLsWLsJCEFBiEesF1VJYKF5oywyNFlD1Iquy9NIaeim2z+jKlTYyYcu474/Y9xM+f/wRz6cnPH1+wjRN+PTxGdMU8Pz0jCkEPB2fEVJCmCOc73B/94h+d4dvv/t7DMMO9/ePmtuCVDaQEGNCjBZxIVWyBVnf3BM7Bm0+bxCpQV9ymhdjYV3uas8gySPj2OCWQSJR/hC1dRuvxGoAsyzCHhN6JmBmPP3lPdzDHe7+8X/C/Tdv8ObxEY/399gPAwYk+HhUlkgGkcA616nsJDJlo9ME7/cY+YAYesQ54b3/D3ymJ3xCwCkBnwHEaj2RFRBlIJnHhsyXFAemNt8KzvCkNjdWa4ZZqSjT6j3VCurtar1f5b0VnVl1pMADOYO2UtaanaukbVnOicyzZYUT5/wPNtOpbiP3wfrDKEqHqLBPx5RMpZtKB15UqhdqpSuqFctHXc55Y0Cn4clBDskMAZyDQ8RDijigx+PQ4dB36DoxCnDelBBO569YG1PT4JL+VbzZKO3o5UNelU1AtOpC+0pFq9HX9CLdpv/X9FjLA2+XS1TfL19uVkR893AHcoT9Tjwhht2Aznn0fYddLwqIrIiwcDPOwXm1DnQVU2/Cpmq8DduTEfUNHWvVP5uXr5Vz9PlrPCCu1XHOAraxCLjUqRc1/vr+f8Gri4rk4yZmaWVmAjSa/apvNfGbY48mRnIDktshcUSkhISAhIQpMgIk6aqEHwlInJQITQgqiI9qhZtSwjzNSqQAn0aPyBHzHHAMHkkFdhKzXKxT2n5bHwXYCoFmu1yBd211pMIlhsfI90jM6FIASEDv5Dv8NLzFgQPeKNPBydy2ncZbNGKFEX/+M8LTRzwnhxEOIYxIMSGEERwlIVuKjGc+gFk8QRwCen5CSUVHSOatpHhMQs0mxEjYhRM6HuHVcoss+aoT4sdilBIAdoRw/xboB/ioAme1BCse7qKA6KLVJ7/hUw7h5lQhIb9DEeqRwZfqDwQ4TeotJkagDz8CYWq8PAwuEUoMTloAJ7Y9CsKRPI4ShCo/QLZXATwiYMcJ6dN78DTKEzFg/vd/Bu0Oa2K/qmdmwkd4DAAeNRdG3Y/mK1luDJf3knv3R9DhPmuyC4NMQAyIP/8ZmCXsFroe7tu/lwToF4q0kfLZtJ3aQO0lQLfpynt7ERoq3y9wz56r2Jb1HDFLX852dn1hq57MopnypnmP8wO0nPN2cOWNCwCznHIoXKgJE84WUZSvSR8MHNoevUwAUR4DlcnV+4UgXO5u8RizpJAiCAmf3mP68T/w9OE9fvb3OCWvnhIJMSRNlCYhmSTxpfTBOWV4/AzfA/v7exx2Bwz9gL6T3BDevJpIudflUGqYbsnZonhBSJsRiYsnhq1os66E+lAtT3M1x/UeLfBYrlNZudUZtOuWnJpgiuQ67BKas2m9sLa2l7RmeNq+tDQSZZillTV9X86qkewLpqFteHU+cf7pjffPEjb1R67/JeVr0SJfo5qz42Be3W9L2ZTn5/Y8ZriprEin29ZuO7fKtZde+sL5Qov9WfiA2/rw2qZb2vw1tWQoesP757BQ9Xu1/BtICDh/1i61/lp+YqGQEiGzwcYsVjnPQ2VcZIBgPQ+LWbgynlec4gzrzdinolXtARJFhI+d8LHOg1zIAiFG5Sm9qNjwtcF2u1iwToGrJqAuoWOo2v8QYXyE4lj1Eq67qYmXi3EJSt0pIUbAuZAT5Fr4xBgl3GtKKeM6wR2Khyvv5aLUrtqp5HPZ2KXKzSRhkORBo6dcWVCgpnM2llBnr5UrsRg1UUzgEJDYIaoQy8EBJMYQzNCwuKwe7SKw/fQU8fk5IcYJMczont/DnY54/vwBYTphPB6R0oSoBmRJY9bv5k9iqEEOfiI88UlDHsZ89iyUZLaOzn2Wj33XYTd4BHKYyWW6pBaGVVE1bRGxU7rqNI5IMYoyygG9hrPOXAcBljub44zn0xM6Itx3DoEIMxUKvYFyXH1W021PN3KI6mBm55MF3Z+Xi1XcxdmvU64T4JhKSK3VmBe/GyrHLlH1aN0+ZS8kKWLxPfiI3kU8hwmnOeAvnz7B8Qnff/wJx/GE4/GEeZrx6dMR8zzj+fkk9C0k9Pjjm0cM/YA3b95h6He4O4jRLaDx+SNraNCSr8zotg0Z9vVSwfMs323kQVdoC1tLrs9WWcPasK6AEsowih2BvMPQ77DbH3D38IC7+3sc9gcchg47BHQabqJ4a9QdMMWTKU0JgAMzIcIhMSGwg2TkKMJ01r7bp9SxPcrFzqyn5Xoh4zILD2QGKyWQW1Xfiizg0k9gg19cduVKxzbhH6vBbiqw1vigW/cUn/m5pBdWdW0NvPp5iSzN03eFlmrkLQXvCwx1EqKXRLk+dA73vcPOa07hei+vhmQd2O7k0uDz9bTihZebebqNFtukuRd9PXe/aZqXi2TjtvtY3Mfi/hladPFc2+Zm976o3KyI+LvHAxw5DMMA50UB4ZxH14nSofPy2zwiSIk558QVllGS4siHMeqZSlx8lrZvIfPlwQ2i/a+obIDa/7HKhnQmC1vqxyphjbmeWYzMGR2CuxPLXUREBCSOkmw6zQghiPVLFCuYcdIcEGHU2I7CfMQobrEfjzOOcYef5ztEhhK6UIWFuWMmDcVUgJ/FyBP3ZXFDawm/MkxyhYFJ1OGIHQIH7PkDSInxyQ34ob/Dm/CEw+lH+CTWQhbKaU5RiHFVjMTjfwAx4vnuj3gaHpFSUAULgdmDIZ4UT/gDAnWAS/CY8YjvxULJ+mgKxOq7xEkkDONH7D//WYRxDXOjXk/V2rFzOP19j3QwQZ0xPbKeBIh1lHPwgVURoYoGJ8pNIg/nPZzvFGl5RRCtAsK5Ym1sHINzDhQD6N/+Ce75E6pWq31Vvrj6ykIa/XP/Bn/ZvWsIu3q//k/jT3gbju2NGcC//h+4Vp7cHv+6/xZ3aYIff7JMFQVrL/prDC0gxKT7X/8/cL6HWRA0zOQ8Ivy3fwI/f5T3D4/wh7egYX+xT8s4+JSqxF0mqFh84sx9EK2Qustk4jq/xRr5NtT22f62z1P9K3/W51SYZF68Rg1K2UbVpc2ly3RzH8hnpBlN0z2xFCt1lvZqG8Ozhav9ukCapNpbsn2hbWchAkoS6vnDj5j/r/8dn1OPvwzvcAyuyh0REIMINwzmZrjn5My7A9A97PD4Zo/7uzvshh36bkDX9fAdC3NdhRVru6qwPSuXE5J6YcQ4a16IgJRC9v5qLYOUvWiPbLMe7Xy3iu6lQqKuo37ZBDZA8WgTTy8VYlGncF1htM2N0j5G/9RM9lahLSWD9TnDzy3wUDFYv0h5Xd2viw3/+yu/zjhuXcPfek6/Ds26ZZ/411EuYYatx2nx6KV1/vJz/GolxPWaq+/X+rieoy2c+dVXfwHbnStGcoU2EZzoXIeuY3jfwfsORJP2WCxMk/4xUHLNNlMrvS98ruI3FSSZPKnZ4641DZAQS6xJpglwvqq/PFvoOlGSmIIBgeEQENwM7zuEENB7L7mUHMGTKM6Lea9Gh9dY3aQ5HByJECiBMo1gfFbJLaGe44yca8Lug8UKHJm+t9XdEPrphGajIHXhJAZ8SvAEpDmAEiG4DuQSiDwSM4LSLEFz8iU2g4WAH94H/PmnpF7hE+5/fg//6YgwnsQQKyRwcmA2C28pA44YdD8AwPP7qGOPugope0/bPBmfasLo4c0dDm/ucNwxZuezjKrQOoW4MxzuGNiHhDRFfP75GYmTGnkSBu9BkPWzafOc4NkhpBHzNGJHOzz2dzj2DpF6MBYW47bLNnCX9EuuMxX+z/bIgkLTzwKxCWoXL1F9c9oUkqWtlC7a/5rure+xtqeaizZ0pxkw6R5ewB9Jwp4wuBF33Qkfnn/Gz08f8PT5I07TCdM4IcaAcZwR5ohPn58lJ8RJzvnucIddN+C7b/6A/f6Ab7/9Dp3v4H0vyq5o+dFm8YRIsQJYVdJxvhGO8dropJV4l6XiK5UKea/x3LRQxQfUxnmOJIaBwaik0QV2+w6H+3s8vnnE4+Mj7u/vcLfrsUtTBZvrf1EtYr0eyluzKCMCHAI8ZojyLPFCGbEeDdq1LfszG6GinucbcM+CHwAbRKrf3ZjjWs6E0m+nXWzZxrxY2AqgZG3nvbxADJyrWL9b5p+q79Wzy/eWVVifWDnJZZ+XfV1MS3vUzryTO7tev1W1qpUWXAN03qFj8fTb9R5vB4feL2BE3USFwn55XudKMSD3kleWtM8ZnvPqzj6j1PglSzv3X6fcrIgYOgkz0PeDKiD65tP7LidqpOqTnCKUDPhQMK9t1k21C87tZb29dcjPzNAVQrx+RWD3y2b5SxalogfltxFt5ypdjuXX3ITnNHVGXNTzdmO/NhUv9dq3kD4LzwyJJ9ch+V1OTBbYI8yTCMrU0yFGTUAWoxClMWCcRyVKJozTjB8/RszRQhtBFQ6EifeI8Cp4o2z9kMxaN1tMYRtqGLOTx6v/UvldK+asJHgc+R4UCZ7Vkit5nJLHZzdo1S7XGikikcRPTZo4minhyAfMc4+UOgAWv9L6TIhcBJwJHkc8ZoKU5CKyIDxaf4WAGTuPj/dvZBWzQIzq4VUDdwjHA3jshPnK59/SZOl3AuASSMMOdS7irpuU2NccM14ttlBZVC+F5SAQA/c8okcSq2VO8J8+gMIINO9K64E8Pg8PSOQzWVUsbsrnER4xhI3Flqd+TB6febe6t9weW6hnZo8pBnBi/Dt2ADiPpy53YcRdmm3oRenyp/8O+vBzhrd2woQojcDzJ2DW9/AE+u//JMzuFog8PIrHhDK+BseJy+wtQ281o9m6t4Vwrd4KJ1D1fvvseevLus1l+0A9/zVOKr+XfcpcIrR/kKR6Rkha3RcJgYqQZTIG7NwAeIUP6kootePYYicz4wdU8YHlfBFZ7hQdM4oVV0qMGBPmEPBpjviB9vg+9ng/9TgFYfLFCmxW2BpzPh2rTqxNGffpiDfkcL97i8P+IAmqhwFD16N3EmOWKFXzX+hoEXJY0mz1XIuz/IVZlBAxaP4IdT2u2RpKhQ62Sm2tq1L2RpkN47cbmrtZC1o8r7DGFeMLo4Fgn2SJT12GYZYby2U6SNkpRsXEtEXaq5S7BuMyzLNxrV5djflLCNeSt0L7fa6q2spv8e6VFvLzyzU7R5ctLQfP9uXc5GTia93nq+XmudxmTC8SuTfdv9xie+E8TXmtlWs0MV1jxG4Yxtk2rszxL0sBv2T+N/bhBVi/fnchfFgQUZs5Y15ZXl9HO0bDjm3PawZbr7A9zU0V4jWrPxgr2Hu+/XOXthlHEcA5DRvcoetQWVuKsti5Hr4D+mGHEBM6PyImwS2Jo4Zcyb2FUQXOeFxXYDHpb4uFn0B5QOK5XUJpiEBNbqbEALEoDsgBHSPzzYycsLbw0Dp1Fg4mJUQ4BB/QhYAUEmIXi9JepXdl3tFsvaz4NnqvpiEKkhZ6xjwilGdK+bvAOs7IkzO+kzBWgqud7olmnbnweCkxQhA+zLmIBEKalf9CxNMp4C8fZsxPM+afRwzdjP1uBGIAc8TxmeGPBJ4nUJgxfzoijJKgmmNsBIGKest4AMRsjlSHZDI6gSBJPMzQ0naD1HM8npCYMXXA7IvR0+N+h93QYfIeyXkAkmdjFwMQEz58nJCC0Feks2O0sYPxI5qIFrZMDoSEFAI+fT4C+x6HHXByhFjRvq3JBzUf0L2Y90JNR+feL84VF1ozV3YWrNDm+5n+zo9Rez9Xu6xb+H0wI1EEuxkhTghhxnh6gscJP356j0/HZzwfJRTT6ThiDgGncVIPXwLI482bd/Bdj7dv32HY7fH27Tfo+x5dJ3z2NEm0hBDE+DBGDQOKVPpf0fllOrcUDdUw9FyXZwo9ZYZRlH9sTssKjjcrrF+crTzV01vaiuRAncfu4QF3j4948+YtHh/f4G5/h13vQC6KIZMlYda6GDmwXdUvCV4VWZQdAR6BO4zwmJAQWJQRlsOzFIsYcYaW081OMi0A55TVxvXgfKnwEdptR2zTu0HLsjWmD6uch6nOVpCp9wIfmyYXa7e8faHPxSBri3ZeKiTO4M6tfuSvqfSJ21VsK71OHd5cKvBDBHjngAhMnw7Y9Xfo3nToXCcyHvVatCXIHmUVD3JeGbGgU15J79T87fVxrfmI9pn2/rk+1XxarvbCFLcyiOW422eXXVvzhMs+naHCajC9eOQ1/OXtioheFRFZATFopvNew6X4HD6F1AvCkoIVq76KgDLm59xMGaSzy9Uj5/bUi5QTW4U2EqhhtX9uL5deWCKQZthnxvGqTtxeXmuN9iVWbCVcxLkT067J0gMiwmP29yIcI7PanbIFb4gBMUXMYUaIEeN4RAgBR03efDqdcBwD/vL8iCkNMNe4gpeMeBfFg4UNEW+I2nWOcw9XhcoItwSypAS/HRMjgp/Sg4Z2dHBJkzvTHX7yb5eVC+FuMSbBgBNLJXACB2FUZExlfGX2BSFFOBzx0NTdkq1UrjJA/lGz3+n1SiC2WWRgGpuxfbDFd0reOMJAJ7z1RzhngssyfzVxKh4Q7bw6AO7Tf8CFZ/EegTgmGMFDhBwXygE4+R3+vL9Dcl1eq9rjoBlKnFfXrPxEA6BE7GoKbhEmhIAJwJM75PEs5+tbDnDT50yk5/Avf/7XlQB+65PggPAM/Os/ncex3/0jcPeuxKfX9z1I4262yp+6LJUQ15Du6tP+Fu85lzfv9TqWbZKyVGfubz0PmOU+w+cYthUC3xzV1jjFEsiIpy3PiNykfGvv8RrBr+LTU2E4MnGcq5J9TL4i9pUIt5CiMSXMMeBjYPzF3+Nn9vgwDQhhQkzijRBCREymCNAE0caCeIeOGG9dwB964PFwh8PuDrvdDsOww9AP6ChIElDrT0U41bBVlBEWXmIuf2lGTJooW5URJUE1F/zJecgVgW0wdgHVqJmillhGXUdZTDtzzlUhmbx4bVE2wii5f8g8uuy7CpMyEblEI7qemfkyD1IbAygLvoy2kmFxO4B6H9T1/kolY8VX0C2/V+v4l4xl68mt2Zfd+3XXKa/+le5KSIAvnOszXS106/lnV22f6fA5VulLyrnUgWfbuMYMbNAKF59fvXz+uXOKxJftk5ZGu6aCOr8vlrBlWU+DgbbfpfpZWlWx6hkzrlsent2IIE2AWUIEas4e9WzzvgMToe8GhD7CezHQYLWyTxqKsJZ9FI83oLYlanJGWK8y8ofyEq4Iw3V8SWN6x5jgvArAm/WtcA8KHZ2VAcwAAsh7hBDFAzx2oohIlofBLREaROhpRjwoOKbaksoyqMJDLZu5ClmlNIrxZvK4hmkiTU7qk4oqS51i4lGE+DIeMagKUegCF5MawCQkDpjDET9+nPFf/y0ifQjwf5rQ+xMOwycQJyBF8YBOAYgRCAHzPEteK045bnxDIWj/g3q4WxLuEjpWORMNQcnw4uluuQmMnmDgdEr4fJpVcFmoiDffEfbkkDxhzpl5GcMckaaI7z9JwuSDT+rZLW86FE8VmzkmyyMicxpjxPE5Ys/Azg8IXcTouyxotaS+m17G1UdFpGK7VDRG/kp5LW8H0DVlJl9qurr+Vow2Sh9MKRBxBNzPeD59wvPzJ4zjCdM0YRxHzFPAaRwxhxnPT0dM84xxDEiJsd/fYxh2ePPmHfaHO/zxj/+AYdjhcDgAIDVkDGq8GHP+FjR/si8sH6XNtCkYs/xgOW5ZijzfmWa1922UJvzOcoj1/NkmqZVCBhmI6kDLSi+yza6cregIjjrs7h9w9/gGb968w5vHN7g73GHnGC6eUJQupQvOvLnY5ZyE1hkJHe0QuUNAjwkeoyoiAnKqezSHvt5XG6RrHR2A+ArFcmEPGkgrsK2qicteXN+SSiMzPK0VqJkHqYezKoyrtEAemxm4luepGUHTbPVlXX/7HJCVEFX9NefQvLiIFHBzWVWmGzXzNepNHhzC53vQw52E8O185qmy/KWKxlwL3s/Kgpv9+JJynba6Sitfo8eu3V/KiExBvH7kUiP25MWmi9xhu0+X2/l6/NnNioi+H0BKpDnn4TsJj+Jdr0y4B8E1DDhVmy4TmrfuiwuI8CKOXD6bwfCXtfm3cnvZODdfUlvZ7pnYTUjUI/gdEnnJ+2BukzkmakRM4kYZYsQ0iTXE8+kZ43jCn36eMQXCHBJichgZiAgVwOM8lvxbCW9APQvyY0oqVM9mfK/FCPsiWAZMyFT2XH1AzONCoTAhEzprS1GZJQnRWmu5KyWK9e+SwqT0rKm7GWfhpcD5+cJINX1bMZY1cOTlzYxkcw6ABDA5vE+Hdp6ozJMRWLk5qnrAjM/8R3iaM4O16lwG+h4JHabTHqwIcKARb92HxbtKHleVtcC6IhA2ir0WucPH9BYJfuNu+5MIGFzA3s/51gd2GP19ebRSzDQKG53qEo6/KBGqKwABQwp4Mz+VVfr5z+AQqjqNwFVFxtvvQI/ftAqJxfqbwLTtoytPZca3nIX6sz0fgCNN7JXpVVr1b+szP70IibNc26WisFZqJDBcbW5fV219WS9fdYErQXjFEHJ5ungzVCeLjbnRx89aybT9raZYGRACU4FrEoJOhCshRswff8b8p39G+vikIeeEGYuqEEgKZzmVBGjMlsgcCN0e6B2GO8L+cIe+26PvRAEx9JojgrhSRJY+CmiyhH8xh2PK3hBxBqegf+YNEWFhMwQ2JoVBNbNdiLp2X+UN1K4VoVqbDdLc9jQhJwzNXqCVEiJ7hFJRRlgOjWI5W5iZsr52YOteUdMuSOuox5P31Zdj3iXu+lsp5cuUELKnVruKNh9+YVmue/2bzzyzvH9D2XqUyrysLTQ36O9NjtfunWGir3Thr7MsF/7Wkb3mjG/ghRe3VRH2BR2d2efrO7LsW5v9xvEQoZFI5HdvmDcSukO894GuIzgvHmts9AwB3hGG3Q4M4Hh6llCtYKQUNSccQwio0ryQFBYuhpE1+w0dAsG/zNVZUSFjJQgyj+wQIyg4zcFk/EQRTzGzJIs1+j4hh45KyYnFd5AcCikWjwhTGGCD1W0NVYxuoxyyyQrnPqhFunoQGE3BOXQnl+vOJoHKpGVZgS+5OyrhC8eECRMwA9MckdKMafqI8fmIj3/+iOdTwvQ5AiMjPTESJkScNNRnyoJLVs1JikK3FJ/QvDByQQ3L0jwr/SNez06VTZIMD5Bgok76SCJ0JWi4G603kVd6ryRFBwFPzyOmOWDqgeQo83SnOQCRxdOaGegkwajtl6hrDFdNYz6DmoyUxNP0eZrx9PEzji5hBOPxMODQd5h9L/2qeJQGFC8UXuXbkq5oYQjpei3rqfnEUnWZIxvIuv7ylK1PzsXICb1L2HcTnuOMj+MRYX7COL/HaXzGeHrG6XTCOI44nUZMU8A0B6VzCUQ93r57i77r8ebNN9jtBjw+vkXf99jtJfz4NM2SLy2UfJKS18WmrrbmZ8RYPIvZ6GJslwwPskysEFtsdH6uud2e8kwxhlLV0mKd6hXLs4gt3kbOtgPt9+g6h4dv3uHxm2/w8PiIu7t7DF0PjwiK1p/CY+bQdFxy0xU+hhBoj6MbMMYBE3uMqoiwHBFEaiiom6MoeLdpbsvd6GxHZdhqCdRpMXNoftWy9FpRkN+qlTyWm8nGQ+s1qT0iVo2hqnfr5sXC5WDWf9Z37R45gGOBBU1evGvCB2421Or25jv2I7snrJ9pLuUjTflH4U9KeObOOXTe4bAbcDCveQ3zbyEOt2jC7UgEZSP+ejwMLT7/c5WrER++UrldEdGJIqLrepDz6H0nDLYSc85MQppEjWUTwp1bKK7+rYEp2p20ZHAuzM1K63MjgU+gzTZXbX2NhVnWcaatIqvi0sdfuNw6vK9psVjGt2B9qs4YomZA3Y8PiMwisFLrhRDFCsiUEXOYEGLAOI2Y5xnH4zOeTyPeH/c48R6xcllmxPPK30r4ly1YawJiYypoBcRbZrD51NtEKPIoE1okRiICLiTpXVpMmGArC7iM+6jHdYUfbNah+cIFuef9WSGBrfoXFNWmcCJ/KVZ7EYQpHirCYxlTXvfMRuJbuXlAI+s/U0SYSnChMGGPNGM3fIbb0qxVRBfXzPGNR2LiAc/hO8wYbnrtziV0fVFEfKYOn/vW60LmoYafbR15nwGoEwXbG3fphGEaS7K5eQQ+/VxQbbNvHSISuN9lQbR9YuP5VlnhN88ArdpYjAeAV0XELV4f2KiTqASeXHpq2LjO1ymrvWU9oG+uxt48gCpRpCkjMsTj/J4xbpmuXCgetj7X42g/LaRusdoSK66UGDElxJQQnj8i/sc/g2OH5O8RQTDvhBiiurPHnA/HYI5Y9zukYQDvB/R3Hrud5oXwA/q+R991kj9K4yuTUc9kMEphcDJhijCAMQVVQsyS50bjP+eQTJkxSxnGFcYrT3xeAzI40t5p7rf3jLMo78gauuwN4VztCaEeoSr0MuMM1VyowKVqqCkt12Gh52wcpoSwBJlkdTVE/lZ5Kc3wq1Dwv15ZzPVlSvTLyvk6FvSrXaHl1fWz18u156/c/1J6tqGZ2roEnm3gfZsAbvc8Vr9aGvCXLuc83QpNc6Uvq9vLsRmd6zZlLrf18eoTZ97bgHvnKjNhuf2sfgnpw/VjF/qwoDkNTlX03q1TwOAz/b1eg+FZRx7OAz45zTcmFu1MBKcW7l23Q2IxvpM9aqGZitBdEb6a6Qq9aCxuylvawkhKcBQLISLhl5Liv3pOZa9LmMQIp8mlnSte4VnYrwqKSgIKmCdhVHzdRSQVpubcDTaPugZndkqmnbLV88a8SxcqIyeUZc1Kkmp8RvFABfumfHB1LiV92Dy45zQJfT2NCPMRHz/8Cc/vn/D+/wwIc0CYjgBHUJzhWGhDD8AT4HynRgHmg0H5T9prx5LnL8xCE0Whtx2Z4r/TvncwTpSJwEm8tbOhAAjwDEKX199m5nQacTyVcGSmIHpWA7fOu5L/gEp+juKdIavnQJXw0cK3Cl0yhoinKWKKIoB/eEcY7h2Si4ia7rqGumswRIvv22euwMS8uPlRW/p8qWmE2lpo3eKyG2xKthjR04QBT3gOn/H5+UeM44jj8Yh5OmGaTjgeR5zGCafjCeM0IwTJjbg/HEQB8fgWd4d7fPeHP2K332O/38M5jxQJiRPGk4Rkm+dxBeBqhQqzeUKkzLPbWch+DLWAGwUfEqh17qoVDK3gIdedf+lZJlrQ/pm+Xc9l/lydY4Lb7eB3Hndv3uD+8Q3u7x+wPxzQdR08M2gulVh4nEwIA03/5IJDoB0mvsOEATM7TPCYECR5NQDTqDmCGDbpfuIN5n5Js5MuRM5koi8ugz1lGQU4zzVXdVhop23viny4mu+c/xi88M6jeo3yMF5Gu5x7umDTMk5TjNXHL7MrN9QJLvOzbmnZfoun2kpp+XDB8xmUVStouIUEv3TOYd8P2PUD+r5D1xXP8VLhkjbe5sNtNrLi8NzQr9ItW/XaE5vQ6nxbN7bU0kj4crr8hrKWlWN1YR29YRsm2uXXeHK/yCMCWREh7q0lDjLlT/NPLcw2rUeLX5bVreif30lFf11FENxv03aNhyzGohG1iRmJOsxuh8QOsyaeNk+IEIL8xRnzHBBiwKRumf/2/TOeRsIUEmJ0OCWHwFEVEBpfdYUFS68aBoDX10vvrVTEFpXfRQZlijoUArbaa4IfFFNwSapbHlgzuC39UnMGa0TLGQEVBL8e9XIkG/fznHF7ffXwAphdggDE60qqOVxdhtgjbdd1tpEMnnpE/LF7D++4uEOTw+BmkHJrxsg2+zPX5MqYLiVSrm55ivij/4vabZ19LJeOEvpY5aXIWqtCINmLCcCH9A4j7zJD16wmGbKoGQLA8R7fp39A5lC5Zdb2GHHnRphCKP38Hvw0CmFR72NQNWfIa2f3W0G5fO854pt0quiX6vmKnDbe34id7GXx3T+A7t82Z6rc12chgohMGNXv537bNVf11fqhyoaaGEf5XnpJm9eZkna7tF3Pg7S5PE9cnVU95QaLmnsFvsinK+MmoMtJL2PeI+HpE8Z//T8ldF2M+Pj0GT/QHX7gHj+edjjOEq4pRPNOEG+ILGTQ/lluhH6Ysb/zuD8MGIYDdsMBu36H3nt0zsE7yhZQzd5STwjLDcHZ+yIghhkxTojZI2IGLDdE8yd9KuO3z1YhsVZw1QQmFvdKqa3JBEaYEqITgQfJd5mLvrH0JCeKN1N25k1upZYyVXuISofyfs6JUJ0ru2yBXxZVffXSzs9tDf06ljUtHtKG853rr/+6hE/rK/B1230J2XqO6vnFy8aQ13TKb0SIfpViuHk9Bon/SxsMPf9Gi7EoV8+CnbU1HG2fwfr+JSHGxRaL0celt86JVUQdQOjIw3XAH79lHHYRP/xMeDpZGBzCMIhxxeFwBz95zPMIIvNWUKGzwnO3OGhLfAwUet8SOyfm4t1swhYWeCDGAQlzjCA4xJgAInhvKE5CwpqXg4VcEjpBBLVEDlCvQs4eEerRkRKYxALZVbAxj6n+cw7JwggmqqBrS59voK923Qx/VbNSeKBMyul38WZAimBEQL0gx+MHnJ4+4ad/+QHT04zTx0mtz4VGN+8Hl2lxIEUGpWTJFZS2AtiRshhmdCRr7wmg5CQ/Q0zSfiWkDDGCiETRRG18fHJOQmU5B6/1uQ4Ae/XgtdTOopRIOmGW54o1ETYnpXA1gbZZUaXEgANijHI0y7YBoNyPEsYdgB0BnjpEnxBCxIenCeE0I7oT3ux7DH2Ho5ckwrmeTJe0obva6P22W9DQwc0p2EIo534bvZK/mggfgCYfjxwR+RkhzZimEZ/ShB/SJ3x+fsZPnz5gmkaM44jxNGEaJ8whIgQ5P0N3wNu3DxiGPR7fvMVu2GUPiGG/h3MOIUQAAWHWxOdzyALfPDesYdMANObnbIvBaA7FC0uBG9UkVq4GtSdVblrp3aSGcuscwbWwvOI5jEfykqT6fv8Wj/fAH/7u7/D23Vs8vnnE3a5HH49wKZYG9Ryb/lT2TK6+6VtKDjE5TMnhOTJ+4n/CZ/eEyCOY5Sx6lt3NzqkB0nIOSjHei6qGbE/mvbsBgCxShOPWN1NOojzfZoApLS4VG/VTiQmRuBm+JWUnlK6s8NTG8GjjOeP2coQLFJ5PLhgPxvULZxqqvtede1WpaZSW3qbmH+VTMm+LfC1/5YT9fMQu7rEbPIbBo+88vPcV37ZqefPX8inhN+zaOUnW7fNQdsNvQZydG+sv/S4ybP+lyfCbFRG+65Ug6mSTOK+Js+oQTFU+CPvt1oI2K1vLetby/zyVs133CyYuM+8boOhrrcA5wWuxECvA/rcqRevZahPzFFyRctTA92sMxywLsscCs1jIYwcmRgjiQmseELMqIUKYNRbkhNPphHme8P7o8CnuEeMgFr4m/KqBO9aML1XXihKiCAAzbZBSEXpQPe6aIVlgbTIGwCaqml9SoTfXe4fzbSmt8N2eR/P0Bhg6t6dvuHxm5bdfxC3rvxwTzgGGcy1U/261f6EDpKyBm/HGvcfgoiRPAmWrpIaFWhDcmSTK+74hjdZnviLWPCLeug9nOnYOcZ5/OhOFukV/iO/wOXa2XVFiEdseXcwbEYAeH+jQdrkSGB/oGQ/uKW9wmhmYj2uB6WK8pS1qrrvqPBziCXef/5SF/xX5nJULAOCJJDEqVfecQxz2gBuyV4a1Wf8mELzz2oZbKwOMQNe4v0uFgaVHv+a1YSLiZV9YPSJyf5r2VUxS1dXAHc3QZgLdmjGpYVYZ9+KaK3VaWIfw9Anjn/8FaZ4wp4hnDPixe8BHdHgKA+YYwByKhWWOMW0MWVlH5wiHIeH+jrAbxBui7+TTa1giRxt43UjurOS1eNxRFR+qBElBPSISTBFhnhAlR0Q9twZ7KkXUas83vxqGwDxTloJsEda4LIgqeSC6KjeEz4lRQS7vNYCKd0Q9/MUaVgOBjYBs7qjyiKBaWdZW+xq8W3fhZquWKzRBBfI29/YXlWs4YmPtmsfPzTlz0+/2NrXvvljzs6Rr15e2uvQl5ddQTn2NkumVFQO5/TOXr0gynw8xdbmc34ob9A1wRshxpbEz41xfXu3ajZdumLQblBHt3jonGNi49Kq9uAz9uT0GavpcaAfxQqFsbPLNm4j7O8bnZ+DpBJiXaNf1IBI8RmDEOIsgwnAUGR4grD1xC9UtZHzbR/GqKKFcnEuQ8FDItFtKQIoRgQgxRbhImosAOTyNeQ2ackMstsxTQjwXOaaihIipKC6ULhFBpvkKVDkiiKoQy4QSXqgMMYuLjfA8q40wuoogAu4inNK71Z/gc/mI0kKakMKE8ekTxo8fcfxLRJgS5uOz0O4W/sj7ijajTPOKMkEuiZWtURxGVxp+hgpYU6bbYvLZQEJ4T9lbvNxfkMTnTr0g2TM6J3RqbVBg1DEDWV2STAlhAl8yjZNfnBEzylNFWA6VZeJy+ZQ8FpKryzkJIcUMjHMEj0K6ddRhR4xRSZGKcpKWKgKpwd+4vTRi34p+z3QMqrNB1Rt5GwldF2JA4AlT+hPmMOH4/Ix5nnB6PmKcRhyPz5iV1x9PM8Zxhtle7Xd36LoBbx6/wf39I7759hvs9wfsdgc475A4ghNjmkfEmBDGkM9V3b8MrtQw0ozvqGymPOZGOPwVCtd163nLoJaQZQXNO/WtlqhbrIXQsoeHe9w/eLx5+w6Pbx5xONxh5wEfj5JvBbYnCq+ylEmUjaKeIkyIySEkhykxnvAjTvgIU2tkGh2AY0JSk7yIttrcbyyayRvyjMIgT5LckVBKnOuw4ThuadS2bNedIPSh5fyrT6I1W6O47JVRV1RP2xV8yEB2s7N9aDRq/r0ppck+Nuv6ViO9fIGXN+sk3lu1mYzAvudPKA4AHEfsImPPCbtelBBd50WRq+8U2YrRZShn4CxEkoeIrOfr3L+UJ367rMmemjfffu9WnuZSr6WlrSv1Wxs79QwtdLPy5AzNbRCQNj1g2x5/CZ9ysyLC+V72UpWIMSekromNbIm5TIj1+y0bsFyuLwnfv5WbCvMLl35xgCMzGA6Tu4dYCSUkCPEdmTDPbTLqOcwIIWAOklhqCjP+44cjPjwDcxD31GP0CCxJqhisVkRAc/AaWN6CcM7vrYHA2iOiENpARdA0Qk8sQnTQYhPW7VN9CRUkXnV92TveePZSWaKXLyWplkKFRgZ3Cfne3HA1TxsInbYqUmK4Q8Tf737G3gf0HvBZeGhJ4SyMCtZwoOK9QO1qmRVKeWPZqavDuU4sVFtChi3EiVgvMb5xP+AeH/CX8A3GOKhrd9qw1FgwBXZ1o7FEhBN20gK1FgtU11ExXque21xS2wfPDn/B/w1IUCVQ6QhlOotw5044uElPGClv68Df/wj++ZOGCUJm+mpiqEPEt9OTuO1nIa7a2WQlBGCZJ7PQOffblfBLpMR0Ne5GfeI96B/+F7j9fR4rg4HpBPzlX0AhVLkzqj7AhBtcMdM2AQn0h38EvflDThJpOWCa+QIEP4cZ+PO/ANOI3qtlncE1AtI4Yp5GPCfgL/4eJybMMSBERggeMZQwd5asM3fFiHASq6quc3jECd+5Hg/7d9jt7rAf9tgNeyEwvXhEUKrXXcaXLDF1spB6xRMihBkpaFimqDkiqrBMYLMxBNiEEiY8KXRvaZOoWqdi9VbPHVDWtplThdeWG4KcxjLNn1WuCCqeEDlXhBlt2G7I69scD2k3h8SQ6zVcqsdXe+x8aSlyxyucUf1C5qgILwDaOO8hcVvbtdFE82omnUs7pa9VYV71Ie+KSrp6jvxf9f+F42/7Uv/YhscvLxtszZku0pf0/YvLcpzL07Asy35+yTz9GmPe2M+sYXpe0PUbSIar712b2V+jVPIj+X2m89vbn25csjOjCydQikB/AHV7+M6hR4LzdTJcQtcP8L7D4XAP77uMa0k7TPq9FpgQVFYEoRutH8mEUlwGLPhODQLYg6goJ1ISnBCi4Hux7KYc2jgmiUkfYyo5K+pJZA0Vk0p+pRBmxDkg9h1S9EguiVeA8ujZO8BoGs0JYQYGytZvzLARNkoMsF1ikMWOz/OjEFsFlWYYY/+RBIKEBZ9PSeLyp3nCfDzh+U8TpicPl4AOhEPfA2DNG60RGQx7snoQoKJXVJDijeeqkouTuGlKmBhy6IdOw2ep4ihG9WIR4wfzaoGtGbMYW3iPjgikwn+jL0hpc4EEMe8jBoA0A2bgAcBiaBIJzu+7ThKsO8lJkTio9Thrrik1DPVKmxLBM7CHKS6QaWfbd+MYMM0Ru4ceuyFiHmaw47yXQQRmjxgPZU5Ry0MqyYhta1vqrTPIDCQSJw9m8QxmaveN1hFSAiNg5s+IKWAcT5jDCU/HHxDmCc/Pz5gm+QxzwDRNeT683+H+/gGHwwG73R7394847A+4u3/AbtihG8RQaZ5n8MyYwwxJeB0qBUPNf9SREGzPUjM242Uyn63jqUOx3VIuomCj2St+wGpfVdLQsNU65G4bQUma63XA22++xbdvO3zz3Td4eLzH4bBHhwCaCWDJjZffrMLlyOgony1iS0LtshLiOQCfZ+DICSdOmDif9JxTpQAOhRv1kLRem+PsH8AsYdE2BKdnp7GaBoPSSeFHY45ayXN4UUNeVeW13bLeJT15hp83ft1gQX7K4MISpoNXG6Th/UwZwcbj13zjhULAMlrFdsmYux7dmTqVR1FYYjxX3kUk/HdHwNARBnTY9Q5D58VQUHkdpkLll27cfqaqAb7g+fNjWs/BtXbrHpzrwyX6t62h/k3E5+FF++QLRn9pfHraFYZ8bU/lmxUR5NX50UIw5RheqnAwJAYosDozoKX2li/eLs+tAM6NlOxNq7XWmFkVF0PILJ9/BXl/1gPkpWVrvBvM901VVYTHuaq/uKyAKjKilBBMhNkNSExIZEqIiKRWErUiYponhHnGPE84ThOmecbH54T38wEx9sUSiBnmBVGPT39c6FsJiWIP10LoXBOvp7zIQZYEQblJzcUtUMQbF8+7DeZv5xBMXtCtN8/14euUi8qHWx/cKhmh8sVx2UVyjA4R77on7NwMT8LImIDPWZ6bjExLM02b9rWiCdYwbAHzasJu2ce6nWXnNxsvlI4I0IT5uqcn7J3DT3yPkZWx4hJrFrkPtNHnsh/r6xEEUJvTwnZwTQCXMVTIuJEGtw+K0qcHsDc6Jd8v7sZy9Z48HqjgHLK65wSax1wtwe6XCe1TwN2nP2FIcxHkuloJgOzBRxrKyBmzrnW56szKkKjpX0aF3QC8+QNKPgwlCk9PcN//OzCPJRlkFpqb8LlYLBYGR4Xvww7YPWR4Rti20IMj0DzB/fgfoNMTWHNjpJRyJ1NihJhwdD3eu0GEHCEgJskNkTipEiIhRd3gXFoxYZr3Dt473LmENwNh3/eaF2JA7/vKI6JdDyHlla1qFBK1R4QoKBDNG0KIbYHBqRm27YXs1mvXyibM61bPVd5DG2XpNUNZOGO5IVwOv+TIAfB5PxWFgTmVU3WgDFZV5zHjiuqzgkFFCVGERqjGcw3uXCslrirl3+dKGUb17AVueovc3p5zvpExsnrrZxc04mJiGoipfd3sQ1bWUXNt2dLaw6NWcV2YuytXtzxcXlLT+WfOxM19CX/1yrKlyM9tV+cwy3LO7r2v2VFr8cvLuV2/GsdCwNA+btBqm7LLU3Yjz7R8zwR/RqveVMeLiP8zfT/TYTky2/VuwgdebtQznT43lih4hPwgYYWZ4VRB7j0QmWAeE3Aefb8DiDDPJyRWsZkKfEjPUraKzt0jWDhVG0gtwGSU3EycEoidJB6tFNKWiyKBEGOCcwkuSfuWL0DeV36mZV7AUCv+yjMippK0GipYbejXTOPIBBavhfqvnWQj6SwMhpE5NnRq/hEBfX3shZxgiLjcvCwDAIcUhS6IYUSaJswfPeLIcOqh673kaXDa+Wz9Dw2hVZFcIpyzhM7I9Fw7HAvUxKpgYjB3SMwIIFBKiLqWSYV9KZb8DcxApzRVTRsTbL8kWF6YWqjIqYSllOJ1PQTfey90hXdOnouck5JTcnCqQHAaQovUo6IMv+xD2QOMYwiYA2M/ewyOkIYJyUkooyw0pA4x7gCIoqzCdDIy3UA1ed6s+6roeAuZo2tU8azMytvPOPEPSGHC0/MTpmnC0/EJ8zTj+fkZ4zTh+fmIFCQss9FFfd9hf7jH4+MbPDw84PHxLQ6HOwyDKBYtV0oIM0KQ/JGJixLIVfnhrM8i6y0GXPXBKTIA2ogmrBQyvURoV8NPaicys3lczu/iXcr/blRbfbdjQd7B9x3uHu5w/9Dj7uEOh8NB8rkxgLl+txYMl5wnRIpTuHoOopSNiTBGxikFjIkxExBQ4ji08Rx07NRewWLnFTmMApotpLhEufkUVPS+/mmKn7Ks+fO2NUv1fkbxdCq4QuF/rq7qP8xefal84ObDgGV+xnID1b/1e1HUrOdhVQhlDuv+bT13UyEYUlgqIeRuUUZI7iEHTw4dOTFWs/C95FBUnnU3DdduKChWZEq9KucNtc6dzRXpUV88M6905n7LGWy8V7exxUNQ+37mNS6FAc/PXn2k6ckl2F1gmnwvc/flNPntigjX6cbSmJGVJ4QxbLIQriCny5gJlzig2hthW+T6Fb0VMhX1t/KSQlhrpIFCkJ4rGYYacZIYIIfZP4BJk+AyME0RDEaIUYViQeOnSrzyOcyYw4xxGhF//h744U/4M97iB3qHUxAPiBjrZNTcnEzDN7m7C6KoRv5tgmpugQutAWMWLBqVVhG/tfVVQ/g0EOnyJPICXC2RNjXP1QC7enJB6LwIZv0Cpe3OBhV29S37ff55IkJHCf+w+xkHP2PwDG/WzETKhChRLy+gCJvbdrhskE0w9jqt8WXV5xLmMRhIQCITSDuwJgRmAH/X/YjJfcB/jN/ixF0mqtkY69UeXrd4y6V8Y2uqUOayeZ0Wn4uqs4KuHBd8mgnPtKueK0nPmv1fN6KInLjDD/yPcNU94ibSr5jIACANwluHj7rzI+79WORFoPxf2yaASMB//xfA4l3a/ZRAsQPIa7uCM+V+LQBoJ8PCD6Xv3wPvnzMD+3b+jL0mVUwEvO8eMLkeIIeOA/7w6SN2cSqKNgvRRIQTPP7i7zGywzQHHIPDh3GHKbDk2AkzYtDcEDXzo5/eqyB+F9HdE+7fvcHh7gH7uzvshzsM/R5916PzpM9S9lix3A6WlDqliBgmyUcRZoQgeSEkN0QUN3pOMOUFOKG29ZDlcEWBmOeyhSRZNl3v/g3cX2TYCrOrMBUCKwRmOOqqsEydwg79JJ/7kccORTPcKpBKX42Al0BgxXuu8uBpPlddr2fki8pVq3xa9h9CD6Z05oWv0ObmS/pZW0st6qHF98xYbBhu5GezwcKiPl5bIxK1WYoKG3X7ENZjf8lcLMQgtYLoVy4r77pL41iSJ4pXXybA+Vu5VBpeaZPXuWWf1cTp7etyfQmX5+TSXjlDKGzWc6YtbmG6d4x/+HvGu3cJ//4Xj+ejg3eSR2q326PrROAtoQElcfQ8S6imuZ/Fqti5WkcP5Rg0gmFFvIAQgoQ5DFHCJXnPgLMErob7HWJIYAeM4yw8jIZ+jTFpLryo1wHLt0SACqYSEgJinBFCh3me4OYeoesQvEfwliiakBMeWPvklHYUfJU9ImrCzoRNGk7SucpinKChM3VCyAFKe2T4yhDLYU7iDQAghRlwhEQEjozjT4w4EabxiDhHhFm8Ih0psaeKBaoEw06bEJE/IyUhwzI5pR4QYnBrq5XAXBlIAPDkQZRAnQOz8AecWA0kGDFJrqzgIlJUr5WaljUUDqWP6rFn+3I9RzpPpB6QvuvQdT32hwf0XY/d7k6TbTM4RcyzKJUQQk7E7X2Prht0vdSQJhUbb1ZPVpeERgy6PB8/H8HPwOnjLOFmyKP3Dv/w5gGd9zI3PgF3Yrxi3jcpASF1mOZdHknZGjLWpXFd0j7JEeR80UIwzekjEgc8n44IYcTT0w8IYcanz58whYDj8RkhREzTDPOa2e0fcHe4w2F/h7v7e+x3d9jtD9jv99jtdkqnOZURTIhKx4oHRKrwOOX1Qh4RstdSo4gAgVHTw6a+qgTDVR2XS8U/GP+lZ4cNzCqJwgt6sa3F6AdUvInckfQuamEOzU9DADuCHzoMO493797i2292ePPwiMPQoZs/S0gmU3JW8ooMQ/W/VPVBZCgezISZPY6B8Of0T/iZP+EpfcbECbNzGtpI5izAvBGW9vsKg6Q5CYtms6zzkFjy3eSEyyvUxBvfpd+WazBprgoJxarcxVK+WgZXdjW1siPjvE1RkkfTdMH6WIxhSfdW5mU4/5N5hKZO2xjMpT5U3/Nnu0OouJWgKJKqAVR7Bu2rWF84g7N1E8r8VIac+b7uc3Loug4uAtOnAw7DA3YPA+53Hd4NQO8TiLq2f5vlZTT2773UU81ApoG3eA1gi7Zaz0WWP9ZPbcGRm6dSHlzW+6W0+gsUEZrs0rlyEg365Q5itXFry4tMKJVasWQcufpZi+S2jGo2heA1wf2SskGgX6vid6G7WFl23EjIAy+fo2U9XBBKU/0Gr7NsqgDX8hepRyKPSGK5EHkWgk8JhxCEGbDkqfM84TROeDo9gz59hv/wI467N/jc73MSN7O0bU7ZYk/ysoO1EiIDfnux7LqGwdMzUaczXiohssVRo7jbnl4jcrahQ7l+Ppq1Nq315OrKx1cqvwwyaOQ+L+7x+T4ZH/PYHXHwEzpniWYpMw7GFBDZGtHmuSoa/q2iwpTFtfpjNaxM2N5YlOljx2IwT1DGzOneZNz7I3bk8Ge8U0IUmRAy2GxwuSYCy8fGCC8SBhsgaTlPK5Rx5hxU79v5iiVddSa6KT9NbdeprlvuHdWjo9RM7XNqIeKypUg5syMRpoXwte57018GaJya816UGl017kKsOVv/RRyEQtQyeIrg6ajMZUL39B48fQYgobM+PgCnbg+QQ88Bd9OMmCK87secs4mAJ+fxvusRGEgx4RQIx9CpF0QonglnmCAJy0TwPTDc99gdDuiHAV0/oOt7eNfBkxeSwckuMAtBoEBTZs6Jqi1Ek7Vtlp1iBWQeETaE/AV2RsWBhWAal9aar6xFsy+qtbMfjcwrw2uX/0SQ46pY2uoh2vwZ4b1WH26VVqFFLVOfcYj1w/p1CfbeCkkMf9e45Nq72+1yGcDiRvv8xdpfCO6zGcAiW+Oymlo4n2duQ2GRDWvsYm2gsPGOPbO+fPtAvgQnbzEb5d6W5dKamP7aNMHZ+pYHzZhNK2z4grFSpvwC9PZrQ2Bt8SMXWsFNNNIrx1nzTGefwdJwawGRznSv0i/qg4SGBl69eIEe3Wh369rFuVztn2t117drXJAyDH18BA4H4OePhGmikry460HOYZcCYuoQ5pMIulPUEIJR2Ubdpwt+NZa4OLCQxUlDKoUgQmwmEYpxliBKXYkTEBkhBIABr1L2FBkxGK5cUWy5F4I3I5IabcUQxSJecWpKCck5uA2YmT3/QBZIaHMZiMSEwsKBJiINrVJvSIuO0I7PBGoWjz+HxwGQAuP0ySMeHeZZw1VFyQtFjjXgu5Mb2pZRTBJWh3MTqx3foH1eHDnKz3h2WV5HIDAlRCI4l0DRvPT13Zgq2q6CtVT92T3rXgUSMhVo4XJ8h67boet7dMNOZ5CRIoGipONmF2HhHp2GhTJFBDGDyISYOs7EahfK8CS48nmOmDlhDBpmhoDUOdDOw/cezhPIM9wQkVDlNkkJFICZBhhkWe6OLW8msahPEsJHacqoNN8Y3yPFI56fnzDPEz4/PWGeZ3z69BlzmHE6jerNENH5Hn2/wzDs8XD/Fg8Pj3jz9i2GYZeVh977nBclxhJitI6KUOeAsH0vXeXMH9lfHob9x0ZHkIYIKuf/silZtT3KxoMZLizfZFMcZB6g2mLrWd9uCBDYoS0kHafvCN3gcNjvcTjssN/tMHjApVNWEALISdCNryn1lhaVghQKnx04OQQmPPNHjHiPmRMmZswJYBK4wwBqycyKQiRUzrEmL1rQYrpO1F5d1Fau1ZSdQCflGZiV1+MiK6mrqM+rCWioRtmSd88Zf22vZatb+6zMVc5tE17e4tX98iVzUYux8+arZaJs19vk3SLDqeD31l6jIjcpNGW90fWPCM47yXMTDnD9Ht6LEnTnGN7yIW52ocYfVeFzt5e1LHbZzfRftfMuV7kqL3w8v8Ow/p2TgN1Iw1X/1nR1+y5vLqm8uaDDtXf1XH9pKNnbFRGdWDWY5Wlhkkt385DPdGp5rhuGd6EIqH9uTfCmYc/fyu+iXJKPZNdCEGZ/j0idxt4EQlAPiCC5HMx10hQQc5wlKfUsnhCn8YQffh7xlycPhHdIuwMm2oviImkYmsaaoTprZu1oQJ/toMn1lAqQrxHDiqev9rD866oYkxVQppo4s9/y/ZxXSaOMINRYuerAbVDwwpLk+/UztwDLX6tcOubn+7kYscIqsWJG9oIwyzCvMWYtoV0bZ35r3qseUP52sdcrgcprMNSifts7zqnizfILKCNpXhJENdlIG21tzPLZ/vDqG1W/lkTABnl9tslmyYAFkLezIGeuxT3tY2sF4eKRPBWu+Z2VAGSkd3kzzMAnGiqms8V1BgVo614+72iJNHuOqrBPVR8yPWmMe6ZnhYT/S/gDHL7JMCw+D2BNyA30+Ev6exCzhg2SXBz6KCIIp9liDzNiAuYwi7I3zKrwTUix5GMovLSEDfDe4S1/wjsHPOzfYBgG7IYBwzBoXggJH+A4wo8/g+OMnGy6Uj7EVAQlMeeLmEsSx4rVaXYdFS+CfGYr4pcsx0d+Q9U+zcV2d1B9mUouH4ENHl49IJzv1CPCA9RJbgi34QmRhUxaMs7ZgPxZ8UD5ezm7BSa1df4W0Pq3afuSyJzqA3NTXVs0aXVdkXAtzD/bwkuF+ZuKvQs44wvKL+9dsDw/52bi3PUF0Gepoxi4/Gfwjsis5W/dka9Qfku48xXK9ATEEzDcww17dJ2D94T/8o+MP37H+NP3hOOR0PkecB28c0gpYISGdplmpMBwroP3HXjYZwLaZsTCL+VkBAhIYEzThHmaEWbBcz0DrgNc18EQExFhniPADHc8wXuPxEJ3JIYIVmcxxuIcpqMwy8wJEYQQApyb4MIAmmfMc4e+8whex5SJHiCL8hXXOMV33tX4VMMzA6JAcQ6JAaeCW021IEoUKAOjOSHy9lfDMEoJHICfjg+YUoc384guGk3AmI8BKTBSeNK8UKKRoDQLLEgSad5otBxSVZtySgNDvVsElIvBQ+QkFtaKX733gCPxhDA8i0waanJvGaOFxUopofMeMQTldwVaOVl8DdmEwlxSOTXZ0AAkIYM8q8GGw+Fwh64fsDs8oOt6+E68DhxHgBx82sGlqLmoHJwb4HwH3w25AfGOFkOVnORWPQ+Yo9JfEi7Kg9E7BybC0O3QOY9xToiR4D3BBcClHokZU0joPOG+9+g6ht+fMKce46whVamENkrM4lnDRv8ziIFDP6L3Ad8/fcYpzDg+HxHChE9PPyLMIz5/fsYcoygeUkJMAUQe+/0d+mHAw/0b7HcHPD6+xW53wN3dA7wTmgwugYkxTiOYGfM8I4Wo4WiLYiFblZfNn/tZbq9t9Ln2eczryXlvweqvSuv1CnV4UJrQKX2oXkdlqyxlAi1fxXXdNVmZ+8AZlgBav0U+yzCGcXj4iLdvHL755h3evjngbn+ApwScnnS0xqcZH+zUIEhhBJz9LMdbt92cHKbkMEXGxIxTTDgxwI4lR0jmmZWib3hjKprFZhY28M3GJeNPpK5KflOdRXnOQnLpnCwrqwhC8fJyGb6wLRilRmhSwn5XGN/ofBM2cdMhfbdUkp89i19tP7cbYrlftyeG1KPM+nCOLlnWc4Vu2bxNqxsWcq7zHTp4HIY9Drs9dl2PzncSZq3BOfVM/o9Vro16zS4YLDu/dmvYYnW9lMYuvSuyyteX2xURWTiSJTYKM6ja0FuTs1148Y2wGA1t5224Xu/rZmTVfnNze1BLS6Rl219qZ3bTXL7MNOvrlJV1Y2FMljO4tCYwJQSDxAPC9YgcUWJvqrVRKrkgQpgRU8pJqU+nE+Z5xvN4wtPEeI57JPZIbid0V7K4nUmREC/6WfpmaKMorjMr0RAWV3dVJi6rWVE4XAsh85kpvy5WyVeeK4BlC2y1DONWLRkFUXvx1aC/fum34rlp9SV/80jonSR6c2Rx14W8cI5ySKYiwLRFvNrYuXDH5f61+VjcvzSVy9BVom9QgpMllEtCEsSfjdKMdEZe4C+BUe3ZrvpKW1erK/lQ0WKjLQkr5EnNQkYyC5gzkF7xEVW/272sOz4fyIWVjLqWrBQZRIiJQNShvkUbe6OOtWy/23kpv7MQHciJCt0yMyQgTKR8UYbDK4O1zzAMAJCM6ZB+nUi9L1jacZUigsFgVTIkhb/C/EX1KJNra7yopD7Jmdkh4cEDQyeCGe87dBaSykI7cALCES6JdZ2AaVnL4gLPmvsiVbF7F8R1TSJUC5HDX6ES/JP9Lm+48rX+qNauvZmZFMsLoYIiR8UjwpLaW86s1khDe7U82yslBFXbsuypVpFdd7LedxWcfzHQvvWFLWZlu2SLsZtrp2YIV8HkWUB6Wx+XnhFXHoYpI0oz50Z1qbb2HV6MgTbe5kVf1127jt/res7FdDWB3peV1UlaP3EFhxZLaqxx01elJX4tpra1Grv9tRo4VXv0iozhZT273CGDXV9H/7Pdu9tZlSt08qKi8yFMFIZyAIcI6vci3FY4/nBP2O+Anz8A00zg5JASo3MdOBFC14FiQowMIIrhFAPOhyxYBCyEtykiDISIYC/EiDlIbrsUE5wXJsMCGucTrfkfQpCkzSGUkEkxxGydDixpG+NbGMwl35LhdImTb58l8TaowrOKcywsU6NkzbQMgdWCONNAymsVWk3pBI5ILElsDUYLWeExzsAYHPZHBw6FFoiaEyrFUYwRknpEIDY8HQggZ2GZKIdBsiS0iWxsyu9xEeA5Emt2zw458yzZ8KmMSwefOMGxCPoTAWAPgOGTF5olVfQKm+U85/AxdUh7EUpLGw7iCeG8R9f16LserhvgfC9GDVYneY1MId6zzmmYSDWoMtG5EsiNfgpgJCShvZQ3JpXMi7eNJMbuvNceyX8cHeJRFWsBiJ6AgwO5hN5rsnSqd24poowQbj8lFWzzCUgz5vkDTuMJT0+fMM0Tnj4/YQ4znp5PCDFhDiGvkfMeu90e+/0d3rx5h8PhDm/ffINh2GHoD6pgkggKiQNiUg+IWQwXC3wwzVK1z/OclX7zwmo98w8Vn0LVWbgFn9DiqeXvfHX7RrlWCaztlfpK69duRixV3dWe7ncB+0OHw37Aru9F8WTbt66FrLYl31meqY3PmElyezIhMjS5OxBNuVMbVN4Q574d//nbTc/OoIyLFJ/NfV6DajHqdSFUOUHkBmM9FGYslBAF9tyC05c9b55f7oP6sVWdG7tP9/5qnGffOdenNR27DQ3Ko8I/SU4d33l03qNzlL3+bioZ3yzO4NX5/BJC8kzlzX650MRy7Vf1LO5wLZvYpt3b11U2kmXnDbOsdW6vzjlPiZoArO9zi1xwa/Lsc+UFighqP+VHubbBhxjce1X/rgjYv7a8fe26/IJ3+ev3Z6t8ObP4kvKKVVMgmCpoaMSfAT0GMLp7ROolDiqmnBA1BCGS53RCSsWdchxHhBhxGkecnp7x6emIp9njYzhgTh5zCo3QjK0zOgQTJjVd1duNssL6ysXyeAlsWx0CNecii570PDTELMr39VEhbakFppv4xL5uwJi6x2dfXD5VEx20untDuUQ1/fL71aDRJcaaIIJ5h4j/afcT7vyEHQVhAsySyhIH6xsGu4wQq0eybGlr/i719tZy6WnKy6fMoArgHdjSHCz2SIEeLWF6ra0K+SxGno1Cbuqx9Rbrs2ifF7bS1bOxeCG3sEnoGnFZq1Cx2bc8W8u5Kv9UU1n/WyPulkApSkkhvAxOOGf5LlzzvBD3CcUlPKmgwizdsDpyeT83bVl4qIrgUwEJay4dS2gpiQ3Nok4S+UWLGetkHb3v0PUeu+Eeh+4tHtxb3LkH3LkdBtej6xOcD4D34FSFcFClh4WAinFGijNCGJHChDSNQAxwKYCTxIbOOERpMlM25NBLOoeWh4H0WVcLUSpii87Q2dQula6NMOeWCwKa7BROcn2I1aV5Q5iCAiXxeQ1XWS1GM16UBwRHLRVQXPaHc3rbcEXb39JrOyCbHMkLyta7N+Z+yDErXgIb9KkvIqQ2kKuVzbVeWgGdYzToLEG+eq5ps2X+6rbcVh0XKPl1mL/m7tk7yzq23z5X82375xfB8otK6WwC89ft8SUL/SUnZV3zBQqsgN2L5dK5aSHAS/ume/mmRbvexjVLuiXse/nx/nq7y1TVeVzjMzCdQLu3wHCAI0bvGf/lHyaMk8O//cnjOIqHGzzj4BxSijiNE1JKeB5HEBH8bPH6u6yEZtgay29T7B/HGVOYMKuX913fYWAHigmeHBwDnqF4MSJwhAuSWcCrxbnQAhGMpMJzhnBdKXtKAiL8jTEhhh5+7hAnj8k5dM4rrvSKq5JOcwIhAU6s5rmDGDZoTkinuRkYIninBDF2MUts46FSyeV053/Eff8Tfpq/w6fwFgQPB8A/3cPNDvfxEw5M6NQgglIQ4V0MYI7A9CxjrY3RHTSUqnSbnIauMnqKBRd7TnApZropcUKIyIJm8YomJI2imCjpvDjlGdTowAte9izqIqG9HDrnMAfK4YNzMuQU4VKACwR2DokJklOKVHlQ6BTJdSGeEc55DMMefT+gc71Y+nv1WI0sA6UdyCU46jK949RoygTyNvcuiddDTAGJI0ISBdgYGSExYiIkOPSdhNF8OBzQdR0OQwdHyEoEQ3/sHUKMePocwYkA9yChuxiWtgFC4xd4cPAnDH7C958/4+NxxJ/HDwjziB/fv8dpmjCOY+b/AULf7bHfd/jmcI+hH/Dw8Iiu73F/94Cu73HY38E5yTmWmDHNzxJ2TI0VTdHW5FTIwD4ZINDz2cKtYviSryy+Kj0Hzom2G9tZO+4ankwE0TUP4DSDH0QJlY1a7D1jxivxKkPoKSeuBpmPM6ZU/0SPZkZUHk5Sb0s+Fg05LPkbNL2rBw6HAff3PQ73A3Z7DxrfI+cvYJL8eSSfXPdLyVRRbDkk2x9cep4YmBNj5ISRU+6ZMafsbG3OMKEm6HwBkjZwu3yWcqJ6UZsGp/R2ctWDcl6MRyndsklOmZdwtWwLplxRvpPFM4x0JqLCYpMzEcSDDJqjkYC8RjL3BKrlT5mcYMknAYZ5lJPygfbdklhbfzK2I4C5pmEX+35j+su4l5Oe02FXTxLMW6QgeFcGVxdP8BTxGEYMCdgR4b4nfHdHOPQM76mEytrqbb2+X5OAu0JmkAGNK++ffeSLCczrdFCTD9YWPsNllDm7qS/UfG56Cxm4ygig5pFuaaOUmxURqy4uFBP5ev3lBZ05Z7X+a5Yv6cM1InslbF5cv/beqzqUK3lpHa8/NbV7WE0MyHexionwCHDZ+rVY/UQlmGYk1mTUc8DnJyE2jtOI8TjieQaO0eOYBiG8lAAsVig67Dz+c+NrCQ2zYNl+rtrUZN/KGWiVEMU6V/6n/F7p05k14eYjlw38uri7dWeFLqo77Tv1CL8MZn49lv4l5Vzf6zE7koTDd/4kYVSWgmL9flkYtp7rm2H7C8q1E2tw35QBdXxLUgusrUqWfa1h+dU+8eX5BbA5d9uWuL/sPuHVl62HFg7Qyly0JR/2jbFWz2Scv0TZ9YucYYPsMyVAnXyy1bnalsbYqAICGluZITAU1m/O9bLltlCC0PiWVMEna8BCFpgVZ6oUHev54DIk9RLo/IDOCfPcUQ9HXoUmnIXnDCGEk7XHxQMje0CkmP+QooRvUGVLO+/1mhQYW4wkREFRr1Ge0vaor9cUbd05L4MS2yWBtJlPUoH5WTlS11NakCVa4x47gyvcYGgjp5yoFRWrU4wCEL70bPF6Yl5TJ7drdXP5QhJwSTPx1njkxsLKRy+imVGt9EYYWb+3kMKuYOMVKW0DLfmiLd+r7+UnvnjOv+xNi7d9rvCtlpO3lI3tcEv/mxN344DP06BohTCb7567vyRwX1LOEAYvLPU+X1vK1U+UduniZFxo64X8y9nny2EWmJAiCBFIAUhBBG/OYb9P6DqG85IX0QwDqBsk31JIAIQ/ATM4BBA5kNc1UxfUVI3UQjWFGDCHiFm9vgdO8IoPGRK+RoRkJYwQOcIQItixGCuoUKtWNre4Wr+rYItTAMcoRgYxZMGvha8lsISLyfQjBLeD1BNQ8LzgvAhDTKZ4QNX/xAEpBbmWEpgnACdwSJhnp54LHhgdMHk4ZniOUi+L94QoOYJ6QgRkqzFU/VK87AA1ADAix8n5ZohnqEvqjcFqmV2M1ZzypIIhLLufzmmNghU3iweDCaElF0PS8JMpFU9TCd8kIScBET+T13OnSh3zFLVxmXeDeFp6mHellaR91MUx0iD3M/PaaWEsYFvE+sQJMTFCMh6Q4J1D33kMXYeu6yREigOIJfyVJnVAcuJRO3NAig4cPMgxHCUkEut3l8+Z7MHoRiSccDp9wPPxCZ8+fcI4jvj89IRplr0IZlEceVHEdP2A+/tH7IYd3rx5h77vcTjcSxz5rgcg40AKiEGTssegicQtBlGNx23/tLT5WoFqZ2hBP9i1fEv2Q8qyjfJsXpNqX23xi8urzW8uvwucPY//ChSQX8aHlG2s3i12R0nX3su6+04UXpRGteCv5WBFtpEhu2vnjhd/YIF9eqqbPBB5UHlw1ShzA9w+d2uxyWfeeFdhFhVzmqTXm7ldvVN/X67j+VWpZ6yAL86OZ7nmmh3YqGzVtzPKhHzmqrbPG5hcm9jL4z53qbx3huan7DQIF4GOHXpy6J3Hzjt0qoTIA1JBOuloWmvADPi2f18rryCBrtEVBX9s3r6daFw+/xLeq36nni79ZwXeMim55JkW79Y8Are5gcsKvZ6ufLlHhPxorp0rdUKgv5W/vrJClnkjU3s49HtSiwxD6HVc8wTG5O4QMGAOCYnFy0E8IUL1GTHOR8QUMU0TPn2e8C8/e8RICLFHQocYGREkVrtKgKdMbJS+W5+3oE5tLVG02vVw1odfaN0CZGuPB/teewdRBTwvnYItdPZSHPzSkkHH12Twf5NSI79zjqPI1idm01CvTSkVNVBJhHn1zPqt365sEwnCEMklyWtcWc9Xj96GO/jM97bhsxa3i+vFrY8vPrfdlWur8QVls7IlnJDyqvPZAqVqXwoj7ZyXa1VCaXsy+3mp0jUrDsyCKS0WdqkMrZUP+b6STabEVaF/SmpZZ+EfTOChDBYpM+OVeeyHXpMEDvAaToDJgahDVrDk6Sx9trARIcxIYUaYZxWUBPXMUKvPxfQBFT2iAgkZViFkyZh1I2QXtEh+f01xVQoFyusCC8ukOSCchkkg50EqOKj/UHlEQNvPCeKNSa7pqEqhUa5pXZl1/f0X2SJCH7yK9vvCYf6WhiwX2bdrc3Hl/i87qtdD0a+1My/tlUtKigKPX0BhFe09XjL2cy2sxUzX61wrrF9SDDH8tdNuv3IRRLC+PH0Cz8+g/Vug2yveqAVtAsu8kyS45DxSjPB+QowJ0yxe3WGay7bKMF1guOBVYJxGTGHCFIMoIvoOnoDkxMLewgVxSoghYEySg2CX1Dred9KjIMoFhAiEAIop/0mPzfqbEOcJIz2hmwnOA33v4R0QvIWq6YoAHEDHkpMgogOY0XU78UhwHkwREQmcAmLUOP5xzsYMEROemeGPe3RPd3iPf8QH/B0SevToNM8SwSUGeEIW/FtwecsfpaGZGiUEFMcDYujgJHyU5HhzYIhrA6sgFFHCw1jOBo3bq8YWnOkC+C4b8IIo0yvOu2x9v95GDHYOFNTbBYwpQOmZBPYBKXrxbugHdK6T0EdDj8777BmRbHwkSojeO3gS62cwkKLgUlHuaGx9Eqt3pfIl4FKsvQBk34nRikyhJHoOmMOMcQwIieH7PTrvcHfYo+967PcDvOvQ+UHx0SxrwTMSEqY04+QT/nwgSTz8ecTf3Uf83x8ZH8OEn8cRKUREnjEdTxingNPzR0zTMz58+ITTWDyBvO/hvMfbN99it9vhzeNb9MOA+/t7dL7Dbn+AdzJ/BMpjOI3HTDOyeu6Kh1AqXjNnBHcpXzfP4rVgWbcAMu9nygbbFfZxVTi4wANqHFbz3EafLsM0bhY2E8+aCyl0pFPvHsonpDyRvTN0jJ48XMfY7wcc9jv0XSeKCHYAkqJHXnZfbSUKfco6HmYH84GKySGww8iEEztEuCwSZ9w6VhRYfQNddCsWTKoIEHkU8j5hDSsjnioQOFK3YXOX57CSf2/0ZzmWrHyoZMOFA5YzS2xzzhWvbsZgAhtL1I6Ss++igop1Ty/kWbkPpgllo58aTm27FPGXPk2re+X7enW8d6DoMP78gL6/w913d9jv96oA9RW/09b31yNHrlf4a1VJZ2HasuVMD9ONOR+uHCC6dt9u1318xVLdrohoenbmnpVKS7WMJXXt5bMeAwvN11IR9jXLyjPi2oKe6dPlcDG3dfzFXhpbfX2x1rAcprrVGj8s6zEBS3ZTy0CU1eGXEJgQiDQx6VIBITkgYoh4npRgOp7wdGKc4oAQCSk5taI19Cp9bRFzbVlaj+VLCrX7zIRelZAPQCW7pkzUXms9931jSc6++8UwTsBH/e9XK78FwrjaJF38CaDBwYX+KWKOX5vlPwc1efGlGMXVp6A+l1w9jOqlF67TLzIBugNvw7P6SttvWrz4S64Tn/kOtLPJy0VaVVTmX3KHJcCJsALqopvvN+cz5fjT+c9CNBnBSUrwcmFCQARHXBEMEEa12hfmdWDM3JrE5fwvKfyDYzgHTVotyd/FctIAoTJuKQIxZHwARvGESJagUrzhUoqFEDdcUs/vgjhtlBAVvK30xfnZZr3ObP/Gq8EsQWFKAhWimDCgUlig+Ws7WrwCy9y2eKrgC3szj2uJX8pSXChk/18s5wnVDZxwK1znKvzaK1HB11YmFIu+5Zj0syGPjJZb7Ltb26Ly/tccxTUG/svb2toLX5k2eE2phB8bt4oicYPWqsFwOxJendHX929rnW+ol16wz88+9vVprWs1Lu8vQdL5nCbX+3qrsOGLRr3ACwDAHEXwi5TxJwD0fcJuIIRY908sNyM59JFBJCFkmYrgKKYCUCyPkHkfpBg1XFJEtFwNqQiWTDDEhhdjBJGEaiJ08CSd4cSAPgMTsmdBrI7BQfkw8TZMKWTlv+FdThrSw2RvBPGOYBFM5vSsYgYt3UwJiSOiGg3M4yxzlxICEkJywOjgxg6WF4KcZh7IHhasAtmkgjpVoOScVMWit5zdBvkXnG8GAKAc8kYIK50XgohJiUBwAPE69IcZCcCsPdf7RrG9NQ+Gg3MOnXcI6s2QOGruKw0VDHOCEPqocyJwc1767XI/pG8WJl1yOEgbzDK3Rg/VNIG9Xod7LPk7bH8brZiyN0xKjI7EmKRzDl3XSWgwzRch70ly9DmIwmRGwkwJwXvxPpglbKaE2TwhhCPCPGKeJjwfjxhPJ3z+/ITjacR4OiHM5k3j0PUD+r7H/d09dvs9Hh4fMfQDDnemgNhp2ClRhpnRYlRZQQyigEgcdd9wI2+9JITjaq2b6+2G2HqzmfPVFqHKsOeWsmRLLynjrV6ln02uZnTGWdy3vGL7mCQZeedd8Sha4skFTl3hK4KlpAFrUvpIDkEjXkTt2cqaPb98Ax96QRlBi88ltLC7DZ8DCzlWBRliNaLFhbUt05fha/Po6r3MgG32Nb+SFa2FpwOKXVkjH+LyO5UKcI5bozyey/uRNr61Vwotz9W/xev7/PttXZqTEwTEAa7fwfteQ+RVRlc3IPjV+b5ZgHBbX19cFS9lpYtZ/YLm+AaFnD7YNrPSItCqmmXC+3a/1uu7nl9TduRWbuSxt8rLQjO9Wsh4A8A5++bCGurWRfkKZdX2r1x+xaFe6IR+EjY95tiAI3Ox1K00uokZJxwwokeYExIfs1VEiDNSipimWT0gZkxzxL996jBODsdTh8DApEnhYo5fyIDz8P2gfWGkOSCGqYH4r1o7MriyPFRKhmbLVeTvJni51QPil9xS18FxjRJ/IWXE76pcnmwjBlIm4E0wbgyHMYjXF+2cKOd1hdaRGxaUT2agYKQIW5hIUdgxV392dswh9eWdu+SI2hKsq9vVF96kGZbKiJvgHrcP5lVaMpk3lBKDvSL8ls+cnbD24TKWcq4aetAIT4U1iUjDBECZZH1vi4jkUl+9HqYU3e7eMucNgKUnVH1/Q7nDmfnR5J4E0BDQf7PD4eEOQz9InGNVSDhyYJKIuP75B1CawcqkmxDE3OpjmCRPRJjEE4IDODt2VxR/BdNzyCSi6s+ekecMN2TCmWpCTGvKsZrRMPiAxHMm+CqWtiWG7ABnXhCVcKUKG1EzccYkL0NMaacyY2ifIGjuGqfCiaL0sM7mKVmApi8wSqn69CUvf9n7vyW99aVly+PmS0rNbF2r7ctau/T2LbTBpftfOA9nmKBy/5ogY/FMg8uv0/eXjInOt7/m7Jor1odf6JBeokCvjud/wGKpd9hB5NcOGDrgf/kvCfPM+Od/dRgnSB4IcuhdD2bG0PUIMcJ3HeYQ4NTiO5xGtdqOME86g/zjrM/EILhwnhG9l5CEjpBi0HxJE+YwImrS3pG9CA2TWqurcgExStilHCu84ABOGpvdRcBH9TocMU+SX6DzPUAO5Dp4sArxoQa41YRE8VAQb8UJ03xCCBOm0xPmY8D48x2QOkiOCRE2gYGUjqIMADQcEWChDQues51qYkGGBXNhAhKpIqM+thXe9c5lPAyQ0h3qD+kIYI9gYR61by4RUhIVidB9EjaLIUofOIYjQqc5FHI+ColXhE7DJpEXC1/nhFYfQw8OQIhRQg11Pfphh2G3x+FwwNDv0A+DekRQRSeWxOaOJH49xwmJLScIy/6A8NViAV/RAomzcZ5dqzARQoqYpxmnacQ4ab3OSbJn/ev7XsJ+gcQwkBkhTjjNCT9+JITOYXzjsHMzvt1/QIgJJwo4Hif87x+POI0nPJ+e8fx8wtPxiDAHNTCUMe73dzgcerx7+w32+wMeH9+i3+1wt7+D7zr0/SD7RhVtiRMwM8YwSUgz7ZPxMGZJno1wMp24tgTOs6JzZMY8a7pdacYbZAcrb4oFH5Jr1wpFSbZgcNi8lhdCvSUzlIXaxZOjKFMWAyWTW+Xl171bHtMUEdh1HYa+K/uRS59AFZ6q6rKf1gLDAZpDIjHhmd7io3vAB/Y4JohHhHNZIVjqS23dX6GsKRW9Yn3WCYupVkTIKIzHWdYoXgw1T9jm71i1aTwbW9OFT88vKQ9snioyeVGvJZWdVcrp7C0m9L6FI1/yRg17WY23eY6xPUc3lpWSdilIoPqzKFaM9+q8h4fHbj/gsBuw2w3ohw7eiVLXkXnP/D7plLOhpxdn9mWz+vI2m7bLgxt9sJ7ceNZe2PEabuU+3f56LrcrIl7DWFXa/my/vlLJLNvZqGbJMFQS+sx4v6B7NyusaftArJDUohO39Omlng4v9ozYeudmrWGBVnmqG0DGBSnqdwvLJAQdIcHnGOAzGDOzhFKqPSHiLMmvxhlziBiPJ0xzwtMJmGfGGL3G9YzZogMQ7bXbGpdN+IKQuPmQEAQZb4YrEozehNOwupt2r5SMyH9vgLYQtr9qq7cC2bMVbL145T4KaGZOwtgAEpfXG0Y35GLPb6DvG47iDV1Z1Futw2YDxfInk+CmZADn//RYYkodxugQ7aVfoNS0yMuwxJKYf03DpZoMpmqB4HIPLQmnxa2MuF90HNYPL5UR1/E7LT7Xhe3fBcX5KnJ+szO8/TXvnZbocRzQ+wTfucrScTkO1njPAbYpS06K1HyKVVKq9nPBL82aZiUEKqWw9kmbpoZkrmeohd/1vq2F/aT7pAhNWs+HonDQMG/2Z+8tZ3aJT7WRdf3I9RXFyaK2cyiKF0+uzV/aas4eOF6/m6u4ciCItvv2kvK1rC+W483M8xZMAOqEa69WJHyNvvMX9uHlDeIyFLmyoNcQ4ZcMI8PQl1crOHoB02o4AizZ6rZpfhm9fb5snLsL4/oqhbZg0DK2b/X46vUrfVudLb186/sXyq+x6w0S5F8EzUs0g9CBHGHvAe+Bu32Cg5O4+pnVIDjv4YnQJREORw1l6P2sD0qYoZyjABCPiKDW3eYJGCs8yOYpqM/EAAIQXQDBI3bqQQDOxibFFMWGYwIgQk7Aa94X2n704tHggoOnAHiAnSRkTUkt8Dmqt+KMOM84PjPSnDCPAWEOmI4TpiNhOik+ZAefDQIYjIAS51v4QgZAjpYcfbMujEJHOIihhiV7lZLAGvJxC3KJtyappFE8GNlJHgZmr8+UZLF5N9jaJhYdjPa4lj/UHhFEknzYeZcTS8fkZF/4Dr7r4fteQjN1g3zvOnjn1UNEKXY18LB9ZevFqjwBNCeY7lkRvrs88LLuhbbJfCmXnS68NCTxOIngj5wXfp2BkBhECewlN8kpzBjBiEQIlDBjhk8z5ukZISbM44xpGnE8PmOeR4zjCeM4YZ6Evyc49L0k4b6/u8dut8fj41vs93vcPzyi7wfshp32w7wwhNdPKmwN6jEUY2z3eDvycqUy1Kku2szpz9Ssd566DTrzFh70JbDOKIzMFdTvnhFy1idlxYeuFCBLJUQmjpF5B33AAXpeaXMM50fVnheweYIAAR4z9Qg8I9IsikizuKoP6yK57cUGL67Bixi1UuWV39duZhlYc5HzEMXJjDfelx8WGqqEXzJYgPw9M/FAhvlLaF/P4taUXhxc1T1afLu5DuvEtaJ7zKkStVMvelNAZK8ctGP66uXGs/qiM21wYmHw8lI65iVTvEVnne1DJce69H6po2pxSxSybGPRhy2W9Vp5VbLqlxa+tMFfXel5ZvlvZYPZfk0dvPhEuSChNSCCo1QsrmNMmGiHiXcIIcjvKHEjS04I9YQII8aQ8G8fOjxPwPGZENGJ+yUDURtOqv0Vg4a2UymqJwResh3MGoVVqEOL7VmDwmJ5C4gVDgC1SFl4Q1ybz1u79yuXuucWw/JmndWXtHtlwc67+b+kFAbIfgnsYKQEXU/NnZClx0rOcd2HZd+u0Edb47npag3YNykgI6cbiyBOwp6VhHQRIRH+bfwDPsU9QlxqrisC8Ub4fE6IcbXko8TVkH6ZDdbuZdwGFGj5tRDWWap6U3fbtnKc6SrpVq7WsDWpVR+cWsEDjflSHkzKjPe6P1Z5BbdeNb0Vs9LUwU27MjeM4fgz3jyN2D3e5b0he1Jj+iYusIRLOCaOs4R1CCNiEOvPFGdJqpkCTICzSHMnPVww241Sorpu/yzhsjFmRQ+Rv2TGzdbGWf4Hp4k6XadeEWqF6TwAs8j0atFHzfKJAECZFm770XrTSfuWGNVVSUJNydIsymsA0K9Qltvw5RX8jab7/RXb0A0EKmVrvV9Ai118eHWrgk8Zd114vVKSLA2LCEVQt/nulTGUbqwFW1Ut2BzfDX2/Xl54VmrjmV8L/164/7spSpfQ6SPYPcEdvgG7HYgYQwf8r/8lYpwY//W/RUyzCoBIPOacd+gOHjExdkPAHAKGocc0zTiejohBQjcFVTyEecY8T5hmwYFj38MBiLsByVEOnTTPE+ZRhLsAQInR+U4SVpOE8EkxIUBDPCGJ0k2k2xDyNQlNGCMcHJhmBCZM8OAoIRC7vkO/GyWHQa+hFVUZMs5HxHlCPP2M08eAH/+vPTh2QHjCPBOejwFxjpimJziINX/nSfIcOKDLAk6nngMO8Alg9ZqQTNPaXRNUiYA9kYd51END+dpvE/yUZOKsXpjm4KjCW+dALPkkHMRTk5U2Nq9MaL8BZIt71vkOIcJ5TcuR6QPdMgR4Z2OThL99L3kPuqHDbneP3f4Oh/0Bu516HfheQliassE4E2YJMZRNrBkpnjT5csy0aKEHCOx9/g2C0CROfpuwDxp1K5FDTGIcyOjgux2c6wE/gKnDcQqgKYIwgXoG//GEU0r40/MA4hmPb39AlwLcccJzCPjpdMI0TTgej0hR9jNDkot33QGH/SMOdwfsd3s8Pj7icDjgcHjAMPTo+10O4clE4Cj8S5iDrs2kBo1FniBrY/NekE2moSsh7lIwbOsKQBU7yOtu3NAqbCeKYH4VfmQNPEpzZ58xXsQeNxpU9qnQl+fpOeNIbR9c48EyN6f1UtI/CGfjkOBB6Ag5PBc5qlgHrvrCyPxQ/Wn0bFIcmkS5OMPjxA5T/yeQ/xHudAJHUtpWfJzLtFFJrl4vwVdDEltMe2mk8DRx83G5tC1QNsWyyQ6I7Zd6LuT7AFGq5haqaFOZVjIjW87znudf/4i5eGakAqPKXrBnb5kOe96ucb5Fi2/rX3W5tEjre5Zfr+s8eu5wGDrshx5D36P3nYTtq/mcrFUxvqng3d9jWSktfwP+bLMPmV/E9f2xWae9d6aCs0qJl0mKbldErAZY3XpBg5dc2s5WRuthCRPBuS9Lo/it7r50X2wJH6WLBo4vH4paV/LaulbjesVues07LUNRvc8l3IsIV5IkjoZXIShjTsDEjBgZISaEGEUwGiRBWzx+RJonfJgYp0h4et5hjIQ5OSRQDsFU/zWTkbtilkSchVDbg2kPS7lsoLeEQ8nBivI7Rn0WKrQJk1F/v6XUQ6D1tXP8PC8vfiUY1/D0V8q5Z7aGtHUvP5MZ4ivnZ4F8eGPtrNVmj56ZHyMUc3ivDFeoILvEKhhUBL2qp34er176MyubGZH2mXpARbBr5CknZGvybCXHoribk0OIHpLOfYOoypTGbRvqVmXE5rqfoZUuoJbbyplNt335DILZuNJYmJxZrps6tjARXxpBkcKWzFht9Gxz3hZPLhmzm3pYEUzNGxv7vn2KQSnCcQBVxLMlvM7EtcbOJsMXxmSmmGNUixVccUcu4H57w2QlQvlSzQI2z2RRONDmb3vN5rDxUkCJXyprVfJgFC+Jti6bqS0lal7vuj+VMrsOA1gGtbEXlofl2uFZ0VqvoAtul86+uryW1yi88yuR47nN8wXl1tpa/H7jW18MOKvXb4IX52hUPjvQ64zj7f1mY4gW8PPi8wuPiJbmON/vlxVSPGq0/PWSx/KlLb+gCtr4dvWNrUdvMQK7ZBH4mwkTruxxTmINHyfZt24nYZp6gIhxd2B4z5hnw0tCPBE5eMdAJ+z0bifx7ZkTgg8i5AsEhIBZQ/JkXBgDYpAwNt45xBhKPHz1YGCIQJoIiDGCHQPOaV6ATAzKZ47NxBBvjIREEZEJ0YsSPYUJgRg0ASl1GOcIJo/d0Iv8ZGRwSBjHE1IcwZ+fEJ4TEDpJkh0AnoE0EWIEYpAQUF5DL3V6HJIDiD2IJJEwE8DsVJBGQCIkl9SL0el0Cp4VObruMyI1rhHawXCuB6tCwPCxKFEITvef8ma1wJcB4iThlOw5Mv/JCGY7y9IXUTj5nBS7eClWSTX005RTnjr0Xa+Jqnt0nSogvIV41LViymep4HZZS/OICXMQul374rsOkqha2yaZc5gSwpU8E0mrl+TdBJAHeSB1PVLXwXUO7AHqAhxJ3gimhBg+Y0qMOexBPOMYPyCliPE0Y44Jp1PIRobM0ifnengHDP0ddsM9DoeD5H54uMd+f8But0fnxTtC1hOSRFyNGGM0T4ioRiypnFbOQy182TkKt8H93NAEXN0v/1IFjm6jbbZark/hmddWJYsOzvAr18qCPCyfRruieDtkw52qVw4MD6NqK+OrS/1no2ul42KwZyujnjUARj5hwhFZHL/kpawxWjTwYtRwZnb5zP3M2K0unq1EOf7N+yY3sCctGbaz3/l9ap4DkMMolxoqJUTV9fwOSz84P8K5zatla3HP0slZKLD6dXYvN0TZ8iaVl2fAMaH3HfrOY9cRBu8a/sdeKeHRbxjgNUHr2ddeTousvBDOXb+BRmrqfUkftqpDvQ4V7Nvkh9fvAsv5EFwoa3HZw0PI2Xa9XjKeL/KIsMRIv3hpz4VeUkLjlgX/W3lVaZR6KiAyq9aYSrzvmQY88x4xRsQYEUJCjEeEMCPGiDkGpBgxxxkxzKB/+z8QP3/Cf9v/v/DsHjDHCMmZZhYLrQJieZ6ICJwiwngEUGK83jQmrc80fWz1Ncd4DVRrhG6/l2ztpbJNNF2494sVO0wtOcXVt19SkXurEqJ+ZqmQuPys/ruiLRTRJ4CdWlZBrLYdsTBN0L8Ngceytcv9Xl6gjQd4vbHLANb7MN82SlDJlqx0kETG0c5njEiJsofExUXdgK91X75W2STlft3Nv13O4JA1jdzuids9dbYJXaqYhcyVnN3jlXJsWTdxloXn5lAta/VCM55akL9p9WUwuCTEy/QsQRQHOZSSJZqWkA9EQBcIQECMEcQRMQVwjOoBEbInRAyTKCZiUGVEzO0WANzCDKcDXjJjyxlrYAaV640CYnHdlENibaiWnM4JE51zQ3hlqiVvRCaja2LUmGllgotuu1ZgbOy7jGdqJvn3cFD+Vn6X5YuVEK95umXAvsxr8XVlS3G7vN/k+iJsIJyX9XtbHJEP9uLORk6Yqm9frXwV7f0L3lryYltr/7vkyc4JnFCuM4NOHwDqgLtvAbcDkNB3Dv/P/5lxPDH+678kzFGZdMlGACLC0PcYhh6H+wNiCJjmGfM0YRxHHMcRx9OYYX8KASkA0zgixYjeEaa+l9BJKWKaRoR5Umtzsb6PnQjEvXPgrs98kuDuGkdrTockdUUEEJx4HMYJHE9wk8fpWejCH6ZvcIo77IceDg7dDwBmxjzNIJ6wTyM4zNjFZ4TEGOcT4hwxjxPmGHEaA7wDfCdwwLtasMGS+NokdFClhLNcEpZgGtkbQgTpHo5ZlAcpaV6NhHFKIAL6LsB3Druuh/eabNl7dF2Xk9F6AoBC2DvWfFzkxN7IiXbEa24EjoyUvcFJQir1HfaHgwj5TcljVtwmhKwkir7z6PwO+7s73B0ecv6FTkOQNEwfc3tMCGrxHDHPI2KIeD4eZf19D991OPhO85goHeK9KiAk4atzHkAEIyHGhP8/e3/6JEmy5AdiPzUz94jIzDr6fD3vwAxmsACIXeGuLLFC8iP//68UoVCwiwWGc7yrjzoyM8LdzZQf1G439/CIzKqufq+sOysi3O0+1PTWcWKM0LDUgYyG1ox3Lw84mr2P58X49vA9DElAaesmvPv9A8ZpwvFR+vD96cG7Ug74mLie6vu9uFm6vcN+v8fN7QH77oBdv4P26yECHCX0CDOGYfCWHmLFI27AAOss8lTomFAKNZKOa/0g4McJRw56LBzXK9Mm9yNJeHOlkV03Fz9b98d2WMcZ/4A58RQUEVzA+7gl6ogUbAHCopUMcqFDsNgN8Uuk7lCDWC8BHTE6xdBQUBDlukvcauasSeePxeCAe8v4YbzHW3uP0eUrgiS/C1Gu6/3/MVLog1u7D3zy0+2QeXuDFyKAowUEQswGlAzbJOjJ9iW8kJWjPUO1rjz74yJ/2o1IoKfNd+Asbz6glvLZVQsQ6Fb/sUDTKK1AE4Dfa3TdHne/usHrmx2+u9XYdwStvKC4gV9+ymkJ9/05cOLa4cRsd2/Y7rM6fZliK7XyZd/5ijW8ThCRqekvaylvreo8k3GxLObCiNZkPdd+yIb9bHWF+oqxNBrZOoa82FPGHWi2AACTlrUwPEcJbwbLhMERRo/4TF4YEbR8Jjvh3f0Jx0E0f6yboE4G1h1wchojCNblTFUUyEKONMj4aNbPJnW0ODDyGryegYcQoLg8PAmRTohDyfSqWOlLm+LMIiTAUeUL+3m19LUpR3TKGT7Hr85TTn7PiuXMvdmrS1kfYS62zkaAntkjD6Qf3Q6wwI0eoCCuYxyHYMEEpYImjlqZ/PnN3wTE4aOe1PiTqt/nU9id6Zwk6wcX/QszHl2PwWpYpsaiNub/3FhX+8TRvdml+zW/4D4V3kUBCepOPduB9AzvQjAXvi/365LmafYlVTC7b89hGk3KiKtYD8Eawv92QhAze5/TXijmgm9s/xdcQTCc/+4RcE/ok3dXVPPuqVypAq7U2jX1rMxlg4RcCBG+ywNvEREFBN5VUxR0pI7NfPbOtF5yQUcJQEpB9+Xn4WL0b7a3Pz7y/3Oc+cvvk/PYxcUzFwYe8N+NxUrCIt/vT0mXlq45COcUks7VX79vz2a7ibW6S0afWEjkD850a6Xebd34eJv7Upzq+tQmun8ZSfZtgskLNyozAAu4UdR79R6kGEYz+p5xd8s4DcDxJBrkgPLBlOW7IgK0Ro8cJgfYzsL4ZvYa4j5Ap2OvxBXi53k6KriocRY0Ac6ICx8VLAgy+OF1kuWu9cpf1o4Y2MByj3ECdobE3ZDySgRwGO092A3gvQGgwCcDjACPI9gNmOwEsAVb8fXDLgRP5eLOSEoVyPQqvKiGgMTl9PPODOZgaZjmkpHRWsnfkl8aqcM5B7KAVRI7QPkGFTlAi9atY1808t68qyoO1sHkg2X7u1spoQOUCEVM16EzBsZ0ce1kvFMEgS4TJgQLTopzIWurKVeT4mzefH4/LzK0sN4uuvOSeQA0I0yqZ2j7YOIkbE7LSEp8cJgmh9EyRjAGowBtoWGhjYXRIxxGMDs8nB6g+Ijj6RHTNOHhOIgC4Th4FzIiROm9RYc2OxhjsNvt0fc73NzcYrfbYX/YozM9OtNH5jo8XeKyWA/OWz44IClrRKarinOxTFKXZ5bjP0Wm7GXCxZZA/hwVSndaYBKfvS4W8Cei1McS4lCZ6RlSfu6i608k/kUYEUEsmIKVz/yuCjR0oOvCJqf4PW1jgoPBiA4Da4yOMbHEGTnvKZ/mTZ+b6XJpi6mL81t82VLnGnVVPveh0mfBrsMshZ08Izs4vVvsUf0y+2RkILTYkCUcXk35pGXKZ2s0Z/27zU2YK2KFl0JGibs4zRod9TBaw2gFoyWuEKjEYNrDyWk6yvJlmc+coyfhKhlPjurnC8KI2LstyhpPob8qltRiTRXdER8vVuwXMIeHddmF55fgv0+LEfHZGuFZUpjGKIx4jrqu2dNZIee5is4Jc8mFP+swUof3vIf1mirWWkz2MSLS0zT6PxFG/NP3Dj+Oezin4biDU38L3nlTWztGxpOrkAcg28qUsepmEH45NQFPnCBC8NNYw/3gN5SyfwKgjWv0i9r7CXxy9m9+mT2VDTWfjdYTar/mlWebUgsIlleGZYV/Gb5GTxP+dv+vOOiTV24iBD/+zoX87iwcbe0tKr5ctj+oKLxeVhi+gfhh785MTLonB/zr8Qu8nQ4xSHVp+Lg1Xboj1lCaOiWU5mMdo3iiafvIPkzXqCAWgiZgnIcmNpGhgNFawGeag82s1BwxbHytiKOMYG7W6iGIc7Deys3a8Gfg7AjnCWGGg3UjyE0SF8LH9LF2hJtOcHaCs5N31ZTFhghUThBChN5FxkFGdDV6GDK3hRBlifkcBVifB1IzySIiaCNG6wjVJGQTkZ21E+6P0O9CEJX2xOXpeiRwln5J19pfWfpwSxM25BbIWG/2jfU/e9rA5MghW40X5wyYswhzeZLbz8/1b6mO69LPd0zXmDafcsrhf878BVAjoMzA40+A0sDtN4DqALboO4u//Q3j/lHhv/6jwTR5TXciOFZQiqFJAhIbLS569rsdbm4sJmcxDhJH4uH+AcfTEafjybu5kefDIL9PwwnjOGIYjgADRgHQGgNJTALFHqdjhnLexYq/c5yd4E6nGED4rfsC7/gGL6cb3Iw7CRBKALM41d2pn7BXJ3RGdKOVZ2jTcAI7iyHe98LcZysuowJjVSvRaNVaAjYbrUCKoZTEZ9CeCUXBLVWxdxheP9gzNEMQaYFHSikf0FSDHEAkmseWGbAOIyZYJZa/WotCg3YG2rDEhaCk/BAUd4QxBmhlENwpgYLDI4I2Gkob3N6+QNd12O93suOt9TSwD0bu73c7id6zddJ3YbDLmkgUKR8LwmVj59QPqcvPgxUljdMotPRo2QtzFBwZQBmADJyvmaCkXgcwLJybPNN/wjBajNOEH3uD92aPrw9vcdMNuB1/Qm8d3j/eYxgH/PPDW1g74jg8iuvkCSBS6E0Pow0ONy/Rdz1ub8TCI8xLv9/L+mgZvwQBYLEsCYIU72ZMXC65yNSvIp4BlAVW9fMzB8ncYHbNU+HKucFTkFX2cKCBbwU+TNgv5bttqS4nECcgrJ5JQxw6UvRnkUnIMqZ1Sp28+y8f98EL2Mg5r9zC/g8+novs/1I5I8BJ+SenDaIQourdSd3iDb/AG6twb4EjAwMkJkRp64I4E/mw6jFccr/UbEgile2TbP0reiqSWTUzu8jGkcQK2HxwRcuBTnGp8pqPtJoIGedJZS1U/fUCTnhFryJx3nYeDbORWsqufHlQ5RzzCDLiqLS1kF1rDU0Kt/sd7nY9bnYG+96gNyKQUCoF1mvr5NY8kefFpc6mcygvnduz83P9i0oXM5UvO8NPD1b9sYQRLUZl3Y+ltCAFWsx3afoQ41/q67mxUOa//oqNzxngDhYQIbiOBTDBYHAKk7WY2GG0E+xkMQY3TNOEd/ePeDiOmEZBWO/HDtYB1nl/9o7gfEDTIIQo74hsjJlAIMKjhU1QbP2Mq1cUyfdRtIzwFwJnTKqqnUJzeaUP807lDMSVPi8ddD638UPFXF5ijYaKWW5/vTz5AVD+ezHr6svFuvPy58QlFeth9t4xYYLGvT1g5C5pcCFpc2k47NWjBImi5V63JMBp/wGbZzbsp2wBq92b2szbZo4mno+2x8kZcY3DwMAGjlXs0byW+kDMOnRRSkLUvO4Plc4wgjbcga0eXoJEXi62a+3MM/NUDDMxTiLevDD08Lp2JQVg0fQ6rdz5kUU/pXBe61KE0c4LGkQQ4d2dkYW1Dsq7bHLOit/raBHhLSdy92H12KgmNFbEapR9NoASUT7zRaVRyBGIQoEHyRoiCBHkPxU7lteVAsmt4yMRcY+IfG4Nkd9By0NcenFRfPWqX1eWLPvwc+PbGzWN5nvoZ+j4J6XMcCUuf8G0zZg+zbW5rA9Lgjvm+V1EDQA4s5SYvUx9Srm24GV5vnl6mtIRb2v+OZMgqn4Ozzf8c7jr2p4EUCWhxMr62yPADtzJXaCVQ28YL19oDIPD49HTXMRRAA0fyBjwzHRA4H6voI0BGOg6g67rMI2jd2M7QWmFcZwwTiO00UJ/OZcJOxjkfeuL2yMIgzdzZ8ue8WunCdM4YBqdxGOwEvyXtYNWBIUBhAngAWxHuZcVeeUzhp2m5NYGEmeAHaKVRmAeixBCeQ1XHydBMTTJOwlUSlG5C+DMtaLX3Fbt+VdeUGCMAUis52Xd5MgqlZ2iMA/kRGgiLUVFutC2KBZ4JRCV3CSGe16bDsYYmK6H1gZKmUgvKgeANABvOeEVE2S9w9wFnEhcGGvv91X66S0cAmbOCZ8CEyx72hgKTAakGQQF0gZQGg4Kjgg2cm68uxa26LSFodHjYRaWR0w8QeJyaDye7mHHE05DcKn1EN0mO4ZYMwCgXQelFPa7A4w2uDncwZgON/sbGNPhsD9AaYNOm9AFMBx48m6qLKJLWOctICJTP0NeC28agQ+Z4bmx8jBOzmFKnS/PW3/3bazhJk+8h1uWr8nFfUHEVlfHOsI05zs0G0eMg+KrjDhsylR0QUFckhlFUG6Eillygn4JJvo8QnpKXAgmjI4wOOBkGZMTC5106soeBIFgNhF5AwvtLoy/kZJrnKX59e9W6+T5e85iNNR7z98BWe1behpp9DlVnjeSM2wq5g1Xz/J3VdF581Tkae0XyZbomwqjmtNZGS8rwVkFBY1OK3Rai2DCw2GVn73N+GCglUKxBRz/SppmLpwsXs4LNHDNmD3UsIqnNup9TvyJgCI2yiZ8t2YeAAWPdKWp1TYa6emCiM/pLyZFAzMWRAIsJqLsBKEaYfCOd5isxWk4yuc4iDbPOGCaJgzTiN//4PD96eADkwZ3Tl7r1Qs1al+HQEWYeUbNFmItv9CoAoqzsxB5PB755DDu7MJavfyvQVjyy71K2eN1sLME6Dj7d6WSD0kTnqHlJEsDqF1Sd1bPjFVatd1CPXItl5EJ/zx8nXiWXjMy7JVb/YDf9ffQtOzjuTWI63FZWvi6XGGO2DsG/jjc4YfxJZz3V2szU9N2PU/dEA1GzCbsqxWL4JLUOtCN2vJsz773M6ztmrojAd6qd5HaqIizhKQGxd685DVMrsXhZA9zpNFZi3FwGIcjxtMjhl6Ed4MGnDEAd+IKgE8gN8G5QSx2rMSGmKYR7CY4NyFq+3BJoCR0KJialwNVWc78feLxZ7VFRn898BzeU2KOCKcDUMEHr8SGCLEj8t4BAYcLjIHMwq/RNiEJPvI2g2bQdquIT5nZ90tLT4NMv/x0HdF2ubZUXvTD+dJt1z0f41k6uF1749m5wlcjCI1qfoa9WsDU822vC4g+hUTZ58I+YQYe3oK0AZnex1S2OOwJf/9vRry/1/g//pvybnHEAtBZC/Ka4iGAsDYKCkAP+by7uQU7h2EYhI46HTHZCY/HR4zTiP2hxzAM6N+/wzSOsOMAeFqKHYOmUZj0BB/01wv1vWLANA4Yhkc8PryHO36Jw6DBasKRLIwmaE3Yqx+h1SNgLSxz0lz2OgHWer11UpF/LM8Z1nohhCYobwnRdwbGEHZGQSnAEEQAoTL82uOtAY+QOQr3torKQCHwn4bEXzrsD7DOwZhJliW4LPKujMQ1JOAmcV0lHbYlD1hLX0KcDaO1F4AQwIAxcq/v93sY02G3u4mxJ8AOVjGIxOoBzGCnwIagnYMaDADC5CZMk8WxP6HvHhHcXyWFp7C7kmtHmRZhRzpLsE7DUQ9WgO53Ivzqe5DSGFljVArf6513x+qDPTuHV/oer7ofceIRwzhi4AkTLI7HAXay+MNw8pY3o4/nJcTnfi8ulW4ONzB9hxe3L2C6TgQQusN+f+tdiJl0WpyDZVEsmcYxs3qA99qVCx7yo+YfzEBAcMnUZhrnsfCKsqQWgXYe3wz+W9JPrLHDbem5oG4QigSBWq2IUswDFR/+HM4tRggUg5aTEmuZxGdOXGlNYsG07w32nYEZ7yVOYlXhEvsekP3qdzYmBkYLHCfgfmS8HRlHFpdgDioJBAvOOPl/6YlzmnhWM0vngJbMhAapLAMonetn9Tb2VbSe4PwBZ8KAxNAJWSkVlMOR9TuxhjK3TincRJaXE1wL7bhqYLOx1hvkejxtUyJEF3nBsYQIoRV016Fjjd20x36/w66XeEpGBfd47SF8EspCeVqiy65DIj9OCvjiloN2bo98ILTzaYKIM8RyLul5JhR8ua1qdooWP7WNkaWZEGxhleN4zo3lKVYQRfGk2SmwT66dyTEm5zDZCeMkFhCPg8X9kTEeR5xOIx4GLW6XPFPU5do6jf7N9sZGJkxiUJVPuFHpXLM8XQTkEdFS7Xa5bKpjO5Bs1fF0Z0ic6uH66fn0lDOZYJsXDGQMtkv7sd4rngG/JSuBupa19uVO91hgRBak4MlqvJlusWzmmCO07d5fM/b5eqj5i+x8OjDghNQ52h7OUaLBUk+L+rf167qVS7Ei+KLWynR+BhuspKIXiwU2tLy0l2LtfuOHuB9M8zx1N4o667twjZ9V4QQxYFmGwzbrXEr14LZs1ooeynFc5834RfNygp1GTMpgGsV1gSIhRi1PIJ5gnRXBg/VWESE2xIIQIo7N41DRiiB+Xxtswm43CbPzdSQKETNj2cJKYXb4Q2eEyOCaWG62FZgvqf7CIuISnGkJN95a3qfyPH0YnOmJiocfuNEAt1qv1udj+1ot59xmLbCt7PXpStj9hPafO8ZA0pJr192ylPBv5vTkOS21WuNuNm1PP8eL2X+Ww5RYSNekMh7b5WWflrK1yCxjuEUwpLeyps4Bwz2cNoCW6A+KGJ2xeP1S4TgQ3r0nIDD/vGY+Ip/Ua38CQNACJULXdVBaA8TQrgNpBWsnaK0wTiP6XS8KXsNRLB0muWNU5Ng4b2E4hd4KY5otJjthsiPc5EDWM+pBcD6mxaQ14DrvDsnG4Yq1uggbQvyxNBui9e552AjWDFprdMZrWBNBk7hmCsJ6wa8pthHmQOUWh35uKMRfCv+SWEQoZgTGc3K/46I7qnj2HMDkkAfsVb6PSosAIrQdl5gCPaCiaxtF3uVQxKnJjyFjFLO/yQNHGcKgFbfFDqazUFZDhhjohmRFaa2BcyoyRLnXcOQwGoOARhgF7PYORBbQgFWEXllYx5jcBFgHayec3D3eDu9xGieMw+TjjIjXAuecxJlQGroTJQqjNJTWOOxvJBD27gBjDPaHG2hl0Hc7KC8oYgYsSzyOEBcsxPiyU7JoLR0H8XYwsXi2Mxo3pEadrtLUboHpuIZL7Z/V9KVZ8cTiKqlF8ptKaGNPY6ZOZH0pK2zfvMv9Enjq+6bE0qG4wxDmTv4IjM48Yt8T+u4FOqP82fQ5E8su9oT9uWX/T44nWhgM2OHkDIbJYXDv4XCE4yFZRMy6/xQquVVX6vvZuyUbX0mXcbZpuNm10hiHAxMh/aF8Lx81QpHnrwsiyUSCwGKeZXlM9YOi00iZchdxi/NVrlF+93IjVw7TQABx4gsFyzMFJVaAxggMVkEBS0UYUxC/qy1W83YWp1jDaWulwBkVKi2mK6rxVvrUxBmBVfphEe9PUsRWS4v1FXUXJefwa97NAAfrtjMF4Oc8vj59toj4nGJKgDYA2BCkWjQuLFsM04jJTjgOA8Zpwul0wk+PhD/d9xiOjMH2cI5h2Xpz4cBo4gz4BoZP/GeeKANsqYdllsRpmp2NGYCkskyhWd+iq6g8xNFqIseHZkjJdQycp5znlmXJh06J/daYyyrfx+haQO7zGCvnSOWk2cDFsrIDHtDhH+23Zf5Gewu9wdZRc34WZnWs/U6lo2ZMYOYWdX54AXAzMbDoA+iDb4hzI17vwBZ0BoAPFogiEPnMogtA0wR5kRbyPj593RwJd86QtAwzbTKrW+Orse756+X3CQsiRhTEAN4P8GgxnE7o9BGn0wlggiGCNRrMBoYcDAYoFssH5slr0E1wnoB1Tghc8j5SIwsih8GZBls96sQIAKC8ifo1G5+yeorW/LPIbACIki1GvsIxYDfyOlptZS1kriI2CyEyQvGTSx8L8D97+sV2/AOkDz8XH1pB7/JUjvny/n0ACu0TSz8LPvGsKaxxditTS7s44VAAxJXgw/eA6YC7bwX+O4t9B/z21xN+fKPx5m0HZifuerzbImIADlCaQDrFOyIiKK1ECMGMbt/LXci3YADWiVuk8XSCdRMejhJI+PHxKJaIxwHOWkzDCdM4gDHBjhPcGIQQI8ZpwGk8wU4jYB2c9YI2JrAmsNtjVHt0+DMUbIwB4WNSizIZA24aAWTukPzUBcuCrjfQSmHfaSgSxrkiEh1oogwrB9gFvMm7uSIDUkkQEbDXoAJASmI37LUW90FdWCGPu/s4BNN4grUO0zTJPFqGNgpaE/q+R9d16HpxuaTCLgguqKwPEA0gxIVSpCH+gpRXPCaEQL1BcOU8TSv3t4LSCrAE54BxEhqZjFhUSowMgEgDJPPDUHh3PGCajOgcacC+ZHAnrm6CwvOht/j6xVsQLE7DCTRO2J8eMYwDxuMD7DRiOJ3waCfv4kvGFHSvZZ8p7PoOpjO43d+g6zq8OLwQS4j9C2jdScwMKJB3RRWCXo92hGOLyY0eX5vEmsI5EZY49tEqlOBfyknIPU8Pp7NVK0qlM+i8tKtkys2ZoDVjLdBAQQiS76IykadT52mzcNTjhnEveyHAugJxoI3zuyXgtyFqxOVQNVfqjIzeEK8M8jtnHQcaUZHFzeEHvLhTeHn7G+z7HuLErGYEh3byZ1Q9BwY64B29xjvLeBgdBv4DyPwRPJwwOXHP6pjAVFJCAQY/701ZKWkVlaeFKma7FkDMymH+rBIOFEY+xXxlLwqNssx9a86HYADsQJwpNC01XDUxE1i4Rhnpbf7y4lRPTbxJA62WmEN+HyovBFYw0Djsexx2PfreSEwiH8sk0F0cQ3MGGjis2XwPXp5aZTfWN4MP7bqIUJzL9KqthP3BE82+XFb8I5FEFwgiGgNhlETzrMN+FGe4gk2aeim/r4uKBy308sOkpBhZMkiaeYHEM1rKtHGRo3RxU+5696yXIuQaHtyAywSQBkMDSjQ1LGm8s8AfR43H04DHx6P3iSnaCZwFB6uFEHV/Zr2rNE4LCWQ1rBxopW9pJ5Roy5yBxc0OzB9FBvfaPg4Q2afcuqSZH3JBh33CZ5Gh1jWwNc0P2JbSDbyw+JlWagEwr9deVXz96c2vq0tqaeBe/kV12Lj8Om+DGt95tY0Qn2T2atZAmSM/3XPhVwkJPxxMbNcahStrB2VDjef2ZvO6mFEFOVnyvLdpWuFcy3LewZaQrl5apmBJEvZKjXy28VtBaGn1jC7eT2v3a108gG+Cj6/nRxUZIUdMYwc73WNSFtPEYNYg1cESg2Ch2UHxAPAE58Q1ANiC2btSyMi1vG/xmddiZg8sc7dIxR6vzy041kyoCV0ZoODAecwHAiEIB/IJI19/PXkO4HCHconnEyehBQWyM8MdcgHEJcnjXm0q+Eqks/i2hoGm3d9una8GOvlwLp2S51EQLyuJhPhM6yD+c3Unzvpape1ui54y9OeEj09ag2bZjImZ/dt6f64vTQKxelff3bl1RbPSrB9F8aqvLUb3PH+j1lZfL1yxOSY8L1nmOVfzWqfPlL1QW/Bs2UsSp4hZc5qj1SXvNiQurQ8MPDwC2oD1Tl44h51x+Oo143hSuH9kMIsrEsUKTAoOomQg2vbw2vaIoFb0kpXkB8MoOfudUhKI2XRwzmG/8wKIcZTYfF7QcDo+YhxOOD7eo398gL45wDy8hL57hdPbHvbhHvBujBTfQWHnryOG5QMsK4AfwM5hskIDyj0OOJsxeRVgfHBqRUpcb0ACMsMzdEurotLlSwi2qiA7xcEht3+QKcnv9+xWIhSKH1IReQNcCte3dwel0PUau36Hru/QdV4IoZXU4fGuoMgTFXqCqjQ7ODcC0B4HcoKruGQh4qBgCbBgkO7R727gCLBaQfUHsNlj2mmcbnVkyBGUv/M1GIRJKzhLOPQTtHZwhwmsGKOTebPOQrkJ7+7fgp3DaRjE9ZN3s3QaBlgnphNKaXSG0HcahMDkUzCduJfq+x7aaOx7CUK97/cSA8OYeNcwJH4XWCyu2VtduGABIZKHjKZPSxTULxL6k/IUqOum856Ub5aU7VrYRxEXgGidYEfCHYMi8CJd14A9QYs74MgBY1oSPKQ+ScuOQ/5Qf9lGTr3E37X2NGSIzuOSIjrzFlNKOhVceAV7qENPuN1rmBD/BENqIAiPWhMVvwYBkMREcc5icIRHJtyDcO+Agb1rJnZJaSsMHXx9HLPYiUBg1evSuBsrXI0B375DkTmnpeuOBdw+45PBe/xY004P6+PJlswVeNlEmvX8X6Q2XdVG6E/aQel71dc45/HHMm5/qZeOhDeIOEsxAFLgEAuHCJqAPTvsibFXCjul0CuNThkvOGvNRejzeRrkkp4239Qk4ULemeuv6j0v5Iu1Np/7kebC1tae3oqSxWNxOa4kUKtF58iXpOQbGinzzeiVC7bSEy0iKEHylTztZXlCag2weYk8b7pECPHk1Brj2bmuCl/SvXDpB7MtD6Md5PpiJRquxDuwUphowA9O4x+HAzC+h5p+krLebBMu0wqtmIO1GdSqhnnNZYvrvAZYWujEAnBptrUAYvgSZ0x519vaBkW/AjZ0tt5LLoq1vAsAI5u789s7aTmsg+gzqUmcrv4806un51tYrviSZ6/LX7OrnpdyL8xVhniUl1REKWYpMU3myOpKS5vTZWvQzl2zlZbSMqoEJAZsNrIInGmh4FqN5071cp83KVKdmfmZ8IbSm/gRLct8iUy4WyIQNQFUd/QM0tzofcVZDxQRnLUYjg8Yju/QG8Y4aBCOONEArQ2c66GIcARD84QX9AiCBLNmWDBPcR3zPe6ynsc9HX57yi8QgBzyUMnMKLB/KRjfLSGegaUC/xn9OqvgLiK8K++kuCbOEyXOr4EqT7nQilI+d8NUumQqRjtbiTwFZtlzp+wGWDwJ7R7l6TKC5tNOSwTE9XO/lVDYkm8xx1LZ6i5ahbVb0hMqyE9IC2tbb+wKPKMh5H3+VMLixeuoxhmupifO3S+1HvGW/Xzt3Jwbw1Pm/Jlg3ayaRr1NNML7WXp8A+gedNuDwWA74NADf/s3Ct//ZPDu/U5wMBW0kzXAGsTGB66W4NVMKmoym3AHAEJnkGilKzoAAF6wjzbgA1VbK375h9EHHh6OGIYBD4/3OJ5OuHl/j2E44fF0xHT/DuP9Ox/L6YTjT7fA487TaA6TfQHGDeBOYDtgGuUuG0e522zga0GsIFSvPINJib95sA92a8XSIfj7B/sYBl4Y4e96In9FEsOxkqsS/i7MFoCCmQCCyph4mo9nyl+XrADSXiChxdLEGIPDYY/D/oBd18N0JlpyRCU5TtiTcw7kAg7kYiwr5e97Clr3iRSEIwVLBAsC9Ro71cN1O4ynPVgbTEpj6hVwp6G1t/zwKTDa+BZQxHj98oi9HkTA4CyG8YTJWhzHR0zjhN8/HjFNFsMg6z7ZJBRRSpjKxnQwvcG+P6DvDt4SpMdu18s7Y6C18nGo0kyLiyUROIj3g1HWzIlGdrAYSYLc8tykQOOR/Zh4oeWA669FohlMLIUQof3Ck0H4kl0LfpflXawYZNl32qJrfZ7XEDWh8zGDYv85/pbvKQxAsKgVGoYCEzfyA7Ig1L4nwc2XTJiCIwWnCD0AxQQDEQw6f86Ej80AS8SGu53Gq5sevelhVAfCgAj/Mzw5NhhQ6Ejvk/8ljMdpGvFoO7xxGj9YhfcgvGfGiQEFJ3SNIigQHMRFXBRENKf2AoSiEEhwVYyrtc72UnhXK655XH5WPzjFZKj4QNz4FgCUyxauxqbDbpYq064ohBD5X+hvsJTw7tCQwdb4LC8TWgpWR3jelPAW8mLl1IpSCloBL2FxqxxekMaN0dibDp3WCCAxzoyvSgUlZmQ04DOia8v6eR+InlqMZRPgR6a0/dypQarU48ztleQIXNgPf/yujfn2NIuIC0pcCuSf1trWIs+z6eaaV9m7K+tcWspFQfBqJY3aViqoyVQHhYF6jKzgmDBMCm+PPYbjCeZ0FP+c/iLIL2NS3r+kc6JlMWvzzCCuXJ+LgMlSn4pTGU/ZvHghdX5iytqMXxe0vBNqgxnRVDCS6ot1qd0tA1iZ1hKZa0C+VoEa6Vlrup6Ga9KMk/fE+lbSrOpqAARssIBZq721b2tCYb51qH72CaVtJ6k09S5LL52V9VSeqKW3F6YlXk8rMcA5o3xGtNWI6TWNr6dmrQHsISP+ikKiDSXBMUeMwwkE8UPs3ASAo8YkY4JTo5AiHOJDeOS7OhdgwdueE2WOrh5yGqtAUJIrqNw9U8YeSscuaEElh65+OnKiQp7XrJW84WXGIxcll3Itl37utHym5n14xvvwTHpuoqHpXnAJt1vRbmqlpbV+1hEsteGfz3zPxrQo2k45zl0a2REpS54pRsgE55tLbcy30GBMiTExm6Maz7qwydkdNSu/7A5kaV8nV45LeoLrOP36lq37eeUcX4NcbBXKXVl9UcFSm0sV54o5WDoHCc/e7xx+9bXF/aPC2/dyjwhDlwC2gBbmEGuxltBagYm9v2yVhNU144C8/3cfg0EpA+cYSiv0zqHvDKa9xc3hgHEccXp5wjgOGMYR4/GE4TRgGI6w4wlv/kQY3ms4O4h1+yiazTwasN3h3WkPO2nsjh1gAZ7eQqwXRYjQabGI0J2OVhUh4qgjcXFEnqkmDG2vGZ0x8EgJ19+xAwUeXzZmxQpzFyIMmynoxKC8ZCQAt+pgnIMxBqYz6HYHmN0eZAygtT8DnNwKxdVz4kbKN0emA5QCU4fJKQyjkfvYMcgA6tahMw4venFVdLKAY4XJaexPBruRoBSgFUB3FurgAEyCvTknMSSsMP+tswA7vH3zHvc0YhxHOHYSUJodxlFcdDkn4+16scLZh5gjSsFoA206GK1l3HoHo3sYIwKQEBsj7N9p8vFEPB7jbIj54LwrZit9ZVfz7ItFyuFXfiqisCbi5I0jU6X5cdx20HNc6+I0Uzxs0PcNS4X5HdGsPPHGvdeDcM+lf2V+CgUaKvH/Zsqu8QAvJM6KcHWdZ0gze4ETy54nUSlF1xvsdj36XgR0PkBKrDjyDKq+sH/nDQF8jBLCxAqDIwwOOLoTBpK9K2VqWtVXWgDzFcJ867K28tXk0rk9xVWBWVme1bF513H9M8eT53CukHhenLj4aLJ35tpYzX5e1W6okCCCT1Kwxx24u4W56aC19n/K32tpNmo+Ty30nKfL8JSt1g9b2qmn6mxNZxSDctdWJfybr+DMOmE5a7PcajfXq/gg6XOMiL/WFFRKw/c6RYBAYDJ4wEtYAhyPeBwZPzzucHwY0J0eYK2F9ZL84K8RAJTW0KbHNBzB7AqWTOvr+bThiFxcX6MQtb4vIFQe29gmkFjvf24dkbSkpY1ZqRn8WXCTQQ02w8J6X058PpGNwkBk5m3R/MyyPAczPUcL19Kydv+FAPsSaUqWd3uxxoV1QZOfRFrieRawiotLOyGc9UDDBZ/qumwuKibEJUXXq/OdAaIwjoGoCZUzAD2zLHchMMf3FvbwFcczuJKKU0vhH99WIKZYiGrrLKZxwDgYDKejJ3gkMKSz1muAAo4cpm6EInFxIC4aypgmre6GM1q7fIjvCViHHfldc25C6vcE0YIF4naLRFrQXmHAa3lVMhVJ8ZqlogsfQvPm+VNNyT1varkt+2Wny6DEL2EHfPj0887CnPC9TqPrU0+LoO8jU51PPfOfHj4Tbi7p1M2BcXsz4Y/fa7x5T2BWop3s3ecwM5RyUM5rpjsF1gqAgVIOPuKsr5lmrYhfJ8A7Q5oluYZE2O/YwVqHkyWcJsLo40kMp0fYacBwfICdBhzv32McBxwfbnE6WRx/OMA+KnQ/aJhpgpkUwAOstRD3UsIwkmDUECEFsbdyALwNPUQQIcGkrf8M+Ipy4qJIucoPuv+qSBTXKHf0wxIzHH4elAKUMtCkobveC3CUBEPtepjdDrrvYwyKoGHL5MDRWpGhtGiMK0/vysA0HA6wTuPdsYNzXqFiT8CO8PrW4W++eARILEaYxAUXVHC9ZAFIzIppGjEOI6ZxwjANmKzFyQ6wdsLxdIK1Ft8PY3Rz45zEZkhr7+NWKI2+76C1Qd/vYLRG1/cwxqDvemhtxP1UFitARiiMaBuCS1sL52NrsLd8KNwnZ8hYkl3Lw/NGdoGZnTNSL4PxM8uHc/mRt7UhtRQKqcTIZgFkq3dlU4RZXDAPEkKAai+KEPgXcMmA0xKSQMH/ELSb4nLkYy3agT9PEDdpUHJi4n4O95mT2AOKGLveYL/fYb/fo+93wPC24HvngdjTUII7JvlHhIuEyQEnp3B0hMeJcbQnDPQY3U5l3az6zpduizMpnecZPdiiDeNgzlRX/M56z2tug85XGYSAM9hXPOJGyVlFqdDseUrE8yE9S6pZaGE/Q/az1hqaNdzxJYhfonu5Q9d1mSDC21BxoDpX+GOf3N3/nCmDD+ASD11hYDQFEiXAuK43vv1C2PwBJ/9JgohzdP31psYfOJ3p19rrTbEhcgbZmXTt2p5T4OH4b+YMhat82YNgqlZephqT3mGEhhsJ1jGsBZwjOJdMCqOZYKVt5qwF8yAIaOxNYyzZv7FtwLvhSL/LnLXBecrC1D6s7ZZz4FdMXt1so4/zRVgCpQmIbt0cZb5ZKY+ktErMU51xnrPeT+3tTQvfar2Hjee+2C5Lu2Nhnj2DdOZ//wOAnEXpM7aNtMRZ0226fu2WSMh8XGvzVT2pz8NKpz/0RZ8b96ZnWQqTEhEbSvNUdC7LtHpOlx+teBcvqp137nlShD5e0xAIREuO8PqcmYB3MV2097P54xxRbbeRtHA5+XRmgJ2FnUZM0wnjcATgoBXgtJHvBOw6goHXvCMG84SAPCdj9WSJULsvKjtC+cfS69jr8KxNZNa7kOsrLCH6zGByIFZgciJD8Vqd0X3AjPJSMrHhRU7MExXEb1K8y889IX/ycbGpFqzb3oM1mLlW1xb4fbEQ5zz35MlVZTme8PbnTEtztPr2GaDhnLm1DpWfEwJ74q8icEvriOuoui1brq6NqvPe7m/rTF1Pz7SLP4GSPdcYL+DtGxNvamKNmbEEdy7sk7PA6R1AGkDysS8KXoybvcN3X094eNR4ex9bAdj5oNAsdBErYco7wCkF1gxyKO5Cgg9E66tYOpOBwRkCBzsSN0VEhE4BVu/gegO760SBYLoT94ovhRk+DCeMk8XuiwmnI2P8cQTZCT0mEA+w0+jn1nocTmIJsJ1A3v+8AqCVHChmBj9q4Gjg3ATnHE58g9F1UNqISx+lwTF/ORZpREVsTJPFC3OE6hz0zQjVGXRaBA2kNAgEUhrGGHSmh+o6qG4XZAN+3rzbYN8WA7CeCR/EJ6QIBA0iEUDoB4L1OiLUMeiFw75zOHkrj8k68cMP2XticCGxsMZxxDhOGE4DJjthmpzEWwgBsp0Fg6GMgUawipEg4EHTPTD0FCloI+69jDFQSjSLxf2JFq14kBd6OY++1C6WRDiFIIBANu/5BluC+0sgsYBrXL6+4J7dLITg9XO+lBrU/jpAaVw6S1ZzS2BZcGfPYmTy9Fi4e0gEDl4okcj6dbu3iDtSZk9BHgZEa2IFxQS2E9w0ggjQRmF/2OPm5hZGaah8CAX+2sI6w70IjNTjRDsMtIejDhYkLtwCBCLnrSkWAoRvwWrXlre4tKtLlbNnXDxs04g5jVV3INIAyL5zdkRanczmL2+/ou3K9qt+Z2dwMVXDZ/B5a5rFutYKXoBveJxJ4vQQjNLolMbB9djvenRdh85o3BhGr5ynzRLTnfP5bqSflaW8uh+fUG/BtE2woV1/qyGexeSMe5PqnOf6kn/NCGdGEk5gXZnkGr7/ZkHEJXVv68j1hOjF6QmCB6BB+J5hhiyljyHNqzUTym9lvhKWcwXXCawMJv0KkyO40wRrHaaJMFmCdQrR9M8jykGPNmrx2glkpwzBafSodYcXzEcANNPpT+1UKTDIinxrgokZcxMVYMB63kZqgJFYbaqixnCWiL8yXzEPxTCWN+N5wm8OsGZtrb5ptDADnFs2f43lIu2dhfv+6eCi0eYzp9l+yADHjJjMcy5tpKt6sCWVjNiZcCrmeq6UwdEcSQsIfOLOFq2mLiaUvXpRMXzK81SWb6zFwqVPvHz9Xjc37CkHxjzoeJkvatA05un6tHDeii1YBYCPKv0MwIGthR0HjJowdAbMFpoApzXEFQVh1ykYgtf0YwgjI8GzsMzMOe6Qr33em7SCtefzeC/na0pb4F/WZHNPJKJAhBAKUDaLdZcRDYGDEhBsZAEN46hyAcTyvcjIBFQ/U1rCfc5rQlRn80z9i3f5pk5eOT9VuauJOAAXQ8VPSklnrS/rDIOnjuLnnIUlXApAIrzi70vxhPZ+WFPw2L6DtvXjKVsslb2ukkUmIc0FzJsZirzkQsy/jk2c73NjuS9LbgKObyVWxO5VUZ4d43Bw+M3B4fd/At68E8YMglugsK88Ya9IGMNKKTBr727I312Fuyby+7LsediZlN07IC02EwT0kdtoIksuMc4BK3xrTN6K4tfjAGcdhvEkGvqnR7AVy0fnLNwkwYvZSuBsO40imOEp3ZM+qPH0J8D9oOGcBTuHn04HTOPOuz4CJlBGFzVWQfmREaC0w83tCd0Lh5vfOujOwHR7ibFhOhDEEkBrA6UNEOM6AcGyglIHRRgUZzGd9ZATPl7iCzdFxo5YFzhYN2EYJVbDNFpM3sJgshJfYhgGcY01DBgH/zmF+RGXSlHAoBT6vodSCrvdDlpp7Lo+ChpyQYTSPkC4ChYP6f4MMaqstSLg4BBTRKxRXBAOudIfeRB2hVgPi8exYnyeexmVtS9MH8JKMhcuU+O5kJjLyo3xa0MZqoZfM+yROCn6ePy6FDhQxBXlRXLrlGmotEYV/wsGPsKS8RYxJNa8bppgpwGKxGf/zeEgggit5Hj5s8fFWFptEliiPmCiHR7VS5xsB0sdLBgT5+7OVFVFdX+u0ra8wo52HQABAABJREFUcd9klTDKDZcu7upZjqtnGVeFEJy9zz7P3lsc/21mLV7U+2optShNXunnvD9lPUudK8u03HrOdkjatFBemGqMBKXe0Q6Hvkff9dh1BjfKwigFFeIJEc3o66cpLCzgX9fWGc/iFe83AcL83FVzXWjJtMpSA6G5FF8901aEWyvCiOuYIAA+u2Y6mxYJ8QvTxzYpCiAwsGaaeRZgFZOC1Xew1MGR8Y/Fh6a1wPBwxPHdIyY3Ig9eJBizBGVhTlYQ4eIt7p4VggzxQktMqdxdSMo9r6QWOqROpDKFNL7VjwbB89Tlm8914+JrdSZO2urNffb1emppX5zZ55uOQWlcvty9DR1fBHJrA19g8hWvt5/nlpBry7zPAgGdayPLGeNIbFnbJ5s6VL1cGNsT7pu6UwUu2G4ugwSVlCQwrs9duYpqU+q6/gpBXkrCS1hNS8WXaDchUtoVF0JiT2i2G1tAMDelss56nkobuaqfHs5bO8FZDTeNcATYSUHB4LDX2GkCWHmXCuEcOJG/FF0NDKpMQ5rC90xAlr1bTbVQIioPLCGo5aiFMhVmhQLAXuNTMnMKSI1A1PtaiDxyHRA2yZ/MjtNnPaR5Cnv8SqTyejz+OQ73X1l60gX8Of2MqblqVMHCM6jE5ekph/OXkNrje5L8rTZd+ciptGj2yVrg+A5QBjD7SOgExuOLW8Zv/8bh3YPCu/uiIn+/hICyLFqkzkYt+CCIUIrEuI6EwQMSbVMAc6FLc3rC3UUIbmUkcKyU1V6frAOBWaNXBuwcxh7CwN7tRHt/8gxtZ8WqwPlYT57pTT62AAKuwg7TncX0qxTs+OZIOE7JBY0KhGHEbRJtJuhA0PwGjAZe7QGzJ+xeKZDWUN4SQKkUIDkJuzxzN1gIeEYX+2Cv1lkJnuvkFndgb6XAnok/gdlishLEOXxaO3mLkhA4OsyLBBJndrCTwzSxxHZQBrudxm4HKG2giLxFg8R3UEqhMzpaOpBS0GQgLpnCeMoldjZZY3IWgyPG3uLsWVQAYU+ieyyM/XmKuFKY+tRYS0i4xVoB4KgRvzU9+WRH+BCYDfMac5cnuRBirVMJDW/h6OmZUuSDQp+rdD0V68Ds0co2b4B8EGgd40MAmsRCCM6BrcM4HjGejlBGo+sMbvZ3uD3cQvMj1CTnNOAvS64JCQrBFjqcK+fE9RxYgdT32O/eYjcdMTGJO9aIFzejICykmgCZM8DLfi1oZ5/lm4Rxt15li14w+X3+RTpMNesMcIciDFroT/xbTgQg6azNiLXyM9TXyps6t9BSElSWRdnTgKrKX1IzShEUgIObcFAKe6XQawNjdIRxxYpySWnOvhZjOp8+Jde3a5w1rnIszsHqsFsvP9T4Ey1aqnRyleey9CyCiGUNlO0sq7MI6jNqkF1rAXFNVzYr+yzM0bkDtYwU8OzfpboCIyV8OiKM+hasOoA14H1WOmbYiTAMJ5zGQS4aIkRTvHhRzVljzDyDZ/KyTeEFppfwoerjOs9fttZ6KshJaRLIVRUBub/8KOVar/Xz5b7Oci8SxeFS/RDaIqmRa15tPwytnLz45kwlBZKxUH6W95KetRK3s26BJ/58LWVtoX5F1RUD9fJ525C30oYhP96lHVfzdLfsTEJatQLhzYnOWY3pXIYOcSA0POGZdkHZi3A3JXlOfearzpVfni21oJyY0pIIT3kmgop7BkBGTF6HZF3KJp3lz5hAYQ0FN3fePdMEa0coYjirweRwo3r0WpDziNOS59WEM7lAC+bbNa1huZZBWWwR+6Dyy6J1Qcbor/1iBiEQwYEj6ybsNEH0092Wu89Q/p2fKCERMVuFmsMwuznTy3Qa1tc/nNurcaZNB/kc0NvY9kbLiYvqvK4LT8QxV+6hjelaV6bnNMqf5Nv16j10QZvn2ljUOL0s1eUSNFvALItXGXTeBEyfk16pbsUFDbvnNLJZUp1I8O8MJrPYl3nNW/c9n0GynzL8c2Xb+BkDPIGGkwghukO8GENspdsbxt2tA/4IvL+f1ymWAwDYAY5AjiJjPTDqiRSgAVIkLngUARzumsyhV2NPhruL4BC1rQOzyJePw/HMTIYRRjxLHArLPZhJ+PnMgLPpXvNMb1nX3KpemG7uW3hf9wEB8PhMtYfn8y/w1OSTX93neX2AMD5dZgkQuwfBUUDO41EyL5YtnAOsd9Vk2dO4IYaCe4Rji8FbgpzGQQQPk/+0k9QX8BsvbAEznFVgJ9YMSknshhjTQUusB6U0Oh/TQfyl+7ghgMcf4i6JAgUJKJ0EHi4KQGyM9ZBwEFGkiHNMOR0MqMw6J+HO1U2cWRKE/dRKxR1z5X1zEY7qxzKzRqBAa2ERVhTwZqbh0kp8dkjJenvu6m97ovLrxjqUIui8qBKLG55GwI6YhgHjeMK+v0PX9Tjsb3Cz38O4I8iflzCGhP/m6xnG5i18/Z9jBXYEZoJSb7Hr/xk9n/BoCZoF47WUWx1lg2tagNcEZbWnaj7c5VOFRmfKtpa61CzXviPb9SZrkVzB7GKiLHxEmiOfo0Q7EucPeHZOLmBMlj9igJMM3w10GAV37fJdK4UDGHcE7JVBpzWMNt66KxFucwwj4BAtqvkc3bFtWBcnnuPR5yw7y/fpO1ffZihmnJiM4qvGxc19mGpLxhTtPq1ZrFadrOpu9SVYSFyfPltE/MWnSwnkgL05L91PF8kwMf78ALwfDVrXS6qh1N5d7wGXL8NByRDrmkU3Z1hW9TXR2hLoR/S90AaRvogSwmUQjQOQbj3fXEkOrNYut7UXHwoSL7X4NJ+/ADbd580yW4e7mueSvtMKgD5fNBdI1AC9QKa4PDutfn6QVaYUB0A+8rPRyh++cLkUS9ORXbQtFGMhc9l+BhOiuwKggFP5bG7bItmFvzHn86UMWcyQgDgaXoAFOS2efYlM6AbbrZyV5Sq3jtEbc4swgq1nAhDuOsK+VyB4IsdLHwL+GgQCBQ8EnlCOBF3oCcX8eS/rlYpCitm4rz0pInwnVpDAkX48cPFcRFLAExlEGswE1krWIWy+ehMWm99PSJ5nI879OX1On9NT0hkkokmsnb+5PvXkoWr8HonXkGFGQOf4CFVl/0pTmJYwCXYEHd+AdQ/s7hCYd+Feev3SoescfnpLePt+jlclRjZAZOGcMGoUKYCEyUwAlGfiKO0jQejkuknu0OS4MHaTRLmsfJPTb+lulg9CcZNyeMJBlgGxCgSCBQhAXp7PyK++eJuHu957bHFBEOHCPRrKeUt6b0HpfNRb560YEk2aWy1IOY5WAIlBzz4eg3PJcsNxEFbYmA8AJhdiPoiAwVq57110ZUQAK2jVQxPQGT9uJCdJ0c0RKQBi5SDrpb2muqyX8lYbMb9ff+vHE/C+ZN0QxuvjO7CLOG+0ggAXcw2/PIs8x+zlnOJoaMYToi/yD6EQt1ijP2tLbkHC78g/JyRXSBekiGFulujOmXJEJHvWd6SYJyLfLyrm0r/Kj5KMyQ+ipn9K/a0MPnvcmVjaGYcj7PCIaRrBPOHLl0e8fq3w6sUBu34PpU6ipZ/tkTo4bQ7rMygAxwqOFSbHGKcJ76cHvHUPYDgYAqyvkzmc9aKni/OZ6KGtaSVz2DcxZwBwGeBmLBwQTvnSgSzL1g2hRXXJjLnQblb+UkxiGx3b6t+lKcCdvN5GbyLRlnoXfmqtoKBhH27hzC26lz12mnBnHA7aAnEvISpyxRhLf2FpOeBzC/8s4YUv1KhzaapqurhuM/XpuYJPJ7jse3+FJPYqQcR5C4itz1cbubzMQtsXW0CcSQlon8vYenTZAj3nhb+mUcv5DceIGhgMxOeTY7wZgAergMydSA3+mEN9iE/boKzBNGpov6X7OgHwRXDL7XVpXRBSUUWKMSAMWb74onj6WnHz62q+2dP2hbgtXVeqPW5a+bUwgouazwig1X6s1XANXEpfuX5Y3zF5CmeBqnazy6bNCKjryVb5wu4npHIZ2StI1VU/ROVE0MKr1f4EyoHL80zVZ1rronBWRzUmLuuaoY0L93vSDVvez9drO9U1NRJXOzj8LsaT5iLt+6wIkLRhigZbuasOrbxKr8v5EdzRRcsIdgo3ncKhVyCvuadJL/QjEPA18pTvQj9qogznDRMQmC/xZ/XlulTsJXKeYGTACyGYMlhbbDvnNfLYU8LcGEvdxWBxQe1t93OlKzf60tSvMkOemLZWUcC/J3Zh69Rca+VwSVpqY4nQuMRH/7n+n9WsShlX61lNKwTZ09Pahl0b+4c7rOfm/OlbKmkuFrC8aJuK/HlaH/mWzi0zbVZrXtq3z3HGNuyt1EyDiHcTMEygDuBe4H6OPt0eGLc3DsOgoyACfhUiz8f/4AxXdORAIFiSu0U5JxrQXttes3wGFy3BdZMIDXItxZxRFOY/fKqC5xSvPs7db/j7D2n3uGhJmBjx8pZ9nck3ft4vANCeQcLK051e0BB5fl6RzVp5b50FOBMueJzDulEsBDgx6KOFAFtY/529MCIIKgRn4Si8ADvxcc8MO1lv/S/jIVJiPuIFB4q0uB7xbpa0j9cgcR8UdIjl4K1XRBghAgj2TOrQNjytzDF4dRhHEH4kt1YhzoPgha5YmbjEkTjOaP1sI26zaMhwvAaJLnujfZfmMORicJ33uaiT47hqBlounABWrBE2dmbmrmm1WInLzpoMhYs6Ah5LFVnjf0RJX4br5qRWoP/CXIVikWOhQAwQM6w9YRgeRVgHh1cvHH71tcLtYY/e9KCwFxEgUd5ZL0TNhhDyMUuAbcsE6xiTtRjsEY9ukJNPErNCEzD5gnOq6glIF+V95fJdleJM1oz18HtxX9RrV9KXMsnpd7GO1aQFOBhp90a7BLSNROoMAaDmfanL1PTfkxJXnwnSo8YVghCcJGasIgV3PID4Dp3q0GmFg2bslEtTF+BZJoRI9w/HNraMhtYynsMRrsAtz+HXMxdw1XfOBHRADUtLKDjHlfjskKSNZf73soDk8tQURlyQPltEfE4AZNtHdyeAR+4sLADrGI4nz2jxYb3IX2KcmYhGxM9FzY1tjRcsp+y7vyDrYNPURlhCWmKgzgKDFhicf1bgYBdels9AIK6n7cBiyQnQh2eLpB7Mf3281s+l5/AhOMMbKhy2zsw1s7G4ac6sV4WEXd17Wh95Qju40Ng5V2erjtav4lHQ4Im4doXQVxc1gUCaIL5zlSe0hXid7ITo69Qj+qG2XOMu7+p8yreN9zmEEYt1I0xPEkKE57kQoi6zmtp0Uvl+bTw1EkyJ6AOh0OYKzh0KLSL/m0gsBRSUR1aTRqBSQvDHOpGEDwhNQhguhPp5Nr4ooELqXBzk0vConKeIAAffuS7SLQSKzIQQBSlqkCqAWQEqjT8P/keB0CwmnrJaPh34CGC+0T8CU/2Xm9aoyM/pLy499Sg8aas8tfGaxP3Ye/e58NznhEfn74mUx98LQnEXIDJZyZXX7tIVHNG6+nn4hz09w2IxKVrxBKfk1pmsLe7RaBFBOR7kYiPhrg7vpBl5IMxxgJ3yV3fYFxZAsEbwY2QkRbUw8syKgSNzyQFsU7mKcRjcCVk7ydgmC0bS/LfOSr7gez0wdxSSEkT48++DMALBksGlyQzMH0B76wyGV5MQ3IUZ3PvFi66VdDZffl7JCx4KetXjMqQAcggRhMkBDlb6FgJHu8R8C0qAYTz5eB27cu4C3pOTr2nHLKZzzPnn1JD9YKkGU/53LYyINE6t2NNKGbNzLUu7M0UuCCwomakxd8ShfV8VAQ4+XoeP+eKEpgkCr7TuiTryO3peuSKJN6INyI5w04Tj/Ts8PryDA2D6A16+/gpffvUFbs2E3r0Hs83OQz2u/GTLc7GEACwTJgcMzuHBAu8s4cTABIYFRcXRpMATcOQaIi5AxZh1ndDiLOviFRbw+bwUZ9+b5TK6JaMd1wilcpXyD+d1khwCHbSkCBitZYq+N5trtO7S1/xxpMXmPV2uq/W96muRK7jlcyAlFntaS5DqfWew7zr0WqPTOgprpWA6K7WATRrxFkRc3jPzztDSm5J/ssD72DLFl0DG2r1v+r1lQVs9vB4/28qreFYLiSvKPLMgIhHdW9NTaduzxHsTzp0rs61T29btI1/uS5htniVeLcuZOMSFALxZqPMILYsgIAD4iAwmLQ/xIxrGXY2/RiSqZ5ztIbnQQjBX/z1D/GupIHukJE/5GJcPWoaMZHA6Zw7VpqBL1VxPGz0vMbgUlHU5SsFK12dY1UKec1B+ScM+YhIracN+3po+BMNvS40BF10rvziSZ2UC0mKH45XOy3kkR6OnTdAzr2R5vRaQUohjHAqaFir9Oa8l5hzBVmVCbVTjYk9afzmnazzap97nM9wZT1/+gt5Y6V/7lR8zqBTyZkyNBFm8oJo520tzJFBRItzLINUZQ8UT/O3YEMnVRNjO4Xet1LZ97tLNKPcOJJh4QPQ5Ic2yPs6TJsojzRrRZYVKdabpyrRfOBFBQcCUt97ao5vh1tORqgyVq07zlVX/HDKMpflqalxueFfU0az6ZxjkB0ofw5IjpqcCu4i7XYoHLIPCs750Qw3nurpy1V07w1HI+qzpMvzzWgXDNfxznvdcJ7ZWtIUSr76U/KRG5oINVrQle0ZiAjGz+P0P9yTJ3cetbnkypEalozIvs9xHgZlJBDiWuzTch7nwPqNdGGHN2AvzIR1BWBOCm+Rec97ve1DRVTQBcJ6kCwxzZO53ExOdHaIbIXYOxBPA1lswhJ4kH+ZBEDGOIyTIs42KbczAxNMMBgchQJqf+n4WRn9AVXI8IfwWHEKV2uk5fsEExRK/QWmdcBAEBRfysTrCOorAI6wDkwUwpfl3Lrl7Csp6QVAzY15K4OzAtEz7hNM+8j0Ja7KJ9ZJtuCbTjmj5qDTR/Y/D25CRcvtZwKEiQh7FET5f2fVzft5TxjN9al45C4Uinof4T9BUTsKtQN8QXNTMShZE6dAhgzG+IwGuKAWjFOxo4aYB4+kBw+kBut9Ddx0ONy9we/cSPVnoEKg9VlPNQ9jTfgD5FhRhBGOyDoMlHC0wOC+upHoWqj0XJ4wX9uqGeyir4/wO5PI7Z8+aYLxV47Z9HlD61AaXcD57vlR96srCPBR5ueq2h6155pkQInyuAorGsxyGUvmsyqUUQSuC1gqdMei0gdHKu6ZL91PszUwIEX5nI2R42nN9TmI/WsKJLYLJlbTk4uhc3tLd8Jzhv4RjliC93A/pbj/ba6yvdcpXCCMioZq1fEaq8RSa4S/aIiKs/8e5Llvp52v5acmhH3/CSAZH3Hqkc0KvLL45DPhheMRbbw5rnfgGd9MEa61otljR+gDKq6JiaawAf88IqrIVB2ItZa/X3IiV/Jaa4ZKQ+Dqtg7OF9lqE5zPwi5bSJWGR0xuez0OrnmYV4ZJf6dVS07T28kzZM022q8oru14s8Vynmxa+fyzokd058UnaBgtnsyVRaeGyjTqIgsYdx7fCdE4B+gLRSiBoUjiYEa96ixeHHb764nXURh+GAeMw4n9/v8e7SUOdHkBukjoCgUKEpEK2xAHasgsyBIyXTSOXwVONgKy0RBcwhnJ4tzKORXQnx89zLb3iL5U/kYYljb3ucfBaLkqp6IYA8FqBSME2AzKmlGgYhvUuhQ0UEdWouRn3YmIEhM+k2Zm9L5gw50/W2lUSglOHfRjiioZAnBGOKIMQnLpuM/qBjsIU8iGts/uFEZkhaNTyOX1On9Onlrae0F8SDfBxoM6nMCNb+tDCfM4mO4AefwCbA9C9KOG+UvjmK+DVS+D3fwLevPXtVBqUdTsEr+9KPmZEfOppmMCcXLrhSewQY8VTYH4HRre/860Tfr5z+bWPoIAWNVNje+E9BzlAsqrwl6Xz/wW3QsGCngIjPSqSWCkb88HjWEl8T8JtjRq3gXELPwcBT0iKAul5FBz4tSj4afV8k2e9ekFLpAUdI1pHMpKyncdlOU4OwGx9XpnIPNZFmIMiYHdTKsUJGeAyXxROOa5Qm4Q35tY5W1MQhK2ljyWAaDR8UXoOLd9ri+c4KQAwKVlPl/BbBpJFhCO4sCn9fl2b52hJTBIMXemdtOYmnB7eYHh4g+PDO0zHR3zztcLrr3p8/e0XuHv5Cka9g+IJjrUXMZT4fey7F5Y4AsgJPi9WEQw7OQyDw5tR4w9W4S2AIwOTEndMPpqaQA6FqLA/Y+ZQ3maavQ+2xy4gqzalqq4AA0rymZGARk5sLVSy0E6wPMgAb1nFIj+tfl5NfiPJVpy/j2S/CvRKeW8JfUe4YYtb1rjtehy6DjvToTc6g9cJnnH+O9CjDK9Mm/VhUZAQ4HSedX57X+1mtGon1Ncq02ojKmcX+UId59c+zcLlPL3tG56qT//LF48n8rnPj08fSBBRgrRWWuYPb0OGa4bLcrENjMZrJTnPZMrypPSEPrSPNUHBQbkJGhOgerAlMFsomnDTjXivRoCS9YP46hTXTIKIZqay0lD+ETVzqtfzw1Zt+pivoWEbM1COlK5NTzhYFItWrW9Ls72z0GDxmBrPGozNc4Bz9WX7baxxoyR3O0IQMeZFZvqitimnHEtpdSpaY73gTD/pFIc9lzf9lPoW6rmkj1t2ZKuP4Rk3n1bPNgySeOFUecFAsLZPmvBl/cyiWG6IcdCMV3vGr7+8xX/4j/8Wb++PeHw8ATxhGE74l39+xP2RoEaArMu0ilIPkpHH01eIt+yvXGupqU1RPp79zpnTS4CMNt1wSx2MeHFORMe+z2CvPLOKMCiF3gsYctcQMg5PTAXhQhALZJohQTiRLB8QNTUpW7tcGJH89yY3RxntluqeUTcLOztmq/ZzmAsiyCZVqawT5grC/UYEYm8lWODNCbFL3a7WKcIO9sjetnO1mJ6gkbKcngbZtloYtMr8bAyPLF3T/+vbui59iB61/NteWVPjW5k2t/AB9ve5u/Kp419em8tX7YMc7w/U5gzUXTTcawjubZ3Zyphcok7OdYHYAtMJRAbUCUdFhOsC229vCHcK+OkN401G4NTCiIBUBrxFLbAjipuNK/jkHzJpwVeiICEwxRwYDLbiNoidA5wDrEfMPKPdhVqjK6Zqdjgxj3IhBJjhyDMlObnrDb6kAe+aCaJ4AheaDIhQwimCBQR5i1itDBQhKjz4l1EznlO3RPCvhLLNcU1GiwYJhiIOTEmhpWAehsDZLp+HQA8D7PGDqNQR++MqoZFXp+FUx6LzEEoZK8VhRA5RthlmQogLjs6a4uu5+48QghPnT7Y3XKBhK2e16EcbvftgaVsMn4TrAihogdI3fMSOEdcw+jbKvhcNZA0FRR+lAViws5iGR5we38ONj3BuwM3NLb7+ao+7uxv0+z3U9A4qSAiIEQixoiVK8WuC0g+xivvcMmOaHB4t8M4CJ2JMxJiYYQnJkwa8MKIYwLmFIhRuYFtCuuJnmNv5WS5Q8s3pHJAPWeawtiieneviHWeF+LL+MbPQ1UsHuxJYzivwcGam6FbT6Es9CHAm3WkF5e7pwY4Je1LotYbRWiwiVFA8K7ozF0IUQ8nw0Pp+a/Vt6Q3x4pSUvVl5m4OcpnePtuCzNdfn+jLnw62lcwLXhTullXMRIQ5jCDDqPLC9BOf7i7aI+Jy2JwqXXoT7DsQOu/FHEGu8dz2cs7DuhKEzOO57uOEEjO9ECGEnOB8QjF0ClLlpadzjNeKUP86ujnojR+EChPnT2uccisc218A8pcurwGZy8+alolR+rqaKgFiIcTHj254TJmy+PLI2YtbzV3Tyu7mhbk436hL8WbxEio3RbiggRHlt8/JVgTPp2ej6ClncGloh5n/OvnxKaUka6H8H4jKILB2it30oIhjT44UZ8G9ed/ji1Vd4/eolXt29QK97nEbgp6PBy/2IF7cG/8OLB3xF9/jp3R9wPzzgx/2vMakDDpig2YFD9AK3vD99p8+MCR553HDL5rAhMuEz4pVrhKa0RCkRny3Ez/q2L1qv4XN4Efwqx3cBlvN84ghekOADM5ICxf+8oCFaOFDUCg3xPcq/pO0ZQWvwaEFh/BRjRBSDyr5E8k7N54uq+W8MpnoWEGPxCc7OB5F03k0hEcAE0jI/yU+3MEfq5W8u4Sd9+FsE4Cfb2c/pE00fiT/0i0qfT9EvLXFE7Lh1F8bk7zJ7Ah5/APpbkHkZakjKEIFpHuiNrJmqNu/tj2NekAR/Js9gnzE9q18UrSG8/jPrOA4G4JQPkGwlFgQ7cR8UBArk8R3nHKjGS5CYJkUvfB4NodeKYKTMqXVXcOZict4qI+okqLLecL2HOz26OoxESGgj59mFuIUlPVbHapg4WIpYz1/MmHsMBGsGl7lVYvJzGQUQgMomKrm1kn4F10sJDwsTmuZoPqvkZ3NOK4efBRNvNq01vVlmWMQhf2YA/rEUElqBqnM+eG7ZmjLO8fRE3Zd5Z8o+oYbVy2COcxGSGycJAq8A0hiOD3DDI96/+QGPb/+IvfkzXt0M+N1v/wO++90/4ObFC+jOgMcJzo0Q9p+KcCjfcWINESbAw5AA/xzDWWC0Dj+5f8F79Wcc+d67Z3JwkGDWTLkQIozD5QNZTxE8UmNT5vkyJmmAA1l2BiVFoS0prtP1+y5p/Nd1zj+Z0fBa3Wh7kbGy8KLqQt2/S5UsRFHKx/cTf4CgjJYDKWitoJSBfXgBq1+if32Lvu/Rmw6d0YjWaIG24mw/sLRSzn/gBc6F4KFX+ZiWEjOQefO7OC2wMCqark0fzfu1PPdz91TL9f6sqdX/bJyXKZ5cIojItUrqV5e1+Sx1hPI57lH++IDp0ln+udMSR7+VMiBOYBg3wLEGWIPZitWDIrA2YDohaNJIcOvEwnI1ss4VnFlgbMmVV6xuNoyAtC+jJvW5ZVROiijfLJyNNeUvAGDZueyXv7Rne6FmkmVoY4bgXJOo7lN9e63Wu8QFK+uus7c0hhZT0HTaesFVVcfRVczFlD3vRI6AN5C1DV1gtBCAlbRYZ70OW2EQx462rpprocxTodMau/aqskmC2Kw5lmEGB4Y1AZ0ivNgZ/O5vvsbty9fY9TfoOo3TZDFYxuOocNMTHBPuOgI6YOosJvUARw5MDMUOCg6OtJxsr9xO1a67dJCrgcebkzdvj8hDp7B/i8mjTEhRVl4SPvn7BXdROagtEPSqr5EA5wbmNa8gwYyKEZJpygSiqbBoyEpEBr1/l8BzZu0QhBCUqgclQm8mNC5gfP2tflDD9XRP5WMNt5rMpUtana2KszGV2nGtTRLOfxL6lpjWcpnU5MIePneIl7b+wjlda6Ku6nornRrOb69rjhVcA8XWyzzxCn9Cy8/YznPir2cm5KqWfkb8evVIXJF/ldjfOs78+lxp+ymz9lzjXqw/jOFJS/ucI26nxf41yJUaSsmHh/PsoOwJbHtEThM7wQ2VglKAMYCdqNIgb9RZNBgE3pKim7/qzkt3IsV8kdXoXwY9aAvrxy24iAMApUBOnivvbkk8anKJM3PCYdt7Itx75QRGBlRmVVBoyjpXPvdVOBZ3iTndJRYVrupAULVKrj9yZ1JApkUauPZeKMIhgHa0WPAzFbOHeBeZCg1DhBGeHiZQPjQkvC0JPFoMqoJ/OaNN07OEpDCKxzUD9IJUdKfAE9cra7knad8xLSqnfl+hpBWRuHp3lVKD64ANVd85wfC5EKL1Pf0iqtZsXvUM5y9SvgaVtUhyOSt/zICdJh8X4hHD6QEv+ke8uHV49fIOL168QmcMFIV962J7JY4aYqIBYC/moySEABOYFRwDzjEGPMDiJzh2mJyDJSW+/NnnreiTcnDLe2FOR4Yn2X5oFq/bknIR7tWCivB93uDyGVrMx5iP8dyFwvXThTIlLRKohpouo0be4ls2zlIYsXZWMsokEWxJ8QqEIKAIggnYHgoHGNXBaA2tJX5JDssLUPYRUnZVfcA6lzZm+XwZPson52sEwmWMqjq117jVhaZ84cIVSlfQ9nIfxyLi3OJfuzlyxIWur+YvKi2qXW5NchEpD7RD4FHnJAbE5Cbs3YBv+Afcn054N3WAtfLngkmquw7KeMDsULLcqcpU8nkXiBOePfE/MkSlSL7FwBgOiHAFqOMvFvBc1F0xrxKmsdBkPYbZHTobOaoHVS2U/6ielVjtnM/IZf7KPOPsdZUTyzViulSmylHdqZC9iLN7WrRQXPl2JgzI+5RdCAsjCqOe3TGb0kLGAikLWRtIw+L+rutd4FA0mqmHv1DThiEuI5Czp9x6QbNvBI9IswWrDvZwiy92Fv/TVwZ99xKD+hane8A9MkRpfsIwWkA5/Pgw4Ue2GO0dbL/Hly/u8UI57B//hNORwe4IawzevPgfYNUOdnIgZ9GPp0jMFqhjfYQ8IkD+XRxSjYHUyG0xVQH7Kvco/Li5rqf6UQpTyRM47UVP8KmNxvuX88/qLxDLASbXAl2FoJGlIdpSSpBRpcVqQSlhZkTcNVhEiB9RQrJuCIyV8BfqL0dUjlBsLgBEZNi/n8E96X/JqKl2KpVv0nL4cXmCQiwinCfkGEQ6IeYhIKlCnGkFJcEuKcSFyNw8VdKT4JZJ2s/vlXWCbZ62nuS1Ohdg4uw+Kr9/xr8+pzqt3V6/pHTp3m7xNZ5W49byW2Z5nemw3LXmhX5R2mRJWPamaP1n20O5Il5xbeb3iXzn7DumI+j+TwiuCNXNayjzAr/+FfD1l4x//GfgpzdZM/GL1FJjDKldJEWGeDdT0dUkqPd3C5X3bZhL4y0knJOnjpW04RnyznKyAIiBpL1rIpJ7MVcmyHqacKeCZ5ZhLzFgdrpj4+9oQYH4LLp9ChhQjqtUk8RZPdK+7wSHCGOpY7kdaCSVOH/GUWDE0Yojy+urpbR0xTzMmDPNjZytSut9pS0rHy5MR0Z7nTufJS241g7Hn+nsFwKj4p1/D7/nOFk7b005Xhux88byzrwJpNzLdZ8RTLDfC8maVq2AQ3/KPfoXdgTNOpF6FmhZIiViAOfASt5b1YMxgdQgljRuijEWQPAWBhSFh6KsJS7KaBrhphGPP/4ejz/+HseHe4yjwhff/T3+7h++xTd/8x1ev9rjwG+hTwOsYzA0SIlQzwenAFMmcPMa7gyIhQMAOAfWB5z0SxxPwGAJo1WYGBgZmMCZBUQ49xXdE7d4DjPRmGSFKCCcT7ukFnCsUokNl+saA9vki5bFWGm2W3xWGPCsu9VZjgpeibksAibOYmhkDeQ0Wfwd3MLWzxlU80CqmYhctTjl9TjDZFSmA37vAQCUAquQJ/Af5BCQImij0WuDG6dxpzRe7Drc9QZf7BV6HQTi+amoTN0Qqs3u22IMtVmDrNc2mWO15y5J84PdqDelOX3e9ufR6kkuhEifT8EX53fjYs7YMVrNm99j5Za/DN6H9DyCiC1iprNZaubAxonPL8WlZp5LDFZN8jmJT44cfrC0MLZ1u4GUB2iMgzx+GBlEDoqtAEB20LA4uHsMbgD4DlHwELBN3kKIpQwz5l+F2MzWtQb2G6a4rBEzSDBHECM0mPUFEZGvQP1swFT0L1VVX75t5HOdaKsnrVpvLvdAkqfMiYW8vkWtUkorWqOdpan65ft9Ns7a+opz1GZWGDU05FDnDGHO9tezHMsLK6mRlyVthICoLV1+LWRnlmdpndEElInNPDspjTqaFawKg1vwQIhpj8TAQdkJbDRUp3B7Y/Dl6xewfIO3J4CVV1jLCVVyGC2DHcFCAwSYbg+9u8Pd8B6dHXF0A5yzMIoBLYRsIAhAAVFOeGDORpiPe2n/LQyyxnsaljKFyXCFqaTH89k7pyUejutsdxTITfgURDZZg/GsbL7iseVcKyu8CQwJQvxeWDIEQhV5VskftGVyYUP6VrYbibrGTCxd963HbW23moAJV1vQJuME7MMgUJvtwwdmm/evPj2xiq2JZl/8GFJf12/gLRdmtikrwgALNW9BlxdxjmdIS21f0tJTe/UUa4Onx2NYr++avj3deiKdpA+MCV+XnltFLiReH2/AI58/bamzsaZ1X+rfM2L42r5fvw9at2Coc3MdQdFo876+AjAz4vwRO8Ce5J5SCnATAOCwB/Y7QqddobydFUWJGDTOsr/kN1mMZXdwVAyIdYV3SjQw2Qd89prt5C0AFQdhBcQigGxE+vL66p7HT0r4Rq2wnq9twkMyRnaNt7hMmIDSuoB8fkYSQDCnZ4m5l9N9Zf3l1HHWTn13JUSJYjVhj+UzkbdR1l/qfLXXdO6yo1FXLagAFs5x8QDtVGN/6XvE21fL++bP5lhLsg9aGHl+tzUD0yKcJUpnZfXMs8dfKCIyrf28lNL+RjnnNdjkhNFKAGsL0a5iBOZuEiRmhan8U0ga6exG8DRifLzH8eE92I7QinFz+xIvv/gVDvsdegPoaQTZQc42vOcJgm8/HzOBvIC13lFMGo52sMRwcLBMIZS9fFKy7eWl1Y/7PI2tPb+EGCsintN8YqvqqX6wkGK3KOHxnLVVd7tZJZcvuH7X6Gfj6BW7upBwZ/k5vOP0udSl1Y6H1a2hcytvViYn4HJ6JxMKyGOCVoBW4s2gNwq9ljgRnQI6zVjGeaoDV4wrg+1UCyKAWidwPV2KfeRw7gLCciW2yzIYWoGpT0LDufp1vjJa2tp5DbPr5nqq7nOMiM+pSIGxzJBLhQjQ5PCaHtAr4B4MTYAmBdJG3DLZKZkKSiX+Iqs2JlUwnoqPhTS7adazLGSLiMm5sqtHKV0UweSwBOU1Mde4LPP8+UVUFM0R2ZW+BNjNofWaWRQpjAzZXe4M+byL7fmP4qqjGviU2turKQBmV/4uLp7sWwvMBW2UufUIEKxP83Wv8Zj1xGeCEp9Bws/djpG4jyhwWXeNL1yEdLXflQKZur5tdTQrzbd6TaTwvKZApFkysPtb9HTCb91PuDlovHzF2N+8xFv1JZxlWD0B3hw++jQNlldwYLYgHzzY3fwKOHwDczjCTRPu//wDeDri2/GfoUcHZy1OtMefdr+GhYENhAMpaDuhGx5jZwW5kgBthZl9C49rzWN9UTfxPqq2bjAjRkJUG/toCTYUM58h1pyvEWeEewgW6ZHd6L/Zf7oMOc7Nw/OYDyn2g/gOVV5bK9IbgWha2HQBvxV4lllKZJ+zucromKLGrL04D8V7yjMWc1ZXl2uByneL6FLCI+RRw1SJphsp7edELESIwndC8se7nopjHhhaxQDPbbzWyLe+A4I2aawx7qHzCP8Kuv4Xn57V5dHn9Dl9TkX6dE7XAoNtU9GaRri8LnGpIegPEQmdtkzhICgKLd09hctEz7jNFRUUeQsJtnCO4RzBOQY5T1dkbpQSCMw5GUIvcfko9S3LHgQFpfUB4r2b8JM80HPFnMvqijy8oi1u/q7TJWyVxbyc92Tel1KQgGX6LJTifA42d6+Zmjsvn7CnpHXSd2MKDM9yfrcK7INlaYgnuegy6jmQFkr9qnQXAzLu/w+NCeObQFDE2GmJrnAkgiMFq0Q4ob22uWJRbFHaQHcGqjNgchjGB0xvfsT45ke8+el7vH//Hn/zHeNXv9rj3/67X+NX3/0ad8aiO/0A8ARmQJEBB3sLTpRnUOpJeLskETAAjsTd2ETApBiDisYUaR7zsoSCNpylkvyd1zNjNlTnvC7QmPeaN7HYj5XXV6fQ3bzfsY1KeTdBBJ+P8wo2NlQ/uyQtEVThM9FNxT7xSSkJRn3rLO404eXugJt+h77r0XUdlNYNAfvGngWB+Mr99bFx73MgaInWTe+WAWQQtoQA23P375elNTuZpZTgbWDSVSUXjvW1XX2SIOI5NLg2aXM0274g8zNv0g+hzfdB0+aLG1GiH1AAIkARoyOHngg9yUWkiLzvNwZPI5gBlyKxySXLmFk7LPFU6+dX7yxa+lGaLz85NZGX6uEigpNexG/1Kd+yZjUwaCCxFDhI2ZPFutaY29lClpYXc3Q2zXRxtc6apjz4X/a76tZsgnKYkZSASv/4hXIQbQS/lOpOuFDebrPAYtpyOeaXc507uclqVf40vGnW1kUwMsMea24lEIDIvKEcFhBgIUS0UoxeK3y5v8PdzS1uDjdAv8PgFJid9znKEMqbAVaIgojgDi4gY8qAQVAdoGmC3t2ASaGnEzpYaD7CMPAjSSBCcbekwEqDWbSU8n1Ldd+XNvNq4oWf6xRQBKXzGs7KC5vPucqQaw0G4jYgyMiEFQFZrtuMTPKApFY4QdweuZZXyitVeLTW503uI9L9E2uh+E/jrLQnpTlNNMc6KH/n284tRJp3PiU3F3lNwRVG2aUWkp9nqu+NfM5Q5Fu+GsI8PQ0/SWRNIlGLrmVdnzOefj6c8OfEyp6DEHpqHc9hAfEXmT6U1QPSnM/m+qwm8gfoS2jqg1S+gotcmLZXsZTzGWDMxZYRednWclZnLzwNX5SHauzEKkLpTLuzdcOvJxEKyx0d7qqr6PEMkNcMn/g9CktE0YCZoZQDx4Bbyo/Z4+AsxESuCCXFPZER8PkaLfIXT47Th3r9l/xx0wCg/lnXtXWa12h8yjZA2VbqUMl75GZf5nsow7My1PrcFl3dw2cLpy+Lp22F0bd2jlKNG+jPM+kS4UNoJwZR9+vFF9ST1VitxRpMWuAwZIyQcD44HSkQhMcCCr69vCscLvsbrKoI3te+tXBuwvh4j+H9G0zDA9gecXNzg6++eYWXr+5wc9jBkAU5C2TnUbTZXdHjElUlxGgRnJSjHAiOgJEdTpjgvDunwLIoySNGUXFz6pYI9OIANQqnOW0mbvxYoKPPPMhebQA4Z/vDJeib0WRr3Slpt3bfrk9zEjfA/mSBntRMK6rH00KGCR0bdNrAaAOjFYySmI+JVUDA4Jnt2CZEOHdqnxfDa9GR3DrY6auxM49Wy3VmxPQqbMlovc3L+7zYX6k80K67fn4NTvXZIuJzkuQv68CEcVpBMcOgg3IOzgFEFt/tJ9wrwjTuoGmAoQc8qPd4//4dBr7B2H0DnqxcYuygGpdIxXbJrsGShd0CLrzyax0cfVgEKG+jXWSu0b9a8yVnecYUyqsJyBiWM4UqGIuXO7fK59pchbrsHEkvHkSatl7Ned+iqWz2mxcYbUt3dmszVV2JDxnLAitBZOsCVb4Lt9ncl3/G9HsiQ3E95Wt1qefmNHuzwIWo15GgqjlRpOBI4dTv0WHEb/B7fLU/4N/86rdw5gUe6S4i4mIJMYrAwVkopcXFATuws0LUuwnBd7A2GooUAIPOENSXL+HcLYBXIDfB3P8T7uwJvxv/CZOb8Dg9YDK3eHz5K4yqxwk3IpBgwNgR3XSab5Ji/lZSa2twPT9LkK6sYvO2ajFJRNIg08kctRgZ7IMucubqIOUN5fJqksVB+PSMe8pcE1FJvCmFaBmQ541ChlhHPmDKBA/rKRCYhSAytN3QQE1NUP7YT1+WnwINyUjCrtR/FcZMCspbO8gQFIjEMkLiZqiykao/5fMKwZ9LND54krNHWd8yonDexbhHkqbPx+vr5/Q5/RJThjn9VaW/zDFXF08GB5OjEp/z9A6YHkGHL8Ddrb+D5q6KtqTEzApChEjGXX1d5MIIzuC6d54JwHlhhA5Ng5XgXsmSgkRI4jkzsR4QWDkwB8aWv1/9HUue+Sk4v/PM2g+wY/zhi8oGjclPigiXpiVmTf3lfBc/dFq0DvgZU4KLmSXE0mQskv8txjaa63xx/1aEMqEL851EgJKNTh7fVcxwpKBYgeGgvIWC8h4GSGlRDnMu4ZDaQJkOAOCGE+zwCPd4j4c//wGPf/4D9jcPePUF4+/+3X/C3/2n/4Tvvr7FXTfAeMviycd6UVp+SywYjvHYuOl/3ycGLDMsgAHAj+4ef3A/YaAjQD5mnMcZCw3sAhDlHPiaMYv574p5P/udfy50e159XqZi7PNC/mafFvIGwDYDwkt7hsXdcKS1qs84zjAH+RwyxLLC090cREctPspyWmBXld+98CrZQpR0ktEaRmvg+ApqfI27L1/jbr/Hl3vCoXPoSEMpEld7Jw31j69Bk8JMSLvWz3w7/hxwiuI/s+f8m5/AdwOALSC0vRpECXqUMOZ6bDHA0vTreW+W0sXz9el5BRGrAKDOujAhH5HgvjT94iwhLk25mqNnBCoSxoQigiZCrxiDJnTGYOccbnoFtgbDqOBOEyyf4JwF2cn7E+zK+6eNIWx4kp7z2VxPS9cIH1LZ5TzLmp5PG8cmMPVUGNREWrn9+9z8hWJU/Ub1HPmZyxDThS1UWlSUvkVrL1mL0xFx2Bqd9OWij8+FfPXYziYqPkprk1buGrkpEYLFsgvMwyIzLWWuk1+D6A80ILJcvfcr1hDWCCrD0Aq4M4wXuw4wBzB1sJQClUWfvgHpCgsUGcPJxJUDMucRY1YKpjdwVgnh7BRY7cFM0M4CIBzcCaMFrH0A2MJSB0caDuKOwBJFzUXiGLatOSXnpo1bSHNRQZye6ssF985q1goJz5Fc/z5ZQczrqlnkZZNrDa9PTKbEhmQFsTElqcJyU4v1yaIlAwZKeQuiJ0wGz/tLmaFyEMA0BByX4jWB+dPs9cJUb7WEWAK7RRtorXebwAnrH8fNy7hS7gZAsn58nOov1VLgFzuua3H+c+NdqPe5Y3G06txiIbHhlv1AKWP3NQS1n05qwZwlAP9z7v36LlyhbYNmMktsiL4Hbg7A8eSNO/PrOF5p8zkIlhCBVosCj6dIITakIIQvBA7evzp5a4fM2/7MwsIj6vKe4Q0kvHKEx+HZu5SMlh4IAgOsLPOcMlzeERfslwVyQ1Cndh1p/aiZp1YOS1nm/XpukD6rbqtg5Ax8K9wSncNBz+GDRc553hxnmHf/wr1/5qwkXDzt4bPCiIQGpVqyYRN7N6f+rOY0o8ck07hVwC1VqthZuGGEfXyEu38Pd3wLDD9h/8rg9Zev8OrLL3H74jU6w9CwoBicOZ3NcoQ5Qus9WRREuN+X/iw4BkYMGHEPxhRrUCSQSgUBZJyDsK/92Z+RnisbZmbJVB9Irj4XqmttTK6/ZHh+0ce6w3Wflho9l9bGnX0pBBRnqpiNqZUCnVNdNLgEH/eQ2dMpighaKWh06NUenTEinFCAJkApb4VzItDJQA0deEx7/9Ibq2B1PBeQ3HhvznIphj12QMeb8LrziePdmR4xoC1gzo91/d67vC+x9Bm495T0cSwiPiXc9nNaTcFNBhji95oVlHIwWoGY0RuNPRRu9x06o6E0wXQGyijc3z/i/vRHjI/3ON3fwxx+A3v4VrRuObn9mDPktm/upx6Dpa147vA26MgVuEXZv5fXfU06W8VKI89+POvJWTVnbb1v9WjhijwzyXOri/L77Cpe4B8UCBUt3/ecZduWAgG5MfuM2XgGAWu9W9oL+aDmVNL8mcct25YsKZ/zhz6gwIoABYvXzuG2U/jN119jf/MN3uEVwICCg2OJPQNYKDDYWVgnsSIUKe+7n71/Ygf2MSSsHcFsQQRoAL1WYEVgKDincL//FaxjWGtB0xE3bgB4wOGn/w6re9jugKO5wbvDVzieNO55B00aSmt04wlmOqYxhvHPkOWFaZ/jffM5br3fmmbIq687wNvw6bwPZhZfy8yQ+USeb9b76khLeedk7p2Po5Aj84y0ZZLiP2X1Ze6HgjVBZL7k+QKhSyluBIUycl+pSGxVBMcac76gyRKDJBEajLC3wC6rVoRT0qZYeQTrCEXSD+X7lpF4Mt+5kGK5Z42+rl44aG6+K1PQbBU3ZTmh2ibkggAkrIc7R1xm6XrN08/pc/oFp2fQzv1lpouQI2yHklvyPdd8b2gruiCqi2bwnwi//Y7w7VeM//qPhDdvG/CVqmsqe8EI7m8pWu61GLeXCPebGo5cz5wIIIIVRuxhdEHDeU6PB3hI791JBbyJPMKsIHgIFEBMcF45W5w/Mcg/cF6A45j8EarvRc54bJfutbwW9uNuzEeZcVO66LhX873sFukvDYTkuAawdXKfg/V3aZoz5eo+JB5A2P9gfxpI4kIwKR/0HbCqA0DQsIC3inAEOKUBpaBML2d7mjAdHzHdv4N99xPGNz+g53/Ca/Mv+Id////Cv/m//t/x3T/8e3zxq1+hs98D9kHoLweAnJ9hr9AVcebAhwhCDznKSWkko35Zzp6jdyDzL+gcY2CCUQpwDKsIFgQLyZzkDrkwYoWAzlOmIJVw8rwYV/lmFbR/sps/56yeWF+G89eCjCWaj9KUzs8tl58MxOCDQQId+8HbxxWaXgEGNamTr3ussShO8U/+S8Is8iVkX4sleKcNdl2PWxzworvBzW6Hm12PvjPotI8ZOGrQ/+8V+KSBydMWnnZoOaZuD2Q+xqcqlrRmrXWLNvvkD4X6w0vgT5feEWvwrY4BxHDfvgV/9dBYq+21PjXVcK9lQXlNukoQMdeiWcqYf/04l8VfClH7HPO1tY55vnDouLiUSCkoEp9vByMX2WANJteh73tYdrDKQU0DaDJwNADuAc6J6w8OzCq9B0gvaghz1ov62fzX8++rOjBOC85tFUIkWFsB/ayOM7z07eljChvW0s+mVTcn2fI3a0/bJFx571HkPG/oxpYU+PoRVTs/b2uwnrKN1LzW4/tEvNW4dOzBFguYpWeh7jqPZ8RabymxI4sbraD7V4C5AUeNGgew9X/Ok9xhUBI0eNa2Jxodu2g4EfIEdAqkQLoDkROLCe7g9C3YGlgnZsq9OYJZYeQjHAxGAEw9GBqOFJwyUGwT0sfL5C7Hf/MTTo1MLYg3q2j9EHPeXlUuR4Ajkuuf1DB4aX/R7EvVQfl7lts3k14QEoEULBdqIcRit+YVR4FHVMFMr2IbInOQuappk9hchN2pH8HsvujXLEm7eeuLcCcw+COgqGaXFn/MWkw5cv1aRr38RaFlcLp4Z50HjXNY99Fwww/JtXmOuj8pbfRnTi3B9odua/a4fP4hZjvhduu1zxmomM3NtXjhlnIfwipke6rb/lg029JNneV4lm1awTYvhQ9znrsxNAZegB2QFn+Le2b9MnRkgEnkHZmSx5yUS3dR4T5x1mUSXCljLOT9qBWZpS5pNTIhsjux0LxuMmx5tk9zxnouoCYkKwmZIsr6mVe/9cRU76PwJbxdLz/ziY1kSdpEh3GpsL0ViLqF0W+vc3ZPtxh6F9W4VN/1cOVc++vW4qH0CtJytv15uZqGmcVPKfKVI5B963sTwX0SHiY6zMMIKASMssAnSWwMyDnQOMIdj3D393DHd8Dxz+hvLF68+gIvv/oaL7/8Gjc3O3SGoSJISTHOKHSRfNuFtfrsREb6KUabZ0Bc11qAJlG4YYk4oSmcatnvzs/H6qlcXPCcZlnJvMjs3/o7PKoQ/dAuN/IVn1Wd2faL8JhbrdYV53+Y1V3vtBmUqoQ2285xEBM3utY6QlSfEVlbpQiagA5ArzV6Y7A3CjtD0EqsJZTf5zwa0KRifbmHiaKhhTTzHP4M+OQCtriZvgIINOkLW13od8XTyL/Q0IOP0/kxb5kTxcBuOputgHHxnNSQmhaeb0+fY0R8Ts1EiiQ2rJeEai0bzBiDAzl8wxMetIKjPbTWUEpj1++x2x0w9gcMty9wejximP6IYTxhGkYMpxPYOehX/wDuX4O9NJgzyXOOIHH273JqHIgcs13JvVprRDwEWK7TbbQOs6j9k6oHy018ZKLx4uYWBgh4+LQI6iVLU9LTKNBE8ussJaOLqufrlZ9jHqROUL14Sx2cpSx/TQ9VD1rTkuP7l9zJqesrlHZ1dHL8LO9TJBaLqtL8kSozhnNOigClcK96dDTi7/v3eH17h5P5FqNTMJ0guHYaADfB2TH6Lw2MY2st2MeKUCECFkO08q2TWAcR8UGMfdB1nWhuGA1tCYO1cLrHcPMbMDMmx6DhPXj4Z+zdI+707zFOhJMDvudv8BP/CqNSsPqAfjzCTENB+RfIdoEU5p+hs+XK1RBvMWh7thZLOzW2z34/cRaMmjPXSzXiW9Vf9HcOsbIqaKU3qc6g8BOFeWfSkq7DjFj01Tl2CM7byrIqlc33RWYpQZgzaCR2Rup73hEhC701BAhEGhIXIo8VIX1hpixOUgD0HOFiHQ2p9imeBtlKM0BbjLuuY17LAuxipAVjxsyqpGoqEBNLigWf0+f0OZXpQ5q5f04fKq2y1Kqs5b2Y30GzbNnzgrHu4SnTkjCilZbv15p5Ou9y7EzsBJHQgUzBzX0IVF32GagFAwtMicWrjNDCSYlU0rhE5qap1UbAN+MMcPG87sNM2SB4t3/SsawR5kvq8/hYjS8ESnihnkthyYcXyH9genVhWZ+jD/Pz4fH1Gh9d4i0UAoaKxmePv2aux1KFCqxCvxVIG6HxSEED6OwEHI/Am3dwD/c4vfkJ5vTfsTv9F3zz7/5X/OZ//s/47X/6n/Ht3/1b3HUn7IY/QWGEUozJigW09ta7cNYrhPbSno12R76r0o/odJTl7JNTIKfATsGxBrPy4wAMKFoBW4gumPNCjPkyzWmgahazfNmjpc+YffFF+X5mzZDhusje1aRS/J5bVKzBuDljJ9LMMeRcaHtezbz+cnxRAL31PBdkXP6jQQM2jhBVNAUDIK2gtcYdGF8Q44t+j5e7Hl8fNG57oDcaWgttFKzHOZyBoomN53Xm5vl6WMPFtyUeFRW5Ws8vbW3+K684bZDyLgXU97dQP97I6zNLfg7G8+0J9nc/APrSuyDnCfCG59vSVYIIzpAUeZD1pci48Hy98vL3wkbbmO1nTts79bG0Alf7kPH8CPABIvylRASllATgZMBouXyM1nCO0Zku8i+UkwBIpBT0MEARMGkFpRjDOEK7I3h677WXGQ4OxIB2Vi6yfgfRQPYXJTLcbK3/yIHcufmsK6uJjJJJc14YUVU9y1sf2izb2e4+BXG8Yl9l/WmRXvVe5TzjU3qxwHyMvypwU+bjVTCYnudX38c+c5e192FQ+rLWnD2Zo85L91ghsJ/lyUjAiNiFVghMGgyg4wf0xOj1LVR3CxCJNQQHNzgeUXZOeid4MhQIlkOfHcT5Eop9keJEyEPnBRHam0AHHEwpJW6ddAfHEizO6Q4D74DRwjiBcS97wuN0wqN7B6f3sGoHVlpMpuv9ys4jh+fO6wKiPJvFORpK1ff5EnCc8ezntm4spTkd5p9nroeC1QIXxc40XnCzi0u8+Fn+SMhobqHkAWlxunMCoMTCs991P2TuovAmuw9K+E+xK0wKUJ1Htut282GltgpaoKy1JFzmWWYvpEwGzYgAswOYwPYUCZZZygix8lwHl10E59xcKKQolo13biAa472RQ+VW09vvtE8BN/qk0zmq5FNCjp/TMuJTGpdPF6GIudY5MB9PoLOeqS+rM751Lq+jMz9SuhTnz9eg/f7JPVgSItgRmE5gaBApHPaMl3fA/SMw1YqKM0SwYo74+zHFXJiXZ5TWDlEo0bLMyfrN2R6MPCBOrhFnsSLg68vOdxQeBME7J4uJqBDQ4mm0f7afZngPoQIvC0KOZgrdmSnELee9NhVdmvVvie9R5ktLeEYYkQlp2u2100Uw5AOlzbhCvmbLUpvz9dRZAk6zJsQTTE/ajmeQsjPDqd58b4dtTFJHcD0qtI13XeYsMA7A4xHu4R7sFTpNb3Dz4gu8+PY7vPz2Nzi8fIVut4PGCcpNmGu712fy/DRQxOnZ/0/imsmjey6rtsSx034rXdfyhk3Eja81nOAq3/m93ypWvuf0e6awVfWr+F0Dr3NpJU+riaLP1fnn1oDONV3dHxUs5SobZVZ1ddcVCZ8PVkPZPTrT+dgQ4jlFqWSFzlkVkVKjy+autWuvvbrTcaTid5sAo0u7utBa9qvRZ65nKSdNrYL3ebba/AxdaKXRgB528FpyqayxbUuJQYMGz2+ZnRdUzy9Pny0iPqdZEiRTC0MGJNJ0QJBNAE45ODA6ZbBHB6U6kDLY2Qn7fsK4O2CcBgzDgHEcMZyOmKYRw3CCnSacTg+w0zuM4wBnJ0zTCG1HfPv+B5BSeP+rf4fJvMCj/gYMg8AoWQxUPLukGjlyQM7eb31VR2RRRShRAegZzp5A2azpxb40gH58tA4+zgKXZoY14NDAjGIxKrNsTHNC7Fzey9lM7fw1q7FMtZ4xrQz9yomunj/p1lpv4snUQEWUNN5tr6XeRRwtIPJ3DsADGSia8Dv+V7zUt+Dd/4SBD9gr0f6x0wCwBbsJ7CY4OwAAlFWAUiClBRnw1onOa5Lk6269to/1mm7Wihsn5xhESgSeAGAUwAoOEi/COQvoHkP/HcZhhL2f8GI34LdfOuwe3uH2/k/4Uf8Ob+k7uK6DNenqFESI0Q+P0C5d4lFThSo4wfmv2tg1yxfqyehonuVtpELzZ+m7TBh5poCCHPlwTsj3IgQjX6LBRDjtBdW+HDES8RJ7mmNU8jMwMZjhNS45wVhiwCmAGAQFMc/zCLEiP7eJ8UF+H1Ak6NQc2WOSvJmwwAWrPE9RefkX2AX9yJxJ7wlNpNgJDMKkDyCzg4EVt2L+TZiMhNSnEyP9TBqqBWzCMr2cK63mJYrnqoN6+SuAHeyb34PdVLnWaJl1+3Eyw1kLZy2gHJI7D/IuhUWgmBPlmVziGWDT5/Q5fU6f04dKa7jYMyBXZ6x/5Rpg8PEtcHoHOnwF3d/id78mDCPjv/xX4O37rCADoBVFKH93xgC4vv5lBT7PemoII9oMDBILVwYCh5WjxIOglORxkSMZGCiZuyYOjM8aJ/b5s8sp5CNvkstB2cCFS2Z5fXLli1WMuxaUlD8bdbaYfS1MLR9Xke2MQkjF2Lky/SVYWZ0/gUs01tPqjlaxlH7n7c0tmcrfkb6M1rCpFvaHtG2VT6mMIpA2IMVQzHDWQQ0n0PEI/ulHuPv3mL7/Ac5oUGdw8+13+O3/+B/x2//0n/Hb/8v/DS9fHnC43cGcGGoQOijwOUKMFvHIRPEoiYDQY7qUnZ8cp5aXYDCsI5ycwugIEwgOoY2AEQveHZX8XXV24s+akmnxILJ8PHuxnOLrKhaEq8oFmojr7Nl5zM8mA8hj6eWfEbXPf5cwJsXPaZ33+jnHSSRIPMSCzua6TOt3Smlvb+NFJKU9vwOK/Z6IDWU0jDFwjy+B6Rvc3L3Eza7HrjPoDEFrHeESI1SVA1xC3qe2RXjer/odXzKssmQQojfeRQWF4lmR4/IGyxYqmjB0Kv/IaeZcIYxW75Oy5/NxAAA99tD//atZWffFA9xv3lQdYqgfbqH+fCdPqvvqOa6c5xVEfIg7cElbaCHbh0iXKl5dwlr9lLT9ctiQnEtABBAkCKliArOCUhoGhIMGDBjGAROJ//dH1gD1EM0ZuZiM1tBKwVoLo+Vz7DScnWAnA0wdiI9QzNA8wtlHGLwXFpljRD1jDh1Nv2umSkuDImhGs6/LdD2gNBztIZh2HHhCEagEknWi7J+noUehvepVC8etE6+8O5tWseNNlZa+YBcy0VpN29q5KmXaly0CK//4AI0/KcvSq4DPXNftcpc+beg1aZl0bOotGZ8OR0A5vHzR4dXdHczNHrrrvbkmC5KXbFYj5eBYLKY8pzwKCtlbTOSwP2+T4XwwZQZolEDCMaOcbaM1FJEwXsHe5RPDacaEDj8eJTD2XTdgwAkTv4cEZ05E6EA3cEqDlYEFoJxdo2zTrDGEyVBDjwr7uehuK4QQ51LGDEBACXPkeQFJ49H/TbHL4Qs74DhagAiaAVIECwWtHHYquUnKNSnBDMfARDJeYobyeRUTVMSDKfqkZVW7U5LvygsZtLe+KTWwCfDB1chzV1ixtwAI6+KF7/6bS1VHYpXIeMTeiHBMGShlQKSFECEtd4ruZBxKeeLPH9wQcFt7106ZyXPQNA3zn49NnnG8n0u4mn6T7qC0BlgB/T7FZ4rLlN+d3l2XYxDEhN/xhMmOUJCYUGG+yC8Eaw2nxEEVCIAdQC4FZmE4BDcdceqz8eWptU1neSJavg6xMrL/l5k+FBJb1/spWBJ8yD4sjLe25P6AmMdFacbUqmmeZ9oXBazIhNHyu8z0ceelxBR+3hRgr/xaZ+yG+7NZBYJVgdwV2X0VNI8CLkMErQkdA0p5eqtRbVu+kHZxsORrwc+l9WwJI2b1czovS0MPAuvcPVNTGEEex/DxLUpcBx5XT8KI9YDA7ZTv8ziXFCxG0ryH58j6HPtKJBb7xVyV05Ke5zhTljez0ticriAkc75ePWdbBRMf9uQ9FzQJ9DjPngJIcReQ5iHxMNLvxf5leF7+WR+oOX7m289KpjMZaDYGcRBWIIJcwePC2aG0mM6C7AScjsDpCHd8hBtHOAK0ttjfMF589Rqvf/1b3H35FfY3B/SaYewjlJsQsVlXjER6FOmgkumbsM3Ud/a5GAoj9TixwegYIxjWAZYT/z5gX4ycZuHiY/YZW6k6UTJ15t/DOqevxfPZjm5u8NaBXgC8i8/nVTbp84Wrol1Bq5tipUzRWqOZ6YK0YLPsBcBpHyPRGVTmI4LEjdUijOhUD6ONd9Ve02dV60vvQsyIxusWvsa83MZCAwiL0aKvZv0s2n0CHFvE5coNT57eT0/buOA59Lmel3l2Auw8roUaOvDbXfXUgY4dyCqk6zy78+ozjst342eLiM9pnuLJ88wN9kwIZigmAMFHKMNghFUWlhysY0wWeKN7kNUYzQg7Wdh+FIGDG+GchR1HOGsx2QHOOdhxBLODnb6FcxZmmqCZ0bvvvVRfJMLOWtngznnNVbkCnfMxJpzzyLiLElhmJ8GypxHOOQyDaFl/8eWvoPd3OHV/A+sZSzLkEvlYhJcVfMhTfNS4Uy5KW+izD0wxrihXIVqoBA2pBspNCeNaa+VchudJ1W26pUWuM25Z0IWKnxMdL5HLy9MWMcTSsON+iJRkQsBzsjjWwAxyFnj/BkYzvv7t17h79RXUi5dgb6UQhRDMIE8wkFKwzsFaK26PrAMIUCTCAedcZMiGfol7HAcWH06w1sJah9MwRgKTiNDvehijsdvtweygtcJwGjANA9ApkOqgulu8UQd07g1e7wm78S2+Gf4M6xiWHRgEC8K/7v8BD/QaU9cD3KE/PUDxlOHEvDyZXD6Yba+MmGqtyyx79mURtfbMfgYiXE+rttBRTm+NewvGCco9CKHLADmOsPqHhyPMSaHreyit0HdArxW+1lpiD3miDMSiSakYg2Pce61PpSSuglIEH31B1k0paFJQpKErrfyQtEeAjTHCPGcNZo6WMVppKCV+TYMLIuf8+yDgJoAVy96DjXEflAqfImjQuoNSGn23gzYddH8AKQOQuNsw3Q5ECtpoYfIQ/CaVvU0q2pDIrDtUCHzQgg0m+4GGzCwpZp9SUpGW/f/qG7k7PQEjyyi/2Ulwd3YO1vn4Ks5hsI94sI/QMNDZOJUX2mljhADpjETLePgzwEMkop31hFKODH8KzO/P6XP6nHxqnccNZ7RmMF3V7odle37cRAtDypkcidnYYmoGRqkIJTw+RSUTeVFTNDCpEG6R4IKSlsvUVVTCCP+w0HzkCk+JQwtWhuB4VxXCCD8/gVYIwoiCkShEZs4jQowJwR5fiMKbbL4JYFZR2BApkGo9ckZ9mPNc4IHZ73qoWRyJs4z99v6u+3C+joU3M+HMLy1dgwdQWS4Kj5bmIuFEzFzkD6kOrp0sUyvqagHPmrcY3mdKjah3Q9hEwSIWYEUAEwwpOAKsUmC2oPEInE7gtz/CPT7Cvv1BlGU6jbuXI37zD3t89z/+W/zuf/3f8Pr1N3j16g774c/oH3+CYwuwt+xlktgQgNBXEItWECQD2Mc8g9c2T0xFJjEisABOaoef1Gv8xIR31uHBMk7MGMAY/TgVILQRRIHH1mepxfevhRCtPJHvHg9hkScqxC0qfzUYMcUzzsoG3LVd1fnEqa+xjvmeEXDHZT9yelEYWhBemwN52jj9ubmFR1XNPLXv/HBTxNglYXMSifIehfOX9jRIaBJjDLre4EB73OoDDn2PvTGieKyDa7J0f5xVJlp53Sobr6vVWkPK6NyLBBiNvNfSM0E5Ydaz0C8G+UDyzJ5Ozvu9sdlCpWBhOzd5l+/3oPd91bfQj1SGkAsbQ9/SRr50dp4kiJjFiljMmDr5KVkAPHf6mGN7ZmWpZiqYX9llLsyYjFkCBdIMBQaxwsEQJgVYIlhFsFqDHXCaFCZ2sNrAWQvrjAgi+gnsHJyzcM6hm0ZhkHhk2E22YKYEJDlqO3umCnsAHbQ82QsvnHMYJyPWGEbBWQtyI2i8h8ZPIOqhFQmXJ8BgH6Q74SMezc0vDarmJzvxLcH8ImMwzmQ9/7y6wBE5bgD4mogpG1IYd18AZKDZCRGRAcLQm/xYL6FfCIh8+M3V68WydT1PSY1GgcbcVXP0DC0vVXBdvdtLPbXfNPvi08JU0sJ7qtQ/ApLiqUQwAKs0mAi3O8btroM5fA10d6IRzhKgmhsIWRAOpn3oEWmQMFG9FrYEVBRGquRVUMRBvVC6MiVLKQJhUAMcG/TTJIxrpcBGo+97TOMExyIcHccR7Ajv3Q2APdyOoKa3MO4RgIIBcOvuoUCYnLj6sWRgVQfnCW7lrLgdys5D61SX/iHbS5L/XqoH9fsFLESEERSJfqBGYDLBEjEmKDgQ+PgIsj+BxlOCv0hwOZrh+radc5gIOE5WXDmRtwMILp0YGDOCkMgHflYamhSMFx4EAYNSwtwnH68IYO9iiaG01NkFQQS0gIFxBBBcSSlo71rLOS/gasyT9ndOcj+VB6ImsTwg0QZS2kAZA6U0OASu1l5oorXfh0kYQUQgHTRSyPOf5H5VpNJ6+LMU5ur79w73g+iotc5nFETwlO5B/7kzhG/uWKwc4BlWLKeK/ViJGeysCP8AAAYgG2lBRwQHAimOxLPROxAZL1hhYBoBdnDTsbhbtqYlIf+iZUStLRTz19nqO+5z+qtIa1ojP1Nag91bY0c8X0/yX+fmqH1HbU/nbqxzeZ6Szt2YW8pjQx2U6AiKP9PbfH2nIwACqw5KGbx6QdCK8eYtY7K1O5eQ5mvgr4/4KMoUaiWIVm8r5avwPRSXn20rjYx/hTS/8plcwMTOZLgdULuryfkaYe9vXq1Aimxa4zPvNzSaXDYtdSZVlCw8PCsuMCFjdkJUBglFK68yebY8NkfezpZ7LeH92dqspI96Uy4wNZokSkO4kPOZAv0R+BaFS5e6XMA9Mxw0Pqf0e5XPRTnsTMokgTaPy+s/w+4OuGSwA3fOgqcJ9vgIHI/gx3vwaQAzQ2mLbufw4ptbfPm3/wavvv0V7u5e4qYjdOM7qOkR7MY4F4GHQXFsKu1aRrLDXYARiRwTwcLEInQYnMPIDpY5sMqhIHEj5HdNy8x30Sok5daPmrGSDWSxooW0RFBdUkmzj/mj6hkvfF+rPwMxCarKr3j6q+kBGjNOjXfNBcgvqmI3ByIwFhD6RWgcrQ2MM+g6g0NHuDFBoSprIpZfantjWsCFtmEj4UwG8LGlAxlG9AT88VzR0nVudX8C2TjP9yEXrofGm6U4y589yy30ZZ+Feqq+lKA3Ciuu8bXx2SLic2omjp4WElINJQwMRcJeUIqhHEMrh4kUnNJQJNYMN2zhjGibOgaYFd5Me5xYw9rJa6KK7Fy0Vb0gghmn6RQFEWAGW+dxWE7PgsaOK3+zd+0ShBTTNEVLCGtt/LTWgnnAAX+CIoXOdKJ1qg1EEiyMI6WyQ7kCuATh8cFqfT6vlD0rF5Hshfq4GA8X+Zeei9knzepu5YXqMd19DdY36KYjlEt+Dy+TFAcCo1UmH1tA5PIxXtDMuT6caXdepCR+clPUvFgcGWNuRr6SLgfDy9fLjOQ8d4lHzZ7lukqspYnmL7ybv6eAVEdi0yMhULBOtNCH7gAixj98/RJf3b2AevE3GJW4agOLL9ToezP6wiGAFEixuH0JQkiPXFvnME1TQuSdMF611tBKtH4cOyhFcI4weSGnC5fo6NCZDr3W6IzBfr+Xs06E4/GEYRoxTSOOwwn7fgfsvxZN8K6DefwjzPh9jEPw7fA93Ph7MVlmjX/e/XsM+hbWiob5bnhA1HzJGRMR+ThHGCeEYrYSqweJPWKRSOLwPJiEp7rjombri8wUmDCQwZEJ3fuf0P/4f4Bud+C+y7TrZa0EtlMSBjuHkRk/PIrrJK00goWBWCcQlCYEvnz+btfvsO938XcQRITP0MY0TZ5YQxRYiCDCRMu5vO6+75MwWztMYyIeQ1vw2kDhdxDCOxvgqVhGdP0O2hjoTgJWO5a9a7SOQpNcCBGEP/ndEpZSZQwg+S3vlEec/9v3Fn98b9vwIjv7FDeXF0Q44PUB+PpGQWv2rBFPNrKFcxNgLeAc7DhgOh7BpoM2sp7KacjZIzANAEgCI2qDvn8B1WmYrgPAcNMA2BPw/g+idacCAX49Iv85fU6f0+f086UtsCvhwlQ8S58zdy7Hd2C8A91+C+oMfvOdyMz/P/874f19KJdhbrwARpnBJP7aFWf2EOcYIJ7OWbxPCHJFBHY6J010EZhL7CbOmYJPSAHPTjw4bldLiPGtFuuKDPrG74IxOBeybHZptJYvW7pobbGYN2cCrtGZeeXb+/lzpQvIplSGaHVca3VSwn4ifpv7pM+fp9qyj+rAxNNbP2/h4sX7VEN0U8mBTyA9ZFIg5QAnro+YHdw4YDo+Ynr7PfjxEfTjj4ILKoX+xuLbv+/xq3/3d/jdf/5/4MvXX+Pb19+gn36EefwBcAPgJkAZOBL8Fx4WiOKK4Jsh0LQJ5z6SJl6hKJIJIiCxDEzs8OgcHizhnQUencPAjJHEpapihmJ4S4iclg7c6JLZuS3NDuX8/bm66rO+lGkJfs0WdkN97JJsp8meaLUT6Kyqwwl4eT5PTsX7dW3Ul3dz7sZ1npuQ4COASOvUdGHIqTRFl0ym77DTO+y7PV7tCC87C0OiKJbzVK53KV104ckpzM06nHluWkVVv6t1o5JGyhUA8tXcAu5za64tR23BSZfAztC5/HFjanIO2jUzt1kQ0bpEr7EAqOvZXMelF+4zEb1NYNLIdG1rq8hJPTs5I7d+tgEmz2tfe5k2VbjChY+SmI15J7T25n9Gg5ygrc6RZ/45sGPckkLPBKfF15hz/upjz5D0goTJeQaT9zUtriMIJxdgdXC7xBGAl4IIcdvinMM4TrDWQmsDaycY0/k8grAYY6BIwXhBhNLeTZNnMi767y3mKjCPxBoj9S+Am5wpFCe0qovL3xzqS66nyrozAQNzhA6FwCHkQTlnjhRAj3CwOLgH798779t8jLl/zTC2NKJKD6lGOpZ43aFvxb9Zlqwe0gbK9LDoYSk3HYvXyqzP8xSpgqx0STJW6Om8z8UDak3VFcAgn8UzVW085IvjiE8XKjpPucZ1SZcUp+cETKoDSItQD4yX+oROA69f/QaH2zvorgdIiQWDNzvlGB/Cu4iBZ5T6fcexWS6WsdbEd8oBTnkFdIXghV97ayd4mGItA7B4PJ4wdQxlTNSkd92EzogmPU8W0+RAwwjDDAPGYBUs76GcR7a6A9g4PL5/wDhNuNVvsecjHk8THAvCz0pjoh0CEzoQKAE2EDtongBQdZq4sc24+ECGwJR5cvJX6gw+KEsVDBG8ckSEs5NOBEsKEwuxJLipN9llqcux80JXFnyLSNaXFZjFeoWUuDTSSqMzPRSJmyWtCJ0WZn3XaWhv6qu0WBJYt8fDuI/WCMoLDFh3YGUivBO3fR5GKULv11PgJ2MY+iiEUoqgT30cO4MzR7fSd621h91imRFiTwCJZgjTZ2wPUtJ3AmHyFhadESaN7qyshVwoQoAWTCLKiBeOaxOZTkQ+IDTh4cRCSc6OaTp/Ap8zlUq/z04j8N/+ZMVayA/C+rtZBPMO0+Tw+Mi4f9AwWkEZsX4gsiDY2BYR4cubIw69huEXINNJ0EIChuEEuAlGHUAa0NpIwOzpUYQrCohKBWHOi01+Dp7np6Hg9tS4/Sy3NPdLd2/xxLSAw2zO+9zpZxRQPXV0P0vPC0baE1Ml5D5n5b651U39y9uoz/RixVt78CwpzkOF0qbP7CLwYKxMQes5wbQSV/ZWndMjmB1I77zQG94KId31nN3flBOmOYcn4EiVRnbo5lyhNOBX5yhxj0/kNChnY8rcJ3EFg4MQAxXczWelwjqy75RwlRW0NfWyxGvy+auFATlelH7XvZPvMzwKFOdzWQiT9b14LIWoWLO6nvWBbgUBhTui/AUvj3bLWWxaF/J8JrfUmcfsqZ+37umlYUs16bxyeJgJz+I4G/CNAtLlFUQo5Av4SXVGqBidSqSQ3x8Ebx2QMQTDniFWUGCwE2Ee2xPcMMA93IOPD8D7B2A4AY6h9YT9rcOLr+/w9d//Hb78ze/w6tUXuN0bmOkdyA5CK0FwS86Znh5OFLOf4ZXBUidkDoISAJHXIvQVAU5htI+Y+C0sHjAyYD1xxiAwkcexw98FKTK903ktP9v1cRxjo8m6G5w9DN+beZo/Go1z9b2sKAoKOG8v5HHRPW5h/hSCe7NLdbJDspnh+Lx9apZS2MOpmqRDmiysZFtQLJME1QL7gxBLE0ErBTMq7FSHQ9djZygqlZEKJyC7klpdugiDauXdcCmslGq7a2s19TRML3daPa+zvhMbd0CmZJZwh6Wq5ndsmcnnqbpDtYSBUmmpNtyArTsl4RzXpM8WESvp3LR+cCJkQwOXH8Ft9S7VLC4NxU0FB6Dp8yulobwmrGNE/9NBKNAFQQELGGXPXeSAKAfGXPBZ6C8KZofBafxkezDmgKPU+ndg2Gj1MAwDpmnCOA6wdvL54QUQGlqLFqvW4tdbm8B08sjIFkGETw4O1l8qcyHDvGydx3l3GDmSF7R2W23n75csJ+py4fnX/E6+dxznnas5zT/zPszqDgjLSvnik7LfCJq5WZ0hOHlWpucOXf8aJ7zAo+pRMq4WLpNythaeU5Fl6Wgksq6uc16CV+pZTARwsbtX+rmW6j0CFJdYen7dBS71VIQEEj7HDAy6B3cddl2Pjhj/Xv8BX+wN3N23YN3B9DtB0scT4JwEV2MHZitCx+ivXxifgfiOTHvfJhGJVRUzHNtYhMnBmE781ysFrVgEpUSwjmCtCBemyWKcLHa73vu67HCzl0BNu36A4xOOxwHjOEq+XoMnA6U6uO5r8ZmvFKBElX84vsEwnvBy+AEdDXj/5icMDDx+9W8xdrc48d4TLIljEc6ctiMOo7iWUpTPqnxkIbzLVCMjDRogzBX7+D5EQUeKI/4gsTXEsiHhh3LGJtI4kgiHiRkaBoo6MJQEmXZWLCGCb0tS8sca7AiOxXLFqA7GdNjv7qBIoScNowh7DfSdweGwQ7fr0B92IogwGv/0/R7/+tO+GC+DgUMPdCY980Jb8siz9uYVQZg9WhvhFoF8kGkFCv5y064SJNoTdEFwVN4DXHzQURB85Qm7EI9CyjnZHkGQQYGRUWnIMHwspPlK54pJygslkhlsziDJYaLLDrys9sPA+P/+0aaKw33rWFxuOQXHIrQZR/JB53SYYK+bIA0oOJjHH6B3Azr7LajfA/s7OAD3D/cAEfb7VyKc6Q/A9ACM/wrl70eZqQly15d+ldPkboF5W/OV6a9eGPE5/ezp+hsY2zmRn2RaYihIqkfVwLCe2PY15ROdk7RQXcRegWS9VpdZZPFzqpOPbwBSoNtvQLSPND2hXOZkkZDT/Yzgdz494aRhGT6zOkIqGLRNYQTHThSM3jwpeOUPB0BBKQdmisLwgH1Gbev8jsruFgZ8vLA48oT7hYnwjM+1Naxuz+xpYPO07pnyTpeSQfzg8QLf54BTxz7Ho3h+XyV9nYaFxIyZeS7lgcFTFfk6LVrdt/q28m5DV1bq5oXveatZjsb+zDGdWK7J+ApYIDx+gzjpKQ5ETn/mKbOchfIGBB6vohDPK8fc065QSomCH08g56AQXGx6MSQFxrTwPzS0PJ8gNM/wHvb4CPvmz3APD6AffvIxHIDdfsI3f6fx1d//Gn/7n/+f+PKLr/Dtt7/GbvwJ/fHPcBR6rgGPz1LEMzkbVbCERjGCgH6xZzgrf+acs57HA4AJ7DRG9w6O/isYRwwA2JHH+cm7ooXHsxtLk69SXLp6HSkBgXjOVyprglbO4if4Q+rnvciTCwhivvB6jV+Qb3YP4/J6In/D87sCn8wFwUTevkufSPkkr4txPOo/KmBFDldr2JjRmpREA1S897RK+J0FM4ffD3G4JFT5Tit0RmP32OOb8Ut8/fUdbnuCMQqkCcG9LpwLOs1puqu257+W8fn2qlx3p89ugQZN0KD65PnFJMel/VuAkxktiEUUcGlekcHQegDcnnaOuyIrE2DnfB9VNW5OzyKIOKdFs0YnJjL6cmLy2pRf2mvvw0ye79kFfT/X+KVVL+2r56i7bqMu7pkrighQKiJBAncZ5DzwI3FDEYNLB2FEYITE78gwKf8cnnnECi/NPMp7RDbiBWjhQHBWLC4mw5isgrUqBbeFCCJACkYFC4jgLkT73zJBLQ2itWmq0aVZH8E4Og3nmUZ5bucFJbWU1gUN8RneysUfMBdGlOVC3qosOGoLLwsQXES2c6HKuiAiz1u2Xea1KS+4KYhQjqBgQXiEYhUmM+2fsADI5jQXwLQ2MSPDiDgWyevKk+YJvR1QviYc+y8xdi8ahRrA/qJ05oBuphw4+7d+daZw4yYuvb4zRtJw3q89A3DDA2gE9geFm17h1e0etzd3OO16uPzK8QgYu2T5xB4xC5YOaV/4zrDfi/4SDIGrhbHr4j51ziXCg1DUF2LcOBZt+Wm0eHh8QG97GC1wou9Fg37orQRssw7WiQsgYWCLWzqlSMyrQaL93StM6g4OE05kMU0Tdvc/oDdvYdQ9HGkvXhHCxmqDsRPGw6C1EDBKxhKXgCR/DeqZAWUHoI5xkBPrCZT6ggGlIBBJcGnE7PIspAmEkRRGECZmqOEN9OkNejri5uUt9nuDzhA6A2hN6LsDdl2HF/sXMKbzsBXQ2kJrjbsXd+hMj5v9C1g2eH86YCSNse+gjcI9NNSkYI4G5IU8b9kAfYL7Ef4qHecQBAnAh4RiO29BEdZdsbdwYGGWIAgXgiAiBPQLcSB8EEGZ/zRnYaLTfPqkCFG4F4Jnynb1912ok0GkweDEuOJcCIG459OYhY0TNkMumOD4WAiOAM4CE0jlv5mjuzSVlS3gsUukSyJhZLCRpPX+gf90NHh7ArrRQusBvbmH1sCe3kBrAlkLZXo4Z0Fsoc0BhidoGmQ+kIj7AIqz7TdLi9Cw5MqdLRePSUurc62NotKPh6/+1aW/orleI6EXrRLSod/WyKcqsLiUFqrLXZpiM/NZ39KVBHNT+U09X6SL/X0Q62XQ+ACFEV+9OuCwV/jhJ3HVtA1EccR1IstpATQGgcbWdFZw26yqvbtzBn9AVYRBl8VSaDa11N8rGFGxESmbfoY7Oty7tQBlS1veZWljELNHz3w0C2HUlk2zsPG5/KfMs7hvtq5DicluhWdtwVCZIx3xhjDC/5aflYUEAHiL33QifR01Qyj7np81IoA4KFFSzAGIBjlIgViDwCA7AWwxDe8xjSeMb97AHh8xvX0HNwxgKJjO4u52wt1XN/juH/4WX/z2b/HlF1/ixb5HN7wT3D80USJra5NYMg9zoc8ss+cNOMBZh3FymKyDdRY28BcCTcGpAspWaqkPCz8WSNqFfZXxidayLSaefVmuIJyFxTPFAWBkebPquMrb7kh2H3DVZvh06d2FPMQwtypqupdzH8AfRaLBZ8kAcoiRp5WG0Rq9Vzi86xVedoROQ4Kj52fZEvhNDz4ab0LTXvMLhlJe5QBQa/OvFc5TAD0BsjRgUG79Vj9fSzPB6WrH+PL9C8zvyqVm4jjb1NDqWc15CVVdK6f8onX9bBHxqaZPmPgS2CTGYkqFoFdyIpz3SaiY4ZS45RCmH0Ozip/CkM6Z22lLJ+ZJxtZn4LDQm6TdQGBHECG0aOs6a+CcaOeG/EFjVgKD6siUIhCgWhqw29M5OOIYeIsbTP7o5ciiY9suk1k8tEzJXCE1rxhLZz6jVQVaQozzdcRBr9Q9F5jU+ezZcmWZYZZ3qWx8Dtvse7SAXKgvn+vbx7d4/e7P4YEfOuMPX/8veLN/iQIRrlMkei68a7ZkXuK0PUdq1sVARpiO2mBQnc/sQG/eQI8PuLMDvn7R44uX/xHd7gW462FZS4d93IcogPB/joMQKrhoAgT58v7po7s2TkSjUn4hEQVquSAC8DABYnEgclMpYyeHYRzw7v2E/W4HYyR2xW6/B0jBWsYwjjiyg7MOwyTwDCrEDkAUXppOQxsFohswM2xvAJywO/4TNCYczE8yrvHeM8k1hv4G77/4HSY64KhfCbESEEcCtFJQWuYsuvPxeD8cA48O5IZEoNVIPgO5e4Dg91OgdEWEEmSePVweSIQDjmVdzP3vsXv3f+Lu1Qvc3b7GYafRGQVYC2LGob/Dvuvx+u5L7LrO3xMM3U0wxuDlqy/Qdzvc3bzA22OPf3p4ATYaXdcLcswAWYCcEmSYROCoDiVOn58lmRAV2AkyZAJAusBNQxxlFwU8CSFWPhaEIOCiCReQT844OfnU5jgjVXNOxEXmYDkYGB0h8HVRYVyi7N8If4IlB+DIWyX61+nODGb13h0VB6uM1AC7EI8l04vJmfGe0CGwxHlHBtE8whvOJTuHP7u9bK/JSP9PJ+y1w7978SP6zmE8HaG6HiOPUKZD19+ixwgzThkrgYvlvAYZRzFXn9Pn9Dl9TufStYAmMXFm7KQGc78ZCLrMUML541soUvj1tz0Gq/H+PWMct/Us3Blzi4knpkU+YOVqKaITG+Y261sR62FJCkGIdzzF+Q+BgMtA0EERYLHp0ESUNng8MjBWojAiMKtLhkuebxZ4eiExsj4FuvaJV9ai6yJPU5ftb0uzfJHOKZ+12HUfI9EZjnvEA2fPGnkzYQSQNL85tkRJKQUJR8rrEj48xf1JUKKUCQizHk6UllQPBY3gsMbaAc4OGE4/Yjo+YPj+z7CPR5x++El4JkZjtyd89w89vvzdr/F3/8v/hhdffI1vvvkO3XSP7vHHeA5WtTc2JM6/UPWUhZaarMMwTRimCaMNXi5Y6KCaOxzIkKu7lQnyIrhdgAsRMJxpbAast/ZlW8Y4dQU8qM949ruY9HZbuZKnCGq962/HeSYAKGJHhNQU1VF6mzeZQ7eYlFj1CC86wUqtCUYbdF2Hveqx73Z4tdN41Tn0Xuk43xJsCfSHO9CjkXauBhWrkoR2yvbkubpbcCKSJXT9dt6mZJ+Y/eRdLW4SJGPlaDxLWifMzgkjtqYnCSJqa4azlhF/zelaxnaGn/3sqbpwwuEkpSTgsddCYHbixprFXQczQbEgYtozRIDMMiIgaVwClYhQRcZwmIeSg8MZMHVEYEViHskODkr8xoe96QPpKh2Cj2qPRwjnRWJDJGZdRK5DV6o973uweQoZwEsvxMmhssxBcAeV5eec4VRD1TBvuSld6muamzR/+Xw5ACc2ovENV4xvUfAQP8rLMK1VIoiCcCkhcP59gdzmFh+prSUhQ2rSP3dl3c5LFnKrG8D/hrf8yMaQW4Wk8kh9zT71oYO72RXPAcahY7D60d+62Rzmix7GEDI1Uj6H6Xf2OS+RPptVEga6gVM9pv4GIAVjp5KEZkEyBmXitlKO0bmS+i2qn8bofgYAyFoYpaH5EQoDDO5hjMUXL17gxcs7jP3XsGoH+ABWzrqCoQkXXBwwQEHDSAEkQgfnAJBYPeQCyzBGwDMAKAgkOAoicpBCSD5Mg899ITIY08QYlMXD4yN6Y7DbC4w43OyhBxFWOmvhLCdE24kLOmYbEWcGoEiY3f2+A3cE4m/BYJDeRXTHWYfT/QPYOhze/xmTI8D9GcrHUiAl7e+6Dv1+J1omgdAOA1IkptJ2xJvuK0xqB+1GUB4fwGcmakOpQEgxhAU9au350Q58egt6/z06YhAxXup7fPH1C3zz5Su8vDtg1xtoRXh7v8cwGfSvvobZ7cB3d5iMaH6BgBMxtFJg3EI7g/vxgIEI/W0HKA2tg7sqDj2S9SKAocEqf5oY+rIQ5O+dUhgRLR0K01Ke2ZVw1maw3uPUOHILkRwwL1/HLFIPB4QYJ5y7W1I5jE8xF2r4lsMMD+RlD3GwlSkuBrD3Kx4DEjonBK/KRuo4E+6Fdvy+8K6tQuM1uR+sH4HgkCTp/MGJJZ8yChYO/3Lfg8iBDWNnBnzr/oyu7zHtb8Fdh8P+JWBH0Hjvh+DN231gtk8Kf1zC8P9aBB/Xaq1fks4yEQIQ37gvzuQrmaef0F57Ylq08KnH+DH27iXzWmsrr+a9ukcLlW2diwznnhH+XLxPt9VCZxc4B+kGlDvNGMK33wCPj8CffgCm6UzfGBD3igAp9pYGlL9anL8gRKmzUITyl+2ZxOwviyYrRU9jhT4HlsZqM/n9S9mEnSu31r/EYCuEEWvlgNl0LFqM1I9+pnuj3ulr1oBXMZYq3kDjRyNVu21hbtowev6MK/hRuBoL9GJFXOfKSsFHUYihEIQGHuuc74x47DjiabGMx0sDlqTgtcTtBGcnTI9vMA2POH3/Z0yPj7A/vYMbJnTeEuLF6wG3X97g2//w93j57Xe4+/I73Bx2MKO3hEiDzObyue6zjLehDEbd42Q7DI4xOsC6EBNO5ioKc6LCTvi8fCcVVrGzTYvlLRWZUZy2VSC1C7y6ppUr4rp1uJv7kjP6IoeQVVuRKVDh9vk7AIB34RToBc7LlULM2TiqIbV3QONpVlWdJVhY19mD9xOcCNrucNjfYt/3MFoU+EgpUewCidbUDwfgUQNTIETWaKgte7egBM+U4ep1nbd6X2evilzqtafMf6afrfLVWV6+OrhEt+ot3mqe8xeZBeXqifV7fYavPV0Y8dki4lNMnzpxFPYjEj9IfIL7V0wSiIdzBosH0wywCsBVNxjeZVOcM7lj460kzBFxyQQQKTA7KOJ4SIRP44OeBhccpJAuUIC8OxFhbtWAeOWwcXYrnEk9GMACVdFae64RRq5f+3/qssvIJgBYJrynF95djJ3lW7WCqPJdWrYQKngt9zr/krVDUQdz1BBgf4nL37JgIwlCGA5TXNdzbTK/auZ5BeBlo82ltttaTO18OT5SluXIwFuaY8eApR6OOth+B1Ya3elBhIYhEWCVxtTtEXSDjBvRjTZqWdTXvXUTTnYAQYnPejdBgXFj/4gdP6DvOnRdh69fv8Ddqy8x6BdwUNgpA0WAnaYYO0aQL5fWkhAtqBDgB8L33IdraTIfrJmUFZ135/dF2AtQBLKE6PJIEZQDWIkLN2sZp9MIwMHu9jD9Dlpr7PoeRokFzjiMGDHKbnHsY+AwYIWJGnFEJQKO3WEHUnsAt9JjJfFolNKYxhEP00/Q7h6747/ADffQb7+H1gbadOj6Dt1uhxcv7vDq5iUMKe9V1o9fG5BSeLsfcK8mvNXfYlQ74GSh2QVAnIh9lBofEZpmSIVTGoPZy5w5Bt69R/fH/zf2HeHQEb799jW+/PIVvvvmNb54eYvOW5X9l99/gcfjAXz3Ddxhh9NuhylzLzVB4O6AHsQKejIgAOZG5i2KUSvNyMCQYY/YJkYNEB3bKgVQsJbJSEcVEOkE28NnFAYWBEHIHhAyCjIDIQ5iJcFc3/+MSF84g/6F4igkDcJR2TcOrDRI+YIZws8I/ckqZi+gc5z2LgPJt6zPr5W3ishi+SAR0wB7iwjvmokoTkqCKzmRkNpTpNJUZnNGJL5qnfPBuI2BA/D9cANmBzcp7GjALX2PfmfQTQNw+wru9TdQ4yMwHsGwkX4MgqttBMnzpc/xIjakD6t2dXX6a1y7pi/jXEh66ZxcQG980Pk+t8cibHjO9sv6tm1zaoAooXekjhyWZvdPxhgtWs0aTe4kCUYT/uZbwuOR8eNbEUScYzSy11J2zFDeOj0XSKQmW3QGr+6FqEGeMbFToOHSEoPZy+OTxlWzrq3LSSAwsVhP+ItXvgtuuHUdc6ZJnefs2i/0NdSZnw3O7mYOjMTs93Olei3WzuZFJ6fKmJedM+s+Nr9iziSVbqQzGHIFwUN8mtE0czXnFKS6/EvWqDVfUzAhjkxkaIrB5kNJBqAgHhmcG+DsCcP9G4yP7/H4pz9iejiCf3wEOaDb///Z+69uV5YkTRD7zN0jAOx95BVZldVdUz3T03zgrOEi1+L/f+YruRY55LSY7q6sqqzMK47YAkCEu/HBzFyEALDFETfz+L37AIhwYa5NW4erTcL/8A89Xv2b3+Fv/5f/G65ev8WrH/8OfdojHH4BzWbislk9dXZMa8jwU4eje40DMw5jxDEmDAy1XG+GQj+Le7XCmOAm3zlozU0s8t7mMlfT4O/ThZnbXOgV12V5MctlaQ2Aup00yc4wPk69Fk2Q04wVV3/22wQVuX4u+VdhM/jWMOpagNviD1nQW9GHdqZ770G3Pbb0HV5cv8F2s1VBBMGTUysKEi2oP1+BbrtZywu7dxHCU3nOM8BPnlqTZ3wm+2c84whN4OgMEmHlfJ8D3q7KxUurRkDyj7n1n/zDC3kbvOXsXJxOzxMjourEl6zj4raeG4/mamKemlbqeM4mniU1mgXGTykHvSxXKtpDtrEUiRS8zJA28aFd7ghDrkrepunSbD7cLaednS6puyEnjEgzu3TO/IOrhrEygkyblNSsrJhU140tADF7xyvPL0j5Ni+Hv31U6NNsj3C+rJYT8ySvJg/CS2IwRbUYmINe88VW0QimWfMMwpF6MAUU64GFojBGVumrXZDZdRe366WBUC/kUq5m9lfMYa3LmNnG4GZS/V4uiELz3p5XMNlvWFsVkpG/V59NzAsuVhe2xuz39DNblGSeYxV2jCPOCiISY8tA5AGH8B4MQnC3WSu8oDEOOyqCCE8Deuzz/OTx0PpjiNgFhiMHBydB4GPELnj0/hpv37zBbneF3//d/4DN7gV+Th1GjRWW50cCNDRzlZE1hd9iOQAeKTFSYhhPlB0BiUA5xoETSwByIBNsGT4HjSXhAYr6ToMyi1ulMhLjmHCkAfd39+j7Dm67hfMO280mM3STwkxRXM+Jf//saAZ5I9uZA9JLW601kABEbHfKmOe/B8YDHL/VIM09KHig73EMPT7GLQIRPNTcOyW83ByxCxLLgl2Ht4efEIZ34Pt7gBPi7jVi6DGkMq8Gl4tH7O7+BcQROUgZMzbe44rFAR4xI2z32Pzd7xDCCzj/Ct9//xqvX7/A9vVb4MUOgyKnL77zCKNDtwvwAQguwjlhVIMIjs0NnuK2WVDS7OR8uiUW+wYmhwQv2v6ZSFTS0OzBs4sjMyF2ZeyJipDS+mkWN4mVxrG4RZzHQRhG6mYwE5QM0+JsCGGyfVnfF+oHajLutn9SYrVaiSC4fCchrxMtSyz9Sww4hkUDFMFthRNAX6P1DQ7Ieq8Jn4bXxMhrOTHrkCkiSxJEOrGMpVOXYUwE8qnEwmYGx6h7zK4JsQAhjhgT4w+/Omz9gN8d/4SQBhxevRai5eo13LAHDbcgZo1bQahtMwQW23n1aD5v+mtkaF+UvuIx+UuyZnhoOtf3JRee1csnERQnGVpPXS/n4Dmt1v/YRlEjqBOl6ZzlXPV25TzqhLJzl1mY6/sPgO9A3bW6ukjNGbXsfknGhqu7bEkI8QBwqv7LAKydk2uMCBMgCJ9nKU/FONErzwJTr9e5TE5cKitthBH6rCXhVomVlcfL+PcFgDycRjxXpXKA10BZJVsXQaGmwMlV9Iz9ONmO0ev12sgf6hazqkWWkmyUWliThz6jbaVVVz2Xistakf1kihnFggKOQFwsaplIlJ3EFgJ8PIDjiP37P2Pc3+H+p3/FeH+H+OEeOI4IXYfOJXz/3RHXb7b48T/8z7j+4Ue8fPk9tt0G/f17eBoF9yNp2vEU0FPDtpLP9jVqjLWdTGahO44x4TYecBMPGGButROQnODjjHa/2oBVz+bfLoB/uk9aYC/YRxNCIxOZdWy9lgqZf1+BadrHqbAjCxWQx1noQPnL1g/2aYGtLWacbeQs0C20KjD/eS4xlzlO1eV2ahbqK8A7hxA8Npse136H3WaDTegQvFOaT5TGappzGolFns3TOgwtvVUDtQY5L6yv03kVxiYLrXz/DKkasrrL63jdHD5aeLVapFrDay69Kgxpgj+ul7s0fXUWEVPE43MIJp6Nnpkh/PmfJyH+p9IMYfwEaQ3kco7JRm5pBFmg2bR3tsFFe0GQhDYIda3VcK5fLbPaTuWg2jNFa1zwBrOCEFce0rcijAAA52sLiRNH48LmfsrMrnWzIFv1BV/gq98vLTGeIgeTFFCEAPPG5wjJSRgnae97RL8c2aPUyUhpbH7b55KFwVLrYprNs/J1na1wgjPc9t9S2fNWGsX64lx+VmRnySLilNVExmNmzyPW4l4swZDSnXzfGqJEVb0jmD+2dW3W+sFIZAh5hOOE4XBAHEdswgZd6PDD9z/g1atXeP32e8Bt0O0DONpcq2BG3RpJ8IYSpBf1hadIv3OMEqBaqH1iFq1z9W4jF6VTQsSBU8xMVrAGlU6uCgEtySkCTURISQKyASNofw8A2PQbOOew6XswJySIeyZmRgQQKcFFl2MPqGdZmGDChJ0EFPdgUXJurjYg2sK5V8D+CDdcg5wHhQB4D/ZeXSUFOBA8AZETGAlbusHWHRF6Agfgu/0v2Bzu8GFIGNhhfP0CKRAOQ0ATHweEgBF8+AmBEjZdD0eAJ0YAYZM+ovOEvvOgDeBe/YAj/4i79CPC1Uu4zRXGzUvs+60IEDmhfzWiy8I1wDsGUYLz5m5B5swpgl3JfWRfEAAl7ljXZoIDmMDOgSnInDdnNWVikPM9W6wocvKlMQayQDpzLZJYzkGJd4YyxKmCvdlYaM37gUyQ5kYyl16tQkzIXp8bRGAWq4vM/HcaO4ns1iTZHw4aHEL98qIo4OX71XDo+tzT/zK0zDlv7V4ksbkycxpLg1AHRxdhj7ouJIDIK5GtmoIpamVmoq/l4ojIjHfjDv3xHq/xEzYeGI43SP0V0u41OiL44U73SDmLP2Wa0DLl+TdhhKTf2Bic1RL/CvvznBCt9b4wENocxpj7FOk5hEPr1h5c/bvY+rSmJ8PS0Fd0ydaoaJf8hPL9dVFiBo43AHlQ2Ml5i/kctuMyeQ/Fy9kEFnPGzDkQ6h7JtVwGoLaOKPPVMoIN5y3umBYaqvG9CYmzNNby/ATnkWg5bsPaoV+lmlZapXVWn1++1qgG5qI1daa+yioitzBHWyYPlhvN45b5fm1F02GcK4dRpbl7waA/IBUlCf1tCotV/ZyhLG0X6xsZ7DY2hOSv+5mD9ZLWXhEkzqSNaonLkKF0qjyTSBVcHImbGhVEjPEIPu5xeP8TDrcfsf/pz4j7PeLHAygBfneFzSbib/8N4dXfvMEP/9N/wPbVW1y/eIsNjQiH9yDHSB0KHoZyLq3xKs4/lwqWThDtPpgJMQHHlLBPR9zzAQNIMeVq7T3o6F84j+ryS1u8PowvbmtayeQcmq3ftfL1u6V1TVXdXF4rXpzbYc1TCyAyXEIfZUGF8bNq164L3VmCuGHDTZK5J15LSoLZzGo9smKc8+hDwG7T4arbYdv36LsOwQkNSRrLcb36R+AHS0XOIT0r59YSilD4aA9p6FOkybqqm+b5lpjTKzQvl/tl97Y+XZyftXt1Yb03F/TTx+irE0R8S7+VtH4iNlI7RQTm+5yKWRra5/Om5ptDznhBtFPFhPfwMLdM1r7ABBSTsxKYyiS4WUCRIy/Z+ymSt9BHfZeZXI/Eu+owqm01cknlIVwgaIzZ3TCCrOhFQF0A9BybPVnKuYREh9OVEMQqoaJGyp29hAQsAVWNVI0IVDmOtEMil8fRPll95+e2Ftqu88OIFQbMW3p+Nnsv32urCuQ1X9XHrcXEzMqCKxhzPcKQbmGbIOTV86QMefukadsTqw0bgyVhRCRGIhZuaALSOIJjxCZsEELADz/8gN31S3wYr3FMhFEXdlQf9VMLiAKxXG71e2HkC4PUGwFqxDDML77UW1w81S6c0IxN8AFERTiUKjdVRA5dkDMiDgl7XbsSmMuDE8M7r/ruYhHiU0J0ESm5DLf503fqL9N7ZVSPo+zxJNYCXi2wQgjorhy2fQDBIXiJb0DONf0Q1F+Y1Xv/CiMnRAgj3m8iXpCHDwPGBIx8QBwjPh4+Iioj3JPDdtujoxEvf3yL3nu82O3gwPAcMXCP+/gS290WVy9FEzMEwhB7vIwdrnZbbDYbdLsePnjEOIBTzAzypEHnx1Fc9QQE0aTniFq7Pp+wZL1SygpK3CnjmyBCCHa+MHKMIa6ro5q8euWjaGpM9jVWUnXUJACOs71RddzaCWxCJ7O+qCeJgOQEtTWCVfdcXoxmGUMjWC054HwO+id7vZ15OAZYBACcCOwAThVsRCLcWOhoRkW5jBmrkES3MNSjh86Fg7ka05sNJiiCk75RsiCFYoUEswohgLz65HAAxwTEiAiHf96/wc074MWvf0S3fYkQIyh06F7+DnS8RzrcQEb99F00QyW+pedLXyHT/lv6liRNENsH5b+0zCV1LhHgen9NHs/w8QtbACDKHnrvOVczeA0na+mQXFKZrnLl6N2jLo2a3A8QGuVer0gIWvdEyDBeaqVgGF02iSDOd9aXExAb5TSlJzKCfIYCKonsbp0xjvjiMTrfhgmH2uc16nG2jtmaXmfPMdbnZiqgunTvnaK323gOpdrSVoaqGgMq+0QVQEwYMe0nzFKX3LzPhntaflWuyeimsz3q1ZJXlNSGwy14OOLw858x3t3i7o9/wnB3h3h3AMaEzWaL4Biv3uxx9bLH7n/8n9B99x3oxVugv4aPCd4n9B6ABxBkn+VYh6tbeDJWq6nMcVnLE6W3RIiJcEzAMTHGZFgaixtawZjVillraKZPcM2zq6DuzyzO3bm0UvPa5qrOqOXyS/UtPLNDalqX4fw1jatKszR1q5pS6S9z+5dqgQQm9S12uLxYPd+nBWXeJP5DVqVrcsu2IGyQ8AqMl36D602HTd+h7wJCYDifZIswwH/ege8DcAxSfznhz6Rpjvb3Y4/J8+W+JEVx/nxcXZ0nhT513Q/FnT5v+uoFEWUB//ZIT67+zfA/EePgc2fMZ0wz6VrNCyLkA61WjphqGNUIQ5umCFv71IQYJRC2XtAgeDikVDZ3DrRpMOmPbBlB5gdbGSlZ5eKB41F6/LCCKMji4gusjUaVrcq7ZK5xDpG/iGDi6c/qwcKC9BxRArIuVID52imaFfJ5CuyWQViVr+Zd3hJ81yG5DUxD3nLxtB+Yj9X6byMiLst/2lLCPtfzNs8N8pX5XbPSsMDgxEboLVtirLUtgoiESAweEzgyEAWx6rseXQh49eoN+t0L/HrbYX9McKqQn+NC5AYwS5xhZR3f4p6JOUlcBhbtbUOOioWtIGkp11txdjU57wHHSMkhphaAHDOGE8YUkY4JKUZs+h6ELRiiEWLR1BIISRkEKRpsUo8jDTpNBO/lmo0pgtT0liBCT+8JXfAg18G5rZYr2uicSqD1wmNmJNrgoKIJBhC6W3QU4S1Wj09gHHGVbhFjQgQjBI/v+tfw3qMLb9EHj9fXV/Bg+DTi/WGHu9s3wO4K9PqFuITwDhsGtgD6vkMIAV7jESClogFGQILMLyfZu2Zd5o2ln1jPWPljIJ/FMlsihGBSYTL5KgaEmH9TVgUrU1xfO9UqaheWXkT5iJzkyL9lAVaWMwxubPUZ4gaKIC6I6uDTmsfWpDHoqfRPzh4hnBOLdUhEgoPY2tdhorMFUGlAm9eD0XEZw0oQU/bPHIk3bESWvtogcIkIkbV3rQTLamUUiwiwV9dY0gapwMXcEpAKRawFsAgiPvIr0OGAw4dfwXFE8h266zfwV29lLx3utKvnidBz92GTTqsBTbJOGCEPKPvk9DUgdV9jmozLQ7XuTwVm/ZrSc8/+/Fy8PNlYPXisz9V7okw+0k+2aWfTPM9lTOHLRuOyXEtEfin/qO1cFWpcCBFVMRdKK8y02I5pfGfGYH2X4PQYL/eo6m1meFefKAz1lgnMpeQ50qjmqfCFZVarMiuMJ9LbBenC5MvDYQEWaLNHdnDaRjUX1mrZw0WJ7SQ9tfDtZJuo1gPkh6FztZCstY5Yhv2SZ1PouAIir8EpvgTFchqEYWnDQPA5UvfN+swUN0qJYgWQrZ6JBEUNpDisB2JCZMZ4uEPa32L/7icMHz/i8MuviHd7gIXxu3nRo+8Zb36I2H1/hc3f/RuEV2+A3UtQ6EEpwbuEEAD24pI0MYAojji52muYQNqO2Yk5NXob808hl6XNYwJGFoo+wrwF1ecKo5F2VlXV0J1c7RkJXwBp+n327Nw+4goJtjbOlDF0vKI3FpuqBQuM+XfOvomLgBhpkq8SOjQ0DBeY86MVQsYeLi2Hs8fMfJWwTSmJhU/PwCtHeOE7bPsOfecRgodzrDH1SAq83wIf+3MNzkBsnkxe8NLD85Vdlv8h98Ta2fSku2ZpkeWKy5GzhkCdbHq+CNZ5t6fO3YmrxGekjb56QcRvOp2+f/9i0pLQOSPBDNSBXNdTdbCezCIHtPybmk9kZNiYlwTTrDFmjaEVxgBz2eWEy0hUg3osXTxLMPJC2SkCdCIJf40WzqCnL6Cp1v4yIdcCumjO3/yuarDLet7wyTpOQTxta5oK360lNpaOcibgio5gc0NFZSmxaWXXjUwxdsLkAMY8/yr0yD5yUX8u5jfkr3qSu2dAFzNCqXeN/C4IDmtFnOtmDUQt6zMy4UCbjHRPhRGWz55HJHERxAwkhmNZu9t+A+88buIbHN51GMnOhrK3jZHMoMKwrfdahR+KUCrBNM+dUuIjQ+CnYsVkAo7EKQtbaoQzJbFe8RCLBh8CnPq3MZdRcn5QjjfBCRhTBPMB4zjCuwByPmsnSheEgewI4rKp9AZkbnlYtIE8ObCXs8k5h77rEXxAv+lmZw6zWHlETkCKSEkEHVmI6hggB+/UTuL6Rzj8gAAPcZ3jASa8fjvqHEc457F78QLBOQQvAgXuO0QwOEWEEfjhFSH0AX0f4Bxp/YWvbuev7hpBqDlJnIAYy4JlCQbuXF62SDDBrxOBj/NlHcCJ5UP1CSfxIUwIYVtg7URcEgJPLZ0AVpqgJgzEIgjg7PpI9gvL/WHab9qyuAozZjuLMIxJx6fAQCSupSzQdCPQQxIrHmJEBtgnMPVZGJZ0z1mdzu4G50SYRR5239XdW7qHtdcyj7oncpwY3SZMlSCBS2kjh3LchkwLFUaPBWRMTBp02sGRnbYEeF3dlLBnh//Pnzq87O/x9/t/Rvd9BF68Bvse/PJ3oOMHcUvygPRXgmZ9S09MU+3dv+YYE9/SA5MSNIbPFHm4nW2ap1FyWkCMFWe5CBfmBNq/Q8cd/v73r7A/OPzhX4BhXOM8LJ+EhUHLDYN4uU1eZ7ScSa01RCb+2t8LbpWagMsZrwWytmeOMbHc67N8mEtgV1qxWI5cTrs9pP7PIwu1NVkEQWuhRKduiwCUEFcrsK52oVo2dXVL631q3XDpWZzz1THZGvJhTt2yKSKapepsEsrcEMx1TUE2iSyuZOXi1DlRNAJATixU4Rg8HIExYrz5gGF/j7tf/oTh5iOOv/yKeH+AGxK86+D7LbxnvLl6h37n4P729+C3bzBevULXX8OFHiEQtu4jAiUkp/Hc2MExq/0B8DzYj41ZtU/rxIK7RyKMQtWUHGRLRV3tUj36p3bmqTNs5TdXi5IX8ly6t4hxeiM+YJPOglKnAmcm3qvv+Tcy/SHP6lgRtdsmLvXWXaibPHUwNj2az6vkK2uIJ68sOUcIwYOHDdLH77F5/QrbrsMmdOh8gPNR+Hw/XQG3G/C+ZS1nlspsqU4f/DXjZE+4yZoD7/KMM97tGRDWb5KnpWcRRPwWrRU+d7rYsmOqiXdh+hyKe2uwmzbM/EWFPU4YJqWs1T1rbFKAcxAzOctT+5mZPzYW1WVIRiMYxkLG2lFGj1PBRX6tnzVmtdj1M++XtZW0N7PBWETGVtudDdBKZhn8Ja2UUxor9Ri2mjYLtMoCvTUDLbczT9O2HpbOIRWSPI8A5rEoBIM813b7PBd9iGDFDvwJsj7LyQAqjWCu1n/dZpFPnYahWFBU2TMxKOsikof3VyiCiLbexlKCCJGVQa7PvO6mbb+F8wE//dzh5j4hbAnOU2Z+lnVCDSE/XX0W3Iozk1M0zwsRou5gUGnI1wM2E0xVlhg63d55MBKiI7V+jTCTbEPumIGYEtIxIboRITCChwRPViY9nMWZEMZDCQBm573Ay1QxJxxJ0K8uIHiPrusUUVOUPoloNWo9KSUkFUaQ+p4V/7gJgApG/DXgPMhvwBTEcgN6wTNAKYqrqN0V4BzYOSTnMAQvQp2UgC7iajOqAEKELBoTHBK1QYIsC96qLnrAxbTY6jEtTcO5qbLwgBJ2Tv/Up6jMuboegmssIeDqTbN84s0Fp9pavfBZx7gSPJWpYsX7TTAh2nFMan1DZa2lpFYQFjg902+Vj2xC0RQkQo4XkQcF+e5iYomDkUYQeTGkMLCS9blyTUCQeBKptGXLLlUEi2y3TK5Xn0Ug0Z5hukG1PhNe1PRfM/h5qzkUZQCdC65hlQoJjJED3g89UrzDDx9+xW57DY5HEUT0L0HpAD7cYOnqPXXSLdI4Z9Il9ZbMFyJYv3Xm9hT+z8E5e+YxW6tNzp4JnvOsLX+dabrOl/DMp1qLPGYc11gQU0jO1T3t12pfTlZ0wbrXO20u0Dpd+YpI4rxAghP4eAfvAn54+xJ3B8I//4lAcamPis9N2qn5X0WIMtWet7zl2Spdph2ePVdcjajglbWFBBtSZXjgueVmMKLs23UXQPWnWhUujuuJdcH1T8q05pOSIUHcPvpUR2pZ/xfmx2RsFy/dCe2z2rYUqjHvdnnNV1J5f9npkWNE6D/CXpiWlfXXrG02y1FgzYIIC8/zXiISfDe7ShVlouAIJlhMjhEJQByB4YB4+wHjzQccfv4Z+48fED/ego8jtq5HcAFhs4UPjBe7iO4lkN68Ab98jdRvkboe5AKCiwjYwxFnhRziovil6ixZOakZq4tGdFpieWOyYvoRonyTIPHNchwxEkUVp1CB0QorTra5lLj5WHr1oDKzbp3DJM9k5ekLLn+Z7qj2/VQgAUZr/ZCqOrmtduF3PWplC9nee+Th0lwcjAU/fkJTpg083qCnK/TeI3gH7zxE6c4BH7bA+00NsH6l5nRoYJ+ugyVEgNZW58PSg9HbT4HPnwTidC+nZ+ocfp4yU5ZqQZlwzvL+nP/Mtly1jHjC7HyziPiWnj/V3DzwkhLMbLMYorCUuPpHzvRUPlfaN5RlauUgvxV9IfHhjqrtoqhBi+dhA/6MwjtzBjQPaLbhpzzVh6W1knTm/bl38/dLCiVn0/SsPZFvTeK6JAh7mPl1uehLCZfrXULBJnTEvLqLWGBLPTqhHdVw/iYQTyjES6XTTVtV/cIIJfQuruE9uZXoNoh+C3HnwogpamwGAWd7fQ3ve/S3hMADnJ9vEDsKlFxAZrAyKoEY6f5W9mYUbYuaGOWqUwQTbJRA8ybo06sWzhFSYoxpBMFixDC8I/V0IzEMYhqlfdWiCsFpuYR4HHGEBGF2XoQJ3sn3Qgx4eLOYyEipMOe99yASIYjzDpuug/NeYkIAWeATEcEjshWEdISy+xsCwXkP5xy8D3AuwIUgAgoCQEnea3wKBjBGgbEPwuP3wvOHc3b4FgLCOSMii1s1p/0Qr0sOnAgpRYkBAHnmKKhcT9pyrgN5D/gOpLEfiByo6wG1iMjTqOPHcNlKibJPXtXorPbbHBmvzzkhnSzQNKfiYizFKOs31ZpLZZ7qWCp2xjtiGawqYDMI4KSackwGIZrg1o3gm3PwdE4RzCJcgo4zRYn54pyH41DGw9azrn8JiEhiiVTFyG42OAPQu9Hu3pTEpVmMSXadnR8W2wFVvBTbY8waFFuFS816ZiDJWCY1O+fEos2aogSL14D0EvODgaSkc0y4iR7/319f4m95j9dv/wS/ewl//RoIW9CLH8UqYrjHt/QXnn7rgptv6TeWLmR6ztgmNQOUm4esFnPlHqpYLNSUfiCoBMoMfr1TyRimbpZ9Cm/GTJmVZioM2se63pqDaEIHictXxykoAgKePCeIpTotw8F630GsI4hXtDArfooZUZyBFrNc9SO9p8v0TrTuq/7UOUQRb25t9eVcwU1pixOMLRjtPadchYSnB9BX9XC2uP/6MmtfrK3HmVBjIjgwl75LNCJpHwynXww/QBLlQCpxuQ9MTvBYUgUgEnrBESEQkDgixYhxf8Bw3GN49w7jxw84/PoLjjc3ON7eg4cjNhTgtj12mx28Dxg3O8An3F+/xnAdEF68gLu6QvAevXPYdQ69ZzgfABI8yrFG6yKhZ8TitB3th6elkoXWZJaxTkwYyWFUNNxw9HqtJMWCaVpPU7PS6w0DZQGm6ZqbKJi1cNafXJP5EzCqg2LhKMj10KzgpC57XgWatr8m/gOXGA950RVL7Ky4lctNrCJQ1bMGz1Ki6ux/dLKDVfZPCAFd32OHLV7RDtfbLXZ9j5eB8dLvEX7aAbc9+K5mKVeDTEDRnnwEZFPByCPSyavuOSTEj61jVm5pcWLynqqiJ8quVlXv0nP5p3yccu+t1fnQ9CRBxPTQ/0sxdZ6dR89R14Rx+KmsSC5V3HuutMoIrRHwfPEsZ6uP2UX4q3um/PGEcVozfXQtKmJShAs67iRMrvw4Cybs4J104VT3pj+qPTAvzyfe6fvZi3LgrNW19PN0eirx8ZhCy3XM8I3M0ltqd2FE60VzUbIQtAZW5fNzVvf6us1tZ9guy1c9XSVUOC/s9Ul96Pae7dPMbLQHynSeuY0qvwe3wRh62DodxyjMVE3O93DdBhxGEUKcPYzUTUE5HFHPjBRNGkiXVFseGUdiKJEqG74KNF+gB9p1w0kYtOQl1oMjEm0eRQbGfNiQxk4WP//ClI1InOCZQFFMVaMjdPCQ+NK6V52eLYr0mqWDc2J55b3Pn957eCeBrpmAlIrGS9Fj1/FVzSz77p0IGpx38N4Y9wxQQvBiqdEFWd+DzmvnGE77rUMK0aNXGAkNC6bxDKfjkGM9aMB0C9xH5JV/LsGl4TxAHuSCCCGcB8iBfAeAxAVTPaEAcuDqyVmMal6y1UF1UjRg1pLvfHdwdtvFnJBi64+V8n2SstBC7gvR9icNEC0tamyIPL/lHqthy0YBjtQdlGQWAXpEcQ8FNZgg9VRGEAsg0YADi/svmdtyv5VzonQ1x4cwmFjaZY2tIm23weoJ2h1jDCkxlHJ5iFsDJaYs2B6rIKIZaiWykv4xbK3oJCUpN5DHwBu820fc3nzEljx2u2uRkPlrIB6BYd/0b44OPzCtnEfN2slZ7fyZtPYXguNenH4D/b0Uwq+/J7/d1N7aTyvz0HmangvrbkUfBt3FuZf2CKNY8pmGEZlVJHLQ3LaaNbiVRiHAe4L3QIzVuZ+/6h2mAgxjcMh1WO6LJWuIScMt/bba7eUYEdVtiNlpXT+ysThBrK7xUXLbylwsigCGM00Ib31q9GirZrYs6MjCFHuv4zh1Z7QmjPjcqbh+BKajNlceK3fhHGuWUc/zWa3Vc3uCK3r7XGyIAgpNfq/mXPwqKIbe19nNTJXB1jsXy4jl2tXEVcuz4dvmmkldMTk10iVKwBjBcUQ87DHc3eDw4R2O737F8df3GG9vkcYEpISw2SH4Dn3fw/uAFDzYE4Zug9T3cP0G6Dt4tbQIjhGC8SkKLWg9c1RbX18+tsudp/zvrEZFBxOLS14mw6+1BKHgwXkvTelNXvy6AvElmaoFPUU+J8Uv3Y9TcGn6gJfrNQS5aV8/06RczquDWufPiHbdr2re17px6hg/9frksNRntymVOQTv0IeAreuwCR5d8OgJ6FOEu+1A77ZYEpC3V8lkb56Fbbp+TxddS2vFGpLgxJ14CRo8q+MM7TBr+xSfZPJ7rd75mcvLnc9bZX76t8Wrm5J0TdjVunJvPiZ9s4g4kS67Rv9607lFWCNyqy+BfMrONdO5rHu2c51LMNrpgUVSR82cyt/1i1N/5M5JTtO65Um+Sc3nH16yWKaVzw6qpUKFaDjFiJkoFK2DsPbwIefJUt8fsFNq5Giq1UI0BeZ0vc7NL761xNNJygfqWv5Lbh+crmS1nK3OelaLcG0VkVt9uiy+yfXw5Pck98yFU3mRP5xL6NNHpHCF6HdwiIgpou87kPP4x/eED3cDjjHmOjNZyBAGdqV1bvS5cx4McUGUCSMHEIuWXTLhAafsw19c5ziAkropYkXQnQajTkr4C/DJeziXMCZAXDWNxhuABwFBgleHMSGxCCfABE4JREAIHqNi5PIJDAdhzHZB4ikE7zT+g1chgWlgiX/XzUYsA8QyQlw7EZBhrefV8FUAIOfgSU0Y9JkPQQJHu6AxK8Qawqm5eB8ATwxHKihyesamAWJmznqmihAkpahna1IZgmhf+spPkNoZYEyxPZd9D4DgyMu68iJwgFPrBqca/mTPO+0vTc6eavVRwVtdReCUYaoywMZF4JOxU7hJ1lSK4tpqGI66psxNWzKyU2olG3OUesmEldppKuvNwJbmzS2VvM87KiOcCcwjxnGAuBuLAGyNiBCJ2GJDOA1aTgJjCpnIt31TRozFJZOdGwwVrJi1AqtrLxECWD/NBRURRAhCGluJOVtHtOeBCTDMAmLUutS9llCp4DSCOeo+B8zptAhBpB1GQhqP+PUQ8P/4rxG/f/sR/2sIcP0VqN+B+hegsAUdPgLDHc6lb3jat/QtfUufJwkNIbgHsISfTX3gr9Z0gnltrv2squ2G8O//gXB7x/jv/0QYY9v2tJZiiQBIjCJhtJ4SRMzcsGIS5NraOck4eUCqhBFT64l5VrljLOZgFoCwBSq+kIx5AOy1wKOxjMi/KeOsjNPz2aQpI/VZ07K19WJLi2OxkHNR2HY5nbaW5kKIS+pZyWO425S2qeln5krxaUILMYQu817wdFWc8T5UeBcDSIjjgONwwOH+Dre3HzH+8hOGdz9j+HCPeHcAJcAhoL8K8J3D1nUSmw0dHAN8/APGbsTt9Vu4Fzvs+h59v8Hb6x1ebgNe00cEwwMBBJjboyhuWzlqP/wzLCGz/2ot1s2CN8aEgd+h6/47en6PdMyqLMjaTMnwz1U2RjvmT0HYpuv1PKmsbVb4+8k9utCRJRol/+ZSn1kyZOtihTcrCKW2C1MLilpA8cS0csKX6itaiuxKm5QkpQk6TnjjgNfdFi/6LX646vHdlnH9/grhdgu6D8uN5ulWGuAZ+vWYtLouP1c60fiSwPehVecpXRRKrNd59s48k+G5hBHPEyNiXcQs6eThcGkrl3Z2csmclFDpP2tVf8LVO7WMmFlKrC3IrKmnP8+0sp5o4UBaKUZrLy5Mq+vDkLj6/cKiyYezaZHzIoxFCEGtEMKe6XwLr672IzkxJ3zMnJ8rsySEmGnrnBiq/O959vhZ8Jcy0Hrb69XoWiT7p3r3iDEsRNND67qssVmuM8XO1lrf6Q8fvEkLxrzkxeXdFqWM3zTPF2mFjJ3r74VzsaqruVTyPaZadcQAokTacEGD0BLgepD3uDkccLs/ZOR5yY+x4FzqzkmZ0eJ7tWilU4bZ3N7oyKgQoQGaWiJUqpQ9LpYUsmMk1gHBsQTVNdc1ZkVBIA1L4OCSCTsrMtyRhO5wLEGpGeKKJgFAVAYuEJxD6kQg4Cp//+IOKahVhLlQcm1f9CP3t8ysxpXweQy9E9dM5Mxtg9EE8sUDjXWDswBtKrThJKclk7osysG+WV1VGeVFeT0yF2azaGMpg94F+e4CTABhgZqln2YhYfmMsV+fatNFT/Y/8tlYZjmf9/UeknGjgvy3K08tIiKYozLkdaSp1OJsDeVfNcPg/B5vGCK5S5zfpTzWCYSk61dTIsBFpGRou609mbvsxqIhFwt4nBePEENi2ZGyoMn2Xi6d7L322ZHEv2ANpI28XEozbAHKS5wNi6/EMBhEYGjw1NqIRZFMxmJIhI9Hj5d3A4b7OwQK8N0W5ALgO7AKIfJx+cjrWRs9/Xrh2Vm/88+YfgsWxaeYpl9tG2vlPsOcfkvPmM4p8nzKtqo2zzGbG7oj49Xz+grOcnpd23nvHOP1K8NTGIhLZ1Zh0sPqZ7mVjGkPWt5jU/dIa2TZ5Eq4gPluVoxrgoZpjYtVIF/UbDgwZ/ykDsx8ipY6xcNcbrPUnS0fUJE7hnTW77NABWcYTAXne2oq1hA1xnFhWoBvja4p2crYT6sCoVmDlzS//nteRwMq1zkLLrXUspGW2Y3X4rwQBPuqLHiduuSEWYKOiOOA4bDH/v4W+48fMH54h/HXXxDvRqRDRBc2cCGg6wJCH9A5jwAHigziCKSPSBwxbH6A33SiWOQ9tp3HJhA6PsAlB/I9KIemNrtli8glCk2r2vIPTHlJG2ppJAMzEg5w7j087ctYTktTwXOfDszanqnTZCE0KPFDYeDJ51JdPMvSVjE9XGyh2WDq81QP7gIMzZqeAbMMds68dpauwW6043THyFkmrsAcPAgbBOx8jz4EbAJh6xnhEOA+bqfArqSamlt7O/m1dAd9inSm7kuov7l8c3qwrTc1vysuuBPnVbfwZn7a9E1VYHafL87CmbbreX3c3v9NWEQ8bP0tHAYna17b4Pb8co3r50gN+2l2R04P55WRofbNcg9PXdkrWU+00WSfnq8PSVRYVCnVWp2GZC3UrEyprMVaMw+JREtaD1vKDXzeeT2fFo+nC5992bRCZ00yXFjXQ/JemofqX1Ni9vL2pomp2qMPZpKsMFvyoV4j+UvI8tNSLY8wXEn2betAlQBlQAMxXIO7azjyovXvAYbD//HziF9v7xETxM0Q7BwrmllcaoPEC0hIEM0ji4MgrmESQAxKDp4CmMTyQdzpcDOftckyIPxts0qIAwNIcN5iwHj1+y9nShwjOIk1goNofVACNsEjJgaNMddu4+PA8HqOJGfOrAhDSkACUkwYnIPzQEoeXdjCOwcXAhyJWasIDwSmqJYesfLNn1JCihGIRvBKwGjvHHzw2nUCnDMHQQAkdoAjQvBiIcEaDyNfcdoEORWOJOF7A+L/lS1WjtN/nAgS2NRkCDqfYtHCiUuwaSfzSC4AahEiMAq0SWN3OKea86p+Q86IHrkwEnPesEUDjQCqtb5sBKjsuWqfmCVAuYSUUZESEEek4U7cc6WxMIiIhOAkEmsOAGRWEE7vC2f5pqQBy0HAth6BZASZ+bZOYoHBaUTiEYxR5pqjzJwjkMXlSAniIEzITXIeDj4L7xLbPClsKjRLJjxQwQO4WLhwSkjjKFYT2ZWaCdMq12pOtABNYJNHnHQMkllssdJV0k9PGlK+nsu8rhlQd2NaBcZUiMY4ROzTDW7DiD/8dIM3r45463pQ34O6DuqiOA+7y8ScrWdZn4llvxaHi9/St/QtfUvPl+S6qOMaIBPy88zmVoVy3mkgaKvzJIVKBOIId/ML4Hrw1Ut4E/A7aJwig8ME3FoziwKAsDUSODkktYR0E7qWSF29EMFlybS5kVoCuMW9TJDNCWptqcx48TWojGmGWTQArtBzBLF+NXZPrTBBpHGHUPKZUsVsNJ30v+IIXcQUzZdTvspheIMiwBPhSUWH23isMJBmJPsqOOfgXKfonySEWIDiEhbDOQ7DMjl0pgx07VR5C91gSL8OaOX2JqMngCjBJMHFyLIoDsGGj7KunyTlgjWhIea8BE+DC15QZyeWpMfxgLS/x3jzHsPNRxx++RnDzS2OH96DjgnuAPR+A79z6DY9fBcQuqAW3x4DJ9zf/2cc4kf89CIgbrd48+oVXr56gx+vXuHtbou3fsQGSZWWCB4MolS5ctPdbZvyKZOtFYib0II7MXswEiKAgYE9E4bkEeERYTSBK+dCmsxRNYPZLti2RfZgwGWRUHnUZD53OOYyBZ/MDxfXsBLsiSZLkRc2au5YVWd15jCqhdVQihVg9VrWzqSmo+15mjeftEV1VXW7VXV1ooVvdTJyqAy3KbEpTZFaGidB6Omw6eGGHej299i9/A5Xu616AXCFTpo1VoCbjsxaqkm8dSx+oePtkbEMz0XpyZtJWn9k840wok4PBovy3quVIE5ZSORr7IK614CSOh7X+YsFEadYX88V+Gq5vedZHIvpoov7cvnurP8XFFytnRcWRkYQ56Wb+ZkUPD0r5dCeIcpT0E7jERVsD5iz2ZqpEUw9/FUbdK1WiwPRaMhS5XqJKGsKyyuaVrD244Fp7cgtl1xu+iIE7wJoPqMW5Wn29/RWXM773NBedOacyvMEgJ6miUILFdR7mM9crHPE72GpIpYMHGKkNFl/Rm0DcC4ghq20TIyYRECwHxLuD0OOfYA0FWc0FWp5h5RJz3bPCrNa/eMrIz5lZM8pwT3pvqo5OSflkiO45DQoNcR6IyEHrQaKib9ofpC2zyUusdI7mciBnTXlvmPpLjgxyAEhRYzRqyWG9M+RUyavU9dRwoEvLGHoUcfqPidlxrOTwVKXT6Rwt52viTURtjokxIpArRm0ks9Yw6nxiwu1sHD53OQKK2SSkWIkDUotGllQzbHikkkFEWVhadNGhFRtEmOqdu/s7M5gaV018Z+RrWoodI1I1mJjaGMLTuAoFhFIYtqeBRo6tjVhawKK9vwo+Wzs5bUw4ht6RokOEXyogECiP2e3RUwJjr0wbOw8UBdPQjCV+5AtYiGo0E62dqz+/GfxPDQmhsWHMOGAjpfFTMm9Iw1CnsoOZqeWSUr8N1qREAZNUf6y9nX9J7Wg0LGTPBaLQlw0xcg4jhEf7yP6bo9XwxHkPSioSy/nka08qume30j69hPcib8Fa4XPQX59jnG4WJN2vYJLG1p/94mtJZ5lFGcqeJe1uYy6Pwyi51wFMz7CxUC0/V+jJE5ZNT14PT9yXRi2tkIdnGsUGA+AYxC9bO9Fq4GARmLADGQXRlANfb1ruaU7m5gHWGFIVItnqR+mfZktHwBRClCcqii+PMAaor2YYAIBZJRhXs80eLZVcm7auPprEYulDk8eVPkp30F1nw2dn7qQMphr0n5Ji3VtUMqabsb0kiX6rOcbLX6d7ux2u07pjHnxor6gfzRpx5Af+71Kc2r7htxNBYmEggcSqWKIbTERQqQ4Ih33GPd3ONx8xPjhPY7v3yHe3iHdfIRPHVzqEDqPLgT0QawcLAbbMQEDJ3wYb3Ebb/DRvQFCwNu+R9hssO16bH2HjhICMYg0QLatX9jeqkZJ+//UO7k4WiqnVL0fIgMRlJ2YXnJizfGylRz1ObYYSHrhfLBH9fwvrn/G+maoJn9afgbzQh22hovk8nT++t3ZrffAvfzY1IC+PK9kcQjHDh1eoPdbBO/hnZ/RoU+GdaLktb6sJ/fcQqHLV+j0DllLnxYfzBA0IJT7ePW8PsFzrihkHZq51WDef3xChEDt+2VsS9489iT6TVhEfEuPSA0j8zHlnw2SB7db/FoLk2QxKFO+x9TFEilRYZo81P7Bvn/OvuR06WB+OWbHb4DP8nWmJwzcSfkI0elVcwrHuqhtadz2ltN9Y/GDmdMsryhjF2T4Zhhwsx8QOQliApj7eNSkbmEISDlocGZnGiUCiexRsTsAuRIYt3gJml+krGVLcHqN+aLCS3kuFhbOpaz15/U9osY70NgTTt1EBVKBhZ5BLiFfyKxQgmBKeMKshYhIhmFESoRwt0fXB4TrndTrJM4DOXVxpLEWRJuckeKIGBPGcchxcMwiQsyzLRh0RSwwA4ggdfuUOArjOZMXIlhIfiNaXs6DnYPzQeY7Cw2oICX5rCSdc32eUmakQ4l9YRSb9YBYE8C3WjIZNawF3fZPzRSpzuosDWoXrc4x5b1Dk/dc16lrO7ESknGsmOwSW4QM5nxHANnlFExoJq1MbeiK+6IiUJuRLzqvKUXEcQDHlGOh1DmZVIPPhCOZ2KRaCqauwDhbk3CcCCASAxCrGonDIEKIFMXKAqlmzpibKLW/SIQYRwWt4A9O49nUQbxLBwFGykwWm5MiVBNhBwEIGjhdtKhkhYpwBPj1Frg9EH734R1cGvH6u7/Fy9c/gMJruP410t1P4OE2z4xYyZhAjWWP41v6lr6lb+nrTQtstbOJAYwuAZ5BTmLskKoWtPxxAthVmJHcBYamZMxJz/ApNTQ7P7MgYXqXq/UqqTJHKjiZCQDkjNZznmvc7XSSeqtxOim0eMxonmjbhByw8YHeMWuM1CVYymfheXNh5uizKS5bC8saZYYmtQ8XhRCfOM2YjzM+2BTrv6S+isbI2GJr21jjc6Uw16gaCAwPtaLhgpNnnkBiUGKYIgypZZHkcQD1gAOSA5gjUrxFGgaM9x8Q7+8w/PILhptb7H/6BfFwRNwfQOTgww4hdOi6gKvQY+sDAjwcO8S7/47D+B7/OTJ+Zsavxz1Gt8Xvt2/x4voVvnvzGm/evMBu16PfBPjA8E7drymuXyuIPv9MC+ZWYZzNmCcwIgERjFHj40WjLZ53+12ezrV5Ei6hB9v3PCmzMNIPYuEUWsdonFmeTOCdqnyylx471sacn5yl5hrZTqGGwHHi/jeEgE2/wRXt8Kp7gd1mixACnHe6Rr9h3V93unSTnsm3fik9S7pYENF6rL5w8T0C7i/FKl5LJ32BTjbhNG8tOaq1I54I0GJFsxgTJ+CapnWNoWn/puVWYHtQoYV8tQXEqfGvhRAZc0RmHi19noThK0pnIfza+/BsC345LV6An3tM6IJ5OlPB+nY4zVjjKUHwmLSyN82ncHkuprjmUsiEe2Nk3B1GpEjVfPA6bkVUackBEjwxVXkFSRT6VQaXQerX2IiGJDhchjVlZmTDNHZeCW4TMABJLSTYNP5V+AFuNa2JVJxBIggAqwVAsrNkilwqC1orMN/5Y4ygUdxNsdmB69iVWB02VsWnfw7IDRQl+Xyyt4yBMm4Qdz05pobTtmTu4EP1SSVgtNP3tpiptFOEE/Jb7FxUCIGWoCv5lahroZv80tFuEP8KhEkPaxyI6rctpdp+2k8Vast9wnkuKHE21c9raWFP0eRz1ggXxg6jxDsygUgyq4OURKjFZqmi9zVTNgiRUeGF1urdqO/VVYVZP4BLjBVjpnBiFUyVWBE2f3ls8rrTZ7q2zdd121RavI5TMrhhE5jvb4YoFjhy+Xcm1nIexhAJYyJ8pBG/fLhBt7vH1dWA4HeA7yS+iPMAx8zIyeNUB/n4K05fgifwJdK3qf7y6YustQfilBUrSIt92pVD+R5p76dGsNwWUADPj2YiiPs+iGXktpNy8VhR5gwUf6GFpmuY+5VVgZ3Ts4DBSwBUIJaYCYqfVfXU9ckdWM8CTT4fkGaTWa6/1eoIOZB1248z9PAl8CnN2eBxoAyQ1FDf5ZwRmTVhBGDPzsP45HQBYymv5wdWvVxrqWW6DdvA7vUfqnGcVsdlKTXbjQqOYQKICouzeHGA4q1UtZddpoobzfG4Rxr2GD9+QLq7w/jhPeLtHeLNDVJMwMBwnUfwGguiC/CmLR4TkEYchnt8GG7x5zHhz4lxRx1AAeh3CNsdtv0G265D5x06p7C5ZSz/U6V69OuzxPA1E0jU7HmeFUDz4+mr9xxz/rHln1q85VO1B2P1c+E7EWYx19of5TtNn527I9YWS3UnZXAy+SXrviKnUa8G5wieCMGRWPl0HUKQNe7Yg44Qd05PSg/D3afXwHPxfGb1Lrx7rjS3475grV7azyWa+OJyS3dCVWF1f9XpOeQT3ywivqV5+oIUrWhmalCmyj2EJUM2amS/xIBwMJ93WfCQtXvxbIfWp0tfO3zf0jytbZZPTPQa4/fR5QEmglvYY4UZrUzWsANv34DgEEAIwcMHjw+/JPxycxSXNC7zQ5GJKiyMTgbbGLDiokk4/WJrAAjRLbz7JFpKLPEZEgPO/CVpU2JBpWSx1u2DVyVxBYoYjhJi9AAi2DmkpF6SkFRT3JA2FJdOzEjkQJyyMEPqSwUAJ3EWjOGQOIIjsD8eEdOI7aEDM9B3GlWiillTE6spsf7FPFBiY2F++1OOs+B8UCECADgwdYgUQK4TBNIF0fjyHYgckgoenAkmnFf6q5yZgDCiC+PEyBCzeGDAmPioFGhmSOxaarEktvHjasVkwpIysZ9xJGP0ExabyhBXBAJnl0RRrAei6XPpn7Zh/k4t8HeeW3BZG84WuGZIpQ+2zosL2ML8T2lEihHjeBRBUxwEXgLEKRjn9Z4DmUMoUoNVBimVucmdjSBOIpDLnyyup1JEikNZU3lc1FKhzIB2h7Pv5dLL4hIsmdCjOntqfoZr5oQ1BotaRlACpRL8e+q9O6WEyCN+RsDHf/X4h8PPCJHx6vu/wfblG7ir1wCugdufgeEeRj3Va+irv96/pW/pW/rLSjRnLOhj/bJ8KF1qIWCVsU9glxCI8HJL+F/+PuH9TcL//t8TRkN/QHJXW0DqSTWsCI8J5cECeyNEMJi5OlB5fri2wog1sKWM+aq2ai7pdqHXSI/3wvAvAgCaFzpVN09/nhNIWJ1FWYCsPygqA009TQdp0m9DlNVNVmlF4FG8IePHF66P2VqqGJ9t3bOCq5MxE0IsruPyrFZEyprXXIb85NXMpTzDT/KqpSjM+rSaZsrFFR1QHE5xG7OpKHiqFvYe5BxYrWHHJGx2z3twHHF/9w7j/h77n/8VfHeP9NOvwGEA7g5gZngm9L6Hf9Gj7wI2fQfvO3gfEJPDPgK3h/+GD/uf8H8c9/jzGPHzfcIhAdvvXmLz4gr93/0Ndj+8wZuX3+H7qy1+6EdsQ0LwPYJX3L/BQ+vP+fg/LVH+JBT8n1ktvJkxcoJGGZPxPtf0dF1dspTrbmYU/pHMqDX4TlW3eH6sjX0D5HI9pF9YTuaCf6e2rBAt+eds2h8Eb/1e13/mlVE5F4iyYmGhvYwGFBfGIQRsHfCjd7j2G7zc7XC13WCz7dG/2yK82wDRXQZr27NHps+P4NPCt8enx63lS+/MeUE0a0qW5IJ7prVCzwrM6fQoQcQp7fu/pjRFFC7RuFlT6pkpJz+yolb747IFM43xUUqdnue16msk4YLGq3ITX9Not0TW1a2EEMaYMncd2R2TZJx8nza5vBHbfGub9fwcPiZ9yR3VaPMuPJ+mJUSepr8mGkMXIaanYFzaY1+QA7WOGp5G8Gv//Q9to23n8UlorGqxG8VEJBrIuv7Zd4Dvhcxl4BgZwyCxIcbMMycg680swN1ojxSqbrrSWu1vgYWzGom6bpJodFILS/yXlBG9QkARGfli687l/uWzAoAEXpO+FwKzWFhIVAQCWDSWkrmBmdB+036nxIiRMcYRLjrElBQRIHNMI3iqaeuj4KT1kjY4iNrA0M4HJNP68p0ENnYdQA6kggoK8tuRBZB25TMLICg32CpzEop2pQ2m02CUfHYRru6NyaKfrgGbvNYKZM54qN0BrUJgA5oJAGTYC5Gdj6eFDlTrNNnKre4mZl17dZFUPpnFTVKKsBgN2b0RA0QJzGIpZHDmPZB/Q+OlaAO1RQ5bgOqYBRAAi/CE1W2G5rG+Z0YUuHJ76Cq4oe3K/CcLMGoWERoslNDQT0hcLR62uuXTYqZgOlY28FpRZMIQHe6PA25vb9Bfv0a/HeC2HvBezqI0gpLT4bHxOkeVfUun0teAya/N3lnYfoMSqBav/ZY+ZbLxfcrpcFkdcydG8rXcafncRMUUOLt+S6vEgCdC3zOOPsGnKAJfAhiuinWkuFQ+Fjm3b5gUGOJWcEL/tU2XcufgrC0i8ifNLQBK3LEHCGOmbUHrViFBRlP0M7cPe8fNXbWMndRBqTOCWb1rfhYY7P7K7y9h1kzqrIG/cKW27pyqIOr5n6rWlamdSiuMVq6qmOGGy32pvpHg5YI+POyko8kngEaLvMbZStXV/oKOi46pqjWVfhHEcjjjIxAljZQQx3vE8Yjh5gPG/T3G9x/B93vg9h4YI2iMIHLwPqgrpg59COh8gKcEn44YIrCPwE26xwd/j1uXcPCA6wkhEVwf4Dc9NrsttrsdNl2Pje/QuYSOWGNZmgjl1KljE7w8pvM4mFPcuap5YbCZHNgFpOSRIIKIaJbdq4mbj2dJPPlyCklYfPeU05/bz9U9XfZdtQMX6pnWwdUftGT7/uzuWepec/VM10H50vAiaFLOiXKWg0fHvcaGcGK54wEfPegQzgB2BvqV4+ASPupajsmMPeDEWZ65kuf8+lnnh5+G5lEWElZ2pUmum+T2ayuMmMBIwILZzidP3ywivtI0Z7s8poavLK3smswMyZo63CJVdmhm5Kp1yUTqC7IEWq02d27y0vG4JN+nGNvfOjm6dNhOx2ntQP6t9/3TpXXUh09cfJfXa5cSW62cQGEHXP0IBiNGkTRwGtCFDl3f4X/7p1v8059vxRJBK1sMJt8gkdzIpOQJYaoZLYIGgE3zekqaEEDwyD7hHQNMWUs/qT96qt0DsbUEeCdIfqIE58TagFkIAOFrcr7FHVH2xU9gsBMCy7I46DnFE/hUwMEpYeSEu/sDhjGi8w4heISuV7CUNZvECiylpNYlqtnlnPqLDfBhA7/dwYce3gdQCCJsgAfg4H0Hcg7OmQsmETC44OvRm6Bb1J7JE2S0fsyABvA2U956/ckYqM5aQQZ1bDgjve0KKcvDFkaBi5rfQKOSWHKgdoIwrZwZmcFPLJp11kWHStDU3BGpksmpv20ucNWIrvUvGXOfGWB1HQYGNGB4ihGJE2I8Sr4UM8UuAiYGs1g/gDTQeSJxHZUAICE1QbMpdzAlCb4dxxHIgg7ZP0kFFFkQUwkDOcW856W+lO9ecM4l65zEnZrVnUvRyvTZnMhwyLixxlxhCEywIXDwThhpAkbEmCJu9yP++68HDM6DwHj53RtsrnaI1z+AeQRufgWGAyxQdrPfv6Vv6Vv6lj5BOmvJMLMcyN/KgyVhxKk2ATh1K9klwKeE7nDA7jDi6jDiyEB0DtF5RPRgckgUKi/7tfvLysWKKUY4nvWNKmY6K9zZ9d/03cL4NEKHSluezzA5SBkhIlxg1YCnfE0VQXg9PrVQgtWVp4HIbeWLY/0UZuWl6dO1UbsEM5yyZmiuUQnTmWDF0YitvkfAglJW8BlzNXW6MlsrszbZ8LQpnDrHVcslJhrgWfaLrG/V9HaCAIrwLSEd78ExIt7fIx4PuPvlHxH39xh++gAcRuDDXUZ8yXnQ1Q6d+szvvcfWi7KWYyDd/Qvub/+E/4YRf+QRux8TXrwO+IeB8W8Tg/uASA7/zNfA7hV+//YVfvfqFd5eXePltkcf9giO1fd+7ep2YYyt/8+VMiJXrQjfYdy+wmEPpETYj0fcjvcSD1CVl2KzlFfW9anl/nQm1wWNPLVswYlPlcuYuaHmFY4OxcdbPDwJbp+muDmX+BG5qdkpe6YfNW1U/+bmN6r90mwyArx32PQdQtzB7/8tdi9eY9d1eLUB3oYjere9YO7+Evg6E5pr9vaSPn5+xn7bvB2Up/COKYyfd+6eJIiYWkac1KxYrwRayWKdD4bpkRoWlp7Vj2iNCE3qfSKY84qeAe4ydhNYVzbRSQlgruoEXPUgZCGE1kzz9dRYRBiCqpqzWYO2ep7hnIAwZaCsgbmU71SXHjsFD1rrn0H77yEWEI9LD8dATu7Lc5vpM2pMnkMZni2wHD/PfGQBHwuzES4guS7HWKhNcO+OEeORcHOfMMRY9a3+psKFzLDk2fxkuqSydJD/zWzdVQQn5Ruhzovqqa3YhkmqRFBhqRZIiaBWFA5EIrhIDmoCrqUZwmwnUjc2lbWEaiwRUq6vLOnSV2s5pgQ3RgzjqH0fy7VvuCqXoI4iTCAlSsQHre96uG4H33XwoQM5tXiAV0IpiNslc7mkFg8l2OTZlTl5NkW0i7DKxrzUIwTePAZcNfaz6hfWbq11SZMWCI8gkHnlb+XdjGBOZZUpkwOFw1HmT037OZlFgQnS67qlLIGzFVJxKUiqpdcSDlbW6iy4BNQtFBdLC/GDlANhp6lQf6aJtTBWU/pnKasJzxSQ+p6uBY3yu4wf5y5YrApq5rgZ98QYIuPjPuLl7Q1e7XbYvbxGn3YgF2Qvhk7qGgaItMMVgB99Dz8+Pcep/pdAtj0lXdz/z3iff9Xp0drkXy59EnJ8DVF/TFWPKrFMINRM2VNLdg23rXFFQy14PADRgeKIDY141R+xHx1u1EVGcgkMB3bTvhhOZliMfGdqLTOnWvYVMDm215oQYrFPbPZ9hgCYFYAJ4FGeV1gGyuNM69WuoLKgxD5qAQh4HhtiUuUy0Gc6tZQeoD3aWMBwGY+1dtdjN7ZrplknioyejjCXS7a5bC4KCobH7IhpmgnjMO9T7dqpGZCFshmyiiFv2BUZnqj4lAnCmAgg0ejnOIJjxLi/BQ8DxptbjMcDhg8fEPd7pLt70BDhYhJc34sgwgePEDy60EnMKxcA3mPkPY6be9xijwEDGAn9C4/tdcAmApwI0TtECtimHthtsO07bDqPnQO2LsErDujWujwby7WxpumD9ufp4lVyYPK6vyIYCTErfShNMV37M1zx0rYec26vlOHJ+XGy7rV3FY1QkwwPgvMMzcHV71pAkbPq2fgQ5tMiTYWFBWV7vMXBGeWuckToCeioQ+936P0GIUgcE09G9z7Som21Cw85a5bo16ek022fPAufC6HKXZhfCA9FcWZ3x+RIZWDhDrF7+BPhaSfSN4uISVoK3vUtfYLExS2ExYLIGtYAhMlRI0WtFQTIhA5ONYiBbA3xwOn73NO9zOj/cmvu23L/K0tck2gVcuQ34N33gPNILFr6MUY45xCCw3/9+Yg//PldQwgukaRZIFBbTNT5jP7S/ZtcKUhs/vvFtZHgZmoBQVU9SQnPKX9WmcISB4GyH39jDDsnPpSd5youhNWTzKNNYW46gCOBUlRtPg3aTA48AqYJz1TY1lMEOI6i/XJ7ewfvHbquhyMHb8ggSJpyHo6cmG/7DmGzQwgd+r4DumtQdwUXgpjM+qDB9hrSpeGlMwB2agmSzEj9hPhqpvnDqKULNcKqJ7I+0VgGqo1op3iqUBq2MbZ2ykfFf68ZOOcOpQnBWqVcnSLyRaAt0S6atW8xEdTdEBcgNbB5VWPdFFNeU8mEAs341QIAgiOP4OW1xDghNcMHLE6Hc0LwOu9AkLnN9IpqtTKsT7LaklpCxHEULT+NgWF9FouJmlzXEVYN1zSZVR0oGVm2MWnZVzlotWvdI5X5dHlflNUCxKTBsRNnYgdsHnM5zygR8P7e491dwvDxX4G7n7HZ9NiEDfxug+AD4tVrII3Ah59Ag+5VAECcrYdv6S8ofUNWvqWvLtHsW5GnP8d6Jbkz0oh4+FeAAjbc43U34P/+tx/x51uP//efdjggYWRhHiY4EAiudpenZ7TxwpNLoKQYgZszhy3ZUwcUV5755TmWheJXVD6njPPaVaHcPSqU4KzWkum+xvKh5Gz5+mcYZFZuwmVcz08AqjbBUHxh3s/zdbmqvydwmIqvOA0CPs97Trv1VMfqUhOErKBCD0gF32vrnrRFrROagoW093dbrv7uYDgoOcOXIoAEZ7EiyEEjPwtDPY5IccRw+w5pv8f9T39EvL/D/udfkY5HxPf3EqeLhafQba/gnUPXe3jnsAkOznUI3uPIHjfRY+x/wfj6v4BeArs3Hv+QAv4+JThPcK7gVx8/djgOW/wQ3sBdf48Xr67w4kWHv+nvcO0cgt8geKdeHWwc186O57sDqZInFDedhn/LWo2RwQlwKMGLjVFu0Q4enSbdNDx1ia5sC11S9yTflLap89TKOoZ0c10Hl2e5ioSCl9fueus67TMJrVFbQMz+VKEImn+h1w+Z+XK8TM6Oiq+WfwMZ+XbBYUPAD56wCzu8vbrGq6sdrjdb9F2Ec+M3HumDu395gfnp/aQdVlWcGSgzPkCJ+fRlhBGXCyKWoMr3FVc/L5OSzRZyfQZWdVaP5iA9gwbMJfVeuukeZRHyG06XaWQvHJ+1dqd+rx8BmFxO5aCcCyFaJx3tt9NwXjpNJ7WZHoMUPGl9rI35glnrJ06Na5a1caDpz8cC+di9XmP0j6ziXP1PKX1C66muffHts5x/4g8UPkgcCC8axykZUgTcHxLu7xJu9wljTBK8drLYuEbA2upPJAKoIEnC8yVBwkhNFMz1Ekoe8VNaAj1TJlQtg/kGrnY+Nx8Q5rAD1Ec/iMFwmQjgbPVASM7cMMkV7ZjglOAVDSxDROeXu6XEwBjV9RVFOJekDRLNeGIhnLxaP/iwQaeCCN9vgLAFfC9ManIgL5YQ0PPQ1kIVvlfxjpoRARWm1INymvmAE1snt8FVjrxguUF8pk0Kfl5ZVxDyeM8MA3JjK1BWfIy1flQrDJkQSACcxWjQNVfVIsR/XVsFWJ53yt0ke27djiWWCQAQq2AhT5sSfM7uMtcEzZ6NKSi7qwA7ENS1Blz+BLHmSXkOKBNQZZRsbThdu1yNu82KY0ayO1fBTo4qXv/yuZ8FkFVb5Z3exxXdl59zcZcVEyMm4OYI/Ov7A76/ucXLV3v4TZ81FJlV1DVjCn1LD06PRR6e4w56YNvPhV9/KvrhkvRpUJELa/2C/a7Ts4/BGbXBT40eL98VT6mv4IbFXiDJ+ewACoRND1xFxuurhBswDsyotTPMVz/Y4JMz25Q4uLIgEFS50LBtAORqbC9Uz2xjRCiuRJy/G864JIwodbfOF6f3vAgn0MSIKIILBRNU4kQoPUBVDdlm46x1w9r708/XhS8Gi8XzaAOJrq2nMvzrsD6UzmJU83quW/PG6orWYZkgAjMIaaHJjNTX1Rs2p66YQRpnt7Iwzbkj0ijuK8f9PWI84vj+PeJ+j+HDR7GAuL8HH0e45EAJ8CHABYfuRQfvHfrg1c2TA9GIhAMiEVIA4uYGfD3Cv+jgrxx8qtayYHVgANvRw/eEK+oQtltsuw4bHxCI4InVHZPRHNb1CR9qMmJrtMaj0nTsq7Nhpp9kY180XHIdD8HDcva6DE8+p89PprrwuQrWKuSFrxXRkh/VBGVqnplyzrwdq8f+0uTZpO4pjI+ZY4bSC+Vcn+6pJjkIDcIeFHfouy36ELDxhG1I8IMDHXrQWLs+fgA8S81S2a0nIHt09adyrF1lX4SFW5Gnl26mqTIfN2v2dGP1+SLXLlV0+2OEEU0HHpQeYBGxdtG2OaaH51reh6QlcvdLEhHf0kOTHdrymS0h9EBOpnmZD8tyyC1ZQjiyTwu4qlc0fR5m/CqS90UFUE/dD58A9ourfP4z43zdz5G+5Hw/LeUrg1mEENe/E+YexBd8jAOICN4T/vTLiP/6p1uJWeBdGdGa8MMSXVoxPqtT3Ige0zST7V5c0BBXAamz83iGxENgEBISj0CsyVNXiE9KKLhgheRwscJy5Ir/YQOeASKNdMDF7ZJjD07C+EwZ9mI6yzxKUGAyL7VQotsEG+I25jiMAAExJvH37EXTqus6/ewR+g2uXn0P8h1ct4ULPXzoJXi4s+BgDJgfWWZIXANj/goEpMimz3Nh/p0x2xKt0H95TU9JIvvgiuJnqD9gQ3ZTAojhGu0eFss3G7tMNLZnt6Pa4uKyPVyvFEzuGKrmWjQodZ6TMnWSCKWskuziIOl9pHDmu0n7yNqGQ8nnNWBojC3mYnOCasyqFzoG6qapDBea+CsqsU9QQYOTINMURGuWSdbCmAZd06TrPpU1LiOs2nBtrJkaj03OwaVU4CEHzwyQQ1Kd27wGoOuopuOMt6FjZoG6U6rxRBXg6f3vLOAqR3Aa8d5d4+Odw/Uf3+H1bod+K8RR0rZN6fG3bgjx271Jnpj+SpR2vqW/vNQynDR9kuVcLPPYMdg5pC4gJSByj5cb4H99E/GH24T3/2pWpQnZrybLvVYzKbJwIIkrp6R4z5prJgIwjdq1COlMO7+6SxUBycoehefRaGQ2+IjdmSx3lVgPMnL3rMxCjAio4J9IVVbsH6IyFk2bhh8IfJekVesLMuRYPufCCL0T9R7PLqUMNm5haGQzk/RJeSH1ZC+ygGj+m1ucYlZPlW+puozDKZ0v8+8aWoNAcI7gyYkVscaZSs7rGmWk4YA0jhp8eo/7dz9jvL/H/tdfEfcHpNs7IEa4UXCZbXgL5z3cluB3Dv2/8fCO0JNHSsDIhIifcOT/DFwBr98EDGAc0QO7DmnXK0KonaBihfzmpfArwmGHzeY1fthe4U2/QQgE5yV2nVecvh3Seow+0V1pdJg2l1hcWTE7JAYGZlHmx5wXV1N4Gbm8YDmu9YTzvxNEcjU3l+xL/HvrVLXfixDhBKC88r15mORsVaECy+Dpc67+xG2q0Wr5WZNHO5BOBQM/k2Z7ivNHUTSqT/ByPtmic+TQdx3csEE4/B2uuje43mzwZuvwXdij+/NLuJ9eqJvcT8lb+etNn29Ul+bwy8zrxYKIReRiYSPPTDct/0p95ywj7EJ+9NBccknPYODm3UMtJNZiLfx1JW4+mq/nLoLM51oWQogVxJIQotaEuDw9p1XDXzJdvThO1GzUy8pcnH67btIuhXp6tly8cp96V2RCCcgcPbIYDaIVcbdPeLdPuD0kJeR4db6XrrNMQJ/SUKSCyGatNntC4us4szrZ/BmrIEA1/5hjRqaFialMVqtKCVCGMG0BYeAKXVvuMcoxAIDEToMYMygxkoeabSfpkyM4l+AdY0ykZeszDpnfPLv7rL/ZFU8HFwJCt0XX7xD6nQSiDls4H0RQRD4Tq82uMldCFR2AesjtqJ1NW+tOZwpdXcaCPNcM87UkzG1k3FY0Mm2tVXdCfQeUzjTt1z8zurHUdNW3ORpVVVCVlaVcETIV4mGEbDHrVxcAaqlg1gqZ36FVmODJ+Ur8YwSe1tMCPIcfzjVbTIavYvWnQlSIEEEyOa0nuQROjECqO5uiCMl0zLPAKnHbePVh8gvHLMIIQAUeuvocifagNar7xmmdZTx0PJu5K32vzz4J4s1IlEDJZYwvJUakhP39HW4/vsOLtz8g9BuwB+RwoMn8fZn0LLfUY++6L6mU8wz38zmrwGm+v7p0ij55jvoekp7Y9meZwbX+PQT25x7zpyQ9N03Tnylh5FEY191G7hwi+EMAiSgX3oTXKQGudruCwuw2JMW+M1d3dxu4OlsvUlEpWbXiXWPO6+08Ez4ssxIW0QG0j9q6UFkXNDEiKqtFFsyn3EnypRFG0IRBtwbcgiVe1kxFvhbBlTDC0szaZEEI0+6WqYXEeqqH7VwZA2NdAWURqZpVnvvNWGmULj7nDR5ZcWY+qopGRp8oL0AUQIoLWMSENI7gOGLY3yEe9xg+fMC4v8fw/j3iYQ++2wPDAJcIxB7eBzjy8F2A8wFdcKAgeA75EYSPYAKOEUjuBmMf4XcecSvIrmcCByfwZjyz+s6EDwcHcAcXNthuPF50wLUHggkgXK2Askxjzcaea/HZ+txgKU+DZE5yKU6ewBj5iEjvkWgPhgkkphHjalyyWi/TdVMTRw3Oj6VMmPefJ195nm2KCzZVLD2f7+HyYEpEYfl3Pj+rT6NxmNtyyQow5oDX8OWN+bA0mffp+jh1LpDuqeA9Ou6wcVv03Qadd/BEEnaFCRRnAYieBOMDClbfL72Pl9takp8+GJqL+cBVA4/CI8pGOiWQflzSu2n2uMA7a24CxJO6punRMSLmAZLyC3v4aKC+qtQw376lx6R8XifTNlYmw5KAJzN95BJvXDFlRpBrBBC57KdOFwofnsZ8f3x6vLjugfB+2w+/+WT7JTUIUyE8Qwj45f6I//RPH0FE8K6NRQBUF0/GoSZsckVcpujy9FtNvJVXusfZIamAREowUGn/c6wROM6u2kx7L7+KCSBh0kqbXqwKGOrCqUWmXR6PpKEiElKKSCkCxKAEBIUppqQ45lTrDZn/XOPmjiQegA89QgjotqLpff32d/DdBt3VSw06HcBOVL6JSuwMzkNXEGIbQwvobC6Y2hPBiAcTQEzPi4k9Y4Vvs9bdbH3jxFcjh4oOM4Y2sdVtFdaftLSQAGUqgCphSdvcSipIfnYBhMpSBRrIOalOf3b/VRA9giDd8kME3k4FETDfw67UmKHVMl618iz2SV79eQ8RbK9w/kdiJNnYCSwLHABdB2zMJHMnxSE3xkhiwQONHZEYKY1IiWX9chKLowq46bwnHQxnwNcTP46qnWp9l3FOCkpKFh3EaX88NLKKCkLU5D/7ywXqINZixCFzNo5HxBjx/qcb/JHeY/viNQBC9/JK3MiZMAJP0CT7lr6lb+lbujB9EWt8O38dgRFxOH6ACz3iy+/h4ASHuQeC3rc+JXVJ7pCgLvUq+GsrBdJ4WIkFr6kDKRGJhWwWQDBni/SldF6YaNedWZUu3HGasXat2QpPUHQbSNn3Dc+nuMfJqml6XWX8VN83LpIybLWLRlaaVJCZjPLwlN46wSQjYBrYtwhhWsuIhYGqK5mPU93fKusnodBWmccXFL2kCFddzriSVzxMcCrnNFaBem4l1UrnNAJjBMaIw81HHO9vcf/rzxhubzB++IB4uAfvj8AY4ZgQ4NB1V3CdR9ft4LwH9R7OOVyHAO6BgSPAtzjQ/46PKeKfI7DtCb9728P1HQ7bTcHvSWKksbpLzRinIyQG/tNPO9wf3+L/+n/6Dq9f7/C7DeNFN2DrNwjeqzUEWmvYSwb1Oc4iNojN6kSqHTnhgI84dv8JKe4xHCJGEEbWcAcrAqdLmMRZMaXmr037kvc7Tx+e7szi76pjjXCgzlcvwCmtMq178r2pu2pj+qzOm+uvnl/Ux8tS3ZPGI4Geg77K6AgSFyUE7DYbXIUdXocXeLHdYdt16DuC90ldiC219Kl5Qr9hnlM9YBfs2fqOXFoLzy+MqCtfbHIh3/MCcblFxMpzOUvatzNrCSpMiJmfu4r5tdrgEzuckZnVDGfqnwhXHmQhcSHzegmUk1vvN8IMzoehIZXM5bv+RoXYysVOBYk0IQTqz9YKYpYmF9uDBANnxnXt9VlT1E+d+IH9nKXM/XpI7sVfz5GeRbD0Gebgt7EL5ykTYGEH9r09BADcHUb8cpvw/m5UCzearK0pcohMbFGVY06s1ZlXHjMKxajPSONFFNcvar1BDEDdOCnHO58ZqM5sZiVsAHL2XAgGRwVWeaz5jTFqQYlFRRwu9z3BOwf2gA8apjolMJG4wbFe6vnlchwAIIQA7wO6boPQ9+h3LxD6LXy3g+s34oKJnMLcap9Mbp5MnFMO1qt5am09AoxRm3HwxTuPT+7/6RuLPcBVhjpPjQaUdbCEzNPkVZvX6nnoXsuBxFNps6D9ak3Q/NXQUP5la8ruGwmOaHeWK0Iv/YdtztSaxwKmV6wg/ZfzL2NE1PyKEvugLs2VzLBm1JR+E3TBsQRAT2TrthjXc6LSXq6d89g43YcTWZOUdk7dbtlDcYnhmJCoMLmapI+yRYmdDUqUJUZmeNXvbA4/xoB/+gi8fHeDbnOFF7stAoVCxxFPGvtC6UvgZb8RXPBcuvTOX8v1qWizz56+5vl8Kmxfgol/SXpkvy6i2Z/lPJKDrjpykRg4pqRarBv0m4gfX0fc3zM+3CS5uVhcL81qU06gWYHWbpGaYNAVB5/KFTS5kVowC81XjQDVdPP0tz6dMtTPpnLPZNhRLEdE4FCySle4aO03wgeDAZlJOlOgWIOiKtTknQ3Q4ogt9ioDg/k4Ne0u/OazEBsY61YWmeVRjWd5Ms/3kGlrYmS0bwrO7DwAEoUcEMwiIuNOnJBiBKcBaRwxDgPS/h7psMfh5gbD3Z1YQtzfI+0PoCGJFScRnPNwziN0HbwL6EKQ+FwEeB7h40eMY8SABKaPSB1j6Bw679FtCG4TQMGUUerpLTijjoq6ryQE12HXXWHX9diEDt4TPGnWRdbBFNOnNgPR8sqcrokz79sWqLIyF8WRxAlMEYwICQUubj5rSqjZNKg2zwy4miaZbMxZngsXVH3Y1OVmOOFawYWfuWPcwvwQeGqaohZ8KPJO+v3yqsuqMIpcfp+pYXGftXXaW+dE8c8fe/Ruh023wS44XPmEzvnF2JArVT4KGbuc8nx8bc/CVjqzx3glX3NOPIMw4tOlts0p/TcD4hlwukdbRFhqCWx9ljUuTmT6TOkrRXv/qpL56c5CiIWFK3erMRGN6YP2e+Uaowlw+5nSdPOvEhiPAOpcb57gnOwBQDyNEfAt/TaS4FgMuAC++gEgp3FaROPh19uE/98fPkAsIXxz3zAbq7I9W40RWyuUcB0bYPU2q3A0IK9BI+6YOQsPiMXdDCNlFzacPGptanJe6JfMYFWELSYkZvjg2itWBS2GrznntA9JY2VEIeY5wWUnyfIldIDzQlQ5ihiiQxLHzRWhT/BBTFs7L/X3GoT66uUPCJstti+/g+s6hO0VmDySD0pIO4hPUSUuC3UI9Q8F0zAvj41Qi2CaCHwnyLbNWZkaaudiIoA3XwNz8rEwSeRPNOGTEjWRy3sGYN3KLVmgTIh/a5jg56nJxs26b4vWfiRu5DykXSRSGQIRhJ3jtN9eP52uP7WWYBUO1OsJEEsLAMUKoPWyzUhazuY2VbRLRVApcFRtxASuOoUyj/qPIw+xFkD2NOGZkZITIjPFprxYKAisAongcK4meFQBYLr3kxKdTBbQGjp/qZ51GS+kLMhgDezIaqkRo5w/jli1dJNYcXDCR3qD/bHHy3/9Bb1P2Lx8Dee73AVv1iffEL5v6Vv6lj5HesBh8+TbjLm6OQiJAhjAuP8I112j77/Hy1cD/i/hDv/ypxH/8T1D2IeERFCG7mrVyqCvhBGZKUmFfk/lJ7BC+8PwtrrnFca1ImxYYavO8xNUUKK3LJ8RFGTURZijbG492dq0nhQYKONXS7fdBGZjuJpgYy336ovnSTVNDKy31QpKzjPEgBN0blPxqTkw648K06y/V/kceQAO8B4ifPAKt81zQuIowofjHsf9LYbDHof9HdKvPyO9+xXH23uM90fwYQCGhN4FePLw/VYFED2cd+hCJy6ZnIcDsMUIx3sMN/8Rt/0RfxwYvgN+eNPhRR9wvdsWb502fIaSZRyx7ZNTl0uvrrbw9Apvr17g9fYKfUcIHnBO6Bv1A1EP6NJETAdMeSTL2S9NdX+cbnAmIJowAsDIjMgJI0usDCng20oaxumpBV/RIlSfIlzw85Vip1ONM3MBI7/mtu21iut8l45rDTdXZTPRUVs81TBUMPP0XTMyD08VPBaLrzrGmzZEmB3gh4Dr9Dd48+IVrnZbvN55fNeP6DzDuXD6IvvGGLo8PbNFwdPS+l6duhP8VNfY5YKItUGjwrxo9zzX52V+Wywjmkqw3L3zK/shg/K4FuoKJowZq2FpAB5TFRbW56M392OWzLnG1uqbo6PyL2chBGdmzanm25vWjk6i4q4pu226ANrHpFO8+EWE7LJHq0/btpfzGIFwKvGiBoK+m7xY78d6O+dlFA+bjUu1fC5KX+gCfI5mp35Tl3fSicarDJftdt2byvjVaLxwAPZDwk83Cb/exnyum1J32dEnAFw6t5ao1ZU0z0bVR6nIGMOmFd5gjITMIG5qdA4OYjotFlkGrCvlQEAdYBpJjPQNG6cEJg8JsB3h2AGO4b3TayCKGyllwAZHcA4I3sE5UksIj36zhe+36K6uEfod/GajSJ6fmGZXgpzc1/q+SaWHzfYva6kZovZ1O100EULIw/zLwu6tnFDyr7XjrN0SFJJ4sufrqVXgOdk5phU1CETpYENvT3D7BnZ1nyR8BZI10G1ASQJ/O7VuEHMVX0mv1OIGEgix1K8alEhVf6h1CsSEZEi/UyFSimX0KkFFCd6ssRsqjdG6L0TzsZe9ywXPcpOtprFQKLNXxHLIhAGudgkB1YJ1CSkVFxy54zYDKqQAWk1Su5MjRTTxKiBxWCKnZp4czKzf8ILqfUpZK88YO44cUmREGvGnjw7pn2+we/MLvncJ3m9l76QDmEVnr90nlOsq/aEJemRzUkZ97ciann9Nvq9Zk/0Tp8/hGvMvbnT/GtfL19bnZ4GnRXLKtUXlD3iExn9JdlrnU4xMYJBA6Qg+vkNiAjrg6orxN28ZN3vgwx2jY4CjnLlMIpiQk07uZ3NE5PSOM6NQ0ea2C53yPZT70/S/HY8KdWjuMVP4MG3PYqFQhjG785zQwrnKKi9Y8D1GAkE+C6zIt59ZeiDDoFaK+aogvW9awUa+DajgLzwFpqK96tujmWsub5fHTAZIlAZ4gs8tJZp9bVYhVZAonIwai+A8B/MkboYaXHOh7bo4T/kWKLeq1EeAqnUU7rnh8shKiKCQ6XyBMcrsRXGLGocDeBwQD/eIx3sMt7cYD/cY7++Qbu6Qbg/AMYGiWINS5xBcB+9U8OA9QgjyzgU4StikX0EYMbwARnfA/euE/cbBvXUIWwdsHBA0JlYFe7tKbEwM41KLUS/Cla7bYhO22IQeGxfQEcOTuDkzUoWaeqe4Ni1+pzKQj0wCrS3nZBAwxJI3CX6aAWNC45+sHoLmS6HHWkSWJw+n9UwOjczUX2qr6UbVDuopmRdoLI1rMAz/m7bJ87yrqaqb62DW1pfUtgOguBrmSR0VyCvzO7WMqH8X929GB+m5PVUUFyQbIXh06LDzG1yFDXbOo3cengA6dOCbLei+u3AcHpaWu/e0u/lyntW5uaVMMiyleqmdqmmWZw1A4wVV9+S0xYuxiIeiGwv5azJpVUY42/8PS0+2iGgxhccunBaRa59/2rTW8pesrL2QVvJcVtPK808zrq2lTso+oDkpKri0qYxpM0Nuy+08tYR4tvmamlhNQZvBeqa6hQwZeT8Ly+R3s60qlP85paiL3VsIEH0K/Oma//Rb9pHpXCceUtNXQExT9Tm9BNYui+pFchDKM43iU9h73O2B//iPd0gEUHATy9bitgXA3Op11qauo6yhvwC7lltd+rZ3KoLPaYcTCFlCwJzpAyInzGVSk24jdMw7gTF/WTTCS3+MEBK3O+QITBFEwlhOGAEK0hYPguB5wCeg6xk+ORAYY0rZqkLMrwmbXrSu+n4L73tcv/0dwuYK3fVruNDBdVs515ytLGVgq3CAlUAto6O6fKzzMcH98zybn58FXB7Q7pKQIes7QOMlZN34uimeTpZU2nDmFXvJsJhgoJ5oznkYyqR2btJiqX4pZdzf+kIkzHZHSHDg5ECuQ9i+AKcEl2KG3zVjD7ATho3dO5npb3AmoAjZq+VpQiwbbxsITpkWEdColM0uBsQMHkqEm+zLKQx2HVolJjMRIYYIw8q5LYQ7EcM5EcqxWfo4AGzuzBgpGcBJxkgZ+TGParWH9T7P25IrgqeipG0kPUn/xiGhCFrVVZnWkcBiRWQCFY7CfOBSVyAvwSfjiJ/cC3yIhN/9y5/wKkSEH/4W5Duk+5+AeATo0KxJc8+R97n6cjbyu+AkHoCuiUcd71/BnfAtfUvf0idNNQupZb5OEOEaPxPE5NFtGqNQWilO9oQ5kkDjPXi4Q+quMGxe49VbhzfbiD/8a8TdLcFFRpcYgyMMzmFwgtMIyOLDnqD3j56XRZBgHZC8bZyoOYOuJncYqOI8UDMEWQAxHS/7Pq86j2F2dMjIIZJMnJJjNeWuVAKIBl9RRg9QrCUqTkvuOtsMQCU1NTuJmjgWDcg17Lz4oPnMTCeqGNkzpKzCsZrE1Tcpqxgy6oGt6RbmlnQo+tKs8aPYAFouTyYqKEoTqSIKSHkAGVfVNVx0hATXdmQx0FS5yActn8RiNQ7gNCIe7jEe99jffUS8v8fw8R3i3T3ix49I+z3S/R48eiAGkCd47xBCB+cJnfMIzqP3PYLz8L6HI4+RCMRHXKU/4BD2+Pn718AuYfedR98F7HY9iksoatZoq7Jn30whCbkcOQfnHbZXW1z3L/Gi3+Da9+hpQEcJpgfjZnPa/jasf+ndU5JgPpnqUNdL8ouiWHdLbDEA7DL+jgqlLxBW39cIikYYUZWrNw8vPJu1ceY5Td7xtLKV36bHgjTJN2ljenjlM0tPZ43Flv+SfUemJSgLJko7s5lttmD7tlkyKxbkRQiB/Onzpk8AOSRPCMGh3/bYjhu8Dju82mzwMvTYBocQGPR+B/qX19VuLzAsQL2cVrJ9XsyZmo/8Y7aOl/Ktp7WV+bhUNlbhqbb3zuUt2+1b1z1/f2pnNe9o8qCxfnz8KDxdEPHINJnuGYP1uTSsFs1AJ3XP8J3zlVpFC+8mFZ3K+0nTnF3Ks1FfSw9dULqYqwVpDBI7dBf551NBgD7Lj5W3UZiMl4LzMPhb4fCkkYU2TzGiV9ftQ6d/KT+v12/B2Szfw5qqjqmiSrSap2mXCkrW+hI9kbQfqwHvL0nPxCyi2cH+gNqecU9PLSMekmby8TWwJhcIIFpDDML+OGI/JrDFUMgf1e+FrcGTH9UVWhWa++I9Bes0vEFBeKe3IEGIGPmURzWyXtZyEXR6AAyXZKxJtbyNeDBmsgQkZgBOLR9cDuxNyWuICjmYPABHjNQxKCWkJOrpXi0hutDDeY+uv0LoNgibHUK/gQ89yHsRnMD2GLdjnr+0SPPSq4YktjG066fKXkanGqOVNCVm6+dcN5DvAIZJfVrkR9eC+gkq+nnr6702588CAflhGVZhFrcJAJyHo+LPllQQVVsgtAh9atZAdiO0gLDlGBTZgqMh1fP4tLoaeqHlM1NjSuh6yu4JWVa0+C6uo4faXWgticjAuUoQwQnsbF1rO0aQWOB3FrdeEoxU58bpeEe7gxcIwsY9h7kN0z3OzerNReuzTZhBxUd0PR5EDKjrqCnibEttGAeklPDrr/f4aTvgb65fot9dg7od4DvgMEj/a6Kdyg2FvI6mtrmcz5pmzU/PvGbN0+z9M1MkX3167B34ubHhB6dz/XqsQshz4AyfnZZYAuHTw/DsQaG/gnE7lU4fJQu0GwMasRcAkNKAONwC7ND1HtevgN8PCTd3jA93EYmdaDmzWP8lpwwOKlXJOS5KKKQBg03oIWc2Z6aICMPtnCxwJbv3SO4ZIrN4q3HCYmFRx4lcjBsBnEEeDbdQnAysIcPOx3coNZkVhiCqtWBg2na5HzjffWu1XnYhFBy5hQgZpuW9MMUTofVM3fxYpgqHqbtFdhtWd2bF2CzYSrv2BDuuHU4aTmfJrB0MZwEceVUoNImEz3gKg4FxAKeENByR4iiWDuMRw+0N4vGI480N4nGPeHsLHkZxvzQyiD28FxdMFDzIO4Tg4b1DRw7eOfQU4EDox/dgjLgB4YgRN1sG7wL46gi/ZaQ+AEFgZAO+7ruhWaDKctTN3htt4AFsuw22my260MF7D+eiBAg2HMgG6gHpwafZUv0kwgeAVDkF+TywoMYZX7V5zLRFKpUAKETHQyBfKcAr72aPauT60vanVejeyG3W9dQE1gJdxtXn1HqDJ3nrz4Y+48fjE5qmx1RNWZFmyEqxmf6QZ945eB8QQsDGddiFDa43Adc9Yzs60M8buNv+gQCdAHTx9SWr+RMi1/moXobjMZhDRXWcrGuRf8Nre2R6p9BCntPtreXh2ZeVXA2DRm/OtvCD0xcTRFycnhsZffZUX+BfSTJVjy+UUs3swRoOWQ6kYpZZ3C/ZwZmRIGWMnB7px28EKT3lOjyw/KcmdJ7WvYe10/zUuTojeJuaNZ+sn5cJj8fAd1mBtavvcYP6OQjxT5qUfg0hYEiEj/f3uD8kkG9dqNWa+HzhUVdGtL1Ml4URy8hx1vifEZQs8Sw0oxALIlwoQiWX2y+ujuRMkZgOEAKDVRsbLNSzamnBCAQ4cbXkvNTIhMQM8iZ8U210p8xdRxVjGqql7tCHDj502L18i9DvsLl+qZYQG1WH8nnEcjydZiAnY1ThtLU7mfqjaP+VAS9n6WVrt901lbbhZE3UsStkXFIeb2nOZsZ8M2vKkcJLi/nqytYGlTBiDdAZpqf3BwDy4kvb+4mP7EwslMKJGZxiaUf9FBNLvBDTako5kLm6FYqxEmwUwayZuSej15yDI4LzVQBGkAYlN3dOKgzTcSVnhKqNATdzSCqkkADaNhyu3L2tlF2WFOteMa1Dkn6Q9sehWAtxskDs0/FmpUO5EKT15lZNUWaGcwRmQjS8wCqzebL9o76/uVrXzoQILMKg42EPMONPf/oVfbzC6x9/h67zCNuXYCSk4wcgpRxoFGbpQh6m7iY1Gwycz0JjK51Pv/GzfyE9xW3Mg9v6LK18hem3jjN8S18m8eRH1kYvrxMBSAcM+z1SdwW3eYNX3ye8eR3xj/844PZOcBwLnuuYMACIegXlqln0L0QI77MLqAYfZEZBq0yY7DIsILlLEzMcpRx3iSucv9YlOHX21HddVkxg5FhYJjk2fLHGKS4+zzI9ovCgxIrIVgraMbaAS3ke7N7Se9/urhln5xyd0eLKTolfw6+WrOK5yl/XQ4AKZAqTi/OvikKjAiJXiJ2LrqlNaPQJuIpDMDcseA2LJUIGiU0iNRiN7+DhzOUlORi2FaH8gsMdOA64v71BPB5weP8r4n6P4d07pMMR8eMteBzBwwizqCDn4FyPjQ/oycEFDzhfXKGSQ4CDYw/HCf3xTxjiHf4YCR888OL3HtsXDj+8PoJ6Am834sLVFm4zRfrb1iRI8B+q85RiAcCWCHG7w9XVFfq+h+86eDeKR1CacR0+TTpx95S1gdlfIlS2NbXdzLSSlbV9KUpRnUHzOnj5HS/kaV4sVrb+bGY1UVc1LVesndtyZlJRfaaq7mdAsdZmcl3ZTy21VeHNKY2bIOvPh4DQBWy6Hhve4Hqzw6ttj9ebEf37Hfy/vFKtqMvgf7ii96fZAcwnl/08TRf2l0TXJrCszu2naLJqe77X7e5bg+/cPbecPp8gYjqK+SCfPM7Z591fyj9v5vwgnLO+WKthti51pZs2wXzdcim11n9ufp5NZ68tKiP1ecjKkmoN0cbv82Rzz13/FPdMwoxphRGXnyYP6HFm5EyfL2SdPHys1cNTUY6ZxcEnP5hKYxdbSlwAU92PB4/JBfPz0PRQa4TPKYS49Nx7UHIe1F8BvoPregz3CX98z7gfGp86ijtVN1J+cQLYxeylF3Jh1cj9wlhmice6vhlbWdNat6emxQRxy5PZwlnz2gHEoOSUeJRi7BKMgMpHtqHdFaENSiD2IIimPIHB6nc/EGUGMAFwXnzRdv0WPohbIN9v4MJGGOTGkLZeriDai1YDRvBmJLp8TF0QWC3NpEyY+zn7EvbWCEbaWBJTGIRur4lvG0JhRhMANmaBacVrXqt3dXfVcK0xLjIzQeaPnDAREmxqq7XS9lwFDpVlDRGIvDDnXVIXQiqU4KTCrISo9EZ2p9AMahkDl9erF0aPWmoUd8yFsDY3ULMglFqjPUrmLilrPOk5ps+RBRSTu5QTEkP6UgVEBzNSHJB8EM1E7W9t+RGTCDDIpcxIAoqJv62LrDCnTsed1RNVIMAAXAQwylClhEQJjswxVRW8nGR8UxJ4/rzfYv8L4ft//QnghJdvRcBD/QslDi3YpQPSCD7eVKOnn80ynWr32a/ZhbeYHhrz6HMx/R+SHiKM+BotIR56V34yl5fLjX3a+r+l9fQV7bVaw//iFUHqAsiQFXk4K29xgBJHHMYbONfDb3pcv2X8PQ/45QPjww0AHuDSCMce0TmMPggOo7hTUveUMDg1FpX9yV0tlnzLVpXiQIoMv4IKmqtg0bmmbO2XMsO9KDZQHifDK5b4Aou8NxThQHHPZMhBFbuKdO8bf4UUbwBVMEtDxHV7rdJVEV5QhQdZ3TRZg4qdrJ0JnP85mZbPO7VoqVvKYyj9meKTs+2RcYTSiMh7dM6qMcyKAnVZxXMM34EpUmi94o7xCDBjHA5IKWI8igVEvHuPOAw43N4gHgcMHz+CjwP47h4YE9wosUAobOS+d+KKiVxA7xw659Q61KlSB8HH93Bpj7vkcQQjXUfEzoGuI642hBc/EvqekHZBFJXIFd+RzUhPR95+utlbioIj/nK4Avk3ePPmDa42Pa59xDUd4IgBRxLM+lPeDVPccaEtW9MMdeG53SElD46VRYgG3XapuMeNYEz8Mz0GwJXy3C7MRWbS5OfS93NDu1TttK0ZeDzPlywWhP6Z8EEQ26o/9Wf9fCGtLD8GGkFwDUu9dcsZK99rJd+cixxCCAgcsD1c4bp7pQKJLcLPPdxhO13emFKk55bv8oq7vLwlfuBam9e7BInRLLyWBbSyRmdlH5mmN/kMFrb7Qn9mjwIN9ZpLl4+SZ51HttIHWvyqy0zvbBNM2T1dwffQ9PVbRHztKTNuag7EX19qhRAVE+JMyhoB9WcOGFshP885tAtCiLWNusiMLy8vb/IZ1sbM4uCpOMCl7VZCiCXGTM34PIdUWeDt+WF7CSBLjy4Z1/U8zRq4gBHzNVpCXMpAyvnIAZs38KFHFzY4pCN+uk0YIxfCg7lVgLDjbeG+OteyXqM1IOcAnSBnPPlmwJBqXAUU9qdq5jmCxTVozKsNq3KZdFTEsaxx5NoMFtLzSetzyhjwRigLcQSnQghlHnsvwfG2V6/huy3C9Ss4H0D9TpjNzk+6JwO+TipQ3mvGNK6LL7t0Wh7fxRnImke8OkfWLkOJbC7B7JxTcrfxIw3VxGFAYxBwNci1a7QJeqr/EtZWWaMoNSHe7V5JcmjBceVya7VnrG6KjHb21X5I4tYpRSBFveMIEv8hgQmII+dZqvuQVUKJ4JyTNUCU3aIxbH2K8MxRjvatYzpP9tSZwKHBFqvtQ9IZp31xrup/YqTiFFcXPSONA5I/IiVh/Ce1+DDXSjyMSJDxALG6j6I8ttHoLHWv7LuQY2CklBDHWEZoHAGMOp5idZJSRLHYGMGs/nZBiElguaFX2I+EP/35Z+zcgG2/Qb+9gt+9EE1eiCCC4cHDPfhwm/GLZi0RYIIYypZUf73pU96BX9/NWdIntQj5CnGGp6SvEQf6S0wNVUn1LZiR7fzJmifBg9OAeDyAtq8QNi/w6nvGD9cM/m8jbm8SXIwIKcGngOgcCBuMLiA5DxAhKtOKWQQQ3o0KkcsMfTniTZBeOQKhpDxcw8cKHkXJntc0lfylNHfVWjPx6/1pzP4ckFkt6UiHhhVloFSCtYowAhpvS+qduoSqLSGkKrWEyO6ojG40y04y1LC6QrWeSd1Ls1tGoX1v1rqPPY0EU1U8uBbkoHIjuYAzaOGsAZ9pO/1R1qJhZfLpdHES1N1XpuFVYUfEUgCAhAhGREoHcBxwvH2POBwx3H5EOh6x//AL4jDg+PEOaRgx3uxBkeGjKDp0rgOFgND1cCHAdz3Ii1Vx5xwCQSwuYC7CAIzvMYy/4p+iw3s4vPrbgN0rjx/+JiFsAd55xVFdZfhZ5ruhUadH3woBRHEEYsLPt6+Qun+H3/3uB7zY7vDCD9jRCOd6CZhtiiZf6EwtOJEkdh1S/wYxAulwzEpdpuhCzsEz2jX9pGvzDAOgsTaY5OEqT027nANq8dWUdlrLqPAY3l1bRCx9NgGrq3dmJn1OCHFpyjSz7czyOLt7zUpNFYXiCKELCLHDq+Pv8F33Gi+2O2zvtuj+9CLH2cuw6tl7mu4/DfwXRx8e0P7z8O2eYYucWCaX1P1cmG1hzUzpqMKzmcjGLkpfThCxYgowIeFnz+fVnOntqffa9nnCSyCa5sowGmIzgV5rPwEXYX4OTy6/rzzVrkiKIGIlsx2G1W9Uh6SZkBFVBwDR8x5cEyHE0kGz+KyVWpzNv9784zpTB/sEagTxmdNkXBaFEHUfDIGfRS9eSNwi/eUxL+yDZbhq2PLvi8Z0LU/b4OclstfX2SUWYfVVcBbumjAiyvPw/uYOd3dDXk+sDNCGKFyAs+Fz4tKLrpyL56a5xjHrVssxqf1gEwBY3WYFkQ+SZmy4WtfMZAYSIKoQXtNuR0Y7lfhSAs8lsBGnzLC4E/bnVNu921yLJcTuBXzo4bqNaMO70HTUiOQW6bbxWIuicMmIL6yJNSHEJUknIwnQQixXmhC5fkI5Z53dcaTB0V3uEU1Mfc07Vgs/Vd8zIKsgNuuHAEpT78epaoSqxSgjnbIrH73xjctAsnZE61THwll8BYcUI+ACuJLAB2UmONt7TuKBeB+Q40+g8sENIxZsjMp9Od33ZSQ0IGR7JCOETjPbHnC57pzPpTIXdY0+IIVeLCJUMMBKVDEYLoxIKWYXaaaB6LQ/hSYUJpAPgmaaYGMYY24zpYRxHDPuEMcRMQ4g1dxMwxExRaTxiBgjGE4/Jcjqf33n8PN+j7e//gkvrrb49//uLbabHqHfgMgDvhc4ti/BaQANNzq5rpxdnFfMZzv/Z1a4n4oJ/oh00lXKA8fnS6Cxl9IOs3L1PfHU+fgM6+ibQOBM+qR7is8urOeYntl9lp8u3YuKO5LcUy4OGA8fwOiRNld48d0e/0M4wh9G0HDEHz94fDx4UEoILuDYJTn7Hes9R3p/1RAVjfoSELkFpQloarhmYrAYjjZkr3nlA0RIn5K5862EDwvCiEvHrAgt9H6156x3+kTLtsGOuOAOlqvg20r2Y3kZOMMXuLZ8oIU1OUN6cgBs4tJG8z7TCFK+VuwSeERbXYbV5gr6JmPA7QqqGnGKlzWYgeJ0hQoteF0duNrMRkQZPILTEcwJcRiQYkQ83CONI+L9LdJxwPHmA+JwxHh3L4KH+3uxwBxGUAJ66uACIXRiSRrUyjiEDt5pQGoikPNI5DCSR4jvgHiDDwm4T0D/t3v4lw7cd9gFwvaK0HWA2wVw0MmaTSRPvnL5booi9QA22VkUTsjharuB215h13fovIf3EY5McWOqob6eTsaReEj5CuT6BwGmjyE9YKGPDnHEh3GPYxrhiRBgal8OkQuN1KZ6cE6lpZ2TkcfJI6PNLuEz2NlTl63LVXNZn+PTvTkjx9gWtn5XAYNZQ2BBKJHrnwa/xuKnnFnnu5g9CWc+4nwd5T06E0LIc0cEHzy6rsMm9Lj2O7ylK/z48wZXY4dWIVjxdbuIUM6apr3y+ny6kGfRZqe115dV/eg7ee2kX0/lTL6M5s53yyQ32x2Rr1Ru7q11yriGudzHy0mfLwzqlOdYZA6uXFILdT8E//kkgojnQI+nw5GRn9W1wM3HZY2cwyTbbGVgbWKqX40WaYH1NLFQHYKTsjlYCU1LlMW9XOWnQ75PubApPrNX2l8RQpDWS8pMIbSX83T4lhjwF7PW1oQQK8XPWUCcavepAodPXWYpFV/s1Pw+ObxGJJyZg9pv6kmC/8ywzWC7JNHsS4bqi6fV7bK812iSp7mEVtaB4A4lp+w1QmTgw80t7u9jBYcKEmuNLN2Xk/vwQWlyuj3gjjDBZjnfa9RHKFlDk+oGNVCea1suQ6QBgpVYdNqGEMxcIeXQTpfzypH54HeZsKOqgGmDdVcv0fU7hH4H8gEUeo0JMdXKr5GFtdF9OCLUFNUvS+O+WCtzji9Ql0l2zud5QREc27Ft53j2clQoNnYMSnYQVABk7vX8zG17fmYMuM1P7WrR26UiVKwDABhFJ1721mQ+SE3XUQQQ7AF2Ds4zRosVobU5VpdHxk0wf8Y+iKWDWsSQtt0ml4OBCsGxNAaswoz2/CUC4Fu3GTn2BJUaZJ+XeA2G5ztvVo0pCw+yBQ4zyA8ltgqQNft88PmckO0k8Pkg/UyJkWLCMI4Kh2sFHQCOxyPG8aiuPYDhuEccB4xDgI8jYmIwieAiJsKv4wYf7jz++P4OL7dHfP8aeP1yi216IZYnnfSd+xegeA8MNxnHKKsyLYz/cpqeY6v5Vu6nqdbvQ/J/zvRcTO6Hn/fPly4ZubX5POuu8RnG55sg4XHpoa40nzVlzdaMUSxme9LM5kO6vnusUsr+/wtMxSJCPuVOSHEA7gfw5i148wovv0/47mXE5m5EuL/H4S7geBNAMSE5D3aESAkDA+w8krpeSomzlQNTuT8ZMfe0nKVt7+1uIwdwkphHReOAYAw65ygrCRtNaEKIRUuJEynfPZhYkNvdn+uY4FQLP+1btpRQ6wtwcTMqj0uMCChWmF1Q5X5Ypef4DmI9YtYM6wQq69y3938iINGCm1XFZwwPqnvZ/mpxpqRTlekIdbdkmtZmhUwGEzE4RVFWSAfEOGDY3yIdDxg+fkQ6HHB8f4N0OGD4eIs4DBjuD0BMwAgQkwZ0dui7HuQ9+r4DOQlI7ZxDcB5eXTF5EivSPQIGDhh4jzH+jH8egZ9jwr//fcLv/sah3wQk76oB8dXQTtZDTXNME6dMX9QDVS8f5xw6IlyhR3+1w67rsPEe3hQ2nOLHC4om0zQVQnyqWyNbO2e01+GQIj6OBxySxC1xIAQSXE7JpAp6bmqbQvpkJcolIV6jvMULA8nV84X3XM/3JTBU7dqf1dM8YzTwMTALtNYILVqQDBeXtIIbVt+bHKZ8lHkllUCh2sfkxZ1pFzpsqMd1t8PruMXrn7fwzoO6ui6o5VtFovGEopyCuYLfXLp+eVp+UTBxJl2IY53jX32SnTdBPqe1F9yZGv5ZW8FZSuSCPHX2Ke5R34Jl/xZhxMObWEq/EddME4bAQ8vOz8SlB/MnXG26OanySHguTYtAf7G0pME3tYQ4UVg+9Ht7sRZpbX1gPiRNEbGTMFjTyF/a37+lZEyuZ0ifjSh+hkPrW3pkIgdsXoJcB/IdXKr3jbmmSRXRAt0wDziLzszv46Z/goDYEyJYqLzMnIDuZdvXdfwIQJngACAB5siEDKgEHiZTsMvWiGY2Ei5lP/5kBCp8Rsx8twX5DqG7hut6DUrt4byYfxeZc4knAaRM6C6P9/qoFSKyZkg8w301EUakCvE2uXsRQFD13VXv2hmvoSi0cVWvEvnL/V1ZB2tPlFmQR5SQmQOkDIE6CklZV9M2qamDWRkrLFi9cwA7wDsVY5irKtWQMssBhq5HcubMazVlIYQJy/KSNubGFD5qiQb7rdnNIsKeiaZmcWXWzAvZOiJ1FVU70JIOp5TyfJv5trN4FJUQU6oQQYRzjOQT4G1NCYKdUrDpgg8O4xiE6HWEOGyQYsTxsEeMI5g9huMBhhMmToijuImKxwH/z38MeLE74D/8eIPdtsfm+qVYJW2uQEQIV9/DxSNwvM1rhE/OBGbjMxsvPO7+nAYhXXr/LX1L39JvKzUCxvVMC4y1k7We+KXJeBXTl+M9EiccfY+0uwaDEXyP3/1wj5fbiH/6lfHx4LDdR0TvENIVkvfgfitWfq7LIGszEHxJY0dkOk4s4giuwiHLnSNifsWdEqMKjqT1V2oCS4KClT7X1ry1y8p6sMSlVOWK88Lxnwsz7IWUzxAqytLippfM74QbZUljWzXX/DQx0EQCz0ksHSuqO8cXkSItztMqNBEchdzHPAtkVRXcGkhIyZQW1LXicACGPcbhiHEYMOzvMB4PGO/uEY9HxLt78HFAvD+Cx4R0HMGJ4VKAA2Hbq9tKr9ajncZZ61QQ4XpRqvAdIoADCD69hx9/wXBF4B1h2H5E3ERcdU6CVb91GELNQK2YwzWtcxZHrvDyie9pw7dszL0n9CFg57fYbjbYeI/OEYJ3RRjxlQiii+WNuplNDCRCigROTvGjJBr0ADxTEx1mfZWfoxsXSvLkh63rJUsIm7vpZ37PZ6aUyydNn2nK9EgFQ02zTAUPddvN5m3hLIrVk/YqWmGaaHE8af6sosvad4U+JEfo+h4dBewOL/Gie4UXL7fYDL1Y8zjXunHN9VawrY1tIzC74N7SND1nZ2vrwXfmX24qQzGhr7MAHxdM1MkWTrwpgvkcD4KqvfGI9CyCiIvcgqzlmSENtPD+hAz13MLkyWf14vw9UAj5uinKbmiWYEXTh8av5SkwZ9K+M/lnm/bTXWpniWVeOFQnZbK2ff1JZgnRWkS09a/B9KAONGXWhBDPyYx/qmuDh2gNNHmfck4/tvsXXBCNNsTkhqnn/FldTl3Un/Wd88ncXzXNr5wh+fXT12SuQQUR8D28kyC8hSmOzKA04q7MGQA6LexbvfceO4QL66k9XyTeAGBM5ZoQqGAwTrQSoJRdAbiMwxlTWhDNtIz8mIUFS9tSNpUzTCsjOPj+Gr7bwG22cL4DhU6CBue20gSlrALlqpab/VzfVlQu/zxAZR7W5urB02FM5UzIVpYQipk6HQ/SMa3j/sxgRg2j4eZc0RAVUrW23mokv76KeZKnAqFBx+tgmQqJof9TkMsOoPKk7gABBK/8AC8z6bQujgArm5u56ENpI6mqtiEndL2K4qEK7vPYVIgmqvtU4TKmkPmIzpXmoNW2vAy3mSCQ9Xg6J5qZ6ioqx6sggmfthwoMZB9aG7Edw5oxlyqfs1V71mz0BN8FIdaJELseKSZ432EcBxyPUeERIc/xeC/nmPDA8NPe4XZM+F3/ATz2IM8I3RYuePiwgdu+Ao538lcfWLovmyloOzF9ooBfZktxbt89SuhwDnd+UFWX4anT/KXpc/jqPD0XtvU1k6bfrB6eP33dAjqafNrPC9bB7PKpkTPKV0DOVammNvfb9FvcI8U9ePcduL+W2EAU8OZtxPfbe7z7OOD+juDSADueU+iRXAA8YXQbCeBr+s8WZJVEaYUVNyoibbkXhOyvLpSM2xREhTKYU6xgeqFfknjya4UGu6jmOZ1SypuGKjXnf+4pmfDicX0x3CnbdKwxVA0vmPBXJGaZKbkohkPmEtcgNZrbHJmWdeucNyjAVJZZynNpLpiTKALEiBQj0hiB+xvQ3Q2O+3scjwccb24wHA4Yb0UQwfsjeIzgAaoLJHEknA8IzmHXbQSfDGo92okFhPcdHHkEv0FyHskFRAbuGABHjMM7UCBcv3boXx/Rv2TseofYiYJQxkhqLfYp87hJhpgUnFV+nqK1Kessee9E09x32PU9eu8QNDi1y/QDLVdzaXrA3TLlWNW/y7RWLmKTxUCDKN7ArMFFGOEgwoh6Hyyv84LkPj89bXQA69HE7Tvt0xyelbqmiTBZK/ZZ150J5wJL83wBLE7LYCysp+VMVM39/M4oQoiaBqBJNkIXPELqcRV/xJvNK1z1W2zYwTmCzwrDEwT9VJoIIFp65oLiEwl6cSNXgVCv+QuUn5+aLqnlnKXP9CmtvTj9eFJDbZXQ7rtGGPHYNBv46etaGFHBUIHykOZ/IxYRX2OaHu1/uWmK+E8DUy/lqZMxpkw7uVzEJYBoq0H7jOlCIcRvLrHOQ31KfM302bf01SQJlOtwf4j4L3864n4YMYwSdDfFmPOACOTMfHlG3lpl5SsvXMWPoSc1neQ3GKJFs4fV1yUkTYjjebA1Pc/0QaNZpwhZo+FP5siHQaSuafodnO/Rddeg0IkwwgXABdEMV1MLYytkGBY0+OzLg4avPtoWCp2t54RA0XBrExgDALmpJVuFiNYSgIzDJ+RYA0rs2Hdlg1ZkC2FRUX0Bvrq/XGVhBhK1Y5jdJ0yw5Lr9nA/tmLXupG1N6HcjQAF120Qw039SwZO5/2qImnqJVWMrmSv2AJXsp+S+maUwXfrTjGaNw0W4NHVjYb4yXH7C+XciMdXPNGT/YWEAAQAASURBVA84Mz8qlLih5YhEuOLhdX9J7toxklPXCUawkxP3V0QOIY4Yx4iu73VME/gmYRwGpDQgquVEGgj/258IwY246j/i9fUe/+EfRmy3Vwgkvpv9y98hHe7Bh49Vn13uQ+nCbxQ/+A2kZht+S9/SbzSds2x6ljaqa4thzMP2vK4ZHJk3UKfjLVIcEP0O2F3jAIbvN/i739/gu1cD/vAnxs2e0KUD4AbwYQT7DnTFYBfAXlwTJi9WfRES64rJKXxOQxMr0xLNTTe7Y61HRUGj3IMPccdUmCIPCzhv9+SM1zjNVPFa86e+yHIVvaDNd3eeJ7JrjlB8ey81VuOulRIQT/s/Lzfz/8/mYpJ0XkjnadKeMi1d1TYDGO1SV6Y9xwhwQoojkCLSMCLFAel4xDgcMewPGMcjxsMR2N8Dh3vEwxHxOCIeB6TjCMQIn1gXcoAL0mZwwtLugocjcZ9ELgBdh45GvAjvwI4w0gYjO9yngMPocIsA9/YeV3+zxzHdY0wJ/bVHuibELuAYHJKraH+2PUOZacyzMVliuk4UDWr0jcq0yRwnkPI2xmGDMb3CZvcCuy5gGwK23qHzDt4xvHcXnRnP4papKrR45+ZBoGq/SgyuxC53OQsjQHDEec23SOkTCL5HE4pLD84QQI3FwuObbgVbSxUpLGtWE7N0wQwbr2xWhKaZ8vfGe7EjOC9uz3r0eNNf4dXuSgRmSZQUi81LoQtWh6hWAKwhWyJETg10nZXtXK9fT/gLFyjAfh3pU2C6es/kIWj33UPvwsdBUN+7E9AemD6JIGLxil2nnNsva/l49uUzJLuYag5PBcKalvDCpDxag2xt2CbFl8yaVofqiZpzWQBxQggxM09uLCGArD1riCjoSXBNGl/8ebElxBkwvqjwYm1Ov/R5TGf272oxQ7iNTGkvv7X0OYi/S2F53kanG/uZ2jYNh6wxQRhHwrv7iHGMYlrN4sMdZAFoC2PUjsB8pU4Q43r2ZuN1IW66RKLN5AX1W6phuQCp139qdzwtWCaMqIKO1ZCRmstPNBVFdd0h9FcIKoxw5OF9r75gayaBuHMSYnZJIEJtV6qxy8xbqvIuJl58NYkN3Y7LbCwW6mwKFSGEqzkJSxXX5au7g80p9HSYp99zFYVQPLec8rBSi8y2pMCJdaPrhNgiRbSMgBmOU00bayxDzm7APMyFl2kSNkDqZW07qkGJjCeQd9hS36f3l+UqhHiZ4ymRpkS5xbOwaKIgZB9lzQKRyhxDtF1p4TYsfqSUQLez2gSB0ltGAhPBcckngScpB/L25LMkJDmPfrMFOQ9HIjg93N8hpYQYBzAYwzggOYd31AMJcB8S7g8H/JsfAUrArr8G+i3c5iWQgHi4kTHNIK+sh2c6hz/pnfUUGKf38Aqcq3GIHmhRkcs9KPfzpBrW52r/r83y4bG9/azz/Uic9FT6Umh2ffvYPU4LOZozrCZfCeC4B4YD0vUGCB2Omx2893jzwwBcJ/z0S8Q9A34YpFyMSL5DDD2SD2B0AHvAObGCIK9u/KSBzGpTzXtx/Wd3rtwVpyzFTyu4zoUTNhiNoawx3dgUR1C0Q2f1n0JM7eI1uwQgW0A0+Fdx71gLI+pYFE1+tcZcjhXUIkKGL7T9r2e94HkT50qmx5DdLGb4S6OFFqiqA8Relw3/5QTEERwjeDgixRFpv0cajhjvxe3S4fYO4/GI4+EAOuyBwx5piEhDBEYGot7rMJdLlOmLPgj+2Ad93ksMNdf3CI5x1Q9IINyAMIwO748jbpjw08j4bneP3/3tHQZO2CYGOgA9AQiIUKudTFdWI5fxDd1LtcILTz5p+m6CrzNaC0+dC04BcNfo3A699+icQ+c8nPeZie+mcSYWmsxzVT8/i2ufTlxVIdNc7wMJUs2sggiU/U2G92lzZMu5hmu2Rh+QVvf/9AVXiPxkworG1ELZhXrqtHQcrBFHM+FDjVdf0qbkXz2WzqR1dMNosUKzNjOS6TYgeI+N63C12YgQIhRLZFMett1jddRrZ97ylGizc2xK0C6nRthKaKcRSo9VozU70y5Ia7y7i2qZZroQGTCKcUm57cFpSouhvV9q3sspYcSDLJ9nZ2ANThU/6dFY4WeyiLjsaFqfngUPFI+t6sGpZYRM1v1Cx07M2cMSTxt7RPGntD+rbzkmxJoQgtoHjeaso8o/4hQZemr6xEKIryU9W2yItYP5MxPWj5HgPl0YcYoQ+ctIInxwwO4t4HvAd2Bm/Pr+I97fHlGb26ckWk9tkPISUPd8Y/rBduEacth8rBWrUousFY15fVYhOgvk9zxV7TulL5Pq69X+hYVuYbGcnR2/SmyXWx/idIfguyv4foPQX8F3HXxQP7ZOzzZutapS3T0Y8l5qLebgS4itQXNqRibjXz+eCsRP1CIZDH4l6oGiCV/FHSiaf1XZDL72LCUJgBwT8iBXhE3uV3UnzK7YJVxg0rAseR1XI4xKA1o3zeupytszbjK0bVigyELZWhOc22Kg8X5U+8FuUWrKecWdtblkMtipql9WcEFtKSOCRLU5dt0P+TepCXsyN2RJ4ixIbJhqPqjcMTQhtC059R2c/SJlZnaBUn4zQAxy1UBkBkHKQjnJq24ldJOIGyYSWt8D/aZHCF6YXBxxOOzgVLuQUwQSI6YI0rvBdx1uksP/6w+EN1d3+D/jZ1xdv0Doe1Dfo3vze0SoVcbhI3C4md1DteLFGp3aPqzm6q+MQf1bSp9DmeFb+gtL+a6e0z8zzfSFe+axqQhrZwBZ47P7ZBlvYKTDB2C4xzEJm5GvXsDvXuP3/+4jfrw/ItzdYhxG/LdfIu4PAzwPcM6Duw3gA6i/AvsA32/FTY4PcmcrWedIxMyFa1XReGomIXedA4vvP8lDrPdXysGf18aXM4Km5RgqQmdRHiCZI6qE4uXmVDAyF9pKtooRlMfVAlFT/q1AFHgNZyOpgNVxDcgJrA4Fj2KUe3oyO/WHFlfcVDVPM8ZblH4KbWvWkA5MvsIeazy3wilZ48GlKHdcjOCUEIcDOEXE4xFpHDHc3SGNI8b7O/AYkfZ78DCAj0fwOCIeD0gxgsdRxiERAGFoul7akrgIgKMA5wjB9RLzod/AOQ/fbeBdQt/fgV3C3g24cQ7/7H4A94zuxYhjSvhwjKDdgN99f8TVJuGw8YKHc+UutUau2NaQjUF5aVloog/TJK6/LuSY7vkUERh4f9jhFj/g77prbLqATddh0wU4HGWNmleIE+nzxW2s9hUkptkYEw4jcIwRIzMis1pIlDW6pIldhBEPTEsxIEqlmEzEcprSHkvDlw/Rc5U8A19g1YqJm3cLZNkjElWEVMvbsnNMLJIl7opHwPb2JV5uXuPV62u8xDVe/str7KLx6JqawYSsojRpFbNzC3MrrYt60NAPwJTxaxZNtVLWJSlX94WZe81Z/dxJtwhhLox49naACb1b80Qelz6pIKJI809leni9i+fLM5wbF7U3PeD4TP+ekk4II7Iy5SfcWzUSmAUPKc3eTZMdfPm3HYgEiCWEaWWjjOW0I9P6afZlvf1JlrNCiLX8X0P6hOva0uphtfT43IJbe786n/YeFwkjakR83vZJwB49q1/EMiI3fuF4YmUeiSSabreD67ZgZsSUcHd/wGE/FMKaWfyCcgKxy5TvlJzNLejZxJPnNW46vRSrHEs1rubJvzKsZVhqFn+me6u88zZszyvHNxOVazR+YQRnmpZVS8i0vMIGvruC63qQ9yDvs7CVAFAT2M7anPexhXhltT1gEReBUGlliT2xgFs078iIi0zoyjlu8QtqYS/XXPc6VcxcpKRMgmovq8DM2BZN0TXo8qAVxkAL/Hx9om4hryErW1rO47Q2YGzjsEx4GfKew1FwNc4kO6Psj9KqMGiq/lVX1AQtr67O2QXWJh0jGS61fFBBUEri5zlFiWdh+Ey9/kQoUoaatN8J0EDW3A5Y1Z60r77Ea19bDOSYDNX+oGwpI/PETtlGxHAMhBCQvINDQkoOoeuQmOHHUbT3xiMAICKK+4NASM7j/RCA+4j9/gYhBHAa4cIGYXct48ARlCyINRX4K+FD0t/2kcdkyoxozifJfI4geGgMMdTtfgLkd2rhcKmSwFM1sJ4zPUVZ49KyX1KQ8RVhqV93eo45qmmh9p+2KfvnkiZX4JrvOaVXJjDkt4JkFNjaiw12Jmd3TuMBCQfN4kC7V/B+ixc/MsJhj+79PYb7hH/+NeHAhO54QCJCSjsNXE1g34PJg7y56JOgtkRJGjKNjwocgl2zpPciw4T5RZCu9/CUFqgYnFSde/KY8l1riiI1zl7wIMronAyFttdc1HryN00XywZmw1ckfxFm2r1g+FBhOxFBuXjVXXlBEtjl7qvv4nZMa1pW72nyYOdLPRrTQz5J7mOw3LuckMZRFETGCI4j+HArAoj9HuMw4PDxFnE4Yry9E2HDfg+MCRgGIEWxmEgMxAS4TlyRqlWjEwMaeOfgCOIa0Tl418G5ALfZAS7A9VtZS7sRyQMHeNyB8C/o4PoBf/NylPk+Jly/jHj7g4xjNEGSmTXUuHa1SRohRDYNnizQFfpu/SagWS6XErwnDOgxOtlXwYlLpqBjMC/7xHSG7m1+LeUlsUZK5CAumUQYcYwRY5LvjOoInJ6FC/WdTLO7dW2EK6x3UcDBC59rddV7mtvnJ5p9ljQFc/pi9pyqf5fumAV6dvq9PiaoWudE8D7Ac8A2vsILvMG222A79uhutmLx4gaFq7YGK/eLmy64yZpepUcuHNOZQCK/0POfL9870zgTZ0t+YqRqiap/Gn+pGtxMZ65yDx5R/cKA1FruuRlbs49r91uMiCenmpHwl5caywe9oPRByXQGobbvpIiSfTbnySLh1yLi5dlSe2fmYYK4/dWnb8Pwl5/UEoK6DShswAy8e3+DYYxIKSpeIsSjIwK7bB8hQgmXKs0zq7NCCE8ISqWWJcTx/HlZqjfmtdXGC8jMDFup4JzmLbA7EsUt4urSbvJzW65+qgz40F3Bhy26zQ6+6+FDgPMOzkt+iwlhpVPFzK0pYlawWqTJCGpAtN8tFGRLiM7GhCpEJCMm2k5BKxd6pvRZdeTmMxs6zxWxWxARJbir87WxXzHBg34mJWzMSoQA1bh36sbKGd8ESYn/xTObbUWIa4apfqH1NMNF7SyaACGP+YRZTCi+k7kJYG6MkvIrA5wLK1LGSbUul8fcLB/amnWXcAIiZpqTxrBprBUW6KpCknEZK9Z6E5CUCRFjQkoR0QQRCgMBetdzXgdWr/e+WBa5eiCUuWFuESwlVoFFTUwWfCJxgrmr4qRnj0LivMRfSXlVpczccc5h2+/gnQfHhDiOOI4DmJPwWJzAzykijQNGl/DTbcRIt3h13IM8gfxGNEJTBG2v4cM2nzv5/ElRiPFYWY5UE9ISe6gEdASKR2D/7sna9yddJT1WC/Fb+pa+pWdO9eX4nLWSMgwLo9XQiCU/95T/AcBRlCFI3N6IvYIgQAxgGG4wxgP45RX8qx26HQGHA/4+fEQ6HNDd/4LDkfGff36JYwrA3Y1YRmyugNCBt1dIoUPqN0jeg0OHRAR2voxGjbbofSSKB9aflolVtHkrgcRMGEF6bysS5Ti7UsxDQQUPdRX2Q8g3CeDMKqOChZAFP0UIYYILyWMCFBM+NPlQngGGoNS4mt30S5NNOYdck8WioUlrqC8SXIyl7SiCBo4jOImLJU4R8SAWDeP+HnEcMe4P4Dgi3d2AxxHDcUCKI+L+KBaUwwgw4GONJxDge5AH0On4ENB5gieHzgd47+DCBs45vPa/ogsD9pseo3e47ToMPmD8/h60GeFfDyCf4FPEhhL+ppP53QaxlNzFVGRcDIhQpYwFZcTH5tIwh/rOLmNl8/tovl2NL4Pgg0fnA662W/ira2w3G2xCh84HdCEAsdA1X4M1XnaJ5juk3RuMiXC8ZdwNH3Cb/hFH/oAxRfOwpWHQHbhsg8ePne7CJ/FMHzN3S/mtH9PPplC1jooWCko0nAv2aP0i07UVEBesCQNvsQ+zZ5TPSnIE7xw22x4d9XjrX+Pt7hWutxtsjx2C9/AMEKKclBNlvsV2qf1yUinqgWtlWhfbRn/AtjELtL+alGn+5xFGnJ2yWYbHnWlPFkQYET9/WKXVnfPcaelmXhvG4pPy6ffBcgfNF/gMJkLL8ak+5lWvjW3DCTkNXUs3XzZfC5Vw9X0xUWEZzYQQxsiiwsjKTBcUDZZlINYXEK3+mDOwCmzL4C+3fSotVbSMHZY2l+t+CB8hC4eeeNCcFcpMlugJgBYqv3BTPcclcbapwkR7SNGLkP+npk95LhKBui1cfwUiQowJ++OAYRiRmBGT7U1FSJsVYRxNXpjL+bl6blhY62Iga72t5qu+2fnQEnEXpqXjPzd9CVY0ZyoI/ASQEFehv4IPnfh+db5C+pBpoUw0LSKKQG2ZcSrbSTDz14qAN6SNS7aMYy9N60K1tW9/QMssFFyCe2oSnxHJGvUmYfkLdVmQZtSI8AV347T9VlAwvzZLectRcpq2ZjNe1b1Z3Wyap0WORXhQxQGZAV4xGjKzYjIyJjCbMGpm65ahVijV3mWUmC6VBj+zumSqlAo4iUs2sULgvM0IKAIjl8VRApNzSESZt2Knq1kMkGpg1qcuM0ToonXmNaFtM1ji1KQKZ9JxJFfH6ahWOAE+eDB6+HBU834lPIibtlgtP+5GoD+OiOMAn/rMOAExKPRwwWdhQ0rqPmwcNXB3FOFsSgUSm8R6X9gadnqmktcxKYTmJSjXYmqsqzDXHF6ojxaeYfp+BRl+LheQazEknqP+r4Gh8y39haSnrsfmoil38cNAaGGgqobaNeS84XKXNSoNPL1LBTY2Teh4AKURw9ULJN8BaQsKhOsfBvhDwtW7AXe3CX/AERxHOD4AMcAhArFDRELqeoxgoOsQHYEpgMnLuVqNSXP9TuAR5n11DlmGmmatha75AoW0w6QunVDuQDbcdoI/kt1plfsmVoaiChtK3Aqu4MiQ5/cWhDpbTJgFA1mPSc9tuy+kjlPrglUBwYQdrcKC3mvTpWDDwhGUVLjPCRgHCTg9DiJoOB7A44i0vxeXS7e3iMOI434vz29vgDhiHEZ11RRlPFKeJWRXy07+HLms1ASX0BOhc0DvCd57UNfB+Q7XfY++c0gvtuCwxdFvsQ8E/v4GoR/QvTjCuYQrjtiA0QfOgdqRxGUjgVWrh5t+C5JAaC0teTJIeeG0P6ti62llvipkmsghBI+OOnRdnwUxPvNGspOstr5VkmjhYYPUPvDumyHENkIOHLZIkZBwxJgGDHiHiHuhFVncMqltTbaSWANxtV2g3cPn0jky7UnHdbVwLqnnEpJxWvW0AK/+aJopX2gxW5nG1YXT0ilEeY9659H5Dtt+g23fowsBfpQ97AyhnxrxtxUutzcTQjway12p/5HX86dCD2eIdbtALl8qD+jUA9bp0v3yGJ4hVf2Se60mrnlhHB6eHiCISArUepq+qzcC1sxpTlRYX71n01I9zR5dOmwuWaGTXfgUrbYarrrKlfynPRKfG5PlWguRr8jUWj713VxcODxglWmgyey2g8wkUQjxjPc9Av7VVab1t5qvS9XUi2L9EL8sPQ+RflFLDdPt8e22rObih/WLEPOfbfiWkFFLD+j3FKeofn/24cuXwbRf9W8xE/bBwTkP5yKCd7g7AH/4NWIYgRi1CBHIeZDvpCQRHJwQWBUdNgFisdX8Soc9WVBi03R28pL0s3G3xTxXkskMY9uvVH0rjdVlnJl35mGq1gBDEenyLGudZeFBrYluFlxqCdFfIfRbdP0Ooe/gfZDge6qqRVU9MpZlPJpzz64kbi0hmntTejNDb1qBw3KqEdqKftZaCrFteebWB7Ty3F631EyxLJmcUEYgOwKxzw5IM2mWBdTamAYyzGXrs4+t/so6rx6VCiTKbcwXryBUDpmxS3VAtrKyuHpqlc9ouclllrX7AWTfxWjzAJzP9FSvzdJJQAlAGzsBU3uljJSU34srsGiuExtcUZjqEv9E6ubEiHHEOBy1a9KeaRgmFlcOzAmUbPxK2w4kro+cjCEnBnhUsA0onRUeZRpTaSMlscSQuDRR3UOZ1YY1xXC6p5wPQki5DiCXtfJAEvhys90geofheIOolgvJNA8Tgx3jfnD4wzuH2/2IH1/+jFcO2L18C88OAR0IUm/iIzgOSOMBPA4YD/eI4wCwHJZJfWpHXefO+2qNEYiCEHyhA4Hguzey5p2Hcy5beTTMAJ0jU9qIaUTipFXqTmFGuv0FPBzgnMUCkTlx1r7u9RQjstKH5WMTjpXftka+wO3/LX1Lv7lE9R3AtYiAALjZZsr3zxPSkj58g/vw/GmbPHIcHxb8xJTkGHpMcwTf/BlR7xACwX3/IzwT3NUr0P6A//nqBjwc4G8+gOIAGg54f+jxX/78BvAdQr8F9z3c5groN0C/QQobpK6HKRtYXK3CIrZ4Dh5MjOQhzG+w4AXq4z+7dcwWCax4k1lFGsJld492V/ESZqhVAmVUkuDlTHQSY4KcWkimgqgJCL7UrTRxPjkNb6yahTZF0LzMENdVhrnOJzLfmRm50BFKcl/mi9EQdo2DhKRC9hilrZQkKPl4QDqOSOOIdBiQjqNYQowRw3GPFEccjwekMSINg8TtGqLgrXHU8XFwEDdKBICCYMUOrHojcve6EEDe5VgPLvR46d5h524xbK8xdte43bzFsdvhj/2/w9A5fP9v/4jNdg/nfkYPRqIjCAnvfRJBTprG0TI8TddC9l9prpksX80gt71RESMl2wQpPrFHl5gVhAr/peyKqgsBu75HSlvs+i1ehB5b7+HHj3CcxHOV4gucGE38LT075GO+l+f3dI3kne/GtLJC849ScBhB0cMfA8bR42MEPiTgAwMjm548lRJpPjhyCs6psrRIri5QLladxXjDRKPLvHZmIVPdoRVKaOmx0RWVRUXj+m4m5ZsVXvg+LVLlyXu4gnuqRDIhU9amsiaJ8m1UESPNOrGz0wG+7+Hh8fruLV71r/D2xbVYQ+x67NhjR4ccjNz+qXeH3nANZETt7+rhM6Zqfa3U/VwKM+tp2u5ae6fWzXOlC+qvweW1F5fUS81no1hXz70tukfOw8WCCGoOmzMLbQbLqUmbflvKMTFfOlnT/GEuvcgQWCo2rU1/Z6n36fLTg/lUNprANNXknBXI+c7NQasVs1gPoUGiJsUhF3zLsGux7PY71XAZoa0BqqEaHmv9a5iR07onqfDO5nlp8nsC8UL6tGT4Q8/khuQw3PQSC4jVg2dhPTe4z7JmzqpwYkmV+jGi6gfvwZVq+IRm0SOn9XGCni/HylmcK+cA8rCAwjUxywzsB8YYLdieoBlEWq7CcgxXd0/dJooQ2bECIkH8qOxAzn8tgqgVlK/5AqwwN25ZAvKFinl9xg8y6Zpr5apl2KlJFRKmRAeREPQu9PD9Dr43V0yqDeZs3U5h/f+z9ydNkmRJeiD48XsiqmpmvsSaS+0FYICeBpq6ieY0x8F1/vAc5tR96iFQ01ADGGwFoKqyKpfIzIiMcHczUxV5zHNg5rfIoqq2+RJpHGGuqiJvX3lnZFwxC//K5q6Srt2Hc2R/+rYdofPW7xJh0+ylTAudOfFTAcQU7E4IEmZ3BwATYJeqC0e6roMNEV8hYpYeHml+0dsvjqumwphGGHEXqDG2GZJmq6GmKirCRaQwV0QEgVXQ5RqahFA0BQHzjy25rPruZ54LIiDKwEhpBIEQSak88XgOXr+wxxIFOXtFfJ8oA9wFKcKmgVmvSCO+COY73Ms1n9TuFko4ITErA0K0QxTMfZoTniFqgGxy5pMRR0G1LkUSQgwQCUic8rzqkAlGJqRDwDYk7Ic9hmGwfakMFw8O7kIBHgfIeAAPe/B4UJd2ItpeMEZb7xQ6EAhMQCRg03UgihBhhNCB4g6BIih2QIwIvQV3rZZZcm3PYAK5cdDg2xlfIkAYjAggZI1Zt77xldCcP35XT60QcGRLnK2p+OHuu3PhKVxhPSZ8/CP4YeG+c/DkTIm18gXIzE/DGQDvx2O26Y7j0jAM6rNiUtK4L/oTIQKbDQQRw8UrhLjHpTDCgbANb0EHBr17h3Q4YDP2SKmDyB6JdxBm0HgAxgHYJGWehwgKwawkzBc9kVl4UImOWjPkHQecKTHOx3J2tXqymtlXz40nMLwxh16QKmj1rDjKg6ZXGdsc85wksmHWoMTVvYt2OgzRmfRMrQoFrEIREbVoMEEEMUN4VCFFsvE190ucEmS4AdItxv1BhRG3I2QYIYcBPCaMJogYx4MqAwxadnClJLvwg91FwRRDgtH40YIghY4QIhAjVBDRRYR+i9hfoO/36HrG/vIK+90L3Gxf4qbb4Tu6wBADvnjxK/S7ARc4IEGQXLgPC4jsBIfNncqfpBmrfNXlCZTybIYV1zgJFpbQyq1Yb5K6qMWzye9bdc+0ixF9IHQERBmANIL6jdIRa+fBCTrrFBl27slQu6wpFucMcAA4gBk4CDCI4CBAApCqPCyow6rM6ievw2o4/wT0zVUTTpZ7CQ2/z9Fao9v5e8GdV4vND6dvlhbUpJJama6mkxatBiZiqCkJVK2Cmvb3ZV8fb+V80f3cIeKFvMAreoVtt0EfAjoO6IQQkOBR+kANyxlAEUIcvZfXeEaPDu2mfJil7X3wjGMLb06R69P2+f1G5VSdC+npjFRy7O20nhXaO+M/d+/Ze4wRsdS46SUxhWdU/dHBsKBGmbWRBNsmqYJZVhlXyixCiOy2pCKAs/buI0znMSHEjwoyL8EPrScmrrxOQmbKPcNHDHmfThBzQxTo8kvQ5gLUbyEi+P2332N/GHAYhoLqZKxRiQwGTNPWCbfCGHb8q9XoMoTx1FIxIURiNfH2s4HFzotAhndSpuCKxrvXF0r/rM1AZfmwgpDkdBUS6252sqxDpOCJ+Vypx1UJsbjZodtdoes2iJseXVRBRAzhTufQmvD3ITAlZZcTVIg2tWugQX0dF51M7IzWXxJKTtOATMAg7TOvek3DxcufIm2CErGhZjCsteDYtDSEWDn3GncNqNaYEbuZWTDB8MTXUd4/dV3tvEzPdWWsK5HC4oG8C1Nf3Qvl8JfgwE0bBQASaewHAEVgo/+MyQJTurshEXAawQcNTOexHglq/SjGXFHFNNc4DHa3MyIEQcNDA+IuHG6hwe593LQdnAaAgOjxJIUxjgmH2wOSBcpm5nw+CJAtIXw/x25EoIDYJbXcCsrQ8pgiIRC6rsNmu0OKA8bM6Ce48EOZRwlJBN/eCujmgK/TgBC32PQbc12xx3D7FvubdxgP1+BhD0l7pJTwn7/b4c2hg4g5zMo8DV0XiRkbJPzF5W+w7Qn9Zoeu32B38RJdv8E2XoHQA9TZ+abeJlRApNMyjm51wdV6QhFKdZ8BgbO7rBAjSBL4+huQMPpNp30eixCD2fpvTCVmAacEN9e/12F0Yu8/wzP8GOHOQo5PdY9wAr/5LUABb0BAJ4gvtgjY4fDZV4jDAfTmW2xv9vgfXr8FxhuE22/x+5sd/v53L/OJErcboN8YtzqAuy0QO/0MHbjrIRTAIUKIkOxQZbu/RhNa5ODQhoG29g8hv0N+rsz8gITAsY3ylJViyIT39twUJTwlT2MdVedx1swHFo9Phgpa9GAngPSA1/uSNciz6N0JFgSuAkqLIAwJYAGbW0AeByAlva9ZrRuQEng4gJMJGTjpnT6o4CGNDE4MHhmSyp3CPICFs9vHCI3lEYLiFsHwWQ0wTehi1Ls3dqAYQd0G6Spi/LLHxeYNrq7+AI4RHANuY499fIE3/SWGDuhe3GB7sQfhN9iB8BM21YC4xztiJHP3wxR0LkyBoBnYWv278GBRRShHZrhJnXD63X5TPW8L+3P2iDJOvAyEwIwewJuhw3V3hVebl9hseryIe7yQW/QU1EVVmGDVdX8+EPiegqgF/JCAwwjsh4TbIWEY2QQRio+KCw2p5UtQ/pPGKoJRYrg1DHixaGLVHmygmbopXeYb9Y7nsVRrqv4+Kacoih0rpyrDE8vkb1LqMaDq3/OgVqmrKTiBCIFtXLu+QyTC60DYxR6f9a/w6uIFri4u8BJbfPG3PboxgHgaae8e8IwXfgD49Mf7DhYRd2S0nMp71mks1aVzdvULVbXMqprf8v6hviALYjuLFH+icWs+d4/XqQWvZakDU9euTGZNWihgHgOCmqRTAcJ9GOtrQoi1/pwcmY/qwJTZ15kQ4pGZl03tLlk/BzE6yQA8I81kX68ReGedJattWHlOdZInHNRz4DG1BSocgLoNqNuCSBlPh8OIw2E8OiaFMVztqzxWTgjm5NXpsDAnMv+pvDSGCJl29yQA8yzrtLGhSRmqtTU/B6f+iCcEiX+tTfobpLcwmonUbVXsevSbnVpBmCsm1XhTgUrDhF7okEx+3xfWs/v5bb04slVq107+JH/QqTmpzH9luj/rHy1B2NTkQutpHs+xMFVApas4uyjn83/0qMhzUk2OEVbZYmUiZNPuUJ0r92x6jkh+PulMnaZqwyxAcrUuXcmkKIoJiEN2aV36oYwMMXcOzX2ekrpjYmV0kwApqUUCkdL/7p/b3RqFACU6zZw8D4eblzuThZWxwpxUG9ZcCnEAwIyUBhVqiLqnEFEGy5gGMCsDn5ktYDYAMNj3FwpzKAR1nRQCI0S15grU2blH5v1I3W1wcIaGE9lK8IowkgDvBuDyoAKQED2YNgM84rDf4+27WxwOt0jjgMAjmBnv9oTrFDINWsJh6rpISXCA4HsM2ARW7yQbBkKHXhhx0wNE6IQhMAaMCyFYPzVwd8rrQIUIBR8jc7PifrpBPQgjCFHnMW+Lyf5t6EMtrxZEnjqSFrdSIwQ/716+G976DI8C07F+aouBIzBlCz5JHZmWukdNPlaPPEbnrPaniJ9SFXZWsqYF6aBMSop2oQk4RITdJdKwQYSA+htcgBH2N4jhFjdDwg57vYM4AXQLSIcRHUbqEOIeCD1Cf4DEDiFu7Kzv7Fyzs95uYg+ubUgDJBRBhJ+IXN0RnhMAgjDIzk6qtJDZBALZgaK9y/zpfPe6iUD5oIycSD5sa5cuPs4Mc2nqwocseNDA4cRJ7880aG/c4kHUCoIOCUgMSiMkMTAewGOCHDTQNA8HYBzBg8btUPdKLohgyGjuD5NAkvaZXblBGAAjBBPhmKJNMIFOMKFRjAEhANtOssUDxR7oN6CXEfSa0F1GxNc9mDqkEDAGwm1gHAJwIODlZcJmc0Bn97BwwVG0FUUhqGB0R9bq2gFCwDI/eyXDCrtJ39VnwKmdq+8DgA6EG3RIcokYt4gxoqMRHUYQNnB3mjOl4Q9MgioQRPQvmeLKwKq0wWCwmBCwCtYON56XFgvP362flXOlyWg6nbVG8/mkUqlEJu9A1TxNB3JxQSzUM30iaFZkphWXfld/9dmwWvpyg2j2Zf3IJir4/mIZmQ4svLgQIjYx4KLrsd1ssOl7bLuI7RDQ3QTEFEChUq5aqvyuONuj3V/H6l3eyHe9S0/ho0fzV8uztOCOvKpz4S5z4Pt0/eXJYt8XqvheLCIeT8P6MSf24yaEzroD7wGnhBDsmhlc65CsMZMrRpIxloJZRGSN22OV3qPdp4UQx+v6mAngfI+hzMf7EEJ8aHh6/34/XlgmukkZbOJaUKrtFFzDKTFA5hfU8TcKIAhCthr2A8iJvCNX6/SsahhU0LOhYopyOuiLGJXAoY0x1XhBOcUZbl6YEirFV/60Smd01fmrptXUimmfiRSisuC3buVA6LY7dLsX6PoN+r43P+8mjKAqBsB0ky7t5YZmfci6nw26lbmQUoB54I0ymqBT56I0HncoayeunLbN2WzCmqqN9rQ9vDOdkfWzctuXhYXtPRCorNUj3fDezOZi+l7LFmtXWCyXld3Q5oELEgCEmaOuSXUCVMxmtgCTnIqwwNeaSGrKCUQgpuxjmJNpO5omlqRRy/Z4DPY+GcNDhSrmMiIUotEtl5IwYiAgEJhHZeYE1YzkGBDASDKCiDAOByRmHG6vIZxgrCOEoBYaaRx1fvoOutUEwzhifzioRYC1fxwTWEYIjwgxVpZGZfBDp/ER+s0WMQb0sgNF9WMNImw2W6QQlXnPyuqAwPAZggjj7U2Hv/ttwGEY8c///BYdBYR+g3R4i/Hd9/ibv/se/+3XByAyEAMCbUEEJBEAQ55RP0ok6RgPY8IgjL+5vlTBS+hwuQP+NL3Ftn+H17dvcXF5hZf4Qt05hd68a6hgJo0jUhotdoYybA6HASmNdlYQNpuN+uI2d3Ax9ggExP4VCCN4/wcQBF1fo/aCEAJEBOOYNH1Uv+duQfMx40XP8AwfFfgZaz9/zDtHNfgPAADpAhgjbuQdaLcFvfozhJQQb67RHfbYvHuDV++u8S+/vwYdbkG3I8Lhe4TDDf77mxf41bsri3kgmVYUCoiBsssmt5xAiAAROBieQEEtK00wkaBxzNjdPAUyK4SQGdtqvReLdRmcTahCdbGYZSXig6Vhzn13nERfVJ/5npfcp2IhISAeQTxqjWyxG9wSgkWt74TB42hxHQbN7woDwwBhuxOZMQ4HszoclYlvZXpsCCSGW01q50r8KAQTPJC6R4x+P5sLwRC3IIog6gCKoM0WCBHS79Dv9nj9Z78E9YzDpscYCYeux/ZC8Or1gBR2GOIVDmDcgnGAINEbRBFcQBAoYY9aJUPbwFDXU2xxl2rXVcVVkI91PfY5Wf2lXrDlFa0lozbtNO8d+BbuBSJSQN8H0P5z0PBPse2+wqbr0QVGMEvEEOZ45AeLz+j1w/RIQGAEJCEMLHibDvj9cI3rcVDteiDHKxND1l2RwSJkASjfM8ZPxYUmgGZOfCoZBKLK2mgKFe1XNCoqvkiWdKxh2+2+LUo+k/eLowNkMYoeDlhYiFa2K+jYdw8Wn+tdbh4tfDt2tzhGPI2S4e/8jNMHhK7v0HcRr168wMvNS3y+eY3Pdlf46YVgQ4rnB6aWziHv03prP16YrwNVFHzC/kyqPEb3vTdYPf8+PnhUQcRx7eL6Hc12WjEwQpPuMXmUH7O7mUVNsVVOz4l8TQEVLCSZu2WSjLQtQmYyVccnVfEhzCJiTQjxFJYQUxcZM/xiOjYrF/9dV8eTajCtwIMsBCZw17ytEeC5mVbGZPXx8TFcasN03E/HTzn++j7wsWl61trVzDI7fpurMgsjSH3kntmFU5dt0bqHEZPITEH4MwCI1elfI20NE9IZ17WlQlWTa3NPj7zqyNB3xyefQBmLJnP9EroNus1WTdRDLYCYHzamx9fgtlNh4uOfE8t9X9K6OobYTpJOyjECd7WQ5ZKpfnfuwjpyZDQlTAQe5wohmt8rc5Gtw6DE1MynrjWmKW+qMXUUpNAsztAw5rm7ZhKj4EhgTJOKWAt6z7oWowZ8Nm1DEWAcVAsyJTsDUv5to1V2Fmt5wirIYLNu0PgPKohQywEGKGogZ0IWRaVk2pjGXFHSEhAh61OCBAKLqtBxsjpSghiOl8w1k9Y9IopAQiFx2cYrMoOCx8voEOKIiA4SVFIWKEAscKaAlMrOc6JnYUqC/QDc7AXfvR3QjwM24wGHt3sc3t3g+5sRb28ZcavlZV4YCnOqLAeGpDK2LILEIc8NjYy3B8Y+ATwecJM6DOEWIfSgkJAYGJNgvLlGun6HlAaklJCM2TTsD0hiwiMAF7sefRfRdxGx67B58RJd16Pf9AgSQAiINCW0fU37El0XkK3dpcfPeawfvCvwqSkffBy3+plwCgdZev8e52Na+1PV/FSWESdL+6QWywpU/adsO6AmeCKqzS9dhB7pO8AEx6HfYNsH0G0Huo2I1wnxZsDFgbAb9F7yQMskjEPqkCRk2hGhs089+91FnwsmEKKhhhojKVGAmECD4Z/K6w+kcdJcOF8s2PLJnZl2mUcoJpwVta3wMfBPVVqxhGrClu/mwvkXIKklnd7HFhPJrURY3SISM2gcTBAx2nM96+Wg7pNkVCtDGUdTKPD7XO96nghBclN9PEkQZUCHwfyTisV+AGLXqUJD1wGhg1Cv47u5gMSItN1CLgH6cgPZEHjTg0OHMQbEDUMuVPiTbMEHCCLURRHMFSLBLTH0PcPnojB0a+8LLZNYJp9rIA2+vQ6nKZY7Q8UPCRRA1COGS3Shzy5o3Qpifu6Z9W0tjPiQZ4fhBizACMYoGjT+2LCpRU0RPBg7GxlrsOzLGMkZMDUf8d/TNh2bWpl9OZK4eidYyYtCp2Yk3tKIK7/UmdfXMU2+TbvRur7yM7nKMiXe/D0hC8lCjIixQ4w79N0ltv0Gm67Dhhg9qRstWligTVtc8W/WgwX4KHC7+aA8NGbYHI/w8uToT7SP5wkfEeaeDNbqeF9Y2HnwnmJEzFgb1Xda+b6W78eA5b1HWBmu2m0DANMYrGNCHCmSJgwmt4KYnoqrVgsnK5h9PUsI8QyPCme7a3rAxfOpMSQ+FnDknoCFC9ZckKSENCbVSk7K+KMQjWCaMo7sI6hlhKwd0flR7Y6mpQI8rxsLUAiAMEIMYDBGTu4c3TS+Izy2TA35lzMUSOudIm9Nu/JYrLugIy9LbI1Xo5HdBYWA0O+wuXqpSNxmgxgCYlAXKG6Rof21M3QiECiCXTxoj6z34kxQyr1Q2rNS6nPbGeTel+o+IAuSLNURXQ/y5ExeJa4EhZmPojFV+PhlbS+s1KbesFbHpD4vd3rv1fU1aSuhQg4gXA9RVrssmdb2THYv5J2s6mBhDdJsAgAxN0XqSokRJUI4mMueojnoASS7TjXbD4d9tqgQZvC4hyTGMA4VnSR5PglqbdHFqG2TgHEcMY6DjQhjGHVvpFH9T8fYIcSofrdjb/FkgDSqFv8wHMDMiEH3TwyOEwggpC4lWK0hhmHEMKplFCNgHBL2wwBOA5gPUFdDIctoksWRiF1AjITL8Qpd34NA4E7jH1AICLHT82aj45kOxrhJowkL9DKL3Yg3hx3+zd+NiN0NYp+wv77G4eaA/R6IF2TnFxdFC1+XVBaCaq0ekBLjMJhAgkerIyElwt8NarkSQ0TXC7a/uwXhAJjbvDEJ4q/+O/pf/6MKdTiBEyNVFltiTJ2r/hp9GNGnA7rtFlf/07/C9vPP8fqLn6HvNrjYfQ6WEbz/ThlDXQePDQGoUrFb3zwWPGPlz/AMP16Ihom5sj0LgHEPeftNuZ+3l8DnfwKkAXK4gQwD5HDA9uYWm+s9Pr++xcubPejmB+Bwi3jzA8Kwx3/53RW+u92Ahj2IOeOFGTJiZuzNoPdpRxrouoPijZK1zSkLF2C2eTO6lgwXMJTI9SOKVwAtgUbD70zAwK4NXQkeBDDrBMk0NFiQIK0bIhNECJffItD4DiJIo99Tes+HcczntFtOEoBpRB8CICEUHQ8ijbcRuuw+9IvwA17E70F9D3Q9QncJCj3C9jMgbjH0nyGFHtdhhyFs8Hb7JcaNYPzyd+g3EZef/RwgwZ4ikgl/rjHgxsZMoHHnxIQ9LGr1AKiwqSA81fzWf9aPwtOt37siQZ2+1jJvo4UsIostR3UhwT2AoIpKMFohqJXhtu+x2W7Qx6iuIoky/qjhmKRan8jCiLppH4anoTgGs2AUQRJASK2Zo+0rkO6lRJKFDxGEvmpxEUI4vj3HDzI6SgAJqYDK8JtFMonqDFaC+Aspn1OhxXI3Tz2YEB32hW3drSU2oSSc1mvWr5S/bGU96WBFXqzJVFrPMr5vCCXzpNRO45Jsd1vs4hY7/CVehK/w8uIVLvuIvjtY/JclaYa2oqannzk1nx4Q2jhIHyu8t2DVGZ+YvXCulS786Xj9eBnNyyMizXjcoTS/0BcYMzWjciaAcE3Mhknj1R9h9FWfLvH3x7XbjXO7MZ3nlr91Qggx4YWtSj4nz++6sk5JVB9FG37tFlqBO1kpnEhSa2bMtDWWuA1rzLw7wn3yLmoK5GYdL+9jsVp4cjAssJhyCyQsj00rWDAu/Z3rO7Z03WoqGFOWVEsMAI9jEUQoZl+Y/RWONN29R5QWj547pig2I+j0nbYjxIjY94hdj+jafqFql+eomNzeluq0XWxga/233NBjoz9H6h1pnFQnk1yE5cHKB75kghJY2kcTgmly18zjTixDTYTNGP9VB8TPnKa4pbvlEfbzwpjN1sekrcVlwzSHn5dLh2ZFloiY5ba7VCgyQnctJEndUDiTI1sTGZHArDU485rNFzVb/Ic0jhUBI83YEgSIJbaJSCrujGBuonIwadN7FEYaO8UZgpKdKQ0mQBkBhlpLsEZ0kWCRXarF6QIYZcYYcZuM+Z4SUkpQ92shB3N2gapaaASMg7mFSkkFFs48ijr+FAKCtZHZ3FpJXuHKLGLBfkggDgg8YDgkHAbV2swGT7REglXEoJ+v4sIkRkqiFlqcwOJxLQgcNYCgHBJoPICGg7qkYsHmzVvEm2u1ruAyj77GyMZuHPZgGXC7vwG6W3z/i99g84cbjO8GXFxdgX76c/QRIOoAqHs+YHLnybwnjw7Ts+MTvXM/iVY/Ct555DJ9YpihlY9d/hNZRtwFFm+CqabvU8Jd+9Hg9lV8J3Ef9wKMQ6YThUewJHXFEgMEnQWpjQjdBWhzg+7yALqJwP4G3U0ADrfY7jtcxgA6jKDEwDgWpp8IwqgOEK95q3Z2dSzjCt9wF4X5jRiO6TRMvrOtR9WFPseb7F73EBECCBjk7ortDhZ290zl7K8FxywqpNA7VHKaYtEAUz7QuwiWVnntyXiZbF5nCAGMDd2qMMguKCFSa0ZTTEAgcAzgGEGhQwgRl5vX2G024H4HiT0kXkHCBmnzGSRuMO6ukGLEPmwwoMf15gXGfkR8JQidYOwUd0wQMAECdQflFpuFuQ5TdMiDVqFGU0uHygVng7DWf/V8LD2ffkr7+6FwDi2ecVG1nIwhGL1QLAMIFV8EFe26jB5+GHA+kFg8ESD3nUjtboOoOzQiyX2LKMKHIoQotAQbrTVj4d+Rz5FpUql+a+MK0SXV79Kxxa/rMFtU7bpq1mKdx/94slbLXpi34e6TX1EY9qXljfk4EchceEZsQsCm67DtLrDtLtHHHl1Ud2IhCzIWJqQu816tfSBUaPaD0twt4XoJC3e0u0ytnqxWNX08FSrdsTVnvZ1ul3lV7x/fW4L3Joj4dOFjuSnuB8eYrmLMAEck9Jl/C2vZKmY/VQEl1zWQT7axlZosvztDCPGpQ74KDGn5ENYC0yCW7UsYj+2BMV8+jrPvRwFruOyU0S7i2llkLlzm85il5wDIAkkrSjrfa3UEmUXGlvM9829jDgIIcQOhhHEYgDSCTTO6uELqEGKH2PUAqYl93ZfllZcx0cW3OUWFqHrwOEUe9AwLRIibHTZXr1X7u+s1HkTstO0V0ToVoGV8NWtr1fhn9eMRz6yCXxzH7HM6qiLMVTlkoiEtRhALxEzMkc8FFTxX3091qKYPp0x8oAjDKw25tuXl7J/P8Erd9zlj8pxONg+bxmEmJiUzCSBunaQtc0EVgSBsc+JqjFYsZy1JAUvKWpBoxgTqnkcSaEwwpwY6L2C9nYkg0iMEYLRglRoDgsHjASwjhmEARN0xAGZBImL7OiIGhh/3KnAYAXO9kdKobUvmYiJGve8lIcaIEDuAXCMUcGZDShYFMwQEIcQu5tUpgFlGJA1YzYI0MsbEOIwJ47BXSwkJKqRogjgzui4gdOp6aRxHxLiBbBghqLVGNFwkxmjCzs7ONY2NUNYgQzhhHA6gcQSGgOFwg3Hc26oSBASE6fKqaTOPb+HCFevfMI461mlUq5O+AwcN+CrW7823v8PFr38BTglhTCBOONg4c9aY5RkT9YcBYA5I44Wu1X/3a5D8I36I/zsuXr/En/0//jWuPv8MX37xJXpKiMMbgFjdlzh3jKjghR8Ax3iGZ/hUwa2j7rtr6jgCnwYQkrGr/PI1Dz8otgcCuXkDvr3WJxW6OF5+Btm9hiTRWAmDBWHe70HjgC//6g2+PBwQ3n6ncSWuvwfGA3B4h5AStu+u8W4f8W+/f4VDCpBR7yayey644NzoWDKXQBAGkwbJVrwXqONkFezH7m34c3e1BL1/RGNBqdDA4zBxZtiW3+bWMOMEVR4gu1xkY2Z68OiZFa39jZ0KGpg6xYu7gC29w8/73yB0AbS7QOh6xN0F4naDuN2qq6VND96+Bu9egnEJwRaHeIEx7PC97HCLHm9liwM63IYdmASvXvwKMd7iLdS24ZauAdrjcvcWhD2+kwNA1na4dR7r/IsgewI0Cz7KTq+qjjW7pjCqM+OuEWDUf+xIQ1Ve/c5wphmD2HGpCS53J6AsaJm/aRGDQEDXRfQI2PQRXYyIwVy5Usj4coaPavubYE1UMWSQpHHC4HZF2vaeCGy4p1pD6LMIQqAJasRaKpFkngZQ8Pccc64SQrlCTCml2awFZsIGp+EmaZt8/sPjOCyNQ7V+6rYZvliSmXtOW4c1XVPWXLUes3ZRW9Pd+WXVIIveRQJkHlyJm0hAIGy3W2w2PX6y2+Hl9gpfXb7C690lLrc77CLQdQkhhlzOap3PsApzJe/T2ME8xbkYxX3nYprvozp8ADyyIGKNIXGWxnNzYdVfF54/EawyVD6ENpdLeR/Q7zUhRGZK2gUuqBDktbK0wPzpB95UCFFbQ5zVxoX0c2HDaSHEUWbYHefvw2jMVzfMQ4s4E861pmisbeysXd3TZ231I4lO5V9o6rQt5/bn4fBxXNIN7uUEYhpAZCbaAHpjBiaWctaqytqJbtDk80jlKIimfp/MizP7YzQkdczEmiZNoBjgTtkjOngALccLl1pReGp3FIaSa/dZvhDUAqLbIHSdumGyeBA1on10AKpnq+usHqSTUMqYZTmLmejk3squ8LyVJVRLC1Tz70x2P49dCLFGYDlunpsp80SGrE+znRqeWsPsPnjWevCyZXABrQffc5qFpdpPTqQHsy7y5kkmWzLhLP7fjMia1luL/IqGvAcZ5qACD/GAmB7wmsfs5kkz2Fp3JoAJnpjL3Zq1GUWtIzTIZvFzrXElCYnH0twQsoZoZvSHpbVGxlPgPA5ubTGOCWNi8Chm1aFMBhVEWF6UT2ENukyk7qRCCEic1EJEXFvP8JIQ1B+5uYdzYSNZGySNYCKAQ7ZCKPNwbCVS/jeQRcUwAROMmcUmrWAWBDA4c2wIIwFDiMAwgIbbjIvl9VQRtopu+d1r52HQ9RtSgnDC9c2IfbrG+J/+Fq+++hK7f3WJy22HvtsYY2iqkdriVg+F94elv1/4JPo1PUQ+UesTh7XWf3zk8x1Aqltu5d55KsWj5q67swBSDN+fnOkzpp9ARF3SZcYWAeARLAe9dwiQCAAB2F2A5EJd6Y0HhE0AjXuE694EERegcUDc9uj3hCvZoE8EGaB3WRIQJ1BSRh/xaJ8aIJbEhPwYVBgQGNdpg0G6dh6McdigMKzM9B32EAje8hZJaC6IgAugXahgQgergQGIXYpdOCDKwd4TkitkZKI2ZFxKiFQQYcJ8ogDqe1x0F3jx4ieIfQe6uEToN+h2l+o29OICsesQ+x5p8xJp8xKMHVi2eCOXGGWDYdzghiP2whjASGEPoRFp8wYUb4zBKuggIDqAwgBgLNaYed1Ivq8Mm6gWg/ewWs/OnOXqe7N2Ju6aqnKMOVHS5efT9buAeDbtui8s5J+wqIigCl5jB0DjbnRg9DQigMtVe6TI+zVtsqcfVpgNqwqc3BjIoVABhJD/9Hmk+n1pUvBpprlLsXXeq7RoV70epg3K9IlnEEdkZ2VW1M2ZbaiQ/PxYmiRlmU3WZ533wXPdLrY8LMqIs2FwHlrB6QIFdF1EFzv0dIlteIFNt0EXAjaU0Hv+s2j/9wzTas9hjZ3NPltK+Dj9LPesr8WVhJNXTtuc08HzW/owfuL71pN4LxYR957mT4IK+DSgdrdRm5HywoorjKb8ID8nc8cQ3P9zOM34XYPHEkI8wxOAoARp9UdSuWlyWGNCrhU7WW8Pcen0xwyLZoL2r4gg3P4BoIBw9TWo2+GL1y+QUsJvv/1BY0WMAqSCIU7nespErSpo3s/rX/pheGNQX74dQqUVDYz7PYTVV34IAVEY/WaLHhtl9IWYCZ9jxMU5+LjirsqMZFvP7l4gbnbYvvwMIUZ0fQ8gZN/qJy/23Czz5V8TUCvtOBuO8UOP5SnkozLRc+VU4cj2LzthXHB8nTNqznkXRKxaTeXqS92FWJi2r3p6JOlRuOu4VNPoiGPrlmwdsrWYaTI601iYJ7ltXcGtinIB2YeycCWEyMwhZ+ZHcFCmud/X2dLCXBmNacwufALIgjwzkgUD1VgDjDQeAKhJfSCooM/azcIYkfJaIdIWs4xqqZQGsGmgggXJ20CAxBGEDYIEPWeIEINaSLj7tXyeiK0HKZr+zCPG4YD94YCbm4O5XCqapL4eVRBJ6ELMwgERYH8YMY6M2N0iJUbfbwEA0dxUlBgaHTiYkCAyaAwWcJ4ASRiHW3WhIR6UleECNp1jZMLBcR/jzOW9ELoOAawBRrkIUngUc5kRIMGD2KtA5HZ3gbc//wtsf/cbXL57k+nXLKwlDYtNpP6n/bwPRBpnAxrMdBwThIEbeoXxXcIv/t//X/SvLrC96PD1z77GxZ/9BUhG0P47rT9QFv4uuTR5hmd4hg8AIh+tAIncBMIuLJ7SZkIVqqN3FNkZidsfwPvvLW2AWEhjvPgpsHkJfvEKYEZIPwFJQhhuAR4hwy0ojcC7d8A44q9uDhrIeX8LpBFhvwfSCDrcaADs/R4YR8hwADFAKYGGa4Rhj2R349+8+yl+s7+EuPtCNqalQIXVAAABB8IWA/48/lcMQvjPw19jQA8mBpNZOVDhqzOgLg5LeGu9MlH8+33R/Q6fx2+B2EEoQLpe76l+A4oBYaNulGLXQWLE4dULSNchbLaIXY/t5RViv8H26grUbxB2V6Bug7i9AHU9qN+pRWDXI1GHhA6HIWIYIm4OETwEfH/D+HZIuBj+Bhf4Dp/RPyDQO9ymt0g8IpogIgI2PqaAMFUgEc5j1WDjZKNhY0kQUPabzxmXyaOmFz3sQrJCKgsI//QB9TWYvyPjMoU2QPn+UNLyGDcuu93Uz+HQ48CvEXYvESngRdjjldygQ49gLnBmFAQVnPqDgtMKwkhCOIjGiXC8SEHbr9YQlC0iOtJPTVHzjHx6yCiBUCkkAUJsymhlmJsYEdOxr3/OhA+T9/m3rxEsrIljdFz1Tnyt+u9617tikP8BzXqUqr5zeCOYkDPUPiQ4HkglQUVn+PPYdYhdxG67w3azwwX9OV7ga1x2L3AVA16FPToIuhhBsVNh6R0Vs348cJe9dyqtGE25lHadb7Fc/glmy5nlLNO2DxNSPAW8J9dM53IX1phrx59ozo8TiVuHx23vuv+y9ntmmqzc00eFEJh8r5kNd7U6qIQQ06wPsYTI2oNH6/4YQdbvSJmlyPAY6/6YZURd59Rd1EwoAZx1mc36cZfzsOBF55efszz9zM9itay8fzAslN+cstn2NVdsjEnVoL3cRnQJuK0tTu8yEatT2KJT0+s0CySg7lQQgRA7CKkfd8qM/5Ipu8OpCzqjTWvg4xRIfe0SEWLsEfqNuoSKGii3nkMnvADHLwtiW4aQK6WuvGln7S3FTstfOZPXOrKwlsqjGpmGudyqiCGaJVloJOXzNCPBPh/n7L+8Vye/c1urB6SNIv+O5kt1BzSNXO/AyoCuCh2a9ARzMj1LloVMi5WWfurqUCLJV7T63T2DQCYnOkrDGvqjAmeKiGmCwl0+VYEynViTUNxyiZ0P4swYr8QIEneFJNndgpR+uQDG/vO1EaIFRPag8+J5PKPujyIS43wuKe++EFhaRDE593XoFh7uzmpMCSGNSJIQOCDAfHSjaLkqM98CXwfJQTxByP3TfeoMFJ1EFzrN92n9zIQRwT9NGMJBhbtmHUJGpOZjmQKo6zR6tIFbyJAUtxWzs4JsbRIBYgLVoBZbQQQRAt7v8c1//+9IN+/w6vUXuNx2uOx2ACeQDNb+YOtg5a68J3Nk9Xp+VO3N9w9PQbI92UhM5/QuY35njfn3Bw8ln+9qBbcGS6f+dISfYpnfNdbFg2JjLIDeHA3xZbiFXVhcn482KsIgMCCVf0IIMN5o+9xCV0w4YK4CBQEIPQ4Xl0BKkM0WxAly0E8aBhAnhCGpIOJwCxkTZDyo2yZOCMMNwnALsd8Xb17g5e1GBR0skGT3G4uhKHY3sqCnHrH/DBDgxW2HjYTsbkatHwge5SAzWO1fLUVjA5n0Hy92X+JiewGJPUAR0vVAiKDtBhQjun4HMkECYsTmxRUkRnS9Wududpdqpbu9AIWI0FkMiM1Wrf5iB4oRIZhv+NDpHUMBvRA6IWziO1zyLWL6Bp18h4A3ILkFyQB1taQChgB3vVpwldkKMjyp4FILBMEUv1zbwIJ81/oYZiZFU1hGrqtH/syf81pjK3jA5qxQX4LkMT5wxLvhAtvdxpQ0dXUEzO9SQ3Wb1n3IW9FHjwUYecABbzDiGklY44I4XmbIUX3H1+2efpf60/NKxmiz8O9k35eOr9yIqtCVpVhRJOvlLdY7x9WpejVd4836PFHZDL9q8DwprpXroZ9YPWT6DCocYldWCREhRGxiwC5GbLsdNt0OO4roKSAgwY9smY7NOfAx4Ahri+ZsJOGuO+6c9DZ3tDY0tkjromSt5PueCCfyzcbn7liVcxFWV849kJ/3GCPiAUetEYkf9rj+NGEalJrrz8lCWhJCuE9UZxAGC5KVGf73WHSPJYT4qGD99LkbOD71CVgO1MGt/ffJPEsI6zPcHUyDLgs+gIlgqBW77Pd7DMOA/e0tJDH+5ItL3AyEX/yBkfixjteaFCu/M8rqezoAAR367Q7MowoEWDCOh8KkozArt5S1dgEuJG/e+/jUjDxB7DbYvfwMFDs1ew+kJvFemxM8aAk0zjRRCV4I+FlbGkKOUTbH5enBPnc68qjnI7248Mlp6vOeaJKzrcxQXHWxQ9ScwaeEEF77qX09Oysyjp3JlEkP23uheXVHcBdLugxqtxVo3ShNBK2NZuCMSCm/WbnJQFBmNrsogi2OQGXlgGpMRSoNQ0KxRsl52ARksP0hFhPC2sP6W5jzp1s+Emka7R4X10xJ2y5AthQQs4ZQzVHXTKwHgkuQbUCtC0hdrgUKiKQlDoNZWyTTHhMTloizcdQCIqVkzVcmCpmFBQXK50CweR9EhSzDMEAAdP0tmBlX4wEhAB13QNDzhKAB+QBWTVOWXLb6xhWAR7gGpzINArLgLK8XZCFcPd8EFTx0sQNkRBd1vgI6uIsD5DIJIj7PAMzSwYNbpjGZ8EjHTC0VyOQUVIh6Z9a4NUaMyvBgAVGH7eUGAQO++z//Ld783SvsXr3GVz/5Kf78L/8KcbyB3PzehCYBKY0Y05jH5Bme4RmOwx+d1igVhrs76PERCIZH5aOxIEsTJl3IrIuABGAE3v0atZWmGH3JNYNfgH3fAX0PSKfnouxAIgjCQH+BePGVumMaD6pkN47moD4hpGsEvkYa1ef9F0PCZ4nB4wjhlO9I2B0qJhRh1lgTwJ8giOAvkmmHG47Fjj9SzDiSn8d6lRMkdGoNF6K6/Ox7UIxmCRGBuDVBhH7GfgMKUa0bQkAMWz2XYwSR3hNaDQHDNfD2Nzo92CvOkm5ByTC0i5eg7goHCTiAcDUKDkHwdfhv+Cz8Ft/Tf0Hitxg9IrEJkIIoA3R0Lqjjs2UxwHGxrIAAF0ZQmfcqTyFHatwbcE485c8KG81rSNBaQkjBR+p09fsG1vZqTZecD0tXZAiEGAnfjVswf40/ef0KXQzogiCSW1zXNIuvEcUgPgp+hqjIZBRgL7d4R/8Fh/AOAxgDA4MwCCHHigDK9s4Byxc64nhTky/zsKlKJQvf66+TuZ1O6yJJ6GdQvZ4WylqFpbVUB6KuyrJA8zNriMLMmTR2GQrNQwAVYcQsh583tgMD+adZD/c9Nn2HL7otXu8u8Lq7xIvNFi/7iIto7kpJIGwWvktT8Qz3hJpvaSdaQ2DXtLc80pivryk/p5er+Hgm/D1aRJwJSwyKc7I50+cxT/aP4ZJ4ADRIsxOw4qjkhNg+IoTwGzjUDMI1wlUKcroEa0KI1i3MOUy6Ns0HMW88p84Z4+zIxs/3lqNkdzgk3kP3Zz7/MdcwO7vNH+D8u6+lxLE+fUhLrDkzlyoEyBnfxrAidad2sd1gZFbiyLdyLhDtOrrTHLVnTf2Eska8MeLsAqZACDDtMGZ0FbIaQix7x4UtdLxJVH1Z22bTq5ec4RmjMieDk1cFYXCEsLaCKDt06udflitCfRSUQV5bPU2KCqlpv1W1yuStTN9LOXfXtKC9XgqVEIKqdycIpyNj3rye1X9qF03uJpTxL7/b+5/qtXYXsHlrmCR56AphUXfBW+fuh8oCCbaWLT3bemHkdePa+x7sEvbdfY0qMaexXbQd1s8QEMTcJzREubWpYqgLvG4TILCokIFK8HVfrgIy90JmTWHEnCK01ar08aiEKt5W8rARbL60M+Fdt1PbFgxX8HYxOAs2tIqiIVvX7+Pmba3/tD9KbAWKeTzcxUi9w0U8PZQgJy6CQ/twi6zpGlX+grksCAFdCAgAkt2LySURdU4ps0QhgHcXOLz6DHJ9Dbq+NvmWU6AqvGEE9bfs519F6NZCX4IGzCQRjOOI8c0ev/4P/xHp3Tt8/dOfoQ/AZnMF8ABJQxkXzOGuWtez/POeP8OHgiU84RQcw+8fCnfBiZeye7Z7VU1W5RMgoJNuUUvgnN3gJ21jqaT9fYIuIbgNVemIWxFMV0rDYCW/GauqUfWP/IoxCz2vMKdMXozhs/aOAQoMwR4SBIgJCKye7wR66fAWYHVbKCKIiUHMiPm3CfHZBRFaN7uwnFUoHCsFAfHm5ctOLzxXzMv0MgWICdVBQV0iUoAEs4KLUS/KqL89aCwC672Fg95RElynIY8n0i1cZOPjh0qBQsYbCAEja4wIjbXEVo7YvcxzXYoV3HGepMK7ZPrO1od/9wSmfFBc2bQKDnMFtVnjqnLRlDtv9Np3b1/9js7fmtXBk5c3C2IQxBAQui26rkeMESEwKCSLRzXHm0uvHdP8QDclBUi/g6CDcACLIEnS+F2iUU+SBBM66tw5HeZLQfIeb/F4ooyClh0tlPHnjNXTwujX9Myx6Sy1HXm5tEaOpVuvoXx3GqDK84DjOtMtNY67cLbWVblTpsxTIzIhZtTYO3KFjj/DZdjiIgRs4TR2tecCA58fIPsA+T60rpi9bUfo6VnCxcY+0j12ly0yv5QeUO+E8XD23Wl0w6nxe4ytf9f+5bNsed/UXVznpfid8/D5fY8WEfeED3hGf1B4QJ+nJsiZySEPsIQwn8tHGf4nDpxjlhDPoDATQtxhj6+6HXkimKMez/ChoN7DUp2ZIahWVYwRBMJXX7wGC/Dduz1oTHM0/A7n7VF6ZYafOSILuAqWB4IGBcRMlCgzkUIwwafvBUfmlwiUOSxery7QyExGY0oGQowBFOPcNZSX5wzjqm9Zg706U50+za2YNeL44J6/m3yi1i0hsqG7N1oEQgTxs93rzDxXKmd/9ZcpjmNYcf66gNQcQViOuhRcmkSXCshyeflZpodLmpNn1eq6cqEBCiFdQ6DiTkfKuuCUDAlVZjgbY396N3vsBLZg05z90MKsAtRKIXFSbXaohmQIAaPFVmnKs/eu8AgRcEqQBAysMQpSGjSuQ1QGf1CzJDDB4kukrCGap764vHYuPNyHtCbTVRVhTIdxqPYHbDvoHgckxz4IREgQjRGTZ0rUl7YRvwHmWxtajzfNXTMNaUQYSYPNSwBzQCRC6IugABDEvPCtjVzibwjE/GcZcyAYqWfxc6hiGwCU80Szntpue7NGMauNccwKc67lC9F1oOcyYfzsS+xffYbtL/8eu/2NpTfhjgAcGJFhZvdUnTmc0/niJAI2mw2YO+wPAen7a/zD//q/4u1f/SV++k/+KV59/jm+/PKn4NsfwO9+q0vXz7unZHo+wzP8yKAIi9s7rHz3S/UTx4+l8AmjM1bgvTNLUDKLiWw9YX/kjBiPj6Pl5OsjM0OUm5lPIEP1SARRBmPuhwb/UIHDLeT2NruGyhgYCSQCEgJYOr1/RdsQvVOOh3r9uX0miKhel1YvwZwmJrssKRTUqX1n64QEgMVwGufM0haX1HcNzlMxcPVW1dtx3B8w3v4A7n8CpkuMCeAxQMZO/yymR922euzzFT1DwNrEGa/0Z+J51Aoxz7e4a0e1NBETRLgyQWmIXZbN/Pj9NvXTX9ddu2Oq2st126djRva/4tHnCCOmaYiACMaWCZfdBnRxhd1uh77vEbtBcTQyt41r68dw8g92SoQI7L4Gc4f0do8xEQ4sODDjwIKBBSOrJW4UyWuSoNa9CVRFRoGN6ZzuaTlMpAIxOBp5hLBYWH7VSXEGKVgv1uozL9i8SOebddb+uth6nU7KbM6TqgCvanpFLAgh9FyZ0wpEfiw5Pex26kEtrGJAt+nR9Vv08lPs+E/x+fYVXnQRl/GAHgAk2NkMYCOQP70BrgPo7VUzJG0bzxnrHyE8+P4+UxjxEcP7aPvZgohH1wq+a8/WklP7o1wz9W7/MCtgWisdfVsnfNji58yYaAnVxj2HtYgmh2H5lTkOhSE1PUHPbHdh/LVCiNm6WRFS0OwLrB80+X2kbY8JJ+eH1psx2dX32eDH9ttUon4XyPoZshCUWgtfzLPw8BOC9bFsSYIzBqPOWyNaTw6uYdJqyIoI+PAOwglEnZqHkwZpvhSChBEv391iPzJuDlIX13xd6sL62jo9+brGLC05UQbD68LkvPEAseVfca3wE1XT9DHlSgACAkWEfoOuU7+9RFUd3kvx3tqTKbJqyHnR8Flq2NIYzCGfYPWhQDR7X6qeEIazOozMoukYOA5buAHleJ8KIo60ONe7RPC176ekwyrpMTsbpdWqIsrjM8OXj2y2Y4Tgygu45lZ5UggjZxRPsxj7IBPeIkDisVRVEczubiklFT4w1/c0ZyJNQHCNQl9oqiggKkBAREopx0/Q57E0S6y9ADSOCQOSIAhqcGBWQErvM4TNZUWVT8SCFOY9YswBOIM+ATKCWU34a0sP4VEDczZ3n5FPBHRRAzCzWQAkBoiiEUWanikBVLllYGVk8MhIIYGHESkEpFHrikHdZoQUEAMBtSWnlwmA7N96DxFBmQMCCDi3xWVg1WR7VwACIgULYspZc7eQu7p2hMRId4GIa7ARogmLmTkH7swnuSDfx2rN4swc5DXW0tlk8Xd67NMW3//hFr/5d/8n+M//El99+SUo9sDmBZAOQBqQGTszqIjhurtnBrheTPUEaNpdNcc/eHBQg7NImjvkOzf/+4Cj2NId5+sp0Mk7Wx1Uyl3tXdbYidm/pqdqDLtC11gZJ9ZfadLDZnKxb2v99TbN3k97W860omBAOYHjGpSflrNj+TyYIC8LqLaXlw/nSbvIheUuTPa2QEDVWezVNZYE8LNVTDmUips6+30Ulkg9u5szrjJNQNbACheY2oKUC6kekHZgfD6a8s3NEpnrxESMREAKqt3Oegmhphb0GjEVATH2v5/7x6B5X7dxns+HYbknqMa6nt8lugsoJpezWkr6k9s6r6rJszmumFviX3zQDT/uuoiNdOi7HtsQ0JO6hHT3kt6/PF9LTVnWf1pp+XI7gTIlx46YJl+eb0UihjTi+8Me12lEEgFXc+J4jAohiqvJbPJqqJXk/0qHyRuXp6eaKzIsspieN72d917cOOMErJ1lC8/lRIG5XY732meOMVaUh07CZGkLpMRVq0jUpZbCeTP1/JJASBAjIXQBuwDsAmEXe2y7gN7ch7WWvZUlM9XHHGHJQmXxySoBPnmxcGY/7qU+3wnT07RJcJ+6fb787G7eTWqfrSMb93JNrtwr9x2U+Vl5FP9aTHmcPl6Ywapsu3ePJToBH79FxLlQI29zzOD9tmUF5Nhm8AM7L/S7tXmGNFSHpC78eYUlADVN3kA1g8mRabt0ZwfM5OfsddOpUtZCplXhw+oD4OQmeu9wZjsazuDsyDxRw0Idj0nUe3ukWDucTbg/6uXyPmC+9pdhuh/rE/dUp59qbbaoijK2rEZfXsJIN99pULvXf4K42SJGZVBuLxkvhxGS9vj+Gvi7bzVgrLtem7KOWwHXenuOI4emy8GhQomkQsLdXUoVe4SKS5ZiqjrF2hfmoRr2Gq9iuzAJBOo77F5+rr7tQ3HL5NkFNWLtVSzPeTPLy7d1u4pWkReZrbY2XZt8WQjgud29jddfIRX2Tw4KPNHqLEIIQ0xXcPo1gVRNIHsKrpCaY7uisYjgtg6lV5cI1CnxWAUrnrz1d3UJTXtrYmqyoMXbJ5IVJql66eWo0MGY5c44rtKzCSE4McZxzBX7bnZBHBuhAEkIwrmuEDqd3a7TIPSHPUSSDlgAQt8DyX1tKy4gTvCBwZzMZZQyxCEBzAlsQhFhr6ti7hhhTQCIRYN8hoQg6iZKxgMQAkbpbAxZmR/CCGzBmY3LQdCzposR264DyQFIpoU3AoINOiKtB6JrkGzmGNpWFqTDCAJh3CcEjCAa1E1SZ0GpKUAkIMYOJNYX39ju9ZwEtYMisfUvwc6ezEzSPNPzR4NUBxBFcCAkEgv9WflVl6oYV+gEEGJAF3t0fYfO5pKzYErdY0kVtiIxZ2uV4s6rilcjOmddF8G4QHrxMwzvbvCb/+1/g/zLb/HP/pf/GaHbIl19BezfANffYkJl+VRX5275V0vXRSmrAox10vAZPjB8YCHM7Mz95KDaE9XlWugoynRTuXhqFxun766PD8oJkHuyRA8alNNxYc+vCkcMN5iSsTlJOeDmFvwlcYulC2Cunaa4SJPffpTfYbmdZ0OFm5PMi5I6TQv1iavfZPKuLUdgVyMBJCZWZ0Iw14gpjBhJMATBCLZ7wkU0ejclq4LtLwEmiJj250Rfc6MyxoeCPUu+m3JvFNmfbAla+QwAudJA1R4XQhUsfdLcc3gE1eXZnI8t5aNNrXBjs6TebHtcxR0uN1u8iD12CNgQoQ8x61IJFE9YlmsdxfjPglNayy3dURBdnX9GEgIlxu1wwDf7d/h+HDAybG34TrJ9yuYGkgJqISQEEGOKa7aG8FqcFyIgiFpPlfVRLKgkZ0azTopC2EqnjykY1Z/Spq2VwGQ2qILCV0v655Y/R4URbTt1tieWqKFddxOKp8kbRC0gMq1BAiJG7AO6TcRnm4jXFx0+Cz2uesK2i9jGgEAoikQCtXg2q2Qti5zkWhyxY0/OA1r8uj5XD70XV/KfVXf1vhZMP0pb/MybFpi5Dvco/655zk3frr8l7EWfz9/cpUVPK4ioEIQHQX0hnoNI3/FcP8Vgz49nz09VIutJHgH3XAoUnC0gqoCU8+GnWV/yXvOLak0IsTD+1Jwv84JnFhCTMuYWErKcblbzQrKVs24535mTcHa6Y68cxVw61k9vkHPX6JPCMZzusfgMT8C/eLjh63L++5T6WHyAGf5ev6v+JfMPK/u3SOkA2b5AiJ26Bilq8CBWpEvi8oAXJH/KllqsfHkfehE5CldLfDZZK66drJC2pf9+gEiVYEKd5iOFQBQQNzvE2FlwXJpp+Rb8VGbFIb87AxbOxuPnTnH+Mm1P/mzGa7oKQn6a01iS5X1QnmXBwz1W9vQMm13B1VXYaKNKKxSorQ5yZ2viAJgvgtz2aZuQiRkVzi0wBTxtg337XVo9qTqUAwbn4OQt6p7H0RYRp9TsSa1PjJmujGVvqNgYeEyXrMHZNAZqtQCzPLA4Ck7oUu5Qid3g9TMj4wXOANJ4BshuoVzj3vMUBSwVBLAwAoLFnUBug1gQa0hS/8JZiKAtcCsLd32RY9fEgMgRXZeQRjEXANJqPVZCLIHvYxXocEoYxlGprDioNQSAGCKSuU0Si8+RpyZr55kLpEwYVwvJYunUxEiZx9r9ZUVMJhUWqIVKgnBL2IkYPiSS20AEjBcvcfvFTyB/+D1oHDP/zMeWnQfjwgmZrGXJjlLyuvO9L7HHd4cO+PX3+Obf/lvsvvoKV3/255C4hexeA8MNMNw2Yy0CJVLrDWbjMNVIPIr/VW/Wfs9lso+FTDw93Pc6/yA9/EgsQT4mOJcGmK5JmnyeX5+eAfeBj2JfZByhnMPNqwU4O97MNN/ZTbrfHJ5Kd/4s3WFeVtowYVOtvp9ie1PcekkA7DgF4Q0ifQfQ6IjGNOlSg4/8rhDRGWJ2CvJNfsd855Q5LbIak2lVtPSjueUnicp9GIhwwxHCG0TaYdP36GNEFzRGBGhseTRYdmW87JrncWGGj6PFuTU2BMwKYrpMaUYWOH0kpnThFFrjhnNxWk2oQTAlFftsEIqqcUtrQ9ZWzV3X0nxtNyuyaHsZueq/M6Jerft63UnJNEER27qrtbGkSLwA9X53XJ8sxsyGBDsAcbxEOLxGf7XV9RjVPZhaT0/2rxVCHYCf3kKuI+Tb7kFr8dycuSUn7uB78VmmdZx4fhRmAspTldcb5T5n2xMwwU5VJfWP+r001R9vSeHD3LXbPx6LiD8yWEWgjQCV5jahihgu2q/5+iMvzzV5JkKIwkE63qYZs/w+Qghr2bSotTobKvgTJrQ+Ahrjk4GPYJo/giYAALJZ3AooYzeBr78FhQ4SNgAFC6imTLYAqIKHEEBurhkmZSxdLsvXfCGaWiQ842ok5c6qMmSXO1PGs2tCLSLxXmxdYN3EOelGIWJ79UoFERSMd79ACj7injx5NFFxOVQz/eomrdN67bjXX5oZmDIO85FcWT+gOu+XqJc7wLm0qcx+FO22rFTVECb1OOldcaqpXBMRDk1HpVmj0ybV7mlUfmICAFHtfNfUJLK4CwSzhhCkZObbKNrxLAxOozHsS8DkLAAIXgZnwqssBy1XUFlbEDT4u1SaViYooUBK+WXrDNdU9LIAIBUBRGXBkY1PgjHevd7AIGEECSrAQAAFHw+LX8AWaDRGrc+CV4sF2A4BCJHQdQHq1LsHIyG5Zhm7n4l6JtyaQtdpYoYkwn5/sHwq2BBhcOwQLQbCOI4IgRBD7QSjPm+M7WDzGNw6igEO6kxJAxRSk9fnzSdIQBhTwphGpNF1CL0DAdqcuZXq+Ppz7F++QjeO2F6/Q0oaKJVFxyE3xy0lJodxjhfhI8X+mxD6HfZxgx++2+PX//v/B5/983+OV3/+l+DtJdLmEvTu95DhFq4hmZX0zPijxv9cz6UWvkl9Znzk8LG4ZXqGTx8mt+6nAadUp39EcI7g4ViaB6I/Vv7aj/vDIrv12LzanQ78Hl34BgGHo3jZIrNOpl/W65rmoZXXsxqdLpgK6pYa5IPgCIqsJT4ygzJJQ3VO/5fsX1PGrHDmEALeDB3epSt8sXmBbb/Bpt9g0/eIIamVJKi43YHe/AUrL7jMXeFhQgsdr3KXqyBiEMZoaGO2sNTOtnnzN7P8nCiU5emopkLRZ8qY00hmMSrJ3rW0z+IyqZfe0uZc3BgnIOeZ0JxT7qtZNxe3sNUATQUT/uwYHTmtU5zGtecLebJC0KTfsYuIXYcXMeJV12HHX6FPX+Oiu8LWLG1jUDegzi0gG7+s77dh4KcH4G0E/aE7Eh/nj+PuaOAhOOOd79v7LOInBj8Xz2xW3vt36Mb5MSIWWpE1Gyc1UnuiTws6We5SHU8B52mZfwhE8251ZmsItnBVRvAvHdZTKyMXQrgrCMpEpQYHqwUS0zLaFtPs5ZoQYmaNscBEnN0xp9bBGZo5Z5f1nuBeGk5rY/c+4Qwc79HgIXfAAxv4caySZagD0i/6CsXCOcsM3H6PcbwBLj5DEsGLFxfoN4IUCcOQcDvc5iP6MDLe3UxNqrV0v22ceSuuxQzAuG2QUDEzUa/3wsyTCslzTW1m1kyBEEJEoGhnUblX6tYU9K3+NiUuBEQB3WaH0HXmSoWK1u/ksp3uzPZeJZBJ/Ru/z1OtyYcsoFUV/7ZNsx+zfKVjU8uxNmnI2anJunBG5TFaQMqXYImwkBXGf8NQtTHOyQRF5d8sR4xwPXesG1q2WsMlpgEAQuOqp517KW10Ii6pBUAMfo8i8881IHLKrphgRJfGhkgmrEhNTUrwBEBCFhpEs9zxsUwuNHBqEnkoAGGkUTXy4X/uKIjNXaMvWVgf2Jn/KEIWnQ61nGLdzyyiwQlZIIGNaGUEASARIBeSFKuHWC8q8RgVKgANMFcHFiuhiwEdSxZYEIWWN6GUO0Igk7UIODEOgwp1CCoIEhF0UZkBPTNSjBCEEjujHEr5ozWG8PgbDHAoRFvjO6TKYEInZsZ+v8eYEg5pBEAIMSKvVxA8ZGoIGmicko6J4l6hwqsZwgQ2ay0S0nGvzhmq1i/gVigFF9S+MIZhwC0C/u6bG3z38gd8df0Ose/R9RtzRWWnplGpmTnAOlYtL+JpCaV7a6lP8p16/7HBQ1t3dv4PyIheauNaa2jy+ZGR5wVqxS6i8lf9PNb4yVG0Ao/Y+0fcB0sBu5fef2i4VzuW+YF3rfihJRSYLBSaPq8gOOM8t8P/sfbkNbmiyiRL+27CnM3frdymkHMQ6QlNgWqzOHJSkBpo9O/KISYhX9zNMJNgqoA0rWnxBy2mWORPgBQvijEg9D02XY++77GLCRe4RkeMbGlNbd4sjCBgjUY9dlct0nvnLrNp5wUqTBBgZMIoVVlEIMOtG/zLsrrrSbPnraL5VWtByqpzrJAFGEXjldTuJfPaIFRBy+cdc7KkwQtnfbsH5PyVxXC9tjO+zSatMWdmUnqY/2RW6Bxm07ie1lFooqIZovRrQOx69H2HKFfo0iu82L3E1WaLF12PyxjRY0AEQMJG9JhtsCgdCymW1GXZLdnlewI/f867R9am6DHv9TWPIydbeEpQcFqD8GTbpnX4ibtW9L2ujMlgrrUqb+3peJ0xGfeSqZwJzxYRR+F9Ei73q2tRCOHPy6rTjxph1gdZE1YJYD/o0F6STyCEWLzc5z/PIx4/cgLzGJzjlinDbKw+on6fILY+TpiPX83g/9jhWFuXyAuRBLn5AyhuMIQtqNvg9csrhBDwl3+2xe3+gN/89jsNnsuMb38Y8ebNmC8fPxvIsL+s4SyiFli5XUnPko6U5zZpYglKZgxPC7TLKUEsaC8FAsUO6KCaHBVFvxBLy/o8/5ZHg1Sosb14mQURSvcc2UNO/yyTatNkzR6YF3t3hOVsMAxyWkPjmXri9ric+24RV98LR+rK9KU0n6vDMxFCUP0s08UVqVsx1utAyc7AB2DCI9VOp7Ayh07QtE1pGCc1rcBWLwMIgsz8redUIEXTXNw9jmBMZk0QQw50SU4twSwEmJHSWLWFkSwotAvgfPpVQENgdkEEEHoAiLkNnINTezNJBXdiROVwgKSxCjytfyypjLnvY2h5pQ2VWyXAiGlti8szAxGYGcH6lwcYyHUQ1FtRsLFM2VJCx8/NxQOZpUIMiAL0DCQT3hDYNLny6lGiN2iwxDQmJEnYHwaMo54fMUakxOi6qNYRncVgiBF9VwWt9kWysufcosDxqWKaXy2cijnErJYQt/tbjClhSEmFn/3G9pfGqwACiASJCUgJCX7GmQ9fF0S4sI5FLVJQ1m+e94oaZ3P3JTa/YmcXC2McRoRwge9uI959d4M3b97g6sULbLdbMNlZsWBSveZOom3Axw/TM+KTRFeOwMc8Cx9z2+4NkwW0jkec3/v7Xv9/TPDehIkPZmo+3kQu9XhxFEitahVfrU5tqdpT4UW0sOCo+VwWUJTPhQWb35/Tf71zWuTZnuV7dRIbgqpWiiALJwJy7AKpy1qYyDljVBberLY4fwYKiF1E1/fYbDbYbDa4CHtcYo8OfY7jVTd5CS89Wu2j0vwlb1Ygs2FlJhwEGhcCKpxAxSzNwgjrTM4HxgigM6YRoXKk62QeirunEcrmP3j8NLjb0jZYs+dfbL3TBYWAWM4we78GdTrfJ9NGVM/zH09+T+o7ugeWFkIF1Xopw15WnyvvUAzo+g6b7Rbb4UtchZ/h9fYVrjZbvNpscNEFbHBAzJo2VcEiNlu+7+x1CCCe0Lx5ET/sXLtrCXdd7ado9eVMKxfvY941C8KIAo946T8JYlsKfSoc5UGCiDWNo0Wp1PS+OrM3pzQuzoH7Ht4PXYfL3r5P5zoHWjP8InzIxGp1aRQBRHWrwMfUBBAetLR2UzIl3o5emDRLc64QYjo/i/WcORnHm/jhSKJmTzzCSfw+hRBn78H3SN3fp//L7Z8/O2edOJPqQ7Mzjra1YqA2jzkBt98DcQO+eAUiQkoJgQifvbrKmr1dnxC6MVtpuvayCEOSM71UI5ktaJeI4HDYq4/0hbaJ/ycCTqMyR9OAYWD8cGOuTwjo+g79RUFv9VOO428rU0FE6DYXGhvD3OYo3rU+doW/R4DwyVnOK4GmzTv2a7Gx5bvkf1pCZlpYFkJMztWGb0ozbe7aJVNDLE1hgTmZP8+412s3P94WR4SdYVolLhpSAIQroiNLCUy33O8qYQCxdW210O55lwwZ9z/oXcohIFRMfhUkaA6Wss4lt19jKxADXAmEAiELGtjc9ZTeOyGjAommwSJg9jWv/3BwWttdMo2N8M98q1nciYQ0DhajYMxEkwsxjDQEWGl8ttgQgPEFsvsmRzwJYIYY85+krIDmzwJZB7SW3cHdOlmfRRgkFgeDSMeJdLw6/QcpCRIYHqy+7EBlskQK2eIKAMYxgaMgDgCPFgS8i4ixg/SCTd8DAgzR3GdRsf6UEEDMpmFGJfaH/VusZaZBZ1GwchPeeHyIZFYyoXJDl7LAieHun5gFICX7o1s+VOtX9QZJg3avSWArYG7TmCE+iAJYBIdhAP3+9/jNv/k3+PKv/xov/9W/AvUXwOUXwOEd5HBTxqVaj3rdTbkiy+e7js7T4yen7um19zT5vA+s8EpmdZwDDx2pD4fVrsM5bTq1msuOvxscoy0fQgNkITHQNL5cw8fwifMYJE9C6M81EB5e1qSc+1kc3C3Pqbl7VAWiD4ja32mGjoxJfUYJCPu01zhx7K6G/HZo6w0AmGAKR9P75EhlNfM2465zHHHSARQ/MTAExIUPXpxhFE1fzW8gRD9F32c8o7rHvSXHqL+lJi5bmhtrhYIqWBw2oPGn6DcvEe1OV7e2hedR1q1MNPilIMVnkKZna6AfTdY0QP9PqlwyMGEUx+AMN0PRJVOFhQq7I11XYgo8jq+avn1bW8OsR8ZXkfO4MktLw8wmRuovS7O2RgSeSF6vV1RtFejguOABYr/rINWT9FbWMZIt322TB7NxM2JVP4rnEsBiq3UddiHgRQx4HS7xevsCL3cXuOg32HQRXdD5KiilNGOcFbpga7EX0J/dQt4R6Hfb9upY+DYd4lNP2jGQI6mOw3Ha/diZOK9TgIffi5j3Y7bcGtp+uiqkSvZAZdhZ5+6aafq8PaCK7tVy4ffB/c8XRBzr0ImGncz/oWFGXz0Sal9dQg9FktbKaS0g2sV9XABhF0cAyJ0kBDh3Z1L3SpumTDZaeH6mEGI25necgjr5483fE5B4mbY/vh7WTc2mY3739TUt41Qdd4JH2zr3L+j8IOSTL9MxXCtHxOpYwyA/EKwhrpNuiSTg9gdw7BE2l2AKKogIAS9fXFoawauXjJ99lWZri0fzf26a3vVfSgm/+y7hZn+AM3mdcavlsmouG7NU0ohxfwPeA7ffbyGmZUQXO/QXW3hAWydUmi5W2shS9382jQH97hKh69VrVJFEnBzOBVrsSPrjBVLd5ty25bRZzoWKMzFNW53j5/SnRSZqlPfMNVwxYqZCiPXzR6ozz6uSUlZDwC7FchCzxreaLWxAoT0Ngba9KE3eI/3K67H416+tCzmvO+2ba/3X6bxV/j4AEKIS2yCEzORnc5cESLYQAMRiRXiw6pnIMK//FCmjhO7GrLaICGYizmKCiDRAkrtBYnjw5xIfQlR4yFBBoseTsEHxqdLtqwKBzDQXm4AJMahyIV2HjkXUhLgHWvYg1BQCArFaV5BbRviKtBgZzqCoNqLALC1ckCaCkRnEguACjjQijp0KIkSwTTttVyJ0Qd0lZXeUHpTa2sBBmrqyxVeoCJnJ0hIRJDEBSEpqJQPKNB8LIKzCFSLOgcg9HkfsANclpEm5EIFEypZoDkur24UmLf5gzBEBhuGA7vtrvPkPt9htNsC//Jeg/gLUX2DksQlaTeIrRfLvNZjLAH09fUT34wPgrtj7KczgIaPyKY/ofaigj450XGLO0OT3A2B+tjxCobM6HkiXPlS48RSdOgL3ch11BKV6z80/Csfm0tkCzIJ9GpDS2O4nsjNaih0BUJQJMtZByAzLk13POJx/yHwTu8Qta6f4d6ouGkIjbJgKH0z5KSOE4BZhnyDwZ7V7NuFFmbT+RoDFftgi8s/Qh9eIgbJyReEXV4vIvtbqDPVFMbszT6GxC2u68FnaIhYyF745E4QJIxOSBAiCClrIcClBVior8x8M+6OMIbjrpYz71bVlRr0z9V0ph9CKLWThe+nLrF+zDsrSw2nXkU06mrSnEBxrfwYu9eWyKsvZqrqVQkGVJcjCbNq/6uJLycGQE4egsSEuu4DPNxt8Fl/g1fYKL7YX2HUd+hjNXaz1zenJeowzPWNuOXsGfXWA9BH4/QYktTL1HXG61cPTXx8vZ+mkWc0zfbwylUu8r3N6c5/j/miTZhoH7XpfFEac04gzeBp1UYVOOJafJnU7DTQZy/VNeRIexzXTCax78Xy/d13OePjjgSUkKmtx1gwUqReyfWYMmXJZZL9VI7ZYRNyFaFyzdpg0fKUtZ1fzDM/wxFAtxidRR/vwML3UyBAZggA3f4B0Wwy7lxqPIYQmz5TI8XgIFIIiRxIRXGOY1ef5ZwJcjUkZrIIcXFVEGZFiQoxxOACckMYN9oNgdxlAMWLT9+gvLrB98RJvBsL3N+prPd8zFQNetLGVljZAgdBtLxBCl/uijEfABa2niH0v2y3HS5yCelxRNIXvsW6OCnhrNylGrGW6atLOoxTzrM76TCat7Y7n8TEhxLLl1/TZnMgA0FhCVBzNXGqhW0+4i5k3YPGxwNwKyTz4b/ZdK5I13JenWCb4jQWnBsCkroJcAODBmwXuUspcDkmlTOCWRVZaICUC00EgMeVa2AgfdxXlAgYeBjCzMtclWd9QWU+UvSomwCnWCkAOQlxd7+7swQamed+Os5GopMQpiyjzvBHeSD5XApEqP+Z+IsfZIACRgJRpPDE+hK7ZFNRRFQUCJSCZpcc4mrZnAmLHiHuNx3A4HMApgDmh6yJ2mw26oEJPPRO4Ci4puc26vb2zDJESiHyqzaadB/peXb8xgBAjOhOGjGLzLwypNnIt6FKhlddf9hZBhSWNtRDQjKtPmAsQIDCrDG1HCAExBEjc4JffAzffvMWf/vA9ttsLbHY7hO0LMEXI4V0WSNzL1P0ZAJwki57hRwp/dHN+V5r8R4hjfxBYHXOq/uavGjTLz3crK4gzkkXdAWZereH/OU7DMg5X4NQcN42Ycumg/jdd0OCNnlpGVMII/02MxoKiHoJT627xQq+ZtsY/MZeSMUb0fYfdVrXPYyWECOSKoO0tYOosLf76IS4KCsDuBQQ9OAVcH67x9zf/Gd8Ob8FmhRnI1kOltKQY6lRZtV5rLbZAJqoIGhECvbBZt6q7phGGh3tOU5jQzDUD1PFTraqlx+5wnszWmhXaTHmNU2UEtKSThe+OtPtekWlZNZ9h9mT2y9dEVpapFISV9g7YbHpstlt0eI2Ov8bV7jWuNht8vgMuY0IXB0QyJaW8yMpiK7ENtUKpYu1pSsLCgD3DY8Fd+AYfegqeeBmcH6x6oRWzw/Ro/uNw6hxu3MN8cGHE49V9X/PyTChPNDTrPFQe5OetEKKYeinz60Rbpv2umFrH3jV5p7/PhHNTP2VMibVcj7k/p4zfk1LjOyD1a2V9TFqL57TlzhYvJ5I36OeSlkn9vk7zsRBUS/jzNMnSmAkDh7eQdAD6SyQBUkrKJLS4DPmMQLXWiEBREaNaa1xEEEXQ9b1qgo8pW0nUgXXpoO5q0jhAkCCmHfNnAYhdxHa3w253gRcvX+H/98s9fvjH722oJ+ca1u/HbrND1++aAcro9OJ6WLrfGjJkcbrPGPqjcHRPLvhsX1qdDc9+sSz7t2Iu10KIo9vj1L3uAqqau9/kWyqgnG3ZwmJhcJfmdpVmc8R9qcYlwhtAjpvAMploZM1yF0SMKTVlrF8GauXgQe3UbL0wtjPC7/EtqnzZfVIm9AvhlUTdLoXQMhjcjZL/MY/gZKbjeZylKheZQU0QpGSlEbKgMCslEKDEfdF4m7DBm3kWCIq7L39d5ZCSraAbNg7iLpzcNUQAMwHmJk4SmoCJwehVdyMhrJYzo2l2ggUsAV03IoSA4XAAx2juqnp0MYCoQ0RE0cSwsy4Hx2zj0WioBhM8NUQy4KQ0gRC7DhRYNUpDQIxmTYKUzxHJ40c29i6oBWohhAslQJTdhU33QE0X5/Vvcyys1hSBAkLQP4QOe+nwhzcjrt++RYwdduESYXMJiVvIeIDgJp9NS9aZrkU7PUyrK2KWpy6r5F044x6Inz3mrfzQshbYEH+UcM44PnT+zsGF31f8r4fg1B8LWnknmG/i5ed3BKdXF98dsQQ4Bee7hj67wPmzI7T7cTixEx6D90HlDPe7jAAIudd4QhAB60Ojjdr7cLF1Ur+omLT593p7IM0XOI6qjbP71oOd5SGoHUFWN+CSKfODhk3LJijNE0JAiAE9d9h2Gn8qBirCCEvrNyem6MJy8eVnpQRWkkx4AtX9O1OsmhQ/588EYPsSQA9+x9inPX43/BJv094EBSZQARByLLE1WB5YLcVoPos6odEnFNdRVCdalAjH5iY35gqz1pVoWoLjyPpabeHCs0mReR0LKmRLUKwj6k1Rr/WlM8E+KvzoOA2ouBuFMgcUNEh61/UqjJBXuAg/x2X/Cru+x8su4TImICSbgwjU+Npsa5TF1yxDx+WlDMXRLXTu/jqVznHIcwpcS/KYdWCOxx4p8mSTmpKeWvl12hhpH0/bfF5LHh/Tfg5W/QnBLDD1ihCiXXuGZNhzMoLbGRoU6tTS5sMRnGdNCLFwMT5bQnwKcNfJWVs3TwsfMs7HjwUaoS4BJAm4/Q71nLopbqjGW/oL0ObKtJILZITbNIiDa/Ru7JkUhz4QIAzmzkaMC+rWpnpAWRCuiEOI6LZb9NvPwOmAcbwFLfgHUVqJskksgfI5N10uNDmfTuIAVYKCM9ztum4KqOqeI0ELa5tKnxaJ54o560zOo8VVQumVJAXm1EyD+zdCCFnKc8Y4UdWKPH/VPg8FAa5b7KbKRWOIJkUSnKG7SKA4YVEHZa7GEuLBfxkpMaTi2EtmQqtrIzGLBjaCWN2UJYzjAIGatzMYi1Q8oV2jk6b62I5pACCIMaofYo3YDWaNsyKcABZtp8d3KCWgxHxwn7EVE4d8/6pGfvS4UW4tibJmGua0AKqBaHucdRS8Y0RmNWDnQQgElkqwyckEKKXTedqD4iYyqlBGbD78fbTYCzFa1oFVw87kRRQAIQ0kTkPC7f6AEAhdjODE5jsX6LrO+uV6oOQLUM8T++4L0E25c4wgoma8YyDsNhswMw7MUBdTeg7F3FhP7QOv5aWkaydlC7J2XKXSUC1rRIo2IQrzImXrm+rMCtpfEeAwDBjevsE//uM/4s9ih8+++DLXZ7KQfB6XqqQ8fwxoGErP8AwfMThOc+z+p/Ywf8ZVn+FDgl6rZp2Ilm07hRq/Csge+7OgP+N8qF+g4IQZj5sgMFOm54wJWpQj2hYK5i0+k870tixpozdw/P202bq9lQl8zRHf7rfY0gU+j+qLP5rVYQjB9BpqpRcr77GPhDtdyI4RWnsUfUViYGBgSMDIgiQlvAZRdh5keEGxji3qMm0dkv8tT7zmgKKQxij1CAAmtThdHaSa/zlbR3eAxTN8gli5Io/HgoDjtmVdFjwQzfPFhs265KOqnaFpwrzgQh49fxe7iH6zwWbc4sXtF/jT15/jz192+HzHuNgkbHu11pFAhtNbTWKCxJqmrwhGjYFmOOkFg/7JO8gPEfhme/+x/ljhIevnyaBt1INjRXxC8LBg1SdmkuqTY8bUaHfmqSvjxwbnIqlLLiNk4XlT5kxbz+sqfpA9JsQx7c5VhlnF4Ftz0TTPs/z8obEhFst5ZALgVGkTPtIyfIDz5Fxpb+sv/m41KDy8cyfXxVrVD6jjrkXOepu1Ms6AYxTAfeAR1lPWupEEHN4ulisNYR2AzRVqBlrD+TZhp1tTAFX3qt80elXKHKMuKt1gx5a6cgIGEcS+R+x6FTSkW8wHrK0/t6PhCUzXVvvdcfnpkVo0l3EScSkBZieJ5kenPV7Zc9Uiq9era5sv4iUL/alfZvJjMh6zpbdQtiylQ7l/shBilve8BVpcA8xb3AgjpNwv+c7Ka2ptkAlkronaOgvjtvj8155m+pr0LU+Z5Up9WBc5a64rjmMjLRq/YRwHTdfFKnCiabtTGaP6/C2WcAWErR2sWmUBlSmFqHWRJHMDJSqQaNeBMdDIAmijRnLLDFfJ4YIOqs84+120ucxKAErgsAgCe0Lk8eCqnxTK2cFcuYVCIc2c8c8wKwmQCSEoy0DrANeqTKHErdutBAkAA2MSUEwYDoO6S4pqlXDY9KAYJxr8lMei/EZ1llTu3/xXXguSY4T0fY9kFmGemkiyxUee8zztOlls68bjf7gQQhlJAuKShX0CXMhbCZd9DVUhRDKRGUJE4oRxGMG3e/zut7/DVz/5aWGgVOdYdtedhVaYw5om9ANgzcL3ZL4H13x+Wfdt4weFj5yofbLWTXCUjxWebHoW+rzK4DhbQ+MEfKRr7dEZO8fKay+XAtPf57Zprbw6CSYs04yeFYa/1Akn4Ld9bWcAuwdKFImJu74p0nkHsqht+eR3RplWENNTMEOGpw2bj6NjlNlicYKnu4X4QSJ+kC0+Dxt0RIghWLBqVzwoONo66XfmWXSSOSYtXnFmebUuTmJBggkhcpIa59b2kjOrM+M+EzRHm6n5zS2nsLrVNNzRbSWoKq7NWa8tb/zklS/qxcGuEp1cN0sbQ+avM94q9SabN30JqP1RVllNaxf8UOniongVuoiuj9gMl3gpP8HPd6/w5Zbwok/YhAFd3CB0sfAJk9FqAhu/BSsMV2p2GrMX0GbUZ7/dzobhaP/OfT+F6QJ6iiukLvtY+6Zo7RM1Rwtfv3MzPr/W1rs2ajK206E+OvSzl483Uc8WEZ8QZEuIOkD1BGjyy6X4OR6E+2CuhRblo845edCmO0sAscBceoZneIaPA1aRVprsb2c6H94BPOY0GaFFSQoiyO410G1bRnpmXMPDNCCJBpejVPy5OgIspn34+lLwP/4F4RffCH5zy41W9qTJEBA2F1eIXY8QO/j5dwxcw3FJCLFOILbM2Za2mVZYGIQF2SzI+ypU52lGIKXCWZrq6oIq3/V1XdOCp81ebDUycmo/cEr5YLlEw/oW8RYxQpeaddcygtsZb7tsTFJnvls7W7cNUs1zqbz42zdCohJGuACuaepkbt31jQskzNgcYxpzkGoAxpxv+6wa/i4kUUa1ClucZLPaXRueLa4DJzNlN413F5SkQecnJQAeyFqsjfqbCNBo0IQsRGWdX4Ix+R03ICA4+ekCRlLftN4+xY8lr0/mBKEAChqXwYNyc+JcTqCAaMzwlFKOjaBnQkvNBgpq8UBAxzDPxTYv1o2uC6BxxGbzO4D3GBhI3OMtfwWANF7HYcQt7RFiwKbTtnU3bhER0cWIruvAVHAj7eWECeGzx5UbKpsnlkKsdzEgkBL3Tp8GJgiFTGirqyTKc8FJBQ8jJyQLHq4ew8QEPL73fL1z3ouFadBSwz6fgLv24izQggji9QG//D9/hY4v8fM//TPEKoB3JkhpokX3qCYRz/AMnw7UgscnY0o8w8cDn9okT/BVtr99+hUGfAvgJt8hhhUVoUQFBJjgWkGtIsgv/JZr5dLqJsg0Kkax43BiaFbFwK054g2z2PEexa30VWU5IWUfluDHgtyZgryePXTHYEonBQroBfiMAq5CDwKwkz0ueEAX1G2k85Hz+DYBuCvI41Reu7ueJfdMjwFZAMGMhITbxNgnwcCCUQQjA6lK31ARE7qPTYxA+b8W/J3Om5fkcUYUQlssTnOJPc2RDh4VOswQcm1rXpa1ckf1V69JIFt2lPYU29Tl1jsNNOXSwejsmmFWaIH8KATErkO/2WB3scPPLq/wz3cX+GLX4SJGbGKHvu8Qu4gQo9IfbPST7z1BVoJqFd28C6IhVgy3pSsG/bN3kO968G83awP6RwBTQv+Ppe73A08qiKjN0s49To+xfp4MVu6I9wnzCOQy+y0Lz+u8tPRsTQhBcybdrPuTBI2wYVUwMS2ztOM+sJZrsbyPgEBe8qf8lDDz2/w+YDbO5x+U71Mg9VR1LaARGVbn/X10e20aJgzgo3sx895apEiEQWkA0jBhzpavyq8KQH8FCRs4St1UDmgUWriSuIAKFy8jQI7v7XrgaiP47R9ErSKmDO2qnUSE2G/QbXZQxudyF9sjdD5gy5q/y2WdgvZsrhDLO6wHMoJOqght1PzTDEids3pTj9O8jsUuN0x8S9XQmnL67pTq5VIaqVvod0UVmK3WyPdCGgqvJtzaZE5AKL3ARkt4MGYlrEtRLYM1f6s0zQFoAEf2mAvIAjOtR7I1hDN7ARN4ePF1G80iQJtSxohq+sa6Ibl8aS00xAQRuc6UCSgNguxEuo5Sni4jdHwYNUZgEUIg4whmik86L9lVmzEHpIS2hAfbJinxFpSnYAELQ7RybP9bfIs27lc+pEAEcAAiAiR40D1NEq0fkQgUBF18Bwp7dClhoC3eyudgRCRhEAuGAYgcNQDjQBi6ASFGbDajVaeajCGoViMLIYSp5hg1E1NczpW1FgiIFIAAxKCBp1mgZxf5LlTLEMXHAhCoCKVY12g93xAn+Etb2N/l+aymJS+keg2JCTc4r4kujejeXuPt79/g9vYW2+0Wfd9nHNHXtk7LBM+YaZv+OGCtR6c0qRt3h08F9y17qe0PbeenMPdP1Mbaiutxynu0ohbhXi4epuvjU5jvjxWmYzcjvGk53anyVvawXhlF2JDwFkm+ATBmXCKnXUDgSNpbrWlq/ay+A2ZoGhUcbZEukcln/dwZvo4ISSmrziNcjVmdbqm+Y1Bw0AVqAO1Fqu5qIwh9CNhSBwIhYkTPCUF6AH1bbMUAXpyxugr7fkwYMYsVUb+b3EPrp7zhqqLChwGMUdQiwtCQCf6g2GIp1XBvKlaxjqEUlav52BXQMibY1ZkwRfQXJjuvAymfdzm2l5ZlU15jbjpLXHq+xCtpf+Uxa1Aq+10nDgEhRnSxQ9f1eNH3+OIi4jIG9BaLLISg8RsDqU81MuvhehuKZEUr36bztWRPtwxcJOBAoN9tlnkqj4XyTFkFC6yDR4Ol7h55X8/lh3GXtNLgJ0I3zxv6h7xt4dki4iOFQgg6EwGLlhCNtmjDlAPU/ZJpO4aQNZaXEJi6jGPE1H2EEO8FPgIhxKcNz+P3o4AFvu3iu3Ome0kDPmtXHEGqr/8AhDeaJmu6G4QIvnwJClEDxcKECwzzhQ51tSIoLM4g2G56bC9fgYc9eDzkPvS7K8S+aGrErhABggV6uv5n8aZcINLuiXeE6QBNiYNT9GeFDXhAwSXT5UIPzie4nOXLlRxnoE0Jv5JHlsaP6q9+J7Ta4lrMGpYPZFWyhVfTPHUbWoEsIO7YmJ0hbxYCroFfCTuU5lWBGCOoRhuKb1wiUjU3b18wz8vMVUxEd+NkFggi6Ez73m5tJSyNqaua7phPvmuNiVpUOPFH1jERBidCSiM4JWurQMYqVgTURZG6dBr1M8e4iEUFDQBIXTQGUpNvQiz0Wk5TFBiIQhaECBMQ1HLCiWaBlkUhIFja8ZAAIoTYrsmUxiwQoUAgMSGPFAupoB1E5ModETgzQWIkCG1wk/4EzLfo5dcIdMBn8ZcABfQUkGSH6/1X6LseXSAcfL4EiDFgTBvwRhBCsCDWwQJSan9jUEuOSmUuE+a5SbUWp/YIMQSQWc3Ufrd9GZFZmLiCCITVbdKocSLYrR68ymprZNywOUMkK5AWIZBawmiskxH7/UEFLkRIY8Kt7CE//IBf/epX+OKLL/D69WvQ7hXi5hLp3beQw43VS6XhedvUe+4Zf3iGZ3iGZ3hvsGadtn0Bia8hEtsQDBUeV+Nw5V3DCW2gxiIXU9DkxzFmXUOjtDgmVUoUmSUuVTplhBRkIAsq1mJN1HACkc+o8zJjmyGIKDSRB6wOwWiVI8W729mP4ZZ0nnxKjFESDilhb5a2idQaou6K2X9mC5uCxyi26H0D6pF3rHWCb5ONnw/Y6sAIFudxdQHeHRr8bVaflIGaWkbMervUqHMbWeFTUrZ0XsaZZ2fBqbdb9HyFl+NP8OXF57jYbrHtO2xCh77rNOZZCEA0PJ0AkICCgH1iaT7mAlH82+ba6XbwCddAz/BHDWur/K5b9GxBxF2kQHOmRst6oPYmyk/vBadGgpYYH0cY8UeKXG3hMema1Inud4LqWTi3iGh8+9N03CkLIZTQtcsgczWW+lHcMJQ2z9NUHzMhxJQgPVtDbCWZNK/XtJw/zCm5PJvH5/hppantaJ2C9+nX+NEYFWcUc7KuufpoW7Zgcl4da8w559hTzvkCHOv+udNwYp2uFiMCjPvyc5qr6wC+yMwtcpav0RxAHZpLETxmQaSArt9gFAa7730CQuzRbS6wOGMTfEvqfxa7Vz2fft4R5kZDlRCC1tOuEnmiX6ZihXwON8KIeblL91tzFk0R06z5s/J8BZaNsyXjv7k8px9X56JqKOYdKdNY8pNh8c2cZ0K1+OAnUPaXlHERsVzZzUDTfP1K1bqSaj69O9liQcujqMQXcYLbXqh9gVRtO9b1if//quOcRiRW12YaAJDh8SIAydZGKowQE2qQWicwNBC0F2rKCQGklhFcu60qc+q7tbSNjGY3YWLVHS9WROusxD5Zw961/TXGA5kSl2AaDyS7ygqkgiUvH/ooBELCCzB6dPQNAgZs4zsQgI4IBx6B9AqJAGYVVA4AYjdiGEZQCOg6RYVHqPcqCQRwQAgMlgAiZYjM2PCVVYRbyZSzk0pDa+sCe1jwMipriN2dVsUo8rWJXEDGB4vLZGnakIlZtrTBgqinpMKdGNVaYxwhNzf47nffYrfd4eXLFwhxA+q2oJsfVramt6HMZ73nfJ3Ozqjcy2pspgUtwNo+uS/+ct7d/kcKz5rvCg8Yh0VN5Xzm36kR96h8eUW3rgrv0oT706y57nuVsFJYXeAUf5nCQyumeRHnDMcxjfW71H3W9JPjQNWZHHpIfwkZE2CxhqgpTKp/l59Mqz/dlDqH41HlzXKfJriftzMLIyqLh4zwVYh5hds1ac4ZuNkCPZKvqrNYwJaswbEiZ1yjak++75d2xNrCfghYpRUuvFS646ksgv24x8CHLGQoq2W6AmjyvcZ9MpY/y+mjpAok+slO3dXFzvoxLWNhfs7ZJ0vvp+tw8r30VNbTL65lmabK2PP69NKsSGrGxfhyhqd2vMVV+BJX/RX6GNGFqDFKLM4XAhUvWNXQzweAmka6FQ6mc2Ju16hDK4la6c99z717eRG56xZqJ2U935GmnFpyj72razxX8hpbougXcy+nWTuC7tYyzM7wexZ5B0FEu5LL5jpvmP2Qao+vqpyT+Z2e8wCr9W0wHdVz21SyZqOzI2aT9xlgOvLLIZi2Zfaj7peEuXdoLpO18XbNQtMkVK0+AO5OwZ+vtIFCYTasl18TlQ11eTzvo8Cpk+PTg/flvulDw6l18eECPZ4xA6faNldRXypk5fmyr8onh3OoRKrOg0dgTmTElkfQ9feKJLNAYg9cfKHawZ0jsRVD15pIAvBtQOx36F9tc+MpTq8wml8H+c1CV2Q57ZxIWkxUCkZZ5zR/gcmL+8OkyGl/aHYsT6hBKYgUZW5lm1ScKPPfi2NUC4Vrq4w6odbkAgiNFdDW5/pljjPP62nbnufB3MtQabR+8wi9IWhP2N3cmMsiTpbOsxUGDQX1rQqxQMpcrBFqFwaSiXso0l/RsAKLHUDqSxiAxjNgxpgSiAgxRg1mnQbTwo9gtngJ5pdJ4yt04DSolQOPADPI3qfhFmlMoC6qUlkyawzReBJjMpLSJiZZHBafd3IPVWBkK4kAiwHBCM7AFgF1SugAApY030M2SFP02INRt2ux4DU+l8IpWx+EEHQMzWojWC4OKigZRSNxeAwFaLOxCRqTL3I7XyMLCDd41f0KKbzAftgiBEFISYNdB10zPRE4dghdBMeAIBFMDCRCjAExADFEbaevaXZ8TcdqMMKeEzdLmAyHi7G4sXJhDIWALkSkJlC0uqzy8rPwZ3oGiS/j1k1TJvBFsmBJWIn/cRzRdz1CF8CJkXjE8Mtv8e/+X/8Hhv/7AT/96VfgpNY4AaJtJlLhkDFhBIRaDZKjrrXA2tdI6kRLaQadV4LK/sT/C+p3nJr18fHCvdzbPMPHAY+AX/qeyutXSoyWMC0/K3TNbuF71QuciTr8sViFnzuYq0zOx4cnoeWOcrwEGbGyTuqJTUhgDLjFIQXsh4Dt8Ad8OX4LxoA9qqNbKteMsBhXBNOMLncLV+e2tsvO/2yZaM0Q53ham2q8rRJMzPohAIn51zfhg94djGzil4UN9W+/gGod/ZL27PO60XhH005XvcgocGCMnLBPA8Y0oKMEjAHSCSQC7g7T0ZvalSzlsjM1VO3vh3BPCIq86ZlEGRm2deG8HRFV1rF3twx8N97gP17/O/wwvMONMAYhBMfLBBgJIMfCvO1BEMS05kGgHClC10gA0Fl/NB00PhYII9Rj0GAuKA8UqrXWjn0eobwPbCxrk4FFgs7/uHy6uUFDM9hvm3/KVjUJYP2t1r8ady2vSR3Vqv6J1U4zNa4YVd8Fjtc5pVVRQIQmtUBx1LiJ2O16XF1s8aVc4i82L/FZ12MbCd2mQ+x6c8kE3Q8sCNUy8LgQuZkE0KS9virVgp0ACYWifSUI//wW8k0H+V2PdnM/MdQb41R1T3XmT+otR/MSMXRPWNVIPFXHXXlQS3vmRN6V9e13Rf3u6LW1AveyiHAXA3rgNZzoJm2t6aUS2qqBYsg9qgcVLGuVODOpaotzQNaEEdX9V+a5PgqqOid8maYFd0HyaPblCL+vfVNrVLoQYskKYqlttRBC5RLFHZNrFx7ry7H3d7GAeFqCbYr0P2FVJyu5fz9niOs9z/W5jvSRtKtreE5I3Q3as+Gcus9eIytNeRSh11nDIevjIZi/u9PaP78Xq+vloXDk4p4Kac+q+1S7RAB3rcRJmazbERIiYugsSSb3rR1Bz0IWROoRulaT2Iut23ysefUdVGiPI/PWECbzb/rr3DE6OUDrT9ujd7XFR2s4gSVMNYDmwoVpHUUgMdUPyCmN+HEt+1n7DY2Y98s0dBpbZVR3oxRvOW3rUevtq1G9oPgUlkk7nSBnEELWeisB1p3gIOQADtOOTsqb/mr6ZIyqbDmRNZYkZ/B+UyKNayFqHC9GOHngauX1BnPjgyp4tmnwxzpOg32KuF6CI1Rta8n76XOAvLFKUprlcesI74kGsl5CUGvdOeR96FYaFNo8ILV8SORJpShmWVNDxn1KlzxtAKMP1zggYs8DBBGMgC4ljOOIFEfwaG6iuPRfUVbJ61rPITTWHaX5SsCxCJLNBYWQB4yQDTrKOq/HkmgSf2PlaG63J3wtN9ugLTxnYI8lUq1rZgHGAftvf8Db794gpbFs5HzG2pjcgeTwN5Nbv1hw1Pv5nvAUcRmOYXp3qee9oKXnwhKOcu6F+VhN8KrfZ1mTvj0abZKVwyYrvKFDKb9r6rzDcNfZ7rr+mnKqatfKeOi4PAXFd25vH586e2KY7r3J2E9x0XUar8ys2N0rYi50JCExYWRBTCM62aMTxn5WUrFxzM+J8vm8VKNlW/sxf5YvA5rLI6TgasbsKLe7oIxNZhLXuJdkYb0ikV7l2syfer7SBykoqN7zCYkDhBNSEsUZDF9c20bTNdqcHA89gqv4YvNXlJOQiCXVsykJ4ZYT3o4/4DrdIgk3w0mACiVynqniXDnjMHnLUEY4JJSzkggshIQABiO5woKN85zWkBaRyPillDZJjVAdGyMpa8gTc3Uu1s/9T9gENyoYI5/fmXDMv8+QsxUguMPWtulO77S4MgVCF1UZqA8dLrDBi26DTQhmERxAXevis+k6oeBvGd+v10w9wBUOKgIhtVSmXkC7EfxD7df1ieAoElZ9X4NFxPlMOFLuY+EwS2fB7C1NEziuu1zm3a7vaeH1DTO/e1bLro736ueshnPg/BgRXGrNJuO5+ooNYweEHS2TPtcIWY0U1gSFE7LTQIEl5WInGySwTb8EDTFI05RPuNGWLgsbB9cUZDv8eGEFNMGLzNKBUEy39FEogoc1C4/V9tFqsnPdMD1rjz3DM3zEUNMNx/b5k4Fkwol4BN79Fui2kKsv0fjuBzLTlolAGwaiNPdE3Wovt1EsWCNMHNds3h2hIqQdl7X7KadfeHbOuLb6V6dhyvxfQ3Jqt7czfD//dERa8riVtGJ3zWkoeUynjk2LfUwFWwjFYsAzsSMVFtR3KnQXbwec6KusZnLbWmLALSLcpU+ui1Mux5F/RgRG86fPgpFHjInzGoS551Gtt1TqEYZHAPCVKRCMKTXt9zZmSwMvF5RjEsA0/fO7EIAQMaYB4zggwHCDMSFxQmAVBI3j2IyHV8ypCp4d2r0l9dwwAUINXafDEsq4+3wEd+OkbQykv+FxqKzcZDhjjCEjtBrjwtqTzyFdb2wxFgI0MPuMLUABIiM4qaspbWsEiBCDABJyrAlfJ8HEBiyCDu/wgv4bDukFrsevta5ACAjoQocogg6C6AIiw6/qOAuBCH0XQWRBqYE8viklJGYMB3UdF7oAgvqRZgF4NDxPGMQqPGEmcFBLma7vgah9UEfNYowEqZZ1Wd/Zz3e17tjmqrHJsLMnmOKPumjSfRGjWcNgxDe/+xZ/+4t/wBdff40XL1+AbgFJSWN+aMsBEkgwYpR17wQ72VTjEo2kRneG6ktqmI2i+xlStTme4Y8CatTjxwSF1npe0M/wSHDuRhHFRtncMKZRMBCwHwW3g1rqhfquEGR9iqXVmkzQxoYHmk1pYVIbDlLaWDFhJ9CWv4SE1nidICuLOLPXrR38t9dd19tUP8FZ1+pf+m24p7ea6m/2jpkh44jDQZD4LfrtDcarhCRF+77gYcfDNT82FEyg9Ms9jfrwEgL44guM2GA4AGMSDOOIYUgYWa1KGUpvJQgSCAlAguIUbk3TutssoiwWE17Aw0Cw8ae0/tHSjEAlhKjchPqILTLLS33a4ZqIPbJZptOclUOkSlDWn753wUNlTZEtdOoFd9yrQVlO7boqVIKgtL/gUQyo5kpUvPDicocrfoGfjH+Jn1x8jouLC2x2QN8nRLNYLnE4Cs5YYgsKEG0xuDEHSYkFYfi9lIWCeuWKWUi38VPq+07zPT3v4Bk+Png4Rnc3iwiCmWNNGkFukGU/0RL9zXr1r0tM9umB4ufQZO3Xy73RiqqI5QUydioHKXUJULQAAGodtHlF08xngZ+nk31dvZcmsZr9Hp/YmrHhn+4Owg/9Wgix9PtYd2bWDwuVZzcka9YVd9Xeqe+UprrzmH0f4gCc1vkg89wTWde1ZE7D+XE67juG64jAvdfH6rQ/3Tw/hmblvX3xnir3Efs9FRCvlX0fpclpt9eVMSn70Ick1Foc9dglFgwMjBYY95xLr22D5Gc0fzwrb3Xa6sxSjdmpZTx9f2owpY0jsNDEpkmyWMc834wEWyFCa20zqX/PrsTT/XAasWGO+n3IVCiWqo3ZkoEox3zANJWgLKSFRVq3u1gziI2t98wEGex1kLlGUsYzG8Oc04gQozHBkZH1IuByC8ZcM1ztTzwwdggtbp/dSk2RovW7TjzothFEDHdhAP3txK/to+Am7+KuqcqYtGNZYhJwAEJ2p4NmHfrcUBY6uBCiIkdD2Rcl2GTBSby9XDFFPK2em1p3xpdQhtWNNHLZ4vksi+FAYYpslkpAlNDhGoP0qv3HgjQyUscY0wgkQkgRgRhMpJpmNl1aJEOgDP0Ygo6XtYftU2NyGIedAygIOnJrESlzQWWMvP8hBKSuQ+p6SGJk/1ntjNmyl+bZTGt25czwOjkHkSzjffvuBr/95e+wu3qJq1cvVeAQOjgfJp84Pug8AhCQdHmMS4PqBviO06zRC5zifPe5cNCOxRIcu9dX0M55GZP0p9J9svDUFhKy7orrcTGmpapbWuusPE/UlqN1rrTtIev8Ho04/vouRT2sJY+6p54KP390aHC3cvoupfO7XRCUgSyExMpkPiTBISV0puDQ+oJoGQH+zYXYkv8m1OdUCCHV96UOGMypxHyhT55VOJ6/z3XVuNak7qp/y4N0DCZ9ynfdNI3e12lk7JNgDIorZnwyt9stKnFkAT8Oj6S091im6gltILRBwoDEgpTMpaSQKkyg/cvrQIoVKmDCCOPH+fiTpUlWdQLUYVg1vIrBOtPbMf4p74+qn9a/upCcbrGL62NQ0TdNikkSqtZSxjdnGSbtadp7BuRpK/NX8AylDyiqu9IQNuhwgZfxc1z1V9h0AV0QDZZOIfP/GsjomjrX4kBAkqq5ZP/W2E2mKg2NE2cgAkJABGgrwEiZZKemwqriDwmnELtHaN65vZymOYNcX6ltveQV47qnhbx2Z825M5wviIAGRlx5CT1yqD0/APh01YwPWUGYKGsVKqGTkYWKMM3354R91saOkEmm6ZKhWmbhBTTdIa/jITObmWsrxHFOZnpjXLQ8RVrEshY6wIlu03CkoDppdXBqrZVyJ08KGyYJ5kyS+bsP59v/GdbhrnPyPIcfCmh2Ln1geI/7mWIErr4CKOa6ldlbX66Eb98Q/vYbDS5bNMiXmlpjg2VcC97puidGiLoH3PsM/4lhmrft6cb1nBW01sc18qXQelPs2+qcdLCUb1/YNeiUAGTlPpvGu8mTMgHj+Y0h64xoErWCgWqPe9E1Q1fL1nnUVaRxR5Qxb6nYYkNkola1mtRFjX3C71SAU8hCiJEZ45jQQUBWgwBgi8egTSWIJLu7U0WIcrOWQYqf6Lho3QUrsHHRqMw29mxaSN5+dcXEqdLKcm19KVr5NrSQqMVy8naUuczTJ8VVEzMDrJpqXQzZiiFEZcYLM8S+U1AcwwkgJy/9tzMymFVQ0PWdErEp5YDJwpVX4QrPa9ZZmfay1qp+Bvh5ENQ7QoBZlVREnaOBojiiTg+DGTiMCcABjp9tnYHAjNh1iLGzmBW2rG3sWDQOQhct/hZ0/NSSJuEwjgCAHkDsOoQQbcW68EgyXikMSNC10cWA6y9/ipvuAhe/+QV2P3xXcELbTw3BXI1T83CB8ikMOLXcCKNq0nVdh3Ec1EXVL36Nf//b75H+NePLr78EXf0E9IqQrA1BzG/yuAfxgO7m96A0Qo2DdAIEQHJf44aHStCx58S6RuwUDhpmfaHBz/AMHxd89IzrZ/jjA0dpxGIm9ZcYu9e4HYG3B+C7A+MPe8b17Tts+Bp7ZqTqHqzdJNWM59EKF8ehvK7a5UvGc7yQynVS3Tj7OrujPF8t1BBUrnCq97keaeuUqp6m3qrM6WCt/i587swSMYG55L6Vft5eA7/5douLP90iIam1gKgGvSsbNN4r1uDRSAPJ1g9LXSWUeR9ZMEKwH4GbEdgzsE8at2EUt4oARggSBAfriwsXQGXo2ZhlIgUP1LqAUaTEirCmjFC37ixkfMCag0oV0lcvGk9D1fOaNlk7m/OiapPYWiF/bzQDjA8HMfze8O78x9X36Xps6py2ac5qVh0stTYpr3QCJRgu20VsthsEeoGOf4qXm8/x+dVLfH0V8dV2wLbvNN5XHV9s2n34vAuIVDEmuWZNTRNX2ZW0kUxj1ECfDwivBsivdpDfbes3k8rXKNNpuud79f7wkfGPHgDnu2YCAL+UJrDCz0fDEEJZ1GvMfamz1V+rcyQH2CRBrVvjB23+nauutEupZv5R0UxrWmyHwYxqr9tz/uRrU8V8YE8ZOEb4gistt0KYT4URpW+lpBwUbfpZtf2ohcNCuraz9c+1/JPfj7g3igbH8Rv7QdYIJ2BVY/ycOj/gOfH0lhBVEY+FUZ275h6pMmdW3TP76vyeHvsJ1psfP/2Cuc+Ynmv9c3opESh0QOiBuAGFmMdxZvVDhDEB7/ZQTYy+IEw1jjQfssmDikhZwEdPwjnaBqeFD2cU4u2aEHGncjxkh0j173lQ3S0TTbYGBa8JSpZZn0DNtDSlkBCKxbAJJ2oFgykBkl8ZQSEwghC5DZTz1wRGNQKZyVusC4STliMMkZARdxEPVu0Bsa2vXO7z6dig+VV3nIwQUptSJ/WL8GCyFnw8cxG1zUIeQUAku1RwzbPpIs3j4y0yoREHDVjoig2ZWVytxQDTwgqFmMx0ZXW0ueIE4Fp37sZKqjVghBJWtOO871gAwweJ3A1TS1QVwaNkXBIiIDoA0iElwpgShnFETBFpjKDAIGazjPBhJhApsZ8SqfAAgISZLUKeM8mNLj3Lc+R7o35OBNrsIJcj0PWqYGLrtLEggYtOaPZ87XzJI8qKizIzgoQGl8Q4Ynxzjevvf8Bwe4Pw4jViv0PyMfN9A0ASgUKvFtJJWzO1tKv7O2u8N2qGf6/3YRVOXDrnxJJYuY3nVd23Tc+M7JPwUEzvFM71WMKEs0uhhXPsCeHYOr9b4N6Fx/du1cPhXBrwQ0J9z5wNJ+bk1JlUo0HKtw+Q0GNEwsAJt0lwkwT7NIIkqRCiuut9VGtshNFiJycbV/+ohQr5s2AnlH9Lwdmai32hxgrPOW9olxJNn51TUGl3Tu2or+E8nDaAdIVJVee+w1nzGOvaMYFF3prUTdR0LCaQEA1GzjABhJhXSMPSXPlhrTfVFJdnUqxq1CKiJMn4bWmxd2CyHxquYpWm8O8WA6Cfe+Q2DZ/ga7UQgn1X1C6aUNLN1u+6xd/5bSKAAkIgxK5Dhx67cIWLuMNFF7ENhD4yYtC1GMKcOtczoR1Pgqilubs9taq03y0P0LvnZF62PI4CbAVykUBbC9SeJnyUZsPc5UScFfAoSe8FR8o996y/axNX089o7fVcj412Nnv0bLj7DrijIAJY3vnH0xYGuxG2U6Z8HkvJH+TUJfIe0bwii/idAIWhjrIJC3FEk3PLLSjqrpQQl1nzUsq7uvdrzKl2ITiBBvM3JyjLt5jxsT13H8lsEssQvL9+SFDzF8xXb20JUQshzuIvrwkrPl6c7xmOwn0Ojmd4hjPgEez/KHTAi58AUf2hOyNRqD5rAQoBMUZ0PSFGAToBAqNm+8mahV7dxPoeQCG7HpMvdEoIURCX0/DYAlVHEM/q75JkoCqI4AgpNVnE/PU7eHDllFImenNbUDGvp3fn9O6xfFwFh3N3OY7iZsKr8inMUO37mlBIouRV9pUsAGVNNxUsOKM80yOsOoLCquXPJlAR+4wxQIjAPGqA4jTCGeqAxkaoB6rEkSgWHTmGRbM+BRC1HiALkpfdAY0DmMc8BilVrpfy1GnA5DyuNV4g4g6Q2rUmQDKN/kBqOh+IQCEgmSUDdWYh4RYRMZbYFkapqLsmJ14UPwlEGsQ5jdpeF/rYnCZm0+oCPE5FHiUu2oUwoVQMwQQEFTHrAzKBLICoKKVtvMaX+AVu+DXejV9D5FBZ65h1Q69/QTrVJKsqGEeNATFE7dtu24Og+JgIsiuumiDPralpWRYwMYgTCOrnqe87XF5dYrfbYbvdYjgMOv6pZNSuhMxcECBbH01EfgWoWBizJIwJ1l5GiBGbEDCEEeM44re//hV++Z//A/76n/4LvP7qawxhC6aIZPjonglCGwwvdiAeQW9/B+KUmQTuokqgrs585Hq3fgMgVLQBpyyHZ+zlGT5KyJu3nNcATgrCPjg8C8E+OZDJ9zO4LGCzdrtNgjcD8O0h4beHEYFHkLAxmIvlg+YSE1CoBrwYXu0KArPGACVeaN4PE0sJVEoe+VOqe1+qv4UON7whwxPJ1DSawMyy8Ltiey9y9mTtxWyQZ01ymmTT4+pyg59++SVevbhEF2GWkXV6mZYwqepxz4zMx6/u23bhOO9JcGDBngXXB/3bg3AQYC9iFhEeLlyjO6WlCr1Ir3zSV1+TGmeiWEQ4hpKtIWZDRCtCiWpOF80+prUvrS1/3uLbjosXBSUTOljMVslWyLVFRGWmPb0PToEgW3KjjpNHWmoIAWHTY7Pb4urqCi/4Cv/k4mf4+UWHn+/2uNz0iF2PGCNiiO0UZ1qgxgTdcwrZ3g0qjPDhsPmrlbQVkRXD4wtfFUKQEaCfDMAXA+QfLoDfb4519QRM98GRHOcKmZ7hk4N7CCKmUFsmnMXt0JVf28HNbtp6M5T3WWvONfyq+uoYEbNWCHRTldSNsMIKaA6/2n2UbsDpQbvMlGutNMrhqc8Lk8M1Epqgm84kaQ64STtQDgZvdu2CafZ8DSZlaPktI+jsy/L5cJjDZEweqo31MWkDnSffmiJmT9KUDwzVvnssYu9covZ9E5eVwNI1rqfNWDpzBDA/45Y/dJBuowIJR9bro9wYhomB2wG4HUSDdpFUnPCm9PJrOiQTIcRimjPA8xyfmmXhw2qZ5xyaZ7a1Gbqz8i0kODYwRQJR0pIFH3bEtzHbl1LeRJ2qQmnnleQLbqJV5MRr/kElTyawqPTMCImSshAfnNvGk6WnRIhwqu5wK4eVnewCiNJvN0PXvC6AQVYWUAJAmMsYSMY+3DmY0fWSm5npsIw+6A/HQ9iUE7zuZQuM+RgHKsGoi2KZj5DkrM2UOf7Flqa8QB00PpfiVVslTmcJkBUu/Ik0/07xKO+bzqcvgRAIbosCIDNR2pxzoLqdxIjYI9INSG4gvEVKURn+Y0IKERSSChQoIQRAqDA4fD5dICAsQLA7j5BdcGVhk1nVTCH3kaH5rX9d6IDtDml7AUkC4uLGa7bXc2GT87gehiqxwIOCm/CNLWB3iBg5AQRc//AWv/yv/4ivLl7hdYwI/QVC7EG7LTgEhEjgsAFLDxoHULcFpQOCCWjsCC/7inX825Xiq3Q+X9MnJ2/E6dn1mIzhtbLWzsu19I+JJzxGGR+KeX5OvWf27y5U53uFKe2Iu7Vx7vrwbj1ctIw4D4n5qGF6RzyEJrpvrIj7bOPHbPekoKoO5LubWYULid9C0juQHJS5bLyRjJqhrEspN1bFX6kTSPu74VHUhVV4n5VIExzweIcqZugsk9uM2jvXSJVqMGih7TT5sdoWv7HKTZVzkfrrFyIMHEBhg6uLC+z6jQUKZtVMr1koa1fBhM/yUFguxsegsmm1oRIWDCzYp1sc+AZJVFgwwtaN5bDIF2jGzLV5pXIsnId85S4XZFx3FY6tj+khmhHkYwVN99wZeIUNUo2XZOvdjBhL/qkJqh9LTVqKN+tpqV3tuVGBELqIQBGdbHAZd/his8HLDWETCZ1bQVTrzQudWdlO+ipEAHGbxPms0yZW3WpoSwIQBaEH0i6BLhIwBGBcoP3vBWsbQ5bXwlJlp/bWe0AaHrVJJy+eJ8KG6jN9tV7HNyzLPZrwCIII4M6dnzrjO7cKqi/1OkpEFU9CKr98DSJWf3HGRcvUWpzKGVJ3YrQzwjd/5pLKbPmQGSaygBARhAtzxl0cuOTd/cKVmBHLzTkFnzBe+snCY2s9P8MzPAqsICQlJox+v9P6pQC6+groTGuCCEQd3Lf87NQzS69vfwD+668IIxi0EWPwhWnpTdPbLx8X3LdVp/KdW+5R686Fu6cm9OrYHDkLS46z4K6M6vszE7SLNGhNaOodF4iqO9MJzIUG1wi83XuuZaepuaSRlgBR7fqi0USolrsJHIZhgPtMNY9LSCJmFVE13csDwJzAKSGNI0QEXafBrYP5yB+TKxuwuhCKEZIEo7AFyy69LkIcNV6nyh+txjZIYB4Bc42ULF5FdH/8VhKZxMHbUE2c4ZbuLmiCB9XJDd8YRdRSIinB7QNKgAoabBCZORPs+s4EMS7gsTgKbn3iLq58/Nk10qDMfRazThCzfhJo3IYOec3x4PE2ogVORH0YAJWbryy8gQp/NniHL+I1buVL3Aw/Q9eN6CIhiWAcR/ScEFOHrtsgdl0enDTomHPSce82HSJ0vgMRYuysj9r2YRwzgwhwXM7HJSBhRJSowa9DxGYTsP/Jn+Lm9ZfY/eK/YfPDdzpugFr02Nb0PSZilhcuLGqAMrpdTy2zBuiOY8Bus8O222E/jBjGW9z+7W/w7//uN6C/+wd0/+Qn+Pqzz3FxcYHNX/0F8Ool4td/gmFzgbeHiDExJALhcIvdH36NIAkbUv/Powk7EidECqDaIkIkz8szPMPHDue7OZ18PsMz3AMaJvjRVI5vqYAeoorcaQQuxv+MPw9/ix/wzvz8A+L3BmA4E5klqD5juzNbxM1yZATIH9WxE4A2ToTnl7aM+nqaeqQAIC6Rr/cRQTuVEbaKGUxcDdYyE3bCdV3g2Rl/pkZs6tdBAwZvthtcjwGHdImL3U/w5ec/w8urK1xuNth0I0JgCyw8x5efFiqEt/wCsvjf8Udlq+8TcJMO+CH9DW74e+x5wD6plUTiyr4lz8N0QNRjCIkytaWpdDoHk7GdPJ8fmOdQNEfSLLzyJdMIgASorRrEV7/hoOoCtYov57hpVmKaWv20vZi1oW4eoeCk0FhncJwwBsRNh93FDpt0iS8Of4m/fvkKf30p2PQRvcWF6GOHSCHH21vqfMbwbQ6JCIEFiMh7nmZeBVqeqH74vqC8HpxGCj8/QL4egL+/gHzbT3MeGZE1WEr/cdL0z/B4cLYg4s3bOHmiLjMuL1YNtxbAmRsNPZ9fVUWjtX7AghslPzzahUtQIqdYSEzfLlUI5CCROWn7vrhImjRiqSxDCPxgdgGEE43uykIFELV0sjqcaal354MqNaxv4CWtjOxWQlCN73rec7RJHhqs6VztkXv56HwKmC6ryRjVmqefCjwIpToj88dk7XFveGzLiKeGtfZmje6FLIYwzeLoLJYPIG4AikDs1AIi11szTesmFbdzLMDtyBaA9kRfCmWF93cCHEc5n6IVa7dNzZicpl2H4+dQvulqS4hcn2tYWVBoI3IkM3rhFxCURK7J0UlkJ6ruiNn1Wt3hSwRG/XiiEU7AsgW3J2BUjFAnRjhbPwCUXRiQAJwXIc2K8gCFy+B6hk70TMbIGfCAuTAy7XnXKFQOdiaOXIOeQq39lG/uGXl3FOdZGJbs+KqmJyfz48HvtG2kbaGqoIzm+ZzQ8rGYx8/xIm/H1DIUNk4wIl81I5kIpm4/gUmfZe08YxAJPDghsyAlMeJaEJJaRqgASAMtl/aaZQqTCWAAD9ac17OPFZc5hr0v+wF5DcSK4KNND4Jg3F0Chz0kJRCbNmgmBpthXAEV4gjNV2ixxm1GS/k+I+P3v7/GP26/xe7dO8SLLboNQNevIf0WuHyB2L8CQkDa9CAkoN9ovAgeAVF3YsUZWe5s7kN2q0alPc38UL07H4iHPDb8SDR47qsZ/qRwRyuUaeqzenImvra0x6R+cM4yWLm/3huILH//xMFPtMewjMhlvofxOafd57dC3Sci9Gp5DAIJgVjAvEcv1yCkfJva9Qyg0lKXurTSAMeKpmkWdsPiI893tC8NjkfVb+ceOz8itO1w3oYYXkZuKdEMDfz+L42oNuPq8NdplB5JFHArHQbpEcNrXHSvcLndYtf36ENAjMGUQ0OlHEpNHU91Y+iNarNF7Rwu8SMYKnAY+YBRBgjYoyA0rPmq8HLoZZ6avfD3qNJMvy+unzscoDMatfrubcufNOvz8bK9fUs2uSgbpmnDcr+We7LyNONwlO8iDSYdEClgEwJ26PGif4GrfodNALpIiO4a1dZY3id+pli5s/gQXkdAPh+Ku9aVZto+lGkSX2MMoAMoCngBv3w8WLhAp2TNqWX0iI177J4eocqq7+eeHudRBfOaVtLfG3e5W6azBRH//j++nj179XLAv/hnPyA2Morzj1sln30VUf0Czgg/jWTU22Qh7dG5rA/DSUJufwKohBGnQHJ674cTupDih5obIQTy5UpEJqmUlrA9VmO+s+sDdHoxU/5QLUIP2F099wNtzf86LS/aHwUz+Ynh/bBIP615eF43HwDq8+QIQV7Hm2mSnxJCAAAC6PILIG6BmSWD5y5l+BkXTPuISSD9CLIAtLMjcFa9n7kLTfnQjIAHwKmmVwrlJc+EPljPfMe6vS72+4xz3ASlGVsxQyA0Lg6Fqzkiu9tJMsGm8aNk1hkSQNy/qVTnaMsfRyEMxPJJfk8EICBbcngshKJGr+8SJzBr32CxLCgQSJRICBTy4DJ7DAwVFASrKAQlFjJnnYugQpPYenarADYjeEJmXLsGljADPGJMA9JwgHDS56nqKpCFQ40kBpVrJMdnqrteL3MpwwYChZjxAy+OiIovWlJteoyjznHQQN6uKBLIYyUQMqtDLE9lWVMsBjQNCyON6hbLZVj1nmdhMKs1iQbniwgAUhQgSQ4q7VRSsQDylVHfNLpi8hgY4TaOjEMYEVPSWBhEEPQIwRDcEJtFJwIkMA7DgMgBfdfrWMUIYcGYVIhxGA4ASkwvHZ/aKkSJUEHZC10XEcIW1z/5Od68fI2rf/hv2L79AYmlrFexOVukzEua7A94ATgxWFKeb8SI/rIDEfDff+jwyx/2SPIf8dfxDS7/y9eIr1+C/6f/BfTl13j5P/zPwNUL7C+2SJsLYPwaONxAfvgGgCB2ESRKpALq+sGxdBIVeh0J8/MMz/CRgQlfGybbKfiEkY9n+IDgF/aaFg7lk582L4DNF5BRgEEQGOgSsB/3OKQBo6gwWrGMgrt7GCmumLDKEzDxcYOKTZivswulvpRksuQn3FrnOYjjgBWuYPi+JuIc6VgtQ1vPF23Qz1AhOXXVlm7xnlnuQ2HlaftCjHgrPb7jl9jSK/xV/3/Fy90lPr+8wsVuqwKJSOgoZYFEoPdL2Qpqdg9NPhVHZ1YhxIEFtyPhNgn2STAwNGg1DF+fzmHWErEi6/AIAHKcBW9I/ZLrMa4X1AqF0uRfOjdl4fna+bqUFoWRPqWdpOpDtv6xH1lLhid9WoE8Ba1LSrckcGvhMmWqcddtN9h2ET/ZbnBJL/Gzy8/xehfQR0HfRXSbDl2IZn17vAnSVFB1kciEHrApqajxCY9Tt4/RdTU+nmwMYkVLPCk45riwxz/5K/aTbvwE7teXswUR4zhdaIT9PuL7HzYIYVr5+qKcMtXLJnUCWfDiakS0lp0njHgolGu4/Y2WGs7t8bSTQ3ae25gNjsCKaTyW37Xdw9yd3MphPU2RD5KFttY8x3zOUvMgP3cEARWzB5MhaC6g6sCaIhsL6bWs41YuTR6az3+xdmnzNPU/xr6u+nCWAGGS5KGWEOdqqpV0pfCzhGULSR5jl52q+0cneLivBtUMwZ/AY2lcrpQzfSwCIARQtzXkyc/jin1nZsfM6re8IKxSFVqQYKEICkVKXWu4Tk9Pt4TYj4K3e8ab2zpV3dgq52zoVsbygedBO1an5uURDp/pmYkV9Hutu4JFxaDCnJ3QA3doUzkLz8nY3hDtG0Dj81JGZN2KsSaoSKR6rndHa+hX1kMZjwkzNj/JbFC4BlTRBXArD2SlgUZJIlR0LwEQUk13SLnPQjAiw/aPFE34vPIFJnwoM+oum9z9kAp2WOsXFfbUYSCWDEXqe2K2QqfE4XQeSqIil7Qy8zXrPmlRNKQg6rJKlRJ1vBhAUKSkWmvStFdK1/PC9nFXt0nFBaVLP/x9njervxXqLO0SzT89QerfkQb09BYkO4zp0hKZSyiYNURgiBDIbEbqYVXLiILJhRCQwFm4oDjLtE3i/+cx8r4RLAA4AqjvQLzFsLsCEiPe3oDMHdc6zCmzrMhYpfA+qFAkIQdTtzHtugCRiN8OF7gaRvzkD++wG0akf/gH0Ltr9K8+R3j9OTY//RNIiEibHsJDFgqFqj9VrzMrrFjWLcOir/snglkNj13nffGEJ4bVdTR9/ojj8dRWGAtUXK53VucdrC+O7jhaWENNi+7f14/BamXat49zNT8cijXb2YTa3dLfG5ZXtaEioNiBUoJ6+DeWnQARknnIzsIrn9L8bsqXukv37VuLp5ddsLIfanRfMKEnPD7E9N2U/lja35QZzzX+OlO2zCiH3VACIKirycARfeyxwxaXmyvs+i22XY9tIFxQQhcEgdwqgpoDYYqPP8VtNhfoV/jTZG0mEzyMrDG2So4wmZoqHkdbG8otPi8/J5kRGUufVd4af1sTdM34PCfWpiykc1xyKftaX9agHp4jdGLDrK+XtRMURAgxoOt6dKFDh1fYxZe46HfYdIIYkwm4KpfspTNlLgr5PelWSx9k46NT/UO7fqc8SjKlRLkYgVcEXMdZrIiHAh35Nev3HY+qhygH3y3nA9WQ3/Pd39R2x7G9D6r4oBgR7647/Ke/ebXUlNU8y40sO7OLjP/xX/yAFy/u4vLJYbJLHgWakxrnzYq+c+0ZFz64f+QsgcwHby2FnLc/m1U1kspyYAu5dHUBeZZCCEo+Bz1v+9wzLDEp11w5LU7o0uN8KZc2tocjWb4qY26mlDRVvpkg4zGhLndtSZ1Z9wd3FzUFmn15hg8CT7wujgghZvEWAgPdFnjxE4TYmfZuu0dj1yHGCGbWwK7m893T1QhSE/CurV0RfVLEN/MbTZP4mzcJ/+FXgymdHKXuf1xwVwTqTOTxIZVL843y3VXiQuhbt2yYQrF0AAQErkheImM2u3ZOfhFU+y2vi5CxZYIyg6W+vwgo2nBL918hUgMACcZIH/UdV8xXdosLW9+UgwgHEDMkRhCJMYkJiVNmnoMsfkFwQhZIifN9WjPlx8MAsfbmQMbi8S4kB6cQ0XZIGiGilhCBCAghK2URV+51vJKg4+hTl5n4PifzQdL1EgoeJgIkFtA46o4N0Ygg5DGSoNIZFou3wWqBwaIiH2YX7nBWcnB3mwLkNST6A0zu6isARIjGRAjk5ajgJ/g6tHmlAIgkJBEEJ8zytLuzqSlhWPC4i/ADdvQWN/w1bg8bSB8gCGYZIxBOsDjOcOSmuA0VpJR0Lm1Muq4DxQBOjGSxGDRmSFkDbHihA3MAB7Z2BjsPA/pe/e5ef/0zvHn1Bb789d9jc3ON0eKRTGHKNijTXQkFSPvvr1gSRh4gzEV4QAFf9oxNSPjH/i/x+0Hwf/v23+HL3/4Kh29+D1zsEL75NbY//Rle/+v/J8LL1xguNziEEW++B8CMIECggI46MEnF+NI5LIfYH8sh/ww/XqDq32d4hkeEhj4/ItRSvyuKo1g+5zAkqAWEu+Ap/FmpiivWrfWz1fas8YoXXjbcjUbAUKUQKRaquZuU+5GFEUWqAGfi6vfWPdMSb55Q+ksrrqtLPnXH2MUO2xDx04sLXIXX+GzzAlebDV5utnixGfEyXKMjvfc9iPAsNNed8PFHAirT6/EhWIBBgIGBA6s1hCYNUDULqAWjONIqUPy68Jt0PlY6k60FpPmY/c5XfzUHM0US+726rqba8RnZrcoyRRARlJgmhnuzoMSFqPGRqq1H13iBMrfUPCCYokxe85SXbC6QCKHv0G067C4vsJNLvA7/F3y5eY0vLl7gxSZh098i9h262CE2ZLHTMK6wm7HUFZBCe0XFy5MzAMXUfvNmpbadItn9rgMnAUgQfraH/OQA+a9XwPcLbOUa1/ujuyQ/Mv7fRwgPDFZNSGmF2VV9n07D/EC2DSQAEPCHHzbYH5K9mbjloGnOZY735QXj8tJP2Qeu/CZ7a8a4/AYzIYRkhoFUBOSJBbrU7hVGgpa20s/a8oGoknBK/brqR8U5sTqnzPRCx1sZs7HwA9nrODIHVVuW8R4XmMwa+uRwStix5tc4vz/Sr7PrPysdsHrCHy3iMW6FI8hxTvFjvH0cY36KojO2fDrtKSuUU8cIRUjYqTVE8EC70ZohVR59LuJxG/TcrjV+i9B0vjdyvY7MEHAYGd++05GMgfGHG4Hpgpc13SB5bZlPIeS703WxaFpS/azaN4tjc+Q4W2rCfDhnN+uxlq7kkcWndaVigob5Wad1rgudWgJUmdikzP2KcUNVArXuM46t051GeAo0WHLbjHpNWLwCxY0rGkgKfYDCjHW6xddqiX1RE+pQ5jagbpJIwFAz6uYuJ90TKjipiDa/Y1EJcnhZoz0r9JFZW5jVkeMS2fcwCqFbCxkAmNXCHEozpeAA8Put3uPWWh9zKVYH+ueElGlm+Zr2gWMAsVoPUr2bNaquw0eJsrZWkXoo4cR2F4sIUlJ3V8IBYtbyimPVK5Eahvuk4pwGEASooMeFJxXNaMyZtp31vxQKZSkAKAT1wWuCWW1Ts9gWZojBTOZ2SnLlXkboN4gMkLmmKsNXuV06eQ1PcROvl3PQ84pcBkSFTMN2B951+PX2L7AfvwD21+huBBf/+A1wYNz88hvELxP6n32NsOmAly8gwwi5vc0WMpS3dWXR8pT3Z93rIwf6jxErOQuma/C9c8keAU7cvctZ/Lw6k/Y6o8z3Bfe1jFhK/dDZnub/kKMk1R37oWHVS8AC3Kvdi3Sen9h2thLgHo78rDWjyvynaZ8Al75LEXZf+T16t/qXLrv1C7DGCdbJZMc3qtYQ6X2eegT5DH14hU23Qd/12HQd+iCIhGwJ0WirNzyUthX3grXsNP8xv1kJiBswIjgRRmbcjANu02g4rsmAxHDVZhylDC011eTX5bOaA0egl0mONk3zXubP8vNJIYvTPX1X+R2pBBRNw2WSd/ZsbW0SCgMtE8GTYXKqg4ruVM6urjpDFxFih77vsMEWl/0lLvseFzFhE0StckzAVS+lGU0GWB215xF9U+g0w/NCgCTOM1a8vdSl2fiZAtgiP0xIkbwoAHG1Tkp+bespNKNNf5yibM/Ou1pGfHTKwcfgAU29KxrzMMzi/g09WxCxdFk2i+pYG2j2xfLTLB0nwt/9/dXcrfjZ7dLff/Ynt/jrv7w5r5BHBj8A2IIcKkPBY0JMCQAUYpmo+Z4JaZoT1I1ft1zU9FDyTeoHpBLDekgBhXiuDyxkX95VZfMDZCJYmFs5SvNiNeRERkYmB0opyAhkms31TDDxSDB1BfVpwYdHxp/h44a8l3xTdxuEq6+N0Wuo01SgJjJ7N7eAOA+C+aEHCa5vgP/0mwGJvVxzf+Ix6FbuDsUT39fefJw9tdTetR6cZtE9pO9TAnQtmeTP5eklEAmKdY1ruLf3Sb5+3ALGmNkBBNXiq9YSUVlrhb6Ga2hl7aXSAghJFrK74oIQAwwkIzwiUWESu1aXCwUcUZ+OhxFJLEDR/A8InWpYqSa839+UTfOTBZf2+z6Q+cK3+BSHwwEadyGY++KKgA2ajiEWy2IEez2BEIRsn+qYpzTksRZnWuetXRMSFovBuBMav8PSGHPc7z3tR7WvnRg3v7IhqJVBiGoqnoUCKZlVRd8uI54zPdrBrlZ7IITqHPJFpH3XPrMIDuNgAaQ7iAS1RpBKcGPz4m0trrIWfMzCmTWCkRm9qDCWrF6ImHsmJbTUhYEtTqri2ggjirlngCDEWLYQ3O1w7eu69FtEY47oGJiPaVF3DzFGbDcbMBH6vkcXIw6iVjW8QrQ7zVnjMvmbjbkG4SakMWUrnOhCJwgGViuT/VcvQC8+xy/wc/wmJcS//Ufs3n2Pi3//f+Dy8h/w7tVfYfsXf44//dkX6F9cgl7+NfjNG4y/+Dt0Sa0fGFq+ECCxGo9neIZneIZnaGDC2jwOFSoP6L3OQc/XALOGEI3RI2KoVHMBz2nuxcbkl5Jxhtnz2c+FsmUlzzHwpGtZnAOb21/u1mwFUfVLWQdTtmuw4jVWVTDFqy52CLxDL/8Ul/ElLnc7XPU9rrZbbCOhw0FxIXNdm+v/mFgHREjb1xixw3AgHOQafzhc4zrdGO6n8b2yTYm0rOmsvEOkuLXhxNMpz9+cPpNS1lLKZv3J2m+HCcbg7k0XFH9yNi5tkBIUpdSTs1T1NM/uOImNEIIyrVNoW39niiohgKLGhthsN9hdXuKKLvFl/wpf7iK+6G4QY0Ts1UuBC4yW9FlaC/TCV/S6yxjlppo7WS5dneydMiZmDTGRJqzq1UxA/miCgZ2m3J9hDvcTRCyN8+xZvVjvMDHGMHB6cTVnpYG2BO+uO3zzu03TlkKW36k58N296RmvX42VNvCktMywUcJbshDCfEUvSMjJiUVnxoCyiwT3yVwdIxW7pPZ32jL9vXx3nZRjSBizpkg2pR2XI4eFNP11ZKTqygQpkfxpQgyppa3lmz9ds7hwSwob0TbNIx5ujdurU4jZEZgxZGXl+R3h9B46sT+blE9zUDZtXKlimXk8c5xxdp13ZUYvnhqrRdDRn4uI9mPD0rpx9eQ1oJU5pgDqdwBFUFRmmjI/e3DokLUoaiYbBcM5dd+rcra605HsB70giM01vEA0HEbGt29GjKbpfn1QTXdHeqvjdn0ZPHTIV8o9vQZpYQ0sMAHPbGA+vdeSL1RXck4zzVM2143Phcx0ndpvi7j39KFU81Odm0585F1WEYLeBtTCdnPJNFnLWQgx7ZYXTQt3X26Ols1cCKjm5rC9QyYAEaqJG9fWlhKIGmLBqskY/QwkoJj1S9b00Tt+7iJKbHDyze24iwWxznEOiJS283Ext03iro9ILULasaruSlSxFZrK2xu3pK4LQsFBCJkBLyw5YKQmCxbXI0AZ8u672UsLuTBFMZYW93zuvEXFUsaxnqq9JMYvdwK4YEYCpS8JrVaXE2IBAUwMJCuzMSPQOY90i234DkFeQeSF5aNKMFMstTJx526wKMAteVyRI4QACZLnRAnhysI3m6l4gFC3snFCP1hdASEGgCPGq5fgEIDh94gHAWME83Qk65F2TKxEPKlnwYNma0D1FtiehZu3AIDbq1fgGNG9vAJFBh+2+P+z9x9dsiRJuiD2iaqZe5DLklZVd3W/fq97CAazwAYrHKzxwwEs5pyZBebg4AGPNHlNimRWZl4aEe6mKliIiKqompm7B7v3ZlZIZlx3N1NOhQvxHvlf/gFT+oAP//gF6ItX2PzqN0hhRDr/EpQyeMrgvAPyBycgI9S1chr49rfY5t1gnm/1wP084DGVYtxabD4fpaoH6sc9ylmMF7GcUM9uuw2s7nUkhdzfnZhZR5vk79x52Z8ipsQiavyR4VPUuQa3oUuWLSNqMNuWZqn3EABhqOsfQ9y0iNVDKGkYNR5EI4RY0zxvgNAznA8npwU+B1f6n/2tXtthihIz5jLQ/j6INJeBgE9c7g1uU87XbL1IzSZgShlvboDEA17EEdthwCYGxEgSqFetewVn6irpy+f1Y/V+cZBIBU4y/0GjEJOeUcT6p3HPcgamnLEHY4JEFcm1KG0oADYbEdc2BorFMjeZuvuZC73RZcbiTc76T4/X966eeuqlBHlz9XXz36zzbDi6a5vx5sqf2Q25ZzOMw8cupeZDekeV1nDj18c+Q5Bg6JthxCZscJGf4Vl8gU2M2ISAOATEgRADIYQ+dH2L27Vt879906nJJxuSy7S3IJYQdaoYmYDAbX9BKBYT/HySKt6OLlaELkLf7xOgxdB78BSNrafujOiS3+c+vFXOYnniKr+10vRdMVxe/rWEOJ9czMmH/y3StnBP10y+AXDjdXjg7hpM9zbww08jfnw9NmWdPBf+HnWE04vnE/6P/4d3C8G52wNPGAziHzinLq0R+4DdXI0AogolgmhMknsGRvHd1y1sqo2tTbGmFQ3mrqkNiuNMCi1908X2ArCzn0zTtJlTuwy4Zm3SeYxgCQlzd4R7fHRJnLJmVva3WV0cynN83XaHQDkXT9+cH9+8+PBxfwzqfN4Pkbpf3tPHd+l8Xa19ibp67OmZMRIP9Y1q+kbDlmZrVQQMEbj4CohbhHEsGsPMEnw651yYZVUjqI0VUfBCEp+iTBkNq5e7Me4O3es94z/9foddRilbGG2321urI0IHhuzUA2Rpnx+p/tbWGc05vJJEp7ObSaltdkfdvj5/tlbcXddRcyzIs4Y5zChugFjzJUPaFQE3ARNxNQWW9uoadQL9Rvhgz6DjSo7+McSYCYXp7+64qC7FUlJXOlqSKKIToNY2gQZwUA36zEqEMgDZA1OqPvgphKpZH0i16qlqwEFiCeSUgKyKBM0V145p0B2Tcy5MbTJfS4EQWBkHeZLIgpzVNyspzqBieVsfVPdSHT1XpaejGKDAaONy1I+gc2Fm+lKPEHumMRgoioVCUMsAc0dlqlr2p+2bKRBYQ8onlY4EnSYmkthXWbT+TTiSshDSmatVJ6kmXwZAGZUsKzhOQBhERVQUQ0zgKm9NaW4T3mI7vMWOCMyXCAgYQyzzj6B7JpgwLUqbw1CtUEjqoEAYBkGvwz6I+6P9BAqEOAyogimuQl5ojIwsvr4DGBQCIgBwBFPAzbd/ibzb4/zqCiMz9mkSArGZeCxci86tFKHMD4ORckICqel/ZYClnME5YfvTHxHf/Yir4d/j5vIFnv3qC8TdOXj3CsPVD7j53/8X5P/2DD8+e4ftb/8KL/8v/zfw8BzXX/0PSPsd9tdvQPvXoA/vdUGQzgGBkG9FpN2dlGyBFr49wZ8XnCyMKFAd2wiO5Sy3ylOAiN0Zx2V5P9Tabep7RIHRE3wqUPwIAGHS9aOCaorKZowOVzN1i4wERoL4fa93v6nxLUSRLIiV1uGv5aY9s4cVD1McDaBylwEQjwWFLpFLNgDwj3PznlEZy6alrTG8uMaia9s+68wiMNf3Ngr2q83r+AAEXE8Zb/aEi2GLl9stno8DLsYBwxiAgS0shxn29hW2TXukrVoCCDMLAgSUBgWWMQvMCCkBPGGaAnZTxg7ADsBEAYkBix4iOLd2Sttems/1uq7hSiqyUQUQqPi5m5fW7njFRlzX7CoCW5Iqzs41D81iPpSFJkFSmvRJ67DnWZ6Vz4R65ms5fs1b19vW6/BToZEtGQGIOqYZDA4EGiLCMOLi/BznuMBf57/D8/ECz8YNzjbAsGEMA2EYBTe2GF798urVlZuG6RjWJ1WzKEaIG1gWwZXMMdcuElQJq5aVwQVXLwrhFl/v2x3wzR74zwH8xug935zbbIIlBszSLnfz8RiX7KnwUHXPcJJHPDyOwm07dTt+nMG9Y0Qc/q1Pl5CllbttXsT6BBwjJjyz3ao6yu4qJ4kOaWFgALtdwHffbXF+lvDFq33lAZZ/oEwNlMCXzbw4gh+meYjgnkulwburWNyMNBs3I2Ub6Ma4kZOSe6GJiza0MnAYxxFdc6PRIAi0PjNL/sRpgVkheanZlLMYGL0w5gQLiaYeRjO+xvRazbukfdRkWDkoT92XB8bhkOZT37aDwoxDY+1gnma5VB8fwMpfgsOM2lsctJ+a7nqoy4bKPwsXj09Hh9836VD33ngBGpyLFFYXOnFEiLHwCkOggpvZ94o41P3gXcOxBtYVdyXCZPPIu+9kzozvXzN2e8bEGTcZmMlmT51Th4u2puXHgbp23RrmB9nty1jI4qeXFpbDIS2q9QpW7kNwWSaWin0DMsNbGpDdM7pWWRtkeLyh2AQx263ufqx8rvcZ7LyqAogq+PatbO/r8pTdOMHNP1ub5S9nOy81NlPpuSQxGUGIAZyk3QiMnLRfmWtcJ/0TnX+WuCn9fDAgUU2kzoyAoLRgIHOFlHVs1cKhWwgm0CGguHLMOalVBpc+t+e9VV7HAW6PGi7hY1jUQaX6leutWmLWoXWx1dRZkB2d/aL1hfJ7ppRgzVtM0xIRRQFL11gu89vqffnV4UZoAYfnIqixtuaUi4umZsc4DkklZqEWIGZrUd1DmXDKt8NwJlMsCUHcV3FAsTow61jvXpNCqPsNGZwJHLjGvaAAREbEiEDAzbNXuKEBfLMDMGmbl3d+v3bq9LFakUjfszQSIQE5hOJSK6tAYp8mIE2YAmE/RPzhm7/F1e5bfP3DPyBQxrv/+A/Y/ekK48u/RvjyV4h/9T8AEcg8gugMYXqBnPdI+5t5m5ba/UhM1gY7vXMdy+f/qjb60uH+2HArpYZfHixRTrM0J9A3t65XFveJ1PFxeIhZ+9hoMx34dSr0NvCfk9Bltp17gVSDo96h/OZbvSca/IpFtFCVjeW/Kb/FPr8F+KbcjQsiiFlNch6u8y3Q0eNLZZkzn2PKB1V5ye5Zu3O9tnr9Xa0gy0igKbL57u7VphVL9LnnKrA2J1dlgxCwoRFnmzMMIQgjmQgBGSPvMXASN4qNlueBIToEd1zeBOF9VBc8BZHToRW8aGLCxIR9lmDVZkmZuYogDL/rlwDgcDjF02ZjvzQ//pF9LElmCz6Lsh5KpQ2t5zJ5gYPiTRU/9WX5Z/a8s3jg7l325Xbts4ezA75au1Z3tZa03QFQ2nuIA8YxYhgGXWdbXG42eLHJOI9ANDedNhvduM/PxCMnL3VfWONPpKwx2Fr6i9xnnXcfK4LLXZeJEALrlr3PWb20a0/Nd7/b8nDulT59xnjVqSNiouxl6J8//D38QBYR6/AQyMMpJdxfk9wI6+XKiQjXNxH/9R8u8OrlhFcv9wihXYNsmge5umcwTc8S9FErCapJ6C0eTABRBBH9hrQDYOGKlffWVntgH+0BZgEUSxcbatpd4uT8dd8GjnLPGvRytS1+Y/RCidJUn+GIZt3SeVFcR7mm3WYtLcapaIQnt4CVulcFJCuFex/Zi3kWHx/z2LyS8cEOpWMjtVbP53sJnAzHhA23EUZA5j1cvAJtLrvX9YwrRIC6/wgQoUFlrWWY2xXLZ8w8ziJoLUIIDc66BMzAP33HeP2egTEJgu+Rq1tJIcwSwBFna+fYfFg+LSwMTznJu/b102349KE06/tT3gnOyKVez5guOLxjjtrLgnCSWc3rDyuEANPIC/qs6oxCNdnrfVb9mFJN5c/85UNaUhZawvzOZyUajMGviYgqw79oEGVtkLoWilGIL05IST6rEEDGIecqkCAWNzIxyKfdw7bsjWEbiMExapcCAjFyQi0P2g5lkJNpFllXc0aeJqRpktgLXjOimU0TlNiYOSJoiT1ueEOhP5xQipvlAHBGStY2Vy9ntUYI4vhBCS/zLVzmHJBg3hrzwJgIlW5ZvuUyZwSNvyAug7LSgjZWASFXba3KnOCG/m57LuNncWkGIkz7vVq8oBvfeqZU4RZEUBSq8ISzG7Aw7wlIhRAUESOLZcQ0YQJAzCXmR9a+gYEIAkUbZxR3SZkFn5QzE4iRkIeIH7/+Nfbn7/Hs9U+IaV9M1frVQs26cJ9OasGAKnGoRQYxiGtQ+EQZSAnXUwLv9zjbjMA44t9+8z/ix7TDV3GH4c33+P7//v9CfPGPoLTF2X/3d3j5t38NhBGJRsT4HCOP2N38hLS/BgGyV/BZ03FP8AT3hPszR+7dglPxxyf4DMExiBziRsjlylO70/LfPv0J1/xPAD405TTAC8+sxCbgbJ+kZUCWe2SGi7J7ZnhnFZpUBq9ZdxbkTj/NIkLLaWI7uXt/3sDmeUUPPP0wHwrDxQy3EoOAiMgDzrbnOB+32ISo+B8wYMI2v8NAESHGrlMfG4xRLS4oheEUyjAxxP3SxAE7JtxkYM8SOyRlwTUSo7j1sjFbGuI6pYzGNKJkOjQGFadaLLR/3SR168EnLkILdjghq5TFWzqwc/vlnve/vRCkKR9N/T2GbVtTXC+F+dZRYsjWGkiUVMbNBpvNBmebLc7CGS42F3hxNuCLcY9xCBhiRCiKSg6Hf6ClVmPTBXE5WzrFBQ+3+4MJJRaf/CZdAnVM1kWeD+Pr43jXV1J86utv7Tw9CT4OA8PW16cYqtsLIhbpLiXQZs/tqWcWHy9v6cU6M4lwO/89p8ESE9ee3OwI//q7M1xcJHzxSrS7TIuyHP7abWOgmzYeYIIGagUP8K5K5q5VbiMMmN0FheNl77kpU86c+U65kxDi1tCSzkv3WGWcds/RItgzi4nF6ubl9AKNRgBypEji5XxHqlxvHhYCg8uL2VE+q6/Pt1Lvna6E1Tmo/atS8oW2HIRT7C/uVPBR+DhH/AlwdKGtvyeXhsYLIG6AMDZ7dxZoOnBzzng3TfZ76S+EgAzRaPrhdcZP75MybLUih8BMzEg54yZBbho9A4Myo336FoftqZUKbHn6pCfS2uz+bdbYqefcbQn6B7jV5+Myf1+b36PI+rmUtVxUjOJFuDAozUwXlfhkp3Xt7o4Cdr+5nyZsqq6XFuIYlKZUSoQ9NWT3KudCYLB9pkkZ5End04i//ipUYW23u8sKQl3rKdrp7rcIDxghFjqixm2qGDtKIOhs1o25UibMyJyU6ZzLuDBRIYyyfnLOSNOEab9HTlNx3VTnkArR3v+VrhVmOYqgojIdzArT4xN2eJdJhAlvzNJF+sAav4IBqnEtbCyq71sqLrh88dI/GYMlcpQZwnhXVwdiNB9gli0hqCuUkIv3gUopZ2z4Jwy4wp5SWTaClwFB75cYIsZxBEAY9nuklDWYedeWMsb+eGkJLAKcJmTF95oUBG2zxHigydKyH5ZK3HocJIuLjZwncGaI57oA8YZFGGIAorjvHEKoga5Rl14R/HW9M8UXFNYVyl5gMAIymDWwPEgtOIAJGRmMvbpwmoYBu8D4/dlf4HJ/hs3wL6DdHu/+43/EbneF8D/9Bwwvv8L4zV+DhgAOA0CxBIuXWS4tfoKHhoqYHU/7WUjrj8BaG+/AZO9Ov3tBtQYlt+/0t55ExEs47jKskW+3bpeNV4sg3Gm87goe37p3WV27PycLiSWYWdvfKq//QeWJ3ct6O8u64izCceWrhvwBF/kNrmiPna4euu0qOrg4Pd7cXJItqjmrUh6YhWkpsBdClEIM/8tuzXZ9KDgAowlmZZ+Gz7UZ5t1izBT1QwgITNgMA4Y4IFJQ2qUgUcvd7OHIOuUyP6fBqpeM8pOUXpfvPD4DY8A+j9gn4Jq/xx7vIEG5oUKIoppWh3NGd9gE9/RXN3DzH/PmWomWdTW5K7tvTxEm2HttmwWltt9eWJH9Mx+XJNe8XihR1qNfn3XEZ12mha1DZUpgLtJiDBIbYjNiEze4zC/xMjzHF5uM5yNjGIKkobnVrZR5x7PPj716QAhEEp49MJhJ8OtK/DX9VTLETp+GbDCDYmIgf3kDOk/AjyOwb61DjjbsTqm6G/2WV86tkt/p/uTTK+nn9lbVLa2LAwV4HOFk8OfBw8DtBBGf4N4/qcqK792vLqPIjrTj6iri7//pHF9/ucOrlzewRVYk+wyAHfPFXVjClBHN4t4CYm4JcbcO9QowiwdZBz2uei+4T0H9hqDTLCYAHDOIOIwM8jIy0Aspuqa1KM5S8Qc3+BJCsV7nqpDCSutcUy1aa9RqToZGwNC8qP0391GfO3Hwc4Ol4WQjBlSz2Ls5obPnCGcvZkIG+6wM4aqRDaBaN/Rp3fdgvtIhgoc/vs74+98JyzA3FhGKsA0JMDfyKoioTLCKgLNpqmBhuxT8or38ZkSpD6p1W/hFr1nPjG5o2goF565IXLmrABQBrwkitIzcFFWZ3NDnMVhA6FDKWsOTTGjQCwaKA38lDjhnICeJn5AzOO2ROSOlJAKBMIh2j60Tvy4Lw57K2dh0W4n6SouokIGj9bDZF20+oASSFuxeXPJwFssGI2bsnlfSz+pkjc8y7fbY729UEJGE+HVxWqqAxPLn4iLND661Kbt9UgWA1O6rgqOQQx7K7lRa08SPfSwKamJi1PEhVEaz0nidsoYn5ay9QcnjXAQWJnUQi4AQJAinF9AQJ5yFPwJ8hbeUZlYq2Z1x27MzgAj73Q6MSeIg1JVQWlStFaxjmAGpcMRy92D43DBEANWCLBuh3BQqY2b9ylkCpqc0IWcJmB6jnJ8xEMZhQBhHDDFqLLEsrjrK/pYvwSw2MprRlBEtycpYmtBJYlTEguNkZuxZBDc7AsIQsB8jkAP+Zfgtnm2f4e+2/2/g/Y/46X/73zD+6Q/A3/0GF3/zd/j6138NHiJSHMUvMkF8flOG+KyKeIIn+FkDzb6433dhXDxGKVZYRyB+pvD5t/B0OOz6Yj2H/22/uPyqShAouAEw5Hd4wT/hA3bYQfHvIDjyTCC2uLDC0kNN3zP6qD6fcWdrGQTREw9Nudx+FW0Eh++5P7hPl6flbaxZ9bt7fI2+oBr9BVwVR0MMiMMowggy10xAYfQTqYLGStW+qscgM5Q2r4KdQlzVYdu+RI5nmD5MuMEOO/o9Er0GsBe3TIonZjJlJFeOAftC7Tu68WSX7pbdgD+S1k47X6HQA9r52rYSzsHHg9C0TYyIXC0kssaKyLn+YUEQ0bWpb6HFP5mhdUBjNAIwxhgwDBFnmy224QLfxL/Bt9sLfLvN2MYJ47Apbj3NFHy2ve4NlR8gGGrS/nsLH4LFpwFXq4hCGxC1V5+5pf12B04T8D6eKIh4SJiP0sfX8/cL4Zd0kz0OnC6IWDxE213np58WNuPtoN/Rh9L1Fd6tvpYZv17e2VnCN1/d4OJSAgUKoZb1/HWXb8d5qcGohUlRtSsdg8MxB0+63VagH47CVISS29SnpVnaQ98PPWuHjpp0R32uri6i47CmWXBMWFCGu7BHPgZjUsdj8SlWCYWDVh+94KHwUKh7vM5cWayTl8el0fjpENQlt2JN3mNaIitClPnjQ+vpnvN4gkbhnQTKdwCvdbd0ttLmEjSegcYtyJj/+t5/Vn5jz1RlXO+Af/lO3HPIO9N8FgFFhmjFgoGUEn58l4GozEU3MUXYYLxRQjnnpLLafG5/wOnlSFkz+qHTJvZj0AkjDgrt3Hj2aWdzuTC5RxEbnn/tm7NWwoIsVsemfDkBFHldw+dhOPmBwoxodYSOBTPufaCWdlKZcnVb4xnTCw3paBtpMys9WpzYFuKBcxJhRErgnArDPltw6SBIM4Vm8RXIWRkCSZn/jrk/i4kAiJAA6mppSThcXNioUIACwBmUghB2zEhpkvExmkIZ9yaAQJJ4EGmakPZ7pGmq7h2JhejVttmceVqrmYOFUTZUKjMvWKNQ87Xvp5E/BLFkCRQ0iH0Z0YK3BLVGqTk1t3CeVWjCReiytIcyMyhL1I36njXqosc15Xwq/c81nkR/W8lYidgshogYxJ1CyNm1wO5j2zfmFkrHO4urOqayrEEkwhFj3JuQxkQ2VnqMURhEMWICME1TbZmNNaHwB5mB/c0O0zQh5QRmRoxRg4NLz+IQwZsN3r/8EunsHLvdXqw/CBhSwsub9wiosXuyMwEKoKIN59cHlbmSPCEATITX58+xG7bYx1FoTSJMREgxIkTC7otneHce8d9++z9j+/oPOP/P/0/wjz/gp//lf8P0+hrn/+5/wrB9hrh9gcDPAP4KvPsA3r2TEfoY6NYinHqWHoCu7cfx24+EMJwKvwQh/EyD8BHGluffizMcqvccFSRroZknVrWGJ6zhzKesuXIWnoDTdoWfluy00h4UHtdCwt8ed8k+RyhPpStp9o3KPdyWWZUSUspIibGfgHe7PXa7HXZ2v5nCErgoqzXlVaLTfazga+6jZmb3ac/8+NV3TS86vK98b5jdSg+UINY18/HRtAu8r7Drku+Ca77hOzFQiQ8RKSDGCATFMW3vH6cIluu2+u4KzJUuKNOpl/lwCQ4bZAzIGdgnws3E+PH6Cq/3120cU+t01a5ZXvplfpbWgj644/nrV5AgJBanTnHg0r6+fq3Tu17qP70wqwgpUvvb3Dl5IYQXWDSD0E2aw5saRqJ954INg4gwjiOGuMHZ9AKXw3NcjmfYjgNiyIglthjarWS0UUfT3BbqduCmnMILKLgi4CKho3DXFBUvVhGWhFTQqTgqIoO/2QHPE/CnUy0jHgva1WWwulJna3g5/8PCnD/y0aBXTjipuw9xgAncL0bEQv3knz+AcKAQiD3BTX26lQYtNOMw78XHYZjXAADbbcJf/faD+LhlJ4RwBRfmi9cqVgKwfJpAwgkg5u5C7okQNWBtaX665+1n25d1RK9/XzUTavtrVYfXBN+CmThrx5EN8ejM4jnuuUJ4riN5h9CZcimvwPzs9EjnQjtPHA8b116A0QgoWOa/aBofG+xjdRd6qR2r5ZgcswafWMnhFISlubOXy+fS8QqXy1rjTzTCUaruUHpaIWwvES5earJ2n7efcr6V4K2laMLVDviHPzCmZOnqOUYEcMjgKMhbNgQwLjG72wutBit2fSx4pFv3nmDwd/Ks/P5Al3UxF7jNUzen0YIQoi1geXJvQ3KspSykFmP53Oha32/ZBmeghRQLGmDzerjeWzyvqdTlrQpCvbPK0+aOQ8WTyd4tuerpfvj2stwhbMGzvTl1zuA8yV9KyNNehBPTJIzfkCAubAbZLzG6tSYubJghboBUQyqDS8C+1oBCLH0iWkuvgpq7GAaWHqwa+JQRWTTb0yQaV8MQNAii9NesGXiakNK+CCFSSjp0fk65WGgUP7jNnnE0A5wLp+zOaKPp+vXeXE06lwsSDgm+TEXW4IUURIQQYzkvSjshlgBJx5ItDoeuOZaLAxZfS9pi1hBBmCe2ToU2LevUzkFZIlUIwaixbuy9dScEYSTEOGDSeSkdLPNeliEAw+8cThiMSaF3XvFnreW4+hAIEREcGSEOCF7gpZNhMVRAVOZ4t99jd3ODpAKp7XYDHmKZoyFG8GbA61dfYrfbY7ffa6WEs901vvrpBjGnshZClnGRAKcAUQBDBEMeX7d3Mo2yXt+cPcO7s0ucxREjgAmESAEpBoQ4IA1nuD7b4l+++e/wbLzAf/gv/w8VRPyvSDeM5//n/yvOvv4VLl5+jRifIwwR+7d/BF+/a46GTwP3RQrvT4Q9GhyUxH/G7b4vrNEpD0oA0Mqvejr5X4s4wwMJUGY48oFybpP25wa36cupQosZ7TMrx+o+WNkJieY1108515uwyg4vMjxlSsCUgHfTDrtpj8SW06zQUIT3VQHJ4xi35TXUtjX3aDERsNprmQWnbGpZqK/EhOjxWJ/Wfc9tKxbTrPWLIXPkh4AE1wlMiCT33RDEFaJYhkeAAoxj8yC7aIlgWUzW0jqVJnb8IwYwXgDjM/DE4MTYZxFEvN5d483+ptkvMl09DbHQPubqjYtPGFuDpUHi7rNJT/W8trYtBrmuuDBB6QOPH5uwpbR3KS6EBaf2cSXsr6vQtcnztIIbdjIE0HBhcCmKCKAQMGxGbGiDF/xrvBy+wOXZObYjIYYJMciaE17h0i7xC/Ue4MeXqiK07dTi0M1QxKZKdePUN4MqrUHEwLc78I6ANw9gGbG4Thb681nCZ4JvHaH9LOaHkTKnHWz3H/e7CyJmzL7PYaCbUV1Pdseb42yb8atvr3BxLm4gGKgBLRuOQFedF0KQc8kUQnku2ajbWH2j7weVIUmNEWPrTqE+W/rs3/vf1b+8mXa6NHqZEHDwwDB8QLLcss+9VK8rR8o+PPGzOmf9PNIEvXhmTD/fsVU4nGDN4sO/9+1YZaRae06Fjvm/5gJKgrour5daNysTk09b0l0XTloTd8H3F4s5MN6LHL37w8oShhdCeMFFfW/J6Oje3e0z/vVPGVOW55kZN3nCzY6RKImdJnligWb8ZGmnlb+ieW/Q400Fn6woz4zQWCqPDc2zVqHMweF90cJ9Zu0hTDwVnz8Azem8mMLWyZypzEtfZ+cRq3sYYxZ7EqTg3uxcbrH66c9BrA7KGWDrMdSmUnEcAHBlAPFsbnOpjAEgKyNZiQFW4oCVcCCWeAvmook5qYXEhJwnba9aQpBosAdtj97WxVuQCToypKyUkwg2iuscQ8yrFaONRwjLe78Q/IXIz8gav0J+k2ju0wROFudCHBExZ+Qk/SaYawCUMfU4hlwlyjQOAHEodVvvCBChR7d+hKhgdx/ZmDMC2+FjljCyr6MNKTlXP4AwzSmXQNDmQiqrxYOtnUBBNfKlvFQsUXRMCmOeCvFGZtaVdR1ylrHLXlikhB4zUvGRvXhwFK3RKSVkzoWh4EuynSBFsc5dRmSxcrExE7pNvvszTORkXFwv5SwWKCEGRAwYB437AXWFYEGoG8JX1uW03+PmZict0qmiYPhhDd49hAAMEUMUpxcBQNhEvA2/Ujccso/2KZXxFxw0InNCmtQJlp7RRdhE4oaLAdwMm+ZgyGAklgCXBKEvwxjBX7/ENF5jePUV8vvXSD+8wc2//RFv/9N/Rb5JOPv6N2Bk5EjqQu1+elBP8ASfD5A/rvWJ/7GOjz/BE7RwDEOVc53iBtheIPEGuwRcJ8b7PWOX5T6c2OPwtega1oHcsjyRKcKrPwqNXwUvBI8xGxlQ+LswvAYF72gKW1Cm8Q8KH7VJtnz/N18Xh9e/cLifY9BmiLa3EmKPLss1+rMGDK5N9LSp0dKG8wmCRAVvTkmEVDf7jKvE2GcuiiBz6onKBNV14gfY8jlr0kV6denZ/AzkRWJIccX2ADXktamP7B+nKFLWQ7FkkHFoLB9gn95lUyeIsHSztdl1kA15QsGZjadXh0xw7mEYMIyDumQ6w/PNBV6dbfDNkHARCWOU2BBkCksrdP6DgcOliyKpxoooSkxktg/aFxIeEBOD1Ao8dIUWj3HOV9Ux/tX9+vF0t/6c4W6UADUfWD3dH4lZdysoB/f9i9mMCX/x6xvEmISJUbTwuK3AMQyNkdFbQNjvYgUxG6Z1BtSt277AtSwHeClzzsD0+Q+5ZZpbRMxH28aDtcKDWjvu39uAMWhWgU88CI8IHw6WoYd0qdIYCQULO179IVjP3l3wxw79WxzcszE94AKqd9Hk21OrNpPLeV0zja1aeMnbpL/HxbYa+6IWvr6WpTF3rvtwuw4UTeIixWiHgow7pHl1X2ri/QT883cJVzvtBjLyMElZi0oLDtF1/3ZH3q2gEUIcTezRYUu/UGNznt3/zC/VP1hJWp5hp4uj1hFZZETFHJqtsiKA6NOxIsXcI9eKzBehEqs2fxYBQGAAJL7opemGJTMIFtg2VEINACsDPuj9aP6MuTakbYPTYmIlBKStGpjaPrP/noSBb880ckWCMHkRxV1QhrlORHuWqAZ6ShlJhRBcu1ACEhfhabnv11Z8PZEymwVA0t8kOv4JpQ8+oLaZkq/RyT4Oi0wXlXgTs/tZDxETjPuCWM9eKmtN+xXmTAErNei5Q8VevD+LK/Ge9xLXwIJohxDVEkAZ8Cl3LSo9KiMoc1C5JpzFh3HO5lJImQM6p7lZz+xKQmlrzhk5Ce4WQkTh65dW1IPDrEmMJoURzIbP+Zw6DlmJ25yz4jgZTGKdwwDiMCBOSd6pwKK4ymKz5hBBzjRN2O93IqhYwLeJhOcQYwSYSxBNWadb3Jyd63iL8GW/n8romFXIlBKmSeYqc7WAMwUZGVdZd9UnOVQIIcG0CUAKhDwGhJfPkMM14qsvQPsd0r99h/13P+DDP/0zhvNL5P01OAbkEIAQEWhEhrdK+RnCqTjAp6aDHrgNJ7tafYJ1WFMUWk2+/ObYXNDC94JF9fj2HeezL/dzh6o09xnsS4OTEFe98BjgYQRvXiJNhN2ecZMYH6aMXao4pFcIr1fsHCto27HWhkOEib7vrCFcq5suGHN26Xnf3fqM28K6n4sFnLogGTCT0rIkiLQvBCNXGWhwXEDX0l2WUYOXO6tbR+IcEka0jWcwiQWpMcSFKS4xz6Yk6+NmykhZ7u+Cg/tye9qBu/FlwLjMNX7YvD+r5E2/hlaEELNB8nwF387FterKYEZ1teTeFSGE4t294IE7IURfx9p8H2oLCGGIGIYBm80GZ3GL55tzvNhs8TLusQ0BY9ioIGJeaN219zuzHFbcfBAgfEnOOsVU6IHqJYaW57sUrvOrSkESG/Lh7oVZ1SsFr96hD9SOnxM0tEo3Ao786NLfnutxH1TwAVWSZJHawVTO6c9AGHHK+KwjJIztJuMvfnON87MJROKLOptvaD6E1JjbAiHshFiUQ8bcGSwLIazV9x+3pTbJc/+zXr7HhBDHYkYcqrN8Y6Bx7fFAQIYIrSago5tlbRmsMrwXD2P95Jqv8LztHp415L5zvYo93h8qV3TpZ00GLn76Z8fY7Ocy8laEFLMXy+vtZMuKBVitC2iFFAv9vA2cIizpj8mZMKJLYM0LZ8+A8Rw0npd2k5unf/6O8e66ar/v8oR9ZlxlIAnvyhR84Lu8uE/8mcHWRs8lm1EGgvNRVuGctsslaFftMoJ60vndn2tH0nmYjbP/+YB7qm57138d/4rr9kJaBvcm04fq4BZV7ZkUnIX8y5zRatFrJnONFwyfZHF7tN8jRDVXjwQKNQ7DMG5AJUg0YFh05lQYukDVwmr6r4PSokqscQRYBZtGKDDASX6XP3nPGozO4gCztkOY5wHGzTXtb6E1GFOalOl7g5RqIGEiwjBE5CyMWdPgB4SRHEIuY+3nElafIwSRxW8Ap4xM1gbpI7G4LkIQBm1WqxBFFRxvwgsu9D1D3UDFRqmBAQTKYDL2sTtM9L6PprGVXfmF8IKux2pSzpDhD5mhUin9v+7rrPNsgcNzziAKGotY8SDi2gz0ZGcl+m19MbP0Q8czcxCrCG1PYkZOjJC5XP3lLACkflBh7t9c3wAky4HUKqLGB5F+nYXX2OIGlH6NKQ0YOABMda/qmks5dXeS4sC6ZOWRnUuEGAfEYcIwDAAm5Gz4IcneyKlYkxCRWG1EGYeyj4vVkHR2jAEBQ7FisD1pOOo0JcE7OZc9EQOJUCQFDDEgZS5zZ4uLqCxbRO1iDCoEzyzWJTmDUgIoSiDSYcB+vMR/evU/44y/wuWf3mEMA/Ifv8f0zfe4efcj6OwCdHmJaDgxggojnuAJfqbwEcjb+2AhD0NJPsHHhQ4P9QS74SIMpAzcZMb7CXizz/hxn/EhZ4xqEZGgwmTUO+POq8mQqyNtbVebw/ALDqU4XkEufLvmOOIaXfCQQO7fon2gyiIJwryfcsKUE1JKotgSXJZHadVtQF0uGv3ApHi+WEDcTAlvpn/Du/wGe+wxMRX80IDMgoUVi2zmoc5h+d13uj9o/O/FAVqZYw8NgVjxQ8BwYJu5qsgxY4VYPzwyW/qyFJTau9pc6KfldQRzBjc6fLXrksDceZ1vz7CJGzyfvsAzeonn20tcbjfYDgljFJojqCDClLEMZ384WnRhUowPCBT8r3SfNAoJUxl+BoMygQNAFsy6bx/RbCruAxVDX+vT4ZrWlZSX8v3yb8zPqYcPLIgAyvZjxxR6AGHEevbuxan1eKbfgSkhMIYx41ffXGEc1c+x02Qs2nmQg6O4WSpUa3DMwSCBAgEXuHql4lvu3sOaHe27RuJfPudWD2tCiCXly4UGLbaEy0myMuqHcJoTYI2JLR+82KyTtepvmdf7bgTXA3y9yAUm6Wktgxyzj3y0rAgk3CMUYcSsdQs94RXG8OyCtOrnZfSWFbfScKLldhVkztdxV1ipoym7FzJg7t4LcMnKvoUEqL541aL++j5l4I+vE/70tlpt8ZBqe7xKMLkP3aOn4PwVgVcm3Mo8c6tag5792L7iLoU9ljqOnz8Hsd9ZPW2r7og2HcCj7XUVQnD3Vr7Ohgg25567vlK9EXg2djRftSqCKI1h+P1S7wJiZWIroTKlCWm3Q9BYxDEGUCRxyWM+cxkQrDTARpFZ1lpWX8ZFa93HLdDx4NpIGEEgAYJZ/nycCGPytznBQI37wAAog2NE4ICAWFIaUZ6zaIunaRKXPd7iQP3klzvQhA5FwKBEnPnYd3ca6fiL8MDtPSMqTNtK8wYi0WYL5AgrL1A0V0ZzRoC5SgrONZYo9tm5UjpUMxlqAhIzbJPnsI6nE0b0FJ2t4yLELX2XdoKru0qp3+3ZfkFSmWo37vXTrCiJqAhoTAhRCMBc11coxCE33SYAOWVkSthNO8QQMY6jBgQk1RrNpYEb+oBIV8j8slhF1AaXoaiCslDviLrGuMV1KCAElmDZMRb3X3XsWOKXqKCQdE5DUMLUCRRJ9zlBLDtkHQQVdkRNJ9YQBjGbkFAFIuOAEDJCIER15SHrtfZUvRurpqW2R1eBWRHFEGoAdhowxS1+f/aXeHEZ8PLiOYYwgN+8Rnr7Bvur94hDxIBnMiYIqPHEfuHQa288pHJWf489ouLXmovWP3vLiANDzv0ht5qu+72m8bOW7gToMY8ZudXP5xISegBOxLx+dlDP9+WeFfrnPh1nPzvu7l64OE1JILH4/r9KjA+J8XY/YZeAwIwEdTPIjAyLp9Ti1m17FxBQ/+54Bw6+qvtAeSgeF/YNmQkoTgGHs9zp+Ot4MYqvmvJMsQLMGSkldU8qdA33e+SW5++96XavfMkVD8mmjKCuGa/S97jJPyFhwgTTlag7tlJxh4i/Os5rtF47jgt5ZxmOEE+k/bJPl8CLUtqz50BdHR0Bty7rHvDfl4Bhwh5rSd9mrsnUCjVgM444ixu84K/xKn6J55tznI8Bm8gYorjx9O5Pm/Y8+LVe1zyViRPr2oyKS4NlrQSC0D5UeRTWd0ZB9cswrBqN36O5fpu3X1YfHHjqCz7y6BeC3yxxBdoEde/LcM9v9McYikdw0nrnm+CTwKGWjkPGX/32A862EygkpMRFe26RKWqMet3gBDgXTEEtIoBZ8M7HOGBmbVtuq2dAtc8Z5JgIy3frwzbeeCO3XedLpkcN4khdOm4y36r85vkxhMOfxOQueZjrhj79wpo6VPysjZ/HYWnmpP73obRrsOa+qcnfWcAcsnJYqPwkK4tblengNq6fhAntLJP6+lRLgTYXCOcvgUCCEMRteQ9ANKuZ8U9/ZPz0LuPtlTKTQnYIqzuf0PwDa4whFYdkyLTwi0DI5r7Hwxriai+Bsv5Lqmy/uw271J5Vos2eHiHmH3nvUKmjzkGPb5YA4H3bjuCggk/n/kBo0yg2WTX75WlhnRsDAgSiCAqEQZ9NIHXhIkGiQwSIWLV8CHE8Q4wDKI4giohDROEAA8XkuTL6q/aWEQH+t+C7VUudqAauLnEjOKnGWnU/wPYfV8uIvN8hhIAhjAACsq7prHEh9rudWEXs9xBLByqzxBrTqMaN0KGNAZHUHRCzuFuEMH7JBBSckaakroCqS6qyBlj6EQLAIWg/KxHZ361NgGM/zWoFUXzSunTNDU9+z2s/WVneQdxG1WDjrSBWvGCxuphizVsZ29KdquVY/rQdWTULzSVlGAYhaJjBpH55S1lchWhmQRHECCNX8w0kFoubMf0BnK+ReEJiPz7SH+/6KOeMaTcBAzAUl0ZB21AJKoYIPqYpI+92GMZYGPYUSNxtBZSNGSjq2olFAcW7qbR2BxUUbMYNAEhQctMaY0ZOqZh6xCFi3G4wxFisIhiGOVKhk+13LIKIilvKspO2l3AYgYqVUCIgkDCpRg4wKxYbZLYzu1izqbDMymdxZ5Y0fgcCgbcjhr/9S9z89Bz/+uE9LvEBX797g+nta0zvXiOMGwwvpS8ZTij+BE/wCeCxseYHKfsQEvYEv0Cop6K/w5mp8k815tFuSriagHd74MP1P+Bs+nvc4DuxhmBxn5cKjuTw6cJj9YSO/dMzQnuGrOMGLtKsHY7Z5zXljKJcIpahFh+p1AmuuEF5Nh+rUx4dhMK3cflZXEju9hnX15fAxQWmLWMyDC4zzA2VCCJuWelDbmcOAGX5ZIA3L8DxDHsOmPaM97uENzd7/OuHd3i9f4/3KeOGgUQkjhF1ek0fBTC80lQibE3IOcR+/hfbc6B/NofZJS4EzoxoaX9w964TStR2S3wrhAxkcuEjjLhmn8Wt+wVYmdpqdSufwdFQTSNJaKSzzRabccBXmxHnwxlebV/gxfYSzzZnuBiBzZARgyoWkXVtfg7cH+Zj1nRQcUPiDIK6aMotL6dRnizTIr89GV74oCOA314BNxH4t7N7B61eH5M/B1zyLivh0LhQu/51nxRBU9GOfFxM6XRBxEn9b5fIQ+JP91L6WRq/widZKkiO32HM+OqLG2y3qZiuM1etsXb/1oOpMgfMGqIKIYqm5Vr77jVedhivvJ296EZg0eLh0K1yvK51bZ12rdRi7qYfMPOveKi0k8fnUIWnJvGInmoh9xcidH3fpn7HaKoVLuS/n4pOX8GR50slLNd/rFlyxx1v+6r1xUnzcyBWCbfrYbEtB+o4WDYwE1KwMv+LMEIFD35dEBFo2CKevxDkN1BlHDXML8L3byZ895rtFUDK9HNNX2p+YQU7YYQbBMzU9hdwr5NgLoVrs6tmcPOQSiO6Ni+fe0vCHF/3qkbPQ8IxZHc2CSv7ZSkp4Bi+1p+21+1dpcz9WRWV3KXg/NGSuV8SJvQ07ZCmPSgwAmVhwAfCmDJSHBCiuGjiLG6aClKtBGd1K+Raasx8oCg9QfdO0f6GBT8GYFrbNofaHVst9lmY1mkCEME5Nn5XGRK7IeUJWYNUUwgAxbI3slo0GMO1nOcmzGmEOigEdulviVshjcxFWKSENzI4V2QgUFCP+VWUa/MlwzQ/84vVgOFcK2ustTDQx2qmQLBYGB7dbM++YtliVh4FObWwhaSStG6NsQVm1tQUEKjMkiWRGk0I4Qa1noE1YVnvmRHxFoQPSEhFGAJ45Ym6AZlF+BRy6Ajutt+ldTlrAPME5ih9R7WEEZP1evaQxf/qaFLOXM/0EDAMESkPTbBsNu1L9a0bKGAcBkQVRIT+cHMDZ3FMQjDBi/QhBLEDqgIm63TFQSfOiBRBFCVge65hKNuzg2aeOVjjtkh8CTHPpxhAr14ghYAfnv8WefcnvLj5CdurK+TrK2C/F6GS7utfCvF4rBdl9h6DqbxS3ho+exfrhXv70vd1fiym+lI/FzT8H4vEPhkV6n8vtfuB103PzJlh9Gv024kWEmvl/tKhOffv2Pk53kst2q33RA6Mfc4SqHoC0v4HnPG/4AoTdqwWEdkYzG1w4aassgOWrNOW8MX1zpmrzZKm4L3V577F5tJLvOCAtT7G6spZw6Nx6Llv4Przsma1+swJ+yng9YcB2zBgAhflk9pOV+BDWULccpsLG0GFECAgnCEPz5F2O0x5wtUu4f20x5v9Dd5OO+wYmJjUuSm1a2OxAn9CUp2rQwfnjGBxc9zhzLM11ozjUp4Vno4hOWx4Yzc35NIyHC3bIDowisJrh7dVVeq54tWubI9NkuBn4zBgE0c8G0Y825zjcnOO880W2zhgE4FIEYEMTwSKpagfYzemt74JVvhjy0lJ3ct65UV3BZUjQ74U102gah2rdRmbg76YwNcZ+P3ZQutni8U97xvXvSrj80u/ae5z9x/Iy9ylcbSXDu7HGNkHtYjg5pshMo+Nd64t4vp68a1mqwEb60QMQ8a/++0VLi72iHFfzf/htTqNiDXNQJk46qQMJngAue8nQ5v4lLzUHVSe4F4q24h16p7bAB0iQD6rQF8KRIcZwIfyyZcT05+QkBvqv96VhmZVCw0+mfGuyRcWw0relcv084J5++TcOGGMwctz0Z+vt8lb2nB43OaM7rbs1XRadkPsMcTFBwMIoSA4tDkHnb2A7cWg2rTlgvdCCv1LKWNCAkeHzPRNnTWpDli52wmt1a/+c3BWCAgcxGR5ZfyWXMw04P2V99RTv6dOPYKOJfxIW6Sua0/5WPX55K3KOhnmyqUSB7WfksQbYDtNB6DELCpQmjUB+QbEGQEZQ7zB2TbhmoE8SfBp0TlKgsunIMzaSWIC5CnIXRclNoNp66PKzKR+ayRL7AQqLaweXylnUBYfvT4mg1jrFRsIi3BQPk0LSvBlFSTkDA41jpURQabJ789nG0HRVJe4BzFG0SxXLaeUan9k36lrHQ2yjTS1WuZZekbKdOacwIGUOM/wYkJpHuvaUAUILOw9omppyXVd9Md+FVi0ZZTfQQJpExlvoFqkiFCFRTADwpQSBkCY+qVVpDFC5AxiVBd95nIIWr64JkpIqd5/QnxROWTkkRFzQc/qUFotgcUZU8qIzKrxWU/a6oLC1r+syWiCGHXhNQva7iDnhLzfI00bpCGBYkQEiUCXjPAvS8XVrcUHLnMfSEzzYwgYNxvx3bwfirVNYejrXI3jIEKbUGNEiCWGjAFbPg2uHlHvgOZ8DISoQgopvOJ9zAEDR4ADCFFcsOUJWdtSTw0JVpI0CKpZaGQwppxxhQkRAeesZ8pmAF+egf/Db/D6zRne/uN7fPNTxNnvvkMYLvH8NwmgjDSghnr5c4LHJ4qe4Ame4GcMS+RL4f0p/pAzY58Y1xPj3T7h9e4Km3SDm8yq6V5Fvcwd/7YgQS3G09Q+uxrtuf+cM3GVqtE7u+IQoqhRMTU1tdR3qqSR2/TlkuW+nn6k7gLkEKDqXsban6eE/Q746e1rnI3n2OUJEw/STMWHRGG8KnHcuSX3ug8Ub1LLxZyAFIDdlHG1m/D37/4/+NPNj3i3f4frnHAzAXsEMASvStlwzFocjMdQBsRweP+bDw9/QSEcfdJYQmBhDVF3P/q1aGsFaJBbawsZ81zGI4DAgQEOMCUSAbEgIQgTvSJupeNdBzpa3s1V+VaeGf0iEGPEMERcnJ9jO2xxTr/FRfgSz86f4/lmxKvhGtsAjIGAQGojWm2Xguueq2x1yI8CAUdjY2p3QhBB5sz1GFoaqYkV0dGTnCBraMF96R2a3uTtV0A7b0/wc4JHcM1EK7/6xfGQiLjbpZ3mzcl8KqUkAzHGgfHFyxucn2ckR6y2Zx9ZRv3QA8oYiIUxWH/7bAe74srF8s/2HXWJ3IG1NhtNF8jS+tnqmX3uoHXFLLWrvSdOuLBmuedtvs09ffs7fWEuT6pnPR1zOzZsDeOqoVgYa/b8hHoZy3EulhFKzIUWhzidfblL630pG62P2UFN3Vkl3RvHrD8Ea2VTYWyVByt573gWdRoxa9OyVIfNf20DSqBvS0EhAHEEbZ81ggZDBPv4LUUIkcUsmwuyZWl8/YfnpZrm4Tju/9BH+dqa6OuZHXxd4lPaxc3HamkLWeb7+0j+ta1XCMUjSH27lZ0FgNcgX2lsEVz5H3BCJyPEAIhA5AbIDEJGDBNSzIgRUJ5ke/2py54chBAilkSBVUM8RldnuSbV1z/DBLHSXHVZxdpDY7ZmY+pqwiBEUtWCh/tEXbsQk3XOGUwQCwRHKNQxssa5Z1wTsKPSyn1Irfa+CSGmnKRP5mrAlc/aZ9Z+ZRb2usVUqGQ8nOXB+sJYEiiyjmcrjJgLIerM+7IIFdfRNus9xaqJyZmRAyPkjOyopLCCtPg5qkoZdX9aVVK/lGX1LeIXxtAorrncKWZlmBsL1PUmY6JMfRgNvD62mbkEMM8WPD3YPAnRZYLapVJEGNP3X9wz2R8DssYtB8tFQS20AAEAAElEQVSkhRgQo1pNhG452hhYvwuyoTicG7SgdwoHG3h9rbEFiRkEEUZIjAgjJHOZrEABsHgOLO6phOZn5JCxV41KVrEUhgBsR9DLC+zShA/hFTY3ETdv3mG6vgaxmMeI1l1axwy6F2uowArK/HnDIwojHlJB6HNUNroXrOz3Zey5z3vnSu+Xfa3+B5iaY206atleLu77M39Wi/B38tLzB6n0Ydf5Yl/uO1aGjuu9JXcfMGXGLmVc5wmcEiZQeVdwS80P/1l+rNDot22mVdIIEbh779PYT2uos5Arwg7Usu7VuAUwpMAXacVmgJGRE3B1s8fNfo9kSiVZBOk5Z2SH1965GStKkLf3DRFAHJBZXUtmxi4lvN7/hNfTj9jrs30mTMW6k1y3HS4LanjKzTohWy+Cg8/738/5wtyV50tz607j2Rqx78dxYmledc3kyJ6lmuqDpu0kSk+Wcek+dPNX8C8lui1I9RAHbIYNNvFLnA9f4mzYYBsJW9pjBEAYWvzOmuIINyuWZg29JbDipkeUjOXPBr3i+Qw03hIOKnSaBDTo4eXQ0/Vb8cDcopvDFvE/mPd+cBKG8DMBXvm1dsfDDfpcye0h4EEFEUuk7seDhcOMm90iH92Z7+/mGDL+5q/e4+JyQhz3mBIjcWqKbJh/VkrZtFV7jZSAM4Jb7jzXngNQ25a7J/aVZmlLT/z7vipa+mGNax17FLcNq4fVkWty9XS/LZw2ZvfHBu6XvS3oQFs6aboglu5yP5y78FmW4BDuu/7gUGUHLqoDv5bT+5XqhSkLsTI+Ktx94vvrd0EpfWVS2pmmhf1Kwxni86+AMICGWFM7gaYhKrZDcs74//3bDn96n/DhJhekaOlU5lndHiHvGm2IXNcd6wO5Q3VxBXfllfPN+XzvSqwPG2EDKQPanUuGLRd8zWFtCyB4HZW6jeFax8PqPL4uTjqZHD5dBb8t8VMC+842wnzWikFergU3qUxzPrXzmvWMn93SZR0BxBOQriCug4BMqpkeIsK4AWVgyCMC9iAk0ZohICNA+adgMHLaAQyESddpjEUoD6grGUDuS6AQmgSbn1D6AmZQFvdI2Vl/hBi1HEmdVLkus7pUgq7xzLJk1B9/tjFRSwTzlx/UBVWaUhmQnCU4IYgwGPM4RJmznIXxHkjiQDBjv98DztrHvg5xQKGimIvFwTRNwhRPQvRRIARiDEE01bwwgEgEFlk5DEH3Qer95fTLhmy5JLF4MI364mKyElm2BEuQRrfUKIm1S/GhlWV8grfk0LIb5hWZggMD6j6p0YI0xBakYQZCvQs5CeFF1X/xlMS90ib9HoQrZOyQ2eJdwFjhFa8ri5tAIWLcbACCMBU4F/1MOweN9k4AdgzsmLDdM2JgDEEFu0PWmA2mASa4n/VF/hFXYnJHMBAYmTXocwiIw4DNZgPs9sg5I0xQQZau8UGL1uFgztIom5OUxAJHDwARsqhwhDQAOgghysGYtY+kAokSC4VF+GGxQoJaOtgYliXCQJ70PNAXxACy7D1igDWodsQADsB0eQFiYPs3vwXnt5j+y3/D/uIZdv/jG4SwxfDyr5He/wi++knXi/Xul0LwPcEMfoaCDdsN5Vw0C7+y11s6UnCR4lzv8VbzsYJ/fkN9O7jrwH7m41LOaY8XljhUkgIQhvM+R1wn4M1NwPVEiAgaF4KXjc0YS0/du+YLrLY5s6rcDnK/cfNInhtd4FFbVWaofZObvXTLLhz7XrRe+sm2OucUyfpvK1MqK/eYC3dl9XKekD9cIb2P2F29x3RzjZgZW+xxPv2EASR3NLwCxvqCrLzqNcKk/zlPVxTzOsJD0TEgnAN0gT0H7Hd7vL7JeH1D+GlPeDsRPmTGVSZcA5hcuYIFzWPMZU+0GIElSCiaCa+T27d44We/UIyOYRTBRuMyqc6zrHpdc2zOHQ05ye65y1bowaATnWFYHpNpYzjcreDvnugNHU5d12NWQtx4fSEDlIA8EDgQhoszDOOIZ9OXeBW+wLfPnuPV2YBfb6+xHQjDKO5tOcLR6qrgxPNVQO7fu0IrYOpA55zAiGRKMEJ7ySJjgKqSii3GEm+OgOCVbbVQQ8O9M9ZDvVjbSYuUuR0zvJoC1eHqfeCUcf8ccdf1fTlr7cxdmT23R/LloYURj2ARsQBLDT4yp7exZViuRA8YXniFdqyJgBgzNmPG8+c7XF4mpJThtU2XXRspgUv1UwhpO5hq6/rstztKuCugY4G2PKfKWKp4wELb+wyW1iSly0KIRcFE/+yQtHr1zSHobt6HhmNr8dbE0xLitJ6supPSTb6QtDlElxPcYs88ANy1qq6d6xYeHwMep+JlZUc3f43lg7aE3J4kAuIAjBfCIHW4p501lidlVi8jjMTAm+uMNx9yKQo4oZenTIDDyxqCAQ7ZY79OT1j/hoMa1lgqWGmAMjWrdVmo7XFF0pHzolyipb31khD3MHNtkbUSZ7eOzb27lmb0kr3mdgSXS68FsVVQcPf1MS669U3DO0pDLyhhLjIICZx3lVBTukDcKw0IGkxN3AtBBOualkmjObDGQnDutYJqV4eCaaugPjikXyeEiVA9+LP44menka53MgVlnrq05b5261DcE2SEnMGkJQc44VkABUOs2zE1AZHMZyi++OWdMOaJxEzfLByYs7jTKS2rFhRGJJmGVrG0VAydFHcgZfa386vlsJlud1Z1Cn0sgWLZ1KU7tE25e1H2iq6HoqDI5grL9j8rHiQ1lxrVZL7Bb80tw0KbyCwNbJz0M7O6REiMEdeI9AE33c5cv3nFhVUwIQ9ce7jm9Y8yS6DPlBlTUiFBtjpqva0tqd9uLG3PqK7qFEcMqrQia6XutXpWcGt9pBqapkkj1jS5XCUlnQ2cCftszykEdZ8V1N1VFSACDF1/ft6hY65CO+9ZAaxTWONkwgK8cwjAEEHbDeLzS+DDNaY3b5E/fECadqDNBjQ+A8X3ZY1W4uZh7uXVGAn2/kFqefiyjtb1CAjTfcs8Go/CK+D0d+tjaaIstWnNzOZYG5rDC6g0VL1i29u6T386zMfnTsW48/SO+R2cPL+PMJftmD4ALODnH5UEOXVCVrg9TAQOESCxqEuZsM/AZE4zuTg/8tdbu4Z7hHZWjeGZhmuvY6n9Y+72yUEG4KFJbS7zhTGzu670yxDWI3Wxy9tUpi+t3mkCT3LXinUwEDgj8iRWv9igukPko4toSeHsULpD1kge45ArmAGKAG2QMjDlhA/7Pd6mG9xwxp6BPUQAYQKqSnusCKasCi8IauIuANUaUx8UPsYCbtdbycysZbjOUUMg1VVMbJgKFzdGRaGFO0ve5V4tdFKVRbqDJtjadf2blVmmVP9jU6gSpZ84DBiGEWf8HM/jF3i+2eJ8CDgLE0YiUNgILWPCAe0qYXnvE4UT+3UicDPgtQ2Kk4ZAyCCQj9mIbj2Q0SP+bGlbGeBn5cjFxE0Nh8Fv2wP7ivnkEu8JH/UmuQMcGoOy+E4aqluwfY/CxxFE3AMWUL8TYTn10hiHwPibv3qP58932G73SKn69m03KLWHLlAuohBi+f5RLUPsIDTm3In1zl1F0eL7Y8+eoAde+b7wewn5+9Tw2FPcbcBHF548avF3PZ3W55mGLejZ16BhbPbbUiwIAPjn7zJ+96eECQkJGdf7Owh2liUnlYlZH8zmbpnIqM8aH+wdF6vk7RFSfyYRYNpgghzZt6qH1DSr4K65YarZt+KHvqSr7n0IKAQKw7kBUqSsJ11qH/t+LzES6jvD1Ys1RkMt9jVwLcMzyRe+eSD/ngHBdKm+o/qFsAen96hCwRaRjyECQ0DmCHDCtJuQJgYFdcyj5YgrAEMygWkSDXjKMn6Romhda63BXDmRCTdkYDK1okpiRpqmov1PRAgsQgtz2cQiAamtZkBM60WLXTTAVLMpB4SoLn24lsnld3VcJmsoIA7yJFv0RwJCyLIu1EVQiRmlDGgLRpymSYjYoqwwYOKMdJMRiYCBAHKCB13jgUTRK7t+Ve8FLY7BOjbqeWp2rtqayyyWHMKQlwKrCyg0lhBl+zU0irLxTUNfBUJiyKDaXVpmNmuUUFGnsudQ1zTrusnsLLgtPZsv7IQ0MaZJ4n2MMEdAfvPYLm7xsEAR42ZEHAbEcUBKCdNur4GoK57X7ySxiEnY7xMi7bEdBccbsgkSSAViuSjlyXFFlSzL1WIkBEaI9fwOISKEhBCini2E/TRp7IsE7IA4RIQQYdKCKSUgM/bTHill0e0LIiQLZEINKu0wqWgRAgJFgJuVOCvtoYCsQjlGZYCYIAJgidWi1lgZjIAM5lTbHBiRxYIvDBEYIngcgSFidz3hZrfDzdU1CFuMo19qvTDiCZ7gCZ7gzxjKPe9+AsCwBZ+9REoBeUeFsWxQaASPD/kSFs/XLl3Jypjz8HheBrtPrl/m9IEVZpeRD4prmuceB+naXJBlQ3RY/piOk88m6S8IMECdlbAJckBA3GywSVu8evkCzy4vqocLyB0aQv39kHDQ1U1tek1vlsBEyDHi3ZTxbpfwn97+R3x//T3e7T5gl1ksR7WA0lcAxQ6U8oExJFQlBzcnvQCyrBXHIZ6Vg0pz9kvUsnD7Q8IM2HftBasdrSGTrD0qltPiIhW5++RcYoSVP+uD64aNlFc6afpQ6CdppixDESqEzYgYA14NAZfjBl9uX+KLs+f45oxxMUwYY0QMVYn5JPgE/DfvYt7AlGbJBBC235kAEoWvMn5Gixj6+cRD/Mjw80Cm7yWIWGa7PAwsDd8aI+iUctzdU4AIGIaMMWY8u9zj8mKq7h9Qz0pXQvlum0qI5kr4ttYED78IDl1Qa+/alniNYp8CJ1+qv7ijZEFr627FzOd7hoj1P49Q3Y9o2D2HBQbWYwAf0lp5BPgYfbrr0mnaFgb5G7ag6I7mBSHElERL9+2HhB/eZSBmcPCBiU+DgvT6w84hl6cII6ycruB2bTdfPXExR/OauhwCUxGaOmqlyVhgYDl6iZz2lNeWL/7bOYOJik9RSV4LZK7CiKaKBmGu3zo28OxpFU7wQsPbMrmtyBVQ7ynpo730tbeEXE1ic57BSGCeYExJSc4lvTBNCTFIEDx5r8x/cLlcmVtmbgl4nHWOI4GMj0+kwZtJmNmMqu1ELq6JliXBGdU1TkCZt/LZEb3Fykbnm1NGjfwmvvBnrsHIDavflkYscGXISkJzw+iG1CaEIe57VLjBUCtJ2D42gQW5ympDlC2Luna4S6PpqAoRyn5jKrRltTZyxZCOP7MQDezsGtxiatZwt6R0WuUftTARYQQhO4GjacgvL03nasztB6rZRbjFKhRgYXoj7wHiNvgmAG8J5RUzQiBx5eUYB6yumez0WTp/CAngPXIekHJAYsZgghNuczGLcCYU1TbpH5fPdq97fJECIbAK4BRvZFvvHETTTycxqw8yi1th1jck5kodDmfxHYC5Pb64AcsqIQpGQFv7yQQVdSICBTBlZwUj8wuNnSFBroWRU87sEECDtG2CuDrL+wl5mysRrmvRCyM+O7ir+tdn2ZnPC47GIfgFwOIdfmv4fNbSL22uKr7zmYzxjLnike4AxDPFfaZ6tzho7twebsua6NvC/mGLdVHz6xAYku0KNu16r/DZJLH7ndBaU7qyGqnJQkc9I0iQMU9NoGjGEyEMA4ZxwPnZFpvNKBriMPwNKKjbQ/B6FoigxT3WpwEXXCwxITNhl4GrBLyb3uN9eouJNSC1R6oXm7v2wp7rp81R88yQZ3TvT+g3t3XPKEpbb814yPfANa25CGtwrfLn7IOKGaeVeYgGK6uiHXuq2GaDBxLAJK5cwxCxwQYX8Qznm3NsxhHbyBgDg2gQhZUez/7Y52ovSDr0vDuLjCb2UOla6jIpH2FMQIrAFI4uj/4IuC88wC49Asuln3oirsPxlj/MvXXChHR79aHgs7eIuD+w8Z/mzwH89V++w/Pne2zGnVhCGPOkSP1MSm+bzrTNAghBXFVQQKBYCEsBp1X5GYAdpj2vcUa4fyZ42C8BjgkhPiugj4eEr2vS362se+U/ccEfIrweRCsmboDLr4FhlDOnFL5cx79+n/HP3yV8mCbwwAURf4wZPHW+Vq9hU7SxuAyW0iGuczzcUDwq41G0nF3CJeGDr8PSy3FuSCcKQ7kGCeaK8JYz38Z9gUpo6u6IolVoubnVjdBSzv69R5YrImDa5PLDIYaFuYPyrvSHzFR2Ak/vpP3ia8mRlwpBJociIaQdQtxBAvUBadKYCEbcKSM0aJ6sbpVMux1UXThJD1QTWyQLpbHZiiuMe2HAppRgAYLNZVlKCZlFS56zMYmlLBNeAGpVEDJCjBLLIDshBMGCXeg6MFc0qIxcViZqzmVeQkhAIIxxUMKUfDcKbbbfTyAwaIggChjUasATTUIryRxQIZBRGNztyvDlBwRiTIa3wFD+WBLP9giJRURmFhc/MHmCCUZ055GGZDGzBl1P2VT/VYoQEIGIoiXIKYkAITcrSd4zq4torvVni+lRrVIsNFfK4h5pPzGmlLHh32Og9yBKAMTdEgKJ6y0Ljk6EgCCa/xQQh4jtdosQQxEO7Xd7WU9GRKsUqbriBJ4NP+IyvsGOf4P9/iWmlBBDQHRpABLhAAHBfA9ndgwK7avGOakuwQgxBqQcMcSIBEIgiX8ByLpOKWEDgIfqZm2a9sgpY5omMDPCOCDGAcMwaNyKcgBqPRozIkQATvCjp00sc0N2mNTIZKQTHuR+CTmWtsn8BXG7xnIe7DQGyMiDWGjEATxm8HYD7De4eQvcpAn7D1fYbJ67VpTF/KC4wRM8wUOCoQfiqx0otBPQ3d1P8ASPAx6dExmw3KMlfJCtS8NrmsvfsfYOLVhGXew+Hzcvgdk5vfa8g3LfmtBby/SBj/0nAzC3hHYRmrOXWfe047MmVBze/jU3luTuaqU4EGLAZdwibp4B+Vt88ewVtsOAIQJDEP/5QS0RPxaser1QL5c7Am4y8Kcd4083Ga/3jPcT4zpBA1S37kwdZlY/egGC42edNK8lSZe2rEudh7I2LW6Dg0IWsio1GBLLlU4oz3NJW95li0U2qSaLWURMhsBKPrOQ6KwqbFk1o1wOeddHMrKbALUa5U0EYsCwHTGOG5zhL/Eif4uXZ1/i2dkWm3GPMWSMQyzxZD2e+DmCKMug4sc9gdMpr0k6qtMMgBMLjfDvP4CuB+R/OAf2h4JVPEpP7oFd3nduPs+5rXBi+8oxcMJ5cAv4WQkiOh7LcVjjUkEtIYaMs7M9Ls73yjSpzJ++5noJQJkE1YFvyyAjnw3dcbbQkj55Td/3s1xA/fMFBl11TVDrK4KUSv01DM5ljVrgZEbrZ3qQGvQH/X0ZyA9pAfGoxPc9caWHND+tzLKHK/Ne7TslK59Qx12bQASEKDEhhk1rCaF1+7L3iTEl4N1VxusPCYgM1iCqK9v3SLNd4gNaEYuWEdY+dFe8Q0bZfW/7dcv1Tt1nD6XqA+UuXQeseYzIMo1kQKwjUOmmJutavxYfe2as5a2MY4/M9WUUkmFBGwhY6i8dWKt10sRHfgJYNeqKBv1SNjO/zQiUy0wLg1UYwgQlDQOBG4en2nzDWbUvXLH4wpQ3YkPIk1JLmSMZpgy24MTdnV2Y+jZwJpDQcacMcKim3d5tmEerTBjBaopfmOPZ1yXa35ShTPhK1HoCj8DquomRNRg1Uyz0WJlHbUo1BKfZHuumpNbnNNd7LaVs6xrd1iHSgHiVwGNqzxATWvVntVmiNIWSEfGlUY5h5+v1fa7WBX47WdkMUmGSWcQwiHcIuAYQIYIsYYZL/AIueA9p7IUQROgSYtRmcRHuHBQugzDQBGDCDqnUX60BbNuqgEFnrnHz1pyZ3Gxj4X1QcddFylgyZRazosmcQVkZCCpYK8IwQIU/0t9AAVmJ6tbqsOKmYZF+INgsM7Hz54vynMBF2FbOLma1HpM1lHNGIpmzQmBrrAgMASmoO7QpgTvh2imwZn33KKygo/f9x2NA1So/fp2/OHjEMVwu2nCgT0cbPQxZdqSQz5z2OxUelQ47dYxOWaNk4VcZGROYryG+Epcu3Fv2aZbcHhxql8OhF3Cqpj0ltphlNVxQL0FfFWtaDqgBqqxwzceuNkPAvFBj1hpyBoI9vix3JIGQeAuEM1xsznC22YgSguJ6Yl3pmn9gZO5D6x468w3PZYpgBCQO2CfgOjHeJ8YuMSY2SwnFp06r9c7t7cd5fe3ZfAGtdQUW8lQ6AIZfqSCCgIqL9MIK04bhvPDM475SRrEGNvpsoRVL3yvtIV3gQABHRGywDc9wHp/jfBiwDYQYAoK6MTVL6xoj1A9PIRTvBf1MrpZ4YJ0ZzjdvksxZQ8rYNtbP/jmdZwCTvjitf+2qWOnRAVpJ+qCv+6PnpBbcDj6FIs1aneRStE+OtNGOYa4//BqHe15m5h7HxmcmiDiwGezztp31KxByDhEYv/3NO7x6dYNxTMUSonIH6gFRODQwAlcl5iEACDUodfF3fatuNXDoQuuFEDPp+InPS2leG+AJHgd+Gbj5o8NnT2A/YvOYIujyGyB2lhD23hifytz5/Q8Z//B7xk2awEM6yOg7Bg9tAWPM47lVbjGJkJ8em2nOvA5FYFTmqMN2CkLEKIy3BrpukTtYuf1nGQyZgjLZukFuhRAdw68rxnc1lDYoc8Jr3zDXBL5kzsVvf7A6yJdJjYLKDLq5EM2WBJ7eAsjCsFxbBmXaTJNatc3jgBgYU75B2mfV2GcMo8Y1KQHWa8U1QkXtIWfVwC/+fR0xq0GkCUDxRRoCxB9/tXRIGiA656R3OAqBLk23e5+LRn4RRKCGlTCtH1IhR2YGqeubNKUqcDHmPFW3S0aY5mx3quABMQQkiLBGNP8TYiDwEJFzRoyiYS5dcbEamIV5rpYTOasbm4Lho9QjbaoWJoKGrKDapFYmFMr6zlanJgiq+sTQtAGK76DUXcY/qOVBaC1Hraz5+dIuVLZA5BqXAzamWV38gJEyITEwZULKpL6QUYSDkQiMiEEFBVBL1RhE42wYRg0YOIBzxn6/w36/x34/aVscQ6EbK4K6CJsyklorpBQ1dkQG5Qy1I0ERIERZ1zm4/aqQde2ZBYhZkIQQytiGGBBzQEoA54ScqqUPwJj2e1mLugaHccA4DIiDWOUgqX4h1wDskpYqwUx1fihQKV90E91pbOdRziCOSCTu/0wYMk1imTSGCATGxNKuKUsYyTAMMh/bEdhvkMeITIy024GnqV2bT/AEnxiW2GaLTKK1zAv03y+DP/+L6MTPEg6zjUTJIvEPGIZ/BPJPIovgmkkxBHfuA2KJ0LGkDzI+V1mw688VQadF5U5yPQsQbQ511eKl4HYpFXzdMayLgILQCiNQ9uIsvoRhSYX3UXEUKSoggHFBhOtpg999+O+x3b7Er776Bs+3Z7g4O8d2TBhiFoZy2e8HcOgeShN7IsV/re1bS2P9Ymbw5hJTeImrG8K73YTvbyb84XrC20y4ZsIO4vYxMdR6RsNT966xlurwlZ2yDtwUSRKbwKX0ug7KclT8kmoWc7dUNVZyofsCM0LB5bP8ZXHfSTkDeRKFhyZGhIsPkZMNopRhMehglvuuSyXImV9ThjsJbcAEDOMgLr2uX+FZ+ha//vZX+OriOX61STiPSa1qJH5E5THakHZj9EDCiPuA3X8hBmRS7DBVniqTuWNTCs/oL85ADqL41ZT3Ke1dqSgj/bmAbMVH6O8SsnQPuJcg4iHZWHOtu9vWfqw1QmxtxoRxyNieTTg/SxoTArKpDpRiGorySRD/0EoQNxdr16alw/5Qc2fJ5pfEXYQQXB4sCSGWG9NfhOt31J/Pxj4Z7L46MjYnH8sPOMS3ZUBX7cv77/jVMh7yMLkFfCx3VPOKCUxRXDKFUWJDoI510fTWA38/MXYT4e37hHfXDI4ZCOz29QlVrqXrhLUF1tauv4Q6nufc+PHYwl1ok1enUMRmad0UjSB2o9CqpCtuxNUlygktKomo3gjze1cw5bkQgOrb1YoqMjtPUg6Otq2aliwwn78WZswPN15lfCZ5lgGmBEC1kp1m2FIzSn4lBqmhNOydamFzBiEUgcDiQPPKpyKvlfB2RuR+rYlfn7o/lJFubn7qmvGfho659WKSrMUTWF0zQdwQZRUGBW8hQNYYE05UzaYSLNgRutaOEnxaBVxkLXBtZdj+rzESlo7N+pzm696lAVACg5eZW0hb9o/u4krQ92Xafqv4RimTeGHS6ri6ikp7OHNlelvfITEKSgzyvAPxDsZAMRcKCGKtYy6aNFCFWAiEgBDVYgBiXTBlESpZMPpj57+OhBDwGXUtFDdeUo4PpyCTOR+3embIGJlsSdaPEOyhCLUY5uoLUMEPi1BLgoCLECGEoCb+oZQXkJHY46QOH+zORqA//jssWNsXwOrRrBeWGyGqoast+Lk7GxEC8rDBzfYlbjCW/Ucrh8Qpc+IG273oaIjuAF7EPR5JCeIxlSuO4ZSfk2LHbdryOcSK6Ft7n5asxcj6ecHdGv6z7e5jwG3Xc4NULtyf+r3gNrzDBm8B7JfLuy3TaDX9WiEemWOYrUaDvJ5SIQGLVg53Bs8H6XGWytOR0GGqZENAjBFD3iDElxg3r3A2brAdB2wiYwxQd9ye71OteE9rjvFfev7Kcdp4OU0AhREZCXvOuJre40P6gIn3InyAsNYZplCUdXi79bUa18Hf0x53xkr624LDlVb2ir/x53YduTWAKTSJuWDS+BBFCJFrH4pgIdcaOtS1UGLs7ydHaDBEtmf45jDgDGd4NrzA+XiG7RixoYSRuFjAej7cYn9NAL6QZmmWTr1lV1DA1fKqlTQjBEJK3E2GWmEvNKKOk0vvpUwnrPfm8eJ12vXg0AVux8ypygWPBXep+h4oXTvSd+/3mkXyvRqn8MAWESc26D5qvPcCxl/8+gO+/uoKIYglhBG9TVtICVsQ7HohMv/X7lPTfhTEvxCNlfi/7XNGHfrDTf58CJkneILHgk8mhACAoJYQYRTXTAolSKnTZgUR/vgT4z//a8YEIMc8Y3x/7J4syi48ljMzjeYTGEPsyjTCIQuTzvBAli9mJTBDKDrkrbqQseu4YpfLrtXkX2oYifN2zvNSYUBz14dSBrt3s3tnGTWrQ8qCPwf5HmCMx8oY9K6G2vYlIL8DIyNTUK2UZSFEUA1v4RVm5FRjLbBeIKHcf9o+Qy4zS8D03HWERayQmd0MVEJGrBIqcVHGULWkGrKHq19kMCNlEUCI1QIrkejGutQideecEVRYwuAScLsINgDkxEjThOzWODMjDlE04WJEIMKUxOcsUd2FYjFSA/4CouXOzEhp0rUZNa0EzOZcgzyytpFCEPrJnPqXxUFlzFvk3274uVUVKY5isooSsyBXyxEKYtkQFElXHf+mDlu7QQNkR31nFhHMGSkRkmmcKVjcLRvH0qZA4i4LddumzAAxsvi7QsrAlBhj/g4DXktcDgjBZ3iYW2aq0R8wbsZiEUFESNOE/X6Pm6trpDRBdDAJIBNQuXOi0EkmwACmnDGlhP1E2KaMHDLylEXAY7ig/pWud5tZhAvsxkCsN2QtSPowRIy6hlMijRUhMSFyVu0+AHGzRYyxWHuUwIfaFUJWixZn8bFKfLXkaRVvK8EcZIxCChgGYAgBCcqQCbruMpBDln2u95e5aOIYcX32Elff/p+QBsZfJ3Mt9QmJwSd4gid4gs8cPE5I6NR8VKB9xu/wl+FP+Cns8T4Z16Iqmi/TBnN2plOLcK+5pK6/PEfQznHH2GVWpqHHk7mmLYotaEo9eh04hZjTobF5UHKq4jXB8XBoiIhEON9sMIyXyOdf4uL8BV6dX+LFyPgivsdG8bsYAuJwC6rrSNL70aIMIGHihOuU8f3uv+Cn6Xe44YwbEBLJOpiYkZDVilwJKgoosTqOjj/qHKylneEYR+556ipuSKa6Zsj9rmuQNUZVtWBmThIjQv+glhGi0aJWmIafmkvYbk2yU3aRL14A4ZqX3bNhAMaI7cU5zrZn+BW+wF+cfYlXl5e43I7YjjfYaIw6isGTbXO8zFns+HcPxWdcEmSclE+VXxoLJ0E2C33FgFqVQ86qTGL0pG3PEy8Tuo8N5RAlpdlUaQwfCws9JCF5gpMFEYfXzW0O5Dbt2gF8vMQFam/BzGm7SdhuctGY3G4nbEb7fUQfnVAvLifF9DEZlmMs+Pw0e7ZY1aFxuacQorBJZkKIJ4HDQ8ApVg1H0/y5nUsfYemditx9dA3CuAHiAA6DCCQcouORD2bGzT7j3Q3hpw/A1STMYxq4O/bafb8Gxl7UTAfTSXE0e1arOfEKN+TV/y7Z234I87glUhiwSLolZkNpyxpjzT/v+3ms2coRLVYUNH/dMO2YVdu88Ind67YiT0AeH7m5bYkg0XYpzbG5BnEla2uCkCH2p5rKAbP8tQ5to7rOKZ+mYYQMgsaWAKkLIWPDLkElXuqQuoFaZZA6koOzMppNE1DLYxOUqDkwx4ZWJUAVmWrLRHfblBCUQa7ECJsFhBMGGiO/uVdJ3Bhlas24rVbSNsNY+uR2U2EMq5spDegdHBPbxnOJXq8/3X72BVujra1NJrUFMJ9ULtuyK6XjZyMpI92EOkYY+jqlte16lpIDoKE2mcXUO+s6YQaIbxDyhIAbBOzVFVRQi4BQgokHMmsYFajEqG6o1NVWEtdKOaVigr/ctX7UqdCoWQVfWaRhEp9nqZgDw1bcb/mjpUH1qLhrYkZxQdYIS9BaQ+gClTckYxqaZXFsDv0+a8820vwEaBwO6H4nFfp1eqAd34E1P4eIPGyRwtQmDBE0bMWNQprwmPCQlp0Gn5P1gcFj9PNjQt/uT6G9eKcaG1pwmXl1d/hEc9nhO78UKGjSJxjWuerjQiOMQevuZmmzpa1KHZwl1lfkhIJvAKAABDaB8AE0q694pkTUNmuGk3L9WtPYRcAL2ur1XcUBUX8XmkHT+t9NHpd+qaGow+geuXdhdg9TIIQhIuSIMQ8Y44AxRgwhYwAQyfAdQgAhl0DbTQ0rbTmFq9XjdAcgRIAiOMRCKzCAxDtk3gvOAuXBg8RaEXDjRjCLzsPni58D/e3fLXw98nD93QJ9JkrB3OJVjt5guDXn14rFgzCzYv+HTghR2uPwH5sL5mrxWpF3+DGjGEAxIGLAiC0uxjNcbDY4GwjbwBg0PoQGIKl1HKJVsX6H3/bY6u+jPv/B8kzBrgiF2NmkkMyFo0fr+dbTJnUj0sUEDhG4DgDTiWfTEhzJuNQxbYopZi1bWiznuRMs5luhvW9Vxj2bcCK4LXfii9vDx4kRsbrKHxALWNmw335zjd/+5qr4tSVKsECXi60pTIcqcKiad4QYYk3zGP1YbFSt7/ZCiLvAAUr6CY5DwZOMwP/lIfJPcEcIEbj4SmJCOCGEB6+d/fvXCf/1+yxKHAM5Sy37rnDidr0NomtpT1+/HWHhtM0bosFprBfNKcAJhvX8UR/0gFgDUMgFzyQ9rKmrvfxrvMZgZxlBfOkL03Th+K/9LPQfLYxrq9ldwdIaxsINclXM1bWfTU6yf5rSYChjIFQN/qKNIprOIajwqmQMrsyMPL0H8aSIoj3vaEf2yJgy6HMGTxl5mpA4I3EuQWk5XwPYS+BqgjIjq3sd649o3KvZNNl3ZZraWBUCdD7OmQlGMJiLJGlCVqMC0b4WrfFJNM7HsmIcw5eE6ERd00V4kc06ICNpWdN+j/1ujxiDatVHiTkAqoQcKSMWUdduLoIFm7uUGJyT4g4McEQIATFGpClhv59KHolvZ5ZRKnBbxM5Jh00EZcao7ofQiOwQy0oGoLENiMBk8Teo5JctW4n8ElBc3L2iLtOqmFFKZiDlBDCQUtKlqGOevaCoEn5ihcGFycLMYoVCJDEiiBDT99jwD2Xu4zAgxogxRllvVtwQgcyIYZA524yAzkFKE26urzFNCdN+12iJyjguDLPDgWzfpZQwBSBPCUlxwgByVge6P1z5pTTWcrSsqsji3qsgOgaxmIkhqSsm8XGcWWKWBCIMwyixIWIsVroyph3Dqig7Lu+x0mqGCh1zOcWLy4pg0S4IkQKGYUAMuQQENwhw/clKrBoOFOQ8p9CODJ09RxgvwO9/AF/9tDQRT/AEnwwOChKKZrVj5PX3OAGHiniCJ1iF2cVEzSuCKC9c5x1u9jfYO/l6hLIMiUvaimqdELK4ZPAcOEZ7jfTM3Opur/VLzuXe5+ZZ9ymInr7W5+x+g1G12F05a2PU98UE6iaAcOi98HgiYgwY4gDEEWdpxPk44GLY4GxIGIYdBpLYX5ECorp8TPel76m9n0+m0TaXwPYlaAKQdMwJyAhixclAYglYnZmRuFoSl7GUzsPwyootGl7nXBaVeV6AXkjR4/UzgmuGsM7eC9YeQI2wpE4aGe7mlmgRxzQBqjU2xMxVU8V110ErKEidpdWDXfGa8WzEcLbFs/w1vubf4i/Pf42vzi/x9WaPs2GHs2HUuGVUilut9zNWIBD8jUGZwckU3xiscWckziWpC2CWWB6ZhA5XfiqPQPjbK+DdgPRfLlY9yj08GGaL9lgj97pJ+9B133Ve75v384ePFKx6iaEj0K+FBwF3KBIYw1AD7OVcie2l6bXLqfh5Dmb9YIEgVxr7QB14CEuIpbLYPT0Ves2qR5mrjwgPpSHWaA36jc7zNJ65+bnAksY78HDj87lDrx1wki9p4J4Ln9QSYgTiAIr16F3SnttNjDfXGe+uxTWJ+AFVBhGh0dB+TFhiYB26FlsEqyUyCk5LNYAVu3RFz8IqyJBgV9QyzMDmZq6i7KXGgmucflr1+anBbusn98i1K2FtyRQrl5LVC1u0dpe5aMK7s7eu07ahXBBjt35YLCDYEEa1gii7vaHO4AZVQJSIlCFpJs5sFhHq/1etIvy101gG+sZ29MnKKM2+SZDwKszJ0O/u7gZzbVuuAi/Tpu8kQc2Xxo0VrAwRRhSmeXFzVP25cmZZk06zyARLJbC8jQtLmy0IdnBWERaE2hjMCAGUc2FQ+7EIjlBsR80qc8g1tee63x1FOGNrhqorLn0r6U3gQwBY1zbXss3NU22nCJm4jx9gNBwb4eee+zkx1STXaobQjOAM4qRNESb9ECNCiMrkk3USQOAgbhNIBQQMBqcJOYklROZURqI547Wf/SL1o2iuxXJZH0bkzk4y3VJdf6m+NN+51UK1WoVQsfAgZA1YHtTygwMjajwIe15w1HKH9BSWiwuyNDmSCUaXH9qmss+hlkB1nZnAgkHFT7an2UuZFEoge1P0CSp0SWbVcSuu7TLe+znDIs37BAfhUWJHPIJ04OAynB8vHw+eJCGfBrpxX1Po6emx8tvuz5WyRcDABc8AeGbMUITDhlfeehHy4tembzOcu0Jbp7bVZ3T0QfleEX2UiwlAK4To6+pwdn8F+qRH7orEhCuOyDxUF0xEiGoBgRVcbBHWyMj70tkFcQhCRyZhtCe+QcY1AtSykNUagrnEiFhcAWWsDamruHEZvh6ftwp6PLufn+XFu3AmcffXgqlCyFsCLFZeGZOlXF093Jd/eC+cMkshiCUEMAL5DNvhHC82z/B8M+BiZIwRGDSuSAgaS+yEgm+xZNs2PyIPx2KoZIsvT/PhNRqz0hJA1oDWjVw1ALxmUXwQVubs2LG2VInbxlVpzf1+dLhNJZ/uDj9acz+2d2jqRxJEfHwoAQ9zLtqS5ht5yUFAsYAgNTfX79H5Tu4JcFdb+7Pl+NwNSrOMsKOTnq8Wpwf1nwmv+aPAKmL5GQshnuATAQXg4ktg2JbzBegYuFQZSj+9zfj//mHSoKPmU5LUDdDRsGjHQbW62zbehhHEc/zTERnF7Y0ig5zdfshNKYXAyG6jEIsmrrnkAQhIioTCvOVSEUZUZn2nMaWMVOoYtLUioGFCek1wVIaa9M8sMvRdGT/vhxaFKJwJutTiI3PVRvfXSWFoz1vpgjTXnyETuPD1pA85fwB4J+MnjUQJZNuX7XBywdFVAJHEEiKrK5ucW02qnFNhLovfUPO9i6YSfw7WsV9mjMq4ysIIFGZ0bXFhBMi6gPxOaSr+8wuZxeTWDYx7ijJPRAU/sMoFNxBrCE51gZrGOYjU6gEatJgRQ2WemmCBsz6XkYIE4FaLyijMc8FJMqZp74hvBhBVware6RTIh8/Q+bRmO4a4rm8qQalZ9xBBYqrUgOKy9c21j7kekveJxaqBAHWJVnUbA4lGF5X4ILbmbCFVQWLdVhpouTx0PAIKILWqKbwGBGRIbIik4xmYQUHmYRxHjOOAOsK5xAYBCMNmUwR/U2Lc7HZI04TdfqdWRdUeoh5/ngnead+5lTslERxN04RIhKzCEGt5ZkbginvaemYAwc4wtn2RkTkoTlbPfbFyCuUzpcE2AHKu7qbGYdRA3MEWChbJ11yqLeXMXN/ISkXRcFWCrApl24M+BnH9ZPvYnzNiJVL7av0nBJFBhICsQnQ7lwF3lj6pkD/BY8M911e1Bqu/eze4Dwufkmh72oufBJTP2nvgJOgzBogZERoPwjHRDMMKyocIMIvaw/XNwEk1mL2Qowvs65nUXJU0TFFEUOnKCifVTGd7rrinFJ278pzVxRI9Tf43d1uFDi9frncYa96bTHi722IMl/iLzRbbOGJDEWMAYgyIJktfwqcPwMnulm6RttXfyJj4D0j4A0J4B7NkZ6WrDGetCjgMJLYK5S/rygkr9RdctfzwL+aJGctpvaIauE3f4RpG7dqaJgTF4QIkfqDi36489uuyfGpdDS4NvwBWYE6nl8dEGDYjhu0GAa+wyV/gm/Nf4dfPXuBXF8Dz8QZno7j2ioPgr/kUa6TPGVQgx9QOncQ/M1oPhcbKhvYzwMQaEQ3IyQ/6wQmocJ+rSA6ek5N/8oDWd4C15j4kz/f2guzT4GRBxAKJcwvobtOF535JrsFJA6oHztk24fx8wvn5VLQmc7ZjirUuR/yUOsgxiahYRBQNZEd4zhvov5jWL3Xv7g8zIcTCu6V2rSPLfV86QnXGePuFwQP2a1kIsb555yP/8cZ4polzy4P3l7Ee5jPgA6ras5OyriUdzkRzJQ7FzQXAIAqYEuPtFakbGtNeYby+hgohUIQQNU4NCuPxXrAkjDiap/koxbSWQUewf7RM4IJIsrsFjNoy9Xb9qlgOjNFaEFCHJK+bNh/oK5ESWly6UAgUpQilqfO+LQunfQdLSTCTYUZ/Ht8OETMCtV5He4AzCKn2wcrt6LGerrOnZkUgzGr1pZ9z1fSHWR6UVmgD5m2X5gX4ddG7o1nvpxFIltCVUShARta92vq119Whncz6u49VDveTfDe0rBrol+oa1fVhDNpqjaPjXYRt1ExpERho8UmFKnUIhbIluAahYhEUUIRUVBJ1Y+VHWdssbhmsIXyABKpzWkdcCT9uZ9f8T1sMA0td1aEq7mQCDhNKztc5VxqxeQpQvkbMOwTeaZ9CiZ3g10AZEybAvZ+SCNVympBScgS4w8rW0FLUs5XAGMM1tgjgfI5MY7GuFWZKUMaLb5MJR12X3brPzKLY0uFVvikmWAxBtDI5xiLArkox88DkNpRmidU/r/2r6eoTO3frTzsTekGJnzfjW2Q6cCPpup5oxHfXG4QbwtflPiMgjgjbS/D+Bpyn5Tukm/cHgb6sj4TTrFFDP3c4Rlncq+wHmJs1HPfO7Vxo03I7160mT4WfA1/kZ9DEBmaoxmcCxaqyIL5Aizd7nMjSzu9vO9LlTq4UX19GLaHcIL41syflgRM6tO/sgjA83qVnV2JBRn0e1OceWfX19e3wA9HgGjRL2wt4TFkEKYGZsMvniOOFWF8GYOQdIufCGwrmJaMMW4dgd1UWXGKJmd2lqUUeWJAhAnEDDmPpFDNwM+3wfn8tblRhfCwUBagW5e/m2itjFct1t7CYXWY/567jfi7RpW3y9MBtMv3zWvRk/YSMVWdXA8O65v30a7Ctu6EuOtS0wbM9f9C+qALIMA4YNyM2eYNnwyW+2GzxcgTGCMRoShuV5rd/qSu3HY7jh9Jd78JTrQubt4V2ce0iVrqkJq68VcVtFYdltsDQDcEqrjpfTqCbAH4XT7o87nwH0mxbtq/7Y0LPzMUYHo98Ed+n+DU8/yHgsYQQwM/IIuL0fSfMhy+/uMG/++t34JwKIVq1IOersmqnisafmb0HI/hoflkcasOctHxYONaW+zEpD1DoT3ACHLp0n+DzhiWMcm0/LM1vf7AE4PwlMF4sIg83e8J//BfGzV7PuMDgQTBBO3fku31SiyTdEVrz7xap9gz5LlP7s9FEQUVY9F1DX4BRVbsrgSG0h6GRhqAxxHYTAInLF9NYqv7YfTnWlsrwbQINAx0S1HQXrIgT24PSCyUwjBu7JoRYGCjm9lPw4GpRsbiaGsSeOkSo3FwoU0aQ9UUApw/gvFOGJzX9bZptiKhra8XVM/KUhHk7TUDO6p8eqFYGzhKCeLH/2c1B4ziLCMvKVp5o5EYnvTZb72clAEQJX+52s4bwRLhpo2clyqIixl6bla1cU822PRYCRqoBjwGJrbCoyKUETnERtbBvzFKC9HuaJuQ0gSAWCdHWNKkAxDGtJD4IAWSagjUQcd01KH0LKujMKclaiLKGS4BlN1B+qXOJHUEoDIGgljeFcCcNkmyxbXQ9Z0YOGWCJXxA11sWksQ1STiASokyde9UzolkDpHMGxPwDRv6+DPUQo8QmGCJijBJ02q0NcckUMYyDaGLt9kj7HXY3NzW+ClDiSjg/cWXN+LaU7UXAs+FHnPNP+Gn/G0zTc0xTQiSI+4biw7rmlm5l5Exl3Va/ntLvnLMSs2a2r8IoCtUFBDGGOCBA3mcTRgGtQIZq+y3+mZ2HQX32kmtjcRfnxj8EQgZJEHOzSOogkAS9HGIAOJRz3dnMOKK7G0uSOq7DOf7+w3OktwF/W/YjEM5fgs+eI7/7Dnz1Rg/mJ/zpCT49NNZzDpbwuSeq6QkeEuS67rEbsyIwbXHq8FYAzMUiouDA3DFffSWC/M4rX0pccGGry8d1EDy/xXs1rb6X9te0gqCgprEy9R5d1FZo2ti2m+YJYLg8E0Bm/1f6x6CcEW8ycgJ2/C3Onn2Ds80ZziLhIr/GmAiRNhIXgmrsKzV1fFA4ymQezoHLr1qyi4Gfbq7wuw/vsEu54f80NJrUoGOqn6HHhQxXcTRQWxhawQTmCWZrZG3+PDJtZVZXPmXd6hJoqZdK85mlb1YXsi1C5v76Rhva77eYGwtTEKL+cRS3WNvzM5xfXuKb9AX+cvgN/vZyiy+2e5yPW4RxELzVcHJ4+qCncFbG5lNLSDshhNGVxbrD1lHdXCgWKyyeEASVa/FRgEGbDPyHD6A3A/CfL4D0iH11ilJ/TsAAequ6zxHuJIjoyceFXbyQYZ6roY70wUIqKcLW0awayXG2SXj+XK0fcsblxV4vOdXI6y4schd4+Y/M7UBrDTGrbomnRbXc9TFou+4J6SZvOQOD/+kK6Oto89dD82FXnxCwfsbWy7/v9dyXfLIf/1lBS9y40+o8Gdh/6Vfw7UZiTer4MS0lHhU+g27MGWCLqJrDAxY2fDNNK++HLRAHIAxNWiJgnxh/es94v5OgYjkYcxdgj/wsIUelgkcYzIMIv09SLctaXLNq1hti2RA/PeFAbcHsEgoBRfXM6ZBJXpq3Rqii/xiXt8erdepbntd8XB1NdQD8Xu+QYMcklJSuTbXraEfK3O7UfGwEpZVCBPAeZvbeYMuOH0hAE5duPmrWQa5lwX1nG2tnyREC4iBtzJOsBavehDu+BT4+Qg9uJcGCcHsyyhhBFCw2CGAuuApTt4xnbYlbguUeKARyleyV76Jxrlrn5ps/iHZ9Vka9Z/76LzZ9fS/n20msIRisLvNFEGETa0u2vwekz+0N32BLinGaW6dK12sap+UmXa4Bor29go8HVebTnW8tGkPlnOTMCMG5G9K3jDomFoeSgGKiHXSfCy0jlmGZVTCYs5GkKgBxAgI7WzQfhShCKs2Xk7jrWsKWaitaixbfM3bfJj7HnkdkHpFZXEZNOSBlRlCLITLGD/ncdSRMq1WWn+zVGiuCVCAl7clQIpygOGjQceKKf6q70INXQGlGv07WMgiTZbZFyuLUOtXePmULPi/pbE7r+cG1IAZyIDAFMInQaDsOuMGEpHuZci2hnQ7Xftuv2c6iA/0/AotDsXb/PRAuvUbfHMzzEQQya3XcVvPyMVp6W9z/ccarCvdOgWJlfI8RmeGpDSL184XbTs/HkEeu1vER6ZV2rSiuWEwj3HoiQtYrxXQLKkPXFGpQjt7AQIRaEcNZEc/o085vTW8O6dpVvhfBAZc2VCFEfVazeRx5AQdt2sHt42NgyRevRX+jz98bThFI4kEMIYjrwwgNtAuIa9bqApENWfPYbnnWPDiyjiqfKZPi0oUnJNVlzkAcQfEMFDZAEnFKYsbNdIWb6R0mXBU8vYnDRxbfjlp8oHdV02jaHGjw0tQ1/W2xxNa3aJ/50KHGC0pbXPBa4+sVmYh98UIuz4BWXLHWF6yWg8p94grWYXMEhGHAMG4QeYNtusDl8AyX23OcbSI2kTGEiIFCsV61dVFrmH8rI0BLqW5/Fx+C28ZdKoorOgDFHa+ENnO7msuZxW65mUVEd5MDAPKYwV/sgOsIvBtmR4wfoKpKfrv79ejI9UfN0tFXCrN1vYIz9W0rW2Ke3hexNr33u/6OnKGlL/eqpCvz9uXd2yLi1CNldpgItb2eiZavqWKq1U3ai+d7/Pd/97aYzTOLH2Y7rKqGoTL3lXFRXTCJACJSLJqFjS/QZiGRK8N35fByr+ch1TvBP3OJqjYpzctoKDDy2Vw59z20llcSW/DKJs18dj8ZrPX7I2jY8eKe/4VQD79QsD3ea1HUo+kQs6c7B0peOXB4+xIYzwsjxs6UEAKu9oz/+v2EXWLwoKgo2SnSV6jPO2bujFl5C6ppMa0xvPu1yt0nlCA3hNBezLSaUCwNPP5bS7ezyixAINq8iZXRhsp4MqSULWByjSnBQEX4bL40H3cq+NkdWcZEs7knmDMjdzE54qZttY2gWWiQxlGoiFfhAXtiDSgBWgvCYmkVUS6/i+9911dlViJq3AK+AuddYS6v4RW1+fM57tFDsAVAZHjitByfNIACMGwSwpBw/SEg7zMQuARSJ1QXtMZg7Xn4Sy3peavVt3FLHNk9X4UEQeIZcNlu7Twa4m1OS/UZBZJYChRAISMMobjDMZyAJ4lDYa6BMKD46vc4prnTKXhKR0/b9zxNAFh8DutfIaBQtbwyc13TUOS/LG95lslpH2ZCGCrOwGAXG0LWdnCBjW0c2bgZgTQ+Ry70tOnTF0FShgZHrpZJOat1AkdQ0JXqJ5sCODMSZ/VnLWVFyshBiP/MEhtiYkJOAZxESBGIpF0hIMaoQSNlk8k5GzRIdZT5zxk8JUy7HaYpuXWnTH4vDGzWnxGmNna5CKau8pe4Si8wqdBhnzJACVPKoEAYU0LRnLP5KcdgZSp4cjxkBkcugq8YIjjGEgxbjq2AoLExOMgYWvujziMVhNABafulx9pNt6sWnI+z5iM5EPV8pzJ2ASRCdUDXXJZA3c5HXIDrPDLAOi4kljYMCcANAEMMuDzbIBPjJk+NsVzz6ftGfizbm/AJnuDRoDC8qsXlCawNl+4h1me7X28FD9WEXyIcogmp/HM3uAfNSXZfwyxA1So4yH2XIyElyH1Z8Oqsf6Gc/oGFySPsczmvE8PdB7Y4ZgcvxCess/grgglN3+C1irvo3UHZlaeMYbOmLUzi8h4osSKKtYeWmY+PX4NPWtMcKVChEiDV9RUK/8bc7YwUMMaAYYyIkYHIYqCtWvcyjkaXaFs7xaLStoN8GGq+MYBJGVyeQsicMXEWvHv7JQgBYc/YM2MHxrvpe3yY/hlTflfGOKDiuXLvkk6luJSs5gbafhu8XmmhGd+Ki5Y3hjiUdUMolhZlbtGskfYwCi4/lTXGGk2BzIrcNcjwKot5YS5joYohJRbGjAjSKMtMnQzGYmO0/QZ0/qgKIkCiTLHdnOH8/AzPpq/w7f5v8KtnX+PF5QUut4yzIWE7RAwxIsbgYm4s4FwLcI8TZ6GwhdJucya5M6wKVFhppyBCOr0bZf8b/ZVBHKowQqsNxiOw2HMTgzcM/psr0E8j+L8OLaKsyUu9q3B8NDkbj8U9b4anrpmPcV3OFWIfB2pUvDkcq/XO43DL7jyMa6Yyed3JVYAW1r4SFdw8qvkX8K61vtUYEN4CokpMS34vaewEEUEPnDbw2PF6l/z7HsrbMwCb3wcmzzepj/Wwetetljc7odcrXshr0vXHEKad3Ap/OHbQICbNi8P9XCMxlqTGc21wf1W2ld9HK+pecGRaP6qVxUeo6i798XPb6Cv0XNMmU1NpN78kprNxBA0bUIxF+/j7t4RpEmRzNwlBwG4f1f3coc/cPVtZqHe2pnFjcEwIUfSnudsXB5d4b7vgd6gSKU07FHsJfZ+5IjyarJTMom9hjDPvHI9KAcf3v2kpLyIozXm3FodibRaWJk219xsJjdMocyUFBHAEzAKCeBLmu2PJLeKcQGt00iF5RQjhiUSgMA+JAxAY5Exs5epULXVExAChnDhVgsO0pzHXg3Fd7QgGBjt1tqJQh+oWqQihMhdXNV56wWC15vflUtHiluYRENqZqIKcahm5xHwq8RdgRGw9J0xxYO4LWIIyBwaYxI1QJcwqDmRaR9xNkoy7J2AcwlwGicCzwCFtGVaH5WvIx6L4UIesgpbPAJEJSnKh3KyMzBmUg7afSjtJh9yaXYSXhkdY/gxQusLI1wh0DbMcsv9KZbb54ebMgnTnLO2ggEAZgajsp2Znrh4FflTcI2P6s8bx0XpypnadmKDUxlu1yHQEXZnV2rUZd78ugOJeI1sfzXrAM0KwdhYzqiWGd6NWT8UypA5XLnvN93t2uFAJdG6liDactt5Zb6D0UQYwp4zd9TXe/PQj9ibwY4CdPK67Etvhsea4ffOp4JhG4ecYR+vnGIjxQYH6/ba46x+2uvsW3hCAt8y7pCJ+8vyfVtkno3E+d/CMvG4sTxkznn3Tsuzer0jSAq9BwNDooD7ds8OvtDC5o7yWjtVljuBJ75IGmXT5fVdm32UDtNvg4XZco3ByUvraHUAUIxiENyliyhtsz7YYxwExEIIqSgRyyqk9egeazS1Qz/5T7gCjV4LuVdKLMGdGDhFTPAPTBpiSWF/mjCt+j6v8Bj9c/Qk/7T7g/ZSQCt6rgig4vCNA59DjnzZ2bkAKotaOWYnbZ+bWthZm07iUefFH/V0JAld/Vw5yFaZoUHNmi1tnQjjX/r4dXa2FbiqfLvaEw+ebNUsBcRgwEuEyBFxuzvDs7AIvzgJebIDNIG5Eo1pTo6yN+W5f26/l911wh1vmOckyoimzPcuIWGgp8xwLOGFEpZGNdsjckvVWfAiVRliErn23vW/KKnd0VH8vf2qU6DHr70/2WqevdK6ehYW3d+YzHYAHjBHhtvbsXli+KJqAeuzSubOxEjJ9Xssmh1dms4TQQ6mb1UbwoN+DEzyQBafU2BCNNcSB3s6DsByGY4fRMThZCPEEjwbrQoj5xfyEoH++sGRRsIRougwtkENeWM1nQaDNJcLZi6JBHULAlIB//p7x+kMGxgRW36KnIKur79Zul1vC6hrllXRcxBE13SIyWvFJL8BAOS/1rE65zVWYbG4uHM7MLIy+HjXx6hclwLeWlwtSa2ov1BBQnpGomdqi4R47blidGtb/D43lnAHYI+LZI+IFCCHKmHC6Aucr6WsiN1QL9ytQFMx8rbN6jXhRCwwiiBY6gujXMYFNGIE6N+JSiJEGAEwSX4JVGwsQhrvdU+7fug5Yp5WBDiGShHaXV9dLrNp0OWeJg6DpiUK5j+E+bY6yzY8ORpn6RpihLplMiztniS+V59YEwmyPLX6ibRAChMUVEYv2OkOYrRGMGAegxNtweJDyLNi3qYPM9rgSaxL8WFtRCCi/COo4lMdlTQv+IlYObV3N1rM9zCjxDUJnLSOWKRITIjiBjc6QbnnRdePMrmliAZESY8uvsaXvkEMWF02Kl0GZBZ7pQJrXx19IigOGQIgxIMQo53KaFomcnj2ylAKQKpiAHDTOBwEpZQwhyFrLgoOGDHAMhVHExvRllnXU3C9GqHa1KSVnwjGAEKMy/c1zmi+GPUHBzdx5ySMzOe08V6cFs8zd6UUeX55DLxy3WBzC2KnPg8WxIQJyRpr2eP9hjz/87l9x9vIVzl6+cnOrfdFjZk7Em36XSRKf8Ku7wJ+9MGIBjp0ET/AEHw+8CyUHeteY33xjWBcBNVosk/Sh6IrIl+TpVX8GFI3wDrkm48kY/mw+FvV700RP/Pb0cL23y71raPkK/XA6dMTQwpWlKGfLWiIChYgpAT/szxGG53h5fonzzVYFEcInCkfuwvuDlBtZhATC2M1IOSNhg+vxlTT6ZgIyEBLhHX+H1/yP+N2HG/zh6ho33kLG1kfBB8RzfyEYiHTNEMCpbUqZk24Fsub3VjI9lLksCDbWE2sdXiiia5mYEcr68Yo5IoQodEGW9Jzrc3u2Wm9Pa7gN43l5BIvtUEsJQQQRl8OAb7YbPBue4+X5M3x9EfHlZo+zYZBYZnEQwVUfMutzACccvT20YyfKKLmeEZBzpVEcUpqZdRVmkIRWKbiw0emPe/+2dHBBs/X7Ws0PgBV8FkjFjMr4rOBugojVftQXfl7NZYF74tL1z1U27G16Fs7+zSbhyy9uZGlzwrOLSVwEGIOjaHa2dZbgeLoJLA5EEUAs9WqdL3AUuutx8YmHxYvO8AD7dIcld4yHsu99VaXsY61cqPgAeG24edbHurCPw3232VHhgR24KwKIjyl86BybPFrZS+UfskpxmW5b6f3y3xF6IUS7p46vBwaDxgtwGEHDFkSEH94FXO0ISc2hr3MWzXGLPeP6ttbNx72YD5Te0BPdOtf35ZwpHEvWVIZQsiIg5h5G0gSqZtgW0wdAQZCN8SiudvS9IZcBAMX1Hmm7RPUCBSWaa7cwjIHHRbtmQWOj4GyubF6bFyOsVsa1EyJbFhucjpdYxkMsCyYACURZ1g+ZKxhaXTz+1l2YQXeOZSApEu80uoumeeKGZmxVpxkUMmJILQLqiNzKUG2HaaaCXRpFlUmvr42gNia9dwnWWDIUzNKIXnJ16PqCrTHU/mka70bLx6YAh1Kv4BmqIafM8pZcaRdInWLR2IoxQIY817OD6xgxd32CL6618uy1kMA9M1k+AswlpbfwqHiFWa8UXKdnkDML3RpkDjJEGDG33mIJJK2xDax2Urc6ZrHiGyduezJSZiR1LwGYJr6kzEVwo2Iuq7comEDPJLVwteDOxu9w67dpsd9rrlnFN7fOhZUXSQQKCWIVkbKb9yyxfkJXC1NffF2bBEePobbVT47NTX/ONmOoz7mcq/LUuzDywUtlTOsZaOu+EmftvDbtt0ZnGZsyzrldmMW/s6qfCv2bMU17/PAm43/9zzf4i18z/n0cMI5bDHFE3F5I/v0HcNp3PXDtaj/uDEfRjR636c/2I3juodgLHw9LXAa/d+8cg+0ecGqdt23LrfxfV06E/LS2zfIfL+vW7Ty55M8P7kPjdEN+cvpS90MO2G0b85BVl7P7FnU7vLr5K2WqPIHEtSmBnFc+vYMzkIhBWS5HuxubQgjg4mIHLTKp5VdtDv+SQP3zPu8h5h6vv7oLtE2ud6Xgk4pfx4iAgMBfYoMvcbk5x+VmxDPa4RwiWCfFuYPhj25RLnpluOP5abGyBFeMmMIFbhDxfpeQMmOaEt7vXuP17nvs6R329B5vdgnXibHLhCkDUwYyqxWuKdeYxyuwqJ+bPN8ufENSC8HD7hlQTqvZ/df9sDtf8RArw+gP11NZGo3iEKNYZutfvSVtravlA5tVRCpCiCzaMHU/cd+Hlbt7YaoMBbJ7wBRe4jhgu90g0iVi/gbn4wucb8+wGRhD5MYawvHZF6tfg49hCVHPPV+nt8ZfzQhFiuWsUctx0nXkrbXNbWehC1UxR+alliPtIPAmAb+6Bl1F8Ouxa0a3DmfP16A5Abpf9Y4/XIrbEx8R7lbb4Vzr+O4p4/B48IAWEQJLHZnf8byy2WwwZJH6QHh9ivOzCf/+r9+BKCPnVFw1zOmESngVIYQTPhSriDC/YB4SjhM88wfsnjuBo/FTmnQN0+BjcW//3KDcb7YKuXv9cyQpnuCQEGIlQ4FmztUSYhgGEAX87ifC928YGKtPTho9Qsy3ul8/2q5eoL8bdzBLedQpuneLV1RzsnPn0tSjaUwQEQhEEUTqix+Ge6qFG4vfydzx5SpCS0DgwpRD8R5T74CGiQsUhnZ2mjmcMZN1VEZvO+fkGtG68cHMYr2+8GNr4+PG2CqjGlcEPIHze2GyUjBqsyt47fypLZ4J6HUOcp5QgrtBXUEFcbUDchaGrJpVzFAfSAiUQENGmkgFBUaMKEM5tGpBNf9yk22dZGYneEC7vnJ2AbipCk16rN8zXaHxCYLT0vZjUfqXgWTtFwihMrcmtcSIQ6wKDQiFiKqCq3axZSXSYhiQkUSgQbIvMgUEFQSw4kfBNaxXYurRRlZ8qQhSlKAFZC6pK0sEEloGiTDFfvtYNI3ojqHusDICSDSbnNTO5m1KGSETRJ5IiAHI6rSZQMWAvnA8IOxm0f5T1xHBkBxS4Y/GBWHxe20dKTz64uooaRyKgBC8abjtMHd4LJxz9sqPVyCJkRBjlLlKCSknTFNGDI7Y5qzrwLq2wlj1f55SbfxqW7/g1rYlM6LIzzWXP/loNQJN8O3xYaHtna/lcjaEZu1ZY6o5vijtIEItoJLwBGx062GDOtA6zzkjpR1+2hF+ugq4yW/xzasNnj9/ic3FiOHiJWj7DOnN78Fp30xN3dtP+O1Dw5OFxAqYYHcFH5u74XuENnxCpa4n+LTQ0/blAmz4YqZAksVDJumdRfXcB2StBj2jEwMTWIJeo6KdFdTV4/wIr8hIz2UtDIv+cq3ppAW5/AK5/fVQxw+t/NDxEJxfFSVUEBEx4iz+BZ5tf40X5y/wfBPwnK8wMhBDFGZ+QLUaOVT9nQSnMsDFUiQDKQy4ohe4Ysab/R67acKHmz3+dPN7/H7394r/EKYcMHHAPotFxMRBUAkKCCSqG2Qxtos/KkgcjwAgBTBVPKYCu0Xhn/e4QX1GS0IMNntHX5Zfw1ZP7vL6RSH0n8SDkDgXnFO1jjCLCP1ETq68Hl8qhP6sR5WtRg7plrVOIWAcR2zPttjml7gMf4MX2y/w7Pwc2zFhHPYY4oBhiBZupBmjJaWdzwv8KPRt43kaPVqCxi9DoSkqPWLJizAis8S4gbJEFHflDNAWwF9dAT9sgDe9IOIhgA/8eoJPCbcTRCzNnOcnrJ6/s+v0hIr8Zqhmitsx4+uvr3B5nmAumMQlU7+xvVChEsHyLLRCiJmU+3YXCS980xasdI3Q+u2k5fRE/qP0ibp8XaL1dt5i50lxSxk+LlK8jM6499wd8lWl7+Erd/X1VhD1/WlFfxTaor87Zq9vdxQXDeSuwMbF2kPDkT7cBypj5cTC+2TDOTBuy6s/7S7w/r368ifgfWLQiBI4bbEPS8/48OtT4dYWMiu4RyMwqYUbftagl0Bl+tlfQ+Sw6TuzIoxciBpCFPJAAzELGpmRclK3QAwJbN1geS3Dy/hvDcHQ3j8Vz20FJ4WBDJJgzcRtUDMVWswQ2WZ45nedtGx1EzrGLAp3kjGBeA/OARQDgH1lBTYEYNOrlSoWmEzWf0XesyL3xkwPQHF/lDVIrv2ZUCCbJUlOyqCV7IU5HGRevZYN6zg2v5fa7AVDboBNYFRpXk8Uw81Nd5dbGg20HIIFoJP58qz3evURgmLLjXF4ri6VSg7iomGeVaBjtJ8JNzhngARxDyAN0tzuHyIXeL3RVHN9cUSVdd8EIlLIyn7Vtth5TcTI2XAjlLk65dyw+ck5o+IpJjwU82vZqgRGlH4F0oBxpD0IyMhIDFD+gA3eYMCH0mXS+ckMpDyBpog8ZImXULrkcCcCYgh6bkyS14Jxu1Gcd8+dYrq9CcAuv8CEMzCdYRgCMGVkDkgpq/BOLCI4q8DMBKtBNL96FZF5nB8GMzW4gOG07riUc8jK0fUh55XlbTW92nNYR2fxzLB5lIrsrQSdrvtG/OpmEElAcMo1r9CRvtz2nCW3Ts3NlCna5pywv77Bj99lRARshk21srEJ1qVOJabl3JLgrnfkQeznkRG0U3Cmj8GoWKvjJGvXzxxuZRnR58WR9TGrS/5xp+mt6sJCfV6D+1PD56RktaRU8nkWemLVsHlu+RcG5Rbxyhue/LQzEnLnGI8gwN2TZE6V9N6HKAgwhGmdmYtHJgmMDcGBA8BZ8Jv50JglIsMcxZfobKYdXRq50DX2h/xDQ3/3AiZ4qDETBAfbIGAIA16cPcfl2TnOxhHbgRDDXt0zhWIVYWWtwW3iQjRpSCIcJJ3LzIwpMT4w413K+H63x483P+C7m3/DPr3FdUraFxLlDQZ2HDBxxg7AhCC6NLoOTIaSPD7pcGcJLOz8uPpo3rOJd787QUVFxdmtUxNCcJefXX7v4svh/gyI6ooJrJxFBJtAwgkmiqUE1z9HP/hZ8Vi1ruBKvGgK1s0TYsCwGRHygPHmBS7PvsSL8wt8sQn4Iu5wHoDBLCGaCrwApp3z0/kOj3EH9zQsd2/7M8nfUn7dijJSDqJsSZOKnMo6al3X27kCzmBTaCGlt0sN3NWzhN0efnQyrA3tPe6B+96Vt8t9amo/j/XM7SijxRH/GBjg6YKIpf5298xD8oBtOs2kR8pnbDYT/vI37zFEE0KoL2Z4DcS5FYQR9qLttWQJ0XfsNh1hLAUEK+3XNs2KZ5SDzx1P1nD/sdCe0y+8u8DqPtSD+bEX51r1axukjTdy14NguVc9IbOKYD0itG5PPi00F+sDtElQwyODedsteUq9DSJ4IN0ioQDwsAGfvSxxIH78N8K//kAIGwaFJAjeoOTAbe+LB4BDY/oga2mVhjAEMKuSvSGVytxgdR1StFe4uKuysQSRBoWV4KYSE4vBMVa/m42aODvkmT1GXNsKmDq+NtEx0x1zXIpT4URxE2OaVBDfpYUzZohXFWaUY0j/XWM0yDNDknVslAlHeQLnD6IZnoKUueDf/RDMj0GeveckCDynCTZvBNFKz2wBebkII8QFq1qRJBFAIE0QSwEhWocAMBEi1Xu7Qe4dYbDWQrb26Y9qHdERxLNr0dzd9FYYrMSYWU8ERX5bIsGTIR5Z90GyWc2/pR3tvZ45I09iMWGGILLWWQURJNY2JG0MyoivNZqlprEVHCngcAGP65T4EJjfVbItWCxA2LmesryhlmtEQTuuPdLqlqsSehQsVoakzSz7lQIQcgCiYkIiZZEA6GY9ksW1D+X3uKA/NOMpR4SY3KcJQBR3ViEERMXn2ObN8BKN2SC0DiPpGl5ccAvnlx+Dm/wcN/gC22HAEEKp/0boKHElldTSS307m7DSRC1LF4vhKiXwez9fmcEhi6ChKYOc9pm4u7I8BOfxik0YJk0KgWXwSv2SqHada99lYYp1jqWx/WthGQLpEdriJFRLcOXafjT3X7Ipks7J7uoaP373FhdnF3h2+QxxswVCRF3PtWzqSn5ImM1Sqbh78xEEFJ9TWY+pZPKxhBz3EUjcobLjSY48/4hkxSeFU8m1jyobaOaP77xm+pPwtDwdnUH+BuGKELGehwvMQwusLNYPqrKjzTDFiBAIiRkRIjZIel9mvW0m5eMmLTXN2FVaH5F6X7GA1hobqeV1NeApxxl9UngiQOO6pXI1j49hR2oVtIRUCEFUi1b3kdsYQbRBHC9xcX6J880Gm5ERKSCSKo7M3Om2d/ttGMxzYYXRGShCoZyBHQPvJ8brKeOPVxO+3/2A7/b/XKyBDc9lkrt/z8DEARMxJmJk7SsxIRIwsRvFQh/pqigaVyS4DHKdB8J8EzYCCE+DLezXTlhR8jBgAgjDr+FwJxNCZKgVLOdquc6Cd4nwgcFsQgj9NIGEq4f6aZvx1uq8aAtswkBRrCGG6RKX+Gt8uf0CL84v8HJL+GLYYRsGDGFApKACqyp8aaifU+7TY+vHjeSDw+wSou41N98IYjkVIiHnAIRkB0fBb1sskSGux2oJAJT+dyfCKR18iEGYlXG3Qld5LQeK8654b1vb4df9udreae7FrKylknsF5JMU1W45jnd3zcTNR/3kh8XVDRHYbDK+/foK52fiK9sIwEJUNRo8ZjnQfm8EEOX9oQ7epiOnp++FJAXhqC/a9+WAhPv9cZD4GWg3bzs6j9iU+vveRNPn0Kt1+JyEEQYP0aaTD63HnB4tu2qe0vxAH86AUX1YM4M2Z6AQ8Me3hJ+uGG93AWFEDfyqDDJfzKNolt1hXE5tx0z4ctKtudKYwgBjZcwmYZpBCaZAQswYM1HryzkXT0TMXIwiiCD+6jmLxYRQWQAIUZnNBkWL3f8jFRSE0bedGWoVYaet/GsWEa0WcxVEyFw4wqly0mZjYTEDFBNXTecJyHuAJl1HAUsBZtfAqiufitBXZMLqZjVlTkUYU4kAGVfkjJzMBVIlAJoKIGNODIxbERbkSeoMNrEzIc/CeMx7ArYYIiqEWBLaBG11YUrr7xCqFSUzF20nchpumQDKJpggUA4IIZayG3ddbF0ldUyk7pqIiuuwIrTRPEmFcJkTSvwRmw/XD7tQ/TxlJcLYiDWERg7FNqyFWCShtS1Rh2PaOKacQZBAzgaE6jK4CNwyVysLh394xQrOuj9MwNJok5ngToRYIjeo+JhoYopFwX4SP7+Uocx12zsq+GFGItkrU0pSToxqVWLjpnOdWX0pT9hNE5L5Doa2fYmxzEZSASAuwqoQCJEJQwiIQ1QmQZkucSWVMtIkwbljjtI21oTExarKxt+mRVxydcwYj8u6tTDzpR9I3bnZXNe9LWlzEdrJGAZQ5HIW+Lpkvh1RqGeb8Za0AeUsNk6PtdHWvG+jRfKQoOYAMilDTIQnIcRiNZTShN2H99hff8D+5goIEXFj+ysUN27k2/GZ4UAPBZ+fqwaBR7V4/VlCx5x55LF5VMbTE6zAo2Dqp0Nz17fBXw3HySBM3IZc8uoxwQkjihAZkGDHBERlYGciMKveOYvgWu436G/h6RoqUHg8bLcm13u0XN2G81UcykNV5uP6qiKtPuGtoCi9sHXcAzVfiQISB/z+zSsMwxf45uUlLseIF3SNcwbGaIIIKrjevHG3o36XzorGPWwGGANu4jNcpYgf9hm/u/4B//jh73GV3+HDXkdODQiyCQzA2CNiYkYKEOFRDI0QKkLu9qr4QoI7GM6YTSihCIBNOtvYmSkkDNlw44Ay3YW2gk/TJICtC+/y1Z774g1PzipoKG5Zk7d8SNWynhneshuKDy1MW/MgFPshlHXMOl9xiKD9ANpd4PL8Fb58/gLfXo74ZjPhchgQQ8AQg7rR9ec116HT+u/qdaVCw/G6YxkLOam+YP97llHWiM9PMAtuQKyOOmUx3ZNm2cv+ucUXI0KxkDqfgN9+AN4NwI+bEzvwELBc6DHF27sIIe4ORwpdwiFXmfKPc8Pd5ea8l2smXn58WlGN4OAwEDGGIeNX337AZhTfytkTbW3qLm8VQnhf0l4Q4SXTbRmzE2ulM6clk7pqu5q63MFX0/WFLglPlis+OCe3JXi6Og93lU4ei4eAfugbH+13IhBqiauWEGs5TxjWT0LP9cv6WLpjcJs+nFr3LeEQ+ndMA+5kjYT+XIgb0PmrenYFMdn86YrxuzeMEBhhqMycB4W+vL5rp5xBD7YOeOHbEiyT0KyBp3NBHkUzy1zmEAVhmqWkDDxl2FdHp6UTWZliFpMiKDIkTK/qwikbY06ZyL79nE37piQX4i9roK1AgqznyrREYbpyaWNFwo0acwhZqZSaumvFkHXDDOYrZZoG9cG/RAC1ZVlRDQ1gz2ZpuPhTNbPmSixWwUxmRgn9puNsxKrcVTYVymDU4bnZq0//oEIjapxPScuZDu7hQlM4IYS52KlMbR2DhWJITaTNc5C5sSFz/RIIgVUYoQiy4AQaayAAlLjQN1YvQIXgMJwi6/xnddFTLYAc4VTG1wJxc52PspadsEytiQoBs+Sb2Am5LO5FQfSXzgsT6qmwjiyztrW1IulEzO5MtKdZFxshy3xGs4yo8V0yMYIGmQ5B9l6WwQUzkJgxTRmULIaGCRfqGmSW98yMlBICBcQQi4sfTxObcGA/TUgpieukhpCYgzFTmneqWRpJhDZDCJgoF2FKBqtFRMaUJFh7yKwCBpt/840MOOMFGbvMQMgIZklh51q3zVmtxXxrYWcS296s95Rt7yIUBUBU11qJHWGLxB8vNLdpALO4mbIBznU0M+ey3q1c4Ymo/ZGuN1uTHFjPCRf/JCXsr66wv7nGtLtB3J4hYqPCKh8nxe8XfhA086T87ea/e11d/j6e0EOU6ct+aPiYrppmgrcHqvMh42DMm/Rw43IM1fulQT+Wn6k87qNBYxlh+KiilRUTVEEE2puruGUiEQYHiNWj6rjLOaz3Zg5QAYQ8z/CoK5vhG4iBHAgpG+7nrQNyE9sK8Ou1u88Mv7TrrnF46ZIcGJnDhA+7NP2d2T4yfG/KAX989xUuz/8Cvx0vcDYEXOIGWwCRNhJ4mDymquX7sgo6ftoZsESfFudDGQACdvQMH0B4PV3jT/u3+Gn6HfYpYZfMDbngnRNkJQDAFIAJShORuN4qeC1UGaBg99JeLkPlLtSgOEnxLapaXoarNLFDnNVBITx6PKZ56TZ4/71kKMoRWdOQ0nfmApM5Fxc/oiGSqoU9e5pGLS48IVaWi8xj6NZHoT0AhEgYhgHYjdjsvsbLl9/i1bNneHVGeDVOOIsBQxwRQ0AMwQxvUNxrurGd4dIn3hlLdFKPp53O/LX5t1OkbQvT8XII83tUFHdQZAlevlSVi3wzGEV5rKwlnesNwL+6EUvqHzfz7fyAsDxuvPrz4Pjc8d4it+4Ow0KCUy/LPt3aWTUrzt1Bj4iJ3NkigrvPkxIXTs/pHRrHjN/86gO22wkxTGKqb8FNO4aMHfAW6JQ0SGOgqBJt0S4NynBYvzfach8aZkwU6p//HOHTtf0Rz6nDlXawpET/BD8TWFpAcQRvntWXcazCTCL84R3wp/fAux0hBtvLdPBiOeqG6tTj8T4LfmnDLBzobMhxQSoONcx6pgcaAWCCBcU1BhIr8tgGRzW3LaG7lSsTsShnw5ipglqTMSuNqU46F5rH2s96ZywydGdjIlSfaHBY3wTMcsMCzDGbBnkdMWMMWsyAhmEPUpy7R+RUcBICwMLYr2097VBpzx+H2LMRiEYwcBVE6DywGuabQMWGIxijmqT8YExFHczi59NIWWaMZ0IXpKRbom/+DA93hKS7eqWpjJyTT4zCICddO5rOGLDCK1ZhgQ19CdjcIe+N4LoGpZbfutfZhDNSRjRXRDrgmc1yRNKRao1PKWn8DatHnueUq+DCEe+Gi5cHXFoJUudShcmd3aA6AUoZvhK8mWHkZy77z5Mi+i/Xtjc0JFpihVkFEFSFe+TGGlBXUdb2zMiUVXhUKFutU7Qu9zkjZsZA4urBxDFu1SIjgzKJ9YRSeDEEhKhCR94DDOx3O0xpwm7aY0q5DKOcTm7umcse9vNPBNzwC+ynZ0C4QIxBBBFRz3WuhHxKYqmRpgl7AmLOYKISJ6KUyxnijwtlv4m2PyFzlsDwbrbmTGo2uq3MQ/kwYpqAnAk5SyDtPAmLIoRQaAlZstXFXDkP1IqHOMneIrFYQdMCiGDN7yE9S1KaABYBAwfZa4wsLrhsH7umUyAgyTp5l89x9eEVwg97vHj5DvHsAsOWgfMXCJtz5A8/Avubsgpte7Ip7DwhXE/wEWBxlVHLImq259OyfIJ7QruMHFIGQmLCdX6Ht/lfsccbFSDUs5kBdXdieEw9Kw13ChmNcKMYr+qZPZG+V5Rh0iqWj9x6p5Rb1/Amh3PUv1xxUUHQaz8XPqt9qxsLPzYzZVLPrNVO2f1sOBUBMQDbsxFn2w22mwHbOGAIGTFA7v5AqrwCNJu9qeN+wH6Iklin7HLAu/0Vfkj/hHf5e1xlRmZCyrHgP3tk3EDj2HEW6xiCKK2DkJIopwxBrGkjCKz3fy54gCgaFI0Om3yCFES2MnLtsJnPsh9f1xn5UnBA+ezmt0/HPHtf8XMTNjCQkwakZrWizU4I4dwy6RqjRiiiOK4FQ7Hu+XOclW4jsTCOQ8TZdouRLvHti6/x1csXeLk9w8WYMcYJQ4wYY1SBVcWVuSw7EQKVvWdCqBPXxmPAvepW2qbDnOu3oLFiuCrh2Z5tglcbfaCxIkInKCJi8LMJ+HcfgDcD8ON4n1bfDZYGyjXzaNoHhV82QnEnQUR/Vay9NzC3FvUiPQ2IGDEyvv7qCtvNhJQc48QYDqibG6CGWCvumILFgwjFf+Iy079vOXdl3g8WNTk74rKv69SAdp9ciOGr5/LPI9Z3vL+3HZuGieef93050LVj0s0HUrCbt+l+hd0tvevDUS22+aGwDHN8cpa+6G12Gm59nbfdE1XLR8sMI7B9sVguEeHtNeGP77LTtK5puEGusLowGu2n+vDjQo8DLiyIdSGEnzBFQhpixTP/3Lh45m4gJ4SojNBGkQaoFBFngKMnuUpQ2hDQuGJhVAY1GI65L6iUI1PcuWXEirnY0izqvkeIOz8uQn7V5vjvpt1TtXuLgKcMj6tHCT+abYTbLApniTETQsizEvRZNYc4V+Td6iOwuiJiINX9RgXhpi40ktzxw8jIgZGUqGr3ARqE1B7W5cJN8sKUNSLJRkYHzOaTU+tv3xjfTBqvQO/eQpyynzvU8v19bHiCLpIGn1CfwcVig3MdY4Wcsq7LXBgCAFxcks5SxNNm3O7DVpDXnitFSFclXvKf00QSek7y56ZSG2OINv+MyK9j01yPZQ9bu7oMBHAWN0o5i7WYT1SXomrNMxdfx8ExyksNOh5pSoWRz4iI7sjmzNjt95imSSwiyhlDhdhszrHuyCUIyT3xOa74C2wRMCqzQpRb6nrR4UTKwDQlPXfUwgFLzoNM4Cf/Zc7CCHLu444RN574649XstOOLYi2WB9QYU61eKxH0Wr8FcA0H5fWgVisuDvLcHGz+IkBwQS4zR6vrba8FtdkTyOu6TneXDN219dI0yTNGM/B4zlw/RbATSmKAA0Ebg+68+WWcOxWqwnvh7h9rm6XnuChgerHwv69T6mfcgX1WrmPqR15uoboZwz3pYHr1V2LA2B67RmEm3yNa/4DEr1v+fBUvxRlCqAo5gQAWc9nU26XYMm+PrkvzBWhvcswPjQ3qT0WHBTHYLjyy33ikXrufvfMautzBR9LwD9dpLWawXMMd0DuRgiOOI4DNpsRY4wYhqiuO0UpxSxoi1JTwUM9zXDazvZ0pN0HBScw9EhCHmA/Ea73O1zlP2CHD9gxwFnxaQDMAROAHdQtEURZg0HClA8BlAEmUXSgULHnoOOQmjHUfhDbJQs0muwqjPAxI4xoKVz3dt7aOdc8fTpeytelzbqymEEmkDD804QQrCtThRDUSHfa4tteO8ts9jin8Q8jhnHEeTzHF2cv8fLiEpebDbbDhGHIGKJZQlQXuqVH5Eont2ZmbViGQxbja2nvey4fq7N9X3FrOZkYHBlINXD9MjFha9/cgpoPX90jJLRAuGDw+Y1M6Y+buu7uAPNVcHKGu70/lHXWh7Uxv30lx3JUlPxQSj748zHgZEHEw7bl8GJnFldMf/mbDzg/nxDIhBCtJi0AJ1SgwnwwFwvGNLDgp/5A+IjdWc9A3e8uzScXLpwMP5d23h5uI4T4cwV2DIaHABMILF2qXghhn3cm8h0TBwAQR+DsJUBqshpiOV9CCPjpPeH3P0nwtkzAh8n8qHdMnmyoN7flf07Q0hGV4edfFMytS1xggThtcD9jRgUhncogBTFxVNPhMAwS8DZEsNqDmycl84hkWL+5YAKbJ3LXlMJNJGUUcnUfYlZ0BYG2MsWuItWBKAWKRyavD05qmlkZcXDvLDZAFbbou07w3axXZW4DE5CvACSnqd2zHslGeZVn2c9UMRG2vlu7uP4WK8ME0TwSMrPG16hM7UhibWJ0QDYGthsFEEAhIhBjey7FTbtuf3aNrwGUHbqoazKzaJ6byTOpb30dOvmuVLYf10KsFsJR3qXMCCGVIOomkCEQKBAi16C+QqxpX1XIBaDEmbC5Nr/E5dxyxKW0wZivag1lgb+7ISF1zL+2w0xDzPtsJ+0fA8rMp9pvrv02PcUQYo2f4YjAOfPHMcil8AV6sQp22jgmQrQaoRGCMsdtbTu+QeT3uKQ/gMPOsSO69eDSTznJrt9PCOoSqbgpYsZut0fKoh3I7mZqvAmU/uoTHa4QCEMgRATETEUjUta90UFWCmm8DWCa9gjEyPtJQiJmBjQ4ouNblEawrjfrV109Op7G4Gch/DmTjzXdgCdAmRlpmorFjc2L4MKE6kFcc+g6zTkjp6mcUzlkhOxJ5lC+MtBYlTEgwe6Zy7lrljEZJphp05eWu0XH0x67mxsVXkElFaTCxGag5MwqpXxk8PfHEzwB4ATcT/AEDwN2PakCsvwTN+DtCyQeMU2EKTP2iTExEHNl+1G91hrhQi5/hjtw5TeDEFUZoDBk9ayNqPdYYIDJueEz1i2pVR24xPWpN7DHQes9apiJnO3OtSlq4sratUdVecina3Bl7RTrJ6HiByC5WogJm5zByNhvRpxvB2w3G2zGiBh2qhcVnPJoh8Oi3j3kWroGczfgqIJ8FqWdxAM+0HNcpxF/vEr43f4av99d432ekDDIfBizO0scCLFOVcUWP56ZwSEjcxBrUgTFYRiRdJ6EBHMxI/rOmdtIe+YtWs1Nkx8F1PQNTs8V1ywEgxM6tUREm9aEC8wAO4sHnqolRAlO7evgtu3sVgihmy1ZP4VeDxExBoxnZxjyiO3VV3h5/hW+evES356P+Hbc4/lI2I4jxjggxijrBVBlHiuz7gAY/VksyNE34mcFVA4m/Q2AlZbNgRF0HEzJqVCuLgZcmQ9zkWtvmEAc6jnzag+M74EfR/BHsozot8R9pmouOF2q7eMshrvVtEaRHkt7OpwuiDhQ/jHl59v2XCwhMl69vMLFucSE8If2er4qVSsakC42BB4NYTxWKrkLzTPB6pc1ocPp2vzGUHjAHp5at88ye/Jx4NAGOzY281gQC4Uv1rn84hS++D0V7D57OLoebYzca787za/l0n4vZRrPra/D81CWwCFPTdYQgc1lgyzY2cEMfLgh/P4nCFNoEMZ6H0i44GEH9kDDPHrIvbK2CXjh58LluKQFyw1Cqf1bq4O73waFGydau0ZdFXdEMQrjO1BxuWE5GLYWPKK9ZOZbz1G/joq2rosy63jXlV9b0gvW5O+Puaq9x7c7bXBGZW4rAnYo2HSxwuEM5utqCb2AKvtB7X+XYege1PXoSFLuv6pWszReNOmz9bXYM5Y7FNmVxrUlZdyVgIuUETIjTW7K+iYu9oPdX29p0O3ZJms/ZlweFx/9nJEzIXh2tywy1eZuDqR5JbouAi0EbTP3SMW9FTfFkGmiNYQW6jgTWqKFa32+Je0WtPNJagvck8SFswDAhxtw+xndPaT7lSwfuXJ6cBYZbdIqHBGiGKWNxbAJAOEaZ+E19pmwb5jf+q3bOpkhgQqREEIGW0wZVVLZT5MKeeYnq2+jCxutnVcXT2quHxhFEBlCdfdWVywVQeeUCDFI0HdOqqFYNBBXcAQbe7cMilswew6o0Gm2sRd6JQWa61LO7NyQunmyNWZCiJJHfIJX3oPb13Z08trRr2PNGShxedxB27WatdmFgcuMlBg3u73ESXH9LbO0ei89DNwKbz6l7l8YYvdQdMUpMdyO1XUMvbsTzIjYW5Z+n/FZxZG5S6Z44wOv/bvAx7CQmAvHP2YZVO+yu8BShaeukdkdDgAMpgDePEOeAtIemBiYcnWlWVMuFNk9Fx699bEiAQTB/cSyAYYyw7SU2ePPVi6zKuiINrrdscHQ7p6GsOGwRnH/ZnVgTnzXXlhNrnInMQaIQscYIsYxYByiBB0mKgbaxfXnAWFEpef02QnnmreIyCxuFRNHvOcLvM8Br6cJb6YbvEt73OSEDGuQVJQDq6KHQ74YkHgO2veMEtahxFdTd12hLO5OUNTjeWUDudfdeJorxto+dnnYfbrvdSDq79lasTysrpcY4AxS5bIqoOBaDqPGjkBfHs3OraomYQip4EwhDhjHEcPuHBf4Fi83X+LZ2Tmej8ALmrAJEcMwIEaJ49cO0xK+xk03P50Q4uF4oD1dosWjsDkbRSgTCNbUTHaYcFGiKlkZIAQ5RM4zcH4DvqYHd9G0fKI4gtHSreC+B8vucdbV82sZq75V4avp5lUt5SSXtut5m+6EGCJ3ua/vHCPiMYBZXDH99i/e4uJ8wji0MSEqc9POR2d6WLQOgwaRdC4UQlisy+CjWx7YbjsihPg5giEhP9e674tOfwY0ws8e/H7okbdGCHHnCgJw/goIQ0G0RFtGdH9I6yUixBjx/TvGf/uRsdtn0EaFD2br6oA7jsmj6snxylo9sP56ocKhfAVR7m+nFqtv2mFauRXqmQyIuTCrf05SjYkQ1CKCQjmnGyUcmFWCmeeqkMgCl2XRCiIiUCTEISKEWLR2Rds3F9c9gQcJoOwUeozxxspYLPEElBDpCci5GzJB52ExF/QzmEDLiJkGGYf2NwH5CoQkxM4JF/0SVHxe54RNW7/VsDcZh2g+BwkC7AphtTSBIYmqWR2Dxq8AwMhiIq0YdYvqi9Y9jKBVAtXGuBBtxQWT+7RStP1La9zu/dJkl6gwNsnyU0GcfNn1tyQ2C4HickDrz4kxTZMEPFYcpFhZxoCcRBOL1GxHHYFp0OosY8aElKaGoWrulYoLMeYmPoqkk7kIFOGDSKuNRjsGjpgj98zWtwmkCBChX0kpaz4EFax0Eh4bI0ezNhCixjyxfVKzuj4ovpYZWYlVIomN4GnIKtCrOF5zfHZHacpJYiIEnTUtL9m6J88i8Lhjxbmsuh2/wA1/gW2I2FBApg1ilDUf1fReiE0732w/Z+QMpJQwEWPa70EAUp7kuNPYEKUNbRdke9VIl1X4DhXAmTBHOmCT2ZRmc8kamDsldQWmVjsxDg1+LEulE0pyBnMCU2zuLGMimWZa0DgXdQtaG3SfFUUf0vw1UORMIGNCH527H/Zb/O+/H/Fh+xZ/u9lisz1HGEZEE+qZxiyh+LleWBa3h18Q7v0EjwP+fP0UsMwCfYI/J+DCzJRYR4kZlN7jFX7AO3zAh5JOgECiJG5WnPrOHHC2WPraCuNydptnRa9cYbxGJqPN0OBsmSrDm5XROKMfYMoJ9Tvst8MHbrUD/JHuJSrWJ1DB4YYQcb4ZcLbdCOM5Ur1n7X5eEEJQ+Tzt/lji8Ri9kTMwTQHXDPxxP+H1/hp/SP8Nr/ktJs5irR2iBqGGxh0DkhCqxRWOTDArDSH0liiBcBERcaZCGwUyF12kcdD63jkMkIwWcOcR+f6bBgMfObDc6ivxHOCsGYBWeOCDTttfAmUTRsz/2AR5xcrGt7f2cSkEHxFh2IzYbLa4vLzE2cUzfDN+jS8uXuByc4bzMWETgSHG4vIdNrYyqfLNNkhBlshGCSDyamE/P2jJhO6VuuaMsiZ50mSyyedFKD5dtF1s6xGhCQz9YBfgp7lNDwvqW3ruUdvXV2WPj21bn+7AkXdX/ufjCCLaW85/LCfX1ocgLplePN/h2eUeKaVKuM/Au2Ryn0W7kIpG2JGm4cEmvqHcK5For9qWVIJYPk8q8ngTHpETvi4w0QvkwAo9tVX3IQvvO0Y8+7KSv0twnyHv8x6jix9cg/7BiqpMifvAqqCBl9afXmBrm8TjU96slAIwnoPiZpYUUKaYIs8g4P0O+OmDMtHErrcysrSCVSFE3+bK+T4NVpIy7rLXj1/si2U2tIBiw30CRQALo10xPyFWGKYibCgYQ7SOYP41G84jF3xWznXf3rnpKwBlaolVhfnvB8SlTlYNGVESEp+pQmUsdqNFHlv+6go4hjdz62+9WNdQ0wfrFFEG8o1c8I28fE74LC3zMtT6D3dzxYASJ0Dh7qqphska5rXZIMgnAf9/9v6rS5IlSRPEPlE1d4+IJJcX6+7p3iG7C2ABnIMH4KfjBwBPWBwAe7A7OL0z3dM1XfzWJcmCuJup4EGIiqqZuXuQzHtvVWqeDHc3olRUVLi4KT0pEe3PL1EvFGDf57IaE7hbL7VraLFubSsdk/8s4YLYT6/pxBaJXbHgOA5hXEQJYV4ZQEhU3rWshLQltubaFfgkhb0V8UUT8z4whM0ch2v1el2jdtuaoDYK9wXmUr/PrIGF+VSn8qY0YaEwN/Jo5OVcL7qniTGLpQ3X0PVmjV6uz7F5zFRG0KtHxL8IgFTDZ8nCCw6f+AIHfIJMgyqPClIpMN1bTELY96NA8MtUROk5TZMk6FZFXT+HghY7ytP245LCM8zjDC6aZ+HMvFmfmUWne1qs0ZgNaFJzw+xbqSKZtq8snheON31ua6eb8HCoz8X8K3c8YJoGvH63x831NUAZAwipqMWm7Zfu/LzvCdh3w+rsDZMeWm/LYL+n8iOyjH9MWev/ybx4j6xfb55ZS2j07FfuKexYYwJ6a+S6/ZrLbV3nN3tW105WSN3n03dklTf+EOD/GEQwoy9XiZkz+mG4XeotDFA5YMc32NMB16ggOqtN+ZklJUQsMfAOAUFuKDg4UlYEORfV3kOUDigSoknJCfdCRT0a2jwUVlcHZQ0fFZ9Hc33x93zwiF4Q8rAp1AlMGTkPHus/JfGMbWkuXidGOvC3aBzy4jnrKsMdS8JYCG+ngjdlj1t8iwNu1euy9seUERPBaZ/ZZJhnosFMYZQkz3OIUUnWX+5XIFJgLbSY0qqGRKbueXvQaN61cYcb0Xsh0hmmhNCwS8SlekY0XAjX/5aommvbnUnN7GsDoUTIeUAeBmw3W+xwieeXz3C122GbMzYJyDQhk3nLI4zT07SH+qmBzcrnMk7hg4fIek7JXx4rP2J0+b/iMpsclxKYJgF/ZzKFVreICAxnmeCknd6zOgkS3vPY9jvd3/s+uP7GQ8+b8157HK0ye+LYKyv3Vqix2Z33ce4+WhFx8gx1iMP85AjglXPB3/7qLZ49O2Cz2WO0OLcdB1OTL+k/CuGXUvWEsKTU0m4JbTYd6C+uDGD5uSUU3ZbgTgfdfAsWtuf0ZTZ1P8byAzJGTzYnP23e7qdVdF/MrWrb1ez5sZboEYo32L42h600kcCXn0kOCKcSshDo2oeUBYckIry9Bf75j8DIjJIKxoIqcFM6gps+hI6eUhk/sMhh3XGk3dfFTbB26HQWwvFaLASnI2BzS11jZHVxp5AxoRTUQp4I4OShi2CWxibo4ikOVtsmCB5VNkn7UUoBxgk0idBQckyQeF1kTbDMLNlkp0msc0HitZCAhCwMlPVZYTCpYiTl3CQfayaTZa5MKM0svuxFrZJNEZHS4IQWEJIEE8E8ISSpFwFpPcqsgdTS/QbquRKa9tsE2+RMiyymM4Qkc5byIBb+UDiYuFKKUIs2nf5xLMogad0k6yO5mKqnUNGIxJvtAWUquLuT+kiXggKzBIam2pPvxBLaKkHCJdVEz6K84RLj987nw7woyWPNm3CRfE3aUIkM8QROGKcD9ocR0ziCS1HruYztZoNhs1F+h13AGuFDRwgR+meBDU0LaCGDoOvNkzGtSRRmZWpqG0g8OjMRJk2InQAwqcIttFvxjtRp1m7M7TwYU56IwJSQOzrMQCLucUZQrvkzQm9JQkdh7KdxBPOEDFW+Kc6cmJAYvu4gYSNHLjgYjLJRdHB60dFRBfImRwtRhPc6FzMeE8o0Or0o796W53g3fQrQDtsMbFPBjoApF0wJ2A4Jg3oUyCqRKiXiOhH2RcQ0+/0IZuBwOGBgRhkGJM51QktVkAqPJpampPPJKcO0H7JnLaK3IWAOzcZRMqZpwlQmBQNCThkpa9tIoJxlrnzjF936BAwJBHlezsEKq2JdWATmrOMBz4AAyln2qwZKZi4K/+adrOEgEjVhDOxMoJxQDnvc7fd4Nb7D14ff4/O/+TtcffIpgD0IxekDT0JpNME59NrKebxG2btF5T3ri3XWR8M5eazO+5SlQb8HmuOvvVhIzqr0VPrHjccEkQi8sIc9iboyJ53ed3mPjaxV/RHijpVAsN2XLyZymUVy2iuBpwxMCVNJmJgxIqEwYfITiRRPC/6SrF/tKjl9AsmwFrFTsfNBUWylbYzOE5pNKUKBbTUyIAKmlECT5nAyIbIxEEYTkuVuq+3A29Hd0imGEfq8ZLdfp63Sc1EH0FPxKScACf/y+itshy/xNy8+xcVmgw0VDAQMGRhIwzESzd6PbVsEUzbyKvBH9ZjjygeQed/K58gZIxFeD5d4NSb87mbE68OE76eMO84YSwYTa4ooxpTUgyIRmDPAGcAIolGpem2IC4BR1zUhFcIech6b921R3llk96n2NfBZ9ZPR8tYGGQRChgNONDixtW945VBncwKHejkAh+d/iPkhNDdE0ZivzB4C1BZf5pqN0A/woV4JpkQhpacJoCSJqa+uLrHlS/zs8Hd4uX2Jn2+f4Ytdws+2t7gYSBKaD2rgQXFWAtVsdGeFOgDGCZzABxH2f2TnuvW+yWMOzHCcy2MhuMLzJxLru1QrdPhg37guSqksaHh+qVdN60d6v/Akn3oq9vN+ZVEJtt7KA8vRyblnmauqlpVbT0twPLlHxOqZO7tRB5dzwTAwnj874PmLO0+21+zH2bumkYzKiOTMz4winHcIBvwx+eWx544hBbszj1dP7fd7KCH6vR6v92//kOXH0Acrx6ypfuoWZA8uj12gB7y/ug799pCHj1vBhdwvch5wIBDburihbo3YIFDeAZtdu3n03JO48dJGSoSbA/DtWxYR0MaEINYHtBXMBtT9XlFMPMwygeuwujb65FH11jrh3t/v+xYx03pvG06iEpFAHbcRgknpRsWDKRD6BBEyz+rte0JKnDqhyrU5/VMoITNCIjNumYF2AhpiQWSG1UPDyO2mW6E9gnVBhPOSa2H58PZWyCyMDzCL4keVnrblsBwnXyWIokfCWfFkbFeBhTYyvkaMvM2dvArhnf8jC2kVzzxGyoHNZCNGqesn+1+LHUxxXWOfWcLFBOdqeY7is0HBZPd9PtbWRhkzhq8jVMAqCekycsrqqWmC2thWbcig2hRAbjymcEhMYeJ0CS1ROBn+ZPFgIEJk7KO3FQf470cm8gybRBHEO8ZSGGRTGiyVwFSu0SIAuefHyJaPRcfh4gqqggHjNVh0Xc6vouU32hYCStdRLIsHluaB/A3Z/8YsEph2mOgFhiSJHBOJcEaPDFFAdR4w5Eik4ozCEGFQKciThIIrqajS0ziqAhEa1PMgjkDONsOHVBmkuJG5bdrgXa6VgMup9dwxEDKLSNRuyPUETgJr1YM4nKNL69LAOzVnuAljUtiQ1K0u+SYngBLKNKJMI25ubvDmmwOuPvsCu6tLlAFISPCwWAovUUt1CsfRwhm3NpR4bYkmads+XSLOf1/U59l9iuM5YY3Zl7822rmnROx08hA0a8VRs1oZhzjZjymxSe6u/VBL42f/Yqlnx199ofPmokG9dsax0AqRpWGuiaernwKF/1pJwDmRPK9ZfDqKSM+Xvps9eVlP0PqLA4bvvSfsTDPjohRqLE2tldqm9lJtqVdSRFIz0hp+fU6NJwIKEm4OL8D5CwzDhSjuiZEJyGQ5Itr3FkGdlGpd2gjUDBA9HjDFUWHCDSW8A/BuOuDdeMB1kSTkBbpm6mliKEU89pXGpKJ4RkPg+rzVcIZCLYsCyxc5NRO1UiIdEAkQDk9YPT2UcP1kWMfPKJExsPBNjMrLQQ1s5Bo50HJXPwUmYg61DS9ABGQL17XBji/wafoKLzfPcJUHXGbgIo0YkhhrmBICWBoSVTKvbf7+5Z5KiSeNmLHcQP1YacqU9RbVrOizDF2OoMWoeK6ni7Uu86JIkBBrgyawMcWZd4jDm4zTcN2+HsvSmy09sDzwJWXpenkoQLSlbWmJSji3ntPP9zxuXxqUe8/ypIqIo+fsAiejAVDwt796gxfP99hu9iiTWLvGiUnoklAbw0bksXAtxjgF5mel4RPX7/tem9j2Pk00ljUfy8fyEy+n3AKXylL4D68vCoC2l+CLT5s2qneUHYwMLmIHZMjIiY28lXdNR6m4YsgJb28Z//jbCYcCEE0SZiPDJT1OvNx3eJF7eOQeXxcEsN8/5d1wzvkQ8e68Clpf40h36jMmRCW9VgqDEoNTgrv1MjxMS/E4/G1nTSjrxI9aKhYT/luTKtglSNx2FBaldimy3pozKLmQAKK85oKRa1uVb2RP+kopqRW8WCjHxJGseYzs3Go9fAK8aoKGpB4ENPnJgQed3gggRsu0OAUYbphDfccUBymJpwrZ2uhkWyoIt/7X1xPBraQpSx4DUywZq5kSg0sG0hYJEy6eiWHTYY82+R+JwoNgIXsKZCanapAQmCHpX0Ih9jitkTEAlHdBtOQz2Ojpg1ona24HE0JvaEDO2f8TSb6Hw+GAaSohBFjdg2DGkAepc9yjQPIZgBk5Z9RQXYyc4J4QpXCzh4chuacBm/mgL59511TcmZLNO9vCigB2Ae8UZpRxdEG2GHCQegdJjpD2NUIvRrX4xpaj0LsG1L5pDgnxfLEnxAJvKoxxnDBNRUI4h3WKcCpTajWL6qnPR1G5vma3eb8OfIE35RfC1KggMRMBtMHldiPwQ8CQq8V+0rNhGGQMpjCJwnVp2Th9Ccc0lYLxcAAAjNtJ+puSONyQhEygOvE+lwzWsHLCDFOMb8zssOWrwKL8SoqXClf4IYIrzixfWpwPouywBQCJJn2uwofAnO4Z8zBWfF1USVfUAyOp5VvyHD8mfVH8FzgU32dxzZMIl6ap4Pv8CW7vEugV4/nLA/DsU6TtBnT9PTDegdTqc5pGiJKwjmOtnGRLls7WXuAF3FuZEOvme9AA9+UHTvCH4UHtw0fh8IPKuu6Gjqztx7n+WO5ZSHC0FYbk2pJP+V6INX+BcjiO22sCXlM6B8oJgAWQMcvwKBIUYq+w4HU3rFkJaB+oEhBYQzu1Ii3vAbM/JzSZXBNaX4XsgJ+zQajiN+ye8QM+WVaSGT+0k+lPKA24Uxrgs2cvcHH1Ei+2OzzbbLDJA8SJUAT63o97oGPlfEKbPEMcPt+UMW1f4m7KuNnf4d14jT1+jX26wav9G4yo80Jsiie13ldUXuqk2CToJEY+TniS4gYirM+VQNOzEVt1bv17oD2djrPfFbriR2VE2mBc7qXgrymd038KoVH75DRQCc/adfm+ukwe85YC/Oh1IVyQc8bu4hIb3uLZza/w6eVLvHzxAs93F3j+7BJXm4LtFhq+64jxzsfSlgyxwbEcekrDJhSw8RnKsgD1u0MzhXtf7IEXB+CPF8C3u66hv+YVOZsCfK9NMhq0c6/yaEXEQ2lahnhC5FxwdXnAs6u9MDjFDsT2RKoCImWy7ZoLdsg9IRpCvjnVTpVjz9HCz3rILYeVCWxxsBiLz69bjlcmtb3cPt9P/5OCYeQWQ1+q5dt6uW8/Zs+fy7Tds50HVXgCxs80ePmLLb1y4FF1mesouj2VNqDN5WwP2X8X1JTRkwbrQ+2O1PcPk+YxA+FuAt7ugbFY7BCokPGcBT1z0dcEEY/dwOH99dwnbeiqpYacfeirWDrjFprxSw3uba2miGo7jdIElYEh1BBG/VRU9mMWVbZ7WmChqMBLrMBUwIhWaCBJsTrGhvo5a1v3VvSIKqyhorgus8smmkGIIA9JXYn7eyuwdHJLzV6b11PHUrq7pOsCZ2jq7EahVZx9UmKR9Nyt+9DDEaqiiYjBmpg2axiqUQWPgVWCTwaxEp4cmNqWqaqCWThHFrdX9dWo73kYjX5eFHeYcNRHmwjEIkDOmpjOBL7TVDCVCRnZFZvaOQDsgl+29V7clwYcFd7Z6tCpruvO3WhQGbDILds6ruIk9jbcuty9caRRCzPia+iC97qT+zwfjTGSNe/wEfZBcRZcBc8WoiEDICSqtnWAeW+03hhMGYxciV9VVNWE3hW/2CxMtEXBc8jIioetzcqAut+GwbBoItzAxSd/puxoxwtV5EzMSJrgvCpdTVHA8zpsLYGqaFm0pJ6vq+0Rw3OuzDF6uSdbne6s1wonVwZJpVN9HjXBonWByfZghYWq7OMZuMdjoxFUmXJD15qZMTLhriTcHUYJFUcDaNipYE7XJ27UI+WUFf+aYkHQz9Jcn1/6utfqXHjxZL/PbXN2P/ThPuN+8nLiQDtn3X6Ycs+5+UD8wBr/0Vx/8LrS/VjotfcXyn2td3/y/NVJuJ8/VumyDE4JZurC6lFGEGFdphrux86yBqUbZRBoa+N22nua2FjpZ+8DWjxe35tRJnKemmA44OqleuoFpUf8XvcU2RG7MIc6YVXcjEaY6ZOo581AhEwJF5stLjZbif1PLf0xxzHdedzzEM1zbbG+9OMWkmgDThkT9hgLg+ktCu6w50nD+GRAw9lEh4KGZmcCVHlSG22JMobmWKCkt8yLIvTIFA9c3/Lv/Zkbl93vcbh5qsS2lj4jbHVw1jxb6zJ60adlCfNQ9wn1QE2EzZCxmbZ4lj7Fs80n2G422G4ytjlhGCxsr9GI547zCcsSgnhslfceQ+QJj9fV0J8KpwKHcf6MJ4DQwdTvoHCI7RhpV8DfRR52hk2W3r73KI+fNUu0Obo+LdDuTwAuq1U4Yuhg5My1ulebsc5uqA8d4vtJVn2i2PH2q5+/waef3mG72WOaih58LbInIMTerOFTCBSsIVURYRZZ7xtBUPMxU0LIz+SCgVkc61NKiI/lY/krKr4fUgLlLej5V4iZe+Xgz6Ccm2tmCU1JrD2YC3hK6sLKzXNyJorA5G5k/C9/mHB7ILHQh8TL7K1dAROmncdAnCwuBDjyQks/NuNdZNCXz8RZG/7b4/N313si0+9Jh6hHevHwsT4sWVu6VF5oX0ICcnbhL8CufI5MkltcO1Hq1TgdWkJb5M0zUBjjNLk3hFjOEihljWOuduwq9GZIXW69HRaA7C8DrMloxdJYxlqYUaYJZRLrfWkrwcMGMTw/RcqSxAvTO1iM9kdw+F5/ZGzYFoSraic+LI4C3CjqmG3M+kni4UA6qVy4uteyejpAz2MzANB5VTZU2iYSIafGLU66xsNmwjgx7m4kpv40TT4foqBo0mFDuwyAFS4YKAVE4sWRzGSvkM518K4pLJZyi4YCfdH8HkQYHNeYQDdhP95hHA8YxwmlFKQdIWFwuBwDrMrusbGIxX1OEppnGovf5fBOCnhGYDJst2AoxgDKFOo23OUoM6iSbJ+X2i+wzE/1ooBLJkphIFlYLrjlXY9/2JRvDYstFRX1IhIHGbHw971SJG3LYWQcDhPuDs9xu/87XA1v8HLzfRWicA0ckXRuGAlv+ec44Ln7e4+TCM2TwrApFZJayhcuIAzYbAbpQyku+t5mwsV2UEa6IGuKE8uVkHNGTgnToYinHa8IKCLcs+TKIADjOCJD6hPcIviOEoN1fkWxNQUFSJLwX8W8U1jHwbosiksjoKA+m8iY5dT1VXEBKTbXpNzMMrclJfQ52TzkqWbsZkvAPakiqejcm/JR56N6wFg9SclhEmZ0xlBXDDa++TOmu2vcXPwch59douwP4GEDUg83rzM9PtRR70UYZ8rbaV84r+KFs3qRD1ju1HltnNHmrOqFPvT3F6t+WI/+IktUvsUiR3kw9zii8PnJlY8A8EELx3OGGCXvMD3/HBMPGKeESfFgJoATcDlkABfYc8HdJMYeiaqBw6RnvqGHntQ3IaB51RWnx9Ub1fJtqaV/lcPWnF5S9Gxl9lw+FEJsk56zxMHgARbKlJ2PIMDDPZqw3JQv7bZz6rwqw5uU2/UxoXGEpt1uN9gMF/g8vcDV1Uu82OxwNSQ847fYlII0JJcpnRI4O+/qT9lomi5WmRHZTOqTLP9RBjAPOHDCngl3XDCCwJjEm9JfgOY0EBqfdLKYs4bwEtp4xouxGaFMfu7633gOR4WDve+WMn3O1jg13F1TyHKiNf4u7XcOdSuMyPXwv+j5b/cijxB54AAf/fha+ppETkCE7XbANmV8tdlgt3uOX1x9iecXV3h5eYlPtoQvttfYZsJmsFDwsxH/FZWep7Sry7Phxkj2BAvfXdi84FU5AYCZlF4nTQYuNQjvTSISShFe79vPFWHJ2YW678fqWurje4KYDwmIPY25DA73Lu9dERFhJg8FOStSIsbl5QGXF+oJISeeveV/qfklTI1pMC00E6glsKNN57HSMxwzjR7In4t9aF7qfvjm8YOHjn7W189bzaUks839te49pnSM46k+LJWnpmVnKOYYg/UjMqX5UemeejlAf331tfkDJ2Fh9TYBSUOWEIHyBjRc1OTQCHuqac/+Uw2RUqpltgmzxkKYJrOEl6HejoTrvSgkhLBgF7pKWYaXRYulpUejwO4hp8TqK4Kljim7Vz0bYuVM8DiNjMXn5w7WhgGpClBXe7i83KTMBIjUQ3du8d6Q9JZoN3ZjoVcxHJ9ZWxe1SK7EKs333jl70RgRZahcuMy5EY67AQ/gliDCULYTLE1OYJ5AQdn2kFJ5hiOMUtjk5nq/vObaaRd06j8CSuLqcqmgw9C9BwLUIIDdBEZd5KloPF4RwMudAtYrlEhzMRQfkFnqxx3k/XcFyhzCfA10gG0olFrbjGeJFzg82zNrzKqIsvxVdT1n8OkUt3wYbiHJID0bq/XGFWlxXOGT66swxR1B3PcLJPExU3WBbkdc8UK1Ztf7dq4jzC0re0DVMyiGI2v716+H4hhjQshwhrRZinkRMQonjHyBgj0mbGv8ag1p4EnnSfKYMO9QcKkPMQpGnQ+hCyWZN0BJSFuehPHOtlBsOEMY06zwbooBECuvY+dIguxXnC4MUdop7imliGcEFxAnZbhCRSaslAGHM61OZ9BrhQScFD4MhlS448nZ67KLB4MpQkxgI7CyNLDIHFasTw4fvkcNfnPTubqvulrrQKrHlQ+vTBLK7O4W2F/jcHuL/c0tpsMBZZwg4aQGgEdDrD78H11pLMYoXA54iO6vSDlKrp0DoGcoK9bee6pydl+P9ONeYzhHOdP9PufV98pSzOpePuVP9aHijod3tqKcFX7zRN0N7d49W/nr5Tp+RGzbk5a17bQk4xEBPIHzDpKwOlh+65mYErDLRQ0xqnffVBgT8yJ8R7i3U9+8VN1MwmgE7nA6t+9TPAucpmE0MZ3YKQB4zP/QG69rNlm1jSjXqTkpjMaQ70k7GpWFdV7lrWkakNMWm+0Wu03GlhhbMAaMksA7hCmM1HPtU0sP+eU5Wbo8FgBIGYTBaWhCAgowsYSbLdpmsV1SnfVDJQ0xjkrDQ+aY0AFVICBhsx7o5DBPDQ2L/ntfYr2Vzpy3beuP8Hx8LsBGA0+seoc2VNPx0i1gmDvPW6bwkilhSAm7dImr4QoX2y122w0uMmGXgS1NGCg7n2lk07qv13suDW9zxrOx9Es9e/5Ufev4evVdI7hR+WRSmrR3jnADJKPHvWozMiJwZtCuACN5TsNTQpmOOl0fw73KqTU4r40H9WTtJV5+4FHjPUlorHToHnTje1FELLXPYPziZ9f42Ze3kuwRjJwOytjHQym4laMyg+b5IJ8S+1a01k+DEJaI+3qu1ARQx9qSPodYDUTHPz+Wj+WvvFAegBdfiQIiEYgy0rAgNLbn9Y8RoBrLQkKnmEBUBdGlMP7L7xjfvatbrqSCQoxDsfeamsP3gBG6g99+nsbP74OT6vsW2nI6r8Wnbaf0nmY+qyKhSrHN+71A1C2eO+RWTZXp0E4GQZVY0DJGnvxZt9IFi9XDNOmrHJgrI/5r0nLSGOhuUVwYTAU8yX/Re7TKKSKxmGZmFEwAQa3227FYyCGJ/S5W8IUZiaSNotY7JnwEzOpGPS64gN3Mi5BNSgp0Z8D94SQyV7NvzrxRIP9ZjY/0F9dxghIo58ZiiICa0wLcMJu2pDUcEwVLFVNIACg1l4f10ESaQMHFBWMcCeMNKswwyxoWCX/UJvurvUua88Pmuw3rCOfRmgnBfKbj+T7jnVBzMQDQJN3iiTEMQpfIO1z5OSaYdbrAC0BpUI+IJMs/1s4Q5Lp1xuEF4p1gXlolwJg9TJYIGZVXS0rcs1qrS/z96iHiTHSyta/jdA8a35PCLCDk3zA6zBgGyR0vIYecaVe4I7KcDtq/qWAqjMPIGEfGQYUqeUjY4xO8ml4gJwmbMKmHUdFFGWhAogROGwxaoYS+Um8bDaWUdMzDMAAoGCXxDwZ3UEpOzW0ykLMtfACYlMQrIuXmPImKI4MbCr8YYuk1jRMI5Lki8rQBMCFllSaoq4vNdykJORm1qcoPv19hkWVSdW8aR1mfiYIR87IQT4oEDPD8OF6j5rSw/RZAC+Zx7HGUpQs+B4VZcCyAnFcUqq7IkWJ4vJTJx2qCzOnNNxhffQOeRoAnfPP11/h1uga2F/jkS8Lzl59iyAnl3R+B6U7XpTKxSxh01YvwR1DWvDEeVBdOs8Ta6IN4j1PhYe9VV6znxP3Zc+f2/8w15/C5SNJwPU/qHHCg/47EJX/i8uOE4o/lfRShHavEwWhGApCYkcEYaELKz/B2+Bk25R2u6A0ukQHsYNDy+nCH68MBRWkD8/51+a89aSyBtjuh0hNmMEEg9TxVutgCQbF5PZgHxQQuEybzULe2LB+Bn6Om7Aj0aADyOY6x05KcbnKlPao3e2XnyI9zOW0YwzQBTPj92y+Qd3+Df/dvvsSzzRaf4hoXzMi00TCcxi9EDBFXZ96/uaCz/pyjrIR09SVAW6RbCeN4wYRUJtyMt9jz3nOCsIazKWzGcgmg4rSnVJf0DFQsZnwGC50No6vjYjekRTzgF4a8kiNkvYR2gbZtVybofTMW49IpG+z+pNf0U/OttQCzgh0DzQpEh0oBIMoZmQif5Yxdfo4r+nd4sfkUn1w9xye7hF9s77AbErabTWRvqt7mJ4iUmRFZ8fu/f88bFsKVNPYnBX6F9IuFRha8Ryi67xLX/e3hYgHQzw7gLw7Aby6Ab7ZLjf74FufR/Tmbylt48+nm4hT99tDyIEUEzb4cf3IzTNhsJ1xcjNjtDjWxJy+EY0IAPhcgtcKkxVwQmE/42QqKhccicbpcixAI1YVS/9jDa0qHp2I+FLAf4mrdlw9FTC83frz1U337qXhCWJkpqD/E5PfT0Ld59jZ5fGdriB8ST4i0kfwPeeMJpKuAc6UOIhxGxt1BDjgKAa6nkTFZ8s4CvN0z3t6qaysBtBECOFq9HJsAE5I3C6dCkLZP+jzX904Wbj7a+pauuWDFMFPwKHD6siM0u+xB/nY3AHbL5zmwUMRra4PQV6vVks4RWUzIbrDWTbXCquhSe9Gsv1DC0uWEVsAUhOFWPVfr+brEixyBd31+zxZUmKgylXZNOc7zwgo6wVeJceYJlmz1SfZ9nNKj4BYZj44JiacckSb8q/fsLJaf3IZHMaWLW2ELG1h0cImSKiGiJZsxkayKngDP/RjOQd8KmlxszWsYAZeCh7l2dnblzF8qLozSMSeiBUFwt5/YmGtW0DN3elWIRTyIYOCglkKxT4FNtCGrfJg8ZFbzPHfd4vZd/xYrXpTEtbcbr9OFCaxVUBhPrYRhXhDF87cAkjiaUhYkrcoaUfSVmnCTsuQaoS74QpLZyykp+Mr85iQhx2oYzzgWg88aAsKvUwWZ5S16GigZcEW4e2ZRUubaOsJ11SPuo3XYXMJQ7a6qfTP4IypA0tBVFuaiqyzitV4x3be5PvoIdPbmnAY2+HTAtBGUEWW8U4UI4fp2xHev7/Czmz2eHQ4AMpCGKoCxeVKdBq3ReguTuUQXvhcy7IMQd1LOZlOfgCZ+Cqr6mEfIMc+R1XXu6zizH6YQ4qbdAK9Ko1RhWmghKEaW2otK/yPo9azerw772Hx8QPj7WM4v1Qikve6/Wc/wJB7iyJvAezGYR4BvkfKIlDfAOID3WcIKDgDTAKSMPE7YpgkTC080WuUdexBpBTNNKs5S2AljJ2Q4LbhSduzKCDt7WJUZce9UmogbAgWnN4eyEA2voH89R5kOqPfeNbmkkIMJzJcAvcAmbzBkwkAFGdycvXFpOPzteYX4nFFy/p6zHPOTWvjeLTjtZQwFyGze1iWcnty9K4xFL0w2r0qtHGJ1xJXuMF4k4rEed3D3xZs+QgX40BogCo8agJVaX9OOPm9yQPeise9c6yixgq6yNVS31HW9lpKEjR3oAtv0DBebT3C5ucLlQLjIwDYBQzKacqX+H0u5z7keiYWV19ZlZw3heF4htN7g/rrKYnRTR/g2BYW15roFYmBg0Abgiwl0OQGHBB5X+Pcz+rY0ln69H0U2rbx8ssp+P55B5T1Y6XDGAFfRRVe8h/eYtAcoIqj77H3G5uXLr27wq5+/BdGEaZpQyqRxCFHxiDLr9bN6QuQ8VCWEJRF0AZSUSEh+mNwL/REUzoFOCfFjx2Efy8fyXosTd7ofTAnx7Csgb+Q7oiDmuCICAP74HeOf/iBSCA/NBGCi0a3VxeIToC1VwQWRh2laL/MDsxlOpIYfUvjx+KoyyJVRjoxDSytGxroVCYvQbbl9V0Cs0qH96V0/at+gYVag1ATEggo1wbMJEy0kSkqmjJhEkM0au54LzEjX5pCynh1qvV8sn0Gx+KJKKZMRugwuJIbU3m9Cyhlg874gz2tQyoRpnHAYR7GWyrmuPYtQ1RlL+2uWlBKEVD19GDy+gYR+OU1QrBUnvbtl9pVwhk3GPfNM6RaMwXb4Qk2pmrpMKksgie2b2EzntDGFX/VMAdVYrJIYOIEhCeQPZVKrOmW2kjADQ8punBASjogFvJMZxYVGBARvCB2lKiHM6jqlFp/MQzVFAZIxS/1MCwE9TaKISiAMQ3bapJQJE4tFuDnYgzRniMEG4Aoa2+8pJVHO6b4tsPviiC/w0uIFBsClwDx/zDuUSsUhslw2InawNwMzEdQnROWkK06NHiPDlQvw6VOoLHen5HGwUUVNMvjR/k+jJPo+7CeM0wQuBSkl5CGLJ0SqioaJZM+zhnHKFBQHFPG9tJm031lzBm0GAjNhoKxzDrgruHY751TrC8y95USI55ALI+ejdaaJWdWMRbxJ3DNiIyKgVMRLg9Ik+8Wm0oUcVfxPoXqbQA5iDnvC+XNF1MKwsXqUiOAnK87KgHsR9+uFhJBHxKqr61sVFEbnkuMaG0FRRYspd4RGT9pX8rNKcA7qvNo9xQGFga/fbfDt4QpffHeHl5/cohxGCQEnHa4hODRx9lEls01UHO+xcp/zeE2qeKJ8GB7lPZUj831+FSv5OXoDiSNKiYe02V2o113SAdj5UIyuMqGqC8kKSkkoSe6T5dvhIrnGnNQIeNb/PGE5xeg/wTp9LB++EAEoDMIG+fnPUdIgimT3JniF2+k/Azjg2Ra4+8MO1//5b8Ev3iJ9+gr8+QXyy09xgYyXwxscVBHx5rDH7TShqJx6cpzeGjSxWjdMjttDeEYgKANN8VDcu46nCTAlPFcvQs8/ZDH/bTO4fLqegUtlEdKVlzMDBI60SVSKGG2wGZDTBlf5CtvLZ7jcbLDLA4ackVJxmnGeK7A7F9tOeK+dVvDzjSsPZXNWWGPkAxMDBZKAPI2MNAEDJFxkVpq2sRrg0JNidHvolHtcc9vPYhNtdRlRaP2KIbQWxre0JJGUji8bouP4vw+pVNQTQj+dVxPe0N5hLkDRUIzmGVFCXZUbWuy8sa7+JNcblBK2uy0yb7HBv8WL4TN88fIzfLrL+OXuDpebjIuLnRjJZIPKokMkbeojbj1ZKOxpSsIHMzwXn8kjLOeiebrGPGLytuSZ45E9lSF+cQd8tQd+fQV8t/khRvcDlDkP/+PqwSJiOFnuoYigo98bplmRxGbD2G4nXF2M2G5GTM5ohBAK6LWN0fPBBBx62Ghyxb5wRNa0TuQ+pLQeD00z9YJhPJATfvfOAfFAhuaDlPsyWY+o69yWHiS8PdHWqS3UC6QX+YA15mClv/3jP6blP+UBcdYahIPInx+2YrqTBiBLyI1FC1siHCbGzR0Ed3BdgVc3Bdf74oIzlUMDJMLSNtybeEAwNFdE38F7Ftfi146e89LCV2OEa19mmvj4vWGU47vGRhxH/vP7DFrAp8dGwwhMy1mF0bv+SqLqYvy+K6Dr4AOS5VpPtLTyq8xNyou2XZunMEajq9ksFS2MTHAPD/VYyB8UiFFup2S2l6LAy+q1TlVLK0ZNFveIjc7dl/63j5Wc4WjWfoboqD4b59zP31gXA4mVWa0EpterQmKZU/kmyXAJUCVRikRm0tAuxCgTdXSBtFm7szBn3dhp7Tl7RM/pGW4jQmKWfnI3k1yFnTExL+u8NkYRLHkNuLFqs+kzmIztwi39fE6OjcHoC4iiptDkyzYjCI3ob67ppwvhCpgIyaXw9lgNR7nSkfWrCzjMmIvCNSmmgB15OKZs3jgkbtkgQkmScFy6Va0WKeAKC7dmNKK50QufnkK/1D+H5BwwxYfcY1cYJUqyzrNRzL+GzTKfDGWmOeKQVHS9omh/aR5PK+NXhSWA48mKM+uZyIArg2ddBjsMRqgytGA2sQKj0TdF8TwVMBvOqPuRAM9JUQVb5M80fWRg4oRSskZuqKH5Yh98z5+Yp2OKirVyDm3T13tfmvShJ0CDoh9Yx4+h3Ndj+RRfd1Z9a89wj+16mqql1cg1vPW+g0N/3tqBcr/hnlWO0XwU8fyjGqf1eTunnHi3P4sdM54A7sd06b2Xpc51A1pj+RsSlAYQZZDSEwmM6fYOt9+9wzROKIcCfJ+Bd1uAt2BsAc4ot5PIbXMGb4CyJaRUsIUYZ3GyM6B6LVh4RQp96PeDdgqRlgdrXglmD6VYULTeONbqsbo6RwtzwF3zM1J/4W0Of40I2mODRAl52GK7GZBzEhogJXHGXDPAWChnPUXNRzOflm55ZMZYCg58jYKbhSeBZsT+1c7bhTaVfm68Iap7RoOz4vwsj9AQF7WA2vQjvtf3u+Z/k1tFLSeU/ws50/r/pkzyejqevmkrhAZtumHNNuAroazokJFpg8vNM1xuL/FsIFxlwjZLGN2k/Ml8yNEkJFT7IQ/jxfVaoOeWttjyo/r8OWfo6UcW23PkUte8J80q3gm5IhDYT0ioYICAoYAzA2khD86RMZ7ubCw/5kMGeHT/nuAQNT6mwdf3LE+QI2JJXCkA9vlnt/g3f/MGoAMO01jDJxQDQBPQmLDGlA4Spy9rjN6URQWW0pzdrrEUTx9PjxhiM9Kq4aO6uQLjuqaE+ElbQX0sp8uPmjL+AYpvkyjkyqBnXwB5B5AQgZZ43l8LBOH3bxn/y68njCjgNPkzU2HwUC112HFDyzhasTin/V6eP2kdfcK15OajCoQiU3sEd1VijOMZXis/RkcuXdeTOsr9TymdvM2GGMScK+D4X/srmebE6pgLpvGgFj0i/BuGDAJ5VFFnaAIJ3wjVUEITdo9g1uBkxKzF6CcNj5JI4A3JrR1NiVWgsfUt1gdECTHuJ89xINbbgzBT4RzjwnVeCOCiiWkpqaA9C5PHNs8zsun03M+erkDF3Z1+MSoh3lF9Jl9wZYX2LdXzipRRs1ifgI47s1pQByZFlRbmUpuKvLfZAKUQDtMBZhFNUOv8gXFxRTjsM8bDZMumPUkVKhpDB/nThq4VwE5OQyTNBlA3h9EaSccGMmG7Gj0MGRnkCgORgRZgBKYyCT2i+RHcsrsw8lZyCpRxRGHJV4HCSMkSEEgpGt82hpCKvQe1XgRxVQlQhll9LxI17xptZOuUiCQ2tCIKE95LaAJ2wBFhKoNTCm2pVwYzLGcFa3ShJcRCCz/8WSY1iBOLyWmS3B+s+S+GTNjkjJyT5ACwJM+ZwJTFe5YsrwOL9WIWl3oCME7aR1VGDKonkqSTBBqyz6TEn9X7Kel/M3qBnE3JXKyo7nEPI2X73IYazxTxBnDPGBDKVEBUxDPChAKFah2+p4wnr9lUEM5AwSUtXFT4qP8a7OD91XwOLAqCwoKHpBstNqkQad6DdUk9xAVUaUXAkMXDw5oqiGH4yL1Ukky4V1Zpf/OYELgYx7HiqkzigTaIF5r955TUgFI9pBYU6X15KN198q1IszyohfPqXrz9V0prPqWR2azuph34PjWrTTkWZJe4R0QpIM8PVcClnp+NMcw9l2umr6b1e+vj4acRjj1Akde8+gRd+KsqbPwKAPWSTEJoAsy4/eYdbv/fO5S7gnIjeQ9oGpFud8B3X6KQ4Pc7fIpb/gTlP9zg8O8HXKXv8aLcYCrCP41q3PX6cIdRYTyBRdDHgOF2y7Fg54ALkfU8dHKb1QtCZc1seBoIuQDqGRr9m4LNOQAxVmEg5JyDvyeG/27u0srRTWDJphgpyAfxyP1muEDBc3zx7CWeX15ht91gsxmQU1ZPa6VzG6fB8zfuTPmIIB7yjgmvciiMAzOuxwk34w1e0T/jJr8V3obV6FuIAq8HIEuJhXCxmT+bIFsmE7qDWVwwvEOBDrEJbIZqNIr94dqgKzRQ+R6vQymJWKevOQfAsE/N+VCMpxI4IfOcKSPcc6J5L3TtyBpJN8zoTXBzGjKoZGxef4GXu0/x859/ic+utvi73YjdpuBi2GLI4qUrlZhncwgf9IOWyENyd32tcP3LJx59wuKGK4kAi1BqtCeH84ELPOiqyiM49pOSK2Nd23+yLGyUh44jbJcffVnq56Om4P7yivuWeysiqhC++fDCzNhuC3a7EVcXBwxDwTSxxgTuGDkTDCgTHT/NIkwSI6WIdZq2us619/0wWFkF6n+ur1ajhCDq5iEIbk4oIZ5q/793pcZTWXet1PPQ3q+N+5gm9z5bZ+kslq89k3/Pcoyz+JGUc4TRwBmw51sjUkoEUk8IyhtJUm3PEmEqjHd3pF4PowsKv79m3E1iXROJURMwcogNIedTsGGLxFXSt1whcU+Sojvvj+EW70EDPxFG+1YNR8ybW1JCrJV1t+b2xagXssaY5n2K90/SOIE28HFyuMzSD1biutj8qbAbgBPdMSls7UtYK6NQlKBhS1BdoCFS7Bmo4IB8FlZhPL6jf4Wh0pwDntyXNAm0/mPLX9EN1oSbAMCjTgAdn8dzS+jnDCT6qUN8qOFcKjGfCFxU6O/Z26kqbuxca5gSYTi4xiN04bMLZy3ZtQvDNQmvuuabGjElQs7AsBkwjVNgWlEjNYViRKHb7DvP1ElrCAJTlisCYQjhdyJCMeUJJQ/3QsZEu9BUaBNx5lE3Yq07LishgamonYLCnjHWMKvBdrFMURDXqMUZxn5QrbeDpdT9tqWKcO/VdZR18Dtp+uA0P6n6KPTXO9nh+8YoRJUZxQzhHOaAzELfaSQkFylbvGPSBM5k0gmStcpuwCKwIwoxarpuuoQUJoXVHYI8DJQowRPIleGk4cAcHZgyNa4VZlPvU2EMq/9WjwgEZUC7ImEFKiC3pD8v2d/VNoFmKWVeCCiqFIgJqh3X+3Ci1WFbLzHX2NOoY48gJBugdG9X2t7CtjUVGxxEgOUQei0l5MstNleXkjMEogicJktUWeF/dmw9dTlC68yUAU9I05308niylj6WpWLosVlipykA0jPCc1mxXbdHGTOe5D6Lxv1+pKP3V6t5CoKDzm9v8dXH96ApPxmB0JllNh4i0HABDBvFvwJL+7dv8O1vf493X79CuSHwIQEH40MMoacQLk9DPr7eA7+X0HaFMg7PR0xbYDxsUCYg0yhhMgtQUODmXhRhWgwTiCLeq3Rgt1HQqMbj8xyfCdX4mSc/jMSvr9b6LdPSEhhYrfVx86BM4HKBwi+wHS6wHQZsqWCDUWn75DSD7Zhe+HiSBTJ6daHIPiBw2oDTBhMTRmbsp4LbccSr8QZvpluMaoxQeGl8HAavh1+Rz0XWohmADo5rb+b9i6Oxr8YoUKX14qREZUbD97Kf1XClGipUOB3A9b/5iTCEHmgSbbNfBxQGO9rEJyB2KQ5H5YpZ6bxn22d4efkSl9stLjdbbDJjkyz8e5hCAJbXbUlicO9jvx4S93xxsbLm1+ncDu8fea71QUhBQlLPeGPP6hEaDEt5eV4tzC5VYHxQH1teBfPNE/BHd+HJZvJx9cS3aH65R1xnNvIwkOxx7v3LvUIzyXlUp2+2doqMPnm5xz/83SsAE8ZRLOBKKW1dZMhfLNMAIKkHxGCxgpVZbDnstV3/dEyA16inUq90qCxk//kXUp5KCfFEz//Q5XFuzX9FpRNIufJNhRF09QWwuUD1fJL9xUS4HQn/33+ZcDcBtClOmDIDU45tGIfYJkJLMyGeuYTqR6m4mIgk5io6ZL1WOqJwzYEhCsAbWg4VNzbTRbHhnqDwN08geCNxm0q906fIkqaT3QMMVqF706nlwiq0Z4SkYrr++lqRhzAVYXUszv2QB21j1ASvKuBnABzCeoREr0b1F55QuCCxeSBoAEm1nCnTJD/LBC7Jp8jioQuByWgClTC7ZbZYZ0seg5yyCq0RlCYQAWM32TJyDVHC1yCePKnzo0pH6weo1uuVCq/W1fYnrIn9UXhJCbDEGT4Wv18t8EX4LmxmKUmZ0na/W6MesUmJRy4TyjhhPIgVX9F7KSVsSKzgD3cJ10wo0xhici8zZY2gaCa4qWECklvzh77VCQDAKhDXfBXK+I80YhqLe8KYFT1PI2hKyEn3SBA8gwh5SACSKmBM+WbWXwAX9Q6NxK2275Z8GmM5LJEIy0P4Iu89hbnvYMIVZVRJb7vnCNZ4wAie/Xxyh/dCO5RquKpw070xJM9KQZk0B4spExKQk8zjkICBgNFykGh1KWlsWO3OoOEUbI1BBOTaXfeEgIhhUtBucFIaMyUPy2Rt2HWiLLGuSxFvjEk+TZkAbnew9aGJX6/rwYVRNGfINI2YpgJQQVbvLJ8rXW8T6Bgey8g69wJHfc4Q3wAqtXBBPknOmwSoJwv5BmDNm1PPQutDs9xarXgoZcvJlgxmdK4130ixhDsNzoD3JXp2FJa8O0hUc7zoOJjV42XY4NmXn+Ly8y+RNgljmXBzd4epTLiYJhCz8wzFvdF+gLJAJ58bOuixhkRnhaO65ztr7z1lmYfw/fGUU/y6GB4wiCRHRErs+NqUl+ZFtpiM9yj5dGIuotL4yKOzJT5zjteNWM549xjMn1vJ0fof9/5PrlAGnn2JkgcN7y/5fr793e/xr/+334NHiOcN0BxGFL545DAA+O0V0u8KDrjCIRW8/r/8GndfvQO+/zlS2eHTPGFDB4zThNHPPsldxUm9fOzgY+MrFKAVdxOkTQszacc40C2/x6Gs9DPCc0KCVKMHV8ToE07zCLGFQpqa2fiFsInduyIPSJlA+6+wKf+AFxdf4OXuAp/QLS65INNG8gBQNUiwHkVP4OMl8DyBFmAdskwfAZefY0oX2B8It2PBq+s7fHt7jX+6eYt30x3eFcadeZT4e137LsWFKET1tuXCqHMN+V0SqpbEXtR71q/Y406pJB8kNEs/Dc0iV3jwPHINT1iqcU+TNyJ4O+hz7DkkJq3XgllZWORIsyzQtP2yALBIK89zwm57gb9/9kt8evUpvnj+HC+2GZfbEZsMbPMAcYxln09G4NeZTp4VH8tSEeO8Qub7IItTCiAGM7rDmX1+Cxfxfo60E6vhXC5YDJGl784OjoUFM4+Nv4TyIcip99XE2YqIZXFZe3G7nXB1OeHZ1QEpFWeoo3VIFO63jIp6P5ilmmotHZYaq66lXkQueX5nse/Njf5uN2J9pnaDmvd6b4iTidV+QOrq3JbvzSwdsx5bqfuxzMhTeUKc19YZz3Strltg++n4yF6daOcJy1F48G0S9sGwg57ospfzAFJlo9U3FcZ3N8Dbm4J9kQRpFNXkR4sSIyp09eAihECnVEKNAHEVVhyU7A0l3I+00sIZkQvloha/f8e/Lwj1bPwVf/T35ZA+a3scmarWO4P9a+1zG9SDqCVMw/FfOxkJQJ/ruhbVW+RIf8CzFpYGZnonoZupv+1hkYqmC7GE1wYAIuQSTxsJmGQEeRhwY/Er30uJ46hjN1go+hnHU48gaV/4Aob5T8Q5P1ZWE3nGgSO23b9/Du9E4a8+rPPWW9u75bJL85VRdMZLa/KzPbYAMInVdE5ZvRMs23j1OABpfP+BkAdlR3ueaHm0oU/Gh1gkUanArVYbSbv1eWGewjWhQUQZkQIM+OsqdJpgdE6Rd2xXsTJ+1ksO6xMvznZd6foenjWlgjHOxqwGJW2tt52panVOdX8EPEbKCBTHEhWW4/T0JV6TdjRRJdSDxBMhC41nqoSaO1nggeBgiJjA3nCixXE2BUsigJmCwoH9OoUQCwxL9J1c6VTXsQsPyG0olpqXpuLqGdi0SYPqTJigshSHD3HSUbzF0ATuAms2+EQk4eIWNnFUarPhXrT40b9byIlZLV2xMbmCXmn3UsOokceZDjiv9qrC5VLlYX8U5ponBoZHveOyxtMB2N8AuARlY1vZlRZt9Qt75KFlhe54bP4HXqjjMRTbKk+z0tY5bR577ymLnxxP3FZf3yJvEPb47Dpz3LnN4229p8jTtT175I37guzKCw/xgCDCIp450dQZ9Xbn0fyJMypZaf+cTv1UNBiRFxx2oLQFq3I/JkwvZQRPhDIFMhPzWezPJmISYTQDnBI2Xz+TB95k0FiAyy1KShoasOBuuwcNwG4Sgy3zEJ0spwRZ/PbIT7CH7yOQ5wMyKtO88OrhrmfbAv3V8AW8eLUZd7MfOT5ETpZmyhiGLYbtJbbDBkPKGGhycrSX4c9JdToPnMiarbmUmuGwmEiMhXE7HvDN3R/w/f41rqcRd1xwKIyRlWLsjlepn7s58QbhjNIahebMFGkdgZ61e74g4YRhbddouB6HGrPhRFPfdn8h0g8+MV27PR3b1iujln6UHogin0r6hSTEu9Dmz5DTJ7jcXeByu8WzgXE1FAxqFJOo1s2htcWhPKasnUUfoPwgRgA6r8Jy15Ce0M945hrI2UPNPX+HRFn0bAJPB+DdAIx07zWKVOvMQ+JIXUs03vKDD6RPe6ZqoThW5PNgae32cZ3NsTqfBo7O94iYMRnzE+STlwf8u394LRZkLNak0yQWq5bYzRGIMoXR8yEnif2bksQMNwHIjEhaOLyOdHyFaqeli21hPXzswHckTw1umsnHTNCKluD+UGTRvabnY/lYnqjMPIcuPwG2z4LCsVqh2ud+JPzjvxa82xfwMClGOn+nMBfwxBoXU/drFDQ7sSxCH0414WlBpWA5bmi0e7r3ZhBclqqFsBN3Juju39UeNCevzkk/Hv9rFt/tTq7zd+Z5psQhNxeCaNTmxztiTo/V8rq2HZ4JRCvrOGs8WCXf+pjyqpR28ZoL+KRfRT0pGj7CrHgohjqqZ4lY2BZ1Gy8ABrHQ1jVjTTjA+hxPag1kluW27kbDq4C2lBAqhMx61zw1uPbdTJciHZ20fwpnlKIX3ZGlaoRzK3z0WYid0eQgMBgNpV0bruvdLDgcFiLTwuEBJnZBZ2rdDur5l2Qdh80WiUZM44SpTBjHydfUQrIMG8blFbC/y7jVBL+sngQrQ4UpHIAK16RJwbOxEtQykqZs6QkuV164cBhIwyCJrBUmrE0LNTVN4uHD6ukzZLFkLxND0zg2NIzLHXQnFC6gQkDWTa2C+1KKWn6rKqswOOtqRGF6UFyxCQuicMP5OMGBwmxlgNgTSkYvGGtLaB9jFOuazkrk4m3uSHNlMGEcGdNUXBmRVfvAqigghiifoaGUkrpfM2teDFNcsSejHnUtPLSTaiKmaQIR13xizsTKBh+UGU05yxyzrGPOQ1USsSgip0m8OBz/614WdNRbPcezw9Q3KsApE1LJKJOEHOQyieKckq6zeG4IoyzXSxKPmkmtYdE15R7GiockBUU9Gwxu4hrN6VQ4c2g5dggs+ZeYMY4HTFPBFgNYPUZcTWFKRAAmCnC6OMIEiedLYQo54kqdu6BYIGgenpyB629xmK5RfvlvkbcbICeH68SsZ8wZNPxfaDk24p7+P3d2zuB7H12WVuwH51XWJIxnE1nnlwdVt6p0mF+/d6gyV/KuNr66PqeMyeoeX57f04JdrnTZA3oo9PlPBzcwJaSrL8B5CyY5m0aNoU+OJvtcd22pMgf9zY0BPagQLv/x57j4XyvZWi4+x5gEt067O9z9n/9n5M2Er17tsGGAuGDkgrdFzsURkgh70gaIY6gkCp2AhIPiokrshOqhGWhmQjhBK525hhna01ZNKGaPCp3AlJCTeF0/G55he/UCV7sLXGy3GFJBTlNNUh0MPGpLHQitwlOlC0zZQh0fypC8XVMB7sYJb+7e4dfv/iPeHK7xegTuJuC6EA4s6RzY55JhIYmkSylMuHpXmuVF0Q2z2E+qYZ1sLP67WcRA6NsCdRuxUULol4YeqnwS1cpC3YHY4hqK1X83n7U940SqTE1NjrjS85FHBgOTyhrzdotMA1L6t7i8/AqfPv8Cn+0G/Gx3wMWQsNtcILunZvRwpTo8u/jTQSuz8oN6ACg9CPUmdAWp4Xqq4UvNy1AMd0wW257JRAD//A701R3wz8/A32/a5sL3pTC/fznlpz2we3hE9CdfRVCbTcGL53s8f3YA0QQiST5XIsMBgtnBiVYs6QEgyUPld02M2cZLDoAXrrRTf4agZzam+f1GYEThKUfsFBC9hZiqfW2scoKgkcK1pyiNh0koS4TJ0bJmOXWin6fqXb/f9deJWWCJ/Jit0RMxBrTwzVtuzkwO/Zt1pv35AyKDNcv8c8sK2dJ8WxOKmzDDr+UdaNiC8hbJc0HUcChEQox9/w54d8vYl6K0UUu4hYaO9Lta2zhxCyN+QjETkyJJiS0sjAitrW/1nVP0hlk+L3VX6KbYfiVomSuR5ENuaS0Ay54QrRJCid1Q50pPfRyNksQE9bX2pk91OWZYsdbLYayh6gZXaiueoJdrfVzvurCvlBpOKQGaOC6phy+DLFF1wBfJOx7GpijZc7VNI5hIXT2lTp980jwBgCpLtPccYlZqH50hdAAhn4NmjhhA2YugvSHiz8ERdTzNcnlP1quZed8sPbsALpW5S2HdjRyn2bO1qnqvgOG211Tvij+ECpmHjGGTQZMk/GyOWE2QnFNCHgqGgTAdgCkyt65YlO+9X02fU8EE2r1mp4nt7U/Xs6gEJVmCuBO7hWfftgJEFRB4Z1VZJQ2ZQiplUZSZMNnzb7BaPtYMKl4/1RZ8vJG2snW2KTIvAlKCvkaq05PCBOnOBHDF4wbj6s5faZy47h1YhXVhxYvEpiicwhwZ6VQNTUyQYfMn8y2tSI6wlgZjcHOWRG/UGd0S4CERaTghUoCX/BApJ1DO4Mks9osolTyeH1nvmv9xk3KBKCCVJi4kng4MEQ6UUhlzRQ6uJG08GQBP7IfYRoM/Yri88FzqFIr9uew4r859Wwnp3EwSTmrUsFR56BJ4AhSESo5ktao57agqN/WGKK6QBkxx1SYEZlU4FORE2Gw2GIYBm5yQ0xWobIHxBh6+b1aqJ8nyyXjqdL9/OVXTg1p6KK/Qn0X3rW/t/acoC/vzKdtqzqbZeANd1eMzMhwa6B3Hf0HQqXuqfZ06OOzw/4yH6ID2CdmGc3kQx6kn+KmjnhI4A66PSH/O5pdONLI6BJPC/0DF5+cMAK90jJ7NZlxTGO9ev8J3/+W3uP7TW3jKs3sUAjylgBzr5NF5GAAfNFQiFxBnvPzXz4DNAflOz9fCABVssiipMzNG2oPzNSgXDLs9pj3jcGBMIaSpJYu2sIPMDE6aj4vFa6IKIJsT1ekdm8c5qJAKKtUgyfZlmBzigsQTNsMWm2HAjrfYbTbYDAOGPHgugDl9w81HO5PrxcJf9rmDGASmBMuVNTFjPzJuR8btxLgtjJtC2AM4lOJRjWB1NQwHIEmzFvIuOcQd21eVeqn8T8BfDiyLI+z6VOlw+aIhlkppFi3mVmhp7Tl+Pqd49zTEJJMaRKGZFb0HQI0ottsNNmmLT/IFPtld4mqzwW6Tsc3AoLkhXJEUutZFE3v6Eox4ziunnjt1/xSM9M/W6eDZj3NqiC9ofSmBJkFmxssQ2Z63xNVGV1fe0iGXKsj5wsc1Oz6chSN4YTAcvyoC1evnnrJhc6724eR0cr9/at2+kvblyNL2MqqmppV7H6rcwyNi6YKwtc+u7vDv/pvvASoYp1FjDNp/RqIMoqwCI2EGBQ1l94BISazUotV0ZbSXUhPR0Z/N5cDA1lpqeIlq/UtOCPhTgcmNln99KCa7Fr//EAvq7Z/10PJTT+lCfr9yTwz3wNpPsaf1d89A/GUW6j4fuuJ2iKfLT4DdC7FsBKr1uQmVCBgn4D/9vuDNLQOZQcP6JC+RK0RAYkLRZJyFi4SU9Djb8qTtbUvmVsy9NE0ADOdQiKGun9VUu8XtoTOmjGCogFrbWMoHUecoVBTxkp6qp2DNBHDtkdQS0d6PeGJGhp9rEmbriqmIPdeG9w3Ne9K0zHEJgsym344bdc4ns+pV613yIEmYtMcFLHkBpgnjeJDzYJNldEMCRnKjIEtsKlbbKQSClzl0U+sEhT0GHw4iDNxswchuZW2HeMoZKAXjFAWGUjWp0JhSahjbOi8iTDPYJpAqMW5FoJnsmD1rccNKdkWXs3qjhHPKbwZr+IW6Gv1+R46wKwvD6EI8+VmtIWasMLgaIi1Z4j87x02pNIDKhO1uJ3QCigpoxTMiJaMLGBscAAB7SphujRCrSX8NBgp1fZIJEpoxATyZ4mrQaxW2BR/UED+1lYKJp2atTZliidXFEUZzg6j3QDZcooJkLlWwbXOfEoGGAVOx+Ldw44uJLYa+ttnlxhKmmTRvAlzhYHuSYelZGEQZBGF6jVLzl1gED5PFMlcFiOE8y5dCGoM4R+G99YvgHg41aatHZdY5YvWK1XwfZB5GCSkRhhxyvmgp+ifruGq4IlRY4+rVlhQ/mwdEC6PqEQWxwkqQ/GMMYOIiYQLzgJw3yMMWBQcVpEyYDgdZV5cIJBBNSGTxsNnHaSHaZB4KiiYMnZhRSExHKWeUwsgsAZdQCphHGVtOPgeirJIcIwVlTqN1HiquTNJwZ40gRusDEmp6GvIE3exwUZlNAjBOjHE/YtrvMU0TtsMGhJCoSeJhwYIhZq2lKKxRphpiVfNvSJ44qAfIBPCgwoQiSmLzombGpP9TYaS8weXFFS53O1VGPAPxhLvv/xU07lu4ge1hrrpfO4cQlGBQ5YfO88fSlYcqQM6qOpxZnXL47HKESDpeWxAmhKqiErM5EQVVBsUpVChAzqea4rY23HsYBMMGWuv6OQzG++XCTvE6i8t0hM44duWcW+1z9xu7c/lM9311Vs6REbp4oKHH2k+5f6LE88088caCd3/6Fn/8f3wnyakDrm7b5Fl7fcUUwvoQVXw97GXGEhi4S/j0f/57fYsx2usJ2O7MpqJgunyF/PI3yF9+j4tP36K8zhhvBxx4xFjGJsea5btiZhy2O5QhVWP3JmRTJwFgw+tzwyxWQpZJzr74ntEEm7FgwwWX2y22uwsAl7i8uMTVdouLzQYpk9KdZoSlG3lxsY+tnrzHLHS/OxsTUCihEFCKyJYOBTgw4+2e8WYPvJkS3k4JbyZgz8ChWKpwy60QlO1B/lRnRmkH8xBMpPyPH4Chn07Fwg9DCjQYy9oiZZ18pRkjkR/zOcioda1YrsfkFoF+riLThKpNI+gC1maCoQ84oGuK73HtleJokDqi6zWCRekh0GZAGgY8e/YMl8Mlfjl8gs93z/DZ5QWebRJ224RNVvo9aW+b5Tb+nsKcnou83md5WB+k9+/3PDneOmFIg/BZRbxpC2uYUiqAygcKV1LT8kc0HBFD9lwOxnlPtCx9NQbtx596n2VtvdaUEeE8ONrNh8qpn3bs90pW3XaAsdlMePniFs+e7WEWXq4JL9y8SircEiJOmSHzfoiayNXWe4Zs4ZmZAP3YZqvE51IdxsSsWtodq7k7VM98q/v9yIV+QH9n1x9Y53mj7+ddPu/r8dBD5XoL87bsiXt7WTyFZuI9Mnv3L0uwd4/+5R0wbAFNaom89VAZNVEl8O1rxu2hYAKwH4G7IoKbSrlZ82cyZgS1rBFteYElV47hNFTh6FYbUkoRgZBZOosywgQZABXBVdzJKZquqSCWoAT12SUI6k89ucwB9tWFW6Y4Waibw/XwjuHmmPC7MnNwayqrn3ml/kigscWZh6+Fxbs1+DJhVVFC2nIJ+Z5WOYVZIIpFeu24h9tRDj8SCz6mlNTiFpoIu2hIm0DWGAG8BHfKLFEHn573yAlyjQnrWSuN5LLfDydel4mJbo9y/DjSjhP28SL5XMZ4/Pa3xY/zc7jie2q7xKGPHOrRdpLmixFFBSEn24PZ53caClKaNEQOfB/3I7RwOGUmaKrvRat8H9IRPMwQZZcrUH1MtQ1CtS5PmmvABzzro2CpCXHOYt7iMLAIL6vLWRl0X7NwoVJqTSeEv40w7O1ZH4IFjq4bW1ZI1H1Z97s86yQfVyMPAwHBkXBlTIrJim1+EwFTQUkd7ajo27lMRJg0YVN3fsT5I1sbG6cqpxU/+JpxQANrc75Edzp+0v5wXTe5brnO2BWoAIBUVGFEPs5ZA3FO2UJwLZ3P3FzuvSya/sgDPp0cBFTCAJo1a4Uh6uvSRXFsSxDljJ8hJtwhH3PMG+KKbsMLOudcCsooHhlcJvA0wbUKAjyyPtvnQD7ItTIB++sImGFxSM+izpyJTAlxnM55sjwGfT1PQUOe29biIz88/XnfPsxw1b1LK34xJUTE2L2ixMOKwmgKbuiR+kntvjI6ktDQNHGPN+M5BQ8LEvEl/vZsL4OzSz0H5l2aCzHmvNTj4Ez03/cbUz0auNc73bucs019dUNj3D7gJ+XibBABwyWQN3IWKq4/XL/Dd//yW1z/6Xuz2HnEdM5WKlLrzR5Ibt0RqBQGMFa1Ld3tQK8/A5UBdLcB3RDyuwyUEVlpeZSCScdyPbzGmA8iHS6E7eWIlAqmG1FK1H1RLaSNTgGL4RSnBM5inJT0efOGTkRAKUiT5IJKkEiXiRLe3e1wU15id/VMvSEychZjCInGUXmfZdSyPuk+bwR3/nGYYYNdAg8XYGSUQjiMB/z55jf45u41DmXEaPRSOIOdrGrqWuqKAgUD7gGUSu1QswHWPAhRcVAU+HuC646mtm44fSBrXQmo0I6f7dw9V5NPt/VHAoyby7NdpDDQZePwZs3dZTNskYcB2+kKF/QcV5eXuNxu8GyYcJnFDqQ1LOauotpOXIB7H0OnXjhH61k79qgqnJ85G7dWXLAkQ4hdWg/ZJ2/bVjdZMMcOs/6h2j+hIaG5aqwa7Q95o8DLUZQSrwdg/1QGJg3FcOTe0v343NIB2r52DjjNIbTO6Vrrj6cIVmpYvXz/Fh+oiBAm5WJ3wD/8m1ciKCiTuuGVoEk1Qo8U2YulatK4v/7fvSBaIvCcHjmaWFVCLC2vAXElHu2j/X3882N5P+XYpvpYPlSJK3CCWd9ega4+r4pFO9R9Q0kopn/5U8G3bxjYFBF+EM0wUNx/wDIeaMOfWdpTTVllxJESMyLDsEMuHnYt7nBCNBkxmuQILOYhYTRVaLsUz01hNjnrcNvhkOMPr5YqZ+xeXjkvncdVorhd1er9Yd5qfR2NV4VeKcEixptW9M1MlUA1hsSEWhaKBgASkHMCNE46Fw1VwiEckoW/IrVADBbupmjwPjfCAmiYnwQMLPFsR2l7mjR3QB5cAtwL3RDgRawyahtG81uYKRsTCB4D3cPJkMLTI2iiGQtwBGZ6kODwpQo/ofF6tdMLQhXZN0Zyhn3UoYEKycoMArpWyyNgLurVIvghDxngBOakYW4J4ISirtREhGmcQBkioIwMClfeS5sXOSXVntmkeEx6/c+gmiA4WET7Mut/s+iH4jMT3LOa7dvzRr/kQcJMljJVNirQyTlniHt+8R668BoqrFWpRRXitoRdZJgMz7EzgHXY5QSsTLrfjFF26q5/R8dbUkEy7xhCEzqo6EDbHCe6RmzWZQmUinrAaj6wQQXBrONKJPF8p8lJSKcKqYZxcOE1xHvFcpPE0FnOmup8pZxUARlg3vJPOMxzNwFclSsq/Iju4V4S4KFFAV9fO3fE4jK5UE3yWBAIGaQ5i+bppHXfwfAnkNj2YX3W2HADNlvNWaiJEG6BoPkpVDDhvB1YwkhNBWWaCwlIXgSV6knWFMXHKZF7QoDI+QJe6D9Dc69A9jKPsvZlP2KijHIY5ZwlAjKhJALRAL76DMyMnAk83oG/k1BNSRnTRDUytcTmNmWE4mVbx4+E5gcvD6XvH8t39bRMv5Nn/Qr4hPSAIcNV5hFBgeY1j74g0LLcK4tyiCiwOTq2SO+2Z9v8STsb3j9gn2fAZdjloW2cmBosTkO9/lhNxIkihiZ25iwSSHrPTvmlNSLQ5WfAsHNaFMy4e3ONb/9fv8b+toDL1azaE9AbCJAqqIotU3wMGs42VNOTcWmE0AMMpP0lhre/Av+58gNUGBlyThm/MWhr0yf/Bbj6TsIVpgnPfvYHbLYjDvsMHo1mpCqa1i1jioxSxEtu3Gzq/qKKzwFgKAWbaXQ+YNhkIGV8/fozTMM/4O9ffoHddovtMGCTMwbKyGA3UngUdtGXuVtz50e3z8B5h/Ku4O5wg99e/6/4/vAGh+mAaar0dlgQX6eWkI/rbN91k9hlz59E7aDWNoorIbQO8mCqcGVE25H2W/SS0DBcTjg5XWrKCTUs4Enb0HfB9XtQZohx10q3de17NYTBMxKBUsbFxQ6bYYtPyq/wBf0Mn119jpe7AS+HA3b5gJy27sUtpU+WYZ/kH3/NxWnORxTJg1ac35yhLje6AdwQJYYMs9+w85jBv9iDRwb+0/OZIuKHI/MeSu2cW7eV99XGh5m583NEkBEe4gnxySe3eHa5B1AVEBJbt/pjGUNEiZxZ75UQUXDZEnHn9qtlylaeghy0lYGfe0JUxBbr7UMwrSkjnl45Ye3c5+l7tvADKlROEbHn9uyDIpgHWLFVO+33P9drh8OptutBfuQ5mtfDeQsMO9CwW4Slb94wru/k+1RYElKH84FmX9qfvdBisVseUDwBVMAgpJKCIK74OaaDbeeJJ4AlbimIkNSF1qP9WELYWQwYiHswQw7Bo3M8xxmNuMuESE67ReFPK9itQjiulkRHmVM9CBOBSguPBGjoIhPOaD8AFy429Nd9GEI2BgXtuLQ+KoBZIzk5PQPfQExToD20M5EhqTomsQYyIaCEbiKNnw4NDSKdkhjtlejkUglgfbnOLxFQioRa8TOus0Qw2CITxFkfT+/9fug8+7G0u5cEEQaXwbMk0NWmqHHbtg506hoHT4JZC3PiikJdHCck1G1wDoJ6qiRY3g2bZkaSvccZ2ACbQrgswC0V7DV5tQUPiuHQDDhsfySEDlmffE6qdXlVvIRq6kz5yxzaokRIXEPVmHV/SmLdbooIv+9crgGy4prgPcEavoDseWMwvQvSNqdoGR+YroBD7Jp/75WGqHkbWMMvWcgpr2+BOYiTyfUpwStOH9b+2JzZKJPSgyKoFppQLJ3qFquesWFB7B4kxjLp2IoqOUopyDl1cFdxg3nfukaQoALEpOMmz1tg1sspEcqUkBS3J1OcN1u5bcfrtq86Hje2UZhiPZAYAqfU19uhizqr1TpsGRcHox/FgAaLpB1KCeAAu3W56nqb8jSxKoGjJ4wpvlAVtM14zdM5VfwcQ1fBxqvjcnwclIVUBMeWacS7b/+Er/814Zf/7t9hs/3EZSKUB4XDSWbx4gVoGoHDta9jPCMc71GAcwbmNt33K++FqjvBWzxVnrQfssQR3Xc0D5/zhVA9kbDhuUDL9g1Aej4Zv1rPLM9riIi/7AQJOOKYIHDW0+UrzWkc6Unun27bbJTZi7WrQG9GSs7P+geXh8AtnUqmfaTuc989t84FmUHLS3TPR+9dwPNSMRhp9wyUBlWWEJiyx94v5YDrw9d4s/8zbibCVAachvq+bfvD9fei4sp6FH47WWKUEDdV9T0hrZ+drtfvXG3Id/tPkXmjrRVs/3CBtBmR3xAwRVomhjsUSq/ggP3wGiMxJo8xSBiHPfbbveP2vC0YhgLcJOAuYyiW/2mLq90Wu+0G2yFjR3vs+KBROoPh3JkJRWb7x+BC5feNrkDpoDKNmErG3WHE7WGP/TRhPxUcCmFcIrcigRWvBfq8WTT/btd1npbgv8a4nbcRRrnSABoIMCLTCXzLEeEEvx308qWY8mGqv03xEHNL9J8La2PQ5Y9YU2AwibEZDQPyfodteY6Xz17gxcUOn22B55uCzSCJzJPyakK89RMe58OuvufARufI5U7Jz04cOY8ti8qIys5oH3pCtiIQ1jpc51MqrWjvxjycwieoYt/a8i9KEDMvhuKb7avZ/cWL83sn5vK4EcCRc3SJJjnxKq08errVBtOvNHaiP82tpwGwe3hEMEDCMG+3I/7+b18jp0liv06SnLpJRurMdnIGPeVcreGUWTEm/bGC2sX3m1WoP+bhl4xRmSsd7quE+FF4S/zgfXhM+z99Jusvrqwt53ABXH0O0lwQ0ROCCfjdtwW//9bqYGAomguiFSLHL3Efi9sdH+HfVChTs5sikVjvUqnJWAE9+AJx7hbiBHWHhnGVelGk/MmoPzv0Ig4QycyRCWr7Gsv9CIQ52x5pybngKjKr+ofZrVmlP/KnFyYJTdlaN4vAxlH7YqkyyCrQQxBaIVwTuiGFRLRGNTW0StdUwM/BCrGKRGM/2OtISWBTLHwhVuCas8IFBWyMj1geVxqnKsgBjSs/HsJY2jkoOgBKBMoq6Hx0bIAzHlllJOo3sxCWpLO914I1ZIJ86JyUCmcUPjleQN0eHXFTSmlfUubS3HFzzupFQt6oeeYQJRf2JyoovMHhIAQnT8ZvBc8cXXdX0jmpbDBnwVm0K/oEqUeTQ5IqHTqwRE2MK3lJUpDl5mRGFtnhps5CzX0R6RGzoHUvC+unSbiin3+ENxMsVe1eYNZ0zaRVvTyHU2YovWaL3TJZFQD0muFHHYN7QPi063rHUQccYt4A5nmWUw7hODtcpXiJlPHQCuo+TAVcCMxiWRfCBmtd9l8h0oxecoaH4jEY03sFNVQVoIqglEQYznA80wgg62zVthxX2FWF45yRcj3zxGNCcENDngJYE4yz5r6JHkCxBzWlkc2r7pGp1F56uESFxwg6Dlusc0PIyEiseXh0DoKzs+SCqFgUBHZFhOR9C2GZwLKHDHergl+sXdWCsrDgy8KSN2IEXv/xt/g9vcbnv/g5rj55CRMy0LCRVvcTKA9Izz4HH+7A443k5QEcLimsua+c7eXF2f5Y/mpKPAiNpvOfIcya84gC6e4BkZSOCbRv3ZsR4fufWjhij5U+dU9EC/z+lWVTBcVNZ9ARkfZulRJhHj50WVEwnHzGrj9QIrcsnGpDdJoSYa1E2s+PJ7kB3j4HbZ8pHlYatBjddMDrw6/x6vY17g5b8GE4wmKsjSsg6kA3eN/CGGeJUPVwoEX4rO8IDRVy7zCApMYNQDBgJuxuv8Du9ovapdf/0PZPn29aUzpt2rwBnv0aOY/g8eCvTC+/x+2n3yqfBqed+Pc78OsNBs7ImwEvLy7x8uoCV9sdLjcDLnGL3TQi56ENzdgKjBbLqhIiVOFwwcpvFMZEE0YccHt7h5u7W9zuJ+xLwZ6BkakRswdqdN4Bsz6beVCEZ6u11sooWvpu1o4vHodFTPUdHRsImhMiKhOmmifCmIegpCD3nqieEXJrqu9Y2CajM3s4bIYVjIusOQCcgLwZMOQNLvZf4PP0S3x59QU+udrhy23BZS7YDlvklIQerUzf8rz/2Ep3Vv0gXcCCMuKMtwDV2WX1jJgKKCkOZBuafGFFnGQgZfRpI3ON+Lrtz6nerSsNzq3hPuUUtfkh13MNP5zfh6dSQgD3UEQwiyfEF5/f4GJ3gHtCGOMeOuVMZ+P5kF3zeEwJsUzwVGEk9YRjX5ZouHDCRhw6V0K0bSwpHh6thKgDOf3sGeU0ERtvfTi2a62thxK0a2850d8xEB+yxA25trwzz4gHwsGx6XuqYc+aYG7ndNgBm0ukzYXkhVDBhQ3tz28Yb66B17cFkJCe0r+lEDUBH5plS11T239s3VjvL0HzRQhe8fwExf507Rhd5cIrOdglxBOhICGBNSqEBeTo1iwINkL1LQPa3LFxLR+a7b3VkXrTs0dV0NvQmN5dFaalJlJ2e/CjJjp2RY1WQHVwMtdJiQSuSavlthKOFmaG4Th2ElGW0JhZ69R48VwkZI3kGRqRc/JQBzaGlAiFNaRIgMdmHqz/+t9CdVBMrMwSfiQlSIDQUEopYrmdq8DMdq8J1LzlsIzEKuwnINGETCoMu+ee5KUfzB00VQJwBgO2D8JvHz8A6nwFTI5b92HHlFqdyoy4zo/lbaETyQKjIYKJDyPiZkDgSdhXcFJlB4mHSgwpxCBQyhLfdSdM3eFuxIiQkNt4o6LWMCZQ1rwzJrhVPmidNQs8nfRMregzqbcnvM5UGEzZX6rCKOO5uPJelJCyJpcuU5M7K1FC4UkSV6tCwEL8WF4T6HzJuAqYk8CoC1btvq6nA367fv7F+8d10ESauJLmsK1fox6k+DopFLrixWCghKqr8J71UUkcXRtxXUjhin/Ajmdi2DAqSbybwlz7ujGqMFD/ZzV+SVlI3YkVn6syxICjcKlbQGlXyfloMacJmQAmo2HJJ1tGXAAIQ2uwIEoX9YbQcxKUwpjCjDc0qs6WTXh7SNb56TepwpTvbS4YLccCIMzeIIo9VxFzVRLYe4nEmpCTCAOS9aewWKXpuiYbj/fAQm9Z7pdq1QrAw2DFRL/T3TWmt9+CxzsNcyhjmyY5Lb67Jox/usOLf/oXHG5v8MXf/j02V8/EiFb3F4E1R2eCpn93PF2ND+Ah6eSSYNH74ucnK2cQa2t07I/C2OkR5WEcwNOURsSgeHM1RJL+pvAmodJTsdKohDBFu9HN6zzBSh9PrW+osx1b13cAoJXGjxTmvq5ytE9zMnSF9n2gUuB9lvsKU+7Dx81pMwZtr4C8A6cBMfwMGChlxPX0Na7ffI8//09vcHjN4OkpYp0vjHJ1DeK503XfaUObAzuZ2OXVzJXPi8qvSsvE06w905YgjEEgvgDuvkJJBZt9lQVdHb7Ey+u/qbJy+3OTgNuMcfsaZXvAbgAuhgHbTBgSwVJFGZ0XObe1sqqA6OcnEEsMwjRcofCAfUnYjwd8u/8Dvj+8xm25w91YcCgJB65tJCTxugZgXv4Li7c4U/5hZuFHM7UbXRF/hjpm9IUPshJyRrNyXZNqxNJ7RYgHBPMkygj3jChCu0dlBsJ7wftcW2uGZoowIIQjHQbklCQM1+YCn22f47Pdczzb7XC52WA3FGwzq0E0BTbe6NE68Ir3jgDp0fLws3rNONt38xnKiB7lOut2zzLDe7EfDylEIcyhevAaAgn8LkdlmOFKopCPzNFo059zenZaCfFU5VSdATkuPc6nxzWTOZ06ax+0dAsvPdFRfg9FRMEwTPjVL95hsxkxjhr3tRgTUzcH0TwHxCwkk4YEOWYp3C1PU2jh21qpTdQEYna9VUIEyxZ/t95bqq/9fazHXYkn8wNgf/bKPQjN98XGPHW9J2GcH4UK719ObO6noK9/SBo9iDvm96IyYtiCrj6vwpRoVUKEr18V/ObPDAz6H/M9s1g6PCx8IsHiZxJVgqcKoMIJS4QUknRxIo39T8G6h+p7VIlrq8SskwmikkiswlLWOKIBgVSmtI3wLfTBEr6I67vu6TEvyw86WuoISO7eoYBjQvPWi7YfhTVOa3ifNWJoUMyS3jC6swpYueaGQJ0j7xNXy3NAbZQpgTCJlXaRJKUgIAdClkSyByrFYW2JX3Ko0JsRRo2QIWYRCoM9PA4BGiZkAighQZXlOXnYHIvdW1Octo2bpXFKB2EgEF3q77mxG8I+NhLvxYfbE9HAz9jYon1zmjvUU08ibuDWKnMYp/heXXsmtWTueBfW/lu4G7PIBuBnKqvy0BLkRm8c8zLAAGy3BZbEepq0Aq4CnwIBUnaBcrvpWFUui6thBG4cs6wkUq4wY9xrcjwhtXmISeh+8sS8wpTnNIC54DCOwXBDhN01nGVliW2emfs+Kh7mEBc3EjMlwijFxauzoUyyeasQGSMpY1u0nBXJlCoJCCOXRqECxaXel1B3bJtsTTsay2BEdMYxL0NYD00smbIprsIONJgJtFrSPZ9zRsoZOQ9S72RW+RqqyQTmasVnc0qqiOACD88kIbks2TY8WoAoXm1jkMcbzoo/XPGQlNY0OtPXx3dlnS9HbrVfzc7s0YIra1CVAMwYx9EfTiwKgpLiXoPjZMMLkkuD4dr6JPts4kmE+RLfqdLKVPdVohrmwNbGFtQ8K1LKaoREKHfvML35WhQRpOc2CNM0onDC2+kC+2vG73/9G6Tbt/j0q1/g8tlzUTiYUsN6ShlF42NUmGMHT1dOLGLv91TuQ5f/CBQMDzytPmh5aN8ivlSU1qxPEzqTF5L5BsVFFWT63YW2YLoMh8HmmTMUDgu16t5bf82ENTOFwjmlq1vqWheGx0Tc9f22zdl6HeH5H1RmGp4fA/T2hKlyFcMVaPdcLk1T88jEe7zZ/wavX32Hm3/aotzcI2BFbNGsBuwqx2cindYRbHrWRLqQ4j0twnLwbIy2J7jZNPXevM5Z1e135Ru4bLG9+4UPzcu7rp7ugNxf/Bbj5XdIG8LlZsA2J2w0UqvTwPXYPlpOKaCcbnJaQkTkZbjCmC5xd32N2/0er8Y/4NX0HW6nO9yWgj0nHNhOJfUo5ISJgeOhovq1g9PlUFqY+luLg5zDaa2nL3GyFu5X5jz8D14RGpJJ5kcMJKiYh4RJk0O+iGLjrHMttLj0pX4PU8JCd9GQsbvY4XJ3iU/xHF/snuPFbotnmw0uhhEbVURQo4hYGi/Vr81jUQWyXGj2pZmso++eXc7EfWuiq0YeckY5+dyx211fTQEBIg8n7HV4f+vBaVHHyL3b5ZxzOy41FLtXv5rrJwJ1LoI9L3y7TznzrX5YPlWzBe3uL+GBB/aLV+88upx90v39373BMBQQRpRJklMLA2ga22DlRV0uCPeGCEzZiU3cn00PJdGV7YsXAlKhhnldV0Ks9eLUkpzTazm0HjzAv9ByEth/FMTmX145Nquct8D2GdJmJwIWEwSoEOrPrxnfv2O8umEJw+TeEO8LuJcwo5wW1ZtJEmZGywog5otJ/jtaDcwkuaT4wsOwVCHS/fmguULl6NORkVgzbQjfdQbqWPx6xXXFXV+l9IJFat5qaQgTykalSqzMrKXrdXICvRQLhANhcINFrVnRGM1amDWfGWsM/gROCfCwW8VbrfJYEzSwf7rADfCQLz0Dbba7xRKQm6KECJOGC3ErdFXAmyLe50nPtpSnBUHBCvH+kEJAdZ0Ol42Wm98KgjkfcBUUgrw6k4JWxqVnVAD4nNo8Uj3DqGtrQWKSXLAha1ByQtJ1LoBawWjseGPOUkZWnEJJ+uSeODbmRVyjFuuFkVA8QlNUzjkHYyGEQGCy9jUZcq67omByy33bU0TRo0cs+8mTwBtr1e4TnUrpW4oKXaNLLOgwV/zTSokC4clhPa1ntfi+IHsRgd6hqmiOEgPHU4yJAUZBSUUTv/eAV/ti7UaFQ1UILhh2JNKtL5UkgsfTFq8oskWDJDzRIFAB4GuoK+mOJUvOw0Ys9HMWCyzWezkrY2uoqkegdTAyBgkpCmYMmTBxQtK1BrOECyLysKMydhPqVQVHUuUENHdNvz0orpWJi2ZnRLuzawgQgxlbu5qnx0MJ2usLZ6YwefIzeccCBxsEAVKd7k991vLAmRV43Q+iaEsWri4lh3XD67YmDjPqLV1G8YD63Z8Zr68LyuZ/wlc//xw/+w//HbZXl0AeFJcxStqALz4Fj3eg/dtmkKr+djj/oMqIj+VHUY7xkeeczhEt1ANnuca+LjqngdkLfevdvTWhU5Tc3LP0wrXoUbTYFnXCG+rDOHWc/kKf5fh4up3YUK9UvyxNF4FW5/FkmQnWQh+4XXDaPgMPOyBv0HgjQjwh3k1/ws3bV/j6f3qFwyuAx+gzGGmzCsePkYtUAjD0cmYBwLNf82Ascy/YY32a3+vosAXyxvXxpyrvqt3cfIJcLsC7PXj7NZg+AeGyrZDNRAVurHascLen6k/xtDBeo6j39N0I7Al4vWe8vZvwr++u8Wq6wZtxwvXEuC2iPK/8pAlY6zik4RV33mZ/Klz15/sMGZ2opzQX6wVXFgjvFVdcvAs9M9+8cgu35KGcihqsWUgmrusCnishAKeDo2FhS3gKLOVhg7zZYjg8w2X6DC+vXuLZbouL7Ra7IWPIjCEV5SuohblGwdYRtAtTdgwc16Dp4Xv2R17uiUZ9lok8VaOHAi7c5RMl5QsFtxZqRDNOfx8llU/0d/5qjyBPVHD0mdVN94FL7MdD6IP73zmnnK2I+OUv3kKsESWUQOldrwBN8FqVEEQ1VmxOWRmcFJi7c8qZA5wxdFQvz2i4irhaJYRdpvBs/+767+U+nznOTsO+Vh6CxNYsVH6MCHF9z/+IWMYVRuBskI5lpqJ+ulWZu5Me6cbx20IApAG0ewkMg+wd3eeAwNj37wp+/ScGZwYN4UWcud+1E0tMXLXUPnV6WHtysqXEKBrOQwhtYR5J3V+DbbEyJe2gfV5EQuSCIrPutGtr3Vkcpp1v94Tpxed58Wu7lk5PBQFXOGOrERTP3tdhewuNRZBauwpN2lO+5nZus1jdb+1Jp70Rq1RiAyboFm8UBCW3SdxjTHoLu1HxuxCtxYPIG35nSFJjUSQkV1homPJJnm+UFzYXSUYvuVQnt3y3h8gV7ZbkVrsxA/05xCzKKXo66CzOU2o6IsboqjemLFXibgZI5PtS4CV4Luha+ZQzSUibWEUQVLadkQVLDJQEUGLPYWLMHFlOi5SQ84CcGZSz98MmWSy1ud2PLmMo4Km4p0+1SJ8P1c/+RAAXTKx4DjUU2aRwarkDzCOqqNDVaCNPVm6CepuzbhVsR3jCPO0NUfC6IKphtCpCWlhV59ea+fdwP45LA85D4AVJr+njdR/oni4qYDbFRfJJrktLNseGIiNtZbg50iGzKNUq40t1/mBQrTkLLDOk9dWUOMWUEllhZlNDMxWJRUspa5gg8/KYnTgzBEgAMhGQk8YVZu8Bh95JOKgYyq/CfLIE2ZYk2wXiPG/a5r50c2JrbH8IIDYPhrpuvq01Nw7cy8F629HuZN6Dy3SotMftrR4fEUK87YojC0vopEQ5KCGSKvjUSyIn5CIeG6a8AwAuE8YD4/VtxvXhDs//+V8wvv0OX/7dv8FwdYWiScq5FGDYgC9eAocb8OFdwAMMS3IvlcaD54engs/lhVYooB91eUgo1g/tGXJ2awSlLysduESvc4OAqSohfAFX5mQm2D7es5MWuQ8BlO6lmWKixwudQQeYF/od6M7F+arn0KNKj5/iLSx7kYge++Ftx1dbg0djZhSjbi5BuxeK05Vy1f6OZcS7wx/w9t13uPn1BuXdxSKbE/M0nSrcfR676oT67Ln2bIu/rRuLXVr/caJQtzeURiGI1621F3meperFmgXD3UtgDxy++i14+w1AfweEU9BPu2C01M9ND5f9b1NMJJb18fQGzJiYcZiAGxDe7Bnf7yf8cX+LN+MB14eCWyYcUFBA2BqdJAe68KXFCGmjI5ZoFetIzakQGLr5Z0NudCdKrLqZCyMmwvfmeQ0VwKT9jJ4+gRhplBAhBFOjhFjwhGgWHMqLLFKN0pthwGazweX0KT6jv8XL3Se42m5xsdlgOyTkNCETKn1+Rumf8uhXuD/66Mmmn3w585xpsIqRmUqz0pDAU5GcfYXDY5XPiqE1l+evo6WP9GtZ8b1wdbWOMwbdIMdjnTlvAk8/1eNPb3z2yxWq5wzjyfq3Xs5WRJRpFDRhSKQURBFeMgFMyiASl3j3jAiWUqA5Ml8qFaQqwpk9YPX4xxLR1CMbavkQE0qQfY/vovbiAxPHH8vH8qGLCelmJW+B3QvQsEUasud5sf+//X7C168nvL0BeBDhIdPpXW7yuaZ9XmKwjqC4uE25v0Ua01tyPYjZtT2sAakNvxgdZXgA5u3RxvRGECYtkfVVaNdfOzaW9mhdYvaWXuHuPRt1pIwW2L5534IVtf1tvBxDfTX0jLZv44143VwlVUhvyW3NgyDlqsgyK2YAyEMSwx9TPGhvG6UASdz3iSEhZXQQZi3hQu+kYX8abUKV0pESov0EedgntnEG/K+C5DKNYuXL7enkCqoUzp0HM2XHi4xEhdVdGDCzxotbwkM02YNK+LsFCsQTpLgZCtf1jd0+wgvFvgEJLlfvn59xrxpKyEI3MWPCJNGtCmAqJyLCsCHsLoBxTxhHsgcgcuVUdcT2V6XrhQpSIQ+D5AAe+R0g0ChAUQmSfBBYw3MVVZBJ3itpsDDcE2LIGcwZpMxz0f0ioZgIKJPQUtOkMGu4NAdmOGAXtUZP2r+EBMnSwEhFJlkUd4DFzBdwr4Spis7AVDRHQ7UnqjktBJaMrisO/4oflXCa5fzwZax7RfZXQlT6mCJPA72JUgIEcXNhYLL9DlfoceijMdgm6KtJsEVJlYgw8UFwh+aBSDkrcKgHQlZBtyYKDxtASiJoXAT1yiANyccAJ6AwhpQwJQZRQWpoYPWEMABiYax9NRU1mxJCtS0wgGu3GXtOmgDQTTGUJjhQadegcAJBvC+UPhejoNzARQUTquscBEBhWR2mEqWAJ+EK/mzry5C9Mk0qeyjgXPNnpJwR80RYXyXEW0gMLggJTAXjfo9ChN/8+YBv3u4xDf93fPHlZ/ib/+5/h+3lFTbbrfAguy3KQODhZ+D9HaabVwpQMgjL+FPPzo90/V97WRNs8NIzYdvadrN9UcmlhyTx/HGWiCqWeODeA3WGNAI9uuZ9IHzA4+frmGLmqdte5G4i3W108e45aLgQb4hQSikYDwf85h//M+5e32L/5g3GO6DcJVSU39HqPg4sAuwSqUXoYHGFaalTw7N5iv6xzYtR+A0sy2lOlu7gC4NoxmMGZvXrwjTo020aPAhksHoyFxBpKHGuEiwoP9GXZu4IHe1DYa20bypHP+RnONAlXu8HvBlH/Pb6t3i1/xav7m7xdhpxPQF7JhTVYHi1lsuOEigZTVcC4R7Gad9n+Ri4XdMekc0G2dFA8RkKlTBqWw4n8V2dSze+CZMT3/Fk1t1/8FwJ0Q/ChAaWNxJhTTSv4GazwXa3xSUucLnZYbcZsBkG7C622A0JOe3DVl2DWVre409WHlP30k7/CReS5UzQpO0kcmYLg+2Jq6HLbvAdVijZ5QLg53fAywPwpy34biWsIM9/zmZ0dYrPmPsGn6I5G+Ty/davCRS5cj68j/IhlBDAPRQRk2nxSwFrPGcAYT9VYZ0npCb7XM8J0ZdI2IRjfV3rSP7EvG4/4ypj5RZ/oa2qhKDwOW/7fF0EdZ+nyhJloYi2IwIDeffoMidaHlb6955EZ/MAS6r3VWa0dX/fSbQFQve+s9o3sjKZx+b4Pp4Qs+YDeneYyxvQxUu1Ok3uCWH7+/X1hD++UYJEwzFRs3uP9bWnk/heBK3P/ZqGtxFMJ7iFkp1+1gP76fdEEFKVECocD0KkKIRuCPnmc5lomCesXuYu5s9VAZDgSH2P6r2AkrvK1vszeyV1LysxAIgVsVt1oYpzIkPuBKIKDVlj4bu1oAoDK8EqAi5pl5vxcHTT1ATWlIpY3zfWTPKOvJpAxDV+ZD9Iql+XafMCpHrO1bjrxa3a5iEGBYjImO/H4EFl8AKfNx/DOdvEtgXF3yqIKy3OoiL5UOJ7S3UBpwgUigAR8OfxDps1NKtHSaEayx4AKBGGBPAApNzPr+GsqnIpqjwQ2ayJH3XPLDEiFPBqV3c7BiEukwlLtYqifRUPilo/T5MrCRIVUfbwBMtHY+FoLBSTz1Ogjn1vGVwZ30YtCW3P2T7gCOh+FZozRcbB5F8bfMYwjwF9V/dz2JqrJYbp7KipgOpMcZeQCosiDIYeCOZqbbjELKWq9X9ymLEEySijNqReB0p/WminqnyU2SnG2Nj8siXNiz1mrW8CgdTDt6VJA7grDozC7mZmVEFH4KCMEZwWtjUrzgwj1q8z8pL07LI+eFirQNPG0KiJehf2ClMzgaI3auOiGnIMqOcpAYjZc5hRJk2K7WcVuTKCOmvE5pSzOXGXE0Y5HFAIeEc73E4jfvvP/wV33/8Zn/3i75BSxnYzCG2SM8qQMW13mPJr8O1r3Xu6H3S/iNApNWv/pOUJ63vinp3VRnNcHHn+h6DS38d8VLzXSyjmVH3Pa0Yc5zwl4tx0h/WZsNEYQbRdWixzHcBCO6fO4G52TSlY76+92L8XaqT2uaUuLPJJZ/JCVQHeXe5XbuF9IUcfDlHzKrsLwwVw8VJwWGnzYE2HPd7+9gZ3fwb4+qIqwFeJL6p0+DK7EHqxLqbqry8/1xB7zTPu4YwOsmcVnSQSVq6v18BAzb++1KRdi3Wo8JuL5KAz9wW2e04D8UqNgW7xrrczLNWQt39IF7hNz/FuGvHmbsSr8Ru8mf6E6+kO12PBvgAHWEhMq4nl7CbSnFN6sCOJEV3Tvbg+3gG0HgXx80gx7wQdaYWtUAfCbwv3aGf7OaeA9b0Y/Rz+y43QVkMNdGPlBaATgxULz5mHAZthgy0NuBg22OSMzZCw2W6wGRKokIaXbKH6+Pd2jMdo4NP45NxTc7meo2ruRwq8f6iSSJK0+15w0LPzR4DS9r/nhAvjs9xx9OkB/JzA326A2+PtPmZ6wo5pL/hPrvcXlZznlkDwm7zjVN8eM64TL6/efUSj53tEKLKycAiV0QTEIs1CMQ1ISdzXSa2nxErvtBIiFhP8yPf+pv4xhsU1BfZRfxNq6Bivd1YnNffbz5/GRv5YPpanLqKA+AQpb0DDoDEVE75+w/j9q1GVixPe3pnbc2RY7kPcr5DC99h64v0QiS5pX5JY1hBLTGXxYDD6PgqTkgmzAFj8eLf2MHJ8nQrXervkfxwR/fydGMaEucWD3BGFs4OwnRCrUD495E0J/WblacKB3gkOjcCteR9QFQqIeJe8rah0YC5I1hbkrBg2G6RhcJq3sNh3u9II5DItjpPBasieEjhlMBt9XsIccUDuCRaCq86LhU2pokJmaOgQ896zGYYb/KREGFlCE5pAlEyEqBZNhDu4n0w7icdWal7Ogfsjz5huR8g3IeznBkY2djtjg/trX1nT724sFEDNf7TPrxMu8qcYo+gGDhLeSCzyR/A0VkUKiZX3xWXGkDe4eQdMh6nyMEUGXrx+Y1XkC5fqPdMEXnbYDX12S7EKW7KfE1IWpkes9os/SqS5BAhutFG0iZwTmEn3U5G9RgnDIELUnBJKASa1OvME3jCUFBRfjkc6Qb8JKcJYwEa/hecUfxW3aoQL+y3hdWy7YewVUZpV/BoLp72uzxujrgpUURBUq/iUQr4YvV6oKqKiFXvKWRNHVwZUnlG6Mw+inEgZpH4LREDOleT1ROE6/gSAEwFIgrdUWZN0MlmVm5sho4CQ06RhyEpdD2bUeM6kaxxxBcJ6xhlTnMQCN0W9b+S4qQIOF8L0562DRT0DKRGGYeNza/9dpmIom1EvoA2NROjg3tdJc6Io3rY8KjJVxWFfusOQmwyChXMkz8FCzMgEsHqUJMMjQSFngqBpPKCMwO++mfCnN6/xu7v/EZcXO/yHXz3DJ5++xC/+/X+LvN2CNhuAtihXX2o9BTTegO/e6tIQluN6fCwfy1KZ41pTzJmC+KPX/BOXc+ezJ7Dt8hn0lhyXD+Pxl+qn7RWwe26EvuTVo5qD6e3hd7jZv8K3/3iN/fcF+z8fwLdU5bB1IOGvtVfxoUPjrAv9WBZ+B56lhrcEzFgDgdanUAfHPjX05bynq6Wji+dz2P52ajOeBxSuH+G/6rCK0lIFzCGcok8n63h4qRptr4WrXlhnRv7j8Axj2uHdlPF2v8efbn6H13ff4/c33+HNuMfbCbhlwlRX0+kuluRYGuEo+RyDlb602E/GtNjZ7WMJP5z24/Db5rCj592jYmHsQCCe5X0K39F8Vxfmpt3uu3Uzzt9iu9w+09zilnDR8LspJdCwwSURXqaMTzaXeL7d4dnFBS53Wzwb7rBLBQMb7RlpYttRDaF7Nsv20yo/gkFF2NXfEuoVII/spR7aHPhS2/tKOxYz+jLZwYLhwDnl/Hfm9fc76uF1H6thqYV+Eh9flpQQy9vzyN58QDlbEcGlZcob93syJYT9l6R9wtSI1at3b0mmgXAzCJ6qJgyzdZgtS2B0K4NcBVLSZzQeEf6qKx2Wfj9s0y4mTnmfZcF6ZOY2i/6RHwFC+hGX3tNh1eLIibb3MJ9BQHyqnPKEWOvfTKRtbaUBtHsOygNMSAEQ3u2Bb95paDaymvv470e7UtteAM2Gplp8ZwWeobKFTsBAECGSEC11jK0ALz4fGEsXTBtRYvPQ9DZ81nsz4e89iwmUZ03BhIXL+KypoHu9aIeiktcVLLGvgWisNK0QfpIEtcZEBzom3AWZmhMionGCJJHNQ2BvlKCkuuNindalAnYhFaUEKkVDgAVcq2e29YY1VE2j1A7nUXHCnHw8/i7XRMJCAbXhUmzaPHY9RjCPAG/gVjrLK3NWqUN6AH7xObdZhjMAFaSOAWZ3hrL1JKxXjy8QLqF9ZK2wTLJ2jTW5LZyz41LcGxN+LhM2G1Ea7e8SpqkqAkCdMsUHHnA1B29LJy/Iha7Wr7rKwfLLhcPqHUZAmVry1K5P3PaFUlLrvAmepD2JG0BW+onZcpTAFQL2ruXX8v7pOLg/G7qtaM83lruY84Ng2WO2Dg3N1hxDsZ64Z9u62v5QxaPGREeIVqUMNfBJFe4akKvCclJ60zun/2M+BjkBpK0a/ip6/tR59E+rSzTZjvrNC3DIJtxncNEJCuvFMBpZ/1dngTCM3ltEioQz6vZYM7H1DHJcZasQjyGy0ExoQqQ6g61nh+Dn8CLFhPIAQ7y/kuNJqcND5iXxzLFesQs2QniIoAgzJZjHsUBd05QMn9t8tnPDoygdb5BAd8D49XfYZsLLu4T9l5/hy1/8Cri6EiUUBvD2hcwZMfgWoLtr/R2m8wHlKSi96mXHs+tL5UOyEz9EOZcfecw8nL1ujaDsCP90os9Cwz1u5c59/YPym13pt1PlPR/fr3PZVCHl7r8zn5Jvo80F0uUnQREbFOk84Xr/Hd5ef413f8wYv74A3xB4XCTyZ6ViaDsDRFBn9O6crmtO0g4OoxKiUuLa0fqUH7xLJ9GZC7tOniz+7kulQ1oLaAAtq9d1R2dIbplhBcdHq7ceLLTrWgcaknKuQDHDl5E2OOQr3B4mXB8OeHf4Ftf8Nd5ON3gzjtgzcGCyYKNt1xuCi6Bm+wCSxs4vqAL4SEf1HdHKGiVE+O10lV6P+Rr6eSTM5fUcaCevs7ixm4Ula+CjYdAinD0QOQQ6y+qllJCGhC1lPB+2uBoucDEM2OaM3SZjS3tsUDTU5krcBWq/NPRZz1b4k/fFH/O671t62dT6g4HviY0+5VmxNpDFNthpY4NNnz9dl8IFVCgENTWjQeOnuMo9XClVaWoGVD7BPWI8UtYeWpjnE/XN1uTcuT46jx2N6LfOHuDJPvUGsm74tVb9ysH+ENA6XxGhIQ4sLm9NRt2GYIphmYgSyG1EF7p31qYggPpFMAKws7ZTRjF+nwslzSOiu07958N37EcB/yPLD0lR/zWXlMG7TwANc0F5AKWMd7eE//qNEE9TmnA3ou45o4IfWMJ5ZFewtufmhLQR5Zjjkp6o88SmAbFSfFG+mk2uxx93S9u2VItrI3SXeaDzmdBzLOr0OA79TxpyxIfS0HuVUGWI8qBEotNwZd8CByKSKxGP0LYoa2aDre2IJBUMdqFh0rBew1a85sxKu7BkAWDLO8SMlDVmPiTpW2EGxgLW8CIiANP+F3LrZSjjPydT6zzLMxO4JAnxBAKohi2J43G2gwELO8hMHofW9BhihS0egU3IkRW4mK9sR6vPO15/U89g6YosMHxOqCjA9gR0403oW5m033FT8ZxviLC9oPSy52MT1gtnzjXBs3xOoniYJpQyYRxHlHFEKQevJKlwOFnM+VxUGDwJjExKtipicXGqjq0wRNjNFkJrjnFE0VbC8IQGIY3bS+5VIy+K0AFq6a2XTZECuAJBoo4pDIORswrFSQw3KBFS8Uip7t1hRgWU1Cm7WB8ZmcK6B57TY+iqJEjD+Dtt5uMskwvLWQl72z+R/jWPGWbWlAtxr2jqwCVG1tYswJqxFj7vvkkqQzHjW9neExye0qBzmnyOBNbUqj4PSEOGawBY+5yzeH0UgCp0+DIDosTgrBEcIHgsnjNDTmBK2KQDOLF4sAAhfwj87EiaNy01eSGsqva3DNfghsWxItv8x3Ulv+ZOgHausSVC1bHkrNMj9Lgp1istT6CgXGUwMuUm6XTimE8J3mcLvZTc20HXMObWiZNr4JwIZZowaZz0w92d5uMpQFELty40oCndLCxBORSARtyWgn0C/vE24eLrd/j+2+/xyZdf4r/5P/6fsL16ht3zF66sKhcJSFvw/g345g1+6PJYAfXH8thC4e/CUTtTRiyvV9wTfXmaJa57/kMX8h33sRyj42hzBVy8BOXN4v134x9wM36LP/2Pf8Ld14zybgPeT63gOBRuLrV0lp2fzASyJMGkz/UHd/8+A1APTqeR9fkW3pf7ZOfgfCrO5wMb9muBJl2oeQaBfhwu1NG3Y/TSLPSSC/p5bWufXcrmGUp6httC2I97vLk94NXNAX+8eYtX0zvcMjClASUVMFWhvefRK3LYO0WSjGZRvkbSagldadb8Yb2aOfJxMqrBBdfnezqty/XR3Gvmxmj2Hga4Dbk001zY75jLwv5T9/nQQkBKyGnA/u4FDvmXuLh4icvtFi+HPS5pDyoJJZHz+LV/VOvoRua1U+ifGb89rrd/dcWkMPUCOSw6FDgvwn72CE0sES9M/kGay06MYMiDgip6AwDw31wDdxn43SWwT08z5yuL/sOd0PPSb+9z+tXToq1SelGwtVzPWT2cl7MVEda2W8RRVUAAbU4It0aDWIKdVHwuzVQjBFkIP9A8Q+E6Vca0kdDN358TFi3DbNcerFdYwK1LB+rxJx5eTsb6MiQQBASxPGTY83imawD7/ojb5TjH95jrNc7knNJroN9DeSg89nPe2scSQBm0fSaKCBNYUcL1HvjTaxHu0ca8IIKX0X36sLg082P9KFO4VF8YidNXi2+o9MZ/trNgRMYxazeXB4HbZa43Zm+cK5BeK0vDbxSu3oHuANIfxRUJQgiSVbrWKZb7dvDXeOVSEvWbRAkDx/VlRtuaMDVp7HYLCyO0q0InM8AFzAnVq0wI3YKCRJBk1mEO3Cui6U97gHqILBXkFWYkC6mTwl5Q4qiZFSeWgiDOD/vaTtLQLX72GNEdhKyrZQa08wX3lsKzHO62ygOTUtqO6Bk+/Zu633Y/dDeuqyvCjm76rl2hMH2OqxKiWt+XUlAm+ZzK5N+LfocZHOSEBBE2swp4U0oYMdV+tkPpfnKFqZU1icOLghibIzN2cCs7nSPHGxzrYccxcovqv0Ri4cOsMfOh+3ned8dH3FS+uH8dPPSZwpr8TYXBDPa9VWmAVOfGFHlH17gKHtwy6cizjadR39+gFGrGuNQBV8pU+rI9PeTMolxDANW+Wqi9EuIzLLRDAKkVojDPlb5kaA40BnJKSKlgmuo4TAFldKPgO8JM6dEOKU5Gt78qPeqPUevdEm/2MgVy2KsKCN+LBBV4LM1zYNy4VFlXaLXmRGl3EofdIx5KPQVv1Yq30zRNsgdMkUwJVHiep0j3NwGitJROoCTCNXbYH/b4w29+g7ubG/zi7/8tUAi7iyukQUJUlYEw0QCMI4C3xuLWs7CbS8fh8cYjzvCHlvdHST68jffRp3M9Qx7XhtZ97vNAMGxAi2dO1HMMjd2/nFNJuwuPPnKqugfyQEss9YfSty0bAp1+5l5t9PXrgU3DFrR7rm2a9b3SMcy4vv0Ob27+iLtvgPHrS0fSS3xwc/Yu4qX4pNJZa2dZvM5YeTb2grsqwg/uetugw/sDzAqpdrxEBu8+heNo4+fDgHNGw9CAabjCtL/DYTrg9rDH9X6Pd9Md3k0jRgBFLGgk/0OaKg1XiuTAs6TVTsJTexTpteXzurse1zoK/nvaXe83Yb/6+3bo+iSaoUw3Iw1tyvX/rNEeWs6BnXV6XZkyz7XG0wUwfYJN3mGbE7ZpxBYFwBbciqxX5BFrZfn8j7viXt4Rq7z3faRjZ+D891Ue2RwBwrsrjOgyKm1aYVX4WoaFLZPVE46rkWV4v0RByy9G8MUE/PGirvhCnzvstz7IGWo9Ab1rwv2uRKO2U+XcKV9+bq0H3D3D7eVTcuQz+3SsnK2IsNi6VeEgQoBhyK6AqHEyyRHn6S1FzUf9WgUqM90jpQCw+luvE+Lv7hyvkI4ZRvF77fU5MXzutN/3YF5CtB+G67GwDR+qrge7Lr3n8lAa50OWuZBqTgoulRntadtOzIpRLj4F5Q3SsAHlhJzFE+Jffk+4OTBoKKDEcIvKeVX3Ki1u62fdlH/hgA9C6SW8OCMMl4j8KEwJ1iGMus8rTrFayZ/r6+8JBvbn2hlhs0b3h0kP4Tq25vkjQNh6IlBFZS7ItzA26smhCoRSJvdQkGElFehwRaGBgCye5bketrbmi+vdJKPWeOJJvFBKMaJbw86o9TdGEUKP+wO4TCAeYR4Q4laZISldJWQNlxIMyEpNQMcaOiSR9AN2alQr7gJ2qx0RYCaJSZ4LCBmJCAWkcdnlfAOAcZqQU0LOcjakYavhQYTJ5MJIG0uMO5nsTQgh1hVioFVQLe8YX0u2XjIioDTkPKOuZQemET6EoEt6ZBa3ZhJvEl14Zy7aPlrOBj/JbK8AnQIjDIAxszyz5IalU9I6w275IcokltLjAWWS74ULpgIwJq87J1aDB+Dq2QabbcLb1xMO+0q5+hZW6attywSqRvIEcOCmXHBfnMz1gRLXOPsmwC+WA6JI4umUs24tqdyUflyKK+CYk1jwpASiDcQKPOTf0qzDRqskS+rLAE8FNY8Gw/IuEzq+D0rWEzDq89PENTwQCyyUYriAmvH77NEscHVY75ozE5vK/gABAABJREFUwCZ3YpHIE2VQJuScK1zavKBuBcntUmmuREngQZkQZs0fwwCljEwDchZrfVOsVhd1wYs5D5I/ImU3lmFdRfHkMHibfO0pepVZB5XxKQxIAoNBo4WxpkJg7DYZRIxpHMHMuJuAUbHOAMJGk1rnBFWgilC+7mcGQfJJJMXHEqqMBY+58tgmUPsa1qERplPde1xkbtq8G9VT2UI22RYBBW+Z5iwkyYPBpmhVZr8wpklibyPreeaQI/9yypp8R71ChgF5yBhSxrg/YH99g8P1DQ43t0pTVL4iJZKkkn4e1zlzjz0GuEzgCdgfJhxQ8Lu3jO9e/xl0+3/Fs09f4pO/+RVefPUz/PK//9+C0gYpbUEXnyINzzHdfY9y+z1Mleg4A6jwwBVefc7jYfix/ITKUQqme7RjHhnNPuvJQ6/eH1467983wNy3/rXn3x/feYrN/FBKC6DyTidlFEanLzxGm0vQ5SdAGvxsZma8O/wB1+MfcfhDwfRNwTe/+Q53bwrKm01DxDWQwS19F4uRkNWgpqOlZk+j0vN6hhhPVLyx6gfnHWhmhFs6M+DIFvRpeXKOlDkY3APmTmyn2r9qeAU3dmg93IWfEu9alEnvpHY6fLP3DZLTi1OacMANbm9GvLud8OfrP+Hbw7d4O17jegImOzTMa3ZigIqGmq1GVFwm7ZVGHjEYTQmJgcm6UiBna2H1lJjkYEpcFQR9dxloLBV8kFxZgLVJnSkWDC640i3MolThAuPPNM6qfNr1kNNP6ivOm/l/ivdbWKtQqnfM43jaY1sIF9uEzWXCy+0ezzNjKAPSRNgUc2SfAtVfad9ZdAVUOK9K5YgMWpgVMt16tQLPK0a/9ytrxEfbJnf3juG5D+X5lmyKHX0pb+5TLwZayBCYmOSzsMC50YkEqsZVpQCWv4w01KhQ1iIb0KDO0kacI174tnZhrURTxPl758zp0jP3Umi1W6U7QzgEBTrVl04JcW9weDj8nK2IqBZVwfPB80NQ+ARmhwqtTyy1f/zqLHTS0ksWu9vYH1dAUPgMk9NblvXXzxLGvz8ibYlIXrKOPFoeqFCI1ki9h0SF4w6LrNYV39ZrS5TV0rsrNx40qpX+9p4gHU13/7I0H/ddh7XGV+rp91MP6lKnP7xSNyR3QsqgzSWQB1CWfVyYcHsAvnmr4pqNvOBGivekPdcf7Y5LF4r1e0ETK3O/p5eqUkJmsdF7MKNo90W4GJprEbcRwG3feLa+bJbTJxmzFQLY/hrsAohhOUSIbQm1Sz3MA0w4kQWAnAitBCdDhaiAh6iqbYY+MZxxb3IxWO0sAsUYJqcyEwweR+mjWiq7EsmsebkmlhbmQghaqZ1nyk/SDggBaSNkHVpYKLVG1wmrfXJhnCk6AJSsglw9d0qqrqIa1skt4iFDuQ8GaHAQGfhq3xuQr1BXh6KxMxfwWAsjNUGbQVCCGGgdoyFYK3W0nur7oNr3Cua2VnEvd1vVGRd9sagCQAXzwtBbwmrzZC8qnLTwQAl5kA4IfE4I3cKs0aWxdXvQc2Gx+jiEiizEWDGFG5dgAb/QHLdKU6FPJl8UEbwDkuzaYFHnI8Bj9bJgh9+IxYjhQvK4jAYjQuwrTDm6avvdXI+joHq9pZ5UEULBE0orMmZBSLTUtIMwp2z7zmDXO8jepr9lBjBZwxyVUWGi9pU1LBMFgbnBgj0qU2/YpOJpi9evEw4Yg+MbBABlHR8jEWNISZLlkcgVpqI411AKATSPyKT7wtY7bB7U8VfGt10OoAongPq6eehYHTa3vR+GKbLNvKent9yQiAHTdJFZoiULSSbvFFUiAgjMZD1gSMNRUcoSIsr5BaBMI8a7O0yHA6bDWBUmg7HEqjVzRQo18yCecFXQxBbGLA3gwx7f/vGPuL1+o6EwGJ9d/x2G7SW2uw0ob5HyFcbxWnA3VyXs6pHMAUcvPfAerPf/EsoST/XDhqRaXieH2ob+PKeuuH+7c/zMtk+X9zFfx+qMu4Af3Gsr5/KwRkY+tsQVWTUgP3dUAb8qQel1i+fdAGwuhWdSD86pjLi5e403t99g+hYofwAOfyYc3l10OLItvP6ljgdGrnJL3K2UcMoFXM/N32Z+QtvNGdS8083xCn+yVuZ3afE6d08c3QWzmwGGgyaf/ECuT/p5GoGPaT5iahsSYWiNST+VEYdxwn5fcDO+wx2/xoEPOBRG5X4qXQKuZ5udKULLy5xG52piQlH5mnnhzGBpdZJaugpNZvSWDqzzZRXG542+0GvheeJKE1eCPdA0roTgtm33TjXaa0bB1r5Ucg3sBJbdJlApyAwMeYM8JGxSwRYHJE5InCXUJks+K27GZ62psiryk9Zdqk9JN7vJdkNJ+20trOyFR56B8x2n59ZR3LKCDD9UOaPpmlOtSwjPqDzjjOYN8ABT4olBIwBwYiAVUOl5kaPoeHUuT43v5Hv9GizRSDPsd7yuZSXESnt9S32/m2n/MPBytiIiJcsNIR4QOUdPCAOgtbep+2gR/+y9mRIiEnz61YDOGM5QZyR+U195X/eacuKvuPSCvVXmbL2Ge7/xYy4fSlv8PksUxsgHAZRBV18Ag3hCIIknxM2e8J9/T7g9MEpmF8DO6N6T1OHTj6AyeuJ+Jz/qU5VsWV61SoB0BJzfZ7iAegmE+/PBqgr01eww4EbsJfY2jAYXtXkFWmKs1UW0+1IqVovycBrFxEMuxKfYpZoAuMeADLNS0EMu0nvdXLC1UIon13WmTcdSWEMgZRUSgpBgCX0nHPZ7ME8Q62ASZZg2QIkwDBnjCEwHywNQrcFN0DpNIwAJl+L0KREyiU9FYRaChNVCoAgRXCbx0kiQsyIPWfqXSITgmhBb2Rixxiax2k5EKImQs4SCmcU1d2g7HxeuMc6zMiOoIoG/wEt0zIMI4FU51T1v8EBq9eN5KMhof2piyAsMESSpLTx5c1VAWAz90BeG5mEo4vlgTLyHZJKwLfLJDuOVUUCoX2CkbKCNs5/7xZRzqHVwUc8XLlUhqPPnsYT9CCswK3EzxDC/HJ05FdBa3ooasmlSr6Ksyl3FYGHa1LKHEkA6XiO2AaerpKgHg404VaUwA3X/6Yuy72Sfu8A+MteqaJTIZOo75IqMBQB0AQwD7t6O+qnhgkDVSKUmPPbdU3khFQjUvAXkT3KpOyep8DvlAZQIWT8xAYlZ50TrJzm/kmhIjK2EC9+DXKLmcyid4oJqrhoyzyiG5PbQoRbZG8OQwSQ5I8ATJrWonEqGOBzkus5Ks/bfKxKbT7lNb6Vx56XStwQS1IhSxFtH8lLA554S1TmPS6ufolgI82E5LpRLcJztOSXqweSnLVfm0HIC0SCKiM0waC4f4PD6W7z73b/g8OZblGkSDw7diqwhr4hIhAiUYFG2yJW+2ucEoDv7xrTFbw4J22/3eHv9z/j+6+/w7tVbfPbLv8Wv/jf/A/J2h7y7QEqMIZGG+iPFR2oxHBRqvn102tiEDFz78bH8FZaPi/+TKEZTGap8il1Lmwukqy9EkRmU2Nfjn/Fm/1v8+T+9wvWvM/hVAV8zypgiuuzKMeZhuVTZ+hqfYgImo2ssDGpkVsIzVqdR9MZXAE4PeTPhWI+GGk/NDj5ZfXrmtcaz1YjWz0iXBSWh+W0+fIyaZ1ALM8DbK0zpOW7GEe+mEd/tR7y6HfGbm9f4rrzB64lxV6D0iIQVzUgYE4DCmMgowklowyJtFz17UmPFoKFfUapXXpCF2TN11mwGjfAJSaZ9AHoh0iA980DhOf8gmOGIJWWv/82ojIMnhDGLlb4FY+6F0ffB2gqTzuE7GKAhIQ0D9teXwN0X+MXVS1xtNtgkDeEqM4apFMkPl5SvAYeZMvqTm/1cp6CXI6IrHaQGr1d5vhKfP7TNwhJf+kHkWw6OFFiuBdqXzLNBaOXIozLXvH+yG8mNUMToUL3LwULX5QL++3fAbQb/12egQ8jj538Qrp2YhxXmnPtv91H4xMNptfZ2D8Qmjhl5H+3FUh9Xz6jj5bHGJffwiKhC/4rQA/IOB5I9XzuJuqH7+85HtQvREAs9DnA1cQoPmJSkF6st1D1ra/k5YAYC9y+R+71HXQ8OlXQfgDjSRu8h0cxDEHgAa3C70o/Vyx8AEZ4sRky1h5DQIiFW+JGlefB+fOTptCY318rDX/1CGUgDMGxBw849IVJKGCfG6xvgUADaiJ1A6urSVueNcvNxrMcr4zj2ZiWsJPTNGqmq14k0/uBCy2vzrRMp8QdXh9f+WLzYXlndI1HKv9zTUBY5jo44a9+Lgk2gMmVN1UGg+ZAigjt4P0gJe7dW0L+k4Ueq6kN+lSKC6ERFhUwWr5490SgltbC1kEzUklHm7ZFSDdcCwIVWbrltU6YgIgLpOvjk8WviwV/PAWdc7PjSCRVhbp3MZi4fsrWPcWEL8DbfNzbW1P7ub1s7rmk40Y+GMbJHopBdJzMSQ15/hQUjKi1HhIf16phfe85cyiU8F6EUS9gHINAlpmDz5HIhrFXvqr+KPpRAjuvZKgXaYsJgD1vjzL7CpAvcyafHQIiVAbb9467zvEBDhRk0BtWG4/H67UzWOjqHjRkT5+Ol/gQ2PBvXjhFn0wrBplmejwmxm7KyD9q5tc3oG0yFz4IHJL8MQCUICtB7QZjUWnFMEDY0E6rzQwZDkH5MQXIl9xhiNylMjj2Xk1hEWpM8VjfzpWOMuu+rR37HBK+WMOcG6kvnJ/k8Bi+RyGzblHNRd3dROrAfgKQhzVShYeHDQh8brKe4hFLgGXQNSc/V8XCH6fYteDzom4q3i6nBJR4Uk7rga7gzU476eoHhiejsHCTCARJC7/rtLSi9xu5Pf8KwvcDN21fYPnuO7W5QV/4MUAGjAMWUKWEOm2Mg4rBueTqa+CHlfeRE+DGW+3kdHKnnzOdWUPzysycFDQ/pwY+w9LDWj/uRa/NjKPF4f7wSgiSsjtIjlDbgYed4tJQRUxlxffsar199g7vvGOM3V+C7At6X09Xfs/gJGY/L/gg1jBXwPIfPqKiIL84EXKEuaZPatsKUHiNbH1JW6+PZl+OVoNJnRsJWuoNc6exnC3eDcuqnEs5ylmZguMBUbnA4jLgrBTfThOtpxDUfsC8JB1bdDQHqYglCAiflZZwOU2KE4cJV82St0cZjunAOc08VIJwgODKDcX974uzus1l/YPYj9jsqNYBWweDAVtp3+n74K137Pt6FkRDVkDzYYsBzXOQtLpIYoRm9wxAaOTmNZF6X1hK3MO2tart9+IfuZ49X+ufjT1Z686mKsBW1gVXU3TECp8bUNrL+3CLNuTY+l4ceacv2IEEVci2uMrA2/il6RTS8v4Z95csJTCxhWZuO28cTn32douBUiTxWvbBcZ/9zTQlxnzE5Vbvy7ofwYD1bETEMA6InhHwCS8TYTNCvnGpzPXBivYdEX49Hno2MF4AaqFoPmKbBWP96+QmTkh+smICjozmWHtQv9Bc5sT9Jz4ildaCknhBbpGEnQh7d18MwALkAw6iuodET4nGLuo7PFln71SJyomVlRP1lhForfOpbWDxflVARtEXhyY6aIBGOzGroD43+2llECJ84yIT4K1Z3p4yoyaX5pMJdSER9OnrtUsS74XknClqBsrxjMEM1EqeGW7IQftKgWPskF84KM5eQAM4oZcI4HjAkwpC3EqY9AeUwovDoY2elSljj9Be1PpKwoab40MSyrM+FkZdSAJowqADbLHZttaO81uZD5kAfKgDRrc53taupZQlvRnhv4Yrtl/4J9Jc/wOH67P3C/p4csV2MKCe2q9WbrSmJ37K+O9X+REVWqKz2TcNkhVwoDUxwyIEQx8fFLdPNCyJ6Qth/aIimwgWYZPSbcUTKCUPOLuhPiTBOIzyOMgxXQEKTEaOMo4w1T+JVkLP2sVU0GxFrF8SKvLjAH4YbNfE6AdUC3faQEtN5GISoLsFy22kW9qTt4oHDvibJGEsWq7NSiguDDRZV9O373Wgm62cJ3gVMLEmAwQ2j6HoTXSpLPtzI7/sQQmGunHHPpb5nAmSHG25BVZ9JSazZrP2UkkKTCr3zIGubsyskAICS5Y+RFlIaQKla4aek+SnUQ8oGIhECCsrEkuOFbXaip4LMidQF8CQXOCe1RGSACZuNeGcMSeo9+AzVObeQYwCDinj0pFzH33jzBsNCn3urs1Ey6Xc2YT9k0Urx+234yZprxHBzXdPqcTdOBdM4IqWMkorkPEmsXmbRYlQY/2EjcdFTyjCXBZ/NJGuXlLZIOSOnLAmqpxFlnLSthO12W+cAEgqv+Fj0juYBKimL91rOiudlLDll3UOylxIzaHOJ17zD/uYO6V9/i/27d7h58xo/+4d/wN/9H/73GJFRLj9DOrwFxmsUUsGPnkmNsVRE6R89If7ySzjzwqkFIOA8//Gx/CWVaB3tLMSwQX7+FaAKWuMkjEZ5d/gar+/+K77+/3yHd/+YwIcMHscuoe9SCXQzw/MjtU/MhUSOkgwn1yPZnzL6jo0m687uFrIDfWaC2pqQrektnWAoIqVwupyW0ayXQL80V7u9inpmOa2IaryQLHeVj0lzRqlCPRCRiKYYzGY0JTkg9gDelYLX04h3ZcRtmXAzFewZ2KQs9FxKyKTfWcIEgWqyaNY8eiaBZVX6c4kz1PGcWq/Fym/pLA4TlOCLShTCJ2k99pyFJ61At1wIAE8Apkq4WG5BD9Fk+SF80kK9cTahdG7sL6kChsJrRhwlJPW0vErAsyFheP4Znu++wL99eYGvLhlXGRjUKwJENZRkb3QTANZkPI2ynOq92TuE+lwsvq0DLjmz3Ncg4fya9Xk+sa5L/fElcmyx/jxoPh99H2Zf2vZI9yfSpDyRGV2x7iOAfbWklCLeLmb0RQka1rlrhuPXCnv3Kf3T5LhzdViLhZaaXuxL5LtXaueV+0vyqNl9dh7shyj38ogwizRjIIE5je7P978WlBBVAWFt9G8asZfCfa8gMAorn/7kmWUNGJ+C2HRN4HtsoyuzzTJ74GxMtKyMWFe9YjmQbnziA4D8A+d0dnh0B9VakQPseN2npvzeXb4f1VdfyhvxhNB9vD/I5X1h7EdJUNl5onblPIw7H+8M6x65t15cGYEjls0rk0P9jyN4vRLd8fQ6r5/1sD1GyT20BGsnriyGEXsM1MTEevl+sOXUV9eqN+LMjQneKm1GFfFap7rpc1zfCPdtquRhC90jlYrQ12LFV4I1jJHVuj6lOBlKsATcRfVVyUmQGqH8HCbmE8fNLQYwAjwIrlx968zSba12dvu+VeLZn44Cfz9DQ6dWQDnyly3k6KuRqwOqMJsBsxazRLJNaDBjbL06WTtjDGry2cqIMFflGJQA9fVlxkQy5pzEF0XyB7BLg23GzIK7Gn1VDwxCqrm67a8xRws8h8OI9tdC+djcUE93UPUQkBZiijwRosY9GhdDaH8FVLbZ6+DAuxNXvxK3/l/fTmgV6TY/TV1orYr6SViCaVIpysx9nQU3J999fgOAhM8SvpkaAYwxn0CwpNeQCrUT2qYrJkzInrz/begFa7kqytZLpS8lRURRgbisN5Elv07IYKGLRXsVJtLwIwL82tpwmPsg2Ah/7dYqU9qAAvm2dtwTFOhLHsC2L9g8hgzOCovCKh6qi4tu9WpejtATqbIKAMxDxfjZqmCU+kUZaAoRU+aZgk0GWriAOCGhaE4bXWkOYcKUrzBsBMooGHAYJ9zeHoDX75B3f8azl89x8903GHZX2O6euUJQrCKN1l2f86em1P9aPCH6suYZ8dOcj59in0M5xZ8+sD5ixhPVeO8S2z1XdRiNIsk0xgAobYC8Baky1WiVUkYcpj2u377C29ffY//9hPJ2N+8ArKpTDFP/M9LOHT0PBFy1Nr5wJjWEX/zs7jVUQj23KpI/dy5/wNKTSjoA/0ftzUa56FUYHRFp6WjwRV4vg1AYuCt73PI7TBgxMWOCKCkSM8zboZLR1PJI3tHKXwkJaDSZ1dEsXhgG1Xt29vbMyBF+V0rNl9Qktl4qIRROS3DG/3a/tPUYLe3wHb83g5r/Vl4w5Yxhs8GGCRe0xW53hWe7C1wNGZcJGBJ7OEqjC+JwYojFOqTKcwCoQnhqd0UljY5D+czr4IzSW/Y/dbk3Rm6GzbNrTennaekBwOG0P24aUUug5yoSstd1JwY+idVAqNvaFRdsJmAi8GHOp5xT+qfqa7z0cUYN8+w657e+fLs9L0686VoTXn3uQd4QD3jlwR4RzlwrU+UMPDA/qMhZH/1tlxXRO9eFlffS7Dp1n17xT5wefKrypMQfRwat3Twfp/tHWk4sTAyxth8J/7/fak6I4SDCAieY1jhyrCK8GYJ+D+UYfux7vIhmgxBHEdjxxhpFaqTq+kq5JQiPlGZ6Z4dBOFCjFQJXL4g+OW189tjUUxBwGWFWmv4m5FSZkyj0Z4sPHtu2Skw4ZaHJldh0AVsjaK7v5yGDJsbEBzmamVHKBBoPKClhmibNFTFI2FFmjOMo10mElaVI0lgTcuVBxzgyLAZ9IhLBmwnLAaAUFEwo4wg4m1HX1ZKrNgJDnxpyGpfcjHx57nu+qL3T1xss2hpCHY1wsy0azqojtp35UTi3oZgSr46z5VR8fazjpCd4iu7MU11Pv8grysfacbYE1OrFwkU9Hop5R8goEiRWLpImlGVb3wngIsmqUwIycHEBlJJQxoRxrFs0BULWYuBPAPI0ASAMSkOIcZgmyvY1b0vR5NQGx4l8YtqVSBLnd9DzMuXk7xUGzGqtxuoP8CaLIatJak0fFRTGRLMpGwt6XYaBkewVB1UJQ6bKI6e8ImnlzFWYN8AVKt4+oFZzYoUuIXcYTFNTmfMOIaGLeS0lC++jMf/Na8povqS5IyQ5dQY0N5klLwcYRNlDuZnnntks5qS5BCgrOhbBdinVq6UAzqg2+w16NjrFmsCYJHwhJxBN8mwC0kTYDgNQJIm1w7fDSaCNuQCcHB86vrD5ciGA5afoU03D16OeG3HebJ+b90OyK30NlXYO505znigTSGQhDRiNVwxBPCLASJS1LbFEE++LhJQHINlvaWoaRxxu78RamIGUCKx5eaD9YZjCESr0A8oocaeLji1NpeFHeGqTkJqHC4EwDTt8g6+wffMWd6//CbfffYtXv/lX/Pzf/7f45X//P2CT7pB5BHTfJgsh2OBfwI5El9l+JH7/skugV+LGMBxsOKfxxv9YfnKlEy9LSRn5xc/ApB6TJIJmTJOf/9M04frwDb6/+yd8+x9f491/zCiHXThHOtKAV3+sEXWVZlqh5+spzZWVsfe4s2wHAi0RKzQlMDevVaFWpV6Nfozs07mKibVy/ttr83PiFfuv560dq9VDAs2YfKRBXGXyaAYJLerUs77MAArwZvoNvsPvMNGt5CXggokBcMI4FQxZJVok3hBeb8NMkS4CoUyj9BkJ4v3q1F0l7IiAVORA8kRGkebO8jshLCXLgcYk9BkD8DPevBkk59XMQ2I2waUaJRWlYQrDE1SzPuN8gP2udbSmNGq8ogtT7L1EQMoYNgO2my12FztsL3a4vH2B59NX+PzF53hx+RwvtqKI2KSMnAiUhc51u0qurYYF9+YdH5DRbqTnfn2QSe3xT/H5p+Bz9bXjLz5KvXufV5c2p83fwthPGhGcUHiXFiza9or6fxudp7nDPNOdKzfYz2gHtQEo//AWuMnAvzwH9cqIrklgBhbLXQ70s3LOKxV212nh2sqj8jyt3u+VQydhIygg+icX4bm/9B6InXslq0YgwGza3ZXJO0kwAU1bqP1wxgl1kgNBx907rVsUxbtNfbP2HHGv9OdDlxMb9dRGXgOxc0bzKHgKygh/n45p9B6BKPHI1enmcAYZDyWcWuB88nJOt457ZNgzmH3znzQAeQAlEYjcHgg3d8DbO8Z+gu/muQxkDcF2JO0a4j2zLGrITzxzdlnDSeHXDDHbU70yYvVd/XamMiK2c+p+FQ4Hof7K00v3orHMKjA7/U1OlDphZkqFTtjMLbZe77/+K8xIQdCdNLRJ6ILQq0bDcgFz0mSprTDc3iDrrhMvHBLOFZAxlHZbBZ+cxNK2WCJkG5F74fXWUx2pYgK7I2M/Pivzn0swWL8vr/kcdo2h6eF26WU7zw1sl3YCVhdYlmgdFht45ADLLAJbye9R6rUlAjf8E+YESKrASKloYl1A/XFbmiTSHk6sWt+OFWrHzJVQa+iW2ApBBOAFEtYtzC1rfeIJULnfaKUnjC43dTIpj9iskcCCpWaz0ZjwlINLctz3Ni/cdf+0YteSY7fQCJgbew8c9TSSLdJszuVGvJ8ExGSSoKD0Ye88oeZ0mVOOgQ7VOa4wyEHx2q6xKU9SMx7BeVUBkNwwkRnI2ZJq1zoaWG5I0OU5qGsXyeH5husv+XsU71PzrAmZNO1CM94ec9lamTA+Ptz3OLrQk+XxsbWiCtv+BheU8YDDzTtM46GuY8y6bm9Q7Sy7Ng2t4jMlUVTYulh9+lvWUuooacDIhMPdHW5fv8a7RHj76Re4/v47XF4SLjZ6ACV16zf+xvAEh3k11DpbnfPLT9Pq//2UJ5uLE0KO911aHHdvEvCnXY6s4bmru3aCPGlZYSiiJwTSAMobcNqA8tCcG4bT725v8fb1K9zcfoM3t69w9/2Ecr2b0RUdug1XF67NLhvttPyun2B2mHOkgXsGrT+3F3sQ7tX+LJ0RwGmy8nR5jAKvo5GWb/mFJUvhtiftZ/u95W/aUOH6W5UAEx8wYQ9oSFQ7+ouFFrQzxQmTJSQR+iqEJAomv8eNEP/IaEzL0RJXlah0eqryMfN+cP207/0zlahHzXFW6v9YV6PUXaaF3NimX4yUQENGHgYMmy02eYtd2uFyeIFnm0/xYnuF59sNtpmQUtEILlZXezb4lqBK08v0mASE6n1UpcN9zqpHKQtOV/7wV+9zKHF7Pp8KzXTSm+NI0+zwBriskQNsgSWnSoIoA1VuwEnguLKYhgitKPxvxZCMdiOYMmifuvbbMaIf99Fp62aE+6sdjN8jYozD4lprs7ZmlbVvdut/FB74dF+WX7sfgN5DEZEr4+eMJ0G0p5URdXezhjFUpqRXIARhD9o7tVB3fVbHOYhh5eA/qyxbpf1VlgiwC0qJj+VHUI4uQwKuPgdtLoDNDmNJ+MffAW9vgQMxaMMAmf/R/Q+T98F0mRz1vTN0PV452uAKYY5IsjapzZoiY1Lyxg/ZWFElmuQsDkJaQBN6WkudIO0Ewd10OgrK9FpSa+1EUO8HFfaUEErHCAayHlRC1hL3WmzNet6KBZkklzIrbsLERYQ/KakbayUcScdapgIy4SEzUsoSS14tsQH2kIHTyFq/KDsKT0p8q2jJmclJ6WYCMpAnc8OXwScdV87V84/ZhKrwJNhyjVa2i80FsPpInZ72p1LKJtSMz7CeqfP64jWF5xUFvYVlMcGlCQPdrtx5jsqoCCEu1if+LEHgIzIksUmFmYYBKOpZoN4r9jmVSWDdmSZLSM1q/ZwAGpBK8j0xlQKMjM0gz+dBBNPjeHAYJEAUFVzAySxlWoJMjPI9Um+YS1v/At91Cuf9NqPoSZGLJtSO9wmEDGxMTC5tmZt5LoPnMCklzIP2RmSk9pbNr0xtaWCjmf76HRSXMzBioY/OxNakzI3lL9HcbKlRzthzgHkhWR4Om/NSWKP1RELfJwli6ZRAFPNCyHXWeTFvkpQl6fA0mccJI5XQV8MjJHkDDqXiEZB4q5BaVhVVTiaNK8zqAVNKwTQVbDaDJsvOYBRQSSAasdtsAQbSzQFcGFOZkCbFn8nVr5Vkjjja9gvLnBuc5FTnzK45DJFZ8LKvp1kiGv6OEyvGihKKzGj3bKudDC7FuwAQ7+ecE3LO4nEEQwVc2wWQsqyL8AaknhHQ/ByB+Ve4K1PB7fff4M1v/xmH21ugiHCG8qA5ITQYm+a+kAhdSeZQc8U0x7KFeAKBiq411c9EhEI1vERKhLK9xM27a4zffAs+FNxe3+BX//A3+OqXn4O2W9Bmi5xFsZL0bOQ6BABUQ2t/JHn/osqyNWCgu6w4Tonw5jdxPm/5sXyI0igZFh8IhyBlpBc/A+WtGrLw7H8pBV//9rf47f/zDyi3E6brDTBtA27qzmCcQhUBz9jfxmBC6I/4G1annSnxDF6cg1C3/VZ87opqsOf5smmJJenFeNl+UfMrjmxtLzwCeZ7YXnE57dxCKUrzK923FDKnscxYbrTd3TL5wtMMQNkiYYOUBgwJGBKQqABU/AxGGTWnmPAbiRJKIkm1YH21Z9Gud+1HuwKzziadgJKqGx+rO4TxW+qdKb8hRERisR5PSb0hrD1VKOgZ3YRsavgEwD0dGm8coxFLGJDBdxeyKRglyBssfEAmCcN0cYmr3QWeX13hcnyJT/gXePniJV7snuEXl4xPNgW7TcImbzDkJB4Rtv2BFjh+iBJ47ZPPrN12Ouxh75do9XfqvaV+9rxqx6ccLb2xQPe7BGVPlXkIL1KUtjbDLYYayBdtVz1xAeFT45lMUI/7zQT++1fA9YD06xegsXJiM7zN9dopiJnn/W4Q0Oz5xZBdK424RxCW53fNC2NNwVCPqcgcnnh2ra0Tz59bzs8REQREETrFyk+xRmA+KnokZ07hb1apzEwJ0X6EDtz34LLWH490ztUgPkYY/1hB/lIPT8VePQcnrjcYKaIfQClxRhszEdxj+/UDnl8zBLQsX1y+SQDSAPOG4DTgZk+4OwDXe+BuYqStekI8sH/v82xfI/CfrszJ57Ot65bPsPXCqAJ3P2K1qkhjsjEIxS0DPI5335gRV8cOoH6zLz1DHa5OcGvUtu35u6QjcqaIF/rB7AJdIQy0Pj826vlSRbXs1vZkQiUOgsYqwQTR3DqbbV5dmKAMlzN6DOYEi7XLgAi1EndMlxFEHeNFp/PCnCqroBOJGKP5XUNggsmzagp6o2OAemQg2iQXXQcXqFa4sz5WEJP7hQti/KDiY7CxWS6QVjHG+l4MEyVjSHVAzM4XWT4XU6pElkcu1eTliAy4W4nZzToP5rXeb58YHkmud7DSTHPcV5WMJmWyzMsnJRJlyMwTns7jnxzYQ4K2RblY2Ak+12iX3+Yl7MS5wZw8szBt9WHbpzDYpRkMhi1caUxbE0/GHOr1rpF7wTDGer+JC2xVRyVT3ct1XJWOFTymMBYxnoaLkhBMEi6MKInQ3tYv4Or6v1+DCJnkX32P+lDjvPVzH1eRHHf1W9iUxoU1EkNcdFS8bVNs4RotF098rlrbUvOuKJ9r+LtFPsFwwXjAeHcDHg+CE1KYGhfw1hwabKjG27A+sO8/CedHvla6PBWEdT8yJXDaYhpvkG5vcffuHa6//x537z7HODLyIF5WyBZKS9+1H04T2F4/tSGftvyYcik8tOX3OmNPQYSGOjos9fi6/5JLP/dPAJv3Ja2XWaJ6Di11q1GA5w1IvSEoq1GA0rFlLJhuR9zd3ODN62/w9g/fYXoLlD2Bb6O3LUesHq6u7ZmeVqj7PPI9SwJpw3WMoAhbOeuPF6OJTz8fhbqtAc6yCNK4nMW6zuyZfPLC1SP9bJ5ip3WYgUIZnAhzo2Raq2DebkpgbMFpADPhbrrFu+kNJkwgJCRKSJTFeMTpVw0HGelOn8PQIMf2euDQPwyhR8CoeRpWhmOHprVn73JxekqaTxriSe/H54HQTlREcOimERj2bBhMdW8PY7HfPXU9H0fNCTFgyBtscYHL/Bwvh0/x/OISV9sdLjcH7AZgk5MmqU4eeqvybVw9jLvm2lDxtTv+7j1x2gz27wHCx2SOp4wNjwmL1yz7z7OmX6lvpR4z+Kql4gg3EuPw2+g0rkacpoiQ68ojFmuJNLwqQJQUBAs4LGyk02zeeJiADcAXB/Ahg+7yfKwULpyBQufrfEJkz3NoPw9TH114+ViEnRU4lBfObv/kcw+kwc5XROR5POP6UxnthuEOeNCfjRua+ko+licsD0oy8rH8oKUyzk9dCHzxKWhzhTQMGDnhP/+e8PoGKFmUEB7ntmn/qWDo1KDOJZZbPCc01MMP5fXSSORW+nJsTGuHup0UekCn+qwIelIQmnONZ17MUlTf17WiVAWrFqKlSf4LzNaUmFqho3VVLfw9LjlRtVxXDwMnHDm8q7HeReAoFfe5IIzmFS+FInFP2ZLPFmkzZySN993sgQKPF14ASNIAGdSQB0zTAWWa9J0kCYvNqseHyU7cNNeKxewfwSVrOCahjiQCvlgFW/4CVwZpLWSWRM0a9z/O29BL0ZCMXwFrfoKmtlLv+8PxQn3YCOK5QBSugLFKxLqrpyd075Xl3WTCTiMmLd9CUWvyYt4JQMMUGBNlMfstibTkYhDlhFmkG1HqrtYp+7uFC2gkt6JPWekVDd3kVquJMKhAWsZSMBWBv5wyQEUZTJ01DQ9kykCxuqnhgApXbw0KCpAyjj6GSPMMm00ddxELMwKAIQMTQBj+/+z92Y8kTZIniP1E1dwjIo/vqqquPqp7OE3OcIE9hwfAFy7ABwLkEnzgv8yHIYHBYhcLcmdnuDPT093VdX1XHpER4W6qwgc5VFTNzN0jM76rOjUR6e526CGqKiq3YD4CldQrQhlFIoBLw3/M8NBODLPSVHA6TiGgSnYDCxFlS4z8v3Geg2BBx5VoZQUHo3vBOS4tFj2AJY4mck8lgwGAJuh27GXjyW7VJPkfDEckWMLjRCSGfhTmx+eT1ZpdheKgEGLJ1nD1vANAVEaYgqjC885oxgnL8yHMsI2HAQ2XMO13qAzspgNmFNRaUKl6zhPW0HJxY9m8iXJV4j+DU0vunQiJE2rREA/clKCea0SZaWOuwXImCJMja6OW5k1XdZw1JWRHY7Z2EzIRMhg5T0jZvFKS95cYYewKM0pIaVKmP/k+A1ThSGh9PhxxeDjgcP8ALkXyRKTkghtK2Q0hLCm9tZ1y7owk7Ezk6J3DIvQhtMTpHlMYwBETSvoc+/qA6d0t3n35JQ4z4+bZJ7j+5Jf45GeMPc0qkAyYlrStZOtFz0rwcm98LH8UZXGswlAcNXrHfn8sP+5yyRxRQnrxcyBfoYKAUtTbSmi/+e0Rb//Na3zz+9/jd3/3e3ABuEQhbeA1lEReKD0Qz1IVinH/rhndsP2rfQ2jssCyFVTzbu1kL4qnO4OJWMdwn7vBBPpR/1JT3Ee+ojfCWJZeINvLhi4rG0I0Xl7aet/OfQZQ9p+hTAmor8B87PvSsX4LiV2joXc34Kufo84EnoHf3f89/ubd3+AdH5GnHaaacIWCfT2iIIknJqC8mUQRkVwTjeeQyoOwHyw0aaTbO/m+na8cvq8ARJhLmDJfaL/aricaHoa2a9FOrE+ELu9DtU8jRiLjwGFMaP0c1q+/m5w6VdCzCJQTgXJCvtpjf3ODF89f4Nn8KX45/1N8+vwlPn/xAs+urnG93+NlvsNzOqhhiHlQN49OW3lR/xO4uSXMwvX3VfqfUsSNZTPs0eJnf2HdY37l/oX1LfvV/141ilpVRC8YSWeXR09fp4tXQvwK7VrVoE2uVX1F9lBGJUZioT8ttoHQr2G8VTpeawHvZ5R/8gB6e4X8t58CZWDAeZy70/PfbKvW+Kr1sv3I2gbWb1ETPLyyVArFbyvIcgOtvlf5QHnzozwi9EtofLhPDVA9nNrJZdZnvf3g4oX+3RMT4yhmsRFOVvqjK+uKg63+f/CyOV8i4j23yIKA9NzjT0a3X9DIiEIuV868/6Fj5f0E4E9T3HKbAOQ9QBmUd5obIgOFcSiMYxVHCe859bVslkDwBHmGXOLxof6+175S/fr08Mp9Q/Y0PqI/N7Dtat1NvLGC288vWHYMNFw/1254xHFm67kIWI2A7hCtfkQxHtAfKm1iFgJuitaeWqHx1sMonBnSzl5OUMENZVor7QzgWmAkuMXdNKEWGbGMYNVdGRJLRAbj8q0OR/lQwCGHRCN0tuapApW0ToYL/WoF58AkWB2BqZM6Q39OlFOYfKTNN9ezwVTntOeZ5JkaK2OzlOYe99E4zxC+hKBj7WfO12trYOigvWPtVlgIA2YNv2SEJ4KyyysdBXptf7iSQp+TcFJWl+UuaW/mCeAq4WIktELxteJrhhFcY8N8OlzVyp8GopsgAk4V0JuQwITY0mfuQNEM822H6Q3N0cOQBMgpVZSaQakClECau6SHyFjC5mbb98MZtKDHAkG6sij7k3PlPR9Ju8nxmj6xUCj6dSAmiMTwTl/LyhdKSKa8HPpGgAjGzZqvY7CbknZ9zdn7zYPD8aKG3IreGoLPZK5yysi56nMSds69ISprFIQRpsF6P5ydDa4BRhG325S68Ehf8PXW5rs7goazvbPbJRurrtGofQrnTXfwA54oPJlSqZNQ9eNlrhKaby6iXCkVtVTfR5zgeVUWgi1Kfko3BUGScH2pAc904g6oMF5A6pbwa9K/Os84PjygHI+CZ2BnzwJgPppx24w05kgLP0X5YzIqWoPdD1EeDdNhu/zRladeY09YX491Hvnm4AnRkUHTXg0NADGrneDh/5R+OR4f8O0f/oDjqwPuf3uPuzdvUQ8QmrHrFXcfi++rzMV4zWq08IH9PUZPCxot7zSRa6Pjq+85DzR8TdQfCatynkdXfUHh4etyPCOLMzZSdxXYH1CptLnWkC5rrY2Y3+p3voZF8VORUCHrZOYZRz6CSSrNiTAxYZcSZhZDAQ1sBDPcGRixcGiPY9YvcakxIIYQ4+gHnmiz0HJjEdByR5AY+7jJuRIerIYhnUakNuD42Hij7/3YfBfFczO+SmL4k3LGlCdM04Qr2uMZXuD57gbX0x7Pdhk3E7BPCZkyppw8ETlG+h02xpW57ta84Y11pE8IdOKJYgYkPDJsAQaXlsh/rykXeITlRhtLRcWpRpc3uQPqep3x/rqsR/h+72vd6Ltdsw1oHwxwquAqHsopVVXKqkc5CWHJRs/p+jRFIENoctrNSM8ewKVXGBGaF7rL0yJv8pCB41r8kIbD37ssXmWYQi1ork+/GhWC4zOBF99+arMzQ/0XXT5bLlZErG4igjLm+nM8nDY9IB7T2BoZEjDL8uRYee59yw9Ncq4N7qfAlJyclI/leyiCPBNw9Qlw9UKtUDPylEUxPFXQHm7l8mOfrtESSK92B/Di3pOUywHTmISh7VUTghMHgioh6lzEsprNOlkEbGYxG2PdVxe0VaUF46EKx8XsW1PDX6hl9SKchsfxN4+MgUAOoBkFR6yhdpjNIl0FqyrQ4/kIpoIawnkgZeRpFypuNRaIkClBrNBraXHcocIjDrkEKMJWx10DrBGF0O7KqdIweRq1QpMgi4BMjhoWy/RqYYQEJJyFyLHQQAE0Pv1rxSEaQNuuNaFpDE3kD8UZsWchuQVMWikEcLNoDhMEF8z7byPwWjDD1m95tnIVy5SQ86HjZ9RSqhaxJS/zDGb5FHgpU5c135Tm+EgQYxWXYzLAljPC1p/CIOkcIwVVXIDvfm8/diiVUXAITI7Er2fmZhBW2RUbUXDRcUJEzRqc4Fb+Rh9LWH5SpQlE4Mrse9SE46RWX6xzZIRzRfNKYWbkqQACsuCJRC03DDVJgzPGHfcGmJZkXI3RM8WO6SZg2Dq3baFTm6PAn5knlICquUuQe46wzzcAkOYUcGtAhUNKSZRHoICXLBySWtsrI5yz3C/zrOF7BC67KSNZbGBIskKujFKqeufMYPNEMQAqLhSmt9GbCeI9MO0mnwIOayRp7or9bg9ALPBKTeLsQpITgRNJQnVDFt06ZxW8W6kOj2QeL5W7mL5mKejnIfXBR7uz3PeywiJI49jydCjuT0SgrHsqJTljKHUM98h4mwKCNH+ctdWfPTKOWioO9w84PDxgPhxAlUFFmMfEQCUGU/H2bL80xUPYo4BfnyjLXppn5UdsTuP8mlLM9lJFzgnHMuN49w7H+SCK7pzFkyrJGnYnFm1WplBybYTt87H8sZdROKjFc+fIr++3Tx/LhxUi4Poz0P6ZGzoUZmCe3XCilIJvv/4Kf/Mv/xbllsFvZqEV/agNdKT9jKgHaOfryL+EOhoNBxGS1f56+FhctxPDDHuAQN72PfF31I9Sv/eYdXGWoPGIcm41AqCn0k8XE8a+zy5ZZf0W9a89IhNSXt7j+ItvUB7uQvvyBrlPSX9nUQ8rr6Ce3aUUHOaC48w4lpjXTJQQ+0RgTphzwh7AfaooDDxURmGgaL4jViWFeQ80wfwwMD3XqFr+tsgMaI+TzcgwAh4+R6j5YWb1ZM0vQXABKLK+r8qcWoyAhrgHybm67h0RurRQ/hjcyPvhuRNtnaWEq/0eV1dXuLm+xovyHJ/iGT67eobPrp/h06sZz6cH5ExItNe8ECT8GCSPnAxPaSp0ZhjafCBoOwit0z5bz/UjU16Fdf2vCe/Da/bMOS+KLUXDec+I1cpWnz1ZmMPyO/P+2NXA5/TP8OrzsY3IZ1Zm5cMthx8h2aJRoyAJ5Wkz3Squte097B9Q/8o89sfGNzAiA/kfPkH6+uZEvy+E50WSeyNse0pjU67QdWllXIsuh28r/bnMJv091lEol3tEbIzaN5s9117o3tt03htx5sqEEm29rUzGgPBOOwo+ffmjT9S8Zk6yVuLp+YEguXQ5rzbjgifq6vrgWTpXQbcMre1+JJeCclm1IeO+EwsvjLQzNwcV6OxgCT8ZjG9ugbujEENEwXPiicpZB4Ju3CMQ1oEyKiGCvHfjANmo7lzfhsceMd3tux/M59/19nRAXd4CC1HDHakpn8E6if35oIRAq4eoFy8avdeOtGYpHleSRXqJHhFeaPjqDMoIMR0lAZKAVgVdzADL+IgSaJq8NhuffG+JgmP2ErcoCmOyNTISmH13GKBgXQ+ztm+Uevs6JEbdOvTtv5O5F068231pP+xS7amK5Qvc5idaYlv4HeZ+f0f4xPUehfVxDRsDumjW6uF+HMxtfghCeKZEqCYsBkTJFZRoUKYhUZLQR7WCLbk0AVXj8vu+Xxg2WDgpbj0juHLNWQ8ONImuySYV1utqVdiWchNSty/2fBu7eWawBrUnrY9inFqz9jJBNkmYIWISgbTtkZw0Ua6Gl+qIfVJGgCBJxS1sWE/P+5fYya4o7TRAEiu/vWWnrYYz7dwZoqBPBpOYANl6EulE8zhY6U9UjnV4SN2wKaniYrjPinPifl90Oc4vc4OQKlBF3CCeKhLuKiFRlbBBrhxNHf9iioTKkuSYbH9uwmvlBjX4LO+teZ609h0/m6LZQ3oNLRnMk4rZU7y1PifNUwS+b1ypOYynHI84vnuFcrgTRVxVRbgfEe2gY2bNo6l9WW737jxkm3cOe1UPTjb4DEtUFIUJeb/DdH2N3bMb5KsJNAkMWKsAG+wbovMUOWub50x5DK/wXXpCPLLbP8ry3UHnfPnJs3zn1tb7Mio/QDk5FU5bQzwg0tQYiCQeEE6nMuPh7h5/+I9/i/lBhFP3b+9QbivqA9xzVivG8tvKlYGpMLzL3e3AJVanTFfPdObup+K/ILxUeq/DdatwOXnXS7/OyRHfKuo70+iHy2Xeby3SMSMfdp2H6cVN2QTYEgF7ONBaQ+jQzqCBkRKQmXCV1ZuvknhGQBQSBxaZvfFXLW+a9tlqY+ral+qNbh7gYVoppdN4eG8JPyNS1iaLmtcIZak3WSx9DReVZL0JbR4BZozAuA8GqqNf3FpnT50YuU+UkGrCnm9wRTe4yhP204RdmrBLFZPmEiPLD2Yvx7Xq8qCVleiv9HfOKSgWz8Vi4A0e3GMdXTgmCs/Yu77J25wucy+cL4vHw4XTSo/Vq36Tzzy8Gi5oDT0GPnYs5M9a2mZuL5MZPSZUqkhIyhs1Q77RmYCQ4EnSCerFxIumjedsHhHtgXp9AF4QcD+Bjsl54TauC+bnwjnkqxm8rw6IdL8DHfPpFuKZcbbNlTmKvy4d1weQCpd7RKwUY7aXNxSJuHBr/QA6sfw339l6djsp9YccfgMV8bF8LD/ywvsXwNVL/01J4u6nlDEz8O/+UPD2AS74+uGWdiNcRkVD91S419E1kbha26YfxD8NxMeaSvhUny9pgltdNZHGtpbLtbb4+q1LpPHTg2UrIJbjaoHdBGw0EIZmydzENy7LNSGpD7gPCdWTx32xd1zYFYfHarAAdg+OSS3h53lGrWJJ1OKQs1oBA0Qe5bEJpgAREGlc3qpCank+KTHSoG/jTwY7tSq2xMkCYw17ReZFIANhNkvdArPisrlxIX8/kRsQkvsjAbp4PX7l8R4PcYLjrUYocQ25FlQB1Qz9m1Uz69Eaz+1u/0UlxKDEAGy2e3hZjzyxmD2bSHLfJVUklMZ0EbNF4Je+pISJCDK9WcPvT2CqSCGsjXkdOAvn/WNdcxZjKrvwn0ESk54SMoSpyim7x4In2GXW5NSqJFHPGBpwZYNdAqEprMx7yazZk7WRklv4g+DxSCklsQZXhZyMKGPCThQ1RJjnGTOzZiMwQpBkDQMoRRQRtgr7XBztS7OWcmpcGbdhXamQXF4TGLS5R9gI9oOakNuvdG+4IpFyQkoZeZpQKzArfvNoYOb10OFbtPBybF4mCJbyBBBjmsTLIlsOB9IQUIB68cyYS0EpBWLV3jpqSovGBPZrk5KsmTrPKLVClxAyEZAz9oqrdru94DWtr6qSqJaKSgm1FqTaW+SNx6+tWbPeq4mRbAo2SG1XrK2gIgFlCt45Vjer1xe1ehKpl4fG1lVFQ0q565MhEV/T1nQJuYyIEMNnze9e4e43/x7Hd3eopSDb6cGaIFrrZmiCWCoAJcUd0D2Etj5cUFpl3icRMHocYRWWtN61TwajcMF0vcf155/g5Z98jk///BeY9kBmOZtcUQJLcd+MPXOVtVJijtqP5R9RMVw+4KqP5cdZzNjh+hPQ9SdOV4tuunYeEG9ffYO//3/9GuXW8IuSjmtJvOwB+9jgCYSWWryBzqBGaScXtbFdwyALCvQZRDmeuFlQu9/BuCy90Uih8aK78TU7V5RNcJSbtl5Yu/4BfFh/nD2+IuvC9GaP6cvPMb28Aa7Ps7wC29AyQ+ggtpx54u1YSsE8M8rM4DoDKCASD9+92NRg4oRChCPE4+a2VByYkUpFYcZsuSPU69xml4SsCdxHFR6xKo2mRigg1rx5qdE0NMCL+3XmgzS6wsKtuiGOrXULcRloXv8sEhaHZ8lvllhDCNft9mxs3ewMfCr6ZuxqTgnpcIXPj3+Nn+9f4uXVMzzbX+Nmt8fVjrHPVb0q29424XHSvG+W76qjh709Jwb76xurZTNW/8ozlq9qVYhr1YzPWL06R50yg9t9Nj6M0RQU9hvn81M83oLd4DvQVD7dY33DDg5LI+JLXnunDUVbrqiYwUhIyDBPNtJsbgkZlYT+o0QgVvNFg6Hiu8RCzx6qcFXk98ZeCK1rPHYHhc/fAp/dIv/9J8jfXp9U9KyVx8B9fnmL+U/eSl85YfrNJ5i+eQ7v/OmGVtoa96T+oOUjqz29hOR55LJ6RI6IrRtnNqoX3T3hMmE5X23hxRvGjYaedPUsAd029qnOX1rCzo8d9bsbUI+XH0uw8uLLZvuXlLXHT1fRLO1cUDWOYYPw+j7LWuu0dpMe09P3HNPKkt922VtplZ1mvqidzoY97cBZ/kyAQCBJAJwSvroF7o7AsZrhxAfap6yAaMRrp1+OBxgHmnj9RSPM+8rJ3xtpr81mu0GvQ6Dz8lqTFOl1UiTfUggsqe+GzwKhMdL/lZX+a1biQviicQFeg9bDrCFHNOa2tReEQ42msdlu+DeGBBG5Erdp0cNXwj1hgDvDutascYVLaU+xQ8Oe084FmJrwHADPAbyN+ZHpNQULgdiEyxKjlJ3gbX9Ov5kiIipnlNiogeggVN8vTrqSIgtuSKMladWJrz3h/FiUwavfm1UIcx+SZbE74pwMSaTJ6jDClKE6HbPMb88tT85ApChMhNhr7S0t4MezmgFL1hzvEbnlS1tyPS4U7y1GakutU8iZu3Ud5r6oG26qss5LVabKFlIIHxPdvg0SorBg776PW9fgOrasC/iJvlDWedLEy+0m2jGqSbAJorColSR0MTOQ1btlIlCtsHwL1n+LZ99hmQBXu9Ydz2fOauq+c0Q78ZRRAI4WkaO9kN2Nc99qigpOuZxaWIGmIQU6RfmAvG0rOsNBNlnetOAOqCLPEF/wMmNo+IE2mmht1rwzYqNwWDs+SwTKJDnHM1lkH7GWJAkNkNisrgzPGi7qU1l0OHkBv6EfaOP0XuqkVRcuaPi71JQ8AyXtIagSSeJof84WnWumBE6Ntrf5rG1MetmnW5XatVTUKkqgnFLL5+BTZqdbavgg1CltEJA57CFqFfhYwn8OZ1V+Hg9Ih1vkekB+8QLP/+TnePlXf41P/vTPsX/2AonvQfMMT07v68B6Fofd7yWOtxBh0eONU5aMH4XafVkPE/Adw0gV0tZ+DItox0mHETgo89BvgzOyiB+2rB3+8d4lz32npSGBc81vDiPvJEeeVsc0GUEKZsbd/C0eju/w7b//GsfbA2qpmO+P4AcGz2mo+amB0E5rF3StndUcn4c/b3AhKO/AqnQnCVTqdiJbTa//ABBwd8Tj/d3VyleXynuun4HaXX1grLr7zXDPUyAhsZxtemKBQgVtX5vy2uh/XqlYzqJCwKEAt/Mdbo+3eKj3krvZTgsWhUQi+Y9ZDCOuGMgaDrYw4wiJTiDJePu5bQdkg4YcewTW+XYvYHbTCUSvmLaUjC6PdLMVO7+NRgoDjs8SQZI5JbPwEq+ivINbmIPUAs2MlTh2ohvHokTyzqLuEAGZwFnovKu0wz5P2GXCNCWkHSkZZnzEiVURGjbv5DPdWP7umJWtN2JpGzGaSzcKqikPOjrO6DpXZrQhwPPBNJLXFrIcX+zLxijz2O3KbRyt3nVghOMw9Ny8MtpvOP7ahr99a1fGNpd9GK+QhnNtXqomKzEvhyTKqCrhmisRkho0evvWd99XZkAztMU9VLo+G+l584BiFiqxjhVw8viNz59tAFCu7mWMBIAq6vU95k9GuEQuZaBNFwqWSNdu9HCjY+luh3Q8rzZ4LMr/II+IkcjeJhL75de9o/fHpbt4HYBIUwyI1H1udHC1zdOIY6uEei5CQB9azk3l6bYjw3mZG1dEsGt1r13bOFJ+jAzVyQX2HZXYTrd8zmuqTyEWu9/x67sblKtPuhAViRLSJNblf/tNxat7qFCCNqZoY47PLJ/LkE7D0N1y9MOA/Tzbfp+77kQoXjy9vmRp+0kjCjrCZolpmKhLNmqWon5Y+40aR9ATtWHcrKbB0dUXMIttS5ysJHOVxJ9lnlFqUQtvswZOIQRIEBxRwNEafsIsP7k2QoLBalUqBK5zNSxWQdUJjpYUlrJ6JWj8e8sHQObVAAJbmwqfUo8SnqZYHHhVmfgwWXMEFKAQaGJkENJEKthi75NLF3VtcxEPAQsHZULFUtHirnNLT2qCTEke3JaKE1sWxkzztLFCqs3d+lLCCvHZXeewv/VCS6jbhrV8H66MstwMAmXIOPSazYJ5NxCpLbLOKYGC97dZNSn8Y98ACamEtoY6wiwyLJ4fRBRMC6GjjsmVRZZcLElIoomASoRCytTUqnkiKtxK36zTrE23chQ163wEABWuEpDVelnyFbREdmOJ+KQnnJVJpeTnaVOGoG1NiFAaAHKavA1XHRDkPkOJ56T9LEI0UwLlCSnNqGWWfV5n1JrAqYoHBKuSkDXDRqoQ4x6bbxm7j2SYR4p4gH0Lt34aCtMxUQcUVpiaNwkCo2XvyYvV6245MiS5Y9HeyL43Zbkk8Cbdxlk8EXwOWojOlk+dkPUZU/6oBlWZf8kN4YrMMGfMDOSsAvqEanhHx8Bs3QuLRIXTnldkEm8uhpy3+30COOFhgiqJGYDktKmZ2142RSPEsrFycr4+rsRmAAKnqfrjMSoaBeZkeQ246m9N3KgeIwSZA1Q2h7P2jE64M78W5sr+FBYmzoEqkmspKnMwBRaBsghoSyk4Hg8o8xFcKhIIu2kHU3ZLV9jDdnkYM0W+FnYMpII3229TFgWUz3v0Hmz5SFy6c6yY3r3B/sv/H64+e4nrP/8l/uJf/Av8s//Tf4MXL1/i+uYG9c3vUQ93mk+keOJswZ9tT/CKAvJj+XGXLU7wVKl+7jRlRFejHIatAdhDP8L1sQaAS/mgS547OeD35MM7+nusYkENDS0wsHuOdPN5mw0iD3laasG3d3+DV6//gK/+VUH9dt/e5KT1jdh2nS9ufEj7fzSOjGyC95URBMno8H3L9TvUE573uyrwrUROiLqgvYNfrIs7mPmjgBuxWfHweHZ1AAMN3xczfcHmW94+wSE/+kYGkgl1FX5UZeta9CFiTBBPycRZ6VP42Uuah05ynjEOXPEWwFeHb/HN/Dd4Pd/hOJPMAQGA0KqT0iGTrogJhJkTJjAKEx6oYmah62YAs/u+Nl7PC5F4CKIicdJ8cLADXyDg5Cg5fe8Cz6ghNRqKWWjnSMt6m+TXXUhOCaCd8qoVnBW+tQBUAPH9AOoMqHV6aCzMVL8jOj8bf0wUEHUi1H0G8YSbnHEzJdzsE66uEqYb4XVRq3F5HQ0v1SSYt7bQu5ciPtvHFH5r3RdXQd1XWl5t+47NW1ZVSkr3yFiMQFda1q6bQoqkr5K43kI4tefj1hev74YTuwGtoul4Mfa88Rbk/V6rIsKvOkTPnZFr9RA01C0SqgWQZg2aytVzyJFmzSEkCSFGwrsJchOjFjf4jIlLfP8EmEdtzCBLnb94DXw+9HtJLOh1m8utkXP3XPdYMIosn70Cff56o45le7HPvjcWfVw7Y5dl9w+fY3p4AWDrPHy/8ohk1duNjht79cnN1/n07UvLUMGIUuO1BVkwAD8OZ0sI3NW4BZvHUKPfofnMxYh347nxcjuvHj9rW8PsYB4eej8LqKfbII9vuW974WrH28+N6258prdEVrSfduC8B+e9CxHMAjKlhK9uCe8OwGGmJpi+cAyX6GsvY/AWpIH8+sA1f/btAebdNT9kNl49BSQ/vHlEFoGDOL8GnX3pDh4jCI3hID/sRegsAss6F0m8agIYsr0yWCePCNAImPaa1G1xP5X4rDY+e5WNWRoJyNDOGMopwNp5gI4uGwjtBgQAYkHkxA1L8m5YKCeiBX1QWRQVQmwmpKAAWhJ+NvJxHLFSuHWJ3SMicGJQNaIWIExg9dKIo2i7aG3PcU/NDgymx2HlRrJHq7kxtqh/+LKOFn2NmCWuzVKMdbx+BgfVnrXroAiworDKeIUNd/pNlVOxFyZoRAv6I+3IUzUwSSLEJoGtmK+LtUuLydX2TASrQ52RcurG1byHbK/0dIC5+wo+7uMWbcfpb91pxcLbkAtwybrsFlDiIUL6PVECS+Zem3oFtuT4ySlJOCMVZFs/1xChKQID5IdRkxv0E7Wzx7dGZIJtfZGOC9Gy3pTa+jsI7l3h4egy4ktq75L3CLIyejwmjzSrJreUi+ehPWxKhgaIFSislIAkWnJmtf6zsG+6DikqN0OZpoxaJuSUXPhla1FwLLcwCN7ccH7otfWzd6Q8u06PjwLQ8FSaVBro10tU0C7przA6RQSq45PE8rD9Uh3LGtxSlrkSC+M73H37JQ5vX0HjnCHl3OaJg/UuGZYR5agpJBxNAc17cBaBTdWwWaJIgSeaJiJkLpj4HjjMqO8eMOGA6y9+hhe/+lN88c//Gl/80/8VXnzyCTLPKO9eoR7uwbX4mUoDXFvYs0fQl6donPeibR/Z/tr7H/T205U18uwx771Pe4110f3wHfJdqw3/UGVJ6Fz44mk6udW7FNv3r73HrPUESKh6Au1uuvO/o5EU31KewFxxKG9wKLeKg4Gv//1XePj6HvflW8zHB9T7q9Xwlx9chrXVCS9X1oNj/dW1wj7W/sjXkes9i2tuxGD0ZN1q3M9ZGudsSQa8d3nUHhjWUneev2/z9k/pFx5WJhNqUqqZyVeRPSEeykClHY7ThCOucSiEQ2UcK+PAjIMwDP68hchy63uW7wnALhFSTWBiZAauE2NmxqFSy8/nwnP5Swi7ioTUMnKiN2Ya+I+wR6Uu4y1q/9s8j4elQqEP0lIzfOpoEMCIPt2bkUbT7854DjFBqcHZ6fJEoJSRAVyDcZUyMolcAzkh0YypFiTMNomh/2sLhTd+UaNvee2NRh9H/ped9r1kUfa7Z0HfGe/hY3jaAyOKLKQ3gR7c7qbO//Ki0WSCosnz1Ng7/ZN9A6ZEaV4Vfd9an0c8JfWLjWRQ2Pn6JP9p64FRUUESvo4Q3hFjp8qDx30bdhvIylws+O++o4vn7Hr8vRrGKsKjxVbu+kBr7/YEfOx9PwfDvb4ffftrZb65F0Ms78nTlA/ziPgjLz807fhBZRSS/kTK98EX/BjLmgdEZ8UahS5oiJKna/D1Z57A2BQQ0zSBiPDrVxVfv60aIzrEkfzei/bYcfuHT/Sj+btOCHbBYzj9/Ni+ybB7WXZD7u5pAGOVAPAQgofNKl3fI3MbJBS2cERAKTPqPKtgXgWDKXg/OJHUkxHWlAnKkv5q1jVtMFHA7GEKqnlZRJpTCQSGKksaodHAp7YlZp1j4ZCMmImwDMmpLbktM2M+HpF3O6QpiyeFAZ0Saimotaq3j3j9sFnZKI0izabmBWLw1j8RyKqAtlQwJA5s0hj/SSTjqEm8O6DxYindqEX3O4APDdYR7hhWEZuQLfbF4FwDzLWPTiGNRINTlgCj5Q8x3qdaXXK/NqdCEZCbFDC87xagPSvWj4BkZdn6Hskb8TpIYAJKqegQu+VQ0LVcmRdz4XOvDBcTiTeDK1tN8UMd/WSWHrVKvgfDg6ZksDBgo5C8qlWNtV+ZNWY+vC9xVkXQT0vLKGrqNdJwOK09eb+5hbNykyZkZ1RTQmgbUKVyTgmYJlCdgSoW6BLqBr5243KA77NuyuSP4NbwiRqcaXiwE0gkyPlheMbnR88VQpcTADp+ssE7zBRG/p5aOCWz5AoIweBuigrrvL3vnW2l81KxsnLWtDW0xO2WcJpyUo8tqSMRWs6loGCquof2e7GqnXYTylxh0QqM16+loKakeEo8FcfWLSKBfRdhhgDE8Hk30R2s4PjCGPmUktMGgg+WDEwUNnmdLGcVeX7KxiRnjbnMeh75/k2SNyNnid87lxnHN69x++v/gDrPqFxl6+80Yax6c4nwP+K9MO80xCQXztGZR8qqpNtJSMqsHqFgxp5nvDh+i3T3DunbV5i++Bz5z/4p/ux/97/BP/9//N/xMu3xHBPuvvo1jq+/RKkFXGtY2y1MVO/99NOjq638dHsecfB3WDbp0n+kjMmZ8t1CZV0wQnmH9PznMGFmM+gJnqHEGiGm4PXDP+Dt/A9gzUv29f8wY/7dDZgnAFOPT8/1Z01St/hQevJUldrmQvnA4/3YvRVai1kFVnYuyMFttGULOzTUb9cCCTgWIjuhnlrsdKqcP7tjOcUD2r1GNjTPPx+XCssJAFNGAZqHMMVzDqiccEw3uE+f47YkvDsQ7mbC/QzcV+BOaQRLaUZ6jhmciSSBtfxOqEkEcJWyRL+vjKlK3oijt2lEhHpuB4my+QAwlJ/TObe10tjKgWdwJlC9yc0jopaWX6mDaoCyMRK+KG2NdgwhnKhICW7BwFCCoj9HKRAgJuiXCFAJaTdhnzI+SwmfpCvsU0bOGcgJOzzg6vgghg8d7Xkahy+XVLy+vsotd5r1ly30u9EqZws3umFUUEahdtf9vr/fi9J8LBsbzPeWTasqI+QeheeWCupONq88kXynATR9Um4DXwIrvyY0mvPIAw6u1ThURrVoYmx1JEwkPlAPmGHruB8hhvZDcvETyomt34vr4/Ph//79/txZrXWoc3xmbJPH63aVV87csL7rJ29w/OTNWg8+qHxYsuqnsgy6uMET7XL/jO9p2kIt213qrncvGyIJv0+dhJeU1cW40fwHlvet++Kpe985XiCgWOWAxn7CTCCAxfq85N6ohABDckFM1+DpShn2hJQI37wjvHkAchZB2v0RKjBpgt9z5RJPiK0heJ9XztyLlsewn9Y9kta/d+g6rpOVPby2rbdbGcqgnfbLQcC4Zl2xXlessmpozRBmhgkWC8gsJqoK+xmROO0Pzhbn3Fy2Vw5OSAI1qKeFjUj6rslzTTDs55MpPkSIZwJeMuK3gw01+lMnNhIvoNQMqH29KCEa4Ed6vXAFFbWIYRF81lparjWQhPIwoSk0vAJbUuzWs562lnBYYq00EhPCEBCbhwF5THUTxLHWkU7Md7eauDGKPmZV8rhgX0OKiMBZQ8EYGuC+Xg6fVict7ul1a5cIXMlh2ajsvn7rsE7LgsTs2zDGQjwXSKHFGqOnCVIbzFgFnuCWnD16oYhSCahIrjSz4DBVF4krGWzfgXC108Ha6vP6BoYj4tyTCKoBpilK0BEYToIQYJL+JcrVekj3hG5iqoTmXN7XBxfYB4+bWp0AH/vX9WVtKByuK8+YArwNatb/NIxnARmFuVnXs47N9qBNO3TFmAICKXn4HwvzJuF27BljaLFxdp1CsgECikIjrFIYS/ukTjnVnxGyV3xpUlv35oE45Qk1V+SUwUnCQpliCtq8h8AzzxaIMEqiSYW5ZxuDKjvHQ6+b4N6jwa4nkCoh9GxAsLhbmUkP++HKcpkPCfPUQqmZUtK86EzYYiGbSimYH+5x9+0f8PD2tYRlmoPVmfU5AVzF46m6sMLa6EVgRAihCpLk59S6CNBQUxVcGFRmTIfXyHwE0xH7ly/ws1/9Clc/+wWuf/WX+Pyf/i9xk56BSsGxHlFK8yxs4aHCvl5yzu9dTu7LM+WPxRNiLBEFd9cfOd7HcB+nhDo83udmcb+C0P+4yhqdaOfcqTLMVR/NwzfS+ebBct7tn8vZYFSFKTuZgLwTEwSuLdQeGIfyFvfzNzh8CRx/R7i7f42H41sc6y1KvVfailBud0Ehu92n5Yg3YOC4Wkfg9F33wIpiYp23cXJspY7uXTuoGeJJGR6rdgbz+X0R7SLst/Rl5Sz8kLV/6rgOZXvMH9I0NdpZ50fIw+j5Z/SdAMTOQwaj0oR5d4WZ96icUZhwrBm3xyO+OTzgtsw4VjXsQPNeyDD6yegYMbHKBIt2j0qMKxAmpcsnPbsrMQr3PFUKfIPRHs0YyNZA8GwIdISPUw3dPIebKR5cIWG/B/g7ocRKzOhfXIj+rCJKW8wLQVw7wI1eNFqNkJDyhLTbYbe/xkQ70PFz7HcvsTNjg5w9DC8h0uTnZUkNHQ04yxfI1vv+Teljo4PaO0avtDmK1GVY2cH4sGsxGjyEPm+fV5GmG37bxwV4d+uoNb5vrbPj5TUcwcO4jV6079y/2fVDuYXYS4jHlxDhtZLw5VzVI2OJnrzl2pge4d91bmqjjwlAOiZMD1NXQXf2o03PWUXDxjO9gmFxt1+/DMy7I8q+xEsny2lFx7JPY7i/sT9byo3lc2c6dqL8dDwiOu3pJWXcQe9ZOgS6Ut+pZi48eH/48gNT1h2n/ZMA2NMXil+Hg2xtevIV+OYL3w9ZLQP/cAv87g0jUQUlBjSm3vtN8fvNxXuvppP75YLD1L+c2pCXENXf534wYX6L09kpIgBwsSTWYgla3StBhCYpZ0+YaExZo5nIw96YYsHaFdpzhgiBZ4BILK9NIOdcDrvFjaxIC4/URtEEynFog8Wv3xMBmYTwaJbFhkxN+M8aXigRYa5FLIopgS38RlICN7hWMleUAux2O7Fm7u4FRq+NDsyQPBtEbs6UVGJdJfi+Mmsa4iRJAqxSAZAww6zcp4QUObf+OLTNzYuEqw7FFEAI861CfzJZiBLtJPO7MH6i4VMZEo/QyXCrQYm5GXDOyAR3X8jbZmcyfLoFxknWiL/jVEZPulbL48GiTKqRIFKC1f+89QmJNAmZEbKsHg1BGbGbBEpRSeWg2TjGA6XWk7+qRGkKj3hvWZeFdEo4vQ4iaueUkCCJjWNXOgVRsA13rw0EJjtSyicGa7lNogBZPFig6xl636IgBa8r6zNBuXmpv3kIaF8SIeu+bhZf8rh7VagiouWxoUbnAU0Y7GMIDMvi20BcK+ORolWj9sUVHGmEjcExqQeIta8xZzW/SvRYk/0uSjLziMjTJDkiULq1xFWUyLVW9/IiZnCqbfwscGU0vODk0UK5rrCKWZSDQF1ygIfcGXbOxITQCGs/KJ2JZU2KR5VaXTrz3DO6SRVOSb3NSpnx8PY13v7mb1AOB5TjscNLbTZlDdhak3wQYf4D0+onCRne07ahe0A9+ioA3L/F9Vf/Dvl6D/78czz/1Z/jn/9f/xu8/MWf4vO/+KdgTmAmzPMtHo4PmOcZVT3fUliP7hlme96u46dXfmAK/0dVLrYsjUJAZvcia/TRH39x3HDhcD8EKo1qTaCbz0DTHp701jtjP+X8q9Usuivuj1/jm8P/jPu/eY7D//gZHh7e4aHeQ8TBz+GnEPetbff/3GjGGrjhUQAxVOfI2tDiey+SizRqb1VsoUqHCs1myTQPVgFZPe3/2HJM2mxnSs8fRYUwhrfXfm3FiQ+PneDxGqm58tCZbduRqQGYMU9eHIvnLgNpBFwLUdQaqkpnlWmH4/4LzIVQDoQjJzxUwqv5iK8OdzjWiiMYJDp7ZIKEiU1Q+gFOaxldUlHVYUCuzer5WlCRKlAYmBUH1QCbOF2LuYlhlyw/g59f4bc9gyq0Ta1gLrKXitAt5jnuRW2WvB5hILX+wevZF5/SNInCBIWzPP42OjQnTLsJ036P6+tr7Msz3Mx/gee7T7FHwpQSaFIjlmEV1pg4OIKFg8U8xzDYFJ6xLp1aaMqvN2ahG/G4w9j2lxGLdq1rg739rk4er4/P957kfieMdf3NrSuXYO9lDUaajm22LTjQrZEfONGm8JnL/hFVEJPekrwszMqbR7qWxbRLDGmaISGcd0xIZB7qMnvTPOHm1XNF5TYPYz+8gfixvD3M4/AaRlguPGL08+7lO5T9nfMvG5X1r55RkmzSQIvrslbPGW58aLlYEfEYwuv0Nt5s4OL6pZ6N53n4ERcUGWNsD/aMcuuKIYy+zqDI0z5g8a3vC69/P9ftSwoPnVqr78wzlzZx+Y0PKN1heeoxee6DGIHlBJ5+zsrW86G+S70JzrXdGO+hqbQDphtgd+0C6JQSvnxLeP0AvDsEQQto9cCNVZ7t74AbF7cvheVpClTuR03y1vuLdk41vLy3+nQgwtcLn7i3rJ9DX91lcaQix/docPvjPmRTE0qJJQvloAwwhkwrF4KKXNAWSJQwJCVwh+TSzkSp1QvrYU9IoGTJSFNviVPVxdz2ZiAIOExrDHlIUGv8ztQ5UhFQi53+Tq0FxyOQp4ycPW4OUpJQTdWSkypV2XD5GtFg+L+iliI9zwJHd6lWBYHkxK5K/MJMn5TWl3fMunncYcEmuvtodIq0EZUmQw9h3jBmdQ6suP5TWzsc3hbeI8Z1VOICBFgMzYVk0r4bIaL1WCxQO1eFOkKn5HJBuOHqFmbLGmAWTwdiRmEgUUVWWJpXjFlOg8z9XEdUxRPb8kkwdLm68sym3yCmHmOoosiKi6ACNQnj5/kpwia1RLrCgGzgL2NyN+8Pn2H+nRh375ra1nAoJnSxP5uPUTZNgCbZVdDFpglDUmRbT9wUmYZDwJ7gXKZgxereV3Y4WwgAReVCLEnxSEuA3Hot82xiDw9rtYaXmdsr4ZK0T8F2RJUjlrsmgLTV2Ly05Ibh1Ib1hYdODqO5zh2u8zBwnJGT4KWabM2HyrX9ypJjJlV2xaeLe9hC3CHgX329DhPuDUSadhgfD95HAT3Jnq1NsCfaQM3LQqBaUSlsidCPlqickC1EShU8erh9h4d3tzjc3knC9VJUYW7M4jiGBILZztlZZF5xvLLuokpOBAMVFSgz9oc3uEqMX/zzf4arzz/Dza9+hU//7M/x7C/+EtPVM8yHI6gwaGbUwyuUh1fA8d5XYQNbPM/gZwmheYbI5b5zl1LGgrNGvqSnbZ9K2P00tVhlT1DbBp4ca34MLNebeQSfcoLB36wlLOWu798Be/RDFTtPLnkOwPrYmUH7Z8B0tTn33hYYjCRtNkQIMDDXe9wev0RFBVfGu1f3ePN3d6gPM+Z3D6h8wFzvwN9k8MNbzDUoQBdCn43+D7+212Sj5Rrd3uhM825ea8/lXiv1L5/mri354PVxMcBMjhwlDKqd2/3ZMJ4U61M8nO6by4CG70H5vvXKopx5cuP26i4dnzUalSVROdcCLkoT65knezmEpzXUnDJ4dwOmHWqtKJxQOOFQb/FQv0XBaxRWcX71xsAMFOV9ahXa1gKJeWhUO3QSQJUxMYsnSyLsE6EwgCrXREcSxd8MMiWC37F1EQwGlB+gbs3U9slGcES42bkXlBqAG3d0mz0YUWn8SW13JbxTxwf3YTzZQurmCTlNuLq6QsYOV++e4dn0CT65eYZn0w67nHGdKp7RHXZ89Do59JsjsacS8nhfnlmu0OZNsXE+Dfto9KhYW4uNqk5h9tB9DxW29zsWYMBd3I9mSwmxJQjvaWreGu5a08sLC8G29eXshj1LSpjsYVmS8HYk+bwc5RnfA8bogeN0ZWBzKBGoEqa0Ax+B3buEfMxw+YW17/BaP0NWDds48P1BS8Pd89TBzfhqtNtgMKbjDtdv47rr21lre+zjeG+cH+tSmWYc9ofFO7vDDtNxt1rnU5SfjkfEe5cPBRvjiUn5H1n5Yx7b91yecqlsUcB5D77+DGmakHJCzhIz8dv7gr//VsPLSNZGC8XeVTZW2yyhtzu+tYM6HOhYeQ0MSpw2fNwJ3jsUv2gs3n0McJfP0qnbZ+Zu61bX3bXxdHWEOIohyW9nTRCUEOzWJnDBiMeq5mjVGqxntaWcczuUQ2+jZbf8FWf42EygYZaw+j4JIWW6jZjoUQRZ1OWYoGHNNQLRbsq9lCehazthmo8IlS1YjYsnUUtBKQVEe/XeQLCyTuBSnDh262eoNa8SmcIwxllilCKeD1x3IiT1mKOi+Kks0m9iS/hOADUCnbmiZvY8usZUy1yHRRFofqN5K1fpszFEK6vNif1kyZcbiANtNQgceTELzTvGrwDcJ9pudTYBrluLGd3a0bHBImdQQgCavHYYFVcGiwE1JhCqxVqptCro4xADlgH15GC3gGJKkoi7A7Qx2RrmBwlm3W6C/IoKqkAZCTMXHjeFzVqJ4YOWNLtvhg0Ewg2euifNYr7aS369YuaCUitKqX1bYS6i0GAkkKPY34X56GfG7tWqyomkORxW+r/qrUfwMGhjQljzgpBcEpZwXgX/DidC88BoXlfGZAXIOU6Q34ZLo/eMWh76klhyQU1Bp/s25ngPz6YwrvkImGcBwBKzHPJuniQ0U8nFGhVjAcOJbGs/hINTxZsp3AQXmFeYdEbyK6Th0G1gq3Ec4UYN+7JnFjUEV5V0fhXioYRSkZMl3JbwapZz0vL6uOeR5suYNPn0cS6o84z721vcv3mHh7e3YC7ISOApIeX9MIcM0pBrRfeR9bGCA94Ul3wArhT0+VMlUwFAxyOu3v0Wn/78C/wv/uv/Mz75i1/h5//Ff460u0a6egbcH3F8e490OCIfZtSHb1AfvoaF1orKs04RYUoIB3btgf8jLk/aw6cab0fwnHgMK1vxaXqwWQRNtNNxmy5d680W5fcTKuPcBHy6+cpw3q8+s38Guvn05DNmRNFo3hC/HsBxvse3D3+DUg9gZrz9Q8Hb//EF6j2D74vSMS+0tret3rV2Ws8W07jNORh1wV5pj1PbYc41nElDTW5EACdR+jq6XntDK6PpxUl+ElYARKgEpE4ZMfRjc5zn99npJ0d4fWB5TAUrz3rqaa7gIp7VnKC8S5XwLPqbjH41Ipd24P1LVCbUWekzEI78Bgf6GxTcigEUB3k+ixKClC/LRNhBaIAJcdaU36pAFioaU1Jr7UQSlilp+Fz1kqxsZ6MZJqEtKKGM9UPP6MD3NKo/Xmu0cA9D24uiuBmwYZjisGfVw6JPjjW8sLrXxPABlJCnHXbThOubG0wPe3z68Kf4dPoEn+5v8Hx3hV1OuMkVz/gWU6RcI53TrYdx/8SGjcDQPvC60UOrKtIuhFUr+WEBCigl+GZPq268u3LoLELphPH0XhFhbQXl6FozngiahxtDWezfsFgWCo9zG/WRiGDlKOp6RgRUslC9MUKDdUzkLUbjG96OXraJMiYCiAn717s+if1iLfQXRv6mC9G1YaDS9mt7rp0Scig0gz7p4/5hj/39oAQYlFE4cX11P6Bf/Vbub+5wvDou1tzu4Qo3t8/G1p6sfO+KiE3CMmowv7PGl8f2+mMf2JcLiGx/dKttLBfzo7uBcwTFKEDRLfHBlMMPWxoB+MRrqcMm32GJ9acdePeszdF0hbzb4faB8NXbDE6CbF89aLgLEzVRnP/+W1/iIUL9NV57/pFD2eA5F1rbE1rcDwX4lgxw8VAUHKKHxnvDQQ85JrOEGdI3maAFRtyE3hpxEWJ+RpExq8IChZUIZhBlsTTX5ORwwqx6g9JEDQxVWwMiDK9ufW4JOy3xLFl8UCU0LbSQH6BcV/CmeWlwm2dqoWsWU9Ed8E5uIyUSr+FaUWtBKQIv0oRoVFqIoVKEwE4q/EQFKgWFTVAaQWHMnIToTpLMiiHD8bmrFVSqKHlMaJkB1mS2DS5W8Qox0u0H7Yfmhujnw4ilAE53R5V2zEDJoGSC7Lh/mzV2O9MYzcNBGigoVX0HyE8BnzdGS5IeaeTGi2jvTUDHvdCe3bW17ShvniDWUApxBiNFzxATUNbqyZCZACSxXiK1KC9VFFDVmCayKRFBa3KvDKDtIhMu9iuws2KHrcCRCI022fFFuxb2MrXbUZ7gugAOFvtxPyZd30HoajjB6nVFSKdYCGGhYgI50ukGD6OxNpvNXTf6MHWkA0mORxoBLQo4E7onr9XgtQzBRB7ayDaUe0mYNs/Gyegsc2n4Qp0FVNs7dhzaWMgv9fMr4zFPL7uqQ7M9EcbLejOGrILi3WmaUGoRDwBLRrGqzNHTesD5FurNlSTagRqUYQQLH2TvNeG4bzcGmFpsWZsPF8yIDEbDTxTPXyGBIMjzLthqslBVpEYOSZN/Vi6olXE4PuBw+xZ3X/0D5ndvwbVIyCRUMJLkKiLS3CAyBuZZbTorQBVEgmuSMoRJYVLe3gFlxlW9RUYBZV0v0x40ZaQXz3H18gZ/9b/9r/HpL/4Ev/pP/jPsX77EviSUw1scv/ktUCporsjHChwrwA9dgvUtz2inpb4PHuUJy5P3clsq8H51XFBOtbJV01lPiEf2YexLRE3Lu38EZWVuo2LeS/w+XSHtn+u7jY80XEp5J0JRoJ+40FStBW+Pv8FcHgRDHSuOvz3g4e0B3/72DUopOJRbp5PKXUa5K8Dc5nxtFvoTfpz7/mxv3+Nb8W12hqCzT+d2JjgNFoVC1GqyM4j7qv1+7/EQnwl0XXyAAU1XDAu7Z0Y4Dd+fWrHra5c2f4w9/g7X/kVb9fRDAs8KLkeUckApOxSaUHEEMIMSgyuBagFTAnbPIUH/EgplzHPFkQmHmXCowMMMHFgUBBX2B1TSUKDKVCSIglzOcZaj1HCHHtB+ohMBSZ9hM3EAsuYPg9ogFHmsKSNY80shsCBOXeuaiDkdwrpc5pKAdDBZ3H2j1azy6GmhX53mt7qjEiJWHNp1Oso+pc2UM3ZXe1ylhM+IMO32+DQ/w4ubGzy/2uPlVcZn1zOupywKG6PLTsgSFusAusfZ+Eq9pnTy5UdDg8H6K9FbmAFqfKzhi811221ta2TZPw4dMB7Mvnf3x07SMM7FFh72s3fB6l26eo0eEauNrtV9UaGhjVa3hCZWErmack6jE6QEsKWrhvDvoGbAqLV49IP3LGZUG41rt57RH904yIdD/X1fLit1Ks/XnW3MziPFFtZPMj0Xhqp384Rnb54Nlxm7ed/xKY/yNr2gPIki4pJOfbib8Qe8b92jBdyftidrmsuNd59sGgfh6eI2tvu71YcAruH65b1eteoN758PrbW2aR9Xzioktgb6Q5aRMKWMun8JCxmRckbKCbeHhL/9koDMoJ3MMo3ujojLY034dKZxuxouXzodPfF/rtklQjy9e7buj63T2Se9Vns87KfFbh4rGgRIZ8sgMLT6EhGiLXeskrvYm+TPkz7AtaLJwRl5ajkevF5uYU9TUiKMRbBCbMSq3G8W5iyCngSQxi4V8DBMMN0sASxALTeorzCunQAV5NR2T5SpsNKEcQoo0r5XVUSIVwQhT1O7HqejSKz7nCchApRgiUuttStxJKv+WVpkI6TFaphBNYPrJHuONFlaTQA0VEtHjK3gv7AsozLCiHSOlrb2eoI4XsQ4lSb4Z+4t6pRZYEaLXRLg35hfHRfbclei3ualE9LWpmzaOAFECQHEMC8N36wEqxoqkTBiQEIGozYLdus0KMTU1YTB3PsoUBUvHtkMzS1cthv7Gm90SMSV485bEoLRqnAZpogag9kPDKM9aVRD2p6VfVVtJYQ+tLlo4dri6grhYoaRUD+NHpvYQuDY/Pgjvia4oSga78tbmZa0sv0ia806whb+CSBq3hVt3WovyDwlBig2LdzQSh/6qSmU4lyIwqRbuQPT0cZKXT2j2323JxjO8Ng7smUTEiXkKWMqWXIOEHo40zrErPtV8YDtU479DUvUFJeOq0zowMm97Sy0UVuHrR4TX7ArIUblYeuTKZxiImcLSUUgFIhi+Hh4wPHuFsdXv0c5PHisaWYRmhTIWUI5ST9JFIJslpQAJNxEyH2ie/3w9h3o/g435R9wRQdMUwZNO+RPf4a8e45nf/5LvPzlL/Gf/l/+b3j+yWf47NMvUEvF4f4e93fvUL79tdRJCVSka8gSLqo/y5pyqS/sIbe/6/wAY4imH2V5YkZ0tYnHPj/26TvoYzT0WfUI+zGWEwT8aNV5UR0rvynvQM8+DxQ3B3JFv1T382t96QjeGbeH3+KhvBZceM84/Bq4/6rg9a8z6pwAmJDEXhzwFs5MyYlh9koI++w6aAMKV4NRB6KAsSn17VWK0Annp9HyWkMkUEO7HL7Geke6TGhxIhKazQw24rC6sZ4pFz12GuodFFfg/yG7dFH3av1isFXrEXV+QJ33KFRRaQYwS14HIvGmTgTQDThNYEooAObKmCvjUBIOBThUYFZSswCqhFCPCDJoCO81synTq5/UTuVQWwtOz4HV+1IqngBU55Mk81qtGs5U2y5gpXM0lwQzuvBMCOvIFAocf6N1XGkx6Whp8VDt+ap1OyM1KCfC+o/7ZW1WOsooJSBn7HY7XKWEL3Y77PINXtBz3Fxd49nVHi+ugJe7I/YJyNgJZReEr7GtU7Iq41IDt3p6ga7Ud0q+Ffc5YDkI+rp7vn5RUf/Tx4TFO8uwTNw9t4rXVy6tK2CtDXtN53Sj7qUCJNIxVkla4f+W/Vm7H5W9CPyLKSPY1oMRrRyjcGg+REhOCYtES8CSh7YbjyiXKiP6ouvQl6Gtn+42lHlq/bM5jkqHE3JgBtyIJoZHFo+R/tl83OFGQzC1t/UzbBUaz+4PLD+h0ExnSYzvqPwEKM0zyogfQ3mMEuNJV/hPtHCawLvn4LwDIN4OKWe8e0j4w1cZbw4A7QIiOTH9tjziDhohvHg90hUrdS0K9V+HIwowgh3xAOPu43zZwAGLTg31jx1cqRVA8AQ6AZ3uVjvwxldayKv4fn9QGSPbuQ6GikhPSY6/B4FY6L0IinSdJFJr3NkO6O4leY9FgCSGLrUJA9VylSghpZaHhC2EE7MKTjnE0A/W1B77vfZEbNBENKE34DFI2ZpW4aFJyhmaIFrGl1WZUsoMykmEcaY0IbOrZ03Apn1Sl+daqblfmoVumE/WkFicmrLFBMZcNQYqtyTanISwkWGw5BvohNzREqaBxeegK2G8QZKcAHUxNWCyhyRxpUTtCVDiUZgW7jM0HwU7zCslsQo3T5qYXC4qirhP9EbepK2xMM/dljNY6x52gtn+C8qCKOjRd2tWK2lmgb9LwkOeFGbMxwdVVM0yH3NtCbp1jgwO0RKmm4nHypfS8nmzWD9VXMALwBKncUrglOHMXiJQzpLEMKemhDTht/1ZzGOtcczDLM8ZI4HhMOBeqUOElFXZQs2DJikBb2HQPJlzKLJvxzBW2itd0x1WJj3bKKklHjQHwfh+xC1ocbBtXtXjpgVUC/0BGoPWAC/VJHLlyOrR4ucWg2rzDEjUEhuzEfVa9zRl1Dpht5usEYdZUq8PC3VnOF/CNEGVeY7Bgj6R9VNHpcxXHVBYU2mHA3+Ya1ZcujhPfV6TzwtRktBqRMgpO34GgDoLrjwcH3C4v8O7P/wD5vt34qVHCXmnVtDV9prgavuUMwXtLEg6Yp1LYsbV7TeYjvd4eVWRrgifvvwVrq8m/OwXv8DV8+fY/flfYXr+HJ/8+Z/i6vlLvPzkM+Q84e7tG9TDHcq7b8HzPbITH+qxl9Vtv3Y7f1MJ0UJ4/bjp7I/l6UujVx97MPwRlC1hWd4hXb90PIS8QxrjwjPj3fw17uav2zU9v45/KJjfVLx+fY/jQ8V8+4B6LJjrnYaTU+T2mlAPSUM3NhpzpKyx8TteN/xMnSLh5OCXvzpSOvI1RoO1ayOrwGjnWoyMwhgqRlOMmnCx1bNCM45d7bxPl+WsEuLRty/cFCtA58X/2F5zJ6o8/UYBc8E8H3BM9zjOEwgZJR8AnmFJxzg/B9MEniuYZhQiFAAPTJhrwuEIHCrjUBilyLxcpYyXuxu8KUcceHaDr+YRK2uhGj/IAq0Uz2Zwtx4qwxNpEyTVOgDXFdREmCB5qSpXZEo4MlBQUZhQyAxWgneC8nvSGQ7XtWLttXeQYstKhaiHJDl5Z171cQ0GXsEujqw5wzcAQ3gzyhl5mrDf77HjCen+F9hPL/D82R6f3Ez45Q3jZgdM+0lzdWm70cs+roeza4gRjbv4BGpfq4vX9piDgbs9uAgFF64tKI2VseiN/hPLsXZKiIDjun21oKtbHeRPh+sL/BLrDt8dfS135Lm56G8vZ2Ep4LfxykKsddaumEJCK016LQnPzyw5AokLqilrh6Xa+mPeyKf71g3gEXgrttm4m/hl/Xfzcmvt2bmG4XpXjfHefst47KH+rum4FoIcytqgtQ6/X7lYEfHUrhg/SNmiXoayYES2BAonNFDnuvDjKBF1NMGTIaQP7et5rfQFRJELtWi4rO8/pQLm0gF/CGAufJcpgfcvAI3DbHGM744Zv/6ahEaYTsc07OpjLA2QwpfT1ZzZOCdediLdcXU7TKJ880wFYf55cU/ompV10l1bIRwWjIYi80WfAlER3iFuyD1ayPYny3Zxy380ceT6c/1n7IsMkVxARCYgC8JRs2aP7xpFKGGO9D6x1iMJmzymu9bLJJH0LWZ9VBSw9QcIuUl6DLM2A1bi8TKGy6lckTjBhNMpJXGH1jBL1YXj1A8vMHSk1taUip3caDM+9MXjnMIVEUbAe3gc3TQirLO5kOR3RjiNR/lKQ2FGIizVqi0123XjDSxsi8ydWcCoAoXbGkmcG6Gg6zMSyqxCAzeOIhEeSjJhCLytj4MiohE97J9NiRaIHeo+QOFpr8ug5Cb9QdAe3kp6PlkCd7OeTznDlIHMFQmS74PBaqktsCyo6JeVKWEGJqybr8XGa1MXYC1zsyTpYv87ZaBejuGEEqvXjrqoSxusOQ50X+s50ITmZok/LHvtcq+4PHUWG86TZ1Imz5HiqzjAyvrCFNtpda3F4LY5XdsMSRVfRBmm4GwY24CcHMeLMmbDhot6AtuSPtveis3b/IjiJq1b+XDDTbbnoQpfSprhgOM9IE8TplqRpwngKongLewUhbas32KqJb9ZQ3tEHBrgaTkfqGMqR2ZB9qFtf1HOhnE7Uurnicg830zhktSrQ7y/RElte5Exl4JSZtzf3eN49w4Pr75EPT4ILHJC2mWAE6jUrt1E5OoITqZgpdYnw8/MuCl3eFbeYPfJS+SrK9z8/AtcPX+Ov/ov/yu8+MXPcf3X/wy7Z8/w6aefggAc7x8wH4949/Yt+HALvP0KACMTHFdSShLSkhFwtZ2f63u9Qas9/yF0YNfKBo37JHVfWD6EpP2hy3fKm0ZmH8B4mv3Uy2VeJCGfmV1JE+jmk4aHmQGuHQYCMx7KK7w+/H2oioAKzL8nzF8Cr75OOLybUN8V8FwBXLX3AacLopFOOKrkjHjsVPiB0b94klaLD/mXoIQwmjA+s8JHRFyygmn69TYoIbbm6rLlf9HoHrmsL3s4ztfG3fCTN2+dfX/42p2GdUYtR8zzAWV+wIyMigMIRT11djhOezDtgCpZk8TjgXDgjLkCx5JwrIy5MIoa8uxyxrM94d1DRcERcu4G4lAIPVSOvB4jsXwSgODoLGc/s3sCyrlFiIJ7sCgjmAFOCYkrEgHHmkAp8HOmiIhJp+1TiGntYx9JoRGlzdtSGrc8B4FWDvzIcl5OTGCgQRhJPSUzdrsJU7nG/v5z3Oye42a/x8t9wqe7GXmXMakxjvVplDE18cK5xaNjaITjRm+5AX1xRwex9uLqO5FSHc0ON9odxrGAclA6RK98jvexVU8bfwtJumxF6oh8RAvptYb3TksO6+bdLRnI6GXQt8lgSCQDqhmghBbKWnlzjZdGSGJgWHvLsfbV1cgNLt3Q35POuOA92nxsibcdHsr3LqC2YkhjYcG7hPFrrYV3lxyt9QdokpOnoYN+Qh4RP47y0yI/z/d2C4d+6Dg/XI3xj7tY7G/ShNSv7gj/8CXhfgaw402hzqkShWcdPY3lnNfxgZWntvhx7v+7QAmxsVY6opR7BDseuNazgKCX755bk5F8Xbs3XuEu6fRSGSFtkn7n8RDgvi4LgcNGMEZh7CBYtJ76E5maFwTglt8cCTaG11/KEbUUzPPswpgUrGFTyr3ATK1p7F8MJFO75GcanxExsXZbZDos9D6BKu40hYIrGUdwNdd+E5DWWkGlqNDMBLYqmIdY/lNK0FQCSJQliV8icBWPBhmf9bECLoRvViKsMOAyo8yk9KcHiVFCYo+KHTIKurBJizkPxK0myJPwJUG5o2BQSKB5Z7S/GEveFSEkQsRKhFQjpJRgjUoM24feN/bYtHF2BM423yzxdH3qqBF+1tvA19A4zRBBJnuMeCX2nDbshYJiWRZznaAJD8kUEQGuYFApEm7Gx46mqOnqUAZxwKNika9BfTQ5+Clhx1KZHusMSpo1vkTf50QgTsh2mZuVfETS5DClvhlfKQARa0ig9oCsJXZXe3F8asoum3UCQImQM7kCzoQtJkQe0bApBkyBULmCWIT1grdogJHumqRJ4VPDM/Z821V9SXYuGuR0/yadx+gRYbjK8H9T1rZ+pRRxXO8Z4jDtxqvu3jBPLPMusu4n9UpLmKYMZmGc7VqyMSv+MPgSanBCGvCljcX2L0OVVkCmuGM5fA/nWCdAgMKibdLEsh+zJhIXbw3xhCDKoKzngobnq7Mk/Hz39hbz8Yi3r1+jHu9QZwnlkLKwFZQnDYXNygZqexaCiwhEO8/jk4hwU+5wjQPSboecJ/zZf/p/wKefPkN++RL5ao/9p59iur7G53/5F9hd3wD7Zygp4dXdHcAFfHgAHu6R3n4N1FngQAlFh2+BumB7i5KvJShO9bl0BYWt2bYG2nz/tDiCj+XpyrgufvJloXQBQBnp5hNQyu0SAKQsAlwl0h7KK7w5/Maxzpf/+lu8/g9HFJ5R+di/CwB3E3BMOB4BrnOLNW/P8YALB16iHeZbGRCWpXEAtGARHAToMKdfZcC9p6LwDx1thO569/6iLR4+461Yv5E2K/RDOPPXeBZnEbt1St3H4p2NupZPnSsra2n1ieX3sy/6Ix0Dtfjq8lNmlFpwPN5jwh0OBwJqxh0RMmVMxwNAM+75LUCT8nTAEQmVEirtAZ6Qa0Kqb0H8Fa7oDjNYCY6KN1QxOb0haygFZYTwAmJABZZwSrCzkRmpmGEQL+a/KRTaVGZjpBIjccKEipzFcyNnRiHGXBNqquASxb8tDOKWML8HPsGoKsk5CE1SwXBLlO41Du9FmsQur9CBBOScMOWMXZ6wpwlX13tcXV3h+voKV1cZu8zukQv2LFad0eCmUmK1NKxhBoHrovi1vQulzc5gntX2FSbn9t+i0ZV+KLyNZmm8nb+hX9b3SVeVX2804viA09LO07T6HOvVYb7XutwzLt29U4YgrX9t70D7RApTXR6Kr4vS/AmWOYIqoUD4x5xS21A7xuHnB+CBsHslXJiPUhHJKVqv0doXIC5/dOvZNRgGZczaOb3ewOnfK4UWv8ZdZXvm8nFeUi5XRKwN4okseL6vsgW6Tat62vh54bg7huU9YRXR+uPKKeGJiR7Ghdp//T6mt1nakF9Zf1CvfxedOrenznRt8dwlz56spx2QSa0o70vCl7cVTKwCnt4b4lL8x5s/1ro8EsutwXEWlvXqgeW4s9W1qoQY53eVS+Bu/mPvuv70Z6QL9k6e/usjWT4w0GgfpnDj9tcJleUeAaKhdobCJFUE8kRkcj2ZoEgVLlXnQHQaNYBZYnLXWuSvWHLf3IRzbrUbE3kqOcyMPvSKEc4GE+6umzKCXKhPYCY9yEZuUK5F6zsbo9qyOlxavyT+qwnRUiKURJLVzQh7VMn6Zj1QYRtUoOghpGBCwbhAg4tmlcTHVKsIsizkitYpgkWBMchjjsioeOVY9+nnoPljwPIFhDVrcIzKByOGo3JCAtCqgDPSe0FhYeNow5S6KkmSuuTTqeeEhuRSCLUZsnY6wVwra14C8mGEnYRh4bD3ZTmnIDROXT1O5yapL6nHmPUtT5KcN6XkyQFlyC1XgTN6Vg/3a00Y0QqibN3qSrSiXsUpCzp7Had0OQ6M4UtqBVfL8JYxoxoKzUMThRoDDyFwbAkrW/i30EdSb4Swn8lDFYXVatNjL8VhUWgQI3FN7YPiNZl7oqb4jPU20LZz0C2ABuVs61fjKXzPBivEVje1wRtjGzXqK0kLlwLHJPhLqzJFhHkMmNDe8g+Q3hPFi01OTOZdgUoSC9r7qPu76z8HRo8kdInHeDD46/iHc9KYVE/ajrYWLMauJJ9u82KeEE0J0fBBKQX3d/c4PDzg7u07YL7HVKqMNfdCS2PhVKWn88VgJsnhkzNylpwan+4yfv6csXv2DPn6Cn/1n/9X+ORPfon0/Dlov8P07DlomjDtMxjA/PaIUgoeDu+AOiMd75EPd9g9vFU4ZFSfb8XtkmgIQArCouUu7b1uGxE4hlZ8TDn5+AfSuO/31ulyebzjD6vvfep+Ek+IU/TmJa9/eA+++3IKnsO4ebhMKYGunoNSExUoikVlMWIpc8Xd/Aav7v/BX3z9+wPe/t1ziIhhKWboe7RmJcuLbzz2dyDp10fZnXr9nQ2wDBi1OwOlC3ZGxJxYcT32QkPngcL/di6tYp/hzBpvL34TOoGsq3zt/Az/LY6yrpqG47bKZYpXPvmzXXqC/XuijXaPwaWi0IyZDpjnjEQTDmWnRv8zAKDQHZgmEAstP3MCUwZnEUwSCgjvwPgNEjGukMFUUROwo5azQWg0IfwbaaG8AAMgEvqOIWELAc3Xx/67X/RGtsqPZBcSYAnVktYr3qXV6brCLcG17bMG+5hZLJZI2zLcvZ40bKJ7MBI8vJExG+Nm6Ym/9aIGIYkScsqYIAqJ3W7Cbr/DNBFyKuGsrr5HFj7tC3y2sfc7mkloueWeM0hdgp2WLazfajOwdXf1wsa4hKwLRmWuMLDXtsew2W9QizCx6Aov4OI40Obk3Fm6aZW/nV8B6OnwXigf8G74J10ipOTp3OF0M7EkpmeAEgMZqM+Mt83qcRzbuBxbrUVrOR+eKrS12C58vg8b9fNwf3zqPDaPT4z7+unKR4+Is+UnQWp+LH8sJU3g609BeYe82+P1A+FvvyU8FIBSbkKXS5flKfy3gWMicf1+xKIcDmtKiNVOLGKKP66lri79jGhXjp8LALaUPrVWhqw+DG65BkLzIqg1AZochAC3707INaEwVw0zVFXQ7ELpEH4k0SAQaSMDmjeDjaOaoNqF2sI0cZW43seHB1FIoCKBkKeMnLLWk1vt3MhXrkMM4Ai2WkVo5VwReeJVqyzIKzuC1egLke8zkrkvxDkgW0eN8BAha5Wmk6w3IcSBuZQmxGN1eaaWF4Bz6jyUuShBEg79aHkOVehwYWAWC6c8Teq+rMKpWpUgFELZrLVtVUTYkb3DGuaqVnApPj8V1b0WanXSqhGcXhENX+0dWT1J3astpBFXi+tqkzLMhyqaaswYrdfYv4f2OmF6/EL+kMiQ49gVpmYCnqhdR2+5bt45VmfS9tkYa8tpARZ9EllYIWHEbG8lZaJMsduE3N0SE9isoIqle3DtFHUNhm38HK4z4PtitRjPRz0tWmtFmQvKLJ9La2x2UHpFoQln3qz/6gkxZfUe0uTfrO79ZDliQk+9lVA1h8Ga1VHjfyIhnhTm8IERCT4TwX1CDB3kyg6f/9YTz4GRWhYWq9v7NRLk2jfZBxlcS4ONH6SyB22vsGUl1grM08o81Tw2rTE7VTReKScgw3NBCGyr78Okwn3zWorzxIAIIQzPO+4KTKbhDJgXCiRfDqXOKjeeEm1b63q1vZUsA6YqSUBdv0nnxpB2xD0PDw94eHeLV7/+d5gf7lCOMwiMKcu85jSBUlv/5hpv+U6macKLF8/wZ3/yEvn6BXbXz5F3e0zThJ99usenL6+QdnvkKePms88w7feqkCfQ4QA6HFFuBXnnckAy3FmOoHevgDqjpgltNTLIsnvqzIt3vmXKWCqrtoXhp72jPpaPZbX0x/+Pt1BCuvlMctMx6xmXGjGodOUb/h1+zf8t7v8jcPhvX4iXFGbYIMvtfruJS/vCcQfjQvi1s4u7a7xyvVHQ7Zc81YltzLs4CL2EjtK+nRIyRaGdKzDkitMbFw7L5HcEYyFSozL8nNePFH3glK7arnr4/XgEN0Lu8jdOX9p+O9JiW/XrbD9k0KsXKDeMQ73D4QHgOgE4IiUG4QAm4H6WtM8JCYyEggxKe+QrBtMRNb1Fmf+Aevx77O6f49nd5zi8zLj5NOP1MeP2OGGuFaVq0mgwLOygzYMZDs2s/I4yILmIZzRVEYaSGp7QmIcB7PmjG6zFyyGBVWcgNN0uZxQiSBaMigLhx0qStVydp6qtGgBdqKbAcnVwTqRKEKApIwBXTviLVka+Va8l+UuUMAH4tMy4gXhI5EnCO6YMSNpwBkpR3gHOk3Wzzls/+jKqAZdd5OHZtTqWw1mvkFp9zjytPb/+9uowAl4ZFRCPD5fUVaz/r3sA2PptfWg1X2KxfwqPn7Oy52ENmsFg46OVtmeRk3luQF2nKZkHflEaT7xiqUugza2T3OPtx5ZLDCUizBxqq68R+jW5WWH/81z7Fz09rIN+aZ168uLygYqIp+zKWHVccY+os+PAFl8fVce5VqNL/3dResvL93lfPpdVXLY8Fzz9d8qAfXdUerSwXi9nBvZ9MRBEAGXQTqz+KggPc8K3d3LcJgujMQowtkpArv1ZSe1++LqsbElIrBo5j5Q94rnL3Q3uO3IWtsszfgsZm4v22lyecd8+cdC398eH+p5FBcSysQ0ulI1cY0icQyMKbb1qJSrg7wWfSYmw5AJhkQWqzbpZa0XmRw/rWqvE0WfNl5CaR4ULaq1/xny5QKztpUZutLju/fAkUXBiu7s+A01ho5A0vKf0rQjCzFKINWkaeSfi3EgYprAI7X1W0koFZGTWPUSqUFJn3wHp2TgpAVygiqOKWopY46c23ea1YPlQ+4WwciDZ8+qlgtq+S/gsCdVUAtPbdYwCk+Nrg2GMAVd2gT3ALexX6Npy++ouisSkKSHGfjBgCrreqj1Yrcc+eaNWv3WgrWvpblgnnVBahekc5iXsCUp2JtuehM4Hg91ynLq5aeer7hwbzwp7vraHeweBYd/a0OMXpy3C+gbQZUUYLGkqSwxUd9t3OOknw+TpQalTFWeYIkhfYA3bZAmJFb5cBYAuvuiWmoaVsyrQK1tNYeBhbeI4U6ulY8yIJCRTyIMi/WzrqfMY0f6Lxwa6enwrYIMWI1NYVE8s3wGRoeMb96sNwkJ5hDUQUIwouvQ5mxRbsyrEI/c2MDgMh7jC1WagHd2NqfR8NR1IU6wpgKWnTePIyODLQCUNm6SeRUmVFJZTZ3HycsU8z5iPBxxuv0W9v5PxJQKub0DIqmCSuQKz5mdJQM5I0w75+gqf/MkX+M/+9/8Eu+dfYHr+BXb7HfJuwtXVFXa7nSvQynwQRe08i/DvOAt+nGeAKyY6AGBQIdB8BA73EuLOQ1aZYp/laE3GvjYPjwig00qICPjvv4xre+znU5Cpl/Iy32Vehveu+xHvdSTa2dcuqfdJoH/msuHgx6+/xem1yV8TaLoG7a5twwN1BvOMeT7Iq7Xgrn6Dr9LfYX7zDPzbF0BZ93wY+/DeZYV8ouHzfVtY8gaxsU7krfi+hnu8+t4S3uhpAfR0q0+t/YhnXPjoKqV4I1ymgNlcmb98kk78ekw5K6g9+/7j3liDWyyNkqriFFkS8JDAO0ZJM8p8RKKKY67IBBzTEQTGEQUgQuIs9AjtkHIF8g6c7jHj9yj4Fsf0LfalYv/2GehqD0oJ1wRcp4wDA0cqmBkoWK4DozIqJDxTqU2QispIXDU3RD+wRluOnMDgKYsWOpKIkUnDZRqNpg6wFVDiU9vummsx9p3fsmf8ubj7GN1Ifa0Oa8qsbAJdZTyM5I1iXFfgighZwwynTEg6BgmdacZkptSxtpYLYWG0tfLEOJrVqgYZxvhGFPr3fEODC8dnDa8O7Tjtu3J7c48xGh5iNCUE9++dUmasFmUBxqOmhQ4+r4BY5KcwGt2aGPBX6842LloatYb+cHE+H5R0GbOwlyS5IQiseRAspLApISKC5rZMg/L5HI5cNYJyjL6c7zjo9v/KQyH895qiYVxxJ3q4eo7C6mjM6HBn2aZ0ZQ35vt858hP0iFiSDaefxSOej8++/8HsqHmworzo3R/M3OopCOmfahnH/v3NgW/zlFGvPwPyHnk34WFO+NsvJ7w7QuJAYmSQ2d8fC7fbXTtYud5e6pFgr8QaBCeLxvqGm+vyhWsqClFDh3kDaa79jsT9sqen+jGwIKvo5Rx6Hw77aPlMWB8IA4XVGr5IqAhChVn9eu/M4tsEsdaeVykCdOIKrqShayQmaocqqxzS9XBErQVlngFmTNOElDLybhIBUgLAmuRXhfQmbERIUJ1MQF7l2VqB7EJNBkioXXKDFZ0ZEmWICOYiTISATiZYU6Gb5c0gIiCLeNWG1cK7UAubRASaMlKZUHXMKOzW3jIVYqHMBJRqwlCz/tMOcbM7cvKQGDVBLC/morqQnfQoAfOxgGtBLhXggpx2G/hclA5iElX0r6JycaJSlBEFRRPCmneHhS0yIj5Rck9pEaSlIGiHht4CQkClAHLu1zvr2q2MqnGNyAg271d43Pa7/k6apVxgS52FC7N5aRgs4xrX/rRoVq07tuK1n32oGriFO+uc1VLAdYYl495fMUphHA4VpDF6EwgpT5AlFcKPaT+dmDeGnoHR8go2jg6gFFaMYnZ3Q6Y2bG3TkrrHBOjNC0bwQi0F81E9IoruKYbkkojKAW64wVoXBq7qvtLxqZIsa2i/TI1ZI4N35RYmSOdVg5nBCH+G4iWGKrwoEPQQPKBHCmk+EMkHkeVPLW0ZhMLWJwqKlABWvUKkXgwIwnc9n5rlEoXn2WFcFYdRSq1S0nwWAee4lR+SeycY/q1cNDaYekFpXOfExkwnVACZJnBi7PIOtei+Bnyfss4dgZoVok2CKtNky7GPy9a95bTIOXtC8RgUwgemeCertwkZnktJPCtJmLWs8+JKEwISksfJtrkEA/PxIGGQHh5wOBzEU2mXhTZJSbzqcvNWISIgZeRdwv7lF3j5p3+NT19M+Cd/9hKfffEcP//VZ0ickdli9VbQwx3Kw50Ey3AlrcCg1gK8/RpcDg4vC2AmoboFZ/YMHfsaiZT9sFJ6/umHIwc/lu+1BDyN5bRHoxD5nNBhJlJDkKYZXcr0nqw8ptYVc5yRDg3X0/WnwHQNS2ZLnEDHGQRC4Qd8+/A/4/bNLb78/8wod4zydkbFjEJ/CTxkrB6NiJA9v4U6cYcrXAdiPJxT8iUK2Qc6/sK2Il+0eIfbRwuFGfroDyyYoKEa9aQz3oix+Xywo9i+zxtjsHxJetHIRIcOxecjAbbo8KPK8qx+XF1bS3O9rDy49i4B5eYb8P4N5t0tUJ9hmh9EAXEo4JJRS0ZKhIPya3OehU6eCYkkNNCcb/Eu/R1qvsexvkbBjJwBvLzD/fVvUCcCHhL+PH+GFy8/x+/v7/Dtw4yHyjgyUFkss41vKRBh+qxC9aK038H5vwKqEIUEgMnmEWNK6VEJRpq7ATr3Veg/cQR1261agcRCzc5onhu+Pg2epoCAGF4JbtA/84xXAo+8P9aTyGfId6dVKPVPJPE4nUh4todXn2G/f4H9pxnPMuMzfosrJBTzymKVqVWC5ck7tcj6rdY/t1TsN1Aijmqt+o0m+cTtnm8R+pvCpjRDHOYT7a600pQRcsnCMtt4R/Tc829rvZPOuN4oPjXU3XDjAFt/nvuLHU+4Nb4eR/WKR3K+rJqHsgVEY1mN9k+MOyEhehF4Whbal1BAqQItM5/Q188y+FjBB6Elm0xmgCSvfu0ubhuwhl8bgIhnzXrZolvWn3W90EpXtuoYPdy8RW6/uvvvSfxcrIhYk6cs6HW6vDNLQuk0qXJWQD/eDn1xBHmxpdNlnMfJeGZ4P4J061C/lKDr3zgD040L77uYPqQs1tKl72lnfxAFzqkmtyYy8jF6gYgkFuXuGpR3oJRwLISvboHCBNo/lpBffBlKWE3h2fV51152ROxWlY0oeD+rtoEpvHBK1x479eraXurDrpyuoE3hkuCyJyTG4BaFr8JGFbKwEXdqDdO3pQcv0XJNWT+dKeJGlKiFvTDJQkxKyJ1ZhJzcLKYl/I1Z8BpxUfV7y60wTLG0U0XAzKhgTj1TwUM3A2yFBM7dg90YvYnmIWHWxj5/bER6QFxK6FIWwRqX0vrtRDoAIojVUPOQCOIEX4UuVBYpqBPhQpOLwgFG+KhiqZYCAmNil+H1S4ABUXTon30Pgkf5UEGcxpOtFaDErpwiMoGxWA05cIIirI0kwnSYJAGAflfrd1MaJA79ChMY6vaPbsn3KkECPEwXp6Rz1/Y7wWnMjdKEEwPJLKULi6Vu7cTwcPXU3mVd95JEOIQFkuH7/vCxUfhclJFUi5KELTumcZzSKwuv43Q9m5JP9phFbDN5PYXKmr5PXfudlGkMj7njy2/28D6uvLC5NYbVJBm+ZwJIuLUh07ImjWprWdBICIvlCeScA3OBHqWWKHsN9LT44r0Ybhh+81+KY5bUVQoKqbgqDf/aLvKtgmaRJ45VMu9JBZPJQlKp4rKjQ8Fgpi6dTj+WLUKMXTHScqeQ94m5F8e5db/C370yPJxZOFtSbrg0vMdgVUpIXoh5njEfDmJVmkiVGpqTxcI5AeKZlrLc3+1x9fwlPvnTv8Cf/ewZ/sV/8WfgzODMSMcj6Dg33Ol/JYQotOEX8PEdMD/4paYuHTFOe3fEKfZ8f/HEgb92lL932SIMl324NK7w++RUWHhTfI9E/1Z/v68+rLUSSJrhuh7Yjm/HxSSbt7/aaOZmFfrUPUZYL+ttrFKfjmszNLYJaLoC7a6VnmEc7+7le2Ec6z3eHH6P228f8O53L8B3hPKOAN4B2K22c6oPZ0e4/PLImk/sr+Gp1ScW829nsYqh7IxG2H/Dy7HuRn/1At/N0WzSGeG6NkDh+c6aWtdqvNbzb219Lns/ILtH7MnY7TOY6+I6z1azqKqdAjXfoV69AZKGaa0FXAllThADDfOQVJqHNSjSUUIe7jKAdMADfYNC95jpzuFa8xHHfXH+5CbdYD8B7x6Ae4holAmYlaZi7Zcpo1rXg7Id7N57iZXz0nnW3apKJu6NfAYwOM2kExJpRUokfAQ7O4TC8BrEDsmU+aaYNGOAyKsAwYpC2zUC1TrAw/xEAt8WpFxLBKAS5ocdkK+QU8IuM67oiIkzquEa1rTDDDDqyTPj/Pm5oUE1z1cnwzbqGT0+1tomw7vDff2PqeVONBpdbvFm29RqCNsz8g1LbwVXCAGNSlpRHqzXvdJ3q3ulrfbgsoIY3u4U3cLh//aeQoqb4VOXlye8bfsSCtOmVGGAEoir+IzXlu+NAHAiYLKl3u+xp8BbC5558cBj2zi3xleeHAU03QMDXUhbz8WfHw6XJ/SIeDJK/QcqATF+LB/L91AYEIR68zmQdkh5h6QxlCkTaLJ4kXii7bVGrmwXt6ah9eZ75m2VKry8O48sdrAoGflexUnEkV4CGrIezQJMcN3Vw43wAtASdw1PGpFQzeJZw/C4e6485ISJUpC9tSZrzNqiygZtJpXWlh3QXAF1jKhlVkWEEJM5Z0kOph4R9m5RZlTC2YgNudviOFOtwqJSUaoR44DpFRp/XJW5lT7kSUR11bURS4LEQ/wYAWV90aTGCQByhilbWK2TY2AuQssVUdRqWZqsSGj5BmTiLeaSMQmSH4Fq9TrAKiR24gYKqwIcIQI3ISMBSH4KcEHd75C5TxgMZnDRMCPzrAnDZxU2N8amaAityqzOEyKQJiakSkCWpPWk4UZqtZj7jOhWwDZv3m93am4P+FrVPpJAlAig2ubG97sxukqIszIcsoQZqBp703IDBFKFAeN8XPFlgs/4OzbKtfoaabjGbhsBbnupMSembGC1uiJYImazpmkMufVVQsKkEA67roktt4Vp0H2nFubiCryO6Bho/bX1HMbSGgPylEBpQlWcYTjZEySrG72FR0oq2O9gqonIPRyTzRcr0U0NngBEYeRMZQN7FO5Dx2CmnKJjkLA3tTKIRKOR2CzlmxjYBSUpq1C71eED786/hgyt3wRRnFGYy34u5JmUxJsq1eT7XLUjQQHqtvzupGfrGWhbyHJJlGIh8FgZeHkgpwxMjJQyKovnWAJQygzihIRJYK3rWhQkCWnSfC6luLeZCPTboFLOA/xtrfdzlUOuDxtTSgkpSy6gnC3JO+lajZ5fZgsu6/I4H1Frxd27O8wPD5i//Q344Q7XUwKnK51DknEnQpom5P0N0me/wHR1g+tPPsHPP32B/+N/+UvsdgnlcEDFjEozklpoGt4zRQS/+wZ8vOvnlBlUjipkiQjuY/lY3qeMlNxwl/sfp5/+MZX1nhqFkm8+Be2fqbRFBDMoR6DMuL97h3/7r/4tHl7NKLczUCoKClAn1LvqebWesqeLK3z6CR3MxlxsdY4Wz/iR1jMy3VN+HgN+Dlj+tfZcq6+9F+gpVnqrhvNWn2xmDIHQr+i8bE4NZ0Dx6L27lB6m+OtUWYHdyP9cUHjx5VFvnX0vkKsbd6WU/Ts8PPsafPxEvACUbynFBO1yjmgWBsxH4QMS7UE0YZomzBNjTm9QqSCr0Y/MTbDsr4RavwUf3uHP3r3AL759hr9/wfhyX3GEeHzODBRtnyDfUS3cJjCjev42YtaQttLLpL9JWzRDEuM3lWrq9QJt8bbfgOSjgDw6uQGLrO+q+CDX4uvdjKHI+qvX+0pXwE8AePA09IWv10lzE+aMXc7YU8J+JkwJABcwCw0pXui02uQlQtCtJ7ZCHY7hr9qv+DwNFVP3TmzcebCVfjVDuGhGEXHEas/7XjmuCc2YsmsFp63WzJt3Vt4P9T5GETHQrE1ZE4n2Mz1gdj1RVGq024xDeRCaHxMk/5zyNMlwoOydWhMSijhBq1FazTPuXxTQO0a+7SN1jNiTecC/J4a+vH8ppE/VcWENg+LhJH4eeNX4c7HXnpAOuFgRccqapj1z+j6wQjxsPTuesJeWE8DZtiDqT/XN1i5cdWsb81x810tLIFvW+/AEipQfgy5mnMaGw9bHedH63Kpzcd8Qz3sA4hwdHDc2aaiKfAXknQqEgWMBjhUqfI294M0Kje64pFOCQE9jEeq3xKL/4byz1sPvC8pZYvM07NkJsti58aHzh2vPbHrjGw/AT59urfR4XgWzRoQtcYMoHuCUQ7OPUQKkY7JoeJnhliCWxJghCofIgETiBOYNIdYsDHi8crEK74V7RpibhbSTSDrXTVjaUT4d0+OgYwt/AoBTO9m4eTq0ofbfKdQtChghm5PR3Aa2uDZdttasoU3g2pKLj0LLYYexepCkZKJkhwsQCEYVnLl1sl2uFYVsrnrcxVa3W/2qsgHssYcrG4yblQuzrBtKEj0mqYIiGV214BdDTg1uRMRyp3APQwdC/Lrk+jnCL1I25lEhC0j6tiDSm6U7EwnDRS2kQJwV38FsgpS25vo9yD6UOFLxdDHr/Z7ZZw1DxjHPCmgBy3Gddknjt9AUwwdERqyHvT0Kuapb3wRFQABEUuaXIAS0c506JGlKcz2o4N32gXeTEkBlQClNuebKUB3e0MXuTOjyWOgDrriGvd/CDzEFxUoonpfAROH2skx4+755InBEfEFhtYb1FVjsEGnXx8dgysPYDXZAJEgM6PE8lPdTC3eki4l1jhNY8pUonFn3sASqkvVdA3NHwGLtdflYdJ9ZWDk5F+W+NK27Rue0Kahi/3Q9xiod10GVpRVlnlHmGXy4B473oqjNqcF9klB0lDN42qHsbjBdXePq2XO8/OQZ/vJPX+A4V7x5d4DE850V1/V/AIvXgyoiMKy178T79Qnp5++7bPEW36eXw0+lLCCyASM7Yewc3irvxSM8tqytycc2qwc2UQLlPfJ0DdZQkIe3dyhlxuHhDod3t7j76ojjK0K9S+BCAOVWz5IUeLqyhktPlTNH8Id2xXgbHq4vn8RARvHy6doeYruwoPW3y7ln/Oz1w8rOjktrWG+PW+V6YeNcHSHzCNTzIWjq1M4sqaDsZ7HRKvC9LLwLKe1OksQZjLlKjojdJF4BBUfUdETFUY1J1AgAKQBI6N1KBxQ6YFd22JUrPGPGNTEICYUSzLAkA7AwvOKTzRKuyfnAViog3gg+UJZwSxxoe0h6bVC7toyj375HDkgoSvOMMG8HDfbrCggWGllpn2bE1GihsS1fDSeWHCkdktRLMzEhMSEnAhEjQZUfIJgx2mJIWA+YuiwbOD5clj4b1h877qfBiWqVLzx5nvSl3zX9r9Nnd/+cr5zG/Cj+4q4/kaY817fVVoPyob3HjifP4m8GVuP4Bf7qPM1iMA48y6JIwnhSL1/tpXj2kq1hEq8ISgCrgSMLbc565GWQ7G+sYjjr+qPKsr/n1+bJ+k431j3lz/o0Lt8e6ZnOI2Jc/k9IXv4Ec0RcUn56zMTH8o+rMCXxhMh7UJ5AKWG33+H2Afi3vwUeZnE/O2cY8+h2+7OkKz2/I6TKWvORSLcr3x3Pu94D6kiq2LPThbd+dJLHjbpc+MNBoLXyfCBS++6ZN0RB1aTH4rUQrPb1dU4mdLJDsFmncGEwF7dgAWLYlsCMEJqgWy2poV0XjwgSC1vxiwWH8C/eEz2IqrejljtF8hcYMW/tJj3YzTq9mh+wmjF0YzSCOip2lHuy64kZhTVcTq1u0WuuIEZQG1PHgIZKSUgJKCTZ2bgyShIBGwEaz13CHHGjwWVqEwNFrKNyziKM61ySFRYFAIr0IWVkApASat2LQLEAwIyUp1Z5Lah1BpeKUma10JqlfxaCSeFXquQFMGGdkcJirV9BLAwOoTE6LbY7aa65deLRiDkTgFvSYLiQPSjLyEK5DMWXt7EnWm+VPiQj4VaQGKukm5hRSbw8JGTTmhWVWb3XeLX7P5DjMr9ZxsHZYNT6G4lemeWqLvAJNcLsomJk6nipEebtuvW3NhSx2pSyegSkKWPiHWg3AcyY56NYzBdJ1msyaYNZ0lhUC2FtmEspZ0RoHMUZkfFZjsmUwtGjAIAq5Fj3seUaMQ8meYyIkLJ4UFj+BlP1Ncg2nNZZwtt4qI1mkaS56p6hBKLoWUO6rh2DCNyZPOm5eajUwGSBCDmZ4lHWdqLcLFgJmKaMQkDeTaimvuQKlBmMDNFSSklJkjjb+rVzlQBJqmfVantZwx+ZzsiWWlKFgOBUweuGqxiCRxOJR0Qi87KQ8Zt3XtXxmWcKWGLsHg4HlOOM+eGAcjiql1HGlHNT2uUd8OKXYCLc84wZwLuvv0aud3j48i0+4b/GN29+hUQZGUnCWRdGuX+Fcv86Ljsp5YitslBgfywfy1MWV8yGSz9QV96nbO2MfPMJ0v6FPFBnUJ0xH474u//33+Pd7494++4rHPmIcq8KiD7yiuBZQaZP0s+RFm+kVS84CXIn7cdAVz+a3z8tOI+KeQY8HJPHo+cgfPPWG33W6gE6wbC9My4sarXI8MLZTN3HMIoIh3Zaj3zcaehcYlP+lGVN+BWuPpb0OnmJOtjWWjFXIJd2VoIkVFEFY0ZBShnT9Q60e8DX+/8OyAWU0c5MGuCpdF4miJHQZ68wP3+DlwCuARzzn+KQnuN3hzvczQWVRLhfwOIFAc3jJYSGH+ocvGds7Un+LqEdjRYWexPx3iZdn2TPCjPhn6Te7qm2tVnBmDTJb+IqfI4+Z4ZrqKaQ4CDctr8WjjEux0a/0WK3kcIqJcLVPoNmAn5D2OU9rj8nvJgYP7864CoXcN2BqYQE8WFusVy9Fy+f7sGe/1waTq20xK0P3bMrC3lck7YkYwQo7sI8ndmT/g6359fwp1/bhtGl8Foqt6LMZ5s/WLAh5lWD5XNLXmi80HjT2K9GC4bnNSQtSGQfAISHJLgHhO095iRGwdqE8SLp+Q71UIAHN81c6fm5sg7hNSV3987ixlrbl83ewivmBLKNIbCGh7/T8l6KiH5gYRGcIFA+nHTpa2hCh8CYrj7/AYA8R3Cd2uBnJnDLO+O7mHYX/n1HvNuWMGWt/JgYyHOwXqyxrQouGVKkPVOGqFz3oojQUA8PM3A3E24PQjCZsMArWMWFK0T1VhdOPLa0nAkNRbzk9awdSKeK9NMPnM1urwCzP6PXnwltbIFjHf+2588No8v70CHswbqf9dBTYetCTmlAZN7qlDZIw5lgVqOqVKhmo98PxWlvNmK2NqKWAELSEDXJ+1yd6fSHVvrNFii36wtpuCNjgszjw8OWaH/Mor8j4LrFo5YKznwFLoz12cTOELc3w5ywKPB8FZtMTfvuU2gEp1k4aQwrI9y6fxaPwNe9EqquvahOSEpSYAJqchi1BWb5JZqixqyN2D/jPMd578AU5ipMvDEfNvDxOQZiYPqY6I01xBN1zwT4Gvwx7IM4Bd6MCZLVGlv3bE8vartEYzSpRYnWLD6clbrGDrWzhiBrtm9hQSSfJmHW37UxrwoMVvoVcQ31z1iiunYBolDL6tUBSHJuZuMVYVBGt6Zbh9j+tz2jHV81stWNGhU6y8dUWK99Zx08A6Cwtoy5I8V1zOrBo+tBe4EWmohat20JOxgMuCcmxxiIlUf8mNZnuvFRG3folVwblKftnRbICEAfPokApCSh3ZLkcrBjwLyhkNymUJWKPkv9kBZbzCe5P6Wj8lmBayGrjCxnf6+3mpWGJWyFH841iVCFVXFeNAl8nLdESNMOREmU03mPQhMKAfe1YC4F98cH4OE1nh1+g/nhZzgcj9hlYKIE5gLMR2A+gEPOh3782/Pt50qDwjad9pjyHRPLce39kOXH5C3xY+qLlbZDe2HBj4l/WZRAw9N4gxIo7ZCmPVBnoBa8ef0Kh9t3ePf1Pe6+YRweEgoy4GMfKx4J9/eHxSoJvrYONpBih/+epPQN8dDBjsbmdo0Q10qsipefCGvdyHED59pABpqIxgv9HflGw/UVMq0f2Xrph//I/flDb+c0y9lHxQHiu1nPW0t0CyYJfcqQCARgpMxALjimWyAxJtp1cIwwdDpOaZsyzaipgiqQKzDRERMKrsCYEzAroXuEeEO0AJGxcjO8MdoXyoeopwKaV0RhRjajCQSvCFRXoHX8i69FM1xqSgvmGsIkavJsVUK4RwTLu06x6NoNgR31TjASo8BS6AOJxBPWjDqmQ8Jut8MuJewSsE8VExHIPIeGfA5mcNVh5/dapub7ahcDnzE+v6h/u0Hf5osNx3Bl1oIXONlYd4/7nx2f2fjG9V5efN6uyjfHs2Ho09C3cbdsit43utRHOhnbin0KbTg9zX3F7DvEuQAGkCqDU8hxSQASwDsWo8+VTi7JgHXMuiX0Z2xMzmbZgNulb48H7niTFljtey3fo0fExkn7vbRzwbNPSGD+GAnr77f8Yx//ehHkk1CvPgVN16CdhGPK04T7mfA//UY8ISrME2JDqkLxy2WwPq+EiPHwBmFVwJlNCfE+XhDS34Uy4rFb9lS7JjwaL28+f/HF/hZh+6T3R6PnRrjKRlTaM0HfTvDY7pYIkSECLBEGhU9u3gjSJ3Frde6GWRMdKwFJEOtdkniIoigRAS1j1rYk8TGljKTrkI0QtvjdpapXh1iqpCyhSKBE5VxD3gtoIlgSiySqIrhjiMeCgMSIAnORFBiklCS2fEqej4IqIanWpOUgaOuy6lhtTZMmI67zDIA1PmxyIWHOSVyz5zBDLDFcqVTUtBYUWYkMHeOxMigl5CTWxpyFma91lvnNWZeLWRuZC0aDEXc1Sx8qgFoZpcIZD3PFTaxj11j3RC1fRgBI+GwWRQxoboJA4KtXgihFm1C27fX+fVH4qGCGGkoywttWrgtH7VqnXGtwZdY+gTwGvyMKJZS67TYQVu4HQlArdYjzuzKdcxFXeNa5SJac12S7MVmxmWxxBSoNfQaGH2H2huvchhGf6/Q8+t2UzsxFX0oAZaQdsJ+yK61qEUUEp6TRHppXFIGQJ41dbPNUGw6xPi6EE6mFR4qilS60GTc3eIIoFZpAW3AZBeWHhw+IQGbZn0k5AEu87POtL7vCCyZ8aWtsOJJk3RJ5qDmBuyqFQz0yELV0YluLyXFTVHqmREgpg1FCyCx0ilsGw7yupp3s+6rKiJQImBLSbkKqYmVpOXUATV4N6Z7lJBlmpAmo4nh0HITkSQ4dj6Pdh19pScyJCFmtOomiklT7UyRvEKkHGJgxH2bMxxnlcATXiqvdHpgyju8mIDHSZ38mCojDAcd5xrevvsVhnvHq3VuklHD1/Bq5Fly/fI7pao9jmRXnZpT716hvf++edgj9jOUULf1Y0uFj+VguKeP50oS85J8/mELiPZrN158gXX0q79YCqjOOhwf8m//n/xdvf1PADxk8ExhrtE5omv0/vbJ+7j2qKG0ZpD1dzcuzPjb3vu2e4g640StKe3D3PQjTeLTu5UWHo2W70VDcGCmha+BHnHumOsmxus56oS/1/304eAa67UdXlH5YuwwA9eprlOtvUa9ewahQM4YQL1jhXT0UaoUYaKSEtAPqi2+BdBC6JLEabbVzdaVF/Z+dn0uAhmz6HSb+Er+cfolDeoHXxxkPZcZvy1GnTHYdpRxyrVVXjMTwu6YgQDVFgRk+RdpIEl1L1UorlgLL18eBJ0SV62QeD5ajomoOjVrEY9n4R13vnrdyKLTyK9jmtTskOazylLDPGRMIL653eLGbcD0R9hOQqCp7I+qa2rnqU9ymq+WxS3dhnNFRm17rCexoT8AHG43qYr0u+7igbI3DKXrFn4O8PXwuKzg/iu7h/nlXeERPl56P6/vf+DLpznYwLdun3e+u7hTELg2I9q0T+nPF4fgOxIQpX7nBDBhIIR8HEYmHBAiJKjgBCQnzdER5MQPMmG4zhq60tpxtWMMMPF44MfYRcKef7/pwceHuo7827K/vuXwvigha3dRPUzhsivHO6UKLQ/7iHq5qCu3W2mpda74xzfLzI0v1x1g6IRVlsHlCTDukNIHBuJ8J744Jd0fGsWgkE+prwfiTVq6/Rzml2R0PzMcoIcS6d+0hFVxRq/8xS39xiPPyO6/c+tASoAIjhFojkWtdCinNM6I/uzrRoFyheL9rzRkgVsEjB4JgfIfAet434rvJqZr1cRsGtxicFtd+rSMAwJb0jRtDQJKWV4iBwMR1fbIxyDtkMU0HTXwflEWEoymldZfOtXXDLEyF83mNGHSBakfUJoh2hPq5tGeV4He7mQBLD92isVRFGLqSXJ4rRLCNMG/DUJT7dOJusY6sU0Z0VbFcFgmwyuqVOo9STAdLb9nhyiWDk8LeLLS2S0+wWCiYcS7Wz2Pqharxjs6bBXmigRG291Zxig+XgyV76xPr+450qIU8k8d8c8BfD+unG97qvPjwLioRJ6xjKZNKiEAcnFAxaxJw6v7G91xwDzj8HIdQs/5ae7ONrQlDun4b6rM1uJx2G2BHoFtdHYiIlg34y7FjEb/R4pk1b4neE8b2bmhPYSeRFgLS9So0VJRfbDRal68hEcCizOiSiyZIUmqyBPJSD7MpaPthPob283nx5NxpqVgy2DJ8M4snRK+skS+hL9TObZFLFA0b1xJnMwiVRGhSFa5HJBw54TgXHI4zHg5H5F3GnkVB+/z5c1xdX3dKHNQZPB91QD3GeVyOgz8iunnUXD6yjOvox5or4ofsz/Jk3CrrdMx32/CZhzbXRcBJETd6DrodUt4BXAAuePPNt7h/8xoPr2bMt5a6VsuqPGJkBDBsu0ccfkMTvRJiGP06qfT9lU6ix31flxI3xM429oC7TyVGwlPrcFvQkAhnXXxmePjcLFwOzscA/tJnn2Yyz/F3nA/g/S0qVXDJAA+Q46XglmFGWgDKEcwzsI9Q3YasG31EssMSSdMBDMKeDkg44FgYNAN7CL1b1fNBPBhFGchIoFRViaU5KHwpBj4w0OvNGwLw/Wxus2r4ZN60xrd0Htvjp7+LcN34hGUZ1+t6CkoLlyM5zBIIaWbkmrDLGbucMGWSMFcwXCbw4DoKsCl2a2jl8YW7CYTTbOOsc/h/vSL76MwLV3p3Kb5cH2DPqjY8xfH+I8v6WTfKegToRl6ytjtUNNQRTiVeXz+htfFCKM3YjpnbcejhiCO+lk8PX01tsZjZoxnkEMkuqqhIlYBUZXlllggMyNsAtabGBX92AoaRjs9vnYmPa2TjFV5e0kKLK+3qd1kep4hYjHuLE/0xlu++oz82gv9j+XGVev0ZeHeNlHdIOWO33+FhBv6n3wB3R0ZlUivxc6TW40swEPXf+m3l6UBQD7ELlwfTqTZPKSOAcwmzLy4d0h4I/3NltJzVb01nvtWgMo0MF2yuKSG6/nWwECv2lgyJmjwmCtLUIsU8IlArag3m+y6zbNbLknesdNYvKTVPCBB53H6xClLhPCVJfBYZ4kCwcq2SF6KINwRg1sPJY9MzIOE8uMKFvNqvYjFKs1owp9TeUaKXk4YMYiE5UkqYdjthFFQZUTxBdJwPIxuV4CBLoipWy5TEkqjMMzgRSpb3xRp7Qkqzw8v7BBkztA4PkRSnnyWPA6zPKSNb0tYg+O1iq3b70CzuScLWwIh4SeIseYmrKlCaxWICKQE1ITGDJhGK+jrrYN8UUpGZdkLS93RFrpCcDSkPa7G9ZyGdyCFOfi/uoUbUUOuXfbgQuBHmXKsIt2tb06YcMBg2vmgIYN2ZXnHf5ECfWtuy5yQwV9T+Wr9rAWoU0hhzsokYIhCow7Fmb2q3l1ZGvSCRUkaa4LF5caworCmNKSGnCSlVcBlrbusHRGCNSXyW/XHlZAvdE0EaMZeiGMn7QC2Pka8t9dJJWRMRKs4hEmujlJK75hN1jvFDjhrv2tDz1teu70M/+0rkLdnvinE1WWJrJ6lcXL0kNFm9rf2U+9/TJORzUgE9K85LlMAJyNOEVESAjyo5XwCIUJ/IPd/IGHP1/JK8O201dmH0LMm0xqueUgZAmMvsA23j1PUjtbgXWIcP2M6eJPkbUgLPkpx6PhwxPxzFk4MZ9/MBtVZ8O+9wmIHjl1+BQZjyBDBwZEbV8eeUMO0mvNg9x3/yv/4L/Nmf/gWeXd+AGZir7Kp6AUm+RUO4dfpHkvtjeWRpp45h+vVF9MOwc5erSsa32ncd3dVzTM+/kBwyKADPABf823/5r/H672bUY+pbM8HjSd5g+/IlZSF8cVpkEI5sGc6e69t2a+v3u8ON++/eM3b6TmjVPlfYupIhVlmbbGxxmnbHWBhepEVoOewwTyfJkfeZq0ctv+V4L3mu0XT97+0qOE7Jgh6J34/5FnfXv0e5fw569xKU9p2ky7wyZY0RCgOUCFPeY2Ig//YAviKkXyVwMuG5/AXSv+dbhn9NkK60H/0WU0n47MsvUO73qJ9n3O4Y35SCmRiUpfLKYrldSNouGmGpKJU3K+3L5p3AaMZDSuwan8VlVoMlsey2vBJUW4hYQDzcofyFh4+09R75FiitH+cx2aIN/GdH28Yvmr+KgJwIqQDpy4od7fDykys8v97hZpexz6QeEQSusxhF8GAeZTTu6mLhjetdz/3PqlpulpUwlmfKerO0/LqWc2+tvg3lwBqIHfY8XF90Z5BTPOKgY1Nqbbxiq2TBcCiQl/t8pSIdxxYesHG2ELFSb8vh0/AsEYJlneHvEnpCgbeG8IHV+JW+t1tQoo1hxMurK2hzr2zV8nRlC/aGsb7vcrEigtdW9bmD8KKK+7rGsmkt5v2g/qcRYTReP1HXstGNNgdiqbvFJ59Z1DhYP215Rnz/S+LHUR477mj9tYVY39frxFDQ5gY9iScIoAxOGZwnIEliambG23vgvhAOhXGslngqaHfX6j0rcTnRk0X3m/BtOZhIcr1/iTBfzstj5oPXcRCWR8RZJcQIwwVg+AIBxyPmZ6ieSONQRgvstQcZwQLGftcFE9KtSwbcSVjzDvgYdbpbF4UQNecGryuMQTT9WletXmfl5rIcBYpUK7r9EpeQC77CWImc8BXCmhuVr3WYoK4TigcgMKMxC+EJu8QqyANJOKvKooBJHgJLhIlVQwO1wUMtJjpMj0YAN5xvBDwrNW5eJx3OIUj4mgCTbgkRtXwJiSQMlfXR8IISWbUCKTHMgqotEGVLNNaphxQIf91SCf8Tm4dDHNvK3ujfWozj/K62QfY9sfYYFZYvgRQuvqu5f8dCuzSFTw3MU+Mv+vloG+FkXwlwrYldCnu1031sVjA8wwNIGYsxQc8BEWDLHvVdI4Pw9VEVgSypjoH50T3i6zvAp6eR5GqKShHweg6MBUMDwDyCBq03RZiTJjhc4N2+N5FZ6NqOQ1ubwO6gsMEDYGrrKlEXcoGBoDzse2T9TiADovyOCuMBJ5myl1LopNN4ur81lJ2vSd/g7Pg6jQoLXcsC0y66tAwzabvd4qSG/x1EcX5EeWAaJfMa4yoMWq0iDTnWglIK7o4zDnPBrBs06VymnJA4Y7efkKeMnDJ2O8LN9Q2u91fIOUuCahalb1uKvZfUwpvuFN1G/t/jy6MY8I3m6bL7i/rw3r3+WJ6gnIV9f9hc/t6pNi9+ef3BU6t1wMRyLSVQmpBqBdWCN69/j3e3r3C4fUC53zWaAYArIb6DMp4x1sWREvFv3Xn43e6SZd8uAILTboGI21gvjHqiSuq/mfKhO2tXvJPD78vW8SUPvk95+gWzWeMavTz85nQEpxllOqLmCnASj4jorQijh+FrkFlp9qkCxKhpBidR7Bs/HmvodWShoqFYFgM5fqvSbffgXHGjHtLvuCKDUIxG6TkQddgmcBK6xcwozGuXYSF+ba0xYCGZaoGHgwW7AoL8sKqezNp4OhtLn6fOaOsBEC7hpY68aNRXVFs0epMgdE0mIM+E/ZSxn8QbQiP8Oldh+6fLFcAU4L1KAK7Ox/LSMiTm+J2Z1vFXz3XLsytdEbqy1efhSz0k7vKdEx3WywPGiuSu3w0woKGqUanT8V/L+vtH65n7w72+Yc9Rt/n8ifqc8/RxtUgAHX/lCFm9/GuVfROHqR4Swq7L3mOuqDWBMloexAzUqwIcIUnVx0Ij77Xe/3N4zX68N0Z9xIunjHUtJkH8/Z0RBqFc7hFxau3BcKhMnguGvnNS+9L61xfQh9XZyjklxD++8v0s3p9KqVefALtnSHkC5YRpmjBXwr/5DePdzGC25MH6wvcCOiMJrPDweb4jcQtdwtNve0icb5J5Y019CKw2l6lSVWf66ueh4jr7XBIK3B5kSCxSPfhkWGa9Hw+t4FYIhgiYjQio2p55YsCJSSMoq4bTkHrJBVpWP0dPCDSFggm+DZ8XradWRikzynxEVQFVmiax+s1ZBPnMKKxWL2aRC7ilDaBWyDmD1EMDgIQr6agmbn8JyMiaiyI7ce/Eg44x54y2nts4Tbifp4xaCeUgxPl8PCKljN1uAoGQpwlUWhJuO75MoVOZ2j2Nk0xQxkDXdSkFXBk5TwAyck6AK5xEGMguhBXCilmsntq8t3nNSZmEaUJhSabFllSbq/AXpSqvU5CSxZsVJqytb2FKzLOG0YR7FOZJEjpr7oEiMeJSx16QMlUmWO5v9UWUJU1BRP6gPxqJTFNEicQXlZMoWtg8X2wPtTFVZnAxpRt7PTCrrlqBBKRKmHIGPPFzgiWv9jViHTFal1td1n9fXRFXDyCIAndLYFxUkMt1JRwZy/oS3CjXk60RVDDERd9wR0pJwVbAIBALa+qKmCrEt4UIa1lDTMjRcBEDQA2KJfUKSSokd8E5J4873NZnG62fHO4+X2UMjTD0epMJrENug63wXiOo4gVhfGNfDJyyvt17RjtIILFurMl0BADZ+g7rmlqSZtI+W4Mjns/qNTTPR/Xiskdl7lISTyvrp1lZpZSRc0beTUgpI01ST9HcPwxG8pwzhrd1bnISbyWzqOMwvySxly1fDRioKeBVhUutTSFMENyZU/Z781wwz0fM6p1xmGeUMuP27gGH+Yhv3rzBYT6CpglTnvD8+QtMOYMZ2HPF9bNrpEzYXe9xc1Vxs7/C1e4K+7zHoR5RypIFiqHXPoYp/Vh+DCXK5kcF5Y+hrFA7Dd0CLmQUweSM//Bv/jt89evfYn79M4AnuChizUCI+t8dO9+jlIv6OJbmmdlwQdSL9PzI+0L+MoZqWbt0xMNEstGnHARLHCTSEY6D4Gmt6aBpkGMhhdwQ1M627Q6eHcF7ldMStaepePHV6LatV5f348rgQJfU/Teoz75EvfpG6RvNlxXOPmYSj2oGmt/ChJQr+PkrlOmI290bYGJMOaMp+8kbZuO3AE/Rxei9OY32ar8ZnCrmX3wDMONZZVzXhN3hCzzwHt9QxcxAJvX6BqMSI7OEb0oEFCQc1Jhi9vFIJ4yn41o8hyCXo19DrUg+Yi1Gr2nIplqFt6hcggFMnAZGMyBKjV4cx9lmp9sHRndlAnJOmEB4djXhWZ5wvc+43iVMmZFTdXq2qtdK9JAin4THrfuoVAFIFQetjnUMLzux030g0tWh/vhWMFLp6e+nOkUizdtaj31ocsm+TV6o0oaRrG5GcjnDSVxwVhB0Yvzd/Kw106u2wNy6BNt/y1l5OL4DEWGfrmEewXKsiOEhQfZxRQKpBxQRIVWAr4H6J0ekV4Tp2917jHcYF43XT0EzPvB+6+aEX8nF738flM/lHhHDbyd+GM7UBp4zKCPOH2Ed8TQy+G5FdmFl67V3r7oQ5pLXVxba+mbn1fuLti9p80PeCwfzEpZ6Z6OycaiX4sz15z5s8a6vt/hAP5hL3MseZWn3REXCKGRAlRDMjNf3wKEQDgWYC5AHw8aT5cQwz1nnrVfWE+vx3e8EPETrHRyR8pkxrO+x8UBda/90ve3dMwTyWJ8TNVE0t+whYCAgMf1wae0Kw+UnLIyu88tkFYW6hRgWwaZRbpSSMzitb+yo21ulKIyTei1EkiVJY80N0XCyhfsg71cb+fL4cmFcSmGtcrMOMUAKh9ELpbRv7VAPjXXK7xEu+i43oSWzja2ioo1FDHsjWw9nOIipWxNNoIsAX2B02wc1SBCRWDiB4nQq3JSpUMqqMrunir1rwmq3wTAmRMMpeZMsBJXNt3hQtPmzVzvhio+7QoJEAVTh8AHMsIzQ3IUiUdh/jbioUySg9cvf93EarKVxUUIEuIRqmA1OwZ0c7MkhLb9HKSTMDFli34TFNlshtmKiytbblT0aIOHC9PHo5YabuhpW0ISFq2IjPiPsdA1IHu31fnT7Wa+IF46t3ch4QZxnFv03Baeu22DU2Sgn/TN9F6/BJiKZRismwwMrNIoLo30MK3gk/t80XU35UEfvGXtPlBFQ5lLG37w1PB+IhliKfWotjm1H1ByUIoERtRctHJUpelJKEpJBz0QGO+w9dFWiYc1S1455zEXFYjKTQoLKEsb+R6A0rwxTMB/nIw4PBxwOBxyP8n0uBYf5gONcdBrVeCIlDxNFkLi7OYsyZEoZWS05W44a8n+Wy2fcBlvewWt5h5ab7cdVTtHc78sTbLfVw+1jqNj3K7yyJmP5oRRla622a4EmSBmUdqA0AbXi4fY1jnevcf/mAce3EzBvhAWh4RNr2DeU7eNw8/HH3/w+Yc3D58qtlftNBHB+v5nF6TkZBC2+fGB5D1TQMPbl9S+b4RNfN1+6pAr0HAyjpiPm6VaMdg4TTFjd231waNYOZgBMoKOGsbyuQGYALUmtkGONqGW0M4312manoYYixKCpSKi0IkTpdX5AmmccAcwEPNQJDEIhoDBwVIMSVtpkIkJReRsTuUcwKz8D/XRa3wxyVIDsZw4bH9c+q/ITY3zMZuQDXwwdvTgigpVt1FgzoTWmWjDVhEyEnAg5iRxknxiTWbhXgFNvny39oDgpuLyM4xrUCUboj7yA5fcLl+vw1JKGoRU8Sn0l5P9tD2ONkF0xyoymfGOnFoaRG021vq8xJhx4YF4s9172tNWCvH+p/HHN8yNWH1hef2NNYEPOeyDMsdQvt3Q2ba8FuQMRgJwkX0Ro5nEl7rvxzplKddN9gK/E0IMnKKe23Hs28wiPiLhhKQgM4kM0Xriob/H+aWLr1FMfXsZ+nmtlyxPiY/lYuqKCh5wzSgX+3e8ItweGxZ6PGrsOYSzPmycsPbXwPkvYhIynGLeTh/XJ3l16eG7kcth6IeKszUrVZmA8+RYleeiNKBDzgy4ANdI4pMKvSizS3WNFf0Kq8L8qmcuBzNiYKBGuV08sKu2gxWPPwnzOKt1uwn8hmFJCCFWiRDaz5oOQ/BSSH2KGDhopSz6ERFpBLZqX2UVN0oRadFtf8jQBBA3/USUGOcyC3FxxLUF1UsEdIU1Z4plarHWdGyEcEsSyPFr4t3VEiZBYhGRcGaUW1AKUuejeFIVNzZPGcy+yDljTY7mltbUZVkFOSAyUEsJW6WR3jpsuLDSCVOPB6lzX2hiDpjxQRQ01LxNmArNZMYnVvCTVJtCc3KKjEbqtbo+FKR1RRZLlyhAhd3WhrKtQxFJ8iE/fr+xRaKgEINSaKT7W0ejBIhLRwkXxkoktnUEwfKWeOmVGLRXHeW6hwyBeBZWBh4eMyoQ8hRwptmaUfCdoCCSFlzNe/WCwXoK1qMGLYu4TwBjXMOS+hog7XMiscx9UQa4cUK8ltmsB/9qnhe51JmpwBWdYv9q4midOQsrNklCYEHYm3tZK8kZkrjlqLIwpUIUSwvseAsnXUfvzFH8UwxZFaLe1TWgwN6+qaqEGPERcL06x8EoU5mrhVZHaGqDILAbl6KJXBORuzyhzaHOfCDknZPUiSFOWHBNJcGeZzZtK8u1MeXKPC984iTQ3SHIavKqHFKn3Us5TS5LNQNMi6fMVfoaQeQglkQLMhyMOhwNev36D23fvcHd3j+PxgPvDUXC/9mTa7THtCNO0Q56S5tkQQiDljOvrK1CWM2faH3F3OOL+cMRhLmAGdnmHmiYwZfQr/HFliXU+lo/lKYrSXYDvlR/CiKlr79wDoctpd4P87Av5XQq+/vW/w1d/9+/x7h8y+Ms/b+frgraNB/MoMFvviQknHw0N7j5WMMCWtMpuPZZb32j8BH1PTueFtWC/hUFQJWukR/XdbXJB6Bk/7pX+6t5bCidPsSxr1z5kdV7Ee/GSPY003bICXr27yXcOhmBjj7ijqWRRzOkd3u5/C769Ad0/B+2ugJ0zN7503FZI6ahECRnA7g8J2BHKi0jb6ieTy5CFpDNvBJXbs/Fg/b4isz7XXF2JxBujUgUlxtX1l9gxcM1AnSfcP3yByhMqgAcCvmFGASMTUBJhygkFjGPOzjsUQEPOVrgRWi3Kj+l3tITXiSGnrvGVFhrXlBluMc++5iMNFb86hJRG7mjmOO9JaK9EhAzGi8MddjXhanqG3USYMuFqInx+xciaO9E8++P8d/4X64tvWXz7Gl1vSGtL2hgH136PT7fXyfHEwniiUzg2nsyM6pxa3LRUWG6QgTs5rQNbqeFU9sv1Csd6eHEeGo94vtD2nt9ovsk+5H3HDUAPt0X7wrcEzkq/sC9tq9+MtSoaLSt6SAorYGsuLi/nICs/F9juka38gOU9D57HJav+HsopC6LH1RMquriyAYkMV/sD9P0W5VjnpeXSpfiU5PGW1vOHKJtwe6oF8yRFD18T5maxSqKUAQK+vWM8HBOOlVBY3C1TGFGPcEzC06q1qx0QuHv6dO8egc/iIbto7DF1NhlO/16sz+MmXkAArzR+kSfEY+87AdZTwj1PxjAWgoajKhLKS4JdLXNrEsLPtDlrHeH4tTFE7BJIIW5YT1ZhitgFfDEOutfDYTyebGxo2S1rjBg1zwi44NqE1WtC6SiOE+UAh3eayJF1PG7eEIDFbPFMBc4piZV7dYNle8EYgzALG/iAKAGpqr5D6ksMSHgsYUpqatYfPo+6RpviLZBzgW6N69oFr8OU9sRum5dalZlwoWpwhYkKhFCVJSLmqoqIzlOjzS1rgrE+NrzMca+8USuhRLrmZH6TZZFOCagIse+HSYsAiSPn/tPc2235cCTKoWuUzGLF1kx3AjuMqyrMLIyYDINFmcUMEzanoJxZy6oAbuFhts73cd3FYsxGt/QGZWRfYcMQpjxqcXmHukn3KrftQolknSZZ+4BiIxurQZRYkv15vSEck86BHVvJwkRQ28OSa2RgzkyJQA2Wts8J7V6EXYfzdbxLhrB5LjVlwVZIv/5sEh68ecgEe0WfMjImgxQK+n1h+RuuRfrPoWJnPGQeUlDAgkj2sDH6rDBR7wHSpNHQ9ejKjWTKWlP4Ga6mNiceKYK0XsCUH6Qh/5Ycs8LVjhMiYdASwfJ1MAOlFhyPR9zd3+H29hb3hwPmuUhoplp9H2UNxZe1r7WIUAUMJK03afg5ooz91R55N4G5os4z+OEBmB+aBOfCclFoRwzLKZQl7/wImnFjUz6Gpvq+ykdPiA8vPPz/Y+AuekwUrqYEytdOs1Legyjh7e9e4c1vXuObr97i7auKcn8lNOfKnutohY4niWPvoXDJKlt95tSLFzEyCH09NTcbNHX3tSOwVx5jf85WgwuwHrnNIr1oXm5uNAJDR8Gw4VQdiF61C8R2Ei5b3b5ojY/gO1fviee355nP3o+3ar5Hzbco6RZ8yOB5AnHWc7H37oxyIV9quyM4M8r0AOxLO18jnW68lnEtRpY7HWpndRwCD3+6vEmMYIgYSCxhLxlImXCVD+B6FLKEE254wgzJIVFYvCQOSruUQI26WRmPnVmDpQn3WZe3PtcpHdjz9bVXFb9YWEhq1xm0sPbuCznNRwDKHSEjixIoJVxPhOusgbCUJmqGHI1OFo9thLkI495YwSMPbx4gRn/1z1o90fgp0r7h2ZXxsr3jy6bNke97X0tKLQcauusHxxE2/oK7hbayD0eyquu30I2dAdLY7gkEvGkQ2UjpJymrNIxPY0QqwZt9bJz752Y+Kh8rUjdm2YuJk+bCVBpZ5StiVKnXKUlEk9L48O0ZeI/yWNnXE5alWdX3T+28nyLCOOGurHFAP77yKEuWLc3gR0L/YzlZBHnx/iVw9QKghFoZ//Er4PV9FWtBtQ5XiQg6osH30Trj0ZVLCPf3LgMhttHYBzVvRP452nPx3saTj+kM8+rjRgABUK+E9RLDBnX06tCNJZugJEUC3BZKKFQnBttfcwPu6xNipkIIWRPIutUyVOCVg9DLq2Zvk8iEa41QN2GoWeNb+BsjwsXiVohIE3w68TUSPSCAWK11sydoZdaY6LWishHmuRG+tZojhdSRgKyhBkw8b9AgJc5qLaCsQjkdM5dAyBJhmjK4EIrm2yiz5BHgLPcpJ6QCVBLrXa4VnJuAlSmBuaBWhieP7cYemANmpMqA6CH7GJak81N1HrlingtKLZjn2eFOMJmv4Iyez6jdnBtDIL1o7SCs587iDkBRoXWqGTHUFtUgaCUJo0IpgbjKM5qDwvKOeK2+J5bnbFvDMmZKLXEwKWXY0Y6VVS9iVmU9ycwwTxIRoBaNjwsAU57ASJDwTg3fJs19wBaTyBlJNg5o0e/lOIauOEypCaOBoEjS7W2wqpG1arkkZIjKaETaOtn8A1zVG0It4AkJlQlQwTuRXM1Tbnsasg4FXgF+rnARaz9poyWGj3kgCGzOSmpJ2LxjWtoJDQcH2xvUmFZldB26nYI0MmsyJutLA3q7D8NZQRkgRn2Sp6WFpwPcItGgqWGLUnQIC270zeNhuX69Nb1vYRFyyj5HBu8evtLfnCZMKbcE9Hr0VzAoAVMSb4mcU1DCSG2S+yF7/hCDo+EEEWglzb2z0nNbT8oRm9Ija24HZsbD4YDbd+/w9Tff4utvvsHMEG8trSVPE3JK2O32mHLGPu9ABBwPB1FiqTeGK6EIyLuMz774AjfPn2OeC/j+Dfj1H4B6BEoBp7TMGXmidPT7RzL8Y/mgYjTtxi1uZ9aPeqnla+RP/kS+MwuhURm//R9+hy//1R0OuwmH/c96wZYREoDjIinBhOQEr/xh8Djz9lIy1v82oRfFSyPvtE7Z+4fTS/2z7jnoRFZ4wRXL4V018Dg3lFF4azSj2QGZN2Ia3jtd6+ny2DnafP5RFfHwsf7yOswa77Pkn8Z8Ba0cr36L1y//e9Q3e/Dr50jTHphU4Kj8zyKvlynxEwMv3oKngrvnd6BcMU0TouV9tbXmwnHpVdX9FCPLSvctb5l6Fyitrm9DeAlRRCRInsAEgKcZ+/yNw2B/3GF/9zkKCHMVJcTMwNtKeE2EmYE5CLQFSvrN1m/8c6iyER5wz1thduA3OK6ycW+FczjS69Rg04qu60BfUgXuvt6B+Rqf/8kVbq4m/OLZDvtd81Z2r3AzoILtk+QC73VPyrW9EWh8XETiw5njzd/jOPv2o6dDz3Ip/cqaIy3khhmrXeAmrdflExGdURzYOfzQE1yP2d5bRlqA8i4YxrKs4RGtjW0b6g11EFSxp3yIr0uVYRgUifFwuAUh4Xr/oquwoirfxmjJ0Q2manwzTcgvdqh3M+pDGWYFly2qCy1kvk9a49FKiMuOnkeXD/KI4PBF5FyqndIF0cH3gwbwPpZHS1eh80qI/hAdrq48vliOjyuPUYo8uoTTfGjnffUo5977TodzrqyttYXW9sM6OBJVW7Vx2oPTBKQJoIS3h4T7I+FQkiPN0zWst9ofM7S4H59ZvL2+tDd7wX69r71ZA20shnNrzQUb4SAd+7YgZrbKiY36aOKZ4NDyGOPW04EyRhOikQrO1mtle7o1w15DkF+SgoMDUUIBVub6PVhLs5qmu+eCVkhQ69hGhJuwqSNKNQOXWNHLb4+N7wRHgAFa+KaOebX5coqxB74LFFNwe2SWRMPmTmwukYHeY2Wqa5W8BeQC2exhnbwfLGGc2OMAWX3kXgOtQ+TJeJvHg44PhEpAEhbBmfHKzWrZvCkg3UMaNlDLWTBBTSxgiak9BKutgwGexkQwM7gUZQsYORHASeHF4bPNV5wnK41Bb9ijhSQSWLAKDm0duBUZTFhqAmfxaonG8Vw1IXeA9QIgtg8uQHcUegook5cA4hYns6O5/UVqsGfgqIwMebh8XVjOjETG1ti4IDT3e8t+bwt6jfYJ/dd9vYnSvLJegCLVmbU6qzdEAlICo4JqE+Amo7cANEvL1JggXUXEliNB5rThAh29JjoGBRxkvUs6isqwveVKr5QC/FiVk9onIhWOZ4ldrkJ0H3XkZ9lei0oK3yhixa9w7hhhrqisSs1aOmbJcTfLGKomoa6uPG1tOD5WePYz4rWJAkj3xTCZaL0mwW8aFiHG3mAfY0s0nil4QjjzavgZAkMNyeSt2b61tiPcHOeFs8nnNZ4xGtahVhyPMw6HI46loJjiKoxfYBdwjs5kKVXCAGa4QosBoAC7tMP1/hn2017xBcPCypkUzmxTF9tDN98qNtmgbdfK+9K7H8tKOUebPSUT8IETtzgihuuLdbUgJwNt4Pii7adlGMhQ+Urf33c0rZ9DDSmDpivQdOXPETNe//ZbvPm7b3D7+7c4oqCgAiXEmQ5CLKs1wiJgw5N9eq/xjKT0B1S4djZ7I6caZsM23D3uIZYsRKY2EpUP9sl67qwOJdBHprRuFxrJH8kGp7f0Y23txnPoA2bgRFlsgMe/xyvXws/tKtlZiFPNm4CQiVHzHWp+i2P6FnhIQN2h0KSehy0PHWmy57hPGQD2M2iq2M0JxIxCAOdA9zg5N/LgvBwmww0T4lrpZ6pZvksqbRZLbB2TeH+3/FQ5Adf5DrUCcxJFxgGiAHmoCblUpCIhSUstYC5QTkNxwQakHciieLDwNfa/J/f20QaaI4477r1Ix/koubtGAKYyI1fGRDfY54xPrzNeXk2SJyLU7dRHf9gHReH62NZumHLEexOmaa0a37cc/RTkd2tlfLvRYQBaKggN6UUd09Tg7AZfa0qOlc516TFiDxiB5j1zBg+C2YUO5OS5O9Bp8TBl+dK/vsR9/ReMYNycW+nb8KK1SYYYeiwZq12GVI1V6XrTfciV2wYiRs0F857Ah9LXvmKosDY0Cs92D62M9akx+1bf2t2xxxtQOrOsPsST4hGKiKGR4Sz05WmMxdpiPHNpq/Dmqh2rDM8RPelkniqPbceZzI/lR1cuW2mn3+b9c/D+JVKWuOS/+Sbj968JaU9IGZ3VbN/gOprg4fclfWxWmXZheHJl/XUIi6Huav2Nzqq5PR0f2OhRaGWk3zngj80RrYoj/Ntqtzbe7MgqZyZ64ZWH9uDQvyo4xqyGKSW3sJUD2DTq3P4Ai5fi9ScTWKWsVtMJDBGgJQA5J9TStPPw5NM6p4DGG2UR1INakxYSI+0kd4HmPpgthn61g9SWgAruGQDVFlJEPRUEIGKZAkg+hJwz0iSCMemeKhOqYuoahMYEUDYrYI2db8TzfHShISWFk/a/ar3EjGyXKSNRBmXCsUq4EJHNWT+LCMUoqSJGBV1qRQPoFquMPE2otaLMM8SSukr80iTCBk5RucQozJjUoqcAHj7JiVYyUp5R66xgewakhFrfASgeNqZ48ji1zlbFSiKLQytKiHI0+FTUJLkyXDhSQ2x1VusgBixHgiMKPY8bAxHivxJ8LTNr+x5eJuwX5ZpzziptzKBUJewc2X2lA4lcTB1qCP9b14xLo5Ycb4XEkMHJGpelMZzrKtAV2CWJl1sZDw/iuH7zQsPwR0aUQ+xZZodRSgyiNPTA0nf3bbZP6oQIrvBDWyOsCKqDiFrojbBu5nFZ9TsaOinlDtFRBsAFlLLijY4T9C4m9wS3kEU93qy+/ZOHZYJ7aok1mlndgwvYYETyDAOqcFcPCBBI3Q1qZYAS0rQTa/68A1KWXcNocCMEXZaG9YkgsTGnFHI8yD3zqjoej+BaUOayoE0NtwvTR94OFJejJiCrAs4FGGFeOcwjWr+zgVyvV83pkMCgWsHzETwXV8wktf6vBN83osZm5DTJ/nJcYm1lxxEp5Z6xcSUmAOSg3IDmjmkLQSwlCe6povitcMXxWHAsM+7u7nF7e4vj8QjJPNPWieCcGVwTSpmRSMJFAIxjKaAKTHtdNqqbnHiPT5+9xOcvP8e02wMgFX1URX26f3xEK4d3UJSN5QeloL8z+v0jX/D9FVt5irsRaDaY4KNR4ImaFxqYXCHpRXFrf859uFAh7oDuDMk7pE/+xIUcVCtSnfHNv/4dfvMv3+E4HXC4ftCdHPL8LEoTj8pHRyFv9Cjc44DAh36uylsGmcF6j1rV8T2jbWgE8qLl8aX4deSNAi3gvEgwxHHDnPbMkonpUYKc7amB1LpJZgEt11MwRDi185cw2uC/LioXrMjFIxvvRN4w0KOXthgtu9eea7+bgJOpok4FD89+j9v9fw9+vQN99Qzl6grzfgeaJqQpaeQBOY8TmrETswgu6cU7pFRw/e0zABn3n91LnivKTVFPCGd/281G0/nhGNaKEFZ2zXghoadsphIZ7WkeNdzClULXx1SQnh8AMHYSTRa7yti93YNf73E4FjwcC9I8A6XgISXUSQysRLmg/WmEr/alebgbz8Ku/0gg9dJgXu5ejsYtrPhvPAt5eY1I6Jybwx32DOyuX+Llfo+//OwGN/sJu2QwMa6m9zTysRj8L0Sshi8aLldY89oO9s7qO7S8bjU4LBstuYbj4gicrgRa7gj7PD+UULXF5/TRdG06/6H8L3ztrhfyvdXOv0uxCy++9PXaHjKc7efCQqkzXO+0I+NpstIJm2Ma328IeNLcjEaPh92sC6qCq+TuTMSoREipAMiYd0fMuwPoQNi9mxY460wP1/t8onTH3sazND74fk2tPDHO/ndPk35gjoi4WHDhioXxdvL10WPcfkHw3+UVfiiB+D5l7N1TJT178qXSnQI/HHP0Xlq2rZ17btENr7kcYquZ8ULaA3kPpCtQSnhzT7g7JLw7EDgpvd4x3loJraF9Bm+0vNhqg0DEn+Pxy7J0xHN4lP2/eC8QAt3yOLf5W8+5qzgwgCeIWOW01qrrX4lf4kERumdEgLc8DJTDPxjjASiT2SoxC/YxfMhaF8n/UwLG15SQOimRCHhMtKNuvL7+VqeP+2+RsSEaEgqjPy3jRSaYKiTGQDUlRNsywfLWY8jD++uwUzARDEaudvEOWGJmeV4plCjUJR00M5gkbJE4FmiOiSSC8KRurWuWcWzKE8vt0MFKBXIpoZo1NxuJ3gbd1cnw/nqYpKpKArScEoAlrCvS70JuRNnCXlWFQW2C8CTJXRkZeZpgM4Eq1srWF1OIVbDXJ4qicL+jvqM9Vyiaf8GHa+uSlaT2BhlIHtkUiRmZISGsUEQZlrLUZ+J62ypLPiaCE9a7DheOzyljp44/be8FFOIhgqp4AIlCwYSyFGCvEDKlgDITLTRPXKdLoU1THsDXq50Pa1GZO4vaoR4fxwpQnLcjoDL5WChJrgeCfjKaV5BjNINNY3rlizDCTaMie0dyCgicWu4CeYdrApHsI6oaOo0C4A0P6P6VhOgVOewvSYjewn6lpPjAN67AwZfM4mzuFT2mhLC5qapc5VpaompuXocuQFImKxoAEGSMNVUkln5mADVJyLXKva2+K9xYzjzmth6s/6bErqVgLjOqKn4TLP9G83yIY2xnivwl6yAMnyeHk81eEwL0VJKfB9xQqSlwTCGciDDPM47zjHmeMR8K5uOMUmrAJf1JPeXJlUSVK47zEYkIu/0OKSVMOSOnDK6SlPMXn1T87KUorgkWyqo/t3ooRHpguyxWyPdBnj5xI6fp2u94QCfowSer+wfkGS4tapO6cuMELbpd2aL0eOFpingcZtDuWrwhYLRbwbdff4Wvf/M7vPrmFsdEKFRgSoiRnr+orfHL2ffbSRivjE+sfZ7qA4cfq6vqFPvRsRaNBtcviNgmXo/KCKtiK0zXuNRXlRB25oeuLuD73uUUAC58/cTNxXjDO1vKh4uW2hklxNhq3b/D8eVXMEOpOX0LPOyBugPlCSlPnr/IaBk7JyMJIeewGHxRZpTnDxKrMeu5Gp61fnUz39HXHRRWcOtA+4WzXr4L/SFGEurx6YeuKRPsu6ytPB3xbM/YpYpdnlHvKh6OFakCqRLy8SiJqjtBtIyCVuFNSs+03x0xGoDR0WIDBu33dHufmJGOR2SumO+BjB2u04Rp0rnKzXvFWQHGirKBzWzucgSCcUrYl91SKduPpN/XfX6qxrtaA7133GY/Iv0M8s6tekSsFgIaFLTeAS/5fJuCYQBkrJrggG780YmeDDh461xpYZpsn/SeEgubW4WlvIMNGmULz8XNqgnDXejD3bQyGHN5UNyQ/V3hD8zMjZQXrmBOEt3A6PKcQLsMnuvJsN1PWZ6KkjpXz5NTbI+o8MmTVZtgqWfM+wXEW+tpu9YLXvjxE74/mfJdMio/8vIh+hfe3QBXn0ucegJ+/yrjN98Q0rXoKCzO9wKVnwD3OBUfxN8trBTWH1mbfs8RcPHS6B9sMoioYFkSsWvCv9XtH3mJsaG109GTOrdjuVdCBPusGh4Ihw0BXSzwKFBqFgVYFh27uXxXDTqaEgMJmHJGJaAUGb8JqClJKB4XwgYGqQeSEbiapNY9NqRvFj99wVIwxDKIRbBkygXPOwB7T8mmZMLL1Cy5bB6qWYyJ/biE6BACswniBcq1FBUgGsHXhJmLUiU5NSYCUQWljJyShmDJME+M9q56XSgMUxITXYOFOQQkzU8w5ewwp0TgooyLJmVOZHkYLDRJUWYgi5dJYa2TPSIRlwKujFKOADOmHetakn6VIn0u6nXDREBKSLtJ83oQypyRZkkEy6WgVvkTxVFFDYqMGEbLV3PYYk7cteXiDAUr7Aqxekckn2vzjlEnEbG4pIQ6MVL9/7P3p0+SJUmeGPZTs/fcIyIz6+iqnp7Z2cUCuyQBLiiCL6DwC8j/m99IEfIDD6EQICnAcna5WMw9011dVZkZEe7+zJQf9DA1e8+PyKO7uqcsJcPd32GnmprempCZwSmJBbgyd25JjxgmZrUVgoCXun5FCHWcwYxahKCUHA/2PKknhCqGMjDVCYUqcpZ1N8uzUponkLzeYoEiNXYqhjGLLIO3aMq1kVFlrTMyaRWrPWcW6WERVviqeUmQKnqEmWtxYA2WNUkwGiME7XuvgGNdk+x9bNZZGsIpZVcUWE+qKsFSJRHWqzbKEqqLgoFEQQHguByE7qcJlAlTnrRegWv5zKr9SBLWDI3BPk/lkeMbx7eqeFiWk3g2FfXgqg1v6Sr4/vb5MUZT59nGnXMF8gT1u2hPkVmxpqgjdWWE7Zmqa15KwVI0b8micEep5chJqRuPoOyk+LuF1oqKBol9ZN5GpDR2gyE7f6orhWFI28FMEk17DViWBU+Pj6KAOBacDgeUZZF1d6gxlpmwn3eYsyga6lJwWk7IU8Y3b77BNGX1WktYasWcC/4X/3yHP/vVDtM0oTJQloIYEu2jyx+AsPuPr/xx8wZNsGr07g3j/cxT4kHwrC8pY3rzrYaXrKBagbrgu7/9e/zl//V7lOcK3pu/kr5zKTH8eNCZMCf0QD44IJbtui5ORdeFNS06/nS8deG1/oWNiwHfN5o2eI0G5WgfpjMoIVYwcCkkU8C3ds7acd89GwYXhLmfV4xxfs55677dG8Z/dS0udqFXir2kivLwA377X/2fQO8I6a/vwO/34N++QkoZmCWOO6kyghIhJ0mEbJ6AMOOUNAGZME07YD7i+OYtOC/IeefGFb4QkaWLgMjjnMXJdMI10Kr+RfqTCMxCNyQmAKXXy4Q5N0Mxy/+Q9wX38xG7WnFXKso/EH58XzCdFlCtkrNpOQEPD6i7HWI4IzNUIm7bWba0yOzOyT8aihD6xGx3nJa3vlsFgbdLxNgfn5BPBacfvkSiO+x+ucNuFs/6JGEiLJEEEPtBkZYb+9L+nofd/vuolBieBoLwXozO+me39EzOT1gNZP0a5DytCafjIzptsoTzu0L4kx5JrBUH1tYGMtmoOip8rp13ki/w4iNaj4zfdDX6coc7tgyxHAZfRNsF5E+6bn7d6rV+MQ7LIwgJ+91rRP7UwqbLHqkSRlm74nnr5hnTqxnL+1MI03QZbf8+qdTzPFVfft+U9McpIhzKxmGYPW8D6tUT3Jh+YA136/2wvUE+lUdB3/anpyw/10LfVO84yefGd24ur73fMcOflj9cCXKujvgWxoEdYW0XcsFIbHPLUo8BIO3AGquVcsKPT8DjgfDuSJo0CypsONNPx5L9oXp2mTbm4CLIbizItaXe+KH0VSADVuPZ6H84edxift2qX4+3N6sPB+Ymiti6PtS1JqyDZ4R/slu8SwXJhVHym8bh9mOLfR1IKElCTJJ4FhiE8Co0C/2pFvqoXw4nYkwgRUBnDZRA6nmgVnFROq1EEClx2pLktpmKHjBWv8U1ByCWAqkJXKv2kVGDKI/Ukn0tLPd6nfhXC5uR8Kwa6iRnny9KCSlniGw+rJF2vxpRUxlEFWARwCVY6KfazRvreF2F3gEfBdQnQveUSPNIaJ4LXRARMgusl6UAmZGnqgSWKA7qIkqFpRTYvjDYFTxBQE4gTKipiosoJ3DNrnwoVTwuaqlNeRWA0JRJfhIzvC0CqReAbioWV9TC1HJeqHtEVUVEqkBK3HIMaBgaJkl2K+F4JlGaqSW5C8O7yWSH3cjIxPWWPWDeHlUVQPJcyS2ZMIXxmoD/yAmlQsPiJYUJaqGYtB7SWE3mVZOiN4A+1PJS2DgCLMhAVz2PIyJTOnvoKQr8yXpOgI17iVQRkICakZImcWdfqK4Lvpc92bjtYbF6M6SRLF9L0qTWZF4Xqb3nkxWYPoJxxgCJUsFjC3v1qtSYZlFa6lpYnoPkXlJxrIRrZ3tk1KriZlYvCKtpxP2eF8em2V3/Hds4bCRKqFT68YJdcYLIqOAcLSJ5KmpZNGxU8dBgSUP5NVSv0DUexoYTbV26lmyt+vkjCop0x1eqoPM5EIUeaz6N4+GA56cn1NOCcioepo7h0aPDpJpgJ4OT7E0JyWR5fhKSRnmutYJTQVbl1ucun4Pu/L2UlwzgM/Ao/xTLWa8IuXnlXflzadnWZ9uZRiI7sKpQkK4fTSRhTkjPx8fyHX5T/j1+OP6IetiDF7fnl9dr90trHE/edvD5uXoRHtfY9hpEGn7aOjW3qo89PFNZe6YjJow+te9mJAN4yBduhjmN9rffNl/tXL623UxYZR12S/yBTWo5esJAV98+pNyID3jrK3ffN6v6IHTD3TrFL7dUV6cDjl//HVAL6JCx3H2P/OMEPE7A8x2wzKB51vMyAZN6RGhI2pbPzpTvSTiAJErz+TkBp4zTXumrFI1EYj/XnR773+8GhaVu0I1GsTeIIB7fpHm+oF6DZFPHQahqe1ZzQDADLHkhdjvC1/cV5a6iLhXlnlGWhO+Pz3h6PHp/jId0D3bLMbjft5C+BOVLe2iM4NoE7Vsw22gmoasJGRlzztgRgfcz7tIe376+x5uHPaZsa7Rd2yVZXIfBPgQ+N9/hfrCrZ7hveKuGEdi7Qi77BKIHzCiPOvfuGpfz1uNsnN8N5czc9f0Jnsg3zXXj/WR4BFO+bNePhhSpyQDWXV1f72BV9w93MBpzlnDDycoCiyxANr3tNwahgpG4orIo0wgATwtOe6AeCug4jvbcLHxk+UR07cuq+d0S0y9QRGyh3hufD4kmo1bMwlx81vIHz538XD5LuURoGxF8BXQcjqc78P3XSDkjUcJ37wh/9RsC7RhpDxeSXSXsO7nSbSdrFIxYpzat5m8ZD/c/HHl7dY14F3p/oLIjYa/P1/Fw3RhW7+EWyTk5vLrEpEBQQljfGkMVcQsQhFdYM5zRS8AOeLIOrcJ8KHFFcCFm12MjEDpFiB2B3Pfd6k0mVGpKKmYGq/W2KMNaQmc2gjJMRiesIhKhn1r4ylOaxNXed4ZLiIJutjeUEMa0Odnp/bTEftSGF+bLZJXQMYDhQnRxcWAXqJlniREB1YkWaAJaCZ0CWwuShNVgqEU/AoEMf48BkAZyJxZhHaknRNKxp0QwvY8RJSlyIhShRuYjZUJOGSUVUCVN9lqgJsHaF8ayHMGcMU2sQmAJI7OcjmI1vZykWoMrHUBKhEQZrLkbahZhImuCbmbGUot6VxS1UBeLcAlPA3HNZrTkvUFRIdtW5t+2cNVJkhA84lFTlXs3SywRIjNKBXISK/SUFuQ6y3rsEhIDRMlTHYA4wKISos7wSz8qRWLSFIAMLi0JsUF94tzFuK8qZBFPCY3/y8A0ZxX+CnwWhTmuAgNTmiXmtynBgkJKvidRcMXQSJZDwSzjw1jCloQxM+L+y6IDg4HTCKjxPdkwrgRXBgUptZ3KrOovgDorV1n3ymqlY7khfK/LfVK8I1ZohJQm74bAn7Vl4cYUPm0QimvArIoF85wBiq1izqA0YZp2IdxTU0gkzSnR8EmYkyvHnoci08TUjlOANm/+rORicQ8vw50cLe7Y3eKLKiHGgzIjaU6DpDI9bsxV1zm5V5YFZRHBPmqV+TOcbAoghET3Iz+GHi/G+YkKCIfB0L64kSvsUVNEVM1LU6uEX1qWE54eH/H+3TvwqYCPFUuRnDSeH8K8yBQv55QxT5OGhatAOaKwni0mQIF4hIhX0oSsCktCY0oDev8dszs/l5/LuvReEPG6belmoPBpGnxZTYEaEeEeLEq40BTv6t/hf8T/BafyBerzv4QcAXFM0Qq9UY/X+IF2IscrW33nDV5g/cjAppz5sdUDjFzO6iWTcVFHbjcatgtj2QhWf9nWuV0z/gCa68nqDbPh3WuKYbF279cMgb45p4Cg/tIHlHNrAx/P+PUc3F8H9PXzfObWi6odSr17jx/+l/93UF0w//U9wAnzdw+o73eoP95LSNCd0oKUkPIEyhnZFBEWpinSb5QwTRNSIsxvxUO0fJWBxGqUEkJHos3RanwNIIYRNgMgHYXfjTCRdMFrIlCF8g5qHMUAU6vHg6tVRmJGsZyBXACu2L9ifH0n9ytL2E6uQP3/PWH58bmDfePRfI5zQtl9A07im8oMNaC5vlqNlO1FvRHWp5yQiXB3t8O+MtJyj1fTPf7ZL17j1X7GnCc3AmrGXvZ5jRi82sX26DDuJnA+V6/hgnFTNvwAumTM2vjp9khsUeqOSokbRjHUt/VEv6c7cNU+uKdWfG+1pcdGBMdfVQSs+kqdsqXDe0HxYJ1gCI/i/EggFiuALSQpxlcjgpNGYzhT61NSmjq1x6QOZjAJvZzUF5jZDCml3WU+gacj8mPChHlj3D+t8odCX9+siNjacJsxjuk8AqHV1jf3J9uQZ1vfrK0nz86Xc8qOD/Z8+ND3pDMX+/BSxYzz0zc9fA2xf+B95yo/P9iPiHDTO+BKHRd7uTGGFTGSZvB01wRY8x3SlPH2Sf7/eAAws4doamuqh4/WZFrYDYr/bNfWlqQ9Aj6nwOiHtX7Xl5b7Oy2SAvtBYVXQ+G54FIhKCPa+rZTgXX+27g1VG5G3Yjhu2wONoOT+O7cKO2WB4jQTgHvPouDMiLxNZqknVgltz0vsfyHAKgtzWTtFbXVBvPXT1qHJyZWwkGDvTakxCPJNkC19DT0lE3yF/vW9DZ034olbbPpwu+p1C1USCV/WvrRqoyVMmDGfSzQGUF8SoqIRlCkJwxGCkYR5t28GKxLWiHJW2sZ2X9ijOjcV7DkREOaGHYZVOK95HUoReGCYB4H8tnUrdVbGQ5QCoriQZN0AVEgJZag2ViElEEucSlNOUCUwV8krwWodznCFQ6kh/BOLd4a12x/BTol189cJXPV2qpJoF+phwrWgJPGiyFnazVkS6louALJQShF3eTxabiANt6sXhkrj7FdLQKwl5dpyDZBL2yUEUyLkKet6pkYAs+07hS8NkcVeRzhFbD/bKrgAOEwZzpTNG9TGZfV3JSp3I25fn3OsAn0Rik+qKGk4QepRwa8xQQqDRBbeQ3FGzirszkEwIy3JFOheszl2DhkwrzBXRKAAlbDb7QEi5GlG0pjN8GfVO8U+SSaVoOG1bMTdPK9pJVeqWR4dRUHiBaLz6bi9nUEE9pyqkiMo4FBbF9v/VQQCLSm3FLne1khoVgv7JHumFs25sJxQF/F4mtIktpgD4xVHJ2GlKpBJY77bA+QKAQvMZGRDVEJs0pEkeKCWgtPp6GdAWRacjkccDgcsJ3Ex51MBwwScUSkHx/O1VCy0gMjCw8kZsCwLEhKmeUKtjOPTCQ+vEu7vX2Ge9+IZgmDN5wK/rcwq2zTdMLjNy5+SDB2FIp+1DB2+1v/fSZ8+tlgff0Kc8BasnXtu/PbpenC5XOJoKU9I+1egPAsOZ6GRDn9fcPr/fgv+9V2PBwIt1dGiTrpe3mnro+p8/1u4ju1Z3nzzXHUb+FFPwMszyP3aGe0X6XmnB+2enRSR/vfTY+gmofOSbPSMdbuno9tQ1nRuqPITFd78Ov7s6ZCeJlnP7ZnZXk3Mi3rXClXU3fdAOmKZnuHhbZhAJ0LBM/Lf7UHlDni3l/OPEtIxAfNO6IeUMM8Zd7tZcg1o6FbKhFMlFBjNQZ6jSfJIAMuXz+B8AKYqxi1I3RpWhw34Zzhx2zDCLwKEFytrTkpJnu51P+KTDV8SaXNXr+1jVqW/GGFwreC6CE3GAKNqyKUKoOLNlwnTtA90fBuILyER6n4Rmh5APRFOv0lYUPE2P6/D8MwzsL/reWHowLiFMko6j7tlwcwV/JRR64yHaY/73d7zSVHq94bs07Zn+7Kmi/n8rQCmGxhdn7++/y6cGtfej2u8Lc2A8dNAo9lfVrZ21vpaB0vYQuUDbt2olt2jeqh4sw9xUfX3mAs1biy/TG1TdOfXmeJ02sCndcu27jeDcVqeASTktAs3GK5gUjmF8OyMZLwUCGnOSPsJ9VRGS9rfa7lJTn9bTecvnaO/YbyWt3xzax8RmukMpbm5b20L2M0eWm5TRpwrYdi/A0H4z+W2cgPZ+JMu0WpvLJxn1Luv3OLCrC5+eMr4H/8hgebqOSE8yS/1B8HnKIG86MZwE2M7EPFOwIdLrRC6IJGrXkRBY1Q+bJG6PTPUHOPC8R0tGayjgWHwD7dA6AkPIQAbh9BiTspBJ+PXayrI5UuHoAmCGECtQUC98awvCXeCTREcE5iLCkx1ofxsrq6IiHG1bV57vKdsUbA+NsGkxXlvSoho/aW0wQaAeKimVVExvRFZAZW7gLDCBebgkJjaQ6AIUUJOdMDn3i6YWJUZ6GLyM7sADERINQGJUXncsArD5jFheSRYLMFFMKmWx2BXAJmwUbwAzHWWdKClEcmaQDrnhGI5K3ScKUkIqVoWMGcs5Q45sWLEqvHtFyynEwhqta85IhxZBHpM5lmDXSnDkTmBwZhi0m8n4NX7BKxW44zldEKpFctSAGb1ELAGCLabGqMe5hAyBx6rtgBVrbcIQM2MkgpmFmElAHAS7zBiiOVaaI2D0sd2oqESg/lSKuqyiHV5Kb7XUxHX+8mt3VpM/ZzEAqsGmDKPCZ87zXhdq+475B78gxICpKJfs0xXZnUsBiKXCnUPBPzEjSryyvzwiTSWnSOaYC0lCYtDhn8KNNmLvJFlzhOZhXzsTEsaTZSQwh6VPhmkStglshwI5plCykCmDCTdYwmYJ01aPO1UGDA3iyTS58nq0/m0uMCO1xBEPMOc6b6ryhhYjhlLE1iTwX8NcNtbJNq+ivZwMjcK3YK8UCsjJVEUM9CFN1kpKMzzolRVnB1RlhNKXWDWlc37rWfgG68ka0CkllhmrqXJpdsghrlxhVOPq8k8IYrkcnh6ehb8Whmn0wmnwwGHwwHldEI9LajHAtawFrGH7AwkYakLsDByUvgoC0AJy2lBooQ978GFcXoumB5mvH71Grv9XvOzRJr/D6dcogP/aZZNom/jmZ9mOdfzcY0d+36yxb9eDw2f/XUCKCM//EI8y9wimnH424r63/6Z5hELbYVz3KxMx+tNWy9tnBMxfNpte6GyTSWE34SFF4wn41bdm0oIV4SG5wS56/eNe1uCHfT43/kLirwGt/S1q05+xv0xLBWHv/KVN5+TS/G54fMzFKaKev8b8PwWx/3foU6L0DenDPzDPeg5Y/cfvoHHNiQxxmAi0KQ0EBEe7md8+bD3EK9JPRDfHoHnavRh44+mPIEm4PkXj1jmJ0yeuwlYrZezgW0mu9ULbHBiaBhVDjSoHCCN1aHGVyCkt2NIvjUujVWxdo1vc8M0CfkouegquOgzmkeQ1EPx9dcZr77OXd9XqMHHoHTHj4TlryY81SOO8/vAh8kb9f4BfHfv8B7Z5Ch/m7JQcQ/LM/a1gp++QOZ7PHz9gLs7VUTktJFnEZDwaecAb/v84eEW93eUbu23M21XdVPpDFI+pBIHpBVEXW/7Ik0y0IHhSvu+MX+3nHNbjzA25QdtXOGTh/tb7zGLIpK27m8tWKQrafPOqhCBmHE8PYniMs8AyPcbMQMeglrCjqKyhiWWlU/zjPwwgd9zlyvij7Nc2osf8t66fFSOiFFv65uT+0OtI2+YITG0yQ9sAYJIGLQyKhdGRu7cc9h8yrowUp1XJuwPQMGxPYIRKSnCP/N0XKez63dLXxjotZ+fr3yUsqOdoFYZDEHy1vmQJvDuFTDtMc0iZMk547v3wG/eA2+fGWkGkK3KYeYiAf3RINUO2E5mNZTtdtZC85VQny/NrFlYBGtxJ+a1EkbvEQGsiQD7Hp4a2ZBWg05ewC19vEKzcqWzuMClkVpfE7qGsEcmxHJLYlr1t5uFYUx9uBbGJdzStO7WXkiORbSdEy/Omym6PGRMI6KrE66BCQtWJj7XVwCRyAemBKvhkH4mbDzViG6fGhW+b82DwY5Rs5YNN9z29u250J6PPyWkqhDoG9cBua2TKgzcohsisKsVkvS31qEdS2rdr6OHOoExPsLcnOpR1lGVTEYxluUETglT3oGRkPIzJgaWaWpMSidUNwtx9cgRMTBGiz4CPBarTaYrFdks2yW5bE6S2Pu0LL2XzYDz21gDA8IWUoXcpTzqkCwWrwmBa9FQXEUE1UkTmDcGXeLiiscR2+6TVXN4rZ54ty259q1ohg8DGQJKSWBO+r4xB21/itKCYR4DXBmVJLSVKZPbfLRzgRD2mFp5Mdoj9k7cFc7rx8TBjvhlb8STgawGR4TmOeQbRBjxSpqqgOQZzWJPMA8WiNsK0EIuSaysFvrNV9ziR5DGCJI1AkjD+zBQWcNMKE6tMqaUdS6SKnEmeW+/30nIJ8AVouax5eGJKLX9Z7kXumLzMOAlXUrzumqHnq50bfvDFMNQwZLhEFNwVMfLNDTBDpOsilL3YvAzDx56gzXeuOdpKUVCpel/CwNmS9hZ0loOCB8bQ/JLSA8NF2UiWZuAs+BK4gYf3dkK8ZYqpeLp6QmHwxFvf/wRiQhTyqjLguV0BJdF6tf/FolrJsIuJSwMFG7zIB5V5HtFFE8Z+7s95nlGnibMqeBP/zTjz375gDev32C/U0VEPQHHJ6A8N8HLQL01C+MA95+gvKS6rePwUygjRlLzbGN/EOUF/d6ct0+zrh9TLq3nQGZIobb3PrjyC20ayovniJOCKSPtv0CadkBKxkLjN3/7j/gP/89/h8ffHIDBEMOF7t4fHtonRIxkB4Ny5hf7vR5Gez+ebOeHa/t87NPGM90D7Xk7pXl8phO0q5J+UEJEGsquwWifWNsWD7TBtxiOFzm28QtbcELnf30MKgjTuJ6PcHW8jDZXn2pL8vwOPL9DuX9C3Z2QHjPSMaHOBTXpucsEnMSYqfIPwHIAn2aktEfNGagJmPYAxIvBzqc8JdztZ8HHRvsjYTerF4TyQEmV9zkRJmhyXadXCLy8B8qitLeGBYLk1Nteh0D/B9okPpqU90uNUdKpF4IvUtlbX8dLLSyT/ldvZjEq0+9KC7m3u9bAob+Bml19ty8UfvMdY/7nC4gZ/yy9CntF7+cM3h31VcJTPuKZFhx/ICzvlD4FYTdnTDnjfgL2NAN3O8y8x343Yz9PooRIW17xZwz64hPd/eHhM8jHQ/86mqT1QzcUo4U36ZZz/d3q6kDjRnxx+YiRflNYwIDy1OCJO8MoAjp4CFedArtmxH1OdnO5n+fn5iVG47yx9254C20TbhdKIfypnhPQfQw7B/UcqVxBNSkqIgnRRBX8XDojs9+VMfwHR/M5W+GZ61vDGWUs4dle1n978x8UmqmP2V6N08Pq2LYNsnLJASw8w/n4aMbAxY0SUeYtJaD/rYW7dTGvPHed8Lq9fHSoJn8/gIR/udbDFRmjv6+RlIHTexGy2OjB6gD54Ko+og+G6AdBRd4BwRMi6+ePz4y/+VEiZNOspD0FTwi+HdTOlZfNw/hw33hjtMJ6c4Od27ralBHsEnOGCxicuI9tnSP0Wq8jObUagtVt7bCzUQicUFeffBnajXyIMScmqPckuQ3v0FhfGBN3NwahRVVYst+p35NuxR4JXa0j8giR7fLjXfGhCeIRCbpRCWH5LsCtz1ptD+brOYydugSCBjlukSym0kC10EERj/fEOCvhlDaab5ZMMrGsYYFcQZSSRAoiSwg99MuSfKcEVE1LRXAvJkBDPLFkh4AlkK7GYAbsrnVXXbecLA57bntJGYTMKjxkoCwn1JSQ8j2YEnKeADBynnReqlpkWRx+idNPbPkTBuEqmrBAupjCtNm3DIdtANMkxFQ+Zc0lUWCeiD7CGl2/256uTK1FZ1z6Fgkk8A4RyDIzcikCuZVByTxgZB0TEYrNax0E9rYXWeY6nq8SFgugWt11HkQ4LRTwLDfFnsySCk8ZBqOliMKkkikc0wrHmnLAE8CH+W3E8Uh4NQxWN1x2LTQQE6/m0eoYcYpMom3W5P0Fa+xyZiRlQKpw3ZqHwXa0MOfSPe67CYIGKW6jTvAQa7U2ZpGpSH0a/sAk8paIeXd3h5QSymJzqh4QRJqXInhChP9xjIQesrq1N/xizDe3OWf1/OFq+GeY9wi/KhxYnckBR0b8r7faNbuuXiQG76KEkNBMRa+N3mxRKdJwqp0DkpeFwv6jVJFZwp05CezL13ASewPNc6qUgqenZzw9PeGHH37AlCfc7/dAKajLAoCR1MKU1eqUCJhA2FESYQcqEk2eC6Smgqph9eZJlA/7vRhm5GnCnoD/4s9f40//5Ct88eYNiBKWWoDTAfT8nc9dD4NnygcSf5tC/49sYnzuk/CBZ4jdc/3/1Lzn76d8wCA+sWLqXIl0q5/nF9okbMHPBRr6DKsbUaDV0Z0NlJEfvgKlGe0MI/zw69/iu397RC0pzE3D711Tm+OggJSGEVD31Ebhjbs0/Br6YOcYmqhn7M66xnWLPVVsCLAhQjNC4NqUzlExbQ/2fIQptPuWzhU/A5weguPztUwjUg5nKvuQ0vEIYS6AYT7ic2wgdGGUfrCGzm13crzK8zvUh3/A8dtf4/TVj7j7ywfQd3ssr55R7xeptRLwj/egwwQqkjdqwmuACLyTkEuY0OgDhc95l/HFq31IKG27hJohliacpiSKiExCuzJBjSQIdHgE6kEMLUg9DvXdcRpWnvHKo9iKGotgigABcVPccwfzbdJXK2JvQql9R0HGv1U1zKlcJdyi0emWn8lofadTtq3Y1kL03hQk7Rj45wsmAHfYOf/Ql+rw/jaf8C494/Ed4/lRnJ9zSthjhxkZD/t7zHkG7XeYscN+N2O3y5iyRZLo90vzSjqDLF9cGgUZlRFj1RuUevf2Jv97cd9GYo3bpfjEgHejcmGzxuF+Tyf0sOSPcv/yOE665srdHvQKL78Rxt13N/TqMk65VHP7McDxFiHHG11x+rnxI022XPQdw52k4ajknORaXdZSpwUlL0hTwoQczqErfdoqN9E1t+6H1Qo7n/9BZeuY32wHrgT7kHK7IiKA+GpgGwve6ANLMNrfcBztHNa6jFq/DxXGfnLt0R9EGQ/PD6V2rrdCEVq3YOEPpVDACURAmoD9G5hlZ8oz0jzj+yfgb9+qi2ViPB4BT1Sr9QCN5rgMfQyYHIjtsOjfaNVGVuW65cBma9y+XGCZzhRFND5HvYV2jM3deDle1RD+6NOBAIuvcLyP1hY7G6FvrRmgFRB2/Ap7CBM2U2INKVQ11j7AaiHTCNyuMqfV9aDSs8zyGJgyoFaN2wnALd4TACQX3HoIIzZr+jYQZ2w6YX6YQxPImzLY5iYkNo5MV9XfpES5CQVbxegItg5eBkIoygfMGwKxjz5Fep0s9iJ181f9jJAVbQy45YHIg/JbBc0afsQsdhkJnHWcFQDCXBqYVgaoqvVvcovnnDMIFTVnCWfEBeCkoVO1X2HAzV7J1jR595ZlQdXYtUTVDdy5SOLaed5jmiZRRAA6Fuqs8lktn4jN9ZokcfOKyUjjdmpF4ZIgMJeYMM3G3JhAu62oLJMyNyERMhtuC8KZqvDVGDPye6UsoEo4qjJmUq+DPOVA+Gl4KIX7Rgz6Iuu2E+8J27+nY5X8v0nszwyMS5X1sn1oOgAJrVQBEsF8VpiR+qXiJjAmtWyDt++eEPY80TrMRaBtDN4reGgnPM4+aW3yuwXscYptPOfJvXFJpiZrJ3NJPnca7Z+a4s3ODFfYWT3q0m91EsG9FZIlUIR5WRRkTTBofbffOYnA2sIjy1qLwr4pHqxvgHtLwPBcmALtR6Qj+362+eSQC4Uh+KXhEMEtFPA3MYewru0crRpujUiUoswWqqn1KRYPf8am+K2dt4aFiPAlVRzek849biSuKCWh8gKAMAGoScO9kVlw2ZxAaRaZmwpGXRZX0B0OR7x7/x5Pj094/+49drsd5kRABZL2I5EkzASJ9wXlhFd3d5jnCen5Gc/LCSyVg2bxgLi7u5OQdLWqUQZJQtGn7/D6YcK33/wrfPHFl0h5FjBnm9eGI6SLH864/KGXNdXyc/nJFKfrBtgMG3eLsd8gd9dlAPmulhG3UUK+/wKU9/5iYsbh6Uf85i//LX789W8N23ulrYZA8G7gzNb2dp6WjZGdq2BjIOsSaUnyNnvL3dindZUhhxQ3nqApFwIvYnSl3Xcau3/OaVOYEuI2XEQ2oHBEw862/lAfxnWhvlsLdx/9qnP4xcN9bh+tKpus0ANawHe/BpOaiUwFy+t3bkxKC4ADAQsBp6SpnWUWiADO78H1CemHhPnxAXiaUYlAT3dIRw7LswPNdqYRXt3vQDmhTpMoDQwGnM4gTEm8ImJUDPG0tZ/NSEPOyZbjDyDlI4DlzSNqegJ21fO5WU4D2w/2p9uuTrbJl0ACKc0hT1aW3ykJIcrG93Szbn8FNqvyNOL5wFiq8Belyu9SKop+Vr1WKzc0xW39x/0+YofRiKgpIngkwrp9y8N1gHFXZyQmVD7ilE6Ys3hC3O0mzFMGnvaouMPDtMd+mvDtmz3udjPmrHnxRiXo2S0YV2KglW8q8n5rj8Gc4DKM7rmBXvfvDUbO8lwb7W6FOT4bweWcnM75NBquRVpqnBkW+nCsZnSXOHM+DKMI39dPnFNP9OPZPj/Hc5PGyY3nbsCvvi43ItAW4lQ2jOCJDMs1aGIJW3Th1eSPyDY0CgKMpwCm3YT8MGF5Pnn41lY2TtbV1N0Cvy+kk7sFv36631znlWpGueVLyu2hmXxxmhWerZzEbbSeBmYD9jw6aLF942OLkje0r/J5XfwAAQAASURBVNLEbZPYW0e3qjan5mMVE2OfXlLfBeK2u39m3DcrVYKwxAWZ114516cb34sKiVu7ea2pa9O1/bweuB+ifImvpAzs30iSOA3fkVLC+1PFP7y12NvSVhriRt8y/LgiYySrUfH2YUzrcMBw+xIJ1NvWagMZOt0TLUnPIyTa+ObVjJ0I9WwpIOK7fgSb1cJqT6HVE6lxl0CJ9VQLYQSI5CWpgMypAB+rP8dsPtlOkMOIS2YX6DJEEBwFsZ48lbm1XWNf2/McKIrmDaHtRkWCzZEpBmJfGxvghJTbIFO/KoIyrINQhbLhbuqnODC7ThP5/aCgcuVGICK44W5fS2pzniiGR0GPx2pta22CTl0fseDV2I66RkJzVbAxKSQJi0GEBInLnhJBhP6AKxp8wowMaf2QHNIEuCJCLaRrxTTNIJKQSKhiUZwImOcZoAnTbgcwY+EWBsyWiWtFXQqoFjCKJstSpY2FHhrPx5E+D5OcVADvoaYiHPh6a3x85j4BV0rqe64JeZeCUgtqoZaDQ9cSzCqgFYtsIkLR9ucyCeOZhfDzhNgcwkzZHjb8R9BQTjLeZWEsJxOiAiCFAVIYSA2e/UQigJMI1GUeCKAME1IIjGpoIschMrfmCdF5x4yokG3l5XuFzl/YE1vKCLa2bsHtbfM5voHWI5+tU3FlXQGQNa+LwZrNPQBR6ZTAxyYkYnBigX/d30QsoKBJ4o3ky9OElDJSVotDO8w03Jjl8jALUundyA6HoXZEHA//hqk3by+1GhxrJFAfBqk7P8J8VRY9FhdZ6xpxqA5HzxiEmixcAiynD1dfdx8zHERWJ2OrXibTFKi+1ksCsq5RSr7ejedhr5cZOC6LKBML4/lwxOPTM56fn/H49AyujNNuh0waTg1iMVqCMCZTwv1+xp5nnJYFpRYsVeJWJ5I+7HZ7TFOWkEsqcEn1iFflN/hm9wW+/vIrvH79BilnNK8rchhutPoLGayPLJ0C5ydQDBIdNgfa/2w/fyoD+AMuK1jo5pSNlLWnL2CrD2l7wHedVhi+n1MipP1rpPlO2xVF8/L8iN/+9V/i6bcnAF8rXdN1f+OH4bqh9xSf6z3Qxj6tSqQxbpiVTtDj74wVXzkRu3HaOlXHK95vO8sG+rfRovaHt3Q158egA3GSQy8qRb4xkssY7mO4uo4TCuPq1i6MTU+OCzUCoAVl9x0wnQAAZX/A45/9DZDVS+cpgX5g0PsZ6f0dEiUPx5hSAo5JFBSPe2S6c7osnQh8CiLM1Az3Uk64f9hjmpKEZnK+pvE6gJF5gdcBQO4hKr8kBCS1JMhOGpJ4cWbg8OaA0+4J0zxL/51+b7C3Mu411GzdR//b8Qk055zNeYLlgR7oDl0l/Wr2DpLGycIxqUKiMop5RVR2z0+jnRuNJOu7BW899dmudKwaAaPgMsohVrBKwMwZc804gPGYTphzwjRl7KeMaZ6Apz1yvcfuix32+wlf3O9wP1t+iAHbBGXNdou37Ch9cniVjZ7qqmLhBTZ3YXyW4seZ59dthi24LYtaKX1u4AY6obz95dV9NwAf6nMx7WourK/XPB5ejrO2zESlq+EQXi311nm7PYc3nDyNr4TsUZ9rEuMe9bOHm8PauQI5tCipUWNNGrZV6k1TRt5PkmetmtSmDWvjxP0kpbVxZS9oh243xj8D21bXy1+9qbwsNBPLwjFZ/CzBUg1ZBeSKdlA2wYdukkCRMDhswPVIPsqtxLr0OSBho3xStmqURP9Bld/hpH+KQgm8ewPkKZy6CZQz8rwDaQim75+Av/6u4mlp7pxOAL1guFvLGonHlfJlqNwsW19S1gzXuFfPvOB7tXttRfR38dC7vl/pFJ/fMzF00XniSmfHLF5VqGLkhQmSXJBVjfFQAs6ESGrdasNOFnpErUW7WOGVUVFVmKeXB+sOBtxC1sNzmPRUCWxKzQpWYoxXn5M2SBGSVxBaAqUW5ob6R9Wrwjw72K93ChSdN4vtP9IJIvPVLxoXvg/NZ6cbYBYl3DIldutH7YceiNJeZ8VQtR4TWnm/yBPSxfBOftwzDUJGwBUSVYiHwuTup947rtCcykiQMEGURUieNckvFRmPJcamOP/GELGl7jar84yUKsrpBGZGPp2QctVQTBWn4wEpJ+S0Q87ANInVWXauNoQPKtVjzVsSXOZFhPzcEqSHyQ4f7LyOu4fDrOVtA9fwqZyQHukJ5LFeAYhgNiUVuAKLwuppWTQMT7/Lq8O9nGHpcERKJEkCU8KUm0V8WzZRUJAqe0sBjoVQj2LlvZSKWheUReY95QlIapkCURzJN7Vy4gBaOjFEBDbr/NSwB6vyxDa0xA5Vaz3H7Wumoe0JZf4s4bMSpI2B2WAwrp3tEQ8MZ0zHEAVa3onm2Iwz2IZ3GsNtypJEFQWinIthCbuwRKgSb5kZKU+qsNP1TcJYGk41b4lJ5zrlyYUBUh8PY4pwsME4AU4vyt+WhL2WBWDbH+EZCwOllbDFI+emoPWK1RNOXDkA8IKqYfRSZY85zUnzR1RhUkoJYcyYJYGk7qNEwpALPkoqHBlyZMTFVKmJw61Kx1IpWCCW0KCESWnwyu0cY2aUZUFdKh4PT6iFUWrB8bjg+ekJh+cDakgAn3NGmsyaVXC0LGdFWSqm3Q45T/jy9Svslx0OpxOWWiVWfUrY73aY5ln6UE44/frfIaUTvvyzL/Hll1/i4dVr7Pf3ICRweQY9fQeUo4cKrLV6bN7B5rQt+h8s7ftz+YMsRCvC2+jO6AxLw+dW+SgekPuvzEJHZhQs5YDfHv4Sv/3H3+DXf5mwPN0DZgyAQA8wr/pgwZ6k80bPDIRffJoJHeq9xNNd2Kur3W1dYKtxy6f5cnE6Hhp+FFivXaQVjYdomvb+3g3MlCtSaYABpQVHe5B4wgBXOOJLNwf+7BzNx/EF7qdDvoZQm3e/QZ0ecXr9FjyfQtsEcAEvP4j37tMEnCrSX87isYsEFAI9Z6SakedZ+WQLcaKK9xTpOzOkAkCEu/2EaRJa2g2giMR7OJEbfHQyoQC6+kJbAwqrQcb+Kf/nZLWEH8TDM7A7gSZG1rM4UfJwK8bjCTsiRkNMBCqNqPKuEODep6F7Nstqy9Dzr0azB15MvCCAWhcwsyj9K2Mpi3pCWNhHC8tU2nuBzm8A0nbc5V0ZvqXx2bDjdbDndojZ53zxix1evZrw/J5RFgId9sDzHnfTPXbTHr/68gEP+xm7uYVkio32e/DyZtjyMNgcZcdfbLXR79t1Dyj+gHNEG/iOzv3gcwYXA6HrTY0rwX1ftp4ZuunoJPD6/uzIN8JwsLzZv7dRzgj+V2/4heHpjZdvle82xcq6TsaYGiAYag7ve+dIwooflkcQE1Ka2/4Z+JK2fyX/I8d5MLxzpt8Xcf9N5WNr2IC9m5+NV6/0gT+8ly8KzWRMO0FjZ+kGo8BARSR29koHL02R8UHT/aI5/kAS8dpGCZq9LZSDjWurGs/07cVhpTaeH0NEnKuz01DKhZe17Q36n1j5h9U1Vn21ay+cLxKiiOcHkCaDk7jvdmA2oejzAvzDe4VSMquYMdnmC5oekOfmtK1Yn/Pjs2fHg2Zc7mGr9k93QhoaXjbCt6kGLKaqMwPx8XTG7TtoP3gDX/gFZyDiEw3jNyLVCE/y26vjXAU7nXWUUIBgBOEUswu3jaiNwGYyNGOARHZJzaNlIK6aEJ8BrkiVPLlrU2LJPJmgdwVRhCBMHwiSDbwZma9Yh8yp4QJveqsxmKK5TT3r2MkngdHyX/jwB8Ku6xdDhJ0XDu3YjyAyDW0YIS9CrFST1Desk5wnKlx1C+NQVxWBYdUEwBLCR4Sq1YTWLAJK0R2RVyxhI3k16JQSMiUsVQSBpRS9Ljkhaj2BOYP5Tvqe4EJ+xP4zg7MmUl6KxGWvkoy5agz85ipq4wnMDcPhPHWSXANebgQXN+utCMMmqBClRNtnMngRvi5LxbIUjKtZy6JCStlbpvDK0yQJc3P2OL5G2KeUkDlJyLAMLAUoSxIPiCNjOUns/aQJxlIS740eOwnENTRk+0Dmw63kUkKGxsYHJFRPFe8Y8XDJbe+PcYM38K/hpxraA9p5eo556etcMyBcLX97Q2qN+FV40filRj/5l8CEuECg9UbOnsQaqqzBO2CKiGZpKDhMw2Axh/wqQriZdb216OEOzCNiCCfkfe36Z7/GeQkfDKjrmocGi0ovx+0pvGRf7SyJF8JcR+EAmJE4oWh4CkIGJdl3pLkTpD81WCaaQk/XKUE9ROCwFJlv1z/YX6PNvHvqfcTiCVW4+DoRJQ1FBZ8D2R8FT4/P8rtUnE4nHA4nnE6L586olVFVgWdhtWVPQM9DxkSEeZrwQHvMZULKCUupWKq4s0/zjHmepX+oeH73l0h7xquHX+H+4RX2+ztMO4kvjbIAx3eipAlnrivkz50Eke74xEqJW6o7R0tdq+Maub6lY7E2Vp4RP5fPXkaWBxixgz6HngY4X0bae02D+XqfPVoUibigmUFcwOUZ3z/9DX589x7H7x5QlxRcozokOVQYeAgCWogK4PwOjGfSWF+s89KVdp03vp/rwfnZbTS6hItTegfDPPvjhu2jEsKuwEOjXiuXlBCNjh/f2aIUbiwjreqfG2OItA4aSchguKVUBI/EqPNb8N0POH77d6j3T12vaQHoNwzUDLy9Azgjvb132liMONTAYFJjPFdEqOLdjDxcEaF0GgF39zP2s8bTBHpDIj8PDE77e2HSuwO0UTRyfaWMUEMA7N6D90fNV6aKiKiEsC4xOtrQIkp07a3WXO4nDD4n7UCXVdF6qu7bYoYEfj4LbV88KXXIDxESU1ewK/Y7GOFrsLc2Xru+b5uicKteAnD3JoPeTEhccHgCcNghLw/Y7/fY7ya8ud/h1X7GlJLYW21sGoORWK+NabjS6M8bOEl/e2wzLGRnNOfPB4OR/sbF+mn17CZVu11dx0AHBW13fQNnx3kLyHaFFgnuVRvbtHCxvEWgdI/S5n2/ckGh5PS3D6nN/WY74zU+d5+Gz/DN10TnzOTXobulHpGQkfMe6xNhGIOf3yzroMv7efweupY/4VsfejJdf+9Da749NBNkAfotsI0IbumuvEmOOZlJhUYvsY2I5XMDws/lj60wJfD+DZD3sGDjU55dEfH+CPyHX6uDVmIclkZcbZ6YZxvqn4u4vlNGnN04a2S4+cgNWIBXX/RHJG7D9Q3U3ghgf8eEMUOXNGyLaY9FcN3qcSfSDW/hzookhK6x4pbKLlG3LurhMPJOKtjxPjdzFajEWYl3rSolNBdfgpCYNk4RbIsTLtnppIPuCQmxZim+6JwIqZIIqpIkK65FQwNZX2KgerQxUUpqCTtyzT3x0EJl+eseX/3cISt0SIsxHztgZLTTbUHh4+3rd7vG6uVgSxvDW8WuDd2QnyagVssqEzZWHWfyebZwLGIJHxkSsYyvGhufmreJ5eUwpqdWVCYstAhzkgiZE3iaUIuEJVkfc2viMEEt/gEcDhIGZTmdUEuV3DJJkndzrXh+fC/Cvb1cz7sdKFUkOgpRqBqYnAlMGTQl5CJhTsz6urfqhgthnTEJCgm2BWEGsyXjLuI1UxiEluhXwkqxJnu2oQvxKcwQ8OOPz3j3/oDnwwnHUuDKWCMsSxM6EhhTMqWLuGPPlD15sVmbpylhmicRcu4IUOYx5wl5R8KkFVkL8/qBKjXES1NXX5ngos/64pH0ZwGQagXXnmmGzW2S0ZgwvUerZ/B03G+3ChGtWad4DMiaQEEY0zTEIkYPi7ofuW5sLAp5R1ZMGEmSd1thv23WapEOSx1OdS8qxb3KYuuciZKHzCMAssYyTUbrtT5sc/Vxxrljwi1G8nI6oZQiieBDOCRXitA5K76GFBtKasIsroyC4paIlr+EVHtSufpatz2mXkq1Kd5qSphyhkn6U4oePxS7oVMgHnjJzpLgaNQsIhdV/AGn04LCooCoteJ0OKGUiufnZwntwIxlKTgejihl8XqWUjDnhJwSLNRLIsKUJDeOneWJRSGBnHA371ByxakK/p3zhEQZT2+fkeoJ/+Jf/Dm+fLXDn/35P8MXX3wt59TpiOX5e6Aew4KzptLSPbux8v8UyhVe/+fykyhR6oEg6/iIhTt7NPR4mygh3X8FmvZy/nMFyglv/+G3+Kv/8yOW9wQusERYgX9gbJ4/ZPSQIbzU8E7sV9iQfLnD/cOr9noaWLvQarNujHTgZo09rethTFURa2Egg0Sha8/w2Yq/4TW3c2YwK4txOfooDNXuvhyj+TFwhrSQa2F920e3Rk0BARhDdfzqr3H88m+Rv5+QHjOW3YI6L+D5HWhaQO9OyE8ZeDeJp4OGYazPBKoJaZqQkJriQT8RDAxgfJJ6+t3tJ+x3OUxDo/sZwDypR6DzasZLyHPJNpuT2C28ZqyO2+GNOOcJzasiJ0IGkKYJSIRDfkShR2DiZmjoXooEi6Fkq2j8hKZVAsDeXOSGGfZq9XCjMC9JvWYePFX5TPNsFq9Kbh4Rpaj3otDhpZihXPVQvzGE7zmgifutTV0Pm2dRWQDnQJEON3W+lQ40A6F5Skh7gJY7zPUOD/c77OYZ05SQsyqEyPgSwMJ4XtyJsUkeL1x47RKuDjDXzuOOeF4Ju1dUqhnsBRhfP7XuQ1frlT56W5FmGN5pW63xMoDaGI1kP86tJJoS6+wZslHZWAyvbiRukJmq4Zd1e6NXNCy68ns9+9N/890blA+tfnTouWtRjXsSaVL7Es6OrWFWGR4l4LQ/YpkW4ImRTlLrT86O5IJy6OZy7rVPNNYXKSJWHQid6wgNbP1oLxgucSZcb3WbzTXQlyduc1Nt7bCPKdessz6m/kvvxgn5BNB9zbti9JxYS5bPr0V/Zwvwt0nOs10KFgibLWzhyit7rBGn+osSeLoHTXu4xSIIgMQRPyyE3z4tKKotBuG8lvyWcoZOXe2dCxXcTDwPgi15PXIc4xy2mke85bt2xedEZcFI2JsGGghbvH/GhKfnhsH+J1yILnGBaI3ftd+RYHdyJyaDRptRF5mbcExDacQYpYj1VABU0azL1gsrBGRjmqhWJGgIE7NqCFY/Ywi7kRcWd+YaxsXx6abIWM2dwoExqmapdI6SOFuMELB3I2M3vuf26SDqRnWxDZttWwbWusWQtkqOA0rCnOvcizVLOy/sfCF3vTAlt82vwTI3ZQczEiqASYiSnDp8adbQfU/DrBA0rJNEiQWApRQkBnZssSZl7ZZ6AJUMZkLKhJkk+TJPklMhUdY5SEBmZGawJjcnEsYlDbstKtYYDZaaoLSoBSGp8oaRKlCIQCz5A6oKPJuleb+fWXNUPD4e8fbHZzweFpxKEZf9zurdPFBkT+1dHiuWZ0dl/rKFq9G4sksBdpUAmpAnUV5kDeOUU8JJLdNsXZoXS5DUkzDTpYN/GTcB4FolJr7OL1FqTBHaO6Z8kW884Ix2VnYWaStF30bZQvbeeL93JUyS4ryA185XFc5ane9ozbl1ShNBmfpm87byLgpfOpxBhP7MFXWgJZdPKaNvcz07EZf04zCvg3a2mHdZVW+jsoiXjOT30MGkBHGWOUtYSKtRkBHoHQt7BmaURKBCqFNF4tRZ0MZ1N4VEnJcEgFNubvMekinZRCrOlO8Wp9q8LZAUx+ljRfekCC6Aw+mIWiqOqpBZnheUUnA4HvXcgXpGFI9dK/KRAuYpHJUt9wQZDd6GgQzCrMImLnJ2JI3vzEsBAfjF17/A11/c4csvv8LDw2tZz7qgHt4CqOJNEmHEFVj9+fWpy0tI5nO04zXPiHP1XGt7Sxmx8oy4sVzr22Z9LxWoDwNqbX6u1Qs1r9r+dGVznRrB2Pfmswx1aEjPMNrdI013SitWnJ6e8PzDexz+fod6pEA36/urRMuBWI80KgXc5202InzTIpbDWp/dJ90A+huDMuJ2fqfrRFirRtdUyw+h1+NB2TyRI7xyNzXXyjAap38Ba2qckG2Mdg10tqnneNPOneG+nY3R+0HvLQ/f4fjN/4T5cY/p3Q6n3SPqvRjcEAipJNCJQL+dkU6Tn/seXihnOZ2zRQnQZ8x4RD0gUk5+vu12Ex7uprNbyGbQafSg5SEipDHOTIBXe8fplvCc0Tp2phkD4Z63OYHzEafpCRPN3nejkwayBsyam0xpqQSgcmdL3a0Pe6heAa5q8KrXWPk2U6S5QZEpJGqFKCqqh/Q1o7PKZkTHSgf1coBzoNyTjO1Xdz3SneP+3tioNH4hpfk00GNO0JDWM2aesZsn7OYshg8rOvT8ybXlJcuROBnGcqaWM3s0jo9cGbJ6biC6+9DLTQnR44P45XLfbhmBt+XbYsRIY5cDXXWGFtnqpqN9vhAK3zZG/L3RWzEEai2x4yRGjPfQ92+YwzAzjiu28nnQ+LUHYFo9oNxGkIVZV83YiBOrkdZqaLKXqco4mFGmAspFcCAmX6vPpYy4SldePVk/kOL+TOOx8kGKiJi3IYKGExq8RpP2d0v8ZbjQFWPUX48vrHNGWM324Id6VNxWtsiOf8rl08z1MIu8fTCsDW0GBmVDC+vvdr8S6v4LcN4hz3tQnjBPE46F8O/+PuNQgEossdARiJVVPTeWjZfWgvs4nkYQNOHpS2FtOAQc2es+YfsVXdUC8aSPR33QlrIBq99tKNWGUjVkmUuXB6JahT9NCXluNPolhEvpDGNiu1qqch1mUQu3nrU+KNGoNZi7rlkBxYPTvRGcEJTxZPFnAFiEuyoWQ2FGZfGGINSWbyG39SUAeUpgREtZ9hj9IjyqHt6GK5TpEDxrwm05pGuYCxNkKkYkgjCkGm4kGfGObp3h77a1tnlIFutc+2JW9KwCtRSS6LZ1pa4d+fAetvWmxlx4oi2FFUnQJglYrZ22/XUdkxAHpvgwBsZjraeECgJz0XnV92oVj52F4cnJAWTSJLHzLAL4WkAWL97nRsdB+muakHPC7uEedMx4enzCUo7YnXbgWj1WPgNALSiHJyQ843R4EqFfVsH8VJFzRp4a4wfPbbJNbPiWTbLOU57F64afAbXwrqViORwBXnBajqqcUOanAMuh4O3373E8FRwOR9h5mi1vA0t4lnePRzwvxZm0SgCRWoMNfUuJUBMhkyhqElrua0vBknICTLgJkrwcJSGRxCaiecJU97ijhHISgauEfbPwWYycs45d1iSj7dWwKcC1KMMo+wAlsAR5UsUEsKhtXkaDyXHeTeEiMBZHrqtsFzTfgMN3t2C6E6yrQajtCgEKZJDicRPm2m6zZN5uWknZYWfE0kAjxD0XjNVH7F4h/pwrbhQfxn1MAh+UEqYkOUByyrAcSlqJ0fDek96zsI0TYQ4stJ3n8KkFy+mIZTnheHiSvAhFPHw8XBRncCLURcMYmZJKObNOX23jIJL8BzaXaoXIpWBhjRWdi8CYAm13Zhrrp+OVJM0AMhTezRMi63xlmxbHpbIGkgy8MlQgIx4lDOB0OOJ0POF4knwpx+NRFA+Hk4SBWyxsQ3UPB1T1QGSggPBcCpbnAxYizPsd7nLGXc4gVVIeE4EzUBOhZsLpUHBaCp41R8R8f480T6jESKngX//yiK8eMv6zf/2f4+H1K3z99TfYZcK0fAeqBbUuAk/FYF3mJ2aTuigo+Ln8JMutSpl1uUDgbbaz/v0pIWVbCWEYmtGQVupwEwBHWe01pcUutNcLrAYeRw+IfP810rSDCIoPoHLCD999h//+//hvcXjL4FMKZ4SdMa3Vbm2a5M+T8ToXs5JCOXGBGPKx1WvtBS/Ckd92Hok33n0p/+KVyqhUCewJe9k8IvqaTVbJm632PVgZ0wx3ot2Jz+QgfOv9usZ751rGDXe4W14enw+kTd29Q737NSo/g4/PWHYLynzCgh/BvyUsz8BSqoRaeoQqFpIxAaA0AXvzCojGCxq2KGfMU8Kbh3s/r9q5BVhuCONlzAOym6th3ni4HulXQrCb3phaivAbrqeUkAA8FcbhVFEpgScgvTmCdyfQTJrfahJPZKUXidZ5zojUOIk0lRbsJG5z36CH1UhBc0YZz6J8p4RaAiykqXl4giUnhHk8Qj0kxCBI2mweFqFtozeMRrI5HUCpmzrjibBVIi4A3AtlqLAphFrckpSExj+9ZSzPjPr+Hml5hf3uNXbzPb754hXu9xP2k3pBU8ClToid61KPp/xbt6V5BVvUPT0ay2wP++ZiNJ5g6FZPJx+6XvEI/+3GGncOWPamLrbjKigxbP38zKDunYhbzlfufzYKN8ObgLti3ZvY9tLQKI79chj0q7BtbVs4OM9NKUZ2z6dHJMqY0k7kCUEZIeGYBSdQDXySDni622PChNPjUffqRpiP33u5DEPj2jjneCvhxY2vfGm5XRGhnYlIKF63QuGSW4+dezj8InQvbgKnKSHWyohWv7I3A4Hw+Yrj1OEa0B8SY3/PvbMqn0u19gHlg2bz/MDOXB4Jx0i8X3t/QOKbcCIEGOc9MO1BSpRUEBbO+O4ReD4BmGoQaNpQfn8M88BvfHgdQz1NKKtjCwI3syhfEcNGRDhSsF039lOwdzucWiWNTWgWzvZgUwu0XsZPXwdPONvuGhsZG2mWJELsgYWB6J51YsKOfYJbr9qMRETbTAgalBrR6IV1LNXfceLAA/MToAnTmhuy1EjU49BmuUOBENV5vYDvpJeELsiiMdcO3GFFfBF1XV16J5ZQ0fIo4jhv3xEgnCJhIhtWZwmx3eNwynCzhI7WQNtW1G0eoiLDQvckFg8AhHNEusjgwuAECXFjjBVZzojSr3HkRHRuCVAmKiNNE3JlMD+5mzVASNl6KIyFJJwDaDmBiFBIFGApT8gTY9pp+KI8wYTuolobZo1kPRnQJMsZedqLUBgM5gWgBZQq6tHi6aMpktT7oZwKnp8krvzj00HnMSFPGdOUsBTGUhnHpYiFNrOsq+EIY5C0T5HfMMUQkabEMLhKJAoJyLw73ASEQylpwm94f1e42JjoJIKapNbl3f5uCAHs1ubs82eKKJllEQNHiJTna7zonx3ec2K94UUTuDbxdf+u7TkRwNcmFOgIfzJEgO3SOkBhvvsG7TcHNK6b0vAOtI2ohAB8X1gha0cVVS3cQW77Dz64NaG7YiCTWBvp9hJvMn2dLTH0glIW1EU+WwgEg6fUhAJEkgg+To8rVcIoDPQ4KIxMsFgl54m9kxKDOG+vgeHn2kJZmXeVCU/IkmMq2LmihCpAteEZIjk7dc1LkZwsh8MRyyKeD6Uwng/PLvQAZAkzESZkbUNwd4Xs92VZsFsKTrVilzIyJVSy8FOa6J3a86UsOC2LKCISxLJUsdi3bxi//GrG1998i7v7B9w/vMKEBenpLWA5IcKx1MIyniHwt+Zzq9xKE9/SxlCln02+dweaA/39W5v+JGR8PDh/TyXi9xe+2MqN67LF1J6ncm6p70INQQHcP3uJqgo3ryzJaDVrlGa1i4qMab5Dmu9AyzOoLliOjzi8+xGPv2YsT6IWZ+9gT2t6x4P01vC2t7ghwLVzZS2IsJrdRh4dbbZ6OlqMW59spNxdvbWMVB43UhrNg5g1t5MPpevDqq8d3dnMYmKP40s0fNmcwpvKtZGHOeL+s60vwFTV8EZ/5yfU3Q8o9T1wfEKZDjg+HOX+MaGWDOIJtBBSIZAq1D0HooWfdZpDziS7n3JGnjP2+1lDaRosB4WElhR+t3kbJm5jJqpCVQvVpK9s0rr9+W0XEoQGLwvjxAzK8hvTUf5TNDQzJYwfTjAnyl6EaDzQGu1GWtD4MQv/a+ER43+uSnMr7LYwY6y5phSmq9Ef7LSN0YimFGGOvVvDSb+9+zXq5i3sj254of5hNfv9wARmQj0xSklA2SPVB0z5Dnna4W434WGeunxwZrUvP233bdOGTekpbfX9jPRpHJ/hnGHEDirbbd5aSPmF1HmabTZ5qRb9G/eEjCfms6E1wG/0RR8fhuP5TYaHz8tGdV0ujWPLKwGGi6NSmrujNujvXzZP1K9rN18fQgdF4E2tmwDUaBRqfWYnTzzvZEBxb8qSab6cXUI6kOZ/6Uuc8ZHWvFTODfHlsLuxZmMdHY3WcBr4tgwYDWxfvi4v84jQ2RxJkfOKgU9VbGAGHNfbUpD5jH36ufwuy4fCGIddT0Tg/ZfAdIc870BpwrybcSzAX/x9wtOx4giAJjQh92eFa+ukfQkU2AjmnwqUh3pMgFFNMNcd8/0+l91HPfbeKh33wOHvQAC4YiJcNyLNq6KmCI8E1chIoR0bkUezQ8Et91dWHgAzKaFETqSO7rpdUcG4EVYpSPtaHE8hyjklyX5mHhk6bnPHtbj5SAl5mvS54sNKdlpqE8kyK7PG+Ac5YUvUCFeCHpAr+jOSlQHYHA6siz3lQFCLI+rhgRJWBnRkMeWtaq3flBGVqsMIA83Lwl5x5QPAbj2EUGFU8FpPogIFaCFthIMwuLHwSQ0uRPhXzTNgEWFj1vAy05Q9lA80aZwX74fuFPX+2M0zMiUc9nuUJeF4OiGVgjxZKCCrQ+fcEs/aGkBirlLKSClLKJSUNQRR3E9QlKHeAQS39kKtyNOM+f615FogVq+IZ5TDE55/fEY5FRweH6VFZhyejzgtVf6fVDiZzDrbtAdweSsR9YnPCKq8JB+XG1qqwFqUO/KIWdKnlMVKzxnExiAn25c5AcioOQPMas2GxkAH2LHZSaqUEAEF6fopbC0M5iLCbCIgZUwpiWu59g2sSYKHetsHO16JWMXtdrIJtt2/QBi3LaFMR9pQU9KMyojVeRTnPyjNdZG2CNmgLnL8nkgYSk257cnrYvu2Fjbn5pUhsEmdx4AAgOFjw8xtqIjtO7Niiaer78dai3pCLKhlwem0YFlOnsyxI5IJQbG0FpaRhduTETd4ropiTTBT1GvK9qdo7SSxPZEmgK++FsldtCysUliaoGS20GSrkFUEzWkhAQ4ExQn1WlTxdng+4PHpGY+Pz6IYWBa3vLTkldI0gykjz5KrY+KM43LC4emk8AoclhPePT4h3THu5hlFz6k0TZhVS1hLxfPxgMPhCM4Z0068R6c84fTuBJqAr//lN/j2m9e4v7/HvNthnmfxfiTSvFAchjgw3GyemBcsFn8uP7kS98UfWxF9wBmBj8HpplDvg1rDSOQTBA+hMqhWPD2/x//wH/8/ePzuIEI+w6WBzunr2+JX7LCOiQ4GYZJZhFu9zgtsNtG6TeONOK72PY60I+M2W4mNtFPDaUi089avxSlh7msiwCN0Dk3QeLEdHf4YDQ++VAmxcdKvnxjZKV6/F8mP5eF7PP35fw8cGXgCmE6o0zO4FmBfwU8Z6dcPTqilJYN2uZ1B6rHo9JgrIOT7m9d3qjyXkrL4fOfczrFRGWHFvBLWE9afd2Np87oOfdypiozmi5UZb6TjyBnITMLj5wR6V1BPCflXCXWXO6/uuN5d2oWRReX+pvOZxjuxGvMob2iGOlXpQ8uv5kZVmk+K1bvHeELRQ1Rvwzy6wUZH1T5JtStQ23nbwzCNgD7OvHIvcXjbOzO+I3QM4fiWcDoAU9rh/n6HxK8xl9e4v3+Q3BDzTnOF9RtnRB1rebkRZ4F2cDox9o76+kIfu4nQiqndvX0T9x3T93uh+JlOnJ3D7V7Hq9ylWbimkPBbHT+29eyIDEM/Ay3NK6Dvuti/y21PNuUAgTrDR73/wrOz2+k0nFurflyhS1bCEAhMMMAk1HfyEKrcUTom7zGqtapWkJJETTnsn0FzAj0y0umy50brb9eNzeub791Kf13QeFxUQsTfjmdu7NOHKIfwAkWEC4J72slEMBeBoCNArrfUNzAQNbdgD/ecuOnpl5WXaOFesiRbTPrvqvxOhO3nylUIb5vpQ91+tAIwZWDaidWRCr6WCpxKxrvniueFnXjTJvVNPxqGGi/M2zn6+tpz8dYLAejWx6PG/WpfItPBW3t5nJNGMPpta67LyLbRYV7vr6YMIfTH0NaEGtG2cc0ZGWDEDHKAGzF+fQ/akBqjIn9EBqYsklsIBHEMszXmYxONhSYqTZKlAKVqP0gshOPASWOXRutSn3UjRDnQYYGIu8AL9T+DMmO1GUJFNm+X5soJGiFMnNSJhzC25lwJc7MUQiSSuJv39XtDF3UVPEE1PDUEKlJI+ghRBAFgjWkqyikR1FUzR+q7L6MLcJuShHWapglgFsGpxmpPKZj0WX+BJnyFKM9E2Lu4AiLlLMlvw6QxGtHOOs6UGClJYkLxXhFlBnICUkHaAakwGDNKOeJ4WECoSNQSPFtc2gQIg4W+3fNlm8totCk5fo2WeI2p1R2jY4pKR5HL21roXnVGpc0jhaYQCGSEOomhMXxVIUVQ2NT1U88IRoRf9IsOeA6NAOJdSdY5B9yARMfSEaUyvmQDP8uEbDOMbV6un+ttC9P6wCHDAHGtLAxDU1JYzoAxf5Lb8g2KmrNhDh32TMmgYZlYFBLy33AC93WFedqm+6xNHVMvLUHMxcE1gRJHANC+ZOlXSlip6IlhqTa7JgdBjyVhtwd66raHVTBEAcKsHhGigCjLgqWU7qxrtnl6hllMZhAyJKRcrSLkqKXidDphmWcJH2jnRVCSWD6KpRTkaUKaMqZpEmX54YhdSnh1/4C7+we5rsmvg83A9bOhYeawNvGBj6H3wvsfQd/eyvSNff8YYf1L5+OWfS4Pfvg8tHc/ck1uKB9H51+s+QPf+/B5u8xbkZ8zLYeMYgWWfC7vf3zG84+MyoO34K19Nlzi52Q6/7Z2Rprgfsmd7qP1O+cqOlc4fuFGFp99nuNHVw+HumzXxB44y0F9V892O3wdycueH+T1SzcX7r7y1nfEMVdwXlzgXOdHnN78oyghisllKLhwJqTT7LSWez5oHi9LOp1MsaDKeSIJs7jfSUx/O7PaeR0E+IMywj4JaF5+YYZacunt+UoR1rYmHf16jG07jJN5PWgY1ZzARwaOYsyUjA7se9f1Zb0ea540KiFUDyE/q9CWMbF0VEiYItH2mKg/AsMS7jfDuWZExyEUmT/TlUZzRopn9cyZr9uot6+BCJ5DEVXopTTNyDQjTzvMaYcpz8h5ljCdAR6sN1XVPonOCG0db7VR2Kg76vHC9iMMcDhoEW8+N8f3+0769y3q/EVHbsBVACnu6mmYq9XRefPrCPMrUh9bSHjd2hreeHiNwnN05pnbSzfnPMLhB0xufB/xaCORT/k5x/6VTfrAaDIMZgnJzKKwqBkALcgzgU8Alo0edGi//aCN9fhoY4+VMnGjvrHNs3TXjX0ZZXcvGMKLPCKiVbohVEqmUb0FKLYAPV47c7g7RWFhmawv5zVPn1MZ8XP5PZSrmt4r5e4r0P6V5oQQod6pAv/27wmPR8aJhWB7yfa/BvdnGcr2wG3PfVTpEVKzpPALMMqnWa++FMn35Swb0rWJRpiFF/r2TQBmXgMBX7Rud60JaSfEilhjm8DRPBJktvPAoCUNWk8p2N/Y4RTqNgsUx39h0EZ0SkJRzdegcVY5JRFiKZGalDilpMIbMma0WeYQyRhSEitwBjsDYF4TVa28J4LbEhHaeerGyWoR11xk21pEgnZF1g5CURPkiR2AeFxImufS3umWuVlEoxoFyH3dQ1LwSMA7423WLGZRzlBhYs9htjVuQkE5L6wahSuFg5QqKpLnAmieEYsK5mRN8pQ91nnVGJAOv2HQwsyJ8P/+/g7LNOHdO/FeOR6ekVPGvJvhHjcMEXomQqqWNNZgtmDRsDA5JxS1PDcGMRHplJLpUlBwBFEGMVDmAzIB027G/OoVKCXsX90hzQlfHL7B4d2E49vvUMsRp/IMrsC022GujHk6wdgkB3QC+hzAYRMGRXELweI7yV3KQcIcJkrIk53f6oYQrTYJfnYTWIW3CZwzTFADQPFDwAO6xhZmBppDQCZKrVyMkYKGzaGMlGdM04wpT5p/wphAG0cbuFmpNWu0MFpTsAxw6XAcnu0svZQYbg803LRVbG48hrC/lnyfnkXhHGm28BypJxdSgH1yr60mfEia38Oey9p267AYDDHMC8XG2fZkt2k9/w7X4l4RtgeqJqYuRbwiuFbHZSZYkLwUkJwiQ999ih2/Gy6TG0wCs4bPlrSg1iS5IjRJvaEnasCm+LgJ/CP96sqAbuDyq1TJZxPTV7Ay2qyJpWsRpcvz8xGn0wnPTwecjovka9ntQMdTC8dEhHk3a0LNipQS5n3GlCfc39+JVwMxDqcTHp+eUGrB4+FZFEhTRiZCTpJXIlPCsoji51QqFma8evUK+4cHvPriC+zmCX/2p4/45tWMP/3VL/Hq1T2mu3skVKSn3wB1gVHdvMXcfjYh88/l53JruZUrtLNWwTgIXz+2xBOSQEivfgGa7gU3FQYvFcvbE05/kcFvCVjsPLpl/xiy2mrtwivuqMlOY3kxWpco1BLra2e9/aahDj+qGLDkvSslAw0ow2jArWFTT9u1VpwkCQ1Tq5vakbtZotAvHNFb490qvPUr0tc83h3eCONhAPXuHR7/xf8LlRfwOwbnI/A9A08Z9Ns7mFGHzDkBNSHtWs4HCdeZNKxSck/LL17tsZtCSEoSY4+cJ/hRbuc+mhGCXKbN757LbpipRhtszFs7UpvueHzOF6y12e45AaV0AWGihPpwxLJ7wun1eyz0BNwRYDRD4DdiSOBG9ilNAnh+Ev+BwLvWKkYtFZ77wfNAqBcEYB7YkXdkp4sbLWm5T8QIy66DGz/EoQ4PLdvBUKNtLkNo3MU9fXupGF2TU8Y0ZfAuIdGMdHiD9PwGd7vX2N/fY7/fqYGC8iy+sPKZqtJlRo9tt9b2H5Gvyzl0dmnUK1QYgW5oy8ugIe1ub8D52Ta3Lm68aKSl5Z2XLra1Oo+vYp9veG4gy3iopOWVWOMlCnxeqzTyH1vPhTl0+fG5Tq5JxjNNbbx3wViZxpeHPUAAmFDrgkM9IWHCNO08N6O8weoIzahMSLWiqgEOqbBl+aqA3hTkf8xIx2359KhkeLHS4QoN/RIS+4ONPj5hH4CXeERgBe+g8KXfLrwC7pcWx1tx43bKiDO5IsKLzZ3m48otxGdc0Gjx99K211v3D7zcCJHjU6szIV4fDoiuLdd6a3I2+z2rJ8QkFsbHSjguEo7p6dSUWut2eUAUIxI+N55bx/35GPO158Mm2Xt9iVaE84DACEH4qAIaiHCly1rUt7rqXxd/3YQ5aML0oCI4170mQIzNBmF7o2UbYSx0aRTjGyiNTqtdK96yVSeCtECk6j22aegO90ZkbiM7r1kJHg5ERrNGjkQzOQGhpGUgto0p2SRp4jKwuunb5BMGJUQr3q9YVcDT54pbS1gTg1CS7bM2jsyYok7w79t93dY5hZoTQmAFTdKw8uIZ4Stgls/a194SLBIn+pdZkswi+TznaRLBbk7gRZRhBIBZjt1E5JZ6Eh7MCJ1IUKnLt80JJ1dGVA8Jowcw254DSjmBACwniRU83TMok1g21wm7/R3K8YCcJnBV4S4sMbUIcisPIbG0KWF8AWq6p/N4nraq0LVXSay8GuKtoq2R/XOdUyJQTS1huyxqx7DYJWDwRuq6RWBKKrjOEn7AkiwPBCrbHDdEhQaZsVIX7ffXhwf9mQ4PjXVtsB8dzr1s+XRuX1iHKDzsuIkIzTMsKCFCSKYmdGgWltKdNg7bv2Buiiwd80pBE04LDkx4jJ9c1SuCa8sfsbbCJO9j6/+AX8jmPYTT0/crJDElgVqoJU0c7XU47jDIivUCrkiiNlZhLm1iWD1xCEQVMCtngqUuUoWM5IQoteK0LDieFhTdozkLfJZU3JMrpYT9nAFKqLWASMJoTHPG3X4PEGH3NKNyVcMhCfl0KgWHZcGsHh4JCTmLQKWUorg8Ydrvsbu7w34/Yz9n/PLrB/zyzQ73D/eYp53CcwWWAyie4WEv9uTC+bPhj6U0WuXz0Xe++S4y33845fN5Qvw0ilNfSgfKuS/3UtohTXtgWQAuKPWIsjwDjwA/a/zLm+aHuo8XFReWG5Id6jzfGqIEIF5Zt6F/OLYX3jThKg2vDLWNlPJmU43MPNNn+7Gu7foZeqls9youHw/fmpB1geTp0ZOTgJqfcHr4DlgW1Cehm+iYgGMGnbLkZDIPXjM4Ig2TlFQRgZYTQqzZCfM8YZ565cK5z94Lsr8+fvdZC2dmf+2GqVstWt8nf8ZokfCSeLQmUK7gaUGlE5bppAqWISxibNppenb9lysDwgPNs0HoG/naQiYxWk4I5/OszqiQCn9dymCEZVRC+KOBX3Rg6ved0UPdHJ3diNS9vg2fYxGjNGICLwkJGTlPSLTHhHtMWRQQU54wZ1FC9DSf4Sf22jZbcdo4rOzGflwfcRv0sj9EZx+Vnz02a6i00Yqr/r2kxHeI+wmPC9V9PdPGubPdUdnIdAz7ZmTKVpWM+NwMwLeb3e7i+fPgRaSJ0zljLS8tymds1a+yE4YYIwKSRL4OT8vZSJJXkiCKihSiBU0k+XuywPygf7udHhx4vfH6i0gl/kgq9FYZ7uqx21t9gUcEBYM906HS2d8b3QwbGheeA4JNsL4aN5GygQY4fMYz4pyw+jOUP3YC+qdUHD2O6zsSC7tX4N1rj68+7e+Q8oRpmlAZ+Iu/K/jxueBUjYjqq1m3ekunzpTt7dAhpbWA5uPKphLCiSvALDvqgCAvKd3Onl1EEdMKkYINJaD+MAGnxclE6KrQrvHgbwqlvj52K3CA1cLZxhaJSPVOMN/ZKDwiJYTICDgjfBrReKsFXIJ441VoLP66KDCtuaFkfVSCs1TrYzhkGM6MjHPtCaNrAnPRg1NezDm7p0AUVeaUUEnjm1u3oIJCmydrAuZ50WImunDc4DYQ1b4KvgU3LOq0ZqKWl6Qx5iaQbgn4hJAv/p7I92mzXrOKBuCWR8k8UQLz0LWhr1gfUlIGrYrnisWgr1UsjHOWBLwpTwAVoBJKlfAobsVcCwiibEgpYZpm5JSwLA9YlhOe3z+isLjYp5Qx7SYnfnTYks8hJbG2qPBwKswFy8Ia556QNcavjdP3idZUlhO4Lnj/tmCad0i7PaZ5h/lhB9rNePjiDVIiHN5+g+fHH3F4fivTnBh5EovqshCwFDBLiBbW/ZETYeYJzEuXI6Ep8UTYamMCa+JbtWQXtUJyS/rCFSlbfhaz7oNKgVnDZTWBc87J15OS5iRQBrcTmDPEZTbm9mACKIlSBgDRTtZi3iFNO6R5BkPCcBkLZLFOzSU3gI/K7c26vp0jOhHtwQ7mUoO9ePA4+WTtBPzRk/HtL2FgkIZzZAN/EQB2SzQVqWv1YhGZPe+DeT2sQiDoXo740UJVVTbPr6DI8vFaAKMIK82SEK50KOpdtig+1ftgsbo0Twe15swxzASpMoHI59rmxsIk+Vop7smw6a6yp1RekVy5EN719dKknobfnQmEWp02vMZVFJGFJeSRK3h0blkVmbVUSSpdxDPk8f0jDocjailICXi4v9cwbcmVBTkTvnit+3kRxWPOCfv9Hl9+9QXuDkfUWvDufcbhcNDk1gWHpYCenjHnhCkR7qaK/TTjeDxhWQpomrDf7/DVL77Bmy+/wL/6NuGXX8749s1r3O9n7Hc7ECrwLJ4QzKWR7Of44D8w4fjP5Z9YiYJHK4pjG8b8CDDueN+QP0FpQVRGLSf85vnf44fDb5RWuiXmdOStx86xhFBJ/R3nP5wfMOEnnL4jpb222jg7B52QNHxjACra8TwP1p6jVgr06RbnJXStnL0UzkoZQzhufM3sN8Xuo52V4fRctXV7OcMj+jj755j7VxgA0oLy+q/A9IhyfItKBcfXz+BpAf+wgE4J6bs7SLhNAjiDdnN/loQ46K/ud3jYT3putVCjprTPeVAs+Jw1YxoAIXSTXDfDpGTzR+3wC1SC02RtOm+Yz9zTOaPx2Sokk8FM5K8wYU4TynRCzTMSzMCk30emcPDf3P4Lf8mOD6KBm99D9GQQqZUZErgBhXZ+g5ODAwZDLa8ZzKUpNhitfvSGWWPxFdiYlvGNuCsJ67N6swVtgJKE9CrvCctzwrTb426/R+Z7zOUBd3d32M07fHWf8TApL+NhT7dq3tpz1I2lh60Bp6xAija/9o9o/TH0wLVeDXj1zG4f7o+wHB9Y1+D8xbXKP7Zs4NZ1d/qToiduNyo7W09f4+ce2tmih+wt7RMIpS5Ynn9ETjOm6c7xuMkgGBWoCZWK8qm5nS+UMN3vkKaE07ujh3te9+nG2TgjZ7n6Wn8aflg509jHKB22ysuSVaNni7c+z5VRCXFW09fN3UbtTrVd8YwAcE0ZcYsC4aK7z/WXPxgEPgEIffLyKcL2eF0fcd+hYQuZk7iaIs+geS+WrjnjUBK4EqYq8fWfTgWHpSeiLvXkrIISvAnLF1eeI5K4sHPWsqfrz23c2DrygDVxfKnwxrfWsRDr2fZ3l5Q1vh2Ju2bhCkBDqA8MzgahKYTg0J8GFLDBmaD//PY1YRQN67U+MldXbA236laLXrAF3NAhxMetb9VZs/B3GFLrbUdxUiKgelYKCcvBqTFfw5CaRXJbpzWjFJ9FCFUFVSK0hxshvzEJAca9P57EtWf9otzVIYbjMRrPgdbX3tI5Tlbzqlh7zIXBIMQbJbNUhiZatSWyNtlfc+swb7KF8rF1oApPvpynyfEEgzR0F5Br0vwgcXitZmH/JMRQAauySuKy1iQJLY0RjEJVMMC1oHAC4QSAUI+LeFBAwkLRNCHPE6bdHfLpGaCksywK/pyyWnrYelTBrRBhb0JFqgk1WPb4nFknRkY08lHabyaAarDUs/A5wQpmLRgK+9WeNQY1higgUTAxp2aAlFiTikv/LBRBypMKsdOALzZgm8wiJsKADfeGs9G2sQoNmBE2Qd/yyHyFKnScl3H3Vm8YYU8GxOS5IqAhFmx0wxnZLSlb17m7GHHKCp2HK+4B4Xs7nA+1KZLZFMlEsiWCa38CofPgMEXUmKDVkE3YL9EPkimeFTL+Prb4y+meiBcKi4KzlAXECcyaG4hU4cgWkon7ZN1cZEw5IU8SVnKZks57lXBvk8T9LuplkXLClOV6LRlznjBltZzlIovNoiBcUMCVkFGQkNwbY5oIeSbc7TNe3+/wzVc7/MnXd3i4u0cmETBQreB6AmqBKH635+GDKOEV7r6RDv8A+vRDSdpbxxX1V7eWkW1+sXXkmdsfys5s1PypKvpJlA6FXX36ZWMX1BrPi5G6M+JH6Icn/hEHvAXo1a21XyiBwKaNQTo9Fy9GeGvn6fn6x/OLV4+48qFGJUSgd7V/l/ZUIJPcC3ukzWn4jD/aWX1BkbJ++0rZon/DbEaiPw6ZKup0BKciQlE6oUzvwOk9lsN7AAsqPcmjSwKOE2gRq36CJF1GSsgpYcqT/A408W7KmOcJTfkAPfuUfrVH9Xxvr1K7bjDrBklo9Fewdu+UGR1o6/1r82m3ub84wt2WR0RUVjDgoYMWXQc2D+1A36zbQtAz9Lxjb9QXvKFtLY13UfgOqeTitg4Lv2J2Al9sNFHkrdgYr1WfexgP+KWTPfHGt/Z7JNHHYryLcCMKPzWBKYN4QuJZBLaYMKeMOSfscsKUI70XCP+zxWj3zdGtr9HY29v3rJHct7/z8WddFEeu5pn7z0vnD1ll19o787xxvbfKNUdl3di7lSLrkpzwhia9344TbhjrSli/xbfF+sZTI/ArvkbVc5m0vUf+KnefEcdAcjKWtIbRm8Zy9ZHz794ywVfbjzTAur6XyA1vLS9TRDi90Qt4Wj6Gl+SKuG1jd21142ZnfGijT5+qfErh+8/l05XxAPXru1eo+y8wzTvkacY0TSAi/MXfAd8/MYgk9vuxoBOw9EzINURryOpcL671fTh1tgZ1jWLYuH2l0YBgYmiRM8zuJnWybiUSGk4QxqTU3KyszOpf8jUA0QofEMaCSRkSp9ir73NWYV2tQrjJOpATFO1oUWvcankGROHhwkkTUqER4XGwRpBGhiaGJbH+camofNL8FWo1lDRZWSnSdwYS9TNdaxXjHK4gJrcgNhKBkrji82jhBSMENSEyZQnJBHYLHLdgViahEdIifE3ZBM4N7mUuI56jxrAYoU/krsYtnrvFQ5Xf7oZrM6kMZ1ZhcfKkZbW15Y/3FkTrA1VXRNeeSMMV2JwFsO1nu1/bqns3qVDdd4ITIeTW1RzGWdQzAuoCn3KCmU1XFCQGioblOh1PWIgwz7OETdnvMM8T+FhwOp3w9PzkTOSUGfNubgyIdtl6L2GSJlCtKIlUSCmx82HrSGLFTprwHJSAInunlAXLUrB7+w7z6Q7TbgfKGTQn5Ls99l/+AgsYKd+j1ANOyxNACfu7GXRkCdvEFaUAKQvszVPGTDNAJ6SSsJwWgWlqJ3uN005Qwb/kv7B5piyeHZhIFTYzsoaF8sTUKpD26jR3u3lBuNIiWO47LDABSZRASYXdlav3kShpUkZxL0cS5ioqS81zLJbOMn4FpY2BTGnrmaYC6F/kBvPmprbZhLXdFDBOByMyV20Pt/pXNXXfZFzsIarO0Tw2vi2ClNlcm3u+f6QLXQFhnjK6PswVqAW1VBSW/BC1FMdPEjaJNds8KRi0nBApZ0TvOQ4T4ww6QYQ51Og6BnzeLWF8xCGNKVLcFBj9CnS6XbtYk5x3pQieXMoiCaBPp25tmEVJUSurR0TVnBcyvnnK2M0zEhH2O0kMjbqTcxTiITJLXClRNhJht99hv58x5wk1V+ymSf7nCSfAvZNACaey4FgXLKcFz5SQ0oSUEn75hvH1V4R/8y8m/Pmff4Gvv7jH3X6PCUlyebz9B3A5yh45J2k/Rzd/iGT+5/ITKJHO+uMrDQsb/RlGaoSG45KX1EwXfilPoWddqSd8t/8bvH31PSr9Z9ax8w022QjCw/1XAsBFadeByTCJqktiW6V+ngQau+/0OYalPRLPtpj/i8GOc01QrpR1hzeawY/RyT09XEnDbFKS0HAkPY1hGo3UJL8Xa9marPPLy+d+dUqVeJcdnOK7TBXv//z/jeXVr1F/IKAUMJ2EbTjNSDWDjg9uhQ5IUmBQQppEMZByxv1+xhcPex+gjTtpPoTm+dErEhLgv21t47z4/CndnlIf7jiGNwQadHQBKsZ7hvYBF+Rdmuu20Wjjel//iROONSHPe+ymHX6kv8J7/FryrwU4lex25rXbeB+N/Kh8KmAeNmNophEvKJcaSuNA7H0Lz2R0Dszbouq1Il67XGN4ysCfDRxR3HWNnm14qSO/yca5PcW34nJTaOWcgSkjY0I+PSAdv8E832GeZ3xxP+H1LiF3zidxvqzH2/yZ/A20wWrZg4FjZNK3L2wXExobs3lD6UNRB5rx3PPD3Ubu6NhXQqXuY9VmJ2+N9a6rWL3vMx3oza3nrl2T6/Wm57bfvfnRs89vre5NSohQofEvvQw7njNtvZLmJ/XziisISfKQchHaH8ab6B5h8v24NZhbSeRr5azS4YYGzsLWOJf9n4v1fEx5QY4IFTSOe932dFBGrEsgYAb8c1ZxsYWnhjYdcSndYoLJ7tFPNFGX6rlFSXGO5LnQYPfcT0kRcnVOP6Cv1+rcGn/3BiUgZSBLiI2lTjgcCbkQmDKeTwWHhUM+1AZ5Z7aY9utcf4dhjvvi6hRcpwriXtrce/o8DzfiXPZQhJFC3i6fEtSMEWGoYFqVA5Hhgx3sMSNDHAOr9VMQggPi8paCpQ6oG58dHP3BPRK1I77YGkRjxGKfROgmfar2WAwjp2PH6hJLPgLiYHHbiNVLcNnUPWYFnJCoKovWLGqSKxTUEt+VEU7B2yR1LV1X6LI/Z4myW79DCKcw1qag3hLCUqcMGVD7VtO3lxvoUqKWBI0C+KSkCaBZLN8tvwMhwkhT1sRi+TpamChZqzxNAvvaZq0VCwHZBc/UQjS0Hno/ExLUSVtpWZ0vYlRKIKrap6rcIKtnUsVyWkDphHJaJDTYLgOJkOcZedoBKYM13JTI9bMqAxJK5Za0i1UZlhIm5TZqaQICQJiyGM0haf+jEIDClpKQTFkVVhYOzMbOHvJHZ9znoxM4mIDIQhD42qtCTmkTYlNAalJmVS4hZW/P+ARWZSYoMHm3lJcS586k+lU0wHWoC7/b16Y4vq1NBmSeYhvhq8Pz2fO2YSBR6jG60JmxBBpvXR0HHB3PJFMNNphr+XbIOO4gh9A96MqrHOo39n1kDNLmWjIiFNsA2GHNr9JwinB7N46TuCnCXUHlDI0IQlwZw+oFoQmyE0ls7ymLMCmpYsJyuExTFsEJG37p5yNr2DZTbDQLy4hf2zozA4v2cz/tkPKEu13CV6/u8Is3d/j6CwnBkCgBtSDVBaWegLq0zW5wtAGqYTteL9eUFx9Zbqnm3G6/ZnF27X7Uv7yUIV3Tg5cr+CwsA8WP8wzsS8rvLrRtBM4rZSCNbsX+Z58y1BW6MfZG2mMsZcHhu4Llbd7Sg99eDJ8qchIPvHH83MZqXSXDe3FEZxToF5vvJ5HdgKgpIbzdykBiMOvZr3RzOxrOr5uRuoJk+lx/hvcbvr7U/5dumNAnDj3s5tPoZYCpok7PQFr0d8EyvUPJj22aGOCS3GMucQJVUnosYZonoXGyeI4m9YabpuQTEY2zGo0EmAKinRVtrsYzP15rcxjD2MKf75QMKyQfFRxYtcFX6ZaNNQm0X1clE5AkrGTOGUwVJS2eI6OVpoSwJarMqhPjFsYTQLeowItoO20JtrDuAWQ0H1d0/vBO04dnYh/ONN3TNut5YTvrV1DZ3o/XLuIwhyGFDc5IPCORGC/kRMiJXfHDAf4bTumVIgNEDP1c37U7zRLdSsLZSVqNV6UNkdRuVV94eePcPVO4m1GjYW0+tuvoL/OZ69aV3l59XWf/O/Kt8fnL529vcGTreK6N0LttBceNOHZrGmQWN+o8O5dnrtuib05XoJMdUaJbd5NnrPZtrSDN4VZTDfFeL4PMxXvojftX438Rr7k14K114uHry+b3Q8qLPCKiMoKVkooC0utCLBo+P7LYJBHgYTWu9uHGqs9ojF5SXkD2/nGVlZT+d1DmB/DdVyJYm3f4n36d8TffEWgGkAuKE+LXDtx2EF7bZ64Awxkl3bnqb4CKEeGMCGm74ohUxkOoCf7DCNfVfOCydXNqBLUKQCwHApsnRLV4tEZTkhOwa1SvCF+JuMoMLs1yPiW4izARafIwFepYbojQuc4lO4y1sglxA7sSvkv9LJbYKnetVeJ4EwmTQDm5NXelpOO0tto4lmUBCBLnnwjVKcZm4S9tK2EVlRnMqFUF25SATKhIOPERWFQozADNmtSYARCrtY94EjSmDChnYNFHPsI0s8Y7L2rpGyzzswiVxWNF46JDwkWBoB4Tqa2xH/yyVh531ZgXf46BmsBpZWeyEhArCy3vEMIaxPZIrlOM+24KiZafyJJYU42ePOzvJPWCkfOwIlNC4YJSiwoQTsiJMM0zQIS7h3tMy4zjcsSyFByenyWHDYCUM+ZpAmAKDMj66+ASZbRMJGp1bt40FSj1CCAh5yLCfPXqyCmDGXh+fIfleMC0S5j2O+ynN+LWf/8K6fkZaX5AXU44PJ0wzYx5PyFlwm4343gqmtuiAkWScE85S66GyjgkoCxJ9jkYxQUMSeEcyETYTRlZmRU14EbSpIkpJaRJyBETpiYCSmk5ZcCWC8AY4uSEX0riB26eLk3mrDkAOskEgsBC4bGSqHiW6vF4LSRQ9IZKF841Fza3Cxv4VJlgYgW1nlHzQtI3w1fGNEUhQsBUjYg+ozDp2LvhYItxl12BGbrPlZuugdrZZOGuyIUJkZHs64odsVBMlU3JVNv43WK2JawGNLF7bnW2ZZRvWT2Bsp7xpQheYnVXIIeLEAbMp8MUBnFS5A9p8u6Yh8a93xQmag1nK0PbakoUC2dnopBMyRNCl7JgOZ1EEBI8f9I8YZ4y7vaz5oGx6ZG52u8mgLMrSHMS/DUlyX8yJTl/3r9/j8PhiMfHZxyOB89BAQg2ySQeQZyk/aVWvH64x5vXb/Cnv9rjf/U/+xa/+uWf4G5/j0wZxBX0/jfg5QDixfNtxzkb4bjRGt1B0r/2c3lRuU4Pfs7yh75iV/rPIx5u+PEcL3izfMrxd/+CKMkFj5THisP/4Vcobwk4NmHx2eo71DXyDVYquJIR3O2m0i5KnGpbRhPBz0qnSUec3vF67Nc64VW1s1Fxe0jq29VRNdEna8P22Trq3+PxzpVQfVgD306qJ+3WsXX/pZC84ptMFjKsgXV1FCw+/+ov8PyLvwL/FqgnBp6PwBNQ/3GHdJJwS8RJhOeTGGgQEfKUsZsnfP3Vg54HLReS5NVKLhw2r+g4BxTHrV8stxHZzETex99t96ICYjWXjTBZ7ZmtiW7kRKRfNgqNP/rBRMVKShmZJkzzDtO8DwqI5BVx/0dDIgrMFQ50SICxLTy77u7GAHRPmVGL0ZRyoaALP6me5bJfNLSvwVVk/2wkyQyNbI57hc9ZXf5GT3uB+ZlCDf+Rei1zIsntptdky1YwJ1Ro+Edrw3CLRQfwjXE5/01Hkm0Mqrt0o9aWTUnCNrS+3otKTwzwfGai1wLjHjtdNFhggAfjnq1mRNYZf7frZytGm8cuQsbY3Y4fWd+/XnjV544HeWFdrU83PD08GPd0d30gR33PWTH86kZ+huvZX1apEWBnJhFAFc/3j8ACTD8mpHJLjqfYlfEM31yc6/X4Y9JLq21s7dLP83V/2EqeK7d7RLRd223cUQh7XhFAw+fZljbeidf7wzISBszbyOpaueSaFC183crg7LPr++PTKzA4s6C/T1L/ViA7G7pBKrnp2Zf0acuFyMMwpIw0zUhZhFoLQxJRW9SAjbX5NFtJAP8mxpA3kIrf+vjerJQQPb382cpKtaHjNOZDhNfolRD2pvExluCa0M2lMGhVhMfG1IywNfaG7bAI3MGAt6yzcp40Joepxy/2zBp7cSMkNXRPTskTRbukjNGEXvpbCF9CqhVMkjQOANwlGBZKSl5iCqL5kTAnZULQ4hG2w3IYLGIVNNzX2z1lp/1qXhXs9XtLXp8xsOSx1lsfLsF3EwKyrr3tqhYeyVJEtZZoxcy3WXGK7AyR3Su6ZG00HNbZXsLbEmFvq9d0U0akS1wiVbDUJMJCI+BzEsUEgFJOoqgrSuTk3O2lFfOmyimXByRGqhTmr8r+0DgxLjwHUHlBqcDpcAATMC8LAFFY5GlG3t0hn54ASC4dV2hp8mjLnSCMhsB8SqIIm3IW6Cy6Ny3ngAJbJlJLKVGO5aAMJBsXRUsrQ9eD5TnBn0mUdF/JnotMEkAaKocAV1qM89kzBlX3c1RCwGFv3HfniysNtoqDjCGVywwPDfPUTcRY6SA8a7cjhdS3EB9suDEoca6UJkhSDEDjXrPr6+76QeFdbMKpFsovjkkzpqTYZ6DlhtBQS8qgi7K4+X24V8O5pRwmiMIQPCmnz1lTTF2cHzuDxjWypbezUT8JLRH3RNljf6eUXFhSlwrioKxWJXxSRUQiVUATwJVxWo44HY84Ho84HYuGf+BuhRIRmBI4qzAnMfYz46svHvDVV19ht9vpOXcEuADmCWH4fZyGS8z5OM/h7+cuH0KCfgq6DNg8ps4+89L914R5fQVjfZt9ONexoRNex5m+fIgn+u/OE0JK5M9WTXe0RByL7fcbG7hhTGPtA9UuOPCQwIc8nFLj91jbut3NnnRAsUZ6FPeozlfbo/1ubcdZ378oxGp0oNbrxiaK+2JTLHiblYZcjWJF07ah+NLWdmGAYH32w3HNWiDUcBqPT3EPCjU9oaZnLPQOFc+oiYGZQKcEKgmJJ4ATdnnWM2CCCMLkf84TdrNY+idKnkA6aSi+Zow1Jq1WJXq3lkYP2YnWryt1E2rzOSghAo1m7bRXwtlI3d3zc3uWFgrnvRO+1kYcjHi4ppRQU8GSD8pPhjEMfai+UEBVYwiOC+cwNPath02HC91SHZkW2nCY97Pf8l8F6InC4a2mw7aNBnz93OO2soXuLpZINVC3ppkYc6pIMIOuHks063sbQ6O8r3XPf/MARZvo9pbB9HTr1r7exp7UwSlpnzabHKscjXWuHBPxKJJ2tl/gUZq+3fzQ54ibe5jr+rj5zEvKQBNc7Nn5co61afd5+L16YuO64oYwvgYH7UExkFxc6ePzYf1huGeO2DwxKql6LUE817KGMj0z9lGefmYQN5f2aiTO4zl65f2ub1u46Vx7H15enqxa1bPkgsPPyUQ0ALq9nTj5H9DiCqibhSyADWYbw28OffjdMFj/5ItqLlPOmOcZ824H5ALaFxdMhYc/Qwcair1EcJ1nal8Asx8C3o5fVcy5Rcwbcbmh7IlPwQRFoVonrgLRwcweZqIWtYBVy/KG/e2D/a9YRSUQNDEvJGwFs1mBw5VSFhfcXIytXa5mYV9grqRuSavEbGSixDpX9nlS0yrLR8EYHT4bI1tKBZcFVDLqogqBRI0x0pJJwr/UygBV9+hYTkeJuUkimK6lABruKKWWU4G2rEbI4rZOYFRME8u4qsVdZzCKCu6aFMEFvXaAbvCjPpcALCs4EUL80qgUQMf8EEkYHNoK19LBrsGSQgAzVgSRKoFLkZwaCdDcCv3BHQVcrK7OpFbKplpo+SlsfKLcomxjILEyKrzqDwGat4PdgttgSVh3EYgnTYTMVFFI471rKCVKSeK8TxkPrx8kj8SygLngeHzGNE2y5qDGSKvHgY3MGE+B5wTmigJh2ksRQqcU85hYdNEmjRvP4GXBux8rdoc95t0OaZ4x7+5w93CP17/4BkjA448/gOuC5fmAPE3I8w4TS16U0yL5JpbTCVwZ+7sdppSR7/ZgrliWkya6ldiZGtUIc56QiDDNGYnEqyGplYnFLTarqqQhZewc5US+J8GSm8PzYZAl+ya3Urc4xub3QykoIpRLtDA1leHWmW6lqYrSq0opqAItFFm2yAieIf4Ysh4RSxDQm+hcQfIs7497RnRArQ9Vn217SudrxO0ED4nVWcRe4wIge1CWp1nldUqUgJ+7vWUKHz9TLIQRNwadoGGXkuPV2H3xhBFlGEiELnI+iBWC8OaKkym5FegwgNA/OwN7rwcKcxNpCkFptcNtxuxxLQ1f+hqwKgZZAq2xWDUmWQDM84wpT7i722O32/t5tZxOKLUAmpdHPJ6ASS1m5yxeV5PBLRGWpeDdu0c8PR/w/Q9vcSwLDssJiSSZZ7Jk3SmDcsa0mzHNM371NfBf/qs7/Jv//F/gT371KyxLAS8F9fHXoOVZFOcEsOLKPij4z+Xn8odZyHCw4y1BNFGB4dc/lI1ghPNh83bHOkY668IbZ36deyXS36bUDA2vGkvbtwY+gEJ/Eegn0bOqh6wpm2sU/EgvbKSdMLOTo7SnGMqLs9DqyQ+EofOG+zdm8HaJQjzHg7iK+2dGg2zjawjAaf6PWPhvcXp+i/K9nS4J+PEeOEyCk/cZ33z1GvOc1cOh0dYxNF8Mn5hSDmeSjbc/o3pFepNh0Dgrg/KgVzoQWlzj84qGVRjDeD3W3U/Uan38OI17r1MwpbaPTBGRMqY847h/h+P8DuV08DZ7kZzxwcYjVOUv2xktD1KgHUNfAtyb0YTBZoIIIoki39hyFnKtYFQJK2x0TjVjBKV5RmknQvs6kEZiBrx0CUtswG2DX+qmOe5nm183Etpso+JhYny5h4QJrpEY0vnskUTADWcwlk9BTxOPuPO8gHxjv3dKqev7f2v6vQ9sS3G5ljrcPof741r0z5+v/9ydq2eAKWDOzt36+ksUEWa8vWng/WHWINaJlRxm+0F7fPg9KDu7iBUcv7S+L8sBx+Mz5mmPebrrzjVAcAdxQkEVg0SSEMo1iWJ0erUHzYT643PL/bfq9WpDXizXHxuYzXOhc3EdVmwnf26jkdsVESvs9JnLiHCczV0/1kdVJ9devaSzlye6DZ6dkIxH27nfIyK9tb3f7XR/KJBdfO+MhdSLFFedEOTMe5SBaQckSUr9/gQcniueiy1UI7deOspbDJxu6WLf+CXkf3luVk+E8/0lh8pmubIsRgP1tSojwBGZmhBGBXwmtI7CsFXfyIk5+bCEYtXrl5xeajnOAkcxNrbXaO1vKVHO0VHWNdvXTGFdWfUhRlBbO4GJqk35kTj1bRMA0qRxSRNdEySRdi0S99+IMg1tw7WiglbCcxcQjgSjCsoSJVQKRG1NPWNm499S7W8VXVcjLKoRkJGADUmCB64Ra6iJ98Y14u5b3LEMUS+Qrg3F91nm3z1RrN+aL+HyBtY6iNyqT6bGLPJaiCcbmSSpiti9EbXNHT4hUVGdhoVcEQG9EfR5yph3E0ohlNNJvGpKEaZalQ2mBI/7vj/WEhLJ3CSyhO5B8MkkyjhmlCyeGVgIS0pYjkdMAKbdHVLO2N8/YHl+wry7Rzk9YTkePIkwAOSUsVAFkcWxXzAvWaw/SKz2oPHsSfWNhWV+JlXQeWJhIvSgzYgnZUvWrtjbHmYTlicPxUSmiHDmgrwNgAL86yzanLrSMljDhaTxBgu2+B90DlP40oCmQzXnKzYlXXvAFLCkSoxmiTrAuOOxds/oFp+NMF/rflPf9yuFhs9zB2HEBkrud/edBw84xgUhycJurdtK6rHT8j+FMdgHNWHaqle2Ni54jNaf6JQQ6/dHQZ7BVszNYMouETpAQxRaW5YbhQiYcsY0ZU1WrTO1UmboHKFZzLoXhKvgEgpVjX1dcSqLJxEH4Dk1APUySQl3d/fY3d/hq68n/OpPv8HDq3sgSQ6iApJEsGYgQMCteUleXFZKMtq+Pt5/YbWXXr3VE2J8LpxON73/KUoTVp/jNW69+OnKOvxDwxJjwsufZKEz3z9FuTD1PluvAJQKPFEwGub1c+Od4Uyh8I3D94aLt2i0WHqcdynGdydQ4eG78QGIhixhPDzADJl3Bo21j72Tu1E6OHR7q8fnRnFxV/Sah/C1tVt3jyi7R9CSQAtQqQKJsaR3KMsROBGS8qpgwi7tkHczKCfkLDkgck6anDoYVmjuI6OFGs0vtI8pGxhmENRyYQEhpCQ1PLEJ4sYfoH/eLrlAOtZzRilx7d7YOK8gtK+j0WOR3pMxS460jJSThNc8LuDEwI7g4X/Ogu65PbBBoDkd1z63LKmNxbL+xTqdxoEpr7irD+Ol2J2xz0PXt8+zsM+cBghrfIYO5f4p+XIk0HMCPyfUkkGVBMZdkUKoMY6nhrQZEVYzSjnX3cFQpxv3dlnf6TKhKSppsHvtBBzhMZCI0M0G8/q+XE/r30jTr9saiNQL5/RZof7Fs70BDPs893eN7vW+c3z+crmkhPjQYv1E+Nga+mXPiP68sfvnDG/juJv+ipS/tifsHGWNtCs8GXMFcQbAKLkgTb0nzUtoryZvHl99QR0f8wRvn7zrIXzcer/YI8I7RtD4uS9v9OVKMfa/4xFK46YZvl3r4OVNE4GXV4D7c/n9lzrtQQ/fYJpmpJTwN98Bf/e26KERLDfOLXFPI6xv04vwxna5tM/P8Nw3n24fer9vVduOSpsbjunaP2XWHCJw6QUxbaBbSE2u1VrFspnFktUcKCwhsuQjEI0zUnJrIK1E+qT5BkwZQmq92SsmGwHU9cr5nqYQMcIhujpbsVwQlStqKUhF4vPb+O35pCF5ssbzLkQomkA4pYTdPOn4xYK2liIEdWA6xMTGrPBFUFuZHR+mnJES4XSSnBy1ikVwqrPG7zTClRDZ0LNr6/NJ/s7oDWHeFs1qyiYxnBGAC/F6F+T2rP/e6FZl8Sxwgj5V9ToQ0tAsqC3evhNXLBuXESveIAA1TBabJRklEfTGZHYa/octV4TCszF/BhY5SfgimXuJU88sOUGIgFLbek+U8frNKyzHBe/fvgUz4/D8jJwTdrsdJBSNU0DKc+jKGUMIo1IEvhhq2V+BpS4SmkU9I1I+its6FXAtePz+LXb399jd32O/m/H1t7/ELmec3j3i/Y+/wQ+PP4IZOOGIKc+Y9zMKi3fKUgrKYQGBMZeMu7udWFjPkuNi1u1edA+Y5bWBcVavFhmd5hmhhAxhvKcpg4u8b3BtR/E0TWINrhaCIFFy2E5Imlchq+V/swRrClHxsrG1UdzDwrbIkqohA4mNm32/lB9iVQzw4wUHKV5Do+OjhphiWMhx76Qkr9RgZeNeSc4kBdpGAWdlMBr+xg45iX1hyCPTohdWNNo4TNs/65sc9qzWrftcQlK0Og27ZvMQ0twhpLlpRCkLENWmmPK9Ok4CAaQKRouHnmL04jA/FKhRHUZ3BoL97DudTn72CV4o+k714WcipGlGzklCMU2z5GCZxEq2LKJAWJaTKxKSJZ1laOgm2U8gghx3cjba+bmUisPxKIyreo5O84Ss+zJPE9I04etf/AJffPML/Kv/9Av863/zz5ALcKoVEwizJnVnDzvnaOlF5bLH5c/lj7ZcIzl+isXoFxgeumb/+uGFIec6E5DuJqR/zaDvTuB/vwMOtKbH7Vw4J0HEiObGvpuxhXzvJB6G0yLN3NHPG42FfrnC1JX94eytwz19reUTMg/Tpl5rgxl5CKcKO6OBOMatcm4NNzgTH1P4iBIBPwPs+vGLv8O7/+S/xfT3e8z/eIfDqyec7g7gHyZgmZHe7kHvCJQEb3/15Wvc72b37k4pu9cvAULnOPzpECkJnZNoUESYwN14nkGhnsLJHHDvSqYRBf+dgYd6l6JXRoxeEBGUbvKIQHi2I4y233W6T59aaMZCM9I0Ic8T8B2j/rYCvwSws9BUhL5xO8DYJhUxY97VfR7WvMF7/66vFxukmhJCQzJBcui5d4RWGGVSPLRH3U/dE46nznTV+qr0QzNvkrFfote82Br8kEF//4ACxml6AN1l1IcFhRfUSn04+vCa73stddhMZ/HbuJ+jBwgNWM0nx2ZjezWJNi9fLR2OYeXDu/ouV9jRia50vdLWbasTYPnaM83Te6S/iFTZ4vh/2NTek/O9uebpEhUu5/HwNiy0db1GO0ZeKXyP9XK43+Gq8Yyx7kZjy8ZTkobYrazzliQcM5F4Rj3fPYJmIP9we66IcWhOa4/I4Ja6/O/tp15/d2BwVs/3vz+UpL89R4R9sX24Imu2Hm5Ax9SQXpyWdb8Vc6/qJn/eGCD/3OhPq/1TkY6XiNCtO5fbjSD/klr/YMoWRL5Iqh+eM0IKxvgzQBmcd6DpHmne4XFJeDpkPC1JLHFpzTaMc97BII9Ptovj+XIjDgyXeuR2+fCJFZ2BgJEgPoM7O2JlfNbv9f08a1Vnf/1Q4HCt3WveAdEy23rSCNYocGNLVkpeNSy5ngl2LNSTWW+6hY5lvQ0CYu+jMY/6sB20jVkKBIHPj80Bw1xlmU0AE2dssFAF1Kp9kZAcnsQZSjElIE0AirhdMwNcAMi42iyzj4dNMWO4r7LG7MewUtyWgRIoZ5hipjJLsmV9w/MipCQEMLA++PTT69e1NqayX8uwz4aNIrxj6D/QYqMPbbUWxytqjaVEe0JSTxKgkngEtCTWSiQEeLTLXAFKDcgq92EFCZFoaR4RVl8URlcdSDvkfZp8+SRWu+aHMEFkEffsQs1qOSXJGVFKkdBGzFhKASV2obobbCOqVbTdJOHEjP4nSpI7AlmtN6rvy8oVlU4oAA6H90CqOB5eIU0TpnmPeX+H+9dvcFqekd/eYeGKslQkVHCuIAKmSZJSg0QpwQCmqQJImCaNT1+rCFV0elK3pt0mb/MFeFgmgsSsFx6bEDPiUrawBcoUq8Wg8wLKbLtC0fYSmkBEwjD1cJ8clq2iiH+3RVB2nNH4bg8WG2ic+udW9L6sbuI6vEvDc+hh2MdqP+KbtDrHOqbCUTNt9DcMyAgvbcPxG8L7Xk0axhbwJcGJeD8D/J/cT163JURM+iwjaT9WOSKQAVQfmhkjVGUabI5gZ4HjiYGKZGOW+/4SWp8txnTz9oTu84Jai4TaG85HQ7i+V3W6U9ZwSSqQkpANFqO2asg9Pf9s3Ha2UUJWgVTVgTsm0+hlUyb/MeWEOWdkrWPe7bG7v8eruxnfvp7xizd32E+zhHerDF6eQUXCyAVIgMH8FjkTQag7T9pU307fXqMZw3n/0vIRr27Xd5Wq/4i6h6rP9vmqQALhqB1PsbBOoaFODvGCMgqKjO//fLN0W3EB2diRSPozEIUfZwufsewdqo1VO96cdkg0C/5SGjYByF8+g/gZSF+BkRFnrdE6Vxo8e2+k1/QQC2u8/fpwWK0YDsOl3H+H8QLw740n6N+344W50X0OOKFNp4F8Wlazuz30s3e2xtp/cHdXz4DpGcv9D0AB6Ego9CP4KEZTCxbUAtAyAbQDZVM4JNztZkxTlnCdueH9pAYULug3HsaNftqZZnyFHJEtlBMIbqwCfx6NZmd0uIO6qaP23+/buWf8lL2k9XWS3SEahcFSUGhcnHWyULDNi6GjSwIvZ/VRSsh5Ak+MJR9wnJ5wvH9EmZfNBbeZ1CCuEk7JmjiHD3yCwi/P6be+nbCSybeHIijzWMEGIuH1VYf/K+W6uOX8fonzTnEjVAk5JHSOhCfmckKtWyGEtzoSDQEVpwV84MfSeFD4d6mUqadpqbt/Hs4+5CwTnqS9J1CjIUntxovORg1X6vRl2G/exzaOdRNxctb4cbtD3GBp4MGlzUYXb+VfdP54RYj0TdxU6AL0bhwr7cYNDYzv29/Yb25zb2GkPV9oN0/6sxYsywGs8gwG1DmYnVUUHpOAVBUmkh+racpiQHkqfb9ulIf2hpHXhr8FA9vvXm0+0Ihb9WwpTT6kvEARkcL3AHsuAUHPu9uDgCshLpZuo9Fq6P1R19NNH1puscjqRRBbY6Az3+3toc3h6XM9eBFO+0Mp0VTi/EPtK/XrjtoS2fK0Bz98KzHMd3f4zTvCX/4gMRpjCIexrFr/jBzReMheKtvTcpEqwq2I2fiBLqb5uWUwhaF6O600yirUq+HgazG9AYSQFGLhr3StjTEIrSTlg+aSANT6RyzKLQEwuIJLkXjupQDThJwhQqlsORQYBc37otEjkXjWMEXF4oGqXYif9e2QtfdrZVQuYM1VQQQXLsv7GspF57KUE0o5oR5PQFnUcjvBlBBpSkDNSNMCBiHxAjBwXI4iiM1GfEsfSq2CdbMK4JglKoaFGXFFSYMEaZNQisQTL0WEctmUNzpfZBIqhQ+z4pco6gSggjWkFHNTBjm5GGPVOpDB+yJPiVDcAY7ZZiwwpu22eDog4AlloMyMW8NfiWDErJ41LInFJdX3qlq8W84O1kTO5uLuTK/CQC8wcd8DtGRkSRQZJEnGazVvjDAG2wMkcY7nPKEm8YhArWLdDEk4m3LCbt4h5Qm7u3sspyOOywKUirIcME0T5nny2PiAWTK1WPkMTTSbde4qI2WzaslgZrfK5kXNo2lBwQGn0zMOpwfQfsLdw2t8+e1rgN9gqf8MNSe8ff8e9fEdju++R94DJTNyFoKqqKLx+VSBQwXzhHkmvH4tVt1JRomsRIx5RpAR8KywQaLAIAgDPudJkuVS1nXLvheMiU4eYqcx6OTr7gshlmahlKrKGFW+1SqA2jPk3WlzFbU2prwXuHsInKBsAVr4HAupVB032oKy4k0JQyYW/SZsD7QPGl7ucsCg4Wi31tK9lEMf244c5w1N8LHmQ9ClQqD2Pq3q4oZzrVdB+estJqvTmAQJBcZgF7wkHb95Psj6qYWoJI0BkXjR2AxVU/xSyw3DkknOeqp9anPR3XGPuoJoMZV0rC5Q077bI0QE1IrTsogyvpR2+Nr8qGJQ+ix9l5wpWROP2lwXFCwoqtQQD56KlDTfyiR7JE3iKTKpsHKBns+loKJimhJ2c8LDTsKBpDwhpQnTPAOcwCA8vPkCX/7iG/zP//wV/nf/1T/H/f0d9pjwzAWnsgDPv0U9Pg3z11byGovUQxhf3Vc/l99RObNwHP4KaRQR5cdwJsLCm8X7drufvwQM0Fq2ba6Ir8dUSc4tRF70ZfNA/keKnU7T/ddIu9egUsClIFXJLzX/s98gvXmL8t+9RmTTb1J0beH5FTO18UJD3xgxYxv4KHlAwHEBlxstHviCZpikL25Jav3cCed+h51bH7bB9/y63LZioX8GpRFlMXehvk+vfoMf//X/DdNvJ8x/eY/T6Rn8Fjg8Eeopgco90pN6LO+y5rcifPnFPe52kyvYk9LS0WgqKiDc+9iFr80bwkIxNQUFuvlaCfUjzePzyQE+srfRwiL1nwjtGD0mVZHSVeN76N93uBmL5fSyeo3O6kNwRrhMKSNNOzzNb/E4fY/3X/wW79/8FsjU1TOO2pQFIDFsSCT8B6ucIaTEcNBvPL395+aN7bUbbaa8leVJQOOhHMQ4TgN3nxa1KU6VD4M2TG+HC56Me1VzX5xmtHBe+rcbuy8zC+NOFQVH1EKoC7CcCGXS98joUx7WrNGtNoe3YP0t+cnlyCRtj/TjHOu4zUK9zXmE6eI09vkXLhSOdaGfIwBj3q2+DwOCv1Q2+tIy7cABi61ubqGYqXvHHq8BGDtI0fvG8wQqMeIA20M39N2x/IdKt9eVrfuJsHO3NwcAwlKOWJYDcr7DnPeeO5MrNIqH4CMJhWy4mN24bn61B07A6YfnkGfyg7r+orv+1ArH3Pq67ONPpXA4V14emgnogJuxBesXAG2D8Nj8/YKBMrp9/Hsvwz7dvqnlIjr9KQ3qM5dry25wximD8x6Y7pHnCY9LwrvvgbcHeYiD4K57+Ya2rz16bvNtLdPoBXG27bNLfHkDRYLo4ltn+6z1rCkcPyw8Br9VYoIXy+dqTp4dk9EzMERqu++Eq1akbIQxf6SEi61zZRKBJnPzrlCkSMMBaMSgubsaQqCz2DISQ+wzah8cxs+VgVRRq1rDQ5ONRYYKLtNv81FFYO5MqzENyniQ5QEgFqvT1MKwGOPY4ourwNbnr81zT6AkX4v+ZmCrWNq8hlkYEEv+xs34eCmOxfnEsBZh2nsiRQlZwImdeIDE1TJxReSfG/GugmYSi+FUEwye/G1XNJj1u9QXFWjGC4vl9dZJJuOU5LJCW8mcSB6HLsSMxb02AjgqxLwqzePAFbUAJS3tXkqYpkktjEToKDkjlJhPljzXrC1CxTIyIJF4foA1dJUIYk2RBPJgVhIm5nTE8/v3ABLun55Ra8V+t8P+4R4Pr16ByxHPjzLO5VSQJxGY5pwwVRG4FwaWsgBgnE4EMCGnEb7Yp4g1gbDkTBGmPKWkCjSlvymske2GNCgeBIja905YpkxY2KNs3j/2rM37pZ1A1hUTNpNf76ClO0DO45wg0w6Eva4X0JSK4r6j6x3DKRk+jrTBtdNrDdPnSC5SGNueEt2LOohxb/pTsQIfrE9kVwzju9eO4215N0EEEGlYe9kSKSgiAnM2tNC8FYyYDv45vn2rJ1YXdKzh/arhUnmjwnk1eb3d8uG60tbxpNwRYYrkCGJmpCzhk1ISRQRRBqXsyg9R5mtOCWi+IIaH7iCSEIWWd8XwsymyllJQF8lJM6UJ97u9LTJSniQR/TQjzzu8uZ/x7euEX355h1nDBC7LAj4+IS0HoAbPjjPb5dwuGqHtc3oM/JTLSOdFNPGpyPxxbs/itgvreL5yDsBPZ/t8nkGl4VugC5rI4ZOUa1bX2+U8XI79Xf+6rYynNkDg5Vlxz+SCsYSEh/oGp6XgsZLJQhDzJVwsZ0gZ+7yZPeLxy4jX5U8Hd6aECDQqb+36/ojvXqdmYhrubWOOSPWN11fDWHVhGNfAs43hcUQpfQLv3qPSgpqOWPJvQT8S+JFQUgWXDHraI5UdaN65ouF+N2OesocQ3M2zGG2o8tkMLJKdq2S5Iaj7jAJ+93QISoiVwsD2Kp0Vm9pTPt0t31psC91v5220bud0/LX2ezyf43vrokYrHZ2nbSgdrIsBRganLJ4meQJODH7Ss2rnp24D24G4YQRlROuxz5n12ufNz36lXNio6ZFzubRD410efl94Zfw6vNKE/2vIf/mJex6/N3qaPSRxKcXDUTYeR8dFqaP91nH8P4weuPSe9WELS3N4ZpVd/lxbVpXmJzTe6ixG2sCx6zoJppYH4Fb5K1QUqrX3wo/LZZPsjiYAhufinRBCecDL7Ts74jWatx9bv9vt+TV4Xh/A5bD57bmbyrje3D62uYexHcNdA01bq8od1cSCm0dEDGXdjsTL2GH74vY7l2aQ9ImzZ++F2rpvfMNSfWT5MEXEVrHVvMyv/OTKTzVO7T8lJcT1oggSAOcdcP8t8jwhzzO+f8z4j99VFUxsKCF+DyUqIT4teEUrodWt/ouenl14CS3UEY5DNFYXsjQmwgR6poQw4RGDRYiuwm8TzLoQ2AnW4WRmcYYVQbz1gVriLrWir4Balra2lExEcjQLNGVFPFSFYOgsMriRjb2bIfnYPR+FWtRbSA+A5bBhApulqwrQko1Vx12LhGianAgzkliZjTyBACxLUs26zuvARJhAShgRBiVJgBTjwsvzPmI9NPqTQ7pWRbmTBntEiucqDXhHPAKc9FE3FWEIIqMQ2rUZDufBWFye0dPvsPiVDEYy74ihMKoa5FT1hsjgVJV7Io9FanArrpTsay/9t6WX69UtzrknMpQxZEC8ISSdRItnXCwEmcA/De/aEM2DJUMUDaUUAKJscEF8ytjv9ljKgpMmtT2VkygSpknCNWgOCps4W3f5lB3BSddZ18WUG6XavpS+ltOCpTBK+S1OhxP2uzvsdnu8evWAsrzG4ZtfoPIJ797+gMoF5fmI/d0e044wTROIGEs5oqDgdDpiWQg5LVimhIf7HbIlMTA4gnndCAOQc1ZBLGHaTZimhDyp9bpbkJllffuffD9vAUcgn9wrS+Eh7ndeg2ZjtqWMewwIXmBswoJu86DF/r/AeBlwhOIhfmyN9HezcBSPrB7B9Yy94a2mHFRYdvwaFMJdFxU/RQ8nPkPmuwJSro7nkMekThsnlOaaacIptNjIHO2DyGNf+95wrA/PF5Jy8rPF+t6vQZuyuP4pcGZ+Ztg5JhU0JYQqFGKMc5uH1iM0Bb0rPUJfzYOJYh9ZhFA5I+Ws3mry/3QS5n5ZCkotalFFmHIGaFKlBSFRBpJ8JiIgyRlSNYfL8+EILoyMhP20Q371RnJNlII0T0i7GfevXuHhiy/wL7/Z43/zX/45Xr26BxFhWRYcj0ekx++B0/sVvH0OIfrP5fdQXkqcDsrefxLFxksb115aFRpeFXqTUR+/BzMwvfolKN8BABIyvjz8CfA048nOdbP4MBfeMQnsxVbb1+2en5N+cX/V8FsgzLo3NFRNw6fNOKmPoz/Qr53AgP18lSZ5GEJPnw4jvDi6fmQj8Rmaj59+Xc+K6YDy6q9wmt7h8e7vUR8Tyl/cI1HCQgSqGXQgTHkHmicPufTlm3u82k8uYE+mTLbwfErT9MoFhGvB8CfwbutnAfMqMDi13Eo2D2vwbfelmhAK08DfeZO+fXTX0c5k0Ob7W+1uFRr74Py99JIJ4LQD5ztRqucM/pFRf12BbwDap9C/Na1ic8XG3xG7zNwigRI0ZKdvD+GclGMLfDAGXNozN04X2ViMJgECsEUhacMUfa2x3j6DlTdPPILzmV6NJcBA3G9key5cVD7C6JS8LChlQa2Tj5d9PMK/slb+u5W3tX4rWbu+2wD39lp9ecI+GCvGiKtacawV9myndAtPNRZ73H+RHlvP6RYdv9nJ2C8nb6n7HbvDAW491HXsU5QbtYlqHXnR8ncHQ+jn+py6Ki8dBA4rJfPQ0qqbUZ6ifBSHPUvKd7AqcWtlJKpybq94SXnmqlFO7ONmsr7L72+fjufe4c2fl7frp9vLn04RMZSXdvE22i5uwGsI5HKFtyHETmR3tURG9PY2hhb/qRH6lwoDTAk83btAj6Y98jThacn4/inhx2ezlNjQ4t86/Ss6PCKsl3U4orc1vlwLkcb3tx73blJsY+N5/SMCRzsE2JmDc7BFCAdGbIHh4ThcwRAUDaxKiHMjiIR0fMIQZIfaqc2cE2gmEELpDv74Ed29LX9BFHjZ2DkIy11LzUq3sbml6j1XfgCMCkpJn69hfjn2dijNspnZ4prb3hbBUlFhWyU5tMRil1341pQJDOYC5tzGQ+buzj3hYjwqSfLlfg6sX4ajWF8nV4CE5dB24KFdJKcEe/3dmgaCpxdSjSH2pNLxwE8qKGWrx9oOdbd3mh2JwZ9Y4si6V+ZuSbwOy22RbG+EDkAtGKhnWAhwAYCEmapATb4fkCTZq3hpBsGAC5NtPXoij7TOJnQupg9DIkKeJlGEqTKsLAuQMpCjcLrvZywtt3MT5nJOKpiXvpJa3HM54XR4xvsfvsdyd6e0Y8H9wwOeX73Gw5s3OD494fhcUJaKI51EgDon7BZJpFg0Fn4pVaOfSRizyazXSOE5xP+VmPiTWGer+yr73ipicQUJtWehC5iSy7PPk446t1Ws3D2O7xax7m/1hLcTqfZeD1Im3xfLqKj8UODtmxoZiLA+jugUlkP9Kcm6GWNoYB1p+7gHW591XnTvkodfk+sjH9MpegZm03tMI0tFgY9qdNj4+9w56OdJrI4JWAlfoKHJmqLY2w6xseMclCL4oJqXXjvAQAA8VZ/uharKZFNY+Vr4++yMhNVl1qom7zGHDxOSWB4HD53hChPy8SeNa23rDJBbw7aQJraWliNDk5mCQDkjEUQxoVGuK2KeJOnbRAmcgTzPsj9TQt7tMD/c4/X9jF9+mfAnv7jH/f0eRLqXlwNQjiBeYEqsLTroFlL1KrP1B1p+p/KUDyzn5r7tpeHaTZWywuhL+ZTzE2bY5WNh5Zzg5yUl8mzutRmErVdbsE0x1NP6eLZhx4sEwpv8LQplJLzXvC/cExJOP8cTLNbXGmTAQ0f4GbL58OVL7dYWQg9KiEBfd6FSY4lzuTmv4XyPR/tHwAhvfOurG+ll/ckMTkec7v4RNT+i4h2WcgTe75CWCTTvglJBeNGUhbbZTRm7OeFuN6nxhZ4R4WwATGltZwtUgSGDpo3nGl3RKyg64bs/GlQDPQvVlWaIE3YShXoCL+deDjTCdz+uKGBdt2n3It0R62z3fZzJwgcRkGXuc87IecKyP+Hw5j2W3cn5gc1il9twhZzXcKFVL6Q4VwGWGw+pwscaeWBun07fMVZwywwP7dvATv/3z0qbtYdLCm1Gou5FW5k2nthYry7yqPFetQsbWTXsqeHMTvZF/b4a5WQfU6LF//aRZFhyRcF6X4wfO1dGwwv/rXlsmAfgZqv/PPyxrpXVR6u9oFEjfB/J38hHbPXRj59LJ9VqqBSW3Tu0er6HTQ3f5FNn+zUePOte8Ea958slYX0Ps2Moqe03tvZgP6Zrz5dyElxBGUSpC/GdXJYj+6MqzqoADtNBvK2pInHg17Zww+YwP/TcW793jXZd3395HS8tL1BEROA8t+QvgrIXlHAobf7u276uHOPu83rbfwBcxx9N6WGIacKyewOiSWNBZky7Ge/eJvzH75Ro8eTF9El3yIdVZbB1obLA3Lyk7fbaBmJAg2ljaMZ7QE8Y9l0mfbIJ9mMdZnELNgvR2p4zZOrCc92hMW4pTOhj4WGsSSHgo2DfLdVrcUHzqtOR31NisN/P5COyg8o+3dOA2a2FDHYk0TSj1BY2R2hGCnMssczbeFvSMp9F6zdVTbLceiXJqrPOT4MXSUYN5CTx/RdVwJgleXbBmhx47kGih6CkwUhAApp7oBHPmofDEjOFeaR+2jq4YHU3TESoSYbtlukGJl5jsHxzGLB1Ys0BwT6pHBMMDWUkEdifknW1BK6lViRmkCb2FQeTFmPeNk2ziK+dwEKiXqkFQ4Kz9x0BSC31nIdnggqUTRlhMAhTQrHPLRvxSGYpLSG0SpFcCgbeKZGHaCqAC0SXUlEzkNlCuqhg3mC8W7/WbwJQLX7lNMkeXhaBARPAnk44LBW/PZ1w/+qVCFtywusvXmNZTjidTvjhN7/G4fERJ7XSvn+YsNvNAAPTtODpuaIsjFILsFSUMoOIMM+zKB20j6QJ3EGEPGXkaYdpmpDzBFDyOVzc00Qtx2sGp+TJxqPw3NdxQJiltrBusTTrtPbXUFik+aIApbOy13WSHC/CxFgbHUMamXNdfxFkNTgALF+NwWZLYmxrPMaKZauP4lj6YsxV2zNtHGIppeemzcE4l2j7bVR6AS18RGeVZ5tdrztO0MkdVPRhPmUwgrYIYyzoRBKaSo8OZBd0rPsmSjthjiWvUIhnG8/FcAYU83wL55Z5pjhE+Bisx+xr6XxhELykSWJ/S9iNBq/ynMxZTsk9gqC41NqrLHHIa2VMkyktNCQTRAFh7+Y0AYlQCuSs0fwtSc+FOWcQS8yzUiuOpWD3cI+7r77En3+d8N/817/CPL3CPO2xLAtOpxOmw49Iy6MoO1KSfT2UTyBD+Ln8nsqIF15eAW9UcGuNP11eaqtn7t3UkO7LKu0ESX7R9zsFNGO4KlHGV/N/Atq9BuEv2jv2wWNfo3V110rXnCnNGdRQzlZR3NfOww3vCxoedx4AzhewG2cYbdi/anRRpAD7eRog1cZNL4ffePqsxmL9Hm61cQBlesTbr/87YCngf7wHUUbKb+S8mpJ7PmisPFE65IwvXu3wam/JqKN3nI59VCJAQMaU0/L7nEeE9X+4Z0oOe86UHH5lvfK9x0NsI16n4fm1YNRCzjZwtS8jPTTeCz2jVr8ttivyg6IlTzN42isNmXF6eMbbu9/o/ZDgYRyr/o/qA4tGxUhIKNo77mDNjRJMEaHhgGuEnA6IjEEy2kKi83PgF51vQnsOoW+2t5yMCVX7eBjKtwwblLrOb6167KxPF63Wyta50VK1AsU8IqbidJQJpzuy2/vei3Y/iUKiJ9GG5Y77vccwbg5JxiJu92EdSsq+kTdh3gcrLH9mWKuIUL7Hwlnh541cWZkCnclvEfTUZxrH9gMd32i0KsKSb+OM3pFn3SijjWt9Rl1b98u0wijX4jN9kIe5e2dTvnapPRZzgFIOOPGT0MzznW7vCoKEMKZEABNKZeVdJGTf8/wIAjBhFjlIPDNfWF70xvDw7TLN8/P0OcrLPCJsow/AzuGBF1mlfAZu5hpSe5kSwmvd/HqtjZf061OX0bLnU5axvlvm8tY+NCI1oU53YJoBaBiCnPF0yvjr9wnvj0psOQE2lGtdutKdD92Am+85EgzNu4C0bYNb2uwPzRHLrId93f0rfmEX7DfSXYgvD3ljlqNKYDG4z8XQEcq9wJAQBcJWzQCnDLScEzFGtwldq8ejrBrCxi1UanOTdY8HCHyyKqtGDbRbRARFi4XmAGGV+Jztn/dLiLKk1iAuoEqa3FC9K2opnii5EQvkfQAY1QNOyWwlECrY56JyVYZYvSzc8rdimrILCBMl1CrWPU1ZhNAWPBQJKXkMPTSt/RrWibP01dIVNJLlHJFmINCS1fpc6xz6MoScEW3vU/emKGgCoWT5GSChmGop8NAn3MYVt3hVi6Kk47Uktg2WJQ+I8C8EC/Vkz5ilz0hkyzAJiZMaTmsYMQrEkRF2us7uGaMKIxP0cWl1kgofayUUWM6IYS9TklAzYX8RghWJzbczpiIAFaULA5VQqQIklh7HwzPev/0B826H3f095nnGm6++Rj0tqMcFjAOIFuzuEuaZMM0zmGfc3+/U2tr2fBZPh3mnDPgkaxXyaJBbhCdUVuZ1EcVSLcGbIQE1AanytjWhzTOHPcnKdziOisRw41YcK3Nk/AxWLf8NVsXlcNZOX9twJrXv28xD2EeBITHrP9N1mveMTIGGIRs4Lw7VjKHC7JwxGKYhZJDDDQ8VmSDdptP3fBOmtL/ovp89eVZgbMGX0CsXSKwURcDDntCFwpxa2KSqiuilLO1s8BwLgj/9vGHzmFFltwoUSD1ubA1s3xL340vZFOwWr9oGIuuWcxZ8GkJJRE8mU0yk3NTTFcVDVZkMIWkM8ZQtlEcTeGWNNS5KMVHM1qKJsBmYspwRGcokpwRwwm6a8GpH+LM3wJ9+fYc83YNoErhYnpGXA5J6QoA1DIXChIUVsZBW3Rr+bsnbn8tHlo/hLwX3jYf9xwPEi3jHDygufIpU1nCeu5BxC/G/pHur8dPwyZufsscEH873d/jFf7rH448nvPs7oJ6M+Go0HYfvYxHySulgamdVi95C6zFx96GHTzzdhm77Y+wTyUYH2bnVWutWYDWdep5cBZ0XAm/Xdx7u8HolAIDTCcev/gaVFtAJKHhGfUxIVQwnKGVQlrwekutKcPNuTtjNEyhLKKHdnPq8PoF2keEGA4W4HvEZxBwRCM8Nxg1+OfU0YajTrgEbshr96VxIPN8ptO3Pp9amv9POuFYNOeMQdp7XqyMEqNFhFrIq1tt7A5N4CU8zlnTAgZ6w0LGjHTrayH8x2HNWDStPcM8hTwbtpDT7XmjhWI2GaPDtOS5c+dY8M91ICcLtNQUd+72IjEblw7gH27fe89ypW0bgQexOv3kcIqhbxW4KG+aKd4W2upsSvtjP2OUYz/9SbP+N0im2b0SyOpSzioIz1fS4xfB8sO4f69HntjsAxLGOCpxzU9CR2JAH3fvOWvPJb7u1tUxgGrUZwyBD23HI5omBbp76vS28U//WBoDpGOK5xuMjGGHhtjRHEccM/Ygl8ClbZ3v/bHv+qkxsfM/e4vau57q0fQsLwyRjNNPFyhVUEyhJHonpbgJOBD4cAXjOa0Q5SD/Edv2Dwpp96Cvtz5mHtvDQh5eXh2bibRozdmtNZvQv2AH8qcqtQu4PU0LEhj7stZ/LBxTKKLsvhNiAhCTIU8b7Q8Zf/QBB0CE2dFeuLe9nWsdzSogVEY9NMvDGEpUXPVZvQn75jNbAq9AbY5ci1WMEutVjIqgxVnZ7tKMAXNCSTFhjJ5cI943gqk4sGbEq31UEiMrF++jkFFfUsoAooWZVPnB1QVQbSyPuXFDpXWb/CxaikZNG/mQGqgiokmq3CXrw2EFUzaVW/jNXuWbMQmqEXdW+1VIlrrcf4pauqrfWZ0o+JyklTV5awZVE4I6sIeN13GUR628wpknjjas1dSWEw9P6I4KqlHrYaJ4hyefP+mn9MaJobYk+wI5DAnS9qb+thHfLv+EdkXAy+j3ClxPMSdj0VCsKScTWqgd9Fx6V+zi5rqQqsjYc9g8zg0sFJVH8pJQ8bmwYCXpiywHT4V2UYWq5Vf2mhI2r5pkCgQ8dt7g0NzhqIVuANCUsZYFbb9cChtibZ4hssSKp9fO4twdkRKqCSfJ+YQYnVhir0s5zBdcFd/evkFLCPO/w1cMroFRwqTgt34PoiP1uwjQnTHkCEWFZqljG6Fo/PUsv807c5ufpPsxhDyNImsBX4+zXIuF1TPDOqYBSRaXk4WlqsCxMupbGDJr3lCmafLWMoIN55bRpisqHhkK2CUOp031RuucdWgaG5Jz1kgn/I1Q1gYMImnuPMAYoN6WK7W1HyQZHAGVTerbd4/vPmEuNu9yNLY4D0fvBtgOhCSBoDXcruq87ZFZCPg9bRNjM/5FIlFQVFUjcLJPR1qxyRVFvnbIsKhyogsctEXa1PENNyW2K7MiaJFWBNiUNGt7T8SZNlE1xXgFQypIvKE+6ltEjMJwL7ikocMsqzLC8RO1dRs6ikJRcEECeTBExwTMlMauyuwJFrC6nnBsVrnOeUsaUJnzzmvDf/Be/QHr1Bim/auEJyzPS8UdpW7Sk7jmIMH4/95wpu5QG9efyx1YaRolXrPz0maSGv60YLu/PzPVItvDdxxQVTqLNqQi2K4CM12++xH/9v/1f4x/+7u/x//jf/ztRRBg+NjwdaR4bg9FrIKVJZb+asJed7lqvpFYZvrQeXs7t2ox/3OAg4Agnl2jkhPS69ZjalXPl2gqs6+d+UNw/w8OzzEDNBzz++f+AOj2Bvifw84T061cgiFc+pYSUVCGRLN9Vwv39hC8eJriRRFQ+p+HTz5ZBPkL2397V5+Jv9PejAt+Np0Ld62O6x9k0ftJ6PRrP2fqOsf7Yduh7/6xDJ/q4P0FRgzAv/mpT7MurEyjPONCPeEt/j4WeG9OxGhkCuPeKdNsJlldtHdJd4L8yQv4oTdZcxZvSW+mEnYHeYRaeDepN7/ypPRd3GsLe62mylYzB9nMYZ8QHGD3gN2eGhnnriETQ8LS6a4JrxcOc8e2be6HLB2/zrXL2Lq++XCm0MRmhhs01HOnRRlcL/7ZR11VZ4fbZd5uIMUZZCO8P3XT6MbZ45hxq3hl9D+O7XHsaO1bXezqFOkZWeGMsY+6gMeSV8b+3Y3BZ49gXPanPdA7oFShDneeR/oWenH8w7iznvxSTqM2UylvEYyKBMN3vwJlRDscW0SJ+RKVcHNbY/+3OxBduHkf/oOGvUO3VV2/ds+fLB+eIOEeP9dtyPBDG464dSpdqGrW1PaN/GajXGtOPn7TPWT60f58k3p4LOHjz+q1tf8wc97J0EcjkKeOwZPzDb2e8PTmVtj70Oi1dgB8MmGzV6Nkfq3qljhvmetjQ3Q/b3bxV1wYWOl99q2e8fw058MZzelJEzbzF1h+noNPe+59GFLvFaBAor05YI7a2mBRmpROsHRf9OXIvywILk2TCpyYcUqEiIfRJ2zEiV61i/IA0gZXHDYfkFOAKS7BtfWIlJgGAzFuhJm8vqeU5ANRSUGhR4VEgNux9ghOstQJLWZoAi6W/Mu6KpDkniERoKXmzxZq/LADNhKZjIB/vWNYJr5swsBG9MtcpKHmMXrU+2VJ1ni42RPd37tuqlthJD90OX6iVb9sf1hm0PW9KSFOU6bq7MsUXPbyu61tNGYasgm21LldlT2PcWm4Pgb42T6xMEbqQPQKhOQkRwiRCdRhdEZU3lcOYNYdDSFRcS/G5TimB5gnLUhqzUhiFCzhV5DyhpqaMcIvvuLbSW1iqd8mz0DxmKCVMyg/WWnA8PgNvCfP9HXZ4wP7+Dl9/+y3e/ggcDj96jhITctcClCJJ2EEZ+zuxCJz2Ek4vp10HL7Z/LC6/hKjSJeeWkJ6VyeLK0iYBxMELhNSHyJmIPpF7ZM4jXun2QzhwelCTX2kL11Ng0ijEET937nXM6UA3D2tl4dkcD3ObM3t5u5XwrAu/pY/WZdsQIgxpnhBeu525q3GGqnxP0nB/Tdt1fe+7p0WALulFy52xeS4afvZOCNteyiKJ3U/HEGqpulBfFLny6YIxR/gNRgiWj6IpH8wqM4E0AbfOVwJcCdAQg1i+EnkdEpopBcGQjYu6gUUPDgBImdQAA0hTE3IlyxHx/2fvP58lyZE8QfCngLn7ey8ikhXrme4esnsnt7JyciJ3H+///w9O5GRuh+yw7uoiSSqDPncD9D4ogQJm5u6PREZmVaAq47m7wQAFUyhXU2gwYy6ljbsychB22RowESoDO5zwKr3Fb15+hZuXXwL7W4AO4NMbYH4LKkdXKrhSTve2L4cyhq5GfzrZuUmrPNZU42OUj8E2PHTunlUG/sSyNR0eEG6LZqY1/PBpiiuCdT9v4VZanNmHD4OBISnz2Eekl5LHpweA3ZcTpv/9e9S/APW/fQU+mSdWM3JyOt1/kbUQmsb6rWpgQRpyE2EhI21uf1t+pc6qNSgmI5cTjZSiJ0Sc1PXh2710XRlpm/G3RW2/Onl8svjOVHB6+XuU3WvwhwJgQn29Q5onpLxTflQ8IVKasJsybm52SJSQc8J+JyGZAumhdwl1f6MiQsbRj97Taw0KiMVnbT9+j17oY/tLdnM5g223t0XpDNmiYDTQQgCcng6MAtx7MtDvrevIxxtNQf3vkXahBCQJyUTTHmnaob6tKK9n1MTAYYUOiSPk8Uk88yOtFfZx7Y3eTAnBzgsG2kWVC0bncm0em6LYb6FHXUdhnwE1yrH8ExGqJaQ2Hjc2i1MGaWdJxIWP3bk7g6BWDrH1K7hHsemFQ+zGC053DnzoFVjAaB+Z35U52fhOmodurcZoePQwBQQArHtGbLcV8a3BZzRbqOJ36ZCtdmWajGdaK5HOH/M7GR4nfUZEi9GBDb+fo/n6e3INFh7qnCuGHzp+aeXTsv0VPLcyoKuoj41Kp/kepRSkNCHRpGff+JMWqklYhyTBuangw+691hOZRS/70HVqzFiA4xy0tDq+c/BvltX65+/N56DjrlZErAuj1zcUrzxuetV42Qxn7lz/DZCz9dYO/eOF+33fKy2P0D24XILtsQqGpygmrlU8PGdIplaWgoI8TTidMv7HdxmVADoYQbb1+gZcV16SD90uXf2FAmIFIQz3/dbl2H190DRyo4XOvNssMgKYkRkzGp6tkQEhMdp8Ox1kSgglmKlnVgxpMiJDw86omfBN/lc78B3ZV/EEcFLIQzWxx9z2kESKo3PmQLRBY/k1QtPqs//P4ArEJtvchonR9kUornkYIN4gRmxK6CARdpOKhNuI2pxWZqCKgsVC8wCAcaW1VtRUkRmIwiEncMHINcMTmUX8q8S9Ec2e4FnhGMNoOXRVrNGrCnDXmPJWP+4Pav91GcXg3gm+t8KFIduG0HYFYNd21nFY2JoWiV6SSFcVUMt0NdWVThIkDFJt0KeEnCxJuSUi17dS67sReIHIiXvY9nECNJgMzGPFw0q5kWBjXGy8orxQpoUZc5VEeUmFoZQzuAI1qZW3EzEEohrC9aDhnxph6oXLMj4CWNUTSeJSo4oi4v7+HvenE+6YkfIeh8MNXrx4AUqMv/yFwPU1mGdVGlRwkbAviW4kJNPNXgSmOyH+M+2VyDVBsDF1s1qCR6tro79JSTpIGl4dj/C5jXYo6O8Y0wlUJhdwd/NC5oa9vod72XpIlNxVWvnLG9dRuI8abtuoaPBVFut/DR+0Sh0GQY9u9+VYHDlZLTuPvcKYxz7i3TS01wQcVi+Nr6yOyxMztskV74GAx4zBNHI+tiuKWLU1IvKcQKUU1FIwn04qkJ9h4ftMAVGZwXXu6Aon+klDIIVQECmEQDI6wxKR9sIRqy9zmnPu7j1LLG0hmKLu1xj4qspR8+wAcUvQTSQh95IqTYnEIwINP85lRimsie01z4yFfUNTODMBE2b8wxfv8a9/83c4vPwSTDsw7THP36G+/0HxKrkCwvZXCuP2PUfolBaby46LJPvfVPk5z8UaPf84PmKF8DTEvIZnIsF5VXn6JF5tIbjSJXU/NDpBPmxv/EYnrjTvbDH5nWN/D1/e4Ob//Rrl90fw//yiKSIASIiU5rUc+1fKRUkwC8HJ7tkmqYLsgli7YyKPwBhBZ/+t3R/NQKnnK8ax6qfVuXjI+m6v4pKv2arf7fs848Or/4J6+xooBMwT0ts7JEzI6glBedI7YsLhMOGLu52HyhO8b964NhpyfBkF8lFRMY7a6eAtBUSgS9afpdj0oo+FsBQWY71P+toUGI1+sDEMDEa4L5tXRBsr6Z0bohhQbNugS9oHYbENzLt+OgCHL0FZ1qO8Y5z+5QT+qgZFxFDiuRiv8DAL8bPTRbV5Q1gOpup8o548v9ztDLKGvzW6vnZKiKq0YFRIyIXdyBT7SU/fuKU7qMex9HRbxMeBhxmmOG6JQFF337p+FFAxkAOY0xYmWZROqRJkPWfxMvX1GxDhTxhq1xLRCp3S8JbTNwtlZf+dupmJ78bxrIPf11/ZfUaaOs9CHQRtaMt3aRzvZjHasfUl95IZqFHbiwv4es+REY6Bg1vv+hrc7vLFvp81UmTLaPpaGd41Msy18yUhYN/jdv8KeTc13haaCxMt+kdliTxQiXCviogdTZDYBK1/4uV+C4Cu/jx6nSzHtT7f19I/q7fmhf39mPJoj4hlGVnH8GS4eNbKpSGsbYbN955BQ/O5fKJCCfP0AkgTpt0Ox7rDv3y3w/tTAnZGqAPbB+yBxe+xdWL7QXtpIWTaJsbtZ8sVcQ62Mx06s+B0yhq8VocaUq9rCejC15hAVfmWoa7PmDxUIUYCtYRlduEZQWbEnTJDKneCEQSSrDYK+q3PCLtQa8xJEkpXFTb5e8lhZbATxkKERCUAgaitdwuPw20OnSLkJhCsEeZ+PkSR0OZaoluQKwrqPINTcoLULq/oTimC6OKJcG3cjGY5K4m0G1Ngl5FEiKqOby0fgq8RLFGyJXsGkAbGwwiTRKDCvaLGGGWsle3N2is32KdVl0HWJtwRIuBilV1E6zG7B0z4l3xdzIIomVtkZVUm6BtkIYCEcUgaEsh2lJ0dI7ay9m+KuSan1PEnAhfSPayjcjq39ZlSAooI04kE7tm9aoIwmdSLhhlcNIkx5KxkJKScsMNOwjNVOy/sFuCcMxJVWNicCAdYQzGwRqolBmUCmESpxbpLCHAvoVpxvL8H4UfUuxtQusHh7gZf51/h3RvgdP8W88mszBNymjDt9sjTDmmaRKCpcFRN/G5nrCmFip538wCh8JcDc53UFVwVe2g5P8xy2wTHMcnjFs3gpLIy1GKp2nOnuutiPmYPHxVbGtEFGGD3zArMiY3fztJGETAkwigbYz8wP0aw2tXRkZxDbGVWwhjUcAW1jjqGOAoM4vj8m+VpsT0mFxjWZzlOjN5PhkMVlxiitq/s44pzpDMpl4M7yVX1BJiPRw3JFDwirI+Az03pgAGfACGEoM6NeSDYPUbmGWF5aHyK9IxnqZem3GAeBIoicGihBmWs5lXHrriA1k/aX5pSUIKIMoOIPazUaS6opToOzdMOiTLyNGGHim+m96jEODLj5e0dfvXbb3D79TeoiYD5A3D6C1J5r2e/MXxsONZWgCQ0oNxXpny6jmo/R+J8Lj+P8nE8xQfc4Od+q+6nKT50Ewp2P6KdC1wQoywk9XHjN/Vqu53a3/LhNWr+gOnwCpR2aHmAgB1e4t/O/y98O3+Lf65V7mrDb4YQ9T70xLmKJ6y3ChZ6UANYWyx8Vjq4h3v8PODvoU4bCWPx0O+J2MG5WXwsoliDi9d+9h8YAKji+OqfUKe3AICaCsqHCjrdCS1VE9K0R9KQTFPOeHm7F9yeMnaTeEJQCgmr7a4NwzFF93jH9kK28PmMAkLa62Uq/jwMcPSY8H8iYKG0lrhvm4zXCCfAaRMbhd2v6gUf7g7S3+Vno88aHx8Nffx5N7wGMxGBUwblnefhON68w+tvvsN882ExJgA9PRH24pDBTgWwjd9pXupq9BBCMrmhAyttgpCDKtC5El5YQydyxVyagZIZI0SlQ3V4Iz20Oqxh3bC2pAIT9Y8GUjd83j579uSUZny4e4PjW4CQG35Qzo58Qnvad/xMK88uDXSd8+TuVe5/bh95zfgowrhyN/WkfqsXn1P/25qiYmyv3QSt4YViZkPA3LoNLRBd3CMLoL0vgYEVN126hq2+taQA9M2Pv6G1vWh+MecRL8Qm1YuPwm8rsPIKO9K+WrjeQIRfWXhUvMLQneI653F0fRODOEm4MqJm+Kke0ru7A3BknN4fWx826nP38WK819Dgw7e1d9buhAttL6SdT6AhH6WI2GYqxgftomqX4YXBrigtbG+Nf1ffxxrR0f/yFG+BJVH1wNd/hkqSbevQ8wPd8ox40vxSQp3uQNMOOe9QasYffphwYiAdGpEGrN4TDyvhYnBCBNg+gOfG5UqIjcunp+0W7/YY9vrifEKAeWQMNi9H7uu0EbA97BGXCu1q6EF+lvNtVpsekikI5jvlwmIMhsRrmEeByqAh/0ffsXBBtYK5OJEIzmrVqWNRAphrBWXrr4k8fR48/0UbM6sACcwgS9INIEicu41nbajtWWM4uKIWoJYZiROYS4tZbrPvYaJYkhYnWVNjXGz+apVQNkTJCWmjWWSeJcSQc81BUklkboJQoZitj8amDwSq92tzsUrI2cDt7ITxrJC5Dqu+Y29U+05ARlJ9kcyJ3RnO6ISGUkoqtG+MBrtihYf5VYJNqYVaE1rCKR0DmvIB5rVh46oApSZoBEKSc38fEAtE0iuvn3siUoKGm+LMCECoEL3WjhkxGIXJTcAMFBQX6tdaG1mbkiu/oIS1hToCh0ThNqcEEGtOkFold4KHiaqYj/fgeUaaCLubPQ6HA25vbsHlhFoIpw/vUOYTdjux2p6mHfJO4vYiCZwAq6DUYAVcCWfhcph9jnx6gxIiASi2nrZOppRTZZlYjiePv2x76zyponaDFgfD12IERltLAHHYFz0qdUK04dWOveiY2wU4Co95udTaFFldYnX0uX+6pqjtswZ7xKZKh2nehYYz2D13osfDKr1K0RCA+7vL/vi9GsaNNmG+JwN4jgN8jR3zD3Msz4smpT7NJ9RaMGuYvhJyGiDUbwKRoIjQiSdKopjT1U85+3nzZN4Uk0/DfyOCe0Ik82AbCgPipOb3NHdjcRxH2dcvaygmiRlPHp/dBBTiCWKhmYrATeKVkfKE3e4GL6eC/8ff7cCZ8JYLppsDDq9e4ebuJWoiUPkA+vA9wAXUKTANhdFAh9s+kTXvc1AZfOOmsTW3epcptS1V96coz0WuP4QkbvjrmTr/pKXdwf6V8KiJXVK4fXnSvhlwhmGr8RZ4TLschMUd5P6loh7fgiiB9y+AnCD+n1J2dIt/rP9PTPx/4vf4j3a1d/gVbInlmxdxDMHhfDNBkG0ip7mipNJB4ur3rdPETh9zXzc8885iocWHje8PKbz6tQmZ1mpxB6b8UnB/+0+YX/xZ7ryakL59BXyQ/A9QvJ5SQsoZ+33Gy1sJxYTU+B1KpLojSywdbBhWlApAjwujkoGu+G7tds+7vvq+jSbtiPwwQZ3YL9IP3XtOYDhtFp9ReO59+30Z8jt0d3ALZyvvNsuPeNd2facE5Kz5ORKO+3u8++ov3Xh8fZ3mkofMZpjRcXH+LNJplpTac0GYMUyt4t2odJMYxukZZFZFhIU2bLRv8ZBOxqsGhYOeK+M3hTUz5UgAsx3VoazgmHModuvo0fZXAlDyjHc3M8r9BLDhKPb/Is5c4IkVGUUsTFtAbb+0Luyn5XNqMoHNBs/M19rdYvx5qNTDs7IX+4fDjRDw50U5YUeXrczbllzVOvBP5C3IHnwgTg48btc+xyq9yUoXwoqH9wC0vCZ2/ttTG9ZZ2ij2DRq3RAfDtTQWcaOPl/LOuOeVx60JTBJ9gThJzlEi50+nwx6VCvD+vl/3cEF1KHrAAY8uW8NddHKuicbHPVd5gkdEvCTWS89GxlcfPpNjW2ttL6bFdy0/uM82rr8GZuAXVIgwTRPStMduf0CuBGjc+5hfa3tVBiQxEl5DtauVEOdKx8RsP7LvcStunhF0+GmlIjvy6K24lhQ4w9zFAiEwANbjueamOyLA9loT7LjFpoaF6HsWYq0GQq+nroSwAyzRrBGCdTGXzQ1Nk/wxiVC/iGDfhFCJyYkata1H5QSURhjFBJsMs7BWRoUbQeVhKZxm0AUc8nMazObxIXRzEymQJpbmKolXm1dE/NvmSPKB1RYbHI1Ir2YVRxiSdEMJ6Bpi0SIQYQQktbZNBJmuGN+U4MSkJlQ2poqrWGiD0eILx70TNmtTGvSEaFR2DZPnBA27ckTPpAkA106J7jmuLbxMYckbULmCKqEQi6eAwmTWV55/oIMDqKUqwd0LFZll3cRrAe0gBMGsuW13JJ/zZSJcJACcJxA16+3xnRQSxTIDs4b2SqmFeSGQ77eqzFCpFdMkiRJTIPIiIZb0bI9WOUzkCbo9/BEzajnhw7u3mOuM25sbHHYHTLsD7l4A9ylhPh1bclvS5LunEwBVRHDDIS3psvmf23gb47qGfW3srAQuq6u8jQNoDGDWdlyIO7ZpTDQGy8SYgLltB7hiCoC41cuTTvEbYeH29tJiZPjdcTo5WmmKBPtvg0Zkw2Pd4DqBhayx7XurEWBwVMyhBQenm3/EORuK4Zgwa86Ye1gCzdsg86ChxZyyh59fa8pxho1FH9cqyq1ymlFqwTwfNVHz7IJxCuBYMm7q2gvrrnWaRat4HyWyvAyW94GCh0Sw2iJLjN5xIwC4xZB2pdncnuteSwRA8YJ7Zfj+DQqTFPcig5GBxJh2ezADOSdMKPjt7i0O0w43L3d4dXfAr/7+N6Ap4Qti0JSRDjukMqO+/RNoPoJYYDKcM6jOOm+hlBKYWlLxdp4/l8/lAeUZGdjnKYFO4VUKBcA2C+kC+83me6I/kvKBnFaaMYEoO240BWQixuFmhxd/9yM+vKm4//NLEY4YBAz4vep9mGGMmcbovwSgsiekl2s/3JPWaQ1zEe7xxmtcWy5xOGfKGrkYPy3Znc2Gyv578O4tSn6HMt1DQmNUlPke9JeXQCYkTqB8kHxXivtzzpgS4eWLPfZZchY6fa+40PKN+R0eLhjz6kX4PSoKWkVdf/19bMfum/E3/xv66yiZYJzRfuzvwfY4KukbLAB1SbC1oza2Dh4bY6gHM1DTsWkIJoEtzEWnbLE+ZF447YD9SyDvQHnCEa/xvn6He36zut51UN4bX2X7JnKAQgYp/6leCp4LokiSaVMgWDgl33RKQ4mnBISfq5bjQd6dSxWDCc3lJHSBjpEbDFEJ6m33C9d+pDZPPNToX+5pMwnJCozLFtuz9Yhbq18bQPjc9ZO3rqy8UC7I6azNVUX9ipC//4kXOQsWnmAXQJN3jB5l/9tCKWET1TV+wRAWbTwP7XT8W8uDl8jCy0bgVvZH/BZ4zMj5sY6Jx60ylJ4vCvtg5R7g4Z1FDZuujQft7CMoK857fYy3drdHdC4Xd+5Vy6/rTMHgL9w7H47vcJzvscs3yGlyfopJPaSIQBBDVKZmUPbu8FonICR4D4zeOJru89ZaXbmdtyicUcbS6nU37gMP9XXlATki1n6jzWdRKw7Y/UMblUMJAp6zddaEFqNwNTLYod1OI7cK+oBwn1C2vAaufe+xz5+jj49RrpmPlCbkPKmAK4Mm7swXOiFJ/G3UVC6Ir748pxLC/l0oHjYQpD1Fh4T6Jyu1Vuv0ooNGdG2+4KCH8xEJ0o74UeIgDiwKpqD5BVRw60qMQFBVZ9S4Y2g6CwmLqW9EWai2GLsTbizJSGtRIrGqcD47ASsBmTSxMFqyKkrctechmdoELoj0MAFO+ons3ixbRHicshF3SqTbHqkFTElj3psVjY09WuRAmEBTyFjc1GTgKYPJLfGzzZYk8mZfnbig7L8DkkAuCFYrQKmKwsbeVgbAcGan8HAiTmGOSdE6QsMogAvxP+NatOEAUE+B8N0Is3GH2L6zGKxJQ3gZvd+WsSdko3WEeZSIcmwQSxO1mOvc8mrIwrQ1tPNqIDrzmcS6PykRKcoogLnomGSuLWkvwfpjzRcifZE6jVQGuGjcWYOrVvFqCOvQCpkBmuNTx58k4YCShvEBSfgbrgWn4z1OZcZECVPKgpsPJJbYllg8nAVRsMi4ItHmguKwFgTABjz4bDTmiISJTWQh5djxi607M6NSuyTcAm9krlbmRdpuTK+sr/+jPwQruA7Ps4cLigKp9Z0e7xr4+fckpYEB7IAdG2vdhPEQNL5OOA2BmI/t29BW7quRSYhClP7qGu+DdhPbPLiirAtlwOp9Y4xMGJ4kgWh7AvAxWZtVw3mVKp4AtZw0ZJ3lSMgurCE9hDGcnK1zWFlZf1M65KaAyGpxmfxckp/5aIHa8kKb8tSU5E0BY6EdHA4AloMkg0GUXfBlioiGu1u7bb5kfXPaAQTk3YQ9Ffzdi7d4cTPh1VcH3L18hS9+9WtgyriTNC4oYJR3P6C8fe2hzpJ5DYa7ypcZwX/QknAbDbes/qiyqmQ+U87TVA/s+yOTwJ+AxL5qTUa4fjpe4Bk2zGbLer9s7IdVAVaAiuOdsjqJK4rYkaZevNEexBApPYndbkP3mlQBjD1iMPY3e3zxFYPrBxzTCxV6ct9i+G4J5U0YY5+JIQKSyu4ZsT4j1k7DlqtKFyN4VssD9xVv7JAFXrqiKRX0GBi8fwM+fI/jzZ8w794L/mUCff8KOO5Bkyoe1JgjKiJ2U8KLw06MQYyA0b9OOyS9d5orRLuH0GiL3mMR7Z6Kd1aoH/ktf238LfXfW+gm9H+9z1CfugpKMwCLJNP2wBUT7V6wNv0EepsUxpMC7NZ29MQb6B+/x0nqTXvQzSuHYS5HvCl/xMzvdcHbEFpk4aaka/SbVDZqMdIfRtuZdyWjorgHb3U+r+cZjVfrP3uSalhIXW2zVrDRagO9yEBLUL25ycPe6GfOPy+E9N0LS0v+SMGN2wHoliTQxet4YOSrtsr4WPilyye7k+G7QmBRa+XFSPMNJOylTmmrn/WuuscLHG3rO/y+0qbpGKKMyozIzOOtGWiu9Tk0qUR3m4fBU2RrLAFnmRJkHU+Pv9Pqx/Uf+rNAsDtwgcRW++2+WrQDBdTvwfG1a/YbQ+RFo/IIjDIfwVyRbybkNDVQjNfVepX1jLF+z+/BGTjwBB6Md+3PQnE2DJRWsoEvxzjAfGa8V8lnBhjWvj6mPGOOiGWJzNpzlc0QIZ1Qc/0QOhL9FNzBA8qnUBB88kIJdf8KyDscDgd8KBP+8x8TjkUJakWg/Tv61+9EHh5sl3ZZ2g8XTtOZNeHFh76PM40OrTxg3XW83CguZaba4y4uZuqR8SJU0kj0quyX6nie+tubIC7KAn1TQjQgwnuBCGweBGYp3Sz7W9gZhstjvBl9z7+au2sIUZEFrhb/tqqAFm4lQ27pbxar3B6Gy6CF5hDyTfCHTVgQnaqgibkC1SxlW12jsYh1rFB3Xy4e5z9amBIlSeJLCZnhwlhzGfZLu0qYEj8KuhawmPlEElO/yJzVKsmNpymLsOxUUD2PBUBJNfRG/KtwtzKDahVhL5F6HXC3xm71pcB006leIk79R+YsnC0Gt3lwwXUTchshFY+6M35qJs+mMEgMqDcBkVj/UbDAImgCM0bHOAAAzeqJ4glZAUL1cxHhM48esWar7skQz3+z6hdlRK2EnJuwlkM7vgOdvlQBLIcJTYSs4RuYSS3FIcLOykCmThivqwiquhTap8fcZzkzctxkUSkReFL/ozrjw7t3OB1PEv6F1DMkT7DzXGbZ1xYuy3q1/dSWOq574IIUgVUEK06ddxOmGFEH9RJKdibMWq2yMw0gtPU7h4vZrELh68ZhT7DjK1+ZgGub8imWyMzFq8ktfAhBUdLiJxPZWdeVMAbX2zVcZPiUZD1VmeGeTzq9zZuIGjwDCUSAh5mw57E/FwgYKdzhUBNIkCtFeS66JkXhLxraYJb1VY+ILjeHllQBToyErPhOE7iXGaVUlHnWcyI4fdpXgIoK+4E6Z5AljA+L4B9deGJWrBkpZ0wpi8eAKiEkgbUmJzWLUoqzoEpgQOI+o7bDpHNY5ln2q+Vx0dwhKQWYoOueMpCmcN+1eak6TwSAsigyv0rf40Az9ruDhEV7cYPdbo9vXvwjDvs9bl99id1+j/e1IlUJH1Xu32J++x24nACYhaDcDykQDzZWxzd2LzftVJhHfC6fyy+qLIQSTq8qTh14ATkmFA/sarvnqP0lqR1oZL8nGPP770DHN5juvgGlfRN6ErC7fYl/9e/+N6T8e7z5n7Ois2BYx/F2Cv1YqEag0cT6M1mYpgAhd/PATm5t3qFX4QDu/mzNzWMVmyNNBgDl8CcU+hP4UFD3BXV6B0z3qB8AevtCPRgSgAPSfkLKEygl5GlCToS7mx1yIlASb9Y8hfsZaMJ/+y31WyQKey26YjMK6P8YP5KcJmo3zZpCIv4WFRiAmy11Cg+mKLxudyAiPA7M8D4Fjz2HwxT8FAF0+OO7MKi6uUuLNoTmbXcMhb5F0UNG1AAgvH3/Lb59919xrO/QFTszYcfGv/7ZcrXZL+oBVEM4JcnDph74tZ2Hnq9tnz2sk2S31hCs4v1ca0Gdq3rfJ4AYSeMFm7IvkviLgxVImkgmjKz85WLC7BR6CH31DhORgupb4UYXG01p8rnrDW8bI3ftK9EEef2dwByu/GrvPYh0iet9Tgu0Bg+feT4ooi72rXMtfbLP+UqT62sQ7zG09eqrrK91BMYUaavAhrPXKTqNEXIGZHsF3EuDZEDjnb025auKJQZAyfc7VuqeLzreSnAZRnxkhnHW6UhDqBymlgrSHBcpkYdEFsOAxaZoOIZ8EN2tDuMBL4L/yAt1hGfl43OWRyoiLh/h0avgknB94aWwoi4NNNvqBG8iv5HzbljzUZzUErR1xHcWpo0yxnp8zrIc6hZsdOH5WG+7Veo+UzizvVWi5Ia4QZoOAE0omPD9+4pSSZJS6avR4njs9erl5MWHlW/XXVQ8fHrMOV0fT/+0rzMQ9Y7gN577r9sIxdonkAvl/A0amgd8fwoBLUL/COOCVuM2Qz0Bo54QHSHWiEN3QaTWLrg213VVTHgy26TWJgS9eAIStyRiBDA3AaV401qy42bRCyXeZaQilG8ETIv37xdPGFdTnFG3bmz/sgptzWomKCIokYbrqaDaPBSgVusUJlYsjNs6yfkYclgwfEzMFUwJOSUnJmI6a7n8JbEhEdwNlPWZeBqYiHlFANtt5HCbciBEwv5ZIxZduWZXL4nlUO1I0LWz1tbD1yJ6agQA2zUTTjCHvVnVg8YSXluzNb7coGDovNi+dIrRmC/ZQ0jqdZASOCfUAlH2RGG2TnY31kFAkpNZJydPhG1wg0hzYFQN5USe1yVrO8F5wAkcRmNiAT0niUSjVIHT6YR5Ltjt9sjTBAZBEq+IEsRc02vREGm2Sygr02VMaowD3PputKrZ/AgcyzuUfT4pDetme9zG4ddpvP9bkmbBdwx0oetsDygmsvNl58DbCWHN1sriGpXxdBaRZLxBagLqmOeC+z1q8xWFZxJWCxoyTSbRrG87wUecAN3TBGi4tjZXds82RQkNe76Nh9pHx69ROWzws1sCmiICLYm2DoxAqMRIKgAzEk2UXDNKrRKKSZWpRMA0VSBVUGagAnMhh2xBC/gYVQASPB8kyXpTQojiUJQhKaU273Y2ABU0VFQujofbDDNMWcKqfE46JpvrlAQ3JZCsQchVYotRq+Ubgp+bxIxf7wu+OhS8ernDtDtg+uJLUJ5QUkaaJuxfvEBKCcdakKuEZqzzPer7H7WPIG1wfBNwM8HPhP9uTDMBxBxn4qpyOayXTd5jqKjHlY/V1VMUNFcxmFe0cvapL/VzcxmfvmzN3xpHNQptopXzWgsNX10Li1Xl/jfuf7Pm6+k9aD6BD1+CKdxIRJh2B3z9zT/g9Q8fgPQna2TgsVofrXejgS1Ea0TnIfwat3uuPTVaRn+5ZmtGRsBfXFY583i76Q4ABmik79rHSq8B/AnzzT3Ky1kfE+jtHdIHCe9DKQHTBKKknhDyd8qE20NWOsvuC31fUWfzjDD8HO6ecP90uQ4WfD35tdQ9D3+tzfAVzQsBXZtGa7Z72dok76vNUxreD/dPuO+6cFGAa1U8vFLXf0JTHmideHfa3eKeEC2sYY+KrG5QdlBywR4zcF/e4m39HtfsHh6/1bC79SwKj9q8HorzEO2vkU6RE/Hzzf3f6iGEhd60PBOaZawPh4aAg4ZpGEtcHg8vOtKJuNIDPbQ1/rqJ4lQWN/Ikjde7cOZXS3y6IJz7miuW4IsV3uxswMML7NyX1euRe1g3jaPXQWs/cv98w5xppRGb93PKm40HzI3285/GhVp5d+Cf5MguTtXidb9fAN248SLpLoruEzNr3UZzjztttajwxWEgUuNPGlY+vrK+fj4vpCNhtIgB8Tkv24tD7j1ONGScyhXERqAuvBsaze2tIPLlDyMRqeGm+Ntm2Th3z0KXrpcHKCLSxu80/LXLcFljUSLx5z8FZLqmPAjvdU2d6YMQCEu72AdKqIt1uLhkzpVzyOP6pY/1n481eGjva++tlQtthXUTfBMIZt8uCWV6gUI7FwpMhxeY64T/8F3ChxO7JaDEjVnpeUDko4CnA5f7s8jxAeDx768dYiTYm7XsWHokS/7PRnsRgGEjOKEY7q+61ufabQAE4e4KhIk0ljY5kVXJQv80way90YhXWqwLob1jeRAa8mRPhMtuIStKhCbEDxb/KmTzoUQUZHknqlrDwmImSr8ZACe9OFCBWro1ZvUiIABURWDNYMxu3U4uCAMxshLNbMl8UZ04Z0vKi1msXaqEgEoULE7ILl6ATXBlly3ZfBWbYRCJBl2iEonVuQnDTPhqcCKRC7xOM6NUsfSawJJoL0M9RkzpwZ4AN+cJZrHDLELklJIY7EAS9bnHiK0hKaHLw94ftrYR4dGrhf1MozElgI/N3mzEVvsFQBMK+79yINwwwQWv1OYHQKllBa1xt29deWTC1JCITpZKLeiGvR/HG9fJLKpkrgVI1sFKDocJpHGdqxFLKqjt6YbkcBgCKFDLCveMaGsre6vCfTvJJt5GzH1SX2XyOqUAoAR/hqidqhJ0wOn0AfOJkLLiDRPIa3vJQg2Zsk8tMGcVXpIqS8Y8JB3KprZ2DFOGscDE4i1hwllLEml7K6Yrr5q4fSQlbG+CG94g9DQ62fXQDjE8GTkAIINhaIl9zdoOtflnv5JcfBsJZd2zHuJpVo+BcJ+1tTGmGKFvRSV+EULCCgUlRBOSSNgu92rQvezxn1nz6liOgrAwldsXAjykjzwsGiavomriaMNJZmFoHgLwadU+gimpeVkwC846HU8oZcZc34H5CEqMTCx5pFJS5JJ0uxH2NydwTajHSfeJbaascozsc5azKCDyboe82yPlPZKFhNQEpIkIvz2c8OXeBFnse6cUwRHHk3ppnN6BuWCe5a457m50Tyhyqm19iOCJyDMROGdwAnKZMZViB0CVIVkEMAnIeYcpEb5+8e9x2GUcbm+Qpwn72zuQh2RTvF2OwPs/gwGciIB6guNGbvRY2GW20RtqCGfJrHbPl/U68fw9p4nN85vr/DWUj8cw/tJKJwRwZNZoMcVkEvbPzSsKKgo6AWjDtH2OLAJc6/sArZbzH4RFmHXmgvndn0F5h3z7DRJNoCKXfgXh7sUBL3/3J3x4m3D/7dcAizKTyYSpy57kyhG6Uu5ldhwcjSbanHFHb/hwyeiC0Pb2APuvC9jWqrd79NI2Lnc/4v5f/x+g9wnTdwfU/Yx6U4H7BNxPKPQOSBP4fgIX8w5MSLRDus1i4JYSKE1IRPjibocpq+IhEXZT84ZuIfkab+CyhPG7zmukqSzUXnenAy2ReQrKiyCL6JQY4W9so6OjtV8e+uqRfWiL0PdFQiPEPpxGcRiaAsLqsL8vbXBUbvi7QcbShaOMbde+HiVQ2oFuvgTSBKKMD/VHvJ5/jw/1hwYmhw8UQpdqN4nFYAdEHoKpnUI9Nx5Kkttnze/E4f42GsD7S2LYI7NgSd6r/+f5/6CUdAVIaUIJX0qg1BIGy74Q4M8JuDuZlaOgIATdeJdS40vHfWtz53Xt90AIm+4j1hGCDS2kZijrAsyn3Nuxva12VhDIAgx6EhjsiGq18TPv9D9sv9nzwG09H9bnogy629b+ovv2UWlYP/tnurZ9aI1005SuoNjIuYPAnw0AjWByYNRcNqK8o975xh+ttdLgXezsLlVq7S4xa1f4hEQJNVUkpJbvtBZvhwmYZzHIo2kCMnD8zRH0Adj9sPMta3eMy1YUR3s4bI7QXVNWR7wYp/3O249irY2+Ai55QHliaCZaILu173ZZdmVQQozDss3cCD6Ca7s2oFnzPqCO6W/9Ota1hR/6flwJhwHLMfVPrbM1xP00NH1t7wsX5DOX3rm2xvcuoUezzqjpAE4HkVwlAtOEIyb85QPhVNve6RCZ9cxrbQ4/R4WI7oOA1uGL3+2JK4u+Ulf23Fjkru+JwEVDW7hiAxFEyj5aavgzRpu71QYElkX8cKGCnEFZJSGoJ1UWI+Jm5b8GmHsxcHXLZLiyw8Zia8IwRq/FvIUThlUFt/2cCeSk7XoMxcFSo6EFhsf4d28C842I8TSNIBevi0jbGzPHtSqfR2H97ENkspbn04ljJhCSCvFs/uIB0HlQqtXmRIahdjgsIZcyZUShueecsAuOCGIZVZywinkpEhFEllsWBOk4i/3fZmm03PMU+u7xh0zXiqU5h7tiWO8Bi4WzFqpp2BiPncvLOja+Zv2kgmxozgnl4WMydBdWLOaC3QvBklH38yH7MpEot1CBSsHqapgrTySu+0Haa9Z6xiw2r4AGt4VismG7klD7kgS92m+4XxveDfgBDC5FebJJDDvigeoEP+Gsar82PAIsgcsaVmq8q56+EpTZnfEIQecQzYAGmm5AcQGCFQtcyAIfv5IV8rhKo30oBX0vHvgFwaX4knz7DiMC4lvc4YVwT7F5DCTl1S0HQVOM1ojH/NXwxc5WFETYf92FSkPdtjhEtrf7UbYO4AIYrpaU3PL82H9FpQGmIDOFlV673aSw7xfZ26q8KDPKfALTPShJaCcCkCaS0HcMMGTxCUDKLInikuR6sawMSceTSLBlggj58zRhmnaY9nukvENKO1GwhNB2X78k/P2rMXk943TKqLXieAS4zOCjKHKPxxNOSHg/sXhIEQUUzj7+JAaemHJCzQmcMm644sAsubEoY3fYI2viVFDCbr8X5YVa8+4Oe1BOmA4736uOJ0sBn97LPRLXrhtIW/owOIzlWtLoEgnZBCdnKnZn9Uwb13b6EctP2fV4y/wcy0gNLJ+slK1JfIBgf/31JfXb/LDX6RK7uf1yosv7VW/zjTMSYFChk+PbJmVYlHp6DypH5JsvIbkMpCkCYX/Y4cXLglKPOOYi2IwB82Da3ic2A/LXvegWFbnDVYu2vIO1EQ9zvvb+Bl/Rlkvp8MRtelZe4P07HL/6Z+S0Q/7+DnUqOL24B7AHfbgBpwlIB1Al0InUAy4h5YxMpJ72hJQmpEQ47CfsclOMG2vUQia2ZNR2L0Zhfnfdik9xUzCE8H76JuLam3B4S/HQeUD4+9ZfM1SQvSh3BXv9YQ/7q0ujMlegdJRNzO0gz6057vYvwV0Vu/6ozVWEXeep+2rhgrqQTBOwv/M5mOsR70/fYy7L3BABaD0v4bGROLz+UpOdWqJp4zci3Rp4MW6fSf21OTYWwrZErONV0Nq0ZepAe8DdYuOMhgNb9XpadKsr7nYABRrZfosY1PvnvuK2wHIbtz/snhvxzTr+WdbvaaUFDE5Ljb+3dnsD6vX3VyFe4f2vrXuBNLpYelaVw++0AGPp7SK8pclTzoFAi/e11PG94I3ggwuwRfkc7G6+rrAmMSNlDBfX1agE8r1LPsYASVfNYe9OTtWoCOP4Wb3WxWC0UkKqVYz4bglmmEoWQtH/wv+uoqyH4IcH7Md+2c+t8hpADUs+pDxaEdHiGPe/xb/PURzZmRKCebX97bBMV/bjmrfzsJ9v7tMxRFJ+nizK6CFzml6iph04C1O9PxxwqoT/+O2EDydCMRy0QaT/FMM8t5Kbd9tWW5vnQRHdlrdCd6H39ZcCy3VgaPGL/d4uYsH1HC6jpolfe388g6YwtHqVgxIiImMXkgbLk6reCv5sGIMrIeACYgK15NT6n06YPzfg2Zgalh/86vHxWTxLgdWSFCO1/BUEQk1AIh13okacowYiXWA3z4a5JOSaQNmUAZ7MoLvGGy41yxwGiJGywFlr1TOk2nWtnyiDE4OzenQUWzGSuKZ1RtZQI7tpAmfG8Th3QkHLIWHrKaGXVFBNZvWsCaPDGGOeDiQIszcQqrKvlneE4QPzytAmxZX5wlkyC6Utat0YPon/Tv0GZnh8ehCj1oRi1se6/8wyXMK/BIKLhQiiKuGXZN9Iszkl5ymZoZZTmhSSJUa8Dl6mKwq5kzB6iQgZABUAiVE5iUB1mDuz8paQLWJ57Z43KalvRBuzn6lS0J2rjlGrmEsVhQRZEm5hZGvo2yywiibntrwVxqCPQoek79n8WO4XS/4Hps4lNSo4DQ/YHZAoCTG3C3lS9NiWIPlPaslueTpMqJDiPjRFEwJTbHNizLkz5qnf17GZuDi6f40NhOE3ICRnbmfXcnSI503YooqLzFpe5qV1Y4rbNtciWKecxSonhfOqLxPkXIAtHw90Tkk8J5ajgVlFNkWMAmLtBXxlOW5KUY8IVUK7lxX3oeds3om0F4biE1U+MIPpA0AnzDyjooB5Bs9FQsWF8ypzqXjcJGoJyDcyj5PuZUqz7O9UgboD4RbT/oD97R2+ebXD3/3qFrtE2E+TJqi2uQS+vCXc7i2RtHYAUTpUZs9bwccTuFacThJG6uQWlIKvLGl3KVXRuMYeTxmYMjAlTQivMFNSBUnWu0M8HcAMfv8dUGekUwZOAN8PQhBAPFR+pjTh5/K5fLqyQtUKMn6q7uPJ8ESqhmvF/PqPoLzDbv9r0JRAux2mF7e4+fcv8OHPP+Lth9+D3t8Ab74BquahMgHMiNM5fODGWy/oe/T89DXGVg7/yrTaPbH2fLWlVFDufo+6f4/j19+BGJj+cAAnoNzdh9w2M+h/vgKfdjjlDFRCfn0HKhnpZifGbSl1dyIR4eXtDodddprWlM67nCA/6d0X8ibFEEHJ6P1IL5gAyz+GkE6AepxHGclgzGU8sjZgYY/86ncBWXxL//U2rWpqvEZotzOHoDAE9G0TZadzXGEC8jxU8eXk3w0gCnAF0L0P6p+hzXEYVODhSAlJ5T8YKG+OOP6Pt6i7E/AKZ0rY3fEjDfvQwO9+N8/H6rQoUMP5HDdy8t/acJMIGa1rHgBBkG/pv0LfqNETlmczvrN8tv5rfNoRsGsVtmQVFP5zKAJMLj9gH+bPm/JY5x/9adggvawjPt8e4Taeu35WNkWaT5jYXr6i+5VsPGtzsXo7dOfkTG9XKWhamCkOOIicRzSwtOeN94Exas8iZP5Vl0+7x/wcO4e00rc+ff/hNe6P77Df3SHnnQHQYAuyK2INOc8sWR4H+Z/gnXGexr6b/OGSuL2FULtQcbuFB9Q7j4O2yqMUEZfcxVZ+bJ+vPEUdQaZ/ozLipyyL7q5cz7PVNpQ4Ty/DDRuf/ETz5ltxAMWywxeaUJMoISglFCTMyHh7BO5nBuVRqPmAvmnYL1Z4vP6XMK82FkunQeXlGNeaWHxYpdRX0MxGYe2ZHYKlRnMTqLWzqdOklxEN7a2jlSDuN8RtT1yqxitciRF3hmztUuPw3Yfp0Lb1tGZYhZEmwNILlRlAE97Z9dFCdLDDxt6qrWO85poQWX4LFnI6KyLXM/uzwRpOhaRcK2oCMhsRzW2+49ws7hy16uXsEyCWa+12NGG66EXMX6ER9Zas2cMKpSxxvam4ILdLVaaJYR18tco2nqN5AMDnKIK/ahw3loDMheYdLnjfRHFu4i6w5RsYgka9wGYHxjguiinxxIrarJ26/pgldFhCmCNd65UzIrRS8rbMm8JK1YTYZLHmzWSCBNZECZVU2aThiqiKC6edl+Uw9PekISXI1qFZOjons3K++v2q4KYKd+uPD31WqXuxxdBk3wAc6rcpVWUAqWW2y6N1TautYfWexkK2yUj3jYYKK66UolZPZl2JOQ19lVLXahfabJgPGj/5/hpg6uYAILakaEuhcDvDEUjda0ExEqalzbd0ZChqsV1FOGLCa2pCjoUGZdhI1Fv+tDHaXAbOM3ymUEfwd20KwqBkrnqORBHc9vHwOixLuCR2FO+Kmk5I+QhQEaWwKtIMBVaWXBLNIjU0RwzKEX+x5resoqjKjEyE3X7CYX/Aqxd7/ObrF7jdE273Yh1r7aY2YI0JThB1H3ky7lJ3sod3Mt5pnuXYVVNMqSKimpdHcWglRwWBMgEZTeClScan/U6UD44wEsAF5X0B13skDX9m4a9iuUTvRau/h5JbT6Ykr+WiPhcvPy3X87SyvAXOVR72wpV8Sk8ZrDzf5EXbffUpyuY9jJ7uBSrq/AHEBbwvkBxTCdNuh/2rO+zfv0O+e4PCAL8tihso3D/r1LvfRQBaPrVAtiPSwleNSMcVv7VnXLfXiPMMjxViJEs6oezeoB7e4PTFn0GFkb59ASbgePde1zCBjjukH14KH5mzhHmsGlJvEpqbkxmlJPGCywmH3YTDPiFR9gTITnuh4f6ofCCl8eRrcnQMAGaIod+aAsLvV3SfG23ajB7Gv56ta6RPBqH9QrkAyD4IeaYanIE+jr939/0AqzEA+nvzgLDE1NpfB+QwpgAvBhiW3sumONHnKYFShsl9GBXldMT87h78oowHpmtnbddtnIiNhyP/2urJnekM6cgNXeipB3jEBvEEe501wTg33ue6kQ5Kn1Votp85vh2bNTjC37O448KdfzXmCf1clp9tYqAL723JG88rrWnpZtbefNBF3m/wXhHymNLvi7hsW3MRlQ6uIECrfwmUntc6tw6ksESlRC+UP783xjPTUwjr8oCNdojhnoaxV+qrQfM4lSIhZPe7W0dznfiRw9yR8rwWYpsAZPHgpoJGo8iLG+clyB+upmXOL9TaOp47Vuvr3vPV15YnhmY6X55DuB5RuuzLrYX5Wy4/cxZFCZK6e4mSDnLAibDb7VAx4T9/O+H9TChMEoFgQ/AD4Dk44BX4aHmqzp5AJZgvMfoXQOCLF/bwmidNxUKw6G3aizF4eHju7Y6KML9U5IKtqB76yAQp4T6CewIYemd7lzHOsYXqKBZDvKpVfpekOVp/Byq/G5il+WL3iDABmAmJiMaYgoTK1cObmEWxCYcN6VteC6g3A5LFKRe4aq1iaWtMh+0ZNsalwWttF20r5eCRwTIfFS12uj0jTUYtoXzi5RuJQIGxJhE4p5Td2moGidCvWlggtb4FaXgPQs7Z16kwD8n4CCjyZqlAVsE0Qhx/cL/vTCkm/wwWCVjh96nlzkhJ3XuZdL/FPRTwvRHmFRp6Cp74tjFNgVlMgcGxs6rdq7OCWkYnzBYL2sFTF07dJ7bfwIDk7WhCXg8/ZrkjrB022BpLWcGoZQYI4pppDK1upZRI9hKy9kUokNA2Nh/i9plAukeYK+qs29Vd/+Ougc+NKb/mMvtzAiHnwPBWoKAan7+Oa+36TQlmwb7Ac2x+SLIACTI2pATiCqoWSkz3ocbRJEByXqQ8tqi6Pfa5l9wpEpvXzlRjSgDUJjTQY7VAgQM/HocIY+8YtHA374Dq3mMfkyQnVHwV8s6A4N4Q8f2WELJ5IfnZ4qbMgs4UaazVnEWYMk2aWNkUBoFrFOVUUARoAmYJU5ECno8TaDvEZqh5Qshf8fziWjGfTpKw2cbLmo+mVN8LvjaAWp0SsuHYUjDPJ5xOM0D3yCqcslxC9l47i+x9WRxu8/gwfGG4KOn6JwLAE1Bv8eJ2wt//3Uu8vLvDb3/9W9zd7PDq9iCvpDYP9e33qPdvYRNfg5LbGVSG4FwmwQPQzCGKDjssbrmAUvXfSPE+ocJdQeFdgk8JNSTZsXPA5V6He72r+ufyuXwu66X3yJVi97fjPPn1anFG1761+Yj6XGbcv/mD5DKYvkDevcRvDv87br/5F/D/+h/w5tv3eId/Br97AX7zK4gIpXYN8Qg5Qz3IDIcNfcff7IcNgciSxVhXmvd1AFDFu7/7/2F++S12f7gBHTNOL4+ouYCn92JI807ycxx/VYCSkN58A0JSw5qM3d3ec9zd7DJe3eyEPlB61hTJTt8SYUoJKWteJL1v4XcqeZ4imPHCqFigJiz3+9FoT9J5puaV2Oq28CBRwSGP+7sFquweN0x7Pgj4saLUiDBGgsfbotBmeG40RBuazk9q4w0w9/2Htjr6KihZqMHfzUfXNgHTDnT3DUAZKWV8KH/BD8f/hh/TP+OH3/4eJZ/Q3Hzs3l+j04K39cC/+KsswXiNwwQbYanGFRCaQ+g3VRUQGtvqvLzCwPa68ZUrvH5k7Gz0JO9RSiGXxbJU2NAt4P/a2RSqiSLdsqB5w3vU47ZuubqVD0Po8EsY0srYfk7lejn+dRVHRdGVLMPFtiIMD7dq32DgnE83b5+mALjUVougsQXr9vtSt5cRrCsprC+r1Tbt+d76Wzbq64yXi6WJbNYWikAUoj6QnCTw8h7tPtg9U4XXdTmd8oR2IgEN3kcAdsD9b4+g94T9d3sj8ttQQo5c+anHldfu0a1ybgmjjnF4svGG8SkPg+lqRcRWGKat711ZA2oL0BWB8BLJbRFFP0Hp8fYV9c9XOhu7Cw9BO0/bjM9dRrqHAVTK4LRzAmkuCTMlvJ8J72eoVWds4NqOzv+kpAWWc0SrH5c/cH/jYoWY2QLPsWFojVegaVKilVYis7BNnKyCrsRFZ7lLzVpmtMR1wbgTQXVgShpmkoRoW0wHeevO5FW05NcuoGp9NNjDXARavM2a/Ce5EJRgjBuum8J4itq7BgPFZ11MTyE2m7XWClel44+EYNsmsR+dsnjR2pwFxU0iQmWVmm4V1na0W7OoT5SQEqOopF2WsAlFTbSbEqFWeLinMBQJkxMuVu6+Wz0lwh2OwLwT0EcOXZaeACbfJW0/tpwKsT9hJhoxxD53erV3CKf10mbDJs8WiNxC3bwOhMfsCaX2mnkLBB8YFgvoCgalZoG9UDB228/2roT66sgaIvFAr0KkVEA9UUJSbQI47BFBRxVc05D2Ymwbbc2UOTLmPClxypC+xS88OJ/r5dvWSfc9Ly23umnT8yVTZ/AIZ0PMHgrTcaqtS9gPfrRW8K0rXgJuNIawksbcJBYPFBUw98qarjGfr1HUJJDLeJ0QaX+GmotJCE9XzkboF9SUEO1sRvzaQlXFkA/mBZGCUq5TCAfUZeGF/C+C4m0EjA3AHg/LsLgpgrl0CR1HTzebh5EmkJ+LKpNnlHJCmmYwnfyoks29T1a4BW2MRLrWEJzleycKZURZmNOEu5sdvvziBl+/eoG//7uvpQ9VhhaI9wVzBZcTeP4QllVxVM/hBGZKsCwZXlrcQ/Is+VyHM7q4RHXdK3U0geEW7lp9CJ14gVYfytXWiZf63ILwU9Ly+KRd/02UcX/G3bSY+g2aegUzrX4/t1ON59hqc7s3fd8E0e0Hrf7087E1R47tmMH1XpT4e4CwwyF/gXpzwsuvvkK5r7i/fYNSJ+D+BBQCSoZQTILHV7f5BqnW0NOAZVbqj3jIXmtkVlGioilfnWpLjHLzI+a775HSC2TKKPsj6r76PUa8Fzy+J+A0gfgGCRkTJNn0lLMrIvb7CYd9BlLSaD6kwh7FxUO+hqZcCEYLQeHA+t3obM/zEJP9Op4np/+srdEowGgfX2tquNhh8KcZprxYlHCRyjj6hxTatfpON6w01hQEXQf9c0Lb8w5XU3YsXgvP+mZT944Pxc+TtZVAlEHTQe5VZlQUHPk1TvQep8MHtJC7xg8tN2ijtgE4PRLq87J2t6udNuXwiny2/GgLj9ahJecH2j9nSuOpiVZAHPqQsx1pzDUsgk4JcU2h8dPGubfxuxU7Gn20IsrD6oNFhecp62LHHrs+BX03j9LzjSz0Xld1enbVry7rXfEw1crhnIXLaNyA2x+ghGjwjO+s9d3vA/MuuX6tdF1Cv+u8xzblsGSJlC8NCpMeYsNf1UNzR90Ka3sM4ftNHsaJRXGRCXyK/JrxCxTZHnlMK8Z/qyO4UHhtJMt22jxs0GfdmXpceZbQTNGl70nlip22QTs9uVwF+zN3/LTmnodBfFw5D7mdGzucbr2rwqfDfg+mjP/43R5vj0BhJXZSE0w+V7m+pcur0UQgj2tpIaB8zC144RKgDmG2dyx+tikhyC3c9bm2VzW0ksXhdy+MyqG6A6F99oIGCSmjVu4slrPVPCLY8kG0kEpNqMxo1vfB2r0TyrVY22YVv86oNsEmUWvbfncYFpeR7VyNscsydqYKJkJvgUoAEii1xIZN3yOXa0VBrRJTX2J9wxUoVeeiqvJALKgqKidQsBywZGak/ftFB7GElqSr4hlBM6GQWWADc61CMDM0Rm5CTtAwKGH9jFkjiHA9eIL0glF7g5u1j85aqtXPsM+o3LyNGQp9RTfPaDnQWbczYLZK4uxhAnjBJ4liyCztsLInL25KsMBMyLYAwba1hEsRK+3FRtI1Untoc+VPABfZi7VUoKh1umicunsqpYzEjBPPAOseYgntAtvfYS1yzqiVkXNLuC6LYfsAACVwTqBqll7Qs1YdZkCZAmprbILnUovM7czglMQzQhkq81gwy3njwAyPi2VcktwMFt4KPDCqjX0rGqImK87JueXhkOEFZaeuFdKYC4rgIblUQk2QGPucAJTZFZ1gsUrnziI9tiS/Jmh4ARrylUAFEZH4s83cEWUDHWS/kpzeNve27/uElAZLp0CidmdafxHDuSeDCUxUKJIshjJ6TOafNJdHnjIILf+EhQtCOMdRYNLJiUm2v3lCnOYjaqk4zSdwZc99Yji6qmKXwrvWKNcZx5nBuAfyEUwFlGfZZ1X2ShQWVTIYgwBDuHD5ngxr5zaNkqUdxAmod7g9ZPz9b2/wxcsX+Mff/SNu7m4x3bzA8f4djh/eIFNCShn89nvUDz8CZUbLPD5wAz7B4bBTC20XlnJ4oW+DALRk6klrNUWr3EG82B8U34/gfC6fy99oWTmh/vvFdzt6uT+nl3hDv5MeURoLv+yD5UH3uWpeA94fMOEb/Kb83/Hlr17jV/lbvDv+gB/e/zPe//4Wpz/8FuBmse7GKxs4rBtx+G1Rmbtv/dNolKKlHr5HufkWXN+hHu9xejGj3BRD0KivK+iHr1F5D+wSpuMXoLmFwaM8OR1CSEgvJ+xzwpe3Owm3lDXPAxJSIskJFPOEBWW0XUBj8mloPbkT2/vsXgrqOaH3onsvyEPA70sztLCfliGLXLUQFRz2Dhqd3Qxilpje3qf2pa9Bw26ytsd21i4R+6EjvexNJyThg+xA7LmWCFscf2yfBtiqOxyTeL0kWX/xgDTTsH4f6hXZumMNpht5RaUzmxcjQpJ2VWhYmE89/6S8g/FnrN7iNm/F+6/+jtFTxl/WGn5TC3Q7hv30NExglIzlwhoLK1Fm+E7Ij0YbLd5Ysa3yrrpet3DlqBCrraYTmwFe+zzs+09XlLblftNcH9LmGSF5khLi0xdTOj2hBW1n+RsAZYXjw8CH0bX7yBSPDckIe8zeR+x3bTyd94niFBEhDbIQJ/bljnj3/gcQZdwevkBKk5/xKDaqLLKSmkhyayJhJQhA6AP9weyEI49Zi4EWOHcOHtRHxGEP28MPUESMnawBdwboSwdw63lgkIHLROGirFTfbmMDDQecu/7qNkwXob2kTV3A8vFZz+dQTEeEwUbUqYXJsWbMyPhwItzPQMqsQhojzgaC9rHcxbn3r2hqAcIlOJpcZFVb3gj9tcGtQLEmCItt9vg6wGDEbItJZ4LxNsdGtAT4qlnfKjHh+KqdwcbQRDAFJ7jSgCHCf2NooiCYV1icIHRbQ3yR4IqEYkfVRWJ+gI7d9HptjtfWwuoy2qiNuIznw8jn1L9rY9S5Z2ZNC2CW3nH92OuaJVPDNxz2Dw/vQQnbrO9KIlYJd0RtXpQArpyAWpFzRmzERiqMl82jwGSC55Z3Y+XC7j5RI0K7Z4F/adMWlsDmbLm/5I40JUTfm21Vv+xtzyrhwLr/3WIpTF+3hLbfdU6XhHfDR/3ebfuWIeeHUsjrEJgtZmcv/IGdrSUfKMozSglUCyillpA91PF3qYU6svl0xaJ2lCJfa5PnfEM4XUZXVRajPFuDMH6bb/KHAaw1vCIUnL5LPg+ke028UyA5TLq35FnbN7q/FI9xCMPmTPISPVlzZ+6M7Xt/eT2P69/ejeOR+WkJDKU9w8tQRw3q1n9xvji0qyVRE7C40o9ofGX9qiIg9fGCWjilWG/xYoSJmxK4VEmIXE2pm9rd7fhnfF8NE2pBrQWUCohngCqIquMi69cwrOWC6fGhHayoWG8jSfBI29gRcLtL+OLlAV+8vMPtzR32+4PikIrKszAFpYDne/DpPrSnC7YxseS/c3hne8vR4kvbM3HqfHzWluKquOPO0UFPYRif0xjkcmc/YV+fC4Cn7Y3HlOdcYWur3eHt7Ier6io4NmR9y9IumjNtP36UizH5t4bvBFe1XBFp2mO3e4X84oA9brA77jDf/YjymlG+P8k9WVkMYYolIO49biPaWkJzGV4vFeK9lU+o+eSV6vQOdfcOdX4HTifU3Ql8qBpOlLA7vgDxHilPoJTcmMP+y9POlQT2d58TDnsJSZgstCR65ULv3WB3c+AR4jMP0aReCEqsWrjNRehPavduUyIEAsvfD9+7NUXLr2A3XBfGCd53eys20tpc5H1YKz7+C/WsuOC6b5vIyL0hjBTFWkYztm9dnwPc/l6k8aAKKFVCCX2rRlj3BXxqHghmeAIAUF7AjItMQcDdf0rjM4aZcLO48F945ryQkxwgM5Byfs9CsQReRDkKVnA63sZo4AGOWEZ81gTBTol7nQ0q9sy3czXPF0bjGyIf09Z9IMSJNvFse4WHH56jNJ4odtGeUVfv+vLwXLUPrf+Y8vgurnlR5usxnhBAD9taG6PxFzXCWl8674G/VWj4EBVQS8VHqGxnzcn6PiyVQMdaW+UAXMGoKHVGh9iUdm/vhTaNXyeg7sSokYq1qjhiYNAYxpKsMSQXqKBBpn6+buB9ri4PX6NHeEQsSDn/TRB0I6ncZQvXIrmtATweMdGAyp9CgBM9Zor/Gss1K9oE2WX3CnW6xe5wAGiH//z9Dq+PkmBXLFr0laUs4ekTzosPXWfPceV1sTZX4G0gnBMTWQOhxogwrmKYepgWcK4MmCEW4RZuQ+i3Fi4pCsQjw9QhMgruynEczCGRqSFtWmljZSgdvAxwy+VQNQnqYMsVcL/Utx5rzaAUYtFrxebhENemkXYU+m5WLanxNNZeimunFjBEQCWw5iOgrES2XjCMqp4JLUmvEbhkFHUSi/IMI/LYLzWuFbXMmJndUnq322FiRinVLXEk1FEFJ1rMt1yc5DkGciKUSr5u8wxQqpIbQ/vo1zckGFZFhsV1b4SlrWUkuy35HHtfHhOeudvzcZ+ozsDSluilzP7ZPCYkjivaPjGPHiOYVcCdUpJQVSggnTe3jms5FOVdU6YRayJa0nBaemZSRe0sH3rqYcpZdmu1mLM9kRwLJUKG5JJIlFBqEQNtVzLoO2Y5rhoYCWPLKOptY4lxu/1K6pUQtnz1s6mwg5FqVcaT0FNg6/jf9q99rrpgxpCVUj12c3jDcx32llue5EatSWyu254RtCMK7DxlMEu+AYdR9wk7PlAGToUEVbKFyX6o6/ixJzx18zmSCURmGE+a5Ac3cglMkCkdGRqiZ2TQfFlJ1tYEJoB/RodrAPIz3q9F+CJeOUSi1ILiDpYcMgR4uAlqC4guXITinMqMeZ49r4OFVQJaPh0Zq+6RIMCvmg9oPh0BnJB2R8GBp/ZeIqEJ+hGyC25MKWYCBSPkE2VZU0sCo4iDEmHPBf+3r+/x1dcv8bu//0fsb+9wc3crXhlvfkCtJ2Ri8IfXKO9eg2tBZ8J0ZSFue1YnZKjg/7SizASHf2P1zo51DU/oP5/p0s/lc3loeU6B19NLpK1bERwqd9QR9e0fgXwA3XwDTFlunGkPShm3xx1+8/4FXv2bd/jwxY8opaDMM378lxkfvr1FSUCtBMmSGfDNYMiAhbDlcqFTQn474fjln/Dm3/5/QO92wNsdatYu8h7p5S32KYPmhJyy0Kwvd0jIgvNJPBzIPHeJ8OomIafo3aAKiqCYMPpEcKHR42bYlvz+9H+cX7O/IuxOmhui0QEqcA9WHOR9NQWFL1hwwTRlhr0Vl9PeMXh7uriHc9yh/o63sbaHxx200sqZrd8Zd/Q/xNtoWW+tRyf1xjlf7bnt55e/VUVEdiHd/PoeH/7jW5x29+CvlA40Og+Bc1MauSjfWYLXJwc6qUYYmAELL6k0RSMglfcc7vMWMkbrVZZcFBUo6hHqRhsY+OVAPwpPAPGyDqQ1QeidxAIrD+McW9sS0tLaX/1nbR1o7fPGfukkGjpPJvOL+2Rd6aLv8tZ+eJ6yroT4XD5FOafEiM9GpYSUXpNnCoVtme6w7orXe/mF94jlqcJS+bBy+MTQVPI4SL4hxru33wNEuL39CjlNIJUbOK4ylKGKzEQJ2DOOvzuC3gC77/fwvK3j2XG5x8aJch61G8rKzLQP7P+2F39K6ugJyap7gZ3/6khFhVIdYrrU3vmyKVy90O7Gdb4Bw/IA0CVsvFGeZJE2ADFa2F/X9Din18HzLIrpIDmklEHTDmnagVLGjIRThSYPOwOVH5LInF8PFA9/x7JY1u5QhlY2tLerbV0J1TrTsVZzhK0B+dh5GTvprEVqE/K5eKSnNiIlswItIU5kr8CQZ+1ffeAavv4iWrSHvk6H1LGyX7lF0vcY74AwdhRgWOyQiNMUJyxGPPq7DhdF+CKENDsP1LeztrdCHQbEYpck+ZEKmqMQv1n8K/NCBKqinCi1dHultyiGCuRldMJcJSRq7pdG6DN6QecwPTBLfx7WkRevDIsU98i1hGLcAtp/zFlXUaFRgmWO1CSJbfxELUcBxvluDUXiOnYucz6S90pkRI8e5rA3GaasEyMDcgH5ehxY0j2aIEmySZUm1c/qyittQGE8HP5KUt++Q4acezuGDM0YwSy6sEeglgV8+l0UHEODZCAPglyGxsNc0hkGqEW1MUUYpUER5vemrIEln+7cyCHtMFv4hcVuH4oSrWtMXLT0CxcMBxzE5jVhWHGN81OFjSm7XChhYSOG6vZ5fVuYcKXty2qhEv08WGM0/A1ts3o+1KbkbNxx3PdL2MAFDAvNNwNUQFRVASZeV6RMwmg8Yktvv3e5RRT3dXe5vpoYmJixz4SvXt3hiy9e4vbFS7GyBaOWI+r9OzAKgAKaT+ByWpnBMLbNoM0rtPBKjeW39bttxC7r8NjcK2YdaMSfU2kmAY9AJh9TSvG5fLLybLv0yv1uAs2fos/+sdJXI+mz1oYLr7sf0S7QAuAE1Fn6mETST7sdEm6xKxXp5QH7aY8ynzCfjji+eYv5HQv+rYDaaDdLTL2bTFHeC12ipbjCMoDNAFJJ4LwDphPSviIVBpUM5AmcJ6SckaiFEM1ZFRGU4aGXiJAnCbFkORYOO0CiLyldmwjQfD8UlQeNiNB7xBQUQRFhd1pYiBZ2lFoyZktWDaOng7cCWv1Fe9wUHr1RQ99fW+ZVhqC9MSpQutYI2/IFwmqjAwzbz4eenBfony8UFWu9RmVKUGhs1G5NTROIJgCMygXH+g735S1O9S0KjjCfiHiEGo2i+7gG/siUDF3d8bYO/43nNxomGM8TOm99ovHPjOYN0Z31jVudQ9gbPfK9IUysiw0SdKufSMxdwpfjOgVqpQLzB0Y9NeNEo7OdKvHv6rls49jA+LFOG9zTythE+z5SztfeHf13inze0KbLPH9CMuyhfT0cNr0nOtzxuLm77p21l9aZyqvaJz1QEV9cORYOvFp4Gya7cNo2eGxUFqNXOcQb7Yb/VYixFWUC7YA0abL6wtpVxF003M0jZP0dvTkyZ7NHHoTCp/D9QQv5sEV/giLimqJD4XEDP7w0F8Qr63efLk9KdHl7Pmr1Y5SfH5O5KH4/yRZPU8bu5gY3t7eglCX2uVmnByLLLX1XD8gjQPCmlkjkuhVmuCCve3ss65dajRd1eL6NGLae9ETXgwUNK3imqsdD1biZbrlRq1syx75iXEqjgLaEJB4Who0w00dEsDBGFIShZj3UG6E2xkIBQNseFRwFaUY/6msGLwPN6tyEee6GLYKvwsX7lbbENIVkcjRckVnISAdmncXMkh/AJlY3HYf5cwKN5V1haqR9z9NgMHoM22bVBQC1VM3bQM6AuUAQLf5hSiwMX06gSV0oZ83zoGFcxGI8XMhUnekjgoduSqnInFe5CAtVgKJQNK4NlDC3JTNmIKwLbPy+nDJ/3As1GXGftfUkQI2TzCshNMvscWMtbE9NYuktlt+DF4HDZsxckvwdOl6GWVY30biNG/7MPA0aQ9qUxIFB0zESEywqVuoSE1qf3AToPnZqlvGVUKlinmdneOwMt0UIy+HMtVhqzbOsO7VeQZDk5WA5BwYyURJz/qqBHHIWtQ6FGQkKMLcS1GHXUXkTzqQsYzvoTfBMriQZ9D5+D8SQU46X1WsjqZInIalnCscG5ByG80nq7VIsabtZMyouolTjqw6jeSnEsmo0oO/wynOb5y7Egd6DFO9ExTMp9FcDfhV4koZril4Ebc6heCcrLikaSqmUua9Mgm9yyt6vKQbsMNcyo9SKeT6Jpw0XQV0WQ9n3v+WtEMJczveMNL0HUUGiWc+FtDsmCW3z6qC1Z5VgJLzPfZW2JOeHTWjCxAX/10PBV19+hd/9u/8Nu7uXmF68FLjntyjvvkP9yx+AlEE0gbksdGFrZZUvQdtvTXm7UoZ70/BkC9un1Xy8tW8n0hKR2f05k6yfy+fysyxrTDY7bcLDWV1TiLES5tu8CncfW4/noRrryT3J4AQwzyjvxDOCb74RSX0iYL8D9hnpdEK+vwXKCZiP+Or2Je7+zYzT8R6lHFHKUXD5fEKtM+p8ROUZZS4aT9/uvopKBe/v/gLW/DeYM/LbLxAJMAajcgIjI08VX+L/gnSXkF9M4JxRc3KP3ZwmyWmWNLSSeiOIFwRwlwsymrwgG/7X3BhGhyUkiVDleRi67ARAIjC30EoU129YRxoUD8nqWE4nR9ry13JFcNfO0GaghxYrToAnth7e93csz5tXUkjGplblKk5QPKrENldHSEs40MEZ21qvxuOaxCpGYqrS/76+xZ/v/wN+xO/x/W9/j8Inzf8QGT8pCUKOsHoklFpRS/Gch4AcFXZONJSuPe5nMYBZUdXjutHS7tWtHu7F+Brz8N7AEU1IvzZ7MiJKFVQJZgRhdFFEEvH9syQBLZ9c2inxebkHfvzvgnKmbDS50C/nlBG9puF5yhkSzWv0RlsDY/EsRNM6FKPM8+dlHPJ4WMxD4Pr6/bsfp1yxlna2CapYWKu/Dt+oVDI+Mp5bO99pMFCN/G3HoxtPxcJk01xU/pNw2N3g5utXmN/d4/Tmw2J4jkc6FpuWz9vDjaFuhbqKsgTqF/FiedwaP1gRsXm5RlA41lU2axTSeN3n2Zxb0NDZp33plRGthShgO9/bosUr651faxoqLEC80PtT8f8WbGO7vpY0gSmbqAAp75Bzxrsj4cSEUmVPNKKr76j9269D39kGsIYcOLTTb8hlk6ttnengitLPWVuw9RGdR4ocv66AtaD1xjMWhTaETnMLNqSoAlgF/upz6UMTK3FCIBBDO062EVA9vobBmUCoHjJllNZ0Ih5Tbti6drTjYkP6e5LYOFgYkXgN2ADsf63HMxhFGSdJXlYBjooRm1TvZkn7uVLEq3YjbXFt23smqE5JmJioSzclhyX5lXwCpKBSG3ecGp8iRvIE2U34KF5sBELtzqdi8+X8cGMcXDYfltgJbt92TYm0INIHBk1ZcJB6ldivra6tocJI7GGtTHBrwn5hZNkv2OhhxjDvkDgs7vqKPMBaGQm1tsbct+Xt2L+WoyM0TghPzSIwgbhKKJ2t0E7d98CxhHl2y41q6wnnX00pxeYqzhVMaeUeMNyqSj/D6czr87NypBQliecDmwLLwmeFfraQte2h1Fam9xkYQIjbZqW0vgOHF+6pGC86XivR5d9RK7V1X0wEAdGqqikgDMhoDdkBqJOWGjx6vikCFfZsdx2YIo8NDSVXRCZVCDTk468ojmMXVDUG71wII1WuqQcEo0AELHoP2Z63Yz1MIKGbet0n4r0xjsmLhZgDsEfG11/c4MuvvsTh5gXS7iBjLyfg+A443YO5gIoK+FZWqp/48GllA1HY95anpj20OdUdZmEd9AIQJmbZ6Eg12PXSX/GGBzaB/9kU9rV9IlH6ufzNl8dsd7tvDLGPdyePXyISugDF+fPXbv+x2iZvHD73pAFDLBFmoB7VQGMGMCMRoyYgTQROO3DK2NEeaV+wm0+qgLhHLSfMp3vUqt9rQZmPzdsNGlKVCurNDKYiIygTMr0IYegMQAKSKIKn3MImcU7glJBIPB1SmuSeyam7b4zm3NEJGbXdaXYvBgMi/4vmEaFAyL/JVtjyLFgb8SIPoCttFS8hgSeEZLLr1Inbcb2oWzCKzwd6NsLgSo5AS0hJaG6KTUF/Hd68UGeFHzj7/liZ1h9sGpt2Aou1uVs23eg3Rp1POL15i/nDPUo6qfGS0p2xWeOljI5U3rAZIkl7RudH6qsRbdzRyQA0JKh4Jjf80aheYAUXBb60PduiYdFCsZ9jLkIrDvvAip2nXy6s67lHxkJUIed4InBq9DqU9zdlhLxj37eVEZd24lU0DQ080Oo7z0scyVDOt7ktQxn5s61n231/yvLx+7+mgzUe1z6v12+088PpZXain51va1ERIg3AHQgRVZrcrTPg03cY3O74xKhTQUmlyaRXWMiV0a0W2khGfe6dWOvifRJrP3JvPEgRcY0SIpZegP/LYDyW3hu26fTrRx1Gv4qj0GpR7Wc6pXW6Rd1/4dbZN7d3mPY7/OffA9+9KygcibT+FpWh1QUPP+6htUNkLn4dabA4GQ+YtPHdtVdHmmLzILooJTR1oUGnnRoS5WFiLlrI+DSw/43Cj5ZEmhsR1iZxOQJnGtRa3yguBjzngRKIxtBI3eqCFiPzSN+2xHXJhbgUaFfdEYwGX2X1EFCGbG28Ztlu40piqQLVUBOglubyt87NYibuMmlfLgJbQUICpQwU2adicTNL4lZXlMj6JEvS7kyRxP2XnHdmFRUsxI25ChZDJuistYBrQkErFQSk2uZzriAkpEmT/iWCx1kFu/UXF80fUSo4Sa4ESoRM8l5OSS2L0O0FaccUFoB5hjBY4/GLVYDdnXJ0WUPf6CRy2B/Mvka2K4wpTMHKreq6k4aNsn4bXPBzQlo/1WaVZDlQdtMEJtlrAFBKcaZZNyOakstYjTG8n4mrbQ3kzEQbNmOiZQ/IG6WUYX0Do+qEDrDmOi3W6qoCIoCooBYSbxcTEKPNpSfsMxhyBjOhzLPvJSCEXQp3Ss6WlE/Gn0VV5eORLdCIOc8TkgHGugqgWRUqnvZOFWbzZNXZrboGsofheyZOl+EZWQSZWwpeRfoBLmgA+vwUFOqeZcp0vcJ/2rTAWzug/HO0wvO2Ulv3VSYsXhP6X43hgHTAlmsjq0eE3yiKPwNH7/1UNpzJKjfKSFMWIZG2l1LycAK2FlxnzRdzQq0FtRRVdgbFqwPfwC+lgCGeEECVd/V+afG9G+4Q5SH8tDXPknbvJFW2uOOCnSMlNlPeYZcIv72d8Oqww2//zb/F7asv8OLLr1GZcX//Afz+L6ivf4/EjJQmVCZXbm/Q7DYZbZlsnru1ayFOfO5XGQYevgPNPtOe2dzUjn9vxh4DRvrlkNify+fySUtTNjfeTu6SGj4DHvrgkcz10Cniabd/Rz5mNXqA3+ehKUCUEG//JO8wI3EF1YpUJZxN2r1Aun2JVCSnj3g8FPGEKPZ3Rqma66eIkLe4olm8Yu/wD9KdCX9fiGtnR6vr3z0V3NApKA+Wd2fzFog0kFHWOx2cKQ/0Wwr3uN1pJLRtX5oxjdHt7mk89BWWoj33d1sf/pxaTfnecQo9/jV+YYGTW78c2+DVKgs8vyyRnlk+XeNHt/QF57sZX+oH2ytd1uiaxs9sNoNG/pAwb2BmzG8+4P4/vcac34O/RqBze9pc2Iuep21Gdub23s53IjOpUmqe1fvQiR+ltXT/ZBY+SpzgG3+A9lVp68ZnMw8nnIAYW7KXKxEiF9FoZMMVbY6vXkLbZ4DSJ9TvrzPv2VL21F0YMMwQT+mmoIxodDA7z0Dh+7nyYGEmj1915qJX9OfyV1yuJH61mvEsS0XSGG5bX4tKTLYtnHrRZWNErSYIQQbDAJg8h6XjIbAqChgsVqb4gPc47Y/AxNhjP+SalDKCfi7iEF9QmIVJWb7bhBNnS//6wy+YqxURa0qIa8ItjcqILeuPy+0sCbTVNlaIuGtgjK9HAdd6uKZ11Py0sg7n2R4WjPHzotxrLwRGAqe2lTjtAEpIecK0m/B2TphPhPcnxmxCm3Fg44U9wNHGF2v11Fv3zATv/rQ15F2vEfeLsfVlsQuor7hoZ0QYW8KnM0A0GVQbk48nEMuRgHblwgYsJvbthHmLypHwGQRxjp/awE1o4nE5lVgUgqYJWpwWI0JitIS42t8Yk74pUQKNCMYyoWiExV/2P439gx10n6tYzp05EXbqXJMRwCLgs1BL3t5CwNnWKSF1Ca77TiJzoUJ3bdMSpjWBqE6gvuJhg6oKZSOljIbPWtxXeb9WyavQLq1AVIZ5bBMZGCpGR4wyGRPXE/TsmYN173WMQiO4PTRVmJ7ErrYKSxgYwWpbsq0lAx7OyQTvdvGbJbaFrTLlCREkwbifSW7vVbjXjtHUsP8qgxMpcTPcF4RmDQGGeQ651XTYLuxIZYkP2ebEzqHFNDZANOGyKRq1Y0jy82KHzveCNcqAJN8mgJB0L/dnK7vSzBSLEWb2YfS4NayF4ZDAMC/Rk+2Btt9dSB1a69AOh3eINeRSzwj5fgwLYnunhdzaOovWOmEDey9g7t71ResoJ6x9tO/GLHIPsvyxeNUaR5sWsAf85uAHpZ2Ox/CPW6UmAoZ11UOqYRBqw3N2bgH4BiLDidDAyBVVrXSFua7hLhBlnFwJtlb9PeSeJ9YH+vGMcyYeHSII26eEF4eMFy9uMd3dYTocpJV6At+/AZ8+yHkFg5G6DXWRZrcOw7rKL7Yhh7XuUVar6cvR36UcavFCK6L7YnFhrwtMnxIOddzp29TZ5/LYcoHs+0nLani5lfL4HaX9POXdCwzJFsw8/O0+h/vXlaqBlr9mvKtng5e9SXvUfe9fWfK47X4LLUV8wZZ7qG9NjB1UAEtVwrtkQcAZCTUBhRg1E2pNGsYmg10RAVdEEIJhQuDTYsgjg2+igp3SGUarOL1idandpz62haDa7jGjWy2cpb6jBjUpjcIjbdfrRgF9U4AAjcZzKPqrs4Oxq0Id5P6J+6rt88p9tdhbo8JhAdvKTlzcl/Y30KzLt7p5XGu06bpX7p8e5O53Ibsu0VLD52HQlA+gvAcgcdbv59c4lbfguRjX4ORuRyPy9ojC0PqJD5/bru7vUpt/It1zlSF/wjxzq+8QMZz/Xd7L/W+RY9nymjJYeJjzoQFp4Yp7/1yNbSzaDsguZ9wcdtjn3BRAW/tqTRmh7YQ/HQo7R2/EPjbrBb5tazif7t7dWmEp4zW3xS99+vIYgB7+Ttsuy3dH+fLygA99d3ts3K2R5x3pX4NBOZJhMZpCUfowWuI0H5FqBdHUNxlfp4AvNCkjg5FTAu0nMXgtPT/evb4Cz1j5rKJiHAviDF5PBQVorqjflweGZnocGbrcLD/fMipsu3BNPeXyU0Cz8tulzuNt+9MAWqcD6uEr/04s9n373Q77mwP+zz8Q/vSmoG4QNqMF/nUIdwXJOJPfWyoAWMZ7PdPS1kFag75jN9akAZfKJYrA6aOeeRlPUqPrRgS6NrpgNRI8GLoY7NaeMhNmddvcngFRPLDnOCilusAqMngg8wdQgZjFXiWGJY4O2BtNIivCmKZ0MFgtZ0INTE2bF4uqHWPud/I6zQ1geSPcQmVt43UTHWbZ45pLnL9S5kUCV9J6MobWXs4ZzBKPvYBdYaBT3WLWVmljShlzkfmutWAuBdOUkfMEsQ6qyAyAEma1Vq4suR8m9YywfWAxeTMBXCvmGWCuqBp7PdZtc+v2RDo+Fbg7U1dDXoDGHJoHjFu3K7NgBkW9J0Sb42b9nBrzMRAhTRFjrELwrnAGgVGqxIc9nSQm/jTtfHuJYHWW+MWT7AWLVdzC0LRzzTYmIhCS7EM9Q6VWZIWH1bLb9mWiJPinBPUfw89e22PbzKYrDClJ8kYQUlIvGWaUGQBpxpBqbuSqNCAGVbOgl70n7Va3kPdYr1SRAMzz7HM8TRMq5xbnOVv/CQy4l4VYlDXBbtX49uZBlbIJzgemKir+QTJ3tXlBsR6O5qKqOVKMeIPluiBUkluAlNt3VSN5gKuGz5z5X7/XLfwDjRaVCzTRzk6sJ0tKblHXlpQRl51W1173t95lo0VpptwpMlmtVWOoCxunKRAMNkpASi1JKCitJiRnxbnmBVGK4B81+esngoGU1UuOxUOMpndgLpJPAhbySxW5Oq9sOJNI8/Aobk0N9u58KMp2jzxmJEqYph2mxPi7uyNeHnb4u9/9FrcvvsDdr36FnBJKvcf8/jX4+3/S7ZZh/ioEUcIlH846nbKcoKEOd98CB7n2YryxCYyC6m5Bup/g293vKsnZo59X4fhcPpfP5SGF0fAnV/9ls3LPqOvfzTM40u1L8cfmm6HRjs8ALNA9KDHEpdWwRpbQDhXIXJHm12CWsHjynlJbxCjJ7tCEyoQqVJR6Vxr+rwBbfqmhROWC0/s7AIdWBeQ0k/4QntByLgYesVIzvInv2X1gtGaELlwV/XtKzzKNq9szh6ZPd6LXnzX+ZMES9B9Vf9J2yngVLHfA0hrXpyzQud0+o75eT8f0Iu2V19avNc+btg6LvbYl16IwlxwOSlc/8mLx5zRhevVrIO3ADBznH/Ht8T/g/vTWz4J7Ghg9bLSDrel4J8ehGU+pnEkFiyFcqBm4B4Vbwjyy0i41dDSmdENow/jf7au5ySr8JYIYH5A/RazSRrTudXytscA29rGZ4KHWcte+enGDf/3rrySnWKzJ63vD8N74fKvuNYXBbXJ6od1V7y/H+ZTy2HbWbpOfY2m4ZOU2eqZyvq2tZe0NmPp22jPbJ1c06PXb3WG70uTBEedGuR8bwQ6AueD1m++QU8bLl79RnmsIB6lbmBMDtaKm5NEapsMBt1+/wvH1O5zeflgHk9ZxwWI0156JgI78In3QGj/uTD1AEfFcB/YjlzXE1B5e0QAtmuj01J0yYmxv5QIfwNrutYfw/GWxfHOz/biPNs39lLBanuhFv/EiYSRw3oNppxeokpZTQs4Zb2bC8TXw7sQoT1TiyPbukUO8sIJI5kEMOm99GwXy/mHlwlNEtLoGa+d4cw4GRO+EzAYxqQSdE84rXRjybE2aKNRppTUKDo2SNxc0GsYOJwRFGdGSXQuRKGtl4TQ8STURqFqCuRDMhvr1BClTaMJqh7FZZfluiIOvIgxlc7M1cPulCl/6sY8Wxn50/LwrgYqWC0AEfW38RKE+IwjNEea0glJC4qRCtf5yAkGthnUdEomlPtqaMqrMpYXsCYMTJY0luG4TwCmJQoBI8gxoeJTKLMmJ0woZSI4hOlJ1SbQ2DoRtLok8dqvPnv2zUEL0ZfHMQmkFwIwpKtp1inCgzb1Z+FuCZ4s1LEukOUQqucIyEaEQBZhlnBaiKFrv29EYXTg7hlXhBJPv3wU9F7xRbB67Chxm2hk8DXuWxLKRqLbwwoiW8CTtqVUXaTJHoiJCztrWt7KEeRDvFkKtBaR7r+rccE6LlWM2rCywmkupzBG38YS1aidK54/gCqsOdTIcp/RzIXNZq4oiPBxEIB/ZrDMb1mCoS+wCF0vPITxzWAGzUt+4G+ybSvWH9Jn9aVnrOtSDertYQsykL6SkuVw0aXav/CbH176/9fcmj7EzY3inxcH2ExdxreaEEKWShewQBZbfO6kpmJgLKt8DNAMu6oefUx8ftdFS2JtE8CB2azOcrFMdRyK5WQ6YcUgJL27u8OLFHW7vXuBwcyN7tRbM9+/Ap/cAm8hqDfM8kjh5YCvxbqYwP6Oo78kQctgXTywR5vXn27N6rvQ03AacZ2n6n6ZcLdvQcg2oD2zyIb0/ovXr3om3/ccqVzPNz9HX8NlogehpJ3+lxllr4wHu685CP+89Pl9+j8Cu2bsbKhV5qQVK1LtXL1zRrxMkVITd23LnZTBqMhqFAJY7orXTwG7nlfpnHTzU1wsg9+83+MMQW/LPTvjfVsWMdsaZMJ6FFnCi3Vtrna78vObpsAzfPL6sL4Z7btFIhGkVgOWTs3hl0S77Cx3rP9ACQLjyV+mSazpfwkC0/A0gpd14MT4xDsuQULJFadGCwifc37zBnD94c/5qQEhknXLXW/isD2oNBEm4t7j9t1D4cPiyMQ3jz/GVjr1rBG87ThzekY1/Zk+sdbJ6CuIWOAvzdTg93NWkvGNqHp6+5QOZ3hqnrhXjsweZLFbP0goUvm/H8bnCavvtSHFcU9aauvzm2oFb1lhdTupZJY7P9NMGxroIFdDPzbUkFQ1r2Nq5TDc89Dq/pv66B+cWdXL9io99j4oN8krrEVgEP/RUhXgpnZtrFn1/AmqpQAaoEgoVHPM95jxv0xJ8eWwO2QjAoskYDs7kNiOv2+O/9bV6OP324GTVn6qsxc2ME/x8BPLYEvc0FqkAYxSsU3xffog/XQvb84whEDcjpR06ob56V0zoEz1fY4gcIkbNB8z7r0Q4Uy2ed0Le7zHd7PHf/kT4w+sKMcFcg5MXMHVwLmuvjrM7Lhv4fxHPc6usKSBWKapeaHP2Ej2HIxd9muZV27MpGvG9WVx32tkAw6h1NRhr0+z2EA8oRwW4qbN4aBZj7qXADK4zeBaPgKpCq8qMlCUxHdJOw8gIoHViEXyy5ZAwYlmYHbN2rta+WuZKX+Z14dkpQBCRFwEoXKFBPHVe1NrXlBdcASSf3xZWRg5pCh4fChRikmTpTy3PNeRI5YJSZ83hUJGyxW2XN7IJ/ElttXMCmJDzDgAh5Sra8Gou8OLNkKZJ3jFzZVNKcBVaeibkKZwBVriSrgmAQlUti83+rAApYdrvwWBMdUKtBafjEVWJy0jkW/Ll5fnxyKo2Uf6pFgYluDdGhcQwtlwK1oh5L7hgnxE8HyLSlf49kktlpCyhWAzYJszsEU3Ksn+LKonmUjAxkKbUCL4KFBRwYhm/hb0BdJ8ySpUQBQlAcfzaBMLi+VIlRBSJFbzt0T5vgXhP9HjKFMFhKpnRVZLD689ttrMpFACkVDEjuSdQrQyuxQ9JZYVFLeCZq3gQcJWRMWCJiGuRNlIizEW9QdQjwrFhMrWP5sEIAhxTUrbFBpgqNFAUXGmta1qDh1M2jxqy+N3NA8J3X9x6mgNEzlpu8x+UErBzXwFK6rkhapV2H6qCjjqrwKBUMzyh1rM2BiMFzMsihovosapauVfyfeuTRW2PCNpKIacOXKGWNcmnlVKr3L+2x9STwOoYTkkpy75JuVEmvpByltkxqSobzLuqFNQyg8sMLuLhUEtxD5dd3iERYa4FXGYgvQND7gTrJlq/drepT4UqFnR/tO1jFqx62HXvyhQTkCZkAL89HPHF7QG/+9f/C25uX+HVF18g54xUgXr8gPLDv8hZCGuRIDipnb2B0ULbv1dZMS+qnKM0OMxDU2ueLT+hgPZzGctD5/55KPnHl8f0f1mo8EsuMrowRv9jFtZi3MEaYpOyWdGngL0WcobVsmTgry+LY761JI4fuavoCl8OZASnAIPcq4kTEprQ1bmYwdSbRgVLx/MEYNbgpIjpVvj4xZgCX79W368u88aIz2ioOvJGDywjn7y5ihu/r/zcwUOdlGBRNk/i+Ar1HxuZFAZwzTwEunLR+TCRV/v1rChsCIQulFJYUxZ3TZRaUZT/OOZ3eP2rP6BgltBIDPFQYG68kXOC5B61pHsv6WNhXdWAjO23yG8Y3YxWIYBouf2YE1BqMLMYSjwKxkcps+G85uK4yJzIeRH4WaePNo5WnLuOV4J5pPdV1rm1sTnun+pX89SwVF5VqbWWE669Kbz4QO3ZYIbeH2q4EN/iAVdEkONfDM861utSV1fjj4eNw+6hzauEVn5b7e8xCO5BM3BF3ZVNuNnvY/u+tjwn/RIUkkR+ngS/tjDTqyDI5eWyE1PIqx3g4i0xhGTHeZiAe7zDcfcBlBl7HDp6ZSxk53Cc0ihCUEO/8ffh0mhjj88VtxruWmv/KeUnUUSc1ci6Jd11I+qOnzLw5i4zoNCVtx5WzACza1MvkianGCs8tNvnJvwvH+4zdAyARi50v/k9LZMi383itglJcp7w5pjw/gPw9rh0xVvpqF/Us0T3CrDx2cbL24TkFXO/btYRuIVesL/dzqWO2P+NSoi1NiJIS011bKcRV6wwh6fy3BULQx++8Tk2i5YHQpQBpRawCaxqVWGzESIEBCTswjIWSVJKWc6SCb+MQLP7ygSbQr1J2w38bl4M1OgrIXJpsWJe7kFTQrATiDpFQ92RAGefSwBNcA9jZys89E0AViHyFrnbV41TaGsvIZeSJroWh4jebdpgXxmaC27FYyLMTQUSS8giwMLGqHU02WW1tJRai88o4AvsUZlQqSLV5AqVNmj9wwh7M4j7uOHVZtUXBtUP0fF+Y0qXbor2eyJCTSKkr6SCBvNOIAZx6s9KN752s1TI/NVaRegNDSGVoEq6mKxK17RLmsYBsDia8wiiI+q7N1vybpCcKXE5Z5jmxvyOUlJjMCWSwAlEDIaGcgJ3llkEURAkYhRqcaJJLeCJzbNCPUqU8LK1M3m9Yx12UkaYq/XcYP18+J1ghLueIZP+R+JM15YMRlM+AGpxIooOrgRK7GeQ/NDz9n1u6LizQJG6Lc9EZPrIw0G19+0Q6BhcYtT2L2AKNvMiQ0fMiqdD86CKMaHN+yzmerAweOGfNq/ep7VQXYHElR2nu2KLDWe2kFummGJU1PIBlU8gqAWPbYaha5+SoLgyLOKKIxjONg8O82qxRqTfA07YJeDVzQ1evXiJ25sX2N/cIOcMAqNqTghRyMWT3VM5o1jlcQzy5XLulF8KibH+w9P6fGgrl9p6rGfET1nO8iP6t9spj1AAPTYX3nOUx3TZ3vm48J4j8a9u4znmdO0aXj4+U+Oh5ezJvwjFVc1z+ys0prVsSndtlU1AIi822lfpsUWcvkZj+h2+GpN/Ce+awPrc8i3aHeqO+3RUqvfV1+7yc+twab5lctes+a9va5yPlTt5/evFh2fn7Sr68nLnsR2hAc41ulj5zd5pdwfkHRgJtZ7w/vQt3t1/hzdv/oj742tUo08hvJNJezp8osxK4wGB5TqEvRuIXVNEGu90dg6MDjFlSOjH9obXWdsGG1vjEhdgOz4c8xXAVl9qp2WDvL2E5fjEOH2oOL2rQz9rhJ19vIw7o3GRt3IBv3fGTvr6ilp00e7WT9LnRl9nIXlk2bprr0E/wDode+WdGF9teWW266w9H39v9R9yj/00dNHmul6Y64XHRWisx4CLHkP7yjfViuP9e6SUkdKu49kQ8I5wq9XlqpaPsu9mmT66cXC0seUNN60/v7jvfCxrGGrgmx55YH4xHhGfrGwIJjgKL7rrebioPzqAH7c064BYZGSWoDdp8t5p2mG/P+C/f0f459cMStxZb66VSDL4hyjAuFRW6sWD2hDIFSuxiYGXhHn8g/O1ru6T/SuvvhyRap/MsxWTeUYBe1UhHdvvEGKLax9TH1hLlhcYGP1XQnNIzPBSZtRSgFIaqiLyhM4uOEtNiJ5TFm+HaZL26gxJbtryQbh7vAo5RYmiArJuTsiF3QyLhd7GFIWE/bjUOiV4WJDPf1LB+8r6V5nLmqx9NCtmE+CZxbXNPzNI8wa4EBI2P8tdU4sIhEnNejKJp1HqPCvEY4SREehiX+Na1CslJbVekX7Kqcg6ZGlvShmVCGXKjaDjnrCxfWl9+NxD1zex+IjUdqkWFKSqDDBZsBXBmR6+a+PTYierAAEAAElEQVSELJM2cnc0SReqJcWGxpuHMwYcKici5GkCab4IgJugkqsoJJLFfFVmRAXvCRIXltyUQQW0CLkw1Itinhm1quA7jKElfg4EgQ8Evrcd5DV0C7ScACvrlLN4+dCk3gWACuLhJhjMjJT0fBEBCUg1A6ioSc+CaStguIJRCtz6zBMkMyPlLEnEqzGJydej5YyAKOYg7YOgCgDSPZ7U08JILMVhxG4Zr5MW0FSbLxeeBIE5JZKcGASI95IoxSQJOUPCvpHnZpF9JOdqIWSwPWH9R4BIvURCGKRmhTkoDQkaNq79bndTy1dhCqXWvysgQkgmmUsjMM0jR89nEnzgnhDqEeRXio+XFmfMk0zXCq6z572pem64VhRVNtsZyjmL0qkWFLwBUPzO8DB34Q4xpUpLfNpualNw2TwC0eNIapkjBJLU+OZwxJe3E/7hd/8ady++wM0XXyBNO0zTBD59QPnxD+DaYGptY/P75/K5WPkpwwT9UspfA18DoJEkGMIsoNFnn3Kg4867CMoG3yQ4V+/gBW0XPcLift/e97youwXx85TFPIw085VCuMu1tuNt9/z9NZ4WtIo7VgWG18rvfkmH7iHKQsqgu2/AeQcQcCrv8f39f8Lbt3/Gt2//C2ZYmEebP5aQXXp+Iy/hhhTKR0aijYznC/y70erOTwV+2H1SjX3iRr/YX+dLI/2u/xrtJtvAaOFzKnpeOZ+t79a24eCePo4zbnA3cnJ7z0Zyd6vM7wp++OM73P8lA5jWOON+JAsebnxuo3h+nLGm3IiFzj796y9xXVbRUbhG+ufPMXO/JCTWykL+sF0T7iXk71S8ff89ctrh1ctfgyiJfMvkb1HuAPX+rySGeoPBncOw0fdlyJ46/30fLVzyecgulScpIi4R6ddo6Z5M6KtCYIH4gnWrI++r4W3McWgq1PNOhIxbPbT288dDeY9achoguroRbpbMaULNN+AsIXdSTpimCW/njD9+ILw9BSv4sf1NLuZK9ubK/bLW0ri65xu4dNWuv9PVjkTHGlHZURnrhKvUGAlv/bWjkkKSZlsnbomCHQgVyDShcS8kbbDbECLhpMKjKp4QRcN0oJpHg8JDAKAhbpJY3Xd5ElJCYjtbbqIde5G5C//JXNZAYLaRC9PY3o5JrA1PLrZhvCnYBHvWjlnyK6HUMWdNEWNbto1tySAZXNTNcSOqJQRQH+bIx1srWAXbIntLGnal7yeenATxnDCit9YqBHUy6yE5x6UUCXG0Swvi18YktvIhabDNqc8Je8fulZDalpK+SJQ6TUvS5n+d2hkuzKCE8PrxqxH7avFf4nrBKfEYLifOmwhmV87d8FMiEWL7OlV27wqxjIIqlsL7EYUEBmiNGFgnEAbCbwXM1h258kx0fyReKUnJIhZLCxFQq6LN5rEmv0f7v4C5n4rXQ0JCRSlFl4xFoeH4qw91FAF3nGQjdfoqMIrhoLZwbepZwOS5L/xeDVyYxBe2NW2W9gKauNHDBP4EUEpYBZd8NG0NeRBUKWwpHO7OUpABdIrMJe0hc5BckSn40mfB+2g5dprixIYV97lC1J6FX7vfqHkY+BO9KyxxdK0FXFRRbQnVvTtCogxkO1OMud4DfJLwTdCk7TYnxEGJqWNybBgVFIFRNkWVK2kCjlf4byZgysDd7R1e3t3h8OoVdncvkfIEAqO8/xEoR1FC1NbPWP46lBAU/v15l0cpgR4i1HpAiTTAp/Bc+Fssz8ENbdLJz7CGSzL9YW0+xRPose+e9UKi8byNdH67w8y7svElBlf/yWnZjt9GR8O2/p5WthwUH9PuNZbW52os5AMXgFjdOxvvrHrkrb5+eeSPutPcKMbauK769g/n4fC7fHcH5D1Y+SAP98sVFVXJz7bvnIJUQtBzEjjorGyJB3NsA4okj34wPgkQoyQLPSxKyKXozgxNSPP8WXSWAGbrj8/NYl955HmWvGT4yFDO7MI6dfTUopnVtnv4BhywMh4XRJJ6Uy+UnE5QgyNvEbsfmr1GJsjjPh33wNDOePY/KcWkdIdB91PSHutdjT/ySj1aqWu0k367uGx2gntYtuWry9JEBh+LJnzA3hv37eU3lf9UeVFioNgTS+ZuxqtqQAcG7xmnV/dIHxLyabfe05lJfI6ZOj+2p1N1fx0eEUEZsRAGryCl5+zWBA7rm/PjOqivXFfnC3V//MM1MDZBElBpwrx/JdaXlJCnCbv9Hr//YcL/+FHiN4t14wrAmyM5D8mSQbiyrAmIry4Pe2/7crsk6BwI3CsI2IaI5a85rtg6yd8KF4AyhMgza/RqiUeXsAWRdROKm+WHhuuYi+REKLWA2OK+N9hECSEW/IkSKGW4RImD5TETKheYuyxXdGFBXAFRW/9KNqrArp+bqu8Jochq1aLCzpVlsNj0zVNETpV5+rB6MkQL3qrzGJcmhg7pz9cAoOV3II3bbsSbOg/IJcSyTkSYdA4AtYqmLOF3VIlkFj5OxmpCZ1NCuAeAhZBiRkXFfDpJPpcs3go5ZSH+mVtEZFtPtljqjXLohYjwnCXsHik6Z1RB1Lw2GrPAyviR6yjcecoINaIO74wkEPn7MjdcGaCKuKXtTE45oyRCnYt2ry6O2kYFqxJBz1M8G0o8Nwuo0D+zKtoSUk2oydaklaRKHbYQ9VEncuW9FM+pe0OE5zK3GoIKpoyoQIV6CcEFsqK0Z/UeYfX+IE9sbvFsbTPb+Rtj8pq1OlRQnpIoYjxskq2z7SfuwyfajvJ72/Le2JxDWTRGUyxC17gOdzqZIkYJOcMBJh7hEL6RCBmAJfpuoSua587IU7pEhALuNQUBemszt3Ixxqtvyd9Npog0RW1XRQ5FV8cI1YAHW9H7tnE3vgSRIRW5fmqJwl0hbXeC5YQ4uaeLWe7Yvk85O1xAQcVbMGaUegKYkaad4JCka25KrzBGguYsCTNDIFjiFyLB3Lq94KHhdK5e3AJ3+wm/+fI3+OqLr3H7q99i2u8xYQLP95jf/BlcTx+F7vtc/lrK573xubTSDCzg+Ar+5xeisiTyO3PruX4I/9ovxkOvvah8rr9Efq/K03Uh/tNmrQ9D8WTh04X3Pc/YVe8aTUrhl1EYdAGcMxWc1rlQ75dY2hZMoNuvgekg35kBVPXk5fCfVoftAef+2iyx7UFpI3r2DDI//ZXdGKoqTVVKDeQSgzgjBYMSWxMJk2vGSYvRoRFdPPy6JedwMSTsjA1km7fC+gO5sdeykExto6m0ja1d1NOdDcQutKg3fH4vjiTvqIzoR/a4+/c8Sffx5H3PVz6uXPB8uQaX9Hv351TOoehPWwxrnKtCyFl55QpU7s+B7YrKAGpFoirC1FtCvWXw9xX5Lx9tAH3h8Gdry6wO9nGLc7UiYo0IeNhh799/KKIYY65uiWx5wISe+ftcdy5f6/vY6oUjLl0Z1yLkwZPKRWrmGZrcmk07+O1yZRMspYycJ0zTHu/mjH/5IePHo4VWoM37SgR418HNW1/oHMRXtucn7aHrY8K1vjRLou2Oe/fNx63rInRSwBjs/5lwqe1pVksTTwDtiohBoGWY3mkmdq8KE2xXS2SqjIJZ7JqgSwTmwXo/WPfKHbd0hTcBfw0ho1rYlaYUiR4RW2fw7GSGDcj+AwIFxf6xVkJKIrhP3ZzqfKL99YRErvii8Lt9VVKZC2DJo0nCG1V2sSwAE9zKVxEkaxLapCGBqglO4cJ/Ts1y2mAxIXQGC+GfkuQ4YEaqFafTydcKBBUgQoWFdparWh3ZXOkeWSVMByJmEDauGgmpwNiP4lCnMceNIdDJBciXTVwZjUD3MD1GmBOyewi0O4Rt7ZUpkfU3Zp5dGNtAJQ9z5ucIkofDvBAqt9BTDjGhKSD8jIV5orb6S+sGBE+AMMOBKjPGShSSlnC4NWAJuGGvWBgeSMgiqOIuei21BZB/KKyBedowWMMFmbcFQjg+Pe8aRqiUIt9TBqjlJ+HIecU9FbaSC4MIqKzZCDX/Cxgytk6RFXCfAAwAyMqlMRGEGtS/qrD0tba+1eSONKmFoTBXHMDoC2qf48JxwNlkoYWiVR2hV2zERW/zHfM0gG1tOdRbMoEAibCf4YpC22Xu5VTtXmCwh2BqIczgeE9ygCAlZNE2odb3YMwo5QS2FO69NqRfO//FnsovSefCf/N5crSpuAtIeYeUEu6mjK9u9njx6kscXrxE2ktYh/ndX4DTPWqdwzz183KODfxrE/r8XMovZV6fm8f9pLkiNub8U4pBzpWnCo+uev2By3BN9ceC/dB1GGtfYDeua22VfltrTQgHGp9E2n5b+3EVRF3LrO/RyttPOEtbbzZS6XzbtPKp/fJIuMY+3fCGztf7Cctm1xsPOkrmHNjhWeUZ707/gnfH7/DDj/8T96e3iCEVpcjcCKk/8PBOSHKo25RZ1LUw1OdWs+niBo8I5YmYgZTMcEeMMZaj7w3VxiFvn9EIaQMzKiPQWNXVMtq+LPfs+d7HmgSgzsD7bxnleD7k0nVl4P1Hdmf9OFxoMfKc1+PVT3Wkum4HlqP9No6DsFLzIT3JL2cG3e7gayam309u+7RYz8WtcVV7m7UevWbrOKmnO66FNYwzns0zpdaC9x/eIKcJOR+QkrCensg+dstQmRi30L1k534pP+smfzA2eFTRLbYp1uQXAPYN3ieWvw6PiKFEZcAld8snlSAo2IDkY/X8ExZTKiQVWpvwIGOadjgcDvjjh4T/8SP0oKxQjrwyE7yBa1fqDR86IvU86BtE9aWLahPTcY8wpDJW0AJaSKMmKOxb6olNhlrsbsC2dXnExE0uHLX+nSarzdrVFBCa08HjuDdQG9wmeIcqLNQTwgRXOgARpqXkCDOl3OU0aEJ6bZ8Q4uA3QVetURlRVeAblBC8tDa/VAgjOR+I1AgDoDFExbJaiNGKWlXcmlhhrXIRMHxOGRUWRqSacBFwLxFC2FLMqKXAYuNb6CogSZgbDqGXWASPpVQNgyL1UpK47x5yJCgWUk7edq0CbynAjkVQl1ICM6PMM4q2QSlhv9vBrNp9V1LbdzUkEWSfL/K4qxu3leMLHZpay4ezS3BPhBpWyvey/md5HOSdYD3u7VCwemoKNtIcGimJ0Dx354v94l6EIEOMGWv3iDLdHp6WUTTvQaothn81TyRmMEEEt6AuIba1KXOcdI8ILqkP2eA6V2z/sHmEtEZke2WdJt2vM7tFhuGLiqSJmwHq2hE3dJ1o/71UzT7CqvQq1aqHJTbmTvY9CODJEltPENykSpAYJ6kdAS8WuigxoTADbPuKkZHQknyxM5k2BMtPgVkS2FNKSBVy1itAqUJUKxURcqERlflLCASh1lFKjUN8ABc+mmIQ8D0bFZaiiAiDXY44zDcEf9sd5AJOA9JglQ+WS8LwNCEoh8xisDa8ajkgJPfPLMmdDSI7gykhk4Ufqyj1A5iPmOcjmKusaVoTx9jYh9/iXDidAY//3PHTRCDKSNMeOU/45sUX+Mdff4Hbb36NfDgg7Q9AOaG+/RY8H0OCeJv7iFv+GuiyX075pSghPpfPZVFGnLVV74lKlIeUiz0ZXWQGIxdbC6MaZUERaQ/KBsIgxNnimx4zNT9rlDEIAs8qYf6KyxVKiIeUwif85fjf8fb9t/j+/f9EwQmdl5I07lMv+09/tw/m/eteFa2ugdyaa16ePd/dfCvsnW58ROBqXthVPCSw3OZjGDQ/litjp+Ecet9O1628ZO2lfoz9Uygt9bA1GbAC5iPw5veMvCNMuwc1db7h5y4/wTkkEr73SW2c+b3Tq3X9PqlLbeNjTP7Wrn5q3ed4L76/zme1PC7979dv1O3cQn1/BR8+/IiUdnj14gCowS4s3kSQQQgrb3In45PMq19433VQAu/6hMLnGmEA+BKEL/AsneHZFBFLFPyxyhj3zfHaQBDFcB5rouO+UX/wrDCaG+HjyiVgHg7sEgedQ4dSupA1eQfON6DpgGm3x7t5h396k/HmFCw89fWHjXqYJ24CJP3hOvSwSRD2mH0LNhMYrb4f3100EJQRZy6oRZxwWlNhrMC1AlMXAz2A2eWEYAYsrFHVBNAucLJ8CzYuFag1tUR7xgyGKAgaTAKXJFFNnXUvJcsP0TxkeuBb35XRCcEMPhGMNoFioxirC4/7+QhCOZingcHTYOAmsXMFB1hxAsX2VCAb5qMnYE2AV+AJzsjmBSL9dbPeOAdmpVtNbuzPhXcMXhWqfHAPFxOCpuTBZJoinEU4mySyYEoJ08SYZ3m3KJx5yiAiTRiuyZorNO4/AciAvg8XDjbliHlEbR1CP8ms+SmIwdyUI8zi4eFXNzfaNNHQkAlWTbis26/LkWFJe81qQP9nluOVDHbx9KAaOO1whFooK+4Ezc0LBxsEPcPogsjsdI8XQlFZ56ZxYM2/0Sy4O0wVGa8RXxhRTHqGJb12jwI4LFeCKA6yeMaAGVX3DHTvCa4gv1d7wmfJSZiKpiqOyfqLJ9fWPy1pNyRPjLqeEkn+CsFVijcYuiF4cd6bwtuILgKnKn/dc6DawqpiwpqqqAykqgm7of2wJqDQZPApkRKH8AkkhuTTUI8AOZuiuIjxcU0Zn+J3AG71r5qsHoWtW+87noLBv3Jf2P4zGMhupMbgtv1cHcfapNRaUYt4QhRN+t3CkjWYJAQZUOs9GDPm+YjKs+wAfR73BoV/1tCFe08aniHqzjYBuk+A20PCYZdwO+1xs7/Fr7/+CndfvMLusBc3l9c/APUIqrIekU6P87lFC35WTjxveZQw6qMwyWc7xBY1+HMO7bAplFqwNcYD9Q/WTWceCMOT3h7aevBcP+8+6a1p47zZv+v9jXCfm9MnzbfTeOu/nxW+PVZITsuPbO1Z4d46enMdH7xcz7e+17b0cBCveOOh+OxjSB4/ZlnhwwDZ62fxPyWkw0tJTp0mbYpRTzOOf3iP0/EeNddgUIJ+brp5ih4TQs8YzxC0FOcX2KoJYd6Dqv82/rDhVMvFFmxXhnevW79V2mgNPudF+3x3WxEmHrR9NtqoqeI0nXDMFZQId4c9vv7yJV7e3Vxsz40rbT90oHdYZQnLRWCvrAp0OCoaez7meI0hsT9FWRovdU9X6g97ukfhZ+tefzc3WuryvPZ3RpNhLJ9vvff0sr7/It9/bTuruZFWQRVagrni/fsfQXnCLt8Kv1YkFDeNe9ONFQG+IdzTPfLbjHyf14fCBNAXuCzap43P0pChOuUeV16/CSGYn16uVkQ8nTCP2P55ink+RMhMeBJ7XU7zOoEe2wX6Q8ne+NBX127/u8fG/qhlu/3n1H7KHs/gw5fIuz12+z3ev57wT6/1eKVm1dsJ0TbaWoHWn3JX6UoSfm2sC0ZhA4DFqwOSWlGMLCl1akK71U7XwFu6OT5ozQLTxJVDngh25YFZvZonRC3Fw3BwN6iIgMdxBMGUy6dECZE1T4jFKPfk1KkpJ4wGiaFSRNGgHgW1iCCsVMkXYTkbOiWEJTFTum9l7sAtZ0CzODZPAq8CoAIkHj7WptOZXXNG+Jk3hmmjoZ4AEqIKtRG9LWa+zRLaHBjMuk9qlc8JJIJpErvlat4PJrT2vqWtnDMKWCO963rrnIkSiF1ZITkTWKzVE5CRXUicKjAXUQrNkDNswmjJv6B0uQpmY+Lawa2l2xv+tTJqyPkt7QNEZeUSo829X7nNb9J4+a1LUWYlV9IQzBKwqrdHhcZzZQIlY1LCncbiUSKhrKonV7chiUy7InFLKKwLI/CBkVgTnKugnxGe9zLdxZyxJnqLVlhn8ecCf5EzI4kZ1XMftJYMRVnGFPOMgc0HMohEIVJTAlkOAt3ncgYaAI530EhQ85AAGEQJ2c+/rod6mFSuyDkjZfVK0NBWsh4adkzvEzuBlRmJm9W8Ca4dBsrar8CWalJFn4QVqx6zC5povABEKJD1qlTda4ZSAqrd3SGcFTESiYLUoIs3RVRmUji/Am/wpCDHDP42B1yOMM4KbqHXwrVD4d9hlX2tKbSVlAErtWgS6tnrmhJYFBIFFtpL1k1IbdkzkguopiOAe8z1iDIXZAv7ZIos7nfvEk/7E9Hp6Hl2hU0YQ1LPupe3CS9vd/h3X32D3371a+y/fIW83wM5gcuM8u571NO9b454kq6hwZ5DOPtLKWvj/Mm9Fj6BkG3s8jxD/1x9/vTjHMu59f6p9/zPQsGzIfsa8VZXtpbxI45ns+mH9nnNHtygUUbeuuuZ+l9W9/oaqD+HPbAuh/p5l4fM2zPjnQ2dw3Z9XFBGHF4h7W61baWT54rTv7xHKR+A37KG3mw0+pI/U2MTpxKbMaAbma1vwJVPwMoOl1+Njgv3RUoErknoRiJUk9wNVHzkpc/hPgof1matf9M0H0sqcNHeNWUQZ8Qyp4IPuw84TkLL390c8HfffBGMaujsvmgyurgfBpnHVQA+rLT5HPt8eGgp6tr56cp1cK7XOad8+HjlUifjRuujgCwVEmd6Wop+rgRxo5PhPrhm7rcMMhuPut4Gc8WH+zfIeY/Dy1swJ016XxdtNpyRQHcAbhlcKnBsons/VyT1gK8Bvm3DuWrtV25+F/Fs3OvPuKd+ktBMD73EHtb2YJWB55ufc3t71dL7I8DwKQtTQt3dgVlDZqQd9vsbvJsn/I9vJ7yfLbSECkT9Mh6KbuirrxNefHgY3DhDUF9sconhnNbZGNtm5x+ByI0KgWjRb+AxByG+Clvtt+peESrUYsZoTuFnKQrGoEI0EJDbZwnFkVUo2AgTMRXpsGkcQZcUlUtFKUXjkhf53RUEbINSA5deuGSKhmhJL7AlF1hbvgRXgtSq+zSEz9kkVpenWE49DzW5h41aiBKKF58RZCRCTs/TEbps64IFXjNvDiLxWNAsFSAQ5nkWQfA8gy0klofLSp4A25JwJ80BwFn2RylFrIlZY/7nCUSkyb5lrvtE0AxLPmwTv2pNocnAAbSE2SRj8Lmr3MLerKwEdH5FcE6ag4C7ZxYPiCghZ+Akkw8LpYWcmyAYPaMkU96E5GAJQWPCVWj4HiZWGXnwamCDAZL0Wd1UEsG2mJ9HzxhhDLzhy7rEnT1LFJmZvl6cI3tRjrR4RlBSKwvuarWiOS9kfdmVUGyKJ2ZVGgXPELb4vNwdE+aW1Fi8MiYVNMteSzk5EEJ3VVSdQqpaT/M1gCuoWt4Aa18nStfG8h4AFoKozRpldjirtc1w3GX4hFBkJxChVJawTZnVU4MwLAu4MnLW/myPWMO6kESkyiVdNVM+Oq3ShPaL4uhX3m1JqQMutr9niOChOcX55nXGXeLyWitKnZvCw+bQtoh6uKECBQXzfAJjln1jzw0uZt176Lyo/JE23BQX8kNMFC8fZf5v98DNHvjm9gV+9eoVvvzq19i/+BI0ZdmDb78DlxPqfNLs18tJWROKjN//VpQQn8vn8jddBvoFMPxkd3S8Zz+XvoyTcrX057kB+QWUx4z55z1Pzy3HMZq+8ozXx3/Gu/tv8frln3Dkt6ikpiMdv+tvhh8arysGYdpuyOM2vrkoJsdjpekDj2b/U3LT2zDa0OxsOtMz5TOYlv2OtJXxPJEu6p77aBv9Z79azUhXje9eXUZ2VwdH7wnztwnlOzivbx6sjzJeYCxkDh+/jAN7BuT+TM2sNarswnqNuNBbrfwMjB/Wy/qkjSHJz43fnl/zWyzDqQO2+jjTTtzvi/YCDFE23OCiVokhEQlydu9/kc+oIZyusak0O6lAIuxub7DHAfP7e9RTAeFLAAfBEUQg3jdZk7137ZZwdPs4ZPLYvfdMiojn3Pjj7rDNu93HWrim9jYvNtyD52pk7q9ABoJvn/nm/kmLCBRKfqHJRRNynrDbH3B/yvjDW6llQqbw1mYZL9fVPofPV+N6DvUbj7Hd/IPLkhQYB9QshpdvPj0RX/9+r4RognoXevp/JmDlRqB57HtuNIHvU5084t5qXYVGLd+uKKFSsN4PVQciJaBTFoEiV/WAqLNa4xb10mgWwDjzrxF7MUSLUcoJEIt/S5obBMYIa8HVrO17Qm650P3Mi8A2tAdLaCyTKddQgilnemltQ9a+XuDQFgeC3+oJHouCVJl8AjQuvs1rKRICZ7ffIWk4JEAtnkFgiKA9pQxkicfOBZjrSfuqLlhMQYCcPJ494Mo5g9AthuzypbD/WpgccyZMAAr1+0MzBPSTHu5PE5gmxzd6L+i+RxLmIaUk8kh9zvLF5KPtkleCmIhUWQJUsnBSjakgCrjEF0Yak6YUBlVWIAVWQkGts3knjBeR/WRnVufS51Fxig11C4dEZRbacWYSrxcmQq0lHsGuJCJU9eSQuWJYqKTKriVpIaCYJZSTc0CGfzTxcdF8DCjgRMh6VvOU3UMLIA3RVcX7Rj10AFFGEKcWUsnPi66ZoYCwJ5OG6GIyPwYh6iShYMRHMkZPDq+4pqLdZaSdUcqISQdlrtQKjknDOBm5x57bALr/HPSwPh5ijQX+bjtQY3qbVxuvCNiXSghDF34OBxwmOL+FvYttS16IomNYNpzVK2GuM+pcUOYZTCEkE6miUkP3kY7F8QHaHlHoO9wdvfXb2ooy92YPfPki43dff41/+NXfY/fiS6T9HpVO4HpE/fAafHoPLrBj6cX7I8MwhC3m+RdNqv2Nl3j9//R9/7I3zafyjPjUZbFXOtr908zFxf17ocK5Ndy2C1rjt5ctB0LsLAzLjkObESFfU57jQF/q6iIoY4UNmFbH9FApzoU+LpQm5P554qQFLat0SCknvDn+C97UP+Hti+8w416Ml7jRDKZQ6EcWjciUp+PqtE3ji7ZpZyfBldiOfEwkGY2n9L6KVdDQxHHNrp5+4xWVnlM6det1QU0h/ymigUXgMeOnR2yF2BLfE8ofCfyjEpc9ewYF6aoj3ZOkHH6/cr9fI53eAKSnEXpauodueA+j2WF48sC5bXvw3IuyI7fbPve8LdBzkSUPD1V0jiayM+o1/fcxxN/WfdUL+x9WFtdevJsulLUwRAsezH8I3u9rBwbNE9wN5KrIMJKFLw77lSH2jcJHJ+wOB+zyrUQRmSvArwC8XJz5bUxyZswD6ju36s95y/xVJqvuyrPTlD/PS/5ZC2XU/R0qTSKMyZKY+t2c8d/+lHFfVNBzNUH5gL7PILzumrWDutXXtX3SebLN5YTn2nDm5SdgYBg9kRU+w4g7iLIhJiNFSLxrSgWY8JcIUWguAipLHNsTt2NsdmuPw9tUAaIiQsOBepEwQbMKv46ijCgFzMVDt7hQP0x+m1kh+0TIniVcSGrJhi2sfCITnifEsBsSXqh5Q9gcAiYE6wlKmycRjOncubhOhWlh6eXuMaKN25yAwgXLHRrpBIMw+Iy4lQFxZVSqSvra7JPCSJp8N8Gs+tOcJNGRXXguFQdqYhf+5SQR/bOG7CqqqAIVJJZ4/6zrzipgrb4mYq0tAlhyQjolxQ3apnlElFraPrK9ZELayhKmfyBXjTD3i1EvbKvDmm/EwjcRETIlEXrPaBb6vo5JYa5OxtfEIJa5rZo7wHOojNT3QPD7+rCGRqvcPD+0fdYwSC3cWGxOV52bN8KSipQdHOeLV95vEA57WM+D73Mdn33uGA/th2uSFCXcznmzbK+BuZO9IAnew9mFrDeqnL2UEnbTpM4Oup8tPNysIXimjMSMhIyqqcsJIpBuZ7XteShhBkA1EeTzm3IWhUmqYKqgqtYlFifLcWdcWQlJJGHXNGxUaqL5CkhiQFXuaBYJDwdWFQbb25LgO/XLGbRLiaoSrFEhoUodMLrcIraWWGMyBgbH1wG+58y6sDH45h1XPF9ES2ljuD4FgppR+T04HQGag8Iywt/uA1MKguG5hcxzJFkejmEgCRCPOxBucMRdKvjm8BV+9eIrfPnlN5hevgRNGYyK8uZbcPkAzCcY4W/YU4fqHPIlRvlvTQj7ufyyCzU09zdYnoH/4nZHdbRpR3dCab1Gr2x2HfDtz71c3jcrFaIshXrr1cvlr41fVgbjc3l4IYAOX4CmAypl1HLC6+M/4f3pB/zx+/8Dx/IGhU+Nv2ChNQH4xu3kh8Y7aN6v9p/mueopgtjMekmCWImF10sgDUcpHTof6bYpa2dFkfPINjjtbeRf4KfRWMY4V4aKjJRpLUVvbvZP7cW1cv2eDRgPfCK8/RegnjQfpNPd2+e6V5AMMHAw0HkgXI8t25B+ety0npPhPFzuUb/5/BkAe2Q5ryAQuJf0Sz+eUfnhR4r651dA03/Sf9ZCol9u6pyKcA02QpQtdv0pr4Ja8e7tX8TAe/cCYBb9Zge98XQKQ0o4TvcouaDmk4cRXlhexyldgH1h7L344CcpD1BExJ3zFPAuIcynlZFIekwvMT54//tGqz9Dq6jHW2oRQAl1ugXSBELSOM0Zxzrh23cihLGY7BcLd3+2elSCYknOL7tY6ZTjh8uCB2vnWazZLozvsd4QW5ZqHDq0ZM4mdGkhmdQyGdEzokHpdhhkBBABiZzgIUBjx0ttwPaT2pR2XNnAyDHEOlykfn0dhcG9H4oley5wi91OWNuJXLVYUmzdlyTa5Y42NOGehmXqXOqCN4gJ/BZyvMXItM2eI+u19j63Y1vcCFi4DLLV8e7bWrkyyYhMJoA0rBIR2Cy3gwBT4pRSywUSNOv9HBjxLockp4QKueCoVnApqESgUoQo1/crm1SamkDThpGMYBAiNRGpFb5Yu0v+EkmQnlSaqjqdAAuMTl3MvVsW6HpJeCljDPS9oIgQYad4fPA89zcXEYjUUj4sQxS2WxJvGRu5p8Ba8bXltgecELfY9yBJCO6CfDZguu9rBFLHuOiaWUKrNazSi1g0aa9sHxciOIEHo2/apBNanoxaU+cdYuemMtSd1EIlsRNKDTBZJ5AqJkGwnDG6G8Bz9WT1iRMmfT2lpKijqpdC27trxKXAJnBYwmbPyZCSbirNe2B7xdcszLXobkV5wRAvG7DvWbA0I44vyYHgCknKXs1DQsfLCUSSzaUtUMPBNZlKU/OL+InXM2N5R9Dw9OqVRTYZYX7YwqjZfubgjcKuhCi1NHxLtoSqYiHyMGTS9gmge1GwsHlCLAlgMngprAmTJnRv3hApxf3S1pJSwk2q+PVdxW9fvcA3X/8Or774CunmIGtWC+rxNfj4ruEG3xDtPvT5vsA0/62VT2oxu7IWH5t8vqb9iGGua/PpQD92HRjnLCY/TrlEw/6UniFjVw8ir1d4jP556Kf/R/t+7Jo9X/kpcdY4WqcXhknf4tt6edPyvfOdXxKYPGIetpp8aFOXEAafe7jV5uPxwccuTz/eSkfu74DdnYaJvcfb0x/x7v7PeHP6I078vskBOBj3hPs8BmVVaV54p8KMS6orG9nPfK+S2IDQ6EYEvmOL7lo0QB6Oc7u68B/dO96L/BNliltbvPXB4eVxMOfgOPNcSXoiQp2B998DORHy1POcIzTbCoiVuhz63jyTy8HHny6+j3DH9izXuS7Olhi6ervOeh9bd4c3ydfeL1uCdNr43L+71vdmTxdgXyvnq0aDzNjHNl0Y63eC/gfAYjxZx+9ina5Z8uDLPjdWsvVJg2/5yCsp73k8fcDEB+z3pOeuhS/u+THAdnOdZhSekXLCRBnseVAHyRWF79cclrUqV5yP56D8fgEeEefR+sd9G+HtjQPwM1RCPLpQQt2/AqdJBCIM7HYT3p8y/stfJtwX04gPOQDAy82r56IRDf3l2z7DK13e8+du10hmXFZGPJahIPu3e/1xyobtPqj7bELRFlJIrT3YJrgJmMwzgF0hEa1D4O6lFpPbBHZMYoHvMcktL0h3ggyrN8rH+jKliFTjVo8BdqGYwloLGFVDMfWhQgZ77zAPgFsXJxGg55TdkSNZOloTnKYmfG9kaLA2VuLWhHW+DQOcdik0IaDlxQjLr0qfBUVj7RNAkl27ycZq1ZUlNeIWJUM3XrIY63IJyfOqeQlkc6dAFFJKmKZJBYxV4/sX5JwB0uRqgFpEk1icJwkflRKw3+8wzxVFFQymaEhVEvraBd7nrRDhZkXLOZFUaw9I0m0PSmS5IkjyL1igFEUzrb1BKGlSTZt7qah70hJD65gLdF4QwkpZ4nNto53T1lFjOuBKnFoqPNcHKQG+wVx27A3bWjVvIJKJcfdOHnCh5/MeFQxnmJBYd5GfhNTzx4c67i31WtFk3qbAsXZ87jyBtBJAelaTeR64B4K8l60N+22e9WiEs83DGbdk9YDOeRTao29vJPAhVmuuLDIhE5sSTxK7MxhcWrJmAKqws1aU4tPx18KwmHXErImzqQttW1HFE0jvmcri4dDijgNi39LwRXd2iEEerExwAECeu8GUB0SifERNAxce1hNNEctcdFqDB5wz6WgMfhHca2ufU8SV4uUkBgiEWt+CcUTFEbUWEODhtmw/ybvtu+Tp0XsiKcri2l3K/jWs6w3u8XKa8esXL/B333yDV7/+B9x++Wtgv8OMGfzuz8DxA3j+oBtEXp71/ayMfgziYPg7lugNQ9SB9Yssv3DwP5fP5ZMWM9Z5Pir+r6gsJuUJs/RQZcSltsayKql8znI97A8Z5V83/ibQjXhCcN4DXPCX4//A++N3+NP3/wEf5jeY+dQZhrnxnPNpcqNX48UCLW45D1lp72p5BqF1mP2PNWpnPXK3VpLS5M7vrQ3JWT6lmAIJKTRsXbzSPJqXbZL9E0QLvKhwqWxXWhtn97uLVuR/5Vjx/vsZ774Xmvzu9oDfff0Kt4d9D73yVi5vuSR4uQKmzfpbB+qhDT20fIS2n0JvXvKI+LmXh+aEWGnB34tlbCMqL4RHWjl3C1i2FqZnVBb2V6Oygqh75t/MsAyaQyY3WRarvAiASbMGiEmYcgh7eri7xZT3OP6YwHOMJdFkc8s2Hlh+oovpakVEj1+CtGizUMfoxc+PKQtPhyecZMNbW6NYnolhk40wDLB0Qtdh4M+9riOsD2p/oflL4OlWFBF11jlKOHLCD+8JhQkpD6EmAgTdfBpRvya8O3dZbSIk6v6svdSEZpduphGLXAaCVj5Z3Q355KPKJaTRCSuNmLIvlluBzbLeZ6aBziYUM2Fjr1RiIk3aZT+gp1RigmJ9zBbuSAm8qMkWwaxYqrglN4sVruWt8HPi8sn1k2maZhN2S9gU1nAv5FYcYmVCIaZnN4Nqbc3+fXy+9jGuPxnV6SLVpugJs6JTp0JRy+VAcEtnV5WMG6iZ5ITmxJNEkuhaaLT2isT5l7mR6i1sksFL+jtY7IhSwE05TeA8+8XsngFV8gFUVD37PRHqQmYVapu3FKCW7WAPMcO1oiYgqwBW7oWAiQPeXMw4QfMv9Beu6cSsn5xY9rBamxtTYMTA1jHt81q0fBR2HrswUt1K+6bt5qWSRpAiVSixrpE+79aah9i0uk9CpXYGg4BZ1pkbfLF+gKXfWo3wMi+YkRKMSplocZ64Kagk/0RQjIF9vSVpIKNAEpwDcO8sowvYuDeI0D25sDyeP2MgG/6ieLksFNrLFU4pSTMaEkrVVQ3ftJlE7+TOQE3qHUFdX8IUy5qaQ4gkNFecEGAkSiCWeYo0TKIEZ0oDvjQGvKJqzhEbKnt/fj7Y1hMgHwMc57rCDq1dO6uVLUSTKDoktwrrXiRNCi//FRSAjgBUeYF+v3V7V59RxF9kfkPG5sZ5l/1FOvuHXPDru4LffvUSv/76X2H3xTeY7l5I8kqewfdvgPu3C5QRdq/Cs30hRyXE8BaWJ/zjltbfyl31TKCcG9NP7h3xVEbgTOn01A8s4yvXxkaOZNJPVdaUag8tH3ufP6dhzrLtx754ze+Pn5nnG/FPuJsefGg26o0kEM4c8Wv7NIHbQ6bjoWjlYtvXjffBza7Up+WlNHx/wFpdNbdPKFe8H6gP0HQAHV4JXVhnfJi/x7v5T3h7+g5HfttoWuN1GACa97rR3kbmGQ70SJtsHq9V7e/kvYafWxvNAGVtSC1ccU/jBF6stdjTzSZcXBAlvVc8tRdC5/2UOnnMsfK5NW3yJRvHU0qdgXev73H/jgAkHKaMr17eYcpps+ktsc62DGzk+zbKI9HhKm3zoLYMXsI1F/3Wkdg+tn2jDzuSm8h1+P60u2QB01pzF+EehUnnc0K03/s9H3nRqGQ4B1z3TnjxnPJhNLBajmP9u527br90DwNOoQRUMTQjyi63Sqye8N5Ag9/bUNjyfodMe9DbBJ4DPPany/Gqf+MUndtwPj+PxSMP23cPUkSs8RDt8zbADUFtCEu6ch1pf22cL73G2rIqHEIo9Qu3BpPw/aznJ2JaOyQb74QRPPpKeCxn9Sgig9p/lEDTAR9Kwj99u8exJlSykDiheoRr+Dgc0WV38Q4aL27bKwvucOzLLCFiRVYiYn1tmkwvPh+p6KWgYtGWPg95lcdHTvxok62lVSS6hDU2zUJjtfaV3vFQPir8s9jfNgbS9UzWmhJx5BawPQwWMz7BFAW1G6T8m8KYVIBo8VoCI2fhQMySup8oIzCrw+5CdM9MoPPiMIuVLqUkcfg9cbGuefQapSVL2cVcZ9unNn4V0FdJtCsKGnj4J/lfUi+ESEo1OD1PhZ6jyhLHRULIB7KoAqDaDMoJi+3eecXoWDzUETNqBmKMdQ9plEgS/arCQWLNhHrmnaFKgQpNvEuiZNzvdqi1opQS9qeuq3vitI3o1tWkuQBQQXlCSgmZRWlywiwhbVhyMRTWGUpZkx53q6T7W6WwMAt9bnNlNYNQ1ATL8zx3CqiUE5jbbMoeM6WEjssVYgEGEwrHPTPwAqYgqazqpoCXAFE6iEW9zC8SiYdJQo8QbB/X5mY+ep/A+jDBP/Vk9qiQIFUCkCZQdgXCgNg6i5ANhYSNSGBVAocBZNvppI9MiVPEK4QlNwNpeJ/TLNb05rQ6TTuUqgJwEEqtohwzYtHgMJj0HmZKg1cSROCfWdUMtljwO4spixdCLaCiyhdqsDujym7Xr9/bHSyi9MZOupUeoNGpBnwjtbyNlnMhea4T5opiibaH98kxCZqnWlgbotTBEHvmoGgAWsL4at5pqoASr7JG7LZQjIJDSmGUMgNU9CzYvlxeaK4/5d7mL0EsGW39KJkxQ1vn2z3w8sD46vYr/Kvf/A5ffPE1Di+/Rj4cQFxR33wHPr4F5mNDdmyrwXLEwrxvlcUc0/azn7qsUW0fG6J1+8zPpZXPc/PXU+JpCsSiXs9gCRMq1QjiX5VcqWqhJ60l02WvsABPA23tu/98fU8fQdeHKFC9VDqBL61gmUE5v1bvU+Pkx5brpBjPg10esiZXNHZOh38FHMDWqN3buFY1coLLley/avn79K8zamgUSuPY5CXxghBvVzF6a7RS5Du7cxratHxfvhp61p1EIaXNlE4rVTzH2cdRQ3uNNurPn/Q+nsloVhXZG+dX1As2Gu50n1SAOb7XdbuxySh+cLmIflbjlJTEm540F2NHdK/3uCgNhJGBi8CM8pUR8LjLl7TnudLReL0IYOsNfW9dJtNqPAiMZyw0smrPVK5p8CkDtbPRt9ErJUY4EiyUWSd/XGt9cbio+zvKVDD+SuHhAg4aX2x84vCXgCBz6fdSE/cQkAFKQM4Zecrq2cVi8Feqn0MvisAoZyQinPZHHNMRyHfCW3q1Ef+ENq5dvgdu6OXOedj7jwrNNMotrvNOIH/3YfW3D8dDko4w4EJWQbj0sMn2F+1DOFArwp3485m74DoYtjDpY9uLbdGwSe1iSxllTvjxnlBAyNmsi9Hm4QwyvITSePhkRL03331Yb0EEow8o8bK9CGX0dDAEOJDIIwfSXXJOPZxdstGNar25XvDj/ep/hsA8Ljj3F3ZjoCLqpI35bRc+mSICg0AWGkYE8H6hAvwOVCUK3Tp3jdYAw5QALtgFByGTQhuVEDnLPtWwMuA4xjh7bVY5HsY4mwPH4NpoE+z6oBAINgrNjzu5PbKVZVTVTpO/y7D5qN1+XFp/9xPGgOZI4DCn1HhnY5g5MCejcJdt3ZSQJw1xA5Ikz0XzO4w4MmqjO7BMgKtwaMQZSoTECVQCCdlZeQcCxNq3PwQfn4WDk+S/TeE0JrMCVPlVJGG0zSHF9QPUcwYyR1u4G71gmMhyQbT9QGFr2Mb3O0kHwX7u9L8EmQ8bX3jXXgu7Ps5yvHAbXDZ3Q4lnfA1LmgKCun0x3Aexb/9IAHHAh41pE3yg4ZsSy32R2BVmpVZTLSlzk5AAJMrqAaAnnoYx2b7wIckMOaZiNGE6JZiijAPhane/KYREMm57Q/GNJL5wxtSOV5unts8BdgcMX4Nhmt0gpdqCCH42hm5UhHkIMUDmLizuaMUvoZSkvvRdhznTUEyId4IqjQc4Dcc5VWPKm1pRqnlBBJXr4i5spAOAEDZBd7I6xmy9T2BMifHqJuOrV1/iy1//I25ubjAdDj7vdHqPev/W19KnO+DpLdJnzduhJ3seQDM9U1meSQ4bppWfHrJffnlOocDltgYC4icsl6jfh3hOLEiN8fm1fNbzS0fGHvDUU9GJtMIVzJH+cmKvu+RXoIkXwKV+N9pYQQWbfT13uXa9bP25t+5+UD8re2htX8UTdeXUPgCOS8+N/n4eJPJR8PeK0Pa57jC7mh/aWvMcBiyss/9A5DRIrTNKPaHMJzFg6s4h2//lt3hfG0R+/LWu8lISkhZqPOcNdHRZR5aMY470yEIZ1v4xL3HmZoDXw2kgxlaXHcanrc6SpgKU5B6aGaNxdG8awNTmbKkA6V5fFiXoyP+Lfbd90j6E7p2/ajR7HN0iR92iwrJNA6rDB2R0/Zl7bWN8jaPwmRjea/v5+rY3MfzFtq4r1H1ea+/a+zegc3vzCVDRmbcXlMSZlowHjnPf7t8HKSHQyOn1vCbxncYLtq23RWfQAhByhjXSC9ThUcsB6PxKEtPgxCEqie1nbp8tzC0MNrajSahTEUNSqpKn0+YtMqYb+3u7bEsTzpVzO+Ca8iw5Ih6iEHhM/c/lecvaEYvLkYiQdjtMTEg568XSx+7ebPuKteWVT1iBaf0lI0Aus2FPK2vkdiONmSPSvwAJDXQ4nScb+7thtNY+X5rweYAh9khLJrW9K2MzYsssTGAW1aE9nwMWYbt5NsR6JigMOLh/ygwggZIpfmhQJgtyl/Ahk+eHiOArjevfyP8FomVwi5sec0JwgDHEFXXiS/92278xY2Y17x4p1qb+XpPl/WYk0suHZJyxPnhU9sDHSLBwR4RaGYVn7ADPgxEvVNKcD4XZvScAu9Qa8Ve5giqjFBUIZ3meU0ZUxHTzYJb9gaK3PaOnwpMPA2pJY8oM8wKgHkcQRAAcPZq3ykIxEiaqgcXK8FT4MJj7MF1GZNtp4UjYC0xeu1N2qKeVnR+r6zDZ2bHxd4so4bRYEm1zsOZurIhazLNJrttpA0EEvCmJhwBrAmITXNuKDIxRE9SneEjac275IUa83XmK6B4QCy2n8JwoakxEgljq1yb81zNXiygl7+/vkVLGzUHO8bSfUOaCU51dkWFEGENwEemahYHpvtH9E/AEk4SIIicOfZcgZ3GDba77tnMBroRKpdVP5N4Bo/Cbmd31tYWDGwv5eSf7X2r7xdbK4yEbHopnlVmTnKu1TEdUN6Rata0IhVjvaR220xr3VV+yWtroSUap71H5A5hP4FrlGU2OJ9vZTwPRLeP1XCm6lnkak1wQDjji60PBVy9e4l//5l/hxRff4O7uDtM0ea6SGrxBRob4o8s9P5fP5XP5Ky/8JETy8ZUvn8tPXjaNMj6Xc6WjRYmBwxeg/QtUyuAy4/v7/4oPp+/xhx/+v7gvP2KuH2BGey1sqXx3eaDxwdZ2bdxH1QgArHkhLJee0TvxXDuJavyMs8p9HTMIqRy8TVm9SWvzvCjF+qwBxsbbktPmCUAZ6MNo4hb/XZ9TDhPbtuX59y7t4UEOqzSsCT+VHxBLIViIG+eNjNYeRJCRN+4MhWiZt5ND105zK+G74IW7+aD+nRVJzdoU8GK9Lwmo1579NdCc6zz0ZQ58We06Oe6St1xVHHTxwMdO7b3+b1/HIt3EPmhxXrrxU9yDUX3YG34tz1wEoGsEpnztahvPp0pjj0jCjMoFb999jynvsZ9uwxzQ0Hbcu9JmmhIOX94j3/yI448vwGUneDfOWcA0l0usZ/zipdL395jyJEVEFHJdSvgxPn+qMmLr3bXYrtcKxh8HzfYiXHm0r+zmeVri8DduVTFbzC40KBWonCVZZWm1xnbWQR0sbcO7UUS2rNBmbAslSftnOl9AemUDGwLOlZe1Ce6+X1ropRKin5+ude6+xV6DYG/5jtNw5+AfcOYIgOdsQHWhINQKJC5WtGQxYX8Fu8KiG/iGyZe3qJSWb4H4riHclEDZwoM1RQSjBuJXdjUpYHEutxRXkXBcPl+xOhiOu1nk8LBWFL6IoNQuIYTN4MD14rmuzyYWJ0IguhlJwy4thHPxvlX4LEUSiFxB4QRjsAIkgubf6C/avkkChsuu7cuWa0FwisaZZ9uYZvndWjVlRJwEISAZbqm+nJiuxBwO3fHp9t4GRg571ATaHalBbW7WvQvaGYx3oQyzFxCTEu/kxLZtZFvHtlo94S4Hl/THMRSTzb+d3lEsLkeM2jwFBURsx6dO16gjOvXfpoeIioi2p4VBScAE99YyL4mqDB2q3RO23wLecD6BQk6MDYt3jvvQ9nc7kxx3GUkeC3DLX2Kn1YcarNJ9bEN/q6jeFqtTSAy37MCFVWJfi+3SKyhd6RJ6ANDyO6jyy89BbXuiFT/FHWxEYnhQy0m92WYwTrBYzZKTB2DNb0FxXQLh7Z9sr+pjdx52ZbB4Qnz9IuPrVy/xq69/i93tC0zTJM0pkx+9t87hgHEanQG9cDl/FEvjT9DH5/K3Ua7dSz/lnvssjP945ZN6QlxZfxstP0QIol09qPYzlbXxPZMyYms8a6xF9/vWhbb13NtZ5WTOQPgRCoklL00HYLpBLSdUPuH98Xu8P/0Z9/OPuOc3QqMxeiWElZHH7go7SSCGYIaDmgfoOq2PfqJ5Y3c6nW1fm8eFhYIyJYjX7ySXcPLPjUqof2zzNMgaz5ZNJcQ5gcnZBtsfZT/AhcEF4AKgEqZojGM0rn0+01/HE18h7+ueb7BqWJtDnN/fcVnGs7HqkbX4Kf6wls9g4LUWMshLi/N8Z3O77/U+R1nDNff4+vjX+eL2pfFCPYcV65+DWXmWxYbvOzPlg/9EtNgbi73i7GO4q3iF3xzmisZDDcCTUQ8akwUMenaIJIR3LQWFLIoDAU1is+TNwziIgHxTkNIJ9LaCS+zL5vyx++vyrWFSk6eWZ/OIsHKtUuI5lBGPKY9eEl3PXzq5HbcoQwRbTAl88zUw7ZGnA+5rxn/604RjASqLhbWeOvv/xeKCrHMzvoose8RBaIKa8a4/N8JraUiHIDR8qYsOBgZW0eeGsuPshdn/E8bd5r01G4QzUQAbCKC1QgpH+8Jd39Icg93aQ0JzcC0woba8EM85D//qKC26iCFjHQB3SJZFILfI6SGEjiSmFoVYypMLzAAjQgskMnyzbu4XkIMwq4a2mxW+Ea7mAZKSxXKHKz783HC7DL1NJYYb2AZj9JwhcaEDoXl9bC0S9UtEcKsUZqCUIsllq4S4Mcsfo71jqJxSRVGT1No556wCSk0iXCpYBbRECTknoIpnBOvctRVRYSUREhJmniURL6v3R5YcESJnZuQsAZ9SklBapc6eJyJVVXZQu+4oWa4H+c+J/AWhs7bBFd94rhS9IlOfx8D0IU5D6Nqb9ZN5jjTCW0eu60mmJECV8D4U4LR514YlvJWGJKrs4YOs20SWVyRwQ12CLgYbQWTz5IoHdiFz2zYESgziZunjOCSS4ASYh1vWXACmMLBcAr7eYX+Zq5KjDducmhicwRrWSL6loFBhZsynWfKRQBJIH08n9XQSYfU0iSK81CI5YNCUWrRxXhqppUoRdXktZdZJDuunexdESHZuW9wk0JBpoeWgaYwo2dyj0TaRSYtgJlXEuR0Zs+DNVH3feVtIqrcj90qoXDTkQKOTkorzoyJY9rtlx2guwBzOkIcbSA0OSpIjIqWEaZq8XsUHFH6HuXxAKUefg4SWO0LUCI3YtvMhIeHs54QU927bfNjzEV9N7/Hlyy/wb//hf8Htq2+w/+Z3yCRhp8q77zF/eK3jr+By8vGqLu1z+Vw+l8/l0aWRr+z3cGcdbfT6Bpn2Wbn4uXyMIjTNL3RvGdiHl+D9C1SawPOMH+7/K96d/ow//vAf8H7+wT0hPFRkUBxET+5RoVBNBsGA5NcqLe+E5Sa7IB4bjSQ7nlv7tL9ehdn7KEWM9CRqgHxGBBfCWzZe28K1osHlPJ5zJhenNkpFaP3BVWUIX+/UL4hQ7hlv/3TE8V3F638i3E4H/Pt/9RX209TJNJ2TGWixyGddK9obzIX8twXb5+RmlGI9thBG2eMolN96r5Vfxhm9rACSv8x93YfIZ7fkWv46tdBCvAlTtyExfqGF0L910N3TznNpJW82RNIYeZKxXx5/WMJKhBZ6mcYZaJ5D8sfOBXd0BQPOE2fK6rHfPORNrrTAWTB+n3A8fADne3B+2ecN7TDG+hjOl8seEc91Tz2LIiKWaz0fRovM+M5jyjWuP9QePrDtRQtXv/i40YTy3Bx3xDqAWDdSBucdKO8xI+NYEt4fGTMn5Iw4cbgO+Y4CxGtm4RziN6FLL/je7N331vmljoTISnhmxHGsLwMvvkUhkcCCTjM74rroahWb686FIaXuucmyHrg/Ogk3FlIdIQ7ZBcIWNsQsbuOkObE2ZDczJLs2XhC50sfIRSPIXJ5riJ0IoKThTDKSJUxP1JIuEwUXWxsY930On3wCiMUUxwlfjk/hxAq1NjqXU4xrGFoP77jQMS111dtEM238DhcwsiwM2KPuhN1EFv6nwtVUzOJVgpZ/vMPDXVKoXtHkKXxdyUGNEAgMPSBTmph9jEk1/MWWhjVJtiaLIN0rVb/YRby1dnKmIl7pa/aEMZROaITAagnIgmAC63EFjKlosxJRknt2BGhEV6UhunTnxOYo5vKwn+1InkVggSsYqfX+QNiUL8ZpfQEJTC0BeYe2iSS+/6go7BgSrTeifeN41LfdPZtcSVdRWc84oEmMyX9PDv+1dwhcX776uwJHiZAoiQK0BoYkkRKF9k6c4yUsnaIY406hBch+iiRzc1C0tf1MaHSTK4B0H8nY2POLMEiVAnZFsK9bf37CGgW4Emli6hzXpIB5BvMJYGHyU5cZXEen8DIifUdh75ArIVLcLKyeEMR4ecj46uULvPry15juXoF2B6CewPUEno+opw+uJOvmccA3W2fkwuOfpDynsPJSW5vMoN80K/f05/LJynMLsrfW+WOWx3hCPJbHezQrdO7Fkc7mC9fuE8rPWXn68XDDYwf9kXHTtYsx1vtJLpMNiucCzJ9CMbbAOcqjIe2BfECtJ5Q64/3xB7w7/hkf5tc41ncwYX+jU4zYi9Rq+9wM4OBKCOOBREnQhHcIb1P3bYQdnd1P5HbA/RtctY+qxjpVDSQCD9Dnxmp9qI1K12Bjw9do+PXSxrOkw695q6s+vmffK3C8n3H6QDi9T7h7kfHi5tDC7IIW+PuhR8LfP7OfG0+68e4jy9IyvX96bV9mXHiu/rXeCdeO6SF37dYaraOznq+1erGNx09730Y0Xrr8xvlvLf8i2kGDrDGFZ8pVtTyCQ2PnlCJsHxdbse/DvzPF19FkwI236/rWfBCJACRyHGbyy9UDa2yhGohzriJzSRWd5wmvvBtHcHFRLy/6c9E0z66IiOWS58MvIVfEzxy8zeLypGARuaxDmKdX4P8/e3/eJUly5AeCP1EzjyPPKgANdDeH5MzOct++3e//WfYYkrNks9kHgC6gqvKIcDOV/UNOVVNz94iMPAoIzZfh7mZ6iN5yy3yNw3TAwgX/v99f4f09UKciVkbU1/oQIPYw+svrydYQXnbDYenrpubw3wqSOuJjCNI+Wnf2QmBDZNoLqDm3+jY77Qv/5ARL0hLxmAcbeC4Yb8roT3Cusma9aUebxgcn35sZjgo4IxnGaC9IktlgUDpfz7Vm84mKbp4EeyMqIJo8WLVXouYMeoU6k8sFbNY7bufREMJANk0LLq8XAqiINYb1LY1lrQwqNcZdkWfXim42TlgVlArUQirZDysLUIEEANZ14kIrSves+qunFeZep9Yqwbu1/cZMWOuxtVLXCkzAVGYPTC0I/Apm1kDCjNoFdgomoM61zoNo0ktU6pUZjEUEVgBKrailYF1XMDGmecIEoNZJXL5o/IbV+kKi5z1NE1ijWTPEB6vNUSZ47IJu5jLNuepNOULijNTNto15rcwoGdWftv5DR0dNo0Gpa6cUgriNFfhrXVFAqnufESEjxnhYfwhcrK1UlIBpKmLRovuVAdf458oa5E405J3OMAEjGC4cpXBV5ARAOlNqYaCmOADdPjVBazNSilwxINu7VrFsAnB1cyM+du/vAYhW2zRPuD5cyeytsj5qJWzCpmxwehNa2RqJ8952tQgvp7gPq9xvhUUcBh23ynB7g9xIFgIERWlnps0V67rWvZXXKYdLtoz4G7Iv7roi2Ltr53aIpMgdGYWBhRed52pXhLaVLVok7gOAsO6oDJSCiSTWzuFw8HNgqR9Q+R3WRYNJ1vBrXBBnjkNlgo0+aZ/iDjCrE8IVFvzq6h6vb1/h3//9/x0v33yP2+9/K1ZzvIDf/4Dj+z+B1yN4Xbd1f8vcvOf0nJ7TLy459jc4W3ZOuOf0oPSYM/v5nP9FpsMr4OoNGAW8MP50/w/4+fgv+MOf/r94f/wBC39UIQKQdl5Khnuykpscj8BJ+FDdEsKsIqB4cIOO7mmmtC36/mcgxe5KtHg1N5EV68qwuInyNsWIUFzUY1dUbo4VylbF3voYJmm3e04AUQVn+vFU3zjGwsel45U2lIdlIgKm4spBogRYwpoCuUguT/kj0bTtb3/I+4HWL/Gu8pDUronmzYPrHylR/9JSz0iPZEGjH1TbtppoZO9nej6C43R7Bv9mbenzkvkwTgv3fKYd2K3uPmsLdMvbQrgt7unh3bVl/CUSzwnvPvyIqRxwdbhxa3BQe0pURutOu0yYCTh8/x7ldsX9n19prIhxk3vd2ct3ahnsuY16aHpy10xAC9zI8qF/n58/1eYetedsJj2dh362sZ2kTfkvIZ14gnEYjqXdTDSBQeDpAJQDqEzgSnh/BD4cJXhtV3C3/uEmC57eHnDNz9GCb10yDZCWEYi0bdy7vA/MySeXrEnTduX0ewNqc/APEDB0wxI8yEYQ05TMjHYFYGOH0F3+3dVgLSQc0IQS+p0BmNuSNA9BvBHGPgBz59OPk8GJFVNSZpYJAii/GxXZrI++AUr5LEdbpkHadi5GOc8qmM1Fz7aJQlCrDc4FATO5Mz5mByPR3pgkzmJi/g33BGxPtrBX4WKK0CIFzPW6qiC3XHYgSIIqaULmqBCwep48IuxlfPaooJA40gILwu+eZGx/klpE2Ib1PZDWXNNb7h/4J3eWOi2iQaDBvuaU0YRBFcHctUkiYBPXYgyI/eQtTNzma8FRESGHNYohiN4Zcly+S7ofOd9XpmFEo8ZCm0NjEDCl+eQCmMVEg5l1Qggb03zcQC0+qICogqhgmmdgWbBm2BkuOFuhAd7Z+hAwW7yVPonVSUWhMOHLVwHFEAb4uuhsqxQm1M14nrvIAsex7z4Wul8soJ/Fa2+ry+dmALmd07gMqh23TpSP7uA4v4hC7MlF2hGXd3qG1RXrekTlezAWVF5UCJ3O3sG9ukmekdIjxgRDpgsOBXh9e4U3r17i5etf4/blC117K+qyAssdePk4Rn8eTh1J//pj4Augbw9NX4Ld+cxS/ctOX0Mj+tL0RRXOHkk7yZEaZTMK9cnQXwLSN8TYOmch0f/+ltcegLNjuwf/p5yZnzoi52B6yJhb3oxLyYNPW9leLxXxrjAdgOkK6/IRy3qPj/c/4MP9H3G3/Iwjv4db249gdwUYow/ZyThT6skWEBavgRnKsM90qaELI5/+aPIlFBQiYuCgexmOCykJpbBYcO0apTksudn/pNSfJTu4uD8KlC+q0Pqpt1Du+oLt2w6GC+edwitAFmKAzJKbNmuI+jYamqHHxds8YQskxN8+XusVtHVe0J+2npZJfGk9Y5x7r8mnufsuqedclva9zUc8DEuPvVgY27WaadI95vfYI0FSzOrWyG7iyOuCiAwfpf5Q7p9RMtv6fRsO6Je95BRmt9a5bRoeEP3UxOhZRaTKv6gisFzb3mlW/2TrlY3D1QrgCP6Jtez4DnroajyVv6//sSv9s1hEnHPP9DUtJPz4zkyZv4IUvsIJYGC5eoU6XaPMVyjzhMPVAagFdBDmojOYBiu5XeDBCHmcECk2vjXHfgFzgv2SWzYDJgyxvQtjD9IND+oBKVsynBTSbAvmD0WQDC2Ca2g4YsKG9HAac0Ms+8r327d2ekRMtEFqBOPirRCiaY9yjb3QUTJlxrjfddWq0fl3dQuL0UAQ10xpHDnayNq5DkFimDc8UQKQ3OCwj1/0JWDNyErYTOQ5IdXIyQi9aTebsKBvC8xeowRS8OsMBcAKY16iwe/yqBORaOtTOmd1QxbSYNZgiCUJ3Ke7WT5Mq36WSfZbDQShVsZaBQq/xEsRIQVL7IcFCybA3e6UYn7jC+oqPlqJJIbEihUrKqapoJQJh8OMWgsq3wPaVqkELuz1EMRvPaECPIkQwALuJhw1GzyasIPgXm9gflu5Mri01ia+jshc9FQxPQa5b1e3SClAqeo2ylanWv4I0WHa77FHq+6XtOR1ntp9boSS73+EVr88U80xDo1ysS4tmIqYmq6ACHeWxYkjE7CQrUurmwiFJx1LJe/80NHxaOIiQDQywGo5EOgPQD5mbR91ZjjOb1jMiMncrElA61pXcK1YlwVMyf2br3eKcwDqai+dV5F0/Cur9YsJU+KcLBpgeYmaBZY0VrVUl7e0d1lsyNixMRK9iyZXvtBzzIjhFSZEsbglsn5M2GqDLjHMOwRU7wDrH6f8gJydpHFeYuFxHN06/7PGhJhKQa0V93d3ONb3qPVnVIlOCFSpvRSCBG1Lc2qBMuy86+8XIkw+ToyJVry++oCZGLdTwaubV/hf//3/Ddcv3uDl938LHH/G8sM/gHhFwYq6ri1dTtQMBfveyIPT/f4rwuue03N6Tg9LfoPku8/u78C0jDuAS5kTz+k5PV16DC399RLPL8A3b8FcQLXiz3f/iJ/u/yd+/6f/A++WP2DhIyrb3R7KJHFVGx7WWglbDAmzhKjV6NLqVgoWq0HKGx+BlAXQuziJ75xwPQY7PVdrS1u7K9yqAgl/b1bxxp8IerK626agnx2PAkDJ8jywf68maE577zilkhEMoWsYcGbnmbQREKTxaIcnLLvNJROpRQQZInhpG6dwseZYHeRzZbn02tggiiM/yEd9r3zX0PoPS4/UifmGUkcP21Pn47VcvpiArly3kanPP6g/P+5LncXdG+WxrRDC2ggeRjy3mH2bZDD1ZEUGK0kYfGSaqoyyG3eDTu3RpvuEaZpRygygYoXxi4S2n/R3NYkn5CyhQri/vUOd7kHljbQ/WJ+092vDrNhL3NT7zcSI6InwnE65ZTpX317aq+tUuZHlg5ynwnw5xzTOWo7BkNzP/0XSGVi3byfUxGDlMgPTjDJPAAo+LIS7pYgmsgenTvUO67QXWYOzXag+xnvwn5ju3Vebyytycn6jQG/XIG3h1OytRtSp+Q2GmWuKZwC87TjSL14uhmggkBKv+sR+i5M4veP21bhMPxAW3Fl7F4A0ldphtznDmJ3B1i4cbvKMkRBjtsolslmFDXZmX8yMNs/KudTn2QC7AVPWkTTCzpmD33VOt+422a6RaG27Fs/DO1oDFDArTIWKhsGojlxTJrgbjEqQ8JIQ00KENTGCoYz9RvObFOHvYDJXNVXdeplbp0KEWqSuChYXOSwwGrLb0P++RGXE+iHOmjcZsTGiQPocTHNidoGF1V9svfmxlN1BoV0I3rCKQdj6v90j42R7OD8xgW5ag9y2TTKKKJT1hgjm1iufE806dKyJHWaCuCIixPkyTDq3BSzxHPTh2bNsgMdSKeKiiQqoSFD4CgniPTprpR+2ANKzPh8DYh5fDFMzKGEMcz+kTJCh6z4LpgRZrCfHI8PJG+Q7wyRnBXO7J60X+wbpqVMUPkOzsKs1b9cPQ8q1qyMr1UIWo4MBLKi8YlnvUes9KhYEMy7tIx86ahbsFjsAFNVvT3MCDsS4noC3t9d4/fIVXr76DvP1rQge6gIsd3LnYNGDNSH9o0EaPczSvV9Q+quzUviK87M5N74KFM9pi7WfTnt4ziDjxTAEKpYQSm6raG8ez/XIdAmO18P0GdMDOWkbjfq+up3nj+nLl2DwPfkYX7pGGxge+CLhphdX/JjjNi3Vc8e1WEJMYglRZmHS14r7j+9w9/5H3B8/4Ig7Uc5JCjdD0AzF5lA8UurOGf/V6BitLvL0ZEI8IVBLBzdkWAgATJDQuoNmNPEROWLumRCicWXKNeqtAVs3aP0DH4CGROR2ro2OcZ6oI8PR1/ZRPmkDd28G3HfudqLdI4F/xvPREtwKIVL+YYrne3nisdEv0R1qM1yUvLcZhX5QFTGmjxVGfFkU6ERjvTDBSxgt29MZ6ZTPX5y+6tsd3Aqbetocp3mqSs+NYPCqspVFhoGAsi8M6BXqNnQmRT1W/f7Qbu0HLzmISV0gM6BKtqKgaUJNII4hs4xi2xPGt50YNGlf17p7W1ufRo9PJm7HqQmy8wnpkwQRp4QQ33qKA5u3E5LznX79Tae8qZf5JdbpFmutqGDM0xXKNOH6+horF/y/fj/jw1H9j/VrLX32DIi4808h2iP2UQ/sqAy2zBEaZt60HXjHTtvcfhE85GLSqK0jaUJkE9E2cA21w+Da+Slegv3NiJCePP6cQ1ujjX/QsH8Czq7rJS9mBpgqiEld99TQ+rC6Papx7nBGIICh40iJFuANmVZLM256PhtMfTCs5jhXjXwdumijEZBYp/bnMhBbwLRo7PIyxmVJjFHXHK+CeNTsB57TaDSc83EyiCqLRrgzRVlDShtCSzavc1vSkUI7/EMg4NYkKTAwoWCegcoFy7KggrGugsjTrFrZSbgq/vNXrFCGZUka8mwaSauYHaxhAVI0nsKyLmgtVWR93x/vUUrBzfUNqBQcrg6oteJ4PIKrwETMWKigFBa/9mSWEYQ1EQCmyd4MKOBrUNzNSD9s3kqJcgQJdF54lfpYfOV7bADdo+7qp6rFQ6LOGOls7QQ5kfQQNQIKJJYkNuZpL9h6lLUBFKq+V2w8PW5IIdQq9jPMul6pgCcWZXaR6IByXAyKtR5ImroiqoKsGLFVOaxp5H/RLUYgt8xKxFEaF6l5i5QaQ74UkuDyCodos00oZYJZElXts28Fim4wc5Kx6tmpZ6QIVVZUntTtkAFhrHGppep8+DjYua0CGjEr6ikM0poE2TPtliITdAJBSObNnaAgPUac/f0lxuGvWLXwZBFJ/yTuiJQpVCTYthIR1ahgncN5nlFI1nrlj1j4Jyy8Yql3qHXFWhcXVMDOQhfa2P+SRqMB0+fZ3HtJJWJ98+L2Gq9vX+F/+/f/Cbe3r/Dyza9Q795h/fN/A9UFrLFkTt2+v0AU8zk9p+f0C0is90d/yETML2wOvV8izbtJj+WkPaezKbGE/6ITH14AN98L3lYrlmXFsqx4909/xvt/+RHLm3usL5fA35wkJnET2aw/oWkEJVLrBI3H4K6YVqEDJF5DCAmMhjEUJNfYK/f4Oy1Xq9F4an2h9EvjcYAZ7p44vTMBCRKd6D3JAgpPY2ao06S6criO8SHW8TE0SymazJmMcplpO6gJMO5DSbSlWbmb0kqBW0Q4br/lKzycR3beGiELIcIq2hR8zvXPepk5JMZnsF9bWuWh6aFH6LjLF3GAH5j/BAD9/hiCszM2me6FjmIQOds6NsUzb2dEKw4btZkbvmurSvA0goig2/riPIJjCAE1vzK8uy6p9HPjUJh5M0bEDBSg1gXvlx8xT9e4PtwAkPgRnioDJRSECUXovwmgSphvr4FyheOHewjzZNA5iq/7ySjvQYesGzvz/ND0WYNVf2vpQe5ymnItw+CLIBgPPdm705BNal0mgAq4zKK5UIRVQZO4aHh/JNyvM+4XwrKyX0gCAzbrEEiXbPrdmzVtYNvrzkO6OczbM6LHl4+BsVNDwxg8DVNmIOa2+PSFxMrs2sDafjZfXIMkgM/Ch/NX02WD29RnBJlgQ/uFekn25oSCHvIcY9W5UhLkBo4QtNdNvi1Z17NuRDYkD830Z6lx37eoajxJxlQ35qv1yhjFrvmuWKBpxVhHnVfnYNs7tJ9+Y6X11ufj/vkG2m1+6t7bM1IGKtk1HHrz3G1wm3rRuGe4LaB2zMYALO6HiiGnxhglQk2wuUbRakGbWRBcwXZVaFDV8aoKMMj0qruujs4ifZb1y+VezEgDNwUJAArAVfaiMcmpwOc1KxKZex/5nYgMyzQQQtjRK0QRqWsp3q49zuOEtGf6GtPNY2NaZZ6oFPXwZcKzvbPWB6t9akKRU/eN7c3CQN33A6q9GZ4FZoUBgga1F3ddlrdoGwVVLPfIXF5pGSf6xlryIa62/Rh3WPgnPdlFL1lAyGGSTSssCyG8zA4x5EuIZY4Ctx8TQAyAuvPR3H5ltMOFf1pH6SbDx0HLFBILpKJnW+Ujaj1i5QVcV3D4xzOAu57E+ZY7ZuhQVhKIfhEKS8j5KyLcXr/Ey5evcfvqOxzmK6AegXoErfci+NI9MFpXsTcSXC643gH5G0pPafHwTVtPfMOT8Q2P2i82fU5G/Jdm8uf71qynO37Lw+vshRoXdKlnPfbD8BQKcZttqnh1WH+eBvScZcSnpM8y7T1dfKZ/n7PtTeon9Fz+hAecfP+QMo9NGdYyiRIbVxzXj7g7vsfH+jPu6T1WOvq+6inWRJk38LaKdlWUggyHRlLAG6AqhncD0HhiYVW66UL+q2i+r48shGjw5gHVpOU2MQEvSA1pYc1s0fRNGRE+UIsW7RbKkz/I1JLaWO4Y633ZvhyVSUjbuTNhdH6dP9OCLhcyRV20amdPlZdxSvBR/yXaeHgKIvFh5/IOp+akMvSGwH8wD7Opb9v4Fh7EXTjKa39DeTSeIn8ffqOgKWmUbwTNlmYKWt9gaV4ET6DhB4wqyevk1LiWdqgoxkHSdm+FxX1Hp23ahSvDkX+KUFCUEltb8+DhdG0VAg5HoZs/Qn63x+7g66k+n9nTCZpPSb94QcSeS6inb8cqf/KqP09SeNfpJerhRWjPqqbo9dUVGBP+87/NeHcv1yuVMQNw19jhIesv1CZPg+zMOccMUnqqwW/QiFYIYZ/Dprj74MQgU1ibdSIVjaprTC4N86jbAfV4EIAge/IwhGpW986FsWEyJUqECCJrYBZLiFrBdVVfntwOf3PRtMfvXjLzMlhdLIikXQwTAUxFldmpaWKInBIANqTEEMBwOdSW285pCCqqX+62H+Yi/gOLqYJbH1hcFYlZLCC8whXGKHXmYKFmzHlzORlT1RZJXEEZUfYLRrV9XEhjlyk57ahlVSPH42pIUGCpsrpW3zxPDQJf19qck86QVjdJqOxWEQBUyBA+77kKq5YmQxQnlGnCrDCtayAx67KgEuE4zZimgukwYwJwxSwWWvUeYGBdxUqhUNbKzitqH9XlWmHaGQTxb2983RhZ0+xRwqEAvMiSK1Q0QHPrrscH2wkjQQlqqpzRCdgg7m8sXkMFA1X6RwgLkgA+rZN+30mFMdcKO6raHE1qXUMi2Clevq1E+kxhlaTPbM0UNoulsEbIGWVvFtAU6zX2YHtumQl510EAKhRTIbghuxbPA5Axwrqk/qrWmuZjJoePbLxyX/WwDcsvHesa8JoLJnlsFk66x0jeFzYCIyxpYARR7lI3nvGjQ/NI1hhtnlPqq/UnVU02TwUTTTLHKozo8HgXeFm1hIKr+YBSCNM0oa4fcb/+CWs9YjneO+xEwFxkXMX6RqAzor/x60pI95yV1/caCJvKjIkZ//st482bl/jd//afcHX7Atff/Qq4e4fjn/+nzHFdXUhaGai1vwNifM8ywD4DzvecntNz+stLge5nJYB0jlP+YjgFoT96/iKsIoAWoXxOXyc14//LmQshGSRWw7qu+Onun/Cn+/+BH2/+AT//7b+ql3Mo3qD7CTBzUnhflfYV10sVda2NBfe6VscDDUdGwvsCowsah8xtSOJlSBbStoweDHoL3Ft0aycTRZer8nGogXNfMpOc/jTWEEbr9gSA8xNatqc7ZOWOJnecPZ9nLQwbXIsIvDJ+/p8FfATKXLZoFTM2A8H7eFlrhZCeurC3pUGjmQ7vRBxTJowohMFEDM7x4YOdQbkw0eDbKSHncHw2PJtBQd4fl0clXxd929Rn2/AH0puYE+NAGb3eTUpvSRA7YrAu7J49BXiStvUWDn2Q6m3fthYR5K8JjbCA2r3rCmSbOnNvgH7HR7ZR/n6spDxN4uVgmiaUaRa3yMJNyCemOyup+rSUgnJFWH79z+D7Cfz+dyj3V6JM6b0YpM1B8JDEn1A20sWCiFNI16mN8bniKPTwZGuHkX/kPq8H/vlkSC6r4eJ2+nE+N36785J1to2xJwwNKoSf7yccecJxAdaK5MriTHODb76OucvXDTBleHO/ui60LodSSoefa1j0TDt770hEhqFfM6niSxFxbj6CaeifelFsFtdWA/1UI5tcCb5dn7lD6XKgLVl7t6+BK7dumDacyL2DdFub/zLEzudphKJdNh7yIeMXhGQEC3NmZGKQxQ5If3355dgwcGajuSJqBEUcy5vyQy0szNxeU/vC9WR3UcLv8tAzNNQvsTLXu0udw/0QcnwFzjhjCH8YGsRZGbiFOg1vb1cZ70k4RnprN8sjAVuIwEWQWePhW50MYK0rQBAmryOjGjPC61JhFZO6axmPo2vwUV4P7JriFocgNP18MKMz3t4OUkExB8Mzydb0zmFFHlRYRkHcezGIi0OV12izVlOdhUoSQiCssJlBlVELUFBjwBHTcvG9Q7LOxDVfRwhxh6NlxMVs4Qdj0J+DPRpEpUjwaTt2mFGmyc9RAyKEEGEVYWszE2+5WH9tVm4B1KgX8ELJ7ZBppUReW1OnBrDpeDsGiqSHWfI2X584LwkSxJSmTggBoEWuY7DF8khM7EFArR+x1Hss6xHMC1hdzZHugzgxZT43xGtDDFlb8bqQWGkUIlyBcDVN+PXbF3jz3RvcvHiF6era7z+uK5BcR+3dI+fSQ3lnX0RW8Wh87QukHrYMy+cenG9QUNTtxl9seijJ8DXTpRjwg9ID9lTWeN6+26ZzQ3mpMCJjof09eM4S4ly61JqhKdPhCb0w4nOsqb1+fdX1emrILoGr50N4hfm+3DZC3XiP83Hk3T5+7LX5NKlMwHQFTHPCyxjL/RHrT+9R1yN4WgW2pGBg9IngWUaoRLWG51Wwu6M0N0zO6L+wv2wIhtFBiU7I6BXzaAgT3dPN6ui7/KBoKNGZBoPns4+0BAbklD7XW0rxQD9JFMdtaFI4unhmUw0WTgXWjxXLe0Y9AnAaJde9cTDjuHFTbddUL3BAB17L8G5hHPGUTRiRm+YY8AEQCdamPx2e/pA0IAZPW4T0Hdl7nM6NzBTQNjdBoh+TbE3ugOSQDOfNsCYrb/Nk64W6MmUzp6fqz+U3xSiXSy9GvKlmnBq7GGzTqTFN/UUe/8smIAvTWpp6p7zNTRHadK1HcK3CWxmde4l9IEpghDIDK1fw1YqVV5SlCE3Xdmnz4zFLansiPC59VouIrxHM+VKJ4SdLFn8hKfsYL6XgcDgAJJYQP9+RuMm4RDLb1dkcxI5l7DHltNyw6u0T3nyxg48ahOJUaoQR2DKntgoo6XI+1/+mEvaguxmbaMbUOj4egGHtriFhT4xZtGGoxbfmmM/WLT2207QRa8Q0WzLTlTaAM8ynZAtyj0EFAtkAa+d4CcRG5kZ/6fceWdoIHn1MWqZpM60KlwsrVGslZAik/jCBqRSgFGX6AkD1fgVzM7RtrB0J5pwvW4W3juHOkDZMclDDFGSwaPmX7ONe3R8pQsqsDNa6umUHabyDuq6C1Gv0AyoCY60MUGj9sMZPEH+g4kCHuYoGEqlWuAoLAJJ5qyakqOJ6SHGSaZ5AteC4SnA6wqQBiqWHy3JErSumSdzySGwAxjqJaXddjdBIBDtjM8ee0hJhtRYqZRJf+YVAXGKL1opCDEwWGwOJ163WC5nJa9rd2szGSZnD2QsTAHLBr64LFldKq1qRlFJ2XfpkprrAIflqjee2ZwH1HVmBaRJ/rjZuq8bIKLZ+RufGAAeU2CWk1iHVzyE500yjnxJi1VCRTtj5mUEAma5aov4IEgNEai8xRwDmeVYNuwW8rKg1LLSIzCoiCSJg97nNBiOY6fLdxksEbwKblKtZfiNjkM5OIwZGuMKumzf7nAoKwqpoY2kzLEwinEHEkiEiTPOEeZ4R55GsuaL3d8Aivw+Hg8fKqPUO98ufsKxHfPzwHqTzTFQwT0XHGr6noWcMyQqGWRn52Wc+kXXgJppQCmGeZsxE+H9+/xZ/8/YN/vY//nuUqyvUmytUAPfrAqxrKEOC0jyZ1rH0KwQhaopva3jvEv8rwOWe03N6Tk+cxlzIxKd5Plee0yMSnyb2zvMfLiByv2aab0EvfyPdrKEksvzxPdZ/fA98V0FvLPZAFHPnra59grjHLRh1ZdR1ReWKZREcdO1pWErft8wIfxYqFvmd5khVtqgcO7JDCFUiAKqXHPxCUuFDQUGlFJ16gFsPU+pDxqf72e9/C1mxs4YoLLjsvemZ7umc1yPw53/+iLufKggHhEab4dQVYLEad/wt1Tmq1PBGp20DPBD12uzWK/u9v/4fg+pRANs8eTq9kGZBDt51P5s9Me7QSaHESUhOZNR53a4n8tcBZPwexoEAQpGxEW6k9Reafx0Y4/aatnvYvanBeA4ytvlsDdLufT/aY/1kjeE9AQylWtIS6WM+94lRUNcFH+/uUcoBh/lK3NNlZQEILVZZFBLNkoILgIlQ3wD1I6P8CNDajf+5blyYngo7utwi4gGVngIuFsepGk9f4OeSMSXid24/6jff2CSUbpIyx+Lx83YzcwOLCj+4H5BO9mcwDsPLd5CNZnA5gDVgZFGf7D/fT7jjGcda9FJtNTUzD2lY74bptgPezoNQGvDBTtl4UI7TiKcvGY9Rpm6GhZEP5HGHhmspjYWB6XWk9uzFcBby2dVdOm2mDrnSZCamLX5FY2aifnEtiIbBqW34bcJaOVkvkHrkDN/Gn6f6zs8bodlD9qJflwPc0MFQJm8glaLlTOHc0ytohEmburnpJjZ5g1EZkFIzcMLIKxo7xfYCOx0RK0dXGfd6IeIKqSgzsNk/SuRS7ryNeAOvic18cyBnTrrwgApPhDnbDoP3ytZAQjjsG/mvNJaULjhn2MrPWitKgcSXQfTHelOZZYnYU2IRbnIEwfa+69oSYUh1JKaUInmzuyPamkLn0YrxEWLB9gdDL2VDOhB1AsFoJetHUxU3wdyz5pQ9z0KCOA+68ZcONOssI9YmGE7cVsT8pn3vHZY9Z3G4GXGP+uqWAexGChrEmds97a0NhNAKjtRC3pfYcnZX9rD34zBALKnLx+l0J26IEyKx1qmF4a6biH0swJxMTtOaD6lh2yfmBkoir26THOlnHaP+ALclQBY8L723+6OIEKI9Q9o8PjbNZUOyf2qVOAsWNHBjsUjpPxACopjTyhX1eIfKR6zrEXVdfH9vLLi4q9uA3kGkGGqlQcBMC2YiXJUDbqYZ33/3Bq++e4tyuALNEqKd6wq6/wAcP7b3WL46unuia3I8WV8o9drGu8TeHj53CexZUPVLTY/owzkL5r/EdGp4vkb3L52tT3VHdKr0g6t+YAHHgBzPhA+2oAcVXWAsIN1PtutrEl6MLPCBBqNLbffwPM0+/5R6+u3qcG/JjWGbp7WAL0uf9bg715FTRR/Qt2YOLmzuYmua0foiunzTtrVZDVZ5+jmgkYdPHQqQ4umV73Bff8Jx+hHLzXvwYdm4J/dShoun9lljTNQqganXdZXg1EmZrYG8j7W3WbMtHrwDfktCsjDcW5ov958dXSOoOyjtJDFE8SlFy+ZTO7OmMch0OhulqaBRP/4UaFmas/zs1LpNVHBT3ul+VTaaSsGrmyu8uDk0pQFK6LWdjdvxbJ7Z15PbKeOxl23ZzE5veT153WYAcmkdhx36Zzel/m3O9s2aTJW15CCauwWnx2br6vZ0Ooc/5dr6dRCw0HYt0YAWygKI9N5U+FwJawN/i+zvMfg3v3qaZJMnYOrXqMHk8R273X161LoFbfO5d276uToaLwjPefTesjErDWnB4ycwqrivSW1I7FRVzrOyhVAmAh3uUbiC6LajP8/18cunz2IRYdN7+hKznKdqeGjaK5MIaEZiCkWgTlPC7t83C7djUueav94UjlOdX2A9vBG3FgBomlHKjP/50xX+fEdy4RRjXKSCGUe3R3JLt9fqpsMbA+MBg04qaywYE4OsRlEgPR81uXtP2VRxm6cP+HN5bBGFg+2bMLpCU7hjpNiBR1196d5xTXiWyzTHOGBAtekDUcv3+wBoOJcyMaC9MlvUVksBgilnyJcgYBXVfXQ2gKd+9WvFmvChddgVO0vgZE1jr8LnOgjFCBCcDutmzNkvACJCIfWTJ+o50j7bPMmnexjSy9JiQcxlFgMPPfTt8iKHST+5ykZQjWpG7B2iAqZq2JxoqQOxtyiZudrUWF/8si5AIbHaUF+qhpRad2WaC2gmYLGhlnyG2BaNVcFlkvgEVXytkk6paYRzib0XTOxAAEspMEsZQCxGuDKgPvULrF0JLmyuIQsVlGkCiKQsM+ZpEkuOKgzlZV1QeMLhIIMxTZOuTpnnWlcNaD0ZOiNWDpWHZ5WvS22jAphnCYTssg1dP3VZpC7dhVMp2mZNSAF1LqkEMXffsX4f9ISPPLfYKLbew1JBLCLqugKqjS7zb21GVeZKqPg6kjvKtdHtjGFZB1WZ9R5fQ4VQtS5K4+iZk/rg6wm0Re7IIimEWN7WrNYEIosZgjwQg9QicaRa721InIIyF9+vftMyi2l/ow0jqyW7FyoaANvWbJkonVetJkn0EU7QO0mY3Ux1SK+dx4FDkguUvIc2V0RuzRQWZgk5Jq+xAYgS8s6omKZJLI1Uy6eKqYoHwDaLGbN4midhoi3rimW9w7r+gMoLlvs7MFeQxo2ZSie4yRQ5IZ1v6qqOOd1L2udpQiHg+5sj3t4U/LvffIdXL97iN//Lf8R0uIow2LUCdx9Qfvpndctkh4xjGH5XGEgPTo1w41vDxr7x9FXH6zGT/ZeS9vr+vH4/eyJ2ZQk7AoURuoqlJgiECSKU0CIPbaJhcjyV2OEzJr3MLxVGAI4Jfxn4HpseI4x4bJe+0CRfTr9agT7ziDpPOEBXtLfwN2/lBYKDHPEn/Fj/Kz7c/hPe/e2/gAmYqLjCj9O3qisjCjJV3W6yWL+CsSwraq04LgsqS2wI6a/1UXATVxjqwloaeiVleqdKg84h9iY73VhTKQYbesziVraSNjtpTDYALnyQH8ErsCHr4tUJxU2A4/OGbSuMxAOP9nA6J/fC+t3HsiGyedr2mSmdT1GB0wQvbq7wH377Haap2KDHEqHob0P7N8Nrg5Z5TIOxT3R8+3ywlnvaz/u33d4NSHnp9svhsWlUnk69jOfGEB9n2z9A9pW4z4xV96JZI0pvbAUMed+n9x1N5AKHRBPLh/I8jAYeABbDZfD0i2nUqVR+wI/1+gD0/LdQdOP0sW1zPAPtnMV4jOGlhgEZ9DrQjtNeFay0PBXGVK4wT1cAH7E4fWY0m5xZ1fljYqGOGaivf0S9m4B/uwXcE0Df034u+6f7aTROj91Wn801U39u+XPXyEPK8XStflltqmjLmBTA+BB99Pn3wOERS4gZtcyiH6sMi5/vJnzkCfcrKZMh4Lx04V0OojItKPW7Q2T41NSfQRovxSm9Re3gQ9xxtbhrAtYZUePLIM5TO6Avg3VU47nn/UEce4r8twnalLUUCCFHX3L9gmNYHebYp20zLvPBRIpUQFz4MDki5DD2ewbBBLYwwtjA1MGp8Bkfa389xK4zt0quhU+KYJWRzrONkcJSlFLNCFkzYrGPXLPEcEs2ePtyO2kHOQlyT7WQCqHUQTAxg0gZ0YLT9pl0PVDW6O6RnNGllS9wmz1yvDTWIaFhGHMO5ywa7pUB5qm9Bgv5+FWQu6gZjYetJPbf1q8OCS3aR83GgLhS6+/ljNynBcXMLuQTTXW07zgIpWYY7X1Cwkn8Wgn0qsUgOJgiSIWBSm7+nIPpuXBTMCrvp4QpZ2FQ2xzZZHCag2Zf2RfKMo1mRm0EChUJlDWciO3NcX4vjn6RM9RhglVWQU4pwDxpIGZzKZQGmsjdDNn2NEAYEYxe+iqC1jTi0le1CLLvPs79+Z2G1tpu1loSAg0R5iS0sBnMNlsiOLFyRSzHyERm6cy28hRWCbbAK38EM+N4vMNaF9R6D+YVYVUS48csrtqqLwcR5mTripgt9stt5nuUWnHgF5inA75/+QpvX17j7ZvvcPPiNWiawFzB9x98vfNyjyC6nygZfGfq/CbkEpf0+1PH5qEdzQTlI8doF+RvYtAtfX5YzjFjP0lr3evYeX9h987V86C0N/EjJsCDq9op6xn7u2Rzm5xs7xTp4XkuBP8hFiKXMuyfeut8ioz2kvyXCiP6up7yKnh0Ogf2FzzHQhv8KwxM5vT7oy0/g8oEmm6Aww2ICEv9gPv6Du/u/gU/v/8DjvU9MEEFEARXRhMCHJxiczFH/K9VLR+WuqpFhLlp0ph2io/YyFTF0TakWPpOWi6edfhcMiBmdOfCkMaXVABUKihJTcdwRsPOTPHRquFibYS9Q2FWfj4BhUFVrOsDoASv/XYYMg6ssecMkQeCt2u5aPu9fZDmydqgGOHskpXamvvKPP+QNt08pObjXHJcmHL0vbxstxV1Q3hRK6PkltJdvoecEKcFLNx8NGV2F/qJtvIa2RQP/L6hO/J2yYsJ7RqIVNIU5veJ1tmbc/+Z1tOecCEgbfrgfRlmJ8/W9xe+D6O1louwbRub8QiogB4Pae11mm7u9MyzKi/BjqdaK464F+8TxiOpVZVJrSccEOi+naYCmoByfQ8mxno/YxSw29vvEaM0F5uTkHlnnM50dCd91hgRl6VL0MLP2DrtLOJfaKrztVhC6GVYimgo/+vPB/zwkVBmZfpkH338RDNg5yh39/hogNsbv2EgdRk81doJEhzPuWQOW6bZnkl1TiasqebvH51WPqzt7ijyA7itLP8cEqZJyHESslRX1spt+rdXFHALH7fuUE1X0rpz2Fb51iEp1Asw2gNYNHorSi3ImjebuBnG6Nfyazbj67IGPHG52Ry2BrSBdkQ5Biljr2i8gzKFlnE7MYr4VjXTZQBVXKSAqwhauL+Mrawy2dVywPTuS5haRD9IGcwdgkHgsYZCl0wLfPAGILU+sTXK7BrznObZLjz/6VtvO7/ZQkAIBKBMxrS0dWtzUzAVuSwrk/vy9/20rhpkObSzjalqQepkjdUGJvvYMIedhtoKGo1xz1yRY2MUV3OSlF0yVWa3HBBLBGWCg4BCqKih4ZT3K9tyN1iFc006TtNUwBVY1hXm5qvY4AMgJlCxPUESgNrqofDr36DW1UzJGWaeST7Hth5Y4m/4PGl+Ej5/HtOQoeXDW7S1ZI3kjZmRuTQhg9+bozYzRyweB5koUiwBaq2gecZUg6DrKytFAzibsCgJb0AVRJOfE7UWWXtgYJq0bREOWeyUBpmmTgxLSG4cty6ZpKRZmMSraZqaOtpzmt0lWRAcpBYgk6ydUiQLx/ol7fc0a7D3tYJ5ReV3qPWIZXmPuq5Y1iXRteLmCaSxYMCoq1qQObJMSdiTpopjPN5MH/HmasHff/8Wr16+xW9++/e4urnFzcs3KNOElQp4vUf9+ffgdRlP+l76eqjgc3pOz+k5RQok+y+KRnxO59PXn/GvyxcZJQJA0zXo1d/AGHt39c/44f6/4N/e/w/88PG/K4Mq033mdUJpNNUUrmAVPIgF/nFNlhC1Yl0WmBVzhqCo6bVb/vbO1vN3BcPZadRmosIwQ3fBcHXUT+CqNi+Ct3exEhv6NnSWAXgMO9Z31elT0WaeVojCm7pOjm51vAQCqMdLlcZJx1XXT/sVY9APmVtTpOTxMDBIjcAq05FZ8SoxpRH0f4YvM9m36oDtROT3mefSkYNdmfF369lDdljm8vSwnhK8jwR6F+3tvkon0vbL94KjcSaLYRjjn4UOjG1/GkZ5qrtQx9imxD1q6h7Dwt7PWNPbGBBp8Rtt1jzvYLQqu71JPROe+vWVR3Uz+OO2aPDM+RG4LKW9Y7/dTTQTlmXB/d1HTNMVrqYrrKb8WBlcKpg11qLy1Ix/NE0Tpitg+v4d+OMBH//4Fo3icHa57LwC2xWUQdvO3iOEDafSVxNEnFGoeUDqD7f9dnqmX7uKcj27w39RygzuflOdOih36xseyORv/S9DmVG2YQk/3k34WA+4WwtMuzILIS6SFWyg5e37xJAz9xrnJ5O7r7x93pcYLJxtK4HwnEqXCCOcl+s/tN6W9w5n7HI3ooMLIXRgzRQ0t5UbHALtbbRCiG6tbSen7ZT2oSojP5i50g8Lptsd7W2d3L1znIIBLkAJhm1zOlduqjBXUCK4QONnU/IRyPzDp367hkwz5nbQ6sVD0pCNjQRIJpQydwhMMOqrMe6B0EavrK5EdOztnw6/IykMZ6AXY1oGehCCTxMGsa+Edngp8uQhzztWYivkedB9l+fDkIHVXF6N93XWXpKA1bEoWd3BeGc5CQkqbAAAYrBHRSNfq+FmKIgSIqDWFUQFhaaAV82pzSrCzxpbs+l8DrzM8rQCBcveIhhQQkD2alz+Ua4A6kRJ2pWA4FX99ROo6lgRNHi3Nk7teSrtx16disblqbG2bP37blNGcGUGcVF/1NG/5jhRYYoOPbKAsOhz0aAwTStEXQYjA21weHlbc7Dn/HZz2I5utMEK28XrbE+YABPSb3DEDslzaj6D7Qw0t2ZETcsMcb0ROKueIQO4emEK6d7bbEE9F62+TV0WpNwKqtVVWB727Us/fL7SWV78O4XFAsIlU5mKCBWqONVb1vdgXsHrHRgreDUriHxexcAbkW8iiIaAIXuuZ4f260BHHIjx/e1L/OrlAd//+rd49fItrl6+xny4Qi2TwPrxZ/B6L26Y7I57TOrL7eETZ/CMgbLno9PXZ1A9p7+ElGSmXyx9yeb29/yn7Z9LLEuyhdn2XZ+PNi9anPrBAHa/9+Eda1I+Pl2ynvqz8KnW4Kkx30tPDcNFbZ4Z889xvp+zdBi7pemZ8E+cepTPHvcKFg7UhHL1ApivQVSw8kfcLT/i4/sfsP7pA3g5govg78VJvMAdHS9TXEYCr4pS07rKf4kPUcF1hbkrNiVAw8eqW9vL85pogYzfONgdbpswQhmCwqC1HQ4d/cCVu7o3DOlEZzkwTuIqzWVud3VeiSzAdwFVBpMoJzmNWa1eazFoOoeBhlPY9v/UMxrk8H5k+lYxRLJ2syLeAHc2nL6h1frztGWCb/hkfCmzvwt6PSJwR/3UR00bTjufGVUewHKiSNPGJcdLhrcb571xH7ZnY76py6yopa/Fu5wpgaaxmD9EOcvTCAASM914JG0fxnDHeMaa6DJ4u7Qps4W36e4ANgCNpwhlh50c1fYcifZyGd48aNVk9xCK5r3T5FBlQcZUJkwkNJ+5YfL2OPGdKmmIK1XOmxj1ekXlCjq8A9YDuN7oocZNj+Kc/vJUzjdgEXHJbfuUwxILql3I28Pwl5HILzcgbShlhPzx4wH/9nHCPBfRYC4lLbhI7WYZvPSHg/nS3SBMtWAFKSDndrgzRJoObGDh7sEAjr0L50QaCSNGyyCYnS0z1w4kApLbRPKDfivljy+ZCc357UVbIhhXTjh1iInfq92UyFdFhGqOCZGRA1GVlm60fai1OhJmx2yi3eCACNcVerIiQ2cuSYTRuzb1g+0oVFhIETZFivw/Ckic+HSEBWmgNK1FffADwDTNICLMs3xGkDTVEK4yJhbPAIBoqgDC7K1Q3+896pr7BK2zgIhdiyfd/Zv+eryGpsZx4owIZVqaRdOoJKSiKGLLVUZDBCyjvSNrlTnF2EgNWlBq28+VWQInUUjgizKF7XqW2dGAc1bW22OsywIqReI0QLTbK6pQMUy6dmK/V9MS6Eenmfq8CYKoIiUEJLBTMIBNs7zZN3qJm1UEa9wJKmJFQ6T6TEQSoE7FFu6KyYetW5PTBCoFy1odDtkius/M3z8VFIuTUsOPrvcvqkSBxCchP5e0HE3ynkqsL/Hj5JoTMqZV93qqVA9hTkRgg3Rx2m1nqeUNOugfdra4ICILhazPJUKhg8Vkn+sajI8yyYrL9wQjxkIbI2qFVEhtS5yTFkQ/wxPMsrRkbW5pnXR2mrukadJ2Nb6D7QODsyarLSKUkvyRW4BqjvMELLFPSiH5pIL1eMRaFyz1ZzCOWJdV1uu6tAKb3HcOjURbxyEIgXMLzI8wTQWFCr47HPGbF4z/8Lv/iF999xu8/O43mA/XqNMEBuG4AHW9R3n3B6AuF6yN5/ScntNz+tIpI8KhuZyvQGO4daWe03O6MP0SeQmSenqYmUHTAfTiNxL/DcDH4zv8cP+fcfzzB9z/t3fgVwvK93D0UZRpgCBQzAWkKXpJLL1lrVjXFffroniLKFCsaqlZkyIbFRJBB8jdThdi9RAsCphbxyPBDO3Zhq6rqDhPkMoc+KdDL4osPW3v9DGFIo00YTi14tIMYQoq7l0rqYIWo1LQwlRJ8MspteX92KEfRzyRRBdmZvBwVVL0DZCxDO70/jq2em2U3FqltOVaIUTG8yOm3RYk2h641P8cwaYwbXg6O3RIm2n/jOecjS6ERYsOFKBOljHBZfuzGTfu4RnW3I51vGl5RlZHFtLluvyDUs2ZVsPgOWjbPyFyN+w9GvwKhaiu7gTnQ4RBkaWln/PXnvXYlisYjssm3/bBObBG82uJmcUF00SYyoxSJpRaUc1nAUNdJ5vyYtB7hQq4MO5f3qFOjPnHI3C8xXp/AxdBdJPRn5FfKj1OEHFGU23E0D9/METVj5MH7BUacrXPlnqqdE4L4hLG46lUacJarqK9cgUiwo/3E34+HnBXiwfNPCdoyazVi5PuBrlfjQlk7GmtMV2mF1dpufvT2BNt1+HJDpy4UBvJb6ouMYiNIdTWODhlOuFWA15w71wbuq00UCHN1tbbMyMTU35309icOFc9rDA8SHYF3GRLg9qQBiXeXs3b9SxMrNyFxKikbb+yUKfdH3kCDb1Jl5M/aeeLYMGFE4HpSJwhjqpJXMwqyG5W+RREsKo7oc6XuQZYh51NzTobYXiKVPbaOFl4kCqphqgyN8PbaDJslkV7bXocBFKtIWPC2xiY8MTkK9UYuf3ZjZ1kmtuCOBYSIQOqap7rGJeKZBWBWJ8clhHyirHWFYWBtSxwgWXuZ163CoFZZ0iVeWBMnKfzmfJQPki0iI8+y6U+2VgRgaoIc2onjOBKqApnAQnzWrXAshAiD6HtcUaFWaJNUwGzBu+GCsNIiShu3ZkZTLZva2WN/9WdMz5+ZgKu81KkX0XrNaGvB95mANTGD8jjKqF+xlpyo5u1nRfyZxjkbU2EN9XH0WHBVoiUeDQtftb1S/BTxa8c6bsIr1SNjihZGihxGZi4FUT4Pe1nU/ttY90f/3Yem+BR66i64LL1kp99+eDs93naL2LJJW6eJo1VwliwLO+x1nusLLEgTMAkfah5GrRSWWvhsiCWWGwMXQerCKpuQbg9AH/z6g1+890NXn/3G9y8eguarwX/+PhOBCUVoLqA65osA7+dNJLlnUtfXjfol5Ueh6tH+gaXyTeX/rKG6FFUxtM23391PDQoj8xrsqugO56/mfSYPbQp80Qb8THWHf0Z8iXOhIvP9b1LYw/IDfKXXj3wsBxpiX+NtCF1FIWiAizTR7x/9Sfc3bxvyrh4z/FNwGJ01arKSWYBwd2m5Pja1FkZKEBlZQumfOORNfwz04+JwtQNLTEfoPhl4JPWC2JypYyELDWDIe6uEUooCBwTqnAElrgQ0rEiLl9ZlNUEH1TLaDa8O+izYL6O+6jVx+j7+dUjqV3ZFbj784L1XtxFoXe1k+lXpTOoG4ug/1se04ivsnUFNN6LoiDTQ0Ld7xMzT71yYld+UIw5jdlDYTm1twfb9mR+W4ujV0TIgeoo/Yl9Giu9oa0aJg1FXD5911glpM9m/294vaXN6esg2uk7N5qHaKN4rqiOUsl8MbdjtN0agzObBjmNHtxOcwP1Kd7eXvKzpuFnJZDQj922XdXTRK0rjqucFUO33Ka0Zp2ZCog16PUMzDcHVExY7xN0RveN2u/d3j2gvw9N34BFxDeQPpWa+mxpi9blhcxgrDTjOL/2g6QU8Uf+p49X+NcPE6ZpkmclNtJnQ2d2EAiBu8t6ARCyPXbmhq3WIB6GjXZ31cj09PT0m0ZqQOStXbhsrKhZHvhBwcE+lepsfvoLVFMJ7eatNU/kjPLc/uZggImGbVUkKSBwbXo/QZvovF2n4IzmgKcqo65nFlNTB1dO2vkBp/hgH+i1kLWFzeAHqOz9s31gPtFJYXXXTMoErVUYr1yFgb+apnqiP8jGHBW1mrub/XUTAcF7SkT+CHIrvxmqec61YdRrQIvoGwFxy3TfkZicVX+pEKmoAGZSNzcrVl8HIySQqMQ6tTEAgytAk659Y7auFmg8r1HR0gc00HGpouUDiLaTjim4YF0quKimEwmSEV1qN665KGLVgLKx8967Br29VOFO4bRWpTdEnHy2kgedMxSJC0BVgtFVspgRDKppveteqQQNMjc40HTj11rdhRCR+G4EMxZdZ2tVIQUJ05y4JOSroJBYZLC64WFrzxFQ3RQU2p1V99+s63zClBCVWJ8iiCTUIsx9IyoYprFVhVjqZiYLidxFmq8hNHPXrDDdwI2Q0HKl45wAWcMJoWUwiIojZkl2pMdUOp9VGCDCG7jwhszdk65RuUZsPLekjguB+t7Q9rvHXrIYL3bfqpDU3QzYOLIGGdM96sST3xX6vBTMRcxy50ksItbjEeu6YFl/RsU9luUI5ho+W4nQCLX8IEl3A0EEcOkUYNj+LqhLBVXg719d4T/97Rt8/9u/xYvXb3D14jWm+QoLA+u6Yv3wZ2C5i3mr4QH5k6xMdeyf03P6S0yXuAZ9Tk+XesUGQ5ncijAflYFoNmc9tTU8p19K+hp3ybd+f+3zcZtEwEA3Rh7cH97jx+9/D2zww6DphJ5Sy3N1wbTWilrNerM67TbeXUlpgwFRsCjoScuALr4b07zRM9E6SeNDOGmq+HxfT9MEJfa306RBT5YSuJwSOkKPcowFGHDXTCiCH06sCmTSYkn0tfakO46CnrajS+6T7SicSnVl/PjHOzCLu8+9lK0aQgiBsPanDpdvyqbnPh/d9749jDxVjHq1v79MqDMAafSgoecbUvzEaF6C3+7lGWn0j3oTY28LgDaxUUJQlRdJvxZTQ57fynQbZANatM2em4II6/IMxxft87ELuD74dc6X16D+3h3bix/quFP2vL1T9oG0zGB+TmQZ5pGg7MJRWeqKZblHKTPmMqslhKIu1c4BFfBOhAMIKOKJAUw4vLjCShOO7/u+0OAbHiyH+ARK72vGiOgJ1YaV8ej6HgnM7oL+pNScZtS9avvfQ38OmkoTlnINLgc5mEiCUv94N+HHuxnv1ylcMZUHrqg9npoAHr+Dvx386qbs+FRjvny+zAXQCGlqGfa9T0E9VQb93oz9YPo9QHWC1Vtrmsnzt3OSpcFirxSNEGKcvb1FyftD6ZMaN4k9k1EYjdGSaEIbchiIkTPTHMERZljDjPY6UyArveSoKOLQaKmbiySzJtGylWNvCAaFuCuTMKQf626UOMNUa/QX0RdHFNUqyDSiGRD/6qqVU7mC3VxALVMNgMD5FMbEzHOkLBjCLYPBnu31IMYlWpSasssZYkWSWediW5mNiJjkuRsYYe9P0yR1liL9tTLKsM6bgNLykn7omHl+jU9hAhttW/aMxvsoSRhBKRivrX2qUrZq8Go9w2ScDSYbP91ZPoYiGPFMieBjHZ92lGMt5dXJ/VjuEGY+FlXMIF2wa3NFSO664MIg3/O6YSpVX48MKVOYsSr1w1XMtANWjQFCUMSTvc9s8Q8oWx+RC5LMLU9NghOTqhEDXCaAhSC0tkXbTAYhENTEsN8Mj/VvvL5j7Dp0K62vQXXd3ZCRJD3ruHh5O/qYRJtMwo1kWwfb67oSUqC/LEA1t0iB87blSeHKkJlhCrkgoTTItrm2ciFa36M0CC6Q9OZljUkw7iLxSUCo/BF1XbCsR9R1RcUC0aSDEsTSvmi3MXj1aCdpnG0d6dlUCFQmTPUeB3zETDeY5xe4ub7G9dUV/pffvsV3v3mLm1dvMV3dgDHhuDLWD38Gr0dgPSL5UPi01F+hl+BlG4Hv43C5Ebq2p8n0nJ7TU6RfrDAiMcKePD1RnSM1rhGO3up0pPsSjzhKdkiA00XiDvji6Rtae58VlHOV9xPd598pf3LOvubY7uBWj63M8MGewm75AWH1bAoVRmMafWa0Fqq5YOXAmIyOFDkDmEVBJksLjE5wepHgOFeDa3LQcMbbTDxTAKR6GmI9UJhQi7D8SlEluZq0vQlAaYUQUbH8Nxev5v466CkTEIgLYJHqCB02qbIWV2poCFYCmxIeOsJCbGhMWS4RbpHn3NwWBq9S8zQV/PrNS9werjvBQkLabTD1XaudHX1GzpbO1eza6BQj/xyT/xKczNwibfIO6m55B2er7qq7AJbMd0rZg4GfnjTV+WDFWhgKfvqxDxrV9wkBnAJDN/UmZnumzzg/TfUE7P185jXbp8SsolFfS9N29Nkepvy5f11zJ2djM27p2t6dR8KZWselEpo05AHtPI8MurlJziUof2eaJmAVnoKw3eychbtosnkrNAGFcbw5YrVzZedQ2O7ksz28KNe59A1ZRESHPpdcYJQy72k3UNOTNDSgctEyXXLb3H/xQ0GZGzRjmV81l10p4o7pn99LPIipTK5tDNBuW6fZTNsn3L3kjgfRHxyCk9Cmv6OkbLAGwXNhRJOvd8UxSqfncisMs+fxxZjxfZ+14KAV+9Uy8JyJVTlgbzsUHx3Di/IfBtzlD/Vjneti54Vmhr35pg/rAcnrSEKx9gnid85+h8ZK3NeKqFFcHsxpAPV0J3UTUoP7jRxINRAZQ1K6ixX5WbuGxMw3gpvlegRhVSYeFcDNZhGM2iTAYBPYdEx58x7KIKBWMBWIse3Ujjy1F3B7qO8gPoxoN02lI9ku6GJBlhXDFsSx3SMy1qRCFf1NJBh5RjaoRboAvbyUUet94dE6lbEpU5H4AhVJQCWINpG4HTKGvQktzO+rrU3mikoiiACRXrTWn6KEhO1RXUcOAvv6iZGIy7cFl5tc1l97X1SQ4ebXORFgqgEibFnTmrChEusJOWOBbGPU7OcqGuuieUSgou5s0tnIAHgVCwpxKSRAWB909OAkUTqYbA8SSK0nBCEpQJiOQyyAZjI/tdAzTgNdgcTvLplVhsUNif4YUeXbnHgojAjk1n8lYrDfDzEfzdDD+g+3hAEJukohrVK3VglxSASy7Ak7a0q89z1WMI2uCpt75LOle58J4xJINiMEEK1Lsny3UcoMrKguTCCS4ObTNGMqapHCFSs+AnSHinusVMFVLCFsbu0stbkk2aBptM3aqaSpEUHETan4zdWC719f4W9/81u8fPUaty9e4erFKxxubgA6AFSw1IplXVHf/xk4vg+hLed1uHMj75zjXzJdgl/2eUY4yFdPXwpJ/otNn7r+nmb8H0Nz7OGuXzxdsM+BC/b6hWfBqT14jpFPlGa8y9oImRt08xHjm1GNU/PT9XlE4zxJesQ5+6WEI19V+HBB3kf3f6fYpS6qH5K+6BlAw68wug4ATMlNUBazMA+3t+6SSZUXCEoDVqBSAUpFYbNctXhsgd8WIPAkfSCoWAgODB8S8ieUXxxVcapO8dZiwgghawuXzkK9H4hslpuU3jTmnOGsRhMQifWDoIiCy1Ep4toWAIrh00Irobgkwo+Q0fkguD5Ec1qF2sKYjJ4SbGpavDNRME43zFPB775/jZnm7brqBjEU/caWFI0QogyEEF1/zgoeWtRecOK9Mp5nRJQMsnPb/iVHx0jYcgqYpn8Nn2MEXoufyzsbuLIZq+hnyUVSvkR/JYFDX3qXuZ/nrOk3Re6+7HA8tv1urThyae9Eel/S9zQHPbx94vTKDohUztUVeVwJD+C+NKXmtu8GzwNH4RhjYj87piI0Ya3qPQHq+g7Gn2O3SieI0KIWxoJ7rCt8r++0ik3/L9yXn5K+iCAiC2ovT5//ch0JHj6rMCIaGc7epu0s1VZ1YC4T1nILLnpRqMbku/sZf/7xCj+v6kOapuQ/ewBC/80uKmd8DkoYsp5ejg9sbbdrOpCwXAE2bZ69AzxjYsbtd/VEBeRw2bi7+4yeCWuIlTEkTrSVrQqkqDLyRkKIZigGY5yHUrlxthbcGiFTPnoguamWBruVeoUpxWxQxEEXgXLlt2nCB4NfzcAcWtH+FSa/IEt7zDoXeFi71ma6JMdbLjGQ2UYonjHDLRocKh2TogihxYQwRrwhZLWu7qs0ayyHRN+5rGktmIAm/4q+WXbYZW8Myp2eRZ9SeUfWYm324wm2YHA7O4UAXhWNr9VdJWUz4gZpVSEEE2Eq7EiZw0gxV5khRyBMZcLKEjzY6ivkvnCS5QJUIAGstfVlbwGTmRPyzRWckI7oqgnCMmJl4zK4XJU+oggzANOXd5groxYLhL0dTCrscSCMyCL33aUz6IgNu1GQLwtC4zO/1awnZJc8PsaMGGm3erCK2d2f+RRpbbb+V14NOBdI+PgQxGQThKJztlR101ZXEVyxrRUSwVvDTOeYm9R6Q7eRLe+IXSLniX0PeDYERmDRYgkkQ+AIlJ14EsxZs6pFg0G11hDG2by5BYQfdGFBADLh1OjglcbzLZX3qRCgUdTq8ZrSXrIzXoqa1ZCdWaJMIHEgCqbJ9lDFUt+D+R7Md2IFUasKtpDmImbEF36vJQCDd0LhI27wAQfc4Hq6wncvv8Pf/frv8fr1d/ju7a9xdX2N+XAAzQesGuW81hX144/A8Q5Uj0EQgOOeK2PCtIHxKwkhov3zCPQvQhjxnL5iyifvF2y1u0u+ujDiU9NXPgsUCUpIWbon8TVm+K8jfe1pP5c+TQizPRtGd95n2b9jNHZXC/ZUJTTNKNevUeZrEAjL+h7v13/Fn9/9T/zx5/+Kj8vPQleq4otbSRutqy5nTSBheL/FZSiAKwDxBFCV+GlGq5GiZBmXIiLQFPSn0cBGIztVSUKluqWCdSvhpEJ5SAyIqhbKU5nkrqftGnUcMEg0xd+Q6KSgpw0O6QtF4GKSNrkQKhdhKNaq+DYAToIOIPqnqQHLrEaMvqFQFmQmo1p3VzOBUI/Ax5+A21JAb0hDqild3hCx2j/FX08zWAPfpu77Nv8eDyC3a3kDR98tQuP922LxuX1ucl2SegHE/j7uzgF/lPvU0kJZ0NVYxXi5RCN5Ky2T3uYpmqNUNrXtVW6f51gjxveibcH0PME6GscdIUQjMElj08ww6bhQB2VeU332pjOjF10r2janjJ9yOgcvcIBM7J7HHEWUXRaxPGdUXnCvEoXGo5DTuhWVhWZnVSosENoSB0J5/R717oD143XimfS9TIP8BRCgxwkizlycu5crR9luH6aqv0CvR2lAme6u21zmU9oDtm32dXZSecaE9fASEXyzoEwzPi4H/OMPM6YrwnyjfqoTQ2fDJcq7gPcO4dP9O9n9boIbIQR3NSeGWg/BbtvNt7xjTgHFzUeo2HZ5jImoTM+GiQRjFNopMTpYt2NozH+vazR4vH3vQo/B5eJdjuIwIUR1i4fqPsqzVYN1zIobM0wuH/agxpY/M/tBRZXsKTSMCYJoDa7//ES0/+FtySHbDVe3F40xqw6FPJ+Z+q7rKoetxoMoZVIhxOQIkI+jMiXXVbTATUs/YkKYj8Jw02QuhfL8+8JI90AwKa3cubUczELWdmRMxpe4Mbw9YG/HwN7k5xyUmGHMzpqB7vaeCTesz/1xnKfG5l4k82mtsDK4axJ0wdxCAcCazg6JQSCfU8BUCNCA6XZZ2jrAWZag7bnUM1s6On7RfU7z2Z61gOVVAiIL1By2runN/aVl9LmIV9rzmBTjkzaiB2TBpRnD3nJ0UmOCxJlPhX3NRjBt65rcG1wYExPWmk3HASGC1JJoouackBkWMU6QONu7IF9vDGjsFx1L3zfW2THCaqd5RjodGc6bDEEM2tVGaX+aRl7hgjJnc3srIGUL0yaOg7Vrd0WeB7OAyAHfZTvrmiqRX8Da3nOtj92CqRTM84y5yPe1LqjrirV+AEPcMtl5TkBHwMX6bE/iGEUZvwIqE+Z6j++v7vD69hq/+81bvP3V3+DXv/07HK6ucLi+csJxWVkEOywB0/DxR/D9uzi/7bZ0occoxs+FeN0noFQPTZcIIzZlOgCfBRPP6WunL2kdEe5ML9uou/k+Axc6azc+JClG3JbskOy9kf0k11q9BL5/3bX6aYzxr5O+VWHDo8fygcUuWRv7eXbWxQX7fLhim0cXdoRm0M1b0DSDQDjWD/jx7n/gxw//hD/d/ZPY/jqNrMhqitVXzfK9+09gd20JCP7KLEo/giqWEEQkaEkJRlMwcyuIjskdsgFlzyYvSlah+IVncUlagakQKhPqJHRGVlbK9P+GOZpwbwGPvG2D3dghZshtSjQiLFEUWF0zMaeBSayNnuy3+Isa4lrpB0e4Y6YzHZQrSNVzBe5+IEwHAl4bTho5Nu5+Blr5XrXRThT/27mhLn/b1l6Ku8dg39KnbRcvvw+Ze5guKdWPyYX5odh7XkaJb+Rj4XwLSrHf4Gt3ZF2yb51iGQnu/qiHjaITadkFEdfTXtZy33ETxu2M/+a5zr/zPUwYN8p7xuJj01a+Yk/OD21/+Z8nwPLzXtJHI7IXyFuX/MzwggVY1opaFxDEMsLuj8oVpF5MKMWPMCv5UiaUA3B4fYd1rvh4d+P0+4YHvJnnz5s+m0XEt6ipYzBl2Fip0VOQen7Ne3ZNf45UJizzSzDNcgmo5uS7+wl/+NMB75cJ080kjKM+onqH6DDzLvwcp/ymjoavN2TYYFw2KgEYTXDknVzdpUvxAnDkx+ugfFQQNpduLszdI3N5Yq8zUoV4mNk6u8fr5jI16wMkZG2MeHLOgHxxDBsbl1XNE9P0N0HElkuY6ndHmvmSbFN1np5dipLfg7MC6OMWhNWF9rmGixLrkgsxjBQ0wxGpwMlKqz2fJ6Z1bP2MbiiClJDAPPdmAVHNj76+K4oNZqRtxHLyZ2m9xPgq8kAEuJ9Qc9HFfQ3OsGzWVcNYhCPAgehbZl3xebM0+8CyxTlXOeI7FHJSIEZZBRcENMzVPolLpkDCjIlqa82CKmctGACqhV9Qqvhn5Vp1zCUwb+YMstymDh3rM/I+hSukvq8Cow+y1hDa57Y8GFJNRcW6qgl1UY2L4KBvZLhGYBF3GkEZITUsg2N+PfZFHnTf71DCR3tLzUpJ6y7Wgo0CmJNmGTBEDhHnTiOUUKHiNIkm2rquqtGmLqg8el+cD3bOueCEPcpeGitri2Ksdb+RfVVEm3uBsPbNzMv7ngShY2dSChKoe0yEcAyuq4PDalniyHUSRFAa5bwjWwS5Px/lgcXLsX1qAtNGSyfdV0WVBCYNPF1U6CPuuCa1HKpYlgXLKpYQdb1D5UXG2vARw0kSPO7CS5+XSS1FyoTC9zisP2HmGTfTG7x8+Qp/9ze/w8sXb/H997/DzctXONy+xKQWMe6+zPw5f/wRdPwIXu+QYwaZ7NbaqpsZ+3bTY4QRz+k5PadPSN8Cd1qP9EANHwfT17bsek7fbvq0tfE115VjkYoiKSZj5gnG4TJJAQezPiG7IDAKs/MKhOIwx6VS1sgMNjxwFSYkFYmPVlQ5yV0oKW5LScksK60Y9Oa208JjNle8SzeCD1IKgavQtvOk9GsR/MrdTPl8hkLclvFrY5WUguyPkrhECPqpiBTElMqoUCgOedmgoQxeo9eYU5w02DlGTjcS6RRtpjfRx04LKD1v9E9Hv1l/SmPxGiPbCC4shl4SQoxokq3roKBXR/maNtrmH5RGNIV5gfCxObF/L3XLtBW6yGdNtDcBya2rrudEd7gwx9pwCV6CgQg9Z3s7VjaR2zWb6ZstPzTWgAj0Yu20FFriXWR4m5po8y2ISts70lA/vy2PL/dxnKjLt3/HR76e59N8O9HY7hvd96GYl3Lura/MY9YNLvJSAqhggnnamDCVCcu6+hkcMXmElyMBuCfn+/CBcXy5YGVqphVEKS7Nxb17svTFYkRsCb5PP0weB8fjBCQjYcQl6WxLWXV09FzfVSpY51tAGRWi/T3jwzLhX36cgLlgurGASYQsEfcqd77TKNfJDp54uXsws17EvLsBg8eaD4AeuvMjv6u11XUt1+xMupyP4/d27EY62U2N0X5iykc7W9hOardjvJb87uRgvlX1+W6BqZvC2im3EKC4ALfHfMd0S38Lqclrco+S0aTGfcAokLkhkATVoKGUgYPhCtO7pnbsOJjT2iELhbARCDHHeIulSMTJSADFIVy302DQNVp3ioi34gQbSwY609WGScupjmZB5gLK3Gw0cnpkw2Yk95ebd0AsAUGcqweFaxjlBqRyjtsxSG2zMFuzmycfIwaYK6gWz+PMfQBcCKKjVDdaCtY+Q84xJ24ogt5JafF9yBt1qTTOHGg5AEX2AdAEIxLcsoRJBQvRTQLauOtpNBgQxmyprkmT0S6C+LnlNdNlOo9mj05JiNKcdwxwM5uNcCzD0OwxxE4BzA1RrLk4x3RtqEGHIZYWxFxAEZ+TpYiJpwePNzw2QSvbpagrrVFqNbxcKCGDohArppUQ3CASu1M27RETjAIqiNBYNcIcZxRoYMSApK8oVUndXuCon1KLzZqAC/VtyW0Fi5vm3I/wpPf45JZc6k6OxPKgLguY78D0EcwL6rJm2YkLn9pxD6KcoOczEco0Y6or3s4rXl4f8Le/eoMXr9/i7W9+h+ubF7i+eYn56grT1RVQq8fdaQTa9++Bu598AMzVgijiJa2twUJ4FFOmL7OHt32iJOGUMOIErSDv/Zb6RBgGg7Zb57Pk5DkN0pewjPh0S4hPaHt40m3TKZrBzvER/v1ZUq/F8AmpwT3z84z3fCPp03jwT9eRL2X5sCk+ugN38j7Zbn3Cbb+hBsn2dFVXrIlegOHahg8k/EDfEVsMBHYc0COeGb4NqD4ShXIHGTS6cw1XIomzZlanbr2AxKdlY+UqDKl/FgNWaA3pRimGkws+Wg1es+LnmhScYnSC3rSxCsaxb3ltsGhHTSPe+bXK/I3Y3Jne7s/0iG8BElweEJKEyBQ9jYZrz76OVErvklDHGOEbhnRXZsCM33PF1PB0dpjzp/JEvlZR77FLfrQXR5YapxMN851l5JJa6WRmvY27raPmNxCWPzbvsT5CKel8n3zRNesrwWGwaNm+SlsXA05EgnVQ52A8qJ/IJIwIIUxfcjuWFyU+5UNh08ggB2ErwDlbTJomO4MsI53Mb+96JXkmEUaYUiWhuJBKSLEUi4fILSTyesIErDcr1mPNBywA3uneqXnc9PTCfNv0dYNVb1fzl2t6JJD4FtXjyoRlfgUuE6ALb5om/Hg34V/ezTiuBdONMNfKCS3mlpeVBv4R3X0snhiICxwp2byHbHrbdBnGsC7oCRJc3I89ZllfgRNSOYAxkA6ROC5PNR4MwGg8Wwrk9owxHhf46bpzI8bo5BQMrBqTXpEsUNRtNbMiLDUxEqXvYiba+LgjuRCzFrw8ZO+jMeQCtDOLxZAyLVQNeXIkihODUCBuefcaB0IvVxPGUFkh2tilQcCqcocLFWBCw6i0QN4gOJNeJ8QvhLxSQoM6EkEENNWl1jamgGvSdNPfMrOsBXahXRZoCeJO2OwBdfFiQYr8OZn7LFkbMh7qLxBVLSAMcW0D60IZkRkJMs0dEwoEHkWiwU42j1XNmwsmGzOFW7TvobAGgRNNi3lhKWm+DRaQMj0rTOtJju2xxk10RTB8JrWqMPPpqutf67bPbFXG6PZmW7OOm9bpCGQB0eqCGVuzpTBmvXZLUf2wGvMv/l25n96Yz+FDSmVY6+4QOZbw6qzUyqr+aMsk+2OeZqxk5pyyDurKAK8iPKLiS8/qtXNXZqEAGjQ5BA97YxZw2xpqRS9xVxDFfSAnheRzV3JqUWDMfRNYztOMWmRtuwWg74XUvhEDRBJvSSJqSAwQ8z+cCAIQ3PWAna/BdJO6rI04O+G/SymYp1k/pyD6tIa1fsTC96jLAqxHgBYRAkCClVmVdjc6ZAQUYtyUOxReUNc7gAiH6xtM5YCrwwtcH27x3Zvf4Pb2JX79m7/D4XCFm9tblHqP6eMfgDvC2ow/on/MwHKHOMM4iCkF6pSR5LeeviUm3nN6Ts/pyyeOk297z7ZH+bmKntM3kB4thPiFp08Virc4heAtx/oBPx3/B35690/4/U//Gcf6EUb0bZiV+r8aPgRGJRMVQMrBLPVDvYqgdBkB1KnnOg7meG1xXBRKi2Y6XdBFox+tR2odzYGdWmw8g1RIGCmn3k3Bk+F5BcVweU4VQekvQlgCgJo4Ef6lKimtiLLgtgWFVjAIXIrSTdwWTPh29jdPXKF6XUbCaYmgIaLImF+R10vLDPeH8S59j1ej59Q307bZDcw5pn8wtzPcQ1L4RFuS8vzvlDhRW+I8NIKTcflxHlIXDD7Aad0kxVACLGi1W94YreT8GC1D2AW7t9rJsRfzehi5WOqH3eku7tanlynN0+1ZtG2j+bT9nMtupRHbehpm2qCpHUFNk/Hkkr1MKDdMScGt6cto8TbrRd9rFgtDaPTlshyxsM1/kWwem0e9NlQ5F+U8Eq8TVArmq4rp7c9Y72Ys72/R7ohm4E70ejMKD8jbpocJIh66409VhXwZfP30IDgeMA57OTdtbW5zJe5RsE43YorobmcK7tcJf74rEmB2Oj303P5JTx848pvOjHo3qjMzlh9I9A/Om9D8GmQYdmmMMNkrxVqGr3pd921blL7rZ8c87q0hvPL+2eYgOH2ZG7POf7v2qjJOszYwJyTB65YLpfdNv99dZcoV8rWoaKaX5PQ/f/OGu+5mrXPvSpor97fe9dVqt0u6OPqsWtbVmM6s/keN6S0li1+Yea+WGLN0eZAJKKnPj/BF3w5UZ3iZwc/528n1M9EYvla3MwSjouaqMOQcW1A8Y8MrJWWKilWEO40iAhTRJmTGosVxsLtTGNVFEXQTUJBhRgEyBPOefK/I8VVkmAspU7frH1KgOFJ9psxoZxaEncJFXLhS2nY/lhWHMDPQbam/MiqJJRFxrxrAIbi2eUmDa3X63JWoG4g1zGuq0owAuADILwLizEBv+pTxl+6uMT/9xJPPCxzkLFQtqBANLBMITAVgtYyw4IOwYOelpv4VZP2SfI/bngxhRJs2T8jOFfmxtfKwPF0dZMNYgCIErJNQRBlrk7WqY2V7RRcXXJhmlRaSeDRqtdIKXQ2YVWcoNOQSPz6Ac0EE63Erdc3zjEKEeZrajnEF8wLGBzAWgGJd5HXQNJPqLgBupgUzFhywYJ5m3L4+4PrqBr9++xvMV7eYX77G4foGt6/fohTCVAj08R64/xkS5EwEMd7KBm/IE5FXwOm742TaRZIGiPpnTHmbPbTZPSyhEWBJxibvo5hGu1LKx2PSnzrMn9D0Jj3Wpck+Mcjp7wPrfBQkz+lbSnTR+dTjcTT8ejYN8EG3rrtwXe+fJe3nU5yMT8Wsv6hrv0Bp76dAfGnZ3euve++/nf49RR8OCOeHJGNC6t/Kd3i//CveHf+An5c/IgvtGsINcW0bfxyJSmzQ50Qj+9mtn4Vahqy/VwZu0DzkPBFW3IVgrj0FAEqW04nEiK5qXndxRBqvgmw7qwtZMJjEhang9EL3xr5UmPK8GF5p+GbC2cB5hDu40/xR+mN6MzZubIhuYbWMyAKfnM4cYiZkMJLTFc0Uuo5BGv9jHVLX94ZWznPcwbS1rBgCuIXD4blgbZNSJ0pbD0jFYXt9cuEO0QDeLYzetL+3OQytIpnanh+hroST4K0By+ltBO1t70dMgJ7BPaLNlNaOqtp4DFZVIUpNbOvqBQhbIU2bP9qMfmTlR3uTuUmNtwfuZnNnYs/jqKfP0w2ufiHS209Jc673a2VTOPakzDmLS+gCAAvWumKig8a3QRw12gDXEL5GHMUCmoH55R0AxvLhBcIyYgz/JelT7srPahGRNQWJkHxY63vPt19H2ndPkkbEiseOAIQxu5MvOIQXtINPRWLEEqLSAcABRBOmecbHZcJ//8M1PlZCmRVmD7BrZR+ArPLOvMSJ21Rkvvl3kwVMshHg8GPeuj9KWAFFO5TarlqFj2VGHpqLvu/pYI4Irbeq0TRywGkwepH+Aiz5hxYfjiOc0Wma/v7exiMHgkZm6nFc7tCLIgs5UhKXTFBhREXrxzKt52zFII17Nzj1vaIKI7JMIFT3a170AhUNFDUTY/byFlAiZpMUYbMBIQSSK8+qwmtthy/7to+ZnWDMyzIVTFP2kikjVyFmaStWMU/zMWyDbE0k8FcWRusKtaowABjgQiisZTVImiDKaoGiViiN4CeNgM+DVenupFqkzd2qqXZE+F2NgTDtemN8GrLgcTtAKMZIZ3YNo2xTYnWPGT5JhKLIgVkjuOWJgs8sZsBEBdMksNXV4GaQzkvlFVRJaQhCmSbUUiSgdeF0WVbNDw82XgiY5gm1EpZl1Vgj6jurTj7t4oaMMFH00tYSw/C8cPNlXTVftFBE57iumJglxgdB+rBUrMxq2RGIlJlOyn7RP4V9a1EpmFJeCyC/LEtyr8duWm2QF1L//DbRbK6WgjgsFokgzSGln3VdAZK9YWfIRBmW6t+JyN0DTdMMKlVcS6llFarF+1Dhj65LQ2xApObtxQ47R5BtHigWVJdI16dVlbVwrHwQYC4M1X1iVihx1rDPbWEC5oPHPpEipbtLrA9yJFYNnF6qLhpKFlcqDKu676lMmPLYd/fiZKfAJGM3zQexhJgPABhr1X2CCuZ7gN6D6xG13iM0BqN+MLB8vEc9rijTjFII390ecTUB5fqAqRS8vX6D66sZL1++xXy4wvXNLQ6HA169fIsyHzAdrkB1Ab37Fxjhi3r0sybHjWlX5el0Mb7Rp3MFnpLD/YC0h/49NJ1k9I2Q4a+SPrXxrzNHf61pj4b5Qq3nVr9Qm0+ZDGZTOqkQoe+CcKZe5BwkAGR4Ejm6ZvHPDBfbG4e89zkxLC+Bzn93ZNip9CmC1K+VLnW39bj0aXV9ipDm04e/hz2UXZ469XUSKqjMmF78GqQ4C1bFkF0JyizouaHZnTiA0aAsjGJeFWddQFxBdYUpBgGm0J+oxiRocOYZhQKcEUCGVzob3/EYte4tiGcE5e8k5ScAZl9qNEJOgs4aHSP9r7WCS8S+kBoMR2an5QwuMv6GwUUFpVYXzPhqIaB1yzrChxMfghiVlOYGq+SnQmyEGUwmQKnYF04oXah9Ox6P+Mc//hm3N1f43XevEBb1bRy2+Be0fkvrBs+i/WzHeGhJ0fQ/wzpInN4FcYtmB+Y6m6zbld9WvYWpp+e3P6h/o4/NPbGOoAsWtA2zok5rHki8n2T1kGHfKFKlsvE+5oYNlga2WGPnemoxFred3zuZ8thv6xy6/7K+O0yUyLQLaJFuDZ3DjZo6u/W5k6tvsP3dKdOBhEuziXvSVNHBnNeTT57y6qrweObpAMKEiWYUklgRzIxVz1aaCBNNIqwoAE0zCECZRWh7/+qItRLwp67flzDkmw6OXz0kfTnXTKf3/G56yst377ADgiGz9zu9yBWO27kAlrZf243AKFjoBigHTGUCqIBpxrHO+NP7CbUQyvUuCN5G+2U/40YgNiyTDvhTnYz7zZnvIyGEM0dVLT7G2wAKBmEGqp2XxFjcPymk7MmJ6WwfBppNbX32dYu45DpCA5mHE8LWLiNdGA279MTBSvkhXHDiBgosCFFzOeVgVDuoNnOj6SvmgTY/pvUgdSmJFl1MQoQWbFvxFnAYiIVirmus7N7A5/UXGhmbS0I1ToxGFL2RksrExWmjQMk1kK1RWwJF3bTYRVjURZrPXb92KLRS7H+7Ytk1hmyM/ZJ1ZIW7GBaINel7SQW84K5vysx2eGw+MrGQwM3fY9Ep0h5zJEXTGVm5cUcka0sIAA0/rWBrf01eWgqIWQO1sbvdgREItYLVnRSoaPBeRimElRm86l7OljwmDKvi69B66Mx6ckdvPl7MkHnVCHIMYLU4CbqAbdZF26oVYsUZF58uh4XusWLnW+5jlRgMU+mnArZXLX6FaSYFz1++cKVNnpxkDZsdOEBlggk0wCH8EcOUAjY8twiSwwwhcmy8GCAyyxgRQcpAt4SWBfd2WPMAYQ+d689vu6cBE2qz9x+O99qeySRRo6lH5DFsHCHXM3ZzxOg+EiOdAiq2a4vseCIlvbOAt+1LDgpogRntrDSXTFQKSplQeRUBHTOYVwD3ILoD84K6ClMsTijIfgGA4wocF6ASaCp4PQMvbwnTiytM84zvX32Pq+sXeP39bzHNBxxmiSk1Hw4u/OK7I+r9O5lZP693zoQHIl+XZn8Io+wcE66vy5fdmTYuYu7lG3mQP7/XB+cqbBKnF0+F5375xA+azy+VnmI8B5hW8/w8cr2fHj/jCZe2ur6KwO4xbX6N8erbpvjqCLM4pRut4x5/G9a8KffwfvYl2jN5C8EeTEpKtPX2qOQj52Fz3n1CGtXRUj6fWm/g+Q9Ol2hZS2OpreGLR6ftjXxaGNGOG3fPTs/bpk4qoKsblOkQAjjUGBc2bIujvCPAQRNZcGpSxQoyxS1VPMvghCKfUFkgOP1qCmCU3PAi4cXeCyJxzastN+6ghkIILekMX8DocLOuYCNFrBQhCRHgORXdb0ZcdMrUNsToMG2jEGPV8TIqKzPeLV98tz+Gs5EGsBVoKlehraopq2UL4/GqsVVhGHStjJ8+3AmGnwYouxttaJEO5gR5w2/rBRANDIle2hdUbMtxpWaf+jyfugup+zHcDgl+h6fD9cGbqhLxrPWmHEp/Us6DRJfA+Cqda6PMc0GMbdN4htHXC6Vh6PwzlK0gYjgKHaz23Vcg5SeXIr6xYU/hLKd4tftwbp89LCZwZ3WS69t7MWjfl1Ta11kYtFPJoD2tJuvZVvJ1xHrACD+qKH2u/AVW99gg9fYQ50ABoU6Eel1Rr2o+nhxWvz9OoyCPvl779HVjRHyryTRdH7SIT6cNipAZVkA6jQuOh1dgzCjlACoTDlcHfFwm/OPvr/CxFvDVSCo5aqnpVPobF1C8PtfPB6CeCckXvqlqT3QCiB7kEFYIAtBW1hXpD+aLDsLRrrJL3WC1z3O9TQdqrsk0mUegJxAkm2p2t/iYIl/tYZqtKZywUITPAvl6uwXu+96bJjusZOGwIoZWTa1reCWCBvCi4mYpdvH2wgXyunJsAk7rOzEG7a33WSQmHsvCYY1+RxnLE4xvMVssaagNqaO0HEJw4gzzhkpTpJlFx6eqRUkjA8jYJQALrCs0rAgMuF/blNewNWX+RRUppgLibA5pZEa7Q0YBzkNjXvpbQSilJcCIOMHNYBaGeoyx3EB7CDkr03qUPFB5KiPzMWHlVTXkNWwaFxWCqOBKx8otAqJXqBUSJwGMdRUXOGaNc5gPAB9R1ZVRcz6zjS+hVniQXrOBsNgfgTaRbmEK/I1tbNFZLRDmaZY5q6z5KbS2qCTfjFD/tmk7EqESufa8uAqqqKvOhTLL83oXoqagchUNBxYibCoTChUUquAC16o36sBM2i3+Rq2yRgoCgaFSUCxOBzMYFbWqRY7NvyI4MmzNagQrxShWBkoM+aEE9Bo3TmBkYi9/O3V0E7VnDqV+pIKyFqDnUOyVogh58XgPItSyVR9mxqzrPc+RavNBz0Y9pwpB3W/ZLVr9DCebAztzQDgcDiB1g8QM1OMdKu4AvNczsAIajJqrRmlgiYVS746oxwVvr494cbVi/vWMucy4nV/icLjGr3/1Aje3Vzi8fI35cMDN7StM8wHzfAPwCnz4QTQQ72TvrWCgrmpVdPGN/pye03N6Tn9ZyfA1xZ/3jsOOUvB7nvOdhybTE6UnovI3tM9zek77yVgLWbHpjt7hjzf/gLvlJ/DPPX3L8T8/c1pHLWvZYheKtS2b+09BXEFMojADQ59K4FlF3O+WSd+rS06HOZEqBaYMpTQOAyChDSSvKcvo/lI6xl2XZCYxlPo1LZOqeB1TwtuxYSRGeatFFXiIXBjBkRH2pGX+JkFLcOvlHZv7WhH3iBVyDIIoHAn948pH/SxTwDhMmWa2Og3vHgghGhx/w0juf6P5HfFNafPuUhaccSqCjh5k8FE4U2kj4aIBDKmd5l3pxsTmLcc0kXw2/mbpI82msc11UHrSCGwyDZUEGgrLti+Sb3cUdhiL/Z7Y2E3vMyQb+LbFxutiL98obZSo8hgSbTyO9IANlfhG7Q6u0D0hiHlLMGGEvti9hR3HGJ4j1ngxX8qAKmaKW/IJRBNWriD3vJLctLNZb8pZUKZJBBi1gsoB9WoSt9HHumn11HZ6yvRZBREnF9eD1NVOIImPEBQ0Phb7d7DzShZSZnZdeIT1je3DaI2lS4apgMsVuBxAaiK88oSlTvjzBwkmOd1wCqY6rns0XM4mtk2S0v4W4fQX6eyNw22sudMyzx3Z73Ju5IRsZS3TVpIYh3vXZGIkjdP+PDwVTdFf98N54HjJ/YvBwbzRWk2aJFkI4esayn5NF5+fzYlxm9sVmYjpeRCEhZfq4NFhHoeiCQpC48Q6yvG1H5f0PidCD17UkfGxMOtrVxWD1R2T5QmUcP+4CGQ6C1SGezeWuPX4vODKCF2GI4UBe3vZ5ZgdQFpT+QCq8rwC4kamxwwISRPfQWj7cArkHSGE4NwUZ0DKT0ZMKLLNgMpspI+OgLMVadc6s0j1DbbKFWQ+/im0oQKZ355jJnCg9C+YDeTWEv2RQUAYYaUL3AapFBFwsGkZWB1EEUPE1sNm2FQ/q5jrIhH/FHVh1I9vEBNwYo6JVDtBCZDtyakt6VgqXL4XoLqGXlaFUMwucBLrCEU0SYQnpVADk0Fpwggpp0KvNKZIY9zgys0epLYAtucnNfm4y79d38xWB6cs5PeIHIG5HDXzaOb70UK2TGKd65LOHqB6PBodO4tDQUU01KZZr2sG8YrKR4AXULlX83mGzMXaCJQLCHVl0MK4fVHx3Q1wdXuF+XCF71++xovrV7h5/Rrz1TWuX75GmWdM8wyXnK6rBK2uEWti3yXbp6U4icd1X4rujfL1z/ojee9M36vzESjjBekzY+qfM42Qn4emzzOon5SecpU//Y55Tg9N51ShzugcSh19FRdN7Ol62zp5+PwsaTJqdYQbYL+fT2GlcC5d2sap89zzPNGZ+SX6PWj0E8p+yoW0pRecDofRf/H3U8dGaPYVR3zAR/oRS7kDOvqkZQ5w278gesRrrzHF1DWRQUgV4IJQKNFkTO9iRCwoBYEOHoR8NaJDrCGK4f5DUqbnf2R6xJ8IUaAujmywI/YFnLY+WbvFK+OkTb4FoSvf0kYeM8P6QqJUZkKGTJPKmLF1CkqYDEg+AnYsf4a0RSK+nf7u6HH/0ZRry2/xt5jEraBiBFGmj6h5ShTvxx2jyNxXG5lSDbSBP7XWlGnzBdHjghtKimI2v67M1s53W0csMsr15TaDunFaB5SY7KnbPe3Yn8N9cOuUEeF2ffB68Lh3SLgniNpLe2uqB6sHJG2HM21Q9zlqarxu99q3NjerkPvRyJW0898Wcw4Fgu9KvtaNr6UrwvmsFiuWuQK1hCAinaOYCEV0LFGdZ3Cmg58hPVtEpLSxgBgw7B9Y4fCxWy8CsmpLBTBhuXoDpgMYMwiEw9UV3i8T/usPBxxXgG7E53h/TgxbibXbgcTNZwDVX8yUutAx15iazW4Cm74d4akkzQd95prUGZEYwEQslyx7/m3af3NhMpzK4eWdAR2XBaUrqUPA3Cg08cQMnxEm8mVtNXPGHEiQMk2dyW2JZIxl+arEvSSLCAZWXYNmAeDa60QieDVLg8QYa5BMrm7xINq1Nc2fMdbkOzcWD/G9psDQMUAIOQtbF9vOxaVr2t8JbVDkywP9GgYGs9woaLe4MP9qXcGmuZNgtIs/yrAGWrbYEMkaZcMUT2VsLPJIsDCHTabIdm0zwRnQu2uERdJfisRU0D1mOEszFYAySoF1tdWTNFgS/A0ilBjinBA+L5fqJyJMZQJBTISp9lqGAW8BgEKYMLlmVLRj665iWWVelgUS4LdMcpGqq6aVGaWa71LpOAPuninPoVndmOZ/4B/aTyrwcFhk51fFWm3+CwiriOr8TDSRROD7zVrRvjc2J+lMrrU2ghXtuAteYlxFm93iHIibqohfYBYfjRAmIa/SlvStqMsr0eYKd1WrwmLJfdySkV3Rr+2dYKbgBTG07dneIM4ZyUZ89RulWe+Wl3NGiEZcwGjIs9G9sY/VxN/8gqWNQZ2rLTubG2uLdPY0RHEJiFtLZ/K5Id0P5o5gXY7geg+UdwCvQF0EVkM0aZIYEfcV390y3twSXrw84GZ6jbffvcDL1zc4vHyJ+foah6sXmA4H0Czxo8oksTDWn/4ArMcgyOr62YQPzynSANV6Ts/pOX2TKYgjUyJhw6WxPe8b3I/j/tvQRbmFDd31aaTkc3pOllSlJPgVCTV6mmSOJQsW/og/3f1X/Pjhn3D/7gNqXVocymkUs+7X7xKwsKWv1oq6LqhrxbouuvsUWywFtBIwFdcKJnsOs4QoKFPCwSyTgUOK4yveZ0o4opSj+D0pX8GVWpDqYaUdgVByir6yUu0VrbLaNkXdrrJk+BjnqTLcXxV5OIQNJgxpXStbmWjTZBBMBYWruGBRA4kCc2ig/d0FtVMQVSQ+hA1BF3qMgEQPhBDCypE/N8B7i4deKNEHJ25T/zDNfT6vPVvBuLMtzTHUpIf4fmgEK13QZmrWRQu/t+FWNqIUZJY9xvtiY+iTcTOyy2zj8W3HVJ4GbedzkRey0y+ZXpLEiU4OaFPdlH93434SyaUh830zc6MJvljIkPsZKTxvRK5cvn+/14KPCW3fkb0YMepP1NyM84l+nqxT2yVzL60VF32+VjlnQcA0SawIqBCiomKtYnU/qQeDqRQUJswTg69W0Ks/YXl3QL1/gXb0vhxF8zBBRMuJOJFtO+CXanFspHMPAO+pUrtJH1H+AqLf+XwESGC0IkKIcgVSJtexTjjWCR+OEkR3mroFbYxC9EuGmw9ngHL/3IBpYW7mYLPx2gskPXGmaWLBR+uZGcJaAW37ksfeEK4tFt8fn/2Py5OSE0Fc8HZNjqrvYUtD3dR9KaUi/T19ULlFiUtIU3N+4uaLOTGWkZiThHD5b4SY1UbdRQdGaB2ED3YbrtrMLce6tlwNcdfO8WYcuM11avyo77+VYsG5zGzWhjQ0w/W7whnzH0Tlue3rCK616t3j7XrmmFVGV7dhkf285/Hb6Xu0zXqG1A3y0bhb4+h3ZIDj2i0iGl/MjBm5bkiw7moa/RlJItG2l2rX6AeTCEwGyJ+bMlorVHTZrC4sy+67LD9XBqYYL2l0O4kuLmCkeW/fmwunWC9wAU+DFCItKwbMtRQnuByU3NG0FtvjlUe5fSnJXiwqKBRhTrUYG2SaL+069LMpNZ2JV4PBps4EsKTwbLRWOpjjqbmgIq1PhTNGyHj7G3S0r8zhJagZ/Cb3FikmJER/U2MQjq1lUMxPAwvBDHfggnbOeVMdFi/G+9lOrAh+EWNSF3CtWNd7AEdQvQdRlVgn0PDQRFBHUpio4MUV4TevD3h9/QKvb17i5s0bXN3eYn75AuXqCigzuJQQ4gHCFDjegdcjLvZx/YnpnFbr55B/+BK+8M4/ly/ukh0caPB7UMknpZYAfE7PaT+d21J79MdDrMcvck16uoKL23qq9CDt70TXBL7ZYEFN9gHv6dHpkqE5NVWX9rPV36HBwxPtd2fiuTP3oqX1QBj20pNYQFwKw5bwO5NBnyZc8GJY+kHsyzfo/EAYkUB0ivSh0i8igCYPnlt5wV39EcflPerdClODC4eW8RdISlnq+teJHlNMSopv1funMJaSaMYOJghOFcy4oF98PSQrXadrGkFN2sQbdHI0TtkLQCKSei2vndTWyOl/4N257XaqAiNuccwnO4ZOpg3G7rwEnYukWNQKJrLgNvBh+721isi046jlaH+TOr5Qyws4t+5H3g4UtkLNs1YAYc+c6kvvgugJS4QQ5GR+TAg3tuOZBhWuFEXtOLXr1dq2MqpsGcEK2x6meImp27nH3Qvq8o5WYIK/eXx6Hs7NUm+9PipB3M13T7/27weJU7HenVgH0HmYrc5MS3NPBbfr9uQw+TqP/hNBYmkqHc5gpYUL1AGv8/Xkf1UlyrgvSingmUFXR5T7vH67c3kXrpx3MAoPuHqeLSK69KRxIbSe1ve3TZAyv6hgmV9jpRmFDiAqmOcZ9+uE//KnA+5XkejL0VHyKt/rwfD3rhBiWEPkbQ9378Xp8rr63TQI7Rj4ZtbPzbXOsTl7plpmcp24tzZp5OpIGOjqt7/2hMipquNgaxCnpjhhM3qb9/LQtZ9T5gyL+bgzy4I4JrpLioQRaGuYrN9UBmtaAoaZv06fD9pqGLMGIHbLCeZ0yA0QRwc8a5pFty1OwWgxWn75aN1BZXm4CAPaINfSBfO9GNYEDIBYtJTtmc2O+NJXJi+HNYSZnYaWhMKrUuWKKhdBjo3RjbGtM3N41TOpBS4HUBm6xtjOe3B88ecLjysnBm4316l4ZREOFPfFSkDp/ShmpFLOnVJqML4TBCbcIKkUYHbXNFxbDYmqsQ7KNIMq1O1PjwWJL30QUFikDHWtqLRiOUqr0zShslgOYF3BpWIqMwppMGtI3JFCHOrqrJfxCtkPCdk0l1JCSKU+mpDHIyVrTAEWLXZClThxUE0XSoijNuoIgc0zwoLDCTFeVdMoNHmqWttInAoCalFdrDgPiksrKDHRc8sRX8PkOGaFFMRPgRGQLJMEUEEthshY/mbitZFkCuDrlFHV/1XJ+0Hhk/2d4pQoUpRdGwV8cU84AWeaRRm5N4sYQASEHHFnuLQwsMNffO3nfhGTjplCMdx6lAiE9JzTfK8V0/wTwCvW9QgL0FiXBfXuI8SyZ8KLqxW/enHEga5wO7/G1fVr3Lx4hdevb/Dq9QvMhyvMhwOm6ytM8wGYJzAVcRNWK+inP4CWO1hExWlZAQaWMgL88yc7E57Tc3pOz+lbShv+od7JYdmacLSL6IoWx3/KtNG9+orpK8iUvoH0y+n0p/IsGpyeZpRXfwOaDwBNLVFun0a82BfO/9U63uNArGBeUeuKuuqnf1dbYSJMPIG5otAk7lOZk/6bapQbXUo9zB1/QQalpT0TfkyKL3OfP0sHUrfDMl2tt+13M4YDbe28iZugg33jAhMrkEK3J+uIESciCXkahT+OtnyaNmv5srViHhR6t0Hyvc+rcJqlcCdwaGIgpLRnKRHd3F/bvQAuflr+euLs2vaFLaB0F8w5YM+WEdYx40N185/6a8pkMjzGr0kBpJ3JrPWQNULhkksb2/YRzgOiqBAxB+TelILL1I9nP1d7+c4kIrSBb7dpsxLzWI4rvazdC97v5eIT76KKyHGpgHmzbhlpkO3ZKcEG+/lIVj4oXZ/TqcwgsK/bVWMAGh26lghazUVoY4LwgOp1xfHtEUudgR8c8gRw/p2f9Xk/LX3eGBGDZ79EIvVUTIlPSkXMDWuZwXQlGgFMuF8nfFwn3K2Eo7kSKen2Zbte+i00Zlh6vl2G8Skgu4v8TNasZ8T2l7eQDq5tLca+YTdl7ICNSk4CdXq+ODVn/7rybWuew3CwxB/bb8XGJOXL23sUnMaYllmrpm6Qn5ZSEVDSRZBeRLbBJNrc+PmYmH+crnTHNc16wILCygobjsPwGbfvbA4VceQ+X9MXavqT11fTqCGUNn5MQJH6zf+7acp4oNkEV7us2vkng9W6YMV6wnFvbfD5E/DiMzJfjlY3DUF3YEMGtzNnnnm7tnxdePO0qcOFNySWEVmryLT/mStcZTwaSJXIo2IMdMiaM5dFpcSuFAES+WdqTAJ4567oUiFUcG2FEcaE5m5CWds37XhfW35uqGut4fkYpID1f6R9bdvHEVAn6nTMTNLDbbW+9wx55Qiqxxa8ztEWfWeWUNk0vY8lAjYr96Ynm9ThKz4E3XWzdwy7tZALI/qK81fyz7a+Foke3Qd04lu7RWScZdXu+EkF4C6otFGP0YNV56YCWAE+AlhAfAewCE4JK6iuKGXCXApuZ+DtLeH26hZvX7zF9e1L3Lx4jcOLGxxur0FT0eDiM1AmVEhAa14ZqBW03gPLva6HJDi55L7+BtOIF/DZ2uoG6Lyu06iSbk2dWOvfbDqDR33r6bF4+ak5eXJcf9T+E9NCn7LGPnl9fsvrO6cO/bQfQ+z/c6+BU2PmuEfz6NHVPXR+9tbmo6b5kWvjk/fHp+yHsw9OT8bJ/eQETJfnHLwNzRTj01i6oju7ziFhUSryTQfQdCUKLOuK4/ED1vU+cRISApqBs7Yq0DDIK2cCUhhirsQFgDUeGZdQ2gEj0w7ObHXEraQ2B8QWG3XYPvecBMeVHGXKimL63vkDNeDiptR2CO1L4MNtXm6+BewbnJQyTtL3MQPP0eVNGh14F6SezktQZCFDs9YUj9izeghGd78WR2WMBNs+jwxAvw3b8gS6wDJYhEDZ4iO/Kw6fKycZnYY0P878tx6FIAm5bnfpSrm0DaZ/F5LPzKo7G4UGX+stUCjls7GjpvAYz43+5WdbeksSp3UX8Oe69s6bwT17Im2refydTIMNInT3JXWqECgLxnbwBtmpI3wCW/BPtc2RnbsvAoueCeqWzVs03osf0RVVXdXVyk5ri+CQQAcCzYwyrWAu4DqijtE940+Zik36hVhEDC6aL5U+m2oKYTm8xlquAZoxlYLD1RWOa8F/+dMV7lZCJfWJmGFBv8gvGRej7tMiyu8GiTdfcBFzwyFUBISRkTLZzEU3QBTqkRr4uFuTfrzaBnrklOTAx5mxXpOf+ma+m33Xanv21hr7jWo7+RlR9MtwRbTzW9VKwwLOGFNS7iy56IpK2qVbtffOpHgKA2SuicK6IjS1Iz6EWVAUCvc/kqWqlvYCE6zY0cfGtezPJiL1IUrN2J8YJtjaGWucALkFj5nBhiBFTYKEIBDSRd9sgrynOBUePHh7+QaOXbVfgFtDBHc/ASEMakZcgDGeWoaKLwCHd2dUNlQIFIHiGLPKjFIJnLWhff3qWlIrEqtOYgGEeyEXgum5UwqlYdH9a0hT2ksZCSkaVHrxYQ3LFfGVv6KUijIfAsRCWGsKEkzqa7+yG4JxrcBUQGVCKSumUlBrxVoXGTvH/SjWRtoPBGDlKq67SLQELP5CIfKYLW1cFJtSVpyQIkC8nhk1BdEmwIVBTl6YxNLmoAJ7d4qhpxWi2VBsc5Nox7DCwTrn5u9WgnmHplf1cZcxnWaJO7TazjINLYXNrRcCx0oQcYN02flLqXxOrP6CmcJ6Ya+/zdJplnjep6RbhTy4G0p6rmMDW5tmRcKi9REnbbpJSGJMuOaZbV2Fs9g5ZGtXx5EgFj9FrYgYEIuHuoKm9wBpYGhi1HVB4SNeH/8Vc6mY5yscrmZ8991bHK6vcfvyDa5urvDy1WvMh2vcvHyNaTpgmq9AM4HmOJPFPVkFfvoDcP8OReN70LqmczWN5udAWS5Iv0RFk+f0nJ7TX2dyxZoauJFbw8LYCsCWdrqEJs2H8APPxc9Gdz4cjK9bwXOK9PRjuVlhHdP548c/459++H9jrR8hqj0dPElpxn+7WyaxqBUqSehHj8XHq/gwT7RvrUW0dDFrMGvCZE0VozuSZrnCa7HW4EKMAK/nlTKKYtdwOhaezfgVkPjUCGEKw2hgpRObIZNToqC3i1B8LAkwXGmF09j5PBhSbXEME95shAUHwGaxLIb81c8xo0+ERsFgD2a4rPPk7Yn7K+MzGL4c490fS0RxTmaGfS63/fTSqcy23pPHoB7BjbZ6+pYFC9ytgyZvUVy6i/MQrm8NRqV7zNrB/ip9Y79bN03kY5npj0YRz8Y6lzHBRm8xYiOdxk/owQYirWPk/glD5demyralcd69VwbvRW186dQv3B14emVeL6qCLeO5yJPmVE4zKlXtNH0WNmBzFjtvz/cQiycBZjAXLMsCsSqTc3KtK8AVS62YSKwkCIS1VvG0MEnMYcyM8qKCfvMjlndXuP/5lQ3EGXif7j56GkFEHrDBAuT091zKWsfn6n1o+myWDQ+FgWZxr0AzUGZQmcAo+LhMuKsF9ythqYQyp4PLLsVHNdo/eFj/tyzQQR7jbqbLv9dWd0bP3gHg7dkWf0ii5oBAqsEvng5HCQZbPNmFrN93Vo7aLHuJMwDpUm8rS01wjF9YH6imco8cbMBMwDJcSxoEZ1SagGNTuqsyEDR2ZMe1XQDVHEnXf3PhhyBJtrNprXftXkKs5HWTEY/dohx4MUIYQsZUN2Y9s+eRETi96rw/5yEOeDfSoaxZNLD8wQn3Jtzn7t4RY2weKTDENuWEHPV10KZcW5VpB8AJgIwdmZmxWDQUvTtT8HKuqLWodkG0Af1LLrSTi9/Rq0xYEIkportW03VO7fiZyyK5yDPCmvf+znDC/PC2p4NB68um0aSijdm3wd843eJkDdBC5UwQzeZ7bIQfyZmQV1JbpZwdxZf79hzTnvR1+1G19XUsc4Qo02D253dGtiQYreRe5Bi02Ghd56VH/q+ggFXYFAKGhMybQMPr7O8cas6GFt20s0WIvfX+CK4LDod7UKmAIodgYOaKFxPjai64ur7C9eEav3n9GoebF7h99QbT4QaHm5eYDgfM19cgmtX6gfW8XIG1AmsF1QpejqDjEU5Y+NQJfC2J/PDk+/nC9KSasw7D4+s4VeZJ0L49CbU//rqk1nM6ny7R/h8HsvxlpyexyuHNlwcW3y/3KIukJ0jOcEyQtLhwvpAvq3PrZ5p3z6aR0o28aJDph5+HJwoEo+QJ1sS3lh7QpdOWC6O6nnCNfspFl1KjICIPMpq81/g+WADAFQvfY6nvsdY7LHzU5z28nP4DGOBJhiuF4pJ+92eGYxpNago0ue7A/Zxh6zhq0HmJuo2RGY5vwvucLrE6zVLDnks95kq1PSk6Wr6jqVplxQ6ePGwZLq+jo8dbsr6hb6v3OvX74o2QsF4iXM0TDvPU5nBGPKXfVlppc2ox9617pl57v79Xt0RIn38DeUfjylroaWTe5IuPfE6T19HAb4Ihs4ROc9TEdoCNz55QIq2XRH/0YybfSrSxuYuo6x2aOvZg28dheuFGHo+HpSywAvK+/Hop9uiWjh3lPk0opLOHEHS8v27LGi9jr8aAIeUY0beaOYVrBUCJ3aMKawxYHB0/LpJg0oWXbGtDgmCXuQLXK+i+pmNGvg2vwRGgn5Ce1CLiqZD1LIzgbtP9klJoPreH7XF+gaXcoBSJCXE4HHDkCf/nv6klBIr7WT/fRjB0Iv5E++6RwAMIrXeT/FH7OvoJ0W5g88vHgeK6CxeSWBe9BNvjDZhfbzu81LtI1HNqSzfAn85n8DFHsGV7rp2jQluGm6dA+HrkgAa7VjQTwpVRQbtXgkHL2u1A2JgZ6xrBZ0pRKaZdUN6lIHQatEc5mVTYFSqYxe8+1xV20OS+lRRoVZDCiloXcF2xrstmKOQgZNiRL+twknEkwDRIJLwCu7/63H9HnHQQm97pQStbooOW0hZL6z8O4NrOLRXFNVV73SfvBEnWYp7pe0EhFl+nxrT0vZjyFsggWawP5H3JysePmBynjtFAMPtFJk0YY7pHfKKf8qdW1RgxDrUOZGXBkRqZWSHwOgi2pBcxIHuXzGWSrlFmCcQray5pIlUAZKbZJSbRzhzrWgGICyZzmWSwc0WZ1GqHq1pFiM/ZaZ6aNVCZE/5hVgXQ/nMg0QmVc7kRm1Fj8f45YkeiEV+rBEMmArhMMEsOtwRA7PVSCMxi7g4QpqnNt9ZgnBMVlKLnaq26jyKvWQDIsEgeAJinCSDCrHE07u/vYSYt4VJIeipnbs14si8mEVQVtTqRMykLWHw7MW323kbgas8GxIx8WgDCbn01v6x+an+r9och51QIpRZgEuF+aEXZ2SQuuQoZodURbn53MdjOSI73dnZUQPwcryt+/tcfsN5/wP/63Z/w6mrB7e0tyjTjcPsa8+GAVy//dxyurnH7+i3m+QpXL95gPhxwfXMr8S1sXkybiI/gFcDCoA8/gO9+AqoIN6a6yr1ohhzF1rme6xbTg9NZfGEyYvNbIB4ek56Cz/r4xvGUePlzek7P6TOlhOY73tzx/BuD7Yely+i2B6dziOFzevr06DM9KLCnTfssoSepXXGoCcDCH/Bvd/8f/Hj/L2CuaIUC2IFj8KxhgJnVEYOruhs22nAFCjHWsqAwg9cJrLiI6BeR44+NQori940iZFWLjASv0z8NrktOJ0omYedXiwPhfAGlW4xPYW07Lloc/w08VRePEHdB7xmtWD3iW7POHCf2Ayi7CE20rNG2Hvwb+hvO00A1HsBgqmIAmyc3VzP+w998h6t5itiVibnsNgNOk2u/bV42uH3QPtFmfo/m+Ri+8SbcOw63/vz7fsifLCxuYmEg0ykUcelKFgroemysV5zKiBPAY5pYfmtx8jLRl3R39OOYx6DjDW7ocgTcUke4l9rm3x3dM/dNt66asc2PFZ4d5Pwh/MkYo32hfoIuxtph2/JMzh2nrbtgo89YlRrP38kN12REFm9K7O0DW3Yh2IyhFeFBUdq/sHAIVwkkiJWFZlyr8O5WqoB52qGCaSpYrhfcv73DuhyAP8l6a9z9DWF9unS5IOIhC8aKPBCYbyntLa8H4SXGpKPJOQcMgMsMTJP4fi4F744TjjzhWMUSwhl6Pad7UL27GtIHWVtgu8lPzci2Z/mSdp9i3vZgUydmYXCq5BByPtVgAK2dzGyMA4dO7nXXrt1UCGWmPUKTaAjg5uvwQWZG9+V8PKnXgk8MWEWAvAcZIfLUjYmP+WhOtB5jJBrCYtYNXuVW4GcaFpa/ejDnnCmtz6aCdNGzzQVkPlVbeW85UvvH+Y3oLuXQBMrv2u7H2rJUse1ptDvSOs94r53+xqznTYv6zO8o24yao1+oIj0I91YJkWGrZDCv3NSV9yVEYKcdyUGAe02iQNZTV0/stR4lzKCZBlNyrgSzTOi70NiDpP1gbbQ9srpMK0mDNAMawC6vBhaBB2X99Q5qQlaCij0QYLdr2qaIs4DHxLLWhDIzzHpDiY9u4UjA9BwzQ//2AsU8X+l0hyFgBNoEd7ZsVYU/mWgQkBiy9ovjVNl4ZpNaTM6XDXVnEWMAR1pEp+7LZjfvXA5n1RAyAbgBwYjWHh5bq6KB1/fIhdR1Ba9rLig5lMlf6h1oPeK6fASmI95cF7y5vcLLV7cSZPrFG5TDFW5evMR8uMLNyzegecZ0dYtpmjEdrkTQUY+AwuK3mdHSyz2wHsXNoUps8+3RQD66W/nTAllGPefz+HH/RIjfHthx5jysvl4+ttEkfUwlF6azc/BVkeXTONap9BRa9r8Ea4O/RAuJby09aj8+tq0e99ms4wfC8C0Ruyf25BezgEgw7Fp89EUeC9sjil3mJnZU98No6CdNT1g9dV8IJLEh5gNQAK4L7t+/w/LxDuG+Nsp3fP7+9eaZ0CuhrLWlI00ZsaJSQQWjJKWuHoMb8ZgMxxUcLtxDWXtBLgVNZrh0ps96l8XmYrpdoQqUBnQuiHUduGeGK/rocBvdgEQLN3NcmnuZuYBKbTwZxDq1urj9vhnnUTs2LASigsMkzMnNe8/Xf7Za+yNLCKthP37EFqChEKHrzEmmLnflMk1AgFkdGF0flg8Gawl4TRjhAguCaXU5jeFDkH+T99vaacciaERqvtDmd0/Hbn9YiU74YQKVwQimhtunZ/GbziXRht7VL7b0d+p70JGWx27nHDa63mMnNuU8h9dyCgBbfWZxkA6Q9PYczHbOdNkdpnyAdnO8qQuNkmk8Ng8URZZ0TVYYVGBCy1orxAF1BXOB8SILAaVA3AFfrag3d8A6Ace54YU8ZK4eeiX/QmJEfLkUjK2nS8t0i/XwUuoHgDKhlILD4QqVJ/z3Hw54fyRZNIW6Q2As/dtDpIzx8DAhRPeeoUznRHcbU3RUhkUK3/hbzdlMW9WlzAFr5I8L1FgsZg0jDDDt25nDo4WNtuPBasbYMPxpe1AMzhk+9RJ5TjgQr4y8mFCHU8BkJOSnrrB4FSaUYbD7dpNLBe6Dn0ruV4DWd0OQqSrsN66oVS0iWELYyBDE5SVIzCpI4bqg1kUtIsyKwooQBGvNl2XEELC5Mulxrda+5KyGLOaULuFSzMeh/4leCedXmvb7L68t075vBR5UCCAOH6OWX4OfRVBi8wOZNL4bMKUeAmtwH5svICx3KM1Nq10jMMY8l1rEOiHjGgTfD24gp2six5lohgZqBeAXYHGXRWDRYGECsEo/qzI/KWlZ2P4brnGN2eCjUOCIsVk0eV2EQIJ8TOI8Y12TJtXJsUEYQEms9KAnqmhPWRDfMmGa1GqoMqoJuDSmgM2J40gUMDBkDQpo0ZYjH35kiF0EuMplr/XYXVGrEUCQvhhhYkxyjeNARVxVEQdhx2APHC3WCeSiCido/PySs7KiYsIkfSRxQ7TUY8wDAfN8ABXCPM0SX2BVy4cJMrIZNgUmzilt389c2YtVJ8FjZNi6tvO9WyuNC6bBd+9jd/j2ln3tZcJ+3pD2w+ck56Eigekb7jihqPSFedVxWVK9ECStssZkWLGuK8o0+VmkixoFwPfL7/G6/IzD31/jar7Cb3/773B7e4vXb99gmq+wHl4AZcLh6go0FczzFUBFxEFFLGfq8R2WH/8ZIrwWy5dCBK5JWy/vCzIN3go9nfyoIdtLAGjoG3icXJkhjddjcKCnEkA8p+f0nJ7T507GtMjnq1s0OuPpITU+NeX4y09fTPDxnB6eHHUg4Um8/BvQfABRRb27w8f//Gcc8R78a8VRTYDgDP4Ub665/MnEAfpfaXzFJ2vO6+RrBZgE3wIAPgheYnjNDo4puLzSpbUqrVodV23iDTpDVmsqAFBB1WjeGgooYPC6JsEJAk8tRePMiYcHp8dh1rZt37RmEWjUqpbUq/Ig1ELCwFM2i1lZZGU+c21spInQjjXFhdC6g9VhI9QSQfYySRTsjeegRONQOgfz88yL6WjwbBEh7IBEy3tq8/Y4/4YZ3tMENmBtbdFnr9bazjBQ0PjF4m0aXaHrzS0J8li4uwjkWBGc6MfcJnwcpFwpfUf0fWmfNVzIRAcCIxZ8ppfI2ywbGHrcfnBf0c7zQcoKPVkYs60PERietuTcydQcK9tx6786szCfFvnDFDT7cn2bm3fU/TrhPrvLpw0P68oq54PC3VdZi3YkFV0PEk2HYSykpWqsCF3XR15R64qyLOCJMS8zMAHLOqNQcV7KYZ6B7+/BL34P/uNr4PffxXg8MD0UE7pYEDEexvN5f9GpYZjQ8PnmHQCmSf4b86jMMPcRIHkPs4SoE5a1ILEVtNJ0kVzKUECs+WDndRkenGJXxoHTIhLBMEnNpIvOkZ1eyJPhZGwYGY9C6wdjlcdvd8OfGZvLh46bj92CNj6OKCVBjpla5rrsMowjST6dSRmdYHtP8PFw91lNkOqEAJEdrgjizJiOjlKeTs08J1iTpMCJO+7Ud/MUEPRitjPcfN6RLbM43IlNDz9dgolJaszeXX2AhDRGvYkIpXa8kZ81Arf2hMy4lYGTtsgm2Qg7HtBYmqTDAImRb+DAj5aoL+POXYd7TXhbLx6IqZdsWB5mNZfOdiDbzcOKNAcAfR7pQ9V8YVrdjUnqc9P3ZGJJBHFvU6s/t/lmRDDnWFw9MuY1I82yl4/mhAiIarJwNSa4VoCKCDsn2+MEZfizrqyidVexkkiwBWLSojmG6LEH2qsAi2snTv7j7LkzqosIKmoVd1BC21XAXBM1a2s7JtyMCTwGxqnzIO9jf9YJIMalRu+7/Zda8DcFIBcGmsAvzlT4b0KtRcsrAaeCiDgGVAixrk4w2zzzKoTk9QE4FMabl1d4e/Ua12rx8OLtr3B9fYPDi5ca5+FKAmcfZqmjLuAEYy2EevwAXpdY0wxUOx+ba1bWmX32Y21wtjTzZTeo3SG/WC3vDeLw6f04q8Xbtekr5SlwmOf0SWl7tj99MpzrsUuNz5yhl6Qs3P3sadPGwzr+FAzpPRzuQXVfgOtbtqc4RywNY6MhcIIhBI9u/nwnzy2ZxKO8KP/FFSPm65NV/h6xpC62hHhwou5zUNOlg/4Z9/NmzH2eCVTEtcf9+jPujn/GXXmHIz4EfRrEfirK6S823wOTDaZ77p+vVIYHXu3fb4bWajY6VX/XzgrC3JUaTE6TOOYIiP3wmnjaqjzodDJcqQ1cnF4Josv4GmR6pNErSutNlQvdvZPR+omGZAZo0sqdFA0lSUHpQwBAea1x0FR5Vrj5fSr1CrCDHE4WJno+8ySM1slrirry3SQOhRCj3wElTMhA6NezNO4Kq127GS5/YXOn80k2DmT5QhBjFhKNRUSmTzaM8r7NLV3tbeV33aKPaqPH3DeFzD2k1Oc0Dps7ZXeQLz6Zg2oe0WkpH3V72p+fa2mA26uAcvQ885ZCeKa/dWvtxSb01nr+bmrDhKOyBE/D3lPwHcD+V6m68aCb5MFe6++8lyyL/BIvO1whPDQGwAvAJEqXVT4Li2KlFDLXyFK2HFbU+Qia7sB1Aq8mJhidIj3Qj7u7ni0iUto7iB+qJVinayyH1+i3nsV9WOZrHKngn3+6ws934iO6ECWpaFwwG2bc7toOtGBjdtyX20mJ3Sd3G3Lbg95z+CM0xnl1BhCcOZotIZxJ1JdVBjwYIqH+LEyRGMOeDrSxd7PHYXcvQbLh2EDLBEM8M+TCYgYoBmGaDeuyBtJHosUumlr6SdQ4sSUiFAYqJV/6GVHhsLKotSqSJWanRTBAFIQZoiBiorVRq/hB5xpumYJBrxoDCotoFBQU90VvYyoM1KLuh9gDF7djb6rgpo1WXNs/aTwTQFxRjbAjNOZqsWIrUBNyWkraIeSfptUAd6sTa5VAKGVqkKucVrAjmL6mYC4cA4FwBLRzhyVxCvRizP4LDR/xizMg9l5yPxcx13kcRFoOmIZGIWGmF7VkqA0DkjrNjKjSZF1kQiwloKkQVg0+Yoh/EwcgIUWO2Ov+qHUV5C47HnVGcupFt1ntQrWzZSoFPJVk6VRRMDV9qVqHo4MdkuJnZrr4mzHQMV/XFRNJDB9Wn4wisLO1RiDtVymka1PXZwUIjDIViWuxVhBWR/xKmWItsVgtiaGSxRAoPm7rWgFUzLNqNRCBJ8KyLI5gEEmsCJ4UF1GiiiFmmTEOJqCIs89WUa0rSpl8rAlALfLHhCJOwHWbpJ5A+KxYxiltD7AheWTrJ1a/3WxmjCVnYnEEszJ7XAcAHgdH3B7JucmQsa3rimU5yji5xYP0ea0rqBwwTROmecZUJhw/HsFLxX/8FeN33xe8fvt/wdXNDa5uX6McDri6fQkqM/RURcEi800Aljvwu9+D6yL/AV+v7i6OxOrEx418aEETpJ86aFXvULJ9qNAXtXTK90Pj6/MEjtNajzynB6dL8PTn1KRfrPDrOf1iU75NAjfb5voyK/NcK/n9Q87lx5Z7Tg9PfzlnWOV7/PHu/8D79Y/44ft/xMJHMJllAOCETrNnMs4eqdMHc/yz+gMoTaE4CgNMVS3nrbLMHO7dBVk96mq4VvC6Yq3iRtj2ddwxRfVBKegqDqWloI/FunpdV4dLQGGnv4kyTiyWEFOKIWc8DRkHpREruyWEWNwmYYnSABZE1h56nAZA4oExoSpdka9O55+Am3FH+jRlq2aCELi2p8yQj4eRt/9MtP52J5BVuXm7K4TYSbnNIS/GqtvgFMGPaPDcYg61jBGb3hPBYrfZnObfHkizaXwwXjYu5nFiIxjQujflU52bx93cmMDESxlPwz63Q3U+nShkr9w6J8ctGJdjn7vNi5PJBRjGUJRGduBKa801sijoI/MSkcrnc+aS5Iq/gUScL3PxBNDJn+YGDmynla0QWZeVARBjnmYwVfXAwMC90OLLsoILY5k0RuW6YoYovoEKZvWWsFag3NxhvvkB6/0rLOur87AOn1+OdzxAEJEOrabd84PcMB3P0Lp71eXs51tMm3dzQ8Z2bY/l+K0symg78acoP+hhpAKmGZVmhUEuT2GqAj8vE+5UwsRUcKzF2xq5Y8oX/TA1e+hMnv0c3XvHOJBHI37rs/6y64taCTvUR+0npqbXH5ZvWj7XlUDwKoJ51sJsAKWFwB0MznTMC7QDsXk8uAA5P+HsAj7KE4VvdT0ka94IerDUPnaD9dWtA4zpVjbXVu6GX2zpQHaCywMrs3MB+dQB3zG2Q4LfXXK21qmkS9oA0oHPDO9mYXJU1S81ymw2g0Tq9lVFaObAlpQf1XltUP6f2jMVA0M8kk/IQCDyGgokM8bfnimS6AhgvvCsEWUE+z3bbxwI5uka8NBAZGjWXHMUZUZ+apxBaAK956nB6cTdNDGEzdq4cdF5yq6mQntqt2Z9XyHh8WzoaXs5EGAWIoFkp32XkUeHM2ku+eYw4ok2S91/NpdVzI+AKzEWOJlIm4s04uJCr1oZpVTUWlBKDWEX4BYFhYoHFhYCzNZrfFqxqi6hrD9mAWICRXN1BgSilIkg+P1iuhd25soazz5yN+OhdTBaBE6mKRYS48RasvMoahznTo9jXbdnIfmPIgiY9YHFNN+CAaJa4ME19U3cw4FZXc7ZJRv7gkASn+F+xdU14fpAOMzANAM0HTDRFX71qxnffXeF61dvJBbE9Q1omlGmSd3lAeAKOn6Au2KrR3A9ikA3CXWbAXfBdRyXOZ6JD4wDO9Km3Y6rEW4+nHsT1Y3/yXQuwyMZzOeaHbeVCl7QbJ+V05PHQX0Crl9Ieux07hKe34Awq4fgc4L08Lq/4vg8yUCcrmP09tI1trVG2uTsftGw3Kj+fRg43TnDRltSJ92x/TsaPBsDdC7DAwvswNMekPuPmqrGFV2ULrNQ2XEx0tAFD28b6Od4W8nZahMT63zq8wzaC0QViYBoa2kUYM5Mzi4c5++vfP2PPoUOXbDWBZUqmESpgxYCPhzAZQWu71PHWldLjg0afSnEz2a/eHuWxekVcXfreDXFNGQSJnBYwbktaHNlU6CrXi+xmCpMzQCYFryOXDV6L8Xy1D64ZazW4/XCyN7QkjdloXDB6x1scPJqyoCuEAgwOp5Uon/JBqBCaDkHPs6+GMvU7GYZtfgue1lzTzU+WzcTB+t84AAh0Og08Xe+R13n91BH4hrWv9u1pgcxUfrM3FAXnzeQiiM6YQQI7vo1GPtWpgT4I//+xrtIgoNW6JPGaciDiTqbE4HafCbEyAqF3u801w9PpwpFP0wRNEO0TQZ958KqDyC9U8zc/55LMUZ7CGvKy32+9uZuamBy2plIV96Abs6ANBCforlO7bFR2qN3CoVQN/FjjP8sAltC5RXVPisBxbwniBJxKRMwAXQg4MhpWAb92du6e/3aSQ8SRNiRFyvwy1Ba/fkypqV3KaX9d14XbX5v2tQHvp0GwgierrHMr/R0rwBmgCZMs2hW/uHnGf/2sWAikkWjh0evhVzrmc3ZwZ95Ne2XlGdTLi7+UV7Tfg2+hx66usA4athK4EHq7z4Oc989jp+YVmdoVnhsgfYE0MM7z9RgBYwWSXrhaEEWfJBdbOQdtUPGkQ8Fv6hGvQUiDgY0N79bTC/qRSHViIZohDPDfGyagGBdFjAz1lohFhDC2CL1WQsfH0NMKCYAoiFNOleeKK5rRsVaV0F+zCVJmRJio0VYNIizo0/mNDcZO8zzNs1i3qv+LcGr/NdxEaYnYKZgBHUhY3PiiA2iHRBQpoRVMVgdmYkjdAK4+tkc5rTpkiAdQ0UeSl6Xzky3C7/VnijJSikY7cmsNiGV7YpLZ3K1eUZaHOl8r+yxFsg0vAFwYYibnVV7zWqZYnWZJUV/SXPgwUXGQax6TXtaQhYxov9Zq2GUCsFjA9RKLmsinc1qMpMU/NfONd83EIEIG65u7oPUMkSY6Gop1Q1SINdq6UJQdzzwsmUS9znWp8os8RhIWbGsVhgApmlWYRHrmlN3SensFZmaWi/U1cenVmHeS3wCArOs57ooAcQVtaiVgnnq9DNfCQ6uKFPRPqmLMdeOMiFHUcKqBjwakMrW4rpWEDGmaYKZSTNZ7A/GCjEnL0WsIFZrQ/sNFYyA4hz3WUt7vOoaLXYv+P0Qwqd8JsURGOd/HMlx1nbTnBJL7JWiZ5pJqFX4UFBAmEAk35ZVLLewLoD7CxatNkDm0Vyvca1Y1wVI60yEderj976i3AF/+5sZ//7fv8XN7Q2urq5xfXONw9UBL26ucbi6wjTLmNu+INIDkwBej+D3vwfWI0wInA6B1G/teY072e84nyJK5x98NNJMRX3p6M8tXYzG70Yv/8bTI8Bux+fSMjvz19foOM9zOpVGAotfjpVERvYux9n/mtLDBFJfft7tDtunuTrMigMPalPQFdwxW+L9Y9Llp9TJFkbLdOfoepLUtPOQeR3lfRxwDyrF/ckuz06fRfvv9pd9ULDw+54cHYsse+Mwej6GYytUo+ad05EQ8pq4iotTQ1OMLmMGvZ8w/bfXqC/vsP67jwBxWDbYrehkaLYAD8UQ93igaAZBtXirWewLlkgTgGkCyqTuooq4ElHam9SyXvC8FViPwHpEXRasdcWyrOqKFBArCHPhq76TzANFGhYqFSuVYIyqQMM8FYAE5ydYPD8bRFGIKerWxIe5QPus46MKMuZdgC2WhcJZNc4E84RKUA8FxS27JYweqzd4BtWi9G9eS2HdJc3mtRZfOJB158OIRXcimREKgEq5+Terulmm3WILvnowxHsLCEr1NXB2v6IJpXX9LMsKrtY53SNkMSbJkWKxYiHxjkARa9Pq9JgQBisBpkjcC36yZUXw8GK8fexK1Nns0421Qic4GOzpyEqD3zEuvrI3FkS5ojTaroxFTZ7xEZbyucA2YNo7EimPQdP0mVNa92Mvr9gTdm85t5bf7uUWR985ObvCm8M5/tKoD7w7Dg5M39TOvUx5uCiUmcnmkNu8UH4EAKxYUJkxlRkA4365ByqwrkeAKg51ktDVdZJYm5glvuQE1AkoLwAcJ+B+AGu/1qwL2SX3Ay7giwURo23Rb4wvm/ZW/GlYtgLZ0eGIhIDopTdimqgwoqKAywGVDoigvxAm7zTj5/sJd2vB3SolK4DCNJTyxZruNtRgUkeo8Bh9yYd6rnNbaceaGdSW8nHahMaQSi3tVR5CkA4EShoQ/Xhv5pXz2/YRtz/7B5fsj/ZcbWExt/PGMM3MuG6Ek6wg78xAGMDZXZIGpjZhgzKlQ2o/AHSEQNN2TPY01IUJyi5F3TSRBEW5+mZ8KK5aQzhCwyfMbEcwZFnNphv50rOG2K750VXUV+5//HcIu+zTcrTCm7hw24PWNHssdoa5ItvAkfAiKxe1JKTGx8besp8rl6U2X4/MiXVGezLsXeItI7Sr2+fT1rwGP0+Ik/NLx8DAhH7UwGAlNgdz+hol+vutwX9H3aLtK2lRYinkbWV7O4MWhjIUhRPqa2udPYiZMtzVPBw1mPfNnDoiG32PcWs7Ysi8tSoaDqVXLkEO7udaEXLbeBD2Bp/qhAq+v5rzY6wvHsPU7g/yduGz1pTzsz32VrtN8zqQzVNJBf+I+0GIMxIitmhMh7qI6bua18u1zalfMqHMjOV+wVwYLw4rpmnCfLjCVCrKPEtg6Re3+Jtfv8J337/F1fUVDocD5nmW/4eDCn5EeIXlI7Au7RqrK1DVTZadB+1lh1Ea3tWO8LdlTh0RozP1siNle94/RaKuK49J54iWT2FgyyqJvXiZ4GYERFfrl8CNs9C9geXL4+VPYQmx0Zy9sB8DbHo35+n3l6dH9zeXO0uzdHe84QyfY6N+g2kPz+vnO9SUnnZcBuj0mbRHiV2YhvO6xf8vnv8xQbKf52KYLk2nKz97rvc47mdY919yJw1u+E0Gxzsd+do546Wa7SPqv+wlAs3XoHIAUMDriuXP96h3RzgDTnEvrgSom11jsLcwMcCi4pTdsHqcQctuuJB+csY5nKAk5aMG7etoY8LBwRZgWvDtdV3VdekC8d1ZUeos2r6JWjE6FVBhExst2OKfWWGSqEBUuCrAYcUdtHrao0yieFRz3EW13uBswSH9KJXF2oIND9Fkylykml7ulsng35lfbj7aGaf2hKL8YhcvPbGLewHDVgKW8tqH9Ut+md/+Ht7It4WAnGAbt9H+Vg6F0Q8UCn8mQPJ4F87Yd2LDK926a/JOR57Ut019mjLt1HgW2M7KfqKufAzu6WLpL1s9nN4m2nCYOJXLdZ44a3KbW9p+pxkOt2l9NurmPVHkw1rb9xswdp+xPxxDKuQuObz7NacaR42cOMPbdbEPsAm05ZmdVwwqE5ir96ByRakklmPqDtjOHFGuLOBDxXpTgXd10+QpUJpd/AAU6BNjRHx5QufBaQfhp3YGm2cjwmd0RLPWv5YZx/kNiNRZhEpap/mAab7CP/w44fcfIIErsxmfwZTu89ZV0T56dBZx8ouIu8f2YoDe5wseHavXkaOG3RIwD/Dakg9eQzhq0g5FnhLVPu+kvQS4JrHBn2MCbBOnvwksZahlZrgjQBst1QzB9uKOh9GfcFVjRpuptvRTlEOSqSprTAiurq08Tbp+NHhYg3RQ9MsECL5kKHxKel9JG9VMMY5QvLHCFDziHI9cfgw1F1PLWDUTRzLXTH6BE9TnjGvGmE90G6WzCripXREAFYDWhIuOd0JoJMinxa8AhcZDICN2eOY57xG96khzVX+kdV3F13zDrJWqTFfFht5WXwdk06Yxbe1cOTMsCGSofWftMcN1AJz+7DDUCKaGFpH2TNsJMsRfrIditxAEITeLn8BtJDzzqpd2DibmGkOdz9MYIvI1kOc8kK7UfncMCUwl9gBkHQKQuCVUoVd1Gk/LZ01J/lKKPlMBBtjhMsuZyWM4yFpf1SdjKQRCQeEWtsnqdGLMiDVDU7UHRpDZOxYLB4s1Ac5IUKzm8H1d0WvHUAoAbwiECYrgZUPzU951ouZYVMPEOifNVDmyr+vFAB7cvTY2YLWAgcSEKKVgMkEEr+CFsZpG3KLuj4zAK4Z8sS/nuqw4vlvw5sWC/8ffMa5vJ9y+ukaZD5gPN5gPB7GAePkSN69eyViX4uPhmlS6ruq7fwPff9gZgbM39ZOnvxL+5HN6Ts/pOT0+8faEHgu9euWJ57SXtmP0C+ARfKW0NzKZrEl8pacfSmaACqabXwHzFYgY9eOK4z+8x3H9CPyNEBBOjzgTPZhpZuXgtGJmthvNV5OgwYQSaGNErqu4CzjQAVQmtzAQfI8GPHIWZZ+1ekyvRfG/47KKJazu5XkGCs+Cthe1qXXCSXB+LkbzSd0Gt1gtqOW9MetqVXcmCFoS6tLE+qZWGDXRXdXrkzgWXCuqeQwgo8Gr0kJKTyPFD63qXoomFFpRiXod7/Qjc1AGyoTN+2CSGz2TMjb0oz/e+d1bQOTvhvNHmZjUoAt7+Nt8GwrP0XBKj8gtFBqrBdJPxd8Nj89WETB6M1tCUBJUdAvR4r7GIx0wr8eonDYP9WW6PrdjOx5s6n7n2u3t5jTe3G/cPidjSe8dNjrmT3UVjpoZrNXNvTIE7/QBSVlz7ySRdPkdpmzAB6Q4Rx5W5sKctsYBsK1xFvq+rMX5EgRgqRKjsk4SvJqVp1GmCfW2YpkXrD8PBBEnYMor8yG9fIAggna+X1BykP2E8GzLZLqkuYsydfVb0kveGYHOVB5ma5nczmiEutCZ8PE44ef7CWWawYcJH1Y5lIpbS8QBmRHhRtMjIx7d4/iemU9RH/X5N7dQy+wZpVN4j9UZzPTOnUrXRjtgfYrLxBl76VV8JJiBxODqBqohLoIzuatF0/Jlt33eMGetnLUQGg4wF0qb0YtV44zHpBXBvDoz2xABUuaXM+n8gIl6jblmzNXtmqXxmLMNjY5PdkdjkI72bP+clRlrsFHxQOOEHC6Dm37buEV06gGMuV07B1gQPMHufGKFGdiNb97lcumnuBquvTLSKsl7g9Mnu/9RR1AV2Y4DwHurvvrUTym3h3mzrfPS5c11633Sivy384C5/e17IFMzDXrXXuo5h517VnSE/3Az7Np/F5IRWpOC3IEo31/e8qyds6ZdAB7ngskDWDnulDM28OaTw2vxPSuXNRrBpsSAiDllxcLFzVInBLU9ZO0VccPE5p+WIyhdKZzmKQmubIsOJn4ovJIhAHNN2nJwDRFOf2GwFELJazAfzf1dodPXWgR2efp0ArfanoR+2G+ryRPKUQJAIwSPfa2m7szhFzgoXqAyliNjIsarw4J5IpT5CrgCphc3ePtywq9/e4P5+gqHm1txLTddYZpnzIcrHG6uMU2TEyzr3XtgufP4PlR08no3T9zCeQpR/ZLMLYNjJLjczWzpHCX6DaRPtZjIe+eUptanpD1t/6fQ8t1AvDfhj0jtfXJxgf30AJhOj00IsM/tpXxnfrF0SWNn9tqD18ZfiSSyn29XPnFaqLu7ePQU6QKOm8U/P+cxd+E8ea5B/tM7I30nepIzJto9t7+fopEem/nLSD1qdelQPcRSrKUJUhnPgGaZMyo+HP8NH9cf8O7mT7iv79o5zniVP0tCiCSogMc/UDdmqK5sY8nyVyDesdBpUGUTcnecfUdYaVahIY3Bz3VV+iy5ZiJR1qFifoaDGjBqmmGOP/P+tzfJ6p3EqqL2eD8Sm0AHvTChUsYipA4X5JhFhNLeVDTWGzOmtC6K0qgFBVxYXaTWVhkm1f+YlIUIJ1djz/Ae8Rsuam9Eb9dU/al6aLN/NqA161odQSuPItP81H1vBAdkPAP9JHRlOnga4U2MoyvCWTsOeomszZhcMoaZXg24+jT2aZLwJU53ZtOlHZdOUimAoMG7mtOP8R18PiQED2hQ+NbdK970c3DP5fes8DVbp3+/V24AcfA10m4/iefTpvz5dHpP9L/kKJU1x6ucNUZ7myvKWqvEAYJYk7kggghUiyhWlgKeiwiT62Wr8xKI+/QIi4jPS4A+SghxUcX5ShgsVGUwZWHEqP3muOf8QSCaQNMBf/75gP/zXyfMNxOmG5FomyVEEw9CuFVbVs/gzu/TKUSwQd9GyKdryo5LRguh8dvkYEMe4rOpkMbazcHF9GzyWVoTuQxHHLQJdkUKGmEEdyW9+49EY1MfRoIrBnRzsmo2MCz0uGXqxCrOvHWLCGWiLeuqY6NIRzFtkGm43cyPfdaiBmmwJe/8aN4F4VTU0P35W3wCTGamui0al3m0AMBdsZBqsJD64AQAWtWQNWvSoPfH6zU1Y7vtt7bv+4WBZGVhJq5534bVA0VcCGUWhwWHzVGaKydYo26uFgRt9aDioo2TGLw6D6HhHjFArEt5L5EFYO7mqKUS9HF/WTqhIQi8BRxm8zVvQhCi5LYvI0P5fKDxOmMo8z/tR7t0wRG7wBE1KMPejrZ+Ian2ERf9HFzCRGL1AiNcDMlq++n3g/bI/kVL6YshkV5/nFuT+VlDjIP4kw1BqwgEC4zv7OODCgtSJktLxqHW4j5hwTFOIoxIDIEkkckCovge5zRRWidpTZlwu9n6gDMeKjOwMiSeAjaJYyHlaXI4oKearacNeksxdDbOfV2+jhKC2yKO6UH+9Hptn7C2L66aCFUsIWpFXRYXRhiaz8w4flhxNa/4T3/zAS9vD3j19hUO1ze4ffMW8+Eah9vXYJpQpwkVhJULaBKXivPEmJMZC3/8EfXjj9GH7iz08dSHj7x5vn76K2Fk/sWkLzJdz2viOf3SU1rDzAk365kGcKL9c9O7n5Iu3ZGZ2fXX4s7ry6Qtnv5V0p7UoUkD3JjhuG/le/zp+N/wfv0DfnzzLzjyx0SvB70ZzwK/tT3EXJ3Gc0uIGjSa0ctI5VRuITRhgXqNkNgQYhkR2vQBtDHx1aqgLljXRT6XFcty1NhggpSWUiSuA/KWTvQ9lWAQdgxKOyNkiKtYIXBVj5tOWAEdnEyEwgWrMbaZHWaLOWc8AABYwShF8Fq3DDAatUi8yApWT00MLuuGlzTe2Xu8Hh2DRGNtLeIHJUZ0+ahe55+01hBjIcSnptTBzHuyyS4mXAgLiOy9wQQPxX4TYHEuQ1ARwoghb6hpND+L+rKgpaFVL2Fycpcv301N8Wg/Pw46Mrfbl/PuRT1bEt570Fjhb2BL+XqQT1xBVq8LOjLcly6XU/cc87aaZqAyh4SbTCHAaZ8DLR/DhBLBi2rnelT+8UnnOvehQPnZBC7F6eJpEoHCfT0CK7CuCwgk8S/VRVNR/uM0FVSewHNBPRBwRKOwvAvNCWHMqfRAQUQ7hcEY2Q74U6eHaqgFkyAxe7rF0uc9lTgxHLnMWKdruMR0usJ8dY13y4Qf313h52PBdDOhzNm//1ZquZ0m3nne52oRBNDAdMkYmoMLar+/ZzZFYvYykIJSWYOxKU7qNmeOHgV7tOOlpTI9rpUDn57fys06zeLgQWvewqAPuZ7suiRqMkZim9/dN6lUMZetzqBXM79SPDj1ltHVHpC9S6yWIaY5LQ/Hd0cglalnjHNh8nenMkJzvBkLR04tble4Z7JLjJHaMmQ12NTpe58YoVnPCTlMl3yqBdYvt8FIew5GVCZWtQklIB3rJe9s/3RuKkzbprov0rwGrEobl8Dfu74F9rJ7wY+PuUDu4zcg8RZEqFQqgYrlS2uPAXc3hIFwzNdAOr91vVj53b1la0njEHhXCjmiHkMQcy38d7VwGO36NPWNbx9Fa8gQpOZVnLEj4aghV4U0cH03N7Hy80SwBrxO6zSDy9AAdpSqM2Ei+cWdCbE9lRC2g7pB9PQNG7GQctva00Dz2c+pDJsIFV1Ap0ITFzRSai6dYdZ2jJtpjcX8xjpSOFU4FEj5dowkgrbAK4662rvOTczZkLV+hFqhOLOs+7WKX2A7eflYQbzizc0RhwPh6u1L3F7P+NXvfoWb6yvcvnqD6TDj6voWNE1it2/CSguEPRWUmYD7D1iWd9Hv9T5BjHQotuPnZ0IzqGQLv+/YbsqCqeH7y6v6cmnnzDsHq7//fCjkg1I/9qcUP07Wc6bjf3GMwUv7cyrfA+mIvar2qom7+lOJwEvSI9pIeP3J999AegwkGzoo0RUXlB7UZ7CcPi+1kfwDgUtlK/gdpselnWX/cwEMo+Lb9wP2yX59W+2OVMsonOfeGbfFyT7HyvtUAclDSn5T5y1h673gAWnE6DrR1Nn3rkKky5/TOubDCv7Ve9Sr46BsojPB6sWWfT254t1OH5irBj9WS4giVqglM/YdPoWLK8CqyWtM/pUTnbbqniHMldt5b0kK/egpo5aGMlirSk5MoS9ozh6DJseTW/oyYmjU7LKqQuhMUyCz/OrWFfq3uvJcN6e5kNENm1kPuhEVuP95wfIReP9vQL2HOyjw/mJMrrSujNrj5tKr+zEMy42VdizSrvFELyrdZzi+CyAST8AtHpwvYMITpalKuGlqvFJ4//uVAwBBj8Hfk4O5uaP6gdvgw6nNpvlcruWNbKs/yWQwwNp8u/yIrg+bK8eRrO1ds7tGotPuZrkfpr2iXT3u2SE/3V58bbN69nlbvNO/Df7S4niiZLl/LgcNa40/hujJNPqgXl3PBIggkwu4qss4FdLWyqhFaGgq4Sau6Pk1UQEOC/j2A5Y6Y13mTfdP7d2HyAMe6Zrpl5f2hBCXplxkRcFxfo0yHVCmGdM0YZomvP8w459+mkClYL4ZuGLqbjneIMXYniAbOPxWbDvUM9hPVNczF0dI6bDlxHxG1avYmX4AlCk3JAT6A8kvge2CzVLUHm4tGkgx7W/lLDDZVNL0bJvGfZAP0fKvgZhsmJrpiyEc1T7Nb2ZVRESQD4DUHdOUzC7jqmmY2ztrJNM/DeM/IYWNYKAyWONvuJsd83+/oW3yYRvCEwDqX1MueGGIKrNXx7Bygid9MljnJm/O+NnPq0Hg/DyGIHAMR+AsXxzOKtQBhUumfna7vrL2z+J2VNW6McsXjzOQ3N1khnu4zNILu2TkJWERCWYb4x65aPYcYv6cwQeAuEqwZLOUTgg7oaKiSLBfO4O6Y4ezW6S9c6MRKuRxAkqRsQgES+Ia1DUEOn0yLZHRWVyIdMsqIWNnhw0dJ00ePUMKkRknbPrgJAaxXsoCW9c9ec+BLMZRakx/O5t6okb3rwJZSkFlAmPVdSBm12upfj4SpTFl5AWU1jm5EJNi0KTZKu6IWAmV0PRRGI24t/Vjfn1tjel6YBgcaT8rYi6WRKV95yusFUa0uCs1eW2NSZdJ1or3VMqacMgsamIkYgZdxEkQQrAC6yr+gGVeCtYjcE3A//VXFW9fX+Plv/t3OFzf4sWLF5jmGdfXNz7hJsiw7pn23TwTpomwvPsJy09/8PXQpzhTt8/sCP1lY03P6S89PVA29g2mT91ln7pDLxm8vo1f9IB/5fTpp6qh0IZi9CzSjMe0LV86b0978gdOd2GdmR4E0FzOMJxgW1fGijnnz4y/NsMF6TKY/xqtNRyn/crdpu6/zz4ZDQHw9Yr6tz9BOeby3veO/Ddr9Qp1g8TsLj8EhzZON/yzVnXPRJAQfvOMadYYEaboiVRMBRBc038W4cO6LliXBXUVywgW5oK77JSWsuAg8FfO291p6KC/EgGmMQKNXmaBSaI3xJhSxM/bHv92ABktLvgswVygBPVMIFVKFLq8QPFzZ44LcJnnwF1T+Yl9qyvj5z/c4eN7xrt/OQC14OqK/FB0vsEZZmIW3rqAhIIWOq/J/mmLv3Hnmr707peCP5GeudWD+pJIAgqoIMLvgiZf6qv93TC+W3dOeRCE9N2xDrcR6R9S/trxEgaZ+m/t0TqYEMoltnffKLmL5G6dt02N7qG9ZKPJQw/Pl6c0N5muppFwTjPanZho/jbraGztgZTtb5qaqwABAABJREFUZWKPVaw41fEeX++FEFYjI7xTTDSppxKI0EHzrrWCNF4NqacPYoJ4rBArrHKzgJZ34Ltb1LtPDCl9In2+mr9UukTqciJPHDQtIiZJGYo04Viu/HBCmTGpEGI+HPDzXcEP72a8u580EE5ymZGvdrvU9xZo3gQZxh6uUfkTiz4YcoP8NNKQ6d53AgjXZa9JCIFgEu0mQuuPfSRSz21nLQrazo4DRaM+JmwCeUzJNyo2ZaItWw+uqax1VXDjkonTxt4QLmrCWddVfbKtgWiYJojBROaSyS691BPXGNP14+d+n8cYtPKfNZgXd4hTY1IH0yKvYC6CrCnSFozMbm35pLMja+F+SFy5lJ28p1O7EgNNTA/Y8TeYXkrP0AcJ8mZBvhpGqQ6iw0IhpHGilKEMypp80IfmDRRxZEMmHfoQfLXrjULZosmdQB5e/mxAxbzpniDvB8VFSltNcr0itV8h4htpCLlWYCfkjG5WbSbPkwgj7KzL/bY92593WaDYMPwzw93mGqyukrbD45Y8vlIKkIggq5xJg5XDkM/qk8EKkDRHMOsRR14hnXPT7c3pPDo/IMKOvO6g5yWpq6e9KO3cvqICqDxDLQoAt7igCSbIXFd4gD8bOztTwHmNG3HBij+1cIjRgjqDpIJqwpNLGAVnrmIjikSQEKewucIi8i7G1ckAWIjKWoCq0f8kfjeJCyUqeD3d4aYwrt/c4uZqwu/+7hq3L25wePsrlDJhxh3KesT64Q6ACVLljCzWmI4tk8w637+/rE8NZng6/0Zh4ILkazxvnA0QJ9oa/xw0dAKmb4BJdDbGwzcA4y8h9cM4FLLtDeWXGOMHtbFDsQ7uwmHpC8iHUYq6z1SwudLjHnlAI1rX44AdtfTIbp+s88F1PHQtcffF7vDuWHyIwMCOb9fTGKPy49JDOmy3qd2XZ+Ht+/2JaXSX9/SGr1BXQOrurXMSzJiMx8N1po2HjMbDta6/RAoc+tE1bAkLfX6+XLl6CZoO4hp5PeL4h49Y7u4EeU00prh3HTEHuftgny+jzzxD38VUhisLrl0mYX6RCCJMcz36oox/D/Qcro6ym16nzSm7eN0Z40TzGY0V/bDnQaeHJwOjqQOvtkMk75ghRWftMIfCVZX+VWZ1z9TsOqdPGqq4IS/aMe7R0lO7iBmYCuFXb25xe3WFoBJTweF5MVpkD98/xrB/QIn4m5gDcXYrrae0UKMkqXSd8/L8N+Cum2CKWOk5yPcabdrS9jcwhmJYC2zHk0j1GY9nk/Lw296k7gF6YUiUbc+DRPs2jyjo75NJx39kMUA78F+YRkz2T0mN4IHHIyRkcL7/trMJ2t9DEavRzj4dnxPwC6+lf5YaO5FOj4ueC8Y7cbpWglNXruE+m81N3IJSC1ZeQZXA6o64UMF6rZYS7wHcE7AKvycLQHph52PSNyWI2GE1P307lBBPnajSBWjJzPfKwPHwAqDJL8t5PmCaJszzjA8fJvzzz+JHXAKWZuSA8f9n78+6JMuRM0HwE+CqmrtHREYmWUWyqnu6+nSffpsz//+XzJx56WW6yCKLTGbG4pupXsg8yApcXF3MzJfIdES4qepdAMEmkF02wvwLZXY/C9uulZkgcvN9EDReWtndOxxJqdmErSM2I0O+6f3cnlrgzwiozbMd8GG9vw/kFt4MczxhiHjOwBY7nGBrMhMc6ATT0hQjrNmjGfN6WNezKgTMAjrV18QKGEWF5skbIitCpDvNV8KUYFaCiZCIHXNTbebGmgS10kFvRwg7HRuPcT9OBLwPTkTl/lCw2fbpyooZQZqqF8Ynr3W6sDTZ443mVNBuFe5zSG594HC5YNYDwjgAES5LEog3/+Qgdh3gIHC9j5kwLflAyoRbr5Rxq5E92s6IXE6KP3+OsQkxsRH8q7KgiHdEd92q6uqMeoxw7mHWh/2Dfew81qhVNwgLphRVhocIHSbWdd8RvtZmel+E7hAdAwwmnWMmj6daiuRwyJZRFr7P14ftP1Ua5DHoYZZ5M+VMbAGxsOq8iBRnCG9U+mRftj4SE+RJzqDhpPReMe+HUlEAnM4nsWRYG7g0UDkqocx69EhfVtvPZPQSeVgpEzZIFy3RttDppRWgpPNxf/r6uZwSfLFXlEyHKwKZ/DpT4FMb00IMboQGzadTNPl8qSi14v/x+xX/8GPFDz/+AYeHV/j+d39AORywHl6D2wn080/g8xliPSf7G2AnTMNyS8Zh5bCesb9p98Z6Hhm059Fju+UeGuDFyzWh02+gfF4B033lk1oD36uM+s2V2cGFq3Ttc8uTt8RfwF76zZZMznLQLJmOu0yIyct7YWY+bdlZ5y9QNh7pio8GqrK7pz/maznXN6vkCixfSqH8pc+Ia0M1js1VeGmkXHJbhPrwA8rhNQoazqePOP339zh9fAT+jjsDf6HJDLgdKDM9ZLzKFSWSkpvC1RYx4qzLgrIsiBA6wa1b/RKJwfJDWLJq5QU5rqGYhdRlvrP7qYC5ogDJEIvFkKipkRqrd4bzgEAfSVaBn0g5ov+OSyS8bvCQI6FNHa3qPKXzln2XkrhipzCCk2UcSsF//PF7PBwW5VHY+Zp4ZXumusAeceuWbdSHwntiybymV6X8TIqEQJb4vJB62YQiIodOciVEGTwfOqXY4O2xBWoAcSvnCg+L9Du65IVzfQTfT0RxdzyrRoNGhjFV+fktuP6ez+H+3GRZT1/ltfncgSHdJwIsrsrsbGEflctt+XNkMOuP2XE1/KBuvLYPbcCyNejdMz43OMZNm5Nz7qmk4TaijKFql2jADEyZGwoV8Q1rKxpJvprSzmh8UPy5qkKY0F4R1qUBPwNl0VDPzatN7d150A/lBRURtyEVW0B7goq7me1MFN3wmMNB4/14gEE4ldcaooLAVFHqEVQq6rLg47ngv//5QTTuhwUfVkTC5e3JMyy4dELs7sctsNnaYO+xfMj5Sbe/57VuTA8Y03KZZo3TDeZcARx/0dB1tors0ayE6LDYfAFz6o8Lrvyd9FQ+1Niu2SHPm3HYYyNc650edwi4D8kU/5ofxEKIKIMDRltXrG1Niog0Mj7+cbh58iQdHyOAmlrhN7AnWs5AuoIDgWtD27mqVf8auSoAwMKGpYRNcr6FxUdrDWzxfvwQlIXVOD3blDhrMdZOJ1Ge4Slrk8a5vzaWINKMENTfraX+hCJJknyVtDak780bbLBctBZiizf/rO9mV8MBC1hDS9m1fq+HQnL0cOl73BMmMUYWW9WGtWOAu+3HujK2B1saPUhehn5Mx5Hu8aD9jvVlnw2y7o0m4gRzGRSGJpCPOkaCJJQp3vtMSMvG6i0w0jMi+JdBEkKS0c7yQCSRt1JApFYBhpssETQbTKFQiQM8rAsCp3AkhZos663VkGwOBm+sSawPxHrYk7hq6wAKVJpjgdPYVz13LP9Ma2sivqN5YS4EOXQ5HTpCVBRBjuMZuv+LuNvz9oy+eF5nAjVtfaJMMPf3uP85nCmMpuNWSBnXVrGUgj/87Q/4w98+4Pj6e9R6AB5eiwL6/R9B50fgfAJYcKHtfbIG8qe2w12rdi1dYE5P3kmzPLc8UVBz8bVLN58jGBrps726PqnQ+Ma6+2NZLz2j7zeUlxJ+9czUvM5nNTXSfL+FcsNa+yIyz6dynC8I7JecyZsFzbvPDbhkY+ywW2H3GTxVLzSdyI761y80xv2fGdSfHKdkWIym765Pfu/GswbSWWg8ACVc2Z3W+bHEB1xHPHsC9s+llPjSSggrPppGlgxDey+cPa22/TQasWHF2+/+He+Xn8B/fACVBfyH93AGaSzNto4Zghl/BOWz7BfHfghWCbb1WGEstWBZFtRSUYslEk7AGq/VViAZ1VnC6gh1DIcmjGwGwcRYlI83Xm665JT2NZ7fQi3nHBVjrjx7Lwad++vdGIiSI8QlgZsIjN7CxWQUzrWnoTVeKvCM6zXSxDMT3v6R8eFXMfBxSeClcUpyBx5wJD1pfU6YpiulDwXV/w52wmQa4fFQqKBINnS4AqLL/QB0eS7tN8ifD4ULdX12QTS29vad50MaG3/DNmBm1kzWYn9d9jIZ8K7GgXkCYO71l0JsZSUE2fglcLrCA34eTrO9+Y+IAvNn+vv75/pNvBZPeDIzFLxJS4bgufvBzGCNTTpdZ4a9QeaNL8R8zpQR07p3ynYs80bXr4VArXgeyQaAmLGyhBtf11WUDuuKFYRaKgqzGNWThItfv/8IKiv4Tw/g87FHqenL0PrN5UU9Im7RCTyVCBvfu6oRu6EZr4P7+hsIp/IKXBZQWSBxoxeUUnA4HPDuVPDPPy1YS0F9hV6QfKEHHaOrl6bP3dCZTqg9fstx92crI/U3h0rqHxnEL0kB0TXtr/cnkxMkjlRzI3ZodCfjFgjsDNHsufw+wwXFIUje9nPmTNd/6fvidacwPZ0ORx8xt821rVjPEq+ytQYaqo/9EsoHJ5ysTxzWHgDCyh7kiMwPAzF7d+aDeUVbNZmrE0oGRDoUih9F3iez+ujya3TjGe3KOEeSLV8Ps8HsCGMRvoqehXWKon/d+FufYHka5Htn1e/jMsSCtAMNBHh4Kp0rI6Nb87BbSOOQlTzdOChhnMMl2fiEQsGUIpQOnbB4yettY8lge40ZMDdgu8EAFz30yJITi5pqD/c2hgjkuwV7WxmVEBn3+NgyYDFgWyuujOjGf2D6iXJy8VBGODXlRJUpUTKB1hcCwQ1djPiyEGol3gvCL1m42xovkPVhChYEsdBYPJe6thmeiHlDI454VXG/7R/HoqoEtDUg6yoPASl6dPbEVwqVAmJGBXBuqzJmUp8pKEaiJCsLAWiIr8Ddllcauu4aCEUWz01lek4PilMvSWGVnXp8BZiAZBjHZuNWK5bygNeHI37/H36P3//ta6A+gEsBUwGfPwLv/gSsH2Mvtx4H2hrNEBtO6/qVmQPe3r9avoTE8xO2ea3/X8J742sRJt1SXhTWPcLF23q5pl6+fNXAfStfURk5neDfBlw0Lvh0dhq9aHQdT17fW5P5/Xth9vCYn6voud7xLlO47PdwJSmOky12V0MIanb2sJEaGxZgOz97nhBf0kPi05d5vzKHFIKCOZ8+e3tj/wI7byK4T7CbOr90xtvv/oQP5S3qP/0OhRjr7z4kRQQF7ZUgdyWEMn85tJF7l/teY3R9TgKjUsUTolSJOEGUSU52PgAMMTzj3jPBIzQA2qbygs4UTAbFuDY2/pqd7nUjNw6IjS5sXdvyu+ZBGb9v2jQcNOAf+9EuYYrM6W7b8zqRfuf6dRk1Znz8M+H9z4Tja8CE8fvNRruJQ4Ovtw42u355wW7lhXNcsq2n5+v9GQo+Cs53a64RVzAUuAGdP6fe1RSKCcAUD8k41PmF4uMIf34yAuO4TPekleA5XQC/reiG0uOJDNl4FnS1+vANsI7CrUl7l9C7bdt+rvrnebi/Pc4v4H+e/JyMl3gqzQ05N7AnXtTDQmPf4KxTOkyUEf5cTKi/eYvSfTb9u3srVZHnktUo19pubXWZzbqeUQphbWcQSU6dRhVVDwoqFeXHR7Tv3gHvfge8PY5NTUG4Z9V+VaGZPmdhXZjdNRDO9TW4HEB1AZWK5XAElYLDcsCHc8E//nTAhxOBHgiVSOTClEM79Wi6r//SXexe7WC+9FY6OCkvh4zfeXxPY7DP6JxOCMvp7wgqeegTv5cF5JDNWuxwclhGLLJPrMt08bArTSAdfc+HfDAgGg+daVeg1oXHSd3j5I3QeRRYv9MaMqtpXsW9SZQQmkBLXaJ6V0B5r5C4DYYGmL1tI3qywMytRazbDISA/QwGpM22SpJlXr0foYAQ+FGKCsu1vobO68MIzZR6KxCmnTI2D5ZIDAWgFNjED3vL6aAsjNF+w5xnKwILgyWwmRXM2lm/GGHtialtU04Ot45gTgSoeUQ0X0f5Pe7+RfeD4O72iRIsWRmyLTHmRL0CobU0pjkBdfNvvhd6b6DmrMae7HckRvIDczIwj8N4KIqCICsYmFnDH6k3itVJsldyGKm+TvL6QA2bwnBLfnma/FOUMYLHqJ92Fz5zhzvkOQb52iJvQ8d2xEV2LapICL1pv+ajR7ZA9cVutbuAm4J48ShIHaaJhM8NaIVBmp9GwhPp2Ol+khi5ZHpLSO6WnFyd41O4tnQ4EbJOnX3tpUVFRqSxE/+3ClpsujOR7AnKhmJ7y28pX1k0LOJ/+cMD/uFvv8MffniF5XDAGQCvJ6zvfwLWR9B68rnLM5Q96CLcWp5c0v+z4iz6T2ndb2Ae5m2vfFbB1G+lXEJCX3v5rcL9rXyBss8FfCufugT9GoqJa29cnyv3sJwggi+J1i5BfrVX35bpJysTEcR+ubJ4lOq/oZKxQQKhCVVqG6FbrLY/MgcIiFmTShr0FVc6qLdAeCpYGKPg+bz1Kjzx4XDAcjhgKaaIEELPxQrM4gnhBjfKGyf6Xoz/Mj9GmitQhc9EQOKdrV7zpjAFRsgT9F8yAlNbv6CxG3vOClHaWNyCltGM45lmsgT/D4kvV5qTVPWX5mBWNle5/xK8Y8w1N+D9vz/i47uG06mBSu0YJl9HJhPoLKzg8AFJZuI3J8VJ5qdhv42ywT+Vt3ZGglIoZFM8yDqy9USlKhyqSCgWbmmIDpHWioVrkupDrkDdXA3M9gzZbwT6wb+O/fSyixv2bpQQiNtT3VpXOAZmnvIcDQqpzMnIx7CikrhkV1+SmiyTZ5LOW3+T/u7H6vYyG59hICaosINf79+SNHvjATEoI3L9PZ3x6Q7XWG4UOSFLAVhkghJ+SVZf01yyp/NZToOyoFEBN4nPR6WAWkEtFbxUtGMBnzfI5VnlhRQRXwEHNpeU3fUqg7CWV+B6FCFaKajLQYQehwPOZ8K/fyhYGaBDoFYakfWAbHqR1hWSdociHhUCswc6AWmHFdGFAtkT93O6H/Vd1yJu60kKiMaupMh/N+2aMOgK1cy0EeXBhcH63YRxnRyR9ldpFozJyPXYnFOduWWx1hngUwJlXVes51W9IYR44sIqEDThdA69EgBaPzyvRGsIrXyCNaTqSbAewvq1reqdoaQPS4z5jujJhyjDXV67WJWuVNqJBJfGqrHEc/fZ1gNcSV3kWPqzud7MEQNhaW99i/6GJ4EQDYXIFStJDJ4nKAhDZnBb47uP6QgNDx/sluXZU8EOfrI5TdYW9qdzQUfM56hgg8GIRBzDYFfPlzTO/s2lton0o/zMSJr2I87M2zm4UMJzJMObNx7LWIx4TYX6oycIwOIqPNmvqWsGvBeJe7h1jWZmNFPY6CvRbsbK0oAoKISp2rYvCMgsR9jnSWrYP3oM841MkPdY3zermOLXEiWvrsX6hrcpyreKIozYGlZaEuo1K2ckiUbGlY01GXUCjHSQfM35cab73xd6WIlwdCZ32UYojcQ4eZTupHMj15coXR/JIoqI//QfX+F/+x+/Rz2+ApWCdVVl6IefgdMHgM/deJfNJEnoM8t3UwC4dcGlw4iMJh/2z/DOrcqG2bG/sRzaqetWJu+LKj6uSfp+42VkM3ef20ESz/KQuNLo3tBPed/PNU0bru9LAPEZyy0b/Dl1XSi3rs3fWjF8tsF/l3gop+WlBiderjIeuPhM9ljcreNzFbp8Jg0Pp7/ydFcHo7v/KXuxFUBduf4CMH0qL7r98CP5QkfhXcUHVyG9oStdWF8y6pvFy2BSfHvka0obcfrtuRRgdPIYwjjoZHvL4SkFZVlQl0VzcM6s87V2U3CA4XkimIMvbMl4yxl7NU7rBOeJB4SFIGbnfYdWQ7lBcKVK0/d6T++gY9lGKfFxdsOM/FxshbQTaWwdvlAuK64S3ElOGH7nMjZvfzrhw9uG1mrwim4w1w/8ZhqmF4zXt3kb64j7t5RpHQN8FmbGeapOPhIeEKKEqmKgaAoG53cGb5mk4BA+MikcuvuqJENqN0E8M6jqx2vsr+3JK2Pf3RkWQsLXJvCWpwJLdoLy4bWJX8MMJPDYOcp88hxiM1Yb6x7L1vNhOMcurP35yZAv2T4yjMv9VvM3Ez/rw7wz1gmwS8qIgHHmIRFzeTmsFS4+s1vSXhJUWxQSRiX107ToLesZZyo41IZW1CiXhGcupboslxaIjGZ9OWrgr9YjIhciwqm+QaMFtBxR64JlWXBqFf/nzw9YW0WtBasGxiuTBZyoCQSFEQfSZTr38oReUkIw4Br7Xt2xj8hGTR2DY59SD85F2Cfj4M+78FpxwN4mgx3s441ZX7nTwMb72n+znHdaJ0ZBmmeMGgkaPq0dq9wEq27ttEMkW3vMwLo2tPOKtp7R1pPmeJBNLRBFDD45B0njsZEjsMaMc2saD5NRi8R4K1Q86/1WC6LeAuuqXgORTCssnzP1a1YPxZesEXecrFi6/nprShWNwSLR0Lj046qEIDfpe8thjy6ybsrcqSdAdofdi63nU8SaW4P0ZFbXXQtzZcl7Wzv7+ARRqMRrOkBZ10IbhOzskCbrlhQiKWgnO3ASkU0zApBhXgYeksusiZAPJatrS0KYl4Rsu6FetWy/FGJgxB1O2AxT7fonJ+gT3jOL8c2+pzQeaYyQl5quq4K03+VabN8JQYetR4S8qnNtbWcCwCc9EQyCVJHnEarMaOcz6lITUat7Bg6oQht1O2HtRJ8+E1OjlhfNQbNcEaZsMgWJD3HXP1VIVHnZvXvQ5RyUHhu+GWANJuoWQocV15FO0+SdNJd5iBmseSjM63+2RrquQTypINoCKqKm0T1OpaDWKu20pjGEVxRe9a2smIr92605bcPWj59HJZ0vvI2jbczlqJhK0/qtfCvfyrfyrbxAmYhfnlWC+ry9Vqe7/2KUZUYPXjyGt8UELfSXHDrpaylPXfmDYDPRn0bprecT/vn//n/j3fs/Yj2cBt56aNOJUAhZtaqXhNJQwqqwKgcsabR8j/aNThJ6uBIBpWKpFbUuwudSdUFyR6ebEoLZvREaNPdiE7qtJb6GSGjDWisKSfLVkoTLRlA7L+pKDXaPiwjDHLIMZtqOTdYyIOqWW4Zlsi9E/7jxgRb+dcPXOX8b/F/wuhz8u13T4uqlxnj7byd8fLfiz/94wuN7oJ0XFdYnr30KetYVN67AuVMImsG/GblsuJu0FmKcALini2oE0HkxkHpEoIBqdaWEbQIWCSvMgLH/pyGcdJ3YezEmO2L7QSEx7Z3zH1lAsFN2x3w7Rv5CqtYF3aOg3PkU6j5jnnP718rtuOn66OR7IbS/qIC4eUl+zefVS1M2Vq3Um/nvQiQK3xUe/WRtJ3AjrOuKSivW1lDainVtqIvJHBu4FCyvH0Hrio/rK6zn5T6a4UJ5niKChy8umOl+dgvpXsDHNRPvjxM3NJY2cZw5HM9SvCeeEA/gesSyHFToewBzxS8fFpxYwqwAlMLY8GTtDJ3rHpkdXPeU7fPWp3lNDL5h6ztKsy9jZelA7cctylbwFwe3V+0CvS38cXazCoUuwDrBwQx42KTtYOgLlyhtos3jDlOGrXtleCfMJcDcsLYgxOTtBmazYtc60ifpH4K6bnLTxKqJmKH8phE3HNAZMWXKiIkiwYcv0RYhq1YiDEOIIl0D3dlph5zWmEOdGFyxavTwJiSFzrC0usF1cGDKHSMOTYPbvTg709kEnuz/hFBuURczWlsRyJq6KnkQ2HaDmJnYEUdZrymO+hm2yhYkPa6M/mVLO04DZy6D5IsHHS6YL3fDCRkaGp7YkIHIcx93A75OCeFtcw+Dz/8Ik+0lEWzbypkLxN0veoqKaAM7vF6DKaMyvas/LdeG/ImcFJTWo6yb0gpQMcxZajGtOflNmMW5tJkQBSvthCaCv9uNnyFVXQtOnGs4rPV8nhJcREX3RrqXznG29ejw9SsiH/k2ngJKfoaRX4t3+t3QdBCI83z39VCqrxme1fUmYyMhwJqvwQawUlm6XmIYYu06A5fu+Ppha3N+3gHYKPIuKVTn79/1+OW67mz7an3TPXpnHTdcARITdAEn3dzmAPhzrF0n+smbysZDaFPxbovT2m4r985/T6cD2MXN99d9e/tR/RMH26u7gWOdNH15ze3V9UKc12csn2IGn1w+gRBgQ5tvaJrLC/2pEI30a2dIcZEX/FRlPHBvfUXg7ei1kaaZvruLNC6XJ66B0TNiU8um3p7Pv39g9p/v5/qFSie7SF+uoBy/nWlbXYIMC4cSazJ7wDZe8csf/wVv3/072t+f+zHcRYHGT6dnjDVh9hyJETqJjbqWh3L/1KO3VDW0KyEYN/4USqvJPs5hg8Wb1YznrH2rO6zgpV6P80+ZtgWyoVeWXTiraoJ+ZnCRzrreIQ/UZNv7vrfnOQSDvRkewTFXUkbE/sztcNc2b5/orgFCO7/75SPe/3LC238vWB8LDkfy8MESpkUpYKL+KE6yCRhckzLr/qWyf9yntWqwdGNiCpvwdHEFhRuIaUgm6BooBZ4vxBu3kEw69n5N1VWk/JIpIdQLI3tVdwqFa/QLD49cfP5aUr6RdpnU5XhA9qsrI6YgUPo7r24EectX9c8EOnsKzZTHOOH7IbLLXTVePa62Z/a03Hp+DWfpyBv045Tb5u7bRtZ4qa3NBBoO0fVdmuSP5AqTpRmOW9cVa4lw8FxEZimBFMRYuh5PoIczqBwALBfFqvfMzs2KiDmbNKFWrq3kaT03PstZuEU9nTEgdcVdiBNjKwwECOflB3A5Yjm+QalHLMcjzlzwf/604OMZaKQeEPlgtP6N5vkdwQs/czuR/C2zw/njwnYz4SrioIz2Z+6N+811Fr1sm0PvTBZbt22S0I0AJ0CKHWqFwmqW0yLh3h10Q1Dl3zRY3hrRA7OOiKpjitJhZjectqPumTj4ooGe0UihWDAvzKvAsp7B7QxWIbe8HR4NFqeS9TqUSDJXqXZeNfSPjE/pCKlEeuQl2BqYRZu5ruYoqxYrBBTurkjdRABb7HizwhevA3Jhn1NQiKS8aW11a1U8MOxMXgEwFYipdgFo9aEOrwbLzEvIwmBZjyvAkjMhkGZ4zwQayC6WRu81oEEtoDn2in6u6i1iChfHECRnnVtrTw4ns/gRKxxbdMlVsxBGYs3wESPgpDIhNrTdvKfib+64zMf0UNT9Ko9ZH4LQNnht/Gb0dK9GTDi34z7Q/TYCfo+EahNQ7T3lSbRPCq+jh/SidtsZmwQSE4m7s48RZB+RrIfWNIcIVDHAalGTehLN9Yo08YgDAHEBJ6wotTqxKkdNS++TWyMVVsVGscSAWi9R9GMsBCccAw8F0eBEFcFzNQihIfunlCKMmuWXGfN16MSzrXnbBC7oj64QMcxrahgiuGY4rcMYt2FcNy+rksjamDxtugBXuDbJt3P6+AHUGt7/dMD7nw94+O4H1GXBiVcJtaR7jTq4Lh++ptyIC9I3w07dRuHAP9Pu3VNGifBfaJmPy3b9v9QIPMul+Znl7tbGwfmk4G4b+wTy4c9TaOf7DWWOcbb3n1j9C758S2W/1Qn8QsXCumi85HVdcVgOLrzKgT1DYMl9iMnEvriBx85xvqWbXrpcWmAX7o1HzwzEC8jhmnXpJ8G7FyRKl/fsNVhug3Xs80so7r0u/yNfiJxRnCytPYIa8PVGAGcDECLQ69+hLq9Q6wHt/B6//PDf8fbVn9DKGXRGsHu6A5hMdhIhQz0sEVasJFuhgbEy6T/2UElQ3i3AlfqYgGWpoLpgKQcsZUH1cDrF2RwnTf2feutbxIDGWJmxethe6X4pi3hZWAJszz1hnhbCJzeFdW1NckysWjdDrYZl8C2bnHKzAieMh8ghjws8EoFzU+LtbLKR1oKGJIiMu1axVl7Ug8NzHUB9gln7jghHxSzwmaoHGNZnZpNKQakVdSmgVnE4VBwPB/wPf/97vD4ecFgkLJYoglQhpD4kBaGsKJYzATnnZVqjzmjM1un+xpBqzPOhdDynhznW6yFHCYWEza17MFC1haDPFv9NOk+kbQEp3FNu22VHwQcQLO5+linaHhv6t6fZnYzO7rGxeWEzwNMHnb9PAryQe93a2G1lD9+9JPbfSh76K3vGQ9l4z+bwagDq6XTxtQe8/UvHYl4jwrfb85+G6C9sxpsqnSkSTG/lMxoYC1XBI+eGlVacz4+yx7iKLGFVnFAqzm8aznUF/8ygDxnefifcS+k8yyNiws4kTBQWi5fKdSXEdvJtX5ELRkdYZsxtXAskQmj1FXh5g+PhiFIXUD2irYRfHwkfmyFVSkixr/V6timLq33f1GyE3pP3TQlhoWu6TcohxOmQD0fd0+LSQhPcTp4x4sjgNASAkGWhMTjHerR56k0J+v7NkHZCIki3XQHjMSFFeOsKBzsYXFOewPdDI2Bje7ZrdjuucywTAkK2HAvqCWH7wSIOhoQ4Mtg7VFa3uqC6IGyImcm67HzDm/BQlRecFTxpruLotDkrsNj5Xo8Nbkf6wYWfSONLzLGXMvGsk2ViVi5Fw6o0eFgqIcu0i/r8gNd8D3g4JhP02loJheNIoLvVTNM2XKjP2sXIDeH3iACWfrWCrfdNGp6WCOtY42FVsY23aQRV+pmrZvhczK6HFU3/+gbT7Ryg3L2YkMNQV55vh/yW89GGw4TYzkWQ9yOe2byqEbQCn/LsQW+IlEakro5+xaaxsnmmBkJVtC3JnzWt3IB/xv4bEaxKM2UkTLEQB2+4fWbIm51XuqKps7TPZxj3L3a4ZoKMdeBst4m1i9ZdgMKkSjygoiGg9aZT7qBR8Zpx83BmTCg9ppEsnJWUUyJXPkGpWyOQ7PHAWM8rznzC48f3ePzwBg+vv4+6IYoIR1VxWDm8l6G02RwA67UU83cv9GPa9EUhz7yOT1VeVBjdnfcX2tS/HXH+CaTis9BaY3sDVaD35vV1exa2VuTKFUhuAXeC2G8B6raqn1Zeek4mtJ7fusYkJoImf947AAktXN2niLUqIN472GMDd75+oaowNtgrL7+fvlS5h8nd53PM6jlivJuwRuhTo83vZLQz4TGdjs+EyMdy4ejee+4l1syte+Qivp/VYbTaqBCYV3Dxbpyx98F69Vy7A0VfqsnPLUVS8awZlCWDmRkeZPacaLYsaXmNcnytq7zh48NbfFzeBiIsDC5DS85Gkoe3ZAIaNTCJMZsZAVnug2b5FoxXykYhBqImpzZFAcyYxjsU/EDnhWqCfK1XFB/5GbP0N+G1WbkP+5qNsuzDBdt3A9a8L9xsiTKGCJ54b4MJX5KM+7Qdo8iLwiaKGFWYWAuUauEWn8wxtLC1MSHgmw44FzBEGYFaUUrBshT8/rtXeDgeUKomB6fgSSj108Yv/+vhsxeCsYwxmiDFzSUdTa8bsBwQ7pmgSgTSsEow3gwEU0JQUjQIPLKuuEtiDXQ5OhVuAlJOU+sfuULI2ssUo+3Lfi2k8Rivi/Bqcz75Ps7PTuWLN+CqDufT7PK83FL1Dl8yeqzdQlPl5/ZR6pYyz8J745vzNslonxymqGFmlr7bJnlw4IuA5pNmroyg4UHzUrG1Fu/vl72784mzNSxvSahyMcY0xWkThZ2G0uPGKaTeitYquLDuKwKOBY0asEjYaJdY8SUorpdPkyMiCXXGBfCsQv2CzAK6iTTSbiAvgFN9g7UeUcuCUioOD29QlgccDg9oIPwff6p4/wicYQjxEkA7i2Ij97iD+UQgKH9rkEIGvcu3Sw/0gAFYhU8DGvSxVCS5qZe8jthw7O+xWt7KowSUhLz77m3602OY1M8hf1ZT2PxY536kzNo56IH9ydveMWakIATxHdQdchn7wrZ51xVrlvpScfdHs3DwkFl6+Jlbqif+hVlS6HtOTMkBXEg18inBmBFTUm/xcfFQMyrkNaUVqEl4lnTA+hogOPGbQ/lsVlopKG3Yj62JFxFkDRQNpcOliWAUMRbz2UgEFVsi2XC7vYZJQgGh76cYpV4tWPNnpJjx2k9TWpWRoEDMSwiMs9U8fH6EhpT3O+y3Bzz3IyxxDPUVmwsM1tpBJnVlfgDaflbLfCI5RLIi1/rjjFZf3z4e1L3iCh2eQub0KcPDStnboTS1fSGj1pJSVPZCjBEj8L/tmfixJfBaa7omI2uCEJ0FhTnylqR7xsTJb7USKta+7CXWhEFGsIi1THjtdG7dICcEevgyjqE0iQxRFm4TCbqnz5rWnbpDhNVO1NvMPb4QwIGXDWdsmiBy60+G4DfPYTMOrued6ZUR+0L5fK4GzkkVOm63Llj8XHmEsLYzwA0//3LGH//YUI4PeMVvUA4VB1rcss1WI+8BdaG4Ymdy/Vv5Vr6VL1xekLX4Vv56SmcskFA5dedSvt7Tvl9fjOmvs1xS/n6K8nXG/+7LS6Is5r6unBsOgNBvlxozBVwws0BlnP+Hn+VnbUHTKtxGu7PE6/DesMLTGuu/zMvCDef8r66LWsTSvhSS78Y7hqa/o+ud7gbDc7+lew3sYXuq5g+z/IrGRxsUktvNQvSy552w8MYeXspoVJeLCH9j5HBvvugj1dOaI5tkI2FeBovAWmpBreKNUEzAjkRXMyI/RlPjPLbx6Ne+8Vu//usJH9+e8Of/uuLxHUDn6rkzagnPCwuLVUzYbwqcss2j0LXhcxrTlhUYqbcjV7iR01h4JRfieJtF82gGLNBE1N0z+hwUflgeCR1PUyS43EPbDEVEdMJDNjnk1P3iGIArcsKhKH9nxmPDiMRwdGure+g6G6MAdvgBxqf2j96DMveVCf0cfhI8bH1Ka2zazGzIvuTZQHCDv9tzWrwwCCaL4gJCg+TPUfyyEtYmUUIaN5zPZxQqWJeKpSh+UblCKYTDUlB/9xGgEx5/+Q7raYkxf+IQv6giYhTi3LJJpxtxt9K04DeLivND3asmJAEIXBZwfQUsBxFK0QMYCxiEM1e8fSS8P7EKPvZ6ePlSXObbF78L5obnE6EQYjmXcnXCs2tlJKhzGyGI3IB0EeBsORBTxQhNdpYxRUeyCqFMYnFz6u0IkCsgErBJxrVBirvE2Gxh3j4A6ZXkEaEmCk3rF69A3fDFjmaXbqrORuMXdu6ccR+E3hRjBzxbC+4ZqoJPD6nka4WDMKIGJlEYdLMYJy18b4W8MUrxWy4Y9v2fQeZ00E9KfzXWVgA9rjFs3ujc5lW4bFY5nK5DYe2X1lzomImFGcaJB2OysgKT0+1p6fYPJ2p/8ugIgFMV/c6eo8iEPZgRFjfbZ+Q9C9c1MueMvue8ubJb/LDSddnVSeNDw92sOLEr6UneYM6uCMNCnry5n7vUUpowBkCNZd86XWz7IHK/hJdPVJjzJ8T64eSBMMH1GRzb+J7AekJ1pTPDlMubheY8ETuuJUrY1fBAXv87lN5slvbgH/Hz/gZIiCk90m19Y2qcmoIwYtTw+PGEd+8Ip9MjDusR9VCF4fAKku1L3mcdBPu92Zujz0nT7it0XrbeWXlqW7fSPZ87ZNKlImeXnX+X4eLhsc4z4iUB+mrKLvX4zGpvGK+vahxeqtxBuD+zjGvyt6xIvQXyS54Q3RkwYTGmZU8gdCM8X1MZ8dZ4/cKb3a/n5d95mVEbLXDztafC9DnOo1t7vxU/bN8cSaxQ/vBAUg0EVm6HK2gtYFrFG+K70wQCCnrQ4wGT08nO/yWKtzHD3CTG05H8pCUX5ocFetfD9A8Iobu1GdecpyMMuQM0T4T+zj75qRJYyCf7ZXWGjCNZAOdBzyOsf7Y0Z+aUwuqHlF80AbupHlBiXLpZTPBIeCp2A01nXaw9TZN2enfGh3dnPP5KOH8oOBxFMVNLkTBNNk4IHl0M6shx31YBEb+DXYjfHdQu7qD4yeNN7SmFl4LLcog8x4OF7HJFhBufjkqIpHDQUNiRyDoSXwPwEMlx3WcmzbG1k+Ae+7+7NiZ8trFrm3eGsfQHEx/Gt+GpEVvQiCxg+GLy7h0omib9zHXueUjc2laWZ3RNcWJRL7GXwN0H9ShDMZ48h7m6BnjIqgOOGRWtyy21pXMzA/op51Nan6yDRjAZEIvjkBqogsMjwpSdjRlV+1CIwKWgPqwSwu5dA05R+9DkzeXTeES8eLEDpkf6VvLxZp9xyMjVU32DVl8ByxFLPeBwOABlwf/98xFvT+quBsKpkeWkmY/mDQvaD51rO8zO1kmlWVAa9HIcxvbB+YE9mIF8WqA7tVyZoYeZWRcY8iglhOEJNvJ31fKhWQRFgGrENswSWRexm8DabhGGcCXDAOVfSWliHc57s3MXnIzFRtjmsNkDadBd4eFDNYBn/We0tUmylyZJouUwrw5Tp3XXxLRipaEWCYXQWDQI8pudIKg1tPqAeoZocu7mLlXN54VBKCWsOASBBswWX9IO/0IFa5is6PgVUFEvl1agptc+Ht3ha3BxA/GqdJb1vUj4G7KcFJmoMbQ8Pwnd+mWw+DDtthEMMWHhNmyeEJY4rVtLm02jcwS4sHlz0DvBGs8LmHHIkhHAm8Vn653Se/B9lglrGdsGr/RSyU1lNwPEqBoZnJUx5F3R5M8xKEFwM+DJmrta0y/biy3wAAC18olnsjWCjTHYFDxmMTUQeUjjwtzV2YEiyCdNTcx1bwXBvqbyXJJp7dwTKs2TjxnDXAZqrVjX1fOPUANq1umQ4RgCCou3RU6kRzEmuUeMpAxWIiGsdEowSLk71lfW8E9MKFS7eSKoZ4TjsIzsrD07SxSuhJypFPG88v3RE99dPYprjBGBKW3MasvwXrdv50Xwiq0vCIPcjZjkBXr37hf8+ad3+N2vfwMU4HUtIDJmPCmIniH8+IuUg37C8tc0XB1z9BdfZmzUU+r4Vr6VL1eCdGjp33Nqor/QQ4KHz2/luaUPA5jKhUNk17OEx+fiRvc8s4TOVHKe0rQWXvD7P/8dDh8W/PT7f8W6qBIi0eLZix/G75EdfEFniX8B1Iu9N8K0kyOvKCIJ3y9JqoVuLBSyBXuQAQ8ZwskLgpW/a5oXsSkPDIhA2qz+PRG25Q+wPIOcjNUsooF6Q5gArmX5SNcbhCzF+ChmMDUQi4CvKf/AjT2EtA+CyjzEUJFcMVCqWv4jBOhk42DyhrVhtdw2bdWchcG/GaRv/+0RH94+4nwG6lJRDwU4FyzLguPhgP/p7/+AVw8HPBwW9xopRSylQRbWKhJaA/Br/b8Yl9Itk54P6YvmmfB8mVZPUV66KgxVYaiuRCB7tiwqP5F16DkePDF15IqId+FJp11BAeNLTXbUyxOzMugG1qVfI/Ye9fe2GHUrWxgVIXE/Hp/JDil3ataCA9PjicsK4sn6T7BuByWAfFFvBNp+D3nGXhtZ8vHUdlWy9pJ9icpfuL5t/Z1oz/dLBdcV59MJa+rb+XwSnHQSo75aZJ8sEFxVqeL0/QnrYQX/xMAHU0LoubAj0rtUnpcjYpiQl7Em0F7sTXan1etv9YIdq4rAKOCyoNUHLJq8qLH8e3cmvDsB1FhDT/D+II4ynAkYLlrbhX/8uRXuzR7fPjeBJeOfyYadgmMD5Z9XvDiyht/kYLPnjV5BzAvr++HRMFpbT5qb/h7WgCNuaxgX+zy95X0g/z2fie1r4b7JKcRJ9M2TH7m2Pw43F9hlxG3buiAO0IGwzGBxIpbYujAIpuPVNMcsAs+mrlpk1KFDEwJVtBHWNFbDWNC4JvLjigjjcL+01qxP7P0MJQQ5ga1kTGIwzbqFeyUET9ZPBtEFv4kA8PU+EFUUyrR8GLvVx2RhG9Fm7+XIQ743jCiz32l+JxD3P7tnzHqH01q2v2kMM4aZbeORmBnaAJLr8qRYv3pQe+G4LPZ9fC8W/xNgdM+52+OVtWQDzUNbMX2pfkOiimjtbO3OmG5tTObbuYiAIZQHhqcSvuEGX0MUa5LY3xrqSX3TKtmUKgMcvgJ08XnUyPE8svtZwjoqJzYHTIYlPTfOc+53GrN9HjtDbvtfXrNrH8+MXz884vF0wnk9Yz0/CuMUiHC6h/u29nH7c8tuHS+oGLmV7PqaZGUjfpxZt75U3XvlpRiKl1ZG3GqxvmXun14SGtq0Ih8DfWTlrjG8E94rdQdaef48fk6LaGnw8zQzK7N189m8JO4Z3w1IA0V+Ix7slff99+CjEn23Od92ipNPk7F7wTV5GyAvVcY2987G22B7Do79FHtyD5xPue23YzCKtQd5h52Ffr+vox+PyzzU3tlkYo4CwuHxFZaPr0Bc0v6gybKKtiwnQSbhjdSa8ysJpgHenvxWGrHjS6IlS51ovLYoJULx4fSr8XKWUDoLJHS8ObcBU2KEB72HVd3IGxLQHW5RPpSD5szykvhCwaJbdfFH5VBlMv5huMbNjPQaOLeRQD1/bHj8sAJYABYlDNeKw1LxcFzw3asHvHo4iACfKHJRbhQNvUdE/iSXZeTrgIWI7ed5wl/ZO8W4q9SeKkbc24FSeCUAEXrJ5juUGG6IRNkzItaEw9vx73AYut+bDTS7ti2jQiDTuD1vOOcfN/VlGlm3yC4NaDxbbiErHTJgemUuZL8Ff/d8XFQRm+R2hceFVhK43G+oCZzbNpI450ltWq0xTnPcO6KGq5Xz8DONX38SPKMkMt7lCrYXCgGteb+a4hb3jMgyQ3tvUThrQykrmJP1/tW8ydvylXpE7DA9GLdsCEdNS8ppGTCAtb7BWr9HORxxWMQTolDF//Xzgp8+Es6tWi6bTe370KWDhiLZyOixMFAb83qQNiaP92eND4f8SIzr341WNb3vr9lhbAd77pfVNxDldthNUiPp83og6Muc+9nSr9lQa9vmatg2sKh1huN3O1zG/idYxyZ8tvp2exijIk8E7gRWzJknUfZNyxrQpkSeJDJXwTyW8sOsC3w4bOwqyyHC0PiZIVgMpAAwqxfGukpMy45oyvPcAPUMMCsSI4haWwMGIo2vGYdWKWrpUcjXh41DoeJJavOgc4vEZba2YlCt/3owTObIx3uYOeu/HSgMoIwnS7OY9wLryCtS+tvRAkrEeBz64QTq6iB5viiBHIRTWIj0h+1W4eautXnvAUmorv88UbfuzRGunZOVOO+8sbB6r5iSa6yWsPWG6FFD57LsjIIRsvJPFAgpZi0sbwFpP9t0jr0tWwN26O+gZh89AyO6keRnRsQ1gEuqqreGtLVfiLxtX++ljCMiY9BlsUsEnxLptVaY1xQzY10bCrFY+Sjj0TQ026pmU5UraJHjuZQibpCdUsQgIW/bFaFkiVtICXwGtYK8HtqwPmPcdY+TuLCTW0NRzEfuJ0GVr4mxYzuX7Vws6X5Da0X75SPu4xl1y15szfZOrLEM9p/we7z9UPC3b8/4/s1HnH56i8KrWNaVgrau+Fa+lW/lS5brNPW38pda5sz6lykjf5aMrozEcL5pFAwkQeesTu/ml1jrt/Gtv6Xy8lanX0+5IhYIenf3gWvl8ktCcYmxBnHZeSI+2T8TeEb72nXutpVQei3akqgHSZCO1oUpFS8FpXGpAdm4iKGeC6vwQ21F9oaIf8FHl1LdA2Lj4W7Gacyab8Foa0vSivhM/S4E91RIQZQSXmDNRQcX4DXz1DBXkRh9SL44kxOodwT5iCVPYB3XJCB0BYTR693UCa0uoagq3v13wvqhgNsBx0PF//T3f4M3SQlhERe6HBHDJ4BuHIPHoSnONIToBpfUrynnKSyUkn5KWyU8L4qF1SqSkzLnd7AE5y5f0Xkp8QxpG6GIshwkBmzipLJ8Jo9lV56PZ7cCfzs8bqyb9PnN4zR5Dj3jbuWZ6LWf541Y4sq7X38un22JNR6Gh+Oc7fQpySG+dK+FRCFdPqQJ6w8gFPAKrOsKXs9YzytO5RG1VDzWkzHkqFTVg6tiWYD6uw/A8ojHn75DOz9dnXDzm1+GnBxa1APa0flk8TMInJL1cjmAlgcU9YQ4cwWh4sO54OMaAsKL++hSx00wTcNvf0eR8diV7YWdpm8f9Wkf0kAlkAJGIyoSJTF1BR1e7oXeO3DMBKddXfvAX0JUnQZeiYNLYteLlJ9ZP9hzzAnlTKrKdekYMLN7e/aAZu29HnB+YMbBbrbrssmSRbTOnVwOYZ2SPG4FEsmYkyAXcOIo4DZYMyI1O47J8BBpiglyTapYXbO34ZE+R20757uYjGkiyPoRHineTZFlpX2wNcbSD06vWZ8vbiEdeNL+btqy9ztpdUDNHfN522mc1/Zs3fLwzecO+3hvC/f8Cif6RRIQMZjHeQmCOWDG8N2I+Xn7ZI9MtOO2jjItZezJXtdsNVmybXun72y0tXde9asy4bEJrpKKwiNhj1a0NRJblGyrex0jEJyGmZRQ8bBYjcEl8HEm9nMvvKNTWNIaNUqIk7r8Ak6UacsdsrZ25ns0NRnGsrvNgruISr+PBwgskm8hQlOl1azxcxEi6rRCGMr2EcAKHA5S76ciWvbOp2ub8xMQ4J+Cpr+HsQDiTL5Gr+xZks3O+1uZlc9mxX5DeUnL8rH7+90c8eBQXmR8Aps87fU7YLhnQe/g5KeWz2HpbeXrWbW379+x3LZGh/Nhby1cGdMrZOHVZcPpIafr/FqiHZ61X3qK9643n7WmXnYjbKMdvFjVV9u69f4t43X7fjY6xfiZm167qewLHuX701dMrm/4eUFg45zXpQZH2g9A8J65bsaG9uvup8e0Bucfc4woZydsHQe/wlBFgYXp1SY9RBPYjWEMZjMmEvo69bUDNfa9eHU3v84QNtkNxGxMyITeNLJIMCO5plR2GJCJ4qBtsOsl4VPmrzjGTsfbDSGHOhmEtjKwGkYgtBNh/Uh4eKh4eDjgzcMRb1QJQblPsO/6L62RPQ8Jl8Vgwi7YAA1CNjcgBcG8t+Va8X/upWFhlSzReFYslfQb8He7Z5A/LSJFCnmFhO9HZclkYvpdvLeBru/kkZvLV2j2YIItSYxuazv1dcRvzzlyOg+Yy08Ov4dwzVdgSWzwDfB+Cvplp2wA71/ezmM/059TFxNtxX5l/WL7OEeKYFi4Ogv9ZvlzwsicqKA8yH38ysD56fB9pR4Rt5R+0lmFVOdyxGn53hHqcnjA4fgay7JgWSr+9z9V/Pk9YQWh1lSPL5RhdXTJRZPQCsNCmq6qIHoz0rpFCcGz5y4V2nyJXwk2jyXYWkDHsBPf74+j6zAZUshtUIiOehcsqPDQftv4GoEgL2dFDWOIqW51EtS6N/dt56DIeCHVY3WJpXY8L4RM6/gRAsf7yFOUiCH0UxcHbP6t8S/Tgdy7BFIamzy2oeUXDxN24sbjY64Wz7IBvILbapDHaLilhyCMdRVrErNAqAh6SoSC3GNjC9lUmwiB1cylab3m9liIQNVicBoxZ2uJQChCUHZ1KwLM9KgxA2x7Ouagm2cj0FS7K3MV3gOtBWE5K36GGGIdcxBEI860crpm8+hxJ33egN6tOe76umkc69zvKhHodVj/5QDYP7V4emvrCjkS9xpCqzBkgiNsWD6s5iXGOa/abj/ndU2p9aCtuwYMB3Rrt++lp3KArhnyvtme0n3FNKvCr4kCJlnpK4OTCTxTzpQignBqIghv3GCeS84eNJY6bf6KWHRlSyEQaV2xvhs3fVTzqRQCN4iX0kpYqYnFEmmCqFqxqmeEnSlF+93Y1HDb86afTFMu9puqEHVeEowIs0aGExyPA13CwnRm+FY2JoxUpZD2aXiTKcOYA8v6ejb3ZUKlslkN1kuo99V5PeO0nvH6KDlpnFu9kzD9Vr6Vr6F8TiZFypY1vv292fP3cHTfyrfy+YrtraY0WLALtOExvhXAzuRPofC9pmT4HGGZ8n1KdNLkiXT9ElzbhrZCtFv69cy+J9QcFDlciASwJDgzIW8w5fPmGSBuILPGb02l9Ry/kyzB3smEv/FlLvh2rYJ6OrQVxA1NcwxKPubmXv9dXoT0b2Xbx7KHa6kS2ieHKVU4jHfNOSHMM8LkALkrMmRCa1ciFM07QWq9bzy3KUdI8Yrw52ecz2fxhl7ZaX/pPQdYCT6TMQAN63p2Wr6xRT/Q6AvcD7WVd/92wvtfHsGssC4Vy2HB/+Pv/4DvX7/C69cP6gkhQv5aiuepoKK8PJlXAjqPCPt0BYavrVGONq5F5ac0/Ij8LIBaWJvCwXNBqLc4cm4Ibzc8JKDPSSJr0rpSKOvMjzo/phB3Qiy7E+t/RD3Gc+708L5y0/YfcE3m4RymgZHebSzw6W/PG2Gv/IX0Y4+EfoEyVVkZ7ieJVYBS0WrDaX2ERH4Q+cr5fEYpJ5RqXhAm7xIcUWrB6Ycz1mMD/4nT8Xh/h+5SRIybcEYk5MPuRYsJeUz4kVtkgInQaEGjBVyPjpDO9IDTuaJywcIFH88Fj43l/hZoFfJYQ/t94P70uFr2lAojUriofPC+c/p9qYyY1BsN2iARDFer84MyhLICDYWwKj0a1taM4cZO9Rku7h4dBWszW3qv317k7fi6MCy1aeNgng0AxA9zfNV/5z71hFsXr97l0Xpou6AyHTAT/n8cImvNBMghBDaiKguFx1kMRVMk5rOY+6mNJID2WozKUaKB0BDW1QOsFJ95LTkDY7TAbP926yOvL+RB7wj5PfSS3WSvF+ph7yvytZEudgDQ8CJt+tXXZ9e29c7eCIXXdZy0vX6J2Bh5hDH89y0sVvAWRuAgEX0GvxJ7O8M4jlffi+3mYyck2f9u90rOKtC/3yvBAPA4ZgCRHN0hzB9wWx4r3wMWgsosPaKergUVylv0N/N8iPO0gLCqshSIJJqWoI06hjZjSMPDedymY25obRIDmCiffzYmrPPKm/qYuItDanD0CBgpfNtYy2w9Rx/6uwRh+lr8JqCWhqUwwA2rKvZEuXkfITQrebnEOfnEem99b65VfFqb95bguvPX217dwbdfk7fCtTKegfeUe8dr7/1PUvYqH4xGbitjB3m4NdvPN5YbaeF9S8Rv5anluZ4Qz2v8Uy7+C012xAx21u+lOga4d/jva0L1LyEYekqTU0/5J7XNF3/feu96O/Pvt7277ett/Acwx5FGu+3bMqfah1cHycsuOg9acIRzK4yKL+WhopwlVrgZx/HwaJYTZDmAKRKcDuwECty/l68nplZCijZwKWCW8MalSZDjMFqJJNVgoGlI1bime6xESKGcjLiDLfHPEuIpGRdO+EerohBcuWH0+BisFUjGZtxU8RKeDHtzx4AbKVm4ZxQxcAoZhY5B5ulTHe3E4JWxPjaczw1oC9AIYBmP42HB64cDqocQNmPH4GXDMyF4OiCtrc7QEv5OXBm5nuG7L0gNl2ShmSjmLD7NuwGdEiKuiyLIPR5KijRhbTlODx5k6wExwOqv9QzARjGxmcWRg48vvvdN0Ud7b83rnO1jQQ3XsUmPkzhd20B6Q4k109c/bdnfeYkyg3mv7dnRfH8b6f2p2OXes4l0hySZyaSaUdQwnZ5rbXeyWE6tK3+shpMmSSENy9YKg5rKHxyHqaI24U1XRFaAFwbVM1AqJFfE/fP9oh4RcbbdB8jVpymhukndzMCZjnisP4DqActyQF0q6uGAf/z5iH97V1WbQ2AkC8wJvWBCKD9s/dGZgGt75Z6e7ykhpkssn/uzh1xq04tvTItrQn6zxoYdeqnlrt60SZ5Ee/qZO6cGe4SqT3o+hr5zdgi5dUMiYsY6clvz/cvdXJpVeltXueJSQhNS2yG3rcvErixmA2rd3JJlsfRSLA2St4BD3BOWzYVs7HUbzGIR3tDQ1AOCI3MXgphLzUo/1cpjXVe09az9dXtql+9ZXEUfu4QFSS2XmQqoNKCJUiIvDMFLYkXRmNXKXN93moCS7DcjyuinU7qc+p3HaqcEjRmKmsvSIZvXQM49/a8wdC0HYROC96HKPfjAvq7N40fVOh73Mta1EtiNAR4cenc3ZL/vd+HYDONt79mTXod5nNjrFNb5sh4JREmQ3jXR9DVCWqzRxi6xrompDc9JZu9uvds3VkA5V8ix8im9wwWyF9gHX1y99XpPMGgKd03y7jkVIInfGdBYuAQU66flRCgKinlXiOUUrSuEJpfnjLE6n89Y6oJGzd/PDBOUCSsIpgKchfBpDzhKslwoTVFoj5PJ9q+vVUYhtoQOQ91abWJSyGtCP/Y+5hT7SsfCFVYd0W37RebbPWEgYyjxbIEfXz/izWFFBeH9+4o/vHoAkVrejQvoW7mtPPnQ/1b+6orv22+77Vv59OWlFSAtW1KD1EZosJblLV9yXUCuLP4XUDI8vezB+te5v7My4u557OV+cflZFsmjGPK2p3MIFeNpWQW15XDAq//5dzi/fwS9Vf/4wUAHzJr3QHhMErddoJ1BbQXaKslONRdhyijt/Ivx9pYnDQAKMVpbURqhrSsIwKr5AcSbXfj01iSvGrcVvEquiNYYaxPjExP2U6kopaLWBXVZVCGR6feGBkJrZ6G9z2t4Lqy90iB0BqQ8mngO1FKwWBtlgVjy1+BllKa1/BVrUy+G84rVhHk+g8J8E0MjVJDnNCu1SvLwFk+3xjiv4mFxXs9YG7tTCgC8/+MJv/75g/NWb/8VeHwrXt1LrWrZbKGPyGViZulsOSJIIzgQSa7LMUdE/uc88YSvBxAeZs7j9gmlzfOBzDujLjpn1YQKUOYIwJhDooTnROI/s2IFsDoCPuNSBilT6kf/vG+ejYwJNxcjqdnlSrPcLPNKM686QHxVLmLvB9s24p/n4vU9+cGnPC/sPP6ETWxa5JvH+6XKy5y6lrfW6jQO3UKiMRoxamEcDgc0rEAhrOuK89pwPq8gOqmHWSgIF8MZdcHhsGL5/Xvg8BEffv4efD7cDeXtioi0mi+yqJ1wMn2/F7Jp1TGcVpgJjSpaOQB0QKkHlFpx5gUfTgse14KVIeE1OOG2yy0hhFesB3f6LV+mb27lfFeWksuJOH527+S+6hNJSJyfm6GEKbQmyNoFupdFXJNLGHGT4b9pvgcZmXwfBGNZFZy+sgu1ZqjhMroYGQoVP3bCa1kBug6iwbhD4VhpayrJZF0BZPEKXdgMnSnOiq1mwHgd/i00SfC5Z6i2ciJotO9kwr6w/Ejqpn6M9UuP+GK9m0WzDAMBhQHW0Da8rTOvzxhq8oN4f5UimD4fg+j6eOht1+RtB1R+zwWnF0DKz7IxqT4mI3GQNs3QilfLQ982TetcudC5hz2ImnmfMiQvdXDmOQgrpbG1vqcW3ojIFBOprh7UTWuyrOajI3Vx9+y+ZYitCY7tlLayeTAVMBoRuDHm3gy5urxZ8lmh402q6mxG3DY4ASy0uNyzHcmhHMn4Awy31jJBvVlibYjJnXM3DcGmGOTj84Hb4PtfMg92g+AMECX4ZjT8tmFSj6w9IrZvx74FDgLMDftADQ+loageiRvQSt/hcQ98VtnQSzQ21vFSSoLPMBB71sBPFvDc0eZYrsEgKMIW9biH7jhUPlO5htuvQpQNJjbI7s552fT/Qutj1Xx5v34r95UvOX4XbT/Gh/Zu3wr/Xj1X967RXh0B41+etZW7o+tzz8Ol9m4gcC+9vTMot+Da7SNK+3D/+yXKc2vZ0to8vTcWZ1NHGrfjHeXOrV4lM8HjzYXGL/EZpl2C98txAbUFh5+OYG5Yl8duHctSFkaE8nfjvU0BkaUNE6UdtzTnHY+olrcsCojWgIKCMJ5s8JyI0LC7agjFjRNxOArVReCehcge2tjinltSaYWfzQgpDV+BKCKsPhPIgUqKrOHUqdPu7H02HjwrIXpu1vhoCYeqCbQJaCUWlFgmW7JqhOyCGGdqOLcV69rQ1gJuhHYCsBY8HA94OIonBIiQwxeZAaGFZAIZj4Gg6YGkeEDHQBkv7EBumGutaPBsyF4P9r3kayWFCvP35bMkjwgzppzlugh5SwbI+OL+jvUR/sSsjM/H91vo2CzK6Ydpy++MTXYwdbLYHbzcyVTmT/Sw7cF/Ge/TTEFzY7nOA+zX62KvG8adLgzvfv39w4LGg0/4YuXWxnvhjOOajuM2mYIa/BUq4NLQVk6iDXaFam1L5IpgM2gEQIR2FJxFvzxtNbxsjoidA/YlWLStyEJ+tXrE4+FHUFnwsDygHhYcHo74p58P+OdfCxiEUhEIdqx0t0w22IZhugZ0CKhuKXHgz16zQz8d7J24zAMkiYDHLXrjQJTq+wPRiApvG+NmS210RNWFTl3TXFg/SOPUD23K/og2XUMfd7ETgOXmYuPQjBBpIvwlVx9qHDU/uLJLGkFSUslzrciQU1GvhhbPFoPf80RoP0naMldLETrG2Q1YICQGr9Lbta0K6+rDb9BIjHcfWpcS5jwSM6RtsBXrV1oLthSLCVd1DzVAhbUIQq4xiBrAxYmqWKfemo+B/TY31B6yoARd2ZLW45a4BsDZwjtRkkZc+LzF5Z6ISiWtyQQ6QvkwEgbRu1nxZOKcflv1JXKWsLYrVkNipbOBYQQ1UbZmNU7dK3rYy4ZDPxuI+biwXVkRj4cDa8YAKDFSSrc3zFPCrAgkBi1D3PYCBMnVMHSMo50AdAucoJiwmp8TDnoCW30MZ3iK7jWJh0juDr5a3RAcymXMM0KJPiZXcHh/2Rg92EXdN2KxJa8XUeapMmJtq1j4KMKudcGKFbzKfl9XuV+K7EODmXVfNDAKX5jHNO2c5oyZHcs1jhwXZg0l1qJNlTMp10OcKnGWMBzXuVVpOptk/BPTkObd5tAZlW6syapwvFwIKHVBLQUPVPDjgfGwHEGl4nw+A6WJ9VfQ6y9TvigF+q18K3+BZSSxn0XVfSt/yeWl0G/wOujWX2fpSzScVfltxmbh7pWcS+lbSSWPRxaT9Fd58vRYLs3Ec0b9xY77jmV+uuDupYqxU43UN5cIhY748ed/wOPpA/78t/8N63Kyp9XDl1E01FDRvArUGsg+uaG0JrnU2EhRUzIwsJoCgMFoauBe1OO2Se4znNF077UW0QOMBmYViLX06bwVCpZaJSfo4YhlEYPUUix4EruXbNM8CxYlYD2f3TNibWJB3DjoV/GGICxV26iSb3QpFaUsKHVxutzzW4LBvGp+ixawqqIjrwBTKrS1YT2flU+yvA3V5TcC8xnr2nBeV4GVgQ/1Ee/rB5wOIqv58Efg48/CRxyWBf/D3/0BP373CsfjUb06JEJIreodUUUJ4AmiU07LknEisPnMvPgMb4ZSwzwgFli+DRCh1AMIlp+i+H3LPQmKHBEWhsmVGIWUZzLZBPx7hiwrTkJuQgktm/J5XwVxrdzq6WT0jdhg7TFr/RtPhwrGgsZ3Y9ZeqHQe9Z/JGOdJSohnnr+btj6HEdcL1THKWKLekHGKEqJipRWn9ggwo2p0hHY+ebi7UioKCPVQXbZRlorz71a0Vyy5Ik64u9yniLhVk/+SC3K3LgKXA7gcQXoY1FpxagvefVzwYS0iKla5iR8rHVFwtfH7QM1V36mEGAtPviEhEbeYpgn6VJmj0cBZHNQ/dwm4rVWwCPd6kPboqmsEJAPbpKmjOdWsb7lHSQDYl31ib2sdm4il1IQdUgQTevagyWMqYNT7NheFWAgZs0CIRQjrUZDeRpwxVOTvyhnvBcGtSUz4mHsqh3YbEs7G813SZkpz4hviyjoftKtQIs0FrhbrXgW9DO6WvwmNd6sHgAHGuDE+mUcvrhvBanoLdAekVNpZIXTIYASmLy7Unt3wr5TGk7fr0ohT/z7rQczXuCZ7Ae1lWKfTeWGrjwra2aNhncSIQZ63b0vU3qkYvRh2CqeW0jK/TojJaPYKjGiPfUoU7sYAccpdkOYm1dlAtiO7PUNpnm0fRC1wwEPxKAiC0ZAVuVZDDBj7GBZNXA3AraSMOSPLlUCKJ0ZX+gRDCPK5/6TwrLAdlUMRjCiUOY2X/RnOOFYFOBc5fIh6xZN9F1xplhjDbeaUMLQ/fRhhgWEKkaUueDgecDwesSxHMD6KNVndxqq8SjvewUgEVLfRCHsC1icxGeM5+dT3P0NT18o81CZ39271cHjRci+jYXv8JbiHoTx5msd67mt1p5a9555St9S/pcl23vo8fO5vtnwOJc6t6/sp++Bm+J+6yXgfl8AEaS9V8vbZqfZlvcEuNOT3PzUMs3pn+H3vrQm+N/IlPzVjCXfhuADkxXLriz0wfmYNtL8/yvmdS23Q5NsdZWf4mQGsj2inD8DyABDhWH/AujBOr9+j1ZZyGKbKePIP+TOay9RbDl1qD837w74/5b3W0+3qFWHPjCyIGNSFF4QlPe5bUFg4FAONI0Rq8356rdKfot4QJDkhChXJDaHC8I7HT2uY0zjFOERfAXE0Fm9elnwQraERiXESUxpmU0RoOCpmrLRiLSvW04r1Q8P5XcH5PdBORcInL+IZclgqDoclvDl0rFyY7woEM/jMngWxpt3rwEanFyQoT2E3yOcFIFcauFKjWJ4NCweVlQzaDpX0qc/rewLH7UqIzph2sxKHd3LnBgSyh9UY2Ky3/Pz4FgPC/9DMpHbkESd7Zge+3fZ3HnsK/p+9QhR1XYtOcEMLV9u7BvetR/n1YeyY4Nsq9Tfj+ckK+8x2bVt5bn8eaWQXxQ9g2TNmZNzUMJZb4EzN7gIQo1RCq4xSz+BKaK0CM7nETnlZj4hPWMYjpdGCx+VHUKlYDpIX4vjwCn/6dcF//fMCQHNBUByAXS1ZAO61xiURPM5DDN28gO5daHoIOgxDXRFCIKnUmSVKThIMhbsU+eEXFsHs710DmewgzQeLrNA5Mrqnn2Rx3AOWXdKVIYd0Cu9yrQxytE19ksfABL5hWVE8/ZQIDeWASbIvPaRZkzeDVTvvYUbsMJXY/+5iOADnGnkA67oCLJvZxsWIOBmahsbimgmo+6bVSiKW5FKEUGsWzgXar94bwrwabEojYhR1Y8ZKADIDjVThov8VYqw2L62hkYwlUQMVcg+HpuF7SmngVnxtG8KzyTDBe567gChNG8PHuVMIdcqk3oJdnisa4n6yeDZMQp4mChrLts10VdlzxoSkv0ZIgyd7hjoqw71zkgUNJQZZBLs9MTMHhdD3VaGe4LxN8qy9TWNz7a55kRi4J+ds3SRlFG0Tfe01IlMYbEuscwd4BAu2JwrpeKZJtfVilvtygDa0puNai8xRCwbFk5+hoa1GOIeVkI8d9KwNjgndPBdGVtqtq9xwF+hCIAZWloOeFKZSigr0q4/l2gRuY7BKKdB0L85gBVWFBKPMrYDIneeDj6fuHelK4IdChJU1z4zOd/VcMhR1K6PJLbzyinpGZKJU8Bb5GiUjwlswaT72pijBsCQNp8rQ4tXDa/z4u9d488OPWJaC9v4DznxGPYgF1bfyectnpa2/tpL34LfyrXzV5Tnr9De+y522Zaf7nbwo6Wx71hh9K88tv/FVNi8XGdP+sdue2JMwxiOjmdH6/k9oH3/B4Ye/Rz28xt88/K84HT8C/8sKfk+gnzIdGfSZMqHC6zWo90MDNVb+0HhMobzWDEsysgHU0r7LJS2UntHfJnkRENhzLlji1LauyDnqquVtOBxQlyNqrajqEeHRjZSOXc+rRAk4nzX/RMoV4XykQqt0sHkQ2L9Sq3xqXoroBinvHfglG+dx5s/BwmM0AhNpLsezGh01Fc6vTluz5sVorWHlhg/1Ee8Ob3H6N+D0zwVv/xl4/0dgOVQsS0VVrxDJZ1HVE6L4Z6nm8VCc3s/KBFdGYCZc9sWV6HbAaO6ik2v5JYp5QhTJ/ZD5GPJwS9a+5n4QQQHEg9x+633jETJEt9BeDjYDXIYb15jgy9Xe85YZdgnNGPti7IHxtzl2wG2nEg0AfVps+o30fUb5jAed8NvyPaKEsAszSqlYlgUNDRUV7XxCa2es54ozEc7nA2qpaGVF0xB4BEKpFcsBKG9+BVrFx/e/A/Pt6oWbn7zHWmT25MZ1aSJ17oQj2wr0s6DRAa08gOoRZVmwHA448wG/fjjg3Vk8ISJx6iWoelC2fegtZk1oc73GWf3zVkjr3t5VSYu1ngWh/l1hGLCAxRx3N7ApPANM49zsnjsREmTeLere5f7OvL2dskHLrFo96i3LZ4114HGy9E2S9qZgcH6YMtI3HaIJvmm7jjO0BA21Y8JTGjptQmUjRAAHAnrcpLm1v01jYbIn1rPqslC0gKkCtGr3WBNVq5DR4Pf5UYWLAcvcKTBlqSsx4ntp2Kyc1p/GCXUdWSI+pe6mnW1OVCFbtiQBslle+67ohMvSeIAdk9dbUjlrOXz2xffIoL31tcf9c5tCNF2ngCq7wH3M0b6RnvZRAtYSKLKux9GaI1RGM+Q5/ggckHxs+sdm+zWNJft/AadSn2PD/upztP2xHHqvhXxfl2yMBCmBPzxpMDukA45o+oCNT6xngIvhGoq4aeOWtprGYSXogc8eW7JTZEwoNw/zZPWQWVizHwdsvdd9abFtGyTUm1ho9f3UyrxdYYo0b0XCZwxInEcCqiWzUsGM5LRQZUKDMJGqSNEIU75KyOBFjK3337tus2iK3XlxfJWGxnArQZnDZRHmq1ax5msEdU/zfRtoYoYjPlG5YRM83VPiwv39wUxfLsE2XeG3tbHTng2FzZ3/npF6iGTz+/AOi8Yr2gfsLtf5m6m7TSMDPMP1vTIZiFuX57VeXRsZumkyJ+M/+XpTMeT9xLLZMzMa9PIDO899znLJ/v95cD3j6L1erqGOC8/k3dxf/0QQb9ZYb6MYFstqbb2Bjjffn0PXjINyy1A+rf7r6+epnhAvY0F727juYP3Nxb0Zu2ztesNZcKWv2eDPyLmr49Pd3sfMPRc6tDurbDblvhyU1rIPZqCtiYyvqDjg4fB7rNzw6u3vcFrf4bG9Cz6Vc4WyZ8CZtpMzs5AG/CD9rU8Imxvr0yzxJeSoCptBDmZivGBWuZ0gH1mYL++FN4QJslO9aUxcCanhjtAgoY+45yEIcGMaYYE1fJAmqNbsEYgQJ/24uxcEO0vRjWB8svKKBFP4FIgXNEh5wQZRojTG+thwer/iXBrWCpx+Bj7+AqyPpOGcRFHy+tUBrx4ecDiU5AmhFs/uCVHMzRhhcVlcGTFYYeoUqQbJeF8Kw6FN6CTLAeGeDFWVHxZyqSoMal+ta8Hu59wQNgfBcye4vHQMlF/i4YnOxHjCBw8Pz0vXdshu4spYtlDkfRlfMrG8BfMaWEPtwd+FEBGz9Tovt+J7Svy40dDQMdppy6dn9Aq5Tst3LZPxlcP4DfUx8u2hTbr9bH86vRJv9vzoIAfA+BB2gbsK85QUmPFVpthTrE2cDJiFVlo1zPvaVvUmaxoNRryaUAqwrOBjQ1lPgltvLHd5RDyVPM4x5i5ZPlMS3G7HVw80WvD48DegcsDy8BrLcsCrh1f4l18L/q+fwhrT8JRKb7aFu4853AOMDDtgxTp/7+18p11sgbtFNyobOg8IBfZWliojg7BVUHHi3urVk17umrbYyCHbzCEYzVbPIkwit3TviAnE+M1hHfqhe5OGp811srDF94s6YxyjK/lLvs+AEjZmjY8wpE+aAPZD1ZBdrAhDY1Z7IUksNRI+PWFscSQVXTcjQARMC8nEmn+C9UZbGxrUSsIO62wdbxYk5n3RzmA0MK9gXgG0dIAXH1uyQ3AFUFZ0BzuJMo+RCBbvUYSCEs8hsZJpxABVHWPywZbQ8ILpJdblWeN0cjCDoY1Ic0HddQGtACWjT/k2Ir3oBm1pFaR9yXZgyqLbJtkLgtfHRQfQLEnyZNsZ38Aa4z9P05zS8aRjHPlKLJ5qKQQmsVYJJVKsO7+m63Pcd4DdJicMTOCd8W1XPBE1+xqUKWoOIyOatQMshOZpLn3PJGxqS0Of68Yc/RlhyghwpvsyKaABlJKy0T0ybH0hLHQsTJKBsjbN9UIFxFaXxsDlAqoSBqkZcEqI2xlTAKxseFE6Z1slDnJ5sSwVEqCpDGeLLJzGKwprSEFWfMGxVmVsYn6pkG49sawiAJUW3avb/cAgd95YVTlZC6mbNMCt4Xw+a6xYceWuVLwmthjBpYJQ3CJMkt2I27idXQ0QRkoyS+sY67jwCmL1/IBYU4DDOtUU6TZPHlPWzqRGqFVi9NZDxeF4wPHhiFoL8HgAzurN1kbjh6cSkE8oL9LWUymuOZ1AF349vf0L/WStg/IlCobN6LNJM1vqarwyvHTh1u3lM66Pz1jSEbRzf0Zt05X745d7IZp9/+2USzTsLe/lE/Ja3Z+mPGPcb0UdGfXus0tfoBAsl9nazmjtDOYzxDhnwUy4GOxEMp7BQKtgj8bbH7LLu+yWGr72cmmlb8evL9QL95x83B+LGR882A9eLNu8dvv1h5e5/b4Gza2FN38v9jrzBJQvkfMkZlDT1ZEALljwN8f/Fb9b/jOwnvHr+3/Df/v5/4vGkY+wSfIE8VhWQzJqDea/UKGW/Sq4LlSwFuFZxauiGcOAWhdQrajLA2olUFUBtPLP4SVvPOKqe2/1BNVmaEdkBikVy2ERD4C6SP6GUhFr0DxwI1LAuq5YNX/F2g8JapERqwVef60HlCrhwEEHiGBdaWRmiN8yqfOIKDfceNRZ3RCCMkto1TOEfS8NALWNQWJj4xEYH3464U//7VeZy0J4/6+MX/6NJXfFK/GEqLXiP/2H3+H337/BYTlIHoiqSp+i3ii1+nxA5QdEct3pdeOplIYnV1rAZQQleSigSBglGfcSeSdIFUPFFBCipEA9eNsAaduRr8I9JZA9IJQPcJcag9F+Xt53vhoo7XMKnnZTLlWXCSE/3Lm7fVkRagngt3KK4A/TjfTQJMBBqj6ZHeb8mYl/vKnc/Ghgq9EDKxAksDeYWb6Yr9r4jFh5ds7mvCXTc8UqsnnnrTIidWJ78Rn0S/Du+SKnu+PTL1Q4xsXyBEcZZASQ/baUBecGPLYTmEVasa4r1tZQl0VC4KkXWDkcQcSeO2I9CvTHV2/v6sftHhGX7t1hWZifJEUiXVxq2DX5lo/KVo/gckCpB5TlgGVZcOaKf31b8POjOwZ2gqb5YOwTG1d7cotVnW74m6YhCaIH8PRrVLRb3974m9Bt7O9Q0R7BE5bwY709AdkJfZGQPOe2pR89Up1WPeAD63+skcwUOOQKU1d/tm5Iz/ZISvWxnUXlBJ1qI/JYf9D0V1LNnRVBqqcTvtuz6BROmYCPsbMxJl3mFI9PIOA83qYMJLnWHxUmRjXBLflEeJipbnQSXFoaK+tmGlSEkkpySOinCds1PqcIudlrjgNJ5qzv1W14JtZjcRwzLUYc+jsGc8xql0h7r3nbn2xqJBOCyxi5t8WWS5I2iHRsMEncfVuvbUbGAz3tZvgi2qujI1JCCQFOeIijtnCVNcK0byo4pIyH9udijxX3twJF7T6XYQQNQk+9NlbSr7XA3a7WydpWe6f1YfuC4JQQSy58R8yNrC8ajqcMcIzzdCzsOsW8ZiW/VbebiyPhDFPcuaKmEBprOENA3N9RhEkkaMg1SmuhgbkE5vDwdD28bo2HWBYZF3bTwZnZ0Mu2f/26LLRXC+PVseHhsAgTq5ZerH30pl+o7K/NYZ/t0AejGOGa2OnCTukfuqvs4KFbyj7xcdu7g7KR8peb+/EUwJ9WXswz4gnlEjk3f+EGcG6of1bnrqDwuVNxYbvcwU5cqtrL/kw8MxHkhTa/RGWfU896U6Fh/Qx7/SoO3F3vl3HtzWVDMOw+9OSy8cS+UPcV8vKOsk8ojfv5liEk4icP9SVFw73eFdu9em2jiJA6PMKtXXs30V03wjKjzWfvhrfE7WWr1Opb3jsuO0rTz9pLq0lqaaf3ADfQ8koExCgoOOC7w39A+8h49f57nPg9Ho/vnE61/3AqKO9eg9sKbmfwcgIfxJiN3OAtvIzcKl4FzLUeQLWiVKHfLGSP5RVj8yZWj1/hjWyMWrcenZ6mZIGfvtuwdCPJyq+xeVew1t8PUz8HekHzQgTvI0ZMnOZBwthaGzFyeZ4YcMNWQBQX4QEfvEc7MR7faaJrMD78dMaHP4txYSmE9WPBUgh1WVCXBd+/eYXXDw949XDEsiyugHDvE8sPkb0VSI21LH9EksGFsRn6XA7Q8NMqk3DlQjEjI1E8iEKheluA8Rnh+WDvmuLBYRhD5ZFxAWpUNdK0E/5uVpwXmewxqWZez7zWntO7+Xzq0DT3/NAuk3sTZ3Cx0Vuw0tCj+1pQo8Ar7Pq0la0BjMzUHjYdacVg1Wl6PdrZx6dzqD89cfV0T4trFZsEYj7OcdFwmoZLK0Vy3UKNZVvT8HE5x04DseFBAj+w5ottd9EMnyVHRMRvD5SShSK9wmzY+K6RXXB++BtQWXA8vkKpFceHV/jl14L//c/+sCda8iW+WWlfkFqfKR3slsE1EupXLDSu4aRg+u3k65f7RsBoc1LCatdjeWuF5gvQ98OpgUQHcRK853721t1TqHXieETqjBT6uz+wrX63vh/GAUBoBa2/IDBJxgfO7QwJu8QSOCO6Hum58klPExs3t+a1dWzED/doAWmuAbWkUMooxrl429szOC30jdShaCIvRTQw4FktSnRcyEdT6wv4qZQEDwdcuh5Ihemqe1cCUAksBqiJlQuaxfrkFOczFiBTr4zoxqfrM2Ud26QYITVbZKwxeeLl1sz1M8HSLlQP6BojVyC5Z4PlHtE5dT1ER/kMOVI0LmiHK2cMxR4dktfT5n4mqmxc+p65EiLXs1Go9oSWE5/6qStqCiDrnnZhNSEExXfjZycjvS0fa1ED7dCjW6sT6WZmRmx/qqC9NUOCfV/SrjOimFtzPGmJyIiA9Szh0qipwDx11aa/HwFbTz3x0BF2GcckxMTWtj4zTkUpYgnKq4RRAzOoFByWxQmO1hpO5xOWZdGcEBpnl4EVqyrLGEQroHiFQECtso4zrs+WPqRKX5ZRMyWG9ayYtVVHoJawwkKstT+8OePH7wi/+05oAarVXcE5r4m/wvJb6nX2ZBqvA7+tvjy5PFfy/q18K9/K1cLpXIozv3/m0k58ajij33YZBWS/paJCLOotZIM1uchAPKvsnWvPrhcTEdneGZq+jz0lZrT3f0KjguWHfwDoFQCg0gF/qP8zHuoP+PWP/4IP+Al/+o/vsFLi+wCU90fU//Y78ApUXvH4+5+w/s0HJTmF5nNvehCoLqgAqIqXwuHhQfIXHA4SUqmqYBwAuIGwCi25NvcusBxurN4VHQdNlqi6quC9utCdm8WEULqTjQ+XfBNoa9TJ6vkB5bbJ+Pji+Qz8n8sxRPESHu3A2izXn+V1gIdXYgTPAQZagXhjU5HQp8yukGnMOL1d8e//9Vd5h4D3/8b45Z+AWkn6uiw4HiVEeVkW/MPf/AF/+7vvNEcGodTFwzWJHKBq3gvpR10kpGmxubJ8eHDZpMoBIrm1eZgTivBxSqMXU1QU4SfgHhDmHZEUIPockoykmNzJwnUZb6HyIpMedcX4698mkupK7OUwWnOZ1r11IckkPvPZ9RL4T7nFF4Kox5vMvVQEgMtj/tJO+VGOcKkYf11rAXOFqVfP64oGxnldATrhcFhQ1oJWmyojhUhoP4j84PF8mnhg7JdnKSKetNBMWI1M3BjSi+TAAEykiVZfAWUBlQVVPSFObcE//1Lw66MJeUXLuhXb5BKC2nsXWwjZNp3pnuryJ0yFff7kBqx4juOFCaw3jXqCIYRdnIaAY+eNxTX9vbUt/ACfEPAUCqbJsPTfB+GgweX9LoaCsrTfPmaSRPsM4UVc2h9nq5e4qAA8P8uRTAgAUUNrlvTYIBFp6tiEJPS243M7IFnYvAUqzcugTDGrBXOB7AX28/pMaFns00LUNIOUY064r0HaozT2cCFjJxXVNdLAKI0lT0YaFBcqKTUWCo1wv7W1s3/gUvo2rMu9ifV+UIKDfS9kea3cDyYlpsdOrBA8W9VZURh7I80vX2Li0h6Hb/UeLzhqo+5a/sHA1n19s8eGCe5uaf+y4C/hHIcpC7ohMBlRehNC0hd5hG2cxoST+rGjoVtDo3k4OT0zdtsrybWRv8hWNcPn0u8rZ5L3t4wDJC8BNRfSMxJhr4pcdgC3gxN9TfgkfbIPTpG2isGQcKXNVhb+p27mvSWh2tTijDWMFDSRte5D1kR+Ra2kjFFghMJGkupVECXPiJQUxc8eXyZGXG/nhNzl2uYyhbuyzyIO/JUZr8A41IJaCuj8AaTh6PJ67tda2ui7czE7568XV0A9gWH42kovtHmh/gzINh8fe0zSvbPgGOr+6fMyoej0+tPGYW8teX03jO9L85AxFZ9vre4zwvd3Luiey/uXBuwxe/65jO7T18WFe8NY7c3Tb0kwHoZo12f8k3ar4102FBeALUkir90G1N5ziXq8uQzU/13vWg3+bQCrH4PZ973nn1+ujWXQ65s381Ob3+M2ycqG3mv0Qj+3FVwC9PJafuagjfyJXx/BQGZTlLjKTAGHXEXozOCtCYz141vQ+QQ6vHH6b6lHfP83/xH144L3b3/GuXzEx+OvblTVlhX44T3woYLeLSgfjyi/fAdePoAOH4x5BFqE4GQC6nJUBcSDCMqXRYTUtTiWRosQnMDqR7rxZZbsOdP5YaWvFr0m9EaR/IS6FrLpi3tdBOOROYIpn9JH79D6mGBqEcuF0dhyTiRyEwCoANzEe7ebp7Q+V+D06+rr9OOvKz78CT6mfCIcjxQhqA4VtFR8/90rvHn9Ct+9foWDekLI2C6qeFg0h4QlilaFRK0ATIkA5EgCrlhKCghXVNg9Y1TVKKpgSDZNFDk7LIk1mYGTyjJs/pKSQuQWQ44PwGGzMc17uzuPn0He9MaAXesX3spMF1wBOrId27b07cz3JBy4VUaMTPSksnvv7ZStZ0HGK3svyT+DMhuh7zQiuGiKv3O1yulemIJrY23HRiinY0wp3R/LcNLcRTc+9Ri42pdLbV6AbzYPwY+w5n5UxSFXFBLFquR3bWjnFeu5oRQJb9eKBZuO5PQio7wd3s/iEREb0g6KUaAUF3qkAnBZcFp+B1qOOByOqFU8In59X/Bff5LI2C4Q8yWSN8tIgT2Vwd2vcv7OYFmcrvfg9VKngUbeh9VPzCvYNlfYQju6YXa8urCC7yaK9b1mNu8Dctmc3N7BBAcnHBqkeQj8dAya9YuHdTI2YXWnd7Ud7trNb/R9J29HiAruYFZhuQrJZKjjYJR1vQUng0y2vIlc6MdGVUGoR6FNyCgjH6fG4doaFgzkRFbCHWkIVLhoRRPKmlts0RwRzV5iViWMWmB4i9pHE75SsG1s1ig0HFQMNGpq+Z3HRQhHsfg3t64Vra1ozKhEPsZXi1tI2AGt1DVyXHxjSkaFRRCz3XmqxDlAbg2DvMrZiK55ySGmshLClDZmHc/2PcOS17BqI3pi6jo1lUlZ315srzo50BHc9man7EPCR6YZse9DyfgCaW1g0IIHXxRCfprGhc+4KV1jxenUj0vHMDCn2YrEb54QmaCKt9QnjSVm3gxdxT4ETfK5qNIFDaCia42kc37uFGBdtWp1sS4wwl6e4daAUjZkJDteBkqxxWmEaJwP3AAURkNDaUWVERLZ2pPssflrxNoXi6XYWwSgloiRzWvDGedgBkpB0XV8Op9wWA5Yir5DwLo2gPQs0P0o1k4KdaFYzwRINsCUT0WVOM5Ygl3huS8cJYmhq8zLAYzfLYTXD0exzvj4M7B+dHO2OH2fwY180fJbhftb+Va+lW9lXsaz7/O3jkSrBb8AGK0+g+4JkoAXLy8xchtO9pn1feoyYaim92bSI3LB+6506WLTNzxvUsK92wm6Fy0bnjZ5ILCzK/vA6FJiANxW0Ps/AWVB/f4A1AXUGo7HV/jP/+X/iV///C94/P/8ig/Lz/j4H9+CNZY+v3nE+vAO5U9vUN//iPL2NR7evsLjH/6I9fcfgv8qFWgMKpJzbHn1CqUecDi+kpxpHpJJAWMGlwY6A0LpniWVfGMPDWIey7KBs9GkekJo3gaiKnRvI4BWsOVUQ/BezWUhSSaQZBMmnyJj1GE0quWR0ZFuNp4s3hAN6glh3ldp8E0ZYTQvUh9QsH5s+Olf3rlF8eMvhHf/LH0qS0VZKl5/L0qIpR5QlgKqhL//2x/FE8K8QarIC2qJuO5k4ZlIrJ4B8ZgQfUDOzwCX19n8ZLlQvo4Ev+d980/LQ2GKiP6dojkhTLkhIcIAU2wMnF7HP4+8wr1KiCdghbvL6I11awkFxtOwx16LnxvjX0GRUQJZby+5BvWFcKltw525mYCyuXGvMuJrK/tstpwhpRCYK6ru9fXcsMJyRTCW9RHlTFiXM2glMQYkRG6Xc8Ga5ZBXyu05Ii6splssqy5qFpOAIq4VrPUBjQ4gTQ5U6wEnXvDHnwvencnD9vRV8+bvVdh2rufjyejVqzglyfH8Eqdb3X2DkoeGbgT4IhE0AKBNjIduR6G4Jnqom0MgNr4tZ0XBZgqof9j6SIjfalsMk6Jb4maRY4lwvAuvv8MjWN0O4wjkUMxCmSxZja0jq4csWZa1PeoQcwfzNfswoaAJYQGnVMYR5HgnNejtGkHtc1MSQQQT5oWHQTOvgxYIU6bWXB3zYJp7qCUwNoRvNtZi+Uyat4+VGPQxBzTmY/RVqkt5EQAnxLitiBwR/TDkJUfdKukfMNCdeOMGRgGVBm6lrxBpnc00RrunpADnr4wH4Dj9JrTPwnuiPseFCpedL7LeGUOce5vW/HbtZRi2rE5HtqW956Cq0NvH2mDJClHOH3sbiVI/9Kvnt8hWC5TA1TEg9F4cDmG8bzDJklRMMc4VxfzGO3aPeoRrLek1SaaMq9SoW6fYvnZlBHwv+ZpUF8XmCscGJ9IBd7sGNzQqKcKcrhWW/daINTIcBbEUC0n2K7FajFnjvOlHzm1Bw1ovpYg3gypT29qEkKiShIpKkTBqqyVPV6aLiuODbn2JlqRfq8ZIKE5wm55M0MVWT8s4r+eMRyCKVSIsdcHxWLHUBbVW4BzV9N/yOXb5cP2ShOX2hDEvl09XbmGQ9i3DntxofKetRek9rXzO2brmGTGunXst5Z81vN3e+bzlS1jl37pPP6eX0q0wPQWW35Lnw9dd+sPejZK2R+enKc8+f14SW376Hn+udTvHnYIUe2WEXb8gbLq3XKtkcsb5rWc0Mb7r7BsmpOCQp6vjbVIFzkdDjfKooBy+xw9/+5+w4DUe6QMe+QPe08/q9V7QXp3Bv//VDc3Wh5Pwp1SAokYyBNQqSoeq+T3LIiGaLDmx5YZvTa15qA49DWOdbLQFSL/dUK8UoFR53wz2CitvKH0y0lWqSXzDyJMIqS38aou8ho0ZpTVwaW64ZsZ159ZEAaHyA28LCIMnhspMZNK4AY8/r+o9wmhnRqkV3AiPbwF+LHj1WrwM6lLVo2TBm4cH/PDmtQjxK+H7717jcDhECCkV7ldNSl2rKAPKUvw6EYHqAvdGKBJZRAwvVSaE8FYIWQKcvjcvGliOhy4MtNVjuSLiutQVOSKyYsN5/cTRdttYrw0/h0KOG7K8LW7379+ds2ZoL17vcc3s+Xuair19Hz3z5emGnjANEzn4YFhfshwuXjAZod3L9V3uWz/vG+w3e6Ord5yrHg59I/G/zykvyXe+RF2u1C4EXs0YmzVnBKtcoOFMZ6xrA9EK5up7uUD4xZKMH6+Vz+IRMZYQEagUZ6KkYCo4LT8A9QFUDyiloh6OePex4B9/VttnovTqeJJw9/EcanOGw6bPKaaMA52H94MAMCGkgTVbQDOEE7KaKwxxPmBhSGkkQLJQQP+l+IDb/g2eFH54aAU9Vk+HPIdxLAKxBsTcEQWmRyvoBXnZyjfDBH2X88s7pdNkko5xPkDUU6C1PHtCdJHCSSbl5X6skd8wgiW5hYKjzm6lcr4mQnw94uPg9/AocMGnMVYMIeBak5iXa45V73Nksdb74m2Pwk7rI1jzRxAkyKUlmdbpt1m1g3JY59Yzbk1htDifq5GWQdB08zusVSUafC34ZwGjSXitknFAFmBy+j7M3U7plnmCIXUq7bWd/dvzvTEnSpG21vLN9F6yXu+aVOVZnIDpQIevjW4b2pu2npNCUdZ1v0f7sh0nnx3f7uT9F0/n1j9NEVLJ2reDTsYC0h+G+zF3wgFm98rZK3ndjYLOWEfGyNjYiQJrnKRsJZGfJaqO/8RyR2By5R6ghH/xmLONGKQHOAHBxKgyAib01zYFX0gbDZozYZwThrqaJ1zgf40TtWejH1RLV5e5YTcu4hFxPqcYuEJEnFvs29WsHoqEQmIUxTfsikWiFrl1srIUSJZMElqJfdz7M1LRVUespgnVsS9Yjgc8vDrgcDygLgvwMeYr78XbSPZv5YuUiSK4wxX3V/h8mP5Kyl9CPOVv5bdXvpZVF6EzOdGEN7zzxcrY9tcykvPypYVg2Vt9VDo81Ur5SWVyxr1Itfq5V3Puuz/PiR7rWZm4DqCxKhmo4vjmd/i7/+n/hXfnfwc9En55/6/4cHor9RXG+t0Z7dVHEbyvq3q6i/wGBKCKYKoeDih1weHhFUpdUA8PIqhyYZWFXREDGFATj19Izq9QFHB2adB+FIBE0UFl0TBAFa4Q0Q4ziv4jDZuU+V7ejIXJFRqvaEzKu65ojUFF+FhCeqY1tRgWq2FRSLCMZ3B/AKWQo4XQTox3f3qUfBsHUQocjkecz4T204JCFW9+qJr/QpQRdVnwH373Bn/3+++dYC6laOikPgQSmQJCwyXVRdowxQRKhGYqhTxskodo0nwYpijoeJ6knADgCbEBU0bYs6q8sBwQmpQ6e1iQygKl6j0h5s6Kpwv3Zu9OHr2OF15uH9+uCDX50xyNXLXM/4x4mIcf19BeljNO+0FqgMizPj6dS7i3uHzTcAR3N15MIXEViBeYy43B26xKEq8IUj698RnM4jHVFMef1xVEwLqeJAJfC2Wm7OscoeR6+fw5Ivzl7sOnkEFYlzdgWoB6ANWKw+GIc6v4p18WfDyXWAA3NT8REN7xRsDF02dG+McnY6K3SoheSbAFMtd9FWaeCzVzqJX9ZSyHgadfGiWZbILKrVAyXO06YFyIGG6JLnYWQRSzukwaTTEbgzj8th22fia4miguZLzmI3ZpFMxCitNYyXhoQlYzOWEAmpbZKSQnZpoiTrNyNoiin2MIH3gCK5lDUxiQx2wk9YSYQMxNkIMSQS27r4IjpqMmcoW14+1bYtxwx8zqZLGaBsDkFiHybnPlhhO9aR5DOAwwS7xLSTzWXGECFUeb0LHLNzA5fMJDhHR/SPxPgigjigvFB0EmpXnSfejzqye8WL5PcIXBQza/Eg80beYeSkLnaUPednx2oYA6nNBV4398/TPc2yTWJ2+IsJ4gyGs62hg1/tucJTsH34bguwU79TDR+J7ti82T87op3/avvJ2LndIJ7Hl4z+Yoe3dwDwMDun4h+gATumv+gkYFXCQMGTM5r1VUKdMsQby2ZTlfYN5GTeI09oPm/mMOhDBuM9wYVKC9kb3NtFcyBCR5b8x6obUVFj+WAI8fKx4TZKkpZK9ZvghYP2KENyApXBZiK8i6kTDipDxVhnZ8ThmYqokPqRT3jnyRsl2sT6hivhLDzuva+fQJhBdfWDg0LSNMRJu9uCm/ASH6zUyJnz/bbm26Pxmrp5SXUEJ8lWtpp2xo93zOPnMo7mU+Pymz+hWXTMPcdkp/ChiM4lRQ2P8MpEaPpbfr5374mfcx+tPWxAscUp+gPAcvXMNLe9554/X43D9CpvVHhbe/tFdXhmkHb19r5amzmpfyqJAQv1W50VPxDe3jL2hlAdXvhLYrVejEhVHxHd6s/yPa4YD36zu0dcXKJ+U7TyJ0X1c84h3a8l75Zg0/BEKpYjBCVYTp5r3gSZlhBnhm+R55JYTLyfgjdZLFgr/W4uGHxcOCYOGTjEJV7s+9G5Rb1yoLYEaDSpw6B8AS+lSUEBWtnZUXO5vERMahrVhXsRIWXrfnNY3ZpUb4+NNZPR8K2pnx+HMFVgKrRwPqAlorXr0RGrcsFQ/HA35489oTT3/36oDlcHCjqBy6OQv6LT+D0MpCN1Mh1GKKiEO8BwvNpMaLgOejtDrtPxUAOZ9rz5gxk2oW/FOMiGxvWj643sBQptas5tNcI19IZbi0h0P2REjjlcs4qMe5t6KJWZ05d8Rzyr1nx61N7tXaKWto8uAOOyrvXm5/IyTPfKWHRskGk7fOFbZrSWHfKp/2T+kwuo3nmeEHzVWl0LPKQEB0bOIo+OhhmIU8v2XtmuyRqKBWxXPcRInbVqxniAEjaXSFUlAVRjGi/Oo8InYm2rGNHcwMBuFcvwPXB0myUyuOxyNOjwX/8ithZaDUWLJ7m/klFsUomrNvo6gs/8jv9AI+E5aF4GvmpRDat3Rt94dVHA3z5npvCZ0a6SoL6/uhET2QO+E5dIHqJyiQiHs3eCzHXnhmz0h4pBTmZ6jbD7hZv3VwRSCoMJpAveco+mFKozMioAyDCdvhhzr5P1uleUxZmSvpN/s4hnA0CVltTXC0lxUfeT7k3KeQHjqsLcZSPQzWdkZrZ1dK2AOk2kmzhpDwMMXn1MLIFLWypiWQBzPEulvnwULHmBLGcSFF0mSzbg/BN8PDMbVV42aKIiLm1qwhugFAL7G39TBaTBBIc1ywCzrnxebJRlH+kltr74dCiUp9Tq2uPSUix36Itu12bFZO33PXfU/lrWj7nPLQxB7xwDi+LkeFYEZQMm7Nw/vwHMahY1N8OyhaYhB2xtO3qMGHwFPo96bB78Rch5rSOE720KxkesRCRY0HdzduCIUhxwNwrwXbZ9BwR9IBgE34z2DObs7o+ubvWZgkyH6RfBQWMg3qCeMjoidlwt9E3fz6NCfFCoHAlhRQ8aXALF4botRsoXBF5JJoTfNSkHiHUCGUVsCVFdfvj3UaNkS+D2gy7zT6Gt5JUK8pTgfEYPxPKaqIKD7uHI/E6MwkvN/K11v+CuZro4T6jH3+S/SE+LQM4Lfy0uXafN0rQH4KBFaCmpfTOBvDzEmdr2md7fM6Yxn5nc/qFfBbKi88JszXhJvPrB9JjDJct8veJbIwtdisceYG/vATUA4ob14D5aAsFoEXoNIP+B3+F9TyA87LCet6wunxEet6xvl0wvl8xvl8xnr6V5zKCYB4DViegXo8oBZNrqx0myUpBpGEOoKeg2pF72Zq2sGYmryOAUtOXcg8ISoACQXUSK16UdAgnhArA2uTT2GpAh8Z20kQB23SsZGcDyuoreo9zNCgUiAirKqIOJ/PWNezhmoKWUKvAGV8+OmM06mhHir4VLD+egS1BTgeZVwOD6il4PiDKG1qrfjh9Sv8/e+/l9BJSS5ROhmFKRFMKSCKiGI5IiwxeNHcEVRA5Shz0HkpmMFvqscUDImCIQ3BFR4TgxLCR9Xup7dp8HtIcqntLkx1dWv96ft1y/lNMf70ydtw7+w9vXMF/34SnJEP1kv1X8GBG2UE4uv2zck43dg3sciH8v9Z3vQ8NO30hwJ801mYkGz2gHBYPosyIsPD/sGz30+tNsPvSkZVRBChrCtoJbS24syM83p2+UXRHJiuzLwDkM8YmikLAEW4ETaeDCbCubxBowOwHFHrAYeHI85c8V9/rvhwzghWBRiuceYQ3A2tXUIGW0lJhnIrnNzUMgjZnaRtvFmMLJIpJXmtoZkSIiEh6iqIT6MubBewyfJ2+smcKug73TU1IgjrUzNhXMDnVrzDuLsgbBQMMg/DJcJjStMT/SZPAxWKjqg36pM6mxExihDm2m+ejk9fH/p6EAd9cctcTlNgQvaGdQ1PhMBZ/SFmY5KVOt04adz4PmaihlSaCkXFJZR5lbXlCggjqnoLBaIC8CpxLxEerqnLIsxO0lpXmkDUD9zluogeivUyw/JNhNKNfVzMWwONffkaobqdl9iD9oTNRxzSZrFGAIk3jJ5cDl8uROo0061F9r4bhU75hQmFvxFMD/evlrTpxDqfIzxRvk6zkbH29Ufx09T3Q3owBNFpHrcbZHivr2IEfuf73jM7xfGZhXQa5kw5AoKesaxfuF+f/v4IbKdsvUwadPeywgC2hNk1/uFVJOu6oaCU5oS7uTcDJbwmFK6iiaotJJclry5K/JsCwK212nxvSK92xlgBNwY455hwJeFAyBUicCngBpyxOsxmJYXWXBfqeS4aHEdafN+9cbVdFFuOY21350fPZMRe78+XfpoDV6aLXVK7a1TrJyMcc7VXtsQ3QWoq93IZvQb1k5Z8Jl0E4xKf11Gnnxhg3MfUfn5FxXYEnrIXvhZlxN7S/QvU/9xUMq/WXe/4qjmt5vdffFoTPZ7o3wxd9zTP7tm7EyZyU/ZENC/RsRsOmR1a9SWVEZ/SE8Kfuw6EfAxvXAPtObDf8u7Gk2N8Z3ad7smfpHxXDtkad4S+c3lB1NVT3ApjO6N9/BlcDmj1jXpGACazWfADvuP/gkZnnNoJZ5xxao9Y+YwTn8Hn71A//ogzv0XDhxTup4GXJmGCStFcX9YpgcRyNDpz6vsUQUQ69OT8qnvwlsQfjrKTJnIMSR5tia7TkNs7BKdti8FmtO/asOIMKieU0jSUqtDAq4ZEXlczBgyvfwZwqo9Y0YA/VbT3wPufKtrjAYeDKAMODw+oqJLjoRYcDkcxtlkWPBwW/O7NA47LguUo3guSiyH4Bg+pSqHg8ZwPZB4Rmr9B+ZiqxomoB+GtJx4RSHxo9ojI6zQUFkGvbyNldIKmXd62q7ef7nER4CbcN6kuv3npLVkbF5+42GZqffruvpcgbQCk/AhNzg4ed3J/Laru52Hv9MpRPGbFz/Xhzb4+Ss/P67l0r9ubHLkgmfdXgf9KeG5ydwLDldNFJ2CmdHgJxYjWvgPbhfoVbTHv/E5lt/7J+rQ2JSB9wYoI+V5qATfG2s5Y1xVnOuO8nlX+UR33TCLB75ZnKSL2XCVveBNAsnpVodOpvgHXBxyWB9S64HB4wPlM+O9vCecm7h4hmDCig6M+8DCoAwF4I5j9hG2o1Gl3XPXQUbYJRlNC6P39hRsCmimBYtXaarOzexTkJdB7SxhGv/TSATzrmmUVHohZ8n8ThlwFzwY7D2MoiCTHTeyLxw2cCExjaI2o4G5MbcZ7V79ekTJD4nK7eYh7OZjh1gbd2ZtwnShCGG09u9DShWs6TwzW1BM6jk0E+p1w2PsNTQAdBEFRIX8QNuzzwppvoWmCagvBYssniJQSRIONhRFlcFA1R0hauc3WaqyDbiKNwDXiYlBCNLYQNQZrUy8Mhltd+IJP47rH0DmhY8/qSmK11gbAyhz2h9VwZOY+IREd1pVuwkc4ONUxvXNTKapgksTJgyCF0hzmsdkgDp85f5stWXI6lDmti6jL8MHtpact+znLjM5Nkhftuwns7bU5w8a5q77GTInR4ZhhzAys9HqqdUvAkb8UeKU1xlJkj1ps2daayOAt7qmuz6JeBysDEfpMBfvedamDLP9EIbcs4BVohVUBIPuX01r1Pu6Ncboua0gYJesjGVzGVKjFwwoA6+rjWg0Hl9A0mPLV4sZKUwWESM7Xj6aNi/Vb1px8Un6imxXrh+Avy88RddgP98zrR2dKvT1J8DO+cmVZX2vjkiD7ayxfpQX9BYXqZwPhheYx06xXmZlPMBdf2jKa8tn/wnBcqs7JoGc2uUeiz2D5GrfSveXaWrkXX1zCl596Wboh0fUnjcCBS0XTGdSXF5zkW/vvyYhnFM7lavYURZ+jXFsru3d3BPlOvyWpzIwemVZ58W5u+v56Ms3XXd9BHpz+Zk6mo09nz9uxOKGmTFxg9H7PI6VR4gb++DNQj+A3b4RHqxIClwFU+hE/0HdYzyvOdMK5nnEq8nmuZxzpP+N0+oB3/P/DY/1XLKWAiNHqrzjXtxJmKHtC6LJdlZ4XWs4M3kYEnSg9F6iGwF0E59k40vgRM+JrmueBLR0dlOGWH6WAzA0CDPEaD8qycZMIAedH6YeFMaWCZjkh1hVn48fZPIUZj8sZ53LG+f0C/qXi9MsD6HwAHh5E8fDqiFoLlkW8RSzpdFkOePNwwN/+7rXndbP8DYDJxFJuCM1T50qHbIhYLGG05oqoMl5UD1tlhslgnCGO392+dUUEpK7Me+nZPu5z6v/slq2wO72PfodsX7584RqW3gqY+1afU0bpRJi2TgHZ6GT6+zPcEbhmCm0e+xky6eaLN/fzSMTu2MI/oven8BJuYJLkViN0gtu2cA4VXSx7eH2zdp0EIGRlxJPKgP/3eAlbi+lRXFuP+fkOvj0leL6EkKUzDC8wLOdDoYKzh+U7q3xhRWnF81wSUUTouKF8kWTVNoin+gpMB0WQBfX4Co2O+Oe3r3BqFYdjReNiCmo5V9w81gbYpBPyUDfM96yPu9dSEsz4pWzhnizsG3tc+ct0DMVZO1kg0ltlXDmQwKjcSGenH+6DWGi/V3pwxjvssQ4NRABJ6z4mvOXUdC8QNQGSHKIMopqEVIT4OsBoNJYTFXAvDVdE2BhopouGho7IHjdk6jArrEaX2BjmpMHRd0FAjY2wWT2B1TjCMj7WBfa2rENWnYUosTjt7t5oicN9MrQOJaZYE4SxxqeiApSmELgQryAL/GK79ARecYSj7+dxcaYrHZmUEuwiWbPEEKZ8EuoNAflHEJc7KrRZ5mlHB8ymYU2EmB9/zL5aCQUtBWlhmwsCsuVatz3y1CJtO5+72W4hEaYOgG8QfhYIj4dyd8ACOe6gW5VklTJvD0sRZKcDiUiUPTBF1bZIUzoy3r+dZ2PTOdTRrT0C8AJ2GYgj9mvjLHTQ+tIXvGYLOBS/o6Jz2nRq3/BbkDEGuuFf8pBFtBoOaWhMKJrg2pjd1hqoNTTNFSGvi7uyJKXexkksCS+x5l4BQxgJDkqLG6MVoND27JAcfOx0Yyh+0zpkVqUm4MyZ56ORkfXcCnpOlDR/gmeTwkIvNmZ1wwSAYpQZLAmfM3g2vnZ4Y75qer5G175fS7gUjO8fVnx3POO7hwcfQ4P1qy79UvtWvhUvZqjwJSTVf63hWb5Et/9SlBEvVV7GI+A57c9onL1nr9MYX7bYAfNXeNAMGyumSb2kN49/3oncm5FLcGRu0kIq3dMeUpvGkxdIuKGichQCTWFjAFjPwIc/ASDhtWkBljc6ztV5t1pFUVHWA+raUI8HnM6vUc/Aef0DlkqoBJyO/x1neovyFuAz4+OPv2I9nEJeYBaA7jXfEr+ceM6uZ+NYMahTYDStcgWrpwJrvXDjJ+Md5T+xZzMhgNLEFiLZeF7N5SayDBHWWRimx59XfPxVwjOtycDq/EBgOuD8xwPwfsHD4Q3K8YDjwwNqqTg+LChVPCAOS8XffP8daimoS8WhFvWcIIBC7mIeIObxQOpdTUXkKq54yIaNej1COhVQWeJ+UkREUuqehs/F+Iut8qG7ml7Iz22fubYzO15hN4nxeGVv71zHAxN7phcv14xBcng3598HwDg9q1+edFxFtbovLhAs1L0zSG0mSqSMa+7BZ88S9l+rcyr+CEh97HeQ+JemYe4qNy5kN7KimMdGBYUYdakgJqy8AuolQecTzqczCMBSF4AXzS15e7lZETHbKKM1xW0ar1iKKx3R6muUIsqIw/KAEy/46bHi41pQzorQTCgYshDMRJZboMc2dx7oP66Dz5PWsxBez8G5EmIUfqWKTVi0M45GDNsGChq6F1IlWZZD6bLDUZu9U0QIlWIcciSe8vpG2GDCNUYOS+KbVc9lC+HjaaW7M8zcAKekm8MlfTYlRLI61vrnh9S8nz6faRCt/V2E6QL2VT1Amh7iNFVicGqjZ2rUKkSF7a6E0boSOekjYJZczZQQSrj5uJEJRcmwST/Xvt45ekikDgpFl3hS8HB4WuSxAURQ2UoJYWnX57QWBmWWwepCbUKE2EmF0qcpIYomyHb5JxJDOe4x+yCABzf6YEStnjQee0X3qNACjG4qpdOhELQ7G4sQnSO3Ssp2sdt+jyXPhR2UJswyJcQUXyss2zN1expz+ttfjQEd35qe6ZPizyRF4nS/G66zujlIktiv4wRcb9t1Ppv3yM8aIgtNRBFqz+cV4EEBK0yJ4TMSa6TGyZMpN5P2D8sZAagLvTIZYDk3Kpfh7BAIOkvqpHTqxrbrmRIUA2XYecQoc8L6vu37UmtHLDNrfgyGMH7pTGDkdXBpFQ+EKY3PUlw36pgIb45n/Pia8eqQ6nFkMC93E4s9yt0C/dSSOvwlCNiv0rthp1yiN9NDnwma/ZLn8QYd7KZ07/jBQd2953YzzqOx8bj6uZbGdg4nzxhe+w0weffOzV+6MmLkBWcenNeG7FNta1aCr6Md7Fy/NidGW70EHDfzrffXvHvW3sWjf5pyd9v34PvpvX0e8P59u1PPre93UN1Qh05l8Gjbub3UdrzR04ZOoyV6koc3pTTg4y9+l+oDcHwjCaWXCmrKn65VElA3Rm2Muh6wrA84nl6B17/DQmIhe37zGqfyZ/BPJ6xvTzh//wHtePI9KaIS5aPTp6eTdiHBnMtoxmB7hxKD2FbliVb9p4Z7gEfjABn/RJ78OXjj1Cwpz6tzQ1B/YKWJT28f8e7PH7BqXgn3/Hi/SDu/vgKfDnh481qifhwfUGvB8XgQRcJS8epwwB++f4NaC3L+h6wkKBoW2zweLP9DH4q5uqdIVmLYp4dRwSL987Aq5sUQhomxF4fVO5F1+BPj/p3s/1HCkUiSbX0xuX5nloh3UsXkShIedJeNcwkapJf5X2IOLhcaXu36nZURI67Rex3+HAywxndH6Pa8Szb3Ofd3gq93UPiTvB2uvJLp385w0y7OypVpmdY5rSDx2sy4lHzh2fTKHYT+3qOXPRsvy0imZ2QSyhITSmEwF1SzazyL4ra1hjMz1vWMQoT1IDi7lIpsXHutfBaPiCCC5Pe5PqDRA1CPKKVgORyAsuCf3r7Ch7WioaJUS5ozQRY7Ar7ZIzfD6J/7L24WbmCBTgnhNwbFBNAL3TafF4DL1Xrbm0V5gaIm68F+GwCH4biG5OlCGjGnmITDvDDcKiA8I9hpfRtZ5pRUF0lzPp3naNfHQRmI5gqOENLJUw1iRoxkLb6d15HZNY+FOHNNMbBFso1Z3ZIkuasJAvMBbNrEjmzieI41wRMB0U6pPhX9igjmSfQOooRo61nutRbbxOqCESrazybINOMpVwSYAkWhzUoI8XqQfhrR0ZDijgKAxsoXWLgfVVfYKGHJPPRtf95NkVIygTWEZ2Mb1zTQ4l0bHc3zl4mKTPS4cqCbv+IophMlkz6vCYQprcPYLqyC8x5NUeqvrbk56aDPWNc6HDPBfwwVeqfaBuJFvFe0fwbNlrbp23dX5e0+GLHNNZTLeYImpSPURmWK3oxE8vswI8HlfI6OX/Vdt4EKpMQJClASlmIwVmVmmnkIJHgaN5AzHYEzJbdLwG5EXtFQR20V74RVE1WHm7X49SApgnOfvGec1TL6ROqrDJudobpfVGlLppAadSTqlZHzblguC1cKabuihKTuiJ4xEl53Wnd5prZKiNRLZmSFtTBdKf8FbI6TspT5HhroW/nKyl+rlf7zyyXObnKP9299K5+umHzsW/lCJfFt9tPotMwVOGXARqt9bkC/leeU69P19U6o8fsueMI9KGP2dOb9hG4qI+vljXK+IPtkPYHe/1GeZ6EbyXL/rYy1PICWN5LXoB4ktFNbUSEGOq8P/yO4/B3e//2/4PH8K348FpzpI355/Gec+IN4sjO7UR06GlbHwYjLJFS1yATMkix6PZ9BIJxTt9b1HLkb1nPiLbiXLzp9qh4EROBHxvmnk+AHU1AQQIWFF1V+tjGwNsb6uOKwFCxYwAAef6poHyvaoYBQ8XB4QH044B/+9g94OBxRlyOKhWSiAloKllpxfDiiqrJA2lNvawtrVYRDEa95DXeFCHlFKCmhddXnCBbWSTwn4r7R4fE+1Fuaos8up3KmGcMXL9NwTPqFu+uZU7texqdu2xOzpwjPYxI6yc6T3r63hNFh3/o1JcQuDBO+3hQinZzkiozgYht3wPM5i8HVf8Z57w/Z3Y2wY+iVj/22t70i6wuUZ7RNxndrmDqmhpUbQJIrAq2hMXBeBe+u6wox1BUvq1vLCygiYoZGhUNYIJsQRL42OmJdXquAUVzFmBb8eip4dyZQVkIA8wWw6WMvlHtaT65LtXplBHcgeS2JcO0FRRlARep2+I19JMPYs3f1hd37A3IfDvDdnZHqCyVECEBHcVEW6OUcABYeBoxOOBRwJwoL0LiG6K5twtB4HYmgUimjj3EDuOgBc4Fyy3A7ouTxiUmEs258JNdB03wPVlcWtnVn8UDbybPShuU+sTApIx1oHjV20T0i2urXCoKAgBIa3Zwn+EcBLwEeBsq8SuKVaE/GpcESl9mclEJAM1TOPi8+X/5XagyichzfYU1S/08YRVUQpQljAmgdvDFMeJkYSBeCEnyNZALJiTD/l9/icYk4LcOeIDv9nay/TtkB3TM7KIcBD/8TW4j9s/NKQYRr8+fG/TMw3fYn42qiYW91wIwA9nv45jLFWfPi+U7IPAB63DethWJ/G9GWmZoNOOm6rRggrKIKChqvjvdba+IhkFYENwYKD3snYEeGA+QePQqA1Fks54KEritoEjdXn9HKOkgd73G06bpB/VIUJnMhzwQTgVzxbM947Zx3LIQ5pAQDQzzbRCuZ1nXsl7F059zO2qHuIYM08mvYvsxhy8RDI615P3eHuvaWnbfJl597iTLW/RSO5M7yLCvYvVd582Xy6/bqxmd2dutOLZ9ywp5WXoLxuKsOpguDG/t6e9XaehrAmyN7j+YaldhZubrT9BXfxN3nv4gnxYxrv/g8nr/3n9PNnbZvXQfXYip35+qta+vaY7f2l6dftRgvGrTU5v5A+7zUasoU4u3PR7l9uQxvfgYpyOf0tLgHV/GVUftkSu9dC5kZZTS8s6GB+pOPZzeQHoDRd7HmEmXXvbuFhd1bgvIbfAadTwADFWrspQmgiQGUKiGaqAhTVKoK6RsIjOPyA2ot4N+/B7jhiDc4rx/x9vHftFlK+6P5Z8d3aQLUNdNrHKwms+Yg1NwN9mIoISyBdITv7QYiGcR4braVcf4gBpi1yGNMrMoRVqXJKooIANw0XBUk3Pi6HoCPB1CTJN3LwwOOxwU/fv8d3jwcUOoRhSQEE4g0uXfBsliC6ar0bg77Shp+ya6HF4RyyPKcG+5VUaooE+1eFdU8Iqr3myj2sgxhyBBGw1mTUe2THeMd6i93NOT1035qBGwr9NrLd6Onvq0sJwBuRal7xNC2icugBG2RlRFyq+cRN9eNz9+DcGMExp0ywt/2Cu4/v/ZevVpTNwUjoTlUsM807JbpKxy8cUJ+em/kdS7/7tqiG9bMuF+cRh754Ru6u8vr3klTZ+Wjj4fIAiRXxBlgMapsJDi2oYKXhj1vpVm5WRHhlZKvbQC24O3fuKjl8rm+wlpexcv1FUo54Hg8gsqCf3z3Cu9OFY+ooEpJextVEbCJe75lbuaQz4/b2fftJAVr0290FxIiaQ9dsJhyI7DBlYVhgwfAJeHMyPCn37x5KB0gPPRyUOrIbV3oDDSNh0gchHonKHXB4wC0EQEAzHreLN87gagf9Ayz2pffOYSQ3G4WL9KWVaBXMaY22Ezh0WJ+5LjVOjvRWA/2Zuhc2ZLGKTFVIng0C5BVLfxZD/jwnJB9UrohI+ilVtIPuALG1wKrpbQlhYEoITzJs4aBil7JE/CnCfC9I/86lzyOZNfmXQD0CapcidY0GbhZj1hfTHkIW9+MxisKD6bVaX1yLBD5LJkguYChNeZlKZaIq2z2fOeylw8uMSmXsFGT3b4hshTfOKFHFvsy1nZuM4fPib7q4a2eEhFyizq4XYnjZ78v9ARP3PJcK11ixd6WJFBIJhYThvCzNOL4CyE9xF0dNBFdngrDhvbuDoHTzSbH3tyisB6DjXUVJbgMD7HjoNnT6dCmwK+OI7SepoRWZX1uw/zpfPockeTD0SZtzXfWNMzgtlowWfENIlJlAMv7iDWUvRXyHrGYsqUSuBHgngeaVycfqzknTb5ubVpb6sEhy1vOVvMeYLBbOmz2lY4NU55jw6naRisaaxhAR3TIc34qBWr3uuOT0BqHMtrPRvO4UmUZMxoRalvxu0PBw/EAPhxwWlesYAkTlag9PzYc38Z5PRZyIW7ao/2u+M2VZ8G9eXmCn+ny7eeWDQjdhU/Q4G++XBqTGb78GkrQl/cqHb54+QzC3a+13CUInj57aa7vGdfLa2bMjmenkOD2yO/miW5pkXjpOdSIEUuptWuhAC9BtPdrl0e5u5nJ+TZngftnntPkZyw8fN729B3lJonRM8otdRuZCwBM+vtG/OiovjfFyJQ2s1xrideI6s1oxv28+4qNhYdWUgilMYg/oJ7/CGb1UljegOsrF4JDkyd/h/+M1/gbvF3/K5ge8ePxP2FdH3HGI07nE37hfwSwKgVZUKhKGrK6gNGwLgfQuoZsQPnOdl7RyoozPco1N9ID2vmEdV3RzidwW5UNVt6vQPhu5Wn4EXj89zMYhKWKp8DhKAmlay1YHyvWXw5OCntoaG6dAaEpCF4/HMCHBWVZUErF3/74A14dD3jz5jWWWlHqAioFh7rA8iCWUlBNSWAeEYhoAPac85bqEWG0s/Cuyt+AnP+AefinPBMmg0FeA0nOQ/rbePUtXTbyjcN1X1Xz9Xs3tk88JPlGuVTLzn1nEC6UsUub21e535vKDehZqw4ehsiM2XjDV186n0n5oYHdGaAxXmr2/m0nRTbKy3zgLe/mZ7qnhgq5GziChjS4UH26qGherjSti+PTH4JHvTDqoauxq/L5uSw6Xn4jk9FnONB8t4w/5blFYpRJVEEMLLWELGFtOK1nNGYclhMA4NAKuHwKRUS2Qu4SqyI2BLIALIBodMRav/fftVRxOStHUF3w9rTg17NYinYJenUeMgLyMhvzXaJXBWgujMj3tpXxcHfSkN/fijfYF0e0lt0MyfE8ZfRM3a/tgubJV8uNoNBkYsK3RMI4lL73VfehLBg9sT0hbeV6Inps8zoC8gM66uw1q7k68h3IVu+eRRUjlCRgV0J0FnZ7Zffm2MM0E9pHRghD7buD7k9TMDE+NlGfhqK0l7ahx2zN6B/zkDDXU6grbNcfm2QlMIwYyUoIr7z7bTCUNP5aYTObEe5k5NYkdXPOoKZeG6Tru+8IgmocR3iYEO7XrJNCtjc6Aikj/exVNAxmJ0zdoyzIYTf80+2V8SBQUBh2KPT9C5mx1aXeJtFRr5OMmPXm2OFRzOHC5X7uZT7zgSRzo++ynqCTfrvXCtBZxO8rcrfFl3daU1JHYv9tj3bbN9ZE0sv2rUyWRgyxrWMeXojv4zKIUFCGozSRtMLo76WDxpuzyS7kMAcorAkA7WIDOgWHPF/Uu2JDIBbqQlCxhmjq9q8qDYh46HKe9dwVW1vsuBJgF7Z7AjoNC6XmbJrBcBg3osF7ud8PlvCwL5QPxnhrqL6fJLiSydzOHQTrjz5fiPDqoBZkpWDV/DwlL6a0v4IOMXwxO/+gyyrTCbYxLp4o+2VEnF+i3Al7nBecpvqGPnTHzJXnr8E0n6Lby3jMfaVlCuONgI+P3bbKJk99hoHa84QYi1uhPaN8EU+Ir7FcEQrNX7lxFT2b2Z3Tff393daf2N74PkOMipobGYlwpsINep7V5uUyq3G3lZHUGe/dWK4Jsvdm4Lm9n62Xp3pP8PB531sGzw2vfCJlxF3bkuOBztv52nuIHs+pf6OEpI9hDDPg6VwLBQnW4Vgy8pEAPoPWM0yWsNIBqK9UmK51F8ID/QDgDT7wf8fCFW9e/R7cGk6nEx4/vMXbj/+MFRLmoxBJklSGGOcRwiCHGMRN6Fol6k2xaFIRp+bUIwLckmEdJxbRaHsCN+Dxw1no5ENBLQXluIiCoFbgdADaK+VJjfNjMDcQW740ArF4b+BhAVBE4VArfvjuNd4cDyiL5oRQRUStBzW6U08IV0SYp7TlhiCAUu4IiMdD9ohAMUNM4weLf/ffpOvK6HAaTt8kP6B0rV9HiX6frMnxPJ/RLUML05IN2ezJQIt79EQ8d+Gxi/t8ihNHvmZTMp9nfP04breXPcOprXGfjsaVs2L0gNhXEPEUUOqu09BmNN6Fe9oB6RotwZNvViHz7E5qaQy7NfspAovhjOW4DsUibOv7wlmiZ8ZTlBHjvghjaOtkL+sy3Mb6rBtHYgfnD7z2RVjGc8BQBMd9w0em9CSCRGdhCWFd1oLeaPZ6uTM0E8Gs/QPelNBmEAit9QGn8gqNDmgQBQRpTggqFf/07ohfHyseWRLQejiZktvjzSKalU/hYmndtEPbBBZ2cyP3Sdf6orW4IHWCfk0bp98dACCsc/2zdY9JZQMHT5DDdDN8+Tk5lDV3tLcxongCXCjuqzIpKTwm+YiAp78SiDYUVpf3W+3MLd9ABCyPOkerpCSczD2cEm0J6cicxSYuJsgF1CLYuptgMStiFHA1BR1DPBqGfiWBoQmJLSQT3ArYIGga6kcEuG1dAbBucutQjBcZYcZAb5E8jnNavwqHxak3ZYh5AEjcevX64GDW4O8O45jWLTGFgsiURZ3GhkJxQ6k+Iwi9k0VlvyknhOt3BNk3IyqR14798wnwdTLsDhjKZQdN3jEcRFQ6nFLcAkHhiG1ycdy3Oz2NB5swPtaIved94r4PGXrq5iO9b+NLee+MPb+lXH9uE/IpeoiblBDd3V4xa8QxoSdsxtBUBqvNYyh+JhMkG3uTeyHWQsyB8aOuPO4IQE7ER+DBpsqEgMn6mnIDmaUAN1CRuIrys7lHUyY8jI9jHeRM4uVhiL2UKCtdN9waWM9YZoWBG9bWwonKcBQSTqRo0Orx6bHnG8BFQraBGgpKh499r8cPxX/ei3RfYR4ZI92bZi12PB7xcDyinH8FnR+B9eReUL6pv5Vv5Vv5SsvL0+vfyrdyUzHaVH4oTU7pDMzU4bfyV1c6owak73vrYXZ9j/6Y1X0FHDxfSTtC4MFOmT3f3yysWv5t9LzzeBdKPb0Hr4/KxxHo4fdAea00fcUP9b+g1UesJEqCx/UjHg9v8Xj4gNP6Dh/xASuv+Hj6IF5Ljx/ReAVOj8B5RXt8FB71dAL/gXH+XQNWRlkbzgSUNeBrTXjZBoCZsP654PwRODcJfurho6kAXHB89R2wLuBfX4Opgo4HoBbgUFHbgsN3R+U1egNUE0SCCD88HPD6sEjIKoIrCx6OR9RSUZeDePwX8Wao5QCiojIyQi3VPfNlXoQnjrwOWblQPXSTXCtOc3c8pfG2pb8XvPhIcXuF+nt/De7du0SGfyJ9X1fy3rlk3Hu9nnt27E4dxjICIWP2e4mvvBU8r8NkIMP9XYC/8UZAlhn9xsogd8ghqD990wWlAOd2QmtnPz9aY6xoeDyfwGAczgdU/gQeEVKyAMmEqw5iBhcAgWnBWl77b6ggoVEFlQXvThVvTxSJqUETeWqv8emguWngL6CQG96PJzIhMrotbusc3wslhF3Nh8AEnh0ZWggvZwSK9TUL6BPS6+bOBJ2GGENI2MsPjUAfhIEJZuaMSB3QnS1uAsPuKEzjloFlFYRvquhK1g/m2Y6DmTr4esh6wfCm8H4/RqHgHDh2oZwJiEMYnyWMGR4VPKfQU1m8Gy2mNZSrQ2hm+/Whwl0OKxizkMhhYlz43dK8dt1Si5qhj93c+broWsdsxKYlM4b+LHfC4FEJkUHNu1AxVTePgcRzk0qoUfzulTCTdZOGwGDp9vpGoNq/k+ufPjNpLdb1TsVwrLOBc1b//CkjYHt4R3y6PyL9hdGCY++5frnGvnak4fhJVzBRP4djHVpDj+uAvDBd6L05KkK5EXhcGbFYJIG7bHy6Oe/PjQ48EssBe5mJZK9n74QLx9d0/rNmD7pTWZUPDZLXIQ8Ui7WZeUyMCrc0EluMnvENk3hIdLHqrxO8WfkRFfLQOfb5NyWqu68/noD1gyoheFhfA2O1w2jPwlLZc881cPgtkfzhtfn0Oj5nrPC98pwp+6LgXwPc12X38+7yNczRrCRTiefV87wte1v5kmO417+9jo/XnwD7y3lMjDj66W2NZbdXibfIRl35PZoRDje09xRIrZXPsUyvlX0PpU/TRk9Tx7UvVbY066WeZ7p3h2idyil26thpyocjIfpOoHr1PUTITO5vOlnJAA3Gi3t5XbbW15j/zk3xCbSegn5uZxhvy0Q4lO8BZrRyQiNGOX9EaQ948+o/4HF9B+AdzusZrb1DW8/g9ojWzgA/AjhjXT+C2xkrHsHlBBwe0ZjAJ5XNFBsIidLEDMljyACfCtoZaGv1EKVMBKJFlACHAvCC1r5HpYrSDpLHoS0ohVAPlp8h9Vlpf+Pxv3v9gO+OS/CxmiQaRUMwLRaKSXJJFPOI0PxzZZFP8pBLJfEipfPclzDL+hyQjIcSH2oTo0Zafj/hvc0uHBQQT96mey9ynxR5c7tjIDNHv7l8sclOXXRrBZv6trldbj+ngv9j3p4bWQlxUxsEDaE+ykByUwNPtali5HkchOn9bV8+E501tn5zo7efsrdVeXu/N14FLqu4/Z3h5ma+0y2VY/Xyu3tpk0vtczQCYnbDxaaLWfC7GjC3hvMqBo5uQXlDuVkRcTo9GsQwAaEJLuyiy6kgwrhGEDexZUGpFYfDAcuy4J9+PeLnjwVnLihLSky9gfvlV3qerMsP9vezda855NljGxQ50Chy8PcCzg3dO7zOkATEnTBEhfIdLBYeI8u6Mn2xR/cnU2kj0OOFVIHWR8Oh5IJmI+6ZXag2NL8ZC7PmlmriiWb1tBWWb8KEtSa4p7T2xAKXU+gVa5sxDnCEP2FkMboLXzJ1leYq1+vjoUmz4vn49Pmxv+nFojCFlQNrvyEKl1U0jOu66udZ3tT94bQVy75rblndE5SbSdD2I86d7ds+NJPlnmWWcWrcfKxcDozcx21eCB/TYU0QCEwl1p0Ms8e72zCGIPeIsPiX0LVg/1rTAFLcn7vd2kthebrxGPagWZFsGdJhM+u12Ifs7r49w2X7fIKMtd+GRw3ErlVDMWygx10nSPdONoKsYTu20toOr5w0Bk8tNvBse2pbW09Mpis9YMjJst07pSTCyI6ZNJ2b5jpFKW/a2KwNu2wEYIc7e+KbTNHm7QdgRkx3XlqEuN5Y91zC/VpnKwXUzMON00uXzyfHgXYO+CfHuvF1Cs+TwmsTz2wN41YUkbW1CU7xfitD1yTplDG2VEqse62cSgwsGwyAe3zZyREdjzMg56fYdjmud4nKkXCixh5uhn93D7zPXb4KIL6Vb+Vb+Va+lVQ6D/NEO8uxnwV138pLl7k361dSvoRk7RMWE3ruXTdlRHNyTWnBwY26oy3lm7O9HV+8N3wM0Oln8PoOLW8tquDlB0lsvSyo9B1+wP+G83rGsb3Hup7xvn3AWs/42MQj4kwnrHTCiU844QMe1/fg06/AL79gOTHKajQlfH9LTokV1BilMZbXK5YHwsc/PaCdClox+dMCWgtqEwXA8odXKLVgWRaUAtSl4PVC+PHhII+X1EH0fr1LIVST2EEeFh3CoooDS04tioilHGEeESBCqRpeyUMzUcJNvfGORXEw3jV42JSDDkYzJ15yw+va5f5aNJUEALeWl9jre0qIp1UTb7bba3DebFvZHX106dR2DG9VQjgsk+d2uhM8rOW93JlfBPv5Wyh3w2nDRJOx/YKdfq7hTeBT5Zftpyok2jPqd/yhC6NoXtlDqSgLgakBjbBC8tg+nh5R24rH8xF1Fo5jp9ysiFgt+U8nDM6nim4yBixWPXMBq0CxLBVMC85Y8GEteL9ShGOaKiG0Tpf3mFDi0oKZ3bPJSRv9xkW3FaKFoGOLNGYtx8IIa2rqPrZt5ja4v55PlXzDLRuSdE6/OtKbUiSj4IYdObckgJ69nImT+NeDNZsOCqzosHMWmuX6mjeS5IMEF7HmLqfMNaNY1JUQg7Kkgwsx9vOpMQGYjpdTIX0sNMuP0NVvg0FOliDG1FYmw5Jhc1vRVNBOAKgWW0RdS56w6AY8s08nhs8Bjxb/3D8HTA5zvTXWHzNxGZK9nWjLzsYquh4KjpjXiM05liBhaBO9bGzwngMhC7p7RV7uAaXn8x0da12zm1YvoSeRBu8zc0nYm+GzSmlnnPqGM66iyX35KhbwCV8NcRlnQuERL0RLoYToabyUjNwXWiK8lHCiGZi7eH6+TqRqXSu0fTpmK/CLoyBjfLwv4fkVkeXYQ+DZ+i4MtEIdrtsFLuP3fHu2J70vBpveJ4AbgSr8HJfVoRj/4tk4jD+svz1MW2EDDZ9DrURd1+a9HFau0w3kyh22P2N80ATXpfIpwjt+2XJvfxIh+zWMxa0wfIWCrT2efQT1Liak08q+XBktlu975/LzT9lTM6rhW7lQnsCRX3vlk+HC2fH2Qm1drUUNJoyZ6tvdGh/dUoKKf3q51v1dsG7bgkNbV87A26u6qf5PsY5ukwVcLps3d4V+t1Z4Oyx7+G30eNgaw932Hqd8Yk4bT+hw8vtKtaY+bOV0iebbIVV38TYB3B5B7QSUFLWAKrC8AYPEI6EuOCy/R6EV7fAGa1kB/ojzeQW1j2htxbmcsNYVCz1iKR9R8Q6tvgavBxSsoLI6FdNY8kgwVqFviYXgPqzgldDq92BewJp3AXSAeNxCFBG1ohTCYamiiKiEVwfCmwfLsSAdISc5TUYQ3/0BzT1Dpei/qr/VI6IsIicryROCyIXHLieLeKbICtOclzBbDWYRSUdtKD91DXVslBD2/dJ6v4ZI8zrrPmd18uS5+8vII92LO6ivxGuaXR9fjP08bMRLiobpjVznjLGeQpfajqmZ8Vf23uXp3Zck3VtuzR82K9cf3RnbTiZxXz+utrlB2Mp/3ySgS88M7/EMs272GLtRr8tMbNdvxTB3lZwU3PBIUSPotaHzDGutAURY2zrNG7NXblZEvH//HgAEACIJiwA4FMyhrV3La6zHH1HKEaUuqMcjjq8f8I8/LfjpQ8GqHTFN7qTr+nEPpXXjUN9LiGW8YYdwdxKnQ394OyP96MlkWerNNvS7t0QwhNytiNSGLjxusXC4kxnFO2kRu9W0utbkmO+ASNHkzErtM4GouSV/EPU9Yd8LrfqDkzVmY36lNRmBtp4BzpYZOmaeU4FcHCjt+AT4Vc7joHU35l4LThSWwhiKH/TWlv2xPlh/C4AGTo1Ft1sS1ElegwKC+rpEq9wEvvOKplpFoyCJingtjFASQJC4kM3iol8oI+51K/x1FauLEs+YtXwpLO6s2qc4qgT2jZDFF9hw2Kcly7NTbhSEqIU1KTDk9ek8rk1ifqolOUhSDSZbc1cYMVShpcmdu91H9mzekf3vqVzYp01zaKhHRLZEiY6Puz2tYDIFSp/zJXYax5jYWOjvba0brsXX7BzlDW9wKAK1KXRfLgnI96hEra/HNznFm1WdKuJ8sM0I+7555HFnRiPyMHMZVbuwG/34Zcyqp3hXZ9/tfSKMOfWosSeozm+1ZpMha6wofilUwIVjPQ/FrP2Jtsq0WDNaN3P0x7u1nRhT3pVapA5Fxuu6wsIfCdzk9Qi4BA+PpvPLZQzJpOdC672MetppYGyAbt5i6ygO1J+lCu0BZvC6oq0MWtmVKk3n2c+jnbXzrczKlUPkW/lWNmV2xn0r38rXXBKf4/RO0Pqfbj1P6h1o5FteufOBb+W3XjaWNsNtDN7I++wVgJ47md24RR64r6i48A6U7zRSnBv445/AVNGWH8CQHAxEFQ9U0RrjcHiDtTUcjyesbcV5PaG1Fet6xrqecT6dwPgIxkegSTgo4ccaVihfTQ2iiJCxOrcGLsD5b8RQlqqFPzpk+xYUKjiUhh+PK4qypZWAJXQBwad2vzMPaBeNEFYFg3o+EArEI0KTWpeUpFqEHl3lzuuMllKU53POc9ockDNYuyvh5csg0wp4LrWdeMQ7mtrfKgnnT/n6/VZk3HZ40N2W4ouwlWmGburQzkMj333pGczh/msumT/+GuytXsywqNvOgZhMXPkcA59QbpNKMIW3L4qnTssZOAMrN7T1jMf1hGLOCzeUmxUR5/NZhCbMKaFrEqJBkWwpaKho5UG0vKViRcVjq/jYCj6sSImpc0+TtPJCmVtDXB5gF+nduuomz/kkDlYDt9KPM0HhlHZIzewOBXUfHYyy6PowImwQOALjbXv2X1L+sL7gSDO9xEwh+NqMV2DJWR8YKrjqUYIL07oQJ/7EbERTPzqBE8cY2BVVQoTwknwcBjF0MCQqePO1s0H+89OgF9Rb2BfpcyMxynAhGYdyS4TarUsIG8K0aIqGdWPx2W+WCWh7YEgszWZqTfZGCgGNCb5yXR4Zz9jvUEAkoWUen2uHpj+d2hs62sVRtHXXpG6yfky0xNvfT7N86/scP3lHBzQOxYzkI0C1xhSEmv3tHkzsMQ1uul2jW3iffvhsByl0SGEJv1d/p9Tk0UI+PccBp6zj1LKvm20/Z7os2y97Pk0XmTnZSIoj82zp2CseoNywMRcMRFJqfVNzPdA4J5zXcoYr4ctOWcfeOVN2mVcGMfXPwLZ2svzsW4+R0f762iKAmUSBQGG1dtHzJoMITms+2XJoPpqNEmLvd7e5uH9R174ZQ0D7mpU7Y+Fc3065ZMX5WyDiX8JC9FuR8twhHJfLVePAoM5ub8TxgTVy+6vy+pdbJ7O2n7vDdrtzrZ9fdG9f90rYKzT5dlfLF+jET702nJb+UoW7YwuAnXMXXnkKvBvp76QBm4hL9fP26+ZMugG8J+eC6OjS/fPwc+CU8Zz7lOfeXpW30tOzp669yWlFUoKB8o9ZoTkdzru/Ej9hVbuH9vj0WK8ZVfY8oF+ZLPtMxvVNMbg9gqkCvCrN2VDAKGCx8q/i/d0WRm0S3njliloPaG3FspzB/ArgFVhPQDtJRIEmRjWttTBCFFIdB5bQx+eD5p8sSleSiMNMTl8IOFLD68MjioUmRXg6d/yBfaPouMli5EOfSCGagmalzkNC6jcjnn6/iTc9YUtoDNN0kTecXujW0FZeNVlfeX1eeTZfHtfqtT116e4+e5LX8vU9m+ULew3djGdo86Wr9pI45Coc/qB9bPd1/23/yqXre+PKU9BeBv/eg89n9qwzWJ53NFD6uC7E6uRymem9hRaYlA6vzgRIE1hFppRDz6cm+bK8Rt6fyFqQKkly+sB3GpWgEHhVLN7aJN/zfrlZEfF4egSRekJQQWkWt9+EAoRzOeBUfsRheYNXD69wPBzw8PCA//Z+wb//JPGnSxELx42AZigybnQLpXQV9pH4vYV/6wX5gyfEUJ8VOSS04iRsGpewt69fsidE30SQzLYkd+U5nJ7jEBf3ODHvlPTRNCQQswvBUUgFXQ0NBcWIv8ZBRLAmLEnjYc10G3HYeLuCstbDvylKwHTeBIPfEWti51ayoA4iMOao3wiFzn1ID353n5QLkjshhZDKAxh5ClQwbgoF2HeZBSKAC4Fakbhqw0HJgBJO8o9AqHVRpZ0811IcfQeFxHKDuwnVvhihQzFMFtaoaQav1pSI4tpvCBIX1a1f1rCSu8UssDaysFFCUMpf6TMxa64I3kXQHiqKNcYdN0ktwWI1vrYVrJ4R5slRUMzYpB+Hcc/0DcKp09RVX7rDduf0Q8C3mYtBH5Mnz1rcJUJ6wDfvdZ/pwqw5n+uxhvS84Yfc7iD37escp2yPWBnxpB5gVMgvKbYEgRyHmBJCd0y0MRkSv9whOQwAXjgbNkSPCM03AnN9lrRuViaBoLjC4M5J1B2/aJ2a7GJVkMq6gi28VlrzNj52fDA0ZwsgCAyEHnOME6Rt5yUZvevaEFwFbUGSPzMz1gbZW61pQujFK5NwcaliIk9uzWCQ4pKiru7idSH73+Dtzqvk3kE2Jz6gw1TpONV6wPH4CkuVWLumuC2lBJHc9X1cIN/Kt/IXUEYl3bfyV1O+YbTnl6CF4fxrRyMpAdiFq8FA23xGWJ8z38+F+fP3+C+jXBq3y2PaUcA3NDScBbP5zkZdXetG26bre3Q9EtyJV7rYTwWtKb1nhjxdOCluoI9/RgVAqygHSOnTpjTtsQBMjEaMcznisf4g+3fVsEvcgHYC2tllGesqdOyqv0Wy0fCqvUXBGUYCmwC0kEPlcowCRqEjegyRZB1G83fylfncGe+gTDuEXzZvDI0w0uWEiHHPdeZ7Phk3LZaE40bYhlk0fmGPzLgVpYzPjQa9t4Rv2VvaLl660nlSAYhFrdjk+7ulzBp+YtnD5zcrIe6uuS+/Fdoh5N5zIcC+MmJSVFhw88ia7PmJg9XBdhegzy85pFMYLmIjb3lWGzovK8TbrFSJ3LKy5JY9nc5bZ4ML5WZFhJUsvGIQGhcR+JaCFRWoR9ByQF0qWlnwYa14XAkfmwgtHNnvSuQI1CH6of2ZoOmCcEzWX09MPrfM6nDNP1JM85kWeQ/YUcjnz41W/5O38yZz4SgJ4jVknSeuq4eT0DLbZKS6jeggVuGwnZAboAfo+lOsF+4mgfrYZzk3tkLU8blNYa03woLkc29cC7lqFweakHFsNi01twnhHSWEmsmzwUIS/qSolMy9CBLx56FEEi1I3Tfu9ww7MAa5v9h5Kfjj7G2EkqR5k6SKJ0qeoIJryGvo6tsoyQZPBrZYg3r4b2qI37voysZHdWOWzDwUdiE81lHchIi5VhyGS4dOXotJC9TtZGVe76FR5qt4O1J5XHNyX6c/fQAm+HCAMV5i3dM3HJJZujsSZJtX84a7hm13DwG9O+SCubnMiJbLFi37eQ0SbifBqT7mGc4xECPb2pSFFY87ia+4lAU/XDjzun6pwiPijQZ+GI+PbkmbQhTYPAdiEeqnYyuGKu9SHq6NjfUcQ39Ss1vCZYzS9zcOqxF/LcSolVGLMY6JLWQbS+vnfJ7H+X9OjNKvoVz11rD+fBNYf7ayt4R+K1MwWhvv3b+1nk9Zdpu4R0ry3Il5Yj+Ftnpe03ttj+z2LSLNT+4J4UKWz7gR9saH4Yecn25Xcem23mnte+PI46zcV/JZee0cu1bPc8pz8ixtrLvvgXuo97nrdcPVTOngG+Zsdw9eeOVanf6U0TeXn5x5TGzkpjNZREdDjuiIr/66QE2nb8r/uWdAD6Dzbe2sNKLQkqQ8nj1eSaUaBUBhtAoxLiQRrzGLkR9adVlGKQWtMRaWfBFN+d4DV71mAyQfJa0KQhwNhBKkKYL/j74KTc/KWxHgRqb+lPNqloRaaiKEQVIoIChJwYZ5cSUEDZf299J8FbP2JN0bFk1WRuzVe+n+bvt57nf47ll/TLA6fe4SLmHnuGB8zN0s5VDfSxJ0G8M99DvIyl1es8+G6bM1tSnZM+KaMiLKPv7r7/OFZ4Yxpv6Nex0cOnb4c81dAjKpLpFl0pciWVyuGwMdpHPFLMbQFShnI62aRlS5rdysiDg+PAAAima5LFRw4gVv8T1QK5Z6wHJ4wJs33+Hh1Su8+e47/PMvFf/6vqABqEVDiVwS1mUzX+C23fCCG4a1zUveENMjmAAka/W9iY56+1qyUHcKU9+Qf8swmTDchMx+ZNLemMuzErdcY90zYJa30DApgBEFDcQSy7xDEE4tbCfVDlM51A12IQqgwqMxOawIWnvrfCOTIiHTMEAKd8v5KojT5k8EHSVUQxEirBhhQEEM5NZCURDrg7lhXcXNE+b+yc1JE+R51fpKgVgcu/yQzezDH6+linV/rQ5frBX7J5rHylVipqctwzlnhCNT8Xpp5k3QVph3BADQWYi8CrWA9qU2j1sfY+IDi/CKsHAs0t/WdC6651OnkiV41laxjiUxwazXWovwVY1Zc3yQrNtW0Atp4UJis16PfTCyIjcgzU4BYgsvvDFi/VytKNZQ2uHF55Ai5+4OExGUsS8k7w6DPfmx3bF8PKYwsX6EUq2v15UWBi9Dc2Jw2kMjFRmeIpdKd57RlrzKVzIunR6e+bDfaXZDwtB4MePfLTy53rJRBtm6VoVYwsnEsu6LTqxnhlGhBLUmSfpI/R70eNhbP9KM4OE9An7bIxZcrr9a6z0j8sAQSczHtjasLfKWiLUDRV+NSSw6IxR1MbEeISlUE4vXhSux+yUDI+yLe8wMrB4D3z084g9vGn736rXmEmJdz+rBtuVQNv376yp/tR3/6ytXcMGnL3/1m+1b+S0Vbn4Gw/LQ0WwLcfrGO3e+lU9dXloJcXO7n6WVS+1vDTLsupVREDzTp+zKTfVGmMZYnWMZCbbMwo37Yi6xECUDTdkt42kB9QAmOH8cXIzyJY2x0Am1/RnGpwotqLxMCb7KZBXmVdGUdyc+Ajhszs3w1hh6P+IG8+xIA81Elk5xgDiPmtxxGpgAT2JtbSR+X1i/YXKBDa2bI4xsdWlZ8OiSif792UIf1sbmduLJ7hKQ37B3N/VZv29sZ1zrJgeS4NNiIAYiTWRu79wReuli45svt5cLSoh7Gqf0Z7bvn0MuPk+d/rLlOdP1uRUtt9h7fqKWVaQWyghymcAWoO1+Fpzh6IpIEDRWl58ySDPlAudaAQDreb1rrdysiOBykM1KEsuuUQHoANJcEMvhAaUecOIHYD2AzwUfW8G5IYRzM2Ivw5qQKVn3OQZjC9QliC+RlfH7/g05P2ihkz0qI2ZTDRievzJRZITGpBaOtt1KXAXQjdkXDbl0y4AcNwTHEHcCOfuUVlglo1lwmV/JccnG8elcCVXw5F4EdjiyCsesY0RxQJoAdWghlAMtxsAUEQpcFpnCYOmHIyxstd14Qfrvs2iwA7AE05GsWJQgzfqUhJI90Ikw9IMnExsANIeKweUKLM51cOpU7ocimYjFJDdb8ohgS0zeQhGh71l19+PMAOaud/cOSs4wmIC7yVxfaEHmpicSRyJv0tr0cgw39ws+jX2/jnITVzAL749xmsa8cCcC+22F3FXMUR9t3wBuOByz8gUZI2xrywrbp5SOwB62YYeeosUExXVs/iJGLHmSR4ZguNZDNOwtQ8scq9ms+kdMmt8xxqvfbSPhPr7Tr13exaUIBknxF1tYtDrBDVYnjaRL75lk/dwgrE3R3lNaSzqeS2EcKlCLwdXv8aiC9hbLk8pzmBM9ORWsl1h8V9rb40Z9bm+E4fpW+lbuLOOUbJnlOxn6r6w4Fv4E3NbNVT6l7c8m1Jy188T53gF5jy6aiJ6e1u4TyicRGu9aHMz7Fbmq4uw0OnFb087Y3NmNTb8zXfDEMdk7PZ81xi80Py85z3N+92Xq3+SZsPp323naXunopKGRHDojl0yC2ZddXoe392+xTt/WIzSW0ykTeKLJC7Ckz80ITmCdeUZ19mk7ElRJZcggnCc3w+sWLGGchJpWwx8yI0UVpuU80EDihQeq3UQDNqsjb63wlg7k3uo+ZBlJ/gBKnhHWXlD0PBuG7v1ck3lKW18wLbeuD7KHaS6wxM79PHZ7nhDbhrbvbnirO7fhJjxN3nspn9+4/y8O4CUgBr7/Krx37tM92nB6/a7BmuFau/N5aKPJiXb1jZieOQ6N3y90bvju33rl5Gdm5eZx3IHV5UH+AwMTTrOFPIUv+FHgJmXEHt+eNlVEhGBYDsdVQ7/fWm4PzfTDPwgg4hsHpgWlFPx4OKLWBcfDA376sOD/+vcH1GPB8l6tetUToqSOBOL3Xklnk/H1Za8OvnsjX6gpCW3CUlnucSdcm6/9WKA3NRbV7VsqDKWLV8rRloXWMU+Axgw0sZQnqhpmZ8zHkftm/5r/toM3rz0fI1ce6DnczUMkJeUUR3wmUrN2m8Ivsj2hIJiK5BGZHNIZboBVAcBovPr3EK7riqOU64His9QCQhHlh65TADBngiQelP/NikoVD+AVbW2a08HCMaVEXnkMixIipmSxfjTrh9aplg0VZnVddJ7h8yuJt9aJYMPcOc1dMitlxHMDmtG+rQ3czqFAAYGreg2YZX8jJJP87QLSNrsYuiwZRWaPz4SHpqDKseQYMf4lhY5qgHtC2Poq1u+SLNSV1dzkR3AGxL4OCriS9nF6N7x39LlNvQhqNZGT+bM/I2xe4so+wu49habFlUvc7buZ8MG8ITI0+f626tgDEXoslJzD08PYWLWxf20dX2rZc5ogz2fse9Kmx3O4gxO2n68Qb2R4Ldb45MjdEjPOzNyIwFOdbH+UWco1Z28Th4OoC5/lTYNDvxDd8fltqtQNOkIww9qaKDlL7Tpq3gpERXPDiFL1fF5RawWzekaUgrVB8J/tw5Q82s4nBqOgKo6wEHbygK9pc3nvxtEIee62RSkVh4PM6fl8xnI+g6hg6QfQBu0uIuhTFRnxb+Vb+Va+lZct3bH3rdxUjJ9z2liYJwBwuiIf55xpK+e/vvy58tdSvmSoxC85y1f3Ng+fgPLpT1RmZx6uI65zk1d4lVGW41Wrh/rQqV4pAd9jY7ikrjdDnkYy8WBmMHzPwvO2kfLZlSEjlNrI3BBz6YdUDTmDMh0lEelZUAp1BX/P4N2O2kxQGJ/BedNwf0BSQKKnL0TiQJ46Hu5vhag+Xdf24KCMuUn5cK2458f9r16tl80rmzu+ynjaXZwzArMD3B6/vuV52WUbLkfZ8C22AmabYdr6tO17yudXQtxfblVCPK/syw7mu/lTUmNzOWjcG8v+QAiessf2wzRdPUuoh6ZhRWNGLQUVBQ3nC7FUtuVmRcRyfIB0uohwtyygUlGXBYwFH9sRH1rFqoLflfWYoH4TJZlR15EsBiKkg2smB+Xuo6/3QtkTqV5cv2NbPd6VS5yFTOmxJ2+MiZBvA1cmqhUID800qWLzvh2+bDLEq8+70AqIduyGaccHCWEPSk98XGyKkvrKaCNXCLEnLxbFgIYdUqG7PNwSrMWF3bYmRQkBPdcvD1ZmQsZcEK01bXMPdWeqhzbzwkjjqYtoAw8PMPBtbKi8Y94iEsrIYmWy1qlqiF4YDHjyrXDZ7XvXKSEoZttj6COtqWGv92MxUINxOg+vMbirUOrIoZDsHB/X4GY33bIvdXzQEm6yOWZD1Nb3GVG5Pz/deLpSolspfV0jUWPEfXqHWx6fvo09SHoasm8932MepnBb0/yZzTq+EyEqPs3KISGOx2rHfsuX7HEWRD3HIXsjON1aZyVgHZZLh34H5X5zHLNFQ38UABeKRMyu7ftpQQLQUFGdNwScWeCWZf+5fUpSGcVMLrgZexdj0u3lNAm7fabNl+2wRPdRABwKsGgYJm5n8LmB2zofszQsTnt8Bq+ElysTnDLBA7e96S9YRVdb3637NzWGX2+ZbPHr5a9s7G8+Lr5C4fDXzMjn8lvLi/PskgmVrus0fF6oItflr195706jhVvav6e2zSx/gXkf8888Z+097d0kKL4Fhpua2KWu9x91ci2FHZ21dU8XjQ13mn8O16Xuihw96NsNINOXh07tg3ZTf6j71vNehC3ZSMZA60XnEiiEvcbQMgWvS7kS/daGblN+cjOc1HvtE1ReIQCZOdGe3Rfn5qd4KHoUPwbIXab2BEwwCLw31P3If18pl3ih8eoW016G/5MKefc8ICa4ejf86/SZG2AmeDiwrAQZV0D3cfEMGXfPpAyyhvkjA/M/b+JKLS9fwoAz2t7Vi94ta5gI5hBrj8YckPnVmJwRiMtt7u6X7fXeQGJ/HYSUZNzP6V2E91QHwjWlYmByfSQr7giAGDlyAagUlHa7KuJmRcSrhzcCChVQKVjqEaVWHB8e8Od3C/6Pf1nQiPHwRjtdYrCyyIzja9+/eDAERdMS9eRDtx+i/bK7QQdYzHpmey/XEIdUaOovtKC3RmPaeH9AQSOOZIHLPB+QPBnMul0EsQ2Fi8uT8gFmfWvQOmACTO7lXNaNzf4MgWdGCjR0Sl7Vv9kqolv4ANAgFsn5wJc3i8MuCLtp2221kEimgBA3oDwuMCKCEJ4hpaDWgkIVVAkhbAM8r8LGFccEcRqCqa2igFjFE6KtZ3jH1FvIhtsUU6RCQUnWXiIXgBJYbsWdhfOgkO/pWK+a16E1RiFobHS5yTZ4DMljr/Cat8b6/2fvz5olyXGFQQxgnFyq+84ijdlIphf9/18lk5leZNLom7nf7e6qyhOEHkisBOl0jzhLVieq8kSEOwmCIAiCABdDb6UKRHq3BfGuJWwrngEAsDaeUAHAmh8zZpUhAWigJPKODULpNp0fpThjnGWQK0xFhYyDbmBW/dvz+mNf4f6LRoZ8q/p68I4S6PWgHoDg7bo209zJ0AMxSGOZrB8kUkLmp+ERGHp3Jq5WJ7iB5DirQyP2kNVtGuyUKoQ8Z+bWLv/BIE3x0+lXnw5J28SjxSCPXme1FKwDePcR1zWsRCHNZY9Tin2Ak/PySuwzMKbf9um0vibIFIpuOJD6jImgFltT3fHSspdWdxe0UNz3egeA3gcJdEcYtAnV7QZdtpqOvdd70wOlX+lXALralZ1dbZeF6jCuc7QC0D2x9Tfty+2NAAULfC0E/+vfvsCXr1/h5eUFyh//CVD/gIotMFG70XO73QAhysEv+AW/4Bf8gn9rMGM7zx1kDsl2IvKYfmDY/JsMMJ+plm8VNGumRoJ7VtyWzRv9AKO1057mC72SqfcxnMiUVY16/pIZ9o8EjTKyyH4lnSdbP0Wfd7cf1c3RbJAACADaFYFtZ7tzWKpNLHuNox+Cyxum/uNC2jRD55e9BxMBxMncbHo7b8wW9cwKic89jwwxk7zG8ThNncyrwjzkqO8RzJ2jC8I+FOKJDjxvc89CnVBfTOi3fqwJkOKVOWOXIZ2e6kRR/ajeh3cUoJn5PlaK4udYQJHN9f99YAggXMEBGpg9wpVJij36jOW5lL7gmwjuWJx/4gj274joy8fL7dYCEV++wCvd4H///Qb/+IFwx+bMwGLP0Nrnlh22pYtSojopYs3ZNORb5FBDhPxDcX7lGLg7r2o5UpLn2BOuXvnaRl63Zdji7E4wdmi7aJrB4apnP7NxUcZcMp89/ia3WjOJNOo6x0/7T5GnA5kNekjAxZpuM6YpAQjG2YzF8MbyfDS8Grk92FNB6hsWE4DwuQc7NEAG/Xgyc9lrGMCsAzK4HaGrCXD3XpDytpg2dvg4wEAEQHdzpNFdgwWMqwdHemRDB0hDY53yOAzmIZk7Hqo7FYGKb4vOOb6YWqUKejCkI3Y4+Jiton7PgUTDS2tYe5FLDWShgVTWIub8lzXcEhtAZMruINDJcDRC5LxTVvtOdTRThIQ3ngUcTGSzFQU1gV5WvQJuO/4+pnDBnxCEQpsgg67wQnO48gFQZb4XRJYRTfmArnHyRLq2Qwz3MczJE3mKKkHaquOKxmSkgI1Lo2MQ83UGkSiM74YcFVqUUE0CPvKJLAJXB6VFJia9Hth5qdv6+uSt6H6pFqDjc3T5yD/WjwilX1CdT5VYThV/fF0rQCms98zz3lkKFnh5+QIvX78C/vEvwDuIoOvKM/IG/cJcf+vVwI/Ns/z4NcN/qQYblmcmf7N+cRkOiTfG7jQFjnh26VsptQ+A0T2xMdEEHRovQzpXPYOQwuc1uNwdN2dm6Uqzi8K8S+oyHTENBxBsb36U4d4TaTrXVGf7l0v/hFmz4FU8FH7jRAb8XAGNpPJYzg6dfmlsf4uyV1hzu4rF8nbq+OTx5hnYtuX4ibTvo4pSvjfiUfKN81s7eAeyVLJQ7xBmBqZV3LOCjbbaDArYI5CsrkPw9r7NHdPJ+J72pfDb9YcEua0LmiNHvZGcLzIKhflZTLJaH+NP7PdWRpydiklRwVwG1Q8JIPR5ADeRH4iNKS36R2kI5cQoiPDTTlQ1MDLqdLUV2YKm8ETfCIV5vfjtyT4fdzxlMJ87Z/ggBHAyfMc24qoa8Vik2bwV3RdM02jWg1CR7QjeOcdrSVP8BMxbfwdfQmX609GwNUN6L7gwtkhXuzYu7Tvzja4QGbnAr8GEsC1xvg65q5R3OXh8U+zcXwFHGpxtFbAZX5oZcgAIZUEsIkKB/UjEdiDiDl8AC8LLly/wcrvB1+/f4V//Avh//O8IlRBu35JLPLqgkFGgU8j6FTOHknbsmXD4lqOYvyMpgADEQT84Bxco4g6BWZ7Y4JxeBhfbbpQMBOzsq/dGYbWBCMZVzGp5dAiJ7Jn3xrntawNyhrm1SyQNn9tffS4qfXNBcWMqmlTt/oC2op+o78qg5gMnQGBHOII39vh4odod6VTvrUy57NrX0wKfa357uUkQDbCoQ174ppYUO9wqdMcbsXxoIKRK291Edkt3rt9r7VT1Ox/KC+Dt1mgxnVicyHx8Ejb+9agHaNCoBxLud9GL9r6L5iykxmG6A9W7fN5fX9vv+2vj4/0u9y0AANxu7a6XcnuBUm4qhMjy0utN1awqyQwpw30TKGsVrarXSg9mYjH3chAAFKj0KmVJ/YMkYWGnfLvjgwvmo2OcTJM+B7NLwR/9pvWR8kj7VrVnCPf7MwDZuCdjHFiuxIlDb8Yuc7Uf78UBHjM90r9D1Tn4AtJ/RVdJfzb3cyQr3ZUfJPIDzILQh2L9GTigFmvM9ZNAB/Q9BphMGhLQwazrn/5UIvbcB3mwZda47q8allfIF1NPQCsxygsLli9Mldd/vT8Amm21/Q+Oo1CzcXs723srorFwYBVJE3HbQwEstQURhUICgqJpO6NYF2k5PbBaAIj6FvMCje+l9jo3fQyF+gqzCrUHY2+3lxZcBQCC0nQM1K6++h0/BZ0cs2RjpwEBe3+SgbfpG0Ao/X4LIOg7ugBe7xXuAPDy/Tv89vf/gDv9DrW+Ah/BN+xMwZkRtCONPw/MR74HoCm1Af/zC9qFue0YSfnoKdVPCdGEuoTgg+EZy8TeBI4Ye/Q+r1PWZG9S/QzniXLabsXn9MpYrJ+6EMQ5Zr6TE6HWO9zrDwB4BSztPr2CX9udRlAAgc8tLH28+pHMleATy9wevB/lj7R/HOF2cc0EFw9TybsyJhgtxuc48ob79o7SJ89W9zGY5SpT4JpVGuu06ywjw6Fhd4OzqzO8JO/UdlTbPaXfTUfVHmfHmOwI7jaNOJ2lDIoODkGrjCT31NHbL8iOaQVdnArayQsZvDMRQuXjuDsjs/7kUCjQFQoovMzm1O+lCa70EvWRXStzqZ6FnehFjRJpFwKMD8HO+A/oi14TwjguEgut/DRvBnr98bxnZwFeQVj9MBKeyPw7Aw+zIq1CwmO0LIdvTL9eHPN5zs+/z+bPdGrQGeIXCUcuTYoS//aMlInK08UbhhrENlgWgvv9RzuxpbycGhe3AxG3l+Y8fHl5gUo3+N/+gfCPP825ZrbMTL9dlRkyTLO4nKCsK5yq20BbcAttI/JBgNCww4NF45sBR4ROshNAd5pVdp5FJN2h2vxP/AmhDygeu6NB6tZD+HyFibdmqsczDGhLdSZ5dPdG1SKR5ccQi4ZGoRnUsUy2c4LQrEGQInh1q3VqvslHCzT0C8CrHnulY4QZ7BGAoABiVRZAu+yqYIEKxmlbDF+Gtrd1AN+u1OtpjuAyXJKdBco3DpL0QErfBcHHM5HZBcMDKQdPkHdDBC1GkR47WBqlyJfLsiRQkh9FRouhncXOGKdqhZq8ZqJplI2J68gXDhjtgVfo0t2kj3FNUJ3eoWtYTsQVDu2Dg1vad11bs7Pe8vrIsmHcElj0l4QvJN00I6XlECnNYz+PGDMdZ8z4SRkR0hTTQdToXXRDc1/dT76ugQZpwjD5c/Qk7cvlZhMCnYJwwWRosUZfKCAJSDiHil2pE8sA34Rdbepd2EybNVpNRyHiiRlos9W2q9Ea3BQEPoo/77AhgH7UWwGote0OGxjDNHtdpjrftC2pbqi1wuvraw9iN76UgkDsLTB2iI5sH73WB3dEf5E7gAt8baR/C5hZrk7vbejeJWNC/zpl+Btj7hHmvxF8QpIAYF92hhFAu2qe/gn1jTjmk8fdhE+Eaf2iYbK2jFcp3nLn1rzMBxFPbJG3bJGdFbkjIWuKsrfJkDammQRFOP8ZeAuevUPP6DCbd52BK9TmrZRi4oBVJvSZyTs8yqVk904nycHzoY3Ol0xBJK8EI5SUgUZnsce+atIfWlDWtBzmCwNxIWtuz/hkj/UWsV+7OPjd4KTzXZyVZLXzzPbJy44JBj9WmLxqSR9ttz4AR4TjTqIRNqeRawSODDOfQV4gpXZnXlSfE8XpX3i/BTxHC/NYmY7FewBdGWPvV7fNNSbt9vc8kDWmegaM+lA6ca9s7JM6S577P7w1clameO55nOiNYUFCLF64J3rmwOYx+vFIGka6EADb0fBnxGA7EPHt21copcCXL1/gv/+O8P/8bwh3gubA3Mg/q/yuyh3sxtlIfAqMo5RXYA4D2Zyf57eugcPGzncOHNhSiY+cAIK2KL+f91/VyYo9BRYEG4iQlfKcCEAcoCogJHdE+BryinihOkTXsjUhiXMObdvqqmYy5SGAOKTVlWei9j34obs4tP4U6baGBvS7DhChFN4F0StAvO1aG4UIoNK974Bgp3Hl146PzFeCW3OcmQuqhJxS4IbQygV29DfjkAcY5oflmTXk2iVc/Xx2vg8D7g6f5R0B6CXUtZ3pTvc7vPKOCN6VwJO1vmOm3F6g3G5wK7e2WwGwR+u5wUn6RjCjhB+xDThZtWxpjQ2l74RwgQig7ph0ghagyzf3GcM3bcp+XBmZoE1YyTBg7XRJiSZYUC1J2By3fLTO1E5Qanp34cAQwV0uNje1RPmWDqno6g0irxqAYHrHzOP9Bf0uCQDZKj1Qbfh3pN7YoUzgdaEe/6RGA+ulI2CeiY1udJ1IxxFhYtQpX2fBiLFONJWZWCx2a5JlUVSMyXAoJtkKCw5iuHRtB0RQXQBsROtToZv1a9z2zUED3ulAVNoGAqKmNyu2nRA8rHR8RYVQ2hZtu9e2krTWdp5vYTnQXKrnB2OpyVsBaGNU330B3fC73+/wxx9/wI8ff8L99RUKFMBy6/TzPUM8ZqouRSixGX8SWEmON6Z/gcJTzMJf8At+wU8FZ/u97qBtv6d538Op8AveH5IFIJ8KLq28bTAsZgmdg1zakBfgxNFTvszPBjwHEUsaea4JfWrLQYrrvP5Y4IaKsnwWz8rLtZF1/eDTG2QcrPLO/MiPGIR4rFIyW7FzdNtvTzSHXZ/5U4rxLuj003/nlxgTjtm9njov9x/J40dlznmZJpVwQVrw/Fou8EAAJJQ7Zv+gP+RUih3YDkT8f//xAoAIX77c4I9XgLYa3Dh35suU2uvJG3FOkEvuMlD6JTAl8sjlX4+slBFo6Mmm/fnAGwTb8IYd50O03ziyfCHBq2udomDyiMMqrsDoq/aJmmVRwTgsaWE4dF5ZK928UWe5JaZ05yFqe6o3VOiXYISJAkensjjImmT3PFUc7PyfLV+Vej/WCEGd9aXoJSqDLKrT9V5r+y0BCHWAal24QJT7C3TniHFyIrZLs8wzIo6627L52Cfzz9DFgQi944E06NTrGC1MoqoXVfOl3hKEqMBHljB/SrkB4s3Q248cqtTiQJYsQ/8YfxDrjl3wRu59HuTvotWt85tMGd2xiD6/rTAxURwsEee8EqyXiB0o8k7vzAmfj38LvcLBzcr08RFVUdlNAMdUDSVJP7JBiGZM8bE6UR+QIXpKsQlw6O/x8sbeP9mjHYI/XHeZCOCwvyopeaznwI5kBwP3K/aax221bsXJrgVB1sA3q/1T4L6IJpsb8rVeWefZAJXfAlAqqzjhf7WcQxh3oaAxYpqCFVI4mMQO//bAUI0ol4GzboZKAMXwFdGdBkntsoe0Ll5GmDaFStROh5K6t6Oebrdbu6S63KYGEVcBgGk25bhU52Fa5kKmdhb9X4L3sITPlhFl7jJ+HHhzZqXoKchs190y3mFrw7BKLeiPZ7LjrURqB++Mlbssnk5Bwov3WGc6yujbl/kMeLj937Hel/RA0sdXeLydBjJYvYPmfZcy3hNiPx54+3Ylj+UEG/VhmA5ji4U8TxpjVos7BwdSZMOCHr0zbF5GxMMW7yMcPa1CVoX1ph8cvdyHsffms8GIWZqRxU+D9Q6vyVw1PFTT3tSX34XZ1+7OnVZ6fDfJMxp1yzLOQjxN5GzXzoMRIQ1qWv6W4tqZK4SFZjYIMQQSU3pN/zZ1P3THLuhmHI/D4CV5HCMC8GIz/o5yP6SmsRCn25Tog/N2yoLHg7/U/r4u705SZpUcysuAwLaJ7tByHhPjvwOjR/fGS4R2ykqZzP9nsB2I+H/991t3XDbHYMHgaN0YtCJoPeeH+jimuC9XhMiiMM4zcux/qP+wI0QdYBD8zI1u7M4rcchK0aT2Ex+VRPKmoeznvresaJRaPwecXVNSTzB1tQMXmb9cApmyPH9b9r5nhPRIokIAUG6jM4KPJBL++kGTnaZ6dnpvi+7M6z5q4GNnKKzqF59FX31bEQCQz8bvAYhy6zKLoEERrXG7S4Gg3u/AdxN44LYyO0WI2j2xFhVQX+lvjjgSnjFf2ane6gn9+CcWDvVhEkDfBVGpQr3/EN7zzVjIZ8FDu0y20c5HMLU7Ie71VXbRcCu3GEaRnSLl5Utz9OEtyAQ5mY1HsPFAAKCyaJumEtdN2Ah8Z4Y4CwHl6BapNrUgCPebYo6J0QYwQLoiP+6GAABdWT5TF6Y9XD+JQAC6K0IRsuQ65jBd3N/60ViVnbic/Ma0LRSOt1Zau1QOYkXjpnMV0axeV/qjfg7mp+4GInJ9IV1hxXKCKLsspphFdtYGGvdlCS5IKTC8t3S50kzAwQ2vXTfNRgxLIwF0GextHQ2MiaEYDZRTR0VY/DCKagsuEQAUKMUcswbWKPVn4CKAu5MGgHUrj7rQd0VA2wEBeqRc76LBoc+BvwqlQt/x1T6R+o49UQA9GNGDpjy0UD9yrwJCAdufFCqR0VPtOMiv327w/fs3eHl5gb59A3gHFEhtTJ80Y89TBvZfcAzvESD5Bb/gp4IH5ik/NXy+ettFJnZHKcDCNgEQG/MXXIEdzq3SvI0MUWIjPrW0DxT/6E9xTk4IdU7GbCKSuwyOTFeafP8o0KNEIcydQBYLifWL2GfPvNjoeg0u+TQfhNPO9j6nxsiYId3qyFpfSTbt/bqnCSPeKPjwTHzWmf9mZaZzR3Tf7Rw3oyF3ZSSXDv8F4MwRyqt3Mda4wrvACqc13Ts0yTwAp75OJV293WTTWd9k8LxY124qe9j7TkGAWuA23FG8hu1ABJYC6jPfLMB6kyg8mwHZrxSeTVo04iTDaoqF5x3c/RLtGpGzw3JTsnrZbADzI3XEQv9hlBCwIWEHRjuwohwLw0GMAt7x3XJU892XP9QT2MlEkoCdwaFB1FEJFXgnSy3tdoRsNfb4N7Yim01aaySuSxVaxDFueNGqr3UXByQaF7FpQ+2HWlfZNdCDAuJbD0ES54flFSZoBxCuvx4FIsEDMDIjndzKBXvpOj/67ozKQQV2OgM7HVveCiAXZbWju3RyxRMtvsaaqbTBHz46Csx6Zmnf2ssX56P2IXbE2wi16yfSwFZpCwVSD65nc6q3doDuDBeUEnixyJXBzL9hJ4QBMcR75yOwqw96MYPyXQC3heu6tv7dLWp28Izota8oUoqYLErBwQEeV9su8/bIKzvQ8sXwDmHnCe9uIOD2ZwevBky16qE9F7pw6rDXGu/DYqnHUE60OA7osdRIN+WAhhAb8ZFKIl/K0ApvuDIanE40JkJIl9Ho+3ABKlWCWrFeNkADRu5ZgLwh63VkGYzcxPAi6EfMVUDiAC3GJA4DyCTI1MjRnbRLUbQFEb58eYHbre2QaCc36dgeNYR8edAIPFyZJHpk0zb5CeDKZCbl/wV4lF2n8g824Ej5dOLJec8GGXOVkKpRjSEGGb9Y9jZR7wmI0+Jn1ZxVe8rLFZNnSGbE6INkTH8MTqGi/fRPbd53lJWrK9bdQpT2wL83fy0XT3WnTdrO1OFZnN2xJ67iegYMa2Q2i7iyM86PSyjG/swJFTi3XU4Kp3g3l8MrTWDHsrhDYpscY8IuVehEF8WZ34yCyyIWm4dp9VamzyJ2qN8J0czjaOsm7Z9PLVpZB/V4dLim4UtGwzD4uUxhrRywfR/b6HhFfk/PfpjIq0n+HR6ctQcuQ9LRDgMNYWFXe7RHkA0G7qZN31kfCMNmJ8LkW6PpLcb1vZn+fLzyvjUa9Db3112BoEH+z4yNuzo0W/CZseAUz88OCu49+Y/BF6x+BHlm585G9xvXZ0Iiim8AsUA5Pr9cYDsQwRfvilPQUvIGMpxGbPYyBscfM5e39Bi8C+dlLtuJUyYjgch9RgFoqBCglKSrog6SRjBa43cntzlPH6GAPxejf1bjAO0vtHjkE3qEN341OQFffaD3N7SVqsOqcwRAqtC2CEwGCfHTRf6RPCOjVDQA0XZf6J0QPQ8PfkYeeeW7DCVFL2C2wQJu89ou3oB6f22/nbMfoOCti7vuPLAy4YZvQw8imsCJ3fHQ+dyZzvXqZ2YFtjR67vdXuXRa35Wen9ugAkFpQQhodwDU0EYtltLMhYLNu4f9uCospa9cFva08vtOiipOaa4tAfSdDYZcQLN0uqOwVk13uoNxPLQERABE1ZTX20ikjrcJozE0TUS3F0Zk805sVPLyiSwSRjbkHfMDvczy9l5fgGcGsQ4ivR8iOvBbMxg8csNwNN+9DpSVfMH6b8GltoLc4+U7ViymbsoQ9aBae15F1kjbNFGE5HApXzKITnIEACwo7ebSdpqeZ2legV5n5o3ZeTCkpN5kZnILsB4l2thpRvaJEeaGV2M4lD74tt1E2scd3qFQtR4KYL8H6TqPCQiAj4cqFfReIZS+KDwgglJuPZ+5d0fG4grUd2NZvqGERBrOWynw9etXuN1eusFToVaSE6AkGEp9DGkFflgc4ENF+APhsin4NH7t2Wi/4JPAh+v7zwzRMPwFZ2DOOWsj90d/YRncOerjc8JjNGOwKOTXZKFKVvr79L63LcXOpk6VtGMm/oTqKQ1GMBzUp8mPpnuP6r9VGVrtc5KO7rudUOfCMiwkeBcn+AFktJ7RkcYf8TgpgR/OD4Hp878ynBuv+nx54qf3fiov52NQ7i3hsTn39VKjojJ+M/d7jwE75no7OalAfsJMDvs7IqKDxNAdXd6QpPGZ05+Ca8yeMYndFKNSs851fjasCujOubnDKBu4jxtLAgcc4AhOYb1geIVDPMIgjupAnXAPATwnu4M9cXJpNstZc+wRABDd2/PK3qKigzUxbdpOaOkItDi3HJqHvWrUnyMh6FYEYSDo6uxQB/m+cLxx/Uw5zcHOgYi7HEXjbnhHbaM06MZUmjbko7JceZZmKxMklRfHXPfPi9O6Of/vcqQP8O4U5K13bTcBYQXCArxLosplyLHd+V4IUz9AAHvRvDg7++4Q4T3TS9MLjjVgphNnXYDdy3JHxhEo2iwI0VyJchzWUJz2a77MmIM13Ofc6nPv1VVZxqFpex67xdG05bTTdtnlABNVqMQBgKq4mP+su3rAYAhQSrlmqyixnhUOA/crDkJEu9IFZ3o/4nhyK0GPhtLjlbht7IijO4Jm45WuVDD0G47uwNKZvpE3m0+sjl7IzG8ZOxA1ULMACaG6I7vmNALidB68HBdYH2K/74ZQeZ7JcrDEbGANASTQzO/SfRDcp8374disSgBYXZl23MOAEwwecPICoUG6FqAKlRDuJkh2ZKTqjqEoeW9nbY40BQNwV6zPpk9RPLGecwNpUiam758BWytiswE7whAAneMb7Jwnw6oqcVh4850RnxTmY87e86mzOR13/c9Y9oc4Td4THpyRD3rgVNHrsg/f75asJu0SJ4XPM/AUp9Fgx1/v56uFIs/EdyXgscpDNI6rR845P0X0czMxMVBt32f26BW23TFk2iQPyNRIF06e87t4vNNOKXn9Rhv7ANlRWRNTq31NMi/NBeOv6LYDeYQBUWK8z6Y9kWYzDTwgy6N/Sl87SotbqY5QT8fkwYmiAywGWdyMEwLBfAfD4GTeDJJswwmcZ7vtzM5Fa5QMOMf5mxIan2Zz4ZU+eBRU4ufjkEmtTqk97EkzzNs1Vx6Pttm7wWLuoi6c6QASXvPvo8p6GaKgx3CS8kzn2g5EyMDtCjWOh8P8y58D0PBlA6R/miBE93iy8dEfAlA/riQh8xnHDNjjcTQyZAa9RT4u1zr9yWbCOR5eid2O1+GLm3uteMAMktOCEHwsDq9aZc9Wz8TO9uZ90sxmALOr3q3zSgybOMAQt0xcZd74VuneP8GUUaRO3vE2ZWjLWJtjmM8xr/3II3WgN3p5548c+ZR2JhSnPgBI4KLWcDE0gDljneS9w8R4CCQIUe93qNQv0DaBC2ZgrbUdT1LvLX/B1tY8QDmt3i7wZiOr7RLhnSJaBwmc9aAAX3INspo/HsFkB8sup8QhSTMl7PQV5qmQpzsFqikTpD18H9SLhrVc908RO+bG7ZBNHMi060RwWFhFRltSDrAM2lCCEGYXhDnDHjiPdBGVLQRoR92EiH2rdy+f5cjIjz2Cie+FwH7peDVHgvERWO03l8EOcTuQ1Y6ehjJ2YOvMRZwfxXEWbP3XwDs8EgPMBVDIpG/teXTlEssyYm+aFS3c5wABk8sMEeb54y60gnpJtX3O0O5ZQLPDRPWr6mrfTz1/SNLa3pg5AVZjmQ/k2D6H7c5r0aFMh/JFdhXVCrWyfo24zE/WHc5OvzrTeBy8FvsFR5BdqjlL9++yOozBxYV/wYfDv5f0XQFvr30G4AUWOkdq9hkiQJnR+W+mZz4XZIs2vI18ZixgXB7D+PsX/IUsl4PpnXsm8zN0NqgiYvvESIzYnFN3nOY7ZCktfu3BrD+s50hZnlnp0e4e71TYPt6Iv6f0XlO9fhHhY7g+LdBcY7X6528+K2RtM9sVoQsLc5v46D6Jq3Lw2ecbx0EIfm312aJeGD4VA0CQsdRD2pxaS1os7O+IGMiZ7IJoL8OP47UAQ1DDfBm3KkVHd0tfuwPbOSatk8Y63RYdeVYhdjQua2EdRt2Jos6n0cGdYbPCQrHJXb3tu77av/Kq/+QADssuEyRpDufatyv3HRVYAEiPAmk3QSsUJsc4e30x6vgSh66J5KpzVx2iEicyTlzqTl0EACrN24d8WWkf4CV4AgA2YMZdpvnoewDiblb7mwCE8bS1392hK2et23nV4INWB7yVYheI6rKgQRxWmsoiuTjb5BkVS3Mst8teK1Bpp6PY3QvSRQobQEWNLKafeU21XTTbcdd674GBao4UMkRmip6MnFrfZpedEgrl9qq9jtRlj53+2V4n23MbTzsvLA08yxhyBxwE3cOPw0DGWPV4LRNWMbh1x4zx7lblQdQVbddCq5d3blt9VS37Es/T6F6NO6z4bhfeCdF2/mjeUgDI9DnB3ANo2idiSXvgg03+OcYX3VEu+sM6uV21aXj/ELjVOPq7ifdcv7dkk9BEn4ugkRd9l1hMZjKT3wmhnC+IcO9WlODu/BSZz+S4p0dTBpfadE/7NR2dWV1Tkyfpx0ZdxnphsJHzbcZpp/PjExBgxabfStM5P3780GPqELsse0JlfE2NWy7I0vtOBrrr2Iv36as9I/ipq/YfsbsXZDyL359my/qjZacD0KA85XETbWO32PSfKFJxSmank6F1fWbVfqRJ3oSFid55v8In8KDcPnPl5KM7IYb0PvOAQxewmOd2Vc4EK4X+tkNXmL29K7yFXryCc7qydxMwqDkzsTzAN9IqZ40D6HG+REPbUJp7DrE/BDM3TbM9Xs8cazyfipSuCBfTaLN2gxPhIPmufBwkW+qXjSKGWTPFN90eFlHys011dPqFSurM1PycrpWzYljmJxlperTX5guu5ukt/Rl168IApnOIs/08yPMjwQgLBGOw5C3hrDl27ei8tW9g9BQc09SmkiPvPhpWgQX9jun3iOdoLFmXbW0Il2iSd3hivtEkTQJIYN0Sq7FmScckCHHg0gY20VlO+Rh29iOkJGMBeIs7IjwTz+c5fhpf7ht77MAEUucLO781jXEGzeY9E+TDGDYjg/gzBCRAHYZggxFDfr+Tg2x9hEDrUNLoL9VGgK70yStIbGERr+BugYjaj+QRI7u7pvnwIHafxg7PZ93rpBj6JaNeHQpvTDs1JGa1sr2kmvonO9kR3XHkBN3pJ+1tpgrWodVf1vsdag27ErCXy35Q/q9oMEJ5rTy0oQ7t4815zcS0eobVV7XtPGHnJ38S56hVg0nibAefngAqVMCKAHBvJ6wU5pl1ZCOAKAPSZ+Bvs6dKfTV+51MPRFQJ1DgNyIwH2TItQZiqaYRovtMkrDfrbSXBIQ7YSJCGOZz1Vw32cD8n89QazkkP63/RXESMPoPIv9KpHiAcksdhX4IypPzg3Sc+aMD3wGgZts+2onpYJqgyJ+NWpwgJHMDjnSYk+VoQIg5kYVLOeB+YOi+32/uEcyQ2CLQq6wRdWXncgj4wqBc+C6sBAcJOBjvJZJ3MtK9IkNc9GCNgrFiyGUD5RpxvVp8QLLQBOjBRhKaiE4OWAChZ4UUAKsdjLohrkahWgH5WZH7MWu+5vX+5EqmNQbeu8Gut8Pr6Krsi2l0XBQDuva46UqHUjfvxvC2OJgGXnSh2vLP5dgRaUFB8kIORwY+C6db79yhbvQnPx72pXc4tbLEZd+xboxPoXVn7NJhWM5msDAGWIUGYLO82+47jWFn9qK/eYoVHxtIRnbF1AM54PB4v+kl9bHkk0iadw468SUTKLgwTu47ttI5hMiXr+cwXYx+4V+Bb2Jus5MfzJL39/XFa/HPD6EQ6jaHj8fbRfBUtzRvjxPOZY/Itx2tdOTwUaj/W5jd0B/NZMh+sls7lTiIypK6cgPZ3s3OznrgORggWUh5jdD5s031OsF2b4m6Jc+X2uD1hJxQbqWN1wwMbkDjvnx/HgHxR4gdr2WASXAtGWPCjxzGqcQYX5fozAfvxnreQyeLNyhqe5u/tPHsmUxN1pmZFki/auAnuVTBkCFYExb8VhDCo3fi4IxvOT3oMJwIR+zScyj95sDRGg/KVddvs/Kskz52Ryo2L0I+1Hps3ur4oNFzUIDpItfeyYtMZOnqjJsKxM4NX0qti5pJNfhugqM2Ja1f6qI+VywawW7pktT4fJ1TbrggV2ObSoVI7w7xzGAs7Vb1zFoC8s5OgX6SsTtEKfFQMGluvO6KJ3Ep511m7MV86Xm53e5kzIhtPvcwmGHBnp2y9t+udu6NVjQhzKTWwrETnitRQ28peRNzlQJ3AfNm2d5Zx2sp0mjsFCFrjFUCgUnqrB6VCBAgViLBd2Iq3xq/ON+ztA9UcBG/qQECAvOPEnO9ORO2CbGoBCVOiZG55EfhgsyZGdqcHSruiFE96RItrXxuwUcW1urzJtoCfiKLwzlHNDuXO274Gqn3LuqGZdEoQouMRmejOWJH7zogWXAksF1FqR2LFe+VbAIrLMnk6cunHzOwAoht6Pbkv8B0oHOSxATebXnWXMQLRq0vNY8pNnN3z6DhKFdL3gSdc2NZ4Z5301dATShgnZHnac0dRNX751Q356joONli5E54EC7AS9R1nRiPZYBM77uWZ6vTCd4WwzNt25vHHlbkynki+tj7O99GUMK6Y8Wbgzwr0reehwveXP+HvXyt8vyH8+WeB+/3eaOnyGS8gI2JcPoj0MbDXP6ZZ046xkfYX/IKfBD5rYOVpE/Fn4XkvvO8Az16pf0b98fxDdyt7Y01MPDyWgdEqTegY7MdfsA8fPLAl7Y+QyUW4N+sXPA02fHQubcr/eRT8IlWeFtu1Hwpgb2SO87hFyt1C4TGpvZ5/qG54kB2z5EtOJhyHhfwF4NEm20Aqcn3QBk8p+QObSMsemXpop1wmeiOfUSpZIHtVtPNP8u9nM5jNGlC/goWzAaPtQARlPzKPiydnA+G68WdFzfCR/LReM2D/oaZJOnNWsjsmSQSiu00nDtP0OJfC5/LPaxJX7mjdTQggjnhkfJTWsEboAZDE4dqN8Gp2Q3AQguToiwKEBKWWfrEpdwwyAQh0zib2XaGyTB1M5qgboVMcec2pLk7raoIqhgfqSNbyJGjjniox9ninKgGBMCmQSliXP/rPZOWerjb3dwFIEIL6kUPVrvZX4EuyRVGI8884u0VYhaH9GwHQHQAL1L4bpr1QrYWF60QmO1+uSw4fHwfFPBI5AM/bRiYafHwvRjWBhPYntpcGagDYcd944+nmT8dTz/nsoTZVIiO6gk3lzmqLASg8NoKO0qfKgMFlkQwFEPsGG6u0773/Gllnp7NUZ0efUwv0MA7eCVGN3Lm2kWymPZToWRGaBL36zAZsV4ex4PHZARCA3zlgyrBptAjydCSDpW/efFVctlpf8nA/JeyXfef1Yhwtzx6ILAC0oC/p2MHvOBgBUHqgwJQfxy2eQXccBdvq6rghQvWt6WOimyoQFK0ecl/nrt209BDzaUyYjH9Wl4zwFf+E/+HrK3wtL/D6+sUHSBFNVRFY37Pu2bXYs9WDj95DEDUXAvpgxI5hE+2TCT3TuxUemWdvelaeehzUo0DDlwZR5sJyqLesw+WdEidwf6o22AUzBpweDmYZrvTXo0Lfc4Z8YVzcyveQHnuw/p/ICSR2ZrC5AGwfip8XyngWfMLAhT+C5q8NbDKlzyfOAxk2o8EM17v3WRh2w8b3CU0R1Ew52c7pVOoxWRl5nTPQTZXlYTpzFMD06QrGWURmXpwJoAgmAjfXONyNG23JVdppmTKbuAg0VuwEumFaGB4c2jah7NQkMA0SZWl2vNmOeptRdmBuvjE8w+gHYLnOghHPqo8dS/bEVedz4/TJT1iy6dXszoksGOEXntv0I1VnZWebbWEM2eF3Oi5NI7QrYH8XTcfBWIzPfU4O93dEPKETjfPE2Ojni9T16MGhaYEd5/wT2JmTmhQpwbvBMetoZ9cTIsoK1x0HBzGeyYS6LfxtzvVGmx6pxMfAAIjn02MW/5Ia5CCXLHdckhyBSl8Bj+ok5aj83LXWdkXIanfGXU1gQHKyN6ynA3CBCK07APYr5aITtKYOhe40l/KrkQ3UAR/Nzg7oTr/uOLbn3ZPsoDE0SV20zZV2vYCZHbccvLH15CYhgLbQmDSAwOyxDnyCvlqaB9ZagZCDQz058h+WbhRZaXkIECvrGSCAHpQiuNe7u7ScZUk4SwDNIcltxvzRnTPE7VQBqLS9EoVA2ol45021xzIRyK4UMcZUhhxkIodo7t6N1g0oHix8PYT0/ulRECh/evABoRTjfZUiWtvXynXxdNq2Z1wcaiQgdWILXZpRdhyRkzxpC71TXoMQ1dwTI3gEL+sH1r2Oheb7aiDBxNqm7uc2x0+ddBQd6XttXo+XZWgFs6DFmQm1dEVB2tsS/WC9XP1OTTdaGo7B7n5Q/P6Znn3cSWt9seut2o16GRuw9S7dej+nxu68aLoUoZ1b2fBYtepMQztRwtmExxh8fdLgRIv7TEEopUB5/RfAP+5Qf/zRxy1rguouECjFo/8QeKTwVd4ghGnaRyYkPzN8aIO/LXCQjY6dGj8N/KUq8wuO4DP0Th+E0Hui1KwLtp0z0s/ZDP9O8G73LV2GPhfabL9/52Z+/KiYhwmYv4Jsvn8Wf/98oyrOghHX8aHiHV7CZcX66IIbgNEaPZN+meckEzNxfXY7KMzmM8fwQHM9DcPnKOM8RIpmFJpZpZ8TP1L2FXbQgaJ5j0GGHpHWBk5POAdst4dkqk+Xxo5Ld0Q4J+nZ3OHLbAfEHs6N1DOGHGkoZvBGEKKlt6uutQxxyMmOCIA9Y8h6CONTdWO6aJc4zzmDPT6DDA52alcxtCUIIfcMdCcTQLtQVqsk+DEShr4Mcc6zoxbYsHephP7KPOQ7LkTww+FEzQ/mRQnd645XjwFKHbnILmKU3xJkET52XossaA9kZzqT0JzAukOApG36zpHCTkMzGYp6qkVA2upv0gtfqDPKKoTmXGwOQUJ1dFu2sDNf+EzmKCaTql2A3S7zbsLPgQg+X4mdp/07O74JmkOwkixUKX3lNLcTAELtd1XIMUSym2RsFzR/WYlaWTCnfnnlii6n54MEv4Z9Go5bjghuO0FtnOxRBzr5oJE2QWsmuS5ff08hrR1FM5VBbTcEB3P0ovp4WT3qZNuSnIKlfD6ELY3Yo4EIAx8mVGjf03yOujOGaijvfBAikdRJu1wx7hFA2lIfqrSVUtwxdPw8R4bD3RN2IRnLluiAeMRR+Kb3Z3DnI3GKhmINZZPjzzaA8+nOmhaIwPufQH/8ATz02cEPWeqNvbRd3m7Cq/LO2Q/KO3qfmeIc2BpIOBLBIyLO5DmCXMl/LCwCpUfknu/dHltiTe/BKhjxkZ6zqFwfgCO7frpw4IESs69naFqhTF9PaMeo/yeoUpn5iPbfLDJfIf5kehN8cU7G1pmfO1kjywjyIBZqp12i3Niwmxkmzx9Xno+uah2rgP7bksSjzjHinOfa7h0tdZyjH8JxX5y/ndvOz4CBFoo/z/FmQLcQjngn3XG5aQGPvM7L2Sna9Plje+sIspxsM5/EFPpkdObZRYFsy/Nu2JWbawW8eIzsg11CWwbHRAIzh50ZTZu0EiUPD0jC0K5ne+w58Fbc7pR3t8zV7rPVhcxn4PgY7Hl/vjKGZHTv1oX9WLmXh9Pkz56qhd34ZCRtUP+TsYaGLxtlnmtXN/VflHWmDdV/Dd0F2PWcOhIu23QnAhEPNiWNP5xRYB3qoVh7jv8M3bCNLTFiUttJLFQbcDAGZ3Bgi1sEAUwicSxzPcS9jQhFVq9y3kZNpLlAWz3OZYynjfeyeHW7WfEsRrTxbFuDUKvWz+enez/C5S5HNJFpA77jgTku/JMl2ChOnwIAhBVKd5wTAeCdgI+F4aOKgO4AwFdsE/tgZSzjFdxUX4Gg3S2BgFBut1afUoCPm+KgBkJpi1+Nz5ZCL2TnsHMoy3+9vsXe44Gyel/a9t5X8dsdI9ADHRzQ6YEIKz8S3CjannynNbcPut7NX6mP6P3CbiSAe6uLc0Yi9rQFdA8OiCzyJ5KZfIHuIpF61Hb2Ou/oAPBBDw8anCFxfLfnHCBC3g4BAER30y6Nh3YyyEEfCdIhN1z/HMpOBjOT0vZ1HTNkPwAAApQSJIC7Lt9LUknwcgkFOX80xHpgz/KCiWCh4xXlzDcui8S0BN6Z0/QFr+jmXSc+IOplnfr/vGJdK47YA0J8pwsWyYdogmGd3tUE09eZadLCVrsATsMsUMz62AZ53Tii2dun3v1Ckt8Ejalp3DMXFrOeancxo+h7Dg9nPJNVAnHF/6rO1nHR39k+aY8Umt7PUYr0+dZmdRBf90UCPaaNoQcxELv+53/gOx6yltV+TbCeS8iKU0UBOnojwOsr/Fb/gK+3r32HX9Ozolel7VublE6bBimOZS+V8AedZI3S7ILuZanJ+0gHJs8ClkRvfv7VqgyP0vlI/qt58z6/nxsBN+T0s8KMcvc86hzMXuyWZy2AR+XlmO9xIv6W/v49vXOsA/4d4Kjl4/xSFv/UO9T6JzSbq913hKWYgYp5y/egFbEbRml4PqilaGlJB22TRx1w6pSbmNChrAyyUvVdPiewdLjyFzAb5fKnu5xPbKihxJ3cq/LmPOBSZqPCW/RekRaKcjOWfYhrRhzaNKv54XlYo3kexxBA55e2fPCyO+Qzdc1tqRHfOZK1J2TzA7sAFPo81LoNnHY4US4i+EOj3Uq1BZmSJtouGxJm57HJkddnYTxWj8vpPZBsT0TzzmPpE7nNMmNxZ+uxb7cM/ezNh3+eXz57tMsIHwTK/xqGADJz1IDC+FLIppd0id9oosP8BfVzgsj67Ib3B31pWwb22oBMu9l8D1vIyXCqQYhoczRtwGem7MLpy6odgeH3TD1jopUp1m4i9HIs0JGCzKDss4In7+q/ULcSC/86P0k9rClmnU9LkehlFCLQU7BnnZRSHtjIdvMRocvj6labE712BzrTX7uT7QbYeB/q7n52hM2V1wx1RBLeSbn9HorW5lXzilNQketRSt0BiwhIt+77wj6ueIUmzlZDI0jrGVq4DYrufHCuL+tgs/Tw6v3OL0SuV6tP5RXofWeA0IYF+EgfhOLlm9j00fPxiEov26YrAHjvux56PrLcBVkVIU+Yt0RyzJL4DFmurQOQwF9ari0HfNwLgWl4bl87uQPemaH7DdDQo85fUhoyDXI4u4R5GuO4JU4souKNOCXQT4Vi4JEdqlKjHjQR/EY+nCybOvUskkfks38iqH5DNjJNfanfJeLa3Sh+4S8nk3shoIu7CYSGmZ8NWoy8zRntDZREZ8fEF2GQjmA0rDErPy1FLId2txtOjw1a0NYDObV257d77stcUZjVwV3ADSpt7HiXvgdWbhblIbaoCSb5wLSl7X7Sxj5McHhklyGcNZx9ZZPy+hZyfQzkNwACVoJvWOFL19kE7Ri5IgEmL75yiTa5op4Gdnz1Lyb9YHOpGg2dLytpWvqMBPMu2S57pmti/Dmr1yaiVdlXA5qbwZZLzpN0uZ68HL6dLeG8BrJ5fWkPHVlxuuwAaiLMIejHK9TaUeAp9aX40z+Y1+f8uPEcmI0e5+D5bvWg15L6Po0HZ5dkEs9N7lD74hiEIgtArFiqjUMAhH3OcT/PrQ0aVS+rDerG5f5uLefmeFYefzfM6bNqnGk7ouMIz6q8Q5nMvbSbcrDWtDqNCv3/sOWDDt7h/QROi3VKwUEZM1w2eOfSo3+Iph/b6SrQPuFS5oy683piWq+QJmvPrIfZtvB3iGUlk/++KwB2LtbzzhYr2XmiL9vUIi13hzNm7kG79Nu+fta+dDME85TnO/33Ag+Ct/ejJaTO5JhgLNXl3Kj7I1YHmr9Hzwl4qQrJ25k5+qwFRzOee58il3kG5xUbnZJnSdmoZaBXSv3j6MgglTvu73FRs5UlirIUZS2UHyiflr+Co3EoBiF2ba2xr8U6Tmy5nldZoYrrjPZ+KBCREXWY5sQgxauX58Kz1FCrn2xpGqdO/60hn66MvVGVbWUajtkBAF6xqatVfY9xuyJIhcZOsGJdByepFMW4OeDBQ2oQCg4+1O48rxWAV8L3AAAPDq3uxsQhgkoApdS+KQDbnQZmzwSBDmCZwgIAObMcgOSui94IskL83ncVQLm1CULJHWAtmECmmAp9f4Z02FZf4oIBy00mHHwXRP+hZZBeJF3vtdedvby172hoF3xXXt3fnf29EG17KGqVcgAF+8p0GTw0nxAASjNPinjHBQeL0DjjWp4q5+XXqrs0RH0RQYV+L4XZ2SGrxMRB28kB7EcpaRmsZzT6qu2t/TWZWEggB1x/gyGde8AE6rOJLnCouN8G/Np/9YglllICIzUmuGJxoHFgCxWWRhvcAdA+aFuJlB8DfsM4MvhaoMPXUo/WiXqrvyut9BKOhANpOxrYxGn082DKedWhcOBoVJaa+hqH+9DWGWobPHLJjU5zKPbONWTe2GLl7hO3W2oCRLC6IyLXmgka0JqJeknSlc4vwrA6PyZOqo7Qgp8F+jFwzNPIJ9T0ViZbOb4NjYpNChyJKAXh69dv8O3bN/j+/TsgvvJwBJCuprKc+QXvDr/Y//YQ7NJf8LbwtNjBU+FTEvWpQew8Y/DoHK3033nemWPwM4M4r56lKsjPf4dTCH4KnWRt9I+jd9fO+wjIrargpudx/sFKfJ4+9dzwvXUcbyQGIN4prYyNwYY8CPELfjaYNt/Edn7CppHTIM74M3K8iXMOxqcEb6Mb4oKspx8P+SnA8/FngP1AxI4lNnkvqtW8P0gY56MAAQAASURBVM+i2ENHDE2f6+h4NE6KQ5AtVG5A8XTAdNK3ChkAWqfsqXDhRVCXGwXHJ3BUj53ZHHAgaqvlE0em1EgYgwBUAbDIcUyIAFj5MmvO0y4yZQeWQWi+kzEF2UFtHKqgzvDuMu7/aeSbomZGg95+6XWExEGoq87t7giWUxBnNN8xIavSDQ/tXRBcpyIGQ6MZ5XLjSHALorRvjcfUj4cqnY+yIqtXqZI+QRiNQ6a7dsd13IEAQJ0VegeHBmxMO1g2BtKtH3dwujvPaHAAS17vgHdTgtgFxDE9rlXJepUfMGfpDSZLo5mlspQqjY0RlQgKkcq3kRM3wTX4LUusc9aql8FZbphj+4MdRMnMLxmXHreFsko/7vxxMpWwYRfsjoKIgwD8/QQQ2nlE5tLMBlBm4dDdI24OMg2FBZoCgnTV+ASuTgZSWzMJeMfXXCbFF5wPk4kUy4AVFqEjyICRD3e8AoYdC5MAD9j+P7xutUYjh6y/euQioa/pRcQCt9sNXl5e4OXlBZDuJiiHfrelETJrrqy31F+D3dF6VuIRTamcPAgzx9Fsa/ISl9hYo57vSCNGZ1ucaouLttFHGOLTEiMtC5ty1yWS6d4reN4Cds4e3oUjh+dDO0KCzTgxQZL0Utga/RvJ4I5+eIoDYYbigfHvaXCCt27hjDHWNBABYCvlLMlnByH6uC12vNDik+3K8XiWvOr1Z+mAIaBBEx1+PE2/UPZRAk3x/B0+bwezsfMhndGF9Wy775Q5zPdofH6uzJifbcOoz/XvEYUzsPat/Z2lzHBumSthWfGpNkBWC/mRMLm9dKaNz7XRmfH72QHI2FafCd7cpiIrRlk/AHaZLeFgrZ/5nWFqszMbjNBX+20y6rcjY0rpUbLIPfd5J3eljYSofwdHXPan/y4aGdwFixOa3wpyyzTSEH9HPs68Jmu4Yvtc0QeXd0SsaFsp+zYX3ayZeJOOrRtxmAC043ySHOILdM5D67QFSFe1Zg4q6+QIZ/azU1ZXIyOsJv0OpXEmxnq6XwjAznlLGg4JtSNTJaj3ti253u9t1Xztq+Z5NwR31nYAenO+AjuPK2um5q5CBCCEggWgIFQEKCaIMJWS7pDg1focEOEjbtpmkQI3KP1eiNaevBOgnUvITAhbhakCIfbdA3z3AYkTrX1ou8Tl++KQrxx8uLffpDsgmJ8gjtiGoBR7FBO2o8F4tVWvuDrRoKcFKOXW5KW3Zzu2nkDjRSRHW9ldMezMq2zFQN8J0Y9ZanXpd0z04AMHVAjsjgjQS6RjUwWjyjrJGSToBn33yohE8urOIW9sDZIeRlueCDXZ2FB0cn8Kp2UawdGoQ00rU/qgMZKRsPGtXxbM7QZdb8jxZl2GbWBLygR/tj/3Rw9sgTA9mjam8zYvGRkHp3NExkHTuYqHsuOEPIMYhMjep+ZN1m4m7c6A7tpt4kCd31UR0yrWZxjT4860XqwZK9BFpJQslD4C4+ifWFvM45t5N51anaybHb+d3mRJPkQXElQCSo5JFD2AURt4Gbp9eYFv377D3377O8DvrwD3ZhhaXWq/t0+9Y+UXfAJIJte/4AHYmoH9gjMwTHV/qY5PA3Zx0mm5t3M7cz8ZQr8rrNvo79qbQjDis8OwMnY0Y2YZz/o+1rCcP/97dlhuG3EcPhA528015fVmuXmyj+wNmZ/pc8DPsdPoCjxbOXyWsv468F47AfcDEHEevRGMWNBvy5sGIYD1ncqQndP/u8OZBZwz2A9EuFUH/reVAr9TQCPz9sgjRQIXdL9ZMW+djKbcGUrrZOTvxv2TOlmXlATHsCWg4BgkWOJi2jYS5lHZPG/zGXbHYQu99Hr3ew26YW6IaE4e40vVjt4Z1zxnQP18VTEf2Elvjh1a17XTQuokt459uV+DMxrHbUtmCzEOMiITSOgOX3Y+R9ZxPQnaTovOL797p01gqsiekaEOpQcfChYpox+OI3URkTdBsxYIKf3C76L1MoqQKJZnlSLaBpK30u4EPgDAQR/lIpcS2JI4Dhf9A8E7KCW/TcuykwqHoSUMAoKvt1G6ksiNIqDOzS2HTeRGfMv1NhdwM9/53wKBL55lPtNjpjwygzPjifiM2rMr1wUngus/OuZGQveV8CoIcXpAMoGZZ8G89Gt1jsdDrUnVYI4P3JkWJDWelhQaC1D06xEkvDehEVNO2oHHvuoCNRpwdGkWxLG+PaI/2/HEegug8f12e4GXly9wL+ZMWLQ9d+z/QzmT/mYSdMLR/85gU84Pdz48QfZnToGj1Vunyo5KKJSdHtvwKGw7NZ6nP47KeDunwHwsjjCMf0FsPyPsLMSJ4IOL9vlBn9rsDys+XxWpv8zE9KgaB++fotfmKx32cdgs0RYGAFmEIH7IxGH1xj4sseaNLZemC/U+0kVP3QFINNoQ761vTjq5s8UgT4dVYEQNbnkm9/nhsZ6fwsI+Sda5LOGwnx69T2jZ5fWs/hS+nVmFPlkCZbCi+xhTxnFqt2xT7lG/O2DQfr89P35l62n99HQ2dh6VaFFMcIxbvuY4TvaNmW68Yndk8DY7IfI5qafVp9lxgB/PU9dlWFoA/BFhLtfB9GjehlZXsA/Av5sez4SaLwYj1iUl7yZlxtxsO7jfi/R/fchsctvnzmM8vSPioS3W/c/O1vHm9FB3Dg8m2epg/cxpq93pi9Ru8wYAXQHejVL+nvfJccXsEFgBbYiCfCSPpW+sYevk2FdT287HE62hiGOjWKrADuxWT15V3+6GuPf7IfgCabbcAm4CkB0i5o7pVsnu5IUKUF6gnXte+q4I6DuZojLpbUq9FXobyH0GbSsAlPIiuxa0TlXKdrxHkFXQpaAojXvHWfvugEI361czepbXRjHjzCf/I96R0PjX/Lu8qyJ+Mg3EHkkAvky7P6pm1wxiv+yWn7GTuuruhntvKxcgsXUQnnBQpwLf9yGf1eyQsIC+yUWZGEeqOcTK5DF9uNdD+uvWjgWeyPjZgup77YvNd6vl8fXoaTkuT9ccvS1ssISfs9O/3SOi/SXFaWjEno/Mf+uqavCh9va1dVW50QKtrmtHLXWHMJq2QQC+c0COGHDOYurH1VX9berkgkfRSA2BhVkQAgc5NAW0FPqeGfIg7I9DebrsOAMXfHT9ZNT96iSzPLLGb9fv/Yg10bOIficM92mcjIb9HW/XzkyfrXEfw48wqBCnIa4V9dt2rMzxLjju/2S6cVf6tpzgCWhVmVAsiLheLX0lgnpvu8a+ffsGf/xe4I623jlH+BojoE3+/IJf8LMB2xi/4Bf8ginoshuSOQ3Vdll1M19Lm7NBARnDlxbdW9D4a5x6Nhyrx/doYd+ybFPTExv82ZJ6Mpbh4NEgxNu0yTv0rk/Ued8yFv7Uas6mAm/WLxEQ5zv53w9mXMwdfZFe57NLcJ7z0V5jxm78cgwGe9/GKhiwE0zJThiw74/oy/wZnp41DZ8TsPuF5pfeX4e3Ycilo5l2AglHeUUHbddrFYTov6IzCcA4Fy2q3pHJNNIsCNEQTyjKkmpa7w8824DMIc63YR5IFZRXBMwCdWS332aHhK+BRh2B/UtjOuoRh+Y87yvF2ZFlV60fVZtI2mPmZPdKgcQRJqt0iAAKAtW2WlYuRK4V+rlERuC803AQRCMTjk98ThKoa56DHwgFkIMNUACwAhk+Cme7AYpQgLCCHOHUnZC2b3BJLlg2k39El8Y7jM3qe9794gyAEIkADS40Jx66ophA+5zrILSYugzknuwGWgfG3527SG5DjNTrDO7+hwzHj3Lw5Ib4koiV3kjKMSJsRQ6A4uVk2kwisaFfIHQ+2Exo2kZUiLbGs4eRYbcHjAPf1PkcIO4+GN4n37I08X6KXbDjh0Uxo19lgSQ/dh0zE3UOOuyAqiYpSHGACUhtVNeOIj3zfvlJluGoBuiaMZylOQayzM4pDPky65X1fA/29qiIr1Wo/09pO27A2dVdZ+20R1bQjvr+gSnrpH6fYbX5p6DBtutCn+zscnw6be/In1lR0w1Pq3HjkOygc/jbJ5CHvxpEGbLHMhGMemq5UyDBpTvZ+wiHAHKUHxfkMp2uwiVQcy3fWbqjnz+DfvpMsOswezriZdams7dRjCuEliTx3FTKmtFgf48W4h5sVGLbsTxZ4RTtmKMNrUfU2I9YFr84awpZdLv0OZ6Lz2FeiVP2fpJoulI+zO2XkAUOdu3RQU9zkWP+7YDWZkJ79wYax0FYj/UcONwRY75mbhLjj6JULrzz3Ka/AiOuBT7n7tjo+8ndCn5Hop/T7uhr68Y73tE15o8v88WTJi3t+S8yWt8K4lHp2aJ1PSUjU617c0kvf/M20sDHiXHNwHYggo1ucmK4eymS1Mb+GvLLWYfdOJShYaJUj2gFajsgrIGnjk2lZDlQluOzQ1vH4BO1+zn5iNuyK7wVJzIXzZ7H2jvgZJ2OG1tNsAGor6Sv/c6Ee98FoZdVh0qob7tAL61CO4/bODybpQNQ+0raYpyyWIGogDi9+3N16He6yB4NVfsq4QoApQUQEPpKboRatI2as73vIKnaCUtFgFvhWIG5U8HUS1Ydd75mMoSt3rXq7gLeVdGq2vIVLFBKgXJ7gbbSvh2r1GzMG/CKeUM0sPooNwSAW39FuiOm/671DlT1Hg+996Gn0hkZyCWyAMpv0DbmnSZE974jgtN4udadDc7b6N9zGeG53LkQtKGONUHOZOW0p2A9sHWcvBmiO+HD6wGkb7IDU/opGFnkQA3/ntFg6sfBn/jajllmsBV57e2ROU91p48vLt4z44tEgIWjP955M7pTngfWuKCUMbP3KTZoRqMOmDHQnNOQa/OyGC8ihW3FpMFSsnsRxkG5rbZBELXd5Sl1rAT5mTkfRBR6Wr9iRL/Pes/wzO68yHiFaHYQTSCbuBBAO67PC2/z8WifE8MoEEnouw7rNSKA19fXtmMJsOtWvXPHE6U6luLrX/AL/qqwCEb8/HBkF/yCfxeYWznz9O53t33ZpkeZE7Bt2O94g24H071jIZP/baHNf+f2wDLvryDEBXgbnh071D6rzj7by/5KsGi0Yb66n/W42L1V+o/277lOUSN+VcI85zV5aT4t9ScM1ZsEpq7CGMgxTtrFyvq3gFVTDgGr4Cgf389xHcZEnlDltVyO764GIR4FSn5FWuQXxS8/J4zBiLeSc+Xn215WbRskOMomNPVAb1y5PIHOn+urtozDxzoV5R0XbjbqujQQ6rNJSW9h56Q/TTmT7bw6nhZm4sRPqnUiqad1CLNDzAY7vBvHE67Oqv5HnEfYfzZDqhnOXJaW3QKh/c4HeUcGpyk/BLhcucKXdqQNSF1AyiaCdr8CVWAfr9YzNgjKZGNpV/DFdnyJt3Eyi/Md9ex0PfvTCD+qHLastuM0hC3MpGXKEVXiHK8SxJEjxsD8cXUgcE3BuIQCloTQvuhRxdAGgIi5U2N9HqcJel7XmtbIck3sJW5HNfptzePqay9DRyOwxQvTfhVRuYBLlhRjrWQEEDm3uqg9j/jG/n8N7OBwEcVRCQPTbP1glM80j38PwBdQ8Q4UdWLP0j8T4riA9u+ZAT0xKPW4ueN1Yq6+dqedDchQpNPr1Sw//yRAt3uEzMt0V4kRy0aDX10Um0M2SYX2YbU8azV3dAFaXZ7QEyu1AXFHSZJgnvliRzosM8szJwJGCZ2nPloZf+5el4SUN4K3dqztrD48C0MfVIQHxCRIDiCuFJ1VZ7by8D12SDwHzk2enis2gUfZ0rNPCrP23VqhPBXkNbzvjpi8rHysMHMeHt+Jj7IUq7qDl7enVGlLn+j8BsHf+bXaLepPAciJfXZfjysyp+Ds7AcZebrvzY36HQzZStJHYJifpMgXhtEC39x5eYam58I4p39OWYwmX0c4kUtnC8ufDMGq5IVOndN3GJQaMLwVjAu57Ar4pfMV0U1ZBdKH+zBkD2Vni52Vr/PGikEX2xZ2dwSAPYlA05/qF6dtxaN58LPyPD+9+pE4/V4QLcPE+X25E534IGR9bF1mguODTD7rfxjfeZn1/omeBrk/jL6LnZ0RO2OJ9TFdGedPHc20Xi2cZjAObJjnRfMpDoiR8dbPoYpGBboptUaj3AUhzj73yxSd7TLIVx8LHexUAGir9tGKyo7J5zsyO53Z4YzgHTzjdhca2oIVhB7D057WviOi3vVuCF6Z3dhcuMqBBS0NO/+BQF34fSAnqM3vXgvUQlD6jgYx+qmt9rddRR3sJHdUDHWrFQAJaoXO2xZd4BX9zgDrfypVqDVz3iJgabtLEHsAof9rK6BMOwA0XhHvUqjCSz4WpPSdLgXbcUx8N0TB0mSuH9lj28BPL7gsDhKYevWgQ73fgegO9fUHVKpwv7+6VuadN41uEGedHdXV4U3Du0w+9X6T8MIoGHEMc57CebQPWJlssjf2umHcJ+1LvPJ7BqxQeVeF79+xANBJZmLfE5Dc1cA7I+J7RellS/r+xEGamTRkZN8aWBQvYEH2wbLMrrQK9V0iPLBwWR5fhEy9nQtYsKK2+b1xkTqg3ReDKj6QyUJgSpoh6FMDrN92hq2pw3swhAtIkNWkkV0r2HU2JLqNWuDx0ACIsnjRChLuDUEJ9DsTKB7xxbJpaO8PeLcCyuSE6+mNG48qCFYQn+hWx9KOuruVF7jdCAgRftR7y7bYGaNP61jmXwqO6vZBVvMv+BhYKO9zev2zgncO/4J/P7gqwmp3QJ/TtB0Rxex2H+xezdBxvJfs+dnCmXLf0qn8c4M3hK9waXoawWWKRlyylzPetXWE69+m2Uc/zfNQv9MgSdq/T2bZgnUVxjkbF2DnAe8KSXmRNzJXPtlGV3aVvRfEeeF+2o+B544tfkw9GxC4AtF6FHffZ2Duk0BOFErcUs/aGXHMromOOYATRzPFmtmXC+pmzicA49Se4E3QZE+nOyFE6QcMQ1WCkYHuY6n8VixfGS/NH6mUuaOL+sWfR4o089+NL9i5xg5QToDio2VaWdfLqn40yJivckZ/T8bpbSAI+ydfCG4qLcMwsZlPoX1skIWYbACgfjyHrZxZ/0CN287mNDsW2vei1cJw3Aq1gIcECdiJ2PtVgcLeYUB7nqxiHIEgXBDtpYGDZy3o0XnYj1EiCdIIA6B7AYcyONjX51mgTNPdFEwl6yAbDNCQDXj8rrhcjjMHucgB11jaxMqVQ2KJd/ROff1WTs0zS/6qb3qp21TITJDQHJR579NdErujl9w7iP18WjwHQzHlsRRZlcdcrpQH8xU8AQsEhS40+IFaHeuN1zbfqi4HRU+et0GVDVAQfjundeLQ569OlLd1qSdIz6XN8jZ6/AXve87A6arNIQCwAqvNF6k63rQGKMNmOt4hxTJiab4PzGnRp/ZYAm9GmDbqeruUArebDz7wd2L+B9kjDDL5TMiE601ggV+qR8lDgKN6jyvpla+nIRa1ieIZE4AZjqMz5M/g3j1LlcfOaapZ/jQibJEmz8G/dxP1Ce5sDv/cyeW1/rC0n7l+k/FxG7bbP8P5BjrkjeFUu/4E1XukP0c7TxY+yWIJKWVsfRq+PATD1H9VD8zbcRacSBfkHOB6L3h0EcUAgyKj9LVdHMEY6aSeciupk/n8I8NYXBtil5kdZlji1Vo+1O6UyBTGLzQ01F8xIHZlR9HQXCeDEDb/83ZveuMi00fzBXgZcdfOhNcC8sxZ3xhpOZr56JxiTmM+V9hq712+Tws/p0t25OZZO992ynrv4LyfQ+7n9nNM+330GcwpOJa1mSw9FTZ38Xtfg/op3vKYJp1jzCYwc7h0WfXc70rDb6KmazB5fwQ7DhYCEId3VKpESZkzEsThZY7u4edPBg5CeEdzHwQmDjMRImhrPVs23m1gBMoZz/0Ohr4TolYSgcV+brecnc9Z5c+rM+T89l+EUhGoFECqUAmhULugGStTCOIg7RXol0f3gALpbgNuJV1JXQEQ244IUDmq8h6AL4dWmqjv9Gi/S2k7GNqF0gUK3qDcCpRyAyz9fofuOGhO7drlxfCJWjl8FFNsQwCQ1ehUDH9qW3VF9d7qVGvfLZEPPBIsqHcgILi/vsqdHm3XhJ7zL2fY9qZp9RaB6Hgazmrvlei9iXd08JDFTruSLQnz2uxY+Zv+ZmWc26QXq/Id+qebNwhvVoXhVEHY7Zaj+UJaH9sPIUdndwGthnrWRxg1F2mZLpaW1Q0BEFS2p+OOtHOFSnNjjaAfYXUwfvEOLN7uqgOK6hZti7UgiPM+xus0QT5WrdD2YMQ4EbS02XdsfLaV8dkqem+ItIZRfnCgEmM3kHL0Pe8q07REbTdZCyyaKmxe3B3pm002ptjI61Tn/OfAjq+Uw2UDAlxlmSij4bS8tyMwjyko78c+0Z9i3wEYJkYITYd//fIF/uM/vsHL7aXtsAKAdrGo7Ui/wMNzDcxTsC/efykgALlb5WPK3w06fzYQa6bDTr/++Hr+0jw/AdiBF7qt3OdFlajfkoayq9lBH7d0YdJzYK2ZKf3qaWI7NVnkNkP8U+vkZxP/OZkxDB1PIPOS1HZjDyGfew3mK30eXbhzh9zPCG9apzBvOu+jOyeocWHb2bIQcOwrG2Va/T7n59vbzfSZOswT4BHRPNtf1buyCiePb8j8lWdS7l+oMSbQXNuzYASnmV9sPeKav786BTofiED7lZ0HowGlK8pH1ZbSueNoYYMyOkiZgqMIV3CkDUzF9epjTRad0nnL5Eo9Or/WkDesMLn7Yid4xNEK7WJqcbaqwwyLegttkCPikXZoM27g88XbzgjGbSaRWPWnY7R3+ImZT6Zg3mHRT9fQeAXfVNyU0fwa8YYVgf1h/Xgb7M5RcYb3NeRoXP0mKCRBHuPH9dPk5mgEvp/C1ofrxEEJ4REYZL3/EB89xXdDmIu+A5jhlJkL4kzv9Ot/TON4hwlf3rtrRtj28nR0A4H6xMgGRDyGuatE2tfKgq29KtFIE+94SVdxrFbAi8iZnCsFLM7VIwgcPZhbhkIk6CGytyjGtzFTedZK87S5FWCob2wQYqm2hqKzSAOmJDp9KH3U6p7MpPC4NZAQ3810dqyfzf/ATHA5WI+ynI8pbnBK8IQHR1aCIU1UEJkvOIQLQHpXt9Fdfwk4VwVywCEFHJLLo1Ju8OXLF8BSOBaVpnM0HLPgccgF5qeC2c4IgFEezyPfsvouol438OUVuEn9V8FLC01dxEDbVqEbaTZRhfacKMNTRR8Cuo/9bDLQ5Oscl4XtwpGcpCUdjryfBi67x09k29119Ax4ayeis5Wka1hbhINiz6cDw/dmrqntnlHq8tvoP4a2t18THrq8HwhH8nq8+jpmGC0VV45jUdDjR/3cysST5HL7Xo2Efv92x8Z7gOYwTc3fx9lZyHwFnqhT4sKWpyn0sE3vr7L7Y1mPyQ6kNlc/G/yh5OeenYIIOk+J06NlOePOfvtuStsRHNhXzh85mWfuFRt5NteHsR2P/JkHm8uSec4S3SZYb9o54CBEGiQ1/oqQaY1zh4y0vD0/8FvAbLdwthDVvgXQYIQ+g+R5Wiqca7P9tNd2RByUG4MQzzDtHA7xTHNZ7ByLzB1pG/B2O8M24DCpPKJtO7LXd2m4gImlvxvG3VEnjpfg1xTeMh/sanbURERtl4BcuMyBCGx3HDQHPa8W7iyqBIgEVJXjsoK842enszgHmVaq/c4MAj2OCICodHbWtoq7EpAcG6T1aUcvAZTSAg5Ed6Gg/Y2rlFm6rHx4w17vcECw9zkwn0VumBbN6CbZmkxljJCgYgse3N2MvB0X0nYkVLi/vvbVvK2ccuvRkH7EEwcg7vcfIg8A7Z6MrjpU45CoYpAAFMtqbcEbqr3sfs8FEFdH681gDquagzgfOaiBfJJVX5zc7gsxyX12cZAIc+WNT9WEsHbZmQeaEuBGWvvuzVEzrSzVH+PUBG2broIaVkqbbZaS0VJVw4+WUPa4IBfVfuvGEaPvVAl2unXFPWIenpuFgIjMQMU60Cx5GlXaOghh/eCjI59EJZjYp6cqP6iZyTOfnoioU9H84YAKGX3EeYQu2/HR0+7rwcbkYK2BCKAE5MYyudx4Cfc1iBaIn3hRSqcQ4NqRQO+p4V1injY+vZhlpQdfGd8gm+i6TONDGboQB2Ri+N8GO15ebvC3v/0NXl5ewCpoMvSMU4kDRfALHLzPavqFbfYXgH9bifu3rfhHw/tNev8yQMZmMrYzQgEsxetAN598PsznxGZuCH6QtjuJ0ynuGzhCIs7Peub6GdCZ3mzLLgPb/30xxjPZ+6v7fi74C8j1NbgmiMYjAPsGQFbWhfJ1ldwD5b4fDEGItyLnNF8+Hvie3631OGbu14IR1s/n57Top+zx6xkCM0fIvwE8w2u/D6cDEdFZx7+sY0e9yys8R6E48wqjgShuy57Vu6eydZ2er/OIXHRC2Wo9Br6zUa15nZ0jjCuLQfErsZY1kqM3iHWtV2h8tKvFOQjRzCzrNNMeP0Semze3f0VN1J1TKE70Q3Y0tJV3AfR8AABUeLNAoIhcZr4YFsA7wfrLfiE1H0fULpZm6UgJqjGgFaphmqRCbUfeOFkLjlc+Gks+23MkksBMK65fkC3Mtk6b7iTqwshObssP7E7P1t4c8IjipY5uJZOVLMHAFBF+wxNJ2lse7boTbYhsRdIKnEPz9OoKZggCltgWyWpLNzCRlutrsVe0yWt3HHl3qDqmB0D/RYMQx4X7AGan/EQFjleU7OHAcMZnTn5Pk02ez5fqP3r9V3GouUgdB1bQnC8VdUNGmuwciMZnoGd6RBPRUEJuX6Ln/YYRmh77FwisPRghpVg7zPzg4LHoIPkTycSpsOko3I9nMo6WUn/AV3yFb7fvgLcXwHIztDcdhz1t2iIb/eCM4+awX/oIXI5juzRYCe0hPm2R/foNE8pJ+WcdURR+XJknpWeiL/ize69DTP8UcGU+qmAvvEfVPcPqqCz9htweg50E7uGRYsWa8Ph6Kv1J4ZVNlSnMB+F9MLyz02CDpJF12SrLsW89ow9Nmllpywn072fveqBdLbRYEhvH1gZHsHOvt4L5Qjavw52jJaScsyU/yuTqTpez7X7lPg//cDZX93bF1AbgIyncvC/7tge6+9rOyWdp9e9OebJI5eTYLanPeDrXZuy6PLFxnwhouTXt/SY5+zF8ktiXlpy8ZowcolqNR8uV8QPSntA72Mxro7NO1yXT6f4BhvcQ00j3m+iuCd1zkpI+7gqHvrOai4wnIQR0B8XhViqPazW9zXBJj5x1zUVe+zxd+2YhayCxBbNlRo/ZeyB456Pjen7Sv0efyabN6+c46JFiYIP5nmqGkDcl1jiD12NaGKTZ5nhIWZ4bD84D875zVfiHzk8xvp9gu0DqdiBiKbamt8WjGzJl5oyXHaJDzcTFXtmRG9TEiT6WGd7tfz8knjJGjYeEIA5SbbW65RU3sDqAetnIJTeHWe1H+PBL77ikMOC1P80/yoYTApYblNI/nfIiaMGECkC1r6rPOx0BtGOZoAJSAYLaCsICWHiZvHVmqTA3rdDLuL82B3q/y6DSvSWRI9eLFsgVQuwLWYryuRuZzGsst17PF7iVG5TbCxS8dbraSt52RqxWv/mUmQ+GemfoEAD2oAHLXm+DtpIYwexhAKp33ZnAu1J6e5O56Fgv4W7/Wke3K4j7nRvhcmN7fm2lOwCXxeXZFdnNq+qXoxtc4wBJ43fi3TUIPAi1I/hbn6Gq9BH30gGvMlQUtNktAgBQONvGefp2nOh/+Ik4R82tGjp14KaWdjf4chtXnjEOOW6LSFaUtzc9VUWpzBAok+9a2OzoKZ/NrOqrSne0y93qOYiG0FybLZ3kl2Ck0S5XODNo2e6Q1cBR3O9ukfLU89VKjtnR/2hHNow8aJyJz9vvSk0DkLRTVgvWAUKkOk5B9e3RBF6PljNYiQ7zyc6JiV5XHKMM6F051API/Jz/qrCSDHxoeM71NccBSlFkxQK+vf4D/m+3/wP+l7/934FevgJ++QK3Ly9w/xcB1buUxiEJP3Km5Of1PYBn9YJreC5YdK7EPQM2ioIcxQX5FOYYoZnFCm6V66Pzeo/ef8ZzoBunz16F+gZwRnU/g48ofwwB2xnZeulPcn1rkj8ZHkU67ng7B2f5n82mrpS5314kZXkb6a3kfD3PfEBe+1yr1m6rAduxpc1boLS5D7JrpdttUHSC8BbQbRN1oGa2RWLtpOR8uPZ5LsgEIX+5NSdnG4Ssbp4eZnyIqvmF247wpUigKSNLOBmaydR55VuevXqzkTG6bKamxZ7N4bN4X0t4PBIwqzzbLMFpyBRJKXieT7Ndo4fHba2CEDs6Bbs9BuruUL7Q8HemPw6BwszUqiIKCfv75TiA5ObSmvWChJL/LvNvIFmkjHiyT5POz9BMsqd9bpg3Y8rarWFC5n5HJMbJ+woSwq3tHXa4nwbd3h5wTO7gnEJmz8fPWf6M7lW9ZyXyQ3T6dp4YD3pR9qbbEC7jc8bn52562fM3mNIBgJY0vHEgwjowJiMorRrL43FZXfeeK3aOv4nDBBJSwsQow/e2E1k9dsOON82ISWiIYWhgQVMJ9j5hwyvrfXTKmo8b8fXEgt3Jj9A2CzQju/nEWdHU3MSbCF67MJsvXggV1lSTzNBlxvAC7QC3GmhJP4wBov/6BXTxxtx+TAgQQOXRtDvfNMBgeGyKTViqExzQdI0smmQ44ImTARn2AaBfOixJRm3LTvVhdavZOTLQTspdBO8EakkyOTUdPYRHYwBiN4DnZFwJP8hltAkmz9wvruHVvh94Kg5jT4+02HK0sOkOSo1dictcVGPmPLSR7hkCuyMslBrKbYRl9DEV+jnqOADLu9i3cxgoPsomTZ6NV56k04M75lxuPou1jOl4ABL0yS7O5rRLXLCYl01XWj4OXVWbwmAhk6xj/LpE/97XoiDA15cCX2792Iz6A+jPPwHqD6ffNoqdN+4J3lxdQZpNC3fLOdKde0GCnTQrE5tHIGv/LcaJZIJmVz3tyOSjMns2/6xOGczTTMpMJ/PvDDrj9r9XabZxQ6IIJmUc4D+78vwo9QxftBDeFa7KwWDzIWzTnswx5r/Xduns/c44dQgr+bwIds442htsGh/ocEPXWcpyS2oN4/tszrwuw6ZpJtCuHf4c3bk1jh2J2jMhyNZcmo9kAYDsTvitITjOkdLHAxyqUDclszPFM5D0/+XUxfBxItzTc8q3+/fEsB9+rn1JrUiUYIQs+Nlstgz39P7B1ZgaQNr9QADczLU37Hl/8gPSIGN7PsuYTRWj2e181wM5YTHV2R5JyptDRTh7TclOcXnnKbGrwtVtNSvgjeZe4TceloVOdt1sbDp/56zzl9z+s+prs3O5lLx9DjyG7coovUBz2X65KMAu5fNlTn0Vs8USnoKjcS2Dh+6IULuOoPke10p1PI7pXFnWYa2+Gj8BPjIqdy9k9B33/MSZQg/nJLWv/rf5NNm4CtelzciQeX/7qztSTDgB+0rWComjvvGsLcrvOwv4rgHnEk6GC24OIChywTTpqtnouCVzpAz/1+tVqQojZmY3GTxRuRZsPLjdCpRyg1JuvY5cfO0GeQGEai7CboLULpSucK93J1JFdl7YCndpJG4XMiuoZZ/FKDeJ89KKTpEtKt7pI8WGHRGRP9xLrCUw3ENgHOjCT597OjVt7yatw/2fwnep0ZVJ8xxEdiXIwseMgdTA8Z8AIPKvswTjOWAr8gAAzDFbnqj2p/Bq9TK+tutzhntpjgpmeQO/G4ehyI3sY/ZxZ8U+jLrH9IM0GBEJMPUUw7Z9uuAGsj5cGAYT2qfydTRuTuhk2lJaQj/OgvOHjhkCaHdFIMDifpV5fp9wq4obTnNpmdRAVd2xVThPVm03xKa5bSaiptv4/pnWdwp8+fIFXl5eoJQC+Od/B/rxXwD3u2QS3+myVj8nPG5QnhL8J0LXFYudN7/gLwaHs9m/IryzXH9Ud96Gz0ugjmnkbRlEN+dAsM6zv47e+sidWm/hGHk72OFSXzVNCAVjgCuktA6ZiXfmitMmwl9JVt8CnA2Pg0n6IbAbjIh5PpzwR+HQTjD8OEpKPk6SbuRfTxsvwyp4sQfPa8xjLLwEjBnk/Wfvb74Zn+YvOA3Pai8bVD9aIDYGI6Yp4YpcnwhE+ALk25UghPMPas7uSs+SmQzB2c4660LDHCmTHSMqNorTheKoa2nahcWQenIsHeMZx2veKrW9LahfBC0Cq47R/HJQPmbDHDcDmq/RxGWgep5tjeWDHE0A5vxgYhpbwIJXGDk+Z556U5ScEci0slPQOKHlP+MwJMHFyGqX2xaU0COiWmrsdaIeYFG/epAKVPxMl/DSpA0xhgn4lzEa32pTwTYB9T5ggzqCKZFtjW3YOoHIKhKZux8M3yZAxNsjWfbWW6bdClvD03NggysdG6KTdSAz+JrxNwYX+5zCk2BEmtPoC8N70w+EEg5CLNo5ruBYiYQYWratXf9rUHB+7bhbycOJpiyPMpjrd9VxILajs/dncQEK3w1unC5VIkmPK1E5GgPTpWQ2c0hmKeCgcRryoFUXGcvLDGZYdrMFXvR6EI7HNYAwxmTBeWnQOCqD0W8yOsjfsc9Y3vUcVhei5zfjxIItCHG7QSk9GGwcSc+wYc/cJTCO2ODyXp2UPGKMr+2T8/QILUk3nO2MGGkSZMsyzvDrvSYsj08uDXyU528FO3yMaXb5sR9BDfif2LZuUcWxDfKujbSo5t4xfAkOVUKXyTqCccQ8N9F8BmUr/pzDr3NHjpHL/Wsy1j0X1mbB1T4TbLRT9Oylni3syPIj5M6JIe0uoc8U56O+tUtC7IN94tCmHGqfZtmG5otzEGNybcEk3ZsGfZ7pqZytPufX/DvaCmfUdmbqo35ZoXgaH4ddOGO7SzBiIMJqXFOZJOk5jXxA6wT8or5zpa2qF2JEAz+W82gAM/fxcyCbiHfEAAQ+OTt37YnI3m75BzOsUq6d+ATcRzwOFV0lR+aB+GnYGeKDEUozHSNNXqcygufvWNrbnTIjaoU4L8vz2tiQT1QD53A9VvB5ups85EGGUbusdj9epf3SjojmhyApkw46MdoeHwQ+VmHlKgLyjrin2d/jrPs0ZPUQPtl34V6LLAAxKyFVTsI0bgO/yhjZKYo345BEycNHEcmZ83KGas9f7F0U3OaR9wcM67LSLmSufVdI3xnCn32QxZgvlkDQ6CwAKLsoOo2lmFXhxhlMBG0VeQGodwDUy7CZjvvrXWgDgLbDw3VMJ7igLRyGFGo4AaDdm8GrnbPdENFKMu0or0ROuJDScPZL9FpRre3a8VKeVn+pF3Hz9TamTqMpq5R+/8ceqCyjBiGCXsgy2TCNldedctui/7ZqmuvG9RRjj7W/iqwWbpUMFpDN+xN92ms30D/YFzYIMevKCIBUBlmf9v3hsdIq/lyzs6lZXppyQLcaFLOyJHKVWI6azBn5OULP3Nbm2cjh+5XoNUk/mUSg8iHbPWbvYViZ7rF6U4PQMLKNSVomH39n6Vd85nE6AY28UDq845x1sBoQjsNHTlXDgqyGrkkH0mY8CVM8x/Mmj2Wx+8jvcEP48uULfHl5gdutX1RNZhfdp/T0/oIGx+3zVKf/L/hgeKA/vkFX/rlWYf+C9wIep+1OdCxtB+svXXQdMqvsU/TByXT5GYD9DwHIjur3qjOX8ktiR9CV38ML/bLq63YB2zvA1En/jK0ybwG7NB0IJ8a5AnQ9kgZaJo5p2UHvPG6BgH5UzBkHw1NgvSBzxaBnL7zhNWV+XtzkCxH6LvWgw07SMA1UyYK2luozQuaA/4xd7z1AjrK7pH6Mr+YkbAci2LkafRFHOyGm+CY5V3Vgx8tnAXu+vuM++pOwKbxjR+8Z45dX90euSdkUy9EAEDvxbGSdZHOG2aUQWsUGLXi1ubnKTcq3gSY0TyUFEVQgoHrvE4Gqn6YuxSDJXJgEfB+FcXZTGLw4UkUEVBEkANFvRW3Oygp8YSoR03Qfe5BUY/BmNzJj4MRQ22vsLhRmJ7U6I+NKY/0lkpX6TG1QyPYLNVE1/mCJ7HLCadPAlt8R4ekBZzk1I7zXwQ72Se8mIHHAZ4NWpMReIOUpQGE8TwZEbNzKGds3q6EbXWGNk2jSjzyZnWwP4hQdgxCWg7oCpjd+pHcCoyM4p0L2OJkM24a0rCjBTpMWw3oDoN9Fj629vX6bhgbSoiJergEXriy5bvA6wwIzPts2WFJ8XNiQgwAIu3Ec3k2q5Ad92+G9Hr0ywPsAjHkO2Hd7MW2ZY9iWbx5xekmRKMIhohNQSb9FGDIjQCkFXl5QdkS48VRLPYRhbIZz4+6M5UYbnYLDnQRPgwfdFBlBONODIWs6ViYj5V/M2l9y/D3mYkOX2y9sfrTdMQ5yOuskIIybIjLjL3uXvd95d6JrLLer7yBY+rz2eDbdRTTTJTM7YaH3DndlcLr+11iaOb55QctyztC0hUMmx/xpcaPOOQDMeLTS0ROanM5LxsNn9vvIl43x7Kxj9Snpp6w6h3v3iORnwnz+49/KnJyiHZch5fnJZx733ET+IXhWe53ZRTmUOZqW6fNWjk33BAYIMt/uK9zsjD8XjHgqtRPCztgS47d5YuWNDQANNUravsUfkvmnS4sDbgvDk6NqykBIRt3vjcsrUO+NnfvNSZoXkRruSXp/LFPqk0lQ5esQ7cT+gFjZPTYvYwZLK3NatL5w89QL9vhZe0THrSeC+MtweBYSnkSsDDkKRuR8CO15klendkQIamHGxOA9eHAUK8wLf//Be/c+iSSjDCIEecOtdkJMt8f0SZvavFZ91VZeHLTZAYTgIqJyN0LfEVGrBgg6Agl+9A0Gmo8IUI6ZsnUKiqqXV7uzv9Z7P/6oQq3NVd8vpxCH4XxItfVsux6aM4xAnLtEUJGgUIVK6G9r6KdPycp5cdCR0Ka8Nlqq87mGNkHG0Q1TBG034h0KtQrdzEfWhdIU2nM9O53sBUbLe4JWMT2Ky6ZLnT/Au4qcIAHXogUM+tMtwy/SExymzjlendOBi98LMPZ26/eiQ7gPYZykcx11BxIC+CALSsvZpvb9vjBP0KDWtuLu1Wg41hP7esRitrpW5UnwBV8uKVOFMFZJTCfFnTAmCOCCEaDtQ7Q+csoU5wmKNXPGgWY6xI3onVbSfglfg1xoj479CsPvFZg2EUNKGWVX3XApU5wT27mhsyYXl+ODG8pCLydnIBrnHIyQIINpb2aV6A5DIdj+kQ3+piqEC4rNC8QbfP1a4OXlpdEEfvx6pN4/B7y/vbOGVcMZ+Gxk/4I3hYebO5OpFdJPI18fTchfXf8dw24LkBmr4xxHz0wFOHbo1eXbY8o+qr0+QFYnRX6KnRJPArbSmn3SbSC8tmDkF/wCADMH3wxGzBfJfSDsqjk7OUINGMzSjVN8TBYxTPJ/4k5pzoaQ3+v050vwjdJ+8042quNOlGewKwt+iK/OvT8u7BlNSFa+3nkofoz+JOO7yTPbTlwsway9rgYhAM7siHDU5Gk02DQ6BS/BLGrWPIr5qtOkMD6Pfl4OpIK5uphj2A0RHH+Do8rg3AV3LFD3CKrP1gqEOmgKYnea99X3wPmYRrLo2vN+gba6OMkEITA4WNkYN8ERF/szWsYEYiQAwUdA9cCJOlatN1W99Y1+E/QQjyJJpyCqALUAYW2XVpcC7IBm3xXVzoN+gTVf1j3fl4OmLHVWiyK1vkJOwjzm4IpxCMv2t+7I0yNGTDtzMVHmTJ2zNg9FrZWsLQrBX9SMIVEq+zjg1/HE74kY+l3shix/NslsVTYaR3+2YyPQKmcBGxSuihMerYKPzmlbYzp04iukp4BevDYVt0sl/Y4DhjikGdWaJ2wmLhIYIvNd8qDsihjL2dFtVmg18pGutAgq1aI4uwbI2jwEJkBxAo1yzQceGyJYXHrOZfVJ6laZJnRCnFdp1iFmjmx2/E2ewxMm44atYxSudfGaEFVZWluFgxsjgQVutwJfvnyFW7nJOOz7SeybAcURWU+ER471uGoavQVs1eMiwY/epfFe8MgqbB4GfsE5GMydXRlJJkVbRzDYweBwEdCD8A4d/OzOilO4D99vDgQnyj61a8wGFcKz0bYnZ8+07opTIyBK1j5Ri+dZ0sc9LMdpruqlJ8jvo8GHtwxePKDtpxjYNjvTrM9WO++9i+Qj/Lxx9fxOXReqv8HurpUrFd6yr3T1/hiM8E6H7BjULVpD2uyapsfkZkJLNhex7F7UQRdE2ToTUFJW6lTnQAdCOKXioMA3Ar8ArD+Z+DtTl0j+Y1mifmXf3f6F1WpXLRYMTrztgyzR8OVNuluOp8+JP0BfHS84nxM1X/S/p/vmu2T5/SrviGOafmp7rWF/R4RbjZjDzgVX2+TRuMJby+l9KXo2Z7Zi2A40ITLVn4eTIuNwlzy9Vy/PF7f5U7SG32QVwchLnf82xVLE8WMc7bUdUiT0cua+I4IRMh420Nvk2pyhigBQCbB0xxgRyNYD4I5OQjPvDKj1DrW2nRDQAxJMBJp/Lh4hlSSeO7SX2I5bascCVaj95J1S+uqA2odybAGW2u+9IOpHMiFCKaVfgjoxKONgDdwGJOQA8iqY/ph3JkDfDdGdZ3q2u/JIHGvkCnBkoKGNOn77exR4J4Xj+zAAzByBByptzGJE0/f1sMLB9jFOu6kQWA6Bne4JET5uZ3gM0YCB4Rl1eiMHM2hBrfa+dO8TFpCggKEIyNLFpQYZl4DnwIvAMEOXjexneveIrQfjyNCW7v3AfkMn5qqU3KfHOw1CTCMR/IxfGZ4vAkmxZL8jYlzJNlP92g+D+j60XVGDEbMUwTAwsWPQs1Dn9G05fKcGEfcXHgUg0V97HVYCrVJW4LM5Fop3PNiUWAp8+foNbi9qomh/fj9vb6JFfwL4OG/4z8erX/BXga0gxFPLe6ynrRY6fV6YWg798411z4xfR54U4KlPDWaFWk9DILHbILrb+Bf8tSGxwd8hcP6WsvWe9x38NCD+mXdp3kNwNDBdff41C0ZsByEm79fO7feBZEPEMl2c5zY/APv2RpwRt+0LwwLID7CZtb7vOMbYMrgfwF4wYgZOxyyX/lP4VDIuleVfbMvw1fvpPqO9Fnnx9uQt5PRiEALgVCBifLTTeaNzb6+sudtqKHFHAJ/cOLJ7gI3UhBwMDiEn+P3C6ubMnoWkeBdDv1jYlVWlLCkVW9gBCCTgGQkzvh/oiPV4pOCw1TPv2XFaepp+WbIMAkYKCICwO+HZdU/9+CdxIlWoUEeHu/W3GpYQVHFKsh+MI5ocD+djqe6EoLGFFnSo1IIhte9SoAJQzKFN4lXl1cYQZYw9gVWd5/YxkDiDqQdG+OJo2cZEzI12/FOjiXEhlGJKRWqbRcQpaArrUsHBpBbT6btMyG8bR/PX7A0wwmBTgHl/PCDygOUd/+3L3PW7uHfioIPy5b9oZ4rM+96E2Y6IFG1w3GfBkBbzwCHtjFTkdBwsaQRMMqmA28uHZXfOoAZU7mMbl76rZwzcmUdu5b832oj6yQQdR2tXDnqxTggGm1SPzLOs1SdtSkydaf1gAA1BCEcAV26U3K4wGodZJmyg0emchkNX2yekkk3rSE7mq8cBDQp1V36jS5eCqdcKZsZSDAco0ozPho/Cm67PpwUnWERhQyLX0HdkDRUABIBbKfDly5cWLO7INKj4GJxdnT8zMVzurVW1bwNRR83KPDo7/j2M7Cvn1/9UoMPdeXjUOXA2/YLGc1b7c9vuqH+OO6Mi03PaB9HD7OE1uCrXZya3kS+DzXOQ/2B4eRs4wd+z9WlpeEzIHSBqo+p8isf7vq7lHXXPLi8Sg/TRBspkfycd7OmCnUWI8myzLunK5ieBQ0WqP4a1L5nS6LZ0M1PZmH4ebc+E896XSX12dwq8Abxl/7Q2/tKHOsu/4u+BZ/3QloewM8I89+ng0hCMdrycuqEOGJJWgsxfU84qWjB/HGiFVBZj3q2V4lNyshMXxjRHPJ/eS+GVT5h/RtvmkG2ngOSP0W8nEBNP3ALM7+BIJn787aIqGfw3+mIcOp2tZPX8uvDZ2LO015Y4r1tf9u2z1O8ni6ecuyNigLXdDzYIIeeQ7eww0A/XcQDSPpAK4NG9DA8DBwf4u9BnV9hgXt9S5I6FUe8bB7QNeACFzpRA4EONzrf+usUD+AJpdkaRGdDU6euOnUEErABUsO0EaJ4qpR20AHZ+M353Pmu19Zgp9ObU54mDfd48WBWISleMBbDvTqigTkZAckEBoh5GKSTBCF5l3K/ANkEV0vJs5aqVaia/KeG2Ut4EXXoeMu1C1O+bcM1YesCnJbzTHZDsteDaRszftruwByDsubet1XozjrsEpIkN7Y61rrPNBynbJHsTleQZeTzznKjOfiUV2iXUoOwxL/OoedhNIfm0PSxv3KdpPyO52m4IgFhGVZTVr9cFbWHCay8bbNLxHSXiFDaBktQxYdot3TGxGkutyFuip4Np6MOL8WB8gsbZPQcVRVMvZ4/2AIoQz/zx44nmw4fGA9+XLJ7syECeeKgDxAaDWAdlPMgnRyxlM4Pe9BPS1R8+NfPLPHF9oBFKlXzT+xkR904zG+JGgcgW14ckmIyWRtZbCFAQvnz5ArfbzVLcUeGi9vtzsktHooUy0AvhHN5yMj1QeK2so7ps2VRBd/xV4gs7sJzT7YmahwP7ek7HNdv3+srZVW88yOmcCTh9t4Z12fOJ42HWQzgbvMvqe3alXUy6m5Ore4riQ712Lt9Dwc4hUEHp9yyfmu96b1sbq/s8YFlsgvuBPhnlPC7uGJxg8nDiHZF0c6KG+m3S/5Gr6U+LShpp3MsjNqTknNljajSR/MnS7dN/aELM+tIB3q22mzrLN9P9JJAdXWthFJ28Ud6iP6RO8y5ANhgh88QTOPcSXxDWGXB/akT072q3XwHd/f/YYE2g80z0L+SBLMQ9xLUAIzvrHUmrIESS+mmip/PNZ9nnHzFOPGavRthnxNmFW3Ho3vF17JF2vv7zsp/Xflf6+flAxM7YHkWke7eIugthJv0To2CjQIPiAkONEuIV7rHweCeE3RWhePxNB+sygzfKltH5pTshhIpAdicUAch7u7uvX1cBiX+zRSFMkEJNLwC7ZSn7tO635kitomxB25lX+0t9+jFMxBjIKMFkNmgnDtACGFx9RIQKFZAQsFRoXn7eYVKg1Nod/yhyJoNPb5xinGVEAIAEHBYSSkgDRTGY4lqC2djZX4UHzCkrNyZPrwtiOyYKAQFLQ1I5oFGryELjH9970WkxF38rdDXAuwi6t4/YgLYDruFFpS5HcvrT7kwlTxcH4O5y3sNpsADvcGlnHym/2aigi8MRyyLzlCXb7DBAKydasNYi7kYYiiDTxa2zNfYt334OJ1kctljc4qcYuYYOn8COkNpvqxPYjglzh1YMErWcmldoSO96JNvrxhphCNg4knfcKnNvXj5WWH3I6SZDFvfjEnWYpetB43lZvUR3pjjCVlTSIITyAGWS3QwnFN04xFWmhlJCC0HXa1yXdQDIoi6liH4c0+Qa5dl+7/c3r58Be3JxCuMZR6l8+zeKQnxyONqO/pEOR6HhgMa/Kpyfs1zv3x/fyu8D1t5pNjzvHO7zkz6oIyJgKX0RCc/edIT5PEcx/Pv1i4+E2XxF5Ao+h86cwV4Q4u3peGtAN3f4SY6hmkwohh0QV7ZoPIM840c6l/Fz8v6QLFmoFeaXhv9v0hS8mFf4bWTindX9Nf+M5n1v+Cn6+ZvCe9X/+DjpZ8B+IML5WU5Ei2mzErMgxDYDIi0K0+4VHY6QD2bOGBWHNLl3wwQq7IaYRtEiDyXIYXZABEeoq5Qo0cAzquIUF7pBHY38TJxMqYMxiUSzRtbREvQvQK1tF0O1XkeydWF5qADmiKTxCBx7bJQdHPtUwTrNkQD7kVEVCiDcoQICkHHW9tXw6tKybQpKm/nN0xFx3Fme2uawfkcCretQFHnnH+pKfyzd4UYEBe9QGwtM8MO2I4G9+HtY9VwMQXYwBd+OvktfO/9u9EnuD2akzB7KdkcO4YiV+4jNyw7UNb3kLhUmK1uCRAM1M8DC01ZvxNhyRI4yvhrnfQt+Yr9bJtZTMbrsQzoVSJV5R5AgJPcgBlt0t41CWcdcYlwlkKv8nckXmW9GjmMxC4f30I7TvKvyKTzLM9ngLpc94l/L4Wl/Gx7nOXXMB4Abe+QCr8Bjcdi4jK5Ql94m8eSu+5MnTseDM8cnDWg2i3sGHB7N4qLhOwgX7540SVmtQN9vqon9M8Gwbk8Er3d+Ysg7wdsWedD3zx5JtkYWf57DbWm1dJ0KRlycHblcmd1xCWfA8xGO4xk/VnW6FARJfnIRT5ixPopBSDBztDYl6sfENuu62W+8eIxjEJ2AYb61XfaYaXsMm8wRB9v3PFlT22jrCBO4Jlq7OE7DGRvnkWJSDHay50nJXAAxzQqG9BP/iqfguTAp+p12NsaZyYENbeb2LeN1Z6rgnLTZrH+cNesOy4/BiAXY/Ttwlo4j4XxAAKIMTdcdH+CZlsh6HZIdDrOJylBPPx9JgxD2k/baZAUuL/HvqcAteD4SkdQufFsQnkxgz+quWeJnBge9dng2DIbMG5WTwfUyrx91O9NnJ2iYpL3S3qd3RIix1H44pSDPhSJWFEcaleyH9dv2QrM8UzQmv+9gbpJjHY5cTOLIme2EmJ3DnTrvN0CPLoJuLBPwvQRDIUowsEeMgICvXnD1747Q2o/wqffu1O6J2oXNIMyrtl7smDKMNe5f/0kAclkzkR7FZbKz8U9yRwS3jx8UxKlYNSAj/DbXOwiLiQdv5gc71bQuchQOdporQS2gR2SRPnfSHPlSDb8tj7iU6NwBgHiQCPbVxti9i1iwX3rck8l9HBwAIaGl8fYud180fKb84h3Rb7qia5gwuZHdHC91hMaZVB4HJiv/SQXdrlojAOXjlF7dHZJPM7x+aHiV1wDQgxDXJvcq7t5UmE70wPfJbPdBJ3LM6F6zHNvEIx498svQC/uORgDWZRlR0HXyNOsArdi4GyOfsK9wUHqmn9Hvgcfnwffx7N1I7tmC0NFmhze5dHMW8DaUAPSA8YDeT2ia2iEAzOrGerZ/zi7SRp9+mKxLYpRkFUF0Pv35TwD4HeDH70lFMgP6nGxchVVr/4IrYAXmPScBv+BReKS1YkBiNxgxO8bmF/wCBpmnOceVWRjH9uUga7xj8Dl66PPsqrgGPy/5+Sg9q85eNRXn4DsczREAcG6SLcjSv+cK4E/d3InfRt8ljHvEe/xJBP/QmTsTvA+EZ3DuCIfMT+ycPcvEcxpyPwUkCNF3bqeLCrscPXtnxKP9msInwIEF/aHm9V/Vtv+r1uv94MSOiDDhh5H17jdlXWQO1lm9zEbTHyMyNkCTFdUARgFNlPhw/FL87ZD5AASG56uAjDrD1AGTlzHSDgYtr2iWSDHxPRHtX+1H+bATnO+wQADdFUYerfUjpe0trGlBCN4R4atLNmEoyK8st++Y126yWkmOMOKwBscfNBAhbq/+HoNDu+8yqAWgKO8bn+7999jW0oZCk5HVvrshVHyoEwMiSACitB/TfCROQ+Uxy4m7wJn52Z2300Gux32mpsvOSBvtvcSBvwsUvqtLykiF+in7Pw0KXinQTE3l8XInAafh/l26RRLmOkxbTpjtwNcNx9lK5kNeEIGuOLaBEF9hnoRLzxxI9c/y3SMjNeI8yueHCewHP7KsXb21n4MBeUFyHrI3oql4Ls9cXDwzp7Z4n6zM0IhmzJoyJrQR/2w+6L6HCyAhyK8pj3rQA/s4WGsFuP8B9PsPgPrDlEcGmy/rzSCb4HaaV6UOq9BPzGJiePbR2p1Z7b1lfoFpuysEfRBcX0V0pbDn5Z2iWtiWzypbILDIWlvt6wk6krQ7wQhpvxPj/3a63eD2hVRzzOuB5XzLBv0YVxVIsuuYGXDyYsC8K8su0WS+FHJvmavdVqvVzid0DuQWrPFfOpaHS7uIn+7gPE+jDEeHeS8T9bCT7fFyTZs+i+fRhpSiUE2TbCqEPnl7lGmRkWuDvEfc2/Tuv9bdF3nQ5RRMV1mdHG9jEGIW9cmebVbgGWIixT3Da72Lg4MRBzayS38KMnxBEt/EH4tBEk0R5ku7a1DJsWkwzcPY2QeY/2ZfGQ2I4DnCchGP9Vo4f4OIQD53PpCKlBRddNtk7KxeH8TiaHIRibvA5p3dbGsikjeBObuL3qZvkzkhhU8AO/uLT83vicl3QIGmCHVw/ng2HyeYpvJwot1O74gYB8lAiHGq85vRRzU3jFpPIvlwhQaHmx0slW/kJii4ES3OtomzkxMrAAFCO+oIgG8T4IphP7u+8Bn2UTFn5ckqfF6hozsh3HKdoWdmWqIHHmq7U6Dy3QLmTFQJQgAAn7XfFFXRHQaVj//R1cyIzXBv1WJLqqWBSgAmsMGrqF3TIvutulFfvdu3Od/bp5UT3QGQ7AgBHuQNuzE6S9EY2tCdRbU9q+xcJSCsgL05a//TjkGqrh5u1RSBtJkPOo2NLQ5aYhb3evWJTyk3wFI6HzRNO3KpQr3fG894O3kMgIDlN0G79LYYuuwOH3ROv5GndveFoT9NHFKgpl0dUWCPtFH9EC2DHjRCkJ0H2Ae/Rl9VecpKGWwjlH5qexFR2D6EjRq7o0J0Gxm0Ule2XFgnEW8n0GCiVEmNG+Q2oAoSfJp0byL/CLkeGHl6oHMc3iLpkGlr6k3xdb7xLoSpgy7YpMIr1muhfNadN5H3HK+/bBkAk8iFHRLsFt0IswE57pBYDRF2sxIhyCXrwivqO5yGuyJGPBLMFIxjOcbPliWDIBXDm9wwQgm2ksGtO05QxxKLmnV0LAOaJOlRWgh8fw5iASAN/to+3jhkjl4y9WHZLrf29MfrHX6UCog/4N51IWeyY5SUzw3k+FJ7mfG552HcaeLfz8ZdltVcU9qQX9ZiA1ZSXaD9MGRykD1c2zqPwKSL/XXg0Fbc4cAj/B/zfpQzbw5e6e9M7VLYmHxfnuC9Azg7Vj5V/xOM/d6n330+lth+7hxhlhgUW2WtIB+Hd+h/Znsdik9MQARErwDwJwC8AtU7FCiA8BVK/9Zqc++V6gO9NzQ/EKJEzYjaI3ZjWvwQfD699Uwgnct0sH4Gd6cW21dqBB9yhmcXpB5tOCuEV32kMueR348fd7QPvp5ctgSl1+b1HCWAb5tgZ78FqLsgLyw6vqEgG+9iM9sYhNqM1noM8wdebLTk07zSOt6uGHMwJp8W1aMGXdi46DvTomaa08wRsAyvoc0pdMKHMJMT6zxYg7UQKucxC1cnU9RJDcaHsX9GjuXBhZCOCCaHBngk7H+aDh5WKWZEhHwPd8Is/7M79q5Qzxnocge/SZvPzkdMnRaGmSMhZ54U5MtzwYWTIBwQ5wEFnI7i02VcuyNiUu91Pc+MIPOGb3zwwQB3TA54Nszm76vBVXclKC3inEgkqkBxymtVFzkSwzgrxUEUHJiKwqiyVKs0w0guY5P7A6qUaScMzTZSmrWa9mplMkH2fn49vyM9qkYCHclA611NfCRUZdsssMuXLXdDpJLu1aiyh3c/MFt0UGkyEwZx8gEsCehwvcRBhcC3S5Ch0lrzZSJO7ETnXtxo4sup2yV5nkcAYI+4onuXGQI5e8vwzJExHcRIUo8ON8MS6/me2zuhgiBOfgK2DSbWNoH2I/uMUbHMdEIlkGO1IEEIaFlbU6w/N/rrsTVadDySJ3W2h7RjgTDUk5J+LM7KOAYbZiP2HT5WJ1gibNHdKNf8JLwa2tel8+9tkIF3mPj2LzlfHD36vqnlrgsG+rvsA/ZV9xvjgQzSI+1CM5CUa2nStPrcBxejYMfGxLRMTpVN1mzQJNtFAhC39q46l/IQ+eJ5jHUwqbsSmK/a0BJ5rJGj4UQZo2kuMgVEGlE4wP1K7JNAlwwuwYYSWUVfFAf5CAnu9Q6vd4IX5Ltwqsdh64UFgEzX7JMMe4+Qq4pjJIC3wruiSgxp1z0wED8B1ouc0bVQwKvWHteLR8akDQYdmwgrzMbQPdh2Bj/k5JwYl58ORtqe5aSJw6ItYTP3c2CJysic6bxnOPCzH1OzBs+JPhKskpiUJ3BPeDjT/Xl5j8jtfl4lKQ4AbwPjGKlznGZf3/ugQNBmbjcwq7EMeX5+seWjOwm7znpd5HMUfIq2o301Ds47wYhk0eak5AuM2dUFmxGTR4Mffr46w6WG1EAV0Uhq0tWGkdysrLXi10zJJnx7GqLhqRup1R48qCd0p/hG+ZaSZwWihmCEeznK9HC8dmbm9y9jeyeG5QGkGzAMTrc7YpLOrXSSMTXyMM4f/BK/oXrJu73Hq3onE94MJWZ0HGSYFWe/ErrHtKUXwoQp66Nuroj+GdeFgkjE+UMoKsdvOUhCkkO3WaVpsoQGhLk4uy6UDQhDRjL6wFf8dJ/nuWH6fJph8jvO7/jziLEnGi+W7niz7hsrcJrncA7QZdRN6Bc0Gj+CLWB6dHOSVr8aI4hWtnxoiw04vSNiBmE6DUxJPok+ibmjZSd+eo9BKONKidmmyEoahPBy1xw4uhNiLJRC4/GROublSLM4N8APsJzFWMXE9z703Q8cfOA7GsgEIPowJs6n0j01dqNDBXZGctcgIMLuXGvAFyTXegfqdUrrYXhov1mWFIS26p3rysJdme9jYEacp/xZ7Ipt1IL6p3XC63FL0NvPAxHAne7CD4R2hwYhtNXOdkAR5zbKpJzrgVJRCHdOgNAtlx2bCAL13RC11sZfKy+WuSt9R7YNe/msu5RD3hCl3qcMv7E7A8doe79jwfzeAXF0QzC4mSbUXUXFbR0AERyicQdF4XRGMRJAW+E2HeNUiaPrY3ldUAyYMCCEtjkaiCWw1xvC60ZkglT4+iAzrqSP3/OyrPz3igCSX8k91FPssI12JdD7NqjpIyXT9HszaGrQmHoQ7rgM54NxFcwgp9vu+NCjpBR54/G6zlKNxB9AQP1OFIBSlA47MbrkgzNjW8yf2Y1xIobhmw1etdrz6quyV4ArS1BBH1YcitjLbZcegJuijwmly+cP+AL08hvU3/8TMN4TYSZr/hixSSAItb+7Xm+eDzQlaIRc1qshmCn853FhZuzuCATZL4/YUe8FTfsC5LI5ws9QJwa7hO5KZ/4csHMHwyQn/Fzt9Qv+nWAm0laFDisPo/2XeG1++tjZG1ZgJ5jxCxSijfQmZcDu6EThc5bmXAO/1W4YXcg036UxBCH0I8jpQb3eoaHcbpNoGkZ/k6HpYdIGM5RnxZS+lzlI9LO9tSAb3TKZmQPgfDf8s2iwfoefcSx4D5o//wKTq7brE2zeA3/dmd1yb0fII2kfh/1AxAm6fJQPk2fnQYZM42RdFs4lh2h5ez4XrPysLLcO3pRlynRKOqyXFUcdDLTHqBoC9Uhv4gRmh6vQQoqTgw/swA80SK0R1Xnr6qGdoXac7A9mxykQ9NXoJkggTpdO/1GfdX7RfJTpB1eNQQhzVA9wECIicM4hMtVqTiESr2nv/mEJOdk7LhCgAgLf3oB9YOTjWSQYwmikPhjKZgRo9NroCGa+VhOI8eBNzMjqlt9YKSIHueHGdHE7OokJEwy7esNvPT52WduorAsGuUp0RyF7NA1WoczKjss2XkB9ytmSObr5OTtZLX2tgCSD6Q7LsgmODuMXETFWNGnlch+pxUfzCcEeV9A5WRv+4HnmcqyOjEat5CDJ52Rrhxjbp2WFWD5qR1vZkGS0eOO/664Ax7oLvFG6Ahfgiqu0LkI+AdkxlPxuCodi4kkQrETDDpam3nofDQP7sKBmShM3qpLP9y3cOlpEhDsWqPACQADlfh/qpUEAPnKQX5WgvyzxxhboOrkshMAFL0yFWNVKoN7IGUIfKFzhXmbHpowKTkd6tLv3Qu6prnmKzF2T3b0gRA75meYPTgYmeN0zNDs/D8obbbM8/bveRzGBqK/SEftsE5+UiTMydPUs3s8I010KkzEcYL8pdu8veE9Zey/YrVJc+PUsEXpol9nJzjakH35O8GU0Bv12pO62YuVehR7nO8u7IzkP8xb75irYVe3PhlV/HFfCr59bOEcrhc+jtHsdbrAtl4kz4VvPJ9NgRGbDWptfvie2Xfh00ztjNO/Iw3wh28gKR/JhfzDzroMohDvGKmbvKDidy+ecFXMKwI7FoZwZj448BNGyneeMePtfPh75mV01VZ00e/UwvFXca4Uz7dUb9q/3AxxnPa3uVxwe5DqnYZZt4gU7pGg/bY4542ZcMEjymcxTJmWsF/+NGOZ3QUxK2xn/wevIK3B5R4REbEndO5Hofft3NsXuZfSV/XzEEB85pPjtadUA7HhhT7ojY2ZwuQGr1auCadhobRlneERs6a9ybAiBnG8/caKJM3/o0Dbqy7j4372voG+r6IH4aBTefuzxM7mKmrSWlR18jNs6YUjaAEh3RHDn4eNQnJFljP8KifHObJQBjO/O8DsBeKU2nznOOwoC27VYs4VZVAjfZSFOTHZEGWKA9Bxy80wKwebwQilXdzZwWZI7BCPYiY0dRzsSkpps96S13t1uCN6loNTYITvXEJUq4F2Pg7KKqRWDxn5QWeGyancGirNRxNs44/DkPqdeDT2yxzCFAKCvgOZdJrpivWdvnd710UaGkYGMHabPkFSaA2jdaCtcr9yQ1cJ2K5uB0Q1igPagEXDAZGYBav+LfFmBBNwMHj4Wqf2MuEiMfFNsfwMiS+ywdYNf71vERxsEO2UWNJBulU1eTxtlnocmZuH7QZi0+P5/VPCkHpYKVQ6GFtYMqsePJv423VI+pL3MBGEFu54FgqNYWSRh/MGCw7oSAHRVeQ7fX37A//Ifr/C//O0blJcvUKHA/V4B7gR05x1+JHZHYy0C4l2LBBBdEhSGo1B21gEYXWI0gdFJNj+Y/GjTuSCHWekSQLpeIiupjKHvVhE06Jp0vifA+WBE023eFAjjOdh+EXInDtRdp+quc3byctNofT6PPwR+cvJ/wS/YAZ4r2aNr2dYRu5PnFzjTEZ+zs7zV6vOfEX7COKUDu1CyUhWT9uz4+7Pz4QgOgxF23uEznnFKNXiSh3iGJnPiDXSvzP8EhkV4AxvYio4vEmQPzXt3YD7v3fUy6CJJ9TdZPPP2M34IeeIXbdrd/AtqT4FrTtpr3rduhitdI+bPvo8Jr5eR4lrRPMj5I1zcJTyms2W/TSuuVZTOsfbGkIO+Qh7X1P44WdXrgYiT5Y/paf4r048c8DDnYoizhiVSBm6lxjkdZrSZyb8rK4PgzEhxdUTiNDEOKPNlwOLHUXU7Eysr0t0INlhAYC4zBoL07JDBSREdr57O5sz33uBWdjPix3Moc45o4EW5YdyAZhBh/xfZviPvmhO/H/lQEKS980iE+WBe8Ve+iDpXTtvRPeuk6vQ5h6elnWI+AA5UEEBf7Ur9OC2726RRxM5N7N5Bwn4MjF2JazpYtReqJ444X2EN0CgP8tbEyfcVSMBS6Ej44z6D95M6jZEWDk5tUNLq4xWpJ2E02qZyYProGV27HuRJ0hDZLyImQCJI3Xma6CjvyCeopOyUHR0Hxw91agNl/C07q5X3Ovj7S3gFlxdBZPI1XUbOSrUsB9PQl2cMGqwuHJLsQrZSbb46mt/n9E5LQLMbZjIyrXcANfP6NBghjyyzMcDhIYcALE1EAOEoLsZp6b4Vgt++EHx7ASjl1gPYIGMy1QoVTFCZvKy2XWtKXGSJsr7Jolxhb4IIGH/Pxvz+nI+SK6U4HJQEXVjXkfRFf2ata2fW+yy2G0a3svsBi/+RGYmB2eQm35kg3w5wXj1WaI8nQnNMG8qM1sMu/ZGWj1qtvn+fgKTI8cwL2E97AD/jTogpGDv4feDZfaXr9vjUqPkThewle4Rblt8Exq4GYU3U7ghJ+7xlg61ZPU33GYMQayfUB9I7dVis+8eZnRERVT6WJOUl7Sx2ZSqMx7Cr33frd07WnjumZSvs82DEPI++8J1f0lnXSAQ7HzsjDyFt1JF2PpDugrHpgxzsxkemZ8F7J8msAv3jXHtO08/62rJLTIzImJKMHKATBIBkjjaAEYvpbpEDmnfAhleO7ZpoZfLP48aPr8c6jBUQfXXI7z6mjhPsJU2xzEs2gyuL5nmPHOVH2DP+HbX5hB80ff8AHDHvQIaPSFHfOjS7aSPPjMQd2A5EyL4HJsYZ1Oc6heLMv6gznNp9AX0VvjraQSfpveOIMWmdJfxpHRODsyp0KikHxCAAgLai2hqurWBTF6/8aqfdnYvvghD8qY4QvdDS4oq7FJQfvMLnfq/NwR46pq8r9X8twCAXf/ZdEO3+igpEd+OYVkcPB0B4RRFDW1BeoPSV5aX4M9EJkmOG2Inc21Dr11bmy8Ddj2JqaYscKSVtwo0U5W8wKnjywZ8mUCNHjHB91JkEiHDrl3pH/7hd1To4stEk4s+kZ/P9EbxbpO2IuAPUe+NXPwuK3VquLt2RxW5g7Z+G18T5mZaesfNCA1ks709UlGD7hDV6zIQPO5+lnYuXWKETtN8Dt01u8Lg+jyafHdOZf8LbGd2aR1KtjIDhMUqWPD1rT1wqbSyYiPlkhhLsS257vvBYVo24LEl9eRWWkZXpjowhO/cpapeXd1LdZGhW4V0RZLl1F1UfjHzcdguH/fg9GoHa7+JxXazPBqwUG+V4hEb01GSrw6flGKjdceu2Ffd+iF0JTzdAix7tQWgZZYO82mEsG19ldVO85MyWU9zzckP48uULFEC4A0B9/QKlvsD/8c9/wO8//mjHB4IJykMLKvwP3/4GL3gTuiqPY70eWmagwepKpgTRp7NjeadYAhAIMlYwHgyBCKu35B6MoMdsX5S+i7oT0LNOA+FhFcPYpyOE+rtfoY+cdwSfsEA/AWDk3UpFBGii/3PV9xxcr9tzrYnPCEeXBzPMePgAb4Mt9X6gSzQ+OwxzOiK5N48DzFjKtCrDNCLi/UD4jEGIf2eYmrMnxpIBJ/hgRLbo5VnwlrifDWx7j8GINhrv18MYrkQfptKOZGRYoNY/d4MRUk6cHK4g2vNvxJus3o/aU86e7vNd9ZVYYH5M/DfwtnpW52Wt9yHsWxTvBmeFbAmBuW9RxGeFD6zfIzKsatHjYNl91rixH4gg/yUtOjpiyDrGcyG0zmIrjByEIPllghBcXC9PnYTWScKTfP/OF03hN4hTw9cplmlfDJrL0GkMYSD9TAAB9G4I9tyFwIW9l4EvlmZndiQSIQiQc8aqc9YGGECctuya1l0ZbMyPGkOdUnZrqVsN3R2axA2Cvs20COoXVAjmjrdo2gNPKAH6HQhAwyeGHLY8GZMQ22Xag/Mn4j5pAPHyBgTgnSuNRQRU7xJQ6pan+JgI2PhAlTEWE9PGulum4S28it7Q3HCZvNLmzIcDSJx42nd8H3VtK/kZTZPSqYO794HMUe4+yeLLKyHT537ezGxnwLwsUyiC9gMvTPGHXyS+Eo+BZ75yIgOL7CisXxUkQtNSYmivoQzL/1GWtkHa/KA7gW0D42gNFGn6k4NgavFPDFT5ro2I2DUjy1FwDA+Yh+DzkriGX+R5ZxJLfW4yOo6H45pcF0TXJselQDs//8qsejL084s42aFOVClFxiHehXenCj84UAsAeixYCwy8Et/q0zGZYGsmL7zCXi6k78/5t3Xw62XsfUFAb6DS81EBaFdV8H9RFzRcpRSACkBtgBmCOsIutll6moLqNJOJN0eshPDOl4NmwiCOlAVm3gnGolCeZ8G9OWlrmter/r2+desGrL5XZErnQOG/EazmA29etNdzR+kYrhz59Rjk1uY8+XO5qePJwn7YLHOW6mqfPANpFzTvsuoR/+NARNTJ2ZitLx35rPvb9wNdI7phke6INZP3lyb+h31kK9nHwGNLZx8Cv8Bwv3y2OZrDfMTKMJznb55bR8+W40dMzWM6B13A89Jr0nUNJrZ4sP5TyIIRx5OsA1hmxTGRmTq1ZqSU7qkuMJ0ujYPY6SxyExm7VIIRY72P7oCYjntTlj+gGOKil6HIJyidVPlrgIpsOpk7aDp9nfSvVC7QSMQ5mbOSZIMRPMMfscUn+CY60btPjMzaSEHOZqVrwYs4FY7rEldVGXeIvW/gtM3DaM3uZZvs0jrxF1ysqpByuYvNuWzHpEfhxGXVccJhyTsiZcVcbVypcg9AsHOcV+b6AQeAV1CLQ1OI4FWEIJ6vo50QdsWoNTgZabr6Wh4R8LLfdieEPTqC+oCVNSc6PM0naAS+D3QkuxYIgCrca3dW93sEZFBhHohxI6OO1o36ESrU0vBv3hFRyRyxEr0VwguQQVBWFrEzR/jRcMu9HmDbyQSLOu/b6uYq/OKC2E0luyOkVtT54rkpK7/dU1Xw8aIdcVoZB09brVpc/Rh4NwjV7myKp290p4VOjLQ+umvBO1julXe2vDbZ73eg8Hn8TZab6UVAskJeeMXyxUEqilwxQNDly0zKOkEYFOgpv+MiCBFJ4XrxUSaDd5rRJEFBK+PNEB2PbRq6asKOxkMTLIO5ykWbcQHTQWrm40v00jxzbgDbh2pXmQETpQf5QVx0BovNA8M6gjjmucxIsj4uIE48Oweb6ciBd6wrkgKS9Ja+oxru2XQaLIhO0nFuV4W3TqcZe2UMbMffVvfI6ORoRtQxwOa3x9iciYdEc5L7SDtOyBA9nVDwGO1ltjnfeTKthQmNnKw2XVdeXqD8+Cfg6z/gv/34T/ivf/0XvNIdXm63tuOQAIiKsZEJ/vX6B/x+/8Pxp31WJ2P6nOD7y1f4+9fvrgH9LoUqeSrZ4H+rZ+11wmL2jATDGs0fHv94F+E4XJPJ18YY3hEYx1rZgcH/hKmhbezYzYUCmDyw0a45jA5OtdGOxpCjPjfeNbGkpNOzxrkPtqPupL+sQZ8Asde+H3xEqbaPnD2ui9M/trL9I9v6FwCoblFdnvd9tyvd7FIvpe3kRhfgNcid3YjQJ3e/4N8RLuoKa3PaVfuK9vpRgyuYmMGBtuM8Z+E9tWIMRgCcmbBeBbYJennElDxQNHmZsMW4R6zr3CIZmbxeLPpt5O9TgLPn+wQGuOmUbzaA5Byrlr1xMcNbkg1v3I+S+bmwaiYLR5ECTQhL6i9UTGc154+r08Dtgy3GIrHLBps1zO88hEmiQ26cBheA5oVexGVA1G1mR5+X4It3RJAZTydMIs+InKwQhHDBAHLvpeLdiWF9l16R2iMMVIBDqZHU/mXTk+gMCe67JPXl1RDMJ/m+BAQIq5Od76gCAPHp/41XA15xLjA/FbW0hRjY/TPDM6mykteccbO2F2xJldmRzM5RaWszILjyQyBASrCs6o1AAHIUTHd1Gnp7XdkZNOnjzjEDSdl29mMMg/FiJRrrT2ywkO8bfDk3B2IcPYZIaQOvjLnv9OaMtq5+5+c0tg9qYccQAxagbajPyCUdRcEM9jbQk3zTHGjSax+3R4XZerNhEYt1jrfFqKIGSdYZwOWdOrkH0aUUp5o/Cx2E1Jy5C12SBhS4M6TpfbKjC4rnRuv4fFy99ZgxEHdCOIdtDxza9n3Iz3QZ/NjQvuiruArkHMQVGa1DZ/VM9XPXHWNQ/i3mbyEYKxO4kSxDXnPy17sERSv9AHj9He6vP+D1/tqyF4TCgf/eLVj93KMDyelGHedsIOIOflx1E7yemKgfhVgJ9J6hBrz/4QYFoBSpu9cPJnV3rktLdD0kfdeO0VigVAAsbQeGDUZAH6tcYILvqbAssEEL+84FLzQdYJCQpUIAP3kLqFp1joSLxp923HtyP17phaurezasu/Tpas3AYZkmmLwu+xjxOCyt83yMbuWyx8KvBCNWv7dxneWDMxGvMfEogBLf6nj4zEabGNBTKuyrPTrmK79VWHWMJfdbH5P/PcxzTPD2EZouptvJ+5QVw7tl5+bpx8KmvGRTtQ8FZyRYh5izBpb9cvRVHFdqqbvMXLBNYfKZ2WO8O8i8KVw7dXXBiGw+Z2yanMz5jDPXC2bBl7Slb9PMxj4GH7KyBMU5gwtGTHwxZ3S9GztXat3RwbPVaG9fh6nemymlWR2ztubFnImpacv3spSgsX+N7Uuh/V0dlvyJdT7JTgw8OpN1K41VGPlivnGhUKtFTtJiAjiU+QDYINQF+RxEbZV4wvtxJ1Ritw72SJLMT0WXdO7CUVeyYjUG4cKRgelCtHNwKhAR9DaArFbDmGqexzB6CEJ0naY7ITiPX7Uui9DdJLqlQ3mFLo/S08sxq2QcMREIAJLjbXgS6RfK6ArYtgq27ViwnTkXnNExRACyE4JX8bS7BKoT3ullmtjvZqi117rvOOg4Ue4zVicNUQ3OSI+bEKC0CkKl4vnXv5dSQFYeATd1d3iU0u+UMB2B+VVJd8Jw+b3d22+5uhsAqJ/gpA4hDgT0odlxlnVjGxQ6ltAQLMbNmWl2bUQ6e/3b86KGZFFD092jkTirZVdFb+d7vQPU/tlxI6DcVwGlM8E4yeSC6953CAigAvBT7gkFgmxYeR+cdjYlCcW82n06hKR4chC5KgBYitO7boeGec4BCJYJCWQldifYPFygMa4aDjty+jzOiNQZ/KbGV+f4oSODCIBX4hkjcHTexxJm6ALPuAqF3aQ6KPrAY5enYNAMAQ1LJ6DPC+COgrES1H5HXuC1AZTaavkqq9vbMTzdJxt4Tu6rk60HZ9myFTpEbYjQiVsk4+zKI2/gVXA7XeQ990rbnlxNm16RiYz3wbntdOBUqCuGCA6P+LGo1ZBXcghA7kJw+oO4Aig/gQDuf/wB+Ps/4Qv9HQAA/vXHP+G//vO/wev9VfQFlwXUdnE5HRDkltPzDgorC5yvAsF//fjnUC2LV472INW5AncAxAL/0/e/w8vtpuO33Rlp8UK7OwVkV09fvCBt3HQ5VWq8KxyAKGZc0j7EOs0GFewOQgAQYYr2UfwUmyoEOqytFe96QffMD/Du3UT+cfiuwjJqju2h5gRkEhNLzdJm6eL7x3TNDqjl8/4wO0zgzcr7cO/igyDqempN/QTwgbSv2p/H9jinkzlL36EtNlqR+30cGhjtn4+Uu2uOzV/wqUCdGd5mTHTn4MDiuee5SdYZ4nJS3x2uFWz5dHV1v50RHaUDAB3qJ8XFPhttzjWTzXwa1c80wMFCujPgF3WtJvsDEfBW4/+O3kuDFwPDPI06x3GItEz0u8k9sL3cf+FxIHFeh5DPtGecQ/8ssBTJg8qcFecjX4lHvI/3veCRxQprxG9YWZnXtcYaj/a+BicuqzbfncLPO9l4LnXXbO73vIwIQyluwgxe8QQF4ho8+3rUcAQwC6u58/m604H/sUOmXaa0rM1IL9nPSHDzHCEVLlQcEZK01jY55c5N7IKsYE9fcngRm3PHkmnsJmYBYXcAMbWkzkx7FJUGCVD+QnccNqjKMgg0LXiUNRc73sA6zeNgg6y8EiTOscOVtoaEp1F3JmgUPTq4KdbKTm6kzqSXmndGbNtSw0DqBzF162B4HjMrDIOBnTi/9TKp4ExXotbZ4oCUBiFShDQ8krsjhjLJJ4w4knKcPEEy8My8bFl9nRjlRlIkQS7jPmw2ZRT3YSNOQX7UEJP+vbIgDuzUXWNCV96wfqnjkHIa5oyeirt06cm4594gxF1uLu1hlzL6h1bDVNZhw7sQUZCgQUg97f+iEtUR7nKGFVKqJ9d2QgY36A54QLhXgtf7a790G/yY4voL647c7OeQp5BTlfcE1HZSBNBHjfly8XXSpKVJJNw5mGB5IXrNMsaMpwAAPcDWRLy2XRPcPpyt6+EWwyTTtD0ARuaOC2DbQIrrX4x0IvPRjxjxuCcwzyyuGLxwNqExWBG7fTLVEV6O9F4qHsdtP1gpky6DG8Wk0MdsVx4Y8XLdKum8Y5RwG1Kb5Gz+A0047IQywiijmZX5BaZtug6rZGQ02u1vNKFKVwFfKNuLwx6ts5WWz4AZ2uz58yy5vcrs7t55hIrWT3n8Zh3idW/sopllvCoj/2FghoqO0wyr312e1fiUIaP17xkc6NBzREBiUJisFzvCsPtuZl9HOk6A9xlk+iKkj+xe9kbUrwPiWPYRPp9Xvy7mzwmu3fY+1nOHk7Xr41xEHXke5hqYzFv94h4haFJeUpehH3NbGn+HsStdVvJf3Jw1lQU0aSd8nfSv4X64E7Czu9DNfsMittPlGT5E/ewc+QG/9TEN6V27n6NLF1Qd9/v2jP0/e0UNwZNQvRnVvjpB5wUkDzbJAbSKnraZNvmzTQLM8T2r/jT099nL/fFsJu8j+Pn/IX3J8yNzftbNfb8aG66to+F+ti5jB/YDETUpZVaJyqsG5Un4jBnUSJ3pY/WE6CAr44AdEMQhEsgTuzQ3VKeQkN6+VkdL033UBySzclJrsbCFmKb+nUCdGdZ4xuZgQKwAhEC3UEfDQIlUdSREtR3903dFADspBW//XUIPZocCMxT7auQuhC1Z7Xq/qFtRnCJt1REflyVCTXovte4gYDko2twybyN1/i/YSC6fykwnyvvjREg0E/tb0OIE0l0pVNsgxc4X6YiojUUV+hk6oMeBeOcuQb/zQz5BfHt8l4YQWMdaZ2cWipj0/IOxPHzrzj1rtvb6U92fnJ2ZUNh+GZtCxZ/lAH0il55guHAaNc+gG6XQMY/7OrM9WZ4do2wBBo9GINIJgenO/UHrj2xfcL1yvnr9NTMYRYY6DdYpmsTg2IoTI9TLF/cL1DtRVvUW+jhYnMuH6nGU7hOR2/sVmHa9F4QAwF5OvAFd780mktJd+Tu2ctA0vrP9jX5Ge96b8D0f7G15uXFr03bdaNE7YRytpdEQm7joWb8dTSAjUf5FQNlpDel1gqbDtuyg4NGiFPjtt9/g5ctXR1PsviwWaGLxktAombgrgOWSRGQsNfYZl9PTA0DhMWSi7v754/fAB8ZR3QNniPJf3v3Yx/3fXr7B379876TlMjvSaZ7c7+55nqtBRMtBh8IBCXkW86GmB73zBzF8dpuiiF5EhwNDHX1dV/oNQrqsYfbGMQtxdaCqAQpiYjrvGznNf8FnBRrnGL/g7SFzvBndZ7VA/NQdEXqUJ/a5iRtJ+Q4+mYORseM/BmZ2wjTxL3gOvBMvNVCHw/OzAZuP3T1zoBUnVbHm7JF9MkVHOr9nu3LVZ9o8R1J7Kxq9bdPQP+NuoQTYtDdoJYgyEv3csg8gd+y/UVm5Wm80ZPb8JL+kJ0N7gn9lup3dhba9Ov8ZMDN1d8HMac62qBb9KBETst4Knk+ug1Xbnw0iPIuGYSH0Q+AZqDGITO55rrhf9sU7ImAiwcZZYpxHK7Db6sYCxgo6J2aYrA4ROsh9YOqb2WHUWr2I01Sch/yX0nYYI/IBH43GR1Oq2CfFBEQF2kp8631hjlkvmnEKMW39jwYhUHmJeulTdnSRHbSt4e74yQGKjjueaa0ICYB4BwUJu1z7DrzZE2wClhTvqCPPIVeYOL1dvdnpRJKPCNoOFyJAKMaFh0N7pythoa+sFaeWaedIi6OeceoDddgnPSX61iy2yYDccO0PqMQEZXKe4VmOfCwDSR6w+ZrcNHYrM6Q8Zp21MnZ8rPJl0kG52CsGmXWOusaEeLoPWCW+CkjYPjcPRpwhEXvwMhLZ6JHg1kQ+Ig2sq3zkbxKM7UWOPgb9IUEIMEGIjKcRoqyrgOSJY99iWeNmN7R69cI7w8Do0bEf+DpSROJpRYQscMQ18d+P+6wL8Jlnlsa4ujDupkp3V+GYLyVTSO0MtJM8+Vbg5eWlxcPrnwB071hPGFRZn+ql6LZrHc8AYrf36SUV8rucFiOtVt2LnkxzyVg5qtJ7j/4jEYznAPcxicenCXusnrDBy1u56fMsKkcEtRTRd+SQKXYE7fuKvza6+/mPWPsRi8VIkXy1AQ+/syJbiQOSzbZbxxfVDYDYSOp0iFWlkD7kZueDZvA0mN8uOBwWcszghFTvw2AM8ON5aafoyPh4Jv8M7UFwfXaPwzMu29w+UvGAphmPRT9K+j2dneLCiOvt4f1K2oBFG8V+KrpXTEXVlTNHk9d1BE+vfbRpo8k70+UzMnbn2AdgnXbzRCf7WhoIf4yf2/UxRtqlvnIhzxZtQ3uPY8iAL0PL5mYix7Nm8uon2qU0psuxLN4lMjSbn0zQTkUsvM8sIhB7RY8JFae+Q5waph1/Pq7YI3uWx/HsDf0hE3/wFzcpB4BVQABhcHQl8x6eH7f5i7G9J+MqM1hC7maumU9J9ipsi5MslLw01HNb29NFmk5P0qO2e+w/2/0Tfdqhjw2C9wwgK4ZDMZYWMt9bztg51rZe9B2Oacjhfx4c4zszPhyJnJUveqDRvA8veQcHOjO+uygzh7x5uk2oEgZR1sakRw+mcCIQMQouhvdt/mpXgl8DNAOJKwzN9wkVEexgpUeO0LTB5m4hQeIMVdXZJO+zQYAn2HYSYc/wtgEIFnqEtgKZAw+ApV/MyY4ZU5DhebVGOKfkP8IuGyDgRwilOzxkA4yMqjIeNscFAgBUQGrOeFnRaY4iKaXhL6XIJZqNvrsZGIyp3zZ6tPs+Y1CJ8jW7rLd3RX56pnF3psVjGdiBQ1ShEkCttTulClAhOTYDmTngZUsuojbBJfu70d6OqyrYtrhQ96pwmzlR5bbVZgHZ+WHT9fpk1p7UyyVHzWcPjV9BCJgNwM4hE3hpFSaQIJQ4rA0uscXstkyQQEDbjTMbpAGWy/az9PIjKBg2YMkMRIibwQj0/Eeu9nhESWNJxKl5Wz7moWnopeB7WeY6jEYniG7FdglM3w1jjbCOT67qYcf1mr+F23YYM5rTnstGNMfIoC/f6mx3bnOvzxAo4Hzm/nJnUJaRYax7tZ1VudsyQiXMF+nZwp8xXbwfiDrNhhcO/EgkJJVeAobyzcQlvtPPTFjIDQtyP8QJGIzVLqolPLfzm/YbrTS3PLcCv33/DX67EZR//n8A/vxnD9ySjGujcUzSLUKJA6WtHTQYkdZHnhfz24wL2/yxgWwYg0pBZ9vdmq9A8N9//AE41cO+L4Qvqm+BVZjK97fbF/gfv/0NbFRs2FHRMxLzyvQ9qtUUqX2FOcR3Zsn9NGFHhL1Yu9lFfM8L74rw6SLY99amag8lEbidFTagNIGmr9Ekb31maG8ebidysHO0wXPhWBc/rZj9x7/gF3wIxF3vJONHhWp3F6OfVkYcPO68Y7znQ2GYc/+CN4ej8+X7ly3QMWc9HqDgdhPL/YKWsJyUvA/EYMSmXNv52sr2eKudEXae4hzBnaVSj6355wgxGCHPTV2O7Jan2zZO7FjeHXEgk/8sb4qzt7+ZWCSzPmjzKFL0sTv8hVXhh1Uv8vndykVx53wsIaA+wzeiQOZ7T4Wz1J5Lf31HhAPr4N/vz6xqmzXYMqofOzpD2ZkPC4wLCoNDS7GCV+qJk9D+oviNTB2CYzY/PkDfuWh9Wqj1rhivJNhOlTQ211EudVVnQYtqF52kozoELY0oK49zgQpuMk870yuBDr+S2jsyg8AkTi1OM8pSdyyNHACO3vuotjpk1BuWl+3TcVCgGoexGeV6eZm0kGLT9P1oGdfM4J2kxAaH5QFjk0tOVfzA2iaYOesMmSuI74Mjx/dtbbuZsRcWjeaFBQfzVGnI8/aF7DMSDWEMbZVedUN556cj1KRqqJOUjobRuJsdizVA4jtbwsRwnKD0Ks3pqp1yWF9oeVdsz7mh3oMaXU4RQI56S9tm8sAH2nyAOM2W0qiJXRCCX86CEWsCO33xTdIZokWivlATL/fjoH5agjIdbFGzbE/0AozVY/7qGKljRo4j8oEk0O14gdi7uY5lrbcVQCxwu92A6A6///kH3O+vIPrX1OOMSbS2Qtb5/OReyN90TqEEmhgXog3NMXO5fmov2HEjV4XMUYJE0KR8N/FsHQ0IAO5QAaqO8m5FhK2o/aSGsZQCBfpEDx1nhDr+aLsH27vK7c2TXqoACG3xA7J9V+R+ELb/QvcwnxrksEfROfJPBCScTUSafuwX0WRJrBKesIsOeRDMGHlakl3GUZ5jOS3tqpSRksv1M/pttgJ1fafDuNPlKKi76DC7HXvMNht40L/HDZ5F8iO6nePWduFUPjL8CwHSHbZFqZmZmlafpDbEMCZG5La/GU1KBHKkLpY23vRjYAdaMHmYEX32/Uba7fHl6RGSuW3Q3uLYiM7ansFz6Dxf3ZnsrFJHyZnkOVCjx0CT7xa5+XmynGOd+ChkNmlur+aj32RMdCbtWAkMj8mlteu8Sfo1EoodQmIL5DLbhuvVZcX+Pdnx0h5fPuvDYud1eu0EZKyVqR/Pk7q/g42vg3ad7p4z8ht35MQFbDLf7bRPx7pW4JQkErpHQtxCXpNMWtS2pcM4G8cXPwX5tMf3n35+eW0OMRlGrA9yJmdJfp39+LnfvjoarAktH8f31uOZUzgvcTaOvesanVCwnT3ujydPHmcHth3h5wm0aYtllthmc0uTDujwbdXlhbpPBLs+pZk23W/oS4EIBGhKF5tBymMPq4Vxe+GByFpPOJJB1p4VLpSdIYLXmqztSZxmEhBU86tCTpu9eNGtErRKutdwHAiDYHRjOF/Zp995ohpXyjuDn+uLzAnSf8T0aMBBVvZSBap3WdXTZLkAFhaijtusRlTFQwB3kHKc0wMg+e6h4cS2CwIRChZZHQkAUO/mkurK558T2LZ1J1EkYygCmHaN70lSDFPQGjoNQTv64tYNpr6UWmSaeVvNubLum+UDS2GVCbTUj9MQyN0QBAB87j4iApSXXvfaReDe504cuOiTqMF48WfYByJbiuGc8sgY/ullOd1VwXXjtHawtk7rvsOF+AdA1xmgkz8r72TLnk+K4mBsq66kkNIPIPwp5r0NG5ZeT1df6rJPBFTVqSo6oxu1yrMuD6LOCICSo4xEl/mHaY3FEUPunp5mlHKSaNTYOmia6NRRJzGadJ6Pdnu7kATK23QA6k6zmU+r7ZRqesLVh7HyTjFiXVs9f1vH6Wwu6iedKQRXykBsi9ceZ4Yg7EKxEh/0I/Yrkp1xzeNLHBMCj7vTRMmywSAENpJR3mFnjfZzH5jz/UTJl47v7O5slTnvcNO6KCJeqdWq1sfhItSpHYVgLlfmtAQFmh78ckP49u0b/FH/Bf/5j/8d/Hg7m+RgJMhUcDKIpGkDzvB8iWFmcxFI8IET2t1P2n4e2WBOzNH3Lzn9XvZaDiKA//rzDx3rQ1a/nCIWhvA/ff97u8OjVkkvQzgAgIYc/LhEjR4NfoDoH9HPtwqFj43qhBNxGXZgUtmSErpe5fHBBoXVzrEo9AcRAZbSbc2+0yJ+j2XHoIZZeMLuF+x1cCzsUIYxwOPh+jN96Xt9aL7HNu9ZyDIg6RdHM7OhCNJxPEGRaEp9PumWO6stcajDLkSdSyMBpyAb+5LfCZlXS830wiM12C/YtTKMleoyd0ANZStbAcDZLB1delTMkF1fEBlhlKbt2qBWqHSHWl8BAKCUF0Bs/6hbhawPEUsfRzmQS8d948mwH+zewnbyeTbqrc4Uf1dJ3AdSeXTHNJm/DbzgqblRjGN9rNtZ7eMIYxz2VAT5m3Aa4ZC9uVN7Hx5Z5e/r4N5MqPHHl/YvIUVSyHQRjLF9OSnp/Ayp3QuGMqcwY79wvusBE2Q4HI9E9EMDHbaVPbp2lTgwtsu0bvof5w6PwnhcpW2f0V50KbmNlnJktcvIs0zvY0x/2B8OxiGxWQ1jB5yj7mNvGM/ZJHc2yZrw4LCHBToEtRAxs1vWcjAOoWSmnlneHV0w0/1qC/Oc43G4bq9Zk5F1+o4INf383HGN1c/ZQIj6iVe+CgRdzX9UwPz90IXRfOH5DcshL9p4gE/bgYjMBUDmizjLZsRMw2MbyUefSA4zS6k3ijoMjXI3q9bas9zoVCFwSCcVMUMsjk8VqTWJouaZWt6xYkpfb4fKl7mKYhekIkS6AhHMZJKkr/PEX7qAdRJrMjCYU1JHHUeiRy1OBOTbQJegA0IOOE2UdE7X7jBcZE02XcgaXyH6BHt90nlFBp3OR3lUbRQQSTzoS37l3YT+jEYjM4kvcpptCxKn9hR6G2YrCR1xCP7S6gPDkcKn1a95htAv5cNOarhPTYKUFmyHkMERTQaffmbGR3Ktc4YdYbNqEHgnGO9m0V1KEacWOBpwUqqj1evJM4aydjzVPY4ELWXqlDhRWsiSjr3A9Z7sDNka9A2mWSFHaLrsIBh5OWIti9q07wckEsBLkGwDhs8JGukLBAh3+HL/Ab+Vl7Yj4t77kzlK41nTrT3DMtwNEGFmt0hu84CCLE0c2AOexcT7gAxx+PE9C868sfQBpkjs8XGOB9h2U/y4/zDxYz8m1aBsdE0kwQ2Lu5/Clt9Gh2mNYgXbB69q40oNqrXZOkU6gLn3IwYiau3HTq6DEPMARMgX2s62ASJA5aO/TA2l3Se1R6Z1ttJxAlNRouGLZoiEZ+8IdCIiaGiZrx1PCKnc5XRaY+74EtKMJdNpyRzNKYg7I33hWpAfz/PS90cS++PE2HdmSWLAO9jEF0Bt5oWNkgUhjsDw3vqXmmogaPMZp/mgLUHpdunOcaRvCBpC7WOw0RfPwL4Dg+ga/cDjodd+R/L8HJ5qe+7bk4vpzRTHnFpT30xvZTl3+lnXZZSojigPs2rHOVKcdyBgUNm5MegXKYUUZ5rxpFJN53iztBRXcMNSxNqRzn5HhDoJOI2n29pex8GIYfTeBH8324AqSe9tAG6jQPwwjFs7Lozbu5QyDw7nJp0HQc/mSG0+/b193OVB+nFsmdlU3OuY7oAnpM+H95lxMe2wKZ3OpgsFo/meEih2Fwtxq4/6UU09w/jytjDKnDT9u5Q/gzbez+dP4FjGfW6JERdpMsE5QaozaJbwrKDP+7bP40czEXfyJzKgK2h7dHjkyqGiM/S1T9LOGnQ/AsjBxsRZOCDhBEiFwTugLT7d6uvGS+uENZM1J1+iwN3D/pUN5f6P03ZnNRFBrRVqrS1iFpwD2FFYM9LdD6EWO+gdBgC8I8CmkUhYcNJG+8AaOLL7g9oeFd1t0ldGII3MnAhU7c6VtcA1DSKcrEFi0rwmkMZiwvmM2LDj1tbRSmQ0BEWICEBXbZhjIGxQCHjvgNlVIW3gh05fDho5S+opH5OBXto2fZ3CaEjxQKpFuq2rwKtTd0zOkb48l5Vh+7jLG/qkZL5z79e/UhgQ8ErcXrYVbq5nYJhdLU7cXjgaRZ6EobfYJj0cd1JnVxSBRFpcoajtH/G6XRPAfDH1toZUnDgZHSeqxtGrhtNgMJPuBDEFiGJFl5qNrh2pMuW4LrqyIjRrdBIIvVtAh+0p5PAYiMq/9jSOg7mYpDuZBmrIScV4Fwb/mCPSGNo4/vNIY7G0rZz9mCLWgQTwUv8B/5fb/xv+17/9X+H79+/w5++/A+uLLWfrc5eQPhcCbbYfLJvojCXo0o47LBj8qskcv7Ub7DN+8q8ff8C/WPcnkzfeueX6SNeH316+wv/89T+0HH5p+DHMNxEAKvZ7ckL/teMazW3QKMpx9Jaye2IfVOD3RicCyL1Xgpp/h0CEBH0DXgmOiK7lVpm3O/WE9s6sob12ZCvmuZiutcH4HuUl00K+vQFAB2c/aHmHtCj9lKRzAYln6weveZfBiLeEi3rvk2rLoKM2AbuMUXIpfdcLlVpgu03R0PRtMU5ARsXPypwPhPe/+4bLHb7AhnY7V8bq5VvaFsFhqEH754FfaMQPScbk9vNqqe8vD7sg9Sb95PsJ04GDzBwTQeySt5B7tevRtcMZMGbTcdrZvP9Zcm3mkXaH/Va+Z9OyVaxxUkBuY7T3YU7Evx9VQRd8IC0fHPDWEGZ0i6+nys2z5Hrcec20ZM8+Vmfozq/nG2ofPQ3Vst+WCHu6xjP67f6OCGk8R404MtgZPss7xTGmBjADpxiKm9CU82CJqhOJ2KBqeJOUxgnm3/CAQWQUrtAMMskk4DrT1Omgc2iezBsDOGURG8fdmO752tdqBIPrWIfBB60iiuj5RI9+LFCVwI0+VzLUSRsVG5hnLW13JvEFl6RtEas5U83DKqbojACzQrA/1NWsZFg3lupWkdj6RiLQfh3p9Jd9kk08aCZRVhgkyIyNPMGXdg3K3DvY1UEZZSwFfpEmtrwdV4CT+x7aZQKtvrxS/zpkwQgzfxxpRHSXrM5oG5y20gfHCekg5qMQ+ybfGne5AhQZHFKZycRgyHBgy8vnelKNrpxRNY+rei1pKrsJ/9wX49QbnKR+QuRzjgFfRBzSAsH0kuVhZQyY9rG2KL/vCbJaMy/TyeKWZ8yT6GPTti8ZrSATp8BnkhTO+hFW4vpeC2eIZ2lkzOp1ZTqp95ktmc5+a4F2bEdA+PJygy9fvsDLly/w+udtsBdmYmz1aeZAd6Vn9gfTEfOu+u4QdUn0kqU5YViKevTeT8tYwnAECo/TmzgSOtIujghms0GDAg5koUGXpT/rqxtwx64zllT7vUjxTgsy+h0B4Ev5AgUnR8YB5XWQapLRDyatDcpa6mqV1wiov3tauR/L5jNBChuUsPgjB1ywN9IgkUA7LrD97NPwpePPBx1HfBPmfSLNC6n6XuaMcL5qexmmesf8dRo8F73k0ck+KRlHZCsrZ1hpTyB3Mp2HvCSzB/yQHsH0xjN2XjQh9+X133Zc1MVYpseIPguDtRuLctr35jDHaZ4BXjOGd2d4n9k2ybicn3v+/DZe98e3KvU6HLb3EIxouc5CDDQoAbpo4HkQdLsVjU0McSfEsMsax+fDbgj7nMY+RKFPiy0yIZIMLp0ozOyJ+Th9BOynYnvaHxRjvtti7XSNNFU6V8l01QPNv76nSQpqZrTYdecLzPh8xWWf74AY542zMod0Ubls+TJzQDOWjAvLkt2uO9XnbhGb2uoWKXFF9452zfNkTnB+prwyS3iTYWVJynkxmNpWPhihheXTQ+uLNmmYt9HfEuFBvfueAbpV+Us7dXBsnIOHdkTYVZC7W6SWIPq3fTmjgKyT0pLCA3Bto1SI3HX1HySMPIKGxcx/TfhFDXCejFoH4WEPa45xvsdBdpbA2GnB0E9Ue54egABqx6h3HBXsLgYhptV3GDy47Paz7ahgvvn7EtofE3SadhAZkQCw7dRofba3hUwOzMAbvdRcr2zsEDmxCo/r5svmnRB+Z4dhieQg+Z7oUxBfCuez+isYCPwFgcwRkL4+Wl2uu7XkKgDVdsRWbfwz5Bqa0D2d9hY74C502q6+25owmQAKMqmAOZEbAYMp9H5Hg3HZGd9xW+qVCATs5/jrWwkJBuWq/TsOXr7UkRa7osbqBntHAgAa3eQNkLUe7HiLT6tB1/5r4G90APmy+e6S2ewuOuyHQdrozFJaglK8vLq6JpAFRrSOVk8SAOHoe+34m/wVWRlCk3JtvyfhvaezjRemTSIaiXBEYuJq7dgXyH3rIZtu89KYfjG0SHsiAVLx+sqVRvrDpjFBCJxUMyvXEib7jKS/eAJam9xAGqTc4MvX7/D1+3f4+v03+POPG5yBeTDCaPdTBt0Fq/cqdudobp8P2552XhtLPKhaNs7Isz5z9tLqYWaT9uEA/vuf/+pyauyLBWnaL40eM2Mql/dSCvyf/va1Hf0UAxVh0sF6wUmK2GDnILtkefYZd0u47xHHJFDBz+JRUOk7RWg/wtjzBGkPbBvHLO/MCZbt9WJpYWZfxXklXWanHuZ+jHB1+PjnR/wgoMdOITrqsBN4i9XeOfC4RtAONu1zgNqOrb1B0T7T+0k2LfoF4BnRdWkbZvftuLeBsf/wkzelBN+ohBCMeAgiAuuU/onlehaE0KkednNynOc6n027LCLB1V2ObCswzj6fY5Rz52Yva4PHvBOiBSPE1SnUphBEnqBXY6HwnxGEmOLOHJSk73aDtVcDsGd0ThaEeGrg93THymf1w86lrKiTJbHOcp6ipymC4/n788aGR/CM3H7kThyD5OdWqgeQ+knMPGnmBz67uGY7EBEJ0tX7826zfdHP4Us77fWGkaMpc9yxk53AMK/6iZgbqC3+XqI8myvX0bGUgQ6G4szvniMx8XiWrWOh/GbHbu3BCBECAqDp1c2BAp642TqD0qKf4UgmMLwR4WMnf8IKak54qmAc8uwUqN5pNIy/B4NnbBczQDdHYTfqwqidToTZsdIvXx/dtezY1fZFdiLjOAhvDSGjB6R/8MXYBLX2IAp7bySv90ZixxcnllZinwXEtBpjT+Rp2de1cVKdsBmEuLiZceBZhk3GkyiDngCT/7hIPjIIAFwwok2Cg9hzOtBVMmn5GVmZ3hNYdaLxGAPtStah3N/1Vfa8OsBPDEbitLq8YwddviMjIPZX5xTvEb64qspVRKuxBTPDJAZx0OKfFGeDO/xb03BdguIzeoyRYQ+wHNWv6T1+TtAuSQfgHRVH3VO3pGu7cwwBswiPJaWGdl+MhaKvugPoVip8LT/gO7zC12/f4OvtBrfXfwHef5jJzKM67FAxd+KsgJ0tIu+0u+IXs+oquYswrQONcuZez5SPUHbwGwDRCyeGpLrJp529eVRLEWsEgNrDkD04x7ig69cf9RXufEdWM5b0u6mjalt9Vamlf7nd4MvtpSf1+eTrgt7BVpbAMjs90fQz1Yd2ThMXtkyDHaUF0vkzBi1cHqYBERCrpHMpk6CYxzFvLUu7XW2GWb9K0SSGZELaws82wRPx7bXjNRjLeBiGuZf5SyENomuHltKPQ023rOl7lrPo+ThGwNVLLrmPJe5oJsjFMI45mV0wcxjt1HGXD1Pz6ITdNGbdbIM3cK7sonwksDhn2QWDEIxORtOvu3nD60Nm9Tqar8x2D0U9N8jahabZ15FH+SLg4lcscZ/w7Ox8W8Cgn9DMAwhkMdiwm4J0HpPNp7SpeX5kdhdKuwScjh7akt+mh00wgovkclbTNtB0PHfM5lRX9MAlHZ1kSQMgyXi0wsF5eMHvUxzaz1drp3XlIB7BZNAV+HmdV+LBL0crxD8Z7cOjOmTGG9sg5+of5+yPNOuuw/tpC7wMLsEXkD8am8h9ENfxnS2L4cw9dNdGV4VLOyLUCXkchJgKwAPGRo5Qn1EQFAIbwanyiVimjqf+TTi8ivAC+AFJB618QtpWuJNc6iiDENPKZyxL9uacrP3uh0r3tmiej0uyljhrKfmMvYJXEBJIkAYAaj/uqe0gIEhvZpdAgl017t+3Rwhgb5s37LR0NIcCcsWDw4B/xQkAF2XqYfgHBftEy9M7lG8GxdlOTS5LVx76N06El32VWBBH5K4dmgOl1nu776O3Nxg5kdXRxgMpjr/BAVINe46VyUqBZnas8n/szC492v5hCjsBU6M+L36KxdPAjiCLjgOXyrF80ipWw1R4ONc40cChPtKjRN8YZ5QrwnZwGHZCWPI4cr07jGSTbeeY6vopGt/zptR0WABKsatw11SNcuhreHZcjsbD4XbDKFdkH1NijcyQgAkmGloSO1Bisv29fLdHLB1UXFUdgUQmkKDtPgAn18D4x68+gch40s+tumaVVFpae1yekSKRK0SEL7c7/M9f/wG/3QC+//Yf8P3rDW5//DfA+79aLd7KAvsscCbieAoyxciD5AH6ZTAiHcTCE0zTRL0bBtU9KKOesnbAP1//kIfWBnCLKBJge4KA4H98+Tt8eXkZxgIKYzHns3htd3DpE+eFedA+knRo35uJqb9rAuF2u7kAR1rXnhYQRRe7I6J6mvjb0jyuaR9llbquYHL8FnhOEy+D/4v38wlcmwaxTPFPw7tF37WietXZ+7A6fkozZxMKu6I4SU7U5kxg+o/I+qOT0V/wVwY3LwoBCTEF6Xgl84kSkyfPxP+5Ybrzgd9P+NPGQ4I6cVrLYjAiNY2jkY92cRb58atNwA+U9p7txjKFOC4G2zb2A+wGIZ4Ng2N5x8ZM3qeLQIX1505IOYIP70sHYnIUjDjEDWv8fwV4z/uKZvo3+sy03Z5gK30wxB3iw/cw53kE9ndEBOWSETiu2hrxzM6OzH/13jp14s6IDQp5CELoBGm+xVTLJBjrv6aBQhVMg5EJQnQDWR37lA8mVKES9HsW2mp5ziPK2oAq7HmnYOeYOCup17JPxqcRc8PDVq4GLKTKREDNYwDWuRqI7P42u3JXClEazWe89yHyWd/VhpeNDrB1HOVU+WwG1F6WuNLEOEomLmaerX7D4+NAYqSfA1C1+gCEsEwu2TPkTJFPyn3EmzsLxsU+IUla/x1XjeTZXT6pn6/o2HKsIwKKicLwzrCEHotnqnPGtpkaNgiyopwdRxo46nk5YGQHtIQ+Cu+HOgzGTV/VHpzPmiPIV+8vcixTAMHCdbLMHIAdWCCOaf7NgYDdgXpcrQ+jfmJ90tPwUXwY0lB1NQmSsWs5J45E8vcBzeuif8S4kSGOwO1ekNmKL33AN5KibzBLdQSinB3eCHGonJWi44JHTURArxWA/gnlt+/w7ftvQADwn//8B/z+559yJN1Q3iH5zLBVhjMGxaSMRy3NsFgj0vLQKh6OxiOAGyd3gQtdEhGfYSIHzzBTQymOYXz+7bwNbb+01NgAoawSJ4I7Vfj99U/REmJqWD0qNh3Zn/KO396wwJdbu7fisCFnHmJjB1WDgwMG1dgmQx6up0mPpe3obN/1wm23Y8/gmx41pTm5UJAxBwEQSg9GTNomo9tgi9ken9gFe/JRdAsEOzsKJMVGxa44TmIXzt4NNA2m7VG5MyZ4u2xF3ymIxqKsJl63ZktV5ahWpnCHFmdrDDbuLM/47Mhv8ikcF27+qeBk9YRz7EqdnsmHaKXvp/Uwtt0oCLvBgvlcwRp6ZgfwUwUjx3Vm9WvP8WB+S5GZdwf0sznjbGc9t0IBhKqzQ5Mkv3haRsswvnKwIPaGYQ7F9lZObVpaTMM7SZWEgzkJzx/l6Kg3UCAnxGFZ/kL3PUL3kTNax/rzgbzR96D2z1JX7BeQ/5Zp9jwYMUjk4Md0vyzaS3aP952NfoPWr+zc09taKc6s329CtEVn9PrfR7KSFqRfw/tteZrY/it+rdTomeAU8eTF5M3TXeuDz9I4+zsiTInCLMgrsO4UkgqOqzFxZNPCv5KkbY6v6hqlXZ5LZqDhuiwcZOQVG7CfCHWAc5NX0LNYrbO/EsmF0w1dVdxE5jfj6fc21NpOPJV0rbQsABTkr/8gyxA5ikBXTvMKQGj3TFiclr2t4aV8Pzlg93pVh2NoQ54QE0+MAR3XoGOZHnEgjRGqh9TiIoXbQQfoZUdLFQypw1hWGvqdEd4cUUWHPXesj8UtRoR9KrQaWSUzX+/0KNfGSrRsiwDQCcDQ6OI0nSEO7cHOjDigD2mnZePeqEmu9nOc5kt2fAz3EMjuE1Gixkyx6JmBkVTG9h/nOFjarjitwwxGdGSem8HWrvhBgNah/AQBCcyFtAkTex24/ZuRjUZPVZ84oRIRwpFAOCSVY6K4R1ijwWRxdfId75pVloDW1SPVgK1PLX2ZsDsXSXWYxYE4vz9lSjsbaaasM7BIPnaBfiggWXnEMCZ5B7XofwK4v94BfvwDvv7tO3z/23/AHX6H/+2//tPoGGOY7XrPpnBSIR6htQbm2dU5B0GIWTFbqPmLv4LGB6gAziHdgh18+wpr7vyx5UUNpmlnMuPNojByEMGP+tou1AZjc6Q2QpbfjPVE8PX2BX779hvw/M3azo42Ir1AONo9TAfpfWJaTZQAsg0acR6xO42cFuw7Ivp3ft4+YhCiv7Y6HI2+xYT/aFabJ0ENNOm4oa3+jne2zeDsirifbXdV1Pqfi/xxrMvTaF+IOc/CuicTjMEIcv/MjMUZCPZNtKln/b/l/uuuUl/WahYw7fCeK1V/QQbvK5Nv1d6nghDtBYBxiBYEqGS10AoS7UKkfRyVHgS7Ot9Okq/zYaDRjulvFKh+Kqyq/0bq4C31zCoIkRCSt9GMvhMDeRqM6MKyjH3BtuCfglkgbwxGfEZ4rI/Cpl06zbsdjLhM4dMhtZnjnGeS70z/PH0003QitYC5cCrzbZ+xStU6ZDmhj5yPwjFO43Joet4GHvx3h6JGuvogheaKob6alQIedQprEIKA2ijJ72eUmyBB5eOSrKN0cuvc1EjupPCODD3uSetvV/5J3biByNAr0btYTnheydOCpStS6zhkerG5ttaW8PQ9AQDV2lb9ka443oNQa0TAfsGu34lgjBCK+a1hwv8CfudLUPqI+wmBtp4fD2VS7/yq2YATfo9Bk/5d/RMDON+GybM1AYv4TL915TtZCQNFqPtAHH+1xEeyoqMkOF48Km0vV1/0Zme6CwP9M0eCqYh8ly4/lifpJoYE2veRO7yzqPt4oJqVVSYZGw0gcu3xoOOP1YVRMyTQnecchEIEZ0iddQgZf9f4rlcUJeBxjG+r/AM8HACxRNrAUPDDi114hFh6gO0KPMHKsi/mZB6xHbflj5MVt8llRh8F3GS0QRybh8wjXQURvn37G3z7/ht8/fYd8PXV0Ru+bhI1lrs/CLSGQqt8pynJJNncOj4o7oFQ/2RDVtcGn9VjjDM8mI2RVhCDEXd9jhMHpkcmk2v+NVvMjg005jLjg+jxzGk6kMljmUVvxnf+ggC/v/6Z2sBRr4q958ZH8540z/fbF7j1YAKAOfau94Xa9QWHkeNBm/J+Sxf2MphX5linLCnvKJX04dPZL1jcOBG/A3id4vXq6A4ajQYuO/B/sC2O++IALslR/kDAI2If4WD2f2ViezUI4s1hP96LqXqCnmzn417pJPOcynOoWgWfLjKyNpnX57bv5aWdGKM20zyS4V2dkYuJw9Bmq0nGCveZPBmaAZ8ZtTK/gTXnJoLGkoz6Y1H+bqeZDr4X4fzo7E+4OMI95n2WU9jNO45sKmO+PAUGXcP+A78A0dE2zIcyYvYIVKczo+WJw1q/X4Hp/O6phdivvh3Fdt4pug8cV1bQDzt1ZC725CDyRP5TPh+1ZxAlG4xoeMCMXWfh8Tovjxm9gm+bptZ4R7shjkoDsOyPZY92m3MvEWz3RzfEuDkFzx3OtMVzZPXwSOo8E/RM+4YO7u/aALh4WTVPmGYGhuwOOPAPuLzEs7cgKKERgVAvKlzRa/DofQfeUAXg8/lGYfR6S/8TskEvMqrQtgI61UYA7YAQQ0efodpP3hnh6eoFV94JQboTwtBm6fPciO3hONJ52viiq+Z6Crl4tBpqEELFgAMkFrOVB1mFx8VZmisBlaT9WNDJTF6sA83wSCegcUbZ2zUGP1w5+WOLH0wJovQRwC8z1ddKoxPc/q0qA4h8e1jRDmIQOeSDIDafR3JlgFUUo8GAtv3ZeJB656Nh3GaLykApLPYHLjF1Dwx5B8KnGmG2usHh4R804R6v3jS/x1V+KNtkhwoYHnANnUY1qlRX3oz4hAwE8OcnkaJCAIkc2mORRARVJ6FlTTqp9D986ywA7S6IA7yxDoqCv/UqNw1rj1Sx8ufZkVu5NGtfg07LtwYPAckF2ap3Y95WZ4DYwj4ZhnLGvh9ZFidokeB0GEMta8Zu9r3MgxAjMU7dcI24zhHJgJQAVUgBEOHb97/B929/g2/ffoNX+n0YL2yhZAmwQcal0bOnD3H4sZL27DCgkN6ovLN0UTQLMhCV2FsB7Qtas2SCa/hp1e5mMMIOFdvFJ4lH83K3QkpBdFxn+OU1P3SO8r1ayKifOOH++fpHOl6NtJAff8wX0Vvdtv7t23d4uU3M9257ERGUWoEQ26dFS6Es4OFvfM7AY0Tc5eDqFd5Pd0RIcKMMY0XhxR/YcfD4JWOpjo8Io54Wevvvcf7UFSKPxdLXc1a6nJtCTelRQfbZ3E5z47+rz6ysTcIuOni35p6TTIP9PnSPk7ZqV7HsjBnXYRkpN/2AjzVTMWXZzBTPXp3fFD6cgE04kqlgP07TZfieAcHBrrF3X47YT+ifJeaL/WATRuDQwblZv51+sXMaxdmy5sWu8T5dXLmfW/0XaUhtxNzuceP5rN9DEFERmGavtkuum+WHKW3kcGwD286kOzBUTnlHxnw+sV9GAoMNxPMJZkSeLsN/FCCwQQHbT7YCCzNTHEOaJYm6uyXzr+yADbrNjiOb9cH0SJ2VsWx47/0pmYY5aqjndVDvl57bTQ8HuJIq7QYh5kfuy5Mkz7G9dzYm6OfKbzumr+iKAYijttFFVbYCG2MS7MzHRzi/I4IL6ZMVOzmKYB2nfucBJ9gp7ARt1BtbrAr/Tr8zu8jRyIUKHs4XO9VsQgDUV+FX2WFgLRe3Yo54dY6dHvr0/KXKDgFW3P1P/+J2FhB05yUmDi7ljQ1CiPN6ym9rqJgJBgHAcKl1hsc+WFh6QfZnQQjO51eFG96COa89TKr1KAI1HtRnafiotwCDrNDj8pKxxJ6oIoEvAsNzw7NeB8dzZ8zCzI8KI9MCIKoMcPIZmgNIdb3YJ6hlnITBwW5IdX6jCSHKwp6DNs7nnxlK1gg3Q4XsgOl4XTBjUe3Il7hq3tdB+/txwNZ+xsQJQVxf4a0xwExVAPvglDjQieU3lHAggcZxpLshhjSLAV2rWBz/sQBQDQ3Q22hwKmTjTU8nOkEFrNPTTFWp52Rcy+oquLUGaxiY2MejNK1pNFPm0rA5MtCJ+R/C2MjOvS2ih0m4khx4J0h78L/vJLyVAn//+3/A33/7Ct/qP4Huf5hgETkZHMmhGaH7YIMZ5zJaQh6j4SqEYVXZFHT/kkd7tEt/PWGJH+mJpBSh56T9G0qN3yd63znSz5QxAlM+6Avsu8O4iLU32T8CbzO2j9Zv/qyvcLcLHKKu7+NjZTvTmB4jmCAFEXy/fYGX24vYhpwtjsdyHw8HOXiyw58hveOJfC1ubMYy2R0Bvkwdw8wYYXVk+J09m6U5Ah/wO0p7XT+96wr3GQ0PkJBNdq0cXT6X2NrQbKOJcKPMa3jRAtUK9/sdKtV+75DKpx4vhoJCFmb1sUd62Hs1x88ShIjw6Hi89qS0j5VOP0TdFpNEEilBaURM0ovcuURhrFr12e0gRPIsjOlzByCdaoIpns38GzOR6xCQxTntuNqcpP+K7WjhgDHR5rDBiG6yykC/1mwXAXkuy4Mb15ftfVvWO8PBvPcaypO7EjqL050yZ2l7oD50Uc9NgxD8fYZymPKaBxgvO+/zSBzvbXjGHpC0j0zePx+0bqdzhiDQzj0Ly3LYz7bg6NUgxNlgRywrCrYPND9v99oz4XQgYghCbAPmwYhJEYr8QMGHiRpbEOrMjndDqEGDwLs2yKGTidwpQe1GcA9CyAW06lIxRkQNOyHMpzFuNFAQBLnZzcArrB0VEwVrS9LdCu0fX+wqvJNCcoEWmqiaeplOftFY5Hovh9xpkxgHIyez9IKZxDrK5gq6sHPTeW7Bs4ba4QfsQnSTfkMvmbq5HShMgxVzhH4ZMNMP8snGEeEwFCtZXUkKW4IRK6RNeBnFuh0/NrZlut1y8i4FsjSQ/PX+2SM8WtGp1ElfScq3fW7Iw+X79m9NYOtqS014hZ4fxt0mRkIbYOe15IwkJE2caxD51/OQXQ1iHUHW8SxrTMFqeBH1nUHMvG5z/OTW62VGUvllfocgycB5xNipO6qFtTmpxpmLoDKZ8pMj/hLIijLCZA70T/qELX98GCRtA1g5BVk4HuG9FrWqcqDJOBWl/oiA5Qa//e0bfP/6Bb7c/wW/1z+NviNHgtXpzwQcfhlNsqV+5okuk3s23yo9EzE0Tp5p5IdmPw5GXB/757gCLcsI5gEemzXzQD0A03FrJ9i1cgjFYDAR/Hn/AXC3aUZUYj+K7atYY1+ifqcXAsCX2wt8u93U3qtxsYmnT8sBZ4PtgDqCm5ZD8yx+d3nalx6GQDdGZLsw2pv2jH+XcMTUamyzaYaAX5IXJ6Iq6SiRbnkV7e483RTewhsQ+8qMhjf0RCTWzTo9NdnkAATVFrgjFnRjNyhPSf9ZWT6Q6/d1yLw9GGvMfR6l35/gw7yTZGlh7Bfb5SSPY9Fz7RscfUGHbq+qPi0QSW2tXeSJAdsvdoIR0cb1TjOPb00lf0arfB/iApajdNkiO5nHmSCEX+iZ662Ry9quPhgBOp9ITGPXEoH5x34kgyMujkDQmW26y+5CvxjKH/mfzu0XDYug4+qu30z0cITYrqaM6WRoE9wirhN4hmIXeQ+Pv5nxZxDVCa2k8y02xz3qJqCzYERGa4TZAo3Yp/KYzGxegfJN6rUDpuseLRxZ6o8g59lc/02c9OKHjPSMSXfv2pj3tWOePusotmdy6lQggicvPPnY8Zz5xt4PRpgShxrPNtb5SDilDLdjCK8uIwqdnrSx9LNNxtixJs6vhFwgpcHOOJrjHuRuiCGrMzR0S3FcOc9OHNnCLvmr520izbpaDhR34JBxPQCF04UtP5i+nA1Z2+kEEs1PZRsN5Q0Q/ETWZJYV8gm98v1AZl3MYda+/IMnJ9SOG/GtaifnAY01ZjtJmyeMDwPPQD+nsyv/AIGGnSuT/Be1y2PG0GZe4bcvL4zfuYYM9h1/y3RRa/siMhBbhtePopVFm1uERyWi7ZYCYfCYdXziedqNi0wog6OKHS6Sk9quHxuMiM4Z0aqqTBxO4lvfwLN3PWD2MqaDZi5stj+oUxwg+KxkTgCgbWT1eKOtJySLvxHt7pXgqscua2nuk5FUvBAmfUd1rJtwcQ25HoGPEigXMsjJYoZTJktydKGOUfMJxtielqs6KIVy5Ct2ecrq7hNb3YrQAr23W4G//e1vAOUO/79//nf48fpnH6N8m01FbBKU3YfYx05CqgOeAMux5wyeRR+7gHM/3+aINpmMZnYiGrFM9bZ5vuPj2oEs+2GtxGl9ppxOvDjURwJ0fEOnn6K+V9sTodasBp63zTYo8u4VKvzz9Q/z3o8Fmrnhqcn7W7nBb1++gizzIGNv2oGKAHQhiJlbdLHwdnbobAQA1OjOggqZQ2AIWNjvmkjTWraZIMZqN8Xs06ULy+vt2GNpyASYjwb5GBht7DTVkz3xFDv2TnqqfZ7C/0hkVcatzKIiLu8tFPsveG+w/ofjxItkPC8Hcy/kzjh3oS8c54gp9vpliukTizlFfQ/ad7N3R7DikB1d/ELVYyqv8n4JbNDIfOXt2+rMQqy3IwI+pep1rfxokz9SvwV/bNABwAcjmuk1BiOuQ2NC1kfmMvT+hsss4DALRpzCDc2WiyiOfp+D9+8M760H9u+IMJ9uQrJhGI7bYs6zdjnYm7mNDUJYh6/9iI/QDmpcQeP0tEOemxMZ2sika2VXSWYDJHYLYRtPPSeGIIQ4ZHTCjohtC7txljZ6WQvRqKy4bJkM2tU+oU5onmcNJfcvsGEW0mF7gPKcjX7nlvI4qWPiU41kwhChdfyrriceP5rozpXl7Gx7rqgGZEA/tcJzTSSvq2FZYigjy5XteZh8H3IOv70YUN6mB5m3DO6MtCwL2m1tJNkckp2bc8GwOcquKSuS59tmdAjYQJlzIgjNJrX0M+7QNsiGSR5D09AOY5/wbzGkIqlL3qSoH5Og7I7+nq+a0M9l9F6pdenzfGxA6e9IorBc2of5YrWL3eeUaBHrLNwUa00fNJk2OMTa+uCC1fexk1DWujZj1zEeoawOc/pegxCR965IxnHUt2Nm28ddHwm6yvGF6eL3bYwqtxt8+/Yd4P4P+Mfv/zJHyRD4guC0NXfdjNqxaXoZMqA8lYBcoU/xxRemY2ao168nBJwDbee9zsVabEYT2rEVvO6weQZdcaCbDsiaPp/WaghC7PERkVJlhGjdXuY5gCrRUI6t8+0Wt+5zDfo3IiC4uWevtcJrsgvC2Y3W3rUpuj75igR/f/mtjfNi27Htm4y/Yk95q0hWQUZa2C7udN5DkCDi4udpIKHbWkeBBDlqkMf5EMzPcGfHQemKZVPXGKwYq6zvbLsPunm0Kof8IZ08vdJXaPiymeVE+k2ismGqHc1EUGttQTnZqa5trvtAbT79XBYSITcDngQnkc3Nn/MlD31JvrmiMtgtfjKKJbTMcszTRlakOpFgHEBCQrVw1F4b7PuJvF7vW+cz7JZ1fmxctdJS45yGuJPf7oQY7NUQHM8CiZh8i/mtmeWCEWB1Lg1ZsaiEzRfl5bwbnjrdYe6IIF1cNSsj3cmwgsSu3NkhkcGRLOULg0e8unP/sMjDNJcd4jFfHG4zvCeD5UegEhXlhNTET/LMghGAPH3cZa7BO+Uj220qtG/mv95g6yBPMtd5u2DEFA5wPlLkEb3PqI6GrLzFNpmNDOnOwP6OiG7AuUKmE92NFTsGkT0uyR/HMEfCkyGrGKJzWFIS404QgJkoxfoBgF2h71eqtWlSM97JTaTieYXptsVhRRTJvRJup4FMlgrw0RZY+Ls6m9o9EhUKItRhoGoGeDPKeSeDlmwd8s4YRwDE4ngLpOcB64Dv+SlOZJ64oVl3hAjFnNaiuGR20PTsRHFIwMVz031fbTcbFPdgBfDdEKYOgp3UPwZ1zGsMZOEN9TNpySXQIJKBIo4IDmgByEy+V7Gl2DvuRtSCzd9XTPOAtWX9G0NwNxghacngDM4G/rSLNtHSEHg2IcuVMVBnxDPW1+od7ZeNw9q3jBEQL6KWPMEwRdOKUiF2THii3bFw05rO6zV779spb2gyfRMD40WFGX+U9GOcTz8Ej5nZVzCr/wEAqAAiQN3cpTPYhKYfO7xO2Cw9IMHvuIPA7VLo7ct6hssa9EkvRsWT+VdcEiB9P+YP4xECLLdeS59hOYqWcQCDiuvtDHyhjcfr6I5JEIVHyrtgogTnaLxSnQDhayH4P//tD/if/vYC3799gR9/FmhnzZhz71dHazlaxnbnV8uJ2HPmCydgx0SbtesZ844FlE7U8SQzph5+u7LckLNJQ9rXQM2tDNK48mIc231xfrqmuIj1yDYGCp8geIYky/wdTP3LoH7Q8Um60DTDnKlkX5sgBSLCv/780+TnIMWIwY0DZHosEfzt63f4Ul5MDcmlS/xNWmbQ3TK/sPVlp74MI+avi3A1ybbPNY7R77ngcamwJlUbwtoTdpeHK8eOa81wNhSZ9GIBGjxd1IZR3nVG5iD6upnXcy2QjWEwPrNfol0HoQ2zrJOi1YTN9UNKg+yCuEOtrwDwAwB/AJYCBb8D4A0qAlRsO5pbP2i7wAkr8G5KixK9QTsSelCPM0NAWq/FeD9tjosg1nEV5s8LD+Vh8n4OuTXpOd2pqWO6hmLUWST2jLHxkm8+H7+ajQkUxqg5l/Np6COtkjv5zkmhtc1mQrVuPUp+zco8NgHmZQ0UyjCUDiTgfTzJum95UMV+0eEgDiRGR6Lii2qPOmFmGDkBRk+uGChHQqHPswFlI+nqfXZUzfHOdt+fcytxAxCavyIB9te9x3n3rYnDchA3XyMde5HTsvPf7LqUwZoSebOI7U87kdvXHVkwAoi6KK3xjItw1aa1EP2sR4t+Hjs1A5RdqLOMQzPf2SA8TmkfEjxJ8G1YtJsUFuv0cB0vwJznizHOQj78hgT5yPms3re/I4JmPxqM25DHhs2yu4lCso18pmiGI3f8WzdAuF0FY8qmRIYZTRtVpC8PdepDE8t0D0ZoIIJxJy2LaTd3uDkhguGBCUAgFMDCAkJ9MkRCr+obYkokAEF2whjq5SZIEHnLCpcMbuhGn6+nDTwgYJ+cGdlAg2/0NDZlnrV9EkywsBxUY1pJrBqOLO3mIkSfzshXDXSSGWL6UVlW/JZqyvQdNBNyo3+jXW3a0DwnNaxSm+GqJmG8szyTyjlnL/COnP7bOgYwscnCA2uXjeX48rQl+oQyiLKmsTxGszAVXdMPKiSKBeqPrDe4wS4iYbm2uiPUJ4cwuHIdTIqJ6hvK58SJFna+Ze0Tvu1sQw3zwp5WtlUvjaFFfUkogvz6CcOHaNMBiO0456kx3CbvBxk1JQtXKIiFTUfaarZTZzu0WHvrK+r8C2Nj75vjiihL+Ui1Bh+iYvGpxq9hLFzPRZx4ECCUUuHv3+/w999e4PZS4P6jK0pZNZ1YR7OFDzbNUPiiWjswMdqO5wR5ggm6w3znwSjUeWFHL0ascahO0am+kADCEcNsp5olnXaoRdolIgsr2RpzzEhxacjv7NqhYz/wsIbDEcPowWYz4phGfsyxia6T9uvjFxH88fpDUs2an4AXOFn7l8eK9qfcymAvSLC/VifmfJ+FTrjNeGwXvAC3T8uMuHdgwTAuoBnbw3euA/8uMRhh8I3HR4XnISjBY4jcwRT0UrNheDeMXdsWlLEyQ/g0G/uGx4NhwW3PKO1YfF3TkSP3KBeZf/13XxBEcAfCe+NveQG+KJ3TUcRAZkWgq6uVofaJXfbdGGuTG/tJs5/s4KvkzihhWcls0XNF+XkezIQA4q4tqx+n2jYlzI/7tgYxhugL9E+NBskST54fvWvlsGo5z1crl+cpWDv5POyN6Nw6Wer5YHzVnBplAcNnXtZAIQH4xV+jBZi1vzMxqtGH4ZvLidZubhh4LAGTk2MjMi3yq1aTEmxZ6PLkfv5m9JP97dCPFkrk7gy25NiwwDttdzImdo5BGXcwxsViK+dudvyiff4ozMwxNDx3EkTYF72ZscAPYO071jnjY13i80XdnKQiyPgPYIIR09w5GbSzIMyQ9VZH+qg8W1toHI+OqJUg0ew9r1oEbtOsGPV5rgM0XRZw2WzbsPKlx1L5Aw1H0vTLZ1YDz/rxdTuD4UQgYqJEjdGc59vHOR7hlBivJ1qzGQvZIDAaksNAJBM1mIzVdqVMu3xaj1PyhljE6d9Ek804/Up/zoMhIgCWvnIeeiCiZ5NoJ4LOzMi8Jn2WDly+bhCSuHoxX8XA92nt2esFUIIQbrX0DPZ03kixDQAlQYy5jCamUZ/E9Yw+KZfDbQ2JTJoL0iUQtqDFTojZym0mqzGnkI8FKMGh7fuLPcopLTvUfm4Czh5upjN9hqI8segkM4t8cMmLWtLu8pCurAio4+6S5jOw8mrKkH5NpnoLefazVDFOdHDro5N1MqAJhoX8fg7rOlzclHEAHGxBlXeppC+HgzI6+Nv65p1VdeeioyO2Oytmu0yOqwArOcmRHoV0ENpOBceBPrkwLR6cRjOk3fxLaDGOOTIBFd/A3glgkSY1OTQvjfjbriABjSlj8FAnz4f/ntfp/X7B7J3g6+sf8B9wg6+v/wn3++9K1N5GmaeBtmw60F/EuPv0LSFoy169NHD01rBjib/RBGYPntX2Aavw+rhuH1X9rVrPnNOdbTbgotvd+dmqYsXprqbySJrjj3qH1x/9vopkEs1HoMrz6ndUyAGY/MG2GwB8//IVvr18M7haQrGayT+Pf3mVCXW7CxP6AMx4YQMVPkH7sOkPOmgBxtWc6bqbtqtcc3/cMFZObOPdT7Z+xiCb8lr5ZN9dNO4trWBpmMkuir3cCZc3bYNys/oKIhTs9jQWaAMPK8l+P16384WbtsAwVg87gG2aWbXPsGMiEplNvEq/LqPpaW6puSyi+zzbsmelgGOKO/merka3nT87sDlrecOx4K0dhhmk3WYJ81Qz1fiYdrE7Odu3YvR2Bs4RiTq3k7nbppGl82PjvB5Wco2LPdc47QxmMUXdxvh8eBuL62NAT/Ro80cJRhD0O+ziWPhzwae5O8QMsenp3TvTDMa1SEc6AMKWc2USjfiIHRLPA5p8fz6cuqx6Be7MbQe+MrNBcBbZjO+PnrXnUppLNzhELV0pJpckHVeIj6zqBmvtFhOvWCKzbBeTb9IjhqgjO6jMBMMdyWQHTg1CqKEObXUp8b9WyysrOVYKaHjj7FMEdmLa83hnYFceXBX7cQJkycnNoeDv9Xlm5fCkc+BNshvHpIs4xdgPZDmey0RVV3C5SWvAx8W5O0YQZNWfM0xslH3C9IE/SbrIBrcqINXRbkp/CBR+iEN/O3/nf7bV0/BUDlVos/yWt6/Slh0WNlgKAH41mG/vGR2KwDshFOf8HZfSIu3mKLEN8IbuKHdDi8TCByHIV/IPgvoA7PgwXReaKqWDx9xPAECPQOI5BQ6Z7NF4/Dcnc5QP5V6YLiABVa6P1QEJvhlPDqorMpsYconaWePEJAG6aZ1x4PC41WT2C9zh+w3gdv8dsP6Q9Myh6aQs0jxQEPtnzDD2QR0xRmxpYQfUTJMNwcllaZcglq0lqRXv58nHVIzD3J7udYu4Qkf21o5DHrH4RHPm5vkeMKLPjk+DKjzQXSnHE/t0I9fbwNG4knQwnQuwLZTj0LUXQXmbSe+93uEOd30dcMRd1BKYYBus/9DhTecC3+ArYD8nVPq/sZX7QKDlykKX3qPYO5rVzdSaQp8fLX1+vdB3YlN2jvFiiVL64onSh+emY0vnOyY2RHPS5/ZxvNsiP7Kg/eWFUOMwam2grmj+/+z9WZskuY0oCgL0iMilSi31me6559z7MN/M//9N92le5mzdLalUlZnhxDyQWAnSaO4ekVlqsSrD3c1IECRBrFxI9YTBZt+cZV6mzHOp7MCgGMR8CEVCOjDmM6qe0kfGU2L5RB+0X9HmO8ObZq2OPNXKP0uru9U0pmV7exJiOwRFW7kOETLQkrYs5stOn+2kW2nWJoSMds7XfSSvd4Y6O0XCwhwDfbfLUE05v0i4ui81JaDz/XnYN9GPFX43lhb4GCtTLLvABCNO4OBt5iDXVn2ykLHCivO3N6d4l5NN0+Vek3l7xJvWy8dGfNzz2G9HsBbt8nBVjjsfT1u1JsEIznxgFTww7cyJc3LHrpdUfS6Ra7vwd6t2JiXm72Re0vguq3ohtsf33OCJPI9lw7tjGXGGb0U993ZYB4CyTCdBnsflYYEITVZx7U9u1ERml85F565/VzUPAcgdDRTKsqA9QG5kXBx4aDB4J0SltnqGAxFAAIQFEOzqfOy6MZpuIoDKz0uf8R1f7EYGoO4qgPa8s8D+gfpTAg8VKjR8tA8Yce6P+eRl+062uneYeueFheOaB+yIaoZMGXyekhYEmxlAs6Q7UezW+ypO2nEHQlK3KBDTWkToyNoEV5/J1+FznqRxgkimlA2CXTsV9Hx8x6XdePJY29V/fNWE7KIxClaG4hlesso7tMbhCY5+ilX6MNGvRKk6yeiiLOkprnDjfkb9oSA4UOMCSn1MorJ31HkbyjDO6GawiMjhiiYvdrwRwET4OZ988cbGMKVtvtnsWEn+9esUjGVLsWxvR74Tzwa6J+VjXZN3aPMlDoPRCUPH46oAtYipS1cRt2CEwzHg63bXMDCTUbrSPzbgumwVnoL742Rowv+edzYyjtRkWSkX+PT5J3j58LE70Zgn2jaeQOmG/FqQwAcjboU2MTdmDPZWxejm1NvEH98DhUki8+0HQemmtEU1Zk4SnTULf8S0wB7Tr/NnB6tQx/zR+OuB+eBQyHZfvmKFX15/G+rQO9S8fucd8aobZ+n58gQ/PX+cDq4sZMk8RTTmk8UQxIuJ2nM+7qnIzojSZT96No1eert9oEbvaraG0d8hLiKyAQq/YMMgLR/8XrTWQZ5b3QXHx9YOkNml31Ta4dDVog1T2xljZWEpQX9w4y3GVKC3USCzjqVgMLQxUWqmMFfpmEM4X4yI0xs4S1TMp/Vswn5rITM4iw4L7INNSyc6eJbeXLjerPEsINIwh87VMFivw68Da/5UbfckHzAF4MsrhQ/GoMSibIhFiH4+5B8Aqc3edAF0ccxHkNDjqeRB6UdSQEM6TYVCB90/gJYtEQApbd1Yw4+VmEinvo7JuN7QbOuDeFza07qP/JCZO+aHSr8T4+KhgYjZqlQ+K1edROcIYJbmBn93Fgfjg5VMy5izY3zc8658e0C9jkpAVJuzv/ZN4NY4sUaShdUFnWDCl6QCAMkyMXOmLBb9VIDC6eyRRNYTR7VvLQY2aNg5Hnpvxhwdc7WrytzrkNRQSVfL7sA40t1zUL4fjEHAhpgWGB1GeCQU2TaR715lk2AX2X5KGmDr2BLCbPBM8qaP/UrAo6b5uenhZBXsMFt2sMzK6lFh59LKsIrKX3+on2Lc6mtMfvvVJuSnizFm2fw9Ol4o1rFMHECIQQdnkJsvmINu7dDzTBlPDI11UIW+1wOD5q+WToR0Nh5zgONjxz8Uvjo1ZkrCAWG58Y2vzKXOXFe4WNpfem8dI4+U+N0wwckAg+1zz8u3SM20L52nQKCrWMccW+MaSxJA28J+hYIET8/PUMoFau2OorP9lwaTx/q3xMk0GDFLsf1BpgTcVub5+5pivYX84WSDYW78JCI+adfQG2eGkjz9OrmcVXZnWo3FvNBIaxmsvUrNGLhX38diWPbHnZbVrbS9XS5b2d+fC22auW0TEcA3uurMNexUd1Pzg1FnzGSO+rRK323Bu5WzXmadUbmHJxOzg9ns9CAguMpv5A0HrSv6GqW2qCmpsmep42OQndYVwO2IcCoDAuKlmTO80KeYIABFGwN7XlW+3JCxs4/tIH7GOxJDI0gcO13mItcc9BGrZ5p+0+CCkWBk8e15nZIVv4H4l+wLYtRTfdvoMPGYUKdg7iavE81znds5fDTf1cTO+eEj071OnfyY5xzodtBhkjntjqC/j7sMYl1Hab9DHnmMSq4BnoXAKQsYar+spsLoT1jrWGuMhEFM6kh+R54QKiTguyKYx0WdMCIxcn2GwZXvDCOf/b9KMz1tO03nR/xldoSYOkdJaS0n/h1k+YSnrE/o2KMCDN9uCdgOw9n/+FEPtGp4/ygi+pPDQc94/1vzX1Q/kfOr5tZjDvA8DnEBw1kxMxNTJLhTmm8Xt135EDKE7Ct5ootPboWVF4szd0eXOJlO9OntgYhslfmNaXbsEp9L5h3MoMquKy8coO1KEMXT5xmmr0S92ck/Ck2PFwBQhSpBCN4hUWPRHkDoyr18mjqBlVZ1ZrIDsX0pbrUqgjoWZbV7rVBrbbjUa/vOn9R3aPSAhB8kqxhrz0iO2l1DtTmIKl8iqlp7iPp2I6VYA2bmQdtjtPOjtwyu4myvOt4bmtMMg7woG4S664XrItuHPvq2RmAjxUiwd4COOMrul7RqpiHI566QxwMV2IkGVhPlb7nCbgAME/nXFaHsqCAMnzuJqN+d23lHxFs+E4Fm9JCo9EzZvhnfpZlpeSLkzn7mMcU5YBb0I3grbd+eomJd8n5H7Ir7WFlDH93vvSm1EtoDemnadbKrEgvgugyVt3eMTG7D+0Od6noxIQZaXZwdKk6ySd188aZzKoE6guLKU4IxcBXS4FAyckAq6P+YLV+uv8E/ffsf8MefP8Iffvp/A5Qr/P/+/G9wrVd1utm2/Z2nx5sP59NRoNplnL0y32U3Vwb0aCIHFWUzlKkFtp9vKAlvkqKAANh1Kmret03fq2cendRvhf63eZ71+njnV/5TzNC4WAEAoCD89fU3/4wVrf7XGvUU3slnX0Tw8/MnuJQi9sZr3508O0pJbKcVXfW6R31Mrf5UbJcL+IVS/gJX1iODHxZ0l/TIAyz+vi3R6ci/q+YDhBZaQWl3rRXqtcL1SvB6vcLr6xXqtYpdxPoc23CFcebnLLHsZDA4z1RlG/iYH1c80uL0ik1pdjoS/W8PoCMZXu51yZ1zrpv6nPHnNg582sCcpN6Qazib/9569vjtbU4mzRYXNAWFSWr5+065NMlGgGCLTB+bJHIIoqTKabeMlEXQ+hhsIoIWDWalH6dkam0D/m1PGCQgCWSNR9I8do7d393ZKHLC4bkPuoC7u3F74doPnHQBg8opAAA+jpYXuU00kjfDCgCgqQ4sKxM9Zygzjt/3SG8Q4z6d0uMAabyEGrvNwnP3TIDLV7FT7juMyWx6g/K1yN920n4gYrLyyK4+b7I2x8DEEPLnq0KLNJ7TahR78nnm0IzQoEk7zR9RtAVFGgdIdHkU8NbhyoKv9RuvWLZ1okrEYnCSqkiOhWpHJlUNTvTLku3RPK4Rgw5E4Sc7IwkIaudblI+HxRmtO43bH/Ln83krxa3xjqiYDAb46JDwc50mSGY4U++CQLCOxmC/MXenY4WHiUxILvSF7ftVEOK8IJj3QXZEgqvHWU8H4HF8vIMqxgkwgacvsyDErCaaND/nK2tEYwNHZW6r3KzOW0iVqJPcov2wmFqJBeJhKX8adzysEZ5PvYX0vDl5OPGOI69uR1z2DOF5clZLYuMiI2WymftaJO+oDkfaso4NLYUeBoZ3A1T9TVThI/wNfnp6gpfnZwCq8PXbN6h0dY65UPnQHocjQ9/l51maOSvfIK1n5zsql4bvRWV6zBvoYvY+jtciGHE4C/rAHvXIUc/l70ed4NTY30NrQ51BrzlIP4Bd9n3T0crB2ftBnk6k2LAsdkI5LKqY5wd9+lqv/XkMjpPRu1SuZYYoEbXFBIW6fl2gyn6GMbgspcXZDl0lIcH1SgR8ZCwvbsmOoIrzk/p8RsG574hwgRjShWAGJttBBVoAg8jLmtJ101L4rgu++wK1bgCjE7Tfpci13dDs0B6AqW2xWFuY1QMTlYxdZMalH4PY9rRbOwq8uTToLb6/PH4ggaKRDY6MzfW1F++urnWKx0KZ5wclCUACGd2bAqM20Ph2qk0Rw0hgTwJdW6s3g13y1tLx7MroVRMGmdoJ4bCGTRTezdR8UBK2zL9JZoI1sTdofdLwRIeZigiRvHZymnmZKCd+l5ypUMbVX1Q9Ez827jFrDvOMYcfARFHbnVOzt7Ny47HW3qZYpdkYWF4e7RIbjBhsqkEHXU2+DCFb5jH6tvWxucWB0vaRmoM5NYc9cF9n5J3E0wEGXUgbcFPyXcNYJDe3ljjt0RwjhjBXtyONzHA9asNxcGaeOPAQgxGt5FjW61y+jvFdXvfAiwLsY7mfKBu7KZlKIuZOgjq9IyK3USsQlUDE3bC3din475bFZrnItHC2a8LPJlWCt9rSlV/ngkC/uslu4SMA3SFABNaI4FmCAldhFsAeTOj/rBMHePIr0TrHjxlkmWTXK1SqQPW1K9nXpnhf22+qFSpcgfq9FRZPFYCkgLmdpP1c2YiqfoW030aJ0kxemVQKQtvJ4U6hNVWNgzMGI1p9tTP5LDVQyc6E3ZRoCZG2CayR5VdLSb3BcRbn5vlkVJRMGGRPHB5BePUJyIae0pbH+wwXOhM8auCT0XEyVQ3q7RURoblUmwCoUIFX3tl6dJZvqLlNq2iga7LaMUpEH81x+R6xntfhNpQJpRI6ZuOc3zdAKSW5uR5fqoI1w3SiBPTsfAeIXzg0I6azM2hXARnn1iNX4Vg+LlyJ+bbMRUaABJG4GkiVmgluc5IzP7hvWz15MMKC3JedLf+s57DLBDBzEdscBYTnDx/g5eMn+PTxM1xfCX7jdtxgWVs2cPMofo8gxBsu80ls6LdNUQZaHjSzano6xPUwQvJ26bRebnjsLqbOKfG+zfvPlw5okdPEdZBk9M4MBZ3nXxmetc6pDRHg1+s3QHgFoApTVomjg2sM4CPwisjPLx/h08uL5LOyasA3vAMAd48V72zkIIDdye5q5tUmxEGBtmiqdPvocmm7yFlfNcj0L7y7slmHfCxUszcQChbgnQ6v12/w7ds3+Pr1K7x+a9+/ffsKr99e4fX1FV5fr/D6+g0AAS5QgOAKFSpcr31H+bXtshZ5HXUfI3R4CdbM6a7rz1Dwz5LKs1zTO8OT/KifYS6jFTM4ATtZEWjb+LlV6ZC9E9tVZ8qjBXDUAz8mExXWc8SDaOz7Q9hTGD9iGnmCvDF2QVpyj32fStN5QRTXpCrPGmxnRc4GEO61K6Lqo76X70/jp/0tGQyiw2DEQ5MzEu6yGA4q0bbp7+pyFCpdtrzVWKLxjbBtx7iozenyM3JoyvY/78lRjk8BOA2xf2Yw2xilPsgzSRZXhWCEgJvDmwUhZkEGXy7x4wS9basnv7PI2A5EYPI9qCa9Y4ziBb2zQk9E1Xh4mVW6SHG8xtU9zMAN6K49TV0QwkMI7N/J2IvxqSt/ChD2XQ5ofJexI8V2jTgEIpa2td0PICt9dFdEw6+2FVO9jOwMSTucxjqsoOUghG17RJ/bDTrm8VOrmjvqHSMQvL1xFFcbp46ziEPW7GkacztGTKZOMfJ83oGJRmPqDsfK4Qoi6RixAno12ew1QjLAnwoBM/GPVpxYnN2csV2zLnqcQt1O2ReDzyRnQ1L2ODBuo2ROcYhI5NlynpnkM5H9M+ZXL6w86K1TQG5/GyIb1FHLPjbAVvGymVD2mQIZZtNiA4xLZ6JygyxE91xwOwK5QZYblQdwOTDlo/OyQ1+OUIAI4Hq9AhLB5fLU/12AriWXKwJ/NErONDvNezg/VrP1trl1XOpxdQUV+BjewMJOGAI7RHjkQdidQzGYyo8P8lH2LtZ/VOfN79evU0nkYI66xETl2a5yIRZ/H2nW53jwPn13R+sto0peerKOeiELI+yO+HVVtTvshVtn9SZ6mXWA+KzN0Ub9e4sNkB5ryTKJjWL+a+W0cViobnvgQhK4ALpzu0KtBRAJagVALFAL+GMbuxNQuhB7IKLvCGb7g4MhAAT1em3/aoXrtcK1XuFaK1ypts96hddrhVL6URVwBeqBCF7g5RySWMa2deGHpt2rXRGEeo58LjiNseHqQbEvziY5OiupbWyM0Z0jH5rUzcFU6PdJPcoPPtFIpm+03K62fVaHui95+2Sd7wRU+PE5uMdxNjoyHc6wbzhWLXaShTsbJ/VP7A1Q3M1wD635qbjQiUXo9I48mgoHdlO6AFh4Mte5XzbLs7szwtV9a5rhfHJwpDjz1qyfok1L9lfnlda+Sdo5G/dbg1JDIG1IRseUYb7J4HxIwi7YWwB/ohcDACPrFl2a5/p95V8gk+/+5u76yHydse4JD+rvbtEHzqTZbk+f6f56HnZZ9TiIvLWWH6mjaor34NTznTB2OvX/R+VtPtn4/gJWXgNDd81QpVb0eSJR7tvk6MqpOAGhw24re9Apr7NJEKWvYVzEq++pKcdAbecDVajXK0D/JOp3QxD1AEIFki3cHFAwvWIMDLEhiNoZtKCrmtwYRFxRn5V+fBSvUBqdvkn7Bl5ShakT42IYp13VHoMQ/rgQyHdkmHYvE3cKAhBh62O++LuOk384MkqROK4LjnWFW9M0INJra8PrGWCOWfJ4A1k5ezjaVAE/ct8nqyGMEE+4gMImvyJXdxlhXqjvgBrq5EAYzz+Hf94vab64sq8hY7TdvJenFzGHIJON+mX8bFp+kljgr7KNuzAY9pww3LFgbt7mJaZ8OUleWLquTfO03yOfOkTKvr8p2LNShAiANoI5M51w2hjNIOMm2Qw+CbwyRM5FlHswpgYWCmjYMRHB9fUV/vK/foHPz9/g4798hk+fPsPT8wtcXy+mLZYTznWB90ubjO4/WTrskcCD02S8tKw/zQy6c8gFXpeuqp4UhceN+Hym/z3S1L3tyXpqF+Y9Tri1YbpVfqYidaes3yVhaVPvpMPOu1dHFUQDdag24cltPl0SrBt//Vqv8O3r3ySz27m6cKy4ozWC8+Tl8gx/+PCJTTPRoRxOgHJcEgEB1WLUmG43gp+3Vequ8qxDEpjebqpwvbbdEF+/fYWvX7/Ct/7vy5cv8NvzF/j119/g+elv8O3lBZ4uBSq9Qu07KdqRTtzWNs6FBRt3ecdTjpXqNkdxg6MD0zBk+djv/0P/fijX6wG6DuPBY5CX0sI3rzBF7DvC7W6MZg+dAAKn+EMSlD7SWLNEW2/j07fny5lu6t9/X/mwrj2x4Q/z7eRP+NYjUtbRUx57ZGP0z13swkDHoMRQP+y32wVKut40coH4dG9UD+sWA+REoYP8s2DEtO5HJALgwOkj0uG8MYYT+10azTV729IEAdvffr6R4LyDDajfsH+yDK2Dn8K0wYpd6zM0RQ7WTNyd9A7dSNW38UbRmRBgNi+i4z8NOp6wJWxC7ljxq+Tt2N0JcbYPHkflG3XdaL/dFIgg85nV2/gjAblLDwIbuYOn2HHSSbJikFaps86/A2HKQYgOv/0y0xhBV+Sw4Y3q4Fr6gWNDshdkWEElqHTtaFWgWgH6RWsE9mJqdp6Cg+GrS+oThysZBXzSLyGpEcGRS5tb26IFeHLM1UQ5x7Xj43jA4jJiC1GU74liezg5ezBCf54IQsxAWvym1d4pcMWAiP1xXJ8aLAe9M5UJ3liddYw1jAYjaVp1N4V25AEbsyulH2iqi5DJkw1a9C/kbGe4/cC94+J2F0S2KyUPwoJ1LTs4OylC0/ag56cDyjjgp+cR8sq7NzKkUllDwwuL57TgTelYahwmR288V7qKhVbeLPjjIDeOMYpBCEWBhB/bfPGYqGG+b3VCc70wPy/1CzwjwYfnT3ApF3j99ivU69eumS/AnOSxZ9O58dzs89VymMU83R/RN0wHw+HSwoI/VIBD2TYHDjwCtripp31JNpsvnFpuDnR85jrSiXTkbboHLsAAOxfDc7p7xDx6G/q8BTMzY6YGxlmn2aPSfDaL0W8cjxibAIFvJ2Tl9JDMlZ00vYFqjh93JJTYG/rbNmOYSfLe2Bh8dBRQKptbnl5Pn+pUrA7RdTKoDnYB1oNig8xdM9Q5Ttejaj9WkxcP1f6PgyDX6xVer6+A1wIAl3bELVR4fb3KHRO25VdUVwj3bQGUeyqoNEOlJot+eCT5qEJEMselJvThjEdrXw6d6X9avVFGmvuX7yFkHc6jODj6Jjr8nDXi8F10bPN4XHjgoMPCuFjWO9i5FuphEDqxU29KxxJ8r4pdPHY58VvyOV9PrnmP2sBMRYrPZ8edCeSsaYkz84wj+yHrXiYyOMXDmKo7davTvguFoS/DAbETo9nZubvpIKu1Sb3mTuG5RSkEI87iNEV1BgM7X3qveRGSZRNmaoz9wrKm82+ToekLceHmBJAFaBN6jptJrlu7aBjHoLBnd3/EI7UzqFt1J2aEqs++pbN8Vu/JbYnzHXPCvHm/5FTAMzxyZvedb+DNOyJsxEiZjTrjnRJKAAMBZYba5ijJ1lsOFPQ6VOGCjcmTCzMJOnC7qrZOjjkCQ5xFL1UbHWDxV03xGghfkGn5JdhQe+ChXruizTshzHFNXI/rAvIwzTuqVdrGTv9sh4lvlHfIzZiHRmTHBgsEw5zYmLBnzOp4KHy0xgiyoyyw42B0T7cYjdo4EFK/aaCXq7WvkKq6yl+rd+1DnLkPJ8IX1HggO073ph6MyHZCtLqh97WZQzAxDawcWcoBhj1G0RkAgu1/fmCzDEQ0AsqbNCZM4EHvZ6simW4SgZPRraE1h4dxEnha8J+et2V42R+TVWydRzo8FsndDZG1KcOohfATVqy7yTxKGOaX6sfbhtINElp2qxnl24Jrefg5mTJcHeZdmNDtsuNOTtkYvNw1JX2VqtRzmnMeP2aYfBuy97FrNG3ofaetMu7K3J/KFf5f//wf8MfPL/CnP/43+PBc4H/9j/+7y7AFXRKMZ/W+W3oDjfEtHNTvnAYy2Jm7j3LOB91jWWXIN8jfCOcO2Xuu5NFEurOfbm3Hqtxy7LL2vDedv7d1R/Mqw3TA1SpG6boDo24Ym1EOCzz7NR0G1m2DLpw4qLJ3Ay0YeVYB4C9f/wYkneB5u0gtWTBFWp5ZhOEnRO1C6j9++AmeLhcTiOh2jNgJvMO32Ut8ATXXSV2KFWxHAbadD6/w7dsrAGI/qukbEFV4/fZVjsJqaFTBxfYMAgKWthOiIAKWMuuaLg05CNF2kNsLudWGGu1HBJQ7NKxc9hXp2IjehTq+7q/A2J2jRq+/1z45FOaqVButbZInAX8LSu/OO35v6fb+8SO1tn8enc4cW3OKrLMIymQujX7foAclFd/trAzieDg2954KkmK5GKJQc+f85BdIfr+ZNz174UZonPaMpO5+gcK5zQJAAmDXn+RFkY0GxpFKzf4zE4AfTOVBCeai7z8yx0GIW+GKKgIAOemzaLc70my+NkasvZxD8P278vvp4rfumLr7aCZmMm1S9MltZog6kL0CFyO5KeLdIeY1Wet88g5PdfB4p5PMtsSB6JmiskzLPElg5SoLK5j8XUtZruHLOEhkidW0rbIC3Hc8VN39wM+gfxcnI9n+6i0Z6o6TwxogjMyakqQLE05IzDkXDibuIwyKKaNvt6fJ1uLINBHEIWudqGZ4zdjZOlZblXslRLI6U/rVfva6ompl8RgaFnDhs1sx0O1UXzurxzFNTvLauTtPhjZmjluXJwYhJpLOGFOkT/pngHyGr7rxD/M9wmE6tRbrEQdNAl4SUPLZ5P2pxLQQ64HQT4uA1wDyHAZay+SIJrsTg+HLahbSy5pSRJLn0rYDBVlURzRPMvyMB4bbMCjj80omieFNPA1bKZblR9TnFjkabK8TvnfziNofkUsuyqFB60CBHWozHx9fED59uMDLywtcLgRfvzTHTzYtvcxfNWSBxmAFjk6eScHpm9NpMv+PDLHWvY/WYE8w0mjlhLk58Gj7fipwaHwXjPolNU6CEEMZg8cAayG/V+kWVX42Re4e1VU/hyAnWBxiuYdZSPfCeTSd35MegEvo/LybIzNdwcuEXKAuDJ8bafCHGboYwKz0GAeoHclpAww2RSuq/e4zWOSM6trtd4UrEUCtAyReVsUr/i/l0nCAtuMAoe+mgLZzoTxdoFxK28WABbAgQNEAgfRDOCLH2ptyfxdC2619aY6eIk1GbWV3BpWut/AuiEoFSqmAUDT4El0crOogQqld5+vP7NGzbtcuqj06LIoSe6DX1RtxRkVNd+bKQpSZseIgnNeJp7j4uvZmbrC1RmC3YvPQ/LN+9r8574laJ3nfYn1EXAw4z6ffz7Ul0WfW6oXoKbkz0uo3M70NNe+gT6KvawaXAl9BXx/bT3cHIxSgxzukW6rRhVA4ANBuIfehfD3BMUPqgTSZ0QriHipTmAzXRpthpJ10HEWeoLg5zWMdJ+MP6CJyguzCmvHKsXv2LvdJ+qqHFHf/5UXZGp5Tq7xxk2d2JUA2D3QgKMtPbAtvSpo3UGtZZp8NFOVt18/xPRrDiidjnOigOloofja4fyIQYRhl9xbHFdwajOh6smuMgtmKRWaOkt7oyvWTZzCi/slzilWnXUrS2X01jdTBCjlvE16gCSYYQQG+U2hpgCNblcmsvGHFm/iuBAIiXj3adkDwTogWsKj9boh1IoGvK4r6SPKLAwi27eMYqm5I7ntSuOVBk6cbMCThYKUvVnQRoF34xv91xR4zfG6ZrLaM1K1HX7mjc4JjhY2GEXCOx+xYp0HIL70z6zTrEl7dxHQOUMwUv004aRAiG28wY4R+etsv0+5TwXIoO3mFWQaLjTaR+ATazVGxbH/5KDB330saCGgDdfqIpCzIlTntDuAc5p5ot7ZNskIDfL+3acbnIY/l6eAJn4nJE14uUHywtI6r/axMstW11wRA2C+QDMqjnYOz5HjoflLS0x1RKC9MHgcbzxsn21Znp1uh+D26211ThIhwuVzgpw+f4KefP8PPP/8MVL/C1y+2/gZxiXcGezvnP9JbJRm9dzBqDmtY8dDBQ3COx+6mpv822JEvv4Ftktb//dOWRAJgeXxr+tEZQDRADlKq6k2j+p1+o+PH/MqPJjng2gc6rDq1fJ1o/jRdr6QGqTP4R0PMQWUZ+dfXX0Ea6vTB9r1Wgg9Pz/BPHz40vbY2TeapvsLT0xM8PT3By4eP8Ak+w8ePn+DDx4/w4eNHePnwEV5enqGUAq9XhCtdAQq03c/Xviui21e164v2NCvRI9AuQGPdut9xVwmukt8GCdqOih0O0VbE9l0XEGwd8ud+F7S7LVrAwo546Teju50YBj/3W/5YFFWJau3otgNWW6rDGoNaR/rx2jE19tWPwe8el/b1SZS/j+qDv4u+nC7+2FyMtFPFCR3ZpkqJzrwrKm9NhwRyT59sIk8Jv4fH0u65xIun30mBsFEPMP2AzQZN734wATMEkqMcU548SXL6Ay8OgCA5Oz2yT+27ph0yghP0IvZya98OWyX0NKoaU/99YDLoInj7cA9jWdRq8L5/dkx6TEDP3pPmEzhJcnDa5y0Yn9oRYZ14QuDTvO0vEp9LeUDo3KADxmB3OfgdD6PKk2GH5m9UaD3xLNHowPraYLSquSce0g4bV3AQ9yn/ZobBL3X3A7dXgj+JTZ0mrsNgA8nf1h7li2YWD23mvIOR3SxwcP1LWV1t1wwVNLsBNMDkq8vcvche7UmjwfepPPJOYod/D3S04TPcRoJeysw5LnvKKWLasz5bjQQx4rbu0OKE18zw4iOZZoSTOz0JqKLrGqXlsDupfxlWB0AXqmQN6NwxSq7UgCGwX7uAFzKpogeK35JVxuUJCIOTWua7xb9PHHGER7hJXy4paKpMw9ThN9D3JOhA4bf7YjP072gb66oW8Zzik7dvU3GdJTwSEaNxTWmDGViGDXk0o0wOQGOfyorJvNJJd/WZMbLANGf+XDiG5DqtXEaC4OA6G3F2nqUBDQdEccACzx8+wcvLB7hSlaD7UPyEFuNkuU2kOZQPgY5ZWKl3RMV5vfcqiG+X9mfjQc6l1h2f0/TNu6TppDgYpyjrOc147A4OLLu7TpEca7+B67j2aylTcHw0x/PMJJv3w2reHM+ROZWcm4f35bh/Hp/ANpVDuYzeg3zcPnIjZZ6eOu+OJtN9jiGrDFF/VWyynZNoppDKL7U1k/qMvlmpwiu9yr0Nl1LgWtquB0Rqzy7P8Pz8AV5ePsLz0ws8PT3D09NTO/oInwBr08+pXqFihVoBrrUAVQTou9F142LjHYQAeCG4XPRC6WbLYFscZm73bP2iF1x7GWYXb5k6+BFRXyjSd09yCQJ3ZCwhAHKwoRRA7jqW5RUFD3d0U7rivuu0iUGg91a0OzLaLaajxoHmGyphmHemBIZVr8OQM2fhgSefzeiqc7cz6ecbifE9sOQ+3FevqsBMt3KPXKUjBjRWJ8XZ/J0UDXWteIcqcRm7O9vdBDDI59GuGWvKdifsucjEQnXQBPqk6eow9vVhqLdbrUFL13oBNEw7qMNRYc3qX5lcZPT4o3RioGKAe0ZKDqSQc778L8VhV2SdwZ34boo9kGs6zg0Ydik0J3ekBUHEfw003tZLkmzUswvtcht2T80bfSVhxDKRu2LPPmeszM+T6XjOdE7P83eSrBceZuIE17T9NNC04E+2eK8jUVWEmzgmbH2B6PE9uNh6P83Lp08xfF3MOdaDGs5azy27ubYDEewAr7U5xVMFIV0hr3mHqJtTRsA1WvRcI3xEvEmksH3arbKu/Ah2eKaCnwyRKCW1aoo2UQxX1JFyTbJKTgiWGCKsACBHKnXvU+13SBB/Uu1nxVWBrXdv8HVznArIzg3pL1MnmNmBCsfngbaSps1cLRGlnLEt3DQi/rScikY4He8CBZzLji/J5uoKKyBaCQch4vEwMREo07f3lXAUXI97auMp+CWMyO0cIMZeWRMr8TXCCDs1+HxE7Zo+BtmkNWS2TK6rhd1N3kM/J5AvKYxtRR1IQMNgLKARXw0g8ZyZMD4znHopYZSiZgYRtEvazVte39WXe0HpfdoWHBDoAjMzVpTgFJiOP/LHfDcSiMcyBrPse8neu9cpzWEsh6FdcPBsB4Gfe0ww/V0Gx9CHOILNFv9UibU0aJVHaxv0dmaXU7IjAofO6bsvFoG52A409UZc7d0Pvmc97IJ+vD0Y5REA0K/0CbhJp3u8HI2R0oVFJzYz7tqRwJ4lGVT+YeeYyRFgGKXJlQ2MIB7t4PBi3uN7R80M0w3I/agyUuECtB0nCAUv8E9//Gf4/NML/OXrL0DXr7L7RnYcOchH6YgxDtxNSy4d7CB95cpEWNaB82bpHui7/TgrG+hGiALyviM0U2LkA5pv3fe2ZJaL4nMyFHlPk7fSah56nGyOvLWOIQ7wcgdyK5ctEPge6WG1zshhVsEBj9+qh4Yv75umNJQ9GzsIHS3uJmThf7agSzuOrKZKktEfDL7MUibo2bfEOn/09JGXX4UArlThP377C3x8/gD/9PJzs4/qK5RLAcArlHKB56dP8NOnP8Kf/vCv8PNPf4CPnz/B81OBckF4/fbULrG+tCMDa32F11eAP//tn+H120VsX2lCVZxeXr7Ch09/7ipct5VZV570t5en/bPr53JPXn8nOjBVYR16XC/b5a2utnOiyyezEpf8H7VPBhsWje6AfQcFV2rGindeFN6d7gao5y2c2dtCHIhBrrE/L+E3hN+YLGDwnWoSAczyOxk0o2cTQZpKI/7Mmdg4V/K6VPWjXjNPnD0dwLfGS1F30gLbThOM8hpnhkEGYYagjmdmJxwUdrWsSpbJc7/gc1Y6qwHBEf0MQ5st5PYSnkxrDJW7eTkr20tZ2aWe1jmOB0N1z06RWU958UpyzLXDZcvBkSXfoHzX356c8j66ntx9POAaaaFL26a4mbzitVUe2mRIe+b8YBM6FVmCAFCZH4Yx6N2ctT1bQJsvdM10aX0QOerKEzeACWIkey1lBTVzMbsxR9JKMBmBXicWA8L6Ii07ks/Ao7zoS9U3AugLFkh+5x0Q8fYNaBBi6OQ8v5z/Vtqd3dm0u4BR+BTrPc2zfToYsR+IcE76DKMo3OL0RP89GPIaIR7ha9WzlhGs91uYujJCpTlsLqOBK5QXM3tIV7Z3NdJMoMZL+CK0fhk1mKOIBE50+BqGuZjIq0Thl5kuqaxiR/38yAWj7IDaOAjgmKnUFIwJOa7FiTD9KTQRLomx9DNE1MnXNQYhuN4xGAETOHY3hG16O9IFtGwiOVZn/TtgpvjoTB1TnC9Hyp2SjtKlpbH1KnMLJ6nDcNxx9ccCFixa2YVuVdCiJQ/lmBQypmrnigsKxFHRx6qwd7ozc98aUnGFuIe0l3Rlgx+ImepPMKGh3QE8wMNWjrJldB72WwkcKZMqDZmWZX8mitRK2T6bhIUEuRXkvldsu8ru7koJo3GWMS8nga8i+mLs63MJwy+7AqxPMmkg8zb5s1Un5yzQjoIoBeH5qcDT8xN8gyssO+rAcOI+oyT7djI8n+JzCGQalX1TPuKQ2C7LdDb/d0urAMIB8sM4RVgxSHaESvbrng48U2eYB5oWxlia/cEjvsNHdtLRks+jfNtp3n7hqIs6TtU+FaZnae0OHG6u5RHFjW4R5Juk04rLcRZPkpnudUxrnhYOGooAffO412d6uVLaEYGXyxNc+nFNl3KBy6XJp3rpxgtdoNYC375e4PpaAOipOdyR73Tj+sjVUV8/i35djb3W+oEg1z+Zf7VPXvBUq7ERTcsrApRCcHn6BrIrgkhvPTXimwMKxHlc9/LK69EJ2XBFDx/8gpEWR2iL3+xRT7Y/mi1YwC7cK4pcQ9UGJgAlbiC/rc1nu60/db8Qw3tK+WwZSGmQ7slzX48/mSHLBEO/LkD66TGZFzNbLarFujrV2CrbXqFOFTMRJ2A97Ts8nc5oihvbKuKDcT5IfWNfbHCCm9KoB4f3BzxP3QATuhmeGGuOLICkcNT9pSiZcTE+jZNpcOYfdPLKXxdxlhwJXucw3c89Lq6a2HlbsCYPJVDs0+gO6p3p+jS0ZbB/j3Dizu1UK9NnHVTC5Jv9td5tNOmLTZXxKH9KtzIl/CkDTpRGBBP+KCI7zJU0id/WPiLBceEunPyO7TpSvuyuqHw8rf9yxdsHyMxTJTDGDxeFj8Zx8v4MGzodiOCzKJ1rKg7KBMZsE9Zx9IVS4oh5VFBnQiQTA9RBe2Uvwy11gllb2mr4nTuJUtnxlxUutUWONEARmVAH0OG7OyfEIW4d5CMMYFrjYILBVFE1gtCWYyHTCR379yPezeEge4eIOpPVkc8r4anELU9MWwValJh6N3BHdLpzyqsmve/AYyVNld/oyqBqSENimMtV2wByxJTW6Jk7rwDy9fQdPXHlNSFgUbzvOcfQBfEIJLAS26OMPquLcZkJJR+kQTN7piAPECbgBWckdJUm9CpUXOnN0OJdMoM0QUWUhZVcJNVTsXQnDDyhixmpZAxGmpFsaTeVD4r7pApbdml8mPq4ORY2yZejvUcto/aZof4w/PadnRtjEG2fYGZxxJ1yYz3GKLD4kvIpH1hEVyw+SnHlH5bv9+MLJyoHKDPfa9s6We3BtqSNVzT02dY51J1ssseuIbTzuS8AHz+/wMtLgev1t3aG94Gxs0y3DPoOTIhjBINyKz/fAgeP0BvCviFJJB+OldTkdejGab4tPJKCt67qG9KuM/6etOqM90xnly4N6W1oNBzQ0p/9WOl9hjCv4aa67fx9p/QmLDJX8VN9hzoSRNR2RBSE5w8v7d/LM7w8P8PlGdvRTABQK8EVAeo3gn//5RN8/XIBAIRyQTnuSNtmmc8T/PLXj0Z9UHuPMZl3g7Fru51EoU1kdl88Pb/Chz/9OxSsUKn9Iwlc6OKu9tmCGpV3WLDqSmFn1WDfRc4NQz+LfiriHrk1ml9stg4K+Y6L/hN9EEM/uQ0Xh5UGWFC/Mw4YdFVU+Iqd4jPq26acbUdvTOYsn7LO6RxLqIC052QhyE1J+64FI1KtfjEpUfBxyIXxV10XLfIGxrqfOBgxWsrB1mV21eeUtWk21Q+fFrJO6O2Wvr9Hj036YMgxgT0MY3+QDm8fxlxH8g0Q5+eJTr6l327q6yQdLUM+D7C1/dzxhUdpdCkfBRxnqdljLA9664WMjOxoDp8TOH4fe2N2n6fLc2KSzXWOBsP6clteuwBcYWR+CV3g7HnVYWD6DdJuMGIsKH+E1tt3OByHt0onAxE08s3g0FmtDlClYU14mUK0SYIDDtPJ3tuSOtiRJ3YiZCcr+QigHb1jKZqoXXHGjmbedstOeaJA5x6TYeqR+ULrPmlOM4uj4kY5UF+Yv0TnTJqUgm2MmAMlXKdb9d0DDfZKCcG5/2qBFC8gjQbrJiAbHILRJHAljMcwkrganTMyzHgXiVe7fS9IJQxvYYk5gaHIxa+Tsnlbx2i8bj0j8PSZOYaTmsb6wmu3M8DSDvpHkYZmARYZS5kn4I51wwFjVojzcUmTsTpSlRy5bY1Wd/nzjJfbWbStNDklcxMBW5wFFRc3iviIQV5ZNPT4NcGKPoNhYYR3exbXN8Dw/nzqpmOnb3eG5qqUs03mTJUag++7RGytKyXAt9EZ6Gm29SZpNjB90G+RHDGiPJqVNQc1eBollt+mIMZy5hnqcwSCj/AFfnoq8OHDZ3h6Lrq392hsjrKw4ZWUWxbjPAmTpfQLDh0XYaRqUQZ38hsYltRxfG6tQWf5O0qvo3xKKUlPsuKaGWmOhYyjJ9x5xdcQXVB/qHsodguvmKREfoz0MEs3jNZaWOgXRPNrn7cdo7Ihh47G4m7DZQ5gH/RBzgeSyPm0wm2N2Exvykpv99V0PHcBnE8PAy26q/KWOXmq3kqsowIAQoGC7bihdqwQX7SsusrX357g2zeEa0UgaPc5IKAsjJE0zB8zYoQDj1oGSo2txkdasa0CAH7HAyFcv32GigREFSoZm7LSQAwtUNFthGr6JeBzefoCpejxUw45Mi0w7c7priPP6o69KJSuVjsExNpFgtfnNcZxDbpGq1+CGz2wwX/Q4YYeV+Hv2HZFBOzVLYHyIw4x1z9L7s6N4W65IXf/5L6KDfV2V7qYMrETWU+0cgKRaTLRZ0Kdo6Y4yzvSWgowPhWdexwbxne6q2BYWOlTU09oVE/e0js4Ues1eV1omm/A0fRJUqrZHpqVh0R5h1Zo7U9wNOXr0kAPU0EY44BGasvu5HEZblQijA4ycqwc5rBgGOa6+Bqt42Uvo6tQB8me3nCWNIdFq9B5OY7B5QlmI8z38p6HZHnyTpr1epRI8+YcaVX2neoYiPY5JHWM+sjDFkYtE/MWy2PizsCQO9iZN+vyafNWxt08nQpEWCezN7lxkrcRGjtvZpHLdMAIROD4I4miGyYOgk1jXVI/GTwjMwcA4jM2bRmjvJBQJ+9MAAOrH7nEl03XHpBg5Sy2S46ASfA1dOLZqAoV7OMyH3YThKjmdzJbXd/K1lyQtk7Au3eyU6N7wGtlg8DQBPZLHG0kwnxjhTfdRRNWj1NHkj+1vRN0u2Kmjk/UF6Ef+OzVuC05ASjlrcNRtnNPcWl9xQuegAiabYQuz+6uCK+YkgTBxCCj6mkeAPiiZep3h2AUaDAT1v0PxbmNbi7xozTFfL0RlfgCPjM3BHwGzBgAA35zgeyMmPi2k7xbA78Ios5moCqB+g0J9Q4UV6fymrj9dbgnIqHbKbyF8q6ZGWHs5EwLwu3tmBhXsTeZ9lpiq1qBOQEemrefvDLt0V310VoZbK8qEBUTJIm8yUulqAwYUh7yaxnzY1uG59xleOr1FJ86rfFxCIcdH1YvOpjGEEdEKFDhv33+M/w//ukT/OkPn6ECwV+//K3hmAXFZM5tpqhU7RbjejNLnuIXxyyl8BLG2TQw3AfAvBUVOOj/www4ZJJvfglfeLsmeh2WfQX3bPo+PX42HQ7AP9IyvR39fK/0GIo40y8naotg70a0tdYtILD2B3+axSxUqd1lUAqUcoGny6UHI6LpjPCXP3+A3367ANWrrJQGgHbGdMbTPFqAfYdjsY6Bw/aYX5Q9syudn+C3Xz4AAMn9bG4xU4DFdjsfCcx9Y+0AxAo//+nf4Pn5m9htAkNODvYLyrhOa5+3jwosA4ZjbSVANOuJqBflPSf3Urj7KWK6wLAjAuf5S9d/WMcvF08cshBKfAOsB3EGfY5QoJC/N2uwZVdE0RQL94jI61xE9jnnT3QzC3NnlTcubCaE0CdjBp0jQW8yn051nKLkdeqI0aCmAfULgeHhJx8OmCX9s7bRs3dH+k4+p3tlweYe9VEx3yw/+U4O54emzDlxo0xxssKlkeLyU1XyFPOyPd38GGyTn0bXVNz5qLVdafSvOm/p1M79zjSBiV/FyKm3qhRR9QgO0foj3UcemwUfNtwwPj28TaO9NU4ISwdhJ0Vf/PUIrPxO5v1JuR2IGKsDJSCwA1Zdg1ZO1EGQWPlllRdgxSnBZDK5ZoJYlCdTNxEZpyB2ZbINrAdjpXAiFglAj3niIETV80K70ig9JMdt9FWojqDH1bHtezVO/YBD5J2k7QMAXRUjyqEvmqXlnEkmJQs9WaUfghAD8AltrB0h5I+cksBOzXGaQmVGlNOo2wnh5rn9YRkW46PVcU5eme5hk4AWDDFXvtcrYzJHrlkJRn4nhEtcX1pvMDRGrIBsmw2sEnBMaS0ZZGL8iQDIXItknKRcxzRZnVf3oocqxTpYmolp/E01PuUmQwMDYzJZxhVM8UH8iR1c391wg4PSriTiOXPmyK/szOWcFwaBSMdy1zsUFO6cPRCQBEv88900g60rJ3k9fyp1YEq8AJ7+HFqU1Hu8FkSEezyeqXf1YIimjUOhWVcrsuwxBmzUk+0cSJHF4YP7ryDCy9MzfHh5gcvlCeD6CvD6G2D9mvftPdpQt7y29UFGWRwrIyKjBGE5h/ZDLsBe1r2YCCmV7Sisoc5slqZ1z3B17eg60CLfCi+go51kkbn230GndHmO+mRchnac7CrWUF4wzOTATWkGZGol6nPulyWcjfTIANeSL+wCyOTIBsApse/Vmtcy0+/Ppn04C4rIISVzeaemuUZ2DrcDa+4Yiwn+O0V1Mu7Vy7opO+1kjvc7H6DLeGRduesWXM+4d9NTjhsbxq/rmyN3y9qp9K8LTmIbAXhxiNct+RnpbvxU7HcboN/W2dTrwFPxAvT6E7zC1Y2P1cclcBGCGBqHIOlr/d52WFyevsLl6VV3ZEhBMuWtzGP7RXL7RrGX1Yytg0Wt3eNiibm+JXpL9wWUao6F4sVvYuOMvgG0eaiA7C21NoaoXTq7B3wQdH0emTq5PYm5oMfIZPOBA0jg595s3k0FHibf/G/VGPzMsbvZB4Zm6HYlsn0dk/zGQZvDSDj+TbIr0132ALbxGifr0PQwD11NVk8z6oHMhQ7fzZ/gXJ1jp7XqYrgUw2WaUs8t/T3pCwEXHo6YmvIxb9ohBOPRTAS6WEt51bxXQl9ityjJz4NdNTUNTIX5TG7MRsAjaeY08T6r+cHwU/7JdhW53wDQ/R/53ZyabV9jOZucnBPI46LdR6ajcWAfyMyXg2HSRT9gDEYscVEFNNRxf/+eCkT4aMeYJAjBysERglEwuq+q1MRnA16ygnuOXVNyjOzrSlB1DkqzStkapyN6nQApvODV5qRBiL4rwtblkQfdJup0lYYsi3R2zKoSyf+4hIftziwDaGeIQhXcsv7JH64vv+mV+Z894FHdNmDjVIYCqTp4JrRoAimtT8yF36F46nAkft4FdnDM2j628QiLtvfFjPU6paArDfaOhuFuCAaPHm6OOzOWvK+a4tnopg1D1cCEqUxXB7HS7LXEw7tBhnnn9g+kbbDK9GyHFJFSDJp/CySWObzNoHP7MKixqFJ4ztBBgYcMfaiENAtCTFeC2QAcQDpXZkG1eJagPIPbukDYEjCdZHyF55DlO0eyQTE6Cka4357FJEU8ncbdWFlSo2qdvEpa+lUlPJhk+opAnAqhprR+Qw8EALKTy4gef4H2uk3jDjM1Ee1lj5meF4P1Dm1UaGKAlwIFCT58/AgfPn6Ep5cXgC+vgN9+AXh9BV45qbsUlYZEWT+lEONR84e0yp7VrJyGBwD1wzre4wDP+PQBbqtkDVJbZrQ1EkjZxHJenAOYMxgOQZy2+1zq+s2jNf4xIuwllgmmPLjmf6SHJPRfN+ljPqKPMVh//PR7pWbMTJ3kQdc5gKDZZNWYS6X9VwoAqLyr3X5oOkoFggLewsiWhWX0kvftXN/RBmU74iVX3D3r7NOFfkL6nrodMGOl374+A3zpxZzjT5UNcvYQDe8Bxrv6CCp8/vkv8PL8C6hdyM5xY5eQXTzVcLjSNR1v1jsR9F5CMjDVLkmMweiQlS9KD4gFyuUJ7BjHeyxKGBN/zAhC4d0YaHZhoNF3UMtFO6RYG8m8j0eZ2Ds17A7TcedEYvd3xx6E4Aa7+1L6Jo97TCpB7UQ9Xmxjh+l4FbSn/VYm4LTjBJg/3ky3F/anDozjkjzV11yzbTN1bwOC+h3MRJ/WpRhNntHi963pZL+F/oiLMndU/jFgtcoMpoMtDGu39flo+eEy6bxR22Gn3IkkfqYdwLdUrvP5LRKC8T+JeaV9NbsL4Xj8sxzr9uul1GGRb6SJBM4Gt3toOm9meb+J8CKZ3q7B75K2AxG8Mlh0JSu42LHafhzjzgZs4ryyq1CtQtI1jKZaVHIltDNbb8YLr0QQeyR6Hm0QRzs9wRumBzpOcQsPK1EShCDqQYjq+8Y6vIfVGrYirs3A5/oGPhYVZC7Sgh/UzkYSRdLiq81fOa+kt0JdPnEbAUCdgtZrBuqq8m2Okfd5GnXSZHVOyi/H9q39KGYVyQqfJQwLDbRvOpISYIIMRlQkweWb7zTyxCEXPg96mVdks0ZkQQg3ByYiT1YNHKRxGyEYOoWhc81UtUiCNBYZqme0JAbsHlfNsqm+5+cX15Dl576tht+NDRh/HiUJRqzac0LuHlWfXaStQNHxpKxOj+e8Ns7m2CJyGScpXf22rKwqnNTleGYaEMjQxE2BPOGPgV9Lm5zOZYU/uffCLklXaEoZueja9UZswATdsLOR5WVEPIKK8xDz/kYAwFKg2fMX+OVvv8Drt1+bo0AnuSAfFxqMEnjRFMm5O1YQ+t9WdgxAZzIPLtqPdHVJCvVWRQ/NKAcBsQ0y4Oi4k9VMB5hmC3g6aQ1AWXEzocjBuDDaxqBgP8oQVnxX059sPjbypPoH4XEmbTpohmLxbTZmfw/pzEKW1Mmyen825WUnGsA+pFlQ0aaDcX0M5T6Q/g/Gy7ITebDgC0PrKeiy4hhGXxbJ6JDHLVz2cjBx7ErV0wBFJi30/SlMko/GT0u7bw3XlDic2d+BNDU6KDSgNhgBwGWQoQWAPsPrt6d+T6LaQJWzit3Iixk5sEAK34JFgEt5haeXr2bxBAEx/Fp9OdtjbNhhB1hD72K7N6RW8g5+51cAqDXoO8HvYN70/3XRFwb5Yy9Cb7aD3n2R7cDgnRulFPnOfgcEcLRG5o912Cu+RXVAaLJuRam8Ctg2085NNDkjDoNZEoaHFy7N3luoM4sgy2udtH6VdWCXRzJxaq8vUiKXor2yrtLPVRTdD2NGbZ1ZdevryuozOtdU2Tc6wzmv5+1pox5a6DJZ4M39nLxLrjcbfC3Y64zO6mRti//d7TUlXkq71JZbdcNQbksuz/PM6fF99V2939JcnM5ztR8jDpM+z/sykwPyzYqgiInISvd+NijbgaANWMvk5+WMH+Xq4qw+JUzXhncY+hM7IrowHeY2gQQfguPSOkudAxpALm6OtoBTOAhEGdHVDmOv8ER250FmygDQdMK31Q0oqxz0PHZwClfuqFBlSVe8tyCEXhTm2yYKieCmv+zEA4YFqrz5Y5mS772fiGpT7NhpSXrfgV95Ol8B0frWrgtu36Jx0PDTVUXsZOeYkV0pgU2vAjYDFMLcANAhiMLECFwZX3Ox8UAHx4nvUzCAHSIEAHi0mhrB0zvZceurt1MtCzO9xYIBPdtupEOuQpX4OtK86Rt3uZszPnhO+zaF6jQDghvQpU8Aw6cBo3PcPLA4DihQ+twWaDIL80yBPiy+A+oSeIi1W3BhK7Z9h5qn2xZTxLcM1wG+VHCQ+lw7B36AwHSmU1AbZOer9ulehYNxACv9V+eoDexRRcAyzlFnVFIY76XAjabdrC2ZQtzLiGU57weed7zST7qUcZswSFHaUjLPCU3oEMqET5rKZM56GtNeUdnLvYOlAJYKl8szlEuB//jl3+H67Ys4CwzyhpXcpvXoiBzw5SMgNxaZBSQeUccUDibsOQQldkEloM2DZELuJMZPFp34dw7PwbkVX800g9uToDAJSrgaO79QuRY1oH+k+5MaQn/vSTXpM4V+DFr7UUaIbRPRPhyv8Il48paiDtyCvB0dRD6bomqN5RLV9kQcy2Fsp3r0mTEd87oZE9AcVg53pxfGhlpoU32UYYYnrG+Rxc7w8g7v+voM12+jvcaFrT5pAx3VbHON9g5+/AIvL//enVMNRjX2brObrx5v50vouzFKhTEu03q2mkWP0+OFk1SzcTWLvzD8tp8AAJeuT2W7IRp2COVS4HJ5apepF5Q2iapp0YRAggZuwdrtTr+fwaGuCh+w8xQAzN19qPpH1BUDHmaRc/9CYJ+c4nKI5li1g7QbjHjjdCYIkadsdPNHrq6p/DjZAe8ZjNhMU+fqYLOvy4kJstsdnQH7xXONv2Zdyo50LkdmPi1iKtvpETAMtEcAOayCkHqAhnpfTpCPdLfZxswkknkxsTtaXl3cLjoGHAQa3puZnEzHu82+TzqxIyI4Po1C0lY1JEpSF26DgjQ4j3p+o/o5J5coD4M4neDq38VJ3r7zhanjKgUmPDTNUlz4Dghw2hdJLg1CdM3Atth2AgwHQTpgDIedy/3YJw7gAF9SDdJHIAqWBiHEAS5HRI1JBTNzxt49rGRz9JF4EhrHgnRQHcZT+1u5NYKlC+UKhLnb1dWxSG01jJQYlI2j0gBxF4w69fcSwnCGu4EmWBLoBdJacorTEc6Cp7RflQ4hP34GOsfsHLFK8YizaV6Ww6A5V2M7fYrNF4CRjvNYr67aniJITrbL37OO/HHo4vwGR4tk8LJbq4d6EfvxTKrMO/rPEED7OOetFqdlS43QlZ5hVNDjHutQVFAxmcvuUG++Io1xecTZgo9LR62JfcSc0PSO6VMPk+w06XmsITSvW8REgqYEJcN8GjgH2jEMtra8RCnrk8Ezws3R6gZphY+v/w6fLwgfXv4VyuUJXunbpLRCMWpFrH4pBnSVWMQ0K4TzV0cYhjJoQLm6t2GfQWLBLwBc8EOcArs1hwFUPooBltHRrMxmhX0qxBPc/YRIkMoeYJYpqfOAWLLvWdYJFo9JVl/AB9S2M95xzGKm/uyIN+M5XGe5xlo2ZYJbQNHroPGdf/H9UobBEVY3Yz0ZQ8rycHonWWz1gdMLLZwmvVebfHYdSR2w6DAgAHFgs/4/4M3KD/KyLS8bbTCVWZ4MBWjbhyOYVrrt+uHIwzM9TnT+/GiL2TGv8hxYB1EdnoKy0/TIKLQZIWPndTtgQDXak7106Xa016RamxAArl//ZEBUvbxbAiQmkGHsIgDQI6KAfNvZuW1s91Ku8PzyK9jVzywj3b0XPRWoLojiSpDXo1uVYa7SxS9okmC+Hqd0qQWAACq2wBoHYdonLzo0QMU84x1B7SEvwpQjp4ydIhiwzSI6ZC/vAiXaFmScQ9JgR070M3thZVtK9wxlkkwOVv7+oWkH5oF88sc4xbKcqf+hsR+E7l0B2z/IxoSbXw4Hx+vICd1tOWXsjFiDgxJt7FXa1HGXDtgb9YPG07FPzTkM59eE3nXMAHmHBHj5tq4YB5yHUVgd8xf1pRTGvsYWd4ydcXbbXQ9tId1IwH6Bdl80TZZWLV7KYwfMwzxSGWF/E3hRgJKHeT8v+LuVbtgdSuH3kC98Gqz83M3K+IZmWGxim+U2PW757kiW2+ncHRFmZZtTDALtWCHEOyHi2V9cNgtuuECFKBc0EBfG7Rk51jB0o4xd8cIzMEonHCOaJiAAvLJCHP5dIQDj/JfIGoAEIIQZjYoMt1d3V5DcvSA7GwxedmcKUW3KSMexbXelWINL1k+c9iErmr1Kz7K8kBui76zQICgtDHoImWO/lM6GcWflLDLjqNltpjGAaRz45Jnz9ioKq0CS7RP+xuPas4ezRhV2rlpps8mV0Xmj90JI3RmSkCuMqyixy+egNXj2kmoJkFh4C71M8uuPDnxi8JkyfvcJf9zIFS3/6eOG41tFz2jhWfNU71CD0PR+jiuBno84SVIaDX9NEJwpBi7uan4TQNj5Zsd0pA0lR19P5JtaxwEhbCevfOylRd00zyb3+AyCnwsF1d2wfaZRgD72xTtAluh3GsQ4B2aFYvOM4af0ol/YiIzQjhxGvIdulhAq/LH8G/zzywU+f/y/4PL0BPDNO0J4XsQ+cPHgzcQ8U5u/W3ieb6IfLiFh+HZrUqq6rZDDYGZ5xHLZ7wjL5ZsJQfR5EphpvaDGnWbIRmExMkkbd0fjcKzPEsTN6S0rSsPa5i9nW9T/cIfN5giljq1H4vCjQWJomeNhnqRLDgLch3kXnZtN5/PpuKeO6lEzYD5n1PZBQCyAWKBgck8dgSj+TgRJcavHTvaQG91cu9Tn9Q6UnUSmTNQDJvVPgK8Wf9hARX53GcqRg+51VCQzfACGxWaZHRPLVj7GMc32BF9+/WjgkclK7jcXt/qrt8MSHEht/Kenb/D8uQIi3wPZy1cCKmNdVxFdbO9pg8VaJq1nbHo23hr0QESolwsQEZTS7jzhIMT19QrXK+8E6bCRbXiQ33rXBe9mbTZ6wTLkYztRLJcOr/CxTt0G6jGNdIHTbHfHUZJVyMjawSiv1JkZC/snZ4OfIzKRZ1D+/AHJaUFon5jqmU7C3R3WF8AwIDxr+YOuJsHHkf4UL7MqfGZKpVVgfMDIepj6uMM6Jyc8Holh4XyRuTUl/rAZHzWfbXx2xh/9V+o7i0JQN47dLWkV0PNusyyfWGUphGmdZwMQNnDRO1KCERtppM0pFQBAHoQ3VDbgl9Y5qmIJyNEuovjdmGT2d0BZ3w9+h3xuWn+EVDBgsJ9S3DglZt6tpst2IELPdAySnZveuaUVPiykTC5XlgIsezGJC1IMAQjPBkaiiYoR9miW9hwzdvQ8gBslbRKlg5US0r4gxo0AoAcdKv8MSpGFbYlEmJhpAwdeKp9zyc54ojYCxAKXAo79CCfZnmqOZTKT+3B70YKnatuMUmWDIHoWk3wMyg+CKjdpJdxxfKxQ6DfkZ2ZsOHIwNOBYQDS+EZXDkWZlNQpZHKy6MIFvxp8VUtcu1TROJsWZ3JiYupI0U2oarFU7JJOZA9nOE55rtk87cybtR3L9Z3tQFQZWOX2ggca8DBdzxh3HJ2Pr8ZEL9AVoLGycAp5XNVQ424EwTbQel7RIdFyQ7xW32gpW5BfGx/K3qMTCyNNPYDzWbOh0aizOUuDnHJxzcx10J1jsXgIy284hdBDzgMAzYosEZ89J0P0N77os8IqtrsQ4TEdZTJ8ioNv5BhbTCsK8szluJRqabwhtdd4FCD59+ASfPz3D8/MLlMsF6IvKMe+gTmhmrGA77Rc5N6fuTimPWGtuNzR/XmhLi7bIcX575NcBRub1NKB9AEJ7BE1mOoG/r2qjynPA5g8emG7U6G9KfYxhs48c778Pz8g/TpcPYihNgW52Mb6lVW8yYqsgROLxybRgX9ZrT0s9fEMvfcjcmsA9U4/ROKUAO5qrcbC3I3zRkHBTan75yzN8+YLw+noxUM7YEp1J0ohpLKkr3ROKSQm06ykbWEgNuK83ZvoiJvrdpPAWnUTxdwgedXV+0qUti4UBYXUxuZeDPScLHKP+Z2BwgKGUC7x++2cG1EFS/2mPJOb2NPuba7ULz0TfJIZCvb8Jnj/8FUqpgFAMMuprqNgUM0QA7AEI2V3d66/A91OOi/gAlLT8ETIqa4uxze3ObTRluPMRGh78rvRjzyDUwQBE84yBEZMBfeaOk35f+g4cNIR2rwmatucnJWzPq1sDDqv5c6DXcPAn80fY7+KbiFWbv6OhQ0CmTXK3WXSKn0hJFd0uZxwZI7sgy+PHc2YaNMny7iLlmMkiAALY1wyjK4qo5tFd8l7mFQ0oStssr4llKb9fYpWW48m22DIQcL+0150IKpMbu+68lQDSwI55NLbb46xBdUrft/r1i90dMaelNuIcPFruitiUiXlZBrEe2Bkvi+VP3Bp4U8ro9mza3xExcRxYXoGOUFioBGljFYKoHIQOjFtnLPMwNfnCMNJAI1qEeEGXXZlqYRCAOtRFwWi/68DQIo6tQ6ooKWT6zPaFTugIk7GwgQRVbPgd19U+7a4Rzlv7cUmSz/aJ67HQle6H71ffW2RwgX4zMlcUJgiyEaD/AvihgtH5SGBd0k7ALlK+INTTQt4288IIZh+MCGUxlDfVcXPsbgVXyGZP5M6AITFc3xO23ywesp2W6R9dgZFlxzqNUBSy4rmW4AfAtG2CdmYwWFF0hU270fzLslDVs0oJvZLTpVlEyifVvcEN6FGyTn1ZBZQS2bTeRxxLNIMxC0J4MvWKvm17DNpaOMR3jnQCGHZ1nJRD5wMsjOMkQ/KCBK2sroksgj7XqXEcFfqmvdXn7gh4g9Pg7Prb8L/oMDikjYMuW5c2HDROrAh/wHsvtRWnAC8fPsDHjx/g+fkZoBTXF1aSD2z+xmRpI2HJ83KLd1EKzobmsIvQfaiPhPjpTgccDcjGgN3gzGfeuM0hjUPGTK8jzDQDLXrkBP7TXEEO7aX7+fXj0yaVbzWx9UnM+h6tPkNXLsmKuvSxLzYJRjyA7bQ6bigzatgngWYeH/szY1ZDZ+XVqJkSBO5sDGK5O9KAj6mTMpnlOjKxIYzQKch3RHQZLCKd4Ndfn+Bvf73oDvKBSEau5H6JPomGh429O8rfZATcY6eobiSjy82UeP61oDGrkxyOb+Lwbt9z/SL2zZRUnbN8nXg43TPRx7xuSgDd6TpZsCU2gZZ7/fIy2IUMu5GZrcM8M+80aGHbT0AVAC+v8PHjN7hcXkOHkDrIrNO40zDb0+Id4Lsp+aQGY6852eysacWnsK6LZqFm9L2wE5VFr9aNAADpyklEQVSDAh2Hy+UCl0uRfMMlv53ms+ObpndnAMI1BEes/WKPkHW1YeGB7jSHXcZlc7JZM7MUbeUhbegRp9Wu2HfBJhO7PyrVJof/NLAsBEsT3JcndKx5Tm8TcTDC4uDKToIQAiUJSsS88f0O/g2/WXkvIHke2bZ4Praq13NRpmgbPB3ciwH+gKP4InCdN6Kwen009IN+lRc4smOHcizioj0MOr/B9XWOazQRnA6Q4XHcaxa6r9RUNvgmDp0Vb5cy2b1dNpYL7Zg25xYluKftQERNJh2QbbAi6c4/9/IUdBUBTQkYANT5P/Aeu5IFNWAAO+MecLTOuCEixsJfDt4HN7ROH4krPakzd9E4+hwjqZPn3Mh89YIu2QXhmLKu0pApxHh23OUYJzK4muGwQyMbGA7mCo+HbadTpCIftz/MBeDa96D97wbOtFkErY69w4f0+06yDEqrNJ0zNjpVwNkp2fBalNcC/lPBt0/sQnabYRnFNHEy2+SdqNySUbGX3iZXOKmZHdEJ+84ElJnzlodTHwukpi9OJWC0Luw87UWU8fdnXA+Rm+I+OmmV6xuTCUK47cPRIcAVcnNwrHnYpZQaZlYIH+M+HGUHoNvjzXw6o7LJ2FPHGQ1t3SGItjAg82VX0eT7WAw/uSXJlvKIi8hFqyhFlYlh8JfATVaK3MD39HO6ImInDVZbT5U/KhS+MDEalcy2B5AISAQfX/8XfHqq8Mef/gAfP36Ev335GxC9Av32F2g3VlaemsO0N1P5d5MORyBRhaTtE2X6vjTKJNevvJrqAVUPK2cNzAw2wXrqMl3cm6Z1L37Pyg3z+iHjFYFs6BFvnU7pIA+uGox+vF3o++H73dMOEcb+eQzhvm+KzqiT5dhGckfUAIJzOho7wjlt5WWnTOvwo2BU2TIMz1uMJptkMDpBxN+XP51o+mOjYM7Pt0s6EHnpHZiZo2mmUzk1iSwK2snxDiUkP4xD/V1JImlUYjNY+2Z4YRZsiV1rd9uAsWcIAJ+AXv8Far0KrsTveoF2SkJ/VwrAtcFDRKj1CrUSvNZXqNdXuDz/Cpen3wCAZLEj+zSco44/a/fy9HmASNJqgmrKJ33FwZB6gVovY4bJwLkdE+2Bs83k+CgOSJm6xB/U7dn2aWwazmdgD7aX1WlLyUlhCIzk733z4hyKhLw7qwLRLoplutgCGiOmuCEGPnmcPHc+yCUKrz7XBaktT7XzwXxanNDk/26J7cmb1A8C3fG0AA97MsC6HA5PO1mmeKdNihk8Wk8dd9/1T+GB5J7fqvLprshYPxyTcEhNNuV9/XtVS1d221unm3ZEHDt+cWDEVmBvByFqnIgivZwCp8KRJ0lb0Wv93ZaIOVCS6Y9xFwbttNcwTVEaVAMxbWDViAaGwfXokUoMV51ooiRIWzt8k5+DEGTeD6lPovbVMhbt37GN+knuC7n+0zrQfgCvrmAGLNuxEvR8kCF/r98NgqYpuvo/S778XjDBcxdeLc19IYGSI1KZMC7r5IyMOEdHFV1KtWkler8Twq5ysXjBIe52zGOSiLwRKpZOTI+33AQA2GeCU4r1x2CbDcozmRaaOqzDnuyxIhbbpBN2WbDtQLM6BxPB5IMH1vA0lsZBitHtHRmX8ayohJ+WlZEncpvR4ufrvcVRvl5UYuGvO4+d9YLZrRLWGU22Wt9aHZuBUBmABbfEXg0tC2qu9DhDfDvlxpL9zIMQeUXdbIc/wJ/hT88Vfv78X+D5wwv89vVXqNevgN/+BmiM4Gn779WEpvzziMfPsx137dSbEd7q6Gd2paOnzkuHOT9DZqPfpM4kYHpriobEEmwQkVske2CAHyW3BVwfNsN7zBzqDnlo+OLqmCZc/lRZmbzbBhrp95Y+C4MTQQw6SswRWORhW1ifEDrflXBc3il9+uhU+RuS03FugJfR3gDjAdbsjZG9AYNZu4Lj6lTXH2aws8IWCjQyQ00Ulo4i+GNnkqrA22tRHrITzFc/KAFLrh5lroGZ4Z7heiQAsqKH7D7XZOK7o7qFg23XNU+y6p3sswVPMg8sn+Iyg7aDRneKXWf0HK+1xVqNUuzBu+d10vl20SMAQX39uR2tZMC7Hc0GzhURrrzID1Avq6YrVKrw/ALw/HIVvwLj0PIpknxpd4XSvBKVO06RsAtDK5mFcKBytakU5k4Pg24MfnD+8KQPiLap2ascgGCaaM+KDSygzm27m0O+AwAWXljjERD8L8F2CUGM4Zk22pXhPotplzdu2Xc836wyjV4Paf2i9Hksi+08n+AWZayT95M5IGX9TCQAt8tBVYqkbcBtRpnfxHlyJ9GkBbel6Fy26o/risQQG/qGu+AAxXznziTQYMguzRN/2qB6WrmX6zmsSR2Cy/4cEFvH0W/oR2bU9oj9TfgWn6YyHs2GQynjXw39a6vY1OceS7Jz2IshHVAIY2hdX9OxPI3cmR0RNQPfV8YK0wdAvhdi0GMIoF887duG4SuBNAWp8VERtuCVDOYCxmHfjhXRS6hFJ2K0OLLOkXgbDiMLky+gNscbmQ8A+75fDs0Xa9faY4vMNHX01GVqFBBuAwt2IkDi1TkEGqkUNU+UAg18xOBOr9MEXr1zi9xftlfaEJhZxHjwxdfSH64zVDhwURknO2Dm3EvDB4kFlAsCkTv6hHkHwxdFaphBZqZERma7J8oFp/OSz+Bzml96jnwe0PAKGwcOLGzWu0Ipx4Q9zySAqn094oq9f3is7XzT/nWXSvNDxzD1IJpZbwyCt8sIYqXH0rAbH24hej0ukWuyU4RcNQHXDDPN1YbFKKGuQ5n2bL00vE7bbvMHesrg2O3E0hyjPLJD322XNkFIq4idTfkWaduQwN+GdpsHlii8bjnCCMVVgbV8HqBvC5LxYVlCUsgPwqgYkplfDNZqzWjm58gXrGKvNOIIzrVJ5pgZ5WFYuHnGsHLDYAPIBudRR4qMK5uN0PhCAWgnKxuZ7HjJnH5khwspvmNedqDFPVZ9FR0QfPj0E/z8xyf4+U//Ck8vz/D1l3/vY1B03I1MrQaONZAh1HMq9WpwufCoEaXWG5t7U80jHsK+4oTgDKGI5SXBIFhiNBAOj198zv2PvjKH24TGuPwwhwgA85mAYJyuU0HioQ8vpbvaxOej4wZlf2GATlderdq6YdDGo+8sqjeyaw/ffD+ClYz0ZkogJ4WZbKYlHWlkQmGSRAZG2stbjNn7Mx21QmXy/AHcwFRiBNi5yMlj6t9szDjTf5RkpUZL3tVWgaBCpVcgqO0YT8B2NBNeoC2Iop7PzFzWNaHLKyNvR0kUlCWnQik2vg9Xeusqncm/lim30NAx2w7yYPomfzKtM7EJsny4mXc3DcekGzmatTvyLbdmhQAKzXhhk43R6VpcXs1vxxENTgAApWC3N0uj9/rPUH/72bSp2YIFNPBBRFB8FA6Irg53GQciKJcv8PzyF+BjZOJSnEu5QCkXE2DpQZBus7bjolnXhpBacIjMSxXRVnb3o9VAd0oA9vtEjI+DgxBDf7k8/AKhlMtQttkhCif7zZxBFqTZxWkhn+AyzBdbVp8CZlzH68920anUE9SmWZpqeo7Qhi+KH2CggHmyCybjmi7jIjGfQT81vpb7hdIcSLarRCmv0w71uWaQFs7O4+indIBFOkakY0hmzhiEFrJnrIGmzycISYb8xXLNEiW9uCKCxbiNC5rCDg1q/WpPYYhVjVUjF0zsozGbbpMbedswh42AJ/S/D+nzAWrcvmV8bBWgdBOaeUqJPu6hUi9LlekXPO1upv0dEUMKDk7jUXUdZBkmAdjV7k5IcIaYDDNXYoiTUIUeQObIsfXhSJRkIHaBa++IMNECo2x2gq0VKvB5jOywt23JhULb8WGFNXcQuFyWtvkvclbBbeiyhq0RYuM8HM/FI1Of7RBWOEi6wChcpl0kAt6vOLdCPUuW1IUhL2g5Cq0RnlE0MOZNYDvGcTSJPJdpwQgInevpHYigkn1HDjeEWJ7HItIy2Y7ygsUEQbQ/rdA3BZOR8Cv3fR5Pg76NXkR2jiytVJppd5iwM9goXMStXaSOzjQPyp/4MMmLyXtkbH0lWVbBudN1nEMCQjIpEOT6PUMYna9jdTo+dxzHw5gIClbok/SzjCmOQmWmAJxTPqj/jy4Pz6NoYOnU0Z7NeqCafmwrySNSreGO9R/KzDDXkwZluGRgpd+D+PLx40DsyeQbDcARG/6LoY89srES/coBVpT/FIBDt4ztf/nwAh8+fYQPP/0Ml8sTwC//7voOAeRiMju28xYlAnRohpYeAs5j87SY+eLJLlR2uIImq9zikK/15uBPv/ksw07A7qLgaTTjFr0u6vUfyrwRq3Q9N8/f5MWozgYdUYQhaT+ZcVEImg/cEz9Rxvog5IdJjlUa50t2/44jxzC00QDH4ccaq0w8zX7zs4wLjvXkT1OIcb7F+WXGk1w5A9vo9L4vYgsn+oqDMWA44JgmSr8us98neSPAg1qli87SaaxnAjd7l+CwJdojjrvMKku3BmaIMeq6FlSAbpsJWtBWThfkY1j6Cu5ZneTCqBMCUEGWr2Kd4T3vo1BrmPfrubruvbXesMxP4xtnw9gsG3PriETOkMFx1tn4+p84vLRay7yXZm9FvuPA6TQPwSJAfjyPRNQQdZZZWp31ArV+HPrRHnvT2KQNKpA+Zz29kzdRhYK/wcvzV3GWxiOU+bJq944qIPSQHz+a0S6R1KW4qs0u/oXq7QRkXdX2Y1Th+IE5Ktp+lvKk2i4CIBZxKgsMxKEc68dcP+/WYIVf3glfsjCNnMSGGpnniLX73wNlumAOQVuF1HhGsWIzdrP1S7lZO1K+YGEUMr07sBMFGsV0NgkT+RPibu5HiIvZYoKL0vRM01unoYTwsTjf/Jx1orMrdlmOTCf15YNMMfPvmPHpnItVKDaWPhzS4cGCvwxBPBBl7xZns6A1zAGLHoXv+rvw5EAlcDv6g8rHTvVOL8uACnS8hIf6uhV0WCQMICdukCeEw3RzH55OFt+ZTLH9xB3V/HXLu3NA+6Xx7dvadEcgYu7wlxXdPLkIwK48kUUnS+gg1O+PxCAlOCMMVWAFvBzRo5m4raPdanXqK/4rKCF2R7IIbMa873qQHRF8R8NaswEW9AKLQH57RhyVlyQZhYLbSEQABdtKciO841gNBMPNGrRNw9Bs+5PUiPK8m5T7Qe/GGAEPsaOo0BiloC0nQc1nagrIRixcQMhOLD5K6rhxNHyl7J1DhL+xUpL3sfLGJGrecRsDME50Dt9SvxkByIXFAqfPr6gdSKeoRBS6lnHNKxlkJPg+l4akfe4HMO4isbmGSjA+AK98Awj/yupmOdjKzBSXBIsYbEqHOSew2cqaW5I6NbmBhlccKSY8H0qiHAs/a7+sog4A4ny24Bgf90BUewEcvpKZC1YxMsrD4Llt3+3F4kecKn17i5zFEVpc1XRQq9Stuo6Rja4IB5HQPmrdQSNJW5of0DhaRRLSpRQoWODDx4/w+dNneHp6AgSA8vWvgK9foJ21SHmzZ8myllUeq5Hj8NL8jIo0alAEj2ni0ekmtW1LDt2bzlTwSGSiC87WoOd1zw3GojwKulzAcdHFm6ZMsM105Uiud1YbHTFDu9Mo7OPGT5oa+e/oDTMG5RG0SQem0Tl6n+nxndJDqPiBHfTWfU3xy2TaswnVHlGzJSpBrcbJisYOdDCOehXD5wrbvz/K4x4Tm+E74vKfImH4cqAi8sprVZ81Qyb3mv5F4Tu5+aM7hMHMMQK8XKB+fQF/1JJo5T30x5IXgCr1UzC6bV9nVGTq60ZEKd/g6eOfAeEqJ3LERZCDIc9+HAC5AHPwaVxD1chhgmoBD/aLrdgFJ4JtgYB63wQHJrq/rAU30MM2fq4hyGE/nQ0YeKMxw0vXeYZd8MFaZZcGW/apY5jz5oZD85VhGBNrl2XE6+y5asDR4Bfw30lxAdt3Jcl9nLKaHATrFMe2w6FyRxOE/Ayt+QGr4OZxWt3hIXrqIs+ZRUOHaWXbrXB4T13aVQxOHWSn+tQDQ3750iOwvt0+HMvxeMtisJNIznxes+pR5mVWCfMZo2jRHr0hgFv0fks6HYjIjLpcubPOluoEGgAPaII66ttpIgB2ituz8hvFWdzQ/Z2zWVCJS8wcdZdC+7CCVAVrC0iQPHdwnU3IwpmkbwR+CEQEzEJ71oQhxG2YoPIU1HaBITIr0cLYzsWCq7S/zlcMz5KrNgqhoSqrXGW4sWCas6Z7+OdZE2Osa6HGL5l+BEHD/MsuqbJDPgs2jLiNz2wgY9txLvQ939lyiomaarwShstB0T6YZDJ6vlWEADxjTfF0j+aMPf+VlV0oKLOSpnN3Lq/2ZblbMnoMqLl3jYfw8T2JHTApOE+HKxUmaVQdN4BMV9Hype6rIl2ak7ZzlDbZA09BM+GeosZ6L/dr1FNlCiQLA0TEsuyZzLjYCBy+zhE0jLEgwqUQvDy/wPPLCyAWgPoKWL8C1m9ZzQeIHKQJ4UxLonFxu7ILPjJG8A/yrSZPlmjI2lBD/w7DnB0vvrk5HQXA20vWaTivoJVmW1S29ywFzpSMIYs3New+0qgxsaF31HXTZtzA3xTFUR4i9D6TeQqDfI9pyuvRr3ei/izWZ/NrxhP0mj5S+hh0Jev0sngsnA5Zyludlzqrr51OYT6cFWCr3IL3oItvFL4ZgfgAJ/nGbCnXvrN/XNVT/WIiMJ1Z07S7eMSdvBHatIsbQrJMZKmuHdtnWXrEcAIcdfFRLQfvad26demctpIhcc+3cVumTfk9q3J0awzffG2WvjbrOsuo5gqO+YpdVxwzoyoSAADiuMeBT5vfYssVuL4+B9tu5O/C88U3U/sBEBb62D8yJ4mA8Cs8Pf0GQFfA0hd6UrYYrv+sBOCOfmp+GgLsi+Foov4zsH6g9glbyu+WYDHedlxxEIJ3YSG23SIAfLSUPbnB776IgYrS9QM0x5QLS6ICQAUQW/sq42J0ivbNHjtrj7dJxm9saHetJTNgURDB+guDTEHoxxHzeHl40wWZFr5baHnLRc0xf8BFHpPq4KJd2P6jjoHtl/7M2o+HqZ8awSTe56r66sjpijlvneloptxUfiVF/cSe5ltUuoB3BoahW0GDwlvWqZWYbI/MpvYOTroz/0inGcdkGJX+4L2DEcOj2eJYOVcsXxjWC0shbcdtaTsQoZdVNqbq2dEYfVVHZJ+kzugIkyFQCTN0nb9tlVuVoECH16PyvOJ6PkUM4VKDzMzDn2VYodK1Ha9ETajJ0ToA7TcASNRdIv1G0TVItK16BYazzkCFs8BLcTfRYhPdU8ExCuTWf545K2K2fsWXgwBgcEk84GM9Y8Wr7Hk5ausoZByHsuEoFSlGHkfEfg8IhiargSGTlt+bSa/Nb5lZcVm0dppcoGThjHcXeKSAPJ4y3tR2j7hdERPnCsusPPCAoGft5mnguUEZWeFOtv87LP2u4tyN6cAlmLeci7jGvNJ3RgBocwyP6nmURPaUh0grUn74IggdK03SHcc4xGCUD0jmsIM9sp1ku3mG70JotRNoCOQsD+NMtbrabDfEWJk1pjyGrmGIUERR3B3PTGovUAHXnINauqK55A0J/AQhnSOm1i5AbbBf6Jrg0Ic97LbQCQoUBoxfFQD40+ff4KcXhH/+45/g86fP8B9/+V9wff0K12q32YMMFkEctwSXGaJGH7Ewz/BpZki3Kk9TsP3vOaMoyzsKqNrHGmE2kGNrpnrRzJY5lTLIM4C4QOaeGo0JgsbwiMGczbRkOQ9OYlceZuyfqLzedWVYLcnfVxrMSZtnAzkQoUIA+UWUk9/7dZzQwybP7yG/B5DvzfX6Lw+Feh8InP68C6z/ssxlRRSofdbu7qtVeUBzCLbvOIB6gwk+YPo7TEG2vi/9f+eeY37mdOkfbDRnjD6jcwCRFTKqLIPCsbrDeFsbVB75voiLG+MxT+2Zrd0n9wpfgL5+AAC+MxMAui5pMyp8Y6QSyZ0YQBUKELx8/A+4XL4qrwg4VLkHU9tgf8dP+73yEW+MOtijmPSopsIBB94xAWxt+KObAEB0euw/7IJf5xOhAgAFoLSbb7Bo8MPaU1ZXQIB+f5pYEBLkcFYShjKBeSLAcDS1dbvqX9bFSBtHAP7EhpjWGoqtIX0fjAtvC6/n8PHiOBroB0Dv0uWgEEC7S6IU384s2GqPISObKWa2U4yGx7B1fNIRC3sjFncPWDk+ulSQWePmwbq8OPuzd8i6eJ5nCEIMuMm3NRIeKAAZX81pm5FrHIMR9+8Cb8ixndEqmsNj3kC4QXtJ2t8RYSO0IO4NRqFnQTNJLAOPKFum4DsfAaBAcvA0eCbS9U2tI8U54OsYphFHlSPnJBF3DjA0hzRvQySAfgdEZecKM1f29JjuYt8Qn7nVYKAIc2Y2DNpDIIti/8xaSROHYpykxii38trV41cbjLXtE5dMDt+odCKz8XAEXvuptVnYkTiqVfDaKP+g+FicWNZZRpIoSn4lJZnCSVtMFqOyhJyjQjG21/ShezoqRCucVjU4nJdpohRgbANfW9uFajV4RT3ANo2FsAP1IJPHKj/uuc+z0w1u1TxalcsqYqaqYUXqRptE/1grWfZtBnW9sofHPsmTVCtHlAHINtWW1VB4LBfn/hyNnC8MTwwPG3LkyoPg5wIT5isrnAiAhHqe+xT3BQ0t8mU2bNo+FhoAga9HvqR5JQghQifUeSK5IERIXtLG9wQfLq/w0wvC5w/P8PT0BL/89ld4/fabJ4yVvB6QweVv16UnNNJkKPbqX6WTgZCjur0h5Ge60gWBP6A/kU7GMTxWwN+PZW+OOO421xSeFVhOjCFlUIRD2TPIrN6zlLXhN/k+jxlvEk2TdpH/s87PcjMJRqQyIKvQrmSao7WVotRc0lw2L5f9uCkrpyQV6gvzwzY+qibbVYY67unLFL6FeQj8fO25VrqCdaAvRJX/hEE60ssRLua1Yx+q11a5RFEnrj3mZKgm6O2+tTsKzXukO6hsNh6bS0UH2bkl9m7lMo+aTcnTnDVMQHR+JlHjXNdsb8Z3p51LOwyoVboJJM+I5gvxg95Eac8ABl0fxPWyEnxWEQNu/m22rXlXLkCvTyAQWEaKumKeGQDxnokWvCAo5StcLlG2M54EUNQHBAD9gvseZCAAkkV7jAP58shHO6E6TXtH1B4coFKhXWRcVccmXpI4Gafu0wAXRNV+J2iBCLmfwlzkjQwAjG7fAxBFhqrt0sDaxrYMk6Hv7ED9zqgW8HZKU7lWupznIOmCtjR/Dq+tIscAFVI+Z4OJ+naujwrXErZvZMYUbTLv++6GbSN49ju8jTp4Wm60z86nGezb+PJN2oklJbtKv/frEKO5y/neUjONEAbSPFT6eew7b9wxEpjnhsCB3amZVDHAcPkymBOZsewvjP6WkKJfzdgTZ0/oOLUjYiTtoKZ1QW23xWQNHY6RMVzMn8unOyCIqCuVbZULEOi9DOwk7uWz8/FkHMifSce7H6hWqERQ6xWgf3I0ndvWmJIGK/h7R920oePfz8wmqt0eHpU6Yru5fwoMQLeawN4r0fDlZ6aBg09ijIrxSn8uqwpC18L7M5bheLBoX8uGviaQ2+1jxM4KC7Kfw2xB7UuGCb7tvCh0SveZ4AKQy1jjcw5u2Saddjpwv8aoxGGxkZFx3434kRes2qlLhJV37AhIn9Q5Juwmz9fferLoNGWUKc5b3ZzU53ZFyRGmMQdj51EgyUuscU/wR/vFzROTj9sy49U3BlLe4gxGpROrKK1RtCuA9lBaC+Js9dRsZCn5tk4Jz0AIW3czfsb0yLzI86lHuB3iSjprUPEzXuw0yNj1dLaVtA9ut1KxhQYadUl6lsUwJogI/hNkCAB/+xt8eEL4/PEDfPjwEei3v0IlaiaTBOtV9r5rkv7Jn59xmK2TC1XuZD8Jvvdeoo9loJHLZEQkDPIRRstuspw5wYlmc38yfmkKnJ8VrXmV6/TOpLpbpwtGEN19TusjkqO5N6sBYJcSfNG5zLdp0BsmWLxlX78l/MeNTIQ0n2NvlignNaq1/eu7IqDrGnwkSi/aM5PXnz347z6nYvoRcTpOO7PqEWUW6RE8acJDVrrsm6XUyIGBQNJgsS3m9FHNcVbzbj8QgNReZftIVxRnhUxl7ESX34m2KKhmk5/0hIzo47j+C1zlaG2Fam3r8AWACEq3uUsvx7szkP0xAPDy8he4vPxFsSAKen7XX0JwAIi6akJg/UnE71ajYEwIAr0Xwvrq4lFPLnU7AfECAHbXhtrd7W+3KZB3UvSwCZcnW48AdvNBIBUPE+CSKeUKCy2MkWjO2EYWfvOv+TtBPGgen/7HHEU88w01x+9QeQND6j/JcGZ6Ebq5gVVJ8BDJ/2abz9e4hAQQfQYD1ziftosawsbxsR6i7E982PGbHO466IPEwYgOeNuXE4MJ7MO7pde2S51RCBoDCw8fK7dukdrbgQi/kQx6VWNXHQYhhl+G0SA/QdcaPYZHFcadY3xaWYXNWAt+QiL9VoheTxVHtxUMRrgJYkPzlBHz36mxHzGfZGEcurDhIMSscjMt+yN0YyIfFEfPCO3wOAqVGDbIEutrHIxwLyw2NJ9u6MlD0ZyVmXaxjp0TyLvznACwn+8ct0/ulD2bhGahMUAbLCJgYaWKzvScN/80eW6UxUNc7xBAEdIBX7eKWqbcW0wQ8zwxn6M70SkSlmnY3OyIIIKJYqdvh6djoORx/XkmHW3Zi+8im52VPGwPw50CUEZN5pnLzsPll4tzMSBCkSGcfT8YFGmB5BnDXacz2kCouTP/nNJxGINYpatZjIu0JlfUf2FcdN4NsmCCPJutWK/whBd4ulygXAoAVd1Kf0Naze00Ca52LJUgMLxzqvWNQcMDRNZvFoHq1LkGXSZ0mhhEUSzETur4zgZleCo1Yb3EPQDfy0ZmHPgj4h54q3xzjD7AsVVk2DkWMbZrOltjmUl37ARyE6wm2Ma6D5LpCqfTEJjTuhaIpf39uHQ7JzxZyy1zNiKXewXGkYodFfjuXf2YwL4b5gI8wJx+57NsBc2+O9bFHtJnUwzUNrGrm1vFuJCNCU4TM2vM+P3T3YtXTpaPY7hXfEIb79GXYQHODIctljIhc6ut3nrMxul0i33pfmR6eTZbZxXmHebbj9mHJyKvwA5+E1sL9eMXVdjpnAcguLDdQIYHEADUD8IXJL/+ac/6b/uOfU3sK1IXUPuCBFDwtR37xN3Jl3n3YMKwMCj0N1W9l9QuYpS7SQkAkEDvD7A4ax63awF26BkBoe/SkHsqStAtdZEvAJpjhvoRUAAyZsgaewiAsK6JVIyPzOzmZojmt+7C4Jdh4iH1AFHQ4Vf2rYewXJugU6N7CiQvgnXmugWTqDRkENW6BtN1PYGn/EpsGD/O4qMC6Mcgw9LmT0yG/rnQACZldnD3fX+kS+RAZNH20JemXJY4yODs4FEuyOJpsY3GuSTPD4RXGgR6C+V4Qw7Q8IXbdKfGPjjZzx93fPpoJvPAI3EMQL9Ku1UydbYEdpJTh1+pAlSQlS01ccTPjcqZAsLOXLMTola4yo6IfuZf7XltOf5aUBkB9MlrlV3k44LQEOSiv8xdEk2GVf6iOxl4B4c1kgMz14dGEe/tJLn3ArqAJI/SrbqT4xvc53OlnwC68AUjWI2AE8EnTTEO+CAEgkfGBo9UMTAIot+l4Rz9NtC01egHcBUjobxKhe5isUb21QWWbB/nfT2j/3myikJE08KcNicIEV0h34uijWnPEPBbQG8lSyBW7loqXaNwuyI6TtrX446qiJ4TqFwP19LC6QfBlomhcqNBeLQVTqLzN0XGcqVhWGmF9tgYMGMnGt0hDNf+VJFJ+o1X6qDm2d0ayDRJGeyD6U3JtzQfGaUGwPBuw8BTHn4MO+I5c9y7XRmiRNkMpmwKgreStAGOK68AAbAUKOUCeCmAQIDf/gr47Vcn17bTWSfj0E2BCNN3p4Fu5V74zE3m22C3oSZoqw4hir4fOIXJtJpbQQ4CgOxsYifEev3pgQW0nd6iZw90wBtS4y99flLvmw3U6VTg6feeLF9f8TkwBuuidx6k+p1KDxqu93D8vkv3RNUBuu5u7IRaq+y4RQQopXjnmHybd8oj2vKWM+0tdtD+I33HNBgXd5R/EBoA51BZ6fxpRYPyZBHAIbv7QlYjKADoAwkjbv3TvTfaPFntw9sDzr9hniM8AXz5owXc0JssxBEI7ALh+0L5b+U26Ofl6Vd4/vQfDW7P32zbK5DzHUWbv31hv1mt2uZmr10bvoPtmw1evzg7sVeiU5yfAoDsRIufF3wO4NmWa36zYvxo6l/z9q49NsqDQvPevBN/ks8XzR/bfWTKNZuxON+Bfkbfh7bLKuvIO31cvr0Zdn+AM9KHeUPcjHFezMo8Lm22n7Sr0Rlbj0MuBiOiPj2LQdx/NwOILd527TBXuA3mPj7fQ6HVtB+ICOnWrpbmOueJZYI+f6XGrEXJTJLffpZIcXfuUX9kndr9X2WOQ6rMpvU59PtfOZevSCa7s2PG2hnWjNDsro3ZTgg9jiNPrTmspCvcOJN2iH2mYEShx843PepEZzOZAtI+q3/YYbS+i2FMVPCJW8K1zyOqtNdw2Z3ccZWBKk0O6gGTPmCUR8yCA1Hy0ytORTot02LPtPNcwgllDwGgLGUcPkANBVyewxSCEMcgcaybmEZ9rcf3L+DwRKqRz+j43ueqaCThDJe4A+gWAZlRUJsOqLwSouDeJKRtdLidvosy0Rl3LMVg/dnU6ugBPwAYVuVMG+EpZhnEQ5aBpvSUbj0fSdWH1EiYoCfvMc3I8CU7Bx+ShQkcFH6tFUr9BnB9BaBr2op1ilqfx2Y+lPm4HA39VG4elMvykJkP4cUpOFrmWEodcUVPiWhk5KTAHWmm5+hTTD59HpK8/mkTt+hsvxF+/5YpWtPcPG7mSINlO2y5BL5hQfmw7/CPx6Zd1h9lxFFA9y7y6VHgsa8PeBfm7/d70toFt8K4Lf8poLlqtF3pFv+6Uz5OK07np74+LL/5PnWm9L9q37XnvChMZFUi6/akefb+uLdP7e7bhDnqdCd15IenDcZ7N8wz6fs5Vx6S3gv9Qwa4OZut3npm2BbtRJnRu2XRqOnRDlN5w/qQLoIk+6K7jEx5I9QHu4iegeozyKy19u9U+JLYqCwHpaWk79kGRSS44G/tN5JgTnAFwh7ICItM+dnIE/tODQKoeIVS+EJ2g93EB0aZTSl2Af/xejDWvri0trNV+LJuauc6mS5mn07zt9SW2S1M1cDCuOh3CIIgyJFT7qSV3rVyUbBVKNlPFXUhoUQzXlyeLWCrW7tO63+cDyk7pcLgcIO9Hm1Ibq86pEnfwUzfC7r3ARpn0fR1LurC8X17jEK7uuiGxvJZcnxuklkWoqhPg+tVrE2QIvCQ/ISSzNbJ0PMLZPUi64DtTkNPy44DHG+kyZ20HYjIFT7fPXoRDGknWsnEzufOrBAq6EpLm6Xlq7Wt/rZbbOcTN+Jr1Djn1WE4HXZtFxRJXfzcTFoFrszMHmFhGSE4ouX2dvJKjYjkITOpqm2XexEgKKiNH6uTwQCxwRb/rxoIeYfGVc2uXmFiIwzb7wjM7JUmAPvZfGSemXrsamZHTwa27GbgcTDMhYD6AtzA4PonrxsoUye4pWfbHzjkkO1hMPR8hASaK4e/TGQhxnkwYx69pwbS4sFbrZrsQn75Pqu2O/5nR4cBujMis2AYMlg3ptVCMAJq1YFxDAZM+z0hXvK5oJYDZevj9ncFhypTpKhf4IpsDHSiwcSVGjrvyL9PwR0LjONdFO1PU1z71fBBabS9PFtZMh2EWb2Bz+zMEz9mrEgaaNRzDXIi/+7x6X+dHDtGissNO68C5tPS034Lik6oR5/iXt8LOaOHMZW1Oc6szP/bf/xPwFLa7sLTystRv8a+n+U/rYUdp6NggtNRRoX0ccnIohhstG+nMi6CYyFG4BYOLOrdSsvusvJwR0Fflcvkoi9rHw/y+m7lejGHt8veh4OXCZQEgx9hQET+ws/ugf1Wc4TTCrc92vtHOpMmSvEjwU8e8QpCtRJqu+sP+h0RBeFyufTFYk7BdHbnqoYfKf1IOyHu5QJ5mtkR/0jfK902zt7Gui89kB6cr0ZBD4tydkVpxpvCbmA129WJQgAQ903Y+/k4O+IL1K8/gwXBtrH4UsjwBfZhMW8zQY9WaQUoV/jw03+HUq5emwo+I4tLxLFaO57roNELAqD+mtJtyUsPYAhoCWy0P+Le4WAE+30AAMsTFHwS3xvKGVHgfmPBXp/DRHRd3W3B5byNy3j7+2e1XX6harSBAy2pAwqyxLs7qGJfJ7HSaxm3FJTane6IJoA4JquUBSweZ9dEekoqx+x99xtjD0YQbDrTohWwSH2IZxaKBClK69N2PBjr3ZHmIdHHV1WHYAQ/t1N5B5Ada3F13Xlk4BsFI/YDEQfvh0umBeHemxSdou2dBCIJdJsN8aD6IMR+6nHvdNIFpzwAc/TYIvdd6dwwrNbw7p9DYGbk8lJVAtpDvePff1rh4d6A4JEBsTF7bh7Jf7G+kBKQZ4MQPIbq48AWxbe6ZeiXKYMj0yLf/DTvyOA87vPCFhf3a9RFupNnukBaHAP8NWdpR24IC07/+Ybkl8sughAeRYU06/5Jv8VeITtOizQXnONLCkTSaIjbm4kIKbjBL48JYo9pozjxrAqzgpvWRSG3UWasYNqGx0BhnFvzXRShvPkux7glq+HtWOAmktO+NTxmdCJm6q1Bo/N9w2IMamt68YBxeOfjVjTmS8ABwcK3i8NfgEi3i3o2lK8phdtgCo70MI5Nz2+KcY6CCIUKIBaAAvD67WvXE88eycT4BIZqlTgcuxHlTy8R+d6EzFZBqaM09M5AP49LweyBMzzFBiNUz4rQuRLmY0fYLKobvszzK2qe6bT27jA7q3tMsoTVTVzMlHTgyBSzn3PaeJRRdkMKvNqP6yYP3iZ6NXq9PnNfSqFYnFClCR68H96557PKaYSxm6w4OVR6boRvy74Bb3mbZGQFp9xM2YAz/tqWegQgzjhgzolNb++Lw/DWsZea9kuT4HHEQ49h7s7bN1zE2OAzPom2eAOQN08P8aF9R5Zv03qByy6QoDgt2Pppjp8zdxgUSJs/YRqprN5Mp/pmOq64+MlKw2ThHhaH9tAi5OVcRv8HaMcEE8jFw20OFyC6uKqd4dK/8iXaXJ/a0O0+BTnmGwAQX+GCn6Dgq+am9tb9R2YHRocl1/AaBsM70Dg4gfgKgKMdIG1kTLnOyYI8ZA++sVXa3RwAfLdF2z5h3tdWoBSEa1xkJXX4xcUIoJdx97+80LhIIIJvpSB5r/aT373B+29ksTK1d1RNA6WdilfrE/XhZHTMC3Jn643O8v57Awy3Bsb9YkA78Iktwo2l7uPlO2jTSE00Cuf4pbZg51/neyUbDFN9gsa077jcomyesv6YYpc+Fa+OXehm+v+Raf9oJmF6zO1YrSv8VRJCcZHgtqCWzPv+l/0aneGqMc+7FRqj021F2IMV6Jg0MxT+wVEpPlOfcWYGyp+V72AwDJWjoxQiltK8YKEiFpAoKtrcCEDXMBkEQ8VJWAyBu5iIGn7N8Wx2EIQkzAhATW1iwu7nAVLfBWGi21C5Vp+mvIi0/4ZXpPXaFgEVICAovJgaxmgcmkqV8VuhbKLyRsBG3KrxBLmAiMljvwxnTGdlLD6DskwSifX3bCQTWpwZlhvlHZ3N7/asOrqJsE1uKbNr+Nh6ogNmqGsa2R0ViFbGMgYZ4bz5zEhET+3KmHNoljmNZiA7SrzIAeU51+P50rAiPJGFBoigbQXX6UQaLLTgBU/I505cDe3eMdyO4G6XuRpsIJjAnmQh9ScD3lowm6u2lqzBwrs0CyY0l3e1B+SVua5sWqXH/JmOsa2JyJA/Ho+1sKRFxsnAHJJRDCwZoxQJTdWdB2AgWqllRMD2Roae0l03ZsoFChK8vLzAywvC5fo3qN+uAKywGzpsMrZB9kF19AzIYWgIJUf5pjRT4OcpEmoE+CDEhjqTyw7PVCXKo/5cKqXdYFIN4WS7tnkgddQWSvCsZJDnw4sod2Iw4tEpRXZQGhYpzsudfAGFzsuy4/iybjnEKPCMMTgTiOgRxkkWRYyBSZj/HF4sUFKZbS7Xe9hqv3+kN0mdLwkNTvRpWcRm+DQWhHK5QCl8fG6kXwEKW/L9e6W3jCxMU5A/00TmM2ppt8ytW5XqN0r4g+HzyKSrBv1zng/Ao3Gi/YcLG6JCzuX2ioz1wQ7rXxQ+SCdFc1yoqG4C7/Pw54L0N+xsXeIyVuDvuNBsYk+LbQQAUAFe/y+ormEkcLgMQvexGFlJRIAUMKwNUul6/8vn/wnl6UtuKwJAgSsAgfjiqvF1STuq85JpDyFBu8B71CGdLyP4G9QHxnAAdLdDwwpbQeDAdUFox0khth11bsGxaQ8HMTjw0TPJ3RjsNw0DrgFy/oXd92fbG2w+EVHjYtSZxa/3OHrdW0GPdVid8i1Fz+CMVyIN+ZgNt/nBC55tkuCEOGfOIS4+5zeM5A87jN5IrtwqddPnb9QvJ3ZE5M6JYTIOCNJACOb0Lb0g1hiWWRTQin+erMJck15rNMxGmKm7f7dBCIcvG63WhrSTlOsGZTYtCNEZjGN40anihbI6ls1zAo/PbLCt/s39haB9YjJJvdKxFICY9sk3Y8yaMRnQyIIQgk8F7Jf6UFdwlqs4BicUC0SYl5Hm6FgbUnLQ4q+dCaoXsmYKaGfmgMYHlc8TfXPkSEjf6Mc0j8dPxgHvY3DatysaMHVawkTIG7XLGWlssp7Gp4JxFoxx1SUBkeO6Vf0567XkAOHAWyxScTpqqZ4l1BcUE+ZxaTDiViGRKgPggh59KtvXHd8MXpLBtHtl13GdS/pFy7P0y8DqBtiKYKbvWDOBWScKPS/m8BzTrILb0qA8Pi5pEBmG8Yo5oWd5KRWeLwTPzwUuTwWQvgFQ3UJQnZrgxzIx3mTlWFTgRi10gXdoxa4gGArOfz9sWFyEM/AOGA2TZXKRUnSPPZgeWJc+VG4UUXtUmrFWe9hdKJF8FU6d9n8K6XaxOAGC8ug+0HcxB9Mlo8ymBN09PWj9jPjBSbnjVbQFs8Zx5bpFaVXrIRtDQzczHGZAdptr9fXDTKHSVI89TyPfxX+dpZMTcb+LRwWZSP4AgOpU7ngNW2SlamzikZcMelsC7+bhSclmskL73hR1uGDveHZMZm6Nsme/Q9+iIbclqxcCzG0rq8kPeY4GeqO5fu/1wqY+kyh8Iv8Ish/WTRj48oF9luOCSbkNxU5k74OZ3RQcDlnWw5cDinS1AQjs2PCxdIDg7DT+QgjNH4VmVwMCAFzAHo9uj/9WqmqdWgDMDo3+HqnvbOgod38DEQEWgoI/QcELyGIkQanxZOwLhdWup3bqgTneWf52noJ4BSxXACjuOCbfL+FX/+Oc+1JHozUJEuC1P1IFqWBp91wUDkQAIBSwfhaE3veIcvQUv/BHOwHgVftcF3hw/bp7w+vGVnbZsuNJLGte4PtBgxPcUef47f5OiNvy6YJa/auKW9cNexGUP9ZWPMcZRVKx0x2UBveWdCa1EY9n3rZVUYdbVLFn+QOaqt8GiwVtDltQe3tYPP4GwYgTd0Qw0cbh4InW89ky0PAkaHcwtPJ9mM0qXW0Un3dX2wXVZqJo/n7HQOOpwJNuYEVMgH0nAD9z590lDnnkRjIjSOnONLiFShtzMc8b6NqjuY3ntU/SM/TZUCRe9d+/d0Y+P2vfd7JzHvGv0Ga5F2JJOKoy5jLfwBxwqC4g0J4jAFSotbTodS3+bDzHgD2DBekiizsMZckyGu4GbO30ClGYTIFi8p62EWqA2XERA+u+a3Jq2TEelbQCdQcJzzX+0fUSxS6hZU87DJPA796YByEy1Avy18Yb0m2IC2HJ71qTdf4CauByJy6Q+SfRXCZvvziad+2JfAJ1wCurU+Tm4TpIYhHLFa2skFshQjrHCUfRePsWyVk5QyMYnrs56YU/z195bZV2JdPpOHIbU4drFIJpMCYoMc648QHUAfbAH2g2NCdSFPYJyR0NnQ1CpG1GHQIzw7bQXsm6AS+RxvCnz1/gDx8q/PPPz/Dp4zPU6xUQr8C7GAf8ScfkqLmjzqXax11D8UZJ1LhHITfQOT9+69bPwwCztJU3IYkjPFLITmwZHt0d1sORie+Rbo5qPSgNzvrRjMiwO8L6zUkN4JjxqTIzvtqFMYUNTqy/a6Lhy07m/5xp0IeP8hvbAFj/m/BOE6wY00ridP6UFXVK5Vluekv6AelD5lZw4vyIwvt3kqarna1+fZYWKHy675YznoN7G05HxOEte/HVmL87Kea8jyTJLJxSeCSH2B9URhmHOeAZbAt0KzSytegVazYMgh5brvVQzAcwXlwhb4w/wPiCUnvq+gHgSoKNmLjtj5blhcHMsyvXF+siePrwV/jw6c8QA89yLBRVAOonohjsamV1upW70rdMtU4fILYgBEKRewEYX+f3koCA3/LQdkq0Y6IQWjDD+kB05wX2fFweZTdFdo8Fso+KF0Wb7x2drGXSJ7ahhWHG7Ro/WHLHIw/OcKvI0TiFjnxG5jObeVGOiR8DAh3YMmyLm7yQZJ35X+4VlWb6DJXu+NEAvM4kfO6BwYj9o5ksUv2v89fwTgLw5M28xTITLNwAU56UyUHNzKc4agDxymUErqeKbao+sX7MEUC7pMeVNG0IQg4tIxRcxBsgkxahpBRDvW1Qa49GVPcyI/jdLUoD/sBtFi4J3GjB44hmBmFGrn6/A0Lz6GRrIzHlf2bMc4UKReAwXArlLCj7Qy41zub5CWYk2RKH5Dx5BIfq0NJnjtb41Ct/bvjQMBA0ZZxWwGh13OyYIblirk4pY+sdMVU1aOzc0QWynyzN+TFM+AZkpGEFvMGqC/JtHAw8qYWt2ZBvvVunQzmo27ZjdYeDzGXz7F5nUXacmQRE+YGtY6ojW7oZJC1Pb5PXB5XWcVKb0Y7tGDydcks7TVK+ema+mzKDYTGvexwrdO/HSbxGbQiqmm6K5qM/xG/kwD5AaGVdQMMQa6mv8AIEH15+gueXD/D1y69gWbHlorNxmdJvZIW+6smDsXha50Gmseo5Rzu1OWEjD6/XoAT44SXzcETFHTB6uhv69K407ak897I+r5PZb5TkQX5r2rgHexefVbq74w7gLNpj5aOBYaTXtIqsNsuTD4P+rrYUuXnh7S7zQscXmwM5zqc6xRTKmw7ro4BvgI4yz/CAczrEEUcP3PNBTRSoU/0DZOqzLSRcGwsAXroKp4W/fUN4/foEtYYOMHXY+bPdFKt7u1K5zrGlMx8tFknGsJnmHQe3YnBLEqXV2K8UX/yIabraZQNvNfchUsG4oI3S76ZIgkOo61iA359ODddjkHkIlO9OZnGwjnImjGqqx59LnvbGjok1N2c3Ofoi+46/M88bLlTmQnwYOLj773R6qPJK8ASWQ+BkQQGKv6H7EAuXr1KW0S7wCkBXQHnKOLQypR9jXZwdSnLvBkJf5EvfjL1NAPily5WRozUbRoMDEjAh9VO1N3YBqKYrtUBRrf2Q1XJRnHvJvt4aAIrZnQFgd1OA2W3h7uVFtgvaMVK6YA0TeyHYE718JQ5mGAJJRKI3ToAFDKySpcXz7C3X+5od6nUZDhRY1V/rJTeow1FXhzh4eJbO03lu8GP561VzXVw6wp7VnryIfb8r60z/oH0QFh5uH+x9R0DiRCCC+mTss4UPXTc3zLvVjl0JbA74aiZ3PO2YBwoA+sp32QnQmRr2iCDVtjq6crS0r7TW86pZAzX9SNTg8jlzVMEu0C6826KYQRCEGk5trA35o27R0hXWSojU73ZodzxUqNcKtVbZFZINGK8/lOOVmFBBmbEjiTj3SettzLH1+XwnxChkZFeHhcl9TXESWfzMLg6z2rV0BicIMxqsDwuvQxlrgUqNDqrxvktfJysPW6DJsgiE0BTgKYdGHzcFTL93Bj7U0snLCQ8caRnyxIKGA2R+SAy7FBzMPSuWvju+Q6CkIRfgMVOhQRrkLLCCjfnqzoSR2Y3nPo4MS6YRkRNwqcFlHdUU1zvEVpFpW1q1K1+kv2aJ8fJ4K+DwWYobxIxZ2zb6eRX7jMInKxqlZ+/zgVTxEUzcVFgIw2yXBY+NbTjjbeqz0HnFBwJMdosxD2RGrOUpXVk/zmVOJeAsdEi66mQ6ouR5hwjdjlcN9FziXAqI6nzQ7ZqyAmXM7uDEutq44azZyh9iHSEPgo5r5AXD3RAynxB0SUnPw7gQAK+mGZtTRXJj56GVWryBfvsGH14K/OEP/wU+f/oE//t//hmMGQAJszF9kSl4yZPIK7e9ZtOB2c57BoIfU52pq11KXob4eqMK7rZln8YzzLWDKOmpdm8XmtNC1BXmmagfNWCeSREr6cHxPunLyHJ/qETuw6WR4SfF8wbtzhYPytwFQzkfUuhxB+pWBab8wWDYVRdR8d1u3Ew/s4syArBbOu4haTK7pcumBKK/SGX5TnrEgoYEqsXoPlBG6SDRZyPVqd5BVOF6bYvSsBQo+AIFPzUnULkCIkKtCH/+9w/wy18vcH2tngxFdK54Y64njLlXg+B1rIUqkdY5Vj7r58zoWWRPWNEt7HLU4nAkix+NDwd1/+5psdu+B06X+9Ocmh8JbzsdBeFO1idawYYOn9NonPuz+sIK86N5LG/3evrseFgej2BstZAh6xb0f6DtsDiWRaluH+WtMUTtrv/21DAjfAb68sfBJBgDf+oPayxYfSgIBBcOchDA5fIVPnz6H4BYu9+u2W2D/OxtJ7wC0bXroVV8VWpT+wXHshCa/XFgLrwW3Hl5GChZ9l0SWJqt2z75H7CrACzD4p0NfISUDWo0+85ceM72nAQ7Sg94NN+mihQDY+gOf3KIxcbmI1Bx7dq4TBYiuUfeigWAHuxhfNz7hMb13uFx7sazBNq9x97n5fqd/PYhmTtCv5YeSD4GuzBRouemiu8P/3zs2RogqG/B7PPghSmxu2dmR8aTTyz45bQdiLBI8u+hz8hcZAOkY9+ZgF9JbAfLwgj1pg2KjvFOGF3BkSnNE5/s79AomRhtIgrxIiSZff4URxPAgL5FjICdUcaxdyhTzQ4RK7hwQqkuCEFSb2TW28kwx4BWx43szwXoiTJDAHxnBAEZZ5gy5jhJdW4ETtRprZ1bOFMsaD6ZTqQMp6N8w6WPXbHZPUJniC0ILBSdPrVLY3t57EadY2KEToIQs2cZAkf5zOs450YmvT94aa0LHrRMlkcA+rkP8dLdbRS3pqOoYURJ/nVlnsea7XSmbIQpfDK8nQdxRh6pSmO2V2YCJe2MCa8bXkd+sEqbc+6+4rdkXienbNrHM9Uvw+Ugj5XvaLEPApqVTgRAQrhggUtBuNYrfH39GqVOMnR5v4yjnatfNg+Gb3vJ0ripPwEx8Pu41WSB2+zX2eSNgY2WRp4a4QyZMeWNAzADKcqLTVE2SYzDBMlBnje6yBZiTWdDzyz8mklrTWLvnA50w++QbDBiTXnakVF2HNZhIOSg71Ta3jzN2rrDk2+sZpPlrY7AbHD6u3fp41Qhnfw6Sp3e7PztPJ2g20Esr6DLSV1y6rEgAKp4OP2W+IXuW9l5O7uLGK95jpnOuTmOZ4c7tal24cfKAh38QPxultRVQ+7ZQaFzz4/yiZpraDotdkOHTuqavpfnh9z7OM2N6Nth3lxpptecUBIy+2Q6d+7jufvW1apOSlhy0HmHJ/7l1orpMJbUfRduKZm1Oaj7NND4h1we8wxgdIAQdP8SQIUeYK79hBPxefBt1W1dIcLPgFChAPXlmHVoO6+lbP68a9cpCSrUHm4avG5AAFDKry0fX8otL6uB12DFwgQAcq6UuQxcbSRpMAC0E9CbfWYW7KHaLghX1+ftNJd+LBSWvsBaF0LKCPNYuyFrMlXNor5cLdpJluW3DNB21oD844wz/ZGftLtKcuODR7wt9EP33kEks9xWTA809Vuwvd+w42faggDGac/ah/7kJ9scZKLXKU4RSm6f2eeyQyRkUdu5fbo7mztfQDqBu6BE472NB2l/RwSv2ouKXGQwRBJRJOrRxYVEpm4EhyGcJ2Ilk0DulODVoCaKyo47CschidhEM2GwXXpjJ0RjCQamMDre6hRnGAEzIarXtgPiWuFar1CvVaKmPFUYVtY3jSe1/hNGxLWQXxUpbQ3/7KTYSwT2XgBW4uNl1MCtJFfSwJHT6VLlXFH3iqicpUgAtfdTGmwDcNsBbaS5VuqbdSxbi186aoFR8s4P39sxUfhcZA2l9qdl2xondszIFad1gIz9rHbqfWveup824u0NufNpv5zuurB4GUa6WAV8Bh1aHRw+KGOTPEa+OU/YDmKdyR/3DLUYZtEVG53xbVWRBy20T+VvnMNMcx3QTSNv6PZoNg2FTqWo5RtoU3A0fd+GZkYfOcC1rNW6rDNovfZdeenoZPXleOVH8uoApwCH5dmGQWFXiWABOef06fkJnp8v8Mtvf4W/fQOAahR4MvSWYBNTxCBzNgNYOdjblEdSf/jkA3wRf5q/OkhO7mF8c28/NRjfs8tlAUPCt39/VPBjpjHYNKcdXh22pcP/XaVVWzPpt9s3Xm87X+ZHTbfjuJbrZH5Rswug2QRuB7NT4Gawfg/pjcf5zbvh90CrPpl1owufxsMq0/Su3XSPvff7Gk8A8E7V3yH6v5c0OwZneM72YxyMhe07e8MnphCHCBJfis7jZ6ivnwRYBQJI7rZ0tRLb5NRPsu5yyLiJCAgKXuHl4/+Ay+WrBCKu/XQX8X2Kz5T/se1vZJu4AAiu/I545z/D8X4T9tm6HQvmyC321bVARd9p0e+xQHNPBae2y6KY8ePy2N9zWZa1Ph+fqyP3UfCdGYxJGf1O3KRSWj2V5XhvkTtxoPsYY4BEfKrWhuU28bcW4QAIvlDpfD7OHMNzAgDkE2icE0V+W985v0Z+QeZ3SK6mrSBE/hwBIF79QUpQminAkAvUOf9GYv/RGYZ6bkfEEQJmEKh2gpILXU3HB2hOjTTOBd0yw06drmD2ycl8onQIfEOF3gWtE1SITpw3/Nm3PLGX0XARNH91yqYth2aYE1Bl5bcHYboi7HbuIAcVYo0jWN7X4A8KIp1YnWmRyUu+R6VOh+6kHWS9/PyX7G9TN46g4hYtA1nAigOJsN9VoIAY92zLUjxmRGYwKU458SvuHrPZBDui9k4ZsgUpcyAFTdISIYIc1bjSOMn1yQQNYKeMCbb17Dao4OAZ4WYvJjpa4ep41tBFO0bzZPZYObIoL0J1E9b4MsFvUHhmdWNC1fruLQwTRldX9x0LA/c+mQ9ZF4B5JkIEOpW74iiZBjn9BumIHnEz310p9HtOB3mlXsYHhzMOs30oH49l8j7rkRbDApC7koORkD0RwfXbFaASXH4u8PR0gUKvQK9XEGEXiS18tfyPebuqiZzPB2Zthiwof48xPKh5SUcOR17NYKUM1HzfQNPXMR/U3eGOfXsfPNZ5bsVmF4NEyZA3oX8sT9pVgh/GL87qEIv0AzlERhFi55hS1K08x2nuHfTQ/EGhmegaU7Z8oFPclGj501eQ5N2qeNK+hBfOivnFBzPYKAPN4z3y4YiGPsmaPkMplo2/9ulIlFn5JYsp+j+xvUzdWDxmSz6+xGUm848b8HAdZZo2dPJ3w2VW+Rswu5WhcrbzB1E0KZ8+3m1fphhYRQeCbOMcDxjX7zr+PdH0x6nEdiHxj+/dtjtI7UdJU5x2lcnDCmjTdTCbx/lBsgCN14sJInqMWa1NSemuiBQAuacic3VciKB2J07TW8jJH7OuHgCe4IJ/AKRXKN0ZXuQd5f+hLuAeHMbSvq9Q8JsEIviTaxe8nd5EYG8hlxoIAakCIgH2eyyAivoqe/6276MINP6iR5nrMU+tauutQVk0zrs1Smm7L/gYdz6N3De39WstfHQUuDrGXesNP77kW8FosEYX4CFAbfns7pyhu/tCaaEnFFIxveM6FSLlSJAN2s4DYrDm3cwhPBMvS7UzR0MqQUNh8uFW/nUccdEvE9zSflmkmy6rjljoimaeEGZHBPcWQp8QwXkrndn+srMRAFwER3Za1CpRRep3LlRRLkmjoGQYQ4fpYXdiRRDiFjWZtByRPp91AHd6C0K8AtUK1+sVrnwvRG1MRepHQQlYalpmwwRS+6XbHbqs2G3BAnPmXG+r7hQhUwEnBInoASQRP20PAJjz1U0UUR6Z89eTrmGGZHpIttERO5DkZXTikt6lIXj7aviIGf6v2khk1h4jGCxucr2Hc3atJaseb2NjsiATOOqMADA6zCKG2XDFJgRdVUWLmUfGYR1TNfPCZqK+NbCUy1BGgk4TnN3OgI5DbJOgvLEKba2HdOHF9HDCvhhWdfL8c0LKfg2CjTt8sK71eJBI77ekwcEtY0pC70Pe6KxkXUgin2FDuRWm4NskPNzhdEOaCCuFZfj1ZOCOHL2az9Qh/Mpm2AKzTGds16O8TgQeJBeEiA/Ac6B5d9mev7EzhEH5R19++QL07Qov/8cHePn4AS70K1yvX0z/k+gEGkibYZnzSFaZEIPC2Zs1jT0v6pqmiTx7SDpE5q0qvicdIf3IDpvBCoJvmjqX+8eyxoenUX+JdGHHLrOodur4MWfA3SmSNU2ev0XV0yDEkBMsM13x1D14hzXl784ApuQHAcihGtRWStZaxU5k/bGgcUJI3UEvSuv5/abZzsKjdH/zj4j8HSbCo1LWGQ9HfcJbf0fddHu6l9q6PoznIc0WF906b/7TpDvpMuW5O2mxkziig24Q/dsMfRHRRwOf3I+hRbzBQ68fmk+P77UNdSDfRVvNYuJo95OWIQB4/vS/4eXDX/VOi2p3VWiBuEr/WtuCbg9TbxDI7DB/pHMZ+qaYuWd3Heqm/falQlFfDiKUS5PHchyUrTP2EbZABN/rW4IMF1z6c62nYaDr48jlK6Xt7K/dR1mQF9ZYn44GhhChHyVvfW+c0ZaBnIEIbD8urtH+K3Av2vy5DxfdR4QUgwpukV/zHIG9v6QFTez9Ep2m+NQaSPhjNAU20v2BCKVkdYTzdljS1zJoNmgw4WA+imac67zChaobPLfbgEiCHwOTQd1uxPEAdPtVdOJbBjDysEBsPQopl1NTFQW4KcHkPCbi2GQEyf0Yo4HaAJBOJZ1QEsQYvD1s3VlnOc8Nheu3c5nibNuDZbgj423OtXwsWxACws4HlPsARoey9ns7u47HyXqCyU7jG9OM9vgzOHpdH3F/gmF0ADbSqe3pkx3Sk9pCCvQGMtUD2na3kK/rOBmagQhj5WzIk73/gnSbxyRvrGMPto22Q9ru2K8JEvbYHZ2K+7hM8F72ea77pLBJ5qoWGBwJli5Qd/cMK1YtH5jUvac/hhx21XpkEtPye3S02VUDfOY/MQhx1ngQ2hzIKAd0ZKDEoNEQVHDfwjgPAQdI6T4Ay/Ho/CdXUBRXDVfNAequvPbt09NX+PD0DT59/AzPz88A9Gt7HY65OwpCzJvUcBLMkAP2Y848nSMCleXn0+EOCJuCcn50JJYWCrJ3jk2YUCeZXQJ9dlTevVJ4qNNe4h5Vn526IiNJ5nBXPXLGup1WfXpLf59Jt3HLu2o8WExxSx/KEKgJIepwWtPu3JzozzdR6iPIe0/Y3l5nxnpO8TEMnzloNbatPhpklbWVb03jKpZVZl8hgSz4JL6nD0ACD3FHxAmkFo8fyQM3qt9sQrTrBp1Fum7Ef08m+RIOaI5QUizTO27sz6VC9kZjFMEOtvd+YUdKTl3r/cPdFOuM9TyKZ91U6Jhubl+odbJ+8a3Y9wpJ2cpE5xjKrWu2387Pn/dOj5oPE338tGq+chycfuEhLuZ+BkHJYnXUZNDdSYqY92SOEb8AAMGlmOwE/bhoAIACQAC1bwmwgQjQJ07cXcrPgPTUdlkQr3CXMEYrQwDOTwgEBdQnyW7aUl6hlL95+W0qZLtL8AZQHy8knlz2XTgZg1DhChxE4GPxCdAdF+XB2KCKDS7wjghjLRrfnftn8qiNpzsqStE7MuRIKeG8FMapwXfBDgANIOnacVMhAG95UDZjdSgIhRbJ6MpaOEsjQxuPAc4ESqfbPraI1NuejWeiE3YH8lnush2I0P5sAtaumrHnmpGcyUl6dpcJQqD5rQSmgyQKo627O/j5X60+EIFCNCCTV8fJXNRS+Bb5Yuqz9WhbZFV+HPBOo1wXcuCiViBq90G03RCvrS/4/Cg0DinegYHtUhXCCp6gwm6Onqpx3KvjjeTTl6E+RqjtZKWPVCmN58mPK9MyB0hOZt6cUaFPAH0LEgNvOyTs5iCGLJwRAKAYmnBYjTg1+se2wyW0YMTXH/s1FTPDHDcb+ex4CkwOrpE0hSe7XqQ9n6KHujIyDilyezApb7EXoJp3jU8cF61zVjT6sKa0ZPiA2wlhlUaHJ3myiPV0pipIEOx24ZCvzZF8t0hcvXCYeE7TDJmuMJieGppvqhQFwSGrFmhUZpwuTtC2Tka+bZLtYs0b882spXOmhJUxyzLCC0EauDJ2okE+W1mxKq/4GkG/RVCtH7zc8f3lOF0MiM5ALtIqWFyhQqEic3HtbPTK33/59Bv866cv8M//9F/h5dMneP3tF2j3oNldPOcSDt9a3yQcf9LsszU+OG3xcMvF9+nue6Xo1Dx2Sj+k0vDbfJ/VTZPvtiiojvNYSnlEfzweq0ckFSFnx300hiA+If9pTaP7e/TH68u3T/NdrJqyns1kuIFqlDon81j+vzU/WCVLTF0J4gVxzY6rUJB3vyf6owHj9LeFHvv3km51Cj8OAVZOHjPj/25S7w7tFWtXGF/EeyDxu01znpYGIZJEQT7tJl3c8580bfXXTqbMjrTvEv8DwKA/Rj63MzajLRIzmOfplJxbKLp42hMYQTuZQncx8PPEaKdnqF9B35s7LRA4OAEgZ9V3cIUDEPweCC7wG3z8/N/B30+qp64wTgT2xJvuWGEnfHM+CK7RSa1YIFB3+BNdARGhVh0RhqN3X1idRp3/HAgYenwIVoBfMOzcG2Z3RrkAIsKl6OL02v3aAMUsYkc9Uqrv5GCdQ3wRgWzLhcTt5PTimeh7F7HMfWN8SOaTiMwF7CAvKLYv+Jt0nPfT/o6IxCskjtYQhNCLmTW11fAEhGbVOBOG5GFjB4BXkLdGVyGIdvk0+cajdpyFJ0CxAJTm/LdBiNiWNsn6hDaw1AnaYUl5kkttOEBS61WOkGKYcdW5BEb6HQlKjcaBZiaebRHJKJt+sJ7fzArpfYDcVwcadmTh/EHjS1dFb53JDMCOd2Z53Fx22Vt40nbje7PbvGz7Rlw4yBNGdiXHps2xygm5vyRVdMvG0AYRgt/qFBXJmQF4PG2ZWUgTHSiSPAA6LzkQNdaISpfclpBs5HN19MvRynA9ymqdrD9bItXSqNxpxwpHXJUgAHvbZIaJzdP50CFWpk5LgkAwDxxAJ3+rFJj+PuiLKVTSBizl1kZf+/qYOoMkOsJnARH6bo3V5aaSGzlIl8+CoTmTjBr0m3UBmrJxN0myJXTB7HYCJH4X2ViGqIsSR7PgugtLuF1qUhOTI9O4U4RQW2fUn2Wi2HYjO0BWmCA8vXyAD58KUAH49voVrvUKUOF8AGLgQZkBqUcb2m5KtxGfqfvGdGoHRJYeaKNmuMzAj1xPf+fzb5xTtzmld5PqDrPuxCxQepLvbWMTwGqVVmt9ZNrTB/bS4wjSBiMA8nl3FiuRDxM07eN7evltKCNw0xlzPYO41Rs3kB5U3fNMdyvZIITX7VdlTE0Tnfu2MaX8Z8exqUnNJmLbseHQj4AoRWzADNdJLTdkeGyi8GOits/LH+Cb6avWcjndXmf/GRmTmqdhDp1NQ6C8g3ska75nXp8EvXrvbEkxbN4Di3sgPwb2zhAIrRofwrkKvM7OTGV0ZHORyM14QMbV9G8XmHigzrAp1vSFtvfhKQUZ65q023QJhZHA/uxMMGJiCSZ5N2FacgEAvpsVjX6VUpzjp/ZoaAK69Ne9JC8E59X8Xo4btkkAeEGA+i8A2I6IaoK0feeAAEI7oqdQ21EhyyMRgI920vlAxhdGUJ5/AcRrf2sWlqL8knIc/CiETX6T+oKjwUztrHfPCiX4YP03iceEbN4WiCgF4Vou2of9zl8F2LBtgYjSj3UyfhSK9nN7Uy6ktrghgGM/AgDfyRHT3Dax70jeyZHywQ1F7rLf3sukXeR44kRJdb4OsGX30rkdEd0akVUwHYF2GXP71+5viATjk7vl3JIggidIIHVsVD7vk+TMz4ig4AgA7MBEKD1qBRq9csW6oOHo37VNsiohywKE1M5AKwh2Z28l6EGIawtA1Ctcr/qdurKAhgDt6m51ZjZcGx5WcCW9ONUoCRxnAd2WJBe8AIp/1jPntYgniKzc5ESQGZAydqeQAvCZY625cxqZ3QfAwR0gPrONJ7hhaph3U3Qqp/WjU/VyR2j/ZH4SV/nHH2LEQ+zZYwWikUlrUMmYqYGQOf2zS79bl2lD4rFXI/xcaAsE7m+K/YUAaB1WmMJxQUsjGMQBaiuTdnX8knMaTdUiuON4ckBiRxKkOBuRGp+lgT701U2ncahvGL8VzrTeCRCqGYubv/NcAZcF1HUQioZ842wYZ0wGg//WSV02kEad78rumKAYzObjEAQj2O5rnj9t6Ey9/JGyIa/WeqnggAthiyIYpjBNaNjl6Y7llG820QcEpetubSXIh48f4ec/fIIKFX79+jco1yvwTiFdITOv1jYH4wP57vtLuTPAXY7wY9Z7Lj0S1qMqwOVP90RX64xVzVjQW+6MEFpOU6eFbOEJrDnG7yM9mjgfk3bE5SEMgXWufSek0u8+vVFM7aY0OC8g133WMNrnY1mFChdyT1QO6u78bk+U0o9hgISIbu30dxisRJ1caUb3drPq+7Jc7B5gqp9MukroA96EUH4/aYOUdNzFiNb0n7Tb5unIfsjy929iX+7r+Zp+XwNxv7bxoPYezvuT42mOio6O0vuDQlmP7fekLGY1v0lfgDB9tgMFrLOADKzRci4MhozUJoDcsf0C9dtnUxqEMVf32/yrPTih3neAWrUXOD9e4eX5vwNevvo+cNgyrnzfRb8HtoOWOy+NUWnvAZ7pk9O5S1yecemLFEqBy0Xd4vV6hdfrVfSK5pfsAYh+eXZhPyvE4JGBfdExt/dW2N0dAKPdD9h8FTgJRrgmkSlvT15h2YvJQmljo9thZMwlyKXZBgU12wGTeOiX6cSOCMEtTGlV+ipUucRiCoPqaLxGR4m5VISIoF77sUy1X0wM4LVbmQQBJppzv3o0y3p2dPtTlZ0Q8UgJcW7z2WHBk0igF8XUHiSRbUtg6+XvDWj3h61O6uFmADM4Mt9dl/ITN7G4D1jvRinKTqI2icN4IWfqDM8GNzKLH1HhG/TiCpszCU1fuctV+IIUaWdUbuf16K6WEZvZJc9tBIOxQzycVgiYArE7SfNEecEjeewCpemROU4+dUa0beS7/u2tFaYk1sFhyoM++o1f8waSvGynOfPeZSXQc/p6H9uRGUaVqM8vnWTksDpOLFxO6yyJ8oq8+8ldZpTgbghCBLGy+jnmpH3jAkcr5S7SrgEDCIBUgWY7yDJq9aS00MnGFzYYMUU3cZSzcjUjeb+bhyeJQQGTbtA/vd7+7mBa7ayy4Rg+gqWFXF2yysiqcl0XkPDoDr/lI0cPIlsCnx3lAUC7oKxVdqFf4CO+wj99+gSfP38GfCpwpW8gW3UTMGnC8GUg7wlHXNC0SquV/Flz3NPpNBh09DeA23DwH1YZDJ05FJbzcKyMbKZHrJoH6NM0lcu6a9Y+NfbMtO5sh0ee7/j5aADe116flgyUsZnU+yC6zmoUHWOs7xFBqbsgDM1e9+GEQu6qc6CPFbgNeWLTTLa8ReBirUPOG+aKDQar15nTrOmE93LLlhY7wD1vKyUJSI6zLVjEhpvTadamdee+1ey/J2Vm2nkYC11zgH6Omc7wk2EeFk89vmffrIp74MSunCiF05HJXsyGZomnlSuLsUvm6qN2P+ykCQcyH30B2lFbrcpK/vmsPZb7TBESHWzkUiZD+BbfH/HhN0pBRc5qol0UEl0hz5fx+QypzeSOvF3r3DPsKH6b2I3tFW1hmc2oVNwuugox5pnUKjsoRjf5QI1mwSgzEwKAi13ww0GN9gII9KgnAAIq2h4phRWA/gvA9QpDj4pJTsZ+pBbkIADquzL4CPwo93nxZRMb+l6ndYXL018aDmACFwA9kNJ817IW1/qoiPd8VLj20244Q2nnPMpdF/kSW32q/uP2pmC//xbNncV2wa64b3p9MRBh7TvUEWZ/rLOt+T7RDrQocDMQepE6j31rF5mLqj0/WvLfk+n0ZdViJJNeqmKDEI4YIDdO3A3s2O4L8P7vTmb9yKNr1UugoQcMDDCw3cfqOkLbOgMF5TISxURXyshOiNpg13CsFF50kJtC24wwQp4orT28U4OPZYKuALPiK+eQdQLktmtXeQ1kiK1h24nCK3q99ASZXNZXLYRpAzBSlWEeOhqgXi2ehKDAJV/HXaJ3Hr71R6VyZcGpEXiieINB7x0BDRYZtBwPlWYaipDZiWJIj7gZBtzfC22lSmGi9RmHcBCD7pPCd1t7UlGjB8wjrudSHzuHDesARogEi/pIR4jzvhczteAAQAULR2ypy81JReTLEjTeAYDu8manNGAGAN3rKELizplZEiGDhj4oUTgNHpmzOj5zF8kPtXaiT4JR20aANC80kJQvNg0DAandX9OUhkH7MTCPr2I/RGvTGnTyU3jYUduNjOm/58kHJi1atxhaPZSovwkHFj4WCsrCMpEh+TAHWQE3W3rRvhs06mxsS8tHzbHz4foX+JePf4N/+cP/B376+Z/gS/0C9bWGmPZRAx2GD0mn58EjK91JGw1VvcQGI3wlj22dY073TWAIcuN0UppphgVMG2vl1REe3I+7QYjddGg3351259Aj6tnPO2v3PIA2tsMtmOivxRh8aMK0F1UDuCN5M2R8/eb08Q4pEwfm77zcfocsgxAuU9RXIoJGCWNdnJoiLqsXSxl1LXpXifGQdDddPbTB0dI5Ap7PRoDHzJmDdRs3AoXRmHsD0IfJmjYZHm+E41jP72fGHNqu7ot28FmuMKfq4xGeq15z6fXIFG2UZfXHr0I60Y87DGBpN8U8zujTd8jjm9eVniSxmba4H8HGHJq9R/91KqPbN7sQT45p8lCS5vm3TtRKd1p92vgs+txxfozrB0NfmW4AwI7/Jrr1O8vn6C/iPGT6kv8KTvgK5fIVsHwDAF0kTtQW9zq/leif+ptPLbrWV3h9/Tb0kC6aRrG1MWRq+kaRPm3Z9e5i9dNyEf0t3mzMAhEhrzn5Rt6zUm1+S+BELubuvVrt2LRgS3MdkOmbVdJ+O2u5nAhEMIPug1daVXJnQwVwjiwwRklvyDi3lenIaliS+FY7iolq6yF3fItHiR8iQB+UtvqlHcXkgxC8C0B3LZDebWEvl26gzO3oED1SMjEscQPJup9WvrRyciyUDYhIt3mnOuvQ3HVyVLh4xseJyd2iC1gtIZvh60caWQimWtu45Lv2f+7Esv0SU+5wUh6p7jEJnjDI3jm1z5Z4F8iejECIQyi4RjoyZOsyj1hDnHKeJ6M4S9DQJ9PI0EtJdwpcPkNwKELm2/HUHy/+Zvj5rhAJNk0Qs0KIadgpYKGcMj47en3LWB/7oQ7z1z4lGT+C0o9QSzDswQpGzKuHY24dr4CAvGdGz9+JxvKROG2wIaOvfAX3BitfKW5pA1lY+JdpTQR9k4ppk+FB23BuTmv16AwcIXvL1wCaPAPo9AdpA84Yx3urWLljH9FbRukCGoeX5StErjXh3/0tf7BeRgiABeFCF/jw9BF+/vkCHz5+gueXj/DlyzdIQufLNOdzibCB4/5XrWOcfxlfDDtXj9OJKTlNpIBkKlllPcD2weBWagzOz+rpXwzPizSwLmuqDrqbX63zqJTDWjmVIq1n+biPx3c50LP+lVn+x3XNjkpvR/axHHhW160OQ8eDevCa54INGTi9NASVBjreaPIjKVWqjPM14f2/I39dSwf4ImCiZ7HBcq6Xz/fNqo5OSSSSECq1YyMuBGB3x++jmSkDec5H09cqxXl31I/IQvwMlhMZclxujoxaeGFhxj5W22ltr+TPD5vJ7GnV3wMbXjFK5Xc7XD6m5c7Jqe3aa0vezyzcLVxmVd0C7HSls/rUICWje83lFqlZ8AA5SqFDb++GMyVz/fm4xKK9ExPm4NXtydnO6xqGeUPjczR+GJ91tFlGf9QEQXpAOw/TAocTlUda9uM9sw1W+iTvrrA7jtSvgwiy2G7cJZLoDgDNESr5jb7uJhG5BXzuSCjTUnaoN/74BAX+D0B6bbj1xXRyuAaS0Wew+Ypqv6KZCJAqXOgKBN8A8FUUP7z8BaB8AV3jjVLG+sFlEVS4MLzdxTHZnYmgAYpJQltrh1EEGd19Yd93hGR3KN+JwYuCKl+D0OUKYj8QChWGPVbK4RP9QCeZ3bk7Ivo3BDDRExOdIjYaqHdCD1qwNekYc6Mo7MexsPIoGj6RHnNkzvq0jdb8YhlrxAex3VFtndodB8VXfrQ6jDtDNtt05RVdRKpCv7xCnOTxWAoOYiguHIFSdDPHgx4NFY1nJoSJw9jk4b4H2X3Breq4VjBjlSdhVimnjgLdjMcELbSf7p1RT5FpPmrahkHxo4nDyqFM/q1EL4VpjBlz+WPGlifkULehg6DScTCLg1DumKXNNJeLcS4AjIN2Lu0ercGiKFNkXHQ34Jonk5P7ydYUPGEm3tleowk4SD4CvhDe4iEUYPnIRsryuWdx6A9StgpFxfuq4MQSFSWMhZDv/WPUAi7UAy0ylqyALSDRct3D6ZQ7GT0jWU2lFQmzA79NxzGjDUpp0EtROJP8KkzQwJvPdJuxkoyJcxTyZAoXR0I6R8Nrp8MgYCnw8vICnz+/9EDEB8Bvv6i6uTnoQ7bTxBKYu31CIVtsHuWPd6u7PQVl7QxMWcyxmnvpV6moOXGz48O0N2b8J86jt7ob4tEp7y4a3j2mOaepKikPUxizkcfwdj84ciuunUoMumq2rogac9pKKNLLf1Pzyvl2Z7pnis90g939Xmmw9C5asnC4jsckCy9qLxhzTaKE3n8QMVtRevKO1R/Wv5GaPO+726koLrwgbLtvj1SxPShbsA7rmah9x/UeZxwXCLVfc+o5sA3I5LJ6SAe11f+7nfsW/ODWsZroGwCQ9oOlae6rM3rBmh/S8C3KilnOG9XcIzTuA7pN7/qByZesf53v6cY0XxAxg/nQXn7f9FChMmn/FLb3wVgrOvM25GDiZBzf5uVo+fZUuhHMlr+CVj8jj4fmU4FNShRG5flJK89OPNjn80B6oUWGvK0Y9Y7hi5lo1pfH2MhR7vVDn9rteCbri8b+XDkweid6rf2YqFco1I6WIiK4XAAuT/4mBD6in4gAzYL25s2tMWaSdMNokCCCv0NVCvMcQJtdy9nnzs+FULAFIJ6fnntAoh27zNcL1FrFZ1nQnuIDgH1VfCnqD/fH1LdyZ1na+TsiANwqWbsaM1NNOZMRtf1RvwDaKq/sxO0w5cinDrIAAmFfPc0rcMTJAsC7Hwpemg+ez1UCNeArEZB64o3j2GKIcq8E9h0NLdKHBo4qvnxPhEBAnpAmEAFMHCj9QR0XF4Co/Mx2IA96wl3MhCIEqQt8DEIEreyioPw6kamjwzqtMDyM9Qhy/r2ID/RPMcB2ho4NyoRAj+GhCzxs5cezw9YdV6xqDh5bNq2N8kZJ3TryICVuCEassFYlNheUHMkUn/Wk7uy5Eyams3N925jfmVaQaNpYvHo8jNIYsTN1aeXDOffU+tn6X4Uvz4xRS7YE/l4KrhEhLxvTKgt2p0xy2fbcSO90d1RnqmjzJ3OpzCmJE5rPIL192rMvN/EJsOzF1kR9g5/5bcckdShlWhuZvAnuQ3sCXfI3FvY7HeCHKtBK/4hBuAFG0j5d9a53hFwuT/D09ASfP32Gn39+gtf6Df7813+D1y9/gfL6BahW8OfHH4zN1rKJ1kkusJJkeQxVvgVtP8hoAchp7oHp/Wb226RjkTpfxLGkr3dIU9kX3s/evT/qttZ4k9aYVMKje4jD3NX58sCZc5i+J+0/YvXtuyQZEDMy5OWHveYLiw1W6eRcByFWKaf0vP9qt3Q6LfVjCzLdLRNXD1XPv3PqErT/+o5M7j9L+iHohpJvU7W1fcqChbfE631StHea2dYFjrPyZz31yBTs0r/zNJAPmuUHswWk05TYNObNjJaXYOyjs7TOjqfDs3VvS29BHUe6mX1Ng3xE994lBO+TO65lsoYylpwMShfgzVanaTax38VPzNCbz7NIIMJjW4n9Q2ietQXxl3qBetHTWLD8PwHhTwE/gorV1Gu8VKXrI25nRMejfAG8/EfLGX1jiFCxDovxrT/X3eOb9UfPU2vt/dd2Q1xfXqCUAk+XC9RKcL1e4VorXF+v4i9ti+mL+jvtkVJmkb/eedH9asd3a7t0YkeEITiyhsec9DhaT5A5t4wHhjS/ehX6fQ2kOxXQOOEQsDuTSDoNsO9CKL3D+jZcPfecwO5ksPUJXfY6JArEW1GY+BkMEciKm8oP1eXMTmrZypJ7yyWYUSUAQf0UqozNsnZsPs0rdq02x27xjlkmWjCfmQYe8BvqD4wqZonz2x8BgkM/aPAMhZDd0gJiPBP3fuieqUzB5NO0nRwsxsY6uY/FA9PEEPl0yD5CwxthHF1Qrdup9pw1s3ry3SAwJR8fWGrtz21QtOD3sWL20+eCPzIgv/jYBSGmGjnoLgrRYxdzBDVPmi8KdzMYQzCC8u5EgBa8kt+zzmrKNgdCPa4G8sg+RDGbwR44kt25ctJqP3b8zXhfhlf+fLrONsrtDafDGPpymyPBjhoB33ukNDbt0XhBu8mvbGoxJy1u5GEoUP8lG1+7sk5wKLaNCJdS4PnpCT58/AQfPz3Bt/oK3779DS6vfwO4fjV52eG7o5rupD6/z4Iah2YE+6YpCpxMpkeEsveUft0SJxZk4GWWm1jFPsNiTYGPSG8+GMcYPBCF86B0pmN4vgOLAA5Pepvyh0OsNEXcBgY3E5NB1iiTocecUBewsmne3Nv50xGtDDw2mVDkXo4Ap+3A/P1R+btSpjvTKBd5h7td0SdtHfSRG3E5lNXmW9cNEdg+wpCRYqEF1LfjfmfTqVXz4fe5VlBo+gP64EguQ3wflcUjHL6/LLklpba0SUOrjd3RfiZ6Xficcbx4ROR3DUa8+fAlFRxMKLfDZx+qfzkt7LX8WXrUDrmtNENmalusYal9aY2ts/M4L0fDFxh5zH1McCyMfCzzDYz4QWJwr8qT0CnuWV04SbLXtiTzJ6d34pCn7WIEryQmuqX3acx9RnGxrQZYm3e8pmNGUMLabERs9yMUduQ3G675bJ/DnQodhvMr276q5sJt6MdDMd/+C1wuvwDfYRGwAASAK121sXz0FFg/trazBRw0VboCEcD1+iowL5dLw7cUoKcnqLW2QMT1Ct++XRueRN2Prr5kvmOL75fgd6VwgEL95mfS6cuqWfm0RNac6JwBjUXUO6uyzqfEi1AAsAKJywWAoGWs7OSnGobZE2O5aC0ahSntUgUEZ5nJToO+daYxRzIo9SNcpCOLBjS6Q6nRV7+Q+vraL6a+AvGWHyDZidB2VFyAL8xup20xIbcgS62v7YLregWiq+CYST0d1wJE145PI3DT88AOb/Z769FR3UHuxiodXpBDQ1DZgXXckjzNChvzqhNkkShaA6q7R3hQg4Osv2+Xfrc+t8+3EzOwHtXzc0OFv2WU0annuWiLxqIsn0an2ZF+1R5S8vYsnEhHLij5PsKpUUcbWJLxESMPRDBahp8z/zhfbTt1BTQ77DMYWWpdEdSlQCotD88/LyjtvqFWtkqf5rUb3ND2G4+l9IJCIOY1ig+keBi+4msMz8gMLLlP76omLdkj00HOjvMyRsf9y8UvkDml88wHSQign1xFrgwSTRd7KNWjH1ND//KF8kBQRyVAnNQV4TognKnNyUy5YD6l04ZkruiwEfj7GuY4yUqLgSp6uX4UWMS5h5vGEgaI7iLyKw0QCIadmSly2iVEKGc/6iVXaLLa+0oib2lQ7NZL7ufP5Qv868dX+Jd/+hk+fvoJrl//ClBfzTzTnX6h8APSSYVaBvhR9d+ScoX3fJk7s5p5FEQNuDdm9dAMtNAY6PweROUmWu+Tgjz/YdPJXlu2Z3f+HfO8JeRpxDNBrhOOlYisLwyRCCuSWkUzcA9IEcqoB+ibVadj+jWHvIPHifJBjzhR6X4i+xW7TZGMAgIAlM5+M4wiQhnN5H3BerPmsUZ4BX7ddtJfodZvQPAKAC/QTN3+D4uUF8jBEevRvLUTg57o9I5JiQkZWJ30lpT1+rAT9y5i6Y3rjsYtP8REzzwudHt6xE6Xx/GeVR2zebKQzRsC+F6yliELHbng/O+e5rqLHgVuk8ihDezvb182jnNbydft7crb02hYpfbJARR7GsTZqn0tgRfLNzRtDjg5Xsq8J0Wyf3b+eYDumdZsBSEmJsCbzhMHfEcGz97N5sSB72EGmUb5NtyD51TSpB7vroCsfc6uJsOqetkyI5Si9XA17LUFRLiUBrDhXIw/IE4kDVo4RMDrKfKlPEHBD80vzEAcbVVod5z0f6XrOV1vrt3B3uq8Ar78b4DyTXGh5qOu12fxA7erAjTIgKVIEAVL80VXuZ8ZxCdxvXq9n4+6Z3+DvHuzQES0FTJbwzF5EsIhoOYAh0Z4pVyAsEKFAsV0KPVS7NivfcZ64wcAjFPZKQXI7/u/AuYS7Qp01WOQLGMjLtsBIEI7HgPBrWqFjhXUHozgz46vZJNBKQDlAryVhZV3voC7EUULQkC1RzRxW/nSENsBdmLp6nt1Yo0GYutT0O09RON4cj/whEH/zvY3f/M7I8bV4OzElkiZgTCyOK1AnpvvI73NpY5zKvdV2yjjq62lAHesI2A4YXzKOJSO+RMdpUXIllkdGdumt01UGM32M319rELIOPS5Qp0+MWZL0kzw+Klij/7xxDST39HBbXuH+8L2lnzno52GVT2+AdnxOjRTYCSLVbZnHWLyTIIHoRd65TjkU9oPnXQ0pBL8SDJTnJtshqLzAbFC7tRLdB+gTHbEU8YkGeAz53qPfRFzdGpwuK+VYj+XdP6pQxXDmxEAB9Bs1QPMoZk7c9HiqDspWmARQn8mjJs/GD3hU71lYRWJrXrvHhgEKAgfn67wf/2xwB8+v8Dzywco335teZweZgeFefp8XKb1msFPMdwhJ5I/oQxCeDP8GsqfXSLIq3zuNhofm2QeDCoADX8BIEWfacJRZRJ8mp1fnd33dUvKimaOpvcJQgyM8tGQD9ox2Y2X6RUzfgonyBztRYVZnetOH/Tvjbwx31xzOp9GSZzlsTSf6w0zeh6cFm9AJ2k/zuq5cU4oS5yNnAl8zxAaz+MC1hfPI2N+iixsgYhmQV772wsgXNqiqOHcAN0rrnAzHLO0MZAIILteD7LnM9hbAbcFDEab0H4eZD9RB4FsgwHwDYowo1K2BX/Oo/wUC8CNLrIdJFnUsUZ90qebw5aPCc0bfmM9syKpDWGSLqlM0g5Df3Cyu5Q3Cwwptnlvju3VNzpfDxA71MnZ1ssk46GhOHzM0FnRuC6yS/jR9vgTOHmRAmBb1TzZUh4yZqOP7ybRFYA3BT76MFZp0gs34DHRaw5rnNeaBnKW5Bvz49TGkBwIQJQsBRxN4eF3c/aj+BABQI8fljI6kch+Kfy8z9WgWug7AoJnIPrYZFMPYNg9DSh3W5i5j9B3WAAUCV9UQLjC5ek3QPxNdJpa20XdFa9y1FRrI0LzQfmTD+QkkKq7LtrCettT5AJLbeGiOQHoZLrpaCaLTjXLNVn/MD4E4CCEP5O7imOaAIY7NFlxY6WVO6ldoMFnferaZCeG0Ogclcy/qltWeg/KHWYAQJ1UC2LjjcUwegKJJNGVgwjW8FOnDzt3UHZUMD49GNI/a61Qry1SRZV3ajD5KVyOG3D/2kAFYAG+QJbbbZVsd/cEE70ZRsviyc0Qm2e+Iv5whZisqPeDy+3gGnlCE9l32eraGZ9SBZUgKu7Q8ZgWHlqlX5O9HzzM6OtJscL45aheL1ntqmVux6I2APD3mKxxs0edoPuwTzXCmaDrv4SSJqvb4THDZ6xDq+i04peQL5OuKJ/g/4jk+m9UhhWDTeXQptNLt45oIxhxR7ojZl9ndVBKDj4w5BWGHQe4fpkYZicHdVBvex9rgMHw+yUgUhk1QUGC2gZslsv9irr4UM72J+NJjk4KBzFE7hhFwzLBKVLJc2xHFT4/v8Dnzz9BxSv89bf/gNcvf4bL669A9CpKj4AgOEm/85RCuQW0KE6jofPQ9MMuv29E9RbYidwJc0d36PHvDCeFYcvl+f+R8jQaaY+G6F/SirEtYaLV9Zh/3RGQ+kf6UdKhANNXd9fTbMMZLF50ZY8u8KrsuvxD05112B2MtwchfseM1I5bYqMAvF/rWC2fc6v7Mdm14d4iSX+SHqudmX534XdedX9Yyna576TT5th2yu/q/L2kXX40z2WJgZY5pQTbkr9jlnZ7+t6NPqp/9IOcB79isCPzOApGKE4Gt2ACjt63PEk96oRtZawrAPuuC9mOYVwLBOCjEqhUTyB3SRRBhEB3mGo7JH9/TtAv76YrYPk/AZEXYAAAdt81Nv8z++w5aMCn9SASXC5XuGD3T1cAgOajxst/QLn80vwlxLswun4VuxksrnvpRCCiHydCGAYsOIr7S+tEtE4K6g4fNJ14xFQk5IClO3aKc8yONEjyl4jaDgbj6EfzV2uwio5xoDPNEMhOhup2FKB+sgNInO/86RunCnLfFVH1+I1cwHfzLbxyzungGBcUWREn0js1Ui+kN/y1HbGvNN9UoDv/nB+jrHmWkUhAhLgvotNoVAqObVg7FhtKVHgfWV9WnbCIAfQZhjziFds2HhfADPSYjcb2W9gZlrOF1NE5bGlmCdDk9Sv4F2m6ZcU7rdy2MMnB9HJQS9qAJFumxJL7CA0Sb/AE9NiHWZqugrMy/6CJw2tDLpZXT/PLi+hVJEcOq7mldHfUz/5LunAi9ZerUnA2RYc+UFJJgkhGE259gdVOkuTnTJzbs1XOYBQTEw5HZrwIlijQ/1GazDEacCgAgFjhqRR4fnmBr/UbfPv6Ber1N4DrF8EnQXFRzzwds2dDpycdmKPcoOG5TadJ6Tt6zoeao74g7T3Rqp59Jut3HEGrLomLLHbL7bw/kocreOf94lF/uokJ2Y8HpLO6h71c+FSxsUo+38/CIwBdddSCEQrnuNU3mrbvmmYybtilfIJP3FM2TQ8jsFznXMeV7qi8C3flOQd6BKmtNRwZ8CBimsnnlbNzKmsWONl6bhv+HU79xulWhQCOVVxWb+b2156OL2kwttWATUEsuzW+PCdLp7JkqhqeH+Nsdb0NRjj4S4G+WeF3JUNr5+wT463BiHkZct8Ek6NKtgjw5CQ7mpsrcHMTZfmAJi+iOmHfivZAh9x/+fZN0s1V3kJUj4Z8RD+Ufo2PUrv8xkUmcwxGYj3yLfgjvoIfifQjrc8qNJ0J2GBxtP5lLlv/Wb/XwflTzcLH9q0C2aPRBYEq+Wxbot+mBQUKQH0OjWHZ13wcdj+orQe7vwGpwgUJSuk+aqzw9FQBn67AfuTqTvBpcAlAdlucZZT7RzPJxRxezInj2D7j591pT0T9tvDeYCJoBzMBIBQZuDZGKPZLQWgrp7hc/8NHuEQhye66dmRWiwLV1yvUem27IUgJFS8C0VASAphbwW3j6VoBoAc0bB+w78cc5VTQHM3UO4QHrMoOiCvUa/+s14Vwp/Bp2itBjky5JiEa2ZHCd27YMSPyz3r/znZCtABHG6C4IFjZw3Agj/YVAviNH82VR0CyQ4UNCNtmz18Yt5EhDS7bs0ww40amezG2mPT4lO0gxKlJas+Ln7dFKGEj2JIelzHk6VDvNNjcaJAZYFfZpG2GwSpeewgdKZheMJn60B4pNS+7HgsvaGb+7Bicu0d1yl0Cc9z4mIAYGLonPWwVFw1fDtPQx/L8tvlfiVWK+RSg8C4GjLIgxHwjQkb/0GVhQm9mwB0ORn6NwTnWuKgJ16DIzfrq6fXP8Cf4Ff715/8KHz9+BPrbL/D67S9Q6ms7+ZARfUDaD0Iwb/DvZ067/IigHYyO6CfOvEN3CTyqrwTSaXAn8Y2EPgV7u7B4q/jNe8aFvoPpm9R8j8DeHeiNmjIPAqj+qDu2vl+vfc/0PVc9PzYFGwTOq9xna8vr74ltCrZ3XHSR9Z83RHCSbtvJkMB5ABgerfM4vX+/ac3fr26/YgvfRajcc2ThI1PUC/8+eNb3TI/TlR+W3gOdYNOpFr+2sUDeKpKP0na+Jz/78dM5XVBKiW9jPUrDKRk30GBm2438ypVIqum2NRk8ExZP4QLo0eN9exKRgihHe1t05PgyQY+6L7vX3pRq44teVEZ9N0OWSvdTP5m51k/xwfLfoOC/AO+AoFKB/doAoIvcjc/iTLr5aKbDerhzerQkLWBp3fIa7C4d8i5m+TS6pG4fDJ1QAfgehlrbroPm7C5eqbHOdjaOBoc+AN9oThAdzjz6fBltA4JlPIeU+0ICEowbr9qZTPyp7EcAjQZ4ZVxW0xJ/jkEIMv/4r64i77+cszSs0M2WPp1SoAwzInXijTshYhWWaAJE67QOKJ1dcengkP0BhnbJDq3BMdR9h1P1OP9o1B4FJLIysYlpMg6FCTbhVx9XprtB7uQOWM0ex4wFzSgoU2eteSc/GXjWUKbpiRwVp3Bo/9GKYQs+/Z6WXsCPhXHMK32XoOac5sNgZg7TCW/qf8a5daNwjgproIEhEBhwE3a+Wb/bRRaV5GRCHLulw8SPDpqNyT0cxUDUzqp0WAy3eaj8gnF3kONXIQAxx6OlZ/oKf3j6FX5+KfD09ASFKmD9BnKU4BlCviPlR7yN7cl43627KEYuI1DC94SXOvG4zr+Fy519GwOg/WmSM5Or5q1B/w2H29bONb9LbQBjXx32/YrR79Q3AZPmTVdibeC0hGkDAzgQfhrQM/rf+uiYUY7IAia0Tx+TbtFA74GRwp3oY9mzI1l5uJPwLG1m7yYw4njyIrA29KxDss0QedyNaYwuhwxeprbsMx5sdSBM7LtDZNz33Vl9T+DhbXy9sW9mDDwVEjekG2TcTA2d/V4UzfE5UXJKc6RNu3mc1gUPpuQC6kaJSR+vHMLppfQrmO+UHhHc03bfSu8rG+lIFt6X1k78O+2vg+5Y9f2MpYhNN/zyR4DlkCf8fZKO7bSI2mZ/PSBAeH5e3wng5sLreU/JN3niFiUd1HnCVg/L4FP81qcyBJho7e1OixTLzFo6kaE3kwjb9RsSwvok+kkI29VWuYLbpOhv70+pLcAH+AQEnwCIdyL13RO9QOnlAUlxOUFq+zsijGNIrOxZ07tXtlJ1N3qXEvLHIyIQ+rGdfSiwACABVmvsqIPHbs5ivGqtQNer7Dy4XttdDNw7BRCw6K6FWV+JM1zOGu23jQO2aB8iUC1QShVFWFai9r0eANoP7XiotjPjWl/7Tgi+sDrXamRrpNUNM6IPc5OAo1UgQQ6SNtkOC89kFa0KZp6g4kyWnS2JYcVPNyzkZkDYwAYBkL/QOi+Hjl5suwFAzn23qRlNI70yDj5FA7J98tnrFqacY115DGsoe1a9mSgyWcBnBWWx2m62Ytgc8BLqT1XTpb6SOkHt5ywJXyfvgE7bf9Af7OBgYz+0RY7piyzpAMXthOP9ADP5mD4+68g6sBW0rpkBukrSmQO0VvcI7K1XdE2nhBl3z+9sWVXg7b0jaGku1NVggvmycfNH4DuyQ05QWinznd92Po4cjDBD0cRwE5oIvCOvmDxM+yCrJrDM8bZ9SsQKBcLT0xP89NPP8PzxI5TLExCQ7Ax09biVFreZdu+04PBUSiTHYf6H4/AD9clJcXQW+sPg/Eh9tps22fjpvEs4g5jtkI081rzk+ArOiGHa96o5WL76qLa8Vzq7o+H4HOPfd7q3bfNFETFf0F/D99pBXCvBtbbzkFnaDwuYgl46czf8/tPaxjl+/og6bwSxYY7IML7ZsGH4/ndEHzT+TO3rg3J/T+lRu5csxMeCizL3JPxbTMB3SIc6QIbw369IHdN3GbC8UpXDR7Jkam32j3ONSsNRokdG31bPT3OurYsN7cI+9QvHnRBHrT5+mdQdCpL9yXP9DjrXkeCjq71+L2/LWKjp5uIU6CcJgeEhxn9IcDONnghE9I4Tp3arXo/wMXnAd6a9eFCcJPyfdPKMVA5cAMR/9KwqINILoGvtQRAt3Zw22I6nqHnPeQc5SXsVCwIsAFR5AvRz6kNoyt7PwHdMNPwAIAlCxMXYetkjJhGr0GfdkaZOcj52iXw9Cx6AMhamLika1X5fv7ieKBZezCLHr2ZUzI48tD89XONZnoaXZqjQ8CWtP418APOLWHbmvD1KW6zO9Tr/cufWbRjKWyvyhj6zcwH98JkvRw7FvFcsbzFPqdcU+vLI+B3v06D0+QyTaT4CoC640oYmQYh5PfzlJAc3U8+RL04U6cTgUFhZtOQAn4HRv30axlNIIp/YO86RYUZv2ZkoIuueIwOO7v5wDkAgwHAWXhM75rIsMwnnZ2VyDobh+YQNRPBdTOXyBM8vBZ4uT4ClyBy1i03nXXbecJ/xjrgC9/uktw1CPMKZsrMa+9HpdrzHgocLoqdlJzRvZOLZtN0uo7jfm2YGyqJaSPnfTl23vEmc6n6n7AhiHFOVHwSwXBQU03vM/kGvCb9PDJEUfFQwYvuus5hW2ffUznHG3aTfLvTzM88n79jmsbaxLAoSAQcyJs7a21R/pK5JvjQ2t6lSnU87BVcK4G6xUQefZo6mIsCcxjZwmenja71jJx0R/jvIzoOaj7pn4L2PQrlNnFPZH1UtwHtreeTq3snrf8/8DpR8Owc9pmbyeLjLvkrcFnO7c27zrl4vyxy9R/8opfsJc5yeBHEKtTOUe2xb3wLrEMT9GbbSvgwKuE/p4yxDWuUnqSIdv7Cq9Izl2czKVndcrKkYzYQ9SCekdusmDm+dZIjYvg6IOV0Ou48aC2Bf2O5WwstX9hXTLaa+pFOBCAC+KkK9EO18f+z3OUBfga+fNrUdA6UphQVBffaqHG6Lg+6Fao53AuCdELVCvb72z6uJeBUoWKBcLlBKASzNyUJIWl3HG0lZIV115Sdw0KU7oIjaLg9eDc87NsTGIgLieyXqFeq13wdxrUD1tUXbqBrnbQfOveD0Pk85w5gTAN+L0YJF/XZ0MmqKKVA5YNPBYilQzPhEQQfQLtRenrktjOLc1BNGhspoNKHUh/ITp/kKEhAUDbzECUeaXw/1OqMi6J0Q/ESMGZ6jUz4aqduLXH9h9+6sngjihCNaQzgGLXga+E1LGAH0uB31O196eTlv3t8tgqj0BfZzt02WBmnRr7sghc30HwSqPEZn/GZljYfkntMdMLfz7knJhRwnRkp7AMBcjmRn/FLvDMb72bS8fNMJODtTZk5GhqljmmX1Zxku0olGnb3obtuyhN675HuZoELb00cqMwrjobvZAHSuzxQjd9ATZkHung8LvLy8wD/900f49OkzPD9/GNuNvG8uajj28xy1HAcj3i/ZAM9O3ndG7+8iPabPvLxon/bZ72BV+tAPt3fMUXuNKtRk4dr+04Qg85wQACuMU+PAoxtl45mxWYi4HzexePo90OBRunuuZp6xoz6Jeq2x0SDISWo78InYBoo6ByksOqf9/12kh/HaDTp+y06jI/D3zrOFIv0jEoNluXc0XWbYgU/6LdJJLfGNsMgSGxrmd3TA5I6GN8HkVMuD7f19SNf7PkY+vir6VhhHu/N79sw9Gb5nssgF4wdxzEPDlxxmX2C33Gw7qA4+WG352O7QxpMzklobzPgUIz/wJbfnK5p7ItjXeQObm2jd26V8f7GPaNSVtB9OODeSdDIQQfJP2Qg7TNilR6MRwk5kiMf+wM6YL7DRXRDt3oV+HFQlvRcCtS4s3VnTgxC5fySuQ/XGrF2Vz7yLV6a6xrAj3Ox80H/+vomVXWLfp7vxCKS/3SLlxBD3qJEbJh2f4DyysAfHMAFlBgQuVpOv0okZ28Yv51K8et6u2G2wz4rwxDXnggmHmvDAASl/7GuRalDKjFh7B0vLzflDncH4tcEIX15yzKrKf0NwtK7SMGaUfJv002Ky5KulghFq5SFSmL+dZg6aEeuZCTnR/Wh8Dgd1OPwXdS8KLiog4Q+8wF7k3RE5G4YhMA4k/NTpspJbgS/be2uIVv3i+eC0/ownDr+0ziX+j1oCbeD4FW4scxPcwOxIisdOgG3mKIfTlLQFEeFSLvDy/AIIAPX6NUjIAG0aczivqLTxHgHuO/LuKWtA+C9HGZtc9E/SEocxsc2uGptk232mr75PGnhkYPM7OtJBDf0Tp47g6Y7Gk+ltbNkZ0GMc8/Ymc3HmdMqq7nICkYXIWnDM+kRlL5x2BNCJeXyHibGGezYo2tv5QwUjDtBf3/1hdMepXmf5oi0H5r2FfaZfMsW024PAR9Ia/LJghOAyI1KP1rZD4034wFDLfr4NHR4ADGuYyI+j1Varhp/g07fDOCh/dzpCYF/POTQdpy8Sm+n0+B5UjnaGvE+aNeE+F9e5hAfz3OGC4/Nl4YM0lFqoJJFjrmoU/wcs6OUAJ5w+yHHK3qhNvx7pbTYRc+KxPWrzHsNP8kdT7KaUzN+T5bZLxC5iY9/CPCS87drGylM5QS6LItfe2fsaIqGPQ9910Ph+wMfb82syoZDHHti0o00e2xKDbb6d5v6zmIuSHOck46S9SZVHPOgond4R0T1BzcEenY+yusQwFuTjm9q/gghQEBCLIVId5ri6vL0VS6XRNjNVDkBcr0BU4fradhnU1yu03QEVEJ+glAvgpbSdEMjHQVmFynBpVkr7Z8Oj7RYAhL76W/MUuLZV4t1LJqpvhY5DC4pUuSPiFa7XvhuiVq0Ld+5HcFULwg3V6vqEd4nExCuCMwbFuw4QEKgHGUShZ6V+Q1c0KPskdE2pwCCAU7GCyON4Ve+GbQwjA/b9MrXdQ/lGs76fmf9SaMua+Xh3KopQXXeG3Xl0hsk4AxP1121KPFPN6Awd82XPJoLpQSkNJHb5xf6PLBgxPZ4Jx5+elCKcG3DeLDXNFWmv49Xitq1UPEZuXYu2xMJYpeEotTMd0Scy76o58tvInNsCiyOhCe+2tDKWtZ9HSXcGQYpc46cizIKnRh/bz3gmu23KvI9QdjrZq6aOAluICKUUeHp+hg+fPsPXL/8G//2v/1/49vWrbwfpMgQAlF0aRGM3v3/KHWGrfPHRLlc0lHOcNwmw+PcbFU6SBnDSt7cDPqxzP38WfMh+q+GQHwE6h5+p4V3PJN4tdL+q/vbp/SbQ2V6QxShs5CUQt2nidDPZZuiy7IRj/7uzpN91yrnh7cGV/dGwx8vK3O16GxG0hWe1y9VaZTEaAEDp9wJqIfBwMnS+v/B6TIrNONWsW22Cs+m2vg4utf9UaWlO/iOdTzawMJC8312sztLvmIzbaulXj2YepV9H2PdM+92uGRC7o9IzxTP8Vjg/eKi/F+UMtvRgh5zD7DC3rZB8Ce8PM89BgxHer8IOm1h77mnx4tveATHaK7N1FFpV9G1717H3yfp8TQ/290MOBn54I13FPsAbpoXx2Jgniru8Y5+w9XCgxS/4yCH29P3pfCACbAP61mxQYwTi4PYBYEc3gOkO1z8TAjXEK6Rkjk7qGmg/5qjfw9DLsf8HCkDB0oIIpfT6uHON1zoSORlcOZBi+qH2S6vBGrQcqAEA2f0ABAAVODDhnV5aceYcmi3o5W6hTqxkO86jkSjb/reNkub0HoIQByleKh5AbSY7aTIn0fHM3DGM1g7VcQLbp7b8CIafZxzuuBPYiadHzihDF5YYmGPLiY7h7iQl+0V/Held7HM+4Sw6ncJ4svErc8Y6vPOhUye89OWk1Tve71UywQj53SpeF9sZt12vX5Ll7LE22j83DiYm3w+mgJCaCUbwG16Fe/vBUAxq3YcxhhJf6H04ZJ6dTNpI4Jmrzy3/NkUSstQjmQ4wQF/HYKD4zIBU4QLf4PnyDJenJ7h+ucK3r7+G+HYbTNJiiwDHrWNmCWf13tezCsykT28QVbe06NF8MWMtedsf51C6hT3OZWT2HId6omFxjFPW0Q12HoRQmbKQDO+YjghlIuRcCgzY0oj0cd6XZxMNX9bplvkGYM0FkgdZGx6x62Cnh12GrBEJv579ftixcw8mXdEpnSzKcV3xhmwXiQbb99ruslG3Tpzd1o+RNXKJj73FTDo5fWSCw6N12a10stJsddk2SDp4zzA1Ow2PlZ/vkd+sspndldjHWe5UXhylIx1D3+2178hgOp8ewht2QWRDcJYcJ88nPr/TcN47jbbtpCV7y67zdEx+N8G8qahRgbbloM18WoPuc2amtuWoLfN9j7SFwsg89wFQ+nU/TUXcjZ23ja9mdDI/sF6RJdkAk8/sgxaspaDXD02yC3DvVQ9HEyK3KRSX0FAJAGTAp7WexDKWNX7VCTTnf4lVrsTaHfLppkBEr7X/i5EemxAu9tB52Y3AEPpqVyaloGHyahb+W4gDHt0TUvuOg9drO5LpepVVM4gAeLlAKRcoT09QSrsjAg28jhIAFWjBCOPY7ZEg3rlRSj9WSmi8BT56JKAFHKoNiAAQ1HZJdb22nRrXhmOlq+6GcP0Zeg/ZyYS5TkkcIOhhjWq2JG8SBRa9NFzvqDBj0NuyYpzqtFNvdBvm4hxklvn0XhNwHlszWWZOvom1s2y1YU41cBF7ZuF0N1lqOM+NsUaHVoSTedefOj+BVWB4bBu9ExQoaAqa4NNqTWKO242r1xChmNr4o4yDY76Rb/AERwLtswCCq74puZVzsHKSJpUwjU21np5NPhVpbN6RvJpYVgTSnHrvuRR5mYiAUO+1eWjaQHnGp5ww5C8IIIEJYpWjUz7ziUNfPOrcidsJyM7VBH1UXhkacZpAlfPFmiaW/mbyTq0uQ9oLiI5IzjMU6OlD/Sv8n09/gf/683+Dl+cX+O0L73LQHXIRRQzgzK/zjfnB030t+v33xw7Z+1VP2fOhhPm0eoM3HGblZwGGvI4c1x8rGPHA9BZNGYws9+JNUXGkNdGP+RLsdxvFhQN+q3jiqH8UDo9L+U4Xu8hDxeq69/eDEF53Vt2bhAZZl2r331Vo0Yja7ahLP5p3ic6y9u/KsTcXsjyosuQZylRvKrEfV7YK9kl3MyMPcQm69ZunSR3GefR3JBnmiRv6+1dXHpqyFdQ3dxHthcEene5ezHWqrv7pGXhLGHO5h0OnjBri+6e7eu5gN/Rxmjmobk/vQwk9YBBlPgcjrHur//H+Me8nUVLq/t6+MH4uhLSS1WK5U31hfXlwsh8niyFVr308pcdgviwwMQssUZ63aq2vAuW4mcdyj+1AhK92dD9kg6BHc3hnkcJgQzOxaJOGtmyd47NCwF5y8m4RvQ+iBRPcUVDDyhFGpxMGa51I0G4N9wEU21LqOJBcjlYVf3bWmIABF0qHkaBdnn3gXHPr4KWO/ib0DQcYuI/lWF/DEFzTEqQcpm5I/Z0f9oOPfXHHs4jR6rrQFtXfptFTlkFhSDMhF8pT+GaLINi+zii600M6CfmJx1ZxnBlvC9uC6UFWhVvF31SZVy3pVNBhwk11l0XP4PpJacC20a6gk8B35jAwfyMMQT1pQ7obYpYYD4yMeJ69i81UaGXttQV3RMdNjByV1w7lgzabw2+lMZn0jxQsswDioJDmpQHYsOXfHV3qf1DmRSi2ixvzSPN9ZeASv7f06Ii989cjgoKgXzjcZ4VNTzj9XLBKc6d8Hf3XON2VHyEUqPD5ucKn5wIXIJEZbqUp7NDNecrac2is+mszze0dj88+xEkFo/4UecS988/CG0gr/bELzT7zQFbjFIMQ9/pX98r7TPfWea6+R5nFb470zWnNIZOnYQDe7G6ErHpUHfhIHt+K55n27OoDt99jEx6jsa/OpoyRpGmw+pYLXeJisxzWUeXZcxomu5VSsiBKFUp4fUV4fS1Q02PsvuccDHVHPYPTQ+ZSPgYjV9MZZB1ANs9ojqzHc9bDmOUw2zfXLhC8c+hu7NOhicdIrFRF93vprDqs5v70o4ijY4LRrNEHMOOR+4zuMB3dp7MHY15+Zp9kC4JW+bnMWLPPYT+mHZiims/zNAgxhbFZ1ZAeN56+7qS/jqrYZSUH/psM4Fj1eb41tOkHEXksgfh4X5c4GGGFDbLdSuB3TGR63xHX3aCf4VVi21kxPS+4l4j/ZAb9qlyma62cArf4CWnSdee44OkdEUfsi5/a1fyzzHy2PmIxq/gJgGq7d4FrQ8NSzfNa2z0QtQcBoEI7n7q0+yAulwJYngDLZe4k4nEhXvFh7m0A0IAGK/VcN1Hb5dB3QVzrawtGXK9StlI/jqkSEBg8iVKaJKQWcZK+QigldJwNwFAFXvzT6qlA/G4ckdYu9p/1/ihycXey0perC7PKHr2EXbn3uyLaj8LbocOmGVF1J5SKuBKhCX79C9nPaX4y38106eX8rpDoZpsZV+Z7qD1lpgdJg0pk9f8B96y+VYqXVAdE/fcErGx8Ex+srEefNuR4oZtXo0bBE8SIDWxtpHGXAmgwgnn7AaxZMMJk6LTXO64bTakQJNsm0vl8txbga5qppozVGNyEpPM3ap1r+He65XIiZH8Cb8Pkio4CUlNHE3veifoFqIlWKIGKJqtk9CYrGsa6AQZqOCzm28/tnneq3Tmn1JqHKfw7rsliWArA8+UJfv75Z/j54wU+Xv8Dfr1+aTKbeE7kahvtzPszaaUb7hDZDJf7CPR0ovAZv9+VxEmT14shz17TOWdUru3uhCNIo2L+Xul71Pl3kc722z5B/adL//m6pTsAOABEx/qVljvIYQ1c/oN9d3XXwSoBFIJmG4HlAWrfMDp//fMz/PUvF3j9VkF22f+nTmKZed4pcqPrji6n2sVWYzH7phc17aDkc66Pk4yQlwrTyRTtuh8g3SnfblWnboX9w6eHyrHv3wOHdutD6+IvlD5fBiF+iMl0MtHvFvGcMt+JXM8sJsoDJYkNPQwFl2eZviMHgr9B3aUHXeNxTRcbA7S7HQG8MnTUGda/IL5x244jDp5bg+K7K6B9Sr6U+izIgETQy3ctXlkt59J+IMLgpCpHMrjc3wAwXZIZnY8Dw5yccu+9HfqPFaQCsguiXUxtLqfu5R3M3q+ASW1suVsL3mlarW6q17YLol+MVrujRl07BO3m6qbs6i4JD9p9FW8Q9J7hB9WAJkcsrIiT6Y/jhDpO0ZE5aKOuhOsatM/FMdh/JQziFJXOHIsAyc4EMn3A9eOQB3qe1n1nkImMYJ1YRZ970gLTMGFej1ZslxmDcF7+XcrHjGycIZLhru/izB1KRMsU0Y2jPyHH16FO70ULHUMdqSMrKSiF9osAQZyzO8uUO27z1IDY4FcsvUwZL82q8NX5Es53jtrHwfKMs2aoliDdVbFKYw2bLV/VcQ6Fsbg9RkLGhys1fCSra4n+CazMMLhkZY0Xj6BzQF9kK1EdCbhXpjFWZgMBAB9HWODp+QUAAL59+wLX61ULBNo6Un9uTq7dv0/F/6b04A6NrCD77X4Jm84VbHLv33pcVnLzjWqk7HimXT4vUBbvHtWGA+ZosZisVD9zHFDWA1YEjtyHP42cuXMeb08HrrbX6bSSaAvEoksdsj/fxWMzzeCleFIvkY0bCysr5x8VlRPZDwuaUZ6hcwhgvC+t5x7gnMCVUBfsGJtL7ZcuzbstWIxTolaE6xWhVjGppPrMrngPvnOu7bO8iU43BWv1nPEekLTaxa8GLXoIViXik7c8Su2eOaD9kuJG0x+nk9c8V/Xclmj4ohXv8rl7JPKbtm2A0XX6idiZrQp/iKoZBnIc16k03Ui78lrn9rrcyc7PWMsExDQIkZXb7oa9dpzRwA7t0YFURt7nflnFaCeltDvLdkpb2Khzv9z5aXqGox+NwRyWyh1vs8iJJFJyA5d+2gJxfaxHJriqP2fOu2UWzgJ1MzwQgRdVHMnS+P7UFBqmKPmHbOstleajCudpPxDBwSXu7LjMXTDRlSUI7ZLorhpKFp6f1gFEqKvs2PlOdIWYWtm2E6CS7j5ABMDLE5TuQCmlAJQC7Z4C1FWakS+DOqKo39sgCjQiAJR233Y/CB/5LojXV6j1CvX1W7/74bXtgBjufoB+RwTJ7gmK48s/zOlRrUGl5+nTq7aJUdtNbP0OjQ6XCIiqmXxN8urW9PZCYoSou1YAMZzzT0L8jMv/v72vbZLkxtF7yKruGel0e76XCIfD9v//U/5if3DYF+fb211JM9NdSfgDCRIAQSazqnqku01IPVWVSYIgCQIgwBftDxKri/gdO8cC0ytWXUulRZlHRjb08uopakNFn00rOxndJEftNgAUHUw7O0kVqzRJ0p6hmjmNhvKviH2ZQnQ9Mu4yMZqtyqIS5GIaQyw7TsTQFKvrZ/eEuFvnPYkY5Os2cHunFMHp6j6dRil2N+Qjw1LtR5krqGfySCQCAUGfTavJ32emTg+XOubYXJkUEfXHOnKhtVIBtjjt6BOCz5bd0dr3m2w79bbrxh2jL/AxXxOQgUlKXSEB5F0MMoQm73mMBPXZFLrKUdKIrsmdAfVS5bEzKYvXguYtLi2AebHJuDruILvR1sfglSXJoA31rGTTE0s32Z1Uqh/abjN+x/i4tyQ/UU1fJQ7UhD8QirrIuGNAjFdcXj/j8998whtt+Jef/4RbuYOJHT/5o8l6fRTISPb0z54dX5iPJPPyYzweLjDv+McBaF6UAc4l+26hLlbucxYS7xWt1PeNDIbL9xyrXSf4o2A0FTgO3n0T82NzPqLinuKRn49htr/mAQk7rl2NBH8ENl7OO+gDdq4PuAMc2qmV2ZG2inUQwBkV2cFHyRgaILftqtLdz6NtEZLgA7UYyNJCWudLe7JmX6cnBHG3WxkWKQXwPWqZEF7wtYGQgLCVhWkv+b7A2OhgG7/a+saInFthj8IDsmKWdVn52Uxcaa9+02UpFcNzJKPWeW1uyQ9LH+yJ+TppWyx5lOxwNz1HB7jV239gMNjkvSwWM9Yhe6+ITm27z/TB7JnF6ddvOK8btk+u2BNi4AtgiCgdGfTP/Xx3p1mHQ9zjTa9cJHcJICdLz4yrS9dWS13C5uiCNRbiMXZwjDplPx+OI36clCJtjG/nvvuw/N6Q/gGJNokf2RRqszDzRjxwZvNB+r7G/ev1aj+TkO+8pz2WmfUx03TqiEqgtdGQIocW0pioOsR8io6K2fU7IlQHCWOQ36/iQWMUNv5CmcXqbZesNfotnmJKU9NVJ3IoQYiyAmZQCUG8lrA2hTrGBVQCIFT/qFyIRuXyapIs16ztbBSr92ZQBmYTvo9CG39E/Mc4svs5FccQ77KwYNtADz47qV1gH3kMUw1C9GboqOmnYtkW73e8+imdXv3qdA/kYGq/oilcCcjOEG6/uT2tU4bfjNwIfU1Whq4cJDLPcefLrhJ2277nnH0kj6gw7ZwbQSfkixPZVRIsa9DkDoAy/7J9S3UcciQ739XTcN/lFjKWvZ2kw+xyae+VdFT5RztSfLBKdtZLiqlrYm9qumysiepSrch4K/8jXET2i2nHWkbQ6iGYL/WeoIKrWw1jMkwnbbYyXt86ZagEgvEC0E+yFhmyHqEg6OdAc4wR1+sLAiVslA4ajXuc1TrEBoPl56PwqATq8XkG4noJ3NYkB/A0NQ3bwnbH/liGwyj2vfgSdN/M+r9fqPRAq6+qwyFovTGi+54z9PVOCfG8Tzgtcw62J/cMI8Y9oEWRNXGqz3AObSuvHea7MgnkByM6hl60iXaflSMlPU/Kjo0Jw0N33XExUIyj3n0K0J0jcEmI3EGLmEfNLQe4+sAHTWwMAa+XK+j2jgSx+Ezhqcu6ak4SOPbg3r7akRYHS53kv1t26rZU5uhiTvm7s8klPjPOp33sVV0U4B5DLKPie21hs7uVvXcwPIdbRpiXqBqu4pW/HaEkC1qh6vDLJ0o9Uh+TMj8a5NgR87A9mfoRMrcDX0/74PUNwQ9Sjgaag/uAGBslsHz/cJMtsOaKhTGkZdo8j1D/YM1p+nPipxrBsfG8ZnKvMEyRX/yxP92sD7rls0ppaT3Iv0LgRQv3zyz9+SLprx8tvg7LHEE1t88TabzzsmooZ5J+LnZKWOduvvghH2Wk2r1MWxL3b+IiAOSjlnJG68gPAAIiKN/lEANiCAg1EIHSqVTvTygY+9qVMuUuDfkgt31C2jYQbUi05R0RZZdDvv8hVTzVO0QQOxao4mu++wCE9sd3UrBDKJPPgYaCJ20ZdbkjY7YCtbZj3R2BijuUXRdx4JyrdJZJI4CaNtYdI/sCSO1CcPg3qPLn+KqscFYrulMc9ait0EoDidUCPfpZ5veVbcOyTbSwCm47y3pE9dw6N0UthN8w8z/R2nqBdnavNEWNwdRlknQ+B3Ldqngf0j6apHStuOhMSpR0MKJ6GrSTgYpSi2yyKY8MIcDbEbYOktp+tfx6W3e7C9TEwTPkgvwh0jta3E4Y+bH12ov3K/O6e6YgI7UfnG8dqIxrpeu7jYJuqnthoVtZ2+yxs5VDzEOx6pO7qURAwOUS8XJ9xefPP+L29g68ibIHtN2/uuVDXHH70A0ZMf4xd6ZqNDqfxvQoHHEJLWIqTa60FB1wbnQgJgN/BXDUmf97g9ULnE0u58njHc5Bie8BDx1b+R8CnmzDASWYtMAJBJDYrzeiyTNB9hei5LnRS7jg88srvm0bviUTOA/iiNu6OzAXcL/c+yuAw8PleS1pZz326WzHd076yFg/OeI+WG2339DuOwHzfhr1zV6eo+X8TuFZrHnXfOgZcO88jOFo398HDx3J6OUjrBgLrX+l4em5EwWM/Q8Hjph2iXF+Pr2pH2VmuXj7Y4g8cFm175Sq76yDufn36k8C8kJ+4wTs/K3C0aWdt+14JRJ5slO9HFUTSyACjUlkIwaEujqn6x7l0A8qX+I6El9Q3QIDeVdCuzib/UD5kmrmfTlYWp04SMABiUxVbEcdEJPVjttJ8jcacyjUJdBQ8VcHNMc8gmhf1QhDFqsuzxLAsPk5zrK3i70f1KMghJ6wyLpKDPvynsS/s/TjAVuDERSmF6b1dbe1lVqOGj2BOU6mN54ysa2E2HHMASwzGfSMdBmEGK0G7ZxqhQn93Tb9s1WQfGKPE7L6ZOQ8YAfagWs7StlyFxY7DltwRgaAusAkUBzxqQYMd8sz/KfrYJgpOH0XRDradwBVGTcLTs3IphG/7iEg55v9AcX+TdQvuAOCTCe5Qsuyp9l/oZXhLIJ+AHyjr3IJyU+W1dT7b6TirGwkW8X2f1BtL1/VADWAQG942d7xw/UV1+sV23tsosc1Hmfb3nXD+TGsVpm5D0HLzZrbDpcw/70C9zos945Yq+l20Fu9KmGPv5coHw3r8rI6iF1C/bFPzttV3dz9JMB6qP17G/Zo8wl4NJDgOsF89hxh0F+n/G7zeC1t2nqxeneJNL94k6TpVflbvg9sW9jxemjsrdRgoJcQ9rOP6rqTr1/1rSdE0mIf2S97rfB0fcck3QEzqVebkPWaWQhT05FM3TCPdYsYD2wH1gVlLRARkO+GqGunTHaHEq+wJ8C9eOlY1gcYwrtjyn7ryxMfSm89QMfk3TLefpveIJ3/YKWUOfaP4qO98jwjq5N847zjbE8GW6ZXmDd5eIKQWs7jC9mZ+j9G0HpdntMVLBPH+I7WYxTgv9dB61uSB3EsFD3iuuA9lLgPF7Yoh9ycHzAAlenpj7lxqTNdNHaM9fM6ag6cFUKfDSuixkAeM/2uiPuCEQPjg7ovtexHQeEgxQSLoO2tZ8Lho5nMCR3WytxtMaqRCLYuC/OqfOxYoVomibonETAI4J0QEeGSgxHycjkquyH4Emlip54UDsWDnsSOhQoptboilV0QG7Z0A20JibaKn/gOCDZ4CW0nBMxKe96xwcGHgOrgrw7OGnVpQQ5wOSC4uyFC0MY2Bxy4xuJ3c7Q1kUywTZAHHqeLdReFFuPdeFIPqPuuV/uHfWcRoa+rKsdXXtrJXYI4oLo758iFuzYYsQqVf50JVZ18URNyLSN/NEHH4yCWugQ4F9RyYIpEHc27dSA19u4ViK6hIvqOyNBGASubDqgg6gMqmHr7UpmwxlIIFcUYoIMPvBNCLa4jyluDVlfGUqOzISm3kYSgjgVTO3WO2C9r/k+Vdh/1A9pmkFXvNMjpDgUjakbvuyZA6adVEPKx28EUegUcpOya8ILvZNH0Aih+lJ6fW6fZMvhYwlj1qA7RhJY/2BY2Y6boztf0K/5L/CP+89/8N7y+vuL9awCP0THtM26aTTRXcdwLg3Y8oeqj4Q4X2NYyv0aTji7l4yB12n4w4hgcuaz5Ueh2Uwjb/qmNtoPvoaOGuABVxnE8NVjxqHFxsFQNDzg7HsktF9Qwon8Xu2yccVJXTZWffioxx+7vQhvrx9w43vCUWfK8JSER8vxsS4rHQ7wgmHsN+5kLdfXITx9wfv5HBysG+PEHBSHmMxFnbO/Jlo5Mfz777wq6AMzI4rNPv6f8GZW51/I77x0ZGpbw6tR/DXCva9x/2p4/tkrclvVR/TGmUJb6WC3kXH69Lh8SfGjIPxCxHNPS59TSVOkqTfjfStg+paP3KzBUhWQ+74Y5Au3jvbO8thLxjsz7sL4joi3bNs/Nb+toBdpKmITqW1fpd8anXo3ZI9BOTkaoLNRsMFHKxiihKixK7a6FfEFzu/y2rlAvDwjlMupE+ZiouiuhHJlU/tMkCjqq560YxHInRMjrdmQjNtypOM5T3n1RGsVzVjHTyQulqxOKZiKOJ/r5u3FRia/lKKc6gMuuk24iYVxe0ptt8DKZvYtNUmZpdGg3ONqK/vKLaVT6gSOayJFOGjvu224Cj1pOj7rySo9dpr0FG9T7UBzfgwiH2t1TAiL5Ur44dggR03HAYW62q3WrcYc/uB+1gdnoHhyLQIQW6uNZTc4TrcfcslfNNuTWIa1jmUMw7lu/6PEyvX1wnMlgnPW3V1lDTOmv2QpSZRR6spm/SMdIl2ZiRE2Wbtuxs+r0GnXVSOWvrMSXY2xP4TSf0GAsBmAvEjnpvd1Mo9XWOeCwj23/CJLQ/Qwhlnrnyfs1RlxiNM6b48GItqCMTNpetoRdj2Rf+Hhl7Rqdmndc7vLRHDRg+7qu5dvDc18Zclx4idrYucvu9FT9UQSTsr17GhrnhC7tGISr8TsHIywF+bmgTOnSPk2vaz3dOiBgYsOv8aW2EdDRIl/vt6lCEYT8cuXgQBfeA3eMwbbKHof43JVT3Q9jaw5x3L9fyyl5F/rZgK+fJOpeVw/4g/R7X/fv62y29etcRM2PQtFv7j74Ydkd7bTGzy6MBrpKY+3Aj4M9WddstdkEwD4+Lvi73YvdtxHCAU8ow0vKqRn/+Jy6AnsWy1PBDKq5w9fa4gaPm/o5fHe8LT663GNyT+qicQS0/+F9e5ya3wrWqPNS7crImQ17b6uQ+/VA4XqAdBLhKZ11wEaaTUVWJpd307vfd3vqqfq35DxCPFHFkH1wlCZrD44mQYMGvVedc1ZiGmjsoKgU7HHmTJvsWidPg90jDz8ADt4RQUBzD5bxWVa3kOdoCtV4y7yZ9LvQLgmWE8t+5TsJx3/dpFD9+AgBiBEx9Euo664BXoVD7Ehi4zIfu5Qvm07K2KQQ8qpsNmzRdlekEiQANcO3/knqzaSTonD4cMAgZkOZPdhU8tXjnsrqHr5rAuriUMO8vNJ6MDmtT4J8r4VFrYNhvMirt0MzVN2jkkzJqQYhrARtq4lXjZfRyin7xB4rxHXjnRByRs87HYgCLqGvt6xjCAGJeBTsGfOKzQylRkBSKYdvb6zt0reMPJ4rhgRQrFhrcKyMoRz4mJLZ0eHzhf7Gv9RRTjy2RA3dFhJjhMcU0IYoXxItKRkidIMQfd6ODkGrI7Xq5wF3rkFv+tXNG2oajZFQL0MiPRW3wa2OP5wGHx2P0ae3/S1f5d0huj+8lqNhne+FmU02B8MwRQ4EdUPqPXhF+mC/3AGiTwn9alGg0CV0Zd1NF0r/dmzQ5IzctdG1ZQB4d14ou/EuMSLGK2K4cMlL/TkPUux9h5BV+wbZY+zV8O/HE0cFfRfXg9IbH2MH9mNByqZZkY/EYleomr4XwXVPK61hYdjX5ctwEE2V6/a5aFvXF6LafjZeJoWitGPNe2cbKBYay9YZgqrJSvbZwgXdMPt0j8USTe2sjwRfx5bPoPnbS/i9brvobQZSHzPoeoYYn6VcLLCxb0KYSCI5T2m8kIMReR4TAuvLyBfc6flrsQko8ReXssfhnmEh8/5u4X7ixnO/5dmgm15OtXoZuYbxdwtmUK2sPj9mNxzUJQ/Dx7V4LyH320rl8EVVTedj+t1z0O8WRscEZVjjx+e0fm9DruB92oj598xCtbuaMu1cDJ4zZorso+CIUh7QUgTBsV1Au7MbRZfebXQM01H4LYIQwMGjmYbOjPq0ufD09nNSE2r2m+z5cFL2tpazzgEyW3qrQ8YaIhw0KJYmUVI0sxnf7n7IQYjm3BOGcWo4s5uoOXlbvfToUqumKrFAoOZIavSX1TpBNATlY6Lypd4ckEC5c4KPseFyW0kxsnM/H9MRQ0sxXF2I0URYPwm8zD/ATJBEIKY+kav+yWEYz/ExSyKPjJoM9zqxbEpE8Z1ojHosAE9zyt0eR4ebbKY8RvaEG+96oI7vuUtDIIwvohATQcqc7C32WZUbMqDUB0tKmvq0OZr5BZl0Q+cUoey2EALWBnzM9NpMG+H97B/rMaYIEGlGmxLkYWUSR5983MdyJ44cFSpnaPXrFPUuHHAaCXtK3oNhZmkLePwgxFGX3zzx5DilbtLa077C89LZxb/9Mq17rmQqTD5tun5psy50kCUHtoX+kEH6oDgTzEed/8/UY6qz6048S1pAjLHx/3Ln2oT2SI11A4xl6V6fukG+Zb6mSuNR2R/uMsyaDJg58b0264uzkneOZ+TUtivv23qQgRA35ZF8tNskK2223q76Mlr55ciE4EnTR0+XryUd5tK7VeZjq/XjCLu2m9gWZR0eDJ9NNrqtkF5x7+fjAg8415WtudjXI/p4UURnZgw69KhIdIrcBdON+shK9+tTYdqmXvnk852yfWivr0bvOHRh+4OK/dvwN2PE7oYIiJGPwJV7IpuRZi3RXrx2iY7BiljqFkAZEtwsPtKZDiQ1fpy8E7wCy857H/Z3QLgvd4rsjO39LE8Gqxk/tFyjFjonmOA1Mr8tjM2zgzUQHfu92nwG43sFD+r7aWX2jFP9dTDldDT7EvalFL8rcPnrDvtraPo+KKBd42c0ePpntNBzwXk/noPuFrkrePrdjKH7fSTYPjBFBD49J1BqxM27wOXOPKbHtDSZ8hLslr+bMgAgPvDf7yQ374C1fF5gO3Xu7BtYA0uuntG9soPUxgdtSjy4Qu3AZdUuLQ7EniUI4N0G2vSIxpMivieAaMv2HzEKGxtSrhixlpRXxJSdC50ADKgHwqS86wB1VQ3EinJJFwcBEtpOCEK9fTtn5MqWlfehnMJU6Aw8kIoTKcSyG0I6moCNgw+J74bgS7GTcPrrARh5J0SIQGy90MTM2BqpNSy4O8VYgiUxHGMwfydExcpxjQPgrJxa2M5ct22LoI6gsk1QqNy7MKin1FNy5fKqT6o5GAsPjpRGPb5pPplIZQeHylvL4WOmxnjcOop/AUCdgU+SV4rbIOi8bkliKNWjn0gIOcFzj6316wOTU2HJKatPhr+s7iLhMSaNcNJ188oOUG2nR1wJkjrBKMv2ROj6IKfzy2zFCHm1VNEnOeu49KlhUVOZn7Ke+/RIOTEan0F8Mu/KJlHv58NRFHzUGBb6aWTZCb7m4LsOwo+8Y6FVxtIfBN/K74WnOBBB1ILA99wvY7+3IX/MAPXfH6TH6DZ514CHSlkbhlF3zN89Qgo5vZyxweBjgZxJiYOs04DI8JdqRSfx/XTOsEzbuvC31B8z/vCOd/peYIei1bn2zQqW+d0ZvYBp/Gt1pclphdNSc9XOaPAEFfKMYxvUT9FUNbC4at9+f7b5LmWuHqXVfkj+8JyRnhQZleEK4Wybd3j8J3URWrW1I/J/zrFMap4nCvwt+vYOWJNv63lqGnyMQ/3xHRDHQNqAR+H+u3O+MxSRz8cL391j/054/vcCT9sp9VcJ1pZcmliZ30+23Yhxemh7aXivaTOqbW8Pfj+4/06PPo/a2bqb47cbQ46XU/zrpe+/uXCULYeKdjDfmvo574e5XSBnu6RKcl1NlQHWR8b9gYhuXjJwH5p0Qf4T0Y1AAoCUdwTk7bLUHNok8ikniiiLdz9wEIIDDSK97lcRVCBq6rw6c0MtgwMR+WwoGYCohYNX6oCorLIKndOoHqshghCquYiP18kXVLedEOT2fORARtkJseTIzV7M6gwZOutKgCRyXWRTO0GLhp5qu+xFZUtBAnNONSVM1kP+hC/U22WXuozsYCQEsunHAYnKFzWHT6N1KjEdY4fB+sCtK5mhWbo/i33l+JGMRa1AVgPWea+AOIUsVtNGgB17hWBLxQj9Lv02/yybKuWYzNQIAiu1VrnWhKZuoTmN3SJFcg5GjMfyarCkNzRU2ZUVQ+2oPUNpQHL3q+adrs4bvRmPkbHzVlAxkxsDp3L+bnblBOfseE8u3TnhlUd46SIaP8/7mflpPI4qx1HbPcUBLJuKv18uV0R1wacVDBN6rFPP6In+6MWW156ff5fBP+gLE4YYOqO77KHJVdVewtc6o411zoiNNDvNZay7U9EdJ+stN9cPfrmahiI1phG1O0Hw0i5Wkval+xryNff//duOgylrHY/qnYH+2ddfukbN+WrwuLOFUqgvfoydZCWkL2tI0UP6/V7TFDuMEJotFgaZRrhmQ2CUTTRDnj8VfpdycoTkaPDC0jCLyNN8zN0/xia6uDLDcdwjidv4a9WOd4Wvbh8yMpJQ7XiW62rBUUQJrJdyKONtLO7U+26ZMADms4NoPf3S7yTuIYh0/TG6a8NR/XK6ZRdR6L/69sbo0ZP74ADYtlvO5+D4eDimd7tUzyDz4boel6VDOkrg8pmH163Lr3tB2BK7uA6Utacrj5L9cJOSU+wiEeT8+K4iwnNgSNi3V6YHNezhcdME/dOkkd3cbMb+CPtVEnILzNtgHow4UjdV6CLM5z0Tj6X41/f5AXtD0ye0n2P4g+/+gNA+eHfd7qUTT+HVrdXCsfXHDODCciCirl4f4pYEaCCRJOMqOyHK0RB8ODwfpZQ4OJA2EAFpSxUBX+ocQHpFPQF8tEXbCVEuly5OdyDk4Abf+1DLI0FDoYR/Jzkx4SOcmiFMYmJWzQHhaOFBmR06AbzaWh11JFuKONhBJQiRyk4Ifqc7gX2bIQB5g0lozgllXzsdJ4IRtfwQ1KXWudky7SFOtJB17hG3oyNUYHZDqLxB/Avf6bcClO8UB6j1IaVCUzevqX0YSruFGMU8cy6YWvuKodmdl9TaYuT48exwdkZ3k/xFgyCXxXXuMzWHJw8JprE4aVC7DHX7WegnJnwhfX+ci0jbtbsv2FB29xCwuFKR+Ukac1Bf3ImF2qZ/ByjnWDOMyhryLm0b7OJTZdcT7G4bpRgKtddCSydl0QiHq+hC7j+qwYi+njKtm8ZxkHar8nYNCtt5tmfmPdW6fFKI4PchHm98Pm2FnNMII3JHvFJ7dYemoFNk/VoeCs9AMOMgBBmIEH2yZEOS3w8sVw4Y8o5J1/2yaXxJPTKuWC7IBtkhSxsc7cEg+ygIwWVb9TYKXg9JcwPbWu8uBbIEzzc9IHeqjXKT0p8a6/0gdVFH4DNwA8pZdxyC+ZSYjxGT9Rz6RjsQTNXZFugohbZpY2+v9HKq1y85pX2mK9NNVHYIq7dWjNTAs6GQq6jeC0jA8CbD8o6Kvm338vZB63saRh8r2PXdQw41LYNsGWPUXK+BnDZCUtFs7TwQAJ4zpTZfjLwnIh/1mycHCUCsc6tptZ4A9wYh+PuR3rZD52459wg/UJ3iGlipyZMafRXdk2XM9wtCgBXZQhrn+Xckc6mwhyZkjIPwrGDE99j5sDst+g8Gv8u6fodOCMBIRR4EqxkWy1Z57h8X+00lT2Gx5d4DVHwUR2k2cyL5ZkqKc2z6iv54ZCrBbr1yFBgNEHqL2XCw6KNHMLVP468iXTJ7oXQwYg3WAxFRRNEoE962wAYEJKQQEav4Nw4oZGOy+lSCnfiiXkiNlPIugFTuRihBgRCinrSx/RqyIckTlxqEoFRpDCVjCCUYUcsuRqhdYoNWriSyXQYsggPgwIWcqDGRoVpj9dI0DsBwW4igB+8ESXx5tpkQVtdnachYHJEhRARRVqW3dZjPrFR2gZiR1+jTjpZau0FghHFy6fJNx5d7k7ZCM/MASdyDAdmo0enqPRuFdyF2FKj2ovw1VgdVfi4dcr7jSP9u9IycUMDo2KS9ZvmIbcPZl6VDHs1RZldl864e/rUCfV11ZJYARGeSzIwn+X5S6mEdu2auHloh5TBnf4SScB4K3vPAK7JWk6COu+rTtXdc0/osNDm9anC37uplRk+3zyCH9bXc/WPYYUygGPvVLJLOsWlxSzTNCfEQWeelzstO5VAD1DweimMurOyC0WVUVanGBetsVB4InCfkgPPlcsE1bIhvf0ZIbyVX0/eypK4mpk16Z9deHfxqrfDojn3Z4WwvtOCwK0g4Q9/dfTChSyF0kMbp36ExXK0yIH96DNwEX6ajYVNjGyac2uFo/KWIKWm7Ehd1Vp2sucJsNtbal1UnkFUVXq5nrqrco+WI008HefeVnmuHKfko+V2WM8IyoqvHoTFoWSxtNVB5zivbIfkBe1W8T67soOCFEFJnTgtcDQK5z0nYVFZXyQCv/LLSKC1Ns7nWZMxg0rBTXvuqgxCDfKS4oAN5H488frf8jyq/S4CBUlt8BAAhBsRyDG5OTUqDTWmDbz/cAyNfhcUq2Z1aJffZezApmu1cvzvQsJDND0Is4PTNo4+FgXL9rgGFIQwNF/VuxF872boH/p7oObo5PJHHwiI2ojZ+al4e9Xu60tqrx+gfjfFZL+72nYfZVeoTIg68H/pXVgTYKqw260Nid2aYC8Tsz9ilaa2nVlTk/nxmne+Oi0ydcj2/lDdkZMXHCPDqs3D5YK+s/rme5/j4luygvcnDLowQHJCsS9nGvqUd7NB0+YZIL3rKYo8DZR7aESHpYKdEPcIIAREJSLHdklwHd2+R5B0CbEACeRdDuawz8W6Ggr8ercQEaKbUDqdioHL+crwT8fwGgiYU1CwSOFCCElighrwZ1EwPUC6yyIETTquMfHbxBGQna1mZw7shuCUp4613QaS286J5z0vLG9kpgxrswJJ2tbzvYmhUlV0Qg5fC5yYnGVR3HHizz2ZAawPHuuL60iz7i9Wdu6s+mlCqE5QaONJtofhT0ss8IHhMOuLHJPiWgEd6OxICKhghfI4KHyl+onrkly6Jm8B3xOz7jSNCSDXwUOlPBETtCNZOzRE4AmyYkvwkJOrOE3QpS2hgFrSurDAMIHA/UzsKaVa10dm7Hb2tYHRBiND33rEghAmdDPJ27Vqb0kFa5CMNvKr1iY3CeelX9OiswgMaQoxFLu7TRk5fqHYblN/tIPEGsNMpo9c25UiO9LuDTLBPOMNDneH7DT2QREXmSeI0t/OrGEogAhvi219yIMIab2o3kK6QF3h4dGVZsJMGg38FxgGRuTErHf392Pfvl+hKts62YidIfH6aGVYmQeiPWToDAbpuNhN5z3eJGb1fw2NTTeWtzLOr38Z5p/J+ULHDTslnOvyEPabahsz7Ccq5jusJIP1zF/YC92uT8Ad3LK6Ah1yqODtvGSqfOVhNNCSm2jReDvmvDuWslk5m7rRDKGz/j8s0SGdkdYHq/SwOEoGm6Wi7UIx3yoaoR2ybITilOvz/LFjh5aqNyHcJH6FoVZc8G9SwPzSAH6BTTQaOSY5uR9/e6tsPFUoMnZE4LrvYzO58yMMxLXGt7Uap7msasYp6KjuOYGzEtDn9fKcECVlyFL7vCFuDI/PKWXrv+T2rsR8CY6YvWsf516gd/OQ7RY/nC/JJN8ffoXEEftsftYykBveplL/22lZ4iDo6w+hIzR16m+urWBmi4urYb5V4zbKyNGI076kJF9p2YCt589PZfKEuuC3tVk9NHV6U7hEQhgJ5b6HFGOfgcR1/Y5xH5/vLgYgYYl5wksrq/WLwJUrVeZeKhy0ar6eKaLkzmuzUpuKI53sdKKX5EFYrPUhMrCmvjEGjNfsay3EhBNSjrzup1kRNb48SgIQE4dyu+ROUoxuhOtXaMUwReZuwdD4EyHsq6k6OGuAp2CpjVuxl27Esg3GWNhCGudN6FROJ/rL2Y0Ur2odqGcZYrnhMr3XCwwd9A0X5LO0+swvU5hJBioS2mlfTMloRTiiTzlKfztfapKZDEVUhQpV+vwIyGMEsFmqD97gtH5BL2ygYMXbqZLw5OFjXzEtHs+E9rZBXIbcLb66a6YIaVZXfA3KwQNW/4SK0LXWzgFFgxq5IhLw65M3aMQbcnRDGhbAjryVpqr3CAVHvJezJMoU4RIzefQQEzW893xqhskrHB04w7MrJVU7yz/3nDhLtICdVpZT12gzGvUB+e7vh7dd3/PRTwuXygrfbO/746xd8u90sxbDRyNmuh062SgNzMt6kvFJtO7SV7utbfcCaI3MNTRbDrqPcBhhquRpf05cH6yHxi9mhpsqzofZ22Nw3tu89X3uEZyUYkdNhLNe+MxwbmwMYIfDUjmGuvXnUjuZSSF2TfUjgcZtA/yKx2GCNyqfC3FTWFA3l0A7yYYLS3kru2z5o+0SrRDSmzJB4KPN8AUTZjgzTJvBiX90RhOi6hEg9ZDsqgepO+nzcLhV7OiDGi5z0GcQfZMOccBC8flicPA7z30tJj6tb/PM9RZNdACThQT3728MHjr/ST7W7jG9KJ72fjt+vBJn5Hay/5SBmwgHe21GsvxHcO4w9Ner9Ht9s9gjHWK3p+6DcnGLe1vxMe+UcpE5kW2WP7yXCGsdzD9qevJcjJm318GRghdtm8ETpJHzuI+67p7T1y6oDIANd1RhMWYATgBjzsxx0oOaEszJH8gDEroUS2GiO+dT0hh00XI6CErhI+Uim/H+7f4IdODkNmYFIsBgzmUG8K05fyhWXRz+15yUv01yCEJGP1Yjtd0qpCqp2nFT7ZGI4kCM7vPqqQmtS2TYgiCAET+jRgY2s8q9+KLaJCNd1xJAkHy5ypXsGr5pv+IjaQmHBWDzfq/M+gYWdJFUYl0/yL4ppPlhyngc3Mk2mAWb+27bDoOEZ2kqlev2r1KcdgHXq1ONgGH9ld+aZdo6upknzDKjVZTwxdqqk/Ns5UMFHhekwI+ndEEphyP7VtHnljdS2YqW9NPKhoBFcfsA0CGHzShwsp3waiixSnibN0x3Rd4ER3MOObPLxI6Dx5Ugi9bDix5XjT5UXWgIKs3UMlpa1+s9iwnJc+rsqxrshdimdvS4ot9uGt5+/Ap8jQviEW7rh25dfG91k9eOg1kL+VSk4DMTO260Guk1A4hA4TjT1un7zLUYyQTGPxl0SDC3djhJJ54DePV4MJljY47cZCN1uVUdn+uBTZ3Vtc1YeMO5dfSmCUp0jRnw5OG4HxT0PVpBX/X8gDyclXt0p+z3ADNQ7wPDgSHB5PHWwQNfe8dBY45T610fAlumMfJm6lr8o6YeP9sZWINufti/Ks1BmBs59ZD0FvFCLCxHlTWjJorxfpsNzIzstG4EUTRMVOCGCv9JUwRP/l6jagvm/duwn21BHOSbboIeyiLxjuDtgu6d3ZgtIjhdWPgeDT1opQTxxq+Ywoe5k//kjDssR2QtWASOQo2C4IGJQpUPQDee9fh7gIGnR7NhZq7QtwMQCOVjyM6jScnuXgx4ZK9R9GZAUVlJ5iLufba3kcbr1ivOlkrv0w9MM5iUfK2WXReQkahF1fTnfdbmjqa0XxHyVuR3rok0F/LJl3awYVEbT0VkRzzNmumfNuHJnTEK8a9vOk/uOT6W+sAtqV3TBwMgwedjHYpd1rIFPx/qc6Yge07Q9R50f0CdKnzXLaQ3bOqHLgYjETn6U1SZbcfbzWZwh5l0IMXcsN18987UYhUxfzisvpSaAtvasTLBCAHAplyXzzoLYqGK7VCk/d9Iknflhd8VYCCUNMb1lkssPEnI55fgoMs5grnu+WDsihEs9lkk5ggEkSkgp5cup+Uio0lzcdAF8dAy/YCEiHAmJqmLgYEZKknVCTS4nBewScc+xl11HrLwWhxzlOy/q9mg0d0WigAhCXTUusOqjpMj0b19Or3t0cCs/NPst2AFjEAfxb06cQAidwG5Kwg9G9PUY0E8oOwT6WbG366IzKkm3gRYUoj+D6Ee0qvNFtTp4gk7iZR7P3NypP7X7oxWr+EbRWHBEiH6R021H2vKW2hSyjGF6ZxMdT6CSrlsLTJXj39zAUuEjNXZDl85dMaWa1FfAje/1C5Wa6zuxbchrDzMBo9b6TsJCdO2/UMtt+UZ57cghkNcPtjiPVv7K/wRGIp23SjhrNANlfc9xKu7IdSb4VVdJIvqM6pPHXBD1VG0sWNGRLpCn4Lagv8ODrBOrgzYfE8jdGyiH8F/DN/zdT/+Kf/rpD/j8+R8RwldsW+lJDrYrPSdcoFZ+1BQ5yO4ygeT3SreWyzIw9BQwY8x/CZ3IOvePOo5mkeju8fEQgMwbp7SZQBIB7u7faRvdCc/qPxd3+Wx7mrs++rDSj9ZrME4+jsD7wB/JnkJtXOXJV20TyPe867LZDiwHpdiqMsqUm+1hoFuEcbgdJWZyTQ+FWBpR7sDprVGpotrCILM6X+VYvCyxBN2Kpjav+gxNdjWCWq/2u6Oa/erRyJRKu2Yk09zHkxwT6DJkO6OcIAogIBEh0RuIbgjI90NcwhURl2KqNJ5rC1c8W0XWEiII8ZhgtKNotONL7mzuq32s5Sam1h25Z2m6GdSDeMfjpEfl8OERXTYlRxnySpOqGq/imBHU2Vl3gjbODmb8XuDIy6eCHddsM4v7Sg0l91DQLPEpFeWHt++WBr/8OZQc/v0iwfZ+xP6LnLgP93bXUj5Pn5bnNKgTT2gAMacY1VbaMBr22qS/gYTnbXKOJ+arOz6gncL6DIE/j/WelVxH7lPzuUnsLRDyhvsi8NzOODPabG8sN/VO9VLutLqC6Rf5MsBbTscIgnnm8UlL16eWPyRfjPh6je7serD2uGefMo2hvFpA7jWFwKTq0VXjiLLVsByIYAd8KrsVgHwHQw5EBCASEKgaVZUxhSNFrnzOAYiy+6EGJApu/qsOmliRtdUWIjqTtMHIKepkxtQjVAwzCM0/EtDsgsRGPLeD4HoiIxuY5lj/ohh3BIBKEIKDGa5gKP0fZGN2HioSPNKCEPWeCV69T/ZsbyFEmLCKXwpSlcUlUUEJQuQCPAEydon2l+lNekoSz/1UBr5ygIkBGtQ3W4deOYXihK8rqljYFmGg7ugo9DfHHYk8I71xYOAOZLFuLdLyKGhe8UUh95UsK9SxyOl5tWkdQzVKJNpN9IlwR6syM0vII9tC4zYSKYNAKoIRLgw1gS3cUeCijhY65aNWSA/Xhasy23E9wWdnpazMuBAN2OTogFqnzH49Ywsq6DehGXFC6XBx7jAeghosrWzqkwyzm4AtRJBWNdcQhRnfXnM5rHAP6J1Zo6pZw0pUIABBTLobXcQvG9ZaeWrHePCgDPVVwSOPzkPZkadREQGBEl7CDf/p0y/42x9+wsvLC9L2VnFUXaf6T3ZGX0dVmRmozjRlrJzVOQTm/1GZezBgjoed6iT0QcOf6uxRfEbBEyM6zA43Bu3c6lezkMThQOAg8TH19BBo9XMQm5B9Stw/SJNfVMbaHye5V6b/ppMHE+jusRF6wy2jvu41/hD2SFHv2zgb9pjRH+TQKmVxxqXlP+usKmqBjqfVXGkXhCAUJXUoOp3l2KbkJZZP5KIYIBuqxskqSPEDD+Z3MwbGVbadUhFzvtD0jCNrq60xkhPVWb52zFvXX5L4veFOXvc2jNUUJUKim7Bz8mIwux22s3QkcbWraDB38aEfm853Gdgu9vRKMKJl2jN8hO01CnhXen3oHe2rMD5//25YHM+S4v7OrR1UozadjDmZpO86bzLScdwiPKLJ+jyzadLj2OeJp9PfhxW1tqeHhZQOk2ZnMCkPk+IEF2Y4OpXipte6ZdeMFu9HSY8+71NMbOpVFAczdfPYPcPF0cW+lp9iaeAZwdJHgS6xxnLIlhqgvRPmQ2tN8Wa12Lclz3Sp/Cs1vJpz8oAyO5WPcNK+iGjBj/zFs5F3dNPQMJmMm2I7WaxWhgToNuwNM0Y2trN6ATBK7/NmcKg4BF5xrt1LxSWxzsjrgYjiXE0pAYmwbe1iacTMiAlUTeupUZrsEUx1Q61m+rICOcRo2rVM5Ivz0Dc6hGOxGKAk3ilj0KxClHIn8xl3YShBFpOXylbg+qzZvLyJIzttsmlMZZdC2rYchKh/tqEixJYISMEhB7owxUU/iSBEIYoI6n4K3V4Nf76c2ShBKVSDl7dVnkQQosprx9BuwmV8iWz1tQDCeKA6LrtdA4Ed2qE2Tm4GUv0cah1NZUb6BaJfTdmd0/AgjCYh9diFwyhDoXFmmElnGJcHuMXxTgBnS2l3N4loAnYb5NhQq0vNo1iMqiNO9ulu1Ue6dNG4bUXJQNPkGBAXxyQYgXEt7A4giYIvzu7SOprAc6a7x+IZWrxQoAx28nFle/U7DiNcxbTxmuth56+VF0+AwdaL8eReELJeSP2UtB/B0PRgwYPsmsnvmvmYin7ne6Cy7gVCKvH3aulxNbTRvbq65gg8xneP0jNYjemipe7VLh/AyhdWVuJRotZ5dTxT+8xI6ns+RioY3KTSSgK96XOAEh4URPo9WBS8s9w7g3Q3QOFMeDwTXsLzOff7YVfldLcry9ceHQf6y9qCbiGD54uC172A287XVPoltIOy9sjSnENoY7PZZVoGdmUoXPLJQUXk1XPP3KS1dNwO46VBE1LYAReaPlDdN6Lbft+xvTnN/lF+rZ9YlkTYHc1mjsH/kPv6KcDzFo9gLxjxEbrUo+rZpTx6L1AHdxDY2u7OsTYre8CjegGATdjb7HfTdAd4+u+vD3KbSxu8kwizbWjP5utd0HPCI0GIJ1MAdAL7sbaQ88nxogp07/XCxTH253N7X9/xrnsUPSVo0Q81ypXm7B0yeF4dRft6PiiYo6IHxS5RYwyuVfPlUBnAFKu0ceyc6K4WFVMk18KYIjUtMDPFv4s9gF3WasGM546z9UBEcU4gaSc3oTisaND9HTflgAWhKO+UfyPxVlmBqOyC4C23qPlQym4BCVukdDA231p5I+drww4WE3pm3kDK4JbZpV+g5g+1CjUxic8agCAqmzqI/6+k1w6vgs2Bkje3BzuEqA0wNblzhr+RMe0Qq0aMrFqQ8iTE9lbUT7ZNMwLkRGeugFwCDW3BQVXeVJp4YrJy5IVDlqJwT2PY4ISkoc+/ZiR3k8OZkCi6biwiNN/WS7KVftSr5PUunJ4uOc7kRH1YvBwPgiV1cK/Rdg8oZ/veob5K+R4p7yB9o6TO5JeQ78OwtI+CECzPWrOGfdKYfK95vLxih4vCv6iLvEV92u5xZ3d9ngXcTO5g3r9M53DuccekRE6A5qkcw0Q6lwUuG0jUNPqPOpnJsomPsuNdiQBCiJwrLxqY0D07xmOUp6NOC55x0u8FU1urtzkAo/OG6vqINS9k6tS6LUKgDBJeqeMTOSlUGjKxrXbK73xdsAqj7tXw8RP+aQkjYTJKXmo1S9FQz9bh0ZgvmAxrB6wY3BOVHMKUwQ0eqlQ+Ag8P5a5/XI1wDN9ChNfdVdjtIFgJ2AvbVKQd7pSc0LCSR2RuxatMmpGsHTaUcwIdAQhVOYdxgKfODzQOAP7dC6uiQFVH70TmRS/BpFdVG8ndhafdYh4n365ONMGIIQUW0Wpwb/p0KB0Gv61NJtp5D8WDcFx29G25HOjZM9MYBmZr6MbZkQKOpp28L4awlfRzjPdLab9ZjY5snTEv7h7nm2VTO/BFwq4bZ+VNje0e+xFwJEaTkVVW9qncoxDvoM0zJSZSCIPGXSus5vTzzoIUz4B5vTQlj0Cbfzo2lnU5jNXxPmUzng3BraVn9Y0DyM3XVoeAIFXBiBYxduyYOyzZVmSCQOzqY0cSOqaOn8YWZU9t6LMNsK3CY3yq/ZF7mESgb4WE2s4jC2O9puuBiA2oxwiVI5nyOAvNwxFCXnEfIQS2IIaQja5yF0JKBD5GqJIdinsz5k4OQbNBrne5gJp3FiSh6AJQj4bilqpCncvpRVy9b0HgAZCPjcqE5/9Lw5P5Dm4LADFEsZPDGD7EdUYNRHC7ZOIJcsKfDfTYORb0CulMTOLgEB9VJSaPnlDXK5e8zfJqRIsG5sy88j40StTKkNaeIUi3dago5QhZ8wGww7tOgSBVFl94LvlM10niDa0PCy8d2YHgTbj8C8Jpkodgz3vjNKEw/64zXdWrta3k41D7qpU0nDDyGFIdYiarqdBlVp9qJ/rYlGChFwAgBgSK6M6f7wQioQY8DC75/YB7xRYAnhTKIF7DPcpF0wKl00JN9Cf59C6hFdIpByPqmOvLG9Iu4OnGnxMR0D+DSuqBTL9gp82KFniasTsaB/74LlOYGXJ44weCpxp9/EVonhq8zrKo75HRuJxBPhqw/W7HAAG3b+/48m8/46frF1x+uiKW44Bu8Yrt+hPo9gXYNgdr7o1xEKIfQ7oepn3t/Rb1632j+XFIHQPIfmLodhvoD5nReQFtke8Yw3OwutrJTuaZoas9yjoxAKDIOtZWLIgPzkmwtEpLRRftt+ajk8Dq8PRgMDnrmZf6r3tOCKPr+Y1ki752onVqOaMyzO402pfXHz1ySPzLstQrfaflFstyLXcHzyr/6IUzq7Q1e39Ht9bX1h4vOsTYVEd1bxfIWMt0YHj58tuO40qDCEasYT5IllWnyHpM7nbmnfYp5cVXeSpa9Gjo5XZ/DKx5L4jrxOUC6x7xpU6T3uOU/WBw7yEhseitNthoHAn+nTrCHoUdwWo5eqi4bdr+ZzXZSeYdy6bR7qHvsXO3lvvEombAY6lWbTgB/W7UqF9tztRgXZP0ODXsYTK2Ix2fu31/eNxW6+pwwO4faSWpZfsk0sL1MLUx23xEuqQ8t/Pz6ceyMtQ+PLaXeTobqtdbo/mqotO2kG/4otZxaHdy/iccu2cD7Svj/6juI6fv7wY9sm2QrOq7ufI2eKQ+2rM9PR27QvcMZw/q6PCa2k9vd0W4rX2QxgNHM7WjmOR9yioAoZb/C3q4H4qznPjC6zJJ6ypcnC8xRFMnawKnMrBTMxSpHGdkHMp8/BPnrbsaQnN47k2Wqk1FzYitTFGXJMfaHvLYGpT0ASgBGF59KlagArlzVTCCxIe934HZWuyESOZuBDR61dn2jgEkB5kU1XWSNBvfk5U8mi2as200afWhHItFKU94uY1Cz3FUjv5inNXpZhwffS3XxJeeYE64RmqlnUmabQt1/4QpZtdgNSyU247L3jsdcTypFawMGXDo0ovm3pdHLXCgV0MMYLIyxYa6Ontg2aqkesRJQ+5pfhQ+XMQLI+tmOsjoKJWvvhsosp25k0rj22D7sJNmbEQOlFsArFDyHdu9I3E2z/Le2WDQXcbVIGqaq8Eybu0yMFl6CN7T9ntpZYNcpVF0Tte+5cgfSoR0u+H27SuAt+q0yXABLi/A9lYbUkqPftomgQ1vYYB7qTyjfYBrF2Z8fg+QYR6WZ8EJ2vcqF5C2vZThdsyNbc77weKi/nHw0hllk+tBzaZqOdtIrLaPYzQr7TqC7+iMGEUXmZKA8ZhVk7UxDvGws63yd0+KrYGVV9T3qEnfQ2VDR5V6k26dl0e939fDYwiJOlwjaPfM9XbnXn0fh3m/SJtOOxsLRUGmE/hEEII/ezVt2n46IyGV7pAek3ZpIdoOizavWePTamLxYpF7ZdlITg4L1YlaUCLbZSHGbBfaBTPEC6cyjqrZRncSVT22Yr/fAc8ONOziG9iODYFIJ38z+oGCgQ2xeaQ5ssOTD89oEoXSl1rqu6sPvV8DO1btGvR1gvpljreUz7+Lj97RT49BNZJEG2g7SnHWwI5egSVzb87GKqPV0FZLB9AD49QKNn8+CWApCDHMDPi4ZxV/FGwbP4rnIzKS/uEtu9W/57ObeTneZECzjtK3u3Og/Qb22HKdVXmMjouYzWOXedU3OJfH+26FhH/tyPgZSfj2hLo3eiHj3Lbt/JzNWMKowatp6fDOiE4Nvr9ALmISyZwfzpHckyL3dP4eLAci0q1dKF1PaQgBIcS8ojlGxBgRLqGcP10anFf/i/sgQGw8h3K/xEWJ/FqhmH+FpEcwr4LJlzxDOFu0k0SKknaBcBsMAQHhklMKHkbLRlmfFv2TqNxtkRLSxudp51X3lRkronK+dCAAKde17CJJ2wZKhG275TowU8eAGFtLUCLAGDYBRqCV3xx7EHc1gyfO7m6I8qw56aUapl5mlHqFim+N7dgBxpMBxqFhZFKUdgmxe652LgiBPh2eRej524hDnkQxOV0Sj+7AWU0x3H5DKTIiUJApgxHAwZuCOxoBWW9S8t915Jp5iuxxCsLgpgXSYuaZYDinBpQKyDsibBd0wRdVAXQE5OGQB0QdXxRAkaBGhGD0rttHTpnVfqjJx0bnKJ/N0ykFwXuKTGa5cMfdDoRDu2/GaPZxtMBYkxF7WPPHcfp2FoS1Eh6seudYks4nIqjLiEMA1GQzqFfOCAAPSmn4VHk8YM2ZgXR7u+GXP/6MV/yC//L5/+Lza0AIr1VPf/70GT+9/if85ec/4ucUSh3arqVrekPErdLNdB4/pmkGnSXl/3y2IwcAkLRdQEXQDIzCbuUwlT6biQ3XsWWMRQ92h0vHjb6MF0WyymIZ0F7H8r5s0eb6lsaJTKunVjF3knbPnzAvfhRGAcRBLHr461CZGLDCIhA7ScQCm4q4S/sxzTxzhB89O17t5jUrzsT+12P6zaNLlyoeiDesS4mPKDhSF2mk0lGN/J3AkdfsqBePHHO7e7cEZU4lS9/N7zRaEDZq4EA5D4OUEOIl74qIEZd4MfMItAq7HRL6F9Wm/x0IKUDbwPb5hxbb4z/iT1qG3ZWm94CPsI7rpYVFswSrBHujiH8/uSGtXWK+PFUiFZvnFl+Rwkst5EpfEdNN1e53NJLE2M6QQsAt/gCmMOKGa/o2y3wAAt7jD+AbVQMSLttXxLKw9vH+4D74hIQLXugbAt0exPn7A+EhguwDR3Kbh+unJnC6ffvFcrNUTihzPW9x3e8BPnYU3m0n1ExtAs+4/LkUgOAtZZ00ujJyfHuSJoJqbwHIbMcl01uRK3nc9JDyJd4Nom7WX7TSKUIu+fXlhdz38dIdOyLaM7nllXcARH3WQm5SGYQwINcwB4zP/WdsHHhgh0ftJGInuWmM+r795Uu1I9juqI7MiceKJ3qU8o6G7XZDooRt20qAIa8QDzEghXLZJyICNiDGXB6o7ChJLZCSCBvxsReXtr2ZxF0crSKiHag6WdnhykcS5SOaUmWyANE/KSLEAC4xNyXBDt864MWRHgElUKK8M4UiQgnIlLyJwLtN6oqkUCb5qmtMe8swcZ1ktPh18vIUXFR2g+RAUSrbtEldJB4QQDGAKCKIo4BSbszm006tfrn9SvtUJ0UZdiHkDTkhCr4sPG9IZefrPHoqFGph6JCibW6BlFk3Vvat/UCN5lT6IRmBxhuZZOCJEtUAGSVn61npGsYfQ8jniSfq6A+ldZllcmyFg3S5geh2K2M5oZhl+bW4WL3SB6r9ForsoRLokj7CzIccNGUlVnZu1U/R3tw+UQbbJIR29BGV7+Iy26bL2oyscnK/TFLnqSWId1ynmlZppZq6XhBembcEVEIsj/ujyWzN9gwFVTf+bVcYmjTtJ+k0Dg5r6CkHvoPTs0Z63RLcud5oTdxYzQfYinpGbgsGSPlGSoFDjI/Mt6j6U0ie0h4AquwNpV8z7pSEbKCIEIrsqnK6I0/ot4ocdHvH7e0rPl++4G8+f8H18gLgtea7hAs+vX7Gl5dPCJcXdZE1iEAhgsr9UNU5zc565kenYe1qXkNpR73dDWQdZuO86HnnCAQoM1OPx55G6ogLdWjaVcJSp3Yku2V0pB2CPeepGqUsaoQc429slBNQg9GsKvsz8y1uD1xuHb/eR7hbVB/8EE5m8WxUbBMrgh+qghMtSTKnxre/L3EMbvUH93dkdTSqS6hpGkihKXmWB/N4vPV1Wqnj2OaWr+1ZvJIz51p1D/pBKS2/9klCfvZ9LI/EbHTzQJIfIxkypczQM8LDNPiYh7LWsidxX3ot61sPtu97fd6kiEQjVxtq+sRE02m/Rl/eAR/KFuAEYCPCLSVEBMRI2fqMl/pXp8yXgHjJ74vpqWU85fvv+kXux8eu1yOjecDqRdXDeYQXSHWNNfvChxEfWlufezlLifGK/m63sSjHcJGx8cYU6Wxy3I7SaFS5W6kSMTI5x3i1zTpr1blTs9E+G2/7dGi5dm99DkOVgxFbuGQ8lP0tPKNR5pvK2uvlGbgBMY8k58W+7I3YEFvwkgDC2yjxGFzdG0C4IFXcARfwLFmPglUbsOe7AEJEwgUJeanvDHrdvcLJJZ8xPawZONtlOfPTHgNpB5SFv54t6dzrBIeExqdS30DJjaqh9PQEcgzXBAEt0GlkxbDhLE3CPumarNgbnnRw78VRfDkut1JacYz38q7ZIQGWyBVtyv1JSOhtPpHO1c9zG7N6Pye6fZQ9m4SzHaDWsMq0U12M2BEDWz+5MHwPZkccNleR5oPsA/fHRT6xvtl4clx47TbY4LcLxy6rJoBXY4YYEWLE5ZpXmoRLzEcpSacbNac731swtQ2iGLi14OJqF475lDbWb8W5nZUcn22dMRBoIxBSzQtqZm+K5RJsNj7ZKcbllTsD+I6IbdtARNjShrcv3/DHf/4XpG3LgYispfKukEtefRPjJdvIMeCHv/0RP/z4Iyhtzcmb8vFUKW340//7N7x/e8flmu+WSKVy7GTUwYjmbK9tSynfNcq4iZ3qlHdZhEwXrw6SkPiOCuiVtiwhYgk2XeKl/JZOcSo4eFeIoLV0Tg5OxYpH8nu9y4JZW61Y4mdmekKoTn55tBIHdrbthtvthu1W7iCBXtkVkdvher2Yye2WSaZSvSAFf+F38SyfQVvoi6iBiBr44MGrjPVcvxj9QaCO+pLpLlEouF7ZZIe8DkTwfSGlYMTi2LbHdsV4qX1TkubgWNoKrk2WpJQa15MDkSCoFdOZVwh/wP/GS/iltWUpL8bcZtvbN6QEbLcbbuEzfg7/HRReRLCg9dIr/RE/pv8jcOQ/faQMRLBP98HlUngyXgpuDmoUGVL4ojuSIgQgxnw3e+FpNVEQ/c35+51Djd9rOvU+tLymfMtPrHBDwcUGTij8bY2PkTGYjzpTb2AhCLoFpSq9UEsaZPnUxoWsZ78ln7r0FXjLl+7uIrs5P0rQqCcHadwWHkg8ivfNOK2yNYTGe1sLBgPQgboQEJkXr1dA8ArvHYqR+zI/JQC/3P4ev6Q/FNkQ6j1EWc4S/uHlX/ApvnV1uhbRuvFdJSHgFYSfPie8xFTGUaxlElENtH96+QH/8LdX/OXXP+HXb79W+m94QQgvSEH0lTfr47a0ASZu//pv3w/MByqfHHKi4/tSH5vl5GMeQ7XDK3UOvwKZV5ShV9JVce/JFHgSgttqYv1izreaPPKatuKo74nUaVQ6sFWNpWp3sgwIip6xA2oNYk+rMhru70+JqwvyVrkk5YhuiK7bjezXL43M7JK0/m1nDocuoQ3k9k0j2wYqhfyp9Izhu6Ze5/ymViGpnMF8sF020Cwdw5N90OcyfdBwCZv/MGvY+uTyOajsDnNqfSqDewOR0DLdSePQmUtemq5HLbbx+0GfzM7xH+pRIQ+6YEzX3w2P3LF7SV8RaXPHDSHiPXzKQQfccIkRl/iCt7c3/PnLv+GPf/6G//XPf8Tr9QWfP33G53+44L++/hNefvgD8NMfkB1VGz6HL8Df3fCX/xew/VJoTkGUk//jxTttZ360RN0HK517Dy5PH3pKZlU/OsPTG6U8FDubTm1/WShP1WVgEyzBWO9pfpS4gU52i/R3lWXADQx3der1lKQpGLlYkDRSVX9LfgjiDknmAD3+1tvXA7YvxRgJATe84nZ5bfNrS2N9NG5E6VqCoJtlcpCJBnkZdqvINnex/RIi3uKPlUY71znUZKHoRtYlBHwLP+QaWfKXELdGlTZZKnLqHZ9wC6+jzMK+0zjXShY6sFFjEnn6JhtadGDcDAiohbfpXxLvjH0U2rM9q6P5FOQkMH8klPtdVRGDpUpsA5S5kZw/dvaMoknYiB2RPfUDy8npEDvXGneAdjZzal8msT1F3XOPBoVA8O04WSpjZUSyUmuyJ3bGUHeCiXrnoqyQr0kddCKZL9WXLRALf6uy9ZWPQZ9EMIOR/KyLIj2brczlPPuO/aqmkFqtlNodz0quH1Qhy4EIbO+5jITs3KYLAgERCdlHF5F3NAQUbw8SJQTaqtO8rvxMvLaTAGq7IKIw3pVba8vep8CV3lJRPASUXQgBEYGaAMoOjOyU50uLxWtcrwlARIwoeVkJJwQiUCmz3NIN2m5Z8NzekG5fkL79kp218hLPGIHtArpEULwAIYAiQG8B6fWCtN1ysGDbSmCnrN7/+gvS2zvCdslKrxKa6gBpoqYEZIrTnRLUyv+U8k6AAF7tHkEhgIqTiWJQBke9fNxyTnFspxCzo63Up3lkpDFTmJXk8SPFER1DjvwzLbWLiwkkBZwYCNXoEM/18VpBpWHn+fv7O97f3vOOCHGkF4vzyEby9aKCMolyQIltZk1Lcwqy85xpiOXYoaZYUY/sspCbLyAV2q0ssk5jbjcOIvEI73YdhOZ8bsJjqxf2hQAgFt6yfR0v4Igcr2oiagFEDsDVdggX1Q+p3NnBgQh5pEK+tJ1A4V8Rw8+FYJSgTmvL9O0NMSWk2w3Aj9jC34PCFUEcU9Zk+Z8Q6F9a3UtA1HNmg7LMkEwWLmW7/iUHIljIMq6YLoo2CTFGXC4yUNEi4d6E3Qb9OJ11xuu+XAxEqGo1Q0c6Bd1dBmbSb5XMaJIk87vBA9MGXrmeEhzVVY918S6xzgiqrnsBF4amOHs6PPptOaMy2IkPoI4ZMhc8Wx6JW85zSRwUjbpdUmufaru8X0HpisQ8GqMIbBIu+Aterl87ui9lZ9BGKJozv79cLlUmyiAhwEOIchD6Alzitd7bBCDrBAAxFVdNGXNDG4R5z7YzyzZvvgK048KMoVYtn9Dzd6NxRMwKNIOdCp3V2S5SEetDIqijHUJJF2LFNnWyV4Sk660omsxcXPqBMDpuglEVw5HrEXjc1UmYyYCil2MUCJzPOyDzn+Axp6JrU2QH96DtQrFhuKflNLU2g2Q2hza93KE8YRYVOnHUMoqfSD+vMrvNpEUCq/e0DSXtp9Dl4eekCx0Cdd/lE+scU+xrZKjCY2W8o0uD4UHlJBBvjjrR9P5crRttW9eAPIm+ddK1J8WOE7agfL5CnfrlOB3lc+uoG2IV9rtfHjl1dIa1sQnYJg+iX9QIYc+nBasOQIi4IaagCMhjLBYH20t+GLPWQ/iEDQlvCfh2I3x5u+Wge9zwngCKr8DlE3D5DIQcwrh8TrhE4PIzEN5DflzHLK+rpTq2mxP1uHyb7YB6jgPYK5QnGHacQjzw9aZKq76R+qhvxdBXdq/Ha7N6KiZjhh7R5ENb7DFudZaozbSw9Sq2zHKXNBu80emU7hoBmed1Wb5LST7tZelIV4ZKGhGAS/lNTLeVc/frbzlCmk5sZUidsLqQwtLDuAOaza5Otpjk1VRqsHZFmalrbFWX6vnCSk30Qi5eTAk2Ljt5S07fGIQFmVgWJr5EpVsHeIb83e9e8SCGvtG1LZPr4NtsIR+XPJk3qtSdrSPp063LuqLHaynUZVZZHMSOJOEzE8SYoJEoS8gQYWGBxwHVyVzfvqP21vLbphq0IWZjbIcvaqrWdzzmujxFjvDCDLv4hgQbj2y7HJDauTlNsLPDCs2CU2YqdfqvQ1vuS0yesGehGZxCgTKPtnYjF23sZZ4bW79GZ7fpYBURS9J1G70tBjK2tZVxpTu96hHKVQSj47oDIYUEkrLM1GkVlgMRn7/8z4o/hgs+ff6ES3zB6/UHxOsV19dPxSkIpC3htm240Ttu72+43d7x9v4Nl8slOz7AK+1hGiFbgim9589yvM772605zdEcPITsQ82ruoujvTjit3KMxPb2htv7O9hJHmLeufHp8yfEywWfPn/G9XrFpayEud1u5eild6S04f3tK9K2Ib19xZZuoG/f8Lq94x8vv4BiQvHwVIdwxAXxEhEvFyTKK/i3PwO3PwPvb2+4vd+QbjekbcsDMAA/IOGnGPByueajj6qz8VYd/cy8RISEhIQNG25IzCxlFTzRhnRLZSdEcaAj4IJL2R4ZmxIlXvlOkKvdsmOt7HSJeTU+b61kR1SIqM6glDJF+SLyLHVCUY6RSxXO8pTK5eJG82rnmX5OJFYoGUckAdiwYUPC19sXfH37CtqoOuIzDqY70/ESLojliKDMWzcQCFfjuWLldL1es7MxlJX04LsbUJ14HO3MfZFqfoYY81nboXx2RoI7sQsIoW2stAKphOBq+ybKY2RDERBF8UaKCNQL25dwhVx9zbBhQ0oJt7Dl+qSU+aHUP9PZjmrxDIpYeOeC9xywYM8IkjquiJ0KMUa80Ff8Pf4H8gxTT9CICAHvlSe8frIwUsSpBkYb3/EkWvGWcX5KR341shxHCr+f0TRy5q8a6B7MypR0jVY6zpTpoxNl6ez3giReMGAUILD02vpJ3MsTnp2y9mDUVl4gYxTMGdJKOd/fXv4VP8Y/1YBYvF7qzqGAgGu4aUdm15+orhVJZ5b1JaDCtBHvMss7/16vn3H54drhHgWO2rhd4aOsDDtjiPr0Uv41BwLp34P6H4E60agTvRaocf0J2v7ObWpp6MgRkr3q+ixbyabqJtnyh5kM5q1bBbUwgBWuvrHZ1mi2ZwmCOc2oA66h7oiN0d8V4Y35PlE7DmHWd0PH2U5/z4OXZdrV4Q5yhl+brieh8TtA4tMEe016+dTTJd5zWxdGZ4/gsv2m20fqvw69Q3Orhwowj+gxjgBf3yX0Oy36PF6APQdoe3ttFdRRsG0aO6GV3E8/bcbZ5CKX0Urfm61ZvKPxsxco76HxpKcfV4P6nr0nPy293A4y2zD4T1s3bvI8ZUMi4DVlbty2b0hbwvv7rR87iaru2sq9fBVP4LKAH/7uHZ9+JGCDkHtUbelUdpvGKgiP65TfIhBR+zEYzivVJzWex3hkjUd9V9Ri3R3a+l4tKTwM0vG12j4tECHEtslqh6N0+vCnt5jMRaYJ9r4uAetomXtVn3V4qupvRolybBVx18JszwLbXxp7vU9qQLuLcUE+ZTmGrtGP2H/3jD+pA/bKGuEfyds9elrZ/NfP43brRD6fNotonl/ZmTt0evXzHeiL/VAYXbppc87iX0pwaAvNRhI+CJ1E2hcBdjVTth23fDKLwAsEEaxuR9jmD5a1/gK7GDyDcjQyeSG3eHLEHu6ejVdr8Q22ldcQEF2bS9sU3iegF37OPj2w/hf1DrK1msLT8ry3M0nY+9HjRS6PzzA3IHcSjO0jFrYkfIR1JqbxUnvP2eXiyVUZZcf/LL+121S6bfPbjfk58REVazs2RrAciHhFu6jnEi/4FCMuEfh8fUW8BlxfUz5HPwSkuOGGG97jOy7xHcBXEN5w4f/EZDXEfNJ64EudibDRe17xj604dN+rUZgbSDjNy8CI5WgVCtmAjLSVi6W/Idy+IRKfMnYpq1A3vFxe8BoCrmErR9cAMbwjhYQbbkh0Q9p+BbYb4u0rkG7Ybl9AacNL+JY7QESLYplEX0pgZEPAjQhIG263HMSg93ek91txhGYevL6+4IKYneNlFTwRgcKtCmUS/6WQkMKGgPe8RSy0yFXCBgqpBg3481Jwl3WvdRdFQDnKqXNuX2vbhiACCWLgcd0zPfkv49Sr9KPIDwAUeMVl469eIBkGDBD17wMRMWyI2HCjX3FJX3KwgoSgoEIT5TpcS2CG23bDDQDhiqgGMUeBr7gih5kulR5BmlKKJSzjpGsrj7lcfl7rKCdJLczQ0aT6KsQWiAip7UQS+GVdJVxxVfkZLjHXIWzvtT657dqRVqqejnwMVJxTlDu0OopLszTlhtrhMQCxyppQjWrNL8cngiPwHDPy3SzIkI2a55nwjwYh7gHPeL13YrziaDziXPSCOYr3v3NbPQI2CGGf7wHX+xJuuMatHaNU/gA5aV/BKfiX+90xjGSAIYaIcHnpMYk08pl8Z5+75Ajaq4xJvfNT/Q79p4V7+UTOY2yAct/4BEK4DNNZ6A1GrZNXcOj3sRvHy47FlMBSmoQMHpVZ/8C7zca07sqWhUDEnlw66rxp+PTuOZGjm4yOwDf8eyPdnfwPHBF7srS1KSA7q+bacc6EIHdVDcDUwwtE9DT1sqhr+7TB8rkFG4Ro9qcu47C+OhCI2JvQzdL7Dpd9OT0KRIzKXtXbRGzzj3Hv8dwwgDCQk9wGck47L+OlS5dxbAiUd7rmXdhb/kN/GSvPF+vEXjjFJd9erkAMlAMR1V9ExQnDgYi8Y7/tinFJd/ig0TKC5g97ni0pIcnSSUqHBb0M5tSev7Wuy/P5clJkqxN6PXYMYi35eCBCjG9jX+zJWsurIiVm9XnEJtU0rdu5nlPOBiLyGNC/cyBCp38UlIPNthVZqUeK/tU5w1hG9fbfatuNnOJ78MxAxOrvvmw+xlnOLdZw1KCQ/3ghEAGEgW20pzNHbb7cD8R0yiAENaojYGvWFmoYG8lAszHy8dLWIZXShhilgAgA8QyMB1erdxBy0Kv3oAUHFNrjlNfHjnih8I0FgBeI8HhrHIhQ6YRQPRqMmPGFsd6a3pW0uA71Zp/NbHIvELE+F2z8IPueW1RJRIIU1gVvm5es6sLQjAr/UyfO6aUMq+VtuXxTL16wFQKVEw76fj0CgT7K+jnhhBNOOOGEE0444YQTTjjhhBNOOOGEE0444YQT/urhSbdunXDCCSeccMIJJ5xwwgknnHDCCSeccMIJJ5xwwgkn9HAGIk444YQTTjjhhBNOOOGEE0444YQTTjjhhBNOOOGED4MzEHHCCSeccMIJJ5xwwgknnHDCCSeccMIJJ5xwwgknfBicgYgTTjjhhBNOOOGEE0444YQTTjjhhBNOOOGEE0444cPgDESccMIJJ5xwwgknnHDCCSeccMIJJ5xwwgknnHDCCR8GZyDihBNOOOGEE0444YQTTjjhhBNOOOGEE0444YQTTvgwOAMRJ5xwwgknnHDCCSeccMIJJ5xwwgknnHDCCSeccMKHwRmIOOGEE0444YQTTjjhhBNOOOGEE0444YQTTjjhhBM+DM5AxAknnHDCCSeccMIJJ5xwwgknnHDCCSeccMIJJ5zwYfD/AYckB/ttx+TSAAAAAElFTkSuQmCC\n",
+ "text/plain": [
+ ""
+ ]
+ },
+ "metadata": {},
+ "output_type": "display_data"
+ }
+ ],
+ "source": [
+ "plt.figure(figsize=(20,20))\n",
+ "plt.imshow(image)\n",
+ "show_anns(masks)\n",
+ "plt.axis('off')\n",
+ "plt.show() "
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "00b3d6b2",
+ "metadata": {},
+ "source": [
+ "## Automatic mask generation options"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "183de84e",
+ "metadata": {},
+ "source": [
+ "There are several tunable parameters in automatic mask generation that control how densely points are sampled and what the thresholds are for removing low quality or duplicate masks. Additionally, generation can be automatically run on crops of the image to get improved performance on smaller objects, and post-processing can remove stray pixels and holes. Here is an example configuration that samples more masks:"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 24,
+ "id": "68364513",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "mask_generator_2 = SamAutomaticMaskGenerator(\n",
+ " model=sam,\n",
+ " points_per_side=32,\n",
+ " pred_iou_thresh=0.86,\n",
+ " stability_score_thresh=0.92,\n",
+ " crop_n_layers=1,\n",
+ " crop_n_points_downscale_factor=2,\n",
+ " min_mask_region_area=100, # Requires open-cv to run post-processing\n",
+ ")"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 25,
+ "id": "bebcdaf1",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "masks2 = mask_generator_2.generate(image)"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 26,
+ "id": "b8473f3c",
+ "metadata": {},
+ "outputs": [
+ {
+ "data": {
+ "text/plain": [
+ "90"
+ ]
+ },
+ "execution_count": 26,
+ "metadata": {},
+ "output_type": "execute_result"
+ }
+ ],
+ "source": [
+ "len(masks2)"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 27,
+ "id": "fb702ae3",
+ "metadata": {},
+ "outputs": [
+ {
+ "data": {
+ "image/png": "iVBORw0KGgoAAAANSUhEUgAABiIAAAQeCAYAAABVBSJEAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjcuMSwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/bCgiHAAAACXBIWXMAAA9hAAAPYQGoP6dpAAEAAElEQVR4nOz9WbMst7ImiH0OREQOa9oDN3lInlN3ruFWVXe1SWZtpne96cdIv0q/QE967ze1tVRmfau67lRnuDzk4bCHNWVGAK4HwAEHIiIz17QHMp3cKzMjMMPh8AHuIGZmHOEIRzjCEY5whCMc4QhHOMIRjnCEIxzhCEc4whGOcIQjPAGYD92AIxzhCEc4whGOcIQjHOEIRzjCEY5whCMc4QhHOMIRjvDzhaMh4ghHOMIRjnCEIxzhCEc4whGOcIQjHOEIRzjCEY5whCM8GRwNEUc4whGOcIQjHOEIRzjCEY5whCMc4QhHOMIRjnCEIxzhyeBoiDjCEY5whCMc4QhHOMIRjnCEIxzhCEc4whGOcIQjHOEITwZHQ8QRjnCEIxzhCEc4whGOcIQjHOEIRzjCEY5whCMc4QhHeDI4GiKOcIQjHOEIRzjCEY5whCMc4QhHOMIRjnCEIxzhCEc4wpPB0RBxhCMc4QhHOMIRjnCEIxzhCEc4whGOcIQjHOEIRzjCEZ4MjoaIIxzhCEc4whGOcIQjHOEIRzjCEY5whCMc4QhHOMIRjvBk0Bya8P/xf/2/j54xGABPpqci3USq4iED5GF+/RNo3cfMuQRShbHOo4t7u4L/5qKqeTrtqOCZ1+G5vJwqdx+wKpqK7jIAIq6TJxjA+AkbOHiwBww7tP4S17ev8bvv/wtM06BdnqFdrLE4fYbF+gTr82dY2q/R8a+xaBdYNAu0bYe2bdB2HWxjcftsi345wBgDIkqfRASAYEzspymnR48BTQ4Fq2808Sx+Z67GFQB8fOTTO88M7z3ADMcDmBmeHcAMZg+WT+8B78Fennv1nnPNsV4GBxxiH5sj6eJ3MMAM78Nz70PbJB370Fqffue8Un45LIztT38H/PQt4EM67xy899hsNvDeY9j28N7jZssYvMPt5hbOO2z6LZzz2G57DM5j27swRAxYQ2gbQte16BYNTlYLrFcdFp3BorNYNUBnOPTTM9wAeA/03IDJol2fwbYd1ufP0C1WeP7ia3TdAicnJ2ibBqvlGm3TYL1cwdoGXbsIuGINrLUwxgAUcdobsDcY/IDBDRjYwXkHFz+H2F/nXBwvAoFgjAURoaEGxhh0XQdjDBaLUFfbttist/jx1VuQpVAvGRgyGQetARkTSQbB/v4C9od1mncupmNqoc+sa5V5jjxoIsbM6L/6CcOL6zTvNU4xfMI1gBM+MCLes4dnD2YH7x287+G9g/MDvAtj6d0A5xyIPYh9wlNmD7APaM6c28a6DYD3LuBgtEF7rwlxXC/sQzof2t1836P7XZ/WAHkPYkZjgMYSXuEZzrBGYwBDBEOAMYAxFH5bijQmzFEDAwIBhPAcBJjwXp4DBDImzg+lMQ19QRpbqDXORV/KOTYIdROZ1JbxzGeaIJ+BvDg47zEMHoP3GOIcDM7Bs4fjSFNgAAKMsTAwaJoGRAZd14CMRWvDb9s0gfba0BZrG/RLws1zi4uzc3z9+VdomiWaZgkyDUAWvunAtgXBgCisPTJxbIjAIPSDxz/8yzvcXPm0x0DoXUZJeboLscsMlMcmkXF5neaE4X2gz845MBjODYGWui2YGS7Sc++GiGMeQKSxkWbfnnyHd89+m34vvunRfbNN9GMYXKSJWwzDgO3tBm4YcHt7iy0c3v6nLzBcdLHMsLYIHMabgCbipDUBJ0jhoOCD9x4+ttd5B2aEefYBH5zn+J7hOdBVBsEXQ0qwceykZI23Hhy3u3oS8h4b2hzm2ZpAc42BaikyErPMSfjiEPrQ96H9zvn06X7/Gtv/5R/w4tlz/Kvf/Aa/tqf4S7cCLb4Gul+j/WyF5mUX8NgQjLUgMmEdI7Sn7pPGqYwPXOAHfOh3uYcLvWHV/rimPQPwGc/AYF/t76osog3axT/D0DbRiUmaQDLG0guhReG77CVCi0yYjJyeFI2qmSGqpoUBZg/3ww1u/+sPgI/zzmF+Xq8J358SBtfDuSHxHM4FmuOcgx8cfrMxOHeM01cruOV9eNFxGw95Nc3rHViFykz1wEzmuUPDDsu1Oy/termn2gNhlP++AzpRGM29eADsK2maWsVvj9eMsnCeekbhxSgNoz85wfazz2HbDl23Shm32w2GfgOvZBACsPjhT+iurgIPchf58aOFx56Ih8CusZuaYP18X/6p9Hete1+e+45l3tnHJcyUOTccTwqPVVluPIPjOpqax5zOwuDMvIJfneDbz7/GtjtD377Cxqzw3fIVTu0Gf3vyLRryZX4CEHUnJpUZ+Dk5WZtUOxP6oiQLceYNRioJlXlOd0Hqb9ZHJGkkZufEA4RqvapHc4t11Zz4zlCOn21foGdePc8fzAwX80dVRe639CXy4WAP8uEZxTJDGT7xZHXdgAd51qOoysbE78Px7erNBt/+97eQht/c3uDt1WVOQBaAwWq5xHKxwMUaWLWBf/I+yAjee2z7bZQ1Mi9ZAxmDru1gjUXTtYD3cN7DO4d+GPK8JTbGRJ7RRL7cVN8p8ZPSb8+AG4bUPlZ4ZIxN4+qjbJR1U8JnZp1WAcxxiHZQHELUmwR+Pky7VzourQPIn/X6ET1heCLtj58a76hc/5LDxLn0ANgu4V/+DezyHM2zLwNb7QeYYYOF34TxYgOO6ck7EByIs1aASK/njK9hOETe9Lm1apy88zGNWjtFq73qf1wjIk8wpz5B1l+iDyXkHkv5SVhLCUpNcZmz/LYLpusH5tnOiaXwqPD//H//vw5Kd7AhooTHb/19SqSpfHfhW4pZoEfu1v0KYzAcAJcWTlhynnts3C0G7tG0C5i2RbdcoV2ssFytsFicYNmcY2FO0PIKLXVoqUNDLSzaoLyyFoYbWEcgjko5H4ipLOqg5CpobgWjLXMyRbmEOPYj/uaydKEN+dOH9GnntHGRh39pM2EAngAmkGeATSYsShlLjKSYCApcwLNJbSGELKQIfdhcwyZNsU4SRSwDJiophVhRKj/33NMATx6MFq5dALe3oKjkysrOzHQkRU78b3LUZXDTA71x8MycIVFtQwZMBtZYWNugaRpYa2FtfGYMTPqMmyuZoHyKijEgbEgcy80tEMIqfWNVddxMDUCsjWChXkMG1i9AZODIgqMiyLOF2bYgEwwgkk86RYaiAImAB4Mor/X43XEtqk1i31bAOt1gQTc2PU9sAYsBwkQ8iXl8NByAFF5T3PMIcD7/9gR4AjkCOQMTcdxwZiZkARFkMw74RIrxpKgsJmHhvSiYGUwOrtmE8lzIz3EdcOOA3gNDYCaIPWADLngTqFXah6kirayUFGGRyMhUg07IQgyqQop9e3I6iADmeu5jaVHJQFGJSEUKKTfkJaI0r3U7qc7DYrBk9SKsDfIexgDOB7OPJwMy4TkZE2iMJXjL8JawaFo0pkFms0wYDTLwg4HvTVKa99bDkU9pGYDT7XgolFaLYklxlUbwRCudtWE207NojNMUQ62HwOg1sJtFzOFhYIG2AbYOlj3AwQg3wIPIJbok45LqhjDNYT5I/dWQUmi0Kb4LMk+p3nVCztQ3IihTQHVWXGBJVea4xqmHsp/Rjr25KpVVCznQG1F2d12Lrm3Rti3adgljTmGaDtxYUBPHSVVSClXzFDUZAHQjil4LHmQyWySVVCMOeT9eMwzYd/Bx/TJ7ANsorFRb5py+UdIyo8iY5rRUVQYDCJVlTLW2MTDrFuw48hGBftsVoVkSeOOTkZiU4QNQePwQJfbHAlOk/0NBsRcJfAwN+3Awt8r0vvdIO8wjwJ7WJHpSK0UoUqD5/B8Tmt4d6tZP8zLjdxo+ZM/37XBT6TUckveuddwVIi95lyzvdWF9+FXMAAYa4P0WYJ95DALaxqExfj7jFBqTcGGRUysZixnI8/TwEZGyhL484ijPsEM7yz+kch7/HI3FqJz3gzvGGiwWNhpOgK1TAVyYS200TXH3U3zkLsiHBscw1mqRwrn8IPO3pOVe1bbEzmF2WiebUPRF+NMD+jQaldkhmZNtdqeVru/OUab3MGCyILL5IGng4GHySBWtIRK9ZVkyRVkLI9k/vA3yfKz5gIUusmCZjGLW8QqRVR+qZ1EBBDpwR00/HdLAnyHc0xABPOZg3aUk0QtQmv59+Q8sfTbZfZiVEkl9eqYXlsJ0ypuWB+MdBgwAfDRCEBls/ICfrn4PsoyzL77EYnmCs2efYblc4/TsGRq8hHVfYeEusBieRQVzA0vhdO6WHBwGtNeE9lZaohY1pSexLZmgzo8FqwXL9eNiLDSBz6dx4+kJUfTHNHJ6IBkT2AEM+HCEPCq5Si+KrPgSyyQXln8vLUonL1U+ZCWqZzmlG9vn48kE6asYDeT0OdTpY1Emxzl923yHjb0Cui9Az17i9rv/HXz9UzjlCkonagcfFL/DEE5BBos5p2kxxsAzYExUeoKjN40oXDgRQEOAnZgpMuFUa2uXINtidXqOdrHE6fkFum6Jk/Up2rbDenWCpmmwXCzQ2AaLbglrLdq2zQo/Y0DGBpViVDx5hNPhHvlUv8w9GQMTFfEA0MS2WNvCGoOuXcC6Dt3bz+ANcNXegA2w9QbUA+ur82iAkPWgdvIaL70woaTwrETP8me9OfEoUWYOeJRHG1/Mn9ag79fxhShkgUQBfD4VwxCLfFTOipENwcsnGLrCSQwrHj/egaPXBGTdyCljMZwJjsY2SetlLYgHj5ze1utg077D27O/B2NQJzI8YBn8JYP+uIH50y0MQvu6xqCxhIvVGiu7ANjAEAA2hVHTUDgFTPGkiBjdjLSOAPIAmzSUoX/FqYpAq7xeYxMTKzgiIKeYDRlJAEI4HT+e76wUFyOjMVG0UQxQEu85nF4ZhgHeC80ACMFw1/fB08cNwSNiaBzIGnRNC2MNuOkwWI/blcf6ZI0vX7xC2y7h0IK4gUGLcK6+Rf9midsflwn3f2rf4tLcoBZ1nUs9Rwka4/fsiRNKYLED53FCwg85pe7E28Y5MMJpbiCcKkrpPKd06XS74L9nNFcnOLv+y2xs9gycMdqfHJqtT/TxjflvgPke7BlkLDpmEByM9yDvYGybFcmBTQyjEhlEPTpTZAQU07IYx6YyVENWK+Hjlk9x/QuZkb3mEM6kZntr/XhNo9K+WggtPuHp7fUNFt7hV198jucXz/HZZ5/h+fprNOuvQdTCmA6miZ5vFLzN0kkqAGrhFK1kQHkHZg8vMbQj7plA9sJKHg/aG0I6mfqRx1WvTw15mhtst19nHsHcoGt/l/KkMUtjWRkRJnpFyfDDpZFT5pak3VkYnmpfc9bB/u1niUcQHsIvCFgR3v3La7z95jWICN572DgWxhgwRw+zGb3MxwiMLKiH31yuunoy7gWfppr4CA8ArhCnJgeUqTsj0BojHpBRQyC8M0gUKOll4OdHKi1dyRHnfj7wKERoFqZL/qXgz/5+emK8sW/BuAXcl5A12TSML85vsDQ9aMAEoyT6gvxKvmfePKcdgeZldyS7D6RzKxNlF/LoPtiV7g5t3Z80cqKKIc1eqXes7J4tmIPlusGv/vIi/f7+G8JPr9+mthEBZC2apkHbtjAmHOGVzohskX/vag4nXtUXuqEJ9QDlL8we8ARHDOIQRiTIJASQiR74SOUQURB0w+nYpIcLZXPSLwkPH/h94efjQTOKmpQoDIy7NJIagj4kKsq98OHJS+euCMW5QyNQRgRSv0Unh2CEuKFz2PYUJ6sTmG4Ja8Lh3iUNYBu1Az6PWZDBAWIli2kawAhKBOl74smD3iHpFVPemDn5UIX0Wi8Qog9k+SVUGMom+Yx9TQYKg/h8F/0TkwYVnSA9duWA/+zhjoaIclBo8um+Ih4+sPn04iNZj55grg9ncbhIHERzUZwHoXRwV+j9LUzXoOlaLE8vsFye4/zkS3TtGuvmOQydA/YUzbCEoQZkG5C1gDFgY0DkQTAIJ6wpLb/CvFh8VUtM7UvlaeEw/pG+7eyiVsIUVJ2VtTIq1qGUyCE9pcWd8rOJbZMYUpGwsxG1SHYZZNVGZZyQBhWKW8nvVXv6Lez2GqNwTiwGCs5NUJvA0t4Cpg+KHDRo/TM4Y+FsYMI25kd4t4W/dXA+Gj2cB7yDYY/QkrwZ5hOSNXbFNOwj8eT0NB8+DwYt0zQwtkXbLdB2Cyy6JdrFMpyMbVq00YDV2PBZuhrmEF6qWjA4Gh+4+CdrlGL9Np6gt7YNysCmA5MB2wYeFt5StCPIaf0gIBqOgqIxOSqGtGFGkaQNBKqpozEr+zH1Sm1CRfZS+QYAGEjhed6o9D4WlHTBc0f2xbC+KOKiyePnKYyFR8A9H709fEwbjWDkfVB1JgWg9Fv6ztEWEnFVredULxjsLWA7MFvlrqvKYQtnDAa6AcwW3jt0PcG1QzBExfnwFAM/eQKbsJRMGsLMIAQjJBQzFd4l1V9FZ6RbkjYfZk3EKU1FXivxfEXyiDC5yCK7MBmx7Jgm0zVKiscSDxC8pn12y6ZI18KYGQyGYJiDUhcMZyy8ITjjwZZgFgs0XQdrO5BpwbDYesLN1gPGwJBH3zv0bgj1E2E7MJzJ0122KTOnO7e2qQ18gpCzokOZSUYOrcRiKPPRrdglmgAJlZfeRwMEoqAgymXBZ29A3Ch6HReJteA2GO6Cp8kZDHq0wxbWD3BmgAPQ3jrAEPx5CxgCU1hrQrVy6K/0IM1tGhbOOEikldUceQ+hPROjW5EVUntCMSc6nSLnqRmyPqp8pL7t5DHqpjFAg4d5c4t2C5ycnODk7Ayn5y+xWJwCpgvGaiPGhxxOLfyrlXO54LR3yi/ZXncgX8Kj4kH4Vxh8i67swmZZb02iccRbVR8nLz4ajWTVMCrHluMzWddMQqdScuyeEwIsQOJ+7wONYE9oW8LSANuuRXe6SLR/c72B3/ThEIJnbA3jxgArorlp2DUsd4ancL54bGPEozRRbzGPXfYvDR44n08CzPDEFf8BpSeZC8c0vT1+bN3bDVNEYSdHMJHuoT2ektE/5lF8irZ9TP09dP7vD+P1NFMncTxc6CDOvbZlmMZhQRss4IoIA/NFZpki/Cq9EkKb6jbubNkjwVzpd12DU49Kvmsq2Z37Nksu7ljSnZJPCiHhjQFsin4ALFYtzs5XKbSR8waeDawBGhMPZ1YTPX0ivWK2hXdVepx6XBM+zfBeIbUP+igEGcLDp0Onu/sOJH0CKvk8Fp71bsKDxtzKcCF9kDBOUw0VhT4wk+Q+wHODQgBFWVoQkgiAhWlXMN0KTTyUZ+BhwSl6A4Ni9ABO2ZLeR2R0KjSQ47YoxWTymFcGivApk6cPZZf1lC4SWseg+siK/ZGC7jC+Sd9aosRoF3566v1h4B4eER/bUMwtuh3Jdz94NJg9wJaQPzPFGgICEsAWg9/icvPPsC3j+Re/Rrtc4+T5ZzhrX+FX9t8CbgV/dQ6/APyaQQsT6jUe3iAYIOKKNTG2eFnf3VBcn1rUG31p7dcnQzNVzbHbROGQLbJZgQ0E5ZOPsQ+zBVdOWKa6U7nqnbjHMVJ+lryx/Sx3NejyorWWJeZ+KsPDXr/Gsz/9QwixMxqH3N8anmXqG3Re9AJML/BH2+DWOmzPLrExt9hee7iNw+DC6eHWhxjqFh4DgG0khmKFNQgHUynF4QcMPIhdsMrnSJlIKjhqYUyDbnWCpl3i9Pwc3XKN82fP0bZLnKxO0dgWy+UKjbHo2g7Ghjj3wRjRFLgj4Wg8I8XLd/EuCO/FO0KIq4UxgI0x8rtmASbCrV8DzmLrLIiB/myTPC4MISmN67AgauDTxjKagTpuZfU6M2r1C67Ssdrsa+DEOOi82bshsicxHJJnF5mMoMCVWPos3gcqZj6Sktan/DoGKftw8kM8IgRvZRmK9Z8LT4m4BjnHHpVTESG+osH63Z+lctP4RP6LPQOfMd4sfot3q9+j+d01uu+3uOZLnHYteNHC2gZgA2MIxBw+4ySK0cFbMSKYvF6BZCwp/dzUxo9AFxljqi+oKR4Q4o0RQosBOqanpE9zFhkWYSYDsfRgbwByupZi9oljP+LceSexP8OacxHfmT3IWDhGiLdvLZz3uFl4LNZrfP3scyy6FdiswWYBNmu83hJ+fBMNyDQA7IDuJrXBR08NLphAGTtFke6yXQszXCmCIcyxoomIHg7hLp8hrPfo+eBc9IxIng99uB8gGiCcG0I9BZ7nfQWj+oH+lNCvTaTXFh3+HA3+FUy/AbstuPv/gfxrvPzDFkPT4/W/X2NY2GDERI4DGmaGo4Eh4AXFu00EfLyHwQBgHwxBHgRjGPDBwweh1BByKw1f6IWvNn4jnHjB6aq9a2oqVCrJLnNAwkArI4VkKuig+koA7OUWZ//1NZ6fnuNXf/YFPvvVn+PFq3+D1lnYDWAQjc7GpPtLjHjAgfK2ogoP8yjftVHfp2fg6M2Y3suaF7zKpeWQhdnor5/ndVqMMPIslJRBj++8B0QeyymjRBpXZYyQkRaaFGQV6bPse0l0qppLwUOMgGXP6HpG82yN7tUq7TU//vMPuPzTu1TO9xjwk3W4IOEmqlGYJpkfHYyMEe+n0o96TD41uKPE9ciVa0l94r3MddznfTRch7MbwUta3w1DYMhlQdNmxA/W0184vI9F+6mX/zHBPebLA+0QwstuvIe1wNkzB9MwFv1t8ICGObjkWiNRvlGP4w8tWUxL8DndIVSAEA8pjGTNO9KQgmkZ1z9dnuIpp4pUSaZTKp47KbzHfZkueK7Wx4WLFyc4vVhh02+x2Wzw0/cbvPupx3pBOOv6gocHoHRKh7VNZHDvfRl1gSiF3i7Sxz/hQJ3wvS7e3Yeo7yb47I4HQcAQqpfSXMtBQgnXLLyxNlDI9/Fxmtz+Hb2Loi6rM4maFx/1bDeQwqOon5HxCPIKQ4wQSSIlApsGxiywvPgM7fIU58tluLMCPTyCPwtAIGND+GmT+elAEMJB2xy+OYwbqbEUXj0MkBgbGIiHdFnCQZiYxhSCTaxL8fIsbdCGCyDLHZRwRPO2UyM7M5STB39+SZzHHQwRuwl1nWLv5jEi1ndoCZdl790oHsv4sFdnP78R5PdzdRdqBzB7bIcbOL9B11m0qwVOTi/QLs9xcvobLM0zMK9BtAAPDWAZBB8v841KAwOAOK452mGEmG/vaC9KBLn6q4hgoJ/5WVbmZuUD1MW9OVa+uMSJglYUYzn+fVFuYWjIG2dWiEi96lmkDukUrzJAwA+g29cwjpMRA8xotpfhohzvISqIRGyl+ztGMamLYtiY5RBO9l7cPoOjBc6WBoNx+GF4i6G/Qf/6JhCnqOi0FPrSEMuVIZH2hTsS0sXj6ZXGszDnxlqQadA0bbzAPFxk3rRd8oZoxBPCGJh4MTSlf0nTmwS6ZIzQxocUsioqTESRRYTGrUBowC2BrYFxFgyb7owQjVu6wBjSjX3EndVHxoF6bmo81k9GZSrlmk6hcwijUJSh8TxdtqrucYAet7EhIuBpUJyGy1715awS6iS+52yAyGny+ktrhTOTImFRBs9Av4G9fg04B+PDOrBcrZ2MRamPp0sHOyxwTVvcLDZ44zdoN+/wrDlHRwaWAPIGnhjwsc7oehkagST4hxMakXFIeDu1mkqviRElLTy7KK0PI/hDSjFIVeaJauMMJnzTLaL6G9XFZboGg+BpEp96ALfkwY1B03XougWadglvl7h0DSyH8dv0BO9DQ03sD5tyXEYRiCdOptS86byBQtHa4n1mhDNOeUUDYig58YRgMfDm35BL0VgME5zxXvaOYj3KHlERVu1FyxaGLWjBABO622fAQMDwI8g5dO/6gNOnNimlJHO6pFoUyKASfxiR5oW4xRxxkyJTq0N8zAWH1Pjpud56Zf/KOffxSuHgTSgoK3M1wtYliHdhSOaGAXAea9vibHWG8+e/wmpxhsZZWC/GO+31FteLKO2SI5GKf1zTv0x8VMMrQ2jMqL8XxidOfyrcrXBfd71IOEE7inUtbtWYpgF7ILVZ06/8qKpQhKVxm1ITmGAYaBG8HYRXWa1a9OdL8OUNeMNgQ/BV2Llxofvb/wRZ58vbV+gDK52myTsS70p04PwfCo89nu+7/I+9/tGamhUCMz/IezBG+ItfapzmaThoh9oDj5X3rnPywbH0FwZz87NjPSk+M8iziAfrOPJhmstVMm3ND6SntaG7TFff/3a3lV7qaGZf74HSz3Xq/aHtGGdQw1nRu3vA3uys/j4V5L6SJTTWYtsbuB4gz+iseEPIIZGiaWU56jblkSpPXikdUsCVeMfAbC9FOhLNC4dwrqy8cibuNSh7xpknrnjqohqodnPmIcedDTha4DkBHN0oxMvobvixn5ZKj1O/CrY8yBJMHbhZolussOiCEUJHXynqIhMO16aiovxVez2A4phFIUsiqqRy5U8UpAQBGHoQcxpIGfFXbVykqTsn5DCSmhG1TKd4CtW60Tuef/WzhEcxRDwE0mTvSjOzLj8NNqNs6QgdC4lNFpSB5y1utr9D0xi8ePUrLNeneP7FV7CLV6DtvwFxgxsyMK2B6YJF0Jom3BFgTIhmRCboD+bc+euRT+tN/U1K//AkzwWrbImKZ0WDEFcA9X0OPhkconLLu4AHXk5B+qQQY3C6qV4bFoR4p3JG9XKOn8+c772OZXm5+4HlvYfZXOPiu39EM/RZbOF4BlufLJ8ayolhrQUfinW/2EQyefN1mpdt6/F3Z9/jyr/DD+9+gO+HcHoLjCUhXGgrBJEJAwx6Chc4N02DxhrlHYF44U8wAoAItl3A2gVWq1N0yzXWJ2dYLFdYrU7QtgusF2tYI7EWgycEUbi4WgwdQQkWbOrOM5wPMdt7N2BwfbpXQLww5DLqpmlgqMHy7WcwwxKX5ga+4WDoaLKi1USFoCj6Jsc5MRojTE3fEn6odFNFpN+FEqwuVZSvOj/ncuPmU6wV7yJuBYNTMDh4dQF0jKnPQ3zv0zoIxfj0HJUBQhiVYPRxI2NERLFoxMjGEjEucFwvznmY6zd4+d//v7DDtljXmhnSe7R8b1ZnaFYn+C8vgH/6C49/+Ocf8Icfv8V/MH+Jz5bPQNwErwcAbAjkB0h89XC2OjJ3UepgrxTCqC9/5aJ2Fk+H0ayG/GLESp4Qck9FxMlJWqhcLIUJTRRHlhznMZaBIQoGXoPQF0PhYaIpYJh0wsYAZNEbwtViQLta4jcvv8BqdYpmcY5bXuDNuzUACxPvUEH0YCuYknGXC5pUfHKmQUX20ZKI9DFdqq7pfHwf8Tbja1j7YLkA2cP5IV6I7OJzl/A63RGBEq8Rx1a3dXLDhzBzZd/9ixbsGlz88a/B/hbfd/8Zht/i+T+/xbA0uPz3n8GtbPIgEtff4BWBqIDXSmRCDCkaGGEwPAHO5/UgHk2eDAg+uhDnsWX9Wc3RHG+5n5/RKxEThZUmU1lvzAw3DLjdXGHhBnz2/Dm+/PWf4bNf/S0W3mJ5M8BSMFKnmLbKuE1qcIrTPkJXYo3lHOZ9OX0WgwMEA608naa/kFWY0ELTWdYpEo17VJg4YZeec/ZMYU7bQB4rQqYVmJjbKABJmMVVDyz6zLvQZ+dYfnGG7//+T7j8/l30VOEsaz1uTx8VSgFrZ6IHQl4E+9fPJw4/687dAQr+Twi4eh2f520+7G2s710T3ni0KSZqhpLaHeEIR3gY7Nu1Mh1ntaZrzqPighRw9X2cIik84+V02ZtYlM5cZyiLLZSeu9qyH+pi5/YvddB7tllTZe4f6cAFlzzZrpY+FcdxSLllj/trxuW3A4gHPFt6dE3wvBfhN0dMFTqv7oucGbwg/oRQuBxDXAdxMepQJDxymaPkWZMuQHhbEw4jkgd5k7MB6QR/Gl2PQu9V1DE5FqwOv5RpCv2HekYkh0QfurPNc1vpEBNrmSC0m8miX7xEu77AxfkL2LaFteGQnldu5EHeVTx2WUEaAuk6UQxiTqLniAcV09iEBR8lIiRDgjAAampCao7389arVIhSXP9xjglqzpSRIryWBUzIl2lzrjst7rwqp2b95w4PuKw6w0c/aHNr+UOBJpRqU9syw7HDZniDHlssV0ssFie4WPw1uu4Ey8ULkD2HRwsgXiIJBMWBnGaMx+JTbPRC8UZTjUg/g25hYjurNl69ORXKhLQAhQhpRUK+Q0CesTohXnowyCW+Qsi0okG+5+dZ2ZHLygaI8N7HhoZwQoxh+w7ebdENA4zzMAwYdwvjesC7zBZx2c+9U7sjXSI5Xp2qjcyQJeD5sMKSgebsC2y2t3hzfYXBD3D+qpC3ksNLDJ0h9zhYI8YIUeiLMtPCNi2apkt3Q7TtAk3boWnaGH7JpnKyEiq3m2PnPADnPQbn4L3D4F0KzZT6H/FPymTTwlED1xK8iUpZsMLRyCQmyTCrMjRRHrtHRqLN5TM9EXPTUeC5YiZYv1cbesZvhXe5sPBKjFxKaS0K2HCJdwzR5LWHQzgpjhhDP/Qn4r/PoZzEgCDrwLODEy8IHy+xgodPd7UHwXu4vYJ3A1abazTeZWHcezTba2DoQcOguwIqRl1AneLZbsAwOH3r8HnfoN96EG3xdvMWBMKL1RkWaDEQwXqCcQgGCQqhmAzHEDsm3OPijYmRZqbCdtS/88Y9zQ5lRaAoKkTxUPAS9dRPMnPjV4xMS6QiimvNmBCsx8QLxbJiN9zVc2sZviU0iyWWi1M07gUwrHDlWvTcIMQXJfh4Ckc8fLNgNj0WgqZTy2AEPE4QSKfCseK9GCnE4BW9nry4ETswB7xi72IaV6RF8Zujp1CtvFadmCSiM6eSZM9bdSACFrcvYH0L8I/B2GBFmR7caLNg6yV7Qo2EU4k2I417QF2CIQNvGOQRT+tFY8TMfqoVxzvZjlxx0ef0jgHWSFsVVqBrhQg0eLQ/3GKxIazXZ1guVrCmhWFpO5JRLRjyIl8h3hBpDZXlalrJ8kSMn6jxSFHSnLF4m8MyTQ/PFKQ8e1MGKFzup1NMv+ZREkSSFdg4eZylw/k2IOOGjjFr4kNmxoLDabzVyQLOOVy/uQYPHrwFGk9wXQjPNtX2fWOws22fsPZ1ej+4XylzI7sP3u/wfYjJ2lNn3p6fuPrxOmZj4boOvlsgnWiUUJaVwJ+8Ivculd0J6j3paL54Sng4fTvC+4PxbO1eG+w53HNY7LVlnvruh/2oMFOnWvv7yMD4Xc6hyVFBYvIGP23k0OXzuA259H0dnGAEDx2eex3cqAWN9w9hvIJcZa3i6ZL+p5718ThOdaFkq7Msmvn3aRmEU9qSC02Kb51GeL4ZiaDeP0ZvqZy2h5+9qRnbAwrUjO/MI9leJSCuMRYwDVbrUzTLU9imgSGDSaNImk4qymPOLxMbT8h3wSY5n6sx1nXojT9+KvwJ/LfqTFJoKYGuGIs4s8Rg5W1RzItMWpp7qWsKds/B3twim9Ti6Ee+ZT6KIeLDwj1G+IknZRcqjQlZYJgdMy7hsEGPq+F3sA3j1Rd/hXX7JV7gf4bhFbAxgDFoTQg3IQpna0QZVgnaWrE7rcNSup96G+SK4GWCKnmDvqHc+dKJ76iUyJtD/qfjgocwHTlMUkgf84sbg6QVBUdS/EbFrVIAi/FBNiQvZcboTiGEyICrd78Db97i2a3Dwqk+qAuu65m6+2IeEy0AIdQHIyrWGTCEhg3+1eYMDivcnFq8G7b4b+5H3PTvsO3/CSEOXiyVw6lvQwbW2OgVYdA2wXUxGBPixaM23g2xPEHbrbA6PcditcZyfYpuscRisQzhmpoGhkJZdYgOMQ4FIwQwDAO2Qx8MED5cojv4IYYFs7DRCNE0LYyx2GANHjrcrFw4NW4MrChvSQ/VLjGuPvErP/xonmZLyFYzlDirH3N6XxvCUitSMfG5GLkE/7yEVpIT4OL54LISNz6X0DZgpJPiyWjn1BrRawihDqdiSmbjRsB75z3YOVz++A345i1evfsRK7dNfdOhx1y9pmUcZuaAN9cYNjd4eQm8JODG9ujtBv/8+rf4p6HB//T1v8PzxQUYDGsIDBNi9TODDMFyAzJhLRqiaJgTnAuXOgNl3H4AxS7MyJ4TydYq6yNdTB1DfCWF6oSXjSLWMvXiVSKKeaEOnkscFKbGGAuhsWQU3aLgVdS0Czhr8HZlYBYLfPXiS6zMc3SXfwG3MXhHA2CEWQs0PvU13zZfzYSapjxpCbVrQxvrXELz03t9T0PGoZSLowdOND746OGQ7oaQ3+IZMbj0HJ6TAS4ZIKr7W3T8/7TvqG5rb4VaTUwEwAL8ogVcg4tv/ga8ucGPi/+M28V1uOw3XnIPNkHQTbc7IHxXxnpdvjEx5q+ncD9QNDAlDy4KbdeXOmeakckMSztHyBexSOE5S+2KCR9lIZUOdV1jgcjcDDj/xyucL07w8q9e4PT0DE3TwoJgzQBDIQxfuh9C3OrSAEtZeb4EP0parGmkGFrjE2VE1d4QadGlJuu7IaRIX4xdSaN0uvySwaVCYySMHABzcxDDwmYUDbOR7zDPoqk25o9aIHjn5UEUoslgtfVYMMCfn2P5xSm++y9/xO3W4d1VwN3uOeC7w7rxPmHfyD6+orYe2cco6hHLfAyY2QZ/0ZDodfjCzHDLDptXn+f9M95TlkJW6st7Rkt7movUT4/jfoQj7IIDFZlTEPlt229h2YBNk7yZQ8mK50MO00oqv05Rt2qqnVPeBntBK0nv29dRq+pydNkUvSbDSf1Dhjhy0Yk3k++jog9qP8/8fEjfHwbhfkxCQ8EQYSJzXRxoxVgFnWCGkLMqQ4uekwFFYvfToTRShoaUOMoZip0wCAeZ2FehpCICj8KKKTzLcu5uw9Yc5DMyc/zN7jK1DFMo66WpIVXsgy9wzjYLmHaJk4sXaBdr2HYBEMUDwz4deoo385Xyai4m1VA3THjtYAwwydO4OK7IsWzSctLUOMR3ab1JOnUX3WhZxHU6Z2TSujT9juKBtw+4nj4GeJAh4jGGbo6uaiH7o4G9jcmtVuRjb5Eb9hjY47r/CT026JYLrBYnOO/+NZbNC5BZgBoDwMaTskYpROTEp1JozFLgcT/CZqUUFxWBC2tE2XX1a1EcpTRaEVFeRB3yysW4QRnhk2IqKhrkQmkRGEQJKAoH1koOyZvDinggKL6QlV0Sj7zfvoN3Gyy2PRo3ADfXwDDAOM7KkFTHxJDdExGn2I0Uo0+5sQl5tSC0WOCEGvxqbbDxa5ytHLZwuESPYXODzbu3MAS0JjihyeXVo3AaFJSbxjZoug7tYoG268LdEE0Da23yWpBdrtgCZJ5AgA/hSQbvMQwDNv0WznkM3sN5B8cO1hBgGH7pwAsP9otwOtkLUxkUXGIwS3c6TeCqwsg09omdYi7SiDKwyD83YVx8VEotlY9ZjYEyShTligeDtFOFnPHqbodobJPY+YFZ8vmy3oTvymuItWFNlRO/O5a7OXS8fsb25gp+2GB9ewMzbECXP4H7W1jXA84lNM8Kv3p8pliAcuA0owdmtGhBvMSp8WC7xQ9XP6F3Az5bnqCzLagLp68NmRDCJrqqhhA4DBPxONwVEhR7RHJ+PTNopAmbZg6FDmIal6T1+S4K1aPC4Fh+SzYmLnqMTGDj6XHijM/EUYlLINOAYTC0BN8aLFYnaJdrdIsTWLvC1jB8E3eL6L2UeilrOPZ/qkOafykMZDNGJJ02zXIytHCmzalgMeZGQ7HcBePlDgjl8ZMMahnPwyXrCIYZrTTW46wNf8x6CupmQ+5kGPvCUHK3p5MG3C6wvP0Mxl3i9scNhpXD7Vkb+FAigMWdliPjOw0U/1CMS0omMI3ByCV4KkauaXrD8RWnAvObxC1E+pV6lb6Qmq9Qtye5+omj4jsLAuWAca6DCMu2w9nZOc5ffI3l4hlsz7AeEX8j/kHRZGH3d8grmT4CrOnJDA2Z30IVbqj8GV/mc02Dg7WXILodC5Uqlb60dqyY3M1ACSmRy+yIhELInh6K0CQnTysVhJcMRSOdnKzKYs/Ch3CILQgbY3DVAjw4vIjzVp/0vg/sopt3hXplPho8WcFz9Wjseh8V74ePoxUfFxTHhRTfG5lZyAEmkQMOwaMxHXj4GvswcIiyaa5P9xR4JvN9qHH7+NbwzxceOr4SHaDcR+dKpuJL5pUJpZpyupxKGVjDHtQvS9SJ92UM+/6oZprZdkb15hP549P5uzRm913Le8rh8aPHgR1zAwRZT+7FjAwr+/LwVCoG1bOp4mvmhxlT9+3l14p3K1k5JKU1KTacOGFc5LjT0NUYz4mPjM8I4B1teSidPlSvpXnY1GoRbuoVSrpVQUM1mAUau4ZpFiDb5j16hMPCOHslf9C4ncK7M9IksCpGeOiRzE4Id3gU78rq04XzRFXzGEGI1AZBPYuEMsyzXpNz/jS5j6Vg9TCY84zYl76G++o97wofhUfEfbawT5atqGk5A1fwuOEt3vS/hzEDvvz8z3C6/BIX+B9heA0+I7AhNE1QVhnkE+tkyjjO07uZ1oRkZNchRrIiSytgsyqg1A2wzpUMDOnssFaoAsheDypGODjfCSGX9AZLQrZqS3u0cji+06fERQkblLZxH5G0MUTNzdUfMdx8j/ONx0m8jJqUoDI5VY++CCmNmVQg7FNmoiyWfIKOgLPVORx6XOMMb+2A33ZbXF99j827t2iJYYyHoRBGSsJqJBUGGcBYmLaDbToslmsslidYLdfolmt0i3hZtbWwxsb403FcwqSkVnvPcIzg/TAM2PY9breb8FwMPgS0NoSi2Zz16C8c+PtnWNyeoLFy0jYqWsnkfahayRojwVFdrrweCqMZkO+fyjtPXdDoYeKfFE7r077hq09pkiEstUF7YdSXrsc7IWKoGg8G/AAPjorZfEm1eEqk2Pux7oTXPhsgxJPCR7x3McyN93LfSVD83rz9DsPlG3x2+SPO+9uI50FN6GtcL5TwakB4avg07ShZ/dav0PoVfmV/xHM74O9/+mfcDgb/02d/gRfLM/DpGWzTIHhvBYUngcFWlGk+yhJRoc+ITCYHhkNp8zKZi7+NhDEKCFUa4uZmP5+oElrH8VcRViu+9yp36H4oP+BxiE9KYBhjQx7po+3gLWFz3qJdrnB+8RXaxRKnpxdwTYfLbQ+AYW0T2mwqRUpi/rKbcEF5hX758WyV/eZyrmv8TmtNPHIybWUg4l0wOLJ34ZN9DMXk8kX1LntGJLz26j6gYg1ppiv3YcRv6jSCN5SNEZnhIsAC7nkLindG+P4a9vf/H2xWPf74b1/AiSEhWQZY/avqTcKhCDsMywQYhuGgOCZDKcwesQHgijLStAiDy1ySqDjFIszkvtXzh4SLxD7ckwJM2D6U0Vbu+yDAWMLJ6RrPPvsCZy//NZbcYHETPdjiyUOjeQkT26Dc1TL9VeuIo5JP3fmUaQRPfC2IT/VZv5G++DRXiTbzVPpclzE92uYbgIYJo9wuznE/V1nUFeeeo7BoYxGF/DtXpNA1KTPidLgckREj1WK9BZYe+MEbXFmDH7oBb63DM+ripetRqH10XuURYKL/mpZ9tLBr3o7wYUHT1PoZQphSJpN5GPZgjxSqdd/klsqLIxzhCHeDPUrkIt3uR5n7IMWBBBhzxON0SUaY0dFrDqTkR3MJtYRUiKwH77kq4Y7hYdVWQjxkEBlR4Q2LAwygpLieKnOyS9Ms1CcEgUe1xsKShTEcw8TGXnEcYq1/Bu7AICUt1vSBrriN1IrbkScDPDgeeOIoNzCCvArOfFvKL4fXdDnxbkGCT3qtgALTfbmXh8+9oULkpIvncl0RgWHRt89Bq3PQ4gQU4mnlRKAcJWTk7WFUaVIXaeIA8slPIa/XkXGpbHuozuhHKLwdxPmBCCnedTI0xEsB84ToAYiGDGljlCKLNNKv6ZX46a7N+8NHYYjYBbMntQ6erQ/HVBZLdaK9t2A4CpdeGmqxXJ1i0Vo8W/5HrNqXoMUCMOHySLKUjRASesRERUxhhJDfU/3OjRgbIZRQnHUIY4WRLkcrIZJiog7LFNLkkDJRpSKhmJRhQZQNOSyDbC5yyU5oWBGCyWvlIScjxNC/w7C9xmLo0Q0DaHMJ7j2s89HjamyA0CIKjybufng0FnsyViRXviJ1ABPnwMJgQUucsseXwxJvG2D7+VcYNtcYrt+kMZITAczBcBCYlKBosk2Hpg33QzRth8Y2IXwSUbw8WJ0mIA8wJeVRUEAyhhiGadP36IcBm+02nCnmcNcDjEG/GDCceBCv0F22aIYubqzpiuKg5Br1eUL1JvOcGAMWq0RBviV3Vlju5hJTXlH6y3PBb7UAxgYIpUwV3EeJr8IUpVj6WrEtJ8s54DQk3IvgfOXFUxskxOgQFL+IoZkC/jdvvsPy5h2a6zfg/gaN6/MdLLlLY06F058dozb1Rq+fgNONX4BBODcDmnbAn9orXLaMi9sNlrbDS3qB1jYAB8OBMGb6AmpjONjROCjiUoglEy4QE6Ob1JtZN8GrCTVXYgIkm6JpomznUuGZjJlC8SJvwXIzcfTwIWIYeLDhLBSYBkzAsCBw02B5cgZ7sgZ/3sHZDltagbkDGZv6Zyh6M0EMinps9T6i53OHESJ1UeG5omlcvOdghFA02Ed89MghmcTowMoQ4eUZZ0ObGORS6Dx9AVvVfgBJYx/SVv3RinkOasygbdaK2zxW4hnhTxv43sJsLKwfcPLjFsPCYnNhoydapMFS5gTml4x9QNDa6TCzsuUa0qXV6Cf507xUyuvAw8ZME3mVfKqfVr8YIMBaA2stFssQhs8amy7OkzuExHCn/AMKI0RVu5Sex0bjFfQL3alRE6ce5HKEvlZ1pN1gZFhTuaMBZiy0jddVmteZluyD7I0XVexcGsp2ghhXE43RhjUO95FEt/XlizVOTyyufrgE3zCwBexAcEtG1LvurmpvP4omPQIc0P/3DXdh5aq0h/bmLlV8CjDux0fWwwnED/TLZL5qlv7MFXc47n7cRrUDOjyaz0PyPLQdh4zZfcb1Y56LjwXuM893Hde7pafiT513as/WBzryCqT678y+PsGdjF7UBoj7gWyq4Wv4mOI185uDoC6i0kDPtlx1NBVxl27OMVxPQjPGsL112FwPuLkaMHgPa6PsHL21U4hU4ZuldffQzo+6qpGsnNZpnXf0/PfRY16MSsXByXu0y98xz+Pxc2WhpRmFE/aGbgqXTkHGJQuzXMEuTgBjwWRSOCKtDYvu5tmDvFjl8Q/zpJy/s5tSVxSaOM5DPk8pfTG68lRfaJQKyyRZ8mm1nIG9aNR0ISrbtKypZfIRTGR5yt36Q8BHZoi4L/Px8U5HwuUKPIAbOGwJINuiIYPTkxc4WZ7jwvwPMHwKLC24CcoEkhjOCMo7I7tsYR3cPX5ZeSDsNmfFUHycFW+cMykFQ7HdsXrOjByeISoLVOilYITIl/QmowUDIawSZ4VUMmJIHRyVYjGtMjr42hAR022uf8Dm5o84vXU4dz4erOQkk6ReVDvOPCZNCSdTqadFN6rS0ETS6dIsFnyChQMuPPCDXeLyFeHm6lu8uXwNMch4BjiGT4JBUNqShWk6tO0S3WKNxWKdL6qOxghCpL1Jme6CVTrePdC7cDH1tt+iHwbc9lv0g8NmGCJ9NrAmlLU5GzC89Lh4/RLrn56jMU24QFtcKQV/ab6/8kJhaMIDP59cjfHuGYydTLielWm1QlqMX+XmUxrtRMitDAbsUrgaCV3DYLDLHhMQD6GEt1AK8JjO5ffeezjnwlw7H0Mz5fBM5z/8Hhdvvk3jJF4QxfpN61hv4/dhucscMoatP0HLa3xtfsCm8fj759e4OnE4/Yd/wenQ4D99ucaJXQExrqdtGOQphmYKdM37cOmzMTEcDoWQTmAExhORwVFrJ1wILUp8oOydxguqmG+lOGVED5P4KfOv1wZiYWRA8aJtRC8OD45eSQBsC7YEftbBnqyxPH0FXnd4+6XBFoD5Zg3jW1gbvESMGd/LQgWBEEGjNCBwQS9LEEV30cc0X5zwWGhqUtpwpqfJwOAcPIvBwcffHix3nERPCJbPFLoprw+kdqPoB9TY1oa/eTEyhrIxM2ogSxguLDy34D+1aPsBz7/ZYrM2+OH8BN4CYJPqllitO1eCbLfIZ1nKuvX4hl/aI2Lmqo/AH3hEy3NtpK16Hpnn2XrjH22qNcaibVucnLZYrlew1sKigRHDnqk81GYVAspAB0Tck/27MkxAj2WmPUVz54Y64YM2QkTDbEF7pa+SZzyH43XBUVDSKgsFJB9T/d8BggwyP9oYwfoCdNXHCWOjhGUCxCWfA+6QwemX57DwGG57bHuP62vC2gFtS3CmFm+meeJDuJfHgClO6X6J7gZPp4bMe8eD6ngSrcAvEGaGUVY1ReOqHJQBkPdP8HQRjIpIy2yXfNJxBo/wy4L3jfH6cFH5VP+KZn8ApYcdqaW7t+VJfz/mVuZglgZo3kfzKPNVV5xuwSDsTHcXiW2ccswTFZ9PxRTcuXDd8/C5uRrwwzfXGDyHu1Kt6ICCDCy6BlEyaHnqoDFLW0WIIlDzk3JavzqQrzJnHkF0TXIBWMAJHUnhsLEgAEwU/GML+ehD7URxT6zcsQtxNbPpIUqA7WBXp7CrU8A0Uak/xHyhTz5+MyB4YhXxySg+XvjmHEJWtWiqlaOnYqhi8XRIqWVsSXlDIAsauZcovCKkWWkMTHzk8yBMrOJ6/mvJdy7dzxU+nCEirLD49eH2Z+oG0PMr4LYFXy8e3LxxBfFzUtgeo8wucrEBYwDDISDsdvgJxgAv27/GSfcKWAVPCNMYwCIqcIWwRkE6LtJD6JHXiyl9CKHNDU6LoVgV2tggv4tdNz7JRoh04lt+ixID2gjBKRRTJrCqDnWayatT45x+R4Vh/Geuf0J7/TptHu3mLZaDQ+c5xigvx4RnicQuUBqHnWlqmFF83FGyIQZWvsGvhwu8bje4+WIN7wjYhLFx7EFs4nxHF8amQdO2aNsGTRvuhQiGrYhH0SDkfAwrkk4gEzwz+mHAMDjcbqMhYrtB7x22g4OxBsYakLFojEHbr9C8bdH0y6QchhghpKvVBjIauWhUEVyQaQpCZUxVTR3Fdu8MpagrSUWI9qg0QrDCw2LZ8DTuo8BfpbATA5wyvOV7InyKnZ+NQKL8Lo1rPoZkEsOD8x7b2yv0t1dY3V5j3d+iu7lURpSawZ6ytrNKp2AXeh80voSWVyDX4utv19gsLJwhmGbAN+++xUm7xq/WL9CaBgwbL68O/IVJYUls0tUZ48EU7j/xnsNBR3iwN8mdddTERB8LEWXcVEXPpoZHG6o0Hkp5FEP2MDMMOHqtETZduPthcbJGuzqDX74A2xbtlQGhgUETLwgmgDLznD0hKLVBfnnVCFbfZ6ehSjtlrAh8ckm3M86JESLf/5DuhlDePYH++hFu55OoGvcUzhWGEah1VA4BGMW6FrEiSJEA5N4IymUBiGGTWjTnv4YfLmEuv4VF9F6JTG/G9cBYh9ih+/YCYUZ3LJSJx4nUK3oyOlBTp63zpYdln8dVxl9bB/unt1j4BV6++hucnL0CmSbexSL3W0SPCMieUDaoOGyX1kJJO+rujtaNnuvkHRnLmaBXUf+eaFdJhKHmqORhdDvucgqOir95AA7WG6d0AVnFGFHiyJz2VCFuCs+Uk1PUliwHgvFA44GNIbxpPbYGeIkYBo7KsfgUISuX7gKfiGr4EzNCTPJmM+92ZnwyKCln3sMjZ6dOn+ocdd5yy9WNr1UZSb0Uf31a87kf9lGOQ5nCXZhTP7vvGN6ZMB9hBE84NrOs0S6BN/Az3jbw1ozS6V/TtEid0j60a0rOHJc89Vs9nuF9DgIlt7J+dkCBY/408gyEin+dnoTprh6w9p+EsdCdnqIJpTwk/GprBjSNR0Mq6oB3MdqC4E4ujzEuvpYXRlC/EBlNtNSKKQ5YrZl5LiaW9W9V724e9Wk4uYP7KyCGnPs0hwCyFtSEEOGmW4DJhCu8RT6cmgeRQzjcjwZkeUnujyw85WOGbMKsVkksS2QZUvhUpJ0WP8uxEOacuEo/sd526VLU+91Du6+Qp4X3xba+f0NEEVNLPX5oucseZtmDX6/BN4vHnbuKNk4J4HdZ37dwuOUY3gOA5+/RdUs8a/4dWvcCWHbglkDWqAuIERVfAJkJA0RBy/MCK4R9tXvq7zk7j7QOHDsRilGnFNN7rXTIitlAZ+Ty6ajsS+GDYhqJry+nlUTBEUN6eLFY+nARdX6eyxNDRHf9E85f/4ta2Kzarfo/mo+7IsojE4UxX7ETTrzFiT9D123xx1+fYng3YPiXPo2D43xBqTEmGiLCBdVySbVpbAgFAwAxhqHjIVce2+S8x7bv0fcDbm436IcBN/0Gg3fBNbKxaLhF0yJciL05R3N7hrZpYYyJMchjOJ2Is7WuNTYh4V9piArfg7fMBBOmmLmZu2Inx7pYt8oIAEZhFBMDRVYAJ0RXHxq3OSlhk1eDGB2iQYERjT4cT9SzMtTFteHlToj43cVwTM5nhfD2+i1u336HZ1dv8GrzLuO5tLlgsMfjMDtcB6F3TDQpvAOdP0HngdOfABiHq2cWN4sN/vGHf8QCK1x8vQaaJcLBFgLHkJHWiFIUAX/JgJlgilCOJhxmjwroAmJ7tEpRtyu1vmIi5Runedd0u1aqqjKFJscExhiwJWxXDn5p8ezsHO3yAu/oGdB36H5qYSiEyiETPCHk5E4+3V+uQc0R1QpgeTEmGcksrPBBv0XGu4JOioFYwjFxNEJISCafQjN5Cc2k74aQy6qVcUOkgDzkPGoL6/6mFzRJC8ecQwk6xqgxLZbrP4Pzl8DmB7DpYckDRHBkQlNk/uIFY1qYm10/kYcZkzLdzz0NrZOkHzzbd51uqmlFexng2x7NP/yE5y+/xvM/+yu07RrWNPEOFnFlJ4CUYTp1SAwdrItEWh/TWJX3fih+ACUfoiecMwZgsleMIkVKJviq50oMsSJw7N0UKkE3Kh/vwnzrMGrx7FvAIT2Usa3FheSjcmK6KsyCnIBcb4GFAzo2uDYGP3UO14PHC5q/bP0IR/h5AyNZc5F5J2OikZVkzal9TmcXBcWo3KMC+8PCcfw/WXjI1BkDblq4xgLDgGneNosdadeueeUDmsEV5zHmaOZ5h6k9nNXfUd4dbMionZEmSd8P4WAmecGJH1x/f1/w4MqUTGgMrAFWzZDvTVQyhzBv4xC3d4fa7JyVzZG/k4geupmVbpOZCyMFJ+ypdAplxZmzzVU+4qQ94uyP1l7ZIzIWpmnRdCs0bTBESPh2zQ1L9AZD4UAig+L9ElQibpRZjBrjsYdzxcPHk02SSspMoZoOWmWxDQV/HnUAehAmhVkpY9fzHe9ny/z5wJMaIibkzvxlwhgxlTfh310qfew5q5qaxdfxCcpR1ZVgqdPdDj/A04CT019jtfoM5mwVF66BMeGSzHAqOLsUTcUPT19FaPfFyMdvSilUNZYnngFQJ1WBHKKmVs7WnhCiFMhtEUVtKFBikedTs6WCTSmhWRRjoQynPCFEyWtu3mB59T2626usYGSMrM33sug+GtzhrN8EUzV6B2DtWvzm+iu8vn2L79y3cM7BeQCeAEfoGAAsGtuhazvYpoG1IahI8IAYwDDgwWZhjeVC4+Ct45zDbb/Bth9weXudPCLEotAZg4YItlnBtGewWKCJ7pHGaA8e3SWtaBVmUCmvBFfkO7gyQnAxDgyk9h+67jVuJOObUuCLkrbE+5Q5jiEQwisJflcnwuP10AHfo0eEn/KEyOsGyRgSLrsOp9ElLFMQsu3b77F+8ycst1cYNjdYDxtpfh7NuXF46BpI+dUc0mSCPFSe0F2tQHaJr6lBD8I//vQNThYrfHn6BVpr0XhtkBCmjYL3Ixkw4lpnAsPDRrYwMTPE8RYSpH1bKDOJwY11o6omqz3DV0nT1CAYQQLuMxBDMzFlNtU0HWAN1icdsF5iWH0OZ09gfAtubLqUOhiSKcfhl8/kRozMIKXtcnpemTXu1wnyus7pOScVvGcUBrSAx055Qjh4CcOkcNyzK4xu4HyZemo/UNwBIW2AfqI+SrIXWdVxt3I5ROqehymgOG8Wth9w/u0W26XBu+dLsBFkCfvR9BimRqc1lvaf2MOAM5TnAtNFFcrpOZD2MAHwcb+n4jUmdpPAG4j3VUhjQVgtllh2KxjTwrJFuxlgfb6LJHuyR0IdTxbJosl7sq6/HJeSJ9ApRJiWZ9W17zz9WbLkaQEkuhxq8fl5LJvJo7E/ArSBuH5HFMmjNCecKu3GXcgkQ9zIlS8F6ffZGFGQzSgchcoo1R3vqU4X5TH7fFeEMVh/fgbfL/D22zfo3RZvbxkLAyyWBDKy7ubaOg91uw8DJaAVT6cG4DDYySnNlHXnZu/isUaF/jKVovUQjUdBzzlNP57O+DCYmRcdzkUMEkA8zGBYkffoEceM9uYGdruB2W6hqY4oSPYrKI4wD3cZu1/mGvtwcOjc3GNeChp9xzBCzDAuHhapiiu5CtVCtd8RawUvsvIx8S5cfhaMcdWJPZtoeYQp5xnzSTt4px3lz6ePzEE9KPEADustWZNlrvqrhR4NI33o1OgroWjE5Cpmrh7TAyAfJKrrNOEA3jBg1Qa5Dn6Ak3vqFF9e83gFmzXVtPRKhTUmwMRBTIpuY8O9d5ylxBIXA0+nh1nqDod4TYzmwxN9VG1jnTN+Z46qxNgWmko3UZzw1ErEPEgXNmvE4XzApwhBUa4tEMBk4RZn4MUFum4FYywMPEh7pSu8TIYJAsiYpAMMTHGcCyk8GRGUd35qd+7giEtIF0lHJJABUbRjfH6J88O0rjQzb5Dr1MhFOZmeCG3IGMmd02uSi4U9R5lpIvf9eJhdOPIUXhIPMkRMiyEZxvNZP5khhHeCQ2p/hJGbqUa75Iw3Tc3Gc8bROJM9vwO1Duv1/wnL7hV4vQDHkEwmhuwQfVVWFOzuT6lkHX+p945EONSJxUKpW+0HtYI2e0GEMlh9iuJGLu/N4ZZybOmiJUoxy4wUksn7oPTRvzn+bm/f4vztt8oIovp/j43w7jAmxnMw9bZeQ6m0maIE01auw29uXwGO8Sf/L/AOGDyFewjIwzNBDBFyJ4QxQamblIg+xMQPQlzAhJ7DPQQ9wt0QV9tbbLZbvL29xDAM2Gy2MMaiaVrYtgWRgWlXaPg8xh63IVajIcQ7iGcJl+CiF7xKeBd/VQpNgp7TvJHcJQyHHltlBgmfDMjFuvUFu0VmBsRoIAzeKGwNK4YlekIgXh5NXi+3UAgL3vuYPp1GjwaJ6BmxfPcjXnz/zzG/uscgrZ/cvzug5v1hqi41TGCguW3QEuGECDeG8L98/w26psFZ9xzLZoEFKCpHI53zHAwTzCAT5oWMCfc2pOuBPSxRPknBqg05wGQkl1M4IvOYPmKoOMoYwZEBYECuJTYAPAUjE5uIlxJiqW0B2+D09AWa8wu8oxfgfgHbBg8ha8PlwIVbqSHNryiyy+lTDHNz91KjmvaCvkcGqwzPF2gAFO54MSQU/6Ixggd4FkNENqiFO0ycuhNC0XifVjQKBXXdVuiJq3+VaSfJCENd7oxRSgNCMFMZNFuDi28HXJ1ZvHtuclL2ibHNkm1uSVpjae+RkGtiFJdxpLwH8YSIoHDNEMrOSp2qHaKSFWdzLVRnPmCq34HNNwZYLtZYditY08LCoLkZgueRbRJtzqyFuLaXjc57NWdamAwDargU1ubsU0jLE8958meNP5wWamWwZoDMAGN/ANE2tzvm2cc8k16EdwRpoxaASVUs06zboac759ACkgi2JtLBgMknX5zCeIeb19fYbB3+aRhwsmH8dbeIoQlkz1R9owLJJvo+/+swoIlvTwRqzTxZeJwJHntqBJ+8r7Pw/mreSXuLVE/Qpl2V16hMKCZJjNTG2ujl6iDUV+5esTdX6C6voqfqvgqkmg836x8HPIw+HOFTgvusa9l8FEeW1uV0WYnnZYYdBlhygOkm0+xq3ai1aR/U5hBGKdrVB3y4YFfLLox5lsT7aF4olhs+VfvnLBIT/P8IxAs3KSUZtdI7NSX9S8ex1Aho/lY+qfquDnWx9F6XXNeWOl3VsbNHVd2xm7GrY1mHo74i0HW5ANq7IR5+krv9GMkozarMsqSixiI6JkQ2CiGujbBloHh/gUyFHH7KGEagOAS5/+LcHK7uDJdXS+O8Gq+Mc6T+sdLMCH+um87V/OhOlr/LUK4T67B6NM8vq44h46G0JyhzCIiyLi9eAGefwTZLWEMgHw0RRFG2DvuyRFkWqT3d4VDgahoFJDmdddhupJFKf3liz5Y7KJDvmpF1IgVpiZT18BbhmfTgRXmaIg4o4wRFRj885zkEx2gO9bNacDgUkqv14Vk+BLzf0EwHm+PuVCg+7CgfUndIcwuPHh6Xt9/hFldYnrdYrp/j/OUXaOglGtvBRkUuxVPlKXRHYYiYrsKnza8mQqqd6aPcKNNzJb3nV4ogcPG12IiLDTmeCpeQNWCAoyK28J5QvyX0EuQC6nhhsoQdYvYYttfY3H6Pbuhxsh3QbG/ypdi56ZPj/zQw3kwfq7TpVoenFi0W/gTLxRrtlyvQ7YDhZgO0CJb7SqmUx1gu4nUg8gBcnLdg/+95gGPG1g/Y9gPeXl/hdrvF28t30TgELDqDpmvRLc6wPP0MrVnnMEwksfPjhmEIkFPp9e4mm0iOzRR/RdyYwedigu8y/DXuAxXujNdEcdY6Gd0qHNYK2OqTvYeHj4pZzp/xn/wVPNfrIRgfwp0Q9u33OP3pj+hu3hRGiLROp5jc90kW00Y9rlePrXWMf7N4icF6vLn+PV4bg54tTro1vjx5hcYYWBNdcG24NMyacDolmtHgyeRLreJpCScKPBvdNoVuomyPjFX+1IrW3AVhNIiUsBG5czkBDTKBrzANYAz8iYVdLtGtT2HbNRp0cNSEu1QoMGbFhdRpneRaSzqWjUvFkE7soYXxeHJiIqalEzko8FTCKsll03IvCbsch9U7MSjH9+ruk0znWRkh8p5Q9qFu6N1oaNAxhTzi+lx6G5TlEXVozv8C3F/Cvf0tgmkiSKN+rm4mtZdx2t6kfm2ECMYaSI9ne5nbM/VQmrFnLERSQ73UFK1kjncBMRZLg7ZbwFgLy0aFLUHGQ/U9FYz9rBpXX7h4xmqdhT9jTC5pr34/Gkc1+JluBz4jgXhdEqu25/Gc6OKjQiKBjIyPh1hBKpC9kouOB0qx3jCsA370wDbSEgnZmdI9BZv9HkEL3vvSPYlimAFtzD7CRwg1n8HyMOzbGjeICDbeMeXVyUKeCveJx+boj3CEXxIcro+pUxIILQVPTlaSl3AEpP6CJb/a30eruSIQkT2Q8nToUM13g+u8U1yJ/qkZoNqDPtc9C6PXY76//F3Keqk/0sdRWyfCPHH9YNSpElIB++aXq/SHgE6sDtRF2N44XL/Z4vq6R9PYoMj2SPcmMueLnIM8EHkuE+7VIjIwJLz+fRgjSnpnuZ+VWONm7vl434hyivfwxgQvC9YhoKMMWOv24mtJMdVqMUwkY1M0VIXsT7SDTbl1C4+bGGDANh2oabFYn6BdLINdAnmlFolji8NPpTgngvZEEOfwPCb5flld2sjeWQ2euk0mt0AfAFIGidTWwlol94Tk13rux/x3pFzFRCpqdfDa+vnCgwwRB5CjDPcc4z2Hue4ADylgh/Z/Mq0IUpz+goEtPK55wJX7EWTe4eTkL7E6e47l6hnMcBpOrWuFblQY6Ng2k8PI2QgBvTBnulwaIfIumFUBrNJWIZmqlNkAIVthVEyBc9iaqJANdZZGiKS4VRtp8ngQRY9c+usZbrjF9vqP6LYDTrY+hOWod4N6cD4KqNsx3simU06337CBpRW69gT2fAl8dwV+O8DbNlnJxRCRjBBJMU5FscwA+3A59YBwF8Gt67HZbnF1eYmbzQbvLi+jcrhF13SwsFh0p1iaF7DchlBiKiRT8IgIrvFEub+6VzmOfcbFrLxEanuZUbOekv+wTbfA4MQ0KkUYc7EmEn7W9bMa09TmrKQFa0MaZ48gr40GuZPJoCBKYdbGt4D3i+s3ePbT72MZYyPErvX+XmFm/ck0NgC+9gTnGdfvfo83hvFPtxYvVy/wonsGZxu0hmCit4HhXE5gMigwoPFUQ6IxxPAGkGvRJaSNHpdyrIRxnWw0tJdQodQGMiMiBg9rw4nl0xUWF+dYnp4BdgnrLMAWhsKdEOEeCDGSSC1l+RrvtSFuLz3PZDzrs/XD9EXd34CMc9lwJngsuJgNE9pIwWK4kFNKUo5nxWTrJpR4kMZzygaAOHNcJir6p9NHY4RmUvVgGWrQdV/C2Tfwl78Hcby0moHgb6A4yqodMvZqpStDEeL4IK3bkG8HszNDqnQL5qlZjlVLeZLL3rL0OSjf2tai7dpwuIEtQAMk/NJIiWvU6bCicZkGKu6irFDjaCU05/VWF1xBqQkY5ZlzZ09GNarfz83BUwlprASpiIUUjBFMVHiDl3mAg1SfDCx7oBmAhinxiEWEMRKhZ1we7cLLDwG7kX0MM7Rix+sHwpiafBwK6qdvzYNLfh8DNYHOcvYmLCvZvYNnBBBD18UEQUbRReUCP6JV8oHhvhOpBfeH4uvHtfo+ffjw40gT3w2ADoE326a3NY+jf4/3+nFwksgbaz40yXaRr9OnTKo6ZkEzXCOrv+ZfuM5wN5gtu+LFChlnosa7VE/1eKQXMwXNpd/XdyqoBKD0WAr6W4e332+CV0HTIBw0UV7YsQDvo/wS3eOD93rQpQX+a8rsPDHEo1bKF+G3DDwx6nA5ubBSnuN4Dye8BxtTcRTIB4LiX2aA02kWrhox0T5WJ/plHUzxSo+wqWlKPBV4TX6bpoFpF1i1S7RNC0fIRoUpoPIHRb45hGo2APko34V3IRSXrF9VM42KKtYq6+exSXLRe9GLZNFQPL3u4ARU5hDVKTFCRBlVTwSZJAMQl3MoZf0SeJEn8Yg4fOAezcqwBx5a/pTENF9meXeEXiAEwGK5OkPbLfBq+T9jhS9g/BnQaCME8ilFFY4py6vZ5JaEcGRBXa/LcU9yPr2BFEaICVmeY6b8Kbt7rcgV5au6tDd6QsgJ2swIiPLKl6GX4gnTHIrJgzZXWL/5PXjYYj30aKM/ll7TJaH9OSzf3X1gZjzrl/j3l3+Ob903+M5fwXgAsDCmQWOboCCNoWm89xhcD/IuHR6VcCreh8h9jmNIps0tbrZb/PjTa2z7Adc3t+i6BU5PlmjOOtg/70IdrkXTNOEErrHJo0cuq66NEArLosFKMx/CNGp8nh4PwcPKzLx3PHM4j/i7wF2gVtRC6qkY1xSSLCpuw90a+YLqfGmvh1bs6nI5lifKTDmF7pyD94xhcOhvL3H77ifY6zfRYygbQgojyWgIdo3J+xRE1Nzr4SSDxXCBZ2TwN+0K1Ht89/v/Ct822C47XKwv8MX6JZrGouEGbBOLBQDwRAC5fArBAPAG3nlAX3pdjcOYtJXKZRnTKZZVR+8BDIgMyBBuFwZDS7hYnaBbnuGaTuG4A6ML3hDxUmpU60Ezi/rEU2E4rBo+aheX+cs+TtN0rw0Pid66aIRwydDg9b9Ix/Wl1MEI4ZNXUTJC1IroWQ6Ysh42P6o6N8ZVVn/0QRUwQKa8ELhgPOO/duPx8rfXuFk3ePPZMu/UREgK5DQ2nE5eeTmFxQgXyDPHK48401MZ48hQatZUGqQPFaX3whDHXD4KUmH8aKfuvMRdhtl6rL67wcq3+PyL/4Dz1XMsNh4WQzAWi1dOMhRTMk7MC5t5jEcSTWEw0HNfPtPfuHjlNStS8CKFwUzyKW+IULVD034PwgaMIfMVMrZTSvnkDVJLLo8M0yh8WMKEJ5Hfkw9rcPbrZ7B9j9d/eI3bmy1+uh6wNAbrtYkGz3Iedhm3PlZeifFEHg9H+NmCYD4zB6c2H9aNAYENwXiTD2+y4JjOebwb4uOCmmM70oOfL+xYd1puI+RwnGkhGzClyPNVcVne0oxG5h/GUsF886q0BUPj1Xf9LgdJmi9etztzQBB5D5mvFrpVpBeeJ1ZS1JWaIg8qr43MjVX9rJ7fC3blP3A9E8FaiwYebdOD4mHJ7JUdhztGDyCKtNwYGGaYyN96kTco1M17DzDGtovujgjEE94LKXXoz2SYWOFf9b4EMZzng3OI7SsO5+4dn6hIT8aRp96/REEPdS+G4vGJYFcv0K4uYBdrkO3iMHDBbiqzSZbjKYdRJjEeybm/aGXwqpgxlqq54UgjYuKp0eT0TmWVH0V7p4LwS5U8MeSzqdOzMXy8vPhTw+GGCO1685DBmjxy9xRQWbgeDPvL0MoPKpZKVG5EgmObBZarNVb0Nbrhc7C3QIOkNKa8KqPypDJCpNq0uUMtM87PJntSbcjVC/VzKr864ci5rKwwQFLSJs+I+B2auCqlrITikbA1PpYhSi7vHdrtFVZXP4LkMs7CKPKh4SlacFiZa26x2j7HjX+HbzzHE+QEQxbG2KRwyeF+HACPwYXfzoULZ12cS+cdeudwc3OD69sNrq4u0Q8e2+0ASw2IDczagj4zMBsLexmMD2JEs/HEwH4jRM0c8W6+hyd+aMPb3JBNkIHSiq6NEKrY9D3i6qhOjvgqxjVx/KxwW5SzXhkvErMYn3lEBW824Pmo5B36DTaXP8BtbvKJ64Lp3DtYHxEodoENGn+CFsAZE3rv8fqHP+CNBb45XeGr5x7Pu2eZZaZw0bMnH0JRxmCdPipQ5SSM6MFD2H++g9w6ZgIKdlL4EhW7n4wBTDBC9KsGzXKFpj3BJS/QbzvYxgZjhboshXR1VeMSPZsxxM2R7awhrp9rXEfGc0WjJewS0ql+wUlOhodsWPbROFx5ScRB1wYO3eZS2JswwuiRkLaSTj3ZtTBjXJYlL9L74hXBm3Bp9emPPdAz3rxcAkRIrsxc3RGiPETECBHWKeI9LhxjlEoeUj6EZbNSfxiTxgg9EKU5ZaL/O16TYyy+v8VJ22L968/RNidoeh8MG00DOdmVUDCFaoJIQXO1jr5q/qN4pXHygD16TMNrXgYB7xKfoZUIDsa8BdGtSnNXeDoF166ZZIgwNy2EaGEtfbOE5csToB/w7rt32PYWv91ucTF4/AV3o/zjEg959oiwG5XvBbW4/4gFPw3Ujf3k9akfQQd2IkBQyjACD0CRTzA6jJniH48Grxp2Uaz75ucd7w6FJyAmR3gwjNQ6rHasg1CmZijCnsi6nPSKFR+cOb3pE++c+Rkl/0HJgFJO0t/EdBPc+SRvJLxJ8V7Jl6O+1WVKq3j8Th8ySd1RPdf9qDqZ6i7eT9Qx1aTDVnmd6u47cs4xr4SVQ7mGPFrr4J0YIjgecg0z5ZlhotdBMEoFz2CYeOq8KJ72srqshYukilNGg4kmy24ClPgjfB4zlxes59akzo7lvrrtVeYngLQGRnXEvkcpydR5ote/XZyhXT2HbZaAbTA27wfDSb5gPldEpI7RkIRC1nf6yZiI7mRywapZ0OtFHuV6hUcIibRgNkFPJud8YoQIDzAKlbrdXwLc0yMiEn7cb5gfFz58C+ZABPJb8tgy47L/Hrd8hWevnuHk/AXs+QLsLKgNJ2slrA1BWV2LsBR6t4+hIJLSf2qznWiTbEojgb8mfl7lyQy7VqbmDT0ra5IBIhoh5MS4Vs6mNsf3IYR+tm577+GGW9xe/gto2ODZbY/W9aDRXRBTJODjxYfDd47D+0C+BdjgmTvFv/LPcTl4bPse3nmQbQAYMAPD0ANq6xiGEF/PuTBvQ1Qk9oNDP/R4fXmJ280WV1fXAAys7dC1C5yuT/GseYXnb7/CEqdobQNrGjTJEyIYJfLp2rJfEWWT0jNvKkg4OBWOKY9KpYSfZATi2IhGUr3TTFk2oqlyNW5rnE1rRurPRgiGhGSKp8bjSQ1R1EK8g1L6ULmLSl05dZ7mIl1O7bHYXOPF1U/o3FCum1n4UPhfMhPTUL2PQ+o8g9ji7NlXsGYL7t7iZvsd/tc/3GK56HCyavHy5CVeLV+i6xgdLIBwb0TmE4NqKlwkLTbccPq7bGP+lmnqDAOse0WU8FTudjDWAsbi/PQE5vwMK/817LsL2AXBGcAYIw1JfKu2VpfKW06hu7QnxIhMAxPc8wyjKkkF9wBwMpj5UsleXbLu2SGFE1MhxhB/i9cEixFOGPfKEAFArSEZVxW0MO1vU6efp2hIDZW4yHmcGaWCyZg1umf/Fty/g3v9D7Feym7QnOlT3JbCP86h0kQAGnww3nqO3mZAmjuZDjXV03MT/yRPG6h8yY0X6VOMYICP7thaqSYXrgY8ddst0DAa28DaBuTD3SkpIFOyPEyJTRPtnOtHwXaMOfTiyU7jaZWMNX3m3L+0R0haTkIDaIx7uXVK0KnePpYScsrz4mAYWdSiQJbmHUFoi7ecG4TkwfMw3Knzs1emytRqWfFDtUXBz3zUPzGIVD8qLjz7fGcLxb27ILyy7saYJHTxl6USOMIRHg73oolTe3fipaY4jClZKHP1RZnCS8RnpXKeR/kPbV/J24pOTF0TncXGcdmazy8ZpcyLQpihLC+kv5pHqrMrmTW9LRi5clzyM67eoXy2YyzK97tfZ8iGhDEEou28x2YYsGgyq5fkFWSe23sPR4Dx9kHRN/Wc+MBWZp65wi9DpO5mFV5+SpbJTxMfGwWVxMPq1Pm8LfRgTpeNihl6Qs4oqSAphhIqwTYd0HRolqdoFmt4CveVolgnyjgQxyAdK9nV9KTOSSsjPi9DMJcWILW/q3LHhgIZVS7aIPcP0tT6nWqgSqMNXWGK9QXlR9BwN0NEIVnPGyOmaMB9h3/G2IVyce4s4Z41PwzSBgJgQDRG4ArGXmK5+BWW6zPQyoJ7wFiTFGc5JBNKwZRGpadPVoSwSFXJtmMjhJS2ox+VEjgXFDfLou5IuaXrXl08jDqPbLaioA2FhBOnDs4N2N7+gG7YYnnrYGXDnW3sxy4OPr4RIiQ3IDZY8gIvaI3B32AzDGDvQXETYEY4RYCgOPMAhiF6QkTPiCEqxDeDw7bvcXNzi812i367DfdCtBZt06DrFliZU6xvn6OxLUxrgzIkhmKS+030SQLdpaRkil3NRoi5oRidtZ3A3xr/GSJATuK/+j4yaimGLOEsSkNfXnPaMKA/feQkJCQToMMyJeVwVOAGQ0RIk8PAePhhwHJ7i+f9bQrLNLV+qwE74KkwU4+9ZqY4gSmoVLQc9pHWLrCmYKz5drjBf/3hLVYLi7PTJZgNzptzkAEaY+BizEjPDIpGT4/gERTGEeGeCVHojpBMt6FkSCKblZQXacxFDygpyYCMRbtYY3XyHHR5Ab89BXUbkAkMNilDhEbGEVYrvBrhZkrIqJ7sHHW9B0HKBjKNljpSqBtEwwMnfBWsSx497POl6omeA6WxWdZHYXWJjcxKVYmfr43tk5gzy2BMGS5UnpFit0HTvIKDhSNlJEriY9qGkhEGnC/F89EjRLzHRFBR29kk7OqTDkOaZZPxTE6Wouc2/qH4nJkjPbZIBxuAdNAht0zUbVSWlehe1eCpTux9djgUPSp4D52Gi18kZqCKlu8zDNwrLNOe9PehqGl2pxBI8CMazIhLqh0uq86etB+Lcv4h8CkZVN5nS8d0fpYwPlpddy75KQZkaoObRHIlW4jCJF0em+mfMKDZp4ZHXMC4wl8K/BL7fITHAlJ/d8Mstzfx6jA+Q/gCUVZreVGpPmf5tPHxnz0ERzPumsdNLrE1A68yTmQbJRRmVLUtfXqdPgkPBe9W8qRZ1tJJ9BgVA7OT7xt3Z/rhoZzI3IQEGd57wAlPJ7y6VwPH6k7GeGBs6kDKNDc5US0jeNMn5flY/R/4LRP3l11cV0DmZKRgdX8XA0r8mc5a/Iy4S3os7ghJofoYdL7qNxHItqCmg2kXoLYDG6NSz3EVPH5czx+NDwSMjmVSPSJKsCrqU3UWRY7fU/TI4Nl7UyZAZEqu27snC34e/Pt94EnuiHgKKPemWdL9gaFcBrfw2GCAIwtjWixWZ1is1njZ/Z+xvP0KtDgDbDjRRsZEjwhAQiek5aO9IsRSLgqgmRHQljj1VK0/tROi+DpVGoTJ5xSTTylePQPphG2MkR/vfYCcCpfNgfOnnIiXS4acZzi3xfW734G2N3h1s0XjPUxSnEmfPq5ZPwx2MF5FmvvBsnuB7tUJ3mx/h37z39G7cNdDPwywfR/u2TAGgwvKb6c8SZkZDkH5fbvZRkPEDQbnYYzFolvg2cUFPnv1NX711d9guThFY+PdEKap7oSgCn/zXy+4K4Yn6bVo9dQwFIpaHXsTakOeYVD15j5GFUZW9ubfySiWuMOM8/lTBkzn81lJK6fEk1cEp3epLSztl3T5bojB+XTqunn7A55/949oohECqY15jOp+fVjQW+jUxq9hhiFhwKLD2r3EV7B4/rzB1txg27zGD+/+iD+9u8Jfv/oKX5+9RNd1aNGAaACzCTGgrY2XVcd7UbwBG30OJZ5VSkx7iXe51QQYBvkyNr+REogAsqCLFs3pCov2K5jLz3DVGvTdBq4NJ5XJUPIoLXpfKFg5nn7hbCiYGElthNCjl/jKqecJ76K3WaLVXFw+nS59Yxfx1iUcFvodxkoZ2AqDRTZC1OHHxp1HMgxlz4iMA+n3IeRyBtL6T5p9ATEKGYg3gWGfPB8CjUIyZLm4psX44BxKQ6HcDyFjf/AS3MVuZuOA6lGVXvJnRl5wKpyOt1guVzhZrLDeMlrjQKYFQYwvQYgyJLwFqSX4+HRkTKp21VGtSc57v8TVze8HNM13ILoBYwNt+B0JfR8KDqy+Rvc0w6S8hxBOzxGA01vGogd+chwu9iTClj3cG0ZrAXcWaNgRfknwAKL5qQMBdrNB99134PUaw8UzJQOFvUsMj83lJez1FWi7mSqmki5/oeN5hCM8JszoHDN46CgMZeK8KvP9m3tUdpRTS1GJzzRcsBk6Lr1kHq/6qr4Rgy4/6zblhOm4i2LnxspVJBkzH7BTn1puVX0rG1J/13xTlm3TP6++p+ZWPOeojsdWmYqglMvc3PR48/0tthuPtu1g7ACGG+UU2SnonYDWe8DYnEDdV3owiD7Ac7grOSNQAAnRRAYGfsIrIiZLDyM/ClPOubxLgpHIUMnHupw+MPQl2cUBon1CyCPozQjIUY3ioVYCh8MwxqI7/wLd6jma5TmoWYDJKI+CenfNeDe307Kur3gayiMDGB9CNI/0SCkfaREnlCBjpewFgWTIA5U6PpsfvTzhVPQxfpe1PEMzivNQ/Ms0Rnwyhoi9wAA8IcX4ql7dB6Y3o90lyrJiBhwYmxirjghomiWWqxYtvYBxzwFvgYZS3DlBSBO/yNZbdyTvEXnhFVsPz2C83vw4fZvSFExkmugzIymesjJNws8E5l9vplqpK0pAiUnu5bkf4DZv0PS3WDmPJhlc6r7tavPHCk/XxsYsALNAhxP4DeD8gMENcMMA1zSQE8q9cwj68VJD6gE47+GGAUMf8nlmWGPQNC2W6xVWp6dYtudozSIYH0h5QhAFt/cUe1wTYdV3xQvxFG6NGDAuhq047VDsF+UpiLlTsSX+KCNBWgusfumNLdcZQjGp9iDjc4HfqhztwiueEOmiW58VoOw8/OBA2xucXP0EsMtrLHcC1baKjxPm2It5MGxheIkWwCmADRi3jnHN1/inN5d4sVrj5fI8XgJtYH3AN2884AneZrdoYW/Cp7jxKqOufE4OH4GIYUBKPIr9kTiYywaLZ6dors+BzQn6bsC262FMA5BJF5HtHAeN70DB8JTzjdSjSeNa3Q8tvEgaCW3nNT6JkVhCNEV6y6zKFdoMsYelZykmvzZCeLW2Rfwruh/HQ4alGp70kzk6tEyP3S7smhQIBIjAJtBE4zxgEF2Ic/9knCVEkyi406XUsl7TeM00ZATjsy/5iTLJHGyN4eJDbA1N26EzDVrHsIyAi2KHSaVOXIL9wUmJ7o9aGVU3AYdwN8QljLkNF6gjz0MyRu0BUvj5pF0Xo1i5nRX7Uz3bcwIJAegGwAxAE8xLgQYS4WZwgAcs7IefSoE76nI5rYsnUgIfVOynqoC++5776NXjnk14IC0i79DcXMNZq+JwK94r7iWm79Hc3AQ8m2hnyVmVjXhy3Pzg8FhUY1c5D0GSI3yMwNWU3mtmZ9Qrwq9w/ZALU8NMcSkhSt2QZj6rtKMGxfQ7LxVQeRNPS8W+r/vG+oe8qstWio9aZ5Nl5FhOLTQwyuK5eln/1gnn9EeoH+ux1R2vv98F8pgPPeP6bQ8PoO1seThXNyfJI3rIct3hdZaHiOoSkPtchELPcr14WoQklHEvbTTj/haYFBnSUN5uvptHPaghjwLXc/ceQEkpEHk1GCIM2sUZFqsLmKYDGZtkZ72097UyyV+Scd9dCxTCRBEBTBTv7gyZw1SHMRdPEik4lzhdPhfUZQK35dEM7k+VONOB+BFp0iMYjD41eKAhIgz4x2DB4ZsO/P0puLf7E+8qp/o+caB1L2zgcQMHF0u46f8EP1zi1+v/C87pr2FWL8AtQG24F0I8IQjaAFG1SW8cophUVthDO5YVptVelJLp0+c5XSLmjEmjQog5Hk/KorzEdBSehpUrHYInRDiF6kGDw6vbHnZw0RNCbSi/wAV6V1idPMevnv8t3HCFm9c/otEKPmb0g4dnwNgWZAysbbLxQO4TB8Fai4Ys2uUKJ1+c4/Q/XGDRrNH2HRrbwMTY49ZaGBtjVMd41Vwr/4V5SnibGat0Clzj26wBIqeRvOlH6mP4zB4RNbOnShR8FjxWWixtWBAmR3xuEw7D5Qt9U9x8l0+K12FuYn1eeQ4VIV+cQ7+9xvXrb8FXb1J843SZ+4h5nGd+PoyIt99QW76fa6Uwg4zGL7Hml/ii86BfXeKPl3/Ad+/+hL/96m/w5fnnAIC2iUoIANaHcGTGcIzvL4bgbCBLSmrOY+grfENMC+YQBxSI2lwGGQuiBrZZoOvWoO0S3HcwNiYRzzZQRMQJ4weQDQJqDZSfZQ7Wj+qxnHipPRSkLu/FeyF78ni5K2LSSyLfA4FE1726U4LzfhQb7quBHM+yGb/doTkuGPqUpNwrpxRDU1gYLiw9xeLFfwTcj3j53/4R1+ctXn+5lohV8BzuLUl3t3iGdwzH+V82UOSKpAVmYhnwxLda6Vw8EwF2ov117rgTI/BiIVTeYrlAt1jCxIvS8xpQhx6E/zXjMp8C1FDdPW+ixeHkZNN8CzI3ADaFQeh+8IT9FhJTP0tfeacxAkC+KwJBIKa4Z1lr8JsvXmCz6fGP3/4JW3b4w8LjOQivQk7cf8QfCZ5oaGtD5y8JpnDkFwGHdjyuj6QwMYihPMrjIUc4whEeGaqFNWdAmILxKyr4vRReslIEEusSyvLqx4x4QS4RQB5gidGfrAcjOpO0XElcyLwZwRSGzqTwTNsT5TtqUrnqfWLfJ5nFEehXtfhb8Ml1mXsL5FxgIWfqiu4AhyiQi8RjcN7j3c0NlosG58bDBOGibI4SmILsooeeVGgg1uJ8+DIRNiGggkIADjKkrcZg18GVXAb0LqQazAgnhnQ3OLcxjUqQHVlwblTPHTmBnYa0Q0Har9oGwHZL2G6Bxfoc3ck5fNPBGxPCJrPqXyqjaBjyfMi6zO803ytjx/BB18RB3vJEIDmMZKSZek0i3qtX7v9ap8R5pReySh5hLdhpApHpRvhWE8EKWdKymFgfqYqPgHd/j3C4nl2bqbQUO1poNTwey7xzWgYLvu6Afr9thXf8213nblE6iMghzM0WHj4qo5hvQfYWS/sCjX8BohbcIV8ETwST9FVhcUf12agRPq2gHZ3b9Wxmr5lMWKxWvYTjwpXnOl6fIvia8Q/Pw6fXyitGViS4Hui3WDrG0qNwYjsaIQ6Dziyw7i5ABAxug77fou97bLc9+j7/c87BO6dinCtyS4A1Fk1jseg6LFZLNBdL2FUTLqNOManlcnVTKHr1ik/YUihbJzinArh4p7AAsaiMhxUTob/vQpnSE0Ib9bJCNf1mIJ+oDwV7ZBz2IuRK2qSg1e1XzFJMl05Vi8ECgB8G4PoS1N+mtVEwi/U4zfwK3wMNUVfUfmSwe00HlsOi5SVO0OKFtfBugz98/w1e37zDZugxeBeNmpw+kT5rPBip+GZqlnFDEn4M5ZGEMYAxsE0DY1rAGHhLye5A+cuOvmV2qF4XCqOhsKcwohV7UfkyPGJFr5mLPPKMIeHSfB4/bWAIBRVrRdepV2U2Us/0d9c7nah4Vg2g5ueofMHyTP9LjdOVAIQG1j5DgzN07zyaa5faVxrNVagmZG+R6TLzJ+n69fO6eTT97n4QOkCOYRyHkHm2ieUTMquna1B0QfB1LJvdGWQfmE9wt16OBWoGmVsYcw2Cz4a8B8KTUUjewTkKjT8QitkzhNW6w3rdwcAAhnDbELbEMzmeDh6Gux9BJaOyyxl7eNWzGHDv0t5XXbvrmCGIj1HkPQthZpBzIM9h0jyDvAOcA4X4eneoYJoy6/37CEc4wuFQKmUPSE9I8mW5CiPPkjyPc/npkAUU3x7LkYISn15zYBVfVn7Xui/VwFG7qPq+Wx7QbR//qvPPj9sUa7Wft+QHkm7a8f2Qf7ENdatiuG7DDEMeRKJD0LKTltWThmCyNeMK5oUS5qoevSfdiRGo5bL5ZmjDkuDr/rruuGEWutt7gh4HWWy2gWmDMcI2XZCRZc3V+UbtyXJ2Ljh8kv5Nah3Lm9gfgxButqQSsm6oKnf3qOXnteZpoon1s51Dq16O6NncGvplwB09IhgPGiTC0/PHTwCH9noLxjUcXIxF18CjMQCt1qDVAt3yBC13oKYBE4I3BJVW/0JDUbQgnKQGEBRF+XFONUnl8pdicXGZYKQc5shsi0Irrs7s5eCzEhVyolaMDKUiKwvbpeEhnAaPyrDtDU6//3s0/S3I9bGOHf06wiRcDMDJNeEP6wVen9ziut/CX16mkwLsGSFsTAsiC2u7YFjwDuQJLTUw1gArC9t2OL14hrP15/js3V+hpRWsNbDWBk8IuRtCQjJFA0VmDpQyM376YkfPO3BYY1xu+BAczGXV3hKTuMz5lCmPQrUVhVeMTMUN6FbEikL7fYHHUKfGOXo35JPlnNaJl/A30fAQDEHhTgjvGcPg0d3e4IvLH2BdH08TcN3JTwDuskfMK81M/M0Aum2Ll8Nz2OYWZ78y+ObtH/D99Tv8h1//FT6nFyDyABGc9wAMDEU8cRy9zkyujWSaKcxZ3QzdHsX0GGF6Ljq0FydYnj9D063x08mAjb2GswTIJchFf6QfnOmqeMoAan3oYSlZaq4TlC9UNkVnoeiz92n9B+OZ3BlReTgoLwjPymic7j3xcCmNL9aMV22ph7NmuMI2N4EnD2QxDgU5qSR3PmgDRNiTgleE8x7O+eAF4VndCyF9DCG8wJH3Vt2ou7ULAlPKEd/G56hyGfW1efkN9R6nv73GYsNYn71A27SBOY8G43CHDxJDT1GIr67hm2ltjs48136uvslXeSKsDbMSPw/mCYW269+5nlTMjrKYZwT1R8A33Y0nQV9CHqwoWzGLMCNetaQEukPm9AhHeGx4agK+f5XZ2xuYb/8Id3ICvrhAc3MF++Z1ymrcAL0edrVWvzuuoCMc4amAkW/uUusueUFEuqL1iokFoCoMal1IfCOiYwq/Ex4Ej1DF2/iSIqRSKYR9RfSoCJ4UcoLaAOxjnbmtSTue9m8pM6fhUHR+R1mGDR4csbvFyeoxNSp6v2vL1yKuJqcPIXCzp+31ZO2Dcu8gS2gWHUxDQHVZMAPhToiiziiDe+H1It9rDLw3IPLTTZxpi3jBsPdgCzBPeHLP5U68pgpVTbntiS+OXStO1RconHH1URwaHg0C8hjThPs4Vp8BZ5+DVhfgpk3yrU6bF3cIpZQFcUrLBUD0XIh+T5RlIdIMfEIVhmESp4ewxHyuK8ka2utYQhSzRv55KG4WifJTOBFeLprsqRX6FZar7iMnHj61aWJCf4lHHO4XmmlmNewiOSM6dw/Ct5e9nSmzZib3Vb0v/Vw7PBg9fMrAGAAAjW1h2zVs0wBsY/gOJOOkCOjp3xRM6KDm3k/9DsRvjxGiSM+jb8V7lndCOfWuFstmpHfakJGNGeG9c1vAb9H0N2j6LcancI9wKLSe0AwG1hr4BWHoB2w3m6iQj2oLkjmjaEiwgGeEqDLhZGVLBrbr0K0XWHRLdMMJGtOBWlFsRZ0rij22gDT98UfNM5Rf9cYgz7lMIQzZCCXkfX4xd0dEnS43bqIDNccWjRCpY4zkyZC9IcoixZCS02QFtNyPwh7wzoFur9EMt1gPW1A86b9Xu6aAJr6V79VmvGO7e1zviUMo534gJlhnsLIGFw3h6voGby832Hz+NdwyMp9GjbnUzAzmHI5prmVlZVmG0PIDEYHJwLYtVqdroF3AU4PeMLbWhXWkTp6P2JwSnVX7qvaMjAtVa0cZ5LHgaVw76bM6SRQN2gn/GGPDWTSs6YoSLrMYn9Wa3WGE2AU1z6DluPChJo3xEBSaAAO0C4A9zNaDicM1U7K2EbqV74PI70KDM1PJNDHPJn8v+jk3QJoZnyOoKW1EaP3MA/Zyi7Y36J41WLQqTGXBZOjHM0L3vSDnlm+lcFwz3pOp7lvlI6jbDyhhtKj17xkEpR2sHU3vUXubOCHETBsh6owPg7uoFR4d5sb+IfCo9OQIARQ/9RhWvh2QsFpt8OQdaMPgtgUNDtT3sHIx9SPjECd6d0Skx4ej7PepwM594a5LY3ILlU1UvVTK26nMWtoBkL0h5EAnhXIDj6xWMFW9YL17auFA6ubMX3HFz0jIJ6WAZHnOqcQdmF4pOwlRlj9cJtRiaa2iOSTv4bzDLn7uAMWWPGHAOwYPjMYYWBPT0eTUTPyueNC78liqHeKFIQe7it4UvJjMzcQ4TTJ/wdBB8j3JhpmHCyGJ6s7dn4/TQ/Agg4YSYogIZC1Mu0azOgPZFiB1ZImlJzsaA6RQVrKG8oHWMOlxZ48GDKgIaEpoYp7BMhHgeYQ/+n1ekrvGWChGakDKm0SAIjcVecfCSvgyXp+VXP3EfNSHhnsYIh5dG3BQeQ9QYanveSO4y3K+b48v+7dgc4kXp/8Op+2fgc9O4YlBLdJJxYS9hSZD2h1b6DldmKmZ/ES7JhVTXBCDhOxcvdOdVGWNFCZK4cRSWjwWqj0jkhFBngPJApkVXxwVPAzvety8+y2weQfv+lCytOHjMf9+pDDGYvId2Lfg7WsMfY/h9TX6dww0a8A2sKaFtQ2YDQxZtE0HGxWo3vs4pYSFNbDPF+j+dg1jOjQ3DRpjszeEtSFMk1XWCAWCP1kprL55xE/B53BaO98lVHtB5FJH90LwCJMrKN/qtaLXh/aMmCshf+YeRUQf5WCpS9ZB9JSQPvgUg57hvYO9foNXf/g7NMMG8C4rPBGW2awiawTvd8MqmbO67l1sYp2eq/SlQJEYkb6HcT2ev93i9O0W/ssb9MsBnW3QsIX3Uf/LBGYK96F4D+9tcZgiTFnA97l5lxMNqW6ygGnQNkssujN8789wc7mCRzh5DrLC9arulkxYqehXBpMR/k00Kjd8/EobfIF8YVfhEcHJ2JDufxBPHbmrJBmJ5buPnhHxs74/wk+1p57XdP5rLxy8105ZlnYlnxAEbHOO1Wf/CbT5FvSf/w9cvejw+tenYLVXiVeIePtpb4jkXcCqf4xwgV3CnMyU66nj+kGE2qhbCg/5VBTRmPYDjGG7RYsOf/nqFIvlEnABH8XzkgxFXFUU5SnYOWGyo7KAIq4nZj9/mehH0aXJ8uWui4KZo4z/9xU+Hwdo8utjlS3Ca1GNDpVIcs3e++Gf7tLFQxW2+9KpUTjCLw0qNiHpA4o9gWGub7DY/BHkhlLuPxh+3sL/ET5eSCzkz4zAHbyi6i007eeKZ5HlLqxEpbSgiW8A0lkh40uakBT8o9BLAFh5Jkh7WOomELy6GzHyPNAsjpTLkV9k5JPhKO9VFEWsZJZmpd5VSEGKv4JwnlFZOitX7EAsQrhHY+/uqvt7P5BT5JwqBrY3Dj/+yw2GYYuLbkBjDSToTjjAm8cqhVJGlu3TgSFjIj8dvCGKgUwFVA1KiojYLkaQc5jAnpXOLoYCovDeEMOrS6hFxzU6/JYYVIU/0reELHl0PloOJzbLNi3sYomT9RmWyxMAgFP6GkqGBTmVpVflnOCNqtshjxG+lsOh73yZdJTQi4NZY0pDiHdaJMORSTKVpA5LVOS2qiEU6iPWl5RXjabgGcUa1/aIOWq4Ms34hcEDL6u+G6Q5BiYmZXqLotn0jw+HbpJZkba7NI+gFWvsKRq6ANABDae95dD6smvQtO/CIY1l9acoZWf20oMiLxjZ9Vk/LZXH8pfLMmRf1Mpc6q9hhhsUNw0d4X7AIeyGdQamZ7htj6H3YG7CBDXhUmkCYIyBjf8QN1VjgjKVmga2XcAulmh8F8N6yF0QotjKSlfZoAuMKHgerYwrT4HLa8GZQmFX5K2YqNoIUQmokmdCB6nKqDMWrRrvCvFVWAIa96cQNxvncnFZER0Uuw7DsEXb36LbXsG6IW6yBzCMnyjU7FaAw5guYsA6gwUMLDHcMMA7ly4xk3HVJIpJTTPladOnH0YHtYsvUaVsDahtgLbB0BkMG4vB2XA5dYzLs4umpzBGrDBM4cZk/wtc3TU+nNKOsJlzXRn/JLY+p+dgnSZnrC8DlnEekeuqYkp/4u8p76RxjgNBCSPy65CNWXACAKFB05yi3b5Fc9WD1jYZalJSPfTldperohJlKOEVpTQ1L0rALMpPycH7QEdTba1B163QNB0GT0mA18pdGuH4TLmFLKsanJi5fWu2lvqU6Jmya7V5GsCyqviAqAdomBdiqlqLsZzExfrz7jCp8KiLm/09X+/+HsqIEVoH9I6jEEgP6c5OuNNutK8Nj9jGBxdVd2zHVL53mGjb/jZ98FYH0JbBRylv4tmIDEU64x3g3d6RmOZH9lebq/9IxvqTg/vytnMb/Y5F/InCY4VjeWrDxs71EXnwvQllvkg4gvyYqEgBfZo8PI98wxQKTPBsDASldmWMmOVpdrE6mheSsCxF8h2NUOlTb/Skz9YbDhww7+YlE8y+m35xCE2caJIav5n5mM2o6vaMvveAZzRtvJ8vjYk+2ogZhNbyM+3eLycWRjAgqBFQggAjXnZed3vfBEwMqPaJUAW9X9DypbShkq2KJyIDRX0PNS1ss4RtOhhj4ZM3RMTpOG4SpqrsX+b1Kb2LXiD1pe+zUHLfepi5fI36NBoBBVtSy2fFnGpBiJCNiTNt2n0MSEs0qXHV77msB24IT4hHhxZ9F/pxuCFCbla+404mdtlUDHZ0ZFfLi4z7GJCHw5x46qunejPM0IDIounOYM/WuFj+Bqf0GxhuwMbAJm+I6rLIAkKs6qgnAlApaIvfu/svp71ZTBo18SnkflYPWdXNqU4OJsmsoPL59GxWtulT4flUqY6h750HDw6f3fRoe4/GS/k7u3OEBNMDRQCebyza12v89+trvL2+hm8cYFucnRqYxqJtLbq2Qdc0wSOCGc4TvAFgLLrVGt3iAhdv/hKWFmhsSNdQuBtC9EgAJdKQWsVIOOFZTmNDxauvmAiNiomRUSfHR92dY0LUukzvSi5ETo4kZpHViqbSm0fVFCv3CO4c4TuzB2LsfHgH9i5dPJ2UuNJncEjL+U4I5xlDv8XlD7/D8uYS3nsYpRSWus17oHdPA9ME3Uw+nU+vYYkTdFjhav0GNyvC7XCNm3fvcNK1YGswUAMPD+MGeBi0ZGA8wXkpX7MaEsupMvwIjpAIOPFy6mcrLF69wtvPgO+e34K+c6CNiafMOZ/OgiqqLpcVztX4rUHT6B0EMdH2ZFSQekM8VM8u0ujwGe6GyN4McicE4r8Uosl7MHz02nHwTnlBKEV9YkzHjU/MZ2D4sjRJ+eV811HvwXX6ufy1BrFsXJqNyEgyCA6EnhmD22LYbsCGwMaCfcCRMLYiGPMkA4vYx3G3NL0rW1Nv33LgQHj2VBSVTHMSkpjiPMt4E5arBZbtBfrtr8FuDWNbiPdA+GfCXSdCt0eLMc/dGO0UU85lunDaiCGnicL/Pp0KE3EjSc6sZ4qzHK8VEEnYNtFF3qNrvwfMJQjbipfM7SlkqchjkaFiHKDT3BFoNEG5vdMZBGvKh4XAdKfmiJhkwPCwAD5/x7gZgH853bm0ngRG7T9kXPa0MZulphOKEP/grk6Q1kPLfB/DfL863jMC3BWmjooeDGW+LBJOS2pFmjvCIR5FRyPEEZ4CHrREPiQID+yrlSosS0qm9mAGDCzYhEM98jZ+HfFCqpq0EzKV5RUVj56pk9SGYeKdEHI1hD78lsqY0pEU4kTwjA1cpYHWezGUh0OMZ0yc6VMqR8kLZXO1EjR6tvro80BBnhClKasCpdjAf8nFCaJg0bu2MF+KP0vjMDWmhwKhPlRSA6uk8oCI0DQNiIE2OpkbhFPw3jt4dkEW8bU+K45B9Nj2JnpSkIWxgBkGuLotM2usXn+McCeFScw4YOI8TxkhSq8NGX8k3jtUnXlTYcRL1Ht/cn5uFZK+XvOsIlsShxDebC3YNGjOv0J38QWwfoHeLiEnAo3gW5RTPDVxHTuku0CR6UAKQxVlgBgjAyahvtKHIo6MGnZCQDXxu0ghs0nGPKxvicYBKPk0rglClqMz6kevF2lzXIusrauxfYxQf9AZEIjl3kQt+Ol1WgnPoQHVxFB6JTlIyV+HwUM3EllbTwd394h4LBP9B4REoDG91O825GPVguce3m+AltG0HWzXgXwDqHBM+gRjUSEDIFFc5B2qrIVV4plOjJo4ThsejzPL87RYCoWxKGKrNoyeqHzpSTSFREXr4DZAfwPLHq06cXtYp46wC1rXYk0naOxr+IYx+AHkAe9dwD+ieFl6YPiY4n0RYMBaNMs12naNxi1hTQPT5EtP9aaF9F2tKFFUssbdGmt1mvhc4yaX7/TmLOicyGPxpQaeeDxeCyUtqDLUa0SfHo9YPdfL9DVtoJxDmkXGqt1co+lv8ppTzZuiRXmTvP/m8FgC9PsXxE34j8JF6Rvf43J7jWfuAp06uS/8ho/01NSDKZxMZJZqpUPmbUXdRYBt0K7X4GZAPzi0rMLrSdmaAVV/suFY4e8UXo2AFT5MvK/KLDcKzu+T8BEvWvcKd9kXWCx4ytHYnEl+Ht85D4E7g+awJmBaIM8MYIl+SmKtJVdVCev0inpxxAPNJAu9m2py8Vtoqq6BAHAw7lIcz0J2RUI/ADMGOkGvQlKQ7+WeSQBMY9E0LcAdmFsR6RMOh7ZSbrT0NIUCQNnIvUDTDLRuVFxHqbM6UKvaNnK16oFOB4BogDF9MtbWFT2IGim+LFU72S/CrooKtKSZ5yi2tJHQO9e+/FKNliEsFh0c9SDeAgBsT4AFBvv++CiZ5ty+p6wo0KhSTLs/jEuYLvPRejWxuT9FLx4Laix637v+JDwxik1X+VH0/AhHmAj7cnie96PCqfnbujH6qzA4NHpfctSR4u9qvy6Cy2c1vzQqJvFY9dtd55+n6MU+JqrkBAOrWPI0de6a3akPjD9sSne1d8883qOm6WIoiWQegI18qUnMYZRMeG42RJaL3ydYxNmz6pNWv1xebnO9cQuSxpInx4bH6WdA2PJCdbZTzprkKO8Nh5bAsGDTgpol2m4Nso0aQ93oUj7Whgd5IgwwcWnUSd8IyQOhNBNMQxS7stw0mUC3SVdWpyWVnnODdIadS6d6IY3b2Yfy3TRvere5vqtRu9wnRoT40eF+oZk+hDHikaurcPFeUOYX9Q1ws/0T+s23OHv1JU5Pv4J50cD1HrYxKqRNXJQ1HSEoyx8n5Q9S6TL0NZWt2xYJcVIG5/RZKTWRj3NNHP9wzCNKmuDZwMgxxhlRa4XkEYGcN/QnxU4Jp8Jdj9t3vwVv3+KZ26Q87xmrfrawdC+w4GdYXwywn23Av78FbnqAz0FEsDb8I8PhX2NADDSeYFenOH32Z2ibZQjdZKPil5QxwujTv5w+Eq4Ivqh7EfQnOJwwCPnKWR9dWl3ge15noowieSwnR0iW0m5tUW3em0gy2Q5dt/4XPCFkrSCeIA99Tt4hjBxz3zPafouvrn5A029h1Wlzqb2mUYec0vulADPwzfUP+HZzg4sXF1j4JQyHkxNy14HzHswGHlzirEzfzCURgk4pDBkMQA1gW9C7E7R/WsCgC+HKImPCI4zLdDs0x0cU1jRddabIydXjmmZTTifEWuF0OhECTaM53VPiOZ8cYu8TrnofvHx89O5x3iUPCR/zh5NInOj7HK+HCSX+fSDUMb9bh9EvGd5dkIURxWClexOQPoniY0MwHPhHNsCkyYAAm+o2uZh00iYohhWpVLggz8r5LdTqI6VDpHPiXRM9TtqmQ9fInSXKAyDR7HiiLhmVxTiBUN8UX5eYpfr9fmFbxypOAgJL/5A1BemOLEXT0zgw5MRhUTeF/IWbNOX371dleFhtCeumLWzzpUdDUSHHxE/TWqz+zWeg2y3Mv3wLf+Nx+lMDtIy3z/t00vNnBYJ2efP/cG35BcJxxI9whCPcH1jt+VnXEWDMRVP9oPipNsOD4UBF4kydh8Kkh8NEE8ZWBVZfp3Jz9VkXONegQw0OqvyZdj0JUDgNf9sPWFhEbwGpN3/3ClckRJW89z5E2/DGV5w6hXBc/HjdEF5a+Lmkq0gwlus0ZyrJEyuoRJK7XEpeZJ6od1f75WT/WOYE8kXRUny4d3FoTsGrF2jWz9E0HWBtobsM8xLmbyQX12GXxMtgsj/1+M13Ue6IIDLZeJXKD3gRJbtaAkx1JRkFgDH5ndy7luUTBudseXhU2wrRPaumkMSsO+rR04rkBx64+gjhYEPE3W0wOd/Twn0WKhe/dpW4q/3yzgMYwMHtCwSwhzUei/YUK7yC4UUMdKfE40Mq57w4RdeUfs12uzxVnZ6IvK83uNkG1Kd3lfYkEatpNS7Xf0XhxoFI5UO6jMZtQX0fQ5TkPh/hvpBXqYEBe8Lar3DG53iLDRx7gB3ge+Rjzh46yAERgayBNS3INCBtfJhU9Gk2MJ9RTEo2IJ2ihvo3fcF6fq4vnkLBpCKVqZdBVu4gEf5608+tHfdhL6T1I/2SdcK5n6n8ynjI+V8y1Mlpc/ZonZ80Quxu8/3hfRgzdoXUeExwGLB1W7h0qTKSMYIizQHkAmuND4zkHS2Tp/A7oF2g2WwJ6AxMZwGygG9ATpS9KDLWveOEI5l8jo0QmM7L+t245Ijkib6PvDpYnR7i4POQ+p0My15amXE30W9F65OB2ee21Y2/TyyBA9GhZBr3QbnPl8959N1wiw7n6Poe7WUP1zXw6yYr6hP9YyQjhCqG0qeql+JwEAEeOTyRYsCDd29WwOs141n/mvqWR0R02kQEYwm2CaeTkhcEqXxEGJWs3H/3XnM8K7/fl0Mc58/OE2NG3aMD8RKMWxByyAMlRqh+5TnZjzssGfJPZANAauW942VkhEkzp40RfP8lBCKYhYXxFoJ41hPYQaHJY9P8uTX2mDXcZTDuRiEeCrrXh9V6GAbuTbnz5UElPBrce8QfK+bMPtS7QzVzRf18BP66J5+ynDU3Kz+f2XpseK9iNR9KGRh13PYSFDNebTfj7sy+KEsUPmwi3SwHUwzeoQNZHyuZ4jznsqq8WgjQULNGteh45/l+fwiyl2wzYMjDGpOUy0m6Vv3LnB4Xe0o69OURDw4h8/Ac+S8xXkiBe/ekmVYn0U+U4OpgEfPOYpO2pGA9I0+v5IQkle0YuMKjlnM5c22fatfUmqq1J3Jgy9gFzOIURu6GkNazKkepOidxXrc5DQCn6Qzsccl/H7K+g9hFKjhjrk77XGSpPYZqi6hGCre0pFTLb3XJ5VdW/3Y1eH8S7Ejy9Fz4+4H3eln1TrgzD/H+h17vh7q5W3i8wzYuRgtjLdpujefd3+Li9j+iuVmC1yG2vpxKFAWBBl/0KRsUxnHG5lona4DrJ9OpuX6ijRic1lEg7NkDIsUjj6dkecobwqtAH+pkuNwpwcx4eduj2zpQ1BbOxks/wgGgMTNv0V9sLnCxafF3fIvX/k8www1oQ2C3gaElmGOYC5gQnklCNpkYqin+06dnS7zlvOHHjd2zxKdXcx5xSN4H9Eo7tvrQDAeXTBmyUjf+SvuCPlBLaUeJdezck3dtLNU7Vm3z4fQ4I6+BMiwQp/57hO8u4r73Ds4zvIunz9nDxDHbvWqPUIMbPDa+R+8cnGOQZVgDGHWRsicP4wEYhBBNQKDVabIiaAKPgOeGCbRqsPjVOdqT57B2BXIWRBaIF7in0/RKbsp0Gyguz55hKDVPfAh4zewoNBWjhHhA5EumWa6BiJ4N8Up0L3Q93vMT7zjx4iXhnPKYyHRcr1+x/90fdueWaeFdKWnqZcXlsXqWODjCwl1ggf8B3evfw3//v+P612e4+osliAnWAPAEF+O47jKkZYY7/E13u5jsLl6w9jzGBZlWIpnjHWMjd3wAIApG48VyhaZdwBrtAaG8HxLvQRFnM96OHR7GhoDQoglTBSFfSsk6uxoRXV6aBjkxVZan0+apMhi2n2OgAW37O5C5Du9CbMFQoCg2SIkRD9RP3d/48D4hilQyp++13nvsVjsX8x2qfvRC7w7vrdZPAQ2PcIQjHOHBEBWymNthuOBC5NshJDLwIlJoPFEvlY3e79el1O0qP8ufpZS+f++c6vf8E/0u3KpQwlR9XHykH0nnxCoNF2My3Z5d73ZAnOiga/A4a3s0xsKQjXKK6KEQvLLTHQSxX5RlEfYejgDDDsRifMqRHNhP9XmmWcxzbHCsmWDIwOd4y1GWm84QbHTq0BGzdgzKvCYjXGEYL7WYLk54vtwW+V16N9SrYsy7h8c0+ZiknUDwfGg6dKcXWDz/FdrlKahpYKInC8kkUeDh0/2hLPJRmKtw/97cBMy/25mL5IYWE4Yv9UvJ4QgmBVKLfNTr6MnvOR/RTUOj5F5NnYiyDMOUdUFzjd1z3OsXB+/dEHGXoX8aeWpMtutqdpDrmRLlGmghBAZN26ExHQw6gKsIiFTVGYmTtm9l20NWNu3qT3qtjRCSP+0jWR2yd0MR5ZXUX2/IzOMipt6ppsvpXDfcwA83IO9gGbNE/ggPB8sGLTVoli0stXFjkItpOXyHy0ov00RlRlSjFYqrmKaAiLdpHuNm7PPJ6XQqu8Lr0itC4VgqJ5/RVggds+T3YoBgygReGyOmFnO5rvYgoNp8pD1pZUQ3H04+iQr/ofsXOpZ0375He/ka7e27uHlPt0M273rT+thjFb/PTdb7HI5JTo7of0BQ6pJcxg4g2sIK2iN4JBtP8KIgeBBM22FAi34gOB+upAqLKc/D1BRyhQuVWU2lqxqzA/SpIPW0TpXWSDISV7Q8GyqyEZllN0v0X+G7Upzn/Sa3ae6Uzfzl5DNAB+L3vZdAuaIIFoQOFg0aT6B4STVFKYYMgdjAGKGZZcXpsuhRs1g6kwRP0jRMvMzCDyTiGOUqMRrUUJHCYOj/6QbUeyxXL7BYLpAkACljQkE9Sc6VgD5Hj0ZPswvDDva6FL11t/W9b+mya5W2rNQCHC5qpugKHy66o1iOzEXubxrHnfhSqgjug1uPQZHn1lFdz9QYy5oZiPHGOjTm/Yo6ud1PvDftLH68Pu9W9nvaVx+hmky/PgFIBkgqnz3leE8N0B3R44HY9BHCUdj61ODQJZJ0mD+XKc6i5eQaDM+rwx11msgXlLmeGCb58zHsN0PkQkZzquXgw6ucqaKWU2faMXo+Enbm3x0A3jG2twP6jQ8HIikql5ny4afEawtPW1eVZcAk6pCo1wjhxKTHoaOf+5KD+YywLbGM6uaD+iT/dJG7H83NwwTMyUuTMtlEEfWjpKdMQm2QVTw1YLMAmhVMuwSMBcsV0TPlJjmD61HfYXCIRgUwZcNKmkuK8oKqUwsLVFIElk5HpBDDQuHBHj/Ks1JZPpO0czNKVX8KcUa3q5af98ChWFr15JNjWu5viLhjfKvpMjAzymNvgceGfS2fr3685Av6TQa2abFan2HRLtGQBYwFDIXTs2M1RfjOuaRMQ7nQG+3uUL0pzCacSMDFV2mFLOCkhAo7QVZacbZMJ2UWUKaNJYlXh/cet1d/gNv8hAvXp3YfvSEeClPsWjAgGENYvFph1V3A/OCjh4oDcw/CAIAx+HA9lJGwHhFfU4xxaMynyCBqvCFIDHzvffAC8ApfkOPTZ6Wm3BGh+hDXAQPVyWuh4Jrxyh4R4sLJlIOLJGNEHg7kVtcs3K5xVWuGYxs8kqePVoDLZqfHxjPnGPsxLj9tbvDFH/8Obb8B3DDZCjFCyNgfLegCGc89A84znPPxFD9DLqcWZtQgeDaEDOEjGSJcycvofccYg8YYAA08lnjnlrh504KMjbTcxNA6ojyNzApn/E14rtDIT9G6A+mfT6io1oOi2WLs0gYGOQki+ZnFK6n2cogn7D2Hd17azmPPEUz8VoolBoKBTZ+8H8EBm3zSH2tFcflBOdGBdWRaKX5e4VI8C2Oa4i4cUHCjIRC8N9U05fnWNItrGlW3pOhCuOCaicFaCc80GTaYU4pQtmcGbwfQ//Z7WEf44v/2lzg/PYf5wYAchWuqVeglAqKNogzRNAnVPBfsGsVfygVCBLF8wlD4OHUwgYAkDFZMep6W7EKPZGCAugsi4BOBogt7pI400ae78JGfBPMe8YMAFiFN7Z9kGJfW439bX+NzJnyO9onaUSLHezNCHAHA4YLsERRo0ecXbYw4whE+XiiUiHHxlfSuYoxk76+JohhmkkL1sLrrEPb3gUJtM1VW3Ljz/j32Ch2raiYYb55+M9qfQZDQrNOtHMvYI7l3ulG7ZZc7DOKwcfj+D7dg73CyaGAMBc/zpDNQ4YtThAYDTkJdbr9E3Ugn5A3DGBNlFBNkMNrT9tQ9DoeSJiDdSzDR1TkdZsDpfLeZkpj2tqUqaTLPlJ6g4ItlPRVyCqJgIHw4R7+CKHPGu/FccwJ3+iWWZ7+CXT8DjIeHCNFBVgwsP6l1G0wV6WAQU/D2SIt7RtAgKi6wNhTupxCBIBkj6nzCI0sX0wE6TuUlrwgomSKOiWZlRSeQ5JdYdq6Vk8xS9oNymC4qk0HEZEbQH4wIRG7/LwUONkRMLkN1Em5HqjILivn8IBzeYa2cT1k3Wxa5IYYlBzIE23TAwsAj2CHu3BaukXMmDcaERwumEw8PgGyEKIrxaUvIC7PYlzhdkpr3NE7pQlgmRjcMoN7BFormIzweRIykHKPQGAPTRAUQA54dvA//iAHnAVgCnwF2FS72DfoeqpFd61zTpgUIyiojQv6VQ8mwwoka1MYo+Jee1JumlAXhJ3jSGFGMiCqvqD7sazshnWxXOJt/S39q3Ee+wLp6Tsww3oO8CyHZRnvx7gb9ctdMOS7mpAE1HXyT8SbyHnm8E0uFwMDI6PnsRSGJiRWDYgDuDLq2BZsGDAvPBhbqYuNJRjD8HfHziPN2R6NrodiuSHLxRaNi/FEY8fR3ZaAoDctx3Sq81hfMp3FKbbtTVyIcuumXY1wP+XQpO8ouJFzFi1gDnDTg3sJcSSg6BMacfDJKGMPwfsq/IzK3nAstqdVMS0n3MFMsZqG9yHsnMFI6F2U5RsMN2u0a9naNVACJN6bgbPx3wBSk0EqEyMCrd5g2jE4JZOXT6RSjd6Nk5QOqnsuFgXXJRLIX5t/le13DSBVQ1Y+ZtqvWvHd+NgstBGC9BYwDLnfgyhh24+ljwaOVLpv+IzTiPqL//aAa43IxPRL8kkTXI9wNPiZ+cRf9P8JDoXY6+tRAJEdNK+W3GAnSTi2ym9r7S9kpc2KHa6k0zPEr06WUou1hNR3KHem6tWpGlKyjNEUzuHhXiASTTeXpfHXiR8avcHaJ1GGgOCae8yEsAgwR2BDII/LeSPcqjJpkovIbGDNo9W/Ws0fRAEHqkGHmndP9ZOmgFVda66nZjPhYWMdUOSlVic/z5765Kmucbiw3RWX6ZHllWfmpAVkL0y5glqcw7QIwDRh9LNiPiikbIOMSy2cl36SelAWEw0VI3ixiwCkshZOLWsZYf+ck8+nyixxTogeptNKGOo2UUDwsVzQVg1LKMSOZBfeH+9G4Dw8PD81UrJA86LsG4jBi+7FCJExAhVyEhjyWjYdvO3SrBeiigXMeaEyOFy2lzEisgd5pojIzUqxJVfEYBRkrP/b2LC3I+mStz14OctFuuvw0fteeEKLokk+5SNZ7j2ebHsuNz8zDp4sMHxmodZgIqNz1EO5/CKcFHFy/Qb+9Rd+GU8CD68ALgP5VNJxdGhhYKSH8i+GahDmQjTMZIOI9B/lTTmQD4PKeECg80S3nVGD2nMjdm2YIGTXzGZ5q17vKhl0M2RgHR1sMBM/z1b65XGlncQI9KXcR78yIa8DH0+jRqDfeuI5wMBDQfL5C8+Uz8DuTQjQJj+I5XNoOUGZiEXaocNofcEoJL2UKjg+W0Dw/QXNyCm+WYGoBsvAwqdyQJTBaGsM81/Ob7224C2gjhKwzADnOafot9UV8FBqtaHJak/G0EJjhvSvuO4H3+TSReEwkjK+5/LyTkwyaerMbZlLMPZ4rsDCU3oWFi8w9EXht4JcL4LqDvbXpXhzAxTKjmYANTPKtVWeZ2ARPJwjuRUY/bb5UKbwn+PSKOQUqB3Lhu2cEEmMsllhh8fozmJtzoLV5TuKl6tpzZLcXST1S89TpLqy1jIr0IaVUWbI3W9nf4nk1lsJLBX3EeBzHrc11PRY8Vkl3NWTkcByMxgOfvwOuHXBziqmNbQ9oye6J4aHVaJHjfdX5EcEnKUO9fyvdEY5whE8UmLmIzQ6q9nclu+k4+0n2K5iMnSJeKK9WZal6D/OQ4OozdWQ6OREKwWSmXfO1VfUl1tSrvV8Ot1Rl64e6fYU+WZVby6mTvMUDdqSozLfGwhDBNoBVdyl4n+UWAoGMAXkGkYGJ9zSK8Ba+5baYyP/Kpy+PuM+D4vHz6fY4XsJzKmOE9mhWHZuph5PRJYtWHO+ayPWLtp6i8n3eGLGrI1OcsDqxjyizTDQ1LQdrYdslzPoc9uIz2NUZuOnAg4dnF+9jUAp3JZeJBBXmJizWxM3viFUUPJ4hgxPmEDlkU00PuEbyKPt6L2MayqE0JMI8myBAp3ZIL/IBH+GMR4eVotdGzqwIBZcjX4ipD2LePjnOby88zh0RY2n08WE3zt6poF3n3u5fA6F3G3hco+uWaNozkLFJm1AK/jSPi6mPO4hLdfKvTCeKp0PaPJFIm9onNlaWv6qdO4tT3932HYb+GvBDVBoc0sYj3A2KAEqwaMEMtP4UjXdgvAazx/b2GsYAbWNgmg4DDMg1WG8u0DXnMaSHNjrEMqswNACUISJcuC6nB9LpEFYnr0OOxAjVvFE2QpSbzJiT2g/7vQbqFFzyZbED2SDC0LdmJb1ysWQmDBIpSdmHZLGfXDfhYY5NqMtBfPfxw9wMPFrbSU6LRIrKnOdEaXFLW3l14h8ZhxGZSopuoGwb9KbDO99iqG47kCrqDh1K1w4LR8cKRQTRZrjFIn19Igp5LCBGBi6eiYEZYIzXal0P4liNW0wT3+4CYtgZ68r3l5cVs7trkM6IIltC0YkRgqI3BCIukKEspDHHMEDxJxBP6SEx18HtuqSRNa9PKXfVQ6G14rpdMAtclCu5TGNhuQl0OwlE+fiD8B/iITA9R8Ui2Tt25eNaip+fgPm5yfnmk6j9TU02yzsWw7ROq/8eAk+l5t3RghGuZzg0bCUBxWG2T1Xv+5gGop8zfFKjNLlRPHEPPqkBOkK9Mz483YeFT5X+Phzu2/EyXy05jXUOmRMqePFxIfO/7wGJA6vkvkKW260WmX9T8XpTaQu5sRYFohGilBe0IpbVYHJZVznIE1UXHd7flzuPdTQwADAmzGgR5hZIunnicLDSk4lySLjZueQe46fwvEk5flf+Lh/iIgY8cXGwWIdnitVleXSuRNb0IfKsIiSMRgXYU9wdQLj/fKttFpWjkrUYPgphlKiBa9awixOYbgmyDaaMF8Feog6BjgTknDg/mehcfFRJasV7iu2b1POUSZMBK09UlL5EdtgxthQFsHxWUR9Er5tWU627h1j6NHa3x4VHvqz6jitlLJUfnv5BMCvy3atqeX49vEO//QYvT3+DbnWCtmkBZ2BEmYHdzIlsMPmC0+lExenu0QLgsqGFELtnSyyUHaKQqjaxeodlVEorlaZQynrc3nyL4eZ7OOd2tuUI9wehsaKIabFEwwssBoeOltjyFby7ws3lGwybaxhLaLoVuGmwGE5x/u7XaJs1zMIqowOAeDloIMPxeaLGHFwn46dWwqdT2ImQR2+J2pVPKf3jA/1ycrN5MKGu145m0FTNotz2Ei4/obnabuSEucJ5cB4L78UbIp9Wx2Sv6iZqz44jjIADJqV7EEbMeURSMTwYU/DTjOBu6dglvCQysAA8DDw12NAKt1drNE0Da6c0hhMCVDKIcPEsfExIELP9K1mbVG79LCZMBpViHWVDmqzPEkeljOi547M3RCgwXjx/QJszc0YVpzb1/eDSZl5rT4PK60DrxeeK5aiYZ8AjGBustelUFkyMmQrENPHeDOgwSlwpvTlfvszZ1CCCK0vbYpmYaD9ziKnq4xD6LCnElFzgExGhaVp0pgthppTxRIwr+q6f4CGxQ/M9C/MCw/j1IzFrk0XMtz2FYpIm6LSU0zweHFrWI9R5j+H8Wd8tdNwWj3AfOOLNB4SfKS06wj0gKzIJNFLMjoFHv6a4jMPkpekadvKNOjerumsjxFzZdf2qosO5pVyP0vjE4nwpwzKA6NGc9TLq+8TBwLGeZ1oeH7Vpopl3g8CfNqYBGQ9rguzh/QD2Hs45hRWRt/UmhEsFQH5ACo+aewoGwl0TCHxw8qg4tImMEPIJooxWd5Goc2nBuxr50NCMMWKEW7H85CFQGSOCGCGHi6ZXxi58TfhMtR5BLu1GkjWykSLc+ZDuhjAGvlmDTn6F9vQVmuUpYFvlmay0FHIiS4/NqFHxT+zrXg61MkqQHocJI8BcYSKnSYPSuOkrRniUIX6Nppo4REk1NrEseNSOuy6GjMPTlOzRFOEfDTyyIeJwSENJDFpvgW4ANX5PrskS3htkpMgowrIjgWDIomkbLMwrLLZ/DtqexAVJoxKmQZFanurdHFHjnJfLl/caoV37CoeaxqSDq6+iHFMnlHU++fh5raePDITQE04GAsPiBw/03sMPA5whbLcbeFgQDWg8g2DDqVodU5zyrkLVKlCYpwwO8lvSCXPjE/5k7ikXNm2EqLqjf87po+YpuEozs5a4bEPizxITJ8GZfGZCdb85PwtGicwcMoKbYH/7Fub23V7kH226RyhBeBHOLFSaNTE8ZK4wa4AjBMMwIV2aBc7JiMAwINME/N95iUi1HyjDQHg2otwF6u/uoioHYyME50WGAlOKzQCJsZzaI9JYMeKdJrKq1YqcwVX9eKd+95A1SUJfaF7XfE8l0lw2mVYDQssnOMFXGK5v0H93jX5tMJxYgCkYKkDREyIy3glZ1OdcPYlaygfBi9KcEdykk6Y8NExEBSrKyZ86nFhjLYyx8IsWvm0RLoQuByCMrKpjbqDeE7lhqXDnuO2HvIb1w/KzMFDM1qWRdNcA7XtSv6Dxo3HlO40rXO1L9cAQEdAYdJ+foN/2QP8OZiBcXDXoW4/rpauyfMA9Zc9E1N6A9yljTwWpDPU1vpM19Slpq99fWz+lURmh+AMaP8KTI9wDdsukn/LYflLk4qOGzIsD07ErqEpVvqRxyj1bHUvS9GNP6oLl3r+P1rHwJ0uttvck91VycSFTq2IVd1m0tXhWVzKRfvSpZd+defYUfQB47+DdBhaAoTaH8+YsiRAFnDBswAYwnsHxHjeDwKcDqPilYLgwZOBNLufgtioxKfDpQf4njpe/Rrkl8JgEJgNiPxl5a2cdNPEjIfs0Lu9Dv9TmFB42yxlKzy4iR7nRceTByAJNh2Z5AtMsAdvCeIbBBgSXFftJXR8OY1EqVMPEYphaHywSaN0eRK+LJIXF9cuYchtJ3HyS6XUVnD+5moLU9l08qJZdRB6Xn0m6CX9nYrvN3pdalPrzhw9miNBAz65Ap5vD0+PACXqvtorgVtZ2S5zY36C5/GuQtcCpiSFuqIijPV53pdJoDMUONTq9zTof80QRuwcir5Ocrtz0lGEhpSs3rFpJwizGRqWY06dwj/D4UB6zDcCMF73B6dDgnbPYeI+hH8AM3F7fwjpCa87QsovKKgMyJl0YZSD4K14RsdhcfArJJJeVezl5jfLkNWtEVUSYq1Lnw1FU6+Q+EkA6Pb+LiYr4Hdsrp8SDR0PEdx0/X/oaV4sXxS5CuhDjEmA3YPPuO9ibK3jv9p6On5jNI9TA2v0x0iqlXA8cTGRIE0MbGSfOl1NLDM4Um99QOPlhLNiXoXbSqXPKbaiapHA/v09eQrsY+FrzzFqNraivKlvfu6Ivna5yQAyCOYVKJ/jMas1Cl61KuwP9Fj39YbBPETyT6046S1YMeObEl/4Ca/rXaN/9Fu27/4a3X6/x9vQExhDgDWAY8JRoB1N5SV4sOfPDSoEsQ5hfybgH44aJYyu4KPFb84kmTNCnUAeB0HQNmnaB4WQJ2yyA2xAeigwlXA04HkPuqX5nY9f7ZJimJf/71p6U9cVkTwlBJdS4eegIHI6dj0+959pnFg1Wf/kC/moD+ucrNAPhizcdrlcDbhZuty31U4I9trQjHOEIRzjCpwW1TLZLApzc5u8oC9b6jsPzTDxN4kbJJ+8raFLvo+QF/VIf6JxvGae0xV2Mozy6Xp4oktV9EVXa+tlck+4CBLD3IL6CRQuiLijynYP3Ht774NkQ76n0URlNxoDYgMhHZTspfUNolDEU/tng6U6GwP5uXhFBNvRgNoBnsJGwqdqgEflrMIJPc/R0UJXUKJqV6dmTOgUUDYpDgH2STR8ErD+4CjQsy6jCFUPhkurFAu3JBezyBGSXaPwlWncL8QSXHEmWjuuA4iFWMRBpOZ3nDm8d2s9dFklmZcak3JdYnxe5DEqOTsVMHIERcYtzmmnZhVHqI45wCNzLEHGw8fhDgG7cnRq4J/EM1SppkIG1DaxpohLXxFdlrOKRnhj8oMGs96Z9RYWuTHRIKU9HBRa6KNVepWCTxOkEvNoQmBnrYYDpGW06cXuE9wUNdwAIz5dn6Loel5tbDMOAzfYWjbWwLw343AKGAKM2QxAQDRDZgq4QuFhnY1zI7+szHGUR47zTMHXw9U6hNvQp8ImWFGhdtzsttNzpgsfjsti8DvITOI/nt9dot9ewk22Y68vPa7XcvzeB82ixwArAq02D8+stWu+14w6ySSjXpEc2yy4UDW8+MqeEgYDbjmAXbbjnBwaJtWAGRixcrjN9Mle4lhX6Bb3fhwPJCMFZPimQrKwzGf9QGhSCo0P47RMtz/Q+K8y18RD5SE9db3pYtlv4wjtaH8p+F7H9laFIp6zKrqs7iGmvtkCiEHcWRHH/jgpuooBbnMMbEeJJrXRyRu1nXA5XmgeoM/fizsVBEPGB7Ob3KZ00s2Kq9YkbIhhjYayJ4ZgyzxH+5XEtynjPUPIpsj4KxgJjnPr/s/efz7LkSp4g9nMgIvOIK0o92a/Vzu7s2HJpSy6N//9nfqWt0WhDG+722HT3E1WvXl1xRGYAvh8ABxwiIiPz5BG36njVuZkZAQ2HwyWg8gKww0cQ3YNof6A2Wvg1U0Ock0P87Tq9B3W+6dcnzMEayVmV+8E6/Mt4C7J1tmP2nVVVnR0WoyHiItFrpZug93gtzBGQmU7Pt2UBTh6/GkNbOvxi4CW5ip80Sa9wCmjp7vVo0Vc4BEmvMPPuEAalUyfbN1hN+LnXhLm8mmfRqR4qp9U7tea/l5p1ar1nkCsfWISfGJ8+3mF/uwNA6ShzANmhDAjvjEFQ83MwCKS0wRgBkXOQZaaAA0EfR4aDvCeMdR2ycECICHKGdvYqZRHhx4PcdhBrO08ix07q9REoPA9qLHqGqU4doVsGIAMYCxpHWGMw+D0swvHqIl/ka5190tYzEP3/+juArjKtooTulX6w01x5HESwqjT1MxuLgpCYTkBg7gxFdlYsKurqEqgypuiCzjJpR8PT13geeLSIiKeZhup8sZMrXWLkK6RcKJ8IGIYRxg7RchtvfRfL5oHqH2e81pXa29fyhaba11sRC66JRXpRKrQAwHu82U+43GciVWkmXuGB0FczBaJreQvLI369fY9bA/yX+3/D3e4e063FsB2w/bsRfG1BLipmYwSENklANvyqXgZylACyN4Zm0UT5WWwWCZUUnjRwIn70uFfWLeplmBHstVc75y1dlMIMfTG1Ypz0+ojvyU341d1HXOxuQpTEkd16nu3tpQFjgytscIWL+x2mD3fYbBhk5aibyKTKXBSMkEKMqLBNET9R2byzwOdLi7dXWxCZyOSU0NrjAm6ky9oFS7zGbc5otoSLyqMiMdRemVU4pws/fepviGqI6xGaYfY5ozJQ5DrQ3G/i4zFksx5TnXaDHmKM6Ixz7a6uns0VfdgIEQ0cIKQY4uhNb2IkmEG+W8EQwTPHy/EiAyttmKtMPZb591HoMZEvNl46EfyFPBEMxzbNF6boUB4xYy3MMKTLtrM7G2VkJfVzuclPB3NdFUQXNGWAwBiGv8HaT2B2Mw0+gENHwBKtXVvkuYwQ3eOnFtMzftp4/L+Gz/g9j/jVmVn90jh4XsxZpbiUKl+QjrPHcpTwghr7FPCSjBCv8AqPBK9ofg6YkcoqorpEY2en4TGEpoolK35329DjoWcKpWV5uDBOFHXkZ+luz0ak7fHtsz/66c8M0+Txtz/dwjuHt5dU6Mu89+l0AUKIbgj3+vlwBBJxSs465FN4ZB/4fEMhesJwcFijNeGhosAu9NhKvmvuXYBoxeOxRGKM6DMrx9GN060SIoZlubRTcZR/Yifzb9FfmgE0bGEJ2Lp7SJRGblOWL2KBebEyVGcFx7UCv2pK1b/W+VQdy6SPZKqHJtUd6iMW2U0VyvnUltz8Gb62Z8CpWv4Kp8Fq6eQwg10hz+qU6+s6Qg47cr3OCVR6d+mpX/UvA5gR48UbmOtN2C42yJ7kqZpitbZQdLLtwEFh9OBiiU2hYi0WHpu1gYHVP7n6cuctHmd9V/j0rBTRK/rwCg8ArQiUIQ8hhAzCZvoaoAt8tf+Mcf8JH/7+Cvbbd3g7/R7X91/DjPmS6rSBw6hNs1QuahOV57xJiwYpKDZ9bIi++LxudRfbNfKlvaZNFTcl5lLp1GGwtBe4LrdIGRZBVCprTk4raRngzi1HSpErTz3Lhcpla7JnfL/31GscDtHiXwLk8WIfjr3yADwxDFxkZIdgWCADxFtPAkg0g7CI4T+LmM0ajANhu7kAjZe4wwWs28BIZEQ8CkeuPEszz2p+ZU65vPMo6fM7RoiG+aq+pByytPKX3IsCH9VW4rNx0MdjmfL69PEWdq8y6I0ht6Vs4QKDDRnM9p2s1sZApL4nZrB80K1LPzt2Wwl0MvaDCbwxmL4a4KcB5tZCjqLjKMQQ8hVvFMfap5JiA6QRIoh4mYtElYvLpynSLDK5bMHQKNNAVwGIB1iYs91+B+wmDCPhYiCM9xOMmYJ5LUVkVlxHxYJkxl41X/MHJ4xrjd3z6Ur+op+cO1+1sWWmhiVCGd+RGpSeV2U9/HobPFgHBMfqh0qAXU3MuZAPszDV7h1BMDfq+K915a9tDDWDkN6cUAN1vj0UXuoOWSHNzJB3UYt6KZ4OThrRow3RLx96riOvHv/AHE72eNhZmlqUtWZMD62Dp5kXvT8KuveeLeVbSneOdj0ZMNA9HrgBRQPlC/mME1GZK7pgjSslz7iiLj0OabvMWkqRA/LTmrcNysveeB7mcmIZXKYooqJ1bq241RXWMiqE64di1OpuZj6/aaniJ4ORZI5XmFOkCd/cedWFudUex90EGW0YDOxgYQA4Znie4NmHiGFjQCm804BoCjwOGYAKThzB890nxypmwBCBjYEhmy5nJoPEo3cXYGLTSpmKwEFkslpeYYS72XwqL9ifCma7HYGM9Aipo0ajYe8yzqZxq+jN3O+yS1r1joye0ViWL8YOYwZjMBjCFg4jXJIrQl+lAo8cURwXruBnwYcu3QMcxjDocqQFHP/3aQRCv/JxVnnt6M5ytV4FV/M6Y3C8iFwkltBeU45O0epiKvKQtbSh3uQ0nYtVVq2tB6MpKqdr0y6JTADOcyxrRL3k/s+sJ6Sp95jt54xuUnnk5xqwbmtq2bp6ouv3zVqtX6wekUbqL9qQW9cW6kFgM2DYbkHXA5z3wGAwwEIrZVLIWUEx1MQuQH0JcCfFDKPcsnasc6gFmoLaKi1E3jg5EYUWSH0WWyGSd3jRh2NQ9RUOgprgYm+DzARhcO9gcY1v3PfYMPDp2yvQ79/jnfsdru7ewQxDUIzFDYkgm4sSKgSfOf9p3NRe1XlD8DMUu2y+YFtNuLOT8OkUVVCu9CjRhIVSm31cj4GZ8aofsW9eooWiAteLN7rGc7WmmZG80rXCsuh9++tLXyFzbOzDSlQUhgHnPTw8PMkYu+ApIymj8SAcgROfxrmUy8csBXOFJ2BjLdy4hRmv4PbXIN7ADFGxS/ESd1J3RjDnE4z0Z4FrnAxcUGPSeDd1jBQppV5XumwgGSHkcvTm4nhEPE64LGszPGcf8JhSO6XWVkyr56L5nowKVOJxYmRqUOJlrQ1elM7n3pXP55VHkSpKX7cG02YEbkcMuyFFhBky8ORjQHekgnEp5+Z5XXiYHx+jU5KBVtoT/nExqRHFtAlCiBePKlKGLvkkIHkAscf+/ga032M7vMHlaDHeTTBmD2Mvo+BmEg0HIpPdHTaCRGZ03BDm13CFt+VD/UgErLxuoeriIq+io3qlsLRUWhk/a3q6eovI/IocZ3UoZdsvSdDhWmNna7+5XlnHK6Fyf4toCRLyFATiNP9HlqlatrKd6+oo+VBS/x4BNPvjC4GENC1j3klVv1/ucW/H7VPch4DqwcuHR24kNyv8FdaMxnKahYXxM4DHNBI8r58fd7aROZ5RP9Ye1jplX4LIKhWJgqZoeJ+ptiqYMzMVH+WzNcLTyGVQ3sfL8gpuJr7yxfs+HRZ+pU2XeL10tE/ZkZRSiQwpp4fqgeKxCras5pNkIHRbKz7qGFyaFVpVQ2oGghkEDxgDQ4AdRgwmRqkz4LwLzlMhbD0aImQ8YjRE5KTzrQAyzjmiwiA4/BhjARMukzYUnIJSk7RKTncrNVnkpigHkI91SoJoEOGYiRHkxRSNLrMVndiKofZgmCiPhrsMZK61w6JEZ9eDXQ9rn0/LoxN+mYrHiOMZ65K+EhmMg8UFTyBMINiI6eEw2QJPGdkZlILcWbQLaAY4G/4o4aSgZpBjfdR5syz6mFHxwDILJLpUWZczukqKxkXkNS4z66HrQiHbc9v81AuO8jPJWHQXYdWMRkCe48JVI54SKhpgohGqcNCdlSfXw4MMEXN06lj6taoumpuDx6ithbz027ru9zf40+5HXF1bfDd8B2NsvEBHa12CskUtubzpgJvIvXU9Yo2/i20v+wCtCSg2tlxW3RrOKzHX3NQUVS95s2Vgf/8DpvuP8NPdql69wmmQiXUmAokxybsaAMKbq9/B0nf44eME/8ct/O8ZZOUuCBJ0DXmlMFKbTKqztjyrd70GqjcPXrWqjWeBSltYGlfkoSRV72bLk/cMzw73n/4KugvHijzxdvJscP5+lpSY93vwp3t87/+Em2nCb9/9Bld8mTfuROCir7ngtG4YiTd0OD3UWovNZgRZC4KFIYoXpR0QnZP3TY4SEs4lG5pZtUwTXiT8a96rcuR7VtPqNMpYpui1j91PNoxkhOCYh9U7xDyLXNcyMMfIkYdB15tH5m9xLg63udgLj2yU3JtjjIf3wWsomCmcmvNcUzYGKbosaShcvGeYwT6+N4GRFtrBAFJQmaJLYMSQc4K1Iwa7ARCOlmqUtQc7+zQ8VO5R5w0Xw9ZNE9KVzhPHQL7j43wbR3IuaV6crYpereqYAAXV/gQAw57wqx83uN94fLiejmxXuVJYsRfJ9vFMXu9ftprysDkB6GP4Mu16qnW8An5m0RCv8ArngOc1FLwMaGgYlw/FGFCDfqLJC9WFzjMSy9BRJ/VYDe58m0uhn6XjeyHNzbzPUVDJDAcSdX/W8viDoRjzYqZm0iTtRHCaAcEOJh6/FNxRPIe/cFR0lMEMglBjSNl+Io/L2Rzj2QPewDsHF/NKy/JF0KXxZjUohXiwOVBsVoiezk6LUMaDcnzmdZriZNNWyURJ/V8b09YCN/NTNa34omRF0X9IpEesWt+pIKdpzLZJdXgZcwshqmptbj/FOc+JZFWJMEG53Tp/8bukNsruVDSbVfv7K6e6X0KXphW8s8PTf3GyrHouUM1iFucmKGd6lAYi1N8Pw2mGCEXs26Gb20IeDqQqW2LUl1+cDhkhVOEE7KZb/HDzZ5iL97B2ACkCmc0PSonSQdd+beeHfqnzdaXFx0IcFpMXa1yWrLv/gPubPwav21d4VGCgPbec6hVJ2A5fg8hj/PxX7GFAv4t3QqSNpLJCUKm8KRXwWZFZtiQmBCu8mNGcHAtFE2V9VW1eW7TeHCvLQmYclQKZhREQj/LKIMh6G43pvMf+5m8wd5/A3h3R0S8THlfWUr5I+z3g9/grf4+/7e/wzdVXuLQXqhXCPAXW1iCGk2ZLcGD7lFuMMRbjOIDsCM/hzH25GaWnwGwxOnEtGQeKzw4t7RkhFFOYcEzuggCgj34qL0RmhYPyXVj7KqpC4XfG84zv6+fxSHb+CCVV6+3zeGxZ6Twwlyh+cpSFCOmqicQLN/Mb/uE6RjZOhTfhBxEF50BSsZccBZNknMjlUjQOWzvAmjEeIUYibalGaTZ7SY0Z8bA78aes6l6enhuDpsHxN5dtadeEyq6Zw0OQjFnrkneLOJh57v3jixT13JmJ8M3tiI9XEz5eTyfMYikKPZsi7VxD1ynnSOq1psjDqWcyNY8PjXeTYZ2R48mBFdF6CniEal4jH15hCWqH81c4oFtYkVZ29tVqLm6+dMtsUhyl013WhfREYf27kAcesJ9qlfVx8vUBJc4DWtSHesbKdERBxhqMhTFZngl3T3JQfsY72xiIOja3jAgMMDy89yDnQNaG9SlMO8QWEbV6c3M5s6aT02YqR5ySCAQfFfZ0HL+UEL3C+KTPDvciULxL7jF5MdJYGudD9JmJg19mZRAL6H3tJ5hpSc/jJtGFYt2KsWkuir8pWexX4XfZrQhlREtqMpePKf2ba4bCL7HeSLRFMiRR64he9xUQWf3pQY+g1jtkTX/V+MYocRge7bLqc0K9aRzs4hPN1x6MWzjcEsPaEVf2t3h7+3/DsP0V6IKy1ZUywgMolLp5qVNEzn6swWHoYPLCnsA1civrePb2FgKU25VCnZQSK0c/5N9JpcWIx9xApVlq3Cs8FPQ6yYxOZ7yJcMHvMboRAzaw1gTv7/iXN1oVJaFL8uURGtobXFL2maO6paeBFgobI8ShGiP+Ut1CDufo+3jkUmCG4kWzcvFwck+WoVVrTy0nwX8dNeLLBK/wABCS4pmx209gfwfnXbzzIHMJRF4Z2XRONWkcmckY/WCGATxQuLy9Qa0SyTS9FFrIim6qKuJXTS9LNEj4BIC1oQFQF1ID6XaCuLaFFsvdJemyajkyzKt3nOmyMPs+0XrB89yOo0C7TKNipytjZn5eq3fm1T3nM0Jo6SL+06GTdch++sLikEXxHFWCYQ94ApMP8TcUGTXmIPd4KT/v/YIB5DOTEKLQOdUtOBFoR77jBABMFNzGYQsaNkFgi8fxJJ4j2SWo6kTb32KEjp3+BpHlK7fvk3AjfG0VoYNqOliXpoxuB9qY7+iig3vDY0GD549E9+WIJuuBX30Gbhn46xbYG4cb3GNXYPIzCTUN/q3NeO6WvMKTwqsb+Cu8wi8KAqezbq8Rnrg2Noiyq/C6RulW0VRafuk3bOY59/iWOhkfSrHUHp55r8s/3HZdMxeMEgKPv9yYusKDSfpwHj7CA7h3Hhs7wlgLwGNye+wnh8m5cKSSDZESZCwMM+A9jCE4H3hv8qKlCDo3ZoZnH+6acOHeQGvkzjSJcDdR7tOy1Okg/LVhgGEA9lFe4XSsq8yt5r57p3qWiK1XAePs/FuqSxsakHUkIh/q9JXyX34QqkiPufWo5OIWKn1KZ2K0cZIBpKOwEI0QOjKj005dN6W8QrG4bLe0gblDHxRPTb26JHK5nbNSP9fpkx6R5+afFMIKzqYjYWsk5g5OH4BHMkT0Vlb9rZd+ufUvQRbRNMLB4w4Oe8MwxmBj3sHufg+634IuxAARCGNWlBYmiabs+lt6Mmuu7X7tJpzzwk3rLi04YQzE+zZ72eayeuXnMkUPqEMRdRWv8Piwhkna8BWYL2BpgCGDcMmp4GjclkoaU3wXj4XiqUy5JtxNYwT3TkCGagmtNUIUtfeUwGJESW2XhZEvwioZwKjohVpdyhjDvi4P6V6wn+sSePJ+xXF1k8PkdvA+3nkQvRjSKfuE/B16HjV9orTBGmvBxkSnG32pMrp4lvFJ1kNWljZET/1u+bWctxjLygiRi/AlneV0OF5gxr2P6aNhzcuYqXYKrdcK4KJzs6NfjcE8AzK7NGnpZ1QhH8vVcJ7PxWS1Xl5nWzxaKosEBojh0uK15UE+PxeOwYCR46AiF8F6/vVeHJhXExtQXXle5CMQLBkYO8DaMZRLWSCjEns7Y9Jnzg/ByXv4zH6QDGqCgUIzq4Sacc95Hg+Oxr15C9rhNAdgXhihLBQAsAy8vydYIvztgjAR456mcDwBZPjOKcxqrniuhfO/DkLa3nvGs8N1PwWsozgKztnklZU//yg9MvzsO/iS4OfKwZ4PhFy/RkYsQ8GLd2iZUunpTGpfKNOfR8HAxUf9+JSyGk4mdbtXqH42w6MtMOrLzdQC6FxKjtUe6PCD2YgQMeDAwZnHhDsgJufhvQunaMhdZ/GOPop3M5APR+lmlxtSpWb+2rMHeQ8T5RNS/zEZ1ceZjhRK+FZXWco9oi8R6cCnthXHZs/QhuCSrPtR8WtL2urVsJ4gNQ5pRdaqIbPFVuNbL61OP7QcXUPdhEaGI6CMPBc5Up5z8YZ03iIXp763LWmfU22M4NwguYC8IHCd9SXHfKU7Qur+zkDDGZ95z+lx3ovp15wsoOBFRET4H69An7cwX38GbSY8aBR7I9Ur7khtS7HPFb8NBmJ8c+nxbnMRL4gUJYAp8y4YIULBDxCqtYRevehug6KIknycFV0MrxRfkk4pB7QSy3NRA8d+5F+MN7sJ445xIbe+vDKxLwKILC6ufg9+8wbjsIWVOyLiGXDz+wqjmOFMr3MS1BtNf1Op8xx60vZhHa3obyd5R2Sl0NWRPsGzgsPFs/FSXzmOKVvbkAYhjwnnT2bAefzm9gO2dx+xeT2i7GyQTA3fXWD/9TX23sM5B+dc2OeNOi+fwmVgkhPIxiGAMVng/tpiuNpiM27gjI30PGZH+ak5UPHACeggBgPO6YpGh9+++i3tykd9acFCGSFYM2oaZzNecopWihEQ8dI2lkgfoflyf7qMiV/ag85Et0XJH/8p98cTdbZ102T8mwJ6JQqTT3Fzj5dUg2DYYc6/rGx2POfWA2ziXPkQMcGkLltDYIZr+knQBgeGkcvWRKhJkZWce8GM7f/xI7Z3Hle//19gh9+BWRkjGiLeYw5Lk1wXHmB1KGUJTtPC6VdJk7l4V5WTGplDpdM6ORPj/Vz3HTwUkhdasXaCgeLeMP5qJ1jYSvI9RpqtCl/TpjOl6ec6Rkx7hVd4hV8eHE+zXuG8IOq3Nen0/pXOoI/Q8N7Uqp7TniAOICu2tmIHTOLgKZLoDHDxkb+kz2NLzvzfPL+2dmfvyyVzr9fBkrItmww8ALdn/O37O0z3Dm8MYWsnMHt457Df77B3e3gwBiIM1sLG6F/PhHTsqHjr1NUq5tczQBIlH/MQTIyu8NAy/3oQXt4juiFF2TJjarhMW2OuMGnz9cjJE/oEirlje4ojkk4GhSlxAUqL6+s3cnRxp4xigS5gn14PXMnJAELEPpQgsDRW+d8kvxLisVtKTlLGHx1ZJWai1GeRtbgstaqwkcs73Ytzpo9Ny7JOlu0597OqhqFH8Rg+/fwgbQniMcchItV2yn8cjiSz1obj01bCaYaIB4yJtqyE4SXgdgu+8+C3t6DN6WUfX/najiwHGFpiXI2M6+0YhT+lyKWE5qoBR8DpOgCF/HVZUQkVvyfFFgBW3t/ZACHI5wu1RfYgLxeU0A8flXPXzuHK8QEl1ys8PRjY7Vegy3cwNmyoxVEW8iEEWuGvvpBXDFbpCKJis00pFlvSMGpLUKyp9tlsXTUTmL4LfmvclpfqmB9trGMfj7ZR+TgXl8qOS4PAeLe7w8X+rrq46nSox+CXuLoSpr3ZgL+5gPsr4LwHs4sKXx/O0wRB7olADJQNe2meLE+E6WLAcLmBgYGPl1sn635Xj8soPJWFViYjwXy76wT5joe23J4RomBoUpSErEvB04y3GodD5ERew01bm3Y/Dm61O2IpWHT1wnNN6Q12rx9z23DcsGUPNwAshx1Rzqbt5wsigSHAGwPjJSoFURgBeuK4JpXpu9DZJNQw5AzRejCIGeOPd7i4AcbffgXidwAbVRMlnF30geDiI3ECTTKF18fDgXzcx780JuQjk+tTuoz/VfHPoHtq9q+lNnTaqmyaK+rqj2UOMUcqjIjgDOOz9bgwBOIBoFN3ipIHOPT4EBzMcu55fEh55zZQLYzZuSnts6liNVI/poHvVdf8AkAL1+eCNcT0ywNSNF9D/fscS6bxuH4GEWFdlVpmXErTV4YmXZLGGVLl1Xsu1w9XS6hHQ80bzLKv6Z/5iS9XGWvd6XLtBwXsByCGbu6C3KBZUALBe8bNhwnOeby7NhiMgzhTTZODd3kuDWUH3/BIBDIqkJzlnbJq6aORAXWPAxGY82kla9dGVgcEQ4MHhwhopnbNxraEukSZiyy/daEnaJ4baoFgpjXUpsw5WBlMqJnfpofdn9UaTfJtXpFaMd+0Q0Sk+IMrfOM6LXT6KO0lXbAqXWSuInsuX0nqCXFqarIkcq2FZ9/5uluwzI9+WEid4V7NRzdEzEFxONjpwFByeP1iruoH13qg5LjeuMLsQPgMhmEDejvCbQlmyxgEC1dgY+k9q1+UreDO9yZP73d8Vii2YsXF8SGyyHz2nAWL+UG0JYqwz2w68mp/9wN2dz/gYv8Zhzf6V3gWoODJa62BMTaGQJbKwExvZUONCky5MyFBQZ5rzdYs9F/Pb4wngWpLeQSTGN4k+kHuhggMkZez9mUdyJrR+J82Ik55gxFOnb3vuWrEif14hRLisDrP2DmP/X6PCRP2Zg8eGNZYYGB4H+LTyDLEozpMdaBlPt2TQKDdFYa//Rq4sJgu4uXWwvR2qk8Qo8O8GBRmiHTChMJYodZOcQxTzpWdRDLNzkYJVneYxIgIwWPP8R4I9UxwMhkQ8zoQ4n4qiob9mzvjNSdCAu1RSE/AgkUeo8dqwBCu/7bH5vM9fvx2i89fbwEyIImcKs4kDb+JAMPBoBX4AlZGDQ8XN27xNMrTmG+qkVHwLPkTn58MCsmo4Amb7YitNxgHC2tNSkAxUS9sHRCmWgbhfJDoKjReV2m6eF9vFtkYzAwMw48w5hOIblXesuYA7YSmn92JfiR4yrqkysogylGSujWM/7Zx+IfJ4p//ssHnS4e/vT3l0uoZ6NDFZxegXuEVXuEVXuGJodROHHQOmylhrrS5HH2V6oJxLDBtEHWa/FvIrqw4E83LNAqYh0PJ/QTmoXZ9Sb8K5euhsZXGzqTpOu8IA3eg0UvVNY8jX5sKDonIWhiyGAeDwVp4FyLaJ55CNIQdMAwDrLEgsmUFWZuMBjdiMo7soBdFMxmEqyII1tl0h4P3HM7yLwX7+WEDg+DB0fGH0RohSvY3350gqKeP3wnsvgeTOBId5qAeplFT/YzznYZTqXENKFwSbi3CwFHSlaiWFyXn/oWLtROuilw0qyMue3RsxEdhwGC0fKkeb0GHJKaGOz1K/I0JWD0+uPbj7FGpwyaJcAdKxCiQJLb/OazFxwDVP6j4SUS4uJD7XtbBakNEiSDPAOeYm6PLONTTTAmNscDGgjcA285orXBvWPZILQ0h2krY71a5+ZS+r/pVtvGVx81oL9qcIWcry5Mk+Vx9wO1vMN3/DeynqpGPsJO/wvFASIYHIoCMupS6s6kGZY5WIiGjWWJeqs+18/wQdCApYmYlKMVq2yzV3phAG93SK+agHWSpSdZILoVVMdlSJ8aNfEL8cV1bz8ifwvSfC56yxpp6MBDmxnlMk8OECW50MJ7gvYfxFI1DQVGsW5zDcuU7YNwA2l+GsN+LSYk57cLIkUAdJiMkWOxLY4Qo6GrZy4KJSwyLpteSTv3nGXI8EzrtrGl8d9U+4eQ+OAKimzw8oUwoYmWajc7SHcGA2GK8mzDc7PHxelRiISEE9bqmrmQwoOpyRUIQWMiXSviSzNRN6/ZEGHqZL2sNhtGGy/wsxbopGyx0w1bB4+zN3PkmPwuca4h0+CNzC2s/RYPZ3KjJ9zyxYjzXM30M6KOajhMQyplcTCZoyVLn+lpEaFzabp0BPg6MaQdc3w+Y7Cnz+3ymhaXbWr5MUDgKHLc0JfsrvFq7EswNxDGIcixyvQ6+hlMiD+YiI87dlqeHMzSAan1Xppdz/at3ecWBqTy1g08fZmXJ3nfuv1/O3fIT/bzK6sAotcQ9Xu0Ar1yOjZIf6gJ65RyNqN1CiudkDCwYxo6xa9GBz4e0wbPaBGV4x8M6OdoUohkVH0H7r/pPBENRwe4BIPDmB4H06Ckn3sKJapnP7N1TUEAjUKgXJArtWUntOKibqpqVhzJe6h0HmIlSpEDta6bXWNEFReiCkYLSdxBV64ALPBPHVyr6245vNkLUcHhfMwgGkyR/iCVF51Nj05RUTWeNhvpNYVpJ5bUFz6LBM8N8rIFqpQHsaDHY9XEOL+KOCA1dNFtYa4+r0s6tESTV4UIBDAxZ2OECgxkCsVx5UUcoUykmztXkpedqFeTIBp8s1VmpxkDyEpZ8+ZiaOiypqZy1Oqx4vNDIV3g6CDhqTDxKTBslusjLmUYDgMITL3OttCGMvFZmZ7tQiuZ6zoIfCT3rNpS4m45J0gpl5SWevMeR+5jWR68/sUxmgD3gvcf9hz+Dbz/Du/0r6p8ZZDh/+3kC0w3++OFf8OO0xX/87r/HW77GNOwB+HARmjX5QnaIAo/FhhGU9jFsN4UdMspLjRXoI7bEMFUcu9XRDmYPq8zIpjVQrKNSYGKVu3fRtOdcJnufIiB8VNwWuKyifVjXK/dFFP16ONTHAiWF/ZOwWNUcxRb0aw7UbTN9g8v9Bnf4N9zjX0EmRBoYGDCi10w6YVTONEXeTyFsO0EOOybDIB8V2/FC8RQZUbWgbFJAPhI6bULb93e34Pt7jNbi8uoCV99dYbvZBA+fsgW1ReJJFbuJ+ib5QgzCCsfTAshHWgGyPlEY0Zpyi9+aWyusTGcBaoQm9Q5za0XawlHomuFvjzE+KHGmaU6a6nCcAeCjowHhzjA+4Q67LsYdv9KfX0B6/hacDmdGzld4hVd4hZ8hiA2CuptsufPrPXqOuqYrJJLCUR8yohyThBvxqtLZjf6A4uXA9pp1QZz4pKbdqHqb2IoeX8JNU6l6X/QrM2KFjuhoaPJS+Vh9M/C4HPYgJoyGYAzBOQ/vPcgABAtjLawZ4nHnysBgkI7MTVxtPN0h9IWK5rPkIwNrAe8trA9HfZrIt3tvIEfWHuym8PmrtvA8E1lGCHpC4jpGhDOy87n1m8u8Hkm1HOUcAIMdcXFxCTsMAJkkL2qJNBgJTKfAcOmy/s1AfpaMDJmfDW2gpBsq37bydPmU1Ti2XZamZxmtjNiYH+dGEG8riOEPFFtcppunDX09apWKGavQ7NGgOvIqyjEFRDw2g8EwWFxcbDGOz2mI0Cvz3Kb+xXoZsBwcFfmc05aJWq83Iu5bY4OFNZHLZWNEuaQ6JZ8uH7bZmvWrrLl6kbNaylxnXPAk4JJ0syrzObyzX2EdyM0n4T5fA6PWLgmnA0ALzZpFA9olLgxVqYNlZT1vGaYauszT0pI+eY1kxithvsL7vER8OoYqL6EKt8X4ENdOSusBt7uD333Og3VCe49RHj5lZMTzru5w6Zhhizc7D7qd8OPtDW7vP2P6eh+OInIengjeh8urvWGYoBFO1E8YQ2F8mABPwSiRMb+CZEAWw0BJy2enurtegIyB8bswTLryarGxrkQZIaQ0Kdd71UZlWCvpfypotq26zrNe6ru0TzJaZr8ehxVVlDQlsM/d4x9BMHwBiwGEHxEkIm1JoSwZx91f04JizUVBl2hp78xyR9WMXG8UoFK0A+I8ehcENYywFxZ2tKB71TaqyjsCHot16xWr6bAMSG3D662tvG7K8qn6tqpdLEIYL+J2Pk94xQBl1jG0pJvn/CIGEcEMQSAPQl0Q0j0xHHms8P2bL/vJM56hwCeU4mSGj6rypEyv8Dpuh+CBQuQXU+ccPD1iHLNvPqV6ROCxojC6dR2dY042VGrC0qfipDat6nqHf1/Lyy/mOVDlbF7lilxL5WW68GCxn80wc//7mUCp4VP9nhnOMyz5IMVF3jYcCZ5l2BQRAS0DK744PZEUtKj+E91cOGXIgIjDnRFsdKDxQWBmgMLtEGtRUSvBc4OoGn9Ex7cwu6yeF53g7o/jgOqvWc5JmGYI1g4wFC/kRuC4fZJ5RI5KDS+35ap/QSRSuCz8Mbf4LgaLNdt8EgkKI2Iv0bxWZG4tzdem0ykjhI6+WZia9UvtGffSpAfkKBvFx80+kmeJwTCGYIeOcWoGzmKIKHQl5yjwlDZc7WD+7q/gDxfgH988Xb0wIGMxjluYYUjeZ32ohGNthZ6vINPvEwdXq5uyJ2L4LeeZp4ukvXjZ+ujZHc/EZqVq8T2KGusRhax423rMUOBXeFYggIhh33zC8N7Cju/CxiyKNn1xdaI6AIjV2fqiMNVe2gqjudxdmH2xOfVDU6tnfEZxQilu8xE1pRd6wO8QySC3o6RNNyJ0r93ZCFEqfeXC9nw+/+s6OCdc4i22fIX724+Y9nfw+3AJmvce3nnspwkuzrUzDkAMyTU2kr2gqLOw0Zhssb9gfLA34fzSzhaZlOOK6SmOePIzzJBnhSOZFoOlDADwKSy5hyv6DoiYWq2l3A7vvfr0IboNGQflDolswMh1FbuSasNRuHuUoSKLGF3DwxFQtLDYXyl9VLtwA+7KwI8DpnsL/GQR3a+QoiCqYRCW3CeaKBcqC9sOiN/Q/P1KUYyKodDWhGg1Y4KAFD4J4he2GbbwA3A5GlzQZfYaMwQEO1ui5a2tRQlxuh2HWJFKZloGwXXJE5kBtV8EnPMpTR4WbdiJ/2rDX/hSNHnJQHbIuPDQ9E8FSxEZKQ0I9mrE9f/0a/DNHfDDXxVePVKfjlq0pP49mAwd7H2FV3iFV/ii4VUMqIAzE9DVLMh+sGLc+vqo7FUc9YYH+Z18zLR2QKvKZcWzcPGmW34t49b8S0/XIwpN4VsLjpaiWw0rr+WZvoV0tXOo+u57A1J3+DgQfxpWTK9zjL/+6RbTvcPGWgzWQrzIpd/WhvsbBrLI7jfSxIqvj/cqEAXFufCYokRVKi4YcIwURTrD3lsf/PnlfoYYsZw6oAUGqdpUrLOoTQrtPiVkY+T2gBnaqML6YmTh28Wakuayxepj71AoWbTKq12peBJvTQRHG+yHrzCOb8Bkowoo8+/h1KbQSA/ApAu7A571ubeyzRldq9RZp3+4l6zLCBOW16XI2z7L6rOtiU8qywirP91AEiMElXJhjt6ab/kDTEhPCAb6oOHA6lcLggGQgWePz7sbwAMXdImLYbu6lvNERKg29Qf3gUO+xtJhPch64G6cr6kuZ1X0xrwglEgJEcgEJYEyKi5CsRCEcBYlrxmvfjrWS4alArR91IrZ+FvylhuvUto21emds4yEIGZY5mpNv/yl90uAFLczTDCjC0c0hRcJhXtonDCLtapIk+jyMytYc2rqrLXHwIquIncxffonJeZmjegfucRScRZ/x/KM97DeqTH78uE5+6HrNhhgYLH3BEwezARmEqIaFO4EeBeYNucnGFgYAAwT71AwYPLw8TI0b4Bp8LBm3tslb8waMViT1E6Gmv3h+H+7dpK/iWJQJUmuo8TDZAzTf1zWwWWWgvGcA9aVqn7PKTbPozrUzM58iu7vbn9ieeoDQD8qYgC8JbA34OgJBFLCQW/frea3pAbh+6odPcpS4YK4cLxOCDkPwpiJZ7QasoAZYKzDgHjpXnMEU1X2ivofG+pR0PxCgZwKlxO+z+Drl2DcrZdxAdXDhxrjaLCwbw0seZgfKdzBFyMi9hTEw8ERPAHO6JadZxy7TV8cgH4BT2mEOHdNx3T36EJPzPYS1v+jwBN2cI6Kf7kGs7ld4qG04JRyvtQx7LMcNQ0/tE29QNv3g+AwB1enPj7XaXUtwcI+mPiQlvNs+T2driOH6jI0g3M0RHX0SuvK+hpmueuVWaj4qJPt7z32e8Y4hPsf0rjHMTDxdBGJhoCP7xcmOUc0aOuB1mSEy6V1C1MkxtLik65IE8GH6f2ciJAKyg/SEUHo7CP1sBPiPRHRAEVr0Yaa71T81nqOiM8UZWmzAZkxGys6jpikGhtsQKfgspTEpQGokZ3rXLne7vvUJ22EUIkPjGE28JUJC7sTxx8SGXJs/6sIkLKE9eWda/eeh5mSo95wYg8iYLpmuOv1FPm8RzNVOPQQONvGMldI3cg5QqRwsND76MLJwNpREdRzwHkEQ1FJ5e8i3MdPOcpDRT5or+6UlmUhtydbp/I5/hPLfrfb4/LOqwtiX+HFAAFkwpFigw14KxdVHxaqxDA1WzQWXquN4PEkyEPKKW0yk/RiOfeycXH+0+3t47t6kVcZ2Dv8/uZvuLj9CYOfTmQ2X6GFEmfS3Rwe8B7J4987F6NbGOQiA2YMBjMg+sfg3nj8aD0MrnHpGeQ5nRuKqAgtt4ewO+XpLjeGZoYjnvi4gbB43HCr2EjGhJinvjNLmHVBPaHPgSwHGi6e+XIkk3iCxIskAH0801Oj4yNJ28Vc9F6Q/EjSSowkXjh+KxBJhDtFcopMCUIwLsd6tQ1TZCou5kfNtmK0g1hhUgSENQbDMIQ7TUw4Mk882k1s/7CZAAa2G4MNLmHIxvtP4g0o4o2VjpUS4aMrfjwcFiUizmQyIa4WfKB+C71Vz6r3+WMlc34kzkn6o6IojqphRXkNzYnQnbQ8ZkXUBOd9DQD+svH4ZO7w391v8Y9/usJPbyb89d3+4Y2lEqeWIdPOn5ne7RVe4RVe4RWOgXojSPwuzyqH5+5sS+U1X0sFX6qqFtu6Zc15T3PiXXp8dGaFsh6llhNZJzzBSa1RYWGuL72nIgs0DVbpz8PVFKVERZoZBozgwOcaW5yyYQiwwwACgssY64M1GCEO3BdR3KoCtN7sHvAGzoc73cjEe7NMjIwwJjtWsVzIXM/HsqFikZfp6EWpytToXNZolFOBx3LyshIIOsRIVonEMRAZmGGAHUaYYYAxQ476jvfHkkIVIoKX3LUdStCcWv4+u91pAQoHZIqyO41WUulrOSbwcuqLqp/LXKqhaN5IuWWTlPGhMEIYgHxKS7HeJLcsiN5rIp9fBogAyxishafoPPf1iP3/usH+7fo+rDZELC60OamiQKQzib2dBbo2RKnJWrd5hq4tFxpPpzMHQt8X3NwoltMi38oxW0omBge9+JsNtn6Xn+slm2wQVWV5cbMuHtZ7bOL+wsAqmvIKTwVZMSWXVBfb4QG8FwJfOHb0EqXvs+zcTJp10DuSo7XYL5fLTdsYTceqPbJYPT2ejhlu2oP3O2zcDhduihcHv3z4Epep4XBXBFsDTzYxrt4HrxHvAvPpnAMxi7oWIILzHje0xwiHDYV4iUaOqKB+ltNXTPxKwpeMCqlOlV9xc4l1S3S9fNeKTaw+KkTt9uv02X80xeJBo2L8d3ZSchHtfRNoGh4pivo30ANGzbjm8fSpCcqAhXCJuGY+U+6KfwmREDHiwQQvMWMGGIMYFRFonGET7SMGMAPIMojj/VRE5XUWuYLY9zUzpDjnxLpROYAnbuTVykA9YeV7oesOoAmAvkSQO7nXGNBV9lru6xga5xnb/HrdSPTKUZLaWVjj5UKYgT0Bu4Fxfw9c7A0+uxdmCnjG5iwN/wsbpT40+Nu+5F7Sx4SndvGem8RHbkY5usupHgceMrM92vRYHOBT4sPzr9pZnuMVOhAH6QDqldg6z5nPFfMQzC5K7hSkZYaaR5rjebpPux7nJe+juRP9uQw9Yb0SbHttXOT3VM2LjQgv3J7hduG42HAvpYEhBNlY6QrJmOR0I/klatYXbdZ8aY+ZyhjDHmDj0yPRu6WjK0F9Z3aFdKu3GFZvqDo6azHjuWBO15gxiShJk320JoTxseHY1zS02jFTFPCzky+7o1RQzduScrBy8OtBPdOLPHBqyUyaA3U1PUyyUPmGukPRW3tl2fVSWtGkR9upy3UXQVluuaLEk/fwxKArwvB+gH/D8FdudXXrIyIO8TqzK1RW8Loh68nRa/ksAtqLahZkyVWgiSMyrnhGCKcigC1gNxZkDYyPRyggz5vnYOXtFF7sIn3ky1tNOnttZigL/Gcoz9tANIIxIRN07e3tWbxpfUjrvRSSLKDyu2mkWI+FpgDwCGFdgcY82nL5AuAQ8umxWUt+Hg5SU/C4zX+p/mYhxg1F7Q1hWgNTIVEzXp55gOU8dVYX6DZMTsDTpTbmH6QelhsAzxj6am8VlSPjLTJae2YEj/H4F70oenPSlMUezoV7ISbvcfvhz3C3H+CmnWrHQwnSK4RxL8fxgt9j9O+w+TuL23cT9h8snAOA4KHhfbgfwk0eZCzcxgAmEOZb8vhEHlfjJa62v4HjSwxswExAcRmZ5kizcbfFDO6n0cypYoiETnOM3Mi44oviRNtdnl2raDRUBEQIC0llxotd0rn8+U6X3Hph8aWFenvqQpGYEs0Qo6bJL0to9ug4m4mDo+KjHLViIIv9rviSPsrZycqBktbWp5mypjM8AU7trtEriyPtSxEocQ5c9BaaWO7pCDyAY8p8d6o7HutIFsYOGKyFtQOG+EcG8T0FocAEgcs4D2YLHiy830RDRDhwTIwaFCMk0gm7BPTPoupBj5tWF28rRbzwGBqbGJSfCS4rfkP4kHynRuZREqPrGcP4A4z9CYxdnpvii8KFKPCl5ick0ntD1XhSl8ylfIht6cfLpHW7Rn9XIbAmAcV2VQ334jVjEBlI5iN/FryWWosaqPpcB73O1WO6AFR+mUv9Eo+46V1+ebZWnlgQx7ynZH8oB7Iq789Q+3reHh3L4z/meP7c5LPnw70j1R0/aygcRCkqLPXmzQyQjWyjBbGFMAxCc6stXrEwmbNL+tFuK7j7tcgI2e1zIgZABmCvJpSrTND8pS6805I6SlGlZMVQ1Xpa+TLnwkbsw7BqXr7Iq/7SYHoUA8v6XdWPois1Nx5uTRNltIcPg6aTMhIW+Mnj+3//jPsbh60dsBkIGxPmf+duQ3nGwhiDwY6xfgfvXTAg+MArgkO0t/MOzrlQh+gvmOGiTUNU7saEO9443b8X+QxjQPDAhJzOI+KWhNbnoclDpi/h5Sy/QPAh8/li4PAmXMotJ5CkUYzjNacDKYY7TWNvng9kT7wgQBgAMAz5OF4c0wyQaBMyFmYYMYwX2GyuYIYNwuXeLukCDQFEnFRFBGXm8KKP1TgW8mUWm/M81XJyGnSOOCSDEKWEtPgjrUjyQ9lpYgqGLsO6OFVaVnX5+CuJs8xBj6nWPGnGSzNShoo1ntaY9Fv/FetSm4byuKT6coHPBLqtMseK3hiCZ+C//fRX7McJv/t/XGLz6x3s4GF5vXnhvEcznROO5iV6gnMJq6fzaC6iJ1XWNS91qGx7qSKBSJ3rchOS9bXMUVBS6AiJpNgqFpJQvXojQ9uWgi5yu391svwyYK3C5zlBXUitKPOsHqRicsqYmfgpm6XGt5rJ0YzQAcirp/7G5VPO78t6OnX1qq4Vs3FDmcddlTb1G+lIHD/twdN9g/x6ZT6m4oXSWP2cF19kNuPxORsGRnjcujvc8IArbELoL2fGyABwPoT27gzj1jAm6+HJADyAk0AEjVzoLYx5Iys3857fZALJ6lMUs8LI6NykaLJeUYJ0+XunTkZpeIi0Xvv4qw7pYVXfl/F0UbnZVeS1Skz5lvXGeZXrPa5ocWd9y1yrHUk1o6QRDOTI2vSskFAx7B3GG2C/MfCDyajBet6iz75HvKAehRFCo5Me4sTAy/FLxsBYGy+ntggyFOWISwJAhGFi8B2D2AAm3G0ibEhxoaPo1/XxOUeQnJMpRzUvXLyo+YxO5viYyMGYfTQQ69x9PAci8mikSZ/VRHdg9lXFlB0el9Pp+rwRYu1s9Hhh9YxEnHjo3hMHt7PtHg2PsQ2+dPZrZd09aaL3/bk5yZ8jUL3w1ZsSDq1NvUh+zvxYDU+JlS9nBfRE9pdkpDj2/ooz1aq2Ia7fSEvWFdXdcxjNOlsqbvVevpS9w40sFNi+6vExrZEl/XOozVqvs74RC+Uck+lwhdMOcBPDjgQbL4eWI3SDbSBciGxgonTiITKASCusxyKzNGDF03Dk99JdmEDWDUPl4axCT+mA+nSnmW4FAYA9g22I8Ji7H6DWW+enve+pgpl6l2Z3LQ2kgk0u8wUeOkRlBwcpYyyC2abVWCTFvc5ed0EbHZrOVEjN5fMkL1OZTHCgLFHxpEdCmvugKCjKI9RjTiuRRMooOlfUN6e7fg5uoa1zuXYywfg3XUzgK4Z9PwBvbbJHroXjDBHPtc8/Zr3NuugPvN4YCojHIZje0UwdJYB+xTUyP+DYg6ah6Xe5URabp/KkhXh0MgPJwz0S/6RJ4aaC5OseCU3Wd+Vy5xv3ChmemNxQIK/pKBD9rrM1AcWeUjxJ+s24gRR3KnBWdso56adAUk4W3q0lXs8qQVm3s6pf9aXg9QoL+zxDIP3OqfPaAiSWYsl7/hWOhVkWjBm//8tf8c2P9/iX2w/4V3+J//Sb/x7X41VO4xHDfve4ZYf/6j7BjRbWXOPShaiJuo6lOZM5T/Svk0/wKTHQyRvcR3oZIyISzVXeFKoM0oWqGiTioYmKKH7HtSifYGWXSF86fTsNKHGnSuFJa26f6TPt+XnFtGoaVKRv2z5LI2beM8L6vfrzHuOfb/DXP1zi83cXwejgGZOPnlkueFp5H8Qm58JcungmqY8eWj46CHhpLEUjAwXjwzCMsMOAwY6wZoA1NkRDxKgIikYI8sDVv00w399je3UBczks96zQOT8eM9XFl5Kols90eoWf2oidDGiJHtdlPB48wZCdHXS0eDI3kPCmdGaF0xkHJrZZ4lBe4RVe4RVe4WcGwvqkbTx8IXiAlPPNin1qfpcoecR1jmQLr7lNOV9kT75U7akzKqE6sPzlafdcCRVZNlVyQ1Mwl5++86rbxuOZg7Bt51nsp8mKVhoszGgxDAOsNXDOwbPD/e4+7v+EwY6gkYpxl0gIkW2clyhaVW3B52qHSIYhB88EwyE6ngBYGxx45I4IUIySdwvspdInBH5KOSoaAGT6keBR1QczEye+NPQqcd/xbUaRPaPAYcTjin3kEamVeY0xGDdbjNsLjOMWGOQO3ChrxraYmNdEw0aes5K3z0cJV8+lT40DnJo/3XfK+XQ5ffyvtFrFgISGFqYgA4DFOiPyusJdAMl6IwxrT7+UmlP3q1qXXxxQ7lqU7YdhgBkYl/8jwN8Shr//CsPVFrAWx1gj1hsivlTZYI2h8QjpTKd07HC7v4WhPUiGUnuWLwxaTTqKUykeiKdNLETakOOC8XnzEqG/F2LIYHULTCYvRa+4/sHw7h7TtAPz9LCOfNGwRuX2PMAAdgR4Ez1tAYjVF/r7Ia0doBRE4WFpd1JY1TFiHSqcq1ZVNoguT0fp32pjm+UsOl7hDeenmD2unrF6Dvkafm/cHuM0wVYKZeBpyOnPOxKiBMHCwTls4DFZh898jw/3NyH0NBIuYwAYAwvGnXf45O8Bu8HlBeBGoJ6ZpBgTZo15xVn7FTWdMcYWPIumw5GhKSNncvqiPM716byZEcp1tsawzEBpUeIorJm1/s0nmVU0ZmsjRGlK6iihcgkr5g/Fi5my64bE8Y7eL1JPORcAgwDHMBMnAUXufZA/H6MgXDQ2Je99hjJQxSjFGhUoGhlg8vFKZMIRTPIXDRCJ+BHBOgPrKEQCFQwfFR8tHEd51t6/lfvUY7YVLRaSqWlmfpV+lLnruT4Vjuk7VZ/t2yejrg/seBkNQ5iIcUcO0+yBD91SUHGsX65MoKEe2gN9OgWDflHwnEcySdVz7NwJTatp38N6d26K8YvEsC8Gnifq4Dh4lDapraLYNQ7WNZ+g4SEjn3iQEz+hf/NZSj76cIYFuXLNm5op6qVqHiteqUm+st3HjFmRVvFMSSmt5kicbihEPBAMmB3YO0zewQDhKFkjMlc2WFUidlN1K1Potx7sDZjCEeTsGZ48LKxqV3DKdBz5bHXfhNaFsO6miJXyLsor+bLnCv+EZeISn4sk9V2xHQTvT08lcyUxQOlPtBAUv6b+MACEY77C2FvQcAEzbEDWKrksl6rEkYLWFUm5msBq7WRHo7JntRGibHC9BnUd9WbfjlbLu0dESxdOzxUh8xrSatyeXb9zcJAwzWFIP9W5yPjqmuKE3097ePIY3mxAXxFoOwB2iEO5vlUv7mimRl/w6BWuGyyNm/L97v4T/uun/4r37y/xW/PPsMYEj9uYclmUbcurnxTvlOVtHVQLNS5sOd8t3fng8/NAJ8JiztESPueV0jgYf71S2AgxYQD7ux9wd/PvuNrv1iuKflHwvGPhCPjzxmK6GPDb0cJYE88UjxESKm2xwSDPtTZiZyg3hPTLdzafIlf4beqVQuVmRKKc1Fxu+UXYsE5dEe/TZpU92EVhGJ7LWZScGIbkqS6b45zXSzwbXrSTv735G64+/wjyeQ29wuOAjKzncOySf2dwb4H/95/+C+xtnjMzAGQHjJdfge0AXL3B5tpg+GeL/YYABxza3pNCv/F2EBxDxv+KYUpYqOhmPh8/4gn7quYcvZAwnJHy5AgID+/17xx14eOdPyXjV49eCUkJffBowMx452eARAsqrnjeCFGD8J0sjF9nPFTb69YVM6jJEiGp1qlIqSqN4AE4BpwnOI9490N45hmYfIh6kMgIMUiECAiOBv9MNxgEfT5wGCMTz2MdYO0AY0YYOwAUPEpSQEm8LI7IhKtNhjEKCSPIDGAy4LgrlyOwbBR6DMh0VdHZaFirV0O+pyrT2XrSFDXPAzpLS6nzvd9rmW1uUlT5mgQZc06m6bVV/XCGxbeimJH7IsCUonQpvicy8J7xw7DH/3/8iNGsZf81RxsHY6bp7Vg+LN2XCj/nvr3CU8MrNr3CFwIdVO2YsNPT8D24aZBmjIgRjtbhJlevZFLP+hyhhhP27DrLXBENX9rjt/vFFN8TnyNvRAbV/L/wlfLMpzQFz1S0QX3OdmTN+JQ7+PJoZ6X+YDbAQDCjARFjvwtOq/d3t+FuiGGENRbGCK9MUUbyynGLk+N6oR+YkS+89wkriAHnJwAD2Aa+yJhgkDA2fHpygJG5W+6dyFhSvyUjDSmA9L0SRu7WCDo0qnjBxhiRxlHm2hdNqsWznhGibAuibkXWYFxH3geZzVjYzRUu3v8B26t3sOMIJhPaiujMx4i8ZlVX1FMm2bfAOajfJY42TlpVz7s/Gz0MlxhZyOCcH0td8ZGRASEEARFlVFIesDhiZMAUjDbNMmJA7mMs6ky/e7SAyzJeEGQnprCGk0OuDUcU//Hj99gPE379+3+A+a2F3W5gLAU9xBH1vBxDxBn2hqMznGAu13QpHL/gAHC8dKactBaOM0msbE3nV8fHm9t3aavsKWu7C6ZfV/2N3B7b3Q6DE+XX4Z78cuBlDIYjwIczxRDC8wDozaRzyWUJJQtV80xIDFOFH9yJQEiIUz+vNZu5rpItrfL1FKdq82qZNNRPclsby3t//jKvSSmJZYZlHy+A73TlkeCXY/Co+0mwPMKyx9XE8HD4tPG49wz+OAUmigHyHptxD4KBdYwBAzb8FgNfprWQz1BfZrHLZdCjigvtLTYT+VOzV7/XtJvLfKV9gaumcfMhAtLRuLICeXv61Z4YuQyxA0TVsC0YIU5Ee0a85JhyvSIIsg9/4d4XFH+eke6ECJdVI/6FBGJ/zSfSVaNNwikEGhwMDwTAJBYiiAk9vsKCorEiRUQ8FmFJDPrMAC/xCTX5lDmbmTRZBkS7+DeVZHfFHC/p+BlJViqj69LvOeFNVCbcpwpH4N5cG5btEsfzh8YYvL+8wO1uj8/RQElE2Fvgw8B4Rx6AXVUudb6VwPPvaGW6+CpFoZ0KZ10HX4YS+Nlb+RSREDPsXvHuySAxrdXnMWv02WftFV7h/CBn83eWwrxWhCu5s9bktmW2XNF89OaDJaI12y9XTErFtwKZTHLzLleg2f4qu/qatDRtVW0FD4Dlcpi4Edu7e3ycJLn8N526L85T3sGDg8MUiyRNTampLHlWkOEOdkUmSyQdEp6efH4NgChGJPuoy5OCVSR8279q3qKDJijUQ9TeiEBEJc8nctrq+wawPh3Q35bSwklCRpEg3AsxYhg2MHYEyIBB0VnZt8UUE9JvbIHdtQ6Ge/k6/VBD1C5HTmqf7hpj9YAlf1la5vBVu2Zqa57Uaz99ZRQdfIjgsAA15jd4N5Nvtva5DBFnjAmGCHrDsG8Ae2lghiHhPE3+KO7mZRgiFmST4wp5TJgpnwIRs3aIZ6jFxw+Roxo9aq/uA/0VvE+eiD4/5vjbZ6WJWHWT97cX7/GQq1ag6PYxczwLP/zzdjfh+t4dFZrzy4AXNh4UT/4wgbhIiF3yooxp5kWschNpp5vTQ/F+LQl8CZ6rPVJvFMxgygxKYirqDjUNificPnNbCo8HDmGbkEihOYXwLGTFtQyJ72R5FT0fFy74PbbO4x9u/opbc4///G6Dz+8tbj7v4G8mjKOBGQhudLBwGDzjjX+D7z78D7i8uIa5FuVuLlOfjKhfCC314ZriLCBkl3CVUNFeBvLtIci4ppdGhXMMriKLsje5KMKLaDZpc8ED6TVYM0zHg/aCScabRC8q1eWZEH/ZCFGwt0VL6zzElMNHE+datpMZ8G4P5yZ470NEhPfxL94P4T2ck++sjm3Kk1lMG+nxiFFoJjB2hqxyaDDxr1R0MRE8UwjtMRvAjACFiAgAwV2pMnzmqumRCFCJ78kLUMab1VwxA5lbyM+09xQYw/A32OEHMLv0bJUuAB2mPM5x7Xn2c4ftxYh/+sOv8OHDDf7zv/05Pf9oGR8vPP4DGVwt5D8eWhrZx7cFhv8sssDPG16Hp4J6QI632b3CK5wFfmFbzArISr6KdUPBI5KyQUAu0lX8ZX5VLfcqgr+uooBlotDGIS/0Yi2N6aaRWOOSv8/JuZtRP9XRpIFt8ol/SmVor5miBP37kYCrIYoy1cSAoyGex+8xuT0mt4dzexg2gbdOnud5zte2NERKaL5T+k/w3gGGo9EjRkoYE+8MZAw8wpNBuIOCwJNEYogApeZedxTBA1wuvyZG5OORoht0ZGp6rnsVhJIDqoaHzZfw/ybZH7K+JOgrGMYOsOMWw+YSw/YKZtyCYaKcmSNL0jIQfi15h3Kce+HntcqfCxl3ua9ly1NlXD6tpMAO7RWZWO695VhMcbV5JdXn+xV7Br3UtyTnKTxTf1zINMhlNeuxaXHd82eDNL36IRHsMIBGwuYfGP47D/vWYxxiqI9njPd7GLf+6NcHGSJOOQORZ77XadTR0A+D1WtXV9bbkKrpYMCAsTV7jJbzhb/FoKhNUh1PcW76Xx94kL+WRKO8KEb+qfKWWeahslDqOgg+BaK9ygMvCTLyZSIcLysinWZdSSWUzA1D04Ma7+ZB72tAZZDQ5VXeBnpDqu+VyIjK5fe6LdW+IQ+zArcDR0gdMvqvl3E+JoTz9rd+AwD4amIY43DzLcDvLDwPIIxwUb85cDy3FAOIw3aoz77Mxi1k5MTxdC1FIESmhSMzlHmVljaX66dkXrLulotnQQmtGVrNJMUS1HKadeJKZVdtm4W1OF2LilppuVzGGiOEtLk0gxxuf1IgqKHmEXDvDPgjwDce8C6cYSvHXUUGXgwPnvO85BbVSlkuf3ckbEbRDHiidAFe6X0WMnM6Tk86YNL72ii0FjrqgwdBmjHVOdadrPkR8vHejpXoV9R0oL96sqO0K174B++A0WwcZ5VCHqq5xtaGOVq/dSxrV+azkRi4qoqCRAw7Ed7cWuxGj/3gZ+b7sQwGDy7gWaBDtQo4qkeV1+VTwRcz6g9p6LMZI05crA+CQzTn526Z+WIw+sXBuUlPi2X5Sb8qYYBMdKag5k2duvhdozZBXYSNA6eK5hddWXWmvRQ3/6ramZyar+f+gIsb/UpGp2GblOBaXPy72JxSnjiQeLk9nS7J3AlLdH/jMO3CMUQby1ln7cMdEbWSn+Ixo2QMjA88jEg2We6pa6y/6zTCS3I0dATnIRPrIAReCczhqFRmOAqRG7UjkRhGsp6CC8OZFhUbXk/pWhK/CYBT5HclkFXtT22oxmB2HRcNiRIByTdxsYvlGALIwozXsOMlaNgAxmiXuVgmV8VH7jmhkppLLQvpIuZ7twhZh1JykPX60+uC2Tdve9hSyJXKORvxdxZYwvdsSioFmtIRS5/P257GkTC1MVLoBq6nDW2f6qKorG8FZJKR6dft/h6eGfbNJYavPcwQDI1mcjAeIbLoiCafNSLihPFahkeXVY4tvET3kSa8H27xdvs+eJU/dFfv7mbHDWgmY518cUGkqIf4LJxNriz0ycIH9blYWZlP/zyhD6/wGKBxU44+EJyl9F+d8tga5nm+AwxS0boVbdBetlXF3KTL2215xmZW9voinXibVBbdqv1ltev69mqEeAogbP07bNnjHz9/j4/jHn/9A4HHAXbzFejOYPrPQgOD8JPuRyEqVsPibGk6qfBRO25kQ5jgFJIXU3EmPmuDF+d8VTkpsifeI8HxLMaQL/p0eUQ3fLknQv3FiB+5UDmVmcqQ5ystLpSZm8xwU8V8q/Jmy+nRnvk85dYiY99rbO9ZW24YV1JKaIZ7Z7H79QXwv0/gzx5+v4e7p+A1RZSMEZ4lSiJUlwWXLHSEr2FcxBtH09/wfymIazroQTAcwtoNA54NPJtcUjybNotCJ4Ce99kyMtVjbp81xRU8hUJ3YdI1M3+A9ynXxLJyLRgJMuO8CDLQc4qCA3D0hd6PAtGL9AgG/PLW4g8/bfH9+x1+eH/MxdURHp0/f4VZeB334+B1vF7hFZ4fOjxDUOlZhGMCTeaJ0JOXNJ8oFwkHzklrHwgUIuir7bBQqqkHBQ9S8d4Ueb18V5mKpp2ppyhDN6zZn7l6vkJObrIo2UHrYJrvmGnnw0CNVPepZ+Cnv+xwe+fxdmsxWg/CBgzGNE1wbo8Q0UHhImtDIEOgeGyktwyyA4xneOcAUMl7ztB2bQgJHx4AxfvyAOcmMCxMNEQMxsKD4AcPR/GuQT9BR/Dq/jErhWewJoBj2WwiPy8yJWkeP41MMmAYZvgYtXsuTjI7ZYUBMinSP0q3xgA+HB0d0NqAxkts3/0e49VbmHELWIupcJKr7nJBzZeXdS72ZnZN1AlyiUlEEVaddQr1nRku6TnDOqDkCNjLE2V074HobFY6B8bfjedeTB/P6WWOAqCSpZt1Wfdwbm0ij+ZZFmoH1pWc8ZyMBQzhLzd/wyezwz/85g+wv7WwmxGGCJvbHch54Ehx4uxHM6VzunDk0D2qHFetnCMbwgDu02KV9x67qPgZaIut+xrWXayb1GqBLXV+lZArhCB+FutnKVO9ABjQhoq27CynVyoCpVxbbuovB2op/eUMTG0NpuIFtakof6zrRUms+3nqp9T51s/ceGA0PEJ/DdcK18x8aoYtv+8VxTMbynxjyy/iefsY8PzKsJcDBgTHwN3osds4XDMweMbe3wFmhP31FSxdwL7dwLwbVkQFcYV43Pk+h+9lhELBfKDFp0yWa0KeGZtAa9VnMmpwKjPxQj3mtmiLbk+vfy2sx+FZ3wz1tTZCUPEx2xLFAGcjev6IssF8S+KUhiN7TH4mpRFFgSI8Hz7tsSWPu3cb8OVYdSfu1JTjEYooyDKpakMOGxZBSfZTeIY3gGEGYCK3YQAPTM4DzsF5Gzy77icYMwHeYBao/lGN7Nk8Sbj4xvXjmkHhOo3C5ZrxT0VExlgZjo5pndgd0tnTxfP5qAiKSoimH7oN3a2NU/70qE7yWDBT+GQAEbPXwzG89BcAs914wv4lZcbT1Flzpi8ODjXuoVvPWeE518Mrv/cS4UR79s8empVCBG/DHVfODmBjFUZTM4hZMtV8lc4R3viZ8/ZrTqLHOfS5DcUaiRIUwjtGfq2XaRHaNmZefL593ey97vYy9Tr6RBC4LAMy4ShSIBzB5L2Ddy5FBlA8oyudMGIGWDCstXDkg8I+8mdMgEknI+RdrXCGqmUfBoKXOoWjhnz4NHI/WzyqidgGYwjL/WtreOPygC0PDyN3cLHGWUTeNjwgkoiCBQle4YSOXK2b1LsfoecQxmCQGE3i0JEdYIYNhs0l7LgBbDQMVjz4HP8g+JvkrspyMLe2evLyTOmhnR18L0UqnSAakbjXZjmeKcxtHa/QLjIuvof+Sr5wPHOWv+UofEbuu8gARWP1R1djmNZF3ccjoM6/PjIiTmQUmD7f3eDOOUzv73HxNcFchEgi6xnWhaPN6QSfpke9I2K14lIR+OcFjS4ZHDM+YgqKgLjaGIxbdmBjsKWv8W7/j+D7d7gfgP4yVYoufasKn3IAQiHeq6cqDEj1JutOOQv3SXmV74bg9CkCtV5EselxrtKSZH0/hFZs5Rb8cuH5Rb6+6pQyn9fVlWk1I2G10rHwqJavXDFKyzixqqaO7KcJatln7V3OCb/zc7U0is0ybzy5W2XbC76OZZ3p9ZYKLtI/P1Z82ZAuOsO8qc8jXMj+49sJdxuHbxywZ+Bf7Q14GPH2P/4G48UVNlfXsMMmsMl6QRTlhpoCu5ijEhINReYrdYhl7SkiTIkgnGInO72skAasytdRDvnsS/Hi8Oq9T54cnbJnfx8PBY1Q0RAH8bxJN5ORq69qH26GCor1VUiSwodJZpSq9zNMYvy6/eMtzL/t4P7Hb3F/uYnGhyhgIRwlRIwQZk1I58TWkJnTOG/eg9nBex+8wZiSSSIwdYpeM4MdsNvt4e53uJgseO8wfL7DYAgYL5JRpVWGUPVZv5vBg9V7ucbojOehmyraRx6nJHrPkC/lnVb6VZd5lsu0ZxCuuSdCaYuScbhCgK5BokTzUhCcGyJWWYUNZPX9BODFOVHREbKcEm3LAsiN8fhoHParY6jXpXtMY/srvMIrnAIvQsB+hV8ErKP9TMA0WMCOwGYb7r2Si3EBpGNsin0y84cUtZI6jjRFjBLHe8BK5nBpu+46AKl6kwc2RW/4Ob49yb1a4mtSlZWmBrLupdScLoUu5YXw6SVf4VCnOqxl0Zn2PBwKzXNZLQIvbAxgrYE1ISrBuwnTfgc37aUXMESw1sJYG77Hq9JG9qBpAjNgmcE+jIk3BPIiTen6EOaICPp4HCYKkcuG4ScHNgxjLUA+XLYLgrUDmAnWDIGlJItwV1ndX3SYbA9mgvchqiNFPycZQ46lYlUOgShw/NnYdV56nWL8iSB6wuDrFOQPkrshtlcYLt7Abi5BJkStBCNRnldpXqUab9aY9JtZZpc0iqR3fKIDVFO/ksvDI9+8D3n0c0p32XK64K+OfpAsWaZJeqQou7G6WzRFeiv9QHcuK7lmHp5z384yIxPw7z9+jz9++gF/9z9/jct/HmHeOgzDFpu7cCeEXFVzLPf/qIaIZxu+umLSL6hIs4OH6249gsxUXEUaNqEs5AVrlVRSHq0AtJaoLj+YnoWN9fDAKWE+KTVyq5OMynlTTIYGIH3PvWRVrl5Q/S05L5xqk5dxKcr8pcNzE5E8H5S2E3mtLRFK2ZVyd9QJXL4XDCnQWv2QNPlR2aYAJr1JzerU14BsChUWF0kazlM2K/lTDJxX+JuSyb+V10thxWgbNt+iMts51DW/rEiIRiQ5CEL1LQPvnMNEBt7ew5khKYzlIKZSXafK4KwIXg8Rd5SidUmB2Hhk+PKdKHK9ZraQ0TdnWW5juSZOw50HKRtndbuHyitNhZ2PzNyh5OfzXTO5jpQGUAZ2XQNFgTOcX0zGwPCA8addYDx3Uwjv3u3hnAecB1sD990VeLQAuW6fmD1wu4f54SaEug4b0GYLu3UYhhHDuIk4aSNbQZjeDnCXQ+ifJxjnAOfgfeBHSOFAGkuNyKVbVB8eLPsczswNX9EQ6Jiu9/sQKEyqcezQIbqMjnClUiWjBKl8D4S1HPsDq+qtUyLCjhw+m31zSedTweMbLI6Zq347DrXuZZtbnrB1yaXvDHWekzl6MqgbfUY6kWBtmb10paLw5wPPgyQ9z2MNys79RcFcf87WF9E5EmCY8Ha3AdlLfMQWnkaIwuvhFSbODg3ON445PZhJo2Xb2Je6hm7RVaK2VVE6b+4KmG3dfF1zWc+69DWdmyvYI8n2RICheIRoiIRw8X4I77P2Mh0xSiYedw4YE45PCvddWbDxsMbCATDs4ROjn5vUPxqIkhGAvYc3LhitnANZm3A/1MUwxoLZwxgT+GzysdulcSEDK3zwgDdg48EwMNG1qFbv9fUiurXRcLASZrdh/SDJokFhTsYEQ8TFe4wX72DGbbgfgkzk17McI/0mXRCKhzkdZFoKSSu0RaIx5PmcAmkGSimO5xcEZ+fB/q6oM2ZdUHGZvAjj2XMq/Hl9fBOjaEsjY+dZXu7Tuj36uAiJJZnvAJ1NbE1w1NxsBry5vsTbr99j8/UIGgcABHIMM7E6l/g4+v2ohohVcG6+qCmv3oTyVw/GLRzu0kLvNIYQlREaB/WOEhVYVObpfp6BaWrwjasX2mM2PS4XWVMOR4LNaiG1Kp+2LU3DuHl+op7rFRL0cGadYN0StkwM9Un4ZKjIMauNPVglFRMeztbkTlRjb9PNRRwHCuf0vlEkUcYKwe2E4/I8G+HY6/HKERSz5au2zF869HMUAp8HhK2Zh77SdWDguz1jD4c/2hv4weA6brAGMSIiHdEUvs/WpRgQHaVQ7g/aCMEdnJjrHdq0wvswAM73QngvOOqTVwaLQS21R9qiyte4WP0+9QABAABJREFUONOsxN8fgbblNrig2W3SH1r42hCY12P42W9gdx8ipKiIkCZEIMRQhubYt8QZkAHZEQaEqz/vsP3THXa7HZxzuL29hXMO057hNhb7dxfw2yHKYIxUqApYND/dw/xvf4aBAQ0Dxu0VtlfvsL24xPbiEsaOAA1w4QhS3PyHS+w3NvC+kwftJvj9BO+88PQQhXo5lAGP5+dC+r409n3oOTKVdDg6bXQ5Ca7ytbxDNridSDdnjnZ4NDjg2RXQjuPl4hHfsHbPY1X0+vFIXIDiYwVujcPfzB0uKAgTjwKHiXUJX6Dy7lng2HFV8DrEr/AKr/BsIGImE767vcZg3+LGXMKZTVD2AkmvkjfHvOcJ+8aUlYs9s0PXQFCx4bn0Q9qOsgO1e10DrMrvsQWpkfpl5NFIRWgC0SOdujzSOmiUPZ3nPThFZu3nIWNgjQ33bABwzsG5Pfw0gd0U+4xwHBJRMD5YAxjAgGOUAuAHRog6CMcrOZoQQyLS/BJMxA15qGS62G9GiMpgANaHaAdrwxG9hiyGAWA/BDOAdyACHHyQvRb2XjkZwRifjQIG8DAZJ0j0L7lpTUSHodgXlFMW279uJiguIZNL17JpFByMsbDjBa7f/w7D1TuMV2/AZMMfHNLtDJFZbWU2bp4UTSUC2KvFAMCY2BSf5aNUXLWS9YLWBesF3QginN7VRot0rCsUeUn3OojBwedy0l9282PvIMfphnH0IrDkvxRJkuurh6Y7Zur5iZJPp6SHgTEEsoTrqwvYK8a73/wa5rsh3Q1h94xx71JNx57O9PyGiC6c5is1O2nqxQ4ekxK8pyUjBAS/tT2tU+jBhpL6V6OlWsDVZrUk0ypSkn5noV8X226v/TLVgu8pFtI3yoRzcYWcZ/m8Qt6sEsSN9RBLkvJx8aVKoAhxvVeXyZJRoV9RrctqbzYhik+4yljUMdcRFDg9Dz0O4QAuMnK7ZL9BNuTpfaU21B0P5zVG/LIiIVpolkV8ymDcXky4Gyc4y0VCoyii8RZv99/h2n8N2pi8Bnp1UV1Pp/KFDahAIaHVRfRNQL70nAF9WXphKIPkLRm15nl+mtvB1T6hIggSbh+DVnHJrduxy30QvV+dcT7mPEwdoaXb16tL5+q+IwLIwtgRNHoYO2BgD0/BR2mwb+BowHi/h/MObgqh4ju+BN8TjFw7IeMt0+k9zOY96B++jp4tBgMcLsjB2DFcnkcGZIbAABIBnwnjXxzcBHjH4F246I6MiWnM7FF7Rxl3CQgK8tNpy6GcGf/UwolrwNpbEH2GMXermrrmWZmgTaGNNBL5sHRPRK4pG9lbkWw9ZO/Zfinz203ZhjmwFyPe/OYddjf3uP3b504DTmj0Y0DC3edXlT9/C1bADNl61tb/zCIj6EEr+ynhi8DYXxTUS+FQFMVTwrFtOH5Zq8tl8yO1pkXRToAhjFcW5io7xSmpEMLV1fz+oaYIT5ucITTPndKUPLRstgfHp6MnnXuf5GG9Ucf3yaShcIPyy5CUyzq0/uV0XDqB158Dmcs5Nhrx8mlLCAEPDGafDAFN6nj/QzxBSVqr3ofoCI5hzJUmTX1SRjMpRJFzOZrce49wnGkszxDIGxgbIyImC6Zwj4SPSmlGuRbK9cFgluOWDNhzKF6cn1hFvxwY1pBBHaeUml+PXI0h1YeSqzI/ySAysIOF3Wyw2V7CbC5AZgxHWKn9l9ioqPKqziqUuNXAcDKssGoIyRFnlCdGHHUaY0QXZDyrNHKfbzUkooMijRB6QLhvhBCnPmLlzKcNFGo8C0yslvssNDIb9fu1VMSBCInZog6K7AQw4afbz7id7uG/u8f2OwN7zTDWYHs/wTqG9aXpYfVprxFeqCHicYAB3MHhlg8ZHzqLWu06GY+z0iPK77Mwc/x4mQayUDnlmUUgbr5AFKXyr1gcWe5rKSyH8T2vUDmkxaQoOSGcwaikBb2XvwRm60uHnmGgIFp82CDRpeWkFIKUtuyHNTYyTgVOVHXLmZ65yYr0PliO0thXEeXMkqqkuWHFei++x3WUFGXFixWQKEP17BUeDvPspyfgb9c7fL7Yw1GeBflHcG3gDb69/XtcD+9BoynKaOuaAYV2ukXMrU9AHY0TnuXPLDDpA4KkeDEiVBEYgqGJQQKyMSJTh5w3p8vvGT2cTj8P8YMVHNTfrimjVyWr9qYu5Gf1nhOmWxJm2qPvilhsEAEwFmbcwGyAgRBtE+GCxds3f49pfIdhCmeEei/7tgExQGnjjc306mi8K4b/ZxdOE/XAeP8jtrd/AmDhYUBmC9AIa8Mletsbhv/ksd8xpsnj5g5wUSALnmZBgAt9poLhmMfrcqQDD1MyHadt49JhTW+r0hLelzmN/Yxx+BNytE+/xfW34usjk9g0YieebXuWNqSqKzqohZ9oULHXG3z13bf4/P1H3P10A6DmcQ+sg58hHEnSXi788qbuFRr4pSLAL7XfLxio/Zn1IlxtzoFH4cHg6r2Bf8MwTmuONeey5OqSncYSx5t46fyeK/6xrEXxK2v6uJg081M6z9yxPKRaQDGR7mmOSl7Zvl6yHp9yjg2wmZAsECWZyyA6zFgY8kFG8x7eOySvFNFrVHoyD3XaC0LkerBmGHjyyJfuhvfymXVpGXuCriPr85g92Bt470Hk4qXV4aJsA8CKIcJaBM93F5XZqreVsivpz+FD/d6DyIR7GMQzKcodGqPrVbEIR8liJsm9WTbNbSYCxnHAsN1gc30Fs7kEDZsgz/AUD5unfFAAyvEOyBqxmOr1Wa8DuQMjywXGIBgjOLaQEC/tFj1StdhquVWQo5E3ypUmK4xA6q7fXGgpW8fy1DPyPsnktaweDBgevYmRPj0fs/nQPTKst798/IB//fQ9/ul/fovt/zCA3nqMg8X20x3G3VQu4xP6epIhYk7QqxUXXR1o51mvHHXNS5G3o50o654h2Dt47MljmjFClL+o+5xVB5kMmCxgRoCvcH9/CRoH0OWyIqseI30mYH4XX64ZKAByQ0j27I6LUnscqsJ8GgOf83it/OIqh7AMqmecFWCsWv9L99I+KxyiIbI51BawOp9wBAofCEibi/YpCFevlsWUih+uvvexPaXSihH9tlCY9Bpebz4lzONZtRUmhVe2chcXCsfyM/bK5iJ/SLieE8aBa5RpdMCLVrZWKn4/N7yENpwCGhPlyceLPXajxzQ4JJ624fJknuJFw4R0UXUxe9zGwRXl9KQK1bKC8UsUNVJL5WlRxK1VZRQIqg0M2lMDGc/TLRGsn2mKzum/2ui2uOV0BkIY6cRQKxmyGffFAmlRedzyDFS0PxkhCiYVyVEnzWq6vC5SrhaBioqIDKw1GIYB44bgtu/hh6sYMm6x2byHNVuMYxxzYYrj/k2U21eMbzLW5j3UXm4xvnkb04fyicbI3JsouDHM5x8x3N3A8xbeWWw3FxjHTZLgkmgjyJ/cMeM/pEazN9msB2Xubp8mUx9t00CqBwXKCR7HB17Xz8XmoY13tQDU60L2rERpoOnmUI2vvLvmIiPacZE5L5EpNVuKJSV6ytR0iZT0uzfmUpdewmq/UpOQ0ED9CdxZ4PvR4x92G3z904BPFw6321qgCo0vR5qKj7Z1Jwo/0myaVzkdhBXZ5pKcUmOPhJwEx1rPjuznl7rHPzc0EXZHQ+b1ztGa454fm+YV1sIx9udaznkJkRGPZkNnFLSs3PYrBpGA/WaD6fISzowAWQAucR69UyiKfSiW5QMXnzgqqG0wbYn6uN1qj1QcY/jm1fu6c5KtkCPblGlLZ/2E1TNCskwkvkR+l/2r50p4W7AqowdaOVs09JiJX6J8VcPkorIoG7M03hM2mDCQg2EDUDhaScskgAVoAGgAkYVw6cEhxWE/7eNxTlO8XJjSvRHMJnbXAcbCeQ7HonoXccip6RbeIiqYATA8mA281+yxAZGFMYzBBoOJpwlEDCI5Glf6XTCMmh3MY0GcjBGZbaXO7EhkhsbPOR6wLiGjVne2YluSgxQZsN3AX30LuvoGNF4DdgMXx6nWAxW/kv4jSliabW5wPEemkKGMlrIkCPkBh4iIzNZyMb4Uy0McKzYe8fqNLCPEtZGMWj63szCKyidHo1Q0KpSXTEuqKOlyma8a4XahpmctH5CNaO38lk/qWS5TdrEjybmqXq5LpTxO1SyLbEY2yLHjbwnvL0Zc/sNXuPj2CqMZMN57GMdt9MOSqDgDqw0RR3uZCb4qAtCHBeJYcdJ6D+uRV73B1ALCPTxu2ZX5KiTX9eqNrN9qAzYWTBuArrG/u4IdR+CSy4KgEILVo4MTFQkNzYUJxm037atcPM9jIek4ENx0o7tP+cPslMrWsszcHl2F5Czrhqpbf/5SoGWezlHK3LuljaebUW8C4kXb5K/VAHKiYY/ilA3QJqywH/Q43oWyEt1cx63n1U4tg689YOJvr5W5KFE3v2L1VyRv+iDraQ1w59srLInqLWL30jKQmKaPV3t8vthn5oaQcVdLguoytORBHh6rUoXZi0S7IoG9dhSKVaUYLKLRik+Fa6kUzT6UNRWeG4XBmaEvISgcOwCkeyWEuHckm5PMYsJVd2iQZr9ms9cJcjxy5nV7BUfwhfKV23Rs9DZcJGkvJ64YNUOwg8U4ErbbEXdvfo1p+22IkjAGIxlsIu6kua8woolsqZvY9E8emOAuBALYgLyH8R4DHBh7ABs4P2C7vcAwXgJJcI+CQfy3sEMgY3RqVyEw1W0pmxTQppNITUHtbVgTUE40U6cQ3iT+4nIMfa0YoDJ3CdXOVRkhesDgeE+IPOAs/c8YIfI33a56H6QgNC8sgjw/dd441rNLMtQdmpn8vIBi/LlIXXwS4X4A7izjnz4Qfv15A//1Lhoiehx2VcIxPMcCZEXvoQJneNFVecoZW1PKmhoevIs/duiOrgpn5jrqtj9Eq9kwtDPvXiT0GtjrxIvvyCs8MTzh8p+tf+2yXdvWdLcBq31MXrL+FdbE/eUGfH0Fb0cEFziX38/s8wVfySGtdi+Varzw3unsdhQdro8xFZFhlpdE7lc6PjX2MviC1nx8MzhojAdUt6B81yfa5QuhLjVXVba77v/cJ1YgxgzNKyclpWUiDNgjOE1tYxdFFxXvDiADwARFPUyUw4IRwvsJe7eHn4IhwpKBjboLa0zg8RHuOmDDIJhgTDIcL0WumP9KLyDH3jJzjAQI7TYm3EthBg/DHtbZIEcR5dwNi5jxX/PWwaGlxP1y+DTuxPKF722mQvWH4jFPibOXJVHxwSbnInFcthZsN8Db34PefAO6eAPAJE7SFDih1p2E6NREoWauWBzUGKLwTu6BJHdD6DthgvmDFc9MFHloRTvS6kzrKcqBagyIOC6zbKBMp0D1IC7iwoGvmBO9lErnwWrkU9aciarXZSNmj1US2WXRUNEnzEUOvS65TEMAiE1ORPIujBoBsBYYfu1x+XcWm99fY/PNN9jsGePOwzCXVag6j+EIz3I002yFfOA9gGyiSiOQkb7YcVbUN9OEjg6itGbXNEH/qLzoGIz9dIOPt/8Oxg72Ir5N6R7AXXQ2ntYAx+o7AOhoiBwylP7TilfJV8xLWqYqWY/4zUxGnUoRjFc4P5yFd6W6pPlSdagkq3/r4sTgQKC4NzD0WYicNoq82VLtktzZyOaYsfq6sCKr8FG6TZFRCsX2Cs2GOLVESgt4elvnfIWHwPz4tTSnl7ZRMxGwp3t4uMDsRnwPDEo8NuduB7+/Bczha5XEa51azfVCu4vcnV8tgyNWA20sSB5eivkp9bQKaxMTxaj3hbo/CXzZvpVk/jSg5svRMMPLLaSPTDAAkFCMshX1lhVoHsGQgbUDsHmD6e016OI9NsMWxgwwxmBzN8FOPhmv8hzEAms622mztCc7AWhamPdu5ziEhvsrsGGY7Qfs+R7f7jyu3A42yBAzssHceGvq2TLHMnaJFtdt79JlRTurPtdYmBIcy9BJRQ+Bc2mBzuRamj31dNH1vUqdfB1+qz62qeKwG7izjM/Gwy0e7Frug0jlLxT8AOiNx+mVZaJ2TvL2WGTy4XWEXs7JPi8Weo18zP3oUeBn0YlXeIXHhWLvZ4A9CD56uyPw7RDnCu5Hr0oxid5FTjjyzuG74ra1zkdLeVrvoUqtv6YUiU/3av8t+eyTVrzmQdXvVFZUytI8S5YzJ2WxKqBg9bKCeF6qmqtgpnc1c87Axx932N8zxokwxKNEVQ+V+o+i4tUkBayMtXOM/W4P7yZM+wmbYcAwbGBjRAQRAOfAHI59ggPIOLjJN8dahXGLxgm1ObKPRojo+Cu6iXBxdrg8m4wBeQuCK/Bpzp8ZLE43QYnCTFHNbwDL6f6LYugUiJNJe6ZX+VvprVObQ19N+kzrJ2YlYzBsLmAurvHm6i3GcQsxaST5MbF3mXeSQaTKcU33fw5zGn6kg6cBDZTCKQ0u60x6MBAuOjepPVT9y8aDPKIeSjU26qR8kqFR9Gm5N/NQceNH5z9f7ghJJ6BxqZUKku+v1EgGu2mPyTuM79/i/e/eYnN1DWst7N0Odj+BquNzOxR0FTzOHRFn4nq1jEUFBi+BGtiZLAcv8lBzVE8XM2Fyd/j0+b9g3F7g2nwndOZkXrNEtiXiL0iiNtwmD+cFLD+VQiuUUG6c2TghxouldrzCS4KjBM0iUUDYpCubnXNdQ7OSimcN0VQPqPwH4jFaJtdrt+LKOk0rjoVR+csNUi4eRd8AwVoxzHoxNFCvt9Zjtfbm7cNJTOovFuaIc/6VWA7Kl75NtIOjvcZytYcwcHMPHu/BEsG2OG8ZQ9YamovlxNV3nS7S6kyyc3uyYlui15RhOXpr1Axx8VlVpvE151P7hDByh456iw/FSHl4RGj1uDVcPaPoY3gkLGOfCSqbLWPUsNNIjFlDYAwMwqV11lrw+A7761/B2gGDHWDtAEsGF58mDHcTKIfRoDH8zIxd2fB81FTdB3GK8uzBnjH5C3g74tJOGInw/uOEa3cH/AoQi0hfx34+irO4VTBVCaHmUCWrSWddh6yLak0UZc906SQbQxLi1hewSkhYVZZO093oZl/Ntak2Rkhb6nBwZsaOGLfGYzpQQTvkkv5huHXWy6lnWZgvZ9c9TytDf/sU8hHG4SGGvUN4Pff+CaZzvoqjOO8OLOX7MvD0FX45UCs7F1Ki2Rk7ZCd/jQYI8Y6Hcs1IPIIuqzz+UHtPZx45V1s5Uyd+Qjtedplzbr7MpOX2KKcFWSIFWqocpf2/OpqnyR+NEQDExQ5A9NKv6i6moZ64U+nWofyKT2fg84c9bm4Y31xtMGxs5JWrQ7eo/K5xzAP5aKbJwU97DGSAISjTDQUPesOAsWFgDRjwgMMEvQcKG5BkKDKFJJGdeYPxQKJpjTEw1oCsBcnF1uxmGcCEW+LlH+c7B9kGJzFPpjBGlCAKdsGXOmKdU58SJrIo8UXeovSfnprQNMKw2WLYXOJy3MIMFkmajvJmngdaZEv767pu6Vw31T4q5zcpfjUc7aWiWgp9Ta6V5DjPSryDrBVD6QinIKaEtB7abbvImOZPt2lRZun2D5g39vWB9JjMFHwc91GPVfdx9YhgDLCbHPa8x+bdO9C3I4aLbTAAeo9h8oW+q0NFV8P5DRHHtuK4OVpRTUCoHTzuJcyPgT0OKy5yg/SvrOrauTv88PlP2Lkb3OANLjHgDRngijBdMzCyGtAe4V/axSOpUR52RYgQABYv19TwHEqUN928gRfLixWBlM262Kkhui01OIz1AgYv7b+/EDinsqcvns9h0ZpllHkSg+3Vr4G372DtNhcgHzoMYraCmdqibi/jsVL2KQRZVj7w4s+Zasuy1ZFmmvlT+5naWjr1yXqpmNtVjZF1CKCmOa/wUJAVkBkxgPDhaof7jcP96EEgbPgSjA32dAemHPVAnW8Nf2fi+/bcoIV29Vag9rFSBuBExDV9zjRfG4p12LC8z3sA54gGz0hsFZd/WsGdFOU+47aqPnaloj6Htq5zQyFcdt7lbSztUz0mXTAk7KtADmMOz7vxEUL65II9sqBhAE/BC2uwFtt7h2GaMLCBGTbhfpFaOEaLDVJBV+2c+gFFPziEvnK83A8ebEO7tu4dNn4Laz7AkgebIMpTOmZMMZxU9vKcFGmZvqm3mmFl9eXM5PEYfSjFDaE2ZB9bmBi7V6VdfJtpWsJSpWDoc6+KHqjh1M0ZHPD2DsA946+6hJjoE+3xEzHUuXTPC8IuzHJBp5X3YuDJzmTp4+RLG45fBuhRf+UJX+H54VHlda3Da14AQIhyIPbw+wk3P+2BvcWw9bDxWB6oj9TmpKyMZQAlbwzRgWQ+cbajnP4pnpWe1fJc8WbCuysrR4/j69FZ7ndrFoomFplMVGgHXi/zH0kAL2sXjXbiLqgiR4VKe2XrDgMRBbbCGhgTLoLmePEve40glBTRWZ/FgPdg7+H2Eybn4PYTRjsiKFTjUU7GwFgLE85jgjEE5nD0LjHBEMGn0xmy7BTuiAgOPgwH78PBQd47GKJwdBEAxHqMsWDrQW4IQ+ynNF7Mmd9Oqg8lx9Soxgi4zxXPpTl1jYf1jGgjQTG1sXAGYFJ7KLWJwTB2AOwIvvo1cPUVzOYaNIxgRDxiDznQKBdaSS1aV78A9Yrg5pmvhKB6PXLxLstHCm1BcR14ZcyIeSm+k7oVrmfDE8eIGKUj6hgPVko6iyCSxjF6oWPki/laMy4pCiwVhN9JYcYhCshasPGYaI+r7QgzjrjwHpv7HYyXo9XOAw8yRDRDs0hkH8aEzc9DiTByYvsEj5uE5L3NRhfRX02h5ExgHE/42+33mNjB0wUGNoEYbi38BeBtWc+acKU5yFubbLJVB6p/tSSazq2PH0kZVRRSGi+QFGAox6z2UO22tfzxymafCR5NYiQMm29gLr+Bsa55RxD1jJDN5UbOEdWHKb1qYsLqTf6+fngUA9ZhuMrtLn6bI3D652ID+m1+hYeCFhQITIzbiwkfL/fhCQEDRjAGTLSrNszqQvFE5vJ8z+8Gc9DB9GbDEhqbX2sjQen5Hf7kPhNhzL2XvYChj17SS0S8s0rhTJer4gnSq4rhiuHA5/RUlhoo/RLmJz5vJLZ2+SlWVCVo9y2dj0jUmZmtr9sA9U7aEv4MyFhYM4DtgMFaDGbAuJ8w3u5hjIWxQ/DyKjm8LtuhWtV5xoUjgJyhm595AC54UHnAm0sYbGDpBta4cPZqz4CsnxTHTJ54J8gJwMVkFlxL9Zi7c3g0PETRWx3F+ZiQBNeGfnCHonQEo4Qr/eeS3jJwtQN2ExUrQWBHDp+JscWI9T1/5BGKy7M0Fp4ZOgU/+rwv4OarceBLglMo1CsP+EuEJ7M7HgGPZYQod/c+ULE/eRA73N/uwTTi3YioA2StFSx5XOjdMPwqHL98zwGiI7stPeu9Ur8yH58VmuuWd5uo5Y2Xs8gunl/VfJ/KUBwdWcvAYrRA9X5du3WrFxoLQjAGGFG6kxq3lKXsQ1LkA8EQ4Vz68z7cYiCGDTIWxAxjDDzHuybicT3hYulQfzPnor1nD2YCew9PBGYHD5uOnQnlBEOENx5kHWgyXV6qVnMG9VkYY45jkYxkCc8Vz1lMgTIqERflNrOQMpeNISBFSQQZIsoqdgRdfYvh+muYzQUAE8aA42XWqShGvoFRShWhrdeGThu1yLYsGLWgLHdJboVwyKoCbTxo0LiP1wHFsnyd0pKqsNOhJKoca1VcaMuxcFwJlIaFaC4n51KZI74TaADMQNheWLA1GCbGOE0wft4Iccp29zhHMx0DK+eFKUQ5CPk1IGzUMQD7uxE3P27h7y08JkzFYqpxqi+Eh7WsyvQT/vLpv8HxBEPA5KeQj0xokDHR7FhZHMpi8iua6WoMtyveqXWg99KsYPJAtYiScknnaRaRV+/FwjjnbacacMgY0Vm3rxESDwGZG3V8UnoTYIb1mCluZsOslFfZixbdOS+J8LkmuMPmpeLnDR3roTQ+tDri7DmetztkZTH0X1uqGr3okSxvKaXqMi2vcDIIa/Thaofbiwl3m0DXtBd4fTBFeA4QG1z6t9hMX2Vjm8ybzF2i49EkR+V6OwjJBSXjU4LKY5690GQdARHpO7jEw2iEyEaM+MkSJpnDJTVOs+e8kpgT/c/EGkd2sOhs80SKq4s9vpp6L4ofqdklo1oykHHlqbNwmaQN6pI3RmT0Y7oooITzYYOxAcOAzb3DuNtjmABDFsYMIEMhakIiEAjxckRpRs2dl4RcUqYmyBM2ADM8czBARYQ3UUC3zIBhWGNhDMGbIGyRQThWijT9eQzg6ltnnuKjRH0fTMa1UN15nYwxTwcJx4/1WqLmC+b2l3n4AvaTB9EVEaWloHM0JpT6Cq/wCq/wCk8JmSfPes4J8HvA7wA3ADwEmi8KhZmza/QVxEleAypdhs4b5TDK6oz+XYG9R/mInELBopw/56BoS8Fuc2bndVpWaeu+pVeH9kKKFzWLYpbaoZA+rFLALb2vN/j5MQ3O9i5eQO2T3AMiwIjsHHhWkWe89+kMf1GqkxHn4Ci7GQMDC/bh8lwyE+AJxhgwgpEiiFNOjXeUB9iHCAgAzjsADEcGJt7fayB8PcHYAYYBK/z95EPERqVrTAYE9NjRYAwI8p0BmTAw1I1G5RIfetOQhp9KJAFHmYTSb2YPD4Pp4msMF29wff0ew/YCTBZMFB3dGhX/QahEZsjyDQVkmbNZL/JMrSsWI0BMF9adlnN7+E+xrT5VofvgEebfe3HQY3ivq+a6qKJ5i0ucZ77XzeNDiR4bgiGqr8pVI0phjdnBYnuxwfaf3sH8M7D5hmD3Htv9hGFiwPmiK3Wvju3lUYaIk4fwDEpLBmNC9m0dIJ6OoehpZ/D5p02sxUMfzVI0I2tgi88eMjrv8NP9j5jcPtsbSATeSKmUIjcJTaR+qUdrR6D1+gzPmugIvdiTJcCjTNSW1418UKn1U71n0dzt4a/QgXMRnIjnnaE/pobZtIXBoT+3LYZ0QuzShrOuPb0jLaXsbhs6ew/VD+oyejoMvXa4eiQbIucNKycoG1Cu53bcSjPEK6yFtWonYU3vtmUkhJQi5p9+HQajv8SGLlF7e/Ta0o9sW68mXGeAUvQ6GSo44WQhuKRnUMxZWUZB/zU3pXG72UdQ6cmXMLyGToqa6zlh+0hMrPrkuuFcptOjTeAgcCbZILSJweHCNY1wVOY2IBiEsG9Yi2GaMN7uYE2IgiAywdPL2mSsCoteR7n02HoVn6G7puoXo5TxHjDhOxnAeBOG1RDIG1hrYQgxKiMxKGoA8o9GXEwo3OKyPnagkZYPovOa9KdSxf66S+O/qgg9JmfgZzoGkuVSqf05MxxJAdLAOXeVvA6O3q96yx7njaaarehkqLnbLxCemxUXpHwOd+8nqPK8VUSl16OU/Qo/Vzhk1z5l6T2lc2DJy/f4kOB9zexAvAfzBEJ08kzH+WJmwZRcdc0Zzrfo8ACIWnOp1lIkPMQUccMS5X+WqQIX/2rOt3faR92/SpoqXs+NxSkS6+H0KV6FM2/re86RRZOVg5V0wWi9W8gUHIYMnDEgH7j2oAM0hc6qaaXnqCcMhgH2LtxJwT5k99HBJ5gjgtORNTDegtnBGzEotP3NazPWT+p7yhAurq7EDjVeULJdftOXkeOaUWNanRgb+kYE2r6FvfwK47iBtSbeL0IQ3WFptyrXbY2lhfqo07K8RKrVKgKSkmWzDFfJrkkn065w7QCkDYV6aZZHqXE4lVjkGjW+rS1It6Unc1QkIMmj8+uhlVA7abikmL17GNZCj6rUcmkcHQh+ygXt1lrQrwf4vw/392wcYCcP4/o4/xB4/oiIAx1iADvy6SojgYmBO/HuJ2DHvkQZrpFkHrz3+NOnf8P9/iatXkIgSJNzEEGtFF+jB2JSAKC4p1FDreZtm6MQXi+k9I8Hqt+yKOuyGFAemdkY4/WA6Kq0cidTg24/ZnmCV3hkmI+OeBgIHotCpqMgqY0fnHGq3SSlteVnWeASkS5xtIzeaUuMZHO2vHXAhSdyfize6CyNyaA11LUBk4ovr3BmyJEQEz5f7LGrIiGoMKqtOdaDEjdVplXMu7zvnLWvj1UJyl1qUbzAr+i1IYxQSpKjITLuITBOimmSiIfEtKmyhMkXY4N4FAFyJYTOq9tUwxpKP5emy/osvIspuGSau0PYe5A+awZUfsv8aMeF0HZPnBzuGCL7EjyHuxnsJ8bbewtvLfbDAGumECFhhnRmrCEDY4LwUzOy3dFVD0u6puhqfMlgsKccIu4BtibK50HYEqYxoGkOxQ5kSGmXz6EwPMR8zvAkMgWLaoK1jK1YUKoQ434EajUOqDGQeg9Pg8YYsSTo61/LlWesPjBADXPZSS8CThTe5PPDyNgNwB8IsAf3aKlOkJXOM341nLPM1634FZ4NXpHvFX550GA9Vd81/8Ye8HuQ3wPYlMmozNLusJkPZZ1wVesk7+F9O/HbQOm0ehBEr6J3cs3vhffJKaR2tql+Z7mgx09pPpvLrmhlMdfpat4FK8exB+14hpNLw3PvOR6t5It2EAUe2hobLoaOTfJOIifC0UvGGAx2gDU28XUS/WuNAYYB3rsgKO7ixebMQQEPRJkIeXwAhKgIgOKJJ+QM2BjAA4YNYGMryYT7S0YT+B9mOAAODspDrD8ssa8SycMc7jKE5yAzUrwgG5TwoyejZelWx/srfKbQdSJAToz1sVYaLIZhi6uvfo3N5VvYcQPYQbQsuTQKUSRF1FH6wnro5o+E4rwyRfFd6hjzKQAyB7168prLMjKJzK6V6UrmTW8UjRG9VSEfN+OqcJd70opINz6lo8pwktliLqfuhLW0RgpfU4bIuD4WmIdOHfAWcc0Yg2Gw+Dzd46f7W4zDW2w3I+yEcFG7FHpmWG2IWKy7nYeD+Vt5aT6njoTQz/dRuQBPmJrNIUm/mJ9OgmcPxw6f7z/g8+5TVDiFdwQCKW9HLdQaUFReGRQY37QBM4oAbn6Veon8pEOPioxZMVwlKjxhOxnTqqkbkCvMvm1xt/yZ89XLs3SeHKeDHOFxnnmoUbK3qSRi2NDVEneEUasZqKZO9F/XZD+VVCD/kaR5YSr6r3Qr1s7jyRzbK3Tg0EgKXtyPDp8vw2Vh+jim+EXlmPvee9LThCucK9ZHYrMUI9/DhR43UtH2KpmspUy/Ja3cC1EXF9IViuy63mioX9xLlkDy6CHingL4FMIUxq5fnk6VmdLi90xjA9OKKHuV90RInV4NphygBvbwbEA7xmZnsL+2mGzkCPIFEsEJwQQegEwwCOj29brC6qxX7UkUIjTimAIAhXNrPQHGcDhaizhGYvgUdh34kiCIIX3PtT/ldr0Kt5beJ2HiQBn1vpXW5xl6ewgJZ5pzPJ+wukGd0svfjQ1iBWhjxN4CezBclLlDf9bua+cQl2baeJC3emC9nbnukLlHg5PrePqMZ4YDOPNSmqngzJh31lJe4WVD4gdWTvdaPfcx5R6lO39AnWnX6NTXKPsQE7IH2J3QyFouXLFnpddZr7FqrzvYtPLo3awzKYsoIpt1Eu7Jnl2JOz3n7rte06g/KbPdPlGmLbJk5xgjRUa1eHkMcuQ2xKEm8tPSZi+OWECKfDDGJOMD69ooGDCMtWAGjInH25qgo/NsAO8j7yPjIrMSDR5EYO/ACA7KMEHfEgwlBBgDSwC7AcZM8D5EXTBcX5hrxojV6a+hbnGAKiSaCkf0rOS7O/vzHsQT5bQacSxc6j1gu73AOG5AxoLJgFMkBEdVJYU1UaxHRr7AOtej97B1x0+38nCj+6nHUQm2kqPkDZNpL8l8msMQ410rL3Ja/fNt1QtYreeiGz0evS7nBOi2+YGgBqaLrhzkzL3fY0fAxSbcDUHOPyq3ctaIiPnBmnlTjcSxQgAD8Hcjdt9fw++DCFWido+g5tI9PP748V9xs/uEu/1tfGdiKoIdDL779VsMQzgzTgwRDICZwJMLluz7G7y9/gyybzBh27SzVoUdg1Tl3qyOfGCNoqKea7eyMrdKXawpLlLMta8UH7ip5Etmq7NOaEY1ycUHjpvF80JgZhQpPjTwrda/eky533U8X6f2khr7B49EEXpWGDPCP/r9aceDZbzWa0a+MgDtoCHW8vJ+iHnIG39kveohFH31wZJ+KXCK6izk+ng54ePVDvtBmNP4rjgiryy5iJIQi7Iok42BIYN8nuYcbgnenT6L/VxhDcn3FEYKoeo1Mxbx0Uv0RIyO8wBY3R3BQL43IkdXpDWldsgEqwlK2fx5u+jactZL0jpiJHzVzyv6AaToQLl8O/HOhGyoSK1Qxgh4eHKYaI/hp09gsiAfeAxR/lM815YMIS/6eCeFarPuZjIa1LwPx9rlWKco4IjQlO5+4Gj48Mh1zikFZG0cHt2TIKJS+mxeSOVHLRcV7SN421SK1Kk5I0QSxPSzJt0pe8k8HH1PRJkb3YFqUCnvW4QWxZ4enorrm+Nov2Su85cMM3LZ63S+wit8+dDZzgK1Lh8KSxq4rhzBSAinUJiKIJS5e7I6KW9kAmrPZKLoxYwYhaDVllq6V7/Th2Y+Dgl0WdIsNumKWeLmM/L3hdiZvblZHIo4ywytN3498OrdrEpMK54fwlSIXBEqGuke1jLGeKeaXDTNKiWEhZXjTk04DMlHGUYcBow1GIcRdhzCxdHRqOGjnEOE6NEdIybYw0fnIDLxcmnjwRMQLw0AQElG8uxhHOCI4vgyYEM4hDGAMRaEoAtka8F+CPdXsNw/4JMcMr+dCe/vMyoQAT4cOSWyA/fmghCcUEVOVIqGPK0Zl+UUFLYjQBa4/hVw+Q724j1MNESE/DFiQssnBBhW0Rlo127ZP2lHuTY0Xmc0zffbzivxZQ3UgoXm+eLYsw+OWj6WJ4r2VF8wohiEKHh9H28gAdLYitnWeqe0+tW681XbC+viOdbSeSC1IKlBoqGpSBGMbR/uPuP7H3/CN//4d/jNf/oPwFc77MxHGPhCrp6DU9m3Rz6aSRHj5mn7rNeJQ13nycDdbMDNYc+lxOrZxxAllZcZN7vP+LT7AKJw6aM1FBRTIAyjwZvrDcbRNndSMwj7+x38nQfcHqOfwHCYDrR3DSQUjgQrrMljEbve/NSPRAHD3yEEy3PDauPOIHq99OMLgpqQLiYseI9TsPWckFWJysk2K9pScw7N7soJKxR82Tgg/1b81UKrl6qocLajZQn7b8RDqnBzRV/K/SEb8LhJUDW6eE6zx7Adgi9seTwyHKOlZHgKkRC3FxMy94qkAAbUo5mSFQsDwCvBR96vowPr2l7vf52dsKNpzcaIzIyxXmnxd+bhauNdXZ4ug8s0C12ovU7SxyokXr8hLHv06bWp129BjZC7Ju2UMFJTlMTiBcVRWa2NoFFw9RyYVU8eDg5m2sP4fbwWSuK0pe1RgEDGwWKzKHuasbSyRYgBQvZXHS2vIzRz/CUV5Z4NuP35kF1t3QqvcFf2lrot3PdeaiP71uNciESR+Tj33QadshaLLzbuBO2WpAWk4+aHo6Am0RDpGYLOxvpwx+Wp+9tZ4JHrLiSDmQiYekwf3KRzROsIlKLNUqXnq3MOjnX3ni8ofj4vh3S+2uuSysM0XuGXB3NL5fmNyeeFtWuIEfYZjgoEa1EOTu1JwUv7XSmZF/df1caINsvaF7lZShUinuCaZ+PyH5Tf5kBxW1w/07LxzPemjLny5uo+H8gIWjCIXHLW69dFSQajigNLuur4LtyJFiKQA6MSldqes18OGcBwiIwAYKwDHAPGhGsh4rFLkGiAEJ6AcJkzQN6DDcJvTyAKdznAiDOTiUezGhiy8MaDfI4sSF1cWAjCdwYcYoDkQnRK79uhCrisHUj7nEv5lIwBmwF0+Q7j1Vcw40UwsIjBjwFx1Er1SHWddjxoq+dKnus3uUDr7tHZOq1HNmpwzcXrghDGfKF5lNqlTZF6PenGCXKqz6LKOZl8Hk53ZFqAQmcR5dy6XoRj026me3x0N/jmzYjN128xbT8gXaTeHku0WOUx8KR3RHD9IyKYrx/GIwl25OAw138q/iT6jJIVr1QG/PD5z/jb7fdVfuB+fw9DIfLh+mrE319d4mqIA08Gw9amIxBytrB4P4Lwb3e32LPHX/c32GwvMRhVRWxHsc6aPU55fPeUUvJvWrSy2OKnLNJZ/O2JVL3EqaaiKT2iM1fVOWWtpwPSdHcW1Dqe5WueB7ShgSreZ4F4p80dyF7iB6vKTtVA9LhGgZPJeNatnqtfrNqilK3pvBQu0oX2yhEusrb06mo9aIuLjBJ9Cc/Em6HcTGS9KQ6oNxCHVECHNOKvsBoMgI8Xe/ztzR7TEE+upIy7Sr2boB3yzOiCPO7sT/BjYCITI5y2k/rYm6qk2vO5sG6V3xMjU0koso4y/xQvb9NbQUxQGiR054KXAnvxLhGPHB/vhsgMUoqC0wZErpZ8hyFcDVGhV7CBHa/0+CJ/W0FzkvdMrCeNG8KlcvoODR8FizxOrq2PpA0U7BXpISchEwDurx1uvrrD9pOBdVe4umXQvQOIYcCRBsWwZmPiUbJzHSoJbLvTl9/yeaelYconOlnSp9ytNYS8D4fI1MJuot5WNL5r2NXPOP3Xry2PxzGQ+S1FGxpkO6/akSmfQ3we0OM6l0JwBAol2jnI75UTQdXON58G/O7DBj+83+HDpaybHiVdhvMacx4PErmbMUa8wjPA61y8wit82XBg+xMOlED4fE3YfT3i6ldbDNsh3g8Qo0xB0VtZ5L1IHlQVkWsrfoWoh1AH6+cCyWJAQbjw1X5Z/Si5LBGcSapKPG92klPlFN/L/bw8alUlLGTVuGcrHjfx7VzdN6fLT97a6lkh01bf254rWMOk98GEMAUYa2GMxeT2oT/eB/1BlN+MHWDskIwVPsow3uejCgyFOyRsLMsLX+w9vHOQo5kofg7DGOfFR6MDYLwHyEWRL9TtidL8BGPEhHCBNcMYFz89GCHSwpohGkU2ORLCeETrxeJ4pBFjwZuoK/FIY3F4nPOnViqnbyzPDcgMGC/ewowXuP7qVxg2b0HDACYTr8oO9+RRlIELoCjbcObP+4YP3YKMxxmN8zOZs7TmOrxyNuhxluUiGCX7MzjqcCIuxbJlCYraXf7kbglGiDwJJCA6o+l2Fis+y16syoJEzEDn7ayjJNNTTj8Dj2KEgKp+DreI8NOnj/iXH/6Mzd8bvPt/bkB/f4OPf/h30DYcZWYdY9y5wnFvrq5TuLeHGyK4+GhelJ7T9eu+t7aPxH3eCBGzOwOOIU0AAGI47+HjeYO65p27wc7dpvyWQojVZgTIDHhzNeLt9RZfv9ngMoZjQS3OxosBwD6m8wAmT7BeD6hMyalTs9Dv6skcapwHr+v2n7pZvTzQa7NofXaXlH9KVoZ6xojHISLHwbo2lKlOUBsUNLcmADO/myK4SFP+VlituTkgBkKo+SFJS21V2rBQNUUXm/kzbvmIDn1LFvoTprzO8uWtmqcFGZ9pAG43U2Bs1fP6c1VhBDg7wZk9xBNFJ9C/1YFb6d0svcXCy17a5omObKiQVSFmMCro/VXyAtk4jZS2RtUC9wumi9rvqcOkc893aiVCH6NrKqJBgDwWnI0QIqyxr8dR3+EUmFCwCLYMjyA8iIOVJ4sBgQd3lrG7cKAdMEwG7s7BswexT+VmYyojn1G1wGx2f+nojmKWq++ciFUWQdTcCw18FKJyGLElRakcWMiqBOte0mx7OnFvPQ7JuuO2JrpiXVtWvK+6OdtrPpRAJeUSx3RERH4fvlsPXOwM7ESqOSvW/RI8YPhqzrYt6iXunrUwP5+SDydZhpXMxANn8PygXYe/eDhm9l4ivv5SoYd/vfk5P8d+btRfdBp8pGU2W6eqr8cr19vsNALT1uJ6YzCMOq5UMeukc6N4u0j0eIFf774oTRytZqWkpATECNv4TH9Xys6eWFrLv+kzyZZ6f4aaSFZ/VfaaP9bJizxnQIre5hUGpFu+Pq5Y5BcWYxARDOWjTtM4Kl5XCkl3oyE7B+eyPIBojIjHpcrRuyCGJxPuWUM2cBUdEN4oOjgFMwEB5EIe78EU+H5ppyEbIz5i27k/NHNDlo5YQlD4H+RZG7mtHG+JuyMgGmQMzLDBsLnEOGxhhwGODEJ4tyvak6ZPN7biApu2UP3gEPTxsKhbJS1MLZXsr+VAyAXkqtzF5Q0kh8LwOMvPZWZum5z+euupXtdPy+ecyuvtvcfHu1t8c3GF8dcD8N5jurjFYAysNyDvgxHvkeBhhoh6zqoXswJkb3eKnwzgHg5OC9edZeDvR+z+/BY8WaRzlEH4tPsRf/rw36DFeGLg+r3FH379NRAX6h8ut3i/GWNpBDuGcKutMelZUfXChhv2DUa966d1OiPk9mFuw1CbE6p1cASI8l0UMsfCqjq/WH6byranwVrq9JcsUKmNj9HZCWZzhc/EUAWM5DniLOsjPS7pQ1KWNoaDDuETz2tpekH0qVgjgPIm9uIVHpmbdHRLqebs0rKTpviLXQQvBhL5jdEJyQiRaHJtONAQ5z3OeVIo6g/F9EldKRJCRwkdOZWJoVELhTnjuKyTRmmuSmD1TSsLG4+muJ6K45zkT9WZ0gEKnw8gdrffD1B2Uy/bcQWlXnL0hvE+CSLBQ8aX9CZl5HK+w2SDEKIgPAifLy/w05t3eHd3h69ubzBNe+x2O5j7e7DfYT952GkCw8ZpIJBhsOFwBi1xwpuANpUQndpE8YkYjbjEC/kdva285+Qd5tml7+Q92IUjpEJWjl5OjwV5TAuczA9Vqjptv6gSH5uiDoLMY/49czdEnecUWJPxSCWreFMuFqnTF7xyNkjWjjflvUsonulPOVsZAD5bj4/GY6LMefd6UnO5Lz4C4lR69aXBl9TPn5Ux4hV+nvCKn6dCQ4aikrcFA4IBOYJxHE++zIw3af5J5HEwtMI7fOvsVpHG9N/PXa1bGiOk7vqbxP4C6h4veUZoaVvac6vHmq9PZXCVxyMrfOQIn+j5rRyR6rryc5EHoNIVjEQqu3g2C1SmW9hzds7DOY9L4XnjWf4+erETAcYShnHEYId4EXWIbPYx0sE7nyIoxBih+WpOEeCAnFNtkC+1DpdQB2UqgUHGRmf/iAHRK56jsi7pChB5bO/BVuYkRnAYA2vDHREWHt6HyAkXPeWFw0+8fo1SFX8cFPEmJSTq4DNryTD89uquEFtae2DNCDNucfX27zBcvsWweQvYEWyD2te40FaT5OlwEa5PlckF1fEOCeQ7eGt00hFLcRQLNGKdOHWBII6AwreHi7z7yCesvq4jyUjQlylX9Wi+N0UyhASZBmic1+ss1tNbN6lstXZkPLi+O/VUE8HjQrgA3mK72eDbb77Bd3//K1z/4xU2FxsMg8W4dxjvJthp2QjxULbzwRER7bB2BCH5pzMXvWlxCNEQPYE6XBJt4O8t7m4YYIdg2QuC/N7dweEehoBRCaVX2y3eXW4SiXh7vcXbcezUIJoqqp+0zV8cfaXgfWrhIK5oKs6T01tsZxNmlebAWll6XewRLxgae0Pv4cuiGY8AxxkeDicQkl6pKgrazSpd/Fc95yJdWz/FVNRMUM8I0WlTwWv1GFEuknUXSdeIp+nFunF9rnXyJaC1iCKeAGc9nFyEQmWaVaPY0KSKtifDQ8fyoLaD9Qo3hUNdYtoymCrDMgGu+SFwK3fMVdUpdtX2tJYWHo3QCxlqphvC83EeIs4soo6IYAATideTGE6qfT3OZzZIEHbG4m6w2FiLPRnsPcM7B+d2sNMdPBtMJjSOvIc3HoZDlLHxCOfJGr2flHSioWicaVToT7zFSgwr7HMoc2SiRYiDMODskc65lQqCY9gicP1rNVFYTz166HhKyS2WrF75KstxyHkK27a4TNTWsbaSVF5RcH8Rz9WrDV3hN8etss3hAUwm3MXztPAcTPJxsL6FM7R9Af9q/uZ8EFrdrHXQI4z4y5/Dh8Dz9+zY8X08rHp5UNOyXn+/BK73dKh7/Nw2vsRy1fxnLWwTAbAA4ln1nJWpvf006WCCDjOlWdp7zzYUsc5sgIjjrCpfbV9dSpN421zWfFRoeN49oUHnmXNmehB0Rl20yRE8GOHegwpDhbGJ3vly54JEO2j5XPh7oEWfVFTqvwfkkFSKzkHGxKNUQzvIEIiNuqy81xeOx7b6oHOMxg4yDsxSfojkMPGC7XCfhBgTfNvn7pPcB4pHSCVdBpUp6lnT8lGz/kHB4GIHmM0FhvESsANgbDmGiwxru/pKvWFmalsDW/xXG89Qrtce9I2DVQ9JF53rKJoEdBZi+ZsaGbOTXiOXcugrxidNSL2+1kN5hHhsH8rvS6XW41mLGUv1Ou8BC1x+NWL7boPh4gJmMDAesI5h9w7kj+/TMbDaELGuGUrYqfN1pVJRJ7alzy1h3o3Y/fk9Pt/e4t9+/N/h2KXJ82BcXln83T9+i2/HEb+9HFM+snLuYHg0kClrqTxmASrC8vPruBgJ4bIasbrGDibPV9Xqeda/XKQ1wuexk7eKFLF6wu1Glcukqo68WRoET1ATxy41CfV1JjpAqly4Ia+uVX2s3ZSfBahUUBLQkMhq9Rc/ZynDWq3d80IRAQmEvU8mrFDIhvFQJ+LlMqCIeWVpzh/tpT+ckTb+lrUTnnshelTjdJww5V7QoTSxzGjXj94NqGhS3sPCu/LsbKCLuHpRF19kjdUH+fShewnwLwpKprJld7Kq8eZihx/e3YONosEqrLZHUXUpaU5ioanOqNgl8jDwMBTOICWOf9CYb+Jf3IMaZkTjf7yjgD2Qzq0UDIkeGCl/PuPVJ0/4hWGLERRJ6PAZb3VEXrgeoior/hD9dO3foL3305hqcqhpZZMXmcmPQoQ2SNOpPvqMdG+G1+s0ekd5DrRCPgPt8NgbwvfvvsJ+GIoO1Ixd+JLvA/EULrP7sNngZhww4AfY2xuYn/4btrc/4e7tP+Dm3dd4c8vY7HbwBBg2sByiMr3gkQnIasgrWqoHldOenfd9FdXhw+8Q8RE8s5yfwlm4fooREQ7kHby7hydxxvAwzJkf8QCnu7U7LPcRAmlIrzyi0ij2886JE6z+a2vwiX/KjM2hhmWkPf4YJUFwhehLZaS9sYaSkhEZ5anYB71zpL72+OAU7q/eM8DVCu4aHGLizD16zCs0ToMe27Q+r8afZnNdU/PRrx4CJ3YzZhaeZrmEk+pYzDA/3719d11Fc7wRl8mOKDknfaTJW6ryyWs8FU5du718X06vnw5OG9+FVTGb9lHgBYgSiYpTlPwKDTkXvD1AYHMJZ6/g7AZkBhBZJG8OynxLikSgkJeQI/FEJJRfUZoEuM9ltEx2LaG2Qzk3tIl7UMfyaHwQY0x5YpGuK76QdPFp2t0JQRGu5F6JkCgjJ3SEBLKAC4hAUPJ7jZGiPx59kMHWvC0XHx7Zlz4YjYQ3DWNizABjGH4gkDUY7Ag7DPGoo8A/MwAXDQDCFyZDRWwnIyjBvXigM8DegQkYhwEmRkR4R3A23CPBHiB4OB8Pf3dZNtN8mOCQdzlimQB4Y2BMPPbJGgw0hhzGgvc7ODeBeQ/EeZKo6zy2ahyTTBlm08DHR2aGGQhzE6RSiX6Od11wuAeDDUCWYK8uMWyvYbdXMNtLcJSHLFyacyKCT8sttNfk3scqTTHNy3ekCv8eoy2Sk1QYQ8e+uGcgrRGFPxT7ldYMFaUXvK5P9yLqIvLK0m2igCgwMb9Pa0ZFU0S9gMyJyOsR00IuL+tH8+x6Lc6MywGYZ82XdxiqPnvvBS/yEwJgcL/f4WZ3g+m7O7z9vzpsfneP7fY9xomxud1j2E2wk4tj9niwPiJibUPmjBALxXpEy+negnYW2ARE8JMFe8D54PVHILidx343wbkJ22GCoJ1UcXVh8e5ixJvNiMvtuMDY0szPqFApFDA1YS5XCMOB7A4wbqGX1B+LQ+N6cNzbBLm15SZXppjrU1u8hKwtqVdLdc/LZnLTHvpLh174n1oH9RDxzPfwW3YnzZBwRQRYpWb1rco7V4mso2opJTNZN/3Cgkt7Ry+dbn7FuCnIzDDph7NQv6JEQx6Z0n9BQAAcAW5w2I+MvQ3cT1i3HcXyIb65W4P6FpljLSBl4M581ntcxZm1KHYcpLWzVJCKHhLDtcqi5ZFeIceQv2NUg7Np1xRSRBDoMY6MLDLlCLwgh8/4xjFjbwz2xmI3DJisNkS0VSUcUmfPghmOCN5YOD/A+AED7bHnTyDewcMn4SjcRQXAR6cEHy6+A3kQE7wJwoSc9piOXxK6pBhq6YMYIYLBJTDJ6U8UyT5UyszY0YCBMnOtBq3qeniwiI9c44sq8ihEVsjH5XMdmTZL84o6q6jOROj72EZlwpbedtcy6W2lfMvqWLeDoAnR0t7aA0VnVo41V2M7Uyp48vD3e/j7lj/tHgGwAlaNyJl4rJ8VqzZrzDoCHmlAelhAnW+rCmpoz0JFz2B8SFXPPplbEz8rbDwCjiROJ5Vdw1JdTzMPxxw791Iw48uRJAhMBkyRTyMxLxzWM4T0mWFJCv+FjI/qFNmoWg7tqwd4hQhz0mtPXM5vuE5Zvmc9UOcflHyET6xBVZcikOOfIQIhOPOacBWxUtB0+NV09KnIzbkXpQgmRg+CMQRmA0MWbABj4t2uZBBCmmNp7QUJhfzP3qdLtOVy5GBUiUYJtjBkwGThWQ6XXzu+wp8zKBqe+joNNQ7Kya18h+BUagYYu4Gx0biH8JyC0FRtu5lfnnciWkfj+joTLfPoWttSi9VAxYeSn1AgFtVN7nVB4zxzuoRb+lxK/Vk+S0aHNJ2HKlusfD3IOljImmnlcvl9CkPxfmMHXBjYrzcwVxbGEIz3wQDh+VHvhhB4+GXVGrj79SB8xoR79qDvr2CGLba//wgaPHZ//gq7G4d//fAv2Lk9iAjjMODbX93izRuL//SH36C8ihKBSJlI4GaE0bJ9shQqjJeylIq9B957ePoAc/2vsFdXwG59348RAYs1dEJZydldiB1QWOnD+7C5a4tnWnekCgLCQiaa9bB7qdEQXSbnEHWd7cyZCM4zQisDlqYkQZGe2mfR+FvQAlb7EqvfpRGi8BCeK1p5/OrQumINq3ZwlRdAOB9SbTIc+yLnsudTEmc25EY5lbnQfBeBPt/0NGXPzx16IyIeHrfbPX54fwtnEGiSMLBHiYaCt0HIMUCaF2FSEUNriWIURDGvEfMrXmme7imMUfheywRZpS6rIX7TBjHJU/MAHB/OoJMug6NXyrFe0NoIfwocUtyKEaBb6aGlIutU3Z0gYdMTgO+/+ga7zYCJbLqDo6hGiiEEz3UIB2AyfYgGkQ/jFe43v8fd13/D/u1nDJ8+wdxc4WJnYPbBE8cYC2sHGE+A9UEQYRPw1MoeGYWmtJnGNqWzaDPTzpzvg5B+MoeIiHxPRHwP4Merb/HJAN8ywSJEURg5kpEQ6ZvwQY300R/iRKe7g9+dk4XSmkRcvT9mF016XEa4eFAEU9KGyT5urdN36sXeCkmHIPBXOjqw25QjQdEHnhsxlbqgM8D00x1u/39/wY1xwOWp9c8BnUQnHn6vxMLc6Oa+FO2gwDMq3c8Dr3zM88ArDzkPr2Pz4kCxzt3Xsl/TALIbbGFhIZcDK2lTPqqCkmaHOsReeCn08oRvM9zNCVDiXuZ2OqWl5s3gq/A1QKtzUFkKmVbXVURDQD1jtC/qkh4KoYEUpyTVmJxpYpQ4wl1/gW/myEObFAVBFG4NSY5BugZhNUgZIVhqzwPEAEiOgyIK/Hl06WbvsSMD7x3gJ3hP8Xu8ZUCPsfxDoQ+eHbwLTnKiEDEm3HEyjgMGawEwzDRh2ns4D8Rwi2KUcrOXeAGtGq/ml5BkWdFfhJRxfM0AMhbjxdcYr76GtVsYa+EIYPhmyXTltR6aJB2ihmXtqiC0oGGB+RpHO23IuidS6UNhntUpAHWBGjGQZeIQSZQbo+WufNk1QzeYVZ1y2sEiPGArOlZnWvPQPj3v6OoqmZtAsENwntvbCW+//QoXf3eFYTvAmgEjO2x27rgGPQAebohghicteuV/w4EWBK9Es1rMA4CJQigXHMExg288YB3ubnbY3Tk472EJuBgsLrYWVxuDq43BdrSw0YouJabam11ITU+1IPQc5Q0O+i0ACSvMm9hgDK63IwZiwEwAzUVEPCcoVXJUTCylOr7cucyq3hfDJB4goXVTl5r9Eq0sJ0FP61iPjFqxXK7z+THi6mtWuOasXKSt9o+qHGU7T0wuVylnJq/yLK8Vf/Vcqr1qqYMlLA1fv1UvTkfy3EAAHDH2g8dudDESQuuoOyNW6xxRUR3hR5E/iQHDI4wfyzKVwrJRlp+kQFLMUCkytGhVLxf1rfHWYCQG9GDNT0CmTlYq1oIGDjRXMZ/pTogo5OysDdEQ1mBPNpWUlrZsf9Jajkw5mcRsipCTDKI8wvs32NMdboYdtuYO4/4D9riGNTac6eqjkcwYeG8Qb8ELnlge4OiRpToR2y90SDPKSEYVMYqGy7edhIBkoS7+58jmQJKarmryetQUcZm3935tOemrahOXj8p9paXrh2Ghc40RosMDaCPYiiJb6HG1s01JaXMVC/3l5ddNctlrmcGTh7vbw33ewd1N4M28UVLT2Ofbl/o18+LbA3A07r+Chjx8Pxd+dy383JGmEZDPXP4SPVxb1zGy46Eyqz34Fc4CSTfa1UeqcS7eEzbewsBiggXIIvrFF0cS6S+BDnFbVFmsUknUx0jWSbMe53hNRSfVTMbZ8gjAAYNELiM+aLS4aj8vZFX1uUY+P+LVKYmLJhMBZGCI4MSyUOFG+F+EtpIBSg4nPWeTpGeIn1FWEEW7MSbcIGHCPQ7GhMONCHJfhDhu6fYi4DFlucN7D3IOzoTjeq3JsoMhAzYmOEOzgddOKRVbfhhWjC0hGl0UHhOCY50dYYcRZC26q6bDEwsaNTJEpzm183ZXXZIe5nnsY71i1DTZSKEh+gWXlXFZ9qxwzbkdhREidzqnSc/kT5WVmjG3vvR8rJttcW5cUjMscea9HufpbQUbBmPyEya7h/kasO8M7DjAkoHdO5jJx4iRp4EjDBHzRG0C4yNNFRlkXLLFFRvcweMGrsqeByeK7iAycN7h//gvf8Pd/gbE38OOFr/67TXebAf80/UFxnCYN4gItpEfDZK/v9YhQYd4caL//eNU5pTV7WReX4z4j7/9Fjd7YL/f4eIie60dDWeb8QOSqza7RauzzJcBhbO4q7Av7uB/JiaZ4ZTNw2Stz4sCPcXNdNeKx4IAryQmdSWVguUlQY57yBt1geFUpqzXdiLmgCLImpgrliAp9vTvnGdNJERRc+QL+p7XgWHj+nId5sRT1MeDaIVm6V0y0x7qfBaUv3ydf+cTT3/+gu5xINh4t3H489e3UA4tiTGtl2hTQPVVykwRELFAA4vL6T0u8TUsxnB5WaonlzKzJRwEZXKLOOaR0V3WDhKpLpSDDcrlNaOZLCmrNb7JHpTvn3g0oHIN9hgl8VgvMiVhI8Ca1ZAiljgcweRdUNI75+HA+OHde9xuNnCgRI9ytAmlSwaJtAcRIR4Yi3DiatmOzf4txv0b3Iwb/DRe4P31j3jr/oS/fv4nbMbv8PX9Dhf70DgmAg0Ak4HnEGTO1sYqqv7GeSnuvYh4Ee6F8OkejHQhNbtwX4SPcxuNFd4QvEcyWhgw0l0OHC/Slq2IKHtDpcXE6nMdZEFtYXOrya/Op3iUhvIzFN4qofAArFuic7zdOUA1NArLel033n1zeatnvUvs1rbDfdrh8//nz/DTlNbDY8NzmjFe4XHglVt5hZcFD8XGFyic/kyhGWkOO8Q3d9cY+Qr/snkDNlt4suFYy+S00VMp1vd8KU6O4l4pukxGOI0mWja4LCZ8ZDEw6jkoKN8I+VLq6N6v6y3blOXFkpPhmfShsrCf5/Kz2lLzryUkrikOahEszdLRShZP77n/vceorV4bemfg5klOlWV8Qrzg2RoYNjDewJC6Q04MFfHu1STjxDank05E9ojHIpHxgIe6Vy3ww+GatpBnsBbe5MhnY0L0crhoutJpaSU1RVzjEOUgPLn3E4ZhAx5GGBOOZbLGgHiAN/G4McfwMAA7GYkVo6odz5ZonRKSmQAE5bFBuPzb2hHGbkDGAiY7XJWCbS4/8OgilC61r2qCfpNwT+ZM8/pI0ebNOKS2hVkwmvfnMkmwF/nknNUkSGVGGcLn9qTjbdPvVGD6TPeKeomgkHsf6wiJw1Bf772YduGEmWNASR1RzBN5JHw3RLh3e3y8v8H07Q7j/30P+m6HYTPi4m6P6893eWyeCFYbIvbpEpUWJoSzmrPuNXRhgscOhAkenrRQmQVgBnA/3cJ5ByIKl0/DYxwt3m5GjIPBV5cjLscBm9FiEM0SFC5UC4sisgjh00k4ogaImmHudi+F/OfFKa03RLCGYByQjlGAEN640Z2Jg29Zp3abSuu2epWPZdKbLrB06Uyqr9Yj1elI+knhvD2HFyi1rFEqzr3oMxT6e2kZzndpiEFMLud5KawvVZ9N3yulrj46sbaUZ3LFes/JkHCMU/p6TFvep7dJ6bZxJ098rRZKSFOvmk47astvb6JmZZeKCK3G/YZ4/aLBE2M3eNxvHJzhxF8Bsr4OEKIepL2iZLhACMxacSk10FsHrbG6RISCrqxl3ooHGh9RfK/peGbo1xjuzgPNkPfmYMW8hOHpr5F5ypvHQfouIblB0GDsrImREBaOTOQR1egIL0Bx348eNoxIl5MnFaL8IV4pBET88GwwscHOWtwQgcxnsBvgpgs4Z2HJAGThjYPcZZJoPxHYqIvnONyHJYyeMMmFMdSH7xIBEQwPrH7L9/hZEL3IeKQNX96r/qoRbr/Vc3AIeilqKr+Qq8Zxma9TGfJZlyK9yg+nWXp0LGhjXHum63w/V41AIXdx/mSAvYfbT/FOkTJN2b7Qsj157OAwTISre4vd4DHZY8WRtUzvGZnjJVioYk3tZ2vhQ45kOqMMAWTJ6NHgi2ZpDmH7F925BTgXP1rnP/d4nau8mg73IXvN9+utqeOy1+r6tF8aJN/GzrvMneS3bhiAcQM/bMDxWJ5UVqO1KQpRb7RzkuRq5zNRO2p56qZspSSh+llRoiqrciQ6VYEnDrKs2qm5BM0zHdZKoNPZBYVPv0Xq+3pcLXKZ6JhaYECQuqjOtIYJjV5lMp9z3GwwSCBc0CvpiGCiFEIUlPXE8RMM8mIQ8UgGIdKoyYEXhwn3RVC8CNuH+2tTdgrlG2IwWRjIHW91ZzpdFRZ97RYtChpSqGtCn2AsiCzyvSvzNF47rQX9fUWrVvMvPIOSM/1mWWxFQ9oy00dAFJ2saZlKl8sMRgiovmUpRbW5McRw9e+KBZSJUu6f7sdSVk0HV8hAa2lNNm3lI88mnkBbg+H9FsOFwWbvMExRdlT4kBbAGYwkc7DaEPGBptCWzrs01lzMM+7Z455DcJII/0ilUPzG+PPHf8On3QeALKw1+M3v3+DN1TX+uzeX2NpgsRRLTqEcmlkbIpiroYcgr97gmgtOijKrOirCkJTv8aVzwUpqTxag0Qyu0JjeJlh+X4eO7X4bCRQB+X6IaMGjcqNIizbRBCXYx02bEIwzsx16JtBTSs2L+mEFFUMQflRslUYVfRQEVwlehEGChA+Iayq2tQl1jM+apdbHP/koMFFvCMrrt/CM1Rbtpvz2p16H3GCzbOTUzJdEYOiIh+JYJmlr054erEAYSRnHV2/0r1ACAbgfHf749W1g5hTzR3o9rSmrSGiiN4ygsnjTpAVQfFcULaej8s18Dzihuoa0HypcYx/xsLNXlKHWVUn6nXhnsFDmhTU02+IjaXRNInQ0RHG8TdxZ1PdSaDzMY2cSEdct52gBzwznPZz3+PH9e9xsL+BSUt8pJHzXBtXiOCMhHLGVgZ/JdMp5h72b8MG8wUf7Bt+8+QveTv+G/V//Aca9A7yHtQMYIdzbULy0DuHsW+tN1eEwlz6dnZvpTvFbIh/g0n0SIV/EE/bwDJAHHHsY9pnORaaMAcB7kAkRH2n8Na/d3eS6D2bmSZW0kCUtD/2l2kLSGKiHxcpUe7Z+XrFnMd+5oCy9V1ddbz4D+1C5R7Qh7V9cbVPZcCOfnn3yDpTjw7LTZK6XFA/7iXb4wUz4/adLvPt4gX//5g4frjoXXBc/eqPBvZT9PtWlnm/SzlvWzw46Y38OeB3zVzgr1FLrK3yJILPICHvjX7+7wP3X3+D2+h1gtvEAm+wLztV+2yuvEeblfsvkdIJwPrhXnESt9NHyJEua8IOTAgY1w1S2TMl2pUNRk1Inzc8Silcnd8REwYtbGshlJERueMVcqRq1cvXJRNAwbls7wI9OyQfCu0macIdauxtFXjfeiaZ7bYAo15lCRyHOSs57GAp8O8CwMEqfRUGfCGAYBhARvAt3u03RASjczRvqLOVOhjgDOYRPAgKPHqMiwuXYNkRKeBf75+AQLkf2sU1LUBojVFrFq4V4GAPAlnpJIN6/sYGxI2CHYOiDOheGcimELOfIKRKcz6hZbKcqROGg4JrCwwodgeCzXDqxUppK0YO30qmMPydmVua0dH3K0UH6dAC5o4RTBIS0Tclb6Xv92/dnraELByWDhffnhDCYLPJsfGZgMFiDgQ3cuMebb97j4ndvce2Atx/uKiHt6WC1IeIQDatDyOvAjlpAZTDu9rfY+x12bgfPHt+92eLqYsRXFxtcbEeMg8VgIsEBFDEB6mXSErL6PvZ8eWxSCi5Jio1Uq3zZmJvXRdhO+luxkPVRSadCZZGfr0s1S1k49E+KPw6ZNnJROu0LZhSbpq0hsolMqmd1MXlLTRtspTwV5VDaXZ52jXegPgm6PnexUsxWQ5UVRfIATZ8KhUmVtPk1Nx6zz+vNOc8TIdOiWWjmtUfdOmzkSvSWZDfDBm7Y4mK/g8VLvD/mZUASUgyDtXNUWkdrB16tRUBRpZmTz2luSsty5Ps5PNgybnZodiNQxM86T89Y1kX5dYTmmF6t94xZV1FfhVmvzMwcMgLjv7MD7kfC3g5wRJGnzLS15Qc6FZHi9SNDyQCKKImYlj3gbIi2vDcDjBnw2Th4H49DchOMsWFqDIGJAQcYYnibGe0wtYEh9l6F/AqTDc6XbEcBLLxXwmhixDkYKAwgAlKI6AheW8HiRWAK93QZRF4jMqhARqWaLs/yogUvvUAzmZsxbKegiuyZQdegnnj42ntQGUdmFWNEm7Wz/qMS5TRoI2H9zmH/8Q7uwx0AxkSM+xG4s3leGXKReuTiKPCAbAAzhftNumdy1p1sv6qmMdChF7NPKlvE07JJK/n1Y+EEevlILTkvnKOBD9lLTqmu86xh55+iISfDoZVxjpUzJ8s950i9vFk51ev95cMZ5nlW35YpmyMDN45gMyKcoSRGCOrThUbmq6okBGdKZLWkNIY0b1c0jrIiMRovUjVER51kULLsh3P0uID+e9mzOf2G8IEF31QxcgfbcCz+ztGFNpku2YNTQCZFJkNrGeZrihHQXpxz6lTRvckQksMZKBqhhLcNvLQnDpc7x+cmOplZYwEEg4RzgPEWngnEDsmC1bRMKxHjHW7egXy45wTGRMc3AhkLa1x0CLFgXn9cSIrE0jxY4/Qh3u3l3LAZ4YcLQI5lQnv6i+5R7k/Et8S25fpEbqUiU/zBCgXRJFCtlX6173OvOjgt7UuGg/CX9JZAdqDWLVNIkwxZhRGiXIXZUbb8LI0sPVheS6HfD9mbK1kBh/YftcLSIMkx/B5777E3e2x+BQxfEYwdYNgDPC2ekvOYcJQhIv8oCbSeH68yzOvHA9J8/+nf8dPdjwARRmPwf/n7b/H1mw3IhMtswiWPstiUlCJa36JE/Tsjc6M44doP9BBh6Cwa8bhO7VLHJNSLdLH8/o4dCOpKjGiIQrm4qPNNNuCEoyxEHHHMeoT/QE9mlXrPC7UyMXxZain3PjqlZiGbYpl5DCqJOmVhGfDnZ2NVhFHxuHmwQEC5fq6YpSphHVEjqWdHYpaRrR+VDGq54upNL28w2gu5W1Y3/xJU6QzhT5fv4NnjH92PeOMdOuFNv3jIW2ampeHBrPlgtiCScmImA64iGwwo/guVNnlZS1E5S/pdw0mzuJipj6t1vtLjakUrlKw1m+ABQJ2x1HPQHqu1tr7MYzCHs1999JByzPjxzTU+X1xginsuVx4rmjUPNCHQXrn7jIFkgAhkLPZDjjVKuQlyV4Nz4flP5j0+bt7DbxhvcY/fOcJlDOUxxgBRuGYEjynrg9eSvrNajnIMNgev+hqNCYn5dTFdaJdPfHQU1MiDHODZJe+xcIomAyYz1+RNFMiM6nyoO/Q/GkFqA0KXSmuFdjneXeqfDNc5Q4uPy7SdKeMagEwbzqnMPDMDM19cK1gcDXECZH2IE4xnD3ezw8f/7Y/gvQMYuNkw/njF8AS5Sx0gRKOV4hDrpsjS7REPtZ4fSkFeDpxhXr5I0PTuFV7hlwKvvPi5YU7jUYhWDIAIngZ4MwK0AWNCPLQylTBHjWopr30v7YiyNgVjRGbt9EXWSr6N6diXhdXRo6RyLrP0JXeknXT18/SRPkVOjWk5S9CFzK3Lr3m2lE7/qbyPDZF32LkYYRCjF0SuIjJJ7mr4jsjne+/h/BSiCDrNJgqXQxtLcJ5ATCBPkAutmQEHD7gYP2AswhWzBmQNsAGsC8cqucije+cweQ/PDuyCgayn40B0DvLOBV0dCGw8hmEEGRtPcQEGjPBsQ58ImedfOQ/JIAFSfLvwaxK9E8fDGMAQ3OYr4OIbmM1bkN0kvYjgbtWNjI+a3+Y5ubd0wmadAQwJPyKRJYBqAXEqp9aVCp+ZusRxdSpHrZApL9AkA0THL4l6yB5W0VgEhtz1UJQnn15FWmjdUHIKKyhFHvd26EqI3mdacnls7Z8+CpazggPGEPbe4+b+Du6bewz/K4O+3mPcWBhPAKZHbdcSrL+suuMFXS/PJJxqQ0X0uGIAd/sb3E/34R0Bd+4ejhm/e3eFtxcjLkYLa/MZVlrNkT6oeqbqzyBKBRQpWR5SsZ7Rxje0UCo3c+EciWm+cFINxLLq/nSUPJBpfoNs69QBGQSocMSFSkSZ092NCTtj8MkSRhA2nqOnwnMxfZTaew6oeyGEUCsz5SsXqV4Q00sMGifQ5h4wG/0CvZGabb1+USyyCrqZZyk3EuWuCc5KWGYO9YfacHrMxlxh1P5sjFAAQCZcwPYKs+DJ427jcL/xkaELkDBx5fD1j+uLBlZ5rwotFeiUbcpFAf3KD2PiWlxVm2iNgqqYufWXny/UV8soVf4lyPjMi4lr75m1tRyqP0UAiDAm0QORF/EQnrHys9GM/sL60y3ubmV1n2K5MSAbd1cMY3eYPlp4P8YIh4DTBlmgDXdVkz6qP5TjVWREfhp5eRVenJjwenDCp4cH3X2A3WxBwwDQiCzA+uAtJMcuko9CTYU9DZJwycehmwjLr3r8TccowXXKik+JDUxOEysu3+oqQ2KJc6rzefVHvbkdSdOX9kZARSYcD5wmLxuRmDlftIfw26XBViJRJHoipt4ZxseR4fZtxGTZ4JXjcDAaoqXZh6nvirfHTE837c9zz34xHGgZmt4+f9GwNIpfQvtf4WlXwlJdXWkyvnkxq/Vo6EcwdvrKwOXgMQ4TyMzv6fNceKOVmcnd5+7KR8syet7Cy3S6bWnOlFKlJnGs+LbE16p3iZcVnij+YKSHqbYGhBeY9wBehoeinDrx4f5mwu7ewbkoG5OBuJYRGRgTL6x2VB6zFBviowKZ6/utlB5SIg9MvNxaxkqO4GUEnjccDh8iXIJBIkQ2ExmQDZEQDMCaKYg6xoA8AxSjimeUGhzL5HgHhPeAixdFGGMBio5JHI5rAgBHU8jrQxm9CPN126DsoZmLJ2ODEWTcYthew9gBRDZF5iYcinkz75j7pMtuV2QlD9TWxQo3l1bUIrurdTJ6HSioYzxK0YrTX+rjzHrMwo+WIFnV2TZ0Ob6ko3QuicRDNL+5yV2oEYcK6mdM+O3gQFuL8e0bjBcXGCbApmO5FmrpOPWfC9ZHRHDbyDR1TGnC07zrzzgUP3z+C3749CeI1oejV/Z//P17/Or9ZbDoIZ5nJpoh6bvRyiPdiviss3izVS+mKTzsKAlUpwg85MXSLtbXfMTCoemJ8nRsUySY8c1iJEQe8NM3DV25PJDoiBQSgar8PiFOyfKZEwCAT8OAuw3hu10wRDwfUGdtLsw2V5/16yUmIGKnLr6iP2lzlE3xOUZG8JUuP2F4N8Lar0AYlIeCUtOuiRwJGaqfuZ/pRYNPS71Pi2N2M1iCetzTRlQRTqFp5bFya+alYrUprGOiQu0d33VwEN1Hv0jYDx5//uoOzga6I8xld+1q0DyTwlvkn5E2RZxPZRJQHf8k+E5zdXaYicTrVAlL7GkxKeNjP011WE0DxzIxGb8fTm1qprkerzIagvL3U5R9QjbE8z9GCjifvaX0xdWHFLlhChPLnlrALM2NFKsIha7KiHUZ5+CIcPPrDfZscP//3eFi+j/Z+7MmSXIlXRD7VGHm7rFlZlVWnTqn+3bPnRnK5QzfKEIhhf//nQ8UocjlHbmc6eXsteUSEe5uBigfsClgMHPzCI/MrOrSqgx3N8OiABTQBapAOOqGTTjmJoR2EwExMJxzgLi/+6ESliHpIuvM5/3zHMXlH/vSfeg5YQT99U/odgbuH2/hOgbBK0JxE4ThZR52YYViRUWupI9JT4bX9VI8S6nFFGjR3vIc0c4RJU9OAl2xAicS0xGK+jfFAs5fdanx4xw9cfLs4kxfMmvzkx3xKAPtgVnPD8+rOMxRAeDwvgfew+E/HwCyuh9bDam+nW1EptbHujwXAKUWvEj5z4HPh8XT5shvEGGea/8GnwM+p+75lLo/J76XAm3xWQBisDH45mpEv7EYWV1avXq6qFraKnnbnNFOlrXW6BhQZ4yoVSpt7czZREcJT9F5BtAniERnGgmylmReDgGSs0qly8YQWa1TzzV2yX6xWs9ewSNE8O77PT6+P6LbEbabcHQS+zPqBYKuMwAEY+fbxcRJv/B+FDnC1zk/FoJyc4KI0RlAgje7FQvOKCS9IeJMQLgfgn2AhhiwELjrASY41wNEGG0HJoQLqREGaXIzB7y3fThuSQSW/D1swg5d79vKxnicxME6xjjG42/GNM6njrudOtkFwkzqQOgP7sB9j/76FfqbN+B+C4SjmQIKdQMUSUhRxRQl38ftDcZST9EbCaT+Tsmvofsq2s86UKxCKnUiKwcU50mcN/AR50n/DVEPpTJTN0XpWqlNofzSxLmsB1Xm1SJhWCyeuxkxBUprZ6b2jAAxoesY1jKwcdi9ucHm21t0DFwdLXho0PcnhLOPZpreBeH/5o1ewX58xP3xo4oS8J3xcHiAFRd+M95uetz2BlsTz3grgaJll6pNiFrhnAClMS/SUd7LItGs5zTUqpdwNAohrENVOQsyqd5rWMskW8WWY7BUVn6TmW5ue2SkhQFgEYvp2/IBNVayF9HCF2FZEFLfZzq41dfPgS/Hy8V7gDPHuaXeVNFIa0ZtPs3p63Dnxkh0gtXddlpIyqbiBkdZgijvSmXEIL2pRIkfgLLRUffkbypphiS0kwBUCmRL/aTn4qKNUdFyXbPZXqPvbmA4aBdNBWiF0J3S1fKRWpz1i+ZCUvOOrHTI9O0iDheDclGYlF8ek3NegaVxV/2aeK2Uc9RFQdFphwcvcD7iIxwsdnIHQwYQwJHFge4RYxgYPXa4hcOIA3+cYNdji43cYKQDjvSIeCYrCePKvsYR9xj44NcA8WffWnGw1sE6A3b+Hhjn2EcgUFBqYzudU60RSFAiyzt31KZD+E2IwjSKYYg8XAQQZ2EHB4Qjmpj8ZXZRoZYgrDuEDWenxzR64SmFInnITCMYyrHJaJ25ohYZiA5g8wCivWpgVrjWMnMt681XK2XaKNMJJtEWi1XP1SELOL+IGJTXH4nVKxrShg8g8PiAXwzvj+Hc8axlAuFm34GDo4wQcL+zGE3dd1js60na+KSWzU/kWA20+HPxwcV58yU8/C+IVOK3Z1Z2ug+fCIUF7zKFnm5jO/3Lwlo5Yi2cKuvcXmiBzvtlSK1zgTSfAtbqbjpdSwP+9cNKBkfBIBzFb1Dy3I6lZFgoL3ubVsny2lLLJbV4WY6YVN9m0NdFUBQVacJnizvhJnJtfi5Blo0yrZISp/pDNrbl4loy87MmylJevZ4J0nmnGoJzKxP5o9bZH7XuwCCIPyaJAeYRAKW7HnyJpayrzUnZSAyfL2xgMDGEHGyKYoA3RMcyIOl4U4OUPZTh8xOz35xghhMGmMHiI5yz825bf3Ph4mon/hwoFgtyBBjVBxCwCfehCGPuXjBN0u1I/wjqwmYiOLOBdFfYbm5gNtcg6sqMJ6dmLfcqd9JJvlovyNfMZ5xivmrmkc5Xc6s89smtW3RtQT+BoB6RHMEt+W+xMRLTTVteTDHVpuIlNXOoR2rgLglx80KtcxNLUpTfk61JAfv5ZYyBuRJsf3cD84ctyDBYHMzgQCGaP1WwFi/gIgx59UaEqzzbs14sxXiJAO/37/CvP/13RSGhc2IEgXg+9J+ut/jHmx2uOxMSUk6OPAnjAMQJB/05A3HO1bSjFdXkVVcxrNOqSdzRUpOocOGbuWG9xo8UlrXHGiKxVUyrntRn0IzExTtO6zAWmvWec0xAYSfwDQo2PTVeVd2rEX42NJRdqj4XQGZ/xAL8AifBEJ1W3kZBcuZYvTQQA4YNmE0wQISNQOL5xQztR+X7KR3PMe6TOOqUiyFhSloBCsznMZH0jxpvm4gUvxuEFQSv6H0fN1HzGnaR9fpXBeW8pNabCbS7sCWs+XWOg1d48YYZm5uvsOvegrlP3jicxb6VIOXcDgxQ9O/IJbWxueA3VYukTDNd7ueJKJ2PGda+F794qhiycvySE8FMnmY/q0miowWchDsiYjSEeCN+jIhw4vCO/4YBj/hW/iewXAMARli84z9jpAFEhI27xtZeY6QDfuY/+ZDtqAgT4cZ+hd5d45E/4J35S8BJ8Nr+Hm/sP+Jn80cMckhD65yDswI7jhgGBhHDsJcNmNkHhMeNXoqyIqX2TS5DA5IBOSqmKYojCNQUoytSXzlAHEY7wIBAo4WQhaPRL/TUFfw43AsZIjYqjjxxMolCniiydJmsC5ihtELCn6dGY+7R93/2cmadTAsSc7AmTQO1daljShXl85wKKmZwMppnZvOylFEy3eTKyzqibJfoQfEqonCMAJCY6Nf3PXDfA/BnLf/b7/a4N3ballYTZ1tDWO7CJyhy9fo+W9S5uD4DnqiQ0uyPZ5ZVPG8fLrBY3aQ9czTbKkXm319Qca8liIVaPzF83tp/g9/gk4GS5af6VngX0vgI0SgYBf46UQNEfc/F1bzP61pNiRpZX2/IOvp9/BZ+pqeTxSQYu6Pur2S6xGOR2b/uB22YFSAcwylJdk+WI4kyH5DOrU8yVPhUnue6b0qI6SedsgBrEofWzarNwa5g/LFJHOwNwfcRfdeBCBilB8RHKqQ71CT3SZRN/NFOXuZO954FOjLMkPDPhX7zxyXBR0REEmI/bg4CVpsnUVZnNn7suAMDYHEQFx0NbejvmhjieHl83QgIO5jRgDsCjL97wrC/zNqw3xwQ8XJ7EK8nfV7YtCfsI+qUAInzdTDB9rfg66/R3X6D/uo1YqRrOMR2ivMSSFvTTD0QcJZExJnOqKBJ9Vk7V9VdmZJL+g9x4wlI416qxmUUho5miBtRMsFlodlqPJuNn7StQOZFwJN5JoJyjcxEoq0XxarABDKMfmtgvyLI/83BXhG2nUF3EJjjqKi6Wk8+EZx/WbVSUosNWfGREO8f3+Hj/h3EAba3cBuHV12Pu75PijiFs6rctcW7fo9ertCjT2UV9j2NxMpNCJV98UHchIg78c1SpVKcwmIUNzE0O5tM3QVZfY2RaDpPWzNXVdeaE426aqNobL3Gn4mCB2pdf/k3lkeB+RITTH+L7dV3IPsjMDwu4vxSsFIHPY1a8329qJcK/qTehnDw6XvEo/HRMGzH2HbG79THkMhi0lFi8mtDyJLgFWhrTb7CewSY9J9Ipkolo8wVhuy5reoW9T79bk++tvCo34a8HlmU/UOF5Eog9Fd3sCDg/h2Awxzmv8GzoeAaFcxKc+mxGk7kCCHKeVICXd8pjGbSNGSYpizTkoM+x6IRIBuzW/24zI9n5y7RYoLEWwtBE4BSLvJULjhcVYYHSwPu+UeMNHgFhcr82dFMCe4iOOAeIGCgQ7FGxUukH44/Y/MAdOY7MG2T8uOE/RFKQcnkek2cCMpANiiH82zjW5F80lP4R6CgyBLu+zscmXHlBOwcHAs4nF0LobQpws5LLsw+MrWUX1R/T/pvqshM2VpWRk6SqhRDCN3/BSSGUtLYuVuG60Ct/i0vvxq1mRKaRRa5QnukmeNJMM+v2lBuRlS/G+kZhLvHDtuBG29DfdV0buIQku03Dg9bO325FiayfPvLS1DJxBPsifqIXBi5aXHzFUxI8oxSZ5/Pyth0Os0z4Xyu9FLweWr9jwAXlX9OKhRri6FQzGWFs+esXpfBZU0HLeA3Y6pwBnAUPeBjwnVricZoIo1LmaaEUl6ZbuzXsmPkz7JocileKTtLS4+sZXsJeBSxsFpXncUxOM+JkgufC88uol2AV5vY2/s4RAVEuZYNWASsnR8bMlGUTzg4TcQ2u5CXKNCTugw75U4bOWH8xUGEvbMLA8lRkAAiCbYQDvUwCD5qIbi0oXk8U0UgDg7sCM5ZjI7ATknxBJAxPiIj3B3hREAkIVh6QWek+UcUIy66Hry9Qmc6dOQCneiEyH1c6x3FOta+kLpeEbK+MIumKmPRoqLKyU5YWkdOmzUxjcZEWicHVGnOIfJC1ZnqOq2No1PFPWUlnxcr2wdk6YwEBJuk32gbO4e/3f0d8tqANzfomNEPFsaqwWv04lmIPmMtWn9ZtVYUlfLu1LP7/Uf820//v6CPCmxvMbyy6K87fHWlz533k39PBxxBuOM7XPsaZhVMmvk+l3LSJWFWxsmZGYiqsUF0Sr/K5QhQexUVRyesUcRPQpsDrjUMN/cQau44ee5/RB7MFJZemVf806YGEShw4n77Gty/gtkfQXi8sIi2EpronjYutGAOfwGgT3Lwx1/M1VGVsiDgnA/rCnNE+LknHDcGfzAmMd10HMNi9zxfwZpx7JytRkfZxMz+0UzUThiLyQ56UVW98M5NjAqZ9ITC3yxAx37zfRgFG8Lm+mu47gb84783Gv4bAFhtxEmwROazHL8WqyQ9JpBf6MLFEZlHlThOiq2MtcmHQwlOtQhUe3IUPHUGKKdMhUwErrlCSB8bdmGYdpES6k8knnullLkMqrfCH+ck+Pg02qY9R3QpIrA04GfzlyY2UfgVNUhRedjze+zxPjlQxNL93oDgx+HPGO732O5ee2+qoOw4osREiQCn7rlK0RCuFJijN0+Uqxy8CqTurk59LZTVhvfX36AjQu+ALtyh4R0sfOUm9I2LykgVJuT5uKY0Sf09CVVW+NYDcK6QXmUscQqyDlE2fscN8peDvIicVCDmtIGT7LhW6dah1ZrJOXoGVR9m/jRXT46IEPUbzUYTCG8/bBZwpkq8agsT8dH3r47VRsSKMa3XnOrLRTan6sVrabPhDN41tyQ+FePTWtLZmdclnMl7ap68pA7wkqvBb/ALh4vqWb9BCSc4pLeGFY+sIYhhmJ7L9XPW/Xt5ABscUckt6mkSn5sCy6q6FoEQ7hcLpyTUsr2UX0UpCPF3Fp304TKuyEhQj2rnusIAtUbZfgFIVYTjYNhHLDCzj1wImztsDIwIjIlRCDTh3xQuoXaOU/SMvw8i10McjlTiEP0e0XDhDjV1MYIIICGqGmB0HSeZmGJZjv2lzyK+TueS/icTF379O+tnDhbWjZBRYNkAYsLGG8GwCeNtPG7OBZleJuVLMDBRYqD+XYyaiSc7+WOvGLTdottdYWMYvRvhYNRxZxIcoRD8AiaK1nQYRW1I1E6iCcGy+YtQdF0wHBYiapRlnVL4yuxJ56udniQfc6uKQ4yOgZwrJ8zMn6LN9fxbV8p6WGeTSvaohm5EROi6DsPmEX/5/d+w/XqHb7avsCHG5mhhRqdqqeviZ7dgLaw/mklNfsArykd7wI8fv8doRhw2R+zpAYfrAbedwZttj7FnHLcWN12XlkiKfyQre+L18dBsSeftndYENeSEza7TZQKYmPMll9EyW5GeMBOcHMQNoL1DZxm8ZaCDcgTS2p3SQKJVQZUZFxcXGFqxK08t/hLPndaT5PTZ/B6F3AvlmkKxxLPpMBlkc0cXdPPJYDJOKwhp1Y5eU/RJl45LGM866qTOfln5eG1JgZaIwOQZGCEclQZFodFYxeGfAPHcxfhqeoSXItIGs45rZEs482W2DBeE7GYy16G1MNAyvtTCAibvCAhOsPnel7lubZmpkhFW/BE/UBs8uXfL5f5TK9CfcPadhHKl1Z19Tq9IHLTUsySUnJmz4BLHmJT8lYVUEoqsPIy9klpozgO4bInoMZ7raGVlLylhPs/U16Puq4h3pEfXSJerOdEMrOp/qr4TFRhNWWR4klgf5SlRJdOsIhpZ06XUIrjfbvF4fYVj1/loBPoZR9lj426wxS1MEGkmASzky/MG/LLa3m1xJXfo5QYAsHHXuME3OPI9jvSQi3EId0MB6WBGAfa3X4HsEZYJnROIdQADwtnTKYakF6G/RUREzYcls34tMiDeseUTk4QETuCcBb/7K8y2h7z6DuAuKFk+ZD2vRhRuzaA0LKV8rXCM/afTiFaMKtpdJJ+SJgtaUUiUqzWVaRQd5c8pxS1vhi0hTOU3zdLiheZ1mkapMxOhwZ3mGc05R6uV8qyofyjlwhQBESoIaZizU8Lw1uLj5jhTU4lR0/g/RwNq/svG4XY7X25MufnewOw5ZW4vUzR9tBYCoQgBH3cj9r3Dq8cOu8E0k1sWvLseMHKWG1qwGRmvHrtgnAL2G4sPV2NZ9cKvCZqn2nFRoOJj5u1TSgRwxnLxIvDpa5zWXcs6c3KthqdIb0vlL9W1Bj7VKJ5RT9FcmT7Xjy8kDC+5eTy/1z+nxH6GTqlb0hyuaVkOPaxs4OM2G1lQ8ciG7ifVr+ZGPYKotRgFUT7T8lB9dPUyZOLKDhmS6NHbTrNHSdRPyk0Tl9JnNi5Ihtd0cXJZdiyzRHG+jeuf11AJX1FIqhjzYbT4OIzYoQcH3V7IG8O9cyGHuyP85gQzgw0F+RZB7rdBR3MQZ/1F1RAvD3cMpKOlow4Wm+L7JqIUT/bwkcn+rgafzMtChkPksvG3R7D1ONrYHqJg31E0EPs93fNA+TkhHB0LjMMRLhxNlWQvNjDdJtwR5+90IxoDTk4Jnnpssn7JcT5EfcJ0wHaLbnuLfnMDECOZl4OeEbo9k5bkaOjpVRUU+i/rBwBAyn5aYxhzlZJYITznyVTMx0y7WRcKj4LNR2K/xPakORM+4yZENFKniHl1h0bRgyjKEhcuuw76lEdNC/ClPF3rS5OeUEviZAlMOs65823hPcUj7mIVYY1hgJiw7QjY9bh7+xbm1Qam68COAIxaS8B03E7hVOsXT4f1ERGJIJDWv/3xEX/6+V9x3A44fj1Ael8i7Qivbw0AA6BHVCY96sprXFB0hN+MyDuDpQI+p27Q9JEmhHo+63zTh1OoF5qJQdRTrrNHYG9hrD8XL6dgtUYvSPai0kwMViqB6rcaB/+tmuCz7Woz91iBgJrejXmxQdGFhXMDvLL5uUR+mvnefjqdTO2eW3gqgckKQSgceVEnL2b8XN+/PBDCWAUhwC9hcVQ5M3auBlT0uFJI7aMsfHtjCKOmw8DQKIgFIjmFkl3qTQjShAXKO/iq3+JREusFTJm+iwxRfJ36bFB/vrpT3hdqHZDMWCUIKulZaG/c7In9mGfwGoH2NzjFCot0YXwkjInfjJA0vnnaCdIGeBBqs1U6UnTgc2GOhBjehJGmJBflvCZmUTguWyFaiYDOKyWNBGmnQbWq/IoLpJ/Ppa8s2FP+mQTTnKTyxGgNGJVjSepFcaZl7MjE98LxRC58hn/3ux3eXV17pcQ5fKAfsed7fOv+R1zJTVjcwrjqaYlcbs2Zelzhzv0ecROyl2ts7A3e46848mPZnnhvHcFf/kyMw6tv4DrBcE/YBo8rBiDOQYhB5Pz2gY5CkCxMu6R8KkhrDhWOQ/ld/PTn3ooIaBzhfvgXYGvgrl4D3c7jGULYJeyieOesYHiW8q6r3EtlZdWeRPUjyx+JXtJyqSaIWl9F/yatJEiVSOWtPwthJPOEKcyvJJoeiii3Vs7ZRSnzK0p/gYaGV+SQya+qk1fLCFo2bMt/kT/7TdbwL1Afk79MMvbf+M2ID78b28vIpE2hv05EB7TebiYvy1TkBF/9ZYOrd90kXS3BneQVjQTx3OlYxh95j2M34M1DjzePfbOYgf2RUpbruzLKn7uR8d37bZL+f7w54sNurNJRK+sZcGbO04LxU0t+MhqfFl6i5qeUWefJ8sUla4mwfNDGJaCxUOg5/WRxpMEUaeZVTdtrBcjf4AKg+Q9NHidITJXhpMOILVzL6zbwElKOCcpNqFG0eq5YaM1Gp7krwUol1Bv7pzQ2AUpP3Yh3EmlzfYKok+RI0xxx6pQxNRpHs75ASRktowIAIHi8VC0Pv+eVCCVnngPU/JrmnBD24vB+HPENUzhWCV6Vst4iRswg+HsjIAI2xl84LXETJ0T1Oq8DWOdgxBv3hf0mBNgE4dFO9KzopBMpyImAHMNxvIsjns7kZR8hQtcziAy6gTGyj5YQf7YN0gZRWwCe9KkEmXwcY/RFByZGv9mADIHcxkd34AiQC5dd5+hff8dFjqohtZ6ysvUJAeg78GaHfnuFTbeFp15KNAQKjlzGy//5ZFvK9FcNZ96EkMpsKWl+aKDJwkyKtpRrclKYs16QdXT1N+puKoufG2qjzrnUz3rulRuPrbbp1gSblLhwekCkpCzDi9Tn0ChdvaCJgDTlEkpyyeN2LtSqECHbmCna4MpqAEMgA+w6gtn1uHn7FnTNMKYHNe8xbmo9M2kuC2ddVj24I374+DcMcsR+d8RRDtjfHrHdAF9fefcmAXDVGRQWgBR2hPTbD5jvzHf8iJEFr901tuh8rrQLXJ+/v0LCiNUuJJvoeC0Bh/QL/ZzKQgxjMISP+Bm7/gNMfw3GLlFqUnXnUNd8vEJhGZYMVWXZyzBltbHp6+3llCYEgBTuXwiFTxZInw6pywscZN18kjMWDYE3fjplbakRyYV+ZlBLbTxKqDLHrCuG0hxNERIU+9v3g9/VzuaZFOWzDsVmXxUrAQHTkMm1+PvWRqN1KqVZXNVn8alqDhWppEijS/nUw//Zya0BK1bxaZ55uS+UFcWIvBkRhVoEOqnJL46Njgz347iEnaT6vFKQvTPi0zzPJfOyCv9CaSqEpzWwIq2uUorHBRQ6fEGrkc8hyJVSPQvbjSfO08/HvqnOnrPFIPRDEsJF/Xa5j4q2OdzjBxzpI27wFh20ETEIlwrH4m6aSegEcKAHHPgDDvwQ1rQ4q8u6JYRs05sNcGXxfvT64KvgYeOVC3gnONKiu6R/EgY/Cem5u3O/VJ1VbDgF7xdxAisO42hh2GLT/QD017D2DUD+gjyQAxFDwCCOwW5clk5qIOI3PQ6I+GbJQ9OT1A9K6sr/Gu7+U4pWeIS5m39LKjGOw/SeprLf1Kqd+Hrmeitg5YI1x7omJK9wXT/3dZ/kn9mYkeFAgncbh4ORVEcRzUEhpD88ur612N0JsOuBcD7yFKad8JRNiOnLlpwNPP7hiOH1OEmnU/ORcf2nPnh5nah45ug2AvD6scN2JOziPRiNgWQhvP3YY+SuzFxVvB0ZemPr6tjh9x92DYTWQZOSz2WgJzLR4tv15Wh42Ix4vxurKLSJkvXLhgbZnZr70+l+Rj+cOhJscS1ZmCNPHJZTGsPT5U8q16A5Zbc5z+eL/CIF4l8DJObf7nwWwpvHDQzv8NPrHoPyZl+CcsWuB68lNawd4EKgaLybUzgyP63ltokjQKDZJN+LTHl90hO0TKtk1KrIyY/V9PwUwm/z5ZZ+zBT2Y4KeYMiAyW8wxKOJAPFRuuE0BmbPaw2H44uC/Gmt8/csWAtrrXfqUXo2Uzrk1NdH8I4FIbKTiWAJKSKRE9L+XgZWRzYBQRYihrDAGH+Ci7E92BJGCATsbTtCebOIWitfpA0va/uTnfymCthfts1CIDIQ9ndl+L5jxM2HWEYU/etaUtcTg4yBM9cYt29A3TXY+EhOfyF3dLYTr6ul41pjQYpGayle6cPNAU+0H+mzWpxFpmlr/KHmUKJ/ydnVhl3SsR1SmyTpT6rkNL+m8nCuPaYJG396g6De7Kva3G5F7KNpTZeCUkfjmTmoJggBnTEACd4d7yHWwJgtmIDNcQSPDt1xBNX3mC/XfCbS6/OecTSTYBgH/PX9n3DgPfa7wR8/dAdc9x1+d7Ut5PaC9JSrMYGKBUVI8MEcsCeHa9piI53aw4iGjrJR86yuAY2EqfwVQs1SPX7NJMAwuCcc6R6D+QDqDAjbhZwnQOF1CblpahzQJZ+qYQUGQV4koPBuXJ3/k0BFNeVqOH3c7rTlGtLKTBMdPs2HL6ErEKdT9Gg+UwmS+veMEBfezU61xZ3CurSolOT6EgUnZtnIPNsOIF1EL+GrUK4r0ktYhzRvzkVobi3Vu/j3PPX+kvCFkNoyLCG5Stb245S9xnNkRDzOJ7MfCeGpVWnU/NqoqaQ7ICoXKIWmdIMBlJCDpIAUURoTAW8BgQZGl039HAPXQql6mqQqSsMyJBqHc38l1x3JdyZEhS4Kql6xEXykn2BgsJO7sBGRhVGJi7HkuiM+EjYMEt0AONID3vPfi6ir5kmRQTih1z3IGty/d8BecO0AFgdyAiLnA8xAcI4SfwSyIJ09nzyC/l6IvLk7XScV9Uh5dJWzI6x1MPwj0O0xjrcQS0AXItkYIBKwC9FslH0Sy9BrJZzrKkWUL02Dop646AiQeAtRniuXhSyhTs8jpjbdJz4ZP1uJJJeRnlR1yOTLTGWZ0OdSTvY0tZeZgoEFP+yciiye3q2kL6u+eiW4/r0FBgNYHQn2dFhcSmg5lTDw+J0+zoiaqfuPjKu/dcDxxPpFeRRbcLfvcLevoy/K7waErx82mAfKVal816PB9Yf2cU+NatpPnqP0xDe1+Db5ftnF/4cbwvvqSKqWJPWy0KDhC1U5S2qn8p1dPzW+tSEZmwqPi7lSMzcq5aAzEZxLLue3tVyinrcGTY14DUEeC1UstOt03Z8HnlPvZblulufiz9f7LbZ0jQ/YAOSNsAnS2jTxb0eRqIGtlH+UhDJn5Gnp40lR0B+zLUs1SFWbkpWinJfwKt4VD2ZqCqUW9orZpOp9rTw9ZWRnBaLcOQF/TnJSlHw4RFqasNngN+adKoaIYQz7vmbOF1ILfCSEFThr/b/Qz1mVKLVvgt+cEGJ/F5sQyGWZvaCU5ORcQr0R0RkLS4ARBysCvyWxZnYFuR4O0RlBnI+K9hsS5PsFBLDfIrHM3sguTqFGtV9Q0jMB+LssuIN018D2a1B/lS7/9rX7KIukB2FaVosu2qLPpBdn85e4Tnom4b+aIqN+E9qSNvRc1EV0tFAoWeK8mU6cdBde2rDIczg7v9VYnwnPWUhrhhnLIv+OimTlfHTBEEJEMIZhxeHD8ICNuYLpbsDkNyDM6GDGRiT+bMVn4PsEWL0R8V+P/x8wWbz9TkBmg/3GJAVnw+wHc7K+V8tA/AnfUU787uD4OABHB9dZoBdAvCruxF/UqL2ok3EgFaUKVdDuG6UkJKaRldPzgQASXDHjuw3g3IDu9geY7RUwVH0gQOss48ysteHqNHM6BZOchHSPwYTFNvRlyV2+XAnVpRHAAthyDJ6v0p4Ljb5W3q3Fs9n8T6s177RVtPVpO2AGorrJPjYRmZGvLkEJDPVdKzrC4FNAHTQ3l2qO4U62SYjUBb/x3TrqpZgfUVCqJsCnnwRfLLRsUL6nswlvfVfFldavsxQjIQjo7BbOOVjewxF8WOtEQKpFr+XZMBWjonCL9OmXgBxeG/OUXuUrYG0EUcRE8hfR9a2Eyx+od7q81HVJgJcQtoxwJJNPFI9pSn2JcApoGGsnDh/o77jHz359goWDP2JGSNDJBjfua3BY+AY64IF/wkCP+In+lNp+pHAcU+i6K3mFrdzgkd9h4If8Lh7NFnC8pxGORrx1Wwg6CFlE7xVH5D2+RNNPpoVCWUAou4oCKCeL9iTyArmA8fPNN+hkAP73d+iuH2G+2wDdNcbxKwAGzA7EXuEi4nDBXxZm44V2kzEqeFgW2v3QlMK87juNO0GyKARKm78CSTxFKwGRx3yuRXPNXGhLn0grWB5PvEAzpBiXNcVH+ZnD0Yx6I8I7JdR34rQNP+33a9+sSNGg+7nUdit4/z8fQHbW2prGctXqdjJRO8FZ/hxPq/h0npVdOke3z0anyE6wxuHVhrD52WD7Y9+Q1S7Hb/adw083R7jJGzX5ZknkCXicm2VmgpIAXz9ssBvLuWdJ8MPtEYNpnOO9NM5xSaAVNJ+WflptdzgLnrDuTedR0PQrhwL1Sv1cRr44DvIkIgspnmM2+A8KQsDHVx3eX1/j8foaEo2myaDWHhvST2LaWtTQzoSL6vaSTietj0Y5SoLT8pzKF+XULO4nM2pRzFzZqSHFhoU0GqeeaZnyRAsSzM7PuXkUj2CucfVt/PDzAfuPFsPeYdNt0LFBx5zjboOM5zceHIx4oz+T36ggZoi1sM75f9bBuWkbBU5dtyGhaH8xtgv2SEd+6yPTh/hLrJ13PHLOAnBJHwAobI50AJGPXrCUutXxkMpYxezVmFNwTLLjAMeMjhjxMm6QwDgOGxWnRyC+YdOBN1v0u1tsr27Qmw6gLuicFhQiIvRSVfyOm0iTymq+MTNPks4iM1rDEv4ej9RcNReik1nWBwM4JIcrINwmIhmHlDmmcRqnnC9tUPgdr7SZke6aaOkci7rNejip9c/SVTkaetqm8QyROkyAFYu/friHvSK8/r+/An29AW8IBkA3WJDVHStVybH0VVLiRWD1RsTf6C+4Mgbfvr5Bz4xbyd49adwWFtbUeRIVTK98OgjGg4WQg712kM4vIBxuhnTwnReNyPms25luIv3s0hJV2aYIWwZ2zHi0A3j3Drz5Dm4I6QRKoJlb9UV1on5WetUuQkFXmlmtFKYq1OZyxSKp2FQJmSnxGUCHXX5iA+zi9FmFR070VNT1uLVwKcv8tFJt9NbLR6YgzRtKf9SnwjPbRcnTgKK76QXWDVhBy5pZzjZA9BiV/TeNwWiUViQJZiMVcRGrWMLj0y3T58EnnGpPhma/KSYRj1tZU0pm7mHkJQtSBj1IHCwdEDcGkvH6LOQUmkkuzkxPiTi5MWkZVmt5XfUZg1WXs4RfnXMNnJKBJhtrS8nDwrI4f+Y6IgiWzsWNHCmVkegdEzWRUImQ4IHeofAaiUULwGJw674GB7Fnz+9xLz/iSHsceZ+NlRTPNPWyxkauceveYqADBqjLq+FZuwu8b79hyOiVKAcBsY82cA7+HFrhQOIlJUyPPAIEvKjrSMineb4lwuPVVzDjHru//B2bHeH2mx7S3cLZG/j7ukzwHiIw+TsuKG2eIm9KLNQcSb/wKCpaRNW3WnX1v/05py4QHieeFP0FMi+pN2SWoU67uJJoGQXqK+VfVL2PEGXYeT5AmFPQJk81P9L9KbrfVpSl+WLc3Kn7gzKdx6OZ4mZERqbdnsmTJzPAGZ7ceHCqCtcLHv4wLFY1oYGTeM+N6HmwLMc8K/ck2SVkkctvRHsl8+ahx5v77TLbfWbV73YDfr45puvNSv6yjpbOggsJWgTg1aHDq0N5L8nADj+ri9HPrXtVW2fU0S8N4qa1/66NaxXFzqvpE5jNt/ywwqtdydIexn9YIOD+tsfjt3cYt1t/xv8KyPqlehL45USmlvJ3UFXP8eUJ+Up5RROTpBTZO7usOBtQC2OqW0BCFZHtNlIlaH2v0kr1vu6YFkyMHLUcIIWym2QalS86XD1+GPD+hyOs6bDZ9DDc+SsWCjnEG/yBTALeFpHllXgHnHM2a1Wxr12WObVhmoJFnYnDXZ257VF3IqKwAcH5U8m/BAazP8q0MwIL9g5QzoIt+02MJD/Nd2k9Bv5CaoJlC474k4CZwM5vwJDL0nGRf2LOCLoVG3Rdj22/wZXpEO99k9BX+T7CqFbH+ydq2qJikpX2l6bgizz56rJaaWdgYvYq06YNibgpEccRWR+Mejipuoo7I1S5onEOmxBS/J6J1Wht/hXtWJYV1y89M3a3oikSxgiTNLFviBjigB8fP6C73eLuf3iN8U6w7QlmYJjRKWfbegVt9d3LW7lWb0T80801urCWuArX1rI4gdSeSDxaRRVYAH/d/4yfhwf8w9UbbPtNyBIWGsrpfa9Tmj9PUxm8ITWv25PZXiN+ErzBxAEy9clZVUoipuU0849XkjwhHNFcM9hWH0zLzG0J45BS5zEiCO77Dvcbwu3AuLLTPnlxCIiWfd/uo/Jpu93PQcOX2l6asimjXmAuh0OujJKhLbFftfGgj5eYY0aEaCjKeZr8RkqqfIHWNKE9ehMf1YW0bUjjmFx245VXuQTSXygagz7FUv7LgSWTQGYTgrWWCR0VE/96wSvPNxeEGRaBGYHb4Ttcm+/AqMLDkYYuZI1CeEPDdZLX7OSJkYXyrKSg5O9JUKoFnFaHtGdPPd+mgknJpOeqoPKP+ljT9/MWsNn8KxhhuZ2TBdEYGSECfMAP2PNHDNintCyMO/kWfTgW0dGID/x3EBh38g162QLghIIr3G2ArdzgRr7Cnj9ib95P29TEWwAnEOcVnFEcft4IjhC8sd4TSghwTlN9XD8wGScGpQWWWgbUIEwn1CMJBVqzzkFGh8NxDzuMcP9fwNx8xOYfDISvYMe3IPJ3eDlmGOakBOoNHEQ8FNYZhVKwF/U7K4Y6qVJ90qty5Y1t9VNNR4NIeF8qx8w5Y3pDesNihsgirav15Ze0Nqu9n+m7w4iHf/kJ9mGAWAcoOw+RP5YrRkHkaAgCvbWgry3cdmEhajDKpX5b7lM9lq06F9Xg86A1h04W+jS6OF1sYy6fKulEoc/rn09H+Y9fj3DdPYAGO10Dp7qOgIEEd5vG3MgC+OlyA7AFrv+4BY2Ex388QAi4/uMGrKIW1konGY32eBOA3TA1yhpH+P37HVxrI+JsyHPt8XdHHF+Xl62TI1z/qUf3aIo8rnO4/08HuL6NQ/+RcfXnjZpj5w3smrjQwTj8/fYIy57fXI0G33zcYN85/HBz9CroGWOrKn82zMo5a7vhXAv5uaAn2oq6ogZfQssu0oJauMvyt+3YXwhsDAQdMBLIDRDZ5nRz8pVCv2jOTNIsMbf1suJOwYoFReNnUX70pBbAn9bhXyaPfOiisqyTj3txKByIKgNqHhYl6+tnxXvdaqk64VK0VMt70ze5rf7Jx58PeHh3xLv3BzwcLV69MrjaOWzYwXDn5U2Xe4cRooSDPMZhR4LZ+E0I1GuDr9E5b2Nz1ub+VWEE0TYR5dkCfwmWRkf+AmweIY5BYYOCgyxsjMkOJgSIWIizGKnzp304O7HUTDqqsPWQpwEAdgSEHcZx8PWZDjGiwKMcnHNkplikBsJ0G5huB9Nvwd0WQsaXFHVdRS8OhHxLtaL9CbrhKNjc+GKOpKgBpyYAGo6Deq2JerBMx7P8GZ4VDlk1jecoirgxQWFuat1Kz+PUiWEeu0gvUZh2apNjMhdRlrHwdg7W2JiSc/2i91lsZLnO6tWKQDCdAQnh1d0Nutst+r4Pp+CpMSqVsc8Oqzci3m6Vt8aUNvSrxfclsQbagw89/eAe8SBHfCt32ABpsS4Kp8aPgkM9R7g+X5rRZ2yKiF8UlYFDgPaJTE8BWUfUy+9pfUEq+aSO1OXlS0YMhiMcjMGhY2ysxZVdKOwFoPaUWRqCefUgflsjLut87dRL+tBEFpNY8zKW58JkmlD9Yq6f5o0GmodMYGIQXdeOxVSzAvVaRb+RbSGpVL+i8BWFsUnmWrhFFDk/Hf1/ydA0ruqvYcE8e9ksilE0R8heFSIwjnDtbnGFV94oe7LQiukLAB3yWxi0G/SwTMwn6g+pQrGpzlSTjsPIdT9FP5kz2FF8V6wZVORJtgClAMSIqwKPKGvS9Jz+AmJTklDqBd8QVI0D7nGPn4v0BMY1XmEr1wCAAUd8kB8AMK7cm3yJdVAKo19+7M9OtriWr+DE4tG9T9FhtIwp4ih4pdLhkQUgwSvrwMLZQ8ch79srDVSLL7pXiVLPp1qKsVQ/BWFfzDmIsxiGAc4eYP/k0L8+oP/DDpA7OPfKnxbl/CFMLtRDoHDBe1rRAVVzc3xqytPzQHsK6kQ1EAXvUe8lJ2KRj2iaHk2l9cvYX9M7NErarB6nehvINJ7F5BcQ4BrL/6qj01Yaq2R0OP7tHnIcAclHLoHiGMc5mTciAIBvBfydgwwAwnH+RdAhLfXMOTDT5zOFr65zMeGpUualnXNgVnp6Dm61TPgsOF3KWfWcmXi8cRhvTt6MOJN9fWUFN2/Nm0lR7bLNQHj9bz3MQBjvjhAWvPmXDbrHpaPLTsGcXiDFpy751aGbpVAthbbKK0tSxLS1sF+V93bwCLz64wbbx9IkMF45HO+OGK/ajmRba/DVYQd6sp/ZEj14nPfdiB+vj7AhzKCzhNf7Ht1mxI83gZfL+bPkHK2uhe7pY6DWFDVdL05itYYfNDbZTxq5MgqFaaXGsVWMTlcFrAMAHAPOEKjvADIgB3BtcK2raogfZbkyeZZFjfk+auFXVVM9kIn8Xc84//9U0JniK8t0JypTXdySHPWi4NcYtYp4NLIyhMP9gA8/7fFwGHAUwaYXXHUjDIu/uwEuBDLkhcIfux4iYcNdCRyl7cpukGguesg7gRQe7ZXsrDEN/ekkHHHHAOA3M8ACS/5oKI8nhbst4I+NMgK2I8iYELWQeyHTUWtApvKzSJC4HcFaC4iky7qDqpHaIBQVparMODmJQWzAXQ/utiDT+76c0GHSTJTyUdKXkPj1M5YdDN5eNs3j4RB1XUE8XaDYkJnMV0Gm5TbVExaO8lYbdrkrgm6A3Pce3byRIFW9uv9y9LlTv1X6ubFs4T8zD5fWfe00uSrnybW+HEsiwJCPsLk2W/RXW7/5a5STW4H6cxaTBf2weH8aVm9ErFkDZ+ekTkD5h4DSMQGOBBxDLyOxk78rIp0Bh0yMcZ4+T0qvoyLW55vL4JwL3rdIk4IAxAiOc3Ger6kNbcV2iVCigOrHwhuUY60zCwTyWFMDwdoD/DKK1LkQ6Kt4cgZU7VpfzpoJkLevfOGNHorDUi3Az4UknqZBatWtDWELpVA4iomg7h+ZwjyzPgfOy695av0m0yyVGU5WUa6CyVlgjiERIET42+4VWAS/23/Exg6Y47v/UaDYyjnREfH1OjNKXZhi0oHP9O4aRm5AEu41qvIs1yPqX/0kKitxcPWGdDam54uyTtQzI7iJrrXwPM80WQon6yitNO6uW7GnXpCtfOpdupNmPUdIXRq6M7b5Vt5iK3cFLkSEDpuCx2b+m/4k6OQKb90/pec9tiAQruQVOrcNawhhi10T67hVJgj9900P7AH33/4VtCfI1T/BmQ0AH4IN9ooQk6b7OG5+TY7G43oT4nRHecXMWq9gDYcDRnsAs4XdOGwPe5gNQN2/g+QW1n0DcsZ7eHEOi88bTnkTgFAb33LfZmUh/kZSNuPGhET8wk0WKW16nsclH9sZX2ehKW9CJMQSj6p51Tk0Nsvnlsi6kexzAQHpoF8KynRN6z4iwv/T0RDt0mpF+wn4rIHCgehSUNPB+rSn059KQ6cS5Pen+nVlUc1Mz6z6dCHPGbMzMXhOXc/I6xh495/3IEuwWwcQ8PP//Dh/D8mT4bQ5fMp3aPpyqZDK+HC8s5MkYoB3/7yH+X1ZthiB28zvMhzvRvz4v9y/qEDrSHDTA9ehIUYcfv7uEZYFrzue0zrwkitz99Hg+o8bzPEZZeZYDZYFf7vb42hOZKLTJ7IvSWI1SChzpqpVUKcrdCwK8hnIe22zwVd3Bn3P6Drvu40FeWd+fNvvGiofamUwen0Xs68QqUsjqP/mUvlSpCEU+BQIZLlcv9PTtr0iSvV9RreZpYQzJyTlL/oqlixuZYtFy8a0tyPeHQ+4+b3gzWvg9d0eVz1hu3PoTN5M9cccAfTuNcR1SYbOo+/b6py/G0LTUTSIi/MOv9GxzOMl6cK4iB0TQZi9rudc2riQ2DALOAnGe3YhD8CdASFcpA1AegfnHMauhzgHohGABNvhOcq8T+sgsHaEc+E0hSBoebmXAfKbFW0KD0YHZozmGrz9FuhvwaYPx6pGGT73a3IQSsp01r+nIq7WHf0mgY7sz47WahOoQg2A6uv42Y44yDpD+OX0fJnXgxs9G+hWCvrV32IkhIQ7QmKfp0iR2nEqtaUx/y7I7+ZPD5irpByt2Gfh3nfcD3sIA7evt9jeXmHsDEQs+v0RbB3G3h8DZoapHPC5YPVGRCGKLA1C/Y7q123jsO5aK/6aSRajKduH/4ggX+RYCRur5Q699KvNiDlYSXSCeDQTJmdEekxfVjiag/NE//WpKz5dZv/c2nmE5+Ay0xWXUebSn5PpLr0ZkcteqH8mQiLvYHtcVhsrTqwLqzLO8IIzTE7I17WHdhCCN9XKRa3GYVJ5KSASET70W7hxh68P99isxvV8uCBlvCisHjdlqDrJkmcSiPoHeC+XTjaA8OIGmRdsBJPLW4vhVd76ABD89Zc35NbDJLnabJgW1VJWzgRqfI/e6RPOrV7HL8l4RuW7otj5Uc8yqjJXh2Y5eM+lOFW3coONXENVWgjCtZ7mPbL8j3hxXkcdenk9waPDFh12UaQvlup8r0GFOAF02wG9wA3v4R4tZPcHOOlA4s+ZZbA/pqnR8qSIpW6khGc22qfumZYQhHknAnKC0VrQOHoZaWSMxwEgoNuGmBL7BswCBxc2JBgQCjIWFaxm0t6qj1ueSKKPLUNbCVkPM5sQp7Od8ZjyX1I0fAaOJ2GiIC0mWxctMYdNw0MkbTbVmxAhGQkpuTXzd52muXYrGetJotbZjHyiVBSPT/OVaaK1VbelojMKmmr+K+p6eopWqnMp+ynJl8v6UpSDeRAj2H9V3jvy+HbhHpKn1oNqgjUhHloXfz0fJmWQ4PDm/PbZrcPDt8cLYLQMiQ/Dc5PHwEX18ym8nES8HQlvxj54SF+m7oEdfhACNSSEGi46HdV3jfWaKBNRMpkuUCLvcABLkGWEQMIQNtjuCNtNiJSYL/3E7+nb5RRzep6ov+Fb0g1mHFUbvDnZQ5Rc1MKptD7V72Xm+wxM8LgAzVeytF6hVLeoTQBgdBYDO2xfEW7eWmyvjugN0G0EbExKT+KAkYGPt0CaO5wuTM7Ga5eQ0M4xWTaKONX9pYWR6FwDH2HgQhx7SEbsL5D2BnwGk3jHHGRZScBgZ8DGgMlHReQjbgKBp7qXIOIV5GLxEQXWZRwDyv59sEtMYm+CSkwEONNDNnegbgcQJztRM2Ip/g3jWkcVA1Cyn5SDHr7kCIRsuI/lxj5O2ycpbdLkFrpIpUlp63bPZF4zRQDEzQbROrpMUikCj/UqzFprwKINbT2OKWFznVFcrhZ9NWLkNcZBLAjA7fU1tlcbCHmOYgYLEoFjT2/rbujRDajbejn+unojYgVvbINaF6ZBAXrAfdiSJcLfuw/4wEf8zt1h57pwBiSngae64ARzRNF6Xj7LHniYPiekXadMWw2mJoC1FvwA9I8bYAc4UxL102RwxRmk8fyJJSLm9qtIOTj5xZPx1XYDAE/2sHsOxHn6ZN1HNYLqx7oOoGjcfDOfhszTR3paUrQZno0F1V/K2VxDC9/l0LSZEuLHJDLqVM44blKSdWq9QG9NgDCJVhD9Z1KpqHWxQRGRP9CTevs/Dohn9WllFwDx6B7JYzOTdb7YOZme/AOpHhJVQlBRZxLDp0UG/LPjiCgSiA8l/iq8o/SKkcSwObx1o4oIiAqZurEzITj1+jxNUEs9J9KnZGFeCYKzQL6IeCGT748UTRg3Dvw4fby+wYfNBnuOSk2uC8hKs5BiYcFbf8AR39O/YUNXeOO+g8BEEvD5aQ6z3GACcOveYufu8JG/x4Hvs1wT0olzsCC8/+Yf8HjtAEPYkeDN4GDiUkGULlMturdYW8vDoCpJxSshUZgQgRMXPMj8PzgbNiIcAAf7s8OP/+8/YvP6Gq//y7fg7j1M9y9gY9CZDs7dwo5fIUaVSFDMqNBYND6UlMbcT0COjoi0Gc76Dc+jB1v6FxdP5XE1B+tZ5nLC5tu2jD8PcUlq9M004akn5duJwlVP8NS/7ZKam39KIdebEPHzegSuDsCNNdhaRrfGAFXX1VgbSvWlReyfWBjU9a9cy4o8l4AT9c7N+ufDM8r7TXS5AGR/X/33w+YbHLq7Rvo8e4wMeL3/M4yMDY33nMFZlryXSvpcM/VLheMri+//14cTqc7rNYFg1zlsLj7fThU4xZP3jLt/2YHHaV5Ncx+2I76/OUyqGL4dMb6x+P3/fo23f93hsO0wbgz+/nqHo9kAIQpColW1KR9mO8K5PXmiedXjsoamSK2OYpUyc04SZRxAeaEnqb5IrzkgpQIaum2hKKhP5LJn27m609bx+1w14f79Ee9/PsA6b7Pb3h3xX/4wYnfD6HeE3YbRGcam80b8WIpzDGcAfPMO4giwFhh7yIevIWLgRodxHGGthXMWhXd/IXN5YOKkMwgkXFtAAHO+d0IEsA4O1geqx8gW648itQKI4+D4I+ikgxD7i6TB6PveRxtvBgjE30/hLMSN1XjVApFUz3PK6J1vRwkyGat0ZVRDzFsOt89DJjgRITqI1joqJfmbkxkiyn+5thJvlHSWdFsBxIXoEv87bSAB3sgdR0KQ0uRNCYVeUsDi2LkQ9Z51Pol3ihR2tVqXDSMgubzWPEgbXKk8yflCnnxsU1FbuRDUk39G7p1ELa6Yi2nPYZWRNNqtMp11XXDctwLcGtj/6w6PrwWyUfiIoDvalXV8OjjjaKYW4meIQUs2jfAjkuAjhnAP6C3ydbDKUFXlTcebnai4uVMoMY3MpkkvFEEWLFLlERHQSDAjQ5w/Fy9zmmS5eLpwv5Yrt4dr8rx4lGxW65GbQ8UzDQZxh2ccIPpM0AvGTJtONHVNT2QbUjayZ0PX6fIabGCa4OLrxhMJMMy1xU2lc3BdtUBHYa7sCh/KOBfCOINfQJwQSSJEROm0rf6ueVTxgsoEjXpfUpf/sljKOtBLIAmB4/n5hYQ+s2auZeqN5KL+W8JtKk6Uk1mKZ1pYCm9UOKfUCJ1EvmxEKR9V5aq6C++NC1FFNiI+r7xlI0cp4KXNCCAJr0fT4XG385cxW3X0D9Bk2sWYk79TIt0TUuOkPQTURy1t9LJDJ1s88M/NViDwzuH6DgKLxxHwGyreI9AFwV2g1s/GJkh56XKFVN04ZIqIBn4Sf6kfBWXHHQXu7/cQAexoQeYAIh8GztxBHEPkDsnrAtm7yos3jOQuFddbLay7CqkiQfysbnZMXSvwV+nFCx1zgumUWbeKzh+XUffr8+GpxZUbDnqdmL6vloPTOFE8MjFsOiTazlStNyN6R9g6Qu+ATfRO9G8VDusqb3l4Z8m9YWiq1/VPboRbV8ZF0arOar7I/SOL8IzyXwK1yQJ8aVgSFF66r5driPPA+2UyjuYa++ZGRIbOHWGpA4mDSZ4vT6HJU3nmZ/lLksFLwknd6olgNw7262W99ql1tw9CfA4sa/Qt3Hom3LoOZmxhk0s79uHYyRp2gLx26DvgduzQmx5H7mDMBv6SKs5lVY5aU+Pu/GaEfr6oHhSyMSYpi29J1I/fGwKXzjNl5bP11G+WJesLKNLPMDhqzbaU+YDj4PD4YcRIDtgavLq2uH49oOs6dMbAMGCYwcwwROnoSMCBCXC7I0QceHSQwUIeLGQABNb/CxEDHqLRoYEc/KpWO3DkyE91DGW2xXpMRMDwDkSO/eYAMUOQj/dJd1cww7CBMcH4DwGEILJmlrcEGweAgnGc08XSFOdFYW+syw+dUeksOU0pQzfnDU0yoiDewoAVn3sZ3akdhSTCQwoTW31UcHREmjRFoZy0M8mbENEBvNE01ReS6lgCaf1oZqrrLHWZcr1pdHC0A0pbtqu58Gy/TB6W8rI08CcCaEfoXvWwXzu4G6Bnk0yw7AB2cfzOXRteTnBbHxHRBEks7vmo+YntnMPxwwEwDvbKAZ2EhUPyOIj4nXRp2iAmoNag+ES9izvYM5MypSNk7Vwxx6jQhTKdc/C7e/oiHVX2Ar7L4Utlgwi1MjstrdUOXUZeYKJfeDw/P3i0ksZ9PdHGkvurb8H9Hczwr6Dju08ieM5Bw/zkf83MraYdqFq8a8rPsyH8FkUyTWb0GSDydMXbL41VPg+wEuFqApCcfqakybckHK0WsObTeRrPhZKqJM/dwOTiq2rHIhsrq3c1g6i+f8658LlB+3tvRoM//HSNfW/xw6t9JcwA+jzL5U473aMCwZEfMDJhA4tI/eW0LseQNF2k536NT2eSJvktCFzhuVM0lATC5JWRqar0xJBUlv5sNyiWU+HemBs1zTXl0NUQjZj6l3475aXTi4eL17nvYoOU53x7V0mqImIEDYqx9EXJCWNf690Zs1R87Q4OZAj03QbyOGL8dwtrCc4ZiAAOLoQve08uCiGy/o4Gr7TF0O/5waG4AAIIh4GJJMUt01b45/w35xy6YYAdBz+nBDBe+wLRT9j0e8R7BMbhDUb7JtAIw28UxDHP4fFzkkFWQgL1xvN8XVQY4nvAmA8w3fcgDIX80woMmBzF2eiaTwLPqGdKVVMay+tBi+/M8aKqnsTnvcKaIyKyclTPiY0jbO0ZhrDkAdQSop7YSSfFpEUBep1C8FJAky+/Tji1LH6xzX95xNZqwx8232Dfv8LBbGA5dyi7Kfe03OGnq3/Cxu3x5vHPYNiJFnICoaZM0ErcKm3tJuSXDs8d/XN6YSoTPa2uTzGVWpYPu3P44X99OOlDOJLgLjq8q4Ku+w7uIwPfCr6/vQe9f41RrjBurwDeNtZpz6dStGikOgk2Fonb2VmbXmpLEqVnTSpZ5haVUFReEf0eeQ5Jxk1JWqjdm9IbpedSkS9/RMeU8mib4kv1ufROJknnobBYVO8acRxhcwGmh+uBb7874NU3D9hcGZjNLdgQmAkd+QgDwwCzeLkWgAlRCnDGHyNKI6wB3NffgxwgowU/Msx9B2d9VELWA1B2alBiHCTLmkTpAmgxAhDBiDf6k2UwO8BxalkyqkfnRPijpIxxAG9ARDDMcF2HbrOBE4e+c367xNngxFgJLWtUh0ADDgCJg6O2jqLX+TgP0tg4B+t85IhLF79LUbbvq8iVylWlubZUZfhnMv2nkxcTJ/+WIoXkOUXlPBXkzQ0RAVyIrHBSyL2QrPr4oSdVF2F6TFaoOyRbpdHVuqZu05r8VRky+fJMEISof4lKkad3ItyPR7gNgP/HHeQbBl0BPQObxyN4dOj3gz9u+kmbEC8LZ11W3WaK/s1J/WEWtCHXG32c9ZPcbkdYdPBLmpqEp2LCZ2toWE4kGqLqMJwZ40Rhua4Mz0BaNJ1eOAP3SZdzv5CypKcfFU+KFqD0LwibEKFpZ01aoCqpzGPMFqCNj4r4YkCqXye8hCLJKMtdUvAnScszDOMm11KUyZIYUL645MLxcuJtFtryfMhMqXrfWrBX1XEuTnNA6nMmVeLFjff1RstEcKtriwbGc2KO5uHLYiVPAxbC7til40InRmO1fl5ClXRkAbJ+k/W8rBHBSkZTAspE6gjClRbozqlsRooR9W/6dg7xM3vvBI9Kq2bFUi+2siw06il078cphGcDYJg8H1MbisUeS+tC02ATFnvaeY8pZ0aMo4UDwxLyXTREcOLAwiWt13isqTWur5rkiODMBjSOEAzppRO/IcHifNg7CZgY4AHENniPMYiuIDIgemVRiOkWMcFhI0sXLf6VNxri5Y6RAUg5XyAgsjD8CIErlY4LQ02vnwaq3llkM3GtiA8avCTx1GYBxVfLBMdIG0dpQyLKMGozIpIgC+KhZetBgNROjRddoqvPLYHWs4kqTatL20bZmXc0+bIammrNxWC6cQhM2ztb9ZMW2yYa8+mo+r0m7yoEpgVfOLblyTDyFgdzC8uuDNYunL88xMgJIcbIPToHFRmBlfSuZSopn5+US57TZ6el76eXsAwL5rYn1fopKeel6lqahjqNGMFwN86Wo/Oo2Ib03ACAZbidw2Er6AaCHTtIZ+CdG8KlvMnpom2ElapcPaqLnsRBQG5rmPnFVLKeb2eZNVcQZf8V/nTZiLpQS9m2mTZOPDWqL2fZDFZZIZL5y1q/iva7Hle3B2xvjuj6DqbrwV7MgCG/1jLi/Wde7o0e//EZOx9tK5sjSATUWbDtQB2Dxnx0cnK2UViWlkPVlHBWPjlOdhsiL8eKEMBS3H/iBGAEL3zyx5sSMUwcLOYkG8d7ImKkhe8USvLaU+ZtjMCQ2E9AUxjIJigJuRycxEu4S/r2w9+eQdNSq8kwmUtLNxnJ9HtWBNpVLnWU6EgIKdpFYbJFO1vsj2hSFSUc5ypif8amZh0sTcaV06S1xJwc7zNtXGtEp3rfK957YsVBmGDeENxrAYxfYnl0MKMLkRArkKgRmTTy8vrZWRZiAWY9yC8KIrDs8Nf+A3bmgD/IG2zQlXLlSuNUec5x8SZ8SPgIy/8JoTj7QOsJnhUx5xxsOGbgJG4A/FLbODe/Uf8Zc+ZkrUBQUgPD0hEQRAiXVqK4mPh0ifVT1fWXQf4FIG4WzBgqkkKdz1gGZTqYbkgoTw4EL9/sWnF+H5wlUJyGxMxaq9sMuZ6uXZKwoAW16GlSfiKF282X+5T2lgS2pFt5fuQ3BRMmjeGR1K4lvJri0G+wAJESiiNApExR9KvavF3Ldlr6NYGxc7cwcgeWvno3xTLRFM2liNTj8hyPl2ElDw8k4QqSvVRyNATUp46uaOHToutTVLdm4aXmzzlj28Soq8dGhUmQWmzyMpm/p7YQplEnswN9ziyLvNpjfMQBf+d/wRbX+Nr9w2wlp47wab5SG1QODugJ9/95i8PjCP73ETvb4e3RwUBCJASlI3Q4nJcclZ3zQK2vYZ5Iv8HhD/9n0P4e/Z//G2g8pk0I5xystUGA93WxECAmREQwgO/Rb96DwP4UhYDf8fANrL2Zjv+0KzJuSTlQXk9J0QBEXPbmeiKvyzz5VLqzi/4MMMMbJ+vEfD8NHfCXa4eR4aNtwvM4HeNRBRy8G1/+aKBPAS/RhvkyVymhz6zjpcr6TU75kqDkz5YA4mqExEevWd7ix+t/Rm/3+Prxj+CnXtyYjDBU/v5CYa3qeNkV4PkK61Qz/DwwY9JUv0rMajepibw2SVGWrEtzHcERgQ2BLIHYVFGfyk6gT2lI1pH5fltjZo34tn5mWbviuUp3z0dKlrIMkl4/rUFi+vRblH6geIfoJ+cYB55iSFgP2sBbPCXC40eL+/cOm7s9/vG/POBqK9j0W/R9B9MZcHB+IHHBqhVlUx+V4CNefKQDgdB3nY+MAIUICQLdOFz/43scPjD2/yqQUWDtCMMdnPXGd0SbmYQNBMmbWqyOUxL4aAyGgMn4HRJHQBHR7rG0zkIgYOujc8kwDAxMkJGY/X0Xhg2EDBwzWJy/a2IyHjNUqck7f8DBb0a4cGQTlclUsZRoz44WMh59VISMSBt8yLNHhEDxTgzEuU7Qsz6ZUgHEqAQKWCW0G9EQfiTXrZPJvpgf+A8pqk6O3PpfstGG1qVTCgh+Y4k4OT3lpkjqL2/n8dti3umawvykaAzCZGBWzq9aDqxLqZ8/DaKNWBcWdD0A7x8fMYiDud5gt91gs90AxuLqYMFO0O1HsIs26S+Tz1/MVf1pQsB8LgfBniyIbGGcofRtKf9JlXT6feZCz6US8vTIICIQsnA0gsggLpiT+y1knoE+i1RWrAuTjY8gANRd0NwgWapWSwaqhNWIfUZoKpZFOwAog0f8PdXhFYfxcXf+hyAvxOfIG58ALlpNENbqNS8aUNp1NgTFE4bA5ryZtd4s4LtU4qnJmTh4ixU1qkDU+b7sufDpwa89neU0RxwDjisCUvPxqUAwYOmCALWIUvldK2NNfj6l6CgQRf1lQv1asWmUkTSVMJ+KyIqywBZCZ0E+xT1+ovjMCqNSHHUKKlPP1kPldz+sUTyuFNxT07dYfFt1Z9wi9x2wh5Gu1cCwsNfl5N8WI4QdhFwRIadXgNgOIYa99Zd0H3kAW4eBGSJAFzcMwhj6avWBZXPtqaDhNe/RMpDdjVcDg3cYRCCjg30YgJ2Ayasn/tI8BsN707ADiAYQWXBQ7JIXGx1A6FMfVTeoQGAAUXf2SPwQQByYxvSdGBBxIFg1DyYNLPpC287aMP/y89raG/O6fh51vEZfnIoUKZ8SHAEHgxQRASBtPpy76bDaWXrCF1uJ5ippJ1ks8tkQePAJWaOFy2VxUHUsqDXLKK7rnaU2rOyGp8OSyvYindtuzVJVn2qJWGwuTd8nQzAYA1/5qPqC784UtFRjk8+9xECcZ9g5VUpd0iXmxfr857ahxPqlSX++p8+xh8yLcvkklKXyKt5FBGGC6wzIMYT8vyTttQQ+jQmpNboh72qTQ1scrnXLGYvGXPrFp9OXWuZPsk+uujFGtRzfqu0UlTQUkicSFtU/pHxgLTAcgQ05mO0eZAyITJJfmeA3GYJjpzjfB74/ovuuvxcBiHKvd85hF+9icODtCHNgoCPAWbi42RCcVmL/+pNMJMmGSazXMmqQ6/0GCYNZ/L1o5PIYhbGR4LBDFI5XB/mQCUiWoZiTMxHAiHdMVty80avLg+KbUxaUVnoC4uktAvg74MRCxgFiR0C2K/XjYL1q0OwpaOoaC3S3dn+71CIQZOGoPMwUEKO1q/s9Z0VlrXcqffNp06QcW2m8O3nSyrMgr4kExFtVsLlh9G96GOPpkmUEWwmbEDXeZ9a3lL3Z0PPkidUbEUs0PotH9TL4AS4W4MlPG+7jEx+KRMLem9kJwHMzFslQMK2tEuCKiUOZUaVkGg+VnuI9DWXp1o049j+Dr76H2dyBcB0PllJIZkGSIcGHVr8RtUkngRnn3eW4azltWX1EVmaIc2mZBPG4hVw3ZakjFVUTVluzILX6+By5vyl07FOn/0tDSxmbHGUQn3A+aCckyHkicwsM2Z94R+ni8sj4Yp1r8LoMRI2GIC75bvsz5wJvcgBYheLFHeWEiOiy8qLbHFeKjERy8vDb5/C1FH5dWYJT5Uznca1HrbkzouZRmUpVc/TkRwjlTO2PYaKqgJg9CunR4ze1TC8w+uunUnu/LCjmjPq2HQz+8MN1SnC/HfH9q8dy7FUEizYElyAx6eRZjUkSLGMG8ePCMUscemqz1STAJSHW5bVZBEjn9qeZhsxJ8hqezvYHgveGgJz2wIr4xRlaYkDiV5i01kc20Wh1owEr9FQ/KBz7PAr2KXsc1Wo7Q0K6ctCXKkK8qynts0jsM31JZ/BmUROwlk9iVAMTeYO65NdeOQlKRNnEgj71p0Dw0fyAR34Hh8G/UP2neYd3RnD+fGXnMFqLgwi+7xlbB3w9sD+6ILaBVLTdynXBh2V7GkPwKEu0TMFzCP64nUjXw/sjfvh//QlX397g9f/lO4C8QgNxsCIgR/DHJfjIDCGFExGI/4p+83e/MUFU9Lw4g8PhOzjZKMLLayXxA/r+L0BQ8CAhQgKjonE17hX15k2IxETTfRtRd5M4jgqKdXZN15LO05AGqCqzyjtFvSUz5c9I42muV4YScU6nLKpK86MQXErZUG9A6GCb5G12KWh0ydrl5WRBZ6Rft88S14MoD62vejZJS3i8ILxw8Z8OzmoIXajRa9fU5RzRjHaxcThj+i2T6EkGvlyh1OmmuZdRXdOQNb22rhxKaVcu6CuhTjnFZrn39Ro9TamfNOSWSd117WvHOJZf13a51WOxpKgnRzk2pB+uDQ53txj6G0C2sOQjJfIyHPlYWXpb5TxBjUmcqCQJrcfqkoNoqSPkScnqWk6fVlbK75F/x9wi5cn1Wc5XOBCSsbuw8+hOUBDN0Vr/KBJO5vOpueIzcBatyiJcEL6YMAJ4IMY1GDx6//0j+6iFDiOIOxjyUQRMFKJwAQnn/o+jDf3rW+EChZhQPpF/ZwxAuz26393DvTOQjxuI6eCjz/3Roh7pfB8rBUtb2ubypz6BieEIMF0PEuc3IYxgHAc4Z2FdJAB/CogdBsA6b74wxtNFONaGyKAzGzjjQAYgOfr71hiA2DR29W0FSS+ikibjJ1M5fyUItT6SIOsHngQdIA69fUC//x483AKbKwgYwlGn8OmSGU9KN6/SfK6w0SpIksdV2qhPxXvfAv3RpKzYrjjt4i0OEvQTnyPFaqSNh1Bfkk/L8iX0Q8mUwsxKuE7X4Wx5Vnq4SLbVFaBXDj1ryzTl5ynuMV3vT3O7qMxKPpkmHY0r4W4I4OZqA9k49P/Pa/A3hF03gI957fHT+oKy/io4r75nRkQsKGSxD1czwJKUi1wCxLMzRdEgTdKGwSb1K/9p1piPYsqUTXUa/Yyq52mi+d+jdTj2e1xt9kB3nc46Swr7DDaXEfbOgdqgg9SYc0SWaf+rw6ZCeY4IAwWjUME4vxRoC4lrcxRb8aGIJCxEIiMJmxLnNf6yXTVtVxKYiicn2q8ZQy37NGtQNZ00frSEPZmgpNWRZaC0drwk4c1GYwAg04PMVhkap3icWidbdHNacfqSoZwwDMLGmvRkMA6b0aRkjgTWKCqNwk1DcVnTEfps9Ch811hNyq2fiBr3ht4gC0+mxS29O1XOqefrYJ4Cy76abgxqvltzzwojxWri52p7aGOOWQwQOBja+COO4nMaMNIQhHmNUhBJJbehHd0x14LGG2n9lHD2LDD2AsD6qB/ikkaruqfiatne9E2USK02/sv+zKU5AWAF9mHA+DjmzbKAZFxifXxE3PhRjg0iIDoGcYqTYpTkGjI+YkJcQ4ASMI4g2ns+SP5cdHJBTI48pKFINDv4TJiM71LaBg3MJCy+aEWpvcTPrAZxE6IBNa+csYN4L779CLcfi0Q6AoKUMhuBWdD3FmRmEFiE59wLN1/mc9JdMurlSUVdqkNOMaMEl+39y4/nubCy9tX9c0aZK6sEtJvcM8s8656qS4xOY2G6iNBY609L71tw1oCekXYV926/mKocF8FofcrVDOhZmLxgI1NaIUCY4foOjg0kmYpzutPRjqrMORKTircqKOV0becpcxR8vAml/aIlraSH2aui1N8kriI1tieV6bKO5QdPAKmWmbqzvVE8b9MwrAhkHL2B3TE6Z7zNyyRXGC8EizfsuyjzJUmPw29G0Q8iADlwP4A3Au4ZYItooHZOQCzqMnWNpyT5PvrUEvlIDQgXMrNutwSrvXMCQrgrAoBji2gVS0c0cQcKp54QWUBc0GLtiT5eOGekQXwCCYdqxE27PCYkDiRHwJZy38SJOJYtXNHdHIaqnKLcabGaZFcZu9fM8UJBKumvQCUd4SLJHlDmr+1aJX4vaxEqYb2tptasFZZpkxdeBiEfQcQCiCHQDSA3ADmBcUj3bpZlr2zxc0SNJ3Tqi94iPDVXPKN1WSNOX5dEs8pfXb8ocInMKBqMqREJUG5W5lopYBPnq3SEo7U48E+4+voOTq5x/HDr39FK1S3gEXEo5qRKQ3PvWsUtJwlLYxmw5Hdi4Y3nZxxbFRf/ZHwn4OdtD2sZ3xwcbk6t058VYoid5DsyIGknWntkLo5kkw/kOzjSgehLfXrxFbIx++akNpRzK86kuWMdZlGtYuammxaXa2Q8b/10wjAWMnP+aBhzNfvOxsP3l5+kZBjbu98B21egj9+DcPxkzO9LhXIGSfE0wtW+wz+MN0B4+u76iB/vDlOGfpZXb84tCwbApXxLoAXcluLh663fltuA7VKXnkdvaiQhPZZZCGcnMX+ekaOZOyqiEr7q9VOmcm6ZNWwYLGinAuBn+guO9Ii38k/Y4gYEgYXFD/xHDLSHwzAtJy3B5QZLmrcz+Nzat7hxb/DO/BkH+tjAJ5iokj7nYHcGD/+nK3T3A/j/GOFCdHkRzRn7ZrUdLihqqy4fkxxMg6jEueQR74LbDFFEy1+kHWUhH0ySlTABAeGM3tx/BBEL0/0Jpq490aCDiD+GyUk+r9TjViqF9Zxu8p0qIiMNINQ4pL6iJTIq9e4XhnneV3KcGAmR3lZzudC7DiPu/+vf4B5GyCCgLsixahMifEm/iQi3bxzu/jCCOpycayXEclakWVniLwE+Z1t+Tf14FtSsSRbeTeDSvXa58hwLbH0XxAwIAGsEJALjzr1D6Plwnrz6H5ZSMU+oL1nPM1K94FCl1if2zBAy8MzGKCvOEkJr+1AWf547FPnEgoWMcZOh1nFThZUe0FA0JZUTHD8keIzXeNcmqSXF/QTabSgt4PPZBT0TrgwwWMLDuAGGe5B7RNf36DoDdyWwmw22G8LGdAD7CAUTdG6Blz9HaxE3GwD4CNwgm7pxhB0GuHEAnIXZjbj+pwPkwcE+3MDaAaM9goXA/hIzvyEQ2uFSBIuPjzDhXhKy/o42G+5KoyHrASAk55zROTgO+BgDQbhPy3RgNqANhzFwGCAYYf3dDvnIC8xtNpTanoqw1aTfHO8ygb9c28IOR7jhCDcewYbB8XpwIvgr4yXRVHIUk6o80SVPHxbZzgS1F1eVnxPEaOBaF5i7eaNEMc/VXE6ef4CPZqGoMyG3I5tZT1lJWwtlnYcmb+fgVDdOdNDq3kBP8oSuMzDGeCLugL7vYTsBBreMwBcIz9iImFE0Fjtgynyo8e65fThRLKnxrspRHocUv9B8A0OSnIVgmLATwMCCzAjY0ty0fiPmuUJMlX+VfFQ3qHi6HlRUhc9LQLeF668hw6Pfvf3iQCa/6gVPqHHPx2yGDASkyJDM7tf16kuKsvMGkRVQo58tXdCiWHq1prYTXK72pG6hEt+dyzBXJY/MqyXkUt7Ga2HHpgd1vzzmcEmo5SwPzc4E4EM3eczr72ZkbAeG5TIyYm3t5K8JxkAGwh22M4LY5WFa+KyOs6T3JIGrenoO7lqxmXndfnXC4nNiMbwM2Wda0HPe0YgBRwx0AItBT/4ScktHf4RSWhS8+N6hR49dPsYolJs2xlQdNRh0EBiwKHN7lTDGGMYSQQS3ZdhBMG4Iw6APY5wtpgF5fS0jB+LCmJtaSlFaaZW0ARE3IVi83OM3i5SSks5eDVw8KSJKTkvHOvpnRMMEX0oKHlL9WiFY5fUvsf7lDYVzgWZ/zENySDgxJdqZ6081f4MS5R+v484iAnt/hHsY4B5HuMHi2AGDQdg0QjMiIj5jI+CtL+t0U6o5vaLzLjVUn4Rtfom8eVGD1wk+L/In0TwJz8DfE/nT86+ES9SgfWHTCQsXKPXp6V9U8DkDztYyn1TDKvhSumQC0xbMtekpfO2i0OLhIAAMMoDp1ZRt2GiKQk6Mh9Yzy/Sl0TEbLNeVd6I2aAksli2hwuKzRKIqTjldFPg3O7D9ozC6nmzAmdAujMTBjYzhsAHhHswWZL3sPFoL4yw612FkBwNGvAciHvXJ7ENwnUSnFEDE5o0I549fSnczGIDIgayDOx5gYeDcDgADhtIxP4kbhj70TjQAiPyxU+wvNY7H9Hh5qLEiOn/klCXvocMufMb0xDDMcKaDNQPI8kT/Pz0MUUpfMBwVQ1GX6AVycQ5WRljnLwcnOMTDqUB+3iU/YsUnJwEUqdJynmRdJto4ZJ6eq3X8lG5aHGlWZViMlJeS3j1O8fhjJBwyrrqear7VrGep3gmcp+euoYnpJkSrSv/QO5FZ4Fpg7gjUI93r90kZ2QWqumxExCxTmaZrJonG3paQlgagNXWzFp7Psc5aeamYh8daeBW1TZDOcMsGjKJRDYsahcl+a4CbjnEUgbU2KN3OK9Ay1+iIDyZzZA1MSO5U5iJDbEAwjQejQlRYIV5gZqFyp76CiU6eVndvONjufo+ufwtz/N9Aw3vEhe2LBplGRTjxwXcgHxIoRIq+PLSWgNyrEm08WNyMKHjB5fppyttWjEIlv62OPJhhMJ8NUr+3od659w/Tn/BzRjBrPpHwTR2PodeQL6BLvkyoVpPQTzcPPa4OHX66PeCnm0N6XR+l0lpiCcBObjCSwQ/bOxhzi2vTpfIvMdeaOXUUkKj5pohtVkdR/y4CbeJG7rHJKt5In8XSuPBR8c5/ZmfsnC4XHcqI4zUj+M15khFBHacYHwp+xp9huMO38s9g6eAvWFZXkhNhgx3eyj/BSOc9qZRCooX0iRjTlEUazzVaaec0BC7wBu+/fQP3OMA9fu91rFDvORcIezpyk4AIQuRHDIjLnlZhXNLdNc5B4OCcv8RMmMLFfYHHxzVPvFAb5aC8KZH7KnVDZVWYxPhUyna+n0ArLWdSeuTPjVdnR96emfx5h7NoVUmXmJWo9F3q/il/u6PFw3/7Afb+ABksjiz4851gIJlcVB2+FLWee3H1OXB+yS+Hy68B0gbYFwK/iS+/BtAE9Usf0S9ocgB4et/Wwk1d1plVfzYI8qAAAAPEEDa4uWPwzsGE886L2wIT3qck8rYCdVpmlup7w5EnRTpU6p+SYaJjhT7DfhoB3cI+PnVRkIsFlrqBbsx8MZcHatFe6G0B4ARiLcbR4fiuw/HD19jcfsT2lYUAsA5gHjA6wAljYwXbvvenNAUja997uZuDPeX+8QHWjhiOx9T31lqI9Ybljn26EQRcHUBX38M9vMaw36Dreo8d+wuokQJ1c6QBkd8IESf+XgMiWKfsjEE/F5F074Edrbf3OAfnOgCEDj2M8UcydV3nqzEEkRHO+X8STxoV3Xe1siCpq1cdA5rIIdiOlDIl1sLiiIfHewybe7zqexgOOkCwgRIAR7XjE4ciQtTt5NjqiaUoUsGs6WKuCXn6ZH1IYnsQp0CWftsUGDCoHXSCLiMqwrvYkQy/c9l5Uk/bQEoZVa1RTsQva7MslOREx/lH1gwME8CEx/EAZxzc/7QH/gDI7SuYbgMc/UZaIJlfBFxuI6Kab1pRoyrdpHOqPJN9IQLy5MmP9L9IR2WFU3WxOTBE6qIibWyJUw+IGxT1sZ76MuZ4KfWIoGy3zPeLGsXcNF8HenLr3qfqfavKZMhIGybSMJivwy/OoXisE5suGF74nGI+K8SFL1+IqY5oAnyEhAD+7D5//wPQWNOLEtfXfW6eVXDOqtSg02Lvbjnz6TSffPxPEV0lQZwNeo7kOkUc7LCHDI+45w6222A7HsHiWoX8BgCy4JN/MwhsCZvB4Oo4ZVtDZ2HNdBQK8UYYjgjErF9Ovz8bajNj+3X2hlpTOTVIeImm63cxwPcpokkejymPXQ+lsnleJqrmVea8/q9ji3TkGjE2cgUiwohDYDsEcoQOHZg6Ja5QwdTT8xk8qfpSHAGUQNFvFHwNQ3YbONvgwvW6KtO7T3KCGILsVB8gyDB61Bc6Ogn/QVanuNz7CIc4Tp7XaT4g5YdOCEK6iK/Q4PXX9lFMdYcknWXShKwQlfStn5XKXUk3rTU6w2VOfp+HrICV/aT1p3xk3Jo1QSCDhQyZl1gGhOc2aNpwCXFsVc+d2b1zo9R8urpsOufnFwXzqsMyXZ9Vx7NLOAeeie+XtDNzAl5mbblAmb8AXew0PEUYifx5nbZV17Akda19ugzzeebsJ0+DtS1bgLksKuwnRUQQQmyyNgQpvp1+13JSTahzhLsO/7LVyniZdNeJoaf40lIdWqcBTLDTVYUHqdbpyzo3srz0iSat5BGMHubOeRmbYUB2Bxp2gDNAZ+B6husE1jqM5GDYBu2NwEwwxCBmGGMg4tANXpcbyR9ZHCMiYl8w+WOQmARiBAILwYjRDiAyANlokEk3xMXf+VJjChdXU2hPdKWKGxZZNhMX2wlv4GYfnSHOwYnzd5xSaIuwP7KJTd7wOHkP6BkCh5R0GO1p6fhXcYBYiB0wjEeIjIAYtGmDtGmvgUOW45PHpkoXj7CqDx+bQ7/tXFaWGemp1V/lVGgXFqPDvQyd5y0l7HRled40RyfQSV5WpFyfZHmoTsOS63G1/gUDaqF1CRLPIiKw8VFFQg7mdgO6QTiSFSoXNSqsdLlzYHawzy+qhiduRGgTgPpSKX+1EjhRrhvKIsVBULuacVCidzGBfOhDdr2sCp32mFbY201SWIg6YGFieSinX97AyI9F/K6u3oFD/Fig5imhyuRJ8Xiqw6sk6y6d9vPP1xyblhYBPTdWeMLXpoE0EoR8JMBizNWXBVo4iEYuUPCHFG948dF7of8AxJ0ILYzkRTL+RhJA2pUWX14GkgdGe2mekMAZ47bWkLJOBfgMIMXH6eTKQJDoPjF9wfHj3zAeHvCwuUJnevznjz9ih/+YGxHrmXlLCCe8euhx+9hXhQr++voRH6+GIrVekKLi0xKGtGh1EUqcoK4W62oOPb2+sObEdTkstHGaUpCcsoNVbuXJMZhLVPHCtLYnpZJm8513Br2uTIVRp7/+irt43VCUCeJbgw5v5R8x4ojvzb/C0hAUIU5h1K1jjEohbg2GJ7SIpMIB1BP4dgvqVOdSlpQyaUjiNdOL2MN/4uAkC9/EBHYEF+5kYma4GBUReK6/nyjmz0ql39jwDhPOkfcsg5bLI0FV678S2JOInQT5Vv9pg7vSMmp+V+TVgmVNlPp3FlxI3b1Bk3Et887OhYI2UIxDlklbGecKKxac8BnWGymVKb05kdOp7EVaPZZr8VkPFxXT1vZX1fdrCnnyJsSZsGrtfGH40iIjPjlMlaTf4FcB9dp+bp7nwW8k9URY6jgKtgUiCBlYGJjRgXjI5zPNDGHbbBeenVwDWrrDTLJCUVffEeUlZEaYRSbFv/2LUpfO+eP3bMJ1hRLiZFJwicOcDUjjdRJOdJjyVlcP06PkbBM2CawdsdvucHO1gZFvsfl45yNrmSDdO4zdPY7HAaO1sFZgDKMP59lvthv0ncGm7wJDNRjGI5yzGMcBwzDAOevlVwCm77yDjXWwTuCswziOkMdHuA2wEY8XG18PE8MQK9pS2w4qkpcQ46U56RHReTh6m8YIYmut3zyxFmI6gAA2DKIOXbeB6x2sHeBCpHJpRY9Sw9NWmFIczpG4BAoRASPs4RHj43vYmxtIwIuYw7yjpJa5SK+EsLHAATOXyzyBp1Sfa9JqW1fefMi/a72gsDOmtHpFCHPPBfk3XoAenTuVbO1/OzU3NWaxI0IUeayFpsmaXdNSVWY7QtkIJ0VUT1tlqbtlu86g6xkHIvCGsf32K9i3Auo7pKN11LLxSxAXn7ARoVV39SUpEFR8pmRaep4LqQ9KnukY3BlcywY76WGQJ1OrLu1oj7Ia9XxaY3U6U4mfaPL333TliS4DfVTqIpxzYNY8p6VIT6GB5WzaNvLzkM54W1Ekgc64zKXMB+hJT5Nxyz9+GeJfpgTKC6Zicn5xr+mkHJZVxgKZfPk0EOWmOtxnLbQ2mGaKegJJXQiqyqhGYCoUr0Nx3jyRnooDnIUNm3G/DKr/1DCdP1Pwc7C+IkIE2A2mpF/yJe03Fi5FsxE2wxZGtnktLEo/Fy4ntJ2CLMacLm051Ty96ve1IXziLBArWgmnaq2BoHUJwsaOuNrvsWfGYDxjXYpaIBjE02OTM4PkMnMTlHJblLDczxP5ZkJPmQ8SALAD5BHk9pCiN6ay0FJf5XNVswhbysvKa4kN7PVrwPSQjz+lsnNZPjjbwC9RxFCbWqGsSAfJSA4f+dDgeVJXoFtUKRvNhC/toFCIcDO9PBUy6xeTxM2xKrqmVLCirjoXCSGF0oRJv4gA9v0B9nEArEAIeOwERzPt1fp4pslxTQHVzmES7TsHzzOEn858gptetK7nlN6E+XCeTwCljvKS8KwazmUGk8p/Car1J4BfbTdcvmGTmXFaVWnmP7ueTwFnV7qU8AzF7JSOJ+VTAYMF3qtcvG1NZnnoHA5KXmuZMghoHkuw+FOKZ+1oCMn/oqGzeC3qR4Hp+SCt70lQeEqJWKNfKelkMSkTQOJAGGHYoKMtHIexPG4gxsFuLQAHy97Mb4zxNxcwAZzvMOiMAaRD329ARDgeBxALuGPAETphOBEQ2yDrOGAnsLsDBAbW9sHJ1Xp6YkCi0dYhReki1h39/ygc28QytV0ks2KQ4YOx20drWETDNhGBjI/uYNOB7QhhBom/iyJ3Yq0XnKZP/6iVV8v5IaNYkLNAiCTJ77OsN+9E3CC2WkSvJnPCKznpzoFU66zPk0k6Rnfn5/qUgHx0eP5LSf+JeLgSPXHTrhVgyeoSezWfcgJAtP1zTqbTNDPTC0qfmvRUC6VkV2y/IiYYw+hMh63pwTuA+g5irJLp8+KYyV+XeEoAO3ONuYAt78yNiIalTn02u2+i4E9V8HyGre/ozd0Wm67HH9wb7KRHxyZYEDh7+YWFLPlBpuiI+FzVWHm0NVumnmvD8pJy5vufCqYIAA4OYi2IXDnxVPlNPNpctcxYvF8a/bmGTrPFdlC8oFK1Jxo2KEyQpaiIOI5p7lIsg8FUeoBfgHY/KUTjAKkHEnacmQAJ5w622H00MqRQspomivX/ZXqFqEU6NaObyYvIzNZJunNjOz/mn4Aa6qmT6g3fNArxuxZqCT40slUK5c94sWo8yF6be6II8qvVHz85ZEHoq48bvMEWepQtA3/++h773ofvGkd4df8avHkDemNUGaciIaaMWwtTzRyteX4KlDycZRd/ufHS/SZ1GedV2hJKFBOIvBXI0YglggW/na9CAt9bSKl4u1caKHn73zw8YPvhA/7+6jXG6+swLSmVr2WCzLliZKX/x0FJYOEK4Six1Z18WnkrU8f1IeOVxtQd4Y5/geyP3smBjb9YTK0dS5DCxkWQL5iYKk+knChcv8X4h/8CPLyDefgA2CHlSqJE5E0Ef28Eazku8DjRnjyU5ZcW7deytujPdVFgVHxv91G+bFzJehdbWBs0HsqfbkDVX2oIXL0UCKp3broJIWW+ovjR4eG//wT74eDPbGbg77fAkQVS9dHSZ4SNBXaW0NVyIU2HuNXHL8/PfuOYvzo4cWdeCb+08V/C9xmybrEs/dL65MuEL1EHPYXTKTPSFC5IK+d2mHjbgj/UxqAjxgbij6+ek6lbPLOAag4FRrV+ZhUKtxbmlVzUTqpLSI4VKk0t8StzsTdOa+8DLQ+lKIwTjdDvzle0F6HYWkn5SxMuE4HIwNCIjh6w6TbY9New4o8usg9vIPcW7usfgasHCCyYBGQ6kCGADYhNkin7roMx/o6y4/GA4zDAGs7HqYLhnGBwoz/uaRgxGgu7e4fhnWD80Hl5N17QEI5wZ/HHR3mzYHZIIs56DDP7zYrQZdHWxzEfh14RC2eB0RJ4ZIzdkI6Y8vdUABsJcRXi7ysgFy7iDn2ZTAtKNShoZ4XsNXkP3+6OgA0EZEdvh6KgP4WGRXmdJzqkC2tJIZxWNVV6kZR4NbVHybQUNxNi1LV2aCo3FGI1KiqlmAxOoRFmmppP8fgs/zZGRoRNCWm1U/HR6KHmKAceqEZNxyEK5VormoIUaWYGs5rP01ODvOHOwd8NQUzYbHrstj02PaO7YdxvOjgjmWiCLZwTYlS0fd1ZOXNIzsAzTXhnbESsR742VmjBKe85+M6iIh2l50wEQ+QvlQzpKCWOxhFSHT2pCUWFq9ojKcuU+No9ncw1uiHiJyANhG40HlczyToLuqbnjG/Ns9K3k1YttSmhkGjjUi9FPlW87FpjcmCG7QjbEegmRp9fBghC96VulHBHkuoklTYu3IXg8rmACKa7g2xvQLyCIMOiVmPcNsYs7DnPcNVzzHyFEapRv6hvc0x8ldw2/2OCR7OOGAoZ0zGh29wAYLj9R8COy8j8yuA016hTnKKKtnE/m8jLAbo6dOisF56FOgzGC7dRKCqq+tzzU0PdDYHVeZSfTjyLGwHFDrnkSjU+UWo/R5iJPHqlpTjyUi1HMAAD8my0YJBz9JN/R5QdLPb0HsSmTEUAIOiwQe+2UYLM76ROPN+OSWREZI+JTWqmmstJjjOpn3UdaiM7/lfpB3PgmOEv7s74JC+kUI4TeA838vPCifhNEslnOZdiLM2sfVHpqvrnXDm2Fb06WfVzvpylTCEVrlQNei17tss9T2gvpm21vCQ1KrxsfaaoiZMDGwYujI8jAaq7IfQmXOZL6neFd8vp5tmbO8/Nv6aAljacXiyUce4S9gXAlxIMcKJnT8A5Hf+FNHg1zOP7hUgWM/AfQyCdGmF+me1u6vZzzTh3Cl2sO7ROGA/UnKbR9UrBQNsp27KHfn5OA+bTZh1BCj2+UBhEayQThr+uXmk9br1/GYNg0a9azldeDePg8PhosX8UOGKw6dAZhgn3IwAu6SYkBDps/Yk3MHCGIRvAWgdrHZidN6pGux78kUpsOpjOgJh8pAQRmAxGa0GDP7ZJXIhGcACuLKzbA2aAEMPaLTBuPMJsfOBFsGVlC02Uf/z9DuLihoX4PQzxbSE1qcQ5OCLAOlge4cYO1AEm3nnCJuDvL2UnoklQDtXfJNsNW3Yhmb9stAAn/s6VUgQKBggq1Y/UF3GeSbU0pISS/0nGz6svUxrXskARzSuTmTHZhEgON4WhrKGKp2dSvJj2XY3YXIENICTbXtYBpRBBsv69DLF9pRY392MBIU1D5KMhjm4EnGBzc43tVzd4NI8gGkGjA1kHtg48uiDTl/21BvvzNiqaRD55dQoud1n1IgQTUVT6wg6l16Hiec1ZUWLtxZg2IUIZrJSqUCj7BOl3rlFhkBTOFjPMeMawo3LnsmxHAUFZr/vcOYfuQOCHDu5GYDuZdwJKRvu4bMQlc34sl8Z4gZevKLlMHTcU1Lw8lSWl8Ut6+CKMdxuD0TG+cxadnS3hiwcp/4SFvd58mRqS8qJbFib6xwsCgdBf/x7d3TcwfYjWmVnD48/JLvLEQ/YsBKYS9NlCU7tmzWxnpdhIxGojzh9BVgxCMnpN5j6pS8kxv+GRrVsEYoPN3bcwdsT4/f8BDEdlcXzZ8f5lQ7t/zloPhfD1hy0I/tz8g+nx4bU/Pz+Hhcbcai7PoVR5Mp8Ngd8t3rUTmi1xLUnuGRQExxOXobXwl9MG1dadBBmllvKe3yWOS3VaanqRnwIiBsgrAxxlAGYfeky53CRIV8Xrnz6wwiselgb8bP7SzAM43Liv8Nr9Ps/rpJTNTvQ2/igoKm9c1wpDYRBWAkchfwaeESMXnL8s8Oxom+Q5pOR9AURcCCUnODiw895ozgHM5N8H+ov9Fg38HrtSKcgrZ9nBWe7IbYov4kV4cVClzqj6y3+oflP916IzjescLL8vZdenQlbE4nhOf2dnSQn/S6pbVEEujWXJTKfOVFVEEIX5OCMjnweXKKMBiXTOLLmWK86Ai7fhheAXZ5N/LvziGnwOvlnPe5nyV8LsYivF01+HpDrXf63nv5wWT7ltneBztsXTuYBh0UGyVaCQkdJpAytQfRo9Ktld6eL5tT4mJqar9fWpcC0Fry6/Fyfhy7TeecdEUQnU++fqHzNAVOGYjWXJsPxwP+Lvf3yENR345hX6XY9tj+QoDOtlU4Tz+unhNXjPALw8OWx/hPARh+MAiKDbbgAOB6iSgLsOBoJ+uwMD2Pa93ywwHQ7HI+4fHtEd9wAAwxYODNOPcK/epXs2xu9fY7i/Qe8cjOnQ9T1MOgYqyEHidUEIYNn4CAn2R4Y5sgjKUqJagcC6KH/7SB5f5iZdUu2Pku/BzoHJwMICkh2gQPOxwCdpII/SRE71x6g6ldI7HREziA2cxPZIcPonIMj5WXoTNGdUwEsfD5VxzbQO5CjcLLtWMi6y7pF/q3ni8m+Bm9ePQ+RDwse5VDbSPREKv/h7Mm9OrfdKW6lUv1OOqLmklrGryjgZ4pb+EpKxP96s7xj34x6PPfCffv8/YPP2K9D23wDs0R0G8GCx2Y8gVxVeF72whEyTntKPZtalM8SVMzYiGoOoaXjGVhE96ij/SgMcj06ID0xvYAzjDlfYooehTinrlDcwqjqmdcbfkwenmXbK0B6puUEqc8Q7Iiy22xHHjjBKZralaqxztuvNT5dZcG2kqklk0nczRaUhDQqwt9POLVpTRT15UQYDb1pCg8flrwVS3wRjSjpfm6pQKCWASF3AJ4NoTGIQGdSsUdZNjLJEygbBtU2ZnFeo5ubcyr7WcDI1c+XZJuFnvFw+UXH9RVt99PpRLX8kOf1kGSJ/DCY5f0xKaThDdFb4Vc2FU0CN0VmTK8N8vtabxGdizULoHPDm+IiRO8BZaM/yJPufrOsZo1bpFa0e8fMjCsFlSgImm9kxiCEagTOPeVlYMt427UdPNirFdctvSiDIDHHj5NxS45mx5aZLWLfDPsdABxz5Mb3dyBU6bFQZT2hGWHRi1pbIWUtYUr2N/9XvEk4njs4roioknsGq7j2KNQfG5sT3ucRJEtZGf89Nm8L06konZn3awqI8+VoSUmrfS8NCHUWw0JNAqu9BCYvKXKwkpZAkT4hE2m+XFkQO//0EknPHM50HJ/jx5MXZs/TlU9F8/hM9GD5fboX9xdnfz4Imc5h/9YuBE2tv49uXDbTwawrLctE6Oe5l4Dlyxy9lrC6L6XOn4cQslfQr/y8eaVzXtKiCnqE419ERk9TaMCn5Y5KwaEj+IdX74ijF8D07GtT5Mw6rKKyurPluDSwnLt/WSj3BQTCA0BuDmw1hwwTmIOFJNCCnCxj8pdFsvHxJPqrAOovjMEAg6DuDDgAbf7FVdG7smEFM6LvebxBwBzhg3Pq7GYZhgBNg7ASdEzgKl1iLgLZ7kHOw4w1k3HqnZXRgg+DP5amLiQHO0b5E/qJtcv4Y3MKT3znv/BNkVMcWdhxAhsGuQ3Sk9o4eDAT8xVGQx6M8G/8+ZQCpkP8E6WYEAIDhDl3Xg00H4g7+TClKUmbMykl59NgkfILxJ9qskioxnTgFKa/bPFzQE7QjrIqGKFuuZ1xOINXT4tt08kE77kR9ozmPi2LmcF/zrKGnTTYh54AKfOK1A4/jAY9W0H19jZu3dzC7HdgY3D3cYLcnmP0RPDp0gwWJwHYD4pHDjh3ur+7hwhH55AjmaNCPHW4ebmYbs9/usd8eZjFVFINy9T6PizwhIsJXmKrNeuek7ukmRDBcUvjO6g0B/U2Pbd/jO/cK17JV3lwhVTToqegHhp5cuvKJeXCaptGymvTrEibPKPOZ2A3iAGstePOAm/4AZ3ocRqP6Kmq1WgD3C3p63EBAM9giiXpRZi23JuZov3heuIPGN5R+MsU1I/cG6bwVnrkYbYX5ZQl5S5ANCKQIYMUCJo1nLy38Uhib5jQIS7vg6ZdWr0GgwY7za5r23RO9NydFlRMGccJqjIqpFwrgYBiuti/SnCVdSZzO4aKj6A0eDXKRvRS08hushKcbgCLH6sTiHx/f4yAO39sxGVgnAskLjUs8yi23JKzPNbFqfroSl7TSz+ZZV9gaD/JJsXOvku65trw2jpHXI3p0A4UhtVZnG6KILkjxoaqE8P7A93hn/pyyvba/R2/fqtJPt0O3ZIJP8kz3Px38+a1+J4SnuZKHkaD08NFNUWvOjGdN0PhyeQgREiQQUREP4nkEx03bUJ4opv48Y2kRY5GfUqiv2m0j5M46eTfE7OB/IaDWmELRicpv+KyduKY6Yf2kHRHRghfdhJhJvzr1Ra3wM2XRPFZfMun8quBXsdvyedpQyCu/uG6cQ/hLFIZ/E9JPwXLvZGOciIE3N8VLdLOhNKapLA6r65yOUrTh1JYPKRNGw02Ui1KeSSIkQ2ahI+jjFAXRsCpVy/J8jd9cLrrAYa6RgglaF4SEQtHrBH/vgpe9hAxcv8HV9RZvNhYbY9DxFs45iNhwf1kwcsLfv2CYIWAIOThrMY4DHvZANxj0vXft6ZiDU4zP23U9OsPYbnf+uCM2/o5YZjAR7DhgpBDBIA5OGMMwYrQCvn0Aru4xfi8YH8PxohAY0wEcbJYEv8EBBDncRw8wfOQ0APjrHvzminPeY1/I34Hhu0gAMiC2MMYfK0XMYGNSlARpAV+yzJq3atYOJhV3yQHwfSUATOiffoPNZoeu28CYDUAcNvqAuOFF5OXqpEvFkRd9IkSWIUkAF80UtYIMTd3VXNXyLbJMOwtV1E9b9fVpnJ6raf4pHV6AfFl1ntM+ZEbCZlfY/FD9U6JT/1aInYSZdqp1Q6cqXQ1nKhAATOCO8cPDB9zbR/yX/+WfcPef/gH97Q6d6fDd91/BHG6Q9gFBEB5xfP0zpPNHgR+7I35+9R6j8b/5wNgdDXb7Hf7hb39IJ33Udf/t7d8XNyLyOM3p4+vgokczLRsxSkSzg7DaaNAGgUKhpqnhgc5rejYArV8CpmVMa8qLeOYVZARkRgzdR4zdezi5A4bdfCEVpMEtZmX40ZKN6sfa0F9sbU6NedO+IEB5KLaOrlkL2djgmULXv4LsCHT8AcDx/AK/YPAGFGTb0anEp9JcFFpHDV2u7PLb0+eXz75yGaPqh5SL+hqDYTLeCcKG4pp+qqxeNR7hI21QqHXO7F4BZICPP5/E7dcLz9Oc14+th0qs8HxA5j3LPxu0NuEmr+pWeWpNUUaJX4QvZTJMaLf4rplNCb7PFqx3p2DBnTwLer6RWi6IBnvP68sjoFDkA65whx47GPSr0TJug63chMMaBRu5BgjoZYsb93XEEEIW9+bH9Hvk47QvnkBIaU9AMNkcpsRQtMg/FdhLgz2UXESokZRUpxbmS9wljoEgHQ/mN7j0oZblxsW0YRmhWp8uka0hbsyVT05BQV51Pz7bUlfOiSTjtqbKrHKTP2X6uqnopfmb5AkfXn/84QHucYAbnHp9HnfXx7C1tu1mfAHOgPMyPGXzgeovE4WxUSbNvlkqaAGDy3MPiii0GVhb3ngBmCv56S3Wk3oyST85fIYqAQAHc42jucJI27PykVs+VPgseAGhp3VU36eHlxjVOZkpvi0n6hcjT34CWNNWZwjjpoMdGHEDIgspqm+DDETqN6oki7AgP8/D6THz9p1WilKDyP4dUaADiqyVwbWGk9ykKSOcVcJswe3m+YfHw4gP7wccjw5311vsNhy87zk01UGcTcbxeFFyvIeBBHBCwP4KsAajPMJ1Fg+Pe4x957emCBjHMRyZ69vSxSOG4I8I7TqDPhy3BBHAMlg4G44JEHjnMrraQ2AxWIIMO/SdDccvBUcf5R0fNYt4d0QyoKfjeyW1DQQ4a+GYYd0ItjZtbBARmP2JLs50EDukIVlwjToJjcChOGr+HRNM16HfbGC6HmwMnLoTLt/DEaJqpZS3sm6nbH5RvBWgiNsJydIJILWeGQvQ+McnFGR7mUuZG+zLDjW3pk0tG00SZcVKnKjfKo6kgUhbDleP1k/Sck5J+Q4lJpWOUsviguM4YHACx4Kb7RW2mx59Z4Ari3FrMbg9XG+reWwRJxcBMGLwav8Klv1uBQ+Ejeuw5R2Or8YCB83DzabDrb1daupF4FkbEWl6nZxnYTLkP0hREZEhcUqK7EOM7OGnPnNhC3gtGD+eAxMdYTIgAuqAfmvhuvc43n4Pu+8h2GGuowqjgpTPlg1va81yS1BYdTA34/yTPCY6fG0er7JB/e534O4r8P29Pyv/hZS5zwUtepiQYFq3P3G7qdrou1zBRR2ek+Flm/fSyngD/3Pk3BzBhbjU+bsibt4C3RXoh38DfsF3pHxumLPRxHfUSiV5fqbIH+V2LO3FvKrxDBypEuIqKAMgYjTDEpFFnuklQQEQL2Gby3KKd2ilSegck23NxyjzbZo+81lO82Pf/Bz5SFDf45xqjDCRwZ18gx1uJ/rtEvSyxZvx96i3H3fuDluXw1XfdX/Gh+5v6wpVsFqXFm98F4G/Rr2yfQiykqtHU0c/RDNQchyo5aRgBY9HMzkIOGrPpMK4I96VoEMQOOg+j+nKsVDYVUVUdBg1nUnOKGkoWaOOhlgp1y1TdNhSSErP6TIjCZ8dNRQzh3pn0AEk3P8Qfkf9KkXOWIfDv7/H+PPjk/lr3IQQLb9pnaylg60SpV+AD59T5VL1TbFH84e1Bb0sFDXPje/qReVLAVr8+cuF9Q3R3OWxf433m29hi03mE/nFH6uROd8z4JOrW2sx/iXogr8EHJ8PJ805ON0L/j1h7AyOux522PjjapZySOb8hW3pBUGycFXIKElHz+w44FXLMX4eS/FZ5i3NjlGgU68Lm8/6dWEKz9S/E0vMyD0+DPjXf/+A13dX+N0bwXYD9JveH/MjAJzfiEA4u5/YwLC/CDoceOKjF+5fQ2jAXj4CmyOECJuuwzakO47e65rJgEHhEmxfgGFG33Ww/QbbzdZHD7sRUcj1mwDkIxfYQW4fgGvB+H0Pd2RsNltQuExakhOaAOGIJhCD2KX25zsErXewdy71j6MRdiSQGUFmBDOBRfy9Ex1guh7OObiR4YQR7zSQ2h62apC0+1XW5WIbDPnIk812g+1uh67fgLsOLh6BTlmWZiDpUlDlZP0g/IkOYYDvH3GKLqJTMgX0T+u2iHjMe9+ktYJi2SwgR+ommZBelvpOvVebEOnYtOZmxQrcY23nzKkCj9N1JP1jZuF9GI/4KAO2Vz1e313jarfFtu+Bm0cMN0egO4IHW+BHIjBHh3ASEzrX4ZuP35QFM4Br4PF6PuLBoMcrfDXTztlsZ8OLXlY9p2aWSg3BbA3YMLhrCa3RoFE/V1M6eoMqFibpOWVaJqnU4zbWSRFXDSkiKgobl6BO3omDfTxg7B8w7o5waWe1nMPpvOrYzMCINc5lo6NCXimRk/XtlBYzD4yAQ2xn7MIqnEuXlavOfUuhQX68w7YE5bH/9Yl0ujVrhO9P1QP1kQ3KwANWBpUw5lAGHD1VZlGt6CCu2kTpPoapxBXaLicLL5WvNMfVe2UZ0zvacZc/nc6YJl6c4ar/PYHXBWbWPxmq5XHL7F+LEUjhmtGglkVWKfLO1TBHYV/aPKLq8yVAqs/6+XyvVAKItL5Khby6Z2RSMk2Tx0QV3UzzK96hJ4rSJahM1WhVg3ZOLi2VUNawMhYbARMGfApy4rSeLOTXLdPJyMdLx9mTNiSKZWAyYQhOLPb8HiMdMIpFjiwo8ZriHDAJX4/8iAPdY6A9AMJWbtG7Lfb8AZaOqiypxlq1RfPlWL/GOb53QNLcNM1EuijCe2U6ZuncU30kgZJ9tNwC9SyWJ7ntaX/AEYSVkBxQ83qFlOMwGWC/vovytCopf8Xaf6EFpChH4ZvFywbuE/yokF2KgU1J68me6aC1KRmNIJ4MWsdC5HSRlvwRCOE5CT5sCYMRWMobRXHe+rbnzTxEjnQloK8t3JXL1TWGYa77289PydXnlHV5mNZTMoGSBtZx1NkWP5Fwi6ViCZrMZjHBxUDzpdMpVxb4GeBp1FqXgFWlXEo+YxlxM7xD7/ag2etPPy/Ua+n6tj+1ly5DQKdKqaWvKc8g9bdM+0uE52Kv1wkvOzMcTD7+Jv1VglyUPeLTaklelICV/Ad1N+VE10sb8KJ0QRQyN5CKCM+W73OIXFsaBsh0b4I06lcVy0RfiDKZ1A3Urc5tTs9o2piUpmL2kyLzg3EQ3H84Yv/o8Op2h9vdBpt+i4674FnvYMXCOgvrRki4KNmEex0o3A8Bcl7utOKNoh+vIV2HAQNkM+KDYRADh3EEEWGz8UcLWXhbVKQWgQOxgI1B13WAuwLEwUs9AhoB5yyIBTgOIBHwzQNkY2FdDxrhjyYiDkc6OUD8pc3GMJz1+IM4042U8jTBQRzgMMLZAXY8whmCsM9nmNF1Gx+wMR49ZuKCc4n/l0naz4xkV5xE0/pj55m4GE8R5yNNyAD9LejqFmb3Fai/gnAHB0a0u3HC2/9NJo6ICQcbTRTqE60FmVbbVSOBRtuFuOxEruZWNYvU39jSLHPGueUhHrzk0i/vLlVsR0zoNKsuGv+YJpx+UM/BRjnlqwZvF6AZkljUN/+aXPUkKbIAw1/4TsXa6OvnjrGFAVhw9dVr3H73Fvx2A/v6COq0a1iJt9Rj04ITTO+k4+0FZbcnbESUjUsifFKOQipNkwRFtFPsu60Bb03ISPN9V2T1BWdWJokgk6coUEZGROaycAZ+u/OjqqjaVr3NKAo2AtA4Yu/2GO0RLl2MKtmrTs3xljLsvdYY6VQ5zdmTF6Jko1OL5jRzrhQvjS+AfE65MiDHzQR/xp1f4CRZKjgzSlTtCSWnS0URlWP1Xq11uvemPfpLhNR7J+DEQnEBIP0l9b9nU+lxZaHS1JEf1nhm3DMVzOTVbYzjHilPsNhPGX/SH60UxTsdcphoVrKwq411QqWoSdDzL76pW9jqj/gqM25COAaDAXas0mWB+dcEVH2+BGh6m3u/+EYJ9hlP1yg5CMBRAgnhnSndZO3KC1yL05UeV3nupPzB2Bwpkckfb0lV6mS6LKZVQ+ma6QN9DmYrYqtco8OcURFV6pCkAnRZyfGGxAv4Vftba31kbT68GyDH4DQCwfTSIixC4oMCwJHDe/4eAx3ARKlv4mbSPG1qnBgH/lhEQuzGV7hxb+BoxKPaiEg9XjG0VJpkVSZCpCSC94JnKuWoJPsr2SNfGl32W4lEJG/KuEim7CCeJ1wEgcbi8ugAsHrrwjqlNmgj4n5ZFcwTkZ4jU+EkKxCYHxRVNqnfxfe1i42WTcLveS5dUgrVaJJOF76VbK5QZ4rWq2VG1B89L0uJM4ta2rHLMuHHneDYK76lm1t1TNqMuHPAPw+QEcBQolT19qSNy13dooUSyv57Gpd4Gd5yHiPWUkCBzwV2zxLdpDX02UVeFM5GpzkBcJG+eg5cpmvX0Q1VM2tJzZ0DIyNeHf6KToI38FOQf3mV46Iwtz5/+iY8vcYFTeFZcIlyXrIfA7eBl2ANHJmG7B5moXJ0bLKGJt3WMkYbi2TuraIVkjwUHjOCHBQfKj0h19aOM45yVH6gGHaq1xXv2miLSoMq/6nRqjppbq7PEWRsABGGweHHH0YQCe6uO1xtO2z6HQx7WXwUgXVD+Gdh2EcxGDb+0mQt80edRhj04RYORxzNXzGO1kdTMOFoLdgY3JABjIMNsoRB2AoQC0DQGQPuNjDSQWSEyAAmgWGAYNGxQNwIiIBuHwC3h/vxBnYwoN5vGPiLtbMeZQwDYGAMdEjx3grf/9kJGYC4FPFgmWGNv5S76xjG+KgNEOM4HLz4bEcIuXBUs3a/idsEku52S8MhWpuM67yLPeF1Be7AV2+w/fqf0N1+A+q3kM5AOA9w2tRTRzNIKLOwnBbOQpouvN1PiqiIgGs44ipFVJ+kUQaRy+oz9Awo3aecuOK3xD5Sk6ycmqQexHmHsAlRHsVcRyuUEncNvo/Sm6fs/SudPrYl8n+t+xDpXQ5Pe2wYbAgb6rDpgJvffY3b//SP4LcO9s0eTASOl6Jr9NW8b2vqqxBvBrK8FJyxEfFEtlcbJzD/u860Lvw9h9hnr0Aq/4paSArP6bkiayaRjT5FNEKRQn0JGyFudBiGAeZA6A8dsIUPBROoRSGD1jsE+mXYHAiTsayfkgEn71qG73MKwBwkymthVdc5f+hHuWgR9M5NOl7rlyYRPxc+V1MJECJ8MIShZ4ANDAhuf4URDLclGIM8ZovKYWksORsWsq6Z6a3IjjqvFE/CNmmxgYbgGUHJE4BEsmJIyf/a50uhijl0MBp8W81J0T8KO1JrjmPG33e32BDhq8M9jHyZnm3PgS/MbrIeKsXjJFC9UhKicXNhdayLmOhSOgRXf9Y5KdJ1orfJgXhlRdXDQvidfDkNmdX5edFSHs8+wiZlpSSNx0gIJsLN4x40DPi422Hf+8sPIYJ7+hF7+ggC4OBgZSz4UDSax9Di2aBDAEd6wJ4+4sj3AICtu8XGXWMjVzlR3axYmJbe5kgg6ZaixhiAEx8FEo7eisThdRgHfVniTLHKUJ1xCMtcgvHjAe/+t++xe7PD7T+8yS8D64/ZKUSSiEQvK09EWd6KNKDVBiDGVZ4CisSfCsp4C/I46fatpaY23c3knnt8JunO2U6SyqOUn9JOMTeuZYkSldGkS0UDCwDK5yvHbPouiNbv/DwheVYfnwOXKvMp69Sq8p6Q75OIdC/MTF+m+AZjSUoKkK0Zzyv9uf3/KeWUuBGefr/URFsDn1D1+lK1vJfq+rVy3znwkmQyJ8ZcCsYO2F91cAcDHPRiMK13XTs1Ra3BNhoCleNOko8U4yswmSkmymzpdzBlO12O5PIToweSJ7hk+Ty1ZLVOXc2mqeI7fecFYrTbWuePMreXP48CbLseV9sO227jox3gIw/EWtjR5tM+gp4LouRUQ5SPJtIIkTDch1dwDxaHzm88uKsPcJ3D3uwBCO6vrrAxjOu+ByScoBTkYDYMJgNxAhf63ovdPYgIW+ePShpGB2sB3HyAGw8Y9m9AsgFx0PDjER3i/IXTSl/J7IryJc+IcilgnQXGAaPp/DFUbMDsNwmMMei6HpB8RFNrjIuIAqUzeFtDuPA64Or7N/zsboDNHXavvsH19S26rgdxB9Eu+02akvKbFjvVxoumXVF4RZy1/O9ld1foDal9WKS4BnqS+jdtcqR/kYeqSpLgKsjzK7dd/yUArYilTwX1ipUoiriQhSK2RH4jous6HMcjjhhhug5d12HjDuDDkOeZW7IhPUfCDTqg6q5Wz11CHjsvIqIewKgon2Fu8LRL5+ao8Mh1A5SiDMrVPa6teeibbZgFJVKoGSat28Vr5IKx0sFhHEdsDoRubzB2AmdchayCFB5FyDsOuUHR5FSYuZThQ0daLAYTJp6U3xep0ypc5ieQipwIvwsvvmwQqxo2i8uXKqheDGTx5yeDDx3jse/wqjPowHCPV7COIW9GAFH+aI/eJUFfEvU0oMa38q0gMkwkxh43Izxpa+YUon382SigeJ5n5BNxeqkpWx6slOeANvIQvEAW7bMEAAw4w/hhewMDwd3xEeYLDbF/CqR2/gJAqvVvOfEy2yg9B+hJnTBdB2vR5QSuoYAchRbP82zjO18InjyIkQ/TKkJoIYaCCaWjzOJ3EK4OB3QPFgdj/EYEAQKHe/wU8maFgkJUgERelbjissQy0B4fu78nZLbuFnf2m4D1CppRBFHTjTb6ZnlaAPJxH84BzA7xOKQkTDclwMqwNamwjevwcMTw37+H+8c3uP3Da5WWiq852CHINFRKHxQW2rqWteRTlJ80maqAZsSFqispc7p+Uu+eCCsy66qjXFv0RTHY8Vnz67qVKOmIirYkyHqVODm/6RC8xFZVdgbMFLhcT0MGXlPFySyX4EKXUK+eWPPZ6J/f3pfj0ws8JD67UCTEc0boc8gp0yjIixU8hVYDn1NxXd4nmhbnWRdOw6VKyjGOTy9xqQvPKfUU//2UK1jNwm1HOFx14I89cJweD7kM58/wtfYEmf+Sv88VlnQHxd8Vrxe16RCL0UlT0SrNBIWTUAhJM9/1s7ry8jVBohEA/rQCwsgdrrdbbDcbbAyjY4Y4B3EOLh7JJGqDh+JRQvEEDYAklucrJiKQdMD9HZxzODoLmAHm9xbkBHs+QADcHw6QTY+rbgMIgRylE1aZCNwbONeBR0l93/d+A8KJgJghbgDEwt3cQ9we7nELjIAxnb+8mvPFtMIUdPbcRxSNCKQ6LGw+OesgGGHMCGsMnLNwzpdrCOiMAVyHgQ3gHFy4FDJRdDEPqKQDgu9HIgCcHN6JCYYZcvUa3at/xNXda1xtdyDTgUwHoXAhvMQer2kh0qf6jEb+ZOyP5BJlTKlyV7MyCMHpGG5k56EoZ85OIfW2PdP1L5fo1O+rJeHXtyRFnMRnKvRC609nb0I8Vbsp+y6WVfRhcspu1BDGuu87QBhgQtd36Lse/fgIPgxF9tSLQfeOUTXn493oH1XJS8lNl70j4oRekQZB4pFCM56JM4VK9FwWNZAht5O4cEheVJVyW9Qxh6O0f+iL/dp+0NkAJCENEcGNFuPhEdtxADsfliTicWVqiVjeJGqLaaojHjL+nrmVD8uoCEnvlxaDRZuUnjVPitOJxzFJ8kIHgA+9wUdHeDUAGwdV7qdX+i4P8xNg2rpP1V7K84FCGCKVrxtfK5BnoyuT+bVyWSOa6K6TnFUbJHrTUlg3wm8XDDQklI6BEUSjjYT+cWEtCQfDkApPVBsp2TBCFdPJnCAZyoIRj6nH9uYt2GyBjz9lfNf1xC8ULse+LupxJr68wiM4CmGZyVSZ2m05RyGtvUz8Vy0FBtwKIescqBdvqb7qZ36SxPlVH7/0HKj8iE4kzow9RRIjbOYx+bsimMCOwRwvYCO8krfY4gYf8QMsBtzKW7AzeDA/wcro+Wf07AnRT7GxczLBxl3j9fgHxNBtfXE1AFzZr9DLFR74Z4y8Dy1thOtX0rUIYLcWH1/9gJvjNTr5nVfeonID75nlNyNQLQyi/vn+SsUHms0XJk5aNws5j7ow3T/xrZJiaNJaqRWWYm0mtVGxgobKzQjVVMo4fOlA1Tj776Xn5NOgXCfiJoI4SXwl/o7dJEGgfo6td44znx6Lp6k+a4AmXz4V/Pq582/w5QOpf6ugnsSXJuGLT4vf5tlLwOfqUcuAMwRrvEFVgoHb46Tlr6li50lXW9mibhYzJUmkel4Uk6bAXB9I9Wsil0/0VYkp06N8+XF4lMR4lV5c8IdVLS/kulj8E+0gs8atdeXEQ4IcgON+xN/+8hHjCLzqtrg1gk1nYMiABHDOYRwtxnHEaMcghcf/dM3O3zEmIY4zRC8kGSaMY8c9QAb04RuAHaxhDDeEj909ho0BBotgsYALkQv+H7yubgxEHAQGLA5Cgs4wIAa2twABo/VHO7m795DxAe7+NXjcAH3vcQ1GuYg/E8GBfcQ5i7+wGi7RhzfaO4gbYe2A45FguAdRiIwgRmd6AIJ+6DECQLiXIt5XEG2ZaU0PQnaiAPKbKWSML7frIOYKtL3D9vYb7O6+xna7A3c9pOshnI+1iEfT09xdrroeRYouKp2Rdl3GtaCvIHtSLIAoOHRKYZIkonA/Rijdlacb1XtwEolQIxajjcTjjbi5EcagTBOP0ZJCVWpW2Hh9EgSYOLYvQO2onfos6nbJIV+thyIA+8vXj27E4WghhnBzfYPddoeu69IJAcUy8qyGlViXBXwavrx+I2JRmVIq44wHW7brTNWceUZRHQcAQXQxlkiYRKnMtFAoA0gELlfJk6A3H2odeQKkJmtAUUQwOotxOGC0Fp3Ea3UktyPkTQQeH2kiI6DYPk28V3m8EoPEe3Kv2i+YI+C6UVGjFYRjQMpXGbfY76EJM0IBiEDMuO8MRku4HgWbk3j8kmCqqk/7+VOKhnmRC+ueFxhY/U58JVnNU55za1psmSz+XCh4isu8USLP+8IUG41jaoJQnkiI1s98QZmOefDrSw5QqjhAmibzfZb6nciH2129AcO0PVZTsfUa+Snp5jSsYcPPg3mG//yeUONXKABLWZbSLFN/Wxycxaz8fGpj9fJd72LP4ZD4T2VQjEbv4vGUj8/BqSa0MArOQN4TiigoB37t4rCpTSBcyyts5AYH/gAHixt5AyM99vIelsZiXz5LyFF+aLdigx02bhclwxIvAXZyA5FrHOkBI/YLrZiC3Tnc/9M9+O8O1z9/AwjDxSOZkDcjvEjgy3Rh9q/h606QFL2T2Igif32v1lSC90+jaBeEubhWls5csY/LrZklI3YaI2RJIqafDYg4x9J+llX+3K2PpdSXWbPbhg6kTYgJXUwn6zRCYpUM+HSY59HNVBcoaxla87xd3DP5Vj0YJ6N5fi3wco05VfLc+y9LYvoMkHS0Z5Sx1Pmtd426To3fc8fpc47/UyIjLoXXl0zfjgmuIzhjoL3sayNXk3UVXzCh4Va7l6Tb5hQITDRbLmZKnNQrIZ96r+Qtb4DX+V3gtequwah2FoVLKrvqogLfs6Elw9btUa+Hg8Wf/vgeu+0G//i7Dht26MMF1fGMfjdaOOtgrYUhgNgfkUrs5VYnzl/AG2RXuLz5kO3cfnFiZjAMeL+BE2CUEcfhCLq9hx19KYYNdp1JlzdzkBWZADB7g70wmL1BnJnBxt/9IAJYawFyoJt7YDSQ+2s4a8DGJOdl3SPeOYgAZjjnwi4IpVH3bXGAE4zjAIBg7QBjDZgJzB1MZwB0/jsLHA9gB7VxJcHmnO/qRJStEzbkNyJMB9PvgO1X6F79A66ubnG13YC7DajrADJwxVwi9U2NtibpID8Wr1Q/zO6JUU0/6xhMco4qyE0aiWQyHiSSNiHSu+K3y3lddsgq21zWNcX4hOUu4R87oCVRToGqb9nEFnVqLZMHR3YCmAkHO2IgwmbDuL7aod90/o6UQnBsLRYtmF1pV4C2lU2LugQfel5ExOxYKAkoXhirX8W3IYl9HCGDRXfVA0YTUbAgxMsRQ5mpP+IiUo1FPtcqI+dkHeGUbZgScFKQ9bN6JMJvZ0ccDntYN4LdCHE88QpPntsS+4SQiZYScebaJbc7Gkz1ZTPK0Cqp0ClupyBmay8zpxafsq8poOX3Wgibq+/Q96/Axz8C9rCivF8LfNo2JkqKhnAgHEnnL23y4ZPZqBcXxuwdvQQl2ytaRtHI94LjOkFO0xv7C6Lis0iOBJALm5oM+IgHjyWD4ML57L4QCve56DnYmhUtb2hJRSTv7iR8qWel9e0XDzXTfTo8vUNmeGX1drqGixLMtBgUlYdLhOBr6tHvUoisejjxao/4nbEzkc+hrI2V5xKdpvlTql6d7mn9Vq5H4R8TyHlPpfhMADAYd/ItbmREJxsQGK/lO4w44IP8ACEb+thHQXVugzv3Fj02M+O60D+Kv97Yr7FzdwAAB4t78z1GGop0LXDivIcYEJwp4L3c2dct8DIPcfRSyt5YNWhaLZVjIHsIzTSHzhkdP5bFxg5N50YzwkHlb8N0PhbJZ3cjct5z5qfmietAAgqnLjuPyVU0RMhfVC5ZHmpyET3Nq0/vCOYLICf4+oEwGMFP1w7OUHYeTf2Vzw2eO67pJJyZ5bmr//PKuETtv8Hl4csZly8Hk/PhNNfWfHhVhl8t1Fz8lzzu58C83v6pESFsfryCffwGx+EGIxkIrLLl6LQTk027SPU3/aoaWkqgntGqAyKgeybK92XZ8Um+XLq4yyvJVi7zbIQ0Dbk9MvQ0M6MeOGlXu7XnQWykqA2R3CNa0qIifc5Omx7dZou+26AzwUQoAicCJxZWLGzsG6JwvwL5Ku0IBKchX5M/ymkcRzjnNy/8MUbx+CoDRwwO6Y0Asjc4/vkadjdifPMBfc84bLfYmA677QY9AR3FTY+MvpM8cgzAEEEYMAxYAGQdRAjOWZA7wo3eI1NE/AXU3ovHY+J3OfwJJVaQjN1puAOFOItxHDAOg7epECdCZvZ3RRAEzvVwsCEqIo/BVD4nMBlwv4F0O+DqK3Tba+x2N+h2d+ivvoLpOpAxgOkgZNJcyqMc7Qzl2JakmXXCwnrRIOFlqAVVjUn4FvTWGB2jNxS8rlP1a4x8iBs+tWIQxiFHRYRnLoyTStPmAGsad07a6bKV1jLSb7Pw720/2f6jhj/dMyJuwFFG3H39La7+4Tt0N3dJfs8bO7G8WLHAjP5ydFo89fvctWWJozyf2zz/aKakmQWVNC74QPk99LYoj+KwdsEOFm4EzMYAxniipaiSR4EqmDUVl4lnFGdEoJS4xgI72TE40TS1yOXmTssoGKh67ZzDMBxh6YhObMCNEY+JqKEw51R2jMRUofohvhP/VDPVi0ADCb+wzGcplN0iXTyDj9Fv38CZGxD9FYTD5xeYXgBmqOQTQpx4mlDChgN5w7s2RDWpcVYoFPVxTrvm96UT3Z9RWobSGEVhgqTaCOGsSn15dUwXssdjWyqjahZmoSZ6LFcZ4Jq4k+Y1xXu139iEp3hafRlwWXxb69klapibn5HBJ1oJA5dZwfPmcUMXmsdQ8x8pvp5T0/Rx+eUZ0KL6+pmUaFRRVzTZJMlsx2+Qxovi42YE0jF/2dRKuJLbQtW6klcY5Yh7/hFjxW6NdLh2r4Oa0WhCQgQlo43tCY+2cpPa5jDi0fwMYGiXo4pxoCSQC7yCx0RZuCRlmFYCdb6LpkSnRq9+KIhCu0ZpbsN5ibrUZCD9NOfJsWStUufuJmivnrHsU2tg3nBbTPZseLIhvwLNSgp5qlZKKl2qUGBFwI5wdwCOBvh5h7BxLpM5Vrehvamlx7BCFk/gQ8/opqdnpcWfl4RLSHNnBE/EFE+qp1ZNLtstZ/Z54/1LDdMXKznNL3eLWc7UXs+vRMMnnzuX1I+o8e3SdZRw6YjlZ47eF6JTE7r7LbrxFYZ+G86b9GflS7QN1bJE0sumNhIpvkv58CIN1kK2TERXbRAS9SfHRwiKmSqVJbDhZp7X5qfq1GiI+lJdUF0fnFRCwjK0l00H7jqYroPhuMkgQDCixyOGHLyxnzgcvxW9/WOBYRydINwp4WCd9XdM2LyREfVugo8QcCPh+EOH8WbEuNmj2xiMELjNFn1nYIypNYxmnxD5I26IAXbZqQduhHMM60bE43O8c5BTRwnlKHCirAYUG08QnwcWox3Bo4Ezo68zlGGYAeP7ESJwLt5HWdJvqtW7w4NNB/Q70O1bbHa3uNpdo+u2MP3G20iZAQ7RRhJHWTLOqVBlFVTpCiGz2Ydq46zs1uJ7wZdEQhwMQi3KFVUkRcKIrlvyey0QxcvlSVTSImIi0qP/TeIAuFTHZC4WwvaMbtyEWnqarsytmZVryFqq/0nJ3jRJHMct0a3/19/dof/qK/B2G0rx7RKXezobswC2DuRegANUZw2X7TunT6dw2TsiEPozbCQAFM4j88gKhRAbMGKkg9+MSNMD+fy48FRQ2gLijCJ9J4KGPAsni++Z/TThCXOrH6Hwbotf7DjiSA7Hu3/H1WuLzv4z5PEO7gpwJGCqsaQ0kUWVm47XqC6w1n9nPTBn27zcGWlxmMACwVVzlCnf3cHwkRzEMeyNoO1AX4bg9FLw6VsXF7T4K0U9cNi1ZwKB/WIXz2pCuaw8SRAOxjtKs/qZsmIQSCdy6ZQf+OpjO8Iu52QzItxXEoVgfz01gkDEIIpHnIX7WiiKFGFmylTlqCM/iguD49wMzCcHUE6Z2a97Dnx5ENh58dsLM5zlnQaNTfWJQhw7v/6k9JSX3LXFw+m3+dKR6X42z4yKEgT5JUheHXXNooWjmcJXQdx8EJDzxzN57ysv8BL5+xUcCd7T3zBgwCv3LYwYvOfvMWCfLolLuEEw0h4/dX/EVopcUpgAAQAASURBVG5w674+38gaZutH8z0G2udycZxLGtIAo9nhw90/w9w7fP1zPu/UQfzGSGTz5AAJykshvDdAyebqkf+Mwn9auwT96x1e/ee32NxugxIZEVWZT3TJXJBCjDyBhHsMGsaEZtELUQ/xVbpk+ROdabOAUhu0YUWmqpD+rN9FvqlTCqbjrtesuKHghLx+7UpZOW6c+Ha0en5OuD0TavpZl+HMN18O/Manf4Pf4Df4DZYgKWJAOOVfglaZHLsUKJfT8Jt0KckWE4+1KRbh2lDTXKCnkesU5SadqdhsiPzVP4tGapHaO97nK8rTHtnJyNq2zyzKdh71wu7TbBtFeSDL/VqL93VU+gURRBwOhyMOhxE/fH+EHQVf3/S42nXYbjfojAGR7wNnHUY7YrQ+HsIb+v2RSAh3KIw2RDuk9vleHIajj4wYBjjnNzJEJPjtZNme+873iXNw9wbuT3eQ2xH45gCEzYurrgN1vb+/AQLrxF9nIJluENrrZUYXdAiAOwHevocce7j3bwDHaSPChcu3CzpMw9eQwYPORg6wdsBAALO/T5KDTcVfiG38xgLgNyLSpkiW5shfWAkyHdBdgW6+RX/zGndffQvTbWC6LYg6gHtvu1FnzeuLqQmSIm4ymqTINW8I5H6K4mewKEq2rVJNci0x0rmCiJMjGcIdEUGHKTcbgs4rWS/xmxQqwiFt2Kg8LqbVkQ8OKTKiLV1PoIjiXiPRFTJuuTalRtdZ0roU7jlMyahc1+K34Gw3uBGPj0e4Dnh1c4Wr7QZ916Mz96B+DzHHkhaDrWtdJMQToSSX6YtnwuqNiHUqS6DSOADR0C4xwiFechiMdMGwni56FskklLfG86BFJOLxCJExRO9Iyul8TjVrBAmHGmefak4J1jN1pkNUr4hiks45DG7E0XwPe8vYvf8D3GggTu2INmZ23HjwfVTXRVUedd59C63GsyeTTmuzo8KvbE053TxbpDThgHiJlTwDqc8N0yWlhM/UsCjrJZmP/XmKYH/eIwFkYoSAT1gaHteYBKY0NycqLV3Y2eJtVWa1GaF8ZFVG7eGroRA/Sf1OeSmJa9mIQ0X+zKpU60KSxY3nUF8aB/ICRxYPdV3tgi7tafUU+CUYh9bDVIhoiSxtmszrlN4slwsvX+01/Jwapmnn5mUz4apkVApfFyISrXNlnh7mDMWVLIyh4vMHuscBj7jFG4CAPb3HgKNCMSPoYPHIHwABbt0b5NvDGphMpmdQukhw5Hsc+GN+PccaVRmOOxy6HfZbHwnokO+MipsP+W5Gt8DVa1iiEClSmG2H6z/cwYTzm4u2zy7G8cXJ1RpxhZ7bkGrh6dfzadoleM5+xOWiKJJQmj+i0wgwkZdqeihLybxGFsZT65AUGKGXn/N9HXkTQpSRIlfmHcjCeKpXz+2O0/nnU1yMz6wsaHaNn0l7XjmXhKeV3lrRfoNfETSJspZs6mcn4NdKJHPt+vzidYJzu34p/almndJanw3aIEP6jogWFiWU1g0kJJu4Si35nHDaKGqpCi8e6R8xilAAyd9Lu4Wg3OhYaXWp61otqJ+A1jIQdRa1SeLE4XAc8bgf8MNPj9h0Pb77qseuBzpjYNiEvMFYLw5WnJfPw2UN0SjuxMFZC+tsWbUInI1HM41qIwLBFuYjIYgJJp4k6QBYghy2GAHQq0cQLLg7wgDYsvHDQSEyQfwIeOGZdOW5SwgAC/j6COkt3IcB4gyc81Eb4pYtuElGI4K+dtlHRlg4G6IsLADuwl2c3vmT2V+gjehIpYz9vu8k9AGDTA++eoPtzWvsNlvA9KBuA+9+ZcLx2lmqz86NrjmjJuRUO1PmwpSIL/mya/1+0q8t7TmbCrMzjaTfOZuWScuoonwkk2QFO21Y5EgIv7mmjrtK87TRERGxqi9att+p9E3TX9nrdaYynY/0chgrKVAl+LshjqPD0Y3o+94fRdYZGENgc4T0Dwnvuhp2F4qEqGmherw6/xnw/IiIxhgEOvaDGQ0JohRU8hM/GfmcPs5HAOcgDL/TRqrPo3dyMOaJylNPrMbUUP1aKaFhQWtCrJxz2kn7C+0SaZJcieCrvcC9f8B+94DtOIKcDQtwVrrDFRiF0YQhypfT+23HNqeTisOOS7nenuBkMv2ZclS7pJOGlttw8/UoSSLuAErA1R/PRLAE/LjpQcL4enDo7WzFXzBMjZpfBuQz6Px8I2xvfg++/Qbd5hbEhO2rR2yuyJ83GM94RD4CRUPp3CFprc+1lXQ0RxlrhF8thE6QOHkU0jrwbQztYH/Wdtz0IwqRDxSYXKDZaUTS6tpSRJALMgwxgVNfx2l1KQn0c8IlZsLz+iCfgtoSjsp1vym0vfgQnBrntmB3spylLEEGSh4qRRn5ezoCKa1rtRA1M75rh53qFSAqDa3bZPwTJgIYcMwgCUcYMeHN/QOuHx/x4/U17MYEXB1+or+AQRhlALQXuISIvPgJ4EiP+LH/I7buBnfu7UzDpgrlR/MjjnyPgfeNPHMlUEQDIoIDC/7eO1yD8Wp0vl2OAA4ROYiqzgxP1msygPIuG/8ieT5JlEl0OaRl47roKJkhbShQfjN93iqj2owATgjsz4SnFD3JUykb1ft6/UgQBF4JwlgyVCgPsGzIQNaXGpBkuTRuMa0vz4XLqb08JYAQHMUzjgmOIl8xXuFVEeER3E8E/NcO9MoC3wg6MLYwIHWfhG7nL+N4wF8Cjr/Bf3T4PBLec6Tlzwu/jLXnN4igdUAEGYDASq6cMxipr8Eeo00ykhljSuc/9YyS4PSvZSbFbJXiGm3A+Qri+F2XKcHROvNcfd795JjDWF6sRm1e6P7RuLl6RXjKAqG9zOuydB8QwTnCz397xHE/4sPDI6yz6f7Ut7dbbPsOt9fX2PQ9+q5PJws4cRjdgMFaWOtgjIEhv1HBxHDWwom/L2EYhwkOw6giIkQgYpE85eEvpCbHXkdGdpjs2ACHLca/GuBuAPAI9BYyOnQdhwupXSgLXk+P+jQxONwVWV7lLIBxMN+8gxwNxr/v4CzKSI6Q0kUv/WC3ynbEUjcQazEGpw/LBn2/8W0KdG9CRASz8X7+1oYoiDA83goN7rform9xd/cG/e4GtNkBZCBkADIADIj8MURJJE8DLQUJNKgOgL5LXWsm0SYyY8XRRRTzUupHZaJiY0DSvIvHlonzdCDOQV8CHi//SBESPrH6rdJO5nkTkzY0w7qnmxOplSc3H6j51ZvjCo0aOuJZ/v/s/emTJDeWJwj+HqCqZuZHXCSTzKOOrq6eaWmRERmZ//9f2K87K7Nbu13VW1mZyWQwGIe7m6kCbz4AD3iAQtXU3D2CzOwEGW5mqrjx8G48xPfGhHtLj/6E26++xot//Dt03/VwX32EmU6wLUODGnahxr6UdDZkzPLxGeT0BOZmuyFCweU6WyPCKtLRlBymKRIYQfmMoCyNzwUYw0bheCmz7kIEB2pMeu5ePpqUwqrIskvHGwB7ZhLluEudLd8TXb5hAD0BN0T4NE0YpxGeXbRY5c1Lah7KipEnmvJDYhXyJv9J402XXypcIjlWhd/2qFsjXi1RL0waRlpLjpvS4NR1cN7i1fg5zhJ9zkSNb7+UVKJQBsBEMP01+t1rGNOBCDC7Cd3egEy3yOwvEpfWrzNgUasg19J5XFrhmKhwvNChFnmDUMJD0PaGqJiVerl4f95woLYt8kmg8J0twRsLbywoMmXbx/9l0iVtP4/A+ARKdi4pHWLtBP6l0hxi1sZbvtMne5Ygb/3UhLDPOmjaSu6Z0jXS0sRJUfn60glVCCHvLUp7j9TfkF3CNAWDxG4aYZ2H3e+h2ZgTfVL9a7GTpH5NOJqPsLCA48aYgCSepv4yRvMQT0I0GPaiqCbEeX2YAWeB+x7oXDA8BDwd/sjx8GXmngrBfRmq9DfGIgOABt5cBJHzsKPbPGewQKO2z6l8olmD9WpvKF9949mXRuLGuqwUFMWHnzLj6Scfvfc4VegpOKxoZQkgn1QqSqTnJwK/I6AL/LZhgmEzy7cpXUxvn1Tsogy/PN7sLzG1EMPPnR67sr+Evj8hKaXPLxO2z/PEX6YPyz9/Cekvhad/nvYoM9xN/qpOOVTN7HquOmflUR1IYqXUaah6snzXeFl2peSgFG3NsTsAqAt1g6JVh0BS+VRfRRXyXEkbT1pvg/GE4B3j+Mnh4cHhw09HTN6j6y36weJwRRh6g77v0fUdjLFR3xQieDgfTkQkOYSCwSCodsL8OB8uo05rE+9m9M6neyLYezCy4jnIJAYw0fBDwTEHHEMQ+Q7+roPrGHTlcYKDpRGs+H4xAIXZ1gIeqX9KL2UY9uoIZy2YOjDkjgsl+8yUZnIyOzgGF5AWY2O6icCGgxECBGsNxARnKBhXRB+atAhKpiLbwdguXhRuQdRlIwSpqA8JrGTEJfyncPhcQUcLHBG3Zj6KnWA/qUsbe3EtykXqG1f51JxmGJG9pYwMIq9IhyUkk4xGeceWe7HoQP65FfGlyShTmJ4F/KXzc7ux7NybXSVb1RhDwTnWEvrDHt3tLczVBN6fwA8erei/RXUazC/ELyWk188alS3U/xi09rQTERdQtYS85NLYFJInbn5HOH08wVsHv3fwHcMQF+ualeti41wSwGVj5Y6KZ77OtE0EjQCtT2zEBppsV1Q+MACzM6Ce4acRd3efcMsTOvYxpFogDDk0jq5ChHeKeIHB0MjPANHSm8X9uIeSAUdTxoWhFcPUG3kbKOmsGldxrE8rFIgIhgJJIyaQsdjd/A48fgVz/P+B/PELeCM/b1pCKD9nSjQueka+HSzueouhG9AbA2MtjKXg+S+nHyKPmOIOzmRPzgZCoGS6NvZpi+J+S6q9c3OXSqXXKpGEMMiRUMY5CHvNgNPeCvk4c64IR6N86ksTVeu9B8BQuIfCkIE3DGMYvj/gj9/9V/T3H/D19/+Czk2/CDHuMekXb4QAUAK1VoiVflqPcdrOTFyoaNM6JnjTR1KlRwG2C/pW8ohFI5FnT7Q1dYKQDejRyiaXP/u1/UF5TQsvjjTESyZJCm0so1AQg8JFcwB8uqQaOZ6s4UhXAu4iEMibYt5SiJpcdRB+2OSQjme7NOc1is4irlaxBvJC0eL44b0H7wzw2x38Ow/3xymCTzi2HRbARHxcBodD/E5Zeohee76kx1ExHe6e+HmwSoYhLK7/4vz/nNqaWaoFkBKmKTpeeCUMchS4GIiXyql3kHechF/24dP74JATTj54fPrvP+L09g7gEAfZfTyBnQcRMBHwx4PDyQInJhgHOA6nIIh8dboxr4WcjhGYGsnjSCM6WHRs87DPSaL1fCz8XHn4hPTLAZBfTk/+lv6q0+c8UfZcSdO7v6X/KVMJpYH2iYil/mCWDdA+FhUTzfNH6U1WSgKlgjPlUacT0l1sopOC/pnLJiWuCv3CPtP3pCeFiJKMmZCsFSQQObWWHVu6lyfsIdbFGcZ2YALefj/i+ODQWeD22uCwvwEQlJ/WmnAnRNdhv9uFkw4i9/sJzk2Y3ATPga+w1qK3fbjMOnKYznm4yYVTD7F1ka8Cf1pp3IhgbQ8ig67rYcii6/oYoUFdIBrYYfi7AcfxNej2BLw6xsuvTeirMeGEAct9JAzKN0DGqZB1D1EP2HvAePTf/gT3YDH9YR+MNarhwLqaiHpLZ40AN2JQCSdLGIDxDmQA9g7MIeKEi+Gogq7FhDskwPAcL28HpRMRdrdHt7sCdXuw2cWuGEiAs1rvNlv+xNuVGir2XJWo1c2cyqN6A86onXQelgZ1vdlZRoxYuYn43Id37Fyav8CXyikHH/egfDLkzo+wjUOetI+KPizjCp3q0a9mQiX3LuGxRd63UgxUyyB7auh67OFheourww5D3wHk8un4xvKJDDF1FsRANzp1T8g53n0Jp9alVOdXJuyxWOsyQ8RmPkgUKfVW0Mf6VTgURJCdPLwDpsHBwSEo3wmG66qjOEe1F5dqp0HEpF9ilCgn7cwU1sxVdepCNKByYoGZg73AGvDk4KYRnlzYgHKkQ6+2+h7sD1G7FB/rE1PUgEeu8yGrtJbHdh6wHpOS57junO4vEQwMuv4ajA5sejgTwlbVF+38stJMFfHLSzLpsYOjITxYiz5eOmUMB0OEyUcNVcEiNAuwRabICHaTAvYpKe4xbYxoRfjLer/Le5P2ENWjEYaqzWCmwupBrgs5FBPHC6Bsh+PVazgygFwW/ksG/Sp9qSPza6GWJLVYKyw9e9ZuV4tW/DzfUMqu94/sX6EnkfngIn8W9pfk/mbd6o3u3dlTptoTp0qsvjVhon60Mi0FHSuoVxQKKMKDkmrFjGTYwqJDUAczPBqn7GQeE80lGG+DlUPjvIVueniEALDrJ/hqw0X5OxJ+C+DA4I+5p8b7cHk0IxiOfEAN89jKUlUWlnPdaqxcwk4xwKX99Ez74yIjhHpfO2YQlmHvudKW6pfCuikObbW8iGUiM2n6keiVCGDqBd+fwHenpEgxFoAlGEPw5HEcPE4dhQsQ45p7BkzyOitHKCEypV1HDEceEwwslijqhvm58E1rtmY5Fyv9xXJf29J52fDZmsHFTT2yY4s05C98rRbS/Kzdl2bengmILq5CC6zP0+Szz9xfJ8hdlLZOwdJqXrrKrfxZ96OI3GrS3OS6tmvO8QivKHRP80Kx/YoF0xUU2qBCfmRVR3zKUOPJz8vPxrCEJpcPl8ep02b5sBYIgh6JGXATgdBjt3MwPIF91MeZ4PQy9D2M7WK4JXGAyQph712QJaKOwKiQzkjOtSFMpMyciUYKCflDVRfD/QkW1nYw1KGzPcRBsuDjCYDvwPcWbvAw4xGOGMaEsEnZ2ahgHoHURzXd8Sczg4yH2UeHEHJgb5GUbBAH4FiriRUwAG7w9OzDXRHEYO/gEByjyMT5U+uSZAIt9JABbAeyQ4hUYSwgd3TotjiZs4Dqc/mmkjieBRjKz0voLDPJR+Jmy7KVLJLDeOtTC7I/fPE8GRaS0w4jGR6KcjVuyDx1xje6/1TkXdIPsP7RfE/LckyCp4VKqF1vxj25EibAWIPd4YBu18N0IjfoSW51kuJ1BgCbKKaqmVqiB8ur3bje4Az+eQodf/SJiHU2iNRfXSaWEiNERbYYDEeMP9oP+Mk84Dv/AgO6LPYrakcgZKGtngQFhiSbviaVW0ShmqzqemOdFcErSCkDzB7jOOKEB7h+QscOzCFOnJFTEW24Sp8S21r6wTE2MMBKEZURkiBN3nJxyVqWVKUoxs7kb5VH8FgVz1SDcDEPolertwPev/kn0HiHlz/+G7rpdGEjXz79MvncbGBLxoRI0A0hWOGNQX97j9010A3R88DEi6JW1Q8N5grIcPFIUfeLr3LiKZf3deJBiqdU/FaktsSDCxZ5wXVBJxfXROa98sq+dIv9LW1PmiolXbZ6+5h9ndnr5VVLbwW2NCMuDCQJXSzZy5A0w6rzlUx3CmtEKryPGNR42a8/dRLlLNR3xagX5W8Zk7SzXaNYVMl64EK3GSDihNMCPov/jBhUDV7zd5jYhQvz4PDW/DsmhFi1EqaGiHPlAHo+4LX7NhowzqdP9i0e6Cc40z4fG+Yby6AQBQhmgKc7+Pv/jrvTHmP/Da7Z4KWLPA0bkPcBZ3uAzLzCWtQQGSDFMFaMP3MZb7lRyWwcT0lrRog5aFBR5hdBXGs5YsEI0SpWXCWUUiYoYY8EoZTluHk6JRtDk/p4F4Rn/MN/fY0Xu18lr6dsgCSM7DDc/R4/jSN+//+d4MYQqsn4yPsZhtw3QqQ2Vvz41DFOPTAaD0eAcR7dJSGalqS6z5p+CQDyhPQXT9w1gvsLX4u/+HQ57/18qSZ0T6cafwWbo0or2qezeb/sXDw3FBXqP2bQeIL1H4BrC/RrJUWmWulRDSqK3jaNBOqEhPBJUJ8Us2SFHycZUdswckgm1XDiv6QT8VnTcXVJ56TLPi6V6taQjA33N7x/Bzhn8ebawpCHQZcGFeY6zri1IDKwZAIPwy4o1KcRbprgvEt6BGsMOhIHnmBs8J7DqQjROzGCww0Z2KhP94gXM7MDEWHod7DWYtcfguK9C8Dho+GDTsdwNYIhwFowGeDYw//xBtOrj8CLj2lqRS4IxgOGnHyQ2PtkDBg+3AXB4fJtgTfxwIec3GAAMPFi6HxqXuCEwTHElMCJ8N3BUWlyFsZHOCKKujgfT0YooAqCDoyx4G6Au/oWuPoK1O8B04HjGMIqTWA/xfnWl9ZGGTIKlgLymfW+DL44LEAJTIuZWX3kfeOZQzgluVgaqguR95X8+XRDPvmQPGv0nhSNizyW30oG+rJU5LyTVHZ6l4zhFAdFmTTo5gjGWoze4/54j/6rl3j1n36L3TcW/O1HGHdCdzcC7rIQ9rWMeBmNqWj7Z3YQf/pl1bO0jaQlFkqQIWU728mMAOkobPWmoBRqoqixmLuoPIwAa6pns15LZ1Z7rDte/6i/589gjZ7g+wkwLgm2GWHWdUTTSaGwwuy0A1TpHD5meSvmNxuRzFKKFW3e9JTXOvyOyjRDIFi43Q3Y2Bz+6hec5j1s9znPzZdVu5NuEgDIgswuxHskgh08bB+OYxanHwjlZ+qyYr1WhtBWoDYyrOTRBoJFJWjKK/mkYU7zvRUu63HN12ylVFG4xQY2Uj2muFgna9F7C8uuIFmL1Zx5/2VSPe7P1cr5ldyy3mGqKXick1UPtxSUNioISdzpUicqRFkfX5gdZ1hHrNqg1apOV7E6HhalvK6Z0ngkXJu80Z9r6XJoaE9e4S0kU0JAOplBQiMJnfPhngUaYAFMmDDiiITZWOOSsocGBr3fg2A2dZ7JwZtpM0wCC0vBMbY/neBhwYYx+ODJTsL0NRTH5+oX2i4MP7MHjUdgOqUYqyW8cDH7W2mblKSVPKvoe2acqGjQWtrII+Qln0+cppGz2uQ5lQ9oOcO2JGSjYFM5Kznid5H/iD06eFxdDbi52VW0KhguT37Ci2EA3zN+ugLGYxbUPMLdDzquNcX2ZcEnAtgAIwPOQPv1bE7reGF9ji4XGp+f3tQi2vNyabQsA+pcq8P6ZVD7lGoGc5HZwy+u6yWHJzLY41b8y5+AWEprfNga0D1H24uMykUb6Sl778uA2HP27HKs93OmrWtzlv9mh46ms3JdoRjaJFdlgjrjhbl8WPJKZebSeYAbn4y6oaSETvlyUJ+kZ0nFnrjmqXgNP8v7z/vQI/YGHQ0YuhFW4e8kSQjTYYJhIWFG5uwwEZXBgf0O4ZgKuYHVVHO5FoaAECYJ8MbAsIfncOrCdh2s7dDZDmQt0HWxTcCwz/fLGokcYEDOACeATxZ+NPAIp0NhjIJXER4oEFhxtiQDsENSYMvaEMP0DAcfLnCr5lfkR8WwNVKcOQbgPdgA3gc9i/cyp6iZwDg+CzIWdriCHfaI8TVVjnz6mWNTcw/8bIRoUoUEh9W+4vzJOePCIDnvFeZyKvQXzmaCEv6rfRSNEOl7sWegnlXrNZtD4aJbg348lUjSL81no6h1PgmYzfP8AwKfhgyYXXAu6i266ytg78DDETh6mJNL5ejRY+KVX2vF1nM+BzV7tCGiFiWXf0HBAhU/NY8usncGXs4W6FaFK8idgWRxEgTimUNYlNSNUqDkVjMLdafdTgIUaRSz/ASApxMepiP46i32+5d46F/Acxci2bGEawmQno75JOAn5F0Q74lISgoDYh8uAI/YKRkkuO6VZimWmCGFhioLfhbHQ7tMPiCkaLCdh1Qi5DZjaZIV8fGuCIahgHNZ6EWBYP+y0+NYzkvZckrgTKBw0Q3yZO6uvwNe/BrD7gbWGlhr0HVAZ2y8UEkIdPAomNn3Yj88SngIr+SSJE3EypGEHOGbVrFnTNBO2oqeHVIr4KAM6iSuqDUxmnmxoBiPeKRCGCqEOQinkOQuFk1GRXkUd1XS7rRS3NPxqxGGLY7HkoHvdvi36zfYn+7xu7t3sN4X87JK/H6mlPvAsyfPUes52F/bVwK+szwEkLHor96A97cgE0if4Jz1IdTYD3DFq8beSK/zfx6u7JiGzbrDhkA+4kWYlHc+9vowLtK4CjwueyhOEBd3WlDkhxLbpU5VKX64IUQGwSTXFT4UEtGuOQn/S8+lozXzVp4MASGEOWSAvAleXfE+m1cf3+P6E/Dnly9x33d4Z/+AEfdw3gHxIj0QohgUxyTLVShe67GVM0og3Exf4Ype4X33RxzNh2UeRC2SHodMOYMx9lf4qf8ndKcTrt95sCeE497iMSa8ig+DT3gkGlrVeeDAjmR+SQRIOj6g+7f/J/h4h2kaG2xTNWZS2FNO0Eh7ygui4HlIF6ficy2dMz4kkDPCO+RaNQ83uwMBGl7L/POwT+1GayPEWirnM0ywV5dXRiBHmllGEuy9j3dCMOKa+aAT8B7fDMDL/Q59Z5KHofxlAB/JYbSMb26+w9fXjH98BRynE/79wx9x92nCf/yrC0KwsemOkOCJBbAnkFUxmNXMPu5c2Pm0VGvz+faHv8C0vZ/rOR833vPc42eaR82oPVvazhP85aUGzcYSDy1FtCS3ZW7OINdnTVUfPsPS1REU2sN4Tjip5d/lXNundI1z/eWmNs+9POrMKQRj+OHGo99N6HvxorfQM5c4B2o5ONQy3UrnuJUvM2M6tG6S4VLsfC0/RmaJfdJtBDlTvZd6Cl2JYi4DY1a+azHqICx6ASxGtSgHWrjhRYPCu7eM8Uj4am+x7ybsugHGhBAuLHUzwBLONCqDfbxM2vkJznmM0wTnPYwYDwAQhfsVQgp8tjUEawystZicA7MHTAcyBl0X7krgieA9w7CHIYNhd4C1HfphFyKtkwntn0KII7IWZAhWnb6INhD4u1v4hwP41Uf4mzv0HYONDC7AGBGhswiGChcu03YYwz1ciu8xO8but3dwdxYPvz+kMRlmEPlSHy4e+/DpbhCRmYSf8uxBjkufogQ/wojFHUIWtt/BHm5wu7/B0O9A1EVeX/QBQc/n40mI2mFRg1kKAa34vkw7srxV7Co9wErHInBcaHC8vruBsz4lnepVdzxIW9pSJRefuwnJGAEO+kx1R0SedOmbU0x3o7/NdClubdGW1rO8n5vqz/iciHPI/rgqTCbJKtYQho7gJsZkR1wdDPa7DtQxXIwiM0drOYTqrGcrpHghy8+ePsOJiColWkPVY03kqcxa5PKg6pKYxUks+ZRco/qQfC1helb8XJsMdbnS8tJaIhh2GPEBvrsD2ytgslkybCgElqvTHt9Vj6uYAKvVtAazMel6k9ooaCvK6lrDioUTs0EBU5MxcLYHsYeZxoW7Ii4b0fOmjazmeUlwYxvbxkrFt6x5SQo426PrDjDxjghRNQjNzKcimmi2+Rl+CKO2aWALfV8NFlM0JUbKAukGzhCQepY26exJzTimDs0um82roHfdUp0lLisrCXOcwsxEAsWWMO2uMPpoDFnp+UXKnEb5reV+/rQsxW7pc2veBE+N/QHTcEA4FRE3CpU7oG6j1absG17LVNSQ70RaZJwSnCDml79xVJHBbAU2jJ0K70vtRRsnJVRBaTz6c9axZKS4JGUiUGI2dZKvVax+IXgrI6146prQew/yHjFULBwdMVEInURez2DmA4gNrO9jSKYWy9nqBGDRw3Cn+JGVHTYnkqlmBsOTwWT7GONWG0sjU8EAEyeDUbks81NfrP8lL3gPc7oDTg/xqP0ah5PrWeLGvlRK+7DwCEOehAWFpzrIc0HXuahvdhLijHK13mpVzeXvZCjK9znIqvn43FgH6oDBAoddh4k9Ji73ugdjBMMR0JsAw3Yg9I7wgoewL3ZH+FGENII4zgRaGk9KTAQ8GBgWr8UGw7Y2cMzp3s+SnqHpx7Ixba5ppUONV4Xc/0zT+PRqFnDFilzyWJTR5nNaVLjm2S5vrIbTx8LtY05EPEZd8jxY+PHz9SzpCWLbjOd/ls5gmQdTLV9Y499SkcoY49YCtueM35TsVpZaqi2nR4FSsd7z3Turk+untRNQLW9y9e/SRNWMbZON68QA3MRwnjGOAGBhiWDhg6NhvI8wceDE6RyHYYanUEsKBakovIQ+yk4hcXdydp4L4Z4NjPfwMCmEqjExDDEZkPGAtyGftUE3YY2SQVJ1IWoGUeK5Ccp/yNtg2Dh1oNHAkZz05vi/SHUm8DdGLnxuwJlhmIHBE8EM8SiJM3lSEUGIo8o9LXO93pTLBK+P4GysV6iWCyiE0bKmQ2eDsSed/i5oXlKEzNZcf6Y53JL0iaEW6K6CoMgZOV+amxn06gzqi85bn4oAZ5lFyujPDVvt3DRs3mErhDhPYU1n54U4yvgiDuZQ3YSus9jt9+j2HagPhj7yHudpVazLczW/7WH8EtPnN0RsSLJc4d+c6eWEeih/sPrdqjPt2YggY35WeAIIx79S6w1++ywPFde+ufE5tP/1iyt8RQYP+D3e9oydvQZPO7VpK4YrNUjh1ASgTkFkoTJNnIr/XUxNo+ObeUJlqafYPjGDDan4AboPuetpKoof8ws8EU9yGCI4O+Dd1/8F9nSH1z/8C+w0LfRUb/Ivlb40q7ltbNqrNHhChM/s10iZMUiXQlkYGwg8hDkwatdROb+JQGzp36ZutzE6b0G2aAgmKwSiWZ7r8CQU+bHtbF9S5Ki9u5wXgREhYcIjljOA8Qa222P/6ncY+h9BH7+PhzpoVuvfhJ0y1Xgs/9Z/oUzYhMla/Mer38BfvQBsjy7d0RFxP2Vld/x5tg+iIBcFH5jA4sVAtMATBHgITHy90lzlFBAP+FJgSeKBRvQfDGjE4WQQOMWqLwXCuu7nUcqcS6T+ZMxUk47wTY83nYZkiicgDIwJzL2hcETCmHBRdQg1F+5dMXEB2VTzGtdp4D3euN+GWLkXhMR/1MATIzGnvGJ+8N7DewP2HO7NBoJwx4H6k5yKKFmUihKK0CO1ZoLMQHFRni5b9EfJOWchoZFBm8hoLeOGanV4sOb7QpykbISgVu6NbVP9O8NqUV/1XCB32UCtjqgnho+T3MXRMsHscfXS4eqlw/C+h/eMj3C4o7kwwj6Mn9Xfnix+e/Md3uyOMP0f8Om9xx//uwu8m7EgBF4Lsk4/GPgPHa5eE66/ZXRMmNHXagbOpgvp8WUVt9IvkTLWfV2RU+rffIES4YulCxb12da/ruiXKkJ/+fT4KRb58dEVNNJGiXKz4Lm1zb+lX3aay4zJ7sBA8aOgp21v5No5TPgazeqc75LQYiUjSKx6ec9QoWcU0Pr8XveDObCQ56IaythSxIoKyRtS4ywEG1KDXapc9EaBj/jww4i79xN2g8VhN8HSNchYSCx+OD0LwpYoHgVQClKLvg88qk3HxwEy4eRC6LVJ/Im1Bj06WGsAD3RDF40QIdSQjfw6jIGxBl03oLM2XFKNcGJBLr4GkAwYxgReOHjLc1y2kMd/vAbfXcF89R7u+j7yguqUSDS+WBtOOfiuh3MO3jnltBPWyO4drv7hDu5jh+MfruOa+JRH+kDyLM2foNXoaJiY0QhfyqEo/Avym0Pgzbp+h24Y0MULwyGyI7IyvgCB2ul3Syr0dFzUwflpBLe4F4qNFteF5dR12XYum3+w/pRTGmnS1FBY70GOc85FHfnOiPRm48AvT+dI5Nz4UJXOHuoLtQdMZw2hsxa7YQCub7H/u6+x+8bCf/sJ3TSh/3RaORUVEzHIA93oojHiL49XusAQsZ0plLfFOjyL2w8XH6rCxkMdIEIRvQpAAk3kLIHrKltN6XLznjWTNQZkCPfThNHfo4dD2k1rU5GGFbRK80sQYzaS6S2VOekl0PCUXU9LWRMfQYiW3iV0IIYRLcarGOeiPItvjLVg3sN7B1Es/NL20y+S/dXaEAiVAyZDcETwYmzoPGwfFOCixCFkhkPsTpJq0pdCf1QK+3qJFtesCVCZqJxLUm/zZMTZjbRU6eVFyoHwDPrXzAelwhogYlhjwN0ADDsc+2v05gh7OoIanZP908SvCz0FHjnMzWnbvGte+bLa6/qXK1juScT5RBi7AegGdBKDMwlBTU3mQnU1cqq9mS5L4t/O9YJJO1oYSaciMraPpastRkmiasFBMa8rQ17yCD8b67fOX/9gTd7CONO0LiD/WeCYiLSIPTrnMEwM0/vUWDIYzuox4XQDrGIJzjGPOVke0PEOE06oRdC8BnFdlog2ENfWgc094HZg7IvQWcKXZNwXkXSN+iqBAOpnuhgPLbw569B8DhJqnfNX7RqiklvA9myJ+Xt9xD3/Tou6UkFLhXGuUdIfy+Wp/H0J9PPsr36TnzMD1gMDCDAGIzMmZjgtiMYKDHG898OEJYv+NL3t4dnjxdUeNJ3w7srBTVGAF/5LEI0j4GjgvMdIjA4hYIaJvNnWcS7DVMmBb61vhYRelC5q87O20eZPzktRl/d8iWd/ar3bW6ZC3FroxIV1bmjzCyftE3xZ4ni/4WoWaWRTffP0BeajYCo2CpZnsp2b0+dxlNgKU8/RzqX93c7r/uWkzIMaAE3GQKXVGeP5j6SPqF8vltOPNF0VPq3i1xplc7z+5SQ6jjB24dTVdlnrqh6Mrmi5peK19wzvCdYAlqIjC1kwYghQKnkRjmGkauW0IYInDsYAIBxrqR32OJQX+UOMF4YN2Ph0SXQ6BR15cmPiCQtQKUv4kqMmxFMY0QGWdcOpjAE8gU8dfN+BrAMZCVeeRgOQiSJfcGgiJwaGPNnhGgoPHjzMfgKcBTsTIgXF+dEmnDUwaPgelROn8oULwLsQSlPNB+svCufOqq0dVS6QSQX+5ycZOBlodDta3JATvumT69G1WtPOUlk2geZzU584fZeB19Cb36t0KeqtgZrq2Yuy0UIh6WdLLl7buUSBJx+9A6xBv9/D9AzYE+B9Mixo/ZeUbbVB1fostn8JaWkpEJ45PepExDwwwIWpIkZn9T+89JPbGRAVCyk6bsxDcXOyyiULy171STHTZ7pF+sfCOAKiNxjHEce7O+x7FwHGp7aC52OGsiD7hy8ZoYnXq4xQkeA0DhQesvIqke01xYj0n2df89wwQiw/H+LnM+KRPul0ddRLT4d4H3sTXlLUuhhDYB8uMkohOJppZZL/KtL2PaUVp6KoyUcmCe96i49dj0O3w94a7G6P2N0wuv0unI4I7sPIFoiZmi/0SBODWT9Z5VEkrOF9O0PqULzfBePWJ51I9qkwkFmT1SgY/pAQWw6VBT6PMhFsKi4hjV6YNHESDxOAmeA5nIjw5GHYYNq9wB9+979h+PQWv/nD/wvwT8Sxf0tpL4DEEzh4yzMonxKK3jYgMcyFshE84vcFBe5siRig+f0GwmxoxjjlusDimk9FZHAUlCtGLkHxMoYaJ6+S7nqIiRxR8/WmHguKiTgm71EUW5breZj1MwyMDMEwwXA4OhBONBq8+eknXFmHP359BPVAMnoXzGNmegVtBDobVzgJaMsqDwLhdvoa13iFd/3vcTKfmvhO55c1K5Lw3VcPMN/+O+wfb8Hjb8HGgDl4YTGbgI+I1DypOcsLnEcnSDXx7fE/MV4p+D7L31RwtjUVxgiB8TQh7Zoy6s50DUAhlJH6ou+GoOL3vM5znZ8XreBdM/+0DBshNZhVtRZASWMknq6sz/DR4IU54AM7vMcI531yiJL1ZSDdEZIiHRu5BwXoTY/f3fwGn4Y7dMMf8P6dwx//TToSYiyHdQ1z/ad+wo97h++OBi9HwoAOHfSFjU9Jl0LP8xb/xaRHHXX4Sxx87PNfYte/QHIEOLsig21m+f5CecNfAlv7c7f/F5geo7fSpQcAAxiTUMEz+KE2Sj0ObLj6qvYdc9R4CyOmZVJ5FlXivlE2PlpTp2S5MbsLLamHfWLqVOGsnGo0oiaP1TMCrO0w9CG8Yx9iLob7p5ycYAjjnbvQ5AoJSDISEE9EOAvvPZxz6VlqP7IWHTpYGx4EsTecRvBO7s0iGArOuSY66EpdDMbkHbx3ETwonnQOeiEYA4oXTQtfySJXE+A/3II/XcO8egs63ANAMnQQARYd2DAse5AzsJ7B3mNybsZb0rWH+ftPmN73OP5hH2X2MAYv7etZS+JcDCEVZX4x8iQ+WMI0pTtBDEAW3bCD3Q3ougHoOuiQvAXYNffMOYFueedonrJ80QZsBqJTi5yK4CQrc7zXIZlqdBWyZeJpF1blw16MpSIcQO7KTNaNqIfSd6nUlT9nWuTXyra4Oq3AUem5qsOkcM+KsYShtzi6CR8eHnBDB9zudzD9BEYMT68MRIVcMhdry/n+C0ubDRHbhK/n4Tx3vsPedE+qLSxbvXO3/t7ORc9yVpCQCCoDzjt4N6XLKMNzbtUSy4rAyYLDzhI+FsVy0iJw+X7DmNbQV6qDoOLp546Vo6hORaiKxRMf4Gg0ifveWoz9AZ4I3Xgs+q/rfd7U2tX1841ptv7y6Dk58KyNyuoY+RLhjQjeUoy9aEAdYGy4ryQZLnQnZ0PNzFYgNFw/jl845qlfJNYOTxt3XTZ7284UxGn7LrT35OmvJ6mtlFr2k8i4JSiPOMSxJ8BYg2nYA8cdqBtAbgLcUniyx/V6a03nPc/O11SfgPicp5taO8uol9kQhBSSzCijXetvOQOfWaOi8Xo68bAdX4iXUWErWyuqqxbGO42dInqZYZbU1qOTrpKhhDTpcjQGcLFLKpGJoBnE4DHFsMToHWPwe0wMHPkU9WHcGkZsgKE1+8lwLqGv0C4aTlR04TL7Wa4NayZtA/Cmh7va4zgYHB8YPQWBnSOeC1lnhLUhOOiv6tSU8PLqXbNDaT0aA14bCnMTJjadvgg9TE/mJyHSi/i4hs22rECNH1QBn9S3aISYuR5RK9uZ5RYKGFeEM2zXRY31sJ1HTwSL4OQRhPOQM8k7EZH6SATD3SjiyMHx7iFCRybEG+6AfkfYXXn4KcSPTo4D8dOfCOMnwhHAgwWMYxiSWMrnJnhLuhCoHlN9Kz2hyUu5wE0j3GiMKL3fypovncnHT8FT1uszr3ezPZ3astTTWmgDWb0/Np+QaDOOz5w+I9M1q/oC+neGtflcISJ/eennHOelUkErndvnpe7BMM39uTj+oXof6ZKlI0fBzxRip5I1C4FjLpuWD7JjGupi2mmgLj7rpXxXvxrTvJmzv0RlwMA0efgR8I5hO4K1IfwRICFi1ckHAF71GHPlTXICCTx2CIXKUVaY4TkK6yssMSGHJ9IzSEDhWM7R0YIjr+OdA0tc/OQkWfYxzy8BnA0NxBZwBB4HsHGgboI3HlZYueBBG8ZiOJ74oOwoFpsR2dwYwO48zMHBjwQcJXRWcinJvKleCAgfXfJ76YSzyhaFUqDbw9h9vGjcqNoi/Ovqi+YUnK3CyiXAVDURS+exlKcf0smFCFvrsn5rf0rlik+OeznpR6vsWTm/se9ruZdezPg1BcmPUGjo3RaMZ8EJ0ngCrEHXd7BkQX4CO5/vfGgmrbFodrF8+VQ0/5nTL+KOCJ0ME3413eCadsnDSydWf2sGXXPwVP3eni4VQVbIsdoBDA/nJpwe7uHdFG6Hj96cnjmNtWid8l5guewWSN6jyQu20GTFXNoLU2sF5XjFGnApupTais8DfqX8Pd5iES46Uu1AfaVSKWEojFlfTiQx1X1/wE9f/xfYhw94/TbcFXH58edfVsok4CnSB6U1yL+jYqY4ESEX4YSjiHIvRGc7dB3no5LFCYrlnvlEDFRfOZEJoPFvfuwOirjUE3Pp2gaoO2uMmBWLzNelmnEF/8lBJTaznbaHTgVwD8dCmQHjw+kg4wmeDAx52GGP/uor4HQHvvsR9aw1mcCfLf18glRNAZZUD0YuZ6PgWWPIwAsDIAaJeDJIvHOyMnKh7hYTdaaz9Um1HIInN6kvSles9gVCyzy3xuGzF1tTYuRXCum5EsGAdDPVZCald903IT6NPkMxcdFTi9nDe4IJgZbwxv8Oe0/4nv4NE46R8Zc5rVhSFsGqSsLkUv65BF95LO1V0ntV711pYhxu8H74Zzw83ON07/GSCa+dbbAsVS/SEPJph4CXA5/gmUHs4YTPULxQgc5VtfU4t7JNS8aIx6Vy7+VNKIy3ODC0T0JQ40ftCLF8olfarsdS9mEt6VqTsMQsOoBES4VK+vjv+qXHzVcOu3cdeAp01zPDs09lc53qR0Qkcs+TQQiU4CEhGhj7G+Af/leLn37w+MO/umK9jDHg7y38W4sf/t7hx187/OYeeDl69OjmPPi5Kfj5SMJiWuTPV/J/tnae4WTEpeM5V99fX6o5pr+lX1zazNj8Lf0S0mXLxSKdVk/jX+bAqnqOOtdQu/Yzrzi1Jv3TEmbZNy4LCB0GAM0LIdLj5BQa8nnP6V2SaFV9BV0vB7eSHsnXS6n5MeeqYcKnnzw+vnc49ITrnrHv9+j7rjx1wD7eQ8iYkimC8nqR4qvIpMuikd5FOZZLOTToIpRzV1IFyb0AnL4LnwL2OJ0eAA4nNvJ4TOoHFCQRTIwo4JM+DEwwNshx4TngfroF4wr2zVvQ4QEUTyGEPpoQ/gjh5IghuSdCC2JxvphB1xMOfzfh9GOH8T+GPOPipS/8qFIrEOXrDBANLGRidBa57NqHCCxm18MMV+ivvkV/uAFMB5ApZpY1z45zlDvvnDX4WtYjxDdLAMqZjxXdEHuRQWRPsJoAjv/Hfcac5RH20elO582wkq0deT8WezlN+uqErKcLy9YOuY9tJtwNYbDre1BH6PY7XO136DoLM3nQ3UOc0+p+5Esb/Qthfi4yRKitenm6gPk2HL3CNvQlP1DEJyoywjrE51varwc4U94s13F2zTkcT5swASNgHAGGwDaEbUqGhEYlZxWfK1StqYOSZ1upYZ1P6YrAULEQAe3fKqlljNBVyZdgeQe8HeC6AfeGYC1h5/gz7adttV7U9sKcLk/1fL4W87T0I1ofltkAGLtHv7+F3VnYnYPpEI42ivI1KmbPAq3+JQRlob+aTrBmBtdGRu047kUbNezJzmbRZzaMESvjeGwK/Fe1eVoW85X1FyaPGSHMjA8GvKBAInjT4W5/A2IPizbcPHYvfAma9Gz6yCppBf3mlLaNyax2gv0Qnikw6VSEgJF9VTDVsu6JL7pIjFjO3dr+lbRyidCyBC8B9lZmTw9fPM/PGCq396jEX+mkg9oUFI0Cmljln4ptJiTBIng0RVEl9tegg4XBDlcw3uKE+9wuE3oc0PNh1ss03fWWrt8DmOgIRyM8OTXMBqHdND0EDwMmg3DoXBhwKuFgIUUWXUpmQQAZTJXItFJHOc660c/C01JuSV9OTRWcUJH9TC+o/lnDXtn2vEut0as+NMqo2S6faXQh6xq/z/aoSTIoAIZloGdg9ASXBDFVcaopnCIKjwkeHDwTAVgyuBqu4PyEiU/od4TrFwQ3EdyYhTv2AUO6ewa/B44GuOsYe+/VWSRCz0bNQyXIXrYsnz9VDW6F3+fhFM41onqztreL6W3xGp9jVrdIeUtCSJ2nwZNdIIZtSeerW5+npzp1bC3/2Fa++L75q0oN3vxvKabPMx9MQUbyBeBmHjCrotXOVA6SorPREn9J9rTyn9HcgUv8OZc/sgIUSZGaLy/OpxF1C8k0UYi3lyllLuHnZ4XqwgmvEhwDji26zqDvga6zsMamMI7BUCBXa1Muy5p/zA6KZMMluMFxLvAv2pGi6FvkzcpVK7oHw4CLTyXMUQjzxDlslMhm1gJsYciDo/wmjREZhBA9hHRqgijyzAZgE4GGZHhgoNQoJsezaMRQPSeilN8bwHQeZvCw1xP8yYDHSjep6LkYqagav/DfDKg5NGCzB/oDbL8D2R6gEB1kHbZSQ8u5GvKInK4wjfzCWid/JZROcWrTqf2YDRDJCLEkA7H0mctnUmdteEh58/7Uv5cH/oypkhEea4SYVyuOdIyH6QQeLPoXN7A3A3g3AnaKYZnWmtrI/z3D/DRhpfH7KU096kRESSaenhhIHqIpbeIh1EpVyHnxzsW1Ppx5ci4tloibcHIOx/EB9JNDBwIswCZsYh8RmGEga8GygpLksuqIcBf9ohXBkpBHYAnbQdHeoaSCHBMExSTGn0aQZ3TpTac0VG4DhCNucbCsiVxCJOFfOu5HguzidwbYEOAJxjAm2+GPO4thdPiND/dQ/OJZyZa24smdrsNHyPxRBJNAhMv7RQx2V7+Cff0PuPpqxO72E/r9Dp14gZtwUsKYrJytO5xCgwixUZwXqzVNJUrOLBFkISBLdy9wHMviPRQLjwGGePc2jRHzAks7puxT6ksAyrTnFNwKS8Ezt4Hwu96d0i8TvbOJEO5F4XASgsgDHOJhnvo9/sfr3+JgLb57/0eAnWLjy3n7nzGdx8qK6RZjA7LRgciE0EzGhtNBJJ/hXfgnXjiVgWKxR4pBmoNDRak5c3ZcF2gNZ85QtkddwRwBKO4JWj5JkxS+S57gFyaFivKf9Ewx/EDD82ZOh2RXgTmeaAknu5g9jDeAcTDewDAHTxN0eO1+gwlHfG//FRONAICOd/jK/Q4GvfL05twJysIE1WuXesX4aH/AvfkJ9UXVm+YGlC8rZcF/SIz3nNddhviEW6XTSSBAEgqIOV3yx+C5h7tuYqmpy1mhWCzzDJemdNoPQOEdpz5npyGoUUf4guILtfM3OrE9Rb6q9NqKwkTBc7WbqSnwFRvsPOEdphBXOxb3VT3EHA1zHBQG8ZSdZ8Zgd/i7m9/gw/gR//HxP3B9S7h50eHH7xnf//+jckDJ1PR9B/4z8P0/TXj7qwkvTw5X3iFwFMDrUx+NERFfzOb3b2l7qgnFltwtZui5JbHnyHOm+DN2eUt1a0bYnyv9z8q//S39dSdvCa7TQbEJwcNbKWRmPBWyUgE1yyyyZokBWycZoLzv8wstf/pcZ7oEVvgjOQlRKt2LE4zROJFpsHb6eAofv/C85ovruNypvsBBMHXAbsDVlcX1wOhNB2MMPIJDARGHEEgeAALv7FnuqMpzHPRFBGYblaZRF+CDAUGiChS8vDBTRZ80Wyn8XOBlpukE7z3G8RhPbgYThbUWZCyGboCxPQDAWJvlMmHMTQYWo/QggY03afrC8noQGF7d3xd4GoI3Brbr8mQnPgvh1ALC6YD+doI5nHD8YcDD9/uGEK44dq5XNJ/BDac2ooBhLPz1r0DXr2F316B+CKcfKFde6Opi5XNoqZ6kfZaVdYkljXVrv+dkqOIII4YAH9f0nOwp+8Trk0aqjJJFwuZhhFNJXl6qqdd7Ve9v/ftyyvkoWquEg4v0LQ25JNcS/hoChs7i6Eb8eP8Tbl58jRf/8PewLz3Grz4C0wnmYbmJ5+b6fglpsyHiyYxTMrXNp7BWsm1R/RRfKuF9rXyLKZ3J4cUXqbSldNzSUeVD7jyc93DmJ1B/A3QvwRAkSGXvKmjLRD0T7KLjReagAJj3N8+QtFYSuLkSCFwrsbIHXtlMUhfloTcmZDaDFDamB2LIp0i2TAe7ewVD98DpvcKkj0lP27Zb4GrxpZrSdYTWeltXGqEgeY+G3aJznYzBZAhuMOiuHOzAsJ2BlUufkkd4Llm3kli+JhGK5EIxhgV5qGjQo9OmwkKoRCEyZ5BY/T2fBOA1ExWgPyl2IQQ6wGpqO7UTnuswO6kyBBhPd6NQNDAmpBcU5oIHIpeAHGXzyVj4bNq2U7bvp7Z3ec20XprOswbJqwfi4RO8gcT7RfaBqRiH2Y5aHeq5/l/EwiyWbtdSw50uQEjG54RTMYdJ1NgD8/HOfmspctvYlqcw0iHB+ZHJrg2TQn/kuRjxwhHu2Ke4jvvjEeQ87roOjoLanZgw8BV63sPAzscsw1F9ZQacOWIyJ3S8Q8eDyueRPSdaPEGj72itYUnkk1MQkCjuWdZbZ2AuBMpalFmthtHcq6mPkdZTUQAJ3or1WtXwL1BTajyrOMM1ZeLSSYb8gMqP5Yzbnq9Mqj6RUnpTtik8p2/yTLDVQusMDAiCtDCLTuQ7gwQHYqzpTY+b4RaTHzFiDPxbUrQgkjyKtIaAOwP/rsO4Y9z3PjqKEHYM9LzuhEQALM+fbcWDhpumslDPBWycafbhfHoKxt7cPS3gCyO9pfSF4keqfmu/Fht7TH41RmCdbjzGUrnQ8lJNP6cb02LLn61LaxVnfA7gEcCxJqN85jluCyrL71v9+fnA4BHp3IAfU8dSXY9pa4GPSopNEWxI5S3LFGCofujWNapM+7iQP2sKWjWgvYsjveNUh/Loho+P9OmIrERNcm/qj8ifUJUvpArn1R7zrTzlIGSE8zweEuWKcbA+hBwyilkTOdNTiIoQazEIDnBginc1lLK9dz6cGmCT5kPC8Ai/Va5HHlPJuSHItfFya+Zw4bX3DtM0hbajIYL9BDIWANAxw9jwnU0XhyJ8Xmyf6nmlZIjAuAsg2N2DjQdBlN8urSchOAWKbB/IFidZpBiEBeye0d9McCeCP2WDh3yhMx7VHPllYyzQDdjtr7HbX4FsDzLtS6rP4/N5U6mWDcYEzSLXTsbFr2SAKnncsv4kjIR82jgRjYGMkkPO4dLUyYi6vqUhbEVvl6QlWWJT0abCI1VmCPFuCEJneuxeDBheX4FuHGhwsH4E8XYHt8fzd9vrX3r2nO0+8x0RT5iWWmC8pEk0JmxZsl6sRit+iqEUVLJqOKU2odV5vZ9wOk246/9P7N+8RW//D/iH26JxUbiUVQcMoVsIyjRUzH5GJBpdJFwkQjgTOF6UWxgjAMwMGLKBondtidNI1c3ItxBx9almoloWsZRLqEiP6KXX7bC/+UfYh3egu48Au3nfPkva0MalIK6qXK99XnGeK0pzJUqb/DsraT70Fj8NFi9vHQ6v7zDsd+HSyugBbpLXd7hDghJjImuZmauaVSq8bYUxEUYv5cjH9IoynyMljCh9puJ3mWmdHtfrEoxjygOXg6dCUpJG5UxuW2rJfSLhqEm9I8AgenWzB8HAewM2DMsMH5XFhqI3Psm4Pjfcf16C1m5wRTlRZ4UodKn4rXOEKvNnMDTEkxDGAOkznwwK96WEmKRGTr7Ef1T3byNDl0AhgoemLSAED6y1qgrmcQMuqnEyWN3to0QeQobJRse10WZT2nhao5BD60ah1zaj+EyL86mO0KScggp7M1w8Bxjj0THjzYcPGA3hP169wdiH/dPzgDfuNzDokU3wrVGW/MudeY+P3Z/xYvoWN/xmZXAauZN6Jox7PJkYcSGhXLQUi5gZHIVDZgvmsj951jJtF1ybjBhRwexDxSmPzJmuT94tGmYSrW7zdZlXuozX2pQSs6NOVAguppLhXzR8VDylqrKZcdGYsZJEEJP1S8/lorkaRSk6QbInk2NA2ddZP2J9BsALWPQIIQgcGO8whTBlPhrqPEsABuztHr+7/Q1+Or3HHz79IdHtfL9IBWN/7EF/Jtz/8wn3txmXvkcMrLGy1oMHXj54UJSl5rzswiTGfHtH6P08UxNGF7phGBimx9Ozx5TbXGZx7i6Tncq9eXEvFtp/zlSNJzmitbIm5H6myqqPjfxLUtmXTs3ZbLOlP0P6HOqLn3VAjfRleOa/pZVEAMEAUbFcJ1b7d87qlJsl8zpKRo0FOVVQQ3UkmBy/67zimZ7ooPoEp1MSyeMb8UQEA3ImItel+jvj22smQPqiIXQJTtfgN79znjEyoTceB/OAARbW7MKhAaJ0/yaszLNDcOKJd3vCgw1hmsI9Ej6N2QOekmf8jNIQAfDwXp0cUZnyCYZ4B6jc6+YZ4+kE5yaMp/vYZjREcDjt3I0jun4I7fQDLNlwMgIGmo2lglMKTJSxFmAD9/EVGBP8y/8AdkewD8FP5QYGE8sb22XZzfvQn8S7i1wUZI3hpUN3O+H4px2OfzbF0udlyfxwPiiSYZjIwAx7dLtrvHjxCt3+BqbfAaYDp9McHrpqcYTUOpqllHklzk+S02QuS2SUfiZKW7F+0mKigHaak0b7yqgn81bsCYERDvtI9l+xB4q98zMRSyo+LipHVMLhPEswQFhrMHQW5jCg+8dv0b+2wK/uYZzDcB9O77ewxl9z+jKXVef9sJps34WjWbadcevCzNms+CR9rB/VfRybFkrljVgqIxjA9a4DE8FNJ5zGe1ibCRppIVb3TwuvxdG8NUYra3OK8EyCQiTkjIQLXCq/mPKpCMnWLpEVJkhjKtWJJXDIVZsEQxwIl93hbv8K3fSA3fHThbvz+URRWn51WZV8fuXm7dTYMRshCrUhAaa/wnD9Cv3+GtaaFHbGiFc4ISk9cjnpUSQfivCUNI/zsdS4+K3YfecI5dm0Ur7cX+lhSLVB4sKk54OJ4nZTewmkhN8YNI0zw1F6CciaKWyiumXiY2/ChaHe+6AUj5dYjcMVfrr5GsPpDvv7j9VAn0fM+nmE9DmbFB7T6rqXJRd+K2YgnYIwBDIWdrhCv7sCmS4w52KUM5TuTEmVQC2z6itXcL6aqqwCGVzh+eXClyeKNCI1kUC3VOa3gGce5ibPruANKVr0sDhNcq7fVH1Wr+riCzBBFLyYvI+h/rj8FIOKIcLBvwQAGHQLNL/CI7N1Z4zmDncwGPwVOvQpa3MkmzdmWdL1A443PcajA9/HGKHIxl5GnoqEa7ShIQkBpWB+KSomGZzCpaXCs8lZlZ1LObdhmNKo0C63dHrvvKK7XW72nko6ulplTFx8ZrrYjKOsK+PqAWXBVU5ByF6W+1Bqtm9uLsz7PutGOBUgEHZmwMvhJXDzgPs3D5hOwHgMFz+Kl2MKUccEfOyC0GzCySMTT1SiwA0VTfYMd+LCF2COpxu0O1Y2OQNyC3g+k16MLydw52eImggwnjHZQGON37YBtmzbGvctcolL8KP3UdWY4aXdEp5aMWzJ02cn3s/BUdTpcZLUZqS1wQC6UfRcLfssacYLbCyzQCoblPgRHaLZ/ntcPZ8p1f05KzQ1Ml802c+ZtkzmjOHZWOeX6Kt+dnl73hqwMfC9TTSDz+3GTK7KoSZ6VnVF/c5F1Q0UhagafySFqGSRCn1uRC7a1UYGcboTLqs2QOhOFn3Uv4sOlbM6m2JuvODyccR9pxPjOAE76tF3Lnj463ZI9xcQTj3xWhbhnqh4jJDjBcuZhxT6LsVFDubozF7KNUkSqGSdfPGuzCEiL6Pycggd5dwIImCawtlPa8dgCOpsOAlqMgwRUTytm2W4IEtbGGZMdzvg5OGHT4BxoR8EBCNZxUuZaNpIzhDCP8V2EBw97JVH/2qEuzNwDw1DW5T7awObMTYY5oYbYH8L2x9guz5cEGbMHAwEstN+UM6/NaxtFKsKPkLlqMG5LqPXVG/Tdv25okI+Sfqi+Lb6rZRPqdHMYz4C721wXgjPm1/Vr3wivxh0Ark1KSFy9ARYEwxpJzeCuUPXdehsDM8tYVK5KTksJvKcLqA/ny4j+J+DK2ylZzZELAipm4oS+usOu6EHOZMrmKUvMS2x74zqhptNpeK3fGGNpK9fXOMrEN6dTrh/eMDQTwHxsgeTyRbCGAMhMZyizGRl/xVkJKbLJKDOQS1l40Q/IApWqkyfi87XUTFLJPdZZAQdL4lIpDW0Na8ozU4BGFnRYSgcniND8Rgh4Pc3+Nj9M7r7txh++BcY75+u6L4w0ezL0ytL6I0bVTd+6HBMyQhBSj0TKCX63RvcvPpn7K6P6HoXjBHWhkuqU3gmI1wItHuBntdSfmcNIsqTkot3BfNy8cRUE3IuGxrGxEQcNtRRKzmJwnFMQyAvxF+8P+Ocx32TFXMmM1ecGSFR/AbC21JOhLk3FMIwWZO3MRC2k7t5jT/ubnDz4+/x6+P/FRnaUhCZnwr4Jaf55pmJOls97GcVUWIUZb30yR9jOuyu38Dub9H1A5wJl7gZa2FI9kXeT2qrFYmLTbChW4mh+BxrVDJmxd0mxfOI96MHFGuEs9StJTy3ovQp8FCRv57MFSQqe1DKKFjQ9XOkP0QcBZJgwCMTBAhR5lr0eOW/A9JQ57ul4icbPAvjzvyEO/Mer6Zfo/OvlvtfDgb1BM8MQipNuxtMv3qDqx9/At//OOulNi6FI/IRAjzHcMdR1PMcvPHR9lI71+PYXPEjGSMWGLo1Pi/jSso81SLTX/aGdC6KWLgSQOdtzUd0jn4X9VR4OpddKNya3CS0RYhLoLDIXOW/gsNIhF8gys3ISpb8V2pLBzBiw0J7fDwh4Zlx6Ha4Hr7D1fAO9vrPePtHxp9/z0HxwDm8llymZ77fgX6ghFe1U0OZ1JXWRPiUwg82RqoMxWnsnH/fGZpN0axMzxh/8wH+4CpYKinKMDFu71xV31ZBrMYM60ngfD0s2XIaRqB3C3MGgvEIzjmPqn1e419N2nga69xqfhEuSpQuFzR2kQx9capq/7yNffm0eZ7/Unjoz5G2LPgas9iuzvUWbugBNwRvqxlTTRXoRdpTO5EpWlp0YUk3FGkuiXzqowc28h0QkBMOEEcPn05CJLmWVb74PdE5LzJfln9nImcqwypv9Xp9MPPnXj/PNHF8YHy8G3B1RdjtJth4AsVLVu+L6eMod4YoFAzDBB9lA6JwmjLwkpWXqjgqFD1kOGFGU758tyjivRocw+/oy8BjzAFhZNMcM3s4dgB7nEwXnPQo3OVguYPcWyEGrthkugfQkAUhOPix7+Df32DyFvzmI2iYYrsAdRbGy8XBSLqweHtE4nmFLwuzFmTu4cWE7obx8IcBPhoi2qsY+DCOXbV9B7I97MvfYrh+jf5wC+p6wA751HQt28W/soUCyZufcDifanlEvujQqlV9Ar6KbiUjSPwnYh4zCoV4KiN7Qda3OB2hP2W+5ht9piv4DKmSFtp5tDFCPVtPHGCKCJ21YHgc3YiOdtj1PWwHgKa4tmnCsXWk1nmY6fL7Cn9J6bOfiKhkWqTJrYVI4BwMtCtfbu2i9Hz814JgygxQEPgm5+FOJzjvg2Lditdj6H8WOkuBk4AY+SHseo2GCqVkKiD58qmI8D7WyyguzkwFz+A3bdSodLmQi6oNhUu26w0VxiGKFa1qyHHAQ+gohIurAXhj4a3Fe2vQE+NqOrdBf05u+jKUSXX2htZkpnCn+Y+jIRw7C9f3sF3wYrSG4wW98V9SuEqt8eLJxelS/VdK1WSAULSrNmzX/SXML6R+NEERkG3Eh5xV/FhQEIRUbrJEiNKlWZA7HfRc5b7Ufaw7GC7MIpCPzI8JSgcGYI3Fsdvh++EKh2nEzXRsdPNxxogllcfnSTX8yjqVzBbLu02aU0ofASVmAScwyyYZF9gYvL96henqJWC6xMQakhNDJnn76ouqi35BuqyNcuvwnPk1Xgb2BtO1ls5PzTwD5cktYeUJy30pCzwrLF+Sh808PBOgwCFb0Av6QxA7eKiBEDyhb+7v0Y8jPu528ImDv6zXsquluyfzCQwOl18XZDOdNXx86h3IfcJk7vDRehxgsC86w2DSxtcsYCf4yoCZhU4FembX4fq7F9i/PiyMV60rL+v3WlzWec7rAt7sEXD5OAVwVphT+edxiYuZX2hx/oYAjPeETz9asJvA3QO60cKyxRA9Ye7hMEn+vBXwAI9R7+o4zQWNSrBqwAzszB6v9y/BL4+YTg+YTuEUA4CCRgsvdksDBphwfwNHgZ+A2+se1hJEQ5LXIAr2S1RGULfG2cWLenbimAA89B7OehwZ4JNfXC4iwI4ew+iSkug0eZzG0mhCIAw9oe8NxOtV+JyHo4dzeSPk/iqGoEpaj1YItjVs1Z6BI+Ad5TnQ5TzgJ7lkNL/mjnF8PZaXcmyAYVkX6z3ILTNLrT1ef2vnXG18xrPM4WRen/GISsqSZ9h64kXSE7H0o5MnDzbAaICpHakGAGDl+qEvlqr1b7X93GzhpeM7l7/ejj/XIj85bRVclviYVpmlvfp5ZWTzMICnWzjeq/298Nm80zKn8s1SnprWtbKyotEtqUl4KS7yF80K/1/kq/rHKCJcFEx7YtUa4+DFH80UTv6GkLNd18NYhjU+06lkVEnsv6pZeNY8u+JkYKxRBoMwTjImha5NJTwnBwWZ8MSKihFHHEeVgYchtFTBQT12DmGipukEADiZDtZP6PwQQnen0+zByEVEsIgKX5h8YoIQ5DtYHD/0QOdhru5hLIOdgTcIzjyGUnjwcKKEYLyBI5/Gm2X+ULexQH/NIB4xfbJwJ9OIMEJJb2CMQd91oH6H/uoa/f4a1PUgY1WYMlkdrQ1Ui0d5fhKt3yAvZ5BeyZuU4Dx7LjxRMsyVvcrLpwUIVVcq396YqZaMyjV/pHbXYv9bvGNZa7o7pFG04NVWOJ/zqYVXg97NM+N+PAHE6AaGsYTOWJDhIkxd7rMOmhrCqBkHeBv2ofEMYh8dZ5f6+3Q8f66G5yC3jzJEVIfFH5e0J4tWTGwVKBebv0Dg/cIpeC8yxnGCv/8Ef+uC5d4zvPGJ0SbxbE3TEzwptY5O9CrBw9AEpYTGCoQYlomruYptqPIiPJ3FZ8ltmxvP0ijT8yRucPkuq1PUWlFG9OFCWYSjap5hDDDaDu93FoeRceV4Q2e/XMrT3hKoLugnzb6gNBTkQ4R1LPe73uLtrsPNbsCNsbA2MBTGaK/v7CVeHGNEyRjV9EjTsHKp9ZE7VLU05uEZ0EaRanrZuKz6UnQgRrsUcinipCQER+JfeMeDSrQl370mwo0+x0LhqGlkgHxUqpqg9DkOO7y7eoU3Dx9wM53mg5Y+/2KlL1r+qSdNG1bPGiMUzpC5T9/F6AbI5eyTtfjh5bdw128QroowsNaG/UE5fFk6UVF/1ycboiAzN6ophj8xUVnkaO2vxya+pI5qz9UXQT8lrW/njZtuRtTadctu5OopyR0R0aubKJxTevXxE06GcP/V1+AuKhmF6OmULOrSKJeXMqt0Z96D7PtYTtcRx/GEPUj7CWb/Hqe7T/ixD6cP9w0PafYBB3mlNF0SavU7BtDfDHjz376F6W1xsiANoa4isWgLSLR6zIgCOFX0fTMOrjJGdjDTPPVK/dhshFjoBzW+tdLy25IwcvVbSq9h6eNHg4cPBPfNCP/6AYe3O3SjxRVbHGAwgjHBFSyCB/CBHUZwUv3rOZdL4BkAe4CMB2Bw3R9wM1xh6H5Ed3PCD/8BvP++EjApG2u/oh1u0IcwUZE2WiJ8e9hj6CvhjnL5tVlcd65InSheeQLev5gw9QBwHcbYoKfplG8H4Da/fvvTCf/+5/v0WzwhX3+9w9e3Q4HbmYH//tMdHu6mTAtWUn1qoxXqrkiCxGNXT0WeRh0EwGY9hyWC3014+PZdCFEF4QnzPMz7mEYOArD7NGIfYxI39R2NpOngajqz/rq2Gf8kb1l6C+weAPIlj208Y/gLcQT0BnCGMXWEqVtYHwDmtH4Z/OdN2/D839IvIf3yFiRja4K9u8a0+xawN0lmCnciZbkTWrYt7pgECv/IOmmBFIpXVMpuYhRe3slnQ51gX6o3soFZaSr3RRQhm0oGMNuVBUNKeML8yaibVYNkabl4ILOhljt3Uhytus6gH3YhLJPcLSB9BsBysiGGWCzq1bKBCQ5cBnKqNkwEc3hn4n2SQf4VnZWBFV6TOR3N5BjpY3IuGiPSEV6wDychjCF4mNzPTA7CfHmH8XSEdwzvAWs7dP0EQ0G2M6YL9zvE8MbMHYwFQq2xKortOIvpxwMcE/pf38HuPRy54AjoTeyPgeihglwYZApPhBi1KjjXxjwMxvDKoX8x4f73O/DJgk2cr7hAMiRjQmSKfjfA7vY4vHiFbv8CxobQU06MOcpBQUsU9bIBy6fHdRIZgNV+WEXns32X91Dmt4RX1MATt3ABu9V+SacfkPeqylvIyLiUDn45IrUsQy8zT4Sgo/14PMFYxqvrAcPQYegCzEzKMLdkrDHeo5s8JuqC4cx5WJfDnf0lp82GCL0plpe8Qp6t/MV8KcKU8myhQK2n5xZiqdf5OaGR5Rx8r8Bjppe5h8yMcTrh5O6Aew/jCbhCcONkJApcN5nnP1KgGeGSfNrOzeoJ4g28Ipyyyqt/rcxksUFy26Lfkct7w6mIupayr3laVd+VYYqAoNQwYWpst8Pu6jvw6SN+9G8xeMLV5J8F9TyujlJIlu/zuWsB1Jbaqaqc0rNWXGzbXWN//TWG6x2663t0A2Cjp7eN8fBDLPxYxijEp3vHmamrHrQVKYkg6RMS8lsjScbMJtYeeDNTarl+t5Q3gRKt7OHQWInbOMBwscUozT+zAVEwFnqSmBlyTFJ3iiEKOc2Ihq0RW0xbIoSZEQW64bhPCbD9Hv31G1jvgfv3c/zZnoJihI99e0lq6x2o+lihGrXxQSt2i/WT9aSiXTkBYSJBFyNEEniQj4eTpXxZNdmYN16EBkpbI4VDW5hgzTDknZQ9pmagWsO/9qhitZpVwQI2Ndjol2tpZQw5S4VvsoQY57i9dtufMsRTWoewXbOJBLpC5cm9WFBfWs0wCB5SABEHYczk/eTJ4c78BM+uaM/yDle4RevGKFZfen+NgQ8RFTAezEdMdCxGygpGS45mq4kw4Au5PDgIcgYJEaU549IzOH54cA7P4yaYH/4D/uEjvJtiSEXlW6X6WRptxVsNaW7Vq/hcLrKL/ILei835U+EfCzwwh5FkWl/A19nLX2WqCixiNGm7MmBQ8X6N2dPtyQC5ypGPmAsmKGA8b6lMC/NkA2BM7484+QfsRguYfaK5BxA62NTiSS7MJCihOzfEAMhHXkyBESPAik2w5gO8eQKshLIL/24x4EDhVIYBcH0t8WyDcN91VnkJItE7NcELczlfLZp9mddhCDiMHZz2AFtiMxvJcI/9Tc2xATfocLg3pQDIwN/vDjhqD9O1phSOPBeWqk4l1AXnoYeOMRng/acJ05ThPrNvBPIWw9trmJ5xc9Vplg4Ewjgx7h7KEyChwYA7u+MISqdKeHXui2HygvY/DYRWFlTVO6P3jbaAwAudFH8g8pRj+DErLNze4fj6NI+GOcPL63SnTq2sxjPslE/bgAHrGCZsIzgijERwxsBZwn1/wIM94FN/g7Gzi/SYvINhhrNRaUgE6x0O9z9g4CO8BSY2eQpBMMwgN1fceBNO2xZtadzvuTpRsrB5nsImXjDPTy67ghaeI21go1S+p/Xg3JTX9S/x1s/D42ced2lUbAjOBJgDCMwdJr7B6F9iwgEHEBxcolkSejDwTSIvIYdmko+SxVB8SGOUii/KryUskXaYa40uy688eyffhLBrQOOqM/l3GprwAXXtMwZ4cXbbrwgJ11kDWBCsyXoCz4BH1pGYXKysA3lCPQVHLY76KImkIXevBR5HTjn4aKTPoYk8guFhigaHaTzCOZfGZhPfjuREBKJgqYXPjAo4Lr6H9yPcCLAbwW6MYaYNTNfDsAvOllGoYITLoOs5JUPhLoaYH2A4DgYq470EY4oyRHTCMBYA5cu7KxJpiQLfDUZ/60H2hNN7E0I1EfKpGCLAWsD2cLuvQIeXwP4VuL8C2CHs3lKhrLG5YhuRdHmkdHfVaSKtxKfEj3Ii82F6850H6aSK+g716ZUOSGbWl2yfqlfBOQMpjHc0TBWccQrXFT5n9xwUFT4Fn1b8RuXgUXCEFbpshaziVOUCblUIK3wldBaYvIfjETQM2H37Leyba7hXJ1Dn0B1PIO8iGgz4wkTYlH6aeHrVOAbB53erU/M5KGGZmnLfhemRoZm2NFcyOCWzXebLvt160bnKVaUVgTBjUMjuLcrMYaiK7VrPLDeeLybWkKr6njfUeDrizk2gjxMsMbAX78Z8OSExCq8AHfyBIMMrTx3IL30HtVhuRXmRLqiO1JxS/aE+QW4g8fouqXOajtyJ2E7YtLlHul96hVYmkcIYTBKMKOhjidB1B5jr3+HU/Yi30wdcnyZcT8tVbUmPZ9FqMfp8nZvG36oorTOl+Slaj/Bthhe4fvlP2L28x+7lPbphB2N6dHIiIh5ZFGUrAeEODiHUs37qBz4xXJSIkrzm+LokXrURojX6LYz9ogGinblMFyyw7JN5HYExMhR8TQzFeKIGIDYA+6AshVc0VAhe/KOYakRFHjiyHoSgNGUKXieMoBSKHhLD7gDTD+jHe5DYIc7MxXOIHpekRSNEgVKXe6Vhr4TDhgYh7QPkvZEMbARQDslEwXUmrC2FOTXGB2WBjfdEGAMywQgR9knGQYm1pcyQcPrnIV5SaasKP8/B72p+FmIt1Qg2P+Zq/whDXApjAnML+2XLZqsTqS+b0RZVn2V1MzKrL9deqlPRIjkdqF6G4GgU9osxHvAGHj6cAgOBacQH+yc4TIqpJuz5BQ7upqKBOQkM7v0tbtxXsT3G1I2Y7DHlSbzLrBJhPjgtVmnwKWFDDAmOxagQ4GjeL05VJjmYhekHeBqBP/4r6HgHck71JAMBVf8i9wGREufLzUoJEAynTZ6uQgZhO6j7DlSJ1DYH4XEOK+X+ZyCduLgokdRV8isavMseVw/TBucqV14/Js7egDGDdhrT+EzgPof5y3t5fHcP+vgJN7fXoAMiP8i4hhVfR3gAbzFijPvBiCSo4EriErN0mxHkPovkLcqIwjgjGNhBUagPuPEVdniFPhh4DeHFzYDDPgjnVK9WtSRL+H516c6sKzFh/1Dl4VnTi+mWOnwzDPMXE4CP0ojKbztAwugs8hbLvKAulrOf7y0T8PEV46HzOJ48vM8XiRfJG9gfehz2Fn+/36GrPO1/unf4/feneTnOJzpd5LVnvi2r/ZyfCFwqN3eaaV3IuV4HA3hQ2zfRYuJCgp1uHnD/63cgU856YcThcg8v96U1/lzCnByuPxxTWAQ7MXb3HmQBOxhM1uKeLB4OFvdXHe7wFe7xdZLzUnVV/YaDc9rx0MHbsM867/HG/YDenOCZ4Ks7WLzz6N18JGwA11NBX3W5/vQXcpxkY2pzWud25iX1P2++9Touq2V2UvSJrS+lJTnREzD1JuVw3GPkl7j3r3HCATf8CUPkpYWPK4hjorFVG8SZ7EZZTPjqNZZWnwQtn5a7vqDVNeMt74Soc+KSYrnM1+X8+tlKb2bIpyyT5iApT/XTOokHP8NG/MqRe2Th50hxo2qCUzcMwQedOMiaeC9VdALiaMyIjqze+TSPRpy44ro6z3AU7n9wfsLp9IBpnJB8wrohO3gRQJ0BOSR5FzraBTMAh3CyYgSRwUgG1ljYroPxE0w3hDswrQWIYEEg4/QEhvEbg67rAAyI1g94H2R364MzhiGC8QTqQv86Y+A9wLBw3sM5n3aWSfQ43CUxvHSwNx7TaYB7MJEFyy43xnRAt4e7+XuYm6/Bh2/CmE8fAHgYVka65NWUYYKUQUnzEmF4Wdc2h6cwnwbhFHWe18wDpsvGfTYUCByne1Wg4TA4B4tsordvvk9F1+OzISIdTcrGLLCPDtIyxnL8xbDEqWlzyntGTkNpGYwa+VoNtHBNcXK+WoBwUoWizigYIkAAdyPs9Q2G3/4a9oXB9PoBnZ/Q3Z9Ackl87KPxHv1Y0WgTQmrCE56eZtzpk9P6LC6nzYYIrr+VdO/pqVHHYwl6ArQL+lXIt4/kOCR+OM1eiqEhPHaOMU5H3POPQHeFjl6CuEtMaro0aDaEqACQy6xZCFwiMQozRFKviGIyEqRdlRl0XlJgbUkaGyVv73h0bI1bmFUSOpAVT4H2cbTGw3h0/QG7q9/C2/f4gd9i7xnXszsj5jPXSmdzrbxsi5+PZ0EDnzGTBuM79akZEgIerMF9Z+GHAX08/hdiRUo4pnixk4kKC4r1NoS9kvlSsBMBV/Ik7xIxUEiB9FYqbTFlddo4ZwUccVXsuRCp7BBS00zBo9SzOj1MMSQagylclIt4AViYs2Dtq/cux31RuFZwvthLQpJxDNHEJhyUNcw4Hl7h+zd/j/3dT7i5e6cn4xnJiKSnEKiawl8gFGU3P5CGI/W+ZMYoHiem5N0snjYUQ5F1+xewwxVM1wemQMKViVdN3BfCHJNRewQKZ+qkkTnybK2HPJofPc3VKaaxmSOPmYsvraRPtlXC3lKJFaWTSfOwXEZfclt0dkVwKr9vwwEhZ6Z4oHzIj0wUnDzBGA5ryx4vP32E6U4wLxieEE/tRdyvaGCRWsuh38m/BK7Kf2lpKEvDVKgs8Nih4oB/05+ZoJFxcfjhI+7xEecm4aJqVFTIaamofH6Jkn9rztCeYsjWtdHpW+LJFowPz4/3ypoLKC3gmVP/wmd5GaTOs6Wl2T7fMLCA8xp9U98JwjNE3FZVfNVf4Vfma/RfPaDvThjvgOmk6AqF8jdXHYbBoO9NsY41u5z4lPnEXZRqirHoJNT6fUEbpYH3zL0FrXZWxlZtrzN11eMNoYg6a/B3ww6TWTBExNRZwvV9cDHRfbITsD/sqrojb12c4GzftdFubyNcl0DwiBoAGMLDDvDRGDRNjPefHKJtdTb/NA3An29LWFd59gNw2AWfTmbg04PHaVzrTS5LBri9UvyHY/RuhJwOIe/ReUZngL0n9GRhiHA9WriTxZ9Otxj9IbY99872VyN87zD1NjijKM9msAHuXoAeJvBEQO/w8OYYvJZjX6y6rDKhAOZ4Kio8sA4gDzgbquR4H5mJDsveogkHxkHbYJvzk1MLC9aY4ly6NL9kX0cGxnMjnvZfYyo4kovSuVLz1S1LnAaL474H8wHTZGF2jP3gQL045yA7vRelGzQXkYdtHKUv8XXJj2fmqT2+wjAX+xMcVki9jJQ58oxM+bu/CC4XmMkNVWyRnIUaF44VAMpfQXBlEWCFpyekWWSWgH3yL5wSCCHBTdQne7jJY5xGiKzbdYFOSZNptJ5DyHEXLr2W3hhMQQEfDR2GLGAJ1ndg76NxACmscahMeOJQj2cADmAK6nmL4C/gyUdHQU4hTJPARBbGdrDeY/pwA3Qn2Ns7wIbLto0PdwnmWP0U7qKAhe0Q73B0kFBIwtNqJykQsH/l0e1GnH7qwKd8GZAxFtR1GPoBXT/AGpPu2pKFzFiP0phFlkunijdBRWtnLsiWSk5If1sGNqlzUShVDcomY91SrjOLJZVcU3RR89g633xki8O8KEUYU6KGdixlIFhejOCKkko1e8RBfjZEsNYA/YDDV7/B/s0V6PUI2gP9OMJ4p3S5CCcVnYc5qzv7EqnVh2205RIKdMGJiFIKPgMOm9OSmursEpzLQJLpLLhsTwtt1tb0ZW+G8Nz7CeM44p7fgeiAK3MFAxsFWpMUCyahoZiIYpgFTmuQSLJS4hUudih/Z1Xr5Xu2CZKqqaRjlU9AMUTbWxNGOuhjg0IRxCBv0HUH0M1vcLIDfpze48XocO085ozH4zfQclaa/S1fz0VzhfEXmqGUtVUt6S8zZiMYIt7uOlwPA3bWwJKBtSYpXEUhm5QRxY6r+ps+8u/kQ1Iwd0KscrGCgJWo4km7Lp+V0oyF7uVGRbee/oUCSaHD4eQQeUrATCB4MomKzvYec0XADGRminYXNhEhEK1wWMmATIyjCcDCwN28xrvDS7z407/g5v4dtln4HjPzl2GFUhdQwfLWtVGlhW9cKyvKNYrfA0MoJyGysozIot/fwu9vgtcM5VidRmKeJiNE3CdQCp+qAxnO048E90vYJrOF6ymRkGZWvnRZUvtAAzVeWoPsiyUcVikKk7Jbd2Kh7mL/CIPH0RhIUMp0zsUYRXcoWKuDMcIQ4IMQ0TPh5cdPoP4I88JH2PC5fSphrMZVGe/pJ63vZZrz5ZGOn41NJ8w3F0NOl/2R6mGaligW+5rRj2UqD+AipQ5SsVZZyFrra3uPnE0b8z+WbhTlLq5gThlrGGm1WLF/2AYn1IQHwWnnu5q9HPXeyHcUAIi4MNVZGyK6A66HK1j6Ed3NhB9+zxhPirrF+m+ue1wduoxXUcJGSQIum3QCze4ruaT0rP3mg4V2VUblfjDLd6b59Zcb5qPOwQB2x/D0CjZJaQssYnjySTWJXPaVKW9Gzvy65v1Wbk9e6vPF+z7jrXpHLNXlDfDpFnBDyHAaY6ipqHCuDf9m7NG97WcGFPn91UuLr4YcRuQPnya8++CwnBIVQ98xfjf06EVitgBe1LQ1t7sPr9OYTw9X+Hg6KENxLsXwGHce1Hu4Xk4+SXUEwADHV/ATYTQGbhhx9+Yt2EpohgYSATDcnbD7OOb5OSLcQdYBrgOmuAf6I2Ad4bSPF2HqqjxjeMBcgV8j2UKBq8c2L7SCEZtPLmZfal4//u5Gr4Lb/XLT83D1jxvnk2aHgdO+w09fXcO6a9BPFv0B6K9cuEcg3vGilb2SRCmunyY2j7PZgcRJK+VdOvtwZjS1OCkNKzAWRxXWD5eAC5jtw1mo6wsmdwObWLSkedtlTl3cXKLJgcJ6iBKUyGT5hgxA+QQAEE7mOe8wTRMkPBORgbV91a8gx3oOZbzEsSeAnAN5H3QTyBddGxN2pjem8AwvBs2IOrLoaIMc48GD4K0PYZS8hy9O2IbvxnQAA+OnF2B6gLm6B5no9S9XNABJ9gCiHGG6dBqiXn0TgiKEUgTg1QR7y3APFu6EFPUgOIha9EOPfuiDESI6ioJL17FcO8e1RUE/F4Cg8WzO+3P5p3hRyLaAgmeuM5aToPdSAXyhnIReCusncoq0VfRseWip7YWXS0yERiYNbq6kWmG+yyZa/L2c56rmUL9nICprQYZCSNOhw/V336F/3QOvJxD5EB6TyzqIGf2UnZvO4/un0rQ27X58bZf3Z7sh4hno99qkGgZeugNu3B4db2SMeWHQEl6zaG19krcy1tpKVnWl+RwVUIOA3aHDoXOY6A/wPYHMd4UFuPZnEGNoQoRyqTUQlTilSJYNDVKiurQ6FMTsSJdCIsVmTEW1JbUcZupRJVynvjNhG4iGOsQbyMTBcSQKHGMJ9v01+ObvwNOEn6YRw8MHXD18OFP/tm3d7FNRks5UU0npvCDQ1o8q5j79pbngDAoClh1ucPXytxgOr2LcRAtrfLoTQp+GSEpaQ2kI9XqyVmalL+o0RO1xqxVgGkoi0dmC4pb2VD01S8xVs3YZD7UVDGutJONHPH9IZMAU/XlqITedXgpx3fNr6ZeEfBKY5sh4cDJVyD42FGDbk1wZBnjD0UMOsMw43nyFPwG4+vQ2GCQWx3FpuhzBt4wQyXGjNeuJKVB5Kypf8A2tNuMfkgpIK8bEKJFPOKRs8bOzXQjLFD/TZe5xP0krbZipOAb9PCmP5btXTJfeZ+HI9Lbp1p6T6rPoRU1vnoFQYwmC4v44x/Qt1Rm2w4yhX2kq7Y10T0RieuOam2AcFCNeiG+LhJuMNRjMDi/dLY6Y8IHehri5G6Zp725g2WLg6+L5wb9Exzvc23eY6KRg/pKdxw3GXX8XPJzxRVa8UQQ3Tp5qzPHgMcuh/DLli2zTk/wM+tlyjxfsc2dTOm1UP298K9Nj6fW5/jQ7sVLgzPu5pBKfN4SslTaIgeHNAfsbCzu2WPNQjwFwA4OJGffE4QRdq7uk/qlBZAEn/80n+WS9Ir+QcKooL2gzs5xPSKwB1Ube6EwbFyeqf9LyMlXzl0rER3Uxqj4bLnYq87z/1Mq7sPnmp0eatRU/F6BlJV1IU1Qn6tp51v5yHwwD+zuCfwi/9x74x66Ht8D66UPpRlnvbiLs3sd+MPAbb/BVOiGxuvgwBrj6FO83Wmx6LkiNO2DaE64OBi+HrlBe6DYnAH7Kp1dy1wk9T/jm5YQ9hxBpzhqcTm8iT6rbDfmP0WBjjhO645T4MXNiGAfYkUDK4GBOga6aiWDEu1mSZ9DRi05lPjVn2A/JUnuhI5A1HL+6x7QvY+zW7Zxfa175lZMdfbjb4ySXfD4PrwQA5IMxp3y4nN/ZEC3ATg3l2JluLaFT4+o7P54vMSHfWyLPFExMncHUE+jugG78Bu7hBo470MTophMcuQgLHD2Lwy9RF5uEGEpZIMtHyPdFIOORRT1mwTPr+uqzb0hPCk9n5sh3cmw7KOZZ8idPy+bZ7S+TPBDu5PRwzmEyDG/yogSa7ZU0E/7quB0xY1Dmm3j3ITPkzkLhMb33mMYJzrl450NI8i7Jbd6H0wiRySBjQtgkyJ0gSXiLbRsYJhhy6n4KIF1uLQx/wjUy1yGkTzA6eBjvAO/AboI3RsFmLMgAwYBMh67r4PwO49trUD9ieH0EEMct2JLiHRGRP7HGYzI+6z2k/xyvt4CHIwl17TC8HuH2E47vemDq0mXfpuvCP6PwLKnh6YdAXIdsVOE6RzKEYJZD7wORF/QJiLyGWa+T943Irlq2LTpYOCGL7IFUJJTzPuPZ0L6Si3Vfqs8cCjnTy1I2upDvW+IzZzVW81c+KtotTsM06xZnR+B+HMEdMAwd+r4DmUlVnKMlrEoMzy8KVWnrvD6/XPaI0EyfYT4iwrh1O7yMx1cv65Guap0ZCE3NxO9tLaY90Wq7poT11/yt31schh4TfsBEBjBT2MlRiVBuipKpT1dfECVCCcrx7dPlgXIUDwFbUFXbHOnVKzzHPMLQtjmlSOYVlxD2aGIdGmXatSQROXbWGGWnibH5u+EapjvAe8a99wD+FVenjw2EVadyTotf6/Jy/nbpBnj0hqmIdiN13RWubn8XlaoGlihc5iThaZAv7RUjxKKaVStNWaFHBsTrO52QKP5C0atMSPTsn2fWuPhYmI0LQn2db6rdSAyrlDca5DQG1VI0ozgNIZ6GJBe2JwaIytiPFO6EYNkvaWwxFJNheB+EzsC0S8xJxnj9Gg+Hl4CfcH3/HvMQUM+RztQ42wLCNMmvNRxcedOSsKgo8Moi45W02QLHFJ/luyHyO1URhfm01qDrbDg1ZEwKyyQnKmBy/3Q/NfwmLK34Na4YKF1S8HryhNT0YUHqTPWrHSe/Z5Wkqav3UI2/L9s4eer0mlH5slXuDM6St0JPwt7h9CLbslvseT7Rp/tCxsB4BhsP74N3mDFhz3Y04Na/gaUjPnY/Rg+q2VZOodfk+Y4P2LnIjyjLxd7fYIdrnMwdJjoVAvl6yuM5uxI1D5H6JmvPYGXPCgJ+uFuidRoCgNjt1hXDqZ8rz2YGjLWa2jmfF2edgbULxluiqvPj3KokWzsMk/cuo3uxx/C6h3lrQeMCsSPgAANPwMlMmPLj2G11Ign6Djbdq/YZgIQ/TQKWbJBonFw4a2xoPNaqIDF0rKaNwDJXyl8IZQXPWtXc3BJx7EsGBqr6RKXSav20xfm+n8PJiztvixW2KjOfkUuKL+yvDbUN9+Xvg7iubkm1vDzGfzHt5erN5t6snngAdxvbBXLDRHAHwmEwuDU2y5AzmOnmReOfgSZ8c3uHnuRy2B7hzMW8LiLCT8cJ379z6blgA29zmCtyOb+XEzcMUK1MB+D6sv7mOBt9AeZSZHZ0Chjo/vYtppuHtSrPrve8zYUCEc8e3h/RHc9fMHgJjNsJwAkl7ljYwwzgtAsKzOEI2Npr4AnOJHJy5VL6OuOz6/cUQno1rVEEuI7gBgJ/OMB8/Aoj3WA0HQbvQM7BmzDeJAJ5jsYIRUMqfi9t3yAcJb5PGyVCRgVlmg9ujmwuYxRMJ4mRITu/FIYHUA7vyZxjgyLODZf9n/dh/rPVt82JAXiG8/HaZHF4M3E/kwFxtaYVnysOciECB4EoMpbh8jWE0w+A88EI4Z2P8pQJ+1idYPCiJ2DhL0wIv5TWJ/Kt8VJow/GC7KiY96Twey2HCX1OspcPF/waA/Ym9MM4eOdAHMPKkjLDkNyDNYBhcPpwBXQndLdHgDjexaQ4k3hiwRoD7wlyp5f3pd7DMIDOAg5wPlz03d+OMFfAeGfhpmBgscbA2i6ezpfBUDL4FNAgsJawt4b7DXCSBAN1+i7pZFgtB1f1iYyq9pOWJ2f7K6+JllXTqW5pI+H9WoZlzPAdV19Sf0opHFA81JLjRp1WEKNmF4phioCn4LDMuVxpgGvGyY+wbNH3Pfq+gzEexD7VoD/X03bJa63WpbbKm4gvS08xyD7ysupnSnGs3T4sjo3HiNencK06BSxPFEq43gzzHBseVSAWCcLLfoeD73H3cMRDdwd/46MSJQKCUGsF4xkRieKmGh8IIBMsyZGwlB4EQf0iylJ5E0JjIClGUdU6RxKt+ZD2FgSWpJgVGWiGdsuqEAwsXglyBvmqmUgfJTMAg9PhK/wIi93DO1w9fLwIdtZRCS18f8bUgFkNyxoHSnqwBh96C7vboTeByAXPbm2EoHj6QTzEKdWbvP5bRKUiFlrxGlwgOBG1pGCVCKCRAOV6t6wEFx+L7xvprKpIMZPbk9o/kSEVWON023umdYkhMSZ6AFCxpMnbBshEDXm/yEoEr+7wmYDcULhEyhCsiuL5cXeNh6sXeDU+4MUYPDp0Xedh9fEEZzlR4ydVb5faYxTMQ5zUUlgIn5S/QgwRuW75Bzgy+OHFN3A3b8DDLjGC1nbxQla5JyKHaErMa3J9LDgx3bkE8zPvDb1XpPcsUKNYqTMMGPNMQlVly9/tVAteBC91NkCkOE3SzvL5UiXEncsqiSE0MQpfMSwTc/CKsh7oPePN+/fohyP+/ILR0LWcT4okfzLvMJo7jHjIzyP4zkegniyNTyGLEmsGzKEdlWZV+XgcPeFcr3C3XkNCMuIBEb4/7+pu80A6n5oq8wKvt4A5fizwfVT+Qfmt6qdSQszqUU4gmW7m9Wu1m95xK8dCRxrJALhli4kYd6QoOaHCiQuNcA2wItzFHNGQN6+mrJtWQKnkycvS9fdWd6X8Ate5XM/WpIulZW7UVT/TPJS8Kvh1ahbTpwEv7uTiHC//aj+q6ey5dGHE+Zmj1/K72ftZy42cszmd50wZL+q4rmOl4LIUX70nDCfA/sT4ZIGhU68jHEwDkiEgA2CEHwb6I7CfgMMIDCxDCvlGGvDRvEHHJ1y7t9Gswuicwa20VSCFqrtqLZiAhyuCVxeeEwHkGfuPAbc8XFNx+irxv232qJmEBw7o0uNEL+GO+sQhwTPw/pOH01GzVngDrt7Xv+uO2Ycp3KlxocKfwXA7h+NXd+l+jtTriWHrC8NXNrnrwpyPB8ztglp5iHC3RX90ywbP+NwwQP0ZvF+yhMXoimwcTmsAwNQF3YRTgSqMB7qJMO4MHq7DKSXfGfC4B047MAYwelgaESOrwUUFNEcZh3xwxDILtFV3rQhzRCgMEXkKkkS6mCRv5hr0aQjl2Bkzkch7BsGSQj5dQixwVnpGN9pEdTfn4hosvliaFhAYkwfGyWHqow7JhGBEXpzqtCgjM8QIDm6EJN9yPClMQHKwY/ZwTk5CBEOHiU5c4vyYxRZOTlmEcMK/HzoYR+muuWlyaYUkTJ3ou+QUQhCdLOQyY9YLJtMEhHfeBSMEAW6icEKiC6GfgnNalu9kPwblsEHX9/DMOP35BnY3wX49AhTCSRm5fyc2JYaS0JdKDmOAES7YsT7gFW8MjPcY3pzgbz3gHDwDzkddHzS3X64+LYEB1z8XYCUJEWrPZAt4li0aeDvMfQ75V+OcDL5xrX2AER/vBNGnKzjCjzxPeiK5AFsbO2ajKp1gG8P/MqkYv1nMluQD7VBHQN8ZeIRL3E1HGLoeHYD+4QSCS3OhW/FEGAcTTrg5xXt9XnHtZ02f2RCxPnNi7+t2NiAsTwVRrmSEzU3OF+78CrZovLJ7LhQ696Bd9sr2OBjg7v6I8XREPp6UhZo1XjcTtmi1j5fjCnUORJWXjQufcUsHIobcdiTuLC8qYbddAwAKBgfPmZ+rxRsjGYyH37/Aw+4G5ocTOJ2M2D5WQbCtvhSM3RooXTq1a8L77HspAJyMwYddj0PfY1AKxKBMjZb/aHgwkHfz+gEkAlQ8UH8TXYtKLvG8gCIuYlkPBIqLijdNyQKRPTfdxZfnAutUn2I4xXigtC4MVkaKQJizMUIq0qeRInJiVnHxVaNRsUYR9hNHYgiAiR44gRh+6vd4v7vBzjnc0qkg1lR9myeuvtNK3nJeFvdI/UIJF6VX6LwreZZ0eYUMdV3yvTCqqSHo9SHCx6sXmG7eoLPh8khrLGy8rFruT0khzBr9TUycMsqF/xWMIzBcxSP5krmpVfjMqKNBc7hqq8rTupS4VfMsrYHIrJpnphtqz15ecy6saV3YnyJ8BU8UMoTOM27vjxj9PehFvPg1Nhxold6vdObOS8aRPuHe/DRjS5ONMeVUOOwcM02CZ0owouJ7/UThaOV1lMGOy07J3lhUkFwCENvSmsJ1sTU9h9L9enLP1QEoRds5PrQotNLGGpQSUIRcm693piWNqlhl2pIi3tuxQQfgnqYKXZYVLZx/UF/LnlLEr6QdGSC4MRMCqqpRNah+1rgd2cChyq+daNg0LWm5t8Owzrm279cMHVRMhnqeaFWjvSYtvTQ15nWZqZyn1e1eQ+4j0ppBQr1fMhYyLxhAZt6Pzdq3p1j0nLkl4PGVpmj+3o7hXz+Ef/W0+l7D3Xy+uhPQj4ThHhgQaUBUhHrT47R/DfKfMDz8CIojGEC4VtSpxUlTfhEfEO72BFfebQ7jCNefgvx2d0VIUZO1EUPXWjllBGyh80ZKxkBwL+tmuHByDP9hwmnE2cSA1v2EZ7Xy7Mxv3f3FdhIsHuEODp58nQGz7m7AQ81zGczFXb1mcuHy0mYNuY3W2ehzBlqOeL+eEuOB4QFgwzju5siKp3D5+dQZ3L/YQWgG+h2AHoweHh06TBjgMcIg3omeeJMgmyLpCZZG1iKNc04oseiYAZSusPEqco7hM9E5ZGNEmKhMQyOYU+y7eMrPG2o0uPJqljYwxRydAifnopNcTCboXUieSSD6JIZwxptpIinxAdI9jm1479PJh6Dct+hsl9eNRTaKCm6SS3o7GLIpW+guBwMCC08buyh8hjHhfkbBIhwnPGWVNWAQHNhTcFqdJnAMn+TJg+LJA0YX7gRMdwCG/ltrATdg/ODBo4F/dQKbEKLJ+zmiNyacukgLSJTCIlkTHBAtGXC835EM0N86sPPw73wau5e5miUF0Ro+lCg8cxxdwmWFDFpg6GgAqjIWMmb5kWgF5x5oGwKn5yKDcHUXEudupN/yr9Hl4mFJTx6TLmEPlluhYnlkfQLO0A0ITxP+WROCbE9E6PoOXWfRwaMfpxTueyYKGIIDAexhxLjdZjFXevy4+bpUDHmu9ARDhLAUdIahXa8DzaI1iTmf6tMQq92phNplIOcNXag2sOrRrI+kEAcD03iE9x3ovYMFgW5Cv8Tq6pmzt0CywgsjyjNdHXNAshxDy+TLLRvjSIgumTVWaaP2smyPC2lXyjgzgaZ8oiG5ja5MrFpHbYwQJ3EfpgceBtYEBtFQCGfzsBtwP1rcOo+bKZ/EqJur2YaGlFT+fc6duSh4lNimFP5VESJ0wy1uXv0Dhv0tOhMuqLbRS8FawFgTwpWY8JnDz2SDxNIyBHoR/0ZKk47apXuH8rNMbMTLSMPKbKbPpvoAXrPUBR7U62kDRzjjiCkSIQkhxsgnlDgfWeXc+7A18oYVgVJeMnM68hvWSTEIjoO7k0e8xBrYXb0CdQM+2B739x2+Ot7hdjpWHV+avS1c8PI01E+SwqV4TDN4XqyUWz0SpljtQ1WvGGxSSKXicjJdTTAy2M6isxa2s3GfqMvc6zAkrYo4eHzEH8g7BPm79uBJUfqXaUgpWOnaYnvq8/ytCkrCqYzQgoeX6Jzg6rq652VGKC8ilY/DVqDkSSVYu8YcqzMgsEFBvGXidGcEjIc3wZ5niOCjAX8yD3jX/T5VvPPXuObXeKCPuDPvZk1c+9fY8VX6LeGdkg63QklavqsWe5aEJWnw50WZ5C/E4TJARumJxD4KOpzzdVcdXv2XX2F3uytigy9M4gXP62zPzL4uIv+oEmi8X+YlW4/rwu28VEFfm+zkE4KlMb5R3xpbuWGbz1mV4FkaWIOAx4LzQVVxIFZSzazRgLWCu4GEWJg3vmHOaj5cz7XwsYFhzeLbGuw0SZgwMSUvfxkE1vyXTm3gIzW2LdUusJUrZdf6dL6hzfmF6OZfq7PxqKTX5aJxtcu06k0UudpvrfYWZRtGkqewko+qOStrn38N/Yj7KBmByxaGE+Ab2mipJsTOp8DDa8OM8vAdzR5vd79d6PVKorLf/ghwoU0nWJ5w8H+CJYf9e8zg80R7fLBv0DbiMK78exz8h/oxEOXBD/YrnEwZjpnchN+Z72H7aV5MpdHs8bH7Kt2TuHcfcTW9i3nL3IshMGXNCbi/QnEipJUmazAev1ahVtttfLr3uDs+Tj5hICpCQyLnYUeXWUp5rvdBpWws4KSVDOP+q49w+4UQVcx4uA51TjbiWMXQGA88OMA8HHD4/etEd9zDC3j0mKiDpy49l955iKwUnphIDBIvhfkWa0z1QlJe1M23UmFsX921GYZF2QNc9pfQwfSTlFwSPzXzNksNZ9BVXpDyC9XEGsYMinOPcAeCSbI/eYDIg7z0Q6pRDGvqR2A8hXdkMHy8D2KcJnjvAAI6MvlEhOky/xkdF8Ip1eiQB6CLYYWzL4yB8x7TdIoXWU+AD86MPnmHSwEpK3INogxGauo92E+BFzbRAclNQY4zNupAehhD6Louy3eMeGoC8F0HmHi7AwOTcwADnXXFCbBw3yZgo3GHo67Ne4CMgQVgu1in9XBhceCJwN7BY4LzDsa7oNuTJViCgZpRVPB11pAxS5nHy6d4K2GFAdFpSGZKr2qYCboh7338V8ocOY9Pd9ilS6uLboncWwk+KtuS3Lr5FCytzctCambVi7W814UPt5bQdwbcW5iv32C4voLtOhjKRJbraf3FpMfRrsemJ5+ISFbiGSd7fmap+E7Np8taHCoEmeUmCU2GduZVQ8vv5oWL73VumuVR5YQGgsNxNz7BPHjYeOkM26h40ibHBmWuT45o0lj3Za7WmWVIP2Zkc42Db1WkOpOuqIjwQcRqaitBYVHoCMqjwLwETky8KExEmuKFbozBse9wHDrsjy5ax32qp5iz1THVMHhBWmUy9Pvl8coXauST9TTdDvvrb2FtILbBAm+i90G0yEejQ/hXGiFaaXlKMoPgUwgmxGeBuKQ7IbjcGwvy/GJrCfoUgp7TacX8rUr9Zb3LhKsB5AqGE99MVDSdLt5SjJYYZdJdLUhTpfhJxUjFPOHOl9BevH83XV4tnDgbgvEGMEA/HEDdgPvxAR/diJtpxO10Up0/ly6D66a+qQXLcXzLRoj6ATenX+fV8ybf01HbQPXjR/YI8kRgMinuqYkMuoneMOkkBGmjRuKWVfdajFPsd2Lm9GdcU1Z5WilJBTUi53k2YFWxqdPF9rnm/lT76gyYbGYGm2WXll02WcywYUACKQYh5mw4VcRZwNW4MP72mPBg36e5JRhcu9eY6Ih7+37Wxo6vMfCh6HUxfdVclj8VM0xAGc9FlSgY8PqzEkQYhYFJQ5u+KN0MHa5//QLdrmsYnOp1bjAbwCrdKKtbzhj4mvSt3dzs4SIBadW+Ume79vZoWw/r9XoORr1a+ycII5l7TmcWKkVVi5OoemIAjpdf6p6larQyqlFH+UivBSUcXWY5gz10u0utzuAtw+sa2jgPz2cgY/XnOd5uNdf6eFFCzQy/nBlYnpeSxuk12QLbW0Ldnp9iRd8XUluekZcbDVmxrWZom9QNSpHKqD3BLUZUla/6rdBEuR8DnpL3ZqoDPuSNSmpNpQ5WfArFU50TBkxmKOqYd3sDhDIAVz7qeQTTWxB79A+5Nkmj7XDavVi8qWw/ntCNH2bPmQEDg2l3jWN3W7yzPOINv0PPbqmnAIA77PDJvkp5es+45feob4BqjV+9CF8JGA4EN8yzhayRxnIPoG/AQlg3OTnxw9HDva9Da8770nIwYWa4+nlBgyIszVjHeV3Lp408fD9hGmrnJZV2Uqc2pul+EIbxgKu3IbSWMQYj7zCRgSUb7wbIvKRcBRwoTHY50XzLEv1dN96vONksjy6zYWqPSije5AxDpDIJ8iTIHmPpnG5MV1y0VndgbVCSZx07im6FVXaJguBj10poW25Q7hdjcFQuu/g5xQusEUMydVGOCnqXILcKZAtONEmOTf0S/Oo8vHMAuRhjwadLjbVDVpp/+c4VPCdHHB+d/OJ776MhInyyZXC8NNhYAxMxbnJkMyGEU/Aji2OPBhNo2TAyUWVUhOA0aEDg6PjJJjgjegYIDuSjAS4q7L1X4aZwFkpmmQpHl+VNUf3M8kDRWN04yxryLGvCqlnISC0x4ikIkYVZRDfJI+2nF8t9Va/PGiHO0v264jPvdZ4l4/VCMV2nIYm2YECdhXn5AvbqAOpM8661bUCwVOD50yo+/gzp57sjIhLWtKlD+L0qcZF9deqp+Lh8BhcUQCWjsO2A0BpJzKwo4N2EcbyD6d5iN+xw7F7Bsy3K5LsVuNp0SnHGnO6ACL9lMrPiX5POz51axxcRCTyRcuxQROpsnRSRvswjxYuDGCGEo7Vg9tgffoW+f4HJjXjnHE7332Ma3+PNiXFwSsDePBVbFSGtTp9/WIhiCnhFOKoz33cGPw09zG6Hg9wNkf4Rpvsdjn7A/oXHcI0YHzHGgtQ0HIq5hiIY8fhlUnAlAwMygRHDA2dGFWBAlS0VtqS+Y3HeZ0YIMIpbtYq5ICwRisclDRAtQhxhmkJ8U45eJtJF6YuOFyrhYWQKsvW7flCOiwiAp8DQMBCPQiApiDh4X7Bh7K9fo9tdYWd3GLp3mI4f4YuTEVso75mZqcGwwkNlvojPizJthVOBERU/X4CL2gc5FFP+lBAiodlQgI3B+2//GafrN8D1K1hrMHQWXdehsxadNTFEk9ynYuK8U8EkCCx78epA9hYKGSLTzsJoyZgyw5VgIY1UST4KztMekydxryVZRf6sGkbaILV2GqINDmEeU3iWgqhuuW+FEhg8BXU2e1y8yP1hIBi6TfDW4+hRZQwDPgoLcodOvASe46lDQribpbZr1umTeYsH8wEjlTeo6sBOArMtLF+MSD0SME/Mt/JGF2/dYFDPkl2Ou4qMhxVuXhPO6xTFsqxnnu33hYJUfi1D6awbvR9LV9NljCtwi6ovj06L9FtoX0XvZNsnQazFznP5NXqJHW49Di89usErPFLlT9uq7JhhwgtvwRQUEA6MB1uSTg3bFH/XU/TiDXDzknH3E2O89/BGgjG252EZLGQNpNNzIwTlDLN6WiGS2jnV+9krgb+lPVDzXIs5NqQSHi8Kj7TldcswwfkdUfXuTJrbbqjajc+xdzbUtsEQUWPOAkWT9t5s81Krv1U5GX99yqrYwYv4YP4u2xwijUonNs/BXTUnFPAzGQOPDj/238BT9LqlboEat6nPPNcSHg2JGXBk8Xb3a1BJ5VJy1IGVA0i93e66lxjNHu1EGM1h3gXq8OPu1zDsWoVSE566Arcc+xv82f7dRrmu7CwD8CeqToQsFZs3IE/203tcu3fYTYRvdzMTEz71X+Fog+KemHF7+hN6Lo0BzgAfrxhaFXApPcs4WPGzlUf1CW/gjx7rTi6BGB1HxtuPThkxwz9z6op2DAWlkiWGBYdID4AEj1b7K+g2fFQSePbJQ5xV/1Mfoha7VqWL9In02RrLAm4Qo4Ji3CSMdDhRnDZxrkM9SqcjUliK+Fm4OS/xOVW98w4uv5NXCWkBMepQrFlkAQb7igcApf6FUxQiu0SFPvvk5T6OI9zkcDoFB7dwuhhRZsp1hmoNiuoJ8BwvkOacz9qAy3r2cI7CvQ6QcEHRIMEhzFgIpQsQslEjK/PFSBmlYgbAU5wMF/CtD3dBkJ+CXA4H44IhJRmFOcgFfuow/uEF/H4EfXMP9hOIQmidnsNpCKbg0NbZqE+R9j1AZMFgdMzxWscOQJxPC7jX9/DeYOQH0DRhYE5GluVUwsAMGrj+UufgGaoqTm8XiricsegW6w+O/DenKKTNsMAEqNAZIY+X3yLDyqeviqv3T02PYWO04FXUpTkPhuYbAs6KaxU3gY2nhu7dEeQYV72B3QH+zUfATCHkEpdVysfS9QTPwpc9W3qc/LaUnmCIqBigDX3SzFWbs2swRi0aggwAl6bHgfdWkX65fD1XIeydD1ZXugfZexC9gHAfBY7Ra57MyipT9PZhVb9MkFxG/Rz7+uJEQAjVFBFiJP6G5pb5Yn4KGM9vjLr0WqhbukOKQ6imbriC7Q9gz3DwOPI9Tv4Oo3XYM0WiFZDpo7fRMxU8L0LkxAQwESayuOt7HPohHBUUbykTvL8xGTgm8PUEZhfcgyWm1WyS5esCcHCAfFF0sfyWMixeDJmZLQmTYFddf3uEMyNEgm1B2I1yz6FsKitUjK4QlshZkTDR4UL4wNhEFajqX2bqMxMqChHWXFrDGyZvUwIMw3iJ+xqVhFFJbrwsK6Eb9jDdDnb/CXAneHeC9w7EC5fbNRHB9nlcO7nUrm7LORRNxFUFVOYV8jBTkCta4o2Ftx2ON19jev0dhqGLd0BYdTG1iR4LFGKpLvWxhkXxDqtBXJSQM7FoPtcV37EppXmKOD57w2hT4vlUCJyNAWslb7mEMkMZMRdGTS6ybk8zupX3WrifRXnisTKja7hQ/Fz6TF6jea8J3FgOhkIfL+IlGTcHP7K1NJpjuKB6IdVyQZPFOZPS+iqGnSOjS/Jb5ZM1lfiz8A7w8ULAc2Ch9k9WGsdH1ed8j25MVX6B10IJtlDn01ndBn2d4Zhz+CyMu7R7a9qJsA+5et7MWiOU+IuBbgfsbz28Y8DnEGVllxr8MgJ57yJTSSBMIJzAdSQPLM9meL47ANYSjneM0502uNa5t67Kkhil4SzXxs1SG1pp8Iot/vF8Dx+Zk9ScrGdT31Y2Z214aPI+Z5tbrbNIDdL7lJTrWlr/cxU09m3yqCoJz1Jbm5M2wnA5ES38026lsRixMGse0FCmDUs89wwnyr4GPFk8dLdwdE5s59nP2Z5NXV4DWAbD4sHKZdLLeZfgZ6QdRrOrsy/LHAg874OJIRAvcDiaqMdk+7P5FmurWTauX67UER/spxO6E0XFClVZCEe6xtG8iG899vQOe19aPxwB2AP+CYaIVE71oaYnV3yl+NZ5SuF4AdxNjLv7CV5fngoDzxTvWgv/crQCgKic0PkIyhMR8q9N58q79uqxrCzV8sOSaYzPOIe1XkTT9QvFG3H9fonjL/np9TwrqZKtxeVp2X2gKg7hI5EcYCScjvcezofwTIYIHMN6ihFCS8oU/wTlPydY8Ir/BhBlrxi+GFYKqr6oEQtMGQNrKJxWAIHZlaha94YZMBLmNTjwUbwzzk0ENsE0RlHuS2NgC38fjkP56R4Aw7nAQVlPYGTjS8EcU0DrPvK04VJrjrJmvI+OGLSfAJ7g4cJJEwQjXbEys8XhJnjMV7ZCWlk8XJEPG7DVoF8lTpTatA6oroarv9IJLvDJvP+5oiaf3ejis6RWf87SG83HUxqfGMXFgMUEjOxgyYcTYpbg9xNAE3A/b7tFU5b8cL9UWpPBnqoV1+l5TkQ8QjgVRVJQBql6VgjjKlpe7EMmb+tIvyolio8W5t7Urs6iSGj8agDAOYzjCT+6/w9c9wmdeQ12FilmNyPG3KNiBNGhM9WXheCS6BGhOGqoFTqtocx9KAuqsFCqnoyAPCXePQPhwiSSFmLOJoSXaDORJ6VxDKcqKB/FAydDhwFn3GgYzAaHm19j2L/BcZow+QnHuz8A4ye8OXnsPGZIp2y7IWA8E1agxo/UZqONozV4O3Qwh1d48eof0Q1XOdyMDYTaGLl012D8OMA/CJNocP1mgtln1UQb/2ZFp8T0k0t4mX16DvGcAOdnrI/mlUxK1Up+KsaLGrTYV9kjkD+74WHet0RgVSKQCs/EkKAvgcWJJ5HUsGrZSbyIjDC34k1AwlR7lQ95/xiC8QxYipdkhR56YnQxT4g/yfjp9it8vHqB8fgr8HTC1z/8dxyOH5cVZM+SKI03d5zU2yUxnosnS5CiWkjbgmCSIaIsFVbk3Tf/Cafbb0Av3qC3BkPXw1qLvu/Q2Q5914WLyuL9ECYymEkRiwgFEeYlZqrETffRi0MYd2lb7wPwOjOVB7fIWTaFrXaqYFVgL8IHo3WZXtWWeKbWLvFqOfP8zBF3GXIPGYXNvGKV0Sd5s4Y6Z7RdSIn0XfZETaGiMSMb6KMgQARP+USEMR4304D/5XvG+/2I//FyggsyEgZc42b6Cob7MyH7tqcwS0kNtTG/Yslrr6CIe9Lxec9VXgDTCPPv/xf47gPcdII+PVisa8VHV9SuodiV/VfvOZVrk3eX7GFKTHvd0nJxBaOL5dZrqce1hJ1kTkrl8hwwhFtRdkEUPFPa3rkss3j/xVMuybgU8MfuY4fdqQdNNVPc4n6zIKQFlg6EW28wGca98c1SSynRcu+D4G8yT1bu/nV8Pc/zGZgozOFhGz9+cSurj2sjxHL9mkEA0koswPaGHqgM50dVYOMF3rtZ1wKPvNg3WoOQRv3p8Uq5FUeUrSg71SAyguY8GvzlvMWVOdYek0qBJLKfEUchybIwBxpXZHxMOfwqLePAFlcl5R+T5ueYHlPHwvpsMTDU1nCVv2I3ZmlWswbv9ZwLGUtYm8N8eHnfv8Rol06AAKPZpfVgWPy0+w4fqpMfTIB/aDWyNW0sWMx/ex40G/vNDWNwd7g9/Snh93cA/sNp/OUBGgGaggIODJP4MQmrrONMaD4mcoIkXJPiEcR5MeHNuJc071fzhno+0mWT+WXNbxpG6C3JHZv5hIRcVl0UMfFkvOhoOHpE1gyANJAeaUFPhqP56rpz68l7D+8mTHQL7K9h+A7w94HXIk532wmrJ/ojL7J9DBXkvYNnn++GGE+YnMM0jUG3EHkVOTku9y0k5yUK+gcgLIkPR8Wj3OTT2Bkc8RnDdgPIuBCP2Hs4I6cy9J4I+C+sTriTQepJc6oRjbRDANgBzoMpXJbuTXDUCYYIm8pxXE9/7HD/7zforx3MNw+Jt7aGgc6CwrUV0aGNgm3ZAIaFh/Ngljs0QrhwC4aVi7Jl/aMj45atmkBhAWVqWVOcRbMjU84Q9BhcwSC3K03zGb7QLFvmC7kuo2RhTvOic7PEASv7KEhAxnJmXp49iT6qwBz1ApV7WzuuMke4Nga260CGMdkJ1DO6voPpLFzBIlT4pGrJW4PJEKxnWDd3K/prSk83RGykeTT7kr9bJliuLhttcy/Iwv2cmVvqSqBVxZbZ5GSR6MO5TCud0My/1gfkExEOD/wBO1zBskv1bdqESjIMSqe6ZCTqn3VHR0SVkGTsVCTeoqRKXU2KpRZWXWRb8/vIfFAcW/AUzcxL8GjIKK/rr2C7eELCO5zcBziMcG5KpCwgbp/iKS7GiH3U3Jx5t7F+R4SHYcBud42r/at48VL2RElsW7wLwo8EnuTCakTiHdIy7EfiASEg8kgpWpUCTPICatVSoTA2zV6V7Sz0hWcQrJhNngm569CylSFvPauJhBgjuPhtmNOlVYG/iASJALmUrdwbKGBUjbIEPNkKEmWNsledhJ4hDoyfB+B2e4xugOsPcNOE0/s/YBgfYLzLa/KItCzD1vBLqJWLzfzF4M7nlD1PyAxvnZMAOGPhTY/T9WuML7/F0Pfp4jYbQzGZGIrJkDCRYiDNleZjzRLmLjJLiXHKOeW9ZsmaR1U3pIguM+rEonxVGBtaTZ0zPGzqz6JBqYG3eBlOzkEEJ4KYDSaLRphI54qGUU1BFIzYULisD0HwIjIYGHj1cIAjwALhvhvysNxhx9fblu05aEMbKc6aX/pdetZrgcLBfHoPf/8BpO5GAqCMEZJ9ZdGKlPdf/Vh9qMfzJ2fr35i9yUNuaGM2zLUmIzwue7jPj7vrd/WqzWQ35iKndww3TuDRgSeGHQmDG5LR8zHgRgB6IB6bk5EoxpKQnV2kTAsWKllxU8PNH9V3Kh/PuMCFgS5241IZpNWXpUGe2SPnjRA1sFH5iTz3j2Y1Ly1fo4KKBupfrOoPDxonic/JYfX7JUPEUn/PpIvLpfGrkk2aWddc8YSNcdfzVfJ9Ku8SuLWQEwtaokaflnq7bVbO88jcDJV2CYuzzEJeuHKUVTdrKH1GXhfp7cKLecb0ZTU3xVMZ5vypDEkne2i/WPQe3prOL9qs+npyK+aTDNAxcKA+8heEIzF64nC1iBhYyIMo8FYa14uH/Ix1jcxswVov8pPz3yWNJGSptFW6wTOqTZbksgXeel5GmHF5TEpe1flZDYDy3LbIZOFwM+d3q6EAzPDOw8EgxH8ZQTyCzAjyyoAjZarNkS6njo6H7D08u+iM4IMRwROIPLw3cOxgvAkXjce7F+ohAFFepRw1IEpIairkBEHgR5gMLFw89SAhKqu5TXxsxRlpWOVysKEOD/YOgI93Z4jeJGYV3OrDyQjfnULYVi8XgYd11fjcECVHXzG0BEe5GMfAhJP33nByWjREMYwWxZva88rOTv0twmCcg8rbMbGXGwyM9ds2JWt1gMtpzquqXsc9VhgZZN/VZ6DKurn43JBqmn0pTSmM24+Zq7r5DKNkCKYz6AYbLpAnQKKIzAs2HlO469JsltW2pwLFb0xPIkdn0qMNEQ3etX67UlYEvfD59XiNF/YKA+JZxC0E4MLUUnhuKJWJUmqd6rez50URhVNkzuSuBMce4+mEh/t79P09bo8EwxZ8i2C5TB1l1Gd0JJBEuvRpNi3hQaZt2rq/FT1tTbGtRJNz24yAeJkV801YNUasiimJaAgxkf5GJohj3REhmvjdGwazxfWLvwe7X+M4ORw5WO2ZTzh++h8w4xG/Gj3sE5V4W1Kb1yIlJOVHAND113jx5r/C9gf0XQ9jCNZaWGvQxfshhPClS5hEeZ2gr8GkCYHg4OUt8RbFqq6NEOk/beVmqHjlmsmbw2zRJLcffP6ZrzuTv+R+b+sFAVHhGWIA+xSiKu8HgJIhNO2NaDQzmI9XM2oQhsmEdTOg4LFCiAaK4IXDJsTb9GQAF7w9fvzmP+On8QG/+v5fsD99jEYRbB5bc7yJGOa9SOmL3rdrYuJK/a38JJAb2yAxuCHPLwg/ffOfcP/iO9DNa3SdxdB3sF2Hoe9h4/0Q4T4VHaKJKvoeYJZncC9MVWS6vEBL/OdrhMrFR/heMtRFSKKqWHNuCnlEDLwyCTxrMshBnE4RBG/KAD9lxvLz3IX2RZniQa6QWt8KgesRTFVTiCJIgDQvilUOtDPsG4CNheeA0703IOOw5xu8Ga9xZ+/xk/nj43m8NhIvXy/lOVN2tVLB4xqPJhAIf2XVTbmVzlb9qGXS+1KXbXoxo8IVj0ur/CcvtL2x0rXeae8zmfu2c6/22MvKgERXQywtHP/4AZ/+9UfQ3xvYjwb98Aq8P6R8i/i6SV7VCsavFJpPNDY4bgDMYjBPCHbVc1rDRkNeUs0GWODZ85y5fr4ZzBpt/7yp9Glb6t/a+J5shHhEKltsXWy8Vni5p3OyEFu6pMxCO6m3yhFkvQIpIB8qHBxXL1OTFxO+WV/Tt4QbMpIgdZfCnPovzzwB0YNY6PO8H7zy62kQRsV+nfENG9KT9uzMIeh8arInzXzrtWmctTSIGS58Ltnx7BrHbBdUmcMaF78alcneUnJ1fHOyV/jz4R8Sl7Gf3uN/pR/wI4A/eFE+c/pHBghXCwRe1ULoZQWVUR+QdLGgGX0TuoIoTwUaSGo81ULVE2YQ7t5TL1r0R7OaHIm76KxCtzk5fhqSi7dlGJy8+xNvrkdawMd8nsPgVJZiDG1AnKYJHz6e8PpwjdP+gMPtK+z33+B492e400dMpzGcetBOhOAkt3s4wAdjBrPHNE1wfoL3LjpkBV7TuSnjX2PQmRBuho2JuhgTnbvyqWdjwiXQPjpypU8ZEXWw1sPaLvbKwTuPEwAXT2MwAZCY+sJXJeE5xYmaJYFcUc47cLg42oXQysYEY5qJdwSG0xwhjC8QQ7iyh5sA6k1mtYW/jM5sBAJ8OJkifLnww9ZaEFtwv4c3B/Q4wA5XIBuOVuQLoDNUzu+Dje3Wy1+Du2wOBDikQkCo6kLmReX3Zbik+i16Nv2pnuf+IQa84Azq2uj6nAze2uaeZX1MwyV+ZEIKn/1xvAehw80//Q77m2uYoYdhj+7+BCYHRH3bMm3KyVuDkwW6ycP6XxYH/FzpAkNEmLXHsDNLZaL8g54t9tw/IzcepbSV901haqW6OsMyI9n2CaTqAXEEWgKmaYQbRwhzEPZp4qDn7ZPY/WNFC0h4E8g+s9J95iAQ+xH4hfwye/WqgS0K3Zkj0ewLa8uG+paEbyAoawnRIMGg/grcAykuomd4f8I0vQURwfEY7/kWVB08ym2zay2ufMt8Vsy97nwaMsElYteBuz263S26bigNDZHB0ycjAChF0IrANiNi4Zm++DQRfskvypFE9EoKUijS5XtNVLn+8rzH8HJry0S4yHdB4+l4IzKDWp+UgCiJF7kGSsxnesr6d7WBEHBF8BY3MMK+kIRoC9Z2YzwMG8AD7uoF3HjA2O/RuTFgC2YYN2Vv6XIW1sddr2EtJGyqpaogiTMrWRZ/hx+u68DUYTy8hLv9Gn3fJSNdZ00w1omBTrx3SO2RuH8kCTNXgLDGxWovlE5rbTycRnqGiWy9CN9IlY/v4ve5caskB1m02UYNVteQyjrmGK+9WOtUOOcUEseKgCgqBxlmUbDqXhZiIdszOqckqgBCMPb3fEDHOdyZwxTKAEEwS33LjXLd0GdNM66hRLsQs7DOUH0R3KE8rM441TZRdsV6PDqd3edn6l7k22tgXKnnHAebuqJpcePbUkoUTdPTOKkipDKCMOyOE9zDCP9whH/owMcB6JZo5XJvl4bc5DEW8wtOPL/ALa7nOVPtGPj8LVWLKzThMft6HWmqj2X6uXl0j1Hobyi7Vs8Syj1PK+TreTqwVr4uu9kAoQuz8GXxQQqJuIUuniE6sz7GPVm00ZjXaoxc425VHdH54c5nrGY2zpVfQ5pzfhQA1mXsmAVPuIsPmIewWtqjLfh+Ip2u2c3WSKhqJ/X3M/AIT8WCCZIXCUOWzcPPihclwMHC0VUqMpgTBnTo4UU3G4wExMkIV/MPxV5kzuAaJhNIfN8aTJb4WuNSRutHPRNcfV3K3OhDMZEqdHYcFjODDaW7nsKoaqLGCx1NCOt832Py3sONE5wLpxi6rsd+fwWadphwggHBuQnTOIbIWcKHSDUeOQQtc3So0y3GMTDAUeEebDoEsAE8I0ROYnjjQyjuossGZHwMEcWpIr16JhkvDBwmGGOjs0acLe8VzVRzuYDDK+yaxhmW2sV9GnQoAueeDQwY4R5Igp8IYMB0Pjlq6j4nvJz61dD9Ubx0u+tgTI+OBhgb75mc9brs/8blnw1ThwxeyZa+6wvkixcar80qqfRCYN0BpHWGfufVu/Bctv9yDz9X0mNbbi/s64WVqlhGQoQAA4zewZJFd9iDDnugA8g6kA+nxc4sUdkHAgADNnkfzMoGxLOJRqyPtk51AKnPkzYbIpoizyKvsyAaKR5SOWLFL9WK6iqWmDTZAJEKMOniK9M9kxaRCYTqdmtR63prIovq96wORXxu31zB3BAeju/BrsO3r04gMwXEyIE4GLH4F/2KwBHDTyTmJ4V8WWGeW6MRpLJA/3hTXQWHmh+JEBD7B6KoPc0CQUKciwprea2Z+uwZneGKshJdxpeYqjBWIwaImMmzB/s9ulf/Gd47fHLh+B4AuNMDHj79K3bTiG9Ofn6cuiKCNds1+1bDRxxzK99kCX/ad6D+Ftcv/hNoOKAbBliK8QdjuBkr3t3GBo8rMikUSVG3WhKiaLEmJK/vQIg5EFwAzC7MX+RYJJ613BUBiW8tzEWxYJoItSCnJoV1WmCShfmkOXJ8DJPeRDHN3gjDqTwYAIQzluEJE2C8icc+hZXO3Z7jRIGdcNIBEC+Clkdu3J82etKziUdlGYZ9CH1K4XQEmbA+zjl4a/Djr/8XvHMTnGeY8R7f/en/jWE8Zt5hbdwzsK0RWtyJad9qJEWN/SujkWEtUVRpSoXrM3EdRJNKAe/99NXf4eHN70CHWwyDxTD0sNZgtwt3Qwz9gM4adH0PQwbWdjFcmUE6RokIxsIwiQHOy3Fl5UnkATm+LJ/ZOBfLcVoxNTrKl51p/McicpV+WhQvZ9Mp4xdB1DFGKcTwVeYs5z7sHXEk4lhHuuxeI4po+A2nKIyCg/ZlznXYw5KpFRytcCWrBrX1IMFxDNMke4YbAt2MCZO+IMxF6j+n5o0JcYDllIBBOF49mju8Hf4tzKMHPDlUgSLLJpuMaWPOBU4TDhDY5Wb+5ZQ9BTl6XYnnUYjtG+HU+3B/jxdaztmTFnl3ysnwYs1nlF+FmGtgpDANsv+llhLnZ2jReIPS+zAl4Vv2NWBVSrdaYN6iLoBVXxZgtD0CGUjOodeGcslk8GtRs4g7BH6yIEhqrYS+hiqO33/Ch3/5AYfXDr/+33u8evkSr168hjEWCaXoJpuMGScaT0zF9BAh3n0TZ5WN2pINfF1Vy8JHphAGBiXcC60qfgbOlJWjRXqu0IIe04XpMXRed3Fel6JBZ5T1tRK8nZtWf+bHrD6fMqpG6RVFfk6X4J9LOvO0sbRSMUOPqX4+QeEvKTX50jKwKnNB22m7Jlg5A1uyT+OfQvlR47SGAWTOKdR5nrIui0C8oeRl7dbydY3NmeoaG/Vzztte0zbsL+6I5BixkFoGqSfsA1ZtPql81a+E/jcaczLPkusoJ8Hjob/G9/bvMfr3sKf3ADEMRjhycORhIx8WQvBkfkHgXBua2APeBJxo1BpqvkDwZroIWb4bA8QwtFrXD1Ih14TvVvQ9KWEVuwqY0BnhWSk4n7HXdDOeeGerHILkPsUoN5vMS6QZ1zGSM2ORJzb+DicLOJ9grqEvTqABAO9wOj7A+xPYjvj6ZsI3t0fw9Q08X+PTeMJpcvj+Tz/g4f4eU2SlvEQyQPDQ9m4K4UrjIhnbAeTRxXmjNN9hLb0Pi8ZAiAxgGOQIRA6a6JswoDAmmHCnxSncA+HcKTRne5AJ8pp3HdB5jDDw4whmD+8kpA2DkzyQ5a0iKfhqzV3A+uEya5LMDDA7uOjk6T8Z+P9xi+7mBHxzDyKPyXh01qcag3xa7Q+mpOayBmEOjUF3fQPYl/D+BUDX6MZPII5hijSaSkIjowhDH1dAKJbc2ZBPNURZkjMsFpAlPCqHkyHwqQL1HorxTLOrJzL98szxlE1gVk2sjpKtIcKWF+//CSH8uQq5JbolqZnLtlqp2i3tNEdURdmSaC61R6jrIPjmO6+e9DYA/HGaQMZibzt0A8G9+QRnRgxHnuOcRmrxqs4CzgrM1ZSf0Y0e1DgxseXJz50eEZrpjKU6pgXerxSWDEJImUJqWaqg1RWuvlNGQlXTcwtUxbqxanKVId3Yt1Z5XY6ArjPoYPFwnDDyPRzdwZgrhAjWJo0pXYHQYJarKsvNthnetmbcmK8m7HWnolJMexKwQgqF4aKotDF4KpndFGpgNl/JfJOUxQykOPHGXEEreACAu0/w0wGT6eD8GLuTB5SZCwdGeeHY2uTUbKuxfXiumLLJGkzDDnZ3A75+BbJdDrtk5DNMnlYmhq2kRY+wv/xEcCNgLAq5pggZoZ4W72d5SqKhwzI1U/NdNYeprcjkFeynEEvWwBJfPCHMB5ftb0nSuzqY6Nx7O8J46i4lDyFdW4Z75Xut8+myjMCYUwzT5IUxZMAY+OiZwhyU6GSAaX8DzwznPfypx9gfYBiwbkR2EakGCJRz2vT8m7+bPduMg9orqPGxEF8hFZMx8MZiHK7hrl+j7zpYS7AmnIIIl4UFQx3J3RBGXUxdamJnMJrWJa0PJ4NEfqz3BWMRoBK+K0AG+fh5MCQUJxwEJupTD2UFqb1zU12/b9jdz6RzOSvGqOBuH7lDhe5VW74x/GZv5kUiRmRG7xxGePS2x0QOkzmG5TQNItuss2YEl0qsvSs50jq3xmyafUnfNVMjNEvzNwTYQ4/u0K94JkceQ1DrSp7WyLaG8ykLxjbRRh8p22PBplVukSEtv8/LbqMQin0pfzOSYiKFdGPAOwdyI7qO0F8T+qHH0O0gxoy63Qy/6/0h9U+XXBtOcGCV3VF7VZWweW7P5TK6B+t76sul5dY2cxEzvLkEwLT2s13yQuXll5y7TW1pPmGNZ1gpt5SWIeiSNMewJb06X+SSPjymv9lbvPWSGvDX+t2ifn8ZaSuXsZrzDG+zdGrhbP7Zi0ulh22J1trcUp45lc88NCUDxNnxkOKWCpZ2zvN4WHjTwfMDiAcYEDgaE+TkdZJPpR8FMZnzzIwVKqe7QArStSwW+e0cHHqFdhZsWMElZnlX3qW2M7OUdVc+laHobBn6JXXG2ozJ81w7wipZcD7g5alAdECxFhh6wtABvfUgG0Kde8Ow1mC/G8DOg6LzCpOL4ZimiFs4qVwIcd2iYh6IBoiCMYsOUOSjc1x8SkiMuxEZJ/4z6TB/WGUxtHiEMNoUp0LLbD46f8mUFXf5pJNnah5lOpdk2zgGShrhuHYCeOESRvijgd9RdL4kMHw6OZKWEDH8Lev2KJ0YIUsAWRAOYLoCmx5MFmY6lZEJCjicP86/6yec5iXvnPbuyaIBz6Cs3Idc5ofIuDL/8qTCn1W3ynx6nVjvri+cLm9VSSuz5xrs5PRLcHoj2PiPiOA6Fy5lP2YdwnJ/WnuewU0nK6FlAT6zb7TW0z/TTLfoxjPRwEfdEXH22Nwicy6fAan31wP6XQfrrcrQoErF0+xVVoIypc1U903Z3OYVz1oul+8SdiDQpwSaaW+nYasfDIZzjGlyuH844oEcPgz/D9y++A06+78Dbg8YjkrJTBx1h4mVkUL6P4O9mEHTVGgFFzLWLqY/z1m2um5LmpkOthQlzApBF2+DuJbieVmMslheKr6XP+erlBiEis9hIFpvBbGGT6+8meW5tbfo3vw3wHl89FNRicwOM3B6+B6nu/9Q9VFzzwoR18w02R6H2/8Ma3cQD+1wCZLBi76HsRZdPwSiLApWa2BJx7o3MeyMSciwULQy8PBjj+N7i6uvRti9Q7rnwcdPIbAQS7Yc0ZTncjwxH1FcvBD3LKwsE7qM9kscc+le3JxmXW31vdg8OcXfiekx0RsCJo6nvAVCMyqhYByjDC4/jq2ygDBilFUQPOTeldBu8Pgx3sMTw0vsb1C4ZIvCMVDDHp6u8MNv/xvs8R7f/uH/RD+eEn5ZplVZaqD6WQHk6nuDocL856xYfkSL7yS93d/gx/0t9tcvsO/7cCeEtdgNA2xnseuHdDeEMRbWdiGep7HBj2VR0IsnGuJJCB9P/mQG1Bf0JBvy5J9X+DKfOEv5Z8KvCC8y4BIv53t98pzkU2+NGRW6IC2W6F+3uDy9reXFI+hhhNhCCZ5wfx4jIH2Mo1JSRE2vivniajSKpmlsUqdhHPGrH37Ap10HvPw73JkPeGf+cGakz419zuDImbyRw0iFUxBRgPPCD2UIFEGpvx7wzf/xW3SHAdRpJjaOTwTqjanOunZkOV0EeG7eUld4hY43G9i8Io0D81UfLpuH3Ic23mS1BswMdoGuep/xwf52wu3/RiAb1tAjn5wo76ipul2fwqz7niyMYWcIjVima/JO+Mz4Kd5r4noHD/FPzhQh/ykogQ6ZmdAW5zkrC/+M6cL2Z9kf3/+sUPgMc/AoeH5iWmjvbC++dD9V+rlUIY9Klxh2/qLTZaNbkvU3tbAR9upcmY3XPO9lsDQXO2q+8AlpyemALjl/FRW1iebU/H3yzQYAOH4JixcgfITrJuBogrJ1J3IoBa94yNgpd5UAPSPZ9z6fWGqzAcInZidDGEp8YgiBEhR0xACbEEZI3zWhK6c4VkagYeTDOCkqz433Bd+t6SBT5EMTr1/yYoh98HLSIsl8IqOzoom6Yy24iiehWS5SZgwW+O7VDr/7usf1jrDrukh+CWwJu55hv/sG0+RxHB2cB+6PHcZxwod3/4ZpfADYwcV7IjwFmk/EwXmRTLxDISQvMpJIpSw3ZbBaEwSdBeUTMYYsQARrbGQ5QtnxdIIz+bw2GcB2Fv1uH05OTBTurHBTks+EvUjTWRv/xeYjLEcENhtD9IqBReQ1cSZnFf0G04TOeRgT7uKwxsJ1HmQcyMvdJwaOwwkBRNgxXTw3YnsQDfDjPwH8a0zDS3jqQXgoeSYZzGY8ogaWZFYpzgUIZX+lCJWcy1CEUQj4icyrYVcMJukODK6coEQGznwkuDQ2/Nw0SzvUqoePrAupLqki6OcMbGdhDWGwA/p+CIZHhH1v4gkkYl0LVxVrA1ndMC/jcAKm3oI4noxgMQA9deZDHVNn4O28rm4M43pqevRl1RclLSch+7aSIVA8alIbNnVSYpdCLHXOPOnLzAjXWZt5xDt11vl5h/JGU/Qk/OYqTyZ+k2eM7PBwOuH4cMQ4TiAiHN0H7Px72M7nUYinWkIwlOU7jWRSEnLwy2CysyAMCLbTa50MEMkjryq8UGf6XrxoPi1/RYKfLlSMl1eZqNlKxiMGQgxBC3ScLt+RKmRtgqfjPdjdQJSSAIo4nPI3rZnqGZke2N0A/QFymiMZFEwgckGBGo42Ggq3BIjBQZSqpD4LI0RqKlIaCYeV+ho/tWEmITF5nhcsIeGEiCs4V0rXpS2myGf7RZqnzNDkPGmDpd8z75+VtL4r1rFPaJbi/JRMYmJiSYh6AHSWC9XThCgPdwDJGCFjk/0QXsVicU4JAExUEFUjpngxrY+W8Qg7QFQheYB6A29u4IlwGq7hTZeMGIMcofROjUufVqtSMeePJHatanPLjQKMqdvB2QGn3S384Ram36OT0w/WJmOdMTZ51Bij9pDqe4m0WX0Vhi08Dxe4q9MjJdeHtBcUH3bRNFA+Pp518KJ817iTkjGbBAZJLs5rmSaWBJkLV4wWvjerXm5TSZ3zqhRBS+GZhJVN3mfZGJE45/i7Te/CYtTGHwOgcw791MH6Hh3t0PM+KIM9w9MEJt+o7zOnBJaEZHgCIp2Rr5oO5fG1WCIyhO7Qo9t38/VeQNDPITC0mOT1lLFcgpCZ4k1o2/P0rI1dlqKAL8Azl99ZP2cUxn0/Okz34R4w03tY42H7GD+YLCyZog5Fks8mWX99F0j4lL4v0VnNiQDTyCFe9NLhTm6zZO05a72oga4NhM+vm1brXrNFy1nP1LRQ4cqr7fP0DOlLGCNqxU/9e2P5z9xLlRoyYr3H6s7wyrsvnErquSX3X29qgnbiDdLPBUT/NNm4ObNEcyqx0s4MzM7t1Qv7vFTbWitLfSDR9Fb5ko6DCYAJHrsU7/qM9CzRoMKZt+WrG/Lpk/BU5ZiPpDILROY5nDRmZKO98MmIdzcoPqJgnOJzZlUfgsKaOV7KPOewAeRwvDKHUacenGh8COsU5TewD/FBPQEqFJLyQFKjOu87bgyh7yz2Q4dDVIRKSE4AgbcwjF3fobMh7Kv3gDV7jHbEtD9g7Ey4l9I50GTgpmjEYQ+DKeojRHEPkGe4pAiR6crOFEl69wQ2FCNdaV5KTlsEmeb/Zu/PmiXJlTRB7FPAzNz9bLFk5M3Me6tqpqq6p4Ut3cJ5oZDC/88HcoTkwwhbpnumu+vWXXONjIizubsZlA+AAorFzM3POXGX7kLmCXc3w6IAFLoCCucmgBmTPWZyjLHW12UsOM4LklhTqHLNROmLV4sJmX4ZZbVc/iIAbmJMe683dtaHInI8wTkfCtnJZrFY1v8rkTb8qZQO1l2AcQHAwHC4T6UZmngpNRTMUugUXVTW0qzop/UIiGkiBHTSDjTRLZRzAuldXD9JQVHfC9CAOHfPo8CJfxdbYIrPrEDxuwHBjE5UV6P/DS2GjVGjG+FAMDachlDtOQImQzAuOSwbTEPZn1v94Dav8UD4LEGX1g6PRmZwjR6ziYng6kCJYBDciTFbk57kiDi1Y3WJCZLKkMjBTAm1yLQDIuI35wixJENWiBfqEmKoBVMJlQEAEqxwfv8dF9Xn+ZI+kGD9w8Mj3u8P+P7332F/+xFkNhiGLT58+gDqrjF0EwyHWM9yCRABRoyaOonROWu/gV6KJ9eLsvn1mSkR2QRzOP5GakwFJs0Xog1oGZpomCiNohltyolTIgzh0yijOzQdlXlNRDfGkY+MK+x7v/wFNhdfJCRQ8ETHABKxqhQ428fLdAH4Uw6geLmuMdYLAtbAULoXIhlYTQrbpJwQkV8T4+LtEf128qFHxNmg/pzE7gt4J7HI4RgMiYmfyunxUgsyG9p69uT9HBFW+VjGaQV3eHJitR4WFsXJFIRigucCIoOzQeZEYEZ+xNeX5bgejHqhdq1zasV/sfGBhBJz4XI0YxjMBhTmy9nwGX9bOGvx49/8ezh2cM5hd9zjbz/8AXR8wHj/czRwFq1moKc3jbmZkQdaykdFzvT6bSzlu1df4/ab/wmmG/Cm7zFsd+j7AcPQo+t8jFFrOvRDD2sMOtvDGPKOCYOwxtIu/YirIRyKi+tbxo2hTwKJUTg7ISFrQgzCSOsqa0PzIN0xRdeZ0+lt2e1swD4eLifSwQgCsBqn6OBKHqxsGrWSl6RPpEpPLDNqzWu5TDJ6TBkq5IbkvJKIGyLYi2IWBDcmCR8U6LG8VyQiOwkiNHquL+r74C7w1v1dHPN7+x6f7A/Lg3Fm0jwlOff0SvD/CitM85z94585Bxfu5vGXCyZFSHb+tBSzgqrMpvLuh+r9wkt5V6/rl0ppjOTLORfi0uyPk7khIwh4+pA4WeJnEhbPaZrLDof39/jwH77F7g3w9h+7YJxgXOyu8fbqnVcuMpoi9OIpIycyAEd8yBW3dr0/f8f49LOPO20NZTRjdcsFTflcnPsp6aRdfgnfW09XOCHWo9hf0kgVaYVD46QTot6pVeRbYiovm/5SNmmdk/6CseNPnmbRMWepszwwe/FMp0TZfP7g9KxVUvYcPGc6FVsU/lRPk5E95xFa5vRvReCK0gpA/kQ+aADM4Dc5kV9rKao+4ma7+Duw1GrTWSQXpfJTQY08CkWuNPgaHSSEUDTIiAxZnmpkxJ30cn6DgzwVN4CJgYKRwtGQA2CjhM0SOJ592CIyXp8m57zDhjnYloLO55Q8Dn+yHeBwoRkB1a5jkTkYQ2fx9tUlXl9d4NXFDpu+y/Yi9jDoAPTGghnYWn8R9LRxGB3h6vJLjG7E4+Meo3PYH/Y4HBk//XQEj4+YHt4DhHDJMsKGHYdxmryzQg24myY4RnRITGCwI0yZQAsfPQAGnbGYAByPB0zMGKeD19vCnX5934M7i7HrQIeDP3kxMSQUtp/OJT6cJGtjrN+cE0JWjeMIBPnMscK1UIIJcJ8Mxrsttl9MsN+MMOYIe/ROHm+zYRCZUIc/QWoMwVrrdc1uAGED5is4uoA9PALsQEYfu6DcdkLzZCDHgJApXJ+h7Tm+7wpXONivmBX+yg59cS6ET5dCUJUOBg4XTjPCfXRxg156X0XXEPmT5cQtUpmXTDNoMBu5I8ukPleQ2uy0MoUrBgzhu9uf4cyEr9+9wXbTKTsDgwl43HawE2PzeJy/q+cUEK1y0QlBGHtvgOqPU32vbUiOCOPQvk+vhCR91pUd+1LLFxDPm9uzHRFrwmaozM0HxpowcTPlOP+qVPD0nWtcPi1gpp2DuaKfhwXwaCALxjO2tgeu1Z4oqoSjczioy4ncyODJ4eP9A+4Oexz2BxzHCdZOGKcRx8MRh8MRdAxx5ww3mkh3KyAYbXw8usD3tAwRyxYS2p80yXgl4tg6IaGZGRlxPJVwU068q1a0WkMoZ6ssFkw2MZfIKGmnh78QS3YmmyiAeUYrhkAyBmC1lKIhJnc8mOZ2QordIrmvIkgRntFRdDIY5A4HyR/7ruq3PcPYgIvEMJ3/izsW1EJKfITDBbmJcSTvt+QU/J4hUYXxtZLy9KMllMxl4WVyk7x965ImkgXBbBHcuma1TyXuZPEAC35TYDyBeCDuWVdxODmrTarQgvKJNRsuK/bxNX1sVlkzJlizSYRC+Dnz4ToIvLvwBl7n4EyH/fYasBZHN8GOB/THfYKQijFQ+F2nJzGGZha9msduwDRsMV7cANsr2K5DZy36zl9K7e+FsCEMk1GXuMtaUe1mJDwhY7YOoiCmd8aH9QCX5Zd1ErlVY9pOM2bBH3W5nqI9cYeEEjI54JYslCzc3qm2ihN/FaXMJ7zhhFB1ZHQ6YUYtnuiell+kyrS7O56KyNYFpzplrJo8Lxd4W8My0YiDeYBDMAIHPu/kvp8S8ObYnuCtDZlyiVx5PpBOvkglmr7KdxcunCPnQI+3wP4BPDVOcswJ6MiH7qmpNb+zDfvJbcNTyGFVbU8AshKSKzQXQZDj8qIqXy7D5EDLX3qXwjyGPwcwT+i6CV1PMGYCkfUOU+sdp9GxCXEqlUxyAYZWYo7rs+Zp7YGcJmA6ApveYgOLrbUYOiOnyxubYIqfMySEygyr53GJJq0sczJPWAGLoLXhOIWPteyZMZ75fE9JS47BM/LPZz+df1VbJQ1vlmyP00ukz+uEKPHKt1i9elb9L1LRyrbOf1uP7suN9yqUXbkmk2qs6P+fIVUixlOYXJm4dbLvNObkbQd5NP6ksINbdOCgzwS9M+6HJH8ygoyBHZzfM1VUm6/uXCfK4Gn9mCcyPlOgL+k0bV0Zx42bWvIRuRPIQhkGWcw7I3yYW0qeiiRAsb8+W2CJTfhbEtImmfRC0cJC0W3ANs//CX3f4eZ6wLa36ELUBJ9T7A9eJzHB8cIm7GJmFw6udLDOgBiY3ARrgL4D3M2A8WAxmgNA/nQCgzGFfJOb/GaLKR2hnCYfEthvwgDGidWmitQ1IgAGsNaPmyEKFyBPmMCgyQAWsOTvSzWGg93QgJ1J48hp3mYxg4qIERAdy0v7rrn2Rd8i8Ehwe8LxzsCCMA2+fz7cjp96wTUyPmKBCXcTwg5gGsBjwMewqS2TMVXzybJQSm1e1o9qTQWy9KchN3KeR8o399Ur9TVuSIzyrQt3n7DfoJoyqr8c6lw7mqOxed/qcvOpWg0FInBR76wMf6qdiLgeujjO5H2FfrOj18GN9SeUjA13qjCB9h1gJbTVBEdjhbQEBrk27U6g1sCSKC6A14nJgOBCuLg23UinIYrxatAX/bYNk+TTct5CJxrpLEfEWU6IvGD8ICL0ux79tvMLVe2e4ybKpoWQKeBzg6IZDpprPctnVKsJL/ITElnhynmS16x78+P+gO8e9pAl//23t/jw8z0s/wyLPaZpBAGY+IiJgdu7T+jNRxgDdIbANwHxkyU4EF21q5E4MdZyl2gBWSYU88y7+Ns3SDIe8dFTBTaldmTjrNvh8D+lzRaBaWSGRF1laSEjWRIaVwnZzwBEc5gUIY1GCeQGPmZ/sVJ4k8kNlYlWmJ96V41MVNB9PhOOVUqIJh9SxkTmZuWERLgoIF5gHdsBtjcjNteTgjB5xCPLYvYXQUE825w+nfwGIMw6rgWZp4LpzTkhWjizCo30Cj6VlbEojYSUzfkKJ0QLioiLMgYaB5mV0VgEdkThi+VSl1hpIuNxN09hdK375QtLFhOUASCJMCYIBo4N0okI+E+Io8L/dr3FHzd/F4XK7cdv8dW3/2nBY/+09GTKQcD966/w8Vf/Fl2/xTAM6HvviBiGAdZ2GMJ9Kn3X+ViNpktrBd5pJ/ynYr5cn4SITjiEZ0B6rpwUYQ9I/J7vBDmvz8kJkRwPzPAOexeECs0PsF5gW2431Sb/tTOWXyjhsPCfSH+R6LOigbEdEYRKthQVyfQ90k7mKGTFMtphIWuJklwb/zjEtQ0QMDMezSf8aH+CUydQAqU80X80Br1+GdXSyBuWU+IcpXCIiE/6HgH/G8B4hPn9fwLffsC0fyzoWnKGZxAyFJ2qmizgKvluOlFUFqMGP677+KdJpbxawdqCRvC4fMZ+t2XEE7/k/foPSBZPQ8hJCEVzu53Dl//OggwwOcbV5gLvbr4EKCjuQKIrEOU9ByKz5+p+kFx6n3VCwZrLuEQ5liXxw395R1t8QVt8c3OB64sBfWeRp1qe0TSkyFk0gs+Yzqhcka45/KiRt9XflZBU6+UZ1zWeaPxPucZOtjmz+UaPw+maX1YOeVI6Oaife9T/HLPaSGvA+AuYrr/WdO4sN4f6Kc6MzHlR0HDSbcl61Jt7/O52IgOYDhM2GHZH9Jsp6PFKdtX1QutEiGJk0hvTh5BpUZ3aKKbayHSooIdp/cpQXnHU50KL8VmSP70dwhZ6rxZec+OQHxkXHDzk5VZ/D7K/YBoKxnBBci6LCUCU7E7x5HZIhvDq1RZvrq5xddmhNx2IjN+YSgBDdIrgQCGg77xOOMIb/224V2PsO7BjHKcRzjm8uhjBbotxvAQFB4foRI4dJmYcHm5x3N9GGWMKTgg3eZvBhw977PcTDuMU5SHA2zhABnbTwU0G03jEOI04HMdw4teh67xORzDobOf11ckfNfH3bflwwjITc/xbYJcNnC7s5HduCs4PJaCXfDpMz+GjxXhnga8IZjjCgmDJgG2Q743HE2MoRK3oQMYC27dw5hrH9wCP92DbgWVznMId5iV5gJNC00hJd0UuNIrhQWoWe47opqwysrxP8iu7eNQi1pVFxWAHJfwG25E/KUFB4YqnKkr7Udm3Ys7O1JxX5nsOY4oSdPjwBMuEjcJ9Z9FZg0vawPSE7abH0Pc+70QwP+1iTa4f8fgF++gkKvWjw7A/FsL9GsjqU+5MBmOfZKdZermi9nUy2DxVXpNWOyLWOiFaOyszHSUQSISwM1XSxgK9QOQZpw4v2cm4+Kwqj8xVDNKMFCJjvmIOlx2BgONxwu39fdndmD7uD/i0P0Co2cPjHY7jHsAIwiit+osnyeF4POA4PgDdR5jOwNFVzisLcksBfgRPt/feC+IVjD/iU2ayQWS6QhMV79Y8NkKgGX3WcdXYGQZMD5IWGKD6IFU3lNv0T4ZfHsVM9rCtJJeKYV45A97hw2EsC5yIR65kx7QSyvKhF2YoAM6wSymjvPeGyIcmUQ4JwT3TA/3gYw1K7EYdlsmfiEjTHnkKknHCrysdckaeyScA9V7wNfrFNO1pOSFYf37+1N5RO5s5/6n+nU8ySWH1FNm9zEix35njAWFtqmflSaB8fS8xAIVdAR+iATvAxeTXlQ9rI/SSIa5XCkKoX2+EiSwMh1BE2ys87l5ldBcA2I1w04iNm/ydEhlIJcYX41JD3iqK0XY4bC7TWgjrYNzdwGwu0HU9OmvDnRAdrLHo5BJ3Ha5M1g9yJ50e2+i2ibKUrAHhB+li6oTfydEQ10WUtdZhUTZs4R+NjoI31QmHQL+lD1SUC+rSectNGQhFaZSa/PhrQLMvdSfKV821mNdZ8ppYjuu7IiKfRl6mHAehcVDzlGia0DeAMWHCiHRFryZohCoWGdQIr5HNAjQMhN2EJQ6mruQrg2L7s7Mp+Cc5xhEUNja4MCZth9IyfeQyx0lyqvlbu8KEYgUfJyTcQYPPKzyZdY61wVmRTWVU7RbiYTPJnLD6x2k8E/xiAOTQ7xysNbhwFwD7jTRDN/iNBKE+dmmmaydEel6AGwHVDlZHwESMkZQiiGyoQQQcecQ0HnH/eMT9PTAe/Jrb9hZXfY8hxJs+hRCVfLVqQ8BSPc9Ly/Xo/pDCuZmZX3A+rAZ3zmk3ky+mkik8pe25uqvX62tcSRJW5F+mHan7pYz09KTxLtLx5QKragXyfrRhf1qKZLDBYp9e6YvV1Kh79seJ1BKoQy3Nal6wD7Uw9VeRXmIEkt6SKfwLbaVwsvlLL2czWRgaYY1DXlkSmkj9yvUkDVStEaXPBTk3FtA8PihFWpsPxsQ68oKGVTZ8ySXXIVpFrC8sSnZF1F0Oso8+tUtpnOX0enSYSJ0FDOUzAYsZx8OEw+OI1xdX2G0G9MYises8ZFLkbhWb83c/MHtjIBu5Q8JfPs3s0Fu/4dHLK37jlWMf0qjDBgeTQlBOk3ciTMyYnMPF2KHrJvSHh3BSIsjDxndkOnSYMGLoO79JY5qiLCUODUOAU2GrjelgrWyiVPL8CvroxaF030FSIk6QRAZcOO0hjhJ24eJx4zFf3z9BtgfZAczXgHsFQhdwTs9Midnthstd/fkmaa2X5vBK9Ukfaq0asUPoBmRckg7loQ06VAaP6FUuL6vraAq0ooM1JUqs4/PU/Pr8lGRp/1XoRJ6DlXPrMB4xMtB1BsPgN0kaAsz+4GlH3wcyQ34D/r4HFY4ITA44CBJT0nsWbCsZ1EsIvJK3tWo4lysyADeMqAxkC2n9iYgVE72kLBKETam51YIbcuSOxlFVh5yESAq4vFWeaGUw1Qit6W8p0ntDAVSs9kJYLXooC/HDp1v8P/9//6sn2qJsqE9P7lJdk3PY+G9qmftjbo6Bh8c7dP2PuL34/+L6+pcwx38PHjcoUYEDwBSYJAJfc0BkaqUJI7FghG+eyemLooU5U6QQFOdFsWVfQ0YDSuG+KZHPJhK4pQglmOYL5aRc5AHKjqwko1c0RFaLNceIOdaQ4WeGlzY+i7hUAR5gNbod7Q4inQ0ULta10aAaBAFjvTJCBsPFhKsvRn8/hAmOilLmE0biZFmE+x/AYS3J3Q/BGQaO77Od3cJowrqLzopTJOpFBPtKcjrR5LIzgium+JR9iWm+9KkBvYb8UKV7I9JF0/7ERAiSJKspcuQafn06K28ry2XKo1qhZhPml9SO/fiXwrs4DrtyHcN1X+Gn63deIAztMgOH+x9x+Pgtvny8xdePn/QQnjdySqMuZ+qwe4Xv/4f/GSC5dNrAWgPTd9j0A/q+R9916LoOtuswdD2s7dB1Pn9n/Y4gH6YphACk3ODk+xR20jiJsZ/HtoTTfZc/2SkiuC+xNF0ShpHw6znYH/WVcLEcDHwY2iCkCA/MBpabP+q6T8A2R7+SitPgj1puC19S7sZ8K3lLOyPiLIlT3VBw/vt8dTelfaHPwv8DLQvx+v2nCxt2PP2bpjB3Lh1STqF42YfnVStN88AWd5VyKXH2rZQ7dDn5ZcIGjWoKOK9LMExOqkW3cYA58r18Ml5GXp9zGDQaiGyI8swlx11lCH1WluB+bWs+i5VwoMvJycAay8I9MoJj3ukvymq/c3j7N0f0DwNu7t8AnORYJ7wWCDT4PF4n2aJcFn5PYHwyQcbkskjazHC7v8UPhx/w/lvg/XcGXdfDGsIXb7b4enuBrrOKdq4ctBmj+19GOnPiP6MT4qz0mZ0QZ1W1MsPpFp8K0ynutb7Nko4v6a/zUqLQr+Ip1WvvyYledAr/elKLD6Kcp6U5S/+ua+8lJ+2vJ2m9RX4XbxAnIxP3ovaiflmABnTYY2CHiQwmmHDXQd5m9kneKpHfi1TPYPkkkwXjg7Bg4p0OAGBA5O9r8HdFhMzaGRFPqlOQRVnJpxRsEgkpI6TM6aRurJbiyQd/ksCFugiGg0xPAESvlg1spCtG/ixOiZcfPr4/4Ns/3uPdv32HN5fXuOg3PjQTDGS/vdbSJSSQVOdCfSbcm2c7f9qjYy/vbIZwOjyEi0l3qXrZxbGD2279yYIgA43TFMI2eWfE61cTxnHC/e2PmMYDJrl7EgQ3Me4+HjCOFpYMjuMIYoNxGrE/HOCmCcf9HsZ62QQMGDN4XQ8dxokwjf6i67TRCBndoDhX7O0f7O1tUZkAqRDxOd6lyZQhZ0yTvxtjHCeMZoSFR23ZBGeNvxvCbF+Bumsc7v81pvE1HBzYOBiTJjeT/isn1BmUSzYlCe0KHw7Brhd0hHSReMIhks9oGyhO9uvoM5lNKJx6EONS/HPhJESKsqHhzDuX5uxp7C0XNk6HZVqupgkIqS+k587rWH4TJOHHx/cYacTffv0OV7sdNkMPSwT3049A1wNfvgO6DgCDjgbdTxdlAwADx9APHU7MBHtg6FQDforrfS6ttnI16ufix2xNgiZ2wvHyE1w/zeWs0pMuq9ZpMYwDJQU7UYdautCD5BEdVYezkxAoM2hymyvqkqbDBHd0uD3scXRjfC6GqooWFf3Tl94In3v/4RMO4zESaclHkakkCTLYVBSjZXhnAkDhxqZpHDEeDxjHB0zHB/RHAzgfKy/cmxQXgwbTEMFFhZFjqKZk5ixRpyXML+ymFXCrh3WNuZGqHs9mKpDfo8n8wqqqjPRIE6ZTToh8XusqVT8KASTzkEZDmML0wpKUCXZUH0unIqMPxSSw+TIeT/1JiG6Y0A0OphNCFbNVKRksOa0J9mJI5Etxh0B6n9ahZm7JO17xlLzVGpBnpzl21WhdGXSiIS6JYy8HUqxbPYqMVcW2l7Ul+VnQMVAyJQTn4XnUkgdSDFclRC3DBsiFa37XC4PDLns5yUNx1yz5ExFBMHW285ckBxxgAHa6hL18A9cNuOs3qS0uvxQCQfk0U3goW4OHixtQv4XpLAyFUw6dRWcsbPjsjD8R0UXhL13eTuHSPDKy1vKFwTJ+4SM6ELRBl4UPiaEw/0/WQQyTAxmjnAc9PWltRERVyn6zykqNnfM+Z4vO57nS0BR4XNEvxf/Ce1Y8Zk2P61OVAUoR9GOlVKwjzodDZMJmqyIXqPkKjjaPyowDjfjp4h6fNiPi3RDClzVdo8RB2xLqObOc+tMC3EwOPTM2R4MLB3RMaVxCe+liuFBFHAPO8I8MYfv2AsPNtjIAJKG9hk9etpy5Jw1hVP+oUEute23bppInrtwBNA/KylJVp4QuBBlPnirWIbJlfqowOCTUMxjG5sLB2hHT3R72OISdlARDLtxL4jAy4yj0RE2uXDDZGoGwRFR/E/QHwxghYcG0jCwyECJdZBI+b+A3r4gsTDCWqs1CVYMz40lltiSIhY8zcWtVWqqkHqwZSHPcay+dmbrVwpxzHFCZ90THn7kOaofhulrObmt2nGYRJcBzotpZefbpCFPamtfSCmrS++V+vIRdm1rNniy0+uHzq53Jw41nrdSSWuZqrljMqnFp0/j2U6wnRv/dOCxOEcGcduoNcZoOcJb/c2mM6fRCBSLnX0soMglP9AAU01wUWovXkWSt6eRcvsZzIoPtZoftMGBjwy5srSlEfSYZhD0s6r4KAHEjL4VVJoWBcIo/XTcud12QAYwjkPUbZ4wN9gIDGGdgJgfL3gnTWYI7bjF1FuPkYkf8XsgB08Tot0ccjyOsBQ7HI6YxhJVmB56AiSYfghheL6SOwOgA9sZO71xApRt7WclfVp7NSSFDrU0u6H2TY4zOG/D9xnYDQrgfBRbsrsHjG0zTgNGRl+2iTFmH0olwlZqcCJzls/bDNu5I/kJPP9X97MSIcnb4LT3yqaDWF1fHPGU7PAt6nkqEX4Z2nWyj62zkj44GJStn+Wo50t8NYfw9lR1h03UYOosuXF7NDPA0gR4eQLYMcRoqsha82aRKiQAmf6E7kV9sueBa9L38EpIiXuQAc9inZ9Zi6vtYIU0j6HgEWwvuB11JrgcpvahCOQq/2IAOPYxr9bednu2IaCY1l/FRMbcCsw76p3eHpZRi8KZXXOBzw4BePHj8+IjHnx/xv/7xN/jNh2+9omUIXYjxlXbOtuZaBM7kqZK47N7eVbwX50P8Vys3OXuWxUxwOBwe8PhocX/3ERu8ws1oALIYe60JE+KxwMA4GJ6q+mW2zPH02/o0YHhLpI5rybO82taSbpGO+ciTOmN6o9jluhj12kGkGplzQsR/iYry81BSwylCkeG1+9Hua9GmdmKo9SG72+WYn8dNb2AdtiMuvzyGPCYZC0oaFBZVtgM+7GIAQz13WR7HU3zvmU5iLslBqCmQXoU5BOuVhUaqOdi6MjrF0DYlxTwPqEUwGoJ56Ywg6YzcGZEsrxJRDax200idSaZSD0KbiY7OYJrSBuJuXjUMMr/OiGMirTyWGJGcX3Tdv3qLi5s3YGa8B0V4PH12ioZTc/6MXK5OEpaPtK820FZ/SSoRxcvJrLXorD8F4R0SQei21p+MsDbdCWFNOiUEijJ2GVIuXsru0tg4cDgJITtDUK8Rl74jvJOdNk8JzbQmeeeUKAiBqpLErNWXWzdLK34RwhwxQ4evq3GoTVMTPPknAGRH5ExVpCqr2+DYn0ZGzkOcUcQtjc9pnYuTzYXTEELz4g6uyeHTdo//490BI8JpGIkRWyAtC7+FrFF5LgPQEKrz3qKij1zKi/59PzlcHze4OgBvj5NyZqc6WPdV+u4UrfZn1WG3Hd7++6/RXw4w1kJmMhn8NcdWkFSwNXpEcxRH91nVPItjZYmltgu+OpPxKSxjKSV2odyQTt0hwwnHJDSBOCi7weH1NxPc4wF3//QzuLsAv7oJdMbTWMeMe57wMZyQ1ZcmvkaHy3DR5fKkpHcTGB/IRcedOOtI+IQ4ZuVhYCREFE9VGmMAY6J8SzMzN8t3SqhOOCGen2jmeytrTtcWR7VN+k4XmIPkPE/eyjcvk55V/+w4nZBLntpcEjueVPZ5dbR0g9NtPhfez48BCzB85nKZCDH7rhRA5JNO8N9/SU9JpV5/Onlekm36IZFXKMo9KXQOVby60iJz0amJG7lDMYe7jRZaxlMtBplawyCbO3TrWSkle+rPLEP5SGqhYvON5JUGDKWjuRrHC3lz6Du8eXOFVxdXuBq22NgubsYCE+CmqJ8oqRUcDJtkjRdvi9P0FFQGZwKQLpwkheg9Ms1+3q3shARgTBf1JMcM5yzYMba2C/L36GV05zXe4/UEf5ICOB73uPvU4eFhj/EwYn8csT/sMWHCNI3h5DvBWAtjeu8MMQQcD3AjwHLSgQGm1F8X5Xv/xN99UMq7LWwP8y72H7GRTA6jmWAmAzMZePsygcgC6ODQYdr/ChP9DQ4HBru9D0VvfGBkZLNRpAbylo/077Trv8T4MA5KL4rPpPPS64hjxYIT/OVYUcJ2ljUY3jkfbUPGCBlc2iqZVkxs/2QKhIPX5Y4wpw6mPi1Lff7DqO+FfdB3ScnN1qKzhEuzQTcAl7sBu03vL2En8n4yduje/5jsA4V3ky8uwV9+NQua2EhacsSsE6J4ZtyI4ef34NFvwnfbLdzbd0C4H9Hs9+je/4Tp8hLj6zeqx/PUNKWCwrFB9/PliTJ5ellHBNVfS5GfqMi4OjWcDQDc6DA+jngYJ3w8jCr7BPGWMoCHD/d4uNvj7vgIYZoGVPznCXAOooq/LyWDs6HfdLh5swUoxenX8frj/lm1AChCxGDyDGJyDHaE8dFhmo447B9x6PZgOMCkXckCn2bq2agIUyP5TqFckTMQnohicZHnbgwKTFMYdSk5tGaxFC5o5t1SSoaeeeYQ4dP1zjGVwtFR1jor8Dbz1HVWOWle4cqeUiGQiaE2CHSCa5EYSr1EMKasTMtAHL3Z2gkRDa4sBrvESDTzSEKYZlwoKKFiJxWjOpVO5ZqbETVai9pdyKcHt5GdG9/m4JhP7QaSyJtORohB1Z+OCJwlLi3ZpYLoBMzCCbHgVOrUCgzzT6K3SsPGYJLdHIInQg8oGsXIaTwwMU+kCcidFf4zNpwgIkCM3xIbPTojTDKUQtFXY8NuA9PBdtaHaLIScsnG+yDk6KIJuweCm7ggRjm+Rtoc4Na7ypP+kYS5uIa4+CsEq7mk6cGy40CXQRSWo9KicEYhj/ZNJ/4ggmSr3sazaHSM/EN9VsCp72V832YmzfuL50gh7Xz4nMwFjuisUJ+1PCD4y2lO2XnlJ/yNOODW/oRPNGLC4E9CuFQ+gUzxEcdLw/X78KUZW7g1BnWeUGuWi0jw2SHOhua/EczoZk79dokGg+DXlDENSrrA454iluU15C0ICoGyyvWJwQhVsWDj7xNouAKcJyW9RFnzUSB9d+KADCHanIMbR9DhFgZA/7ABjj14uMJgNwk3nT8FcWCHQ3gmdocOhA4EC5ES4cP5FX16hOIRBFjy90Kke3+UMxxadgCO7oC76YBP9w/49BE4PHq59cL0uKAeAyf5Q4/hKemowrATTog1jqfyZ1mEZ9+UVQqMc/SsxL15KSTRipKOzdeZ8qyj/SfTmQuiec/as2Eo61o7vwuZVvDG59EpT0ufT+taVatKVT+eCy+DcG8uAeq9EXFFhYJnQgOelz7HYJVJx03XOBCezoGwBFoTldpruVXNIiauwdsW0E/1Sn3mlIlz2Rtu5GinqAvK5jXPvKo8VPxoys8zsutMbg8hAaWYJlIjALUZSQTmuuqoFXB6yBksnPJpPUFpAkFIABA2NyEZ8GPdhY6xmFJn0gMi9IP1YWA2/i6nZCsQvUV0GidqQj4OsXKqvuZjIP11qu8cxd80pwEGRgytauBPXlprYBhwweTIzo+MYYQLswFLPcbtDgyLq5sjusdHH3YpbCLSYBvjwyHB2uDs8KdL490lAT5SPYg9pvKJ/FqWjRmEaW9w/NjBXBq4zocz9n8GDhbk3oBwhREXmALmaaeIqG96XSh0SY6DOAcN5MjwrugJocCppBfFmmWNnKRFSd7NgZV6WT2QNRAcX5oOzIC63LJ0Rn22VCmRa3XZsl/V+ileCT6EH6S+N1Nsk3B/eAQZht0QNuFuiM4SyASMMgYGjKuNqQ6nS5o6h5HvMY7A/oi4jg1R2FQp913OpGgfXMDfcYxh4nyjE7rHh7iG6XDwlu7xCDyke49zfETxXP8uHjiclZ7liFi3N65WMrPEQsJZMbJSwcgXrU7jfsLtd7f4zacH/C/f/ZzY5vgJdPw5LiQJbdMZb9Dy4TwQCbhc8kMR3vAlxOn3P9MnEeHq9Q5/9+++VDH6qeprJABOI0qgRuHIm2NgPEz49X94j+PjHnd3n7ChW4ybERR22xLLDthQf2UYEfiDEhkZQupLHEnWRDew6uIyJ5igwDqgDKzMDQEjm6BKQcmfL6WMF87l4Pyn/kHZeFCzslWgNBTTZpPVG1okCK0SqZ2AX8GAFJ1aWZ11/bJiZLczWOJNs7/7QRlNnd69ne30lvdByGCXr7q4LlkRnblP1bmTjKfBWeRfzh6tTBoWekL7L5CEuEco2s4IQSzZeS2xROPBzcgE9JFjNT6Yuw9D433Kr/0RkcFEQUHNNgMSuimb2WiAzxmRS4Vif32jAodv2ISdBhKTMzoSoyMiOHPjnSgUnQ7W2njywYbfxhjYrlOOiZCfCBKvLOcmHO9+kMths37Gfun7IsKJhyBkRQMkknEyOf7WpflTDIR0QXXCnlrQjOfg8rIRV7TzWO1mgihg4gxTdYb50jveqXg/b8TTlZQ0rXwwXwWH/C1fSz0chCg5xDClykDsHCbH8YI8Nzk80h1+N/wHPJgNHP8DHBt/QixCEEI0an4niLHKYDaHA+1O53yI8hFsCddBh4h3EsQ+u0ivGSgUzbr5s8jpmqTmvyA7UR5pte3XfAmc4nONb602P1sSA0PAKxdOQ7iw+0vmYQq/x8mBxwN2/B5bN+D6/g0MGVzfXAPCW52ftz0c3mNMzYS0g8VVdudZPqeG/T0gnzDhCOedsAAMpfjPcGpTF4n8gOiMuDs+4LvH7/D+O8ZPv2cMQ4++N3hjtvgF7bBzXcxvxDkc4z8quq3ngMr5z4XAJzshFt808KJZUGBbol85XG2MVc/m1tSiwb9N81enJ1q0X8QJcXLoTs3v3DovszWev5jxtoUvbfmznVqWjIV+ZHCfN+p6bTmy+Kn/CqAOwudX1/OMtwmOl03t6ZSGau3ssziNVqRC8jqz8Ar8/gt1SrTTktasNUWG1wim+MvLytQW44S/6ZEujVzqewZBJSTOzZlyRtSFVeviQOH4GfWeoodyCjo+cxydDoQ0tfnmGNmJXxv2qp5W9EOlEBbp8nLAu5sdLrcGQ9iMlWQ/0VdSKKQoV4fdTRKLI+ppcQlyPjLKVgDOrHUqX+L/cV+SqrOzBLABrJdtxBFhnf/tnIPrLawx2O1G2G7Ap493mA57jOOIx0NwRLADkQWB/eY0swlA+LMGY1QGQj8y3h60U9G7gwxNaszmk5ehptse97c98EsHe3FEx8kJ4dAD7h/hzL/C8XgEuxFsDBAjACg9W3lJNI5kUBTgUOvxCVzKdHmX1khZrywjUgOWWwDSU69JCl5wOA0R/iYX9ZEIRwxpw2hW2YS8BWkN+LKtrZDTJLx9lkVJMEr4i2u4VDkgock8Hn1/e4sH94h/9asvcbXbYjtY9NbAhfVlyJ+Y+eU7g37W2s5w/DM+3DJ+9+MUbcnplLL/q/qmwNf2wYXRiK/tNML8/BO8fpPe2cMetN9nsHGBkLnTrNEb5sX3rbTaESFCvKA91TN0ojxgewvbGRhbXqwa0grAD8cRf/jpFtM0AtOI4/6A2/f3+Gl/AI33SfFxh2RUCY4GYyjGE3/17gIXl30IreTzeLoZ+ifPjM1NBEFDIwIubjbe0xsQRrxY5ZgwA2w0VidjP+B3JVMP3HyxxbgHRnfA4fgJePMjTDdiMldgtqGkX/z6uJg0GA3ZnJgMyTXWwQDFwihJHhHEQKog888gQkNxqRshGLoak0bVF5+n9fwcAbMpjei+l2AIc326FNusswmYJgo1LEspHz1KtLPAI9M5DBeMfsvRoAuEC4lEwAjUMzI0ZbxiJAOyOCF0TGvWQlgpZmROCGTPUj9mFm85FiuJUyn2pt8VJ1mofL6xdWAk/FqdCkl4XplpZ6RwKzEraS7ubq3AaMGVGJKXLyskju+EA/lpT3PtY+bXNDrOP1Pm8LZQeCUzRVQxSaGN5Y5ocUBISDIJ4SQnHiTkkjiQrZyGsNaH1ZPdA8nahhIv9K6QKExHhskNfI5ZA531f5yVzYXxunQc8CpFwaHi1i1nhK5JXXJPJ8Iz6eJC7xVIpP49nXLBRz87tc7aIlRrJacwg6IhpPsDFe1pLKqo8nIeq9/HdPUXBx8t4364waEbwrx6J0XCU1kSkTkGfimLk1bTr/XjEej44wT3cQ88CsdNYwLKFeH4yQ708QeYh1uM49ErGmdMZwuOxQJnpsr4PFNLuXmjiWMrm5cVmbd9orAgFlWDEt9X4ZiCA0hOQjA7bK9G0MS43F9h6AYPQ5gS56cLIzvs4TAysAsnzBLcgERtFbpTgvMAh8ljrupxA+gw2GmDjD//a9SnIYa1wIXpcEMbfLEZ8GozYBgs9Gxlzsnsc2ZuiszV6yYNWftorrEZUW/GCZHEq8h459uaQZ+aHZ9HUev6aV5707zzzLSqxIpM81lOrN3q5/px4rrSl0lxmFdObmtaZhysMbsyJlL+c3UixetS+MKWzFs+m18nWd1/hrTcboO5x+cv1w6fmn+fa32rZw7mLF7/VTknJPl+iEGLztgOW0nQxdc5LVOTkurkb7RpUNRnAIQ7mgKgAVIt39UagJK1slfFJj2JNoCkb2u9G0DuhBDdoVIudBuVgKuadxjZYWMIfe9D1FLYvMUGEBtP6HTcXBi0K991E/QxzbPiOIqs47LPGII271mClyXaghijdS7FYxnBKMywIlIHdbPrDBgGm6HHdLHFzetXeHjYY3KfIJuC/ayFeyuMgTEdrGFMQTd0bgrOlmIIOegRMjQFP1pHd/zv6dHg8PMAe3EFe3mDDjdgusTENzEfk21UrVxiFdoHPFJjXKXMCrxMK/L5yZ+ek6JMHdHV47A4I/SmPI4Oq7qPgvLL7UhaK3TNZZqTo1o/KMjKAkdL7uOsnCFv9+37HmyAzWbAMPSwxm+4vNwRYAi3/YUPyWUfYAzaejoAS4TdBvjiRm1qD+GliVA5IjLWkTlT2t2eS8eRcPegqBmX1wpq26+HcegkL8WRub1nTCFMcLJLrIfj7BMR5xzzzMQhAuymQ3/Rt4XpFuI20t3jEf+P//gHPDzewux/UJhNmcNLh7QBEEJ8pItFvvq713j3zVVD99SGCe+IgK7TfwmCZThJEXbhxvshUjavWzjv8Y3UFn4RU3BEOHhE+8XfXWM6AvffPeLu8B7Tzf+BbvcL8N3/BEyBqSq2SUC++5EoHeMXyTegEYHAhkFO70wgmFCT8OZMnBWsZM48pQzOiHjDlnbqwYJiWQsn1M5WPaycY23NdAGuGaW+rLsALA2FhMKokKquWpSLsj5Kuw91qJpuw7j84ghjqarfOyMS/keG4ORkhAtxEjkKCHIyojKyqDsh9GdyQjTW6IvLzq3BquOKPqf28tu5qbUnXb9dqrtUSKMhORQjGBCFkGzguK5rtagYEbUmTUaHKL4UB53eFSLzHIUhTnMeyyDhll9XhaMiCt75siN4hiz0EiBEkhppTggDomGjQFNN2FVgLIz1YZp8eKbghAhOCQp/pqD7meAPqE1PCq8jOKI0xN7mXYwCtqyXUrB6uYVw0mixjGKN7P7Um1w2V1d2OkVsmyfIi+2fyhHzaadDeEXZjroGAWKO9Kx0QMjfobe4vfolJkNwLuGGKCiipHm2p29wUvzvpQhQcaLQ3Y0Yf3sAUw9Q12yGkYzgDgDcBPPdP4M//QAcp8jpi4YWAHmJzpxIlXF2uU3Sn1qOis9OYNKLMQnhl8GJIDjl1F0Q4bTN5BzITrj68ojeAa8+fgliG3mqYxfL7uHwE464YINX6DOw5UtzWbOX9e4w4YC0zcTTYwZgK3lbtKuk2IhS4+MVe+cu4Y3d4RtziS8vL/D2ZutPm1G4mwraoazWMeVzVKWZ5XLSCTFfVTP/Ihk84YRoAVm1NQNiLeKWeH4qlfWrQS4J/xOdEM9ZBmf349Tzop/r6MGpG+/+1ElB80Qr/hpnROWYrd75VDsldAmlP/25PA5PTp8f3nVD0tBtV6flgrPNk5LP/qqcEtKjeCsEou4o2+MXeDPHsqR+52/LJxVvAfKoS1GfotB8kONEvhS5klg5Mwq5P5sDdQpCdCa1mUk2BarX8PadMA6sHRZzjH4hhfomBo6jw+Wuw9AP6Hp/px4M4IKBP4bUhej63v5kyAHGeruODWFs5ZJhCn1SGy3gcmdEugfPZWKsODtE5o5yOBjQmyYoFAr12GCjmgAYw2ALGBjwrkdnDYzt8OnjLY77AxyCTkx+G4aBBcHAdl6hdM7LwO7IkGgj5fgxAxQ3BYsUJa9PKVwpjR978EMHfv0OhL+F6X8JDK8xOQLGIziMMYUATVLaFbVltghOHy38YG5ZABow6+Unei4nTfcs6potZRGGpe4QLaAKWeznX07i6xBNZa8/SxJC0H6hvqevmufK+anMwqNoisjQtrPY7rbYdBtc7HbYbgd0HaHvgHevLMy2w8PmBo4IdH8EuRGt+2YlXWwJF5sOsolT7tJsydlzJyBKvlbKviW+3D4A94+I67q1qVHLD6+vCK+u0pgAhMkBvx0d7h7zuyvPSS97R4RyCjDqQXHHCeMD0A0dqDO4dAM2bGHuHPaHfTZIo3P4/uGAQwyD4YBpj9v7R4yHD7DuECZLkEuxJqV8Xb/e4ur1Jniw0gWoVzcbdF3rZEaaEAKSUViQVCtlRNFYZo1JyIMECsfPFBdde5VB4hxmUGcwOodpv8dxvMPjw88g2oLdCIQwEj7mHgUGioU1HVYM+91wzD4+mAv3UjD7ndfZ5detKoLhUQtHrRMS56Vy8RRKGXOWJ3t8qjbhL6vIrQhKZX1+kljBllxAjUYzJVQU95RBdgNkp4rKuQtwy2MZ4YxNkhjNAhIVdSSBxynG4wLvYIj3OhpRkXuxMye7MJHWmDdgp2wQldFcG9zitFL6vaBqlsPTTlIpx19xDc+U0pjlGm3XzL717AQzje51zfjKMkp4FzyjUIYJcpS05SSMiFt1MT+RkzshGh1RnI4CvBQE0hrOCG2jojTnpICNoVkI4QLUnLF5OpsB7GuntDPAhFNsNrsXgiJNlzpkdWVQiUExwiiagtrXI0IVgHCVbBK8osNBC3GpvjirRLHpBEeeO4NwpZIZlzpRThYz/MgvdAZINhwlJVDBSkooTUJPOj2Y8Ts112YlXY0YT/rZnJI5U1qzpWIJZcacNJ1w7DA5pwzG/u/RHPGH60+460dM7JWZeK+JhisKYylmvz+N4F28pOF4RvJzQJAIwkTAMAKvnMG2YqbKAawb5/RcK9Ue5EKQzP9ZhD/hwJpU52vJfTH3bL0CF+VwQtPwOVpO+du4DJdjjodFX72Pxv3IGxm5spUc/JPz/HVzNcKaCcOtQY9wUSSzUs6BkRkPcNiH+XIoFJKZRZEteZEavTYdxEdKtCcbonRS7OiO+HD4ADKEzhp8uHvE+58Y+3t/YtY7G5Isq8l7qlY9pOJ3Mf4tB0A99Y35nEGP2WU3h86anRRvMzhI962RNA9rQVR06vSqofbXSlSoa0p31L1AWu7u6YxlrgLvWkXnVz7X/RW6dhYUa5Nf72fce1mQpJVjEj5brpTTbDRbOTUJkzcn6viX9Pz0ZB9OseGjVc2c1pNQrTRazehjL5xqqtbSgEqkTN8NfPjAI5kQthVIFnpSPFqVCl9q8zE3v85BHaHKZEUPv4QjFenWiQ1ESnLY5Eki+8vaE9jDR6RPfj6caJF6etRGBvlOAOJpCs4qg7rAYqmTgAMOjxM+3I94PVhsjUEXnBDRmqWcAklGsAD5kDGGOiCcjExNa73IyzUCG6tNi8lIwFGH8v+EPG4Kr12dP2vGD9aE9DvJ3L4v1gCdBTbbDtc3VxjZ77oexwPG4+ijnHhIY1jeji3YTphgwTzlelZktAjoEuaoGGLTxPUo1vkSPsQKmAYwbeDMAEc9YKaAQ/6eN/EniLRUS5wpJVBb65xjnnLN+Pr8pmgGwGFQxILUslWkHkqF+SermqXvkE0vQSYGJ6cVQtjSNKayjSvk0xtcmz1bmdYKBS2ZpFWQRLaiHD0Y0Ba/GDkmPOsM0BvgoifQhjAMFl3f4eraYOgN7nY7uK6HM94N9bHfwcbx8bV2bsLV9JjJoKRiqhZ7KhXMIW8pE7bkRt0HFDZMAJsO+OIG0BFusu/FyG03yr4UPg2AV1eE3SZZLc/1oZ/liMgNCycSC4FLQ+EOE/g4+V2uncGN2+JmGnD38Q4P9/tUEMD9OOH/8+2P+HiYMIHB7oju8B3AE8g5WGY/aWoxEhhyT4MYqH7xzSV++Y9vVbwtfZ9DIDBCUAVJlCLldycrZEUSJIkQTlkQrJXwIEZNfADP5uMQdzbqUSSE2H8TpsNH7N2Eu9sfQHaHjqbgtXZwMDDMYKJw0axm3l6t5NiOB9Lbovz16IYAp2OMixJrEKwvWoSmsAABf6QtKQ3KqT2PALk4nac4iPKTMJ85PNbPq8bbClD5KpVqCDjBqRUXrBDkDLQEcwx2n7+FEBHm/KnOVc59blApBD9CcEJwuGDVQQy2WSdY45YXIFx0MoT34tiDC0dKHcTgKsJS2rVR9E4IdTXvaWQLcVD1g2V482LwRpmKu5Zdo5qI5hm4gRIyAae41lJqzshMPq6+zuUplfeEKywyMYj9mtUMkhvjF38qPMoYbJZfhJNAcma5XQ37AobmQMnZPnEQaMZJQBSB21w25A30OhyB1CcjSJwRxiiHhZYthZorY2JI+n4TLxelXU6sd+5AOfPK3SlB0NaCpfTX17lM+9rowcUnonNBHENy74PfVeEZrMYNQHbua4Ur0Zpo0C5Q1bMeijSlImugBp6skTRyJ5P3nXKi/cjHJqMYin4mIjzfpt8tFRwQznmHQ9it/tAd8ZvXRxxM0JOi0CzVK2FNO5ziPy7y1OSM0Fx+TVLjoKi/yJ1bB7wdjT8tZDjLm7eiiUEKv2ooXTAvuTJZRT71wyVI5/KUUmgLuVHzvPK9dCGuIVVv1X58lb8rING1IZ/d9vtEyVSKypJ20ofNGy45IcTpBeNw82bEQA6XP1+iYxudYIJLjoEDgA8IoZwiga+bb6WK9ADRSecvd1f8kRUfCM6Fg9vju4fvwi4ugw8/Ad//htB1PtxdlIvlgnO91stBjhOQxjCj5cX8J5LRxocFdraYN+VXtLbkh6UMqt9Tzs/SV1n/S9BQo61WtjV8VWdv7yY7r5Y17VfUpGpt7VxU8ztDFlDhgwajvQhq1KEZ8fBcGix7Hudwqn6ydg5KWNISj0LGAnQ1UlXr64nptPz6MqnVRqkJnEprZ/MvOhGyPVgzWRaecnvO2kugKIkXHsTlmSPhSuTd6wTvhPA2B0obIyjn+S0QZ8GWJlqwlaKYvog62D/KbX0gwDADMN6RQIrusqfFjlw4icttgDlEzGelV1Tyg9clRC+J1pmQPd1RZqCphf9arBz2XXu8d/jhw4T/8a3Bhe3Qh1C2BMCou6tSm9aTj3BfQfxUNEUcDWmzRX63pOjY8TP0RSIu6PvyfAgQIIZ0klmXbkgbgN+gy0lX8yPhw093hjFYANsO9O4a48Q4TIy7Tw+4O9xG8A0MQAxrLQDGFOp2E0fZrZi2MMfFhMZNcWq8w/iL1Mhi+CICmQ4wA9hewJkNJtrAYA8yfh0wknPF68Fq4jOAlKIT8awWDhMf4fJhLjME2VA7uyIOAwoOVm1n1anfoj/mUqjcP6JxxTvZgj0puJiyMGRVt88kUiezz3Hv9KuuQuQSmXcdkj5v2oFg4beldcaHKLokg35H2G479Nser19ZbLcGv+6v8WD6iGw/DddV25fTAVePh+hArDZkxx+qpNiu1W+fa5mbzOXZDsB2qJ/rEzQznCgmYxhvbpSCwAlT16b1jog5BlgSy/niMbn95InK/hEPR4fffnzAx/s9LO9Bgagdpwk83mHAhOPEYB79dTQEkCEM2x7vfnmd4o4DmYNBQiW9erdD19noJBCFKxLGgCjtwU6EiWJoPYrKvBxfTyFCyB81IzEApV3qcRQCgWBTi8/MQNcT3v7yGjwaPO7vYe4+4ebiE0ATGNfp0mp4p0RrjjJDFQwYThmsEvzEJnpuKRi508YFCsxGiFqxJIjmZWPt0GhJUsXzJaVP+/OgvzW9f3M4SvPg6NKcf9X02qMB5y8DQ0q9TT5HTWPrHdEllEthh1SbyOFiqJ30QBQE/HcncogSiDgx/OismB2QcnTOIiz1rM1MgBJSEwOeT/XIfY50iqHNPZ8P1+TXUYuIBtxQEjJDUC3gV8BBT+OEyK+bEcr/ydrSBqeyH6Ex9U4ZbiLPSQJbXn/Iq+kskrE7XoBajYK0HmhoEZ5JnMuGxFhW9jZfiZ60F4JWJvQl51W6tFqJXaX8VAx3epfmgvS4xPYa+ETzF1a3sTzMVQAsxr8FIM4GTfd9MQ4CtwyNFrFCyRnEpsb8p39LCOdxkSHH4dvtZFWUFRfgimMm1ezH17ngfHXqJIRzGPmAH+1v8MkcMPIlmL3SWZ4U9ueiDIj0XLEiTR6AuLGiNW+yFIpXaXxrER/wd0Pg0xH8aQRoUxkhS/zT9KXE74ge0TFHCgC5iLt0TJb9eCZFZVR9SHXnX6IcstB0UzZPTZ1B/xdyNisPc86If+Jc8OEHPK6RmzB8NNh0HYgp5mH4/BOAe0w4gtMpHAYOcPio5nYDwqaU51R6CHVMqtck3yjR3Hg6jIDjdMBPj7c4uAPIEB4fGPcfHfYPXl69MgNed1v84vISby+22G26VIfmEQujPyc1r00ZaZrNUTyh4n2RhRrfFiooys5WthK6dhtrj6pnpwVPZ15X54onp6usJITm66VcVd1zhGiWZs5Bth7fSnn0mdTuJCwSDlFvEBFZbh4/qy/PhvMp5RfLrOUTfMY9C2vaxXl6yJ81re34jBhIKOUJjzynRalEE0+O1WoZ9GSjMCC40HTHDj0cHJvqlENLJG63qJTeBXByqW0ZxkL8jZ8xZGmQq2N2nfdUA5y+iMwQhDYkg7x+3pYJ2+9SDmsNrrY7bPsBnfWnxIUXy5+Yg510RHqk+DkreBE3XXjZGSJTI4WiTXAFWwKnltKdbC50WV9urdoI4xFDQ4ej296gDbCb4CYXN30wTz48VGiTwOg3FhdXlxgPRxwPB8ipVUMENgad7WCIMDIwwYU6RIGOI6H0JD2+MvcekdMe+ISLJN2JJ2MnOBfaCePKofok30RFc15uZdEXC51V4ZDI/BEipZNIqRK9pT/asLxEQ0SvyuxG4nwSR5PgdARX8APqM3ZqobWF9ESmN1dMjzxFwXleNstsOaILEsFYQmc7dJ0FLGPYGHxx0+Pq0uJhu8Nd32MynaLDLbpNGE2H98M1onskomMUvk90NMkVtWyVGMCaYZxzCgWLYYS5KDRT5vz0vNBMFSDJe1bvApdPgjtOcMcJh9sDugPjNx8e8P3jI7b8MywfwqJmGGZsmAE+IsXC9cT08mqDX/3jF+h6Hx9OFO/SERFOUCHusPWXOuTEJy64VjJBOfN/RuJ2BQQ2pEOHmOiYIDLBvIF4W302dIUphNnfI2EGg7e/usZ0YOy/fwDdfsC1/QDqADaXYBCMXEYd11Uw7hXNkM4SvAxiFJKQVsyFMshFBUB0UgjBA04gW3XD+3yq9jXSnGJRLqwz0Z3nS2hCJHTUnwBRBCSEwspV70BkyRRPdRiS1DBXHviZ76oyYTzpHfvQXGDIZaoacM8fwkVR+uIgTrs006PcU346nU9iTmKCFvBOZG4Z+UUoeGpao8TOq4PrGs5k2RltPM0j54pEwEUpJ4ZYYteAJ1UZDUiybst1FR2mql+U3onR0n9IrkA3Sa/aYv1K+yL0ao99gCu6d9XW+zyGJUUnSToVoXfrqnootc3lvwq106m39DI6IZCcEFGeYvldzPGZQpWms613OjajwJmLkDp/oEbRQk4VPC0hNApcrGiaMlDPGXs1Hj4pRUctx1i8+hTH8xJHmiaOB+dcjFHLjnHEHj+YX+PWODj3jz4cTuDF2bDFcSRkF4WHQSxPY+U0mWq+qV8XMly2J4cA9zDBffsI9+BAtNFZU+FAsFk9Z/1a9YNieVJtltNY/Crmo86/PsVys5P8DNkgSysYxhOaVmqzIh6IfNRfTo14opVGYPc4YLvp/A48JB4LACMcPmGKO+MkFOARDkcVc/qGOmwWIHogf8m1Xq+6Y1FGRdg0Q4Qjj/j+/geQIfSdxf6B8d3vHPquw9AZXNvB3w2x2+Lt6208LRwVHKHzlUymKczz56B+tIyfNa95Tprpw4lK17a55IA4G+4ThHO9JLN0kWD7RbbnYDH3GXM3mye0NRMuNmVol1tKL8N7GmkGFkLge4mdLE8U5Rk8b8mktLVNZ6L1uamSeVfMYytHpfO8QPoMVa5O5zS9evybQylymmr7JPLUlc5HJA91zi6+tgya8CHQTRFFla4BIlh26J3DESg2TNb0Ns1nZvJdn6Js1C7J2cKLAMffsiEz29DDabOPyIc+wsRpfZlFXggyaq5nq8+yE2JrKEPqI9jryUsD1hhcbgZshgHW+hPiST9MBuRMX/bGq8SP4hQoGOXPSSgm5YRQDogqhWO5TuRUFcqyvNhbZCMnz6cEA2LbDjxNcNMEnqbojCD2pyU2fYe+63H3ccLhcYzdIAA2XEDoyPgNSgiOjVwbCmOVcLlkKwxEHdhPF8X5EVxjhHCwPIHZwcH5O1oZoqxVdes2sl9xaLnII+9y60fTXlnog3pjUm5DasAiDgf5LkaiOK8JnwVfErwuh5+XGkJL0TyZ4ia7tamsM4MprYFlHQMoBt1vijT+JHFnO5gNsN10eHvd4ea6w282l7gzg6cf2XzW9R9Nhx+Hq+r54qaVcqMKZb/Q/nV+yvDrBFEup/sp7PmZd0SUyKEGXZQi2V0VPhnA4ydgfw/sDx/QHR2Ox0dsMMLSBIJ3FnjDPND3xp98sCFOc2hhs+uxGbpgnFJKGJFyFvhPY1IIErmALzJgVrvEGyPI2U6zcNEfhU+EEFCG4uWp1iSHh2F/NIvNTN1hqETQnCYBiUE9wbwFLO7h+t/CDEc49yauc4IJ/hRf1gkDlRnQmgP5UxFgE/DYpbwKiyLx1Y8DhY9HFANRe6Y+gHypnKFNRi7SFvOeIsjM7kxWu8+jgBDCZmR3IrDzMhn5wFgZLdbQzAWmXex7EvjkomDi4OJSl2z5fkRWkgyvAb+jLyyb9BP76tcOZnMqTrPf7PeTJFAkR1pRNtlZ1ynvc00vKWTUFNbDM91+/DnDmBEU1pC/JTTF/DHclMnxltNzohzu7CifwBSNTBSfkbRHSWAVZ4HecSvKhoaPoZi6GLLi/TohGeMPICsHhRQm5MZ6yWNAIW55aSTTDTsvVApBJS8My7h4OY7jb6i29EkIRAOiyxAq26WihLpcvltG4IbPYPF59T7Q4HhnQaA58bI9UKIPEAezGP9TZcJFmZ1yTlEk/GSSETLOQxy3NO56h00aqPBPqT2LM6LiGqeJvuCjd2YgHo0OwXKQLgN2uTNichgNcLt9h4cO/so4J/NbCIdhXYmin7rMatx9X7TiHtd0ceKjOZ+h3eRs86kbR/T3I7au84KKrreZZLcd+9MdSimgjnD9P7zFcD3ADJ0eQOVsknmVdvTvE7SyoKXnsOyq7Bksf32qcWp9G4lW+eUeZDdGcHQhKuWCYxevRvRwIGdDNAIfFuCOJ7lpBhMS7Vla/3t2+FAR+1RgDN9lj0c8bCa+4VAZGeDoRvz88DMO7ggyhP0j8MNPE457Qmcsru2AL7sr/OLyAl9e7XC57WNgCNlcA9RzVo3qKd4aX9e8U37WQ3Jqxqj1MZ+vhCXyrchxCyhW0qTFDC+P2SebPCNHuldvZd1a5jmj9VPDcM77ORH9icrHk5Pme5lzes46XsjEpHlPs/8lfyFEVWRmwAhYEIAVELwGT8rydYlzsJtiFPenJglmo4XDP+WkF3SkGOfTesO68WrXM0PDpEyuwGflklx5gkYXrS+Lsw2iS/pBe4MSYV71LWvn+BkaL1BHc3hW/6Y62hap1i+Bi8I4saHmlYacFV8S1rUtIfH8XOWe0wEDTYn6CaexDbKIl6UZ28Hg7fUO1xuLLoSpBWmtXv6CbhAcFUbCMUWxV+L8OwDqHiwnJxQkvr/fCR9pl9jMdAeioVrCnkYJ3T8WuTUYrWUjR9yIFcL6+E1Ek2/bx1ENF2ZPIoyFzhG63mBzuQ31E46HA9xxBBkLNhbs2N+Rxf5ya84u5UZYUEKTtbwlDsCSFqvvjsFuwjQecNw/4HB8AB02gGFYZrCKBpD0sWzCG3igN8tpREzPmZ0ycBcaWCjj8plJOBy/hLMBJS0LRlep2Yf29nMqc+5DEqvx4kY47xoRn8Wnz7r4eE3W4ETNsyoa2FznfgKNMeg6i4fpgOM44vpqg812i/vtFQ7DBkfTBQcm0voVxluy6EYraECm1zYVz8unjUer2GWZpdqcTXM5Rf5IcD5F+n2WI0LEsWaSScikSQIMcH8LfP/jiC1/QA9/N8QmEsdUpzFAP1j84m9eYbPrs7r9nXrJ0UEg5WzQ90CEExGAd1oAyHbiInmCZ/tH8VxEuCzV1+UdHCnGrjESqsmfkBCvWOWdrgfKfyOE+H4OsIRhZ4FpxHT4AwxZgP8eYIJxfne+cfCOEmOSoyDWqoQGBoB0MRPLuHESrOPam1s3hNwZAUTClwsGRfuNd3n3CxIfsfpEwXLFaTlVEdzFtqtULPf4MxBuULCr5T2VvMzh7oZC0Wt9S6XrcaLyByc8lUt04kXjWXlWTEt2RSDsAk6/hV9IkWz+wjznQlUjFQ6pnFg1EktvI3RqDEpGiWoqlibxqU6IrMyat3SiyghHqTjNtELIgBfU10I8U0454jvmvLrMQCrriJTcmYDPDESkW0PEXwKC40DyhLrEEaHKZrKdrtOoa7+Uc8OIkBaHjYHoSMhhgaLjWf9jWfWPDCCrNMF4AAEAAElEQVQnYWL5JARndUQxjvP8TeQT/M9I4ZxokRUpn1b0pFx3Qk4UOUjfKClPsacyXhzGNe5e84Z0Ys54YMmrcxvEKfN0I0Xng0xJ4hniUDjtIPRws96JpGlB3ECgYtlyuidi4glHAA+7t9hb+N1VXBpE9Pzr0xAChBqzVjeBlWNT0rwwg0ywjnHhBgzUx2larEnhtf8daDt8jNyrv32Fzc0uyUdIQ10J9K22qix04vdzU6M+qp+/ZBvtHC15RW1Q4XT6RsZ8dz1h0zPoJ8/7nfOhmG4RHBEFny1WdXxB5EM1HRoGOz1/MZZslEnVe5N28I1uxE8PP4OJYa3B8ZHx07d+J+XQES5pwC/sDl9sd3jzauvpcXE3BEXaTdXYAAmouZGdc0LUs13LUvOkYa6udoEa3xfw4ASKrMbGGSfOnwabF95Ur9Z1eG1bJ+eskXftmER2kclXgZ4+d2BPyYiZfEbZZ1Z8xtKaOeA1E8uyL+Nl4pdtnOIMkGYVWMFyq1LPxtk4Z8+pKY26pPODPb1gKknKko6UZV7WQtfnVGVO8Mk18106K9Iyq9fWMozB+RF5CKkCVHyeThlun5GU2p+VLdVJ+eWXpNytBhGTEUOfyvqDiNIil0ItrLyR1G5b3sx+Vh1U0n0SoKMMAgCbweDtdY/dQOGOUkR5W1rV94ZG3StuMpLqgqIk90i6KfyclGzt20/OV5E3fUvJaOvr8qHI8zsjogMCyO6v5LDBA/AnHcT5weKMYP/pnRDpHgKw72DXA9T1YZAM+MOE4ziiIwMmg8n6nb0TTeoCcukLBR2IEG6prCajJY5ryyGYwdOIcXzEeNzDjHsYa0MZCzIhz8ypCN0ca1yZoyki88voZ+UXKte8k6DsSIJeWidGvEPPm43SJdS+XMCZ4h6SOM/RIZXrOjML8GVTRQ/PpR7tFLFf7LzW4sEdMAL4YnON7WaDh+ESU79J+q1RREFsG0XfNW05lU7Jb5W4feZmmJi74WjP9zTU9WoW8tTpfbIjIjeWJEZDYG/zRjKCfTo+4v7wiO3BYjgajHcOO5pgMYIAfPGra2yvhqJu/0fWYLPtYG0SSORUg9+9CY8ghOh8EIeEP10RyJRc6JNvIUuLSRmgsqkITFUulcwuvQ53Qmw3HV7fbIIjwtdviJQ3XAwlqXZm4OfbA45H1aiRnQz+eBmTV27v7j5i2HyHm9f/BLhXGO9/AbABkw1GQ29YEsdM1odAhLwgb4JgnOYno1KUypVewcoovSiArUkNlK0El3a2ZtsL9IfqR/OZw7PYRDT0cRRYmCmdjFAUVoQHGWPEHBzrqoU+fXlVoEzZ6RP/mMOOTBdgoRDiJCpjgkZaZglfktCBPOOJlAyn0tczj8dllc0L7TIqer3EFMdlHZHLjagtGlW2XYogXL/Npm0JN/O5PD1SjIrDZHgcIlQG4p923YlBeaHqzFBEkTGSfk/5KQj/IRwlXCktedI/ymAV6HDZrJRVIdpiSCUg0Ko4AolJz+AHxwwIN+OYdhnF7CMtj0JUUV9myNU8R9pLv7O+xXYR79FRwxcN53+ypAbfhPMOEt4phpKLTurAn5XSkhmpKZquoTCj2RZibQtC84wzwr8HQJmZZiaF+UMgDmEnVbqY2l9I7SZ/ebBzE/Z8xD+9/ohbc8SR0s72dkqti5OZg1NCS2El+Eu1aZk7/c4BcA8Tpp/2oE8HwHhlaql6bnwXpU7QOfdN0jzAkZZS2FmfFNRGphX9bmRYO2BPqLpsJ957daKe+SwnMJAV/nHgw85h87HDtifcg+F4xATviGju/y3JQkNeiSRWPw9wx1MKQeYVZ64JMqOBwZGPeH/7Hgd3BIhxeAR+/nFCd+jwP26ucH2xwVdfXGJrelxhwHbbR5lZeMCirb5BDjTv8LDqOpbGVTBwrUxBrY+qjdP3kzRWGs08Pze9BL6fqPspLTwVrM/Ym2ekp0HVxLMZZ1Gt/xXvuXqVbTLQzz+aAT+bHe5Jn1ArayxhbfxeoF8nSeQTMHsx/zmVEZrGi7MB4frRqXSKqjwVk2r8mNNrctliXXqJaAPrU2tzjBZz86dpMmQLkmiGQvsNqRN1qo0qKZ6n51i3UI5FK3HxK0hr2VrXtotcNy9kfMFV0SsI8dR7dldE0/xAsW5tQ+GyDWQvGz3xz5PzQ+SOCfd3R/z4/hHfvHmFqy822HYdLOUbCKS9WDUFO1mWT2Ta4GwIArK38YeS8Y7nOMPNfsRtrGJ0kLsdglAql3Gz2CLibxdlVnFgMDtM0wTnJkxuwjSN4XREcEbIpchOtSf2ATgM2w5db2FsB4IFfQKOxz3YWRgHjJOX2zKjP+SkhwqlQ3p6VMgupSN6OCaMh3uMdx9htleA7dBtL/2cGIMQUCu04k8amPJS8icmp/VazjefyqfWaYVMRT9B6HealzA2crl3oVikS791JQwdPaDcZBpUvBdL8/cqnkitpRZ3ffnPzDYr2fQmBCKQBR7GI/Y4ot8aXFxs8NXbAV+8svjYEx6UcBqXrfwu+Ji/5xeR4OlutWTYuV63xAkddtl/nDFmhY5eglLL6oHL8VKe02m1I+LU/JP6JypUYQIexyM+Hm5x/GSwffA+xQ15gI0h3Lzb4ebdhWorZyJCOCSsR7zvQYwnoR25F0L+AOWgAKVLqiUMBRJiS7y41kBDlCvKHRFyWfVu2+HNq01QCk1CPEWzMkNXWMMPB4dx9DHumAByoT9B8XVwcAwc9o9g9x7m1T+B7ddgvAW4C0vI+JMRRoicnoy0YzlhSjCyaADVwvG/OZ/wckgayFBlWVw6LfGiVLTm5gPVYpmHIq/9vAUSCBWzHjmI4Z9cyZoZbDwxjhdfVQyHU72gKPPER+E7x/mQOJXhQqhw4ZLA4ZmJUTuilSBSeaaRCwwFVLNpJc9sCbRlNYuJZSxybJWXLVpax7tcamxZHavVzfJ96yLRwMTiOqLE5HimpowhLY2KX6MxW3BKqAdZ8dbQk8BUGTECndF5GiCWY5LoOkXHLopx8fWFEHCGijY97urd+L5rThVmXZPvWyRXYUzUzpCKaWdCR8MBIRWq33OOh7LeCG8cD85C/CWotarzfEmspSgqkPIX8Q4GT0jk0JQ/QJUITSXACI/U5JlU7ky4Oa9PsdVEUkGFIJgTwXYtUUAUxYnTDnUXhGXnHI404fvdEY8dYRopHD1XiFE1U+JaDgs1czY6WeQRNiyoG/Mx4A4Txh/3GA4jiPvos8tbbfNZT8JdpOcZfqyh1Qu/1UpfLHVqpihNtAeJG2t1AUJt0BYatbb0Ur2Lb8OEcSH7ZMPLADsAE7A9dNiYHh/5EUd2MXySL5avUo7150nIeT7igcpQ4nHx5C+l72lMw2ke5/D+8QMmdug6i3FkfPje4Y3t8IuLC7zZ7vCrq2vYEONW5OjkhAQqB+TCWsl4x1y+VZN2KhO1PuK3yvGxHs3U13bZ1ThXOvLPLa/qqAl+g3+vqOZJ6fmL7BmVzXK25uv1tQsjq0u06jiJjTMZWs8facCP3YWa0lkmVD39HH6tJ1f5lIKiFLxEP3QdK8WPzzB8M/WebmkN70v3g8UnT+n22SlTp+PaWqJjKjyZok1R7lF6S7vX9RqIGyE4f5+FFp2pxX/nSs7KNckkKMm/+X1daZe4ZgW6jTmnTaxTaEypw0qfKjmt7Bhnz1N/vNDx+Dji+/d7fH1jse079J1VMgGiXUlMxumePeHzRoEnJx44CjVxg1YexznJsVJO984Lo6EuCeHjMqeGbIJMtgn4XffSP4Yvww6OpxBiNdy7wC7VjeQ0EU9BQg+DYbAgsjBdB8Bgv+/AbsTYdcBEmJyDIXVRdjQqFCciOM19tPeUNpPgdJnGI6b9PbrDA8xxC+43QKfNqqWAXq+Ic23r6WRHPh/yX4lqsdniYTK+cyyfIy2rjEHw1TgjeljWR9X+iY6du2s/FIrdKV7Ef7NWKzpA6pUKaSw5GiAzc3DmEY7TETwBm26DzTDg1VWH1zcW9xZZEEJukTPVfAzfBCT7Rp0twlU6Mma6Xzshqu9rk+bbaVTbc0aBrgi9OL+9J56IyEcju8CXAIKD4RGfjiM+HCfg7oire4O3b6/w9h8u87LEuLzZwBqNILoJivgc72WweeilePoiU6zkeX5awreZFC8XHRGKwGY4a9I8ULgTgvxdENtNh7evthgG6++IMMjaBaW+eO8jB7nMT/KbmwFXuw7vPx5wPDpwiBEtRJudw8QOj493mI4Ot58+wNoBmH4CYwfCFYh8OWIDmHBCQodEYb23gAPDMqDg6fULQs9gzTBzQjO/FtalZaL8MvXmvxeNgVx8mtbL8CsIiqTr1ATCqXEkVAYtP+2JxflHmmLliaRNIkx7wv2PG9jNhM3NqMjuhGyPh+CxMtBlzLDA8/bYKCa0Mp1ipsVI1C+BnCGsKB8vFNNpTkmcf5HBUCU5fdV+mQmwLPUx8jktC1OU6vIU5ygVIl0m0A2u39anTdS4ZHnVB6l8+TiaXMFI/6Qqwj/pe/pidH5KY9+WO/QC5Mbz8CuEPfMCqZzsMrOIl2otb37TzgkuhDGki7n0XwmPLFlW+yxPeeJWpOSwzp8VrUcgIh0iio5L/1DT+maJvKbMCdHaHS/liy9cvF1xkd+TUpSDwykIZkxOXVA9BQcEH/Ft959xS/c4utdwboiXU+db2nK454TawMlnRLp53lWNk0puP2H89h7uMIEY2DrCu8lgF08s6c0DM4zBOZjvfwO6fY9xfzcLh9SXgFEARcO+WqdKlprp0Z8h/fnazjfEIMpv8k4r1qeioM/1QhvAteiRnVKAOgFBXpH+4+0POLhjvJOss4T9o8M///qIaWT0PTA4i3/YvMVF16OzHTprYKwJp3lN3L1Kcc0LLBpnqlGB4CXDb5qBwt2s3BOmbhb3qiqLB2e19UwiNecwKLM9pc4/Z3pRED5Xf/gJVScF+XOwp6Wk/XQlTZ+h7qrck5C7rmuhndUVnF0m0ZLmSehqA8myHDcLz0tM6FOH94WRqYrLXcwcAdU4vTQ+t50SjXxAdtBl5+5x/fiAu90lHmkHibuQy1INeIvKvcyqViop0Q3pUzTFXJcFyrvm2spkQ8/MNhIVwyyi7anBZgT9RARWDbACXG1KzdtvyM9x5wPQW4O3r27w6uoSl8MGQ9fDGhs3djFxtBcAnIdbNCkSSB42KdzBoOE1FO6EaAj6DMjlxNEgHsIpTeEzGvr1hq8gL+mLtEWe8l30jodpGv3p5mnCFC6qduH+CK/fRFOvjwoBUaWdB4scePI2wqvrLdzlBhfHCeM04uef3mM8HDFNQS8spDZDNsjBJpu68DKMhn94dAaHo/U1mAOsG7GZDrA8guDDyIv8lqGBvGnplREPZpJSscrS+ZxKDpUrLid1eXjIJ6GYJDSXC7/TUXJ1GkS1k9pI7xSoFewvz3wp+6rnJxt00QFNAoID7mR3O2VzlMv/xhCsNV7PxIR+c4XtZsCnzRWO/Q6P1AVsomZlpZYZdXUpsTTt9JSha+m6T0laBmlBoSRyzb/OtIWc4Yg4UXEwunIgnGRGHMY9bg8HXBwIV0eLV9c7vP3mullfzgC1IYQBDpc4GoqnEOJRMyQlTS7ajJ/BUSGOCEAcFkFxIn+htKeZgqBFP4XIh5/+DghP6DabDq+uB99+yGf0vEVDhjb+cIw5fbHt4DaMT3dHHI+IMAuz8IZsxnE8wDnCfn+P3t6imz7BdQ6ELYgsyPMcOCIYmHCiQtrXfUHi6uSdEQiOCA3l0kyfRq+wABZxdn6RcOPbaWBKYpKNdqvyZj2en3GtE1LuqIkOicyrqfZAhvBK8WhDJDgpRAogSybuH1XwCI6kNTWNBHfXoWdGf+lgLOK6yPoa5Zl0ZRFHGYOLISso7+IglWkGV5rFV2BNJRyWZXIlMgmMyhkxQ3crU2NL6S/p7Jz03XooRiM5djpX/wJMYlAuwUuXLKdKypJzbWZGG8orFiHJf+jn7UGMT8VoJXmFzpHKqXfZNiWS8hEnksD5nMadTvKaCYDzwmIV8z/vY9odUtCADNeUwKbfJWkktK8FrVpBfI6MpY2bCRAt13EG4jkpqn+Udn7Mw6uM03GegyIjS4xyOJJ4voYzcLr4uXgTIVXek0x3k5yiyDCny/VY4vc7fDQ/4dbeYsK1csKm/kHjKWpQNB5rWQEl2KQKMNcDmvE6lY4O488HkPN4NTBwNZEXxGy+PktRJCptcKC798CH70DjpFWLZlq1QyXQsGgAo7kResGkx1AekMhBn6/p1jzWdCpyz/JRohuCmJnDssi8BEcUHyge2JflltECgpcRSFp2+LS/w/3xEZ31IUJ7a/D4wPj44wQ3GfQ9403f4d3FBXprvRMi3p0mMnEQW+MyXx7waONoyG+Vs3mRJVP2dYlztetqt9VuablPJ/ld9YLa388tn3mIV8gnC2lV9paFEZgb6qWK1jS2PmuW1nG3p5KFea3jOaRGSi4Jj57jJr5buezy3NnyyNfKc1IzQsNcnaemYiWOajnz2fU1HRpL+ecAeqF0bttPqno5FJQnx+3GnglCMSU1TmvIBj5g4+7wSJu4ubEsHbTZVaiVuhS05kwJ0LlFxg91Z/p/gy+3Gj+LdxdjH5/UOkbTotJ0QuS1UP4ivjeGcLnbYbfZYOg69MbkMqo0DXjGLgxebQrTYIgMncnInOQQoNSxtFzO4Z4Av0NeTi44ltBMSPqwgiyFZuIEA1R5F05FBAdEPBEBBuB8N5jjVrQMHQRWHgG22Gx7EBmMk8M4Tbj/+AluHOEmPy4uhIb36pF/5jfy2hAhW+ETkbLJMKbJ4jBZUAeQc7BgdJhAAmMcMw1jw9aj57lMWhfhet1oGTGiUHgkzl+tQ2rrk/RLwnOJCpPmu9C7Y2XFX66czffFT9zMu3Upaa95te2M0v9afvfluHhG2U99t6SoIlY2ilug7yy6rsO+H7DvtkoPriFupcwqLA1U2XXnToxdU7h5DgN8HqM897TL2SciquqjIke4PTzih7uPMIZhDUAPwOU94csvLvHVv7rB9qrPDVYR6Jz55BuzKOZOYZH8zBkjDgo/sdoRIQQg3icRCPbrmw0utl1sRIf50IkZmCaHH3/eYwoetb4zePd2BxtORXSd9bHgSMJE5eMS3RChH+QYjrx3kWUn2aSKUF7WGoNh0+H1r7aYDsCnu5/R2xE3Vz2M+wr29jW4A6adg2MDCwQjOAPkd7wxBA41liSLwMCQgwtEFoy0g7SR1i4yT9UaArRe2RmTDUTqiXSKhXnOGQ9KmpOXLn6lHRWxBxFH8j5pI6nPVt73QIFAFAwzhsYCwARil4QHKcoMx0rhDs4JYfaYAIoXGdeL3mmGD/jYjUEwE2NW2rWQmEo6Tln2vRBCUks5M2qMqRZFGo/jqaTliWLVzewM1mKadUK0aDzV+eLaadAtgAu6FeiRjFmD8eaKJbefZ2AIDkmLyRGm4VlUMkn1o3gXd94KN6T0TJ8i83nz6mtRkNQbEXhKZ0SOLIKDDE17OAkQwXBNABzYR90kAziHdAS8kLB1a8oYnbAwpw8sEEvZ7HJ3hZuyls709s+ANuP8bq8dSU15ZU3yE1oIja0U7jhKCKIE64RQmXKYntRIgiSUtIQTkjZiKuiNPA135PhYpn4Xj1MnJJxzGAHcXX6Fu/4dHA25f6B0whWwaYg8S0+bAuIGAT0mWtsQ40A1jW26RiD044TLI7Dj3oc5S4EVm0ntv490OvnFKPi7SdGtRj+reVybzstP2TgJ6iWItKyUDeFnTLTQ85wyppFO8xlHHip4ctP/pFP5LvU1tWcUKsURIuD7+/f4uP8U8dAGOdYQYZoYv/7Pt7h7mNDZDsaQV4zY4h83X6Ajg66z2AQHxMVFjy/fXviTu5RwmfJWMyre/B7FGTV5NM+72mkub0NezL7O0BDiKqf/9QSEeiYO6lOEKzKfxUfa1Gtt4XLM1tU911KF1y3Z6DOv56ek80EqS8ytaPm+IJWG16f4d76hQzfzAgN6AsS/xJTLrMr0vWbtPLeflcB7huT1ZEGtXVX5hJcz5I9Xwt3SVpZT4h23uxv8cPEWTk5Tlzr0XIvqkmg/ZImGcvUrL3u6V1IpZ48y2WxOKS2+ylZNPbE63LauM9tuWMr8+lujAyJpUKw6hCUni8sLi2/eXuOLmw02fQ9rg/1Jyqkqvcxq1I4D3YDIN7VuUW7k8n3QBuvkvOBwIjneCxE+XbVBTHQpJOdDlOW9XcK50cvw8Y6IdLJCa2FRf5NuZbqxskU4BjkDsvC2SBBu3r7CxeESx9GfkHj4+LMfXzPAUYfJvAIbC+r8pcOTmyCh4TtLGLo+tnEJwoUzoH4A9T222wvYbuOjkZCCk5EAVHhMEdDlpKet9U7sMeVmZwBBJwh6K6f51Ccn/LyFEZabwwMixYvJWS6plqpZ/SV5uA18kHMIyI82vUAqyXP+T7QnCP5oG0nSUbLSVcUE+LuAjUFvCNuhw2bTYbfpsRksrKFgwpVZ5ZzHZvTmBD1dmuxGqqSRsLaS+vU5Gf3L1r3aETHbLCHcV+JwmEZ8Ot7DwqAzBptHg+vjBleXW9x8edHcTJSMFEA5tGKXNfCL24TYR2lnV9o5VzsihBgjHUE3hO22w7W+GLv41MT5ME74cHsERv9s6A2udj26LhB5goJB90ONmaF4hMyRg2HABXiZXd6PQvgkBmxH2F5bHB8cPv38CGZgxA8Yxh1wOPpFNlkABCYHGG9H89fkmOh0yHSFYLSIx4OEUZ1DI05q4DlDz5a5CB+mYNhrF07LO9wCSvOCGaCXBNuMhxTlKThbOOqToSdhPPUR0ShgkTCIUCgeFaMAghzuMmE4ROBBVFxdYByOgHjvujqvx6SHPw1ANGCH56zfAzFP6moi4s3hObGLpDUfTcFMOyESKFVKOJK+pJ+sjiLpMqXGXTKf4nmjfKmat3YJZfOk6ms7BxpEsBonlScwluhyipeU56kllteGkbz/ST6l7F0SSFVGRZjmHRDSF8FnPzbM7fHN4Gb1ROFW5ugBwRH7U2zyojDokB5TRoNWcIG6hXMhCsxFqbgeWnXkvS+/NfNxDUd6lz97ot+jDcnseMkDVEwsclPhUbrGE8JTwpo1tH1pUAMdi0I04ryxYzhMGDHhsLnCsWe4cQqCqKe7M/bK6oH0UT4NUZ4vkXhNPet6izn0Mjt7Bcn4e5226DGYIWs31sWc/BucD3JA66p9EjmoPYqLz0uylua8pCEr01pe3siXKEiep3p+NkyqgfJhKf9EnOPGXD5tQVL5nXT3vUONglPpbv+A9/e38TSvtQYEvwlnGhmfPox4vCN0HYIjgnDZWby52GJjuxCCidBZg6G3uLzoYxinDImpwD3pH2k63+oEpU48ZQQafLT4qN63Tz42cs/W06h3rnunSs7KDDPALGb2mL0K3hNVzgHyknUv9vyJ4/n50lMhyMeDa2UgWzd6c0i5nkqfE2XlT8Cc0aVZJnMyUfXliekEgjwBNWNa05s4HAubT85KK/tTtXkqKYPQfJ711ZUpl7hPNLRK9Mo31Z1uM39y7AbcdVfo3BHklqSQJbCUVkEIdy1ylv+E2vnE1Kok72Fc/pWMoPIE2VSneswWlNw5iNjbjLquw81lj+1gYcn4cOaE4MtRMnESBiGbYUH6PlREOPV4ZzCXl3QrnUeM1nJ3g9gkZLOQyhXhj7J62NyVhWgKzot0AkKcHk7ZLGaSZuGs9UlvIKdgY7OGsN0OmIYO/XHC8TDi+GDhHIFsD6IB0+YVYDegbuvLugnABLgR1hL6rkMyarM/1dx1QNehsx3IWnV3IjKBNdsBL7UU+FP2K3UwbXBtDkWGk1oxaK2dpDVkIZzEaC8nZIKDodI8uPiTNlsLI2s89enUkq3XzMqk+qw3mKdNbW1dpm5D4W7g5RSWVG8NqDPoOwtrTVxncWzZb5hstVEGhpyNJqDW3GJXs2+pdnHONUOX/4Wm8++IMIAWmgmM23GP728/YOTJKz6PBttHi3dfXOPrv3mD3UUXJ1JfplE/KyZK7oQIi9vfEUFFCCZER4BcXm3U4Id9ZHj1asDVRY+hNxAPh56itO4TDENH+ObLS68ggmCsnIJAJO6yu0+MANF6AA+TlkkNERwBJrx2MDAG+PLtDsfR4cefw10RkZ2klWt7wsVXhOnxgJ/ef4+e9rjaPsDwL2F//nvw1mG8cDDWgmHA1GUXddcdDe/IwBgHOANnnJ9RJ2uhZqp5qJg88dyLZj6EcH8EDgMSd5KXgNagFzU1HmcGyKInVbGVwgErelpwBiE0orAwqfkTIzmbVA4UQxSyxhcCmCcApFAxCRbHB4Pp2y363RGbmyNUDugRSsRXHBAiAEgGz2giwS5OwmR5G+OUOy2yj+Idt7426qszaEOIH1YCGOkJIeXImH4jNRyFvtgKQn0yi9Rdwr9WacvzaRIS4RZGE46Lxj7HbKWUXK/5rBVB4sJqQ1qyowo0lWTA1cCXiEBtJl/KLFog9SntqPEnKoIQTQQyBg6eTnk/ngZWNy7o5NT3BtMvHGH6kve4B113a85hufAkyWuc/U55W4RHr7+zxLHTKTq+w09op35SXCL/gnZC6HIKMkJwMLNC3XrNaX6tnwHZzMVPvZPKKyrhFETYjTU5xshHfN//V3yiWxzxBZg3nl8T4r1LKZxeqJkVz1Yty8YAOXUZ/0i9by4K0tJ+1TPeTzj84QHgAcObv8XV5gG//P4jNjBhl7rUH8icnIYTgleS1GIZNbmlgK7XMZX74OfKN3v4J0uaqmTP41QUvDWmhHMxXz6FFdkqfU2KySho6iRtEBFMoM/Jaaqpv8+ow3ZKOfn78f49fnx4708iEeGf//kTvvvuAGO9jNmFOx3IECwT/q77AtvXPTrrY0RbEzb/dN7hYDuD3abDV+926Psu3m1GCtdmJ1TxnOyRHkDK31epmsCnYs955Z6jd51m859zBSimeTLPiXxU/pxbTSvqWkxPH49zSmbi0GdrpcyeK/Gnpn7u/fko0xbWZnlOlV5IVihFu7+gpEGKesFcajkpVk5KyR/LmspastUpOxWqPFpoX2j8FMKvrMZnXdHfoD9QrLuFR0meycRBTszhNCz5dyreJpG31tlrefiUwj7/qsKholxrvnNAah1XLxktF58YyjbQUo4ZD3cTfv444Vdf7PDq4gqXw8ZvKjBBqODgBJCqwykIQ8bH7DZ19RoEyjylsWFwuBxaQqAinFJwbkLcAKTvhYj/FU2F6hnpDj65h8CNoy8zOTBP8b6JLOwqWG28jwIyiNJeTpkBeebvD3SAC3oA/MkIA4LpCJ216PsvME7A7fES3F2iu/ol2G7Awy70Y4Sdjhh4D7CDYQeW+1SZQXCA7WFMh267hekGONMhSkYylaQxQ9/HMZPmSL3c/TdbMB95Zqj7ebh4zRG/BJ+17hvHm/1pC4niEqto6rKNblX4P4v4WR3R3nEWPwslspMQqt/58ZkaNsq/MuBla2txmCYc90d0O4uryy22w4Cu66KMIA47p6DWOPCSqdaTy6eUaBhz3Jj/PGa+UvZ8YlrviCgmyY+7vzTy6CbcHh9gjfcaDmRwwT2uLja4+WIHIlYOB6UoBqUoGr8KASGFVUonIjIHRBhgcTxoxS7WH8pvBouLXRfbli9J95SFRVn7u22oO56y8P9KqAPhyMl4o3PVAycnIgA5tQBsNx26zqHvRkyTH9MSx8gA/c6A3YT94z1cN8H2EzZjD3P8Buh6MPc+jB4R2Ci/XPyginBEGIlAHCLvhR32TcaK/EdrJ/bpJIs1ENZgXeBGnqwDa9rkRCSr3PWX3MioWpJ+i21ZmUYj/RaGk8iejKbaXRJ4D8nks++3vuRW42AmD1CqTzi5Y4KbLEznjzKmJVOLxVEoEGbOoSdxjOS9KlEO7aktKJzGJPs267Cqy7PK39i/HnoXpBnSJyGA8o6NJXG4pX+sE59b5WoJsxQRSsfEXC0zr/LEyp8vgiOVozXT7wRQ+80sDqnmVQ6Zr/xyorzayPM1gunMJUHRuzOyujh49g3iBVrBn+eY4hhHsSU7fZELS/XpiyKr4DKXeKhhmpnTuHYLnNCCIFAvp7yKoo1S0OAI5kuJAnJqsOJbxYaBClc4/wkkYUw/W3cSItTkJadMCQOQHKkKPWRX14QRI424M7e4pU9w02sADJ4ks55zjnQ1XQacw1jKKVCyRdnfxnDULxngCeAjg+8djCX0FzsMPXCBW1iRJYq64xIHhXCLc42EPnQGZujiMK4a9nKpLBZ8eeFzNqnhXwRB/dZrYtnOlCNpzjk4ll9ap0QMsojXQGlWIDonx4lQXSIKMvMU5V757+H4iA93d+FoP+HDpxF3H3040M4AziSZtieDm6strruNP/kQHLT+5ITHp84YDIPFxW6AtQaGTCErREl2abDK7BBZfV7uABYpVPNxyF8VOw/nqJrT5XqIzmihoAPV6yWAZiFopfmxy5tu5KPm11ZNJ+peznvO61KuLiSk5cKqlqeVOz/7yTE+t0HVcWFvdTvteazcD6dA4blMiqdWoBb5NeErGdIZoDwlb5nvlPR8qm7Rr84t95S2mu8bBWjhdLAkLoWoU42dGKg1fRUpOn605PasRo0nXp+1NIU3aQPLk9IS81U6bQlRE8kb6utzJJm8hTUYek6F7fqcczgeCdb02HR+84FRshq3BBbZSKRluqjGKJ1a2SEq3SvmTacYxHDNTp1aKMMzM8orQvId42LUjuXlu/90nNrLT0QIdgUco5y/UPxXOwISZhsAzgCG/V2q/bDFOBH2xxs4ewl3cQM2A6Z+Bx96dkLnHjEcffQSOWHtzQ6+w8ZawHQgOwC2A8jE+xrjv5xgV4A1k75Cr6a4XH6o8W3Umeme+m8GBOWUSLpT+qSgF+t7PlJ9ygU1x2ta/Wk+128UXiryNMcsqpMQpQq9YvGzbivoipNzAE/Y2A6bzp84hrX13ZwlaVQ/S1ko5ZE+twu2SfHMPEb8UoHkeF5uPT+tGcDzaz3rRITSRwAAD+MRf/z4I47TBGsIrzZb/P3X79Abi43tsdn28T4FreDLmBh1siGX0uS9ibvN5HLqMiQTUDsiAML1VYfX15tQn8HQpZMUWYfi91BHa8JlF2G5ArQjxSwwXyVYMnlCCEIk7MRAB4Mv325xHB2+//EBh9FFYu+HhjGNI46HIz59vEdne4zHCR39R/T2J3TuF+juvsGwfQPCa09TjD9N4j3C4izRIKb5MGR8DHZywdAzg02sv57Os5gvjKkfhzQzccFGTTEQl7iiT7k/ClFB9aVtH9f5KWZkIBGa7OKlAJ/qGavSLO2QScekCOEECEDE/uIjofMVZSLFFDQfTmKeXOoEFhz0EOkuJUdEOmWTTrRw6qNuZFYITAS+HDYRVco66t3nbfbTvHS4aj0IFAxkzohUyazSsZxWElZK1c8Zb+q+lRh9PliphiRsejKURC//Xs1rVs9c/3IaOtcrP6yCO4R0UXTAYyaQIDYrIUIubC9rzZAtCMISo5JLJwAHuith7GQctECqqkW9QdoVC74pv+i1kC+GxoicTrNhnZrCROn8m8tbllzYGUNIYxS+xzUW8CGeGoxCM1W4UtV/YqkIf0t4SlmZxENVdYKECt8jPQGiAjCFExB6B9bkHH4c/is+4j1+3F7jkd7g7g8jxsdP/rg4t8fIXlj0v7yId0zl8Hh8Myr2bjpD0B6OKPBJf5xCtr3D4bf3YO7Qv/ob7I4T/ub332EzTrCUNlnoezRk+og5C6ua+HKujFNn8PbffoXh1Q7drk9jHWFP/KEUYVqJZj6buUoF4dy0lm6vgTkq3nPFdY9WAE6cBpLTs1dfO9huwuOjxQEOk0MMtyW0Ty4X9DjvT/aSIXx8/ITff/wOctzeGAJZg9//9gG//+0B1liQNRgPBttdh7/fvcLbbhtONEh9hKuuQ0cGxlqPM+EEj7UG243FV19eYugsbCdOiCA3ByeunJAQpxyCHJtkriTvVsMTWD1F2Wx+clbqfmflbGV9MT3rpdILA1RXN1//PKX6byF9vr6cP2VUfG/hMCUejPxOsbqORvFzwWnJDUlwPS1Y/AWlue78VacVnVLb1F6szrMT1ZXmnCCH8ILv0LtbPPIF9ristEWepe9Jwkq/c408yeUrwC7KttOy3ULbgGTNlrpr/C4KtBjMufEeda+qhqsOhhqYsO0t/u6XF/ji9RaXw4BNOAXJciLCFdhCFMORx/jmiCMJsYI5EchdAZl0JWyI9RdQq8ukp3BBtfNOCHbBuSD3TgJIFnXpG4d8qZ54+gHht1x0He+c4DiuolEYhPC8ADh8ShNyR2OUd2DSJBBgjZQLddkexnbY9a8wDjc4XL/zUUp4BMHrm8ZtQdaEUNzs61RaCkwIx2R9pBWWiDEiR3GYy6h/yWcASysRxexr6V3wkJj0tbJpXjXuFTpsdOZoJwPUvRKlbqxxvdw0yNUXgaDuwJ+KeMsai7hSOCGUcaCtyUkFpf7r9UBrrXeK0YTNZsDFZofD9Svsry5xZTtIoH8WPk9K7/xTM7FIZoXiUHQgPc8Z8XllyNWOiDEo16J8EIDjNOJ+3MMA6G2H3dDjzasdOtvBWhtDDkiYAy0PicIvSpQokgzA2nCvg/HEJHNAAPGCnggPyckHQIjA0HfYbmxStgqLSKlesV6F0FmTgUANQOoDpP5GyppUMXcV8SEiOHYwBv7yE0voOoPJMaYx44iAeIgxwjFhdHuMcDjggA07bMYdun4D7i5B3IHlDoN49sIztmgwCsgpF5zIHCTmqYXrfFzmBKV6V2+ZQY8LK2+dNq35TEJYoi+gqnJ5hUdCWsCWCyrFGJc/uHyhS1P13DsgxCPvwGTU5cUBDxjeUGE8VuR0kLL8GolIDGvWAeSCoU2LFym3C3CXDgjtiMjGpxjKcrbnMlShuuLP9riWc9JMrdeCA+Dk3BEiS6H3GRFusBvN+M9p9NmpxY1O152puaG/c2MXlZcFZkONb4uwyDhX1ab16RXrXJoSHM/7rMZABB+S457i5CslB8R6khM4Sp0BF3K63hyeWXRbJyGUvdOUca2k0Xbs8ml6WRdpC4NBSI10qASrsoBQ/q8yRmoWVWTPmuXGq3Zh/6iFmgWJq+r38r/skPK/nfMnIY50wL25x73Z40BvccQO0+NHuPsJ+uLzMrEhYATYcQYTC4yW/I53XkkBxkRLBVahxXx04L1XoYZdjw2A68cDOuYYetKPejoZkWkp2ZzNrX1guN5i83qXP2zkq57RwsuKpiIOUn4OrdGGbCtqNqo/5qnSbN0rklYE2tIZFRnLd225B2DYbkI/TDjsxyykYZJT8jVE8DxqchP20wH340NwPgE8EtgRbm+PeLwDekMYrMHQGZiOcN1v8Lrfps0GodzQWRgTjA0mbdQx1mDoO+y2PTobwjMgya/5WFD9Eb9raWJleil2GVObj1fNity0WI/PU2Za18KJ9hceLNd94m32emFBN8lCRZXXNrsunVHH85t7Qg0ri6x38LSf57oJNeps0Egqv8y0yIwOgD3HktHg0+3G58pnHZqt+k+VZkSDJ5X9i0nP6dRnqrNFShYoCJTGAQCwGMFwsOQWyswBdSYVPqtvQWBeUabl/pmT7kuprBlNYEU9p2g3EUDW4GJrsel9CEZjDMiIFkIotO3Euxu8LmtFxMtSzhTBG+lUAnO4hDo4B+JJhngvBLfbiUOf5iHK9CzjxoA4Ibj8a2nOEvqak4jKosKIndCgTDJackerMQYWFoY2oG4DZwe/UXgcYeDDOPlN0p23yTiGP45vILGLjLEA2bQDTgueVfulw6jKMvtyFn80bi/qmJy+V6ac6kHMnz8rf6o8pb5/Lk2bJQEzFS2QjKYTIkszeklRteyR83K2dzYNfYe+sxj7DsdND3eCny7RjjUUb34Yc4zI1n82NunHS90ZcXJq55F1Nq12RPynD7dBUSEYTOj4AcwOlgg3mwH/+PU7bIYOvfX3HnTWw2MMkMdcRrxjQU48aEXIGOCbd5fYbLvYXkIKEfSE0Mo7qcB/GiBe1pc7KYBs+ptf29I9ZW2nfESqSKVaF8+jkBf+CfH9TCBizgHWGnz1bofDccLvv73DcZwgBkZjLbZXwJf/eO3NAIZw//MDfvrtzxiGj7jYfYfJ/D3c4R/RX75D170OnjyXOWSi0da36seMPGNzQbGNwYicEKqAXSYrhoyMLckZGZHKCYG+6T2NllpkZyB1ZQBlAZfbFVXTnYsYaad5+a71Oz32egmB2MGJaMD+JETU+N0k3DOrLp3KCPnUz244Ynh1D9iwk5woXOo1l/wbJwaT6IBQJzwY7YuVT/Q1DZm/FEr/zhnUiVrLeeGKNSbiKttT/JZheRswdM48ltqowycJIrcFh2z8xfAOxazKvhTf5tNSngWjit5CkaH5KXG5LK+zcP48PON4qkGK+hMQHi0ZxCEyes75QDwVvdCO0CQhcHw069YEUDg15AKbGN8udzI3a5pRziPuVUUI6ZJtjjhHYT02MUnhZcuh0v4tOsBKuoIc53KhVtqPPYinE0RAB1HuVIp8FImXVi2mdZxf2K1yyM786JD3a1Pqk2PU+S67JBSRqoM53AEhiojzMWmnye+aGid/EuKH7jf4gO/x3e4aj+YLPPz+gPHuHrRnWCKwFeiEYalROwDHX9+nIYjD4ZWY7u0G9hfbZJPJ8LYYIQeMf3yEu5uS8hT6aMmB7IDh1S+xPTr83R9/wHCcMDAgu+TFmCyyjoIGTMn5wkBS4ByDnIu77qPKxRzvyZKxz8+OFes8zpX0P1YTN5zoGvLnWqBOFWh6noduK4VgLQNomUrjYbF5JS+dfye5C0T3RZ0CXZmckzrI0zqmOAcgAibg8fcf8Wj3+HY6YiSDX11+hY3dxPiw+Rrw/fl0uMfvPn2L0Y3oOoobbX74dsQffzsBE3Cx7fCr4RpfDZcw1jsatl2PToVV8jFrCb/8xRW2m07E4LDphyCneToJ2aTGPK43E45FZExf+Kk6Yak+ZTR1Em4r8qle3dJ3IMeWhCtZRbNzlMvXM4lXzjG1GypGYQYIoFbiGtcfUnp3otaF5wuJqhZDa5qPUQFSq50VMkqmr6wEb/Z3k2s9La0ctvZcfp4GxZa3qOcvGPnrFgkWDn87fkQHwo/9FUa8yOitS1TP3Odtb+ZBMVZzsPzJxuVPldbgSiazv+AIkITaCZJFSTdFLwUneYAII/WY0APcgcmiXP1JK6Tsm2dFFB/LRo4oX0QRVOmVzVRI/1HBCHVynoeCUEUxL6JMFaHkBHlSFYLuzUhhhOLAFFCqjlDilvV0lbahcGkwEdBZi6vdBXabLTqyIGMxmRCuPFwSLW2RDsHYYndR31K9ZBPuAAjCDzsvCDl/b4ObRrCbME1TkM+nKIvK2CYA2rpMOuXgQv3BmaFON7NzsY1JnBCBsHqU83iZSYshj+vI64TsJVYihynrO8EG0GyUk3qw2eLYv8W+u8TIB+9wCOGeDREYBg5dGDgHYoR7vLwM5SByV9HtcI8hiRwUwl/Ixrl4l4AaLkKoO+JKGsN4iXTUwcSBw0FC13YdwckQ3SS7l4IhThR9ubqU8Cfn/dwTT+G9S3mZ/aEOkZODjia4n68xLZO0kl7lSskps8SvxSDz7I+6vKJTYXc2kj6alAaO8Vb9784a9IPF1hr0G4OLiw7bix7dqw7jjYWJ0SLSZrS4/DKBuE7Rrqr1INX/ufLl42rFUT5SccPmn4SRh3RmW6sdEfvJX4xriPxt8tMBxgDb3mLX93h1tUXX+dh1Rt3h4Be8F+KtDaccijsfknDtYA1hs+2wHawy/gNaABejelT5guYUc5R5y9FRipUorNEQIvGYVV7VvGozr1K1jjxDkQ1IO93FAK92FBvycYEBYOgNHDOmaQrdCjvedl1aPsbhcHj0yGYcenuNnl/D7jaA2QLowej1WoPEXE8AhdEgMRaIgVvgA6IRCxW7LxZGS2hJiz2+jbyrYMAAamMxFlNOu2rix3Wm4mX9ID5eI+Cx6lfsXGCgFIQPGfOwU1SOb0WbfYZkSUjzlStkMxPIjiBDPlw+B5yFHlLFwoodtTIWUahqGthSGaqe5B0PvVGPhGG2cs4kNff6WyWrCZMjOUlCNdinCGChLaYixeWiM5X66UtjVveqFjDKVNn8V4C9lJKzbIZrNUrU8cDCXJbAKSUkDh0LA3VgDqITpTmP5JOD8BAEyHxNLe0gSsw90Wf/vLqUOx6FpGWhp4EqzWw0M3ekhoLTibJWZdq5cKqPdZsr6E2AoaLFxdCkk29StToBQMpIGw3XFPkM8mLeMSPghdcS9kpOcBHlZu+KRSog8xWYGkp0Cf4yPFH0gsArsWQP/IC9ucdo3+BoNnCHA3if4Ih0Sy59poTDcAD2yRFLYTxYRIc9gw9KQIXMZ0MydAA/OvBeHBEAjAUxoz+OML2B3VpsGbjcj+idS/JPNizt8wUc2pZ5puMBOOy9E7scW0aa12LEy8zUzJCNyIq0Lq+msZWcBMpwUr+TX2263Pq9lGbyth7nU1/kJbj9BNgJexyCcZDjOwo007HDcfRvDRnspz0ex0e4iTGN4Q5JSzg8AIdHYGcttl2HV9sN3my2/kSxF5wz0cAfFTfYbrqwWcePqQ0bfWTDj0mDiiguy+/1o6Pet1dzOWw5ja23BTS3CsxVSYjjejJljde8bR7KE6lwQiyWnFtfjTaftDNtAYamkv4coaLVmTOElZdqejHbSVmvVe9ayMr5ClVy/Ww1PGdmJGJseEJXrL4VEkLK/Mz03Cqa5Z+C+61yajLOGpe/ghT70xJIW+NX5jtniOdFyKyy5vJnb4z1eqgBs4EL4WtaEQNEpmmCt3IC18211ic56B+eseeyZ6WoFsW5Yh8pS9JTXj55B8NhnNAbg6Gz6IxEB4EXIMAzBMnnmRvnkhvmv9JJheBpCZuBxHEg6hvX/Y44WI6pEuplAINRW9phvfkoyPhNGCl9SORMz/1kg1zd1wx7gw5LIJCxAHVwtveXTMcLt2UoReiS4iYhn+zWWFxnIutovJMwS3XUgJZ0XM5W7uZK46nUb/0mQ+PsbeaAgJojXX1eKZeVir7TwCiC1u+TANGmLWluqvQEOcbrvVzXp2wZp6tUm6AIMVJNt7Hotj263sRT87PEaBVZKDrYouO1YK34w5o2/vLTakdE7z5BFBx7BC5+Zlxdb/B3//ALDJseXdfDWoOu80fHjPE7uigcazHG4IvXG7y62QIUPH+GggcwjSwR0HVyKTVCmwGIgBllfGuAosKWHi8rnimWeKhT3SzetOfNKMtLDoe5pHHL7xYNu29lBzIxOkv46t0O+8OE3307YpwKlsE+Rt80HvHw8ID94YD7hwc8Phxwf/U93gzf4M3lNzDm34D3X4EpxNdjMUA5BaxeTZ6kx5MqzvdRdgrETcJG7fwVxkKB3HKr3pqBA0IblhRHgCuj6Xzep0ujBZwlgW1/nSkXZjaMlXgoHQcvORA9+RlVicYuVV9mePXMenITDPu1NcUaQ6J2fNF0wRCSACC/sy9ST6uvqMYlN4LnxuX8NEkjNRaaVM/pV6gp7O6UDHPKTLKW5x2ZSavoeOG8SIwhreIy+6nqgJkqQwZurgvkBdY0qipmIBqNU8onWu+V8V0TEc9XFHc2xzGZ5uGkUhlZ7kRLoJdjvyS7FZAceN7w7VJ4JsICXsy1imoKdffSjqhAD8WYr04+ZIfUM0f2U4gRRRhyiEl9cJwbw3rOCCloKgJpKYQc3QxR3IEjz7KLmmPrEgc2zEc1xEHU58RTiAmN09GqaPrmwh0hLu4yk3shpngKYpwmuMlhGieMbsKICUcaMU1OnRzgKITK0WwT+9NYdCVkQUFxH4443I3xmYzn7GyOLhh7CTAd7Kuv0TvC3//uDxgeJtD99zAABsDfJWByOYaM8ac4TTo5JOFxEwkkgCfY7/8Z5udvMT3ct/E4LgVKMMXHpRC+ToqNok92AQsrY3dRU5TPFFhhHmZJxXNgK2Uwkf8ofbQLL8iISoaJvEh4dHQyer7kwvN0+oKwHw/49fvf+YupjadTxhA+vnf47X8+wgTjArPBxabHr7aX+OVwhW/eXeHdq1082WIUTZNxJCJ0vYlOB/9c7hqRT18iW/InhzQs2MrBn/qlh2jh3N7pVCpXqt78y+dNz2uGml8/d5oZuhdMa9bFuenzQ12lJ8M7D2cm+nymFDcEiNix4oLj/2bT7M6QRtbGsyej658zlR05Ywye3J6Wf0+pTopIjxPhMBp03IMHiwkWR/iw0H4fOZWFIDxVP3EFGFlvC/hmdxqXOvuJVN4hFsMsyul+zfIDlIW2ryuDlhVyEBu/yj409LmH+xG//+M9vvnyLa7+9gK7zQbWhtBMQReRjTpSczoFSbHipFex+vObejKZJl4YPSHeB6H+JrkbosBFoVfNKdEbiVh+O7iwy36aRMYfwZxORDBa+mAYtChfBrm8gadJTyH1LDs6AtgBMBuMXY/JWDgnl60HXVcOjvpwIcnxEYe77vGc/BIdEpGe++9lF0PLcZYAxNMxcfxca6Q1loWLpSMSJ4cBhfJy+oHV+4RH+tSOn/PksAjvOb9LdikmRwJuiSETKm/KWakxmNIc5c/am0DSegG87dkafxk1W6C3PS4uBlx88wXwizeYui5mz2wmL5ECvY+jVQ5b8SKnrMtS1unwTGVtf5q02hFhjw5kCJtNjw6Eq22H64sdri626HoLa+S4eYhVa/zFecPgL3PxZTtsBh8zIV0srYQ6bSugQtHROwYjgUkKEul6mhpOS9HVu/GKrOXEI7XTrq/VHivMUDm5ZFSt4oShN2BmbIYOdJxwOIQQS4ZAIb61sYThwmI8MI6HI/bmHuYB2D1ssX/YgC5u0XU3oGkDGjuwRfQWlmBp2H0WigxPjOnRQId0zIyJQ3ig0/1qp5PL5+wazysvhoVGmQajWKpTGAkgYVCEWaZABdo37h8JY9X1hmdc/HbCahhwir7HNTQbnCgKHZyyxvordG8qP9zsf7yrgotcmaBVj1dT3i0YYtl23Pkex6qG85Qc3fQENGsoHukFk8HQ7N7pVBTikqY8UfmoSinmw+oZ0KCZlewX8FVwGckZke6IaEEhlGBGaKJ0Cq0BbpEXeZuxeobfpRJwI5v4ebxoNhIhVsJu7J+maiFX8VyO385tEjqlSy751XztvpJobFcEvDxyngT2stN5g1mT84vFn9RVykTk05Ij0B/Hwfxfrs38o9FYEkDThXVhl5SKG+vY4YA9DvSIPTkczYDpALhxUseDPR5YF0IOBj6/uGuts+B+k+ENBQe8Bk/f5wMw6HAAOX9wW0gwGQdyjIEJW7bYAsDkgnziT4dquSOe3qgEkZl1Mx6Aw2MWCq8lw+TyTENWqeZE548SVcpXZKS5F836yjwnyjzx9UlQGg6LphTH1Zfws6Rnmpcy9tMxKtH74wH76QCGAzmCm4DxCOzvHQ57YNsZ9NRjM/TYbXu86y/wZtjiajNgu+ly+Vj9E/FFlOTo4KGii+1zMfldEZTqrUa1dA3NzeHp+S9TPBXRko3VzzWnBiIUJR+by9ie8Ub+8/vVrrfGOZ9Oybyt1FRKFquZf7VukelcovvOsZXTvZnp89yUnT0FM3VnMvS6SpfarmhhIcvUsk0mWaxODGCED3PTOq9biWpn1P1XlRY2ugBYFKxaRZ9j01/RZMqr21ybsfGYdcNLdSt55bxUyooLAHH5wGO2/Dk2mNggXerbLJiByUWOMme967p6WYwPL46B1hX8d67e1y1qfXe+Xv1NsxzOxjbQghMEwRvqDTrqMdjOn4jIq8kq0HIkkaj7PD+wsTP+T9/NkIzP6b02aKcWlYyom4h2Bc5tFmJI53TyQU5BRFlf2xKUnsqcIpjEFlU0iMpuN9tpPwMTW4zo4GB8SPKF+YiyYtFQk6OUskbMHxAh9qHRGCPfB8LF3EipapGkFjM8jPae9D1DB2UPQpwLREeDKoqEJ0WjUT96RlqzIFbVUfygXBLOYcwdCHGpSEjVsNl6YofeGh/xZ7Bwnb//uLKdPdNZXNF77SgV+03TOZf686Q50LaAIOTVruJ1bTx1BFY7Ii5+BDaXPf7hH75Gv7EYTAdrDfqhi04HG24YN8bAWIM3r7b48u0F5DiZMRR2/SE+y1L4nU48KGVLIVR5J0QulJdOiaJyUHR06OflhM/oRnVSDdVNJkIJ4AR/LLmFR4S+M/jVLy7xsJ/w++9uMTkGiKKH+vrtDsNFj5/+eIvf/af3GI9HPNzfw8Hg6BzevJnw6uafsXv8d6DHX2C8YEy9nwtmQjqtlAirp7V+IcgFy2JNMyT9UMefmMDG70xO4VTCc6UIzJKZZ1Ox56emsDP7sxBRNF+GdEd3igODCRgs3uRkJmsT0fhT/Wb28RspEQsijkbsJuDqSXVpddUJPR1zolheJgosnD+fSyWmt6ee80yhHaEDaWf+bAWqnpkM3DiGuRrq0M1n7FaaG88k2c0rH6mOpbY1rCLQUdZwDK8TJRnVipJ6Upz/gHOF4p2nHH9PKe6nkhjjZd+UCw+j7MgAkUnrLp7iaDSu+1bBnK9bDm3O0a049Y21q9FCLuXOUaWstQ1nDn7CeVkDCGufOJ1aA6CiuRVMR/hjYK4pZFEmkvl/gwLh2MdxdXIxXQYTRcO1MeSP6SunV7m0yulg9u04hLshHGc7sEbnT0OMxxHjNOG77p/wnv6Iny/e4bH/Ozz+9oDx9hN4TPhNzLg+GFi28VBGTv+UIwDAcbjC4xdfZYAKD6QGXfW6gcPu2z+if7zDlyNhG8eUgPsfASJsGDDGJlmH/AkUkT9kbIj8iYjsxIEDMrqi1mIcyAzJ5B9SdS8MvHo0L9uc9Ti807JbvdHj6bvoazlNxrSEKI7rwpoqaquSKMN+yGXnodepHcvOMkBi/x7ciP/6/jc4jIcgr7LfVUUWZAgfPjr85n8/gB2wGXp8NVziH69e44vXF/j6F5foyMKG+x+s3OEg3UPqK6lneozj6Rrt2FJls3pS8Ub+Nr0uf2c8888ku8kczjohKrhOzfpMOy1H3oukJaXy3LJl0tjf5F4nW2hxdf39NPf660hP9DmFspR9ls/jwCjDwtLMafefg8UP9iuQ6eDILpT6l3ROykTcJ1pOzq3j1LyfKhvbwoq1dnZjoYCmo6yeaziqhU8ADBgWDj1G9DjAb1Z1CA4KqVcbp4M848J9oWl7Xp6nUlPDP6zqk7p9GVfooaGeJECFesMdZpzqTF0S/YTzOhg1QOmyzJlU6AMGXj8RvUr4coQz9dQYwvXNJW6uLnC12WBjuxDaXGoNF0iT2NSEp0u7qOr0b1iNH4NduvsB7ODcGE8kczwR4U8u+CHgKBs3aWd0MiB+OmmDHfRpi2mc4HjCOI5wzHCTk0mouaPqV3yX7cLM+5mUe5HbBccsJmdwe7jEsb/G/mKHyRDITTDQdy5I9BA/X4bgd8gHlNCnySMUhID1IqtFKSXBEcvksGnwE557nM5PIHhkLEyL6RREGHflzUn1OweOdz7IHDGik4L9iZWAXanCOCbhMzql9AiUm+GKRKjUUV32WUQSSHOtohjoOVATVNOW7B4cv/aGzuB2OuDuOOKrqwtcXl6i6zrI/SDAwt2zL5EyA0PjNcrhWtBnkjqg8E8XKWX5OQa3JPk9dSP6GY6I65sdthf+eEo/BO8spcsWJQwTkQ/PtN302A4d+s6gVOjTBdWU9SMjKaRE6UoBayN5QrzsYfY96a2EKtcaheOEcXDeATI/QXGeGwhtTIhNNrlg6BEC6E9LdJ0Fb4HNRY/ddY/pyJiOIw6HPR4f7rHffcRhYzDgIzq6APEGZuzDzkyAbdlmgzNLNyIGiyEyxNUOi1+fjMgKUurb51LpXiatWUazs6ikxNYFn/5HdpEMKwcCJwhqviovCewM3KEDWQfTyRHSwARouQetaa2MXaH9WQN3YbBMAkH+vhIiimzLaSkXC4BIjokkYpHAQAuxSMsaGSCaz50R7lbhE3XPpTnY5M6P8uTnrLOpOebthpPAQ8V8h68tgP2gesdlkCayXCWpKDrWEljOSfHeGr2WkN8bwewg4ZvifQagRn/W056M5Ol+L80pAWjQQC9TtJwR61N0r8iJNpJ7ewqFBhqGFo8t+WJ+XFMLxQ6yQ8YLty5YZ5OY54U2LwgnSZMb669t8FECcDyCLBdWJ4XlQA94pAc84g4HfsDx4HB0hOnowEcHM7ow1wzDwJY79LBKWWAZlthr+XZ0BnTQIcb0rLeA9gOydYQNddgawoaTQZdcokbRCEwqDJYWf7QhOM6fmscTKR3Dj3vcF4WSJGOdwr3lXPP+vcbR3zPQnFodqGTk+QpP9qolGxbT7vHRf4uX0CEpgUcwQN55xgAej3sQCIfxgNH5+5uI/eYcIh+alJgxHYHeWFz2Ay77ARvTYdd1uOh6jwdG6GsOp0ef9E73g9IRJOV7UI6ClqicecLyMVBYdFaixo9ZR1DR8LmtUWPqmvO5nKvd7oxB+ZkjsjIVksYzxOTWfJzO2HrtM7TkwVbRNJst+rXcr2WHQKvelQOkvG8v4XR4UlkkNf2cWibycczbY/2Xl/4sMM3Oy2lcWZ7StTxYldB6XJnvRD1rWltTL69pbLZAS17mGT7i34vs6Z0OBo5Muqw6yD6QDSyRmRbNlyA1B4NVeVZPOT1rmDMCRy/KcixLWX2McpNUyp3Ki4wQNS9udGy2d0sp1UVkcHWxwW7T+02+eqNKOX5JoGy03oCBVT+QnDguyOFiyI4bFxvtRqpKSV6SQRGnTXa6gtPmDv/bxTCsKX9ROVQj+idCfo1TaGExZ88B+Ps12GIk7zjzBvdGHNlYJ6vvyDfnNmAtN0pXasVcqtBXRgpx81064dJcNY12NKJw9pn+Dd+K9+m7WgHi8GuAUEGU9TtNVJNeaTqzNE4tuqbHLVbTkgdnCkf6lbQeie5j2V+E3nWd32RPBm5JKXpppwRRjt/iJC2HawWOpf5VmnndrK6uYnAVwqvnT3NGrHZE/Jv/y69giND3XXA+eCXLWj9pne38fRCdwavrLb768rI4AZHgF2WpvKchdS8o4/GOiGJhh+8MPUZ+wpIiWxCB2bbk8fLz7NHpLO1UXOiqCUG2Uz0sfj+/+Y5TCz/2zvhQWZPxHuQ3X17i4nrAj7/7hD/8l/d4uPuIaTrA8BE8PmC6HnF58xqb+/8ZZv8O1liAgOMlw1klaFQ0hiBHlfyKD6gsoQEc1I4HgE0I2cShv/B98MVn0PM52sHJlMayepMt8AZ4FZMr1bEGJRYmEVFQhWgKjTKJSSowaUoGLz9sJYOjWNYdOuzfv0K3e8RwcwcRI/z73Hylu1wx5pLplQ6JhQGrldLQ8TZ/mk0a5VJXK25cgUAkEUVlguSTE2LmVutTFQY6uhDWCi/DY8qxa7Y2O4512VN55oFuz3czN2cZG2jv5yL61BbXOaurA5627pMDwteRH9nVAkjxO7Y6I5DEb61VpPFM4JghGIRglA+1BUlBHCrlOK3Cq2BlzMmowte4iMLJEBIFq+peBJUy5pjjQ1IcvFNgYn9CwbkpkjkT2rOcLtEzDnDGwoiwHna8zU217Oryu6UmOMcYJ+98GMcRx3HCODn8YH+DH7rf4DAdMI5HPH57h0dnvITuGJcHQs89CIAF4+upwyab6RYAHi7+9Ah398cKMg95XU6UV8MOBBNPOXhDchpXvbsVlO6rKGUhKRf/4RzX5qhu1hNKxbNeUw5DzDw7Js9IBc3Nl995bZ2CcJ60z+PaKUg4o3NRDIPyxMEx430/YeyOOEz+9M6vP/wOxATH/j4IE0IoiJxsrUFnGUPX4Yv+Av/66jU6Y9EH44Ih+HCbYU3mcxU+TIZNsgkyysbGL+g4NnHNKZzTNJIiPdJ4Wo5Mg3ZqJ8fC4D755IuUX4GjdBJLmlX/N5+efuroc6bnwETF9xdW9tdA8GI6yp8H/v8+03PH+q9zrtp634kCS7rvjOgE4TlkALIADCZ0GGlARwbCdAgIOi8DclehwBd0Y2G11JBD89/6Z8GntbArOkL1SuvLobxTpzHE/AJl9BX2HyHn1Gj24ZCyJEgruwGn/qYXFCsiBsgY7LaEX31xhbeXPTbGBkeEwO7CSWJfUu6G0DJCORZxTNjPAwN+h7w+CcGMyY0+u3NhvlQ43FBVrVolZ4Nz3sGAINODATeFkxDsT1lM4c435xym8Kfndw4lsxYzo03YvKOHSI2/v5MznHKwPYABY3eJY3eJftyDQXBhc7WNbcnk+nE1SOdfCpNk1LVMfF7IcZKZFY5rZ1qODKH1dCcHu3SfAzjH14SLsnGG82nX7wUXtYMo4no4ySK/nYJTOe/iuKyiLgXvXrTviMyK1PaKlDujCOHiRKUKFJMVNxdpDAnfwsb6rjMYhg4OwPbCYrfdYBgGGGOCU6gE/eVkrgr3PQGNT0tnxOdMNSx6zSFfCM9wRqx2RAxDF3d3pbsgkN0L0XUWFzsf41YunI6wKgW5pcxkC7pQkKodfVlmnU/naunbCi1bHtbsQU3SG6/Lp8XvpalQHAzlwqjzGkvY7TocD4z9YYIh8rtOyRPQrgN4C2wvB1y/3cGNBm4acTzusd8/4rC9hbVAT+9hux48XYFcDxwDkbayq1YRxwymGdgE48J8CsFfxsJY4GVTs816B9IcaOucEXn52Y0QWWvijEjPSpM3F2NCqaj+4p06DLjRYNx3IDPB9kJ4NRCtPbU5h14kFkLoivIldsxUPZvOFpKzyj1nCSMavoRJI+mvHtlEGNfiWzkzXLwr03OxeGkMqhnU93aQKltVUgo0p1PzJESWQfCP41rXLfg7QpZGIwmKjmXfbbGwZkYz3QuRh35L/joGw3gBzQg6kBI48nXFRbv1OkQmyNUCWBsX2oSCohNSHBIxCzXKVX1P1UVMVkzf01rhp3JqJa4Q1MdqQp8L/sbQa0Z1O+5mQnAWqGO5hgD4i5pNGH+uGCPVAqG0wRzuQpMTEKl+UVAOeMA93eERtzjyPl5gjbtPoMcR1O9gTAeLDpYMNgA6Bnr4Ewjz+5yQz73Lj9jPUwyFC8LzAIDS/Ril+4LivRBJ/onvlGxSiCnp94m1mRTQWaAbZebyP4OiNYWiVl+fU9+6rKuMsTk6hu/Zwo+KGzMw3h5wODzisJ385o2Ixy6uS3EIeVmZME2Mh1uH4wNw021wHU5CGGNAxoDIAHFjQoDaqO+hb4tyr1/QahwEsSlmzhRnUr+LwasU7BVzUK/4RhkNc4NEZD9nkPMkKBUOrMnXEvo+X4r0fLEvgfokPXlVqsZ93QA8Mcep9udxoHp8Ng06gUBn1JRgeK4k999HetYo/VnG+Lltri0vRqLs55NbeimKdAr62I4WILiUmpFtNjxVaQoLqmRWzPcpGfkhe5UqkpyHruH8ayajxzfNR1Ud8SPYQZSMXxVcMymNPLkNd74FAvzJSeew308YbIdt32Pou7Cxp5bb048Z7MnGJhj7tbEZDKgwPsn54tSYU/ybizOQjN9iCOd0eloM3Ixw75s/eeHA8b6IWEccprwdLSfnfVSwtJCs+O1lNAMyFmx6sLFh+MLmItVbXW3+5xsqxLFabl8AbGk9eLBl7FRGFvuELpzWanZqIhRuWmxkiuWhQu/oEEm7cDKogBQSKkVA0jJUo2cLUxbVqKwnXA1ifgH7ihTFzHpSamzTGfzJZGv9NQM9MdBZUN/jOGxgVIjEWMMavlYaLcrnBSyUQSgRFRbGtvq9WvJZrK5c7TwLMxQehPWxEgLgDEdE33Xe4BAvo/YOCRsWtrUGr642+Obra++cCNrTXHilufhyOo92BmSC4qKTgHSWmbeNskWduvwq3DmRxJiTGXZiDG4Ewp3el8x46A2+fneBh8cJf/z+3ttNjD8qZIzBNDkYa/Hlr17h7VdX+O6fP+LH333C4+NdYDQOh90j3OX/G7vLK2w+/V+B41uYOwIbwnjFYI0NQu0yQlUSpWJciqcZCayUPUWVsne0fg21qluAb01BHQZGg3SCayy80IXLJa2IE6V86TJrnS1vZDoMcIcB3cU9THfXINTrOtCWm9t5Gywtwf+ENAfV/B0CIuwIbakdOmW/WznWpqf16mmp2d/KWarXTFVD8Vn/KjFiLt8MgKlMRGuFEdSYzfIS9iC0SM74utwpEoFMULKCQRtz0oiEGJpOzMBhTUmYqwB9FHaiYDDDbOHq7tSjEl6UbxIj1sJV7ehc5lU6lFMl9Eo4JNkSJZhOCAOrTg2p8oUvK36JdECHV0JwDkg8VzeFmK5+bJyEkoEFG8BYglU3rekTAqn+9CkxY51zfpfU6J0P4zRhGkccxyN+sL/Ft+afcBj3GKejd1iMDvTHX6P79oCLv/n3sFdvYcjCGuCLMdzNAHVdosghq8nAEsVIEoQRkhvqzy8MTu4IGXsjsUXLOShA4+wt5c8acmiax/PoHDW+nVeB4lPF5hHSa+wFku5jrZSqX5nMWVTCao00Egec10p6vCRwmnD7X37E/Y8fcfh3I0yvlDzyc28DDzYB740h3H1y+PV/POK12eLfXn+B3hh01sZ71Trr74WIwGaXUKfHcn+IyYD3baVsaRceyZGJOA1yEodWz8383RCfLz3ZCfG01lLlf0JnxLpUcqW/7HRSxvozdKVq8i9+OPWa17LLv6T/3tK8xvanaJxWkJ+5l8Fg0JAzlVkNYk0o97uxEnREG86VmHLTpjJQxPzFulG7BVm9F3tMvJ9BeH5WDWcwnZekklTOlXWpiWYAhhmHB4fffvuAr9++wdurK1xtNrDG+BOWNsyNU+ULmbINtzgDwu56ZvA0It0HwOEERLh3Qs2WIfL6hjP+VIHTp1o4TkGs28nJ6eRokDYnN8JNDtM4wrGX99OF1fnQJRxA1BtPrYyoE2bD7oJcGDZ92B5kNnDdBZzdgWkEEcOQd0RoHcYUf7l0Iv/WRtdKFi0TY/ZwgD6NDlbzJhteIjpnyhRY5k1sjEqOjXnUGtChcDNcjQMo45gGU+sMhsKc6w4XDqQ6FfM3N51PEvh8ZdVJWa0vMBBudkg/FbyGvK176DvswhUEdteBb27w06vXuOkNLud7k8uSTQP3ifczvTr1nqsnK9OJ6Sr10raeqguosT9Dpl7tiJDj5t4JQbAkd0QYdL3BxW7AbtfD2vzYd+6A8ABmlzIqA1YWskMZL3LdK9/vXA4iNZ6pN3WFsw6I1MppfFnOkDshEqNITK9GI+38kvY78pdXX170OB4dHveTvzMiXvgAmN4ruNevthgPE/ho4dyEcTz63XybexA5GPsDbO9gxlfA2IGOflW6ruh9A5k4Eqsa9ipv6nApT4R+5WYX/3LGkLDYSPPFYrFZL2M0VijmqCYllQjfyiqepDnoZV4s+VbdrGHw8zS/E1ExlWa7My+rYkUeruttj2b5JVVH+sfJ7+mZhPuKVztoa618z4ZxgeKG/KmYnvTQXrtks6pWqgzJESbVVDW8aYByFrsO39u56nE4R7zWwn2Glk3mqvEj3CfDHO7AIB++CH50o/M5A4zzJQFAyYjxdVrCfscOgyFHI7LdGwE+ikKXhlQPdPlOC3zyNcf9ZSdtTf/mk+Y7LcJS0EsTGD4n9S7eFyF8pjElc2uytX5Z5FiXBFXHDBPC8hn/Euws2CJHsUwYz8dI15vdCRGObU8TY8KI0Ry8AuMcxg8HjPdH8DSg2+2wMwMGDg55509DiNKQ2i/7uWw2i/m5Hov4TvXPBOtxvos8N5j7uWrLJ/6Zol1tiJppeL1Ftxtgehtznive1vmpfqgcDXMOw1PGSHEGpTFYYdjWAzaze2i+nE6ct9d87z+SXqaeAei3DttXhKmXS+oELO0A8J/TCNx9mnC4Ba5pg2uzQW9suFuN0PcWu12HYaMuoSUJsdTubn45YjlHKhQA6e9Q/c5lccLSnOXPcyfEnJyx/CzB3Ma9U06IRfxah/RFg4FjaNlhJp3Q1/6s6fRJiOdD3hr7plS0NEV0Ul1YX9lSqRa7OZX3ZOaXmP2zOv8nTYvo/1ywP7f3cjaVcvznTAXSaTr3FCdngwVLekmfadlGklTPHTPRRhmGJxA79VzkAyVfGvgQRDN94eJLspkoKBmabddySVFhRa/iZoNW46XW25LhEzwN8FogqET5V2UjIQKuthtc7QZsbI/OWMR7VkUn4LqeuIGVAH2EJW1s9cKNXFQcGyyM1JUOQF5XoxCbKOpqynGTLqfmJDc5QBvSnToNwexiuCEXyi6PV/GukM1rubfAYf3TdGDqwKbzIcPCmGrxRksiIvPKuKTNXjEocYS2xSXXrSWZf5kL6WeyHcaO18XUlyi8ZgMUf5Y4Kp+OC/xowKfJaY4gzb7MJ51/jb4zl+c8jXquJp2RDMEav61xYgcyjN5aOGvgrM0QQ+7DrcQNxe+aPVl4r7UrLXOlJRfwLtQhNqLzqPWK3A2eraNmnMLqsp+n0mpHhIRakiPn1vgYgNYSLi8G/Orra39fhGwTzBwQgRHJJq2oaAmDygMokHqnH2bCcLU7q628SNz8iD/KQYLseV3HyVRlby1gRUOi8UWOyCXvPhcLW8KYyBE1aWo7WHz95QXuHo749vsHGJA/8GAsnEne5f5XHd5+c40ffv0JP//xHvvHe0zjEUSM42aP4/C/YNhe4uLT/x00vYb5ZABLcDfkjUmNlGieYjbyPCruHJl+9MzHMSjYOOeDKGNRxTc/O51BpJSCrpsU2FJYFc6Ey9LwyuDYlZq4lE8FI58i8M0nDsJFbQvWbFUJT6vHV0l7MziuU7NHrYfVNKUfUWmdnUrvjJCL0qvhzIZ4DmAtqDC0M+J56YnMdYFj+u60HSLngnvyGu98EYRCCbmVyFTARxWzytpkhLieiA4fim9bwlxjQETQjo/VRFO4LwJ+LcTdMaouSscw8j7HC8LVKLfGQfecs18pa+ak4erfZmpNR0ZiSP3lYYRASRJJyh1Fh4+Gl/Q2nBkUIPLzmNF7eOUhKRMu3nXDhuBkwQrdjDNLBS/3CkmMJRv+xslhGieM04TjccQ4TRiPI47uiAMdME3+NMb9f/0Z+9/c4eKX/w7Dr77CW97gcgy70EmMtepeKSRBTSsa7Y7rrzKmnD8D1FKgIOpQJo9E+UXLGIS0S302tdfOXCJLeP1vfoHNFxdhc0dYC7p/2ii9MlH5ScU7vQs/7rA/Ueep9ktPbbU+qfl4Vd11iZnnevxFVku4f/NLwFiL35oR967AC5JlyDDG4HHv8M//6YgrbPB/uvwCg7HorD+9ai3h+mrA119eprseomxMxWfRhu6vGvZ02EbjomQglZcaYyttz4zWKSdEVhW1fxfly+qedBLifMbXrLcVlqe9Aef8Jj9HejEYnlmRuP1X5f1zDJySHXNZ4CnpebP/vLb/Jf13lf4CiAxRLmjHpRS/JD3SS+8OBIbFiA4HGEzhOUFye95lsjsQ092JqspC/tZ2hKR/cgEHiuehBGePkGLfZw8TlNGOEWoQB4HYNqrY9Q04gDyOfPZJVV4/FhSq8vHp//brC7y92uFyGDD0/v5VWL+Jlx0BmJBJaqJ3EIPZQOu8Hrxw+bTc+xCcARAngMjuLMZ1KL3Cz66BD6dEclg8bqwNd0I4cSp4mR5Bxmd2MaSqG6dwsnr09845FyODZPDq+SKKbZLJDeUsmmehhJXYSaJ0GguYHrAbuG4AmwHkRsRwS/moRk3G6zEc9Yuluw5qXqdxpFGIG86fGC6LkextJUKl71K9RLrSvoRoZ2QGw89TdHiw/Ab89hppM7TPToWtVe1GdUN0/rCCMrrRGqBcF1yXVBlZQ81q6vqiCpfNCZc5wjd/9UDXWzg4PPIBG9tjN3Q4dr2/+9AwtP69JANFeTy22g5XVMvMLQiTTRigSBOjQ6Ld89n0JBZTOlAWDIjn1r/+RERQOI0hIIQD6sLu/ItwEsKQqRWh8FHGtiNRYFudaOskeYYZ7bpSmChNdJmbWvmrCmdgiO0pRBOEV/PjFCOLxviMz3KCm6FibBMouZ8zUAjApre4udrEOHyHw4SHPYL3OTAsGFy+2oIdYG3vnUfThHE8oLMWe3bo7B/QmXvAdl4bHghkOtDDa5Dz21uZwkkJQmI+sdNQv0RpFxxNXnIZgzpx7K10rvZ2L09CRmcC5ZlbI5VRJXuZ+DcR4Mhh7O4Lp4v0BTBTh85tPSMhyuezJJZFQ5T/bMPTKmknmH6M7aA7Rpii0Kf6kAqSdOCMdFbmdlpQ+FsX7pTjEkPFzMIXvNIxn2KCgVGW+ed/t+o/Nz1tzCrW3QCrrPkUvpzT06yc0KKscU7aPLVZL5/VSlmYq/sFSAGR0QOF4Bx+cxSI2nJQfJS6kLcVQE90Ta/mDNBcUVG5aprTGKVT/ESXFB4njCWWNUXdfpwIgX8EOk0piCckA+sjJU0AvCAp//lnYUcUGfiL4qHehkFzwhfSvx6swAyErjPiJXtylFscE5Nz8QK7R9zi1vyM29v3ePxwC0dbwOxwMb3BzeUN+u4CHTr05C+LlsuxI92NNFXx/tLYXY19yNvcsaK+kZ4O2amGGI5S8ptMRjnFxYCojkScnxdwEywikxVvqdVe7iwpBCAFx0y/V67tSrDO5Lkku2VGdqjxzFpWvxtMczZvAyo9Jun80ExSsho7Tg5qg+TMU8tLds2NE3D3fsL4wHhjd7g0G/TWwhobw5nKZp4YVilOmSl+K1wUtFYd1I4xkj6ZLEP8zHAVxVopRm7eaLw8/2c5IWIfM2zOy1ewtbI1Z3rxwZIMKPQ85Wkrra1HT+R8T05r12OjYOvr+eW5gKGx+Mr6xV/dxrE2NFF0PSFaNeucYXd/FsfIbHoZJJrr09K4/WWNw+dKz5BLXyK92CArW4F++gJqmqS1HD7CwwIAw5CDJYcOEwyJc8IoLS2Ujl7BNC8iU/mIqHojZmKzqT2k9oHTPDz8SBtCVQZOsFXXqcXuudjNsi392xFmgAkv4vvWKDOmifHp5z0ME27e9dh0PjSMvojaF1dySwO3tKq/NELJlp7epy5QNiBUvPWlwuYk5iAjcTzdLKcuOGxackG2n+Q3p02zcxAqNStuqhJHUFaKW4U8vFEuilgIHEaL0XWAmWAwIoZWokykQ5onimOewbkklghccwuKq9qaWfz4SMgl6UFer3a7hFlJv1mGRJwQIb+TEFySL228yS+p9vnj6XoV/gkNWKBC+1ZJkY1zUyWFVXU02iQ1Ber1nFZFwa5tjcFkHNgwrDVefu8B2gB2YS+ZXh1tUWSBui7iEsXOUOgBkb9rM+XQ65Iadcw0Oic06V9zG3VeUHhY7Yiw1p+A6IyPlGatwW7X45dfX/vj5kZ23qXOVXFulfLRVpNV3yoBMtXV8gKVDgUqyxUZU1snlKtnDHYyWotB3sWFXTolBLRsTYv/tQHCbmuwHXrfCjN+vj1i/8MDmC3YsZ8PQ/jimw5vvrqKxrmf/vkB+48PACZYYzF1/y8Y22EzbGCMRYcedrpBd/d/A6ath6MD3JX2A7bhF0+1Z06ITIEVQZPy+UAFUSDyvlKBPU25YrF8u7T6HnAmZCyN9PkOwlDaHvB4+ROYpgS7kw+HzeEG/f02w6nswt4mcVmiOJoFtrmY6Y/oX33UoKvSIkJkncsziSZYpKyeZcnudFLrfDFbXMesJlBXE2Lko74zItEJGSfBtVPtLkkH/+2mNsuq8+RkNB/3bDnOKb3FmpuXw5LzjqKTI8zhjHE0/0axnCdFmrYUGgFJP/QR22Kth3/06bzKTFloMtm5B0UPl4T/J6XCiY/ql/RFTpKFcQlzSEqD8utpHjY5ZSTLUe57YvL8hJyBMYBzDhToaBRJRYhl9jSdHQATN6Ah7C6PF1NPE6ZwKfU0TRjHKX5+MN/ht+Z/w93v3+P2f/sJ9t3fo3/7S3x50eHVRQdrTIDFG/xlo4T/PzkHmsMpNHaGTmRrQDslIl0z6rWnr1qUkM0Y9TlPFDhX4lcDGFHW5G9RllXCk/4WtPxCRHpa0t1QY17CUA7tuUbTTDSjgl/r+YvNUyxUyn7lRhT9vrWfKYYS4LTDT/60c1TkCAlbCmKMB8Zv/8sRWzfg//zqHTbGpjshTDAoeIT1OFLKreG3Man+mEPJKBTfhd/GZOOQz0vIG/FA4WvA3VIWbl2s3krJKTcj15T9ExCrev/0PDm1uJZWNzTd6tu5ELwgn1jTIj2zxYLtVJr3ioE4xwnxkul5o/2nw880lJ+3zdWq7Z8eTf8lnZFmVLqXbGH2iZenGYYYIIfejNi4EUQOPpJPvgtY24D8rqBcWmYTjJ46tJDGP5GzGwiZ7zgOebL8HGXQctt4aZQPWypVFSF/sLewqjIfkRaPqO0QrXQYGf/5n2/x+nKHf/03F7jcbNEZ2cQAyPFJV4xZEspqDSH2FQwJx0SMuMM+5lF6kTiPsnGDnzP5Y/Y2EblDTu6AkBMQbvKnLSY3gh1jGo9Bzj/6E9Ahf2FC8q1yY7zCPCbziuwKdwCsFERuQ6HsF4wFs8HtfsDYbdH1R1hMmJR1mYpRrWdL65dKF53NN5cWFiwjhrVCxDXWzalnCa/TZ7wFIcxtuihcnBClXtH6TihPTKRIJZwB28DF1Qzj3PyyzilvPeJ0qJVkjsoZrbANQLhuoLOwnUU39CCMsBtgs+uw6TvYC4vthZwAOt0b//0Egz2XvWvjOHPQHfTqVdVmMDYammX+6wS5fAP+85nPakfE29c7ALkytRk6/9skxSfCl12il75kTogZ3aXYQtfIsJzqenTiQklbIBjPlAOFWGQ2spNJK4OFlK/4DTEAS5HR7AaL1zcb7A8OD49jUhCNNxzJgr246dF1hPGeMU0TDI+AY4yOYGFhHAC+hx1+D/Dgl64FeEMw3KM7XsCNFtOhj8JCIgaeiJFjv0tZmEcHoIt8sDEQYQ5YkY7Y5cXIj0U1gdBo2qbmmWTw4DBO9wCPsNtHkHGIcb3V/SWWDujpZ/hjkP9/9v7sSZZeuQ8Efw5EZGYtZ/mWu5GUSFGi1D1msrF5mYf5/1/bZl6mTW3d6lFTJO/6LWetyswAfB4ABxxbZGRVne/eS10cO5URCCyOzVfAIUMRWRQfvmN/BtI4rx9UT5ZKKn2Kx0i4mzoSMDxhPt8llzJmPivlRR2k/PhMonaIkQTI7uqkiE2DkjstM7bCmsQRS9vZmoYVRZQ7ii8f38/jUhUb5w/FMkt/eDq9Jk0tYMxruzy3hR4Je16RfenuerK8oRoduO65MenRyqmSwCpivNIJwgYWSUbotkPMGoOEpNF4Mc1HxXQqRp3SZM79zYmb0spZwWWV26MOqmoNEJdDf7TX0j9ldmUFY7gzRq1bxT2ulU0Ur7k2BOMNPAHGMDwMjDdgIwy4UeWFkMQWjndIREEh2W8iIywKXi+7p7zHiT7j/fwHnI8nPH7/Ge+X3+J4/gD3eYJ980u82r/FgSfszQQDE05fGuTdYnH8kh/9+JNcNBXzrmLa1EPpIqZydUfpYDYSIhJFbqy9YC0u8C96HPR+qywo5zljPr8Hff4AnB7SuugpiXt4LsM3AKQJYW2EwzPVgr0gX/UwcX0OYVRA7Tazn7Jse2dIy3RQuJ96Ccu1EUlO/A3jcPrhEaePn3F87WAsw3FAQbKzU+owxmAywM92Oxx4h9mEHVbGEHazxf3tLrkQu72ZGiNDbWwR/FuATapNelNN/oixEULxA4qJ2GYU0OlHaUbZ1VhRvcYGRaRlrDtpQ1WDj7110Tsqvx3r0iDxNXh7AxEd1v6EPKtD1vJpIzmtQPg1Y9A+DjJf+20d/q0lPpcPHNfwYhzbuCYhZS9Q1dX98PId9xOEa7mul6rzpy5by2wvVA1X751Xzb2ETWMeBoyJfFSEhq2U5dXHwmcDIOEVFCKRE7vESQYlJWysyZJUAP5yY59L0rQ4xIT2ceIDAiEPl6cpKSQzFqLzrsEUDbs1MNOEvZ0wmQlEciLCBM8UKbvIVlm+r/kn5tD/XPRaZF5YtStfoBfLirKDbBBl4etZ/c/v2rgjpyQgpx6iK1fnGd75Ik9NQNYUmlw9UPUxvcdNWHlWUW6X9JOxAGV//yUGJ+hT4TqB5tB12Lbi+22TGZ3bx2X62mAmg6ErHXRbKDcbETgPpBq3XEcel5jey9irC93lGeo0ywWZYAuc275ojMNFMq17C3OXO3xtTM5A6T0jzBFjDM7e4+P5AdPO4LDbAfs9jrd3mKcpidF12MyLbUjW3WSf8EeRMOOktJZUskIw6le8BepCRqkmXervhG+eziZsNkT89S/uAaJ8aXV0alvuRIyQD+QMky6JqD/qi2IuCatAVJVgVUm9ynVXwnKt8N9QxNaQlnVU+Poa0ZQ1lpUK8tE7ApMgpxal9+Gy8MOMHz+ccT6LPd/DWFO09fXPDbxn/OH/9xnnDwuAMC7MDsZaMBjGnOFu/5esnCeE3afLK9w8/ge44w0eHt6kUaOI3Dw4XXpDXhGsVwQ2pHDcBQaBqHCRVE6oQb8hIul6zIRBACBHPpk9ls/fg5ePIP7vmHaPsNMEIsJs5pyVGTfH/KyDj37zGBw3dngwcbJE5zL0m3Ah1CAXPxOO/9bA78oG7E+vcP/9vwexbbCMLjvzIMq9g15LpBKyYunYZEZDUTh9ZQ7r9CNszBkh1QS8h0jz6Y1BmbG8ZMwCUBo4NoatRPKK8Kcgkg1QbD/RKK5ZLu3iSV3eJcCXw+hkz+pOW6FomrJpvClMveAGea/oQSgi5yPIhdm5UZwTFjSorLP3qk6FFT9j3LbFKHdNGNjZITibqzalNVdlLHAbB5ruQRFdEQwsLDzYWNUJ4me2KCj+94A34HibtUsX40Wq5BySKybP8I7xML3Db3b/BccPH/Du//t7PB5PeDyeYL/5Wxx+9bd44y3esg1GiHjhbzgNEQQwAwCmETsaXNT0H2VhpU5D0QVWszucqJkr6RRGU99YaKmmE2qxQYQGMGP68beg7/4Zi3PBO7CMZ4/PjE3R91QoUK/GX/n0Ut/cu4Zj61OxNSzrQfq9fq85RDUG6kNW2Od0md50AmcqKHObPePxn9/h82/eY/m/O9g3wLIA5HPZchrYWMJ+tvj3d28xuQnzNCUXTDeHCb/6ebgTIu8s1HDmthVKeMVPUwKdys0IeSKXvHieCGX/mPxe93fmt6iKK/v6UmiNUW2KYV7d/hcIz+PjRxP7GSX+kRkI4bbUCKff5lRtB7c0BfXS/ckFwtjF508Iwxr9b9bZF2Be8ceff38Jfwahxy8VT4InNH/tMcFjJsYS2UdfyJT1rCZQ1MXk7XAm0V8iDqdpRRQAh/0v4l9VyZCR7S0PyAuPxBfWXdE4kQUotiorIsjEwr2kFx1YgDd7gQh3NASxNtadnvv96+PpYcwT7G7GzbzHYZrDxoW4oSH0pdzpkNsZXKYCkF/V2gQ/o+wCPRjxIcsFBqJwZg66oVxp0CvlU6Ks7iUIyuuwiT6cknDOpdPPwSDhkO7d8nkmbApaTCHdIJkkql+Ed8pcD2AMDCxAM2AnyGZMAoWTOEbPS6hxlkdGzZWsbupKMOcxKETXXsNQpi+jZS6qcrkd2ibI2HDQU1F6Z1WVnicZ0NrQVK+kFzN+XqKNo8AK3Bw1HpXUb0p/AICMwTRN+OSO+HE54pvbWxz2M+juDu9fv8HtBNzmAp4E6ij0NgKtrgrNmjGCtwL51oB3iQ/fBGGHH8w62qxXeHqnbL8jwog7grBr3CjBKT4UA5t+EjLQgVKWIrH+rmUhxexmVEAqWdtJRWmrnFcmkv1R6gDRBHVUD7IwxGJYKSKEUHCGeSh4acUH6T6rBAdjgsqEPQ47g7dvdnh4dHg8LWU5CBZ8MoT7tzvsD8FvMRg4flzgzg5nDpctejsnZU9AwQRyDPA/wpkd3O5VQVjDsTyOx+4Yjjx48fDEcI7AZ43fSsxRGvIV0xLfm52SDMDPwHKX+9AeAfvQKo2krKi8SovH/ACajiBzCjt4PUdf2z7utiUYa7B7JUq9OM5pvG0kApx+hcCmPokT9vTRw51ZjXmctaq9bAC8I/ip7AfjTnDL70EobxBn9VeQAiG20VAYaSYsdwS/i3MI2f6eGAfIxemAcRa7h9cgNsrnu0fkswZIrFqrutNH71zPdU06uEgfFGDFPpqxYoQ6CHMr5s0opchWMM2dbM0uwhVc036pY0qrfo5dK4u2t/EyQG2CLudE3SHfVGHCf50dC0T9Z3mPWy90n/cZOlK0Qn9NpsiyJXFyC20p8PaAthZGiKb+cdCzqJe6jhuxEcO+TwiOiv4Nl3cPVnC57QFghhFhxBBcFBPDaYgJwJJwArNPhgHEOM9BKIUnhcfzbirngzHYeQYfHfyPRyz+EefzR5x/APj+F7g9eHx1dMD+awATbsnAcjwJAQQBLdIGAjVGiEw7eg3WPwRtWCgN33EG5UbUHVfkldlZ8iEEPaqy4S/FcIVBsrxXCBjpVAmXySSuawNJwlo5vimGq/cicxCMedD0IlT9qY3g1eH43MwIc+ju0oDQLVxGV9elMxV3n9TYafRcwiN8gPg91vg4DUsarGwMMAR4B3z/Ow9zNLhnk3w772aLN6/2uNlPmW+mqLzQJ2w0/0xxHlfLMj1R4C0K92Ntx6gyQ3m6zHKdAPoi9Zrd0lB0l0H1UMJOxfcxDmpq6lTQrbVfXvPUiqdtCStlDj61M3s95PaPaEWNP/rVM7jCVWuhpbXlCpG+qU6IUPXbC8NxW6Nk4wK/jJL82kKfC8TaGFMVP6qrLzfKc7EJaa0YfKk+3Rq2KCd0n3wpYLf0+Z9bGPft1hZ2S+AW25SlVjIugIVmMFl4BizO8OyTkQGJ7w4ltC4rxQl1LldOUZAB2FO8pDgwK0QcToUq107Nhie5NJcAMQ4QPJgAw7qJtVOTzGBJmnx3VzS7iNtE7wNNY73BVu6TiByDUmYDInMjb7QMEjhO7OEA/NXX9/jZ3S0Os8VuigYNeICiviEaNuRaZWOQTgZLfMYNionsoqKoN6BcrvCDmS/18Owgbpfy/Q/RkBAvv2YXDRM+pA9pPVy8803+B2MFIKfRE+VpNuhWPFyh8U5ANu0J7qvKjR4i3xFZME1gMvFXaizlSYMwR4xAkPhkk9+l6MTqtNuiy137NSdZAJ7jWeZ+3LSVTilwk6MWUVn6gBkGgBM9W7x4mop3H7yWgNP3MDDhP6vLsksJhdu2FX3CKo3+Luu0De32vEHZvTtA1TzVJRZ9mvKE9RoucyGI/BaMjIC1hB0Z2N0Od/MOh2nGdLBYboFprsDaQsY3kL61O9LKhBdLiuUpoe4JocTscRNy9AKTNhQXMLMekSeHzYYIUfKRMdG9bazeVB2ZhBilFJRv+kcLLaiSldvYgML6SSkzqYL6F2qM2N+aKd9CtlfSKILo1eLo4Uopp+62JpXqA62Qb4w34tPbBOv13e2Mm8OE79494nhemraJ9fzVzw6xgxh+Yfzhv37AcnbwyxFEBvN0AJGBsWFMPQDvP+KT/0OoehdhIEoCvHPBx/fp7HAGY8GCZVmw/ODg5Fie53RqIsMU/ofTNlnJKTsHRdFVuODw32Dyfw9ha5z5NZz5x9BPCHNU3IjlHbQGU7w0cnfYw84WoB0AkxTzRAxjGdNkMR0I97+akGX0iGDTGFc7gtPHPEbMwMffODy+96qEPIf1aO7fBejLuezB/NvUX/Xl6HkdWQCEaZphzARjLGAMPr5mnN8wlLkfAMNHA4TzS6Jz9rjH/jevQS7uBI7tqw4PIhekYGliqpdO9ozAhInKsc3yIBVrFAXmzAbkJdP2bfGyhu913/Pl9hRKl5LyjitpoYIQzA4Wa2heXcaoOQ27U805TXSG4Nb9yWM4q8oGBfbqaNfDMB3nmSaHRJvZWA5hCWt9ykHmYuQoWfVF7/TCxXZfEUbLo5dq3Dsy/9QKZBWt0jX3rKSHtnTxsSm7lggAwv1uIEzwFAWPdI9RpAUItAAGYBeMH+IuSS6oW3w4su2cg39YcP71A86Pn/D47kecD1/DfPt3uD8T3i6RGvhIC+JucjmFSdEAT9oIkXCLadZ600rFR2i6muzd6fugEKrXAef51A6ASpX/lnE11ouCCUeTQLpETv7E3Wg5dS5CuQDg4tLBjGuzEa6PzykaIwqwlBah7G+ZA0g0XApqFaaq7WKwUP1GkAgNF0W9uu7XqoO5zNdiqpFZJKRm9vCyY09dwhhlbb0pUHQRABGsBZYT4w//5LFbGP/2lU2GiMNuwi++uY08iPA0ut0Z92nDDOp2FiiSdOKiPJ0+fU99Cl1IY4ToKbbHRgkVL+NSZKfeaz8/+hSlk3qtqE58Ofbb6tgatkORvhSf0opVof8+glvwSDHuw3pHdFsSKUQyLuoJ4XJBX1JRXtL/L1hRN1w/R9ow4Pz09NlU3E/d9mtCq+jK4Tlwj7iqhiv8VxEu2jivDkEAKnSMqh5RhgPAiQ44YYcdTrA4w2GBgW/ob7oYWNFojXTKS1cRT+bKJr54MlNORBSX4sa8Alv6Toi7NJHwXziqkehjujtB/hIFnkkbERjgxFNFLkruRfXBX7tB2LYXWIS48SbBGPpKWLe8kSls4DzCAZPF336zx9ubA253wRBB5MOFUURJ3mUYgLzih/NnkW8Sr19v+uTYp9JWAyUEoWAmmX2+80GfZohGBTCD2YX7IbwrDA7OLUkn5L1L70nPEivsccEZGGmC1j/U2Dx6pBBFKfKpkKRk8zLUFjATGDPYTHGc830KolaYYj8ZkQVJpk9eDAmaOMX0nNanhFgnFuZR4W4uX9IYMmdjnG5vGh6W9FVdAiYjGh5Ehgv/ieMl1fIfDHgX04oBIhok2CNtXG1q0Q2rEI5uNJfpR5i3xw219aj3OD97slReaYKfSjjzWIXNvUxhY9tkDfZ2wv5mxqv9HjfTDrtbk/Y7i61Duwl/TnjO/cO5kKrvRB+m8eCGUGBdSisroc50Ah8oXOVVoFRlbQ/bT0RERWZxEkILLgqm0WXUF8OYSy7K7oXeDtskuK5U0vWzfAlOXW8BQ/iTCUIpcAdE0FZUu1pKyaGFcuXvOhHQAjempWcMcHezAxHFkxEOdUiINSLG2693OD8s+PzDCW7x8O6IYCkME9DH3azZJVGEjoIS3zuG8+Hy0fPicF48Hh4ZpxNjcQ7eRX/gYLBjRSDzgjYmkEgThXMTmQKJhzGwxJgnB4PvMas+c/gATw8IuwwNrIkX0MRjjeHCSAOaQid57zNCAcMYYJoIN19Z2JkwTQZ2Z2Bt8EUul93m/qsI/iAwAzdvCfNBo0y1hvR7MfbVWMXgT4zzp/yeT4BMILJ4fJxwOodnIoPzPxP87xH6xRgkYsgMbzweDidgZtx9xTB7wumrHwBH6QIq2Q3BPluc5/Mddo+v0e55zS0sgO51UcFD6jUjHZCoO7SRYdk94HjzTtVBKFd5eD88voE9H3RHlX2s64FOVmjagKp1Cfb0jcv0rF+qQP3XNCca/C4Vtb6sIX2yUsElOlf0GeW53OBEzfBkKaRf4qCNvXQyIlcRZCL0VC+kvl8V9PBWbVpnjqpU5Q9GLV8rZfOHBHPJ/qaPXcDH/Uzdh7hADSEcCo8nERiwcYeZCBUZLtnFYwDHQYdNefYGoSb8npfP+Pjhn7F8POLx+AEf8AD/6lfYmVvsFoM9I+F/TcdNuqNKjBBiCEmtDH/LbXedRmcepTFCKFyxtpz7nXiJ5+jPqLW5lpW8IVUyllEFezGRr1wHVPx04G4Dg5MBr47v9UIZsTaxaT2Z+tDWUeEGupC+ErRyHDr4IBsPhH1yDvj+dw7ukfBze48bu4M1BvNs8fbNDQ47G/lhIG2kiF3Wu+hcTeRcKwlOzvO1NBBQ0bqctG+ESPS0320qrkN1umSthbnz2vA74/y9sD4X1742m3FWS9IJr1xDF0Jh87sOkmHyS8XR+ueL5Y8/XYEQt9X+5cKLVv20wgYk+Xml/xG79M8jbOPg1ouInbxVo/NnFsYcYW8bzrYSI6eWSg9nEQqCVepmY5WkdBIJZzMX9CroeVRe0boquEM1lMVDTsXmbIUxomYWudCtSNa8IzjXBnAwlCQIgnvmoCQNhF42taeypK1A1Pcy3r9z2MHi9be3eHXYYzdNmK3swA/lCaS57wLv4plgYMp9KkDKU8upvVUh7IHWYYkRwsWNQxw3kCZdULznjZOugJUxIj7LXRFR11PMqghII0cUrZB8ZTZJ0ad/mccqWMnIGFE07HAqRCkjav4R5RxoYcsJWhj13LygD5FMo28JWIDVaZI0uZq08TdZLDjJZzK/xd1SGvN0YoLHcEido8ZsQBqNmgOdvi3KkYlC4z7qTpBWNlGlQfCMMQRrDabJgBA2Ed3fTPj51xOOe4MPqfynYERBFmt5LxPyzpa3cVF6iRGa6XGhoqqeWGRHv96Azf3oLWGzIUL7+iW9ypuF3nbaNaFnTEgVVyHgkMzd687aInqM/BdXqTpxldgqSukcMdDTVf2l/ybBUaVNWVTf6z4WusgUiI5HPLLIuL0h3B4s/vDjEcezLG6Bs7zcyhjC7Tc7LKcJn94dsRxdsHQjkzBxqyHKpABEYDbkVJeLROjsHM6Lw6fPBg+PFs5R2FUoSM8r3/+VBU9b+EOX5MuKQR6TXXAzP8KYBwDfNV1sTFDAm2SACMYE5jkaI0LB3rvInAQ/5tYQph3h5huDaW8wTUGBIIqv7ng3g6zYEc5pb94AeKOvwaVq9NHMW1JzWofTBwad8nuGcQaZGR8+Wvz4LvQBGQPzMVx4BWMLIZgR3Gd9fkWgO49XXzOmPeM0vQu7QN057WzgyFBIuPn4DfbHN0hKP1JwygXmpPsjPhf0rQAGGrWKcivtpZZ5bwC3f8TD298rZpTKsgJEmL+/wbTclvFdRFoaTclUaWoOA4Kc5XisbkPBx5QfMhB1gsRstloD7eP0y4ehQYDimNRMZAxh6Ht4ty6/LViUdFfBebngQbpubGZGm28t+a+rzG3n4qfN0Q99GC/kSLhynKnsksHFXT1pRH45z3AijnjZwBsGsYGBh/dBLMoMbSjQK6OlLlYM0c57nE4f8d0//a84H4/49PgZ590b8Nt/h90Z+Erwm5ERiG5wSIzUJhmrSeMJabeimaXgo9Y5amVsu7OcVZbLs7TGLaP01ToqYvKT7KjrlS+CWzYcqmRaanriwtIK46t1sUmO4KIv60q65QrMNS+UcEtiCjS429bMhmSp5wdymF4eMvfYMX7/awdznPD/eP0aN3aCNRa7ncW3X91gmiJ9MXpuCj+jTkWoCjJOpGKNl8YHyZD7pNTzP+8EQOHasi6/6I36tT82q0aIjUhwbUWVEc+gl7X88fSSnli/ftxK19ahXJ0HDdp6NjXenvMn79y1UAPzFKXDlwhPwMH/asJLNHxjGX+WffzHnrNK3gWi4j3y9IqOF/S7yCm4X2mwhJ+O/DgBeQe91vNApROLAWuZLPK8Ua5i0f4zgdRJCfZZf5RysuBBudtM6lbMfeKzKDZDy7dihBBJEXBykYL0WCyOCXAe+Pie8fpAeHN3h1e7GftpwmSyIcJzOF1iVD7PDEa4j81ROSKpn/PW+WrEhDfO/1P3x42HYoQQd5VJ/4Pshom9h3cOjksXTC5+k3xJ96M7ugNwo5C+GMoTtJTmoKon/VI4JWFM+N+rpdpwKlM0iYhFnpIn1zFj9jv1cs4rY9qkrTYgZgVjZ5zzF92HlQYGsokpjTOXOqa+SiucNkoqgJFmm5uH6rtqO6lUeeKNs2sjRF8NMQ6dwQirO8q1xsIaG/SDRNhNBq/uZnz71uCHPQVDRKfPL4YBcJd4rC1tquVbPe/qKbay3Io0PEqwlTY+w2h/nSGC4lJPBKb6vq2k8LMqKG8rKxO2nvBwifnuCUBrsFTIQ37jg/Yp3B/LAVoi9TX2YXHygXQrSWcKMYIhKXj19pFIcyS+97czpsng46cFx7OLx7RUKzgrPbx3WM5nnM8LXDQWeLAiJNlnnY8znplwPhMeTybtdl3iJUWns8eyZGIWjvMh6P7BiXhXeL+Ya6jeT+RxPALUVRwCBAciHw0SLp2E2M3APDHe3DMO++B6icBw7gxjGYevdtjdUOHBiEjcReU+JwCTBQ67PmrqI/Lw+3AEzun2rQw+NXNMt6vEKvtbgvl54nHARwIfLcjMILPDbmcxzwQyUzTIZDdN6VKrWKKHh18I+MTA/8lYJodPu+AT3nkD9h6Ls5h2Hoe3p8QULodHfHrz2wI66YusIBMGSJ12SESvxAFcWYsNBaOJsVO60wQUXGvh9YJXX38zXLrnz0e404Lzq4/g/VlXU3Qt6T9qPRmTnxkAPGM6H7D79CYRcCKOp3nXEK7MlxbP9EY57NDglEcwCYEi/a6Y2EthKzq+FC4wF81mDE0A63ZzHcdpPvRoynYYW6o7VoGOwtM6NcBdLGYFzoiRvKLKARg9GlfGcfNlO3Nf1yfCZTZIhEsD4+m4uMaLU2IU8HzqHoQTcYt7wPt3/4jjw3ucjkecvMFy99eY6IDbs8HsM24n1U5D8htxQaIJ2j9v1SXVnCpU2xVCEANkkX3rnGwMnBvn0oBhyxsbajFCCxy6pLzTvmQRpI9UEZ25Q81bLJUkvaLDZVFNkzRwuYvLwSn17pUCvenKMk9dVck7VG1S0miZXoznUHK4CGUSn8eAf8HAVwRzH6gdgeAd4/e/W/D4mcHOwE5TOn2Z/0eYTDCVJV5PzbWhEaIwUuhTEVz0i4xnIXijfxICULxlZ0x1XGn0GBsh6npVFw+ND0XeNrafdhDRbDR7jpC3yQixhkufS3RX8o8+rbR32L1dBqSeC2vhynaO1u6fXXgaj/CX8Cce/jJkTw5c0JfgNojjr+IcoH8kPrM/GinpNGoDjWjJiJI7nGKTViQEecNUlKGikSLwlOHOBfjg2og5yPuNcjPJYib40SdfwNtlC9Pu63C/mldSceDP9HsQJD2AU7xT899+u8fbQ3TLNFvsogt0aXxwmRPh9FGJEnfyB/dPBXOXulS8PiibjJLPdbvFUCAnHeJF097DuwXirlJ+XTRAeLeE/8oA4eO3fK9EdOP0kjLJSqhlTMWQhPkUL9bIvZAE+6qgDGboTtVnelpCT4fSENCFr/jCRUqWcUinE1aKYrnfM+vnkPJmt1CJnS2GXDtdiumTDrOurCN0dD+vjCWrhMOyenigredSfIFzev0XZSWDsD4ma7Gwx/vlAbvdhFf7Pfz+gN/vXuPRzmN4Ngfq44xuyufWFLUOaXnxxW5tQzk75aSabPRPc75V6Dw5XGGIiL9yUU/4KT5mK02V9zkQdkopZaJe6ZVwVSe52HnUeRTJtW5fXriFxXcgp3SPiVcGCFLK0ErGS5JfGU+BEBofLmJSSOfmZsLhYHFePI5nh1oCFyOEHL1blgXn8xnn6BM5XTAk/5ERn/fhpMPjacLnx706GQE4pmh8OEefgpz+t52YX7J8XUjCVbwZjqFEmzhPp6CDx24Gpolx2HnMU/BZSGB4b8EgHN4QdncEY0O/SC+bZF2Pwj0Bux3w6q5bfTcwEHyiM8DnfpoCeQ6+AgAfGNMhx7qPFp4nkJlh7B7zzmCaAUPREGHnYJSJhgh9OQkzY3Iz+MhYfr3gbM74eLdggYP3wbjmFsLNG4fbr8VjIcOZEx7mPxQtTPNICJr3Eht2RgDZxzmqtZJ6CSAYmHiPh50nGDLBIBGVO4f7G9y+fd30izCiD/wRZ/8If/+AEx4G/Vn1rCg1k8I1jH6g5x788TX2D28DTo+EPfkZLWCHwoWX6qwiucQNshOciSMznEjMhdIvf05VXiBOmrm6nL7F+j06JcyuVgS3F5WhqyCTNLncTkPTt8wtXu6OPqzbQ4XTVf2ZaLeArHd/xpOsqqgV6GNwyj4rCqmY316JHBn4UlgkkAhznEmJ0AQvL+o7gIAL4lo6nj7h+1//71iOjzidTjjPr+Ff/RK7M/D6GKHSytcoQBhAbvgNJ+aUlJAV5gJph36iN741bel8H+3y2KS0XAlxPHpOgbh5l7lQ/SYwaND+CmQp8CKwrRFiLVMgjypdh+Uq4R0BV7WAMiz6NES9BBpeQeCpx3VQNychWSiWzNdAy+zPGPuZsLhwNyOBwJ7x/W89Hj4zdrsd7BRpljXqFCUlI0SCvWOEaGAdGiFyf5T9nMuX/qBcieriGk/p+Z9hqY0OPSPECA8l0DYYIdp5egFf0+prHv8RbzgqV+e9kCujg3G7wvd+/BaABmhq2N5x6HUYQVtvnu6neCvwq9FfNGxr2ypCwnYJfkNdF5KUy4yUL+Z/LWHUAV9GY9AHYRtuaHp+tLD/tYeLzc20V6RmzzbGU1qDwT1Tm1V7xYn6rigLBWlHjBEejLSjOhoXQJE3Et5WMzicL8rOY87qZES8f4HjfRCCGwMzm/iNUBql30Ypq3AzMcNHmh3ui8gbkQTk3NDwdownMv769Q5vDjvc3+xwMBZTpKE+tpEjD20YgPfpXoPsVaoEKGxg4yRXNptaYjvzzovM73A8AeG1UaGQ7+UkhKRZ4FwwYIjxgj0nV03MjP4Z6U7QYF6JBjRPlQvjKoEJl1WbPCdkilCqss8kq9EfgKkMTSjHm1SMnucawktuvosQjRA+zf8wjpmT7WRRf2T4a1mwMGbUeYuH/NwYIOrEw2YNaOyQ9JaVUwIzj0zefFSOXzIipk9xnRIwW4NHdvjoz3hrZ+zmGX63x/fzbfQwA9150HgtlL02bnqT+TqdG7DUF3DwOscqHnISnhqUdXHmRQVJ46JpbefpFWG7IaJSjie6PKp8C0LZJBSvJK6U1Bm6J1fSyS/FyIJVC7dSzo8LzcShhjcpWRAXESkIzOh4fS4nK3T7/pqFoL+622G/s8mX3/uPZ5zOriDoZAmvf3WL0+cz/vAvH+GWQFjykbxQ37IYPJ4sPBOcYzjHOC+nJLwnq3gyWHC89DH3l8wPys0p8E9Ko5qUF+rKeFbKiHNUBHg/Y3IWP37a4bQQvqYFt7eM229vcLizIOvAngA2kRHJ/ydDuLuN894QrAFMvaJrPKMbxgy2hFe3wE1zXUdooGfg8WEg4Fa0Ve+cn+4NzMHixz9YvP+DwfFkMU0EY+Z45GwORoh4QoKMUUUx3OKC2yVjAG9wfwy7GpblDM8Oy7JgOjJOH+ZoUHJYDh7nG0WSEwGMz97DswXDxfe4+0B8RTb4mEELMP8IGDaYphn2zQ43f/8aPBsANpRhCMeHCfz9hOlsMJ1tKmLZeSyzx+nTPdzpJsO2Fjxh/zkYZ063DmyCMXA5OTz+cMR8y7j/xsDfLPj8ze9CG9TlXfPne+we7kuazcI+qwHrzddOdBfaIrK+3KuTpkfvnhgK2vuk3GMFf8EYqPf8XRO8/Kz45iJ/XXZfCbFOiF7QwI/qLETyC6txXMOwFoGQdrXkDCW+rutAKYvlwlvk1PPJmpg6Va9cCKb/p79czRFmeDi83/0ai30MNZ0Z/PsjcPZwzDgtDg+7n8Eaxmss8HaP88nAcsSplcJVK6ADC1K5Ycq9FUN5uTKVH1F9SUbmflAdWRDb5wTOfa+KF34i9a14BeAwLj7SpHbcCpOM6q86Ffr9oPv7aQ1qQsHP6PovhFZ8uJAYCuquEaI0aKhkKWheoz7UfvztBzx+9xmnvz6C3oYymBm//ZcFDx89/JlwsBP+zc0b3NsZO2sxTwbffHWLXbxfqrjnJPLQRvdLxfuktLE3shGiMgiQGvPU1pJ31P1TGw4uGyGk7rLTCwNwDXuqsT+KVKTpfx2O/2gN1/zuUxD4unWsm+xSNU+lI022bh/rmPW+7vHMz78k8br8dertQvxfQl5vz+mnl8LsT637z2+M/zyh/rIhzSKuIwh7fsQOR3jew/EMjYGyIl9FR3rbcKFFRMmzJumHCt2a8vgi9CAxyamcIY8tehNdVl11Hbj72E+aWD1hluMpYu/gFo/33y+YQfjqb17hzWGPvbGYbKSP8TJqBoOdT0Ybjn/YCm9hkPleo3gKcZnlQl7ZKcpKVud8KTF7F40Ji7pgOsj8SX6PRgrnPJxfQppFXVQd04gbVi01jLoxGWnWVGjd2HCyJUtSoX8TR1zw2QSisCGT7QQmC7BL9QvvqWbCsNbmMyN5dRCTT71WCplVNTVMCTltgnQPR5azeNgvMoaQjTMCS4oLv9BlQbgv7YqralcqnZu4EvBqZXHz8DJIdGMZ/c0v5YJOeIMQ7oWwE3bzDCKD/Z3B/e0e+/2MabJJt/1T8ChfikITkI0RKeKJhVXGiIYMPCNsN0RoMYLq2CtAeZa2p1IMKFheQozulqEmYW2ESOuyN1G1gFcIg1TIT9rtQWY666PxRaFlNRoZGhK8HBCv53Qf0+1hws3eJEPEw+OCU7U73xjC3dd7zDcW3/3mYyQ4S2GIAAjnhfB4muB9MEKE3yUZIuRoHwPKMi6W9k4/cdn32v91297L48yqX4wYc0xQ5jw+zvCe8erOgZmwf2VxeGXjhdRx139SCAUYrAVu9kh3V/TGQt8qX8Mps3a/A/ZFw3NwHljOBO877asskFqJa2YDYwnn3xF+fBfcF02TjacKJlgTL662U3SpYpAv6QaIAvPBAMgZ3J4B5x3OZxsvlT3DP3ocf4xzxy043jgc3zikBZB2VMTdD8EvGJjD1V2IijSORh6gWjLEMCdg93uCZYNpmrBze9z9x3uYyRRwO0d4/ADMpwl4tImLOO0XnHcA8x5kpdfXQ/APOAVm1LikQXPnMz5+d8bNGbj/lsE7h/P8Ic1rYc6wWMyf71piXAmPoyNsl+mbwjerTeoR/ufiw5fiINYV/LVBovyW8X2JD+LOJkUP1vEkZXB6QQsvF8JzekVvisisoJ4pJePX1MVAkkaouaUkJollXuAPU1THIJHjOeH0DGEpXigTZDBC04KP0+9wtB9DvrMDfvsB/OjgPODnOyxf/wfQbLGDBzFjL/5zpTGy6YH6SnbtoiaHmHIw9L3ITWyInrxVBtpcSK/c6hciWGQ6FE4PRqECIqBkASEZlSO+Ufr3QaDVVyDTrbExb0u5VPTNtn6itn+bPHX/V7yg5GnkkMvjnRUFSNLZ+cdHPP7Le/hvGbLHkz3w/juPD+885nnCfprw8/kW93aGjSci3rzaYZpMch82akEzrZIRwqT4wghBdRnVac1+N1XGhbovav5TlVtB3uNfe3xQL3Q34VTrdQT/1rIvZK8Lu5DnChyxNRSFKV5xUHdWHPTyj0ZAp6jHZhOUo8Kel1zjgiL6JTv4mrDeN5ksbuvD5+gqeuNPw29PL/WPFzbg/hetLdKwlaLHawYpb3+1/imGl4ZuS3llmpnPmODwgBnHuPGsuAKailFJvCtXJY36PHP7pPJGWsRcGiOAzACzxqJa2GAUbp16lfUiiqQdWbaGnT08aj47nihYHB7fOdjdDq/2B9zvd5gtwUYXyppvL1xqiyFB0f/MP2XaHXg40VOVPHw2QsQzoMmIEGRbfd9Dumxa5HvnQhoX/0se2YTosy6guBuiy3Ai6X8YXLa7mzg/hjcxwNQzR8ZLlUYEkAUbAybZKJkLVCzWKn7oyWrCM2oIUhnVBClScTkyOR7jjtDlRdGJOT3k/J0aczsyjUmg92TGJG0E/R2psruGim619YqRvhmlr+OGHzq8USkT9QIzw1DUlRmD3RTuhqDdhMNuxjxZWBvvXUlD8RI4dsS/rn5e+7ChLnHVr5ECnk0yupdXP4MJuto1U0b0z2cenlzENRkH25i2lsD1IooGCH0kqu7/7n6vSogLynHKzzFRYVhJi2nLAEdUTpkGgygc5aNgFyUy8ARYZnz95oDXdz4ZCb778QGn0wLGBDoY/OLvv8LjpxN+/48/YjkHy7HgOUKYiOyR7n4IRIijCyIhXhHd+IxwpRzdqYH45AWSrOlDJNSyKwU9UH0mxIXZY7EO1hh4ODyeLKajw/f//BG39zt8+zevMB+CcYVsPoZYIPU0TFS8J6iSsNUXXtZG0RjC6/t8ybX3wMMxnMkghUSScj+SkuAOgmBnG04SmAnGBiMEkU2GCGP1pdVxXJgBY7IfRzLhUi0y8EygaExK/h4j4bYnYPcDq3sShLEJYytzYrlj+J0+0inpGHAA/eCAJYy7Z4I/T5hvJ7z5+zeYX++we7Qw53CRECLhoLgDxLKBsTZN9p0jTMcp7ybYiBMnUXqebBrPGTP2X+/BO4/T4wlEC+bDMbY0MJYewMPNe5zNQ2TQYqWecPf5W0zn8qLsnkU67GQpEiFhnIvwcy6zu0SuJAqaUG2qf2vgKCwg4T5pX2VfG+fvBIrtqy+7z9+zMo+LBVyXR2o8lJEP1GYRpv+JBNcPGdIy5GQl7WEg4fOayasp27oQncdYYeVUtzZCyK+Pu6niBqpSuGCCh8OPN/+EE3/A8R9/gH84wnkHPnvw5xMYM5b7X8GaPV4fGVYVEsgcgZMCWwkZ8j362y92veiG9VHyIIROTDaGkaUs9fXg+5ZqCqA4D2TzmeOSZjUu4S6mRHeVUPf677/G7s0Bu1fZtI2iPKWcJqXYIvkWQurhXvMY6ByyXAlXpiTN5xQAtkVV0ZtOQkjKrWAV8IR8xhD+8GuHh/cey+LgnMfpyGE31WQxTeFy6mme8POvD9jNQYghddmUGBQSjAqm2giReESBRdISdbupUfCunITonYLIAFb9RaoXq7pKIFYMIAM+qJv4ieFqI0RnMoxiLtvOBgm6G5NKDD2mIMUov0wvPbeQK/O/zMh+qfB06Nbmg2YLiueroanW5UrKv4S/hJ8itBxl/Sp3QwDH4xkPj+8xzwvsnuCTBC4ZSl68iC340fxBNmHo3CUslBQTWeyJrokw5tcv8cXCg8lmugIGZpU8y2yZZxYFf9YjMABEhb3xDhM7/Ltf7PH6cIO3hwNudhOsDfI5R9GQfdjRLoeFDZnwjaw4uc90WOsfSOAQnlL++6BcQDZEBPnew7lzvBtiiYaGJW6+czFrMFQ47+C8g1/CN+dd2uAqLqTyrv6NgRSr3R2bMm16pJW0SWgKd0LATEH/4R2IjonvIYTT1uJfgXQBBZPe4QuEReoAwYByr8fVFyQdV/7Vz40js3HIiyfNzeIekFEgJAY/9H02DspYtFVJmlpPsE1vMKZigw7sRvJKPQK9iuFYM6k5aQjTZDHvwomIyXhM+wmH3YR5NykPQCFv60RXfaWehwHJ+WVDf63UE1SdflG48kk6HsXkvOTJiM2GiK1MEac/mwu+JvHTihzsxqlD2mlYT+T0UCKOrKxZAUVLaXHBaxdM2iAh6ajJTO2CV+mBfBlRgRgpl2HSJclB4XNzCPGBsDDefzzCORMm10x49c0Npr3FD7/+mA0DXlWZiG/sg2hh9yzHzErmYa2falydfTa339oXZbFN7VdogzkRCc+M8zKDDHBaPM4nxud3R/CZ8dUv7zAlBdzlcc0yuhCnwezSBKxpMIp1td/lNIsjHJd6NzlF2ETJGi5XNpYwGRv9U+c7FsKvhSEDshZyNFEzhfHqTRjjwFjChdAATNR4GmMDavfhaCh5D+sscOZkYAqIzsP5cC8IOQYcAzsPTMjzQZgyZrBj0PsTcAo8AhkDzBZmNrj52Q3m/YRpsSBvEnNmoxHFxN/QllC/YQM4pezdqiyOXbETl1lRgbR/zTgbh0eiYCThY2hDHAwPgHePOE+fEoMmH3bHe9jTIVUheUivGwqztB+4RVadRZTmeLy9rcBbiiHfEkb+iGWGdGG8EJvne25pwJ0R91xPLEK5BTiCJ2om0VfxkX3iEkLqGmzy7hyFRspeeIIx4pr2FmykrBkg+aAte5QFJScDzOVaQgqvd1qJSBUFCSAowoWxzfcEZToYPOGG/4/mHR74ByzffYZ/v2A5nzMNmAj+8BYTzTg8AEb1HzX0WbnUIXnLbmqEaW5k4wYHl8xjS9VL/NqfCdtCwYxpQpw+1mu3/SxjLjIjEPAtR0FPpz98fYubX7wawLcV6nrNbM/3fBUpNW/UfFGCtY5PCXt83XbFeDE7NElWUQzg4SPww+dgiJBTWsYQrLWY4imIebJ4dbfHPAca3PBwlfCsf3UL06kfNefrpgyNEM16UOUXNCgHYyoqpNdcAXOncBrPguEJiJXXpozLloAtxUhhF9JWs2jYsHbe6sCdNL204h6hl2Kr4axO1h2NZq5dGTbihubrC2xUe14YjMHWvh2x84N4TUfqPR3rEA3KS/9fyBj1pxQ0gn2R4p431qGMrQkHg/uvOqz3jpgTGAbL4rAcF1ibfRCX7rsz3msxYNWnha6lA5LWpxHFk+eAOh4xqEe/t4VzIUPWCghWeiCVTIwVyKeDAx8Xlf0xbbi42YNd8Cjw9d2M1zcTDvOE/TRnudZINfFSbcEEccMC2XB/RKDXBqbYCd6GZCDREUkm91GGdfCO8ymHFC9ug7I3gHA/RDgZoY0QSV4Qfcxg+NLYUJS1koyY50bThn4JObWwLOXAxA/xgmoKF5BbXkB2AhMha0TkWY95/MLhj0C3CV9wkjKKSFYfs5GtnVfbgpbH1LyT8gT2QSjXRrkug5wlsOa1MDZCvABOVAasto+VYKTrHm0iy5JxbplKaicDYwP/bi1hN1nsJhs29hrCUhTYwyLqa8cY8VOd9qT0pw3JCANuWzBmQfPrhSHVJyMuFLUathsiGtG53s3blbc3hksM+BUCh8515UTI6EdZ6quJ73WqQVuLHWcKBLm0MAmFUWBNF6xoBo2yN2w5LZAW01q9HIiVIKJUvfgnhonIj8KitwZkgJ9/c4vTyYeTEYsDLQRzb/A3/+mbdFfE8dMZf/jv7wNE/hGnxeAzT2klxNsYwG5sIZRmcoXEqiUMUbWFXcr9shp6kwifPn0R8vuFYTxhmo5wfsH37/Z4eCRM9ggzIfo7DKcDAAKzBxHw6pYxTXHFDraHFvNsLAvqDN326GhrGa9uJXdu/3kBHo55zohLBTIGxkzRHVM8EWHCaQKKBglKLo5MWqsWC4iAaZpAnuCcByi4TCEikLdxjjqQ+P2S+VozDRzmpmeEeyd+cMC7uAMjXmoVNmR4sPPAZwcwgWwwLthpjr7QCcHXZWwfKBhTKBta5FvAs5l6G76wPvtDqFoRd9J4hvXA/nEHRwYnBphOmHafi3knG0w8Ix6fZby7+R0+7X4EF/2Td7kkBmEwD4QJaNzr6LaVX3D76Rvsjq9LRkz6ZkOoZcMy21akrhl3qAmd2xlmzZjZvFRrYjtV0atKncSfj2or126tdynztRBdTe4G/bpejjCXkerqedNM8riDqm5I8azqFYODlMXxjeUUhNTtRdYKggsY7/e/xuP8PviIdQtO//Qd3PtHuOlXwFcz3j46WPHgZiyW0wSDeKpDwdSAqsYh4bkUH1bH1otI25VSrPRAK0c44Ql8ZFlb7Y4g/O1BlASHxGsHumXe/Ra7H34L/+ldGo/VyoW4yo78Vuu9vS2sj99K4TkMS4zCBNX1JlDySZdLYDXzmMoP6dWU7+l7dx0XwBbCjeYdPh4Iv3kFPHiAOM455nik2+LvDm/wZrfDv/3ZPW52E6bZgEw+2SBGM6ShyPQ6QZX6JNLVxPf1TnIow6lqf9jMkltPqOvQfSHPJU4uOqse51r5bkwnVQFlWdwGpmgt6aiWfvJxXf0cnXn9hHV/KazzHBmG3phvK3/Uoc9oz8ZB+QLd9Yzw5aBZ60fZCPYSc4eJ8Mm+ApHF3nnMaZfZX8Jfwp9CqOYiBTWXB8HDwCGcG5fLq6uk4ZcQdBDCe8kmL1FEygYWrrmlls8XRW+gz4BszAqRnBT5l1ZQscFUYILmgeVZNtRlbi5s6PHxBKuWQYWviymXE7zzePeHEyxP+Id/uMObuxvs7ARrDGgK+hQmBMV+7DShuUwAWQNYC6MMHF20VxhSJM4neAKwLhkUFrnrIV04nf975nQRtXfhFISLJyk4GSHUptRizPpBcyAcefExnqtcCUG9aDdcpFIm5sqAYfDpccLZ7nGaLbwxie8nEwwQeotmKjrpAkvuYSS5raN/0UnkuZM36+a+S8Ier/Ri1Dfkkw96rFk9ZtkRrOdjNpxBzWcomAZN6Ec8iz7FudgpWctPCc4qVeZ6eyDW+oiQKrgwnwFDOPoF00zYzxav7yz+6lvCxz3jAbUhYz2snYwY5mkevlQgSF+9yJ0RKX/nAusnhCsMEQ0k6PVeSyYGKZNQ1GfAm/fRh/Kryt8Xqnow5g8d9JJwnMq1MnBJ2KurVTvIkmVbBMZ6Z1nTdu0Xsduk9EHcizS+koVixU3kYUKGPwTGzWHGbvJ4/+kUrdsIJyO+ukG4gNrh83zEj7/7DCYHhgM/MsJ9SQQYhuPgNofItzSF0Lhi1F1Zp00wVuilyX+B4gl+9dFaf14cCMDjMXw/nz3c4sJdFxyOUhIF4moI2M0Ea6syMcAbzZjnyP4y7QAd560hYGdCmmJ2EHA8B2bHRKWH7E8NSnqKl1PHnZnyGy+q1icighuvYIgyJhioyJhIlIOxQsYzWjsSfGJp7e3qT1b5Rw47et0SGBq5/MrpEzPBgJXWjBHuQMqnREDSSSL9G/tEoEg73/14t3tXV5HKIJAnMPlwcfYygS1AZgd2cnFv2EnNLpzs4HPY4SIXTp3xAWfqjG+EO/HIPVxGyG4OVfbkBSu/QUfZhztY3KV1czn0MHWMH6wlqk9dXCo30ao+2/Yk+gcRXBAHrZyDmU5EfOH7ZgpU6aTwpLTLvG1Ze8GpPo35GuVqeTzFLMQJ4AWRNpkqhjgpH9PKaNKkHVsQ+saRP9XCFicFuCeGmOIZjKN9jwf7HRbvwIuHe/cIeu/Bb+9B9hYTe0zihpUZs+PeSKXHgmZTZjDNcMo9jYuqSY3EPYkpXBGcAOTLD5u0USCQNjAUTsyCr334CLz/Dt651flGZQuuaEIpeiXeoRO6irZO0iF9rLPWHa6Hf8W437r8qXi9NJ+q9H1JJcNdGXpOFvi4A5YzgEVIUnARaIjw1bTHV/Mer2532O9sMEIIhydkRsiZpldV+ylbSxW9qxNmA0e5dDJ9vCa040hlfP2eovv8THGmdzSuTZ5+xKW7QS6W1CWrozL67cyfr+zXq7/m1TI03FwAoZnf6rmPEa7BmQIbrWcdba65oqZLMGxK2cNHG5r7dDk6I5UCZT2pPJKScMIOwAxPR0TGZJyt18BR+q08Sxrv6+mrXmuyiW6QcD0k9ud54/+UUJOKhnRcqugnNRxdIGxfqroigsBMYRNa4iapy2vJs+J+irhkhFDpm5YVTe7IoR3WUJsjOtxwiEibEuKu/lQHZ2VCoTzOG3VY8cpJX+GljGgA8B5wDqdPDre7Ga8OB9zu5+TOUfQ2nrg4SUIIvCQHZiJvXOD2nri6WUrLon7zqYV86sGDxTChDC7J0KBPRKT0QWZIzhG0pmwsSlbjoqjgSJlb90XdxrVOiPzR2RmcaIYjk/VKwp+ht7W6qkRkzlSdgqKun6vvqV8ir59nlwxHJ7+Or8uSTHmtNDpKNSb9UPjY7dSSm9bKpirF1bhunH5kwmptar0OC5D2tVJAwWcRon4M8ORANGO2BvuZcHPDeJzUgHLxk55aHfN1CvmG3avzavkf9DRaXJBx6R+0xohnhp4x4hpon2mIAIpWdGoO00MNWEfGqBnw8Xubd8S052mpsFQ9kMW6bYlfP22bQu80y4gtPGgLbd7hHRKm3ew94bNqE4mLEUUEywQZuoQktRbERHTCkSBTXLAc0zGD5nAy4rw4/P77I5bFBwU1e3hnYb+y+Nv/2wTvPM7LgnffPeK3/+0jnPNYFo/Hk8HjeQYtABYX7grQyhVQRI6c6XnTnpdx+1CyHLFfGHCLwxnAeVlgDHBcGMezweI9XDyOSExwPrga0kfdPCNcaqM0MoIfKdXUgX3EJ9aKiV7+amrsJuD1LXBaDE6LSQyJ3J9gyKSLeIwJR8/kJIEYI0oyyoAHjAnWFmtsmCPGBHROwSyhLzHN46YZNSRGxTmHZVmwLNHn5HIOOy5kp4WLl5nHfpyww3yzw9f/01c4vLqBsZklSLOCgoHFkEkKn6z4QfQHikTkydRrZBT0ug3zEwaAR2w/YLzF7vMM5xf4ffjIAG7eMQ5/IPjvz+B30bKlcUzNiBEAa8A/2wNx92yT9mYB/82nYocrwPh8nvD+NJXlK8veu91v8MH+oY5GPcM20UnOfanDzekr3H3+GbofywJ0lRi8DENvVeTXmvFuyxR0LIytxCpMkIe9C1KdZ622HC5QkA1fL6RaZUQa5BL+puldQu5FaNBClRfhRMWr3U0fD7/Dw/77IIB4xvk3P2D58QE3p69gcAM+vQHPwPm0A1M4UZTBCXiKpB3hAYoa6qVYMfxrYYhcB/EvF2r5p2bpYxM7eChJCJBdeIXQl/4jnhDLYotXYwZEAEh3XI6v2WR5E1p1Lct8tZKH2kWWx7sCjqj4Poakak29vuOfoRFCnleXUv4oPJsxBmwtwAxrLfbzhF/94h5fHQ6Yp3BqUJ94FWEnn06oTyYI7Dltm4bK7lFtyP1HVfx1pyE0QN06i2T9NTk8AbHCCo0inyTIXUzXT3mxqidrNa9oQ1GHwiiDIkZ931vs1HnK7z05ppNuLetLaX1fKIzAEZn75cG9BqlsLIs0HruMpznmyREXGvqFx6zFz8/oFUKSezcl/9Oajv+DBOGqw0zdzQ5vXz2CbIhbG3tDaoNVnCgM7XdceNAyX3otWLyw/mr9GqNFWfm7Lp9Swnq7TLcNjGRkKO4lZA7eADiUny6Z9mEjiUHY7Pd3v3qFNze3eL2fcDNPIGvARvEtHpnPIyQjRJBzpWcp8Rw9KEOzREPBCT6wD+62nYPneN+Dd3BL2Cjo5BSED64onXPhrogov7t4ZyQ7TnqRoCNpF3s6rVKPWQziMZzUaMnO8jwH2oU9Wuqc6hRYAmcGY8E0w9sZjiYwmaAD65C4OHjV/NJzYTyri3YS0k7/PD9ikR1ZjjAQ8TpxYzj0Zialo4kuuMDyK3d5SJ359E9WRmyQNzchd60T4XJI0yfflqdkzzyuOk2layFEIiCb62rqGeeXCfeLWhu9VFiPaQYOs8Wy2+Ef53ucycabWJ8TxrlH66FMpOk6SuT1LJjaC6yfzL1oXWjHGLE1PMMQAYyQhA5dI0TNv+kHKhM0RqdO2aNBzfO1v2gK40NvcndCoQOo2kECE+WPWajTO7jzaYhkhLgoFJUPNEQU0bVMcWu1PEpdQpSQEKaJlxTfHAjTYjCZBd4QrI0+CqMi+P6r4L5oWYKrjs9/eMSyLDg7Bj4BiwPYEJy1AILfGlESJwOEQM7KKpx7GCMbf0JKDWdSkixZajUtCUSTlWXfw3kTLtf2aneDUgRlWKUwRlaf4SL3WwiDHYaB6rc8RbqpjGHMc0C1Z1evD4pDTPk/qHyPc40RpoEhAsjAUOwzklMtOW2tupK+JGFskI8csvRvvLDcxcutvIsnIRQjEy7IJtiJAQsc3h6wu53XtyaoNaPXGglRparPLyHujlImXNqUnMDAsAE7A/YWzBYU3XfZB4Z9B9D3AH6MZLLcAt1WNwG8M8EQURHjwDAAOC2AZegEpyODP0ecJYOXW4kTfygrUsyT/m3na0WCFF5JzOUEYCLQeYc93g7b1g11MjU+3aG5hAq5Jh8EYlPEALmZvV0LgFIUdpvRh2CbgXTcL9cT+kGOrdwqpP0tmyHr1cf168gB8CgU4Yi4NiLBE3/EZ3wf4wn0/gj63sFMe5jpDmwZIA/yrOro9GY1JvJqaMQO9fq9NKrxQGExWo2rjCB3vg3A2sCqdz6UYoT0s76Do7yPI9PPsPwV1VSKq6sM+Bt4jq1MJSl+Z5hmJZKqiDxnq6SZmSrzbeKdLg2mfOGiSE03TVSQ7KYJt7sZd7czbndTVvLHXz0e2QgxBKzp59ogoMsWISKlUFlpWE/d/s7XAvY2reZdOxmbMVzH4wXQnequmMfDGlZqXyu+HosratxU/pYymnVRp6rHIP+u44BMA8drm7qPbZJ63L9EuAL/dJ4l9HTzl9fJCEds6d+Qf/s8aOecRZaERsXU0ncQ8dpx2UpRR2nLfJcbVepPxvtTN4XLZOqLhkuz4U8rCOLgnw5gCgotFqO68dhNDg4mXVSd5eURj4qkSAx3BWQGLJ2oSTKSpjScxS3Rb6CjVCM0m7NqXvDyvL+QJm3ZlorUhpGk8RUDAHB/M+PV7YTZGkxE0ROArHZWLeXUxwkQDYl0XlRSXoRR2El9b6PntDEw3RcR+c90MkLpTDRvWriiSmOQ4aa6o8uH2Fq5j090V+FL9gNyRahFWQR9RvCPaQGy4Z692NV6TtRrvQC36dgxZF3cm3Ql4zxbl2yYXuVm3uxaqUyZ0yqZLM2Das7Ko+gAuCilTrAdWi5fi9/6pZnDeW5pepc1iYomcU7PcfKV3HwMBCDy9IzgvUXuhfDW4MHsginDr8+/VvHeT3uR1RgwCjX/z9xLOxiLVcJV4cmIO/qc74axfgFjxBWGiF7hFeixs6iK28xKUC1M9Tvj0q66kCVP4LQxs7NQddKnhTBJ6vsf0jd9EXVSDsdWbBX0q5c8IVvAiWP/qH5PxByShUDKOBBSiN9fhveEeZ5AxHAmkAMX/d+Ln0A3OUw/n3B7fxNPRDh89y8f8bt//ICPxwmfTxOWJfgRpMUl5bPu7F63C5Es4tI3rhKOy5HeyYqA2OtyaVHSdhMoOnEOVxzUWLMuXcoiaKZ/TbBpF/g6eR0ZIVbzV/ShXBvKqFDjzRgXTksA6ZROmqvxeEDckpEJH8I4CUMDhnPByODUqQi3OLgl7rxYgvuixbnIAHkQGfhdNvro9grhEZiMGB9M/kXCF5SFFm3gSlxuLrPf57JWKL2HdROgIBjM5wm3/3KDzzeM86sz8OMR/M8OODlFA8dzlADwwuDfPcRLsnRbY9rfePB/K32BEQE3DPzSL5eZzcHXehaOSklogoGzI3w+E04/9/j0nxhn+h0+3Lwb1lGslzW83yDcdo2tBS3Yvnn4FW5P3wyyiMGByllFovRer+VyTBnfkpcuS5UyFGPSKbzg4Rmo/dz2/VHqVaTWRgc0UXI/zO/xbv+P8BQFEvjiYnn6wwJ857DwIxydsBx+Dj+/xuvPr3GwDDIHtXtL723qw1jeO9BwERjPL10GEr+gyypLVEwRt/CsuW9MhV3DVHWncUbMzZpLY6BXDqe+r0+m6N+cI3SESXOqnFekWpd4DxrP5W1B81llVMLXEqXqHJYlNKeTrlW6appb0uBBAWuVD0AigDi5NbTGxvUHWAL+X3/7V/jm5oBXu328u0jzGUg835oRont5NPXWa706Iv0nU8XW9bQnMJ4dtghM8WdcZbvanwVKZ81dZZDrFpqK2pqxl/2JMFxZt0JhT253VZhCmRcqfXodZRhx8OpNYFohDS82z8c1XJl2i2DZzjmCx8/dEYDHvHLHl86Z6O2VUL50aAw+2NYLg9L+qG15VhBlyB+ncjyn19uyxsHvDY7zHmBgxoJwgr6Upeo5WUKn6HfSU6i+o4rrLZoVldWksnagZ82j1DKaSiQ68EhhUUkN4Z0YgAkKTDnSQQiycXwxhLSRUe9m9A74/vdngA3+0//0Fm/vD9hZA0sAWwO50I6i2OlFwUcenuKdjdHjQebrCKLB6QZG9MATHGaFk8/xxIOciHBLOBEhd0D4vFFQ3wkhLpnEGBFkhcE0L3hrbqLV8IZRZGQvHalVtCq3y0bLNDZKBsiXe0deyxjAToANpyECX+pSP+b+LGvS/PNaGHNGHVl3LLapRy6euknjXO4Xl09CpAvElUynDRPZHqFkC87lBBHmJfAJQ7er+FIYUlo5Kcdx+QrAw6exDuAqSqhdEweXJkmflAc3GMJMMgbqesJF6i9OiJ5Q3lNJSqEXTPVS1NXHdj6XXj3TGLHZENFjCdbYx0ag6lKJnpDVyUDld6qTrDS6XrTptQP8WDnXlq/xbGqqgiOddFAZsiJgbISoUVc3VdMBdQElVisUEz0hI9DWMJc44Ox5iicaYOPEikcOQQiXFgN0sJhmG05IOIfT5wWff/iMBYSzNwhKagNDHp6C8aPcwRAfu2NRPdeJhryWIk6RCHFsH0H8wkXFDRGsNbDRv7MmO0YQ0yg0O486HPiQPA3KHY6rVrdxgUzK0irCJbtUYrOq6ZiZrupbA2F6UYRE7dYNO3h9/hX/kepkhMQFRoYjgeR4E0XZ5lV02FUWRIZDiKZi1MKO70xIqJpHXFadS1U7M1J+JpizAXYEggeODvwQjCsJv9QMReedH11877E+AD6VhggZpxnRQt8sjitCZ/31AwOOMJ8N/MHDfHZgXrDgYaUA4S4vFx1+VlnoAmQPpF3vBIafGJgIe7yB5dvMdyiETAVI5RxJM6dijHNcB+cjTAvyBsS2/KDqWmlykacxuKsqmRyYXFN/6i1uGbJcFxdGrtQvwnYIA8vB1c+RP+ET/RjW7BIvnfMu9Lm3MB+PsD+cU0P4jQVuDyDagabrJuBoB8maIbfbv0P+gtAbO8nc4t4x3hFSOoTtUtMLQ2QrgGRhgJNE4FlkAjFCcPG9ZuRLtoPGzdcZ1G+B2kl3I6l5UxbQYOBiSMe76vWkJ1V/lT3F1Ouj5GOobUNRRlNz1f19gYhA4CXceQKOxm9CvNAwuD58e9jh6/0BhkziKzSU9d8ELzJPInR5ZAxLLVZ9kIwQRcO10UPl3CwIUNm7XeMFdZ7acvrj0c/x1CPcMj3q/gU1D52MnUi6lGwDnG0xg3QawXelQ2SuoLf2+nWXaZ/Sr308XJe0LpdcUW+Dz9fHrMUPnaTd+crFt76c/bR5mPNu4V421qVkij07ENmSjm+AZFRby2WX773voqCobSHXLt0t81jvgn/OiLSVV6X90YwDP3EYs0AvGwzgpwnOL5h84YuzgoGb+RlTFSPPiumitOlKpeosOWoLuiREdhLoFcRNEjFCMAsNFv+9jLCTv8wm+/l18AC8N9jTDof9HvvdHPQRwhcVdXKi61qxmniHC01t4rXojmAyEe8QLCc1Eq8JyC57fSpC3xsRNov2RhQdeqg6R2JIxBDhN2I/QtxrxX6mtpZVVVBvfgQGDjAW3lgwCVbt917L7cjAUpVDRnpDIKhTOdsXYjdln3VdyS8bPdUGzWSMyP9L2Mby5Ta6VyYRQ8bwdBw3DwnOsiXFnwRPiV2aGaPg1o9hXGt9WgN7H+LrwwZGpsdXFa1qWMgu090FutkkENdZi6lUARuHusl9pTHiya6ZRKnOcZLnD7pPVGPUg+y9LxhuUgu6wW9GTRFVQdNOvZR09yqVF+f3LHyPO6xV4pN6FtiR4E9tkbSk4JaWNErsus71kJpPhG5qktnDDdJOSzJ1AEP82ki2yQA/+9bgfPb47t053PUQCZX3Ybes81OMD2537LLgm1/d4/7tDr/77x/xh396wPvPjM+PFif4gIDiSQenfAuC4wWsDCDt8uPqV7cJuZ+tmkOxvyNZh7iSIqHx8f9kLYw1uNnP2O0n/PI/fIWvfnbAfLODsROMMdjNFt98tcM8mWiMUGOcxhZV3e1LS4xzq7LCtJtkGALakHEX5YRcdpkZQU8UrxkIDc84y6eSZHYLaxWmpgEZTkdtxZEnE8ODs2Ehut0CB/+Rjj0Wd4ZzC5w7h3shnAPcAi93RcRLqv3i4nAbkLWY7IzJzmHnKVG6MFev5EQ4itaj+o5E8L20iotZ1GDjEkvkv3k8wrtnwM8OD98+YJo+4qvpA7w9g+MpES6Y8G3sxmUVvCqPezLUlvyajOksVXwqMr8bYtzOHjcfgDf/n9pfVmJxOjVWE7k6xVHU3GlCr1XHM/D5nN8//JtHfPw3Dkf+v2Dmf85LVOqXNaqNcUXdedT1is16QdUGH+a+lP36+CvcH38OGZdUsLwW+GBIphLtEaWqUT7JPu2+w7ubf6r6grKAAC4NYCOGJDWlHT9RcDssOB8f4b87wf3XT2m8+OYb0P0v8OqzxyvLqTA+78AfzphA+VJ4zSAVbVd4T+3wz3DFHV1FE5T6JdHcsieiTTzKMeXutQKQZr6PvsfyVJXhOZ4GW+nfS0G3WT8lH8Nxp5KLdFbuVvLMgGdQPGUW3AcC1XaePOnUZofMfgheV5sguo0oMWovNDaktKjK34z94rgl5fZa5w2+DUAS93nh+HXmt0pQVEtlHdb0IPI/ZBB2PjFh+c0nPPzmA07mHORX6RoLTBYwlmAMQCYz25TWcu77dM2Pgqk1Qmick2HSbhFlY0XRh8ZUXVOVhQzXlkDNX+k/yn3X5KnG/xlhNCMvLjhqX/Qa3lTR5Vq6abU3uCwkbu3w0barEYAa/2xXfvRLHgzoekEak1+Tua78RcM1U6+9j+OqmqC5h0u4ssxpLvN6PQN9gRguw3sJkmuHIHEMX2jsdPhTP/sgI/CcGXR9jTq8QG29Lu4WG1ob/nIHg+T5mHHhhDMsPJzi3hhMQWHtI3eb742o5AdCPkGg4Mrm9x6wKpaqfBRbwAhqhcjrZZxNSCf9U3oXf01wL2pMzB92/gdZksP9AsxgDvdnMgPGh7SeGJ48HANhd2do06P3WJjwd796g7f7G7zd73Frd7B2irQ8064k9RISfCa6xzawAVgTtvDJHWLSxNRXqS9DaYYILjJAYZOgg/cLnHdwS9wA43N9zAjulH3wdpE2Fnp1JwQDxAzDiDvNFatci5WoQ9bTJCUyMayUHZmnsi1QvF78zjKH4kATwNElj/HBYwPMDLYHHM0rnMw9RJdk4uzyEbol9iPJidYKD4dspeuvGmundqZ5mPtTO5cwqT0xuRjeYiFe05pojcmb6IIpaYwRCEC82xVBrgg5BMJ4V4RcyxD7l5Hbl3l3AbIe1HJV1qhFXP7WQKZZnpqiE3D1XgeZz9RGa/ao90EwGfugX3KxT8Wexlkejitm0LJYT4fxGKRs369lv8rZCJnxaYPFBdqwhUcinTAtOv2xE16QAF5tiGj82UL7devA3J0gOoZWe6ph1yv+LyPwMGlKu16PgassfZE4XWTiBvVGbJrzK0m0EEyob4QYCefrLi1STPGjY8Oii0oiVV5mHCKMacd47jsDYDcHpfBu5nB5EQcFybIQfFR4G/KRuAGGDXaHGXYm3L854/j+hKPzOC+Ac4A3BGfCkUbvg4KYiKHx1cWlTVkcMIR0ikH0MgTZtRgVMobi5cbAPHPwA2eDu4XDYcL+MOHmfofD3QwzxZMS8ejWbiJM03he5PHT49DZP5q+dwap08Ttocw4zcDhYPLG2UFajcBqZvJCFdCEgtXAJd+SrE9ASFzMo9yNZDjEsBMu0tb9dAGyGqoyJQnTGOe/oKe6uBhJTVz5KuvCGcayc5iOC+znM/icDZzcy4xqHdfcS528C9849D63PTYqhKufHr6JSriFgI+2+b4O4KiRnVKKY5n9sv1C2J3zt91nYPfJgflzmks5R8lAptISbgZq928pp2Jyw8EdgicHb1y4aHwymP0rWL4rCbb+0YyRTLyKFJF8I0AU70a5W3nER3zGe1Q5AgNKAJ9c2LmdGPHW2FK0y3QuXuFgWJR16T6c4D8wTBQuDFvwbhdqtlIwwUTmjSgzr90wxOup+pL0R+RULhONKCvGN1kvxHC6AksL2gBezfjHaFLM+RXMl0DLnVglU6DYzCH4cllA5yPgzon91iVR+k9N0Yn/KFJ3gooe3gFwId9Tvq991nOCqhmwvfoBrZXnwRhKf/LJgT+fgRsf3ApHtu0wT7jbTZiMSYI3oOA1iR2s6m0NDz0jRL9dnT7o8Bl1I0uDhJo3VH7TsJSlUNn/VJUzGJs+PLnutZTDNl2ckp0Eg0LHCs9tvEbVDVX2FTjqaO580v3TOzFBl/q8KqOXNjZgO9tZjUGXkRpV1lZdb1q7BoRxtqeM6XOQ2HbA06YI7kyc3lgJHkga0+0jtQ7JemkvU8ufQdhquerJ3/oz1vss8ZsvFurF83LFdkPa+a+i6uRVXk82z9tOuR7RuKV5ZcrPPT6ppTqtpJXdi5Qf6rz99adkj4igiuUqvBSL8o8yk6K1y7GKgNcNDML9hx7BUHFygHOEm5sd7g4TJmtgTXTHJHy/kidKSGUsqKX9AmdPzoxty03hlFR2x+s74CRl4jcrOZ6je+5Wbi0V9xwr5UTj1IDr6RE7WmpNrdQyuwxL5L01f9LOmVRyHBMRsML9EB7BJXc9jxmAp4HqOTJ0eeNuXheXSdnl9ZrKKR56CXql1RB0JY04lvl0USblQdYo54CMW11bPe596SbJUF1clePbe17lgulBaOruY6b6S8G2gMPCrk6XU13KQDisN/lc5IOackr+7enUoRzDHk/bjEudhOuP3JmLl8B4Ofq23TWTkXMMOQisChWr2CsYuYjYLxH3VPxKIjloko07EYElmhNTEC4SdtnhlmCOTGJ9CgIprtqZVyFoUYRtGb6+0Ea9n+5EFESfWkjyorANEKz+ISKUI/FE2BuDn38jym3G8ezxvZyQsIFIWQ6XEE/WhrsBlgnf/rXF66/vcPhvP+D3//IRP7wjPJgZMAbOeRDkHoHg+zDTDIU6Ke4QJvHdFhR1JN1okIwM4jcRBFgKBF5cMIVnwt/8+x2++cUMY0Pa3X6GnSzefn3Abj9jN+9goz9oY8UoEXwJmqgsTzsjBaGo52Iu/BG4+m9/ZvHt61v89reMP3wnHdqGq2CLzEc6EcP5sm+W3QbRABHShp0WcrFVYlwAxOUBYQwMEMfGYpqmZCAS/5fiw58uAj1ACJEpDG6aesxdNwuEHLK0Px1L9ald/r+e4P4LA48mMWgMDscmCshapk0vwc1D0eMxuwVjTQ5Yr2IbB1DwuBdKrB57bFSnkEG5k2Hc74WBYdx+v8PP3s9NuucQ+XKWEI5nj09H4Hj7EcdXP+LhzYTPb2Z89v8nDP9fYU+KjD3y8VfhwEnwVdxZVdAHIBlMM36J1IIA7xa4h3NMm1sjx6iX//oJ5988ZGMf1WxmpiFEBGttFSdjHuD23gPza5iv/j3uHOGrBYCZwJ8XTOJATYQGA2VgUYb9ahJpo2PZx9LDPYaUk1FpbYqlUUo76Prz1DTL5ML+ERJjqZpBLMO3hTtT2Vjqa9uojQ/BhR3iibEwvuaHX8P8/h/hjo/ZmFsCmvCi5jmE38heBTdxG5tTVg0pchFy/QJYgCnDurmsCn4thGu3TLk2Xdd6Tat8dliYoS5jgmtha2At4//517/Ez25ucDvPae2WvF4JQ6Z3QKHsL8YNqV11XG69ho86vVXlLRrTqQ/1+4VQWFay4FPwP0XJvSK+FFPU4X0rIjA0Pug+3rC023L7cDyJBtX9c+l9pYxhyvR9dQWslTBePJfWXEYJX0Sf+qcahsM2MBiR+t6meFrHPT3nn3l4Fs75H7bXIG3nJq7y359+g4JXJC1O6Wt5hfKVChKbRKTwt1ZH5qecK7t3FjjVN5W606T8RV8IAYWTiCI/TVlOI9EpCW9PIM/wxgSvAEFJEdL6sJEHZEPRHnDs8f4Hj/MRuP/mFq9uD9jNM6ZpAk1GzVOOMmeWcxL1CjsvE4w5iIyq26l5Ti5PgVDoMc8+bTAFIcnjDgwswdPFsoR7IdyyIHnDiLAF/Ui+O0v6MbjQzW0ob7JS3Fo80ZnniuZohM+I8yHqhpJxSB9F1JOpipZNjiALGIOJz2D3GQ+0h6PgMaJQuBeThqSQ3D497avQ8mNqDsexzGD2CwnTM/YIhXamuK4OIPNjeiskq3RyAollXtdwaqW8OiLBkpOB7F+Ccw0i9MUFXHYNF9+kUlJ9oZmAIZblXooVnF7okVsZDoiTNd0RovglCidj9ClAivOumG9PDX8MpWCqe+VT4sfymuPyw08Srrgjoh8nUzvvvF8Xcuq1Xk7h1hiRdntCSE693GssVKUhOZLDsroB8YvVAbKzpz39JESqEVSKo4SRtbKpEMJpdU50Qi2MlLFUR/RKUJcy6KN+uekc9WZKUlD1hbsiIrEDYTd7uIWxIBxDJJacExB9mu8OgLEGd68PePx0wsNxweIYngPT4n1ACD4RqqTpSe0KxobwbowJyrRoCQinFhjWhksbrTEwk8G8MzBkYCkYH4wxsNaAjMGbr/d4++0+xofLuK2x2O3Crxgv5tlgN+Ud+kk5WPb4BiNEf1Cego9ykWEex+lXCPfTRJgpnOJIiDv9lDtbkpGuTFaFdidvOromjA+jYJxEuSbPMq754utAME3k8eQy0Pluh93d3Cg25JXSMxX91/qh03nVfI94psArazi2IYC5oxgMOjL4o4numAYMBYQ5HFfUfOkSvEH+UbHVmK7Nt610poXzygJSNq4jNqcW9Jrizgb23OZ6yeAXwu6IcHTaEngisGUwnwKTHef5Mp3CceA4988u+oOdgjIz4Ei9+zmsB4tsSCUH0Jkj85MZpOTfVGZVvCDu9O4Ry/tjujiOowhXKqUprRljrMIZUYlKBEw7kAcmTyDagewBFtnFHRxgTGDR5AREcXlXh1nsnebLySoGtKOQKdw3XRijSzOwOPeiYL2UT07rheGImCsxbNtqD0IUq5QZJ2Y+3sej7lFYid62aDmDTp9BTk6VbWhs2YLiJ8de5hk2fN5cfffTACnVvJ9idPKaqIwQV4Gk6V6BTHJxmreS9RKWH+F2nnE37RJPkHi9yiBUw1caISrYtxghrmomFb9aAdyPH/ApDbw5vsfj6Evhm7g2+YWwnrAwzNbfyuZ3+PkyYcu3bYNPsdIqtvxNDEy3iI5wfQGI5mtXfhl/K8t4BgJY79KVbOUmMR16B0B6+a9Egn8yoZDrVw1GnTaOEMEV/Nez8flzQsm0r3+v0z1bgXMFT91ko2EfN+zPhlqvhKBT6KDUn0JhpBqc2ajQP5aWwAuTKNX1eCsRrM6PRsJKCZr4iHA1N1UOT7luutGyCFPchVGkvBM+3TVJpFzosBqT3FC9dcjDC2cOC4N5mjFPNuo0oPpL9GedXin4EpSTq0NGSjOE/OXiX02ntZI5bDbMl1VnI0SHb44AJYmffbxbTkNB+bRBxX5mnkz4Dc78mYAex76guVW7s64+bzwUHi1e+BnUU3K6g5B/U3VUlFkyE1wh8Za3qGWc0QXPRfOq9SAppK36rmXNt/bmvRYRnk4ZisJzSXrDVxJekJ+rv5QMFPJelr8dvi0pK+REg03tMZJiO5x3YaeasfFeXKCxnHUL6tc+/kAN6t5O1Sp82nwN3wq8iMx7D3taddmqMULCF6YxT7sjQsscCVf2BZe10MqDYt0DiqnEnC6gZXBWrnfrovZN/AgrY4Rc0lGmVWx6RLC1wJZ+QciK0fwrE10bJ65npaj5KXb6rTKy1doRRMsrjG/JN3TLZgA3hvGLbywejw4/vF+SgsRPPt4B4OCcx2IXnO2CX/zbt/jql3c4/O8/4A+//oAf31s8ngzstMA5hj0vwQ9hVGaLH2sbDQ9igJhscBNlbY6fpwX3N0swNkwWb395i2/+5g4iKIfd9WKIAHbxYm1L4bTDFA0V0zzDGoNpsphmg2+/2mE3Gcxxp0LwF0hJmY7ioqOqJxsugTrfrwt5HCn/9pCCtjQzktsXiR8e4RrxtqlYccsVTjikC6uQ62PZWeHDvREcL6OWQgzCuIW6OG5TJuznGfvbA371n3+O3d0Odh8uDc9uQhD624SdDWLayxCOxiBikoigOLGGgq4vI1W9Uyd1bY/M03hI2kKfl+BaUpCGf0MYGglUPzwNin4WmZXjIjcD/gRgelguxGnF9WSA+wOD+Rb4fAA/APw7LndtMeP49vfwN58CLmTgtz+e8dkxvv/W4rzL98xIbfI+KTznvjvi+L++D8sjGlKJTMJjQMCPIhgsj0u4WNq7tEa1Yc4oo21iswlhHQluPbzC/LN/wA0b/GwhgCzwmP3NigDpPWDgwWIYBgNsgkvGpgtrRrYdorQzp7Nwtg7nJVR6iX8c1lOvZ2EZEu5pWjOuQ+0WCqF0B+ZjJT4ef3cunr7yAZeSR3B1532VU/gaeRaluQKT6jRo+IbEyYgyXJGYrWHMgrXMd5G+4mXadOs8zpcLkdYYgjEMOxHggssJcfdI0adz2ihR8IZiBATyoMgjqTpCJBXv8lVhi4v9pBOVSS8ZIa4NlPJWsNWJWLcV47QqeghSUwy1n+vM1E/bM3qu1t3AIvhv8PnaQhWSunpIqMfN5W8NXFeVvan6C0WM13WP/9peXg8H/xThhTDRWkOpfOzO7T+30OCBjQ16tgECGHfeH2sO/ZQQbEVAbb6khGqEwwy194Szs5jphK9uf8Qj3eCB7yE7sPMWLYo1aZUZFyfPs16Tldy13jatTFfqN7RaJWkDF4+iB8rGAwZz8O0R+FIgKU1ESZ6IG6IYa8JJYiAYYeBhvE1Ve+9x8oRHx7g97HFz2OPN7Q3uD3PQaRgTNsMKuLKhiIPcLeDLfZdBsdEw3GUzBVyRV2MHB5Yy8pI+9n/kTyLo0aOFw3I+YXEu3PPIyn2r9G3ic/KILt7HO87CrwykobCBycq9C1FnFm4syEyP8FBe+Ce5e4MqObyZCYqnSbQ06kDSaYgJTBO8MXBs4l2XgI3pjClPYJeyg2gJlb4wzYltKzjPcW42RqWTDCyGnG7OFYRBGdhoVRHZmlMJ4SSST9TXACZcVsFR2NNGDhlVKSFdGh89X6QMzYCoxctSs0DJKfrltRz9+P49DkH29cx4d/yMaTa4m17h/tbiV98SPu2Bzwn+mIe2aIy2w7adsq0wh6O50HwYxcVCEr8uTdYSBee/m5VcTwvbDRE9wYK5aNN6fkkz6Ny4EERtWBibEerimvle1TZkwIISPxsjxF0LK0KbFkwlaA1PQCjEqhJH1BqRNbXgjY+oU/NY1EcJuIsTucs+JKmU1TgIkovfWCGOGk4O/ThPgPcWh124BGdZuBxXAMzhqCb2E8gCr97ucT6e4S1jfgQ+fXQ4nxmAhTcmuf2R43qzDbumrKVoiDCwlrC/Ca6ViAiHncX9/S58mya8/uaAN28PACFeOBQUeMnNUjQkmOhiSRR8N3sLYyzsZDBPFrvJYJqUSyaN0MphSH2X4wh17zfDvZUP35asDLUlO3N4obzheukgq8zDKAKt0tQUJTIOXBEpMUCE7gnrLtyVYmK/W0yHCfNhgt5JUq65tLBUD3eITJE54ya9W6LLvI1wlzCUC+P82YEnh5kWaBctocSITwyFy2UTzIHRTambm7O/bFhFjypNAVRvChWzYGPFKyFdszVMt7Guq/oysbNFnJ4RDDRlBgbZAN4kBXratRTnOz/u4PkMPy1gWnCI/faKGSfncToGmnOeAl5iJsAx3IMPd9pYC/fjEaePJxiEE14+Ggs4/p8ZmBnJ4DC5cD+Ej0y/V27QtFI6oa7dDSgadNP9OfYWhmbszBQuwwPC5V0knAnC/QhM8MThbgiDAD8FRpYUDeVGXa56mtvvox1DSrxoJvDakuUq3ZOWGke+oJ4YxCh3MV+ogPVc4+qTOjmmfkP1rOaZEsw591dBmwtaVPTcJiJSGH2hT+3U6bq527crCFeBrqHpaJliReV6VVjno7PA5y1wmgneGhB57MliIgtLNrkOLLpNnuRbelV8Q22EUHnHRojqF4O+oKos/SlFXLEalPFkyHMWbSgnYckfrVSTqGcnMdXphoWslK0jBqVQ87C5qlGf5L4Zl7kmCm0BIoPdz725zFH/beZTr1+bz1/Pz8m/dT1sq2PUlq7qYqP8tjlsHaS1UwgjpHip7Kfme6nwnHoqeVVFjuvpMYedUq4B4Tl5SyCqkjYrjNYgaGUckakIABuCQ9joNxHAnuGWJexasX0motdmzSF1pYxOU3Tzis8rzc4yGJA8YsT3UiyLWvmYTsuRoaDiRSnjZTNlxAkRyPOZ8XhivJpmvN3vMMvdENH94+oQCF9Q6JKEMRXFdXuPR/FEWSbPvGWWz0Nm2QATXTHFS6q1BwQNkGyqCEsiwOE9Z3fbXhTXgKVg2DGg0oKfeGrF/LCWx+qBKWZh1U3VN5lIUX+zOAMnd0RQNpL5LObkLBq8qh4971bX7kWlbZYdpWCRKZVoOcgqvZN7QmCt86T1pD5ygs8keUyMaD196FrQ67XY1M2D541hO8d6Yf3U5cTkhggOHotfYClsRLbWYJoAY7mXs4LuaZibVt6eWVgY4g5da+/6kFg1a+RHZR2ekNgwnk9xw3qFIeJChQmXrDA9suqbUKySeDnk2BgBcOkeYgPgQaEcCmQEwkmCpIGkYyDNLJJ+D4RDFM7iIkD2x18kKpdgVNl7u+GuQxESSmZC19UtS3W2qSYTJ9dbwM0B2O0MHh8ZP350ace8c8FvoLEG1ltYu2ByBr/427f4+q/ucTw5LIvHP/9v3+P9D4/48Z3F+WySwiW4X2K8ujlimgBrg8ukeZ5x+2qHX/6HNzBTIORkgGmyyQWTsQZ2MqkJ5Y7iMHYGQNgRjOS26Wdf77Gb1emLyYBgYGwgYib6fjTRR6O+1FMNDzSCeqrx4cqkZUjrLpDZsDs6GAeoYlakJlFYpiOXvbWZtWCpnrzGJS7eFSGnIeJ3I0yfCWvZeA8Pub/DYDfP2O12sDbfy5G7MSt8hPFJ7mRiR8m7Nh5qJY7YSWXuCn4JydUOix4VT0USlo8O7/6PR9z91Uf88u/f42wXuNQDce0KETexMMXZkE6LgZCq+3Pwup1AbwvcPJQfefhxVFC/uDWUX76MBqKK7iYroW1L6Ze7KsiwLlP9lfUSO8l++Ar242uc3v4WfHD4+pWFB/BLD7gj49c/LHgA8N03Bm7yIGOw/HjEp//398DCmKcpGCTYgMkDbBM+kh1Xb0/AL1w0YjDg2QIc3d3FXUu6EUkhbQg877H87H8Gz4ewSwiI7mYNsNhqVlJaM0GgCoYj4nChG3wwJLLpzcaMI/Svrz9vYjE1DawHvypwpYQRPtXzJNF6XXydgDM+Ss27BEcqgwv+NRsfMk3N9/CECDkVIafNGraqQJUKB9btWOmDQuEsv0W+/D2kUfeERXoKfSqg5hlq/q0Hgv79UkqsCpBLs+/TjcVvvrZYeAEx4ZfTLd5gwg2Hm6tJThspXlDYP80fZjZLcXZFg8sQSm37MX/P+bNwRTlnPfBNCJN5NC4Xx2r0/Sr+hqr3fllbihzDW56nWYd7G/BdXELt81Yle7nDf1DmCizhYTRPnhd+Kl3yX8Jfwmr4UhNxhc28nBFPzfwyIPwEodj5jfzI6pvfGZz2exAZTHBwxwWnjz/Czgsmi0JOy4xP5k41F+gjzxN+lOAkgevHkstPWWp9RwY6yX45X6SXSu8jpxHStcW1f3h1QiJkNaB4GTWBwgZXMjBs4NwC54EP7zzef3T4T3+3x89e7XCzM8k1U+AlYl2LV02Im2WjjJtORKg2ZTlEVIoUTlGkQsLZlGAg8fDs4LzL7pZY3BMhnmJwOB4fsSwOp3Nw+erVSWuAkmcC2VHOHI0P3uN8dli8w9l5eMeRHzKYov7FTBTlBhGKQ98afcKDKG3k80R5J34dSAZdCdcgJEtHEicNmAw+Hnd4XG5w3MdTEQj8tI0JjZprrLKHKvQEyoy/xI4xlJ7jHO8SBCAnXiD3bUhd+gxDT7wN34LnCSlfY5HM1IUTEIGPZEbSmXLk4cNSCHJm0v3IBjQwWPRGChDtZqvsDU51lqs7Pz0V17WKcSlT2qsT5sS1LMIpbbwrxE4ALzjSGWbeYXeYMc828vXtederYO8wiS0Z+zJ0rW8nqGmWcMYdYwRy0gxz1qMJXnqKcelSuMI100YGu08/hqFVMQQEFRQhAHNvIEcl9Zj7NnNcj1FJmyOzIKjj4qROgmYW+uRkxLimLUHnr6SwZhcXpfiLgXV/6CLKUdECW/mhqln58AMAGIN5Zhz2iBcaU/zvcVwAWpAuK573DLIEO1s45/Hm2xtMkwXNjPOJCuO8McCbVxOmiTCZcHxxmi0OdzvcvdqlS41B8a6IaIgghGOAdiLMU3Q/oi6zlt32SYlgDKwJaafJFCcmwvhm8iR5tABY4EBFksaKhi2zI6Pv1UAEY4DJht277BmwHkxnZMcqddGKsXphPBj5yPhcrWgqT9mEMYgGIjFAECB3cpQzUvqdUI1AVvhU7ylb5hnj3GV1mjISyJhnvDM7tskT2IV2WGIsiTlRhLZgnDKj1WWOG+Igr1TGDnZgv9Tw5e6oqJDmFVOqutYvIUZtLJPbF24+XQnfIDlfTgLypli5hiI7w4DxhLt4PPk7LUA4YHl0MA5wiwPLPRTRaGc9cIewZoxn7D1h8kCzWz7+ut0dYIWc5/EiAjDv4acDeNpB1kxaL7FR8bBDZk48BxpMFJmWADchGCQo3iJXzZz4G9lUVvG8NjY1q5rdd1BuyoVRqEokzdZXoUJRBXyyxhRIAkMQ3NQHJbH06mmmqa4AeReUT+PKwOkRePwMHB+0lJKAne53mA8zzK5i3VQfFZspcmTiYQJLU2NUKabDLymc1eBZVV8/30roEsuXJU5p+tTa98E0IkLgDScCOQPyHnezxWsbTl92Iab6l9qPWiCh3M9ahtK8ZgMX1vng+ts1abeFC5k2FFq0WULadapoe+9p81zaEN3t341Bo6q6z586j5tyrsuzHfYB34HO/HlpJnHE83yRsAX2be1ru6yHHy/zkNtr/ALh5ZHB0/M9oayX7LeePmsQ0QeC9cvzoLi2lAHaab43/fkiiiPRxwQeiNkgCNcGDIbnBZZOMLXMshp6btqU8lb9tDyi2jzHWu5UEkvNPo2KGsBWKOi4ioskK+inghwuOJMBnE7Aw6PHxAZvb/a4P+xw2E3By4MwYhRTc9VmqQrV5rsuty1t5NgPPqWUTS1ysiEkVI5lk0vQeDG1c/FUhG/wmRgW0h1dsUjPDO8YLl5+7V3YFEUcjDQeFHVtjHo7pFZ2pjZ1FZ2dwaL8hVRhVKchgoeBowlMJrHh0QlWmgq1rMAc5RzNs6vn3swtRkdt1szGNSUTMap2ciUjaIEpjm00VvR3ufdg0UKMzDsRZkwyOASG1CAKdUA6IYE0kcLYxTRM2T6XHmJvUozyGVvpnpJpf10Lsq5GeifXqxjolHXA9BFAhoLHAbaYJod5spishbcWn80OR2PLSXERwk5Ep/4uzv4Chva1zTk6JOOp0hXEL+1rWpIxB9GLs3FPuyMihl6j6+M9jTsX3cqqMZnmcFaCKVdCJIsiagn6d0UMBJLqG+lF06DI/F12u8lENlFY7Aqdui0d4t+mzfCndVYYH7S0USHxbq2xbqmLO2NUl9NfIStWPE5z9cYChx1HX9ccDRIe7z6f8eFTUPYvzoJsWPQu3gfxN/9hBx+t6OwEYkRhO5xKAMJdEQCi8YFgo2uR5HM9ulzK40R4cz/j9f0EfYKleQay4cHaeEoyl0mEaOzIeWX3o4xPoZCp+2vYdy8XZsuYbhxOJ4PHkwXvzvDTB7A9ADw36cPKq5FOmWCrJ7y81zhzA4zM8BBpqzQjubsUt1g2uMOa5xnzNIUTEUZ2kYoBKZ/YSA/yXgKT8kGNSd8TMRKRIW2woexzNCybqHot+EK6PIzRGJEqMhyIdgHIwBWFeq2/tzJwzaQ/JbCydFdAaBoPVkQfqLolpivhqehYh/FQuKSbYxP01fuF/E/oK11mxRNeCLnF1gDfvplwNMBvJgcXiQ4j3g3gEYQ3ZvjYj4aAN97g3y0WiDiR0qmHKLIoIDwA9/O/g79/2/RLWBIENlPYbUTCYwkNDY0iEh+i0l7KPCvKXS1ZLhrhEuVSSPfkYNquzYZrUWdNl7coiHR6mbFaHpI+zG8yBpfKroU5gSl885FZ97GzPDPs+9+B/uW/wrtF+VnO4c2//wZ3f/UadpK5odoMDob0NZqvaZ3Glwqdt1l1eih+RXFVwrdcS+qeSRoVWX7RYEw4qUnM+PabW/xyf4gnMam5E0L3JdV9kpmFBHCxfGoBesA7tIriVEDFi7RroC4rp+t32ssroXOZfZC65q9++m7hVbuuhm3j9zjcurqMs65FVNclL/MOFutfwhcOnVmqcIGmB0nI34qYNrCXfwl/CU8KBcLawg+JPF7HAOwJR2fgjEHYujKBYTFPJ0x3j1jIwKe95qOSq/3VSZG/cjI/feOKB6+UufFvUhtxP2UKrXCi0mZZss0XGOmgs6V4l4GJbvQ9vvvB43ffL/iHX+7xzWuLn725xaubPXbTFL0rxOKTwjZqPuMGmiTTGqX8r9shCm6GOrngUwJ2DgwfeEnnwN4BSYbwcH6Bcw7Hx0csbsHxdEx3fbbNjd4hou6FORgslvOC07LgvHgs3sH5eKecCW5n0wkaZpAPN0NEzrU/GCvui4UnL4eMS5fthQwa7ojwtIMzeywg+Ch7MSHx3zZtsMryj2wkSxqTNDFZSk5DUEoOCSqITgzgxONnN1lqnIpJ79sTPsrt7lqQfgk0KRiCwh2nYdc1GQLYBw8RzGBMSAYEgYfk1wDskI0QAgOlNpQXz5piPsL4WLSYe9QA8dopiVZLpecKy/mVHgvUobWpGwnJc8punjCRwf7G4O5mj91+hr+5wT/t3gRXyA10GqI/RypdSO/Vl1pTVo1VkiUQhy6uaSUfv0S42hBB5Z9OghqRUDlBN1WiJmP7gCa6AK4Dr+Lyunwhd8oyWthEVmL37oboNyEUzTxOS93YtpCVmkZ5myEqBChC+9RmLuXn3AbOVB5kCcQUj/oFtyP7ecJyAB4fw9B7K8qd4D/QULC4T/MUj5lxqoNAEF2K3BkhbkqMuiQypYsGhckC82Rw2E/pcuvUhUpRLTsLw3s+CZFcbZmy7SYxAYm0Fe9DpNgs+I1hbW1V6cqk0cafdqS0zGSO31b+6reG+nKOJopET75H5ireoSAEIbhosiCoEyt6zqULqisyUChvSiNEoexLJ0DCr/YLmh/ktUJOCV0xJgvc3BnM+5IlXTPcvCCOboYimTKupIkFiWlkZE7xZZ7Qt4nFJ5li1KL0Bonm6ViRt2jboBzRJZSqrIY+1uuLmxnPZQZV0DZalJULmlwP2KdOX0qIXt3Cl7PD6ccT3LsT2AWmz3sK11B4wsyEV7C4ASeXaqFsX4xNcV8FM+j4KeJL7TpN0S8NkJ3Bt68DnU10ql7S+m8ZSkGoKR1JOFp7zxA2PXqBpK+GNFpqR9LlUCmR1K6+MPya6yrLGxkjmnWk1ganfAycjzAPn8DewzCAzx9AbgkCA7c9YSYDM9lkqC16qMfcZCtFsWYKI0Tnu6TJCnaJG43ICrPem4O9bL1mjJmj0Ydx6CklKhQjdIoMxTtRCDbuopLLqQOMgdopG3mz1nrjU3xT6dNpiG4rO/2axqNKPxwnWvmujUzX9esWbqI1QpTIvDc7hmAMjSeXY+ru07zAahua7qfm05Y6r/hUJdza5uvy9z59uZMQXzK8bB3d7hIWU9GK4n4dLtfUkQmfyeKRpjzX/kcNz7QSb5RYNgXN46SIlomtaq8+b9ZjjIrqteZyoRcgu9hHAd+pVFec4tHcT7hDiwDEi39jHJlahUfqf45htN2Y3wmrd+kN4otd11k90ZftLpTHlxJUYFLkD4UX9xw2+MzW4u6ww93BYjdPmOMF1Vrs0WrArAWRCqjBMbWcFnTKyiUTy8eg7GZxmRwvGs53QchJiAWLW+CWeBLCq41yysgqmwMFguSO24e7Qj0zWO+ciaJ3OC0DpEMZnJoGxfmUPU2qgaMQDUG5I0tZJIyLAUxwz8RkwfGOiNQGBCW7jzo67vGHheCSKxT1eja11PKByqdPpKj7M9K3buDqex7bLJnllqRuif+yw67cK4HnNGDvMx4wUodcYG1iX+Yz8iCfj8HL4iVAHYtQSDouDG/iRkxTzNuQJMAX1s94nFuyYdq5Iq3u8K9cpQsbYaM3DkPARJithbUEGMCRkU4a1TIAtA/0Jp50JRRQ1J1xtRWgz1/LyYg6jE5KhKVZ8/PPD5sNESWwWyDQu0j1dNswuKkPFNJVlEty+NgxvfsiZMKnWgoBLA9xSJeRb0Lwsk6VpEk6f1tl2bo0WCpVD0bEPoiYQk/jJ42zsurqdqTSMpUpvrcg5gbWQm1hoVSWXo4Giftbwu3B4McPBu8/LSBj4C1Hv4NCIBGtxUidnkhwMjSEdzFAiAsmuedB23fubgze3E9pvMTgkMZefKPHdznZUpyoAIIRHUg+GYu7MvT4lNGqx9vwgut1pQKFdkmMAjUqbgOLo8imSL3LIDNZVaWQ/k00iMJ9GgwT3bsA7OPiJQMyHO7+mCbYaYadpuieyWSjkTA+6ZmQ7+dQgx7HTfIUaJMo7fZmEEguq4/tAem1GsqRUxEJd3GY3/s94dVfT+C30b/jiE8W5XD8m9z2v7AY2iOT2+fYiIhU8TXOZlVLOQSAZqer0xMoXjMzonFU3YKapStCwXSW8CuSUZXYIbQy/q1FpqidQFVfjMIAXxddxlg+nfHj//Jb+IcF4ahzgMFEg9lXIPx7TzBgOHK5q4n6YEYaZn//30IZwMWd+nz7Csvf/mdgmgsmMbGuieQlAlDq4usmVnDldFWGJp7aNEXBK5/r+AIxs8LJXH6uk1cx43Ze+t4CpXkJmWaF/MEM8/EHTP/0X+I1OxyOxwu+1bWTGgtDJd7T9EtYCak4xekNFOE/SRI91jobUfmeVvtgyVT5dZ6mHdJdAzzUW0xU/um8b8WCo4kstD9uSLCxnwjqJAQ1azHxGSoiCdpC03Ta2gCRC1GgSN/3OmIwLtW4DbKp7xVOGVg1qE73hNA3QrSwr2Qcl915WsuqWh8VFrjMvFV9vQbFlvDM7nxyWMdffwnrc6azJvX8UP36we7xj+Ze77O6Boqivj/v8DJt+KKy1QU25NnpNxcqYVvhTwG7qGGzUULSRSaGgnznaQLDwIHgMSFwrdHFbmeJ6KB1mImEy25bDWORqR9fg57ZivokM8tDgIvLPOpTUeGanKXHgBhBye8cZmvw1e0O3766x7evJtwfDriZ57C5KDFoece83BCQOkPxeFJp3golQmgWRgtjhPdgMLxfwM6DvYN3C9gvYO/hFwfnF5yOjzgvCx6PRzgXDBEiCxMQmSDK91mQiQYMj2WJ90Is4b/zSAYHQKvJgyEiuGsCwHKWwOT7IfQPQ+8dbAab1LxBRcuSgVg4YDJgmuDNDGcnuGg4k/7zsb88A/BRd17BLvKVnhP65A5V3/N9nDJZfeL19b1wWu5SRVfxrMrR8b7J3ohDUTZgjm0igqEIgwl3QySnEDbACUxIJyNgAO/iIskumQqjitr0Kh4k5JdNhNFzHtgIOxC82YhGpifKjfF6NQF0FOWeTyuXcxIzWUyzxX43AQaY98DNPt4PQRau4FGfgOBHfPf1Jf1kYcQPijGr1CZzQu0vzUNecVl1LUDk8EX42q6Quhby9C3cKalvSpZX8fk3ZMmtIVA6g1UIO6Rz1kDGIatlul76agGVdWwUqweWBEqLKSsocv+MYC+AKBjuVWtgrIoQvALKBc/7ncUdA49Hwvns4YhgmMFsAj4zATHqvgkEUMZLlCxyMkIMDARrgf3OpJw3e8JkTcon1J5SO7LCJlRRzRUSI0dWXGn/jEXridAT9kM3FKNY5FkPT1xFRbFCtGp2Sr0/SaOgFk7qvxhvgr9QSkdICRQJF4vbwXjxraFIEK2FnS1uvrnB/n4fLgYX3gGIl1ZnBZAwY3q5yDwgtBerC8Ti2k3cvOUTEQH7rpIbrXyWOWL6fceD51HM6Ms1I/PFdQmxb9OJgM4809NMGzpzv5WSQ0pTM/ypbC5exfVe0b/1BXJF4LITh51EiYHk3vqOMT4BTonJKuYRIqO9O4KnE7xZysZlFKxSI52EEN9HDMZutvj6zYTXxoZjwxRSK13yGAeLIJMtX92mJxZuPgL0e4Bt+xGh3wu3h9onaFs16DNAroxsGZV2zgBPREd1OUTwt2+AeQfBwMwAvIP5/CPIt0fNY8bmjQjw+zvw4a760oc/pWAH+vQe5M7DqrJxJPzx7GE+vQOJT958JhvFCCphtKTJVRMUjuwZIQoeIDW4nFeBHhadG/9S3V0XA6lGZzqsYZbFoRdJfm7a8oQwzsnNYGpI0iWRUQAX4VaRwAK02miXcSaVaUdGCF1mg29zOXUf1htMnmuEuGgYeEIYGSEkqlvVEC8Pa6nqaj615RXr5WLRap2sJB58WmsjgE2I8eohqWW2Yg6Ua/wFhxubOnNTuMTl0Orrc2pfnf+avg8KFxVW4DcVr7lGmMfQDDI+I1xlkXrZ2XFNLZcgVBLuVbmpTjHkGwdQPaVLtuThrQlD4qeAUatWkkyU3xIcqSuY4JjgOCilLTz2OIHIYsEMTwaG661vA1rUwKDmN1F5P7DitQMbTtUlxoTVExSxLVtddJaZOnGjmAjr6QQcj4zDZPB6P+N2bzDbKW2izBMvz6FCXBAZOhkhKKZR4yL9kpTbPvOODDDCyQY5CeHl14k7pnMwHsR7IUQHY4wJJyLk+LZsDgQlftW5cJLCeRfuhPB6w50iqAI3A+EOjSSlrM/aDqojUNcokTsjuz/Op9UQDClE6kREs+rBEOdE8XQEGFmr1Eudx6GdduE7x/ERN83JbXWaU2WJ+aGUl/VY5wxczgFpc4Kllh96835AhPTYMTIPxoi94oVxLYoKHprUOoz6nsze1/vr42BeQ4PC4qgiMgx6LzrX/UiB5zEmXOL9uJwxzQY304xpCm7B8z3nxXarVAhJv2wEtfd8bVjtmc0M+gXcOChKn5Sg2PeZVvJFlHtteNIdET3+6ylADRmIuH2wmLyMeIE15U2sejdroVgOkygflc8IXfDqQH8PQZeSrxAmSabneBKs7mWpkDTVH2mTqFOUUcmhLSyF8NGBvdMXQJV2AEzyY4iMDIXoEwj3twa3NxN+/ODw+cHDsQ9+zuMRPi/W1zh5RLnNihATkFw0CayEYHh4+7pSEAjUJsOljVKFEiEZHsqx0D5f40PR3m4/xN++k4FrwnPQlgCR/b6Hv9pCXyNZglK3roIlfWiIAGPgfTw64uP4aGOEAcAm7Mww2V2gscH/np0mzIcdvv6Hr7C/38Nak/vdyPG5qACiNMLhr+ISwvo0idDkLtAXlqmL70H5lIQ2RlBMl/pp3A/99YJEbCG9vrIVLrEIiggXOwO65XdgqT5vmz3XYWqitl8IcrqoarPIEjWQHYIhjF8puchM1QXVO05o2NBis0lRr2bkyo9rfWaAdLw40B0RHpQwRIC7/xHL4X1TVcELmnHPMzNe3Rr8u/94C2MpHBGtYKsVoOoLADVGPeZVFwIAOIPxfxRFZMO1FFHTiQHu8wD/0xn0g2LY0OnXPOkvllnmy3isqFe/2Anub/8z2LzNXwmg0xHTP/1voNODqlLNSVbwKuUcf/tv4H75H1Ak7Facg3EO02//T5iH91UbB0Az0slAD0Bkyehgr7vcSdOsSHt7/Iy4GSx4EcXHjLq9diFZ08KCfdHfEhDhlyqANJ19CRL35QIlWiKn8kDI9xdRa4gAKI2L8BjFKtBsxMgIUZaW82q40PIfmj+j3vfinZvvbevV/Bjxi02eS+99jNBMh6ZtW0K/zC2pE72tlveo8is4822hEUAo442XtAKNAXjhdH/64Xktoe7j1ZX15ltKrnDCKjP4zKBlm4uKoD/u+A+6649c6VqCisg/pW4po8g+UB4+oY46V0UlVKIsk3gYHF3Y6MdksMOCmT7jEXf4hD0cJuxgVnBXXzFK1ZMR2azIVhkjiEBexUFvlGHQhi5Zn9WtTDx0ICq73OPvw4PB+/cT/v6XB3x9Z/DmxuJ+P2FKrr5j3YXyGGrpUzwNYVJirudBOgXBQHS95DmYPQnRAOGD4UFOQ3jncD6f4fyC4/GEZVlwOh3DPQkMiOvr4JknSJP61IpnwC0e52XB6bxgcQ5uWeDUOGieM4MrCv5wgTWz3CnaH4ikT9IyIKfpOJjunEdIk2kiwFiwneHNHIw2cHlOUzjDw1GW8x5xs2QCHWBxx52FhXomGzUuYnBId0xmC0k8TCAC2pjpICCdlMmAoMiTjRtVHaElsYrSV1amMR0pgzgpnHM7RcLwMVc0RsigcJyilN8R0+cWhURUe94Q2lPQuix/kqSpQm/4RdwduuOlcLfJPFt4An5YPuN+t8Mvbm6x31lYa8Dx9I8uNM/Fp4WX3t7xtPBEGqGGR96hN4YagHytGXp6uMI10/Uh4TFjQJy9qjWJaiXFExlxEcbEopuFQiVGZCf/qhouJk1h7FCFFyU9qUMKdlMVnOObYodagxqMnlDGVYq271uDjJ55ujxq81dl6aM84Y6AYBW+2ROIolWeGY9HH059+XA27LAjWKMWviF4DxyX0CNyObWhYOTez4TdHHw3Z1BFKUNpHshHMV4kQ0/GtZkxSE3L5UCX0zZ3Pf4LCZMNodahOQnxkmKEMuggGnuY4okIgjcU7+zIlgdxjxRoWyRrFMbTUCzDQPV1VaMet7Q4KJWTxjZ/hChcsjFCVKz6BIRwN5Sp2HrTQ5mUfRTKHGEExi20VRAzgQxnl1TjHm3qUT9XI/iXHW8NQz2vaot4bwf8paD6RgMdGQAtZmztCfHVWpCUogK+pji0kMhMKoOcXNjUB8ThHrCIe82OsP96wvTKBo5WbkkDCkGgQlJF64p3wvj0Qk8ITH/aI8h9+KsSCeC3BD+p2Zd+4kMSup4yQ/WKUzNOgcfwwPw9gMecngE2J7i3Lp3uqPF8/TfgOIa//QzCbxQ7omDudEtAPw789gh/DxQ+NGmwLo8M+mFcZt3I3Vc32N0fMN3uBNIGX+imtUYIKCU6JcJXw9UYHdKv4P+aMUrQqN9+mXWe+lmSib0vyUQNM1YHEUS5haAYu7UFSvCfTlg+HeFOCwDgBhY7mjB5zU/WsPejCoPFpSmv1ktLAzVtG1bXfu+M0YuFat6Nyh7xi00/NuWtl9svqwtAt6QR3R1+v1TgOFXnY9trvPLtS4U/DSE5hiFZ2wjjFU25ji2nzlt9uWPuy4YzSExBxXSsT5BrAMz1PDVopLulzK2802UUuTk8fa5eytfuzb449bbMzTTcz1xjetoM4bkI6LDoXmqqE7HQHwJg4K2B283hjj9CuF/AvwNwgqjCt4DTO9gcagmNZiCJZ/lktJLejNoMxDlfTlA8oOTkrw0dzjXJjUEBfTwRjkeL2RB+8c2EN3cTbg8Wu8mmE/segBW5SU4yyEa6yIzljXaUqwGKjZ7hPSiSiw2g8d37cGM0OwfvF/hlgXMLluUEHw0I3i+pGmtNVLpHl9mKHnvmcBIiGiGWxWNxC7zj5EJUjPpaTa27qXW3VSmcI9+9RRRPfVF2U+4XHSf3WiTf/5x486I8RLdSVFUfX/QpiSLE6dVdOz7rHOraxvOQU4ocpRomHcQ5jXb11Erpkk+Vywh3RMR5qyaPmtOqPSnvGsRQxj8Fb4IRqq6yWajzxRAcadQtghI/Ruu5z0UGvVOQsXeTDxdWWxvufqtZ7AJ3EPIRreeGS8j8Jww1fe/IRqO9MgmXXlB6XNPKJ52I6NVEyECigo8gVu4eY4ds6SRqP+rAyLubmdrkmpGPkzXd8ZDSRYRf1EEK0USBNiGl0nXQELa1sGKASL2ylZlsQKhKrTiJvPPscvl1+4anKDpVEwflsIeH7FCwCIjy/pZxd2PhORwZ/OGDx+MxIEIi4OvXBvOcC2UinB3ww4fQ+2IEIQL2M/DmTrw3qd3ysSPTWFE5avmV0o8a/qo5UucVobDs/jEDFz8vFqSL5TJvjvd0MODZwMDkC628rDGFsJCNBmRsunA1X/6eqkl5tR/0lB+I464NY/mpcbhEQKHRpeJnpb0U/XmGsmW3iMCjbRgy1zgivqQSM5mrk+OaqY3Fw7DLUxjvBimDTnJp/g54AJVxUCFn3Ais0qLVkIamBloTu26mtUJlDApwryujCgbx3JDiSRqm+eKcUkyf4o3ne4O7/7jH3kZSzKwUsCp3YsCkNC6KfsoQCHuVzlNU9ZbNk7mb15y0xf1VsqAUIa0LZhQMdZGoA5T+Np6CVfiX7nxfvgJANpVXciHtUwD5HYB36FHtOmg6s7wFAJuPhxvpk7rvAPrewfzogus6BNzB3QUR6nj1N29x97dv1d05yERMg1jhUXmjMqLbstYIkfG4NgTr9DralJ+7dQzDmuJrrRBZj9wW0WS7wDi7Hx5x+u/vsLwxwC3hLXb4ChP2bHPf1HVQRbuGvNL6bCqNEFJXPbhljueGi/YdqWk0v+SpU0YyTXX6q1fQ81szDsMepB462tbffwx4X678L13Dv4bQYEfkFU4detjhWQjJF7aUMFad5IXQ5w+vZFr+EjaE3jp4Zh9X7NGzQzEZruCHN++MGeQFgCjjBbkmMK1+nnB6dQPQAuMXLP4Iwz8CxsO79txALKhfz6A5sqpE/S93BuRs2q1qZLx9WULtFvZik1VSLv8MYNeukRifP1v88H6Hf/dLi29eE7662eFuN2FvbNowyblF8IsLbxYgmCgPiGCAYmqyfmLEOoF4+UKSd5g5uGRy4RTE4oLh4XQ+w7sFp8cjnFtwPp+CsQKhzmmaAs/qTbx43KepEwwXLtwl8XiCcx7nxWW9deBcqr3ypZY5/y1akmRn4U2DnhAJLr40BrF+kWCKzWuiNzAGbA3YWMBV5VHoPrkqQeev2U6GxvXcrnMtg0VvCHmzHscs6hSD5C17pISvnpCpHilV5G/Vt1HUSjKXzNFUlHLlFSZR6AQdnwtRDavGQVkSxNBAMT5Bx3F+6saU02A1NMmkCAYa30CkEukN7YTsZcNaGAvQgXDYz9hNE+ZpShsD2/CvhOa+YDMyWXnZvnnyHRE5Pv6yZuzrSy5ouLQBxB3FOXVddPmiJBcR1EwprwqospO+9atMRVkkwMdVQqC8Ky8Rj7Uwlqa64stIKK0jWimp+zL2C9wyyxmEgWCVBG7q5hv2RBw/E2979hE5QREZwIBNOCExT8F9DVG4M1X7+WcDzABe3cR99HGsCYTZApPch5XKznADtSv/UiBu3RdU/RIJW9Pci5NAXB88Vci7vLCpeubqS7lLmNOOEVJzuLcKdalCJxJJjoKR4bAywmVOFJRsHBIQOxBbEBkYY8Jxz3jUjyKHkncbhJMsZAwMSnNCPB4RYpQ7DChmRWBK5Uv6xH/mfQjimxIkdEsxrol/Vb2okWxyfEnwFji+PcEcWEFcnrUIsASDK4fmh/4tl3yIa9w2jeZMNcJPnVqDcGlJp3lVxwaut+3nlwjdcrYRvcAvVcxuXegT4OSqpBGI631Q4lOaCIefz7i5nfA1Tbghc/lIecXDrqGkVdIxiuPi50L6DePRY7ovDKXejSUPW4dMiSFtvXW85IhMy7jNg54kKUHu8VD8TFqsaoe+pm+dtZ9WGsUD0IzilBVITpEFwUnbINJ/6tAtlLgzPVWdYUzZUev4RsGsCOiK17TmQ+K5Rhkqunwp5O5dWRVKpsqinFf5dLWZE+gbCXqA6rkx4gUUveqWsR56RgEU8FXF1OtJvenNGSWvN4CjW1b7bpoPlLsEbbOrmYlaKC/dLq6DOIKT6hjhARr8UK/NfkVbjTgD0C7GPSl0ETp14FznAl8YqsvhhWX9p4xLzLn+rqbnaFMaVQRr1aXgFlCKakaK3ivL7mbuUscXruQp4aescP3OhaR/uRASi3Mt6BfXQV0g96NT8jEdrCM0DhbHKrKhyvnwHwAm78F8Btjgwd/iBAbwEPmPej98cLXksTEMHI+H/mzv9CtqitrkpHLQTS0yUl5FSeCLCZIXB8LwtmRVLoPxeCI8PBA8Tfj67Q6vX814dUe42c/YTxMmMvqQM8BexOaMhgnpXsxe47RCm+GjYlkg4PTO3gWvE/4M78/xBMSC5XwMF0zLhdSgIKsrPRQTxwul5dQAh3sknMP5tITLrF28E6LuFaGldUTioRDKZERjCalxivXprlbTujvjZdgkhgly0bne+MhmBke3YWciOCo0GzDxzgNKdcV8ao5oGKj4W/MSPg5U1H1EJT4JiIWQoQStQgGljQaSJrZJbgLnAGG6F0KMBcpFlshdzJwu5w52BXHZJGVFw4P3odXxpAT7EC+nbgqjhYTkOoqlgbGNnNpRHnvI7Wn6oHjYJtUSC1bQ2drRAlNwo2INJkuABcxsMe0m0GzBuwn+9S38PGWXcNWSp+5MrAINZ0edsPj5yQINX2KUtP0yM5bYIDH0lIrHJ7FzzzdEpO/5RxPhfKqlHORE+iJHn4axmZho+k3cWqRn6DzhLfj1bcHWyuKekkBaEGjUuFdZp6+YxRJlxeN3bTNy3Eggv8hR94SM1eSx2Lr9dbU9I8SWuigRCdkdyXLRKfuwO4gZ9zftXueEPuTBEHaTgpdUr8pOTD2vVH6qI6o6tLGl04L+y0+CONISH36p48r4hkXIiCEuBiGvlNLLWgzfPLIRW3C7AYHimFoQ2JjIrFBkXizgHYK52QUDGHPwtwiCIYaPwhsZwFqLyVgFhxp/QyAT/HPLqQi5KwLSjpQ+XqzVjGNkRhjIFyiFiZn5HcX5FExqQd4AAvzs8fDzR+yw4JCQCiFd3qQ6izIfVJ1GVAS22Dy+RnQrnNnDjZeCLv4pFAIDCOMazJdZC/PztDpCZv3YwxBt4cKO99v2VGAyK6jLLnYC1ELKeOmGeaxmHZhhD8Dd3+1wv5vwC8wweksGq7HXZVeFr6GnEX69FEY9lujUxQK6HdC+t2iqeV+r7VJ7N/N79fFfxbz0m5sFGZ0nGyNqNrTTkrijTXttLQRT1u8BB4qJ1kDwY0mPyxOAVNG2uj1lG7QRolG469YIPMILUDsvOs6RtgXFAKSaKfZlD783mXU/rwszWYivykuCnjJCKCN4uZlB96nqjKIvatAVxa54sN5c08ruxpik+ZqqXmllaywp26FimnKGJxpaMDt8SI5Qw3q5oGHI83ULCrpYlZ7QsehL92e8fOhh2ifCsJpN1/MCzMCTKQtGJPyPHGoO9EKyDUmfOowAeov+qqpfMrzEbPnjhi0t2N6ytb5vuYKXDdeNxZa5PMILGZsLpTw7iTeYvIc5Oxxph498D88eM32C4SVsUhMBXCki62Xfg7/nsKY4YaQK0eU15LUphCBa77zRRxdGsXaFB9jH1maGLKmCKEvZnoHPjwa/e2/xy68P+MVXe/zs7Q3eHAiHecZsbVbqnpfgLgkcfKtTpDmi25CTEFWrBLokk3DsK1H4AuC4q529A/sF3h2xuBOW8xGLO+N4OsEtHovzmb8lkzZsEhyYCZ7k2mbAew+3LDifHU7Hc3x3cAkSUnJsVrhTelO8bfymdOmJRQvoTslvih9PedVwFaeGC2V3zagYADuwOeBEM44w8IZB7NN1D+JIzFC+9TDXHfQW0iYqqol8OFExDtIX4U6FOGbSWK5kWi6K01GpaXLHA3sOz6osnTAZGFTh3sctlhwMCwwORiRthPAegIeJBgjy+W6JUKY2RIS0ahCQ78FQm3nYqw1oXPw0smGpICnbpfqlzmNUGiJlHkkTS26eDuuLTDgNMU8EMxHszmC3n0G7GeZuj8c3d8Htdl2/hq3iv3uh5JyrLz81e1nXfyWFupRarxR9P0+BZ69gGp7nmmkQ+jvpy/eEYNWOxEqEK/LkmCwYmmRFFqPDeMBLIbIHWIZKo9OmTU05Om/LOOre6IKmYL52rq4KidSOQ3kypOyr5tsKQBdVDQmxUkL2IBOU0eyDcaKjsNIXWhakuDA8qApI9e3KlKsqQXNCpgP7Hy+MVq/uda4/oUH66SUrWZj1hZUMOaYQxifv9SfFHBky8ETpTohwcbgwQgQwwbCDMSb99yYSLtmZQPECsaTEorxc+osi/lTzV33V5egiOH4rjsPHZZ0Zh1EPZ2YzwNpefMaqljKXVAI1BllBL+kDT1zhtyE0sc6iO7bkvVikOjIZ6xiUeomWNBfcdkWKXFj5Re+ULXc31MpcNZoZUM5zQS6VLitQCa8KGf9fm7MfMoErL72V3dHSD2PM2mKsNWbtAusxxOujyq+Yb8nYOS6XqzFcrXv0rVr0l/stw9cNfIGeqrxr3VEozqVt5Wtea4PJJQr44pCCzJkV6qvnVsOFaJJe43qU7dKXVG8pK/+o3f46V/UgRdbfpV9GLWSgcNf6DEzY7fvTzuD9mwmnXbnyR+OdeE5URqEmYfiTxu4n5TF0b3YqXpnM40+rJV4VVtf9Uwp/Yp5nzaXN9egaNN/wlPxXf36h9l2gij/F3H6xOqj6feKce1bddTRtSfWThz8VOJ4ensoLXlf6NXWu8WVrUGrsOxRnLg3Y+CIxGA7KPedNUlyzNTjvdvAmuF52ICwgsJ1h5lvg/AB/Ome40m/pjqZ7OqLQ1+ZT7Ekhi7I/hn3D6rQDytvdSr8WnOOkfaxTB+7fixEjRibFLgfX0p8+M5y3+PrVDX7x5gZ/9XaH17c73OwMdmaCNZSUwI6DBwheGEwcTyMQYOQeg9T7BZjJzY4PJxbALkbG0w3JAOHg3RnOO5xOJ5zPJ5xOp2A8WHxIywF+cRkq7fccTjq4JbjOdm6Bdx7L+Rzi4OHhAUMwolJIurfQnjRkWoZpBJBK8Yw87r04kcCKXEq21idoZMzi1keACccz4ewtlr0NbpULw4XwmuUJ4yYkMt0mEF6OGcnzg46kqEMAE7zqg75+NGoFKLuGl3mZeXBOahsDCpd+629SEofh8Ynv1DVo+bxdjeUl1hz1BMplE5D6MJ3GYKAwRqS4zkrlqk4evVCZX63F8txVPWr5/IKXh7jWDBEsKN0NYapNrF1uLOV/Cg1sYVtN9mVI03rdTTIlXA01CGtEZ0UYXwnbDRHmqYPRDyzKJrFWy4dGUssqqBSSNTdfNKLOVFSBCoExxqBJzPUjRVzXQRqNMYPK6BSX750fS7M1KNt6uFFKdpqU4mjc7ouXUF8BU5GastAtuz8NAsYOBolqMleLvWd0GH+vd4dubE03YbvIxoqRl8Yco7o79aihpN4auVQFafhjflFkASCYoERPyi0DIgNrTMrH8QJ648OJBZOQu4cX102C0KIrJSnPxCOrefYpBW0ApoBJYC52kUhTBHcKwyAEeuvw6LREIOZAyLmdW9cUOFLiFTaAizDWx8VfAgMHTqUi+83zJjWJHBFNmak/Z1NhJaLVbKHgtOKwQRQUSlpdcJ/psTaulqKFzA/eOC8y/i73u0h7t6/9DIXMp6BkLuc2VWNQ0ZRedVSmTfWR3pM0zKYitswwWn3V8FEdUSXrMuIDerBpsNYmaWfx1v3VWaZN2a2RYkTPy7a1qfLETjuKFK4LgkaQNkjxXIKDBdhmvRb0scU56MT30hT38aiOadqr2tkzQuRvCUsPIHgJfPYy4bQ3ePdmSgI+gGb8S8NNtUaL8GXbVW4qeGIY5KcezaNyBF/2BEGnshS2rP9LuKIqi40iswABAABJREFUX2hR1YaS3lV33nSau0ofN/UPVb8Xkj0xXObvN1RWdHEnzdYqVpHtpVCO79YpuN7+tTV8RSiY0HE9m4q6Osf/6GHUU1t4tK18xgrD80XCNrgiy/D04usQ5TVigncmqU29MTjfHeDhYNyCBYSFAOx2sDf3oM8O/vQpFMwIyleFIYNektuq1AMjbtIuPmZ9TM3PJ60soPj6SnphDUMtD4gcWzQdwWl8FF4VvRe3Sp49Ho/A9+8Ib+5nfPP6Br94c8A3d4Sb3YT9vAvuh4ngvY93Y3q4BWDy8dRIlAEmo/ATpe5LsjMrNzk+umXywbDA6f8C9g7OnbEsZxyPR5yOR5yXM3x0qaSde8hpWhfLW8QAsTh47+DOC7xzwRDBnI0YMV+4cc2EeRH/E7UXVZcvI2rZkaTUeIirY1A8UVFrLZTilJDnCkB4fDQ4TTucZxO7MV6nLqwdRSOEgqy4lzj99uhdGCtiivy6pA9pjSnnnhgkpKzssCzHhfuE5NLvWD5y+8qpLvyfdiQFZAOIgSEfdG2U+yckSYqZPM+VIY6LUxYsi1elj7/65INO3yxenS7rM7hMlPuKQlyBLrq4Q40LASjOtVDxyRBgo+twaydYY2GJAJjsha0oSx7G2HUzX9UKj9vSPcu9xKXK6tDjrbYRF+mH0th7RdV4womIVeZbhf4gKbVTWh3UfuVyGjV+oyPqCHK5Wsih4FweA0TZu+Bwp39D9ORJIUmqyy9/WyMEomjOCWnJF25S9oBaY47biU2oy4pLdesiuFRFgn9DeVygdhDlC3yzQUL3RL+ylg4M+vyKCX85Ka281SnXfba+TODqFwVQdmLcwGHxBA+Lr74yuLV7/PDO4NNnnVVORMhzJgdNG9TwyckDQwQYA+8tkmU9pjHGhv/kYOJxVMMMR+K6KI+1sQb3f3WP/es9zM6WczwSXjLRFUlk2EgIMqlbJcikeySkfLFBpBp1xJMDK5obHzRx7R5DLBncQbGjl58gKOZo8K186gdWuC1Oq/hBH3UuC6uNFIQ8A2X3leLnqoKRcYvM6fq7em0UzrHqfF9J2yL9Iys8naiJceGET7riuVvSWqh3nKflFuOzCox6P50C69dOyrQwRvjtUiUXqm76tI5oWMeqoP6XPq28/H00Ks2GhZX2ljYFaiNXwiiV5nGSvVQplfWueZFjCBRwHQQnBjhIgZPnkJ5fJTT5e55vpYufUEphhJB6qo7RZfXmTgFrXX89r7Uhpionn4Ui9Z4pbzYVStyg56PwVs/JQihT/UBEeH0/4xu7x262/TLrUK8tNSjFaYgXUOKvG0FepApVWPlw0QhR8W9fNFQMRH67gJdXBZkvA3lLWV+S7m+FuaS/Vxfdy/6TDPTTQsdk20mzPfZyhc/jOZNY9KIL+C/h+vC8/i9lwyesuQqOVX71ytIkl3NGyYFtyswGG0zwuKPPYCIc3RTZb4ZzFp+O9yA/gewtzPkEnE8QpT37wD/v92dY6/H4aLEspgSGDNx8CBcKk9PNBuSy96appVIzsxlKgxPvrvPswYTkmsZzdFXjgiLecVDEn32U9fwSL32O331wVeO9A/wCOI8dW7y92+GXbw/45TczvrqbcHsI7pisVZs7DcJm1uhymG3YUGKEz8pMVNnnUeiU0xDBxZNPpx84nloQA4R3J5zPZyznBafjCefzgmUJpyZSt8RqzudT0ZPTNImXHoCBkzvCORdORiC42Oc4FmDhsoS5CZk8pys2ZHQ6MynKBBzMCeGi6Gr+xe/JHhWzanfRejowWq8FiYE1Bp5MGHuBQ+0CNIq3Naw3XzSSTCeI9prTZdd5Pkc+ulr3RLr60hmUXLwuM9oYhMMD8agFG8R25j4Pb7KW1N0SLsx3CxN0bWyzEZDzxeahQF/x1iYYVmAAdqpRqinpfogYqS+kLvQhrVy+hs0uMGWIwkOVtCNjaE5LLS8HBhFjpuAa3JBJa7AaqfiX07hcRw+0IHQNXzb69OfBC5Tc93W06YmumUas26UOKyeIfk+njDrFF6ykojyCxHNRmQCIcM9AYeUcQ9jvup6lrBYoVoXBjlBWiaurZXRK7RXS+V6dEtCLOME3AnwEaX9g+m6qQkg+CRGRArSSsq3/eqNDDeP6hWNVJf3PdZmD5MWcxTpbuG14e6l4AEOImAww7RhYGKeF8fqNwf7VAefF4dNnn1Iy99vB6Y8UK0RU9wPFy6UBGCGCDI9gVKLokoniiQg2Bs57EAlRE/pMIGtw98sb3Hx1A2uzt7/EEkQrNfS9ELERFOHLpzYo54sllQTlctianuNg67Rpd0azpUaieEUm3Qbll5X5n1ca1bM/vobjuS0TIr9phVaoTLNDOW0JZ8YDEakLfuE8zwb+tFIBMmPaHVoCkIrnwOr5VF9v3K7vx66SO5XU758y75V10vClMw7l9zWmooa9vl8lj+VGeGvQZE11kZfC9UMDy2V6PXbXKG4FO/Pvqv5X+KEwZHYY3MjXGEBtwJC7IeL3juI+w6nbWPEeakMEgHxZoU5L6p20e6iqF3v8hf5NoCgYSM2XqtyUe0RroU0NPUcLA3HhCmJQ44O72wlv97v03nNjlRdP1dfpRRkhrgqlkaj4stkIsb1Wzav2oSnrvlR0vebWg1JUPCE0+PEJZV2EdwBiEz0as275owEcRAt95TJhg8+uavs2GIq6O1m2yi8vscnv+vauzetr6eiG9ApPPNcw8ecbNHZ+at7R+5cI19ax1r71si7X1HDWG0uqVWn9NBT/Ojbwvjr5hXTvc5i6scyJHHbmAWfs8EhzlH09vJtxxA6O7uFuLez7H2FPP0RXR3IngYeZCWY+4XG5wekc1E7CjrC1WG5+AZpmTFgq3oGKDiCicGI9CgcU4TWRbyGT0/m4y3vhcGnv4sLpBO8cHHucz2c477EsCxbn8f7o4ZzH2Z/gnMfx8YzFOTycTnBuwfG0wLLH7D3+/vUOf3V/wDevdvjmjnB/MLjd71OPa743wEXxv4m9L4YIUzZR2EKOsmO6HyAaI3w0RrhwH4RbHBb3CLeccDqecT4vOJ/OoU1LcONkpHMQynVLuNTa2ODlwJgJxiAosNmHS6ld6AsQQNYmeJkpel0OBhWBs1HGV3OS6ighJDUjx+IcKAl/jXEjqbibB2WUIJP+e4QL2K3adKK51QxbHJdCXsTlwLm8cJrGx/6KjVPtM9I2XTDl/CbyuKW7p+gOGwxA7n7QG1tiMXEAyCC6bWKwYUwI90MQwt0fkHVN8f5aLxDFq+VF+d6MZQQsd3w2SqiTFfky+Lartmzfq9ibPLEIsX/Lduc+jH1SVU+qg4whGGsxkYEVgaphdqCMPq1cMeYZSllg9HnwmkJu/09B91JlIyg259A5r+WrrjBE6KW7YX0WncidTyWpvK7PFQNOF8S8pEDMVq8m9SqvOMyVYVAwoZPy0qCMd5hVQK3Mbw1GDRM1qdfGkYbN5dSLTwkKLZBCZIM0gGpH0Z5LC2RLmrXcVW+tNLeWMUY1Pw+dXNkeZnh2Ct0zOvvTIZ+78bI+48QKjFTg8Iy1qUwTd2xYY8HWwsfTEOw92IYdKOFmKJc5W5L53q5bmcdiaADqtBnRJ7c2hMQg5UatLuhuczMjWBJKVn+4yaVxQ1vfViNEP9la7PPm+Cj08MSlsM3yLZxWhL5iLEtOipLymamCgts8XR2yzAUZy2bLDOI0aVvMxWkOYcbKuUUMsDjSBWH6/Br+tMdy+w48lbuNQgqCtoYTDHZM+Dlm7GHjcqOkGFa5CuBKaAf93jA7mZnqJStq6SE7QtjR1ZvMnfRUEdN0oJ7WZ+yQAmojQN0DGnSUSux8MqpPQ9dppPom/d7hWVrox0x2sD8w8Jlhf7MAn/JkLk7IFJmAwy9f4fDNDQ7f3Kg5ogwEJPMLFSNVtStmELVDbczYatzqpbhohKAynabnm5Tm0Yoedr+JL901rux54RVb3PAOB59PQmgjRAUcmr6u5qKKXmcoivyqtM7YfFkZJUnzX7KSjeELwvClJtBPEp4D+AX+4Qqe96cOzzO6lDn1z59K6LEzfwl/ymE8Uh3ucjX99TXk0FH3puC8iW5mVXoGmE2bxxBOtzOs8XiNj5FvNYA18NMOhBm3mLDDhJknOGOxGAO2YQOaeXsDulVQxeJne4IxDne3e4BtVILHXemGMN3cAh44/u4RvARlaK0m1uRTrlWQOAOCsQTLRh0pDg9OVLhk4AEskwsuiWABAuZv94AF3h09zs7j+HgMBojHE06Lw4fHI07nEz49HkBugVlO+PZmxv7ugNv7PfaTw2RsJYPEPxxdMzl1TwOQ5FeC6OQ5Kd+DASIYH7yPd0J4B8R7ILxb4M4nLG7BssRLqc8nnE7B+LAsLhgRQkVBKc0ezklPGBhjcTjcwtoJt4cbAITl5ozz6QQiwul0BH+K8lBxmprgxetyNJAk9kTkOi2ryJRX7vg5RfelWREVsxtc4Z/zrz7ZkLjuCCeRAYyBg4UzExyCIcKIa4MIsIkzJHigVhBUgmd31aqd/w3sqa+q9ig+uJZLPEQvFg1VxocMJpzlCCdbsixHYjAoKo+dYwCbmOSQn+JF5OHOz2BwCrKVD3eARhdcFE+9JMCNV1dJeIjjqIJFTEe7dbvXmYRWl9L2W/mZ4rdguEsGHQVuXbiMW3LnHXveRCOaoeB6TotPurrrgvTZQDIclvcXSg9cYYhod22qp97cuSAp1ULpU8hzo0jaJuM1QRQl9drJ6+pSwTXJRKKQdV9dLUA2jPc4SfYpXacq2duW2b0M1GhH/SXWuZeHuemtNk/zeVxPm1RTkeulpmvGqK5qlPXSemguUaYNLa3SMIvVvG5zY4OPsdW0p/JBE9WEzI0cKQx+BJk53A3BNp6MsPDGw3gO89FTzp9Kp+6MTGuNkI6yhnUePhZt0P2pGnG1oKwyFMaHQUyRFX3c8TQzwwDoXjQJgyaM1xOImXB1Oor0hGorftrROyqflRWiRblCDMJIZ94wjg9lvmdUDynhh4kA3zeerhknJLUXYQKR/aLM6+la7eMtDB3g9p+6hogOYcAeBm95gkUtcPUN60P+rBO6+bsJW+LbzUlcGAQuhopBLgSOGs1V06MpioVetH1AQ8BFEczlfWwVr5hPYVWVcpluOx0nRQN6vm8ZdALMrz3gqpyU26NtCYevb/Dq332t4jtGiARWxQ/pwpuvZd3roTaK5TlakYyEq2sYRich8rd1PqJmQMb8yPUhyKd5tG7Y4mueMcfdomMjRC9cA1S/Ty4ZIZ5X55XhBfsYaMesNHlUb4M8TdlFrqeaUQZIoP5WL+om20ag18KgAau4E328Pw6DtBWO7Cb5gtNtPYzw2EaA1FpqclzZqFHq66WNDgwv1L9r82HEv11zGlJyPO/7ljCC4eUnYo1DvkzpL5G7d8dbHRPePQyWzsmHHkhsCMvNDJoc5h1jMkC413HC2c8gb8Fk4dhiRjA+sI1ucq3BvN9jMlNcamF3NhFg4yYKa8PvZMMlzZMR9yjA+fGM3/7jGcvjAoqa61bHE5S4QpFFoW8MwgW0VvLFxpE4EkZ0Y89wHHh75wnTzuCXP3uN6dYmQ8TD5yMWt+DT4xGPy4J3n494PJ3w7vMELAv4dMbrww6v7g64uyfMeIAxtXya+Qr24nM/eyjId3Ny9FEfZbrkkim4iwpGCH0fhAv3N8T7IJZzuJj6fDrifA6nO5xDUl4ZInjv4JlxdmewZ8zzHsZY7HcHzPOMu5s7EBks7ozz/ozFLTDWhMuunYNblgg3JZc/jj2cak/xoGWkxHvmjcA9ykpF/FgWZi5lX11hninBxODJwpGFJ4piQKhdTisUlCDR3EqLHXPU8IZ4jn/TDGvWKEnDKBatL6hQwQBgr2WReMaETNKxhIvPjYKXk/iSepc4nHIihvUm3bHBHFwtJXfKTPGb8FrisileVq8v/JCTGQCy4EKlwkspk4bYmjLYTW/WgmBX4I2eMpQ8mYtrdV65LCT5StZdWn9kZBVCD/omOlCMVSdaN2etnKq2NU70cngpmvh0SvgUCK4wRKgqCC2BWM3cCpmlYvL6QAUMayXU3+o8CiGRQnCsUSdQYCZBMMgItqhmwNRe5HWTybgviQxYCSRKXrCRpURBKF6bslsgOxJXQ2mRscuobT18UlKdTvrB3Gj6B02ntjtgt82uRgn0hHC1ErzIK5d7CTzFV6y9hhCZzvmEM72HowOYw+mFsGvBK2Q7rsEQBQu5CcTKxAtSrbGBcKUO8mAORNKzg2GHyU7ZnyUYxhvwxPAcdpaSiTt6qR5mRfGI0gVSep2FPkKD1PW4Ma9NrH5/1X3AcXeAECcCxbsoTGJ+C0VbGvPIaXDc7aAa2M6JkmHpk5/4ZWVdrQqalyZi7zN3/G2qOpLy/tIaSdtW+hX1IePqccBeXLG+ZDwr7kd/3V5YhzBfVwLlf0QgY0qmiAAg+6zsh5aF7zE9ww+dpd/W1KubxrSnE8JyaCsLF6yhC8eo1Uyd01xb0KF8ae6c7dPFboFFmsEud5UOzPkRmRiUR8u5NVjHMS8NH1G4EiNI/NXG2pw8QVikrdtQsihPJ3RXGSH0fO6Nm2rP5jDgNyrWIbEnQDkGIj5KcD8esfzhM87WFRzxNsVuSY3Kjta4s8NbdHmjkrY0dPrCuNX8XTUaF/ibNUZOV/LknKs156KvKe25Nf8l9EOfDoTwdDWt5pGfgoP+MtI/bQiUaFVY+0t40VCusTX+jEFw3ij2NsqA+wluP+Een3FDD3DOwqUtuZp6Z7os+hQ2Bucdw1pgN+1hrQGZHcAWe+zw+BF4+F04cW+Ig1xkJiC65rXGw5p8EW9II2s98GNMgIs8r088MOCcx42ZwfupMP6LeFXAGvMYQtgIRwRjhK+W9Co/kJSuopTm6LaIfgD4A+PgGHsGDouB9xNeLYDzM35mDzBfG9h/mHE+L3j89AB7PGH3+RE3fgm1iNwr/IYPbqn8eQmnGhYPeI7yb+YT5I5f9uo+CGZwPAkRXDB5sDvDexdOPyxnnE+PWM5nnM4nLOcTluUM54ILHmkzew/HHO968DBkYWaL+/s32O12eP3qLaZph/1uhgFhYQe3nAFjcDo+wtoJp+MRnz5+hHPhpAUp3tOYoKH2MGFHfT6GnGDIoxjaLc0PUXkmcvGb7wUJ0zr2SWTeCtk2yRNqs6UxgJngeMLZTHAI7plCp8T5GF0bmSiTEEIckGWOQs9OJTeYXUexgkE2r8V7UPXkA6G8CbsKweaA9qADIWmGTHCjZEDwJjnDUmVQLCfeB2rCiZVgJMuyCMUrxpl80Ap5E+euAbOHgwsXXQMAm3AvSmGMUO1W91iEAYht7Mjc4c2U/HHD42phou6uLOfk9wxU9hql6+UE6ktQq1YmuGCE6JTw5xXKWf+lwnbXTErpX8yRTcaAVgBKedcUAhdL7Zdd5O4Ic92JD0BUjzk6LKqkaGzqq4wQleJCi1ebjRDpuRz0jMz7eSlD0/TpduNDW2Odq9yJSDUF6VQzqrMf3XzuzY/Vzmz7rk3Rz3+9oaiX5GUQTZdkxXkxrsGDpzPYEEAzgPqSzZo46rKRtCVJQSrom4IiHkA8pRCg89HAYXw4CRH8TVqQcYHQGwPDPho3TGLAhis+oYONZOOZfV10Q8ENZRyQmJQIV3YVJQxfZJtqbkoVTFTfFVEm6rWiFUOeSASuzDYyG1BiLmKgkiEktTauM8aVBoiu0LsybTcFmVMNYGocap5Op6mPQVxdtyoqri+NnPPcCv3cxyHxziPO72PUOphRLUJp867R0i2Bq51GQkM1XNeShN7plZVAo7eOknwFG6WURZ+MNhnEbyI4XaZCUpwimsqgIIprKZd02mL6CE7NuAl1Pw/Yhk4Lhn8VwE3ZAnPTv0WCEQS90doEcLesgm5qlNXBz8LW8eMZ7g8P8K8N8KqkmfVpiD6rpPjAzhobiZ9lF5brvmeEWIWhiK9GboWHqnGFpnVbw1ZTwHAKKCtEfsylrh4yUJWXxoz2PQOyAdgrw7CuZ6TMSb8AwHXYYiXb9O36ql6sdRv6qZ0LT6u9x0l06+uxHc8M1518eYkyfoL596Twch17zey/JvQhfCpujU+i+/KA57yrOWRgnM2M87zDjT2CjMEEhmVxq8Jq4wJQbGKIvMTBLCAiWDODYGBoBhkLgxkLM87vH8Heg8jFewGXQAMNASb4pRe+RTbXCd/rgEIZLaRG+IeZJtBkkrzJkf6KtJX4IqJohKBohDDpHoZ+6PBFsYOX90veO8Ue5IPqenYeFoBhg7tXN/jFX3+L4/mMDx8+4fT9Oxwfjpi8KKLjqYdYAfugmA/3Ofjkainxk6ROasCrkxByeoLTCQj2LpxqcAucW+CWM5bzObplOqX7IOQ6CYHBc3AH5byD94xpv8M0Tbg53GC3v8HNzT2mKVywTQRY7+BsuIh8miYsi4MxFsfHY+gnXuKpdB+MQAjzz4DhKd6lx6X3hSFfpIdiZRnnS5alj+VDvN8gueHVdRjAWHhv4aI7Ll8NOqk8QXceGUNWKeSbRBZFqLSFK9oySR2XE+o1K3RCNmopmYODSzE50wGDcHICMV0qX1tNJDKcHiDySaYA5U2WIUU0IJm47dpTMGQA0QgR+znWTb7ESGyUbEwU7QKiJNzEFaofUq/1uQeVnGWLeM3Ql/dL6k8SOdJvjGHTN9rW+KO8cLxuUr+8tQRb+uvLGQO6oejD+LJBD3pt2H4iojI49IRi/b2Moe4YmDSw6wOg3W3UX3oquz4s1PwdlidYSrmE4KIe9XcV9GYlDJJVhoRRUTROkY/6SXeusFYXqrkA6pZU28tcGfvN7FqB1LfdYzHWi2yodZTmmeuygbv72q97tgxrFzg/wbOPFFT9Z2QXfxFYglzoJX4g1RwXhamhYFSIl0dTQvbhjggPD2vD5VfeBt+bxtvwa13AVcYXSCup8JVVq1bICbMZGDeTv7UI56rA9W+xe78KVD1Qhn2bklHq0MpMhUmGhfSMTYr4d57aumui2VTRGZM+9i4+aDTSWwcVQ7ceuPrpGyEuFzXokTzI/ZSDgrmARafjJp0OCTV2yw0CIM3A/T/scbAGNJvoZkedhCAaoBeN2+vYKu5ZiqvLlLQboZjR3F3C6Stm+cq6E85L7tNk9VCD96X+YenVes4pL2wUoJyjHt6aHBIHF16SWi657zddlarykIoLgnYBRK+IUondTS5v3Jkfl7miWEmK0O3WpzmKMpKCfjCuz0PlTwvPoNHU9LUYD8NzStfJ1/BNtXHgyR1BQjL7MDT16Jmsotbm1oV0W0BvpoDQ/hUcPDbhvFDYVPTL1P+FW/KXsCH8Mfr/pY0Qfwk/ZXjujBlvSMjUuJcLcM72eVkAfmfhbmbscMK9/wTx4x92aTPO/3/2/rRNkhxJE8ReAVTN3CMij6q+597Z4ZDL//8/+Dz7hUMu5+ye7q4zj4hwdzNVQPhBRAABFGqHe2RWdU0j08PMVHEIbrllmpHyBMoLXiiV4lXRRWi5EAI4AT/+irGes1q/M6YgSmMxKsM5rAASQAnros5hggYyhgokXOBXCSVtWIzHAQhsLow6XKKwVDkCCMIbooo1Mkr1lTYMVKNUR+UmNd4klFW5YR95XNrdQYEBRNX0Z8Qglh8HAOEEfPwvn/H49QH/+i//HN89f8Z34TOIVyAtyMRInEr15laJk8SHoECIRVhDyGT4rAghyKwh8qrlVnDOyGktMSFSWrGcz1jWM85nE0CsSCkXOUfOEuw5c0JK4pJpno84ThFff/0LHI8PeP/+G8zzjPnwgBAioBrzMqQBRwZinBEQ8PLwCKKI5+cnrD/+IG6hllW8G+hkZJh7KV3te4uaxGKAWF3/BEZW2tjIcFvHMnxi4SHvSgY/hQ3z2WgCDhEIE1aacKaImE94zC8IOj+yHsQ6pXH/2+BQ3Y1tAGqeKh+pdGLBWdyhP9SX7/AqU2KseCWLcFEWNEo4Ql8PGYx9JbrrlH3JIJHXMIMilRhr5oOp9FDxMaJc+8ShvrPOBwLU9VOh74oZB5eYFrWch9MhkB3i6+202h3cJdbxAVCkbuxGh/34k45LBmdCYkbMEgsj59yN6TiJS2bqdOH2EOZR+lPD+vZutLelO4JVm79cBw+A3mnDvmJNSxDRDoE0Spen8jZqtsoOPTG4V58/hFj394gC27bth6ewTKgrs22x1t+MV8tc6ceub3UrJBgDd41RT/0hN6pkQ6V2sIwr3a3tarp1fdy2HC628dryN3kGulD5eGXYt1rxiNE4RbnhT4s7YAl6wcjhXOe1XhRV/lC+1JaLIECsG0TIw4VBwCRIaVCzXPkzywhDeHPRhrk1UemjL+dWrZ+nO+pttCu0/xeXuWK/zb4aMrV9I4OqyBfz/dizHvB92magYb5x2hWZEOrYMQQRbt7vHGw3pMJfusSDvRXOm8ru/cAbhRC3NmpJNXQuWFBQAA6/jELsyZMqhAgeHevXDXdTcn0VeJT65gkcXXO3ZHR3RnGzSrUfr2fFyQoqdhYFx+zbp8HPSyeq/LomgLCPhnDmbZ5mpbv3YsWiOERCT1E091VVJbB6CY6Lvbm3K0gNoP3Xrjm3bnrhRVf5CG9x6g5tOxeEDm37+w9374g3CdZuSxzaLVuFK34Nexj9+IyQDsJOb7d4Rsfh3x+GSzuxWx27eQdryK2j0me3pMq3u3CXq6A4QvZSeu25cVu6jAu/tt1xuTf35AZh65dKhit9KQvf9i7q2trJu1/ZbTCNz5o7+9MwNvcq/SlI8236EpYQXyrtbukLeX+OMfpZ02gQmkuEUC1Eb8TDVJHDXMl4Pql9T0xYpgmRFkRakDlLcGIVSARegVU0wc9t1SCIAAIExAhwCnj6uOD8xCAJ9YApEAhZAkojg8IqcFMCyNz1UlOnnW6MWM45e8qoSqe55K54BMOdM2w4dL1nPWVayhAAdRtMQXzH90plXp2rmRa2qenngvR//6klE3D6/ozH44yvHx/xPBECndViISOvFtdC2zOmuQokzOKENcq2wZOVcS2a5hpHolhDZBFIpISUFqR1FRdMq1hG5JwaIYQdVTlLgOysjPxpmnA4HPH47j2OD+/w8PiIGGbE6eD6KJrvITAwzSJYemCAAk7vzsjMmJ6fsDDAWMsYyjwbjl7naHjOs4+mgLqmuaLFWZ/lbAIJedC6GvZ4dm27YFWBwBSQEZFCxMQJxAnCGdm5QwvwDB+MsHfJVHklOr/UcU5MYYorCn/t3id0vCMipcd1rZR+ekBr3y/+VlpUlEh133g8jy3+hLlQk7xMAWrrUjsCAjiIgQQbpWyWKbnAWxbjkE+5xYvLTnd4ccE/mh65kdavW4XB5gAAkwmyUKyNLLZpVamt436ZH0Tuxw7Kv1v4hsc3XZB/DDiAzko5s99+s99hEWFfgls4GC426svI4/5ts74BXFgE28EfVF3SlpFE5SIAzHxvD62zY8MdMmVzeZCuMDEMrgbQ7QIu2pCb8fE5yd/Lg1zUFNleBB0z9aZ0S+cwnJsv1ILLuLPxRyDcFSegL/y2bU6D+u5Jm1BHzc/r683WrD+b/bvMXAMmOWyAmc1rYNs4iZCBAYQgKGRlBNoBn5FzQowZOUqALZ4mrGDEKFGzUjIksWrjWvOlS2S7FCrzJDcGZs5aL6u3nccCi11Dwub0vlZRLlPTNrKLjgnw1iPltKm2vbWVzTLsLr63n99X03XiVc+5i4K++wZbCAu4M80w5Pre3thHbaNFJPbc8vix7c+/FnWplyX5Zz4omUt20lwVRvTHDBOmj79A+PwB61e/B8990GoxNrWg73J1msYYAUFF+qRxVKwUGU43OtdapHP3fBw+HfXvtnney8Vo92YvPL0HX/HLseK0PXJ7Yc3SYD1htFb2ayvnubs7G3y0K2frqsih3JTRCyP81xV4yVthhOImdU2UTiDUU7HrX+2PF/SWOjYw6vs+ZsYlYcSV5OHcfb9XPw2fDirZqdvhQ41wpT68Xrem00PE7/7iiLP6tt4GyET3nJqXBR/vx7wvN8Jjds9du/9oJ1s7x3t1emFJWQO0rbA+ojp8Tf5NK7tt+9n4GXjmfwTpMn7a53tzGhL5/5x+2nSNnfTG9M/z+U8rXZsuf2ZumKiGXxKWFJBZNPAzEdb3M0JgvM8/gFgYpxbwODMj5SzSglNA4oTvecHzjxmffmtKZVIPewVRwy0gLo8oLCAEhBhBDKxnAieAKCMgIE+Kleakt0Zu+xNUeSaIFYTgG0F82FOGaFyEBlcKajFBIdQLpdw3hvMSJloEUrN0MH6T8vglBgSr0xljgl6ekvZ5peXapyRBfnV2ArN6spK5ev/1EX/1H/4Mh+OMw3zAPE2YYtBA0AlIGiMiBClHpsAndQTlOTErlZ11BeSs1hAJ4FxcOeX1jJySWkIsWM4nrClhKQGkE1Juo0pmzkjOFdPx4RHTfMC33/4ZHh4e8f7DV5inA+ZZBQ3sMXRZD2BGoIgcpS8UJTbkfDiCifD89BmfPv6osC2yFoLRznYvcWFF2LqpZHVGygAliTeZyVxh1jgQDBGgWKxuo8MNr6Ui1vL4mO0rAigCcZIA6zQDWZQhwUGjRagFSkdPFPKdahy39tSngtcXFopjhnvyP0s1FcoBzdCxZ9z3HZrXtRQKX6JyFYoTDHtSLAV8QG2BrrgCAzSwRRlsGRauIDfQ2KZWhDFkyLqlIG2wWPeXeJJ9X8zLzIj+bPojcNYHPV/F0++XbRtyFpprXVcgMF7WBWENWHMCcaxnm9LZ5BF5gnKGWhz+evpTv8/d6jAmxRvSHTEiWn9Y1RdfdyR4ArOXJvr3bnduy+6lvrPUfNQD8MKVRGPCflwn66LkjdnZJVi31g21AI3ykIfZH3ttHd6f46Z+99yYVtw/3wd51Ikr70d17lHGN1Q/kq71Y7Zbp2/3foJhu0Zfd4i8Zi96xvzumKA9uPfXb6sDQs0brcOQheae4G7cUSTjgAnxgru31V89GIwgwcKyICQhCLJbrCRYXToFqpZ0KYOTInrNeWF9tnXcDIbr+bU9fCFtEFB2n93Vu+H7trezuLQa1LZZB4YY6M+7z7mfMslZsQ/S/eNcNaTqEwbU9BmgDm/oWcX1q8wJbQaVCpZ31aLEB00uiGHVsG8EHQ1Bc4MwokvhfATRjPT+h92So3Pelr4RL3X9kyLg7tLphqH9SpUA6N771K71PfjaEturd5uvt6opVgz34nCuCSNAhFDZgfmSEO1Ko7TzvTzRS7g5pu5ZFrYVVoB+yKCFC9rsx4UUVnIvavyHmnqioOmfrZ9rzHtsx4W6TJsaNsxP3Zs7w7u5UwcvxjC4Pvf4TlfHjSjK1Xs5TYTTu4icCJT3hBHtvjVmfn997cHg4e3HujkVyLcxugc1f1k77fxv227HcCyg4pqXaolS/6BjI5j2YLyaxtP7ZdPOgrxlK99ygmzndJxuPTpuGYMvaiCxUxm/kcD8UhYVd7X5JSrZ6/ctONy9JEizz3vc6Q+fLnalO2Qv5bV313p3a77bUg/RG2vdOW4vbRPvoIn1PA1sLnGpKDtxANYQQDEjh4RAqwggcsKaJbBs4gxeAV6kzIkJT58Yn75XvI4Z3Gsb6FlstFsIDCAjBMGtQhB1BxCLp6NkrkKTdJjdjBAkFgORCgVI8Q6h9QQ5iijuWsqYZRACKCgeUd6Zpw1jYErdwTxwhGo7EYh03FA9w3j+Kup91k2VYxX3zM6agx2TNAOIjkaOh4iv/uwdYggIrHEptAGxasgo7nSUGWv72eM1wv+tTPdg2uPGGM4ZzBITQj4X5JTURVMSAUAWawdmo+orLVTddAHTNON4fMDj43s8Pj7ieHhEnCYEkpgQWc0PijMdo/cjIeSAGDMYBxwP4srm8eEROSWcXp6xMCN1B50wcWVyyvg2ZxohszB2TfmxbByzltCYxykrfa1McoaOVcFRBhc6kVpDiEAiURQLFAQR+GxwsY5HptVbr6Qr9V6sLotqHVaegTLuYBGUFbKJMGBLDS6SEduhMOdtjrl7jrp+ujLGjDC3Vpa3UaR0m0gENB6ApncDmG0+xCKi2e5W/S5upzPI3LRS/2Ub1A4W1+cLiWxf6PmaM2NJK3JiHHPCyhlrbqOokhNqjivtcL0+bab0RiTgypX0h8YIehRuOPS3XoY76WZBRGgIEtPek+8ekEpQ1fwtKeTSHjG8STsb4HpBl0GYoYWperVhOZ6FZUXVnz21sPSSvT0hBI3elZ+d26sOsEZLsmS8oBHXzM+w4otpe4H7B5UhsVfrteZ6oq3vWz/bjXDrStoyQe9L+8Gubij7BqJLoCa0R3WbY3e8US+qw5Qw44QpPJb3nn9OLr8JIeSylIszBAJnFR6oQKGUViQChm9p6YwEIKnkeRINEWJMWXwyxmkCEsQ0MgM//pdPeHl3xi//b99iepzag7vZG9Q+uyHdegZq192otjvZX3v9Pd9kMoTALvgLAGzu9+s5X538aukZ6u1K+qmuuH711jOby/GrBMMW19Cf/rwc3xV+7W8Su5yNo1hyeJVDSR0GZQHMWBHrBqN0VTVrZm8oDX6qsSAC2V2k2mBUNdsbgTMBRQOlGYbsf6CI5i7uFa717qa9d9zmGWZrz97+nL83lf4oAeKv7Wq628JifTNR0+ZM3gFlb0x0Gbi7u/Zxs+5GhMROYrI52869h9n7SjarHr+sS5+cEKN/VcC+Ng3X3jNX0+5bqhniCeRf1ad/AIZln6pwoYN4JIS4XBMqfubXzWhPXK6sx32GAohBHU3bvmwn3GlhLDmH8zHqN23+tfI7Hbop3VF40FC//8rx2ePRN8LQ1zfq22ZPXqzxemoYJK+q4Z9W+pPp2SvRqXY70x+W8/DP6Wq6er4po3lNhJRDYbit72bkmfANvsfML6BJFJLTqvTYi2iC/5Beimud5YXx4z8wcmJVXlYhhmLVeQXy4vAeUssH5yoIoGKVYPhmII3zoHhpyRzsbhDGXKFrVJPMBBExTGLJGyKIJLaC/NU71Jz5GmeegsSAQDCERNvWuBXTpPEroghHLAh1sPdaf44BUd0FIwSAAyIFBLL2sEXIew0Sar9OWPW74VuyDbP2w2ASqwNxjwTOiAQEiggUJAaGRNFWB/OuXRtDhlpCACGLO6bE1cVTzhITIqcVq1lCLIsIpNLq4iboGOeENauAImccjkdM8wG/+MWf4/Hde40JcUSMB5lTykr+SDyAoPhKZsUrSGAPgTCFtcx5BHCYJwRiPD19xicSt1DZLA4AkKuxkEwowylMYQYSMogCkgm77L1+yYAGY99OmWd4y0rTTMqzeDoFnNcjTo9H5DiJq7IQEDiAGIgWuprLP/Kp567x/IwAERJww2XuGOf6LRsVZHwBKZMJRRixryu7wVwgVTrCovAcxKqDrdHyXTNy5fGYFQ6rBQ1zQmVqsAZShyiIcgbyWl2D+XyFQ+V4JTrRVBa7TQUpjD2i7/ZC089q0dWMxUAxuUirPAwumXVVsRhh4Lyu+PXvvsfD44x//2EC5SN+9e4dDocZH8h2ANrF+ur0J4PN3JAqPfyWdIdFREtsFM1NdyiU5+VZKw3eVNnVvcX4sfO8a7QvYwdMoQ6oEpgUGvi2yRoLeqnrRexP1nEvukctcTcSQvj2CyLQXI4dgdcJIAakYsnGrq77t4UnKdvB524dbGq/s826brR+1LPqHgGE5LdJ8uvpAndwCOsf6hC5Xct/pCEqBz6JxgkSpokxzYJc5AsHBXM/QnLNCINUAjpxYCBTYcjVrS9IRaCATEGQRUVGMysCqaabIQfRiGdgfVpBOSheS5v9vDcKl8anNdd73cHoEYh70khr0OMa3DztMr02XVkql/rh7AEu7Y4vnOqFVdu2CR+PSw9Dv06t7AbZMSRQkb62VS3WWVQUDYohxO3v4ve/MAw0V8jgkAZjX8/lhulsD51QojCntZ26kHo7hoDykrZD2I1SYSBf3Rsjxr1RA+7d8Oak8ZvXrqUW9v5dwYBL3jaOg32/3npBQrvUjHcj9df5KfTB5XUzbNDghPWlrokNc9imzZD7C1UOmymVDndQg67s17ZN5a4e3dNbScP+u77dXUINzXVxE4Cb7/UhDR6T1U/A0MXVTW3T8HO7lqj5Sc0z33abb9PWFZjK9F+aAqrt71lB6NvdNvpv96YvdufsjdPuyz3C49Kjbj/tnH1vTR4f3ofF8m4xuT+WdIFvcHu6svm+bG9Hp/jgYPoSHVNcgqCxAWA+uv945m+TCmgdbjBWl3TfL1nffiGQSkt7udo74N7KmataTUH/lHkfKMEsz2U/RlhAYgawgpEJOHMCU8KSRYFrTeLWNp0SEjOe14zEjJyB9Znx+SOJ9x7HrKuswRZG82oEmDsbgZSVdssEod30YgidcmUmVOEtAzkpgzFbjAiAKCDGBAoRIegnRcRAiCZkIIDN7F0Z3BTFDa4ESDbsh8QNUJAYExQIkRkUAiKgvu3Fl31iGX+7zjKAZNAHSPBlP8MbK93tfBqaHQYWvew+AZKA0U/PSOez+NVHvavJuWUq90GJA8hlPMFZozVDP43pmwsDOCexiki6PuzPfNt7d0AZFlNB2p6mA46HBxyPD3g4PmKeDoiTBJ82RKDW0+9OmVtZOwEhRMQQwXEGH45Y1wXHwxHLuiCeZmAVN1B1hDSygMddCM2atX3DnOG00spa5uZ39TKQSbhyFbevQJd5AJBSwEozsrlwCnCLhLZ4oTvL7L5lc7FK1itfYIRactPHFjwRbIyvitEMuK/sH3P7x4AJIbwVRLWAMMubXK1lDE5vhWNCDNYYJbaq/O/S/i5iCG85VXDZYRxMg7W6jOLM7Tt9vxmP12i4sASo/nx+QY7qvowY52kCRbOJ6BH9tulBjp10B3xXSPG9Wu8o9pOkfgo28/uKObrdIiLE5nfrNqAjQ2iLBFNo8zXvgBGd7Cm3W8Gs2W3PFAqsMlI9TdKTJ4ZkeO1Dsk3WnGEd0j8gVOyaLYyLzVqvFxb5MesyGmOC2gdX2vYGofcnGnzb/tottPO+H4C+wFird7Tw99f6ts7bX/erwf3yDfKW1Tiu/Erq5/FKFeOZ8GsmlvX+N/8i4pffPOLv/i7j+x8TSE3nGAzkjKye75IG7slF+i3VRTOVDQzOQAq1maDILbP4t+Q4ITMQZ0PaZPPlmMEghFWNOFdDNEhk5+ZXFFxwt3qeuBXIWw1Nu6LKKBAaoQp3mau/RBPLbP0KCnLU+oeUvanwkGPSuMOBtFxtd4CsVMz4Uizj29MbN3bBK65Wv72Nh9qyzbcd5H/0xOEar+uSIas7pVs8ePvCxYoguDgG+jzYWlUEeNgOyfvl698hH57BcdmFNKCadQcERJhgIhRNDgpuJzRI8i4G3cSVaJOtYgNC5+cCTllLaXshNHO0USyzI6iU0k8jEKw/e0KQgRSlnm52k8E2qNRubrsaLi41Fcj17wW894kZG4FAR0YISuDG0udXDwW5uSeqllVQXEIIcNIzFYUJbmiL0u76Xc/OneVHQPWj7CAOVlnJycOzdDB8pZ/WOYOfmrIVz7kp2HT33eZoL/UWL81z9556qJwVEfFo77i6bP5Q8b3CS6kD4IZxMzr6O1R43YCGZvy7s9J1b+yKySmedEhyg5J0dXSAFXia5VBBwHYv1S5cY4jS4NvV9BqCclBHO7LX4NiD9AosF2HlO8anL3kLBLtE0R3pS9SxLX3vfX3lyukaGed8bduvS3vn2fghgcBUtTVbDU9L47kQVyWET+EDMs14yAmHzXn8p5Dac/paTm5+XS+z11JbaVvzPaPLHLDk6Hh/Uk86TljfzXiPT/iKP6rrD0bIQEyMdZVYArwQ8sL4bn0Brwnf/2PG8iT+y5lR3O5I7GmxiODMyItfSg47MoF1cXEkimFipaCWEYZXkuEghp8l1F3JhTFoNJxoSAMprYVRSSBEFRrEEEEhYIpRGNYxKm5rsSgkxgBRQJhm+PAQSIr4s+B35rKJsyA9PEk+jvKZiZEpI4eMQISUCSEFxChugUMMmEPERBkhmNWHjFKwr55vwChKlUb3snLPWd37FAqRZDzSywkff/33+O1/+/9iOT0jZPWWESdAlfEkZoKMZ10exuxlcErKGNXPJMxezifklDUmRML5rBYQKyMlxprFsiZxVjlGVssIRsqMxIzj8RGHwwM+fPUtHh7e4f2Hr3E4PGA6HIR/p6gqazlitdRxtL2FSgdqfEhMB11fhHcgAAFxmkFMeH7+jKf8rJYOjEgAIyCwul6qyMtw67IKUMxlGYVYPDYzZaxJgE7M4tk3iDCicVxBDGGYBwlSTQes9IDICcf1CYkyODI4CQw5SKwIo09smszqwY6HDFJPKKxB1rubXs96P88+NRwGVh6HzUFDM7RFSfdaocFMIKACn8ZKwYQJQHkuAgeN1wlx9yVjrXWyE14wCz+IGTmvwgfKK6AuwqrQrHZ0KErm9kv9l+tzNrdQWk8ZCO7K+982KPVdaHO691ZUBWN6JmaWMQhrRkiyX2Ik/OIrQphqxBERvlid3mrLTVjf3k+Zdq68a01/Sdzo58I7breIcFRZrzC1JVA7NH/jsrAlyBytt9P0ncPhT5jCiHBM7kLAeCLC+iY6KSKgq+SuBV+hzQmyn8ZCiK1AoQpI2jq3zKURoVqfb9vm+/xZX67yxmI9kmcvyL0flWnb3XaxHggtIb0DqF8DXWttc1eISH+RNkCOBva+QdsKpm4qha4D+ks2mUH1+AAciTEXz0eGfPKmYblfRsxcJa6UHVsYYso4JYi7pRITgiIoZP1MxRKiWkjYpbnZ+cOx2DB6CJunjC0joN5pXm8EKD3ktnT9PkoGidvLZZEOLswu2dj+0aS3gsKyhpozzOGYN0VW4O33V4N1w9h++eHfqXBawIdtkOr+W7V8sO+hfie3v2lU3jRMvLMr1xptd4d87Qjvi4dN1WgpNfgjpz/+ugu8ZuWuP+NGd6/95i3rHUytFn4ZqnEtoXk+zsMXgKhdbb9VGUS1pWnwRsu+VRdxw1HxCztebLSI0MXQqWU2AF7toXu3KxQYP7YHLY43xksuplcwnhvLIAB7GHmzFJqJ6Me+HjZUstYeEct6iXbH1dnYvavr8q5j5DNfGi+PE7a/6/NWCNHnHd2f7f738G22vZvPrRBikH837cHfZ9tmuH9V7LS+maAbzxqiyxdER6tcqvTevryu73WBfwlZzrW0OW88w6T8c6UO3Hi/d21dmsFhsMtBHQDc/N4xYHeNbX/H7PV29FznUz9WmpBoQu4DaV1It4ztz7BUrqf2aMLtK+M69Ps5/IJ1G9ViP95QD9v8QJiLKyk9xMnlyciUsYKxUMZpyTgvGjg4ZSzripQy1pSQMmNdV+Q14/NHYH0irCkpUzk3PMKiub7xUWNCCCeMsC4GklhHwd1y5EbCGIqeEQgIc1z7aEzyzOwEEWohz4yQCRyAGFhkCgEi8KcApowQpnKfKne6zLkp99Q9bHwKiSNIgQUI/WR1q0qBkU3ruljporaJAAqqZa9dJ81qChm7R72ONUDCdyVGIsXRWN1iLQnr8zNOz5/A61quehFAOryuDDGjsKOdNjorI1gEAhngBKTUWELknJE5a9BmLjEhmKEOlWT1ZnOXRQHTdMA8HzHPRxFATAfEaQKZNkuZ68rs7TX1/VlkSCmpW6MQIuI043A4YD4dME8zzmFCIO+Bqi5Eb2GS0dZpeWTsKi5W8A6CeGHwY3mB12MgS/kAhAkBjMgrcqBi2VCCKBtyUxjX3VrwyKRjGvS0f311Ax1aR6d96Mv638woQoMCmHvXjYHNLxtD3QkrNtYQ7jtrO6Ksae1lNAILbX9r2+FBd/u5608Njs0dXeT71v0u6c57m22sdWa1LRGSyuIKkTBFAt3KAfdX1S44dC3D9Ta+QBpWs7913t7eF0BEb7eIUBOWQtdUKCoBNkodkt5rddnWvo7oD3JcKmSL2jF6av59RJ5ZtD9DkAM+az1bVw89omjIgB5YpoXQNEtN3vq8ajO0ZE87eGNic9yPUs8XWtwj9uI+E7+b446Bu+nHF8WSN4M1enu1fJ2q8eCO+x6u1//mvlamQVuVHPQSRJpwnBdM+IgYjgB6SeA2lQtC6xVNmizulQBAg05H9f8psSRkb2XOFVGJGTlFME+IIQETEFMCgbAywDk7uG2vuPVPtjdcH5vNOz4txjynernx5rsicwO3Mz7VpWpmuC0sRANRCNcPwhiBIhii8E8zVaKmXTcMDE6KO2sdVHBNvHFtKK18EUFvEDnfbIdAs33nm9rqK+41aSxAYIBokMUYAIjvW3kfrKWuLoN99K7dFSasKCs17CCwDaRwe61DvBUh37mC9JFkKEH/mqOYrg9cx8BtbhE2IsOqye76oOEeq52Cy3s5m8+zCRZd6tK7Xc8EzqGB1bStLiHTflz9eefP9y2E43MERGoNUYEtJ76/ezf4SZNlW39H/HmcYqMd5rO7F69HUvfvLFtOtU9euaNCWuC61pTC+HWe8Is8YdrDr3o8xjQJUb5s1/BmnMc40G1CiEu4EzVlyjOqe8nPny+6cadKbfm9RN3nxXTzOtgZ+0F9pU9XhBC7LfsDanQ2XRNCbPbGz5fu21bNSfqzpB68smf3wLhVCGEvxv769useH59fLHmcvO3itbGva7AXNv5JpeGCAHrrhD0Wl7EkR+8vjVZz/XcCqZFm74iMOK9RYzMAeQ44vz/ggBd8lX8Ac0JKGYEz6HPGmlb8fj3jx98BH38PYWCr//6UMlJSV0w5ISfGumSkJIxu0ypveqYKdVzwAsUXLN6YfQazflCXnaSa4+YZaTg40lZWJmHRsE8JGaqtD0Zecx02CggWjFg1rMWfP4NV6YyJgAkIENcnkTS2w2RWE6FwT0xru0DIGcgEDglIhGxzHwjMhKBumjLbma2+8iGxGxAYHEVQYtcxkVng9/dEHQY2wQAqzm8M6sCM86eA5+8+4vx0Aq+50I3VBTbXFVUYrVk1y9U9TmZwXuX3KhYRIuSR2BCcV4kBkSQGRU65/F5XEVSseS0WDSaomMOM4+GA949f4eHhPd4/fsDh4RHTPCOEqGRvltiNhbldx4DU2qFY3eqrMmYkli2T9onzAceHIx7OD1jWE07niLQCCBm++9VhE5y1dyj0j7Qh8xtUWBJiFPdLYCSuCsP1X1k7uZGs2Rmidah76KgeF1ZSXC1kUA6FjjMnLVT4AuVQ0vuitiu2rrZS6758Cyd3hKXWQNK6N5u37Uh4LwysPZDpVeElGw9T93cRKuj8mxeMnHT91yDo4pGJ25Ydrd8/N7hr7D7U3wywRlppCGoA4J6P2r0HQKp5Zld+y2+5QM/qHMUQMIFxPM54OB5wmGZMcdKYwU1Ltc7xUXEh/Qne2T9jul0Q4Yi+DQ3U/aoEF7vfo3wO0d/D1y7gm5e02asbueAaGBBym7pZcSMByPpSUKBygAf/o6NBa79GhFIrhKDu2RZruC6AGPVlu5nuSt1cXLMc2KQBA+MivO7R1icujb+/DrL9hn31HRHKO/k3NV0EZjux/gkX7YZdiuoCBKSXakBgQiQgxoQQdg5qNs1qvUjqY8dvM40FhgXahSKFglRI8eAQGVJkwIQVmRU5VQSkxGhRf6hhCogPEZsA8jt93Kyhpnt20drlJ89ejyvoGXDxbf+QSvu19GYztbD3DbyBZ7Bdrz9felub3fmKOn8X27nSaF/HhpTlcb7681L+NlGaQOsMjuvgECu5yllvRJIF7PMWEabN0Z47dp8ywK1210avabNoyb3weccnm1+3VQsIlWQcDoDdZZsDfA+oYdv+d1nPVpbtTjaC+y3n8U7bRHsvSgnhXWp/A5qDky+025zgugjsXCUjBhVxqHYztyYPd7l121cbXGQX2Wj74Cakr3OYf6fOW3pzj/CCdn/4ZITbYP+7NicKOKhQwRjyO7yLTiA9bnrbj4rrXQZ43xKib7Ce9+M52cC7yea/UdsvujJf1y6bWwUCu3jtfp3b4+3Wtrb18IVGqcvfvvuJbtkrgpHa/j1nw8+XhlDZueGtSC/N2ZX5GMkh9tr35/GXGrGGB7YDwHYa/d3rz9lxJT/Z+rqUNrDcCcO9gucBejxOlcG1m71vu2GK9TXtw5ODKBZELKKhbztN6SAgINMZK07iRudFBAzrKgGM13XF08eAl09UXCulLJYQjSBCfzNnpCz7ogoiuvvbAkCTWUDkcj+Jlq/SPeaTfTAN293WWsEznDBEtaEz1zzkg66VjcgihAi58rgpiBsYygUvMnVQc9sUTBHM2IoMMHFhHnLOMta58mNq7A0Ijx9AIAm5TBngIDELSU0gjEMTCk+nWz/uC7OGEWCIlYG+C4EwHwJCSDg/PyGvi9zJqojXDqwOjGP2mpAjZ3kmr6TnWbXQRUiR1D1yRkYrvLD5YDbXMfZOx58CpjDJX5wQYhT3WQWWav3CZZIU7L2DVEgMR8aQuhFVCwnH8A8hIAcGJS9SEjzd1A6NrgmhChwYQMgST8KsNqLFp+Bc3C8RAPPkIA6YHLrNo3VNQOFDoDCcvaKODkeBjQEXkLoubZAXgsonNRnadVRgIPfbBoWxj7+Mxr+hSgfWW1QDMutmatsERGDmhBDaJVTrHMmYy9rgsj5rPbb/m87CFnjZyd5yguH2K7uLcEx77j3zpFg5zT0taLekCYZGNXIGiDFPEdM0IZb9YTWX1jCKOcnu3ThdxtHvTW+8ge9r6xqMPxMKcrMggpxFRPN8j9hqf+7gWl6rCbudHg/WHWh4D0yTuo1L3hyMYJ4Ci7SYyrJ0QI+Y7BWRHGqwOw2YntgZm+G3rXYvBultiOwlRP9aKtBfHHfXzz1qf//BzpvRIrpM0DQPqL7ZMHB22q8XL21z0fjHmOwAiOLgzW6F8qRZKozDcsS0HhEpAhSbMuIX0qTlkr+a/rb3aRmFID44ob45oyIjMQRFskSKPjmpeMwTgIzMol2aJzHf5JzUlZNoCv3wn3/A/O6Ab//jtwgPBGGukt6FBpuOq5ub66MJbHQJXH/t52h3UFuqSVwQ97ybp9bSnxMVlSinRtiBffdCrX2R4dhfb6/dvrxBrgaw7d/5l+u++LbBOrcNjoC42M7Oe+velhrpMvg3vLMg/FgR4o9/hhgSzr/4FfhwEkgHOArZviJD6DWoO8VGiN+uUU/kOIS6gKB+Xce97pID5pKUTs+UEkRO591cI/VWJoUY7k/lgjheB6d/bIhzwevJt3V9wV/QeSlpC7HB7fK4Ambmb/drtpgP1s1MbQFHVEi9lj9UYitACSYSLUZYngs7rcBRRRYl4PXo/uqPC6cEYV+o6XdbYENPdfhK70LJ3Pjdk7zW5xaEt7BeX4EL2aAVhQH9VzdZ6AfX4XPeJZln7vfft4Ih+2wHoB+PflVX64ztnWB3RX9nVoufTgBh7ZW2roz64PX1eer6dTW7nwFXv1tjV6vaydffJpt6hkKIm1q8P+3hxP3rn6LtW9Llq/cCVG7mRsf2nYKke3r/U4zU/jB0bzYZN4cwABT3JuP9/SeUrmgFXVle4yqxM15UmdGjSrn/xsI4/XQ4gCPj2/QDiFeEsAJsQgMGfQKWnPD75YSnHzN++AdCTgmrudVJGSkB4mpdHOmYxUNKCZmz5q2udyyYtbkHKvArwyyEqIxg8+5ARQARYhAmf2DEgiyp9nnQOiy/w+XYJGWOJqwMSoFdgVJwqrJEQPWtzhArhsxZfPRr/MHIQAwTYsgg5IIvGfxWZxF4MCPDLCIEZibpdwhiPeyDQYcArMwIURmhAfrd0Xck2vMCt3eTZJBQoepWjZkgLvEzQgYevj7gX/37r8DrR/zwm/8CzisOj0fkdcF6OjtXP+peipO4GmK1sOCkDF79LEGpxQ9/Tis4J5yXBZwzUlrFemYVf/0p6We2ejwtIr8lJsiMOM3CaKWIgABOuay/SvvWVS9CIdOcJ/TunSUmyHZPEUlMjhiFDzCFKG60wCI4AsqYGvOfwiTBx+dZ6BwNVp4sbgFVjwtSz4p1FYuenHQ+c0ZmCVodMwruG1BFBFSeiYtNCiRx+AI5CYZTIi6HgyhcErjQOVvqy2PA/o0bnn68umysilTGZ9zmqYqTTj20rZwV5+FWzVGK61lShF/cWkTYOij5Mjitbr2awIvr3ndWDNQEr67nRYEg19nn8tt1sFuDl9IW16F6UVJ93oto/HnPzFh4RY7A+/cf8P79Ix4ej5jnGRY/x8k1cGEGr0H7ynI/Q/ojBs3S7YIIhD3cuMuH0vFhUFNPiLm89d09bdxeYC8nF9MJW7l2pEm53sf2iNDrvjSE/IZwAuCDZjQMg45YHAogbuy3VPf6Fch+N9/Qmm+qHuJ7xNRlYmtU7iqB4w/pW8puGAB78+of7NStjwMHCQBlaWf4dqeQbyAv3QHclpXGYo6IHEWoQcC7R8LXXxGeTkAqLk0rsgD/V+Cl5jtpm8Z88sHPRJs7KCKhn4GAbAHLWCwisgVPq4OSF0Y+u+B+sMvefqHeKi74aM378yR2/27mdHivbie+1Tz6Amm8HN9erQlcB1A2e6RRx78NkI3GyT4QJb8jXdrXrCuFtvPiTvBLrXzxFHIEM4E4XOgb3DkvyL/difVTA/jByCTU5bc5pmyEDLneOXNhlXQWQpu56yF3d5geC6TYL0GEhp6Rvd/pXdB2S9QjfTCaBkTfxrjli88JraNFO59pUIBK2zWDuQao8HglgB5OK1rXgBcekHOxVL1BXvBtvJf6Ie/Gaw832AghbkWxLuS7/ZbfgWGzrC8B1b7bGzZmgJeMfFrBS97Hlco0U9fHFm9r4e/r0hqo/b4nhBiXQ5lD6t67nJvK7CTZ5KSdBd7D2YM0SFdxs7231xfAsDbyea4JIfYY3N1dth36nXJ7QF3OdVe6vJde20Z/cdxXzyh3tTq/VHD7djOyd18PezkvHZKDc/judrh5Tt3vYQ20pSGbl3BLGcCBJSiv24Lb+rt6rt3gF9PVdVBu4Svvb0jDKrbQ37vCm/PAtzMAnUn5kESIvIJcUFiNd4uMgJwZ57wA64KXz8IcXpQpLIIGxpoWvHxkvDwRchKrh6x+/k0TXhS8crGMWNX3f1pFIJGTMOyS10IG2QUBQATemUTrXxi+gl9kxfokCIIfD8eQJRNC1MDVOQPmVhJQlyd3IRiORitko1JvyrymnLWtGusgsLp/CbWWouWvCm25aUPiUIiGMkkQ6QxQaCoAqdWEWFSQDAcLw7qGBKgM5p4K8TxX+TShguScp4A1EVJaVFM/gIcqP44WyU7oUSqueQqr1taMBgdO+r38cW/RTxVm5jq+yMWigjkj5yRMYzIKorV+AXQvmDJCUSKyf8nxvGwsPK9APg2PCYEkbkixmFHLBgBQt1yBAkKcRKhGNQ5rBqoSTiToAkUoeLGD2a8RNqUgPxtawp2pJoCrVtW6Csr54M9z42uUng/meHyXUJPnwsmo68B2chn3MtdmRVDralpRKw0RapDGZumzXqK1G46GTqVbpz0PRuex0O8O/irUq2uirpGuTXafI1y3sbai5lX9onPbb+YBuRWCxvThBCDgcZ5xPMz48DDh8Wj8rK7QJl26/3qcaqeKy69+pnQNgp3+U8U5f0pX4re7ZgrdwTvoV/+o0go7xMIuEcFNuTIAG+JgB8ndAIJ2nMtm48JcYe+Kic0f2Sg2hCXzUd2b+DA2BObOl1YjuhU89Ijotl+XFtbbF4zXnrgtNddF+6ZS0l3WWqYtvbe4rj/f8KdGDWC8dmoFozI7a809n9cj5uWw38YVbk0d8dECHj3y/db1DAIc0vl//98y/v2/Ify//t/A776zC04HySTimQviVHULQmlG8ArThDEBg5lQsmirREbgjICMkCbEwOAoSCmHGTQFpLQKYpQTzMx4g2lANTQ4FMm+XLiKTDGVOWYARBnsNRz65PZ69VfI20O14fB2txv3t52DtcBcL+aKj+7AVPyL3pku3Zc3V6Fn6pWKbtPEvrfxG0o4AmCoNeJgsJXqB8VGlsqPtobKPOH2QVPe6udGUE1cEW1S+Haomx2YA0LIoqGmJsqikRHcn+TzSG1ZVx7Ocidu16R1oN1WDvujvfnvkcda4x5qTtTnvDzHzY13w3qQeezvDQz6bVm6u3cHx+DuSys6omb8t+XJrT3o2vC5GIX9a4EWy7uqVUhBiS0y7UULqCbu60TxqcbP2ccD67iTZm6vLtf2lW29uUubL4MyRaOoPciv87eolB9BUdLOkrrl7NnfkvImf3/C+b//gOVDBL6pqHA7Vw7G8jGKCdHlRR0Xz9iHFrkkhNhaU9QvlXClDi4q+Vpsi8r7kcuxag3RQNNnu5DuvgUMzLteNH36kkKIG9rcTc2c1e+vodeu7ZcvagFxY1WXhHN3VNNXegWUt/Rz7yKmK+9vhYG67/v5vKrBsEVjMtdFiQjGX/EJxBLf921j8UeUmgG4ejFcq2B/Hw+KeczdmHv53Qw+EKb1M2g5C/MXGedlEWbuJ/HD//2y4vyc8d3fMtaFnRVDrtrqGufBmMJGr6iz2oKn2fNVrSDWVV0zqaa7BR0uuJ+51okRHAIihBFfrBDU3YwE+rW1FkAUxV1OlHgMMU7yu7jPLU4tlQQU2i9DYgKC9Z7QPjQu3UnyGgM7Gw7m5qFiQBkpRyAEQd9CQEJGTLngvlzGBSK8ASMljRqg1h8hRBACQkyiUR9jtfSggJAjcgQyJ0SIax+CuFkyfMrTAd7ttmfEss6VeFBSoUVmIHGNF9xsZsWKGwFS/bQ4DuZuGZyVkcuAumLilLEuZ+ScsKyy9tZ1ld9njR1RLAb0TNEA3pllPa7LghxOWCkgzFE4egTkddGxIIcrK9WjrpVDnIAg5w5AYsJSzjXhE7CWYk7glJDXFWldkNNS4lyEQGAOmKJYk3ijDdL5mg4PoBAxzQdAY4QwQ+J6lP5B5RcZLAElEYmQSFZizkASX2malxAIiCTWDyKYo/I+kqzfiUQoZes0a+CUMh+kikPGRyjKpLn0v03X75BimLR54VgSaFah/uKWBvat6bTISuBKf3rImp+9EMuDL+MLdd1UrW2qYLCZyHpgoMSY6GBtoO0tIUb0NvkvW6TCbzk5EyVf0UllAMQILLFkajNSIk7imeMpvWCKB/yLrz/gl9884n//l0fgYcZvQiiuw7aSnFvvqet39BZLfQWC+Nr0TwSFuFkQ0RMvl/I1KFqhGfYQUNoMVp1i03pt33S02aBw/8Ifxo6loou2LsGy0+vltesXbBuY2Igk2jxsYfLmQIYc+AIjwnXQ0i6hUE3LXpvuLD2ArxkF31f4bbi3knb6d3nZyWcOCDzSVtjWtV+de1nOx/HB439FjojUbalb9w325nNM8IxpaUEkhYEl5eYDEHNWZEGXM/kLxP1xrbjuEnK3AVWEwWAjhpn9iqsRz1QNijQGEGeYhcTQ5FNTvd+qIySRuuslSOY9HyKUgPbHX7q75zy3L7Udz9zZMmj9ZrqyL8zksQOCy7vLxa8mDzpjY2FQQdxf3NcEEPeC88XvOYP/Rm5OXYctPLxzCDaGb6P6zNJC/w2ogdFKsDIyDfX2JGvvqi2cRpwaE7qcknofVJc9Wqa0YzW49gx/0o70grXN3bRHtDf9cFpDTV3bfVPou0Gre2us0q393bB/Mpop87ay8bk4hmivT3Ud0BBB3ivbv3GaYAU86uZP8nl3RcUOws5UorIGCh5Btg48XjIEqwNy52bdK0ctHuLxE9+n/Trq7rsqwNgRQlwTTO2/1bbdAbA5xQdLknMG1gxT0TQtUgOxWTs9TjaAbTtmg5VCe/1m973m9V+Gre+gSB5cW1vbovu45lY+9Nq5uSFdZU6757cIIS7Vd014cSlt5m3nnHvlYHxRYcN+I/JxA5D7OSoT9NYmCzk1rHd48IzTjlJafXf1YLzy/hIMPe3YF1Mt1WYXqrKbw633myFEtrOH+iv/OnyOnt1Nr12cbSWXXzeI2Bdobu+Q22m7NBkJiISYVwR1jZMLVUFY1gVIK5a8IqWMz5/OSIsKJFJGWhLOJ+D5M5BWYfwyi0VEZgs8LcGouTDvjHZpd3Nxl5JU8z/Xz1bhCs74OyATIyAjEyHkILCH/qyou0rO9FA/zQWoMV+BEkshkGqjk4jWE7apWYJcmZ+ZUa0z3OXKdhHmLLhzTkg5Yc0JnAiZCZQliDCAEljXxsEY0xKPIiCwnLMBUM1vccUTECUuRQ4AZRHcMEnMgZARmCouT4ZHkpC++rAGv7XxJ2XKalssrOgEsymoTFApY66rcnckWCNGbHSEm7aXVdCQ1Iomu0+xbKha80RUgiwD6vLLyp4XnFPAFI+YwoqZFpEZkbjsMlqjwJhD2UOUQ50zo4ELcRHK/Bd3PlkDcKughcDtOlI47X4JMSIEDVIeJ4Q4FUGX5z4YvhsCgMyy3smUH+3M98Na6f1AdYirgmPdH8YNIlTeCCs9ZxgfMcGCItd5eyNe0yTefFR8xvEvHD322qNzg+uOKipw8DBDHYXiHPtKY10djZDE457+/r4+ujUYvKsHlVvjcjXUOEjWHlHAIc6YHw44Hg6Y5xlpPgDzXPMWno3WsgvWbffQWzCrcbq+EnZ5wTe3cQPUu/zmt1/yt7tmKk5oW3JoBNqYSdo8aa/RC4hfu3ZtUV5AkS8IPMqBWjgigDr0QyDdksUyYoxsjiov4zBi4tBO/10/PONpr6HrZvz+nUC0NxK3pNcxLMn9u9cybSDb/ByM1/YJDV9N6YjD6eAytmO8Kb+puDJkSm90KbREe48IyvsQbxCC7OSg3cN58GwDIwMIaLWHCaTsT0sMsTYoF56qMJhAvF6Rxu63C1xR6yAIollEgANiZDCiavUwprjCrC3k0hdTyykl0EpIstFQB7b9ytAYEVm0Y1jVxjITgvkQ1fFuUIdGsIKCyBmRYLIALtJ6u2q9MGK77eso+Dm6tD9q+322Cue10n377suAqO0a2OIF5QtV2NyLjfXZDhD9ubjL0B8/3uQZjoQMtGgkdXB7BHS/zXpecjMW1YR17/xgM1kXtS8wiUl5NoTRa07otru4ErjiXCGob1WIpleA+faNCFDtrUDF9Fz1XmpFaLqiKZfXlxCC3llUW081294GJLNfbnQ7fK0hwNCT4F3qzi0qF/yoDG+Y+f2yvzT2e6ep1ix5Olx5BGtbsLV4rJArbsIs/m8z6yP7j9VlnfVDBRCk30sgQLE6Y+pGRYloOSf7GXHtdwKFa925/Ka/z53ADP7MsHnJNfcew3fn+SY2xBVYy7nPdg/IE9pdS7cns1TdWkI42HWs7XnFDSoucAuOt42vgSb/LowFF24LXSzW92OnzXuEEJf22JdM5OF4rTDhjeW2j/wN1u/Gn2NU7kzX1tSNlVjXR/f3pf3O+7muL/hb8jXMj1ekqzBQ+7W5l94y3+6c4Tq+o3ZurmuT3s4suFz/bc3RgDzyPNvXJo+22P2YDwHp3YTj+gw+PYlFAzLWzwnpY8Z5OSPnjPOyYjknfPe3jPMzsCxr1U5PjHURIYbFiDDXS0l93ebsXWkp85TMq4DCpAz3lHIJUp2zCjcaJmRWXDGCNNgzh6CkFiOCAARl0trdIziDxILQYNAhIoYJU4gSwLjglCha9gmqWW99oCABpptxrTSV4ZhJrdK5zSrdD0HcKVEWF6VLwMIZKxhhnRDCojhKpUtNEAGWmA86itKvEAEKiNMseHLOavGRlcEtCoABxqjXeqeMCHNJJY8Co1W0UZo3G52YkvjRVyZ7VldaJxa6IYegBVYRaKUMQC0dHF5WaU5/4lnwZmk0a2DzZTkjpRXn87msuRIwHCgCpBADKMv6AYvLq2UVy4lPTyd8evkBv/xmwdfvF/zylwvevztgihFTCIghNpYCrFYjcZpAIYJ4EvdJirSwrWOlGoTRz+C0IqcVaV3BKQE5yWokKuvLRkDi3RHm4wNCnDAdjsIYDrMIk5JZiyQpo7BFnb6scUJCUNw4UIk/ARb3TJSTyFQ4VP5kEPfQYk2vwg1daWYdwzqP2Xh9GRCrZu9WO9c1jQun6tVza0x32a5qhHiyE9rDbFjVpXdaUyEbvZunroAnLW3RunT5pGdXxQAew0+bs51UKuRx176V8YC23autUhPctLYdYsDDwxGIAfHwgIf3D/jm6w94+Oodfvv4LTBN5b6//+q5967/w+GCd6MPf6B0hyDCk6PNi+65ETktQbhlBO/92L7Y92c8IBB2n3D3jDc/69PNA99oU+ulfhFtM7TE6WjseoKmPrqFQX/p/a3bwUh6+357C+1zsU6wPlH79iIwozHrs9Qrwr8OHKsPSfeWRm2O6CGFtScGullv6tgj7Pv3F5NgcZdejmE12DRLmTtq2Cb48GHGeSU8PWWsa8c89JNs29bdIwIZqalrqEwWUw9RBmoIhKzaLtXljCAlIbBo54QgeZQjl3PG+ccVeQEOHwI4CEIZIcgYsWi9iCWFICDB+myIpbdCcBcque5cusPvSu4C9YxiGQ5C1cozDtl9DW4vdsda45qn+IX0Z+zVeuHiLrQvrkq1u3zUPa9AkCLldyTPyymYWldDz4h/Zbp2MZc5HWY0TVB107SbD22fSnFy+yJUrS+gWA6BPAHr15hnsVq7QniZ6zLPGO773APqfedaO4YK9zqVuyEahp2t7WzWFLWrtT0vt3cVwbSrNq3Dzo9b7rQ+T4OZ3HoparmesTY6Y4rmFdRSoigGUBmhesa6uaby0F1vWwC390mPINA434W+lhKbqtu7bXjFbQZzeGFXMLt29oUQuu553G4Z9817P8P9OVK/5hhweoxYZ7cqHYyjvnVHbpd8Gep+b/GDVgjR46d79d94ApZ1qmOx0699nLIUuGeL3J8uCE9e1e4NdMqt5W8pvrsXf+p0F+Pbnft34Ay3tDV8M5iDglbaGXdLPXcmfz6/Nr1mVBv3f2TWaztnr9u+LYXsn3erarAHh+jazpGnQA4eXkibum64S15LLF7IuwHDMbbkqzC+eQqF+Rt5wQFnLBTBecG6nJCXBasGAn75vGI5ZZzWM3JKOC8SGPf5M7CegGVZnPukXAUQGjU3q/KWt2YwS8fCtA2tAkVWRaisAWElSLUobnHnqpW4dekErm5lxwNK5c/wS7GCkGDCIQREo8lAyEE02imi9IEAcYFDglmx9qcq2pglelVaC918MgBx90JqLaFBlhOB1lWUbbLsDYknSI5kU/dWpUcarNrwAhWekLr1MSKUjDbMGTlTDfydFdoSU0OwW2I45ak6znWMa5BfzoyUGEtiECIwvQfSC3JeZR6Ri+JOPz0jeqpYxbCMiwSmXpFSUgFVtXkgN5empGKsFKP7cmIs54S0ChM9rYxlSTifMmLMOB6AHDLmyOry0yBRGn4FQkhIAaI8Ewz/NBwhKA5LumYlsLbEtUiVgU1OuZQCCFwsIaZpRpgmTHECRREqodQXQJSqNYM2bWuvG7wyfmWdEYSRXy8Xh0NTUeYRRrwqA0EpB0Jxpxp0jRQ/ZNqnGi/Wne8N52R84I1vOPdS+9PWhuZsK30ueU1Y6T0/uPHY1jZIZbM5pdNraYBzcv/cj0/NVPauwzl6+4pGLshw7/rBaB/LnObte1ChpcMUEWMAHSccDzMO04xpiuAQq+u7Tfe2/ULzq18Fe3NNbVfekN6m5PDGtm/JU/gOr+/o/RYRzbPut/s2NDF/dapMlqso9C6CRKUebpiFcDeTM6Mt9XlWQX3m2+v2mntF8Auy9KBBXJs3mt2t4E1/bhvMWuMNCOSlFi6srd151efzcsS8zNhnsNeKDIm/AMng9xiG4uJiUHZHVoByYhbqoL1+7KvdUT5H0489QvhaGsHc+6/vtHGlmIfPYpwwTOOEAYRI+Lf/9j3++l8c8Z/+04/4/vul1GcXddGwNAm6xYhwHAtDikQDwg4fRRo5q6CBEUMEx4yoFhHgjATCFBMSSE2ShcnIZ8YP//kj5g8H/Nn/IwIRiqQAIchnplxhAAEcKxNYA8yhIISeSlHE+Y03AUEEMYH8mtArlVzIQhbTYQteSxCCxPtL9Ou8QUV2QVRm3OCp/VNOi3pA7a69W0biEo17tZ4OI7+0BzZ1vPHC3lZ1D8J1ITncpMy8xgXojUJ7CGT6lBhSIV4I6sfX/jPESX3fekEqgIqAegSJUeNVEGD+TOvvETzU/UZ3xshp4OLWAeD+GNp0t7mvrB3u9sYIJBis++t16wCxvtkiyG6SRn29AsvFxHUZeHxAUAvSs0a++5hWpGd2ccVFKAyBkkfPU/sU7b4t3JukuILRbXYeUTeenXxiWw31a8buyv5z9K4t0yDg/rmenZeFFqO9VNfTZkrdb+H9KZeBNEN3tBZxtT44PwR891cPRUvRmEl1blx/7anrRC9QqeNRn9t892lrCdGvrqZCN6OeuCuZ5F9HkHvIt23XUn7EqVsow3OkB8++fMGz+9VpV1pw447/AxJ8d6U74ewFXbun7Q317ubY0GcjGLY5+vy39Gxvqe3dxLeme2d/pEhW1QY2t0T7U18XNld/DF5tu37f0P8Xzsk/WNqBocDuzstRAcOYPXqfcsB5nbA+RJyPBzBnpJTxjs8Af8T5JWH5lHBezkhrwrquWJYVP/wDcPoorplSMr/8GctZGMzLukjw6cUEECowgGDipL88H0zwulBcyjCLa5xy5zgXRObOSYQR7K+q0jdOWc95QmBojAcN+gwA0UbFY0hyf4UQEOOEOc6YpwnTJJYRQa0tLcDxmiQ4Mi2rBkkGEhISGQaieC61rkhNXJBG7ImsAaazrOxMC0LOSMwijIhR71kTROjMWtBwvdyCMeCVlhVFuCD7hQMixMqXCciJ5TcxUphq3C2FNwRxuxTggymjzGlhcOc21kdaGac142kBYnjA/PjXyKfvsJ4+S9DtLApz0dZDs7BRBDyg2oastRXL+YRlXXE+vWBNCcuSyrlBgYSBSsJMtZEnZLDG0EAgrInw+WMGaMYhzkCOOJ8zfvjxjKdnxlffRMzHgENOiEE8lQVUCwEmtazJCwhBX3gBiLznEGAuydb1jHVdkNOqwgijzeUfw3Pn+QFxmnB8eEScJ1CcQCTzJ0s+gShjSbV3ezdTtRgyLwn2QhWwAAQEgCIQIjhMSCEikc4wE8RChzSvrQuHWzGD1OCFKQCcwSHA3NKStad5702eb4R+rYCLwK/wBJyADJDYGxa/QQQJWc8OE7pVd1nGB/FgmlWErcOaZ8TM97Bcuj6o8FOLw5z2NCp1uRK7byuaYrB3LZdgLQxxQ267jpq/EKOsvcMD4iHi4R3w+P6I948PmI9H5BiQKbjqe8xhg2BvfhNdwjX+GC7cmv64oBmnO2NEXNH/aei3febCpmojHC80vlnee7j04Fl1xzFiSfgXenl5AnRnNxZ/3qO2B5jlZkx8G1bfpp0BETno3zjVIJfXKhDfisH5RzeIDeUap8ukBxB4ApEEm+oLtsM6JlL8zz3tzmurzDMVrksWqRJUBTG+MAcDwn0M5/VZc1eie1h/cQfLBk33FkikCKpbbMdpAYHwi29FKvz99yecFztyW2qlYXS4yQ86hq2gRy95z1ALggwXE0gSAUUIAeCAFKK0yqm0wam6UbILxpBTRkZmqB/3gMzZzStrJCqu4HJFbFtXQx7jvwGZCIw1JDFXHk3h8KalwpS0Ud3EQWqK+9gC1S3QdSRgB5arO+KeVKHor+l7a/ip0rj+nXm+ARhf7J6lYomYEE6PElDu8AKEiugVVNv2kAYG9G55xKzfBcNl0+CRNb+vdVD9uV4C2rOj5F9vUE6OmSnPJA4LtfFIdu5rE4kVOT+4XStdESr3IW8uqutrrJ5ZlZmxd3+MNuqVndJrLFl/OsZOjTlCtVy5B8oJ4M7NWt4LJurdQxVP6LkTDfDunhIEAg2zHN0YXsADNoKGHQ70/vVJTZ6RgP72tHNYNu1o4u2j8rz56tkEHQkYCHMmHDLhyE5LqmlyNKB9t6iMn/+8TQjR11Eb6Mdyu8Q73GkjuGiVeGhQrh3xfRxs26ZPd570F9bE5o3Pe4XhfendxVW4Eazt1TE+S36ydGmcbt5X19zl7eGVO9nt3L22VNrFPMx3ucwgMd8E42vT7XUPeqHInifl/BHFo6IXW/c7c6/QTgwl3+ZbBuzqfnDtXCnTw9mgFIPLigFwrqx/gJAzEEPCYTpjzYTMEUBEymfklMEpYU2f8ZxOePq04vmzWDykdcGyrsgp4ekTYXkhdcGUiiDCAkiv6yr+95MEczU3Ob2XB+t5weuMiVb64N1mVnrEtP+tk1s80+FDDICEMVcVRCocdseYf/6g1hBiCRERYsQUJkyTxe8jUA6I5nomiGIYJcIaU3lGmQoeI61Vpv2Ii9J0wWItqEAiq8VCuZmC4UHVaqSMhzF/iUTpXb0ISzwGZXpyZbQWxqq9z2JBz6EyKaUe/cVbpS6bA6M/WcBFWhnnl4Tvf/WEwzHi/VcT+MxIawZWBrIywUeRifUsgJtGc7mUExfLGKN3DRc2l0YmsAkUSv+NOctMSCuBKOLh8QHnRFgSsHAGUgIvK85MmE4kwrCJMRFhnhgxSO9FrKX4/boKnAkVjwziFotDAMco7aeEnMWKo1gD+Q6rAAMhIE4T4jTLX4ygMOl8q5UzcsuYZ4FHjI1EUJbVcojNQsWvN1KXUFChCQWkFVhCQDpOyGFCshWnioEZXNSXyPaOTo7QYzCPvAAFZdITLKal5NfS1nd/RDtWQ+Uj+n0BgHrVtfqbyyrs6uP6QwQK9a887WkrX1NTT/usx7Y3e0MzWJD3cgZqXwA4Og4YfMFl7oEby2HqxoMZarM1yCfCTQriFYUDJFD6FMRNWQyIkVBPojqqQ/j6wbkL33F40s+FK/6B01ssI263iKjXradmujy7hW8gDm7DeOo697t8hNE4FKlRuxitLHavCA0bsKOByA3ALlG4x1TpiMQNqNgSntfSLhJKwFVLBJf5cH6HkDz8d6DkO9IOI+qLUIPgR7Z+Dpq6Og79GJf1Qd0U10NnDOsG7N02LEvtz20M2kaMttfhSxXYSx7DZBX71W0WTDaTj9NnPM7P+N///Z/j5XzE//l//hbLDwm29gu66atXtyLyyDQk1Ne9+YRkFq1uzmAWoiHmSbedILuRhViK0wyigEm1TlLSQ4sAwJDzKqXPOQFBrCcoACGrRgvs8pMx8brR9fI1YYbtf66ml3b9eCKgdyUHIIWM8/EM5gWHC5eJjLsi12oVYdoTjbWJpd4Uu6kJF89Ln25Ze18mjQiwnzkVxnALR3vJD+botkebt/Vf1f8aEGDj4oTp4y/BtOL8Z38PPpzc4VTXcdXaUsSJqLGM0ALyr6jpoGi16LouiI5x/tkfDy2sda11fTCroSbwuyG8DlN3VoPWz64aWPDW3TudXObmmbv3RlfozrBXw4ML89KgCdQ/ulBulNft5wKajJ8XSJCLMyVHthGZjkllwqfCRDD8wrE6Xf7dbm0EEKMx75EnmyfyS7Nk2N6VYzhqmSpg2bu378RqGjgvpnI00aBER2bsVPchR/x5UlTYuTizT/Ov7PG3Oh4+L7XjeIcQYotCtbjgCCXbE1K0z+lq/nrf0OD5T3vu31X7DUKIP6l0lwDvQjUNZrhfN1153+dp8M1NxrpXLDGV62U3/9WkuNXua2vrttruT71wpSLcAhrQKq9dvJqaHd41QZvne7VcauQLLaFXj+dFcusKbJwJ5zwJ85JZhAKZMcUF9PAZGRkIGZQTwqeEvCbk84LndcXHdcWPvwY+/pbEJdMqLnBysiDTWQQTOSOtYgmRk8WCUAGEBU62v6IoQgV4c3cjmvvmr1woksI3A6rLIAtCzC42wWBw61XtcL5CzwCFbCr3Lyl9JjEh5iiBWQ9xwuEwY4pRhBNE6lYICHEpsSFWDaK9hoRlido3Km5sBBaPe9aVx7rwyw2cWeIQZMgcWf9yAEcgiGP/gh+Vyq0NMvxJaEjStUAg5CRzEoK6gFI3vxyCBnB2wghiZGRRjjPasUdjbfyVFsxgpAzkFVhXYPn+jI+//x0evzniz//d16CUQOeEuCZENQnx4VObGyqUQatCiJyxZrFESWqZwhAraYAQp0ljycVST2YGp0qfM0fk9YDDfMDhF+/x6bQAZ0ZGxAsIn5cVvCbkKeBxjThMjCkQvvqQMRFgPiqCDf66bhiyFAhTmCSm3TSLcCBnpLxiXRaknJA1ALytWCICxUlidxyOmOcDpsNRYlEoApMzI+SMHAhIpCMu1jgARICUEtK6Yl2TjpEKI9jhyESIQf7mOCGGCecl4pxnLA8PSHFSi4is+DkjFCGUrN8JJsjQkdb4BbbXnJ+wukCYAPPQsHsocomW5rFSdtWQtgRbf7a39UEtV61BqvBBP/X8KJYRF4EywdyGU1JvEL1bSy6Cq7db2+7sJisLd9+XO6wyWYbwCeHoFN2qxUb58wi8/95f9hq/NM4iBMM8IRxmHA8Rx2nGYZoQwoREtCFnN8lfvz8ZMvHPydLtgojOIaAht9cRSmHHXcQ5dhgJ1sYG2e05+FsgulpItJpZ63SvGxkF2YNtX323ekTR/6wwtnmAGqelh387YpuiCmzfz/o+5ICQosseMAasKwiIFi88A6xAe3fyhxL0u+/l3r4eE+2XWxquve306UVDgzHANnPXOA2z1Cum1ybdA7lfUbuw7IHj+7VhYtRRLZAR0LhT0wslaAAoX9aCbY3Xfm2yjEXtviDmLMKJzAEBjBA00BQFESSEgABBhAEgpih7kqt/UiTG6fdnpMcJD98egOguW1VRyRpkq2jHKELijQvtsms1bcx8EeWy5/Z2dOWpII6bQRj/rBdsJ9n/qe+vi9vjC9T70+oevja1a9SEPfbr2qjf8vaSQP8SskcQPDUfnpDjGQgJHID0FWGN6u82yb6kIFZoIZBDrkPRamvaJNUEg2nGcTExb1YcbaDZ+VWJL9vU5JFtbO/3atVTa/L1kTelMGFG0SSk2mghNH3ZCmS9LXpMt28RfqHuJi8vIZe/vaf7Qjt18dg1XmMBwnAENm/yCoHdIuveJRBpvvB+xuHDAdP7Q7fG+9QjCgIMde9bsPefXb502ztvlEQwM37fM++vp/FJu/9+m7ffyxvNMScMsnSYAg5zwDyNHYONhRAtXtiiQKP7uv/t9/Fgf/jFi26Gm60yKnvLiPc57jz7/R6/JZ9rYbelt3JRvxQX9p9oGmNyuLwe+rV3VxvjOnbL9PmuNVaueWp/X4XrFZjY1bXTn+G12BaNdsLli+c4d3v5VshvHbjXp5tG48btxiC1dKjKUpUNlRHAeDicRWnjvCKDkJMEpk1rArDg+fQCZsZ5WXF+Sfj8MSGtZv0gTMznj4yXU8C6rkir+OQX10jKVNUYEDkJQ7jQG3njaKfAafczyqfDkk2BmnPx51/667T4rbIiILQBcEzKrkWFTdmJnqNpOUMAKQ1vf5Hcd3tOhk0wsjG/KQEBWEMEZ6ERGWrBnrMYnCsMe7jIditXpqrQX1kY9o7JOF6V1i8WFoYgvFrEDZLmYVc/AoHVgiVzrvEpmVUI2sGuQHsXxQwUl1lJLRfymvHy6Yzf//1HHA4LHh8ewDmB6AQiVgv9UO9/O1/Z/aZQPAqI66wIRsY8zyoYElhDiCLc0gDluSwYmfe0EsAR8xxwXoDzCaA8YwoBmQmZCZwICYTPnwJOMeN4TDjMGdM04TgRaBY3TWUksq19c3skMSU4ZsQsezQrrZ7UJZPEs6jrWVwwm0utiBiiKFjFKPRM2TNc8P/COmfo/hNY2OJmWDsmECRoQHYq8U8mCogk7WWewGEGgRA5QeKJWGyTPexR8XFG/TQXTcEEigGUc53UQsO4Des/bcYYGCtJ2V6uMGyEEHXa22qLYmV977N7PJ7c/IySP72uyPfRZCrn3gCDM4SzNEDupzu7fCoKqPV7+6nldSy8fIiIvOdraV/dLr2kFTkHvKcJUwh4/wDEx4wzNlO17UdX5T0vtjh4h41cHeg/XLoF1rdYPuyl210zCQj6rzHfW+JodyL7aR8xnTcP6iK/rnfu66edp6EVRijccva4Xeik9NTV1rjG6feea9tDrrfQpkx931Wy6V7PaBofpzFNOJyOzq2H+lMc1Ev9A/1ZtM3lx934q2coySG7dck0/F4eyMPQP76p7dpPv0Eas7GCIXRlfCrMNg8CDV9XRv8VIEft7DHjhvNLpV8bJkb/rUGSff3K6KIBOP3N192sRaNf8YnmrmGIJg4yomoCiVsmRoxyvIQgGgIxTqLJwqp9VC7gBF6Bz//jCfOHGYevDohBkLCQGZmyCkLW4j+fdF9RN5SlF3qpNVpEFYMteYuLxDC+mtwAwpiFtox6JXm2hi9ysrnm/ZnS8Gz1Y2ZY0bVyf8h0AVMqlgEjbND93Ja+cxYcjdR891koI331HdLhSX5HYPnLiNMcgN8GhNXcigXdT6bNRsXSSATC/sypHWD1jWkESp07R2JtusXlTDarCioL2CeqnWL7KdS1mC1bWwQzMa6g9XewP6scnkD9DDEqUusZOntns330eME4kb/GHHgX17brGMOd//5Y7Ov0FRc3BK4+3XPVTU6LE9h5Zun4F+/x+L99WwWxw76Rr3qnH/a+nQOfqU7TeFTIw02t1n9Tfq/wCKiL6cpZfLUZ2xt9rp27FTY+sofev5vw9YepPneXDDX9drevGxM/Xtfh9nuEN+1Q03b997a63febS/086Y8Nnv+V0k9q5XKr8OfVQqJRuasclBvz3Q/DsBvlvBVt7faVMcbcLFygh+8Zpf3evXXGXz9udlfXf+VzxYSMqjhXFIVyBoWEx+OCeMyYF0ZOGcuyiLsknLGmhNPHk3yeFzz/APz4D4Q1iXslCf6bsKYVa85FEJHVEsIsHXISdzecc9PFokDhYAZVS4jWRa6/q8yNDGpgYc3FDu/PaO/TgnKNEEoIdlTomczgYG5xuNCEXggRQxRN9hgR44QYonw32KnofIOyWBJQypgmYUTHKQIJ1SIkB5Qw0ra2Hb9kdPdK5ZqPc8UPiUUVn6zDrV1QdburSgDEYkEeFPdkGUFmtX4IWWi4QGAOxfKk4MTs2NAEtVatsFZ6kZEgTSUNUr3q2luXjNPLgh9/+wnvvo345b96h4eQQeEF4BXIjBiyximwRRM6vEzaikGsTeZ5Qowqb8gM5tCsJumqCsu0bE6EfBJ3W8d3EeePwPk8gUGIHMxtPrAKXftpWZFyQvjwGdN8BvJXeDzM+OYrQpw0zAgYYVkgVglJ8c0EQtC1E5DyWqZULDkS1pyQO7KRQpAg1dOEECdM04wYNEi15WGASCyOPLGek1hGJA2GvZpAMa1iLaE4VURAVLdRk7ogm8KESBFMB+R4EKZmOoHoiExTGVFbhbApQnWrRuQUhbkG6AZIhVxBPu09nEVPUeRE/bQ553YN1OSiwHUEiqei2nKeDuxz+6bdN6LiVml0thhv5yJP2Rc1KY0nLpq6uruGHJwMdZO16Y5YUdkZ0/BQak+l3uqC2GiRnjUQYgDFgB+WEx5m4C/jOzzMAX/2DQNHxvdBvJDdk/4ZX/1p0x2CiI4M2lDag1/NQbw/lZcQMnl/eRn4Zbp93tVD3G5dVoaG00LdI52JA+IaHXObSoZKL/oeh268CG2x9ljcjG15MDqgWihjjghhljfa1ijAeGmig9W0HSqcNBrSeghdnBJqCOj6dAjEdo0QcLm34zbtY0OAX1iruwTR5kAdwGEIx1XIxm2Omx71tyKtw4Kb6RhcCAAYAUQSyOev/uo93r2b8Y//+BHnMyA+6K0tqnXqeApq2H43JFQMFDQEFDFymIBIhclfmKZxAueEGBOIgMziezI7kXZeGC+/OWF6N+HhFwcxr2Xx8AgmBA1WRRQKCuuRS9spxY2Nt4BgoA/OVC6w8jiUeoqmDAuyCGJwZNDjCvrlC/jzBDxHjJLfsXuM/p8rbflxfOHlH3GijUi7fd2cZ+7Dgjqjfz084Bxio2gqVRSWPGFjWcznhG8T7nU5m5QYIo2lwubTUqyHRNtH/gbAan1ich6KSk219CGXudWao2Igx94mlVw/7MMF85OPCJO4iWWhq1OxbMnnkFPrucGwudj8fmgJezl3+htB4OTmDO6Q4cGisD1Y8veLZ3MPO9J04MZpZFXnFH42AoNyTrrvnu9s4qbNdV8QitqRC3K4AkQR5qA2VO/50Z1NXf/cv+S/d/dPV8J/3cNpdn8Nr7RxR29CPW440PLzivzjCWvOwIRCQMkSqRffVuPLf7rZuoOp2iz1zeBvV0JXGiPr4ZENil9n5L60ArB2MLdr4QulC+OzXZI7eUf4105NW0K+Pm+fXV1MLudo7W8pjC+SXsmkv6lUfxbvDfetFV05U/osDd1xbzfdeVh+fwmtvDcIT/o11bGM2uLu27jFevbUEv1q3u/vF92zuy1cG+/NDmtSRqhxHxhIx4gcCA/pMwJEExrIeEkn4DnjfE5YloyPv12wrozT6YyUE06nBSmJBcTyDLw8oQSeTjk1GtXF6kG1q81NDrIx86Vbwe0NOeEt2HClZ8vMDCad3YsNiUZ1/gKpFm9hKFKhEXLBm3T0RjS0li04RfdXMmpxsbo1t59UhCURCUSMNE0yM2EtwgsGEJa14DeMDgfpLi/SvplSJxOE2UyqyGL9YhEceP6At2guqKU4VQKYNbgwA5wFhWbU+VG8t8bPqHPBsFDD1ofLO0SgrDRbYgnivYgPYWTOeHlh/PCbFcu7jPDVEUKZZo39kBFjVKtm64/2MRA4iMVsyCsmNtfDZyBnpGTa4hIPMSujPzEjJ2A9E9YEIEacloDzU8ByiiCaAZLQ3UQZgRmRk4yzDdY5Iq8TfsyMlzlhniYcZ8J0kBEKyvjNKev8ZBEWcAbHCCw6V0RiGVEsKOo4+7PYRl08HmTkrEHbmZHzqhYgCchJlHZYZjtrXJacEtKSkDKLlQeppQVB6SQgBtmvkYAwBYQYAD4gh0ec44SVIrKuL9sjqQS2ruAyecrF7qVC7cmKLgeDxo0IZjLheAlcVn/dG1zXtn02GN7NVxejDHbZC5d5CrZXSfOR7qNtMW6+yz7ZCs8bpa8ecbXuUhmxTb0yVBnEaqPC9R15IUTOTTl/v5v76zqS7qwkAoJI9oyGngJh1jg5FKOcfU2vlH5tzOZxIXUvu/G/X/lonP5wFhMOh34DCOIl4L4K7rKIoO5z+5679+NLGcCAWthHYC5N203d7W7ndlNZJWP9SndfIqSIw/lRTc10gzrEcYuAh05rbturSjAOemk+Bt3Hti/2i1pTglF9exSa5m+08wY4Z2EEXNtvtHXGVYUj11DVG9OeFhGN310rexEcPy4XqwmDw2lc11UdpZ1y9XWP6XbvmnVpay0gYMIcDvg3//ZbPD2d8fvvnnFe1A9nNzdF7uH+AgQB8Aw2JoKZwxEJ0pUQwEygFATpVqZnJsJEGZwTgEmDxNWLOi+Mz3/7gsO3M47fHMBBTGUpyGWWiRCYEUJW64hWo8YHU6sxJypT0hCo0seyvdh1WNHcIpmXv6yUA321IvzVJ/A/PgJP72ASfMtfUA/G5kQXXIKHc7oznW1Zdx7slr7lQvw57joPxl5710AdlLtepJ5f7nhv62gQnG3tZHgOM4hNI0z1GWl8UZczr8HZ/PkvOGwkjQeRanBBCqHEiqAQmik0zTTb06TrkP0nTHOeCiE4IrzIMPDundWl2KsbCZT1bfnKlqD6vL+mrAIT/vuWPPLqsm5+tLeq0+nvJlSGZTshNcyi5rLh6fEUJ+AyjdX6i0q/m+S0JgtBrYRCvdIVAiYE4iqyph4XcHU6IsYTMn4cL23davVGzTOfY/+bCTEq/Bvliv4e0n3S30fjG7PLt1kG23VZ3tjQ7GTxQzdOVAg5/rxg/W8/In01A3/xsIFWPQejxvbxMJcO67rZLuQtmqVz2J0FbabBSJC7k12Bfv79Ou5fFOcnbo56IURvnfNF01UBwoWGR0y4K098GgmuGkKU3HZ71X1YbpersPxRpDdN8C1lLwgh6CrGe2PqEezbs7bzZY9GFVyDtF1RPYbXnNIDCfKwRQdaf+/dB9sovRXZG98ft9Zb7m0AnAMSRzCLd/jTHMEHwiOeEfkFeRHhwafTCSllvJwWnJ4Sfvc/COuZcT4tSCnjvFicB4npkNKCrFYQEgMiCRNUBQ6C9nD1p+7oBIGR9A5xVpn2zp8hIXQPxhfP3uyFwnyvrQuIVFEvBoz9PqpTUgZYMAoCEBpsr649ioJXhjgJvUQkpBozQAEUGJEBChlTWgEiTFFi/K10hgkQqmtgt1B7ZA8EmVXUeHwWZzDLZcScALKYWuT+dOcEjYNALHVlQg5AzAxEzV1JMjMvkfgdgliBESCKpa7+rWTI/ZCOiCunAECs9ZcsQq1zWgtunD8nnJ4STt9GhOM7zBE4hAUHTphyxkwBU5T2Sfkg9iftTgicQeEAcMZ0PoE5YVlXcGaxPsgZa67M+TUBpxMAiqA4YflM+OG7WSwWphlEEzJNCHkF5RXIJ4SYQYmxMiO9HJB5wo+fCSECxyPj/TvCQ2Bh6OcM4gQkCdKOlAACcgigJMKYoMHPZa3mEmekjq9ZFwizGVmDW6cs46l0cdJA8JwTGAkhZxUaijDmdF6R04q0rBD2tNBIkSImIkyBEAMjxooXhymA5gnAI9bwFV6mAxYEJNW+iiyzetZFc8jyPOuUiB+HATZMJhhTXkBgEaJyhgWQL59uJZUdrlxzf0PY3VDJldEuF8K1wXnBAJvJC++UtRrI1wSy+JuMEui9X/uSn8FlbwrUFh+NgIJQFfraD5bWZcIIb9HQ8FE4VTh8P7x/JR73zwSLeoDBmiHb8yqhsjNvDsAxTojzhDBbAOuGSWpo/Ja++xNPWxdMuznxGvzhHuUs4K5g1Q7N3NI77eMRwTWqsPsxeNTc94OvukcHA3VxIMaXkn8azxMAKtJTEBBYzR/NRw0Usagdb6oN7t8hSLvMAmzrpMGrcgmM6ifsTtT2TQ/YMNN2SHdqaYQaF+rfq/eGNbybxVOXd5en9t/N8LXjMtKQ3YVpUM/lIRqX6UB12fs13M2/LuLqosncwMh4bafWYNxBsskOcWHbcFDrWTb3lqSxKEj9TAaVVgNABEMQCiI1jzb/lLqV04nx/A8vmN5POP7yCMoABzWVBJAzlWBbzpN9+bcVQtSLkZsLEM6awsZBb38KKIHlOsYsfX1A+NcfkD4H4HftiDeX/EgI4b9vCFQa5t27CHj4jpp6R2fyuIXuwtmlgrYI22665f76wvf/qLp2devsu+5uSZK2tIyOMqgVuSTxVeQsBDQ3B8Tnr0DLjPT4CUgZ8/cJPBFCjmAihMBiXsyqvWE+fFWTIwSn1W4bqu8nc4kVQcVUGKhWCrbe2z42AjeXIRvCafvGN6YmyYJ3k/bditsLwKGK42QXKY9EJD7PxQfjNvr17SaZ7HeBcdC67v0i5KB23bQm/XDBztxeC6TaflWzL6hGFwhAoEZe0oJcSRgAWL5/Qf7v32P+9ojpqyM69pYHvPmsTJTxZT+6s5q7g2o9Xgghv0NXbgPM1cTN+Ld9vrkOHrfdy3f3mMxpInz69oDz0azZ/CZpx7M570aCB59oew9XWGp91L3s8Qrfv2vs2/3zvc/n10ddA/u4iO7xWwQJcOvyBqbcZg1fhf3eF3sv9wu8nkf/6oJvSq2g8aYCg2fDr6PCt2a8Ldtbh2yv/C7OckPh3cX5WmD8mNH2EHpL1femHbcclxvcG8y9enpgPS7LyIcZOQZM6YwDn5GT6sDmZ6xn4Hl9BpaTaJufM87LgpRXvJzOWE8ZTx8JaZWYEDllrKswQ1cLOJ1XZdoKozPnhGLpRoqXE9TFpKEC/myvx7+d8mLBWM9ro5dKLMUBDuDxhnY0O3xbfxYLCFOQKrHsGhTV1aEMST8VXHP4Ubcz3CsnhOC9NBCIGVNmJEqY5hlVEMESx4BZ4/+RcG47xiuVfspdTlCcsPTYfWdUZa3M6oTC5/V9yWC1/jWctGXCNqMJ/8bmsvx5nKYp0Z6h9Vo2+piQg82/4NcBAYEYeQE+/X7Fw7sAvDuC1TI5cAIvCXEixKJgRCicJE4ACFmDbVOIABMoZGROWFNGSitOy1kEcc+Ml5eMH75Xd24RWBeSqQBq+AyqvaAQRVkvzogUhEmr1iQg4NOPjNNpxbcBOETGHBKIE3gVKwjkXMYqQOKE2FyKANECrrtR1985i41ISovAFSJIA06DGTktIiDUeC1C9zPymrCmhPNy1jgRFpRc6KIpmCVEQFBXzbaolpXAfMT58B7n6VHcMZFaOJEw0wNf811h68Hj2Q63p7onLRaJZDct/br+bSZKLRfO334vbT59sVLNtj5C6wSwYfI3fdRYg11ZdLlJz8ryXuneBiMlX8atA/tdNEDdWjFTMGtP89T9Px4nHWoU3LXMh1pgyEZHibUYggisXHycBge6cp21vJgBo6C+lFc/iRaPg2cjOLgPn7gG3yWFnL2yXzL2xR2CCBpORLNpeubpDXOzyUKDsl3/mp9vsSHpm7a2OWBeDwg8FRc0BlrwTHZqF+zQf//eJOLKWO0N3maMDbZ9RPD+5K/lC7l2cfCtNkctc6Xe8ro7aG/d6HcQaLuuJgqOMhhbvw2uEHft44oM7cE7yr9X/+W1Nl4jhmITqAR9IlTfpz3Xcn/IqxDCxonAgnRlVsQLKogwn/cRiFkZlxOYkpiAKiPTgmEVN0YnxtP/POHwi4TDNzNyJFBmIARkTqLdI85BC1R2AXq3TAwGsurpDJisLeogmssiNGHkUBHokpsC4rcPoK8PSH9/kuDE7M0Rx0gHD761Z5cxuvtC955vHfJkfdvRgqhPrrTTUApVg3x/k30pDcgLoFxL+/hffd8/8tMDh4CSzg8TxD5ijAwyE+LnrxHDe+TDCzidMP9OXMCEbwJyEEFECAGRJaBgCSQYNRBbsS6SNsgRcE3/yQg/9avLhqy1zPfOGWGtQTmeDPEXy41GvkNlAwDrsVE9haL3sSL2BrzTwiFqjppmGi5cY9USY9CE75eWq7c23BbYCfxczjGtp3PN1MkhimCiseplFuonq9UWhUpwos4n4M9WM0sOIlyCmvp/94zTd8949x++Rfzq0PWuu+NG99je1eTh7e9KE1IHn0fHZQ+3G87FzgSV9VbXDNN+cOv70u3n5HoI+PiLA9zC7ZIyH1yfmwDyHd5XnnUC/dcIIQCU8a/vBnf9qJ07x/GnO6F9G+1n//3VQohbSv303XtbGjGod/D7Pu5Z+X5rO03+9ny4eQbc+TXK98c+3G9KtPlyR8ELZ1N/KP9kqW+Dm+cbOf6uuwrtzwD5G60Awz+XOOPl+Ihv8B1mPmFZEzgl0HkBpYTn04LlnPCb/7ni/JmxqIull9NZraYTcmYsi2qOayDh1btfygnMSRWIgBhDpW30TjcGWwkmbUoR7shQ3SxEu/dIXO0Umonq821PdTyHXpGNMVmHkMTjLGoga8GVTPm5uAryeCC2x0Z1Kan/FCZgnR0TovgrKDMwMYMyYU4JBMI8RQAZMQawKl8iA5lM+cWQYteeWxfDFe+ECZ4uM4uJCrrmI1L6Ti0KuNj9wuKk1Q6zo52qlrP9st+Oaql4XQdmAHSc6h+pLyjxBkCIFJHOCZ9+syL/gkCHBywUcKaAjM+YsWIGgAmYEBAo1hYDZMIDA5SAPIvQLEisiTWtwpA/r1iWjE8fMz49ZXz3O3X5NKkgLJAMZ2bxzFR6EgCKQGCECUAOYIgwAMr0//QpI3zOmOYVj0cGHRMCiXBAYjck2QNWa1YhhkrwyjzpPLLh95nBlJAYoGXVsB6igMhAERCCM3JeJH8WwUdaNSbEWWLBBGSJm0c6HzFgIpsPAMh6jTHWdcLCH3B6/Arn+Z3S+lk9N7Dy7GQ/M+Cs4Un7YPehp6+2ZzYRdWF/9DAxvE5DSGyOy0JP9HXu3wsbfGmAKmzrcnvBfuorT/W43WZGDtbBMjY2JnVYuKy57THvDjT4eDu234VGrfn6M8zRoxfGggD1vuHOmyJsDuXTBMYUCVMMmEPEFKLOzfiuJTdCG94saEP/eeC+NObTuzb6qYUcfwzpdtdMPd21g+vv8s/3nvT3+TDV261ZqmXTeBK9r7AVHGxhqVcSgRCXA0IOmGgCUQ041DJzrQmnITfoQwPFsJM90dG/3jwoH9T9rpDV3mxK3rOgd3feFqRtznClqSt1hz1u0+VyW6uA21LHPmgq2IvLQP37mxu7EcbS7O7OaWEaEpvtMy75SJByc7Q4RKx9TVTPe98cVVNjCWKUxXljAiiwmMkRwDlqM1wuJM7ixsrczgQNmsbg8oyZkZ4yPv/dk1pGzGpSLLEictDbH4C/dIHqRkkQ2Nwg+R2/sowVURBci1gQOPWFCdX0QDEHdQhHOQyUUNDLnA1zzT3iKxdpo0jfzFPNaRoArQa4e3+F91b5yi0KMkojNAnoHlJ92OMQu7X5JodgXN8PG/RtS+UMatgbHG5f0/hx39Y90v7xWMoeCrrOiMRUVNz32Z++s4DsVC0diimrXYVuPRPFikR1DcvIGNHQdcrNJ9xaaQQSpc5QiM8i6LMqurgrvnHW95ePyRbo0ZKR8UAlHAY5+p0irz1CV/MV5No1ylxora7O7jatHS/71fD+svcpAJRBHISosuO1O7I3OAIJ0zuznYGbbjSFCmG1h5DZI7t39gQK7oxv3+1N3OUd6/250qDI3g2/v5ed8Ko5h8i5jdCnewfZ7iHXt8XuonOadB0q0PSLxv3cE0K0Ciz9F596LbvmVZfHDYQHpoGbWlgvpTtwmzHkO/XcUO/tLb+hpLuDL4H0k7LYdxre7tPu92uaGhTe1rNTcyN57OitW9J28/6TSQby7RjAXbX/JLX2TRQ0h91D+9aBsGEQXUKSuuOGOSBlAs8RfIg48gsO/AzGgrR8xsvyCS/LM374nbi4WZYVa8rl8+ljxrpABREZ5/OqbluyCCDWjAyGoOYt6yiEoLBHAKz+5G29Cv4iKETLEGtcSpMd54RJmfamuW+CiFCej+bOCTZ6pEHdLxnqYUxAETwInlE123OVU25wOlacK+ttVZEENkZgKSh3mdfyt/GyeA6RI0CEaRJ20DRNYDiLCHWFIgITalW/yM4mUqghdJ7F9WXDQBmgDOYA4qzCjNHNRjYo5Wyh4ospl/gQ9U4TpEVQpx2LXIKb23pTAih0GEHu+UziOpVDwDwF8at/kHEJRIhB3ANJLAVh3L/8kHB4FxHezUhTwESPoEMCU0aCxDyw8Tcr+8QiiFuWM1JKeDm9YFlX/P77J5zOCz4/PWFZgE8/zEhrROKITBETIiQstngZYJsNIe4h8eUCQJO6EWMEjR3BSl9jPYNB+PRjwvOUgPcJcVpBlCTmBksMx6j4G6esCno1ZaWJOSttwRJDg5PO/0IIKSElDfSstDhY3F7BXKdllpgQKoBJGo/DBEdRmcrRhBKlr6zuxiIQ3iFP3+I8f4WX6QMyP4PygqmuJoBJ5lXXU1lHtpA8PV7w/ZYO8itUhHPqzUElm21oP6Ucckf7NGdrvUv9TvACs1HbFctzERncdi9CIpNmsrlmqplIzwpz1VQ+YVRNhU/oLvkuQ+9hcweaO1PteWnXlEA7i4jd1BFLsn+rq3uGnstczwAQiRKsnXNRlPyqJbObCPZfr+MzPzfW8k9J+PAlYlrcFSPC0ogQG29Xv8l2zPpvGe/ijw2bNbwxeXRVylr2RF+P3PtPAjHhkI6IPIlgmVrpeg9rXd79gFzoyoag2FTafe8r3e/LKAbFpbZ3E6M5gPeW2X5tdJXg2IOlmEzuFL9E+JByPq718jJoYTjPm3baDFfT3jz7IGbjcqXR8Xtdo0x9HhrAHVBUgezQdlo+G41rD8SgedJ5EiQOGiKDxNdmFo0kEDDlIP4YqR5anJMgrip0yJQBWt17YbymU8LTP6w4/HLC/G0s45UJGgfNnSuFTtKLWC8+QXxMoyZv8osWsAT7EpybCqz12uwZ/+6S1HOJqbIti2ZBoMb/oV30PffMnyGGOFUg+zNDkQXqYdqmjqd8MW2O177uLSg7eWUTCn4yWN9srY0auaH6azl2Cen7KuZC0LUFLsHiNSvaF7bHgroZdsIHF2DLYkbY2V804iweQxm2QsVue+gE9GW9MbdFm85zRWDL2kQVapCVqwSvy7azwOpZ0sgpyp7r8u6e99oTB0vbD3L5AE+I9ub36LZU79KtCHxYNGDMv74HrQx7V7f3oUwhF7/UIKhwE6WNtoOX1qYRFA7obSbUndviBv3dsRHU+6HZwNiWuQneJl8H2aDYCPJxLmxyXS5zrS4UoY/HUctycsNYvEeUcuVVk7cfUyOk7eGesKHSW9veUD+Pgxzb97yd5ytpLP+4s45rle8w0nnwbL+RvRz9Gr1W0Tbt8cm/mBDiHqHOnWP/GjhGq+1S/jbXtRX5R5yuAdjv552Ce9NZ8K1b0Jo/xGBd2Spb3ODWKuXfnAlrmpCOB6zHA4gX0CpCCLwseD6dcTot+N0/Mp5/QLF0WFNC5mrxsCSxdDivEtw2rRpkOmdUNKSqCBAFufuLEof8BT9RnAs+4Zlj9ozQzmsMGisoyDkQzM0O2Z+/D9oTrbVuZoCp8OtMGGFWEEUIIcaTDm9rJ6Y4VdGKPH5a+X+M1kmLjYUpwCizGoIrETNyFFinSQQ40zQhM0vQahaNcg6k9NZ2cTfKC+zh95a5IoQQ5qcqeYVQB6SsIM9Y59ocq+96p0hWr9S6af167pVSqcxTiyMWjJ0g8bxCQIyMKYoWdc65zH+MAXOMYE7gPCEtZ7w8J4Q44/DVEWl6h3WOmMJHMJ6AtAApCc5vo8IajDonnNYF67rg8+kFp9MZ/+0ff4un0xnPTy/I6xH08kuEEDBNsQgfgrp5YojgxLpT4jZSbMY2BlQhAGcwJEbD05N4ADjQinlKOB4keDnlVV1KBUhMDwIo1PFTgUrFT/2fCMgyAwgJISeYm+MysQxdoyLMSGoRkVNCTgmA8A5kzEWAYBYaFq1POhoQphngd8jzNyKImN8jrgsiL1A/DJW80YDesh6N1qnrxeOUVcTZ0u6AuKGGumYibBVhCkrHEGGlGPY0QottZApPbI2+7z/yPTBrIeOBZDtjytyguDrzym0Gi+DqhKK4pjy1SoPV/Vrp3FqH15zyfBcJQs2XgL+MI5Hh0LLuyQaV3Lsg4x2CehUIESHEYhEzGrrL1HyftwPJ/ftTp9cy+7+EQKNvuihmvA6kYbrdNdOG4HJEloDl8tZ3tr09cbupu/vNm29BmW7crSbb8r4NhUlXHunhPa0TQp42SH5v5jyFAwJXf2LlIOopJzuE9jpxqZ80Krc1CNrWaUhX/6K7fmvnLkExSGNqjNyrm6qpR/Hu2/13o34PwdrWStdavlrJ5nC5JnS4m1D1F9ZGcDDe8bs+2ly+4f4aSfNVMBdCwDxF/Nt/9w0+fTzjv//373A+J5h7EHZVbJebXsI2VW69BQI4iB9NJHHTtEYW5Jeg9TOyBhMLWQgMChm0iqYFINokSOqPMmesn1Z8+m+fMH2Ycfyz2QEjPjerOaJdki72BAPQGBTDA50IkSOIAiICWIkaXhPAzwjRWV0UbpV9dkg5INo+mp8AQVwcbJsLrD9b9UfJN7gJTPP6HiGDlR1eyaOfm40/aoz3X32h1N4HHnO89Sbc3iiW+mO9qZp9uUoAsS9xAwg24iEERIiWT6SAwD5YtWncWaA72/dc5A/stZI6oSH3VgkboWL3uxB0Ttjm+1u0ZwSBB3MVrjV5PUzbFkvMlTp823PuQjLoWpdZbh85wrSvXc6m0X5H3ZuG0BaA7R5RnAKKotvebco6mAiFCAdD4kFkIXyYA/CQsf67APrMiL9q+2PqDKVF0go9sNCz0wTGRPV307HWB7Qd0CN8x87w8p6anHL01NFpkg1V8/snR8p1RbH6/93LMlhfLcHBADIecsCHNOGBK/Nq3N/2nK1C43qSN+NH47KbGBtD9x3NdbqfdtCkKmCpmX7qeZG+v62N1+NsA1z13vr/iNIXF0L4+r4AUfrP6QsN47U6vvBU3XLjNqjtJQAIYCbkHAv76jCveHw4YV0J4cxYMpCfCN999wlP333GuorG87qsWNaEl0+E9QzRiGZGysqI19+FCUYRFBghqutCUgaX3snMrAYQooIfAPXSITyDhpHYMMu4fKcNjiG9ihbcWc9QC4gclCva36X1C1dcwJ55K+hyv4sLx2zuXvQ+DpBAwXA4WJkhYyiKBEOf5ToWJWtl3Fu/q0BC+pMVNfMudGOMiHHCxBlTjKIwFgghk8YRq0qhVVDux0E7acFkC9yKx2RGDlniCmYJXA2lSRvK05RdwKihnrn9o3qHbvck64RX9709ptRQNgRVQDOBFGGazPplgtC28nuKUYQqWSxJOASsS8Cn3yU8YUFAxte/zHh8f8REE2JMYDyDWOKecAKenheczmd8//vvcDqd8N0PP+C0LPjV9x+RUgCfvkLgAyLNgAajBpkFgDBZzaLaAnMrmxlBF1PVGA/KyBf3TDlAxh4JnIFPP06gkPDhccUUM6aj2lmkpJr/DA4sgigd18xZg1ZnDT7dxY1gBhIhJeWlefwZgMWZO2cWi6gk8TFktix2HmncvGr7wba2iLDmGef1PZ4P3+Lp8BVWZoTlMyKvMGdYEvfNhAWeVlDN+ZJvhEm06kZ1LbtF02j6aRwPK0MAsgXPtNlRQiGbCKxtsewoOz+IoNHbYWdes8Zha7z+NAXMrGcE65/F6SBzbabWLGYx4eeupxMbAWjjGs2OqU7QVASkuZS77RaqY1G+D/iRbBu/0GwkMUgbt2rAFKrI51fhiBwiVvj+tDh/jQda22Q7v7ozxq+Hf0oWDF8+vb3vdwgi+mO8x1mM6OlB29nmLS1XUmG6cLM8ACXoWl/T6LEnAKGYTApJLr8jH3BYHxpCjaz9HvnX8vK42zyb9dj3y//ebr5WSOPHoZ/M7Uj6dxuhyyAP72yO/ulNx8POWttfgpcX50XieLtcbm5l1OVbCfG7hQ6v2X8bQtN+F+xuJ5/LvYHTLWgP7QY+qv8RYT5M+Ju/+YBPX53wP//+RyyLugMpVe2xZexLvYSJFYGW+0CCSav5YgwRGRmgCHONRGpCnJERYwJlAgcWE1IIUSLIj9S/viScnxYc/yJh/kUsl22FyJkNMoAiiGCXl5sLCFROFvHhHxiBY3lJ64ppfgFNAayBiXk8JM1cmB9V8pd1j/livFb36hy20z/bE12PKx3+bJ9e6ayevbehF3duaG4+sBm8C0KI29GdQV4elW8JvIqC3NgSyRoLJP5aAwlxR1k16wI5S4jOD7ESkBUSR6ihLvdydtm4bMo4pLr5YkVs/5jGUJ1XUQDoCF0t2Nx23XshArgQAJfOlN2h0/H2hjVut8NVXH77n9nJZ5ohKuu99f1f2+zucTcJZYgbmqAyT8wyLwRGzgFECXwISH/FCD8w5t+KkNXDNOi59LKdbrAj1/eLkrtD/cam5n1zze4hZNiZMX92+nw/OT7uoXGtV8rp5v1/yAG/yFMhJHr4R3dtb/1KLt+WLzVWCtmiGT0OiT7DJvlHVxUVmnTf/rtcVwHg5om/oWttvdfyXMjQ41i3VfaF0g3jcd+8vb6tfh33K/qWOq/BtD0ffq6BHgBxDwKwqeKuFXqtMkefdnTrKPsfYMxuGap6TzicAAEJseDYEwP5kJHjijWfsC4r0tMZP/5mwfe/Skgax2FNWQJVc/Z8sPI9g+U7yU1ehLdkAXTt8iWHAwqOQFBvNGQBpZXVV1AEtYgowZ47v+Vs9SszugvsbPEm7Lgz183b0STRmG/QRnJBslHXgFoakPmaByvdLkoGtYusXda4CYanOkah/VfZDr2DZmgb5IaQQAgIIcuYMUtsiDypr3W1AskeV3BdHbYwuoO5zAHY9Nq1n8yi/GU4BVt/+w3t+uieD4UQm98Ev7s9hB6fKjNIkJhtDj20wMkhRMH3VFDFCFhPK16eVnBaAF5Bxxl5Dpii1Bt5AfIJ63rGuib8+rvP+PjpGf/w9/8TT0/P+O33PyIlsUKJeMDx/A6gGWEWIUSiCWKVECExDKPS8cpKN9fIzGBU6wUKJGssECIYsgcSOBOQJ+QVeHk5gjJjSp8xHRIeJ9k7KWfZg5wlRojth8K4ttgs7rfOXZmlRM0SMe10CzewrhlLZqSUkXKuU6VjbYKyYDSMIWkUsOYD1vANXuav8Tw/IucV03JCCGLZEWzNmTWS25+dupLD/bcriLsHhLqauCnQ3h6tUorigqwW1wpDzw8UGLKcM7C9TVugPHxl/+s8FPdHaqUCccllAsxCUxVBZqVpm84WxTM7U1QIgeo2trGSZzs7XV3leTMwF9OGJrmUkVDwT083SywXVUNXt3LfhSMStWPZniRu/jfBInln/KW+t7gnunbvv6Xucdm34RlvAGc33SGI6NS32v3bPe6ILtuklWrbaUU1Htjn8b1WDMBtFvL1kUwqgRDzjGk9oLi7yFPrhsbKkoOthxuoSEsF8eI4XLZWqM+oaXf8blN+h4ndE1qXltlezIF2wdJg9Lt52Lbscl4hjF65D8aQX8vX/bqToromfPDjeZ0F4vP2ZcdroX7Q5nHzoGC4W7g6gGGCCAAF2QzqGqaE4d3swYqmtWuC6huqF3QIUpN62ZS9l9TiITCytU8iracgiGnmDKzyXrQjRPM3qw3q+ceE7//zJ5Hy54zjLw44/uIIs3woJqIqtS/xJtQ/ZhVeaF/0PJh1LICIsK44nhn5ISOBkVMWM1Vyl/JwMvSCB+C1ChjoraU3yM2ldJ8GuYPKpLpDWG9ruatx+/rqbsfO0XH5DPFLv+m9IWb9sLsffX2jHuyOKI2R0d3MXS5PJgH1PrLv4uqFit66f2dEbvHjG8oFVetja0U+K17FjorTZ1yhbPZud1ag1ClETL84iy/mQsBvTwJXjXvQ+mQq7+/AZFhNuL22IkPDCPleufcelhgNyW5vtBaEDhHvzs4emTOhCLvxsHgenLloMwYQzL+xvBNLsYp3VMFvy0jYrisPKtsaJ38yeNylMkvKClPhQ413QP6j3nPN/uQmrwFwlXHeQUS0eaLP/bzspX4surnpnmxHbX+tVTywGwvbixv4WxBqt7p+6b9eCOGZP+jG/PK9vwt9A3uf11yS7Ldxqeoez/yZ0y7T/I4qbn74p53K3v/ntJu+rMXQztltj/f2+u7vL5MKnsDtcrh0FZdzUZmbKcfC9Iox4f37z+CccVpXnHjBx++f8Om7Bd//ZkVKCcuScH7JWM7WGIERJZauOpgBCGARRGRmFVJUjV6iLMpKWfkCqvxQulBwjKwMTmFClUC3HtdRpljV/E3621sYWHZ/T9fz0N8ZzX2hk1vwMgQwZYeWOByFUCwgAqvyFhEys57bjBg0YCkNsH8jKIogRb+rljN3Ws7O5lU+zX2Vjn0gKRqjPJ9nc9EUwRzFMkR99efsMVzFXDa4lF/FhtOEolxKlMVKHFTj6qnimMRHk4GX6TAXTiLAaHA9p3VdbSbkvSmyyVTrO+ImTz+oXOpUixgiEZBMDrclFM1yiYugpQMBTEiJkVLCb/7hBb/99QrKZ4BXHL9+RpjO+PTj9zifzvifv/oNnj6d8Ol3GWkhJP4GFAKm4wMizQjTA0ARHGZQiKAYgTCBplnGKFhwXkKRlrBo33MWxmvQAL4cIjgQjCKnGAFihGkGEeHw8ICcgc/nEyZecfzqnSzRlDEBCFmskpiNoS10dVIte4sPYWtDhkfXfuHXaQrKL2Ch78+JseSMcxKBBtQSwmJDTNEcUklUdyaA4gyaD8j8NU7zX+A5HHBOz3rEZrWekDlSx89CRWRZAzWmScWNyi8vEHRgez6m4cAiSAglUguale/pq5aOE2FjXZc+rwgvNI5KX1c/lqU9j3/Ws664lmY0AorMEmulCCy84MLF0yx7rUo9YUKmugc7iwd3RstwtuO4DT17HT8t5d15oDY/Ol6Kr+u8/ublE+Jhxr949xUOE+GXXwOHdxm/Ri7C86Zmdy97oU9zk++SKlzov9em1woaNop/PxGet7W8//LplRYR3bvRDzITJRpOYEucXhE+dM9Mkt9XZtqNRISYJ8z5Qcy8goilZZ1Sg0w04PV9ZN4VwGz6s/uUa1v+TdP/LTHcHjCW+vgFOyi0EdF3rJ0GPjf8FY8bTeJOXTe1fTnD3ttbiIbrwoY72+4etO68PMp1Q6I2fz/slSFknxeA8XAMmDr9WFVUmdEi1FT2R7Gs3bRrSFxGZZS167sJ+mb7k2pbpnED+1REIcQIZEIOjMAkprtMCNnMlivClV4ylqdz8bGJmTB/Myvh4pFv0w5IctdaLIpCbGh/yLTSIyIDIWRgTZhOC9IDcFJfppyzuIviFtHuUZZyiXttAjNpbUYS9f2F1FyGm3T9DbFfR6Nz9ZbUryvfzg31NG3fT/aT+9e0yrhXke+hK8jRuKcXx9WfwbsaBQM/vpeSLWHUO7H51Ezl1gyE5u5s8FzdqB65VcsDfy8K3uoL+tkih4fVusiPZ9kjRqTVu3o0pqUtjY/A/d1pVRbi+HqqoFQE298vGw0WryXZX0R+TbjJK4T65gg1AqCDybpp1hSEiqwHAmUR5mZtPwRWJgNrXB4dg9ydz1xIgdpf2l9j3QrY4DZl/TTrrsM3rHjofm9++TPfPb2CD+0LIXY6dUPaoGk3lquB87bwNAATteN6AYi+n5vuXkjbsRmD1PevtjnGEajv2z2p79fO+00q63V/BV1rc7fMnYtlOHf+K+2NrM/+ygW6wfPfsNB36tzNdqXsTTPzVnj/GIQeN6Ek1zJt3/fXyd3pypAbfvClE9H4+4US5d4pzDoQxMc/IeWMKSbE4xlrXnFOLzgtCz4+PeHjdxnf/1pcLaWUyz1WtVWDurjReG/mVkYFEEkD6+Zs1tH6O6hrE9PMt5hZRs+wCiJCKJ+RoP7xpVdFcSCrH/tMkKDDgucx9/je9nzYCq3tuzH31WLBMTSlSRnJDK6oG8uzYh+gdYlwop7tjTJuoS/0wwQr7o9zdcNSBS8eVoACKR5nTNVQgn2HEBFjRowRKUnAV3ZeIoqLKzh6p6wcEeCIiITR4GNw+COLmhmTaWgLcI37bXJ4YkNXOfrKGLalr5a9Verww7aXqqxIYCBV2w9BlOkqzzWX4c5sdjYCf2ZhrC8/npGWEziJICK8/Igcn/H73/4aL8+f8Zvf/R6nU0L49AtQPmA6vEOIE+L0IHtjnkEUwCECpH8h6PdOENEvFFKLGRVE1LyACOwCLI4EIyLOBwTOeDprrIYstAQFRsqEiWVvZh17W18bIYQynUs+3iqtsLoZYogQJ2VgzVDri4IdqkAx1ADVboVRiAhxBvCI8/QVEgUgn+rYcAbZnqqzb1tGprfBc6h882uV6sLbJjKBiigcbXWH3APd6z0NXEm1DoqCSlFzfjKzBnlnVKHECL6eumL9XxYwscOF60GCqi3Z7jHbGNzzTnwdfnC71vexrcu0wJb0tugQMj+ivGujVvlYP55PCCHjX05fYZ4IXz0ywgMamm9zGJSp4c2jAuuFw+M1woR7cMNb6h/leQ3+WeupA3ZJ6PEzB6t2F+Pee0cX0ZX87bY3rWp3AGwCsTrNAKoDEVLEdDoCemjJQRUQOSKESQURdaGSwyabc3zYJT8RY9gvpeIfG248fB+6wdnm6Rk5Pv+2vv5HO8a3LRYZnm6RXejwaKHvt7WH/vcWGOPyt+yp3Sw3TtouY2XwYqMZip1Atdcq7+vbCKVuqWtzEw4S40Dfg/EZJ3yLxBEWLNcsIkgR/PFVUusRRKO14jBGlxAO5tNRTW6z6CXI9TEhZEYiiREBMkGBWEQw7NILyDmBmRCCBL0KOSElCaSFFHH6/Yrl00cVTGQ8/OUBh29m5KR+EXNSTaukyKSiyHbHEkrfczojnD8hIGCNR2S14DjQCR+mE6aQS09lCuo+a/CMci/bah4g7Zsx3pux8QzcmlpE3i+bvvXRPq7fejRtN42WSvOu6HO/uk9t2XEtvKttXcfj2o4xnK/Nqd8LQthUua3RHWycWSxsSHZCZqqBCgcI3KU0ttTy94MisBvkWN+64SEVNLQuibiLddLdA9zCy/6zXP3N00L4OorPWrrQU3Og3DZke8nGvHbbCKCd1CPvvN0j9ZVZY3RovVYe+udKCFcCogpFQwaYCPwOOP2HgPiJMf1PD4/3VtvDuwXPr39z72UmyUUgYb+1QMted2tlg1bQdn2hO7/emETLxuqjQlu9ocbuc5Dj84L1Hz9hmQh4H+uLsg907AoOur3fZYrc+UX1Dqxj2N3jdt6FWo/HQ/dROTlceigKrMOyXd3bblxN1H3+ZGmIU72xypsf2osvs56lum6mXrGgX9v/cb9/8hn8E017RMANJQ0teBV+/vOnHk5mQuapCsn1zI+U8P7dE5gzXpYzFl7ww+9+wOcfE373jwuWJeG0JKSFsK56l4VZYmGFSTWcozBbNRCuuaJkAGkV5qYxQuUvY5pXmIa/v7sJNfC0jyMQ3D0YyHSe9C42ZmlOwjxNK8AZaU3gIphwSgCljb2xs/Gr9BqzndkuriXUPQhE0arXoWSIckIwvh6hCCsCdzQl2TAwYIFp2TTRnVAie+YxCpMYpIoQdk8ovQZmiZMHwhQjkCVYc44TYohgdd0kWuWVYVmu8NH4lFz1buYSuDfKHBpztSiRtnh7gxGxCHGIq3uZAMHDxO2+CK9Szgg5ICcGRRYlapK6Ny7Gqa4os6o3/M3ud1YhVS6uj6isz5Qy1jVhWVcs64JlWbGcE87nhHVJWM8Lcl6wfl6Rcsbnj0csC4FeZhxyRji8Q6AJh+MDQpxwPBxlbwSxAyB1BRXmGTFExBjVOsXodVsUBA4aD0ADuidbxzmL1YvGTAmKpJO5d5oJORMO8V9iWX/A3/33v8Xx3Yw//6s/A4ilHuZGn87WGasQwsd2adBEMu5eHWsGI2k8mHMG1mJlI5YQUwyYQ0SMNUg1MVQoM+PMj0jpG3yaf4mP8QOe6YzMJ0zIJTh1EYSh4l9Z6f4AEbhxwGYvCoXi6ZN6bnvLJ/MdQTYW3fne2QHUOkwwtiNIMIib+mqz+innVHPXcB3n4l2jELB2oAxgYxhiX995AUUhvUwJUz1mlDHq+3lPavf69eRUXVWgXWidsicIhykizrKOQgyiHEZ2W1yBcxekvTKvx7G+BAP/tjZ6GG9t19NUPZ7wZWG/3SJiNzqgvi+fIwKJ9nHi9tSS7wSACVs3TVamEorEE2I6IFBUxEYOGqj2hS3UYo5VkIc6kF7yOO4ZD+G/ZQluiFPX5rCOvqGOqG3LtITul0pVFnzdJOfetnfzj+nq3XyvS7et4S0D4kL57QRebmO3++08Vz7D7fXtj21dawHPYJxB+ApEErzd7qxa14U22e4uRvVrWkkC2boZxAQiMx0WLDsgIHOuGiaywsSM0hDiTAgxg3OQOE8ghCC+JwPLNRh4BStyub6sWD4vSGtCygnhfUB8H0XwkMWsmzkj5SRWE0UQUZGrQAExzKDzgoeXE2g6Ij8e1Fw8IyDhIb5siI7BQGPAzXQfiry1ry6OtZxzlXk/rHwIyXgO9++Py9TEbdcOVZgHtRZcqJhI75yBl1u4CRbagaLHL2+tzwMQuGGN35zMGoctgDFU/z1XQMTio3wp+21vjPo9K4ixPOE2g0vdfWZ4JxmKafu6r9kjsS2B3OQtg1oqVli0X90ioQujKdUMovqW89EoW/md4RncHrKSof1NDNr4kLUUrMZR09iuAsFZclb/1IVgD5BIfwF8yMi/lLwTUTO2dc5VOKVEAq+suPfWTYONNwEbIYQnAEtL7aTWL0P8omuLurHE9jy5zvtsy/bCCMszikl2qS45Wr07jW3efE5Yvzshv59AH6YG3oJJ2T3o8EV9g3JRWv4RjDv3d3NPd3OwBdfK0PC8vm4JcSF1jbddGNhS7CIstmbHp+cuJDess702b78ndsoP8bp7bp9hpbttvLHmWzZT287N46aL/AZi8hoEN/fxzYPx86QbTpr76rttmLeFXtXWvdAPDkuC4N7mBgfQgMUAzQsYK87nTzgtKz5+fManHxJ+/K36ek9iPSx8IWWghhlTmBFjRIgR0zQVwYQctnK3pyDBb1dakTkjrWJNEbL44wengrNLN7OK7mvsgSKAKHSDoSLCQMtZfN2vSRj8GSzGEVE/yWE0QwZON5busPT3cMWN9C5myP3PpJ+O4UgQxjr0NaEqeClORgWegkkV/qHF3DN8y+MN48tD/gkqjKjKr2KBTkGCdOcQinuc6r6XhCbL1Lqp3S6h6oceFQ5xqapUYhGMGFroLEUc3rh/bnDto/U3iwIcqwDGLGuIZK4D3Ga0u9xwZT+MZZiML6SToXlEwCPrNWX9S6sEZF+TCCdSxrJKIOa0JpxfgJwI69OMnAhxnUAA4nRACBHT/IAYI6b5qPtCoCBQEUxQEMFdiVPh8UcidctlYrlcxiXr2gKpiyMIDUOQSL4UAKwzCB9AnPDDj094XGf82V/8UoeVq9JNN+Qim3GCMLQ4ao9mWllx7SQWERI/BupKTSwhYhSLpoZKpAAOExIfcaavcKL3ONMBCy0AUGJgGOlRuQ9uzwxWUr/ECGrRxKNcdW8GeGUtZ63g1kpf97b9nRzU7hEub7c4+LBK7sae65dCmo3a9Si11eFj6VimppJymg1huff628tfqdKKi5OuC0JVwopEmPS88rzfmxqpDf0JpVs7NNy5SqcNKc9Budeluywi7LIF0HmGoDbX4GIqu7eBmQtfwmsUmw9w7iKVEwMhB0znBxQ3TAiIcVaGaijICFQIEYJntMqCNMlnSxzKj41AYk+zdoCPbNIuYugwl+6xf7/RuN9yES6nBsb7d9Y1Df+L9g2bhfsF0isR9FvLCt63zddsT2qfb+RG9m7IQOjz9g9e37/XlPSBfYwD0+6D0aVngYqq1q8hTEER+YCK+Jm1swV7FqZfRia55TgAnAmkgbFClngMOWdQiEI86O8QVkFg4gRKCSkkAISVCTmK3/2nX53w9NsXLMsJmTPe/8sHHL6asa5JtDdSLsjxekr43f/vO3ACPnz4Gg+HgK/++gH8SHj5VytwFISPwgoi9a5eeKLG8GsPAgLVdaTWHhURh0MK7HNnn3CfxSHQ2HwdFOdNhlcJLO/axtwiHl3ZrUtMNy49dF3eIRhNPXYx7eX5cuneISlmzCkhA+JbVQO65wBZl0zInEBZ0ObgfZkOGNC1fkXT75raUeZKgpFbpNy862vZa5SVp17ZBASucohyxljdA0FDWe7dOt7Mb1u26EvY2dQxTC17W40SDkVIqCtSf295rvYlwo9NYR4EcxEHcM46j6IhSRyQiaE0ZfHVWsbS4TwM4PnvP+Lld5/x+K+/xvHP3zuawohUNWE3LVNDwM0PtFmDdpD3qFu/95q7f0OQ7e8AEy7YjuyFDV8ise8EoxJsMAGzg9Y1uR4Cvv/LB+TJ7rpaDRHw/l3Eu8eIeRIW10gIUUiaUt7tAvfMv9m1hMBoROodLFXu4YibUm1/DeQmk8GFNu9bkue03lHhl1kJP2/N26b28POfD4pXteMXwAUu+c84kn/06fKp94Z6/RnzE6X97VnPAwaQ8gxm0VAOWPH+/QsoJDyfzkh5xa9/+ISXp4Rf/Y9nrOeMl/MZ60o4LwAQEOKMKc6Y5gPiNGGeZ8RwwBQOCFMUd0lxctrclUmUWBQyllVx/HUVvGg1i4hV6Qi1UlTramMyBrDyb7nQNPK9Wgpk1RaPSRihK7Ewh8vgqAWB4u1sKuCbgTOcxOgmP6Sk8BkibCIJvexrZAz5FBVt+Z5FkcFiNmRIP9p151cKA6poxZwLPVaY/1lwC9OQryDazSAa5zCBdxCLhRgjmBnTNCGlpMGrVUs/s+A3ELpNzDgcRNpnv18EDzBaMTiFAY27R2LVwKTjQZq/0FbST8ksn2Sca1YrdwIyBYnnRxmgBACIWkUIVAQ9ZQqLoggZGiFrQJ9lxeGK2yFGcUOUnDXEmlaktCInWbsy3xNCBCglIBDixAhhxuO7gwjckgZ2DhMCEaZpRgiEGCcdx1wGr+B2ys8yHA9qUWQ+/stoqZDEXCQlVdyNkCE7cNZ6J+k5J8RIOD48YJpXfPjmG8wzaWwOccVG5bOuMRY1PzCrhYMX8riZkzVnsAnfYM3AmjOWVQQ5gSQ+yhwD5kiIGuMFnIXBHyLWPONl/Qofp2/xu/lvkKcDZv6MmRck5T0kQ//IXPioIIJtVYowxlt7G47feGYpaCRvtjd5vqQeD9n2ehFu1dI9NeWTx4obFUWL+QIVkm5Sxc+bWs2VNQMSb0N4puLd2oQ01suReqM7Q4oTJLg+cZOvQtPekf3npVRphLZ/G/6FCR4CVbdjqPdIUNx5niLmKWKaAmKk6g6XHIxf7EL/cnTNT5tu6+wWHeSLz79UulkQEfqVYghUj4yPJoUkX7MA2LbB1oipfJKvgvTfiCkfoMtOd0CASY5toZJZRaDEZoIRly3M3TW/ebdL+V19ZAfixVQw0X4cR/DUfNcQ12sulW5KbO1cWHR7bbyJyh2XvbnGvbZvreBCPs+YKr+bYnJB7IMwns+dnze8uJAu1G2aOsV3K6iDjYbNeoTNGD9ENeMmxgTDIZR1rYtCjjDliMV9WgiCILDmFTPnhBAM4QZA5rpJkOccJoSQETQY2vIsminn0xlrWnH45YxwCFjVQiLlVE7V88uKT79/Ai/AtBwQ3k8gegRmIH3IwCT+UgsDSYkP0j6I604GJxOwcOkla042TMULI4D2LOzTpTN+9G5vaXCbpzdV/UnSvbBbovYeuFzPaOD4erk7Qdp7x5deAtIXMoFd1dgzYhiUVDNIAkNbIDFWIo+4BmoXm3Ot1nNOCyzW73ZO3443NBt4K6DfyV1/8fYbkQtexmU/9XDa49Ji07dab99wvfIMs60vTVuJ3FlErpyCJ/C54IZyUrV9bxk7LWxSlbmTUuWIgtBTlTMQQBOBV1QBRlc/wEhPC/KnjMNfvCvvK7NZ+6jnr2FIUCaPPZOsV+7UIXpXx0HBcW+5gLBZGjqedjfuCyNaMmwIyDA5ra5yoLK7dytAPmZKDsDpMSieiAK/XVjTRHg8RhieKND04ws/AW78vJCh7tPmRm0RBffOfesZWxfSVlFlW1//kjZ52/QqsuoWBvwuQrTf2v231PZ89Mn7W35zsvHcwdu/RN0313l3fxpE8FqOV73fpA4X+SnSF8Frbt17O+M2doXwxsZ+kuTuxuZ5ACEBlEDxBMSEl5fPOK8JT59f8PxpxcfvFqSFsaxyEmcYgzQixgnzfMA0zTgcDojhgBgPCDEixFC066kwkMSCwgQRpoS0BvH1ni0+mwU7Lgy6DCp/dupyUeAQnF0Yp4JrsbhaJe0jAZwF/woagy6TqREBpr1fbkJCfX4Vmdqeyxbw0+5CMsY7yR0lV0d1t1LuDmopcD9rnhYzpzg1ULWuxZy7rdeeW3ZdCk+PdC7NJZApNoTG9WNWA0/rDztlLKtvF5fXzrEiBpVOrDjGNqAtCh1ZcW8uuHNxgeUETqLkQ+LKKQNAcHygZnYaDpSrGuzw3mJ8wSixCHOuAiDvFouNACaJ6UAhI8QZDALNKoiJxuqVtRg1ZorFJC2r0F9pDqcl46zqQqn4uRMRGEweR4bgQWAon0yEXwzGNM0gmnE8PAJhQc4ZmUjcg1ldVomNEWvA7tJvmcAGN+7wEgaptwG1htB6AwHRAlUTKa4ufEJCQOaIhd7hKXzAx/kXiFgw52dQyG7dMZJK9lgfMnOjL1j2sM2TG5xmqbrd3mA4JPuIYO6e9Bn7Un4Wff+rVIHdJ/UPNXkD7r42jzuz/ewCY8MIGxC855em7f6AGSL0fo+0v+s823gRqnLQtWT05aBb/XeQ+VjTaTMerymbSx+LRUSod0yL52iH/5DX7xdKV+nyL4Hr3puuwDRKdwSr7kLGdBTNPjqrl3tRhyzbpss3Bl5qCCAOmE+PiIigMOkBahtADmWTEjeWD81N6wC9IIxoWr9pUGl3bY9K26bZEoe3EmuXCS55dSVeQZ/2AN17f2l9v3Ht90fp/aXfki4xRG6jplqdFR4+/8nTLoHpkRlyf4o7kQpSXseRKB/EFYWor7TSEMRvpSJEFsSaYyxIXMgsQV5zAlFA4gRaQ/kNWsEAJihzMcjen7IQKmuMiDnju//6AzISlmVBSgkprcLwBQBk5DNwmAO+/cUZ7z9EHA5HhGkGTxEUgxBQIaLEz3CDEn55RvzXn8C/ewD/cIQJW22Es8WWt6hZ2QbCi2DtTNwOY02Mbab94b+c5edbgxdO1dsz79R8/1W3V1PzD8pBrj9zpUr0uf0YQ8DEWL/+LdL8DJ7O8kwJozUtSJmw5owUhYBPJBorALBmAmUJbkyBkE1r0CG/fdoyH+8a9WGZHrnZIsDbmkd5Gs1193t8//v2+nP2tnO3OWMaaYEjOprg7eUkLPPLpOcJC94hcHsmdwFy2I/K2A4IxEq0V0TZyuYPwMt/JMTvgenvaq+yW19m7l764Yk7bSuQiDrMCoKKO4VYCSZPa7k5aFEhN846Fg3xBTiBBDX526vm2s60M09XDF93/3ixGvvJxphp1ceK+0BC8REObbOghHtol+F1nRBiIw8sFYTmp2f29EIrj/ntWuNeSG8RQuzuobFq2h0w/SHTz9D6H4Ko+wOka738X2MUfo7kDrGfcFD9srVzw+5rBpBSBIPw4d0zwsR4evqMZVnwm99/xMtpxd//jxXnc8bpdEJaGcuzwC3WDRMeDkfEacZhPmKaZhyPD4hxxjyL2xmaJnXTVJnc1Y1SKGaMzIxlEa3ydV3FteqyKtNXLCQ4rQJ1TpA7KhXXRt5CQiqUoNTFIgJc4kAIfi5xglIOGmsgIGcCm/EC8uZIlK9Djvbe6OscCBNQSR1RvGIgh1xdfWaIAIA0nrbRCYQCc4sP2R0KRU3rnZpzjY8n914uM97fe+TurUAQrXwGphiR4iQWElnmT1zjBolHkC7cVwVMxWUMpVYcjQo+plaliltkiLSIQgBlHR9QwaEpC9M55yCa7WqdIXYyYiGfjPmYcseToWYyg8MXGSgWEKwxCzjpb2fKbRYS2caUWCwZAgGRkJPiHATxWx9ljQUAmCZABRcxabBmHZTo6HBZrwmGtzJltfpQOiAYzkB13qUDOhCC4yQTkmQudQUYs18q4qBrLgB0OICWd5jxL3F6+R7/13/6L/jqm/f4V//mr0EMJPUKQGBklpiMZu1t8Rf6c6wsAX1uTn5MEEEQHDbGiCkEzDFgCgEx1PyBAsI0YcGMH+I3+PTwl3h++HOs/BkfE+FDfsE7PiFBx9ORQjLFMh4BoeBi8pxgbo/NEqfg3ShDhooLF+S+4HOBoN4fzCrC2tcSRfDGcJLHuhc60r4ITqvUC2CxPKmxpEf8ACrr1M4MUYGSDpO2LW7KapkSi5cU1m5LmwVM+9dSy/7Tvt/nurhfOFR+NgqyJdbvmMow/tUUxAWg/YVobs0q/dWeo29Jf0rY0Bv6shFw3Te2b44R4chi96DP2016swH7BUHlKSnBSwgIHDHzDOKI9iY1qS5VgtETXpUKrA/2GPubdCdhdiFrs80uCSFuaK8ndIExEdvXdHFpXGp2cMFcg/PCiF5Nt4z4HkN1IxC+q44WumtT8So49wQEfbYrtV+E7Yal1NRPAfMhYj6L6yK5yLhUddeRInebc83CrjUulxSbMAKmuSQIkQgtgwa7zgAiQtDLOWhtmTUmDGsQtYygSH71TSt+TtenhHVZ8HI6IWexlhBKgEEUcDg+IEbC4YHw8BAkGBhZID1xNxWDIe/tgNIhg94toB8Ohl+4CeDu3zqSZhZaZbNcLEl2B9UKwE3IXUfTH8+FOTpObilz8wu6/K48brHNcSFun5m1vmnZbdogBs9n8OE0aJoBEn+oGRmJAAos5uOKdBoTPIgzXkiwdxmxMOhQdV94bZfei3Tx8OugUxXp2MnXCiBurPfGPDfxbocWNDXVt5XQ2H56gPbe77VhyhhU9/nESB8I9FLXkNdq6yjobX0epzEtIaCcU8XtRTm3ag/redQPgj9n6vsarNvF+nC1NanbL83jcYk70mhvohJ2qIKbQnOwu5BQteMiq8WRQuXtAVvlqZElhOsJUR1iy7J35VPz0c4hw81X83iTilbr5j1tv90qhHhDuljjAAm5Ffu+G4IbKtqNzXa9YFN+B4JX1bn7+o3lx3WMzrT9tv54sIaa/phwmXHavwc277upeHXP6HqrBQsnAhMhcEKAaBAzAMQFPK14WT/jfD7j46cnPD8lfPqBsZyBZUmFERtCRCS1gpgOmKcZh8NRPucjpjghTjPCNIFibOIMEJFo2IMQpugEsbKksyop5ZyRSC0iMsknQZjSBBCM0azBqlmf+bGFuDYR/DwIrZAJHIIG8BWYEtkdwC3dQv6u3HDpNj8bToZ7z3q+m9Z41dCWUuZRxRQZhMFJm93aNMkVZ7A72mvns/1WPLVRiqsXRHN3MUGtHiw2hAoFdJwK7QJCuVov9b9FtktnqiJEO77VckR7z6Lfb9IhESjJGoQJcZgRMpf3ZhURmJRRDoglTWjGr9dNr3hqLrEP7Lmh6BXlr/hUo8gXYF6h6jvz0MEk/WCxmKbM6v7LYx9Wt7cwgAqSQlmfZS0VoCvu6BnZFoAbqIHLM6uQJ4q7JqsvhIhM6hUAL/jx0yeEGchJLJMyq8WRgihCDsCsIfw8XbpdtHcNzyqqUFKEJBVPta4lJiyYsBy+wnJ4jxQfsOQzVp7wyGK1kUrdQIkjW6rhIjCwmfOoaol5Uoay4pSVn6GLt0XbCu1vQaOtPr8ZLlEIpR03Ntv37fc93LBPG5zWf+6g09Q/KL8dfeL3tSdb3no1V2S73RMN/A7Jdm0SNM5ICIgUiqBbFPrCoOsjYMcY9x9bqtcHuXm5kO91td+Wz334s/GedLsgwj43K/pSo/5wdCAOi/hbjUAccDi/Q+AAoqjBb6s2hQLjSDK9BNxneeYpRbQagn6RbbXzqF7wFw6H7XO9mFiRvyHlVZkJW3qiO8Z7hOfn1sx6K8F0T1NfsK5Xtf5PXuttiLLuphAC3j3O+H/+H3+Bjx/P+P/8p9/idFobzdILHuohqH8uCJLHPgURQ5HUM6IgoCGrayb1RQpBtCKiaKWQEAIpkcSSgDJmOQBIQCQQJgATkCIkPH3EhBUAIYQVALDGCZwZMUTklLGuKG7dp1ksHQ4P73E8Brx794Dj4yNofgCmCA7AIS749vgZkXLtV0dDZnYHMBnhoEQMYBiKPNN4Ncjc5G9rxIUjtbq3u3WV7ua7eZmPUZ5brnAaPfzSaQPIlXP6Kjz1nvKmyGIZYTNdr9ySoWIGihfUcePMiBPw198SXgLhux8nfErAr6aEd4Hxy3RGzAETZ9HkikFMtkMrYE99t91Z1Qrft66UrgcGb8jB7k2PXtw3qUOBzc3VdLo1I6Srcp0HbRhx0aGeLHCZFpPHZmo1vGm/HYmWCOTynVGWS3ZZPZPAEYlZ3U0w+0CWjkw27SgGCgeDIMStIuVEQQKFOhN/MpcKHm6Do+9DGQRlEfihbM4+w/xvWwNNNc0bqWPj2obqu2Hq0M6cRceu+CcuxDY70EX7VtwArHifAv5yOWAmIVhQmFCm8VdhaQi58tvwNtJnOgeh7WVxZ9p+wON+/roe7c1rt3l/fzQYcXO/3HDgbxHN62VuTD8tVnWZAvZMt5vg2FUW2a7gP1y6dJLfkm94W/9zGqTrJ92IFu7v0Bsb0aNvb+tttI4vVux3v+EshPXxEcvhAV/xd5jzM/LLJ5xzwq8/fcbLacHf/19PePmc8PR0wpoy1pMy/Elo8Tg9SAyIwyPm+YDjw3vM84zHx0dM04Tj4YgpRsRgLleDuGUyn+VULSGCuVNWCPM8IeeMZRHXMGeNC5eTKC6lVQUS6QxA3DfJ3ZTL2V/uKQr6Icxswb3F4pQzEOIEUELO8gk210jVlWI7wCPc48LPyqYoKKNZm4tlAlfbiiDWsKAk40AaAkF8SSFTvZOJqcQFMI1peZ7LOJhVREpJGMnZhDYeZ8Tm3gkQS+7AhGmKyHnCFANyDAgkxBNTVEFBVmGE6blXjXdPA5Z7yAlFCoIUjD6U2IAhi+JNCCxjkQmimGZOMkW4kHIAJwBYEWKQGIFZ4kNwytoTGaNsDPKigGZ35BZHlnET2OTDBBvyPJvbKxBKGGRmoW0V7hgZU05ATqLQRwQOs8O4WGJH5IyosVBsHSdrOyu2z4RMFmeMCrObU6oLrKA+aqmhAg7OrKY11h8GE7CAdTwjJhAelR6feAKmjIeHRyC8YD4+ADFi5YyQM9aQCr7EBU/LqpxlFhzmklQFjmww6zrOQGLGygkJGYjZWUREEWASACw6RwFPJ8IPH7/Gy4d/gdO7f4Pl8B7rkTCdGIclY+JqESWfuaxDLns4FIepSedsdoJBhsBla7hPQfkSwe1Zr6wZNF6JOmSARRqpm6sKN2XY7HAwnNyh12Wd+HXmI15onMsGTTYXZShtSOByA0IZ+xzKvjUmdrlSPCmQjYCB8isMQOP1cCWHWzCGaXRDNgdkWU92KNU1ZkqtVIDUdaX5zOFECAFTjHiYMx4nYFYL8X+I75FDxKLCiELBDGF9Ox40qvattV7EQTbIwm202bCVEaA8/LrT0uvavk8Q4TZVXVkjorE74Dv8oGqwtXuJODrCKyDkSVwxaTyIQmR1whDh1dhBrUuZsCUcdhj/Bt/mPcNJOWufze93S6tfJuJ2Yz34Md0pPhY8jLd2TfcviLdulltcDLy5jS9wUFyzUrid/r4h4y5Ru1fjfbCNx2OnzcFzIkKIAR8+HKsgjkzjwu/SNlVma3niMG7d13pokOZl2L4UJJGVEUVZ9juCIMtZy2SFIxCrpg6DAyPnUDTJJSjXJIgrM0KQ2A5xnQCWgGvgjBgjMljkEMyIanJ8PEw4HiOm6YgwTcBM4FnHIABzWAoy7W8ub745HPpm6MjlE+Sbsi9K8K7rNpYPg+qvpWG+u7YO7Xzfr2Z7Il2/2HYrvHB8jW6ct2VsG5UranNpDQHbHHUMEY6lCITUzOUjiQ/k72bCkoGXRTT/VpK9IYQUDA8DclBXQU4T3d9Vbg/Wu0v1+bInBw2hHQ/1TTdJZ7LTaNddWVh7Zpq3uaLh63N4sZ4BWdEg/e04tbB552lW1BX2oPXaQkUr0bklUNze+xLOxMgzQ6L32ZliBEWFPZ1XrM8LwiGKFingUBLDfcgOWFjcrKCZCr2jhDEVWGvvhvNR9pB88dqiKP+6MXz1GbNNHpzRfWkWNpltLtzJ4wuzBEdMSVwVBAaOGWL+H9RFSAzojX6dvgv6Vd4zcbyyS78f+jgjo1gvVMpdWsuby//Sz82bi3iNF2ReeP+a1JT8yRQ9+p06wpVuSO4cHb6+F6w7+vslRmZ4U38xQvULpJ9q+t+Y7lmWvbJa+307trR5vJ2lEvGAaXMO+RLlynJHSINvdfXbrmYICysExhIADgEpMwgrnpZnnM8rPj494eW04vPHBafPjOdTRk4MMymYotwtIUQEmhDiDAozYpwRJ/mb9C/GIL7eNVCo+cCX3+aiqVruefwkECHnrPmlsxJbisBBGfXGWLb7VrtcLOCg+Dqpg5LCuEKJIelpHbOKQBFMd3jedkouJ3c/lDtTf4tuktzxNn/lPndb1tgOoUOBCNjiG3CMQfuSffyCyprt4fP3GHS+QoZaQohSg1iyoOIOpNiAwwu5W3/axB72h9qqfs9ZOgsAKjxgtsDhEq+ANFg1I4OZVIkjCKOYob58oP2t7moslkFzy5G1XYfMfhj2Vx97lz0Op2vwIZ3tYBPvx7plgiJzVZJV3KUqpwj+7vj3JTlsbTOG3HSi9qMIrXSNCL5ESNyh9YEQKChtLC5tQGZV4sfC8E0Pi5/aurCJKlYjgp7shDko/LqgXgia2BAsTOjEAc/0Aev0DdL8DmmakQIwccbMCZMffYLy52gzdtx9NqPIZYTqO6WxyhoufECuhbtz2J/13lhd3pmSmucfEnraqq1xADOVf2puquDU937FbXFOX3BgI62NXXeyc+09df+2V6G1GmpuL5jY4Mp20KPpC2tdgQhTkL+gluInikgUyz7eP5PaJm5OPPz6xdL9dX5hJMtXt8FjeDCp96ebBREChLux+ob9HTQEyr3omHomMZ3PjwhpKmsvkAohzKzGLsFgi1qRi4D6e7SI3zBKNzHV94QOe2OxI4QYIcO3Wj+0jON/Tv+cbk+C8KvGkuFQuoe436cu7b2r265aAoCrjkph7Ng5EIIiA4TAjKzIz4SATCVSryLwUnnOGTkQEIGQCGsk5BQRYtQ4EkBKM0CEdT0AIWBNK9ZlBcAIU8Q8E/76b454eJzw/v07hK8mvPybBBwYRNPwOC/IiiKL5XtPDNiH25JyHNgZxoXPaAiJIfU/yy5uaYYuve0iq6fuTj10Qw+7y2+DP9VXFwt2V81NaYh69chGQbRRiV8GwAHzj38OjiuWb38NnsVFE62M+e/OSBE4H2csnzKW/7bi5cOE9T884h0x/mzJgozn2BDJIGOSVuzL7sPaa9m49rm9C3axCSt9IbWjPRqfyzXsk6L1i8/TzeGm3JUJ5f7HqG4e5PXF2AVh9ELHwQbVsWY7B1QAYRp0OScwM9acAIb+llrzB8byHxnxt4zpbx3pW84T+fvxP/8en/72e3z7f/wVHv7yQ+3KgKltmJEJJDzTgZyv6BrIUMlEO2M7JF+YDt69nBFo9RBh/fe2YJ6OwGJq8B7PpLlU1KxIkmO22LjZmQwAFAinlwW//vFJ8sWwWT+PDwFfvZ8xTfV+KT6YbQD8cFD7zLtUqsoyTWaU0384X37/9Pt07wwd/dzHIy8moqqZ+8/pn0Ci4bL4wuTn/zLp2n7xJ9q+EKLPfftsMICP9AErzXjICQ+wc9DnsXOjsK9K4Q1uVA5wORPXPCHlgPePL3h4d0ZensCfGN99/h6nl2f86r8+4+lTxvPpjHVNOL9IYGcLATBNEygExEliPkzzQf1vz5jnCbF8n3GYZhwOIoiYiksmFTyE6sImBLHmK8pr+k8iAmfGpIznZK5hIHQBchTNZEzqsonFhz6LvrMwAkkZ2KYDLR4WpCnBsRCgcRoEPnGBqUJp0hDYRr+U0dy/27ZzQM3zQFoXi794L5wmgsRbcNr6hu9xEBrMy1bqD10onHUsxOIv86wKWoJ7pLwi5Qk5iV//WGCm5uwXNFaY0RwYMYir2hgDksbJCyTzYi5B2S+1rv+899ImnLjGPshZGL85gwJB5Q+KjzBY3RIBpEpcKwIDEwUQZaEhdSyyKvTkbGtC1x8b/cVKT/Jm71cFJE/T1e9FSOECVudsGuqKb2kQXcG9VOPMXP3qimC1ypHnLAI/J4RgTipHC8KQz6KEZ3DkBm4uf4p5wgfRtnVo6F7WgCRpzUAAksW5iBEBjMPhgISDxrcgXVe1tUCiJMhl8VJh2tt+yYrXGT5pkC05I3FGUsHQhIAYAw6TxIioyjcRiTNeOOA8fQB//TdY3v8CLw9HvMSIUwS+DQv+As9i/0CkHkgczl6+Fqq90E1m/WLeF4yyqfn//+z9WZMkSZImiH0sIqpq5u5x5FndVdXT3djZBQhLBBAeQPv/n/G4BGAINDPbXd1dR0ZmxuGHHaoijAdmlkNVzdzcIyIrsyYlyMPMVEVF5eT7sPXWD4LUNcG88VoLUC+8IHGBGDAeMfOjZNUepZSrJsGOgMTFtyPDToJ5fDBYzi+xGnQ6cIqy77O2gqp3G53L+eMk315GVFPwj3c+v8ZgYmmfmyvGs9j3poVFTwyeWtMFzzjBT95rqG0bY2P9uS5D+Egiag3a/S3RZQteDUXJng+G3H1SuxcrIrIAbX7wjAk3JJH5+xMdsT1fISpigFjyQIgHRMWUUWH8alf4mqE7+xtz4nGlS6duNxRoXX+NC1hvZOnOPT9dhRE/389znQSKIKHu8NM2w3PLTxMqag4Aq6sXvv5TeUJ8Cq+Mz1rYCC35uRyXWEI5eDCC4qaZRW1+dmWsRc4jFqaV0KYIfg0R581dzjuVZ0FqQWJEkt53SGoNru7cEGIJEObBitfIjz57UzFcJHDoRBnRdQABXexBkyg1GYyuB7qesL3usNn0CF0ABY+pB9AlBJrgEVcIDQaPEWmM4EndoDMBgxNHbu3iCZRVxTP/5Ed4ra2n8cxPKqe7/0RkdWYenof2TpfntsMA2E/KeNgalkIMYM9wgdD7iBQZxymBpoRdTHATcDw6eM+grcS+dWrFR5qQr1aqtILSmn6rRYqXL+55FNgg/FUYfI54Pal4mtMKK0Q9Ld53nnpf3mqvNGGmyn+FELb+GBNq9XPdwpy0rylMH2votVQxgympFRinHLOYoQzploFO3L/LOzknJEmJkQ4jcADGuyPCzQh3LRanS3qs+q1bpDkjpKtlgoT6gVr69YgBBs++tXNRVZxdr2uTEpS1grl9dc3umBrE5l+t9GRS5TMnaszRfMGREEfG7jjBeUJwrhiLkZwv7xz6UDE+VNNk7ecl52mphCjtrjWxpAlt6Gc5sVU65NS7zxV6Yv31Rh55/iehET/fq/6qFN8p3uL0A5+rJ6fLpZPeAIATTX3G/p8+xvMLz+MN7NlF/QauLichksdEQUORLjBe1Z85PstQUe+6UkU9HwCAOIEp4pgi9g877B5G3N7dY3844v52xP4+4XCMSInVcwwgKgJV+S7h/5yT75Y/wEIveefhg8tKiBB8VkA4Dals5IkzPsPGodbPRABcyvyIeVGwKQg0hBFDQviY8Dwzggw1IKCSKLaePkOIKkQhwwOk1IYRUjnxa6EJahphvjqyxCfgPQCYlTaKcUyxkEam+8nofu1P4aLKs9K2DpfrLcXKmxlOFIE0VElRbNq5GXduqOq3UxkKwUJpVXWrqTTC1Dw/z/IsNU1RzUGmO1RqzVxC5thziSW3hySvdhYBaEmOGd1m84BizJGbzO+yOvOVtO/rDFOdFDyHzVwUWyhRRhTDIg0wlRUVRoxwpYRI2SMIue9lHLI3uHnO+NBST/uf56DdyykVryOpr+tbKZ+sb9kvl1s62WhJ27D1TOoJzLOYYAmqOUeLAnRvwSFQUb5JvYSJCSN6xLAFhmtwPyBqZAPEA1ya4LV3SXlnMkUfIwvmF6Q66j2zwiPV+5jra61XCNX1GziQt9eZcu6grFc3Rdpcg1GBvjz+TOSSwnGOuZEsJ9SO0uw9bbeqNc73qt+Pdlt3TK67bvKyFqpUCleDm12bfU/MiEgIXnCQ5SVqfOIz7M8gvoCZU2T4bCwrgyxw5NS0PGGpV5r/mMc/Wyn7vFJGWJm7Iz1SnuQRsQDZCyD+uBsPgLIZFND1xyv41AkiNsEkyuZ0ZBai8rgz4gptvdy8CVVzz56zjPayZzyaW2iJmZrRXf19hsj5tWhZwRnn7v8PW+YmVVUhJAz4HgkBB3wLoq4kJcvk72WvqEs+ldQSJSYYMhwqAqBiPWvMErMI4yKRWjhFkHoOpASQE+LJT5I4i1PClAJ8mhBD0FioExInhMkjxYjQBcQ4IfQ9piQeEeQSvvhmwrDxuL56ieA9Ot8hBWBCQu9GfNE9iDJEXX0JQhwzgPjmAdMfPiBNseEr18nWEzea9WjImGZunltaBHpBZTp74dnvPl9qGP1xVZ89W7z48mhHSJklIWaUgSTG9PJHxOEBOUGcnxZP95Hxnx8SHjzw//ufPY4+YOc9Du8m3P3rEf4Lj+4fCVeJ8HqUdXAZH856MldGrFFBVFmbrA58dtpXiTHCyf1ApY3TO+YkZ6r/L+8/DoNW2jzDD56qewpMylmvOKb6ucWhrjwmlAE2xpyTWO3neM0pSQziwjYqUJE4vJxfXjHTlq+HGB/+6xs8/PsHfPV//y02X92AXZU8sOQKzIPPK0O1IEWZ2VqJWveFUrbgWp06Lk+UWrw2LdYNWNMtzVismVrrSWX1auWEzY2WlMTyL2lQ3pQYHBndfgtKhWgjIoQJSNNbMDzUyE+TbhYLXWHYTFBWn7cVQ5FMl2ZX3DzXtSKgYcKqPdbUO1VOHrcTOH3l8ucmhS5p/1dy7Nfyiy+rm/j0OTyjwz3Z/AranpW0qFUb7EmwGo8UAwy7xD5gugoYpvfw43u83T1g/3aHP/8fR9y9jdgfDpimCZMqIJI+R+TVujSIECuHVQqSJ4A8iALIBfWQcOiCRz8EDH2H7aaHdx4hWE7HkpC6hoU1hqnlucyEFBIoOvgk1tcpSsx8Rx5JvRmYLW9cjfgUEWakWE2bJdIlL94ZTuKdSxJm9diIgIWESlwWU1UEWOLESrKFGW9fk2OqdCDJQp2FV85SF5BY/LNzOSwPmBXHiLcAQYS5p2QblhOAk3hCJE6IKSKmJJ6DSocAMlWkfI2zhVEjLQcCHEl4LR8QfEByUYR6Ti2xVZJn3gv1xqe8A+s+Vv2saQBWgXvSUErq1ZJQhShzOjZKQExgFzWMr/yFlODUyp88ISXBr/IptHkSBrKa1yxFy9vEwpmWOeKTZ5mrYSVVlGTDiLzmDs6TnB9nZ0DF44nBiBDDuATEWK2btEcgeFMUqEdE5CT5EvXl9rz6DNU9XPbHrquBC08TQgKid/AEUSoSgL7DiB4+iBGfKAaQD29WEuZ9M+cXdS+RLB4DGKMY4IxRQ6spvdT5gOAcQnDqLRIxpoS7acSIKxy3/4B0/Ru4V78F+iuM3QDsfsTN7ge4eERkVXJUtJqrzpdIO3KGmLx2SZdfklSvwODZtC3A8WOahgq4NUZMOmWsXyhZGCle1CuygBqOzPqm4waLpwS7JLlmIB4C+WxaDhrDGuLWUj1f6HEw9My58qOhyVujoDVZw2JqFjJOntWb7Z+m1MwaFOYbnyWJzsk53I57BPL4Ktxg6DoMfUDfeRw0HCBSq5Ru5nTRs+oaNyuwWhrPvtUKfObmL7cslBH5Bp403osVEZF9/k7McGQu/o+UhtNvF9OxA7GD138l+QtViLxSTBgQzIxctY2r3y0R9zxW6FMxUKeUEMsD2Padua11uqwj+LWNsHbQnlMe9zD5CdjPM6/4OXss/BRTc0khTO0sEcE7ws1ND+eA27sIOhtCR4lNs6awc277m1tUo3RrvieHWwF8xrsi2jLlAzmCU0bEafgmAIAHKHFO6CZJ1AAHQiIgcQQhqCtlD6fxcF1yCB3B+4Sra49u8Oj6Toi5gcAbZMWjR4SzRGM52baOOSbwfsoCQvYJNIytdYwRFbUArbKkAQAcwsnDmI/vEwH6T1Ea3u45DSwe/nyDfGqrxRr+grphAlPU9UxI3QgOEvora62aUyaWOl0Eeg9srz0mT4jEmBwwUoI/JvS3Ds4BOyfMASlhTQC8eFNnHFmJO4H56/QCrV2fUbc1PlrCqFPp6mdtn1F8rpaGUJ89cyGR/2g50U6GT3McSfURlnXNpa67ZknHRpgbQytnXbwh1IU/W7gpXJgYtGPwPkmiwnpSGEWppf2YDgkcD0ijJSFEtoDLtEMR75yZCG4Ha3Vqj6xqotd8U2Yzh+WiUO7jamEucXhz907QM9U1RjUvLGENOAEUHRCdZNu01xNAycFxqJZSTo1zQOgcvK8Y64YOq8/CjE6rLi+svhYaw/rrWptrvy4ri3Nykr48/fCz3vuMZ5783DOIJZrN9ce+63OSa09t+3T9R1rK1nqfYTSXtvmpmI+PKM9a4SdOWQRhB4fjpRZsK+2fmlLBVwW2zW30HYDQsSbzjUgk1tX7wx7pfoe72wc8POxxfzfh4Z4xjjF7P4ChgmnxeiCIFwMqrwiYIFUyTiOHdFWPCAuFIfkhxNNMNLtFeIlKaA9AleHI9I0J6UhxUeb5CcXIl0VxUHBXBZub/BDGW3C+Z94TZOwKhGdpYTeVDlUbdx1alg19KvqBjLoKE6rzIMZNlXCSSzuZX1IDArlvnhvLnVGs/+Vdllw55x0wAwjjUXilHZpjfFPU6xzNIGrhUSxkzQWH2zabkgW2JWoDWuayjC31XP3PZSysv6lpv/KEYPMkWeFcznT58VDX1ZjZftXC/0IXkJ4F0r1J5MBUaEsTQudxJdZcF5zHxMZXZK+pat5tHnKfyhw0Bh157iTNdARJUm7rJ6A5XGTNEzPGY0KgCAxzjNrSfEVZV640qhHjl7k+16oABGAWNMyMQyRE34OHF6D+Br7bwLkOBAefEtx0hOM4UzLMepClpBLyeb6aMlNrlFI7roZV0ufs7C7zoq7tGV5cr0T5zbtrXqJWQhSTnzU6e15O0eL2lRondc7XtA4ZfBBAKVvTDqPBV51tQjPnl9Nc5+rNZrzCETXcstkz3JI4YUJCcOItPgTC0BGOJ/bHKS/+RX6gijd4FCacGFbx2luWS0LqP0pmnWGzFm3l/z6unbq95Rk5846VcrEi4mG8zt8dTdiGh6xdflSQMO+l/uymDfzUC/GD2vJTfhuB4BpFREH4c2XE6vtX+vYYO918P7EDPkk+hpV5eXZTn6I/v5b/YYsjwtV1j//r//o13r/f43//3/+C0YRdJ0qLfJcbubgA6juM4DT6IN+wZigTpgkJjgnsAK9u2w4OyRGSxgNNieFTRIgOyftsUcKcJCYqR4QQEFOEDx2YEr78OiL0CeIu6+Bdj9QDD393kKSxThguJmMVZHyZyMuCRLNYTsDre/CL+8L0qIDMiEEjCIuEk8GTB/3lS9Doa8McnTj9mFEphUhZX4+LQclqxacDoo+GOJfQVBeWNSLzxI3VC7a+p8o87B0RY3rxAenqVpO/MUCTMhpaPydds9cUorXzhH/4inAXGX/8cQ8eAP+/OOze7BH/X3f48G3Au3/qgKRWSooLX0+El2bZQqg+dTSzYVM+YjNSmuv7hVBrB11/WdsfxhjTrP681imi+NR81wz8Sndm5STJLVyVVuJ1XD4TxOee1bCN2hr1vcJALvsXk8QkjclCXsSsmAAgQeW+T/D/fUKKAE9VHysYU20gAGJRFmNEjBFkEWM5KrgRIBuZ4ZIwEi7HpF4plUCHs3aGKiV0SbAnC9Lek8vzk1MnZ15bxZoLYlUYz9uZ+YRVStz6L0bxhPC7DVx0KmOp7d8cKHrcTC8wISLyKL0gYLsJ+OJVJxZVdrF8NAoDouq+MtGgQpMWoN3SquVo0KLNujwV+q6SpU9RQnxE+Tytfnz5uRh5fNLyNzmov3J5dEqfP+cf0OFf/BWiwsbH3jM/sad6YwlIJ3QCc83ov3p2O0x49dWIwzhit99hGg+IP+7w3b/t8PaPI/b7Aw7HEYf9JLS9gvuuC3DeI3SSB4DYfJsdmAiJguxDCkofexB5OB/gQkDX9+iHAcNmQN8FdF0H5wBvXgtwOVVRTQ00PGtFHhvv74jUS4GQKRhtyAS5rKFuCo6s4vJnDFLC4ZREtiIEdY4lwgKXz5pmypbKxpgAs3Wl3Ha+Uhtk6QOmyDfhXpN/QuUocFyMTlhCcwISb98lJ6YLXMRnxfPA6EzzEoxIcUJKHik5+Z2KMiILry2NRtVv5pyCU/NlWIgTNQh1pggj7UGh5WoyoayHTlZiwIwvjG8CSnuJc2dEcK+0UI4QZIqsinZUgTpS0vwJa8Ie48NIcwhgacBfdbMOu7Tajj6aaQRY9yWvSkqQ/AdQ+oDEBdN5MXjLOzJGmEJCFDkaPiuKaJ3VQ0TyK1Z7nDkn7jblELN6Q3D5K3kixKW/RCkgRM1RRgwwOyR4MEp+FHhZ6+gc9scj3nx3hy9f3+DlTb2vlyJdImTKq0ZbohhNOZ8XgBw6p+u9nHMoQHMOUyT8gGuEzW/w4ovfw/Wv4fuXOMLBs0OXRtykPcDABKj8gCr6FBqWDer5qv3K+dE0ukEVxc7GVNO55Xq9X4osoOUFZqWhV+c3CwwQXcl8r5392Z6tWq4AzSWT90mlvKrekUFZ1vpaUnhCo3Bw4mmW16bWFtLMU6OeqxmN3/S/NrbK01SYJ1o8VJlVVdcKza35TRzhgRghEIaux7YL+PZLoN8mPARgJAMv9boqdJ4xb8ztqGw6ZO6eSRuc8Yj4WMNt3WmfjC5/ajuyD9rBPbWNy3NEcGWRzA5T8rJBV+a3Pbjyo55sR+ISSezg4DMTGDkgscuJrIzp7WlCwe2nLcouLY89tdDqZdxXH+YWCK3vMQP9duCRtaj5EGcBiS7no8TrT1d+mtwPj3XisdvP6OPccuXCJj6Fhd1P9vxK4Xo/QoCHxwEiuulBRBiGgK5zj6593sdsO5nRzNAa3W60ApfhMdAI3BsBqdEFhgTVosly0DmnTAZr7mcyxC6fKRHgxQ03BuHenPdwxPBdEgKIOkQfgQ4VNCxj5+rc8nFC2k1Ie/F+mDxhcj38OIIoFuInZ/YqRABxSygTJmA4goNHFiDOVgsMJO8Qe5+7lKdqjPDHuETgsyaqF66U5++xM5Fbls2zPjB2mGVZq/aJfvEJ3E3nG1/jN2ZfslXQ2efKBl232a8FwbZGjNgFpM4h3nikTS+KCDA4dfpYVZ8T3GEPMrMjfStFYBiBKTGGLiGywxjFkvHwcATfJdB7PVPmMk3AJnr0SagqAsTSCqgOlCnI9KybtVE1dsdAxzVDJgeTOyANWNlT6x4RTUjBM1vpkyXCXRIWWlZ7J/OztrL1vnykFJi5fDA1Wp8l42oGiNGSanICjwzcp0yQ811C3KXC2FZaydrK0V5UEjGqxaOvBPNJLCGd/jZlbgLBqDeqNkPdYxlCUQjMmYnzc3Tyy0qltQaW/ZHfS4alic+cGJgASg4UCVzBFiYAkRHjEcdpQsSEJnQBCR4J3hDNfA9TXRXzHbBadG4XXrAL5nyF/rhgqulE/9p3PfbcsggOrhHvmT5c2PhHUS/PoH3qRz6GTvtZ0LxWFoqlRYWntZfX+Lkdql/9KGH+tOt4Ji1fP3/R4ycqnWL5Ln1eSwIwZmi7ZM7NA+xcOaUzL8y2iaClkiNGcBHkI47TEQ/7A96922G33+P+4QF3747Y3UccjhPGY8QUE1KsQtXAQii57AUhdLopXI35FrrDkoJaXgiXk1JbPojCo2ee/cRsrhXS5+rUD4tpE+IHsMStsxVb5h6oGqRi7c/5e/WpAnGLNV8zKFwJzWadye9dxDvPiWvJ2Bg0HhIwbFvEuwt4ZqEVFyQtA1no7DQ8k9IFlhvC/nK+iNaDolh1o/lsR0go61i/e+YJoWOz9kuDqhwyWsXaZVb5ZiXaXhWC1O3V82BtCbHF+vzjO60dSfu58mpUNDVRodOqCsU7QcdQ7TegnCVS3rn2NCnj1lxiYFUU2DoJLwFOYPI5/4kJOI3mzx4ReUhC6Ns61x6lQCXDUnqIjA4iKP1KiBGaTLuaEusX2utzUqbwYRUdTQRPLis+nCvBiMl5UAA83SBsbxD6LVzXi0IMAgREbsGIM75kHsChXmGqp7heNovCUD1F4HxO840KFi3KGbo3C9rrfrTH5USZVWoOp/5VCoj8OXsfEufHuelnWRNeTEo1TALATuFeM9uLdW9+rAkIlgR+9e6aNpl5ttT9q2Sl9in7xvaSKk6JEBzgKwX4eicq+Kf/r+He+bQ+teRzlYf0EY0t2kaDMB5r+xyNewnkXLZ3AmQ/oTwhR0QB9JGB+8OwOGTaLQAoCWyNjqmQ9bbbwbmxqi0A7358hYkHTYZlGtqIzv8AR5Js5XQ+hVlvG6Hf5y3lfLcH2wgPIToMiFL+neFcUkJpoar/tfxaPl8hRPR4g4QOif4OTAIOsrUn0YkzLsWQW0q6n2m+e3kG/pXcnhHgsDipShiQUGKwxG1FKUGSxFe+glmwDJOHJIFN4CRI08KhTMGL50QYkVLE7n2ED4xvfxvQ9YSYCGOY4MMImFVNRkx6ntWyIP7wgOm/vwNPCRwj7q9f4uHlK9y8/RHb2w+FRpjNlzGgpHNGYKAD+Nu3hXbQCW3jpwKHm2s8fPtNtuywsv3xLbY/vq1mWts5jW/bPn20wGXtBW2bzSuiB/35a1FG5Ke5fYwJPBzBX/+4pCof6YqRxYVXaSgvuba6l1VwP2uvIdIyDShMwv6br3D44gsw9U29uRcGM4OmCds//CvoeFSmgQEm0JEx/NsEf00Ivwt4v0v4w5sD9vsddvd38AeHhzch739H4m5657y4noYuJ4rMLs6EbHVfJ+ibTQCuIvDPh4Awm434FWH6n05Zzj+P2BAiyT0dq9Gpn09raR67k+bXK+Yy19D1t3/zkARc7w1ADa1mDLm2Va9FSgn4kED/nyM4mvIAQlA1QhEILEgGP7l5Z2SHcZowTZMwcezhnQcckCyuaxT6KRrt5QRWzlcih4iqZknBcDth9SQaE8BVzxqGorUCy8qchrdY20zr17g6T1bHcm343QCavM6levCpIGw8Tnjz/h57HPGwuYN3AdduW4ROlfDIxtkau7S0pv1PMw/dwqXW+6sdxaoSosaXK3zb+vOzNqqfn41yfFQg/tctPyfdwScrf5OD+rUYLfjksiawUWV3CCM2L/Y4Tgf8+d0e3/9xh7/86x77wxH73R6H/QHH/VFCBSYGQwT4LjilIVSRYLniUMfgVtoiJ7ENCF2PLnToux790KPvB/Rdn5NTw1nyYsOtqwNCC/DKuAgoNI0zZYATjwHLJ6cGSOSciiaKkpm4ttQv7VuiYOcYzATWYPLOy7Peax4KN4FT5RW9kKetCLNWF21egxc/68SxxKwW8BL3nBWXJTDYqe0CkI1jmFVYnUit5CexyE8eLkXENMFHh2maEMKIOI2YgkefenB0OS9GMkmEkadg9fLVrip+dFl4Xg1FDV/EMEKUDVTTn0YbcclZUIzXigBaGnQ5xG8juOM86EowL/weJQZRAqeoSj7Nb2XeATMzmEePnoWloUpIn99/YllLJT2TKfPGJRcVASp8BzScsLP8JCoVMuMKqFGJk7lMLF4ukhclaQgd8zql/G7zgigvN5oRICp8juULsZBnpojsvAdxymq9KTGmJLlSWEXDlpsxMiMm62+9/9Ungl3lYSsVnCo6CIQQPLwjdE5zu3AC4OH7AaHzeHX19wjbb3Hz4hUYG0QwfNL9hgJDW7BodGZZqyJ11Nki2XWkcrk16/csrzRWAFzg0nzZ18pjfBJBYWwdmsskg3U7BiONz6j3Y8XPsq5OEmpevGsA1nwjnCKKkkvXTPdHpqln72pGaTky0b5/nUfn5S+uf3GG17xSsfDo9QzbPNVEeqnjNAyg94QuEDpPCJVCoijSGY8nUV6/fwnKLiHg1m7O2/s89N08FNtTy9qzl4WOKs89R8lysSKiWH3ONGz5pS0zl3SfWDx4VqaNQIIowZhiB8Q+30/Jg+HAcBoHUpDBlAYkRHRuBIMwpaG8SIvDBE+nLGmfuzDcfOSraxOdEXe5Z1pt1IeYjFBa2zDLfs6rnMSHs4rnNsMnOwIXHrpP+dJHraY+4QH/FN4Wn+pdC8HGE/pWGT3Ib0PYEJdIQoTHHoyQ91GWw6ztI6r7Y8ROITKbvWhggdttUVcx2X9tZVGQXktUgKy+CvadddOpV4S040hcmgEgkSQSS+TALNbBXejRBYAiIzkBVo4iHI3oaKrobOlTQsKYgKPrkEIC+4DYdUiOMHY93LBp51z7noWVGQFXc2ZWQtUVqVPGHLcDUlfy85TrHcabbTUxK2WFpliUp5zhC8vqEUgEmgiIFbG1BkZ7B7zYtNTjRaXYZ5U55Wb/cPtfeW62N5s6JszX/xIDcduDO4favd7q1s/YnXh1De660scEUIzwhx38BAwPjG0CrjcO7mXA8ese2CdM+6g0lFgrsSNwUM8fJjgNewC1ZhSrJjkgkvCw6rsmcGRmRAD3BHhG038eGenDytRmuIHlfJ4teq5O5YhY1D3x4pow3RIwAH0iLE/FWslx31Bv9tpCKsM6VDx2tYeWIo16zes9tzI3EwN3wiQgJvAdg0cGxZoJqB5XCy1zp6jhYFZGgHF4/wAXHPzXL0CDUyUZCQOLBKKERA4uyQAt+aEJHcxidHXf1+dhfjZQw6cWRs9pjjwvGQYuS2M5uXZ/1hmJ8MDgSKDoJR8EU05mzWBR7BwmTGPCFBNYnM4QQLhmj2vnsRkculCzlib8QvW76sgF6DYzqTMA+KgSYu19Z9+w2tzqjZNtXqJcqB4+Wc+Q91qd+Txc8J6nlpbU+JS030d05GPfXMGiz1JaUPhXL09dt78VHU09jA0SAqcFTjPbUAGjJT9E6gIoRYS4BzDifn+Hh92Itz/u8OHHI3b3RxyORxwUDqbE6jFmRgserqIb1vwWLRSOGDuIIYRzTqyZnXpDWNx7WrIKts1OKyLm74MKBvXJKj9C88U+LeEqmxdDUprMZrdC7orbRMCsO04FVASlm6jIKMwoIOPjimdaIk3K89Umq6aM0+vVrAM1led5yW7ZcPWnM/ydeSXKPAVrwm4Lz2QCaQvPkzRRdYoxG2mJIqPMNSvvYXKdLNSsCeRa4ASra+8qVvx1CNtCV3DVFucxGj+XaYWcdJwgHgAOFlYHKalAnpE9BNQTRMIzVf3CjFabDaH46XDeewS0AnRb47IFqnZmeG9lnxNsX7lmf1CWQ5f4BCYszdyDzYfmGgNLSmpXKRlyyCWb15qcsu+2hys6ba6icRDPBNLzx5wwxahhpjQhNIsyIDlVBC1eOB+7nWlRYiUgK2K8U8UWZM8kSD6K3RgxuQ7DsBEFp/eax0LeGU3o3pRCF9t7uepD3Z+ars1wBW1lqoTVdjJrHgF6Zup1Py1uO8clrWyqtcerKV7uZ6V6az6EAVM6NAqHIrTNz5SzWO2pE92bq0rOo2GuPio+gWf8hclAaP50y3dlDkLDdBfkUuCud+ZlI2dt5zwO1DWBWs+Vc7X4ggpmjLv+8CPr/InKWW+HJygIakO9S6KjXNqHU+VyRUSaABaGFjWyqRE0ymKY1ZmcUmN8Basepw5H9NjvX8LFKwVYDnBeCAEDEonB5HE3vUbnJoT+BzAH3I9faGzIclJ694Dr8PbJE/BoeYxoZ2jCrfp0MdpvBriKa2eTvKQmYH4tzy+/zuGzCmHCgO/gqcNIX8MRqgRSBclmAi577hg5Y+dwCZBqq6hca0HQyafEY1XEqWmotAswoVlj66SNFusZl59PSrhOcUJkhncBKSUEP8EH4GbTI/SE/XEEOwiz5RNeuQ9iYWNkFqdsVbDzHu+//irDPqOyHm6usbu+Wk7sgnhYEri8Vq+qc0qBf7h5geP1zfrNk6Ulnn7y8tvzt4W+GwC8nN+pvp/q+BwG1/usJVSXzc6Jo+pmRUPl92QCtni5AFXiMsg+BQPwHoe///tm0zMAv3vA9t/+ALePGP4jwt8Aw287/HhFmLYBhz/cYf9f3mfCioOGPXAe3nfoQgfvvcZjliSR5JwwmWCkKPvX4gpzLIniGIw/bZQYNW8fY3j+nStG1z7LWSzXAc6WX/N77acnL7jvxP1TcXkz01oRQ8P/qUP/rce3KeCGXVW3WVBkAWnRvkqhTL9Wa4Vys1mlVVJ4UYpcXue0/vmQ4P/fI3DUeWJIHGCjpaxNBsQyDciWHJm+KuvkNDTTj//fP6PbDvD/2z9j+7Va/+iYnQqcnJO4xSCCYyrWQSbEWWNqdL6X7tqqBGhgWdkLzfkzRVylmFt9F2wfze5VKSZOKTf8fgM3eRGsGIzWuukYcfyPDziCwS+8MsIeV67D73iLV32Pb173lTcRAMw/kfdO+Zn9vNF4Q+SyDMtRIC7V1VoodgE/eg5gn7pzqRKCZtcvViCcq/MTKCH+tkq7b34tf3vl1BEnML5JB4HTtBYEh5C4z7QzB4f9dYDnCcPDG+wOe7z98R4fvh/xw79FHI8Rh90RU5wwTlOWgzvnQPAgi1fvSiJqE+9ltKn1QQ7sAsg5oTV8QN93CKGHDwHeB/UQEyW4GaLXXmaXzIEJ7cUhgOBI45M7ofedFxWN5IcDiL2EMCevIfQTKsJMP03au8KXgCUMlQPYOyDOckUkAE68q7PxpeKellc3Poia9kHrYzXlRonRJMCfkL+CqPgp1oJcMbBSoWweqtIJKSFRlLwSSei1pAqIGCdM4xHj8QjvnHpSiieMKV9EtmPrJ/g0xhLXX+QWs72p4SbNG0LCPyHTDwwUA4FUQjNlWpsYYC/8ZALYJaWbWS32dWaV32QSjxhmQAODwzn1htB8JEJj6brVhNhsLzbBeMjpfihbhYklJ6H2w5QllwrziEhthErIMztzxLL3WMMNJZP/2Jqap4EzGltCqSUioeMdiXdQQ8VWXxnIGaht/BVNlnR9yUkIOSIP5zxCCECaVAkxYXc4IiXGVUD2fogasSBy0hxoLc3bdoTyHvbewWeS3CE4yRvjNV8ae8JxingzHtDf3OA316/RDVfoeoc9A2OckDjiwBM8onj2ZuVZOZtAkUpw/ce27tV80RzKzr+Unw04m4M2PbOFByk0su2dRZusjVY5GaQaFUUYVy94tFTKP7ZcMJprhItiEpzUY8kmJZXJqQd04p3m1H+yTkXzc/3beGxOFZ9Qjc3qWYIarIcDznxHdV7IE7x36JxH7zwCOZDz+LO7RnIekZZK9k9eztFtxic8QRHw5HfMy8qrniNjvgTmnWr3KYqPJygiUt5IIugzhMJAcuDokRPFeAa6CKQgf+RAsCSwxeoAyakRgyySxGZTFJwllwKkYyQcpw0YTiIZzMYY2eOIIf92FBHcCKjwf0odElvoGcDTCEfT6kQ2gsPqI7HDxOrBwQyHiEBHmMCgCeOR2zBgXFlZsCI6VitWE7Iu+oHVDfW5y2JjPXX/PqH+s63YPgEDe6qJT2lZ92gfFhjqr8GJClZwijhLvNQC89v+lQsF+ZFdWN3L+XHYlubmqhEUWQimiKqum/XxFc9OKlQj65ueRUOYDl5jpsp9D0neunsAwpjgeqeJs0iFUgyCelAcJvDtARMDRxdwPFJWjZQQiNrDlfEuwyTWFEyZs6xsyNTS7NCvcjT0PBf/qiu/hCJTXHV2RgQWOkcmm6l5Uu83T+SPVslTMUjzuvV79IegJkZJ3mt7z/a4qp2JwJbHoVZGdB2mFy/gjke43QPcSOjvgGt2eP2yw4drj70SqwSCIw/vAjrfiTdP1yFookgJl9BpbiUpSZnCZASqhWyCEe8pn93Eldt8Jhir74jAirLh3F9d11WhHubPzq8vPrldFN4B0ztgl6JY++clObVy62XOwp07DjVBncMoVPfbXBGG+yWHA/YMniY1GrQxyz4VRQSrGKPAVQJhA8JV5c3BqOeGkBJjOk7Yf38HJIb75gVCL8pWOIJLCYmRmVyuGF4igFPtKQLbrciHoJrP7ERtc4D5eM1asYw9w3Kr3bQ5W6t5u2lJtFN0oFSsXhHJDDHL3k2M+DBiOk7YIWFykLXST0cEFcVJpA8zBsZSGZHfa7NTcaIL5cJ885yqd7bu2s1lveXlE3j2VFMXKiGegh4WbcyvP9LB56Cxent8Chry+UkIn/bc2Rk6sZ1+EeUn6vTzlun5nSsk3CcYYKbvlm1VZnuFltVniBjbTvKBTWPE5IHDdMR0eMDdX+5xOBxxe7vH7pYRjwxEhicSwz61EyJABLXKhy+suatfQuIXQTW8fA8awslb8mJ7WHFboSN0HCaQ1wtK7V4ojyGAxADBZX5Ewj5RKl4PYuDoVIZQhFembMgJYas1EGWAJLUmbYPUmpYzjiTlzQUv5X2wug1aAX0TdrlWOkDpwuoSG8/Feo+ELyiCzRY0c7VP6qnKmLWSRVheCE4RKUXEGBGnCSlOiFE8WuRx2SQ5kbWGPTJFRkqVdXU1j43hQYWD8/2K3tSLQI37mZCVOKS/jT5SIanwcVQmISUV0LO+Q8TO5XehQcr80OpncwxnvJitjVPjHtLuE5XwK/U6EIqDjoN5Lde4EYVuNFpD5+QsZOF6rCpcZpfnqVU4IK9HeT7vxLIvVCAtfhCar8FZsCDGNI2YpgnHaRKDWWcJtZHp1pRWlA/lVcDaqAj5nC0E+14iGnSux2YYsOk8gicESogclXaTtNoJhD15OE5wlLJgvNDyVA8774lmrfLt0s+2+0uqQhR2XD0pUKHm86lqx6LA5Dr1i9ov64XOVLH2ivBg+decJTlPhZ+an8X5Jppfk5fyos7aOApvh/nngr/g+aP6qrWB12tlIXNLnhHvHYL3mrtIYEYi99gsny31s49RAI+951Iac1WAPwNhp59t61/UsUfKJf1e6/NTaOrLFRHTWAkwyicA8LEDbjf55bQ9wt8cgEMH2m1F40xeiApnISScMscTDCAa8ZI4FUKpIjRu0wutwyIcqcoRAcfxdX5m4+8QuiNMk7+fNtjHF/n+TfgRvR91ADZzaH/X0AXAlBxux9c55EuHHW7CHjn2Wi1ErcuMuBHLFEJKSa0yKMdG/LX8Wv4axQQwknBOrK8t7vyc5Jjv0izQTAzyyHt5PYTZ/Fm5KLipWLY24T8MKVVHJAuOlLA369a6PwCDohN44sR91+JsfveXEaEDfvsPA7qQ4HwV2xaMyBHpdo/4X95it9niw5dfCirPwtE1iH+qcDXW+TQsEfpZOuUprz3z+CXIqeKFZzfO/vz0hVa/Luvw8gItEHIhHjNdafUJJeH4rNG5Mo5tW2a359xERYhysXzJXRD8kPoBh9/+Hu7+Dtt/+wPCnuH/GOFfOmz/vscf3w94yyLED85rTOYNNsMWwzBgGAZ0XYdhu0GwzxBEeIByDqIxltMIhoiMzSqqxln2uz5/BZ9FkLnooxAd+Rm1aoopytjSUmkxrz9XRJxUaNTMLQB+x0jvGD8w8APH1fcs4AdKH8ve0NWYM9gom0JACC36K1ugACJh2oHaMyTDtdn+MvjCzNkDrCh8pLtMwD9ig/9EQ3leNxbb+kWJ+/rjf/kL+qse4X/7J9AXW6Er1EJV3OA5012kBDsIIKpialN5QRZ+NNNhZ2LGPFg8Y1Tzz0CqE1NafW7bQv3MEhq2DAAD4dDDTz1qoYdZ9tl70hSx++MHHKeI9zce6BwG7+C815jEPocZqcV+WfleSxhQCZaqnBDNfNXMtAnF5rCxgRs4XRpp2fzeqcvrNz5WCXG2nFI2XKrAWBMCPaP8Sir/8so8tMOTn/8bXvMMYQiog6YwGMExvviSQAF4f3sHHA5IP37Ahx+P+NN/O2A6RhyPIzgCnBgOhI0PgCe4DogQce8U1co9J9OmLFPKFuxmtU2EEAKIHFwQI4egHhEhBDivAkUW78s4JYxTFP7dJ8BL2CYbA5QOWvIES1GPKEJkt4jlOLKRhSOPRAQ4NQliEaZLvjhFnkbYZQJ2huOQsgArgTRBt1iIO+b8O5HBeKP3yv6trdFr2/RawcNWj6qaBDShmcz6mbCgFQvtSZrXAnAMDbGlNQyNQcecZTMRiT1ijJimCSDCOB7hiNAfDjIncPApgZJXOkbakPBNUfJQxYgpRfGMAFfx5WWvZUVFNI8Io2dansdonrzSFb+TK6qCgSzEFtt+EbkJiJWm8WDnVCCvLji1sLU6P1mu5PQbtXss1zMUyLreGh6K2TxkkuTpSA5ECc4RUmrXu/5zsllhFg9GXyxwNqPqe1X0aEoeDAJzBCdCihHOFC+qqMnDrs9x3WZei6RrFhWuSPdC8Ag+wDkgTQnHwx77/Q4P+z063wPOA1RyL4KTwhRp15JIy3925ts/UkO/Okk1aRtEBB96BA+82r7A9uYaL4cOzjsQRjAl9AT0lDA4xgiHD+ixxYQb8Xst+VNQ+Sex0axspy2vjSw/VTvFOorV0pxvbum+Gcc3W8uidCmsAC+Weyl7tH26orglYIWBzQ2YoimHVUMSWt08WNj2jc5Lna/hBJ1emJOZB0XzIJc5Z27mXxtd6e+8+4XhqUC2tLCgrUm8IZxH8B7cOQx9jz7o778VeuFjxzHfkp+hPDe3hJWLFRFxF4TJtM2dXD7iGB04ThCvB8AdGdgFYCSJhU0QSwOnCN05e9IwkhAbBkHM/VIFPlBkVJQTS6BdPsSaYITHHpuccGqMATGagoMldhhv68fXS3VzSh5TrDTwAHY8AFlDLFYInibxxtCTJB9FCSM/5XdCgktKbAlmqxb1soW8ROB7SfloT4hL3vHcRh/hQs7dnk/Pqbqf0xPi58BEZSFTRRjXhRDR0QO2PeM3v7nC/f2IH394QEx1nXYgzBZ3tRBu6+5cvPheBFzIRBTYrD6QBXvz52uBkBAU5vZa7udQJooHHSOfNTjC69cEHwjeIas0MzyDKFWODBy2W4yhV8MTQ7BVv/GIRcvqyGdXK6L84mN7hmg6SeQ8sZzEI7Pr3MDfM/040ZdLxvzoEFYbmWHg/LNcX+BoIoDrJOvrsFiqGcYxqxjKT+TWiYsejZSZrazjuOswvnoFsne6Ed2HAzbeY/j9Deg+we0Y3mmiyNCh6zp0XY++7zEMG3R9j+32CiEESWJdARtjIFOciqIhMxRF8bBURNgZFEKVKpfarExpjBK4VUxU58VohrnSY+4ZsXqdWZMQo3pXgQ2lrszo8rPuE1fAT096KvGN81ZqFBFVv/LF2caxRHOZRi/MINchGHUbZS+VDO+qcWi1e054Q1MZbw4xITUCPDwcvkkBbow5eTNLEF8ZLxGIotBbCRqX2GXhSt7H1AymEP6z+ZCS2nnI47XxWF+rKuVL+UwARZ8ZRitzMYwxIxRd40VeW16mmDDdHRCPEQ+ImAIAL15rB3eEd4zX1ON16PHiKmAz+MoDDieUEPq5IqzQCZwxo7PON/XXx/e0m8+kT04oDhYtnVMknFI+XPLs2vN5utYF0z+pR+pjYzv/8PLS5Q8/Ay8/8YGTROcn5Eov7FKzpvXrLyCMl7vr0v5f0LlHWZ5PuBfPnJMN79Fjwo63iOSQ2MGBsR0SvEs4jBPGXcJ3f7rHfn/E+w877O8jpmNEjAwHDwoEDwdPIpwh4cgxMmNkBo0RRBGIkkZnMU7ltRkqXCQATpKB5j+juQFJjupMGC3C6hglL0+AeeAZDD8d4iFTTVnypNbloByChlQ5ADK6XzrHlPRa8WYABM8b3ZUDvJqBI4lFOTkJY1h7QZDTPzgVACucsiTGNdRfsdRp8MVslNIzNY5RlwhTTOT/a1xo42ILTalr5BiUkwQXy3r5X725LSeEa/NDmGKCnIfzExgseUlMEQEutESqnrWwSzWdYPyQWuXXBmA1n1NkONW13Hu9r0qtjPVl4mdHXYw35smIS3/aaxfp1ZsWuKL/i8cPsyipKCUJHabrUntLWM7CBkolFqFW0r2fJLzScq54PqvVeGh+A3nebZ7s+7xefU+NXiSzg12X/eedh1cakVPCOJxudj4AAQAASURBVI4YxyOmGOGdKmJslyndb1sxZ4DTPZ2dw7Vu1M64ejg1KnCEyMBxtwd7j83rHpu+Qx8ActJfD4cOwIYIV0S4DwP23RWG6QGURgULZmRVtT+jY+3dhPrcVH2xZwgSpYTaOidpp2Urs1Kd76bqGu2z0oruyebdZH21hagntdoEeQ8k40qQeTPdB+VY637kUq+po+1lqi3fr8fOZfEzHybrg+p73V5LPyuONF6Nq1t5Fsu1ArMdvNcQYF7286W5IZ5bPhUV9RSB/VyGNy/z609o+pOXz+IREd8OYGZEC/HQMO8EqsIcpYng9j1ADo5GgJIAZE12xewLQ0kk95WAICIRfBDlfZ4yBCleE2sDrj/jFHB0L3OiHdm2Md+/jxsQbZrnlqU9BUVgIEKdMRF28SoLOuzvKjzgxbDTLpe4z5mg0EOWte0EkKNKk8t5Rz3fguivuAN/Lb+skrf5hI37Af6mx//yf/4KP/xwxLt3+xx3/uTjteAOrYXQ8lUFQXGFnIx4tsRqy/2riNiIVhgi0mS93iyAtbYzco5A7MAcQeTACfAd8Lv/NCAExsPDDmMZCBJBGKwUcXQBH774Mls7m6VBW9QNew2GcP3Bq/fq67x6/xdQmnGW8jnFIJcj2Bn5ZzRPFcqJtFO51grht6aQEH5WiCUCZ0KKgUyQFxIZOS9QYegYaRhw+O3vcpvd+3fY/PE/cN31uPl/fIPxX+6R/usdfAiqfBjQ9xtsNuIZcXV9jX4YcHPzAn0/5BBNZkE4WbxgPVPmGVB+Cx6PM2VCtqyCJMdzFb5/zNOhbYORonhjGO3Q9qEwZWuKCnBlaXeizty7om6zfqcoVdr7c6+O+fOPtb82bisi7FmeArM/MoVNStU8QpjBd0j4Me11v5R5sH3jmBASYRMDuugQYxRLRif0Bk0TWKVGLgnthQSkedJEOw/Vnl9A3jymeg4quDUL21UzLoXphRJQmvRwCugOm5ng5VRcWGkpIakCgosnBDPSlLD/8y0OhwnvroDkHTbeI/mIe3+P12HA791rvOp7fP16gPfCWJugZykyquZEfzirly+1NOdSoHkZ2/pZyyVKiMeYhVPC00sF+GeUEPb5fBr3I8rHWoZ89PMf9/gvtszNFCs5RCm/7MmpQGl7/VR9AF/gA14i4j/w93hAh5gk98HmZgJcwo8/PuD2/QH/+l/usN9PeHg45NA5nhy6END5gE3XIziPIQQ4VUo8xIhdnLDfH7E/jAAiOMbCV5tYjisYbnAPhOBF0OMcwXJbk8HglMTiHoBzI8BQHl8mwjnAa1z8dc2s0U+zWSLK1umOJEGxg4ejiKR8NVxSmqqEm0pk6hfhphkScpaR5BlOCnMg3hYOSI7g4NT7gjPtZEoNJsCxtG3zU+j9En7lkpLhXTU+MVap8kdC0DWzKH8aOgTIc6voVClchgV5TClhSgkuRaREiHGCI8I4Sajqruukt+Tgk4fv1HjMhM1JaIkpTpimCZPlikgl9JYI1pFxsOW/KoJMKZnPWxTjA12DAZzRxrN9mNuu6W8l2hdRXMjyYSGHZTTFQqNIWuD9vOkBZs3LQXkcICC5JDuKJXeEcw6RaLG1Syx8uRGjhElzWRGhNCM4113OUz2PNsdK96Qk/EcOsZmnNNepb7C9MyUgmXpAOPUQOrEgTxPiNOGw22G/2+FwPCL4AaQ5YrInD4tP0ZoBmr0+qZV9VB4gkG+9DwAwEZJzOIwT3tzeYntzjW+vttheDdgMckanGNFFhy2AG3L4whG43+IWHfiQ4A57Pc1ceDilu+tk2iqC07PlRPlmJRUAZNHBOCvGUNF8F2KmVVBAuR/yfS5HKJxq5lj1C2m/2narC2sIRxgJICeun3kOZVg/o89R6GrM5xVYyYebcrX8G7Zfy2RkNM9FGtveLZUuNkRxArO9E+WD64C+79CHgC50OKixUe77Za2eKZ9TonGmrNJIP0FZ7LnPV54QmmnSLyXOWNZmKwilfNoJknhREK550KVq07MSBBlCANmFzQSNpSixpIId+yyM4fKTCOLKlntnLZVcDZzfvUIcW31qLxoDnBSopxjBKSGmSRNDJeziCJ6QY+ttuojOJ7Dz6hUiiUUNHJGD6EhMKUHFYySf5RNAf36VFvfOl7P7++wJXl4s7/4Eu/dCRu8iq4cLD3Ftp/GLLHMLnTlyOjER8/iFYiUhTEwm4DJmzI1V2NmINUZMSbdxsTmo90Wmk8DZqtXcfYsrof5uOlneRfmMUwY3NRipi7jQqoIzE/okY/OMh5sD9rRH7+/BOIBSwniMuH/PGI9UcuGclHzL4Txn7bUYw2Pn4+SrFhT3Rc19MkS2OkY62fZaby9XIFQPzds62caaWOuZsEiZ0Ezr5ZZa7Jwt2iqiC5m5tJ9O93Pdwjokt599AL564fDwdxs8TAR36ECjCgS8h+86+K5H6AZ03YDQbeBDj64fxMIpiLt9Z556GsZoTYDPmHtGSCeM8SVOmQFhPcCMyqKrfhaQsEHN9Smf7UZwXwmTASzuMwuMMJdygxny2Xp05ETQ5masfZwUP7fKDS7eHHa9mRdk4X89jvl960uKlSIC9Xjalc3PzttUZVCd6yCBs6BJ2iYJHafzaILxtzQh8hEv//we6eGI17/5FqELIC/hh9wkITHJq7eqJcTGks5iHyWsxmxPzmFbpkw4V5A+TUHaZa4iTuiuT9omiwWmS17neOUcnDiyptTI65sY44c94nHCPRKOHUCeELyD1wR2N2GL10OP1zc9rjYhe0I4t0L3ZVBGjRLiFD1w0otiBSautTCn2k5TVJeXggOXz9ZMbn7jCdpy1tjZawtafT52mt1fPP8T0luz/i8Fi09s7mO68hHPXtbwKcS/5K5ON7O2By7txolnefZ7UU5XqHHoR5ULaZZTTFDeLrys+RSSI0lmNkzbLWLH2BLgecJhlHAju90Ox+mI//jjBzzcjdjtD5hGCa0RyKHregTnsOk6BB8wdD06J4oJggh2xVqUQDGBVJgcwRk/GQ3tnAjpJIa7xm1RPEM2LsWZCQSQGQxqfgizoo8JyQntTBZepxbsLSaxnsOa+QYkDLMKcDVnRIbNnCtpX1l5Zw3Pw+ZxAJD+hvLWBIDVhVoiE2hoJoinBLGEbEpc+pDlCvVCVzjC6D1Dr6vCQ7YcFQyGWPMi6XAIRdAHG6KFF1U+ZEZ7iidtAsGBRMgCIif5s1iFzhaqKUYkN2EcR5U7BMTE6CDyCMvwy5Gh8mqLvijCZcieNLO0YhZhFIElq25XtHxw/pzjITMI0Flp50yfsHwhmSeg8mfJUCgnRalyi1T9oKb9E/7OzGsXm69ND2s6gIDsHcGsc2IL7HJeP04TEk+rRjbWpvrlLEBVpi8bOsyMdKF7q9zPPKwa+tm4vSeEQBgCEBwwpQmHacTd4YiHw4QYZXI7BxHcK23dKnPapbLIAVHpWfOWyLBG/5z26zAecYwJYdig31yj66/QhQEdSbSQ5A7oELEB4wYeX6IDOCH6hA0SBvXxmGrEYpuw6pxtS4OJknPCwjVRPlt2DsGsRmok4dCqMbi8o7hpHzazZH2YlxognGiDIKHfifPS8srT9oXyasrOlr9yNivHYZjR3GrfWJ9iIBtbVkqL/NL596ZDzcsy/CqjBZamRrT6FfWZym/QuTUZsRO+xqLtOO/QOQd4Qq1porI4H1kWJ3FxfRWegBdPPrnMX9X8prYiz97/3HF/9HxdXi5WRPA0Ngyp4EZzJ6yJB8qhlwAIdQOIdV5iJBKkWCfWlMdq18qVYpZZzWeruFjzjJidFkVoGiPTrACyANdGVvpQpf+cCUwsAdSEmCJiHHNCqENK+KCADM7ji+uIV1cjHHu45AEviarF6UwAssSrU0DvJfF3Ay9o9oVmmy/fetqWL8TAWlm/c87evTz3E+7iX8unKdUeK67YGkOVU3WSqjNSHZ3E6oYKzdkALmctCy0NXhQBHKKStirIROLZqS39Ml8IOS+uoizaQdjZFwZLBU9JQzgR4MkhhYQP1zuMdIer+AFII44xYtpH3N732uU6UVsF4RuOhFeOihIaF0reH6/WEixPRmwzWFKDj4vefbLO/N6sZ3RZtXOvvqhkkHOBjW3mM2ilY7NG6/wkJ7pjgl2bR7K8EUYmMpfwN3Uf8x6aUxeM7eDwD193+H4TwF9cg/5tBP2J4YKD7yRJdb/ZYNhcSXim4QpdN2AYtvA+oBv6jAelX61QfZ73oLHSBxpcJ8+tMUzF3beuL4qHqh7H5hwU4XoUBrfJ3zDzsEjIcKL+I43Ts/TCaN81prFqSyz76gSM5pWAFa8OQsq5MZp5syTJZzxB6rKqYLF35/G27ZkiwkIpsIYBMKWLGvrhuzDhHRJe/R9vELdX+PrFb9FdbeAmVUSocYOrrEar3d0w0VPPSG5cAITC+AL1eTEllgyC0B16UHLt+CtGheeMzJw2M6VEOSa5L5yv2z4DUkw4vLnHcT/i/YYRO2DoxHK3Cx5d8Pj7MODV0OHbLwY473N8YmBGQqHQNXVOiKK0KXPWTKDVW1xbKbx85zMg+aI8pU2DNi0OWaHoniyYXx/4Gj3/8SN+ZnmmsuHnV84w84/Wlfqnnliy1GcrnanyCI9wMa/CK9+eSQN95kL15wpJyCu9juwACti9GLB51eEKHlcM3N4ecDxO+PHtB3y4PeAP/3KL4z4hHkY4Bnp4dC7gxWaL3ne47gfxhOgCgvcI3sEU7EOacIgOQZXAIxImpGzdTl7gXFAL00AeRB4gn4X1eQQMCQWldIEjFnm3EyOkKSX4mEDewbN47mVFRDtDzYIW2kopEaW7SA06RFwg+CzPY2306DyE6jLeeYJ5+WVrfzJ6xMI5OYXJXj03xIDCObluMgqOdf3iHd4oBRRHUNW3ssULzjK+wZQR4m4hz7lU4tszIN4ZqHgIDeVESLDkAObR61JSHkfDCMGLEoIgn4kQo4aLPh7gUgLDwwcNfuMDnNd8G5PQR5JTRASjiQkxoRis6NiKMNyElyv8BFc3mjWniiZR49Dsp+OqOctR/QvvksObQmlrU56h8KxVvpNsb6prVGRDK11FPYYZ1KnOda3Ai6naj0ZfMIPTpHRPBEiMckFQeVFCQsxGrZzM4xPwFubcqAubO66VDCi8jvaLnJ5Hpc0TinGReEPoWjmg6wh9T9h2hN4xxumA3bjHu4c93j8cEEdRyPWO4EjoUTmG6jEksZwkZwUJP5WQEDlhYvFgFYUgELj1oCDIvtwd7jHCYfPiG2xuXmEYXmDot+idtJVoJ4o1d0TnBgyOsU2MfhQv7o4ZI4CjLVFSvoRZc1sUeGsr6bkoeCq9FrJHUGEQYWF3zZud2CK0tAxhu+dtD6zdrPcd5bcxSOewpofR5qK2eeO6LYBhYfKTnFUg/xnrx0xAouUGZ3uRGnMBJUyw5QFe0PNzfrXkhLNr5o9SYzuq36vAsSYDFqdxTiOYwtnyDHsP5z3Ie4Suk/3sPSg4pODATmTKFp47NXP/ecvnp01mb1iFub+ccrEiwn/3Ln9ng3zAAumQImxLTkMgTX7rwTcb8LUISOqES40igZYkbNn7ZgVN+TvsucXn0l1OWnCFKCIDPovjkj/LeTVrRwCQmJgpiftivN+B396KkCPGbMkoh8bj7sse8YuA603C0EcwArwm2RKk4AvDi2LxzVVfdGQSIxFG3M36zMjxxz9ludxiLfcSn+so/ix4yQs68ViVn63XBQEOEQPd4sUW+E//8AJ39yO+++4elAqaqXV3Nc1GYFUkWLi1/FAWajahSJjB6iqaLaqzVXPpk82YpSKzSIXElbVW+6WCTXKuOP8Ta63EQsxEqMuqJXjKLseAWYU/HbLzzxMZzPHXah8/Ycd/qjnQDfPY65rx8mMry1ivsELQZJgNFGsQq1szqNWm1ktFcEuIwwaHr78B8Q7h+x1eBAd65XD3RmI9gyDWHxp+yZLLSw4JIcy8t+RzDt6HzDA2lvhVGCBjbGy/92HC1Sa2RGsmVsspyjNe5Y8AuFIcGM6sQq1xnVuiCAbKq6pzZ14OFhLA2gbP+lRyV3GK+V3MLGfbxssJUZO2LTxDLORPKvMjiggNCcRlXLWF2ZQY3/2ww/4QK3jWemVkzwn1/CpeleVdOTSdJoCMOeb2hBBCFefZXK2lv6LwdbjqX2AbrnD8YQ88AMOXV+IFAWAef6zQGtXeY4BGB89dZo3qLd4qI8rxyAyx8H81L7I8X9lE9NS548VPrt6BxBhvD4jHCTtKiGAcKCJ2DPIOzjP2fo/gHb7oOlwNAV+9GnA1aHJVVywmc0zwrIhZ0oxLRUX5tp47oq7XXlxVFlDz69HyONlxAV2SP+txX9gatSPjec1m7mbjf7Rnl5RVzmBW5RLabLb3f8qy2r9Tfb6kf/SEyaWVb5c/05b1vl1E1y63y/O6cHmFT1Dq8Z5+34Yj/o53uIPHe+pmd8tziR2YCS9TwgYHdKnHcXQYxyNiTHj/4QG73Yjv/u0eu4eIdEigidG7gEAO29Cj8x1utlcILmDoOnjnELwoEyhYgl2CS0AgwPsIHxLCNCEEBkcRGDqlXWq2zUwpbOiCY80AIEmiXueRkoQCIo2Dn1LK/G9KScIogSS0Y4V3mhmsXzSb6pyoOSnvS5TlCxqjqeR+zdJmABaeqTEYqhTLdsmpJwMXi3tClQuDtNmcqLqm/dZs9ysckl89oxebPmHlulGSM5MaKlWsTwAvE+4qbcLkkCjlSA0uSnjaGCMAQgySxDpaqJ48NzXNZgYsxdszVfRUpilR0QgN87ZW6nnUxTsBty20isiToN46KLhb91dZ+gZL53lr75wu9UplOhMVrbo6Lt03JALuRKQ5TpAJIpEHIZ8qUzycmiYGVE9la+AWVVtBtUXpEPqWVvabOBFrcmhyGLoem66X20g4HEccDkcc9keM44QQPK6GDi9e9hh625M1UVjNqnU4U4/yPlP6EKk3ro0fAk92+wkpdNgOG/TDgNB3cMEXWR5YxGiJ4D3Qg9AHYOgYoxe4Zvkn8pi56l+96Mxg3U+iqFif+yV9I7+KoQxnVo7X6ub9VpSw68qItr9znrF6dfM9U89c3p7HVMsrmua5+VtTpra1eXal7npD5C+HtehrubXq7ZTXSQ8xVfSjqylWUS6yAALhf73DPk2gOOK128AHB7rpMV0HxIrn+TSUXtvKacpoDbafbOZkWaNTH6ev1nfv+tWfT7lYERH+8qH8qIDzWrGwQ1mxoJqs+NtX4O16HOBTSgXRvmeqYcFAnvssmvYa4iyZz/UtpaGTMiOcMsIVQmsSRcQ0IX24g/v3H4AYxXrC4rFBhES300u85xf4zWuGJwUgXpEFi+VK8RAxRCt9yJrVnBi1xJIsCPwyIvkXU34W2oZfcDlF6J6qjhoBMhxN2Lh38C8GdP/5G3z33Q4/fL9DZG531xq+ZLHGcEksl5wryCZbX6slcM43o2FWInM57/PuG4Pgivaf4cRSwRAutwC3HlPbT0Zkic2eOCKZFXUyRqqKhaoN29gaNurcPH9GiP/k07HywMfLYH4GqI3Ll/VenOnbJUqIpw4tE6eGg+p3ULUTpW0yxqRajLTZ4LjZoHv7I7Z/ukP41uPmW4c/XxN+1A3ovLihmuLBNQqIoojwPmAYNiBHiFQRn5UAvs5rYJ83wx7fvNxpT1XZZ3iQ7ao9A9TxTtu2Ur7fupPrFORzxWgE3bWCAKr8rwT4pY3Sn6zczLjX5tqUHsXrQAQphWifh32ydzkwzCMq96Wqm5gxxYREt3h/O654PLT5tIqCZTn/dY6pFFOOzxw1waQYPiSkSUMsWL4IEu+um+0rXIcrjD8ckIYJ/cst2kC4OudkDFWJm2tn2UUPF73MZ6WgqA8CL77oqnKZ70Xhat0rqLxoZlE3X8jrcvzxHse7A77vIg5ePe8GQvAecAm77gjfeXw5OLzaBHz9xQadd1XIEaoSVVPGKwDM0K8INpQpqvub6ceK2azL4vcC9i6lIp+F2llptGbp5AutV10xBjpZd+V9n0cJceqlNSP8E9GNPxl9Wo9vzsAzHp/Z9fsX9Z6AIuVaPrzmd/g5jGt+HqzAkoY8Va4Rcc0P+AsGfKCuhXpVMyk6MAe8Tg/4EhP2MeAwJtzeP+BwHPH27S12d0d89x8R4x5IU4QDYeg69D7gZnuDoRNFhHcenTNvL2RBLZyD4wQXBRX4EBFiQhcCQlLb8yR2olneo3hOuOKK0ma1pia1tXVA4ghiQkoRlCQOvnOkoZlU+E0oXgxnF7NQ7DLlZopXvBlEASGCdwmnBFCKGkkBAJN6mYo3ds0bF6Gh8ftyX6JHO0kAbfjAEZidRHtS03+yUClUBIxmzGit1p/VMDJ5dwlbRsbOZI1DOWuW14wcIWmoQ7nWvlUsoxMoRRABMYkCQrwcIihOAAMxitdIjJMqNzRso9IqtWFEbYhR5D8q6kDB2ayJq6VLLV25qqA4A8aMSrG9WeRJGhwny4IquQ/yAWjX4xFAsnrCudCe5dJyAa1fjiTngUsJsZIzCc0o3imW0yFlRUQVwrWalEJnMajKqWpF6FOha2uz+UzPJ6Pvyj2hMxneOwTnse0GbPtBlCYccTgcsT8csDsccDwe0YWAq+sBr1738GBwmma9LDDfpsn6mZQ+dgQ1FnRFiQTxdpg4YXeQ3C2b7RbDdoswdPAhZCUBsSoaCAiaWH5IwLYzz1aChwUkms2ddQzyvHEOKcOVE1tPb1QgUfdH4VEyP7R4UVss2fxih2Xyev7c47im9ELOmikG8whzzpFTuUesnRKG9ZTigYHGk6Xm31DPe62VafgBeTLPQG2I17yvyGiLEsI2AZXritdAlPfxAycknvBlJ54R402Pw6YXOp8XmOUjyqdp5RJy4smhQhekcJXP6Gmv/quUy3NEpHF2hddHRELcQIUsxCXkEr+7BR/3yzaoVU7MF4FrTA5SqskgBeXnCVQIBTIgWbuEIiOppUXYqU8lQLL2HyqsFIFAjBP44YB43CPFVCXzVo8IIhwPAWnv8OGuxxQ9Xt0kbHtNjAsPT4asjBBIIixwKMk1a6ho/VvZfKuUzilrg9Wrl9396PJMDmM+vHkzTxj+L6o0RwAFIZxk/s4MepUYzoi3YB3HHs453Nz0+Od/foUPt0d8990O5o1jdGVtKZIYag3Cmp+hOkf6ckOcWeifohIumrzVKP6mbwpDUrJgtrmrDg7sWE+6oUuNlahhnmIS5umrb7cIPeP25hZj94CAt/DYg1PEuJ/w4S0wjqrsYEPq0v0Wdc44kI8sT9QdPaHh5z40P2izH7x6Y1m/Ik4+slNtWW13rRPnJ/V0DZoRV6W+fTtl+VB7RszfUvAOFwK3WXypG7db7L/5Fo4P8H/e44uXAcP/cwB/8MCOJAeAuahS8ZDw3sP7AO8lZnTwPcg7hFDOi+3tebig4Cdc9wcMoUPfGVFb8ZQzZUJtMVYrCGqFhzFA4IrcbZ5BuWa/a8VEPn9J4xW3bdT1pFpFfGfOiFc9HtjaNxjWKDsAs/7Mc2X3qr+YGP/0+4D9MWluDKB4QMQGhqRktETpu7SR8OHuiDc/7LMyYooToiojknlapoQ4isJjmiz8lQR4/BAAeMZrAnzeb6J0OI//ljfzVuRqNVcPCVf1Hztn7XmpH1mwQJXgYrzdIz6M2LuEkRjHOCKFhBRIYhx7DxBwDHtQYPzD717ipu/wLW+xDR067zXEoMsh+uZKCCErC/arlRD1eQeMGSpjau7Nx1ykILOPp8G/y+gXWv06/7mge8+1TfPRr92u6nxyBcQFLaxMzqUeD8/KC/GJiMnLWzlVc85eXtbC2RmZj+2RTj5H8fCUZ34Kun3+imU05+Vvmk/9bFJ59llfF08Ih9j34BBwSAkPOOJ2f8R+v8Of/3iP/cOE3cMe05HBUXK1bftOrJj7HsF7XA0bdD6IwQE5OPOqN/ik+YRE3+7FOSB7UXp4l+C4trU2RF8It0JiicjKcZV7IeNAU6TL95ScehozPJfcEeRVj0GznVvRJPU1OboGg82qWg2bmHL4JAvkYzkEQFQ8L0xIn0kuY6LsP21f65EjODaPCwZUME8kYyzKjja0T4lXMNsXyOKNFf4NOTIT1VOvrEUlP86yjbxGXITz7R4rdIWElNRwjjEiESFOYpkQJwd41iTjBDdNgAeSU/7JQgVx/afry5X3JhcFhdGHXHd69QSsF1McUa6no672NFHlEWHGrnmyCi6n6nu9LtJUmdx2vSjTuacEt4vCddtKY5B4onhyYEqI+p7s/WrGSWoQY8o+61veK4U5qPAYGxABnPaysvuoBY8EI38LPWvGJV0IGPoON8MG274HHBDHiNv7e9w97DCNEYmBq+0GfRdglDvlHBG5x2USrGsw410dh861A7IhiJxRAjuHfnuFcHWDzfUNhu0WvutA3ufQUqIulYT1wcmc9Z6xCYykhjbO9k+9KDUQ1km1PA8JkFBT1S6wUKdlZ6ydrLKtiUogp5pszXuuOr80a6O8wmCQtVFTybVyteyH3A9u31E3W/a/jtvccwxoJIOrruy1WnNgiWHyXHL1GkbrCiLwwsZB2kkmmk9hHlfu6RyRkp4BUJUvuIyqldsCROIRETxLgmrvEZzIrJIr9T5GrvLZSJBqiz1Gh67eX3tktm1PyYNXSJbnlU/SiJTLc0TMtKHSj7YntgmzYoDNrU7cUOnDBFLHirkV5tyjoW139tsAmr21QS7WjtW2lDR1QxXhUj2z/jYFw8aUV0mgkJJ4QaSIaRrFejHFHGrBDtLx4JEODu8B7I49Nh1jyIhfD63BdSOgFABYciMygcqccrNYmnAwt7vHytp8rlX4JBZOn5mbuATIzInAz1l+aqWHiNxtTzwRMpxh4jNh7hxubgb80z95/OnPd3jzZpfJRHllsZLJHg+VIKB5hQn7LARTjEjMGONUCUVnNKw+L0QeCXNg+NEBzOIaLmnm9B8XssRCuogFCeGrrzdwVxH/fbjHge4wTB+AdMQRE8Yx4X7XISaS2J58ZkoZa6Dio8qjyogag9QTu0rp4CP795k38mx9P6aRZ+HDmpE0QnJZCWvKiHL3nDICQkRCiFaAMg4puIrzNprzbWmzxXGzRf/DDxj+coeXvxvw+j9f4e1/I4z/Loo48i6fV5fDNRVFhPcBIXQSR3Poc+x7KyWUgpyPq26Hr672ELJ8Uxggbq22ilVMpTDIUKHF6xlvcsGh8z7U9Yqwv7TJSI0nQtuPWf2cnNvc3pVTM9jC65+AeVVwYeAQc46IOpySfZoy43e/Gaq+VWNlVRYos2JWjDbu8n7GH7/b437niyJiGhGTKiJiFCvTGDGFkPNGRFVOOCLcBQJ5xosE9HklKmZp5aCdwlW1gqlsgXOn7JETmPnV2uBk5RluaS2AMX7Y4fh2h+9DxM6LNajrxRrKESEEDzjGQ3dAf+Xxn373Ei+6Ht/sBngWxRyRJmHNSogSntMEHRnrGQ3WMKUVXpyTSifm8DlKiI+mHdbJuOr3jEumlV1hc7EmrJnVq2+uCuMuLhc+tZig9X035yk+wZtPlovR2Nm+fBJkeNHTRI9Q9Y/soZ+i5HeeAisf06mnDH7lHlHZV/Nwdc3Ta31naKx9j9h3wDDgwBH3kfH+/hb3+wPe/PsOu7uEOApeCiAE53AdNui8R98PCN5j0w/iCeGDGCJofPws5KMiI2JKagzostGC9+It4ZVnN6M96zoZDOaExK7kKiALilrwblLFhNESWQmhVtHiSCHKiIUdckO7lh/ZmHAmsHGEHJbDEjOrW4Mq3UmUMMn4ZmmXje5ihlj4pSyvkDMh+ITJaXQCwasW+t/ot8x+a7uE5a6RcELGly/lJDWdlOV1RmrqZyORIGgC2zJnJUzuSttZsGihLS2BeARNhETqETGJTCfop7N8Co2iwXLkaU6RVJRPOQRnM0Ze7dMp8qE+T4vQP3m4ugi6x80jgix+Vo2jTVFBuXFrIeO2BgbO5E5GkVva7FMdX113QPeQ5ldMlI3yFqGdLIwSc4VvG2ZZBfnVvJgyw+hcVx+bgn/z/mGGOTLVo+h8QO87bPsNtn0H0IjIE+4eHnB3/4BxEoOaq+0GQ+hQqEk5MykfYQmSnPIegHjQgEskEVY5AgimOjIRF8hh2Fyjv7rB5uoa/fYKrguaJF4NE5EARDgkECU4ShgcsAmMiYAIka+7BW9RzaX2l1WJyFBdDkpOlgR1IG7ovpVdrQKKnEeheQlkvLptTuIxg0mVAkI6U+R3zNI7UgCxlPuhoZOblxAVTymlc9nZQzZZ8kdqAI0aPjqj/+2PsBwEtF8KT7Mywu6trYXB3nlDZV8ATsLlOZevldNacByI4B3BO4c+EPogXoHB5122OvU/q/IpO/nENi5+9UXtfvwALlZENFqxE8C5RvZFIUYCcJuRF8vHNdhRI4r2TWRnK/9uLdpahFNryttmylYtSLD8byPNtBhDBSEWPkESciYWq4KYEuI0amznKY/NFBHu/T3cOIK/SpheXiGlDikROHkhGlnTqDAAqpM9KrAwxU4GCIuTXF0/AYwvLc945Nfy1y2NMuITtmNEm9LreV8LfVsEbCzZsZRwwFK5CAMLGh5FFRCWT2XU30U4WN5fBEaCdMQSyoOZ4b3iTeflDFGJ/yhnl8SCB8AUxbX9OE1wU8LURUwUEVLCtI94933CODqJo4lUIfmzE/bTn5dL3/e3fo6N+OY51H7ksQpE5kwO7cfyRavEld09kxpbmToulYVQ1Y0jTKdxG5Kor3AW8tR0fYUd/QbduEP3hweM7wi7HTAMW3Rdj5gsJ5EyOqqkd+RAmnTSOU3qpQx8E/bQlIIpgZzD/eQxhCO2YS8nPCshZmPMeJyrqVFmKU9Xnmhwda+dRs51G68EbdTsohqlR0OLWBgme9ZiBaj1lnlZLT6r+jCYpvlhYH0RRmjuLZFzRDRhn7j5kzZC7rd0KeVxcTUnKTG+/krcit9+GPHDuyOiKiBi1PBMqngwg4dxHHPYJjBwxw8Y04ir8ApHYoQ39+g2HTZfXQPeCCvkRM2F/sldKtsWxQrL6LhV/DIj0jLcnp2XekvX5yW/slpX+ZZwe7vH/e6A8XhADAlTgIQjU4VC8B7kgEO3RwjA/+03X+HltsMXcUDPYiXsVagkioiihCBlbkxOUfj4dk6KtWUZa5k9WlyrQcXaQ59VCfFIuUgJsd77lcbm9X6ZyOZpvf5ljtGK0VIn8ePPaninOvM5xQqXTUBNF54SrrISE3aboAoIJkx9JzHR/YQ+jtjf3+Jhv8d3f7rH7n7C8TYCI9Crp8OmGxB8wMuwRXAOQQV1zgUReqrAiZ0JaUvS08QicJuieN1Fg68KBz05lSEJDswwzXCTuTezcQZcwWoNpsHmNai0d2L1di7eEOzkvuSYqDxK5mx5863FHaYMEPid4Ei9oFXwK8NSvp5VOaHeG8ZDayWIJboYI7I+x9q2c1wpJAiA4BAJhViFu6hoxrnSeSm9EG8OZHFHfb/IKkQkqMJd4/v1fboMZWoUhyXF00uaSukXo09SBKdJLNajCPniJFEupjgigBGdk/k1Xkxpy0x7ZVqpEohnAcnp87BOW9fME2fjgDJt1V7LfOmM0GgaXMNmlWX4vOZMAVGWUJLbMhEcJMeKGLrpNecQYxt+krgWalueEQsH6eBdklwqACxn4py/zEfCBM/zwXChgTlJ6DMLeQQge1pQpvFU6aJn2UKXOkfYDgOuNgO2XYfeOewPD3i4v8O7D7fYPewRuh7OMfx2QtdTXvd2LbRbpBSd9jmh3geqkNGwcQDwsLvHlCbcjUdEOLz44ve4un6BzbDF0Pfw1l6K+gKZGzMzBDM8AR1pmHOUHBHLWSM0+0JhiKlUUgKIeEET1201+5ZLncL52A3ti45/SRPN9+zKIs8PyTpDiizXtCOkcJxY8mnI+AAHD04W3QHIOTwsnHWldLAzXyoX+JE9yYyvgda1a8zI4fBM1mua0rUzSu1Xu2BK5GwsBJToN7Ph2z53jhAcofMk0QCc8LyLtf+1/KzLkxQRc8ZxWZRooboKL48322ZeaYsqQsXabIi6llksllvmGTGvJ2AMbXUD0wpIUTSOQCXoUAEFI1sIRI3tFzVm8xSnHHtRlBRTbsMSLPl7wO8j4rZHvO4Qo1NFRNLERkm12wL0JfY95DAbsQRDAicy7OTZPcPsnnmyrvBJGcuTe8Xe+fMDFsWa5UTfFhKX5S0rp4b36DueWGq0+Kw28yZr9xApYVAPRBRylfDIBHRVmJe64Yzo9dzHSYWnqoiYojpiZmtmVgJEMA4pQQMWzUNajK8ImAykiCAtKTOmDBFJTHeKojxMpAnnp4j7fUCMQELMrolzK+B2ZgpEan9/rnLBmn6io7QmnCxljUpe6cRZUHQeTj2p1Ewg12RiXWF+KLFkjtauLd5FpyblTN9mzwiyQZ4Dkv4KvK9DOkkd84zw338P95c7YO9wOB4xqsV8ZD1LEMGDke1ErrICFwtIcmYhXpiz9sz2mHCFju4QwpTP4jKGrZZGgGzMaMGd+iX/XhgeVPWyED9xk5YvKyKShV7ixXO2J0X4YoIR65/cc3rNNQoJhTfq6p6UMC9tJ4BjVow0bWhfGFDPiOK1UYj5kldKFBgxz5GNkHX+X3cBL296hO6I+4NHmiJ4ipjiiJSK4mEcPWKMyhDHHKJpzxNGMO4DAAfcvN8DuwnDF1uQ92U7VqU2wjPBCnO9zY224vPH1QwlGuai5rm43GBrkW2Bq/kW3MJg3O32+O7DncQY7gjO2z6WUEvmCRG7Ed2G8I8vr/Ei9PBTAJx4TJgFcPuHjCuywQoM1zSYr6FFm+vNx4wenU/UCZpqnS44wbyevL9eVrBj+9L5OO3/iqZevGne4dl4Pw6az3Hppy3nWz0L8TFf78/bl0/TyvrWmu/T+TOP9eypPX/e3q2fXD7x2Fo9vfHHqfBze7PuCyGDzBUSSTx3PVIIiFc9+vEe2+MOb+/v8HC/x7s3B+w/lIAnfXAIIeQQTNfdVhSr3ixFtSYjJ2A1Plcwj5CxMQExCd0bk4YjIbUidiQW0xruKOP5zMOXEEyw3IZGE+TfKNdTAnu5bzR3ShKS0FUkTya0asVYLRDW9xvbYbiFGcJTQ0InEZvolyASOA2HrNbFhsyMYshojIxWJGRvCojlNrHBfcMdMqfOQcPMZuaiWd8Wb1RQkc3cJdvYN7unTEvBtZbzIhszcsG/tTEiE8NxhUsrNCtzoS2yRMXnzPOIlXlKERQJaZrEsjwGOCqCRstjYGGpwfYOmVuutsBzj2UNj5oT1k5Oc71KCzhrzNaUMId3OWrGGQUEgCLclc0GgMU6O6mhG1fPruDJCoXCqZdNgoZsygojmThiqGU9Z1oj78l5yyoXMlrbQhRzWRRoNpXyp3Qosyq2nAhvh77Dth+w8R2cA26PBzwcdri7v8d4nOBDgA+MYTOg8/puymo7zbEgPg5c1CtNSCbplRlF6VwxsD/scBiPeLN7gO83+Ga7xXZzJZ5eXadKHN1fzVi0RfXi8hAPhkJjzmasonFsdqyS7VnJfSPKPPUJWNJ5s7Nlt5hrHqe8IdUhm+Z4pYavOLGHYfKWlmxWyFDVoXpIAMT4zCSGTgeUXAIQUB9Wi1STEZUpFTRnSX3GUSsnlD6XkLWKa5IYaxEJroCTPU7qfbI2AXOKsUS0oeqcuqx8FjRH1TxbXcA7AjwQVCHhNa+EGaUWOHIpgJqt+zPKx7dwQTnR+CnP9TmcerRvZyus33yKaGReLldEoF7PRwjCFQGefSv7XImXtkKFdKvlrGaRbWPO9zjMMqJ2u4MqGlJdrWlnjcCUMyv9ixbvOUoc+6jCU8sFYQqImMx6cvYqIhyvHPhlj9dfebx4lbDp1BGMWnBkyOMUyUvNN/1cwVm/ll/Ls0pGrkpwmHAQUGUccjLVmGOsq3Y8FW+hfG3WuCgvJL65c8BXXzr4AOynWN5VIUwHh8OB8e6toNegGu8UWK1jvYRccpwZB1au5Ztvr3B902FUYvo4TZhowo/XP2Ac9nB4g4F3SGlEmpLiYJKE1eAWhhlB8JRz9giI/GuXeiynEMhS7s6LMc3oMywAUgOMn9XVy0uec/M6mBGhn+217cao1SDCVxgTasIKJVK5XGWtR4QsBKgZ3gRRdm++cvjyPzHijzs8PHgM/QZdCIhxREwBMU5wzudYvobniEXA75XO88764gW/VQvdBa8EneA+OpW0NNPhlsdBcXqzTQq+MuXl/G5hahWm5BilhQbOZk8Ko2qvwQIzWJnsgr/rsHHSduXFkO/XHg32EoFhLPHfwHlcXPJNZEVMpczhUg+qeLB+sCYdrPtm7dnnN195bDc9fnx3xLv3I2LsGg+I4/GIGCNCCKKgOI45Z5Vngg8eDl5S6CTC8bsHUUY5B78J6L/cCtPrCkFf5rqlRRpaqV6xlaNEa98rANKQeNnzhzE9HHF8u8vruXMJOx+xO0zw2QPCFGmEo9sjuYjYB3Se8Lv+Bi/6gI3vZexeGGTnijKuVj44zaviqo7W3g3L0awwp/Vz85oX4IjLlBBPLG3XqstZEpMr0OyBduiPKyFoti9++eTnzxxZnysn1r2tc0ml/8HKfLmfODeNovYMLZXYISaH1AekLmDrRoTDA3Z3t3j/8IDv/2OP3YeItCN4ELZdh855XG+vEHzAdtjAu4Cu68UTwnswkI0OWGEbnAlsilAwJQmjkkCIIIX7JZdUUCF5Sklp3mpeEtSTQc656B10vDlBruDOxBrigwWHWQ6BmBJcIvgk3guCAy2Hw2NTbmdS6JYksqmcuDYLeB0hcasEyotSWw4LEaQLREXBATNGLNbzTmmfHKLJaSx1SGLd2guz2D4qLq3pXXDGgSYLqL3FicTa3pQNRCKpIBbFDUOEvlngUe8/oxdhhlkVDs+5PNTDU2PEs4azSiRGJm4awYnhw6geGBJfndSsuw3NZJuj5ovmtJ5dP/Wj8AY0u0/1/lP6V4TfCcSuoeMyPZdp5NwdHT83106Vhk45U8mMhEyonkDqJWN855zXLduPqOS1MK+WZAPlcmZsItf8qwvtagoi2T+S96VwOllxmBlWncsoa9iHgD4EvLi+wvVmA2DCeBjx/fff4/buFrv9AZwIV9sr8aJN7+S8pqSW9lWfwHmubQ+mqq+iqGA87B7AnDCFAE/ABAa6gOvuNbrNNV68eI3r6xfYdD2C77IMzFqQ8+YBBDA7REbm1RNLaKbCCRBy4ptM24o3ksBJ0p6rRJDlZS5zi/UOrdrEGcWBbTA7Bxn+QPevtqcN2Pqy/sflR15DGI/Apd3lrqjGSAkEUcA61aowE+AJlJx6y5SDajxShhlc1lI3msIpi+tV+C3hn2Lus0CoBFKvuuIJYV5nLYBw1u+GJjHDODX8oeK13zAiFUx1qnTwyhuEELDbXmG83uLaew0DZmvzC6Xt/gcqFysiCIJEy/KeAd4rmEnOW3Xcbc/z8gHmap8ueATb2K2bMeuVHJ7FrB5m5pw8Rzo0+9IIEoCoyDhOqniYJlVEmGeExdieKTvUysIRIW4d4suAqxcOr64Zwddgr+qDQcEFNKwmxOYrW0qsigDOlmcl6UO9fo+9ACi75JF3PRVIPLPv9asubWIO/BdjWev7rPF5lfm7eT5Pjzzw1DE8qTQ4o5zRTOVngZ4SRCwWTzCr7FgnOWO0SIgzwxOnEd4zho1H1wGIGltWk72KlYicnZQY0yQMQE7slQggb72EY6hLtdpSM+H6OuCLLwcc1fthPzGOnPDD9h6HcI/r+AEuHfGQJg1vIvDNlBDrRId+XiRI+ttAfkWWyLP9sSwFbM0BmDWGzz8t+R3zl32il9cI6URzmQCrXm0WIgQlEissymotlN2rNR4wc0EIIi+P2L7ocfV3Hm93Rxze7zHFUb3z5C9yhE8x50apRy/KCPnuZoRezUqJOzlVPVyuJeWV5nx2agshnk09AyCXliAzC6oZnDT6tKuuG65nXtQHUJQWCpscpaqaJIyW3wq7yDXvkkdVKVF5eUl7saJTKmJcrQadKT9UWVESXdtD9o5K0aL9apQRrny+vPZ4ccVgdtgfHKZJPCCISD+hHhHy24Fk/aPaqDknAgrleuOHI6IjCcMxMviLDcz9fyE0qZesQjB5pW0tHsE9Tf1Mt7QMjX2P+wmHt7v87F2IeN+Lx4d3rQcEOcI+REQ/gQcHeI8vwwYvgwjvnPcaK50qRYQyOJaIkyx0ApptPR9tsVCcX7ePdfj2GL1DzZyvTBzPL5xrbP3nog/VQOavL5a4J1530pL+k/rN/mJKA/eeUU5gxgtfXvMAy3aWS/T4m57qCfFY7RbjfKZylg57atH1fEKbS7Lf2rDVtTNFkPCgHuwDMAR04wO6/R3e3d3iw/0D3r9LOLx32DqPQIRN6DCEDtf9ILHcu17yPoUAaFJqnveBACYL0QLkJNUQIb0pI4T6cHDQ8EZmUZ0sHFAVbkMIFRlTYiSnFq+K+8QqVmyjDeeZAZJ4QqiHdCIwV/nbYILKcxNdYJIGrET2BCCCWevVFrPygMy3KFMlDwQqxYcdviz0rvBg9oTIoUHMK0ISZKdEsFBJmQQ8wXrXiawrEk5hrM1XqWshNcF1GGYA5vFAnJfExqlUIQBS2WstUyCovbeOVRQTnDTGP0U4ADFKGOlpmhBASH7S/aF9TIVOKYzggoAr33RjtkZAyNTwAl7VOIllvE27mV4wZQRUBjXj0fj58PgcjMy70LYJqReKI8SoHkWMvE+W1IKFImtNPvRoZZoIQBbg5y7NPF2Mvk7Mst7Mqns0ukzpybX1EeYBXejRdx2GYcDQd+CUME1HfLj9gNu7OxyPI5wL6PoO8BFHjuCotD1XuI/K+Gzms7IEpiQVHmM3HZGmCS4KT0F9AJzDMFxjc/UC2+0VNsMWXQjwOQG5zSBB/B4cxIiHinKVCSXVt2WC02fMvSHPJ1X9bdfblqB42RRgUU5Unc+hFMsvUfAxIxvtaMcMxNh/Zakq4X/mB1Dt5bI32u95VPmdpc8Sks72IgE5VBOsZ6wXc7dL6F3pSqomJYFlsymeYCREcCIQiZwHVRQ8c4khYliI+XIsWtyYx5Bpcfss3srtQpW1cGT5ECVPBDuH4ByOQ49932OAQ59B8DPhQrUPTt+bF16t9WgPLq648sYnyk9P1n76jU+q33maR0Sl3T/XB16Y0soTxU7VrnJ1f+V9ixWi2ecFZQ575rPH5UACErKBLd49M6YUwZUnxBRjVkDI2UzNmJxzOF45HG4CutAhhICX327x8sseL657hBA0mWiQOJ9OmGdyDlkTWFlzlMTVyADkSeWzSKwfKQ3V9Gu5pDA+TZ6Hp720IiL1vxqwJVbhZhLLnZsXHf6n//klpilinCb88MMOb77bI6UJnKJ6CSV88UXA1bUJJ1NuN8ZJLLuPI5gTHnZH8D5hN2oIpSSCP2IhYoL3SNHhy688vPfogoPvgKEj+OAQvMO79wnv34/45psrfPFlDyizRUGSbx3ihClF/LB9i33YAfgzhnhAnA44HEe8/wtjHJ14PiUguyI2M/PMdXkMUK49MgedP5dSU/1n5uPR2XrGnDypnG37kZdXDOMa2bd48kxzjTKiFsbC1njBHReCUBljNgKOi7CEfpxAuwdc3wxI/+sBux/eI94m9P0GINJPIMQ9EiX4qUNAgJ8AzrimDVdjQ7FiWKZmd5uxVWiYjEsD5Viia8RRZr6qT+XiYMoMcibQqCuj5nxgBLMR15n1snjIGheam7ku/cpKUjJ+QOafE7dENxQewBgxs1YSoYy9gwFQKvkoao+umuHI1qBzZQVKOxZSisH49ivCi6sOb3484u2HEc6RepI5pBQRgkeKEaN3YgyhsPee9xjhsPUvJJQHEQIDL0YCHyLGP93DrPv8VYfwxaZdVzaWZXkCKCvKTp+i1bPPQDpMOL55yLm2jOl5iBHvBrMYBaJ36DvxdnOOsHd7jG5C3wd45/Hb7gWug0foPDrv8fvXV9gGj77vmnBMOSyZcyIMcMqYLRQMs95Xgve5WKF8VHeo3Pgo/D0nbS+c4PLY/Ma8z8sGHu3vCSVEzdb/dcvnppc+T/sfQVH8WuqZ+xwTudomtf+bZW2jvWhx33WK+N10wLQZcLx2GOMB0+EBb/7jPT68ecC7hx0e9kfQQXI9XA0bbEOH19trUUZoMmrvRXCXQgCIkLzGv2YTehVBuwlqRXCmagViMHkwRcB5MUbwDgElFyG7CEpQy3+F8foOyqGCi1ICThUMZjmPIrQ24+6sjGBWzwgJp9TKCNeorGo6FfCYFTqYNGyjk2vOvBYcUuWpUHuSmlAXOhc2d0VpwSLkVsWMRLyJIADJWVgmi1cv85M0JGOOnV4r7au9Y/I0tt6wyjxq9KrGKdmIm3XuHWuCakYWTlY4qVVMWDXDz6q6UcWRLghAsm6gKELUGMEMxDDCPD+cE76KIfwYpwjLlUU1xmgUAefUALaf7NcJmQ9xmaz62VqTw7bHVMC5dETQttaR5ClQ0SSfX5A+63u0KKmKgkQ8JEp75fnU/DbFQRZEa45Q8fxRT2njAez9evY4MZg0NE7NvzNLJG87g0AOreUdwcPj5c01rjYbbDcdvAfe/vADHu5v8cP3P2B/2MP5Dr4DcHUL7/Z44Rib3uu8t7I7ScBtuSNEWVi8FRheDQe90l7w4sG0202AD/j6qy9x/eIlXlxdY9gM4vlKBMuETfBgeDACIntM3GFKHofocZ+AD5HxoOOcgKyUyHNebaWatCLUe9EuKMwEcsL4czugXGtVbjVMyG3X5xQlzG3hXApfkVs2OAvOPIGtce5N0ykDDHpWSJSwpKGs8/htf2fPkHb/mIdRSpz5KQu3ZOG5ihJUoIHkmyi5eOrz0yhhZnRte0Yacxh9pp11AwMS7suSwgPsga5zGHoPDh7JBRBZILxfyy+lPMEjwg4XNZsbwGLByerZfc4BKPImzof0IkKSFv+fKswa06+52DSzuNyEeUgloS6DwTHlUEx1SKaUTPBRgI4lW0lDQHzZw/cD0PW4ftXj9Y0wz4Ls9VOt80TBUMf+bMddE2VymdpPreIWCPiSGTs9L4Xoef6RzsTRp+IY5n35CRUtc9C2OqZH+nfudt3+Yx4Sa5dPzfElIFnwCC3xoVo1pZTQDw5ffjVgnCIOB8L9w0EtsTWxmSY3Cz1wde1FQYGSOyIlyacyOgkvsj88IKaI3VgsqMB6EojQ+QDvvRAqnjEMHiEQhoHhfULXedw+RExpgu8Trl4IOUfkMMWI/TjhMI04IuLW3+HYPeCa7+HTHsc4Yjok7A4eE5P0PxOJqDmHhgGoZvyRGZ1h3ieUZk+sPH5KWfG5j8InQ+yfq5+8+HIWT9n9OU035xWXdWtq61QfZm1khnheYd5WxYjAzqMRtw70kID9iOFlB/qS8f79DtOtx3E8oOt7THGCix5jnADnMKUJSECM4kEUk1hE1iECpPF1hsuIyIz7lzWUOBVkvq6DtraFYBUCVRo24t/kApbMm2eTR9V8FeUDJGQDs1iEEmchebZeRLFkRL5OxehHrSaF8RcLn5bJQA6fYMS64wSQJt9kRnIiqElKJOfOJwEcnPusPSdJ3in31MKyGhMAXG8J10PCbp9wvwPqUHcpCRPMXsQ6PiXE6FTZG3HghIMneEiyxBQZiAJjp7sRgLq9g4BXttkbtqTBJa3wQOqfyhvCQDGJqzRPPCaMt4ccXgAszOvBM/Y9ZdsL5wDvJceDcw7wDA4R6DycY7zuB7ykDsGLwOTFpsem9zkJewnBZJaIwgg7BeJFwbAChFRJ0d6l2QfV1Rf3z5VyfNafaWDVmfbmtxbhl6qKj45jFbeVtmhl3J++fFzbnwbvnWjkaZdPlxWh5S+jnGCeTpSffHS1kONJ5ekPmUeVvJZOLKXAyA6Elwwce+B447D7MOLwsMf+7R7vv59wv0/YH4EhSKLNIXTY9htc9RsMXYc+dCByYOcBIkRJ6oAmqS+AOv+hhXkxoXUWsCmPSZREMUsST5zIhMvF5KDNs2jtyohZBdsixzdBmeCmHL8+K+jrPBHarwRR9nNt9X9meawSG/7nrEjOcMsByN4K9YPWfmX+qHiZVRAntEJtkavecuRyyCvSd4rgi1T2QXlu5dETdFG9b3RNajBQ89V5uNXDjoSEsPq2rOX5goiNJ8j3VTJRbMaV4CEVKmrIHUBkHQQgpgmAhwWekli8XLNBWmrkbwq5mnqYEwf171MLXuCMnbAiXCl9N3qx8GmtfKH+zPaceQJXvtc9q+jE1a5r74utKKnRQ/GYsX0kXWPwsgltNxVBfiXEFdq4Oo+cZ0OoR1u72tiFjD/Q82j/WM6qecpuhwHbzYDgHQgJD7t73N7f4v7hHuM4oetfwHkGdQc4d8Smc+i9B1XLkXkBPdsGZ1IqIeFsiuU8yTMmkxsj4L3HZnuNq80Nhr5H13VKr9l6CrwCOyT2SPCYkseYPI7JYx8jdhE4ahqUCMwinSxnXLohsGC++hkWMbJXuvwssGTZdH2P8gQ12JLrR1bOBBcYwNW1+rzK1uD6UhnT7PVy6o0+V4+w6nVGr2bjM+UpksFzTuAcaswy9aUGaJHNC/NySCtlcdJo5ccZVJwNtlj5KPW2IKdhCT0hBIfgCIkc2FE7+R9dnkInrO2sxyHe4vFP1fVz7zr5jsdfvpQ9fXyHn+QRkcspSdjJ6hU2rbV/FxLlq8gEp5mjfLXu55zqaSWOmnCSJeSShmKScDGSDHKy6xoLjXVcBMqWd+NVwPjFgOsvOvz+mx4h9Oh8h+0moO89fOjEyiV0qowQj4gSy9jQfcZ0aBIikauGYpYwn4NFfDZ1/2v5RIVnwqBP1q4iNiMW62MQ2eMQv8iETmKHcRqRGBg1Meo4jjgeR+z3BwxDxN//ziNOEdMkidsldFnEu/cJMcl3s9Y1b6LjYY9IR7jf3oI6DelU0csgISyi8xh3HXZ/fCFupUOPEDohXEKAVw34q68DorvHj+9HEHmIW6AICt/e3OLQHxDc99imPTjucRxHjP/9LaaHiLT9AuzcMi+EIfRza/ATHJFTIPKJIPhZ7/hllCfgIRhxiYaKK7SnnomaPlphRJ477RYSRxh+YyTtPbLxjdg36xWCwPnp1RdIm21ZrOCAO0L/5Q701Xu8+8Fj9+MBTB6bdAX2AZMqI0LsAADeeXRRLCKnKC7m3pcQZzbAMQbsp9cVYV3gRZ2o77q7wxAOKCT+icKzT9TMZLlY02HNPFPdRN0jYU5R+PHMzHOSe8bbmHylNrCz53KoJZhiQ1/mALDFjDaFBHIoJqdQ2pkZFZf1BUiZL4ZZzJkygdnS7HEm6uWT8giNqf3N1wNevujw5+8J726PiDFI/O3RI6UE753m5omqiBDG4T7t0cHjBa4B73CrhrQEoE/A9YGRdiOOf7zL829xwsPLDv7F0KzLKtHccF06/1PC8S/34LEkuGRmHFPE20FHzaWB6Bx6bzQU4UB7HNxePEedxzfdFi/Dy+y6//svrnDd+RyyaTMEeFflfpjngqj2q9FN9tEwdQueiPKPOQ5oFApncMQSrtLi6ynQO+dJMgk8f2LZ8dnPtXfS6fc3ypjziOFjYOGnKr9s3PXMUsOoX8tnLO3myhbMJmjMOFEU/GPs1CMgYdoO2L/YYp8iHj58wJ/+9R7f/8ce7z/scX93xBRFcrfpe1x1A15urnE1bCRMifeA82ACEhySI0SDZ0EM1sh5xRE+k82OGRzFmC7GKHSwnlKnQlFPhJAigIRgCUcZACUgWeghabHw3QXnEkroHXmrehDn3HAaojBJ3oiYGG4eqklxtuHlGtpp9p4sBrOwKGJnoPkcLKyUeUR4RkqGa034RqK4SbxQ6hb8LrQfO/GmICdGCk5DxLBzaqXuJKGtc8X7BMiC/BaZkAqT0dI7ebytUQSU/jB1kOVGcK60ySQNcF4se1Oxqpb2eGkIYvIWs6TPrhdAxAhiDzcdwRzgvAdcAgXZNTGl7OmSFVzaZi3ono+1Le2NvN4n8V89acj03ckiya60bVMM1F6/LodivARVUAaubcisuv/E5V0ltn2lkHDl2hyC1EyuqAOQ6RXjzXO+RDXgQ7XnSku1AqiIzOUoqlGNHAFshw26vsPN1QabocfD7hbH4x5//O5PuL+7RZwYRAGbYQt0EfvDB3jsEeIBrjcaTnjylM+leXRAZQfApLCRNLyXd6KIYAJcH0De4cXNDYbNDb764ltcmzdEF5CcDDJBjHscOyR2OHLAmDx2KYg3RAzYjxP4uMeUIqYEjDqPRezeIkiCkPImPavXxVXwJ0FTTDSLVjELzTrW91HV4aa2zZdtZZu9ihBGFn6w9iJbSVXwLK+1BqHi0k5R/KZyTrV+3j613BWlySYctT4v4WwZSFGvi/xGPHKSeklp3zQUt2YIKcBgJl+FKa3qq9Qq2vIcZv6gmn+7xULTe+exiyOmCFz5Ab33GJ15xsXMYwgvlSf+l1F+DoT1T1wuVkTMjTkFMdpBevz5DM/PMG5n3l4EIKXFGWY50WamCs41b4hViMhkiXeZJUeEEVGcCvFhGjmnicKcA28C+PUG21cBr24CQggIzsMHr262XhUQlhSqxDM2AAlUybPmzLP+38SRBFpFz5myyA3xyDIsrQMemchfCFf4VAHuqWFd5O3xiNJt3hdqgHWNTGn9gVz3ce60VkIUokcRQQIiHI5TD4bPXgxxSjkk2RQl/NKkSgnnEjZbxjRGuGkCjUeQO+I4HhHHhJhG9SKaAJYk1SklHMcDECZcbXdwg1j0Gh6zObD43sc04ZgCpnFEogk+BYzcgSYHHzzI93B9j5EnpMMR5CSWLlhYmZ2/x6Hb4xUeEPiAiSekaUJ8e0A8MNCXOLetZOrsVF5A1X5+TPILOW4/XZnPx6VLkGlJg7DVyTtJFJynFk56IVVcasu/yg9plZSW5uKivRkQhz7TeRalr9sc0Q1H3P74gOnQ4eq4gwsB/SiW72EawQBGP0lIISK4JPjGOYfERfBY6D+HI4ogurhgo2K8GD05BGWSWxjYEu0lImlNeFdztGIZqMGuV+eyUqPm/81iEPPP+t0k7dYxixv2gbQvVFWvR1UJTywshsQrVmGJfFXCH3mtS/zggsfnu8P4oWINJ1ZJ2w1h0xNuHwIe9gnRRTA7TARwimCOSq+IRar3GkoyTWo0IQ2PIVMPoDFBrNgY6WGUKqn0KPUO7noZ94Bna7W4T0CaGNP9CB5TzpkBAKNnHDcyvmTzoNohp0y88xK+gwLDBQkp8Krr8CUGeC/0003f4Xrri2WvkzAdlgNinpyazHhDt6Q7sU1p/i1/tEDlMSUENV9WAPSJd54G5Ss0wAk6brUni6ordHTd3RPjPlU+Kwp6IoL7qL78xLh0Lto4WxYGWOcebgjIxaU5Y//Zyjlc/Nh7/wpMeIMDHy1rAh2HyGJNnshjDB2mbYfD3REPD3t8eHfAux8nPOwnHI4TwCIY68ij9x360KMPHbwXgR3gVBFR2fCaKbZzuQ6cB6kYiBIjafidPMVJ4utDQxgRRODu2IGcJJMu8HKW57B86HYpAq4lPi/8s/w5VcqI8CpJSolKKW/wc+WYV6GUSH8r6ka2RAepsFn7bW0URFrWdRaaKQtQC7VV5tUSAasSO5kyW5UUgOAo5CSwRhO1JbeJwkevKSOaB/ReLY+z/mflT0U8rNIQeodsvXR9mHQfGPXEScJuJUuYLbKNBFKjTDNG48wzohEw1utVbmUB6UoxJcRcJHMezLeAKi8z1ZdlvYgo0wGUryHfk+fWFAR1Z4AmtFc1mmq3NL3Je5IcsnrhMVkMqvUlS76u+w6iTLAQO81s6PmRLSzKCOly6akpjmwPdn3Apu/Rh4DgHW4fDtjvHnD38EGTSUPz0PSAH3GcRjBGTG4Eh656t1KmZHvCbiB7Pzml6Yg0ZxkRohHT3mNzdYXt1Q2uNtfYDlfwXYDzouizrWMrnkCYmDAy4ZgcDuxwSB7jxKBpkhwX0JBQdfhWqletNei0HHkASl+rtWSYh0C9veww1nDDFmNlcfMYuL6UuRUC5xBOmddkICt1F+22Sp96bIyyD8yY2hSEuV6afeb+6Doa/Fa5Z05GzVETqUdtP6qXlCSohoayrj17apjTfNpLXfUjh/sqwJoaS7Fyr5xGXRtHiIgZn3nnEF2h7yvsdGG5gBi6hF46A/8ubY7nN38SeujxlzxVbvqU8gyPiCf0ZkbM1MqIj3rvJ5DA5W2u8R7NfTROchjNM6JJvAtozGH5nDYBD1/1wiSHDjevO3zzdxsMg8Om9/Cuh3cBwYu1geSFEE8IIgfna2+IKklL1rZXHhBokWm5Ub7XAPekIOzX8ossz/WQKIpp+WKEpVhdONxPr5DYYxojEhOYJzBPOQTZNKoiIokyYpxGHA5H7Pd77A8H7PZ7HI73OBwe4MN7hPCA8fUR4yYipqlo2FmTo3ECxwmMhN0YQYrbdJAAjDkhScznDqB/3IOcQwwBiRyiKvGICC4EkOuKcs/yrYDAcOhCRMcJPI0YKWKKE8YY8e71a8SRMFnCvhmU/STeKH9jR9AI8Zo5/euXM+j8DNN2siluvpyvdqLeY7B37hlRYLiFE4LRaShCc9L/OScvBBiH8RrjuMHm2x1CeIf77ztM7ycwHPp+QHKEEHrEKHH3QxjhnEffS76BEAIa5rBiMIqreZIE8lSuExF+GHt4PXtZcW7jUULeUcKr4S28JZHOk6QE83LylA6vmK18A8j5BWZn1uokvWfEMaeY22neawmqc26JNr8Dl47UnZLxVxZL9nZhnGZbSOO8WtI2Oz/q/6Btre80ciL8cAqn/+5r4MtXQbzLNGdVjBH/8kfC/cOUrZgsRFOKEh/2gQ/oEHCTtpLEmgjJMd6HlMfWHyO2h9KR6cMR025s1iTP3VpfIflObwdCBDD1BHS+opvkf6deGd6lLEg60AE7v4MPDj4EfPP6Ct9+8xovY4/rGDDAI8Dl+NVD7+G9KRwqwYNaQPq8Z4sQAqj4H2r7Xb5XAioq1/L9Ga01v79scW2W5r/m9ZezS3m/FBix9uhCVLO4X9OJ5/t7Me77eSGCC8onwOk/u3LBmBifhGf6JOUjunEeK3/KcnknJWzIoAY9BN52OLwccOCI+9tb/OkP7/Hnf73FD29HvP0wIR5HpGnCNki+wMH1uA4bbLsBm04UruQcJhFnYiIxTBM61yP0Pcg5uBA0HKETG1k1HKKU4BIDziNNo9LS4r2HaDx4BEFj2nvKoTkmGEqTnAh5yxTtO8TyVrwc2PAbadz+lEDJlZCFKSFFIJEIuxMIiR2IBa8t96QJkFEJqcqKcF3PEYg1fJ9+JmZwKgqVmmay5wyWGq1jkmChVQjJFQVE0fs4IMk4ZF5IDEFSEV62ViVrRbH/rFpNC9ogRVAuypokL9K6NueXFK7GV9M8EOUUORHkUQnNlKKsu3iXoKKN6n/WNOe/XEO/r52eQjsqNVsu6Oy4Mk3W/wZZF2MXW5ec76n6NDqh+TOjBKMZrMlZCO8S3qsYvppXhIOdilk3Z4O0fSFhtaSjzvqn7gEOjKSOHEYTOu+KdbjRoMworLGG01wVUKo3je5vM6A1L9IX1zfYbDbwjhDHET+8+Q63d+/x9vYdpnHC9XAt0TtCh0gRu90DAu1xHcwAt0w6Uwn/Y0Svpq7X6zLH3jkEUgOTxLg/jHDk8fsvv8bLl1/g1asvMXQDQg9JMeB0/+j4EjtEEI5MOCSHfXJ4SA63TIiHPbqHdxjHhAMDE1tn1ovddU7W0eVQb209ruoXlFl5iDI0j1xZk8Jg5qdsJoTmXelPLZMxg9CihEjV+UoNvyLXzYyn8IDJ8thy1Pw1hS8BALKkIVHeY88Z/5W4GFnLZ+sRIX1K4KiZODLvpP2t3lmmdJ3xrmyjdA2M76DMX5TIMFWDOrXOiVwoeI+uc+j7Tva5d7jZMqbNBPKtoRpwAXj+VOVz0MQ/HeHzVytPVETMl1fLE4jL+Zw+Jjx/vOl1li63WZ9Jai9mtySLYVkh11QpIHITprFzDggePHik6w4udAibHtuXATdXYrkX1PvBuwCXFRAWjsmhDsdkHhGmzjNlR54fmgFOUvKqYaqX8/Do3q0h70UVzxSq6tETmNmPLbbAn5HRWhivLBDY6fl5zJPhKf2+RBmx+ppKkWbAnpkQ2WGKHaYUME6TCswkN0qMESkypkksbqcUEVPCOI0YpyOO0w7HuMc+PWA/PWA/3WPw93D+AehGoE9wqknXDFZiwZsYIUmIpikmiV1ehTTJZCkBzic4cghXkvfFudQSlI4A34HclL2LSIWi5lUUFNEnZbxSlPBqk+8wOZfzUpT1+tjyN4oxjElaXnpaM2vE3yWNPBnBPxN7V+Pk2bX11p8AcRuiiprEZbmKWcvp/UwQK5HOZh0oBwbJdWB02HRHhE3EHvfgqcNm2oBcwjgOYAY8RkQnVurORXGXVubd8Isx5zYuO2MusxoVI07AlASPefLFIqyC/USE4CZMwYFdgqNMwef+t4VbJYTCLVNhEGocvTbnxgwra2wmmDouoFZUtMyzeToWxholGeVCIcH1K1f6Yb+r56otcBpftEITUTqJ98l2cBh6QIyVGDECUyRsNwHjyBin8p6szNLvyQh8kHjXeIk5nnNeRLVy0z5zZPDUMjPMWA6xkiVEAnbkpN1A64eHUrFQdITgCckTuCNVRBBevuzw5c0GLw8dro+tcjl7TmgoTCGZqhBMBLVKRKGlbDea9epZhpWKlWtV7xIlBK3+KBN06q1nWtFiOJ/KbVqrSYuvtHpteaHu7tPotpNU9zPbOP/u+bQ+3pPPSYM+E7+cpbnX2qs46BXB7cmmVuq1v39iOmX9gKwUfnxAn6TrNUOIIrN9cjOElLwI6DyQOodp8Ng/jLi7O+D2/RG37yY83I/YH0bwFIGYwE4EYp6cJHYlp3lsCOY1Jt4Vyv85B+edeo15uOAFI5IXoT7EyCjjFwcN35Q0TJ0DW5iaCp6axT+TWWUbFb7EZzlUjeEJxckFJxrO46zUF1kV5/xrRURUeBkJB/UI5CEUh2/DIQa7suEewXJAWUUCmvjxpP3Iw7A55wruNwLuCk5WigjW96LCtcsNxEa2zWQes9/SSalf9YtWPNxPndyZiqXZ3UbLCF2gQkUYjq5oqpRkH6uws9BZlbs6qkbzF55frN/cGLDU4yjzNUNOudpMqZFxFVXPFHVT8da1upSr2v5aix7RRNvQ+rJH9HolIGVwodFn7RXBNeXP5hrbljF62842gZIonOQMlr7rY1lJkWeGV84RWtrSOYcuBHR9QN8FydEYRzzsHnD/8IBxEgOWEAJC8OLpA4lgQGSGiS1vUu/APIbZNafnIudbIDEKhOuw2V5hu71G3/fouw7kY0V7loXOMJAJkYtnxIEJSAl+GsFMmECLXbdWMqxA2QunEEk5O1T2nK0jt3NcdTmf4SL1bo2OmnfU8PJ0V2ZHax0ms/JKooRI+beN0RTGpuSAKiSZra4oIJLKaVKS9N/mwkYKG0wBQVwZg6VqHIzWI3xtaJnpdXkerX4OQad9L3CxWhPjSZ2DdwmhUjh2noHAM2j1ieicJ9EGNbJ6ehdquH2y2NGqan8Oiq5dO7tw+tw8tzwvR8QzSxaszK/rf0Vo23w0CGzZ6Ow3r982DZ64LwExlaTT9WdOSq0WldkAwRnC84iDx+6bLWjocXV1hZfXHr/5qkPfO2x6UTp4LwoI7zvVyns4X0IyFcENAeSV8CnxDgtzvTL21flYzuxz6Oq2vfl7P6rBX8sj5TmM0OIRFg13IcykWB4Gc5t+mF5jigGHfURKE8YkOVEmTSg9jRNiEg8I+TximiYcxhExvQfT99hv9ji82mMaj+DxiF064iGNSDEi3Ze45RI6hMvvmDKDAog3Uj2izAQogvHewzwk5FwYI+VAYQIFB+8kprjVKcSG/J8U8ccUJX45e3DtD3rJRNfVsvVGvQIngU/z+EWI5q9WTo1nvdent2xFzj0Cvrlu+rEzcOr+6mTOieYLi3aqCdF0tvX2Yol7eeJpar/UxEQ9BzVjaUSnWZQ5EJhSZu53x2scxojNN/fowx79uEeXtnj4cADRFuNwgPMBoe/FE6LzcN4hdB2MJ2XUjAXymfIO8A4QYQapN1Xpf3AiRAmqBLTEwN55gBi74wadn/Dl9gM8pZbxy8M2iz3O01Asw4ywNwEHlNArigdbiVqJIcCwsirK9TgT4TVRXhS2laVSArIqhK1vpc26D7n/1Rh0ZNXi1/ZK1fWGyUYer+0xp3AvaT+IhNH8p99e4TBO+Nf/2GF3KEm1U8Usg4F7f0BIDlfTRrc32RTi2DuM3nCDJRcl7eHpA7lwbfdyjVlsB10VK3nEiAd3DzjAh4DXNwG//c0VrtKAV+lL2TeO0HcB/cEjJFFMuEoBQVTFftZPR5UQwmimZnPV87o+liX4me3PvEAGS2Z3MgF7+h1nX2wvP1fJGOEFzrFqZyDVYkrmFyq6O7d/wTge6/OjEPc0VD719k9Pgi5m5YnPPg+LU9lsj5QaIdTwYv7u5b5f/V1df5rSqVgJfxzh8lwEb3c/JdW0nL9zK1pyR8kXp/jAcUIcehy/3GIXJ/z4/g5/+vd7/OG/3eH2wwHv3x1xPBxxPIzoQkAIPXzfwfU92DlESG6fcUqAhhmaSPMVdQMoeITtFs47dKEXTzlnJtVOcwoTUmLESEiUMDHAMCWF9NMENEQJRAznGB7Fmy6lCMcp1xMUT0q/Ekhz+TiFw46cwl6FiwxYsHZymmKJgQkOjglTApxGrSEFp6YUKOehYEeDQtaXhBJ6IxEEB3jK8J/UQ0SGGyH2z17puDKqLODPcTxkHJKIOyHBAcQg7yUeeWJQimJIheIZyp4yrTG3T7BiYWzKjpPvrvpeTbPOg9IrBA0DJbaPJkcse9RoBMNLxRLb7hKUbiGI14wjOM0fIIYJDKQRiRJS8gAiovJf0Gd5ktC6LiUkJDgSejAhIZF5CnD1V/WtwVvabqYZyrg595Zg0kyz85cQXcbTllya6iOQQ2NDw2QnKkmSbZmlispwXDHsrPnkTM+Req4kXZCGTLOcJVTtX8q5Bhw5JGJRAiYGkZccYrm/YlWeiCSyWid8KKUoucc0jwercR4l3+wUTqntLzOSi+JRoHY+HgGeAl5ur7HdDLjadPAh4s2bP+H+/g5vfniD3W6HAMnPcH39Aj4wjv4vSPEeX7xwINogIiJqjhp5pXhSObNJ0jMIiCIlAZqvi3F7/yPG6YBu2MBvrvHqxd9h+/JLvHz9d7h+cYPNiw6dJ6QxgpgRIoPhwNQjwWFMHY7RYzwGHNFhhwG37PBD8ug5gOGxB3Agg8tG69o+Kr4IkgOh0IplLdvS5AaEZboAKHsR6F5VJyXbuzBeqG5QDh5M4VdCFmF+RKoO5Ad17zskxOq8twoUgWpFicCp5BcRuGQhk6LwOZbbwbzE1QNC3BTsk+FqTwjdZwTJ+WP8DNlUz4Aet8dlUbItWqNV1vluwvECOf9LtdecJ3Teo/cBzjM616HvenR9B13gVQriYqrhhLDiPKm+1vpid13ag7PvL/ttvc6npI7aouvymV7y0ykitPOPEb+NVdqjA6bq/3JpHn/RDg2jxC2WQ2sx0URQ2npCGPCRnc2GzUDgwQNXA/zQYzN02G48rrdetXSVIsLZX+sBQWTW2xp6ScMLGGJkU9+eUERUKHt5Jwt5PgHL9hFNnBLCXdyvTO19vqP13HKqS2swjGco5GRj1cNr7Rce0NqDcRXL9+kGqc9BShKzFUmsDKbJY4oBcTogpogpiQJujBJbfDweswJijCMO6YAxjjhOewDv4f0dkj+AuyNAI4gmTNOIOI0S1kkTqCZmUUwkE/6php5VvFf4pMpAxtBwJWik4s7tNFQHO6/ngAEvqN4zVy64BcllRcQxYRp5OcfZimGtGIXyCJY1wjmvRbt2P/8Ek5eczQsw0XPhxicAWU2pCLtn9aVWRpygbj4KLy/aVNjNyAwvV1qabImnjCWxhZMhJApg9iB3hOsnID2AiTHiDpwmcHTw3GNABHmHBA8XHSJPAKGyhCw4KjkGe87XLG9B5KQxYaVnMVo4g6SJAeXkJS8M7xgJwRFuOsmxHVxEZk4zfV4lWkM5n8XYsgIUeoMzk8/VrWIRBHCJi2oKB/OrVoMEZOueWiEhPRIvSXu3PqsEvr1LHqqeRYHRtSIA7Z2yjlXhBmLVN9qwWPLp4H3C1cah6wK2m4CYJhwyI9LOY0oJEUBy3Fh1ORCSd4gK/lISa90mXN4CcOn6qiAn+28SKZOdlGZyIDB8ICQCfGB457DpPG5eBLx+FXB19Hi5M48asRB20RdFg4bKoExDIdelSvFQlB6L2VvO51ohquLTttfn4z55e3b3McOC1sDmDG7Ja96+49y755cX7He9nxbvfTogbhilJ7VTs9mfqheX1eLlrDzjTZ8aaZ171xMrnjgLcvVpc3VxueiBS1s9w3F/jna1jVM4fQ4dGOpp4B1SIBw9cH+I+PBhj/fvD7h9P+FhF7E/JsTJBIUEcr4ITcGYmDEl8dSlxHBOY/Ub/HMSxtd5D/KVNzBUiKo5C0Bq0U4ORFyM3VyBl1DeUzQFBGLLpSN09Dyx83JmVnhuFH5U+BLOdH2eK0Y2YGDOoqwG5+VZbia/rAfVdczQiGybl37VxhSrFFoGANaG9aPMKSsHYk3XiYkbdsD4BsLCCJbJ6sxQKJlwb1m4qrPoNpX3UVXH5saskZvHTNNjeFxpG7N0lrGbTKSmY5SzymFYCoymMgXVdHI1znbxC+3STF9znWcbb7m/qvcD2WizzheSnywburRj9fK15W5eKDnnk0lld5kCovWa4fY9Wa7jqt1VYTvrnJPfLkETpKcSBkxiPKE5AdUcmyFSFg8z4NV4o+869F2Qc50idvt73D/c4nA4YBonBD8ghA5d6ODChF16QMIOfRD4EaPBobLGq6tkBiFOFC2cGNN0xHE8wA8bCQW7ucJm+wL9sEHX9fBBaDmedNoysyzKQ/HGcGB2SHCY4DGmhDiNYtTI5jHG7ZxQ3beaF1+h7dbGUo2TcruFr58d4/a82iEEMkxoDuc5Gm8O5Zp8FGaSxqjfarxJidyiz5hgxe5nw6loRD6KB0RRQDShmBQmmPbT1n+paTiHS8+UvN712BlNMKvG2FPPM4kcKxEAJwnR4R2iDxC9cIET6928jEa4ZKfw4sqp8sgczR8/ga6e0tSjq7KoeO7J5d7/uJcvy9MUERUSfOb2m7VnH3Pwptu+cu0683hbuP3MmeTZFA9ymKIJSc0jQgUSiU1ZIc875xB7h903G8A7hE48HbY317jeevz91wF9J8IA74N6Qni1zpa4nnUIJiLR3LcIrFh1NAN7jJP9tfztFF4RjlshyvRkVV0JIkNKPIMpgrQ4RiQG7g4vcIi9/mYcxwkpjdjvRRFxGI9IKeI4johxwuGwxxQnHI577LoD3r6+h8cOm+sP4DQhTUdMPOF4LwqI8XjENI2YpgkxTkixKCJyLNFMQDUdVWGSWbkWEjEmhlONPxEhUhGSijtehEOAg9f5S6KcSK5YxioJwZwQR8b9ux5jCojJBKtPKbQ4ksvR0Ow3zyusP/xTl8a68eTGA1DFta2JvFVtWQXLPwPoWsU7z5rDCx9SArJeR57fRzluJakkK/GWWbS6+qPvtLBiErzZ3iqurGJcVWYie0boW3aHKxyODN4+YLg+Inw1gdHhzbgDHXu8+HGLwAG+C2pR6MEAIpMmrAvCnHQbdB3BuQCQJLIjL+du1IT147jHNE3gKARsR+Kl5O0cOyBbsYGx33lsAvDtiz08cXWW2vWovRdqYrupkwO1qutwJs6LMoAZEnYx3+cqxnLt5ZDfhqKY0H6lCq6apRHMc4Or1a36mBtoGfIGFDBynxZTsKA8K5KX7OgSAAcOQO8J//T7LY5Hxr/86YDDMSJNqvStvRyYsQuHbIDRxYDtODRtOkeF/q9Y85wyNTP4hV4x+A0AiSLu/B6JEkIIuNoE/Pa3W3H9D1sM0eHLg8Qu7vdiKesDSs4fspjORRFRC9Rc/X7bXyj9X5yxp9BQp+jMZaN6veKmZnVMePXp3k0nrq92bQXWlD7O+7Vs6zGmffauvyYe+4iyqoP5yV7+1AqP/YYuG81+L9tdehVcuE8v3BY//zIT+jTlhBdYfcRZrHenaYNpCHh4/QL304g/v3mP7/58jz/813s83B9x++GA8RgRxwgij24I8J0oFBI5TAzspglwR3SHA44pYQDDew8MPRAc/GYAhYDQdyJg9JqPqRa8GsDOkl4TUIoHApIHfBJaGgyXgozBBRAIMU4AgOhchWtZhMOVQY+0XoRgRpeDlC5uAEGN11gV/K7iBSjbEKwBszmtZ7jHxFSeGNE8Qxznz0SkXgRrh7vgKaNrTdhnnqbsCJTE2AlOrLydGgw653TcJR5/DtXMLAohzHg1Lq8V5YP0S+SSbQdJ167tI0mYLc2Zkcn26tnT8pia1pHwOMSQRMZOc4QQa1hKKp4xcVKhstCcRX7CjQKFiEp3F6ay56VEmYbRPesIOqcmCzFr6LL7bA8QzQw6yWgA2YdqGF1do3I0KrkLoV6ksgYubx0ZnO2NVvZV4X6UFbOzSc6BmOGc13CoGoomaZgixEq5QyDqVAYbwZQATBr3fxKDIF0jssHVdGeCtKm5ADbbHpuux9VVh75zuL9/i/3xAW++e4O7uzscDkcwAy+uX2DoB2yHAQmMu7fvMaV7vLjxCN6VxM6Js7KEgJyDEXkN5ewxGO/vbrHf38N5B98NOMYAjgNevvoSr754jZc34qXhnHh6JPKiTND2WQPBgjzYOSTvMbHDMTn4w3v85sMbjHHCkaucHY3g49QepMztu+r+cgcUinsNQ+hxBDsCJ/MKnhH2uUGdoyysWTsTFS4iqHIQCnur5/QnN8aQxme2qteGX9FP4wHOKiKUl6IMo8vzqWpvRj3iaWUJE0wNPIeGBuxMt+OI4L3D2+MOP2DEN8M1rkPA3fYaD1fXeEkO3bzxX8svolysiCjCqAKQn1ROPJDRzCpNSHXF2b32UjE+LAfVNPk5PAyKRXZK4tbUeEjUwgQIxEmdA/ce2HSgzsN1vYS4CD2G3mEzEII3TwiJ4emdkwServKCyLGOzTKlHLTM1Gcmsv5+WXkS05sfevojH1se9RDIFZ/IIj61/iXliXM6VxZ8sqINr7Zf73UF6FYXYEzswBEYJ4cpOsQoSjeLD3mcRkwp4jgeEWPE8SgeEPfTPaY4Yoz32HVH7PgBPR3R0Q4JESOLwmGaIsbxiHEUJcQU5bp4RKRGUVKvOVV7PROS2WXWrLSoHBOywRbBU37OfucJKXvBBJJm2TMmh8gO5vF02XLxWYbpfDlDkJ+n1X/CcgLOGjGFZZK9tYE/VwkxJ6AWXaiuPWnKZpXLz+dMvM7DSt9Wm6x+0+mnqsr1L/PCoByfVghRygwsofYcLEGkIkLe54iM4I/CdGKPlCbsUoKPAV3sNMeKxJpOLMmCO1YXdho1jGDISj/vhclLiLB4/8zIHlBM4nzunbnGswqXvfQtimJ02k5gZyxnpZDQOStqBVSCkZb5NkUEZW8Eq5PT5gGMnAOmKCJsDQqRbedbYEWlnMwCmaov+XoJw1TfL/1TIUUNi5qln7M+9c/H9ovAPsMHBIdNL0mgrzYezhHSJF5oh6PCXg33EF0U3gOMmBKSU0UF2XgkNIcIVerR6HuVGWZwVkCkSniSKKHfitXvxgdcbT1eXXmEIHTQMDncTEH6nSyJJCpFQ5VcslFItDjBBBS1oF5wx/PooHxceXl9DaA11+uPZ4HAAmPX713Qp4oZXr/fPPx4Hy8mPPXzI/DYKVpwDR+c7sC5K2uPnVjZ2dF7Fjl38UOPjWxtDU/91F9r0pPqvghfnzln1v7p5p/V6sK4oxEsPfby5xLcS1r0/BYu9SVQjMcUOkw+4OCAuyni7fsD3r0fcX8bcTgkTFNSYS9yiFELzQsSwVhkxpQYxzgJvAsJngge6mmmYWdKXgc3G7LSyMYbOKEZiEpyWxGMioC9SfDrCMTVp0rmRdY1gxXNO2u8Nps1qvFdxpDlt/1VnOByY+tetY1gsIvLfVJDBjHEqKzQiWCJrmvhFtVt10L8ik5jpbGK5wMV3ERV3iUSy29o+2T8mU5HziWgNJrRZ3VugZVJLXTdYifOKEiTwVR8XnNkMtwyWQhV3hJVXg8kSDQUifue1A0ycRLr/IoeK8hxeUoMpIiSxfi8x5hhatBR4Q4rWYjtVV2LrPBCoQMyzq32dWlDn7F/dq96f70MheacT6aNCw2tOZuB/I78aUqkVO/xsgo1hrM5IxIhvyMGU5Lk6UxIrn0dKxRiSCgyCRUkZ7kLHl0vOR+YJ+wPO+x299jv9zgc9qIzI4+uG9B1HZxPiGlEjEfN4+jEu9k5yeU4TXCa97Sa8Go8Asc4RcQ4YpwmDGGACwHwHUK/wWYYMAw9+iBKDpvmDGcIyCoCLgsrOUtI8izHCB+PiOa5c2pf5cLtcq6UtXut0V1Vixrw1uRzaamVsmeaa2tdbaroC07wkacfl+cyvEE1rzZRlXFUPs9cvYsfmauPoO8uKfMh52t6Zi1/hCMxUI2U4ILIWtl7HL0XL4mMazBbw+f1p26iKIFX+nmuXFzxJyyLvrQXeG0Cntzm5eVJHhGNMuLSsiIgnhPYp5prr8+JlfW2s0ChCr2UkigcauFoNGtBDQeREzpmoagDdw67v7sG+oBhs4ELAd0wIPiAYdji6oowbBK8K8mp7c97D9BcCWHJPIu2v8xH0dQz/bz27K/l51doBUFlIokZHGWf3+5vsD92OE6MyOLlEFPC/iiKh93hgClO2O3uEeOE3X6PPe3x5uV7OLfDdfiAxBO644iUIj5MR0xxwjhOiDFimiJinBCTekGwCf5SJiAdUbbmkghnHoDFuVX3OmXWGk8hO/PZ8lXbUy+jrOwLIQuw8rnSubHzzimVhEucwM+BtMzK9Dx5tc41+uTWPq7U1DuWhA8q+EzGhBiRrBWWj3yqnj39Gq2jgXK/7Swtvj1OrJ7qTWb2MJf/WDLDcxO1MrKKsBW6VAhasqRxRmyCACQQSyxjEDS+pjyfADwcruGPCSndoRv2uHYHjN7hh5dXwM6h/6OXXBZevPbI9xg2W9zceFxdR7x6dY++G9D3AzofEFyAC2LN2aeo8ahfIvGgrt4j4nQEOMFDkh06PbfOBUjYHcLUJew2ewRXElS6zGDWQI0zq0+V2IKVgE7qblzmVz0cqjim8luaLAx7JUCplBBlHUtC7VIqz4z6tylDrOe1EgPIsLCmYzgPol53bu/PX79SitBFok2TCrj++XfiuswpYX9I+Nc/7TFNnGkglwgpSYzwRBEf6C4bahQmhcs85v4X5tpreBBPpnCiTI6FDvi//ONrXAWPL3cBAe7/z96/NElyJGmC4Mcioqpm5u7xAJCv6p6uGZppmtMe9v8f9rC3PS4N0Sz1Dm13V3V1ZiIBBCL8YWaqKsJ7YGZ5qKqZu0cEkFnVKUC46UNU3sLCb0YYHWgEzJWSD6UswbUovyMN3Aoq+QXmyyDWlm71uF5GSdcvaPuxPl++WBK2vD6fUJPmBXa+6qR4Dqe++H7dlu3H1/oFtEDyhe2+UPWrDofnqrr6np7L8Hl1buXb6tNnEbovHdvXFH5pMbc3F+msV9T0+SV8eS1ft5yXl5npMgDMhGneIfYBp29v8BQTvv/4gD//6Yj/7//nEU9PE+4fJlVs6xACEAJlXDVrNJOcbGMCEBPcOGNMjNl7BDCGBAQ49C4gZCt7UXQDCkObDV9wgEtkxwG8ZzA7eHbitsl5OBcB75CiB/sEp5ld9BqHIKp2dYJTmhhgwHntP+uxaeF016eVso1W77JCICeJaZEUn1/yHtuBr3mAxYc7A+amz3txF5m8uHTxUWNcJOXObkxzE3Q3H3AE50xI4gRv8F7Gw0dpSgpIHGE4Q0qGiSELI2xOTKBQCyWMN/GyVAtWOAtb2KXs7smKyrxQQ4b1XbFWqIQmkPmT8SSx+CQncQVJ3OGQIySlpxgWX5BhwWst2ogJg2yqMq5zpYv5jMzbwObC5sC07Wv31S7jN27j19VB2KlYUboav8guHmVuCiysz5BK4ULRQrH64JzlctdsAJCDTztiiRnhJKaEYycWO2RLW9d/ApidzboI2IIGDSeSmKUWX9Fil6YIhte4KQGggKEP6DuPm33A0HuM50ecpjO+//6PuL//iJ9++oBxHHG7f4Oh3+P29i36njDG/4zz/AG3BwYQVENexv48jfjzj3/GYX+Db999u+qz8bMfnx7wdH5ESuL6NQw7dMOA4fZb3L75Bu+/eYO7uwNuhg4heMRZPDWQC7pkVUSmylbmmo7JYSbCiRkjM3aJcU7AKVUWEVdTDbtFASfpXimyHZlVZ3MOdSMHo7mqGaZ6tRbFsLzwWTIJOcYLa9GKLtE/zX6pithcadUeExioFswguOTE/C05sFOlInXplVQ4W3uybbpuMPbavqVn6OwXJhO4sY10o11b5qrA+7I/nXcI3mPwAA8Bu77HMHQCp105jyqZy99IegYo/j29wiIin+IvH9BiQbFBBj37wArZaIO+yOuN2ycmhGg0MFLKbpeKywLdEqyHAoAUXA4GljoP2vWgvkeoLCFC8NgNAUMP+GwBYZqjDrX1g/jXdsU1JwqRXVNyS7dMz9JnzxAqjenmc2P7S+D2/xbSJcj7KiJRi9LBfh0bews7zwVWiOhSa5gxJ0JKDtNMmGZSYUGJATFOI+Y54jyOmOYRD1EsIM78gDOdMeIejkbs+AjmCNbYD9M8Ic4WzDqJGyZOGoBa+0gEIp+RQefVZYuXveB1MzhnQdqLL1ygMJsYEoRvSgWBJXJg8oqoejgKSJD7HFsFgKMED1Yt7coJU+eEeTeWEGuvms3PFkZsl/XXSgX1Xj6n1f2KeCLkgMx/C2lrO66sNy4Otbx8MaqwGrjq+6qQfLkqeKOxtLheTwpMWC3EiTBEoNp21qBcPxOYvASbOxM4JXRhFmInnMDBIXYAEoFCAKFDB4ajgOAjuuAQAsP7BO+TuEBzgNOggc7Jbuq6iH52OIeIxBPGcUKMCY4lqJ03xrWLICJEODhOeDwm9IExBBYz+EyctQShae8Z6ip8A2OQKwDMMLDEb8glMGvQZaAIESyZRUUlXKieN3PMVZvYsHl7UYs2Fhh+Dva2nPBF2szwsv1VC3C8A1yvWpJJhL2HXYdpjkhKlMwRmGZqtB/BQNGNIGHimD9zY6JkQYEEjHPksCPTupW2Dh2h7z3e9h123uFmDCAm9VihomQ2oUIRLmTtRsObjDFEyLiT3eeToGaAXBm354/qlilxTWG1ZVos89HF+5e0ZbUCFpk3Srte5oLRskK3n2vca8F7DRc/99uv9dGLyjOq/oVFvKqN1zK3NMxVHO9FpdDWw1XOZnovnDEVON2us4DStgVX6n3uETaashqiyy269vIlNT2bGtqJGSCP1AfELuAExuM44+cPZ3z6NOL4FDGOjMgC6yy+jVeGqjPGVXXWCY4rjK+YRLPYrTyG6tmfT8PSmyVqQepOKcM1QrGIUG3rxiJfGbhwKcPhFTJzcSzb9xdnI5+fnGnu+ky9lJYtkPOpulZmnJ1bWXNe72tBRsHTFqWSMrBY8ZDqvLMyJP6VMojV2oJ1DjPTDIpLUNVuLpC3po3MvdFas/6ZsRCUr6mz7kdm6mVuI5XfbAHhtJ1q/UlOcUr5FbQl5XUKGE5V4Vzao2YMa34DrmPUW+djfQY37r5AYuVDZY5NccXwkTp/bc0i5Zq1gVlQUOXWrLS3bXkttGlH+zmI0560VTuq6yKJ2ID/VK9T3bfsQJSAJHEkUo7hYXtC4Iv3Dl3wWvSMcTzhdDri6fiEp6cjUhT3aF3o0Xc9vBNFpuPpHqfzA8gxCE5ddGmPU8LEjGmecZ5G4Xf5oOu7YM4xRcR5FjzSSUjuBI9u2GHY79H3nbgvV5goFALr/ksIISEpz8LGqebvRYZowkM8l1jo+a35WK66MpcFJBBaMSXV+fTK7FbqkupVnWUPtCwFy1WQS8XG9XaeAkPqoinDeP2FwT3omSM8k3KWl/O/FnoswKKWU1XWdLTsA4PByxg3n83JqPZH0/e8j5EBv0M5T+F85r0mZ/v+Ja2oB3TdjhflXh4hL6wxZ9xaoBvp+vhuf/S6eXiu1M+e1VenVwer3mRMXcpbwd0v6ZMhHcvVsERszBIipijBGWOE+UKLyQLmqq80TYJU6C51DsffDEi7gK7r4EPAbn8H5wWIOufRDzvsd4TfvU8I3mHogkrmPURLo2j1ifZL0fLOB2beXTY+FXaFDSTj7+l/oPQMWLODJP8KY8z+S1GC3j2cb3E8D2IeHieMKkh4PB0xzTPuj0+Y5hmPpyecMeKHtz+B3Qk39AHgCf10QppmfJwkhsQ0zkgxYp7nbF0ke04OPxEkaMB2H/RXhHIhePUdX7krg7rbcIWZZdoq0k3Zq0+jw4djB7C57rD4K17coYUua1wbvk1g3Pl7dO4MF6MibjPgCbjZARyAPz0BozISK9hScIor81AzNfNB+vr0t7DPRauD8/VmHqoRG7YP/6ZTpstsPS0jCba5tx6+vs5FKRm5avyGol5k7a01jySzadE1mchVSGAJYEZk8SMqxnpyeBrfgCaxNnKY8Hb/Ee4Nge6UOeID3Nmj+zRhv0t4+67HfrdHF24QQg/vB9VKF800QDW9AnB7eMJ+F9H1n3A+T/iXI+FpTIjjEcQJfbaI6EAQwvGRGE8PHjc7xn/4TgQcviI0jWA0xkWLoHMD7+QRV0QRI1/q95fDwLQEQ2EKLNZBJagQxkKqX+VvTPuxeckXK89t1EKlLfXnCxxhK7X0K8EsZgCAnMPBO/yv/8Gr1WdUgi7h08OM//IvT5hjgg+kihmlfrMes3tH4i84x7rywlT7Q+pwYIHl3gO/ed+j6whhNAGUhLHOggQN3lgHWjXmAHL8h4qwIv2uwo9IB2prZCSb23j20lFEZmyts6zhwyrWwkbZl+tf1pt1xC6WJvm2Xm+vlTbrlYGw/m02dgsuLltZMaEWW+Bilc/My+XXX+Pg2dhwzdsXk5ZteZ/bjlfmuTyfdKXIJeFdLleEMrCePEKGxismxbWavnS6vga3oz5vK5j9kmLrYXAAUiCc39/hiQnf3z/ih++P+E//xyc8HSPuHyckJpAfEJxH7wMcEQKRBAJNJZaT4buAB5MTIT0IkR08SAToycFFDWptFmq0ZI6182fKP+wET3AakxCKdyfDwdmBnVpEeKea8BLLiRKwdXBmBrrGGDCXPsYxW0MhVv/yLMr0pC6RiZAgFhmsNbkF+KmVEgrK2TLCRLDjwI7hvcRpSJEAdiJoJ2Muitq5CSEoY2aVtQKKMonESVKFJUDGiQAXtb0szOEk/nDyItlijNqzLb5JwVvsQ93Z1YTaWcjG7Cdj4JaJzy6ftC3lFWMlUOIIdiScXULGF5Oem44Js1oYQBXD8trjYhlhfRJFEh09V/CtpbAhx2VQOs3pWW3KZ5zxAQ2ini0i1EmZF/6K96SxyswqXv75Ohan/dN7OI0bQdTEmSqQVE8xTkhMGkvFImsQWNcvZRhYrc3VfPPqunGDpvHSAMG/WePAGa6frWo1wLUYUCWxZGUJII2UxIrKiUtwHzoE3+Gw67DfdZjOD3g8nfDnP4klxJ+//wuOxxP6bo/9bo9377/BftgDYJzPR/zTP/9XjOMnfPubW3RdUDeayHsIcHg8HXGcJtwebvD+zbuMM9owTPOMKUZ0Xiynzylg5h3+8P47vPnmOxxubrDfdQiq0DRlPC8hOMbt7hExOfz4+CYrJgFABGNmxjlGTInhE2NmsYbYAOWb543tQaMQMs8wf1P2jMXFSLbXNG+Z8XbOtzEmtmJL47jJUB7Xzcj5KmXp0uqqEIFoTBpvxCHHtWVbqAonOCVDwAEn8Tc4scQhySZmNXy0kUgaDANgJhAVekBQxetwb2usluNWcx0M704mSG8OE4LFBQ3BoXOAGzyGrkMfOkzOIxI1pf7i6VV4yddq09co57kytt//0qP6CkHEcum8MuVF/Mou1Qdu9bgBKPorsR9S9ZuyWZtZSEhsiAqZ10Wfeg8ODhg6uKGD73t4HxB6QSr3Ow/nHfrBYdcTugAJ6JMFEL6SzBetvuKXcPG7JIJeOaRLbYprFhLP5v0lVtnXoBf/VlNGHtedvPJK3r92Dy35YsvKWEyoIzvM7JBiRIxJY0IAc0xIUYJQS/DpEeM84oEfccaIE91johEzPwAYEfmkwajPiHHGOE0qgJhk76gAwhhKwpjycJ4QvFfBgwjtxCbBIbkAkIObFbn3imQ2gfdqTRXWILMJNDl05x7ZR67zCKkrAo8U4HyXy7DDl/wk5npuhHMznEtwzAguAlGQm4YQyD8CD+i5iaznYIF0vyZ9KZ19kShdZbzcvpeuxYpce1H+v3aqBeBLzbQvL1x/l/wawgq5bIJYV28ujXozzhvDXfsGzpqVFbZtPRXaxuvnov2Uug7kGY4jnGP4wHAzI3hG5xldILgO4B5InhFDBBPBk8QRcErYAUDqZjAn+HOCj4zQRTg/Y0wzOIr7H2Eii7algwgjeI4gBu6fEvpA2A0ybjlovQ0MKfKdkfYKIa+QYPlN1U31jnljuRrxt0RHamS/PDFhRG090bzfoirs+cXlVq3E/F21Ip61PKXqL8r+VqEhAeI6yZGeEVJjSsCud7i76RBTxDwvFzJlF3ZSnGr0ohD2HRE6OLwbAwY2oQOwDx5BhQ8AcswfMgFExo+KEMI0nUDI7zNhjmIdVytrtPvG3i+vL49Z84QW73jj+1fB95JvVfbFupURc+HddvG0fLB5R5dfXm7MlRIv5aHVznj+6Lxew4WPLx14dO3RxoS+sPgvyfXSOl9b+ibh/9LBfmn6fEmRtO+XwP+/QqHlfH6+LFvViQVf5c4hdgFnAMcx4sOHM37+OOJ4jDiPCUnL9T7AK35amixnVr4XH6Xqv7D+11o+pGR0LQPE4j5kq+nKqGa7Vngqft5diTNhsBfVL0it0UzrVNlSlbWljYjd1+dicx7no1BdoMK1ygP5N/PcqgV9YXPbuwodIiDHJajjBWR+lF1Q/YU+qvqVhRBU2mPatY4IyRQLWd0skcSlSHpQ2Jg3I5Wr1PcmIKAS18li5hWFinqcL6c1LV9IkDz3VRZuLoogiR1AEA15MAtzmxJScvBJYhMgVfNtjOfa8kGDogtDWed0MYX5XF7Nb3ttAoqipGDzIPhmrcxJ+t6RWdIbLWqChwqPoHIGkuEV+VmLLzDMU5Lgys54RdbHXA6tUD1TBFymCmPVvui42oIzfI3q2dfxtH0JFYokVleYVpQIX4L36IK4PUaKmMYzzqcnHNUSQixiga7rMQx79N0A3wVM6Yjz9IjHpyfM8QTmG9Q0RdJNSiSwLUWJAWlrIQtN2NBsVsuMAOp69LsD+t0ewzAgBHEtJ/kNyUoIboL3EcFFiD2GdY/K2okz+vMJiGeY8nGCAfICm8gG/JmzyZLZThtMtT1ULCLqL1qFxWdTw1cweImKJNiiFUqGWtFqmWrMj/UP5cDW9RlX5auviPQbKYnN11sDTEpegXGllBq+meBz1X2UPbPeF+2+K4+oEcJyWQkwrxmeIDSGc2Jd4wjBM9iLcLxtwSvSSvFiCciufLt49xpLt6tNunL3paW1B9ZGqvrEq4sX1vGK9GqLiF87ZZxiA0kxrellPIgYi0VEEUIk49vKJjHESxf18bsD+NCh2+/hu4BhGOB9h93uDn3n8Pv3I0IQzT/nCCH0mRlq0jo9SfOBaYu5HMbr1fxCnPjv6e8pJ3M3Bi7r/2ne4348YJ5nxHnGHBNiPGMaRQDx+PSEcRzxeHrEKY3445ufMIYTbu5+gseI3XhCnGbcn58Q54jz6YSUEuY453pE20QsHERb2ut1QOi8CAa83Dvy+Hk64JwG8THLHt1PHbqjh/ciSAidxHYI6qLJ+mb7dp5HeCYcklOkU3zU+xDgndan7pnE/NzlmBDn8T1mnpD+8N/ghqNopqUEGu8xjYyf44AZvh5V5BOWC0hdb01av8gUzDrfta3NNae8zsvNz3Y5FwouLKHL6bPADT3Tn43D92o7Gi7c1zm4vzRt9q0iUl5czqJrFQnzyrYYophLg2lOQbXMzZf/Uri8pGuZGTEEPN79Fp4n3Dz8BeAIIg9iIWp86NF1A+jgcXp3AtEIcgFeib6mHwSAkhAPk0fPDm/e/IgQzvjvD4zTmTFzBLEwvwExSCIidI7w+ED49NHj3R3hH39v7iuMOd0i223HGFvWCxXJvPjgklVCQc2Xz+z5BqmwurI2bdZ9xSKiLUO/5wW+cDUpQaHz7vLAFZWHOi+zB3PCnBLe3Dkc9iFrXa3aZPSdzpeDqwRFwN090I9GNBatTa9BCKn6NjMVlAh32sHCFEBpcyaAC9OgyB8WK2IJhi/Cp8u7L2+Zeu/k69fBpGXtz/Jxqe2PTHlNPV4voHx9cae8PGUK/rM/XtT/Kmj5ZVlpo/5fDZ/eqOhi3b9go4wLe/H13wmMOrUCwOZNe00A2GGce6QQEN8eMBLhp8cRP/54xv/1fzzh8WnCh8dRXQBKPIddP2Qt7ZS4nNfVPnNerOdd6OG8BwXxdQ0XAOfFei0y4hTFUqIPyuhToXAF++s2Eylq4ByYJVYEkgOzR/IRjj1c8gr7I8AswgowvMaCcABUqgILOC0MJ1HhS0xwSa0zyGhrdfHDqbj2cSrQZo8EBiVW7XJRnqIk1WxRxZyFNot9rWet9dP4ZyY0cM4JT52S4tfqhB8M0/wtloOG6JfDxPBnY1g7kFqOQN1rGRNV3j/LdFJGngiYUAQTS24h1lAzl50FOcuyufkon1xkCo8VrQjpunR31oHzIGJdL+J+CsRAmnOA5NxMZZJyHn+ZOGOMs86F+Pm3MaqGtgLTbsNLBDKzUYM1q1treBUwmCWPF4VQ+S2W8Z2z5y4LJ2oBhbOg4664hFwmByeCJmW8JmVSg0U7nNkBJpwoATia+UswV2tJFffMawfleSfnQOwBTqBsEQHFlXUORD0DThwMg1yCSwlRXaMmSkp/B+x3Pfb7AfN0wun0hA8ffsT9x5/xw19+xMPDI2IkeLfD27ff4eb2Bre3dyAH/NOP/yd+/vg9vv/pB3iX8A/4RtsnArIYxfKlxBpImFLErDR2YrFKIhBiSphjwj506PYHdHfvcPPut3j37j3u3r4VfloQuBM5ghDgiHE3PMC7qO6aAO/FrZPXmBpEDuH8gO8+fY+nGPExJY1AtySSeSEEu4z3lcS2LWTsqcSJSCT983SNF7BRXL1nUS6Xnis45+FCP7DCB2YsYYOBwuaxCh0diaKRg0xVgdclX8YUM64gz4onPxJXvQZjiTI9UoLSlDHLU3CBjm93RtWH5gEpGFUhvIHovFc0m8V4UaFb3zF859B3Dl0gHA4J8z4uhHl/S+krCxH+DaZXxIh4fjC4+rtVwvUBzcf/hW/br1PFiJXYD1Vg6vxPgElSIUSBKITUO3BwcL4DvIPb9eChQ+iFwXpz6NB5j35w6DpC13l4L1YQZgHhGp/GJVCuHbBNsBWq+rLYMNdG5aUkxNeSwv1a6ZJm8ostBf7G03MC1rWJ38v6XYK+ecQozKWUGOPsEBMwR0aMjHmOmGPEOI2Y5gmn8wnn8YQn9zNGfwbTPYgnRJzAPCFOErR6HifMMapbMz3MLDCcCt6CD+g6iZUSfEByAdF1oOjh5gCkAHIBw3xA4B08B3h43PgB3eCz6yazoPDkFTpI32bMgvTwqEScHEReBRE5OLXzKojwWbCYoObDjuCix/m8BxMwkUOiCEcRwU3o3ARwQoSvlBfqg7Qg8nJvk1ghQNWkGuO30E4GDa/N6y+xZw1BbtOX7Krlt5utfgmzwwZ6wTTkIoUq778WPFscOwR1RbWm6qw1Lylm8dnl9tZ8zatwfjEE2y3TVlSNKW6z6rGr12FVChNoEvdKKexAYHjHoODgDg7YAzwwuGfV1syftWOmDFNxUcpIXUKaE4augxs8vnkbce4T3NOEOCX8ND6JNbmZQDshFjl67DuHOHsxn2eXiVvTdmyGg/Of+oH0vxnAZZ4lMK5+mu1SEQ95jC/MWr0g1o38xRNVe6i4fKyeV4IjztpNDo41sHWw7rmmzaapmcsgZNd5fhZCbSAJtWOMm1KnqwgUJaUboYNpOsI+RmaZVM9cvpcLaiasvqR2Lq/BvZxvXdbWg/o8vobRLm+uQsGlMG/5/QYMfVm/bO1fa+SygXVLrq/Zq8WibTYBhYB9QfoyHjnh0sBfGrdVnmfq3zz7Gs7E18VXXyaEXLZhVcqFptk+vV7udTruUrpU599qqgE4VXfVvueARA5x1yOFDiMTjlPChx9P+PhhwvE4iyVEknUowgenmr8FhjJMK75oc1vwXTKGqv6DEyZMYokXEWMUn+vJ/PkvcKgGB7XYA1K9wFpqtbDtrMjXKG5jHOQXlBmtgoot1gID4tKH83GbrRyYwappnzWnIW5AajZcSpDg0MbcNkZ9NTsFjyGdjzWjqxVCmFa8Bl62fhoSA874Ujn4r6xzXdDZ4qIavxanLPhCaVfVZsVnc1+uCCAaJYs8ntbkpSWKfc2bXSnruexo1rkDAyJ+SgKvk0NyyuJNCck5eE55qArc49z+eg4EB9OiKyEZadtosV6znKJcLNa04gJZSIEiuIDGGKSivJKt86n9lXdSvqEnOqvtYIGbGBzNyNXzTbI3xF1N1Sbd51lgo39X2KfCgYLvUJnPjAPUbTWNdOmHU+TIk4MLHsF7OAcwz5jGE07HJzw9PuLp6QnTNCMx0PUDQuix2+0x9DsAQEwznk5POJ2fsD906LyNrQWp1zHSYXLOY+h79KFbjlqFUhCmCLgZ2Hc77HY79H2PPoRsTctZMMMAMRwlEe5lPE/nrfkP8CweDaqK1/h5bdawtCimCluwBi+3fo3PKwDKvAHKj7bPON1cdZOKAO/l6TL9Z/CragdKd9f9qCx0XtEGm4mGP1Vv8FJBOw4ZENRVFv8f5Suu1hW1hVSdqaCHNoEwpYhjmkEk696rVYQnQqRqol7c02Unrme/VPRl3usmQH5JVYuKX/7ts224mOtCW180PJfPs5emV1hEXCNHXlI1P7Mhii7CVg1Wi7lgYmZEFTbENKsFhAkg1CLCBBLZGVM5vI7vBsx3PUK/g3cB/W6ADx12uwO63uMfvgP6nhCCmGiGIL6yvQ9yCDrzYVgEEXIelfgQBBGY1CaGXHfm7+nv6YWp1mxhZoxxwOP4RqwHoggd5jRhGkcJLHU+Y55nPB0fMU4jPj3c4zQdEf/dH+F2Z+zHI+Y54nh6QpwnnJ6OUoa6YGJOuu5FcND1PYIPGPoeIQT0vWhydaHDw7zHY9xj/2GP24edCik6fKPxG4LvRHh350CwoNWVz3AKAHPet/M8Z4smAHlfSdBrD+8lECupL9NawyamCE6i3TXHDu7DP2BMZxy//Yhpd8ati+gH4O79CdPI+PTzAbEGg1m7GbnufM8L+KRERkHE5Jht9/bX2egryHgBIeLq5eUz5DKMLWVcTitE5UotKyR8o84G4d/I+8VCCVreVghTRtYuZK5yXsI/5bOLWEou9qUo0qVEuRVFo4+VeCGuCOx1QCUIQUPAjxE0eJx++3t0mLA7/oxwE+C+9eABmG5HdB3Q+b3uL9Gaa8/mQlwyMc77M2KI+ObxNxjSDn/4zQjMEemHCcfTCf/Pn/8THscRpLpM3kn8gN479BQwnnZqaSj73KtpfdHyvzImvCAucjLsrTgtpvoVVeb1ldlKzsUFlaetuf/ibV3vjkrzv2EsVbkXnWw0CoFswm+4RhMpgVRxw6CDCiPazpR9IISgy0SvuHcCDseE/qitCIZRUXankGM5GPlRM720Dw1UylNLi71fX1LzrBCDtMy6+H7LmmIr30ZdV7Mt9kHTtms7fOOd7t3t3GXMnismE3QvBDDr2Bab5CyA0tsVCG6nZVH+y9qxXdultL0+tkf9JfN4Mdu1F7q0WhzhVXVeKve1Y5Zp+PpM/dITphS9hHjP4QgvnYPr6Zcnihq8TmMAXJq5KQ1Iocf02zvMnvDw6QEfP5zxn//Pezw8Rfz86YQ5MhgenjyGrkdwDoFcplULJzRlxnityOZ7iUXouk5gcghg5zGDwSnhNI0InBCmgMDqF9+rhneteV633AEuFd/h4kdfLR/Upz57J3nYg2jWPGIRwYlBrP7ROaE4MQFEmCK0vLheEiVAlwjJRTWCEKUfSg7shNGdmEBJBCqk55G5nWJiJBS3LNeS+SY3BqjTP54d4BjR4gZQ0tgaNsN6FlUr2xhiRdmIGmY6EVXXQtdDhRyOLP6XTjG3tpc1A60WRlxLRWtax50rhcskQgH7BReGbl5raOFS+bV4mpznF9ZXWz+O4SIAtSQRK0jOAXHLUWdjr45THPIYO6gwoxoIc7dbCyJaiwggM99r4YFdo32W4wo6s3xwOWhtiRFR53E5aLyVecEgYsFrXY4i8hxSHjezttmax2o+U8lDEAsbYgeGBgm3wOEgtQApGBxpW1xSd1FdhHcOQS2uvHdgHjGNT/j5ww/4+eef8NOPP+Lh/gGcHBw6vH37DQ6HW7x//x36vsfT0z3O4xEffvoZx+MD/ud//C26Tq2JABF+Gl2hONxhv8N3774DyIlck6sjCAA7QnIe9yfG6AJ+d/MO7969x+3NDQ67ASHId/M8iSIlCM5FSPANi9siltkED6IgfAEXAPILOJexkmy5VSGG7XytUlFsMddi5Q1Wm8coCLO+akuqstuFxdfh8rAWSDDQLKk2rV+sT+Eqz4p3bPCjeMrIFG5toaH3y+dSfKWoVwsgMhK4xoaNHlw2NUPaakylRQaLDe+3M9IyL3rtCD4EfJzO+IAjfnd4j13XYQhBYpJUqO8vhUFcYLf8wumXx4eebcGv1PHPds3UEjNUtKc30rPDuQIy7Z3tAdPAKPEeUhY48IY1RCupkjrmwYM7Dww9fN9XFhA9+t5jGDy6zqPrgOBJ4kCQMU8dyBuRbhYQLh+WyIS3Hji5a2WnZFDygsn99Rf+39NfKxnLa2vOkyIyZgkxxYAxBglEnRjznDDHiCnOmKYJ4zRhnEaM04Tz9AlTPOIYPuEcTgAf4eYJ03hGjOJPMs4WhFoOUEckQWydQ9/38MGj73sAATPtANfBuwEUAzD3GNIOjg+49Xvc7vfqtqnLsSLEhZJoYmfzWyI4Y5jqCR/V/ySRBOdzbiGIyIil10NMg6jq/pJnjOQSvJMAfMEFJE7ozx0QE6Zdh+gSnHcIfkbwExwSxn6QjXmCYQ54bgd+PsPl89KK+OcLsFUxqssrqu1bhda9OL304L+Ub4Od91nlf3bSDtv4PC9Y2R6hyyeXZXieAN3KfnFtNXNetZ7Ks5KhIOkZ+da/7D2QYibQ5CwTtDtVRG3WwAFVbVroUJO4XBAGgEdHHkxA6hkdOvz2N7e4HUfgYcY4z/jx6UEI+eDxdIz4ywfCYedwd3Bw3jRmqvO0rWx7zJe4cP6I13mtB7x81hIbtiYuzd6lKSpr1+DSpQ9o/TjDsbbmTJgWiYVMGRUFCHtP9VwZTYGk60peuMUCq0WLYgFh5YolhI9AYIHZSwa/BX8sQgMj9Ba/1R9qBqYaDVo+p/UVbTyluvwNuLe6bdv68kSL68tQdvVV82ndA9vFJQutLrbqf0mi6+MGYFtwWb3aIjTrkp+NZ/J8G1su0IUsW/tlo2EXS1lNwrVsBN5p3LjVe2GA0DEWRoilIN9VE9i+nyLoHDcq/TJkYimwK89LuuS6YvXBJVoua2U88/65OjbTSyner4ER0GZdZTcjn4AJwJwYIxhPpxmP5wnH04zzOSJFYbJ7UksIcnCqbUZVYaKRbdZ+LlsDe+fQBbEwNqZiDrAL8dEeWQJCi8U/ZYWkmkGwOj/sXMtniZ6jZoXhHCgZjE9wygw1IQlRwpJhXzSflbllDK+UYJ4JOCUkDRpNJqjgBGZfGGQojLnM5CvoRrVH63mumI21VYSdJYxGSECmOp508C2AazVAWYFB62pXdFG1EWvQum1Y3SxbWxQbKtdNF3BAGQrO72tPD40L3lQxGLkwHXP+XDUbsyQzPbO1iuXKeE/5zuaLIOPFCdklVd3bEqcLDWqb8dZ2cnIvLx5nqNfo8vxrhRUZTaUyd/W39cusX98IM1QIQa3oneoW8uKpbeRmr9m70s781/DpurOrBbJcDrmgUpLhcyoZIy/CHwdSRR4TCM4Yz0eczo94fHzA0+MTpnFGSoyu6xBCh/3+gP1+LwJIZkzTjHGcVIAkvK3g/YKHZwIjuxYFQONrOUoFWBJEIBQCnN+h391gGHYY+h6dd9pWGYTgZ4h7tARXB0C2/aK9rP81tMAKbhsPwca5Jp64FG1uT+u5ZPtk4zyz9VS2zLra5jkv7ta0Ay8f1PfPEBl0Kc/md5dhDZbtWm+EF6RyElw7t3Nxhh8SYEKN4lqw7PtqtgosqM5Mxw5evdOE4OD3Ae42SBwf1OJyKbe1x7iUmoPnar7nyfgLGV6NslxadL9CetEa+/oN+yxBxJbP0Sz538oPW5DVyVU+3FwCNYMhKRIDFjZJjILgzHMEJ2HCikAiZv+TzAmtHFoW/vi2x/RGAul0XYdh2KPrPP7wm4D9ToJQOwd0Xch+s4lEM5yIQF49I1cumZYHEGUADhSbLmQgaqjP1TG++vbv6X+UVCOjiRnnOODT+Z0EpZ5HsYaYZ0zzhCnOOJ3PGgviiPN0RqQ/gdwnpHePQDdjPJ8QxxnH4xHzPON8PCHGGTEmgCCmnt5jNwwIIWC334klxDDglAY84j1iCJi7Abv7Hd5+ukUXevRdB3/o0N2JFYSjgBC6xoWZqm/rPcBoBYr2L4QuXwMoSKQGhM/xWJjE1UilceIIiAlIKjicowcQ8ObjDhN7/OXbE+LQ4c6N6HeM2zf3mClgvrtBHAn05xGUDJ9ZH7IV3lk92LxZvfra8Pzi59XZyhcRBTukqfnkUnFfFR6ZdshrmS9Lyqd+VZf74vJK5tWZtlnWpfY+g/DQxhhfwWquDUvN4Mi1mpaiYqtM9UljLS+km51V4nvTyirajZ7Ft7Mj1y51JfDkHEYmilPG2k1r0AEuge+ALnb4v939B6QpIf044afHj/h//OV7xJQwdAHnJ4dPn57w2296/O//eBANL7WYYtN+W05N06/qeXNTXSgCbHu3ITytHC4+nHNnGcjo7YKpvjkvqOduQTTVROmq9qrchiDlxftCsGaXBZnIdvp6gU8xVIANQP1BM3FVpra1aapYrplV5+ExoXtKIgrxuXFVnxtqEiamql0sLGesJuDbgQC2MMLlsL/EYuCSsKFM0Ub9W9uyWVdVButfU9TLYNrW/BseuZn/Uh82mnYxJsDFx5fbbO5Fr/Vqzdb5nEQv/nQJ217+XTtXxjpYry35y9/ugNvWFYV9hymB/tsDaGo1YnkXgH93g4tqtz+dgb8cX9bgZ9JLhA/1g/UsXloQ9Xxeen+5VZ+XrtW5Cdg/L1UTfn2rq3ukyDiPI44p4S8fT/j48wn3jyeczkJ/Enn0gwgSOrMo4AL/nJO4Ds4HOE/w3kte+9V4ZyF4tbgXIZZ5Qo8cgQRM8wwA8DHCA3BemJIaEGHVCyJkd0suCSORXQKrkg68lyDWLIIJxwnBi0Z0cgROcq6YhW+tRSxYpTLHXUKKEY6BSBJTgZxHSg7kkjC4EyM5jRGRROM+pZQtJCII3pXz+9IKapiI1fw5jbfszELaYgM4EoFL0wdBngSsCU9BLB9ES1vqKLyMzCc08LRgYrcLq2JGst4t8LwsYEgmqClCHAbKr7rGLYGBi6uVLNvAQlhh9bGOVsmYG5Rjfuj3BFa3X4oXIqmCCktsEVRKlvoVUfXLgovI+MsYmhEFYGCwwjmzQKG9R/4t8FdQGoIpe6L5t/rJV4bbZuFFZUGR62u+k+uUir1xfplUQKf9LB7OLvO6KklJ/uXqv6LoZnglg2H4m9e5s74L/usJ8A4IDiCX4CkhzhPidML9p5/w408/4uPPH/HwcI84i3XFze0tDocbvP/mPXa7AxiEKc54ejri6fiEGD2IBngS904parPECxyCC3muOyexHG05ybpIYGgsha5DHzzC/h1u336Ht2/e4M3NDXZ9QOedxphjHIYzvJ8KPJFVAoYDk0NEkH8svwkdhE0pFjrOQV00cd5qDeNW27uUHja0fBWXoxZCVCurnVCdsqVnIldd2/O81WQz6jN1DY+yh1dtrwvJMKqK/WcCliU8QV1Xq3wt2dseLcnO+jaj5A3BbwNAahbCiyZfP+/rWVawlPf0cuCbUBSWVz1hdN5j7zv4HbAfOgx9gPtmh6fbvbg1bPrUTtRX5198VnoF3pIB9Jfi1P960qsFEQ2RU2+S5btlsgPwAjOp9qnI9Tdc1j5zEiFDEoZJYwWhDE3Jn9oNRg5xcEi9B3Ydur7H3U3AMHQYBo/QBQydR+edanGL2ZuZwcrBZuaEJoCgTLDDDlKpLd9nFQHbfHWbNhfXerFeHdOvlV7WlNel5feXaJ6rxBDWkPNS+hrj9FxdX1DHBf5plcF+OAv1aldMxrCPUV0XxSRBqfXfOIsVxPl8xnk8Yxw/YopPOHf3YH/EmMRV03mU32kcMc8RSa0QnFr+9F0HHzx2u50IIoYBcD1mtwf8gMHtMHCPm+mAg9vhsL9BFzp0PuQg0s51qkHRySGh1hA6AhkZNH+yKUYkJ66YJJAYa9C5SpRY7T3nhGohEkGEeg6RsVJfukGjMHkn/mM9iZl2/+Qwnh1GdkByOD45RM+Y/RGYCTyPEkAMAHlg8NJmw5Lz2ZkZDQum7zNLJJHDNOzAzmemZ7PqIoNOscDLS2mJzyzTtXZUH3GFUNPiXfNJgxBdKneNJF1Nl/YbXfBaXudvNF/Kuy8FW3UbXgx7Xpu+Urk1I6rhj17Mj3IeGX4JAFDNRT1LjUCWYHS6FwwZrZZ53p1czIBLPQSCUw16B08ABochDfgP797h4XjCD08P4ODgHePxEfj+R4+bg8fb206FjcJsSRVTb4sNwCj92UyGw9f5DR7nZwp3te01sVi+MuK9xZYzJGiQd6oGHK2AYEEJl+9r3MpKpuoTwzssb9b7y0KDTPBrk5OyV7JvbHJoGDpUysxCDogwybQHeSBEdTdSiAaCPzMoMqhpnwxuPUYrHCb3e71SU+9Eo1yTO6eG2Zt2HuwJ4ZRAUUkMJ89lkVUDuhx3fVcIkwXVczHx4nfdmfymxmmvlLhEBLKga1X0dht5+a4iWvLVBqq+lfK8br5YXT6bXo0l1R+8oKLG+qv0dlHk4r4eqmcY6Xk8egkcvJk8gLsemBcNHiRoaqlwUdeuA95+BfhP7VBtDWGGbbYtxgQcW2uMy9P++bjua79cYCC/bKrgQXNkVFVHDmA4zPsek/M4TxOezhN++mHE/acZ4xQRozBincYu8xYvUHtkQXHJC64oVvZdzhucF0uKTG+Kco5ZqmXtTmNg5cC3LeN5mz4sZ4Qjp4YBwvh3ziE5D6euV9m5/EtJ3fFYzAgiCVq8OZByPpZTkaGhIVRAoUy4zDSsLSL0t/IXf4lcTIv7VR4918QdchK8PNkZaAqIVZPtyzz5K0Tg1amO62BMQXOHtGQOZuFCPRbMK0uI1AgrStm16yAZw5TLKcII+5NrLW3Lr6yF5dwp3eDsLohUU+WiH/R63HRM2yVJim9ew0obNZkGvyl4Sv1NIX4uldriw2XH14KI5WQXXEgDqUPWMxnOtwoU0OI4teUnVX3KEhY9W5q4HzVeBwCqsMf6xAQonReBRHCCp8/zhNPxAcfHB9w/3GtMiAnMwNAP8N7j7vYWh5tb9H0H5wmn84h5mjHPETExnOvA6AAk3e8o4w9XuT2VtpnyCzOLV7vkFG9OiAk4RcK7YY/D7RuNR9ELP4CQ1zyyEkx9StnYSIBkCRTuMM8J8fQEnkbN48qkGxJvIc5Wy9PoFVsrci1ZqVh6Vq1A03/KsKUhtqsFl3T31J4J1pCshQ1W3Ho5l0I2MYfmsOKG3s2wZLPmNRL3+dhHvf6vnNbLF02/ZFwzv7fG5QjKE6kRV/XQoTzZLhBCCKIwC4dofpmW4/O5uMRV3HAb11yN6FdA755Ll87Lv2b6km6/ShDxJUzx4tsRzWRfLLE6nI3HMSfRErBAurUlRHbRpN9acl40Ps5vepzfdhh2e3TdgN980+PtnZr4eIdOtbdDEF+dFlDXBQ9zCyMHpLmFUeQnS/bWPSkBL186blvkxN/T/wipXrdbAgix9BEhxDRN4k5pmrIg4nQ+4TSe8XQ64jyOiPgz2H/EaXjCOIiv9vk04XQ8IsYZ43kUJDaJOfPQiQum/W6Prgu4ublBCAHDbsCIHR74GzjvcdP1eHs84HdP3yJ0HcK+U6LKiyWEc3AUQKR7iTzM+2vSLprFr/QvIYUpx4RIKWUTUmGKyhgUlyLqCk2tIgIYHiT63Myg5DV4oPjAnYPkG70oj+1/dAgz4f4+YJwSHu8JqU+Y/uMjOACJkjC0CLjpge/exMr1iMuIbNESqhDS+lCtZ5YLcyiRx8837xB9yGd6g8Q8JeBPT6C0AQs2OA9k35WqFukZ2LPGU7a/4mVGbm+/Znopo55/wTYAgjB9TQHHVxNAlL/rEq/MN22z8bOQM0XENCFFj5RmWfdcmGrrNSHIeMpMkrpwYcQkFlcV7AG+c7jp9/i///4/4vv7n/DH/+v/jXkCKEX8OE24fxjxD7/d4WZ/C58STE3S5R7T6jhlYCU3aLdhIZ4yoVwRuJmkpNaNguzvLfReCmmJBCNuC4ItGSqLklpAoPdAwank84owqsqUcu25+Q4uFHqtTb9ivEfAhCyZCafUE1m5RHkMQJQFEcbMSe8EVpc4FA5IQPjhDK+MzUJkLHF56+fGMLYXABh81yG+L1ro3Y8T/CfRBmYipPc7pJ2H//4EZ0zVQEjf7YChdaNjgqXLVixlXWntlxkuW81d367qvlxO+2VZBdRkyQRbtQaeS+Wbknjj/UvSs+Ox9c0r8tYCsKrSK5mrtX+tzMWD9mxrx2ertrwfLtXReeC3h/Vz5zZyV+mu37SyeE0qrXpurRreol/8dAaOTxvlrMt/jtC9VPPfAkF8KS3d222qerDDFHtE3+H49gajYzz89BM+/jziT/91xPFpxukk9KenoLGOPBz5HGMBAJwnBJVjOc/YDwP2wwHeewTT3Aepko4cs81+5YrJlKBnbFIcN6mSgPSqdLDAd/FGpPPvCI7FCgJg+CSukpwTdyzOCUPRXPG4FFXPI4EdiT97XosEEgMuMRKJsNuR0BPsGFgIIxqtXUDoGao6umIeXdl7pCewHekqhKco9LhTF03bADNjETWkzbVzpbFQtNfrxHJOZwZnma/2Pq2VhytBQ7aCSEW5MtM8ANIs6umNgMI6n4try8v8lRptsfy2nvIfZF/wBceV38QMlxLYM8zf/aYXjMUNG24FwJi+0DNsiZ9kQZmzTCWvaUsvVLwUjpc1lXcI151rzyyrh9S6thVEtH3yri5Gy2dW32HiGk3kXCUguuFmtu/IOZDij1Q7r7cO1vu6GjyCKet5XYgMkBMXx95hNwQQErybcD6NOJ8e8fHnn/DjD3/Gw+MTHh6eABb6+Pb2FofDAd9991vc3N5K3IfEOJ+POJ1GjPMsgohuB4oR4EeAAQ9X5sZwPW2kWBs53T3CgndeFF0SAXP0OEWP2ze/wTff/RZ3b97i5nBA7z08gMlofRRjQVIcGZAYMiKA8IjsMbPHPI+Y7z+CxxE5BmsWqCZxvaY0b7vPbGoX9KERCyu4b/BgcV7qSZgtpaq1YZhaI9xr/slEJy7fmfWI9LqlIaTJLf4PZcpTftvCnLTYA0W82TQ/f5JhCPNqBLZTVUAzbNeQ4A2Yu3zf4HyLliy0Z0zY77y4MdwNHkPXoQ9BwMSS3snp9Xjr9fS1y/t7qtOLBRGblhDL+4tESwWQM0So3qFsVECQLjmExUdKiuovMxZBROKEOcWMoGWJKxu8EUZIHALSvgN2Pfp+QN/t0fUd+q5X6VpX/Ng7B/I++6KHI9WIssOxHJIwiptKH7b7/ZkL+IXE4ktKX5V0jar4pSiJTWrvSmW8eVk+3bj68nSBBPslxmQJf6tHdlikpMhlSpiSw2kccJ4CJrOCmEaNCTHidD7iNJ7w4H7CeHhEih8BPOEUT5jPEdP5LN9NE2KcARbT79CJFcOwHxC8uGIi32GkWyQKcLSHSzu8n94ixA6Be9xgj31/C+fNv22AV8sHckYMuOxKyQhAV3HJmSXWi0RwV6QHnBE9OexZ10iqvmNFetWMljhrh2a/5wTV7irBrD2JZnVwDgkBjPcAEjp/Iz7xfyAgGAEHgAguMB4fzURS4YBqeJDCgyYsbMZfqn7qHwONiQjzYSeuoyp4BcfgAXBzRMdK6CzWCBPDuzOCP+Ux5FLLi4BBnYWdw7g7SJ+fYkvAXPgy43gV2kSL+v9VHNlfrZEvK+iZYX05jFmNcb1OtgB5xXDeSknycErgGBHnCRM5+DlAqVRhlpBXIt20uoCYfVdHJI647z7hiCekaQIl4ObpJgvxlrDNe8ab2xnjzJgmBpKHo4R59ojzDOc92ImJupjMq/7eBjhu0Q7VX8sAVRa13FM1SpUBryH9FVK7JAya8a+Iy4awzcIFl6fAmPmg8rxYM5Q8TTJ/3ajy5XdKkKH4HM91lWbVtCzAYlnCKG0vqIv1QfAZpziOU9+8xs+xNZQ1FR0j3fRA31qtNWWv0vLFxrrcBZAvaGnaE6IL9jVoCHDBgW97xF7OMHgS7XVfWd2h9K882WhKPZfgy3F3clof3M8xxp9NuSG0aFPdULt9lg2//lkUenFu2tMhL/UVkV8Drba6V6d6jqR83hCm19NEzX1Z08+My/JlZjhS8+i5z17ycqOF67qfS89keYUsqcz/LgDf7ORRA8cWiVdLZv0+MvAwCY1025W8UwIep1c0TuHwi3GXZwQ92Gj24kHueob7tvvlvIu3PSY/4MyMp3PEX76P+PRxxuks1hAcVXnHO3TeYa/ayub+g0mUbUJwCH1APwTshh32w04VdVxuiPKP1f0wMh2bxe962IqigAV7lhhq5Mt5ahZxee05ApJotBMlOHW35JxDyjDfA5QAtc41yzlHBCaxJkYi5fdRaawernKiiAUlEoFdBCcCcxTNZnZIbEGrRdtZBCniqsmUDItSs86MHV7WlzJhkuvCWslnlQp5EuVP8jcGz7Qk/U15PvK5CSpnQYMX5zDNG+iyta/C67kwH8GVBYgJHLKy2eIXlbACUItTrGosMSJK2Q1cWwwWV+2k5qkq3dTHjTFCHVBbOZoQgCEoFTOK0mW118j6rJOTIWKFICQ7qw2vMMGc/jUwTSsgwbpvRE6QGLKGbew5geFF+a1GjOyqPnLqX1sDyuZxLC6LCMI8Trq3wdBrAtiBHcNLh3RkLSaiAzkG0gwJBC77JY9FkrFI6iLVsD7vPILz2PUDgif0AUhxxPn0CU+Pn/Dx5x/x+HCP82lCjIDzAZ3vEHzA7e1b3NzcYNgNCN7hPI5I84w4J6QEMHnAeTBmAKNN1GJgdAZ0HMZ5wv3TA/rQYej7/MkUZ5zShBQIN7sDbg4DbvZBXDKFkEGswY4Co5qJAZNDIodUL1+OoHgGpQhjsQuM0hg0+p0s0yVQWBJKnPH8vOYWi4GsGIPjKny1pW1CiLLMS5Dt5XmyPs9sVZSNwqhi1XBZe1Z2vYUrUAYAZZzAxXV9tZKtzHpLGk1U43Ub29ZyrztBQGNlsnrZgOntI51aHLe1hbLWK5SiEoy+8w7OAYMndI5ycHrzJtaq2L0AmVilAqOfTXX/P6eqSy1owRvKKVVVfenbK3eXHqEu/WKXLnfwK3b984NVX0srLapKIq4PSt7yUUbEkga5MldLKcpmm+cZzGL5kBJjTnMxX6wmjACVgHvE2wHn9wcM/YCu67HbHdAPPYbBo+8YLnQaPEwsIVzoigSdHMgFZF+ZBdPJWhmbm5jKz9JH299i4o2bX77VtAkBn1/cGy37qo39FeeLl7dSd1KNpLy2Y8Q4Bfz0eECMCVMcVfhwxmk843Q+4zg+4TQ+YfzmL3B3n3A+n8VV0+mM+TzjfDphjjOm8axWBwLMh2FA6AIOagGx3+8RMeDovgPCDvOwx+35gH83/x6d6xAwwPuAsJdA1BJHJWhwa+mHK7wx+aXqoGFCioqXKBOUWDWfSUgDT0IckBNE2/zR25DJtQRWSySme+YqySnx5KKXfqoQIjghrjoiRAqY4zvMKcD5GYQE90HbooQM1BXbOQfLMssOC1Rf+cOv+ikXbrWOC0iUCwcGLAYGM1LPGL9N8GHGLpxR6T+UhcLA4fYH3L0/ChFTqB1BjHM2zvC0bkBdHgGYXYePNzukM4PPJwmuUeGhbR8MYeD2uiZ6qJS9hClf89B6dXoGb1jv+Jc0+GU94uXFpc9eUhxZNiN4r328xGoqlJOF/6CLSH5iRCSJIQNm9bvcgdyARAGgLjOpbT9mi8QYkVLEh91fkLqIeZ7gZ4f/6fw/o+dB9ggDiWMWLASf8JvfM+4/Tfjzv4yIIYAxYxw95nkW3TDnkcBwzCXuhVCt28NTEbj12FC+LwiuLdt6VcvwGKSqVFQXxLXdihs5K8SuFXeAIuyEEvSv9nVcCQCW3RF3rMW4v0yn5Xf5W7fSwDZXDgkiRBKtV+mOrR6qytJ2keBMriq7WKFRGd+6ne87FMMtat5T9fxaWsU+oEUg7bcdYlsgiID0TbdBSFJNv2U8bUsIIRm3iSB5vUDH1yjtMw+0jksFbHzXaIBWQvVFw9d1rW6356vNXztcqdZQJsTLvtlqwnaZ22m5QluN1XpHAbnSuuiLXHfDwy+1Zflma9w2xvzKJ6tXz8Lt6kB9YXq5xcozZS7Lue2B277u8bWPr78+TcDxHugc8LsbcV4OAPcj8DQ/07QN0npZ3QsYApdFTxuAe/GOqz2SmZwMsGPM73Y4Dwc83p/x8DTjT/884+E+4ekoCkAcI7xzuA0OffC4C6UMBiMRwQWCCw77/YCbu1vshh67XQ/ReCbMkRFTwhyFno1RLQujKNU5FUST0gExCbM/JsHROCWpRwCm6hUX+ECAWjMgWxjbL5EHkTqCJ6/3ALkocglHgqfrlM6pGTpAgxqLjTOBUxRFmmi4hMZ10kjPzBI4monASQJjJ8X9Y7LYEcoopEwFaWXKodWnmxZaLH0nEs1Zl1IjDGcuWCtnqp3zfAkSVBhRBMoazmYUWXYxAXAw988GKQt617IEGxdL1n7mLIBg5W2kWLmXBiNqm8Q9LYMrcF0LBEwAgUW9m8R1KQB5xZBhA9ILY4zaWWqdp3oBGIzWOOBwJIIS43Rq1hX0VQFX4adIPfYsP9e6xW2szGWCr4QRKsDScTSPGUVBvAhlUjPbsqqKWoNVVY0cifCBGWKlxCqMgNK16n4MTPBm7UsMQwWZgKTKdZyCINoOsj+grpChAkK2WGuUXcxQBDx5BN9jCAF3hz28Y/R+wuPTiOP9X/Dp40/4/s9/wnhKOB0VDvgBh8MNbnYHvP/mG9zc3qHvHLwDTk8j5vMZMSbECMB1gE8AzmA+Inv2yHtCYA+7MmfnOOEvP/+Itzd3GIYhr/hTnPFhGkH9Ld69eYN3b/Z4fzvgdt9hNwRxIa0eHcrusfG3VaWwgZzEd2So2URCiEckBo5sS074BASW+YkORapui65e+9WO0MdJ3xte4qrPyxIu9HJ2g8lZbyuPlQMyW1CMewhZWFvBFGsK5VHgBq5kHCnDt2r3UHtr3E6L6ZctohY+9MoI2Ng3tTdtWn/Jqyd5LHjx9Aqq2j6iBV6rZzC3J7lGrgERaSB1hz44JM/YOYfBqxUiipv8BJTJezmq9XnpC8t/FrVp3r8UF1x8fKGOlS3MxdtfehDb9HmCiGepso1P9M96iSNLHlM2TyyWDmBWJE0YHgyzjBAErQysENNzR5j2Dj54hBCAmwHDsEPf9wihx91twOHgMAxOgoc5D3ISoLe4YCI4F2DMAoCU6VAjrgviqRqWejReTFNcSs8V8CIJ3nONuFTGlzb+JekzCaJfomm/YHdXa2Yx5oakZq0Y9dceo8Nx3OE8O4zjiJgSxmnEOE04nk84ncQd05P/EfPNJ0S6hxvPOJ/PmMYR4/mMaZowzRNSjArcPfqug/MO+/1eXDANg1pC3MHxDu/O79DPA/Y4YM+izeVdh+B7CbgXiiDCea+CO9sf3PSs8AXsEFKsgmqTQj1eOeV/omktvwI/ygYjFRAkVm2YJPUXP7ozgAhoQOzjeYfzOOA8B0wpIoRBkCyLdJfLhbhXcFQJGgxRc0q0EcisPZq9RaWQaoYN9hmsKlLo8ps8w08JNEcgqN9OzVLwGMaYHO5PN4DGyzEEPJNVmrkPM4JL9hRpgJpal5SI4OMOblasu5q3DXTIOpFTF57g/RlFyHGBCKmEIM9Dqys5GJj6HeZ+AB0TcI4bWdqDmIEtUP1M2kLNFgjt5km2/LbWutc/lcr1ilB7pjkrwcOlJtgnuhTZEfjWw4ExPD1IhvMZGppSeseElGbE6DDPDm4uhAn5Hs6xnIEqiABDieeEFGd1GxGRrEzeapzseXfjgJGQTjNinDHPQi6mzuHhccS//OkJ79/s8e17MRY3P71mkbGlkbNEZZdoeM5nzI6NM7F9VpdRdaXxbWt9MosuKm0xJhFBBZcKT4BKkOAa4UnVmUYQUciHAvdcI8goYktm0Ww0BnIyxo6u2cyYp+V13R5lJFm/yMZmyfqrxoKKAIHLKLRDtZFWgghsjEeTv1ysCR+qYn9IOZeZujWhV/KU6aUmZ82sLAKMS43LX7Xt28LVspAH2Cp1LajZWCzLqvP9tb5XAvSaKbBY35eCcm61YfNJWXy56rataw33qy6RlsKwi8tlMf4b39KFsduodePJlvXKpbFat+WrpGcafmUUr759rnhmAMED73dijeSMWQyg98C3+2dIio2XDcrIwP0ZGFvOyuauW7bx2QP/QqeIMB/2iF3ARB7THHE6nXE8nnE+j5jOM9I8ASkKY8QF9L4KxEoSbDUHxu0DuqHHbr/DbrfDMHTo+14H1YFigksJmCIoyplpe42Yiga84k4pJSASklpjJE7io91D4b2eaxkpoNyvzP8xOO9UWO7EfWnSZ8054DhbRjiV9tWRF0WggQsbkLMioSLncC6JQEBdOck91D0RIbEvDGBsHLObc4YMT3gBl9e4eY3TqnMZqpYj6blZMxDrb0xREhW+rb8mVECy2A5J6BIUnkZx1SQfLS0f5LfQgPV/qNxeEmo6AvmKmRtLskzS1OcY28lcHWPUXOTrUnY+cKuBFpwHLPG/WM3Ihc4hZOmN4f0MZDeJhillDxOGd5iuOOXqcrs2AZGOTaW0qj7MVLENjbCCWBRaCMXRTV2V4UY2R7UiWIaWpmAXq4VDpU+Ak7XuRZHHO0YUQwihT1mYp+pRSHphSmvatuAJvQ+43d+g9w595zHPR3y8/wse7n/Gjz/9hKfHI+ZJ6NGuB8h7wDvc3t7gdn+D/V7iMxBFiHVSKgI8quYz07VVUjzO/sujnRjkgPN0xqfH+7w/Z2Jx0TwM2O92GIZBeAtKH+dVapdWjeGKumgTE1IiRHaY5oTT0z3G0wmJJQyTUSoJ6uJZYVLuj0kZGlM/vbZFaHtM598sI8pcCD9BwkJWs895tSnPUb6nuo5V2j4A885d4oKbuKH+FMDVltOcmVU5+rIIKo02qABXtcNfn16Py7zmC4MDphDOxCJU94QQvHjfcK4UuoES8OL+r5+WtMHzaSvX5S+Xi+MzCv/cT17Cg34m/SIWEVupNnnPC8U2SjJkSw7s2gUTMySoLjPiHKv8ZYPZIQIQ5r3H47cduk4Qv6E7YOj26LoeXdfj7RuHd7eAD04XdKcumYL4ItMg1eLr1TSfrY61EGLrjDSB6N/TL5OeHdsFMvnXTwvtVuRjsXrAGgeiuCBLccZ57vDhaYdpThjHEXMUl0yn8Yzj+YSnpyc8Pj1h/u4DwvuPmMcRJ40FMY4jzueTBLdWhNh7D+/VEiIE7A8HdKFDP+zArsej+xa7+QZ/mH6HgQcc5gOCl9gqzvnihikEOPJKtKhPz7w/rIcF+UX9Q1EOFzDEl6jJ+JP846iMTWVwpnmhCWWCQTHLTKzIIJdxBM8ijGAxv3g83+Dp5DHPByROCH6CdwwK7YFswgfnfYUkG9Km2mM5MKFrz5cLhE+Z7+XTOgOrYhYDtUJhrfXEDBxVvJK1pexTE8BITX7/BAriIiGBMd8kpFCTYvJbNDEW63E5Z3U79ffm9s84vDnrt23+jPRk5O/KCFRI1LUxYk547Pd42u2BH9eMikLoIB84yxm5ChWaNbp8qadWA9tLXIFt5ln1Xv80OOVyuDeKqFHq5ZVk4FVTG4YNARQI6V0HuBmDf4LnBJxt7TohBtTlaoyz0IcjwEksHXyI8IELYqjzGVWTMcZZBacx+z3mVct1bQYC3QXg7DD/KNYT0zQDSOiix8/3JxxPCf/4D4x3bwIA2W8ylwwmBl3kPi6YMJupwhmu5FoM5voxLX+NwKbsJiMLIFwreKCcz6PiQOfqTEBAuQIt256S+hanuhcGJ1TrlWcwlKiy/laCC7tH1R4rL1uXVXVsr++ywVqxST1u10d5yyKiKb8qox3r5qvytx7Lq4jCBUiwhOFc76/1uqvdUW21afloCYFWq3Cj/bQa0/b9uprt/OtKDDZReZaB39XTal3X8jnVbajOWAJqp84ri4hrdV3I1qySK+vu8nK4XP/lMda/L0IzLzEqFmvhlUQDN/P3mnStv89/S0RiCfHb2/XrXS//LqZ0+RQ23CKxKBlMEwpysdmU7Wd85f1GPkOtTndvMe5vcDpPGMcZx6cTHh9POB1HjKcZcZ6AxOi7DkMI6LuAznkEJ0IIJpI4DF1AP/TY3eyxP8i/vu/QhS4PMM0JMSYAs/g7R5T4ZFA62LRdVZM4RmH2xpSAKEoABMGJkgaWBZD5wHaGOGMAZ/zcBA0qiNBguGKRTOq2SddU881yEhgpkRoEG64v8FLiRAgegCSWeSkxyOk7EhdTIKpcK4sPfnPHaFPXaNFqPxakQMbJCMJEjc7ctFYLoCa1qH1YQIYVLoNoPIr2Y7HQVq+5YMXZzY2uxcqKyqMQRSrW8VKqTxUFLPZHEVKk7GbFLCGgvJGajKpPfGlS+7IoL13Ao62r1SDWeEHBo+1MKHPA1bg6srlTUwFA406YfUXlUrfUpN+7EiMl81uomltzTqb/VlNpSnsJlBJimsW/EZf4KTZPJojIwiRqISZVvzYuRfNd15bGSiEyq3loYHSIgELNh5zGk/BecGPHjKSKXpQCiCIcZsychAbOgSlkP/fBY9d3eHt3h+CBzk2YHs748ac/4tPHn/GnP/0ZKRJSFP7VsHPwXQ/fBby5u8PdzR32hxv0/YBxfBJrBO274HF1Z13xM9WsBZdxQKBsCU6M0zhinH5WF3MEdzig3+8x7Ha4ubnJwgjvi4Ajw/tNeCyBqYWOJ8TkMI0Rp/tPmKYJM7M8t/kkUuFFhV8YPbDi+RgObWuSM7BnmAWD0D0S91o6ajpUnHGXsqcyLY4KLNX1Zrq3+lb/lDvbr2abUe3rfCMX9XRJOZQLzOVyKbWAAi79RYERjAtw7WKqxvYKX+25o3aVycDspW+JdHkqLPGE0AWEIPynEAKS0levbc+/6fQifPRvL71YELFlEpkR58W7Iu3MuwA1OVcfJMUVEyoBhCAxZtIlrh8YUX261OynuSOcb1R4QB689xiGHn3Xox8GDN0efbfH7cHjZu9ws3cihFBGahOM2plFhEmKKUOHpRDiOYT91xJGrMZ6493fYrpG4G3tpRcJH5774FcQTiyrID3MZD2UuWoCjLEhr8UiaI6Ex/Me40Q4jxOmecbpdMI0qyWEBqZ+ch8wvv8Z7B8QTyd1yTSJAGIasxDCCI6hF9dKu/0e3ncY3RvE1GN4uEOgAd8N32Dn9jjsbjGEHrthB+879N0gbo5yEPeAWoN2nYwJS6W/qgVkLl3mKK7WpjgqISIMzThPSJwQ5zFbRNjAGrIIlpgUZhXwdOpwGjshDADE2SNGwjSr6xg1Fw8aQNd3Aczc6IUCBCiCRS7A3C+ZcCJr7lSMxUajM5+qOs/tn9ZykldPmrxGSCzLsBST+Z5lpVe0DhNEuADwXD4YIzBZGRIWbDNxjajU63mBbAE4/+ARP75fIzwLZMiItLarFfFkObnN0bzX3/E2YHoTgIcBiBN6Sgi+QhZX0GNZb7lYQ4PL8KEekxAeENxxnakicOr89iQjsupyMNvb5zWz3kf11splMuM4E+bZqPDFN9YWRdJpcoj3MyIDP3z8AyjJeu77Ed+8+wmcepwf3+s5KBZO3nvsbkYcbk4q9EKJm6QVyrSyCCxMGy0x3p++QRd7hJSdWGdMmZXJ0vOAP/h/hPcf8M/pn+FYAmaCGM5TDsW0FafB1ls7NgRAteGaINMtkXV1gBe1LDibjQBqVUTWIjMYZbCCUMfNybFliFSoKSR3XaQxjQrZ7qqK1q6TAIm3Q7o2iEX7lKpBInO/lBUrandRKG3S6+IeqWJMNd0v42p4ES3HZhNfegHhcGFK6EKmxiXUYrqtP5KeOf+XMIr5RTjctkuqVeGF2Nwq49JdnpOmx837i2XR4n6jTcscVI9VA1p4mXW7vc3TqqyaaF+AOtqwinhB8fnVq9Bc2i7ueWb+hXF+ycLdgNGbUudczAs6xGnV5tfg+3892mBxRlYp3zsA73bA4TnytIUtefueI/BpLLny+3YNG9ziux4YHGLnERNjnCJOpxk//vczHj6OmE8zYowIJK5/Bu/ROwcPOQ7zOnDCSAeRMlflLHUaP82UZ0AaehAErzEAPDNI/dwllzDPxfe9MbQpAXGOIEBoYSKEBGHw6wAULeTSSVILQPNnLy6aLA6itJMSyy84n0siiE4Z13Wu0CplzhROJAa8Wj2wQ0oM50RTnZxqq+sZz3o+icGEFwFExhPo2U19ge3QnMPljHVgdUPFRhzwsgzTk6+Soiw1M1vwnWItkNWnsjBC3UknliC+xt/QZzZWhf4DTFuduQghWhwa1cbgFm/lgu1uoc6SRemm5oyqcYKikADDOYxBresYtA7vXdYY6f/qp4l0LonRWN2ZAKPCYWBWRAVrym0AQV02SVjfeoYo847Mej4iJQ8o/eyUpyRufVVYAY3pkF19Va1bHJjmGi1bBxJE+QWyj2TJSP9NSQZOrQ4SCW0KcdfkaIJzES6KsFH6EUTJjgUXJnLYdwM6H/Dm5hYhBAR/RpzP+HT/Ax7uP+KnH3/G6XgCuEcIHq7zIO/gnUM/DOh3PYbdHn3fC/PW1lRMhRdVwQZmc+vpQRTbqa09NTLA5r9Vv2av4+eduJg7E27fHXB7e4u9tUGZ1qaANoQzgpvhqPh5E2GVA8MhsROrCPZqBUGYGJiZMYMxM2GGekDI39m5qpuila6h4FwKUwz30DwJSQQQupQTnAgjWhSoGoeKviUUWNWktg5os8zAzX4lJk9VeJ0axKJYuXGegdK7InDMIgbhAZi3uQbWFEXFUlQFQXj5rG5Twe63UJclbruJaa8ylR5RFb/P5EykbrDHFBHnE96p8qy/6xHfdUidBU8vY7Bu97UG/bJp041gfvnMt8+X/qqPWqXn5z7lC8/t4dcfzC+yiLg60JbH/i458xUzNmnMB3PJFNUCwu7neZYDPxa/jHJmOcTO4fSuFw1t34mbmRDQ9wN2uz26boe+2+HNXcK721RMe7y4liHnVQDhc1wJsgMYBsS2hRBLIcAvgdsvx/giA/8LKl99+wtu2pe0c03gbRb0sgp/BeFDna4IjYtUuvq19Q8WbWRA/LXPc8DHxx5zZIyjBKU+no44TyMeT0eczyc8nZ4wvv8Z3fufMY1nHI8jxvGMcZTfaZ6ysMN3QTUoduhCh/1+D/I9Huk9iA+4ffgd9m6Hu+4OneuwPxwQfMDQ7SRwVuhzEPfiikmD3636VRD8EoDNzJQTYlLf8mlCShHTfBaEMs3qjkqex9kEFEUQYXSe2KR7QJHS+6eAD/c+9zdF0rJICQGJBeE9qZZwAX21lo7sfwu0rT50nVo/WBB7MiRuwVGxBVA/qxE4VK+Y0Th+XR4F9t2FxWTEUbumCsIBHDKi4hkIU1VoJqOWdZT5q58v26BRO4DTt2qdUSGqhnzW93U7GyTI7jkTVbXwepmPmTE+JcRjymuuCyMcT7nv9XBeO04bpG5riDnXmvFXS4fDjMPd4/qbxflWfoqWm1g6qeVPDkBI1bKpCMbqvMlN1IvHe4fHswZQxyIInJ5X2f8vMfA0Is07TPf/AE4dAIf9/h7fffMJ87zH6fF3ABcBm3MOnH5CP3ySGA2J856vhRHMyJqbrIEp352/xWE+IHKsiBgu/5gx8A7/EP4XpDAgxv8iMAHi/9qZolalC7DcVtUQw4S9SqIi0zr2vPlufW6UaeOL+cqZb79ljDMEISPuC2yEwRJQNlfPGmfk1X1TYeLnMqtOG3xaWTDkcWAR5Ih6JpjNf7ctKbOgoFyf/RZGQilzKeQwK448Rhv01+pct3HahI/b6bkjffW6am/VtGfKvYatc3P5GpSqrEG7bz9uLSsutWO55l53/7I2tm26VBYvgZ6190KVm67ONj/YEoAvNtf221XiRYa1MGF7rq/JpV6NR38Rzk/Nz/O56z3ovqzql1fapq+CTtvKaPGOBsi+31W4wHabVoIYu/h4lkDamwyexSUBuOuBNz345DHPwDQlnI4zPn0/4eFjxHQWhl4gjavmPTrn5F7LIIIIIQwtdA7kPZwL8BTU+s3l9eXUJahzDp4VnTXXTMqYF2a9nJ+cJG5ATBGIorREVNxzOgNYGXBxhtui0M56LnF2yeScBzsTPLDitBpMO+dXl3tOGO4tfWNIVhLf+ExwGgMCqi3vjEEriAIkYK/0ywHKSHbZUgKey4BeSJsoMZUVQXq+iRKAaLJzdhfZltGuxIKjMlDmgAtNY/Gx8r16nyrCCOVnZLw3FbyvCji9ZA7moNOpxZ8NZaK631y3tjl1dEoub9JaiSErU1E13rZ2zdIdopGcp6PBcaFwSNeoxgIDsfLp6w1nOIXhPnW9xdFNmXtBMrhZCgthBExAJ0x+s8b1JoTI/wBimX9WC+KCv230i0iFEYJZMxESpbL2SfuusSJI3StJiwhgYWh7JxYSRAmECNK4hoDQwlFjmzrH2Hc9hn7Au9s3cD4BeML59Ak//PhPePj0iJ9++FmCzWMQOn7oYAKj3WHAYb/HXl2Qk5P1boIx6QXZTOYxFLzUAWQCEoU/Oge2D1K94ZhzUHM4hzk5JAzY7+9wd3eH3d7aQBkfBTP23QnBz1UxtoZV453VPSwCIqvggQmRUQQSXFwzVdgtsjumCvahfm+LtYqoni0GUIrwnDT+h62wCl7AgEBe4ht1VHXVr/Oa0VXCupKNNqzgaUYjCRleLfezzQlzoYvZLLLsXucKBluqyBLgDaW/JYG5BCFbQHcxzJegTr1nMzFtY0xlNpZjDhWGTzzhFCe89Xt0XQe6G3C6G8SDjdV9CVf4KvjK9fQSPnj7QfPzfMZXZLkG+19WN6/f/wo81F/MNVNZ17rA7GSHbWrogS0mquJrWl0wGcNSA3cx8roVgOoIMTic33TgXRC3MSEghB63B4+3d2IG2/c9fAgInrDfefggLmVE8BCK4MGRSv43mIu/hHThbz3VsPxfc/qVhRBATcgW8NschwshhP2LifA43iImYJ5nTLOYQc5zzIGnH5+eMMV7zOkHnLsTTocjYndEPJ0wjWeMp1F+NR4EGOKKyRF2ux26rsPhcEBwHfj+LSjt8X73LXq/x93uLYYwYL+7QfABu24H7z26rodzHp0GcTfLITJBHZm8XpHRSvAwRxEwmqXTHEdwShKvIkXM84jEEfN0UtcuahERJ5wnxsdPAaz+PqUuqJaJUw0zIaxAwHFMSHEsjF9ljhOSBMF2gGNzNWK4LuU9b77XSd1NedcBICALJCozYkJGqttg1YY4vCxxxcDffG9/N/KkCtkoSJ3hSjXB0x7SRa+iImOa5+VPLqs8tIaX+Tbkos6xEGDUAqpSd9HmyHU05RSkT/6I4GRwCfGccjluHkA0t7heVedSOmHilxVoqPtY9bsITsoHx9M/YPrxm+bzxoWA5k1Nv9XCDwlpjqKppVEgs1sci0NUSkResEtEcXTYxwJZapTZviY7L7PAvEM/3YB13YaJ8Om//K9I3GE+H2BEoBDxDo/H7zD/fAtyEoy+u5sRdlMmFPc39wjDmP0UvD99i2HaoUshI8c1od1elzlyGnOm63v0fY9+2KHrB3SduE30zleYf0GmtzZGo9nIWKm9UcWwKJkW43hR2K/f0tbzQlcXYYKar5sVhAaxNmWHWjBhHxqRXBea55DEnUHbgFqYrVqJCvcAqJso0rVVBKjZdQUVeFYLIpoxqXgUi8G+8JzWz8lGvUCetZWFvG+9gHD1fnma5oLLpa4pouojoFk/V1Oqv/96qZRn6/ZSBctBpQvjT+2DPKgt/nGtH42waeOdweftdtUteW6wqjFf+qRuytlu27X8i9bVBbygko0xfVW61vN6va1z8XJ9vqqOL0XQ+eVd3dhuX482oEwflqK5eqvMsSUgeS7tPPDbw0Ztyip8mIHHScsijLHHON3gNBPO54i//MsJDx9HnI9RLRAInhxC5+DJofcOgZwyQCGKMgQxcyAHeMEzGSIwiJzgkrkUUYEEEshJjEIoA8aZIEL3nlkyFx/4hKgxImIUBmfSIMElhtAaKBiaSwyNYQHxua3WeqJBbRZx5TxwTrSOyTnxc0+pgQktDqnub0isH5gjkAgpRVCaYZYSDJdx1sy4d0r/s1grg7Yix2iNi7XHG+hpFtib9bKYcwJI4GSxCFJZXzZ6nEUQyO6SKnomqSullsnNiHVfFDVJlRCiKGq0+CU3daqQg8r7auHKllUGeT5fq6ORqYpqsLE/83e23zINA9sGYoGgOKh5gKH6XXOeUhk3eMAxXEpIGoHZ+tZ0wsrXX7e0LicCw5e2EZCtNrxHEWK0OJgEAteYgkljr6QIl2TdBvJICTg+PQExIqgr4R9vHCa/OgTAzOgi49tHRug8+pvD4jwqwnTZW6QW6Kr85hISImISBdpicQLM01mEiEwI5HE43KLvOnxze4fgCeAjzscjfvrpX/D0eI8fvv8L5jGhH3YgiGtks24KwcP3AYf9DrudeDoQKwgTpKVqLAvgLuOtijJU4iuSzXu1jGQJSPudwYygvIFwQHj7Fm/u3uD25gZD18FrIYyE3h/FDTKl1dFhQoiYAn4+vcFpHjDFgClOoHEExQkzA5EBcd7K4OVkARA6nEujl7RSXn/667SU1LaIgQXuaU9bIFMgbaF9VwI6y1i1xUQBgJEvVp4Kx9rBKRdVNeX5uu21wLQWQCQVCJnVes7Ei741NFUL25tmLceXy6i0qcV9BJ5ofwx+sKwD8Z5VicIUPjgn+yR0AV0Qt+LO4hRq0bUF2a+dPlcI8XUqX94+U/jl42G7QGABw3+59HLXTK8uumygRsIPPYRNcyCJlgfn39pnpAkidIgz89MBg8f0fgff9ej6HbwP6LoedzcOv/3G6b0X7UrP4obJFdcT2V1CFUiyAOyKssVlmmbL7HHr/a+bWkL032x6xdh+rWl4jjY2DaSM763aweU3M+NUOyJ5PI4D5uhyLIjz+IQYI87jGefxjOPpiIh7uO4D/HBGuJ3A0yiCivOI6XzGNMm3hiQGL371drsBfddjv9/B0QD8+Bv001vchffoqcft4Q260GHX7xF8QN+JBURQyyHvQ2ZWiSCCcl9KfyuEPCXMUYSJMbtiGsUCYhrV/dQIThHzdARzRFJXTTHOOB4DPtzvkdRZpx3WzqlvUafCA1cfnpMONCoEXww5DbE1KXq2aHCmVa4CCScupxyJ4MXeu/yrwgwHSEjZ4oX9eRqZ8iJqTCQ30nOwI8NFO1zyIVMLKKrDqdGCaLVByuNqfdpzbvPKo2z32ebfROK0rQuETF61lhTX+s+19QhXdWake9n29tS18Uq5Lbzq97Ju639L7TJwfIsZbar9uWchho2dXkcNHFe7IJRvgS1GcBF4KYumGkcvJNvGEuK8Dqlql8sCN8MbCZj2iKd3YJRYAqTvxF/0LU5OzKBBDv67I/rbc17DoTvB9ycAwmh5e36Hw3irrhZtfXLxFV0hv1lrB7IXvRdkM2hsp67rEUKXrbCso4llP0sQvguAdpXqcV09zmXXwqSl0KG+L/NTcIVWdkB5DE3zT2yqPOAqBkkVY6eUi6yJCIO3CnBcU6/tK4bECbFgjSTIvs61CD8gAlS0eI4FWW3WXhaG1WNVjfFqCDcYpVRl3ICJGbtazIetzk1BRJ1vu0LUa3+db/Fuq2GcVhywChJ8lVSp1VxMK01vWl5s5KvHfEEAPsvTv9AcW0cvSZcFBxvz96ISr5VZSrbV+jnfv6oxq8+u1fyCCl6xpLb78ZkNB9C6rvuc7z//U0mXGBjcrGm24MuvbeoQ5N8yGS9qfgSe5lzXxD2O8w7jPGGcJnz8YcbDhwnTKSFGhoPA3iEQAhE67+EB1bKGnG8KXxVJFcYwi+3oHBO8d+Le0JczlsDK7BdCPCkjxhnDGQznJIirDIi6/YlGO7uMExSIvxxTuXWMypNIZS0gmj3iFopITY7VcgKC4Rbt+YLn5zlimzdhdDkmEUKwWkjAC6NYIgcLvZAZA0oHqUcEJj3PmJqVcAkXXj9lFHyHijCFHJw4YgG0D3o65lIyPs6oBA9FCMEMESYkVisIhqHBJpCQa2UIWh42fsYGjlr1qwkEXvWNFsRkAwsU5ht7NjNpK9yqycpcCRTK+SyuUEhpGsrrhK0+K1YakOtAI5xgXUcSHwRpce5k/KnMy8rNbYUvFXyqfZ8FFFZnXkOCWyNFxKRB2FNETITkxCHT+emI+XhG5wjRE75nj+MFDth+YgwPCfthEEGE7ZUlR5ioWBMlAjuJI5N0P1SdF2o0TiLc9B2887g93GI37PD+7g7AjMfjn3E+fcRf/vzf8Pj4hJ9+/ADve9wc3sE7UbZlyJoKfcBu32MYBglObWu3Wk1kc1uBBjLXWNb+elrB2TWOtdzgWnZRrHw033UIuz1uVAhxsz+g7zp4Qm7j0J/RuxFZdb0aPcO6Y/K4H+8wxh4zB4GTcQTFiJkZERoXUdfmNjiwBhtWsMjE2lddt2x9ZkKObwLUQLLQuDW9mMdlGauupTfbXlYiW4OXukeXny8bzfV7bQrXXeT2U6P5C+1ZhL7ZEzCXdjVNXTWC11d1vrzIFt9ewt/z3NXzQ9pPPecrnJNI+DWexBV48KJMLnuxLp3bpqzS9bcvSV/iZun57J9f9grSP5v/+Yxlrr8e3fNc+nyLiJrm2UgFXFfaj/qwtoQwxkyymBB2cOfNJMQ0e8LxzoO9g/Md0HnsDgfsDx2+eyfSYO877AeHvheLhxBCFjzYwSdCCCr+mpuD8IXEy9/T33T6q8h/kHGzTaDVWECo5szjeEBkj3maEBPjdJ4wR8bpfMI8zbh/esA8TXg6HXFyH3H+5gekdESKjxgx4XwcsxumeZwwT7MKBghd14mf990OXR9wsz8ghB64fw8Xb3AI79H3t7g93KHreuz3B3Q+YDfs4JzL2sjCDCzauzXWYtrNos2klk0pYZ4iYkwYZ/GtGydzwXQqrphSwhwnzHPCh48Oc3TgFADVjIqzQ5onPay5IFOs/l6TwoVUozSWCrLqTXipmsGucilFRGAyDTUjJNVSiiwGhgSUdVU5hiU3CH1V7+W0RMYWWMQrTjROFbpZMagLwsPlntsDi9ucTfWMev3Wgo4G3UEWUDSfc1sXV8837k3rbNnvrDndNNHc8lWoR8ERcxlZyLGqa/Gbn6+HoUZvirzFsL71HLWaxZXZL1f7Hqohp4S3IeotjmQEmAa+y0QgZYSybSFWK9BavmRSmiBihZQtHkmVZZ+r3g8SHGbncKYOHSZ0NON0/xbjcYffB4c7CujjIKOWCpzjZNqOBvfk98gP+O/Tf8KP8RH7uzvcHA64e/MOu2GHm/0Bh5sddrtdJlRt/DgrKcR8X3peAvJlDcBGsFARx4v7LSHE1dQQduWhySacjp+rGP7OmDzZ/VvIsKjgIVTakgUE6t8bal2BsgwTR10XBLDTgKfmfgD5+2KNoSEgTSBibqSa+pYI7gZ8vTpCvByYxaBpeSvGuv42YGUbJm5NUSH3L6fr6F3lF3rRppeA5tW5v1avk/20BUNQ7buNl5dGfPv5M8j59sBtpOW8vy7lffRahCyDves1f/5bA+qXxvO59BxssLKv9fulo3op35ciuX8tOmcx7jnKMvD8uv3yRAD4zQAMAWMckFLAOQyYY8J5ijiNEeM0Y5wiYhTmjXceBKDzgCexKLDzNfuzJpJ4g10HN4gQXfDThDjPmBTeekisBYO1YkQh8Z6IFMchICURvsfoMk4PWCwgs4yImJO4jErCXYcjt1rZpGUKn1e1TWGMYK7oYJdxbZiQ2jEoGl5QjtRakQCcJGYvE8AlTgSZEoJaSaQ0w6vAQ0TnQvODkC09guLzToNvvA506J4z3IWcWDR7sRZ08OJiEgBlV01iKVEswJQpaTib8SG4uIU2wUTtHtUEFwXfK+6YjP9RcGlgC+dl1eoWHKY6J4TwWdA3VH+JBOSAzKD1GSN8FF2zJmxXxn9WRqgUIEAocSKoet6SC0ClxQxAEJ9EGrekiGudl3pCCBJrUD1TZAU3dQuWUAQO5QzQucz9JrDRZw4KQ9QSR90zpRjByQEpYXp4xHme8afhEU/DLLiZIzx1HpVRcdOvswNGNwP+CKQnBO4wTHvcUsDv3ZBxDUqisU95BNQVk2NQAFgFIXNizHNCCD36ANzdvUHf93j35gbeOZyPP+J0PuKPf/z/4enpER9+/IQUEw67O43RaOM0wzsP53p0XYdOXSYnZrikQr4KD5WUmrUk7srU0p8tHipkn9pasLFnILt18zJfoeswJ4fHM+Obtwe8e3OH28Me+z4g6Bob/BM6mhCcKEVKs5ZQSfSTIgNTchiTw5kdzsniQ5iQr8LLufyukyHzhg9XjwkSx0YFe6aUI27EBCd2+XWpj1URcknDlvNd90ojWFAAocCi8D9tnUp5tUeprNSc/1REbHWdj0kLCE9VVVVuwOrcqLsWBkvGdhjr+4pv2+a5cF3XvUgFv2VkN3kLZReBU3pOeYnn25NY//TBy1lcpGbIa6s59X45/GGVXlnVWkR8LfP1vKu3zxT9fN1L4P7rpc8TRKywnHWWwhgrGqu2McwSwkzpZtMQNQuIxO2gEYG9w/muB3UBvusRQkA37HCz7/DNW4n7ELzEfDABRLCAut5ndxM5FkSWri8ZAMsOPp/+OpYPy3SJGAV+9VV1JT07Vg2Q+exavuRjXJr/FZ9hC4nZ0Hap3xUfog6nqceUOkyTR4zCqJ/nGeNZ3Csdj48Y5wmPx0dMNw/wt5/Accb5PGGaJpzVAuJ0PiPNETzHTGgEH9D3HYZhQNf16Psdgu/gxvcYxm9w2L9BF3rshj260GsQa3HB5FwJSu29uREx09lyIDIqoSILURFjxBRnzHPENE0qiBiR4oxxOiKlWSwiWFwwTTPh48MB0+xysDEgKn0aV2Ms2hxy6IhfWTQwyJgfxpAsTEARNHr1i+m9OqF3QZAzs4igoESZBqvW+BDm2kQYeDURYMHLrq+dsmZoe31sEA7XEqupq33XIkotIVIjKcsnzfMVs/5C21jry/mt1BaxWT2vCmiJvvLKiN0iIKj7l1n81Tdt2Ym5ebwWOPD286Z9TY7q27Sqz1pdr9PMJE7WP3XhwBWRy5XGVE0koNVAtPKbdjQ1b7V9maFyxWNm5Znpvtpg9WuQkOxgJjx5YEIA6AlECePxAOY9dnuP937IrhVrjZxkk6XEOZSgP+OEv8T/jkcAu90ddvsDdodb7PsB+/0Bw9Cj6wfB85Whw1ACkxNoBpgdEmadriStzUNJTX+2xiwLXbb6XQuXDCfIxF2xsKLMnVlUQKiY+8UKgfJ9If7NPSRRERYIrNEZyO6TTFhKGUdySWABIOvKLfdSFjyoSya1vijxK6zOsvaAVui1lS7yiJvvaHP8V2UtrwlbPPxlRZtlO3t3sbKLVCwA0yzd3mjXh4QXe6klsMrTNl8hQGm9F0vV19MzDPsLH72g7EIsflYVNbHepOfW1mdV9spyLoz1V6maFr+/RD1fVsB1kv0XpBd4uf8u0ymZ2f/K9lzC001xhA4dsA+YpzuM8x7zPCPFiGmKmKaEaU6Y5yRHSlIrXAI8mdclynAKJF0iRzkwdei6rPAmFhERLjrMzkN9HCleWtaouEdy8MwSNNWZb36Nw2a0cU1DJKeujYy2rjR966G1LUgCWJ0jxGTnStJzxc4jZYIrTkO1eryV3SweZapBzuNa4QqKIxojX1wHlmdgweETKcNRLSOcWUYs1/hLwEiFO5GTmBVJzzkJWmzMR8rnDNUdzNfc9EUED5yDhxdBhHWp5nMUN07ZYqXml70wFYYbrybVXOPKawLYhCmMVXeq4ZK5RcZHhO9PqPETQ2zyXFfxaIrrKMplGk4kvv6hAhXKz0AAecrMRfIe1HlVEg0iFFN8ROJ5QBUvrPCi9CX8S6fl2gSqkCi7aErZKjdxQjyNmM9nfDiMuB+4QteWds0ljQCePMCI4POIkDrsJ8Y8DPit68W9GRPYadhkwwvBsr7UW5DElwBiYsQI9KFDFxze3txgvxtwd+jBnPCX+3s8PXzCD3/5HsfjEx7vnxBCwM3NW3Gv7M09aYJzHn0v8VBDCDLdxjNLnGO4kc2z4uDmbisLI8iphcwGHlvRB4abOFXk9SFgniWeQz/scXs4YD/06LsA7whAQu9H9O5U1ki7svNV0tgQEhPCYWSH2QJXQ92VVTiEoW8OK89Ki7JlDTa7hpAtIuR1PhG0bG7KK+QZ65rnZhvmiBu5efXHNR2agURRnDTYyXWLtaf6py5yQZGXTrXk7kbOcp+0Xa6haZud3FZxoeznYNiKf1BeFFrKBi1nqmEc8hkpQktGHzyCk+DsIqOmpq48zhfQoi3h76vTBQLg9aU+N4CvKPuVfKOXzuGvnT5DELGF5ZRfO4zBhSlUBA8WrFODUlexIMy80SSLgB6agXB8v0fqHfr9HsM+4Hff9gjBY+h36DuP3S4okFQLiKBM1BwHwvw0A440JoQS93bIXhJCfCWa6O/ppYn5Cwf9r7nDBLiutFFSAoPwON5gigGzrv/jmDAnCS4dYxRLiHnG0/GIIz7h4f1/w8wTzucjIp9xPj5ijjOOxyMmFVjM84x5nkEAnBdLhq7rsD/s0Xc9RneDGXvsPr6Bwx537jsMN7fY724RQo/9IAKKvhNBRAgSBEsEECK4gyGtkMPSrCBM8DDHiBhnbUsU11LThGkeEeOMOJ2F0JuPmKeIn+97jJNDQgAnxjTO4oJJiRfz8254kR088ivv1D6hYRwaYWeMNUAOrhx82gQQmQHnwDkGhDH/JJ9pLWdz1GoMsl91o0SvrIZLiayDzQcvO1SYWcz/6zwrIcJ2u+xt0ZK4nmrrCEuCSxUsqMJp2lZXsLx5s2DALwURhqeYVUF9xmQR9QL/yMSQfbdsUzlUmsZsMzlqS4iSR8ZiHWy1MLNr5MgE6jYOFXGuKSlSmoMYUiEeWkFEHpncvoyYL+Z5qz81s71ed1Qy5POv/JZkW9Ojx+E8Y6AePVTbEQnD8KRBJrUNdVBuc7Fo/2yPk0M37LBnj677Fjc3d3j3/hvsugH7YY/DjcduoBydXqwkI2KcwDFhdg6cIhBJEXyNE7IQNLXWKlXfc18XY5PHf7H0mvFa7y0TfBbhZ8maaXssmCQ53o5f+EumihFgGmpUwSACKIGYc9A+c17FGm3PBE/ZksJZ3WYRSorsi8s5RY9gm297HS2vlnm+5OytV/I2slzfUpZUtK1aBa+rerJuP9o8zb5YUwN5TWw1qHlQ9ucyi4Cp8pSWBOyqiS/FhdZ9uvgt0SrX1Vo+Ax9rxtpg80ae9dwsHzxX98b7VzT366L3XxP3fK5lX7bXVsfJqu5r5X9h3YuyuKqSNvPU8Obz684hWwVQajwysd6d54QPf5xw/3HCeEyIWV5PCOSQwwjCfH0DcKLZ3e336IYBu9s7uK6D7wcAcm46PbtiTCA3N+eRM7d5RCqIAEwb13m1xPUSf4JUdVssYRPiHAEQ5jkCkFhw8p1buQyhamzF5SIVywh2OVYEnAclRlH20bOkmgVjuoMBsxKwmXEQ4Q0TASkCyYmQnPTspwhmry6cRChRLDwiCJBg3AR4qJZyXgLrNbl6kh/YGUkwjX8W4l/WQBJ3kwQWpjmn7RMtL7eiRKmc9iojoXnFbRkZD7e2kX6fF3yBgIb7MQDyrhRawcIlrpnf27xAfpNC9noniQV4scCEVwUrX7upRh4z8qKk4FQhQtZQcd1k+BMR4f7tAR+/vcO0j5j2c8EnCLlssQDyJb6fs8Doqp2OerWVYcvjXI0pc3mbx1j9nu1jjx3vEadPiNMTOg+4OeHcGd738mR9SC7i1D3hBxzxyd/jO9rhf3PfwcUk4gwvGu4JBA+PETOiKRtxwm63B+0I72/vMPQdbncOhIiPP/4TjsdH/Od//q94ejrh/tMDUmIMuwOC9+g6cQsn+J+D8z264NH3XpeAuXmVNeEAmFKOCGNSRowoo9M6bz6AKIDcWWMvCpAzpTvrP3GJyxi8R9f3oL6D37/F3Zs73N3usd9Ju/bdCX2YEWhC3jcyObr+XcZhU/L4cHqDp3nAMQWc2OGRHWYWhSKLD5Hyut8+HUri0mZb+zYmUqMicUqDgGQvEsOZ4JPyls/l1fRpw/fO8Q7ypZRr9J/+NVq70NxlXOoTjeq7Go5UsGaJly5Iys0R2X7NVccWCnG58s1GfIVkWGf7azi4Cd+9c+i8h/OMwXlxieg1wPqvnb5m979WlS/g37yyxL9GNwG8ShBB29cLmtE2RtKLor0RlSEhAohGELGMBaGHsXNiCTHddqChQ98P2A0O7+4kcEnXe7V86LIgwsz9zPIhE/tabhMLomL8oPpdE17tvc3/vx4hxRaReiX9EqvxpZtmA+F8fVXXv39e4+7S99vrQMpsHxZJLWfNmTF2OM8DpjgjpYQpisXAPM+Y44xxGjHPM07jCefuCN7fgzCBwhmYZkynEeM0YRxHTPqblJgKqoEVuoCu79B3EvR1Srdgd4v+8VvcxBscbt+g63oMKoDoQo/gg7o287pvqCCmFRKQNZ1Z9m5MCXOKmFUIMU2TWHSMZxFETCfENGMez0hpxjydMc0J948DxslXZ31SfFyBRxW0z5AKR6yBWgtxUpRmqORVTSETNJhLKeeCSNi9h2kdExzg1fIB5potKGHYxoaw+DSGRDUWVBeWy3OruGY2r5bsM9L3tauh5Xe0dVvkByk+07rLZVPtRBSGcmHV4SXriVeIz7LN2/XX6NQya27jYhwvWWdkTTJuv2/bXf1VYjA/q2NVLOBIq6VhWidF0GCWEfaZCd5T1QZjaIMyKl19U5PLizNrMR7rZPmXZRlhYnVTnT33gxlwMSCmiJ6AgUUrnzghpAjgVPKjBGvkrMmZcn8teRcQuh5dd4v94RaHwx360GE37NEPBN9xFkRIwEvZu4lmMBISqYVWSkjKWChyokKUrOapIkaXR4G5L4ASF0aJFmHCxqhuHidt5jK2FZmk+EjtFim7KTCBhWkL2jyVlitdp5Zk6lbD5rYWRGQrDHOxZ22h4uqp1rBUUn+rUw1jYA3hFnvt1fiRcVSWa9DatN2SdUVqdaDEZfN2w9Si4fVslM+bTxdlcdV+UB6E7aVRBRZtcvEi2ysHsCmG1s8vfLJF3tPm/K5TTSNvswn0PGdq146tkZoZd6G/S2HrVo5Lrdsu0g6LZ4r9K6dL87+pLf6qgqvPtxd/2YPrF59fb9OArfIu7QN9urKmeH3KWtuJVGtd4y4kxvE+4unnGfNUlOiEN2eOOwuDzxlXzzuEvhdBxH4H5wN8NyAxY05RcAelh6MG0s2xC7hisWUa1MG5lANI54DRKgVNUhgSMyglpJiQXIkVIeDHYBCy8FTAPZWyqDqPyGkAV8rnbX3OrOesxa+MjcRIOTYGs5zLcMoMTQms7Sw+yqEoVbEQTcxw6rIzL3+q21ATXVUxy2VhLoKo4FNl4TtIsGpxywSi6vu1wLRx02RtrjaR+DeXgbauFehf42p2JC2QctLxM/9ZMKdGLEIdcxWTx6JAZ87tQ/Ov9KXUnZE/dXtl8UHgRTM+VdYRTEByleCqKVfvibJQYb7b4+G3bzHezhhvJzS8lYzntJaYAPIvanEXlXq2UiPsMZSPoZJCh5tzwGHuMH+MwPEM7x2oU0vQCzBmM9n0MMCUMLkRE4CnEQgDITlZ44J3scQjJUKmrFKpo++Ezr67vcOu79HRCTFGPD38iE8PH/HDD3/C6TQhTsLDkuDTHt4X+tuRR3AdvDeLfgYQtRoSa1in61AX4UoNoxpbym6JRbM/88mW425xzoxB7D3I9+gPB+z2A3ZDjy4EeO/Q+YjBnwBsWdUaXJL+JHZ4nPY4ph3OcBhBOCUZtgBCVIibm1ShCttUm+063SMmV8s9UosshY/O9qIByJreNVR0c0ms16UU1Srw1IpnjUCiqrZAh2q8CLmjVHdtAV8ynVm1YXNEePmWsQKYvLxebLLNdBEzvpjq/tqpscLvMh0k/7wjdM5poPSKRt0q/7lt/QXowyuw4S8usHn1At7p9n54XZ3bGb8Az3xFer1FRL0I7IBmu0ZGQkQTshZCRLV8UORJfZxnDQsokuiA4/sesffoQoALHsPNHXzXYbfb47Bz2O0IwTt0XS+msD4Azguz0anvZdP6czWhX4BUpnUzAqj31TaxJ39Pv2JqMNDP+fyvQ11aszPClvcD8DTdYEo9TiNhjhOmeUZMEefzGTFGHI9HzHHG4/ERJ5zx5/1PiO4Ru/GElMZsAXE8HrPrJttXjkgDvHbo+h673Q59P2CkO4x8g9vjOxziHd5377Hf73FzUEuI3QE+dBj6QWNCqKZKqJF3JS7UfDJxwpxmEUDEiGme5d8kApJJBSnT+Yh5HhGnE+I848OngPMUJLBwYoxTVLc1MlcuE2MMoYUUaSRS5K7c127UZFtXJuXqQim7koIIIIqFAxVLB/NF6ntkhlwWVEK0w6ho6uRghBVh1tBrF5ddzfRYZKrW+XLJP4cDUF3xAme4tgMyIuBdOeCu7belYM2axCUo8zNN3UipwYWy9npDXtn7JcLU3rdIWGVyuviu/YwWedvylkS23b4MKhWSzSweVuVWjWp8Lec6auK5PC8Ia8WceWmrasKwrmlB7G+5NLKgjWd6xMmPGOcnnPmM3fEGfezx4WGP+6cOb/ef0AX10ZsiYpr121mtIYWs8E6soT59ukXf3+Hb736H/eGAw+07vL8J+N07j11HGHpFOh1ybIh5HhHTBDcGpDRhniUoIUVS7a/KH249TtVSN4Ke8k2NByjJosR4KaPOq/PRDP3WYlJtNGVgsbq4MYQ6w7Mcv6q4bKoZRVRdrwAOs+A4dtgoDPWVSznRaiyxsIrFDQHk1u1eLICNJVHlWa/e7G7o1ef4FvX3OoS4me8GV9U/TZtquHOtzG3IxsuuZwpWfi6TiFBhrrwzwnSj5qvtupj3SjBiyvv+mbIp/3lprRdzZIE9KkKdFu9fWMO62WVfbnf5yqlU7f9XJ/5yyuBvw6XrXzu1o1hwgUvpmjbktfFUug/AGAdMc8AYxVpBlGnEpeg0i2JNilG/IjhWd0HiiF8sBB3ggkcYeuzubrHb7XF7+0YUV5wXRaNksQ9j8c+Pik7OOCypiz3pX0qA9yIwmJMHZiC6hIQEaLtSEn/uc5JnZhmRvAccZSWd2gW3MWKT4sfOOemHCgiSc2Aok5hF0F9PRKHvi5uowhRmwCwiICdeIgKS4N5JAwm7lMCUkJwIHCwQd0wRgFhRJjLcqXbR84LENfZYgxhqAIe9T1ywJwKywoUJpmoXP5yqDLnsGuZaVSZgcmCSQOdcuXzJrnJqy1pSPI4YpMKTHOPKBIXZb309ITVuWfW9RlAyPWVKmaKM4JyDDx4cPH76x99jvOkxv2WkkJRBDTilkXwWWBlu5ArOot4m5r4Ddg7B96AQstJY7e4r4x4w/AYotu3yl5d46Mb8rumdAjUYBD7MOOMR/pgED3JLIcTrkw2nHfH38Yz/l/tnfDN5/OHnAWHYwXU7OIriwo2A4By63Q0cOez3A7ogthLT9Ig/fv9PeHq6x7/803/B8XTE8SmC2aHrhdHfqesqynMHYfSr62RxYTWCeYJYNXTrNpPgGc45OJ8E1YsVjK2RWKLstijBxGzy1xHBO4nvMU2M033E3Xc73L1/h9s3tzjc7FQpGBALDRXOoNSV50cnLjFjjozzTHiKhE+RcBpn3H/6CBpPGJLEhmA4FTQ5QyFKeTW4r+Bcnq/MV6igPxE4Udnw1Udm6GRKkWQ4nV6oqtMF1GhJb3KhcVV4XK9U5nZ8Ul0Os6HxVakFsiXY+aGu4pTXmgWmWSBScK2MamjjBbRonmZTFRh3+TTderOB49bXeiPWhLS9F0nPWyJ47/A4TziPjDdhh/feo3+3x/zdHjz4tmY7hDIeuGjLkgj8jPTVMbUrBX55Xf/68MrPD1atyTaaaZAUIUQtiLBAtjFbQ5hPu7IBRQjBzmE+BKR9B9/3gPMYugHeC9O07xyCB0JwOSCY83UsCPOnVwVgdDUxVBGeGQuh+ud1fX/mu6/l7/Zz0uX9t025NQFz1q9/kbRNO/6yFS8JwJfP0TNMkcx3UK1giQ2EKXY4xwFzLBYMMcXsVmmaJkzzhPN4xhFHPN48AXSCjxPSPOE8jZinWSwg1PoAENNyCgEhiF/afujR9T1C12PiPdjdYJ/u8Cbe4bA7oO936LsBIXTouiH7mDSipGVQoWKmCFIgAojijmmeRRgxTjPGcVKLiAnjKLErJDbEhKdTh9PZA3pYWvhbHfyMtNi+NPNR50wLQ4ULFVPOBBEZKVZNLlf7Xtdg06LpZfchCzAAfW9IstPnCjMyDBFsHnlQpJUQZGXNWKlWVl4XZMTGxnLZSgVGLdbqcsnpAVyfwXWeZR3U/FL1fL2mTddtWUgmPi/s00t4QHlvZtg1ImQZM/bWEhxYImZWlmGmLUN/1bJ8Pi3ngDfvl0ISqZ+u+65fAFx23IxTWn7MbV1SR/Wnamrj+34xKFzl2GwW1Oy6amNDpDe/9lMqT6Sm/h6YwgzvJ3A6ox8HpNjhaerg4HA7OHR2qjOXYNUqRLC5SojiMzcd4P0tdvsDht0e/TDg5uDw9pbgycFRgPMQlwop5sDUlMS3NEWNu0EAOAq+D0XiUxk/NqKi6lcbA4Ka56Tj0TBxXL1XgI3tskiLSW3gRFVH/gfkWBDqVq4Vjiw1gQqzgmzTZyIfWbCaY0AoXLQYESZgrctc7rUmLddNJnS2BqLK+xr0J1P6n5vK+dzKIPhCYxSiVMBzBV8BbGuHL2NCtMXLObcBU2utN2vrVgF1sa9GIS9/sCVofFEZn4vG5u7yxfn9bMuPfCsPloHGX9Lo54RQz7WBth42qWII1E/5a9AGLT56ubjNVa3f6Nj9WkKRFXJSq1Rs4dd1W68XXQcZ3X4vv5EDpjggpRnMwjgzV6Opol0LdFNchBT3UVc1rP7uw9Ah9D36oYfFGouqkT/HWeEPZdQmKx8woIa44qtdsznnlGGvAnFX8NAazyt0tmtcG4PlbFideWD1CU8gUvhkuK8GbLZnhn8sTwch94tltMWlsHXOxNkVLZOoN3MS9zRgl8fac4K5EWSlZRIsVgSasq9Ne+GhFSYc0MLZ2r5viWsZPZLxNMM9K1yrYdjV39tZbscI2bhT3t8MiUeR95meN9Z3awjpAiOUOB9raNbiAKs9S+0Fe1k7cBro2IuAgb1Dcg4ueKS+x/H9DU5vdhjfJ6SgOAUUHwGKlXleUEWw4QiF5iLpc7BA0qRtrvgvjUcK1MIBg+G2Vi/PehF+2XzqejT3TpQwU4J3CSbwyG1/DZjbOqv035hmjHFGf3Y4n4UO73vV2ibAkwM7ERx4H3DY9QjB4Xx8wDg94uePP+D+00f89OEDxnEC3F6FQy5bPOS4hDquTt15OoMlABgzCD63zdafrZ+ylfMpueoalQWs+4XLDOjYmTVEmglzcvChx7Ab0Pc9ui6I5QaVvVfXtUVGsu7zOQFTAs4JOMWIeH6Em0aBA0DmDCyLa+ep7M8tlKwqofR3AQgaXrYOR22Yu16PFxYHo1qg3P5bACGzV2rPmfIuu0BjVO2thA2siqL5+bMtzM2sf5eJr9zV95fo/IvndH7O+bzbbJSeSZEnTIh44wnBOdAQMA5dcWkIOycu94G2GrrZm89Jn/n1Z3y2hRldzflMHb8Stvfi9PmCCF5siCyAkOuoAaiF8Soa4DHGIqBgqFt20WSGIzy9D4h7D7oZ0PcddoMKILpbDH3AH77z6Dtg2ElQHK8umXzoIBDTZ99iMCGEAeFnCLDGBzxQbZLnUKF/e4mB6wy3X6UBf8X6PzOJ4FtdjiXG03yL4zxgnICYRozjhJQizpPEhHh6OmGeJzw8PGKcRvz8+AEnekC4/R5wI57Oj5jnCU/HJwkCPY4ZKXbk4PuAoesx7HbY7Qb0w4Czu8XR3eL26R1upju869/jcHOD28Md+m5A3/XwzqPv5Tf4Thn5ecsAqPzWQ/sUI+aYcM5upCYVQkyYJhOonBHnCT99IDwed0jRAanDNDNSmgDVlADyeQPSvpjwgVQa7kg0QMx1CVGlQZz/leCthqBltyaVRQNpUOoc8wH2S+pX1PpPWQMr+8mshDIyydL6a0t0hbRcAD0vW+JXEHJcZmbU4GtrK7+k7rYfhmTW3xKWAoAXJTsrF64WjLArZ2lVZ8YQFwTYQits+fxS3fUD3ni1dPkEQAjKC13arCqPvWG5nHHNDXJgSUc2fZar9Vc5R2Ysl2/q9WGxE7JAvhaakCH86/UkZzgjOQn07lzIfqWfhgc8hUccnm4xpAAjCM1aK6YITlH95Er9x/kef/r5P+M0Ad9+9wfc3r7F23fv8fa2wx++8Tj0HYahgycP74IwahwjpQikCO8dYhJhYoxC7MbkJFREiqIwatqczFl4UfpOmTiz/taKCaSD2Aoq9M8GE9nG0FxSGBOiEHQFhcww1kF89laWETBBcI5nZURoPS+t+yQLwCmB7cr8Z4EDFrCygrFbFhFUlb1cm+v3S/KuWTV5HC+nlvLL4LWhO7m+adMlBGWDbmp27dUN3MKji4XycwXZOliSD1cg5aLqS0N3CQI9B4WbfZ2Xez2jleBkUfmyLa9S5GiOkA3hzSrTc2nRtvr82GQWPFf25yOal9yXrctfnqNfA7lewqILVf+rT5f25EbOCkRfSsJrljmxczhFRpyT4rBmFRHhUgQxBJ8HNKguQTThPKjrgD4Ig9ebYFgYz54cXCeM30isWvZyDltgZkdk/PnCMFQBuvMecAwXzUWoCNqRXO4IMxpFP+ecajMnbComkAityREoqY9+VosIVeYxHIdcwRUK9GLAlAxM0aABbfas9NFiRcSogXFTgqfCL6BEICTEJC6oYox6pidhIJsmNK3XQVGCVPZcQ7Ovd1q+V4FDskjTpMKIDSVKEaKgCI+AjD8RVFAEQrKxMiGEI4hgwVU4pIa3bQTecpUoZV5F6VM7d6sNXY+J03lDiQHx0//+DT7+T2+FOQ5SSxlTulI8wwHjoQd7gutcNe+qtbykt4gyfyXHfagEEYW2siYvhRg1LkHV4ULV6+t4doun26+xdU0JAxqDovIo/7WErVR216cd4z99d8LvhgH/SyKk1CORx+3uVl0BRxDNuH/8E06ne/z5T/+Eh8cH/PSDCCAiJKZMCOKKadh1cI7gvc43C94nsbwYCec8CEQODnsILKuigpDFebGlnrJwECbQgNDBzSmma1xDTOS5d94jhICuG4DgMQx3uL27w92bN9gf9hj6DkFdRXGKAIlVEwGZgLK/rP9MmfFpYjzGhPspYjqP6M+PoDRjbgQRMCdqVVl1KvMqtKLu9FSsmoX8ai2gNOJ4xtdhdWTlJrVg1kIMqpa4LzXusd02MhBjrVwAJataBJY1vai0IlXVKNwyeWlisdTilA0uGiGdwa2Xr3v+altklfL2r/e57fQCZ2x9BufgKaDrA4YuYNBg1bPxY9pWS1lC8NarIXOb/k2gQv+G0xdYRNiGYL0uQogclNqCVOfD3e51wbO6QfGiXRL3AXEfFLAF9J34rhehhMdhB3SBEIIEzikBdRWoavCj7O9YmQyF1l4c//Xq3BKlviBt0VW/vhXE9fq2msOZmK6AaUU81yTca2HTkux6SVrl+wUA4qVpuaRZ8jz4WjMoRAuYEBMwzg7j3ImptwriYoyYp1lMwacR0zTjPB0xjSOO4wOm7gk+HcGYMc1iCTFPswjzYgmq5hwh+JDdMvnQw3c9XNqD3S32uMEd7nDoDmJJ1A8SDyJ08M4LU9H7jEw2OCEK4m37eFbEYWqsOLSNs/RpmsQq4nQOOJ6CIvEEIIJYAtsaMk5UkNMSjFq1SSr3SoZYZ0EEioZNdp1UI8XqJ7QEfi0WEbUFBNTsGBYHg0zzpHIsmddM/eDaud4yNZs3Gwze59JzvhBfcrwW9Lxu1NoH/FUNJIUGRSDQNHJV1vN9M62vllGUR5kqpA0V0mJEXsVxMA0qNMQdNhqaG7dqS1XVGimvivkcQYSU2ZLDOVb3Ak1qmtwQZEXbSMptYXb5uNJ7siPQSlDBYu2OSNpQfrfPiXJGmCk+kjAs5jAhEWPnDuZtqxD5GijPtDRZsfGZIz4+fQBjj7dvbsQaYhiw33nc7oE+iGKBJ4+gwQfhOPsqdkhABLwPACdEP8ND/E8nBhxFcYRESYmQVvOmXkv1+BgTIRPe1RxY/hrBvXaWGFFRu8jJ2Vc4B9n/1X0F23JyqJY67OyWrVALLKzIVuBgAScteLUJWu3e2l7KX4zTtYXfCAZfiv+sCQp5SgpjW4uCtbb7dpkrpvkSzjUZWvjDRvm1rdwwiLjSljw3qBijG/t19R2vz4xL0GYtGVjk3QDUF8vWddQeeBc/5wt9eH7GCdvCI9oa4OdKau4291ZO19ZNda6/Nn02xW7jvOQ0vr4Iu7m+3bZW0TJGSZnTlcXOL8WYuJiW+9Oe8YU8dVrvoeXrJSeImTHPCXFKSLO4EDYrPrKzK6nlPnEO3EpOLfBN4cXwo6qNGYdV90MJdhaK9CGlBHK+MBBR8E2xWFAhQWJlHnOGKcZYK5qxqBQCFb9itPKIDHJ1PIlKSAhn542dJSWn/Cnj1uBKlcKGnXmccQAJApvbZZ4QHGufKqsK85Bgig9ce1kwjHExmRXHrWHAXZl+5nIhNInOifIwJF6FMfCqai6ALsMbijWJuXSRgS0njF5lZtkyQOy6rQXzRv7bIAGOEF0QfoqrXD25AOcI4zd7HH9zW858o3FMScGEF86su6UPTusx/KN262ia8XUA6kKPATBFrwyXKvymbn/Vn6Z/aF9vjXu7x3SUbPzZ2qF9o/aLr5oImALj7IG3A8OdzYpf3IV75wEILX86fsLj48/48OEHPD7e4/HxhHlmdN0tPAWhy71TxUDAOVl4adX/VI2JCChStf6ZNug9rleSAAVjAK/sNllxrRzwnrKCnw8OzAE09Oj7HkNfYkMQGMQx7/8Wb2rHnxmIiRATYU6MKTLOSdyy7dIseD0KxGmppxqj5qvnMFcwoj5B7Lrg3Mj0HrBeconMcqdElgGqIWrG2nAvRjPk61HYbm/VFgO71g/K8JAzfDJLsFxmHiC5WJ/0l9MGdN9Iy7P4Ujkld/Un4/elKGpyF28XEhvCew+vyuWmO3q98u32v7zFn5E+4/PPrfGXR8d4ffkLgc86vVwQkbknuiEVBnAOPC3+oOMcG/NW+Z0R05yLKpIvQehO3+yRDh26/YBd12HYHdB1Hv/wm4BdL/7yvPcYBqe+6joROmSfyuaepdKCroj8LxvIyx//6vKGzfR5jSjwlzafr5b8xg64tCkK8nQ938vTr7cjXlVTxmztcBB3TI/jHk/TgNM5YY5HRNUKHscz5nnGw/ER0zzi0/09pvkE5j9i7o5Iv78H04Tj8RExRRxPJ6Qobo/s0HXeo+/FYmi/26Hve+x3e5zoBk/+DW7Pb/Hu6S1uwxschgP2uwP60GPoenjfaVwVB9+JNRG8g+hPOIDFV2tCwpRmJGZMUbStpikhajyIOE+YpxPiPCHOI+bpiHk+4tOnHvdPPaZpBuIsiD4nWMgpC6bqFSE2RLbXfSvmnZSDZmWXTI6Ayr+oBdPOFg5mKkxUYkA4e+ehatWCnGrw6Ryc2uu9MupaRkxLlFky5FeeujUO/QLA8KXCyqx5fen91XpeBxQ3GeVAdegvUKwrTEPDkTaJj1W9a+ZDq+fXHpqbKNdzBOoSzFWD+qVwa/W9UQuuHbdCm22Px/LpNZcwa7aTEoK+zbuCzxlZLG9Yg0Y6kpH1y9gGSngb7puYEVmElhIHKmX8ABAGToTDp4c32O3f4O7dt9jv77Dbf4P93uFmn9B5j6HvhFRy5fxOUZhEzhGiD2AILEwAovM6pOIGw3FEwtwi4YultBJIVL8EITyyz9hlnpqIXjK2GbCYEEYolzo9CF5gVIZT2sfG9ZvLv1TVC6rXp5Jj5GACPcr9MjiIRgPSYCdggok2NTKt3Oh1PlTCqcUHhXraSFlItoXsNt9rn5cU6FbG5dMVLK4K2CijbsslqLhyqfciJrLaGFTjkUctc8Patnw1MmN5Zm1OI7X5aQt2vLC6F7f7mn//RZmvbsqlc+5a25bjtDUvF4rIDXwF4cZ1Flp0cqmNeLnddHGl/hqprvvl69WYHC9t9brkl315AZzIddZ8jxhjwhgZ08T48Y8j7j+MOD9MSOMZPE3AZEJ0CA5LAALDOY9d8PBdh5v+BkM3oKMeDl4sJxzgvAPU9ZFzDn3okIjholgTpDlhRoIH4NgLc0tx3np0XUrqQocxdQSeCW4WyJL4lONGAAEAAElEQVSUcc/RI1FEjDOcA2a1JKjx0npZEgCvgXXhGBFQywgGkwOTB5MHSIM4wwIZmwZ12VUEY4aZ4D6Bk7hYlvXtkJDgND6EnONFp9jcQTnSeGXMiFE0t0MynEPwj9qn+JXtBaE2RGkBQBMYO1suIDMvlK8RxVIlxUqYo+Nso2f4jvrnFxDrVYgj9IuDuIokiiBIvA2zsgBQhBvgrN6drTmS5ItqwWlCGIPlRBI/gbwKixxwenuDH//9bzAfgPmN0Vhkvm0x7TvhlTSgpggkXFbCqkaVAMAXekrpMRNACN/Gy/zlNWvjYUxEV5Vla4PqR9U+bewey9WLQEt7dgNcFJPsHQPZx2bRDPiytGBwSLxvQjcEMJ3hwoTx+BGn4wkfP3yPp8d7fP/9H/H09IDHxyfM84zg9ugGj344wLuA3dDl8WYIzc3MSJEBpxYG5EEIgn+RE4Y+R1E6IoDhZc3lHerhQPDUCVzCBOKElDrEBCTXA9iB3COINJYbgMQaY0bnm5lE6Lrr0YUBw7tbvH93g9/d7HHbdxhA6N0RIZxBNCvObBOjTPO87xw4OXx4vMPj1OF07nFOAR+TR0oOHi4Hq2cAypZA1H+zRMqppn49n4kNj1+uj5KfALhUzqMMJbjwxDhbGXPG6J1aOIngxcSJViZDGAmWGwArb4HleUbNbHtnxV9br21/6naLwEmsvE3Rq8YpSnBsgWsuu8NlkAqBS+bcWWSBzQsUCMtviyst8bVcTSVYQDUySwspidfDOR5J79XbjXPog4MLyHBLaM5l3dxWvNmav37622nJhfRXauCLBRFljZYJLxoEFvehWDxE8w2dTDvSDgMJYsVOD1XvwPsAPvTiNsYHDF2Hofe42Tn0HaHrSIP1aEBdiwFhWs7mjoVID0VlMtLLSaRr6Tmi6Ne1gHgZAf6iTNxqdjZWEssX2xT6xbR+9VIgd+07vpLv+bQyfLgAPNvWVKfGag+UX2YWFyGJMMaAcQ6Y44hZ3ZIljphmjaEwnTFOI47xETEd4cIj2J1B/QiHGfOTWB3M01TMg4HsdqwLAV3XaTyIARTEEsLjFge+xS3f4uD36LseXegQQlArCBHeFTdGFYciCVPGNJFiEqR4ihFxZkxzFEHEPCPNE+ZpwjyNOS7EPI0Yx4Dz6NQc20zEU3N8Kb6KYvEAEUDAwflK0KDIdkZs9RtkQaMx14ogwt5BY0Pk55UgwiwhGu3nwsEr+HjWRlYEulosZRVWq2S1AX95mPDXFoReYitsMrRqBv/VdhdE8SKs27jiS/XSopXPxIho+FKlObmO1yjvrrJm/HS7d5vnCG3dXll3F9rnlkGJl/3MF+VFSopUU9mLpi2H6te5BO9TRXQUrchaVVGa4MG0gw83ErOm70X5oPMIfkYIYq1F4q1R1lieCAazuHBw3oM5aaBNr24GHBI7gT2kQSMdreF2NW504V6uC3xcDWvGN9aJlr/1WBtjoSq7ZjYUweeilKvrbiGEqNtWw8Uq7yZcaw5Aqn+aVO/Q9cuLOxF2ltZvr1o6NGv05RvvElxc7XVelHvhu/y4FrwanblCKixvXXJ9pQy+Fcf0C3CbjQ6vH9Hi/Xa/n8Nl129f0+46X4VDXfz8tcD22m688Nkz4yTats9WvO7HBq5dUMntdjZCs184FaGg/uXypr2/XsrLU71OXtq/ZfnXv9t6W0Mb49Mwl1gEkYHxlHB+SoiTuA7mGIFoIVtRgrcq+ui8aDx3QSz3nboILcddxXiDMnxTEvd9MCazeg9gRgm9qfCf1YVZdnmjuLrh68Y00lhJnFyxNuCExC6ziWpWXHGLynld53NjE3+1NbJ9BllTLL4Bw+hJY9zZHrcYUU6uU1TeQbV3agGAzo1ZTEi8ibbOi4ynxfG5gsGlAGjJuW7keVmUaXvTGNk6H5Qgc+SSWIk6KsGmSUc8pbw2Mh6j5ReXUlyEXkAlCCGkPki9nRfFLF+ULKc3e5ze32K+Ycx3qeq3QyMLeOb0rE41mCVHPZjmoinTXkCF+7R5lzW9FELwAi94adriM5SSlkIOaN9eCt+u1KqWF44Bz4TABFkQM5jPGMcHnI6PuL//gMf7T3i8v8fxeMQ8zWAGQh/gXMgxJLogwp3ibkeZ8XnfcK633qvrHtY9ByzWGBnuRWX3cPYeQlg77G83kuQnUPDodz2GvsMuBHROnTxRRKBJ4BsVaF9Qb4UUySEmj/Pc4Tx1SImQZkaKE1KMiNzuv3rLMIqAsIzHxvQofrWEGZQLbiF0aSfB1k/9pnboxAR1w1pKojq/WZNYiYSy97mUQ59jEalwv1XkWdJZ7T3xRj2c/ywfviwRsl769utawceswqhMZg2gq9qLcoaeHCqUMF5VYxFx1ZLsbzN9Sdteizn9a0svF0TY8Z81v0W4MEcxZRX3M6y/CUkluqYRUOPfT3cO401A1/Xw3qO7OYiW926H0Hn8+9902A0OuyHAewnEK7EgQuOSSSS25hPQFd/K9DxB9ff097RM1PzS4skC+AMoJnKCSD6eB9yfdpgiEHnCOI+YNQj1NE94Oh0xTRMeHu9xjkecv/kXoDthOj8ipglPxyPmOON4OiJF2VOAaFh57zF0vVhC7A/o1CJiohuc/DvcnN/g7fk9brsbHG73GPoDuq7H0A0IvkPXdXDOyx7S4NSZIcKMGGfZz2lCNKFJijiPE2KM4s9ynjGfz4hRrCA+Pnh8vO/BEWDuMEcCYlQNIEEUanTGqXld8F4k3ypYtJgQWeNGkV4L0GfP5dkywLQTjSRUllEQjWAoMScHf+uSqfYjKlOss978tkjfcp1US+F/yPQqBSMjsO0aWDPxJGN1vX5fkzprrYh1Wlt8bd9bWQ0xtMDxC2vimXShMUvk8yVCBFqiILRFVlJzuVn7QhBBi27WbTINGeGfSIHCZCDV3LfvhLD55s0nvEdAnM7FGiJGpBizywUiQug67NDj/Tff4ebmPW5u3+D93Q7/4bsZux7o+x7BO4TgYXwXE0TEJFqZRAxKhJQCCAlxltgUKXggJrjk1S1VQglNYSwZym2h0uG1UKJiWtTrdTWkq3taZ70kuTIcpRKI2viboLYpLzMpdOS5Xfv2vcsMLCC7T0D1PptCcFWnlbNgmFxIV/f96uWVtbpmE7SdvfTZM1kvNEz/XaGgni2iwLBMZhFtw7EFyrB8sf7uS/HVa7DwOgx87vn19ML5u/QdYXMxbfACP38JXPn2104vPzN/RdJzaeG0vP+bTFvjc32Wx7jDGHucZ1JhhMZXSBFznDXm2YhpHDHPCc5wRkU/O+cQuoDb2xsMw4A3b+4QQod+6OV8ZfUAEFVpyHuQI3g4QH2+S9wEoHZdLMxrpWVR46SMEAJccuhiggMh+knazVHctsQEkLh8dY4QY4KnSqO42mZLoGRKPqL9zvk8Yph1o/wrGrPL8a6Tna9QBlhSPoHT+AkJjChnEwBKM0BAUk8J5ubExRkMjxhnEAKStzPSVXCNL4CN9gFZcN/kxGWNnbNk2sl2FhYrEk4pw+ZsjQ3RCneuMElTInjPSCQCgERRO0CqkCxeI5wjJHYgZSwnVdpMUbWaU81YLP30DIz7AT/8x3+H6aZD/BZgX2gkApC8R+wEUXK6vgS+FGaz4QqZR2mzRLIWFSsA8vgAcAmOCcmplQfUfz2z3JHP3FURFumZxqyWKJTx9IYRTcYQ3l5FgirZOZ1HpL1qtjgVvKhhKSvDOonQK2m8Dhu3bfy4xkbICpU/K1BjNAPhm8nj3z/tcJgJ4/AjPnz4CfcfP+KHv/wF9/cf8fTwiOk8ghPDuYBBYUUIezgfcHO4kzXGI5gjZo0fOY6j1EQEhodnD6ceRoyOzfP1TKLFrxacBUzJVqDuQa+KgBwT2BMQHM4zYz4x3t/u8e2797i7vUXf93DeI4IrF1KLPZjxVrFG+ng84BQ7jBMhJsYYGfN0wm/uv0eKCWMS90dcTSczY2ZGZBXUtMjwOi2el/1gzwV+xCUl1RJCyCtCcT5zOqZi52pU67Wn3xpAq2NkmOIkM0jMxtS6luvFp+NW2pr/mWtAfWNcFmITDGhZ+ssaz0c3w3p8Krjw2nQZjyl0TL6r1ulKIS7DAhE2BO/wNI348XHE29sd7voD+i4gBAvefjn9VXgxf+to0r+S9ArXTOqCgU2Cr9YOSX1Bp4JYmRUE9OCVREhezDZT78BDAPcdEAJ83yOEgGEI6DuP3eAxDBCGhMZ9MOZp9p1sxLoR8lLFF6XX0mHPE25/K+TP102v2/AvzXyRs/Gayr440cZ1A6wrJC8xISXKgrkpOpwnyoTCHMWyYZxGjNOEp/kBUzrjKT1g5hPYH0FhxDxOmDGrxcSMOIuJsDo9F3dk3iN0EhOi6zoE18PxAIc9Am6wxwG3dMDe79CHPmtreS/CPOcsHsTC0Z7t51SCUieOGpMiYp7//+z9V5ckR5ImCn6iqmbm7kEykSjW3TPTc+fcc3b3//+Qfdizd/eSHdqkCApAZkaEu5mpquyDiDIzcxKRCRRquhSIdHcjylU4mfVzQvQe3k/q/eAxjoRxBETyZ9X1ryBOSooI5SVyqCUl8G3O65CEbkWAVj5JEXjlCUFVPghNNm1SbNL0ThOerVga5yTUydsC2sFGWlHeW+6JeivIq7/8M/5aBH3bkJT5uHH4Qli27PCluSvuvJd6cAsVvjX4xXvn2lq8W5Ofl/t15jrRdjM3CgqrBy783H53eXXZhLKVSCFxiiyKEBAQKQrTDSHos2ECAGs9egCnWbKmcUPoaoJGMI5+xBQD+n6H3bBD53oMncO+BzonyemLx5bsLVIoYjRURDQGxDHTAWQMTKT8OylP0lgi14Ot1nmpeFxNzPZz64ldU+R5HhvOYuNVfT1ZAmUYtVAQlDVKTPZyF6b3kIn+c8qWcmnZRn2erxD8l859Lf1q2ls8ps+tn7x+7punb8odUfehUgBsCRguNa3WsKv13piMlBOlXNjqz9fCHddh3Hr9V505c+N6aZdgMbdXCvOVOW8aevt83barKmFCvrL91tqT7kaYzSmG/HYfSz+w/dBXKrm3C+Fa2dsXD/gb2lvC4HMCvkv1b/XpyiGrnmGINW5UmtfPEfMpSviTLLgsOQ0T3LQZLhtYY+Fch05pbOuceOjXzbPkRkvCbAAZJifSUh5XiK55E4pnrlrVIymOWQTaycgmE1ASgoPZ5FAdzCWER6G3qMCtxC+z9iftR+1bqrrw+sh4/NzsrmWQyUCr0AoSN74YbtV5IyJFGLX6ZhU8RpUxRDaFJsHtJyMftxq/woByMBVKM4NaZF7DySLwBYBKAGz07TKdRQ7BxSMiC/oWWyMZrnEE5s5KSKxOzkOW0zFhPgwY3x/gDw7+HUsUiYTfF7hqDac4t5csyBMfK31Tow4QknJewtkCBJa4+LqXiE1eUxkW61hV/K+KL5ApoWbSdqvWQh8+v3aZ0U4rXT2bJdqXznttvQ5ESzC9lVeIQJ6Tg++ZtnMXm7IFlQwTOgb2bPAAB8wBx/iC5+dPeHr6iOfnT3h5fsI4Tgjew5JTQ7wOpDDEGpejEwSVn6U8kjEEIPG4eeNzNcLlabiMf2prcxByYt88rQ32obLOQDE+sg5dPwjt3vWSG4IiJKRODmJ2vidMmKODDx0YAcxAiBJ9wc2ThJlCp30xeT9EcM4ru3GiFitVt7e8X65nPUHzZtm7ZSZqWreuP3k96dxzux4J8i69Kwho8ho26wHWXDtyYUnaUupbeqaBXCp7qd/J81XPVeHbvrRQc7CxgEf5IWxcrbuY7xBEURHhMYMBK4oJZwmd26b1z8s2tnikS/fPlWv0xdei4b+0vG5FX0Vh/nRkaC43KyJCIhBiaHJBBLWA9j5k6xKORQvPBFUkEE6PDtODJLvZdR2Gfg/nOuwOd+h6h7//lcN+RxIvzxhxezUGxnQicDDinigxOCkLVUuC2YrK+1v5W3llOQsyE/EMYRoAIaBPfoen6T4TD9McMfsRc5Dk0i/jCeM04enlCafpBadv/wnoj5jvT/Bhxjy/IIweLy8vCN5jnCa1qAoAxBPCWYvdThD/4W6P3vXY7Q/gl3sMv/87PA53OBzusXd77B8O6Ht5trNC6DjnxBPCOjknimV9EH16CHKeoxcGbPYjQgw4zUeE4DGOJ3i10IjBI0wjnp4Nvv84KPF0AhgwGRFypltMsu4xaBQPomAkSZhttjwgFMmapWJBY7HWeWHIgiSAoBBQydU0u5xqnUkBY9q28krXxMcXgpDXvv/X51VB1ecvu/NLBm3THvrsetHq1+uWtn369gjpLUOsF3CJ4bgqaCwp1prniXKAAu2xUugRiVvBs3nBZ/eEKc5FgJCY6UQTwCAEDx/mLNBJG9tYwuf5iP/tf/wzjBnw7/79/4r7u0fsdncYeoe+Y3TOou96GEPoXGK2pbcRJAFiKUi8aZZY3ZEjDBkwSdI+mAgmoxICzX1jKovAavaWgvpmTtJfoivOlYXwNoWUgwoKUnxlycBjFG5RpRBW+6osYKCsrE1/jUCHk3AoVl0oyl0Be8VYIytrq+fKPqlPAi0+L5/ppFg6c/OWKr5audiXr96Y7sjMSOZ/qt/p0XOeEhXM/GrdXk76EhZcgw20eeNmFqxBAzWUvO59sqHX+QuX12zgL8B/N796rj9fQqT8JSf8Eu1wXaBWnnt9SV4IIUSEwPjx9xM+/XnG6cj5XhEGxmxFb42BhUPfOfTDgMPdAbthQL/faRJNq9bu5/slnmnCOxCQDfmC92BrVZlRe+vppxUa2lkLRIazFj4JeyMQILxCmAgeQHAelgyijUrz2nVnchG62GSPCNPAgFgpBXLIxfymjCSHeZIeqQRa7kY1JiiJZ4XWMGBEzdVmrORykgqNepBYBB8ABoIVgSRB8CtjqVSvBKhEMNlQTHgGSS/HMDEiGTExSYgomWMDUARxqlvrMgTLtlhTc/E2UCcIyQcBSGLAhBJI8mpEBASuokJo6KwkUAXEMPPP/+kfcHrcY/41I7qUKoryX+wc2EqMdBljS5M0ycpT3hCNQJGiVnCsjUjrtadSJyjTDtEK3WKNeofECGhYYJHlyPWYvC1zroiivEO1TpwVbLgM7FcIpabHlvTwegssU/PO3w7w7/uMZPp/foF5nnVv1LRaqYbqCvMcLxok4JvJ4B9fergu4tR9xPd/+hP+/Kfv8PT0rPy8RAUx1sLaTug8stjvDuJF1Q0gIkzTjNl7jMdnhOgxTVOGRaQGiMIjQxPKK/1BKN83J0V/V8/nuVRlVuKBUy60dKIN63lIyoq+g3UD7j+8x7sP3+BXHz7gfrdD13fYuSOG7oSC63mxlAIPRPYgYVQjW0Qm+Eh48RHPk1cDyIgRVfQUki/JJjOmfd4I1y+VhbKi9jJgCSFVP3p+Jq/McR5nTQCKUo6TApQgHkMCbrJRV1ZGGNnzJkWTWCgjEryVtTJI2SlK7AlWxSAj577J3hC1kqLycPuScpVwKxuuKIJlXmTc+o8OMEW6cc6iNx0Og8F+N2A/dPj2vcPf/xr4fsd4yXP2GiXE38ovvbwiR0RytUwEW9A4m2pBUiNc3QjREoIVVy+2Fjx0oF0H1/WwzsF1PZzrMAziDTH0Fn0H1bSazLBTYq5NQdDK6kvninRBfxZgQfX9N5bbLde+sKFXlC8Vll6pXT+3EPIvu9w0LSuapt5H28w8oIQcxBU1sIWPFrMnhCB/PohgP/gZcxBPiHEecYyfMZoXBDqCzAlsRnAUoV3KBRE0pEkifMVNzcI5h65z6HqHzvUwpoeNO1A4YI9H7GiPPR0wuF220sqeEEY8ITKDkQhD1vNcKyKUEPCqRBEXUfGAmCeP4ykgBg/2EeNk4H0SklVCMVT2KJRl/mr1AVVEICsfjFE3x3OeEKnfKswrHhL1b80FgTS+1hMiBxZMFkuZkE/Esq5t2glL4eK1rXTmgVvPZ2W4dvW515af57xuw4qfpbxZ4/NT9HW7L0ujkWuvr2qh9Y/zoVUu9ynv6GaLr7AlCiMoJSJixoyAUAkUgGzZx4yIqAqIVvAPRJzMiBOOGKeIu32PQXND7DtC74Q+qBPT5wTMGm+VkvkS1ec4wY7CWFF2V0+eHcVhf0kINIxSNaf1DBRmaHO20b5RXkyWr7XHZmYeKya4eHO2SoJaFJU9TxITce5QN/NQFDlpbOs9sx5YFhxcEghyhpRn5qXinC6Uc0c3hXnY6ld5ZnH/Kgxq7+dxLj0jrpVKIEGAWmjVCKQw4aztbLZBlKUeuWdfBVhXjdBihWg5TGq/XsF3W9eTpfKKi7/4VltSqLS3lK9DAi9raUWt11nt23qRBD0NwbG08Fs1duu+fm35kr2mu/vK8b+9rvLS9X2wTZvzVZjUPpss9KNnhEl41loZrA+isa8mqFDRaL41m2nUWvl8aceslMFZPiaCokaOhQJDQIVeTvguVSBCOvWEUEF3FkBzXVv5Lv1N4eFQ8FP9bNM3+V2Soa4mte01qSIgswcMmKRAj2DW3BYkkRQMpTXQedBxkOabzLPaoKXSVs5FzNoucbYqzg5XVOYuW8gnmJfC9ii8Js3pQUSSJLiK7V6GWuY0GwnUAlKlPbyzmC1lT1Fvg3qsANEYTO8GTI8D/B0jdqIMqkkVMa5at5mnXduJie7Kyo+Yr8Vqf9WeMpx4JYowRKJPMUZk15rbQuw6RJETQYCJAEteAMSo8TM1+Vm1Bim/R/GSSO1egLdcXaN8AjKtSdW1zW2YBLipOANOEq7ICDsDBKdCYQLmKE5FV8EGwTDQR5IQa46wm4EhRHge8eI/4fn5E56fP2M8njBPM5JCzlgLIgtDElbcdZpXRq31YlR+O3jhwaMcGmYN07Y5V+fpp8L61vgr0aOpwnR2pI9L7xpT7XEJ1yyK0H63wzD0GLoOnTNwJsCaAEOiDI2rRSnrHaKFj06F6AaRxRsC8wQTZnjWqAwUEckU1Ei6v7mcrq9ueMLNR9P7AolR4A+3zxYwSyheDryxR6m9VzOHjMwbyNKka+VVgrwaUzX5v7qXi3ZzBWdg99lyjfa44V1aXllu2uo8U1GIERGclT9jCeQMYmfBpijVC267tX9v3TMX3ruxyq+8W3/aUtE/P2e5WRHhvdg1eC+5IGbvwSzWJayurKKdK7Gk53uD43sH63o4O8AOHQ59h64fYJ1D3+/hrMPf/dribkfoOyfhGZyTBCXk1ANC4r2TqWLD55PZElBfhzn5W/mftVzaHwWsl5JIoSR05xgxhj2eTvfwgTFrTMd59pijKCBOpxPGacTnl2c8n15w+vDPoLsnTPMR4WXG6XiE9x6n0xHBB0zjlJNTEQHOOThncdjvJRfE/oCu67Df7cHHB+z+8O8xmAMOD+8w9Dvshj2GYZAY687BOpvdPlPyZgCVNXOEj5ITYtaE2LMqQ2Z/hA8zTqcn8YiYTnh+sfjuhwM4OjA7xMDgOAOajFpIZ5MT2RpNLJQ9IDTcilVmL32aJFBMuSFMYgjanC8mhV/KSacltwQZA4YFjFg/EyiZFFUhmJJFcJXwOsOKjNEbJvgaDBGGsyJQlvd/Wi3hL6A0HOGb3v5buVa2yeKfsoVyg6sPVTJkQ4Oo4RYjPAdEja/tGeIlqTmjEEVB6WnCP+3+L7xYj2++/Qc87L/F4907vLvv8Q/vT9j1Haw9wDqrnlIAuUJcx8TQccoHpZZ4poRrjPopoTCMuIkrDZIMtdpcfHr+l8JX/VI8V7b3eaY4WvmOwjS5bqh4PhSrUyv9rowrciI27U+KW72GIUlJ3a5aqkPqBJKydssj4m8FaBgs2oDh1yTPjbCwEjzWDD5XLFYtsOKKs1zxZPSFxH9i/s6t88b1c325pbXUDgHncwpcZ2bPY9Gfp1xu+1Lv6knb5Pwv15TnbdmbW9o7387PU5a0kvy7Dpux9c6X7vH1+2e9jxZFshRwDgeiL8MZBwLQdR3m2cNa8ShIluSJrByGHsMwoOtc9mCQWgv9yoDgv6zsRFEKZ5xA4MAS8pAlY3ZY5CaoFYmJBzbMsFbyGBgiBBYDIgYDfgYI8PMs94LkVWxQWC0oU08AEQBRuaa0LYOKta3mPBBlhNalQvD8vdm7KdcCJEY/AASCsYwYhU+I0QPEiEHC/oA0H0GUTFzBe8Ba+BAAZjFWSMk6VuuvwtNMNMjYohG6wRiGZciaMgBjZVo45FEDBLYkyhIKYGPAMWhuB8G94qieQsUk5U+ET4aZMVaGGdKXH377Hj/86hHpzeldRNiJBwXDgJ0VrxcjnuPbXEia52LNLOtShbDSnBMhssx5LIajyYi01Fzy4wn9IXk8rAWIIyT8lM6KhhgzJJ4szARmg5jCZbN6faryJ3v0ZEFrLFuwCiezBmdJjKrP1LgyrQ8WiYE3y0KxkQ8Rwf/2AM9KowWg+++fYY4BKfF0Eidl4/FqKR5mg//1qYfdGZj7CdP0Gd99/h4fP33ED9//AD8FzKNHjIAFgckBxqBzOxjbYRh2sNaqVwkwjSOC9zidnhG8xzzPmbYmkBoQKn2h+wuEorC7pRDlMS2F1nkJCJJLpTpXhqHJgR2mSPg0A9+83+Pdh/e4f3zAYTfgYfB42D0h+TudhfgMRDZ4mu4x+j3GMIgBZ4yY/Yz9y59gZo/vQkAAwTODKSm4kEAskj6zrMyWoH+rB5X2IJUbpi81neYrh05iyWHhUCI/NDuygrGsOJ71upxdzcfCOmv5ZVEUljqEuiwjISSNq4g2DNhEURrmPnAJjabVUNHEIqacEXWn8/evgZ+vl4TVCslYjFPBjJkD2DB2vVXDdIvTfof/1j8gLvNL/E2S8D9NuVkREaOQJeINUXJDsHpDZLtoEte+2BnEwYL6DqbrYVwv2uCuy54Q+8Fh6B2GzqDrAOuMao9L7PhkrdFak9RMlyKupUXHhfL1mfKfjin4Kl29qD5HBk7tz7+uQ14rl69O2WpoQgjn2JfpakVo5xAZannkI8ErQ+NDyFYNs5/EE2IaceLPmLoXRHuCwYwQZngfMCcvCB80tFlheMhIslZnHbq+Q+c69J2DoQ4072HCHjs6oO8Omguih3N9zgUhxI7Ngq5MYSniyx5M6oaekst7PyMGSZYlnhoT5jngeIw4jQbzrPsiSmWJTUkxEpMSQnGkCt6oJIxLArcseKvOs1or1UqI8ptQrM7SPf1UxoTRejlUZiG6OVKc1wI7WsXDGeFBPhDL3ZKI6YLN3wZT6OzR/BoWsl8s2/qll7PW4T8dPD5XrjZ5Y5cu5DY+u8fWl2lxX4m/i++091tLfGEnOQYgTiAVils3gsykgoo6TnWCDcpHdGIx1e0G9P0gMbY7h84Vq5cUxi3DhiWzeWH+CrN17oEt4QW11VL7aMsGtHUvvaaaZjLMKt+XfwneLT0izo21rEXFmNTKlGrwmems4dtC8XKZka+ZnqoPmWmhjYvt25u0w41nUpT+Nz16pu1b7p8f/3l4rO8t+LXMWAFIHjyZA1/wfI1F57qFrwa3zlqGXzlDze9X9+Xc81fGxVictNc2+1PS8pfPiTyy/cyWF0+9LlzvJW1q5amz2ae6jaoLryrVGV0c17fQMYnOKIq5C/RUxVtwXcFN5cxAue134V/W9FVqmZXgTlbfBslYRmlVMiIQS/Sdhga2mmstKXgLPVlPxPYeSgIXieQjdHCypK9DHmYehIqCxaBVbifyllU7kPIy5sgEGpojG+imhaYKtlcKRF6u2c1LUtYkrz2nPCgMptQXsaQv+TMiOKZPzS2lnhGgYsnPUcKZsILWLBxcoKECWcUaX5QT6tGQ8G3eD0kgW+8PynHzQZTzHzCl9UH2OJHcmPJ9ssCx70tY6mr+GYzxvsN0X8Qs/i4g9FzWpOrbFuRuTgq34b+K50NKus5FIRKr/bQAEJw8RvLI055tzy7n9VXfoDQnGWanflWwJL+p9eUtIftuSVflPizBxgohLd+4BJu3iEECHCEb5RkGDh1YYh4BzDCjKL0IABsC7xwMA7sADIFhYwCNM7x/wun5M56eP+P08oLpNCH6qPk/ZB2tsYBxwpu7Ds52OTxbysUYglfjnZjndmuYCT5kRdQNZUnp0HJd01NMGE8zgvGqkMhQUULlkAEPA4bdHsNuQN91AiMNYMzC8yqBGKQ6Elwh+Ojgo0Vgg8Ckn+p5lPO2KL8gK5JRRSOOWg3/DL15dlZehywZKEqIfJE392p5dnt3NkMgaDi4+snq3JwfcKH10cLBGpon/NC2t6hthfuRccK61UsIYTmv69Ff5zikw4KDGc5S9pRnGMxJ3vO3cqYsaY43lr+QwOhmRcQ8S3xoEVzKZ0Z0QN71xliMdxanXw2wncO+7+C6Hawb0HeDhI/Z7eCcw2/fA3f7iK4X6+0Ux17c2aixiG6Z+ConBG1AhK/Nm/yt/M9fshXwgknSPR40FFmIAXPwGL0oEqZ5xjxPmKcJx+mE0zji+fiM4+mI07f/Arp/RphPGE8zjscj/CweERL+qBA+ycLXGov9bg/Xdbg73MN1DvvhAJwO2P3xHzHYPe7v3qPvBgzDHbpuwNDvYJ2BcyYrI0pIIkXuSvB7P0suiDAjxIhpUo+O0xExePHaCDOOpyccT4Q//nAPH4DoJwBRYhgSQCnGIcUsREyhUoRQUSuulAuCJLcLQe4DJR5qOucphFTrCaGeUKiTUacY6xp2qgrH1HpVIF/PwsFUMkNyK7D46wQqmwLnvwyu+UWU15OiX6/cINb6mUpLaK68wFjkBZnBRUQ0ERSf4PwzfJwROWD3+CdY+2fY734rodqihpdTazxDBGsNhn4H6giHx/e46x6x399hNzgMXUTfO/Sa8NOoZSAZIGc7LF3WfmvnGldtKO2tVpgEZXpLFOtaK5et9rKAPs1DmY8sV0KCIVgdpuYXVV4NQPZSMAoLE8wy9Z96diwVs0WoliyYSr9Lc5Q/DdXvpvB2GwqQpudf4RSc03R+iQaUyn78OuGKzjSSx79kAq+9l8qyb7z+VlVdWvxLQqCfqFwaEl0Z75dMx0+ucP56a7W02m+8aZqmzokvvmahth16bTsrsXUlg68EXhuK0y+b0lvWu5zrtVJFaOLIZS1EOSD8ZWcdQidhTUXIJvets7DOYeh7DJ16HauXfqqj0JgE1hxvejXjhUSPWiJENuIVodbqIUh4G+ckdFGG7wYwkWCdhKVw1oGdJq9mUq+NCMQA8gbeR1grOS6CjiHLmbOksIXPrFa7kYBIIvhhpHxylHFQFghWcmcRUVdBWZLmIxaBc1R+gSggKc05eOGnvAVblnCrxCB2MBzhY4AliKdIANi5ItTOpLyKOvM6l6vJQxJQL8qMA0nxusoOWD1D9MVaRyOeoEnQH+DDrMZbxRP00+Me//Tvv5F8Gos4+czA8TFiuould8bAUrUfFsK1EmZMZ1x/xxhFKJtCZGvopRSKK8SAGFhzdAIpBFkptTKG8j5MhmJpHy9FKkWYWfs7RfGDVwNUQzGPQ/ofAQ2vw2lOdesxaV6NnHW3Gf5Ffuza6TepvtxnytsRgOZMgVr7G4R//wCwKiLHAPNfPoEmObu0d5j/4yPeT8D/4z8fMZ8+4w+f/wWn0wueP32GnwLCySN6D/hksq/rSQZ9v4PrBux29+i6ndDUzJhOJzFGHEUJ4aeAyEHepKLeIZXAR46gqOd8aRyS94fBCtTphKWwY+3kJaAAhAj84V9+RG9m/Prv3sN2EkLKOofhMKB3A7rf/Rbf/upbfPv+PR4Od+isAzBl4+RmcTJsURpOYUmIBj5aTNFiigYnJkwMRHKIiIjEeoakxFomj7qZdDJqeu2NSOUmhowVujEMZ38daM75DHvq7mayjwu4XCbbFrlFzCHkKgCaZU7M6q3Fi0moeAIZ/WLsWiUZgcOUw+IViJ17msNEoTqsdXNfSANVMIAp7dc0Z2XvGEMgSxLyywJ95zB0Fr014gVYwYr/2eUX6+FtQcVLk/Bz0JBft9yerDpKfOjsEVHvBhJyK1oDPxjEfQczSB6IrutgXQ/rBrhuKJ4Qg8XQM5wjTUKdEs8mZpoEmQmlmNvZQl7Xyl+TB8QvqVwXBCzvv2Vefr5Dc67mmvhLYLc4Q5SYpSESRt9h8gYhBvgUliR4TH7GNE04TSOm+QkhPCPGE4jFE0KsH9QCQs9QsSRRwtDYzPQ4J/khyHTw6GEwoMMOvZUE79Z12QsiJXHPAvpqv6dzGtRSZo7iATF7jxgD5uQJ4UtOiGme8XIEjiPBe4ndyMzZSoiSG6FREEklMXWJ026KMC4JyJAIcMrvpSOdZr9YCRUiI4Ph/HANB6iEYaIyl/JoFZakIlBTvbdvmI1nc5feCgtWHUK7Q28hAN7SNv/08puN0lhn/KXwYmLu3/j6VxGM3tz411ukOi7w5cnn9D9y3GNlaCMDFCOAoC7kDOcNdryDjUYs8HKyRKkr4XHrLToQOtuhU29IEfb4KnwR1Sdbw0VAqXlWdqBmrYvVJ7IFYhlfTdvnmazX/4wSYmnYQAmmbE3X4npSQtAKTilMQtVYFkwlGFrui5CyCHdWORGq+opnx7LflJ+t39uqbzn0rbtnFZrLG+mA3whkVkowIC/eeQ+g83VvjW3LOr1t+TpHWm/HrQsZWpeN1FbNrfB2TTl9faB8dppWN8pJWd261q3VITvX5rn3X0/PLyv+KfBZ2UdX8PCZxvOOqsFu/Syf8ZBY7fvrOOfc+C+iqxU6uH0SL28rzm0vz53opFLICl534a2t50si9VjpXCu4m1qtDejS48aggcvI10UYYowRZXmdc41WvnsL+nXZTVJ6WUIMFvylOCyqwCbRsCrIkecpC1ETrkmheqIqJLLAq6pTksSqLXoFnzI+rSVmV2a+fWQptGqlh4yUBDp5SopyIEZJ5wxQDjljJEFB5SlReR6Y7e6l+UxwN68jNIkrkYR6TOtB7Z6sxXsp/K54YtQKiJh5Jx8iPDGe9g6RLXywOB46eGd1+AbRRESXxs+IPcC2zEpLI2wVeTfqfGaaKtNWnOcmCy0rgZ7QEgm/VW3ke8iheCjnHKloCjXkMmk+l/RR3c1kGc5FqSoKVyB5P5QRaZ+SYHILceh7l2FRur/1TP0uLfq/GAiRJn/WcxYZfN8Bs4WNFtQb7MeIw4vH/MOPGJ+f8PL0hOk0YTrOkox6jjkvMMiKV5V1MMah63boeolUQDCIUQx4JRekz3ur3dW1d8F1mmS73I6vEhma9pOlkouGAUyeYXuD/X6P/TCoItagsx6uDg+1pI9psfeYIH4PBgEGARYBgFcokJIvc4Mwz4+uqra980b27Bw1tCy89QS3+yqfg+rJdEKbernwWmDkkEqLh8oRQ/1Pyc2XQHe5046Mqjw5b+dez6zJLbThkpRRGmEFy8kgMmMMXsL0WgNyDlPXi0FqruOto7h1la+9V737ZZP6heUy/ngjcfUXK7d7RPhZEKvXXBBRCImkODDGwt87vPxqD9s77NTrQeLW79F1e3Rdj67r8Kv3AQ+HqHHsCcY6QX5JKGFqi2hkIWZD+L2aY/pb+bdQNgm8DeCVQy0t0AvVmutkdcsSB3T0Pb57utNwTCNm7zGOoyggTic8vTzh6eUZoD/Bdp/A/gXjKWAcT/CzxzRO2R2zjhdtNG74oMq73bBD10kulcA7fI7fYs8H9P0d+n6Hod/DuV7CnNiuxJ7UswgUZ8egoZgmL54P0zSKV8c8iifEJH2aT8+IwWOcnnE6Ef7ww50m4Z5lXhXhmULnSvdTQnmqE86W+O3ZEjjnhRChI5ToqRm6ooBMiMeiiCdN88eoElQvBHNyXebhsqLgFpixwVASzsCg19R7+TkhEKn5ncqXCcSXlMHPW/6iuPsX0P5fviS4c37vcWbAxd1f0iuKpwNl67uAx+dv8Gv+IF5VqthExVxZZ2FhcXjpwdRjPzxiv7vD0B8w9AZdN8I58ZpQxyb1iDBZ6SnJ6ipBDYsFmfyl0JBJSVEUE4nKl3Mk4yoymAQn0NyoWVjKz1VMbPX+siRm3qAw+UYFR4bEcyvlcKi9IkpOB1pVXVs1FgvetadDG+5ukbAbl+DUl5WFXFUvAudzBrym8ur7q6r6S9GB58ecBWW/WMDzpXjs2sCucUW/dNp9u//XRrN1vxyTdsxJ+bjeRmZ54SuUUt/bQMMloc8ajrW3ORFPG3T5VxjnxfEoLZkXQX7nvDw55FJRqBMBrrMSSrDr4JzLoUZTXHVmBlOEqZIe1/BX8j6goVOts4Aq8CNCtniPLqpCJIUnlRBDgIElhnMOkaN60wXkZMREoBDhgoR7DRl/RyT9CpPEf8/6+xTOCdzSlEofMIkAMcmcE+lQ9vfGenHiPAgUJTSSIYApSFRXQPI9MQDNBxFjFEEuA8Z2YoQQpB6x/DelD/Xp0n4SCmyNuq7EOV2c4Ma4EI4m/i6Fk4TmeWD1Go8Rs58Qg3i9xxjh5xlPhw7/5T98q+GiGFzTEobh9xHjfZC11PkxVQLqzLM0c1ZwfE6mHqLyobovYlVnxaOKgZjUawwgmRy2D0Hqg/Bl6VMVW0DxjNCJM6asd1MjAyBRLCEC0UTNEMgAKy3H6gmTeMUU8kWvcdayJa9Vyo2IN0D6oRVkBca10j7YzDcV+knmIYMAYGcR/vEeLjrsXvY4PI/49v/5f8L/+An/7V//FfPkcXqZwNFIGNIIeK+eLmTgzABnd9jt9hiGHVy3g7MOPkhOmmma4L3HfDoiRI8QZjACyDBMZCWbiyiZF9bpiU1GXvd0w6zo2M2VV/jTXpa56IyBI4OOLJyRsNBzYHx6CXh3N+DD+3f45t07vDvc4/0+4v3hWejwuGyl4lezp48FYBHhMLPFyB0mthhBmADMsPAUEEnPeH6vJijrvjMyhU6VL8A11FEAyOLitgkIl5fylVquvryajTSrcwkUT4isWGSU5O0ofZLbhX9pHBNYzkQK4c2a9yUq7Gd9KCmg06zJkqd8lpsnWUs5m29HwcuX69mqfnPKn1TvFeGVxuDxNJ3wfjhgP3TA3R1+ePwGDx3h/kK//6LlZ+gC/QKG+VOXmxURBUlKISMWHX6QePTWOsR9B7cbRIjaDUq89eg68YbYDwa7Hhh6A2tTMltNjJQFkZW1SRYJLAEprUBIAyZqmoquC+5ez6i/Zlf8ZZisyuBnAwCff7785rP3zo//LadlgXBuLDcvWQ3oAbUkqZAFtwQ1VQgkMmEOXQ7JNHoLH6II8IMkmJrmGeM0YpxGTP4ZAZ/A9gWxm+AREL2XRGLJA4LVuomRGSBDYmmVczxYm5UTkQ2644DeDyrQ0r+cAwJKsMj+j8ygCE2oxvBq2TN7j6CeGyH4nGR7mkdE7zFPI6Jen71B8BEhGlU4phUqyF9gY2XFm5GLnt1E9aKlAaISisJ2U3WSKxuZipZco7OEaNP7BfnXL6RkZ4mZrHF/GQ3njbSMzb8F+5dbrjE0P/vUpbJF2rymXHrnWj++FLP9tJjxrDX0q+pof5+DNLfqdd4aP/trlXPW3o0MgYCza3OmLzUxHzN9rNaBUSyVohLIJjJ2JsBRxBAIFI3mqytMNAGIhvHkPmHGBD8PsO5OaQKJmStR14pFmoCM+jy0uL2xBlSiu1gDqvKDy2gIyBZWMiUFIWbwpA/W00IVkZyVEItFXPFz+rxBMswgVZOWPDaiKKjz9lBmBOvwca0lWbM6qOEF0XI5NwCYfhZ4zZuPNs3dWIq1I+f+tJW092+vd+PdN4LIc2dv7RnyBTA4NXIOiOSq04Jxe/krgdHL+vbrQKiigBbfrrx7Cd7cUlb7+JdRtr1obiuMjSnf2GKrM4QURm757Ntm6PKyL8bzCkR1yViXMxy+3C+uJklYlAuVVrXnFzYu3zZPKfxJ20/KuKLA41SdsUKfJ5q8bbimh5GFP4I2FuG4qNwXhXTM8F+SoKb8bU1tSBlJCUmxbbKwOO2dbDjAUQ2lIpyV38TCFxhOoZcqoZbSxZw7SABqCe2FOa0Je3DujdDFyZpX+BAyUcKESMpUABFkkBN7izJCFAEmmmLty9VaUVpBynRO2Ut6L6N5sQaOpuDYGmcKalWPkRjAiJqvL1R58zxmMD4enFhwzwbHg8W4Fy8NlSpWqw/xhqA13mPtGyfeJF9XHpRlTpIwMerCtDkeREwb8ziUbkBqk1bCxOZUpTnaMGRI4R0LVNpa7MJIcbX3wNBgTQa1K2qmwTglmq6vJdoqzRWVWPxU+MLchL6TTtxlWjw9uNy/eQNVtwpd+/Ac0c0R7tME+/kFx+9+xPz0gvE4w08BflI6U5PYSyQCMQTs3ADnduj7Adb1IKLsARGCJg+PMbdNOUzNijFtp1z3fz4LDNH1SUbpPIeLEbbrjq1VpfyfIYIjA0sESwbGiaK1dzvs9nvshh2GroMzFjbJGlagIZ3JuhhdewkjF5gQImEODD69gMYpy1laOrU+Ufqr2cSvpSoVFgNIii/ZZ5feWNLdDUldFAV5v6f6ajUgN3/l30LhQvuUPSRqnFShqHRdwt5y8UBnFsMxiCGWwJnMMRU+qbq23m/cNvKWUsGoFVGXBSUKBRrBiRwIowpRayUSSOcsjLWYjRE5D1WyZ6q7+lbq8Uuozte9KzBv8c6Fub5Iyi9+r2tZEI/XX1i8vuznlee/Urk9NFMIFb0nVn5hb3H8zR7U2Rx26W7Yo3MdhmEP5xxc36kiYodv7jweDrO43ZADWVc08jnuu2zMJcNeAyJFWytgW2atAgW8ntt/S+WW8d+uaPjrKxk8qoQtslqYqOVOVEF7rUmGEoJz6PDD6Q4+Aj54UUDMk4RimkeM04SX0xGn0xEvL8+I5jt0w4847k44HQLmaUaYPfzsEUPQxExKwCBqAEANTWYNut7JmXEO1km+FDc77H5/h8EdYB46kHFAVkgIgE62Nzn2LQFec1pMwYsSZTzBe49pOkr/pxNCCBinI6L3COoR4f0J0+Tg/Q4xZYmjEr8SESWJfIOa9Vu+bhBZrJKiupun/jIJc0TKiInFVInAxlGejUbTVmXcVojh7PjLgoBJKRkmhkmJBmndv5pjEU18RfBWjyWLHareyQRS7gaDF9TMhtFJux9vPGu3hEVrlI0b99elIKmt6n8uONkSEn8rX1LE2vIWfLdFfC6wpxKrOSSBKl0DeUQESVbNEb/pCH+PHU7+mJPcxyD3EFmScJoZv7/77xjhMfz4f8MdfcB+/w673QHDsEPfRVg3wRrA1KEodBCsDExm0JES43Fm6lLem8KsRznXBLAhmCTMSEJ/rZ70HwKauasFY5klpzWDlWtKzxMUlpgcc1mYVKsJTsXYwlgLyslOKVskghJLmDqWGPBkWcWlnZocIhUq5DEVwUJrYbhc/euH76+RZPpLw5QsSN66t16Ecv0XVJbs97XulRNzy+QvmKQb6v9llVvGuRb4lMLt5VVVWUTytu69tSwVrY0ohdf3mseXfb0wR/XwFzTAUmj/1Qu1f7VQKBVjKq/eJG0yRkJFdA7OinAkC3VE6qOgWulFIsCICroZV4LF6rkmIZ4I1oacvJb1U+bGNniBSfCqNRbRRvUi1NwOkREgIY7meYIhQtc5zdHkAAs4MFi98pIAK1vrIlG6yUuvVsbUE5emUkKpIF+tZ1O/RxThH4AYiiTVsHg8E4v1PjEDxiMywaicwVinceM5GwrrhJYFFQag2UukP1KaKQNoYt2En02m4WMMQAjwcQZigPej5M/zE2JkTH7Csbf4r3//LSYn3iuhC3h5N4GrqdmCYfkkV1tM9kkJIakyQmTGigsNlkIvLRVZgPiJpz0MAMxlv6WaufqV5Yy5HqUTklKLgOKNnmd3XZS4ZLDmh9D9GY3ydYzk9S4GpgxU+U4Kz1ZtK06tJW+wxHOWB9PXNAkyb4lfrzi0ZacXCCzNX1FKSTsxBvSzx7//3/4M8/0LfvjuTxhPJ3z3/WfEOcKPesY8Q/KJeNiuQz8M6IcDhuFe8p92Q25rnmYEP2OaRw3H7IEYYEk8ntikvR1U6WTyeLharxijKjUiiIx8QpQcyeN2E94mknhTVKmwSuFdbyx6YnRGPCJs38OQw+7xA959+w3e3z/gYXeHve1gTZGTJOVty3OkhdXIBWTARJjZYIoGYyBMcwR9/CM6PyFGgxlArMIoE9J2SFCmLKScitdRDTXdT5kQq2BT1WsUUF2dIlHiAinLUN2bgrEpn19AM5c3WWMYRVnBMeVKiUiAIPExpLxOfXbTO8ws/FbifzIcl/C5qIy0yvuc629xLG9tj9LhV5QWdadzq/VXeADNrBv1gicYZ9Ex47BzuNsN2A892FkETYye4OxPSiP8VCX1vblGy0n7i5RbKfefutzuEZG6SwS2hGlvEHYWpnewrkPX93C2Q+c69YLoMewMDjsj4RccY+hrL4gUmkWtTBIizMy/ekgAFTIpxJ125auUrRjMX698yTJ/nX4s93sa3gp4XHjnte1st7G+v25/i5po3rzShzb2bPJ62FJAFOtawhS6IlRmcaf00WKeAwIDPoTsSTAHj3GaME4jTuMJIZ6w2zGIBhjzCIs9whzwKfyIOc6ZVCIyGhURKH6vwpRYUyyuqPpkR5juAuA8XvYj2BjsFeFFjmIsxYLPslsggDkEBI6Y/QwfI6Z5hg8zxllCMU36OY7iCcHzBA5e81moMJKh1jsS39FQ4iUk9JPqQGCMWEyLp4fmkuBE5BEMRWU4NJksNDGdIYkhWxObpK7cRogZZbUKgZwYAE5ESyzwAkKYxdr9rwEgBewK0c1ifabmDRW/mBluXoRGaGhnUCbOm/1XbdEvPUe3PNQ8fwZ2UUPNbzfyWgLvtYXqg7m89pp6vkpvtvtwbe7/coLDcx1rSYlzuGvJk1B94CAMIwMSrgFicTNjwos5YeYjEI/oZoLzA3oCYBnEEs4g5WpohAVEMCPBkUXndui7HZzrSig5q3GIqTCGhgrMlk9hcoRh0zASdTgmXhLj64EmwUQ9WwksZGOH+h6QhT+1EmJlUbZQQoAqb4g6VF0KXVnDKCTapgiaFiROvWp1c6su3LIda8vFZd1blt/XzoPA8NsAW7H6XnUANTPYrkIrZDjX1nmm5LZDuvaMuOWd1Pa5ls+13QDp62TOW8qNsOmnafpWwLiQDl159lrfqPq3beO2cb0enN/6xtZzFTyp4FS7zytlxE+Ga9YV1+tX7/GtdW3PwMbcbwGrRFxVJtvXztJXLdrX2uMtFVLBWTGKKzyogHYVYBtq4GXeewkQU4NRCz7ZmA8CqVTLgKgYQ6V47ZxkOHUiaCD3oYSREsFwjJLUNhsP+IBgxRrbEBANCe8RNQ9DElrVddea7jSuttPXD1VDlypCptabMXIEYhSDJgjzwhpsP8YIMraWv6G25V0XqSPr7vUdIc3TPEo/svcIS5viqe4R/QyOQYwqOGRPiB/vB7zsDF72Ad6KMC9ajWVfOcZkW6RG6IfSalz2nNffq3GmYREAY2X+UhMmb98SMislypaQQYme4HI+F+sm844cWmxrRuuJlPBQixBxRCV8ZhIqCpenv9QDJq9Ly3slIXkjGK5AR82LNcc1Ewypb+kTMKzMcObZ6rNaMAVzhInA+5cI5yOm8QgzTjj+4Xvw5yOePz5hGmecXkbEAHCQN41GKnBdh67r0A+SkLrrOs2roIYxAGKcEaOXfV15EYgCU+ht2ThWzjgvdgXrqLjQJ0Kz1t5KyHz2GqptrGoifnUNEo1rVPFqIEmxjy8TzGDxcHfA/rDHbhjQd514SxTslGe4pZFpNQ5R+olMZY4RUyxnPTAQdA/H3L9MyK9Kk2j5hiL0dTlTWzRwrosL3VArIZZOIKY+77kbRRmRM5fn67WStmoxrXkzXM7VZpTJUiXrXoiAhtOD6jHaFpLHVVZIaBbw1YxuTjE3fSnlzHxz/bVMCDFXef7qrVdNml5MPKCBhbMkXhHGAI7AHcPZNPM/B6HwhvJKujuP4lZhQg0MF1Nwnpa//YWtXpQ+3tbFLy03KyIAACTIy/eEl18PMJ1Dv9/B2k7i1tsOfb9D1/Xodzu8v2d8uPcw1qtVQkpIXRN9RnNBEFJyWQBZEVE2b7kunxc6efH+38q6tJv1r1LrWBUGNj0gsjVt9cnMCNHgh+MDfLBZ6xwy4azxQsMMHzzG6YTZexzHE07jCc8vT3h3T/iH3TcI8V2Onx7niP9q/nc802cQCFb3O7MBccoRIRZK1jkVzjlJdpVcwYkQe+D5dxNOFhgH4HECHl4eYWJEiB4MA5CF+msi6Dgn7+E1GbWPHqfpJP0fj9kzIoQZp+MRMXgYfwRiRIgTJt/D+xnMLvMlhsStW8YgRC8BYCOIPqW+MwbqupqyOIgrdhI2AoBhzS+TBJYAkneEMFpi/ZEYQKNaD6G/OKV/EF6AS64JIgKp33IKgyK0eGYJ5d+amVxQcNQ8mzxOqvv5VvUc5zttvW8orzl6m21wmwSzqbei8jfZuoWV0dlGtzSON5Ta0ueXWv7a8AZVcTJa5UJdeLFkNdMnz6c40Qk2xhjxQkf80H8ETz+iD5+xH++xOz2gpx8Qhid4HxBDzDklUiNGicrh1KE3FvvdPfa7O3Hx7oWpcc7DGiMeESmXglGGRBkXYWBKvooYI2KKgR285KUIKaRCivW83F9bHg3p3BfmtJrAwrQ2DNbW3Cujk/MzUA6zR+oNUTwgXJMDKysmFsKtasm229T1awZVw7/lPWzBlHaWVgJ5JXzPwaKF7nWjk1RVfwMz84VlIU77uWjnV5WMIs4Q/n/d5QzT84XlltpuF0n8AssSl5YblbjnZ+hGLbBbgJVL9Mi1+5dafNteubbSt9ZJ1V+Bf4KPUn6zAk+NMSKEMzYLcZHoKdqAx1lwsMH1M0uSXMi8Ww1xLK+pwp1ScmfdAxWJaQzBOAlhYazN/HGIAfDATB6GDKbOg4yBs17od5NwhNapeDYFes9D0PHHlK14Aegrsd6FZUiCP90gFBWXSw0iJha+wEQrPESMIM2VQYmWyELYJBqsBIpnVpUrUaXoO5RuSPwcEs8nuSCCn+FnMcbyYUSMAT7MOHUO//S7b3E8GDw/jojG5zXMQtw8b5TrTkqImNZP+19o39qT5HwR2oDR7YLITqjQSMjiVVZ6ScYTJoIfbSUmLitVC7pNJZQuLEFF+zedY4DbQLrVnSJQpSihhA0rz0dFHVD+0fdYZDuc+JKKrkH9HCplh0623i+K3IRUhYY16XplpZFotDTxMQYYH/D3/9cT9n8+4Q9//BeMxyN+//2PCLPH6Sh5HI+nSfpmDJzrcNgPGIYd7g6P6PoB+90hr7tX3lm8HyKCnzUUU1SP36gKOFVMaQZ2QgcgIvBcrVeix5BDqmVPqyQX0/UHQ/Jv3IAEM9TT/UtkgCgwT5QMQJwjPo0Bdx/u8P7DB7x//x6Pd/fYdz16MrB5L3G7B5oOkPYvjYEwh4jJexxni2mOMCEiBsYcGTMDgYDsxZsTidSYoh5jBYNvGG/zb/NqOhRFVZlL2ke1Ekj/DLDK98UAKHI+38kqqlYRZPUEVW/lfbyorFKKpJ7FijeLMYVvi8h562s4qXkkxEi16lN20dhos+nKNSivPeO6h2X/JkUjqIIa+ZpOAkH4H/Ugd0RwnUHfOXTWod8Z7A5RQvfn2f95aKJfVvnScf/y5+1mRcTxXrwWrHNA7+CGPWzXoet22A0O7x96WCuaYmctup5wGEiFq8KQ50SKZmF9YkRk2cR0BjXICygEY1t+PjbkLQL6W63uzlqyfpX90zLqbZ1f3sBmHyuacQlr6eK54AtLur5Rzy9XwJSrazEyRt/BByMJyRRIi3VOQIiEcfIixI+1ha0me45BPQo8TuMJkSf0nQdRgCHC3nZQNTUoCmFADDzEdxArCXGr+5G+x0wniHUJMmNgs2AquQ5XhBhF7OwzYDyYOsx2xKfDZ1hj4Do5U9akpHKUXfbsZGEmwuwnhBgwjRqS6SQKiHk6IgQPP53EPdTPSFYKHCd05jMid/DxDszqQsdCXhRrCvEmiQwEljibDIANq3BSLV502ZIFTkrqZ1QLkM+9MSCmJomYeHxEkCogKBGhxIgaXimqwjLbFxNAyeHSJJavEKJLoqYmUIrVcgt7Vu9lYRu1t/I/jJOZxGVeyz4OEFLua5U2LE9xga6t06s+1tZqZw/g+nC2p67iaAhXAVRDCG7AwqWAfLvNBENkvJdje76lbLb2RWVZw/mR3VZTsxtpcZcS8035aj3vNUkLqGyg2r/ZOrJW1IIROMJHD0BiJ3f9CY+G4GiW3Dcp7m0WFgCRIp66T5hpwunUwdk7dO6Azu3gXI++t7gbjti5CGPWYaVq5l3S6rQhmVKbHKVPYA9CVIa1TlYtY1ueY1p85utUYAeAKtSBwpMVIisKv8Tommw5K8oHGKe/k8enxvZOioP0XzbAMGUtmhNanZ8NrUoTSgOVYoPrt5tLud+ZfyDBW8XCkM8fA8JiQ5575nZRKjffLr9Vw4wV30QC2wpoquHjsp51O+fP7SWS5RXw4uLx/wLAtqUwf0vhxDxWv4H22heV18Da6y1uP1Gg35Wd9ApIv1VbgbfL68vjsdWOoOYaJ9Li+UsjaBD8jWXZ35b2SXc2vSOa96oaaaHkXlMLi24muLKenUIf3DaK8vZtcyH5eox6IxciM5GoJuVocwTrCCYkWG3AlQl8pjOZkHIAIcHxFYguOKVYL5e1NmRgTfFCCxyz9Ss4CVA1N0AehSq885nkHCc8RoIPFrP3sMZiChFkBNcaQ7AmzVONXTLxWwLEUBH+CN/O6p8sgmYDsWpOfBZhIfDSfgFGY5/ovZhydKinRxQBNrOmxc7eEQUHJt4G+jynMWjspeQ5ydoHRaHwUaytQ1QvaQ6gOCP6E/x8xGd8j9mdMPMItgHBewQwPt3vMO4sXg4e82DBxHBxxv34SY2oZM5yMmwdavH4YBz7AadhB/HazBgVHAgcTd4TWzvWcsDD6SO66DGcxNPcGlKFkoa1UuVHQISPjBAYz26Hz8M9NIImWL2PYt3JRVkZFTAa+rq9xZp0WtecdD9Qei95Tsh7ooxIp1NpMQKSV9TSEx7Kt1D2alhAuQpEbp94015UJVjnO5hAuD8eYecZfp5Bs8fxX3/E9PGE5x8+YxpHPD0dEbzHOOreJAvrHPb7A/qux/5wL0a2/R7WOjAbzelSGcok+jT3kZDILKShU/nMpBSV9YLu/KKYSV4UnM8fGni0ARMTwEhKigbGF8KQCLCSBA6fPj0DtkN3/4Dd3R6Hww67neR67Ttg6Cc4ExRemExntXuEmr+THzDNHcLcIU4GeDmCZo8xRHgwTmDMOqLsKbJJe1YZKUnWOgm7k7K22RhVocVnrm+7mYafqVpQuYPIHzJ0jKyykZoA5aqutMbU7Ohqy+s88qrddB7AorblUmXZT3VDXP1lWMrI4Z9iuZ7GBYVN4DOT10xMRmQbz+u1kjxD6l4BuLTxZQYzfaFh3frOwQ4djrsd4Hq4lAclnZQUwutSX/O+SC1mLHlhfF+zbEH1skFvpdg2e3uFqFxTjFeYtbIJN5v5uWbsZkXEx293MNZit5MQC7vhAGsdhn6HxzuLf/iNWAA6K4JEYwOscbCmB6wFWZsJzRQbObmZUU0QLueLti18/1aW5Syrc8NzG29W8PS1ZWMJzxIUZ7u1CcCqxxsgRxUCKcxMUjjEyHgeB7xMPbwK0FJojxC8fo5ZAFcEX5xzQ4zjCB88juOI/S7i74dHsGEEeyfu0Kqw4FCseb6Nv8UH/o3WG+DN/xs/0ggHq0SAxOdMyamt1XjiCniZGdbMeLCf4GmPIw44DoB3UeOdClFqDEHSraWQUxEPL3fYnzpJSu29KB78jPH0IqGZxiNiCPB+EmvmMDeCmcH9ET7cYfJ3uS9EUCYICGBVJCRWwSBShGFCjMgWKGWJKCswjGoasicDSu4MkLjAEiKInBClaa5UcGnERESUm5EWGnP9loBJqCyFq77kLScUpzKjpBZvxWKtekQ/EwNJzZ5t2tS3fuw/42RP8jwb/Gr+Bj33zbysjxhV3y7BPdF6ldw6yEKBfBRSd88oObf7sH3osxt3fZBvgA/JtlPgiZJN9bzVBLKe3+3ecvXv2/EBnfl+Femffehrl/O9ugQil/dqEMv1Vk0WPlwYmZzrOTJiFLgZweJRBQ9ED8cRu90Tfm0mTKcT5smDNe+NMF9Sb6SA7/b/iqMZgeN/xD1+jaH/BrvhDsNwwGEAvtl/grOAdYUmyPtW/0thmJJlYYxceUTM4DgDQWI7I3oAHsSSS6I2/yvM3HrOCoNS0R+gxXmh4oqdiWzOdYucSmGMTYoHB2giQ4FbLntKYBWmyWTlZLZ+zaGuiqKmoZEyrKuhVMk7sb0jypg3z1DmTc8xglUNaXMxnzmKhdFdXlrv6UVDW1WeOe6bVWqfajaysl89U8/5g33tyK/Cel55PtMni9rfQuO2xiu3imO3e9TSZ4W4uq2uLwGMX0CjfuEz3Iz8lS3S4vpGNRfZ+kXTvCK4zzOQy/N783rT5XPQ1H9m/eV3rPpODW5fNYm0M1e77FoPfoJCAFmQCUI/wyjtKWNw1iL2Fq43cNFgDolHddAsC1XvK/irsXpM8iJYNIlKjZDGlxTdTkOQGrXollyMnPM2mKwa8EDusSq7ycqsRpbwqmowBE8wkwXIAi5AlC6M3unX3LGEx8ReJ2MSIvF+ziGTbc7jxJQEXAEaIETpTV2zyjOy7BWdq2Q8xEZ3hAGxy/guKyGSkUE0CCRjTgYKMQqPIbZMItRnACHRLdFkGmKOBB+N9CkyOHogjgjTZ/jjM348/BEv/Uv2qIyR4Z3Dv/yHDxiHAYDXP6CfTviHp/+OjoXOIIhhlIrT1Mpddwgzfv/uV/jDnfJ+HJOdGhCF/uecZKLaJlpXFwP+8eW/48AR8ekRDAngIx6XNr8QERE4hREGfnwXcXx/jzgCYdL9hGpPsgpDG8SZvMYFT4ossbxThJXpNRGCp3NNTIi6fzgSYNrwTFH9IiRnh8BJ+dAQvnXy93SPAVFc6SlhLMJfVaWSDxW6KD3IIA7oThbDyeC3/8efsPvzRzw/PWGeZnz/6QXzNOP5+Yh59ng6vSCEiNmL7Oru7gH9cMA3H36LYRhwd3jICrqSiBoIHoVeTR4PjByaJukD5I/axLWGxXhRLf2Sx04eg2EwqRxDQ6GSTkoxZZE1I6SjRnmPsNHfW+SeeiP3TIgz4/fffUR3f8Df/7u/x903j3h8eMDD3R12fY99H3A3PGu1kv9RFkz4/8JTJzWlQWSD59M9nscD5qkDTwA9fw8znXCMHqcIPAGVqR7UbartbF7Vih5O8GSFMvPgWtqqUMqM0vXqd54YRqMQSDS/ksQCBqkoHggtaE9t5Crkdwpc1lKmcoZTh8ruLX1MufFkSyW8UPc3PajrkJURsf2L9TOtwniTyuDqI28nrq4nPjKds+o9SkR8oWHS8wYWYJJzTwCMwA82gHOE+8HB7vf4eP+AODi8N5rDJiu+MmOnQ9igFbTtTMvmyzd48/0khRbfX98LquZws1puL6+5kkttLlf/55+lmxURv/vVDoYMht0AZx363sFah66z2A9GPB9UmFqSNUr8+2TinJnvbH14jpimrYtnyhYkWtD0V8oZOd1Z4vo1ZVnHssos32uALPB6dnKz9be/+bX24oZMYrPUfNeCyVtbMibEJPNWu8TOscMcBhVaSfiiGCNOsySc9sFrIlaPyOKeG2OEV0F8iCETvMwBXedhCOg7D2sjjAnYWQnhFDWXAlCseKpey2fmLw0+8K+xwyH33SjRQDAw0cBSB2sNutgjuoAX9wQgWUF4DHhC5B0COyXIJXdCjAaeIwJYPToiTvYFce/hO3ERnf0I9hGHYQcXLcK8AyMi+kHa4KCfhYkIocPLKAwHEWE2I472iBh2mOd7eDaI0ck5V+8lkcWbnHi6Znu6ycJG0lBLyIqYTFoYYb1s1HlRZiMRtzmpff4dK+E/Ve0XsiN5WyVp4ugmsS5Y7DFQS7Asb3PzxcNg0s2YXwfzDuJqK6t2iid4ZWSICZ/4Myzbxf5Gw9SDPUAnEByYdm1PaP1StszTe7s4wLErlHuyOlLrpaM9qVO8kPn7sMtWTucKKWNad2P1RiY86veU4UgEQAF2Mm35bJSzki3HznXmrPDzbO/PPp77gDN1bsuBcr3rhy89Wc9fS0GsxDMZuC1qvjSQtAm3+pdcnau2M82evJi0uRgjJkx4ohdM9AQXjxLvloP8aWikpHxokimrV4A9Ar1xcN0B+36PvuvRuZQbQtzyi1Vo6+GSjXm0U5y9tIJ6s3nxhlA4V7Qo1aipJdoaC9/VXBeL2GIUUa8Z5fVoroGzgtOkPBApKXVSEqswJ1viJhpIQzmlEB3NUm54EeQ+V2esuNdTHsOt5WsYdnAF9/Lvuo18A8sva4L6amOv799mNV+DqKmqWCX+wzUosHymhe0ra/JX9ne5qrfmOqvzap2r66csa0+5JcS88v4b233VPtxspNrkb+lEQYf6e3FoltqKLyk1/n4NsEjvbP6qdvKZOmVvFeJ+65Qs1/9y/97AxCeYrora5Lm2fxSedXqO8FNUntXBalg9Q17lPFEFQppfoNScP1YhEiuatJ6LlLOunPdCbQrKEzP+GKMY9mTYLlQUSTB31J7GSXGveXRhTApfmP4kwXWMJDkEqDIsSXhEu1zna0xW/3U0D1aBWFIMNN+Vlohb8ERpPdJ8ES0FlL5QjseeBGwmRlCI4oHJhEhWhLlGFQ6ckn2n5L/JeCFgd+/wcG/hpxFhGvHp9AOmMCJ0n8HjCXfGoqNdFa4XCMYA4wTvY3Me++BxF+7glOYgEkvy5J0CgnpniOD4V9Me3SePU3zCFI94OjxiHHZgKx4dMVgsmBAQANsFWHhY7AGOeR2sGkiVsErpDUZSEN1PE/7uuz/jczfgaXfA7A04FNrOZP7l0hniwjrkZgpcTrs8V6PdEbWB7IWoAsOYFH2kQsREcOu7mSxtCV8gn4vF5XquKpot9xvQdRQDmXefJtw9z6BPEXSMePr9n3D8/IzjywnTPOPp8wvmyePleEII4rlijMPjwwP6vsfjwzv0/Q6HgxjdAqpwCKwhvELOXcb5cLze7rp+o4CXxDnh8nIhnauKXanmuaVriyELgbNBTDQEWIO+GzDs9jjc3+Nwd4f9bo/D3uF+mDHYpC7gzG6UBkz1o+IwGAgwiEzwbOChYVeRvJyq+Wpw4NaAKzzC+dLrSo2uFSAVAS+fa7aMmRkMgyQO30rBfFOnclO8uFApVvhCnzb7uGi6AOuKj+RtUiWjpLaxhv6k6m51nalSQgBX6aA07uTxI3wTwaZw5MZg6Ai0J1GcVzzPVlkamq26WMkcbuje5X6fe7lp/pYWzu3xNV3V3l3XXXs31a9uUGhn+rL1QkUrbr7xlWjSqtysiPj3v9nDGIOu72GNQdcLEecsYKyBs0K8WZtiIxflBMiIG16tjEgW00kjnmm2JRasAOzVcvuTv8SyVkb8GyuZgK8u0ZoxqeNGLpNRn6YOL/4e3vscSzwRDSHO6hEhcUBjDBgn8QiY/SgKCe9FIRECXMf4VfcIB4NoolgmUFTCt7hhJi8EtHBb+geSPBCw+A3+ISuja/hpIgFEsOxAhuC8w6l7xnF4RiSGMQxLMwZ8xMQez76HMRYBhWGYY4BPQjtmuP572P45C+1MDEAk/Pbjf8JhfgDvOCM7BnKs2NWSFIoPH/sn/PPhv+H0/AGfv+9wCh1OIfWhZsCiyv0rgMaEwwg4b7J1FVFc0DMaQz0q0ZEVDSEjrRRPkKAhT6oJr4Vz2WVe+09kwIbxsX+Cdz6vzXL7pW+0fQMAwfELOrxgMURM9IhoduVCNoOS8qOZN+e4LoZn9PwRET1m866BiWdhg47RgPB+fsQ+7FCCyxThaqSIj90nTCT96GIHG5woRy6UzAgnprjkDi/HVTd0PXOJHmZlltoDUogFQlFW8PKsb/bnCiJsXmpxQkMzUQlTxxuoY6PLqzrau5fRftqbTe94se/oXIO3xGZe485cVR4frdYoJUBLYZCOdMKP3Sdg+owuPMHzjFk9vgJqZUQoghWIdRWTQT926EyP4fCI3e4eQz+gcz2c62CshGLIYZlW85EUy+oVECNi8AjRI4QZMXj5i0EYwIrSLqTmWhBi6h+JSVOmLJMcBdTls8P19aYK9UQianM/GAtrnIaiTIqHFkYmYwzpGFV9X7ZRlIj5mv6uP0v+nbqX54jdr1XeVvfP5x7905afI49WCr9xQ29+8r5cLl+HZr19vL+0chkzXH27woWlPt74/sbyhUqIjQqrz0rScfUdxqXx/BTrvwxdaUwReNx/MLh7D/zwTzPCJFbQzjKcdXDWgcykzh+iiMhWz6iTBteFK3iccBsBjUyIGxiY8wvpvHBkBCIEHzQkj2nHAPGSKLQ29L2YLacFF82wxiE4j2ANQrAIhmCj5KVLCpXi1SdKCCYJ4RRTmMGQ8lcobmaoAYLg3px7QdmfFKpxRWctcXItPBPCr6GekmDXhghLATx7CTtloLHyZQyexRs9JF5MjSU4etwfLH71dxYvn3/E8fkz/kxPmEMPNgzaGTyEg76DPEYA+M0IgAIMOb0eAbaI+LXSBsKXOFXYiBc7oJoIMAOPnuA/A99Pf8TH+fcIv7EYd3vYLogh0MnkdsuwGa4P6CmCQwcfIzpLZR+AigIJrIoZMQIjItjTjOFlRvfNHaZ3e1Fm+Rxsq25oLSphgCmuaMP2XaHjYwp7i0qJBY3AlayxTfICEmUEpz1bt1uDgyXtXRNl6XtlhZ4E64ZSWC5pN2qUg+A97v7rD/j2//cZT0+fME4nfBxH+BAwjjP8HPD09IJ59jidxKhspyGYPnzzK+z3e3z48AHWdrC2AzMk/0OQvIs5N9mWFPhmZQQDK3hXC6P1kYQfLlRacpFwnj1qppCy1xMRwTByOOhoDMg6DDuH/d0dHh4f8PDwgLu7Ax72Dg+7sYTY0n+KvLLGBfVaEZjFM8LDwMNiRsppUhQSrPOVy4qOLVORErC32/aGma66RVrZJiY6K/yvV1nhXQHtpT9lgi73a1NJIP+WEE1o5vs89qw2C1djqO9nhXEFYZnb18HNWBo8nI4dLce1lBlVDy4O9RpVyn1jJDS5sxbGEoyx2O8MugNgs/PXNZrlp+Z1bmn+tXTVss/r928Z1aanxE9cfoo2b1ZE9F0PIkLvOgnB5BwMWREuGJuVDsZqLoiUgDorHCpPiBTjkSrosFyHSnCyVbboVUpQZn3n4tgWir9XE8NfQjtzfXaBShlxrtKtifq5yjkGQu/y1Uc33r1ygCvgntpIwi8Gw8cOU9jlhGTjbCUvglrt+jAjhIBZQyzN84QQPMZ5RPQB/UsPEw1wmBHtDGsUcEeGMwbRB3gS17Y6ZnmMiRCPqIVxq3lhZJfUdK0RbNWCqTSPAFzs8e34O2BiTVxtYaxBRId31OHkjnhWV0mAsB932E8HSM6GiB6PsNiDOeSkbcSADZ0K+2LlYX8NaYqAdPB7/Or4D5hCj8cd4GPEHOc0DBGMVQNrGCgGLIk3RONeqWANChtCtHgZNS8FqcSbGN7MGN1YmLxl/Ylg1fkMPABsqwmXxZi8X1i1lWIQ4Wiq+t+sZvXdI2aH0uo6vQBhwrmy4js2nxFhL2ME4sfm6ZqVi9QhUl/uKkP7iZ/xglNG3nmOdPxjmBBJGAnmGT/ik1h0bRQXHfZxABKjnLZoRQy2oWMW49u6t/ncmthIDP364csxFtu20od8qRldkBJjNY5Z4YHqXu5T+lWYottgnbR1GbfwCh/U93J83rYH7TNAJoq2aKMm90EmXoEUii6EgIATiD+C4wkcI+6tx8Ey7j3BR69eZkEFE0KMRkR8dN/hRCccTw6dfcSuF6uqoR/Q9z1616GzGlaOypkv3VdmKiWoDhEhBvHI8KqEiOVPYFtyNU42Vgyiyv0a7Rq3Hg/IZEjZz+u5r3dAOU7Fs4HIZgWpUY8I6O9sXZqUqCR/MCkMXFnJxJRt7ZE6h0XxgqBGGftVZIxXy4INOrOdW1rgBuZs493leM4eHWrncVWfXj/H0BT4sGa+rpXlmAojt35yq9ImR8pm584v6mspv819pW1c3TpXiNylAnmznatNXF6/zTq3Sa/by9WOveZQrffh+Zld7BtaTnGFbDN+Svv4baUVaH+tcvnstd4OhMZ8cpNmvnIezsDGq70kzatgjCgcHBC95jHTsCjGOlgArhvQhQBrDWIOixKykU8SQOV6NXwEcoJrxSOGmv2ZZT+REY1aimcrarkZIwMkFtcxEOA6baicVbGxKZg84W/BxQQij2D1LwQZp4tFgcAGphpDQ8M0CvMFvaOCruwFEfV7TAoJpSMUj0tIXqk84UoDwZus9EwrrgI4xZGMYhvlg+J0ExBAiLPyXRA6ZJxHmIHR3XuMPMNTwAvNeDYRv589/r//PGMeJwR/wsk7ACMCZrALojeoFijmISYBW4SNjIfThEiEp53NYYiGEPFuDrDGAGxwdITnnrCbI+6mJKg32NtHoRGmPb75FPDiP2HChE+7bzF3+7I/AZjo8eG7z9j7CRRbS2MiCatUb/Vihy7nKhr1momAfQlwMAg9I3hCjCXIV9pGQt4uhWFcfU/f0tnFdhEWMdV85qGtUtGiuYIELzLLUtE8i2Y5yv5QA7zHjyPufxgxTROCnxD/x0f8+MMLjsdnTPOE4/EEP3ucxllDKQvt9vj4Hs51eHz3Hn0/4P27b+D6Hs4OYADzNIvSS40UY0hGMDGfycagKU8Kr8DVisupAH86V1IPt2fv3AxWrEtTNwHJU17N8lDz52nfM4BABtZZDPf3ODw84PHxHR4eHnHYHdD3BGMkDxtizE56RILzy56SOUjB7sCSV8ezgWeHERYTAmYuUYIyJ3crD5VgUn0ucLtQlBafud1aftNUta5X419U424VNOtX+OzPbfyWPiq8wGvaqIx7G6fz8t9qX5Z8FnpfH7i0DGtInVpMSqnzhFiZbyobVdfSGoMIxud5xN72Ilc2Tr3KqeC5PC/nStv7lUzyrcxRpfy8WNaTf/4ZXl44/2AGiRe2eHMGFm0sWzjDAbzmhdxmeeT8Hr+13KyI6LoOhgw616sHRC8eEaqIMBqSiYzNls05lAoZCPUEZA13jXeawVeIsDpBDbo8s6lep5zYKstEznUdV3mxrR5dbKt5Mu0DOsMwXmG2v0Z5qzXSlylilLk6J3Wgdk2WHhCTd3ia77PiQbwgpvzdB48QxYpBrCGO8N7jOB4RfcTd8z0GOOBuhrG9eiyw5txiIEhCMNY+tcR3SaS6gPZaKBP0LfZrfxbhGCF5CLnY49vj3ylTQ1mIBRJk/8PuhNl9nyv6MP0OH57vAXUhT/3KjE6y0ohRLVoKZD/L6FM5fczA4A/4tT/IeeiqsVT9r4a+LvvCTK0IMr1ymi3+6fsdQqzdPYGjnXAcPhUOKc1XTcxoXxiEY9zDc19RH8WaH7FaAyo9NxTQ07Mk4kOl6NiAN2F1BZCQTZfLmsxfl5BHN+WHl+fD44ApjZ4IFACQwQSveaCqOa6FryHVRQACJjufxdG7eQ87lzj+6TMdjZVwtCr1ulAiuDcK0fL50tf23EgxW/B8IVxer9uC2UpEU97g3PahehTgatwbioIbYR8ByQik7WOqZlEvL7UIG8ToVknDavqWJpLRmnImhkD/IktouogTLJ4QYkDgiEcD/Ee7w+hHTH4UWKtxlXN4Bor4ofsTnu0L3PN/xEC/xn73iP1wwDAM6PtBQzTNaoml4dWqYebwDjEpI4J4Q/gZIcwIYdJPUULEGCCJtBM8Y11brvZVmZniYdCuQQUi2m1KZR+W6+UsJOFWSk5trMTTpmyMUTwliFSZnK9LzbUV8FKfnc92PmeUx1AUsuU7LfZr6utPZmW+xZusnilM9s11tq/+4sql+Xxtl9MUrqncDXj0hrqvdYqRwOGXTfbZniZB9IVnV+FLz/VlgTy/yvY4Z8l29nIazxma6czLW8/TYjxrZUS6uUIOi0det0+ap6+9e26vNziGFhfKO/Xbhf9eAOczbax6xgDOGE3cVFRpICECAYQgVuCkmRdsB0sGXdcjhABrjwB5ADF74NVGLAmX5BCjphqa5g/gaq+mvGJMrOGLYrX3WXGwGj2FgGhs1RIjkVGk1uWN8ZIaYomexMBbD+cCgg8IXUmkG9nAZClvGUnBKYWuS/UXvFSEbjWPkb0ilIZgTYqa1Cspmr1ROUCioziPrQr5k2kRgCLDBw07ZQmGhReL7DH5I2Y/4eXlM7r7Cd3wEd4YUPceH13EnwaAOAAhIhogug6MgBhPQMfZQzSdV05tgxEi6XpE9HPAMJ0QnMGfhwOieig8TAHvxhlgAzYGJ9vhT3vCB2bcn3zep3v7gJ19xPuZwDPwp/Ff8Dn+CP93Bzz3HcqpYHTjhHcfn9D7oAnMCzQxaX3a7Zz9Dcio3wET2Efw0wn2boDpgRgdEBa0YVM407qZTtSE0Quyp30HxYuFytsbz1L1d6mkkWoLnPZ74iHqthkci2eu9x7uXz7i/f/rO4zjCdM0YTyNeJlnHMcR3nvNBTHjNM6IEdjv7tB3PR4f32O/P+DXv/4d+r7Hbr8HweQICdM8Fg+InOg35i6n3Hwx0zoVXZ0OSzPMlu7NgsQNhJ3hQ+bhNzDpcnp1qiTPPeUMNSY91NBkjGAIZByGu3scHh7x+Pgejw+POOwPGPoIQ6HBk6yLYhIsAol3j7ZHGr4oRkJkB48OEyxGAJ7T6hWYdk52siwypoIDL+P/Cm9u4V4stlP1uUJLqhFLs5by92T4pYpXVLCcNsd0rjflRoMvtY52W1DeLw0KvkIyrbfWmi6vyfltMNF2cEW3njneDdyhMgbxJrMIHPDkJzhy6JyDs8ofLc5J2//bymv1DytSpOYR89a70olbwNzFTiwf5PU71+ah2Rznm+azd9LlK8zDVyq3e0S4HmQMXJc8Ijol6joRklqnAlMVXFHZTABWgPJ6qY/F4g7fHsJoRXO9sc2/ldsLb5ybL6mshp1JCTBHh5Pfw0creR80XIivY6PGAK8KiGkaMXuPl9MLpumE3S5gcAZMnzCzhWGP6GPTrjaZGm6UDjHnhGgZictFgVojEKOsm6snLVk4pWA3FCU5MSDJfbqxxzfxN7mPw3xACL7qS9VnKGWPCvFkAudsN9fC0TQbKZYrGDC1O31lrb7J4FPhNrDcI6xkqMc3d5/BKZkuCdqazAmPnQg8CwGWEFWFLPTfOR4R41SZDVFzfzlWMkKwDUatXIyQ2bJWNRBZj6uZwmbf1M9EPO0+wtvr4ZkAYB57vHx+kLnepO6PsPD5V6uQISUSJLNIhEFPp2YcW6vDcPAY8jMxRnhTe7yUuokMBt+jD11mWBf27dX+TvteLzYMVaVMSberHlJ5UX8rCUjV24S2ZTpzHUDJ1rg4i/l++3zyTiNKDuYVjlhtpcW71XehIeVMJuHz1tOF+D1PozMvzvKiDyv8mJe9YkIUlpZk0BEjj/jRfcIYT6oUUM+EGBE4qCdCKOEXkuWjEebDHAk9LHb2Drv9AZ3boXOigOg7yRFhbBTaoJ4YquAdR8QoymMJxTSJR0ScwdHLX/aEUGUIikKYaiCczm5eR1R6zLKGS4VIeg4pBMHqnjxvjEUJyWRgTEpWLUoHMkuFRCKukzdDZUmXuRCuFmyxp6k6Kxt/9Ti/rBQW42+lLV+m1NF5XSzR16E6lzWsoM/ZVmqm9lo5Ry5cNChZKl3P9mQbpm0g07/+okKFejC3b61Lq7V9b6Xwv1bN5kMbHaStfi/GdbWPN8KbinZ8dVH4Kd77khiTIyFyACMInU0W1hD6YQAzox96eG/ASRGRwrCmZJwJJmvOBqu0JnNUQXetbFdhHSclBAMk1ESdFyh5XfgQQST57BIbXQs3kyJAK8j5miJHhGhgfJRQMhpOJnlws3pcJGvpdBZlOxaFd1F6m0rgrePTf7OxUxRDrTS+4lGQsJkmNUYShpqMJzNupPSpO5QjOAAjRhCA2UfEOGMaP+F0GPHjb2fMcca0OwIYgU8v4snSB8zOYPIVjQHWPK5Ct5Beqo370tZisBpZMJgDphjx3Y4AQwisXuSGcDLAH/cp/KLBZBkxRDxZgPcGQcNR58XTtNYD/QrDfEB/7DHNHlmgzREIAV1ggIM+LwvOBATtt23o97VVNIixnz0+xGd87iOO+x2o8zAmAt5lI6zVKWKh6fNhaSBF2ihUFjX1Q8F7k582Vclp34qXar6Z31/QOKtfqRlG5CDJwDnCegs3WuyeJuz+/BHzNGGeJ7jff8Knj59wPJ0wjiNOpxHT5DHPHj5ElUt0eP/uEa7r8e7xG/RDj4eHR3Rdj2HYgYzBNHkJkZbzSYYs1KB8Wqjsf5b8IrJctXJxXXKYMtKE66ismRfEfp6xBY1Yql9i0rQrKP9uvqWtqMCEQGI0vN9JouBv3uPhm29w//CAw+EOvevgjM/rwBWPlpNic9XjWPpwnA54mXscw4CJLUZVRIRqL1FKnk6cvZHW45LvxiidDjFiSu2S1iNwpg4VtMCrAvLyjistcPU8Z/KsXcLSF05P5v7Wa9e2W7+Z3z/zXNPvBOj1Z7abq9+jdkyNuKVmgZYtUd7K9SA2+rpRqJ2b/OqmsUnim2r5hcLBRIuQ5L7pyACDw1695q112bvwdaXeMz9X+Rr81i+5/Dy84Cs8InqACJ3rQWTQOafMde0BkRBvsfiT3VubimwsXHUe2tvt1m7uXAH27bO3jTEhvWWb6/e/xsIs69huqyiAzzB6P0G5db6+psVinSS5galVG5yIXzB8dDj6A0JFMEgy6lDlhwiY/QQfPMZpxDzPOB5fMIcR3x4OeDB7xJ0HYxYConIU2Oih4oeoiI0zQirEwSUtPWVChmoAnYkbIWjLHqytJBicYqjq+ndhh/fjUGg7RhUuKM2nEuA1suUb1i3huqruZiRUjXMRJrCs4lYja6y3Et4aj8d9aK/mH7vF70KcrPBB41CxoVnPPSrMojBCg6wGJdfA9H4h6XjRh4ZQPFMCefzzwxNO3Uv17Pnnj5/v8PTxIO1tPEYU4FCHgSqMQemWwRglYdhgXkRxUSuHte/pp0eHmU2uayaPkx03mAOZ87v5AJ53mYEpoWYWfSJkfCBtlbjHVCrVeV/sh8Vvo6GZaHl/UV/BP9VwF0qlpYJnK+QXUELlEaVEfOsib5bJF4Zj8UCG4Vzdb4mnWl2WT+1S8cDr67Wlbrayb86YsjzqW82AxHWOyLGvTzThyT0D8wTyKZ4rg0NENEHy4gR9SeFL4ikJBt1oQOixP9xhGPaSF8L26LoOnXOiiKBYOWVQHkcRrmgc7ij5fULwiH4Ga24IyXkjnhC5H0nZqgKQNNrcRjUPiRHLzyzXcUWmZMokX0+wItE/KTeEXJNPqIICVLxDkUMzLc5gbmbBxCyEDqQdSEkGb1VCvJZm+OuM03++rHDMmfn42smsl724+tqbabxrz1+7/2X+EM27vLGHF8rB9E4FiS5U+PPuxzz32+T51Zla3z03NsXrN/F5dPHn6ukz91tjhfTslbPQoKc10bO6vHhmS0nRYryEp27Y8wxctNC7VJQvNbAwFrDRIFqx2oURC/ZEf3RuAA/K8wJZKB2Zi9XzQhlhjFjrZpo9wXNCA38Y0HBQABA1PFCeGkQVtoYQYIxBZIYpbIBWkpT2XPBfuhYFR0cj+DIEL4qCbDhQtcfnZ70JMUVmJejKvFj6K12rPlXFqSAgKT5AlPFnVtQnj+9UIiNShI+T4vUR83zC54+/x8uvPX7YPSBSRBgIiD3AFsQMwyeYWZbUaHhowbe6DlW4mqVsXOJBcc6rF2NABPDj3oIAGA4wUfJgTYbw/d6hxssUA14M8LI3AFnNkyD7Lj33u/Aej3jE+wnABGmLGYwIH2d8FyNmTgYQCiE5GXtRWYcMVwsASWu2Dx7Ge4zegMwA6hjGRXCUMFJlHwgNala7gLa/12Cc05zW94oBTJ7aDUV0qremtQhYJK7OFSBVwyz5wmhk0Edg+P0Lvvk//oDxNOJ4PGKeTvg8n3B8GXEaJxxPJ0zjLF41kbDb7+Gcw+PDe+wPB3z7q99gGHbY73cwxkJyXDPGcZQoCtO0hvcKq9LYkgdQ1gnq9ewPxAsYSDp3eX11+hINixbfFa8iXjxX5qWZ3oq2zVslcwBreE9kYIYBdrA4PD7i7uERd3f3ea6sjSg8dsmZVtPWGTYRIAktDEY/4Gm8wyn0mNlggsWkDxUjMVW3MTLvxMs9kPcHVeOQvRNrPJbOB+q5S+PnBn6m7pf7SaZTL9NCQdQcAwnKFZf0enpsifT47I/zZWPbFTzBSZfcGF7x6vnzxEWFnppntniiZVGwdHkkpiitcs2VDCWvvyFYMrBdj6Hr0XXiERG3eCSU/XuZJryJqNp+88zwm7l9NT91W1tcNuS60Z+oLEey3eTlp2rZw+bjN5SbFRHODSADONeBSNxboWEJMqNdKSFy/GIymx37Kef46yV93oCK/wbKknf8OUs949lCRbF85AgfO7zMO/hgJd5/LJ4Q3nv5C7NaQXhM44jZz7DuhH0H2DsGR4eejSab0tipaexb42bIc5wAIFeIq7JOasqaeVwqIWrhbCU3zY2mMFHqYymIJbfDqLFBzVwkRqGpq34N6/O3tcuXvGhzvaFAzwCqzaNTU/6JqFoSuxfAIdU/0pfzZ7RFhu2dugpjDdhYTO8eNL67Mg81E0NptEv0jcWBWfefwRj6/zsc+Y3bDAoew/OnTJDNs8X7gz07tpowXLefCNaIKR4RGeholiTh6X0iBG/x8fMdQlT3WhD2vJjP6uvoTjh1x7xZR3yC7+oY9Wb7VSKACTP2AJahnsoLrYC6EM8NMYOUYoiaa3u/QxddReRSfrnQzJSVJq0XBzVtgJLlTWk8NWeqeptx0upK1RddkyqmbOOJkQXOmjtBn06F85moCepKEVqdoczcIX8BEWATkx9TTgdgYo+P9BkREQEREz+D/I9AnFC8EwI8PEJkVQTEApd0j33n/oCTeYExwN7cY+j36Ps9hn6PoRvQWQtnDKwmmSzjT3BN488mq9Og3hdBElR7DcuUPCLA0g9oElFwBKlVZt4VZrEGCdbmKV9Te+u5o9U9oCSnttaCSPJjEVnxCjUWxnagijYy6iVqVEGxznRand0sjG7PT/IuTUqMax4RP63wNs3P7W00jN1PVtYMSFbs3UAP/jx9RHVcz+yBr1H+CsjWzREvefi/aqXYGWILKETU1r1fwNrVIePOPIHre7Z+5msNSi3FL53nGidWjxnF9Y4sjAM4CjXx+GvC7r7H03cjxhePvh9gjMFhd8BkLeZ5FMFXFJwIpHwTNuOZuu3aMACoYA+rcj9WUi+ukkFDFP8xMmYfABBCCEjeFnK/5E/K4ZbUQxGKOwkGbOU7h6TQrzw6TBJg1hHeSWkb0qTVlD39kmdEWs/aMjuN5ALZXuHfli6ReUSuWbxd1bIphWZlD7IBZvcRL8MTfvj1hKknzOOzTnfIdGIK/JTWQfJt1O1LB7kgehmXbpOkN7AxIhIhWVinYcXImhC83loVrZryYBgSsYdmNRevAXnm82BwqqQuITIoRjw+e1BIxhVR9kVNFgAAS14DULGzkrlP/IjwigaAY+DDy4y73/9Y+j8bcDT48/sDjvs95tkgBpl1URJJ/5Ple9rFSw6vnrP0WQXXQpUwoqHT829qlRBljsv6MwBESUZuPMEdLYanEXd/+jNwDIifAuKPn/Hdd99jmtT7YRw1EbV4QAAGfbfHu3f36IcdHh7eYRgG3CcPiJ2cc8n94OG9KPLm2Wtfiii3zoeWEyWAdJ1aX6E3lQXPXoTzS+Vm+Ux5JLaE98mwp9A0yvuQhi0lAlkLazvcH97j7tDjV7/5Dd69f4eHxwfc7zvcD8+wFFBbG4onR9kXK15ff8ZoEKLBFA2OHsCnP6AfR8zRS4J1yB62kPOYlTYbU5NOmJzxJd4hZA8vLOUerYRhOU0mX5NZWqZebunBUjtBcuLFSjtL1Ww0S8Fo5qo6qc0wtrFZpTzman7SP1ypGioesWk8XW/Wh4Gtib6lNNNPq1vpnySfSLKCVglBSvowPCJAhF1n0fcWnZMw/5HMRv1lPW6jT1I5R4P8tdCWt9BaF159Tdlo5gtav7m8QhHhACJY4wThaiLGYvVH1SdlrH6JAdyAn0X4uXrtApWzVfcrGJjCvC+vX2r3deW6VuxrE+yvL7UQo55/XgGe7cHUXg1lNG8fT7GSLZ9zIDxPOzAzvJ9zHEfxfhAlhPczpnlWAuWEeZ7xq0eLd+aAaAOi0ZAkMSJmwpo34TNV49/KB5H6tr2b0RCstRIiE2QoDEGa9FKTEiIxHYqasS0WFGW+FuCX28+3Ft76zueeaC/n/mwI/krnbhD/nN161Fa/untl/xkIMUmM2BNOd3eAVSstUNHsNwzUxhBuKAb3TQ6J2uLC8Yz34yAhuPQa3NlBISN0VPu2tqpRV30JZQUw96gZZCJghMM83sEHk6+tmioLiCc+YrYvyJNggKAusxUVspoiCWtk8MIBEYXAqJl4qnFFzccoGdo8l6eA9FkCJkachxJDVD/r33LWbH53pQyohLmJkCoKibrtxZ5bTFy6ny3N8v1Y8WMtbkxxqrfop+LdIOuXraLq+9Vc158yDALyPpB6IoCRRny2T4gICIFB/AwbXjSWtCTo5BgRKUi815TssoI9DMYn+wOeu0/4tf0Wg92hdzt0rkfnBnSuhzUSlshQtR6LQeY6YwCzV6VE0ATV8zpBNZI3hCojMpGf9kT6asr6LedmUah5JvWsXesUiiHnfdC8WE0oJmpDMhVv0dpTdDELW0Ck2Y9pHbcVEMtxvcUQo+3D5feX8oWzMLASwtWw+CzEfwXVu4TtyzpXSogb+JDM7JzBN0tFz8oa6IZeN/XeskxfShJeJtt+OWVFr6zpm63yNSnm8yGmrrx4ZW9tJZu8RDdtb87bRrrNx2zXdWkbNsz+5vio2lpblPPqha1Wzlw/92ihcs/RdkzbzySjA2MEMzsLMAzu3hvs7hmnzwHjMaqxHaEfeoAYPkg2LlECsJIKlJNplhEWQVDCz+0+IqTEuoCsE2ni6Uq2JGFholjfxxARNY8FUNF1Wk/DfzSeEUEVE17qqJQWHCWBxdJgL/EnhoCY8Yvg7njuOOg+SJtuBYMJ0OzaRTaQhVOLpSWAoOEVOUhNcQLMjIg/Y+6OOH54h9kwwnhUnMhIypNkXKK1IAn1mSxAXGh5Th1TgbpJRhricWssqXOEEQ+JtLIacmsVdZaFlqUoe4tBsCCQTd67Mbf10ifxq8x/ZMAE4O6F4XhGcctXZUQz44SImMNcVTMn4yXBXsYAloHDFLCbQn6O1Tt+ND3mPsD7JIJN54WSlU++svxsW12XbKFfm+pn/nZRxwZgSrtH9rAYv2A0iB8Z9rsj7v8/f0QYZxyPR0zTiOPxRXj9ccR48jid5mwkOOz2cG7Aw+N73N894P2HD9jt9hiGPYw1St8ypmlEjBHz6CHeSDK7JhuzSM9i4sMzTDSaeTllYeBtOu6NhYHC8mfPI+WXdXp5w+OEuX0vl8wLyNkjY2Ccxf7+Hnd3Ozy+e4+Hxwfs9wfsdoyde9azmI554n7q5LgVHuNEGxEiE0I08NFgjgQ6PaEbXzDHsleN7gfD2USr1FV3Gnl3LianJkK35p1X/9b11S1w8yVd36bt0pRGpRO36qqvZbywEqTIQp2156nXkGM7DpZTmiNfrCpfVsqLb0t65JWFtmay+rlUPOeblN9lkv1sjEHfiRLCOgtrDAIyFGzWvqzJZXLoNl7mNaO+pb7bzn5+e0F8XSbT2x21vnuGFnot0X9uOcu2W9/MJOLbKfGbFRHGddKY5oJAygWRPCGQiIzq99Ja5A3M8c9RznlQbMD4v5UbyhIQ3/RCVQJHBLZ4me4RmBoi2kfCNLfJqGc/w3uP2XvM84TJz7B2xKEDBsPwHhjYIHhfJVaLbdtn4LbgCxako0xCurM+4hVkqRBUFj6lI5IRcUWQL4mJrcm5AFMyL7K8/ko4tGRMv5SsKgwLN/Veq3t17+zDXFe/KnQOrBsSD4gP78HOwhoHOAvjkqdXCjdk6srQ/tA9cY5JW11sN1sDuLsOzx8+ZFfLrTpWZ4qMCoZLIzEKs9R//AQ7TTk2cCKiG7ff6PHtHSMybcO5BaP4aEd8a3l9n5Zrm/a/EiMkZ27mZyTrq+UZyfNB9bwQTqcBn5937Xmq3nrpnzG5GUfzCVNXzln5qMgYMvDxACabz+FSOE0N80SVfiKJMareVkLrdtrEuvBuvoNjVwgvMCIFPPdHTZJZ+laEyumvACDOnAVj53fYhQE5RFySXuTGS31MEc/9EYFi9oiok2d6BPjowXEChScgzpKsWmHrg/H4MADDbBF8yssAZEscVdR0nUM3DBif3mHg3+Du8IhhOGDX7zD0O3TOwtniEVGLryK4TUwdA4LXBNX6F/18ISxTDatKvgoy1S4iYFtI3wrHl3ssbdOkxEqKKbGENTDWamgmJ9ajWRlhy2+inDerXeNWyZ77k/qwUJQZU4Q52Uq1VlRQWtVqMK8sSfCY9vs5proV7OvZp9fhmtba7PWl0m80dW73cU0kZ2VDc3Sqw1E/U15qnm0UgF84nmUfvoSor+tZCiK2u3j2xs9QluO8toe3BRVvK3+ZMa+8QG8oXzrKeoVvmdWfsnxZW8WK/1w5d3YcnWAoYIoHBLOHdWK2zmwEt6lw2rkOxlrsd/dwtkMKgyQtpzwDDJu9BdJZS2NTXAsCGJl3SDA1ZmUCa2x9rqIMinDaewn+4X0QvGSEVZdQtIzgkyIieWlo4eRd6BHDjBg6waOzR3AWwRpENuCYFCmAhCtixS3C05f8DYlHaec0sSwEKoxyAqkJhzEyHZUxapab1UK0CMBnoSdgEKMHWeDwzYxTd8K/PN7hZPcgy3AcYayTGU6x403aF5TnESBRJJjCyCfeK30grRRRlldICEkZDEeAqjBYGWenNdOFT0qIRCOw7hXidI01JE9SQukpiAEcZvz48j1oHjGTL/S0IfW6VG/KpGTKAkhRFCWlWPLWNQy4WtyYBMRRTDZ+9/EFH55GPGPCyIw/7n+HyQ15+6SED5vniAr8alCjzmdxhqhxqc4l16FNGcy1kZfSgiGCAqF7tuhPM+7/+Y/AMWD6cQSej/juj99hHme8HF/gZ4l4kBKmW9Pj/v4O+/0BwzDg7u4Bu90Bd3f36PsBneY39fMMnhhzmMSgMfhCZ7Pa0JbOVx5MNdxOtJcp8JwrGkqfuZkmIORcANUl7Ya03XgicVFGtNUsFHyV7KEeFRNghw7dzuL9h3u8e9jjm2+/wf3DHfb7HTrnq3UpdZeDs6Z4iIAoOz0rIV488DQDUxS4NAPwaHyfyk4i2p4DBpiSsoLzfMi0t7RLUgm1hasPzsZQRuchUO3PUH+sVy/ZhOW+l6VHUqLK/QTb14UZzRjEQLBtKfeHqwlJ39N+qGBp+ayMZbnUVMpWj15LXRT+qbzabLoMBwvcNQkFAoB625GE7O0shs6Chh4/HO4xdBY7ohu69fPRra3C9rY36m/n4cAl+vdC3cuDcvbJcxKwrXLhSZ1q+fj6836zIoKyh0MV9zgpHgARSjQKiXqCz2+qlaXQGcn/eSufawt828JuMd2CVG54fdWn20tWrn8Z34nt8b5lk6+Z2C2m/4sLL38mUC5GBiESXuYBIRZFRAhBwjNVSaR88JjmCfM8Y55njPOIaZ7x/gA8moNY89qo8V1TGKaC0K/2jSt3uIUl8vqF9FkIrEbomr9XiDddQ/15y0Tzxf6/dqlWCPeV77+1nbP3zj64hbCBJCwsuLdyq128k5gVWMJ8dwB3HYI1MCiu6BI9xShvsoRnpaZIaBPkJkJ7A//zap2re8ZgcjeD46o16F7WkDvqpm+en0GTJLkDc5VQMFFZ8rkfwrpHtMWCEO4AAP1iCLTxQQXkLwSCcmlJzNettL9/BIDZtcxN9XBwHoFfACJEV3eLVqcxksGRAhiuCFur2NC5UhIGIytGNoSDjVqifRUEwLBFFx04xqbX3ng807NaOSpBv6kEQV4jpsIIEQMuGA1Xpwxxtdcq0IJIjCe8IJigioh1XNPgIwzPMPEIsCSmZk0CvSfg72nASBEz+wXRizxvkgDUgc0dYN6j7/aaF6JHZ7vKI4Iaj4hi3aXWb0khkf/UMyJ4Ydij9CtlBuR0xrme+7T3yh5cMmbldyGrVjueyvMJjovAQ5l+UyXYNMkLQkMxVeuaBQWNEqK0vQXoStgwICkfaiVEvVfa8Xx5aUNWna+4nUNlpugCTl12knk95wBeGwN+PXZafS0K0ULXZMZiqwvpYtWVLaVETatyvQnlwoVOb1+kRX+v8Tw3hZta9nHrlTOXv2rZEGRq00A9Xobuo1sZty/qFLbO35vKZjVrvqL2JFuO5dLI6qdv5ZnW3UsedRttnavijcR/SxKdYd42BSUbzy3qqbHwa4qhGQYzAg2IZGCYwTAwIYoAnghkCcY6GAa6fgAZwjSfEBvDJdb60GyhfL4IQMrptpAlye+E6xiGRYgeOfn1IQtWQ4jwMcIEg6gGIBw5h2+KkcUwqq4cQgu2uDRmA4OcL2JJjVa4ieq/rBDfoAiJVPCmcDWBPy4VsNa9pN+yMD/RNZBY9JKoWa4aYtj9CHYBLw97zMTA+AJiwNoqrFSi0VLy7xhRwudobUnoXQ8OKHGhFH+BhUZhSyqo5Ox8GaP2Tdc00WCRy16grLCqMX0713XkAMQIDhHH8AIOI6y1sFQUXImeSHkuQgCgYYIljKcMoOSNSkmu044oZy2Q8r9jwMAeh+4ZzzThz/FXAHqAxV85pjWtQ0gSREKf663GQ1goIbZL7nONVxMBp7RlDB40A/jEMB9H3P3vPyCcTggvz5jnGc8vz5hUERF8RPRBFWqEbtdht7/Hw8Mj7u7v8fDwDofdHl0/wDkntG1kzNOMEDwmjaiQxMoprFehE1Li6drrqFpZTnNA9c96ZnCZKFqWsmcbUrGquz4z9Vvpyxk2tXpA6yHAOAvXWxzu97i73+Nwf8B+v9c4/RU9U+2lYtjFZeRUYF3a7eIRQRg9YwwRU2AYZngQgvahVhgUeuwMdOc0+qo/LOeT8kVeLkJ5Z1HqM2pI+yJJF6SavE8TslzXkteEF+cbyH1i5dmSEnP9dv17mx+Q/dd6vqXzkuVRiVc8W/+ig8vvlwotftDmjebeklcGkHTVAIoxlTUG1hKcs4Dr8NL3gDUYKphZd3fdctuHtNqbhjhfWLbPefvEtXdvb6XdufXbGXvcwiu9avjnepkBXT4OjTLiK5DktysirCRmQrKSWHlCKKCqIeg1zHSB2a21vVt7aUsb/PZyvh9/K+fLORx7bSYzM8blk9ngxd8jRCvxT5kwTkEtFkQBkZJSz8EjhoDZz5j9jHEaEUFw6LB3HvduQs8O3vtiNaRxzVsrRmSCvOGJeNFH/b0My1STmst5qQWbpO6u6VotqNqeMcp9Oz+HLbjaQAlpKJulOTsL4vIvVTa6dOWpmiRa3t3GuIYM2FpM336D2PcwXQdYC6uJ7ay1+lwlPKS25rpOk2vmZv9kJuxieeuMl74kQXT6M+pyPz4+YjzcIXIAfED/ww+g2WdFRW21U6qlra9ner5FChSCY0m8NETEgpBZ0zXlek8ev3kcsXI70UreuREzqSCh7gkt1p4I4IiAZ71GmIPDj5/uwZULPIEwuhHPw3OlJCxMLG2Ma6v/DMJn+rOGnyrvMzEwi3KiRHUo1iNMHby5g+EJjo96v8Cdz/GIz2aPNlFkBdNISHpHRxBFnPwADikRJKF0mIA4w8UngD0iF+Xugw34bU8YImEOM2KIOSRE6iuDcvLp4dSBwg6De4f97h67wwG7/oC+26FzHZwlWFss95J3h+TnSXA9aC4I8YLwfhJLzjBrmKa0d7O4BqTf63XKuV1MYpraMINLYe/qDKzWWZUQlBQPBGOcekQ4GLKaA8JJckxjAHI5ZBOhwJE2BOQCF1FpSzpgKmVYUkK0dbVKg69frtNXBa7WzEb8IuL/Gs249UZiEAojtySplx4xjTJiWQ+1daRnU9lSYBDRgrOu8c8tY8DGhL9mIpZikHpOft6yEoxf2EirWVKiculx8tdfXrcfvmqpCCTGlgLwln1Ww5pXjOPqo8t5OdcXynuDsbXHbmgr8c0klrfGGLBhWCaQtfj1f3jAfIr49IcR03HGbtghOAcgZoG+IcDPMwiEuZtBRkJJLIVM4ulXj0f6733UXHaiLDCWRREBIGU5ACKCD4BhjOMkoZVYPDaiF0MsHwJCiLndbAmsHrIcPKK3CH6CnzvMU4dZPROdterNIUl8M6WkfIvkiCgeEZmeSziqwkliiR+zLIxTRUqzCA6zqXJ5N4HPlBgakFwFLCEgjQX2HwLmgfGfv+kwWSuxxHX+NXaUTnXZ3LmbRuB6cuBMa5KsxdOfxF8ygCk2/gQIDo+AsxoGU63e01yJAkhCZkW19Jb6lvi8Ckm13IQQ6+lvn0e4ccKPUYS0Vr0su34Hay36bsg0HasBRmRCjAGU6RGjNIl6tFSCSZFbRhHFBCGjo6Iq9gN66tEPHtyd8O0Pf4adT/DzEYYJD923iGCc+CPibo9Pv/uPCOzgj2sr2yroK0pe0AoHqdeNeBcUO11mBiKhf3LoxoCH//4HmJcR4w8T+HjCv/7+O/hpwvF4hA8B4zTrFBrshgMO3xyw3x1wONxhtztgGPbY7Xea50U8V2cvYZpDCjmq8gTE2OYJyAQ5I3kuAZxDqaUSG+WE7JpYj6dZ5/OlGDoVeMbqnZ5lDQmuXQC7aXclnpUrj5aUnwQkfQysR4cMut2A3Z3FN9+8wzePBzzeP+Cwt7jrPsOSB9KoGoYurXIad7kqXbRgNpjZ4DQT/I9/hBlPmGdZv9nYYrQBwMOAkUJkt0OsMVXMV8rdvM0TPOFyb11Km0n3mNY+5RyMJDC7We0FHVeT3OtWWJV4he6q9RnyiDDqUb+b6pyWejmvd6sAq2UM2YUOKSxYIwioYQBqeljnIQnvmuFtzFvmR5oL24VQ9kqScSVcAVIWXuBV5xw8In4MR9xhh9/0HXZ7C9xF2A7NWfw3UxZoovWuWj+2vrO9fkt674voat0vtGr/y9bpFR4RNn2pNlz1mciAxX4XmJNA/VapBUZlkpbeCFtWQJtC8NzIayemotbPtLlu65Uc809SXsNU3LBxX9VmawVZhzZYt9S2JUI0yjAzRsLoe/joNBEbI8QZHIXwZo5ZseCDRwgShmmcRhynEzo3YDD36BAxGGTiPcVRxRLgVyNpvBwqi3Fe/G4xSvpe7/kFN1RZAiWCPgHm9Vy+oZAQLrkv5/DIoteb8o43w5GfhsGu+3it9stiDqCJgkoAjEHY7xGGHp1N4VMEWaZkugYSR9cs4dqi/uTJ3DxDzUdVliNZwJvlfd56tH2H1PhLbZkyceyHAdxHBI4gH+B+/CiElwqvkZm06rBWygleN3W2r+vttJgv2rhf/07Kno2zaUzAwfhVXamOOwCgfjU9xaqYykd19AjAKZAw61zlrSCxxJv4RZiCKsRPFmSkFpYHKd8ngGVN1jGYAQpaZ6BMKLBhGBC8CfCxR4cRhKMsT0WkjmQwkYaKQxSCltqNYhBxoGcYiuJRBpf3MVUKG4MZFEcRAKS40hwxEOM3pkeIHlOY1YqyHaOMR4hKF8TDZDjs0PU9XNfDdR2scbBkRTZvhBGlYvcpMFatztbeEPKXQ08wF+IbwBbybwX0Gv+ZluRaYaSa32f2a4LZiVnMzD+JB1XOB5E8RWGUVkqKnwL7Vxtl1f/qkwg5KWQlzFgrIS7RIbfhljWdc8t7GekvK9uUO6+bONPGBu1wrRTmcAOuNBeqNiplxOqdtMUWCgkAm+9IlVvjft1I3kpOUvXv+l6b4A/YpqW/LiW7xpfnerfJzlTKCKDiCb5qH7UHb5z05X7+GqxAywm9pi/t+p6tvLm9jbtWZUHTLGnc1yu6Cv45O+JL40h7YuuxqxNHxXqWYobtxsp+PbxziHeM08eAMDNi7ECG0McdYgyYp5PkSwgB0QSEEGBYaERGgRcA1IK+HqPA8tq7O4QouQQY2UQ3DSFGwXfeB4CRldAhxBKWqZW0V8OPmh4hSF9DEGOuGJt8ESaFZqrzdqV/KNHLl9eCIIqUwgQi2RkUoqtZcyoTBBmjyqK1LQYTw7sZYWA873aYrQH7qYVbVCcJrlohVPWtUMJGieCSzUvrEuMxidYltBlQFNek76RlS3H6mzpYQiQZrkde2bPHADBjN83oxxmfQJLDQmkqax2sdTDWgXLLATEa9dSIaIwc1Ou05BqTiWACKGpIMD26IoBlBE9gAwwIYJrwLnxGH044+WcQWzzgHoyIjj4jxADfRcxzxIklRXisPCSatUXCmdWMsKpACdJ68uTxHhQAeoowTx7Df/4BeD5ien7GPE14enqG9zOOp1FkAiHAWoeu69H1O9zfvcPd/T3ePb5DP+xyCCZrbU7oPscgyr8QNLSy0JwrT+cEW2J9jtNm1t+Ja2IIXYpkkFsg4S0QsYjNSh+2YCnrGhbDI2zSvmnWq46WA6HtJH6PIUJh0zl0g8N+v8N+v8NuGDB0QG9fcjiyjI+h5zPWbbXibUAOHDOBo4FnA56OsOMTQoiYIuAhIZZKWpZ4ZsJ0LSjNS5tLIft0VWKPZWSC5nuG+wXOybKRhGGTxlpeagN25F1NaNtG5fHARd7ANf8GLvspNVmqKpU188Hrrxvrz3WFG32WL8m4Q1tMtC7VPdkotPpy4aFiTFUrrNOVnB/ECNb0iGArHm59TzC9As2qz+f3+1YvEn2wTRN9DeOWayhl1cLyhZsABDKfcpZfXFxeKybOVL2B0y/Ny8qoKfUtt5suvr28wiPCotlkWaBRIR9qfy9LKy7Zuluu1ohia5LO5XX4W/nLlwtnJ2v6IwPP8z18dOJmzIzJRzB7VTgwZj9JKCafPCFmSUo9iyfEaTzBugnf7ixM9LDxI4AIH4NYLTTJ3LRvG/1JSICzcKxYq/JZ5NaMOH/UxGH6jaSEoNb1MxMJS34sn/cFAPiCcmFJ8v36mS9v8euVS6f8tn5SFrYYsmAj4VRgjFozS3gZSaZriwKiEgaeKxYXmJ2LneONB0x77Wy7Bc5Go6F/YlTBtz6h3K3ogBnFvX6xydLXisG/3n/e+ig8Zia0qL6ci4rPt+UNy+GffYiaipe4oGl5JQhOROKMb+/nqi75DMbjNwaAMnuFxqoI8hrtU/MBAiNGg+8/3mPy4klI9QMVAZ9gxGRHPO8+IZoAixmgCI+A3XzAfrwrw+6f4d0TKHm1KDzNIES769O+wI9iZ0ltzhOBeREzzwBL2LoHG/HvBpPz6Xjvi/VY3Yh23FgLYwnT6QF+7nDX3aPvewx9j77vNS+EgTEMSx539s8gzCAEJA8zCRtRWaqFgBC9CmpmQMMhtJqQau6z5wNaIX0mhk2z9rRai2Y16mUu80kGZCCwAiIkIGNFSKA5Iih7RqhiAudCMukoFOmsSZvqeSo0VVGEtEqJvxykXjBtX6vWK0O6LqO8nSZcWt3X87oK38Tb7+R3FV9slwuMY35/vQ+3nntLOSfk+Hpl2e9z83B9fvJUVwzo/zzeEUsq69qzuPHZn7nwL7hvN5SOnmFxwsj3YNrDOQNmQggG0QC/+Y/v4aeAP/6XHzG+TLBGchacVIA5zzNiYJBxcNaB+yEjXpETSriebP1NYvXLYEzThGmcFbdGOAasQ84nlDzhfJgQmHE6nmCtBXPM5yD4iHkWHJn4qWIEJoL9gAgfDIyfQHMHuA7z5NBZi+AdgqmNJGoaR0LUMBlYYxGNxoqvlAoJzhoNKWU4jVlhZkwCP/F0z6QuA0xicpy8S4IHuAPmvz+CDwEhzogwmL75LYLrMPEE9ix0AEcQ+0y7pJTKBMXRQJatZUEbmdJ9iOFDMnBP9LDJ5GTxYCBAPStSYRhSkagR2sWocqc+DYmKvjvO+ODnnBernmJmxg+nj5jCiE9z0DwWgKMOfb/TkDk7yT1lRUQj3p8EYzU8JSWjCMlLZW2JSxopKQiK0QejGH0kww5ChI2M3/3pM6Ih3PEDHD3iYZhAZNCZHQDg3vSIsPjwr58QfMQ4RRzvevzh1x8we4swlf2R6EyZCzkHRcqqsxmB/snAniIe//O/wD69YPxhRBwn/P4P3yNMHqfxlEOKEVnsdwd0XY/7u0cMuz0eHt5hN+xxONzDkpUzotqfcRpFbjB7yW3GxZCmKBAqHiHf43x+E01cl+J7zNV6JmPMM0qC5ndLy7Hm9YhkAApylxN1u5Q7bPGL67YaTwrlLWSfSK4ZJojuxBh0Q4fdYcC7d+/w7mGPw26Pvgu57qJzqBSWhoGY6GiTh5gs/0UJQZijwRQNpsDwUcIznVh3JBEotvxm1v0seK16KsoM1LzAmqYo3BnnX3mmmHPdlOmLgpkburZiqkifzzCmVJ2rbfmUatujVkBwdeOctIVRzu66cG6Qq7bTKLm5V02IDqWiU1XJlXj1BYdS3m2/bD21IH3r2VzyVgJfrbOAscAO2A87DK6DIyd5QDZ5+X+D5RqpuJiYzYTStzb1Whq73lNvbLMutysikqsMFUIkf+fUnfr5y/VtWxS1QPstzMdb+ZV1+83dM20VRmmr7S/Vk9z2/rLPP8exXTDRFSW2BqkVYM5KCIkhOIcOc+wzQR01PnkIASGWXBDezwgxalLqGbOfMIcZkz/h4Bh3fEAEI2IWaxhUoUSqPi1nZq2EQEYYN7tYLmj5LJCgAoRJidxWTkLVvrl1065GUPHrC8hQfzlnUVjRLFstvekoLemuv0TZaDdfshKaiRZhTiREsFkoIaq9TWcq5vrqQtxzcfx05oHLyYWWIgADowRzimkrG6II1dJ75zpzoZOv3QCr53n7crp7pX7efEiJrAXeKVZNzQcaDjC9X1lo9C40xFn6956SAoFqerapbhlarf4ViHCKPYx3iz20fFr7bjxeEGA5wJDPk+YisA99nskxRkw4FaZpyaAwZO+qsMjBAyTQhwAYLowiMxASU8qMjiI+YCcwOHr1KOMVXStjB5gi2BCYexhzB+eGbMnnak8j0njPOILIZ7fkqJ4WKaY1K/PH1Z8+sJixtA4FSq1DFlF1vZnpdq02t38Ft/OfKBeS1aGpPCNKHojkFaHwfyW8qZZpoSCv26yQSfXurV4Q5/Hduacv0Rnc/LM8S9ulXpdbQEgDWvncmtQvnHvgRoDVtHW5sUYZUV17XdnGG6snNvpSmIv12Jb2iGe7xdU4sB4zZQD3xrKg/88phM62sKCDCmhvoPhXLF/KNt3eTsXzV+U1o6l224Vuv3Z+rnt7a61fZarO9O5GBunaY2sRynan05AMPAw8PPYIiEgebRIWhdA9OETfwXUWs7GihI4GzjlRlIeIgIAwC5421iEJsBNOZpbE0okfEHwd4dU7wYeAGCJMjCLgWsA9yQUhRlgcI7xTxQFTtuxOAvV2tAVfR1bPQq48Ibh4RDBr+CjDELPrMlFJWJpDlG7NZaI5FWgbrmFlYbyYGTAabs1EsGXEnhAtYK18zvsZfOcR/Qw2DuOuQ7AdOJ7ENYFlnkrK2gTLSn+Iyl7IIXeSlFHfoMTjZbJOx55wW7UO7bjFM4KRcHcR+BmjCYuT1D0CLkbs5ghHBtZQqZ4lX6GdToj+BJ+spzXXlDEGzjgNtWTRhCgxBojCR5oU7teUvHbNXqBCX3Dzr/Yx3yT0U5C1dBJasu8OsEQga3X8HRgMfxQ+3IYAChbOSa1x3jjhScipxQaGCVENBBn02cA8Bdj/8SPsj5/BT8/w3uPl5YgQImbvdQ0MrDUYhh12uwMe373Dfn+Hd4/foOt6DP1eSMQY4TXEqERMCPDzjBgCSu8SMG46mnZGmZKUR7Ja+7KfK1qUyu9LRd6u/616syZqN/pXXVrINBr2hHnxbktHindBOTC2s3Bdh6HvMfQdrNPQXmjrz/RnHsF6hGlqEl/BKuMJEIVsUHgYl3NWC4/KrLRfCVsZqJvC9bpcLFt0yXptSt8qXrPhEVs8k2BL0ydmJC+oMjny3sWt05zb5cVqH6bJ3qprRW/w+mcSHhUQuR77hbJ1tzlpm1uFSp49IjhLcNais+KZWIPiW8q107e6f5XeP1PPq7wyrvTlHDm09TwBjRfquf5n5LYBQm4sm7xQbahV9XBloPXGNlO5PTuqdtIULN0g7NwdKpuwATGv7uXyhQXz9KVS/mVrfHWPXnj35/HO+Hk9QN6wrXShYwU0mSuAzRKO6fN4j8l3mAMj8iRJqGOUuKkcMceTxAz3QlCM4wgfAk7jCGtnfBg6sGV4Z+GYNHQTa0LeteCsCsVeAfkU11QJtBQPsiIwtcsb2t70demGlojX7e/1+5Qqr8UJCwIE6ze20HX53uYpa/q5LrzxbevutfIl4OfLS5qbSxafBIVbxuD47QfE3QByXZPgLVlU5RA2QDNv9dlr4FnjxLBg2K5NzRmL4i1SqS0M4sL0ShgpERoTk1i8qEFFJgho0bsFc7kJWRYXefG5/HENPl0MPXW1LFrn9vrSNfV8qqt0tisisy6bwi9q5nHzfkV5Jfru/f578G6DqqpgQWL4o4n4nTWAobwHhVmY0O1/BNSi8gNOmMlU1m2J8C+EOEkA7ASVAGIkYWN2Q86xhAlR3+9hNSdDRPAln0gKPcaq7oUa3H23/z1OuxeE8Bvc8Tvcm3c4mHsczIDedHBdhLEesBZMEtAgeXJEFms38X6YEf0M70dEPyFOIxA8TAzgOEvS6pYdQ7JmJCo5IlpvAVlb06xnFVbn2vJThuogEk8IiTlsAdOJNY9xAKW8EFZzQhTBQPaKqxphRo45nIlbSlaTG95XRvZHFjbo/YZRrB4/h0NeVxYIlOrrt7xeqNMW691QvojGKd4xqy5t9Z2wnLCztfLmfKyfu9hmXYXZIvq3KtX9vIXXr3XoSv+ahjdv3bbeW0P50rLCeF+qfNp6jRa/v0q5jNOXWOlcuTSlKwXUrSWP+db33nA2Vg8sgN8rz/dXZXlUQZ/629EzLB8x8nsEOihuZDB74QMIKjDpAcvYG4MYA06nEYEZz9MEmme4yeecQUn5XCAoAfA5ufRpmjDOE7wXY6u7zqGPFkOMMNHA6osxePgof0ZzSCQcILg/QE2TIULnmBX6Qv1I+JsQIqzvEK2Dny2mE8GRCJiNCroNRxCJkB+IgFGrewcghadMXsRsAFihrzT0FCkRUns5lgzPoqzpDxO6/YzTB2C6Y4Rf/y+Ih4ciQHF3EBMyDdUSPYgDOIxAZdGeZjTBz+RtkOK8q4UEwARLDMMp+rzQOSH/1vlECUzFAGBkFgrtVISzsjCKHTkiEsFovCNRTskcBET82BucBocPR493UwBpcu1P8xOO8YQZHsamkFakuaYMnOuyx6U1No+TQxqoU4VHRDagQhKlchVWSDxGiFmNTSICBwSOmGNKdi47xRkLYw2GoYc1Br2zmY7MZC0TOiL4YGCZwNagIwN0BLaMMANhIhCKhwhYE18z45v/80c8/sszXl6OmOcZLz88Yxw9/vWHT+Bp1kTgBp3boRscvnl/h67v8HD3ANf3uDvcw3Ud9rs9yBg4axBjxDQdEYLPURNCDFlRxDm3wwI+UZqhlqfgGNrn6vtKKxNaL5la9p8MwSh7Vsg7QKFX005Lxk9ESvYlWkSZywSmBQyxKgs1iFiNTNJ2BzRYWARB6VCQOjBo6FC2UoclwAH7fY+7uwH7ux67vcXefQ9rou4vgZXJ80G6pbS2SaMXL/wISCg4KuMNDEyRMbKci+SDYhK/ovR5OdiF59HFwPUcs4vVogVvrt/z+SAJDOs13C4vvDJIvayoUuLVPF3qcoLwSbZV8ybilFMgf9RFTHIlo+cB0KT2zAmE62Iq9OZE83HaSPmPEBTeJv5M4W3O41dGVS3JiqzH4vKaVt+a/G1OLPFf5XJSzHN5ihgpVSETARboiPCwI/zDrxl+H/GdUS6NOXe+6fINpM9XI+WadjOGuFx+isabRbz64PZlbN+6rc5rVa4rfi3Z9gqPiPZHsUSoN98be4GKd/0JmJqfow/XlBHbllHX23q78qFu6LV13HjgNhi5GhAWjwMB1jESYiRM3mIMVpKgJqsfZngfEDnAxxmRQ+UBcYIPHnMYYQxhhwMEDTqx8GEFwhALn4L2qg1Z782VfIDzv0slRPosy0DNR0ZzhFbxsLhev1QTaq+FDpswhRbf8xLU1DstlqudiHo5fxJA/hOXc30vy0RgMohDj9ALwV0EjfXT1KxteretkZvb5+D/zcdu9dy1F2l9vLlC9lt94ebRFlTf2M8kDGuGu3i3ncv2HF3SqN9cbn5++eBSXKLwWi8m5rM+M2We9N3lPC1wYD12IsDZabNndQLrAjMIhjQecKXshwVgRyR42jOB2SElqY6ZnYq5v5SYiLS4XGBQRTbm/icBgggRQpVXR2fhzN6e7YixP8JZCxd7ONPBUQdDFpYkGSap5V5ShZT2kONcs1pqcmo7RiAGiVOLJCCpmy4weJk7oXyvSeXzR3p99Mr81OtTh83IHjTKQab1S9NdhBhtC9zAe140SVjhmPqBanzL99OLzG88U6vSzt2itddVc3aiz5fXexws3l+8zrxdZ7LkbR7MdVRz+oo+1e9twrv62Sv3zz/9ynLDi385ursQxpdzHHw9quQSLL/+oj7+2vlarv1NwznXyJcwKheqvbUswNBqH2P7DGbY+sr2X7vzLz6vsJbBMOxhiODZg+FFNETJw5RhOwPbWyASOALOdQjRwroIDgHez2BmzPCgaGAiFE6bjO/SWGMQYdQcAuYg4WN9jBg4wkIEw8Ywinyu4MXIBt57DXNoKkqGN/70OkekMCkcPWLQMIsxIMSAGG2F55VurGpOAqMa91Dy9qswqsjXimej5N7wiCYi9gYUVZB2F8CHgHhvEO8N+K6D3/dVn4MOQYRqHCOIAyhG1JRbTWsV2t2UUNENr5W8Jyh7YSZaRxaFVZORbJQLzGbiQgMobmYmjV/OoCjGP2ADQ4RYGyoxS14LQxgRMAcPAwcywBhnjHGG2EVRFjAZUmWPJglvDKKQArWkMQKElLOz2gmZTOLqYulTZFVYqaw5YTaj7ToNVZsUNJT5aPFuICJYwwgkou4uSBLsmSRvRYhpvhjkIygGkCb2dn96gv3nJ+DzZ8RxxPz0jNmX8GLGSBjPrt+h63rc3T9g6Ac8Pr5D1/XY7+5gnYVzTtZL90kIHj7MOXpCDLGegUVZcAArOcAZs/szsLomkVMR8EJFgdCeqvzvkkxrfnO5UkPWS4UzPZ/CB1GTW658Gt17QGctOmd1XgmWZk08X9M8ZR/mUVAt50GGdSoOF28IAEH/miBD5wQNtHH/HO+RX6D292ZsmrUPhwTcTQrHeg0r3nnNGOi/bdAnYCFm4QY6Zj5tORDSF6keIwO19XuzbKwN1V7itYIi82rpL+2/N5Rr6PYqj7FNaxNIUvsQEMAgMnCG0FuD/UAYOwXfzV6oJFWL5c7PNO2c68Mtc3Fp4DcSThcsht5KMm7Sq1sP1wQHb+w3+kIyetWh+rBs+Eq9YsC3KyJSreeUEBslbb6/lb/OQouNW37rJlwgush1YujkvioissiMz+M9xrnH5CNCHHMCtZyE2nvEGDDOR4QYME0TQBM+DB1gLbwdJKGrukRHBcqshHwLhqh8bmzBrGTQcQic59X9xYwgV1crHagSWuUQZkkocX7/X4YJV6H9FxUCsvXGX3epGY9zjqP1miFbGWWmI/1TsuwtauCq5sW+/xrL1LxPzceXVJfJFIYyYLHZ45T/eUvtbUnMWlVz/mwFD5wFg69TRhT8c7U/F/Y0N4+1RE6jqljStMLXXu0iXWqeFuSzWsDnMD+1JT2wYKoVpmo+neStEFVgsWzSVLCHMixKfUjMRZXATuF2SpIZNTRErBSzpduy1sZKuIp+6DHEHZzrYW0HIgsmAyKHbE2V55U13JMkpw4q0Ile8v5EPyOGWRUiHimeb9oqdR9kbBU90nzXnBg1t1AJwrbwQqNQSgoIZdKhoRPIpATVwrBnT4ispFChCJU+SPNJ2YM8n6s8QvqZ+28oJxR9vfDuL1RqQvgNgtKvrYT4OcsydFYLay937CotfUVy/YWzhrcisa823VeUEOeUFMV46DIT2VpUF7j3qnGfa2KFv39qmorwU+Rn+bdRmo0AgNGbT+jwhBN9g4A9CJK34bf/6QHzyPjTf3nCdAoasx8gYxBChLMTfAiY5hkxeIxhrnYUCfxOigm1Qp/mCZOfMHmPECOGzsEQMAwi+TekIVRiRPQBY/QgAvpoAGulY8yIwYNDALwHfAB8BEIEBbF+RxINEsHPE5gIbjawFiJ8NIDzGnrHdiKMhoHVaYlsENiDADg7CO1jTmASq/oYPaIfhW+LkmeKY4TbHdHdfcbpP/wDxn/8h4y/R6P4wAIwFtz1AHxZE65EmZEBtWyvCbGaHCo5r1RJIjFVAajRgwSjF+UBRxgAkUIlq2OQiRKr3tiKLkp7hErdtfeFPsWGYSIhEBDZgdnDUxBvUtb+G4PPxx9xenlB14uBBjugM05pB2R2Qvovbdo8J5rPggHmkAPpFzqngmIavio5RBhN5p0NShgaZSBg9gGRATIdrAX6zsE6h65zMGRgbKfTnHJ5eXBk+ChePDMHdBPjH7//J/zRPOJz/y3sqcPhuUOMARwD7v/7nzD863d4eT7iNJ3wh3/9hH95PmHW/I/WSkLpd48f0PcD3j0+igLi7g7WddgNu5yUGqC8ZuPpKHsuzBpizBc5AJf52Dz5aStl+UR7PwtuG+OExbtn6l6WJRbI9Ca1XOplCUHVJldC7WYcQMlxmAjFdf9LZ0TpQ9Ziv+uw3w3onIO1GnZU+3kuFE2hkXVN9LxF1rw4LEmqRyaMbBCyv5HUG3P/tpgpRrb8vjgpZXbbedZfteCqosNi4vdSXhdOPZH9oCBDYMaiNXCNcjl7vQDJQYRKhalpXni2tOBM5jkmnlH3pPJ4OTyY8mVJnZEYeu1ty7OuZ1Pa35pqnaOSD61cvliq5WkkJcsXt+ohSUodAPx5OmFnerw/vMNut4NzHbw1LR1Xf/2qdP1bKrvlnXpGvh59djNFWe+9Bf/xUzW+kgnX772ivDo00+aGWFysPQuSW+S5A7NkwM57DKQbpM9VzPxXLmvPiGsLut2nS/vg1m6/fpxbjbZzd+t4WpRZjhnXF/JXVoCr0JZT2JCIEAmBDSZPmIKRGI4rBURUQZRHnEUY5cMI5xg978XiApK0LWahjvjJLoVlm54QaPHTa8oKNtbWr/m7KiGyYKmex7cy7GeY7zfVtag24cy3Tsqlun9xpRBCqYNrHVGFRHhxrxIelvrSvS+Yu+WxrBtf9mH5Tn2J11ZAmf5UwqWRufC5ym/o60bZINsulJqI/BpJVJft1RwrmvW5GaFvlRVBv/3MRVaIWeO0phJBDESSMAGFcKD8vGKSXG+Cffm7KiE4K2KFSU07wkCXn8oZEPdjyqtQmBzpU0wC82YYyzFJTGgTTU4WmEI9lMOlZw0Bhj2KyR5npbVY6HHlHRHK9YxLaoK37sFSCUFrWJ1/LOiX9HuL3khKiJzvIXlEJOVEwseqONJnWo1BaT0zyAumtu5Larf0IdWxoZiq4BGVrxvM7+VyfiuvT8qrqY80L28oX5ukO2MklPvH9QSmUhH0r2usvP9VadMrgOvLWrqED74ObfCW/tV76Wq9FxUZiRdJvxNc/fL1ue7JcgGN3+Ruf2FoPwGt9eotu2ApVmfqFfXeDC/eOu4zfLIhScicQtEQAyBCv7ewjtHtrMCOIHjRWQeiiBgYgJEwSyRhCzkyQpQ9wVFyCBmjoXCYJQxt+uOIGIIKkSsCQ/F6jGLxbUCILoguIPU84cvaOjZyMcisr2dvQ69/oXg+RpbcBxFgDVlCTCCWnEiE4gGYvSY5IsLDdyM8BwSnPESMiAODDkB4cAj7ASkEbhbipzYo4ZhkhRwV1RfCY9uWvKxdjZNNpYQAIImmo+BomY5k/yztrvlaEeoRU4kIs+Adl32QnNBG19gU/pIZCAHwjBhmzJjBkeAsw8Kp1wEhhy5RQQ4RZbFtUcyoQCkWGjDzlxUj3ho5JIt8vZsEmeqdwGoM4qwovowVbwRDKQwV5ZbEcETPidXW2cB5hn2a0JsJrvewL0D3zAh+RvAz8IfP4H/+EeHpGeF4wjSO8HPK10Douh5d1+FwuMMw7HB//4iu73HY72GtRdf1agQiZ897NVpUrx6vSaiT91KWN+Qp2WKUCn2eFBurB95MtaAhNJZ02CYW3dpkZ0ph3RY1neM/GduRjSjRzbLuzibjGqU1674u6ektYbMq+5I/lWeLOVp4tgj5PBKYip/F1ymNlCcNebOs8nPoP4VrLnunnc7CI6QR1r1vjN9XW4nz9SWNvnqEUyi9ileAKBtqHgilypoFwCV1RG34dK5s8VaXHkpwuVZK6Ze27Y1KDBnBg2DAGs0pKPAwu+FtbdpFjatjcKHriwFs/LpebuOl0jzc1KFXlG0D280+1Od1gyNcHuHLyopqPJsD0nOV8N4XzPHtigi8nUFM2/ZN7/Ky3bfX9eVt/7zlL9Y+b3wnbIZmya6ujJwILQu2ogi1Pp0OeB57zIER4lGtIpJVQ8A0zeoBMcMGj9/FHub/z96fNUmSHGmC4Mciqna4e0TknTgKKKCqp4+qpR2i6R6imf9PtK/7sA/bvd3VM9VdhSogE5kZEe5uZqoiwvvAcquompq7eWQCCA7yMDNVuU++WW1x2Mpl6oyFZXizy+RGhNNJnCA/MNvn4woQoqQE5flMXtiQMb4KZlW2Nl+WtG+XktMzTchvbw64BE1P9j8baF1s5Tom58BKFQiLpySTb+qCadAIbLW+NZM2TAsKmhT1xVYa5Qv+LYRe9Dsf/rHXnPf+YZ33KxuYMDUOvAZKE/myV2uK+jDLrIEsZ6AaLa3nBECmgZydMYRm8VN6Zro6CgKpoK6FsS2+dMNjju94WkKguxBnhD0ymK9RnzxZ62eYbEZUU5aBgcy8v+oSxxQImvzdA+Fm6LHVe2w2G2jdQXmBhCIFJgWQxS39ARojGDYFyrTCZLF2hDUDrB0kPoQzcGwhPrDtZLxK90v5OewJKUpMA0q9Sr3NmP0UvsTiM0SNskDUvj9EGlBaXGgpDVLeNZMPYE2FBmV27vAc4YvU5lh36E8WawLi8beYj5C7RocaBM+HBMr+f1L+HxHfejbQzPenQrZcXj4+2ByhcY7Mx/Khfo12P7f8WjBNqU9nLVHOXFjt/NMNWT65Rky5+fxLe/D5gv8/bWiucj9USnlvPTHSMdBtCL/4t28wHh3+8N/vYQZGp4TR23cbGGvR9R1GY3A8DTDjCHM8wbKDMTae5eEWGoZBXM46C8sMawysMeKfngjO34nGx0yyZoQDYYCGUwrYbBDjRHirCPbBq6OALVyZjuGMBSkLaAkEPQ4Kg+5BROj0BgQFUh28M3kBBzhHACthzEfhiYE1A4bxCHNzj/uf/wF88wbmy98gSPoUMTQB3HWA9a4pPWpCRPDRamOMqsJiMfsMDqiCONsVy1lFekvuZV9JVCAIeLP4xBeXQaLKJpEIJF5VxAVZmIAg54OlSnpHLmqJM8Pf6+ytTb2LG+frHwHtxELFOof+3Tt0h3cgpdF1m4gfdV3nXSFRhg8H5ZIsWDBb5P7RY+wMdqK4EvEB593hVHhOXNyIArDRjBiNlVOPCF3nLSG6XlzVKmEEOmvBAKyTQOmjHdH1hO1+gHqvQP9zC3NyGE6EzfiIn53+G8ZhxHg44eHxiOPhiIeHR7jTCOc9bu13e9zsN/jkzafY7vZ49eoNNtst9rsbdJ1YPgheKXEaAo5ozOCVFbPYD4WSSlLMiSdtdWaXiiAcFW3qs1AF4VjApxdgci9k6QvKQQhsv6ZqCiogqhSJo4CTluVn+CMnzxPTs6zmzgC5QUJYFsr/bXWHTd+hC4zggB9Tjju36amkIiVxY9hJTPkfhjf47uEV/jh0ODiCQ7Ao5sRriK0AConZM5GmqWKbHwv/kWghsYio1fdcQft4eiKkCXg1p7CQ5WiX51eYs7w0VGs2Wjy4tKaTgm0pZKZgGuUSb62oj/L1FurJ21N0dRGdK6Gek3Aq+2+TKaMqtT/PSfng1ELT7LeE/XaD7XYjFllaR2GovayBHxRaxwLzZNddmdmxtC/KE6VsAxDcLqYFcm2QWmsU+1J4WoyIlVA2KGyY9kKN9TQGfUkY8RTLiLUmK8H8bPp8UmJ4s7pN3B6OhfRP72fKs3aFpIM3jnR+nvkLsRBCIB2kzhGsVXBOEIrTCJxGeN+kmSWE9QKIcfBCiREEhkIPzQo9Ou+GJIQBCxYQyV1HAdmFlhhKq4fL49LhAMm3dY4wBLwhkHseyWjf1386MKc2+tLVLozUixLN4Z5OP4Xt6wisfNDneKkD9WJ72j1eeW0M22x2T3PxUXwNBAzSODkkzajgD1aNBhhH+OApLwIU/7sMLprfKW/nCRkvSR1Q8QyZnUmb0S/V2wUkYa7eeFTTpM4S4Q1fs5LPdjXkJS+zqEJ6LzQw1J0nsSMB3IH2XWLCVwevkOwjiAyCphhHxNt6YXX4dAhBN7mosSSIAtNejuRUX6DnQhrpXz4oVL1PY0wBx8g0w+R1sHgQ90wpyKDvX/SbDSxdOoX2U9HmzKIi/M77UYxpKn4uDkx53NQLaLpCZ2HmTFqDOz2f93yt27Pq78wVl5GbWL+X2vAMfcoITQuNVXU/Fc7lbDAkqreLpT9xQcj1O0H+L4MFhlE+6+28T2/7pKC8zMl58RLQKpsbzJqZppxr23QThSr8z2f07aWGZYFuIwKIDRSNYNZAdLFK6LfCINne9FDKwRmvXa40OhBsL0IEawX/0p0BGyAGFfX3mQO8O0IXaSFh8HvhvE73X7RasMKWscqAoOGcRbAmCPRXoZQV+hnoM58SQTHM12mthbESCFsZA2gGh2DYzvo7WqwoRjrCqCPc7oCxO8H0jGGnMew68L6H3W48DiRMerHcAIiDBnxolmfhFVyLcl4S+hMsJ8JSyxnNDhIwu1lEKskzYEgpwDkJPA7lQ+zmOFd2EoQ7lLw1goOPC5HRewikoGh6ByabIgI7RjcO0NZAsYNWvVfQ6ORTCcONKGsigmvh0B5vuUCZTqtXOArMaqaMaxqzRuQm9c0rp2Q8zYi/kCJviettL5wIZ7ZanEONPtCwcQAGxuBG8DuN8VuNcWScTgOGYYA7PMIOJ5jhCHccwMdBrHNA2Gw6KNXh9uYO2+0Or169xna3x93dK/R9j81mJ2tQTFq8EgrH+CWyT0SQAuTM3Zx6yyAKHdK7uE6C5Xhg4ufZA61H1WJcQ2tMeFqLiWMKqvK27hpGietFvLjBQArrI35PSGysT/BcWUOKAB3WQkSOypbO9wElvxsAM2F0HQbewHpXYUSylxsETlUJVb/XQZ58cdyrucxOflSnZwOmb/O+lw/Tu3iqtJZpoNm9JXsdTzUXtMUR5tSNMMu5i6inQjzdltC82UpofSZCdB/WaR2FD6wUBtIY/ZkeKLcVlV8Ma5fXMvpTti3cUZMWX4rfXaJww2kFF22ZtCFL0xjS+syZeGXAZMe2Olq24Qn420UWET8tWCaO/tLhGv7BuP6M3BSvsYAkyXUczJId7o97PBx3MD4Y1WAcjHvMYkJ4SwgjcSIOxwMcG/z8zR47bHCyBgTjTYdDLIhMK6QGCghiEx2dSR8Oj4Swwl/SiAKogHQSgrAhMI1UtIzIa1lej9c7TkNd1ymxOEaIrnK5rar3zIlFAYl+VmsSMzkQZcwsGu8+cBsUJUSAGOQAR26x1HVANaYyk6Z8rupseQkFXpNio4j1Q0LgRaPIYPfH76Aej8A4ZMiRb0vTdnepN89zpVQqZ6Sz5KcIFP+Xs4GRghcC7TUZd2Sipsv3hUCYPGLmiTBPjOXESWmvAMSgkPFJIoZpYutRxo0IJeYI+PSN7BRXda02Dw5y2vcPHYzbYbvZJoSeGcxyfjrHcJS0uVxgbtgR1hnYUSwhrLeEYOc1Q6MbpyLMXWq3P4eTQDi4ZkgWL+F5oVdJqbcpPkMxDKDsnbiakj94ywhSYvEBH9gRudWETOgEUQtMhiJmQCQAke6WjCisLSIm+/SqGjfXg+djZB9xup8eTEiR8u1Eg/P83d4uv112CYkZtaaKyRnI9ZOFQlZ3YUYxplVHcTY8d/9edn/nt9qLXbzn+Ac/we0drJ+39AMY9ziqz2F562kBgNih6wk/+9vXGA4W//Jf3/rg0nJG607DOcZ2YzCaEY+bDYZhwOF4hDU2Kl5Z6zCOA8ZhxGAGWGtx6jfQAOx2A6cI1rtOMuOA8TTgdDqAASjH0LoTJRlSUCQW4gYWFk7+eXXdSKYRw8KBrAVDwdEIy4QBKrqEGvoe/fYErTQ2fSf7zQstjuMBJ/OIP97+E0x3BPofMKoO929+BcPAaL4Uq47jMe5TrQidj3WgvDckgjC8nfLWBASA5Z5jIN2BkHsPBJBTYGLvdtfFYN+BV8xAZF5L/hATKmeghBhcAJQCsYraxHm8tORKOTAFpXzrWJi1Uli2XpDVRYILaIVOa2yOj+Dv/4Cu79HtX2HTb9D3HbTu0WkfS8pbVhC8FSwziHJch8FuBCD0dFJ69nSoIhAHN8C5hb4q8AjB1Rx4DEGERRBEqgcpDVAHB43BWJBlgC02SuPXuw20cbh/OOL9/Yh3/9PCnCwejyPG4xGH928xDCMOh4NY74wnMCQ2RN/tsd+9wv7mBrvtFnevXos1xM2tuGPabKG9C08mgvPCu3EU6wvrhki/OGY4612PRuXAQK/74SKPefpxbCmAB+3xQOPF3wWumM9vdq56pH6O2iaUymVz3+NvErqWFAGOfFgTmi0/5WTfv/PndthTweWScsLsDRixKHsyegI6QhKMxQICkh9Li72NlhCBDmEArGLnDDROTkGZA+7MESc4jKRA5Kr72v9w00dPvyOaI96AdANy0Zk6bxk/oQbPAZM0nOjwzCGVp+c4jg9ziO0HMFyybolr1HmBGcd2UfzLLILCevDFJ4EF0gGV8evSl3ziyiTkf5fzlM9/+XQWGgMWYiB2XQdWBGw67DY9Nn0P3mzxj/oWrHSVuWxj3rUfDyaEGIDcPVH+9ENDWes12kDFt0Zpk+laphXmYLUgYnExnD0cs4N9QUMJmGPwTC0TJFvaJG2kArPP1sAccbWWEMq1H59aVv3+KQKGp+Qp76XydneZb0bHYvpqrIazDtYBwwicRoY1DGMZxlpYJwi5dQ5HOmAkA8IAEINogFaMjgmaVECro9/zghG21ObWGVH1hqgiZDkgJBmGOykruc0ITCP/NZZ91sR/uekLKaflpiPhHNW3vrY15/tcmgmxP/MupckJ4nmInokaAol6vM/1Prt7I56V76nAaBbNI8oyzR2sK0YsV2VpXc6x3PJlYgS36vCXs0udcfAWEN7HpHMONI6gYZRPa3zOBlLVxjPmu4RrxHXI6r40LWGCZ10dsikP/Y2a8VWS/EGNtPLc0vGpItFMkcSKRMkqyNZJ65Sgxs6k2R0/g2hk9AiXlUpwOucJ3oxQimbGjsHkCWliAAnpjvEgAlMgBqd0WZXtMz+dv5R+F+/zearTtH+Hb0UAaQShRPoMfxTdQ4ilRLEws7Fr3b1x2rP7I90xqZqiYVm+ljZc8/dcxbF9T8ALziI9Fxd5eR1zVRfE8xPqzf6/FqztS4GvrmzD0n14GZx3UZSnbT2Z6+f5UmlVKqlHLqu8KlqY67pdkZdVPLgGRERlfRZp3NWqfplMc6tiwq2YpqhVBPNSfzRuwvL8EDkQj1A4AURwENdF8g7QvULvgN3tBuPJwgxytykiQImrGwDYbZ08Y8aoDJQCRiPrVykl1wULDifujgyMMRgVecGF0EvWW08AQkOBIDEjlNw5yUVLfu55mgnBRa7Ec7BM0FrDkYLVIwjAqADnRvD+BLVV0NsdSGmclNB3p9MBgz1iJMAqAqsettvA9doHpu3gLMNab8muxCLAKQVyDFYQ5j+kHcQqeq0kCmuEAPaMWArnEMkYOXghJ0VFG3bBNSSDYdOdrZK6UbhWU2n+e6C5w/3tuaAJM5oiw1JXiJ+QpY5rOOBNcmkrSFQMcUPSxdhZwuxV3iojy+stLwrsiwF4Gtta5/sk+IYmhSKIhQwAggJFblEZ6JzAFlVaQYPRaQWtOvTeUiPscmsBjIx37+6hRou39+9xeLB4+IZhRofDycAYh8NplDVqHZgJWvdQagOlgO3mBtvNDfb7G2x3W9zd3WG722O73aLTYh1BRMKIDW46mWGNF6d5X04uxD4rcMCkbbvupE15487gHIsN8xZne7m0WFbFy8nKvxgypI8uvI8o+0P+GXHUqaeGlE4Y5sL6zRSsVhDSsa9hbflPB4JlCUFvzQDYI2jO12sorGzUtdGvDFr0TeMZz/3wK4Zk/nNrNIQzOA1KTD/XHclf4n3JEgL5gkUgn9jP2ZSuyPHAOZiu0Lm5XiOMqEeu2EKTRsh6ZAYGtiAoHwdGY78lbHoN42MLLtcyD3H9zjyfzbd6vS0l9DdMlmQB/Ulp1jamebjUaWu6nhu/zmef4GaNLTrXxOfs3WdZRETm3QtDq560WS7kpH2E1VAjR4ykcW2ciUFGH8cdfnjcw3qT33F0sOYAY0b5bQ2ctRjtCGMNvvn0LcZ+wP/y+Aav7A6m68WU0wKGx3jAJ9+OXBxSE/7LBcRszO+1QyZK4fnOpfQgIXgq/s5rX4LzR+m1COIVEPpV8fjSPL+sNUShmXzmFgiIWS2QmCb0TNfoU3X+hnUeSWD2YfQ8seOUE1LEeiTuEmJ5Fts4x5xJJNBiOfkLPybSDxeJjeDWxjgHthb7b7+DenwEj8bHH1iY1bkj9GoL4QOu7xeA9g6fXvFBM7gmUUENpM+fLcHPccl9nls36UTO0Y7k6iNv0txiWjgra7UOjwgHTChZSsmCYW+1ENwsOSdacdYaEAGdIShn4DoDkE3ant4CwphBYkTYkxdKjFJmcMWXI3MUCCz5qeqxavDGJDmVD+JHtgur5+TrIs/wEc0ysYYQ6wgdAymG70EbMS83WLAAOb7iZ6yUZldtyZgKcbzLsj/CRwjwXBz8AswJLbbLenLxunAO75N25edzdQ4TYTYozoUtKT8DLJR9xa38tPl/WgPaaMJ09n88YcMSLK3U4PIG2OEHOGic+Es4bIHgbIgY3U7hl//+ExzvR/zzf/kezjAAYVTrvsNm02F/u4M1BuNoMA4DTqcTHk8nHI+neE9IbAhgOJ3A1qJXhGHTx0DWw3AS64lxACBMfuc0tAqapb04NRfkD8r3y5H4E3cuaJhbWBiMOMG5EdvNBs4dYbTG8eAAcqCfHUCfOPz85m/R6Rv86x44KIdhGOU+P73xgbU/hWUSV1LWwY4WxjmMxkIRoJjAmgJvXXDryOz17pGQsN5o6UfCEiVGCphNCtCC04PIu7NyGK24VVLaQiuC006sUrT4omcFHxBbQVFwEpXjEZTwtGBFEdrhA0IHvEN3HbSSwMkq0BhAeWZEpqC801pD9xtsNjts+y1016PrdHTfVJ6dLi7LeLJ64ZGxYkUznAYwxDpTaQ3qt1BKLGmhVLTCVN5tpMR5EOGVdQzrAAsFC43dDQMw+OK0w4530G4HhsLxdMBwNPj2f4y4PzL++d0DrHE4HB5gRovDQeI0WOPxPmh0XSd93O1we3uH/W6Lm5sbbDd77DZbGTsdrDrFAsc5xjAMYOfplMBPcIjul/N5kg9PL2b8WT/omOJFnlEbTqQQViPnI2T0bUDH4gqpeQEZcONb+n3JWedd/zryLotIrHUo/Z7zSBD52zlzMMMTk0VMwlvF2FqJcBBBXCAWVT0xesXQPuJIjOe+EqQ9JNPhCM4RBgc8WMbw+Bbu8R1gKy5DnCr/PARcwGV1520o6WmeJqjfh4mPxFlgiLTuB46u5vJPH6007n32MRxCW1Tx3Z8dJLFumFPeMKeuWNMc65YPB4dgPZXHupD/2H9Ohq/oDhff54RqlwBNftCEBgqgNMGyw++P99jst/jVzSf47G6D33xNsFvGH4jgfpI4w1oo184E1/xThZXIfT5zSQSyfgCeJIjIFfKerZW11rxgJmstjGhpIF7DTVFezjWQ7Npio+wLUG/mtV2opXJPhYgyyanpGZ0+8JUDTmMnmgzW4TQAg3Gwxon1g7FRy8dYA8cnQDnAjSBtsDWCeHesoFih4yBhztw9hT74TkVSr2Y2BRSunpLZKcouIyYECwmKJ4dfR5QVE4QQqEwYn80CAGrG4rT5527pJ0xycSeV+2+ptLk2Lh05bV3tlRCQ0VwgsdRAyr60NJGZ0Z1OsGDwdgPWGlGTgX2eoK12yYZjJKKqgHNlVHNfM0maWUIebwHhsW1mMWVWwwAaR4kLYUKw3/nVdb6p58eBkcXU+IAsqZ/iZb947GTfaz400TRZq4iz3Z0g3k+FsqZp3V6jJ1o0hBhB2W9n4cjCsQNBAqaHYNXBBzazBVzKj3gHhHWb9LU8zyK7C0oSpBhiyr/nPxrPYvrS3ZPUK6H9gouk5E83ixkRA0dSUXGp8cRZ+cjKCdmoUf8FkI1LJFjP5qlqiG29DIl8DvwYDMuoVXlBFy8OXnkhPNdy4vnjeEn7p+tmufbW3ThT1kJTmjtiqWIu8zDKINFPij+xenNdBztcCx9uH7Xwqj8VBoKcwSUrsr7nGCAHxYCiwefaxrREBKUB0pmyFDmAVRR8K1KAFtI6MVATA1wrcWXS6U4EC6SiVri1xit0iTZ8CBzsnIWDWESANdjnyfcegaGYYdn5ANNG0vt7jG5HYK+hX99BbzZgODBZUGcAVnjvBnRK42gJJw5KYT4YMgiOdLzjI8Ms8M0o3Ji5gIFRaGYHi4eIJzLgRSjEDvBBvSMvi9vr2vn0zom7Jzjv9kWRlOMUoAID0WX5ZLzY5Wco5CoHyX3uH5IiaOWDqGqNEJdDiOBsvZDLLl6OiihSjg9KXfQ560Uct8SQDBYujj2eFOIaQOfkaVSgC7a6cRqilzixyqCeAKfRW4YaGc5uMD5qkCEYSFD1h8d7DCeDd390GE+Mx+MAa0ShUNxKehdkG3FHqTuxbtjsxC3nzc2tBJ7e79DrHn23iW6B2NMm1uN91oYYELKuObd8QN7BubOZJ/d2GbiZWx9+fBfYrnVVRVPWnfez6TLcPsSOzYpfAZekpIhPRpwWJe4sfwyt4IOmt8oPZ6Nkiqua/Xe/FTxHDMZ1OJkOJ6sxOIZl9m5WVTa/z+6eQGHVAhT8oeJ8z7rxpMqmbU6qWJkdWs5PAU+rzBqSr8f5EWmVkCuBNXJm6729a8rSA+2cLP7nUKEV45Wts1Z6KVvWIxNBaS0xIjqFse9gtS7mcA3M4fDnyjiPJl3QisW1VVlvNaasdeQ8tVXnTqizdc1VwH7e8stnkvvc8/PwPIuIJ+DxH2EKwYXTNcYzlPE0ujidZs5fNs7JkWvZ+hgQFqdxg2/vb0RDxYww1sGYgwRAMwbGjP5PhBFvboFP9A5OaTh2+GrYwp0EoTM8Irj1cLlZmgfKviT2DDUSIPCEK2hfskTB5E357zJwUVAfkQdfq0p5JyRmef68EJxBXbj6nLxPiysgZfX75za9fQWVP+XOunCR57dO+5Zv56k3FDvs//g9uNO4//or8NZL4YlAVi4OcjQzzC0mCJ1L0c429/KCcUlmocFVmhCI++9+gL6/hzM2xlaJDN2Lz5YXW8yCAEXfmc8o58ln3QvAyoYkhoW3iFCNM2W2jhIJrt89DzIqaUWBzFYsGszoLRtGWNvB2REODsY4gIW5AjJwZhQNTTP62BAnsDNw1kACVxsElxKIzA5xe5QLagoBxNx29ambQogqx3RfBMYJea0yBaguxohI1hHBEqKxt7i06kv1lAKI0KhCAEEXHpETJgfmLsMLyvtLhLWXy48HL8NwDjjVMnk8zRO+PmOtPQfOUp2ocMmSSRGtkrCe2VRWfG68lsi/58/jj0d7TQa2DT+5rRRYJan9EwZmPI8ZW/4eDI0jvvbMNwvHFtaKT3trRzgLKFbeBaFn2JJCpxR6vYPrHLZui5sbC2MthlFoooeHB5xOJxyPR7GO8MGjT8MJ1sjnOI44jSeAgU4B0BojiXazCowBb+3aAREHdNbAnU4YxhOG0zFq8B5+foL6ucX+F38HfvMaYCv3LN2BCLjHCcqN4IMwe60Zk7a/Z0CKSx2vAex58BGP0UErX9wYibWnuCIilc6ucrnkMyAq2SJAEFw/xEMQKwcCrE/r8V5jAKXgx57BWpjlKs4ziS93ZgQL4rBvVO4qiSjGnFBKQWmN7XYPrRX6TS8rxsdBZK+9D+/XnazUJkp6PiaHY1FhICAIiIptE5QawxgExQtfhzHCvDcu4YsyiGKFKcG6vRf6KHxw8ucVPm5uAK0HvDp02Bw2+O5f9zjda3xzGmCswf3jA4ZxwMPjO4xmxPF08pYPUt+mF4HDzc1r9P0Gdzd32Gy2uL15hW7TY7vdQWkZK4Cks5YBy7AmVzgRy5ykZBLamu1ML0Eh0n54eIJPc3h+BlKSVEaTYRmY8NVBGl1qc6rvHHk9aUPzKaXP6Hos4X5hHy31MbgFmgUiBBdg5GM/BBzWo7SQeA0KvSb0mrzVSux81k5Mx8bvqfr0fBhv8e3jG3x3Uni0wNGfDQYtu8ArhSLO5iZZD0vzg7CkKH2Gac3lf00I1hBRHMDhe1hjjOxJVE1qNjs7B8j/Vl6Y7/yZXqAWsXiu1kZWt/9KjDLvtPZQayGMWI9KlHd/5I/5NR32VcFjUiJ0VwBut8DNboObbQe92+H3m9eAljszb2FR40WIzhKOdQWEpC5ydiHXvJ3n8zp+THhpPsuzg1V/KGFEOADmt8waguDcSD61Iy8xAHNtPdcXKi/iS2vNECWGR249cmMccBp7HAeF0SSzXGssxuCGyRgwH0DaQrGFJosOmxRwxxHIKajgL9yfoMUBm3cxZ0AFgnmBJ0wxW80kDihfIjiCMAIgr9WV+3lL9QQGUl5Oaic121sO5hL4etGerTOswOxjqikyST2T4Brny+wOmPIBn1UHF188RKuO6lVxMPnJcQ6whO54hDMjiBSgCHa3g/Nm4e27rDFKXCTI+Yrns5WpfOPLxIsnnSfEAJlXdTqBRgMaB5B1PrBVVhbVJSydI1XNC31IUv8ruOk7h51S2oV5wkLW9JTFXA/FkzbEPOnBKNdl0YcZra+52Y8I3osgBZwWV3P8CT5+Z9SMdDZpcQYNTBFEMJwCHMTVhLhmsnDO+D+b+Qj2f6HeBtVY7K2oxTU9XCaChxofzEefqjcUyk51kBIGQG4NkQJIy18xn1Ggu4yPJOYClc/yfs1sp9THZXL34iWSlzuH1J3bYHMX2QeFdQTIkzXA/myhjVudhcBkW1VDzdhozM2FbZi7d0S5pErb0N6vLSWKd4sqdysaurBfnidUyjgZHwo8viPBnc9X/LJOPp8LQlknocS0P0IfOHQ4wMHBQoGgwOygO8btpxuYk8PpwcdjgGiyk3OewS34mVKiFdwJVxCd7gAGNn2Pvu9hxhHjOMA5C6UVxnHEaEaoTsOxMHLFTSBJ+UzC8Ea4i3OLRG91aC2ckXLH7QnjdsR2f4N++wqj7rwFguwP5ZlYNmjgs5Qp8QlcHK/gkagI9Ax46wFhpAbXUYoARV4r399rKhviRGZRZF4Vz2O6UK4wuzsNhLVPhGRxIA3zfDmGML1VFEKUusjpbg9CiPweV7qTeAr+k4KlBLPnRnp60QcGJ5WxHb0wIlgzWOtAJMKVFmM0zKGEQ5R4GILeBRfAGiCGxQAmB0UKW7XB681NGP2IN1mGd31pMRhgHAQnG74zoPfA++81hgPhOIiL5MPpIHEbRwYzoe82UudWXFLtNnt0XYeb/R26rsd+d4O+67Hb7aG1jjFRpEsWzkhH2HLE6ySOBMf9wYFWDeMZwC+O5CO/PDuiAIPzeSyHsxjaKj/J8M6G8XnuSdyqLyr+1bwNzn8s10yNb80GZCmIgjugdDMW6793UFsH3Sl0mtCrAX3cV76BUwS52ToRCALGEQZLGCxwsgzDDO2CCyPhcHBWbhlPbx2+VqyJxvooqGkKSfIBLymwyaO56ypbauEcSLRKK8GZQhooRXikYpLWPvCZc0FF3Ya6LtTvqrpXEgulBULrIC/pGdlvnmMXhLwK6HtC763MtEqKoEuCm/XtqhqUvV8o4YLKFgpdwIGpsezqrK3XL4k9zfW6PsUoW5zlnrq87CV4tiDiI/z5QMIB2JtkAtYHEbXW4Gh6fHO/x2gsTqcjjLU4jQOsNRjHAcYYDGbEm1vGl/oWrAQxZ8cioHBJc1uQ2lJWXl5MQhSfO0io8au8kEqmDoGyeynDTGYITAJVj9qHcPyd7+R8Fy+eKmtZR/lNV5b7k9EKn4Gc8HhuOcVZOMPHqB/LPcEy5dZg980fvW9OwPU93v/sSzjdTQtaaMeKZBcu4NZqbtcgrpmSIG/3w1ts3t97LaRkLREQgSm8wIJZx58oSH+unuc/2oKU5U33YS0klphU08fFfMrELGcs6siI6QniOVNvVez5cWkgvdXjwrWJcRiHE8bhiPF0wLA5gJgxaMB1HcA9WFmM/QBFI5wdUowIO8KYAcwWznqrOFfrTuVuHZIQIL0t/yLiBIjyYKO0ug+ppPA8qyfztSvPvDVEeJ4TkvFaSQSzy/ozCawd65DMSnlNtijoWAs/8YP/I/yJwVpcpM7ztHU4caVwRWiW3ehevtsub8sl5OPzcJ+ymKeP+XPqzdgM55OvFe78WJDfv5M2hZ4yNvgBjB4n+hqMDgyL7Z7wi3/7Co/vDH73n9+BreBbbAFjRXCgtPZBjhVIa7DW2Gzk3ri9vQU7h2EYYK3F8XQU5vBRYutt91sMw4D79xuxLB8HIHN5QkZWrVbk4yuJ9nlwyWTMCafTEcfHezy8+g6Hrx7x2Rf/EfT53+BICvp0gFbB0lvuepczyRiwzvdJ+fn2BrbWhTlk72tegTSh7zSUAjpvEaGClndaOL5sjnefCkz+wMzPkxK8Jjdhs+nhHENrG5nZsaHR+hBg66TdGsBE6x7+flVQQWCS732vSd73PbTu0PW9uCLSInEQYYLzwcYZYAIrglIOygtKrHMwRgRJ3Tj6drrY35IOoiQYZTmrnPNWJ9SBFaB6wNGAk/4BpAgjjtir1/hb/XMwE4z3QnAaR5wGiUPyx3+2ePcNYzAjrHE4Hk8YR4vTMMAYi3EcxVKBRYlnt9uh1xvsb27R9z3u7l6h73sRQOge292tFy51HuPxwi72a83HsxBXmx6NKwQPaasF7wO1gnA4g122D4tTOfINcqES+TO+DXnsjribYzumvII1cL1TVwS6udILp0GqiJ/iY5GlUCrQ5AwUP26Koe9GdK+A29sNbjYat/179BqFy7I5COx+luMAlgmWCYMBjgZ4GBnvRqFNew6CiAxPzkoSGpAuH9P6rA7KP1Te5cX9P2HoU9aKjAdUFM2ThskZGQQBsrfTC58nYzGF4im2IcuT1RlniSFKhK4qILSlOKNrerA6wFG9jhVeIy5WBR4nCUq7yd2TnKm613KGbDR2uy22mx7dppe4OZTotqJLKOez7tfTGvnE/Bnd1n6fPW8pr5z1K75Q9QdE9c5V9VL8lWcJIs7x2Aoz6Gsh4XN11XNfVPcTQXwbUCPrc5Ockp3ry+V9LQXNXHzngAT4oKTGsrhisgajEQsIDIzN0IPIgjYGG0j8CPaIbAgC5rxmxJQ2pOLXHJe3vYJKxlQLjZkQUOGiIAgiyOlajFkyAUZZQzZWrUNy0ki/c1uNf+6yjHcstx6fhefsyHQul6akBaPyGeU2y/Cn4JqraelAlZlmwFlhNlqL/uERrBpy+eYgXbRA80rPQ2QynCnOYxdB20idBqEAMmpSEIFGO84V3mLe5O2fGVghMGj1wmqfdamS2Tt/0oyCyr1MmbueynNpuH5RD2hrkNac2fOrOiCSMrNnTLPzErigQxZhfr9wMf05gu1Y4gJZY2BGA2tGGNXBjKOsSWKQcjDGQJPxQm3rAxd6Dc4stkR+ouYC4EDGyNbIxnlxnZUEyTnIaUApO7dQqOsrWpR9TxZKSwOe6vCtiwIQJCFEJXQpYc38N9xFnYFVDMKzSN9yGT9OENu1dT79Qr5Gv6a44Pr2XG9cq/PsXLG86kJZhGvTBmEsmNtWei1LCf+iSN+ylJhovlYHLNcE5yVCxYvm8AoWiE8Eat5X62DJ+uRs3mdTwLn7jpzOwfzYR3zTQvMDHDpY2gDQIAK6Hrj7bIPhYPH4bkRwoaMcg8nBKRUvYsos67RnPArTW4GJ0VnRwDfWyOc4YrvdwJgRw+kkLjiNt7IIDC52cJbE9Q3EDZG46nQYNwcc+rdQtxp3/RfoaAfLDOUYIIecCRgZw+HTCb3mKr5ZZPgD0f+I9sIWsYqAMPnByT1SPEoCrUDxN0F5YUh281OZByTBmsnHnCgEERmDOr97mF0p2CdE6wZNUqcKvkRykjTkAXmFA4rvM6wagWKUpeOfRW6auDS21kH5YNr1fiUfhFvliAcB+424JtqfEPmWjnvYToQU9qSgjlv8/tsDnGPvwktceQVhxMP3wPGdgnHiDsxYC+vED5DqFHbdFgTvLkVr7Lc30F2H3W6PTnfY39xAqw6bfhuFadIOC8ArWAQXYDHuQ+bhIM2CH74Kl80+03xhAoFOC8pWcexaZ7q3EJqFfD01YN2JRhO0MwlaqnsCiEGng9ttEFUCmByHTE+mQzEtO9UfhBnI1npeLsd/4anWCn2n4x9RamspOMrvtGzuskkcbY/DuMPB9hIndDTQo4Gx1nvTgI9nXfdsnuJ4EoRxnTN5qTZ68oaRFVB/5/J9Mz0jE0KExzztWhjcySDmaaLdiC9jYXxqwQojWquXdUyp5LaC3zJwNRaxNP81p7bSp4+pRMrHTVLQfYe+6yRGRIyxhwuWQ5ugXY9SrEmY9Sbr5mqUp9WY7N6rXswqDOaPL1cqrNsEYFUsr4DvZGdItXBqodE14KNFxEeIUJs9Jn+OYm5qrcUwjhiNwXEYMBqD0+mEm9Menx0+gbu7h9pqICAnjhOCUhNwABDNT7M2+JermEf5/3kZ+Z6nMl2sM9RGeZqy5ArlwFyqlGIGjaiY9S14qlbgj6FdFkcnavm2+zcZjWswSybaIoLcIcT88I8n/PAKAYgXCzvQ6MRCIks2ndusSgCFnXnxLtfCKOusIdbVqozyDrQvsEQUMuA80RjIpWsHkKTq+9KyW8LqX3y5zvc7R65bsArZmOBBcxlaA3au89OBK07kIMidq6aN267ukhyEDSSaZD3VS8pZBzMKk6TXR5xOJ4AJHRFsp8HcwXUO43iCI++SiUVg4bLYEM5Z1KQ+IjMgI9T9u/lA0xT5AeWZvxYyJggRhEOSu2GC3/eBhSN/yR8tMqH9uZoEgkZQESdkUQiRwwttpuceHVemMT8c/Mk2/E8S1uBFHxSq6X+6tcaf7zq6MlbxI0CYm5zZMHVrmsjwQClY9PwtHPWw9DOZXWex2RK++O0O938ccf/DCcxeud8zxMgxoBhKd+LeP5RNBFIKWksA6H67QXDtJAIAsXIYTkdYa/Ho3egcD0dYY2FOYklhTidYM4BhYEcDN0g8v9EOOLx+h4dPv8fn29/gy5vf4EHd4nE04hrXAdDK3zvSJueVsgJP33krALbBf7+MTZAbEHmrh07cbPRaLIw1BZdJgVlf6inLExHKKG9tCCo123MLQmJC7wNZ65jC4ykhqLMx0RUSmOEcoLW0Q3cddKfRdVpcPFFA/dmnlZqdx7tzl4xyv/sl48dHqiZRnogEK8V+iKsah9EaiR+hXBwreCZxYO4z6bjOOqXw6hOFnSJ8ffwcnev8XDAGY3D/1uCf/+GEYTT4h+MB4zjg8fiIYRxxPEmsEWNGGMverZY0T2sNpQib7QabfoPb3R6bvsfd/jU23Qb73St0uodWncyLHyPRencY7QhmC+NGb3ljohIJnGhvi0hJgoRDuYgz5kzZGOS4WAthGgOTq0Roc6uK6fvAa03MW8IcTbxgPVFo7MzRdelVuU6XGXLptAm7IeCo+d2yfKq23jrnoHygb1lWPg5EwFl9f0S9xyuF+hWhO41N32G/3WK72YBgANimAk0h9Mt6E54czB7fPn6GHw6Mx9EBx0fcDQe8swajY1gl5woTw3Gu6GeLcq4CjOURbTB4/YJBQZ9NJjSb+PDnMCkv5uIscegz59LcbFzlIkl1ehqPcp5ZFGAU1GC7rVWScv6uAXkFmUpCTndRWusULM+0liDVuw32uw02mw59r8AEOE/rcaDPOVJCcY/Q8sw+A1aWN0m2lK/V1rk5+AC4Ypygl6/qqbBaEDG7sRc1frKeL81D632j0Jq1k+eboJfcSvx8mLhYONP71L6ZdLMLo+xAYK5fdRtS+sgPvXC5B56UvNFg0oDqoFhjb3r05oAeI7rOwNzcg7oBbDMzSs4vwEmX0gfVj9tIQfqVZroQ/jfLa66axm+afxUerGIula0M31qMpehnMLZzzSmRj+XzTpU1uc8dt3GmWowz8v2awdRaW39Vj2rJVTY1TPWc+0Qrt98yOpqlmzVjXWexUbxvJSgsh8oExUrhWvxFxccErn2PVxARhwsFIYXcBdl8cpmmfh/fhf8aY7l2l8ztwDXoxLrS0/e6TAJHbdrAWM/nOD8rcpz57JkUcOiFjtXKNe2CSgQRANgamOEEMx5hxh7WPMAoC2MYzBqkejjLeEcOvWJs9ABAXDE5FusIdrY4ywJhlXVdfvsv7B/WlleTe794H5BZFNqWYRACIedTgLJQl6GseLY3LX4cgmuFYm4CMh4vKf8XhSpSVhRC5NpBZa8qyLGdcyt2PUzP8PNI2zRFEKY8qQmYs65bA8+3CpiO+fUJuQTn2nsJo/45fa81TlOhl5d1eTsmyN9sinOr8VxbkqbZtMS4kqtXE4J4tn85XTC3jvLUoYIza6DxrH30n6FDzmzta+iIxIIXl+xSj87AcxvJFG+CFnpfJGWfLkNfyTPXOzyC0cFgJy+cQ7dxeP1lh+HgcHxv4KBEW1nJpwQ71VFjWSsdcR5hUiswGMqvDHYKrB06RXCO0fU9rHXYbwc4azEOA5wV14jGjDidbmCGAYfDA46HR6j9HrTbQW9eYWv3GB8GWDqBHhXoVgEbBXrzOVjvI34hNJu4XgIAa+U8nrjL8dYEpKQvkV3v7+XJUguMYgai1aAviIvVPMXrky8deI3fhCekOUlZc81wrRW6rkPXdcKM114zN+RW8DiXSwobGSLBbACoqPAcrDZD3Q4KG3bYjcBhHEHDOxgaQVuF207hVm2w7YXZqzqCIo2gYBFcOY2D9q6MADIAf2cxMOGb+wNgSWIvGofTacDxYPH2rfMWEN4V8ngSawdHUNSh7xQ2vQYgQbtJKXS9aCD3mx5d12G32UBriQGhlYwNFPl5EpwszDszw1gDhvMWrc4LYLI7g+KIobSJmAr4Av5W/C5nNMub8SQaZ0QqhrM8oQyPOJ6hQ+Kq84jn9IiZ8gik9NQeVd3TXOQL67XE2YIS2WLLInqXtJSjCkymrOJAMn8ec/Whw701Sk5KOig47HuNm60WixilISGlswzN0U7NCkHSHbwRvrUYHOHAhAcGRkc4BSGmc3AqjFOIOMPV6FwROP8ofhRJKAxM8YKmzxDS5X/Z87nrrqo6re7G2md4i5RUR2p/2gOIeFr+WRU0+avbd+mIL6VPLvaAZPUjr8iTOuQ93BKoU9hqhV5rjJstuOuxIe2XHWVlpnPiDFZzQX/W4w7zaAZVvyocb3KGVYXOLpSSG7CaDGu0pdmGWEU9Zq0xLNtSfK9x44pOn6dHz8MzLSKohXNP0lxiQvwcVPNquPRc+RcIIa4L+am2ts4JZrUiC0/OXNGKILDSYNWB1AY9a9yedmB3D5DD0J0w3NyDnYO1XlMiOBRFebYXQ9dsHzW+lT9Kn6P1xplbba3Dof1g9hyYNftDc//lPWldCaVWBCqkaaauJ2kQnsmTOriGL1C0Jfi1nM5VXtB5Yvsc+362B42ip2nb9S9fscsJ4zWfqNRJjXHOZ/KvgRpxz8d2cuy/GHZXFbui/DlUNmcCLS2L1pUWmdL+ZWIwJ2QoafTPIQmt1VCfOXXN1cA+eXynawSACGtJfMZGhK6uJIsH0kJvz1ediIxJlnqwl+4Z8jc6eQLk+Ijh+B6bjjEOGoQjTjRA6w7ObaCIcHhk9GrEV68OUMrAuhFgB2bj58UVPYldVNMlTUkyERoj3yIRGS+WMmcmgJjeOOFeJ6nUs1bETQMyQUX2Lt/hflyj5V9QftKhIzorR/JGtw8Iv3OGSnVmtM5YZBp2V4a0RzPhSmzK0sIJ8EIH0IvDXH9aY/y8Pq5l2K9J91wBDAHrrLYXC3ha1jkSaO5JmevCRsfDpXhwWRmrKwowcxM25uyy3qxPHYJGFjkn2fOz5NyYLNVNjXGu63kqXOmsm8H760c8ea2gwNjie1jewmIjvCg7YLsDvv7NFu++GfD49uQRRAWynunMGnAdtFZQWoQTGqKprkhBU7KxAzPQiT9+5d2FWgaYxTJdYvaNsE4s1I01OA5HDMOIx8MDjscjHh4e8GYY8PnpiPHhHczDPbr7bzDob3H67IjxFdDf/m/A/tbHmGBYluiy1iuTWSPdKNyfK4CgAM3ooLwgItg8OIR7U5JztKpIWuv+xuOcJUneVRGn9yB/KIVfyb1MpBbCfa4kLTkAKmnh9n2P7WaDTnfQXbKEDxbEnFlhBOU7mXihYZ21gLKIuvScljWz7KudU/j61OHRDiD+I+wtw+xv8ZV7g1/iC+z3O2w3W/TbHbquj+vKAbDG4Xf/bcTjeyfByq3DYTjBOotvxkcYJxYwxhgcHg8wxmEYRjjnYIyNzGyJY9FFoct2c4Ntv8dms0Hf99hst+IOpRNXTBJ3I4F14trKuFGsSrzFg3NO5tBaL3fwiE2uSIE43UisVEr8g3x8K6hPRim28l+fCyHi2AfKah6nj/RkPNJS2lrZYfE2aR+W2YWZcEdCKbSDp/tTe5MgNGCGgakf/ZyRAsFlAtDkUimgi4I6UnzgFPk4LoBmgoih/L5Tsn+dY8BZKDjc7TTe3Gyw6TbodA/Cqeprdi/mX1lEpcja6xzDmBEH2+Ot0/jeaYyOMDKgWPpBkb6hqOlPYX00oxQ/517O8tUaVlmxE1qqPuzrvJyl9xYL4UwqhallWUzwQujwnIu2BPw6Vwap3ZtF8wtXtSu232Xfs7YyUt6YdYm5n8P68SdS2SoFstUn1hBKQfcK/Ubjtu/Q9z3e72/RbTQ+o4oP4AXFwVXYh4brKWRkZcaCl2mL3G3htfHSUjG0FrhSJqys1vLa8uN59bS9e4Eg4gzyeWGOlGYu7wusiEYtVyllonk1f0GuhXk0PlxlK0qOB18b0Z6rpF6K1mk8DDucjIJlBc0KBAWrAe49eugvRc4PvqojNP+lqr16Hjbx2S5T9TnzGvl2r9k77Ww8+za7sBuPz0Gh2TshkhO7KcsQEpc/Z5oybXejYc/mRKRSKfygmXVX5Ulju5z+/PH2gufFucqb1i7LmZ/HApGxqtB4LCyA8vlz77jnNX4W4jpotDnbJQg+S5uWL5x9nxbThOVhmZ4Pdbp6+tfKCkULT5B0zhjsubAm39drgsnNwUVTlquBxpxTx3PshEi11sCMI8bhBAKglYZzBgB7Fw0AKQPrxARcXDG5trVcPMKvtZ8DoZgxOJpVBMsISZjZQKRGhckgcb+UqCi/cl1FSHBZRwqQmLVppp/5aTg3Ekv+jq8DjGIBVrU3iRrKiZ6XhWsTDQmRnq+DuV6oxdvZsufm+UPEzMhjJsymOVPGbM4g4KQy3dpeFUfNLN5WMwda+OEK4GpDZvfFRKOsuhQupUcmmmmT7PMMgXNBnmfP8oVxkClaWrNXXodzbWmuwXV1PxvtoNkfCyVT8a3NHknKA5u9wmc/3+PwYPD4dgST8tF7CfA+9pnFbxAzQysFp5wPBqw8GTWdKeG1B5Y4gaiDZg2lNJyz2PQ9zM7iZr/HOI44vjmK28RxxHA8YTidQJsTuDviQX+Po3qEO72CBWAGH3R4MHDOwgwGxgG0YTjlAHsAfNwJtd2j++xribegVfBUWOx/+UvxkhjwymkpDZGCgoNzCkpN6Rdq0g9cuGMnkLfKUNC6A5MEy1ZaQSuFbrMB9T2gtPyBwcTCt1O5Ox9hfL0ZGIodmB9BmtG5IIRIdA1ZQvegwUywDOxGB3V06O0en5hfwMcsx427gaNbHAzhSArAAOYBxgd5Ho2FMRZvv7EYjs4HkHYY/KexIhQYxxAIWvrZ9xsAhN1OfktsDo2u36DT2ls/bNDrLXSnobXXfNfiCgvMsMb48fYCp2ABYUXwwGxlzrhyMUmlUmm5xXnyNYqOVmzap+LQNb4fBUUrshbxv1qNiI/K5yEuA5+jmQkxZh5D4ue16MKg2BNlCxMyrh6csoHKK8iQygWAnv3ttfyZgxiE0fcdtttNFFTVd1100UQodC/Zn3MO4rbNOglUbVhhcITBAW44QA8PXpiVNb34TDRFs3/FWnriic/5Z+zYpPhJHYWiV6Ow6vXZ1s2wNYTxm1tBZBkYSAKEuRq46uN88qa33bpNz+YNTPGdYJVGSuHAFo40dKe8MF6stSRWUWtXTHoxU+/z8Jb16Pc04USQOtuWsKGXcaLSArrCU+vW1Chx1oYlEc6lyp8fCj7GiPhLhfyAXKQNCJY7/HB8A2MB50YQy8XnOsDthKFENpgUNxhLOf3XuNhbkKrPkYTrbJP8gl9NMC+8CQjtulIWDgmVHUQZcU7lA/lVa+AzN2UJhPqwmiP2Z5s1D1dgovDk19JIz+V7GqxtfYM/Jfl5Og/timh6Y1wCq5d+I+GPebtcAHPDMzkHPKJYWEUt4Wsoj5zLpqFmQqSmzBjCTN5fAvHszMqM2lTBLUCwWmu08RzEPszh/TmR7wmtGNStOo+Chpy1FmYcMA4dhtNR7gIQtNZw1gqhDACdhbUDwOyDHkrAwzB5idinon2RMdNgzqQ0zzzFaem9isdSfJsR2qH9HMy0J/NeaSPXhNlPEhoLYtW7y+C5x+JPDy47bH+cwN0vAMXheGHeH3n+a/dXT48L8dOGhdMTH3ISnhsX5KeHzoSbS1q1veuxe7XD9/96wMPbAWDnXZTA3w8OrBTYMZQisNdQR4fk8iiSPMkHd7wflZgJai1Mx23VGqlGmN3OiTudk1E4WoIZThiHAeNwgBlPGI8H2PsBh4d7mOGE4+ERZhxxeDzgxAPeff0edjtAq98JE30c0NnPsfnZz4Guhwp3ou+cU6L566JWexJCOM7cHwE+BgNJsG3XYAD7/6kKKh61RkncWVEIGk4doL2rKCUumVS3gerEHZZIcjwuRVzueQUoZnw1ADs2uKc/gMmidw4ELTrgvq+bQ4/uv9yBjYJlB8caDkBPe7ymz6UeUgBZHGBhjIExFsMwwIwGgxlhjcVpOMFai+NJPoOlg7Xi+ojjGMrMi2Zxh92uh9Yam83Of27QdR02vbhb6roORDoF4pZpEMsUJ0ogxlgv3LDJ8iHilZwtNmRMMn+GnGGmRewgaDQX3Oh1wFx/OZd+hsE8A617NzOY9Q8mX4r8QaadPstbI+I2BC+AkDMi7mnyaCVJ/IQghRBf+eGzHLtgtVOybWVeVAj8qyRgPbzVAYXx8V4qFDG22x673Ra73Q6bfgtQYqoWAcczcoRByXMRSwwW5xjGASencHSEg2HgdMDm+A6WGWPMG3uQ6I/8MJiFS0/6DAHPiZYmfchl+tnq2Cct8d71LZtzwVU/D+1pN7N8xu3vRRllppe7N6n9lURIrZUGaYUDHKCAru/R9X20lEjn+0/rVv+xoIkfLUxeSyBRuE9+8riGSq/NdWvDswQRf7qE1HK7l/pFCxfUJP+KeXvqQjnn+iQdlxP92pSuOM9qRgqBWePR7HGyWqTfjmEtQBZwToE5M9MjkW5mDazaexk6ErN77YO8gJLmbZVcj02ZMfG6krFvlup8m7DiYK8SpJ8597SRjWZcs1Stk/LyCmjec9SSS6nQmsbZ12jc9L3vGNfPngzr9sPcKL7EiTQ7Y7RqaD3yNeW6ES30lqsvk47N7ajGs7qRS4O0Gplfl25afGnEGapsMSVz7cBE1BS5fMLsUfmlTF7BMnOmSYLEgs71v/V+Krzw1h3ERY1Tf7OZy7xrwJPKCeQI0jAwg52FNSOMOWEcjgActAKc7gA4dAq4uwU2Hccgh+KTNlw2yTQ3CJeSNUJrLUdWRvPx1HUQJkKM9h2eBpjy9cSMoFLEcKBodpzWX3RZEIsI901gBoS08kdRszDz95s3pyLeoyb0B8W3povkkurnNHbOlbXOFdH6dvgcM88v3wjL7TuP5fw0ceYVYz4zVhm6+OS66yE5Zz1y7QDXLWEE4PGrJ9Jh89ZK9dletmOxmrn+n1lT59VtJrdx9fua0PLDvh7W8K8WNQJncl9q8UIw6PEOFh1G9GkN+ftie9vh01/cCGOcNB7fGzy+FxdIDGEMs5M8yjPJWSlAi8s+FaznFEVGo694fkpIBAGiCiCBqBXEN3enAae3cJsOxvRwzsCYV7DWYHw9eGa4Z44fjxjdgLfdW9huRN/9EuAR4ziAdQ9334kLJO8ShJ0FgaG8S5mIsbEDrAghQCcQjbGpfd95bX0d3U+F2IIAvPsgAkIw63jXwjO5NBgabPZyf2qhRRUA3Sl0nYbqRPMWSuQDUVOLHTjEdIJYWSgmbAZAcYc9vgaIodUWVAw4A0eFER0cORjnYB28lQO8tjh7VzgGzo0YhxHGjBhOowgl/Hg4L3AIrraU7qA0YbP1Ab+V9utAxkF7gUrXiV//8Kn9+Cml/ZpRYOdgouIKoqBBBBGc/U5pgHCMTN0xFuCPhwJVqdKX7moaiH18k52zRXmYzZPX8ZSjKZ/Np9KrSTkorcnyixSa2ECZNTEnUXfEcinFfkhjS7N3bsSAKeGOQWbBBAQzJR8OHmwMrBm9jExht9vj5uYWndJQsY3hv5qYyvBt/8gxYbAbPIw7PNodHPWwEAuhiOdmePzTgBP+HTt+pjyuPsN3Lr5k6erx5cZPLtNngo4mmyY1tmiQ3FtT+4eikNjfs4VX7ZV2pbsxjzGx0L/ZV2W6alm3vhY55S7wAmGtQZ3CbrPBdrfF8fYOdr/FbsvQvYv0T+Fu7U9SO2lpbS5d2mgQS3V6QuThrKSnYklZjKWF7FmV+f7PTyJOic505ynEwPpg1VcmoD6YqXpB4V/WlvS+WejFbf0QmlYTf3Uz9bJHV3Ppd2lOruDQ42A+wckSnDWw1sEYAizBOvJMNPnLmT1yqDhfUkIi89rbbU+1l4wY/7zam8kCICciUSZq1RdMJKl8N1dKq92rZrLasOXPuQs/PJtpe1F8NkZ1EVUzFqGmPc/lqzE4mhfnnO/FOVgu4Udn65ynirMzfoqUn9sZ51fimrRrR4mny7BR/vVOsXCO+kKpJIomLu8Q0dyqJeVlWzeyRqTK/I2VO7ePFmifNWMze10ELafG+yAgFkuCtavjTH1nITulsiVLmZpXxJ2shR0HjJow9B2YLTQBTmuALdQGeLUD+g4QF9QOgI1EVpp7BabklipnPuSNIaR1Mb1/s/UUsywwvprPcwQsH46AKE+F7TnZHfxaB5/BzEkDLhaaEZDTNpT3MRWJPjyCPof7rN0JawV2Ldpj/fp96kKv7qo1UuUXacdPAc61fQZff26tP+KQFVVPKLmAH8cHl3V2jmBs7Z9zAohJIesa8jRGUH6GziCGK2DRDVhgqq9IO817vs41/V5yp7sGFAw2eIuRtiD6tFRSdSKI+OJWzByIFPifDnh8PwJMngHs8UKn4LxvIqUUHGuJcSAXHRTLXRKFExMUoERukua6uCKC1uh16KuQ+8HVeLDUsN7FuGEL6xwG4wUTowTG5uEAtgbjMAjz/N0oWvt2FNeMZgQ7C7DJeGPCaCc7Am7E3eeE3as0zr3roUmjVxrKkdfQd165DdDBiqEPghktAgi98Yz4DYaHHt/96wYEBd313gpA3DRprf0YJJ/j8U6SBvpgzL65JHgyA+jxRmjbiHeFfjEsGAwDQ4zRiVujcZRxM0Y+rbMYhxPGccQwDPHPmFAOeW1g8oIEQr/ZQCuN7XYDrbyFg9LJx7rWMT15AUWxGRgeP2QYa73QwY+pY2+RwpkAItsvvpwgECrXWE6HJybp/G6pNOpXWERMBBIvwYjMEI32uS/M0HM8nSSEANL5OEfTZXSJH7PcUgJMEf8t6R2K75ddHCd1lugkNMaPkHOHWHg3zgxypmiF/d4LIrQqaa/Yk/n6Aj57slu8Hd7gYHtY6mHBMOwyGm2Kd/PM9ybEtZM/4/YFEOaiZSkQ5yn/3fic8IhCmVl5RR4HLLjKjSu6RSPUfWpUP49AVHdAbalRl7dmK/Hsj9S8nEme01fFN4ppxW1fEAhr6F2PzW6Lw+0tzK7Hq51DpxEF7FPHv8/DDS9VgDpf4HMyr61gCRo8jqV8FWtkFdD0R0Av1ggjzimfLcFH10xnYJ4Qvww+tLl3WofzF9lcmywTTvYVRtfDURfT6lHh1WMPdkfYmz8C3QGeqyJXIfk/Lg/gcMzIgwaDKQCVecLgN1kfXD+oComEVONxGJM5H4+XMiRKWmD6bPqz8UTaFJ/Gjd7Y8RdD3s8Wx6fR5dllTpNfLUZ3jYwtkdrrelcP7LWYc+v3c7sPZ+aHEroKRunKqTEtlL7I45k1+uT7ZQG4HtOZrl1r5CMDPi934WgoiISgAbJGg1po0blGlJUuFdfaJ412ztXSrjqPecEpbY4gRyLTTcuINWY7bp6OODNpNUHFIfwkalFjws8drDVwVsOZEY4AaxQ0dXhzQ9htQlA7eBxWDu4pXscgJB/ZoSMU31VdOTvtVKULv9sDME/fhIvGgTKXE4lI9O6yYh3kGW1eL4gdQLkuVNo9gSFHZY3Z9+AC4NKd9pII80f4CH8msEQ40czzq0F+KT1lv34IemLuwnj6+fKTNAhaCS0mnYLBlt7CoMfIewRGTa20cPvJFl3f4f13JxzeDbE8Jz5OAM8EVZ31wnOxpgtxI3ot9wVRcD8UGAUlY6hFd8i9FS5ggvJ0hYK4W9He+2AHAlhjqzo4VjC9MJWc2YomvfHa/M5IsGdnAfZBnYOrRY+8ROsG/7d7rbDZIzL0JLYDxf6l+EreIsIzMslbRgSBPAVLAdbgDrh7I3EclFJRYTmMkdzBJPEpOAV0DYx464wXRsjtbH3bjTdvcM7AsYW1I5xj8XvvHIyTWBrjOPjnPti3Z/ozOxjjYI24sFGqw3arsd1CBA/kXUd5jeHoSsp/Eil0qkOKgTFl6oolhR8xXyezk6DECL/ZCyEC7iGKDSJw4Gy8yrLn4xaug7j2L8z6bErXb4WgGd5mD2QHe6Edch6SEKLE41LRYVzneS7noOQFkj8X5Pt0nuDPBO/SDbLLNYmFDKyT9TocMQ4H9K8c+huNV69f4e7mBvvNI7ZdwGsTlp/OuXQ/kcdnQQRmBQcF5+Q7WGFjD/jUDXggByiC9mvAxTErOzc/z4FxNMdgLZ8rtKmi6QLIHoTFWTHxS/Q7YzBl55psozkeQFVpjc6HPTfLvFpa/ZzulUnfsn40ny8X23zMrb2flV8txkJvzAvNlQJYKVCn0esOvRcQizB1riGNRR4atLZP0+b9qFDjDeV13VgLgRGS8wBmYamj18YR8/OSq448r64XFURcYkr9IU3Wn2oBsTZ/gvXih7kxWiuhn68/u1pmygp+AYOfSMeEg7mD5R5MGiE4p7KEV4ctTD/A3L4F4OAyDVB4RJmrdgXkgKP4PWvzBIn25UnDJgLgPF+rN7N7l4Gmhlt588v/T9hT8Z5tEALtBrXKqC6SOHVrUbQ1CNBMWY1xOFfK+dQT9mEjzXOYbFNksJ32XB3r93M77ZnzxOeNvMtWyVR/8XlnTPJmkew1MGsqHcrOxm2hyLova2YyLy76EmZAgq3V1bWQE0ofQUtlqY2U0gdS9+xyeQFo8QpCALsU4Ldarx5plelyM33NEeB57f+YgvLpX08w5ZpcMQcz2DnvnsnA2hGKGM5qsHZ4ddNhv3VxquCRaE9XpbVO07upmPGJBUT69MqiM20u00frgtkxjN3K8F8GRZ/SLpQk68nfmy5qRgmhJmOthICJUrAckU71Fdq7DLQXZ8CjQr/a/U2pVyacg1VH8pp7Zn1l65p6WX/W4mnLAajXwvOR/qfiwOfw62u7Mvqx4anjNLWwC/sE7fu1eL4Wl6iSPz9ReUZgnqp4niuMEirsvfglX2bqWnFI5Wer/L50n86V+/T+n6ez4reQAyAWywg6gbCHoZuYhvP7DcDtmy3uPtWwI0dBBJCsHNmKBQ45AhRF10RiHSFuVyUos/IMzzqwNbdRG2ZIQFDnL3Eq1wll92HQTu06gBnWWwUYbCGWHP7OcxaJIcdyz8U2BFzGa9/7ocrHj4LlK5dsmECOyU0r49GZctTZ9zmwTm/vMgqLRSgAeGEDBxRRrANAXlBAVoLtMnlBgrRHYj4wjLGiYOEOcCyWIdZJnAfnLEbr4zkYI8x/IZqlDV7I4awCO5krpTp0XZdiOmiNvpdYD33XQcV5JS8koIoO4GjVEIQOuXulwvoh7qk0B/lU5ziic+FZiUPmsJaHk97zhGx4CSXMGEOhKjryC2ZIFw6JYjlZxlnIFCsLhmhJlyQcmSbtWg8yD5FVsuJMV6Sgc2MWEm10ZgO2RuLBjCfsbxRuP9/i1d0dbvd77DYH9Mp44RnFNdOuURDtYLHETHCsvHs5Qm9HvLaPcOQwkIIGS6wKJEHBeTTkgkEj8lZOret7jshuPKiftawwOE+bva8Harb5nPF2OB2TRV0r+h6Oag5lZlk5O//DHMb2NuJUtMZiFhbeFfRXtq/8GiStoHs5/3ofoFqpkk6dlk7FR/qxgl59KRqeG3u6quvM69l05zNc0qmcnqLJvJ+zWkhYLsfSZs+DuuALhUU5fLSI+AgFRNwyIFg8RSOWlpuciaV5JhdvBSh7VHlIR2Sl+LNnshGEBsDszp3btxPfTnnj0nWWF71amMYz58WVcLDzxfi+PNu9xDVhxcVxAVQK8fmbczkX3lzSvrOeshfzyt2QO0ArEeKJT2qkvVFjW609sRpmEeXMd2m1v5rJqXxb/ZxNHwSCCmoh+fk5TZpiwcdkTtJme/ks5Pk+NPC0evao6+qtnE5kjoLhaRoCkraYPyfy46IcPS4fYrIEEdgI7ByYxR0AmPDZa+BmR9Bk4JyC0p4B4pkzmcGDR67Tg9KkmxOjpcg0ZRwll051v58ypyJ4j9YMzmVbhjN6xI+GCxYesqozKrJ5WZYu9dY7TvsIH+EjXBGmqoUZzN2ReZ6fEq61HnKsrMKIqy/TB3LOJUz9Lw8yoiQo2QNQGLCj72GxxYhXyF30AZ5+8Jr2aQVlqlFBGcwpwDGcclEQQSA4K3UGbVKtvIserbJ0UmJxX8ZWU3VnhhZkqyGjhRgExZ0nKZKP81B0GQdAJSGCF9oHy8cghg8xLySGcsBtOMbMiNw5TvemCBb826DhD464njDmLcAcA/SGIN0SIJtTPAavMCEWEBKk2VqbMfVFEMHsvGsjeQ9PB0vsBwJYQyuCJnE3mYt1lOfKeedSAMTtklIK2rtYCi6ZFGWxATxywQ7SJiCND+d/qa1xPJjjOJZMKKS5mmM6UR4bJ/+U2axp3ucGmn8qRLcgYetV7Qi/KSXwuO5lbZ0//+ZSTxNSQYtkrq+RBBUxRlie3WvUBDwzF7SUu7akC0SOGGK3+X3rWzYOJ5jhAGNGOHbY37zGm9ef4mZ/i02/g6JDokcr3DzQEvk9IdYPEAGEF0QYxxiNgT3egw8/oLMjLAljkQEJWO2CI/Bzd4ZPsWbaFpn4JeNoqsvnlbom13j1IJ5H+WervlRn4mR592fFuSafzNOVw4sbtejOwjgujUl6dm55l9YQdTnZfZHhAZQJtMWFnAghHp2BYY3POoVdT9jsHWjjQBntn+JDzHbsAvjpUVPTW7d+O4NTLmdcURuS0L9OtbDcngy+0KfcE1cVRHywuA8XQY2ANVJc2LznBI+8dIKefvFP8y21u6jHH0QRScwOJZelydd8fQSKkgyXycoqyi1T0H1cMEtrYknM0/JLvuhJ8ygSBCEvhdPXvM7wyN/O8wdys+pnwBrirjEg9du6W5c3YRVM5m8xZavwDJGc/Go0jerfAWPLELqL98rlo1Tk4PJpvU6nSQOK2SqRJ2+qSmb321oomA/NridLpJoP0+538+0qAb7gvR554xIvrLO37uOkDZgR+lmiubKKh5N+rFjV57HpszBbQyb0LZfy3KZudYQb+ac6tQXRVZ2L+aOUT87bRE4kpJo5EfrMhFc3wN0NQXkNRCid6qmovTCDpVDOv4uYd4pBRNnz2hpiajHxVAhj6Bkq5AkJ8hqHcX15UUx2LEvNnv3CWVvrKvK9zHwxDvLy8LSFvmR1OV/P82AtHjanDfSSeNyHwH0vHfNL/OM/zyL3TwFm+rfYr9kL5CpwTjkiw1KfDBM3jEjolBQ/X/5ir8+u9wzTu2AdPiX9taG+C3NQZKHoAWBg5Du5r4prOdeKDbeovzE4ZwZ6PWIrv8nJ3We9b0PtHIgInXaidcpe89QFV0eBuc2oLkekR9IwFXuRxezIETEvYEiEhUta0/lUBGUBf1Ui0mb+DgSQ3CV5/MIjfU45f73mjDuIlSHDu60SN0oh4DKCJQA7WDtArBIdhEnropWA9coRQRDhnBXBhHfTlFwayadlwVeM9YIKI61VpGSIfB80SRwPrcV9klbKuyIRCwhxjSOBsoOVg/ICpShUiC6UQn+lTSF4dXDFGdxIBWuHKHzg5JCmwNPjHZcwuNK1Y3vPFOhzptQzUfhYoZh3Tut2FgrkvmxcLYxIlcHjWYGz1mZ4zzVlgudGfG2eHp+eQ3WTpR1RxJYLTUDRqqfEtTMBYnTVioK+DfzsCrWPwggO2DSLtYA1J4zDQfYOHHa7G9zevsZ2s8em72WzUth3scLYhUKfJtJoYVwIlgk27JfxCDo9SJBiEkdRHTNMNSZFw695f87hOnVdcWlnv4svC23KibOcEPHC5aKurLggVExH4rQOxIGk7gABAABJREFUORMnT7KflOoFFuIVJtrsuvhJvlMS7VZDijcjZ+WRHYhYrMC0wn7jwL1DdJ0XBKlZFUWsp7VnSXYHtd+v7N5imno+luuanC3V9zJ762BLKRtH4kqoz//sTUGDri3vXHWyTi+lez5aRHwEAJhIsSIyB8A6CdglPrwd5JaST4YPhhXSRxPRpC50DgnIbv/sd4tgCah7wD5a/QDafvVrAcUMhyhjZs3pvz8ZFvdmfVG3kqxvD88cBM9twiVZufo1V/TaO+CqPB2qbosnlVHmr5HZOmkMkj55UWUqymwzPZ4+FMvrmj0GurgUFif6zIBOxouiu565qgJCEjXIPOEXLj0GYABhhvtM0/K4jQsvdmyhUVc+GtpFXwOrCvM9h8lMUaPZriWVLilXJddIgV5SoQB2AAeGvCdhSIHAPkBZxjih9D0UlLQFs1ZGrbGEDBdty/ozFUosEM71GPgFKaSdC/Qt4CStQ4Y8I1mhpIiBgRhwnrhQsYllXcHBBF3/fLsKLCHHH6GEFzwUPsJHKOC5a611Cf4U1u6l58tL7Lml8hrty3A6zphMXKEb4fuk9Mh0KWspeWW533nP5HQMIguyScMe/r6MWvaxUH8f+WsqCPXLO9NbXQBwLjBZvM97iLujJIQX4YDLnbNHpYRSi1+CVtsM34jcOF+XMNitlfgLzjo4eMUGBpyzfixDgGWXMai8NWb+CXihQ3BTFJj+fm5ivxCtM4LVhob0oQ8a084LGrQOCEgaY6IYaDUqTsjgejyGvTBIxsYZaUu01nDJykEa5+L4AT6QNvKxTAui4IFNvzShRTrWbpt+6jLlKIyof8dtETpBkQa4hrAyKpoUZdEkDVGBFZZpZEnENorgRGJqKgKUcnASGQWKCC5OcnWKTBjMHmf2gjGtO5Ad4YzB8fEdDo/vQTdH7DbAp199gc+/+Bqf3o3Y7UYQbC7PKiFbEIHNzhDnpNYRjAMG6/BogfeWcHQSEN4RJUPDxUW1MC8rj/V8pGfz+P2XMrj593kBnOfLC243LFFTFdfDKzMl4V6pvBSbUR6LeeOa9S02on7I02SzvJiVtHxp1e37zZ6OUySxb7QGNh022w2Od3dwN1tslYbO+HmxDDedA2aAJjyTmUlmnr4pOO2Y4QusHOF6wsLvFtFWDXD6eW4+a5r14lY+Gea2Kl24BFOmy+CqgoinWAo8V2PsKfnPZ1lX5qpL7kPf7ulEnE9ydp4CAungGN6cNXj8qy/CoFXi/W9GjQ53wQKuj18qD7q46WON8rMwJUw4SJ52vpb2cRyFh1SiEvMoSF3AwruJgKT+fb21QjPrbk5AEVuzdEvVZZ35fS79ZalKf3dFEy/dYy/B8WvR9jmEi7BeSK20rbXLcfGX6dZ0fVIezS5oQn4jzWJ25RsqfyyPbmYqSOl6bifNiQ6AiJNmHYlAIhC7iUQvG9VyMbS0wJfepBOBp2OfZ3zmNk4tzw9zqbA9unPWYaExy6Kn9H/5rWxR0GRMyWROQoNzXal8/aSZKbYIUXTokBgnicgXgRPSu5jSf6N0fwWeSxRaZM/zz/PA6Q5hWW+MQEhkmmMcZqck1Ij1/BDGHoSqggYbe7kHLeK2l/XjmedbsbbLsq7ln/9DwNpxrBWd5t6VZbTu7g/fx5eCH9eK+cPAkgn5OpecM5RtDmf4LU+BpiD2KrD+4lpxy888X8gX75b6TlpKv2IcLrqPS4x/yhjKn6aDMp7dHNaMA6DBzOL3P0yZ8B7bCquMJk7EnG4a5xIuABDIW0gEt0BRyABkh5l3B+K1BIIbJ6j8xiY44wUMVgmV50RxgJQBgkA+MsgRmZg5wxyOvQcqbw3JBuDghz7do6Fm510omXEEs4+7EOIhMMOwLdYS+X5plbn1ZFGIi/cye+GDH+MpHkCedxvoR2EGx9dKaEvFHQgKutOxxRELo4SXwFv/O0YUCAEGTCauDfYWHM4Gi41kidHCtx1ywQQm7wOHKBdQNFKVz88wVJf4xj+q5VujYbk7ptJSorSImJzxEw5w+/yoz6+5bEtFN5tPGU6rGIoA53FZRaLcwy64aMp6Es9ElvWea437ciVWhIIbLZwZMJ4OOJ0esX1lsXm9wd2bN7i9e4391mCjDRzC3ir5LWEEcrohYveyxb0lhMNgCUcrimAarcDRFWVxlpESke9VdP1ly7JF14a1M8fNWKKFufia95SyB3H9xaKqMsPd4f+rZM6T5gagSINklwlXNyxXX/KraxbmaED/SdWjrKkIa1kpaK3BnUbX9Ri3W7jNFuyDq7drm9abms/i9q/ZssZZhmr9eMHe4nI5s5ializNBlFjnadBm5RT/JybmHIhtM6feViDK3Kx5QoPBQSE2DEvdQv8WVtEBM2JH+8K/REv7yeCIGgOd/33GGyP0/FOlFudEf+l3AEwcgTm5q/GwFgrPi69j8248xvDUOzViC/nJss56hfScfm0vqsYnlGWbzxqfm2/S9riSwrznCdovpyrpyZreJpk/kGj1Pk0s+5xFk6ugJII1bLQikVOTqPQVp6LYQbZbiDiZ+srGNzPaNcsxo+r8wlm12OjnlVDvbR8KbgVaCCDfuOuu9ra81L3JQwXUYi4lrTBCIJcP+zf4XD7Dv37O9w8vsb9BnjsgN37Ed3BYM899rSD2Vk47ZF1RFq7JmUXYP591MTLkLnWVM+7plpCQKq6iIqCck2r6ZrNWPSz+35aHWf/5/hsySThMiUDeDTgk4V6dNBaJ9/HIchmtGYIjBHlBQ2e4CftiS4viogCByDE/YgKnZX2Zhm4OqUtxi0mn7kH6tWwOF/eAhDKE4DwzJRsdVPnyyix/OROimK/Yn8ywi4XRsRnVz4/PsJH+AjXhuds0p8ibfBhDp2fQs/XtKFOs2Z0NJ2wp28x8g1O/Lq4r5RS+PTrW9x9ssd3v7vH/fdHqWfmvM9YAaLDH+6I7K4I146LF3cDSPT+k/azK5hY0U2QDcpkNd0mcQtCLCQOjfZ1B0uDwDhP1hA+tgIyxrsToUGg9GLQ5SpeQ7ACiLiE761YYSp03u1ROWyEgKAlK4J0/wYm2ZKQlYBoKUGuGk8OTEWHoGeXhlysGCzCAFlJF3DZTBDDTgQNOUO5TcPkSFvCAFNbfHsKWi1HUH2OCzbcFG/66cC8ss0MrGRmn6m04meuGxuKa1F+gXxkcOf8OoTg9x4nduQiuk8x/3yPI/6rCKQ7KL2VM8IZnB7fYnh8i+Pje5jTEZ/efolPvvoSrz/9Enev36Drf4BWDOZOcNlWlzh36eJ3oA9U7ZhhLGMYHN6OGr+3CtoCOweMCrDMMBDBnPPdjAKzmUO1yTa4xvy9NJSMiIJ2CnFywtlZElcu5Vt1GQX3RSEQtVigxLO44IO0Kb1cGnaOxpglI4PVt/LrOxecE0dakLWG6nvsNj02mx7QEltnwseIZ2rWZg50dcXzmRmnRIflz8rExHNKfPN5ZuvJqprU0+KZMMWYjJMCZitrpV8g7p8N7bLjCZaxBYt7qJn68va8iCBijWXEtS0hlhbZ+aqe2pYzA/4hztDZOs73aV4bjNGrIwADwhbsCMzWo5TiZ1OQ0mQNYX3gsGARgeAmJW9ndum0NAmCn8OURZZ9OX9JMtdsPgO5wCK7FYqxShe9pFP+IA8WAxWrajpGF2F3VUnxMC5OzgrOBDGlcAi2GWxz3FCaNKauNSG6USwzwRIafQ83G8+0qJbU5++abZmSGNPc1aSea+OZOp4CcQbqW+pc9U+supBavwC9EHdNfgO1Uq0Y3mVyL2mUT6oiEqLUE8wKwKBOOO0O6A+vcaNvcN8POG1G7EhDG0/kkYMxBlAE9gxkDR2Zv/VuWdvaaTIqkcLQeC77cw4msVLrM6raSDOn9ZPWweRs9m0PbofiH0/Ts3EIalB14MXYD0oMgMiQJwAUhBJJwBA/oxAilZOY95TOUUr9zpKm/yfj0UaQEplI00kL90jM4iLSXAsiCC4J0erSI+OjtvMLtw9Vwoi8ZZfCCxwIzQXaOuFn7pvq8Zpj+TJtn5eFp7T/6XU9bf5eQlv1OXHQZsucef4Sq3YtnIs78Nz+L7CScCmB8LJWKm088qmKGnW+i5iIs0o+T1znOZq9sogcb50UsliVRU9HOO48Iy+34gR2dxvsXxPuvzsianMjoc+ppgyXjghmEmwXncs6Vd/roi2uJaZezvQOTHE4H4dBXAZ5decSJ+DgTsRNKglMicBLyoUQYMCS4BTRCgDsmXJheDNregaYvYgkkm2+z57xpXz8hRism0JoXsR7NrQq8P5yJYBksRDaz6n9/g3F8TYxRRIaiNW/POLiMwiDRDDjx9SPYxRGxLpcyr+0NwpiOUPGCoTMJyzQnLSu8s+q4Oq3/0at9OvhXN6ocFH3u0LDlsqp4y6gXeJVoVSCkZqbZ3i1xgBknhZCvyjit0kAUVpzgNBwTZOKzhV+oDTAFnAWZjjgdHgPOx7hnEG/u8Htq0+x299is9tCeassZ4W6UuRaxYMyn7nE5HFVWb/OMYxxOBrgwRC2zNAADPv9jqTCUy/X8km27uJbqtb9HHCZroHmL9N8T4R62ifEFDLSqbEm8+3Ml7TPc3y46mDdhqVh83eCWAqlx+XdE75MW8aRKEM8LPPrWgX6TSmg0+j6Dp1WYB8npy5yTgjBceI8HjpDw5WFzY8kZ2XNpll8WzWzUZUsi2kpVGdoHRvVWi+tAOnMVrgcl5wtqUUHV3XIt6VVu2KuKviztoj4COuhZMbI4aAw4vXmjziSxsNxhyM53G/u0bsTPnsgsAJc72C9JYQEAwvCiXzXZggUqFzbGUzRIi7wbIrFTNk10yXvT3jKf9YIaCrFhlfebXc6kOc2nDzP2U+cPS+yRoSzPu3bG3V2G+fSZ558qaBddi5oyCtraVlHMc2a2zxHfpeSLL0oLr8p6lJOxfMP3yWHNpfAJPrImkI56/YFmNJPgTkXoXUZ50QMz61k+R187LpAyDmOjOhD94Dv7n4P9X6Lmx9eweot+PgzHHcd/nX3Hg92gHEGD28UTq8Jp/EIO76F+faIx28H7HeP2G6AX776W2zVHsyUkJzndpj8jHvBW8LcswFZuwkoP4kow1e4SFsw+heaNlsvoR3gzDMMXH5GB61G+POCw+f07BAiX0EpDYkBIX/KCxyScEH5P0rCi2gRIT1TYhoRj4FkGUGxrsTYbw9AxJEbaWjxzJgSj4G7wn7sXRiXEAMptsev56zxSfMyEZzNKtDS1HkR8ukJ0Nq3VH3W7z7CRyjhp3Rl/VTg4075U4N05mWo7gQC/rLRJyj+FobvYOhNLCHw9sLdFpzLFNXUZcZrlyPOoeLdA+Eq1jhohSsTEYIKF3u11qBIGwM9W3HVItbvDHg6LvIpa7oujAgnOiHSbR6C+0UOTPlQMTzD3iWFlDyf1J+U0Ci4kfJ1qUgLSZ8c5wprgXHDqTqfV8xCMhotx228wMAGQYN3XZN4ZSldoHPjeiCx/giCGOKSYRjda3kXx9HVY6QNy3kL8ThypCEXXKXxymjaiuRuCx/KNPmYzykA/KhumaQBH6aeihZmv6CTtXH6DMIEoXeyMUzEQIGDiveumYAMNI+ZTpUNU9lEwUJIA6QxnB7hhkfcv/0jHt99A3Vzwu1rwi9+/Ut8/av/BTevXkH3HZgtBjvi/x57OBD+WltsCjokbOSgKCM4fiBOmBnWMUbr4O7f4s39PUZzxME5bwckOZkQBRIFzsgQzc+C3i+ngf24zM59TXcVXHUg1/JiItmLa1kG7c0z347G77i1yi9VhrD3ucGLaFCqWdmEc01MfWiuK14ZULi6RxQR2FvxIIvVSEruIKU1SGk8OIMT9/h602PTb2D9cwVEemlykU7OnexMqs7y2KKifQsDwlh0S34WZuY5H585Cii/4cRiYh7/q+zefKFnlJJ/BDjPcbzszH45QQSVTWmR2lh4fw4a6+ADYvd/YqTVEwdbkcNWj3CuA9DDwuJBHbBxA96MHay2gM4sICKjJtTbQto53T/Fc4qXH3LUvDqnKLylxiyw3D/xQPBneeLR1UcFBVOI1v1Qfq/GLLTQLRxuk0OzWdQ0/zm3SrFJddsuWP8RYYrdrwmMdIkvNyoUIoPf1C5eypYVTfVimWgr1pn9ImrUt0aTr1ppK2D++ih/XTAAS5Ga56rxXW9pNCxm5/Vp10Lr/I14YcIo81ZM08e2Jf/Cgz5i0I/oXYcNtjgpYNAOIxyIDAwbsDM4dQqDVhgU4DTDscH7H+4xvrrHzjKO+yM6tYkVkRNkaH45rxmcDG3MiN+if82bOp9r9kRwYERQkU00T1qHD5fLjcpcKzCE9KBAlMNvbjzOEfM20VVUHCwAMksJrxCaMehT0ynkoWxtEhVDO3HRQDlh2GpP/rmw5qsXQbZUDnlmAu2SoJ0ahE3e17qY9j6QQjiLd5QIhHwTLa3LmXfnjrbF4+xc5uouCr/yuX0iLBMb6/NdWCvWtPolrTU+FMPnqvVUx96kruvV9EFgjjg/F0tiLv1yHLaVnBGKu6t8PC3xyTC5xs6Ueen+ntWCvqiQunHXX11L7WuxiiJUA0iw6OgIh42kJEbSclIgraB7DRgbg0SnWtpnaI0O+FsWUSBeNCchY+F29isyuq/liH9YYaJDNJ4dAFIOHIJWkw9Em+EHqbkh8G7WrglSSEg+PXy2EOlauTJpgGDOEMZCITH5fb1ZYklP9TqTXruYniOemY9IsOBg729J2sZxVKLExpcM5uhiKreoYJIynGMRwOS0axS+ICl5TBQ7kmXG3DIslUmm50ey0mjnXwKetHdtvop2pHX1z50JrV8TBbpWO7LhWHmyzrYpfGe0z/Bco7zWP5ojCcp6Ap5Jfk8FQWEGBZ5f46kBz6SItBpjYE4HDP7v9rXDzesdXr95g1ev3qDvOygNGHYw7PDOERyAURM0AE1ZDzhozWdIOQHMBOcIzoniGJsB2/EB1jkMDrAUvErI/dae2fMzU4/PtBhei7JlNbZWhX92yYKJ9dftyvsXqai6EY3fLVFsXWaZjYpfoT0tnGBCoMQsTWFEczxL2i4Ivyn+Dmd0inNiIEYRpDVU1wFaXPeKhJbi9DX7PNvXZ8JVC2uXuYQ9AEG5d47rxPmSSM+qWLjXgtYZ3apnwus4u08uP3mfL4hYM0CXY60Xwyw/7wUm8CcNz+6vXIdaBXeGDGIHZw2stTDO4DCO+O7wA/bbEV93N6Ihaq0XRngZOPMsMhJxwfA7XIAc0daF1kEuurm17gvnyVE9RZYAjq76ElKEKnWdTxZaOidKtBCtXxP6iarnK6m/PHWeN7Zhvs768ZTg8pdJYLSkxqJ4sQjBLHlF0jKb3I/1eHDd10ZGeISxNm2b5MkRl+k1XkNIUV7UF2EqK0CwgqQoU95qFNoakYf69s760cA35lrEjGjKc25Wp71PbYwe0LjKUCn+lMy7rH9h75FczNZZvDOP+Ke3P+DzfYdf//A1htsNHn9LOLGBPZmY13l3As5YuBGAsyBm9F91+PLTNxjsDYyx+O+//x0U/QGffs7Yqx5fnP4KmjZwt+WF0RrWIBjLSRNWANzEBmZhxLITrTCBTucIF9OejW0ohfPt5/PVGkD+S9zfuTZens5r5CXi2n/GRZi5ZagJcA+KIEHHoKBIg6AA9vbeSouWliJASWAy8r5Bw2cw36X4mQkqQh1hHFAyMAqf234scluRyb7lMJh5iur8rX6mGoMWWHCpIO7COLJttHRGke97KIT9OIlliEJA1h28A+ppE0L/J9px+SZ7CWSrBe3zqwyS29DNfAls+YNAvvv/VPvw04Sn3J4/Rbh0bS8FwvYp8Lz1NpfvCaM8Kerl9sCyVVorfYIGa+cDQjr7cu3MxEAM72KUOYAIPY7o8HuQZ9wY+gxMr/HFL1/hzZd7/P7/eov77w6N6jgrK7UAvhZhUIR1WeL/uRAib3p0S+TvzHjqsZZPbxnhnLdUdULHOSsCAMdWPmO8Byd9Z/bX2hTrTG1JKAWQWS9QsM7ILQQyd0ihlZZjOikjuYmSuzmOeuiUR2MSTeKCaUOl8RzaVNQNjvhffB6EMFFIUuFH3t1+1G0rcKfQfk6P8k9AcI2m2WrR0OyzHofw7tz+DTRdfYPXX6s2eygY7026I/XjclKw3OVzgplzLvXahc/gNalyBLc14Y2QYFTUUbuTyXX1pq6UuOwTqWRB6xxYOTAUHPVwyoKUgoIDjxKH00EEh0wkQa1juwiKNJTuADPCmRHH7/4Fjz/8HofHe5iR8OnP/ga//He/wZc//xk++WSLT3Y/gNQJ/3gE7l2PAQwm4B8M4YYIf91bdOTxXyKP0/szzQGAg3E3ePv4Bu+PhMESjFUYHWN0DgYODsrvejlrEs2YD3iOR5anWjkrPP3OKL8vTntD1EUKrZDasY5FptVCnU1hSZ0n0Fr+xiAvmk5BNFLa/A+JpwYf3N7ljq98XpWfM41mBvexIV7B1HNDODso/gKSoAGe7mNF0CHun2e0kFaAIuheo+s0sNPY7ju4T1/jtN/hk1cE3csdlB8vPJ2hWFdrKK9DY6wtI0tHS4utVd5k9LM3Z84qrr9w4hleARaVLcIxNTcvjdLmf62H9YKIpXFYtTjOpHkqMkzlQdZuyrUmsRr0M6P+QUjamUrOE0JpU0/SRaZQWo4aFgQJKGbY4a0ZYJTBlxsIkhiRu/NLcfb8K78uFFAcTVWG/MZoET0RzQy5/e/80pvbgAGbRnE4N7qR1ZMO/OSaqb4I4u5H9aUJcqeVl3x+tU/anH0sHEH+gzBNmZEtOXJJ2QgvNHn6avokxy9iXcFcNFx2rUoIk40oY94+ICdWF0uwRrVnKc3Zc7GJ0aRvXMrOS8KmNU95KVOisPUz908qjzMEu1VGRKTKBZWvc6DaeWc2NbGY7g884jgeMT4abDc7aI+oHHoHax3caFNB/rxx7OJ3sIPtFVwHWEvAaGHMEeZ0xO4VAbrDcDxh2yuhJRWgXJ/amPmwJAr9zPvT6gjF9NNlUJ8xjb7HyqYvhMhHMmXN8aIzZ0ReZ5yLCTLNHo8Nk8jZ85x8miJVgkgTgjZmrJX82/hoajcx+V1bNmTChvCZ9zZqgiG/o8r3k4Gon8dn7bMljV/mxxveGgJcHbihv5S+U3DVdMalVmjDk5CFqs3xPn9KWWvqym+38i4Lp/a5brykRcHccfsc7c5L4Tn5ry3IeRKzpoJrWk98EHz4JwRL88mldPmpFdSFYt0o8/qNWpRdJFhRT7vup+acYPNPOEwuzjIZh+Ijw76zz4wQJRK6SUF5JoyBAbC96bDZa+heTZGHWGVOk9R7WfCCtmu/Vj/SZ3SnUVXjxOzAM5gYisQdIbwLInLpPGDHcJTi9U3xmLQWA4oecKp4f+ZdjkPgrQs89pFwSP/bf7oikHQSRCQ8NLhKApIgIZWDKPiIJaAkbvKxSfc/srbVdcd+IvfpnWFRNb3XRP+LEc2ehzLKz6IMztrpYf4OyOiKRjPqFV435dzRFdxIXb7XmxOAyXjUS616HpXT/MKanB2Taj12T0lrOcfe47sFWi8aBmVMw2Ktx7YEPFGlesIGyDZl0WNChiAjKfCAwE4EEePxAafHe7AzIE3Y377B60+/xs1+i20PEJ3gMOCeGfdOgZTslQdWcIpx8tUoBByeJqvAscZodzDORwwNJCGywNSYzFbZD85/lOVPEodNFRLV67cx9+fBN2JCtIXni41KMBE+8Mzz7JOzptbXMGeJ8jI4exfPr+x3a1waMBmes2RHRTwRghYZWpQcwbsK0wp9J3/c97B9D90Rus6JmURVR6Sr5xpT3I2NRBfhqG16LxZ1Jt/l71pp5mpZu/DWA2f/n60+T0LV+pspvfnqCc3/GCPiIxRQXLYe0dxoi5+9usf7I/DwKCZ8mhT4foeHH26gb47oX5lqP4rv7Al+fRaBAWaRjyY0kMeionpzU/GzgWYt1sWhCE/01VLl8qfvTY7xZxdxhi5mSGz2ZrH7XCQJPhmnDfHpYpHLY8pTMXmruPh9NgxAK2/1ZGZmMjwls1OhCWpWJK7zTuqkmeeTZNm6YV72SAUsXoKLsSIa5ZbbRxZKxE2mFc+9yN7PP6VqoFpXyrw0nBrpPNnB+Rhm1+Bkn3iNPkvojgoHNvgn+4g9CP/h5gZjD/zucw2jHMzpiOD+Le7tgnke0GB5rUmJf9KOoX/1Ch0zDho4Gcbhu3+FPirsukdsaY8vzW+g0QOkwB1gb8J+8ciR8usgasOV45DjRXMyqTjmBaM43/3t9KHM1mKZ26f5eZCpN/h2p+CJAaF1/nvUHPQEfqk9mLUqMu7lq1KiGaN8MDKlgt9aVVj0JBcSk86VNFa0kEh/8RwoNKmyr9Uc5Mz/ydVA00w0+QI/BsEntnyKRmg04/HEZxb3wkcBlDFRntBUsT3kCc9zUM4/Ve1uNHT22VOB012UFRtNuZtVpb2+ijH2Zwg/ui/tj/AR/ozhp7S7Cn7axTnzX5eflQl/oPggZ6DO5qHgFqJK5++WpAntcQKIVYASZ5bREoIsgRXDOo8bFcGnEzbPqJn9SAPHZfqIjnLADf3zZmBoaUvWO+SzkXh1jKL0ilFYCiFaY8az79bCRHCA+vckx6qynmR5XkFzDQf88JlQz+vT4RyhNA+KkjAiF0rUML9vprjOrDDCI0vTKmSUg/uyKAhFhqsqxkZbOFicSMEpBac0AIb2rpGCgEt3Pbquk1gPcBjHR4xvv4N5+wPe/vBHvL+/x+e/eoXPf/kpfv3vfouvf/4LfPbKYNt9i/8xGNwzcGQNIgZlNNPgCP8wdLhVDn/TMboM3wwCBgexyjAEGMXiDlf5Oa4MDWL/5tZSTfTPJQqbOWaaI7C4OBLD4p7QnnPf2w/abTr3Pt9YdQP87yjMzKyrYlyY4qxwmNTZ3rR1pWdhOvRTGiMqm2VPk5vc9FwpiQ8BrUF9h/1+i91+C9V1oE57g/H2ZIc7ab6hflPNST/XKIxeHc4dQkvvG7SnB0bVz2t3a+21sSLRZG+tzNeC5wkirqDB9dQiLtMeu+5s/snRmyuHqjgQsotVKWDTWex6wrYjGOO1aljjNDhQZ2DdAGJAB2ZRPDuylU+pluUGcuPZSphh3F2VUbO6eT7h3HqhlC6ZqBWPV9UgZXGb8U1UpJs78KOcusV5XzQXlo+cLEgy7xqLa2ad/R21VMLLwKxslHlW92blno0aLJF4SZXMWmQslXWmPXmZpSCp1ohpMKPnS1+AQCDUBPGlpciEUPUUyDQcsvrKWryGkgNgAYwKbAm92mLfW8A+wmrg0PuaItHJiObrAFCYp5Y1EOSMcttOzFgJADFMN8JaAzceYeEwmBM6Ymz0To4tmyGSmfIGN741oZjDuTyXIYotgnGZgdEqP5jwJ6Q1+XwOQghkBK4QAbnQJN8WeQNz9wvFvUxp5yShA/nnCdENzG2i7Dfqz5Q319Qqz4QGat0cpnmfm4TUnoRpzRH+QUBS5C7a2RJ85PnTB1VpUhtrIcQ87hPGdI4gad2zU8hJmnpcw86e7O6W5OKJ8FSccKJx+gHhGkKI55ZxDQuIj3AZzFoV/wjwom3JOWjPhNVFLGgfPxeeY5nVuo9XZSIC4KBgwNAAEbqNwmbXwQwWzs4Es22Cx7KYs2Csl49LcY4HjW0SDE08GnLwxQilxEWExEEIbjYIucvJwKhlTkKPeC8E5Q6gTVNkqAeQ1nG8zSoBQsxW/Z7ipJffDUt7KMbEqDD8WujAVT+mbZnUWtazssVLbT17FqzAUZf4fGv2UTlKl4neyjW0KgMihhIVcYKi31P2SMBXBeaD/CactOAjcqlMFyxeCt4qe7c6lPoZ3U8XyjoE8oo/IICdhR0NzOERp/u3GMcjHBvsXu3wyc++wOtPX+P2dou+G6CVxZEZD85TX36cQukOwAMzVPBx7s8AWeZJATMKI5yDdUYUcyjrXj4Pqw7KguNRPUe2iWaScPUyFFdsuScc8i0Uuljka8us21+eactF5f1q0R/T1BMvGxdBxROYTEtNoySIFn8KQKfQ9T063YG0t7yhRLczM2BsTbrPwrKXhvp8WQvtflxSUkHaeZfETyk0P+cLflB4eQGSck7u9xyYlDFDZj6lro8WER9BIF4mngGiFeCArhNfhs6JBP03X4x498gYhy1ONOL3+AMeTu/x8D/f4eef3eJv7r4CyIKt9Yo1QVN/ysFK+7hGudS56+mqMGlZwUt7CtETGELT8qepqgqfClwdyAlz8j+X6wikRFMYe+GgJ7KkQqwDXlhyD1tLo4DQg6jJRJOX8OjVTM2JiZmS+1IbzDPiqg6/GpsX3iIRBJxDfAuXYBW+XQsmrgqx7NC3SyAnUur+uUlTFZUTrZQCDIB7B2c0huEOumf8Wr3HsWN88+UWVidkPcYvYIcQJIvDb6+1HhjF5LXRO0he6xwUKzA7UEdwv7gBM2PAHsejwbf/+N/x6fY1/u3rX0MbBXrnq2LA7Rjuxp9EiqK1wGQ06vVbD0nA+yVq4kWMDKo+18CkhoIgZoBzSwjnz+kwb+G5fG+b1xOSlj9VAgSkZwBADCJBUpNLCJW9D8/KrZJbU5zvb3ZvVWeumqzPXAiR2T9Frn/dhqCd6SLzhJT0XQXCEN4CIvZdgaBjfyVqWxq3ooKccJ5A2dbL4OnnRU6oIiMgZot1+Vk6d3N/KHgJDOEjfITrwhrXqX+O8JfT45wjls7DDb0D8IiRPoPBHb789Wt88vUN/uW//YCHH44XVhEY/gAi4xJY7a6pBZQEEOw5IeW5zt7iL/XTeatRQR3CXSBpg+VrRG4dp7YCaYgYYGJx00mIgpWnuZM7cwMFWpdC2ilu/9T9eU7IsLbID3GDNtvyI2/QpKaYaIZ5NyrVnGXYcqsbl+Dds+27cF1QENb5Ra48XuWYAXIgVj5MigPBgYh9yDEte8XTPFBKtM21sOzccII9HcCHBzz+8V/x+O0foN5ovP75Df7q3/97/PXf/T1+9Vc3+OTVEX0HsG+34+CBVtoVBIbSqnqky1+WGRbAAOA0PMC8/wHaPsIqQLGP2aaqsQ9nA1DR+UvUeni8wOHkxvu54iJdEzM2vqPdzpCmeL60cQIdwfPlFOnZE5vZ97xveTuLdk/bsyg8LbhNuVvvmZOmJjyjNTdVpckvrRW01jgywyrCZ7s9Xu132LxiuK1DpzovuGawMRi/+SPYumlXFmB5xVy6s69wwmZFbD7/FLTfPaklrRYFmjbd5c85uVqMtmdCtVeeOx9XFURM9WMXNsbsOvgxidhl+LOnG+J69YcNcWQwKSJoBex6h2On0HcdrHM4bRhsFcZHwmEweHAnsBkBa9FRj43qZDs1fdzUA0rTb9UeugYysVgmTdfxpYXXSrCxumbDn7/em2PyRH7QExWr1pVdfQu+NItzghvjXzO4ZrDMpXUxZ8qca3yHquKjwiQxWyzll6qeZgVnIaIG+eJpZD1LYM01pM64pN1xbgFwOZMTrahME6ksvayHjQIbBUOA0w5MFqMGhl5FV7lpbfj5i1Kiaj6z74mpnWms+7VmOjnbHDugU+De4IQj3rkHKFbooKGpQ48OZCECE2KQI5mbWV9s+Y08ZaALwbt2LVwbyv2VEN3kNzkXQqyD1ErO/j+TdIbdnl6UAZEvGIu1h1aRzKN7WZXl1cDVX9Xe3FIDpSAmCljWChLqI6/IW0Kb4KDMEuJMVfV+bdWBcl5m24kJCbZYdrLyON+Gl4I/Vwbwn2u/rg0vEVT9KdYo59rxIeZz0oKXQv7WwKS7Lcx27gb50GufZr5nvzOUNVwXBCsMRzgQEbqNhtIEpf2dwdkdnJCXWJw8oYinhyqCpvZL4u9ZTwBk9SGgZElbPFrMepwtWFiEdElLHZFpFy0JGcjsKeIILDOB0zid7/7z14ugS3NlBLyi3d41fSjqeXoL0UD8z7SlXWO9piZWKNl9fu7c4jhP7ZkqcLDWYs7Lb54Z6+EpW+WsMKJqM4HCQvdPfLB2priHwivxcFS5Io34pDCD2To4Z+AOB7iH97CnBzhzj93uM9x98Rlef/Y5bl9/gu3WotMGAxQMEyyQCPy41BojkOG2KU06gxwDzhqQOUI7C0tCyyvfXoeK7stNapaX4/yLes4nQoOKAGyWtXI3VRZMzTq4lf4J0Cp70ve8npn9OpumdTdxUwFzChVRFJcvRfZEOLOFP6igtIbuOvSdhlYKvQas9qEhGHDGgAcDHi3YmosOuKXT9kPCZNQUSfzKzjxpLUxy1FPq6XLSWhTEzzVutglPOe1Kundd7y4fgw9iEfGX6jP4TxGiCZWTWVNKLpdOiyay0x12vcbtTqHvBInu+g6qU7gfDvh//8u/YHj/iOHhHn//N7/Cr9987bVtgy/Rlt/7NcRGO+XF/btazoQ91IKHOgfX6a7WprwMOlPQM2pZuteeUdysb9bqec1fmxLPWaEVK3E+V/t9uSy5oCnLtlxhJWb3fES6aySogsVal15OutsaJ0pIc/t1fJZL6lt3LwGxLy5qy4kZrwLATsONr2AIGD4/ATvGHzcEq+AZqiEQdahTgqMpB7APqugxUiFYo9UE4AKhQ976AgBYnjrr/f4z4Dqg++0bHJ3Cfx5+gH5woPcDPt++xm/3PwOPDjhaKKWhFMHtAd7Vg9rQp8vMaMuzLidG6nIw8+5S4ApRD75H/VjGII1+/DiLGwGuCCyumpy1z5crfqNdFk+Bs3+J5knEVCjKW1PEn1Qgx8lCIbk6KmJHIP0GAEXB6qBGxJcIlBwabsb8uLHLAqKHtDE2RLDu8AJ7f18qFF0NOwVhUC6f6bm1s/Z9C9qoJYNluaikK5fqaJQS6GXlcYQLPIwUR95H+Agf4S8Azp1T5xgpT4VrHTQrSHKmVU1txwAKZcAjnPXNFNj0ENdMUgByQcC0nnTDLd4+nFsxpHYUM0IlMyu6Ycq0gNMIBctJf/8R+zZLWsUAmOBUhusRxPk8GCr4oM9iReTKClNXOYK7ki/3qTEe6vgQcwz79cLC9WycVHqs/MIi/3Qv1KStvR6C5c6HhLYwgibfwxSRX8hJoU2BhKIBEWBVBzBBwaIjH0GAAKsVSGlQtxGLA2tgj4+wD+9h3r+Fefsd0L3F9u4d/vrv/iN+9f/8P/Gzv/23+PTrr9Fvv4Ejg/8xMn6wjFOk6xhB2RQVzh32tjwNKjayV8mTEY4JZAz25giL5K4JULCkYMkLKyD72xUjAX9WUU0cZVDh8DlzvaBt8vTZ91kSOtFEZdqA69d11W1olT9tf+aMq1F99tRx2YdCiOAHe7Yz1ZiAfVzDNqQZRYMRtbTjCBLdoeJXMKKislKimLzZbKB3W+z2N7jZbnGz3YgFj1JQIDhnYb79DjwYwDoAKmOoLO2lvKmt8X4etHo/LZOaT8Oytj+8hX071+ZLap6+DYKI7pPX0K/uFvPkbXoJmPCq/IPnVvk0QURL4ttKlj3/UIo2fy5E7TW0ttaWMU03/Z0H5Ow1cLcDHgeFwXYwrsdms4Flh8E6MAaw6/AwjHhnHoVZ5Rw0OShibNQemjRCcNt6Cef4aHHWXgvO0RCozUFb4xgu73aSbOXPssATf89/e87izRCK50C+FHL+Y6HQ8ZOGc2NYLSiqnhdA5WOaZlt3ic20I1iEhAs+Y3S++FjP2GWzJ3ypte84EAqCBAkhTOl7SFdZQnCNSBoGjw4njDCKoW4NbGdhNOAIvgYXEbOcnJQ625zOwCuekjIsiH+RT3wrW02AI1jH4N5CbUc80gMe3AFkFch0IA2QZpAB2EAkKSorG+2LuE0ENzZSjow+49yfHKU50j5pF0ecmsPTRnPT8bbAMImlPDe0o6+L0mc41lKANEyEEEVDmwWmL6UbQJokIUIVO8On5ixd3J7JPRUio6e0sKghd8VG5YuiIZwduKmb5wiGvJBU+uTMyumr+oyLCcJfvVZljbbKOtfCPH0xdR8MN/wzQQ4/wpOgPrtewjKidE1zPt0SPDXmw9l8HwC9uAgmzTzTuma31vZoeSwTE2ntWXuuLenWSi5JqTj0iAj9TmN/t8HpcfTKEqkYapzDDHFjFI5vypVH8trzq2DByi5nMJRWDBzDconLvsA8C3dd5kIzCChii1tKZ0Vts4+jpngozTN+qfqcFtCssIKa3iyR3bMa/TNWDnP5LnHnE3CxieFtlb/lTmqpxMnTK1+FH+RqzSpJWHf6lb4/7XS79D7I03uqqTknVH1JlkFBQEcAKTC5gFHKmpFKQPCKLc6BxhHueIJ7eIQ7neCMQb/vsf/8C7z6/Cu8/uwL3N5tsNswDDEMAwfHOLEXCBS4ZMLuFRg7BexU3lTZ/0GoJwQWgb0QQTF7MoigCNAxowJ7u4i8lhYl0n7Dza/yeyZt+6Ap66iJ2Rq5j8pZebl5G/Oy8t95XRVNQY2qJ3ka5eQ0IU/Pg2mZaUe0KbHW5ZB9yfdWcfeUGXKqJa5P8SUGIi+Q6Dr0Ww217wCdKY8xg40FO5u1tbXnFvbhhJn2/IOnXVuNJJ3B5y6K7wTMrojJGZe9Gi3cMF7nsFUE1fcripoMePWuVcDl5+/HGBEfoQnhIiRSUIqjZnHnOtztHH712YC3Bw3DO2itoZTGdrPDdrvHuNljuH2F7x6P+Ob973E6HWHHEZ++ecTdrcOv3vw7vOo+TRq02R4uzt/62czmnRyOFecl3xZrGSUAZ8yl6oJJ93fWhrJFS1AzbKcFz+Z4EaD6zJ1JswTl8ZTPx1IY6UT01ejjRTrDK+7cEmGpHs9WVVMDqfCmp7GZ5iylpLmmtenKcpyfsixqrDi/iTxyvESGV+H5MiKO/ZhkWhd53AHIWUIO4LcGRzPiG/cW2zc7mFcMwxawQlA7H/shqlaTbyf7Gj0zVFWEAIPhnJU2VAxdrQlMCspJi13QJDTefkJZuDsG3mxxuB/xX7//R7zmL/Gl+yWgB6jNCXRQ6E4Edwu4wjKiHNp0hHD1IqNEstTlvHM2rwmLzZYeit1RYRJxvLmYHS+k8aPk8wjxnNKfhYl9fujT8mZgeEZJwHBXrdv2iTpHLDrnKk3NAKogDVQIKFbhUyHGgy/NCyPqpNJ2BSWIN5QnFLWsbaWgqIwZAYbE8vRWhmnDC1OnFoz4pf0EmJ6g9fvV5xJD5ioMQpjiGaw10W/VxfsRPsJHaMJfaoyIP3mYo70n6cp7ce7+Eo8rhK9+8wZmsPjn//IdHt+e5GW4f5auzOzC8DcIZlOfuVxUVk5gq4IILsZ1cNIY5TxjzDMlwaAQUyJJJdAcqPiofD/LWPfa00Qlo4cbdUQhIJfMuFneZbizMnwIwCU3ZQPKvJcJIeJFilwZ7lz+S8+Slzx2PsSRxpMv9ftFom4ZimwZ4n2muCR8C37dU76AYlOYU/JrNKdfSIFJ+wYoQHfyTYkQYmMNcDwCb9/DPd7j9PatrBbV49XPf4lf/+//Hn/1d/8rvvrNb/H56wNuNv+KfxwNvjPA4BiWAR0I/UBXKS11OWCnCP9mQ9gS0MWeeBEqi2UDsZIYLk6BnYKDWHkoMLos7puMgcTlC8NYAs9MYovebny20kzK4WmaWniQ0abF91b9JSE11wgAGb/D09PxPMnQ/0QXcyo/4N0znayp3bTS6/dtoJzunCT2dH/e54qciGs3a4HSEh9CdR267Rbb3Q43uw30l3sM+w5dr4UmUuRj65W0bBKwrNuvE27SVZRJnnJeXJq+nteZ/JFxkQR5Adz9A+zDo39/7qBdfq92W9AXnwF0xtXTtIFV2WsRomV4miCiUmub8/l3zhfgTOHV73beiYbAh1KreyH4KbQ/1wbKg3cyJ0GEEt8o6Dv563QH5xh918dzVDmGAuE0KGAYoJUDK8DYDofB4O3pEcb1YBcCWluZ9V4YiL0WZs8N34I4O7zirT7XfoGcSTxlx6wDRsUvvIjJMldLzcjzTJ6zZT5no89rQV0T1lhFLeVtplozebT0fuHlk8bkugM5X9o5kvKStTiTNRBpeXsuuo/zxBkyR4mQmiiTOIazDvfDIwY7YrfX2HQWR3awwRwZjGCSGrVqPLFbxotua/AnYi4n4riQaQD+vM20/YgcQCT+TpUDaMRB3eO+v4eyJ2zMiH23xY62YMNQA7xVRLK/4GgpUSG7zXWcp+HqdVsvMyk9lr6TW+XmBHZZfnVvZk+azaSFPZxpxgd3CSkg/ZmlVDNFJkySNHCUNzCkC32tysiFOBXLJ5BVgT6I9RQpM6KAK8KlbF76YZ0GuMNGK0CF8zYb5zgYHOun7I7NCYwJowrngXzjwqfYEO2EUMBJSONFIq48DYLLLVLkP+vuJMI8aa7W+Jgvd+bquoRh8RNAjT7CR1gFa/H43KXMGkbjNdpyiV/z+XS4Bt35MvAENHr+nLpCR/3dmccMCqAwQuMIxx2IFHQnrv52dxuwYxwfR1jjqZ4Kh6gVr4J7pmRxUbXD87qSjMBr2NI8jil3ZMwghWTMI46XWhUrApwNXTmGs+u9Gup12v5lply5oh6C2I0VUFtHVF/LZ1fkurcsHtaki1OTCSOa41d16zKXUo2Crgi1K5u4jmKV6+qMuD/mJ3yOSm21B3P7KbwtFKFy5aBgrUtJiDgRnOV7R/YMUWDWinKLR0JBzgHjAByOcI8PcKcT2DmorYK+7XH35Wd4/dUvsX/9Bv12C90docjAwmHk4BoJmF/J0vaO5K9MltF4LLSYY4LzXeIqZRJfpAU3WWs5vljjjhVJOUu7FPnmntf5WnX6TqyxiijIgTxN3v5FUfDlkNFTjUZELwpUZ1iCM42r2x/oioIWjPi/KGBZYhhFuNEandaAJnCwhlAhw2R1XDxQrTB4zz+RVlNZV6xj3f1WkJxrfd6uGBA2Fnwapnif0qB+KhZgY8DG+uInl8naamfho0XER5gAQS5EscRz6RDyCKdTDg6MTb/BbrOBUj1Iddhag93GYNzuMZoBwzBgHEcMpyOMGTEMr3A8GfzX3z2C7T3G0wnsDIwdwR3D/bZDf6Pw1X7Ea+zw2+E/oHcb36qp39LEOKkPzumW4Pw//1leogWmj+mNmH7nDFZSJRK1DO1TdPURd/FZeI6Yqvv4rMqeDs2qGg/nEMIwlzPEGhCOdE5zmxFVrXquj25PqjgDc+jMNYmfvDw/JpdoVqFEguL2CpowuQsXx+C3FqdhwD8cv8XtboPfYg97eMT3QwenGI6tL0WsIdjHdYjEPBQAn4ZpInAMiHHOhHf+8g66Rr5ZUPDBpyEWAmwkrTMOZqPhftbBsMOp+x7dDyc8fvM9fnP3JX7ZfwV1AvgUT5+IGtpXAG8QNfKiqy1unB3lyJfPuD6bmij3/ErgrIyIWMtfi44NBFMY1/Jd3cI8r7jqU8q77fMpRXuq3cIwP4RAgFGkA1Rk/Ms9EwKcRVwpPoRo9wRzcb/Oco2sZOEwJTLTekprNSo6MYu1jGMv9MrHjPzZ4IMGAoAjPJobgHbo+xEqrE/fWyJAxSaUey0nWWrEv2V1l/8s31MshQhw6DDqnwFgKPvPIDYTZkyJOjISwShWRc5YQDlRQLCIzDQiSOyInKmmgmbsTwHO3Xkf4SN8hL9MWHNG1TfvdesIbzv+AR3egukrGNzK/amBr37zCuPpBv/0//0Oh/sxXsm0YM3A2R0ov9tJxZ2T4MJEKWG4habxFqTFSgHBHQsRwwXLQ0WAA3IBQ9QIj1dzW1s/3p8VzlkwZj0izsGacAanKMYB85hzVkl5GS5IKpJ6zNo7pbx/Ut/Pt/u599ZfhpXVBFten7M5PhTf5YzWwo1aVUb+mQNH3LJuq99nRd0JgRPc2cdZ0FqYgcyAddDDEXQ8gn/4Du7hAeMfvwN3wiy8/foWX/yvv8av/v4/4q/+7j/h9es99rdbdJoFD83w/Vgbpz65rNXsXybBCUVbYgWGZWm/dYSTUxidYLryJ2Uoj32HskVYUY134KXGvVy95/oHT77OTvvkeZY38n2ywjh7B+RablkRnNLX7Wm2P3+fgGq0tPg+U7YnSoizNLn0Z3avT9c4FXyP80xxJt/mSoBeFQvVKei+wwES1ufLvcSG6LsOVmuhH7ziGIOj8l7Jo0vlT92iT9tVt/2plMeyXsaUr/c8CqfmtS3c5dKAMg27IsfiyXd+esGDwfiH7ybP9e0t9OefTDLb9w+w7+/LAqt1+Jyb56qCiOt4iJ6WKrC8DF7yAr7cd6D/sqJJPwVLiACl/2ry5rbkzyIFkJOAlAwopdF3wN2OYazDSTOsA4wlPCqNB9pANAPkeuq0hlYK1lpopWGthSIFZw206WDJwYwEnBiDIjzA4Xt7j447xMBh8UAOX3kyxoUmcAbOBSYLA8TY3BA6rXHDd1BQeFDv4WALTk9iCJVz1PMGO74tnH6sh0aeF1sCYaymFUyP2VbepzTsWkf3uvpzfhzXdU72Yc2UnK/iHDtrqWVtVPcymA06iOQj90lQ4sZPbJ1kIy6HNsaV8IRdPvwMYDwAJ8PYvVLY3WgMGhj7ROxJ4gZSFLQ+onk+tdPmbcj+BweBRLk2pPuesNAKyrpIdjoiMDmMGIDeYPOJxqN6wNv+W7iTBozGFjt02EJr0RpnIzU6DfkdKg/Yfd02v8Qn+7Miki+62XLEung2BQKCJ65qUEImKrZhi/Qqyxc3ew8HCweC7sR3bN8xtAZutuluDApiwWWTcYAZKOK9IfAzQVxwyVksJr5KhUDRqUU5gaiU3E+BoPItgzBVJK/yav6OOd4jiRGvwM56911VHURQ1Ek7uIcEEOkA6uCgYOEA1p4s6/2nF9FESUlAMqUtydNu2pNCGDaI3tw8JD/8it89FHUyMXQDJiuCvWxuEw3mBXHhD4zRGFgzylgpJeNP3g2VIijSUE7FbmgMILJxhYSyWhqwa7S0p2nC80nSKl+Z/iN8hBzq+A3PukevCBdZLlytngpPK8isc3asV27fBfTS9SqroaQzU5POYYGN9/5cTNYQSMdzONMDturd84W50Z0GJ92vii/HxSFYU8bMGSPxDESGT0MYMUnJVORrdT3c23Kve/yPpvEc6r0XXSzF8kot8aesiSkt4AUjcZ1zaiO8GtPkdxqLDL1JY5C1a465XVtprG58Vd+qPPGOrBjeS7hf8eQF+ScrqE1Jdy7NDE0UL/58fZZrMP89V24UQsxogSwJIaK1baSp6n2a7Tckt2ehqeRxLPKx7MhZwBrw6QQ+HeCOR9hxkH3bAZtXGjdffIJP/+qv8OrzL7C72WO3YWzVI0484NExBpfWtDTBj41qtX/6K+CIDgTLCgezxcH2GB3DQNw9OWbklFVk0ZQH1/OX14TBL2VObX9aFXH1vS4rKx/152Kjpj9LkgnAdNVWp8pMdXk7/F8cgyV6+ZkD7TchxTUsB7tf3UU6InFFq5RG13foug6dt4hQimAXmSsze/nM7TUdy0vxt3jTNQSG7frq+TyXZxnaqyG+pbaFeU3cnKv97CpgbqwdgK0BPx6LkhgMHkcfYDw9vbzSefhoEfERGhC2Xrp4RSGZoP3B1AG4JcamO8FZC2MtrHOwxuIPDz34fo+xG2GNhd2McNbAuhHOWdhx9HkGOOdgxxHMDuZo4B4dRjvigRn/P/dHMLMP3sZw1rtwcv6313Z2zvkb0yH4kE/MJQfnGNaMcI4xjAOgGb/8P7Z48+kW/8b8PXre4l82/xeO6hC5QVHIkCELgOzdT+2X+PXwtz5Qb0hXDV/zR5upWI526317hxcIcitzjUHPNRHnL4DzcA4BWMo6Rz21Efw5WKJnKU+wqrQn00Gz5V6L6bFcTo08t1Nx0xRkqaxyHQdcIgVJDHNY+kcFIC6ZHPD9Dw4nZnzx9x02e41vbQdTVJH5FCWxWnDMADuIz9GSCBZt9uTjMCENCT0NZwM7juUSCEorQCn0SoEh/pEtEZyz/qwxUJphcQReEfRntzgcHvE7/HcMjxsM73r8XP01PlOvoW4G9NqCDrJXzSuI1mCB3GYdnQTF4bmfCATMdPRb85KI5BzZ5fAciVlAADhqNObOoPLRlHVC2Yv6BAvnLDk5cy07/Mu3A7rOYLPZQGmFTaew3RD+6muFPpyjBAmbIIXgeAK+u/eCB6UiEzyw9MXEV4k/UqWhtY7WaDlobw7cdZ0n6rS0y1r/XrR0tNb+nvD3g7UROZMPlvuMRWAuAo7wKZImrXsopbHZ7aC7Hob2sNwBvtUdbYSBrzph9vi7JSDxTgUbEj/6Dp7pnwjhQNgG/6rkXX9NiOL4KR89aYABR18BzHDK982PdxDAOIjlkWUHdg7OOTwcDnh8PEDrDlor6K6DUhpKaygi6K6Xueg6aMXYq2+gcYqLy7FtLOTrnH0f4SN8hGvAEsa5ABzyPgdejun5QcGPRQtPLO/o0gqvSOe1RfPzPLpyqqqaQ5EDHiYGgv6+jhf9/FzNCSNi18J9gSyW1LQDYj3vI+HWsSJyN365MCIxy2X0Cr4UA4pUIYwQEoF9U3NlHJWVC7SZ/m1MPuFCwYrDl5vhj/H/yPd76tpdT00s0WLXtHp4Kn3z4WHKJpetl+PYjfSZQlRMH6BYf3mWBv1E7b2bp48YNAWlkpQ+1B9dXjPDmxnJOgegfdB3oxSILWg8gk8n4N33cIcDxreivew2HfafbvDF3/8MX//9/wO/+t/+d3zyyZd48+YOr/UfcKu+xz+cLH4/EgwDzls2lK0XvJPYeaZzeCpBq9N+TZYNB7fD7w+f4dsj4b11eLBiMTwwY4RYQSuIYCJYSdiizrSH4K2r4vNisMsssSFF0lCW3/cFvVOthyJv9j4/z1rM/Nm6p0mnv+t2tNjY/pzMve0E5nAucIi8LPZKW95tcZZuQpPNNHXx2g4EPRAFY8hXTiUZDy6ZdN9hs+nR7ba4udljv9lgpzuwj5cX7hSux2SehF1uY+MskDIuKgSXCzCegfMs8p3CZgsfQUAyY0G1shnE5Vgvjk720h2OcMdTlcCfE9m50Lqj1vGU2vA8QcRKVTUOmMT5pH/S8CH7lhhHL4RKcHWU5hqnRGClAC8Lt+LoBIrEvcbdFhgdw4pQH9YpsNN4PBJGy7C6g7MW1nUiiNgYzwSxcM5hMCMcuyhQcMZG5kl+ODsvkACLKw2OTMskjHBWyhxNJ8wmRWC2GO4J92zxjXqHDh3ujw5GeR/fwikSUq3QjpARuXcjvrHvqvmu0DpuzU3F7KsOz3r5pLuwedsVd+UkL0/T57DbeC8nW4ImjVv7Gor1JN0EnnSBXGtjTMkxnlwpuQbIpaVdD54kdLgoS/t2WV/tlS7iSYUBIZfmOXb47vgOp8HioHp0ncPNQQOWwDf+WuCG6Xu4L2oiFZC9FQNhB9c6XOwTwfcTkyAGZmaAiAHrEWclyJYicdWklfZM2cCktkJcOMLIAOwWbqOBO+Dh9A6d69DbEXp0sFa0g3p9B9310CHKWy+NDsHpckK36tYUeHrBVyT8cgGTZ6n2xLCIwz1BasHZfA7iuso+OphHxjgmhDhYoiXten9UO8A6B2MVHg5iGaF8tWLxwFAaOI7i3oeUBIKG17TRpNApHYUAXdeJIKHTktYj/sHiTXlBRB8EEdB+nYwAEIUcWgvq45wDeUSr7rr2d05yP+UtMYLwQPdQpKVN2v8pDfbBqpXSYj2gdMDuozCCiEA6nLfkTeYZwVojCY6kruD+yv+Mcz/yPSxGLxTPiEqHdA9m92EUVIX7kZ38WRFCOHY4ukcc3RGaNBQ6bPAKvd6DmeCI4NiCFIOhYBXQdTs4kvEGMSwbABbaHaKm7CVQa8+m5360JuUV7LNC67ZINfP8I3yEDw1LDMWXX6cLjM6zeMEL7p1yG79M+c8qe76BJSmQaCU5qxNNEZ9DzjOFIzoQDG8A6pIgAvFqnkBuuR6f1Ux/BPeHK85fKu+O8J2JkpvJIGBodDylqRj5+XB5eqotjJiWyTxhXZ3tQhBSrGdKtWEdTd1YAxQWWKnVmlt+hICxtZVgfD9f/CR9zQNYE2w7lu8FT+fH6nqbkRrfygQZp2uSMcszI1ygHJHN3lNVZp0vVV8y+6h+PvO7bmOx1wOF6rdDwLmZXcLlOIsz5yycMbDHR/DxCD48iC93MNAB3U2Hm599gk//+jd489XXuLt7jdstYU/v0PEBcCMcw2ujp32dKzNlqmJx/1oA31tgR8ArldS7Au3kGBiZMTIwOIeRHcAOFrm3JU4umUruEcp11FJ8yl/XNEieMDCmOL1rlrHwYI7QWr3Wl+pOvJnWKm9Tcq2E3PxJga7iiu+Rnzd1yWfx75RjwtKicCpRkTQphomCku469H0HfauAG+Xdt6JiU8zt+3PtWwFnL7ly/i9BBWZxogvafRavitK0bC6oZR2xplJOF+KK2kv+Aqd8Dd6BtCvcN/XbhT19Bj5aRHyEJqRFJhsjMERIeW0VWO+2gaGVMPG1dbBQ+FQ7vNqPUbAgQgPCH97d4OHUwVoTmXwM57VVvSCCGSdzioIIMIOt12pGxvgKjEdXM8DkGgz1GmNEuDEMsNbGT/s7i/dg/EP3LZRS6Ptb0TrVor0aGJMhSLeMiQzKOwDv8X0xXoIAO9FM8uksp4u8HNsScZyOPU/+zj2XoN40KbuVVmvgZ7+w2N0w+FWHTb/Dbw//AZ3tQwuyuUf2rPzNk1srLZzWRVwE96oRw6cCZ0hPLL9FKFKRJ/86yZXduU+hjS8WQtSIdgGtuTiTZebVpdfZHASUTehsBc41/EnOB1Ik+4wd/vM//Qvevxvw17/+NW53PbZ/OGHUBvjtBuhQaHfU+KBcxkHoGVruY9W44DfRE77MUXOcPeLtlAJbL1gIK4UByw7KyT5XXtOeSAviZR0GN8A5hrMDtOsABg7dBsd+B+ykJfe/f4vD/XvYgxDpo2WwI/zy7d/gTvXY3zrorYN9DQlSgTBonjGRMYYLqBfdDFK9iINzykzZ/0IMJ7yViEskLt/UUcIpbeSDBb8fcf894/DocBo98eEFwY4lsJ6c7ZSY3c7hNDD+5VvR+NdKI7lQUtBaBAiBLx+sD5RS2G622G228XcQRITPUIcxBswi1CgsItBFy7m87M1mk4TZWtwChn0b6oJ3RxQtNDyTyNlwnoplRL/ZinVA34NIwTEBpLyJsghNciGE+Ogu75Yw3MENVdgSwehDUWh7YlI5tri3/4QTvysWDkH8+iLelyIQBAMO4b6EzBMz2DnY7K5+xAlHnKAggpRb+yuQ+xKA8v0YAJAERtQd3Pa1d9XYA2BYN0DhhB1+52NmqMiA+Qgf4SN8hD89WIMNlsw/5N/CR4EbMjp+C83vwPQ1TEaOR2FEXcWMZCGcruKeyV/wmaVju7UBF2njrIIxJPyT4QUTnnkJBZBjuIBTXEFwlqN/Ubmhhc8vCTLy/LFUIGqixO9lPZOGrGnvQhtyXtC59s67TVtOP6Etn0dNXR0uYfjF9OeESQvvcyFfrJvSLggM3CnKXe3TXKhQlR3bMNP+/DV7PJ9SY1JZHt9zPp1zgB0H2OMjzLvvwI8H0Pffi/sjUuhf9Xj1d1/jq3/z7/Cr//R/4LNPvsBXn3yJu+473KhvADeI5qfrwfDKPEEEwRmj0Ovd6EzaMDDw30fgTgH/YSNKpexpa8uAYYeDc3i0hPcWeLQWHTNGAgwIGg6KVbSESLR0mCs/AGE/pKoXoH5b7dO1C6uVrqatLt42y4WyP2smSuKcp5srL+9jOLM4Ez5wfBX4TbkCWT22nnNXva2BqldBAU2e18tdKQXViRJWv+mhdjtsdzvg0w0e9h16LW55Z3r1RHgO/UDl15lz4Hr1XQpyqZI/I3IPBkA679aNYUQ2lpPFvRhWVVX6rIVDGzeJbV7VxhJWCyJa5/5TlH4nUpTVZVy6jK+ziAIf5lyiSbql6gue6FLhLTQyP4pKuO4IpUUVDzSC17zkGKDSsYMCQbOKLSMmECuwo6hlyY7x+oaw6cRckJnATrRHnfdl6FiDwTCRieUEEXUOxhIeTl5CGLRlArdmIojw2p3OYRyNxKXQIgDput6nkeO56zooUui6Xvxf6y5Ke1sIehOZjMwjlyHP4SIPiC4QZ5tbZZUa3eBQXuZepig7EzCwpw6yMguBDcoxI2KwGzEMDPcOGDuNb8Z30DjMXpQ5GynWHzviV8pkbPKrsPE8js+0troZ3RbY3CJutL27wY19tXiAzO6HuFlrA/r5Fl8EXJUyV1jEln3NM8P0lAZdpR913RUSWSDvaYmDRgDM+ME94GBP2HU77F5v8Yudwl4zNCkYKvdFLD9DvGRPpPJlytJKTPOV7Z1soVJqqOzRbA8KExowxkJpRghurEmBiYVAUAxYCKPWWs+QThXbLQPmBHQapAk0Snu/7X+Pt/Qdbt4DegAcKVAHdFuHnjReuU+gWK7e6J5Iw1tOABJTgBMiwJhfyxWU6Gj+i/wWTeueA1cB2TrJkY+gETkwMDioQZgO9+Yt/nh8xAFHsBImtw3nUzB3IAVm5c959rEdNLTS6LsNFCloUtCK0Gth1ve916zZdEDvgI3FVjO23RitEZQyUr4iOBAO90c4Y2G8sOHmbgvddyAviGAAcA5wg1jUAWClMNIG1locH09xLYQ+K9/WwM4nJW6ggjA+na3+DjE9lFZQSibQ+THWuo/upEDiwgIEMIW4EbkgIt9AnPaCF36o0DYSBD+cYQ/0Bxgcq8WeESZ+PwVhTLIk8n3wAqQghLDO4XQ84XQaoLWGVh0e7D/hZPPAZmIdsr27Q7fZQfHP0Hc3sP48Ow0nEAyUvgUphtYdiA0kpJ0ncuOeDcgTpXMwbuJ61c8epM2nS5YRH60iPgIwg89dAD+FGBPXhDlrpPj+qrXldSyUvIZr9ULT0HKDGDXQi18+fdEObtIQRcwEf95pegTYwWALpQmvPtuh32rcf3+ANRyvB/JMlIyzCfg4fuHYTG6LJG1u2ZALJxg+eDUFZukSApo6mLS8OTGqEAJUh/ungb5W524+rVnzs2cUhR5iYUFnF+DUnYWUxJzn5zjyeYFN0m7Sm7ylwZ1TKqcsoy2gWeazc/U5JXHWHFkTq5S5arIcl+zulvFCq12pN2n8Jo5Gwz1dtaAcp7yipUZl+G3ObMzW+ESbPK+dc4skQjJboMlElP1QWby1ELxZLA0QhA0qcB0AYnHNRI5BbMHmBDcOcI8P4OMjcP8IDCfAMVTH6N5o3Hz9Bl/8zb/BZ7/8Fd68+RSvbjvs1Tsc+YT3xvmA7hqPnOGVxOncSM3zW8HPhcclmYGBCd8awk4BbwJ/AR7XdQpuNFDHAXBWXD/JQMBBJRZAlL7Nr6e09xo0cj7xnFZQa96bNXD9Pcxt9X5SR/5stvR2ZVxXmqzEKadPM6AsTaR780+vVAsX8PlgcyLfp46+5y5Kqj7rX6WFfqCFwz5KQnFJ5wjoiKAVYWQHRYy7TmHbCe3kVNgvKu7Dae1LcIXLvDV1jTW2EgNpl/ESMHcMh23S3gZPryv/OXE9kXNY0v+T/GG7P2NwPlpELMC5YV18f24jXAlejpxulyyuDb2ggRkEBUfhnRxEDEbnAMdatIq9UODzjsFskDPq5X7Q/rAKLilkA+TanIehw7++3aEInJYx3ZPWvwPDija2t4AwxmAcB1hrfHp4AYQWZhGJiRmRMMRicE5MiYglwtXBSbDSSbqggVrmrdM4a4uDP9cobtWdv5+znKjzFRYVlkHfCCPqdziBcZrkCZ95GyZlZ8jHXP7mJ4frOvN7CCTt9SztzV8xvvjK+aXB+HL4BW5Pr3yv2hur8JPXXM9+rWWv5rboGlq4KjWlXsqUIzxLkQY5lbrY0FbxjSzPOTeo+kZQYMrc2xwYGBl/PDzgwVn87JMvcNMR3hwfQdZBbTfQHUlMFwVQxiQFAiM3kSVyGigwXBQmlJ2cWhZECy5CtG4CQYSeEIYrwHA8Qlvv75IUuk7U8q3WgLEwLHEPLAOddnL2eYuG4fUWeLMFabEAcZbhwHh/9x6WDNz/6wD3Rwegh94wPvvlgFfdHq/oFRQ6gEXLUIHhNgy8Jh8MOPU6gEPV6+YEJhWnLPxkmqrMBDwIlZ0/r5R3c+Ry6xafDkcG3sm5TUz4Zvg9/uH+X7HdafS9gnFWLCG8dQWTkj/WIoxmAwKhUz26rsduewdFChvS6BRhp4FN32G/36Lf9tjstzht3uOw+w4dDHS2cIMwwUHw9HfmLU4HObdIKXTdJ9hse6h+AwLgIBZxozJRIE4gDN0Ggx3x7nSf0RDK05zKCzGS9UJYS2F886OFhiQoAEK8CYB0J+d5J3ppcqUQgo/eNF+B8HKR+AirP2YJObxAIxC0YTwCwVyumOwcYokHgcw6BF4oEe9Zx7DOYhxHjGaEVt6tFH8jZXG2J0nhRr9Cb2+wtQTdfwbs7uAAPDw+AEQwu0+guw4b2kPjEYR/EndlnZQlunPVOKTGVb+vCx+FER/hx4a/3DUYTq/6WZPcTSmp9fYJVT+pCM6u0nAOukjLAIlnWeRZeYb1/AM6KDj6GXS3w1e/eY3haPCP/58BdjSpRA7XTPgS2lbhjsz+7mo0w7+TRs8JIyqkmEU5g/2tRGBhPoKhFOCcElxLuXjFtJjIiRGcMeHgNUH9EBMnphc8LhTxu3Pa8hOYYr2+xipdvvbIpwgiF4rpybsjFiUO6b+4rVq7sHzZrb2f3a/rIGnax+nnDPdFZiFflduu5RIqp2pJlqXOXda9Yk9wNvb5dFdCpmkpieEaxmMijIAfnwZtjOAuCTrt5YCLk4rl57RdcNTplPJ7SHBhBRKlJoibJCahDRQE5+ol2ibYAsQOZniAPT3Cvf0W7vER+O6HSBd1dwp3/+5TfP43/xZ//Z/+T3z26ef46qtf4E59jzv1B/wPA/wPA4A1xEo3tFLGOl9VlDrg34m7MBkfhRMD/7chvCHGnZbzTQoQxVF3OmJ3eI/jOOABQFDGARKNEgVzxbSX+3DiT35y7gS6fGEtLm25fC9x3pbs2SQdpumalWb5ApPdz5Wsm+RGPCmLhngcPo9Xss0dW8UyHQPeZSy5rB6vZFtaRnCaz0mTs/VKOZ7tqjRhFYefKiuvdCsYYoCQVug7jYEc9IZwe9PhdkPQWsFp78YWpdDv3E24hpF9VWwp5+3l50RWWxzBkk20qq3XhTQ/1VV+IZzZT5Pk+ZlXLrRrWt9dRxBREMNTWJq0M1lfBM75YE3aJP73syqbe7ByElea1zwJZsuuEaQiU3xAFCSmSrxYeETWMUcEV5FIUJ1KrjrkD4C/lAMjMXwXThz7GCnpkvz8tZq2JSLVgdkvh6WzchkY08EYgnUEZ/s4t53uIO4zgl9W79dbC4KggtrpBF+dH3CXMZDqPOluZtyfNKxT8XfM7wUltQsj5wKjvi6WUQoGpsKIMl8a+yIvOGkLz34mTdrIvArvE/ZR5cvTlnWXaW1KC24KIjpnMXxvQjfw1jmQ+z6OX4H7FEhG7HlrZgAu5yH+30raA9hTll7WyOfq9v/P3n81SZJlCZrYd+5VNeLuwZJVVnX3bG/v7CwZgQB4gAB/HxC84wFkd2SmZ5pUF80M4syY3nvwcKkyM3MSkZlVfkI8zEz1cnr44RUXo/TTpE715cEHS6rzcfDoo2LiOEiuhQD0oNAlxAv+cPeRzXbHrXYYa3mzEi6MpTmYccGJOV6ojVGdaU7yyZPWnEgM0phcBpRzJJskA5l00FJaUo5TDevNHTrUmmjppRgbgv02PorJVCMumQj8gJyFM9AhXvBx3dp7wWCwbxtk6ULA50ZwywtuPPz25vc0LFAxGKMsVg51it9HwYmJFhFodsmjxBgKcfqv3GuWfo1rwOfQLmVNFmuKCr2S+i4uTIXyUvvpD4rfenQfXOYd9rDfg5olF68vWa0a2kZomxAketGuWbYtr1avaJqWxjSIgLUO2wgX31iaxrBeCniP2+5CK4xwsAb0jt3B0tDg/J7O7XDAvl4HBfdHAecVNTEOhBE2O8feQWMjERvPti76yfNeI13Z4TqPJsJNaoGDieOcfufBy2MlvbWUkMTyWQcQxQcBqnrJyXradpEgSW4F6zM7BfPO+psS18Fob0isN611VxEgivpA+Hg/EUi6ug9S/UIiU2MfUJKgUL2CeLZ39+y3e5T/TGPWmHYJxqKtYGQJ7tfYZoX3Dms6sBe0tmPFLpI3Ze1pXKrH4p09FkecUyZ4iRnxAj81nBMrYgi/7PV6bBPP0UYPpJnOacKgqHPOgtKKHhtoHuJ1fOrcyveLKq3cYXTPQdZZ4eF83nuF92Yt87F7pmQJ8aAD9VQjJopKTjKPjqgE5QaVFNNCjzAY59p7jCM5kyN1J33JGrJJANL/Xbof6urX+JD6P+/enXJ/e3QGZtb9EEWo0zzVCiy1J1vmnMsEKpM2kz7hr3FGpG8ZEVP0yioWLWS8L2E/Wd1jSjiXv2dqKCr3JM8QtQBAoyWrQdSGN65DvaPb3+L2O7rrT7jtPYfrG3S/RxHMwrB603Dx3Wu++x/+J9797X/HV+++4s3lggtzzV63/K6Dm9pr7SkYsjQmSN2CBWrEGYlxNj2d8zjvcxy9yjw3VzDW1D8fHnzS11WfzDSgLUcdnxqJ9DwNVKGlxgR9tdaG76qiZfSoukkqXD/h5VIrKA0EIDldKpsTIGSvJn0zmYp6zHSMktzR5vKNwQDWRt5Z27JcLFi8WmBftWgzDo6u3uPu7vGHQ6BDRk06dq5PP+mP3ZGs5w5MZAhMJkvD8TRO8BnwhHvsQXXUcCLzkSbNWt09Yvu/WET8bOFzL/rHQ/aV7YOLpnChE5nMQWvZqA8umIxivGQJsY9MxMAwLD6+oUZ0Uk2FIdM2ysVqfIildCE/mWHoveBV8N6Ei1TjQSPJP7eN/uEtPeaTScj/8MZOVR2ZFzm9B50X/nRzya5re32G4PN7CmqLhylEMwkqyjic/5mtKtDR83PKCD/Ip+FU2WOByTCdO5kPQP9U0myB3+t2VOZcXYqbbHtWTBjkH6VTxX0tHC5Tl8ua+z/a73mrV73nI6jO62NLqNwqY+Lx1JnwUAn1nG/AuQu3T0AU0Y5sPGwD6u294z/9/t/4w/Unfv2r73n76oKrrqNxe6xYaMZ+8ePGJbkiK4hf+p14tiZYUcTWTN6Rmaoorc1otZYnSSvKa7B40MMe66ugyNYGTSYF5x1djAvgHEhyb2AiueIlV6MorbdAA9+HYBIqQYvuIJZuu+e//su/ontQLO3a8+5XHaZT/KdQbtZ4F7DWVvEOYowAgcvuv2fprthdONTSG5PeOokWbGlcEtNDosAF19eOEVPmxG897uMhWLSh3G4Mu61F2gteX75lvbS0jQHnEFXWiytW7YK3V1+xbNvYB8W2HXYJi+86TOtYLQ90uwO7H6+zT9l03IoH2RukMxk5RDUfMdVRUxj5psnkz+1tiF9gjMFUZ6VPZfiUuQsVGosQLGKA4pIvxp/wqqWcIeGb19pgzLOvz5jM+7LnJcWGSJYv4TxQrXcUec0GvD3ZZoS0Pa3V1IQkSBET8wVBhKnShqDU/Tumh6+rIqrZaZRUfxA13jQITNQr99d7FLiztyAGY1tMa1m/WtPIBbo1NM0lBz1gmpbd4hUX7Fk1h1h3PEcyBTQm2l7gBV7gBZ4dHk7zV3nKfdorQpOSQj/L+aA0+hGLwfFrRB5GnisaNGmNOQNbPB/mhmrIBAm/p90RTWbOrazuscTcGLWhElYwgR3rPFN9six0pv0DBouO25Tb8ABLiCLkL3Tq02G6bk1IMw+nCYbllXbq4NlwdT12tT1wpebNNZNnYkhmhb1ZGBEyFpc0JEQr4FUZUUuKexPlSFB+AoIyBiFGJPiAA5sFgo1pQuw553Ycth847O7Z//gD3f2W/fuPqPdI07C8MLz7X7/l3d/9HX//f/q/8OrdN3z77feszS1X5kd+d1D+pYu8laGO12NgOBVxyXrv6TrPvus4uI6DczFOGsFtkC1ZEiosZ1sIMcCrQ75y1KZNKowUpR7Sr6nv55RzZlWhhSFxtuiv0fmYqvbSMO5JH/8vfIg4rok3oXXZGssdN3dECyaWVjb3KTn6p1tJk/hgySVQim3X2BCculkuWS6XNG8X7K5alk3wLNDrlfccPn7C7w+fAbU/cXZkQmwuXX0BMJ5vGX35zCCZfjx3rB4ujHg+mLuvHwpPEkRkOlzmHrxAgceNyXNpITwflNsqSEoVg+CJjHyVwNT2UVtZfQj6rOHistUB23f3k8oml5816cdVj5sUkVHvBRUXXJx4gxeDFyW7qsi+xm3UTE1mmOHwDEFKk6bzTFWDZpy7DRXFqvDVlQSf5tp/l9xO1VOtkfDpIbyJQUeyMJgcjvx+eBOnZ85LCB7uJbiU0jLas4KH/FE3vqonHaAV0pYuT03ve0RcbfFR6poUJgwEA0BgLFZl+yhZSMFZ0xryKYh5usTzmKd21vkpba0+u8bT3VUIfnx+bw78m31fDXOVtzcfdb7xUvYJu9B6TIcTW0GfhhvPS/1bA8K4fqssrOXt4ZvoHojASN9W+azCckjqQecM+05gB7Ivz2UjsFc+6ns2ek+HcnlxyZvXr3lzdYE1Hjo/OB88OQj1kKjPHFdDLYzofR9gDQnpSieG1ygsqBG/iiBJyJbE8ryCuBD0OARQDueCbWxy9BrWi6+M+pOFhBkgDrGRfTcHRcjw6m8uUaeoCYz/fVu10Ug4k+L3xjZoG138IHjb4RpPe3NLt2+4uT/QWc9X8pqVWeKXivbwwIhFplYPEdasFaPQKbKL+8krH24+8ds//wkjYe8YWdGu1nz1K+X7tysWbYM14PcO1HO5bGgbw2WzwZpdGCAPcmiCcOFHgzQG3wR/tovtClF6rpcymDT/Ev6WHSz8YONI8BUokCmxLJxIzJi4MtKc2LT/qrnJQmfJGl4aGSWmbltVb0H+Jk5/if5yfXLdUc6oENzdIaa+SYQQOHpQTlV+OEJ9bupQcGGSID3eY1moV3UzBBEvLptqks/nszmOU0bgNe4TqZZQSBg0ABX1DsGFPh8c2+sDovdsugO2XXFhvqZprlgfvkdWS3aLN1gONMG4H413T6rz54PrvMBfIujgTvhLgb8UC5/5OXkEE+poRQ8prhykCj1lkr6CUHVBPXBtZfwknrdNa3j360u29wc+/fE+xIqYbFl1t0tghBnViqE0btoIYr2lL/F2GDA55gUFw6GMTwYv6mDCyRoi47Fncl9SkdnN0yMYMbUwIl2UU8KJycph1M5iWNHfgyNLgzPaOZdmqA/xlG1+rIzHMJamyjtVTlKuyktypkPjbVQzUqvyBoohyVqaOnVNQ44Kj8oosV1JsGBiWxXtL+cKH0o0blDikMhDCPiVB0zij7gD6hyHzSe63Ybt+x/o7u/pPt6g+44WEywhvl1w8fUbvv2f/iOvv/ueq6++5+pqyYUNlhC/PSg3Hoqrau036pGwEPiugTUgHjoa7g8r7g4te6ccnNL5oDyUlHRUPYLJVSclr8ec1vmImurWcODz8zTv1eZN6fvEMSOCeUQQjX7MvK8fhMp6VGyPNqjWnMb1lduSkO70Pa7jRAxkS4haY3LchrpuOZs9nGihwdrJBw29/RHOWoNYw8Z7nCqv25bVYoE1NlggJVoBCbFdb+/w+z3aU3hLxT9irVZNO+/8O1VH/V4nkj8jfjh7904nHiY/NqMy6Mb5++4xu7S/OUer7RFD9mIR8bOEn5o4qhfn1EKNCISkS4dgXptyxKDNgXEXGXj5TK4Y0maOOV2+ZA2EU0KuWK73gvMgPvitN1GzNWVNgghJGrNSDMnCc1uYlIO6jhJ4E5ojc7BsHJG7OYap/o20MIbI7fGTp+8PNTFjBecNf759RecbXGUx0Ct34nPcPH1w3p5QIfo9HKafs3bo97tc2poEXzofM6P3HMXTFRTiRJ2qih7GzwA+aDf5/JiFx9QYjv+o8JU6b2TgnTHGKZ8sPF9/t+diseC1/4rWR+TRKbIlu47UBeiqQkDiCjp4y52z8MnBBxeZn4Xw+u3+hg/+A4u25dXlindv3vL68gK5fh8079vgqocuzo/3JE5vcvsCAZH3kSjNTNfZIzERvNV1GK2ffJ7ZkK5clzF9ImIhuGcSD4eOxppsGdE2KVCxwzmPN66MUyJO+jLFWJ2QkIkiB1BoLPrrN7npChx6vUlxCoLQoovxaxIf2DUHfNOx2Htkc8f19Z7tvuPV5YrLdolvADNsTWEij1oq1RenyF3cT1758/uP/L/+9b+yaoV1K3z33Vu+evuab/7dglfftlgJrqzcTsELyxaseHR3h3fRSssZZPMa9gJ7i4qhs6GfC9Y9krLsw3BOh/ExKAbsDlaHqgdpnGxgoORzPPY1MeQjWl7q0VxT2B6+NyKaiFipNVsH66iqJu3NmugQY6N7uSj89OGs914RE4hV0X7Lip1PrMWXsQjnnC+V9Z4F8CYKBrJqVLovq75VFhF9QXu/f2HUSoA8yeMRBeKa9mvYoOqjK4FoQb69P6CqePlI41u6wwfa7g26XyL6ju2rb1nIPQ0bgqVaaLd4zfP2JeGv11f/Lx/+Guduqs81rvo5x+SnH+/HEM7nF3eyf4UL3nucBQiRsVOY+X1GaB0Id6qe5AZDRLCN5eu/fcXu/sDt+x2u607KNjQxABMTViPjq14fkVGa8zBnaTAaHMg4k6SLmsL5SHdmKal/N/aLluiL75zl1PPrL5XLHZHYjDPXZVXO0A3TKSnE/Ot4Zw7a0MfLSz+fd//EMc/zrcO3Z7EkRzBGaKuHg1XyTMLcMdY6tkSZqr9qSKZt02+p1kydM++TXtnJXqFQzMEytOBSShJMlN+gWSEOm6yWK/wfQWJMCO8P+G7H4e4Th80t2z//ie5+g37YIB7a1YLFyvCrf/8Nr/72b/n+P/6fuXjzjtff/obLZsPa/MBtpzEmRD0mU3M8nKfpYat6yFLg71qwKrhO2HVLbvZvudsru86xd0qnGlycEkghE+mz3gmTtbqH63HQ0il2xzB178zVkqgcqv11L0q12apPHQ9TRtvnXpyCQY/SeVfXl777Qn9KIFBjrLQ6fXHDNMT50UG5vf70Ry2tuvD1GM+snyv/CsTEYHWFM84awy3KtrG8W69ZLVdYa3HGBIGbSeczHD7d4HfbiVE7dWZMvB88eowA+nSd02fclwWhb1Kfnk45PZsegIdhSSdSz74uL55qGfEsgohM8z5h7p6jjPPremZE+lnX7nQhX94y4lg9wxOhehIvCDFC4iskpDUtWSoELZynmrNG3kf5zXC+CoNI4+Fca6cn1N9LYUar+mheGZCEwFhJAUQLwoAEFx1B63RwiA/XTE/TqH73DGtrUGe+y5heA5khPwM6TBvBqvDVK4/XbhSkNtc8uPAma5moXhE2hyWdb/L8TGdNjLq0JuJThRyXQhPjcGKce0j+kNlfI/8+l5nGQVFUotCsZvDV79Pzqk3pN6kuSt56LeZ8vl9WsrpI85h+Dz/T/kjKEDWzXtVxjiAiPfPeg/H4jzu2VviDu8HofdgzHdhDmSMPuLvBMKPsDsL+YAKjeqmY+M9Ff6cslStzybu3b7lYrvjbt2uW6nEiqE2a2nW7UtwY36usJzgTg0hlCVFoe5KZbn0dQmBq9gjgRLCWBZY/JV36USDivccJSBfiWwRXPRKEAWGySFiWB8Rn7/29sSfFc5DSrnS4VbIkkMqkG0EkaBclet6IxsBl4VgwB6AT/ELYveu42BkuXcOHzUc+7G/ZdB5pLX+3/JoVbV5LdSucF7Y7w4Yd7+XPoSL1yB4Wm4BSCOAbx3//m+94+0Z59Ra+Wb/jqrlkrZb2JjZQwXcteA3CGwS8YjXRDZHAEynufnTgs1eA1qPLQzn+TQwYLVEQsRKwDeTRicRe/jOxm8nFklQVVJ1PTAMN0+7jOvHqw32gFM1MkV6ezFypC6wZLxpWo4oPzfBpAUhZih48PmYLlntibK4nr+XoKirFl8BHvTxVUmyltBRzE6rWlTOh7oHGloZc+QwjrPsifEnjGda2kXhfisb2OhAbRlpLwNYk1CuRRzv83rH54QcOuqVdvqP1jt3rN/hW0PYdjW5o5DazAVSHoqFyTn5OHOinZ7C+wEPhL8ma4aFwqu9TLjy/RN2ffQ/17tNR5Y8vs8o6N3Y6k37YtHPW5Q+dct0V67TvGmFtosBXoeEThgXIZVSK6DNeEvO5L1CoIOJYkhM/EPocqNLlGe7PMUsJjpyt+S4dWkcwFdBZ8v9PWmU9YUTdjvR9pq2zlU7j3z8JJIWcej338JYahk+Gv2WwdI7t+we1chKm5mLIsMyCPEyZp7Reegy8Qr/XwrkiTKsD6SambcCOjEjeb1DmtRw9xfpUY9+Di+qQ16czQCRSSIIedqjr2H76M932js2f/0i3vcd92qD7DtsuaCy8/m7J+qtXfPsf/hcuvvmOV6++5mK14Eo/cvB7/nnvuSeglkakIIGzo5mHYX7QNQggvm3gwo69PKmCU2XvPPv9FnY3iOvwBFdDnkCnyEhbbDyjOvX6FPQOPmpUfHwYjH4Xura/yROOOnpx4vegA1NWXL3skbaNghvJv6OlQ8TBe3+RHgvEQsD3szCCE/VVP6eGVyEK5yZOuYpc6acvCaw1tG3Dqm1o12vk6pLtxQUr29AkIpUU0zCVUU/K3FlUVytTDyfhiIzlkWmPVPjQa/Rpl1QpoNpGdRN0mG645/OXav/NtunErTrs+wQy9CgLlwg/O4uIY/zezwXPRtCM7/GJl8/boS9hjj0fNK9OVF3UwSV6uNASMtkrIx1ShSHZK1PLaXiqX2Omc9it4gOikt4ljc78lzRqSZYPEXEwAxPD+VGpW1E9fSIBOKhSy2k+StND1LVcLUNd12PtaNsupxzBkLE9U8Z0+cLHbcvOjYM4D/N63/V+p88pC4OJEghaVTrKX5fZXycxTfVvKu8x64bwu1hfnEo/FJQMx2DOaqLgJ8Pnwbv+udYQOc7IXUBkbhFqy5HeOBwUPs31Q/EG9DIsQ6PCYRe09ZbNkqvmkm++/oZXV5esD3ew2YKCNzEoeOpDHJOamAAIPNs+0ikmxIaIx0r/yhwyEUiIj884ZN4XIj2cNqSPhqxxDfmAdSPRYkmz5VSy7ErrDYyPmuh+GtnKNQwImv5EST47U7pkQWHyAojBjhVEBUPDbmk4rIWv/9yxPgj/1m340W+53gVBxq//5i2mWaKurE8So3kvbD8Yrl3Hb90nEI9FaYywbCytFRaNZXmx4N9dfsO77/ZcfXvgYrOmuVvRbAxmbyIy7XGuoUbYbY6BkBgLJo9DMUuuhgDAdujVLgRjxhDcGxm8scGFlQgiIVYGlKDMZEFyITzT+EsezP76SAOuaKDoqnWiSiZow7WV7qFSfG1fEaYwCqMkJYw6cyIkQUwSGgLBLVcUrhktWkQh/4DCims/LdwYUQNfHLnFfZjGsuqvljWXcVnN3c8pvQ/nQwhEl8azENkhgyEJGMRYUB9TWJz3iHokCVjiOIg6/MGzv7/H6oHV+s8srOWwv8VzQde8YS1Co/fkGBjVOH0umMOZXoQRv0w4hb//HOf0Odt0Kqj1gyx7P1NbHgJT+zK+Idwgc+2fpZYfDSNXO6dzTLRA4t1b3n3olN/vw1sDvDLCOnkXxNNyg8fSyTrfeb1yK5IqM2FzjZIRR5U0Xg9kE1QIVrh6CoaTGb5aPlWSFYgS4kTEuVKdPW/T0OSnQxpnkqwYIHCj13Nne6zi2ARmPP1IwrnH6f49Y2/JoDGPXaWlmGIVEcobChAKnlDaO11rD69mvKPorbPpYUpTVAQgD+vh3DotQXQjFle5JRKCVekIN6Pc63lJVcKIqRqzQobEEnp7Iezl4BI0YEteA/5liG6gBTS6FhUJOJXb7vG7LdtPP7C/u2bz459wmx3uZot4aC4uWawNX/3373j1/Xd8/Q//gdXrd1xeveNicWBtPrBR5XeHoJMippp3Gffh1FgOoRH4TQMLm9A3LfokGrxM7L2n63aY/S0m47WhEvWKN2fUNrevz06bzpxzOndkD+vU+0LDlPfH7poJQqY+P4YHWxRCJEEAPgob0u9kAZGsa1SJkdkm2hLLn9iAvaGRwQuq/VgTNfQz1GVkqlaCNUTbNOhiwXK9hos1dxdrrqyyED/af4XYOGdtPB13qKs98nNU7eyx/ZQmPbk7g8mb+KmjdMfrPX4Pzl66pdLJpE+ft5+dIOIFfvmQ3DVl5pkUFLakARJjr597sEnmb67EoPWVQrUVG4QQph/zIOAPRehgoguIFKAqBSlNmqgF55lnWpR2FIJPeDwzIx/49e+qD0MYjsykBpTG3HocHTzvKBmWcQQhUOHNhaPzm7opTM9lrcHTZ9qHfCfGc+Sgf9BKFe72Kzq1o/HQGNR4KPApdQ7GL82HQnb+U89R7334XltVoKnsqrwkCFDt/c7ftWpjLsejSXe46lM9CvXzfrB4LTh2qntgtZHGYEoY4UQDwu01hAHoOtQ5ls2SprF89TcLVmuP/vMBf+hyu3wuT3ttHeJX44fBlZr4NOb5cXAJJ5KRPB3l7UPS7E5+6XtCCYna9hKYs3Qe9ICxgaCoiReRSHxnIU7Zr4W+CedNChjsKRY+gTeRAiNH9C2fPRGZy/tKB10KptHqhU9vlbuFZ7nZ8a3vWNwvOXQtf9pf88lt2O22uBjg2xrDarkEDIfLFrPY8z98c4kRxeCxAq0F65XG+xgrw7A0C+zW0LoVtm0wVrBicHSgElzs+bJGnHeBu2JsEBGk9e4iPmoMNB4u9tH23UCjIcifCIqNB7YB06DGkgMxVxZsGse4Wg55/guzpL8e5tCs7Goi7U8J+YO1TjmRVeM81Rz9+rxNdwCe4mZISfFOSjmKOhesLxBEDcZaikOk6mA1tmi+ebLQrHf4msLKn70vgWRvkzSWVAPrPxHTgV4IgpEydMEyJXQ3JvQeY+JZIi7ORblLk3l8EPZ0eO653fwT7uY9zc2OxeIbLt0/YJcti9WvQO/B3xAcVx0XRtTMrRd4gRf4a4ExHfEweBxeXuoellPTM4ExN0xefGYH+KFTPjnl2pW2eOAPh/D8+zZYRkDAbUSEZmH57u/fsLvb88O/3eC65Buyz3DOp7/2LUBVpRcmqrT5Ab0fMnPnU2bBRa7kLHoo3tfpe8SR8nQ/ZeqeCGOqJ97Qs/TMFAThTG8oEkP8AaUcrSHNkYzQxbPrkOr/4dPxs/mYGn0l9nnh4aimY/S2JMxPcuaAhk2Mo1Q9ifvBQ8TXmV78UeEnu2cedijjc4m/IXlsjRGMgDHB/aiP9Fm3vUMPe3Y//pnu/pbNH/7I4X6Dv9uD8yxXa4wV1t8uWL65YPUP/572q6+Rq3ewuMQ6T6OehYVWwLji6rqPYz7kTCxpW4FfN8rKBGFEHIjwf6L9vOC8sPew9xHH1zCeiEd8wMuN16wgNMXDOY83UtOF5+6KI+mmFv6w3LyP56mDUT0TvNn8INPQtWCh8l6gwQ2p5rRaCSWS4KFyy1QTqhNNmYXRkpjLVGiqamv1coXlb8AYTNuwXC25XLYs2ga1FmN80FWKZ1B3fYPf7/Guo7qZphr1IHjsOXky3098xzwUHtbU2cX6s4GfvSBiUmj3C4EaT5HBIf/oMium908Ns9K1KHiQqBkTW1z9T352Xj9qpn/JrRHJTgdcYLIGJpmvgjsHF0zk70jlfinFjMjBPvOR/OAzM1tXPEIQ0ROg99/k97meKRxKC8I8tIioijkKp6ZihEQUTHMys9UO6EbJB4VM1lELJuZhivFW/45IEYLaBQe/zIiAVilHhIae+zsh4uelP24pkT7n0/aeZ2Ko//xYnUAODJ7c48xZYszVHQQRHieKdh51GuI/qLJoF7SN5eKtp2m3OL/HHbpgtkwUIcwv9Lr1vV9GwKtgJOz3+kTJSnl1tmN4qSSkSyn+iSsfyXEZe9UQUBuPVRu8AkF25ZYQTSEw4r1GDaJE8QvZkqKnwVURoxLbY6IQtE9skQmtLJiqR0hBRbl/Lcgry5s/eS73Dq+Ww2HJBs+923G7vcc5j0ODkGjVYhuhXXtWl/DqbxqM+KjRBY1R6Bxus8cYE+Jl3K1p7tZYa2kaG03XA1fce5+Z/hrNiL0qeInaYGGcQmd86ZRx6HoXIlVH6weRJjCijQUEFYsXixqLr8ZpjFhVDKH8XxrkAfHfS11reSacXyFpxmsSB8QCUjwT77NAq+cct3cGmvjbEExmKuGJxpgR6sPaFheD/tUd0EJk53VHrj+5BZCJutOdWIQZWvwaEwnI+NxHJkGKCuGl+DVOzCDFlLsSDfE4TNx4JDcH1RyETqWbC9Sh4tnJB/A77g5LnB5o5Gta8xX+8lucE4Q7wJ+FE9Tn1HPiQn8pAX//kuGh8/1LmdPnxumf0u/H0hmPsU55mOu1ec3+MbNzKuV5YzGfquZYRDpnIA3Ib2WYD66d8rv9uPT3TrFeeBcDxeYCFGxjePf9JZvblve/v83R5ZSEc4z7Ge6ZysllEq4P2jY1momZXbc75KmCaaerL34WXDg2W6cY7xwdfk2kU0LsMl728PWb2vrUPZ/qHtIjDym1trTrTVWcu+c5l/prsWb6qlT48tGqpibo+F5M8w7V3GWLg/J8ftdO8wCOnQE19pfJ7YGyY09RMDduvkcKAU9DEBPL0anU2cFoWviBf2DAWAGxqFjUHVDn6XZ3uO0d249/5nBzy/bHD7jNDvFBeLG4WtCsLBe/vmT1zVcsf/O3NK/fwvoV0iwQ77HqaWywPhcT954PbdUpCePkaE2DFfi2FVYm4PN5LLLb37CXvcLeQxfpN5fwy2QNpZq2LAPHq6AVisyxvTPzZi7D6PmQtpyoraLd+0TjCegVNdcLrT7id6/V80hTDIULBLopPyu+mHvF9gnciojsrdPy/OjKyHUXWhMZ79JylwXlXTGGZrHALhesFi2msXgbab24LfCKu7un22xOLb9c9jlQTrHPAfqAoucxkEfBkJw9kkjreX9wlSXTvGXE6fN+orgnw89eEPGLhlN3xF8ITPHes1aGPuTyOWNlR65j0t7ODNn4KRhUIhOwZluZgAxJZBIms8ocvDodwpKQxcdNXMha+nHuHs2CkekS+7TPHEyttzhW+ZPeqAwy1+3pv89awpOpZ9o1xAHOJQKnEIwRpAqHkYKn075Zb/F6yO/T2tS0TmoG/EQjRoz+Y/VN9buah1HyEZHjey8zPlILFRIenHGT4QSUwEZJ80JTOoWC+MDBGW53qyi86/c1W29oee7wuOSSyismEhqrxRIjoP/2L3T3t+gmMupHOJNMr5f6IFEIsV1MGbJ0qGhBGhLNKklAUQtO6sFNTOW4hk3UalfjI9O0+ItNeJ2iUVHFZdc1QdgYE0j5MAkJr1wtpXozMznmS5ojydLCTmhgZQI4z11fSzxYaJDPrWW35GLXcLlcwIWwW96h4vnqnUO90qnHWsfV5ZbGhgDYtlUWKWaOBk108S60ZdlgJAbeawRjJfLh0xlSfUZNHsWTzdOUoDGfUhrFXW1D35sGbRRjWzBEbXsTiThTfmODUCIHru6PUBkMBuupXkPpWEx7MC6JKg4LRIsgjRYQPq0XjXdJnDyX5tZUriiKxmuyaKnnSFGiHX05cwhrW70LsYwIgiyb5jXmC4ymtM5SPUEg46isJACf90ay0kp3XTozwutiWFHHoQmXnkp1P0IW+qV85VgIiz0LT8MOwKvke0wwUWMOxJb7sNvv+Pi737NY3tG99aj+LW+u3tCxoLPf0+gnWr3hIfBiIfEC58DQ9dbLmnmBDKfw13i/JxwmnZMJv0k0BhT3rzX82CkfvHJbvOyNwKvy2z38aJS/aYWlcSzlPU5bdryt6JRp5vwsdp1xkGgdcWTZj0mI84jYWpEjW2RoFCTUzNJBx7MSA8VqI+G32W1lxJ0fqeN1FoTrM/ZCJeLWz1dZCqp9ZJaeERK+Wc3BTL1FeFQCPUvUWpjv/lxZVTDVarLm+AN1W08tMan6FJqQFDuGQjOtUleViWC8Dxa3o46leQ990+ozKSkiyYtCxPmMCYzZpGhkAKNot4fO0d1e023vuf/xz+zvbti//4Df7LCdpzEtZrXCNsL6raO5tJhf/xp9947u4jXt4hLTLFgs4M3lNYfG8V+cY4OgajCqVVw5zX14PJzIq0HlyongosJmwA1LG3xN5OWnNYH6sCpnafqpRXnOluo1ZSrD8Nk5hWr/rxAXlA2UiJDkKtj302Whw5G8vc2o+R4Kv/IBOeroeIinKKiYNp616aQenhdiDE1jOQC33vNV27JqW7CWg7EYE0RT+0+36G6P2x/OGL/pVr7AuSBMb7Hz75iH36lH9vQT4FkEES/4/GnI5/TJsXrcxfJlYkVMPx/wqPsH/mDd6uBbv7cD5tKgLK2+1e5sin47mTgoCE4MYF0xP4tAQrLWsum9T/09MgeT/R0+P6G9NULOZDztU8tBqgf1fE/5aIzIZUIyR/XBzLtSx5DRM0manCLkGF9u/axyNM0sZDWq47A2B5ByOZZ9UvzvztU9Jxg5d68NBQ0F5gat2iU6XZfmvXW8DXnPVAz5+lNVOXiDt2u8mupVvw2lfsFpEESkMizB3cuiXWBF+PTPO7rrHcaG+ApaVdvTypscgzIXSiFCe5uzt15NPGJcL99wBHSwkRLRlDX6BnsgaZTlfy54pBEx0cJDq20oFd1c1x7LrMYu5QkaJMG6wGYGdmJWh0aVcy0GBE77MBGYUQhhgMa1NAeLXTTBV+t6h7ddxlE77zDGslhvsSYws40xGNdgkklw/DMiNDE2hjExvoeB4PfZk/ZMNnOPAqkgtUk9VdJJqwhqHLrcoa1gWkAMKsEFUxAGRgFE9SkmuWgK66aM4uCeOHJspvblHNFNlSaBiY/jnjSQvGZrmFC2BiuBxFzSGIw6jXy830Z3RWxzWgNFTliIjbyvNI6oF0QsUcZEEoRILj8SvUlb1OiozmKZUAveYjyYVLMG776J/glXUbmreitYB0Heq8qC4CnvBFIyI9FXcpocE9xSCR7fdWyub/GXnubyd6y2K9TtcXaBMxcYt0P1podPnIPbPEYY8UvRlH+Bh8GxmAnDd38NwohzLA6eugceM45zczHpluUIDPv1bPt5iOOns37A2J3GY6piBO5U+VMn+Xf+MlCA+eiUWy9818AKxeodQstB3kTN66Ac4PwEPjjDetLqvURiLdFsRTlJeoTcMXo14DppFOJnRQPWVuoVglXG7RxeRrw7M49tJk9xR9SnVR60BgZlS0TmHmOJMWwbDC0yT3f+8UfSQzPGMc5TL71XAS0etnWGhqtpUhJ9UuPTk5M3aM3x9g/bl/Zi3bK8F+u6E/4nZf2PQPvl9MpMwohskRtwY2tNwa+MxxlBXQeHLf7umsPtNdv3P7C9ucFd38GhY2UWWNPQLJeY1rB6tce+WeLfvkNfvcEvVvh2gZiGtulYLjbsjfJHb3OLhHIGza2kU2M5nb6szf4YBBzeIdEGvFZyK5/FiWmPI/N4GFYy9a6X6Ak1jtHbE4mHqyT+JcGBr38TaTotCDg18l2XV/2e3HuaZ2rY3sneD9f63FhOWNbU9Gagew1OwFiLbRoW1uKMwRlDor/9ZoO738ywJZ6Ge51zbZxTRg2ny/sc+OFMK6YIsFHOwRwNi5t+MFN/wpsmttNRGF6Y5+Q5Di8WES/w/JDx0IiIwckFPo1Gl3fpSxY+1H+DuvNBHZlBmScUEZTwO6RK/tvTmZhdLs4wZuoujho8YIiNlNSnGlo/GT8qD05t9rlgQHJOAacKH15QD8wO/b4fS6+FOBq3YorQGiAFR9tW0pY+mFzuuFYt+MKxBp8agOEajfnO0jjKeYeEJw+6mesWJOZnytyo8F3bjfapVv8psO9WbN0670HnXWDYRtrSd3/ksLsG6bIQorRx4tKrl+YMHuk1uA1KWvHFz34a+cgYz4TrmICsUWxNAcMiIW1Eossoich0FRNAIATtDRrzLrm18mEtignahaa3cac0DlPfk/u3QMBYE13EZTlE0ApMLOM0T5rKTQMIPQFqIIqEtjGI89gdLDaXyIIcC8dFxnqrC8QE93ViSqwcNAQ+V+8xorFNgYEuXVGRCzISH2I8q48Id+y5acBrdtvjX22RBrBNCDi9XICxmGYRDztbzVToj2JQTPRHWs5rVOP5OEasy3leP4/MESUw070LcgbfRSUkV63L1LfyqerzgZyDlWeXfoYUG0NU0BicGz+4F+JcYzzGZ1Qd77ogGFCXE3rnQRQRH4llIuEsUYsvbQGTBV5B2zGtkcFZlQkg4lryIaCgc2mpkaxtMvno0/oPxLvXFNfFR9dQiZDqC67wyWoi1uk7vPchNolqFERE5pAP7rx29xu6P/wRuVxxd/Un7PoV9vINna5R+RUNtzTc8QIv8AIv8DwwycKZSTnG2dLZPlYKqe6pXIdUmR4PKd6eiLBYWX7zP37F9m7Pn//5OtwZxyALHTS5v0dNOPcDg/+4dcTJtiEUH01pXCIeJrn63md4Hd02hUy5nKRBnYQiKuF57WZoODaPEjwMelFjWENLiCxuye0vbS7Cnz4zv9+W52CfPRT6tMVxgUpp/7iUqf4cK6ci/XssaZhbaFL9DxN4XD9h+VG7xISMHyoT+WsBhEix2q3LE8WIjd9NpAWSAKLJjNiE7xsRrAQ80ntHt9ux3285fPxId3PN7v17Dne3HO7uYX9gaZrgzma1prEGVjt0Adurt8jlJc3VFebigsZaFsawbg2+Ef5JGvaqVKovpLhzHmKA7qeADP5CzyHRS4AKXoVODC72O5x3JVh1iDGmUUA5v+LPWYszGRkguP2XeY0mHLVOU6VNykGD7KPKMlqsgzR9vLr2LJBfZCFEivkARRBR/yX6qeDRIX0dH8JXdZ17jlQCX5hYH6fL6dFlgG0s7XKBtC3r1ZrL1Yr1YoFZe/brPXJ3zX63we/2FW8iHZr9tj0OnniRnizhOc7px5bx+LpHOU8/GLwb7Mmzm/K899qTBBGjO+MvRLsoa9jkJ4/tV0EIisZG+v3Y1h2HL63lN1tNH/OcGMIKcYmFJMSnX26pICqvxnO+0uhMJUnm31TfC8JSu1Wpzaezc42hUCK1eaKPvfkbIklTj4ESjG1uRU0NZr9Nx9OeC09EXR6Tfe6sGBJ1UuvmDouYu1Jl+GBcd3ouxfdleFUsIkZl69S6na7q2JBMz5RGn/pz6RMyc2SlPGAeRudBxqeCS5g2xvI4dm7cG8V1i5y56wISDkFgsL+/4XD3AdSV+Ah1ZROQNOb75qV9SEHmZDjPkj76GfN0p/nrvR5cugRRlDdERDCmEcnnRThn4lkeCRoRxXjJvvuFajoknShKZhJDZiSHoYlubCQGwgb6Lrlinb22VmeLhpWb/qwRbOyDKrTdAoPF2iDAcS5wIqxvAjEVA0CnmDaqFsWH+AeGwBBPhyiEfaOhjR4TQwprmLfqvA1UigHrYeXQVqBVgvClBbFgGlJcCOI8aSxAax+81Zleep8phHoKByB9wiDi9N57vAvM8bRuU3C4fA+pxnHQ6I83CRogC71SkMB8vVUsibTepEoqySIiCA98cmWlfYLYe4lyi7SuKrdkSUuqJ0hPdZW9o1VaqdvnQ70+vjN5TYcyDeDFBKGfpnYWIah6KW1IAfW8z30P2SR9obbAyJMY03rv8YcDnVM2/pr7mw8sjbBeX4aYIFxh2aPc9+b3c+E2PWu/hPt9YTzqBR4P52rW/TVYP/xU8JiYEnN5nmrZNOlW9MEwdO+SC5tqQP93RfNpZCJqnXSOhq/oDxXBqWJjBhGhaS2vv1nTtIYf//UG78c4dBAuFLcyQVgdystXRfwyh2f3b9gjINKLEZGZ9McEBDVdWHwxnVPboJhh3IX+GpheC+kdZc5qGnVUSewWtTBCqv6lpoeEDxWMPP/NUvo3YviOpqEer/EYhTT01lF8erIV9dCe1swfuzGby9IrqyYF4nyGZZD6M7jTRTgaqDpxASTuISL9kt2GpjhmQa/CSMDOnHeo6+i2G7rNHfvrj+w/fmD/8RPd3V0ILO89zXJNaxuWbUvTGtxyi1sKu+USFmvMYgmLFmuExgjGeLyBD2qyckg9vjKzZCe6dXRo65GaJJXieaEenGpUYElumaTg/0RhRNgpFQ3LsNQnwrCs2jVzauyR5A8pX4cFaT+J1o/TwVrhyFkZSPvfqX5TuWYaNbzaizOtnaWw03l/upfjd4OMSWHNWEvbNKzalkUT4gU2jYLZ0+03uLv7yb1VKGStH5wJz4OznTd+83Wd04pxGcNRlslfJd/j9smoxqMP+m2brHGQfyRU7iV8nr39YhFxBM5GyP5KYUpYECAh1AVhG0O9iAsC3i83vEtWD+qjmxRfb6I+U2qol9R7LlFDOGoUSJTq1z0oFhFVC55tEQwLOmcTV+4EZm8dSocfiJw8rmtPG5A+QlkhjCTtp8nXk5DC4Z4D0+brx9xnHa88M6Y57Xd38mHUOu+nSmu7RqiGVER4pIOH09dNH3kauigaphvRT5WQ8MI4VotP7NwlO3eBweG8Y7EIvv63/9Lh3h9g3w/i3cfBKpc0RKQ6Lt7MulSpiLzUV81jkmcx0bH5JCgYegniKNm9DSTBcFU/hDgAgDeC8RVjNbUFolZ3RMSjEDQEZSb6ig3B5wShkaDFbhIDO6oj2or5L0CykNAUxLk3HzUky4l4tim8/XDg6s6HOsVwZRraVzafaRJDK5goeIucZ0S7ME4pbrSUoI4amfA0B7jcBtdNtsQ3UO+LS6M8n6CYwISOh6cYGwQSixViTRXnIZi30yzCvFBESIFIDBMa6cZwXqdUIoxZJ3HfZe6O5LkpKUK53geh2aHbh3vEdz2SKZNXqagoNIqDlEsLgkxDIlez1hIGTcKbsChDth6h5vHe4dwhzHm0ugiMp/BbTIMaxahFRNMGCevOk6nQMl4UAUqQtuTJCQSkxxMEMKjH+y6vr3CXeiSv/SB0SW3rk0LE9RN2KnFMgwVMdLEVNaDUB4sPn111pQ4oGoN3e/V4d+Bm/yP/+z//3/n67d/zD/b/illcIIs1e7mikxULuabhnlPwwmR+gRd4gc8OEs8yiWfOiIGU0oWP9074k1N2c7hkD9EJ4BT+aaesDPy7VlmYlDQybdMdQN9uY4jfpl8KwSVhup/zBUsv79A9E4x+9oUbve4+0pWRxNwKSaqhc0op1dgngUdq4/mEz0NiTUTEUUv/MnN+8LuUfaYQQodfng/6tEP9fAznWnCcduf2SEryUULIub2UPgbv0zqhv/Zr4UpcUgHftwFfDfi6wdom8g6I+KLDdR37w47t5p772xsOH36g+/Ajh5sN3d02uHFVy/piiW0NK9PSGuFSbrHi+bM37LTl7nKNXK1ZLxYsFkveXa5ZXlju159wJi53tdjYAyEok3g0uzR9Oi+wjFhyu6QUOsc5j++2vN3fgNtxV+/0iJ+mRowpmRrSuqwPlQesm1P9HL2fopt1YonrRPpzKksi5qpfKZhayu7r98XSIbuCjTRxIZIrAcbcXjzRstl02vuIR2+kV/KdEo/ZqhAjBm8NslzRrpdcrVdcfLOGdw373R3dzQ7d7adYK7mgSLk+fak+Evo3488LyjDFb9PTfnZZCapr6Yy6P1uCs+B5BBEzl8e8JGWc5vmht90Gz/otOI0MfAZkIW1Qmf49X2f/Ej0+esfaXfV7WEh9CtXvHz0Mc60siOE47RDBjs+0/6TOlTSLEy+pfI+EQ3xg6FtE9FfhZzoqR1pTw6NRJ5OV/Ok/PT7pZ2yn2Soeysypp2qouT8q6nTZiRAaNSP3fSbfmc0OSNZAu+TEIX0MtFf5kfbNPqzdf/UPdGWeyBWREHR2tAnGNclgj5ed0xfg9Jia5WFGMsNXBe1wCp02Ufs9MNytBd069N6RrJBK83VQV2xB8u5iKp/FmSCFYPrrS0N6ZVXPakI5/l+fEGXrBMIy+DD2+W14FVHwpOXXJ+Nz9oLMaVHGMT4Gew76/GrKXiplV8LPpOU4OSoTIBQBhgfxntXWc3nnomWDp31jaJYWERvx7aLpD1G3XtL8BmZw0mBXFC/RZY961DpYHsAYTGMLbuxdeJ8FSZEQkijsiRpkam35LhBNLECa4HIpBf1LGK8COe5CRRz2tlYRQ+RxS1hzNYQpRkIixvP+8oHp7qM7Mc0M+eSqq8xCIDhTW6Y+6znrX+C14L0IKnMjIDHoI1EZmhnHEQ/e4aMAxJh0JoIazdqWY00tKPFMQp2ioT6f5ssX11tpLQfLEB+HN8xHiB0RXVNRpoeq3OzELLpesghoCbCdhVq+nrck9kmCvlB353fcH96zvn/NYXtDYwy2XeGlRVng9W7khWFOM/KpMOf+Y+7dc8MvQZgyNw7P2fYvUccLvMBjoQQeZpIOz3e/CDuFj46ixVynS3jK4IUHrr2yU3BtYg6FMznjAbNbIeA3kq0NyHUkzfCiYKEVhgBJm7x/Cw++aOp/hV8Nr6SZ8SqWGmRm/nHuwHisRsMthWbQibY9BXJdmeyq8MqEVE4wNoexIWbHp1LyeSwMlQH1EWVOjVme/ymytZdvWBhlvM49rof7Qo68jG2ou92noeaLT3OZ5FxjXCokSAooIslFaHSpGi1lVR1dd6Dbbdnd37G5+UT36SPu44+4e4ffOaRZYJuGpm1pFg2tEVqg5YDQ0cmaHcJ+0WCXbUhrLcuFpW2FGzkEZSZti7JWjzRLe3XiAHok9MYp0TmVgsvS7WmzO9Gq1gFqPNua2RdyKsFMeQNa9SFFHB224YthPdpPMqo7Ys0TeHoRPjBOo+NOJBp/aGMy19IhDHfEZHqpMOo+ORXjBEb6rW1o2wWLpsGuDN1C0NsOv9mcaMV5bZYjv35qGFJ+UzBexcfPo+Ezrb+du62PpOvdXwl6mzY8OKZEcB5/frKCB8EvwiLiaUvy1MA8dCt/Xuhd9FOXfB/jmS3n9NIYoZpHGjVdgdQ/6uT6KN2YUlpE2gOjg8BECQVPNKy4qpD6NJXi+iS5iZHELAOy6cPP5rybO57OefYTQ0I+j7x+UFnnJn0EoitDC4onLNT+/nzovPQrLizWipGan40PAgPMxgV5SPX5PooMwimKKRKzO3fFzr/CSzDLtBYUw93v/jPbDz+gmw3GFI2aGqOtSxWg6YTvftexXwk/fteitkLuIrUqBkRNbJfPhOaUXkUQIigms0kTtRFrNAbBR3cGgRAvrmniKSLBvVFguo8Js1RUeCBZMBFcNXusEgIbezDqMaYJZq0E5oFNsQRMVWj6TPhp1pYh4yPp3BIR3n7cc/npQHsIKEQmrhJRkoIxqyc6GQp1RLmLGINqqVsFfONwV5syOVYxZgVGUGxurxcfmfkatBaTT10bfOgSg0+LtVkorJKCUUsUQqRYC8UyJJzzURMfyed/OteTBUJpIEFaMLzlRKsA2vHuiAScqAPX4febcJ9415t3ouBEkhWLKc+ziyoT0qSFMFII9MHCod5DSYDjfRetMjpUHX2LCBPicliC9Yw/xBVsEWNDm9QHY4faXKRCIMMYZolRjN0ShAVePc51oV3O5YVVCxxAg/m1sWgUYNRdS+dQ7lutxSVRU6/sfFQ1B7Sv96v6sF/SGnSHjq3ecdP+lt9+/H/y9vAfeCf/B2QR/NGqRC27NO0DWi3d556AIzzEQu4FXuAFXuBcGDIaeqz8ITO1okHCg+q79tMdVdQTweC48D+gLNjyhsaUK8BHV0HhSA9nf26tEu/oJCA2MZ5PiFvkI7aU2lorgSTmlA6vWWHAMMucsl4cIVWJOFTC16Tw7GVQTOa9REWhPBwxn6Q7PdyVaBFnT9OxEg1YlbOFEllAU/XZS2lTDw2X3PjiilF6+O489NhNo+dHGjhKOyeEeBroGK95IOR103vWX0jDNZ8xGlPmU0dvIUt1Kk3zWokEY4KVckaoQ1aN6zOg9prLEMBGnDOFmktWxtIESwhvgvVnd9jhdhvc7ScOtzfs3v/I4faW/fUn2HnMXmjtkmZtaJdRELFoMMawMDcIO/7bNlgU/GktdKuGt69f8+r1W769eM3ryxXbqwPb1gS8T8BEi9qA54eYZL1OPYnTEk8GcXgRTFLi0YADOuCgsFXh4A0Oi8Oi2EB7JFTLDxdJvcYr+i9PY02QS4+mKn3S8SaZ6+4AJxx9LwcM5VzUflsyXltnqwpW6LuBAtRk96SlzWldVglT57MErT43peTvWUlAcoBViLW6gePBkPppWiKlh/h4tpdpiwpy8fw3nqSFlasTa2gXLQdruBfDq+WCi/WKxjYcjMm03Ri01+xzWBXnHTvnrPlHHFqjFjweHlt76Vk664ZraKai0fYriMbo1pgZvgm1hEfC40o4WxBxlOk3Vud/MnxJ5afjy+98pvo4YOYZdc+l0f4hksvrrayKXXmmUGK2oqoMrd/NlXRsYzwIpi+x8ssXBHFarSRrYEu+WNJvQzJlNhXjauTq6OmdqNo+MzDJgmXu8Jir/0RzPp9F0WRlR2B4Kc4gJyc39gP7c0byo2P0hOHTKYz7IXDEHEN65Y7rKK6HHgc6rHuGkJJICOIFpMGzgoggO+fQbs/h7pb9x2t81+XW6hGiTESwqqx2kRBw8Qo0GgnCuF8kt2DQtBqRHdchIjlodWZ2A8HFUYoRMuVeILc+E/dTJ2DdjLqvyTWN91pcvGkggFLZSTga8E3fK18jQlr+pxqDMEVNp6y3Wtoqgz2Vy3C9myufjRKQZY0EnwrQePzC53aKMT2hQV2IikFNiB8gEi0fUsyH6KInuepJ7daK0R/op/Bbeo3TPOXZsq3qex9FOoL8xpQ+I/0S8fvIjPFdYNL7LrwzJuw1YwgM9VJnb5JlWH+qsQquiRRBSNWkbJVQWZNkawklEN9CtF6KKyxqoQUBWunbyC92plsSMRPuyySU8DEWRdDk86SQ2cFXeBJYxKZaUC8xT9F8ixLBGH+k6l9srqhmC4vwvBZqat5r6YgJ8xF7pR7XHTh0G+52P7C03/L6sA/CrKYJ600sIXSkVsiykGnLLwC/BG38x7bxIQysLzEOfw0xH36Kth+z7nlsXIbngMfEl5iCudgQz9nvSYJNpr7KOMkQ4cjvptuQNKFFwOg2BKaVwCuyC4NX8IdkAQE5dg/0GVEJeZJklVae5YDVWcA9QWb2fs/gTZGhprGM7GqJJLAv91Z/CGcGpa4447qJTVOEBsNyijVCtDA8RYTHjvX5kLGu/DEUFg3anH+mUarb0W9b35Jk4OaqutPnQXvtLb+1/DqL73D+mT+G4eqo3khJoYPUUo31cM1Pk+RVLIKEh6VUeW4KniwyVlFKuKPE0jSt01SnRp0WIk6aeAWSXGZGa1J3wB22uO09u9trDtfX7D5+xN/f4W9vMb5FfEvbBD/6bdPSNE0up8PR4XivcK1wbQw0De8WC5rlklXUND/YoOSzYHg2Vfj61NnyBEyoR1Zli2LJPHGn4JCIgaW5OF7f/NuJvTP8roNkU0fEcKGPGP9T+3PQjnTuJbposo4Z6O33czLUySbS6eBz+GLi+dRaT589unIqUaIqerSNlAxpmo1gGhvokMZi2wZJv3t7cqY/D4L6ljm1huYqespuOJbrKeflY1tQ7uN5XtFEm3sXip56XL2f6X91D4b2PP9Y/CIsIl7gMfBlNs7nAB/9XCfXD1NBfTNrLx6kWQMpnqDFhLlyhVJrJX1ROHcufjrC+pdM1P9UcPQiPif3sTGXE8RC0mB7fO0AWSM6xSsIPkc1BrUtacUmbeSCHd79/r9x/6c/sLu+4bDZFmJIZxChjEQXbfjlQfn17w5sV8Kfv2uClk10E0OMrRBaZaIGjs+4Y1VoJnrTmAYd+so1USaUYx5JuoCRWRp/5fOkcnaqSmYS9zQglRx/otZdcT64PTJdhzeGhQkECUaK0DSVm8dHw7ij+fyrZDFxFgwGg03kl4BdWswyMIq97wIvwni6y1u0Ccz2YFq+AGxAIkUwNrZJLBiLbV6lgQozlDX/yzgHSw0fAjBrEgDHuA9Z0BDqy3nyMPY1QlUDBZh9paaVkeNtRPP4apY1PZndNhWGlddiICS973Bdh3fFGkHEVD6Do03J4A6pBSpZJJOriPdUWoIyFCyFtN51qA9+hX2yxkjlhGUZBDtVLzKlrKWcHIcxLTyCqyVNGoJKlLhFgYtGYaGPayNZYWhc8Vk4EsZJ1CMEi4ksYAFEwlwnl1IFQU4uoAaUowS3TD6V73wQotng6ViMqYQaHnVwd3vPfrdns7pEDt/z5qvvefXmG7r2Db55i9U/YfU2KGwFDkHew4V99MvFeV7gBV7grwBmmADHQIHOaIj1I0J7teTv/pdvuPu459/+8RPqouBXQNTmCsJt5DAEC9ratV/CH4om5PhSVcKdU+OpWS0gX8iJuZ7wL8q9hkFirKGxAOLIEKXEA8b9ePAeMZhHK47joakvBZ+dTJwxyGGb4rcsiBnHlsjMnSyMqJg8s90atqfgOOXX54VES/d/Fxio0ZxRXv9LUTMwuZaCHw/zKimMV5i7oKuvEl3XJuXDJBzzYLwiBJehSeAQ5tqALEDAG1Aczt3hD3u6+xv85p7Dh/ccbu/Y/vAjbneg2+4wYrB2RbNa0LQNF7Zl3TQ0NBgM9+4Tt4ct/5s78APKh87SmYZfr95xdfmar96+4e3bK9brBYtVy876gIMnt5wDdPe55zjZ/KTv1WiTLKqdQIfSecWpRtvXNPDPDeksGTx6CIjOHzaJoKrfZyGEVN/T++HnqbopuHudp6ZZE/EH43b22t7/fDgDuOKRAUOlSZOs1tM5FtdccqdrrYQA64sFdrFgdXmFvrrih6sL3ljDuhCnL/Bzg7z8numOfOardghnCyJ6+/bMtfcYycmT+aGP4c4dqfRYacNc034WpffuyQzfwgecrHsyqNSJIvM5NRq7KSSjfjtsxFTpx8ucS5e1SCcLrQ5YSQyk0p6hEEIE+kKIX8DheaKJX9QS4hGgefV/pnZOFPtTjMmTazyyHY6dFZUC26NhhANJqrogpyGdQbEEM39w/oBqx/7+lv3NDW6/L8zVugMDECgaGJHLbhSWO8VFpeuULjUoxyKIhIZqiG+Qy+uVXuelh3hlbSiJmnI9yjgS5xXSX2uvVc1lrA84xjnDmAXLCIMvDIA+Jtr7iHrsRK4wOlgYif+cSzChYrGCsYJaHxjiVlDxaNOhjQZ1L0P8lECcmSQ8KEIEqSwfisXYwDw+BPSIv2LQ5iTorQURtRXFCAqnYnTfRCFNJhwHeTLem95XQzSrZJQtBAKXPlkkpDggeVry9AysIXrtqEuuiH8tgqPqNs0CBI1BqvEuuM6qCA1JGXVmT2v1lxZBib4efw/Mw7PVhc8BxjVIBjKjICQLQv5M5vh63aW0fTcXkziO6YcoTJYLGrvmtbhMq4c2yaAUjUIaz8bf8OnTH1msLrm4eIPYNWiL0QaPxURLnyyMmJmhv0b4EnEsfg7wojTx08MvYa0NLSE+/7qRwUe8tx5ZrQJ7BauKFY1Xr2Cs4eJySbfzmX2dPzISUz3LsRkSIlMpCOTfEzGYZrsZysk4kkiKM11dYpoVNELykv6UO6rJKknlp99VUOsZKYfE+3zkKrGGiWaU2AFHuC+R3sxChJ7QouA4kPoNOUYGY2FEma85b/CPY23MwTmxNB5DL8+PWIUfDIuTeuX1kLG8vkdchDz3w+ZVe3CAc+dVH+tLyi4IKCbjwE471Hd0+y1+v6W7/YS739B9+kR3d4+7vcM7DwePtJambcqfaTCmAQXvHffS8cl2/KjKj165oUGlgcWaZrVmtViybFtsK8GwWCQrS33JWy6NVE3fFAwz/PP5OxWPU3opGX17JDz39XJkK5/dCB18GdEvzJ9H8Yjoe9OqkftxUSHFeY0ebamJFCNFnUJQ5e8JpQ5knCDGYKylaVoWbYu0LYemoVMPnUN8P+Zm7tbxxpz7cjb1kO5/KozLHb97Lhju7PPm+BGtOGvNH+v5dHmPa/9xeLGIeIGfFahWlhATgpGhBoUg0aVILXhIPshTnvL95w0/9/a9QB8yOdeHLzCNZ5KMRwoIiImf8KkuGcGMTEIu2OlXeDE0jbD59E9cv/9ndu9vONxve0RbYiwebbcQhAJeStBcgulvuOmCVYbkxvjMIA0EiCk4VNbw7pcf3DAlJkSZp9C3JIxIjOQkKOiXIUixDDEhsdGoAV8Tt9KfD/WByOycw6jBxhg31ga/zKYen5oGjePtgwlGfGUqsjYyt0Uwywa7MKgVvAruYoMsPWIaQJDlBdZYxLZgTCB+kBIsOrlPyia2fSZKnk8gCxYi51gSM3/Q70I2TuDio/NXe/1OlE2gH1N7pN+eWHCmMSsytUanajw/uGGqGPLehTUjQTPOxPvCGEO2CsoSOYUkcEHLuqlBx6s9CZRynI4uWGR03QFVh3ddhfsHhorENWNMcHlVVkOY96Bc6WPMlAoN98nKIfYrWjYQg3J7d4hxPTxJEBOaF6058t5NLdc8NWmIvYZxSvdy2htpXnyyWKwESEH4ojEmhI8+iJMGVjVHcXE7r3h34Nr/ge0fr9nuPmC95fXXv2L16i3OvsOZK4z+gNVNZjRoWjzSX10v8AIv8AKfHSpcKf+mXCFz3IBzLAQOCv9l51kZ+PsLWBiPqNCoIJ2y6DyN6xCnlZt2ExGSZBNaINFTPt3hmNx+yThN4piVTugAP6o7MHI3RCXUEIpwosJizmN6SHT5F8U5tdLIwI1K4f8dZ66PhRBntgOigMDn/tWYj1b9KvOa8M26TRriFAT0LjyRql+a8FuyC6FzYNLFk9ZrcLqoY+M1FEJMC/EqnDlbNKS1Vc/R8X7UVjcB3+2vkTAkKcgZvX7W2H0QJBTbkmLbmpZ5WO8hhpmgtkGBLvr5t2xR13F//5Fuu2H7wx/RzQb98wfYH+B+h6piVWjtAnsVmLOrtsU2LdY2OGfYefhRP/C+u+PD3xn2b1r8Xrk8KPd/WuJYs/jNr1h/85a3r77i3dUS99Zz13RYY0OMCoQJ0mxy7J8TwloP31UlxolQDqo4fLSXPaP60ZSfsZbHiPSDi8gwat+J/TSg6fr1TQkL5n5Lxk3zcyVa1A/KSs98/7lQ0hfaaKbJx/qTm5Pi9aVH8Uu0XM/nVSLzADGGpmkwbUOzXmPXa16t17BYcFg0yOY9+w+fgvvYqWE42qjHwpfH8GXi2+PhIQu434bH5RxnHt4RD67lSY2Zh0cJItL++VkoJj2HmsCcavCpbIPf5+Sa084ZIgQnN4BOv87lPGBuhkWV83e6rSXf9Ng/bEZK6sDnSi4b4kFcI7nS/1JbQhSrh77gof+9162Zlg7TTafptadq/5Php9xTowUweD6E+aGpkmj1uK9lfl4lp5P9lNYhIyuhU2fHcIzPwc+mtL2eo89StCSSdnKgfwSVJnyq4ljgWYAoxsBht+Fwc0O336POFY7lFL5WejF3ZIEGk+nFXukaxR29lWKbM1JlCpFCRZSkpmRGQeX/X6L1gybNtBpJzSt1oIFHVkTPU1hfynWntIxnYsgKQeNcTDBrztM/h/vGQq3zNC4wqI2xWBRaRRagK8nDTiuwkCBYMDZoZRmDNG2YZ2miN5tktWADkpp+ZwR66u6pPxUiQT671GViGRTa/XwaJc1x1rysH0uet0S4jotJTxKzPk5Kj9Pe7+F0o4MlSNDEL2KPYUyEIpQI5Xt14ZkPrplUXbFOCB0jMx8IgouwqKLpu0KwPIlMEDVotAYqC8jFfqXPGGg69jUIQ+pA1mGk+taGGutIVhwVERT3m6/u5pS2sB7SGA7v8jQWYY/5quzefOX9p3gOHPSezfYDHz/+nma9ZrG6xFiLiMXTYugCcaW5N2VNvMCj4OdgZTDPFPvp2/bcMPQV/wKfD47FiDi7jPh5rITkbnI+d7w/08cJ3pgqbOv3QnAvE/GlVmC9EA6dsj84VA0+x6ZKl2X/rlPIDP50ZwXG8ZH7HKaFEaP+1zgk+Ypm8Dxce5Gl/4ApqedAqsFLTPvMkI8WBjl2BvVdDf0vNQJX5mZyxkfzFhBCqTpYu2Ga7kFCKAvuMnbtdO6glDYOhRFTcqMhhCZL9TtMmtTCEUqa+ekfYIwZWS5lhsenz7mxM07SMIc2Vv0pYyyxurTgQlBnieVlgUT6z5R0qKIu4GZ0G1y3p7u9pttucNc3+M0W7u6h85jOEVzWNDRNQ9suYjyIJsb49Wwbz07guuv4wXbsFgtYGYxVmhZk2WBZsFyvWK3XLNsFbbPAmbCxbdwwx7faGffFcP5H78dYfg/U4GhwaoO7WPWo6zBaM55n1uoDaNuTcJRXM2zKc1R4tBET7ejf4/N3TEUUThHKiS8y/Ti8G81UXwGrpCv/z68VyeVl66yK+BMBmyznmwbbtDTWIA2oBdk79NCN6N5+K8atOgfOOyemYepUfwg8BRN7bKufYmFwahxyovE1NjF3D7l7nhdeLCJ+pjDgk3z5Aj7LepxuUNaopNKozvhaORmL66XyOwggTPVZhBJ9OLdD56T7HIPzSyZG64t1/uKbH7dfct8/L8whNk8/H2o2Y0GQvCpOLtjxHYrifCBwlQNt09IuWg4/3LH97R30vDEduz516qO3apYb5fvf7rm/Mvz5V020lKhTU3pcdzwFGI6M0kwTJvb0oAwTCfDIA6YOBZw/C/0T/MhqRTAbEJ+ImJlVbcpz76HrHGoUYwTjBZMCRadxyzhqYhqUs+3q04F3P+5p1kuatcVcKvKtoK2CjR3BYNs3GBuEEJJcLhmD2KGGWSB0ihKnqR9XSNF4NrO8wleUYQU9xjNl7YYZipYgVVO0nzEQ8qUpZOuH9E5rh1UTBGtVXmKoC8lKIP7VoxBp0lKJxvkoriyMpHWd4j8MCHdNbgQhBaNOcwqO4KLLhT93CGmjGzNJcTBUEaO98TF4REKQaU/SpCxxO1I9KeaF7w4lILVqjs+Ar4UQmucnCUNGYoQsVIn1eM2Eu1ZupcIyld4857UT++CTMCQKDXwMjJ3j0kTGQfAO5sFb1Hu63ZaP/l+5231gc7jBmpZXX71lebHG8R3OHFjqe4xug390BTnqDuwFXuAFXuDpcNKlzYDuGGp358MxffQYqjNFAkaFxgvqwDhPu9uxsB2v/p3l47Xnn/9lR4fFNQu8GHy8y7M9ZSWA9wZEg/qGyf1RVEzlTkkZXavxz1SNnnSvGJnyhXkcznifPWLOd7gWJij0rCJQqphcBVOQOJA9908TwqdTc/cYl1EPg+dh9EwpcRWhQsYqz2rNuGAlu998FIFR0egUt1SnqJU8ZyUQVnrRa0vCBf2AWZ+DsFeCByMRu4/uR9VoxvMUj99vUOdw9xvcYcv9+9/SbTd0P1yjuwNcbzKDzhiLXKxompbVYklrLKumCYpJCrvuhuv9PX/+O2HzK+F957h2i5B926GLBqzh4usL2vY1v373mu9ev+bdxSWXywbsPuxLkeAy6shwPTe1HFzWCrVmlWPB7eENN3vBO0F3W9r7DyycYsUG0q+3xCYOi2eHIeHw1Mq0/3V0GFcU6uS5UZ0tcW+PqCcfz9ZcVqUQpRrfx9hr+YxOZ+up9k+thHr/9HHiHsO74pFlt8GmbDLbWJaLBQdr2DSG1WrBum1ZXkJ3uUcPIXbIw9v3lwW/jB4KFTMkPenvmp504nPegdPwJEFExT+YeXBGGZm8T4jDmUXMMuieNohZu+Fooocsv5oBVD19LuntdPFPKmr0/MGaakPE+5waa7cuGdtMFdUfPUYd+TMJI6qDtZ999LsnbZ5o5lS6ubTHnp+EB2T8Itr/50zrl4Yj3T6157+kxcTIsmk4t884hs9BNNWMZ0+IBeF8i5oGr4qv3A50u3u67QG33aGHmSkZ3GPH25gQn0ACth0s9spqB51VuoZ8O0wS8xO/tToP52Y9PDeB0avlbMmMdIHaikJj+9JFnQjfpNFXk39TtYb4ziFOgBoT8M4kCanGqL4JGw+NU5Y+GDo0FppW0HWDXBrENtG9kgUMxtgQfKxyuZQORJXAyCh19Fs5fjacs9QvrYcmE4X1ATnKqQnHj3rrWr0Y5ojE9PD8zlAJpecgzUWek/LfoHVahVnQnKnvZiLp2oc+ZkJfE4kSv0dGf4q5UAiP+NwPtchMdXdJvrdKn9PiTU4ukmCjKicx+X0Sdiiox7toAUFol9cUYLoiqibHg9FFl/aDQk/uNAxkX4QTaeQljwe9fKlOn9NJ7m+asfDndI+6Ozb799ze/4nlqxULvwbTRKZDG/u5p7/vHn8mPkUz/Tnwub92zfi/9v5/Kfgpx/nnHlvi5NiM2j8m3HsKU/HLsWLn3vXoEyW469At4g3Gd1gci8azNQ7rHV7AaTxbB3LZcFcVAYNGQUGyjpPIzE4a/oGxPbBnjgKGWSFE3f9030tfOJC17kl4xJGYERWeoVnTvfBL6jv+mABiNNi9d0+8N3Q8/8chWuRq3ZaZMgYEaG+d9LjwfZdQ0rsPjzV9sG7rga3a+1QoTa0wzKN0Ur3w8+qr3hS2b0XlR0FGwixMdtmsibEvAS9Tf0Cdp9vcod2Bw+0dbr/lcH2N227x9xtk7zDOgwQf+WItpmloG0vbtDQC1ga8q1O4a4SPrWF7IbhVUDhaOcW74J7yYINL1OVqyWKxZLVoWbSWplVsG5m6wtFzovS8P5aDBMd+PoDXECwiAh7pwAeXn6LJJWvdjkzIDGAGvzzWBB19OZWw/7vG989euilvjRfrzPOpNujEu0GbkuAhl1f9af0sZTlB3Q+2S5mFczpdLzTJdFw6krJXEWOw1tK0LbZt8AuLWIM1imNwbj/Dtf5TerY4BUdb9lzNzmM4hVMMkpyAnrXLTLGjEzfft59bID+GF4uIAWT/li/wmUGzJYRP2pm+XvwFqQhIBowFEOmvtoh4wF2bavrS0z1Z4U+35l4YAH9doBnxIWgJRUzG64KNfotiwSvee5xzGGNoGsOn3/8Ln/7pv7G7vevTSDN3Vo/BPqT9tDBfM7NXYL1VfvPbPTevgmVE73KWGjmkV2AJ8RcJ7VxBP70QzbhFARP8HMR+JPZ3IsgLwUNG0nJRvr4l6saMB0PxeC8cOocRhzfRLVKukYwMJo2o11vlu1uwa4f5DxZpWmS5xDZrTBMEETneQ811yG0MHUrEZr7VRgR6FUxzNFE9DLdUkX7XggHV/nwq0aNsbI1WJ1yyWMgFp/O9qiMVXXWrT17riAkwTgM5bkLsS3/OossmhBRrJPnWBg1xDaqzMaz1QhAXn9spplFdr2aGvcSYJ9a2GAJhKiaduxLn3YTAcCYIlaS6yHxNCPm4vpPlg+/AK647BMGDc7FtURjhPcV1URmpJBgS7e3SMua19mgc1NKMKGQwhuzOCc3pk3WCT2Oas0WLCK9RVhYYXqbqY9JmdIcdB93xcf9f0et7mqWybi6w6yXGNux5B9LR6p+wuieYB8HATOsFXuAFXuCzwiT+XF2NzwFGBfEd1v8B0QbRJY3rWHQb1m7Pwu9Qia5UBDw2nKTliiUJI8JdrTn4dT63Nd0UKRZCanxyJWiyhULGH8/uQbhzhnKA9HsoSMiFp+cQNbc19yu51wx305TAY64p1bic04OsiCLZIiMFAK/7d6ysWggTxsIPhBGD9HVpZZCO9GcYn+J0v0YuQUR7zx8yRFUpM5kGGMjsxhje3zL7XTAZZw4uRkMcrCCEMAg2Ilohq3cd6joOt59wuy3bP/+BbnvP7scP+N2e7noDHqwGIUa7WmOMZbGwWCMsrMWalqaxIFs67rhbLNmvL/j0zQWHX12wEo8XZR2bm9RAftwd2Hrhon3Lev0VV68vuHzVYt7s2LV7rG2xJnp0eMBoPxUyridVPLxMlxhUFZesThGsCI0R8D0d/9Mwtx97CPvQomBu4R0hOofJZgUEWt5PLfTRMh7QnVpZMcQipO6jVuXn+jSYhdXWEMkiIhLSQWlJY/njVk+ujdntXp1Z9WMz3otZ31AE21ikscEt6nrFm8tL7OsrPl1doq3jwrgXntFn7H6YzpGY4HlKzmtFh28Kj0MTR+W56j0NZwsiphqVWCizlhHHYLCQ5ywjYg1nt+k5YOT3fbjqZsw26mP8rwHmtU56qYYPGDG7auZhLqLkKUypKSHE0DKC0bzMrcdzz9Kj6R5xID8N1Zhb88e1rk6X+YjMMvoykWR46R1rw9FKHg19va7nhieW2se8xq+PaHg9j3KhEvyBtniWBCeQKTBtQIbc/p79zT27608c7u/xXXe0uLOeQSAiVAm+jBIxDMbD8gCr+4CwKZ6uEbo2IchKkRjU5fXrOjo+PW20iIzFcyjLL9K5o1rxvAUj4I1ivOAZEqTDegoNqT6Zs/pcDkSmrAt9FgvSGpYoi2WDXDSYCwvNCpomBFU2UUMrE1kS3PL0ule7X2J646n2+0x//HrjeWQO81j1L20yBpzHMpIXlUalVIOd8InxMR4J7XEHcj/OgbB6qsgISonboSlWhu8JK4oGZz1ASaOzrKEkN6hWVIhqXq2jLHC3KZin5P0tJgnUgyCC6l7r9Vj6X3KMFEnuFBLhY+L+HbEVYr6AavpKM7YIkmKa/haZ45lMQHKNlfJJHvAQmB6MBvdQ2XWDkhlOQSM3BNje7++5u3nP/cU1h1db7HKBWAMS3Dj1+vbIa+wFflnwXETwT6md/1dPyPPlx+Bz19cv/ul1jXjygEhkAhlQK2CEpjVcXTUYb9l5JSlsBOaYhN8RCck2dko+zLV+p5EJIsVicBQ/4kwhRFYuSPdKxJ8k4QIxRteUMGLKpdIUvy3kjaybKl+JE9HHoUu8qQoxyVYZ1WhPMvfmOH5zzwft7/WrWEb0YmBpv7+5RdUEFEzkeJ0PgWQVM+xVqOc49NbpZOKCY9f1zSSbzd//nXCuhDdJCUaNKS7H1KGuw3tPt9vguz3760+47Yb9zQ1+u8Fv7vF7h/UmxGCxFts0LNcXWGtZtBaDBJ/5onij7Bu4XRm2rcEvDfoK2nVci74g1AkFvBShUYN2Cy5WK1Zty9I2YR+bwsuox/NBM/jA48YAFwZWIlmNqaxiifyYEjdsKHQTKrqIUQF9GM513HY5efmvfOpM3lMwm/4Bz3XQhlGbhvk1f0Cxii7PddzHnKayWB7W28vzmEUR82uhBcenSB+SIpwidAZWjWXRNJjW0C08+A7d7lB3hAdw/DicyTDq6aPgoXkr0mTy+bNWBsfH5dwDd6K4cdYjhSTafEQTDpN9OWHEAywiTl/A9aX/fFAM/sdPX+CXAf258tFVRQqYGZhoWu2q6riMjLZaCGGMENyRJIRkQhjxOWGmkp/Wkuap++H5237+eMy1/cE32gn4yyH+p0/FB0B1AztatnyPig1Ii3qcOyAiWCvc/PH3fPjH/0y33XPYbPtnr0Si4oxpKpelVE2P7gJITNtQ1nrj+fW/HSLz0nP9VcOP37QU4tHH5BXBmojJoZ9ZatxOc9pCjGY6PRLk6UEsRTUYTohmItZoDCDsEyFbl52GONk8hDJdYpymxsTzyxjD6t7x/R87mkto/juDXLTY1mLaFaZdILYFaUIbiLErcmEKErTNIzs6+1XWTGbE1lXc5HrKJvH3/jSPoUcxBUKwZlwHlUsfe1/GuUbUQ0DJQqiaquxgSTBs6ZmgGhWNQj1iJMa2IGol+TCWyVWWiYyXAVWWEXiB4FIpclZEsJqWbFiLJgb+NjZaBGRcvSIwJf2uRjQ9S+ulJth7X9I9qaiEIOhKCGCdBBLeKHiP0wPiwztVny0jSnVx7SWmC/06VcP0JZwuWRIljVqPZsUqn/JnYVgiqOKmSowgn9xXxTxxHQjpDAl+ymNi8B33nz6xub7jjftX3i3/hsVqzaJdhVUlBIXHRM/9guGFMf0CL/DLgnQW9+Fz7ONgnaAi4UwWg6wapBOcLrhYtvz7ry75wyfH9b/sY0BZH4QQkdEeD9nS7iSA1nSreMBk5YiaeVX65VH6VoKjlubqEhMj3X21UECz8CBlmLNiSAoiyQWgZIvF0J8cz4I+sz98BjoRitVn3+pi6CIp9fMB+MacdD7hllr1o1d3+u3juJgijKj6m4s71qosUDq/2Q+BpGAx1YDhvdW3/OiXMZ2uelaly7hqxpVMZIhH5QoRjBissRgJPAEn4I1FItbr9ju869jH4NPbj+85bO7ZffiI2+7wd/do5zDOYTCs7TvM0mJWQrNc8Orrr2iMZYFFPXQqOLPntrnl9s2C7d+0HFTYq7JYCsuFAbX9HkWro3XToKblsHvDxeoN36wueLVcYo3gTcDnQ59kOHSfBRqBf1gIlwaMDRNcV6uEmGRe4aCKU8389AH2WvqaCjmHFsxLpEqsNWV57mKOtEQhMQbvqs/8M33x4zxTZfTKLrRLltBEqwYlxGTLyaK71Ej09P9y3VU5WeKjE+04DcOhr1SuokC62k9Za6q/V40YFm3LwRh2TcPlasXlcsnqIsaGuL5mf31d2jnViL8GeGw/z9gfn+kYn4Dn5q89Hs4XREzgW5PCgMl+TTCI02EweDG0jOg/fTicczkP29ZT7JzoZ27bjBjt5zG1Pz8YIh5zs5p1YyNmMhRCJA2IhJAUIYSML7dz4BFMgDkm+180P2Gib8V5zecYD/3FDujZjKXBUj1bS/OJh0xG+JNnGpKLn+Q2xdDt7tnffmR3/YFut8d3HTphMjpbB8XL/mxzE3MTKqQoIE6NJs09w2IPF/cFedu3IYbEiBDMVFMqPMGY6CnEzrhJ/QfJlF6q4yUQi0JF/E718+gyEBoP651n1XnaJTRrw2K9hqZB7DK4YLItEt059RD+fhN7lY9iTWbaOxGtPZbxZHOHpLnUqWScLrVD6+9a3f15nipkeyQ0yo66RpX3iZfCTKi/9mGCQM88jMQE8WUNiUIVEDo13PTummQ5IXkYYpjpSERGzTkkeAvKTa0sHGbGjriiep620lBlBkV4oIQwIB4QjU/VIPgoXFF8cv+gQpSXZUK+P7tjEEJcE4njkO87AfGCIQZBl+DdLLkCy4wXiK404lmo0aVHYBHkeUlZNFpLiHp8YsoArutAPLd3P/DHP/8XlldXNItlpPdNNYA/Ldb1Ikh4PJz06z5I9wK/XPjLmcMvd9444JOHjSpWFYvjjTlAA91iCYRxXXYdr94ZtlvF3/uA03lQoyMUqWbiJ0uIxAgMQucqhlJGsSqlEZgnrmeY830mdeVKaJaZTx+niZ9aP4mIjgzv1WwZAXUcsPpd6k/dhnxvZYuEOa3QKu+gj6GNCb8pDR5aBCRhycgygpn0E62YBJn5PgUTbeu9PnIm13nquZkuq+AQR7k5CdcjugbLOEOy+Iw4mQmB2IMuT2DgSmQKe9fhXEe3ucftt+xvgiDi8OkT3W6Lv9/C4YDxgmCxtsFgsIsGYy1tY4KrJGkQI2AcnYeNh33bcX0Bh0tBmxAMu1GwtnIvmpm+kBSbvIQg8U3bslpaXq/h1VLZWxPxogcqUcZ1NUd5T9Eww2G+j6TcpdeM44aXYYY8incOcXtEXYwZmFjuPayf0UbV6svc/k4NiedR79kwzWR2pVgbDBPOrTGdeX1iTU42ZPA9kcYjE5KExFfPlX7bT2mCnQl5lqtq6qlP0zJMJwA28NesNXjbsFgsWLQtrTVBYCbg0MoS+cxmjkiNnx4HGAtGT2U4+2EFwz0Snw22y2koGR6c9ViRwKkYR5NWEaPtfsa5fgIeHyNiaoyrxvy02uHPB1lT9gUeDbUrDpiLCUFGQKYEEH1XTKYngIAvQ+CcLXz4qRbMo1ViHtbev5S9/dcMSYCUXAsVj59hLzVNw92ffuDH//1/o9vt2d/fj8oYr7ZCyNb1DH3Uz+EjOrAfDT5egy/8yzvl4r4jCQF++Nrw6SsLPqHEyRbAZ+S/LixfqAl5l+EqTgd9heH3epk4uVEYooKhnGPBdX/fwF8GnzUYEcQYlnvlb66FdgXN/7SgWS5o11dgLZg29CVqAfZdFNYITZw3E5jSJAFOnzLvIQpa5SswdoLY+10zpNPLAUbac2Ik1ZhoGv8aGQ/PMcm1UCmweKiu3GI9GPuNFixxLFJ5oRkxXoFaghsKH5kZwbrAxDuIJPSObpPCvWNDYyriLRPgSRAhgrH1OEt+n6Q1vX2nVSyI6Ac70W+9/RM1kYwP5gpiotkCKZ5KdH/kLajHeYd6j+s6NBKW4Md3b2/UCMEJpUhSerhnE+9uKXlQxfvAGPLeg9QCnLR+fdlmGvCBbOGhwfIJCUKdFNjauw7nPZ+2/8z+T59o15e07Zr21QWmaQBLsrx5uZZe4AVe4HPDuRagzwUHVf5xF899lFfmwH9cfKSRFZv2W4QQu+Fy5fkf33l++MM9//pfrvHe4VVwCK7yC55l8PFexishjFGNu8T7WkieJAl3S7wjZ87aUyRIlvmLVILocSZJd2SPU1YxNBMzLVluDBj4tfVBvkc1Xb9CielUuYbKuGq816OVabIG7MeJGKsnVqPA6NXwUW6j6VlGzOU5GvciCU4qhPOzLM/MwHz4RXtOjrytlIDXIICNCIMlPTIC1ghGo/Mg78A7tHPgHPvbG3abO7YffmR/d0t3fY3fbdDNHu06LAaDoW3X2LahbdfBinXRYI3homkwtkFoUTpuzA03ovxeobtQzN8pi0ZYLSwBEwx4T0ZuTLAmyDiiwB2ezii/er3kzdWav3vnuFju+J19BRK8OwyFaWcN6iMnulP4r3tlbeB/tsJaEu2QUUw67+ncnnZ3S+M2dHg6hM4HFRV/bJ3ltk03sqDFU2dpRR/Uv/P3mVp1mC+WX1eoGgUGgzK0SgNkl0m19cRsXb64WqotG3xG8hNCS0T0qwp10E/l5CF6JuRS4zjXtFuf/xzeGWNpm4b1csWibbm8uOJqtWbVhrgozoaz76zoFVPTPpHsFwFPbvOQ+6FH9+4xuV1Vwk8Lz9yI82NEzIxMQhj6D/vIRcATClIwKJipF71r/qkdnqlj+Prc7CctJGS48MZwjgbCUYbvL2RD10KIwnionmfmVVofkhlefSEEA2FEeTeEkYTuAYKBU0z22aIGL740sz6ZWz8Vzm33eNyf+Wj8gn15Uh2/UCll8P1p6FjidUHajQBud8/m+s9s3/+Zbrc7HhOiB+MR72lKZw71ME3OXn5EbqWoiczhRIgFYnC1U7obz26hHJoqb/KVX1UZivRZc1yqxmRLAql/S+8OK3ECiEKBoBESTKljaEcDScuwRmiLcyZCKAyCKybjlYvdnrUX7GWLvWhpVktM24Jtgrp7pLxqNnD/Vk1PpPpN8p5DET30kfcwjDOWLQ9dz1rVHJkVJj7xkXjX3niMkeBEOdemxPXMjfKcefSU0nTwPBEHJHX+UqSCSGFGBBGAyXdUvquie8Deaor/qZj8W+o5qDUcAU2CLNJcRWGT1nRRet6/07TKRWxlGigRxRhDEEgpagRsCp4d9k/Secs0Xx7foAnrk6CuinSXmm/U4E21fqK1gxiigUkIYt0L3idCFemz9EQr3MBrYP4AEBgz3gcNrEO3xx7u2dzfcn93y9V6hTFNf6Jf4BcN596lj2WCvsAL/BTwVAwxnfTpoNsrvHewNMradggtRpcIjtZ0XC4bvnq7YLNx3N85FHCDVgTGu8bjXSpemFaMbelfxRXKMYvOafmoyWGtLvA6fkMNs+6Zqlt0+CZXOGCMDK2spn7X1hmjuhJjdqbmQcNjZ4c4y4Av8FAYDPCwuCFjscYRzllzGTeffhnrHMarGPqq6H+eA1ngM9bgS1h5wOPFgLHlNwE3C2vH0zkH7oBzHe6wx2+3+O2W3d0th/t79tfXdPf36G4He4dVA6bFisWIpW0XWNPQ2AYxBgtRuWhDR4M3S7rGcXOlbAhYlr0UbBv0hAqPgupSSnghYQ+ZkMbvWtSvWF4uWTUtjQ2KKlIlpyrhxACWlSajV4MHM3ym+Ffzx3OcPKIyCwH/CjYQwT2TV8VHC+CE+/Zrr/YjjBfGHA4/fH/OCz3+Oh9Up2C0P1O+B67unoVDXZaO3qeRG52dJ6oqitHDw2Eq8UwZE8lDbAjBAVuBpokWESsLl4pvAxU0vEdm634EfAlOysSRE2Bu3CcbNVdIglOLPO6TI3vgHGHEs8BU/4d3aX3P9F+M8z4SHm8RkdqgExfKYKVPLfwvBi/UyU8OtdABLRYRNSS3SuFyj8y7gcBh+BcyfrFunG358JgmnaLBv8QyfrwQ4gV+URC1wRyWrX6LYjPCaYyw/fQDf/7//r9x+z37za6/+DLjsjBMC/Rvpp55+rmIUg/JCoxLUZPL0aip8ura8+r6wJ++NXx6ayvtNqmYwOGLEAjh5PqllG96zQ75CrUX8pVgYuUeC/mMeLyRoBWlHu+jGXY631K50duPNQIiWNuwPHR832xYXbasX7/GNAvMag1i8TYQX8ZEbEQL07k4LhJqK4MsrqgItZQjj3WNHFPGpz8hUlIkAjQJadL73tFbMZzjK4lEo1GPCnRxPEL7qnnuIe0aFIvEY0jWEROYwwOPHvWeHH+gGocQKDm2vxqcNI6prYKJ/REkuggQE4jk9FyhV0KeIxOtLryPz5XaFZWviD4NXPcJ0qcgtb2ZUl+YKvVIxf+MNKWGqC1pVFEfglgHy4jiAim0I5VLjB1RCO2a6FWROEfEfgTBnI+EdzSIoMx67EG8142xeO/iPCjqQ/wU713w9yweCTp3qI9Bq7cbvFM+/fgnLld/YPnqDbZpY3wKxebQEi930wu8wAt8fnhQsPMnH0vlrN96+E97w2vr+A8XnxB5Ree/ptUDa3/PN6/WfPX3wu//cM+/3NzixY6YncOyVUF8EFpLFCxXphPlQK9+zvU+oyy5xUe4HKdgyJGJNCIacJ14/M/zkSoBRKIl+8IISnuSAKZ3o5abbFR2xE+DDOIMztEz03A1GRbaUjC6GYPHXhvnBTzDeiYW7yDbKRdOtTJFbm/5kdMJNtRnGyAJIuoZ8Kh3dO5At99x2N6x323Zb+7wH97jP71nf7flsNnBtoPOsTAtjRhsu0IaS9O20QVTixFLIwGbWYoDDlwffuRGG27V0i0E9xuwjfBqaUNTM9lQYWkiILamXACwBsQY5P4K277l7fdvebO6YNEoTaMYKevyJFkt/S/PhelI3OYJwwUiHaM44p8qTj1OgzUFkixW6jadOhkqmGUK6vF9dLLcMQZ9+p3202SFneliejDV3fq4qIkOBmVPYPvTFPXYUv2hUKzB0jGuJJWxyG2jMZY9wvVyyburSy7WK5ZvWrZvBNvEtfyURfeCmldwZJ98hrvi0W0Zpfw8AayfGKwaehd7fiQD3KM6sOcsI+a5Uiea9YBBmUr7gJ01bVgxzF/1/UjRQ02N0pyBVshzbt5jQ/Vst1qpLJu/qo/WcGMtmH7W+hr/aYQQR5fDEeuLs8t4TOUZiT4CeuSAGKsejasOCQfrcYwsTsMjOjy3EB4xeD+Vq6jEyHxCCWXo8tnS78u8OXbM9ODqFYToM16zmagBuv2G24+/Z/P+R7r9Hn/oGGrO6+jL3MO6nSeeneyDlDskamhLfc4SUbU0nIM1LF65uAvms/eXBm/CGWudsr7zgZEeEePERAdl3wqbteShpqbNVcEIxgetQoMB48NwmdBOgyAmBKATCQRJ45WL/Z6lKsvLNe1yhVksENtgTPAXq6k/kEUJZanFBlAF+e0N4twZkD50uOR6DOxeCdlchHwW98/3wSx5SriP2MIg/DHk2CIDnkRdoyqBCaIer5YRWScJzyjz2xO09BoT/4tBqhOhaJolqAMTCF6xFsSEGBxINHJIVg2GHJGZYrGgXhHjs4LTkHQo3qWjIMD7/DutTY0dDm69QkC7IqBPzJPBeVAv60TQxADRYuqXECN1IxF19BLiR3hjgtGBiX3yySojuE7y0QIprb6aFKrkTQXN0cRoIG2MqEkrmCgUcz4I8+r8sTVhVJOwT1NLUvpoMo7Be4c7HPh082/wO+XyzRWN/TXNcgWmwcg2zGuFa8ZGDWaoFkTWA9u/P+dulMll9gJfRDnhRf/hBX6OMFTGExE2XrlT4aZCn55CxJdbSDIeskP54eBYmS1v7AdEDD54s8Q0wb2gVaXxHnXByk0lfPpYlmg8ESW46cy/Yz/CoZ04r7Wl+rG2aj52e9d9D39KZ0Zi5FOumxoxmWEL1IIOgWxsl9w0TZ1HRZs4zVn6HqwIpwQKmn9Wrqp67azy9kZgwGwc9WOMrxVByTjDcByP0WahWRVPJre/TjzGpcpTJStMDFgRuYyqmHTNTt+NAQcI9QT8p4/TJFo/WZoGu4SyNlxUVnB43+EPe3x3wO82dPsN3d0th92Ww+Yef3uP3u7Rg8M4EGORxmBtQyNBAGGtxTYtxljENBhRjGxRUf6owt56tl9f0bUNXAmyFppFjAFhBn3r8blM7G2lEBRxfoyhaVqa1Zpls2BpGhrjsPiMt9VTepx9VM1YHy1+NAhpbhPmFdd8dC1UdLGkILw1UdRr9RF6tU4+hLTmh9YDQyLjGD18dBzmXk4SshViX2P4c3u5h5iT+zEMUK3Vu5xU+/lyMTWyHVfV5NhNUnMxTxny7HNEo5KRSjynJexJKzStRa1FFgvW7YK1sbTG4o3B7zv85oDf7acaMQ0PwNc+B2o3e08NN1B9rh9NN1vQkedzu/nkZhhcRf0yn7jlx817YvKntujJFhGDK/IB6R+S9jNCjZ08GZ6nnBLw6hE1PbYJD6GwZ6awZtkQGUqBV+JHSGnJI9kaAlLfU0nJHDP55u6nfSoMkbBTFg+Pcts0RBrPbEvfBKp694ymEdP9H++HU0uhQqWe84j82cLPiiHSa8scotR/rChqCNrPhxB3wVrL5u4TP/6n/0S33bG/38KAeRzDD+R7G5h28RkzTV3Hw++T26NHiPb3uxA09jw1s3Rir2SqQbCqfPPDHlH4t3XLoRFQz2Ln+fYPO4yrG2FiVuH6rWF30YbxogToSoSzKBAtIjwKPml+Bdc0JhLtxghGDMZalnh+3exZrhe0l28wtsUs1pkBHlodmcOV+YBSKTVWZ4Cpdlzyq1/eJ8KhcuxQzVc6TxNzYzT+acQlnhW9c6gk7KHpKsHbUZpYDWNdCyMygiVVX+ID9YL3ip05N0dncB6j0sdAGBvEBEJPEdTbgGyvr1ANsQdSH0SkEjgQhBDxWfLhnNyCBcP0RFs4ajsZMdElk497LN+D/XFKSG+gVYJ1gleNQeDCOIeggMGN11DI0JuqaMHQWJO3igDqO0AxJgpaSDsyCGFM6ldi+nsX3I6JH2hTVptdPdG4I05dZDLE8n1cHyZNMuHuV7/v0VW5P5HQ9XEcQ5kOfEeyKhGgMRZ/6PA4ru2/sv34A1//4Ruu2gX2m+/xpkHkzxjZge6rDSqV3+PUVhBJddXMGRvG5q/g/nqBF3iBx0H/jqmvr8oaE7h2wn87aHDH2KNpHg5Dnp8Srr17r/zjruOb5o6v5R5jruiad1gM1lmsKI16rFcWXtkbobPCIcYwUg0CetGoOxFjRaTjuScI10h7jfgnE+elJIyFjHuEO18whnCH9Dg/5Y4RJFvbDvGQxBxPSiAVIoPxijeK+BgjTP3AGiLUN62TFeNVVAKF3vyKyXyCfN9nHLBP8ejoy9QQDTuXkaF4P0kcowHeUAbpKGS3i4PEfQWOIaT7NuQt2FTEbbQqQYhjQbnnc72U9CnuFuXuRSJqnuj5ZAEhMSC1Te4Wo999t0ddh99v6PY7tvc3uM2G/fVH/GaDu7kJLpk2G7RrUGcx1mCtpWktxgqtsVhjWdoFjbFYu0DE0IkBcTT2hmt1/D8Or+mWlv/4P1+yXAptazBICEFV9TuMXzUWeZjSu5hOQKxBbMPqYs3q8hVXiyUXzYKl7LKGuYGekGMM8xP+VFI0YT4xylaYea9h7pwHp9E9JiRBhFEJ+K/JvWW0omb37zhpf9NN5O3RCFNwCmcbNaY8qwnYZA1RW0X0T/yJqgYzkONCuLiGI06ZnkfFP1VfVkt6Ny4tNDE/rO8RPbGf4xJUiD6BidRzEVzFi0WtII1hsVxgm4bVes3r5ZJXzQJrLTtj6LZ3HD5+HM1BoSseD5+VnTIqXCZeVEyNkbb5LGH82AYceV5PjPaaMRR0n98m7ZFwY+bV8I6ZKEGOJND+uf9YeECMiPGzWYbcYDInh3xoETAs/5lW59QgjZkZk9jJfJnDtTpfOYNd/3xwsrgx2/zZmMQzdRckLGh3ZgaO9qdXJr5BWQtDhYn67xx4aD/7CtRDps+40odaTcyVc7RNE+m1fysNXo79iJ9d10T/TwppSqN6h+U5/cz96Fn+PH18zsk1evIUdZLnlEgU/OLs5CXp8PyayTRE7pTgJqVTDre37G9uOGx3+ENXEKUpemnQ4Ol7qv+0/tXD3SeaO33xFX3C+tU6WjpsLg2HheHi1tEelNp02DiwLggwXt14fBTCtAfFaHEEBFI0lERY7JU370OQX/WO7dqwW1uSb//cEWOilgmoTYznQGgZD6+uHZYOc2FojdCuW5rFCtssYjyIaDURx7MQu8pwHAcjFcZjAlHX9J8O5yASSL2ndabBqM/iUZLXUP9s1xIKoC47L5dI8CYCQBLxWyHVmkahnGkp1aCwmaalOTSINGA80oB4EBNIZu9b6Cx2v0QwQXhg9/jFliQclygEUF/HOwizLxrWUKC3Xahv6MFBB/MT2xYCMVIY4SKYroXtghC40OAijSRRiCW1hmMaf0Bd8AFubRCg6XKDGgc+rOoc8jvHTkmMnuCmrK83pRg8Hoc4V8Y4Nd+XR+F3WqlxpmqBV0W4SaSIUpx3fNwjUfCRNG0xinpBsXn88rvY5kO3xyv88f1/Ze+3/MPi/8bVm69wZo1Ki9WPCK4nxAtlpD1bbkftrbv+SJQJ60/p6LqYxuv/auCxlhA/K2H+CzwYvoQFzINcH/0MYXSWnIJTZ8lkgcrWw+87uJAd78wtag2+bVi9WfHN3zjub/bc3xxoMOCixr0xEQ8KZeaifVCkCAoUAYfKx74mZk1Np1UMWQrKoVQChcjgqS0hasFAxuymUJ1Uh85T8omeEK3KkCPBnSegBI+m16a+0kTdxGN4WTUgeVRO113nMdGq1queplFG7AvJZeUStbjpnFpWmZCLfR9iZVkZhTLHUuVO9gBFMQSSAkStO2iMjc/q2A9RWQSFwx7U4w4HvOvoNvf4bk93e4s77Nnf3uB2O9z9HXrogoZ2p4g2WGMx0mAag1hD0zRYK7RisWJoTYPFIOzwwI0KW5S7V4Zta7lqGuza0rYmxIAQKQo1EwqQmkYpb4ABXiqCN0GZpF0sWS1XwR2UNXwSATXB5/7sIXHq9JDzkp0oIgggKO52Y1eyAURW7pKMB+d9N4SjS7XaROdATeyd3MppzE+l1ZmfVUUjemoqT3zmq0b2yhqUo3Vn0mPtl0XpwtmQpmbkEWO8NpJVhSTBhABisMbQRFdlTduyXixZXrboW+FgD3TXB9xuV1ETT4HBufS54exLOK3NY4k/d6sn6GXo0fDzeebTnNPq0bYZZupVU6WWqbX3cHgGi4jPDD97XPTB6OYXgGdoz2O6FTeM99Hlgp9GfAIUhh8VktOPC8FAAHHqEjt5Cx2HB1pAnMr/3PC5/LNN1dP7LcMvdVrtpTsH9y+Ex5kZTrTv3FyjJxmBfMSY/tI5KbHLTdPQdY77H35k8+N79vfboJmdCLIJ3OZ86F+S9UifvO5lAkeEHkEF8OrGc3Xt+ONvlnQLePO+4/LOU1tEQCHOvvkhuX1JOlwGNVq57pd8Bl1slIv7LpiFq+P9twt2F7asv6yCHpDMpHdehOyGVj3ffNiz9Ip97bCXC5aXrzFNg1ms4gHXkJDXmk3a6/pQyEBCZMfP0UgkTOytPj1VzcLEFujPUUCaxUiv2IBL19p3cQyksuAoHAjyxZKENX1yd9hDUqpxe+qmVWdQzG2MwXuPRA0765vclJTH7i9Y7H8VWuGVQ/ORXfvHMr/RrN54H636QsyCtAYVokVDF9uQHV4ASdGpzKhIUIEztiEJOzwCYpHuAnv3FcbaIBxUxXnFWlsxbhLJTv7tfYdqEERgHPvln1Czw5uo1WgqVTuNTCYNcR1IwaE1uGUK8xbXsWqkn3y8x7VixGhv7aWVO1xvGsdJTOB4qfHRWsQXfNaEmBuaCDID6nIJmXgKvriV/W4LsueHu3/izv3IN9/+d1xcXOLsK7xxGK4RdWXFJHxCLMXSyMc1K1U9/pkIrV8mzAWK/Tx1fZFqXuAF/jJAB98H1+WtV/5xr3xnd7xbbNHmCsdXXPzqiquv1/zpH39kd7MBb4ILSRXEQ9eAM5IZjtGbDMZHZlV0V5hiGRHT+MiwzwL7TKTFeEmi8e7zUSu3xvXDDZIsJGpFxDlRg0bkLLheindC5oQPnmPCdz/DKJ2AQoZUzChNbOZ+W0O1BYtV0WB1J0kYH+vNyO5pRlFoQ4/zVO69ms9Z3bd96CPp4bqU+Ear1xPCiIiyZTG8gHiTX8WVMOKRiVZ4bl27hhxpTaUAacFqUrAEa0whKHm4GB46aOJ72N+j7sD27pZuv2X36QN+u2P/8SO629Hd3EHn8IcuKpoYjBHELFhYy9JYpLFgbBREWJYYGsLaF4WOG/bq+CcnfGhg+6sF7aXlN6+WLKxhtbBBqSP1rmetMMSKJ+jHzMMgWNcuWlZ2zeXFBYvFAtO0/JGOzvtIM/y0oPkvutCW8syn70lRKi/LlMKUQs6CI/T2SVJ8+LKilXQu3dz3QXpVhm6Ix1VNlZXyllGkwo3z716W/p483b6ZNSL9732GcL1h49yZeDaYLDZERLBNE4NTt8hiwcVqxfrVis0b0Psd/v2HuIflrHkee/c4qzfPDkOS8zQMF+BPuTf7bXkkq2yqqKcl691rNd39NN7kkwQR51oGTF2fWbo+NPWZs5AYVjpb1+nBGKY5aSFRGjdKFvZmYpdMHAJVrYPCYhnxujuTOjudrCA+X0yhKCFIlUakeu2du7l1Uo13pX3fjwFhesKI8w+E8ztcBB/Tz3vPho8eafXwVAJ8aHHwuYUS51hK6Gj8zth/VT+G+U+26Zz5OZJ7ojWlgHM3zBfkpNTm5c8Hlk4v8bLA2gWqN2xuf2C/vSu0z1R1R5pw/BIrb8fp5s/K6bT1k6BRLWq4vA0WDu0hYR0VtZ5/1hS8hMVntK9tJ/0VnFoiGFb3jrc/xLOt0nC5f9WwXxow4ZkA4pVX147FQbGXimkFe7nGrlrMYgmmiUxiKf6N+5WCSDaZHo7SQ4UQMvyV9/Mwv06u7zCqGjTN83lfCN2QTSPTwGR/zRLP8OAConL1JaVnoqn0QYUjBFIGCXotz2kSSmQkaH2Kt9jDJYLBpP2EIn6BbZelVHkFh3SXAzbEjggBr32wPvCO7Le460BD7ILkwzjNP5EpkYQRREsIY4KPYjGCMU0gwhWMX2KWa4wJLry8Ko1qcM1U2e2n0NgmPvO+QWM6jEfcW5xzuEMIMh/cRaU9UNxrKD7Gp0hBo4sPW3c44Ls9rt3i230WRoS5DsGjgyupGOg73ddxIJNrp7SrmsjAcb4En04QgmYfIg2ooWzxca1EAUlslwoxyLVnt92gKny4/yfsJ8/X+g+07QrXvsIR/QaIASyiBxpuBuuoYvQcPblGF9wkzJ3Pc3jdz1Hb+yHCiJ+jJcTDr/EKl/oZzscL/HLh0sDftMIdwvUoTgQQmb5ngRADSMcf1UcCBe4U/rUTrsyBt80N3i9wdsnq6wu+U8/1+x131wdafwgWmgT/351t8BLOSxWC80ERTNREMZJiHBWVgHDyDwPWhpYI0WWkkNOT8YGEOyQ3Teni8OW+j3hFtlJgXnFpCu8UCu6RWzWwyAjPqjbnoqO1ZhI65LYkuqVUUgsv6jaWcGaauH2Ddg9pz0EPjvrCOAWK0YCvhrEr4OOsDSnHMconva8FDSuzn1x6pTVRGO8S0UsT8YLkFqasFY8H7aDzHA77EHx6v8d3Hd3mE/5wYHd3i9sfOFzfoIcD/n6DdB7bhZhjNMuIKzXB/ZGxtMbQGIMRG4UTQYnDy56DdtyrZS/ChzeG3UrYLZYsFpZX7yzNwrBsLY2V4pusnuxJSPM0wq5DcGcPh9sG2a355u0VF8sFb9aOq6XjvVEOJoyVETNV+GeBtCeswDcNrEVojMb1LHix7PWCHRYvJs5n4c3EyGlJpSMSAacOsiHePqA6MoNb+8kyEUCucbQtevvqgXvmrOQ6nS4TyQEnzsKH/Cw99+V3SguU/pwgqmdfTbwUKgHkIK1QlHzTXiW4DW5sgxrDzloWyyWrxQKLx93ewv4wgbPJoPzjcPL9mffgQ1G0qXafkethlXxWqM4h1R5+O6LbJ56k7+EKmulXRQ/P7YcR1S2DL/mjKuuB8PO3iPiZQ7nExxfSTwpfmK5KbpiCJURgVAQ4vgHSARkelc/8Oj97vrZOCiHmhAtH0jxEM/852j/EZ7+UhURfYDR4hRSGZJV2FlR7/XjI4fV4IUR1+069qgs7ddv9LNU5zyNcUvcUy553GJYsmyU7/cD9x/ccNvelnIH2VU1QjvbEWRhC3cZzUJcjZfZwWQMGXt0o3MTG1diWQN8Ba9r70ae+99H0eKpt9WYTLu6V9d0hnHORMauqdAvLYVWIdCHQMl997Fh1Hvv3LebK0lxelZgQYsA0hSzUiN7puAXZ534l8KUWngwYv/PzkQ/V6RnQKv/cOo/uiBLzWmvNQ63KlfhfQoCJTIf0PFlEFGn+xC5NbnmYXA71mRHoggFalurWluXhOwxtdDdRwaKUYHxL61+XMfIW1MTx9nh/CMIIFwQP6bPbbvGu43DYgVaxRAiyqcSYN02LsZbFao0Yi7UNGpx6oWLQpWSLCLRYPhTlDO31C0BdEJKkJd52K7xXuv2O5EtbInEuRrDG5q579VkQURN9zm9xhy275Y90i+sQw8FHOwavqDuA9+H2UcUYIbmUguADXCH6HA8aV6rBUtI5j3NdboMzDmizK0ecA/FkAYTvULpsTeGjIGO7vafzHR92/4zcbblq3mFXX9GZV0F4FD0fq1oM9xhue7EreudDJBTDffpzPN+/HJwjjPg5CiGeCl/SIuSXDl/CLdMvHV5Z4XUj/N7RE0Q8CAZoSfg5dTcHxtCthzsPv273vGv3uOYtjldc/OoVb98sUfcjm087Ft6h3mPU4owFljjT4I1BJbiLSa6T8NA0yUQtWFMk7egUx0dT4FMUJDC7E02sufEaYmjFYlOsiCBkn1CaS8yNJIyQxICRkVWERLw0CTqypYX6LNAA4nMYx4yIvclnQMIR+1YOCb8rAbFJlRJsawM9phm/qedwiMQc2UPJRc4jzyPRoP1fY/ChfZCsV0cKY9U600oZJ1th9HBGyfHRknghW3hK8AppsEEQQIj9kEQgHofi0f0O7w8c7j7hDjsOdze4/YHt9Xvc/sD+9g5/6HA3O8R7rAOLoTEtxjbYNvizt20LNtTVGEMjRGZ5okuh45ad7Pgnb/iI4fBdi3nT8PbNBcvWctHaqKBSNuoobtp4lAeffehU6VT4cLvALt/yd9+/4Wq95t3FjotFx0ezRCRaKP0Ex2kj8JtWuLJxD0MUQjZs5B07wMs+4KVIxCND/LfGw6FHazykA+fQqtr7mKVnMiFyRtpT9aRsvu7XXJs0vo9WxRqdW/WED6ncRAD4fl6t6phqczWkU0fjLEQCIY1yIn+F4OI1PQhlejCGdtHirGW3WrG+vORyvcZwz/7DxyB86nHAC632WGxpFn0YPn8udGxU3y8Qf6mJysHjc4bprKGcYX1M1jf8UjXkMQKJn0wQUVCU/qIYx4443plTnT0qcExVnCijMOGGqyAhOGl/6jhfmqzR2h8iAhUmUH38rDdNFj7E72hlCTFutySksRZCZKQvojNRCFGInTHz+ykwEkJMFD5ZX/VwuGYf1L7Hdibvi97PZ4e58ekLIfonVkbIT0Ct1VQPQ89CYmYv9tDgER32nAvkJ95vcxdOPmvSaS9VbIMq48TCqAkSkcAcNWJwuz3v//mPbD79wO7uHtcdYqCyTE7lslMZiegrt47kOT23c8cuz173awQxIpzpONU6araailBPBU0h+BOMxhRgeMjcr8pSIxGZrAh0A8lpwasbx/LgsyZcOufaVwbTGuzVArtqMM0SsRbEglS6aZnQnbg/en06d5ynIJ25DxGf9nMXvD+OVXyQjwpTmpmP+fQHIf6GpgSkjR/dKPRo4d436T88cwgE8YbF/jXGLTAqGNFMnktuaEmvxgQXTICkuAwSNZoEvBoQxUuDqkGtjZE3TdDstwu8RiY6ZAaGxrVDY7GmoWmWGBu0+YLOf3KPYSLibwm/olujE+imaG05qBijNLKK/QjCHIkunoy1cQwVo4oWP0gZmqbFLVaIaXDdG5zvslUIKPv9HudcHitrG0SCkCMF2tRYh2jwzawEwUenns4dcl3OOToXYtJ4lK470B32mXWhqzu03eG74DNaEVyMi+G958MPP7K72yO7FZfrr/jqzb+nbS5oFktEbJgTAPsGK3sabuJYmbw0i3VTJfT5zDCs5+fEBD/GlH/o+PwU1+mwzr9UC4kXgcBPB8c0CBNkXOEpkGnU8kCmElTfFfAiiOwx8pGuWeKXF6y/2/N9K1z/4ZrN9ZbWeRp3QLzHmYZD6/HW4puWEC0o3Cvel1pEyk1dmNpSvUsQ0iWFD/WCGEU98VMqYQSoBj1rrXHMGDx6KIw4c8giqpHy5tMeKOWl7zlvfQb4cdygIS421aZ0FSerhJqWry1pp+qEWF5SOqiWWVF1ySkzNlNT3V6Ck53hUKWYVpLKqlkNUjdTKcYcKY5VviErNz0SZ6sKXC0hpkVQRIx4g/eBtnAOt9vguwPd/T3+cOBwe4077Dnc3wfBw2YbYm4dHMYr1rSIIQSeluBuyRhLYxuMtTRNi5EQh8HaDjEdew87hRsPG4XuV2t4c4law5UR5A2YpbBa2BBbS0KfB6PVG+k8ETUy2tvemQuHElyDNmK4WC1ZXlywXrQsrMHaoLBhTH8OToL0Ph4MY6y/wnVSM6q+qAYBo9t3uO0Nsj9gRbCAjfs2x68+5tJossVTm1gHX+M+GR0pE3kLYdL/Lb0Ew4IGdQ2TTTzL9StZ8JDqHe7rJJzI/VD69U4979Ofw93eb52CzvFkKHSeBFomI7tSSg17xtA0LU3bsFqtuVgbnLzHdS4IIKpiJTW7/j1qb/Xl5GI9kWCwJ4epT/J2J4v/JeJM1d0l8bQfzEOC8Yjp4M1c/wc3XO9n/53Uj+svwyX4gLH+PIKIZ0CQRy6bMvJzKt8ZD4sE4jj0kvUZc71yRQZKpKWtWTY5rGt2jNJBNX3zVFUez/8ZYISM5SqTdvDwKK3ySrp4Jf9Ol2FyxdQXQtTp+nVNFn5W+wdlVkz22UZP5D+r2icKHD57nimQB45PfBsIjuNFZ20mtD82o31+vKBjAqT5Fs7djENk88vD7MzNbLYe0TLEYwPlMFFJv58atRzcwXH9z//G9u4T+/stPrqcGbZtGEz4Oc6Yh436XH1C4n6Pu12dn/VY5k7VazASXIkAU2WMEvaZvRJdECnw6k6DKmIWFhqwgv2HhuZNQ7NcI6aBRdCCIjOXU/1DbLf6Kjx9mdZC3YnXk6Orlfl9NX6J6MiuelKpabgj8po+87PcAoIbCDIHYroVMvhe4+9z3axKEkDUsty+RXJ8CE8O2ZyYRFJyBpwqpEh+kQWfTfVD7IRosq4+C2JUbHA31Byi26Fw31scqOJ9HMTomqlpF8FKoQmCiCBQLEFBk/DAxDszx+UYjJXmlkZMo1rytqnmXGJcikiwQ7RaUKUwk8o8+8US66HpXuGdx6kLAbCjFtiOHZ12ecYaaUJAxrYJJVX0mRhh0S4BxTmlMx073ZMIJO88nenCGKFs3T07NlgTNDj37R/x62u6wx7vDnQeVII+nnOe2w/h7GovDPfuPa15y3rxhpW/Cn1uQYzByStacx9cNEUirb5KzmdWxxk4kf4cl0y9fXFG+i8Jz8XkPo2vfj44i2k5M5+fxyXidB0v8DD4EnMzCwP8aF5gl7/xcHxpCvkb0iL9X/XNENypGIQ9Vvd09iv28ob1d57Xb1vc3Ybd9T3GdYj3iPM4Y1EjOEnCcYuKiZrlaRMn5lcfPxrSxT2XSBBuOOOjEIIolAgvizBCCC4doxKMhHskuTcauj46pjyYb8fJoY/t73NSwpvBPSAUuoU4rhIZgH2lqtJWiQoyQaO+ttyoBSL9lo5aKLF8zZjncKBDbi1lSLUGgiBiik6uR6fcgYVPkd5U/Y9fwrqKYxBjXaXYIKmsPKTiwXu8dzgflAgOmzvcfkd3c4Pf79h/usXvduxvbvGHjsNmhzoPXVCUsjbhFAuMtbSLFiMBZ7LG0Jjw2ZrgbtNisO0eZx03TvnklH9V+NErv/6bt7z5VcubJml3T/Bj+j0u8zNMp1AYpFIWySB3auvFcsHlxZp127K0IWi2MaYcEFKt7TkYTv+z3hsD4kjLVzA41+E2d4hTrIBFaBC88XQ+CQ+PwficOGvoh2VUa32meKbndUA49A7KE3mOgY//1QKFbBFR/67bVvdjgu6pmnj81tDRt94ZnBTC0vqU9D0JDSVYuFjBWsuibWCx4GK5Zr1QtvvroFhkK7euwIgnqXW91XOZffA0kP5YHee/jb787ODofpjN8Rhc4iF5Bq3q8cr7d0T/Cn1M2wo8WRDxZXDpUx088r4m/HrPBg2XiSWrVIreQwTic3f8S9RxPgxboj656CiWELN5K4o/CyTyiyR8MFkQ8WDQU6dSqXOOyf5LpAmnfME/Gr7QAJxEul7gs4FiOPAGpUWkQdmw12sOel+tpRjnJSEZD1gWT7uKptp75HemGvtnRtrVaupzhmGCPkQCLQX7CrRFJmcDJL+xKlnzv+/MpQrw90aQtWAul5i2RZolYkKQPkxqbxjvmoWQxrv4GB50fm4ucjcjxShTe+wR+zsKIwoun4L9JouZcGnW8X2AzOyejPeUaLdecyoMPJstTzZn1KOpNSFqabavMa7FYnLgwUR4S4pMnu+CMlo1rps8Ydf4gkZEX9RkGsS0ElxM2ZbkohBVjIZ4BiZa2mgcIzXBImaoR1YHhZR6XI0pcTTSZ2xbWu+JMZDmpPgdDr0OlhCCMRK0FaWUIgxXhw0PLEF4YwxoE+/uIHhpvCMwu8gBtW3TxK1U3HeJCcSOQtBw9BZpiumM90rrUwB5aJYNi92Sxhisgb02dP4r9od7uv2e3fUHZL+heXfALBWnym6344ff/4mP7SfuVgdWi9f8zXf/M8vVFcvLV9impVle0FnDvv2Whh0Nt2lVVUypeRhej0NZ+mOYymPG1Pj9C7zAC/zCQODaKT86z53KzNHyvNhSXcWNU/7rttwub5s73ljFLRZ4e8nF335Nc7Xi5rcf2XzaYX2H8R1sHd4aDn6Ntw20KzAWNS1JeNtjgkVrOh/vnXA/BFc8heGWLvzAtBTi6xT4qiLdCm04LSiYBK3OyUwO9fP0rSLKuXvO+TonpO7RMRM8RZnEwc4HMSbjEUdSkRjjfRRrgBtAdieV81Xv+45LQxDpOkUK45FxtsTMJyhZhJhpIY4Uhy0cdnT7PV2357DZBNdL9/f4/YHu7h49dPjNHt85/N6BV4xvEITVogmulRqLGINtowVE04b4WrZFjAXTImZP1+zovGevykfn+bEz2G8XtF81rET43sDlmwabDaSnmNoDdu7EfJYHabH256ZnrSKCbQy2bWnNisvlkqW1tEYiXpOcR/10TIcO+O1euTDKr1uhSetDo7shL3gnqC8WucGVVGAaOg34qntuqm9yzBnsg+pZmsu595NDPEVIJKJj7l2Vpq6zFjj0FIW0n2bwXGJ5ubZBtVMuQudj0Er5rGlBqVal5NUfaGORIIBoGu7alvVqxeVqwaL1HFxQDM4umSJNWpGCx5sxQVE8DoZrq/p9bNn9Anl5DwLpL8v+q2ei/Yd5euNdbof+Nf34s+BJggipF/0xOMZEOTloiSE03cGzkImZeqd4If2MUrW9YlbkAe+XPKX9NeeCapj4oUtnzsjjc8D81BVLCOjP0Yhwz0didUBmS4j0OSbo56b3If09WwjxnIP4xIY/hAdRp30S8vvoE/z0AVRrHg4PyyFT57ng3P7MTcmX4AMN2ziav2dYkpkAw+J4hWdJIxYVz4F7PBuSZkutea0kgiohQUcak7GUzzRog7IF+n5rB5NYNDnSc52+vcvmZ4zQUlGiNVkXEa3I0JacDsQK+s7AG4tdrxDbIM0imo+n+oaUTi2QSOX2U4QfAwK739IeLjC39s+bnd6BEtdB/FlZQhDP675FWzpT59eKxC72GPEjZD6mO9a+im4ooyqIGpr9K6xfRiI7CXmSJcv0/U39RNKaj+m0dtMgMa5IAGOjwycb8JEUeNnE4NVJaJ90x1IAwB5d2xufQPSJCWNrhCIQirhIpoOjgEyii7E0F8G9U8FyTGWFEzQZg3qqaOW7thr4LHAhWVEoJioKLMTgvWKskGJDiBBiWwDgqnmsfMwCTn2IlBihR6cJ2NbSLhc0YmisoTtc4rqO7f6WvWy5P1jc9pbW3iHNgUO3oXOe7uZAYzbIa2Wzu+TV8msuuwNilaZdBcaGLHHyBsMdcJd4OGmyqVfkePnOrefT1oCpn8fff4HL5oz6zxWojCyWT+SbJJqeCd36OctrXqwenh9+akuIoxCn+97D7w8afatXL87JPPp9iuPSf3/v4N6Vy6WVDV83O/bNN3T2iuWv3nHxds3u447NrcP6PTiH8Yfo3x980+JNsI7ojIVsxRiZziiIj0LYcPeYHkMseQmocJ0aR6yu4HBv1YKBxzI0Rty8I+N28kCucL9BbhnTMb2ZiDheeT9X3/T8ZXySdO/PtbUa0wEj1iRLx4S/J7xTqdqUFGlM75wK93jt2iVWkQUeoZwQYypYPvjO4ZxD7m+QzR277T2H3Y7d3R3ddsvhfoPfH/DbPXQOPQQEUGgAg7UWayzrZok1BhoTcJq2csUkFmuXqLF40+At7JsDN87z6dDxOyf8vjP8/ZuWX//dgrURjK2HV/u4zsilkPY+pmcqlVHvVY37Q/JzK5ambRG7YL1YsLCGxgjGRnyoj2J/dqh3FoRg2n/qYG2EX8XtLUkxyoc/9RJJorC7DQHdNFrEKA+53eb7eWovzvzoWSMM38/N5ZG9lCESKL21UifV8kf1eazOntBksPMftACGdMtgBiTs3GKRPj1LRiS4YLWWw3rFxdUl69WK1m5x0Vi9R6tWdMp8c2XwOdnCoz2bLzOlqH6P3Kk9ptafDh6/7+P9MnM1fDZl3/4lR6Iuq5/U4/6QGfiFBKv+uVIa08yMvwyIB6cMPJdHjc8SmDqhJseOp4DNmMiAMQm7qTRpixDiecfzL9ESAhJC1PcV92Jp8ALnQHLRYky4yZSg2eS9jz7vyVzgabdWMxxiIVsVPAtUOOVkifXmHW3k6d9FKDNFhMSzLGm111kT8lghZ9kcPp1hX1u4EOzrBWZpse0SY2z2y19MeUN9MolAD9oLOcDjKZDqy2TyU2VMYjZpTErZCdFNf8MA0FkYEf8vmoMKhGDDQfMqBij2Wk91wZ97nRp2YoJBoIZ29w7jGoyPAZJtNEfOTI+q4JpHEB9n62MRfCS+etOU3ToUBD3dWiEERgnIqdKELyZqKMZ8tQZn1toSzYELAw2g8c4k00U1FTA3lcYkBkM1LlnwX+I5JeJJoospnwPsKTncdjQzTzSJkFx1hTgURgQxQbhTXFCkxpUzwkcNVBHBYLBN08cjqj3QWItBw74xhoU0aKsYMbSLNbt9x2K5xuor2B+4M3/ANzuc6+i8Y7vb0qnyrz/+ZxbtBa9ev2H96hXf/8M/sFxf0ojBWUu3+B7j7zHcUDa3YWyn8gtFEH4BkHh9L/ACv2z4MnTguJY+82zIsknwvlO26vi6ueaN3aPtJc5e8fofvuXy20vauxvsYQe7He7Q8bv3e7a7A+wd3rbIhaLGoja4lfRWUDF4omVfVkCILgVjW0zVFu19j0INCjsjoB4F55zGv6ZxyyzEOMq0n4Y6y0gHJSbotyVkyGhgfh8tXXUgesjMm9THwUVOL1FdcRyH5MKSfpqcUDP+mcBotKCMOHwe/4ikaGx3PWc1uIzDRCUF52Kshw71Dj2EeE1ut8N1Bw7bLV134LDbI9sNbO9x+wPdvsPv98HqwYWYD0YF0Qaxgliw0bVSG10xLZZNCHLdLMBatF0hVqHt2Kuw9cpOHXcI/o3B/u1rts5x33VcGeE/GMPlazBWshCshwtpf577c8QkjHd2XUiiJ7TgxsDHTwZ3s+Q3316wbhtWTcPKWhprgrWEF8SbUclzlRfc/mnnjE4VoUTEt9jRKBLlEX3+T7B36lvfPk0ToEZop8p5SNlztEGNb09lm6tjfAaNnqd256rPaa8y35gzYWod1DyuTESVMyA9kuiWabFooW1YXFxycXnJ3eWaVjxNZ/JaDmvCz47soOLx0wcsVxkO62Q9E+ff+TU8IO3PHKp76IsKIwa1MBRGJHhg1WcLIh50/k1qlc4VPMo8U+a5758T0gE2vA1m6k77fwLHGC6KfPlPmVHURcwcbKcsB0btGL08EwYFp+DUc5YQpYqqEknuSIr2cPIvmZRDn1MIMUSsTgohprSpj5X/E55ns5ZBP7kQ4gQ2N5utvw8GP+fhC3Axzm7Lc9Y5IjWfp/KAgBbCw6uC+ooZGJDrxJA0kaScKalqb3maHkjld+fp7e8zqfM3Ge3ykyXVbc1CBMbnW113zhn9IxfKYECcGoO8ttivWkyzCIzUJvi1TS5sJAoicr0zC+vYiKV5PKUVOjUacwKN4zu3ZBpqTSchxLzW75jiCfGOy2fRJuqnT8Lr/kVWPrVecOkKVUNzuMS6ZdC8J6BJNZIUjo0eaVqK7jU3zxjxtsvlDVd1YtIn8CasFa/pvqmFD0UAk7UpM3WoUUjfH43AHi/n4xi96vdH8pj1tRpD/zWPilbjr/Es6OEjUUhUYt1J4mWE0k1hNoWKfI8mK848QrkmWW1gQlhS9agIXpIQRLAmCCvEmKBpawzROTXWdlxcbLCmwdornO7ZyHtUXGCSoLhujz94uh9/pJUb9ndbrrYb3n7/DQKsF5d4WeHldRzy22qkPYNFUMHznMM/dw35U5YRc+fOQy0qSr4HJX8WqNv6XPX/3Of1ueGx3f05W6+cAz9V8+sbcGZnVt/7uNGNV248XJgNX5kdzq7wpmX13Rvs12surhua3Qbz6RPdPXz4cYvbK7ggiPB2gW8alBZVA9LijYBpwtEcY2VBvA+UeE9oDNda7pR5vEXyPdqPP9GPx1C9IOMmA1RME6ITcdEUc2Jc9zFGVsGKUplTbUnNUC19yMKILCBJ1ZS7uS/bmOHgVO2f4/YUWraPk9cWwUq+QklCn6w8U62V1CaHL83wHu2SAGKPdgf8boc/7Ok293S7Hbv7ew77PYfdFnY72G3xe4d2DjoFp1EJIbqIFMlBotvGYMSwaGIQ54UF0yCLJWoa3OICrOOw2rFxhvd7w60Xfuw8V1cN3/9KaNWwcpaVhaVNY6ilU3FOTHyclN0T2tWjK0bzP3inwzmqdmRy22qEzUbY2TXWrFhYS2sMrbFBUcQY8Ca7eB2uwVnK5il3TJV1fIZI9RkWimotiAiLT+J6DFYRYc3Jcx7oJ4vS8ddh/Rl/nSowzrpW32sYEkJpzx0TcFaKZRXTbqLN0+0cUxPnwWgliAzeSH+9SOlKemWtxTQLLhZL2uWS7cKiztJIoY7rMudbObdeZ1s7U0zZY/Mn8/Cs/HJ418yJ8IWhWqRDofigTceEEed6C5nM39sn8WyYS3MmfBmLiHQZnAXj6R5a4IzwkVGOZwIdnP0T616OpP8pce4HDflZ5RVtylOWEDI4BLM2ZdKKzNKHmPoZibjPLYT42cAzIQDzPMQvPA6P0GZ6ujDiGCHyFwICYOj4Cs8SaNlv7/jxH/8/bD99YnN9gz90qA+a6up92AMm7O0UCndc5qk6iQjFYyTzYwSy1pp+WGP6pSYD6tjL0rbMgy3u5lKKETc3I2bxLHnXYF5ZzNsGu1hgm0XFSCW4v6lbXq3zHsrawyKqy31q+M5Z94P9NLXaj5cimVKTRMwD2f1PigVR/V/PdW/eNQZt9h7vouueaH0jmgjp5ObpvDkVhHb3FcYto3WJweqCcqcMkOl0DwFZAj5uab4DCgkxKCsT8J7hTApENjtlcLW67hC8kcBgGLkGCEOSXHgVJkHN0pfI4PCZ2VBrp+Vcku7n8L/Plk/Bl7NXn/e89x7fBUY+XjOxkkxBgouoOAY9GjwENBWxMU9gSIVuFaZM6JRUnhCSNVCMNZIEoYB4h/gQWyMUEPwGGOPBwsXVBYtlizEO5w7cf/ya/eGew/0tKh3umwNGOvTVJ7ANh4sdN+6Gf/n/GV6/fYf8e8P64hXNYoE3C6T9DY6g89X6a5r/P3t/+iRJkiX4Yb+nambuEZGZlVVd1d3T0zszewFCLkQghPADhN/4n/MQgYAUAqTscoXAygI7O+jp7unuuvKIcHdT1ccPT1VNzdzcwyMy8qjufFWRboea3se7n74+Yli1FlIPdUn0l8ag/inBfTE6PsNnqNDip3UvgLPMyyecWpdkNZGn5UpnL/4wKm9D5Of997z0t9AnUge3L57hwhcMcgXbHb8KP7C/3fO739+y2x/waTT3g/0G9R1puEF9hx+25ibHd/ngMy30KgivnK8JXI59oCVQhEy4BUzrsQ3YPHVCwSYl838bgtyQullAaWO+6aQYs6T1RFG1s8WEFyUGVtt9hXHf4IS1XdqQIGVOSC1GsVhNqko1rURymhVGKDKVVzPI52Rt6sQlbRUOSvPs7HcgvmG1Zpw2N27CebNCRMb7y18a92gKhMNICsHiO4SRcHsHMZB2O3QM6GFPCtnqIUY0BAsokRV2hA432Pi6TPf7bOnonSnr+H6D8+VX0Gee5Dy3fuDgHN+7gcMmsfvGcdDEj4fIVQe/uO4ZNor4RA94B16UScrQ4PWZh5RUyf6gJlRGp2l0hGYv+U7L9+2qzC9Dntt+s+H51Q1X24FN37Hpe7rO8/sII8rewRR04wR99MGOJhsvw4IMVwwxsQ9wSImgSjDUMCurTMKtJyGf2/E6m+ExDjrLpEx4oV0WTZK1MtYyO8bLHwWlPtpMtmZVFqLz8d24ft4s9awqFZGVxnzfo87xxnu2m4Gfb7d4L+x//BaR8Yi0PFbaW5+YMnv1mMlbGqDtT4Wz6+8sPMUk/cShYVWs0bLvs8yn4KO9V0HE0n/iapp7dv81ZsxafmfQwXeD5YamrCzUZoGubYAXlZPzuE/yUZPnvn2PhFRLdBckJhUk/NzEE5k1owgmqg/x8msvWVy0Ja5lfm+9j7rkHiHESeHFJwAfxNLhRIPXN7H7OufU++W6lsVbnRN7p3JZWyYn8jx6e/TRZX07aRNflPxJ4VSbzkqqjx56Iteou7IjI0Xe/OEPjG9vCfuDaTuZirppQNXovtP+Xc+bo3GbFz2r1er5tEZ8rTawpr2v3x+25S5ruiDYm7IsX1ncl2uhMrOfOfjahBDSdTjvzLx89uW8PNXpurRx1o4Zvt0Qm7UZ97dYVy4eijJILqto7ddtu2EYtMyAQvTrsiPBCF9ME75YQ7StKn5NZ+tUF3OgErn2zMcr/HizMOud+roQ8LPey+fP9IlQGN+rO4Qun1QR1WyMC1+gLJPqZlbKUlJUzMLB+B5zMV/Rb8x8ewqBaHlOUVpsKFxlpE51kKaxZRzIcynl5W39XwQQGs23cwxjpouSCZmkwTGSTAykbNkA4FIeL5e15nIEUk2llnnsUsItTPyn8bf6SBFKpJTnR1ljmPsnzDKjHzp85xAiKXo2+oIUOmQHsIMwor3CdkR9JG0hHBKvv/sWUWX39hXedWZB4TbQb1FVgkY8e0hvKQHKJzrSmF8l1ketf9FIWsyZguO0A/CuAosP7Rd/iV9eWv6pdB+D4f8ufXbptx9TkPEp4al/SaDzf2bwsCE5j3e351hT8v11O3pi37+Nyi3wwu9Qv89u/zxh8wK6K+Ra6fzAs69Gtlv44x/e4DTQjSMpCikF1JlPf/yAiEd9PrWcoDhjsItOGh/NmWRndt4L8/6pdX/EhAEZ15CsAKHlXC2f5MNUy7koOU0JCl5+hWrg1iqbTAoKk0Cg/QWsDe1hW0ZEFhYORTCiLb2b79vel/nFlPaePT8jgaXO7ZSb9h2Z3YsIKt7+aj4Zt9eU+01R8jmblBQCpEQMwaxg9m9NALHbEceR/es3xHEKNK37HYQIY4AUIZoik8YEbgBnbpYwT164xgVT55zFesiCCLe9ssDTwxV0jvSyZ/SeN3juEH6PMF4FupeBEeVwgOcDfHHTxlXLYaeWa3LqgLyfp+lBtXAuk+vcOJy+a8egzFYVhx8GNtsNQ9fROUfnDYf6AeEuSgnt9f7hSNFyPU0Jb24umYzPM4ZETK0LzRI1bU6ZzCRnjzpyL/joIkXFho47ih+wdv/Qyj4g/Yz4Wvtuon9WT5EiUF37tsHvV140eTT0a6Po5b0nOUfoO+Rqy2azAVEO+1twCYZTeM2p82r9YrWaF3RhxagXY9gYTDwQLl9sPzmUqmVO5cm0PqceXcDKM115XfbQx5X8yceImBP7nyJ8+jV8F7C5NWkJFy3OuWnp+rftJig5XbWMoMEDppLWSmfev6f6+/w4HAkh/sLhJ2P58RneARwjX6FyBbKpbnScm9aBEyYfv8WkXCck/Z0OtKOPL2RmNSknhtDyd56nLpGf1aKmF7MkusRxFxk0W0tBvAVBvvTwwuNfDHRdh+96xDv7E0CTEdWZ/ikuYZdlWZ5ahRHu6O2xSH+5I649r8x2IVuwZUJ4JX3B3WduERaCh9rDR1RU00HLrlMjgI0OLtp31qYSu9tLnpDZjVX7rdIWJwzjS7rxhkTWqh83uYx5jZxb+LYt/BCh9kFxT1Q05lBM+7/2StH8mtKVJkpG6rW0sTRbMAsBFEkhM9gX/S1TWWYG3zC9S9ujEYHVgnCZQVmrWRhQuS8KmiQHlmw0+ZONbYyxakGmaMyHGAMhjHWcSn+l7EKqdb+lCn0OIEmsVQGZNA5FQyWySuFJBFFHZfJnZkhKiZhi7V+NqZmrgus8znmiptzXCZGsYUnHzc1zvO9JY+Iweva/3YFEnIPhWtC/AbqR9MV3vIl7/vO/9/zsl7/ixZdfZT/VG0gRTZHknxPkaqpf/osSs5uC7Cs7z4SyHgqTqg5Ro3Dh5cDA99Yf74B8PNRV0mf4DJ/hY0B7fjxtrnYeTdq651b+/PRTk27n8+q3Ab6N8Ne94wvvwL8Gt2P/8hmHdEV/JbB7xjeuQ5Hz8+UAAQAASURBVPc7+ts/cdiP/OZ3B0J0hNu3iO/oNtfQ9ej2mtR1pH5L6rxdiyeKr3TfDDQLL/JZXGJGuKwlri6fa7ndc2FF7ousxj5ps+u0D+eDVKURUABUK4yiAGAvnANVMas7mAQSmauT0kSHViu/0v+NMMLqKJTaiJAVM6aTvcGuzoxgZiIWtKa1YphG9PjzioIl3OxMza6VYpxcLKVI2u/REAi7O2KIhN2eFAP69g0aA+PhQAoxKysldIyIKi7WobPZ7nqzhumlCqI67+jE0Xlvgai7Aec6tlcBNwi7zZeEbsPb7gXB9/ibG3QQxr8aSV3ikCKK8gsC6kE2A5BIoaOX4gxMM+7e9KrmSaITRmVKbg39UBG1pi9hyZA4PTZHkOditviQvuNGtmyvb9huTBjxvXN85xRJCq61pPn4oECSnlu+ZIyOfVD2ux36+i3cvSFkq4iYJIu0HMczEto+PS7kxFy/BH85uVT0dB73seVOkZPLsup6P/fBqUqeajO0e8g8ldw/Me5p2/K1mIk1LgdL32w3aNcxfPmS6xfPuX1+jeiIGx3ONVZpOl8Sa8XKyoWwkvAB0FK5c1JZ25+L4S8KQy60JU/T7gflc8zUvRguF0Sc4HZczK56bK88qF337Srzd9qkercKre8MDc6yksWJ0o8en0FWOFXAPM2MuZSZFWtZHdWhuWmZPaeLbFk4lYOVkdHCCZr4JhVFWyXSF4j0qVE6movtO1m/PUr4uJnwILhvPB+yPpZawo+E+8+7wni7r19OTvJ74SksPi4l/NaYNuf6YB2/uW/xPAzeLy4qJLlC3U1ljoVxb2bUSecI/AwBaveW+zC6nPTk82MC6iFt1tm/LRN9mdND13AmHFlxHbXamExglm4SQW48/qsB3/fGrHUux4SQ+kX5K3noag9ozX9WXH7VXC6aKHOG78lac9zORTWOT8r5Tl6I/KU12TnQ5kIXxGEpQtRc+1jHtmEuHZok8wymFe7jlj4+M1dDzd+sztJ809S3NcKb2quTNj4TY2NyAlHmsDZ9ORVX82kQsDZYt6VfESRlenlC3uazsATxFrcgTKpAKNe+oRYqviFTLyewYOC5nyxQONUiIkYTRMQQcgEWqjoh1XWTze0Jb/De18Y5wRxRaWHYKE4jkKqSjmQXHNWXeEr5vRpDJAVSynVLJR8bJa8e9T47DShdaMw+Fej6niEpfT+QUmL3ypOiEfsJBxG0V9LmQNg53nz/I1c3z4jhgE9DZpyAadkOqL8ypkvuK0WJGqrApLi0KmuqzJWM5FBrp2KWIir05p9tNkcnRlwz3hfAUkvuVLyY+qyxmJn20rbg+87ApyHjTlnwPkX+n90rfYZPA9o13Z76D5ufS3xk/v05mrbNo/0iWyDmw+02wS3KV51wjSJ6h8iBNDxD6BHdIr2w1S/w+57rH35g9zryB0Y7UNKIRG/Ws10PJAsuDCjGlCZr5os0rpWbdTrhMg0epnYvdaOf9rB8yM4OzhqMWE3wXvChCQ3IZ7g2uE9jjVFdjtRsTUAhVfU279XFaqLZO6dzvZwBrUVFMw6t+ygaN1H3bbwyIRf1rGl6T1Sra5zavaWJGs1SQRNojvEQIxoOaIyk/Q5iIO52Zvnw9i1pHDnszNWSvn2NxkgoLlvHYOOe42QIphxR3GiK8xn3FZAELjE4oXdC7z2d75Bui+t6Ns8Ud+3ZX3+Jdlfc+ueMvmd73eN7Rb54heuULimeiCdSV4SKxWJLChqP+RTzo5HpgTb3s+F4N1gOnwA4nHR0Xc+mH/C+Q7xj75QDiWttFY0eSg1dUokFzDeC2aUTwVN6yBH0ilGFpAdiTGjYQwhEVWIyEWgiCyNaBZujKpyqkz6iz0/td2WNnsrwsn1yltdjPj2Z9kQGF+QrZ69KNse7giWciJzZCSRkHoAzi/2+42ozMAwbDkOHC5FNo0BTYn+sNe/0cC+FECt07nwbuxdWu/chS0bffYWdgqfaRubwyNzayuROW2v3Y3I/HrIzg/jIzn6ARUR6cDnzZXT85X15zdCWh2wOq7D28SWtmQdsfRDRszZGbTtk9nP07Xnh0n2dsf7xdHyUKXU6XXGjYUT5otKLmkx7T7OZYcQ4lLgQ9n21on1E/U+c/hN5v5hq50driQg8BWLwnqA5cN+Jdm+JgYILfyT1jA/idqop7d1z0OWDCT5w9x2b77cwnUbeC3iHc5797i2//bf/D+5+fMXtDz+SQqyxXmz8HeK9MRWLJnYCcrDa+5bHcoeYdhpDQKt2dmMhtTYuZnTVEhZtTnON9ba8Wf+4yX3PVAed16n5XWqdSbtDSXHlk+v9ZQ9fCf5ZT7ft8V2H81LLLMRwza0JSjfvm6ZELVr6Ry1hboTettzqpqXMEyClDrk/7SdlAn4inm2LXpx3rhFEzLHbBeisCku3fopOmjnZ6kEEXLhi2H1tcy3HIiiErXiHY35CSehJmszFUC2zMBZ0qmM+ayQXNDsfaOdFntyqqLSshqL1VfbGieG7nOfGFJ+IrJQFLsWUXXAT/0Snkde8JrRaIpSeIj+LEMUMD6TML6uv9aEz5r2YcEBxmYlutSq5JTVLCAqzP1tEhPHA7u4ORxu8OmYhT7EAiBbTIvcJIubbGUfXmwuGlGKuq1lVFPeNLltlkAKQJn/XKZCiEsNITJEwHog5dkhKkFJmMrk8/5zQdT3Odzi/QcQTcaSMV/R9z/XzG7qN53DbE8ZEDCPhDsLvruivQX9uQpUQ9ux2b/nxx2957oSr51/i1dHRY0G0HUkPaBxJYY+GkbC/y66rjCmSsrZpLBY73jdrQxDpzAS+64ki4L+iBN52zuE6z0yol9dLSqkKjGMy4cd8/ipd+han++oeq8zANmi4Qp4XzdrJ29naFv4paWd+hs/wKUM9v6sUuZ4sdj3TwG+sCN8BTuHJl+fq5mRsxjV+dwj8cbR8HIG/2fwTz72HPqLesdt8g4uCu34Bux2/vv4eDjvcm1fcvR35x9/+QEoCrwXpOqTf4oeBuL1G+wE2W1K3QbsByQoaWqwIKdrVhngkyMJjSFK81Ts0uy9MRZGhnrMpCweKu8c5XVuGIuUzt+Cgc+LTGfM+n0uuRNpODRdHQcXnfbUgDcU6z87NlHHLGZ5SWRY6lU+T7+K34qMVnylmtIpkGhxViDHXMRpDvlqZBnOpkxKEHcQ98TCSQiTtxhzTwWI5hMOOGALjuCeFSDyMaEowGo6gIeZZI0BH53ozVsXOCZ9/HXb2SbZadN7j+g2+G9gMI/1GOWxfEvsb3my+ZN9v2f/aoc/B9Z0pmcQ9vd4SNBIEUj9aO12aaI7Z9Ncs3GkhD3bFqpvn9VcX+bQp194tcV05S/+Id+CEdLfB373k5sUXfDlsCUPPn3rHjbtl4xPOZ9eWMyRyzg05WczRiwfuK02ZnQj/fBCuHQwukhghBGT0+ENHGAOvI7xK8EohIsS8xymQdT2y2spUQIuvt61SWSHn1kDKV0dYyvQjWpDp+ft1AuooWb3PMeoKTi6Vx+Wolmfn6lrfLxMp84IU07DJvytCxAJGg52ZaLNipr3O9rUy//OpU7ablFDn8P2AdJ59P7C52vJss6XfDoxDR+cObIcR0VSn5CrNuVqtBZ75jufdMdw3CB8A7ptXj4LHZnDBd/Nl+WQw36mWBT2+sIsFEWtR1C+HU1qbsnK1/v2U6L6c5p/Y5QM75wRVNmk63tP+prizKVcIwBmj6tzBd74GnG+1zlOtJKwIVLWEWBn/xaFYfHzXEyEzcFqfyZURtCzvSGPudAuXWrmz8ZDj8TkvPFp28oWHwKXwUFxhbd5eYAHRtvlo5JeWIW3aU0yI0y84btTx9nQf3LcmL2aMlEN9LY9HjuNPztvF6pR1hhZmAjCOO+L+jrsffuCQfb5qSs2HZU27Jq8lStQUcmaZ6PJKF38lBEWzF8jRt8s8LxwUmeOjrTJdRdhoGdjH+VZErNE0B0zTzwly7XBfmism1zlc9v86SUGVFkk0orU0xLDDhm89IcKzOiz22Jn1ylp91zWjVxtXh6V1kVDeN6M9Y2SeXkszPH9ZBwWSQ7IkpD0ebCpscHqDw+VYBIIkI2dEJRM2ZaI0DAl0vb2y3O+n2TBj/C46Q6dSKrZS0mhlIEipxsrUbzs2129R/tGiyWerNkRVvc5CgNJc75359soWEOoEkRyzILt3ElLWViv1LnNPzQpKmQUKjzHaPiDgnVA1KLPigWqgxPMw/o0FjjblBCNYRIprioSmMVtyZDGeMx060ghYgGw0QYqkEAjjSAzmFirGSIyBlMQEES4HMi3eutIW3/WgZj5uAoM8rk7o+g7VHt85UnJYMwXuHMmDzy6fUoyEcWR3+5bN9bNMvzqbfyK1Ly2A94iGA2F3SzjskaydGZOFtw4p66W5DkFIYnXxWViimnCuY9StMWqkQ/GIdIXirBA1kdCsaSpEHYkaJ7ocMSIxZYFT0U6VMlen8ZikbHpUzsos/LOF9+EK6ynhs/DnPDx2DN6Lu7KZYH0t/xb/ft/wLhNnOptu01TTDmFMe0I5al3HofNI6tncvMD1G7Yo7nDH0I84lN7dEVMy5rh6EiNJN2iKyLAxrfshEPtoygXiSM4jOFNGycoddY9aEr8VZyqb4Bk641Snt/hX2QpzTIc5H6+cY8ffz/FfE5DYVcp1S8c0Vsbx7OxUasCKcirLvDXL2VNcWpr2v6Ll3A7m9pAY7CyN1v8aAykmUwoY79BwZ4KIQyDtAnoIpMOIxmCCiBgZw4GUImm0vF0xisxxuJwYc905UwhxWSHBi1mNeCcmhOg68J0p5PQ3+P4K/yzingnh6it2w3Pe9F9x12+JX+6Qm5FtF+mI9FnAH6O5YsoiHpxCjelQ8eV2wNoB0mmOrE2VBu+fwdmFunJKriPeU2oRCB7Hlo0f2HqPdjA65cYFRCKCZ6nscz9cRnetVXHtvUcYBJ57uHbZ3VvFzQzPTAkOqhxQDhkHjXkx1fV0pi6ullbwa6NpprtzlZQJd6nJG6S7XaTtQj4HJwlLnf+WbI8fNc2Z8PXTv4uC6552Xw9Mk7dVAZulmE2Hkm7yFyClPdLMTRTxDvUe1/X0my39MNia1ogn4aTYu5yAuhfK8nFzsTYhnv5EPK+IOUv4ZwZnDrrmZ0o+J1ZPdcfToUxnzugz8AFjRKxV7vgYnsFnTP09wbE23vJamdwTlG/mv7PcqhDCNDUNaVkygJ5iOM8KIf6M4CFCiKcss5hIf156nzboDMExmBACxyg/I8k1TrbEw47/7f/z37N79YrxbrcylwQx9Zbqj954X9ManrFrK/ImR4fc6jTNzNaUsqZVsnyLNo1Uf/4NoYZWzWojIo8tIQwxmlGvzPenCW0qDL2G5Ts9KL25JFza4kRwX3bI1x3+2rSdi0a4yy6ZWvR0WZOj/nhi5Ow+5svchVFh8szPgapBfUIAcfz9eRARRD3D7htEffvGutTZe98Pxx8nI+ATMptzxUVPy7w/j22uIPJ16cz31rrvLYSbUiw4MiEx8UWkPherMpOVxrzkI4G/FouOIuzP99kdksVamASFKVpsBMmWS1avaX2mTAQUi4ey1ixPZRxNqBCiuWwQVcJhZNzd4gSiFF6QEjURNeGdMR1KTA+cB/F4Ip0z1wlOQeOBlALj7paUIi5rijqHtSfcIQKdz4RsShwOB97e3hJjIoRgfzHWvnG+WMdYE7v+gPcd3TDiXIfzPYgzJgjQdQ6h4+rmGX0/sCuuIhB0J6TfbSB5SCNvf3jN//bv/xcO/zzy87/6W5zfMPSDBbqOe8bdG/Z3bwmHW+Jhx7e/+UfufnxdibSUIlrH23ZFVSXGhO89z37+Fd0w0A9bun5ge/Wcrh/Y+BuEHqQzpouaUp65qCp8pmJ1kV1X1blpZe/1SxNI5Fgm3nU4iWzk93iJ5gZDJGvOGiS1MRQhW7BM1hdzy4rP8Bk+wzm4/NQ+TS99ihBR/v6QmE7pkcTvGJzjX131bK7BPeshDBxefo3+Ys+vvv4Tst/j3rxCwgG33/Hjq1t+/6e3tZ/8MKBDD74DcWi3Ad+ZpYTrUN+jzgQUimDs6An3C1Lt9SicMCWzqJv9F0pw5ilIM5rwWoT5aXH85rO/5WNmPK8ww9OSKVeU8qSc83pyQiQ1/FakCCuo5y4kJFs2iAbqQUB+r4o7mHAgBXOPJGE0t0qHg8U0Gs3NkmarhjQesvA8mCumMRBCJEUljVkIn3GDmEaSpmxTqHRqZ4DzLneBN4F6jg3VeY8TR+c78B7XDQzXjue/vCL1G0J/TXI9qRvY+Zfs/Re8/XpHerlnlEQkItyxlTvURXAJF+wMjaqgQnRZC70Kx5q+P8l7yzE/6v2SKb2gDZbvj5h2J5h590G26EniGDYD127LdrthGHqG7UgYDnTe8BGp8bZaxvWH2yN8toR47mFTpqWaC0nUFBzGCIcIhzGxHyMhWoys0PYjee007SjYaIlT31JzRXQ3UWQZn79Ugap8V12dKavCpYtgRghO67q8O0ud6Szd0Z+W/BZ/yxxXCpAZPXthO8h7mUw9S25Byo+994j3yNYs1l48f87mxQ23Xzyn6yI3r36D00CJifNu8GHn82eAP4f+vlwQ8RDO5HJjETlad/PcTnE+9egseQxMgRbnmXyU4VvwTpaWACfdv8hRj7XZXFiofXFqKKcttjAf1uuwatXQbKItg0QW35wai0vglBDiVHvuY5Z9qkKMU0KI9+rKKB9mk4T9fA0NzqU7n+ZIon1iPqxsJRfDaZP2lrl6eX7vA55yTBVT2lcA2aCyNeIvJQ6v33B48/Zsg0Wyq54WH6kXhQJb2Z8eeDRoJi1Nw/uEIarOL460Q/J+I6WOeiKfFmZ469SOU11S55oTpHPI1uG/6PA+m6E3Qohz59Rxl73bmOtKGx4ChSSYyyDm+/VxmXp0v0wryc9zVXCpx+sWl/qmLKuFS9I+qN/Udmnpq0lQNN2d2l/k6KqlN6ZijvfWmRB2IY2tU0fkKAD1MQFcGBYya8/RaDWNUjLzOaVqOSCqMyObqb7ZWkAmBYBCj6do1gqaNQw1M6FjyHEOwmhVTik/C7WBIlmgkkyz0nlBvaBp8tPsRHPdzLIB1CwhYiBmDctaGVFUI2Hc21rtPWTlhnEcORzMF3GIxjQJIVh+qnhva6tQtUnBuUhSEz74pOYSyQHiMpPdXDhpUrosoLAGCexsjaok4njg7s1bDnd3FgPDmyWCMUJMoHL35hXxcEcY9+zfvOHu9Ruqsys191eFBZI9ZBBDwPUed9XR9T395mD1iUq/vcIPPYjQaaK4JklFCJHsN2lCNVYBVWrie9iq9YBHko19osfJSCcenOLrJFvii3Obn+X6vQ8feyoLgVOxIj7D+4QjjttHqQWsbJXvpYzH0xjvCy6Z7Uu8+2nx/fN5KXMLCXtyIKiwH0xoueki+IEkVzAMDB5kd4ffCm5/h3+T2O8PbNyIxmRWd4eRGDpwHnUO6fao6/H9AVxH6gZ77rrqsjNh7n/MXZMv2GLmbjom8TyZ2S9VkD7pB2MC20bQX0QRWs/kvBdpq9xAFhZMzqNm3acZ98FcJh11a1GY0Kz3XtKoCRZEsyJACuZyqVg2pOwWiWwFsY8mnAjBXKtkwQMHO2P1cDAriDH/HkaLtRQjOkZ0tHMqRUVjPmOKGodGUxTIghdXXGYW+1PvswDCzkXTnDZNanwP/ZbuRU//1XPCsCFurkA6ku8I7jl7d0P6IsIzE5p4HSemdJbeJzKeUhQwmi5e53Q0L3Xld355GmaJ5Pjd2W8r04ZKeDRals456Gyue290QudHczOVhRDrFf1w+5QA1w5u/LKXpQokoiohWvwwTeaqM+V5r65s4NJs5pMQQppy2t+p/OLGVOp3Vv5KRWdsq/bgWBvpE6O/3NLq73Hak0+OCIjjPWG6SCcOuPvwq3rVfHHim5kbptN9XYS3xSWo7zr6YcOw2dD3PXHwQMCNO9uXGuvZo95dWRv3n2mn6n/PZ4tJcY4ftfbucefmpTyv9S8/7Aq+9LmuDxwczdELk703+DAWEU+mYv2UxMunTQi9r/E/PeEyApUM+UozJOs8M1lkchNQkBpjkpz//lH1vlcIcU9Zn/CwFyZtvZl+npgo+cTgEyIYf3KwOLQLkZZSQt2kWVsY94YwM5nF12wMQRTnQHWG4LRw6nlThYroVWFTgzSh5gteEHAOnMOJNwFI469omhGT+5G5BnpBmsq7pfs/mV/q9O0MN134CZ1/bv0lX3jcrzx+09P3A847XDZZl1ajeN4Bc4GBlh+dJ/9Qc1/nHTs1r+nfM9+uCR7aZ6KOze4bfNzW95KDT4v0iD8uo2is14oZ94DiEqu4B0zKzEKhJXmKUKO04xzS2u6tda9VPXpvdJYRPkLRyre8Z+OXtczrNzm/oilZXRWewsc1x29IFqslplhdFBXNyc53eO8yg3rKyKXCfLfzNsaIaiJmYQZhzMGoY46NYIKIMBqz35W+zf6wnaMGAA8xEGJAO0E7yQKLaK7InGfoPV5Hgh4A4XDYEcLI3ZtXaAw4YvZiJqgmxsMe5x06bAALfLjbH7i9va1M/BAih8NIjAdSMga+BcXOYy07BOiGt3jv2Vxd0/U9m+0N3nf0/YCIsL26put60GQClOxeKsVCJkZAcN0tu7tbxv2OThyuH4iHN4S3P/JP/+t/4A+/+R0aD5ZHCOaTW2yM686ptt/G0fp4tz+gCq9ffY+I+eR1ztMNW65fvuAX//Kfc/XsGc/5ytw5ud4EGNE0X2MI2T1VzAKIlPskUHzSD5kp5L253fO+xzkY3Us6N3KTvsdJouu7ae6pWara2EYcYn1Lwfc+CwY+w2e4GOrZke//jJfOqMp/uNtz44V/vfV0LpD6N6TrDeOzXyMx4u9u6Q57hrevuf6rt/zzv36FHPbI7o4//uGOP/7xgOohM9wt0HI5T8Xlw0dsr9dsOWHWd+aCELB7J1UwETFt6ogzzWxxJJGsYZ3xYPEIfpXhrWShb3MPrdCXus/Xsc7nerXGLD7fsz/Eej6rmqAhBaqWf7LzmWj3WuIpBXORqjFkYbQJJEJ2nVoUCMZynwNIl79J8SBbQmYLA3MxmAfRWXwmJwlE8dkW2fsecb7GXUI667Nhg++Um2cjfrOh++oXaDdwGK5JbmDf3XA7DLzaXjPeHIhf7IhpROOBg7xiL69wLuJSysKgCWNLKIiSiGbxqllhIk0jMUOjl0zgGS61glid5GxfAidYukePpf4Uvod4j+t7DrHnbnPNy6srhr7DSyS57HJxoojmTfiI+4etA7EpiiOqMCZlf9gT3nwHY7D1pNkaWclx5ZTiutUrtW2OySKi5A9UIWAlPIrwr9JxK27RZumhuuAqVhGOvAZbIcVaI5tVru3vopLthJsJHU49bwSVOZT39Dy7uqpur9qC5nWt5O2FE6HgnrVm+bMcqYwaSDzTH13n8UPP8+fP2F5d8/L5C65fbEgvzC2bvAVNczpwSScvSv+kYUmnfZgyH7PlvG8Rxjtthh8UnlYQcZap0r6bLCRqV1VNKWbpnrIP60L7BMflXk2xE6rh53Hh+xs6DyraIAInPj3aNPNm1zK0RNpxPGZePRTuFUIsNFeP+vDo9oRg5aHE+DL5h5hX72IisICHflqKfth3651y6qC4b3qs1uGBffJeDqlPjCgtBNXcvRqTkjbzNVOuRBY2MSfbc66hOktiiJPMjl3NbmfM/Ywv3F+ON5+FwOHcs7bsRdLJird9v0irbT5izPMO3JXDPevxvkNc9pUrOf7Gqba3Wde4Zzp/9aEFcGfotpmV0IxQynVumeDaYZ5mm6WmDpcGXNpM50Ddp92y5YvSV+o4oxO0It7He/QkBJfZhKN+M2tTaU8mRk6NgOhUY8nzohVUtBYUxxU+sRkc1SvXIWkVNKTMXCjB7ZwknIgF6NaJkFJcdaMmQCyCh2SalGk0JnoRQBSBRMyCCGPU5DHKy06TCTJSiqQYSAhRxSwdouWrviONe6IYui8ihHFngacPOxNYEElicS3MJUQAHJo6Uta2s7gQI0kFxRFCZAxWbgyjfdd1FF07zfEYuhiNCe8tVkXXDba+uw4QnPd4Vbw3DVuN2XqjWDEoJJ/LOYzs3ryhi0qKwuHNa8bXP3D35jW7t29ATRu1M1fZoM0smBBXyytOfR1iRETwXUC8xx8CdMLb1z+QYsSJN7dNm2tiwvpjd0vavWEMIzHEPA4mxAnFPzhwGAa8eHxvgpr++jne9+jQo+oZxdH5TJTOttG5D3SRdZcIR1bDF2iXP0aI8Slpq18CPy05zX2VXXv/4cZj2Zfvayp8LMuIT9XS+mFgbUgoO1VcgjuFLjOOkQ42DiIk2RB7T3Qm0O17j+x2yG7DsIPNW0WjmEZ/HCEZkxqUEIU4FoJRkOJazmW2WlYCqPfe57PLcArnzHVTcnaf8nNzS+IR8VXAPrEU50KJwiRN+WAuSnjFuqxiCYVZngqNnIUKs+cZu46jCSLK2VMUBKqiQLTfONqzYMJmjfl5ETjke81ni8ZY8QTDGzIOUXCZjEdrIcJlshFx7oCI5tgPmBs/1+G6LUiHuh7Eo8MVDA790hGvtsjXX5J8z9hfEVzPrrsiiGfnetImIhvNsSqK857JvVYR5rRCHc3xkCortTKKy6MlEtj+tvi1zjaPs6u8EgHMzu7jRKxvj2ukxuz9pJgkXZ/dWS2Yuyv7nhS65H6C673CRBploUQyRQ7RNNFaa/SDMHPF1F6DVt2yNUrpdDSChn5stP8nbaTSYU2FHsLTXcPZTz2aTcHmZjZ3dJqaS4HZrKzj8o75actkMyTuuL7HOdZvyhbgOp+t+Dv8MLDpB/rOk3xetqdOrKOHsv74CNbo6kfAY5ZCnToLvuMjKzHNuJUJtmA5nOBAvGd45H7xoZCwC+EDxYg4tbrh/A6/9t2fA5L38aH6yCyWEKqgaca0PAVFs3raOycriPYYqhvXg4ds5fC+QAix/PYzvCNkTOl+d03vsIn9xBgSnwoY/WGaNsuhMSIgB6MNkXAYTcM2JdM+y6lgfmDXkV4J4DyDrAmjhaF6BrGz49tiUEgyAiiGg6UNmn2mumbvmL6rVg+N0PV+Il9ml+1OVBiIFa9tn2vBt8umli0hft3jhw4/dHTO3DEZgje5Y6r9MCOS7GJm5VQff+A53wj5j4rOsTCWaJbR4hPyXIlcEbr9l/Tji6oRVfrMaT+zhKuCmtxVxdIhT95K+GsmWGpZBbHTrIW1MuRLV1LrJrrlt4xLQ7jXrjlPzKqCx7XHHcXfdPHbv8bomjFnZXIsVhkgiSwgaIQE2SIi5OCTGiMpRmLnTUChORilqhG6TuiHHgHu7m6r5YKmSNzfkmJkt99XBoqVG2ojO+/ZDIPRmCocDgf2hwNg7iNS9lkdwp4YIn1vwjinI32/wXtj/h8Oe1IM7HKMCO/FXDp0kzsuFFKyOBC7w4H9/sBut8NsMxy7w8jd3Z4QdsSwszgQzhWPFYzjSEqRvvf4zvPyyz2b7RZB6IcNTrxZH/QbnO/MpUAIjHfRYnqGAykpIZjP7q47cPvd9/znf/f/oxs2dJsr7l59y+71d+xub9G4t5rJsZZf2ULLnjrubxlD5O7OfG+PISBOzErDOVy35xB27N6+od9ecXPznJuvvuLLv/4VY4jsD5H0h/+IfPcb9vs7DuOBMFpfpZQZVGmas4Jwtb3CDVf4f/ZvGJ5/yRdf/ZK+H9Crn9GnEeU7nJiLKiFbH4m3kPEL4fS7wpq11Gf4DH9WsHp4/mWAU8chwv98a0xJFeW5v+NfXP3OhMJXoNfXHL74FRpH9HCHjiN6ODD86pZfv97Bfocedsjtazjc0e1e4w47/rd/PPD6jULYI5lRP9dWzlhaCRbkbP/zYsx2X2jRbBlY7GIVzZrbc2tCwwEzzYtlmaaDPQurDSeQmPMq52cWZhf8xfAJTFDQ0s5JiWRrw2yRnKIpEqTcxuJyL0Y74GLMLnCyZYMLoeaZwNw0Mqeuay85VxULELF4G87OQ+8c+A7xjmc3twzbiOuuEDfghi/AbxmHL4hu4NZtGV3P6+FnaN8xXDtkG9FvfiA6Zec8EWGUhMQ9ffyj0QrZRSMuu1wqfSbZfRVqvV0RH6UGRcrIs9T+L1o7Tfp6XxDtnOcRk7d9tgJLhvqpM+vCo6wqwGTr6M476HuuNwO999kqlJqmZtugnFUY0RT84U/SCe9OSQmq5AgmIILHT3MLe+fEVluH0DX47SxIdSP8S7OyCsFhyhEZAc11aNf+opozqU0z1vXxqT1apylyou1HL1vCtlEAmq7bhK3lw+KvWkm0c3c+9WrvHRGrU2vnd9NTyfNrof0LgOs6nPdsthuL1XNzg3v+nGfX1wyDZ+dCtSRb56Pp4v4zPD08Rnzx0LFYEaJ8YvDhglW3m8bscWaSFDJ90V9/tgTOqf54nNr5qexyVs1W1iJkZIQtH/jtlnzqSDx2iSTTZpjLEpm+vbQZR/7G5fjmlBBixkyd8zNX636qzPsr+Y7vLyrigWZlD5gv9zJxG6xo0tawi3VhhM4+fSw85tv2m6Om35fhn8OeckmnZcRdi59xDHlcKiDV5TpF4eXyg+vywSt44jTHM3GX8t6zCHAvCz2ao/l37gyXhy3HGWLoBRkcXHnctSFzzlv8A7eKtDWVWCLSdVN92CQ/r4Fcr86mmwWXbgj0Wf0KTi/ToyIcKOexJI/TrhIjPg047S0AnQii05gtKnhiECbCx8rItao+qpv3C9pibj4sR8+mfO+HuTXg8bM6pEkRN2nCa0m3IJ5aq0bNjIPVuZIXYPG728YB0GbNphiz+wlMQ56EplAZI04dLmYf2cEsCWIRRISRFAJh3GdGcW5PJew15+dIToyOioEURrASM1MoEcYDMY4IpiUX9jtEleRNSzWMZjGRwpi1HR3qBJ/MvYZzhfDMxGnW9o/ZXUVSZ4z3EAjjyBisLCeOHFvbLAViICaPj579fo84xziOOOeNoYPUYJDOeQuK6RwtZlP/U3N7sb99SxwD4yGwe/uW3dtbYjxASog7hSNMG08Zv8Joisl8K0vKzIfkMK9kykEEjWqxUbzDDR3jfsfh7g73w+/oXv+Jw2HPOB4Yg1lZFEuOMjdiMgaN9hvoB7R/zvD6FTIGhu017uu/Ig3K4Dq8T/ikFuPmxBr4MzgJ3yv8NFCFp6jkYwjip4H3rZz3KcSMmDOU2qcF3vdEe+j4zs/GBOzVEAUFeiJ3YaTLOIHzPV1n7nYUh3pP8j3qnuO3N7C7Qw8H5G4D+zv83QCHO/o3b9j4gOwFiQHCoZ5TmuCwn5TkgMkVS9smyRzf9o2CigWMRrVaONYWCbiM5bhF10jecyXYi9QIImrMCdSqpAWH1YzHarWYSK2lY8yWANmKwXByLKZD3tdrQGkUcoynVHCjzOx1ztxPiTi8KOICOEG9ucHEOZLvSb43awfvoRtQ3+OfP8ddCepvSG4gDi9JfmB3dUPwHa/dwCgdPw4vUed40e2RQdFBUVFGCdUBjZcRYaQwZwuqO3EXch8t59SEYGbhA7Mv53Ov+a1Ey9LNTZtM5/en4Kn4cg2vQYOQxg7BtM/VCWGRtKWtrZqXxGP8QFBwM7X11qopmItNw7cdmAtfmRQ0iksg+5ss31sr9En9TZr5rKfHcgknSdPFi6bM4wzvG/T2m3butb9t8jwvj56fyncJl4398uyY74BzhpfR2JJls84sIboO3/V0w0A/bOi6ns4LItFwVLFxWdazpbS0yf+9wVOiMQXKnr5G/z64Kifoflm/fdgW86HOf5ivt4+HE7Xw4QQRn+GjwDlXT0rxIT/Fg5gW6poxXc2UYhUhOVCkCSQet5jm3y2ZjZcLIX7qMGPUFsbNhwbVrCS9RjYtAro+toiPQOz+ucI6gQvHRg2ZRMjaSIUhZ+hH0WynCdNw+jhdCjPvqx8lP3E4h/kBVrPWADM3rzPOOfMnLx7n857iZC3Ds3B6ehb3UyAqtQ/aCe1e9Pi/7ZHBfGtWhK6ui7n7ulqlul4zM7kQkYv+esod63Imi6WzYOatwF9nOLbh1RNRoij94QXD4cu83wteumx27qpw4hTM6X+dypuVk4n7NDFdq6MlR2PFk9+1woilEKL+3j9Rlu5pinBBaftTqi9o04Cjau2lqtmY6kKc4iRRx94CIZfmW4yElC0hyl9hUmgWxlhch0iMCZHinzeRctDLccznRdrgnXDY3RFjyL6lI2m8JcbA/u4OC/4sWZCW+yZFRDuiN6IyCoQ4kuIec0kUTAARTDiRUiR1Hd55JAXGvreA0M4Rq1sJ65cD3mJYuGQBG7ve3EuRidxkga3DuCME5TAmDofA7hDY727Z7W8xV06OFBVTIo0kTfSDo+s8nfOMh0DfXxGC4txgBFaek31vQVCJowlIwpjPVnM3ICmRwoGwvyWOe3Adu9vXHPa3lexy4o78HVcli/owu9PKTKiUlP1+RFH8OOK8Y9DBrEdUSWEkjgde/fAdv/2P/wv9/gduDt/n8YjZCsL2xpSSCXGwQNqaYLffEUPRlFXSP/w93TDw5utf0T//kq//6/8z1y9foj/7Gds+0skPxnBzriqczHC1T4QQ+Qyf4ZMHkQVD++HQ2OK9e30+CJjlgc6ewF2E//DW3PwB/KwP/IvNWztTBfO26SFcfcWOl2jM5/sYISZkv0fCyLO//ZFnhz3uzQ/IYYfc/gBhhMNbwj7ym/91JBzMElBVc7yecn7ZPl60j0twatSECVE6Ir4Ki+fMxIL3LK25SlqIOc5Cas97LfETNcc3ygKEQkujU2DoRHapaDhDiQlV8qw4EHN+pgJj70AmF0viPTiLQ+C8g37D9VXgqy9H/GbAb7f4rsMPPXHzgrR5QZIrlA07ueEgG17LFW/cwBvdcKBj57YEB+Gr35P6Ha9RRpS3YsFrg76l1wNDeJsVDKx2PoGQiFkoYLRGjpVBEdaUlrRI8pxpbI8yMlgFDMUSoiCJjeVEHb/GOqK1nFiW+ZA1torCLmightha0sfj64746hnbl1cMved28Lzpha9wbCTVDxet/0TA+szmqDBqNOvc3N/F6l5USFmAV4QQvQjdgh0uZKMXIOaYb1XRqfwms0Qqc2WOc98HpSTHZGux8m07FWZz4oJyqjQlz81KtOQ53+RR6Bhmv41VROmM2TdzRv9lMBc6tB0+c42elXE2mw3d0HP1/As219c8e/Gc59fXXG+2+D6xc4F4TnO3KeSpZHc/VTjd/hUpxF9yRz0SnlYQcYbpPV2vfde+WORRvv0QqkknyvgoVhmqRYx++j2c7ZdT9c7HTtbKSBUhOwvF0qH9ZbJ+aONDPITVtnTJMuUxXVxsCXGqjIey/n6iso2HtvPipdUkbIURq0kv2YXPIBz3fb8qIFl8cnF73hk+4kQpUqsZaOWWOUY8eyI9IjDcPAeFcLdDUzINf3HZH32LFp06SdcZvmdhZVzMTZNA8oihujVgtJZ/RXB+Og+WIpHF0b/gFF5SsXUQL8jWW0yIrcd13jRGzL76RBN1cU9FYO366bCSxxxDU+DFiRCavS8taBB2SR3EnqKx5NKQLSJM665aQjTnQJvf0bU29zM6sRDhdeQbckE5t6NVt135rm3XRWeZPoQUtHqbcHgS/BQhxMy9k+ZQ6q3srGH6Tj6dqYKqWT0y0Ve15ygWI1rzUCzOgqCE4EjOGfM6CzVKjAeNFvw4632aIM05SiBnTZDimAkZciyHZIE1U6gWEikGE24AuEQM5mtaxNytlfab/CVbDbnFfNMy1ybBU4rRglTvRw5jIhzsvrg8MpdEGCFbmp9dWh3GiPMj4+FgFhEh4py5sBKRqqnrvQdNOGcMKeccrgjQNBHDCBJRCaR4QNXiO7RsgzJv1xUmJvcMhdGUspZsaX2KCUckOXOLlRiJwQJRu8MOHXe5TxrBVspzKmF7UBaaOhwqaWKsHfaEGLj74TsTgPzDf+TZm6+53l7DVcd1vwFNmF1NMxiVo/I0Z9i9Mc5+ovAhyY/Hw3In+6Qrey9cQkb+FOE+IcT7Yk7OrayX2NR9sE6XJ+BQXyt3MfEmhjx4ResZktszyi2DcwzeIU4hCslfQbzC+Q4JB2TTI2GPu92YVcThLe7uwPbHt/iDWa+ZIMOCPEsItq9Hey5xtLM5mXBCEHZBCNGRSOY2qPIsC76R9/XFxCpu8DRrhqdssVuU9uoeT9Eez3gAWZNcsrVjxndVwJNwkgP/Yi5ubAcv572r7Fx1EDsTRFiQbofre8R7ZNja72bL1Y3w7JuObjPgr65MENH3xOE5cXhOYkvSDUmviToQwsBd8ryVxF4TEUVdRPsd0u3wuVYbVZxGRHc57oMpP8w02JfCBm26Vpsg3+0cqsIFnT8rE6rNv+a7vE7T61n69rsm37V5ft/Un9ER99Gj9hcSaISNWGwI7xPqIzhtVs4pLPyxsL423yU7zQK2CBMNk8E1tKFDqjCizty6tUwWuBPPZt6tsy6ekZwn9qm14Sydr83vCfr1eNfT46RzZHU1n/n7RcVaYUQrWbwPLuZdTTSPlrZW+qukcxUf9d4sIeg6XNezjYlhv2fTKz67uKvuc1e7TVYvf1KwGPh1ywhZuTqd1RpoTaGzn9NpP2340LjWp2ERsT4nPsMTQus+orWEWPVvvSBSy2HSuiZxxa+7yKOJtKcSQnyGpwfNnLe5spBWYUSBU0zI0xnrudvPcCHY0lsIBxoiYeA7wLOXn+O31/zq3/w3jHdv+M3/+/9JCiPD1RaNyTSmF7KIdcL14bCcD1VroxuqexZimFy0JDUEShPQm1k5GPOtNnB+wj+kdpWPrIa8qVh55a175un+1QbXebpNnwUQrmFMnmvsJHiopvsV+Xl4XS9rzbnq6GxvT0xm4Eb8lvOApm+tf/rDNcPd13VvF/wUiE/aM2Bt/k03upxCzfuqCdimnzXr0t56WK/WPhAmYcSqUG/ljFHNvI4SGyK7ZIhx3hqftSydByEH5iy8ZSXGVLUrtSgcqEMk4XA4L8a0zgIG1VRNqEtdD+OeFAIpjjgR4mjBqsf93mIxHO5IKXA47EAhlSDrvc8VicQUOKSi1ar1fE8pkMKBOO4IowXTJLscSiIcHKTQIRgjyWVmSe87sj+j+ie5sxNmMRFjcR114LDfcXu748fXb0nJ3DDFlIjV5QWIOLNI6iw4eiKREtze7jiMgX64YjtGrq6uzS1IZ+m7rstxGnq8E0iRGLts3dTRdQIaONy9NsJbwcjvor1oggWVyVq0+uLNVHWxfun6gYSgaT8JbVIya44YzSKmSwjgnLm8Km6owmGX3WeBquBcaTM4FcRbUHKXY9I48aQU2cmBGAOHcSTtA69v/0hy3/LtH35H/+XXuH7Dy6+/YXP1N2wYuZZvc9VdFaKtnSGf4TN8hsfAjLX2Eb5/jyANg3d2JRWp+iHB67tsbTUhkijfA9/xt9uOF4PPLpsch81fEeQF6dkLSAkXf45oxI07SAEdd0gM/PLv3qBxJOxHi5u0t+fusIcYkP2dWUnsdxACOh6QFJEY+ON3yt33UoXaKZag0TELue25pJZZrNkCRGu8g+TsnI+SUMnu8cQECkX4YDriRbigaMpuoTL++OwmcLOJ4DtUHHQ96hzSD4h3+GGbz7kO7Tz758/QrsMPG3zXs7m+wfUD3fYZ0g+4rd3319dI1yP9Fuc9vuuzJUjHYfSMo+fu4Emj48e7xHdj5Nb9ryA/8GJ8Qxf3yP4HOBy4yoKXqiCRkrUuNeOvBVeY45YTQzgBEcmPpJ7lmn+LdvnSAiLV3Or9zBKiCCF0+i6tfP8uAohl2qVZ+Ywn3BJMwm0IvNHETefx4ni+2RO3e3pnCl8l1lTNOmd4r0L6hwBVcyemiajCQZUsfspCtgkTztFA8YBH6MCUPjLMmpLR6iKQK8IIVXDZUqJMnDKf1naZuRBiXdBg5eUCS5IjwUCb0X1Chvab5hdm90XwdvQ3m+OPhVbKQiOHyBczOsxVLN53Hd47ttsN/WaDXD/DX1/z8vsfuJHAy12A657vX/4tIdN0l1TzY0/T9wMP5SCcfqOLsZp36qfE6FohyD8yfCBBhHDxVF8k06M+W8/nJ0dQPXF117I78oE908jU1a5skUiYCyGq4KFc0zKqH8gQak7go6F7F0sIuV9I8anOlar1uRiYVhv2CJ6gLee0/toiTcth/uBI+HCBZGGZ5GG6yZb23BifqsIHGfYl8/XU+3eFlfznrmbSjGnmu4GDdFVr1znz436qbnNhxEPgHEHdrOfMxEt4C2KdQFyiDQJ9JovT7y6s8kzn2Qnu2iE3Hjd4fO+rEGLJbK8zUDPBWbXryL6BJwR1XZP6RH2KBvwqQ3wNzjMujvNpREvqcHGAVtO8mbcuDjjJBtdiFhDGCG9c8p0biFbjkLavl/sax5tPFnZK+W7Rd8sg0MetK81YL3Mpc1jGc5jFdtAGZdPmQmnOz4k4mYT9yRCXoh3ajK2mahcwq+2M6FUrX8TmpgmEjfhYCu9jjiORUkKLgGPxO7VDzB5e1ZgxTkhxIpzEGRNfNeRYFKkKIUgp7xeFsZNdOprHaNOMy1ZWvZPKK5iYCjTfTHtU0jZYtzHJW9xCXLbCcRbonmj71xgiSWF/GHFdR4gBnzq6wiTSZKSZczbffUZ1U4754jJOmmKjxZmqQUoJxrjcT4prtnIlInjnLGirmA9vn4UHqhajQhAb3uqhYVoX1ZoiZiuRwlypacr8aC1QXX5k1h04c/8hKRHv3pJw/O5/+nfc/eJXfPHiS/SmY3N9hSPiZJwz3U4clo/Fkf7cLSOeEt5fFy0r+xhi+9MhUgu0R8Tjvj8fU+leOPXtylH8Psb21Jn2VOkvgdWcJLswglri9GP78V2KvAqKhXF2HOQ1RdPe+jXiRbnuEx0KvYPYgbtGUsKNo+3V4xaJERdGU0PfxezKaYeGCOGAxAgp0g87bjbZrWB7HqZoijBx7jpFCu6WYzalzPiOjdu9RI77UFNPPIqGTYmdJs7cSorj+vk1VzcJ9T2IR7senEc2A+I9XW+WDr7rwXv6Zzeo93T9gOs6i//TdfjNFc47uo1HfI/rB8R5pPOIs3Mt4ImYUoCIo1ehU8H1tzi5Y3P4Dic/0qUdXQqQLLaT11Sd3agqsfAK1mbQGZK0RcRPY6kNsq7TsTh9pcwLWVhCtBYUMyR2gUfNL5qyV9pz4ZqVxU3FAaTHe1N2EDHRVMEn5p9cxg37UFCxMTV8MoYDGgJRTUHDBFONZfpRP034EFh/SP2m4Pdtqqn1BZvVZXbL/PXE+7Xj6pj0aR49oOdX6jETmFSBw6IgXft2DveqttVOmfhx0l4UHLlQSlLeGa7sfId0PW4Y6PuevhvouEVi5BAjKQjy9hY3E9CcqUtptCwfXACfAiq4mGQXKzLL0cU66ArP5Jh1cPT4o+8Dj0Cq7h/9hw/4B7SIeORsrJP/ASfFk8GnsILeDSb+SfG/PfnhXk6luRCiaMPmza1IXwsRXHfGh/fRUwkhPiV4PON2DieFDu+DEn5XyEzD2f0Fn8zuP/5W/NOEvB0Wf7bVjyfGaFwygvb7vQVCDYEUozH8Zzh7ixw+do3p4reFJlcR8A6vPaJZIyMlUgwZyXLNem+zuAABOpdEyAxirYiDCMi1Z/jXW2Rw+E2XkTmzxqgxM/I/mVStWmNA9etvgodMtjUEUsrj8VDm3KWpl3EOlsyW6dYoPpd6hre/hORrghluLy4zpaUygifc99gSYl4GjRCmPDzeI9ZmyiwQeOmv3J5LBRCXgOR5UKwiWgFEERqU57M1osUSYhLkTzFVpvbGEHP9lWr6DDUGRMqBKUt7U9FImujyzNQ2RrPmsjUlxNm9c54kiXE0gYFotloYAykGwphdNI2RWlFvbh9A0TAShRpQUDXhOw++y3EMTLufFGZughTJQooJlzBmuqPvB7w3QURSZX9n1hSpjFeKkAIus2mEhGokhJGUhJRcDbDpslCkrBuX94R9tua4u9sBMGw3pBTZH75AOqFPA46OJLaXdOJQ39EPCU0d0XdZWGAxX1I6ZF5Zmtw2VUrSOmjd8lMRHF6SxcoAhs7h8PjtBk2JmDR/ZwyhQvOlZGPb9x1d6vBqVg4h97WS6rrrncsqh1OckUSqfd71PaqKyxYrd2/ukNsdP/6P/1devfgZV19+w9e/+Cs2f/N3DP6WgT/auhZPTJEQAnJiTX+Gz/AZ5vCXh602ew9zprRjwv+lMnpWGFsK/3RI/OGgOUcF/X15RcmgE+G/vPZc+bxXIsTrDtQhbEAVpwOi4DQR9Zqg30BMEA4mIM8unEiRm/Etz+JtjrdjcXc0JVIwqzWzzksQIzQuFlM+71waZ8oDph1eLAAExINrz4cJB1fXoWLCAZzDDT3iO7TrUefBb7Igwn59FSj0iHN4tzFBs/cZXXZZAVrwvGWrvwciIneNgqCVPfKCoM85qOOAcBOUvVe2w3/iWfcn5O1vcYfJEjqarAiXz/Osq3CEq03zYWJM1yhrkxYdJaB5/b5Ojkz3V2RHTAmpFlIYu+UPaiVLfZaWFCVGQMvPqJdtyOXFhMwz+IgrWPkNx18dCxTsHO+cYxgGnvXXbIeBzlsgcSRV/olBothFFFLko7MzynipEBTGEOH2Fe5wS9BE0MQhZbeeUtZvg/POOLxTY+qISyt6mAJVq2KOeZvPF7xi6rgfXS9gqV00+75MhmZfehAvpfl+9q02r3TCkcscbT+fU1eXF90um9nzSQhR3CsJhg8iQt8PdH3H9voZ22fP2F7fcNNv6J3H4fgWh+4T7h9+T9976HNhRRnqz/WQO55gT573aQ8h61KJ91ml++GBAqX3CB/MIuJSONJYkdnPvd89pSbWT502m/bwyYRs8me9RC/mHd0KISoDCplcmZw8RDOCcaLvTgohmptLGKGnBBgfEi6q5yLNOcbZUgjxkPPyQwhojpamHD+8tM4fQwDxWEuJ0206Zvh/SDjeKpcS+QlZcSK4ruPqi5eEYSDs9qCK73pjmoXMsOSxY3P8zRw9zQRLmzILNjWbL7fIkGkSL9t3/shc0hSXQdZK7pzFhDA17AWC3Hq7bRj9ZV/N72cBji9E6k7Nn3OzaiZYOHqXAz2PW0TdIq3l6nTIMTrcLB+xCmVXMFKZwNK8W9tnJhp0vbFnZUNyQjusPQ8qs0NqgZq1rpZ1qEnK+fVAAW7Vms1CCC20kjRWLtVVwURBFR/+yjQniJhP7JK6ar1bxsXPNJnZEVMOgpldRpAZDyJisRM01fY55+i8N+Y1U3WKgKzEFbDsTYtTFGKOEZFisHFx0+ikmI0OgrlLK+6jRLV6IqiyIqlfVeZUYYj4LODRZDERNBbvwk1gUbTmJWSN2pRwZMsLLQwPpQqNMuOg0H6qtm+FFAjJBDApRiIg0YQKzue54zwiCbLg07lMFme3WcYcM+1YzXMedeC0flOaXVe5dSDeOdQ5hr4zFwxiwkcXIqZDJ1nw28ZWEsR5oh/Yp2tSvMO5SMxzwaQVeU5pmu0/5XdyrVlKgd57FIjjAW7f8Kf/9D/B4Y5vfv5LdAPd8AwYcebh/aSA9FLN8ZNxyN4DPv4ZHgvLsbxkTE6leQq8bZ0ov/jr6Rh4eMky7YlPDcuz8bFT/31YMqyVMoczZemcxVhO7IL/S7splheze60+51s2zawItQPmxyAcUgnkfKzcJZnJJ5pIHIjyBvUKZGFCB1uUa0DSBpcEyUL8LltEFKF+itkiI2Vmdz2X7RyWFOf8Rsq+Sx3cgi8WGrngSTiPZgE04izYtAha3Bd6n397cILzmWb25hDHGL9ZGQRy/CUbNq87hGjjUDt0wq1V70gIUbck3aJarBjJZ7laP6qYJd1yNHQ5O05j3seoaMs9behZzXh04T20DN21P20zbdKX58tfmvcXr22r56x1E5p8cQ5RBOk8wzDQdZ0pObhogYBlPbta/RPvPxQojsAVQTtUHUkjsQnKHnWykPFZ60aFmeVMQszVEpWzU0mgdjY0hdY5VtOv1Gw25ZYT7ehIO4fr3zcf9P40OrWn1G2ubMU0qKz9wmwXPccfy/no/JN5daT031zBT5wp0TnfEb0n+Z7tIbANka0LeJcIWBwQpxEXYeM9QYRxbe4/aHK+T5zhieAcMbqW7vjmsm90jR+zSK8Pyv0sPHUPt/PzJN/sCcv+NGJEnIMHHgx/NvAObZ6ZIGthjlxqCZGJ08x1qJYQmTF4nrA8PyXPWkJ8BoOFEOIhxMjZs/g9QOHXfYZPAE6cCk6M4eW952r7jF/9V/9Hxrs3/O7f/r8ISdneXBNDYP/27RTM7wmgxcm0bi9z5MwCvPrs2AV8VywNJo1fm1+T0f+lx94q6aRtLlIfWHA5j/PFlF6Ov1NQ0izP6kt3ddEVju0DmSwPSr2oS6lHEvrbn+Hipr7LRht1P58s2jCtvnJZtNBrPAjzfYy2xtmlzPzbtnGtL8r463FvrJ0pSxR+lUzJ7hGW5RYmQfHY3Fbn1F41c6914r3Q9HEV5hs4kSmQdRYkAMRkgY9jEUYUBktTUEoWG8W002N1I4FG6xtnZ+84KmMMVTOy63uzXkjBXCjEEiTZ8u1cXwOKalJiGEmStR5TII4HvBO67KbI53gUIQRCOBDCiEaz3CgCN4+rQionYgybXH+cZn0/oXfZnUWOfSAx1YDvqhbzAhTvBC/GhCEmQkg4Z0ipdOBcxlsE0D6vWAGcEcpJOYQRN3oO456ucwzjgZQ6UjQBgROsHO9Bi6u1ybGGZiusEsQ7ZgLCiTN5ZCpCi8nHcyWenRGN3jmkczy72hBTTxgjISb2hxGTKVhpJr8SYtIa9yLKc37012z0T1ynYC6q1PY7lyClaOe6mKu9lN1bmZAoXwPkdFfbLTElbu92aAj86d/+39j96V/w9d/8S168/JL+Z3+F0x/p0z/Z3PX+aD5/hs/wGc5AZqyuCtuWh8yfA4JccIfMXSwtkubMnahKqbtr5UYWzCHz2Jau9wuRHxT+fjcJ2w09GymlLxEB5Q7lbv5Q4K964eXWAw6nnk4F1EPGByb3Klmokd38lKdaEGFdZHwCO5vjL5OAYk3JQqbOw2ISRSuqWluWXLQKN6YXBYFacLByv1ZXUnog6Y9EfsmYbggRUnAQPEk7RAVJUvUpZtiP0HoGXIGpDjNZQtt+sbMUtd8i/KC4clRre1XsaDNqFSVVmSwfWDxf/uZ66EOIGK1n+UWY+iKRSKZMvMdvtmxvbthut/R9j/OKc1oVes5U4eMKI8Sz5xfs6QhxT0yBMSmHmDgkZVRlTBnHTQrFQyaKxZ23eBGG+x07X526bC5yqM/lhKMqPXHNfP+4d8yWc2ct45nZ+3qOx6u/JWZSk3+bdTMvF3mtllHmSaYllmJY2yUnhb6S1JU15xziHd3Q0w0Dob8mDde8eP2Km3jgxRcj4pRbvO3RCi4mbnaJ0Xt+HCaa+DMUeGRn1K58Gk8pHxM+BF/xckHEuZo8Atl6HxopIM1B3p7SH2ciHPunfoRk7Wy69YSpOaAVrcyEo81yIU2dPSkHaNWqzmkKRvmAik/tXgghFvU/cse0yPZ8t5xjWz0t3G99cDrF0cb0mKl5Zh5dIsk8BVWwkC+O5u9Kq9bK+KlvvAUu678TiQzLOjEdn65/7LzTitBOZIVpPQlvQSPO94jr6WQADfQ314hzxP0eEYfve/MxPk6WEefh8W2YkNB8nRl65Z2hVgX1m6OA7fo5uwpL17f4ojT3ggWCfe5xzzzSybTnNa1rbSEKiXPf2XXvDiTr+0NlbJz4bH2t2QvNSI8LV0gYEDqKxYM082JCdiX3kcwI3moFIYUZK0flHgkgViomyMyXrDLvt5NtXKRDmxHQuYurk/mtSEjPHb1lPrZJNPfpFPchP6PV6lupfO5PS5L9SZfg1kmnY9geEKMFLk5Zu1/VGMyTv+qyviNOFdE4ncdO6HyHqDKOozH5MxfB9x2EiXQxDXtsk8jCiIQzXoFKFbAEVWII5j87ldgOxnQy5c9MOKoiKWEBtiNOBeKIkojiJs1ThaQBkpjrp2ahF9/KQ+fRqESJJjwJypCFAHU/0xEhmnsrVbTElRgjcR+I+8DoA4dhNM1X36He0XkH6uk6I5erVVYew+o2LVt2GFjcBRtil/fS4iKszJRpxogDUUfnLKB2FMVVanly6dHSutbdDnGefnDEcMVdPJDiLSIhz50yD7VaVKRkwc61uvkqZcynpHdmGbF79Qrpfs93//HfIb/6G77+2c9QegLPcRyqZcT6fl7m8uPw2A9lDfFQWuJTsdI4qWl2T/Xua+6n0LxlHed1eth4vQ/y7TGWEbr4rXvAjCZq6SalDWo74S6XUTLvSsus4+Gn2isn3utRkmX91neO4zdy/OjoQT42j2o1Q9zyvR4lMlzlLsEfx2x1tziry4nY5iC50BbPmKrW9st63x1hc1I8AlzE3s410QVKYSeVNMosgwgvfDt3V2aISnZdZe2IJKJAdGaVoqrZUnKy4FyGW0hQdCruoeV09lMPuJmEQmdJ5q1bDPSsv8tXyz7M6y2tlb0ihJgYQqytp/nyz8HWVxRjlnO3eovIAcaH1HPd9WycoxdTsIjksZJFPssW3b8lLCpdK/GQV1N5Mx6B1bMIhEII7O5uCeO+KlFYvpJ713AZl7815ZLZEqS4MUOmKVEsNovbrmNNcWFVU2ll3RVW/EVb92z6tB/oyuXxDr9al8JPqxa+TR1Xy1o+Ox6dGV2mK6uuZN90dFEmK+HonBdc53Cd0fPD4Nn0jk7MSnmX19d8Ppu1s/Pl6eV71uXtO3W2PBWcoyYf+MlTwmxPW9Ylz3dWXn0MqALvxfMFT+LUWf+uTfggFhGPUAydw2lM58IXHwkzXxSr50S5ZR+6tK4ntEin3dk2ydYyYr5PFHbG8cEr5OCQFKYUVPPTy6u0LoB4oPDhxO0nCpfNvbkwIiNql66PlUF4SrdMEw6pJwVGJ7/9JHbUh8IlbTuxWM8QJ9P79zVzF8hZw+Gcapfw+h0qnq7/NfgN3nuki2x/9oLxbc/tP+1BYLjami/dcJuzOdXmB9TqmEqqLyZ8ak4oKDJHzLMVVUt+Hs/38wiHNMmqTYOAu3IM/2qL23jE+7IbTuRPRggLwWZ5zJHlS1G3hzC/Lpk1x9pkoOrod1+ZMAKpbndUs/J21eC0AlqhQ8vgb4UQFdktFat1bPpjrb1Mo5ZyutL36w6eSnaTZYfUhjZtzD4Kjpij1XfBVK356dO+vAw1LkKBqmSXP0qoBW/W2WO7LjEFUMg+qEOIldFQPiiuIWKMHA6HRuBh7beAc0JKwWIYpGCm1CmPT9eZdv8wEL3jsLslpgASzGJis0G8M6ZCUtOszy1WDcQ4gjqS06y56UkxEMeRlJn8kLWtymg7Z1ZDYEKInKdLDu+UFG4t7ohuzLy/BKNOIcd82OTxFASHE8/QeW42HV4Deojcxcg+ks0PnJ1DKEghl7MbpxhIQTncjbgk7G8POHU4d2uMgX4geo8TR98pm36g6D2qpqxoqSgm2CG1OIoNUiK7xFCX96nyN589IoLzjsH3BBzBKVETCQv4GRttV0GRrIrqouC7jm7oudMveM3AMP6eK7evAbxTUlvGmbkZRrNaSSFlCxibh5ESg8J0E4d+QwiB2x9f40Lih//v/x15+2/4F//7/xp1W/Zs6PiRDd+2s3e6qsw0js6DYtl6jon7KTDDP8MafNyBmTGZf3JzZDrptR4ith9MjGf7Xdw2jJ8TTIlPGhqm4ulTtcLszSmO2tGzee7HqSd6qdKMK1kK8MOo/DBmxqfEdZ7jah1W7i/mdp7J94IsjpMcP3nZCf877/AtPiQZ5wAER9KES+bzn5SIBIIoo1Mi0VyyMO3fiRqrm2yvYLGjCn55Qb3mz7VpszL/V6gSjrIoitJIeUaxwI05bZO3SFP8fB1ZvKllldbGdG2s9ESavLaXd+VsdOA7R7/pGNzAy2HDM9+zxeFwhBYnFVCRzAOSKcOKE77bHnAfDTJnxUxUi2L4SVRBYiLs9ty9/p7DIRCTYUc5GozFdADMtaajK+OZx2WikzSjUxOCXNEndCZvyKNtOGiTxjEJypqPKZz4+dCujHPNTNff1/xK+lzVdq+Q8o9M36j1hM1Pc6NmiyVNLt5WR2ISkplii6vFCzQuUuHsaObuaHlpmuOR+F7oho7hesPVzRXbq56bXtj2Hi+OH8UR8/5ZaAGLgWZZu7ru18vV0j/HJm0Xwkmq74Hp37W8S8pu379DPepQtnk0hOCD6/O+4J4zrEm1VsN3bcl7FUQ8GXpVF8d78sl+pD25Xsax5sMleT/w+SVQrRcmsP20aGwybY4sNpd8EMnsft7mQmhOxKg0XXRc8ba7jvuu+XZpdbH8vl7oiXQnOk1WL++fKxeOwaWM/uNRaetiv6tazRfhuou++AjEi54Yl/bdu8KR+5cnyPf+LeO+A/L8mD6sMo/4Zg10OhRWibeKu9s+4PQ1Gg9EfQ54nn31c8L1HV23Yby74/bb7xBJdJv+6ARJMRJDOC7jQlibLbP3zdoo6PFkr3zJDLgPDW/LEvDgv+hw1x7pPJ6BYXxBsYgoe6gFKrQ6pIKE5s207reiRH+LusO8nGXjVt7Nd7uVbxtY4t1ljH24QWKfvxNc6nE07qUy0lo0v9f6Y4oFYX2+mq78cwo/Xjyfzcul0GDRplm2jSDCcF6lquyRCc75gbNeofpF0UGdiKWpqPPXR4G/Kx2Wpnf1F6rWVwkxkshukcxSYcrK3DelGAjRgjW37U+qdGTf0mhlOJdggYq57EkIKZmwQ1gE+87nv8N47PVx0aa3XICUtd6UFCIp+9EuggjNXSy1Qc6+l+KCKgeaL9+oBYCOqqQYTQMzB9gu/ZZS8YMteO/oOk/XdQybnnBIHLI7B22EJ5UCo6pP2LzOgp7dbm+Cs77DdxESpK6j9x2CBRCX6lZkvp4dWrUXpy50iDm7wLmE5hggFsQ8u4qb6GzLtQgLQsh/MftaLqvB+llyuRYTwwhD5xxd15uAKTqzelBzE5KkaGpS+7lavZayU8p9XAhmayUIKUZeffs98er3/PGPf2R7c8PV8xeoXjHyEs8dTlsXJ2Xet8on02ljvKNGYDjDHbkQTn/zfqyl3w88lhz5OE388Djjpw6X0pNHgu/F78XlQTklHgwfTdHnqLrTrtzi66ex6Pdd7/WSWzy4eXIvzCwlLvzi8W8vSy8I+wT/NCpXAi+zZcQRjVzOmQbX0PxvFw9s4g7VxCqcqqieSbDs5HNpm1pOGOIZpLIodDzF9DnJT1x5kQkRrUoQcyWXggs7ceihQ+WGzm8Z+p7eezrnM+4mi/Oh0DW5zHxZleGfoJmnQJty2mdWK8NRokLMbKOpy5uP5t2QscfikrNkypEldElb8xMIRQjWzE8txbV4+hGRMPEg5nXUo8vHQLW2oPknK60Uy6n6fEGbzCv8sHpoWiS+CEGw2nonFgPNd0jXEXzHwTleHvZcp0Sn0WLNNESc5kGqQgiFqygEgT3peLK8Y7+eh08dLzm5eVwE53h/luCC4t8rnGCgrpR/aVUeWuVPP0bEZ5jDihCihSKEMMK0bJoybfI0yEtGZFpN2Pl1Tr+wbDhdteX7xwgh1lKdIRhma+hT39BOw0/TmuDjwKcwzq3J9Metx3mcxd4luvQdKh17HXD+iq//+r9AMtPs1R//kX/47r9DnGO4urJ8mz4e9ztiCCuE3ek6nYM2Czm61ppK86YllSI8l/Hl4+EGx/C3W9yVNwZg3HI1/pLiyki1WN8W5nFGk5M9K4hycdWzv/odaSGIOF3NdSa/MXzvGUyYucAVhH7/gm58Mct7opsaDnRKU951+5dZXkUIUfVlqvDicfNcm39Ns33e9pnAYf5iukxzM2xNk6VWe3ZMdT1Rl0a4sPbu3Pu2SsYcNpdLFnQ6EbPlg3cWV6BzHaXSZhExztwlpsyMD2E090IxNuUUK0ZPJ10eN/ObLU1lYgiVqZ9Syi5ihexrCVLMcQPMT3ESASwOg6oF6TTrAhNyxJBxhpgsvkOO4yBiLHmHVKa6aLJA3L7EwkgQI8kFknPm2imZIAKw+BBqFiBJEyla/s47vPf0Q08JYh0JjCkgNIIIlwegChIE54SUIOR96fZuR8xxQ7q+g6jEvmPoOlA49COdEzo3OeYoWnOpBh8vQrlslaIux6rW7Oui0KDTHmW1yeAcGiOHceQwBsbxYB4kpAgGTeBQ5Jmpofg759G+x3ceHxwhWPYxJSDW+sUYbL7lb8v6NOHEND80mUswERNEvP72e97wW/7+7/+eX/zVr3j24iVJrtnrNRv9I447yp5b1oBzOepHg/+VtTIX3F3O0P3Y8FOp52f49GFuBfFTgU8Db/0wcH87T9Jd+q7sp5zNE3b1XYL/tFe+6oQv/APqpgopMYw7JN2y17iIdjaHzKpsM+CoL/XE7/GDWT3XS81zckKE54TNGl4sZI63HmVz8sEpwmNRq9Z6tZz3LZ/EquRw4oj7AcJL+hcv2PQDQz8w9D3BHWZKPvOyJh6OCI+bZO80MQuum0c2GV43ajIFkkrblLJmyGf9V7EhSJk+k8qgb1PSlDXFj4mOjE/m3/aLNTJoMR1FmQk8Hg0r8SFmdEu5zvia5MZM9SsWEU2jG1z/3uJrETrdnCS05Xi+CLgcIN1vNvRXV6RhIPUDL3a3PIuJbnuN7zyjOMRVB8M0Cw4fIjcxcug9h34Z7aPhOT7aGuKnDB/yjP8Ez+f7BCkLeEztLxZErBHodYM9OiTmLKXZNnx2h1mD9zgJLrKEeJfyl5PqviP5cWWVwzIVTbvSx22MV5n9TEyr/Oucq/fF/LDeLxDutW5aE1acEkIcyyuWQooVptI9XTPTzHkiS4j3Do/AUk8Kcj4gnLOMeGp4lzIu65vTiT5ppkWDnK9V80hDXRWIeH5Ewx2BlyAeVaXf3vDl3/0dh90b7t58h46RdFc5r4jzdJvNycyL8LP4lp+Cr83Xe8XV6l7UMr6Uol2uBSnLyD7FHcy9Z3SLya3stZ2je9khW4frnVlChC/waYNxO9sC5gXN3KkJ5mc3J/fjMyR2zbpoP0yE/jXqTmihHTVhjoX7sMWH67mf+aa1krYgk8B3EjLnfwpBne9LzxRhRSWWXLMHN4z+NUJ96Zap1aw6TnyM1i/fte9TSpAmLSmZAnOQlbTRTBSqZB4vl61Vo8dtbtk5N0FhRltAvkI85nJmQopioaCgppkexmCWCd7nwMZlPHL6GIklCDVFkJFd7KRYBRE29Nl1kHpIsd4Pnc/up6wfYgxTvIQsnRInSBJUE+N+b8KKFCAFyMKHRKhCqdKulCw+RSGoTOs+Tm1wDpzlm1I0wYZTUnL5+zjDBYtLoXKOe+9yP6Ys7LCynFjWXoToHJ332Y1Skb9EC56OzLTxVMiuq5QYFQ2Ru92emKy8rutIMdH3A53vSENi6Du08/giJELMFj3ZfG8FXDDtQ6lacehExFUGyJxAN+uMwNvbWw7jyN14AByu6yte5Zyn67LgTB0hBlzwRuQ6c4nmpAhErb8ipcpTLI+6FUkh7qcg1hUHTAkEUlR2ux3dqx/4/f/43xH/xb/mZz//Ob7v6foh7x+TpQNV4ADrfrPfL6H0aC31xXePjW3xseBdq3f59x+P0L0EV1mmvVej8KNAQ29UPEe4TfBjUt605+iFOZ1v3lM2/unWwX20wKeiYHVxPY75j58UKHCXlH8c4ZkXvjrBwcnYy/zDoxQnWqdzm501DHD1xdoCvXjR5vrMBBClDJmet9VucVxxTX1S831LiTTVXmNOnayZHKWTjIPgHEPXM3Q9fd9zswm82L7ltS/404kNT47zXBT6oHePnqeqZlmrEJIwKlVgUOgtx2r0DRQTIBQ1iSmyX8Yd8veZujM8Kr+zaGIZvyotEObjW+jCRUNdfifoLC7iIztg5VKnstu6KBk3N9y/+jTT5rdtcG3DeqlHw3gPbWtTpnSSKbeIk6zMY65IQ99zs9lyNWzoY8SnxKYfcR7uZDmKZhkxn6bHfDxmr44W4L3wITDHy87QU1+e++rpzsppa7uXkfHwvPPvk/dvU9UL9CQfDZ8tIt47nJrIj5jgK1i8HaoLIYTqZOqVmTdW4hyznxD9yTWHMaSknv3Luj6ZEOKshUTz7FJE4ScKD1nYn4IQ4hTMGLU/GThx2P5UmnHmZFh9pYlOv0el527cggw459jcvODv/g//J16/+i2/+Y//PeObPeku5uC6xiDrNwOyMFEmWwwUpl3MGs9OiwXWKrqVv6Uyc4vlgWaGbA0g65TkFVf87l/MkViWmfcaL3T/bKC7MqauTwPb8Rc4JvWyKhTJiLEAutS8WkAfXkB6vpomSSB2dygnXDetVr9UBny4YrP7xpD2itzOM6kI6iSNmOUlOuGQ81fTHrwUQEwwR9TvFUKsjM0sqHRRUmiY+zOGYdLZs+IaSyuybxVUKYi5PzIZR7IbnUoWlTrOrQSZutmIJNXs5siZdQHTvjZpgufYS9k9TkqJMRzM/VLvzSpCqIIOUYghEGMgxDAJM1IixBFNsVoOlM1HNaHRkbzPga6Vzg1411XhQxjHrC0/9as4MYOIpBz2d8QwksIBTebP1rTkAyWgNWoWPdaGYPUVyVYWU9B6wYIlF4FDlIDDkZKtG0sLaA84Ym6nYO4LOm+Bk2MM2Y2TCSI6gSQWsLrzjtQ5huiJCcYxElMy4ta1E11ImHBDUQ4hoEF5+3bP/hDQFOk6TxgDwzDQdZ4UI5uhB3q0zyivE2NSODF/BEdztlhDZb/bmEsqcYVIXewJCWKMjGHkzdu3HMYDuxAQ59hsrvN8cHiftSudswDgQUCcCVbErFqsvUUQEpHMLBCRvCfP6yuQ44CYIKSsU+PbCDFFDrcHnvkfCf/w7/leR17/N/8tN8+esdls8v6aR3pFyHwez/iEkJAzcBQH7T0SVR8DPiVccAmfct0eB8JRYNXcyNsE/3nMuIN7GG3yU0I9PxZ8MFrvow/ENBuWbb5N8J8P8PNe+dLP97aKd7RfzZil62WUX7eUAdS7nKb9vv203UyLpd+EHK70ZymhIG+NprYhIhXXW2d8Oiun5cBJiT9winV+nMvsDJjlde7j3FcOxHX0Q88wDAzDwLPtHV9e7dm5HpGuoCz3Ifxn3sjywZNAOzSoBaU+KIxJmDC/hqQocp4GZ07axI3I4I7ohXyZcvwRlIgypiyI0ClyXP3RlQwyul67v9BpSw395fy8aB2vJCodU4QOJbNyX3+Lpfny+r4yzXp3hpccrc3pYcuKK7SeuRn2dMPAsBk4bK/wNzc8v77hpusZDgf6FNl2B8QnRDxNL1bFk5mtel57ou+Hm/O+z7jH5X/qq6c/a1qeqrbz/Knyf9LcSqYTsvy+8OZ3EkSc1DhaEjP1n6Onl5RScn9Y5Vp4JCYsK1cP/f5xi2L56PjZNIcb4UPDXKjZyNwVE8y1Z2fmg5mBMt+VzlbjqN6zNBcKIY7yXeuCC8fgrNbbRySIZnjaA2bFqXZ/UOKuaqicL/RDCiMe1f5LP7okWcXKPjLFcqZN1QnJsooa6fkBZSCmL1ARYox0/Q0/+6t/zbg7EF4eSCH7KW8IIhFhTG8Y0y2HN3fEuwNFk9oPDkI+UhRkLxBbOyf7t+KHyXyvSwQV8z8PRpo4L/iuz63QFv9v2jflfG4UxIP/2YBsHX5wCD2b8Uu8bmbrazrP8l6oWeOm9sGZUk5MBYdnOHxJkliRabhnn7LK2PfxquZdkYB2O6dFTPOna9WTOZOxWMC5alJQ8jvu1SOEqRFCHAkmVtqxjL9Q6lLiEBQLiPJey/NG02iylGmEUiLmNkcXtOOpuhzVi8qInzTfUyVjrVum9ykL+DVbQtRyMnPdFP2NGHEiiMtBlbPVw2F/ANSIOpO8kXKMiNq/CgljfOf/AQhecJhmfkLNIiLGfL6ruWLSaAGn40g47E0QEbM1RHbxVAQMxfWSi0KIRRhizsmSFtdMzMYqpYRINB4+ZGa9TUoTVshEeDdHhnfm1ikUAU60GBDee7yLeDHDBC/Qd0bKelGCmABERKryGWJuojqXA1mLCS73IRA10Ql474ghcRhGut6sI66urlAU3zm8E7qM6zjxdZ7YmLk6XxPg8jyxoNHKKWmgqhJiYAyRcTxwGC3Yo89JlElg45y3PU48MSaQgPcOvOeOgVu9JqVdHW+RSBJ3tIZn+h/52tyFTWlKfArnPCkldnc73Kvv+P5//h/Qv/47nj//r0hyxShf43iD6G0VpLXrXnW2wmZtXyyred3eI9y3h56M9bbYPx8DlZFzYpN5SN7v2lefIqP/kjrdR9A+di6dD6L++M6arIQaBlmbZ2bivAtO+H4wyjbHd50s6/T44/D+h31zPw34hD33EVH7d+U7FGhPKkXQwx2kO6TgV8KkpJJ7VyVrwKvWQMJrea4XeOrtqee5AuVoaQIfmxQvGWKgzfpqhQ9LgYNmEkLLRRsgeL0357TJ4p20KeYZGS3kiCLs+56bvseLWTSKm/gp50q5T8h/qRDipYMXXvghKq/SejIn8E0n3DhhaAkFlYoejkmyToYDUzXJFpo2f6ahmBAPRXMA9DLP5lWdllERThX3RinjjYuemflbWizCGR3y0Ll2JrkuHhQhR7vXF3z/6G+RR1PHtVFfPpuNlaxcaqHtGs8kefy89zjvcV2P22y5ur7m+uYZz7dXXPmOYXeLSyNviICjcQBbS6nCiKyM4qNy4x1BhZ2f45KrFb336el077K9nivr3LszmMGj63I6j/MtnFCFJd/s3XGIy2rwgNzKvsxkOX4Kz3pMT17umunMuzqxnrBiHxKOtKWeLOPpMHk0g7Yy7cn5NLAQQsyl+60AonFtQnPAzYQQC63j4yqsPJf1dK2GxqVCiHccg1ldnmgA34f2zTnN4VnZsp7sWGhzIuEFedc63VfGA+Cp+uydiOsLP57qur5Gz5qbHyGZHx+W9W1dIM1fJDp+IKWB4G5IyRFjpO9v+PoX/8aSZOZjzAFnW3g1/j2v42+Ivw2EP+4pjGJ/3eHUZ3xT4XtQ473megBkay2dvNQmil98C5LlncN1HcNmICVzfQNYkFfW9qh1DY46uk7ofzHgnhmR4FLHJnyF02GdMZH3bc1lnjOImO3Ls31vuuoPL+1qobmWa76a7yQEyHOtIO2zba7dx49qc9Se4/1acndO6+DkbF5w3qoQYsH0P8IBFoKIwkydLB50lqYGgK7fp7kWuKpZQzgBnAktMlMaWc7003ti7d+UmftZAKKYqyLLvdC+iZDdCdXzthApVVARMeMFIUTzzd9500ZPMRJjYBz3AE3gOEU1CyJqP7ZttbTeCTE4ohSfuokYxykGA3mNa8qCiMB42JPCCDFQNbcaawQTZzhEAjHHhajTXM1yRMo4a/k8ZbdMUonKlgQtGsCWxj42Zr/lbBYZFrsCMasG7yV7frK4D4MHj8erMlLIOSGmsu+a2wCziEh57iYOYyBEh0+Kd8I4BvpDT9f3pATPnh9AlO7g6DuP74q2oqvBxSVbJhShFBgrwwQurvZbmcdlPpbfGBMxBg7jyBgCCZfdaRnBF2MCFZwLQIc4R4pKSgEZOkSEWx240ys2yXGdSnmCk7TYP6aRb+d5qfvc8kgQ70mq3O13DG9/YP+b/4ndZoB/9W9IXJPcNT4EOu6aMrSOf7k/uZ5yoqnctp4/fXgAelXTn2UyvQuO9RPu04f242O/eZ8wP/EMKj3zBPk/jJ3x2DLekS59Z+HGhx3Ui11HtSiUnG7ZpzQnl1amLZT9OyVFDzsTRMzwcbF9vSFpBDuPzYulvShWwfezyJaM2zb9ype1v4Xq+F9KPo4cIZhciYzrpeljBVqXM7qYl6Wx+pgZVzGrfKe1wgWvSSKMwwY3DPiMq7mGZ1Pw7iNGYzkgpiyPmNP3uT0rKV944W8GIR7gdSrncM6jGetf9MIXfoqDV3hGmgRNQkhCxNkoZ6UMj+CSCSEm+UXGO6T0SsFSihVmM4y1MDX6rSKTkxWwpV+aNTcdUfujeVznyFqKtYx0cSvMo3Jr87fMS5kQocVfaU+1hphPx5VmLOq7RjM2T8TWYuXnGaIKiMVY63v8ZmC4uWH77Dk31zc821yxdY7em4X2W4SQlXZkVqZdt7iKj5Gbu8hu6Ni79R59KvTjvnzeR9kf4mx9UGl5akozR7V9cf7re0t8UigLr+L2C36Trq2dy+BJXDPNl9PD3z+orEJkPWWmnyoshBAViuAhTb8wR6rqNyWPwrMqh0zDnJr+HlK1Fm1ZJ44udcf0GT7Dx4MWEXioRcf9aPknASIzBH1a+4mB71EdCOMXiPOzWDHHDC37HeQlz8Wz/eIbxs2eGtisaJVnIYZ+YW5TjDlG1bLWYExRc+ES0Rgo/tCdd/Rdj78Cd50IP4zs/7QjjoFwCPNm0fS+zIURAogX/NcD7sohG0Ho2By+xLNF1FdmcNu+Nu+C5xZaaDnSBZ81/uixW5N7h+XUPiggOp+LRVP7iBc405TJz+6phjRIbRuc+tJDdU0I0QoKjtPr7Lrtq3ZqVv/3zFdlK5SZAnpfeIY01WlkOjW/GLM1RJqIkjKXS3DmMTOWa/Pars5M+/KlKoRoaUMOAJ00ompxIoyMs5gL3gspWnu0uihbuN6xaIAc9koKJegxtb5FsCBqbo/CYU+MI5ICQjQSMRNLqYYELNYoCYKzdSkZn0gKonVOSRbupDzeSRMe3+ATGQfJOYsozgFJsjZ+jovRCJjMbVMh2h1O7NqLIFkwIeLx3gQQMcebSKnQYELnbUF6b0YKISZSVPYp4Zzgglkn9MMAwO3tHWM4EMJobpqutvRdhx86BGc8j0x8O8r8nFgBZV9zdXY2MSXKesDm52azwXcdEcH7jr7vbY5Fm4BmWZLwTGvDLCNgm+644i1JYrNnKjGZBubU09OkrnOmEpRZ2IeSYsJ5T+89ne/ofEeMge++/RPpy2/55tWPbDZXDNstyT3jkDxe3+CzQGJxdHyGB8B9wojP8OcKf2mD/lBi/POG8hi4csZMdvX+WLnEQJq/CSqWUjnFedwqTpPPkPJl/idlJqaqoDVK8KVjeEG61eya+rXPNGEmpUX1v3BL0yyZHcqlJSfMBC6tvyqtMqc4QfeeeHuF+Cu2m4Gh83gRXiO8TcKdm5CDFYyYtt8fy8t66eCrTnieJ8RXHjYi/Ckqb448Uy3ngmPkBQftCUk47Pbc/v63hNu7LOcRs4RQwbvK5aFgdKUVJeeWhmjVU0QTguLKVxkP1fxvVG9uJ7OronN1BsOXtLrgmlrzONDjS0NQS2HNn9V9/kwXZbe90+Sz1hZZ0n/rE6AoXBW6HABn931vLpm07xk3G77YbrkZBn7+hXLVR95c33A3DsTX38FhXM1/1vgkkwl2i9x+hvcLF2ynf+6jcLkgYo0aaQ7Bcx3VEv8n09y7EU/bXssg+yjwhEXfx5Q/9bZKtIswoiF6lpreq0IIcXaA5JgQc43aE3VZ0USu+R9ZNJwXQjx0+C4e7wuSPVYQcqoOM5cu7woLVYZ7m/0ALsGpvB63lN7P+ruoLg+s8L1rrGG2r6VdMuPfXZvsaeGi+qz0mZDoeUXUDQeeQTQ/5yJiQWIbISVM7R/cC3p5Di/nfdMGeE0pkUKcWVUUZqQcchDWMKJEVI1x6xz4zrPZbmF7x+H6D9z95zv09Q8c2FVBhEwNOOWq2cAJ/ucD/oW329SxiV/idLMQQkyftNdtVqd6dsbCfwzX7tTUzMKIQq9QGPjLZAWhlcuQlVUhRFOH5RyatjZZ7agqhGjuodkT7xFMrBeWi3TONOjbJEz4hMjx8xlO1xIVU67UIOmpaOmnKsxvLTZStsYwlzsjEzlG7T+O9n5Lb/nFmk/KbpEESKJ4dUhBv4oQIjW/1EIQB2GMxGDm2LlzAHP9REqQTJgXxgPauGMy4Vx2tZQFDkWgYG5tU1GwsrrGgPOunulmNWO1MVdFpWPz77J/pWhwmc2FpcpMfdUc4K8IO7I1hDNrCO8dJQSDCHgvjEGRbEkgqPkYwOLXJ2/ahyJCzMLOQ8pJHHQpsdnvcN6x2+8I0WdXWRs2fZfjgPS5m112q+AyUczkIqzsr1mQUk3ZZwsn94MThmFAUjRtQufpu44YI8Hl8U+Kc9mqJm9gSRMS4SrtuXE73pDYFYGumnsmK1cn4WgWAaVcvqJZWJEFWlWwZO6qnPd03mJm/PjDD/gffuT2zRu879i6a4K7IeoW0T1O7ya8cY6SNM+OOSinLCPm37Xf6kqax+Jnx/V8V3jXvMr3f+kCiUv68V3H7xJFgIcqC3wM+PRruAbH5+z684dBc+KefPuYMi7F3T/2dGlbvnHwq94E9u+W2dSrLUWjGaGe/PwL0xFlh3I5d4B1eURlzp5AqueJV67X2lYOIp0KrcKIfNgDRelhZlWxaOmD5Cet1k8WgFhpgo4efXtF98UVm66j8x7vhFuB2+TwYgz8eT3mNbJXst7k46P1qIueeZsPYN3wshNeAnd75fUcbV45fxwHnhMYLEbY/pbxx2/Rg9mhZnUZ401ngU5RYzmmkaf76VQvs8cQOlfnRco5pYwKTjTYzO1THbJ2kk3zavLg1BKA98y5tfm6nKtr71qct9AUq39MaY+EFDJbfhexOcp/TmYD6FzG5fqOYRgImw3u+prt9oqrvufLq5HrTeS7F1texw1Xdz/i8riuTSptXJ/NZH+ZtvxYZ+aHQJkuLePC0+KeXM+cV6tz893h1BbyJJk+YX0/SLDqoon4Gd4NqruAol3YCCEKFGHDbO+mEHfFbFCqb/B5ANr5xmnfnapN875JtCpo+GwJ8ROA+8bmExm7v3SK/img4Y4IgpfIlm+ZjXGy61YTI+gVUZ5VZmCBCak28s6V/WnIz7TR41VwY2H0WtyE4gOnMj+dQ90zOv8cvvkWnOfVP3zL/u2uMk3bwqswwgn99RbpO3iWkEG4cl/T7beWVDtE+yyInZiL5+QHS8HEvWdvk9nEUNPmdesyb+XbeemZAWvXOs9+XrFKTC4sDhZllTq5su+fWU4n+2QazZmmOzBHWi/lPhViLV9PZ4iYdCqXJpqfFQa5yxrszuIG1CybC62EwawBFO0mzbETyjFWjk7zHpYIIRLGQAxhfo4JdW4X6wJNprEeowV7PhzuUFWckxwEe6rLpEGf15ia1UHxOmBDamlSVGIwy4e+7/DOZ5c/oHHMcRcOJpAIB8gCDyeSw3NrZao7cSQHkutqGvem/WbBA82EXsRPvo6NHKlM/8l6Mq/tlFBngsfCE5itsWQ4inc+Wx5YopgsfkbR+q+oRMZLkncoARCKTKBsPb0DUaX3gsPz8+EbOulxwCEe+M3tH0iS2B8izh948+YtXec5dJ44BgbvQWEYhuwWyqHiKNYqJUC3aglKaRUrdKgYu59iRaeacAK9czy7uWIMiX0MJuBwgqqj63ylTycf0jbpUlI0RZtvef4k1SxgUQjJZE81iHaD4pUA79hcIwohpep5IEHWajUhSUpw98Nr/vS73/OP//iP/Np3vPzqZ5OwOJV9cbnZ6hMrAX1kLt9n+AwPgmKttj5vl/TNUsj/GT7DQ6AIHro8hwaZrCHug8ovZXKdM6Fjc4ZkGxMLLBaVts8FRAsuMbGZZ/Ed8rcN0vVIOGY6zxnCD4CKfpdzTDk2KV4U23zb6pi0OKn3HvGeoe+g6+m8p3MO732O5eQaxc5TlX7KM/TSvDIOk+cFZphOTBASjKqMqsQEKVvMiEqNCWaxQ0qbtOLJtZUn2lxIPBSEhDP/oghYDC2UhOBUSUdWMG07m8KmasyTnOwj5tNpLXERJlRBAvN7LdiUPZtaenFFFmulpF0otRTIAohqKZL713Wevu85eE8aBn799RV/9QvHl9vIdhh5s/V813kOeFyjyGW0hebBkClLJnxPM27ahcRzHKMT7krclc/wfiET99O8uojj8GcB7yaIuG9yNoyY+7Se/tI0h442nlPa9kf3hfFz3PetEGC+12ZmwkwIcb87pkkj7ohjdr+lw30WEstCmpo+CqS9fNpJ9JCgiPcx7z4kXLyWjhgOF5eQf9+9bffNi+OSH17f+/rj0nGemLzTv/fBqfF/7Fx9kvmUVY+FSM+b1XxdEzxMRUg8g5bA1sagVnJrsjUFMHtX7iU0bXAgnTfEvzCBqysn5epLT3q5w//4mjU3oi2ICG470F0N8POIbD2buy/p4lWTZj7Oc5dKuviZENIiAKiCgBn2vTAqPjGP1oQQp6zMqgZaRXUn11PzT+ZrtzBGZ21sC2zLXBS9uneVRi8fw0wIsRYb4mKoDNl5/YqwYTL0zih7RtAna52phcf0ZME9jgnZaiUASAmMbDc4VUIqQgULsDwJTZo2VguGciaX2CqB/WFvzO6+RzUhMvVXqYtgFgGF4j9ic6kxuWMwpr0TkE4x772ghWkdRnONlswaQmoUSs3zxnJ10mhZ5dgYtf+LYMa7OldNaJCobhxdY4Sv034xCWTyeIhZcth6sb4XN1lagZJy39axlWk2S/a1HJPLFgRAJooRKHH0vAfB8/XmJVf+ChDejLf8490fCTEyxogfA7vdns47oveICNf7A13fmdsnJ3ndZA3QRiLlmnppbvREC0sd81J/74TtZoPvIukwrTOz+vCguc/dJH0tfZRSmTupXpd+FVKpnfV3CfCe89PZhJKqpFLTZ4GY7zw6RtJ+z9tXr/juT3/i65//wrTsmn3bcHaxedTkcQwrHJx3hCM3eRciMk9JK9+X12Pr+HHh0yZq/9J5He+v+Wvn930M0netzac5mJ+KFfMl0GEBhjfu8r3FBNITHjEpajftXmHETmfa/HcZhHiWxQzjuo9ppou/49yO0rYNOJvvAha4+YJTfvab0ykM76nW4s7R+Q7xjk4srp13QnCSj/Vjym7GjoGTMpHjFk6478kUlX9W6kntwjmGPFWk8NZNLmCuL5NWuxIKTi6zurY0idIGEq91aOolte/zrEyGk3tMsWjC7Cc8Y9bMdaR+PkmXjTrRR/PfU9D6tFqZswpVw+NIKJ04m//q8Mn8Mrer0jWZ6K0zQMy6tRs6dn1Hurnmm59t+OULeDYEfAe/6zpeS7Gcnhc6rdblup08zSjgY6KLETY9Owd6TlvvZHsfiBN9CASg1OlTRTaWW9Yaf6GBh7biqU73p87sg1hEfIZ74L4Fu7CEaANUH33eMgAro4YjVytSkRs5zoPTDLKHCCDag/MnQad9hs/wlwSnGOa0AsrpSPT6FiH7yucYMSl7xqhfktjM1n81waXiVkTNLlcaJm85fE07F7w+55n8c3abPfubN8RxJK74u+x/vkGeO9wW6BIDP6Pfb3G64RxzrJRTkfmKb07I/ZJ4nYQR+eIEktb2oTQPloGq187x+q7BzZWJIKho5BFzvNl3BYoO3VGQ3ZpJpWDmFajj1calKH10AeYhLcPa+sgVRvvCaqLWKWvq1CDaAOLBTYhY7ccFzVLc/kz9YiROcXO0Fk9p0m4txO5kfi8loHQVRMk0R8t5HFtXShbwGU2EcCCEkINJm3//GnQ81zVpskDW2SLBuPbVIL50dxX2mDAkEKO1SzQASoojqpE0HsyNVRxBEzG7nYrZ9VSM5oJJnM/FZcZ7KoSqKSh4bxr8JkgoOIP1ifcO7zy2PpmsIXIfxmha/OI7IDPeEUK2JnHOod7cS8UYCGOoAbedA3W1g2odus7VaRpI1aJTMxG76RwHEv9w+1sG2fDLq1/Suw3/8sXfchf3/Cl8x44Dr1+/oe86tkMHKH3nUVX6rmfoe/phwLmEd65aSEieYFp7KIdkzMKrVGebzSsHeHEMXYdzjpCSEfd5Mnfe2uIUM63vXNV6i2MkamIMgXEcs1VEtohIihLNVVuuS8ru7nLXrK8/lbquY0yEkIghZkuUhL/7gbv/+D/ww7Oe13/9a9P0rMLSIqCdCyNmDIPP8Bn+gqAKtOv1Z/izhp/wGBfMJgF6+5bu7S0uRQINS1bnact1QXsmFqVw7AM1vyz+eyqSOLG9W7anlLNqQtjyRYnN1dQgK3jMmL2tQKJqpxvOZ+/TvEHzi3vgDEetwaHrIxGLp7e5wg0bBHjW73i53fO9bwzGm2z15JFZXhb8sFE3eORR+/McN+L3QXmd4Fed8KITrl0pcbLkjSmyi4m7pOyzRURQmEJJlzbPq2z1LFahEw7ZygiKTY2sNkSa7/J0qo1mJf0DYKlYdpxg9ak080vbOdbmWyV7mf/Wzs/yLTQCmHmpE3dugU9lRZumNhTFpNqbzuE7Tzds2G63/Ozra3756w3fPOu48p4fuoG97zm4zvD7TFu141KKrOQrcz4dMJm5CPjtlu03XzC+eUt49fpEf36G9worc+nPDd6vIOLoYLj8kyW8T0b20q/tB4Wl5nCGadOYGCf3WULMhACNpuhcCOEyI/DYGuK4+bL+vtHsPSWYWPvmMXByTFYefwqunz60wLUt50NN33fp5w+5xN5XWWsudwqc3L8+wNycNHTXy560Zk/XZarnHClSVZwccByOFUEKKIAjyDOyX6ZGlj99oN6epUyASIP4VAZ2pi2cbOjZsN08p99sUFXiGBriRcCDe+7pfrHJtXUMu2d08WbW3qrJ0wzSfLyOGXuTxvfJLluFI6ODE0KIynA/nVNupREsepTvlGfL7C5lrY3nAi0lf3xUchXGNNKPVgO+avfD6X16YVFhtNZ0r7OyJTPL20Yw0xybtNW1GUedaNNaFy0tyHRCyjEfWr//LX4yhdhr+23WvkYAYpqHOdA1munmmJn+sT4Hba6bYnXSeLf25AUgQiHgKqGjhXAs2vFUwlvTaAKYGNAU0Sz8sCDZuc051oWK4CmEkqN4/TXjCet757IVRDNfJy27KWheFUSUCanUuhXfyJJt+i0Qs7kmcmL4SIwQYyCl4t5IsgujZniyBYXvIEWl02lvSLmMzgtR4YfxNeiOr7c/Z+t6frb9kjfhlj+9+Z4QEvvdgdRHvID3B/a7PX3Xsz8crDjv8ZqFV1lSWlxmFYKw7q9l72kou6KHKgKd9yjmiqrsyIJO7ZPiUsxV92IxpmmMsxDCBD1MQrYyPVALfK6T/p5bmItVhoCUvda+KcHZQfFhh/z4e3Y//JHdbsdms6Hve6ufWBDzyRXTtAhFFuvnzwhO7fP3+Un+MDTEY/Neq/u71vPPb+wvhop7PGF27xFO4YX3fTWHv+Dx/omBqp2nKeNrGg74/S0Oww3Q1vJy0refMliMfrPVr+76Z48CmTI8SrN8oNNfZfqmJmmD5LXnMGvPThRR67R2f36VZGrDzj8RXD/guh5B6H3guht5JQMl7tSsCuXjkznPS6nJ1747U0lV5ZmDZw5+iHAnwped/c0zmnDKoPaXVIkZp8iYYf53miETt2qaENUKRwq6v8AXTvZ3vlvSNKtwYpKtKoGdmhNznO1yWOTXztH2t8kzo3kn2jG/l/JvbcpEs9XbBmf0ncWHeH7T8YsvHNeDvduJ5xWeTiZLZi0IuXNIsZLNNMdyalVBe1UiE6Tr6J7dkMYxO0lda9IT4Twfknl2QvHuZHI+8gl4Yg/4qBzPezrkIf312SLiEwWhbPCTFurSEsLSVep0sbYa64eq4Scz/3Cz1DL/7nTFHiGE+ADwKQghPsNn+NiwJDpnVknNu8vWy7FLvZaNPSGlc+j1ezpe2dscjK2itOLYxxeodHh8zk9y4Nxct8zArEapTvniV3/D9Rcv+NPf/yde/eGPhNsdcX+g+2bAvezYbr5muHteqARc2jZUQ2mNUDWwtLTvDNFShMCnTtRGC2bWQwWxPhI+zOMy1ODTp6VXTb2yZnIpssmjdcc0Z4i1pMP6eJ+bD+XcqcKkop2/EEIsqzvrhKaMqiqW5l/WO2Fi+M8qsVLv/DzWvObmqy6XpZnBG0PMAaOnWAltDSyob8oIf7ECmMbPOVffVZc5TG51IGUGcqwxIvq+t7yzdp9zOS5DFkyklI7blwfWzORj41s3B4HOAa0Phz0pGmNdUFLY27swoiSCUoV2mizOhThAOuvj6nNIEC84L3jf4+gzA2Pqw+KWyTmPc662v1iZFBdOVRCRhQ3ee1JK7Pcj4pSuWkrYvB9DqARYYcqnmIVFzlw7dZ1DkoMAEfMdoKp0AqKOvje/wpuhg9TV+ZQUNm7Dv3z2a27DLb+9/S1h6Oh9dgaQ57HvPVdXW6KaxULvO5x31dWCcw58jskhZY7pbNxKbAWNqa4Rh1hgaDFiX4GUsk86Ecvbm4sH5z3jGEiqjCFwCBYroliY2Dq0uVnmrcUw0bpUUokGkjS7svLZ3UJCVIhAGEdu726zEYYQ9gde/fE74j/8hpe/+x1fffUVX3zxBU5eEv0NPn6L01vMRVOzSFeW5sfQ4fkMn+GTh7MMyM/wGZ4egjzjTl8SMnsn+u8J13+AtEdDFk4AkHG5fA0OtPVRTvNuulpgu9OTOZ97enWSi9cyhzMemnGpaq3aaj1lfBSYW0JUwUVT1yO8qq39BQuypq/EiwnmG+sIV+KTuSkGwkmQqeSlSOB9gIjwqx5+jvDMz9+p5tgQMRFi5BAjhxQJKBGKuKoKFiano8KS+6RittYljkTJf2IqT7SPiKLZPSXO8Joj91Qz6Ysu+nTt2SWw9sFSRc7m3Sy9Lv5mwojzeZ+qZHl6LAbIXgCwNaATc83+xAQQw3bLYehJz6/59YtnXA0b3nZbvvMDo+/x3oNz09g5x+FX3+DuDvS//yPsx/m6nF0eP/Sv3yD/aSSR2K+26DP8JcNJ1sgD87lYEPEQIdUlRMk9bIx7nh439GyRy8qfqODZM/NcGSekVceJHryD5vwmSeZJJqOs3DeCCKFxx3SmIXNXHysCi3uEEEddeyGF2jjymD2ftFxPVunUwyeA8/k+SnD7oUwlLoEPyD14MqH5BWN9f1n35zFfZ+fyWe4tRxl9cDjXR5cL7M5X/JQQAsCzZ0IYDUOteCk9wrUxt4oQAtfgga0bHkPoUlKubl7wxVdf8ebH77h98wMpHIgjuGee/uuBfveMPryw74oAYm0i6HShlXhZSbbEOZfCBk5t8zJvgzQ91exh0vSgrk7Y1toA0zyXRY/P8jkVG4KTc/Kc/tfcp7CuPV2H9jyoW/qEfs+I2qrtv15RPdr859fanIstfVKc6JSytfrbN/dGhmEXBjpVu19UzUdQkhJFz8iAcobmAAVTjI1mDCl+drOgQY2xDUqMWq1Vqpcbndo/NWjW+vz/5PHZCaCJpBBCIIYRnMOJadGTkllGoMaozozoYoIvKniXaoBvrXSHtcmLMd9jUkK1HJkEEYYbZE0rLcQpdRWXNTWlz0zzlGbBxMu4pJRMwCGTxSZJSWWx5D73QHQuj1Osa0aT4jNTv/PtOrI55Z3nZfeF2bkESGLM/TJm3bBnv9/jvKPvB1QNHfb4PDYe1WRCFZ2YN/P5qXUsl/PZiVhwbm0EGExM/SLgqrEZNFuyVGuWSQmlWgGVWtRrmepS5t+CjlfM6iymSBhHvPf0XYfGRIgH7l6/4dX333FztSU9fwZuwMkGlR/P4LLT+iwC1RmKpu3+1eyBOsviIjhljfBY64PPApRz8Anhpz9ROEfpPax3HzMWp+joukM/ML/H0qz3VukJ4D3P1SW+xWXk2yO2uEdA3nElj6mWPRkSA0FviEQgEd2O1L0FH8ieVfPBoLPcphO9LeZMg4+00ZuZL0Jh3p7mtlDTTGXZoSU05+tRPUq6NP9umd/i8ni+rOOl63Ut5/z8M6NelvazeTwaWmCO4r7bzBCyR8dziVR55icaqD2faxWzMsY4HohhnEU4mNU39+lELs3nzWSzXdRS2vLmd7U+OjHLV/t/1tFn4L6hayva3mhDniwT6kR7zquxMgfb58smNFU8om2Y+q3QyMVFV+2t5rWh3p6u69n3A3pzzeZ6Q+c9o+t47To6MbeiFPoXTLnn5grte7p/+rapxdGMmD0tv+4wIocRfzXgOmcKW/dscI/FqT4Ia2yNply7f6fKLL9915NghYCX+e29n+pFjx8HJ+b9Q+ABgog0u5/G7Z4IouX77F933qX3DFDTW4UWq0ukZSI1BOhDNnptP61HyaKG1W/xU6CF65Pf1c15TmSWoK3tojhiJLYc+qLhmBkBLt+XX0tyAlFdMFeO2yGL4mT2/Myn7wl++hTkpyGTeP/9eO+8+GjcgGPm0jHcV7e1/e/Sgf04E+CUMHMO7Xp/JFndfDvhciNb+QFFslZ5z0G/BnFINxHLlbGXs4lRGQ8Jrh36TcB/2eOjx13P+1+ktEpW9myd8MclArzEMcuhMyNs5hlO7pUWe2OlYGV+P7MSOA8n37dMPeZjOa9TeTKPDVHdN2lhHx9jEdUKrxBfJxCr2tdi5U5M0gbNFUGyK4AYwiyXie7UWXfprM8bxq2SrWYUjZOlwUxqVIco29PEkNOZ2ySNFl8kxdKGHO8gKXQe71y2JDDGvrVNMR85zujrZK6XLI62I1ZFKqubOIfLDOypPYlxPCAiDF1PTJH9fk/nhKHvCUE5xIRZZahp5XtHHPekcIAwgkZKQLy4e0MYR6TvcCKkMFZBi6pyGK2vnXNogjHEYixkOEEeCodmLDDjDs7hSHRIFWL0g8N31i8pCzrmsyFbRFQy1NZeYagvsWbNsTQkj51qNGa/85AFClLcO2FumHx2LXBISlQLJJ4yx92LcuWNjuud0DmpsRVGTQxuy3/51b/mbbzjj/s/4ZyyDxEVofMCMbLFkTY9cRjwvqPrOkax4OBjingnDL2nc87mgzQTPW8V+xyTI4SYR8nwVNHssqnzuQcywaiKE7Oc8MVVkyop5bmapjVwtE3l/avgiNOatXdF0zXHJCemgIxwcAc2mwHvNoQQGEOg++F3/PDv/i88l/+Wr7/5mhQTUROdA+8ciKt5m9VFGWMBUZKzTnA51I/H5kIVvolYYMq6pSbUCckJNab6Jw6ttdln+MuDavWk5D2tuC1jdQLXfbB8/0FquaQNP2jhf9HwYbu4ZYJOY55UUJzFGmLHITr2o0OjQBQkGdNcMTd/qSgAlePMIglT3C1Wh4ON0oEdO44qBGjnXMWpS5wryUibTLhvxT91uicrgaAZxylC/cnCsP7RXtM8m9pRbmZoJO3NcrRyRIRWPV/LowUFoYkxBTQGdjLSx8RNcGZ5m5ucXEsVFktKbcih7OkCKFbSDzkDX3rhr3vY1kIKspRQyX1Zx8L0alTAFbeeycZkl+DV3YEffvOP3O52HJLFh3AKPuMUEbF5UjtFJ3JGheK2ySwyra1tvzu1+qmzMTWrCyU4w98OThpcqe37OgDTWM/4BJnC0JJmpaPq3EjTrxZ8npqvq9KG8hchKVJcpxJBY7Zgbi1wmvk4W5MtTG4925pn5LdWXVHItIiI4AwzR1Gcc3SD52rTc3M18Ozqii+G53zRdWy9WfU6741XKZi5CxPJqZmGUlFalRHJ/TyLAZbrU/Gd/NhdX7P9+ivGH38kvHq10s7P8DQgtc/r8X2Ed77rOf8Op9Xi07Wlt8JVuBceJYiQdnHNbKsKsyPf1bk97TAtITUXAixbOB0pNUX9ZlGmNpmtbFpHR7ZqViCYB4M5OgxmmpjLl2dg1q5l3rqetHlbiMoihFhlHB5piWZGAq32Yvs7MaNONmZFuLB4dZTmiId8pCXxULivo2Vx91MgY49h2UWP1Vh6EA//wsTv0qcni3ikxPlUXT6c7EJPF3YyAtkl+4aef71MfWK+vCtMOizHMDGvn6SoWqLLRp5KBN0AI6oecX0uryDquY8yIywlRToPG4ff+mk/U8mBXOGoR5eVn6gpKtZ1aRt1kXt7IxfuS/dN3LMVWWIo55OtF79kqM336/quCMVzIce40LT/F8130TP7V9bWnlc/z68cnqFgARPxN4/XUBpstIBWC5qGSzqVn+OOVAZS8XybiZG2llryTJLxeK1/k0Asl5MRkSIQmbvmb9pXOVRTGzRZenHGFNCUUJfncbtlZPeJThxxlKyFlJBUQk0mUhxJ4YA6SCLEFMxVUsqBsKvmv9S2iEDMVghaiMmWKVAHdGpPmQ8ut6XiUrN5LDQYwdQTmkyYU1NMec7ieyQ1V0yleJfdkOXsJBNn5HpbaPAsiBBT5PBifevnXUlS8K7ji25DGgUZPVEjinIYRw77kXE4EMcRdWKuA8ThUkSRbJ0RUO/wPttvLcooc9v8LCdCDpBehFw2B8hWKGUNT33pxMbauVxe3aPmBGK9aJZDlYWkFstmvhZyQtWUhRzTmaYpwbgjfP9P7F59T4yhTIr5ONdnQjNb7F5SO2UqLdXUfqp6VbbhneF9xGU4edTrw8r5tCwt1qmM9XfvqQYL8uxj5PU0wqRMoS3XJ2W9HeMhNek7w+PGal6r9TwebimxUshneBIoXZmAUcGr0q1uKNMa1vprjN2kkZjEBPbpxJw8VXrGtyeXPCtzuKXzl8hUCwtcVc4kKQzd4urSzq1i9bDigqn9rczgtrxlSadw0zPvC8qXD7USayxqJMSISylz+ql91tIURVnnVNnn6K9TMAh84WVxxkz45rJpLZlqvCWHqiMqhJQIu7ek/YGYkolkdMqttr09M4pwCamZ66Itkh+W+VhiMUc1HCcqRBGiSs1fj7iaa5OmIF8yzQ0pjTzC6qdn9XZaKe0caVvRChakcRNWHVO1c20mHOMBMLNnJWWljpYWKC1yTvDe4Tpzz9T3Pc+6gd4JSZLFfzB/m8vOmnePd/aXssRsdnxN9am7SnGrJWYt3W02RH+Z4vk7wanl8CHOmDP4wX1k9+Wwho+dS31hjKdz28is8m3CB7TmxHa61i8PxVQujxFRtLNkCtinlSg61q6sd8dnYIWWGLWsXftyFZs/8ZgpqN7i+YnmFCGgKdW1K/KIfHrvUPrBAkvaYVd+7X2usyw2+9L31fKhDUotzSHYwvm2nRQwNA/vdcP0zsKIz/AZPsP7gvZgOyt0fE+lT4S84GRkyx9IbBj1Gxac3bqXFRcmW37Gs7u/yfEGpoq61Ocr27+XgYwnBLSgfoY8ttvUqcO+9lfbMacOIk7sjyKXdWzeOy9FPo7SncBxZmlO0WNV+FAIFmq/1XNn/fA97hsmrewSiDeMY2XolZgD9ZMESspnmZEmUpjTbRsLsZrSTGu8WB9MbFIb35TMQqAw6S2vRArGjLZngHOEYPhMjKbVfogjh3E0KwExNTdNUmNBTARIFnDINMyqypgDIbvMAHPONOFT7o9yX5jpzpumYdLsf1jMEoHkGcdIOBzwmUAP40gIAedtXRwOo9UpC0iKlWWIgRTNJZHFfGgcBqtmwQT44FBvTICKsokjdytJpzyLKyFbkz4HuBazaHAOJVV3WKhanIcaH0OtTikhMjH0NDPxS3+VOVdQTCdi1io5mLPNKXDSYYGwBUKHOGd4ZNEKy3mlpDzzV/zL63/G9+OP/ObutyiKd5bv4HsGTfSS51bsrJ1OiNFwqRiCpe07cwflHJKJ+RSTjUmM7HY7AHzXm+ss31lfx4hqIhb3SUSic8bQcI7NZkPoLEZFu44KzViZn4q5cIIa88SUUPKaU3KA9Jwecr9kK5doLpoUNcuPt3d8+/f/yP7mf6H/9X/JV998w7Pnzyx4ZYw4KTuazT11WQMzryefg4hP1g3TGkwIiSyMcmQtSnNZ5mLheHxYfPszfDz4cyUNbBtfZwR9hs/wGNgr/Id94pkT/sWGE8IIKhpSXEPGmBgD7IOyG80qMCQT3he2smDa6sVecdqxpZ7DUQ2PSRn7Sk2qicers6+XcMQrX1kalk1+kaykqomZGkFEPQQbXHChOGOKm6sl3AO62JhaBZgpj6QJDYGwP/BW35C6nqCRmK1VJ2z5Q3ORVrlvCyahgjp2+jX7NLBPknHcSBgTIUFMEO1oJyE1ZkQJYF1UepxqnQZCYzGpRayQbT3yfdFjiNi8CsbiZ8IYyqxMTcfJxESsCs/acMorA4+Lxzi3QWmtVjIOj1oMslIjzUKIYplT8f0yV9Iy6+mi4dktB8JwJcl9OZ8pglmJJk2mVeMdXd9xdXVNGraML17y7OY5V1dXvN3Cm05Jrqs4uTQHbJ0Boojv2P+zXyL7A5vf/BMyGv1TYjge9Z5SlZUA/I9vcLd7okscmtouO+AzKvcZHgOXW0SUibacsXkdzbZwKRsLxwuUiTg8KkOXi3Ja1PO9p5UG65S6EUa0mi+ay5wfM1A0HAsfpSzc40Ay8zPqIYutmqef+Litpe11rUn+CaS9FQhUIcQkfFgKIcqz9v5ce6bNc4VJuWSyneqMB+5IpxijJ7O/MN37hGWZ70Jg3cd0XOb9oPZemPi9WJc8cn58DEuIp9CsnCN+TwdP2W7bkpp99hR98wiN06XG4fLbiXYQVIwp6iqqezoPTSlrIHm8XiPJ8qgQIhrjfNsWQV1BtBa+WhsG+1EF51kc9VcrlLh3nsrD9ik7AoVWGHFyX8kNOt4Lj8/Ao2aWE/rouVWiCCFai4i27kftWFSyFWSYICBVNzLm/me97w05xmI1ZGT4qIIl35TJokKsNGxQycRDEUIYQTsRE6qp1kslWyhgLptiTMQYCMGY/Z3v0C4TSSr2bc0PUxiYHaj2qjCJJbelCB2KRYA0TFiRojU2sbOmv+zGLCXMTLyNIZD7NpZA3MZaKMz8Glha64jPu7L0oyZSKgw1JubzQv3Ygg4WDX6XhRu5zkUzK+dbA4M7X4UxqmUezAMDTv6gW/xvBa9Ucn2nPizBl6tVxeIbyUSvx3HTXXEXdnjtICpjiBwOgcMYkDHg+g4nwcYMcDiiWDljgCQJnwU6kyW85kDoml0z5TgkzuMQXC/mcaLtczSPn/WFOPDeM0pHVDfFu6jdb/2jjQbiCtJNnd+LtTVZjxWGVUJKMO4UCbvI7Y8/8v3vfsfVzQ03L54T1ZugJ1cjFRy6CKRyWEvR1nVDGcaGcYBUf9AiikeoGozHqPaD4T4t93PnV6vkcz6Pefr70v104X03QE/20fsWUDzGGuLjuOM6VeZ9dVkSJO+jDo/I+1278Amn5ONjZXx4iApvojF9U8sVbKHwRlRJ6ojqiEmICUJUDlEJBTfQZr/L+EARHre9MZ3MjUVEe+Cs8HQeBxM+dtSgpZChpinP0lS81k6Y8VNOFrlkYh0R1zXhSnXtzI4xsgsjXYxZcJMtOVTz0aYrzLIlPI5HkjAXld61wqkzZTVNUYWoA1E3RB2J2Vo2pkRSISF1zJfCBy1to3Z3wzebqqBAzOOYmjlGzQ/M5ZehAcWFZe2SGV5T7suFTP2qK+lPdkBT6ZXn0/zWOp8K/TKNu86/r/jWIr8l7nVc4qKpuSFNPymZj+cyXus99B3d1TXD9RY/OKIX9k7pitBnkfGUv5j+0dWV4ZUy9aUWIqsZV2kflS4v+PH1gPQ9FMta1nCeiwblDLwvLkoDH/RcX5a17LB72is0Hh/aXD/yGbZGmz8SHiCIWPr6bV+WGmS7iFqhiZg6JSRooTDLCxO93ZumoiRr0i1N0/LCagjaVrjQltkG1yuyj1mdmkV4KtTSJdD6OD8+1KbyUmZkmBZbYbAsGEwN46sQ1845EPPPbPtL+S3MjYksv0/YcMRQaz44yfT/6VNdf+Hwefw+Hkwk0acDH24+qHTs+QatGtrFF/l8ny6WEK//9C0//O4PTOLkpq6qdL+/w786TK8U1Av7X1+jV13FJ11B5peaVGdA5kWd3g9PPHiv7uMuwPlOISyq6yNerUVYF4LUmEMLYU5JWxisJXBzYYbHYr2Q1PzoFmW3nIdm7XzEtPWcExsnl6qmkmgmojWhOiHD5iZXcqBozdaF2SIipew3N5NXGkkpQNYON6TbEZ0QQhFERA5j4BACDAO99BQjiBjGysiFyUJCs29/UhYWlPbgEDGLAmWKs2B65VYvAbx3xpSOoDGYRmIyIV1KkRQDMVosCJLlVzTfYwqkaKSjIIg3C4QYQu3/iuzU8TecIwqE6CBGxoPS9xYjwef1BzngtPM2Njmeg/fFPZrNFefNwsN47il/4+j7DlUlBBPulDqZq5SSrsU3mF3PSMc8ZvauWNU4Ogeos3gLBQ+lWXuaGSxJ+WJ4zr8Z/gu+P/zAH27/mMfHcZPMYiFtN+bzeejxvqvGwEEszkZMSucdQ9dnYUTuxxgJIbDbWxySAaEfhK3rUBI6hjo3SQ7nNPNYsnXM/5+9/2iSbVnWA7HPI2KtzKra6qh7rnj3vgc8gEDDrI094YjGSZvROODP7hHM2EYjuwmggYcnrjxyyxKZuSLCOXD3iFgiRYktzrnl22pn5hIhPSJcex/wevUMb64iLuglzjsu3kRQujAXJUOlKqfxledLtiqmrI3DMKDre/R9h2HYYhh26L79J/z4v7xFP/zP+Pyr/zu24RcYwi+L4seZ50/cwfGAJ+47OE7IOYyFECoosJjF7ExZw5rYU5SsEgf5Uzr/HuERluExP8gjfKqgERCx4wtcxxd4NxAuB+DVLuP1NuPm3VuA32DIUdIDsOWeVC86mPBYbPojoIJYVUSYTGV0EOu1Eh6zuTZqXHOplGOE4vye0WmFXimeEFZPrt+B8ffZWcKT++1jU4FyQ3eIFBimkhmJs1Sj/m57g+/evcTfPnmCXyKVc7n1tF6Q4szgLrzBq8S4ysDXneSKKFIuna8p0U427OqJGTMjJsY2ApsIbBOwy8CQ1VtBpzUhIzIwQPNMlbGpUyJHvXFl1l/JlxEh7zhQyQEiOSeABBOIT+ViFqO1lcc1PJ/WN57zBbyrBepn673A4/uNN0TFufYvgTnVhdZ6SGSe1LOAg9buRpc4kwk2ijYmiPIhOPSrFbjrEVcrnD95is8unuLJFwHDswzXKQ2uXsAj/B21hGv95s06qrttlNGW8jnmGIDw5ALnX73A7tVrDG/eNXeWhOtLc/KA0uu/cjg5ZNNPAE4PzQRAttb5xkmj+wt3JxZahz0iGGobWMueyfCrMqKWCUyRmqebVlFw8NhDon3NytXyZkptouk+fxjMEpE0tAW32wM3z5jgxw4zqIBkabx1EzfrSe1X/Zxsd0cUB/tCLd3VO+EhF8epFmvvk0+4jwXXR90oPqAnxEPppD6spwst7i+3eH3vOXp6kR/+YL7LmJ7q/XOK9wRTQEaHjBVAvioOJn0vIeYcIceM3c01fAjwPqASTADAoF0CXcf2EhDMzbU2enR+8bKgfa9igfdbcx5VPtQijkMj4C9WOW0hs7pPKHNfVdNGHbUuRjl3uFVGtO00Rqyxxs+NgYBVXKelORPZ0KHOjTgfWKI5oDIkDRNiLsZFCVI9Hipjq0yE5lwwa3R5XTgtppqkWRQdqmRgrzkuJJlwZoZnTc5nZeUkyhdlRitK2CHG9axvFWGNwYL8VYt/CX/DRWEhCaObIAnZhAXtOIoNW5vr0cI3TteNaehY2805w3t9kTR0FOocyvST5nEwYwgpzZlXgimNyHBGaKasSb5NSVTXhCU6xCz52eg71ytCIdZVVvDSmNu2qy16A/AU0PmAm7SC33VIkbHdDeiHDjEO8NEjOQ+KpiqSMjNYkldTUsE8SfxeR0XRCVgyW5R+jvKcFJ7Z5i1r7hCl5XwP7taIQ4eYB+1Kbl7lZgpp1NW27DlQeSBzRsoJgbkypgRQ3CJfvcHm7RsMmxu4J8/h3FpCYLMJiTI46XyiB1FUHr8VRtwCaLz+HzLfg8Epnn2n0pmnN++R4b4t3Hfqj+HOh1cmHCAQ3wvspxNO50P2PPcx0ffUxfkRoSU7Hw4O031TSYJ4RPQYcsKQE27SgJscEXkHylFInxEmVHrYzpb2c3+zjHZpG8LTC+PP6aHevjN9fPbc0s2DDbzl/YVxFqJp4elqADtAaWASD4AtiyB/LNA9DrdF68jyNzTjJvQ4imKgtHrUnkpXZxaFRMosYZi07YktLFPzVxQcmG1pSyPNLLQSoeJbTWpt71hopmYQePJ7XOqk/krP1HcONGrWyOmDXP9GoZiMp2geLwZNy/i+1xGmxeW9S1s7qd6qPgSw9/D9Cqu+x8XKIXSEIQBwgKeJQXbhHaf9a3jSKS8PhvFPxntRQaaxMsIx4EFwPsD1QZO05z2YbqWdCLP5+zRpqNPR7LanwoHn9wzFyR5+H3Tobn9O31IRAYw0i6NKlyqfHG+sKQ95kqBnIg1kGGLbIOuvdkOdDGxhtqfPNSu+3SC4OWhGbWB7a7yUW9d2LW1SfnsVo2smAOOSgAnl3RI2obECyGq56ECa6Z5K6eT0D1QsU1tPiFYJccoBty/U0nu14n2ETwROJ5Ye4REegt0ST4hfgqmDKCFkz+USL16qIefgvYd3HiF4hE4UEJZHSLbvBYp4xLg0SmOenAd7lBC17Ft06ogSYnJ0HIZpO+8LhBKP9GjV4yaMizFBb9s7FarnJlcDIAmRWUPUtImJS8YHzWU0C8FlGaupnr3Fm0E4gmr9Qw0LbdL2zOAcxdU8RsEA8zZMkuiZVBlBqqDw0MTHKSMxI6WI4jaexAqK04A4cFFQWEgkFwKIgBi3SClJwuOGPuqCr+PEgIUjIr2WcgJASEkH3RQlkGSTOSYQRxAzPBE677AdEnIc5Lx3hBhj8UCRYnWmYw0XQERqOUVlPpyra8OoNLGWl7IdEVzvQM5jGAbkGLEiKomVZV2G4rHk1PrdyX8AHDqlTbz3YI7YDTukWJURQuuIJ4EPDo7MwFLyTIBZGB1m5MTgDM2bEVq2sSivlo6y6T3LT5Az8Cw8w8XTc/y4fY2Xb14BzHDISIkRY0K/WiN0CeS87jtSyG4rOSBWQZIIXpyvJYeFD8iA9rcysTbKNSSTJrhMSZU5EY4DnCOcrdfA8+d4mxO+ve7xgt7hwg3FW9YQyJQbWfso3jCCY3m6flU3I8qgDMSELbbSzrxC6AJCcNhtt7i5vsbuX/4Rz//rf8a/+vt/h+dffoXBrZDJIyn+bDMhpx5XWMMh4sx9D4dYmHdGqvjOqrACIbQ0PkksahOi1PlazvX2CI/w8aHysu1pfpBX+iRQ+dMQ4DzCbYAXvu1/0kIsppSwSYx3A/A6f4+3/geQewc/JM3Xo3YYqBkNRPDMiIbdvCBjLZVV+rkKc9swSbm5z/U5o08yxu8f7Bw1AmoTPIvxx0iQOypjwtPS9B5Q433aeXqSoARQniT0AU/OA77uv8CzJ+cIHnjnHS7RAeMgOQc6+LAbQzsMSmWjxNexc1nHe8iMbWJc7xhXO8aWCTsAW2ZEZvHEBZA1u1Na6oIhSukKz2+XH1VQbTRMHsnbTuyddXI2522tTbtmzWoIXhhPUg1/DV9NDke5GhjNvCGmi2SpHrRnw2R89ihXGQB5gus79KsVLi4ugPUaT776Gn/zmcfffrnBu/Uar92q0N4l0sxo1Ns2NTK+vbg+WTc6HNPHw6s38O8uQV9+Bv+b32D344+I7y73lHnK9C5I2PcujYmy6hF+NnAHRcQUlr0k9j07F2bRfA2U3/pFV0RdGPNFA1QmZoSrpXiebw8zDWy7gU03iPbt9izj8VOzkEbzzW/qvmfWiMjNpmj+dKNDtVESLHhEtHB40xkTz/uUEKfygz8X96CHhNmY3HMD/ZR487mgYKFvxyzEf0qw1yWmufdgB+Rt9tIPCbYn2P6qe9nEmnXJc4LRlTOCKYCxAlOoe9yUioblu5GwN7sYkWKclc8MYJdAiZscALI3c++Rg6vxWqFtXqBVl2BEhJ1gkXdrT54T8OVklBqN3XhOlss1Iry+e+gNMfqicqZUXoBLEujc1smNuIZPPx1qnnKajH1lDpgh3gsoOixrST0ybfdt3PhreIHqpWGJ8cjwOSekpPH9IWGDoEoVCY3U5GVAK/wXZiXlCHBWL4GaLyFH9VAAQCxW9dnwkqHhl2pfx2GkpG2Fb8s15BORJJZkkyyMQOtrvCAIRiOh0B6tlqw1hqg8pjxs/S5CblWEgBrc50oXkU5QCd3EVZFT9w59Z8bI6XQUwT2X9jlH8OyUUZbkitB+jOitRaDS3wyGJw+vwYKGKKG44pAQ/aD5LsQjwYUa2giAhIZiCTPE2SGrR4ONBTlXQokxUPJHWL9qH7kIkDJlEDs4L6GsfL8ChggXb0TIT7V8Ua60QhorLpd1OKJXJ/HFTXloCiFPklB7GK6xGwZsXr/Cj//83/H1xRM89x6uO4PzHWi9QnYOzhOy6xG5g8sDYl7BgeB5ZzqPOr/qBSSqiIIZZWyWtsljeYY+LBxi3G/z/LJA4m7wEGV8rDE9pd7T+vfgpNepcKy+EQ942iuTAm5Z4RQmBMHeaz8xmE70PfaFu+aKuAvOTR+9XasJo0116X5znoqyWYTJKe3AfA1GFM9gtDH6rW1j1VoGo0SaKA2fns/2e+H6BGSP54PPLPdJCbOWoCjniY7JiC5v8LvhT+rL059N2ZO2tYavpVRymuvLAbGDdz0uzs6w7np455CJkQAEnqsilvt3f554YOA6M3oA/Wwt1DlsMETpMMaQGXEXEWMSAxzG6K/FhzqmQLHmZarTs+8gRw2B66wx2IMB5eI+Go7GnZm6zpbXrH289PbkWltGpTHN+7N6Ljf4XijP8XsLHTkCDU1umFDkcA4ueMB7cPDo+w4vLjqcnRHQAfBU6P/lPX66TzZfyYFXvVzc7Y6kMWloVqsrZlDMcENESBnRe7i+B8dYE8sfGol9U3sqfLRD/y5w253/Fn2aEBYfJPfRdBFN22AKsTvMzQMoIqwlt1mAwK0JokYZYeVUi1jXPNYwYPY8ta1jVUpMFnHm8bg23JQx1Wg/9w32RDHRMouMutFZCAk7HGbFMSTRKkv3Sm4IkrwQlkzSLPXuSpN9SgLuvxb4Seyhj/BXCMsUZd36aOZBe7xEhx19JWGYAFXUhiqgnNVV80J0XYd3P7zEyz/8CTllOO+nxaP77gb+1dYkkrLHEmH363Okiw7w8/58jPV35yqPakxOK2YpniTzhLYwBQXZPWEGqYToqc9kSPz6bHkWWs1NEbCqzV3pgzHVYxrAlE5OIzIWpgk8sw8YE/7NzZyVKRKLJQceJ1wDa34B8YxAljBeYoWv/oo5YrfdFoVLyioMjwkuEaq8XwrOSdqXYkSKA+KwQ2ZG3wU4DwQnAvPEgygMUgI5gg8SWixrwresY06klu2c4cqYSYxas8hKOSHGnQjKQYjDIGGiXCvo1TBKBHhf6RyGCCmkrhp2shWbjfJKqVA9s3pLpATnalx/8cqsFlkpJxDLOqVWEaPhrWpCbaDk+Gg8I8Tqv+akyDkhpqweNgTOhBA6hI6QVOi+2SSkzCAKIIeKb4UnY6WXXMHtzCTWo0q37mLC9WaHVeex7hxiygjDDusY0cUeq9UZQtfBUgLutgM4ZyQveT1W6x6hC6N9K6VcvD02u6HmSgFr3g3Nf6L5LnxmwBOCD3BrhydPEkLwWF/foNecJSgMcp01y99Q8ostKP6MTiYYTcxIMWEYBmw3Wzw5u8DF6iluNltshgGrb/8Z37/7Dv/wh38C/fbv8dWLz3B2dob+734HPHsK/9WvMfRnuNx5xJRxvQNC3uBF+hM8EnqS5NQRVleGN9q1mZbbmDA9wiN8TDhZGUaTz0d4hDvBXJm17xkN3AjLFZQzkCJAmxus8hW2KWGwc4GoKiOMdGLzkjB6raX1GmFkobXaNthZm8e/TSsyMVBpCluQDhO4eMXqc/Y9ZzSWJvWenfXUtKESfZN6WwULzwa2qmR0XE06TIDzHv2qR96s4K++xNP+HF9/+Qs8vbjAed+j81HSGziV0xzXRtwbfoyM1wn4TQD+pqtj03JxrXEGaximbQa2Q8Lw7i1wdY1dSthmxjaz5odoKMkp8mUAznLtCaPA1M7BVBhe+YWDUIRu92HOlplT640bKTOsLv2bKB4kLOo4lGv9a/Cal+o6DpXmN6pSmBF2BN93WJ2tMYQe10+f4ZdfXeB/+EXC1XqFP/QreB8QnG8M8/aM2awxBO4Ddn/7a9Bmg/6f/gzEtLeN7VASjWUD3Q+vEV6+Bf3yCwy/+TV2332PdHVV311qxElTuzSCjwKzTwbuu0T3wMmKiHcpwoNwRmNm9SQojzabPCbhmcZYXyxSW6Z36Zlarl2uZZY4xK3goigleDSgo5wRkzJL+1RCw807pZ62uxOz3SJYMSs5FdBUy8zp5i3jO176twPp+gGMWSKsTdmjc7NPBjazFD4ERwj4Y1YBJ9P/R/RDHwqOeULU8+uns7nexyLxFKuPT1YZdpuGfSoIeDKM1K4NyK6zNOfmeWXEz6GuCnPUIUPyQTCFppAqGB2XXz0hOGVsNpfYXd8g7oZyH7sEt8vIvQM6ByTJD1HKM6WvJyC0fXjoFTcen7JXt7zOHWB/K2nvlJWzlMePH6loXNSStSFzUYCPXm0VDSYIVSFpq/Ao31vTsnLeUe2WEdSqdTD+sorDrZfjts9mtz3Siaqnw/Q5zR9BTT8BsRTLOZXWW6xcYhajAFCzzgFL+mi5MKztRG3bzMuxtsNRjfpv3pAEwDkry5JLqzt4Zs0/kct9cZbQ8FZs9dRwV2XOmkGaGpGJnokKLWKC6naM2x1chqoaUuQmkSRBEoVDFRUtf5QZRQEBrQuM4mXRWnKqD4TmV6izbl43zgel/QjgDKIMRzyWjVi/GbUtE2gprZ56nPtzOHYYYgJIglSELsIFh5SSKFf0DWtvyuJRk3IGpQyjuJzz0p+oSdpT1HyIrPPvdNikIEvqbUyycw4hBPR9h7zpsE0BGQ7kJKQTtUY5Y9QyVFjsK9dJhDHbkgtFB4JIwnekAWl3g3cvf8Sb7hxPri/h12uEHqDr5+BuBZw/ge+eAc4hdR04RqS4ArEDYwCYNdn8BJ2atV/WZzk6l+noU3I8fHj4lNpyd7iPFdv7g31ju9zG+fn0gC1ZGB9u6jgZJd8TA38a8J7vP3G49STMYW9+w/c4X+3Zc8pTkYHLBKwd49zN32J4JHRgBAAEYsnThBhBeQCxyhvs7MLkTGgOjUKZN2fv3nEYyS7ar1Oe94gcwg4gYog1Qa7EtNGOLV3Szg3pe5lRc4s29CWad41AnA7haEImNwnqHSkhIeE6uHCGcHaG89UK665Dp6EpTbBs8rFbSsluDRGSK+KagXc5o3NA59rQqePnjc5j1twQKRUDhsw88ZbhihbTAptyScscrxfG7MEZCpy2CpqWLxQ9bQgW9wKaPjMqut3XjaBqyubps80zU3plWt+sIZUPImrwQ62QiAjkPcg7UAjwfcB6dYbVqkfqPJJ3iCQGSE5ztNUutW1Z6qjxWwT0ARy7W+2brZ0ZACBJeFsiBxeCKFFOLm1a+LiJc9D+TNd927gPCHev7f23c69nxD5xz90qOQALa/8EOFkR8V/iBufk8G/DCv3BU3pJwL3vcsskThCrUUYchwOYvLQ+Zzv1OF41tYKTUVmnNcjKYuKyUZtLHDD/nDa2HGbZiZb9hM266klaRJi+pwwgQYQZNsbN9SLI21PlPgXFJ8UjfqLwSfF6AD4FZvoRbz4G0ML3OXLWuaHZteO4TBjoS0SssRQ3dUo8GcNvVsVXb17j+3/6fSH4zCK/e7VF+OYGu1+fIX151hZZP41ILIzq5P57gkkElIep6ogLSqPmrq+YUuLo2uLDjZzVLc/nJMLwEu9fBfHOaWJfHW/nhCm28FgijBZrdJCGF4ITTwgjqpszSJpgZ6Feb/tF4hmYmUuOihLflSBtKcJfaNJdiDV7iuJVGFxxH885Y4gSjz+lXBkE7+CU4HbF1I0QVdCcOYI5qTAZ4p3gRFBuYZtYz3phIqQ9RcGQEogYiSAC92L9nsEpIqcBw26LYbtBToN4RnAVvRNRpSUmQtuaUyWXKaVyv86/vC95DmBjqvecxka23B6psaLyzsPp+GSWHB7BuREtIgqeLNZfjhCjekCkGrIop4TdMIBZcGhq6xI5ISegDwHBe5lPBoYIANkcC0oOi1ZuURRBZUxMCC6/f3H2Gb46+ww/7H7A65uXCDHB70iZq6x9h4xNEXZoCIOUcb3ZIIQg+R0AhCAeX0MUj4682YDgikCDnBNjO1XgwTxNnIwRHImXRXB4tXmOTQx46nZYkyhpwKLIsnk0BdMiyWprtnWbb4SrKUekLDjGYFDw2MaExBtc//GPSN++BDngM084/29fwT9/ivw//k+gL77C03//fwYunmB7tkJO59gNv0BOG/TpG5BjeHjBa92doim7ABBkT//kSKJHeIRDUBbaqZj7UTUQj/CThYozGyb8l03GC0/4d2tJUGtcOwPI9AQ3+BKDIqfLQEgAbzZAugIyixcg2nOCS+RK8YYwwooLnSW/GtwtRg9N+6Z0NTfPlgvjmoF6uI9k/0wadtPyMXE5bomFeGPziuBJ/W5ax/JYjn9aWdasMe3EOYOcg/MeXd9hvV5jwDn8xRe4OD/HZ+cXOFuvcL5aIQdG9FlzmCnN+oF42+8j42UCftsTvi7yopaAYlhI0szANgGbCNzEjG3KGFgUGgkoBjICSmWMhpYBx+DsKhmOlmSfjOmUd+HpmE9lbRN+Y5FHOXU/rWFAZ+8QqhOP0c7lcVsDGsysfMd4HBagrsqJWoKaTwIcfHtX+QwPv+rg+hVWT57Dr9f44ukLhIuAPwVVToSgNG5T5i3BcHMmV+Q5D1v6cpSffN/IfkCSfoRHfoQPCXebh5MVEZEztgDe5YRAM/uzCSwgpa3D5t4ZOaxoHm6jhdOVEbeAvRtbZdAM9sfDn4a6WJgAPeBbz4ecuVhSAnm0fhb7eWReW2UOT7QHFg96Wr49Z2xg64lZ4z3z7D2rb+nGqB8j9dL0AGg2DVrM3FGulXjII+kej94r77T00gMQ/m0fTtnjHtwT4lSJ79JzJyyYJeXWg1gcHinjJ6V4mI79UuPvfQDue/+hBmq5nOlcS0gPD6YVgOoRMXpOw61YTHOzX273xLqGCYkD0OzvNanWnD034j3FiO1mh+3VNdKQQCSCUNol0C6DbpLEqLxJ4Lfb4g2BUjIqHWl7B582TXtxc2kT3QO3wYZ9e8GsrUasz/ipPe9jwUMCup9WNvT0FjcTZlbq1Zp9+dwrNVLDa7Rm+qRz7hqhuWYrZrJzy6mXBQBygMvahjEG2ZFSq23OmOasKW0hTdoMiMIBluNCCsma9JGchAlwBGSHEgPV2muJq82Cz3nBf3JOFSS5UUDUwTFLNNgKUotFx8L8GuPDbLkpagijIny2adF+Fx1NOfOp2eO50CJjoIpabDySionVA4FVeeS0T4JWXPJSZM4gJmRkOLaJ0F2Bx94OY29V+7MxQBHMZ3aqrKHSRpn3XPhSVmZQPHYsubXm/5gEvi35FKag/XWiDgMyMKQkE0GuKNjEEyUik6siEuW+WZU2WT1WTJHKQFGS5ZQhqNQqZOs4AdDxznAaQMA5gL2DDx0odNhRh5wzAkUJi9Aoipb6NSdHeMR82lwCmsOCI8xuliEoDWJscsR1JpxnQnjzDmGISH/8I+jqGt2zz+Cef4b+61+DnUfqejiKSIME2DKVjbN+N/wsM9SzY//e/CE9IeZVvHem45OA/dbK873ioeB9e2HsI50tLNld4eCrZP1aWHz3hgNCmA8F+9jgnxnQpzDWEzDPzA0z3iTCihgX3nh4+Z9cACEBSFUEPRH6GglpaZWKVyYmvb0tr7oXJudwu/5Gy0R/UO0R2P4j1BiSpELjVlpqhM8Sb1bLL7KOUoVF5GjLMrmWk++FLnVCAA5rODrDen2Odb/CKnQIgYB+AIcawtRCUrZNfJ9y2gQxishtpQfI8pRRklInE76X/QvN2KPeLNemfENbEe+/ZRdmionp/fYGLzzHk/sL9c8q5vllbrH7sHd/fX+2UvYATeabCk0+vt/grhODpxA6kPfgLqDr1zjr1wgBxSPbF958JBQ7oU2Tteg98pNz0HYHutkcOdym41oXr9tu4d5dwzsHPjtD3m7BqQ2RdmLzDgDt/dE0+3QLyfH7d23Ux4a7Nvx9HG+TMu9Crt8qR8SWM/4hbU/YU/c/0QpA/z6ssFqI+313aBfKQ5dpxS7M5Iz21EPPGHJVPpgbfE1yWTe2veGulHmsQgLUd1XgwgcQoBXk1+cm4zTa73lWDu896CfhtRbKKImfsLBRTJQdJYxHU458oXH/9igyHhKWFCSHnjlY1ie22903SdYjPBS8b8RYnufqPtyCQ8YKG/wSzoVi3d0y7sEHeO/VYrxaw9tzbblVWDxvE4HU8qJaLhMRvPfYvrvEN//tn8QaCZU49m926P5yDdOBhx83CD/OCagZCfqJrb19cNt2Htt7ZqEPD1S6XxZV7xMsabAJZsdn1xSdRtdclTYaVpC5s+tnZfokhn9RTsAsvlnzkefKDzChJgZIWFpPZg3vyCE7sdgnFTAnzkhqkU8gzXkhMe2HXZR2O8CrgNnnDPZeFRSElGI50wmEruuKEgLMGKLkznAgsBPhfc4Z201Ezmp/xhk5SyJ2JoeihEhRkmdr/glWZYQjQnC+WJmnJPVbKKMm33cdAeayTslCTI0f0TN7vH5TShhiBIEQfCeeD45KeTlnGdeci7CfgJJcOrf5C5jVO8NV+QjnEnY3I4MSkJiQMqPrPEBUwvswoibhlHBVWY04yBGcJ6QcwSkhO4ZjLgZsztFIJVOJ5UrHMWT8hphwfb3Deh2Q4RFzQspJ8n8QEJgA5wG44pHBnDHEiAyHleJJ33dIOSMOETElbAexVXW+toF5HAYs5QSXnMRfduaB47Fa92BmvN48wxC3+NpdYuUS8nYYea20687m0/Da5lPuN/SkKdR4wC5uwWkAZQlDxj7gae+w8ow3eY0VOuCHS4T8GrvvfgTO1nDffYPV17/E8//5/wn39DmG8x5xGBCzKBlcVnwlj0yMrHRnZi7KlFNSez7CI3yyUNbfZE99hEd4YLhOwH/ZZHweCP+noqhvgBwkpxcXhTkgAurENdSkxevPJghVIfNBw8rTrPHm71nTVEhCZiQyk6VMrluYJvOihbpvWAjDUpUKdatEstY5Gh6ud5U3ma/VEq1f5Rbi5RtCB45r+O1v0K/O8Nn5E5yvejztV0gXA96dbZQ2qrTsov3qB9scqHwUgw9A6UQgZmCXxDNi0ChYYowhfJmFU5QXCZOkIAAYYnMyEYZbJe213Hxf+Fq8LsqczuuafT+Ei+X92h4LGwvoZyFAc4P1hShdrPIY0L4vBRfc9HL5QeRAXUDoOqzPz5C7HuHZCzw5e4LPz57ArRK2IYK8g/dqqqKKjFHY19GaOtxaXvXY/e2vQNc36P/xj6CY6ny78bM2DJM0EQAD4ftX8D+8Bv32l4hffI7NX75Fur6eV9muz8dD8mcI9xO0nK6IUOSpSWcOYRNP8bV5h4tF3yUYLsf5g80uPhXAT3d4+9mTwxO3rNRYsqi61bAtHGizG6PDEDMlxDhJtZVzpBVLeonRwPLouf37s214spNUHUZlTlvgksineX9SeFU08PhCKcQIc25/7mkdNV1ZECbR9Mv+Zx8cjik75pKAxdt3Vpicql48Mr53evFkmOLLwhM/h8PnkMbv4SvTz9MIi4N3F9o7sk6GQ+IemVYgeIjng+6lLX7bdeURTMQ38rwqnhR1fxnXiyKwtGY755Bjws3lO2wvrwsxSI7gdhlum+Guk8S9tSLNrGu6/HB8bz86fbeY30Wl7b4LE43wSc+2tyc9O5ibaA9MY12XIvccHuZxx+YaP3pMwgyxMYQLbWqZIuGTax4QKnhQFe1MgGNLLEyoOnMR8poyZNpvozgc6TjpGZaVGbG6HRFyEbZLewlQxmoyNopfufGEENEpA85VRRw1nhANoyw0QC6jIJ4EGSnGEcNDMOEwSTJ3srwNWXNDiJJFbjkNe+NEwJDreOjSasZ1PI/yRZn8disboZ2MkZ0ZOWd4J0yqzJmDJaJ2riaqFkVRFh6mYVhauqeF4gWhipJqsABN+Ei2iQjuqKWhKV2iJkhPWcMcZSunFag4ODyBg5fQDrQDYzNqRfuRmRFzVta4ieHLLAIRJ2NNdaAVr80rQ9pAzgtjr0qvllc0nKhGKHXdZM05AQa8htRyzsF5Qtf3yJmxTR1yJqDE/jZvHl0/B3a/0hdFDuasYynKFGaubv8QpU/kjDdJ+hupx5o8uh3DY8Dw52+BXcbNn7+D/yKh++VXoK5DXD0DpQEh3ugsoK7jIsRo5+D9nqeH9sWfBV1yJ9izT/+kYNrm4zT2p5kTQ2HfFPD0gTu0/aGn+/ZD//7gg9Llh2FZ7rEMt6Hw7fnEjaB4VrPKHAiAq+Wb0Xtu/sbtOxbhohR/GoF9Kty2rNHzd395fB7UWShXucl1ZsYQ5BF9j747Q9f1QAjYdh7s1WDFPCGIFlfpw3DZp/OCRua1kLDGjgMiCDEz0m6LHLfCa0HJGW5Gqvy3JIjCnuFvbszuN/zaCPmXni8E06SMBld5Wtjk3eY6MyTXW2kHL7yydG2h+D1Q0aqOV6Fqjb+B0ed1zyJHcMHDh4Cu65D7HmfdCmdnHeg8gjuly82ohk6SuGCOgZM3vPD6bXfbzLQtu2r8fF07Wl5ueH/1IN+HMrel9JafHa+umSPEiZ4Rn+Dpfxp80g2/e+NOVkQsh3Jp23AAxfYoAr5JA77FsLfGU8qyn1/6Dv+G1icJY6z09zWnJUdE5sZqmMvnrC2NJWKb7MgEHO2nViACC9tY99Bh8zUpvTb+fio8qs/PN/b5sNL0kclt2/Kp/bnQd5QDf9xWq4UK8z9DsUM4dw9YVPb8ZODjE+OP8GkDla3EhIg9BvdLZHYF+ZdCN03DNc09IE4D57wK86RM7z2ur2/w7T/8k8bLJ7ggBFK4GtD/8fIwUfueoZx9dM8qR4LufYR28+yBs+xegpTZ9r5cViHbVWiaJ8+JdbwoIwALvzM5bxpGQ4T0pGFhRHjrTAmhAvBCCjdyaGSIlbYla27aYMoLGBOlxLoIaDWxszVFheditebAHJFSKlxY1jE3ETEyA46REhcvIBAhdOIdEGOScDqqgAhe8iWklDTEkHpEmNcGiwfDZrMRS3HvpM06Dl7bnlRSm1JEjFEUFwC895AEzayKQvXiQFL6QMOYOZQ5sXVSlSn1r86DPGbo5pyDV0VkSgnehWLx570rOTC89jfGqEZm0u9uxLBoTpF9OMiWrFn3FOfgyWsSDYjLOkPqV+Vjzhmb7QYpZTi3QmbxKOCkdRk+YIUOv4VDAAHI/BYRv18mRlgSOA4xIzNKLgenuT5yThD3DVcUJayCB+c9vPeiDHFc8mn4EFRotNMq6nriolSVgc+ZETkiQPJLCN5IvpEudDg7O0fXdXj7Fhh2O7xIN1gha76W6dCaMqaGBKD2rlYt+Ugyht0AJFlbHUHDKjF2MSKmjE06w/fk8Et3gQsP/G3eoN8MuPnf/g/cXPwJV8/+Dqvf/Ra/+eXnCOfn2F38a2DzFnj1zwgpw2VVxxFLiDMC2IxdH+ERHuERHmEEt1JSNKIBQNji7IBE1QMiseQBsH1Yyl/agA/QlVP5vREOPH2olWYfKuwIDXtrPUNT9/R2aW/zu7woYFkPWBX8joQO8j4g54Dh7Cnc+QXO12sMvccPK4+VTzhzsdAExQjkoEnAhweGw4Zf4DqfYZcJKW+Rrl4Duw2cep87ODESIFahvRqIKBlPrJ69NmYOVSvGjeEGUA1ujcbZy+eU/1BxiTGefJ7cK5WMy+bmuULkWBvVGIYZI6+J3L4/bdfC51GognohvVqeuaXDlO/xkoMkrHp0/Qrr8zO49Rk+u3iGi2cem2cRFAg+eOVtxjWNm0WTazZ3Ft1g3JFqtHSqzGiqSjhdison1/EIPy14mF3uFoqIIz8OWR2NfrQs0aJY/sAve6v5pcLoTc74PsfxUi9faVTW0n7TggfhmQsIdqjMM7iMS2uYat3y5PtICbFUmx1e1l5XNod6j0zhDk3jWOqcn//TsYEqMVTA0ljilmSV1hNaTkJdy2pHTyVEVT43Ye6trEaJMCIQJlRTaWxTAs1vz+QH+7Qbd4EWLyfF3iqU0YLl52Kht4WjCrbREXeHoh7goKDjbdg3DOM2nd6W25J7RiROCjn49OznrYmT+8BSJdT8TZ+rhONcV+iQcQbAa0JX2V8yeiBVARiKIhRwJPHOxbWVlL4zC+BcPttWjJb5QvOL4NkTcsy4evsam5dv4V5uQCk3xDzgrgYJ11rW0QnD3ghbgTHO0XTY2pcWfu9T7hos4vPCxcU2L9C/o7r2KCOYFwZhoU/z8HJ2bowt1KfeACOCn6clyW+bj3Hz2njDlcCtQ664SZZ7wRi3xgK+7YppIhyD1SpbJejg1C5CO1vUYh9ARFLmiGDW91K5ePWIUsQjk+Zq0DE1y/SYIoxRsSTNZvkuioZcx0wt5nNO5RyuLuAoDNI05n3WfBC173reO4cEBnICcxqHKdPwC7YiiERgDWVSXNEl1vkesQG6jqcMSFFCqEKoKDIKQ6f5GCDJoB1p4mWybADqYt9qOmaMS8WTOVR6x5RURK6EnCJImyQ6F4MzITNpCAqq/LDylpSfwtEZJEeNzJ/DGsQvwNgCuB61JjPjLKzw5dlngIsAi2DCa1+dMyZdBouck/yYZIrVqsS1BNzBe5k7xeMUk+KReE9kzsokyv6ZIXlFkJv5IQfnPEJwAAL61RqeCB0HBGaktBOcnQyvzbiMHdczoX5RXGckavPs1PmKOcMhg3iLDMIVrcHwuHYOjrzEM2ZG/uM/IaZrXP/zZ6DPXqD/+ldg9ID/AhkZu5gA2gF0BQdSZ7a9G/FeaJXhh/O4nQZHjWs+OXifBEdDP4w+30NND2bcc/dybpsvonJ2NeiZFrRQNponbtHGWwu79r20xOm+Z5gOwweserH+jwy36f505U1/jT3/DauqNKDkbwZDghYCGWNL53FE/EON3EO0771+DMZ0mu36bWtY6Qv5yfMGlkTB3FxbJLzHVU7ujLzyMEeZDNZnuLSRAbATmnEVPFZdQO8dkiewg3pDKMmzr/JRI/bcuwf+XjjCBQFnZDuUFFiMEFj7lRiURBaVckaE5IrIdiYr7Vo8ZsnoZ7tJzUDq92Y2R/+3c7jouWAdXgrFVOnW+bs8fjY3zzNXT/m2rPZ++ymUH4pyolVUWKJqe6bhbEoPpsZ6Ta+UYIfNA7Hx5RaiSXOQOAfyDl3o4UMAdyv4fo2V9wjeIQUGefWGIKH3aVQjKp90BCp31cxU5xFfPAFtd3CX18241FVQIpYYb0PjEgHAXW3gGfChA54+Qb65AaeWrpy9chSW98V5QTMZ0F7Dup8STNbKiY3/qOrPE/FwCW6VI+JkIpUOP3OSYPeUKprD9h1nXA6bPQ+OBRzHhqojwn/oL9C1iVYPNqh1+QIs0WRqYqiPmlQsiZuNimh0XSyFHYpHBJEKA0cDUOqfyuTHZ4Qg8jRZZGFIAYBdLXJJIDQ5AGy/quKGCXFMpeRGKWFt4GlJM4LeujrWb4w7OdWynoJXe3M/jDbYPe8cZXiXJuF2a/OOPPU94PB2fxSOrPVbFHKPZ04f4ENs20kv0/TCQ8OpHN2EEebxvSUiCfDY0VdgrND5rgg9xfpWc9iUmKxUBHAACtNe3MJJ9iamDGrI30JDTrtTbss6cx4IIeDm5hLf/fd/Ab+6xur378T33PpQGn+bBbRwiaZf9r1L+x871gRT8h6br/HjB4ttaf76HsOYzlryKRis7/HYOp2pEpzVYqg2UPAoV+akpKDNxcMBGIfZAQUAhKxKAacJFOHc7KyrgmfrTKOYBzRJm45tglrKOxVGVwbVlPjeCUnDQ5YQNspKsYWiVUWE9x0IDuxEIAxWxQMYKUcMcat8CRfLf8qqiMgiUPYhaLigLFb5wwCY4LlhhrIxTMoQehWCpRjrOU/G0Ip3hAMDaQdOAzhHGRfnNTyQrTjpvyPA+4aWaJjErAmeKx8lYapEmTDGEFFA1D/OljA7IxNJaCs48ZBwXsbakTBVrGNLDtA/0TflEaspgpOxoqZaElrfASaHTEGSRHMWbxZ2GDIjZkvJKUoQAqkQXxhrQgeffw2iHkS+eG9kPoePvwH4DRKuiwDBRvKL88/w5fkLfLv7Du/yGwQ4rFwHFzzIi6Ih21gTwZHXPbKr4aRA6tXl0Pc9AEJwG6ScMOy28N4jdF1ZZzaHEtKJkBLB8nXAiSdIQADnHsEnODikVYdzvEVIDtvNTrx1yFjGOs4ANJcLwE5HyvBDmcucxANkcAnBebgmZ9uQIpAZZ/01gt/hLTtcuxWeeYeEDl+6Jwg5Yfv//Y/Iv3+CV08usfqb3+L5//X/AQ5PsV3/e6Rhh21+i0CvsaZLwTM4xWETc5zuGvFQQuwlZvoR/rrg9smrW2GU0EemCi1l2jMTtGqi4T0w/Izx92fcteNgu3TWYRBC0BQQRXTDQg+oDygSWJMXE8yKz+SzuZVnHbICb4SV0zbNr+s1pXmoibtXAxYY7cNwRTTA1WjA+Ae7YPQSABMQ2xgsGuHsXVk8+jqmmZeKkStOH2CTYXgPTx2er3o87QLOu4AYAHgGnNBTMHHOnhbNWMcHhC894XcdkEnCKTJZ7j2lpcBwGXApATEiRoddzNiyeMoMcJphzUJDZrUtUVq/kmoSWjUb3zAFnccSNtderPtmI4FCnZEGF+35Qj43lY/2X6sj1/cUx0aKrVYIY39ZaQ5TcFmkEmZhMnKUe7lVSBiM5VyFzjIjFP098v422ReLhytIn3MO5D186HC+XgP9Cv3zL3G+WuOi79F1jK3PoCBGOFIiz0ZBmnWCLIzmbedVj+G3v4S7vMTqHzeSvdwYT9s/qKEndWqq4k36Fr5/Ce8c8u9+hfT0HJu/fAO+vqlD9oDIP1+3zWp+MCOHjwmTPrTC2o8CtxjTOyojbqGIOHEgFgSTy4tCP5fOtfbn3mrnN/Z3n4/cH5eVGXiZIy456RlLI8alJ8JnLpR+cVO45YPIvByGCTDhTmXAy5I2JYQjpAR8/84hllwLqLXNFAPjcqd9NYu46bNEwFdPgVUHiLumCTWrRUBNLlXvNYWUA5Yn160B0/lbSmIr3VkYK5rEPD6SI+KkSE2tJTB41ECzvDzl3aaJC49VZqXUcwIUzfNSHXtvzNt2aj6OcVGTsZw9RMtrcRKM8raeEHoXx/eXj70ZK7SL/d6wbxOcPnNCfZN1mugCTF29zwDDgagTgaZuKOQqkeRczR8DI8LJiq8zyyy4kDU5a0lW23ap/dFuHznj8uVL8HaAfxsRbzZw310BV4MKa5sGNzDbwQvturAmmeHf7EC7jPSsA4Ibr5W7aPtm+9htC5jmV7Bi6x635NTNI/HikRomFvdNIeV+8YwYCWG4CN3RhoyB4lSbH1AJ/2KRp3u9WOYrk9xIQwkQy3lg7L5ezj5UhKPJltZ+4eYMZBSlvCgjJHl2c4JpO43BsMSMrB4DDt4L6eOSxIiJCRqqxpKwW26DKij2wYNmmiG5J0n+MpAkhBJrv2HKPbakzZWpIaoeCFaihICykEypzulo/1XLXOby3eaVmpivYyJA92lGaT/rmBqjYY9nZs1tYHVLYZkzcnalXsCE21TiwxLVea78oOZOYMVn0YSMh5GbpIJOcntY3ofMTVipBgeqMN8uUqlvRmM4B8eueBbE2BahY4dqATi2uBeviOKaygwmDblV6N0mpBdRCQPmfVZ84NrPnJEhlol23Tlf9gIL3ZTByInLPksE9CtCcoQb9IKrurda8vjSap1uox7H4tI6RmXNsHlypFE7oeMfU8ImDSDn8AYSlir0K6yYsQ7iEXL5n/8Jux9v0D3/HdznX8P99t+BPUDcgfIaHF8AtAPyBmN/nGW4q6fDMRgrIe5ax2Hafm+unAejHU6Bad8+ZN0fH+a8x9Izh+f/Loov201mPNetS9I2nFrAMTLyQ8ISHXhrGFN3t/JMf8+wxA6P7uN+q22pp50DXgTCE7OORvVMlXf0/Bp2oJstiGO5azvdMvtidBhPkG2pB0UyMLkvv+08mVPvLS3RNqQawIgywuijRsAMLgr1tqxajn6ZNNdOuNlFw6uWJWgeEVpRrdBLyM0OwTnJ3USE4CL6ENE59XJsSrj7vN8NvwnmuZ5Rs6VRGRJWw5UIQmTCkCVJtZH6DPtehdyFNmxms+2XGBwVJgyzB/bAQkmTd5tGKc1eH5i8V7wYtMHlb8HLwd5nRsEtNPdGHhBN/QWv5u2YnehUTaONLDQcpIbHkQeERg4hIHSSG4K6Dqu+x9lFD/csg9dCS7tCLZ2CWdNdch9OKZaQGMBMMlSPKWgGWPkesvEgGj0lNKSWRXNq8yD5cwTtD/Z6cS/766Jz3i+0a1DhPdDlt/SIuD08DPHwcB0/paRMjD/G7fxdnYDnLuDFKszKEuEFRlr7ljFphS+mMR15QWh4BXIO2wH4b9853FgzqFnwze9bAY2/dB5Y/x1j1dFk52lIDW33IsXVKihOuT4qvbZlqsMYldPcmAUI4TF+HUtevUg08tgTYqqcOAojqb8ds82hdYs9cV/d+xQke/tbzBcWysKyYPM4w/W+N/dj5e87YH4Oh86xw/PEw7UoOB0G9xkyPZnc1v2FDEcZUOsZB4lTXv2ishIUebRnEZEai3BVQjgniaT3tFzoLykjDhE//P5PSK+vcPZPl6CBEQpXt69jE0qXm71gygtp07vvN+BA2K6fIXceHxsWl5dO65x0nCpggenet/TM/sOtxoVHwzQRVYt5U0Jw48FHih9GeOYsngWKDVJhM3feuaYeZZIJIsAHqkKiWGxhtkfNFEuKV6QJiSWSEoOMceBUEjqzMR9EJT8DsgYsYFWWqZA8dEHWQYp6n8VdPWWkbMqIpELgDOd8YR4IGl6nKEOEuUkxgZ2FWlLm0EmeBVMwMGch6vWMNGWEIXJOEXG3RRy2iHHQvBUoC8nE3SUJdNY/GudlmFn7mnGA8hys5arcH5n0k6GWYNB9oQnxoLkSGEHqc8oouRoaCVChfavgz2OPKedctRSjSiPlnFWZJXUlJqQsSiaCvpc1WThruEtvTKEpxcYYJIof8eAQvUEHl3tss0OxpgMUz8VbyEJqmgLEkXhUsMa9MkWNd37R+EM8S5y8Exhd34F3AGgQSzhVIGRwGZuuIxA8wLK3JoingijGWL1mAkIHpC7jx1dPsMnAM7wWIr7xdBK6zabdwRGDYGuOa7xstZ60rT5zRM4El1mU0tqnIUYQMS53WzABL6nHJnhw1+MiePxu/Qx0c4Mf/pf/D/yzfwalFdb/9t/g+d//DnAdEnWg7TNg6MH8CkQ3IPWoKrGkH+ERfhbwKQpCPsU2PcJpUOm8cwL+9cohkBPhJpfjvAgrCQRsNnBXb+FTxNDIPgHsEdzNedh6bwFvjF5pac7ZY1yFwEbC2JlUemRCrgwuigezUtfTp/WMaCs65dAo7HfjUTG5P+qWtUxlAuI569H3PTz36FwQi3YAXUg4666FJoErQuePBaSYIGe8g4U+FBJYwlhGdtgxYZuBba6JzxPnQo9ooNI6dqVTOpLjiw1rpvM1vT8DXv45+2zrMEqEJ+2p+GW4Vr26ueKQfc9j74lSbjZeolFggOvvUf8Mn7ltRVlFFnaWWroZlfc2x2yQhCbu+x5932HV9XCrFc7X5zh74rF7lkDeIbiGV3qwfXy83ouhNU3vNIZriuAj7wjYOIz5jlNqvU/L/+pOMvrIm8sHgFsoIgpng6nUY99ZROUqTS/u/22XZ9dPQ+NjT93ZymrE5NeeGiPFzUZV9jg0YSaa94vblikjHCFl4Ie3HtsoRMUuE2Kqouap8vl2bbfGYvQlZcI3r4F3NzweOBrP7cERG8Wsm9d5bLidY/zyObDq2oQ6k6Jo/41DHhNLsGRBPRP0j6whj5S3T3Fy/PKeApdDRC0pKWaKyplAc0977rAEDnpSFCSdW3efCseVrqWSW5V7DB62tPvA0Z1r/51msBIukKkHo5sJJkefbqwYbcM02e+lP+ecxFIFFwEWZdvLUBWXTasJEq7k8uUr7C6v4b69Al1tJXtekVzPiVueeenULzx9GDSO3MbYv1kuKOpOPRZuKzR7CCFba029736rXKh1N4fGAeWkEfB2blW6l9RITncSI/SpWo6PxpkIFsO0JJ8maC4BxQRSYn2xF9Wtuv3eMhKco7gP5yg5FOJOhPc5iZA/d6oss/6I0znUgos03KIez6WeIthXj0bOYqGfcy7tlZwWGl4KtZ0msE45yVwkyMIAwJrkOmdh84wpsUR/DFGAgBmcEuJuh91mg7jbIaZUknnbYJvngHlXmMC8VRgQav9z5kqBFUWQrXudvIYRsclny19ApsgBODtdk8qoq/BfFA+yKzjNo0FObeu54q6N6Vj4XJUQAJAUPxMREsTLhHNG570K+BmOzXvBGEXzJHBw/DkcLgC4gjZOK3PkxfIsPcFq+AWGfI2Y37ZiEVsOogAqdB3NeAECVAljSs5mRyKdBVKLyhCK4tY8DeqWNz4/YQxrltAAcYjynQK8F88JB4e+78CxR9gFhMwYcta9t+JADXk14x6VGa5hKOyehW7LTNAYXho7O+OskxBhg++w8w67PiCEgHdhhdARVmEN7AZc/uf/jN3uBu4//GuE51+g++p3oODALgDsVRHCEAz5dE7gnx/chmb6KczDvjbe/pAt+vMHOJ/JFlP5bd8bscmSBOXE7hDuRrPPFv2+Ct4nTGm7u4DN1aScT8lDYgkeasR7R/jCAxfe5An1zKPGIMEMuoU+4Gbam5EaeT1M6bBC2IzenXeCG3xucdwBnOpj0wEgFOXJzFiPgXkuCP0rwmFMCpy06cCC4tFzPHucrf1Wv56dnDxwdQEK5/BnakBhBKDRTUfg2CNH7Tb3FPjEAc894alfftmGMeIJBg7Y5R5DJuTtDdxuAypnveCM0XYlvlATZksvNB/T8ceYzzhxY90nO1zukH1p8KRRds0UDIY7JRRT+1txaqR4YFVW8NgzvL1vdPikSSPxWbnT8GLlq0y2806VXB186JDOzhAuztG/yKBzB6ixzshoq6n3IfY+sdsRY0Ne9Yhffgba7hBeXy4up1YxITg777V//Q603SGtVkh9h3R5BU7xcENO3Rzp0KPTs+4DnnET2CsnOxkW5nZ6aU9xi0bGB0eNDj+zdPmQLOGOcDuPiHIIlh8fAE6v56go76SBo8UBPvxmI8ixDQsYM4BN/ZaIsfWAyBn4/Y8eb65pRNjeZZRpcn7sI4hyBn7/Q0M00/wFwoE27LsxEUTOa67QB8Lzcw0PtfjciR4TOIFYP3A43tYbobSlKXOp+EObwL7dZW+de5QU5fasuD3tvu0mPVX4lHJovCfdmqJ6hGOwtGdxM+ijkEkgJPcM2T2fKRns06y1YcJEvVe8G6bPNt+ds5wRkkAWIn8Ui+g8qQvmfaFCvJTw+i/fYvfyHc7+fAm3zaUP7Z45Jmy5MqHcnjs0Z0xI+m9P3AZ+1ihrZxKaM2l8U4Y+t4S28lolwZomKWexBndExVECzbyIMRAV4Wbwysw5TWis+DZuQasIgCoC6idyLon2OGcgigcEUgRSRB62ooiIOxFah14ZyqoIqIyxKUQqXhUmrGHoLSQQJwnR5LwNCuoaIKrCdWVeIhGcM2+CDO+dXI/qCcEZRBYCjZUPEg8MjvK3295ge3ODFLfIMYJ8jdtvyYWrt4Z9z4BHM76EVMIaWec1X4eFRCqSOJSxKBaVur5Zxylrsmz2GdyaRFlRXvI3MMQLxOLgTvEwJfFS2Re0ss2nFRGR4Mo6Jx1771gVoWhkCuI1Afbw/As4nCvTJDiTnbbNeazXa9CW0BEB9D0GvCl4aE02QU42hUkjdOBm0LyT3CEj/rvpG5GDd0DXdWCWfA85ZcQY7YGmVmU69bspr3a7ATkneO+KR5p3hPWqB6UdVtsAlzJ2Q6xeKrpHFiWRTQE3nil6jxpcsDWQsigIfAAIHokZjhjPVxHOMa7dE2xCwHbVgXzAa3RYeeBZf4Z0fYnX/+v/iu7Hb4F/8yuc/92/wZe//B04eCTfSZ6VDBQlEte1+giP8FOF/STEAwhF6KFFKx9XUHMqfPQWPuAw3b6oYuqBFQF/uyIEcmBSG2QVthbauVHw5yzGDXaaEkFkDcyNHqIc+pOGjemj5U5MJQqENsHxEiMsdGH1TBi/39CeRZjcCI6LcHn67lgkxW27R1W0vAIvfi3v6x8BEm4yetD1C4QzyRnqLRxjkdHM6ai98MB8xnNP+Fe9E2/2MqvteS9/O7zAls6wQ8TAEdjeoNvdlHwK2cJA8tRjZFEKWT95/HP+yBGM58n8Fdxi7F8xbf3TP+t0G7IJqN4Ok1BNlhvCPCJyajwnGEV50da10JLSF6OHpxIWQxESGosgvJEPAau+B/oV8OIzrD5bg58D0TNW3muI01ERDw5G//F6heE3v4B/fYnw5qr2u9Suc8Ko0bhpjPbEQPjxNdg55H/9N4hna2w22+OKiFPhlDVWe4Z2hj76WXKrtp8AP40j/GQ4XRExG8T5yNI+YdC9JuC0GTwuEz+1EbrhzKRThJVz+Mp3OCMRMIgQhUs8aRjjWuqmUbVVuylKCEfiMvfNa4fLLWEXa3im0uY7jt0+4dqiqK7sdvO7U2XKvJ7TGrgvdm5i4Pc/AN93Syfawmo7WN3SvGF8gCws3i4Av/kc6G017OnT5Ybxl1eNVlof++yC8NWzW4s/l9tTLu/ZZQ5oW2Y5M1qpYnvdLp+KXKZYmzw+9gYx3OHlZk6JkmN4s0+JcivN8n2hPYiXYX9M6IeFdh8bWdwpQZzcBRhnAK1hkVFo/EiVPxKqtWzT/n3Ki8PtovKulfPu+5cYNhupNwPux2vgZoB79Rb9ZgDFZp+cWdzMuIPmk0sd7S3pEteOOiB+tkJeB3C/JyxT6Z+VUfs5XXvL9Pjh+R53a3kd7l3iM2arEoJtXofpVjkm6tuxWiboSyijRopK9baGELJHpBwHgidXQre0bSw8GhnzK4hItCxsHHs9tJ+5KgOMMSh/EZwi8rAD0oA0bJBjRI47ZGbElDWev4XNcaP6ctJqUqyhktiE9rkKnyFKl5QSfKhhmUbt5+bch7UXSJC4wWBRFMRhAEPyUwAAeQIngHMUQXkckIcBcbfFsNsh7jaaKLq1vMrqUZCbNucpCjR4XJUrhYYqQgzsFTRIu8WzBSS2Z67MJ8EFV5JZW78dEZgI5HzjGYWat8M5EGcV7ouHSNL+QftY8Nq8REj9RxjCZjfrv+IYias7O3zRfw7yT+Ci03eqyKOOA+C8F68C7+HIA6YTaGgNY85NcJ81JBXIgUlCkIliVmi4xElRV7RBnIHsqhKjCx1yZnRdjwE75G0jGClIIX0S4z3G5maD3W6HIQqOdF2AD66srdB5pL7Hq9gjDRnXu4jMYkXXe+CrMwfvSHMAWc6NXHJKlHnKhhAQBwg2Tw71cjMj0UZQEVW5OHQdfAjY5gDyDvybX4De9gjvvgW/eonX//F/RXyzwdnf/geE1RP41TNwfIo0fAniK/j87o6W3g8FD39mH6cD6vr8NOCjTsADwYzYfPgquDmvSrXmSdbQSkaDnNLMfXDL13nfA82N5lS4ZWNOHMuPgM7v10Pi4dfp7ae/pUknYGenekamlJESY4jA1e4lrvKfALqS96jmCDJvtDEeT8teaumUTl9qMTc/SX+O741IjxEJ2xL6zY09CgiAqwf0Ef7+cDlte5u1QeoB6+QctfwQnsSSPbq61ktIp1uCvXNXvDUKp1BFE14m4gIJPWIOyBkYEmE7MDaXlxhubmqoIoIYmIwbt/xb6ZPFh7j5cmg49szXSNqjP6j5LjmJp3U2/E3rUTNTZlm7uL5j94siYvrO5G/U6Ml4lQznPMZptdjiZs0REbquh+sCNv0K3dk51qsV+q5TmlKecTPMeKC9qPDPNOpGFTHU+Ss9td/U4B2bfKCOR/mlNGR4/gy8O0O8fCfGY/du+/2LuFtF+9foKaKfwncdgttaRJ7y+L46afzMnfawfXKNO8A9ckQsETSThXOHBu5/5XTEeBBgHlXBYPRw+E3oEeCKMGCkhGjaWEdCODljnEk5SVcEGw5/ee3x41WxY5s05CEJIhp/jn5S83Ny367vmZy6gTVtLafKuKxp/3IG/vgj7OHJoj7sATBvyOgoa4pZKrvC2Qr48ilVRcQeuNoA//ANI7X0FoB//TXw1bOxm+ZU2D9e5AcIvUO7Gh3eLGayfqtncqMaw56IU0XIvFyuKCBVwsHLdc6KPFL3PiXKEpF8H4bkUCtq1UtP2Zjcdl0ul7VPoTEOdWTKg3kpmS6Q/WcALOZ8bf/4k4t3w1LoJhNQtdem7Zm2kSaI/+6HH3H58pXci4zzf76Cv47wJIbbrVCxXZuVVVmCA3ivTE/BayLEz1fIT/vlFw4oIUblHmVqToB9zxZCb5yzpYSJKWur3ZXrvelZU4nFlsjn0e9RPWzW/yiD3xL9AFQoDLAKkV0rgFUrc2t9VWyhCIrhrP1+XO90HFregBsPiZSkjUmZBU5iXaOKB04RabdFTgPSsANzBlwEOwfneqjEtk50JsQk/c0pIpuFviogcmswBai3QwJYmdKy5mX/4iII0HnJGZmozqkmvx6GHQBG14c6RqQChDgg7baIux2GzQ3iMCAOOwCkMmoWwUE2JUlVnKBpq01dPYGrckTwiMFMRTg+EnYwl3BCljOGpnhLlvfAqVeIIIrsT2JY4UOnyerQtFf2FM6uKiFS0rGvUQAMNxJkrjMBGQQ3Yi5bYYoDkXpLwOGr1Zdw/ASX7yx0nJ27FdcBUSL44BF8QIIbCQOsx2Xs7HtOwqvaADsLQSXMFicLteQNnWteDJJ8JJkZXQgF52wdEFCNT8gBSYRKm80GV5fXSDkCzLh4co4+dzoVhK4LyKnHJVbYJMZN0iTjBFwQ8OtOcoAppmqujer1ZgrkZLG5qXrnWpJOoVVdWY82BIMjZOew6wJc6LBNQXJM/M0v4F46hH9IGF69xOv/+P9C2jKe/l/+b1h/+TXOn38JDE+R4UHDt3D8riLuR4P70tUftfFH4FDbPuV23xf28CkPYsSyxPcu8K0jmmuSr+eBYVo1T2+MzoipaOuDSXbeO9ymLyfzCIWoXC77yO17wHzyivcca1+1UvGMZMQExARs4ytE/xc9+/TQ0jO9GA5pHRNuY1L3FPbxQftkMzz6Ne7Hsdnixa9zofC0JdP3Js/u7WJzw0HpHQIx4B3Bkyoj1CPWka+00ryWO8Kx8W8ea1muQnXUDH9gQuQLDPxU6LDMGDJhl4Dd9SXizbUK4KFeNrwwzgv1Ku6Mwr6Ov9wK9r5FtkYZxQTf+l2ZBf0EwJKoG408bqyMyDUkE5rryldUhYSVO/GGWGhxNdYbYzxxw4wqN8DZiFcUmhBdj+HJE6yePMXF2RqrQADlYuCyJPs6EUNOh0L7SZsruyn8Ao2slia1T/DQ7tXwzw7d8+fIMSLdXIHTA7R1Xl1zf98+tO/l+8Pp+/4JcUgOPHBXWf9JzdNldleF6kMcfvdQRPzUCNljWHxCCSzhA0R20wgiMLeUaYtvlRAWNxgM/Pm1x7sN4XpnZNH7ZRxKLaQCgKaZpf5JNTXUyrSwSR9HSGyYvUCdV4nZchvbU/0BNG1tOVQOsTHEBPzjd0AfeNIA6578vtos770/vgP+0x+zChNoVgdPPvcSWUc3Acazc8JvPt8zLiOp1P5NhfkWhDgWyNUZZdlQ4yUj2YE2Ep3chqN1L1XxQAwJL6FwU8v72ANnSWbrnSLElO+TljRWece8GvYxxfbu5uoab7//oaCj1WmC6FyEr7rv/XANerdVmo2R37xFv9vJuxmgIU1Gy4hYLh/cXp+RW1NCcD7upgNLn6/AZx7cv6dwHw/BcfJhHOXcruPlZ2y/FY+12chirhgfX89JrcwtBNK4eYCddTkLYZ0Z8A7knYRs4jpH5AKouOFQCR9gyYCdzW4Jk9TOvxD6I++CnMd/5ladk3oR6F8awGlAjgM4DpKPgUTQml0UC32RrsIC+hRimGuIo5QShjggxoiYouR8UCFzCaHoJLE35aQWSwv4pee8hcPJOSHliBQHgACfBEkTtYqQ+pdTBDiBwLN1XvNX2HVhmL0jMNeQPqUp5OCcxopu556b55SxzGUOZJwZVblCzEAwBZQoIqw9FrLJebHd8l5wQJQNGTkJoxt8KCGvcmbJe6AJEis/ORXsadJrtVJLSXJ9xEjFEADwpYyYGAE8W1dlB9H2xpjAOYtHBLvF5cUMpJhqbg9tO5zMi2v22DqmQMoMIg29FIImOnfwISAwo1+tpB+mBEiiCvHkizDBcHK72eLm5lrWuAmPipJYvFC8c1h1Acgdei9KEHKEAMZrXbemaNsNUY1mnCZB9Dh3CU+7qPtvTVpoocfMiEbCNgDfbQjJeXgH9DljYFExbrzk8/gmMVa+w9MXnyNfXyO9fIvtn7/Du//635G3CesvfwVGRvaEkDxA3U+PjXiER1gEo89aQdVHbM4j/IzB9vUVIl9gm1fYJWCTGFcDY5sYURXHS7I5Yir514hvIXxalsdOym81MyJZqMY1KPdyEQhXMnAm/ObJF8aoQyMuYZGm5vGDs/uLpz8K3UWApQEHSfgjVkHyhzi3CqejX0ZGS1MRAgntAY3WUe6weMrEBGyHjJshI2VJs2YxMglK07DQyYXvm/JlOk+kRNccBU7Ao0J/NiWP5qeZ35rdvJExNO9TI25o1FAln2oZBwsGqsjW8BMzZcXs08Zx0o92/jMax+vWU8BaVDE1hA4hBKxXK7iuh1+f4eKix+p5gu+dGFERYYm9eDiYIG/DE+SzFXa//gXc9Qb+5dsyS2MjNqgoz7x+J1KUzAjfv4J7d4Xh8xfiUo19nPsDwXtU9H9CVX54WJBnvg+4oyJiWcA1gwOSvNtZEpyAwsdk+Iv13GJpNFpZUTzUOMo8OSCrZpGKcKJVQjgiZBC+e+fw/duqBjgF7uLGt1cf0Ja5YB3dPL54+I6CSLWHRXlpVkrZ9A5O+x13q73TPHpoXnjMwB9f2q95CXuVMApvbuRvsQ0mbN3XHt77YxF+/Tnw6xdLa2/y7mEp+unEJzAXEk3eHXkvTEI0tc1pfxDtacNMaG51Lm8Y92L2DihrrM6l/anW+X426P3KCGlVGxankPvtHrNHEXHIKs/qdM4hbXd4+advJCZ/qVXWvyNXkvOaInb1hyuEH7fNs0DXfCe3sMc1Soj9MMVpe1UFte3kkwiN8/Me6cXqUKG3h4VG3seS0CzVD+X/KOXz0loXaPftSssvCWNtV1KyOJslf21RtdzU2lkUETFFuAy4nMEuCJHPCRLbnfRdDb/kCIwaziWb63fBl3E4HjCXWMfygrZdwzBxFKF4RgJJLCNwTuUvZxHeF4VEygCSnlcJ5DwodIBTi3AYA4wiDM5apikhkilotE+uSRonfB0Dfnnl2xqx4eackVNCTEmU/1lCVKUoSbezhmYCqvIF2RTaGDEjNh+lLp13p0ofs9A3XCBV9ko+igavMhdedcSwlbBULcNWe0kOaqlVk+flLHkYnESuksTNBAy7ASkn3ScIwXs49RrgnBFTatYyyoAJuyP5s5gsrJA0x3ApZ9LIACoc0PsJDNdMytTTKHNGssThOi7k2nVVaUHOjJRrPg7OWfBd6TwhhYRAL3kMdQ6T4r0pMcgRvPdgZvRdhyEE6a0pVwh6H0XZlFPCbrfD5maj74vnBrk6TqKIIHTBA7mDW1nYJkGaTRIFXswJQ0rY7MpQwrFH13fwtMVnofZTvCAsj4j0N2ufmQmvdg5b5/HZmuAzIzIwMLALhJQzhm3GGgHPnz6Hj4z05+8xfP8S1//yB4SzC+RhA/ZOcna4AEcBYtYzTUT6U4JTz4FPQSr9cG34UCEp/yphj9BrP0V42v2lhx/MQ+JYI+4DVY73gEWyFvkprMtbgAnrGcjosOMX2GXCLosC4jpm7HKW86s8qn0cMadKqBS+nesDRxnpVjg1lnsUwe2ozVP+T6+VJxfKwuTSUrn2Nk8fnv68HVIaB1sIMB0qa29RRpTS74b0I9yr5EfTXqqX2drAC2s2KzHnm2Wo9D5nSGo1wY9tZMScCw8n1RhBqJ0zIxStdzT0Sh8S11oWOnaw16P5GBe+//mCokZcl1maPN3ihNGxqPTslL5tPSWmOSTK556u8EIgem7+nLXZ5g3wwaPrOnR9j7BaYb0+w8XZCvkMGDxjZSExF4YKpnm5zx47XYdjQSCw6hG/+hz+1Rv4V291qKd75fTFMRAz/Ou3cMEjPnsCsgSwD3A2zI6CPWX+3KiSIge703E15XP2PHLPQbsPKXgPj4glsOXWIgrfU1r4AHCXAWqa3MPhV12HNUnyRIZaBQNVeIIlokYZa2WaJZGkw59eEV5fEy43CwK6B4YlJcSsrSN53lTorIUsvTcpvyiXJoXSZP8aHa4PCUTzkBITOFbl3tk4JAzcc81CM5QrjHp976F7GF5fAf/7H/a9Py3udgO87gh/9wug88vMSRuaBFgYEmaNITgX4E9JFqF7FvprQubpZSzvI3vLOQX21AUArZJiRvjdEm9P2f6mgum5MmJ8+Nu5kd1TJJwj01l5b8k7YqlMq3PYbvHyT39RK3nGsNmOrPLd5YDu1U5DiMi4lNAwYPjrWNpkLW1bjcwgYnAJOF6fmLBAWMRrWzc8HoPaL2D4YgU+75DPjxxpSziEdkymN+ftuTOzruPFo/5reBcdTyIaMwlGCBoxvacPdi8bId0IqrUYlHBMGlNYrPelFQAafSMBLiMnyeGz227Bmw185+A8wXeSpJe8CI3DKsP7AJFIOzAJBZ5zhHlfgE2Q3hL46hLcMD4mFC/eEMgAWSI5/RRxLySpsv5lsXLKKSpfMQDOI1k7ncT3L7ZRDBH4DgN22y02mxvsYizCfuccQghwnuCclzFjSCJfJzGXLUl1GTWS9eHU4zGyJtbOSeqOBDjFgZzBSbwfOu81ma9DZgmfY/GJSeeWOWl9uTBbRABUyO00J4btVSZLtpBDJQawkCII3slYm8BCv4siqBxUBS/te25CQ5kCQh4VTwgGMMRYvCKMqSKChm1qhCIAmGjstaEkkeQnCNImja+bOCMlB4vUlVkYbCRG9AxqBNqGypYAOqeMNERstls40qTafIEOv0XGOyS8hu1EX519hqf9Ch4JwxDR90H6S3U9AeLRIMc7l/2rrDPjFzU0hnPKgHYd+r4HdkCMmkuEqCj9Uo46/xAFTvDwwZVxNC+UrEzzKgR4iBLIOSqJzSW1SsJ2GBCGQZR3Ot4hBPR9j5gJ3yaPHDNiE/dZ9gXCZ33GuWf8sA24ioTovCi+VJm0i4N4yTkWBVW/AjmH4bPPkOFw/uM7eBeQv/sB8asfsL18BVqfgy4u6loZzdojPMJPD967MJtxkifwgdd/auL2R5jyS2Rnp5w0elwjZmCbGVcReDtkvBoyrhMr/SEpkDJnZFQjk1L+3LV9f1tmvMix91rJVkPdK32VS5mVvpjXNWMiF5s2+31MSrmnteVbIRCF/kwshgkxJ8RsoSUzKODea/PhgFGxQ/7LLHmdhszYxozt5SXS9QaJGYNRka2An41e5OL1TDzijsrnwZG91YZz5PQvHTIhfEPHNj0eyVHJeIlpu/V7MX5q3EK4cAbNM6iDOW2U8liFZ80EMksYQpNLQW5LbjKHs9UavuswrNbw5xe4ODvDeR/EtdST8FXU8IQ15TzKWrkP7Bdw2cxjlESuLGEe91t/Gn4Uw+tpqQ8o+z3cdTr6xO3gk1jUfzXwwIoIwHah8XlQBSPtpYeAKZ4/CPqMCmF0BHzlO/SmgNDwBdN9QdzblfE2jl//HMSqkpnw46XDN29oWtH9mnyoqNk9mnytgsvZUweUELdui5VTDpb5I/Mt/5ZjdEjQWDTYx99ZfGzp7QOvUkOhjA79E9+vL1a43gK/3y4/el90enrG+JsvCMEtL859CgmgGUJmIZpnL8/L5NGLFf9G5badWihj5llxi4PvoMdDK7C/x7juq2NU14Ryo3LeT/dMDdNhBBgBmc6Q3GeFJJP363o2QZcWUITgFiscAOJ2h9fffI80DLUeruPqNgndj9tC/PFs4+NKt4z6Ws8CIXLHAvY6RnUEZq9re8YvTTd9QnrSgT9fN8zapJIFWJyXycVTlQ5757gde1QFjtxrH1sYV6v/BEmdeeaxKjHIqENbUyo0t3wPxfKdxtY3pEoE8WyQNsW4w+7mBn4geA/4TnMFhADnPch5gHuQ6wBnighofHvxbAAsn5K6RcMi2nLZl83KXKzzNbSPY4CqtwBYFBLcMA7CN5qCJWkIIAAUkUOA8wGhDyL0hoU1YMSYMQw7UUYMO/WGUJx3Do4CmF3xLjAvSG9rR8spRyQBFpqJIX1gWGgpFo+IrMwFS38cSd6C4BwG58EuF7Rxlm8BXL1YtM+GOiagdhYaS+eeyBSbYk3fohWhtpGJyn7DEwasJjyXt0o4Sq4IXPYXFg8JMCOlWMN6FfkJ1eebdmCxdYKH5MRVHezUC8aYayoKpaiJ1GM2NWc9MQgoiracM1JOiMMOzgV0XQBhjYDPERFVESHPPu2f4DO6wCv8iBg3otzT8kiZL5lPCbNEDmXsbbxEsQNxHFLazwePEAJC1yHlDNrtQPovsygijL4UbxyPoO8YXVlDmMkIeC9WkC6IkiB0QecKJZwVgdFFCd0E5xC6gFXfIUbCdfQYiBEhyq4yt8R4CvHCuIoeb6NH3zt4It1DEmIShQR10n8XOsARhidPQUNGf34BcgH89g3Su7cYbq5kDPBEV7+GgvirgOmm/5CM7m2JyrvDjEd49Iw4CiePzdLZDwAmHEX9eeC1wzemaDh5ZmREtVTZMXroNNLrbvDh0HwODR13h9t3gEOdNWMgiFA5E24S4zoxLncRg4blS1CFtIZf4tI+ozOr4ejeak9u3/GXuf2m9PBI6VC+shEk9S0el7BYV/v+baCwX43w1c7ZDCQvuZREIaE0pp5bSzXdFi3vIqsdYUO7PXD9IXMvRgZDSoibG/D2RvrAED69YbxmzVhixpqdofXaXtwmjm0dx6apPSqNnyntZVSzm/FjxhfMoDGqKYuBgRKCqcU53lPGrEilDScGNrV7ssa8esb2fQ/qAnB+Af/0Kc5XkhsiuQQm0txrSwhR20KEU5p2APZt0gQxqrG+yG9Zq809BopSqFkyrdR31MR9XbpLs9vt4BHuAAcWJWE5VJ8xiPbGexj896CIAJZ3oZ9QHTrQHRF+E1ZYg+CyHEaWhFAshidEuS1C5VhHiamdw59eOfx4RXhz/VArcw8sFj1t6+Qb0fypKu9cruahu0Bjz4HT32u+LxDaNOlju9BOUnTctZ9Uv0i/9LRXK8m5kHOh44fqPsCc3AU2O+A//ZHR5CtehKWqxtd4jBwHdy65d9YDf/9LGntj0NIYTV+fEtKnJzg/2cviFmWO4Ej7WyUFqdVvmwBr9jSRJKV2L0RITARGj9ELmkSYirWG3SakmPD9v/wBw3ZXhKdEhHS5QfcvbxEGI66VCFO6zG2PWa3Q+GueW9EIfUfNFaMrePScfeWWEDyA52XPLWQQzV6ZtnERTOj6vkgctSRuO98KdeZC3qZpxi4aMT66KedRHoVaah4rgmUVwGvM+2LSYht8CblDxVOCnYQQ3OIKu90O+WaHnHdwXvYIs9RenT2FDz18twK5AN91Es9eky1zUiVI6b/0p4ZVzYVWJQiNm1UZIS0QpYQI4zVEU5JY/xa/3gTTSS32UxLPRbe7EWVJOJM1QYSs92MccLO5xrAbsN3uYHkQQFqeulDEJGGgDHzwkjNCx9x7aXlOGZmqx0CKEXEY9F1GjtZ9iU1LHAHn4HUknHNIhgt18su8macMNdPq1GtCFBJTbxquY23eFSTeHMXCnvQk8uqFAUNRPaMavIkq2PbOi2AdBElmrLgb0wzHODNSTMXLw3mHEDpA55hmirkafMCSJZNzogygDGQVsmu4gc0ughMj9hmBpB3lXaAI8GF92EWEAHCoY+7YFeMI4UsJmRhDHrDhG6zOAkLn4LwHMyHnpO2WMQ+dJCH3PqiHgHgKCc8mCcsBwJFHCB3Oz8R7bRgG9QzQcE7DACQGJ0lsfX5+hq4LcCFIeCYz6DGGnBkODgRG0Hp7HwR/C16yJhgvGz6c9/Becj04x+jgwOwk1Jl6TgDAOyRsIsC9w1kQrw5LRg4wUo6IySHmCMDr2UN4efEMPTo8+/oGHDzi5VvEd28QL9/AdT3Cc2lzRnp/++0jPMIJMOGxHxwepuwPwU8/wqcEUzZWtlw7nyDnasrYxYSbCFwOwNvrbxF3fwHTazG0YAlUmZhF8Gy77Yisbuluo7kngsoRDvOJRuyV7qxer+bFqvebUDim3C/hYGcKilx/HxyxO8BMhixtSSlh2O3wbrjBM9/jGTI6444y5JAtguPb1X8fL6rnHvg6EM5LyijxLVSCAzt+jshrbKLHEBlXu4TL7YDXb15je32NTYyIACKJkiozF/q5tb+v//Hoc9EwbLZF8Zhf4cn1MYHbVjgqYvE3Y8z327tshi4arlR54OIvYRL8NvcEuH6O8GwfVDnZmM5s2t8uHyJ4clj3K4TQoT87R1ivcfbkKfrzC2zO1ogr4NxtAV/LY2vXezmb9p8n1jt+eo7d734F9+4K4cc3e0pRjlvp0nGpjXe28+i/+AK8GzC8fA1O8SE78wj3ggZZeeFaufR+CaVbKCJuv3HehXyqgrml0u7XntsAAQggfE4BKxU6mFBgvBFXQRigfCKoKCOcMtOZCW9uCN+8dgt9e8BGj78s3y4XaM/19kfTx1u1ewGZRzAhtdrC7zM+03cXynoIV+pTylgUhpZDFxOPiduuFn7wJTAk4JvXkzpGsH9O9+LQns1revXZGeG3X9TEttVT4AjsQcpT5udoHUcQfrTmJ0Jl/Xak7HqfINbmVRlBqKGU6hrJtAL752LNYvuS3qtWGUJckrbFFKIpRbx7+QrbqxuooS4AwF9HrF9uQTEX4mfJOh+MGiZoYTSO9XkWnmvhm+2x7cHYvjUld0ZF2K09++DMaq3V8htb9sBn7ajOhbJnrqsLzxSrmxmhziUUk3xkTPP9jMNOmQJ9bAdXlDgm5FRBqmOG9xqKMCZshy3icANyCY6ShI5xhBwzfOgRujO4EBBWKwkV04mVfk6pMJktY11aZkmP9aaDWL5LWyUMU05iYQ/zCrDcCsbXUFGfCWOloRNzHOCRwbkHO8k9wGrNnrIoCoY4IKUI5z0655WJAXIS7yNJchxhOSBKiKuicCMV/uaCh2xhosyTAyJgl7YnEMTLgzzAmgvBxn+sxlMhf2HmJzgNiODbGOJk1xnV3pGKksFoEucAZqefWYTxtofwAt5AFEpZ++k4FwbQrCwrjdSsJ5iSjHWPcvA+gDkDCUhIZa8iY3KbXBiOACYHIk02XuZYHktRlTSJkDRkVhkb9fawPoAzEie4EgdZ85u0PJ+e0cwSOmnIUfM9aDtZ8MtB8bkwoqLEcs7pPFb8tlwZjsQqrut69DHCaxglAJpfgku0AB8cVugRugCvbv3tnBviy/iIJZ0oHFxVMmcgBKfJ5JsBJQv7JV4QjgJAQRKrZwlDxgAiB0QGfAc4JnVkqruQKQujjoMo+oBrF8DrNdyzJ9Kv7QZpc4O8uQGGQZycZBaBBs9+ynDs3Khb8l24omOwhwbaQ7/cxXvh/iEWxqf4h4Glfk7r5vfGY59cJk9/Lr3Y4M0xVviUeifs1/SduWfELSs7Tg7eH6Z9+ATgZPurA7CItaNto/WGyJKoOgK74S2IvgfRDSKbRXyli9py7XQeG3Id41uMJt/znO3rB4qRY5cnfxbikpuHFhq9r00Hfx9BxIZXGPMHcr4PKeLHtIE7u0BEpbeVMoOdZKOiToT9W+rhktZE+CrU9lJDbDATEq+xy88Q0w4xR2x2CTfbhO3mBrvNNWIGIquJT+ExD5gEFF7VNkrCcq6CfRPe3J/iTzvXdp0WcLIQ+qVRzSePLxk9RyIk3x/RYL4iJgVg6bw2WtV+0ag5NG4SCT0YgoblXK/Rn1/gbHWG0K+w6T2CZ5yTK7KPOp2FuxhXbvXcG5bXBhGQ+x7pswCfc1FEFMXDQkk1tPR4vIjFrCg8uUDeDYhv3oDziWfIoeP7FNx7hLnMYx9wHdiKvmMZ1fuEB/WIOEI+vQdgMNO91uQMr5kRQPhtt8YZHAILk2tChtbisOR/AJTJxkgQJDoIhz+9JHx/6fBuc9u2TjfAU16m5v8DtNo+JcRkN38v8U8/HH7fGk7u7wmPlRBUCmaBXwQJDV/REhPHYFlp8YkO6IlwvWX8b39gjB0iTpkL3nMon0YeHq7itDH97ZcOv3xRBWn/+C3j5WV9d28dzSlxsSb8u197dAEATCgIZLrAQC/0cQK5lRBCii7TMEymvPjh93/C5vISohRVAWfOiLtBZM3F8qLtqxGZqOE4j9H5805JbHqWECrHidOle5XIHbdPyh/XJtD/cIP8bkD6+hz5Isy2mH1z8L4UEPuATfjZKI5Kvo0m39D+AgTfLUxQCRW4SMNzCSvjIHMuoj+dY6quwKwvk3Mg7+FDwJvM+MElhL7H+uwMOW+RBoanDEcZjhkuE3h3gxx3GAbJyzBsOhHK9mJBTc7XtqPS6rIPQgTzVGy6xJJJhd8uJSAlcScfeZQwQJKzILGmvCVJRp3BSMooOc7gTIhxkHGjGtanTcws4ZNc2Z+NfWdm5BQRY0QIAZ7EG8B5X5hSS9ad4qBCcZ2TOCCnKHkl1OpPmp2ROYFTRE4OSKkIfxkQBjEzyAT4BTfmu5lZ39dcENJmp3NcPASACc6V/9Soj+BJ5NQJGkbLxkbDLFm8aR80J8wQ4YORrgTngu5JkM1DZecWckh0XBIayLwkjLk13UCbQFuOSF0rqG0HE1Ji5AR8vf4aPc7R5b8F5TMQhYJrjJrg22kSbAthxTameb/YL6aE7bDBsFsjdgEuRFjoreykHexcGadCOZl8hcUbIkI9L0KHEALOztbInLHabpGSJEpnxQnK4rmyWq3gVg6+C0W5IXldZC5zkqTWWb1QiLqiDAEJ3sOUE57gg64unWvnCLnz6FcBhAAgYBi2krQ9J6RC5xIIkvvFErn7XkKyJRXUvMMOHXs8y70oRs56DL3D5fNz4OYGu1dvQW/f4PIv38OFCzz9leRGQUAN0/xXBe+XK3qER3iEnx8QoJb4gIXYHBJjExmXQ8L1zTU4vZN8SGy0BDRp9eScK7wpT64d4C0zxs+PflaBsXlAMNTTwVqiYSnZQlOWPy7GGsUIoaHNKm+yUP/JQPOvNL5gLDlpc8UjIuP11Rus+hV2OSKy0DiVdshg9wDGpfc+DkhoLibJ7ZaBXcy42UW8+fMfcfXuEruba2xSxjYBA4uRDUO8ZSRk6aQ9RmwU4JqAudR5avsqftRL7fy2ZU54ep48LxMwbkfBW1eISGKh98XOhzRktANIuaCJ0U8l4FpNwrh5QulWwQ0VRqYyNUb+AoD3kmvu/GyN0PfA+QVw8QQX5+dYnQWk9RYIgHdCn7cBZ0llcPMxviey2DpfQtoiF1S+ZmEMahn6ldDkiqhlUsro/vI9ct8h/upLVE7kbvAJiw0f4Z7wnkIzVWjFsPvu3A/GyojpXnq8atnA6tlE6MjhOXmck0PiqEIKE1xMCtGVSmUzkusxk1iRMfB2Q/jujdy764E1FpCP23GozNGtyYOTc3hUx3zB76nkaH9+OtsHjeb0lBcOPDil51SoUg6+RghdRuiUenmKC9NKj125K+xvnKD+Pvyo/TwEMQPfv51e3ZPTYwZ7yqYx7j24Uk2Le3HO+PIJABLy4dU14y+vuX1kz7tV2v7iAvhXX0vIm2L8Sh6MDkxPlChs95BxvHWwWU4LkXzz9h0uX75C8a7gGvtR6DH9nvJyTvPWmmTKbBzu2WmgxNBD4ae7TnDbjPzZClh7oTfdCW1ka8rCIXFsme3fkve8tqe3hVGs3nZLSrgStKYQ4yJAbxOLF0WnvTPabqjMqykiaj+pPkgAE2FHwDtmPPUB69CBvC/EqSTuFctw5KheBgSQQ04ScijkIAnYugBoCBkAReFA1nn1iGDSXAel7SJsRZSY9K3QmDTsTLahQMN423SQCbS1HHJgp7vKZG/g6ZyOBOI88TyqfFo7paaEGIZBvQxU2K7zw40VoIRWkDBTCQHgjPZsKMwuGo+IBSjtKP1Y3u+o/Gufkz+CCKarW7glPZdf1hZR91i+hYyg8ZIFh5RDpYpHRamQueCo1OVKLowy1PqqHZu8xKDCPCI0HBcDT7snWLtn2G6egbECTcapHMMNjWPlS0ACS3w+h5yyxFZOSXOPaAJ1cdkBHBUGbFQrm2yFle+tTxARQicKiRBCma/iraTeE9579L4DBfGGyIbd7HTpiyCqJP3U9WxLmolAWfKMMNRTpJwh6knhHTw7EAeAg+Th4KZMnVfxmJABzKy5SzSZYkLGFpIMNWtuCwoe2QG7dQfebZDigGGzwe7dJeJmAzJvGudQk0TOYbol71UmH9gzP12YEogPBw85Dj+tMT0F9uyjdJREfV9Vf9xyj7y73zOiPnH/RmgJt63ivlW3NPgDr8X3hUtGchgpIQmrGTsNNUlxp/SPa2ijCf3AbWmHgEcfewd6drnSDvJz6jsAjOPy6/lYBo0XytjT5L38ydK1pZf3PS80X0rAZrfDdhiQ1OiFVSbEamx1JJLxcZgKYg601qlgfRHYAdkhZzFkkdwQGdurKwxX7yQcKQNDJkTpISazUotCc962BFQh0Non2xYemwO7VHmY2bNLm3HrETFSQszB8rdJCgMqnhGg9jXli63/IyEMj37TtI/TbjYDJd8cjKY0L1kfAkLXw61W6M7O0Hcd+p6QuwHszNhjvs+Woefm93uHKicgIsB5I2gne6aiwygzdwPM8O+u4fqA+IvPRduC+ig3/x9oRlPewr3ZXva+D/GmCaeJth4U9tV1jEw7bXQOHcB1Xb4PWulBFRH3XST7B3PfjXp9iWk5TOpXpltLgAPwt90K5ySeEJElwWH7SnvsUNNoc8Ei5/DtW4c/vjQLPMLV1hjE05iPijRtp9qdqBUw8GTg7LmFeharLhw6zFpXftK+F+p7k7bM2nC44k8KPlQLx8qeOncjbDy0yOnA7YUb9+vXgbdp7489z4+kZVjA2J8e6HL+w4+MH9/ZsUp4txkf1FOg6Q0CrraM//c/Znz+hPA//Jbhwhmy/wUYAU4tyoUuaogE/cIAXv7pL7h89VqeY2B7da1eDwRKGf03N3Bb2cu4cxh+fQFiRvcXuU65rv1Zm6dEmj1ljMJ0r9l3Si0xLKPrLbcx5TyswzUMjXRPvotVBhC+uYbrPAsZAAEAAElEQVR/ucXwm3Pw2fx4K+F1NMSPCYctJmdR1szOhz39OYL6LW9VyNSRsJ3V245HCoUaVqcZDQYsGXWxGNd5KWeFCa9tWzcBogNArAJ8292pWK07WPx+j3eZ8f1mi02McADe+Q6vnzxDzxkdMxy2cBjgvYYwIi8he7K0NMYNkBlhJ/W7XuLWOyX8nVr/eNK8BcVqn5FBOj7GaYt5lwm/WUMuhRDgPInlN4CYa/imzFlCNakCgdiBfAAoIdua8B5gZRS8gw8OTEAchoJTKSWknEDOoet6BLVoJwA5JXgiwBPyEJE5Y7vdgFOuHkGaR6rvV9JHVk+JISKnhGEYkAjIbgA5kv4Q0Gv+gqliyjsviaCZJe8FCDEnGaPmHG/x03Au5SjJjEPQoeXCTNd1SIXfSGbZCCBlBiVG0ESInAjsCCkyHCckBkAO3UoSEDvndOylPUQehATOg9RnbVbzTqHVxBrMwQHkpfd5kGtkXhrAMCQMkTHsGCk7xM4jZzdbpzOehSQ3QteL50DmDHZXiP4PyPkGxFVVZqLxmwy8G4CLDSO4jN4noPdglwDH6ong4eBljyaAiAEnDFvOEZwJ7DJ88MjZAyS5JPq+x3p9BsAhxgyfWfDX1njHoE7XioN4zUQuazcOETEOsu6dKAWJGKAMZ54fDiX/iKU0M+8KmSMgIyOzJASHB3z06CGKHtvii9ALO00Yj2I1yhHYRQY8I5NDgEdAQAbh9fkT+EwI4Q3C9Q7xH36P4ewJdv/+LYJfAf7vQPklHL2W+T4oUHqEnwd8+rzAFEbKwpbeUcVe66tWyKT69gds6V8Z3HVop1KZTwwlp8JHu0poVeaiYB6yxyYBb7cOm+TQQTw1zcq9MW8QaOhRsQxvrxsdkEfPzpoyKgRjQS03w1rCfVDDLnAjVK45wyp7wZN5MVp5lL1gsR1F6LMXMcb8RpXftNIOYSRiZtwMW7zbApubK8TtBj4zKOzwejXAXPflPaMcDiAkzb7se2DvU88d8Jse6CdypAyACRjyBeJwjk3y2KUBb7YZb7eE15EwJMJ1JtxkxhZQRYS9PwmNpS3IZZ/TQbNqi5zdMGMyDwWmvKK1FnWeRsxNU2R1jS33HMSjGMxwbN7PaujDSkFys1/DMIvKXg2lVaGmHdIfB2Qz8MsjunnM3zazou1jRU9yTrxus4bv9B7whO78DK4L2Jyt4c4v8OXFOS7OA8IXW6RAQPDqrs6jGsTgbLJRPZRRQClmOl9U5sD45Pz8CbZdgH/9DuH717pnuFE5JWQTsyh9YGWg8Bd1fVV8OdSbfSvp+Dt3KfWvDQ6Nw6GR17XwHpQR78kjgpr/mwOovd/QcveqwxbDZFCY1eh3cbDmlToCOjhckMcTckic9Ew09F5oaBEK6qIFgbPD9Y7w8srL4htt5odacAQmxO0hSyWajO1+fJm0jUwARmgrHFdFs+/Tlpxkx/4JEX9Hm/KerMJugZ6jB/fe/oDWa3f1LhgxckARQv6U4WrLuNrarzGRuARLTwyZ8OMli/UrOxA6ZJxr6JX6Tonjr98liW/G9uoaV6/e1AKTEm1gUGa4qwH+RhURK484ZFBm+MsBbtgfG6Pg6PxL/WxcaQvbM6NJeXKN93xf+F0GyxIgk9KWVL5bHe4mgncJbrdG6nOJid4WVsT2RrSagEEJYGoUBaMmHVmX8lP2z1nYpYU+cWHIKvHclstomq4EuAinURm6Sa+KAqOdK6rNrMdR61FD5azMRNhxxmWMxQtgIMLWd+j6Hq7r4TjDZQY5BhzAECF+BsTSPydJKp2EYHGQ0EusFtvsREFPmkDZws1K1NpmvhgStsmUDEni9DNnMa4hr+y4DocpYco/aBx/qEeEumcTqTV2DZNVLL5z1vnn4g1hHgMWg9/qIq/nfk7qDSH99nANoaaKFZL1yBlIOh9JlSpiD0UwrwLvXMlxYeNgbuQ29YZDmU2Aq4msyanFXHO2K36NQrMueAAVtLJ67PXMRfAOVUZI0uiMnMXyEi6P1oiMKZc2UWGejT3UwUBlGsWBQPFCJg/FO4RFGZE0SSdnBwdR0LYRIyasm4L44Jgyh5WBZR7AdAlQzV1i78qfB2ePGIEYM3JiyVGSrV2tsrDui7YTZsshwQBlB2PhiByck/Bn3g/ijSJYBqinQynIGWrqes815FRKGZlY1pKisEw9l5wSEqqvUmrkBB+djgOxg9N40R5V4c1UHHkQoyisLIwbGf7oQOXMyA5gJrAmzmRkDPDIoYPzQcKFvH2HfH2NFHcg9wSOnsLTpa4V3Ru4QaIZzCnNQ7A/R4LdP/j6reBDOg68Dy+F+5Z5PB8F7X32LjkrTmzVUov2PHO8DeMn5mVPKZqpgPZUmNLW9x2dh8CWffR+46NYrjw0PHjJExbkBJL948AeBlFOHQ9mr3QEYchAyg6BLLyLBnfhBRyc0uFHyO8DTZm8t0z7z2Tcxypbqtho8vJ4rjfvKRUr5NJkXGJKiFlC2iIrnUmMjUtw5BCoegjXgo7WdJR3npYnsw2sSZQRbe4raLMzgMgeQ1ohJiDmhM0u4no3YJcyhgwMEE+IhJJKrKGU2wZM2mcDxARQnqyXds4XeMMWv0afDVIQj3ORl/wTPPlTHhhmJNMa0mRNeF4rGvuqLo05lTZTYZWaa+X/JWj6Sih8i/AzDNLQBhQ8XN+BVyu4i3NcrHuc9YQhZGRPCGoYMtI5zFC58rhF1/ZQsFRY6RaBuw78LAA3W7nBBCZexOGKFpMNlQHKCUeVdQ2ctN/Yg1bHgcf49BJ/krDXU2L+5IEHF86CA3Cq/ekp8N5DMz0MHNpMluFU7wpmhifC7/wKT8hjzUCykAq2uRZkb77rhmWCDOc8vn/n8M8/eGwHmtXz/mBcz6n8xCwM0UnvfYrU2kPCQ1Okh1fmwwWmeTh48PBFC+WP4zK+//o+PByb1/1tygjY0q/Q0arkcQAq8z7NL/Dqm2/x9rsfsLvZaMkiQeq/vYG7jKU6t21sqYaM/veXsoPFvB/rTfuNuhWOvhxlAJQgLGFZ9KpZ9Rcido4PpN+pXLM+K7HXfJ9WSYkR/nAJv3LY/eYCvA7lWVaBaknyXDwjRLhI3Ar0SkPk7T0DZf3YFyKktWyXYljil8La0szNvsN94jHR3h/vI9PzTa9yEdmPKjJlgHMOl5nx3c0WA6olHREQugDAY50HrNMOw80giiw2a/YsuRcYsJwEAGEXdyKwj4NY42toJ9ENiVBYFBVqUcas91w9lliExLthhzgMBfdTziDn1GtBhMNVKC84xyzhjwgJO+msMAfOiVGX5WCA5s9gyYEgOFATxTtP8Jp7IGmYHgLggihUrBxyJoSVYfbeSxt2OxCA4MXrxLse4IwUJYSVC+IxUvBAy3FaXy7JrmGyaBUZVyo8J2EonROvks6NlWms0vpkuRq8uFvLOlBPDfB4TIy5amIBSFgkwdkYE8hpjOTsiht65oSsoaeIHPxUGahrL1ucZcWbzAx48UwlFc7nLG3aDhG7XcJulxEj4Tfnf4O1vwBxV/pmY2SKI1vAzhE6DYfkuyBzOAzImoi6ILoNqTKkv7n4Bb4++wzv8ivcbLY4W/dwntBnydsgAn0CIKHDYmI4duqtYl1lxBgBSNJ20gTv5ByC9/BeklFzAAgO22GHnBOGOABboOs6ua9Wf8MwiOJ5s0GMscyR8x7et95iqpwoLhW6qZEFp1IxKWeAHALp3PlcZA5msBpDLngRUw2RJnktCEgRGcAOAwBGgOCz7wMC9whPzoFVj12K2O522N5sQFih6ypK2FFS190jPMIjPMJfMUwF+vqZsMY1f4YNO2SmcThKQPZ4QnWDWyqswHEB3em7sQoaGyEyl+ttfdYmh8YKRT/tGtUiW6G3CczEAsYImwMsFY8+FptRjkajyQEQIfQr9Mnj+fNneHJxDqdRL9TUSA1W6EDdd4Mpm/HUAX/bAb3SzTNFJUtOiJgJO3hcxoyrXcKPf/ojrt++RbzZYJfVQ5Ur35SNBrA+HJtoByATqreCvmvzMnp/Oig8uUV7hO7ttXrTMYphnf2RekaMw3zpJ1jzjWT1vtXfnOtn421RDSLHDRp1q5X9UTE5A1jD1TLARGBP8H0ABY/u7Bzd2Rkunr/Ai2fn+O0XCaHP+EtYIRov/0nL1RoZRBkhxRqL29xYSrIaJZrdEYFAMaH/w7dInnCD9BGlXqcg+c8LHlqi+b7gXoqIY7FZH37K7zCsU9ybvN4RIYBwTg4XpC77tj9xyz+PX2wFg5kdYiRc7QhvblxjgfbwcIonxOw6pkPQMN3N53RD3FvVhzT/+gBgY3PvXi0x0DNi8par4gPum+aO997r4Q+MP58cujb7mH5ISBaPvuuQsQbTREoDjJQQOSWkmLC9usb123dGGpcyaZvgr+O4WhuHLJ4D1JTf7qwj1mWvMmLcttFFrr9aoRK3N04YmrYOE25TUyVh8qzRxwxJOqJ9tQ2ZQZVY1fZkfSGzJtZTS/mWGSKqAs5963lmeTaSu/L8miknDpxNIyWEeW2gvTYZ0+kEWlsY4EyjASOQJqiThnkmbMG4ygmWzBpQjwEHESZ7D4Sg8eCF+yEwWAXVmcfC76wKAgIVl12ymPUkfXDFy4WbhGcZ5rFBLHkoLDSTU/yXuZN5MyUEJrjGMEUTSVup4jHleW4NgDVEP5fzX26pwkG9MaDMaqDGFRkiuM8kElzW9wjAoMJ/UR9QZWiN0DA6vuV4jN9jw5VmPssMGiNpfVUb/YKvdSwq2rAqg8QKyxXP9rEFmKEKFZyp9kw1nBiBzM3C68NERTEgZfKY0R+tH/PwMQ+lepP0e1ZFRUysCctljs78GhfdObY7QoQfl00tLSMCA+flj5wDctIE3CydL5rH0QDjzK0B3+Ny+wZDTEhJ6tfUD2UvFh6XNdfJWIBS+qdhsKx0w2PnJEySdwz2DNItO+eMmCK890URxCyePdzkrXA+qH5N+4axp5MoItTbQvspd50o3TTUHRFVTx59nx1Km0V55eDBiJzK/kMqCJD1mZCyK7hEJInvue+RvUOEzGEeIvJKvUVUoSx7jdHcn9yBjYOClVu99whTGHkP/kQhs4RziXZuTM/y5v+7w6eDS5+iEdW94H24Sd0HZsPb0q0OCWskMBgRxfK7aXqlDgrFs1ToQr0zAneCdhM6d4IJJqoEH1nPxYhpynMSSpzVtr7CfDSVG23CTf8IGJuXt9dHjSxfK1lMhe4AibFG1wWc8Rp936nRDEyWPy6LThzfvbB300Ag4IlTmmHyjJG9YqBCSEzYZeAmAbvNFnFzjRQZSUMpVR5u2olDbZ8xfeMGzsb+luMwecdwqOyZRngqj6BEqBgMNfxXfc+MiE3pIDTKSPlQGCNUnJ/i67RbI/6thgOmMhTKCxHE2MkHkO8Q+hVW6xX6vkfXJfhe16d5+XzMPWeBfW+vm6cvOw/ug9DLKS2gquUvRDMgVMfwegMXHOiil0spLVR6WtN+unDXntwPPxZ2luWHTmoHN3v3w8EH9Ij4OIttPly2cUnMud/4NZ45hy6zeEKwCWdk+orWG5UpFwbUckIQXr/1+IfvA4Ykh2h57hNaQi1ZohdGn5+2VvYnCjOa7tPBhyl8KCWEVvZwp8vPBG0v1h3+3e++xtl6jRB8vWHrc0KsvP72e7z687eIu924oIcc21KmHDzHih6zDq2gXRmTwlRw88FjOmxE2AMgB7PgFWPfGUU4qtuIwd0vz5AuArh3lWAlI9pVMJi5JqA1V28LB0Mo1ioMWqQVC6k8EmjvH592DkcJkEsolroGpZ2mFJfzqBh/WT8mDF+7ho3ILUR5FqEfqWu3c8AmM/48RMnL4BISCLlIv6u7sHMe8MA77/Gq67FyAT4x0rBDzkOpi4JXC3gJMWSeCiVpLjlAE+xmIjhKcETwLgAwpQWKENORgwNDjK6jeERYjHu1Mo/DoOF6olpt5+INYeFrGBKeTDwhGMQecE6s7U1p4AhINRwT63x5ZzH2GSlG7ZMwOymKELfvuyJYJpCE8AHgPGnuiK30qe/EOt+7Wo95cTBLXoZmjkyQnVKb2JnL+gGRMsYOcZDcEdBwQKxky1RBY7jhQ1DhcRT0KHyD4pIjTYwogvKSIZE1fFUiTcZM8F0HD/EA8Y4aAzRG0abYeiILtSQeEzlaXg8NKZHFgi1lYfaGzIgZ2Ko3xHYnCSKFjfFw/At4XiPDlbBbln8EkDxdIXisVmt470qS5TgMSBwLY07O1bmwZaRDN8SITdphFweE6NGrUsHWs3h+ZDCc5EpIQRNMyzrIGk4q5wzKFkKLSsLqEDphTB1hGBwGWA4I0Up0uSvbym67RYoRu90O4Iz1qkfXd+hXKwnppfhs+OvIg5yDD76MuyIWnHrvCC2r+V6cibVM0QkAGYkygk+65qJ6xchEU/LIHHGDHRIY6ySeI77vkHPCzWqNoAm3tyliuL5B3z/VPatgJews+AnLox/h5wzNXj0654lwmYB/HjISmefhIzzCw0ORmaq8PqsRTdJrQCsHbIX0pYQDPAKPr5fK9HdrdMTtDaAQp/s4hJGCQKk8B01e1hK2TTEMVI+JSZ3FGrvpJzfFj/pgAzOmk0sOPfsEhN9wQOcc+vUKq36Fc/oFPr94hlUICN5oGXc4cfT7gGKQNr7MGeAE7AbgagB+3DFebjJeD4wUGZsERCZEjL2iJ1RhgxctPzNRVkwP6IISDfIxoc1mUsot92z/JCwqLowvZBNwWych5RaalkuOuMpvivKBOQM5GiGK4hkBnntItNqcIvub9G8qOCtsqOAsG1/jPRAcwmqFsOqA9Tnc+TM8PX+Ks3WP77qI7OQ5R40yAp823ZM+e4p0cYbw/UuEH15Zt8dyQ12n4mRroUsFr4gB8h7rr3+BBMb22+/BKe6rbhkeRLbxPgQkp8AnPLkATm/f+1FG/ERCMxnMdoWDUIapEe7YxY4YAQ5nDjiDWjvaZrZQZ+sBYZ8pk3hCDITLjQmsaPrq4bYt9K78punv/f2vlovLv5uejIZxSQExt0i75Xj/tcDSQpydqSeOynscvE9SyfSJNOmUsTllDu8+xgSGg3MBF2drrFaraeWLYxV3AzaXV0oUSzkgADHDJZbcV3uaNLrcCsf3PMf23AjfR3dRDqiloRoxEPqxuAFOiZqlNpuNxrQqJa4DgYNDXnvw2k/KnFdaE1E2jSOUxFtAccSe1Maj9/eV2zSttH7kxaDnzmLMTa73RZ8gzxUlxEL9ZIzZqK1aM0v9mYHIwA6MDUuyOjKX6/asHJ1lhEiEHTn0ej2nLKFtNOGwA+AcjwzSjJEQRwIhYMz7JJMxhDVZt/GczmWwq+xMMRDQ8cjZBNimTGrC/JgQlVGVOS4LgZybcADNPJjgH9A0doXHdaWerG205OKZcvEIcM4hE428vcgJo5WU4YnJITAhExpBdoMP2jdnSqOy5JapBeHbqTEetLFv1nSDH9S8h6Jka8eq4g9xtdoX+f64TAkj1XhENIx8ESjsY+pqc2Vcc3H2ViVQBnP1NMhZrY0z4MgjUAfHHYg7ENZwvIJDEiWaozJvUEWSc656FjCDkZB4i5SHWbO4XKj7WebqjZGY1cjOPD4snJcokLK2W8aSyzAwpC/elIbFmEXzjjgH5lxyAmUWfM0pI7kko6vKm5gSWBly8abwpZ/Mgt651VpaXWx5Qsqhofy04rD608usiVLS8ICdem9kwxlT+hEktJfgecwJiTPAEu4pEyFpQvjkdB3HBOZGUHEiGApWlKbR9YeFY4V+eALm0/QU+anB+xnDxJLcPpPlUqnAzf8fAx6m5mOl/Ey4v09ZGtgC1ZxgmQe4fANQPDINDWFWUHSZTl3mbY/wu+W4t9O8eaXdsy3+aXnWoeQeUOV9EfQ2qSBGIZumHZ0fDvV6udYIka0Ck4G0S9aJEQNzB+96nHcrrPoe2TmwZ4CyHasnwj32nJa3m0CldT0SO8TsMCRgkxhXibFTejiBNHn5JDzrXmQ5sb2Fjj61I7zw/QQoSqZKJwuKjHkg85YoCony2QQvm3lIoPJYVqbWta+FI6qW7aMasbAjxZWA0HVY9Suc9R7rjjA4h0iM0PAb79P4Yh/fuvDg4VK6AA4e6IIVNBYBUPuVK1/SyhqJ4LpOaNdbzP9YDjG5yUsPHSljTvHfCfbP2ad3hlQOi0a/98Hh4dT1O9lz70Oe/oQUETT5vN1bdUBl8/m1W+GFc+gSkChpgkBbOcqeETW/jXmsHhFvNw7/xzcBQ0R5/j6T0a7bWT/2KCFqfVOmbFLS5PVPUjj9M4NP2QPiEU6H97lWmB0Geo4BK4D8wv1KXLVK0NZrS58EGOi/u0F4M4AmCagXe/DAgo2qIkBD8DZkmx5Ymeuh2AqA273agssYMTPaG0s1Jrzm0p/t1+fITzpw5wphKUY3VMoWgrS2p7StHKxWR1NrM1QjJUC7xBeIpHYPKCEochWmF0KYzEKraU8RfqsVdXM8Fd7MUW3DUhsnxCI5wsAZfxqS5IKowTyrELuJz8sqKDbBpiMP7zsE32GbGcM2qmV0RrdawXmPnLwUo+8QNPpSLVQI9wTAEWKRhOfSF88a4oVUGUGAUyt+zqYAqTkUouVSKExF/WMVZpNjid/vapicNrykxPxn5Jwk4bYTTcgQB8mHoGe/UwvyrAoG7xy8d0jJlUR1DkDwXjxAUkRKEZwivHNY9wEpRYTQiRV6AsBZxlHb5L2UmXNGiqmEzxkbo0n+iqI0UrrE0iMUAy/o3qFCb4J4lWRo4me2vBCkSYwFnAqfK10jY5ayBIUgzYVATvJAWOJGMkH3KKeWtQNFCJE1CXlKCXDiTcPMyDEhMSGBsEti8DFEQkyEX69/jWfhBdb4V+DhCRx1IE8oOSZUiOC1vC50cOp5kHPGsNthSG9wk/8bABnX8T44Wa9ESJkxxIRdjOhiREwJLjv4lJQnFi8U5ztZs8XrwY/WJVsIo5TKHIfg1QNO6g3BI3Sd5oJISDGKok0VH7vNRsIzAfDBi9XmaoXQ9yIAjVHDRAElwWchY01pJeNPGhbKlHgSwKkE+pB7+p7LhGj4mKRdYFlP6yAeTRsekImxTQM68gi0AvsAnJ8DDuoJJTlTOMbRWD/CI3xsWBIInZyzpFHstfDzwPCfRy9+ilClD0ugoUXTj/i8+2fc9FcYNKes3h6/W+i7fdK6u0pEW2+IMc0/yQjYNKQVZjHATttnnsn6lsME/SYEN7fXGuIYwMiFuHnXDLfMg7WKVvS863rEIeD63S+wXj/Fr776Et3ZGq8vVjjrEp65LDTgHfjCEmR29irNv81EOAtCZWYM/BSX6QXeRcLlEPHDNuLbTURKhMCEAYREhJSBxBnJ8GZmrWa8zhIOGA9nQuTpRjm/NO4ELz9oMrbWs6Hh72r4JaXtlU9gSH4IVwzJzIAlAxzFMzgL7VSUDhYOSJOPF6WE8SRmCFTa0vB+ZahsHACwJjJnSG4IIoQ+gLoOb0KH7uwJvn7+Ob54+gS/ezFgtRrwbViBlTY1MvlTB+M7yrqpBO0ishYe2+hMasvi6eMfEIoZ4F8ZvI8e713wd4J7KSKWLXTmG+rtmnvaW3NvgVPKZnRMCERYAVjDIVMuzDrz/nKK+556Qmyjw/WWcL3VkEd7x2JBSnQIZv1aOCjKvfH1fUqIYnxQiOXp/X1tO22Q//oW9nF4aE+IB90+P8HD76Mpxj7aWBCYHTICGJIMGKiCURM8Tff7NEQJETOMQzLRkEGJ4TYJbpv2VLnc2X077hLGGS+DIoOfCPEaZkYeq2TJvnr3AgNjs4rp/boqcueA4JBX8mcFmCVxm5ZkgYzeU3VzIEzmoSiIyijYHtwI8ZdqmfJqE8av/uR6oWG2BCVI+S0d4UnfRu02uo+kPTvO2LB4Q8QiwB6JX0eNsXA1JfyUM+bNwRQVRVCacyHIF3nE9nfpHmtcIBOG1uvFG2A6d9oedlws5k1BUYe4jhfKb1WAqHeJWZTNsIFRw2YRI2tYHa/Jts1DoMx9sW4HLP+CfW954JwSCIycPURmTnUMtaySRJ21nWwqucVm6lxMwpu1TIEOgHPjKWjUd0WR0SbOM++bYi2o69pGKysTaCGcTGBX9q3S1snEqxdB8x/M04WUHzUfIYbwiilDvBEy0NMFVu45iFcA9xryS5V4RAAk/JIjTUquyaGt7pQTchqQ81acN+DG7ZuAeCCJJ0TKjJhynZssDDJbvUDBqdHaL9Wb9wk39Nh43MXDwYlFna4r8f6pCcBzTvBknh6heENAk2ATJBTZVC4z6Vjds1BzjcyeIQfnMgAdT9ec1M1eRSoIMM8hyzsCIiB4FSjp/mDzvWcnPkbLn8q8z73FDvMrDwnv03vhmGD8U/KcuE1bPoVcEdPm3qkp46P3Jw537MXPo/OfCOhGPgI9Q5hBiHC0hXOxPt3QfUcN14/JlEYk+G0m9hhH0VTcCnuNLmXG8cZNihv9dsDE866ceHb+2flYDKIcOAVQXiGEC6xWF1h3PVwXMHQMeKhRiB3fGsZ1PEh7mjeR00zFKwfeK68sPCRZ1DokThg4Y7fdIG13YlDDJDndhPIs5/zkZLSC9gAvf94LqabVj5jKacualuQRKgpdbJ6pEyMkyw9ooZnMSyKrMqUN96TltGNDbT/tbLLHALQKGwYJ6ek8XPCIfY9+fY71aoW+86CQwY5F32Z02QF0OaQTXBrZU+UnU1H8Pgv5cn2yeXDnkc96UEygIY1sjYxn0B8N02LXMmg7CDbytMZT2t60Y3pxymfOHkQZuFtg5s8O3osa5gHozY/jEVEsez9clWZB/Cvf4QsKcMrUFZeq2jgAwhAKOD0INI6uc3h3Q/j//Tlgl2Q3WVQgPziMB+s2Sgj5POWofIRH+CuCj7gYGOIJwZrAtlxXwVNh4JXYNWvsN9//iJd//BOyWoTbY+GHLcKrLVz6QEcsNXRG+WhP+qnUlOd0Jo0+quDZGBAyOjFLzEl2IM4SH5frocoAhq9WSC9WYD+m4Myzu3oTtGTTtIncWEC2Hijz54rAFSpAIcCplQtMGDk2X29ksW3uh8kY7TsUs7wHFfQ7DeFiCWqNAC9Or03ZBMB5xg6MPwwJA0rKiJESAyxxb8EaMicxUkzIrEmCOcOR5D7wFuOUUf6gwvuMcT+K90HKFWmqXFq9LaT9THLi1gS/9TmAitIhZRG2JrWoH3ZRBLSqLOBcreRNlM/6PAOgnNUoKpewT4YRUt4wIrA5c43p7z2ccxjiTsZEaQXz8AkhFL6WSJL8cnYYdltRPnad4o0HIxXvDmOqkilBmNRaXcn5NlOi8lFFmA3xhDCfBEtaLfWo4oicjjcjaW4GBkRwD/GGcN7LuGeUPccYJ6hwOeUs3hKWfNs5OOdVGWTC8rp+RHCv84naZlMemFFaZmgYK4DJgUGICdhGxnbI2A0Myr8C0q/g/ArkPJzXNarbRrI56Do45+F1LlKMiHHAdrPBkHe1HZqbHrndTWS9mWtJzsAuJmyHAd4ThiHBu4ToE5xnkPOgYl1IJcQYQm0bYGGosiq5zANHwjORaopCCDqeokQZdgNSitjttkKvRsGV1VmPruvQ9R26vocLQZewLEa2eS9JrA8DFUVTXQekynHvHZwDuuABzuiCA7GDD9pOZAkHBULmhBQznMtIup9xF5C9Lgjvwck8cP5a2cFHeIRHeITjMJKjkRgdVHmwfp/KiaE0n4nHZ5qIqSjOxPMsOZRMid2Wp0ZRozMSACrFCaPhyATBhQY2+s6eaZMGL3TU+lbKrGWP3luS1C4oIyqfYp6KrtBmRRlBBAoeOQbw2y8QwhmefPkFLi7O8eLsAt1Zxvb8Rjw/S/4sJ4LaE86xY4Li+7GiGUBC5IRNysgvv8HF65e4jIwdgAih9yNYE5xbjgTjV8Y86P5qbA6wwLscevGEc34qUJ68S813M4chiDFM4bU0PwRSkjwROQGc5Ddrjog2aXX7h9qn6mFvH8aPjBvsGNXgondAF7A+X2O1XuP5ixd49tnneHFxgbN1hx86h+QZRKFELy093DM8U2XEQ8lL7+IXYF4R6fPnSM8vEP7yA7of3sBGy3aQwsPqeJHmZBNv3YzuX/4M5x02/gPTfjZ22ra6vX0otcQhDckjnKyIuJVly+GC2o8Dbx2uzxZoW86SxswWyZoIngk9CB0k/u18c1lortZBJAl/tjeEd1uHTRTPiLbO5SE6bdym7z6UJ0T7ZTbCn5Dl1E8aTtlTjjzz1+Yw9kE8IE6t4gOvA/OAYPbwzuNi7XGxdg1/waNPAIjDgLjdYXt1hWG7gxsYLuZCTLttgpuEY5pXzHv3gtlzwCK1VMVtS8TMlDidEHYjrgko5hSMIkivpQjBS9ZYJiX6qT4P8YTgjpBXXsIxLfTFhHIoPd+/1syK13JEzMkHLgJZg/IUGcFmhO10aGxe69jsB2lnHefqIUBgMFPpU+mRtVsvMjN2yjcEMHbMGMCI1ubZgSnjy2Al5DNYhcqpEPISIz9r/FlRwFCj0Jh12gZWx65aky0NU+sAUxRT0DwC3J7ZZl2eG4txUwpQuS/12PxUAhn6rvHFWcPT5JwkXFBMxasBRCU0EiDENan1eZuTb8raG4NU8keo5bsjKkoQ5oyUNccGUVvchD6hBZSZKLtmQLX9lrxc4/fLmBkpXvF3Wn6RPtD0jjHwtcNZk41bzg673oYWar0fLPG4QWYukRiy1pGyJFwMtELwDp07A9EK5IIqQ+R9Z8mmIco0yQkhyjqwhJNKaUDKV8h8M+rheMjG3B9pW9o8EWXszOrOjUvZNyOm7Mqs3iauGbxSvQj9vfei9HGxJlVXxZEkEPfwPmioMQvBpIoHVWTb3C9BZezHe7wpURgsXjQNalhYMu89OGcJf+XMp6TBFXDJKQnINp8hcfSLkq3UEpBpDcIA4lsmL7wljBTHDwSfIg39Pvr5IWHa7o/hIXGnKhd40Ydr+cecy58fb7JE4n6wuie/D8tLAIw8Hitmkf7ilIEUi4ANMCE7ihB+TPXedj7H52ElZZdpvSmFbUmH5TGePD8pY9q0vOe9WTnLMB42mv1GM07mAeqog3M9uhDQ+YDOe/jACAQQ6dlN9q54GlRGZakN+2Rec2hPZE+EMwLO9tgRMAIyPDKHhksAOEVQiqCsxgGFVhavxbGS5zA/VCvb8wy3c7aED0fmaYYs898zQ9/FJi/UxxqCaZQvwj5RPLEr3k3oOOMfRpxuSy/ZJYLzDvAO2TvkLuBitcZ538OvCLRiRCe54cweo63jEOyTKd5225qeR7OoKIdK1PEmkvyL7DrAu8LPgVhy483iKI/pS2KWyA0MuLOV0IXb3ahdt4ZT2Oil77M98UPDfLz30TmfLhn3cFTOTyhHxGHYN1fG/H3le/yCPMgs8xYmvfUesE8RHohV2WZD+N//1GGXNGba9MX3ApMNY0KQHFVCPMIHh5mA9udHxz/CncEh4ikyAkAO5+uA/+nvL7DuHTq17m2t7aECu8uXr/DDv/xJrI0AdK+36L/fllLpVM65UUac/OxIQbDw2PRbsVriQvCZVbk01qgxFQTrc7lIriQUCEiTpLKHJER2RXgKiEA4frXG8FkvllzNuLXCGCJRYpCY24OYGoJsQj6bhQw5LFGJNVHvGOpZYclcq6WOXbewOyXsT9OPkUtraZsSeY6Uhs7F09wH8TzwJAm5rd5WWD4w45shYcOaJJcgAnHtOKN2kYwQ5wROGo5oGJB2A4acEHMSQpIz4rAFdlswZ7GkD5YrQObWlAFRFRdQpQ5nFvflMl7SgCXFjPysltMxSkgay1lhaBRjQowRu92AnJNak6PmfHJOQ+HKuGRIDNiUk4bbEcVDjJIEeBgiNpstNjc38EEs6vuuQ+i6omSypgbvwc4VK3cTuBMJLg+DWLMH70G9jG3wTnIA7DK22630SdstuQJkcrL233Cr4hmKdVJmBqeaV6LFHEdeng1m/Se4GFMWbxAn182bw94XgbeMnXxobpBchdFtLoiS44UZcYhgMNIwgFlyehBIc0FYDg+zoCSQd6oscGpZlpHUqyiRhBPY7iJutgl/c/Y3+Kz/HE+6J/CuQ/ABzramZtvxzsORQ+h72XqSeJxsNhskfoNN+u9gjhYJbzRmU9VqHXXxNNoNEd6RhMfzDjk6IHgEHWtu9rIpDSA0pysKLzhzY697vinSnJNxCz4gxQE5keQaUeG/dw79useqWyGEIF4fXqUV7MzRo0GYGYvd7MEo+1RR6DXKTMcO5GSP8USAc1h1PYKFvdJesCw1cSJRGjvrumYipCFhu41YX29GLUn0DNmdo+Mf4fnVdFIe4RE+KhxSgpBsiGMZ5IS2+rjCjkf4ScMIlaZCPfnlQODdBri5BCltWGI5EMBQy+1Cjy9JddvvJqEj0yBUJB6929L4VZBr4fZq2D3xaiU7C0Zt4GZxmBeofhYFRPWWHd23JpR6rP31XJtyOUZlj0Jn2nMEpWMD3KqH61ZYdx3OuoDz0AOeEP2gBiNiQOFJKIY9gXBvAYTpyBKACwf82x7oaZI/TiHhCTZ4gahvkc0dnPpIADFnybfFjIjq/Suv8Gi8zHuEmjYVz8WWp5vtaM1vntwvfIVdWDCWazfJpptEAGWdKyZlMJS+IqU3MiOPyjaca5QORne2+SKMvp5tzhMKcLzs6v3SXgIcIaw6hLM1dufncJ9/iRfPP8NnZxdwLyI2fUSnITThmhr2HQyfsOyu8KR2Qdc+O+GvG9tCuQ01pmtITgoeq199jZQSbv78TfGkf/9gzK5+/6AH8wyRTn+TGXc3KvlpUB8fSBFBH3RxlUXAwIoIPRzOQAgQraQJghr5RG2pHVDlT5jkdzeEyw1hG4GYjAhtX3yYtj+EJ8TCC3vLPAyT0+FjmpF8StASZKOvC4ueD9z7WLBw6P9VAU3weUqcH7QivTswOkgopgDvPJ6deTw58zjrHbrgRkyv7QNpiNhtt9i9uQK9vqlWqRvJCfGQ7Vtu9N3xtpKtXAna5gY3Twq9mut1yiA4WBwmBhWCxaLXMzOwS3CbhLSSHBHS5EnYpAaOCQZqeKaq3DGlM+8jXghVkTApq3xOhO41/AlN3q04ScpIGj9YBJ2QoTBBbJUpqmcCM7YAtgxEENICYnBTVdNglFwPKYFTRE4RrN4GxBJpdsvAzpgnswxTzpgmfbCKpmjUkmUtY2S5FwhNf7nikI2lCOIhwuss4aNqDH6rsyE8q5UBQFTnsvBYXJJgm8KjPK6u+AAXLwbOdgZTqS9ntTizvik+lyTXKnS3cU4pFkt3mdOawK492mt4pBrV30aRbZztcXtWnyMjuidjbWG+HLnmGqqlv+Gf6gTNO0jC/VANQwYAGchOlFSj5ti86Zg1jUBdxZVzYWUwM5x43QDo0MN7j7V/jt69gPcrePIlOTZniXxs5XhxJ5Ak4Az1YkgqYI/gPIhSskGJCtPdoRlvHRsJBSZJtjkbEtpcGK6iLlhUZsyKtvwadr96RtQE4c4L0+01XJZ4SEiYJE+SjNsFVzx1Jr654/XV3psxNdVLo+7T9VlmEypVgY13DmANWUriEcGk4SoaDLW9qtn5YZ40MPraednLE2E+/j9DqJPyCCfC+8kd8bATEAh4FggDEzbHH//A8IhsnwLsm4UpO1Z+s/xXd+D2pZrIl/TwbKME2W7q9MfpsrdT9uA5LW9tGlXClR40e/1aej3/xg1jlVUbvZCbs7Spc9EV1ejsU+RNkwfaLqvHq/eSr8krzShjSnvp/Sk49WgIzaM3DJzq90cAOhLPiOW2E4gCAA05lBLckDTZshrNQA1WCi3No+GqE2jEHmAZwidUZkPP74EpUzFH2j3PTue2oTdg5ELDB6Li1WxIFuurNO2Bxs3g2AwzJOwqeScGSeTQ9T3O12d4fh7w7DxjE4DkoHZ1xjMdrXqRCj0FPoRIh0DIqx709By02YGGiJajY5iHRIM7Df1LmeFvBjDncf6a6ZTchlY69sweUWjlQU+oY/r6RIx0W7gNPXMf2uf948S0htu39WfjETEFE3x9QR1+7YJYlHFuYkYbtJu6KB5aRYTzhM2W8J/+7LGJKqCaucotDfx9p38iQKPx9aNKiEd4/3AKvQZM8O0R/hqB4TDgKSQsk8N57/E//qsLXKwDgsU5pyb8i36/fv0W3/zjPyH8sMHZn69F0NNa8ty5PfP3byMGGgvlx4LOUfgi5mJhXR/LzVs8emcKJpCWtrnRewSH7ocNulc7bH59hviiV0HxvKAxA9EIAdXKvU22C1YvBCXmCRkoOQeWvSFa5qTtyyj5uAp5k4awIWdSZyXSmpwIUq6UWazI9H7xfMgAzBLaVWuvBODbIeFazZQlAiyXQoXWHzOSDBWsxogcI9IwIA4D0jCUkDSs1mmXzEj9Gs8211jRVuPlonK/GWW+mVnD7Tc40g5ewyuYtZYJ/dtxyDkj5lwSI2fOoJywixG7YUBKWccnq0A9Vw8bQonB79SCwELQkI5FTglxiNhuN0hRPDnESyGUEDQpicW4I0L2Gd6LMDar9VVKUebb6/pUC3MigncO1HUgAIkzhhix3e5gYgZ2YqLvvIP3rum7g/MNIareMyVPCicZZxPuOqeCbWE+xeNBQ05BPF1AALMw2kLMVG8OmwwCgKQhqCCWlwgSBsg7X/YnSeScxfxuZO1WkxIPE0WE8bMS3goN4kjNmRyGBAwx48v+a3x2/gU8/w6eP0Pw5+hCp1ZyQOIou4L+F/oe5DTMXc4YthvxdNntkDAURrCR/cO0Pxa2YJ7zS+4PMQFg7HY7BOew6pKMi2prBNdljyA2rxxd+7pAirIHNQ+QWVhaXeYdw86hX/W6pgRHLX9Ev+rRhU6UW04E+gADqdi+Smk21jbw2p6670GUORrijLl0t9ne64A4Fk8gZy4gALwOpvNBlEQgQciytxBADs4HkPPIRXlZ6dhTQ+c9wiPcH+6JXw2dJj8Jz4jwH9YOP2TCP27zA2Pwx+TxHtfixwIR6I2vlXxcDBCLWZMHlCeQh+VElzAw5fchGfKiANBeUDoOZhzSni6NRbkd6oyiGLEP844wOtZySLDSvOV9sFqtN/xCuZ9rew4PGuqJd0QhUcbEDGAAqMGIDwGr0GHlO/TkwZRqXraG+Tq2On4dgM+90rAA/usWeHvkpVNXO40O6Qy3ucH68gZ9jrjRtpnBTmSeyL64kmuUy4EvY6D0X9njJsjTokA55CedaoyLrH2j90shU8RsCmcUj0szrag8FlCICHCLfiP9Vr3RtrOpcC+5MZazTZUBrDdC3yP0HWLXA/0Knz19gS+fPMPffJHx7PwGf+nWYPKSf80RxtTZTw8IQtqlL14gvniC7o/fI7x8I8vTZTjNxl2UERlq+MOqHyS4IaL/l7/ABYfrgNMR/j7DVgjie5TxCO8NTlZELFnrng6FFWrKs7LaZzB7bgzH67U9Z02ENTzOSVLuCYOIKvTClPmp7TEmOzPh7ZXD5Y6wS4SUaGS9drwlp7X5tnBICXHK1ByPwTpVdvy8V/F76ZUetlx/HHiubcwHHOOf97TeHVpL6vGX8WML15aezOjhyOHzJx287wEA656w7j2Cr0pPQJKqbq+ugW0CXe+we3sF92oLf5PEA8KEqSp4vA/Md+X9z7U/7L0xbdpQgvO39JLsvWM58zycEtAQfpbLByQW140lNoNBWQSBdB1BxOCVAwchXeeGRMu9lcs0qp9bhqlVUszeVbvuhbLtnZI3QpkBs0pqY8eawU7rKWF9bIYPNgGVQZV+3mRGBAP/f/b+q0uyI0kTBD8RvdeIk4gAkIlkVVk1vX16Z/fs//8d+7BnZrqnSVUlQQJIAEGcmNlVVdkHEVFyzczdnAQBMhTwMLNLlIqKChdWDz63Udnr0wHrBQEsEH7Nt5CiekLon409Z4iT0kTFcqxhC5oa6xqQSTeL5fY9QLc3B512BoVpzKW/NWGiz6OHZspKCYPbUDhu4SZShUoOlGLEsiWkJtJYqGUObI1646rqrSEuye1uS1k7ESDG2CWoZrY4/24AAa58NItmGrR6CD0NojqQGrfYw3xpHgI08+IKwb64V0FRFLjlmQAIbhvnsEdFEeQKDgEgOdeQX1BvCYeK4hFRq57NW9cbiAnrR1piGUaseKUeYDyCZCyhl0oWCWuILRk3B2OEosFxSkh5h0RXyLhFCV9wCIk1P6j8V+FKQ0xpMvOUoiX7zt27vtbqLJHRBXwqlt0apsnXo3g1mFcBmTJCkBFCwBAC8jggsXvVUFFAoFvlOq8QdIno6zz7PtBS84RoP4rWtyDZdjejWIoyofSfTZkkxCWExB7qhRr5oFG+EjmOIAgWyHwBki1IpvmISi3zdXp6OUz7vvdyqJmfr3yilv3j5fmqfgba+Jhl4ZHL7RMHr7aKNPUIOlYeYtf6kB58YuVn0cla9uUQn1oxRC5QWrhc7ifa4W7vSDM6h9ozr6n65D6UJqVeK1+N6CqCXvT3/LfU+1KITq9HDtcDOJFzame7Ph/l3XxO7LvSMerVmmC0BAeMAVgNW8SQyrG4v8tp9otwxsCS9M9T1yVUMnP+3l4v74DHjAEZCyQZy1hFgLSbEDe3QExQ30T3UPU5bdmuhhgjzOb7EGi0633ng/39/kJd67ueK7Bi3RM1gOjp7oYGbj6l/Cvlyj7s6CIcpiYq/XKnnM3omGEMGJcL0HKJsFrj4mKB9QVhNwK3rEY1+mztIY5X23foDhh4LLo6lYKSvTWrFWiIY4LQ2CPOQlMrX1W4XENhJf+fAMgJNDDC+ZnS6ZsDfoQHOvmU4+WuOZvj/wejm8/lSeVn5BFx2tbzA+4LWuCPYYGcIpKFWmgDYuzVTh43sDJ624nwf/0t4GbHvreOtfrgfj693NPOkyirOcXyj1Ked8yfPSF+KeXYfrhLWOJPEBLOQWGJ//JPl3h5HspTITRCJRPMbK9v8O3/+DfwTxus/uMaEMGZVCGqh0R5MlvrDAH1NZFdO3gS79EmZvnnRktOBLYMR0Nc1vv2XZrrB5U/PZMigLm4hjIGr2f47hYDAzd/WCNejp2w1j0W+MiclVBMjTDVxyhNO23okpoo+ogConm2CKlNIJuzhcWZTa60HhEkOthSV3PZu0gaxkVA+D4lvM0ZoFwE68XKCy3Z7eOipiJl9HLOyNMOKU6I06aEZ5KsjHC2EEgw5QqTz4N3TmcjW04QFRgrBVq8DJn6nhShZwsnBwSZJuhxa3zJGRG9UB8WZshzQBVrfQJYgoaPaYW3NobMVQCMLAiBMVrs/RC4KA/KXFqMf9U5VAVE9cYJjdWc5qGQnEGWDHvaTYhxpyGOOGAYBs2b4YJmVkGvCs1Z28oW5qlN8GybT4CCQwIrSRenHdy6T/uGsu9I2rVHVdyQKR5ckC0ohohiMmS31ici80JRgTuye5NqomUAiEnhJaZUrhMByeCtookqkNbE0MBX4SW+XH5tidHVQpFpQAgBYQhI0Xen0W3mKTAMGsIoJvXmmbZbJLxD5D8BlDxwNpA94IXldGn5clcu2ixlm+UpCiRl7LYTBibktIJk7phmnU/N5eLeJ2wutC6kd88Db0HDL/WeuCq0ZyzGscC9hxQl0mTcehZUe1OgehWpVwZBQgEUtJ3cyyliXiRS5mRWTLHFRFiOYxHaKCbxt3QNysxJw9QzgYK1E6hTvgBA5ldI8gJj/hYkb3BApPa5fC4fpbR5gdpy6Oz/R+SaPpf3V6T5169ICVfkFuOGZ8mxph2sHvOfPHxezcN2GLPOce4R/OuCbf8u0l9vQlQWfqA5g/T3LOSSh2OaKyLcyOQ+yWChI2ci6mIYopPjZ1wne7czcxcTdjkhgfFyGLBcLnC2AL5Y/4TbgfEjjSj0BuwMPbDhiYDfDsDX4ZH44J6XEtbY4ddoug8IsL2+ws3rH4ApO0VV4KFdgfqirXeJ0U/d7YNa1W6tD5WG1uiZw7bmw8839ZLUZOxe9j1VpaF3Gjrc6TGZ1324352oTObXfG9R81NAIYCGAcv1GuvzM+D8Bc5efokXvzsDLoDvlkqrLpiN/pPWJ+S0cogR+tBlb7pco2CKLmoeFMvF6BvN5sooU1SItJrGAcvf/AZpt8Hmr39DF771/Q/kH6Z8CmB0X3mUIuI+74iDSz5jfPyjvUzHvxwsc2WciGBFhHMMOANZ7GW3qO3rq6xmtWj1zyyEn64YNzvCLlLB0223+p49fJnbI7+1qjlU3/4cHxGovXdwmx9Cs/aqicHTm3omExWv5aQePbLJwwoH3/4PnItjc/fpmuw8qLx/GD2hHJvjOYoqGHy/130Nh0f16mKJ5WJAxBIhLLAaLUSLCXCJGTklXL9+px4QV1tMN7fgH28RriI8ULp2QWYh4d7P8TKfmT3itcEBla5rmYzup4UGaQRg5YtNcDfPTkBCk7nOYF4TDQOUpVj7Sv+ACSVRBPUm0S0rVIzCTdniOpeaXM9r7Q+XTLVve/jaYKQouqWekXsJtAVF0Fgt/r3lwkZqnzxxsCsjHG6AEoLnBoIogh2gSiVq48O32K8fU1UQSf9njKRLoVtrqlIVMwgDdsszCAjL7Q2Qo66Nzz/I2b16vrbT1VTnvSFbl/6+1OecviX3hpCSCBmmVHA20xlOrZfKornA3XtCTOpVY0oSDmzhbwJC0LBMU5yQYjIlCpf1JoOr7GtLDhMCMStGac3SbW08N0RgteAfAhfmVj/3vW/IGACnWPRi84wx3F1Sw6KUgRL5BfaqANhDMol4EsfG26BrnZTRaPZPSXSdBVmSWsZzY5tZjr8mJJE0WxOCQDWppuaGYERhZH9HzgAsQbRAaBQEbIwdAaZgsvgHAsv1ESGpYWwo+8MH6Zd9S2ntKBPhq9UlgIy3t28QRZO3TzEh5oxgScodlxTjN1RvqKZGuAKG2Rhmqt43rqgR86QAwa4Pui1zNugmg9He66vuFNuvJDDf+AYVSKG7W/zl8hpqcoZ01Kj1E0Wh2ihOFShLGAXNmsq1L1ZLDoQc1MsohIDlOGCLiOT1ZO6gbr848qVy/jzlBJQGl3dtHCzPdNYeYIPufeU56OlHtvFgL4T30NU9XHhPn97PfLnRw+G6t1lwnTPe5SZ3knbmSS3W8gnQzc9UHjolHwD8j7fxAae974LnmjJ8Z38egjHrcdyFXHJDg0JNihkPSK3xbo50foecgD98f66EcLLRRa5N/qSezjxUX0tg+vc8+31aKUcftVdQLkh3z2l/4xNIQ1oNQWmzHDLeELD1MVD3RqUvZ4Vg4R9boveEYQhpTolXTDjnyhFo2McRIiskLJFFw/wkEcRtRLqdICkCkkHILYmr9kxG45bJKZM0n7nmMx8B/oPr1zJyczhBs8Hma968d2ATFs/0wiE5j+X5BBvDtxYeC38z62K7amVfNHT1fMgzgy69xOBhwLgYkThgGkcsz87Bl+fgxQgOrXGhGw4dX/zCB/oztH9vdvnJpeUMH/wmoXiTy/kaMSaEmw1oV421NDwbFX4NGRBul5hAMWF4cwWQIJydaUjgzeaeTs1p94ceJs04uuvS335A2T/qj/VNZs99iHLfuN7HAXcismvKkz0iKtE3207d+Oao2hEPujVr8dtRYvPg5cq4v6CAf6EREIvZDOkYDjY1b+sWXhGGai9jJvz370ZcbVyY0g0YZXft9eXuRe0Zu365DoaJagQoXR3dQUpHWv4QFNQcKXz8cqwnD98aTyhdQ49H+Z/LByjHGMayx+5SneidueGIQInQf/7NF/jq5SUczwzDgNYDggfGbprw/b//CfLTLdb/fgWKGWuvxCp3/DWzJS/JlPfG8pBxz/qtX2aH1/yLNF4NQAnRUZggpxsbgZbrHbrDoRBofSLbnEW9F0zwq8phr9uJTbHEtqhCMMPjzIxsngIgDRnio83loHEhXu2YLnmxl7LuiAo6O37IcS41eR7ME0CkJE6uQ7I2s7KCHNSi3DVLnkLDBdXIouFyco2Lq/0AYFbnNKjl/A9Z8FZi8Riocztb3ITCnZHPufia6h9BSn4HEhfjp46mzwAojKDAuEGALM7xMn+H5eYKo/WROUAARFvWwZRvh+h8Xc5mTcqZp61nF6bDNwFZ3RkpJsQYES12PphRRKAOo9Iz88WKW837NVkui1rUDwG8CBjCoF4KxCAK2G632G63CMOAIQxmkc7FA8AVRR6uyH87uJZ9YM/GuNN5GRlDCFiMg443V2GX57MqSgMC1K7RBPHm2ZGISggxIBfcAlj+hmTGGCkrk23eCg6XMcbGQp8ReDABcyqzFtjzVijNpruSQRaEOiZlQIKHcnKlU9Y6ydqadglEgtE8PgZKSJQRmJCEkDJjyoyYWBOiM8DyBUi+BGGNMAQEBljMCwSCbBb4ZLgVlmg9TjvEmKw/GjIok6BGoKoYoRbl2l15GEjn+V8uf4N/Ov81/r/f/Vf8/eYn3O4iwITzOIEHwioly8Wiygi35tNwZgQEFbC3keOdwfacD8MwQMYB0cI++fUwDOBBvefEFG8AEAYuoWC6U4EAId0zZdMSYS9Ok41fcasPn8Gsoadc6NJ64vHAdb2zIOUIUC541pNqZlIPGMoRrpnMbHMQBhAzFuOA89UCmQTbHHHcGK4546iuW27H85m2+lzec1G9vNS8Q7OT7CoD//fOjQXeSw/22vxcfqml0s1UTlDLe8QwPEpIEYjSCkk1VGAGIxutxSIYAaRy/hBSoYG5vNe2i9K6NJ9AVUo4jV9p8Xrd1BC5moPsC4nz7N35J9DlhLgHvRcWbj6D0uzFNpM3ABFXmhvXQlBDFKjn3hgYwxiQRuDfzWhoKJxBk1Pirk41xjf7PeweLrOcIVgw8K8rwcLWXkQQJSHmNbbyK5AwWASTCHYQTDcbpLdXwG4LQYZ6IEtBFxkMYVFGg1AZjrL88zWc9857799mHK+0sDK7Vgw/mrXvilMws9Cg/p90VJP+a/yAez64FzSygLLxLi3MtSIYp3ucBjK+Q4CZoV8zevPAzzD6gwnDYonV2Rrb9TnSxVfA119je3mGvMhYh4SBA4J7fZY8aLNxHGoOd0scHlwOHUYPkYTPBWfOM1u8pfirV5BXL7D4j28w7N42YFBhohi5mCd54Z+3E8Y/fQO+PEP64x+QNjdI33yL4zPzNDqvBYV+PN2XJ7dzetmb2F9Qedh4njU0kxz7QYJ9S6fGhWevlppAtCszpC6OOKE5IS6JcekJTR2ZdXxMlYR0ighQcXNnJiBRPRcPCE9mXb2zzG/v/e7GeLwyOviD9u+dUB5qYfSAip+nnqeWI8Lle0d5bMEPjUv8Q45cv+f9D1DuPdA+IO77IJ4Qj2miRxDN9+N76xC53v7+8nKFs9UCZ8slggkua1x14Ob1G+TtBH6zRdzsEL6/AW4mIJllbWnVkVUf17vAWHOJ5mNpy30WhN2PGZE0/zJXQhx9flZ/y3ig3Z/t9QND2KMPpDIPDf73hRjeTaAsSC8WkIXH3VeBNjkhOl80oBK9jdVTW3GWKs4uyugwq6N26tAE9IPxZ1142sxRG9rK+8AcQMS4EcIOgiC6p6ZS7xwYbI18espRm7u5o6Yv6kGoDAG7Lz85U+vzV3EkBQbBBPdhAGSCZBW5ErElsaWihJgvpntblPOoKH0cprRPuTClMAErIadUQi5qzW61jxIiyRlGkwrr+7npi6BYRRWmn7lYm4sIsiegBkpdLpQqPBSRhjsyF2y2sGAllA4zYKFyXLjsIQeUoTWLLKaSOLhdf6dbXNEnqN70YkorHxPtMb+ofSgjbfeafi95Z5pW2+f8WTEvnWxKD1sonSuoQsMF6Shr0OOHnLPlpXAqkCAZiFGwxBKX4znO+My8CwiQ2nc/ov13Ub45023KQLZ7xE1ANsNbFZcewpfOZPkjgte7d7iZNtjmnW1XQYoJOWWkmLvwAOxKKLK8MCTNvq6tcMP0VoUo6v5v1o0BUAgQFlDSeqv3ir3mOGQmSNAu1HXQ8VFzX5/PQJNDxD/JvDx6l/raN1sbqv1uw4aVuSYqCqG42eKnb77DMizw8uUrTBaKjESrEteBFPTbI+vas3b+Ph4Td5/1/cfs27FSchb9w5Z9oYPJv55UjvnoPA8EPKWW+6jYZ2j3HxqeTiv7EpC7y0CELwPhnMnUEBVIi/HBnpDfa6b2mIQ7K0o2xTPte112vwqNJBUHzwO9N18PVVTIxftgaN71o51qL7RnWPPz8BbsbumnmNGKGRNlQrpdImOF9YsFxnFQQTI3ZixUo2Yc6toc11O7AHcPqissMPpez/UoA27zCkmWmFJSA4acsY0Tpt0Ot2/eYffuCtvdZCE4leAq5OmcCeg0N/NFJPThlA70mJpQTvN93xJ6hbe7Y9wyU4IVXlDhq+NrWx4yZ+UFnGfLxi94m53y40Cz6Dm8+k/7jtIu0v5kAocBNAwIiwWWqxXOzta4PGPQWjAOUK9qp8+chi0cc2lsDyrmNNajMP4D6Y27KOG7O6K4wPNFtKXxQ59dr3uv8F+2XsyEdOeI70UMJ5XZ6h6B8UNI7enl0zwiP41OfZgcEfVEaooz4MeIpJky4iCMGuuVM87DgP+NFgrsOe8dss4QlYOEuBxCatlaXakqz358Y5S+3XHwHe9x268Hltnh9umxOf8ApRBahw/h7vqniX0+F+DwZqTjKpODj6MesMgq7Pndry7x21/9qhFq1lwQcTfhxz9/g+mnK6z+7R14m7FAu48PMbJ3UNb2ygPR0KyeIwzJ/EsjIAakN4Y6SChIV0cVjEulAiRDcmreM0GZWayXdl34T1L21173IFj8sAXeTLhdDsjLoYSqKcqT9jyR+r4LdDXBbA2VU+uXckGaF6kovvX3gXzAWtScBh0D1c6pCys9KXIjIAGg4VsC4SZl/D0lDYOUcrWYnxWve862iaB6l7RPN8JvlS8yNE2zCkI5A5kFnG0OidWzgwnjYsSYRqRdhEiC5xQfwlCY2F70Y2MVoISuKlOaIZbXAGKhl6TGxneBa0zqDQGghKkiIsu/MVMCgGqScNHZ0D5KUXJ4HYFDydOQp4Q4pZLTo03SnEUQoHtTre19HZqQRRQB0hwAKmXNQAhYjAtITshmMS5ZCh0CAXJKqAm0aykCfal7wJN1cwn51q42UExAzNrP9AM6Jt/3pCGAeGYSVmHGBO1ZWfeUEwLMc5+o4IEpRhAThjSCc9ksTce1PymlxotK97lEVUR8ubzE79a/R8ym/MsBMG/VAqrSjNAMSPxKyqnMB0M9DjJYlQV722TOhtV6qi2D4G/X3+G7zU+IcdKcIjljisAUE4ag+T8k27gAUGBllJlBUhPUcwm55Dio5iahZp4r40sI5nXDRi8npLKmFTyk7uncjELQKCgMrXL1oXAaOds+zHmuLGnp4n0c4/lpvJ5kcOvKNQcMdnwOYHdzi+/+138AKePsxTlWL19h9fIVaqaJ2q8WnltlpbU+W7vP5SHlszJivzyHMuJz+VyeqywI+NcFYWnx/gr9nNUoxP9agx4PiKfFPIvt+A2mkUiOmr2+IpFzOqyhkRu5dL1oIZM83xJq+12R/tNJbiq43jfcYzbeAY7nYBW9UFH27pgRKgLo3SWGxQXOl+dYL5YITNWq3c/A9yRwcQo5iCkQkjaVUsaUA97EL5TgyhHIACfC7vYau5t3ePfmHa7eXGGb1QvZaVxnWUqgUu9/ZlQDCZuV4sHQTFLh9/Z7W2fw0GD8rD7kaXPoOaAqP8wYz/56hYLBXaOEgIXGFPuumpjWkEf2m2/GVb2NvTTfisJJSrAr4oAwDhgWSywvLhFevMDFxQW+uCDI+YTFMHQ8xCdoh/BMB517r6tHLDU0+LGtSYAZcPUBp1wm+6Hnqu3mL//Y7znwT608UhExR+cnPLE3dhVoyIG6fPvvKSNmJ5tkwZIJr3jAubDF0EXHqM+10jVxKUy4UGO2ZwG+e0O43gK7NBMYHR3p3eUp77YvOT8/vyE0q/sRDT01PuyeQB53CE8/RHm6adM9tw8TXOX6h+Rm2raeG5PPh/GI6h8KB/O5/WBwZJIdan7WPt1dvrwgvDzTJGJZBpyvz0q4DQJw/foN4mYH/mkDud0h/P0K2OzAqY/Dfri8R1hqYOcQeq5fZI/PkIMPN4Ik8TAogmK1Io3NoBOfKhkvDIrK6Rit1VHxVMiiQss+AGzXhXgZkFYDUoDWawnjyCz8ZfZ8m+BMTBEArsGZmLyLAvewFWf+Go8IKvN5hBmrTwGtMLIVxLef/rh5FtwScCvADgSm0DBHmO17P0NdXKl1OkvQKiFILwCWZ0FyUoK+CHAzODMSu4KkqcMYAXYGoLReQzS6+0HLwLV8KyDdlLlhQhHIlvwGUgRnHnIpuycAajiuTnhP/ZmZLSwWGqUgWN/NVBVhOZtyJ1FJug1qlAsiiDEhW1JrV3QwkyYubpimlo0TnzMAwxCg0W9Snc+scYl1TmpIJk9O3wJuv4favafC5BYcfDWY67q053qGJhVnZoNtrc8VeP5vdsawJClOGoqnpVFsHDFaaCFjTjxsWGYqlmtlkaydLBkxZ+UlbeFU8eQMjCpccmATyjuuoFZ/YGEsVIDOIprcXpN4oFVheoCydgZ9vORds2vMhIEJEgKItR8xAjEmpCE3oaxdkeB+Hk2lTfEAW9Xehdoh6H5yjRHb/dDQfLnZNNZZ9/71kAWe0LQbG/E+brVwMx6eS2GPsUf7NT+ZWJWSxtCm8i5KnyEVlgqsEpBTxHazxdW7t/jum2/wImW8DAPGcYkhjBA+Rw6EgGtAdtYf7BfqPh5d5qTaflvzCw8jiu6krT8yP9jlL5n180N4cpza5kP7UuD7JDq85y2bY/nBipoWp5z4Qtv0z6s8gcdp5/ghzz9D059UefDyK8JGQbYF6Xp9SvHVMKVUfktLD2VBgoVoQiU7S6fEz4c7elaMMP3lSqRQR6+0dTbn/rOUhg840tXmBOp4yeotSwjDgISAOCwwLlY4W65wsRzxxWoLGTI2REWIfyouepMBmQSvArDmY+/010cCvhgIawAkGTEPuJ3OcJsHXE8ZKSntma5vML17B4kJkiZsbnfY5oxtZsQMxKx5TokETGJ5QjyHHc3oSetHudYyefNJtflu1/vA8ajnfR/6dZ6wvLTsSoFWKYI2L4QzB22+V6WlxRQProSohhyCwlvutdmMidp8en1xY2WnpzQkk4brWi6WwDAgjiPGszPE8zXSAIwsCNzkhzhS933lUbvjoec19ftmf8ffIwEp8ELGW1CfFoxmZuaiijCCFEO1si+niOHvPwIA0ssXyNOEdHPTgyIeOS/3FDnw7eddfp7jeHaPiEPTcOhaEdzQPsBLOTgOgZ89Y0KCtTD+mXUY2ZPete24cJGqoIsLQ+ZCCbOmTIR/+zvjzc0zcTl7vW76tffEPuPXM5GzY5z65/q33z8TAfxcQf6+chzlHVNA1N+/zBn5xRcCjikhjj3uRQD87gvCf/qascErJHqJYRgQQiiKiHff/YDrH15j/T/fIdxEDEQY0BPJ98o7TurZ48peUzL74jzP/AGTMBEqISlOdIoTg2is0a2SNjap5JJUVtyq2/MuqPmxJbm1Z2Um4BNp1o2wfTUivxgBs0rWM4YL7u+GZcLubERtttijNGPwipDRWinx12F9tYf2QiodoNNBzTsuuLOkfl1iaINJDup5cJMzvjWL4zBwJfzaZZszF81Ft7SWFupUog9JCTlORthrbBQPayNBqpURpFhPF4skySUnYdsdEoHkqJbsQ09mVGOlyihI+yl+lktzput9D7vkngAgi5NvFv11bqmjL1QnYgJ+SwwMQkn+WOZILK+CUPGqYOIiEJYsiHkCAIxjQOCxhqjhmkDPMlgX5kogkJxBEAzDaPRGVGVLzpDAHUi0yg9dr8Zoo+XZmqn0eanhqOxdVoVGYTYko+Zd0UfZvFAEyrh6GILagNJcmbJa/ouKOEofG0VRjJMqYnko6wKS4jkCuGIsaMVMSACmlDHljJQyKAwg0rwCAvTC8mZWtGn3mDAlDWleCxFnhagKFm29pQyqAUzySaUelokxDJr3JGVGihOyaMLqKUbDQdq/Llm44Zwev1Lzr4c9qnNcNpOojEe9WHpvFWGxMGqN0NU9TDy5vd1PPmQTRrmHgT+bss9r9SJ2z+D5Scd+TZOw6FXDKx5OTGfP+yAg9nBvlg8nRsSY8ObHHxEZ+DoDYbHE5eVLLM5GpOEVMl2C019BsittdHzCvmvL5/LE8tlD4ng5Oi9zHPneymd4/0ctMpdmOoFQSadCh+mJbKEQqXrbFRaDCBnqlcdiYf5IYBm4rNo5neyEBKEmOUbzqQLbEvOSZmdqV6i87OFqQC09+MTJ8ibmF7oj2Ru0vpDmbBMM4PNzLC5e4fLsAi/XjK9W19gE4DVGeK7nkxQRBPyQgB8T8J8JWB/MPdB3CRCMTPjnkbAAgEjY5QFvNq9wmwVv44RdjLjZTsg//Ij09+8AqNwqCiMJY8oZMTMmmCICVBQRnsDaaUttN5UOHNQ5+KfMbhDmF+tYyvMNLwM01GtTsUh5XsrzUt8tvIpBqBsnZfdCTcUjwhUTrpwovJ/3paPzZjRaM7Zyq4JqYW6IGcMwYrleIq5X4ItLyMsX2F6sEYeIFSeweUNwt+ay19LxGfyYZV8We+d1k6mKEZYtj1JItpZ2a5URDR7gzQ7jX74Dv7xE/pffI15dqSLig5VPbyX+0coDFRHzBatclhyTutxb5YzJKO00Ap4GkSxB+CoMYFahxAoargEmJKhNt+7kzoqZHVrDaH33lnG905jQKRO2Ex3oz6nlwPwcfdSFBbT/WNfvvjudQK177/mJ1cMEOB38+t7K/SZr/eN4vm7daREih585FaV9kKkrB+CR1h6Kf/35D8gX3TuGp5Syj06re/7UFxdLvLpc4/w8YEcBHM5APGAcVdB4/d/+gvj6GvjxJyxutuCYD+z1Aw3JfQ+cWB6Kx47AwyElRJFzFsJ+VpG4tXu14HKBcnEnl0pEwgSlRJYY18yqsghyUoKZmudA5ZHaSaAkekZo5YrNGZNRFAYejsTD/4grBPw9yRDhpgm3VvdxVgE2TNBZBMFNUTR/QK1uczKPzU4qGQYxYcuEGxHciMfxdwZqf43mS9B+1b8ZQS7QEEEpIcVoSgiP1KkC4ZQSUnZrdakW1CKQlICc8DoBAwLOsmCRMjiQ6ZFIJzzX+S+hmFDneo/X8b41MONhY4rAVIwpLCEfdX5dYEuWsI+MyTIHYgSqeSAAIBlJrLBXhcTFYg5mnG6tZMlFQSHGqDs8emgviZb/wc+IrAxUygkMwjgwxPJFaL6Fuk5dMnuqygGUnqEw+wUzkguPrecHJrTcawTYqnzIpvhzpkLqmA4BErkHB4HI0l96LFybr2TKIhWMBAQO+t3DWmUN95Vsf8cELLDG18szXITLYuipqEUVZcnWK+dszIzNR0MLEUx5kwGRWNYqS+pkD3UfNhIVV2iSwwLw4/YNbuI1JmwxDur+RCkjTuotE1NCTBk5NdZ5jg8r8qlr0G7agjP6aXYcUnKc+UJb35nUI8z386GVUt1mrbzEwW5hqLwhFWasj+ohQ+URtThkIFBR5PFsH1cQpaYNb1+vF68iMPJ2wvUPP+Htao3Feo0AxmJYFI+lThDg1VoP96jsRx6Rd8vd3y+RczAH3oFn3nc51kaXF+dnWh7mGTF/9z746B9uFXwPt061zznOdvpi/pyXDyk/+YSUVA/1qPjUy/7y65VJgL9OgjULvh5Y87zOlBCVVoWdt/UAY6cNrFZ1SFQXwQyz1QHBPU8zudJfn89GD7RRe7pee+66clgbHWIyjdZwosXl+6O/YyHnG7H1rDi4zfao7PKo0ynFU9g8YhEGMC9xPlzgfLXGahyxGKChmUzASv7sXvdmtH57xAP4MRG2IvhVUI+HQmQ0zw4E/HoAVhZrK4p6gu6S4GYSXMWMv+8m3L67wu2bH8CbDXjKZUxZdK12AkTJ2AKIYEQo30EMcOYS4tR7V3CW48lCCxE6pRMwW4O2GumWsLwiPYD2cpIWgHOtpxBEDV2B1hDJPD390wypXBGnionUKCEENUyT0eRtLxp6Xz8df7dXAbDmfRgWI6bAeDcscHF+hhfrM6zWBFlNWA7mDVHOgjrWduR05Pud5X2ewfeePXvUFjrAIICYkb64RF6MCK/fgG53tnwHaBzxLdzfu2uEd8rhDnX+PZVCI997/nzQg/mBz80I60+kPMEjghrko19E9hHzSeWIMqKwxE07IzN+zyOCCIRdKJJLeI+md/ZZmWyPNeyuiwDhmzcB37/j2VuH+vPUMq+v44gP38cd3Sh44OfLKNxZju3y9vqRyXn6Frunhhncf5BycI98pHLsZH1sOQEvzoUuz1JOPAiPnNV49WKNf/n912BmJAvFNA6DekIIsPnvf8PuTz+AAbVymbV5cMxPAKn2qNEL9xD4j26htjNvoQiOYURgI+SqQi/ndNx6RQlwChZmJ4Qm2klGylmT9QlAoTIhxQKjo1ulWAUDNQ9R0fcWAZ1+arx6Ey43/XThWyaPx07mbaz1enJfF966Bf98vloPhOOr0bCgxkRSUG+Imwx8mxM0b4Vbn+MwwDbtz3mF3GiTyqs5I8eEnCJynKBWdeYVAo35nmJCjKaUsPwVyZQSKU7IOWFLAcQLcCJQyhhRFREl30PDqbS/a7fqLhODH3/OExAXAa0L5x2GW8GlnevE7TmBYqzArH8hhLJuZc6BzqLdGTUP31i9MVKTy6P2PYvCXjQr+TFQgQ/JghyTeQgECDMCM1LDHPo8cKihklqercV/lnK86aN+zkMzqYeP0WUOBzCBAQEijGL/T9CMINRAUKPta7exkNZFOZvQWudJoPOTu7m0PVOSGzMSGZYQQsyCNV/gq7PfGTxwCWGczcotpQiRgDzW8EwqXFdFoXt8MNe+qsd+9dhpS/lNpPGI7arDADHhp+0bfL/5O87XCyxHJ5UJGUDKghgzYkxwr5ZOEdEH1i4w4lOroO1f9GLvBSTluVYZz2wCBXeHB4rSp6+rvGzr2vejX0+LyeyKN9LcFCV3hACMqsDyraZ71AQXPpeljR54Geql4nT3tNthe32Dt4slwnqNs9UZLs4vEBZLEIfST5dBGITt9/2Zyv5xuHeaHvn9vOU5lQ/PUdcpCpPHlg+l5HiKQuIBrTz90WOE5n31fFoyhZPLqQqFj6lweGzbj4HsfjlVsPznneBFAH41WL4He4BAJaxN+z4ZTcqkpzr7NQKS1a25mQnRqL0kbMYaej9mP1NUCeHvHRZWaig/j6FIxe3uwKE7K/WsbAYw5y3FBiAHbsxRNB2uot6karwiZhhBDIxLDLTGii5wsT7HerFQwTIFsClbWiOVQ4t7DJX9kAQ/JeCcCQv2+ep7N5Dg94Ngwap8SqIhKncJuNkJ3kwZ391GTG+vwD/8oPxNsWnLEB4gIOwyFQVEYsCjizMYgdVbQukq9fjV+Dj1XBdXQBitqJ4uypvpgrUjq7RGr3Rol2r2XmchI8270jjSmA+s0T1VCaHvl/C52Xk098p2b+7cKSfKH3q2qeOPmusgt+xHNV6Bes0sxgFXwwL55Qt89eILvFif4WwNpNWEMQQwh0JXa72yV3/X1rFy37l4grzk+QrNftUR6DflrfMXLyEvLsG3G1VEGJOgIFV5tfL23kT07ZyGdx82CYfqPDbVd7V/+N79fdk/7x5L/zxl8Q8h2I9fHqiI6Djc9qPBNc9LuPpmXhDh1zxiJQSkpIejh22Qmc0geXxEKoiFSGMWf/+O8XbDxtARrrbHGpb7EcIjS2HXDlXfnHTzA2uOEv7hy6cknP8Q5VMc70kn6wl1nPTYe1BGNF1oCZVDSDpjgYwlvrpg/PpVwMuLmgsihIDbN++wu75B+HELutohvrnZr+d9cFWzNbivhV5odV/dh5+7+206esRpdRbCxl1q7Q3F0RYyT9xbAcWSx1MyFDgwelkkg7JKq9xiPpQk4WZJnZLRvVSYKjFBW5cs2dvIAiBrDgAyIStpHaTSyjLlbnldrf3RCKDLlPRf2rataHJYAnHALYB3WbCB5SF4ENhIGWMug23uCcylOUFSVM+G4t6v65FN4J5ybIyUqldEOXHNQpoQQCEAEhBNcaQRjQSgbGvjMHACjSBSBPt7SgipORTsUfjudb6VQyhtqfUNm6W3MgwcgsJVkkIb+D0P2diFrBENLaRWVEEjMXHQpNZJhdE55RoySkTTCmf1hJCcCqyqoLlXXIkziM68iKilPTzEzczDM5u7usuADdbbUEkt0Hg4rWjhvYZgqbbJ+fw6pyKCJFJjv9peU4PCOs/J8m54zgPPl1FYZLufcq572+AbWZBEwzFtthMCJUTyuM02ITkjymsIbUD5CwScaf+ZMTBrQmzX1xjXmEVDa01TxJRuEfE3RNyWuZifH3MBN0H7wCCEoN4ri2HAOATElJFYWeUMYIpZwzPtIgIRhsUIkHroZhCYswl+Gu8G338CZGFws0aOE5ArnMMZ78ZWhotaQPq9ZDAkWSzcnTH0rAoiiK9JCxpm6UmNosFhzeFRTD1Z6G19PVu+kGShEnwu/bmUyEgW7R+LwkEIg4U/E2zeXeHHP/0FL9bn+OKLVwAHDIuax6UknS/j1flvLv5iyqcaGul9KiN+nuXDcmKfjrjgH6t8KnMusx8mzkYGIYoqCgDAvYWZlO5ikH63I9Xly2AgeZx2ISQ0IZrEPCWEkER/sx4BSMZnSCE7jH4QKdblSoC1dK0c5CGULPV7M2HSXRNAzQWnbQtNbSY0jZfs0UJK0EhmvHm9wri4wO++WOFiEfCr9S2GUfAdESaPoOFUwl6V9/OkAuDbCLzLwKtA+LJI3fS9AIDJztYkSHnE1XSJ613AD1PGj++ucP39N8ibDbAzGsLsppSmSBAIJjAiBMmihcDyoAnUUyZAlSBZmjCfxADbejGhsdhC0XZ00yne8P4gbQ3Kb+luNPfrtZKzbkYLa3PV6IhmiaklZ9AhhYNYKMjyfdb+gU6Tw/Es1q1A6ZVhGLADcCWE1XqNLy9f4Iuvlli+yKDlUDxnPKLwoWnxQge+fYyyNxuNpuQ+3h4VeuyK02M2AUW/pXuz2aFdD+a5Ini7xfjX70ELRv7VV0ibDfLV9akjuLMcI60ervA4tG4f8qR4zrY+lRPuQYoI2lu1VuP30HLCUdG2jEEIX1PACKqu9iIH2qbua6uEICb8cB3wl58CQDSL53uoV4e30MHBnIhX9pQQ1N0sF4jmN/2Z+bXDDd+9Jg9dsYcQ3h/YR+NDCufvmbZTZvVjHD+tReUpz91XHrLCp7b94HJXdfeZWt0LL/ubU+V6AzKd4/x8iT/+dq2x14MSKsMw4Mc37/D22++x/PcrDD/tThrCyTvxGKpqf983LKcF6b5HT8QeD0QjhSS0ZKsusIU4DVMTCHdxQU2gSRab3K21/EwqVjIw7zio0JhDKANN1hY1GaZdyOsWyMqskRFjtW0KoQihPV45m4JCsC8o9zA4JU8AUHE7Na1XCb8J9C1sUGDssuCHqFxgTfZs5219pZncypb0NL8T83ZDgBISKyWI/cHyF2jRuXKhemF6PJ68jw3N+cqiAmYKyMks4kWgwXXzAVC5G2B16lwZUfNCzIt7KzQzqcy4KSJyUgWA8Z0lLBOxWodxFvV6MUF+sPeIXAg6U7oACDyoQNjeEYmmtOkVEaqgSuZBYXlILBxTCcclBTi6HAiuCHP4aeG2zGBJ1o2Si4G5CV3TAIhb2seUNMk2DUWY4AxhaBQRLiOgolcwMbNzWwK0ic9BhKGxeNf+6ezlnC1mbkAJn2RKgykJtlPCgjNSUN65Cp0FGVfI8haMJSQuEFPScY4qcOA6QGWds3rsxDQh5g128j0ykna5AzdPKK31kFkDOg4gJgQmDIExDIzFGLCNCWxznsVyWkwJ0xQxBEZIWYX+WUCkcMAgY/TR8PDS7C9GiwacJy+hmaSBP5ig38YtZnHWcY+CkvOm4gvLkYHG06KsfS1tgtP+CPXk3hWXVCWuwXuuApl6XX+nnHQ/SQKDzStJW99d32J3u8PNb94g7rYIyxWARYE5np3l3p/iuPOEchrZ+BBO5a62+vfnSujnqLOt+7nLhwzVNO//c7X5HHkwvCt7PXrOafm4MqoPXvaEd5+OfOSjlFb6YMeu4tyODDRFBBQ7O/YtigdPUgyqighUbMYMBDOMD6R1FAE1mQIiKx2mwuvaP+8X2Zei4BApYVc6etNp6Xr6NT1pa5X9S6cUM0KogvKGzi50d8/0+DkvQnh7vcaaXmE1rrBeMF4tb5FG4E+yRILSAXv4uyfl7+4egB+T4G0G/l8rwsvAzR3tTYJb+gOSGNfbS7ydCG+mDd5d3wBvfkJOGbtYafwksITjetZHUi+ILEAmRiCAhEuukOCnODVztsdIAMZoNX3M9VkBeg+JZt3KK07EzGahVU6Vd3pPdP/sFFlu+CSivIuH0c2qoKieEWKDz7UNI65KUmzsL1yVyTktXKl+NTQMuBXgarHAxeUlXl1cYH0REC8AGgQDhcILFDuajmrzVfYvD0Twh57fkwecjjTbnXaf4uTQyyUSwbw/xWuIIcVU5rjooolXoG9tdhhvfwB98QLyx99hesvYXV2dPK6ujSedIXe9/PCKn+88++UejI8OzSSzz1oObJon0PIjCL/lAQsAnDRZoodqaCtuk1KXONEWzoKJ8f27gB9vAt7cqgBpXwnxTB0+oewrIfYFnz+/8hH7/iGVEd7kEcj/5aKKX3Y5BD0ZAxJWeHUe8IevRghGgNe4PAuajHocEIaAm//2V2z/8hPS9TUW2y3CrdsoHYAGNT8+2G5hPE4BoqeAe0Md7NGAbeMukJxf3/vp7qyarDUbsQKiKjiy+vyv8x5gKtY7Kty3Kcq54vli/W7WMaIJwbIzOZLVGtqtc40Jy1ZZjrommqS4WQNjqNrhuPUwteeAC+nIEv+6wLaxXvbxuJDZE7h6eEFqQvV01Il5FXAI2AB4kwQb7UDpz73LXbnBsj6t4LAwEa4wiap8KFb/OVlLqSwvwwT3IiqwZxUlixBysHUTKVZxm8svENOE1dVrhDQhi1qOc84dvLqXSvFo6GCubgCxOXRlQlMD3AXaLfRdaeBWccVjoplr925pmSrp7lPnUeAJnAkZSaSElvHkwWxW4zFFVb5YeB5VTmTspgmSI1LUufXxxhhVKZFSCZXkFv1VYO1wrTNB5hUhFjPXBdRscY89Nq3PE5sVvBP5ng9F19oVaihtF0VcOMBkFDGG8nge9sqVUtKsJUjzQigzqfCVYoTwAKbc1SmiCsLdFBFHY10ywJzLvhVkaNzkHxHoFlP6DUTOdYwhIAQBiJFE99202yHlLbb5L5jSre5BQvHm8B50wn2bY4V34IfND3gzvcMkNxgDYTEwFoPmtSgKDxBiEuxixm63RSDBeLZU+LHQBw7duqC54KosolapQuYR4XOIMm/OVAtLWe8aHsI8c0jMkUHDXmUkxBSRYsQ0TSqYCqFJWEk93iKDDYNFx7HVk8zynJhgKucMYYFbDrplYpomiJgHDREALnDr81xUkUafO9OeUkTa7bC5ucHt9RXC6gzDUpDoJTKtEeQnsGzgO72mrvC5+ExxfS7vvxyk9xvhi/8+Co2fmYPP5YFlD2T8kCBCEsK0mxCv3gJxp6cI+T8ubK0ej0qXS6mXjcATqXLlTIJMwMJIxUQqgo6kZkHlaPP+lQ72eN5OFVTlA4wORnmqDEgq3VbPSin1+nO+y44rEhsivsjXbUN6Tq2s39vHiAnL1QKr5QLLhXq2f0tBKSeieqbpsVaWoV2j08rxJ7PzWRlAIshE2O0YN7cRt1fX2G532GQgZ0ISBkQVTxMytjBvcAiSKSLE9Ag6XMHAwcJ0Nec/axhPgdoK9ZPSfOm1X3UC/Np8OTrepl3HhgfUUfe/5+vqPJXBg3tEUElO7XSSh/dtQjIVGDLjKqk83pyXorJdqNB2UmhGRhgCVssVZBhw9tWv8NXLF3i5XGE9ZAhruMmBnS/sp8jnk4hsjazBj3wWPKlp31t7lJfimvTrL5EuzjB8/xNooyGafAtWuGr6YbK7IgGl6oUd1issvv410s0t0iMVEh+7fFZCnFYeoIiQvW/Hj4Qe6VK98SABGkHd1r6kgCU0dp5aE3o4D6uwEei3FnwaK1GZntebgD8XT4iuV/tjnHX4uUTc7gLWt0H9B83fubu8N4vzR5VWsPR+N84HHe/8jLxjbIVguqeqJ/f+Gc2GTvWEmD//GM8IL8fepQ6GjjxfT61+HvY2z8NmuYh5ymsBWc6wWi/xh6/PihDShZwhBAzDgOnbN9j+178CIIyltn4ER+Gisfgs9MmJ3T5W530wuHdPZl/ugK09RqAbpK+Hj2RGcQkKYVktfanxhDCJ4bxaADXhtFkONTkABG59rsLW3kLK2CQPFB9qV/uQLPOhS/lORkyyxhrS0CUumG3CMrVjdCKrCJLb9qTHkGTcohBhK8CPKSv9T1SsuMtsHuIHZsUJ7ppow9tyhszzKuUiPFcBdwbElWgMkGiseMrQxM82dvG+2I6xMFW7EBBzxHJ7q6G1SqK42nEP2tUKrgvnpBRuWT4BLD+AWlS7Msioe9uHjVDULL9hIX6ICZS5hMbprPUN/nwd/E6bh0Pfr++4Nf8QQvGIyeJ9zEUB5esZY9TQVzkZ02vJmpMgSzJPnNliOmy04a9QYdwVJyXxIKGbmw6m/IGGoasCaBTYLBbsQpaE+ABQUQ9DZQ5FkM2F3WeR2MLzWO4XDeGUIDI0MKAhAnKGJUI3q0sSIKsyJHuiQgIEV4hyhZRfQmSJEFQxoEqnZLkgBLtpQsobbNLfkfJOHXKgTLjTjP3w+l9MhHe7d/j29nucLwesRmU01YsE8FByAiAlQWRVpAyBNJRWyEVRutdGEThoGAyiWTi3g+eV4zN0Ft0Ff7jywIRG6pmTkFIs9C+K+zuVd4vnPDwEXjYYUoUDcZ5PDbII2IQ5ABUFSUqaE4VogCstVBmRocofKUocJ71VOMaQtEOcJkzbDXabDVKMAIBEZwDOQHgHhywfbh8M42lc/bGjbn8pnka5faphlz6XE8upy3cXzfkEov8jy672x/Ue4bkhiT8XKxXrqxA6gxBjQt7cqGdriyCbr0oHFZGIk1gAasglt/0g8ZwSZqtMqnAHSTkvhMqxsdczgYDFc0dZb5vzrT3LquKhvr0nxPZxNLPQ74OH4uSGtnGjIiaMQ8BiMWIMATQwXhNDhLBkrnOIOUd3V6tH7nSXGxpMxAwvACQlwaeJsNtl5NsbyDRhl43eNroii4bl2pV50/xUWRcAYKWdKDMCREOJ+vlPRnu142k3XSebEm2zMyJBQ6+2KzJb34YnqjRQo4QqE4D+ubkiw2HIcsEa0Y3i2d0qIdz4yxQSJLXeUmvJaaX9L0O3P9cZsPF8wzhivVxi8eIlXp6d42yxwBgSEkdNUO2ewLN6dFrdQJr6acYJ5SHyi2dCmvc1SQXRtO3U+cwvLiHnZwhvrkDbI1EhbFmp4Xfadv07L5bgxULDuF5dffBDUI7+ODxPp0/9/MFjk/7wwd7Xh5NAam9p3/+kn6yIuL8rT6Cy5m2JYCDg9zRiRQzOGQkoIQ+6vpAnRfQDl1HDMTG+vwr47t2Aqy0VBujZy0PrpNmXU86tT7r8fHr64CLzn5+p473iRMlzFRfaHhGI6SfVz0cevjT7VA+Ic1yuGP/69QLEAzItcb7S0EvMGrrl5vVbvPv7Dxje7jC83mH64R3aCWitgLq+fkplxkh4X/fowlaI5j+Pnpv7QkwycaELzciFzpRNcAXwMGhYH/NWmJ+DmoOg6WdRNsyKCY+FTZApNRm1xAQVns2FYYQMRpbYjVfPD5QEZKX+brh9Hzw8lJilESyUkFrZc7U8s4nUY4sRmLAl4Lss2JVBU0N4OQM6mxj0W2Sf3jfFDKogulDJhejX8EEpTmZpFKHeAMGmuIZqGYNaiiVjDFKueTz8SeEBV+evMKwmXG6uEVKESJ+IqZ1P5TMqk+OqAWnaiElD+6iHAlQpImwJkdVtvE18qMyECU0tDrKLLlMyBYA9XkJN2ZhDSYauluLuJ+J9JNKQX4Et9FOuygT3QkBypY6UOQTMU1OyhpZswzNB4ZaJkTn311u8IihhqgrpQFwI+gxo3Fy4N4jNKBEkWb6CEMDBMxOIhfCpfRT/bvCn802lff2sAgBXBvVCdALAnoMeDmcxJqXNGAUuswii5YvIRQtlnhBdfdrmTr7DgHfYTr8B0xqBk3mK6HyqImLClPdP6o6mLj+o0JCvd6/xLr3GVbrGEIAhaGimMbAlHrdQYSAIGFPO4CjYbncIlJF2k4Zwi0sQZZsFW0MlUU1xY4lAbUt6+AtNuK1zoDlaFIZdcXSwtMyvCOIUEacJKeUShqz9q8kUpcBuMi8KVbYSQsjgAtcCZJVkkcEzF67BFFEpAeI5Rdh0ya6I5Bo+qz3SdcA6LTkjx4jddqtKO4K5PlBRshXc5X2XUuUHLs9N7HwuP/dShE2fy+fyTKWI+wpgCTItscMrbGVETIRtvsHt4m+I8g6y1fNToOeJm3Y0odr11CGBCJeQfgRYMlkonQCogQqhJJoV1BRF4ormljw1XG+mA6W//jc3qfDPYgaihxf2HkFL9bY00T18uBItRvNm5UGKgryR2RIgFLBcjVgvBywXCyxGQqIJwmJkUA3fuCefs2+9fPQwJqjk0Yyes8TUOROmNODN7Uvc7EZ8e5vw0/Utrt+9xm43IVGw/NJUjkL1WDGPCHHvcAujlNXDhS33B0BgynrGA8p/tfN9iFjqEo9b4H8ilFBNkj3zOYrJu9GiswUpdF1Z79Jgbtqf3ROD4DzL+5AzkBNgIWXnSgj3iqDcttPLsWlvpRyuzeN5CBiXC6Qw4PViiYvLl/jqxUu8fDli9UUELQljGBAsTxwTZnBQatVdZuPn1kDlZ3xoHIJ6D3tVQnz6HvTdKgRqaFmf7zbHDAHg61us/uMbTJdnSF++RDg/wzL8BvH6CulozojHlTuwyN3vyUPFOne19OFoyjv7faiLncIY9w/6kbK40xURdzTQWd/hwHio3pvV2jbQPC4IQnjJjDWxxli2Z/q6qftKFjiWLOmOEOHdlvG3t8YO0onL3TGrz1EsGnGH/aj7ONrYidD+fjwjHlqXVKbxQ5eHY4Y76pr/PDKeI+M8ZfTPDmI/s3IQXjtZ1jGiBmWdy1E4W/dCxB9pm+bfrCkmRsIK42LE119dYAj1QNX7hMCMuNng6vsfsfhug8X3m1lDLRF1rANUn3nCXtl7szAcpzyIvbadwD30UvfogS537IK00R8dJwBlxVwhwW65HkCBAWqszJsNQvAzJhtRN3fnrs9Wq3ntdPbY/FlAlkSvs75wvGwlZ7futrpm8WFb66hDZ2LNo9A6bfRttBwRESBM2AnwunhC8MHnpVjXHJj/Q2sigFtwz5kA31oapsVzQaj1PhObdXq1RXbLMJUim6DUXJilGaeAsFmuMOQRF9EsYmKviCj9s06W110ILdVjxvNE+F5xb0ZH90rMzjhM2wRCPvf1bMhZrbSRGtdwsTlnQQih9qd4W1T6x8PbsMf5bZQNFngLyZOxl3cAd91WY67WI8hxoDF97tUBoCSQ5taaX+r1QtM40y1q7dXBR4FWQCzsTmHv6/6pniWt58js5NvTMlKBi2KtL/27IpqHQyBl7n0nCxz+qPREBfPV2wNAI4wBMq4R5RaUX4IxIEtQ60tRZdEUI5JMqjDwKfWhOqiUTaSt+rebfIOfptcQiCYgZLWYDEHxfsU5OsaUMyIEMU6IE5BixBBCUUK1iagb8QMEpiiTVqdKFsvZOpMFCO2exawGr9fm2uAtJ81X4iHtNB8KldBduofr+57TJFsScDCXfCZ1Hxgub5NmF5DwPeveTwIfhK5nHwyrQBw14VGzhs6bdjvDKfvzNge95/YweFgeglPa/mVRds+Vp6Fdt2N13tvWfQTeo8q8zYdWfkgM9bzl6LDfy3zcU+Zr9B54vucw8n1KHUfFFqeUZ5gOgnsoaIVZAiZcYhINRbijHeL4Djlu22BH5Qxpz02Z/dUW6guEDvWqANvyEblyA5CSMaD2y2hrFLFrF8ZQj4RWHWFW0H7glyPOvfDum7z5fR91wzTUmdAeFyt4araLnnfjGDCOjHEICIHKwlM7PwfhgLpbJVzgUZhpqAA/r7Oe3TkRYhzwZnuOqx3j7S7hertD3G4s55rNPrlhlxlECPts1oqb39nXx5JXqwlFpTt9vaSbO5vTymDbZYvlBfeQ0N9K+7VT36yPzKCuW99K17eXuh+uhLD8GRD1Byohe7tQTH7fc0LUdivLdUBWULpr88IaenmxWOCWA+LZORYXl7hYrbFaA3GRMYagXrKmhOjLIfiUdlk+ankSXuvqaalau0a2D6gnvp1/OdTw/CrvJtBugjAjffkKvFiAFwvkaULC0xQRp6Hl087y9yvmfKbK59XQ4X63+6C/LbPn3s+8PDpHxPsoAk2c9HsacQbCkAUZqSSp7FClwzq4hsogaDI8ML6/DvjmzYCbXThC2Laz9aGxA3UfnwR2eq7yMZQQbdtPZZie2P2POPpfTukkxS01Xdf3KassYCScQyx913pB+M+/W2AIARlLLBcBQ6DiAbF5d423334PIkIYAvK3b7H+8y14E/dq7tb/Hlh8EqwcI9jvqFTak2ZPuHW4gtY6u9ZxmAktcd0bqpQaqkfjp+tJKKTx0YkZNIQiBHMhstPBZjiLwgC5UN6F1fZHrJa3wzgCi7Hg/BQ1TInEpMLgrAQ0N9RjEUmaUI4JoKAC2+J2O5+dGZ5jZm1HBCmpdQ6ZNwVzI5xt+ARiwg7AD0kw+WDdEr3MmsxaPkDIuVC7rGudl2wWV84xuXs2mSUTFYLRw8RkSzRtFAtp4u8xDMrIEEFi0ghOjWa/0a2AaYBwwJvzlxinHc7ebRHypP0i7y9pvFebd7FKnF31MFu9AkwAqlbdhJpToVqd65iySrQbYXBjmVTcyalYgfv05ayMTBYgp4jdboeYKg3CTBjCgCEMiClCYMJek+8KMtJOvXCGMEA4IcXckbaeTNjrJBdCtwo0Y1J5cI8afzkV2GhzbJR9GowBNU+P8oQp4IYQyvx5KCtmVkF7r/3qUEFlNutChxAUtqnOfbtUOpdQi37JmiuDAM6ElDQPxPlwif/y8vcgrM1LIiOg4nmxPUPWpj4hmPLfABoRRCFak5oLImVkSrr/qLHkzx5azJKbm6eMiODH7Rv8sPkJEiasV0vL+ZExBsZiCCVhNciUJATAki8nEQ3NRMB2uwEBWMa13a9Mf9mabmFIFnbNLS2p5icpe9cUqMxViOP73L0k3PMlm1dDjFG9IYgwsOUx4lAUTe5VXFdZiiIizM6rPqGyYBgCnPBuGRcishw/6NBTNsSTc0ZuQFhsHXgYwbSF5Iw3f/8RMf3fkGEBLJZYLNcIw4jBRDA1l0tVWqFv7nP5XN5LmSeM/1w+lw9Rlgz8YUVYEcAlLKMaeySR8leV+vqekzcum/Voeo0PQqUhgOZfKRc9/KZe0nOsGE5wfVekCQtIgmDB+NVblUxJobQGoWaH0I7WU43ceMPb6KRip+y9Q7yQDaLEntJrRAxkxvTTAhzOcfa7JVbLBcZxxBDQKOuNDjngkfhwg8/DMiil0YEpMrYR+H434c1txtt377DZ3CBmzSUFVi+WkpM5ezY37Al9IU6jKPMkWXN/ZPeCMHKNHU7sYq/cpzqlVB6yOwIxL5OiihF/7r55KFSwM10VIMsZj/pM6wkhST0hcgZZLkB9p3kO7lHcJqjeM/mpNMysEDHGxYhxscDZ+TnG5RL01Vf44vwFzhcrLIeESKnLc9WPrMJ0lfhX6p+6Z3+mZcYm7N0OhOl3vwJ98QLD374Hbbdw/ovckIfq67otewOoRmzwbOXnM+fvsacHxDdAgyrve72yZkfvP6Y8gyKCZp/oe3OC4NCfZgCDEC6JcUGMZAlIHUfNJ6B4QNhmVw0vIQrjehvw/bsAt9qbt9X36X2CaBUn0f7l8uWZDI7eK8F8vIsnsIWndusp8/BkJUQVGpzyXPn5lCZnv+8dwTMqep4VVp5LMnAEX0hzr3v8jqbpwC92IRJWACn6GwbGV68usByrIEg/NbRE3Gxw/eNrQIAQGOOPWyze7Aq17gK6bjaPjOMUZN+Vow8/nDluZEr3NnbQ2t+5m5ZKaJl0kTIX8EekWm5nEyQ6EVjCujDXRMKzZglt2J2qBlH6UwrDxYBa/qqEv4CKCtkyxCx+i3CtoXnbaRFLEFt1ApVd84c6spZQrMHdWl2MaQyoxJXJ+o05VAI+A5gAvDNmxAWne+vVTPccoIqArhmLW1sViyu7QY21PIFQ/ImbaS+hq5w7KAqVmoeg3N/rn82HKXm2wwIJwNrnWJzZtfm3dXXhai4LYnBkrtUHWYaZcsiZC3ahuMNLQ/CWlWsmlpgBg59MGl7G84zk3IT20gzsxcKcmDSeb6FLlGElSwQtkhFIWfjku97XpSQ4t76RgJvNWfpo11zYbOxV3QVU2++t5FFgseAnAcDVI6JpqQjoZxPcwEIt0qwHe3LvmQKi5dsVHrW/2XMGuAIRwEhLvFh+gW0mbGM1OKHqulDWu+1LwrWBp+EWm8/ka21wXZWIdaxVWZWQJeE23uKn3Vtcng1YDQMgjCQCDmxjpKIMnZ+/WYCUNOxUigkxaOJyGTw0lycMLztqn4/zfnI7j64EaPGVVPwzq8gTRztsOW4N7PlMUNap4uh2v9XQY3t9kLkXmeG8sjRU8GWHD8s5Wue/xT9UFM+C7c0GWV7j+s073N7cABQwgixERp2L+fnwFApmPtb2+mPJrFrlM9JW+61oC89IC36Mcqz/93pEnDjsu+fncXPnVd7dxQdTeQ8qPUZ7r02dULlv6D3C5Nl6cGyuPwj4f8QtFgB8EQgLAiQBCZWWy05LwL7bO4U+9t9SyPCC8Q8NiTCHWilhmVz121rDEiz8kyWwZmu4sXkBoIYvudRRpB1dX/37Q0qf62keKOZI8Qbt7ErbERiWGMMCQ1BjjBpip9LK+20fuyAz3HWAAy1sUz0bJQtSJkyJ8C4JrmJEnDbIaVfkX4AaLmQLMZWcriuMClWa0Qw/gKDyeYYZg6B6CXtfpK7InILE/LdUOpuafsGuNUR+//qhhREfvP1oeJgOUgt/k1WI7YqHlh5ogbq4BrWmG4VSqR/H1pYs9OowYBgX4OUKi/U51sslxhAwsCCTGavt1VEVfbUNauCp+MxUGu5gJ+oYHlzulYE9DaEJpOMjG9CodRMhn59BFkuE73+Ek85qdGP+2A67lYFp1qQBIA8dO2dPjvXvyfj6YyH8J67L/PVHkD5HqLG9O+/j3H2yIuJ+otEAbb7xZq+pJ8SAczDGLIiUzEIO3XseGqH/MytJDvj7FePPPw24nSqDXJMBdj0/cYQzJHbgTu3ZvDhnZs8XZvpY26f26VMtH5FqeyZNzs+btft5ler6Oif65gRcEw4HQENRwgnk1uF2n4QiRFwg8ID//IclzlYBggUAtTIZAmOx0NjpTITtzS1+/PNfAREEDpAfb7D+jyulsRjgnTvGdo0UlH0qJD6MCG9G33Id99b5MIi+k3lvBMUHaDCjDXPPrLu1rF8QC7UD84YgS6gKADGVynrjGsflwQhMiwtKAJLGMydWa93FjxHYbJB+S8jLAEwTECNS1iSyOUcQBRCPQJYivFOrdAYCjBAdQSFYbriemC3COffEM8VDmqJaU9u5JWFAYeMEmlsBKsDdAvh7zogAQB5HvZn7QqDXS3qMOqnr1t71jHMBr7/ujKqIlDAoZGdx9jERAzyAhxVyiuoFDYEkizjMBEk659mYhV1MiNHyNglAlryZOegcuvW1sFpCe5tOVPrciSoBHB7E1h0ZIIuPz0IWe972l2TkVJMquqX33ChfEyQLOATj0yprDA911BLTUAs+IUZMEZvNBtN2p+F2hgGLcYH1eo3lcqlrndKeQgvweP9aD4cAEQImo6ctOTExWTgiLnskZkEsyd10XJqnQBlkVYioV08INd4/jJF1xKPzVL0rctY9VTwBxLxAmEFmXblv4GF1mWIs25wXUsbpLlvzEAJAwHa3A0QwiCfn1jBXSQgkhMHyHRCrRec2CzgLJhGIqCcrkYX7cjghHY+IW1kahre+uOrCmT/PScFlD1E3frdiC0T4YXqHv1z9FUkizhbAOmScUUIcMuIAnC0ZS/MogDACCAMRSCI8JIAQsMkMiYT1ZoecgfVmC2RgsViAh8Hwn1hoBO0RiyZUZLHQF8yQMALleeh6y1BxQ2HWqZDUroSKk3pDCFQYMg6a10gIADN4GIyn99BHOodDIGAMgCwwjIN6zDAsUXhVRHSwAT8ntA5eDLanFSaTaCzqIQyKa23/MWveNlX2mRUjE2gImDa3mG5v8dN//BtGTvjyD/+Ms1evsDrfQYLiIRKyJJS1PIVeO5YkvFrnPabO/ncf1u9RVR5q5cC1nzvv8OmVNjk8pOa1qUYmRpfO9kfHuu/z8c9TPiCjcp+87M6bnxmqRxadOBYV5oswcg6QxEhZFeURjCSW4wxkOR70rCGlkiGEYjkvTWJhqk1UQamfo6Iv1mvS0UuWPqERqhKyXVBDLyXismQl/4EibMxAY4gghcQtARKLcUpfvOd3iJB0N7rMp9yswl8vITBEAt4OA3i9xm9WK6zGESNlBNKwjBQ8/GUth2ShhRVzGY/xol3fXBvk/SCVBYkQEoBJGN/tzvB6y/jLTcT1bcK0C6ApgCQgS8ZAQIQgkSAzEDNrmKYMABGEqRuzTuwEgA12CDuwCZGVnxJiVVBkLrRseb8AAprvrU9NO9qAogEgQg3d1M4B12ea+nRhjXAToHpK+BhmeSHE8kK4d4SoNRBJTVDdwVMjg3Pqq4QEM091nTcGBU1MfbZeQ8YF0uUrrM/O8KvVOc5fMMLLDdKoYVk5uDd5zx3aCsOzwFO77qBCr95Z7gLyj1x89ed2QvMxtSGtCax0p8Bzre+/Sg2Bb08Mb69A2y3iq0vEr141rT+uHJvKvRqPNvGPcZjt495DM/e8c/HsoZmOCrLu6Hcg9YQ4J8YFETLVJJs9ReefhlCIy6eAkDNjMwX8eB3sUdrnDLoOnbLL/bnZ84eY971CTbfpzicPXb+zhz6sTwxRfS6fXnm4G+nzvn9nXYWipcP37ZZaf4RCoLDF8G4RSxsrXUtDiGCBYVjixcUZXp5VtJdZD00NO6H4K+0m3P70BkgqyBzf7LC8mkzIVfvXCTOb4bTl6B6eMa+noPU6rONP9yqCO547IoS557WDLRb6YE9DwoXY08bsHlOdPG9/7/1C8qC6bELZK2dkNOC+EqHWAG0zKEekbYYEgjQJzYSbxNmlpcJmARATVHLXt9qTWffQrJ14KJWsntEN3m/tyvxaBnCTMjJRN0VH19Z5tIYJ6IIAN3DvpPiMNOx4oTLDnmyOgxHyauKmwl4BmUdFBixUkiBFTXCdbQ0JQYWr7HPngtQAoYDMAyhPqAmIRQXiUvvqE1pmyrwS2qnROi3/BjGECUQN49cct1LiDfuU3x3dUtrnTNGQxcMxBQyDhmMKISDGaOvcKgebdWFSoTpy4wWDkmBXO+rMmjFD0JBeLiwPBKuDC+QXm46W4ZY6d/C5IipxnTUkUZEGNCQVwZM4HjShaJhwdUyRMsHUPKND8T1syibn/YghB5QdvtWTe560KJt0TQ9ug4YD8nF23gEChQdxlrfOUYKFxzLBPwlhlza4mt5hHBgLHjAQMJAAQVsYAmsc4JngUUdUOxhF0zmklJFS7xmhYSCSbd5c572dax+A4x5X3LY4USocifXflW8iNdeDTQvY4hdX3Ms6r7nCDhuOY2aEgauHi81T7yXQL0P5Rg4H1HjV+NlSQ+ARenTvzxEBxIy0m5CmCdurK9z+9BOmL79COl8jZSjTP4fxgkvu9164T6lw0PvviDLioQqK9px9Xxbc5Ofq/U823489f3h8P3fvi4eWdrhVFzczQLmjFFr0ZOruIZ3zNrqfH7zczUE73pGP18GfWaFuQW12ne6TNl9VCZcPC2pUTiSB8wCey4EKfeof+76PTbOl3lrmv4m4icHfw4DSHW1vKv6H0RT1mUql1v2CIpduXtSvBxQUXetk9RwMpVR747nO0jAiWEimwAFsoaXYDFV4Vv1BaDda+ihq3etKpXMzCFmCRvBIAe8m4GZKuJ0yYhKEDIzZx1WnQul2WJLoaoxb6OuOj0rGKhByyZOBvtPSXTxQpP8r8Ol3vXf3bHR3yzk4LwfaK8SzI2D/9DBlDu0Gb/ceadRdqphc+VQKmquQhwF5XKgnxPocqzBgGIFpyCVnWGs8eQwm22P5YVTDbCr2u3/H8yci28d2SJqPO5uy+QkBEjSXSPUO7iduL62d1zBFhN0Oeb2sBCSHChd7HXvcoLqt+zM7q56rv8eroeaZuxt7NIzjyYqIvuk7idUDvXQLyN/TgEtSTwhNrpO7utxitg2FAVQEzMz48Zrxv/4+YhvnDT12eu54b3Y43dvCPdLK50oE97l8Lh+1PAaMm/NjvpO6A4KWiLgoF7/+YsT/9ttlv3dELFFnTbTpJEHGCKaA83Ww0CpsVptsVsYBu9sNvv+3PyH9dIX1v12BshHdqa/t4BjuuHzsiHzIGSIdBXD3k92vucLhCI5uLf+Olmau5RCBVISBNuue6Lm8xmollal7rXgQSO6Ovb4Bp+hMuAgp4VjK6jjBLoLhL9cIAdhcZORBvRwomNU+kwq0RcA8QCRCJNY+uwAzC3LKZvmtVh2ScxW6ic5btDwUKWsuAbdWZ+4FsC6UCyFgELUsUwOlygr2y9OziB7ipi+NBRDB+tivOwE1ZFHbRnN+SmBkCWBWK36xsQk8T1wTTsgYvsESjHMYQKzvujcAAAQWIAx48+LXGKYdLm/egHNGlgS12JMyL1ptTSyekZEkdrRAG24KACjrvtXQXgHFIk5EvV2ccaFGwOrPtDMoaJKaa/igYRjAxFiMCwyLUa27AcQpYrvdYIqx5IYoW9O8DxbjApAM2anlVowRgGAI6rVDHBBsTDnnotjQ/CQEUAaPDB7U08BzZbTEf47JRqO0ULCQUTo1uTD9FbZqyTkj5aRqDlPEErH1IalguoVCVziU+dJOpJRKfd11U37QwBhAAAWNYmd4OWdgSoLNNmKMqeQPCFzpu4qujCHVmbPYvPWscNRcdJVZ6yiJkAm4mrb4t6u/WH4EdavXpci4OFtp3g8ijIMymcQBgQjjOGIcx5KjgBo48qVo+eMUEyITNpstBIJpmvS9IWjOFVZcQkHPFadrs3nvgNTabhiCJpcscF/ztxRxANUv2RRAis+4wG8wxVmBU5hXguU+8jKEgDTFgreTaCg7dLDFRRGaU1QRR0rIIuYRQwrf0ng+2fsFn4qOxfsKg08OAVl2iDFie3uLm6sr7G43SNsJW3kJ4QVW8iNYNuZFJUjJsB61kHq43MWX3EV7z9/rLORPKMdCPz3kvVNKW/Xdr/r58TPjtj+RUvDvQf7t2Lx+nuvP5YGFgOIFzO5xoDmVNNa/aIgehtIKTvdCzwU2XA/D14opK6HcY+fqVej0rNNciqdb3NWcfUQlBr/X5WY+raKjE16JDY1EbZFEL5CY0sToU01JQHvSTiHvgfd8Pm8amjOjv00uvScTWXMAaMCLy0usL17gcrHE+ThiDAM4WBhC15pT34f7Cs37NlPElTsCiBBu4itcTwHX0w4304Th+gqL2x3i1VvN/+HnJDTPw9y/Q7vqdK8alhSCxEqGWG7pjN54yeiPNtX53JhMmmulymZMTm8e5R/bBw0AWq/Golmz+7npv9N+9lnD0Db3LBeagtIxJXGlBct8lVu6z0IIWK1WSGHAu/UFzs4ucPniEsN6jbcvVjhbZZwPk/F0+17En8uBEhjbP/wWvN1g/PO3oO1O+TLbX1Up4er91sDH4Jyqd/dweYmwXmN6/Qbp6t2ssc8L8rHLMTnXKeXJHhGnEdg9cPmVIOoNsQbhjMgSLDrzif3DpPEqcGZUAEyJcDMxXt82IUDqiw+YnLuepOaD+p931VGs6XwM89t39+4QM9Q/cHfzTyv9uu2t4l1L/9B+zOfl1Aqe9UQ45oR0N4wXAc0z9uRnVZ77DCCN1TkOKsQgAhIGBCzLep+fLfHqxXk5qJxISTkWIbPW1a+p758imMw1gmna7rD56S3weoP1dTJFRNqroy2nyheOIun3uH9b5cKeIoP2nznUnf5KDZF1EOjnzAnN8B2ppbgU6/SmElu/fp7mvfHkt7XvB6dfAEwZEgWyBiQ4QcMVXrpuVWvV0mdnggojQDhwLCkRnHvhWqlnPkYXnpL+IR+Bq71BWYfuJPKPlHJeOQ6Xrqqi1Ac3ZyyhN1Mhe8eIRVPEaF4PLsJNv17sXpggCJiGJYQCZNoBKYLjDiURHdx9pM5P9VJBYTK8qFA+I+cmPJASDXAlRKtEKSPweTh0Pkuuwl5XcpAmpmdh9YQYBss3oiFwpmlSITX3HguAIAQGhDUkgjPyIqDBAbcPDSWN5Zf7SOgWa+ZD+mV2bwxn7AM11u8dOLS7ydfeYJYsPBZVePW+is1noVu64nNsYZtynglda8uujNRoDVTqzjkjpgxOGTuZEAhmldj2Wcq/jneSlEjZAKD5XyAowc0szBo1HiDbvMVN3qiSOkcwAYMA4zhgPaqCiQmmlNHwfGTeEJrI3PJl2Dz1+79FFTWvSIoZOSYNuWRKBBUJcA+FrTKVgOKR1QedKrixbQ/Ur5cYzJB5NhQmrlmb+flXByEVVnOP58jyZHg/PO+MJgg3RW3TFklGC3dtno5C3+sNFFra6o1TQtxMSHHStc0jRJYAVNFYEqq2gHGk3MebHFMsHKPJH6pMOHwe3F8e631wn9eFC/q0jbvvv9/yMJ5n7+2PJgX6NCn8Y/zHPhZ9XO1Pm+07GPAHwvkjt8XPpnRoEfDjS63ZEZAoWEhNt/qXDkdX39AWMfaTdmgKi6rCiAz1tmjpqEoDex00q6FtlZsTujgnFHqswYn+i5QD6xSq5YHCcaD1mugf1MImIOYDAKd6DZsfCQCPWCyWWI0LLELAwIBQRuZ8YHylpwfbtePrOJyTqKEDWUhRGMcpQMwLpByQZEJKQMgRnCIk7wABMtzwwo7ocmSSkejOlBCKG2yd/dIFAZQ3IwDlfM4tIVIB0AmSbsM1BGgheNrPdoqkr+8I1JW2umfaz6aNto9ddTL7Vun3g3hvxo867UvECMMACQPy6gzj+TkW4wheMLYjIQeutGxDz3zQsr+sT6/yUUM48SUiyHqJHAAxPqnCYecb0dCzHbmqF3MGTQkcGBhXSFdXNVH7fpO/6HPi6NjmsHEPiJ4+RYdkLMfffuzUP0AR8dTN54isutP/lgNeImDMgoRYQj9U2qXd+DURpTM9zIyfbhn//bsFdkkZsGcFwmOHC3UfezcK6TbfbHsykI9FUH8un8unVKrCIWNEohd4dbHA//uPa43XSYDmcxjLG8sxmLWn7nsVBGdIYo1XKpUgqbEKqQiTQgiIuwnf/a//QJomjQ9/tcPqf74DTVGft3+O7lLZ+3JnqY/f8fwRnHOQCD/0+jHLlHLZSfr59UMPN4qBDlftE+blFzXIsaBBFXoxMoTIrO5dOOfCtPm0SLUUxtz5t3c3t0PB8K1aXFx9ydiNQLS8B2NQK2A2mCkdZoJkzSmgSWk7MWG3/m69HoLCnltYxxiRoirAkAUcmrwXEOTkFuIBE4C/xYwIgTRJte8sHXXVA0hr6dYxbkbAd8pvF1g2Z7GyjWxXGCBNTK3eDdp2zoIk5sEhYp+wJNbm0kxBrdjIYs+Ktq6Jvy8AEVyvLrBMEa9ufoKkCbvNNXKOSHGrfSWx0EtZGW2GKQaqoNX3OWChoPSiDt86JmLW+gRkGWps2ENra9ec6c6SQUzq1VBAS8PlbG5vsN3usNvtkHLCEMwLxHJY5Bgtj4Yx7GbRpgoTtVIXyYjJvLZMqeImfBxCWWcRtfZ3Rj6bksL3pFujE5wWyipIF8MV4vvG+lK8FmoYH1cgFYwgUrwc3LpQ7JMb2qp6pihDm5A6xVtOWncwJVUYgnoXTYKUBVMEdjvB9nbC6+0P+LfNa/z+4jf4l5f/pPy0Sg10L2eLHEbaz3+7/ivexavCn+6mCRABD4MqMUTzoQyDkrYpJQgBy5EAYeSkmJQJWI+M8/VSGfOcMA7mITIO4GHAOC4whIC4ndQDRfZpNqNMFe5tbne7HYiA3W4HARDGqPslZNCQ1V3d/ks5g6apJP1mgxP1rrKwCtngKGfAE9r7trbt756A7PlabO4LljAGz89DZrZ6c/mdLSE73EHD6gmsXkfljLU8QDFGQAQBxmi60Q1xN0M1lwt3SsISY1kKyCHfAtvvttj89gbTiw3yboIMI8CWhtwkVC54s+E9qhwLv/RYBcKxOo619dz0/30CfDkAv/P7h8pnNgXwjSZSBSltmdNIp3uwfi6fS1+Utqq0SqIFbsKvMKUBkRjJiAKGGnIuFgtkDkCcgGlX+B03YCgGEV4/Ki0tqPS35wBLxSDU8r0ZScBceYdiSiSmhGiF2LnmP/I6AaAEkRKn4aThahpb/4ZkdXzf0rntlmp5NKWFuBlZVctAADBp3rK35wjhBV7+9gtcXrzA5bjEYiS8Xb1FYuUf9oyojpRW7ncIf4qt0x8XwKsArIoHqsmxnMbLShvuMmEHYCs6/5kAyrrOoIYbahkiZrPnyUp6Zj9UDWHZBNQQm95nq6RzYREHigZgcn+vXQFpv3ibzfUKZHYvz+qREoZV/zykaq65IMTzQ1i+CPinNLyRdOsBwJQR1XuBmtUSaGgsIsKwGBGGAYvzF1iuljj76iucr9d4sV5jOAemiy2G4B67jbfu/nJ/LrPi+9P3cT0Z6/70X2Xd0fPFw+sr8NUtpl99gfirV/fuy/enjJg3/IlAwAftxvtp7BEeEQ+jSpXwbVO0CAbR9DZrENawsA+uhECP3P1bMZ4yq1YBY5sIt7uAq63FvzvStUNTNxel0cEn69X7R+3HaJG+dQfqXJz5VAbn6Pv7g3qG4pXSgV8nludmZn6m3NGn1OvW4vbQ9TtefHRbh4sKPVcLBmhApBXO1gu8uDhvFBHz/dMIVjycjltJU/WScGEM22bMU1QhWkjI2x12b66QNjsQE8JNwuI2glLe7yKAw5C/j126K0dOxDvR+R0CAT2wu+O7F0Dcx/8WqxgqhO3BN6S/0zEGTjU0bZVQIXftSyJjXKzt1kN33k0nWtsnWjiQpl8Nns0BkAGYRkIcVZBJUuHEB6HEypGToRks2bjasEDMdlYZoyUuHC/g0QgkpLbj9P5OBBE1FPzx0s78/MSqk3AXLJV95wJuY046foIIJcEcMQiN9beZcOWsCeGcX9DX1HpbE4WrsF7DwOonS0a2XBAAkBAQOUDGlcIC38KtzQETyjeKktysv5QOz8NX+QNZE0A3lnyn0Ew9SDVMc4ltT4XLTFm6/BBwuPIuoPki0p3VanHPM5hv2jN8llvJrK8TPPxOZbhyA1dlfpzXI4HAhAgFfq1jpepZw94fvydSwy8Y8UUktS1/Q/bH0YIVAZ4yBEUwkm0us2CXE67jFjdpg23e6jzZ3hSYskM0Vw8AbPMGm6yhjyQLpqThjwINarkvAiZGMliKWUNoLcMIyaS5FaDqt8DAyJo0ElRztbiCxt3wff8XFHTXaSYW+iolZPtzDz0Rzbni27rCvZSzikzxk8iT3Nc10bU4QI02+7KEDej6bQxgySthvgVH4re3NGsJy0XNeov3WWHMRT/zGo7lH8oi3e8Cl5mQtgnbvMPmaqPhmaZJ55ECmEYAE9y85+6sL59emSs4Hur50HktHbj+0D48oOVHvHOkJoOjR74N4KFjuPvZuU6hA819surEWt9TmZNoJz/+HL09BgOn1L13QtrlnjbZq/nntb1PLkdZ9wPrq94PjIgVMqmvgWI/PedYRgRKGAalG3JOJbeBGgrkEh2opSDbU6TVIYgF6unoKHs2ZymehuaXUfC3fjQhfrpPvSelkf3dVNiHY3MGAkhbrV4AFffVEKTWP2nwotNE9jOnAUxLLMYRizGAgxohbSghQjDQUDpykEPu7u1driMnYCRgAOGMgbPgHisAMEAwlLOYwCZfV6G7UnAoHrLk9KzH4Wob9evZLVFaIgzNcvTzLuVfnxhpb6AQlOXrQcJ79rw/1/4debatsygqgKKEKM+ggZsKc3uF9mHoCAmin87jEGuszsWIYbnCcrHAcjFiHAjDKECo4XYLO4AT5CTvq9y1UQ4925a7Ue6Tjorj+JqBcYQsMmCGQzqGDgtBms6160YxgacJPEWdcw6gcaz5Hw+Ue46WZyr3LcJpjT+qjw9cv+NNnNL4HYTHM22BZ09WDRwmjAtTJcDXzPgCASHl4mrf8cXG+fh3NiESk8feHvDulvF//m3ElB7nBTGfy4P7tRFItXj9WJkrIWa1NT8/EgL7XD6XT6wIBUR6gYv1Av+f/3SO5SKAaIFhYIzj/j6pgmfbYwwVIjEXq8xqreuEhlqa5pjw3Z/+jO31rV7fRoz/4zUWO42HTdkERTOMsH/u7z9zeHDPfwpWZUTtiX8phKXIUXyVgZpo7lD3DpgT0Ozzzs419WaThDJ6YoGLdW0jVCAXbBtTkklzCBQJm1rkK261aLQCtdpt4ulufr3AdDFit90gTxlBUEOVMJdkx8MwNL2qoUz0FxVBJIORckLcTSUHRM5qOZ2zlLBMKbmVPhX369ajA8wY2KygjoVkOqn0TH1l+fr11GWk+ozUsChdCCIj7HgY4VoHl2O6cFattvwdKUZLfh6DLfeB5YzweeXASFmwpVyIyygBP5y/xDhtcL67QYl7L0Cp2MLbRLNC91IF+yix74PRCTGagrFKZEuegCNikDJRZZYEnfID4vFz9YkcNQ8IB01ezSXsjgmZUQWMYjCRs4DDgMCsMJeqU7GGEQLCEKwrVK0IQZprwb0tsiA276qSKFiIppqnIXAABEhRYY9Zre/d04Fsj5YwZSZUiJKbZNo210kt7Ngk9NR48OiWtLnLjeeUKNyp0JtK/7UPmoRxu8vY7BK2k+KAxch4G3/C//nmFkNgDEyIRYivdY8LzXkw0YTFYB4srApmEcIwcPHcCMRYLkdkEex2GQzCEETPClMwsQDLgbAYrM/ZFC2k+GkYBg0VxYxs81fDH9WJqh5Hmp8jZVEvDQBbyxUxTksMAGRcWOxrMaafIGw42fOg0SxhdF0Q9YoQQ3UeEiw3+ZD8OhFijGAmpJwRmAEsLNdNzangChNJuSh8xCqqypiKF1vFSc4ZKRo8DobxGsUbbExUPNU8lFNCjnX2Sn6RLYNuR9zcXOMWN0hnATeyBRYrvMyE8PIL5AVjIX8DYVtDkWRven93P0bY/6HKMW+Mj13Xsfrb8pS22qoOCokOyZfKc6dKYB4mAHBlxH7bjaK1P2kLTns2Tvzezn6YZj6Xj1/8TAWcdqt0DIsgQDBQwhkukLf/jF14h2HxgwpTV2t/C7vba8TdRukH1NwQBZql3wOeANt8z8x/oT7ExiMx3EPZlOMigGSlWwqNnPdpfLgHaKWLO6/oOvomRGM1mqnW7UqUlsyhxfisqYGqAYyPPYGQQLghxmK5xHp9hvVywG59g+0gIBrMM7GGULpzjY5cE+8igH8aCV8MwKp5QcDY4WtELHQclLESwhgTlrdvkKcJMO9xV/ZnmGdtFnhy5WawSnOx8QAMJdpb4f18scsnYW7YtsdUPgb3SNum9wXovCu6+0brFwWEGD/gHhH23XNnScNbzZuu04JmkvY4es2NFxDOLkCLBXDxAuPFOV6en2N1Qchf7hCbEJ3lHDKe6OeIkotdynuo92gZA3b//Ftgu8Pi3/8C2k1wmxphMX2Eyw50cqsvt11vZKqLV68wXF5g98MPSO+unn8wv7DyXuG0rfwJcPUoj4jZ/j6xCEYAgQhLISxRD7o9IG6UEDCrTAJZCBbGdke43jFuJ0I8Zrz8xHIaiXngiWNKCGruP0O51zMCOB0CP6Je5H7r+1+W0mYP1D9ImzNGctbqyWLR5+is1cFEWC4CmAdEXuB8vcT5emXX+E64PnjPBYp2L+7UkrJTRKSE6XaL3e1GCYttwrBN4O0dSMS41H18e2wle2Lvzi0oe18O1NdeMUskqnSdfymtiRwhz2pTTigfbO2QEsIsog92vXlO6j/1IRJ1gT3QVrG8trHp0nnMehcAi1fTRFj3bs5CDwFIgZBGAraoIXvQ97/0vYEjKrH+u4FDrbIFKcVmaqQIzj23wKEDQ7zj9mMnwCTtPHVP3y00a62cZuO4X9jWMHPS/Eal/+CWQW6+TrbP1DzdiEX3+nBGlICSd8PeNQWATweh5mDJkkEimOwZT9irqptU+rgPwDS/gMKAFnioCXuLJ9QsWbjCvthY9/fXsWl05ZVOUxXQertFAOtdz1LC6aiQkCusGS7SyFHkdHfTTwJ3F6plfLVONO8egpmjz1kshwkpgoSeXlChe2sxWOvY3+ulZ1Tvu3fE7InSg44RNHyVxZQRlpDclWEhMIQyJuxgGTgxSVQjFfExLCzJOSGQWvOLakkgEAxmbThYPoMhqJIos+YbCiUcmwk6oLQoM4BMkAIrYmBMFU6KsOXufeZCF8lSEn/nWIUyyNnim2Xru69Qs67W7l7dB1bFBUzt1miVBilJQRucs84B+jbb18t5YnUTVXhpx7jXMccpzdHXwnOnyCCghl9o6xUgeZ44wXazwc31NXbbHeI0IcsAkaG+Q71HxFO9An7uYVLftzJi3tZTy135LPY9R9r3Tmv71C76vPUC0xlcFiFa/14L5weba2hAOvrQif18xJ2Pyth9LkeLg9l8u7aC9BUR1swgLJAx9tRrTuAYMaSExS5AhoBMg4bKDAOEIoQSUtCY98Vb1xQDbT86yqoh21uwdwguNGTXbyl1Fa9hycjIJSxTPVcqvV8+m3Zns1E+PXxTpS78LpUzqhoRNQmLmxfMxgDEATwOCOOIYRgwBkZmQSKphkJt87Pu7e0ob7cyFR2pPjKwDkrh+lzo3wDBAkI7AATOQBAB54iQUxlLO9muNyj3/Ju35/yGRwepxGCdjLIOzejmyFKOfD9USv3tCw0glUG31yssKDw3ya79fWkVEoKSELsoIWZ9OxXVNQBEgQEOkGEAL5YY1issFkssloRhaQ4mhRY8sf6PVR5ytrTE5NH3jt24gxY8Voggy4UasxXDr8PL157AbTe7zxDAgcGLJfJiB4nxqGfEp1xOYNtnP+4HwsNV3jXTd7/5oPKY/WjlETkiHl78kPqKA34FBueM6IdjgTzPAdF+qkVV4KFY193sAv6PbxbYRULKhyQ/OMjIPX/ZF63JHg9JH647n8vn8omW6inkFwiLMeB//5ff4Gy9AnhECIzFWBNsnspUO6NYCFE1VcdPf/0b3v39x0KouuAwx2iKDjShevZqnTfS/2wO00cVF9w0AqjHVFKZZGkEUi0R6HRsS1VL+wGnug9Otwst7xpGU3txCbebHj7F47sXWjhn+7MxuBCwVRohgCkXr4gS/ogFzLMzrwjvLJRMypCcIDlVQt5csz3ESUsXMzOGcSwCRBAhcICIWtpPuwnb7Q7DOGIYh95iuSGinRXKWaDxWj3+ekAmwjcxIYKQiYu8v1vLE0oJn+Nz3DJ2fvy5m7YACUkt1vcEqboY2UMymSU9OBjfoHuKra9MXKyms+XCKEJpT1od1KXdk5GH0ueInBNSjCBksESElNSrQQYMcUDOQJxS6SNDPUiqAJ5Kgmpds7qnlZdRDwSxmPceNkr73waPmZG4ImiF/M1Ew5UxMSWkmEDMmsCusToXEfOO0HkgERWc5oRsSirPPeKhcENQl3y3Iiz/ZRUcMw3mnFKBRGyM7pUQBrPWN0t9VaRV4WwuTJ4U2Kix+oESLtPgR3zqLefOsbA62j8CpLFObIsJ92ueAoIl+0CcEqYpY7OZsNtpTrAQAsYxYGDGaPlbmBgDCSLVnCAjqyWmzjNApNAVTRHDZrUWhoDAjOVCFREDjyAIApunSmK4fm0c1PtClTlVWcQ8mPdAL0Rv0WuFJbJpVoVrBkxxmTFtJwCExXYLABhjAoiQ02D1Gl50pZLjQFQlgONFmIKDLE63hxrUkBe5WVuF5WnaFXl/GIZy1oUQ9tZWvVa4KPKqEqbOSUtaq7eLwpu4hEc0T4WeJVw+1WsqlGuSDSc5zQxrTwB4SKuccXtzDX7zBpvra+xuN8hTBAKDQgODcIXUcdx5CI4/BaXDp9CHj1lOyc8x/32X8uLUNk+7bjjUPACz2J8LxnJWBahbKwsfFNJ24rln4PMP9PyE+//YcPZzLEsm/JeRsOQRiX+HhFG9fo2eCNMW4e1rjD9usPjzNUYAa3wB/nKF8ddnuB1/xDb8BF6vEBcjppyRBJg2N0hxKudCoqqY8Kj5LgNWL4JclBElJwQAMmMjgpMXjQdEQ9u7d6rYM0WIXIhvKXzCnJloArXY7/k3N1a18xzqXVgeKcrDrDnLiBDGAWEYQcMZ1mfnWI8jFmFADIwcPBzpXPA822MHtxOhHMfddYH5kdQ71rcsmgMsa+Y8cBQMSRBACKS0s5R5aoS/6tJusnjq8zsYXWbJslCSPXnD/k4JwVQNi7ouF2YNlS7pBt/Mzx7qbNZ2T3kg+79TqjgVlgfL+qbeMxElR0Ru4Mc9JzrFdMuH1R77E9XjV2nMxWKJHAKmswssLi/x5ctXOL8IoK8i8sgYx1FpTW68prsxf8at95VqPGkyXQOo4vNgygnnLbxIzsa3NTXN6IXx1UsMLy6w+/7vSFfXH2Q8H7fMN9sp8Pf8hMdJvXgg6fFsoZkOHxqKTEcAIxFWAizQxDd2hHfANMDd7N3iMgthsw242jI2O8LUKcBmoxbZr/NZRoZSL83vz7Sme8LXn3V54CDuePyjekDMuYE9uPPnTnv/Obb4Y1DLByvP0JnOYp001MvZcsR6OWC9XGK1XNSEr3MByR2wMG132G02JgQl8DaBJvOxyoLp7++QfrouSxw8sS6zRXMi0JQ1tMM9ZW+N/PAsYzyhyP6PqgxoiOuDNdrzaKxOmzr3ifSTOlHbfMA6izW8t5UOPtswGlQZmJrwVK976JdDNbpoVaw+b1//dzKzdoa3GSFEIFqoEWeEoDFt3cJX37Jzg6QI1VpbYYEUi2YPvaPCb7N6KooIq9G9QUy47IJkh9EowET7YV73SqGeD+AnObT2B7wKu3owW3odc+e9ArMlM6GnaerK+UtMFgZHvVI6LysP0VSYOFs7V2IwAZkQLcmciAY8moYFVIg8oFhtOY9iBGuFzUMwgtKPKii198r3Q8UZx8pYeT6MAE+kLuU5gSsBADZBLgHluSI0FphgNBfhVvHaoJax9GYtfAA16+fC5yMQUhR23mcXnvt4fUkJMM1bpbV8fRo238P9VIZW6+Z2jxSA6wic42XOvIrSfDlrcuaU6/wwoSghhiHoHgMUvwYX7Ot8M6lCgczrQeu2/Wfrpx4RxosTWbgwFfmLAElFOgisnhhkcFCTH1s4ooKTmvE3G68Ov1lTsTn3MbtnRErIyfPIOH6g8lrH5NZFLt9boUxZBfJ7FSeXHknrkaPeEJ6YWqTeP1QqNsDecjsudqEUmzC2bbd030lwV6y0ozS8X61YAUhGkmxzJkVJLTZAq6rspxb/3CfUf4wF/ymKgqeGLHqsMqINOfVzVmg8dF3u8/p4Dk+NgvfL7/LNj3Y7Pl3Aag+5BqLgXmm25HNwCkc7fPyeb8T7nrurFETwlDHc8+58TVs8clet73FaP0RplbuAzvKaCWvWUD4jM241jgRIs0eBIchTwu3tBnG305CLPg+TIO8EWQgiA2hijHmAm+NnjpCQkc0ug8QselIE4N5zRidXDUXb44ZmrAYUfi4WDwg/76XeK7SPzOFR6hFKKF/abThf5rLF5t3rnvAews49AmIAy4hhWGAxDhpyx/MyoaUHTyin4N2yrtrbdhd5uKgomisrxwikVFjBQgG0tJfH1D8+8H6rlklyWoNRA3Q15QgtgNK+D0T6620fDilzC93U0kcFadYk1Q4A7T3JNan5sWdQP3x+j65K2z0mZCJEAMIBC5NDvFgCywWQBqiHLPcw0Q750Ix90JP4RNx39LGH36hPPBDvFnqNGXm91DN8uy18iR4xlbYsYZlEmj0E0JRAN7fAOALjoKHoTEY8A8aHdbDt62xffxqhPR/Th2PvHMKmTysdz/DIqp+oiGgYiVmr7g4oEHzJAV8LWfLKXOL+kgk+KjOo2mPmoNZtJjzkEHC7A/5/fxmxmQhpTwnhn+8XFbQEw8EbZT6OPPgzZho+l8/loaXug4onxsD4f/7xN7g8X2MIQd2JZ0qIUzwi3v79B3z/738uuGPx7S3GH7aV+EkJZ427HpMJpMiFTyZ5O5iY+m7G61RMs8+HNgRyS0s5nTmX/jRvScfYNvfkkKXuHR2cEaoz/end43DW4z66tRCctY/KwygRmc2SXOOjMkIYKrFMlc7sLCDFxmpMRWGFhNRA0YS6q+83WBCweyXYDa5EcIGZIFiuiJw0NxEzIQtbxJTecyDHjO12W2L58xAwLEZoYmTzDrA+aQQihaWcBKp0UyZnHNTCOohaQT34GGgIsnsW6MCrnQ/F3llVhKIQl/TBQywRMyiwWZtznZcSWiebzsJEjexW1NpOIIAyYb1cIA4RknZmeS/YccAPZy+wilu8kIhIDEwTBAkpO8+jHDNR7pRV0vSjFX4yuwjdv9uz2VyCyakOKgolf5dYreN9djxETDZmaUoRwzBgYC6CdGVyBeM4YggBcZosEbOG5RlYPUS0H1nDe7nFYANngMKvsFguLDJxAOozpH0Ohi+5PKdrq9fZvI/E8rBoUujqdURNXousRmWWzDnYe3UuLTGmBY6WjDsDJ7dMoBQQIkBIheBJMMWMGFNJ+B2YMA4B68UCQ2AsBjZFRcJiYIgQIsNC7AlIMhaDeT0EC+HEVRkIApZBk8APbDGVx6Ew9FkSUhTznNC5DEMAgaDpTQYQDyiajNwoE8o+l2bMHqfaFQU6C2zeODkl5IkQp0lzdaQMBA/RRP2+FQ8tZkPpPH6kzGk/4/VscAVDqc6Ydg9ZlhurVWDfk0Cgoe+87fZwKBiDNIcJWA2DFuPYCZg0v4rNgdPyRr8XvGDjYyZwGMBTRgIQp4jddlvuExHGcVTPn1D/3KPHw6WdIjx6isD/fTz7HOXnrIB4SnmfIaj6WPb6aTcq/QEBckZmLta7magY6rp1Z0MINQ08pC/973bIJ8tGRB5Oa+zVgSoA/VzeaxmJ8J9XjDMChkKL5op3Dchub27x3TdvISlDzpoKpg3w3QZJMhKd4WxDWE7A9OsV4ouA2/F7xPUVUhKlQ92L4fYakrPmYCtnWuVWMjUCww6e2zPGPq2Pya6rrEfs3HSaRz+LsBGGxxs+qYRLm7cJ7UcbplV5CxQ6ORv/4f3ZGd09XJ1h4Jc4//olLtZnmpB4HJA4gLiG8QXJw6G9Zc+qBqGSTFL/cibELNgmwU1M2O4mTLfvgO2tTSuDkCofBVLfSSFkJ7Sk+cTsPCBAiic41JuAYJNkCa3niiAAPWJp+QW/7mFbpT6Sm4HJ7M/XvcAumu8zz4acjM60cLptbgi0HhGueGvXyGHowLKIewej8CU8DIgg/J1GrNdn+P0XX+BXlwv85692iIsB34aV8j5UBeKCjkX9BMpdKpHj5WFPP0Nx1hIEGQds//g70GaDxf/8C2iKRoeqkZHz/HU/9zKR4ac34NdvMf3214i/evWhR/IJFl/NOUQ+9yo/j5LnrvJgRURhuI7I2svBIcAIYAnGUoDBhEbSamRdCeHCQXJ37tbaj/B2w7jaELZxnhPiaZOyryc4jmJ6JQQduNFbfh1TQjwXEnv/jMgD6z8qoDh24wOi84doNTu+YUZ07T/yyyrPtCTtHiAAFytNDCq0QAgBq+UCi8WittnsoQ4uiJCmiO3NTb1mRMHm+gZxtyv7Lmx2CLe7+lwuojyrywRTHn/9HuZqb43bC070ep/3nj2kHKi29nvgWKZrvy4VtssBuFSiu0+adWw8c672yGNPLL0RYG8BVLrhDH1DHLpQOHfhYo4rPNp9mUXUuVlY11xUmDtsInLImIKABlTLmiN4p8yzd1NQElEDqsBiE+Tm5OvYelzkZrAV/gXAFoLJ5+JI+11i1UPjduKs7XHL281eExyupvbPgMeJbZU+g2Uoj9TwNBZip3RA382FyISd5ZaXAXqua3x+QZAAoCZOzll3ZiIgckBcrJEFGMYdEibkZMzHEQCYJ6E9HNvbt6l09Thd60YQgNMcGQRGYNZcFkRIOZU5Ksl7QzAG16asKG8amsiUUCrPNQIbDE81nTu4afaBe5b4Cjb3C53U5C/YG1PDAPs7eQYFFW2ZlZLMrs/m0S2V4EK4PbQnptqpr5URZAAsxm+qsCI37QdLTK2KA8t57GNWtwiIqHLJ6w1seSBsvrN5MlTPFIdu/R04wDcJZYIEU+iEmovIQ0hRCBZGDVZnozQqCogDlnfzCzY5JWZ2qiErVLEFw48tDDsc2zmFJkl0U/38jKhqxn7H617MoEwzF3fxyDKdAkNmcOL9B9SitCR+NwERQYoi7KhToS1ICTGFimc7VNycCWG9QFgEjKsFFssliDXsTcpJE2sPTX4afLi8CIfK+2z7fXh5fC6nFz9j+nmWcg7XJL0VgbZeTi29568+hXF47HI/C5jMzpUP9OrR8ksE/TMmrEkjRgzEyLSAYLSjQuEw7nZ499M73NzcQKLlYJjRhJSUTiOgyHFTzIhbAk8Bw7AEgp//G4BEaRoAQgmUGZymcp63pBUX1slokjmMey+cgAYaPkgw3wR7HmWoZ13zVPfdH9i3VBeX2TedqBUTMZIEEC0wjgs1DhoScgCyGYDsy3B6vutUbH8IPH1MSRZIGBEzI2bBLmVsYsT1ZoPttEWS6snY10h1/GVQ/rvmDuwbdALd8BL5gu5xZntzvveVCIc3nsyXtVnqekPxgBif1OJOQdXiNgxNwb0y85zQBqgoWSuNdKhr3Xezns/MEGIsz1Y4P7vAerHAYhwRB0EczOiK92k885vfa+bBVEBD9zy9HKYHP2450gczDMIUjk6a7+V9bEBAUl6fN1uEqxuk5QgZ+HBFtcla9yOmpstv9syl0MT3Vr2/X/vfdOD6h4eDp7T4oBwRRWBhzc5hqUyBuYG/ogG/R4CkhCQtu+Ku9lyYfLfWIxAGtvjOzLiNhP/jrwNud+4JcWzbvw+mwJkv/7nHcR5u+uPxRs9UHjiAh47352bN9UukfN9D2VPCkYZi+t//EPDrlwE7+i0y1hhCzQUBglqRUT3i/TcBuHl3hW/+23/vQkkIBCmmEoMUYtakuRIrrVAZqMSzFFwT0KHOu0CyUtPewZIPbP6gHHjcmVI5dEY0wsu9NxrJ/lECwwlEe70Lk7rXj71m9+jITuE6Y3SO9aF00wlIs4JygXTphrgltsa1D0E934ZB8zHkWAnQst5icGXMBAAUKTDBYvEDLOpdgRCADJx9P2EpGT9+KYjrhBwTckiF0XClB5llo1p0WZMWqzzmhJwSQhgwjgNCGEwRUfNb1DBTTQI10pVgIuTA+JsAu2Rx/O9DffegmgJCgh6mmgc6SzTvzoxg9xjrTnBryP1K/Du/Us5lO5tNug/OgpQZbSgLNygwThHBSEoOGSkGpGVEioxtjMaUCTZhgXT5JVbLDS6ZEbcb3OIKEiNSnI5OS1UCtXDS3/ewOAQgNDkACKb8IhViMwQsjMC6zu5psZ0mxLxTTxjR5IbBcmjkFBFkAMRCTzV82jiq1wyjheeEGDV/SJw07m0b1oaJMQxclBQ5JaSUdYms39zSSlTkvDqGYr2l/+io2hjQ0PGKh7nR5z1Mpkg2nMvG+1VkVWVtswTXVuYebC7YzpajJSbCNCXEpHDJQfN/0CAYQsAiaFLHEVDmuuEtQgiqZLT2lmPAMAwV0wYqCasBIJArJFRQPgQdvWTF/SwjQggYLJ8JiDAErZM4gHnAlHT/p6R5TVJMaqlXwrBV1sD5ewJZLHlXy5DlLUmI04QQBqQ0gSIj5wimAe7xIyJIOZW1Z1YlDUTzYOSc90JHuIJNBEVw4cJ9ZtI5srXlUJUaOWcQCMnhwi3QZohEACTPgcJBz03bMw4QzB4bPzXtN7iAGUwBTMGjhCFn9YoZjcbXTtXz++wPr3D220ssMOLll18gDANiTrjdbpGQsFird0zJ+XRXWImPUE4NHfRUJcZjFBWPCTf13GWOJz6lUhXch+dJYVwV1tkwbP2PKsE1U/LCLt9VHjQTd83bI+Hq2FsC3KFpvKdJRxVPXOafG7v40DKA8J8WjMsABNL8aFv6GhmD4mlRevndm3f4n//Xn5CjWpEXJ9E5zQ49WXYLwXYQxJtb5Bvg7CZgTC+w+80K6YxA678hhwheLiEimMyTk1KEZNE8BUqAaAPZaUMp5y9DZT0EAWXpQgtVMeIhIVrPn/l3sz/o7ggqrmii2LZsAIrnb5MWQV9RXo/CgNu0hKzPcX52gcv1Etv1BjdDxsDBjFH6+YQJ++kk+LXxGP1bx273BIAwtvIVtnmNTSJspow3N1u8u7rB67c/YtpN6iEh6rGSRcdTKXdqJkC9sJm4eKyIoK6V0fYQH4d1jt2z2WmqrMZ5ZYyCHr9Yu53lQLM8HUMijQeEj1nvkfPmrde5EgS1zea35ITiCSEZxRNCcl0iaTuAmqO76Vu7J4g1nI+szzAsF/jtb3+HFxcX+OriAqtzxrcL9VQdGnppHzFWHuLTOr1+HoWM5nY2UcFLCm8hDmcF7PaNTYYfXiP8+AbTH77G7ssXh1rBodU5qkv72RedrA+hhHpf83eyIoJmn8eKiGABwpIC1srWlnh45f1GWMHUJ6n2JJNCjNe3jJsdY4qEOE9Mvd/yCb27q1CF3drJ5va8btr7KIKaT72c2MeHDuVON/mPQU0+8645jR6ZPfWhxv2RqfVOCVH6MkAQAF4gDCMGWkBoQBVWGInV/M4pYfPuqkz27dt3SDEB2wi+TbU9yRhc+SAZ2CQLDdEcQw2hUmiTnAFSIR21RNudi9tb/ihxQ9Uy7uDct4S0zC4VKVCdi1bI5AJhmb3flXrY3iOSKB8thpT5/e5XxWNUlBGEY5ZCldhumJQD6Lhap9sbpY6OZO+NmYgKQ1F5BCm/XdgmIsjIYPNdpqzKifE2gbJAvkilfy1nQUewlidm1j5AT7JCyOTCHKkxz0whQJUVURsaKgLL40XmS9HMjcGAzFZtDlYdMXLco6QMysfWznezxoVodKVFY4TgykIt1aPRZqrgARIgk4Z3GgYlN5gHU0hFgAkRhIkDpsVKPVy2t8rcJqoM5rHi09ZIYgUWF99ERQTfo1Q51zINzQRQveaeMK60DEGK4LSQCaRu7h5Sx5NTa9Jqalzi9/wSej7OQ9o4pWyKkCxZczVQ92qZa7fmF8p1nZo9OF//ouCzhNCgDBIqe6wqNsQSrpddhhl475V2F2Vk8/43QXnS0Eyu3SohhyAIwZdE8QLBlEQ2BnZhdRF+NyG3xIQxLWyKJ/zuc7GI121hxjhwqZZIPV2KBsTxSc4lt4PYBnYFzh6r020ifUIsDGk2AU9N5ikQ1jnNJm1gBlCsMl2I7zkgZmeJ1H3eevy0FoI+xyKoSsQ7SkkYzbVOTxxNg74bbPwFdjugUOVXhxZmNLLPR29pbsqX1YDxFWNcDwhjAO0I6Toixax5PuAwnfcEVR+iPDz/Q/+7VdIce+YhpSgYD9RxqK1T2rzrvecsxXbimdt6jvjO1QLycJ1+j+6UTu7fu7cnD+7rkecfsy3okJ3vA3py5OXn2qa/TOGR7oMLJqwYWLKedQkrCBbI0ATLWQQyJUxvd9i93aonRG5yBs1EDkSWCcDIdjEBDGVBBiGJGnHFrSo8hBcYop7TaQBEIoh3II7qQQgUeoSgCudsfI+e2JUHcdZPrCNUiFSqoZP8aZJKt9Xe77EN0vyL0h4153ppol6Q2gZA4MCQEBDGAYvFUkNpcgBRami+vuF9PmnWsSPF6YI2L0RbNEwsIybBNkbcvvkJu5sNtlPClLLljOjp+9IR57vsnNbW7OGSM8tp3UO9mv0mGC1x5Nm9V+YEZfMp7Rd/f/Z7XqR5rn3Wv+8xORXW2s85zNB88dyQh9UbIg4DwnKF9WqF5XKB8QzglRQjxWMU7rOXg0D2ocqHb7RAVghIF2eg7QS62SjXanKGEqJtlg9FyipT541IAMJyqeESt1tITEfbBw7TZZ9s2UeEe2WOH59rXft5eUCdj2z+dI8ImrMye6yYdUTwggL+GcFc0ZMx6JVZrq7nxnCZdVTgYLGPA7aR8N++HfBuQ3fm0jmpNOdf3/+9i3vFhTH9k+3p1TPhxyt5L6jsSHv4SMjtc/mHLr3cARHnSLTGRBfY0QIlqS0aBo/aWOfAdLvBN//1fyAnPVBUeJYxXEes/nSt15rrHj6HRBObHvIsAFAt7JkBStbPRqRE/bs0q6NFzCogQ+ECBM2WaxQIXfvS/tLni5BtVkpOhSObuCR/OqWIic2l7YfRrQ1d60UFWCa2oznOsmtiBHD7rqDk/yk3qOJGD0vqNKYTHy5gr74kzchcsE2aXAzEIHhyWiW4s6QSnxZgDCNUQGzx3M9+jEiBMP06Ii8SYkpgqSF1yLg1gQkwWS2FUtI49qAmdIsIRBqBopgluQ2sWG2x/sNMaoU9EwS6JXwbhucx6PogEWUMYm760yxRmVfmHtbJzcv8QvtZ9kn9LVBlRLHGd+H2/HVSASbTiNUKiNOEuJsQpwlT3NlcBdzygN35S6w44Gx7i0iA5IQcpebuODRcQIlQv9/E7WbJEBkNXtCd18Ubaz6hgq49YsI4DhiGgGiCWc9/RUHnZYoJkIicIgBgOSpZladkCoXqaYIGlxBp7pKUsoZ9MkY8mRBcUoYwAeCSfFjHxDVUFJS5ZdKIyVmSCg4stwOVVn3vJQQKGEJALglWc8E5IMvpgAwPlXlAV9OV1iPCfCG0rZSRBdjtBDEmWxrNCyFEEPPQZjGrw2S5QJjgOSyGEBBCgGUwLwmm06Tr4MmrgykWYtSwEoMnnPbYxDlrHpBhAIeAYRiLooFDQBhGdXiwEFIpa59T9DXXmNRckmUXBwmHwgJX7rECUyapZ0VCmiKIA0JKlow7ADkjEUxR7+HfdDwkA6Ln05EKv64kAWr+Cj1Dbf+R4cB23zb7s103gHQPisK655JIKWO72yHFCCwFYt5gnqC6eCQBKDG1yz8eclXbJWY9p8WSlbs3EWx5JGP51TnWlyss1iv1grnOuH79Bl/+8w5hMQKBCwx7HOl9vPSPU+6S4bug/5Rnj9X5vhj0hux77209vbwHRupRgz1y9h24fLeC5FChe/p0nDbZV9LMaG9/8WgF9/fulMeeWP1HKwzCHxeMl0HUE0IYO/41siyQWc/7KAnxZoub//YTdrc3FnLWitHnHdlmtE4XgRZKre+Wgu0oSNcbpGsg5yWQF1hfixok/GZAXCXE8wiECZKz0ttZgJyQd7d6NhgNkyzMoOXCrsW0EZk05JEewQIQGw1iyaOLMsLHol/mPMm8iABCntJWeZV9sK80XhgG0DAiDOc4O7/E2XKF5bhA4tQY0JS3Glr9DqJnrznnI1tK3+krGF1pobIysI0Jtze3uPnmz9jebnC1Jeyy4Dpr+PEoUB7MLXkl10kp7JddCADEcz+Yx8Mea8kNEac0pU53rn0/poQo9Ed7bf6Z64WZUmF/bWbP+F/nTSG13UYxUXiLAvMGA10bRue3c0CEYbmAhAHXly+xevUSLy5f4vJ8AL7IiCNjYR76rouo093ybl0TP9PykQ5ck/vKcsT2n38LvrnF8n/9FXBZTzZ8AQuCZfscGWY0OgdC3bvjF68wvnyB7d++RYzX80Znvz9ZYuOJ5ec9rgd7ROxfrc6pSxDOiHGOIqpoBAhcw0G4EoJUQPPmNmCXgmmpAaKAmIFtJCRpkOMjenhXmeOUyusdZLfLOMpP8oML/mP2yt6R9GylCErmxODdtOGBcnxlH/Fac/8JI34MF3Xo3bvKHfV2pLcLcJ+z7fdRDlpCPLQO+3xgNZ0nEBEEI0ADXl0scbZaYbUcANvbLqTIWbB5e6UKB24UEZuNJhLeTgjXsfRpuI5K0BSBoxIqko2WcpFQIxzpx6WETM5S8oSKWFx728e9sJN8OPuLT07+AlL2f0e5dTBUq21jTDbcg9S39qraa/r44hy7Q9gHzdzMiT5UwyiBjoOSY3zvptg/e6EIGjzqgiMXYDmj4iSo24uLCXlzyh2DVd2JVdhGMEGYCTbbfmu9Upk00di249sdkAgynmkgXg42Bn2QOVjSWw+xpH1ickJXjDaWZtpaK/QqHCMb2I2gulg383nQEvTY9DXcfFmyQsTvVyI2z2296J7ehyDRgboIsXC07Tsyf77UVQfnBGQdYzkZAdZYxEEyxsUIYiDlqdZsyZTzMGJan+vVaQI4A8ImXKsJ7+pesSBbZe3RMz851wSi2jEdj02weMz+BugzNGGyFDdwgxFPuAsLXdS0gRLaCKUeFZrWs1pjz7KFG6r5R8hM9zPEwvsYE3bgaCdT5lYQqPjH4dMVsmJ9IdH+ljjKnhQ7Uw3rY0yAr6NaQOr6FuZMAIgJmX0OHJe2OMFopCxijHdEsqSDREDwGLysqheChvHiZsACFZAzu5KjxBmoy4gq9HcPgM76f2ZZp7kouOxZgnpGhDAihBGaKN2SOsepJKQvsEFOvfarUnlm/8/lBLr5c6oeEcgaxgKSITFW141Cz8GUCNztM9+TBQNXZNDwZ43Lu3knFGUuuwEQwQ2CClA1LjdMjJgjckxI04Q4ReRx0cVMdtiqK+7z7VPle9/EOsVzqHqaVOuiDEkJMgQgKDSok4iAkloJj6OGRRsHhvA5hBcg3FRcfaAU+ribu3K3zuszUeb3kV6PI80e27djSYpPre8ZkhwfLfunz3O21bMO+20dI9HneYe6Vx3hNVumP0Xn7VSirlbZHvB3EHhPLA9nf+5+4a67Hubv7qfvoEpP7KvcBx/HjBTo9DbeR5mRfaUQgMtAWDFhSWqoIXaW63FDek6IhrSJMeLt9ga7uKuRJQwe75uacp+acyKLGTAYjLKeXTkmyC5BhgUIAST1rEIWUAzgbCEXUwbnnZ5tMWqIxJDs7EpweC/emVD6nu18E/cqho+j31X+2Z8z5WE4TVrUEe35ZyVDlMfbjeC0xmK1xGocMQ4DxjBopCJru0cV3uIdwDPvjv+o7E3JbCVUcynlDKQk2EXBJmnC6m0WbAXYChCz6Oz5+WUGJcd6o2SA0Q+m3FH4uWsvNoisoXt1wRrAchqjNGYz3uCxyp7YSjktnOvZ3J62Ur5Rma+Do5L2s77dw3vjR0u15r5d0tx3zJqXchjwYr3EernC2ThiOTI42NSRG5Ic6hOO9PUZSgvsJ5endKauxGnPzq605PWjqiBQCBCNB2xFkVOhcAUgqlIW5zvawrcbhJ/eIZ+vkMdh1s4d505p7/7S0eAPnvPT3rl3PqXl8vobj+nVvK35vH4MMeYDckS02Vua48GEMFkEa2L8Kw0aYzsns4LKYAQQhcKksykllLFn/MePC/xwPZT4x95Qn4RyPjsPoF6pBz7/t9WoV9zbhiAxBLVHhc6OzQNdaV3YP0o5aXoOP3QAb7yPxj98uY/jmS/YQ5QQv6Cyz76d+qLuiERnEDrDv/72Er//agEKXPa+CwZynPDdf/wZu9vbWWPaWtgkLP90Dc6NQKGhSxwjMMGS5hq5WwggaWgsJ9T0uQwgp6Q4KIxlT6N+QFyQ0xC3HU8pMIsLrVuckXWB1LFJa9rprYhlLw/G8XluO9MIlbxjZRqdmN2HY/HYnFaHE+TczEXTmUpw2xxqf9H1W2xgXRxoa6uEN4GAoXFNC3FuHc6WkyHFSRNOjxbGixgQguQId0VWa2S12mYOTXsmcCXokRU0lvPir7eQVUS8PEMOKw3NYgMiAMMQkKNao6Ox9HJFRMoRnELhsdq4yeoJkkDQ5MwkylD+PQNbZI1Tf5RImsEK9ffnevgipPbHbM9JNs+B1jugXQM/qvaIDiNmfN08bE4nxLW22/qg8OJh1TQxsc5/sHg7DgcsxhDyCB4Ya2RM04CMDEkRkiOYgDAERKyxDQFLDhi2txp3OAPEGYIMJPMySFnfJ5Q+KPLJFldXNMRsjNY/AQVfVIVCiJiAHEXYLlBBaUyxTIGKwBWZMDF2ANyTQYXNGsh3HEf1gjFBdxuKBxCzpg8AFpp7YLsBoOMGMVI2i/FWQYGKC9jmlNk9JLJ5lFgoKTH4FainqTja0y8KOhlAQOCA6LH5DebFBuvgTSI2XWQeF8Zou9JKTEGXBZkdjwEaXVrnPOWM3bTVEESUzHtGvRwWQx/qClDGm7IAwRULwWgpo9VsDGy4N1jelcAWOg1jmS8RgaRkygrCQITlMCALEEWsHwuExRLDco243SLGLWKMiNsNJInBkuIgJiCw4hdN3KleB2J5amRQD5Bsobhyzpq7JgIhaa405AQWhdEsop4KYQCCrzGbUoUgovQxceH24eda8ZJwvaklgm/tOYGaUyQQlVhVbY6kCh92HUCeMqbNFtubDdI04Wy5Ag1jxQtM6hVn62/pZZCyKppo8HwSQeEwBCTRkCIpJfOO0bwXyBk5TcgBKuSSXBQWyIIQRqxXZ1gvl5qjJZwDlID072DZlWmpAjoq52+PStsk437icvvA51LK+5uT/RwRj2nrOG10N4lfBVZejUjt074yQn8zkZ2PWoeGTnPbaWMSyzioP8/b/j5WavABivf5KNl67MV7hRh3SFdOLA+FkEoeuSDrCeUUqZvDT9uH2Wd7nwj4pwXjy+Cw5/RzPbcoGQ6MGZvdDt9PV8gpl/ddqdzCe3fuNa0TmeLBLGQsKiNgXhfbtbaVNhG4FfDrddNnKQZgDKUvB8nAkBDSLXZxh81mBzm/Bl5NmDRxAdw/L/k5l3Ph1wKzeWyi5Dfwgbi5gbMvyhvkSuPZRDo95vRfEfpbHW5sAGKEzSUWeIWzy5e4XK1xtlhgNY6IbEYV7PPZzuLdpYeqCmdKF+mn81RieRwyEaYMTFFwtRO82wLvUsCUGG+TekTEnAoVZcSEN+EL3zUuztu6h4Qby8ye63peeGIDBHJvCqnMgohacJXGgWpZkxujQDeQ8j5XD/F2IuuaUsOQ+N6iht/oX2ppmbpVmjUS4/9JHUOoeSfBwoiNI2gccH5+hnGxxKsXlzi/OMcX6xUWC8Z2mCBBQ3jN2K/aiLRz90soH2EgNocENfxrjYaK4kHcQ8f2jt5A5Thr70uuiD/+HvnVBZ46pvv3/bz+j3mY+/7JTyYrnlXx8MjOPCA0k38pKAUjgEtSKUuG4NyFctJaiMKEEoC7+b/bBNxOHqeXsYnhEO461oE7+ng6IO7r3mfXbZ3nmvpT2qADhMkpPerLU6HjIXNx2o27rLEf2fTzlY+hxvuFloL7T30eAzLGElrk1cUK52crnK1CjQduQjTJGTev32J3u0GOERIzxndTZ8FBAHiTwI2svLO2htIuDNa8AMQ1LnlhJqXQVm0yrmopmRWF59TgJ1KBKTlGA9yu5ZBVVs4Ac6O1v684anEC9cg7x65XS1/0n20DBEDUyrDqcZsf+1LvqhTxv64v9pQresjjlltP56r1jpCU8p5+dUtrIyrYGfnGSrasT21fldZAZjaBqdMm1aOl5fV9psRiwbtgS3JSZs4FyGaJ5uPpplOcHZBqqV0IeOuZCZm1eSUKslgSy45xKLM4K7MFpGN3qjeET+ux947W0MyrUHP6OQNofS3z3qxlPgAz3a9WSNPR6tJ9wMNYmbB1CEGZiIQajsYZjtUZ8uUXwM016PYaOapFdbdQDTfiYWdcAWVuASawtRjHWSwGPlDCK5U94Pb/7Zy5EoFKXa2SURUXBA7q7RWChuOaAVL5xiGosVhR0pBVrX3IRWlR+6M1SLde1EyyGANa4u6XKWrnqcGtpPdqyEzZByhn5pyWYzJPMmcW20UuvmiNl4iFXjAlBcGM/olKKM7AXMIpuTCQiCxBd59kuyqHyQdcPLpY7FwozzjSb+aeCCEo4yNWIWX1ovCcEf60lLncnxaf9rJHCmiw8f+mzDKlK2fR8FPEhkPUDjRlzVcDVobMYeDQmdviTU3cdwCXtAjMFDStorsl3VUfYeEQBdBEgYZAxZT05hUikotQhHwhioCn1udnGdlCU1ln83IyJakrvdq+qQdcAvKg/UwZQgm0YmBkZIm1PdJQdwAQcQGiyQROCZRv+t1bAMfnvfWpIfQrebw8Xx6D56bvH9LWgSeebVyPLw/tQ2+Y9pjSi6XdyKyVNc8VJY5rWzxUIMfgq6Dj5gwEqhh8//hsGjy5tBSRXTmCL563SPPvvEf7Spd92vVpcLY3fyeUhizAw0NVzSs74X0nc+6B5xZzEzwJq0JJxBqChSqf7QxK2wm337zG7vpWjUxmPFBXGhp475bRsv6IkkeK19WQyzid5jn/7VUXPM9cBkLDiADCsGREypANgXNCiBl8O4F3E1KnXDZqgQQTTSXEE7FgvBRQoG7t9Fhzpb6UsIXU7DE2mpW4ysCzkdxkIb8jCEQBg3lDDCEgMBXDjrpnD03sfJqPPzA/mSsdJoiyRsoBKRHiFLH98e/YXd0gx4iY+10j/vJ8Lo615ue/h6J0DCWzAbVMRDMiYwrsu3kdU1N324nmUuFgC7HUKiHsqWK9VL2Z9Yt7n0vzkLfT0vli9GhDz7ZjokJ99HcE5m3KGMcBPIyYeAEal7hYrLBcjuCzDFlKE8LJEXk/9/2P2vaDMdt9L+yj+AeXZ6ji9LbmZOje+swJaPRrOATEL1+ANjvwu6v6SkPLd97Nswa7eyCEszXAjHRzq97G7708L0139PiYkbX9JcXmR9G/fBhY6Jt8eIsP8IjoS5aMJTH+yANYBMmS+hUmqzCSrZBC//72bsQ3bwa1siMTSHmynWY4DypHV3H/eqeEqDxsZWipfa5VQhyr8XN51jIXaH4uH7zcIXvcK5lWiHRRCLs/fH2Bf/l6hcqhNfVmwQ9/+gabqysIgJAEy7/dgnezMAsH1r9FcG75yCBkMqUEZaVCXZDUMIJkdUqpXuonOW6qSXepWADncoDu9YhVyE0sIKkJWA8V6nCKfjsVxR0ifucx8+sBdfhIcoKxhnSrHWPUsbfPF2UDGgbdhIvSEo/WZGHOfW6zoE1Q6nHNYXOsAlwuluMl2a+NJudcFVnM4AxkS5hXhH/GJUk9cPSDTX0gAUQWpz0RUpogcQBk6c4VJddIjT3ucyBFCB+sHbeSzKnmioDNj9dBHIBgAj/WJLj7x1MDf3eVokDq3+vqOQCbhd63ZzwMECyvQHvqubu8nsW2XxpFjL6PmZ7Kzs5G+ELtOEVmhGkTdsgEleO4UIVAHsBMGFjXIqWAyIzbYYFV+BFh2iDFiJhzsZiXpmaSEmkLORswcl3bnCxGve1nyoCkbNb5LgxviF7n4ywsggpVQ4Fh9wJw2iaY0HUcRxWmx9h7N4l6Q6jiRWHQ90CR7bqg1ohv9zrIzsD5HvP34ApBz1khDd5DI0yf4wkT5KZkMGyCYfaO+HPVsjynDLAgEENCU6cJAXSem75aknCP/0+mnGHLbTEM6hERLJcGXCnAjClGSIwl/0K1Vi7QbuGkbB0IEM9NUhRPUnUlJgwPQb1AzF5Sc5Fx0PjRrLGrW++Vuna5zAc1/eiYAxNqsH2mZCEtkMESVEFluS0kC+I0gcIAAoElNJ7AfalnFArM1XwMdReTPysCtXI0Twjvp1RBPKR61WQRiwOuONm9ENRrIRYhkFfkCgxXArnYiIy2z6x4JLiyKQRTRCTDv6kId8t6Gtw7/OaUAAGWL9YIiwWSRBTkEwiZCUQDdukrqPcVgWSLUW5AZpSgy17DR4lUzzs2pEWEEkLvc/nA5SjXfM9rT1SedMpZNPxeqf8OtqNTOlBJJq/KNi6hDVtmsXhmygGkUerECbwOHfm+/97JVT5DOU3g0AvvHt7G/W8f64XcdfOZCrWCy3lbex2fGzroZwYh0peaqLoYFAjSzRbv/uv32E4TsMiNIpzm1TZfCodTD+bSWPErLIH/BCbKIjWAF2oUEKQ99jOmOoATciakPIISY8gBdDsiXV2CsyAIsPjpBsPbjYVnrMYDOasn6+vlFWLYKT04ZKzPBDyg4uyyF42WMPJk9HOtKAip/NbMVnUWhqCeeTfMkHHEYrXCcrHAYhgwhJqblLk1AngCwMzwWjl7MrDLF5jyCjFmTNstbr/9C9LtDfJuQvTDSaTiKPvr6Le2azRHooSSoRy2kPBDzt8/Aqdt/gj3kug2Xos3tV73fi2MhnhIJqdDHLh7+FNX0AyIywntvVKP1OtoPBsPLovThtWEqMKNAKz5wFbLFcJigXjxAosXL3Hx4iXOzgZsLyMwEAbz3KSD+2hWnobOPhcrRICsVpj+6begt1dYXt/0sOK8yExMQs2/5QGju8dXX2BICZtvvtHcZp9EeSSx88m18X7Lg3JEOOIZCXhBA85A8ESRxYIq+1FgKIvVvdwTfnKxlOIq2XDLpZ6SO7Fjdz/vPZE9DEKz58opX39jRlxSK0ZshBbvpfQM+ImPP6KFT7TcN/Cfi6KiEdp8sLbm5Slt3/GqYETGiJfnK7y4XKlghQmX61DfdcvHnHH1+g2m2w3ibgckwfhuAm+z5o6W+sr8W6eAsOtqgUl2Zom65wqrpY+3KT3z2dXYEmUeLFTcTRUQkmIlXomvWQ/NvVm9KI7D474SwhuuYylCp9mBclAJscdQ93frv7UDJNJYwlvbZIIZbkDEBdBlejxxlDQNSVv1Yas4AapFbXPHBJ/CYgqQOr/1UWlG7njYZp/JiGUTTMwkg8XqyoomV9XQNSED+HECbRh5uQINaGDFBOXFIl1b5dKE1hHjVIX6s7l3pQWxMkAUQgmvc2fZYzDQTWphLRsGsaxPvTmroipnSKgodHqYPoIanI8wRqgPxe7vzeG03CqQXZKRQ5OHizEpRCiCShEq2w+k2y9gQBGqn10gpgngt+CcgaiJzUriDYfLkmzbvW6MYjGmpHhJlTFmCBoPhvKh71QhleIYF6K6IDWEAa7oDGZhF4JadSdKDS/p4XFQmGdnn0ti+AJ7KnD162Uyy3qYEpAb2KiaB+PhsuE9LvRax0MCGjIpppK3oPQPar3YNSrQNXLe1tfVcKvPmZBZvqPmovDnSgoEds8XE86b0DizrZ0lNlblUC6MtRupEMwLDVmTOZb9mm2ppWGRm7kObAqHUDwiAN2fHNQjoYSoEs0dETiY0MThMjd5Firm1v/J8BH3J4UpukII5vlAdV/kDGYPC8alr2hRWgMAvpfU68+zcFTcQG0fyMKeintfGM4g1ryWOYOC4lTbMQW+YNOjuTMGEGV4CCrHbw5RzO7BpJuHAQvFpAIAtnUruYEKDtcDR6A4M6WKG3S4ruxL2Lx+h9d/+hbj/2PEuBhKZAcKhiOQIMKI9BKMCZ47wmGgeoU4gqm0AWZnxWPK+yHrZrzJrJF7ldc/hzInhR777kNeE4IcbLfSEJ0xhqAofQE09GYVfrpxgqOVSiM6DSP155GOH/K2PWZ5feDUrZ1t78xotfb2IZh1mmJ/ekrnn6E8pp5Td+ihp566u+dv096vftpnRPkBGv1VIJwxMNAZIi1tLzOyaKg8iEBSwnR9jZvbG1whYcv7Z/hp/W3P8trZShnW89K9JPQsr3kA/Dyjpn5CBnuetkppFOMPzgJaBQiWgOXZ8rwUZDj3bDVgETxnnGDIEZiccqxHARttxDmDYgJt4v+fvT9rkiRJ0gSxj0VUzfyII7Oyqrqq+pruntlpwgILEPC2LyACfjge8QTQEmixCxrameme6pk68ojIiHB3c1MVYTzwISyqau7mceTVKVWRbqYmKicLC9+84gzcSABiMFRyAQ8MHgakYcBF2mPc77DfjdiNGde7e+xHxlvidpadxzgDuRBwnYCXTtuLEl6UOHAFNwG4ULf8OheUecb9NOMwHXEsBdNcMTGhVDP3sVFsQG0cmgNdBDLDMws+aonQ7Lnfx4+cEGvTv8R+NR9IVCbYXzPocEbFYnHFehvvcRhb/HxiaD6tQO6zzjsNGZQH3FHGkEd8dnmFZ5d7XL0AxgsGDY3mTE+4yM+Ekvcv5zR+xradUe2jljXrupxIR63C8pn09E2Tp7hpmCsmgoFR91+0/aetOW+vwllk1JMW8BOt+sYVfHZPq3cj7vjw8rFo0Sd6RMjFMzLhr9OADBbLuirJ+JyZIAU1tfRKbj2SVRGhIVsCEfcpTjZ1nyOCJ//jLK5SkpHN9HFRD/QPKSF+CC7PnxhN/lx+LgCAihETnuOLz67w3/3lVbPsVKHSsrz6b3/C7bdvpF5l7P98QLpTwaIfrsaCmZDtJHEGiJCqqkDPvjOBaxBmWXs6avmgpHgt+psStMT+t6ogiRoiaLctEYR0z6cj78RxLipw+O+yrBLRU/9bU6IsCM3Y9oJWJVVGuH2v42hajy0I5KUpdqvmZgO9XXolRHVLH6jwzWjUxBVpZ54o5NWWzFu8G0TgpYLr1EIyMUxIIJbSCMxFyhlQYRdVYPzyCFwy5i+eAZo0N4Y+kQTFJmBAU5gDKGX2hLPRI8RWxELTUCKkwayg06Ow8VBZQu/6N+73O5QIP4nJ10ksuLfbMqZjqZgRmKGgBGkNSDch1TBLCJr2rp4xjRNsAloaBumnyAqK0CaJ8DOJ8PhAhPs0YFeAfH8PxqRut+L9FGkOwLx1WrgsU/LVWjXPgU6zMiiLEJiJFS1wZ4nvsMm15UNhVqGyZo4gYEgZiRKGQRQR03T0NQQkJFNbHYVMFchXzaVlebaS7o8of2rbC2XguvOvvzXvC00ILJ8aY+YCCKvFmOZJc4pAY0cHoc3CK6CNW8+BLpIFrwOb/X/PPDYnHI2pzhKHdxiy04AMy7eAoPOVdWcN+Bu91RS8fC2qGb4oN0qdxM3CL2XkcYQIv0lgLNkYBgmXxMUVEUkCWXv0gETiFUfJLKB1rK5os/BKdubUipQkh8UwDDpnUR+UIrltoB4wTi93RVlqE/4HJdQSY7droCWlFs8FFsswXRJKSe6rJPnaiOWfea4psHj4rHEcBCaTJYs3ONR438PYGHjDwxpyLeWMlCUWeNEwYLVWXcOgiKgVZS4SNo0BqpJTjksBg3D46g1elT/gs99+gcuX13IGiTRnBQPHAtCAOX2BxPfIfAsXYujAnHoPCljm+NvP5V9vocXnhj9izojGBvpBdw8hwdmAiajakaAGhw+QTaeUDo+Ntv/hhNDduj8jRNFKCRN6Pc/74VOUrX63cOWpd99TOHRqMWlZ5cSO9FUFXxLjLwbCL8eEe/oM97hWuDCaWXF9qTi+eYu7mwNejwXF7p8H+moD5vBP2ww0uD4EoHkjoLkf4L4HShtK/YAxm8JBsnMhmaIjMQoklxcTS6in6xHlatQ3qw/PhnDJ13pnKGR5qkDrzWhqeakyI90eMXz5rv2o59HHmMRL+u7yHseLI4b9Dnkcsf/iEpdXF7ja7XE1Dnixv8NunPAl585DLmzq6aL1nifC3+/b6tRE7kwQUyvUUlHmijrNmKeEw+Eet4d73E8F96VKzgj0Z7ehiuVgAlO3xSw5XR6QTd2CmQAjW8wDGWO14D8TNQMgi39qDB0zukTV7uWAjiakWmxhYN4RbIQWA51CwmggNJo+DqebD7O/Il6ywDgMyOOId/tL4MVnePniJZ4/3yO9AOahYsiDyiXTqsUffHmYDf/hlrB5xC082paxhUW9cBWhEroNqwusP3x/bi/ST8GW48NKvBvfs4WPuIhnKyIYFSMRfkED9ixMlNxvehkFgstdVztFRMbru4w3hwE39w8pIbYmt0TT9nG9kA8tLUWETw2Mnfn1WqEx6sG8WUputP99KCFWXZ4ew4+a6XoU6E/AyHdROsGQjmBFK5/64YldPfDbdzfrHQpGvHx2hc9fXOKLF6OG9ugHYozcu69f4f7dLfCHN9i9O8i5rwyaF+GYyE+kt2OC7XgKI1PU5ygQQYiHMocQxl0CQj2/JohwhCw3neIzGQeDkCok9qvSd6LEX04UWHzAQ/DYLFCxev5gOedn3qgWGGiyUEL+HxNkK7PJzZrZKrpHhH9PvSDOiEAYQ6Ux3m17qd89IRYbEWFeEVxbuKOUk+dNJmsjQawlkGJr8jcQ/12yPnXlTklxvwlzywyuhGT+4JDnpRQkSh5TPmkSWA8Ho0lWyToNNL3UBd7lATUPmNHunBM6o41NDLAdH8fvSyJ0AWrE7Z5zXUQij5sbVrUR+G5WZBDRN2pCGNJD4DDCDCRxi29sWWOkTGgMwMNXJEiYI5AmWSZovg0VcjpDIcL6cb/H/nKPfLjEBFFazVONvaAW9bRR4S6nqBhBUzKdoL+quX1QOxsSRggS15cLzOIdpPkmtH+z/jaFadVwM1Xx1qBC0+reNALDKSdYOEuLACeCrQSm6oJ88jEKHJLma3CKRZWEwhMq004tgXuXK4BZecWwfpv8qOFdw1fNc2Mulj+g8Y5tpBwf6FMLnWThygyelNFU+DCBtTGeDlCuPAv5aRKJMZ7Nh0WAIiHZ2JUf4zAiDwPyuAMzUCrLPqYMqEAcVZKfS5iiprzgIsIFZjH1zCkhJ8KQEnKuwGwrxa7vJpJ6BMKQxVsmOS5J7vGRSD/T+tQsceUW7RM9+mRdZY1zUJxyZUzT5K9nCw+VW36QqjjclWYE5EwYxgE1i1cFJVMaFJAnDqXAxBvekO95kJB7MvyW98TCb1FO7iHCcwKVPcgSnJNa5pYZzIybfIt68yWe/affo95NePFXf4Hh6hLFcCDpfiveo9LGYre4QSG1JcOCG/geyuOXwSl+4odh7PQB5fta9gXrxkr3tXwly8tBIcU1jxElBRrQ74xoq23vK9G4cf+fYmnO2d6td7de4zjOcwvzYgwhbOEZY+npWNr4/H2eu0V56lAaOjn1YLPq5xl4lgm7dIkJl6ic0YwFlCYuBdPdHY53B/zxm3e4P8ydQZDD0+q7IbaI4IISOxKpHYOgREP3F4sN5e2/HNtsYZsqiQ6/pydSa9bm6/0vsXCg7fVuqizhANN+QPr8GltFyQSACMPFDjRWpJ145u3yDhfDgF0mDGqE4/zPljvSqQ4eeNhOma2leGIf6zWmMuIwZRyOM969e4fb2wMO84z7UnHkhKlG3GL86UNnZYOI5X5NzytbcINgvPfY4bARc+g+wFMkLNkMaapQ8KwKCS7ire/1g4cE+jYYhottdFFRZtNgMTLJGRf7PYbdHsP1M1w8e4br/R4Xw4ghie1iDM265NC357qq+GnLqYvgDOW2N2GvhO8/DOyr92JkuATw9b5UQyR1gbCIDqg18LAAwMiv3wLTEfOL58CY1/187zN+DGjOH992zZan75OVNYP4Ucv5ighmDCD8Jg0YCZjnWYUz7AkJpTQGy5QQFjP2m9sBv/9mdKayAeCpTvXvBx5+Wn2wr9QY3VjFv6z8IzbH0vDFRxrwOWXVxRP6/FTD+9gM0pOUD99/+RgKwh/UjE5sZ8WAQs/x2fNL/ONfX6lwxc5Hr+EmAG++/ArvvnyFyz+8w/5mXjDS/eflN7OM9RAky8JAEK2LoAUZSZOXSfwkwKx7Wr1mN90IMvlPI29E6Jk0FBAIFhVIvlAvSI/jjszYUonCXZdn7PipKsZAd1V549IwXMvhErd18VHpWjKaYgGNl45cPNk6E1ywHwnGkHRaq8vagV1JkTQpuFkWVkBDdFTUOgM0gDmLFYRaR1hYpmqxy43RWhw8Blq8SSJPktvWvKKWGTQTOOe2ViwhazhDhGlqlV9r6XNCECEb0RSEF4kSKhHe5QEHShgR2apTZXnITpAU/iASVmuFlsGeKyBsbB3BbRvY+mq2J8vOm2dIMm5PO/V4/LWh/g4WzTq/1s7DoMV0TepNSailoKhxgykFEhLSMGBMhN3FJYbLS6BWTFxBZRbhMVgTmLe+3GraLLsQrck3xqmwG9k7CzuTKIF5RtJE17b+sgw6Tg9DIw2bIoJ17fIwAlwxHe/dYwEE5JRRqGhOAbgle6IkVpDd/staW9JoJgJSzGshO1g0MXAaGrTY7zbpyhVzKc2Cn0mVG/qGWa+xtqv8QGUGsXjBllp6kAzCOtTij8ya3n5KyfKtAAa/bPuj46+uSCSI9wK5UUsmiU9t866WgNzgNynkaCLqYRwxDAPGcYeiIalAFjZNhPYttKgm1k4JyANqnj3PBRiihMiEPBBSJVCR8ddaUS0sE5EmwJYY1cNg3gE5KCIElzUB55IwtXVkWHYDCo8FHBbKHlWE2TqJkqHieDw29DYMIBIliuXtgdLvtbIrfnPK4KHhGPFcEUURCcB7iFUJK9WwnIRgzW7NFpXaOScXEpgCg2pGmncgDGEZGKXMABfMV3vc5Vu8+m9fIt0Rnv/qFxiur8THisiVg9Jahqk6SeNck55tzygV7rLvhtY6nyb+QSgYthDkD62879gW/KZ8Dd/DZ0uqHmU+LjxxA7rIw64HZU8X3Yb+zhrwxvelomBRnC56T1YvrsNjdVdKiyUVv8UXLX5/0uC2yjYN9f2Wfgy/yITfjMABz3HPz+WhemNbKbXg+PYd3t3c4Zuvb1Huy3omDCAI6JaL6+EwGU4zNEUzq41Ao3djPej93nWmNL2DOttNG3MECaDp1RsMkNYrwRx+0L+xS1rUq9yMD/gygS9GrGvrNPTroP/EKEE8+y7HAbucMKZwbJfr+lDZFO00ipGgjGjlLirRfbnGYb7C3XSLw/GIu5tb3N/e4TjPOJSKY02YrGmjWZXu0odbB6gf8EoTaHdeq/ew71/HkD5cnKZ+oJkAT41HMq8HMTCAekbQKjRTiFjg78apGUJWHoL7AVRW449hwH6/x+7yEs+eX+Pq2TM834tCinPBnNe06YkJb/3R3h7GrrT6sFysj1DORH3f1bX+sAxsfZ9F3jKysoLmWPkPXhK/bhgHBtLrN0jfEubdDhivvmP0/6GdnfF+ZBG4/3tO7z3Mnjuc0zU/xfKerYj46zQKcq8VBSwhBYCW3E+Z2t4bIiFnwuvbAa9uB7y5y43xeoxCWtyH70dRNaajfW//Ne6OlnUX1i/y5SmD2Ly1fi5PKT8yJcRPpjwAsowRBXu8fHaJv/jiGp8/GzThMBAVEO++eYXD2xukb+5A7ybg2ze4ONwjT/xRmW2u2zAgsjWxqC/I4gVAkagJMeQXRHEnXdOf2QR2yVwJLQQVFJUtGatHYJPPrKd1rP2z3eMJ6KxiqOG9ds+Qt2iWJPJ/9iaCjLPHhb6MFnoJLsQDjBkSQkKYFA2bpMlg3W5QBa+RIXGhsFvsajumTKjGAmnfJoIM22jTZ7ZwSYFgZbMIF6bLEvOBm4B2AMAsnhIS+kvGbyFFYELzuXjIHAKBhgQiE7RlmPjLCK71JsXFfKAscGHzSlDBSPzZ7jPuoYWWn6IyQRdNrE56glCa7IlAC91Vo3eNWqyYgIYInnDZItqbsLQp7tiT6hLkPHOZIdZkFbN7KSQcd5c4Pv8cKAyaZ/C9hEyChXQxGLV8Aqakq6JcK2VuwnSnVdoWCAwp7QJCQkKBJFBPOQlM6NpYbgWdqisPamkKKwtpIymyCLXCDTdCty7IFmt7tSQntXBPLJ6nGsqOqFdsCX0uE2e3OAu7F/YtpQQTOse4+WZJzxWa57gJd6ud68ISwo6BkhImg/sY34sk9ITBEUg8hJLBAjXDFFIhtPHbCQkV1eUyUZHdwpsRROBd/bvlZqggCTekcxRlgDCj4/5CchYMo3gzsezxMIzSTljLbjKaFwG6t0iiWAAPGIeEXcnINHcK25QkFNOYB1XCGDyyw2bKkkPBcsgku2dsnxwnKh5d8OJkgKN/jSEjsxxzjSBr4ndB0BZizNtFg8VOh6Rw3nLbBPjSPXObswpR7pGNPbmCgtnykIiXGQDJOaG5J/Iw9J4igygdZf5tUHUuKAy8mr/C3fEG9X8CXv7yl/jFv/trDFd7IA9+fmvZofLnIBwx4g08HA3Bz4WcGfb1+pmK/LkAsOvorCp+5s5gYz9sQKe+P0I7OH5/OnQv2a6OXz7R14ou7RpZ0j7rMdFGvx9SooAwftrsokOoTy108psZOf0iE15k4Cpf44hLVN7JeoUJ11ox39zieH+PP335rXhCzM3jEDZEih+W8ogl1daenvyyuAe6kK8+A4Bgeafae/atKSTkn9tqbKwPsIgUxFpnxVi0rwlGvgu9G1m+k/vpaF9gb0fAvs5IdXZaNV6i2+Yp24U8dCn8LrGJWS4sC3VYOeF+Bu4m4M2RcXMo+OrNWxxub3FzPOJQGPc1oUA9BKG8q8rTfE8fFP7b8xqn1PM8qwVaNdL+roAu/N1UMAASlrUqLlj2cerd6jQKwOuk1t5+488a67LhzchwejAPI/I44nYYUPYX+OXlFa72O9xf7lB2GZcJyFRP5O9rRniRp9wqyxO49ftW+XR3xvdb3geHEwDsd5h++yvQ7QHpm9cBBsQI1WU17G+EXBFLbLhc3Q2cuDHOzaE/Op9zJmx1Hjp332XZOJtPKKff+LC5nK2I+A1JiIpSirr/G+ILsbKViTUlhFhMZXx7N+Cfvx7hwkqpfWbP501wRbZ11M/iV4fgpRKCFs9ONN5ef6Q8hqqWdR/o7JGxPOmVM7v6Xsqp+/bEDz+kKfwQDNq6shjQQ+7VWuHBUjmj0DWeXV/iH3536aEWpKumiLh9/Qav//AnXPyXG4zfTkgAdmcNOIrdF+M2As3pGieLNybBLrgiZnAiscCI9CbZejT8xeG4MtbrRSqgMoFaE1g9vRg8L635N+MlYl1nMz7flmmRfgwoDwCCpVEbhxNgWP9tzVl9wARARiR0ZKuF2AHQYmWp94StbEoLlwFNgKfKArGcqRJmh0RIV3V95PoJVsHcb4WT59Xi68ZcDXJ/JWaX44tVdkUpM4gQLKQbxWPxLEsQOMMF0gTKEu6lKSKkr4eVb9Z+ILgXpZHj8XQ0Yjx6cRMg1vLMK+jdatc+NaVGL52LcGNjcIt/3Svq7nV9JyiYbF9M6O3WLJA+LRluysLAlSJW+LVYuB3gftyhgHBxd4t0dyNrUg3obJ8k0XC8t1mVZbUUICXdU8MPCyEKoSnHlKkUJYEoCCRMAINZcoW4QkWF7bVU9RaQtckqlG0M1BbeaoIACyfki2jryuxKHHT4YQOuTAEV6hFaknIJF1Xg1vhap1b2vs2qHKgaGkLGVxlIqWKeCyTMVQsDRAQUbS4pc26he+LdkMK4DN0SJdTC/oTC3C2EkYV3iEwvFM4BakmuWRMo54ycBwzjThURA7hUUIF7KAAbQrSObLS5iUJpSAnIjDEnDIPm83DGVRUgiTDkrClE9OwzA8QupBfPgLSYgwOg7JUplTzRcxuPwVKHWxR2TRkjxplRCaAeYQZ/Nc6cFL4l5BaCMmoJW7ZxFHC/bJeO3UM1sebUkbBXlDKGITXvkKw5dFSBlIaMlHW/XcJLqGUGc8Vhf8BUZnz9z3/A/OaIz/761xiuLlBzUrlGBacRE32GjFsMeKdwEsfd7ip3//gBlLONMyL98iMp7xNH+Dv3DDm3O7lcYXc2LSijVuKdQhv7dZ6I6jF6/dEMJ+/FK/ZjWykmFm2KzpkermR1Tw2KH/HwOLuc7EHH+ZQ3zisb10VomPBZBn43Eo64xoQXTmfKmPRenQuON7e4u73D62/uMN2XBTENZ2sMn7HSBVj1KR+6beP4THFgPcFPBQFwDPgh6Jjb+2heEes1oDCubXqyfYnQQ7CwjkbD2JVlf00x4VPbBCd5QW1SRBFRJKxg40PCzNQAZ+tYLpvnkGuFwwASlJcQB0YwhKaaCnA3E94eGW/uC97c3GC6u8FhYtxXwhEDmBgjjE5OoiiHeq9oiEP37O8GaZtn89Jn5vWyUbXbl35mi/qLlzsFQXwWmjPcuGo75H0wL09vL8xrpYRYjMUBEaqMkIdd9ggSb/ZhN2LaXWD34iUur69xsdvhbj/gbiTsiDASNVg9o2ysVhvSE9FHmMZPojz9il/cMbsR86+/AL1+g/2rN2AW/McECYFrIZnJ1u7UCq536bGxvb8C/KkvfjjR9vhYTyCxRY2njuZsA9gPKGcrIoq6UllsWRM0+b1DyS2iyK37mgWcWypq/UeLrykBtLEQtP64JmBpWVUuN+qfNSVEaMs+ed8/JdTxQy8/Ik7rp1RO4PeKARWXePFsj9/+8hovrwdXQqSU8O7Va9y8+hb51QH0dkJ5e4OLuzvkg8VDP7d/IUR4cY4fYmaXiLWfgloqg4HETQjZCaAa8u4IYpgFb3b85jG9oxBpOYUgWIzPtubCGwTWQ2XVriVWDoWWT1Z387p/94IIRCpt4UIdKwfhWBNGt+6cedB470mVCrWopXhOKrRSAZgLYiXpLzgBQYBbVWEAoMvbwAWAWmuBAFSh2wmStM6cYOwasZLmiqsvJ/A1wL/ZB8tugllJWxgm1sS8pLG+mCvKPKPME/roOfquxkBHEKa9dzEG0pmmyBTKvnC4hIngYRK5e6PtYVSAdYmOVZHQlDnswsqO1908igsY1LveGMElt7gSokKE4DklYJD8EfOsIW9QgaJ4JGcc9leozyr4/h71/l76Y3TCbuF9WWGVVRlRAVMeUcIwyOA8lIGukYdYSmGsJFkO5lrd26HWimEYXMBbq+Y4qBXjIGHFJI8DWriklETPo0miazm650TOGYMm745h6Gy5hUdtebdMYFCNYlcez0KQJWo+X7a/tjeEhOx27fouJJm75GGRbSvGNyperiz8sIdXCzvvSjvAFQ4pjDchKqtY15RgiaMF8IpHdvB5wvZJ8VUNu+UJpxOGYYeUCfNR2qaUQeoJkfIA0ABKjDSQvpMlTFYIyWSGNEy9MISSjrXK6MYhY1eBRLMKDaDwLqGjLD+9CPbJnMZgOEI8q5J47YV1iWmWLDF0Xd0lC7ycdDk5KuCsPVGKgIDBvBAGC5vUivXPbaAwYliUvu2uJILnz4HKFCpEKZdVuQPF9fMk4Vtrqchjg4k8DMhpkATvz3e4uEyoIzzJJIg15JPOuVaU+wmVZnzNf8bb+VtM/58ZVy9f4Dd/8/e4uLzCuNvJfbLfgZkw4y9A9YBcXrdJETQEAINRdCV/OAqJn8v3VE7QX50sTP/atW6KNzKBliklpVZ448ddop50S+Bmz84R6JykhGhl3/x+5YFGZJzrCoT3E0ZtCx8DB6EEa6VrTHSNwpddTTPkmN/d4Hg44k9//haHuwllqk0ma7yEgRMJbQvADUBa2YY8gVOhEYh7D2jWLx6izwTAehFUGN2toVC75HtWTz3uAsXpw9mCl/BhkzMMRgqwsZIYTslfGMmy0QV378LpT5mD5yFDC0FligXi7s1Fi6FBo8uURmvqHfFKNG/wWw3J9Pp+wJvDjC9fvcXt7Tu8OUyYjhV3hXG0OPjWCrf5k3rEsq+1XvQnxtlpa5w3Q3hHS0W/CQ5svNlsvwrc2o8KhNicwyoF5svq6Xvmydz1XRfjPzFX3/S41/pQQ3gO4w673Q7j/gIX4x7Hyx34YsSwGzAOhJSmcH63J/0UJcX7lQ9p+6dzvwDKx1LkJ+wmbUqmtlr6jAGEPHkAMH79GvT2HerlFerVFY6vvwXmCafKd6eE+PCy1Av2o/h04/kulBDAExQRVf3mJWFnL8CwPxIuVj0hQqJqskvnrMPdhBM9wtyu5d/NOnFVj7oxrhg5H/zW876np1ttfAiyiZcJGtHReMIPL0sYe982P4EF03d1AM4pASJPVHiAGv9E1l0Ptrro8wmqgBME5IBKV7i63OPf/OZCYjCG831/c4vXf/gT9n+4w+5LEQ7u2mF6WmE8zYrOjncFXAQbaHcTeFUnlmNGCe2S43m3j03ZYJamZEjOO+2vR2lrcUvQej4dbAcar++fvG6XHyMQUMyBkA7vnIY5FqaPHzpdwlgv7WEZHNySW1ie7k2ykRvDowyOrkFVSweRP8paUiJwkQ2z8DHNAwben30jSHiTygmUGFxJ16L9LvI5E/rWlR6bKjC+kWTV97/mtVMLQ+Kmc3MdTim5csJC8GQkVXTZuhE4BfgwGDnBlJ1TohJiu2y4Ka/eb4yxM6Eak98FnSwW3gj7umyVefmBsFJ82S8kzFQ8JmuY6XuQWPQZOcu6z1rFLAhTSjiMOxwvrzEOowsX2t5bGB+gcJGzoUmsLUSXWP7XeIziqGVOqX2zuUgjAAeYMMG1LIm0zcwerk7iBjNqmdWbIKtRmHkbCPOVSAXqOUneC2f29Pwww5Qh5lHgCosFU2KJ5Bs+kDrNcl5wWeJ2RhmND6ye70sUDyXke0lUH4TjGJ4NaIqIFPElQdqLeDVnmC+LyV1MaF25JeD2xJ3MgjtI6uWckYcRiQhzkgzSlAZd0wFEGaAMqCLC8ThV3zPf60SKUxpIiFeK4J2MhDFnjFlyKqTSlj+G7TNPicZQISjLVGHp94v9ZsvDmiunOqPdMLbdBZEubQY+lKK3nHookIS4yrl5K/e0isGHJUh3AGqLEMevyh9JNMrqKhNobVVwllL8XJB6WiRKGIxHACFfj6D9HtPxiHma4P5ypHew3n2lTjKOfULNjNfvvsGhHPDZZ7/CkDJ2Ywt3VZFReA+UN6D6bdzKJjZarOHHLx+x7U85zFN9PEb0PkoUf8LyKdbDUct6Qqtn1N95BPL7dXNwUZp/qs7mkAJNsx7qupvV71v9PLJhS9oxGJmcbHLjcZzuRpOPvv9ehR5bp41elvP7wD79sXZescdMn8E8IdwAhBlcCua7A463t3j7+oD7u3k1tkj+OUdg8Gf3/xbItdcWFIJ9aTR1IOz0X7Ngt//ZvSTtGV1iYUnXBitxxNvja3fKsnqYssuk/alOpmID5la9aMhUfUEMi4o3aslwY/OnjseWIiuGiYpGTxXAfbnEu/k53h5nvL0vuL094P72DndTwXGuuK/AzIya49pSyEOmXKsRBU46y5g7xpG5eUE4faB/u70Nc4yLF+ny5fy7efd0qXltPHoF2DiCkkQJ+zDO0P7Jwdhj7sfPyt+nBOSMPGSMwwiMIy6GEdMuY9olPB8y8kCPnvdz8AH5f7bef6SBs+Ubpzrg04v++KH4QRZZz8A322EK96pve+Ah7DdiRn7zDkSE+vd/hXK5x/TuHfgBRcSHlgdufPnd8OWJCu+lCOHuDz7aBnP8+J5tfsBQzldEaKxZX9wQKiCRxuSl5H+zMjxECcnDYjzlxl9dn+2X0NaWAqLB51pMsimsC3c5xS84DUQ/l5/LT70wBhRc4eX1Hn/9m+e4vhSr3cPbd3j31TfIbybkbw6YDgdc3B4w3M3d2YvlJLIG3hMj98UNf9a/KH2XwVRV6cCrd5djbaEmLHanCY1MaKMCSBNtnJrDQ1Nb8beK0x6U9smfJkDGg2h1yZxWs+QJFKRZJGz17SIwY0r03ThftwrUd6syKcaoVCUyjdgYxhF5kOSkFRbuBpqPQVtJtuY6DhVGyh5kDePDGkFGrcjUAtm8XmQfE2yXCBD5Y7C6qkoIm1JtyLkRklVD0+gdV7linueQH8CsuoEC4BURjkiI7KTR10++/p5QOhBwoYcphGSfjGmKwlzLWRDXo5WFy3zXW1fNJ7c0NmBUbPrOW0u6OM6g1+L5F0otYgk9z6jl6AwRE5CHhGG/Q7q8QLkD6jwLH1YZLVYtuYDZ956hVnGWuDvAcDgprGELXAxsS6bCYfHoSchDVgVVoItIEhQTScgFTlVd7IFhN6DW5AnYCyWkxBjHEcOQMeSMGeYJwqLwMqYvCK59LMwBH+lALVAx9OzqfpdZLcAJAJMLo6OioarbvAlKXEhvvLAyjJaM2QXTTpEvGEQFDveQsZwhVUM6ZBPa69lDcuG9eydU9frSJId6qsWqnlteBsqWd0KTWg875DyCkiRoriAgJQx58L3nUiXXWTWaNslcUgZngAaWfCFckDiJ1wEn7McBhYExD6h1lhxEDEBxnis2iNwoJwVc1v5GBZGsZ2UGmedNrbL2yaBYhRDhmFnoJwurZaG0mERxMu53IBDykJGTwFhKCvlBgeGmprDE9k0xUkk9YFTJktXL2eOYJ0YKCrCqAh/2MK5AVjgzzwkGtdB2TN6uhRDT2SwgCajTEXOZ8ebPX+JmGMCHIy52V/hs/zkur6/xxb/9K6TdCBpH1LrDHf9a4btipDvs+K0rK2Nkv5/Lz+XB0gk+pAh9gQCvP5cfUjlrT+j9vTG22q+0R8UFfjFm/CJnXKYLNxwgIkzv3mG6O+CPX9/gcDehzhPqXDAdVaMdeBgO/wVYvAIgYYAYEqY0xRe0ntwWeqeB9Vo2WlBwodEVrhQxOgysgmlWesqlxChw/0Q0oTQWAm9052S5RrT4sFLghT925JggXtUgyem2IEf1xluRHr5yXCHhXqobXhCAv8rAgYA/MOPep7nFQRKuCfjN0KZ3aQPUUlk8Bw/8DIdygTeHAW+mI759/Q43Nwe8+/Y17u/ucJgqpgoUJqFJYHyVWXqTOD8QAbUZxbD5VVZA3FK3hsptDkqP9ADVSRtbqaWvt16A0L6us3s0tOdN0RD+xkadkF7AzlbHK36643LCKxWWgy4lyTOFYQe6uMLlxSWud3tgtwOPA64vjtgNjEyNL1wz0BvCgJ/LJy8EAl9d4vjXv0F6e4P09evGx6intu2VsLd6FswARs/SNi/7MctaTL+EoNUbn24wsHl/rHK2EuIjz+lsRYRZJcItcE1QlzzBXmS6JAmlKSPCxRRxyWoyTVspv7VF3hIWrt72y23F8fmYPYzdRlsfUwnxsJ3qpyjL3qJoZbv8jGMfKT0wPrqe37vWasUonXmpnpxQBqcr7C/2+KtfXiAPcrbnwxFv//w1hi/vcPGHA0DAzg/fOtTBxpHrOn/onJz6NeZJiKjYzp2/FQhdYgu7cXo0ZpAi4X2axfMyeaePLyoEbDBnjP99Yid3So+Ohtqez+ppZBp4WZcWVQMbxCZoNUVEE1A2nN0jdktMbYyR1zCldc6tujNJJAl6TQiWUi8rsiqkuSJS0ng01O0DU0zIC7Egs+srjNMYGOlP/pkgrFmKa3z+RGoh3kygm7edzPEWhBuWfCjZz6IO+lFqZfHR1jn+Rn1V9xTZ4iHCoWhuu8Q8EwABAABJREFU5EBUKCG0E5nl0JV/akoDXg5HV4K6o0E2h62wit28uSX3q9zC5ajXZa0zyjx3SIRSQs4j0jiiHo+gKsmtKxgpJGE3lplcgK10jDNM1PADNeZX1ket/ch4KobJ7IkSJB1I0kTUqnQDVNA6SFsprJcq0DIApISqMU8tWXe22Pma0wSWh0OXKaGFKwLgSqS1ta3iRgcBPVtVGK+W00fWjKM1nMJFrYyi68SMkOciMPsqzA1y9FWJ+cDMYIRAkJBylqScfDwpk/dpvZlXR9wyWULBHzmJpb/HQwoKZEmGrGGfWMY85KGbt8G1MDFSh5J0llKSKHGqoEkEIJEowuqArPSuJ14UhCGfFZfEe8TwBevaJFpiXYIpCD3hOS0xVqvaPCHa4fDTqWsxDIMrWU2BgBTCkyYC1SjGkbF6iDL41oMgz0lp+1qL9pcaHmXoWQ6ePbbQLPudKEn+ioC/ZGmbx4grysN0ALEiLrWg3lSkIePm8i2Odwfw7T0OL5/jxW8/Q64XyCmDecCEF3LGieVqwbtuDd+XSP8YpF7v2dQ/3yzfLUPxnZezc0O87zo8ac84fGrCy9j1phf+gkmQO+XDNu7ct79X8FjOO7BOHyqIORss3vcsv99r2y3RCNA1rvIeX+x23flmZsx39zi+u8W7b97h9t0U6Nbo8xZo2bCrRI2Oa+QlLSZgOFUt1jkgUbAqfrnRXdafjZO54d7QltwQoR3gZDijTVpg8SHuKW1VwIK0oTBxZotI2NpDo93snHpLrnBp7REBn2VgJuDPbjm0DUAMxo4Iv8wtiusSJkWxQ7ifd7gr17idC+6OE+7v7lAOt5jvD5iOB5SqIZmWfOTWammYWVPgV7lqgRqI1X6g4b61OIsNljx5xeqdpWfCooRwrY131JwYS+UClOr2rw2GWhvrGa8HtfV9yXmEvtG8azGMyPtL7HYXuBgGzDmDh4T9OGFUb+iW48raeZyHjp/X98ATyschHnQgjyC9xVJ9inKSXNnsMxxAP4z6y25E/cVL4Tm+fu1tENleBZkmtyZW/SsstvuZH12m0wu0oKvPKKv7/txXT4HFxvv9tj5AyD5h30/O8Ymw8z4eFecrItgs44zRCwqH1JIKyvPk1lPRim9ZzjtL0e3Vn4QGKHxsjK8/W2geVpfUsk0f2/uf4J/tYz6svLdr0M/lg0pFwszXgFo3Prsc8Q+/e4ZnVyPG3YDD2xt8+8c/o371Dhf/5QbpWCUUBID3JefNbjs8ePTIdaGKNhkd8t9ag3bqCVE50YUgUoqYCB5OxKx5vW+0phj84Fgf9ZbYGPKWB9fJdhTnmVX+uv9WqgpKay1OILrw2KwIApHZJa9DCItiu91zD+03JU47IZTR1TmrcCyDhixJfWF0A3vIGwlvo+E7GCEsSxEhlsVFN0lo0r2qIa64jV82SuKYAwCptTpLiCUuRSyuSPKeUM4quIbPxSzYE0nCWtbkWT54AogShjyKxTElcak2z4nHzkbY1zWkbBHl1JjIyHyE0hTh9l/ZG/OkiXe5XcRkP3BrpVvL8Dfyt0YorpQ8Wietpm9hr4TpLfPs3g+liOJhniZM0xHzfI9yPLqHTMpyJo/PX4L2F0j1D0h8A56OoshAkROvnapey06+5hsxIT77czPnFs+bisqlud7bOUuEVEkt+d1UTcMpSUJexzZBAJFVaD4koFYClxmZNSeEajdylrxaNRUkJBQbq9I0lkfCPCEsPNpgwmU0OHDFE7PKHRi1TpDcGLZnokAppbjw186eO0mwT1FgDrJ22QxPyJctoG0OvCc7rSjHNLX2GCqIbfWsJcd47DyFfmfArPLVmyJlozHt5+xxgtM4ApQdvlPKyOMoITHqJPDqsM4O+uLtm5ErQCjAzCKs13nvhhGMKp4RFZhrARFQSkEJzJGFQ8pZc4n0V4kCZs/eVkaDT1ZVjNG1DKeFXbGhG0Wqk3XFkmQlRx4GX/uWr615Hkj4K8O7tg6pUxQTqZcH21hkH8s8o3JFGkd4HhDAYdpgwuQYvsNEEnptnnF/fwRIFXm1am6IcGgDBArOhyvpapnw5suvkCjhzTxgPOzw+v/9LS6vnuOv/+HfYXf1DPtnzz1cLGrCVHfI/BZDCNn0fZUPFVD/XD6w+IHX70v5wWJ//PviPmu00OO39/uVLY71Oyobiu5/reUh+WGlCxRc4vPhEr/aXeNisV/TzS3muzsc/us73L++A88l/BoUAvJV/rhyoj2vkjqgJ9GYunaaUDjS7BqbH5rns3JrXz0h3NM5XL5NkdHyKhDiVWZ9K/yHaXP/S7eGzVSkPyN9m9j4Zo2wkxoxNFRsy9aCOSp81/R0IOPfuxz5Ge7rM9zOCYdyxNvDhG9vJ7x98xrTzQ3mUlEoo2ahSfrwmwXVPAqzhXbVmSdo6ENRpNeaxD1EDbDAG+vYCf25fV/GUbLP5gGzfG4l8n5Gry3rscJYB3Nxjh0h1/52oz+D+d8qxjsnoVtumDCnjN2zK9w+2+PF5YRhd1TK8iFu7MxfKPJXP5f3Lou7RVAZtWQRgTa3GgyE/C6w9Dfw2DfMGP/4NdJuQH3+DPnZc0yvXoGnTxeiyUb4Pd3QJ8sJcmWjYrh7Nn57Up/veSrOVkQIo0Iut0gqpJO4zuISD/0riYVIrRPx6GS2LnhanPztxaSNP+HLCYuVdnWuf5O+qXv4MQFsuRTrtj8eenuspXgNbL7wKU/WR5rmag4PPD23uPXsD/Sqee9teXR/EyrtIaFvEi72A377xYUkdmVgPhxw8/UrjF/fY/9m0iZsrc4bWyNAQ00jLLfGuHy/Y4rWJOx2oa5nrPpu1eRXs/bdwB/ecyDw9Hsv2Arj/UAwit4fq986gY13ai+uxmKCP7n02YWDq9eVaHdBIQeCfS0/c8LB3bw5NOaVVWGtOUYsJBO4NkYsMFHuwaaNVSfIl4yK7pO7b0Y4aXdQdx2pxW4tVQS5ehO6UmfJx7H8lojARGBKbhFEGoedMmnYntWSfhxc6tROz2hsnilACT25sy0nRBsOOUFtdeOeLo/ZpjfOemD+PYZAM57JcYXzKOwhaGopEvaqzJjnCXOZ5Z8qJyTiEmEgCS9TdnsgZ+x3O9D9HeZJQmc5L9wZErSxdQqyraHDhPysbQVFaaB5iJJ7Qpg3hwnHOx4MACghgdUKnlHJ8utkpaSrezt4Xo3FPrqyIcxj7RHWbyBrvcri4SB0f0t23bUReIKmxJN/nUGczkPygQn5T8tQAfF8ktGMS2/Xbqhygj0EUUvGHeQg2hx5wnrZC4Fji1Qt1vySG8LqMJpHhIXS8uGFYXv7JMx+zYTESZRa7KyOKBdYE4zniqLJTKoqsSzec/NE0P07xxIu7IspaLaUvguQlSfEksw7MPkpi3rAk2KHEF/m3eBhFuIaoPVbFefYcyulVlFELM7UEs8IDLU3Hf5qQZ1nsGjd9Lfa4D3gEBcUGWxqzrrpcACljGHHqAS8vXuDaZ5w9+0boBL2l9fIkATZFYTCA1KZAX4r49y4Ppf70a3698Ftfhdk6FP7+ARjOtsz5L07wHr/HuniNP3WcZsnu/t45ZzWlkTZ91A2WOrvSo+xBS7Lvj8YpJbzY1OESx69y7zHL4ZRw01ayMmK6XDA8d0tjm/uMb2ZwCND3CO5o6/A7Zk/sJ8Uxa+jXXL3N/7XPPSM3gLD8wkwTBmhf/Ue6MK+Av5+WrQuVLd55YXFsfsikIpNAdEvY/u+dTgXa208hj9Ac5QIbfVL0/iWSNf4zw/2GDpafI3bAwCFRxzrNaZ6j6lMuD9OuD1O4gVxvEWt4sXNKUsDen/ZvWdbk0If8scUD+olKIzbQzPGghjTv8HLJS6g81oBzpbNtsu3b6OrZ79VNKItjiU23kJ+Pb7+4b0lP4uAhal5tU9ESHnAvB9w3GWkccZuqCAMazr5qWUTx/S003dauoP13eL8j4PXNw41CCCNXmFnVrefw67Lx4VqiRn53Q1oyBh++RnmcQB/++1jM9n4dPpJ+0WhiU/U5Ae/eqHHKpw1mkW9ExW3x3iq8mM4eY1P37ecrYiQpH/qtk1i3Woxtd/cJfznr0c0V3oIYtB3b+8fmsz6txWJtwrvYOEF/D/hTeqweccTb/W7wfQ/PLrvsnw3vT9OAnyCDruvHw7KWy08eU4P3e0/kLKaU7RmPmPG24qAhCOegTGAaMCzywH/+DfXuL4YsL8Ycby5w5f/9Z9Rv77B5T+rJ0R4P57Ac0u/54E80MaaNpf6PaE1w7rd7rrOpqB1IbSPMbt7oe9iuBxm4Jclb5+lICz2OcUBUet3bVm+Dt3QXiW3SObQD7MoiuP3qolDm1WfshU1rL08ANiSUXOXkc0EkP1CtI/MtbWX0JJbW5gOMBgJyNQ8BkrFfJw0iZwmN+UK4lGsmzV2ueedgOV1MHdiGas4riR/bnHATcZmQupi65sTcAdc/csd6vUO5Xc7EBEKJGzMMGYwgGk+IqeMkTKIEvK4B2NGZQkRUpgx5AQaNBSM3ntUA3HVzDYeLFtnmxio5pIf6XmwbhUrkaawZ/chaWxgAphJLZxZcz3ZXpJbpQNRgCn7bOFVTABYDT6M6EeDwyijqyHvgPyqYXAceIzxrUBhoFSJJz+LEmI6HsQ7YppQyoy52N6rsDczxpyRhx12V1fIdcbNPMOsqhmMbOtJGooG8s88NaFEbeHia826ZyZEsIT1lohwTAPGNKAonNciOS1KmQWyLfeCwp4pKbgUIAE5j2BilCQx+xPt2u9gMBcwaifkz0li+oPZcxpUVrMP2wPALRwtlhkn2de5SAicuTASsYTiIbFulP2NuMe2zZBKxKW23wSJtZw0pn/yNStFQvXkUTwARrWUb4AQcnOQemcRSyi1BFjeCiZVBqHlkEl5QBp2GHcjUk6SQyQcHFbmZRizJq8e/DwCQMpA1gTTNVVfa5mqebgols4MQBJ6V64gSEyGwgCnEWMBgIpn+xEJjPlIqJVxOzEmBvIFYwfGxUAYRsIwEIak61kBlexr2LKqiZs13ISGjXIhFqsBEMzjwDwSDI+zeHSBQJVRuKrHgJzbnP0kKO0uHsw5D+3AJqGZ85CQ6ghKSXFJU6wRMbLm2zCPhmkSHEhj1l2tYZQJwzCKwnbIEkptt8MwjhjygPvbO9y+fov7+wMIu8Y5aA4LCf9ETuOb4tTvQ8ODlcFlxnGaQYkw397hbhjwnw8H7MdLvLz+Na5//Qt88e//BpRGpLRDzZ9h5mcAv0LiV4EmCjjY8Bk39sMFYWvd/c/lR1GMsHz8Ll4xA52wyX6mjqj0sOMGNH5fW51PzVw8tf1HRSMfvTwmp/uulBYA2mBOdXrGMjwfLvAX+1+AMaBixJ4ItRaxgr+5EQFzZfzxT6/w9s0BPM3AWDERmmWv/SfwFC7yYMV5sCtZiDqRRbOEKCW5ndlqurJWaX9XkKsnsOaIsJwQ7Iro+H57bkYBVWlBN1p2BEn+h3zM/RKak9tycbeXmNeg+chW2XtyaquPR16Vcy+0WQZj6saXkJAXMqZN/eOK0U2+fnOZMU13ONzNuDkUvHl9wN3tAbfHglKAavd20sD26qGe1FjIIaEK1WNRCdxjPxGqhmnyRajki86pOF3heK4xqA3IWHmnODnlq1YTdlymQ+qsQpr3jcOl0d9Kg8D+ogJsScKr9ucXuM7FQoRaDF0jZO1u1j0EtdxtUD5SLKNxTxU0EOgyY3eZ8PLZhPGSMSAjVUJ2tBxP1GrCC/67/9t/6N+nIJv4tAqJxd3UPW9lvZ3fJXJ9uLQbscGm0JwAP7/C/d/9JfK37zB89Y3jxkpqNBjoNdbcLJYrQng+cnwodaOnTlwj3vj09NJBAq9/O+/JApY+ZDwnx/CEWfIK8j9pOV8RIZxi84QgiRNbasLdnPHNTVZPiNPHe6vQ6oN9eWRjXAoSkG+wvG1/efHSA8TQd63NPKOsrSMffeO9+lmvElZn96Tl7VM7wANI8QOIwnWXHzDeH3p5OmCcKAmMjIodiDLGIeHqIuNXn+2wHzPAjPn+HnfffIv8+h77t1MjKj8KjuqTjDUhPceHTV/A/XevsGjz1OPOwhlb5MSJUfI2Ot+yHuGV5UZUWohQpy3guvfV2Vh8jbHXY7+WeFmalbbZGBz7p30uGQZ/4B2yGtFw6KuNtxu19se1MStREW1heGLCKWuOmcUq1iy3uqwQRmQyUIpbNZHOidhis7L359Akg5DdJpuZjMNyRqSZMLybUS2ZLSkLkPQ/aq2fiWCW5ClllJmBxGASwSubZTFUQO/r//TiBFo4X0uY9TVHDUoE8j2PWynCvEa4d1ej1SburMTjPrfwABAGgp3u37zrAYhVNhhNYFqxXhKDyerMuiSDLqhldiG/KbFKFSatpipkZc7qir0D7XbgJOGwTFhINkelEUwht5y/EMIOjKpEUYVasLYhwK3JuTAqlOkK4cSMbDHvgqZElI4ttwmgVv3IGjrJ1kAJ5hh+x63Dba24C/llR8q9nXzvjCVXjwidZtZ9oKohmNDTnC1MEtpEBBC0VV84uKBY2zbC35NYq9W9K7Ng6yPfXKFIgLHcrB4iDoY6RvFukNBKORG4WLi5du4JJN5WFraJenpUlt7OQu3H2+E1865QQGcCkCSJdSEVygPjkLGbxTCnApgqA1VgtQJKJ2tIr8V5DgsOQBVLtodRibmgzHqfhCC4sglayI1agZBTxK0ozZgoJVmBTsBKwYjHN0v3sHkCSZ5A0pwuKtTS88UOu5rHIyXQMEoOFA2blRKhloLpcI8yTUhzlnklm1vSkGqiRCRmsCu2w93OgAlVJLE3yR5wxd10i/l+QrrN4Fxxffs5ht0ldvtRvT6vgXorCcgDo9ruuwYNvg0PEgo/QRrzI5Qtgcz3G5LqxD4ZWJlS9tExbtGcHE/2+X0/Wj7Fej3UZgR2/mDQPptV4Y2679Vh397mVj7W0ernfmeJBbfv04AXWcK/mXdnmWeU44TpcECZxdvz7vaIu7dHaSFzt/wnxRFOr2vPes8S83KHGv1u5Ib+0sKkouHoyBPoC+1va8eEhF0YIcW7kqag3ZYEdHjz4dXd4CHiW1FBs/XqxoYuH8kNbkL/tiikcqzY+UDAwIRCC4lBvFyp0XdxKLUmKGmKUmdMc8HxWHG8n1DvjyhFklNXp54SgOoGQH5va3eVq/AmSfgIo7OZCZQYVCnQaAoFRP1YOXzgOBEOfxpdF1ZR/nSJ+WIdI8gCYWZ4T+lTRCWE1YuE5tamhv3pxrF4Fmk0X4NA7s6QBbsYB+QhYTdUjIOEOjW6qc8NsVGcjm10LnAKXfS0WQ+DBm+fhi5Ywfsj95bB9ae5S55Wtlak2+lxRH2ZgeMkAmqH7V5+Ifyc7mZI7O6yh1KcBuZkTFk//wdvwafSKdz9eaCX5fflvrx/2K/tIZ9oTc/v6tcTsq4zen9S7VjOV0Soa7mFH8gp4+19wn/88w73hVQQsv2uuWd3Gur24+Yb3bflYQ4KB0HkqXse20+PEhzbl+K/5rLiuR5lwn7i5SQ1++MrTdAPAAkznqPSgEQDLvcZ//t/8wzXlwMu9yOOt3f46p//BfzqFhf/9A40VT2LC2HAdzFu3wI9r0mFr8sL+QSt09VxjOQPvHjYIpwOh3SyBKFd99j/034mUkvXIJhbKUkC4eYkMlHfEIyA7S/Zqu7X1a1fOhLbc0a0/BLkTTajmdYeocerLgdiwBL12hhifh2xwhJCM2myUwsWwgQwF0zHI5gLCEWIiJyVIBRh3pAHCb0zHUXoVdiF4Tb3WjRAYJa2fV4pozIjWyx0HaPNT8ICiSAqpYSdxTvX0FG1VtQkVt+UxLOAcwUXS1QLyQsxDC2+60Y5wyEirGzbLwf8gINk3XlN+OpeRJq/N/qLsCX/Eevw1hbpmgMkChloCCIV9Fk4nBhqxwS5VTYbRZmVymLpT+YWrnAiXVtorIJ5niQvxDyjzAWlsMTbLwVzqZhLceu9NIvXTEozmAnzxQUoZ+TbA3YEIT6rCIoBoBR5T5h3ERQk3XMitahSOIUqzCzUkuU/TpZsOOSLEYgWZp5SxkDAOA7OYFoMfFTGOGannyLSlETVjMIJKEVC3eg/ADCeGbbfZm1GkqTZ/SFY1quapoXEC4JNKM4WNi7ESnbLe4CJVRRrFpENDpNK0FmtKEXOnJqlOrXEx5YIe8jCCJpg2YZleQmqwTOJQYtZwYOgY65gtfZLOSNRRhol1NJuN8o5O0qy5KJzME+XcRw15FVSDxwzoFEhhM7G1rpURs5CzxpPX6oomSglZB4AFFE8zlUE8hBsdrEbADB2tyJcmKe57UVtTHLSc+w51RTn+xlaCJz60rzeFk91vEHhq0qBWipKrR5q1/JqpKx53VY0MetZkfW0HG9pp15gg3g8DArDZS6QWGnmUWLCAfGUYc39k/MAZFUeDQP2+x2GNACVMb2dcP/1jHnPyPMs86gSuiJzRbUxWA46SO4IXzdPi5LkDNamQZlLwbfffIucMu4uJ7z5+gbv/ud7PHv2GX7zd/8WebdH3l/gIlUMLhxqyeErANSWnyXocKRPU7bwT9LE5edybvl5838UJZJQ/uADy/Wwx19d/AoDDeJBpgTUdHuL49t3qNOMWiv+/PoWb9/cYz5qRmRH8wupVSTm2IRgkZmxsDwWWUkRkgrIV2wBGy3BnlfKPFzdE8Is4S1Xm4XvNGW2eVGolb552CblFxp9qdyBsWMfyhMGmQyv1unUS9zmvmqO/C6x3KZGz40E/H0mHJjwT0fG0WifRupJG+ZJ6uS5fJhxjbvyAu/mGW/LjFfHGd8eZnzz5hXmm3e4m4ooxympKD0hE1BoAJJ4MMp1UsFGo0Hyd5kXpNFKNiRKajBjVigFEDrHeD2FCxsnU2MIEOGKIxPX1tEUERT+Bvp98RBuRBaTi1mb1ZQT5sEeEmMrrDmh1MH7Yt+NY+feMAoAUh5Bw4BXlXEoFX877nA1jhiUVjC4EGMFDfkT6HiBkb5b+0CLev38w7cNjxr5y6v6n0g38aMoFP7bUNxidYkCbUVNqCPMvtBfTowJhyl5xlpYW6oVF//1K8y7BPzycxQA05dfqfe5v7oqj8p8TvzMq29PQYIG/6e+PzyYByOEPDiMjR83XzhjLh+I889WRLR4wIIe55pwP2d8e0go7VwH3NUWMgpETishlgf71JcIzMYhLH59TOiz2d52ORckzi3ntvX+mtSnQMTpPnhZKyzEytNgBbwPtXvqJH8o9fKRSpMThUuIGzWLx+HlB1u6gZsnxAhgxG5MuL4Y8IsXO+xHESbMd/c4vH6L/O099jeTyB1cmGbrsujjzAVYxwO210834AwF5PIRYf7WNNsmcv/DBuWxGJf+l07Vix1uKgW2kPvpfhjhHOlnt6Re3c/rMUcRVqSheg+OBy4qSBLSbm22CsUxxgaMGG2fbayRtnWLcWNaQhNm+U6okgjYZ1MBGuTuScoBKYNkCVOdXlV338Qadz/cDUmkoCKsslA8bJbDzZqXQMjq2ZAogc3jgOH75MJD0jUhaMz6hE4N8SQ0HOHI/nMChldPegZsudccExkurJ8YpN4LaAcLasG+UNAvyenGgC53E21tuX1vMNLGaIxyLVWZ5ZBzgYXZagJ4+Wwhw+YiQuaZMmgArobsyZwtsTXQEhBH4bspVpAsr5XOsBt3T0yK4HNhKacluVBZ4KZwUb6NdQypyxHAsNAGwmAmIhQbo1rVm5VhW9PqCj/ouzHZswkNmgV8s4Y0XaQx9gSzhgx7G/dI1y0qFH2JwpAofDDeoIX8Skuo8PkHNACody00N4bbZCr4p5QATdSdU/b8MinJGpPtlQsXslvuw5l4tDMb1qZWY6Kb0kTwhHrwuLazWTGK8lO9InLGMFT3eHBhDzbibC/pXmr7H9c14vOoZNgqFmLM4JJALm9Y5hCxe9v7pLCfirst3JghMrvfo2cOoUWA8KYCmDCF8ZsSIWkYL83ZIcoaUeqQZbJ3+lLgFUm9jhhINanwvyllYgg6MEMSajc8WOYZGICZJhz5iMP9LTJl3L57g931NfZ7ixedIWEgJOScCfG6vYq4lda4sN/o9+cWvvP40t9TOd/r4LGGzqy31c1JNmT7hwW1+sQB/BDLY4T7D5qTOa9EXq4nXN6jKcJg4fsYuKABV+lacmSawUopqNOM+XCPuRTMpeD+fsbhZnoPSIkC13D/OspvBgZkSMnuOAvr5+0oYlQ6oaMF2UJutnqmBKnxHbsoGGjufXYRtFWC4siPBT5uxNqvSChPgNtAp8k9IrTXs5wwMmNn4SxZ73gW6nBIwEimiGg0HJhQMaDgAhPuMNUZ97XirhRM04Qy3WOuhIkl9CK0T1Kluo3JvFHiFFgV4UYHUbe0C2iKsM1oxI7zdVsbEvtrsNAIglCFF/W7ZhpseV3/Xhe/8frdU3t6qrvlAyNAUpL8G8OA/S5jPyrNojyg6WI85NMCmmRo5E1iUYt4ueb9SHjx+xrNcKjb+voYReQiy/a3Sl/nIdHGVh+n6229eGp+dvef7AkG6JQSeMxAqcDc9s33InaxJL+YkQ4HDPOIaRhRsxgmMQqWZXXnfxDuOgXT57xnZXlet9ZSsfspeuWsPdquwsuH3wEpcLYiYtAcETln3BwT/sMfRxxmiyXb112yT71II360gx8Bi1bVuGuhMV+xPoHWh/8MouPHTEp+VyXwiA8uWG9B/RNc2aCM+HEX9YTACKQBl7uM/+EfnuH6YsDVxYjp7oA//dPvUV7d4vI/vwWmsn2+nlgeFIhvXIybRQkrDZ6xVkboHrUasX88jOMjLWWXoQtz1iGdYAJbJxA5NrOeYBzjA+WcBNfOaHD83Ii+6I693YCNJfS5KgHvdoRIfwmaJalVa5bPxhCpwkWFlHZXp5RBVHQOImhNYCAn1FIxzTPGUcLvZAgxWecZdVardSN6bQxcxdvClBYAMkjin9cEToHZgqxNqcUF0wwNJwKRxXl+CZ8YlHEI62VWuzn7vnZbDTTB39YKb6AUhz/vp8EDg7vcEB3ksYUWMgWXCgOD8CxsOMTKPfTKcp6gDJj3Z2eAzJo6hPyy3o0YZgvF1cJGmVVUlwRZ69SiiapLQQ1eEKVUycFRRClR5lliL0+yT7vjiGHI2A8DcgJyGjAMI+6PkygAchBYMnx/j8cjMlekafBcAj79sCcU1Eoeyka9C2xNksWxTwmUhEYCxCIbXF0gv9vvRYBd5iagtvcAcNHwMrMo5GxTUtYky1XCVJlFlwv8iZplvwqS85B0DBW1yl9moELgn8xqzZQktkUKT5X96PhaGOKkZPiU/Tf51ydiFg8Ss0CLbbHvPUGUDDlbImEZVtJzRCxZE9Kw0/wQgyoZdGNThvk+AbL2iRKGwRQVGZST5IlQHECAKr4Y86ywV6uE/bE6KnBHrchZFB9Ms3hojFVCa1EFVcLlxQ4pE/ZDQi3tHLKdQV3qUhkoFSWJq3hi453dl9zxuL9EaP9sxVVIRKRqKm6eIGullO6RKmWSKsPksypaLR8QA7UwpnnG8TghZ5n7UEeJq5xFQevKySTeFeNuh1wrsiYGbwMVuM/jDmlISOMOw5AxjiNYhTT1KuHi71+A6wzmDebQ7hSW2MCJZdycdNdzs2olSiA9ezHuOTFjvj0AU8VtZcwXdzjOR7z87HP85b/7d7jHgIl+iYv8BkO6QSUNOcJJ7/a2Pb1Q5idJ3f5cuhJovShMI7tXTN73MyT85MpSAQ/gMo/4m8vfIJMoHjIk/5B5MB5vbnH89o2GlKz46ttbvH51hzo1mmdLHGz9NDqQ42O410KgB60aASikhhBochR5R/NYVXYvz5Z3SPA+W1x+M8aptbs/ai1A1XBBvjZCNZyG+iZIPLvQe2LUyPdgTSsvi3kDxlxJlidtT8C/vyDcVuA/HQlHvYOfp4S/2xF2BIyppVgWD+A27sKEI4CbWvGmzHhXZ6AW3BXgWAmjeiMi2f0rxFalQIcpbS+ECoNJPANNFXOaJSQPJSuMC0GMJwxnKfPifGXjAcJiwi1WuAl9u3qxutEmFo6JOfxtNL97QzhtY+0pfRL5D0SlV9szr82xb6Ht0jAAuxF5v8fnl1fIL17gt3/5HFcvB2Cn3tvegzJzhI2E71KDbHgdXrdQnf1yyS9rXNEt7UmwPr2bT5VKPl0kZefl3Pox7NQGLKyrn6zwcDNRzpswv3yO+WKH4evXGP78ql3BQeYjdK+cj6p0OYn7s3hVLIUXy/FswfZHKOeu7Tb5sHzZbg9r++HGn6yE4M2P32k5WxFxX4R5yUg4zAnv7jOmgqYPWJbu0NL6GZrbFPzPsiXqn5+sv3hvsbv/aknFJVStFuJcsGtWCfFMnBYsPyRytiqfHuTfm11c3C0rz4hThVe2CusqZ3Z9bjlrjhtVKgaARlyMCdcXGS+vJDRTeXfAfHuL6fU74M090t2MJq0MyPCcCwlrSDipfd4QyD5cVDVAOBmOaUGCxB+6jye7ZTSjksiYnjtEF16ceoNW+3fq5GwrQtAT47Efbm0Z4bxocAMsQg/2e4gpxIAn7o2Mkc/R8fOy5bZBbr3V+Ppm2csVEsVeiFquxUNIEamQshYJp8Mtxn3fjVg4M6oIMznI80yIbptuRLFbyAd30FWh7nkkNGe0+P8tHn5PPDxauq2TifXKphOVfWyNyHcLNyJZTV7V7NsyxQUBZtmzsBcKDSxOle1B7NvxhbZtjC+CV0RIylu1XtV/rEqSFkaoCf+LKZz0MhpyQmITxqZuyTmM1xMu1goqVRI/E2FQItbPkDFIZGxJBOfG0EMFwo2ZRaNLlPiVPBAajgcWUgFe0WCm8zwwATJMKWSeDVAhdH8HuQW9K4XaHotlvqIGYnO2aMpVDledg4+075bnvhgLpa6uVVNQWwLNJqSTs0jtfC9gypQYlJJEFSBVUBApAx7CKWiOCLcSJBJvCltL/c0TLFv4MCRXQtgS17CmaNsRP7hwPxFQycICJaQkSckBIOeEoWbkRMjULiJDK76llcFpmRjU1koXC/0+27I/biXfaOSOdaY4F5tPeMfbbhevWfaKlW/wvjnRs4RpRe+BgiYUSzm5t5ifTWbUuYAIyJcj+EgurLMx2I0FP/8AoEogaE4HSkgkf1uIK72u4p1VqyS8PxxECHR/i7t3I25ff4Nxd4Xd/golEYZ2khQXbsyafek+avnX4gmxLKc8I34860EnPv8Yy4Lp+VjtnRMr9VOV2O+5MEUNn46UfVX2NOAqX2JIQwtxpPiyTDOOh3vc3Ny5F8H9/YzpznI5WdvLQW1973/j5Se9hytYhOp6v1Nq58iMVbp2Ol4k3EH22XCt30PWRqQPF9TxYkkbxbuR0+yDS2AY4vDt44oR6OkkJWTg91OoTSR0xJUkavLfbT5jEq7EmzF5SNBUM0QxMc8z6nQPrgXMFRpwFokZEt7K6BKl75wgX0xIQ/cCrDntAiOzzOHQJtLoS1KgQC/Y7ya2uUUBLmqDjc3CNhhGp4Tg2p4v2+gIo9gnt4/dnLaeiSIpDwPyOKIOA2jc4fLiEuP+ArtdBsbU6PIU6AEbg9IKsmyRntZnTdLtC9bxUd7ew3C+8qQ4qzCWZ+ujlqcezej94du03Yjz92cPgRdPw8SHjJouUMchdoyKlnOtsVPiKdGHQFb/o3kGVTUW5AqeSz/+90RVy2NlT54ixzq/7nkVnyRD4+XXjZffY23eZznPVkT8T7+/FCYxZzCLBjjiPZf4wB6EYoy5UfG0rLW8Gvr3Oi6/62Fppf0JuIQfa/modIAiYmzQUj+v94+yEAH7XcL/8e+f4cX1iOurHeZX7/Dq//E/g++O2BexhqGG6b08poTorbnPLA9V7SRgj72wcYlvVF2ykA+zA6dYTsVCZN02L4zHZk7+IvT2oG5dt6e88IJYKh+sLoc9ODGS1CgpmEC5DY6Cta6Njz2MUV1YrVgfTusjjJ+DeIfhVlogTdAKkhjkM6PUCUJQqMfDPKOmLOFCCMhDBvEIMoK/zB77vaoFUNEQT4zB88yS3iEEdoshc1GvVWKjz/NR3Ht9L4SYl5iyzTqeYbnXWNskfA3gbq6oKvR0YrbblW1EGS1NGG0vqhHLbAIy7X/h7exbBgIn5QHYQkpp0lwy5kf2lpjV8tcS30ncWrlP5VlzyxdgbALhBhe1zs6Ug9tex5AwbIO2ySrzLpbps/Q1zxKfftZ/pahreoJ1R0XmLzklxHNgmmYMKSEN2WPRp2FApdn7zykDzJirsEa1yG9lnuX47XZOvgASJiq5ILs/FualYeF3kuaM6Bl0yTdAIwG8BxEwDBnMFdNRlC5ula45Riqmto8kQm0ZQkJBAZfGqFkCZDv/xaz6I3xAjNAEtnVuSXJeSOxhuLC4U2p0jJYFRVBG3QX7xlgWgAeAVUEIRq0tdIV5vIB0PRQuKjNKYeRglZiSKA4VWIE8IFEGUcYw7DT/ygCijNngjbLknBkyLCQWCJqCmjCmQeA1mwhBcEqpwRMCDEoDYFZ3bOcsIWdI+wRUFHDVeeYEzAqfg4QcutzvwJXx9vZe4bmiZoXxyiILqLIpnEWRRdp2lP9panE9b+J9vCxLIS0rR92SRMtaUO4VBHJGDQcAMWkmuIVJc0WY510DqioFLSuJWQfu9iOYIR4rKbmiKCGJN8oweHJqIkhuiOOEw807TMcJ2O9EmTQMTro3OZmEarN45UXPgCnuckkoRMjDAKIiHikBns1zKwHgecbduxn5/h7T3S2Ol29w9/YVXr78Jf7ib/8e+dkBeT9D8opQszBul6m0qV9j+O2f6d+fdokenVJI/28KNzSh4s/lx1lU0R7LjjL+7vo3GGmUKhBleeES7t6C6fYOh1ev8dXrW3z557ce6rLO61CKRpN5WQlljfY1vG53LQtNB4FHl0c7zockawUciQoKbRbuJMR3a8/vceMlzDtOw1/6Mx0XGh0p5HSjJ7fkLlEt3vMgkVaCn6V4D24V3vhka+h3Erjfxkh2cxiqp45Sw4U4DgBEllMLuGXgf71nfJaBvxv1HVf42EyUUKxA+vY1rr/+GjfTETfKj5QKSBhRxkAAcQKlqkYOULo9cg2sAvzi8fCr91edU2iMRlh8Y0ZrAlLVxrU+6SCNsE3ahhA5gR8tyuQUBRMLZ7vYg3hh28JHT4jut4IO7rwd53q6rU2gjgZh1lCqKWEYRuzGEfvLPfYXF7jNI6ara3z+4gWur65wNYxKd5oHjPI1WBS7xxe/dHU5GJZ1tPJS9rhd3lsh98hrTxI4P7XxrtBGdVu4dTv84KKcs2BBy7ZsnhsnHD23CdDQW4oJLHE1ETAX7H7/J+Qxg3/zBSoYxz99KYzRE8tDq+Zynw/bmPcq6y4fA574cYlPH6wO4NOQvGcrIm6PmvBuVqGOWoC5wUO8WbAxWKL486JWe9jdR0Hj3LdnF8ZG+5tla2N+mBzEo9ZAp2DsnOl8EEQJCliRFCdh/gMP5Adsz9r6++PsdecZ8QnKWaN8ylw2qjIyCBmX+wGXFxnPrkZc7TPm+yOmuwPq2wP4MHXWHvLe4wgr1nt/hLwBpGcj2of7XC7HivaljSa4DaFDN46s4m3Yh4Ra0sTLLqj7sWN11yVY8LrF0tYah7Z4Oeiu2A91NT64cJX98rf/bIZ8Ch97y9x+BVSN4e3C1opST0ujVWGWcCrmYpuIwLG+jlPFam1dEktSMgY8uW43rmBJzi1BsK0ZUVyH9tYyyTkBKCDcg5Gx9jyxtSP5D7YPpTE23JYGus+hkai0WJY16IbNX1mHqSVdYKWWcz3Vz2apUQGxdYCAzuVa4/B0+R+qhQ7Yxq+UCFQJqklSpZgKlmtCSYQ5Swx64uQJGE1aJIKEphCpllMhrNQmldAxH+wMI/lvkZIRwEkpCVMaEhMzW9YH8nBZKsWCWHWLB4AxPI25psb4Ow1F4XyY4MJWm2GmXh6FycZrfKGNN+ga+0n3lJkJzEXIrLDscGrrQc4ROOMW6bpALDgjvYmb5KEpg2Chd0L4J9k3STROqii0/avMSMY86v6InElPr4eh4DC2NmFmVgO6mONCBDTG1KbM4MTIFaicMOSMIScXNjVvH8N57Vy0tekLG27VYbdY1gvKd8lUMwsThmalySZIp6YVbYKtRVu+TraHFPpOq/59zwnqOdEUHjFPCnzPGpBxZZRpxnQ3gVGaR05QbgqeZNQq7VhYEFeWK36oYCRwCy9ibi/Evj4+Nz23FTNmiJLnOAw4pLe4ffMtxlyxzwUiJQprAcanki//eKz+P335WGvxqenzc0awpOO+r5F89+WBPTx3e9+T/Hha2RoMd+d+Rxn7PGJHF9jnnePlSHfXUlCOE+7vDri5ucPd3T2mQ4FfsGHwRmf2JCjHX/1ve+xEoCrw4W1H+K4EpKiIdlpg2b7NfgM+jaYPguPmibZ8v9HGS1701Dav+PEz3nm8tPt0BSa89YWX19/qpTtm3Adaikhop0NlHIhwYGBgxtjxBhYmkQBOoDIjlRJ4AVVMQZRMQkf03oZNtbQct3pY6x2vs1jc5VsrQP3jjm4M+xbDCRgt2ynK9D8OF/aQw+8AzIjEiVILL6qfefHuSiHRdRho635KIELKGXkcMO52SMMIGgcMuwsMV1e4urrA1fWIPGShgcwwIS7vCjaof6a04prvA1Z81CPl08qkP6DxJw1sMedOCbfd9ukVCjzB5q+LVg0v5Yyy24HKDJ5nZx08WoUb2LDDNFfD54x0fwRjRBrVcGY3gmcCz/PmUsSTtXy2Nd8To+9/XuLRR+Aoyna26m5v4YlRLpd1+ekBBLre7YdCxJ0xlhPlbEWEhRdozLciNfcTiwR8++6ATHFj+zq9UGlZls8W77x3OXehfmYYWjkNkD+v0o+hEGY8wzDs8b/7Ny/w+fM9ri9H1GnGn/7jP6G8usGuVKjj6OlmTuK7T3Hz2uX1aVk6Wnx4qLeTa6NCD1NGbA2bEWg/xY0bZGQbAzfrdLdS1+dCP64J2C7syKk5kBK1vDjVKhRylr4yCCKor8FyymwTXFCKpeWJit/CepYiCWYrS0y/qu7LSABlghuGmyAMAHEFzzNqSpI/ghk5JfmejIw3gSTE2tmYqgppnxiZxLrYBIS1akJhMEohzNMRlCUuPREhpwFEwDBIbqRaK3IlIJthTrMPtjizJ64qmBDtIeIjnp3Ac8IUJaaUaTXW92w7tYubdqXlgY/H8nmkLPueIHkHTPHVBNuSXNaIdKEAZM0LNLSVMRIRgG2ta4MKy3dQZwm9VebJPSFqnV2xIUoF6StTAoYBO4iHgexfxTzPADNe759jvGA8nyaM0z2O9weAJU+CKQcoEeosMM4WjguAhXYx4pXDWkaLcWPUZc1S2yv9O2gc/aoC8lpLx2hSMtiSuL9EogvIeQYPGeNuJ94hMyQvhDaejOlXTwpfWj2/Hn4JcAaQEcbnv1OfA2LBFwisWEzi6vCRklqoWS4FtZQTcbAyrzoXJKiXg3p1JMIwWPx+1mThistIxtThHyLJ/5AHpDQgZckNARVqM8StmjTW8jjsQETuJVOrhOtBsrBAMsFEyfNpWJJqIlEipGRKBMGdlBOGlDyJ+jxXlFIw7HeSEH0YAGbMZQYlwtXlHsyMId+j1Ip5LpgTiQdNasIrMpP6DSWyHhUvOedO2WznOOJYO58EOCxnnY+tpYUPYWbNvyEKHUnFQerxpWFXh4wRI/b7PYZhwDAMzSuDJVa49CtjSnmQs5l3AWcm2W/FKy60qoxSZ9x9e4ebP9yCX4wYnov3B2mS+Zjg23P1qDK5VrWoDItUGcA8y+mqpojQUFyk2UNc6CJtlGlCvT+Ab27Bn02YM6EeLnH5uz1ovwcNo+D8RBpOo+FmFxhtcao/lx99OWk8w1gQSdTg2wWyESg+La36c3liaQKGUxVgezZSwt9d/RYX+RIDUqd8iOGYprsDDt98g69f3+KPf3gT8jAAcf8JPUT04k3oPdrwvOdxMJxTxYuSa7wz2p2QSZQRYA1XYryH12v/3MPRqAfjJ4ymd28PnYe2J9bpUE9NcrqP0PIu2ESpn/4ZJyEwCKe2J9wLfaSvE60vj6B5I7LdIetXjgz8b/eMQwUmXg/mTQX+lwPji4HwtwPLPcPSGYPAPAB1h4QdEmVkYmTXw2v4UVShnWBGJ8q3mKKpG5vQ0456+q1vE1Wes/tBCFd4XggAYmluOccYLsllUs8JqFZL3UUspJMrISpQTdFWeibFx8ZhLNx+t3d8HG1Sbphm4/Y/RoXqXNKAYbfDuN/j6uISzy6vcL/bozx/hs+urnF1cYVnvybgKiGNWfJaESmcLniz7xU9n0M8PDJA5g+aQvO+OaffrftsTbs+VPvcXwExJHKSTeFvevEcx8sLjH/+GsNXrwBSDq2KsYwp9ion9fJJEA/FBR/MDB4GDL/6Jer9PaY/fyU4oeswzMvP1uMgs5LCdC+s336KoW5fdwtuePPrw1AScc1T4Onhmu+rfDtbEdErGOJ1urxmFY0Yvc4mqEKoE9ql1YeNWttPzhv3h2Odc1v4EL7kg62CNgb5aOzVD2Ko+sPx2FH52OVBQblX+rgj+f4srbCay4Pz3/iJkQEkXF6MuNiJAuJilzAd7jHf3aN8e4P69oD3vaXfe23O4tvOuwzet6yt2JtW/9P0KZckY2FxubDCAIuozyzju3wM8bUwziWzYgR+s35vwtZ4Ea0wfCKPERstpbrXYgeI+GVBGPvTkAPAPBD8vQVzH5tn81qQ73ZDULtkXIgKZZp6wpO3jVkYQhiXinw3g3dJ41EmNGt08nXteQBXQ7RVe4iZ6jqV+g9d2o0xDfR9eA7rKgDQqTMYd+UhC99+3Re7zGiCUWPUlmuygA1WN+1aShh/VFqw5ufg9lyZ8MYkB8Uaq4BRBbqWA69Uxgy4EDslDZGlhloJCs8MV0g4q8QAafx/UtixAESmXOuXw+DLrNXsMbX60Qos0DcpSYxSs98nFjd50hwIKSVJxnsChlzetaSZbG/CTupj/9rjuDU+jby3vW0KmqZsREM2FNpixZj2vh5As4435UnxVfXsG2Ft/WVXgMRQEBE3kH/WsD9hvp68OCgGvYbj0er77usTDon0IbkIOmxq+SwA2UeWfXOhvYV207BCJjyqlZE2GBPmuIw9zjQlQVOAbRUGVDnIueHgfm2b8EwUExquoXUE8zZJqpjJIQybKTOW9zTZPpMpnVouCFNmtxwrJIq/UlELo2bS8NUsWjFTbHRA1v4rXioCUxwCZJMtQVgLoqoZpys4KvnZ7jxR0s3HI6ZpwvF4wOE24f5+jzEDOWv+lzBXbz/wKIsT9p2UH1Quhfft+hMu2cehz8N92q33ErtKKcy4LYy775E1+GGU5QJ8BNh8KhG+7JLiw1NyBeCCLCnugDEN2OcddnmnhjINhzIzjscj3r29xXy4x/HtAXeHI8pkOSMeHqzhkSW30S6ZYORjeFvvBQ53lxUVF5vsDRZOtDXNTmY1fGV8QPzeaK6lEdNyCYlayP3moanf7ZIIE3woRcgmhCzuGT/T3R/uPmHxaVnY5ydXzlwHlEoYdc63FTgAOFRRSPjIAp1TmXEPxl0FbqooZQbsUJHBTCjThHJ7EK9bvQtzAhKx71ObjdGGHTHXz2PJx3ULsKTlTixyR6stNtHacStydPcbjH5qSRK1n5gLAu2vj8Hgkxdz4Pbe1tjjMvg5avOkLGE2x1E8ITDukC8vsb9+ht3lJYb9BdKugkcGZaVJnBZs8+/jFSwgsKNfV4/D+pxXghw7zHfr80Z5gDl8DB0+KOQ+gaPet7dlV/Hr1vw7mT8FqOf2QX4z/lJoRN6NqFm94VtyD0jIOg2dTAyqBE7KZ0RcWBl0uEcaC+puBMYRtN8B8wye5m3a4UnKgtWTs999Wnlsb8+ggxZn8KkjfV9lw0PlbEWEQ9DSujIgRo8fGH7ukSBava22fy4frXwfscp+Lh9WNq7Gj1YmvkbOF/jHv36OX7zY4epyBJeKL//zf8H8+h12/+kN6L6AKofj+HFg6EFL8A0hx2a9jU8AnaTBQgfnDLErUWi3haZdSH2qyxMj6kauwjuvS8JQwK1d1XLXLEWDoNGYALNmBxHgQly0sDRYw5MrJNz6e9GmCdqIwFRgMUmjRXhPHFNA8eoNogwUazZp+10sMapYvYNBkNjwKSVwTpLc1MOBaJiTCnCRpLcWpsPunDwMKPMsv5MIOHPKYAtGQ4H5VGveRvgEIeEtsP/9HaZnA25/w0DOqETIecA4DGLlXAqoVlk3VutvUi8NabBbZwL5Mm2Bf4tH/wAhoESjMFC6nnYN214Hyq7tSoMpF6Sb4icOhlkZWVYvBAanEN4q1AMkP0MtpZ8PoykQlEmuGmZpLgVcC6bDfVsfEut0sFnoCTxwLWKxrH1Ullj+9t0YZGEwxNqZiDQGb5XQOAlIOSHTiFQGHa+MKaUkqticpVeu2t+MjAF5lDAzmW1H5SzknDVnRfXzkbMQvqXKuAxmzRK9TLNb39taJUoYd3toWkMB7DKrNaN5mTCOBJQyicDW8jmkYJkJSJjf5OoMPZ9G3Bs+lfrJo/M0xR2DJZTDUpFk4YgY4CL3QLascPDtWzEQVXNBAA2HJPWKMIG2KQIpaa6BlGHiC90g6StlVSYNorhRbwgL82N5NURxQ952LQJzeRzcKyBR6gIsAQwus4cBA8uvFo84gcGJkVIWj4Si8ZiTJLpLwyD/XE5BABMuLi5QGdjvd8BxRilHlLmKR0Sp7gnSlEUC96xMVUKW0EFk3ojNA3nmZjPonhVEGscbLcG3CvRTzopzSfJxzLN6gSiOVG8U21HLVZJTUtf1EcNucIWEK4MYbiFGqYV+SpQkj0fKkguEZO9Zx277WwujHA6Yxxn5b67BLGGaKBOQdS9z2y2Lb24h81JKiuOH9jskRIpCt7xYaoN1qLWwwa7emVwKpgLgzVuUCqS3EzI/xy//mnGdC5BGUGovVpLz4vIaJhCLuvpnzuWnWZriPOBdGJwZ/APvKuE/HArEP+9naPhhltP7kgH83T7hec6Y0m9QsUfmrN6ZimNcoVzx+pu3+M//y+89B4TQ6Aof3P46De23bz+cGOJUyOqq+dOK3udKj1WtU1llvhZClFFVyJ1dSSvC76ZUF1pdcieYQFxC2tVqlIOE/kH8B1aaJKniQSzLczJvCL2jlL403mG91txk3csdOVfmY+9GWiWyH+B2WNH02q2urltl9YoA7spnqCVh5FdgHPEfj8AdGPOSAbeGqPX3ema8LcDneY9fD7/FsQqfcvjqFQ5//iMwzch5xFgTdijYVUJBwcSat8vWtzbvEl8k3zObnNAJHZPrcn5jBFKrEwxTwkKHunqB1bBXQlTrS+ZBkaFB9wEqQFFLc+vbiE3PJQH0+Ufi+HHie2grjhVGV2l9kjxgaS/5IK6fXWMeLzB99is8v77CyxfXOF5f4nAxYn95j4txQs6SpyppaE/r3c5kCNzY8PoJePSn7ymjXAvjHyjcqMOHqy1qLA7G8v1HheSPDHB1djeebb63td1xrGythcobL1lYOlYcGREAgzQqp8B5IvWUALk3NADQNGH/z/8N5WKHu7/6DXhISL/6Anx3wPzl10G2EecZvcse3n96ZA8+VnE6dy3YeUiSEOr1dc7LaPqE8p5Nne8RQRsLwIvfKf68tXHN2m8Zg+1xEWyHXTd+XqwAnaj3Ay3bioNT4/9UYH6q70dRY/fOQ7U/1o48dOhoidy+K0XXQsj3vZVAPDHEwvvZ5Q77/Q5XFwN2A+H45RuUwxH1mxvwu3vQsYJKZKyXSDk8oVhFOuss7bG+2Le8DrYH/tATRfK+rSeskMLaP7QLNvI2yAWc8PsLGk5e3tx+d3tNF/Q0Qk6IZ7O02phFVELEPpVgj+RgNAxotGqzSnbL/9X8dTj14XVcFie2ldFpuFjDk3hyXakjXScQZVdC6GhbGzakMLmV54S+SjEOakAFW94AxoiluYJKE1ByrZLgl/q6UYgnxFH7bcnHPF64X9glMeN7b2spH7uzyK0ulFn2M2jJqL0FrGGaubMcpoXbLgUmyRju6NprOxSZWFGeqSdErSE0k8ZeVfPw3m46iKVV6WICVInvLu4NTEn2F4AngITZvBGmYRRL9eNB5fFtV1pYGw5hmCLOgtIwuh7RAh8IfzUEk2rKXCmIACOeS6JZZWWHWIIlTE+cwWmWBIYWJihlpFSQSiSoKGx38CgIS19VSO2AsnHuDWZZz92SrOpv8ABsAbgtf0y7Bkzw0uhAW7vuRBBaKDANbUY6J4ELCakEE36TeZ80DwcJZQDknHwcEbHmlPW31BS1bYE0JFekOMPec48GXYmUE4AcHljoI7H+F4+IUZUjBXVGE1BZSDvvK1qFscMw+XeFGluPDU42yIp8Xa2NRvb27/X3sYzLPBdkTuRh0JKGterzkgCS/4N9S10wlbK0ZeHKFmOWuVXM04wyV/A+y16UqnsrfksMUyj7togCClpP50EAqq5byikgt9ZfmKrvpeQ2CVBbC8o8Y04zSmFwTaGBJb3S/nYruSIxe1r4Y5SflFHRU9iKT1ievKYR/4XHlUXhVvDdsRmfpnzszfiI7XX8xlNf9Juya4IAXKYRu5SwyxlDHsG0Q8WoNIeG8Zsr7l+/w1wq7njGuzc3mI9FldRwetvbDvRWl9Q4XOWOv+0uNu85oyI5hmOVFjzfUOQHWJSj5hVBVIWuScFjK9yNK56Ut3PgCPozb8imcIDKb4iMrlkciCU9YQ8Wz08ekwf2l8+ptOi679YJdUg2t+QjmcGYHhuf7lcFMFdgIqDU5Mm9ay2oZQbpHZaIMFDCmAilyh1WUucv0ABh1XG43CnsoVWtQLenvomL22nRfN9RuLiWAGphp1LSME6qoPDvRnfZXzWsAdrf4LkYZrx61AL5oo1jcYcSCb1nhmE07rDbXWB3cQHa7TDsE3Y7xpBJ6indEo0J4sybwuM0LDaym5ZP+sdnlEYObb10PlLrjcPW7TgUbPy2aOg9R3C6/uNeGFoWtO8SN21HjVo/ZLB61La+ifwRJHxTb4aEuQBzgZkkUkoSZvVip3zvmhkiB8wFPThNXcLr7dm/5x24eq2dTd/lx5rm9ZeHxnh6+86cwwde90/wiNh+RmGR6ETlD3chXpH/i0en2v+xE/BbqPLHPqefy3dSFHRmXAHpEv/9X13jV59dYL/LwHHGm//nf8D8zTuMAEYWovmHzUfxim5z9LqBRT/WKTkrBJj1yX3i59ZIFMxE4bX1ge6ThS4yq2q7tD1PjwqJkgpDrT4HBiZezmYFL94KgY6ECnZEwuPMBtsYWKwQJLHvkrDs16bPe8saB76NnQhISEAiIdhLccFVNkvyYVR5lzKQrDbz7FH2hfAvkrw6kzuD+4RcEOqLK7HDjdETQtSsxFqeAKE3NGGyCs7NIjglgDTBcjUPDD0zZq3mElU+ATEbdyBvfG5Mqu2BeUO0Wj1vacqB4sJ7gHtGETAW1/GChTqxR6wW09avDJlgFkQExlxFeCfW5w2+rJeqHgKlTKi1Yp7k7zQd1TtGhPY5Z01GLALJpGGUEpEba9Uq+R+4Vs37Icx6QkbS+P4UhN3Mkqz83bPPcI+Kz1CRpyOOd7dwZZj27WoLEsty82RQKawtfqeYSGQx6Js1PsCoei5BoliolTGrFbpZ5ufcQt0woHkwNN4+iTWaJbCuXDFUi6cLz80CLvB83ySGZEQi8K6m+GFYwGj3mBHrdEmWbVBgyaZtzhFKliDbnS9bbRdEoAnuiSVptClvoHgKhFJkrbMKrCXnQ8tXIH0lpDQIfoB6QKCFWTJBtzEvOUsOl+k4OcynRNhrHgdLHp1V8TTPRfKQTDNqmcULyOImo3kVNPwhFqE5A7u0l1w5SfN/6L+kuRAuLq/ASBjGjGlOmIoIb8pcUFNCKQW5pqY07yRSsgctKaWFCCPH+VHZWCuDyO4FEcTb/rBtWmvWFXGe8Fu7tTtDlA5o3isWforMA4GaUiII9gA4fsxpDErBhpOaeQKhzjPubm5wf38ERhbPy8D81dIEOA47yYQJuVsrAJ7ThiDnuc4S/9uTjHNTYLtymwGm6ndJqRXleI85XYhp9JDEQyMlq24oHYJjtD1D991q/Fx+qsUFxItiOFCJiu96WD+XDygE4Lf7X+DF+BKJGQeWEPiM2WnuUgqmNwe8+n/9HofjhC9HEWJVswJHrxRwpcTW3Wr1YbiDlXWpQK2SRaDCaauitLOxN25oYsYeaP7UrEpkNpxtNL517IyTKh44ZGbqfusHbnmhkiqch2R3Uk8HrBa2m7PSIwj48qnyoKjQWRzD2G4bvdCsffZSdFevckO+I7HZ1ehsze3eBFBqwXEumGbGVCwHBPQ+BPZ6L5easQPhvhJmAPeVURiyv9D2DIcwg5aeqi7s19+r8cGNn2wCOAq4KK5ImN2aOZULzSwZoPeftUEp/AXca6Ia4VcBzAiAij6/RFxUv0zD47C3Skxa/H9jKlPK2O12uNjvcXlxCd5f4fLiCun6GrfPLvD8esbLi0nsWGhoPK1N2XPBaY92j3cDsW+L8Z0A1Qfh3ju2P7zZzko5YTCAjW3aaHf5oC13PNsPvNaN5cEeHxgD919X7Z7+YavPzephvwTihHZnAChAzRAjGqWZKwiJCdV9FCMw2BnWvIvjgOHXv1zJlvy1LcTAjPLNK5S3706P/OzlPKciwd1xEWdzCo8u9uTUJizh5YNKx4U8uTwhR8SJ7ml1dPtvzmieaqF/vjUNWtVaVF6o9Z8iPPwY5adPgvoJfKReIGQ+tJwLz1sI3ogC+9GZ2A8b12Nw1R1CWvTtbVjdJ5ZTc1gQfhUZkg9Cfnp2OeJiv8PVfsA4EKa7A+Z3B5T7I3AsKuB5aE5PG/tT1qgR8Y+1u1RCKPEViPtzx7c14tBN/+gp8BKJ5bMGwW3ebgVqBAXDXMGdwAtmuh0x7wqDpoTo+tY1MiFUnFJkouOFzX7R86aFwnJVmjcchaUw4tnGHEJJ1UaES3LfBLMGNiERQK6QMGFacgsKIWjZ8L7ns1gQtmgKEqOLWS2MbJliuBQqwHhTUQfGvB86WKUGbmjAKPO9IKAmwkyEZiMR12p5x23AffjMoQ9WJYQxrrEVI6oADnkWmsJFch8YcW+v6bip77SqsowQiVIGwonuiHvdLxNwtzFxj/JI4y8nbrnuWBNfK1lJQAvnw01oL4J72WvihJp6BUpfBP4LS2JrJhFkIhGoyngrVWQaAMZCkaFNqhKphcW1s4dmXRUUdkBgeNgs4FVpSMmFuybYpZSEkUSSPpJYykliXAKnhJwyUpbQQMgZM+Du6w1+Za8cfl1RFa+bbazI1TyQlnsaEcPSM07+ncTthI3fYgsy5pRJhftikViX1YkAc6mPP7VF9rX3OvonZ0kA6bGB9T0iiIDHQ3GVsEj96SQfg3l1Aa6EynDFahPuy/4OWTwihjwg51laDErEWiU3goUbamu6uZS6P+R9OM53egbd9q48wxZrJ1NKQVHUcK81YvM02G35OVoOCFqomyVEWvJ22n1OTbii/ZWpYrqTcCdUQxAbhuRKUYUQ211X7dkJ3qEDV4UHCycBiBOFc5J2Z4Y1hir/hox8scN4dYm8G0EDHF8udB9hvOHZE0nKpxhlfVJPiJ8C0/IJl+ex8oGsxA+gPLZ4782pfPflwb2Q888ArtKIXRqUPiKMaYdMapigwqnjNOHbb95gnkQhUW6OuJsmHEtBpaqGEo3GjOIX7vpEh6PjjePksVxM8m71h3qfm5GLPK8hX5v15m1WRk0AweKlL2i1jnZc0pFhTOEB+V/1ejNcbjT64t7pjRb0L/Uf3ufIRI/eXvi+Hn8/jw88oJtgz9gRsAfjAmjeutU8ApROIkYiYCBgl6Ae2gkDA4yKwsCk+cvsrehFHufUjUfvHoGRGmh4vWwXa32+9fSyQthkqKcjMUBZQzRl7xK+72H8DaAX68mnnyn/0WgdH4nQIJRQiFCGEXncYT8M4CGjKH2djc5ZsAd9W8Fjc7Uo5MPYKo8rHrZoFN1LVb4shbQ9P6VtGI2ylCcAOJWv65zyUPWzvRk2HnYn8hx6ZY1++pa2flQ4qfsR8/Mr4HAPOh7htF1zgxC6Fpp3nRHgSfeiVuSbO9RxQLnY9/T1yj2MIJ4VC96HCDSOSJcXqMejeEYsX/2YtNs4gIYgqp9n8Dw/8hJvfjwHcHjxjbpvT4WV88r5HhGb5WGx41IzuSwfbauMMYjcTRvFhzf+k6Dafy7/GkrhC/GCgODmf/yLa/zuiwuMo1iQfvkvf8Dhm29xNc1iib4B2uewKB96dnslxEPoLSohuHsu7Tj98mh5+inuBVX9CD4cITdGQhNrKjEWXcPjSFy45slAhYAtHkM/hEvpBFWL9QmCLVNQwNsUSsE9LU4SDt5UW6WOsDI7QtbEs8Cgl+k8zeAqlkRECbukKcRsLGqFk5DAScaSAQFolSNWTTgLXROhz2vXvy+czQti0W+eHmalzzWBmDEcKp7/YcL9dcK3v2KUOsLsqowINMG/Ed8EwhdE+GLM+CMR3m0uFgVmtCcwI1hz+NJ0SrxgJKVUf4c9/FGtDRZcyM4QYXwMw2LKiLhXkXFQZgcpOdysmU8Gs1mVKU6oJmxtFuqJE9IwCFOPGajs1s+2jklj1I7j6HtptEMtGZyqyBgBj9cM239tRzwE5MwUkxQmyTtSUVHmGUlHS4mQSQT+0RIcqYo1PuuuM6PUAkvEa/towsSUqMVyZnjOiKzJsvOQxXtCPUBIFSuk+SYwJKBkgLMq1SpQBzB2opzLGff39zgejw2GVfFTNDTEXCrmojkiAAlhBafL/eC7UoWF+c0UQy4EWLQ9IRHfxNipRB5yFxEgLcwSbN+sa31WS0VKQE47STi426NUxn2JMKcMgQq93WZTvaKgXkeUqFc2QD7v0k68T4ahKX90DRgV8zxhnieUeUJl9hwWNq+mhCCBUa7uwTWkEUjA4XiPUgugkDQkTex8eQlQxv5ij7lUHNKtNFMlR8Q0zaCUMJcZVBNq3YES+73lXhgw77GWbySlFM6zbWorEoJK2+C2h+13a29QDwP13lH49msi5PMwTxYyJj+PrnSIYh9ZP/nHlVG5OHyJ51NyHFTuCo6vCuoFQEXDmcHy0xCIKohFlObKCBJryOYRo7P3fgFA8rBIIngoTg9CEfSqaXmzIqMi766Qri9x/cVLvPzdr7B7yUj7I2phSW6ob1s2lqpecVkmiBpQ6s/lX1ExxEKEoOL/ufxgi9Bpv95/hl/uvmh0NaOFf1Q6+u72Dv/0//sXHO8mmEcCqIJHtO/YkO04P8OOW600hWgrVZP+iieE0TOsCnP9K4Su1K9GF7a/BKAmoQnslqckQvAuX0kcmxu41IYnA91pPAYAp9vtfhG7DjMoQqvvnxpWNvrY7VTeR3i64BFPNkDUcqY9VHSwj/GB8dawJ2Yc9CIx/nYA7gvj3Vwwz4wyC18BFFkjAGOWfcjIKElCPxUGxlowMeNuZswQL+MKCF8CeD/m1cFQd2GgebNE+jdVoCaBAVMcpDgTWzpuS7hcV7c265hE4cPUKsfpqUrAQOqBXZB40vcN7g2uFpYxHFsWmqCT2amAPalBQoSvBMmxdqCE4cVLfLF7huf7KxzHPTgP2GVGzkVpvY6z0kaaBw9gOHsbCs7ydAg/PCx3sFP5QFP+Y1/Lg68uoiy40UeHiJSXIltuPWztwcnydGMHo6YWlOb6w8a3voWTB7aDlVaml89wfH6B3R++wvjlEc7TE8CVVIShXstsp5g7GKPjhIt/+RPKxR63f/MX4CGLN9nWeMxoERGutDx/hvTsGvzlV6g3txtzeGTdn4AM8+UF0suX/r188wp8nBDPyQMdbfR04hKjdZVVNeDxPjdferg8QRFxTu+h9uqErg+/XVbrZ1t9n54ZbdwuFNf6aUPfKKcRl/fxycrHaX1z9I+si5/fB1/4ngnxre5p/ZPw+Q9eCR9clpcY22WwLLxtHdJY5yf0o1MS1npAxQAG4eV1xvU+49nliGHION7eYr4/gr+5Rf72KFSRt7ds//QF4r9tVHj8CtJfFtLtdodtoMxwwW1dFhzrPbJwm1WWQN5VCG+QEQZ2jS5WSQVBm7doJA42Vpd1AkZMN6unxZCi0NAS6HlSvVabqI2DAtOApQV4nKG3oZdybUxLZ4nEweI9QQjVhGYxHtagn2kUHgEMDYFE7K6zNsVopSDrUUVYxRamhVqCvTi+sF0mHE61JVc14aZbwBmBr/9JDLBbr7TPuqqyxUSgUmHMAtT66dRRl5eX+x0JVNtz/dG8HwBXBK3Ois+3JcDl0Ei0IJe10zjsZLjjxEC7gcgeeYha4pbnoesDbaxxRqpMi4obApqnOau1n2UXhMBQygm5JiAnVB4gqf509xiSQN3ChfneMwrJfuUkbuJ1tnOhCRdz7oW1y80KwMrxL1nInMhqS4XqCSQbvIPIw8ZICKcorWRpzwSpLIo2SdwMpMSoAyMzq1AWSPPcEj8TQWWkKrBt7LJtnX9fKhgWZyRO3wTxrPtC3e8R+AzImxu0qwPMWksbtHPmC0MN7koN4S1IlaEWDshTALfwQG1xA+Tqu6YESdSSaDbtNDTpd0MMlteDVfmbNQl2C/7W7uFEli/Bxq/4r2posEQAJRH+5ITdkHAcJDRDIplnKhWlsMOK4cemTEse47tdNWEt9bvBFsCyt4G5ktBb8HPJ3ARXNs6UW4graablExElWW6KCF33RBYOqyULb6vUdqMqPjSBhi2XRB2rKDOjUEV+sQPtKpCy40xrg7Vdw8WudnGgVoY8JwmTRwtla4Q1ECgHOOnwmiT0zuMOw26Pi8sXePbZF9hdPcOQ75D56HiVfFTSZlPuhf7aNsC3CPH3NZ48VT48hO1Pq2yt1adfo4bf3fBgNYyGywLm91cjTv65vG9ZEuZYkc47IjzPWBenAXdgHhyf7GiE3FWi3J3uDyjTjOn1AfM0422dcT9N4g1RGu2y3EenZZb9+sY3CDDUJGgp0vXs95TRo5WBSHNr1pzwDDBFhz+rUEGc/C3qSJa4g8wwPkafqSDeM+3es+/J7/lw9sKfDft1b9NuUx/JE47uowJS7k7q+kenVWwcKYxWcXtkWSCcT3gcCmFHjGcZeA4gseTiOBbg7jjjcDdhmorSZTo2NdLJpLwRyx2/ByEzUDNjYGCCePGaAr7LIeHdk++70QG+tu5JIytNYE9G3cGo34EBluJatdbRhYPqzp9e6hamNAGcRxBLCNUWoL96iFB1R+7aEaOzpg5YwQfrGEg8Kzkl8JBAA2EcBozjgDETSibQQBEdO5nWb1+g+7Ed+uh80KTNj6dKIHGwDEvV2mCnY/y0GFu0kDu099pisbZN6JURLn9ayJu4a0ZPxKnztono5CS1/ePNF06dYMIap26/sKhHBKQBHqKVG35tngsQ+o0kjHNaNEsAkoW71XfZA6stxrlxBLobn4BDnnHcTYo3CJfpAkMaHr37N263rQWQMo49zt2NwNXlIz2cbre7k7qnfOKNUI4T8Kg3xtNpnw/0iOjL40TiBmG58cu6lUjU9782odtW3ydO0VNuxNUYPrSd76Z0e3GW1vN95/LDXYNYHoavT1Mikdah1DM01Xji/hXe44grYeYT8Ne/3uNvfnmBcTcgEeGrP36J22++xdV/eYfLd3OUC3UjXn5aCv+3TjAvftta33UYptioEVLbPXgdNCTqHfGqSoe0ly0apjCCzp+cBApuoZMIaMQtAKbtC3yFk8Lc+2VAs1KStlu+BxV2q/DILbJVUMeaHK2UgrnMyNksgVWwFyzcPSSSD5/QETJOpLbhunt4TOKkScmEf1JiOKnULdlaVLnYuQImvNEVr8FKGQBKEUvhWo6wkCBQ+AWU3i0VqEWS8GkeAcoZtczwHA+MZsGqm1snGUNNhFTFvZyoYla6mNlyKagrtcMAQaRYGcyk+hkZk1mIcUnAXOVdJiHANcn1Gnraf5s+QnMF+NoYc6CMag3JC1ktjB2s2l4sYUX2us2PIYwpUVWL5iYkB9e2WM53MBi19VWhlvpue6L7IgmDG9jUVoM05nEtKGUCuHrKsGSW2GRhlBioIRRMSsgQZofmBEoz5lk9FWrRds2bpbglIzOAMoMgOR9GVBzuJzBXiWOfJXwOWGLzEoBEGS30S8DV3NbdlqZCrdCUAWyKitKdXbfST5KWOudBYdqwgQr5BxL4qpJ8JNl5JhlnHnYo+Sj/akEtE4Y5gSthnsQDosByXciZ51KaIoLE5lu2pPp2N+iDKyhZv2fqmSBEntNRgDC+w5BdMRLDW8VE1SDxFhGPAsVfWZQrc5nkbHESz5RhRMoDQKJEr6xrl7LDnaydKRr8uGAYRoctArXkGSRn1/KMkAoiOHibUcp6HhIMSkXZqGHussCOnWRiiBAcDE4VlMXLgAcG1Yyrqwxwwu0IcJW8FABhngryaHiTlWFnj3WbVIvQqazCvUABf3PbDDm2tYJBIJW8U05yTkpVWBMFwzCM8BxALmCV9cx5ALKENGsed6IMFCVEBpF4F4EUpytyYWbMs1hFJg375cqhRCjzjPv7A+pYcPFvnqOWgnI/OWzabBInNeY07xqNgV71nKkXgigFTbECnXeLb04K4J7Euspe8GyQxEj7HYaXz/D5F7/D3/5f/kc8f/4cF5eXGMsfkat4G9VaJLyb3gnx3uK8zpf0c/mBl1Os4APFcu90tKvTCNbesmFDTh864J9S+RA+/PS7zzLh318YdbEUbjEmvEDBFy5mSin5npZacffqNY5vb3HzH99gejvhy13FMVelyZcthrEG4eCyTzPISMvkp9TTgkZXW0ge90D26mZ41Qgtuz9Y741Its+er0fu+gT2e54awYJmsR7oTQuP6TyCeULInWp0b/PKkxEGTshpBmm68RZmJLppcdyvXPzS1srIq7ia3Ydlo5FSBcRKShTtLTmuX+QyNpJ1tWCRCakz6gABzxPh341i2DBNjONc8W4C3t0ccXjzFtNhwjRLyE0mgFiMeIZEqCwpiBjAUBIKM0YwZgbuqYhXRGHMENjsFhSpDSTyn5SFL3IgqG25lDeT6tTgygw04mejETt4jbIHoNH3Oh4awIkBzuAMgbRSZE3LEUgFwIyW1KyGts3Cv9HFcb7MCKGMAB5I/o0JGAdc5ozLIeFyl1B3CYcdAVnGbiztEhsvp9R/fQQHBT5g2QC3n0++utXpun6br9G3bPPh/qVVfgsK6j6m9h70hLLUWYn+Tyo2HptHWLnQBnc1H1rTQLs+UGu7BC9okrC2orwTOEsKbiklNVpjFFDLH+HjajhJ5ADb9BzH+j7aRgswM17lW7zJrwGI4dlfPf8Cu92zzTl3Yeb0A23Ua9+sPoG5tBrXF6DrhSKCuhc322t9nlAEySBXzcVv9ZvXkqj7I5ePoohYKiDex2jlPV55sGwdif7YtF8eOpMPk092S54Y/Q+FGP1AK6Ll2x8yrVPvbu/T+8LFx4amD+jaCakFubzck4XWOlp0tLYjMrXmMwqPqBgAED57NuDZZcaLqxHDmHF/c4v57gD+6h2G1wekY3WB6MlVanTk2eWhqkslxEcr79HemgB5BFY2fj61PKJfskvroYvdKcaOmWgMRvvdf6lV84QxqBJKKZ03ROwtXpsbYOb9OvljxGjYppgc2cfKUAbKWJCeLZFkve01sgEEArpXyC3XRcfO7bVGkIv3hyla3LLfCW1WZqIRHkAvBF4tji1IsAjqjI2h8V8jI5YINRE4NUq026rlZE4VDkMxAsWYUftnVuOBQW2u9WsYietNqhTxehpH2BQ2prFozBk6ayILB2NMzCrBMYnAkyh4dofRWDJ1RlJlSaOpoTkRLAm5z6+yKxqsDcufIHHne4vpzvPDdlgZ9lrlHOU8qGW2zKmUBo62p9aCLBNrmBlGzgCQQ70TGxoYeKDBbbIkv7YnDsoUFkos6isYicVSs6Y+/i+lJFbctYJmAKSxiWHgu6JowVyDrrFtUJy36g8huUQic2Ng1DNBouTuzzwR1EDO5hkGkkJeGFW+W+JfEXTY+pjlveYNMUY6KEtizoKYP8FCVIjApYWUM4s7W8WwMjo/yzmjfbD1oQIZC1GUknufOTwaDkr9nu/GEdO4wzgMKB52ymBbPcDqAEccuob+NeKT1bhtqAFeA4lgaxD3GQjhliJNG+DBkrA7fJMp2qp6oLV1q5Uh+UM0WBHLOXF1gu53VoUFF0k4f+QKzlmNHEmUTurlFpV+bbWC1SLFeSkMaZ8Cj+z7BqCF2zJ2i5tADsOAdLHH7uoKV7/4BV7+9rd4/uIFxjwjldfgchAFRMSHDoBt3Z5mlf8QkfKUdsJbH0jPf5/kcVdOEVLnvvc+/Tn5redoyfydKo/d5z+6cu5kzq23oobfs53T7Q5E+DwDRAMqLnCdEyqy4noT2jREyrwDwKjHI8pxclwzvbnHfDji9c073E9HzGVCoYICM7w5NY5wv2/MOBBPkSJxMo2WNL0jfHZ60EDU6GCvy+09w4GxV1Y6tUKMZkiN0jXzDoT0WxNqTk/JJSvPyMYS6eGe2n+wRORtdCnI87OdLLz40vFFW3Ue6HoxVPL/adjBaJ2uY62qZDdPUwZjR4SXGXimIbAK73BXRhzKJY5FvCKmIkmoZ24mQ5Ers1BZkkSckVhgWTzsEjIxjokxMHkyaiH9GTHxc0xCTix53RIFw4IwIfdBdsVVWDxubUKTpQPcvOL7ppT2b/+6MK6+zgooidASWQstJyGerFEzt4i0ZatvCkAzckspAymBhwHDMCBTQskJb0YC5xljmjEkST7HbHTANpAEm6EwzzXtvH4xUGsqPGEnTs6/vh7qxvjyJ9+FZ/fd6EZ5YATX4x1ukRtOs7G2TQzmbmE35xt/We7VaiTLxOaCpFCvLjB99hzp5g7peI8gkli1RU679fOguWB8/Q51N2C63mOqE26md2vPkxPFqk3l2GhXrriZ3mDmY6i34j7Ch/63Xd7hcrxuYwzz79rZ2JD4ZLENG8X8WazaouJ6I8IgB6BefqhIeVU+qkfET618Ipzw3ZQtQfaPoPyo1/xDSi8p6P/q70slBADMvMME0cASgN/+Yo9/+N0lBo2V/c2XX+Ptn7/G1e9vcfl2glmofPTh45G962jg+OUDdvzRTtfV5S8tnjz8wslahG5PWIm2zvlTmYxGZ/R5DBhoVjCd9VN7yayn3EoeQJ1nlLkI2Ig0UQSWFAm9cENbW/pTEzBrf2Xtntg0+EIZm4A2ChejgNaUAW4VZevjF6OTB/puaj/5f4VqkOMgv6ckMchnnjAMI/IgigA36k8WgqWA0gCPsW5rz+wC1KQMh8pFG3/DNiUlZjVk1FwmpCTJg91aOGXUxGqNLIwFlm2F6XRMH0x42vaFAeU8ApOpgxPBOGAWXK6IcEVRxBHNqs36kVwCSiRWZY8JIGM6EjU+gNt7JuBu+6OTiegjJWFK4vxZ9oMqIeWsaxi1UyoAZvbYnLVCBLUKk+LlImskVvFC7VewemMkcBKFnIwmnClAFWIFnAi73ehx9itXkNOIJgBX2NX8FlwriuYPEThawHigJF3YHQlckAvNk8XIV0/2Tp4KDRlWoWGJGMxZ91vna2PIGcMwyFmYWZJTsoT8MVghauvvykZfcral7xQRMn05z0nDrBFXh4k4LwlTZIJtS8Ita2jhfHJWrwOdZF4oYsxDQtqWdyRPh35OBDavIlfepKC0SN6WhbzqlD+AJo4M8Bopf45r0vZpieFTzhKXOJsiooC5CtzmjJyy51Qw2AEBF1eXYAZ2+1HCe8zWrQjxy1xQ8iz7WuGiEQesgEOq3iSmsyJdCwdyw5imIInKHrQ9HnLW9+SA1yBo65Rk3jRb7C8kVTCB9XxArLKSho5262JVMI2qwMnjCK4V0/GIaarA9V4SCk4TQIQ8iueI3Ckh1Fq4o8SCLTWFmCNX2d86qUfbkCUs1zgoHA+6omotVyoyEcYhIz17jvTZS7z89W/xt//3/yte5D2uMaDe/h6YvhTvwlo9xJcJ4gSufiKU6Y+PJfDy3YSuOrXPP5H9/1GVfs0vCfiHi4RMlzjS78BIEBRrBj0tnJIIxgBwweHNG0zvblxJffinGxxf3ePLseAu6YW5W/b2wH6bQnJZ0+h7u39qL7CVG4m7d0jvpAShrckEx6txNFrW6Gwbi5ALKtiuKvBORsdSoJAC7kej+RLE7dFG6/jP7odk4nt76Qw0EujJJY362FFa0jEPvfpYczYPKA2RyFURi1mI0YyoEkjZEMIFAf9mR0iQXBD39RKvpy/wbk64nQl3sygj7hmYICGxWoinFs4vKd2dWYwZ9hC+bwBQAHAWRUYujIKKY40eL9aecUTSJrHSCQrrXf1A/3UrFBQK7gnBBa6QUFp8uYatJSP2jffgINak9s+sf0QLo0QD960JQHX8uJs9Kb1J4wgaBuT9BXb7S+xSxnE34E97wstxwrNhCjRcnPOyRF6J0E5ivzwPXzGL9jsYP6MEUm89tjiO7e9Pz+fw6Yrxz7YGupUAAOYeYrr3Vie27cNKiUT9WhGLhrV8/hLzy2cY/+XP2H0zgdDyRYLQ5AKGSckgtI0rH2dc/uFLzFeXmC5/jcN0hz+++f1Kyba53asiTytXfHX7p80aW/WXbb3cfY6LfNWMJE6+vv5lDcvL28xgaLte+7puu1NBX12Brq5Ojey9ywcpIr77mKYP9cebdXj1JPx2YqdXyOax8XxE/LB10X7f5btAf+eS/z+E9fiQstJMn/PbQgkhhOiAghHPLvd48WznSSg/fz4i54z7f/ka5dUN+NW32N9MSFN1AuvRNXzPDe/JutPzfLyVBeH0cEehbvt+qkqz8n1kFU41gMXyLPo34n47EuVWJ+FmqMF6FkCffNn2vVmNMyqITJCnVzw3hYITpeRflMhvC2XCdEm2BiGdo9ArEEGR2OzyhSoryBXdfp1UehmDlJqFe1xDESJZdEdZVBMUVxN8gtXVXolhahbSFdWVJS2Z8IJaCmtfzcqnywkhg6lV3NZZlRBihZuQhiRJ6ooIyE2Qfvp0tQXzno2xVItrNqWBeQboPpci4aO2EmNSaFoUCNpHEH4zAxWSDNYs59iYTBa8EC3Incj0FWoMh/era91ZYQNq9SzhlJKGEcsDr+p6WKnKMJvqFmqpQZpYp2exfEYGckVRmE41q/Ahe/JHs6SaLp4hkQSaaiEKGsPilmU2nsZibe9eRxQ3WiPZBlBjFGL+BAowF62pLD6/yAAUjlNqBnA2IhKmLlFCtTBPLIJRg/04RgMsG6s7MCz4P/U98LVxzwgNG6Yhen0PLNl2E963Pt1yUufMevYk0TBgwhBT0XrugRwSS3sOghbyKUUgXm4YAgwudgWAKwfIbEIdrqRWSiH/RLcube8Mr0LnmPIQRBUtg4AoxzL24w51VzAOg/D189xgEm3Paq0SuoMhOLxWDXFAAQZNGShzaSGiAk7VNfc1QmBWDb9S82pgbkrvpVEDAy1Xj+oNLRa2dVY8yIkKH6rdQSLcSRp6r0wT5nnGoRbMxCiFuruMCHIWEyAeU9BQb9XxlwlwzHuzha0SmKiaVMNVX3a/lVlwgyXm3mdkJjy7eIbx5WfY/+o3ePab3+IqX4NKwVQncCnIOneHdWrr/DEFAGF7nlx+Mp4Qy7J1gPEe833CNj20p6aEb80Gow08cRlPzO2HW07egI+899DvT1gEFvt9pj0SJXwxZGS9fPeJNAfeTr0wNda3Cufn4xHz4QC7Qd+8PeDm5h7lOKEcJ6XTGHU6oqaCGU35ec7cljN02iiMQe5vxekdDKHRbyeWyqgTo3xNhtuoFm79gZ1+tB5qHGdl8Q5jNFrdic7YqVl5k+PYLkQTAu4NSoi4IlGX39FJ3me7Ldn5kc3F7O6+/uEDnCSf+ByKK1K4/SMAGYRfDQlHQC4haGQh5bf2SiMXHnFfr3Ff96jIKEyYasb9/YT723eYjveYquSLS9zWMhOC4kNo46Q8mqu7E2NXRUmBRJirGaZIQmsbSw8HES6g9KdO0DagNtgQUpI94bXxGfJbNaIyhJlFx8tJh4uFNmVGXFQfGRQY5J5vXhK2CYEXiDQlmxHPgDSM2O12KHnAlDIu8oCREmpKYgSVAoHQHaqHz3OjA5cHkR7EB+06arQWxf4Crb9citb2iTHyAr4XEuOHFCybCqfw0oMyGAWgU9j7oZVcYnW/H0Njq2POsabUWFPh4Vv8SgyxOmQgZzUSk3e27nPHucJwLfrQ/Q+0M8B4QIfy+C2xpMGX7zyCwO7LAa8OX6Fbg02ZwiPw3W6mE6/xxlf5ts8XuBqedS+dbO8jlp89Ih4rHRz8UCn5Dy0/1Xn9eEonGIjU3EIJYaVixITn+OzFHv/4V5fIQwalJO6LOePdf/oz7v+3PyEBuHDC8mljeroSwebyfm1u0aftvfM7PtX/eykh3qM8lfdsFvBm4WxW7Kx3aHVvhKoCebiwjsRCNxBHSze+YLzSrT+DNba8xkwnICV2YRxsDJZoFeS/NStbNG4p9q3CQzLmY7Eg5l2wZG1YlRBJCWFjhApXlFLgFthJhE3mSGClqkIl73YgSqh1ciWOEx7c+rN1L6UggZCzNJZV2VHmGRgs6bAQNCkl1JyBwmAqKJUBqFCdTgtQejKcNSwrNyVLafsuPIE8K6WKSD8ai1ODZTICim0zgGaGr+jEFDKJXSAvAkRtw/ZCvU+aQi1unMX8bfjErV+0rwSS5HKsMJJaAjULm8KQ8dRSUEmECbVUV0QY4WjC6ERAHbKE/4cw2LnkEFdZ9s/yfoAyDpcvUYjx+fTWx+fCRW7jtwG1fCg9nNrLHqZq6ZYeBJbObKZgzd3hXllU7zdB9oJE/M+cPDF3x9aRMKiWJ0bgo0oy5LD2HQ29xZ91X9t5SESSVFFhqUISKBL0N/W0ShqKqNcJ2F6ZglAUGZRI7iTAlZiOB1LWRN4ZlDPgiZ+1HbUaNGG6STq2zlVjYCNz2fCQO0ZxE+wTNYHzei9NeJ+8T1v/QWJ1oZaiuE66MwH8xcUFuDLG3Q61Mqa7SeBfm6+am6KWipo0vw0BnKp4+TgjA8fzjnvZgaiNFe2c2H5Eq9aUzEtF21Pl3yqElm5jDAdHDPEEAVThIDhYhG1Dd1kPGh4la26i4/GIY6mYn+3FY2I6Oi73+8Nyj2ii8ArhL0kna+GfbGZ+fHTYKWluCFPQmvK+SNspJ2A3Il9fY7+/wl//n/7PePGr3+Lzv/w7MAt+mucb3E/3SPMMqCeEe/oghI1awNunZMg+WfmZxPfyJMWSX33sVyqwoNd/Lh+nuOCMMOMZLtIev724xEVQwBevxn4PolaAK8rtLe5ffQuz7f/yqxu8/urg94+3zwwepI3tu17+tv8+OmRpS+lA1EbHr4RZhrbRoTNvY5kwWSOhh/tNc+e4pYgqUxIATqgaZlHwswJschl7mGW771lxms07Kh6agUH/rv93PYmekfPPSvtgQxnRnUfbEw4/naLLloXjq204HY0WzjADAyX8za7ldgBDEzoYlS50+lRHvKu/xFQJBYSJE+4r4XA4YHr3LaZaMfsdx8hQg4uk6wj5mAAJOaQwmYk8tEwh+V7EjkccCRSWLEqrr7l9I4UKn3iAu+Bl3d6D3sVmfFXFC1bzroEZmAsMjruttTWisGd69uR7oI2JFP4C0cWhIatD/TPxQs4YxhHDfofLi0vcjyPq7gK73SV2SJhWvOMCBk7g9wVbjEYvtnf7v+v3nS/eqsm0fKJnORz6VV8LHLLR/3o68V1eoDFZ71NHZfP5xrCfUgIbdfI3/x764s0afYkzccyUYs44wV2mbO0wFXO3JUzqZU9ADXkjXN7RaVHxhHXp59BYkvPMUa0c5lsc5rtu/MvBLHf2AdDYLr722xVf7j/H5XC9ePpwox/DUOdsRcRTrFMeGteHGvU83s7qBlwx5Q1pnzpCayate3+71geVj83cMNDinb3nov8QGa6PsfbNouB8JPhQ/a69MxftUUbGhQt9vcoZBTs8v7rALz67xC+ejxh3owh2csLh919h+tO3KN+8E4KDJNlVd367u/eRAT/6c7TPWDffPdRLuVvXgPz7S327v6fs++Yan3EWVjM5tQanmiIVsoBU5imWKG2dFnC1uP/MWsUEqyYfNUFtrYycm7WuEB5VPGxtvGlr9ksChrVNJURtfAwXuvruWizxIGBlbacyS8JVp41tAdr4YH8IgCaa8tjlROtV4YrK/XkiQEJ+TBPykDFkE1Y1gWFV4psrg5IQwM5YrQg08lUppUgS1FqR74Gr1+LyTKmArwaU5wDlBOKsCpsMpKJezcIM1qGCkVZ3JSkF37FbrCJflpBSpgza2iuBAQZKlRA1qQUAWxazECSPV4sAFAhEq7ZQJPwQ+wKvWnQrP4/2q3Bn4aHEK0FDpjjjEwhIDXVDLlCoDhpEKrhWRsUTCZuA1cLxWHvOUZNYN2q/5m3gyZnBKpyUjlJK4hViElDn0RilVg01o2vX7ZMlGU5YLk6DXemjLpOebV5WYU9M0Wj7UkUpU6pZaiZnMmuVePulFFW6+GFzAUKjaBjJlFap69UjI9ngxPpb7omkZ9aVmdT2m9ohaq0pHoiKCXFsMMWFhS5SW019llOS5JGquDC7dqDtuSgqUmBW19DeYzgZVyJqzAe18EkzN5+XqExjDkyN1Xd4I4UtU3yaImIWrwafk8QxHsqIcZgxDAPmPMOyfJtgG0y+l/ZP8qUY5k0KB6qYVOUz2HKIcLcMBncAubKg/SgVzWvGFRE2f517rVWSc6OiziJ8SJAQFmWWEGhM5MIqabN6svJECYOtS60oxyNuX3+LqRYwPRNcNRfZ69xgxXeMFGa4nUvDKQbcMfBDhD2AnMatLHuYB1FiX4wXGJ69wP4vfo3rz36B67/8Gwz7K8zHCVQYNDOovkYq3yLzneIiCmNrikl7arC+DG8Vy7k8GUecFfYjtvnRPM4/IqPyMQTwJ8Uky6bPZUBO1Hsag/xA3QfoP6c/fpDc0scqH7rnjIo9gHFzlYiAXw4Z+2R3D6HQBUYakCuDSe74UmZM7+78frJwi7d393j17R14mlXpKX3e3UzNywtw+i8axkQpgNGh1OEYdPiyzcgICG2Xm5W5eWd2FunanPEFeh0gYhx0nzf+6V3gFqqBPkcI39nyE1QACVQB3uAH5JajXh4cZmx0RcO7gZbGFlRYi+3HJ8v1lssQ9mpdsSmKebOO9sp6tVgIwFrEiKiyrJnHP1Sv2kC+Vh5wXy8x1Z3cb5zk3zQBt0dQmSSSIYtw04CqkngUAkJ3WrJqskVxggwSBhHybNBwnbtEKBUAMQpBckfYrFlOVIML3XOjva2SwQyUOvRFUhjykMDLtZO6pHW6EL2EfuONT43/cEIx0ZgPdIQAhL5IRKAsYXAv9nuUnHFLGWnc4fnuEuNuh9uLEcOu4nJ3jyHPYVUXSr8o+9oQzLOdw8innIHmOhywqt9hE53ZtiHeNrBy93itoNgeS8RKca4Pv08bv521AJvfuzE8+P75vclqnqb7y/NrcEpIb94h3d33uLRDroYvCZLjzMCRkKaC/Vff4p7uFOZ7GrAHilOExnqEgNFvqozQM7+9JSf66OqvDukDQ1o/XMH/4omRosf5gK/v/vzg3nyKEGE/e0T8qy8fkUv5V14ik/+hZR06QQ5/xYAJz/D82QX+8W+ukfXitn9v/8vXuPv//ovEsHbhcSe9WHREaBLip5UemTmFsbqOzZr4dFmSqPF7QOZPGNv7KCGWJERfTqyR0RjnIGeCxsVHELroaMnaMCWEWsRGKy42og8ALGa6kpULQVTiQazbneZdXD0c+oBYlZEmMAYBzKXdfbpuKUUGRdpABZgqagk9mHAWPY3rxLASAVktjF2Q6T/LSaq1JdG1f6XOEgMy7cBqIQ6yeP4JtRTPMQCwJkwW7wKhw+tiryRsSKkFmAHOI/KBcX30EePwBWO+JNQ8IGncfrKErKRtWyil1NbAmQJa7oBOuAJcNY+DMUjU3Mg78kR/pwwwZz8PkekjoMGMrVszz4itCd/KJCFOanJFgBta23iV6am8IPQDHWuxmVkZ8Bi/mADklGVerohIbYy6nkUtnMwzwtbQEwpD5owhi1mkMx+a9JoJXBPMGsz1YmrpIkJk6sJ5MeDJyD1Pi8GawropK6KSqBcQkscuSB2b7hsXmDfbCzhPaPvYPJ7UM0bhhhU+51IxlRnzXARe2hL5VhCEAW4CFfY6sW7bY1kHQgoWRQCKKjtJc2TYvyWOW0swAABDGjyHgruvm4KBksTxV+E9XNmg9oKknhJqmW6DOoVfbcVd7ZZIYEEzOyZKLYZysEiJVksNbZmnV2CrWENVUBaPCCIc7+8dHoiAcZS8NKgV866INd9xEkEzsa6h3kkM8XDKVb2wNN8JmdcNqVKSPeE6Q84JS/yiTlBteXY88Tva/gPwcfbePO1OKaWgoqJwQZ0LuDCGPKhyoShOkzWzBN5cKyoIwzgip4TdMIAr4zjNKMcjbr55hSNXDAMhDVnCVeQBKY2wGyHsBCQcYHGm3a8IxeEy3RYq0MGOG2VQK4MykMeMnAb86r/793jxu7/EL/+H/wPSeIG0vwIOE6Z3B6TjhHycQekVxvS140nHl9zu27bO0SPn4zNin6x8RPL+Y9K2p202u4rrpf7E7ErEEyvv0lV5KlX6YyhbtPg55eF1YNqj0NLSUsoAwi/313iRh37NmYFaXJlQjxMOr78Vw41qwlTGqzcH/PmPNy3UTBhSFJAxjCzs7Wwj/UR+N4TnMWloIC5Yx8iudNB/TrubsLitqrTPwMLIplHK7R9p+8QMRNxt313YrDwAqCWdJijK1BCZRtsBbX6A2wv1hdp/w1qcxz19hDPB3Z+N5ky41z/z/bDffF+Nr6rgUoRHyMGApqpBFBep66Se5Ky6ry8xV2qhFUGo0xH58AY0H92br1aC3djEYvTBXJErwEjIACTjmREc2k1SAxFmjCRe2czk3j+JgUlpoBYcUWHEBf6LEEmqlLDQNC1RurWh73EDo8asWRvmKVFbmzE8k22Cwb55BLkyYrlJSyBqNwoTJL/UMGIcR+wvLnCkhHf7S7y4eo6Xu0ukiwu8vcx4cQG83B0wkLXQFFJ2FhpYnAuL1J2R7RKxyfL8ruvINzbCNLJMq3rdo9OAL08DzeptRbh/4N1T4zz1zE+zj403ap+5xk9ECw/fRITy2QtMz69wcZxAhyP6ojhWX5TQwHKu3H4TQJ4mXP75FY4XDLzoebsVJltrnvTxYmLd10arN7zF3WT6LYt9rMNWbZtSPn0v2n3UP7ibb3E3366g+FOX71wRscXLfnedP7Xipx/c+o6NiP7D+t+kMbryXS7+d1iiNvxjNutE5addt9h+RULhC4eT51d7/P0X1/j8uVzYx5tbvP32LejtEfnNEdOf34SgoHHcPYLtf5NPTXi8pAQ/bC6PMp1Li4UV8RAI4/caxHlv+irZzevSqlhjPa6HiJ3OFflEM4R4x7WrxaysomVVt6tcPVyNhKlBSCJLLoQHc38knFgLBKPVU+twNnG4JapLKgg2V1sluCtLWBFS6341wuovyEAb+yzJOSVfEIYxarautXvHklbXUlFLQSEdH0nSZC5tDYsKc0mT61r+ikiuw+YDESIyJU14bYJ+WXsuBfM8gYYBVApSHkCZkDKBagJmZZarikNz2/f+5DUM0uyzZR8swTKRJNO2eUgyYbhVMjFaGBK0MD/uwaJW9SpPO6GIQBC2EEDmVSDr5TtS2x67oqvn8ACYsFMVCEEhIXAtK5kCHoix+gERcicksCYER4mW0yqgDYdG8hUo/LO0NxdRQpSZYByF8GIa596SGyfNGlDhHg2bBzLkSGnWU5GZj/iUpL/QjoAm6Qf2dxrDZMobOKy59bvhQ82ZIF5t7BbytgUia9dzHs84LAwWgcw+kjQPxIK49XPKlihTTkiHMU3wwrb+Oi00hSNpSIhEcPzTBEPyQs5RwWA3DrlCglJuQnb7LzUhSFQkNLmH1UxgsCbeNAZQXfijQMgFygE3Kn52ZaYrswxv6yzJFMYq+A9nxkMhJcJ+N6LMI/KQNWG3eZ44cPk/oh6WzEPNw5TpXBlrZRiDNbeCTM/HqK9Z6CfbQvvACjzmeVS4oLDhMG5eR9wwmM2TUtL7gDCo50ut4qVzd3eD+8MBuL7EYI4lRcdcZ7HsJNlv8rW0U6OBuamIclKHazBGjqPUw1NDXozDCFQC3zIGGvHyL36Hq5cv8Zf//r/H/vlz7EoCl7fgwx9ApYJqQeaKTAzQneA7w4XdQoV9MVz6HTBkH7V8ZDK1F9++X+NnKSBieaibE009bhTyAfvYUNJPln3antha5NGLP3bq9SDlRU74Rc6NtKQ9mPbrJnQtL4mAUjHdvEWZSjuLteBwnPHlN+8wTzPm+6PfK0YfH4/BeMFJbaMml/zMcu8bjqUOH0e6IP7VexpodFitqKjuzek53JZJf+3+ZVVGIORfUCFzzGVkNGunmFElhPMGHMbDEqqxJvOClzuWzQMUvUfaGob7fW93MMJNf6r0lG5sY/O0nTqCYakJjPVRjjTkVnt9j0Zpy506oZQjShlR5gG1TKg0g+wK4ILKCXN9BuYMpoS5Zsy1YqqE40w4VuB+BiYWL8sKRoEkDK9JvCJMoM0UPOG5wvxXBLxkjDWM1uwxqGp0KAIGUr2Itl1B4pGofZsKwqj23iPZ6Eg4rAggBMUCvCqcqEwSh5/JzDvCex3trpPzdrfaj30EAlXbJQ0fxjmDcsJ4scOQB4y7PSgPGC6vcH15iev9DuNVwnxdsN8RstEP4LWi8FQJ5GN70OO1h6+O97k3jHhYeKye7Kh/HhUs8mcD//o29JV5o6oNadXlGfcsLx+cGNfWHrRVfvqlaZinLttlzTto/IEtBIUpMYFJ8iDa+oRYAbA3x7zDr69/h7v5Fm/uX3uFDjq2hs5wXn/R5OZMgEjvy/kQ3qa1z4v6cX96vgx+thtI94NcgXzwwqW+s4YnYjXEPft09O9HUUScYw384W7GH/J+W/yPsZTnjmSrr0+/pesxfDR6+WztMoCt/X6SkmV1hJ5eHlFIfFeKhaeUJRJnzpj4Eibdvbra49/+5SXGccQwDHh3e4dX/+2PGP94h92fDgDafIzupgXGOX0Fbv/yMRjQU+VkPMfNy+w8gsMuBq//GNxSbDfSKT0MLltZWQivxrF8Rwk9jliAmhVmfC8oIcyS1cIhxXusWbxCBe8iuEzJrL83QnYQegoYFSa9qpq0mTWMTYYIn7IyNwCjQkLDuJFWtai8RnhuWIYDaGbcuhQ6Ea6L3dSFM0ZO5ixhXYrGJDVFRFbr6ZYMTV42Qd4uq5DT+nbP4Z6grmr9I4qVtsAMyWVQZiCVglwKOA9qJW5CVVYavbegXEJH67GpIWzvGsOp8EGACKIlzI7IFG1hpK/K1afsoQqMCaYGL0BU+bCvrSsGklnMkbiTtzg8roRwOAreCn68TGFRS5uHKiIkjFQKzJK12/aaNA8EeEBNFS6UtJETuWyUIJZnSDJnszNKJTevhmCRZUJ9s8yXMDuMJeHYQ2ATPNv+UGc6SD09Y8TwhnIiCjPtj/FkDQQ18TSHddE2otCc1fPG9F2UWq6Dqo1pfkpJ8EltLkm/BzWTj0dPTMA3+tyOFHolh+GX5ZyNk07GUZuSk0TRZImpZSCiEvHYrJQkX0TY8y5hsHeioeGM+yAjqNnXCm3qDcfwAsF6aTSAhKAipJq6MFtrJkQ2z2BGlAwJFt94HMVIIA8iqG85GcLAul0OOJ9r85BidRgBqfNPz+yJd5090wSYnAEyZRVJOLIFvMo+iyaOmVBqEY8wVzgFJThMuSP3SUpJ9xIYVGE7o2CuE+7ubnCcZwy/eA4AmG8PsFjT1WI6ZwLUs4RSAiMoL2HZIlTJA3J4baukYdsg3jq7iwtkHrAbn+Pqi8/x9/+3/xFXL17gs5e/QC0Vx8MB83wLnv7Fz0HmcD4oJghv9393bu2MasWPFjLpRFmGaPohlicrFN6vk6dVX9FjH3mMfnYVtxs994MvC2lD981o28fmcWJt7Q9lVHrmv10Pe/xufynfFvviI1jAdykzprc3mI9HxQkA1xk39zO+/Jc3KFPLoSVkzLJdo64ixb44Q+Ee69+ldq+Ee14OfKDHw8XNYLmP1aO4qlese8jGfFIEUUDoIJIOzUdobZrnriohovJBXl17tSHcbRYMyPJ0yXqRkpRtPdaYpb+TGr1yqr6OvbtTH4YhW7WuGrddPDvkR1QWx15PvC5LVMF1Qp3vUecdSqqodUYts5K7BKoFtSbcz1eoGMGUUADMlTFXxrEkHAtwrMBUZa2LzqnqzVWVljRYKkY7cdvzkF0vOl/IGFSZlIiRIQoO24FKTfFQlWUjqDeG7q4pKCK30T7XBUwFoIkwT5qkAgQfQFQyOCzas9AXL/o2YvfBIvQg8qByjREXF5fgcQe6usbl/gJX+x12l4T5csKQBiTzkMYJ3PVQlx3qsrv24REup0AbeL8XN7XRbY2nG/MKtfLZdZtxV/uRw5pvLsPGwzad9ULw8tOi7e27I8JfDK7J6/4fWfx+/lt9NSbB8AsBYrgHFkMVj7cmYWh58fou7/DLq7/At/ff4O39a6xCKZ0qfkWcq4xYvkw6JvgLvhqL60vQfICriKP9Ht6+axuOXDxZLL0p9WI7tPjUtuDj0T4/otBMG0TFz+XHU56ixPgumJwfeGHOmHGByhJS5PlVxl/96gKfPRux2+1w/MMrvP1Pf8bx9g6721vkm3LydJiFhnzBeUjS78/1pbitjFiiq9g/r9rrBENnllN9LzGD94GITB/AHQuF1QaJgQ2U7qPZvPLjGqsZrV45/kMTksk1Rjrmdn0bA9GIxE6g9P9n78/6JcmNPFHsbwDcI86SmbWyyGazZ1Vr+urqXR9fD3q6r5LuSD/N3OmZIdlN1pLrOSci3AHTgy0A3D3OkkuxiixUnYwIX7AaDLab5wEgb0asciMs1ATr+FqlmxCwanmbZxeAE1S4TlDhsHpCqNBd3JiF8BTGzCyzhNQo2pY55CznpTOI0fGzEerNNAcSARVTS1QV75NY2RfkPEtS0lCF3m3uCgCav6Ko5Ss0xEmRzHDt3FkH2ETmxYWyw92Myz8X8GcnlC9HmMUPBUKIERQkHvwLBp4R8A7A1HNbWO8K6Jybq7YR+Qa3VMcFkd8xGaGlioFSXbWLW9izz2FlEhprElkkFXwXFzoXs3YOUUPJxMrwbzEcaMPiVDdsbtq0ovK+Cu9mDZZtbhqlFtAkorMXVTDNopHx/AUKn4Ao5AoXnA4JpUis6JCBcmBMcFcZlNww9NSGfmr33dMojT5sy9Y4VqR8I+iUtaYQEDggxYiSkkEgEAOQJOxeUI+CQGrpHkicCbrey++4GERwQldhiivzUZWKciEE8rBMLoRhRrS8AJbnoVEU1KKW+074a0c00XXFsTZ+hbkYBeYsObPtfQKozobnW/CcDtaq1ts7A5LDoudH6JRFqMJ1zw1R10fmpcJ8IPMOI4SYJEdNUKZGBUgUCMNuxJhnjLudjD5aSKqIQFHxs4VDk7nNJSOAmrAjJk6wcGYCw563wDZVw5DLPOTOQlDwIbmnE2zraDz2li6wvR/0/AhR+5ySKKNTknHoiTSfJpRSxBPieMLt9wdwDAgvRKgXxkHOA1V6WOJxyQoS1JMNAKnyM0LCq1E955N5m4yDwP5uRABhd8oYhoSr3/4DhosrvPjiG+yur/Hs+QuEGHH37i2Q70D5B6RyWCh5RfDBVM+JFibWcF2Vc/4Q0G7rX8pfcVl5Yv1NsaHbQM5IKLjAVYr4JiWAEgr2/vx1iAAXnO4OmO8O9UVqtw/j9O0R0+2E12HGEYzpeJJwTEaulIw8i3LWaZyNftHis/3llDDJr/PGT8s6uL+hpI2dJUVD1rArISzUT1HauDmXGU7je5UEF9HVAZuCQ5Qulm/CzhglEPUdEyz35z8zeT9h534TM32Nxyr/sJyH+0Cd8MADbWVO427fXuXf6EbUPM399R4WzOgEdT4BiMfxjHk6IUwHTHNCoIg8HxEwg6iAEXGar1FKwikzGDMySXikIxPmEnCagFNhnDIjZ+kzDSP46jOU4wHleJAeNBMjnAvEa0LHaWGbatLxmpdiaS/h2bNIlQ0M8dwOgIRMBWIISGDMzMiBkc1zFg2ta8osZufh1hNp+0RbNpoBUWN+MlCUf9R+l1Yxxs06e53cw4iThULcFRg9EhFTwjiOoJhwoijn+27E1fOE8Wsg7EhzIzbtLeGvofceLhVrbFVVqyzra4v3+7bvqczr7Guo9Z7pN6+++PS2OIbbfqwbXTS4wnRbb2203ygP27r1c2vfVoOmDazSKhbPzZsLM+xxBSQizJ9dI+8GpB9eIxyOTb/qeC1HjNH15I1tYxO2PbnqxFY5g9TepyzfbX5bd9eQ04yzCl6au23YVpu/M2Mhq/08kUsP1fEe5dGKiE+RoOLHL2tSY7ss7j/RMum+mfppzWKLsHoGfYtoeHr191SwEP7e82DXq/uvflh5rJXXh1iD3fduj1oCZvWEIAKu9gH/7td7jKN4Qtz9cIPDf/4jAGA821atd6WMaO4vaYVVPXZonlmr+4T8rQXMthJi2ZnzY2jr6F5htOEAN9/dUmKsLKr8ha3xbPSTDMUviaLlAXemkFjA1MOBm7+2qp5R6BQmJmAxi1yqoZns5PKqfYy1HQvlA50fD+kiWg1NSmpCM/JQOBKGR+piXhAmDmztWLgSSGQC2gXn08yLiVet/jYuegykyeHMclgtbM2S2iaUoUI98kSpmdARGJ1BN4Aa4qgK1eMdsL+dcRoz8mcZ3CkibN4Zl5CEsgcAJ64Em8ysAYiNyaaFXcxKaqVkBJN4qojgz+k3VhGljr1oeK5Sch0EaT4Pbm0Ea7siYM0QvZIQ2aGosikymCWeLZTxsT4Z0StNcG2sbaOL01wJdRMeuxLB54fVcJ6VMSfVOzR1K/wxB3BQS/EYRUCZBkiScmH+AzHmecaJC4gLcpFwLG5hr+MBLEGgwaCES2As8RltooMlTG7hxtAsSGcJqONkalpTC/EQIxIPEvM+FFFEFBH8xxBqWCQX6gJkIQBY26SGh/Sddg4fyVq0d2MkhBR8dWt+EBVQB01wHtbCClEslh5nudJF+uxtkTGhQYT1MaIgo2SxPg/UrAWZrWrFbeZ1gqYPIdRfpuR0QRHDrem9TtJcO6GBz66wX+MS1PEqIESBQVdYAKIMoYA0JAzjgHEcwJoDBZpnQ4T8NQSVCbQCgMLZFWp1Ypvz0/CuQQ3pYw0cylqSP+NwWpp92ng8GV4miPIyxqh41BSTsi4hRKQouTCi9ud4PGGeJ9y8vcF0d8L0LoN2mnw+EMIQJX+qJStnQFQQotCKFNT/gT1cl3XJACQNETEmxIs9wpAwPrtGigP+7vOvcP35Z9j/+/8ThstLvHjxAgRgOhwxTxNu371D5HfY4ztH+IZxiAR2TdFU4QmbyjXnsSvYfnDp0cVHpmbfp5qfFmPypPIpedNW7C1CQd2YH5Px+AuWNT+yNZdUN4FfimC6xBBG/Gp3KecO1/j3QgcW5OMBp7dvV9VZnbd/eIfDqxO+HzIOwWjV5pPtyG7C5aF2x6taLElvsGNPNi/5tcXQl+vabX6j5zRHkyqM3QuVS6VJ0cBOoyyoFJH1s6/f6CJPeG3GJRamlOs81yVhnysAmqdsOZgFZdN+cd6pP0vvK+T/oKH1HygrUFu/06mZ2vE9WG8DF9zftLCnuUyY5xPyfMRMUUMzZZB6Gtyedsg8QMIoFWQAGYQTR8wFmHLAVBhzZmRVFFEcQBdRvKaPd4DTxw0Ny+aXWDsXSzN9TX/NE5JYIiQGQEOysn63UREKCT0cWcwRQimYjcT1uRTYcdjq/kzAHmsHHBgU41mjEh+20roK08Yz1UlfwHNTZbcuDXiyGj1QDBiGARwSeEhI44iLccDuKiFfASXCjWG8kgUMPe0oaPrM5yjkMxVyizs3ntnsyJJfegCyef3EstpOCdEp886+0L7V9ezebsCWrG3D4GjR5sao2m6ck4HRRnf9znJPNxXPzy7Bl3uEdzeqiFA+jgssHJ2BW6ukbLlTq8tXRYe1TaedKR9Khjzy/TW2XVxZLWZ/ft8rcm1DO5Epjjb68JE9QX9GHhE/jfLzoj/v6a0faFh82abHnlz+KhRXP37pUAoBzy4i/t1vLvDsYsDFfo/jn17h3f/nD5hf3T56jVokvLR6qZp5WrzD3X37vgo/gjX+NGS+tnKpRHl77RysnKFb+nv9KVnHuvHuQwokV1as+tMwNe1V1n8WffB3/J4JjeoB19XmzAejMi1G35NLF6mtuzt4yOOU1yS7cghb4mur1OL453lGzhnzPDtgWNgNUutdouBCK7MCsxAureV77ypPMB9kt9B3orWlPqGxa9mHU5g7y227zro2BleV71HBXM4ieNfwTSUUdS4wJoQRYpOsGCrILQGFJLdAJQttXFXRYtM+vp3A//MG5WvG9BUATfJrioSSZ5SSUaLEl+UaALiDJNa5YLdMKhJL3cKjlCxyQ0vKTOTu/kUVRyWrxVwRxiUrAxwkXo9aFlcms7XeY8j7zuQCyKYUAwCODaxJDHhLSC3rYnFwdf834b+o4VA7oS8MhglAkUTGoYjbbChixU3kwmdRSFAHg+CaI0E8dwJiimrdDVUQFcRpQp4nCcelOMHi4ZMTogUZtEjya9u1+D5aKUVWZS2U6oTvMMURDGH4c5a8W3V8AAlBRgTMReAhU1UGQfdH0Pj4ooiwuqVmV0RoAndrregeLHoGULDUDEH3pSqkCAhRPDNsvmWbqscUkYd5ktGxgqgK8Qswl+yW9SC4JXwDBQACSJNWi0A/wkZAZPu5mV+2uVVFiOFUG6PW3xj+A7Yv9LZ0I7gixzw7guWsMMHXQvJscF5UGOAKX2XKc84GCaBAiDEhDQOGcQAzI4KQUkIckiRvjgLXkogc4JIRwKgO47V9zkUUHDqOotbCpB4pMdZAD/VsNffz9uzWPqoSuBX8R837kGJECAlRlRAxDeqtMlSvERDmeUKeZrz64SWOhwNefvstQBEvfv0bhIsRaRwFEJPifVYhbiPIsFw4KQakJN4wQT1NEAj0uoAmxvWvPsP++SXC9TXiOGB4/gxpHPH5r7/BsL8AxkvkEPD67g7gDD4dEeYDLsr3CDQh6qzmYLCnc6T5eFxBudgntp4NaDVz2eLznxdH8Ev5eIX8378WXqfHe/I1INMVdiHit+OA5JsiovAOY4gIzJiPR5zevcP8+oTTd0e8o4y3UTxuc569vs67FwyeZpShYKYmkSdqbH1XJnPzveukq4b053JHVgMDNzZgWi2b8wjd3q70bQ17ye79YLR09UZtPDZceW20slxb0f46ytA8AzT0mtHVfibVz0phkJEDANQIRc9pFxz7J/zBdiXQXTlTaPl9dWE1qb5WvJjsLW6sn5J14f4dbq8tjk5rkwm6VsA8HYEp4nQigCNe3xDGFHFxcQJjxuH0DqUkN+CZIPxBoRHghFgChtOMcPcWQ844EoOi0E7F+SI4nUaaGBfm4a3nPekbbrTDQPBcSkrHlnYKdE+0M07m/UkS7ZBZPFkREcGYiSTBdkfT2I5SxYQlq/alWxx8RlFSVLI/KvwUY06b1TC+Wa938NHUa1Lh5jWCeJanEDGEBKSEtB+x2+2w3+8wDgmzesIGsjWXte1j2S+A5kG0TM1Hn72gm/sz9Ti/++jSzM89Perw23LbbPWi+Df90mPI9XuPubLdU6m6bHSv4sr7y/n7DKyJrdU7jVBgNcIWX0P4b2YJtUyCZSVUE2s7NZllOByx/+O32IdDp5er++ZMuOlHl41xP0aJ1izC41Zt6/YT6BPqfywVDrWPH5fu/ZtSRNy//R++/OSpbyHrXjXUPVW8b9ud4HJ5SxnXJYQvCbMfg8fyw2+DkOkf1M+P36mHBNRV4P645x7z7P1F1i6CcLmL+PuvL7AbE0IMKK9vcfwvf1LCoL6xovMWZZuuu7+PS4HMfdtkcRSg15Q3h9Ti2pK4vA8KVsf+WQJh8YXOQ1XbZtevM08te9saNL3/DmedMm4UB1q/Cy97gYmIBWtoJguZ4oomhhNsQG+Bz1yQS5YYqSr8DiH6pncr4Yapq32r5Kw3ZH8L4rRVRFgERbI+mOC7m26lio0ZhVqNu9Czj7kLmOCoICAJAybkKljD8RQukghZu0eqPCgUJIkVaUsN8WZja6M+EgHhUBCOE45XM+ZpkqTVJMRMAKFksbxnLppwesPBkZs5s5itxcarzGyRyLPFl548UXHJWVgJY4p1jk0ZUIJ4N3DJ4tHSCLI9mTUai7u2TyTrwpA8DMK4WpiBUvevrQk3s2Rr3ND2BDj91s6jqW6IJKyWxaE1bwgX8moyXAu/BMDHbQlvg4aLEbAqyHkCgRBTFBMqsvBf3C2CWEKjpjEItZMFEiKXvFn1AKibCHVPYl1WChh9x4lnFQS4MFhDDAWGeB0weJbQADqwZo5RhQ4NcHUiARJvDwI8Yb392bMilFcPKFMUklnti4DekiLmtt7u0IEyxAFu72dwXVQRAV3XpbDDFJ/qIdBPZH3GdpGCWlVOAZ1Qu3kLcKEWHMarMAauWDKFBLXzvGTqrP/KrBbdlNYPAiS/AuAh8UKU8HhpSOrtIB4mEvooKM7Q84SbZKM+pjq/tu42r6yKRwAWb6vD+Y5lFd+1Qghq8LPjBZtn9XxLMYAo1lBSMWqIpuDzXuaCaZpx8/YGh5tbvH35Bulijy8+2yPtB1BKvowGphKOibq2mRlx3GO82IvSIyWk3YgwRAwXA1IZ8av/9d/g8lefI1xdgcYB6fIKlBLSKIlw53cTcs44nm6BMiNMB4zlFpd4A2IGUbKgXvq/4d0CcHQlFHxmKsxwA4PtJHfymice+vfT1B9I434Cev0cjfi++Sse473w2Lo/jifEQ3zHA2//GDzSB5f7Osmrn9RQPuIdtUcMAz4frjBauEGGKjcZc54wnw44vn2L0/dH3P3+Fm8i49WwDmnS9cm6FWo/qqV/T5s4HjRaGcu5tzOg4sRWaFKpd1NGLKal+d3DlQo9nT43HNzQXEVwyjJRcFs3czOuho6w0znbOSUd0DPBDyPrWFNhrb4JXOj/Gn2w9HKw36G72t5ZQMQSdOjcjUXxYXJ7yf/pZrihzYgX7T+y9E21Z7fQhaUwOE/AfMI8RwRKuDsMmBKQ0gQQYZ7uUDiBWKinmQOYItiMmDgjlRl0eqdLIDmYSgDuAnDysZgRSAtkpOMOSr/rZQ2JGYr+KFXh0J4zzYnkbJbLUo3+MwMNo7gYmFmj0Pq8N6FgfR0W+7TZN74xHKCCeLQ7EqC6aL7pej5wBSvLfas0pHn9UghIKWFQz9KUAgpR48ip/dc1ONN5+XUGmDrcwd3H6sZWHbzx7XHlnudpE4S3L1if2/20wcN2PN6j+0LKNy0f72pGPz+1nfeWffVIe6tXtc32H/8hsCRW/KwKB2UvWeQlHbyoJzmIEE4zxtMJw74A17ah2n1hIZvvK4s5PyegW761ifOW6/YAnXL28jbceHmQfuk3ygNL9N7lb0oR8X7lZ0Fp/lL+SkrhiBlXuNwP+KffPsf1xYD9bsB0d8DLb/+I/N0rZY4fiw3OH8wdw9fRzY0w/L2oQm7wqB1WZyjMT4LZFnUumY4z5TzptGW9Y4eVkXXSSG/0rIoEtufYhYhVONwIlI3BaRQRdpgFodacrWhE5ACoSQSr66dMksUUd3fxLG7K0/Eo4Xk0DFAM0QVoXZLYhvmTmjUsUdsH7TMZdUwAqFqKEYsVWnSa3OIv2tiC5xlgUibMiOyCri9kgntL4srqFRBYagoBSIxykljrKCKcRxHBt+TQlecYjKKS89K6L/vy9apFaBik+MMB4VgQU0SICfkSyAOjzMaYWrx4E4Qbg9nAFkNc+4sk3i55RplmcNHvLHHjC8s8FmdOFT6cUKQKKt5TUgVThph3kIZ9YVdytH1h5XrY54FAXHxuuPGIkKWpwV90mnwvkP8LFbRXS3mj4wIRCgJCkPlu/CmqwDiod4SGhjFL9mLCYpJwVW1sf2IRnkrCa1E+5TmD5wxEVkFrlP5F67t9qsqOm7j5LeMHdfE1Yr95rs67rQh1v1G4U6jVxaqKTOPdSJk9KyVnzPOE+TRhnmcPk0TqFWFQoJ7zqMJ2BhG7MsDwgQjfISFvQkCMktSyFHjoIFM2CGwIU2uh9Q14qyBHrS9DQLUGVeJfhdsWRsqXWa3rY4qgKMJgRs1ZIHGAa5JnIlEMMaD1VXbblK++BrzA1aqoiFFilpeU4GhKvW2YBS9StBBgNXcKSMOABarxu1XYkHUf5DmDCBiGAUDSMAOKU1UoEDUGcpcfAgSg4h0uRXLykOHWqpj2mOOKx2VXR/XoCMgeKk9RZ+PlAYgCxeYq+HrJ/aheECEkUQ6lJAqiYN5IVcnEhXFzc4O7d7d4+S9vMB8m4DgCOeDuv77C+PwCz/7dl0Cq1mZFw+MxEYZxwO7qAqkE7IYR+2efYf/8S6RxQBwG7C52iMOAMVwgDQPGF5eIY9KwVwQ6nUCnCflG5i3mE0Ip4JxBPGHkl4g0o4Tke4MBkOapsEUt1ORRMubZcUGv9O/Kk2ivX8ov5WdUWPDr342fYQw7KMYFeJQ49ARYHqs8nXB88xZv3x3xp+/eIecMnmfgWMBDweTCyXsae1CYXQ1f/Hsn9DJaUz90fzfkSM9aUH11q2ggj+bR4jiSi9BjMK/U1iNCcXWnwJQKXS/ReiZXrw8zFJK3pE1ed9JoA6rxzd0aXMcc7UQkO497r70Wp4nXpM5SS5M63dZyF/ev0WLEZ5/mjW9ApaceLItzndtrZ+rY3R4xTAWFT7gLhDhHpBNwOgJcEoAJc2bsxwNAjMMdoxTxCmcEZERQGBF3jJADhlPETWTcfZ3EXioQ9oeCy7cZeUiglDDnglnXVTxhnekRmlX7nAGUAlFAcUEsRXIpcVEPwib3gvNdPQg756kJpCPkuBZ+ijBDPC9mnpGDwHcpophgsnMZ0hsHO989bfOVZWi2Xo0XWyngjs57TAnwEJCgIMZdaRBeNAUJ72gRolgnzZrkNfzc96u782AfefPr5hMtDb9ZlojozPMtSmzYhe2+NjtvqYDo5C+r3j6itHC7cbdViHYf/fWzc3wWSdzfx7PToJ7vx69e4PTsAsOfXyIeT0qnK99G7Py87EFCLBpe1hQXBuDMWMRLQ6XVHy5Vgcira/ePaYXhYDXV/tndx+LNc21tXTyn1nvgnP4I5QmKiOXE/FTLum9PZhsWAoazjzVWbZ+kcGWO3vd1YKMK57LPvtm9b+XTWv98QuauNS3YLA8RWz8W4ylCKKIdxnGHX38+Yr8bECignCa8+/YHxJvD2ZwQTS09gdgJV/2f7uBbEpSrn74nFnPVUEbLOu5TQpzzMnlopu+9b4T52XuPqFOfW7WzsceZ2xHLXpXX+8bO6VpMsFtjzJrQSd/zTyFiTUDYsUuNda/KCGs9DCFgGW6tVUpWwXd2q/ga992UEBUoPLGTEbzNVLJfN+aquvKxX1fBKRideXy7FspUOVFlB38Dq2rLBs/PoPftHZ+zQAgeE4lrUyrMM2VEIEIJBCqyOE57rODUBtuEUbmdQSdGGgaExEIsJ1FAZKjwMPRDrP3oAEASG+asORtkXcSVPCPnGblInoPG8buZNDQC21CnTNdZYqGLyVRNTr0epAxPIdcUYqqoMRgwqz8LedXCeLD4saocqgLrM4UqM1xk0bwf1QvH4Dp4GCYXBlOz1XXspEIDtyjX9iUfdkFgFe62eIzqGd7Q/+gu2E9qQBN9fogFEu1fZvg8trfMR6C1Zrf7rQdBYUnKXlRh1YWO0E3oy6+TYtZqBA1VxNA8I4xCAvsx2J4XgXRhgRcLu9TRNI11nxHyrpwx3EPwMACCU4LjrdqnZoxBPF5c2G30P1md5ImpAbjgxYUq1roJXmy9c66bzeaaCBa2rfXocKUwoAL+qgDiZrymUCmUu7OONFl8KRrKKxCIFVYNbnXAwa/5yqMtdkZ6KDCfyzYpPa/Wv/Po6MoSotnnAqqIKKqkDkETaKsHUlRPCHbAqnPCXDCdTjgdjpgOM/KREcoAyhHzqyMSIlBMca7JqHmGAWMYR+yeP8PlxRW++d3fY7j6AunqCwzjgDgk7HY7DMPg65Tnkyh25xlcCjDNMiezfEY6gcEImRAwYaA7Sebu+KsqjqBnEBOpgq1dgBYmaD193dRuEQifviz5jNW6f4Q+PZaX+aR5Gd677se/9zTW6sda7MdSv09nxBoyfdVWMLxHQALhebrGZboy4krCmAESzhMAmDEfTzi8u8G7dwe8/u6t6lPZKtxofWs4y/Hy+e9cv2+wJecXc3MftwTnsgfVyMbOMlMEQ+n04gZDakLhnz2u9RoN/zC7wU3F5YqXLYRgO5xmSJ0SQnvYDB7GAwDkYQ0Nl/k56fPR4DediuWkPR7C1lBlEVdXE/zgNnocp93N9daUa0nTjPEw4W6aMBcCFQkTlucJgQqmKOs4zROIGPOJUTggcBQKlwaEWIBhB84EPgH8bASnQc4PIoSd5I/bR8IxJDnrcsG86hB5NxmMzJLAOts5XyTxNBXjlfRsdvpE3+6OJvYajd6LYOVtgMDC46AQAhMyCJmEN3GPDLIQUe3sGp9GaBOib5+F7XUjuBSSl1rAJRIiwMLj1JRmoYaBDCS5/SznCWsuPYX1vkubm/kB2XZDSzXdX79zP1Q2qGlj38igu37aRncBd1/ZFso624MzSojlvNynzDhfaIVWO/7RP/pNuIkG110+f/6eu75YT+oggJEv9+BdQvrhNfjA3Z4xxYobgzLAxML/B+OtGWDxKirKw8tc2kD7+VjO6eo0O7OWZwd37km+By8uQejePj22F8tNem4hN649nTQB8N4eEZukwI9QNjbuo8qP9U59k4EqvXjSyz/SfD4R2f51l22i4VOX1hmWOeCEa+x3A/7pd8/w7GLA5eUO0/GEH/7HH5B/uMH+n98Cx7LZuyUuam3mzxdWBG3E8tmOnrcQ5MUPPwgfD0+eRPZJb50pDyrZ2mcfee3BKuxfO4irQH5VZ0O1ZBP6Fgl9Q2xWLzXkEiF4otMen3BXlysJ9NAqWeu0uVDmKU8TShErawASuzxExEHitYtMkMF5dqsXE+6aQNqSKoOLeFio63NUF+ZSigjkjHBwOlbWhsEaP7XG/jeLaxcU2ns6PxZmqEASVVtOgQgVlrHkPSAiUIoIOaEUs8aXpM+tkoVCFEKdsudkc1ZBLYx6bi1A/adReAbm4omDCRLj9HCYMOWC0+mEXJIK9GoIFCfACgtzX2agzECZZL5LhtotCcObZ7GGn06anJtdqGrW26QEe+AkAt8IWLgoBiPnqYJLC5IWu7iOsI6vMDAXrwdqqVUFej3xbeFtPc57UK8DqvPJAPJs/a/clFjtU0dsWQuyAkZsFpQSYNbqZsQiPI8k+eVSRHCZJ6BIssE3ly8QpxOeHd4godRYulGsv1NsvIi4wrgkDG7CUHQh09rShLhxsbNedyJYL7owQIUDFg7KEl3qHi3MYmF6OmE+TjgdZ5ymjNPEgDh3IJGEXzIJfPGZkn8Dab4H4WwxBsFLObN4ROj9ZB5IkMhQxAzOQCZ25WYKAZYPxUXiFnqJarislp+1uRRfB4PZBAoJCCM4DGBKABNyLh4Oam2Nrn0jKJNKnTKhjl9gU4Yi1yTvQUFmyfmNIvu0MlAkycwtVwazGj1pEnCFZ9KEGjmrl5WMCGWeXYEpoYcSEApSGFBiwT7tXfAh3LbkRUBQuFfESOaVRTZW8XAwTygLyQQAIUoIupiS5r0xzOXcFUwYBYgniMG0JJ5OiDGBKCJGWeAQIiimmkQ6RLGq1K1naPp4OGA6TXh3c4PD4Q4pJoRR4SgEDOMImoHTP79BerbD+NtrlEMBfzdj/+IKv/mn/4DLz1/gs9/8HcarPS6/fI7AEdG1tgV0vEM+3mFWIOIG73DJGMp3CDg5nWF5NWQoBcGsOz2gmG3NSm21W1Jv9TDX8rftC7+Uv7Ki++aMsKa3TmcIu9xI2UnptQY+GPhEsPKUSs8Jktd1BAB/N77AVbxQGpSwLxFhmgXH5RnHVz/g5njCH/71LXK2tLuMMmfkufRKiPctjWCZIGdJS50sbfTlOFVvueZaL55a83XVj5SURjIalZs1rG8zKy0NOJ1bGoWEFOPJKqzUlg2HqXdr6ZUXpASyQVVchArse48a1pyDw5oZZBhdJUpvaI4IIBI5jrN5a2r8IHa3Kh3uKecEaXp23v/6knD1f/pL+kV8q4Uwn64ywsWEaSjIJSDNR1FAnDI4R5QcMQXCfJIajpZXbyYEktBA8wXh7fMIKhHhWQLr3MrgAQyE09cDnu0vsYsj3t68weHuFocCzEWUDQWkhkRA1mwSWenbrAZCk/EcKvgPLDARNcxk5U+Uf2pHTg0eE6BCqIQJxgiUQFDHYIQMlMCYLbSYvufzWCb5rgQAax+NDwDnjrGrIt46LcsdWI2G5AlvK0JCManFzMv5iIsh4OshYLwApucH5CHWHcI1RKoZRd0HO9z/XN3vvvGZ/XAWqa83Di8+t3vYwrRhLf2kDhVt1kCLuZUfXFHoor/L/VnhaKvn9oSFCl71HC2B1Ool+ue6zqwb37i12ZWte2aQ6bwoN/+q3IRaONG9YB3gep4QBVCpBk9XJ8J/enONl7sZf9jfLni+9Xw8VB7CbR9CL7xf1JJ74GLzHNiu/L3W7p7yaEXEVh8XqGZt3XdffU8+/Nrts/XyY0ivxzb6uOfus9x5X95lG0m0s/zYcm6e1m0tL3xCY6fzZU0zPum1D6Cl3rvcZzdyzuJ/8x2WuIsII9Iw4qsXIy7GKG7Ad0fc/vAK9PKAizeTWy88SLwB2wvZYr4VB7U5kPP9Xla8ocx4tHWbEihPAr77Ntl93d16hxffHw1QLZFc53UJlyuCiKuXgsXul+ebJ02+1JpHkXgFkLbHeo2AKqQFgzn3yiVVdnCZwTl7X6v1cUNgwxQbQhySkcKNZYx4D4jQ3PMUgEWEx4B5YghYCHlQiGoSQmLExUKERlHQHZgWz7+ZW7JHzMJYx23MloR7CeJtoP1uw2R5MlfSsZG1cQYQGumV1JfBLOFejLkrXDDnDOQCCnrdEmU5haqEvYZlQsn6V/MwMCysleSLyHlCUT5AhIkMMTsOosApJPkuOlNEI8Is8FHrJaL/2Xo2ckxAkuOyEmsB6oWini1mMSgwZcRohftSzMp+rYyzUAdBfa2pnVtQH6aoe1FbJbcLB3xe9b6Gj4J6ljAKCgHTMArDdyBEZ4jJ3cFjFCi0MRSbAxVIt2t+FjMtafhmAK0Xhj1gPNmy2D4qGv7BEmLOmVFyJYItQXpwtECAJuxWNrwqyYgdPm29A3H9Qx23HAfs82EhlURBWIdlHhEN+1txUTP6in8MPoLm9hDFBmsmC4PMYEq2YHlHbN/IIiyTn7tH6moRTNCk/VQvA1IhD9eHUJglpEEnqFb1STUr1TmxscuGFiehus/lP/UqUM8CLozMYh9ZdF0KuHro+I2u81XptzgPJaxS1BBaocGHy3mh6snBMtuW/8NyAJnwikICYtQx2AyQpG8Ba/JOxjTNOE2iHMtT1jBOovSIIUguCSbwu5NaYjJCZsSZcLV/hn/3f/m/4uKzz3D55VfgyODICNMEmmaF+xryxPdzNy0FkW8Q+FivsQnbzpMOZincTO/G8X7PgW9746OUcxT+ug8P0U52/31yKizf+ZQeDstyrr8/Vh82yeIVycyLv/s4zCWOhz//cUb0EJH7lFYYQf8T2g64jns8T8+EHmEGHyeUckIBUPKMw80t7u6OePfqFnkyXK7tvscAWyGRdKmvhLvrtLpu51m3jxno3QjWHSMYNVtPjOXT7XHFgCtELEdX9VquVrRGi4tWelGnKZJh7zY0OljSQul32RZx0bN+ALTAY2Z9Xj1BWyVEVU4sz85aU+1w7W/73MMLvITz5Ru8dYe3nnxaO+tGewokD2I2wVHnvmRwIeRZPGiJJJfbPMkclCTnfplEITREWd27CIRI2LEYWjm9DLnPiEh7xu4KmHLClAnxyJruTubT6AdArhVU/g/M7vHMCi+Ba+oUp4/aQYd+ViuGanAWmeexPBetz0rrs9I/XU3MYJTKCxQWbx1m4QGcKGs+u1lvoKc9kx3MQn2D6o2g148lYySZ/zAAU2JQKEgGrUaPFxnr086MJZ5Z0oy89djj4PlcU04zb9xX+rz2hRbnz31V932tIWP716tStYWQbRzJTufwxt3+ua02HiO76WiQB59u3vMvDf5ma3sxjiCRAJizKnpJjyr2HWL50sRYM/oYhgwMmXCMcTELWzj56YffQ8u74jI/mIBYV3Bumbaub5FqSxj9GGTbLzkiluXH8kj4pfxNl2o9HzDjGmMa8L/+wzM8uxxwsRtQXt/g5f/2X5EPE3ank2Sd+tAd375OeNQhviZgt6rtPSoe69fwEfwfnnaanStb3WiEq9283+cZ0nJFJtRZ0PSWKJjVwqRLfmdC7bZeJ3qNUGGNVV4aIbNHGm+6X+GFAXCW+PIS3gWIUcIwxRjluxHLRe6LMUzxXApwl3K4gNzj5BZuu+rfXcGixG4MpjDRsaj0M7hCzIh8csbCGT6WBLgEqPC4IYabCTNr6aD5MuZSA/X6o2qJThbjlGW9JPeCCYIziDR+PcPXqE0sW3KWOKxFLJMJQma/ON2By4DDxR6zzgoRRJhcCsp8AueMcjqi5BnTfELJBfM8g7loOJ6MOWfMuSAXIOeCopbjVAghRRCzWm5LMg0KJN4WoYYOYocFTzmsOTuamMQLYhZEyED1wlnAVjPZjUWbMQVizU+qGGlxh+33QmJFSdD4/hrGx5I3d2GPWEJeEUETabM6q2jDalkocK1hrNRq3a27Y0QKEZHgwnWL70xgV8QRiWVWpiwG1WywV+ez9m9pue+DFLg24fe5ubNndU+6AFYFsqxxT3XJkIYEIvYwTbY0IQrcFcuJoQrNqJ4Ddl+YN4ED0rj/MrfctQvAQ/8SgsKA9NXqMYWBM1mlqDGZutlriLeiSZxBIvhK5gliYEXwhNUxRn/PBFXCMDTeYe1ZxAKvTKYYUMGUebh0Z5u8KyGIklq2imWveL2EOieywB6iCrr3TQFcwBhCQoiEPM3iQFFEeZcFqJFSApcie7RkzCUjzEA8nUAxIg6yB0KuyosYI9Ig+TzmeUbOGaVkVRxEyadCQExJlWikqEv2mecCYQmLFVN0xj+AJVRDiEgpSSLIcZA9ot4utl9MaF8gSi1mxvE4IecZb1+/xulwAu4CxvkCu8uqPAyBkNKAGAPiMAKZcfenH3B5fYV/+3/7R3z129/hd//+HzAV4HA6oWBGoRmhAKER8JkCLpXvEXDb7DdZ9IAZpnj/pfxSPqxsCRee8PRPFgi3x2W75tfjc3w2XOvBVHCBAcgTkGfk44SX/68/4XhzxPcpY9ZcXyUX8X54cun7cVYJpf/YeduGPb1PeLWu736eQsj5xansQjyufYAagKMg58ZjsbRGImo13Aqr9Kvl9PJ3GlrfjR1Ycil141LamEJ3db2arbRXvRVrLgj5bvicLPgWnZ9/7/+KYLmXgrnnqYVwclUFLy7XuesZmTNtbTyzfNQ8rg2G7NzPOfvTRNVbYZ4y5BwcQSTn5DSM2E0jLLRj7QHpOUTCM4wJ868iwq+vsYsD6L/dYf6XW0yZkJkxQ7wjRLlekD3kkfAbs4dNLU7bGHdHDDfaCsK4gLLxXErrtnNdo3+pJk35J7A5SQAAEgXPjceqdABY+UrWDSCfxM31ViHRwVNjpKTFjdscJRWn+0HCx8SUMKSAEgI4ElKA8CusfiNse9ZZOS9lC0CW5T4CfNF7AOvNZpNppOdmfeflAnzuJSFwH+zXQ/dby/h2Py3nqr55vv6HREJbSofa/CPWot/x71XYgbv/DgAg4O7rz0GfTdj96w9Ih9OiTU24DMkHI8xTRs3b1p4LpZmvqgBp+3FWHPTg4Nr+v2953MvLNu5Xdp2Hx09pJ/JoRUTP1p15Rh+677B7Pzn/x6L4bBRn6jMByEdqpVu55Sq+p8LjgRF8lPKT0MWsqIrljb6Tj4HP83Uu7zsg39fDM01s79ZNDwkWQUgMA8ZhxBfPRlzuIwiMfHfC9O1b4DSLiJOWY1zXd/Yg2Lr8SKRCy8N5dbD1SojHlo+ihNByFh+tvtz30PoyAZVJaX8v4cKJDeuPES39otkzZvVcE5E2NLg2ZIQarcYnT7aJi1urE//i/VZiVxknuyqMiiZ+bcbj+gsNTVM71BA8UALQxtB2r8oJXRlilgh2hwGxVDCOQgl6ppr7QR5thY4VZlYWdVvFhalNXxoyWWWXXaelX/KlsFiM13kxhrMKRrmI1b2bzZHaeWeJt3/UkFCWGNne93wQ9peLC5+LhmSR0Cx1fV1QTEAoQYWjQGGxXGZukx9y44nB3v92pNXtthKxzYfxDBIncwP/+DMt7cay0gbT1faJ+wcZivt0Lqkmv3ZhMxnpJ4tP0Lks1rGWqFZGqvEo8f2jAnlRNJSqHNA+yjo3SsOGoa8EvsFoHfSDR4OjiWbtmdWRg7p1af9cIdH1BwgpQOJuMSjXlXIBBMzuUuY5RFUDaXtEhBKKuiFv9VfxuCmemCW/iOKS1mudmvFXxlQJ9UYQIjyshJxzIr6Zk1pXkwOkwXjmk2P4qjN4bfrdvdMoNXsL8ADRflHT/wprbTFFiUFWB8YsQvdgMTIaPOuoMtY4x0RBLR9FABJIFIHEGnosWIT22Cje6r63/D22B4N7lLTDZxWSEFDYPSFsyzFEYWA5Qdq+UZOfw+tEHVMBY55nzNOE6XTCfDyCckIoEtasJtYmhEjurlNQcLo9YLze4+Lr57j66jnGiz34NIOnE8RjTz0hUNDiOYARcETkO9gqtYvzacjTH4Oy/jTlXO6IH9PL4edS1lOyPUe+Ax4ibZfCi09SPg5MBpJQlpdxhxfpGVhDrJTphFImnA5Hyf3w6haHd0fcjoxJ0UrHGRNcAbmiCba6et9h2eBWXl5q6ZOuvsWnf2c8fq421s1oTDaSrqgct8dPy5Ag9cRBvd7SDqbgaGhro2fNwrs5ULFxJHmfuyEvjCOoOdv8z96hR9Asi9mx7vS9WcyZwT+3M1rHzus3zla1bP/87b53bT/XfOWSt2FdTw0hSyQKAjDmkgEiDEmeLTGAkoRlIiJ3L/B5N5rY48oywi4hjhnpMgG7iHIU5wXW+KVBcUow/s1mbKF4sIxVmavHjaxjm3NPaUCot7lOhG+bVgnEcNsd4koxyXHdhmjSh5UGIYd3CTBV90hLGz+0eCuiDUBQ2qbJ20WMGJQviNph7XxhXuUyebzB4yNvGB+yRgv6pb2xZIge6M3WzYY/WwrBH4q20rfKfddaGNjo4ZKCerQsZtEnw8+Lq+cn/GMcYw28dfkqvA1C3o9ACtiFynsJxEknbA84/a5GRq3ikgBEUqMlNeLbGtbTSSzb74977kPK0xQQ2/d+LBLyZ+IR8fNjDn4pv5R7CxMmPEOKA/7pH67x7GLA9eWIMk/47p9/j/LyBol7YvNHLXR/266AkB9+7aN3Y6MPvYUUNWTpE9vvmJ/1u2doBz+82gfEuh8wAWordLT3PPSKWkCjCCNoXgNVqKUiOlLBjh6Y5mFQraty139m8wggj+vNbpGV3eJFPCGSMKZJksVaUukub5lyFwyo7FeTFZeMMmsi5WzWBMGtsIzrYrdOV6vlwjVJqBJhVZCl7RCqNTLgyaRtzCFKyBOC9rlbLLP0Jw//U0JwKzQTiJrwU4S4ASrZhQyTxcJ5BpDEor56QpSGEGJJ+MYFeZ7BJSIFgFLAnCfkkkV4x0Aiyd8ATUpdJrEwnqcjyjxjnk/IpWDOs4RyKUApM+Y5Y86MObOunTIspNbcLLk4CjOoFBFsFhG4FpeTVoYCgCSgdWZMk1DbnEPnQ2GXWeefFsJP2wu2RhanX62vilqQi3AVIA9s3FZANeEfCyMVvQ+NxFmFuBxIeDBuYKVCvu8dtwaMEZEZJUbEYv2wUAXkdeRsQn9CUG+SpwvwjHStPSL3sKlPGTNVQnG80Ao2OoUghL+Nw4DxYgfiEQTG6XBAzhOm01GTJLOHTYoAhqThAzrMKH0KHNyl/zECoyofkT1doGlEPMqXMokq6K5WnEJW5jwLXggRoIxYJBwCsYSkMCvDlFKXONvRa4PP/DzqFEns9wKa8BSQvBMAdI+iY3o1eFVNMN0pYgsIkj/E8jSIskI6FIgkN4LtCc0JQdFgnDCMAwjAMI5qcSgKmWmaEJlBweJ7s+RrSArX3IRrABrFDDzxdQxREk2jZzajeaGQ7D3JDSEKgQCIRwTJXMcYESSZDAIRcs7IU64LHjQ8lp4dh7tbnA5HHG/ukE8zLsKISAlDGuQ5VSYcwwGZZxyPM063J7w8vMXw5jv8KTH+8Z/e4fO//7cIFBERZM9nRuBXCPy6gTpjlucNAIXipl88In4pn7g0sjbgfsHQT62c2xvfjM/w1fgZRg5AmUFlRikZhx9+wPH2Dv/jX97i7m4GTzNKYs3TIjUy6vnUhoA8LzB+3A41wb+LHFsFPQBWQsTbUBzbKvnrSfe4Nu1s2eqN4GCh8/IiOXUp2T8Bdnq6UiQmyCxVqaohOLk0HtB+5rPQNVw9F0yZEGx8nXHktiKiKiGgOF2eNQP++7Hlp+DattvZKkv4Iafj7Z37e9fKIisvpGMOhMbaSMJcFiDmxmuSSMKegjEji9fgfgBdX+D173YSvvNETl8A6GBPeytzzsBwSghTAH0TQL8aMPwRoB8Cbt69wjydwCTeD8K5FT2f9cxr3dpZvdyNZkRxAwbome6cIlHNFMUGh+y0c004ze59KPmf5XtUI7VgPIGGs/X8TEW8OEyhRs53KaHm+KDybb7JjF7rV0Zyb0XCbkjIYPzp7gZpl/CbeI3Lq4jw64hpBCJn5RuXVPYGZPA5aDkHQ4t9wU0bxveeBT++59c9T7Jvab8h89OP7L7jxvrIzYX+fDIceu79hnt65ObvscT6Jb5/suprvI1vtnHy8gJtXG6hot7wOSY47yyO8uxhwMzr3J3PqeLKfbrC755/g1fH7/HD3bcPDm3JTz08lvvLxyQ3fg60y3spIt5nWB9bnmpzW+tdoqk1cH7q0u+PhzblagDrOj5SOdPUR69/cXXz2b+YYH2rPDTZD0zcOQ3zfc9KtSL8TXHAfhzx4nLA9UUCSkE5Tji9egd+e8DA1dXRLTMXTbnV8McqJlxsx7w6r99DCbGgOM/1ews+lgK1zhKI28rpMT1ZHWR85vrqtZYp4LoYK0TfrJPYKDdjMiakcl7rDUTNX1s0twBKQySiVmWHfEcos45QEwpaXzy8Cshnre0KhbZxE/YC1YUX7tHhAmkVFprbuvWsWz1fL5/IjYHC++WCYxM8sobxWe0+s8YHiIwADt4MqwAr2px7jPS6ruwts893neGC+pBanhshM2fwaQIVdotnoHo5OEXLEsaqzf9gicptztwLolT3/gZz1G+6lp0nhHNlBpcVNi0Uk92oVviSoLIE7kNkde3Y2isjouYk2yvHYNY5ILHranNztM+1uEOWuMkFYtJoWLsE0jXgtuGOE62UfdU3kKOHpVW/1d1aOD6EybuwUR3EnDkLVqiB1TJNx9fiRKrMrjNeMUhiYoFulDkCKMghwPKTyKKoQCbY7rD9X+eeqU5cTzfB90I7Fhjzzez6t54hrAwTk7FTFYaMOWmt/sBwpZjhOE8IDUKbvZIaxGLreW59KBi+CB0+tuEr+yuKEUBhibr/fNTUTVCzt6qwx2AMkPBXIbrUBxQiKGpopskSx6t3iIWzg+DPEApEhdSfXOZR4r9tHiwLeRu5i8gVFaZccDhl8pjQpixulYq2LlyK5xkJJOtaioZkmTLynPX8gCthKElbs54Dx/mIU57w7nSL4zzhzfEGQ2Ts3r7Bu9sbnKYJQ5SQEOAMKicEHBFwxLpwtwYbd1ew8HFIywr7n6JUpeMnqf7J/fgplJ9SX6y0OGtp+PKTKWdZ3L6PkQiJAi7CDtfxEigzUDLuDkfM0xG3N3c43d3h7uaEuzvNH+ZJkdvqlg1Sd3W7/Q0KoeUdGlIYzfVKky8H1ygdWjr3XLkHtHqWRFdchbYuiFX6wOmETlFiZz47Hd9ZKDPDov9XAVxTHwzzNx1yxBAqXQ0oPUvdo9DrbUg9w/vnlBDL2eIz08f3/HpU6bR491b+nqUzX2pPThAxODTeJqgwZjRxMbqcydkqVtojUgSliGmQPFbxMXAG9YYukh8t7ALCGEGXAXRHiKcELrNTZoHEGzAoJATrnwvw66Cc92L1DOae74rK2xjctfAIKOfS8JzUwjKb2Vubs6LoM8V5GXueGrh3orrhVTsM0RgMdLNHwn5J6NQARsFpnhApIUVCSoQyBqF9mZUmLIt1xubvJ5WWDm06x3UAXUtdW6v7/U0H/40Nx+jP/w73PbJ026vlgTaqWosn3mfWnJCutawnpMfdWNM559p+3PCtA31btHSVMZyQAkqKwGR7QeC1wHJJKvw2vJhFZUhMuOCEG05oAGJRWj75vj7fM6JHvXcPHfzgvN33QLOP/8J0zUfyiHjfQXzEwa/plaeVj8kZ/AQJ6x+3/K2P/0xhITkmvkKKO/zTv7nGZ1fiCYFS8P0//0/Mr2+w++c3wDFLvPdVHVDBhqVd+zhzbYJns1IHGiK2oykbQXpz7XGN9HVZ/5/C3K3HbCIxJcRc6vhwXf3x/cCD9qWjIPj+pnj5fPueEXaoRKgyVxaKi6i+JCFbcvWEKFkIR7WA6gRkYHdtMCsu2OGrgkqxBJb6xQrGOmnPmIdD8Pezx8nN6tWRPW9BjVGr+QzMG4JZw+LABXCeE6CZDqC6I4uFkbYdA2IMyLPE6iUq4Fi8r10lDHCwdL1wK+gCoMwzwJK/IHBADKKICCF2TIrNOGeNF1uqAM6YTNmDpjBgDH+6Bb4P4G92KJcJnCTnRskzMmk+jgCgzOCSXRAALrXOnrzXZHZALuIREZyQYqCIhTOKJBQmhlgtBbhiopp52H41hlhGInGPa16AUAI4EGKq7v3tfAA1tJfRfW1MYgO/KnzW3ci6qp0QubIrIt8tEq9Ts/ZyyC4c9g5QQVZvjS4urDNALHtHrcgDSczZwgXIwugwWDwGiJBidDlGIMsJEOq4gu7Kwp2Qt/nw0gruu6sudDT3JNhMynWdqzYUlK0HEICQMOwukIYRnCegZPG+4YIYJbeBJREXT4WAISaxjOe2voqkqoKmmcIARLWpa3UjMYgloIXOKcogUxF22mMmm7IKYeHKr3vQcHQpyuxrbhMKnnjZZ61AvRD0/KFGIYkWcqzvTagh2DwWlEIN+hWcFiBKAxSgpKih6WpeCoeHGJGiJA1lzRUCSHgsH4vitZSAcbcDhYCikxuSxHQexhFznhFSFIF+FiQbY/X8CCEAQzsiuNDJ1qkUhkVasmTYZoQYY1ow/CYVMOWN9jii5gMi8nBRBUCeZ5R5RhwS4pAUFzKOt0dMpxOmwxFlmnG5vwDtA8JxBAphHicUZNwejjgcj/iXP/8rbg53+POrH5BDAX0+4stnv8bvnl8j7UZM6iETYwSV1xjLn8BUum3TCth8Vs7Q03959umX8tdY2qMWaHFPxUE/J7j71fgM3wxfigKwZFCZkecT/tv/7/d4+d0NWD0x51N2urE976AW+zDh5+q4OzcbtLrVhjtsKR/jKaonxII+b9uUA0HPkEd0Y1E6BbkJmRioxiZKL2lMfC5iuV40r5vll7IY4lVRXY1ObJwl15CRKOxJrw3IGEHIDlOQK862HFDkNIkMsB0iGZ+A5vwKFUbfvxhmfQwT9bF5/Vpfx+u1zSwUWf3bhEQ3GMo7ECI4mvVzNb7JqIp2QFMhEAEhIMaECxrB2KHcPgOReD/WPrX9tDlyChkg4emG04B4SigXBPwdcDleI7+5QJ4mhHnG/OYlqGSwNCuezEGhkowfq8ZVbEY4pXopuOEXbFuoUsHoMfWG4Dyr8ZqGYnMDKfkLWmdQnjKwhIUNmi8Q6o3hYU/PrNzW9c6QUh8KBMQQkGLEmCR32PMhYbdP2CdJEq5pw6U1VQp2LfEyYn8PBY8Dy4Yj2RzU+uLD1RouOWeoRd3Z8v6l7gHe/P2o3dvXaLjwXFuAabWw5HU2nmzqbLHJA73iRV3d4xUjKCcKPZZW2IqJcPvNF6BpwsUfvkM8TVUOAgI7/AjvZ8aIIcj19O4Gzw4H3OxOwG6rL3LhsWLj9XrzA/fPP/vhhfvvy8H9BaxkfpTQTG6ZuH33g+reVGq2N+5tur/xvj3pwOSpGKZSu+/Z+i/lJ10a1TgjghGwGweM44DnFyOuLxOGISEfT5jf3KK8PYDuZtBckf1K0K+3PpYSoi19eJBeSbClhHhSfRsnxvtYmPV9wvr7x5+Wvt57ury2iDZp2OqIXrwHNy5Z4gK3eGCuCe/aqptKuplpFB5t/1qL2UrTNwyoibMaIW8x7rBxLW8PdlNweLOmRGsEn36tM8ht5sYGxPU9U4aUxm+5FRAsZsoJ1y2PHgZcAOdL2cxFK4V1ZrVUi6HuSGH4XqApSzL5WQl6klBDQhBXBYATep0FSwUqad76Y7kopBSoW7X2IxQJhxKKWH/VjhcBpMbUTfreWOuh9t0ZZhQEDqoYWCoHudbHvdi9NSjprdlboXFrKd8sSFO9xYMtXBCUKfPKId8JluiRm9cEp/RWtcag1wbcKpGrOzsZE69cv/1u9yHXTWAXF123vjwBkzX4e/mOC72ChDQK2o+icNTmdgGHxvOo7lkiVU7RYtabvbjCVO18LJ/g5qzx+W8YLa9IV7pZZqJ6v55ocrFLPr0xP/7kUjG+geBNGFPf6jrm9yVUFCRMmyegJJ8rWHtkfYTiFHR4ExAlgilkKISqYCJRFoQYJVm4vlOKKG3do6wb+8PQ041B8YMkra6xbW0sIVB3PizxvuAmNHjc+i1KCi5AyRnzNEuohlIAVRjNJaMU4DgdkJFxmI44ng64Ox5xdzzi9nBADgVjEcvSq6sr7Pb7euaAQZhBOAlebA8J1PXmiuifTlf/LMsjCIx7ytKb9KeaK+Iv2Z+ngVJ7Tv8YZYtOXN7HGjycwDKsLGUgQgoR+7DDZbyAJYC9uztiujvg7uaE0+2kQkkV9i3ZZqNd/VBsiyHqBmFvdNefXgiZjBpx8tZHb94J9dkHqt7gn+/jU7Zu2PML2szOPiEeYZbh1TuiJRgrrW0CXMGvMnaPwe+02NaI9KxrFON6EtW7+o+fiv7swzTIauRnlu5RcM/3LFBXzf11bUH9fTuBF98akkTfzUglIxOQGZ4QvO13iwOMpQ0UgRCQYwQjIpSoWgLgzCT1PWk6TYVATIhKiod9Ak2MxBEZjBADuAQEDQ2ajEbQceRA6pxD4MCaN5ob6NQ9afAGUT4IrDTGSBpe0RRrzkPC9nuvVOt4RptY1wrWfCjL6WigU79tr55NZVBDOKNr4xAxxIAUZc78/W4/tbNNT9/i9zy0RVG+f2mMys5suA8S9y331MZX3npu/fij7qznvq7P5hurQVNlRx84fJe3259mtur4mKo6ws4Sr4QIZUxSQ2vUot8qvPZSLvM0CpmBnMXQKOwwlxl5I1yoJVFfGadtrnv/88engvpzbXkVUKg3OV1/9ZOWn0mOiIfKYybq00/m3waz9Et5n8IgnPgKFHf4p99d4/PnI55d7pBSxG63w3QsuPifoohAtnd+BHjakgOdUeI9VQmxaooWcdM/yvCWLpOPr9QOo9Zao9ZznhR2efni9lowbs+X/jnU+Ph2RWyj3OwVHSmnVlhFcwywWTmDIekHAbOocrLU3jEvBLUYDiF0h6bkmVBFAyS2uLxg1u9FeayanyJn8YgA0CU/lbE2wnf04s6iBHAkEZ6ZpXkbfoiLWAQZDAYKiEPS/AdqwcQZ5rFh71VZaC/eNYFtCUKU5zyDC6HEKExeFGFv8FwQ2ZddwvoWT3gMNkKl1s9ckOeCAsbpxChTRhp2SJoM1lLRGrG/BBqzvg+aqC0UYZ4QyD0iMIvgL88amxiMxFmt/4Go1t3ubgp26DFvm9kVSI2LM1fyzRLkihAzgCgu9n4TCswYaVV4hEbCvZQFtxYsFSLMZyUAHuaJPXlgIda4yaY0gPax6Q+K5u2QwYTGEpDQi3iZDS6sTyLMp0DKEDXW/SB1PxfljyQxgwoESOW8i9A2zb+tPMGfI9ScEbrmlWaurGVbQoyg3V7N9QqmUpDnDCLJETCkARwCSp40D0vto8yZeicshJGekG2hnASxvGN1mGIRhmnq06b7CCyL48kGmWFJw4EguRRClDwI6nkQgnijSJ6CUD3xurmshVSj5XjEpTOW66UXzm3PJlRIIzlfSEMjBkuQTerhoWMJQe8Hy7ch515UbxMTRI3jDoBcFxSZ4YmjU0QaR6R5QggJmSSXDAHgJPWEWJNHR819M+esuTVM8YGq2NDcDUSEGCQ/Q4oDiIBpmh03ybNJh60KCyLtv+K5UhS0NKdOlNwRKSacThPKnHG6O+Jweyeh5zJjOt0h54x//e573E0n3OYTwMCQBoAZxyLeaDEEUAq4uLjA119+hf/l//yf8KtvfovL/QWYBRclmI2nLXxlGLtls/U8YzT0I1D1v5S/slJptx43/jTKfSLY+99qiCAAwBfjM/z24hsMTAjIAM8AZ/y3//IH/PCnt5inGVXouKRNrB/dSVp/P7jx7pHMcP3ZCuoZaGgMrIU1Smb0Qnra6Mu5+atCNKFtWWUuRiuZsqA0HWBALcmZs+bwynXOvM/1tysqoFb3rDRusUBNS/5K8LzTImSfqEr4TdxYz+hW4f9B5bGgd0YJISF92t9Gay6eW7xOy7Xe6FMHQsVoNCicGB2p3sQADvMBpwIgJT8PAajVvy0XITP0LB1Buwt89+UFwjjgOlQPyLYrlX2ta1nNfOA98R1EQLoewZcJ+399i/SOUfZXmNKMmN+AS0aIYjigTuTIIJRA4kFTAmbJEiF5S8w7B9VIinyeitKMLJ4QXHMRSk65CttsjSmNWXOgKPXrRlRoxtmurO3FxR7s1rJfPCLx+E9quPHt7SuEMeLLq89xuR9wMUQMyQTXxfm5noWmrurN8ig4bmjPHoH6/aduqSpw1xo264ULsB9R48NPdHtpvZFWNSxwydPOP+54qe2+9MZqtRO9Asae3Whh89cq2oVuRn+iUcoZ0jH+sa3LxFgEzVHJQiOXYiHtqozkarjG757/Bt/ffYsf7r7bGvG9xg1uS7N9e7O+x137sHLfCfmXoKmfrohY0iofXFYg+0G1WPkxJrNr8wwktkZd91e2/eDfLKP1xIG3+P/cJnvvuXxgEe9XGBAkEEXAxW7AMAy43Edc7iJSEuHM6Ye3yK/vQMcZNBc0ePT8ID4GbmoIXR9Le6rR4w6preP63JwsPS68rScUXn5/KiO5JBZW/WfVQ6xPGBP2LKYJTottrc+avtHY3UZQGWNVcaGLUt1IrbVoL21VC7gUQsGE/tJnc0LoCUarzWWhHVUrL7LCQM1rUEP6hFCTVFelQCUUQrfWzXrTYr64vudKiOYEN0tdY7aY4YJIeU2sm/t5rgOynBEIJAmjEToFgykD2JIsc9vjgpoKTq+xwbHPICypYckZSMYwL9ae2gmWNZahOmssEXmKCuODCcslnEy2Fp1ZgLhVFwKHIvUUdWnWyTUFgn+WLrBRnSoowc/V26UyGD3x16+qtdOwKDaH1CiFKrUIC0FW6xEvDtlzDIdWMtfsHr5tDtD01WrzpOwsYaFSlqScAU2ommZdOpAxoYDVX7k7WIfbhIWthfdm6fbakkhu5rBVUNhnaFjgAnjYKOgYQhCmPwcEsoTbtbvNVx2TWv40OKbS59UmyJUQrYW6uPigLlr1IuhWkbWuUOdN9Qi2E13pY3ijneFlr1251TC9XmczV6sk3x2n0lStfSaSUGSeIFt6pkoI8nbhdde2QiD1aCBX7rbtElc4CTG4t43sd3g9ElIqujcFrN+q+LUk3TJXtibweaMQurEbc+UKSVXwBMf8wcN22PN1mgNCrPuWiySs7P8KTvOMaZrw+vYdbo8HnDSvxLPLKHMXE+JQsNvtwANhv9tjv9/hYn+B/bhDjBElMzLPHuZL+sKu4AH1uMSX7t7yvpTd4+mGcyRGo4O79/5WfQ/yBL+UT1bun/sN/PG4F+9v8wOf5NWXc48LMkhE2IcRoRRQyTjMRxznE46nCdNxVgGM4JxtXqOpeE0iP3pAC6zuv1oep+Pb2IbwscQi68Et+2SkR0euucEFKoL171XZYKEIXUPvjzdKCKffF/1wZTMAVz4Yqu7PPyx+LT/fuzyEBs9K2R6okDceOicnOXfVqnIhY3e5gRMW4S4BZoaTAWQufR4O2NrVeiSnmeaGoAROA2gYfPY3+8qLH0uarn1Tz/MSAtJFQMmENBD4ROBboeNEGyIwV8i+Q4GBRSHC4mlNTQeM5pBfxaynKq1fCkSRZvkeNMwrVxoaziMYLarKQR2Xf/p2bCDPCDys99TWGUdoDCwgntgxBAwDIUVJsC4psBrvj4Xg2/i+p0L+vWC+glUZDWM9rqYXfRUbD1ZFZwNNH7hhl/TR9rnQz9kGeN7Xwn2NPygT4u7fnne7t+qt9lcdX+TjY6DKTXhjGQnzmBCZQYdTc1PrMnmOYg32RRQYTQXYT8CQcbY8Rvx0/pGzq/TJCrdTsCy2tdh/NvP76crjFREP7uKeyflpEdkbnfmYHXxACfG3V7ZR999iYQATXwJhj3/8uyt89dmoComENAwodye8/L//v5Ff34GPs4uMPnlphDlAc7j9iHhxmZDzMQ2fMcR5zw6gs8Sh9gb4rFPEZhiYhiBbv7Bo1uLPK6Mihx+tED63ruCl+SwMaB6HStlovNrC7glhh6zINUOH81hdcYtRlyQWWUGF/vqQxxMtapE9z7Pmh2Cx4k1JQpCEiMJiZSvVVasCj2sK60tUQZqkaivFLP1VYOYMgogIYxLFQYgRxgTKgWneGgDFPo6/T3wgUAFSTNK/nFFKwTRNCFEsywkyDioFfGLNtVCTU3MpYL0mZ5uTyJ2QNc8z5mNBSiNCkjjzOSYnQSUfhSgYTOBYWCyEwWrdRUGE0MyIMWFQwm9GBudZBO0QgXthqMBRvWk05ru8bx4Naok3zz5+6DyZ9TTVhVJLs4BCjZB3ISgHSbz9OgP9+e+WKUVgmpbPkQls2dfa+ikWVkX3SGhyNyz2hvY151kTDyqjX4SJKnkG5YzP7t6AphNoGBADIak1uikaCi8ihTkkslvdwfaR3rc8FFZUJeA4wIUKKmDOCnPm8bGcKtbrhldijGAOQGDwPKFgVrZHrNoDGMQZBYyiSipb61zURb86Ywh2sGabjN22x1rBO4IIuWMM9RzKCpdaSD0GZD/X86rCloYgQmMdqcLzGCJSGkApASQeB1wYpiCohboP1Gp0DUL3CR2L5bKoHiBWieQgkaTShBiBGpoJdT8EQs5iGRhAgOeQgI/X1n8YhHw+Hk9u+SrPRFCQtXIvCp1/y5GQhgFpNyKmhKT1zPOs9RSEOIjniONK6WNKgmtDlLkrahIqTQh8hxCQkiTZK53iKbgSuWR2hU5KCUNMKDp30+mE4/GIaZox54zDQb6/evcWd8cj/vDtn3E4nUBDwrDb4fMvvsSYEsYLgeXr59fgMWD31SU+f/EFLsYddsMOYxxxKhNyVtu25nytDOEH8+m/lF/KRyjspAZgZNZPCzL73shB2l2z+J0s3hB/uH2JP55uMJUTNBkPANZjuLHgrocY6oHW8wvWpDS6NS9e0+Jy4yHJzacJR/1tRwwAaBUZyvCEy6HIO/ToQl4TuyAKi0+3sbcwNmCnNVoDD6OVa597uqZv1w8DN4aRPGsSdi8oLu/OjW70PafyKRBmayT2lKl1o6b2d/elbQMOD0vGzjKBVQVEhQ9meJirbmqNpgE06TP5KgJGHxByKQrzMrOMhECES9oBaY80fg6iBPB2WCY2uG/6w1gP0alEMpaFMb64RHyxRxnfYsgR0zyB38wofCee70HGlDXfWwZQ1Ou46ACzjadUJRexGouVonyCfDJnICtNobPjFJN5RLB6QmSBbw/h1MDA0kBRADPUMTZjblQIzZzIbEfNJ5hiBKPgIkWMY8J+jNgPASkyYjCPD912a0y3WpNHlcX68AJvnfN/sBlbgNqirvMPtJjQwnx+irKstq7Zkohe8lL1931do0c8td7mi7bonpV76N3FJLMhp4aGXL2TIm5//SXC6YSr//ln0FzzILHzSGIIV7gIv6nyGeKA8c0N0s0t3l5Iroj3K+t+/VjlrAz6sfgcPw49/mhFxArJrikMdKDa0Cf8wGgqQYD7H7zn7Sfdd0u79yvdVGwdsBuL7ATtExt931nZrOuBPjy8xttl+7kP7PFyDjfhrd54zL56sMqPURawLsR7ABAxjhH7UT0hAEzfvcH85g755gg+TI/rzz0DrYfd47BMF2bmI+DJJbn90BP1AHx45A3td7a+B5p7bFNNew8dIGdwS8eILJ5S4Q8HOegYaoUPTaLUHrRG4XZMmf3e4MyAJmxT02SorIyPaLXXq1Ww1SfEtSSd9lBPXOs3odxaodVYXrf0a5MoW5JCGSGsoyb4bxQAsad7qxlNS+QWEYpycWHpalWqyZkSz2YxVIntQAFMLHPFizWg5bp0lVdBpTEDqOefC0Jt3WGCf/OIMK8IY6oKQFUB5DkNYBbY7CGqRDFVUAgoZQYQMROJtbcmrwagyqnZLZ0ZNh0BiKoU0D4yq7cIsow7KFZhlrlzobX0qdK4LYFYvQparwrWUZv3Q4e52eaVtW5V1FBQBmrRDou3Sim5UbyJcKWoUCDmGaFkEdzHUK3LTeCp7bHv2bqnTEjiC8kMCV+ke5W63vs4TYjTMTW+j3uc2zJsDk3UW+kskYdZuxcTVuha2Lxbn8yfIlAT9g3cr1dDxzM0HLLuadmfxsBDrelUHeJeUDUJeccccr9eMtdGfAjYBeqtPm0OrS7b6l34peZJoNIdNdRVTQTqnj2LuW3n0eFZx2L71byjTLgvzzc9tfVtlFM2O1XR1H9WLwj1hIiikAgxenuejyYERFXaWDgmoPZTlIfmpaXKWMPfISBEeUYulzpmtGdKnQfSBSmzKJsPxyNub+9wc3eH4+GI27sDpmnC7fGI4+kkei8K4gGhfUTQfRoihjECQ8Sw2yGl5PiNvR+iyGy9Sdpyjir4Uei3j1zuo7nflyc431Y9l9vfv5SnlVYBsVW2wuT8GOVsqwuCbqCIfUjYhUGEm6cJPB1xeHfA8XAATrmetd1A7TxpPMEanLnsBbdfaHmXVryQPdpSCvWcbZ5Z0Fer4bKTzEBLZ24fEwvEsU1LEHq84xR8Cwzdd8VpDKUjS7PfFvRj2yWlPQJBvF+hZw/s/EA1AEE9A8+ufrcsaxrsfUorgG4/z+HlzYfrDK4RNxpar/7o2l+9t6p+g8ulGSAGl5PkMbJTuSPFGlrMRqLhWCQptYVTDSvEzC1A8QKW10u/HLGvayDJ3QIwwrMdMgWU2wmcGfNh1rGpgUbJIKPbiCSXBCnvEBhUbEysigVTjFV62HJB1HxwCuOeH8JopfrdBwhuQb5ONdbnVruHlgvYQrDRuByAGEj/AIoE2gfwoEYwTOIhv4S8ru4nQPkKqS9DrG4tntBYy6ZWNMs5ImbZVpdA7fG9P4vCmmt1x20ivs2+8tZzZ6ahTvtDdMW5+6T9PDfqZT/Wk9q+u0B5G+/rRwrgHCUc9rJ+IlcS+pGlvE4h2VOhAOki4nK4xCkfMZd1roj7y4fTYR9Myv3EScEnhGbq0ZAsHjZ20gbh8KSa1+XHIvuezOj8Quj/UtpyFv+K1CWEiJTEEwKnjB/+H/8Z5YcbSXSLNUHen+yfpq8fg1l9fA2NQLcl6LePwwcaeYDyO1fZ4pzePtNZ3Fu9np6g6n80wicXAPQH/IIVgVmiF0DDYIpGXmxe1EtEhfFOHJayUVfTZ5Z6LISStRNj6Cx/i+V8WCSODmThP9TSXdvMuehnRskzyjzDLbliFI8IDVFi4+6FdOxhgqJZRacEIhW+cVFLHGgYExtMQSltzHp5j3MGI8OSStm4LYeDEBQt2cted2C19C6QcYFBc9D4sOLAzdFCT8mrpRSYKLy17qlCJAufwgBEKN56gDi1SaheLCECJHH0CwrmLNZIcy7OEJjSx3KCUCDElGr+GJaY8GJtL6FTLOY+ocaSN+KKy6zxZqtgEiS5MkzwiRAQioQMY1IrfIIzyh5KJgYfV0vaNbJmVzSYFVrH6Gv4rZprwe3fRDEDACUgBCEEi4bWcsGzKnwkme4Jc844HY9iyW5WnhQwlIxLbUcsyQkhRU00bjkmCKEUTS4OBKqWjq1CcZuqqdIXU7B1gnMGlhb6Cj1dTcs40CEE9fIQy7/ColQKlvnQBeho9Z5drywZIHNUeOJmBaAMp8wDK4xYHoKUJIeD7hxQyJKrRD1EQpDYYyEaYLMnDZcOaKeKhNYqGvIsFEEQ1o5Y9atnhYc/qzDnOKk9N1A9EsyDC6TjKOyhuYqFKOhnWryxDKYVT5iCoJaCgOq94pjM8u2YwKi1lCPJjRBCUN8LuIeBRNYKGIcB4zhgHEcM44BhtwNiAAdCmUSZlpIYKozjKF4NMH5J+ptiQogJpnQ17w1TCKRhqDl7FketjKH+ltwUESFFICac7o64u73Dn779Dq9evcKbt+9wOB5xc3uHaZ4x61jH/SV2F4Rx3CGlQfG/1JtSxPWza4RdQvhsh93FHnenCYfThNMsAtAhDoglIRaFzfckcrb35S/ll/Khxc6iSh+veMO/kDLiMeXzdIF/2P8aoQDIGcc3b3F88xrHP70F/3AHzNnxsxU/x8kEsHq4NKTUeQHSQ2Vx4jXzqj/9c0VpU3Pfaa6mvjZZ6AZC6JUKixaF0PDKyTGR0NzEak9v57f/NUl/2YxG2K24gbWXZafQ1ikmPzPMExmep6gqvqmtZFX4zHW7t3XrLJvK2w/1z/NiGhe1KaEsHz29sa6vEXIzb/zuP21t3JB/0f/Atxim1zjMB7zjGRh3oCHB4v3YfHgkMs/JYYr/AQgJE9p5o/rZgE0Lk9z84NWcGBUlbwXdRReHC4GZb65QfjUDh4B8N+H29wfkWdizUjLKcQIDiCxeEikSMggTonipCzekGSSU7ygZXOaaT7BIaKbqOGvrU+EYYKedLTdDXTc316rD6vBfo/Y6A0Nm5GE5CqXXQEqEIUlYpvEyIf/6GeYgueO2jEl8VyzW/z7MtII8JyXL+mFUPPeY/dff2NpxhseUdnR8ZUL5hyp/mDZainBWILis+p4qz95aIvD3Kr4Dn/bWGS2P7ayudGx//4ThVHOsYIbm0RNjtKrTLjDTLYPz6+EZfnt9je/u/oSXh++f1P8PLR8uo/vp0ipWPmKy6o8z2NZu6kPa86X7gG5V1ndRJ7De/duXzj7zVDr2saD4MUFuOZ6/KO29XIyHb/wFimEyFQByAkLEs33COCbshgAw4/Tn1yhv7sC3J/Apd4IrKy582cLbPQ3wacuZthi9zc2aXHh4PbYsLfoH7r8gLqnn39u6RYsbLfRsM0Ss//NqKbowK6vNcc/CmAWvCtok9In2Ykmwd5uwPYCVcXDax5gl1LpbgRvJNZ6tJsOzi+TV2qb9Vy1sWlFgtZhzy1wX/rP+bDlDQvCcB8Etqc0LQEV1AjPafxcGo4aIcctha2nJALDmc2iE1sztWEUIWgjwRGjFPCpQx8MFa4hoYR3CKZCzlx3DXvukAvfmRdZ2jBu1VgqAWYWKuZhCQxKJi8Cgj+NcjZbquhcUTxztXhq6DhbSqeaIsPmWMDqIEVQCEC0MjLJMBJDl4NBBBIJ6Sqh3ScusNR9tqXBl89zOq2G7Htk4U0e8YDzY/8SzRUKG5TlLIkkwUkiamM+m28IfqGcALzCUKiVq8sz1DrYx1DBKvbVdVdxs48Xt0BboLCD9WQZYYwXb9gq2h208BWBTMDp8tAmXK74jj7qrYyUSRUypz5kAm7QxmyHiAKKiniNw+HI403Y5yKRZrgVq9qHBqk4UfN2NQ23mKKDNi6DwqErZpdKmXT4LLyCfWZlYnReu3izd3iYCLVaa6mQr2iR/1hSgYpVY8VJgVsWJSplKa2Uor5sir84NNTAlireYJLm35dEwOKdgYdQqPpf9ERCCKZ5DA+M2zza9TRhEqjg8SHIIAMA0zzgeD3h78w6vXr/Gu9s7HKcT7g5iYaqJJDAOI2KIolAIUZTTIUDc22OFoyBeE+NuRBySKosmhHJE4NOTieHHsrDnqlvT50+hGbepiQ/mET9B+cUT4sNLS2l1nsM/yRLAGDEG4IqAy7DDQBElTzhNR7x9d4M3b+5wPMzAXDRk00Y1nmerpWcez4f3U1TP0/7aI8qC51jt+47NWvB/Pam20bQTTt3Z4KeTH/wLbsBo4oauc2W+EXaLrsjXliYgvx2UNg8WmomMDqgU0aPm54Fy74xvEjiPrGVp/dD8kCldv8OLXyslxLnWG9qh8oz1d8iMOGdwPCGXIzJXr18zGjDg5ObMsdWIISDGAcdnl6DLy26t+t5T18+2Xx29ujlyPceVkLW2iYBIAWUcERAQv0wIGl50Ppwwfz+BS0EEAeY9XTISitokkdduSrPthV0QtA28Ovw2cA7A6+rp7tZbh5p62XmNzaK4xNJUHeYTECVpdUwR6XqHcDmKQVAgr7M1UlyghbZLj4Jz5uUFrJa5a40WDz1qf+gc+S9Z7CrkDrUv7V7fEmRwP/s265seQ92PNW28LvcgkXvoh/ZcfGKteDwFt/VUQ7d3Q+X1Y1v1BcJ0sRNP5LtTA9vGv1T4lVBodk+upyljd3dCnLeVVx+7/Kg03GLR/hKkznsqIs6d9j9lYk3Lx5jlXwj9X8q9RfbHjAswX+Afv7nEb77cYb8bEQrj5f/2X5D//AZUWA/RnvitJJIST/ch78fj9qZ32y+siN9GqObJWzv688P3waqGJbFw9r1zJ879b/ckA6+vG2PSWLe0CpMlr+XGY84SsROGVpyesd9kcx0k7ifNlTLx9uF4ZknAAxB38CCC+sg1J4TkfmBndDzZMYU6Dg1JVC17m4EZw+XhmEwhUC3AxHg+unVLJdxpAUPKhKlQL8akgjq5m916WVjpSv8rg5cLOAIopDHXo4QaoH69CFAhF4m1PhtTRwDnOmsExCRW/7mIoHLOksyONVlrCFHUItxYVkOEhESaYDyLPU9gBqh6bZgCxEickgsKFUQGQEEYJN1HNSRKBDQc0uk0IeeM43QS75MyuwA6RgnVUho6rDCrhwgvwlU1x5zOKRdlW6hfHwsZk9KAEMUaHirUrIJM9aox74lGeRFaC8qOUfGNUeG4AqDE5+TQMOABlpdDLN7Ma0JrIoA04BArDIPFI2SeM46HI6ZpQp7FbnsYdxghFulieZgQgngItQyJzYZ4RxQEln70IWz6shZMkU+BWfsDwJxnr2MZvsyE1KY0sPvusaK8SbA1DALbolsRCz5KEaKkCcA8y+yrIDoNA6rqSCznBUxq7pPAAp9Qgbh5KYRIVaGFoKF4mnNKk2X7/mfBfpb7Jti4PISQLXv1DCFq89ZQN09EETEG7wMAMJUmFrgpOCqDyKUga+4XDyHXMOWer15zPoQQ6l6UGBkwvCPNWorLRuFuikfd80XHMgwDAEswrewz11w90PmIQ8IwDKJoiFGtNBmZxYNlHEeM44A0JLWKlRwQRNDcD1E93MjseJFSBLN6eWg4py2hKTV7UfAOJAfNMHgos9u7W7x89Qq//+Mf8Yc//gtOhTGzevQA4gEREy52lxiHEfs4IgTC8eYOCIQ0yG+JRClWqMN+xGdffoGLyyvMc0bKbzHMfwJ40tw71CXRfqj8DDiMX8rPppzjY7GiQ3/KLB/TgEIvcJ1G/Mf9hXieFcbp9g63r97gj39+hR++vRXPU887VpR2MoQHVwqzE7VVnPaePVt97wR9S6Obp9TKlmemngFrtGf0RvtpZ1BjAV4Wv80i3ELaiHm60MNqvGI4s0C9DVcAot6RQb+Z0l77aGdn1LM/BKFuIoWNcTwS61kXHvM4Lz6xXIOlgG9jhXj9o3D/7LZArVVClG6rbXtCCN1hq9MtJ4Dh7oT96zvcjK/xeniDMIwISbwGKVblfTevCj+BCBe0Q9hdYv7qayAOiE2eDhsTGV9i/VzwhS3f2RoJuTFM9flFHQlAQYxiwvAClICrizq2+XDA4d2EMmfxmmZGpIyZhT+YQeYgjdaIR/gX9eSx3FX9JHsjrlTzCdX7Z9atisMX66kC3a23qkJI6K4Cxsubt6Ah4JvnL7C73iP+9gvkcVDPdsaWR0SlxFpcgu1Gt4qv0TmgX47qIQnt5mgXNRn9aj/Nq7Yav7HWvcK23P3y5zrF6T09OVt4kXOv2xcPvcuLlttq6ljOvPw03LTZ9sazflSt18dBO0XcfPM54vGE699/C/KwzHYWKcPFBPHYt/7KuoxvbjG8vcGrZ9MH5Ip4XPlbU0IAH+gR0U5XRRAtw/2Eyp48AeuD/+E23m+WHzOMnyahuk2ZvG9fH3rvp2c09B4wcm91i/rOVFeQwJxwfTFgvx9xdTFgHBKmuwPK3RHlOIllUsuAm4Rt2eTiIFoecOfIx+Uh/TDJTxv7eYEUtw7yszWuYa+zyOV6tz9vNyjke6q3OVkSg48uy4dbyyfrK3jRXo0nXr9s1NscZvKtowiFMGtG0MZ4tmer5RVvzAwLY2m5ALhalbt1rCshmrramtoJJIuxrgxXu1wqwGxjnTsP6DBiyfx6YLak2hbix8djYYyUkDVZmf1bmIVgCOwqDmtbrLnrjhCiH0J4h1qHdrpZlwBQ0dBYOsZmrKZYIWh+BKUgWROEByJkAjizhDBCEfF424S6RF8QYwBwADeKIlG8iN5JQlpJOBcR3GZkn5cyi3V/AYNjBMc2XFMGq7LEFVBbGrO6kev4dM1IBdxizS3eWjPUKZWKvyu5KVTIzKKoAUt84xJkHIDWsemihBUNWvN9Lzvbeh4xALXgDCTfqVbYEr22DUUpU5AOtxjAoAidYxH21vW2hHwu2xZlSFe/KUP6JLo1fra9Z/0gAX/HHbpv/Fo/N+5Z1MKnarIIpCEFgngthKi/owj9YwAhSkAjVYjJh8JUw3x3zL1JsFkCEAWykG+kSgjziAi1l6RzZwKXoAIrnYCgieItGWI0vGAeUCEBMYFSAoUIaPitOnTx8uACF/KvPSWkj9WDSz0KdE/NeUbJBTnPLiiq57XgOQvfBgK4mEdSAaUIygbsDX7XCxUWBU+EgIZxbM858y6REHtlnsFZYjybklIEffCYz/oWIgWkkFRRUhVTHlM8SOJq91RymDWvLPO0iM6rtuHhHPI8T4ooqQsz5pwx54LjUfJBnE4T5pyRFVzMgDqXDJAos0opYBJftikXUAHiwMLPESGmiKtnn+H6+gX2u0uMaXTcLy6A3OZN72ZyWdbs5X131+WnSZv/nMt9E/oxmYAPW7gVuU799SXZtoaTSh84unclu9I1FvDkPiB7H7q07ffZOwFMA4Yw4ioOeBYjBgB5nnA6HvH29Vu8fPUOh7sTSs5NclpLvNy2sPQLW/bg3N2eK7l3FEr3Gz6t1DABnaV4HTUrPWFCzq61jsVQurOhZXumgPtz0M7jRiBleR6KJ+ttaDY7T1ww3lglt2tPlvdBz00FnNDgfyW7hP7XYy5g6SUKdPP6lG310JI4cXLvA+CtZ3jjR3vUYjHvfnktRGzYQLDDBnf12Vtl+Q4TgBmECQV3mMItJjohaxgmavgTIjXM6npNSGFACgljGsBxEHqFjNY9P+zVSFq4bmkOOOroQHW1PAQxogKcfiYAKQUMv74CzxmhAOXuCP7+BgVijAU1SChMEt1Z97fn4+JelN5SMs7XiincYlSGD/qxnC+0eqqOwuh0qPFGEc/tREhjwBfPAi4vg4T5JKqgw+va2m90H77dLLxC0esalpRFk52OetZmSxhfZ4H6HhOcj6xbxgyOyO/3NW6L+1dorXvF1vchZNFb9ffjeqgs+rXEwQ+chdQ9v9HoPUdNhanFiw0/0T3fo2U1jgn9Na+HXJZic0z+Rfvd7q1l35rrnbiB22sPIGV7Fst1vee1R5Vm0j8mebYq71/5ExQRG420AOxMxdYpSOvJpNWXs+Wx60D3/PqU5ak48acnsP+lfJwiB3jGBTIu8PdfX+F3X++w248IIeDlf/8Dbn94jYtpQtwCAhWU3Ef7PYrGBGDC1XPaa+nt+ZqWtGRDUjjR2N2kc7UtiJ+tPq0Ij4eLIWv726CC1t83a8ndFemKCna9W9wJ8GKECnKixsu3e9z91cNJmQwlxoNSZWLxqkJvEDKLUDtGAjJh9sTTWmdrUQwLS5Wh4dCV4JP+BM3dIKE3gHmaVVgtDGkV9DUTVBhMs/KqTSgXKCMWNJWbxXdXePUE1o1lWBtnM8ToCgwAgAoL8zy7dwZbiBC11mWWGKkEBmaIS6UqVSiOmOYJOc8uFLR48BliIR50Xbp4/SAgyFqGlECFMc+zxGPNuYk5z8KUFEJWS+lcWOmY4HHZS0NlCPRLgts5T4gT8DUXUGD885wxAWANuTTrp8FQjAk5afsAiAt4njEfD55zIqaIFIMqiAoYxa3PGLZe8tmJGHxf2jwYTBXJVa2KHWax2k452pD8HVJuOeUBMUbENIKjMOtka0JBovwIV12Z6g6HbFGKGpSJ6j6wHBIC9gzGrMqRoLIGdU9WZp40QS9ltTKaZ+zevcKeGOnzzyQWvip9oIKGnFXJU9gF4sGE5qj9N7zVhwQiD10k71ahvayBDLqLHc0LYrXJb9CxiMaYUPL4pQgMjvIb6vkTuAAxI2iuk2TMYzGrfYHFGCS0GefZrTiNMyyA5o6QJOri8RJlvUMV8hMSIjMQZhRV4plAnEGIcQRFs+YkhCDv5SL7KO4uEEJCHPegOIjrM9vcUT33dH+ZNwAauJZkkov7BMzTCSUXHA8H5JyRTyfU/COmpNM9jJpfwnKoBCJwieCY1csrAqGowF49H9wS1jdV761RRJHKIcmcS+YX5OMR5XRClO4LToqSaFxwjSSsjGAMw4iUhqqEaOBNBPsjUoy+tw32xPsmIJAoMGKU5NC5ZIfbomeuWST6uQDGXDKOpwnH44TXr2/w8uVr3B1ProRoz9hpFmXPNE+IgTBDlAuH6SQ5MEzCFgm7/R6/+/t/g9/8+u/x2fUXCHFwfMLGnOt5sKIbzvIKj7r8I5VP1fovzMGPV1qcbvi5Ap8rIeSXCin1rGdT9gJArvTxAnbPWQk/pZh8XbvRXE+Ywwu8SAP+cX+JVApCmTDdvsPd9y/x7fc3+POf78BZYsRbrHgP3+LKZMAPQf3rRYt65m0S1pUSZ7OI6YQu7B9mYtCRyV5frb/dARb+pTRyPKGh9bPtBlgEfq680KdL2wdVLhShgRj2XcL5mZGCKVvlDM96TcP9laykbhNLn2yWKm1g5xUpzdLmfnCPCIWhoJ4TIiphH/kmOtgEKOofMDP+xeUlTdbeXBq9bTJXKxCo9XWGZhuPdVWiNMry9tOeK+v3Ft0gHLG/+xaH+Rbv6B2muMOcRlBKCCmAohqggNWvU8LIslgB4CLsMcYBF8MlynCBAyKAqHMWjExqxlhhtKKFjfm03+alDK/Iw8AEQGLTK59ZgsChUYJEQBgS0m++ci/o09s34O9fgkLW/SCzdOKCQylIhcX4BgCVhTiarK/Go1X+znKgOJ9Ay2WnRUV1oBVGye+7/UP3lsB+5gxExu4i4foq4T/+Zo94NeDPofqMeNMrmQDDiDA3GHokcm1Xwpbz3Kte9UJCvwod6yurtPc9jdepXPBjm3WfL2sM2dTd7B3Yc0u0vVUnrRa8F+Lf07WFrU9XVsJ3qs+cU37U6yvEhfODkca5btjm9fo7Gk6GGWi1dSh+0JyEQb/rRsV6hZZ0wka3V48viYMzz9qtBvedfeYRhTe+fViNH798eI4IQzrM90Ps1nvAil75kLloju8ndeHHLKsp+khaiY8PQh16+Oi1P7q81/ycW9mPAGT3NMNIKBjw7GKHy4sdnl0mpBRx/ONLlLd34O/fIN0eQFM534VuPzwSQo1IfwJAP2WfSE/0KC8bjVhfm7XadC/j/p5YtKLruNF1HelzL3Jfd2NrImjz19bBKycaWz8baxcLv2NVkHauNwLfPiiZLZ60sRkMOBMSNG+gCkdZnqIAoJATFquaO5yrK2qCtkaY5y+uqC+z7hLLYCdI2KzBjahRYS2TCplrXHkj8DzsCsO57xpHHg0RwhryqbhLfEssVOKlIRqL9K3oRFsc9OKW2Wt4rvkllOxrl5zgAnNPtArxVKBQPT+YLCE2+Xx4guMYwLla1Zu1OEMUKMgBJU9ADmoFLkJfLsLwlqKhm4oK1ENASBERA4Yyqmy2gLMkoq7DU8aloPeysDVY7lOq4+9nqIAKgWOBDlkVEpUhtvkSuTPpGCQnRGT5DCyhumDOEB7XvmmU7Z6tTXWylrRgZn21QeoplSeKG0YXMkrXyYT6KQRgOoCmEwaqYQ8A6Pu6nTWhu32X/VKTF8t+XccC9T3VKCEE/nQ8zA25yr42K/pzmdS6Ha+2YyOUpMNRhNyhoMQknkIxqjDchCEaezbohKugH4FUoREV50D3LrlCVP4k1FpMUfAAkXrmMADZrxSTKEBs9kPUBOnCvE9ZrOuGQRj+EKMK9yXBcjDFrZmBqgWSoiwPbdTNC5HHaa1zRrDk1HnOooAomrTdwmx4P7kJLweUYvixrmcuBakUxMiIkQFEBKqyHJc1mQcj24prv7RvBQLbpWQNGTZJeC5oeLCYEDW8me0xY2JNKWIJNM17jO1eCD4HPkeEDbh1DKD7RBQ4BRYGTJO2B8LpNON0POJ4POF0nDAdj6KYVWUmN38AsEsDUpRk7zkXHE5HhBCw318gpoBhHBFjdMXNbr/HOO5k3SHeFwtbwf6cX+yDc+UTkdBPbPUDa7u30596QJ+S8/nINPYnLA/mfmhpwgfGc9+MOjXzSDp2875XIrieacQQBnyRRjyLEZEzyjxhvrvFm1dv8f2rG9zcTSpcNw+I1jhmMayeDHtEsQ7pi0b3bVXYzGNPii4HTtiea8OE66t21tUL9bxlwIXBhavg2z1JjdZXGsO9c0vx86XNCdGFsWl6QcQVnyuOttwPhtf9mG28qSud9aSJbwbXTcT63lIi3PW9fi/dhLWP6EnC/X3qHmno9LaCFW/WnEtWtb3K63d48RsAiAqAg/0A5juc8hFZvRpDiogxen4iVxwuptkMKVKMoJRwuEooF3q+hnZdlsNZzhNv39/oex2E8FFMrJ+kSdEBd7DyZ5Xf0ctxHDD87ktQzsCcEW/vEN+9xfy64PAuo+SMCQXzJGFdA7Nm2FuGZ2q2q32nNp/LuX24vlSfUmMMoz+aBSSIAmLOjJxnUCKkISINCXe7C8Rxr5q4BT3csIHwNpouPPIYWy5X3R5b+Kf56O73ndlQ27Wvrovz4u0+oOaNp5zJ/dr04+v3OPPDSMWUY/02bEa3qKPb/+fq1Pec3lus5Rqbc71OwHbN97XW1kz9pLQoMBCOzy8QjhPSzaEqqQEJ/6ohs8TblxEYHd80HGdczROOu4AprT2nnlQeueQfjZJ6oKKPT0c/vsKPmKxayjb6epiQ+7Bypu6fPi38Ey2fklH56y0zdpj5Gv/+ywv8u29GjOOIQIR3//vvMf2P7xEoYP+EeMjAgnbEx0EWT1VC+CGxpYRon+ImkevGo7xghFormPMknRwqy3GvmuiIb6za76zKVv3WF9gIDBMgcjNmAhqGQyVnKgyEMjTr9aqdUWbHrE9ICWJI7gMiQLznWT0LNEFwkNA01Tpj8al9MSEZeczZGp9dGK4zGQpVEC5xReHPt0JtqVjHiibpLzXJfZs5Q8uUuZAMfj838XYBSEz6UJ/r16Yg21AtYWsIiE28XguPQE0dJYvg2a1ug4i7xQDcBLwAImDu+PJmE0ZK17u12iolgwhIMWIurKGSxHLdmN2cxcvidDoBIPBulM9cUHLBfJpRWKzyRRFBQIwY9iNCjqBIyLPEii/zjHmaUPKsnhjSn1wKci6alLd47H/T7Ti562BiAkz57cLfIomIcxZL6TmpxbmOu3ARI+cAzHFGiBFDLhJffmTJ2zEMIET3ejUlkAjcHUgdam2Hs/bLBflLTsn2H4siikCSL9dgHQKTUS3BqRRcnu5AxwPGYUBKSeCPGdM0tVDllmh1w4rwV5SCuRM6tEq9Gus5tLU1eK2OwRRFbbGcLdTsWcMd9aEa0oE4SX6DmBXKxWtqBoNDaWIQu1gGYFFyORFu+Erxjsycjtc8u0JEiOKdA2hInizMLXIGo0DSr9RE0KZcCDEBzDgejzrGHWIMSMMOMUakYRTPnzS6cgJEKIUliT2qIH95PJoys4a7kAfyLGGYTqcTctY9ognefRIBWMiynLPPzXJdY4yYY0QaBozDoPOWAFdSNd4HCk8O42DxDgM57p6mCafTCYfjAdN0AgDP2xGj5r/QfBo1TJJoZAw2TJji7QdZJztvPMxdu+5Qi0O/XOE0ApojJXngiel4xJvXr3E6nHA6nHC4uRFlhCoiclNvAOF6f4lxGMSjaJ5wmI4YhoSv/u53GMcBIQpMT7PgtcvrZ9hfXolygoE8q1D0o5VfCPwfv/x18wa9nH4tKv9LlOr9aidnRKHn2KcR//Fij4EZKDOmu1vcfPcDvv3hBv/6L7f17LQwhLb1jKYNUA8CNAezEQwtl7BUHz5U1s+4YQujoRlhZHfzSrOnu6/UPLzRXkOme32e28xos9J8R/X6dWMH8YgoLEYyNYdZNfhwEpergIuY3LggqKFOIPI/oZ3lWVO2VzxugvIWl7WSM6zR3HIOeOvi8pnKV7EtdsMzrd5uDLCW8768xt0/C/5t+d6SNj3XdleM9ppwcfhWDIIQcJzv8O50K2flMCCmBHJlvyahNlrLjaICECREZBpGUBrx6vMLlP0OL6Ip+htmsR36SjB+T+nWpBG7EgQeuNKwTOQe3VvVCwgw0m6Pq7//OzlLuWA6vMThVcH03ye8fXUSI4JcME0n5HnCZQqImjOvAdxuUGLjQT3v3vV1uRJU9xi6aUIHEEZjqYHSlDMyZ7zNt4gl4FcvPkPc7fDD1RcI+9E9gzyCUdtAC2dYtn2/IL+Fw/U22dpIZjC4DPfT81PrWuq/1C22PVRfbG+/Xz6AflGWO6hXKG33tr/STvID/aHGi+6eYrMh80GrNQSqMVpf/Tkc70+cba32j1e37a0yJNx+/Rni3RHXt0e0T4seXQ0Y1Wim6MuWn/Di7QFfne7w/dc7TNfj/d16+NYnL1vH6la53zDm05eProiQ8vDpKU9QBfwz1oEPlbPT9yHz+l7I4f7yqdb5cdVuHxuPr+2h943p118fc6xPlsQ/llC+LybqYiYabfZWTQUDCgY8v9zj2dUen10lpJRw/MP3yK9uUd4dBBmS1bFNbC+HcB4MtwS29wyme/OxENNSkPVwMIGnWf40L9SDldf1bOWaqLzFxj2733TBLZrtwYYyWdMX7MSVVcbNN954tlbGTfJfJagIcOHqQsB+rvPejq+n9dxCtRRlRnqCp6gVssxMK+AvtR6PJdqSYypE9nA55ElbGTakOi4hgiEW0yL19PqWlvVONjf9FAZXR8lwRk1IFQZc5CX3i86th0shF4nWOpt5q4wKa5JkJQpUSBdDqOFlbD3IcBHDOG8KoRLGRJaTSuq150tzbam1InS5IoTpFFgQjxX1cChFmgwEcMY8nwAilCHDrIVKyZhmSUA3zRMsd4CEDCggMGIkEES4y5YTI4ulcS4ZnAumPKPkLLHxS6kKEYjAwZhtYaIV1hQGCBDBPhFMicNFwkjZVEoeDlEY6TAlYk2WyctR5jPHiMhAjEWFnZorQoUcDI24S6ZwgLFCDaQZI1TXXBJxFw9npXJVhJJUSFv3FDHjYj6JN0QMCOOIYRw07JTARFEBtcXNd4tFExzE1iKr7vEWb1lSabNCdyxi+4oNWORnoKDu93YwVnhvjzFT5GnL/RHn8K65IUoCIhBYLDvJvYqg66t4z4NX6F4Lss9dsB+iwnBUDwXzXojqpWJrASXkK54pmtAhhCQJtHW3Fx94BMWkyYsTQhyaRNgRgaIrYSsCVOULnH1ZnMF1vQFJvi0eRZYQWpVn7TuKOy3ZssGVKX7Ew6a2EkLA7F407XURbFjCa1uv2HUQjtPzPCPPs1gmztkVwxYGzZVYhSUPzYJxbfPwwPNVUPOI4kw39ZTjwIR82mtVstT8QMyiXJpVEXx7e4u3b99gvpswHyZMp5MefeoHR5A2NHxXihFDShr+reB4mlVpoQo3VdSIgrUoPJ2xGvuINOInoTv/IuUpA/j4PMrfYnnQK+KBdx9chpZl2nx2fXFNo9s5LWUg4OtxwFVISFxQpgnzzQ3evnqH7364wbubSa35i+M6NL/7brViJe4VE5vT0gitupo2hrSQbxn1y/7v9pQwloIRoxuWbS/6uWjDiF7x4izImnS6mOeDKaWVtrbcEB5KsbCfp8UF83UdqhcE5Eyl4CGWPMymGmO03n6GVqu1PjnZ8LEQo09LQ7+4X7XxIdzMFtv8NT6d7HfXC+UXeXFt45FKKdV7Bper67CegyMwXRVQydjdTgjlCIQI5ozTfMSMAhoSYDxPEiVEiELPmUcKKa0hwsSgxhMRKSbQkDDuLoFhB0LE4ujfGFDzo/mtPtMb88L9O/48wT2IlPYFEyhws0QLDwCHPqF5KY6Il89w+ZsRX12+AN8cUG5PuD28xmm6w/TqgNPxpLS/0aFmvFVx35AiLDpBq5TYLEt49X8WuJCEGosktDqHiEgB+zIgjRG//mKPy+d7CTfb8YCLuTon2ODV1j9fnnRULnDb6t2HK6swvP2s4zduFVSL8W+Nu5FDbftjbL2/pIi3wPscLt7A884UdFfPF81Pub6+oTDwJhtoWEzj1jtUAbEhBrsn+hGaR7btdWOKYdEVGDCvJVAdMxF2YQceGG/MkLHtwwYw/pRI0naaah+p/v4LdvYJioglADzU6/PESt0i21qxX8ov5dOX+3feY/alwXHBgImf4cvPLvCPv6hEjbIAAQAASURBVL1CSmL1ePN//Bmn//pnAFWI1b73uNofKoKpu2OpIfLeZ39VAVtLLHJ3oLAJhdv6FwfGUvlgVlGr59vHlkicGnvphtFo6OlF59f9PBcCxfvplXF9gNEwKY0QiOoh5rW2Aq7lKcRorsszpVgsHCXBjGDWOStlrq8rA2neAx7HuO1WQ2ybxbFZaHHhJnlr6cduhClJiB1Wxsimz5QQbL3x9Waf59Z9tmMumMQMl+B9F0ZPmWGu3iUiLFbvDbU0hjPRapVfegVYCBGcAJ5nJx86UFShfFBrI1IhmTGExk5K0uri686FK4Ogww6g3mMaYmlUSkCmgpIZmbNYaVuMfmacjgdhfHdXKBSAnFHyjNPxgDxNOBzFzVyE4DIPBCBpUq0UA0pOGDSnBquVXskF8zxjLjPyNCHnglxqDoBSgHkWTwmWiUfOZoXIOm6B41AcSFUgX9xq3xj1wAUBQIhFc2QwYszIcxYPiR2LkBJicU2heJgmIgAhNtuhxVRC8BmR53uusISkKkWtvGaHsZgyYog+Z6VIzOvr+YA032HejeCxekOEEMFgnQ9WAWnAbid5e1KKvp8DaVzgQAKDxSDF8gWoQsCUOM18GuNocERA3YMNPrJQUnUSepwhyxIcJ5lHT0gJyKQxTIPGMJV4u467VDkh70lvak4IrYeL5tRovBlg3giSZyBA8YU7VZAktbacCSzKL0oDKARkxS+ZdV7igJAGjLtLxUVqzZ8GwU8pVeEAmSDeLK3aQ6HF23p26nzNWYT8WRVxAmfGDch8FBMkqeCdUfGCn21Uwwm0IZGWJVqS6BLgYb1CS78qU1kK5umE0+mI6XBEKZr7JQYMMVkwcACCFwNXmDHOyBUXlocH5ApwnzNVhvqpRYK3Si4wy1zxgIhwj5CiialPE06nI96+fo2X33+PcjeDDzNO88nPigzA8vXYkgwpYT+MkgGjFJTTHVBmwUkoGDS/yjTNmOcsoaiavW97hqixQtuY61/KL+XHLFvebO09N074eC1+0NuXgfAfdnsMIQJlxvF4xN0Pr/DDq1v8y7/c6njEU9TP00XOLwCgQnV/U8+LU8ObN6fTou8bwrNOw76gtbmnEZeftcblXBvtWSvsQwIZ+cBNMleGecNZvgfDbWa4AVM4oCi5mfUotaTVWRWz1ZNi0SW4MoHMCEgVEnrfPR/sORsLVZzouHFz7E8vTTq7ZsV8YiodyP13K+d4vvqA/+O/74Xodk2W1eDcu4QyFhy/KhiOJ1y8eSljiRHTPOMuHySP25jc8CrEBDKPw6iGD53xiPyllMSjdxhBww4XwzMgDJUPayR2fE8PV7e6KWn4ycUOAup6uw2VUcea46Q0OMnmzp9S2A20w3DxK7zYMZ59zcDbA/DuiLenf8XN6SX+/J//FW9f31Sax8NW1vWmEDBcXcJCPbZ9k2b7sS956WqgUg2NWsMK8f4kDBKcH0SM/UXEv/27K+yu9vguivFHJ0vwoX8Ynmzr4gWQtkZR519c0qBNn5o1O//+Bh7zaipkmVLiweIygHsfWv27uCUeOI9sq3t5o59Ce95TH7eKW/tX69l4reJyvd0IGEpTy7KrnQlSsywCr32fl3oIQ2ceLg0sNGoJQGAUBPfcvkiX2KcLvIonEO7Oj/snUp50mtxztH/q8mhFxKYm6gwhskHObT8PQwjk7z6aRqPVl3uePfPMx0B0H1qWfXiidc7TGLqHxvu+939EtvIx8/XQMJ7azebQkM+EjBHPLwO+ehbBYY9CF/jqxQ5pGHD8w3eY//wK88sbgOFWgdW+oZ+vtjv3db3T/Fb5R//2I2C6UaxvtKtjbYXQSyG9t01nDpOGgGX7vW6pH0j9tXWEd/0rDaHHizo2xr9dnxHidrgrjjIBuxNrW29DLaIBcsHWxtoxPM6krXT7LJfiJ6J7KDTjYGWmSmFYroat8ZhFljM2hDrvyoBh4YZe6amwGp7TG5sEkrxf1IqgJR7N9d2FbY3yQ742pERo3KCtZqfKSyc0l3fI16koERMogMOWxUUPu9K+hVkR4Z7FnRerh9oNs5gHsRI48ozlMZD/JD8CSASMpRAoA7s7IM4F0zMCj8CcZxAB1/MJc4h4DV3PPGPOM+aThLKR0FQBYVDNja4fkYSuEavpCAqMUAglFoRISCUipyQx6c2aT8MIzLMw23OWhODTadJwTrmD1Vb0AGfmyZVlogTT51WmTVkY91IYIUiy9DlFMAgxSQicGCICNLwM2dFu/gAWi1nbUyswUZwVTWSeMc8z8jwhT7OvaMoJIQZcc8EOlsOAMZII64OCbGgEvmBn81wgLcmqAXiaZ2M8a1/ECl4YqS48E9bFcXMzseStOkjChCUOqQ1qrVwq4J5GAERJp5bxIYpKIQJMwfcXNJGmOrgInINFgaewZHMoSY01HFNI0ifTxVFQA3hGIQkEBU2saUI5xIQQWHJGUEDhDISA/cUlKBDG3YUw+2nnCkCx8E+eMwI2n9SEkGtwebsmbeHG+6f1zquRlEuTJwIugPOa3FOnwaKKq1hxWCmiXOmSZjM0V0u/eAzSUFWQ/TXPmE5HzKcj5nkCwEhp8L1AqnSlZoSmgM456zw33nuevFrn0T1JgoYxsP4VtGEEbd7nnJHnGXd3B5mLXHA6HXG8O+D23TtRlhwm5MPs+Vp6VQw5PE5zxolOmtNP8BhzwHQ6IVCQUJRDxO76EldffIbLi2sMw07DYplCTs9W2j7LZMyrZV8+sXnVz7SPQIZu0UifrixooAf6/1NgW36OZSknP/+cIeuPPdGPoM3P/WBgpIgvxytcpp1YGrPQTLd3J/z+uxvc3c0w+sx0EVUpoQeN0fUEgFRwT7y5o1rK9bH9XzAI/rFFG29eN3yzyeaYuLOjGhcfSteD5YxAVULkUhUTQov2tL6HUnSaEa50Bio57AoF7ZHRBkIn1BwQ0YZDzdPNuO4HRRvnwwDLi886GY04vKGnnbdb8AKeS2DVAG/+3oSG5gxvWd1tCh2IdAvi3NA+Yjw1lwk4FIzfzkhzxmk6CnkVAmZkhGFwumJ/EXB1OWj+qYioiv+7Y8CUA6oRknpSx4gUJUwikigrGJZ4vq7MVp83ab9m2Mb2UH/Hf22ddf58c+b0bzbraTyVfpoyjcDAEMBXA4b9Z7gsO/zqf3mBF/92gif+bupBZuCNGEqlIQIl4/b4FuZzMR8n3H73TuXIlRMbYsQ4WEia5blVaSXzDGLIfjvNExCA8TJhv9vh7uIZpv0OZekxaXC6UFotZno5M5tlNX8bzz9ud30EgqLlDRYNt6FCn17e44zaUgKc26DLi1sTeN85SfWL8x82p9w90NfXXW4ZpO22mlTr22XxWkkRhy+uEQ4Txrd3jWKoymFqP1n/rBu6k9vunJu/pyzpRyA3HpTTr/q50ehSDv/oMbz/AD4gNNOZmb6H2jtnB7VSRjy6LBDhR0EYv5SPUh6r5f2JlvMoD8hIOPEVLq/2+A//cOVWFykNSHHA2//xHY7/+Q9u2egVAvfU+lCrjyiP0pg/7n2vYgvRMuAKRza81RK3cIKC9aGzbuzkwVv0N/qcd8vGF0oIq/9sWaInH2pDnBjR0yogTOjWoCQCnMmQermGOzJB1qoDDSGq1KYpaiQ5MmlYDa4xe+03W+iR3LyvbTkzJEKpapWlYWNs3ou4pLfj8vHbuBTv3ot6jci0eVKH2nbA5soeLGQTM8AWHqqG9YrN4rQMZYWVOm2moEFD5IIlCAwFQuGAwGgYRiMhWNdHwsyUYmFpTLAn+CmosJUouNA9gCUWkY679QKpYZbFnTrGgDzLMxc3Yln+7oIwj0CeJwQuuD7dIqcBb5HAEAFemU+YjgcArIxRAGg0LhfGtLK2oQbP4Kjp5zjBky7r+or1t8BtnrMoImaBn+PhgJwzTqcJpTBy7mO1y9xJPpISiq+L8Ts2s5EZk+aNoFlupLmo5TWQ0gAggFNBDAlItt6EZTgjCxdlYe1lYiXvxTzNmGcJFzNPJ+9DHqKEuJnucMGzW70hMDgkD0Xj1eWFUrRkFDBKCTXXRN3QDndVuBA6PB7aZxsodoPZ1R4iF/b0c23fpX/OhCi8Ge502DMBR0gAAgIHFDJGVJVFzrwRQhxkvhR3hMYLQ+Ini1eC5MRgMJnyT/9YLIEKsQrRyfORmJInxEHDngkO2e/3iCFi2O1FETHuIGonaA6EJN4xnutAhQOaUhHgRsizRtwiVMqOE0upSkQiApdQE43KIFz56Wuq88mNy7iZCZgFcSkFlAHEiKhaXVFQQOeyz7+Ts8YU1wTVp9MBp+MR8zSp58JO8+qsJWyGQ7kUZGSY9WZUJs28cPwdvc/2rllW5l5gFmIQgc4sFtNv374R5eJccDwecLi5we27G0yHA/LdCfPdBB4kL4310hQdpJVO0wmhFKQhoLDUTUQ4HI/apyuENODqV1/j81//GtfPnmHc7VTp5xilfvwMyPWfORn7CcpjaNSf7sKeW8u1rLW3RP4ILT/4xLlZk21PGELCby9+jX0cJDeQ5jS4uT3g2z/fCa5j67MqH8RiQIQqpRFTMNC4D6Cu67oXW8KNRxUjm7q6tr937zRfjOq03lly364GbngC62+pnhA5y5mQ/WwoPhetYNfCWFZFRg3htOqmniWV7obnZyMiRLCHpDT8abIrH5ffa2tm//cxu6ghleu7epC361Y9URa8Susl3c7juSU/t4Bb/JoH/N/uM4Gxy28w5KM+TgBFZJ5xc/ta5vCthI48qbcjlwAmQkxJDSQI19cJv/q68WjQ0K3fvSK8u4tOH1gC6xQTUhowDAOKeoTK0bw2yvJZPHdsNceawWgAUAJ1iXCXFE0L5gQNa9ltzspryY/i6yXhwjSPWclGuoDHCB4idjxiAOPqBZ9PyVQK8MM7YBb6cC5HvDr+HoXlTL97eYvX//pSwqM24EDDiP0Ap52NbehKgOTmCCQ5qwg4lQlEwPP9BXb7Pd5dPAftdoju6bmA1zPdPnf+nH++mcvFWf4hpxQ1O/m98eP7tv0+NMny+dXvR1S49QijCkg232G4ZSSAFR24gRzMYG19n+9pq9mZ+vV8rwgYE+6+fIF0c4fh3Z2HNgVQQzKBYR5KrrBGM94HhrLs1s+mrDbJ+w7g8UD6eEXEsk4yxFERqMOIH3qL6927KzGUv9s/ukDfZ+bkSUqIv0LO4jEj2traW/eXzzwVDEWA8iPN8Qet5RI5ru+05Wqf8PUX1wAGlHCFF5oL4vTHlzj+/ntEdQ8t376FWcosK/UWNwRW79V1NATmY19tHq1WMv3vvo0zlZAcGh4uyG89QgHRliVgbgFiQyT7gdEIGM9bE2ysQ9dPI7yVCSn1s+1L67pap74fNwgaY9eE6SZM3C5CxFU7e8f5hKqcWL3BTlgD1MVBbUN/uTeFfhpzatYm8qAR4NrgsqfkzflPqukWan99GVgZPU1krfNqgtJu3E1rDr9ETcJsfcbHZ8+yJtgmdbEkFaZCx7eg0pibmPcBJbDHyiciSRCr4XokNcfsyghjNrs5AzxcFnn7EYiMeZJYxPt3AXxk4UgiY04HTGNGHi8BAGkYwMxIwwjmIsR4qEl8xazfggJZjHup28YDsDPBCAJnERVmSpIcE8aEDykhl4LT8YRSMmb1CKgeLQKD7gmBVnkUwKo0qwkYBWQIqihRS7aSs8SsLowUJ4ATOGk4ILLwOwE+Cm9DGTiN4SwW1wXD8Q7ju7eyBgWIg7regzETkAb22PRmTed5N1jeIUhycQ4EsCZjzgWEjDlOCCFKiKbWw8tgROPct8mDOwBVQG6Vcp6Po7E8rCoCWnGlhltarx+ANQeJEt/KJIsiQsIkBTZPpwKwKNKIRWgdw6j7SbyuYmjrBjpLexTHBQTyxJ4UxDuGVGEwl4JSNOGx5nwAEdIg8391eYkQY1O33I/q9VC9MGqYBI9h4fNZJ6cNk+TKTFWisefR0T2es4fe8FwpXPkAC5MFIlferc9nCccRVJEbED2UmylAmaECDV1nliTMrN4Q8zRhPk3IeULhgsg1T05p8I6P3/YeF3AGSgjIeXbFV/L9ZoKvHseb54ydN2YgUApjnma8efMWt7c3+Pbb75CIMMaEeZpwurtDyTNSCEAM4EjgIFtgFwIuQsSRGZmLhhoRuJhL9kSbF7s9Qoy4urrCxX6PcRyx21/gN7/+NX71q29wff0M4yiKiEATEm4Q6FBxuc2r74MWBuyJDy/17Hj8s8trH8oyLHlY/fVhlf7Fyof2+y/Pf923nks5N4BKB36iNetrVRytyGugiF+Nz3ERd0gkCn9iIE8Zxzdvcbo71deMVCk1X5AgzgwzrAE0Qa5x4WyN1UbPT889E7dStNr3lgcwolJFPbyeZDuHZK8IjoPRx65stzqbvGl27gvhIiHmjJYopRHecv+8eUqoJ11xup4XcBI8+p98KP1oRgtk39v+V96k3/pPkVesv/LiytKzuyojUMe5oE9a/sm4K30cdb7btpc8QmMyoM/Nl4x8ydjdnjAcJnsM9Ys8OM0TSplxmt7K2a7MRdEcVTwMkOmttF0aA549T2qgQzjGAXe7K6Q0I4ZJYKpVOAT5s1xHFCQ/1RAGpDDg3efPUXaj04/rJWnmZ8m0LL77HCjcB2awOWmCNnbUgtHZvGvKMu2Ch9itglH92extpd21EkK7sh3RCVztADXmiDzgGn8vsEGE/YsZu8/+3mkef82MWO4mhMMJh+M7HOYbHF7e4vjm6LTWmCIiCOMwIKaAUkZQIuzGAeNoxkPmIb2kwxbzsiAHePXww8WxnZ/lHdH56FJ5wrbu+/dyh/ruqfcRj/kAWlqpwwnt3m37cK5SB40H8NHWejymPHZcj2z6SS89sMS93GQBdA2wMMTQjH3eCZ8fE8Zyje/GI96GU63zKaP8ADLoycqv923L+QpgjfA+Xnl/jwhHuhoLALQ4tJtHl0DsDNPDOSI6Br4rT5yJT6h8eAqj82BZVvIUgqV7//2B5syRuVm2COgPgdIPHf4nKdqHy/2A333zFVJKHsM5hID52zc4/T9/LwSQWqd3nhD8GNi4/4GnzMOGfGWjNe4e4P7m44ojKCN6F8TuqtIHBtEeHIs+dEoI628D661VcRdvdaPJVkhliyMEnQrti/TfBT/GfKiAimpFtd/W/WYMJoiv9OnCO6Zhqow5WE5DHU+d247BoWqF1Up4XAlRuCYqBDyUTcNNmfgTy8kiQIjpJTxsTmtjnU9KHimeb5Nkb2EMZgkRQIFX8StrPHSCpY9AQxCIMkH55y7kis1sUT5YMj1wFqaHYqxzGIMwDo22xJURTaLrOlLpQ6TGWp4TgBOQGft3UOUCkBPw+mrCDAYPF8JQDQPAjGEYfD1CDCJkJoBCEEEoF1GisIYTUIWEzStg8S5jsyZ1/ipMA+MosfSPQ0IpBdM8A+2eAVz4L9bm2ZmdAjL/FxBqng3b+sFyQWgIsXmeEbmgTMnDRzCZtTtAJIqjwmJhD/XOKFC8oUklmQvS8YCLmzeqnGBPRkjjiFnX0K8Z4agCZYOEAI2VD1nLUgomVcTM04yUGKzvG3mi0KUhhYyJdbZ7ky7hRuDCDA1Js3iO5F0T8K85BhWkULWWZCOKPXlx0QTzDJRZPy13gdBjQT1TAmTPpBgUHnoLN3GUJkVcQpgjzwATKMrcBTJmMaCAMcSEqHkeiICQZA9cXD9DDAHTyTy4ku8PCgEhqZLC82yYcspn22G4VT628GyKKmO8DbVI8uqqjPAXUNfShQ3s6sXVvHMp4hGkSimyWF/cxm1WDKMCrTxLDpd5muRvPmGe5FppFAemECXH2QYPENxG4lUBIpCGe6IYgVAQKNaWCajHq/ZN8YgpN0phTPOEN2/f4u2bN/jzv/4J4zDg+eUleM7I0xFgRgoBJUhMbVaaZQwB+xCR8yyKiCR7oJSCGYxYRDG3HyUU5fXVJcb9DsM4YH+xx69+9Wt8/fU3uL56BqIgygs6YAjfa8Lv87xCX96P+NsW+p9p4ZFNPIamenrZOFhxvv+fkIX5Ecv7DMIJpo/ZkVWx81IpxAdbFPx9hlt6QlfXINgEmmAghYBv9l9jH3ZasVhq5mnG4c0N5sOp4sJKUfrZTxqyrj4DQ0ia50bqq5iKG+B7ypzT6ntHy7bCjDN8aqXhF1Vx+7TRwj1NyyidkiEXRmHxnCuaY6vOi3lFsIdpMhqrMjH1nG/7ZEqGagRUFRH1unna4Swao/6fzbIU/vPirvEQboDiUmtuzkgzzkDldQwYuK+5He+aI2h7oDwJ2jCCwHzBmL4ouJxucfXudjlQ72u5ew3kCYUipsrQYI7qFdzkbLCJ318EfPXl4Nb4L4dLvNm/AE+3iFPW95Rmo4AYJJebCRJDiCBKGGlASAl3l1dAGv1sbennJW1Q97X2p+H5rO/ive0X4PvoLOK2vbx1tTZbDcp07vR34dKsY11vr2XVbHOBCLjYeVcDARe47vr/4qsepzQvAzdHhLd3eHv6FmkKON4dcPruiKDeECUNiCFhtxMjn8IDKAVVRCTEIMrQFQ282HPe/PuRAg1PXL2qXO68aGI1xq7ZDUnlg31a4rpl19b8dtfns9VuvGcKyCU+6fDmujw+9VELOw89e2ZcqxeftqgrVqm791hCzl42bzZ9m5pcfh286XnABFbTwMCMz44BL44Bdy9mvG0CenTnha//Q516zBm7AbSPLI+Rsz+ikto+0XZXPqCJJ+eIoCWQP9j44iHngAVJG9O9VVoAfjIual/466Dgn1i4//qJJPofckb81AsjIuMSV7uA33094OpixDgOmuQz4vjHH3D6P/6M+Yd3KixFQ316JfejD946DPo3Wu13+8z7grUjS36/OjpGuSVsvc620i3kru8vHqmPri5UIrq5sAV7Hmbl7MnrZB5MItcJ6NowRqQJXBsRmbfdUosW9kQPtqJMkiUYdvF4sGd6fGhJ9diZJR+M2I5THb80Y9a9qMIy/e6EPluC1paptu/sBL6HK+ksFxpPgOUa1YdgpwFbTgeDA0KPew3OSDF5I5yTRwqYAqKuaAvvknA1Oe1vz4JNIaD9DaIxibovhLds5jPIcRxKURdwdkKEoAmjIWGJJI9DRglqUc4+YI9EX4UWKlCN8t0E0KUUDENAKIyLlzPSLVCGCacU8Wp/iXncI417WMiAamGuc5IlnwPnglJmlBxQeHIY8RLqOvSMvn2VxFsBIgQedzKHQ0lo3vS5tdA33Ah7QSakZI30oIkfS1E7hEZoDknWm2cC54IQI6YsIZSGYVChPmni7aYe3RdjnnBxusM8z5imCWE+qYKXQWoFzwUu/GUumM1bgQCT7hZxdkcEoZAk7wUIKWlODzVttPj8XAoQzAJPt3UTlsmUECKQdda73xwK/26VXzUaTgx6LpgmOWhrPWlbxvcJVfsrBqkuM+o1BmuycSoR7vEEgMhCDshYhSGvyatdSOG4yuJjUfXMIfGEMCgJsSBRQBpGUezo/hmGEUHDHQQKmO0MJElUnVLSPsRaJ+lc2yo0KLtPGFnPgupZ0hyqRXJC5FmVZ2jCOzXGLm4YADlvK+5psNycRTCn8Fz3ge2n3novZ1HWyX6XRPSsOVkAUS5K/Gltx/PqNEXxv+jIgoZPmjUHT0YBIWVGSEU9dyRnR6sUYR1UYcZ0Ojouvr27ww8vX+HN69f44eVLXO722IUI4gIqBZHEWyUHEu8iTfD5xfU1LnYjvn37Fu9ORzlLMiPsZI2vn10jpYRcMmJKiCkipoThxTNcffE5vvzqazx//kLCgxFAFsqNgu+3dtv8LZYuHNsv5SdazgPo1tq9Dy3d19JXkCjg1+NzXMQ9kmaVDswo84Tjmzd4+/YGv//TGxzuJlegKBFbf0PxjtPpqLSe0VRgP0/u5+YW+3alLdi4TtBE3/JSAMBEKOo5bNR+Jz9rBb2OfO3JfowFWZS4TkNXgawLbEt2L9bC7AYT7hVhoQ3NG/rMuhvN7QmmQ1CSY+ENYWf2malcCoW2pBvbQreGx7LrpohoEhE7r9R8L8arAA4b54batp0T4/RZqeuhCxVujxhevoJ5INioxtcZ6Y6B2xOO09TAQqX5GZBE02EEkXhrvvgsIQ4BOVW6BWhCShKhjAO+vbxyfvkUR4QQcJf2+FOIeFZOuOYJ1SOzhSvSMJ4R717sUcYRYyAz1fA8Ej4HfA4K+nnqdoDStU7LmHc8oQlf1MKy71Bfk6KGa+b5UGGYPdF6zWuCSst1ve17Tqsr+sxSYba8v3i3rSOMCXh2gR3/CoGfYbz+Lb78Tye8+a//Hcd//TP2Y8KQEk7liONMGC4Shl3C9e++QLrcgYbU7fPa6plZ7y7TuRvniyqEGtYSrFZ2fZv9qrY7U0lArHfwvQ2jC0lbry4fe2xtXd98/IaTmmeN575vhqip4v6GH5rzs8hu8YNWl5e10bkHqB19J5F5XFko10lxyt2vXiDcnTC+etsccbxogyHKCzbRNQDg8u0RX+CAt9cDpjGiLx+TwP0JEcvnCJ26QZ5cHq+I0Mnf1q60REy/2K07y/lKHdLqPcICFO4f4BJwvAt/bbT+e0ufz6L4+oh9eSIwbazeo7v5UFPLeh73fEU0710IACIyXWDY7fDbb64xDrFad4aA8vIGx//vv8iZ3hBjtQdNv9pql1frxHfj6Lv/9LFsrcFSCXH/MjV3F5YdDV0rv0xgY3UvajrDssBcCDYJJevfhgKi7QdZ/7T2lSVh+70lxoXi83olJ0Ml6lqipS6sMS+VEBTz+V54ZgLJdl6ieheYoK0sEoEZs9TQFgoHTVJa644LUiuh7soDZciKScwbpsP6rUb0lbnaYI+AakXi87gGTIWFStCt7nL95A1JXE2oWK1+bYxBrZu66riIdbh3pXpGwCz7SGLcQ0MAWZiDwmLtzCbkjcrwUAAiEEqQvAKAWJ2Xpn6DNoMh/Vdu1XHlWWK9p8QIBbh4B4ynDPpixhQDjrs9ZiLs9hcSa71kDTVFPsdlljwJZZ6RZ80PUBiFiuYGYD/3Ow+gbvnYVzGQTK/AjcAZ2fv+Uk3s2MbWR4igFN2qcJpm5JyRJ0mS7baUqvQp8wxmiyGvFtExYbfbqWIpCspoYjNb2Kc4HXB1uMGs8fZzmTAL+AvDzgRwQdZEuabEMGVgiNEt5oxwFeWBWHWbUoECNXvYQvIsYa96Qpj1v9Xbw4DCcbP3TBkIqF9CQzu5MgKMKnR/uPTP6spqsvYQmoSk2irQ5LjQHB6SlVr6WVh+MrIqOHRMxRQvFvZLxhSiJFMPUQTPFmpoGHeeABIAKGTdm3JOxjT4XnblS7NvHQa7saFaKSne6nCuzboKpbJ68fjbZAxPDZ3hI1wIZAQWBZkUZp+zdg2lrqh7RuqquSrM6jarl4/Mb1BvGhtXf97KdVcqGmopjLloUmwV8jBLSnWOkpdDcuL0sCdORIzjcRLPhZxxc3OL12/e4s2bt3jz+g34KuP51RUGAhKJ5W4KhMmUVYGQYsCziwtcXOxxezphzjOO84yMghAIKUVcXlxiHAdM0wyKuqdiwO7ZNa4+/wwvXnyO6+tnCnNtOCqfbl+bhyiQj1moWYefQqlh0pZUo8Lq2X7+RAbwMy5rWFjMqcOpbMyWPvpQ/dF5/rm/EgB8OX6Gq+FK31OFwTzj8PYd3r6+xavvDyhz6RBCp5OwulnDVrY8hh2TXav9L2sXq3ly4lS+b9EgdkaR0CCkxzepTIDN66ybnJ7jJzK60Tw3hHZhtQbnwmrMoGY2FlqS7QzmqoQo9X2n4aHCXX+nDqEfifbVBH4E/wxknqlQpUT7Nvd1LCp+HCh1B573FageEMztGJTmb+h9p8/PwXvTm+5ciYzTs1kOjHp6Y8g3GG/+IAoYzWEUQgAOAeb5PbeTVKFXaojR8V4cCM8/HzHuAnJocjo0cw4Ab+MOf9pdCyw5rUY4pBFHjEgz8HyeZR0s94B3gRBDAFLE7eWA037A51HUEG5EuJyKjSmyGVrzS3q/OeMajmFjd+u3fmllDR1OGdkVEgbHcs67gZX+c+573+8G/p6Aw9Y7m4EhAMOIhBEJz3HxTK6Xd+9QvvsOuxQRh4DbcgITcDmO2F0MiJ8/A1/sRBG1hQaXk/IxS9sgs6KwR0wGdbP39AOAN3D+ZhW6xx7LDywqOicra6vbnNnFtNxftg0o5L3tjq8fX/b8/tLzPBv3H1NZc660MggeBxw/f46UbjC+freYgEYuVRgIEnbavfYY2N9OeD5PuNsnTCO60lNzH7esT5f7y8PS32XNj7m61dD77d0nhGbiCmy0pYyQZ/o+cXO9nvC8gPytA7pp9UxbP72ykNX+DZeeoP3pF8LMFygQi839QPj3vx4xpAiO19jvEna7AdN3b3H3v/9PCdFNhPLmVgUuUse5sgSJ8weNCUjW/Vs+96FwtmLAuEdtVahMq/ecQWOrpwpGn6I5autZXwdaQdF5srknNv1U8uHYnNZEftxdUyYl94K8EKo1MRpBlvfLEwNCuBC1DA+hoURLVUZ4V7VeJrHSZgYoi9tfLsZQVgzpAjQ20rcla+s4jU1w7wrm/rk2eSEAoujC+87OwHAYAcQkYnxWAX6zQtKvIoRcM6fLlWS3hmttgFrLAbUHa4h3F06SCC5VD1OZLaBaGDUh0Hz9lfALhVBUYVGBVazRc8luqSIeDTK/0UI2Fc1tURiBGBISp7dkZ4Un88gIISIECdHCzIjThBgLQkxAIRzvblF4wpdpQE4Jb3Y7FAoSvsXi5UPhJku8+TLPyNOMUjTufBHhP0q1fneYhDGixoCqsLlZ9+DfLdGx/DaPoKBzKsyerkNQK2wAGYxTKRJ//tUdTscmEa3OR9YkmkXDBMUYEUgs40MMSM6EGvwyLkPBV+MMAmOimgejsFiaT9OEeZ51XwYMnIAYEYIgYA1tCw4AZUmyDAAza0Jy9TqJKUnM+0AWjUj23izzkFm8OKKGDzKPAB+f7zdT+imcq0DDmX7mavFvhGuLCx84Hs1ycxVfmtrzxu5Vzwi7ZsnZxdLP/qAWpopJmMGkghuy0ENFcRj51iqFAZ9nFg+IIHk6bH1jjBrrWT2YIInLg3lEKA5lZ5DJvXnaM0K2cMVxzA1MG3xDFFE5Z+T5JIKonFUoU1ToAK/XziV53wRSVcFg3mNZgAEnlhBgBKAMg3wnQoyCt0ueARBynpucFRmsoaGIJG/KOAxutGDCejNkcEFLKM3Ag25T1lBkcAXSrPBUGKAQkbOFZxChxHw8YZ5nvHn7DnPOmOaMu8MBb16/xe3NLea5YJ4z5tMJMSWkMWnILRWiBQJnwS27/R5X44j5i8/x7PoSbw8HTDkjhIQYIy4vL7Hb7cWjyaCfGc+fX+PFixe4vLrGbncBQgDhDnv6DoRTE4td8k6IMnAL+n9u9OMv5edfWroKMBqbGZ4XAGhx+T1VfUQe0Lz1IjLKlHH75g3evrvD7//4A46HWZPUNyGFTEBvIRwBAAFMokSuZ0H1TLPf3nclxlxs3OJs+9nkFGuNYfRLQ3/LvDqJzPD8FNTctxfC4nWXN9jwNKRSLoJr5yw5ktyAyD+qMLfoO6Wh942mtRj4roSorfq31gBAFA/1XBclxEKh3pU6vvuxGq+erbcaQyI09J2PsdLGJrTWr/puZaCYGKfnGXlX0GqiQmZcvrpF1OTFzIxpugOdCvb/I3suDJmPgHA8IQ0jQAEUlU43T4TQ0j1mES6T9/xFQBoDXu6fYYoDEIBMwLd7ocGrkNAUPvX3icSrd6mssoV5l/bIMeGzcsRznmGUG2lIy13cIcYB+fmIdDUgzAQqpvCoIUct9Cqhh83a1OJ380RpvrcrWleZnUa0eTYFWkENIZabvCWGAzqPCFQYeDS+WU3a5qWmrw8X82m1NUopYL8bcOITUBjDbkAaE178268xXF+Adqka7bWNto2dQ646Z8s5PVdWsov2rUahaO13XbivH1u7nLavn3l845kFnV+7dQannK2ijsMR2uL5LRmNIpiHlSCbSO6eIT48J8oCPq5CXu+/rddrHS2uoMXTVCOtESluKaajWgBExcttnr2r4Rpj3OFVLLhbZW2vrf18qNntnVV33v3lfcf5tGTVujrsbpWkgLF8sIf1ldCTWlBockX8vFZss5xTRjxBPnv/iz9GsTY/yPTnsZjlibU+2LWnzpcQPzPvABpAFJDGiG++usbFLiF62A9CeXeH03/9syZ40oMj9B15Wuv9ker0/uqZ+tHeXx0zD5j8td4QXVVNw0boWnUM3lg5sxQHoGF5nFhe9pxXCOIskb1+hpVhYHQYY6Xq99NEfoauksqctES6W05V5sRa8YPLLGpW57gQhoazBBWuiZ4abkmF/6xW/Jaky5gzIomZX2rSXuMHZbwqTDVzGyV9m2gj3bw5s9KG8LE7PkCto59In84AqnMlk6fMxPLp1qNhOU8VhpY98S5sgKpbO1ElOnw+vQ4l+SWZQ090khAJCJLElyw+snNzcn6xCqspiNU6Qax7zWIdLIqdAkJs5oxQnH+2pRfLa/HeYLOO1jwEIkwkTMcjiApe5AlzDLhNCRwiKA3CnGvbDAbPM2JMyPOMHCaUklDKIALYLnRSZUxrLFm1DGRUjx/dx0TmcaOhjcos53nhOh6fw5ofwCGvMDhnzNOEw92E4+1cMYQuTi6Sf6LkovAu85OSCD9T0nBnQYS9CEAIExDfgccB034HiiK4hTJfOc+Y5kni/gYNFRUsZ0sNLBFKAJMJZmqwImYGm1dDiEghdeBXSob5HBEFULJwC6HCXzPGHs6r14DBqdRD9fOe428DRXqeGpjlmOEiWxvAGQiG4JQWnxMVJ66rHSOBLNcAkeaZMCWOUmKGc0J9y5SYCQQEdsG8wUrUBNQiaGI5M22dQ0SMlcwkQvViWeLtOkwAVUjNFYHDrGAtJ0Se55o3QvdAcGGI0aK9IGd1PrqwquIIE5bbvIUo+xoB7nkhQsCK483Dh3Q9UpLwA+aBI0oIE1rZGdbMsyo67cwrLEm4QYQya/4HU3bORZOxyjyc7o6YNDn1nGecpozj8YS72zscjxNykVBv85wxxqC4SvPgkCjeOWfkzBjCJS6GAfnqEvv9iJAijvOEeWYgROzGHXb7HZglZ8gx34GJsb+4+P+z96dPriTJnSD4UzN3BxDHuzKzsk4WyWY3mzM73T2y///XXdlrVmT3w/Yx0pweksViVWXmuyICgLuZ7gdVNVNzdyAQ8V5WZfWkPYkHwA871dT0VuyurrHZbNENA8BAwIQeH8CWQ4gN4P0eWaNXGi5w5f7zyyVkbTUAWKelHpGVnCxre/20Z8SP5fsuayQzr6AI8nTnE+BxzRKxGvmcfEkF8hUGiRM4HfHw/gPu7vZ4990D0sjQuETaYa77y/VUhLsijJUEsWb00Ap1C9FpxE2ZnOz6rQjax9JrSsXnRvsZw2/KiCLomc1EY5uwMikW4IRRQzqKF5rzXCs2P6qOsXPZe0GUz6qEWO65evpVVB3cd1IviFYJQWTejsu6VoY0u+0ZFoIdWka/ACiW8HMPCHZnW1HYoFRR15CAaZsw3djME8CMOGUM337AME4AIPTWw3cAgP7eQlRqbicz0uh6gZ+iiNCQjsHRPVABHwAEYHcbsb2K+G53jTFuygQf5vNUBMXt3Hn6YP7KPnbYo8duSiA1NCo0EAX0QUIzxW0EthHhPhTeLbh2LHyY7Cea7YmzK1pCtzan2gy3FDoElbfNStcYrJZQwfpZ6Hr315AyDlZWT1THM/v5ozNjOXUyrz1o1fcxYOgjRj4iU8Z22GKzHdC9ugVuroSePbHJ51ixnobcjoHnuTjO961+dT94NrbVLnk4frzUx+bPP4F+8Y+y+9lcp/lj7TgLXrmwXSdXeGy9C9+xegOzg7N9bnEW+sN3MWUrq1GY0/ltO03WWqbZ7xkcQPZ3DVVdMswvalrSboxN3KDvNujDA8D7y+f8z7I8jg2eS7k+LVm1A4QTF+Tqo8R4RSymhCgCz5MEzmPlv2cA+LF8L4UJI1+B0YMRsekC/s2vbnC9jdgOA7pjRvzHtxjv9/jwzbdIH/ca77QSWRc2pJ8WemV+aJnApL6xgmdrbbNDtB7gpzfeSSWEu7sin1l0gZv/KuPD8xdgxBzU8lYEXx5RF2XAeocdAb58olggUHsyNYohql2qxFsVFBZizsdz17ooiuVYKLFDqXZKJEUwq3HWhmpiNXJtViGZRDpRa9ggydMii0BLvBlY5ijUg5VKl4QRqAlpm6lyMFUpU8/mFQLYBGWAelDLuIR4XqGCnCBbnjhl+VXJGElvHKqApYHNVmBa8L4j8EV4isLQ5SRCvpxNuCpMGtvAMqvgkRxcMICg8khS4aetm3mziMcHqTeKzInEje26DjlNSJNnwq1uclRJtayRBL7A4bCXeO3jiJAkLFEA8PJdQrrLuAvfgoceN8cRoevR766xjxFv1fNAPBCAOESESIh9AKceearzUEIM2FTqXmpCFDCQLD60JTXmSWAySXLjNDGQgMQiIE7jiMN+wv2HsQIXCYPV7e8RDnt8+PiAh8MRh4cRh8mUsgb7XGItW96BPui+VE8L7izEj+2FgDFm/L5j9AOw2UVc7yJe3Eb0w4COJATTNErIp5QS0MvM911X4vCDZE8JzEzFOt3mJxGDR0Ygs1wnUIwisFClncGeCNNDXWtfCv5QyDDmcMHdnC5lr+n8FqWdvm+JwyNQ8l80cjC/aVBDslWeTR6ScEhBks43bVMRZhBJG8EE8SEU5ZHVJeGf5O1gRDsMe8j4owrcOzJPiKGGJ9L5YmM6ipDCCSparlrXzRRRuSgeUppw2O8xjhPG414VA/JOCAQOASG3MZ/na2fKQwAlobTtraTh2KB7giigp17yjrDsFVOIiNViKvlKmM2jJAKD+GpTCIIDuliUEX4tJHxTB0nuXROOJ1bgyIzDOEqy9sMEEGF/OGBKGcfjEWlK2N/tMY0jPtzdIeWMKTOmccTdwwOm47HM5TSO4L6TfBCQ5NkxRnRd1jjUWXJIgNGHAFCH290W22nAPiUAoogYhi3CzTWoj3hzRdhdXeHnv/wFXr76QuA1HxCmbxHo2DCgBmtEYV0B93+A8n/Ucf/5FE/z4I+wWO2h0RHh55vXuApb9NRDkiKNuL+7x9//5h32+yPylItwXf6Snrnm7ehzkxGATs8zM6wK9fSo0tF23IWuNxqIKpvh8GfB517BanXroebSRNQz2Th/Nny8Kk0o/RClb0JKGZMqoI+T0CmZjT61OsjR/C4fBBwfkFHOTb8C9dwDTDhVjiyjf4vywXlLNOt5AmbmvJz+1/BXQCHYK7th/JYpHWo+i2znKsPRhIzjTcJ4lbF7e4f+7qBkMaH7JoPeUVmb43gPniak+yMOWXgBJkbsZoqHYF7Ugr8DGb1ahf38xTXSqytZk5UBf7MRz4djVG8K49tmc+8Yn9X54+Z3ZUjMmIhYPmMghK5DCB36fgBij366RngYEDjqOBx/56r1oijWC2u8j5pzGFuoy6frNfMaLJ7KCnfijQmw7l/xMsyFbs+5Kssqndl0dTY5judzCsHlSrQjWJ1r4NFcGcbzHuMdprAHhwO2mx5ARu4Y9NWXOF5dI/UDBjLvk0rq0Xw911tp+3qhwn7Fb6aW4Nb2RDWnFQsn+kcVHBf3nlNOvTrHseVT6WwyPlwLz55dVSRQwUNrynNf//n+lVPnxPsrda+er7M11+fWR76Oe+vyeSBbb3/abnD3sy/Q3e+x/e5Dwa2L7un+80YJxIzbdwcAe7x7MeC4yBXxpy7t6fZDLE9TRLhykpheWee6LeansFRid5onnNznbD/OPXbq3XkfP+faXCiI+LMocwx9hiB/fArXJ/200ur8Iq299yi/YEDGSlQjADSAaUAkYOgJX78ecL3tQZlBhwT8/g78/g7jP3+jRL65cD3S1skxfQKwnaZAtPhddPq5One8cg0LvFVqnFVZhPxKhK2T867OWSVrB2VbP6/erDSqEQBmcXN+wxszU68xqkUZilAOBNSEZ54adQQ/GCLKEapq3V1QmIZckuwGZGQEZg0BboSitjNjiEqf/HjZWdwwNN8f6zoZM3JqSnUeToLh/C1uL3u6LlCluudvcp1xi8FZIHJtnL54Yk6fzYDGYBdhaLmvDJlxuaRKB6uINM564Socwy190clSb5SSP4Aknixnn5vCH3jeWrx+xBAAjuVu0nAxgzIQmz0w9Rkf7u+BqcMmA7HfYkMBqeuR+06Yvt4YPw3hxRFMQYegighjqK17uTKoyBUWsipe0jSBURUQkg/ClotLeJtpmnB4OOLhw7EwPsaA93d3CA93uL8/YH844nCYMKakgmSnBCphAjSclxrKsW4uthj8URjZEANyF3A/9Og5I1HG0MszEiKH0EVRONjYBZSohL0pgu2ghPDkYFf3BjFL/g9S7B9CRRkssGqMvE94yKiwzvCfpyzU1vHvjDyuawfLHVF/g80yzsIc6LtU6zWwRmmzjsXmogll4HEUqxIAdX/ChAyaULyU4jHhrfetSccMqNDGQlt1XSxKhgaXLxhkHYRXUhdBjM2vCN5SzkhTwjhOmMYjjuOxKJxkuaLgC/YRqZfF+kUEkEskaYoPBjQ8F5DzAAspREQa0sP6qcntTSgIFGVmCUGnCu2gwhrL62HnhinjglopF91qoY8l30rKGSMmMAP3D3tMacLDwwHTNGH/cY9pmnD/8CC4EsCUJozHURR3OqeSWFuVcBC2MQRCDBGgVHAKAYhBksoOsQOFDB4DmIIqLjoMtzfodxu8/PIK19fXePX6Da6ubrTuESG/B1GWPCN23qImDjeh2vcl5z1NWy7LqT485hlxqp7HHl8b99Iz4rLyWN/W63vqpPPs14UM2ieUVrjg2v6MPNZaXetUJ74nQG1bCiBEBLzsb3ATr4sgfRqPOB4O+PD+AeMx13CfJlS3Mwh5pVpVfmpoGwpyIFMZfFYDK8NrpngIpYlaKQu9zVjYDK4L/rgcW4W+Zj1TyzmO2flUcVCl2fR8LfkesnrFCT0g+YoC6onmz9GKfzz9zqdXuoyhPeaq8qENSdMOt5mGi2C1mOPY5Cj95PZ2UaIA3gvde3izny8A05AxXU3A23v04109ayb1cNAO0v07yW1EhESkoYmAEDuZz2geERJikYviQeBIDErkL11vMb64PbF/gLGZphXFlZ/QyviUd8qtMPvdUFdCDBBBPf/UKzNGUUqkARg3LkH1+r4WX+oKi7z6mMGVI814CVs1F5TeUYOhbAoHrrSErW0x6HH/mong2vaiUAuGa+UibLYGw7T8mXDEiDsAGV0XMVCP3DOOV9fI1zfg2LnNVMupc4RWwKDS1vXOo2M4+0BLhz7lOd+V0+LxCzp2yZniF/gCIVd5wsDlFG3jm/Bd+pQzXfGjh5n2/PD8wvy+G95isrE+kAWc0Ozm/AHlNpwciABwHzG+vJIz8e1H0GJfkeMll2h+s5+Qc8LHmzav5ucuj9f72BPtGvxQyjMVEXUw5H8anwk/HWeYwdnn/BUjWhZAKZDUMq4Ooc3449W6LyrtSfe05/8Y5ZED4o9RPk+TT2PyAENecwblTG8aEBJPiBB6/M0vb3Gz69HFDl0XcH29AX+4x/v/+38B34+I9xNY42aeoVke6/niylr/XeB79wqXxy6cpXlL7roJhucnFJW2F7onbntWw/14psHqrDGRzIrDC9BUXl7HoY3VhKALKqV+mQvtqTJCpYm22kLIS0imVIg+T6xrRBpkO4RVIESkSW+dtW6xTNHfiSTESKQAAqtAy9ZLiNjECUBSwjIJdsoBXIRUEk+cWS3VTDECiFcGi8BYhh2UiIXrk7RHnEtfGwbOpovJrT1ByOxQJo7YRzcFMqqwjdSt34Tjmn5XY5rWA5soSBJsXSuJU58LDNhZYRbSIiysTJfdz6wxxAFVQtQkyrmEFTCQEAI9WHihIO+ZlVMOoqiQfBzCZMk6qaVSljBLPLEIyFmt9UNA10UAvVjTZ1UggRr4AVAtj7oOXYwYdlegccT+/g45JQzjCCDi/g2QemAKDEwj0sf3IPqI/cf3yDHiehgQYoeuHxD7Dn2JMR81PiwDnGsIIAf7zOKZI4oMQt9vdQw9jpzxm/0eh2nCeLdHSkccx3sc93u8+/YDchJPiHQccTg8IH34iOM37wo8RFUWHMYD8piwP46awFYtHQMgWU4EOMtZTOrmHkSJ0qmQ25I7WvqCEC1uvsCvhZHJ4yTJpzcDNtdXoC7iuD9gGkd5lknzF0DyTmjIGRNMsM5VQRKsSak5gfMofR+tqwGhHxDCDpmBIxMiETrYnmfk+bqXUEwVrXjKqCQED1484mkV3acssycKIWVIIbjIctSUYIDFI69N/Cz5GepGMvxFGtqpidIGSHusAhBbDFOQBlHSlJBywbXpDkHDxV0UD4i+GxBiRBeHInCXIcp4UjN/NieGg2w8ueBrzhLeizUcGKcJ4/4ex+MB+7v3GMcj0jgCYFEaBAL3AyhkJBXyR/W+MXLR+lScwSCWntEiOQVZxJwy0nQE8oRDANJ0RN93YhUaLDSVrKRhbA42jgEkiEwEIVE8IWIURWMMHYyjEd2PbhSqlpWRIvRUAUA4HB+wPxzx8LDHOCbcP+wxThPu7u4lJ8RRvIU4Ccxtuh5IEqosccCIgA9TwvHjBxwDsL3e4brrcNVvQRrP+RADxhiQY0CKhP39iMPxiPeHPY4pYfviBbrNgBwzcsh48+YWL169wte//gtsr67x+vUX2A6Em+EbBJrAPMnMFEVPxftwsPtj+fMqZ8wIHimeZrykneVvem7Ta/Wv1uVwFNtD5HhO92iVPNa/M/1bCagBX2Ekwi83r3Edt9hxQEgHUBrxcPeA//yffoP9w4h0mASZZ1MuzkOM+vpV0BsiEDsYDVdzQphQJtUQog19rJ5mRvOawUHhT+zwr3SkXJ3xZaDCaiyVZsqX2HQWWpHLnEmXRNmbcsKUMibNZzPl5HgNU7B6OPPMkyEiDYFqhhGYhZ8tQuzyU7AwAW0YphYchB9Z4jX2/68BNWDUk+NdVGBdDBwy6q1qhFKWC0CgB3T5Q3mue5vBHzLyh/e4P9xrThBVLEDzFRGQ+w7ikSfnuVmtl1wiMWKzCfjizQaHfsA3u1tdU/HszjC4APK2X0/+PLtyUjiq67/YHeQ/qb2nPwgynocD8LsPwJQJiITNsEWMG+y//hppswG6AcFyXhBAa0iFBSpbe6uVxbP10+fn4ZOy+wRMf5hLGF7zeDBDBuOncjEsQkUtbF9t/Vth6Rwvr03xupCZFr9Ku/667WH3hoWazL97j+M//yOOb98BPGLYbTAMPW5fb8E3G/RqWLRUitsm4+U1oDEubNBtKYy1/je/Zk36cTylNKjf4U9/l2j+5Ho5IfGo/ToxHW2H1k8Uq6Aa+jxeVus5VZZH1/Ilco/Z2QlaPcAf163YQGaxqJ+ygAsYMAN4Uh5Rae9gmWUcnwfDSHpWMCSyQjAeKOC2f4kd3eC7bsKe0ini4o9bTiLRE4/P+mwec09r8nnjvlgRUbb7ct/XB1yp5MVqLe25slLW2lr0YcWsiAt4Pd7HxfVzdPKpca+UWs1CPVKrO4HkHy3n1vkJfXxO+bxVPw1gl/NzapHcL15aqlu8VMKA2A344naDV7e9xI+MEeCM437E+M9vwfsRkz9g6BSAtMfRuZFdxootF3J+OM2nYwW9l6tzOmqNyGh6XiXLbU8eWTKrwTNDrNoCl1KmacNbdp9tx+iJBQfQ4hMv6yqEPMTSFWpd5u6ixVKkfxY+o6VY2NdZcE9r00G+fTZsVOdV6E33kDKLQYX8YoWflUAWeC1rQP6LE4NZ3JWmXj+nynC6vVDwr18Ta8lTwPqAnLeyd0Kzp9zkVHOGelfnaS1VXz3nPB739cmX4s6cGZFk3N6CvLwwt65Sporhk/4SODCQ7Q4DTMWiLFNAIBYBLosSQEKxWBKrdo4LMQMUS9/Yd6KkgYaVSgncAftNRNZIC8wZPGk83uMB5voeYofQb9ANA/rtFqHrEPvOCboFhisjJ4xx1njPAaJEu+p7dF2PzXaHIzO+ZYDDCDwk8DiBx4R0nHC4PyCPGXmS5Nj7/RF8d8D0/j0KU9pFUBcx5YyUGGNKSCqE93uaq8TRLQI0KXQViodgluAGVygWdWU11TI9xAiKEV3fAwzkSawgG7zO7GLwB8lTECNyJmQV8FMgFayzcoPmCZV1nBJ/30AvyZWCIbLHI271S6gELwTyoEy2+6ggyOUZ4evJdc+Uv/mUruxjg0bFD6bEqF5Xrt/siE7SBaLaR0OvXDaoXg+tIsISeYuQXawOA8ViOVknYXESaTf9wKSv4gGSG2YcbFawCdM0YjoeMY5HTOMRnCaZ007Vo5yBTMikgqYcXLsOGzouzTxrOIuHTs5JdrQmkJxGoQIsJ0+wOOt+/UplUAWy6XckzBt0XwYSbxFZh5o/gikBJN4Jojsze1VJUD1NCYfjiLv7PY7HEXcPe0zjhI9395L7QTXqkSVHxyZ0IAbMRjiBxKNizNiNokjcxU7ye1BAJFXwBgIHCVc1pYRxHHE4HDHmjG0ghL4rXjPXVxvc3l7j5esvsd1dYXd1jaGb0Ie3ICQVwrh5Xz3gz1GVp+5dSjteTrH67SC/dUW9AUTz/Pk+zPfs5+FLL6Mev8/yfCWEL5ety6ItXqOMLy/V+GetBm7X1BHJ67yZ4ZLL5uOU1WxL+RJuuiu87G5B0x6UJ6TjHoeHB3x4+4DDfoIlWi60nin+c62tVFlo5tD+lZt1DGw2MADMGKbS1NkTa84Tova7Gps8Nh80W1cupPQa7+7pekniq6H6skvkW/7U4AQ+0fA8x50LGDQfh9Hr5WggmLDPckK4qa2k+KwsIWxO0zajd6BWaQiDxayEX+U79J0Ah7RY8hbyiGG6U7qExMiCgIfjiMRJQguCQBxBjo42jwcjyDjK+VQ8BmJE3ARsb3vkfoNpdyVKCFVIVVK08a9czs0K/2EllzWjRZ2n3mnvE6Lm0psSsD8C1MnZKt60EWkYkLttoVvmC/gYdi0QxRZGfPaAo6uYNcSVrV35zmWfeZoPzqgFTtEE935p0viAtulFX5e/1zGnTcPauNewZfNb8U++2yP87j0yj+AOoK5H6LfYbDpgExsBvYX6tO86zLaNuZZPLrYdcAYNC97vArpiVQF1YRGqKrT9eYJVRaUe/TstnmippBNrt/K6LehSMaVzfQ5H8ykoOdWoXZvBY+GV9fezLU5Or+s5u+Nl8WcjtZcI4hGohqWIQXXwpoivsMh+bbhWNcQNusDo+R5kYZDdmP0+mrOJF/b64juL2/5Q85cfIUrnXiOPFUcyPbk8ySOiTOanUIPPKl5/eCERy0/CCz+WH3hZUypc+h5QicqJr0FhwN/88gavrwe8vN2gZ6D/+3dIH/Z4+9vfIe2PwKhE2xOafD64zVETLffYZ+I915g7paCE4Cmx0rHcRKSsxqNMODVIrLAY3B6ElfnXNjSkTLnu2pQLYTHHzQFtRJz9ZEcAsrNoZq6GFiQu6iZEDrEK2puk2J5R0PqMQbGqJHRQhkqaEYhKOJrC6CrDRZpozyyHgwryOORCqErzFnO89knCBqXKjwKwvAw2cAvjZLJdk8HCGFAnpLSpk1dzQ1ATUD0QMFdC1LGVCSdqiE4AJcGeTAUjZ/+eutT7ZWRGRpYwOszqoszVICIzOGS0lnm62DmLZwO8AqcSEqJsZHBwgl9z908ZzBNCEEt4IohFtb1fkkS74cPiyAMMSb7cdwMCBRyHDaYw4TiOSBgxpUGSLJvXC3FlrhklJAwzSTz5rhMPia5XQW+NPcmm8SqeI8JcRbVKR2YMwwabzYBtjPjr22uM04SPU8a74z3e/sPvMT3cI77/DpEzAmccjiOmu3sc9wccpyReKYEQmgQDVPHiIp+T/jbmIuWSnJIJVVmgycFMcWB5BCiqyz8I+yngmw+EFzeEFwOJNXkPpL4HckaM8k4IJsDWdajdRAwkAlZtm7N4KTFNyOMoSX7HowpWO/Rdj07f62IAMjCpssi8AwCHv7ImFDZL0tK2tBm6GmILZR4qIwq4fWfbQeE5hGpB5kMBLgwaHD73oQ7MC2OV6TCtFkwZVJO0m3AnA6VtC/EUfGxooMSM7jrNCaHhs0yJa0qV+umYT3L9VaJSDH0nTfQ+Fa+EnBOOB8mBcDwcJS9CmiSRM7dUoXjXhSasUbVStZwZ1q5NquCM2EVEteZMZDluBP+kKcm+QgKFgKyeKiBL1g0U1RW7XFBBFYzq2WSeEWW/lPWXJOuBCYEJOQj5P01yTtzdPeDduw94++49DscjDsdR8qZM5kGiuBRABKEbehAB3dCBjgfcjZK3ZpoYd/sDvnn3HvEWuN1uMVEAx4CuH0BqOT2OE+7u7/Hx/gHcdeg2A4bNFTa7K9z+5A1uXr7ET376M7x49Rq73Q79MKDve0RL/Mct7TTTG0pfyY6MHwn1P5dyEqf8d1DsHDl1rwjuPwu8Ngi/XBEaRujDh/sj/tN//A0ePh5wPIyFFjLFrNFP9WXS1FiKEctZEEGhg2n9K6aoLZt3rNBDpoiw+qlKYALU+zZ6smplXO2VIjwtJDgXOrooAGA4FKWOIohXj4jMrZV5DW1jFuZVeV/OhZV+Cpmiyl4TohU2LBiJLD0q6663jeaf1du04at0302ZUB6zM4bri96owSzpPV8zbTMOb1JZne3dHlff3CHkEaCAcdpjHB/K+cTEeh6o0VOwEF3q5aywTUTgPoL+4isJE6oj4kB4CIR/7AJyiPKehy83EZ4fauaEqLAfa8U4u1WB62K/0eyyfHnDR3yRD7jjhIcYEfsBMXbY9AMIkq+KC01Fi9bcEjQ8ZHOf6/36vNFTXHK0VVqei0JeFIYurKrRRnB7w8OCo5mK8ZsZAJV+toZw/vPRQnVci3lowXT5Kkkesbs//BYP//SPCA977HZXCBiQOiB/8RM8XF1jO2wwRFN+tvDQ9HlVuH1uRCabOD/aOTTOWNOnFU/PYNn2vNo5n/hYYW7hev2105VROUB8H5fvz3Gs60ADE+t9PNl6U6fQdv5sUzh+4uS3Bme+nVpnc/t0TSefUFEJiAPS1Q7vf/El+g/32H77vsHd5RxT+QHBpkzHnBkvv31ApAO+fTVgfCRXhO/NKh666M1zt+eYwT1ysWUMP4oLntCzk+UJighZiiXS4hMA/4Rq4Sudt3D24bozGqFatZh9Us8+hb5e4/ef8vpyGM+rbO25/074vMs3z7JEFTBzGBC6DV7fDHjzYkBIGTwm8Hf34HcPSL//IKE/mlPHsPOs/bMMybyvly6sg+MLhssnf1xeGqLKte0Vxw3Nx+1zvhT2ivSbq9wT/A0RV9opFJj+X0RI7f8rU2nCjUrUKRFdrIis4WWHC64ocu1L1lUHNnu0Kj+0+qKMcAwHM0AieAs2VyokyyUJtg24JZiF6OeSqFkUdDJeLoQI65P+2KfS3wUJxfPPWkeddarGdP4qzRRTCw2ws3jj2v8GiObUYWHEzEpInvegJ0N2yhc3BMoMRFt0FZ3oOst3Ali+ZxAQIMYPUKWHJlI12BC8IYLJ+X4TWIdbV0KIBCAidh2YJUFsyiyC0w6gEvbKoFXGKDklxNqPJtL8CZ2Ejet79F3nKHdj3mX8WT9jlxC7DtPhIAxmmhBCwO2mwxSA3Ac8gJAPCbyfQPsHfZsRjyPCNAKTxKHPYI1UU+ffLf5i3uc32p1GKKHDCkNsezk0whMiQs6Ew8hISQSWJQlxDIhdzeVhz3v6xMMU6fpYbGOQWHszhEFMOYGYQSQKqtI3qDdFYTIdDgGq8LcIUuZ0ENWEz4Xp4gX6mU+RAKruU8vVUPbcfH4dldzUQ02754vil/k+tvZU8WACdRFcWJg2UUxEjRHtlScyR9B5PtVmOxpBzxqCLddPSVJdE1WnbBaEPnxGnZ01WKyCB2r7SDZfrGGbCCGqd1ROxQbGhF9FSMS63gQVzHCpvzHV0tBMlgeiCW/VMH11HUAoDjuZJa/J8Shhko7HEeNxxDiOmntIYcvwmypsbY90XYeEJOH/VKGbUsb+cMBhN2LMGcVWNkRR3EGUeuM0YRxHdJsN4jCoMmKD7e01rl+9wNXNLba7K3Rdp/QVIwR2832eIPHngo1h9sTZ9x8vpxmxi2u4kOZ8qsfEJW0uhTPrdV4uGP8URqDdXd9n+f4UHc+t9/nzti5Ybe8xS4LqHgHFhIIBzhPuPhywvzuqR28utNBiLIUucHjEnaf1/DVfAb+elTaUK+wtV2oToeEEVkfb1NcUnl2qZ2flAQjVCseqMGOUin9bItslawaBqOLoYNMBDSNUcDQKXeDXwRO3dmK34ZnIprSZ8vLdTU/D38C6y2VM5f9CUzqhc/M8u2qEb+CQkYZUn3w4oE/3pS+ZEzKn0plQzh01+Imd0FKdKhSCJeMmhG2P6WqH1He6JISsAx7NA2KmgKh0IZV62olpZ/nx7UTuG526hVnj2OSMWyRMIBwCIWpuCO4iYHksHuuCB1P3ndv/2t9GI5shXQmrZDSi3WdP9reNNg1yc7XSmO5xNs7h8ULu/9nFxSXX/MnnhacV46t0uAf/7g+Imw3C0CMSEPqA/WaHaXMFjrMVNNgp5yOd7EsDB0VJbGNeHdWsjrD+AD3+7qkaz/5ameKnWO0XLqGhHVoa5vGz/rShaFEYFried9jN90mNfHt9+Vg9V1qxWaVTn11mSs55KPZLvPFaOK59I+WnuY/IcYt4FBkgWx5JJs0tWCvIAGKD9BnDMeMKjLcr0MUnf631/JGxPLrxV3DIo2XlmSeQTE8egytPzBHhCRETMLVWZ+fL/BlauXamSWlVD/11BNY+txYQ5Hso3z9t/mP5hEIE/MXXL/HmxQ0Qtwgx4sVVj5AyPvxf/hPy2zt0RwaSxKQOl2LLhdB15b51AGtwyKvPfY7iidqmDX+RAR97dI6sHhveqXJSBMHuw1l71GlwlB9V4t9CjJhlsBevV0uS+ttrqYvVSUkoqgcQTCglTFCEE1AVQdoMrykBOPfPsnfEoljyCbC6QQcj5FkTnynTlNW6BSFrxgUqcdqBVPCWCfykP+I6GMQsDYkTGCJMBTmhXJBQ51lD3gASRkXClbRa+sLg5MoQNWupltWVCbM+SuJosUA7dc5Vgrzqm7hafqj1cQyVQbZ5F4GkP07F7d4zbsRUQsyXnrN537j8JNAOMlRoiJo7IIeiIPOJEEeeSrgsQJK5lgjD6kVhtkw5V4gMhOK9sNvtMPU9Pn74AM4JD/f3oBSw2+4UpgEmQqaMEBhdCML/Jy+APeLIQNd16LooQt9Q4/uacD+p3GCkPYgiiIFh2GAgwrDdYvPmNcac8S9v73B3TLh9+QW60OH44VukdMSY9sgM9H2PlDK6blRm2AM7qTDCLnmOilCFCEGXzOAWxSpM6oiSILezUEi6Rn7vuT9CRlThKvcdgtvzwQnrVa0EGEwxkCcT4lSLPMtbESIDUb1O+i36YYO+GySZsB9b1TRVYXSueSjqhJAqTUKzH20S/B7xrudUd0a5X6wUT1EvbFPOs/dqsulT7/rUQASB8ZzFU0X2tYTrqRb85rUSCh4mUi8V0oTiXuClDHhKgp9yrjmWfEguPxbLA5NzAk8TOCfdAxOmacR4PEhOiGlCThMQCBERQevsul7mTA0OrE+mPLF+F6FMqDgtB0YOkpo1EDBNEdOUxOsip5l3ip5Tquwkn/TbJjaYok1DWzgBCIMx5QRT8FgRzyEqe2WaEtKU8eHuDvv9EXcf7rB/2KPvuoIvc9JY5yFgu9uAAiFnUTpsrwaJ0Xx7i7v7B+TAuN/v8fbjRxynEW/vk3iA9D36QOgjYQgdutBjHCeMhwmHMeOYGS9fv8b1q5f4yV//GjdvXuPrn/0C1ze3ePPF19judui2O8SYsQu/R8AEomottqR6fiSWfyx/6nIpV2g4uPx6gtLndJXzEgn41fYLvIg32HIHJAZPGTy5nA1KwyoBibkgwz6LArqcHQQgFIRLgcrr8uHsY5nBEJxrZ7mM2egzadu3ZmeeP7frXU+D26d8zzmVMxTM1VvanYvw7/jx2pDYxth6VjQLBiAwlTxHQYXx9Qxy47fzmOzZWklRPszWb9ZUnQH34RUoRm4XkynH+xRa15YYcPQFgeiIPn2L/mPG1YExpSP2xwdQyrhPqaw5EyMONedD0CTlQUOrvn35GsftFi9edBgGamE6BGCQs7QOv57tjfLB87UGB6ghLe2me+okQ1kg2tOb85kmP99Un7OOMklU2yj53YawRUCPDz+7wnjbI0wEStUDZNGH5mhyicBtvdb4VXDNFWbeEIXnRMPzFTjVStjBg+0Re897ppfwTsZLlX8AjI/xk9PO0HpxKPApGM1gKsU99sMdcjhgu7vCSAkjJmw2W/SbAXkYwL3SkeQmzaDcK7PWekDtlxO6rZVXHh+NRy/+6pJSYXd9Nr9klO5lbTUvlcZ59eHGM4/nA1+Orwj89b91IxBqnmtqmct9fKWz5wSrOyxPp3j/2gdf1VM9IuY1Nr8XbT+yImebVlkQmwecnm2NApBVGSH8IZV9rZiRAl4ML7ELjD+EIw6YTrQ17+NKn5fL566dh7qnUdjPo8cff+tp9T49R4R9N0aYFSDQrrMtz9NKreXkeQRBEILb5sh3/blPZX0KijpTUbM5HUp8attFJv3E985Xiu+h0s9b1vbd2v1Lh8Aqoew7oIuEm92AF7c3iJ0IV3g/gvdH5Ld3SN/dSciU0rjHnI4AQYv4zvIkF2kgTz936u1Lxt+GRTrR1FxRcWm5pGNssE+CKBZ4tyW27SWvyS8EilMO1ARDdujyAu/MD3gTgjOjxNGVg9bW2wgdY1A8kVowzaL/mdnyiyp9YfHoAaC6t0vdao2dC7mt1YhQfm7jUVutfbM4vQTtXqGJjWAN4MwzAacrNo/B33FEsX2W8difKWyAJcCvE/MLBdZM0camJCj4m5bP+l4xCpEAs1BAqMnK3XirxeAssdW86KFlc2lzw4l0PrMokJSQJkvwSCSJv6kyGMYgEBg5EKLOm4RgEcEuKCGlBEwicA0IoncqEy1rGyChWURxpQq0lEU1xRnMQQSRauElmbfJZBUymMCYjkcQgMP+ASBgmCRZ+2EcMU4ZXb9BN2wQQgRnwpQ1pI0KnmMgpCI8b5VUTveje3G2wU/8LJd1nxWrdL1YROezDc1gledSCeNUQCpQ46ljr4vwpJ7/No4CdiTKPFJFROx6xNgjRImj7a2SLWdDwZm63nPcbYpTG1/dpPPnqOAMv6/afH2V6fczUcdIq7i4CTlw4oAiBXxrmtmUA/XTFA8xBhXqmyBDBBsgzAT0Bsi6B3WOOFf8X/o200IY453VG4KL0C0jz7wjLCmrCcGCCxsVTOhP5Lw4Wi8cCylQEnBD8zSANUUCIeeMGAWHWFdtrNZnP/nzcBQFT7gQceUtOzvKC/KsKeqSWv5OU8I0JRz3Rxz2B0waiqrrewAdpnFCMoFZCNhtNwiBMKkHVNcHDEOP6+srAMBut0XKWdplxpQSDtOE++MRmy6COSD0HSIIKWVM0yTKkRCxubrC1YsXePnVF3jx5Zd48fo1rrZXGLY79P2AGBiBEiIOCJQaSLP5ac72HzAd+rlK9Qr6VO7jbCv6+SnU4g+nfH+eEJ9aPtM8rtBlhq13YYub7hqYJiAn5CmBR/H8cgfYGb6i0st2ll7ILTSzbtbcyOJpayf+43t2QYnP5CZOCF/CYXrvBcf4XgAGfnTmQSIfWWny0D7sn9djNZTztZoClOfcWe6vVSq9GeHKoCu+t/Wzr5YDCXrfeBn/eo6qCEo+79YEGu8lh9lE4OmAeLzXUIHqlWehKBFK+ErECKZOPP4CIe+2mLZbpKuI1IVCKhe5RTnP6u/m+gkFhLvl3j8B9LNiTzq1y/IBf70B7wrz1WNTDSkQkPuAaegwpMv2hPGM8n0dh/uQSTz7LDQNuMnd4tnytsailvKXljRmgaVFh2fTPJvzC9Eqn/g+L0SEzBOmcQ/KCTF2SARwBKjvQMOAGCO6GFzuX+uT0botTzhrwS1tvX8J3XBqyGv0MM3dFVqytIW12f1H1DxnOmd1Mi5ylzjxyNpc+OoX3gLUfl8K8K2cWfnTWodTL6xeeeop/7mpGPOeW23JJjEGcB/BCaDJ0bQM4f2FXUaRQekEd2EAAqMPQBcgxqK8srMenYSGGZwfpk98/fzTn49EPS8HOFee4BHRehdU4YGx92ukyKmalt/aMh/Q8jBbKCMW0q8/XvnhEtD//ZVLYWzCFhlb/MVPtvj5FwN2V1fo+14SR04Zb/9v/wXj794DDyOKRSPW1/LxjfpYr9YI9BmR4QQ5n6fMSJ1C2Mi97CitU6htsZ1OzIM/lBmAKR/mh4614xPMYW7t5ARVa9ZdBC7EvY/aXoR6WopLbHZxytEK+KX6ImpXepbKfLXjX1kbxzshAJjEWj5NCYkTyOLK+4kgmR7TpueckRIKo2ILwnbgLVrW+VBBFyexHAbJgRdj1LA1gI/THTU+ao1Jqk15Sx2unZT6q0dAGz/Z9dVPh8KYwVlDSDcMi1d4qLVa6YuuX66W1BUmCDalwXJEzNbemIigca+87FD601JkJpSNHFVBElT4L/OZpowcIrooQkrqIlICQgY4meJJraDSBMoqqA8BXd8hdgFX1wnEEen4EeOUARaL7c1uU5T49kchoA8BHDPCROIVAUbiCcfxiJiEwYoxqsV61OS50QlKM8bjA9J0xHc5YdhsETfXSLqm/dDj6uULhEg4fPgS+/v32B8+ApDQKjEG9EOHkDLGSechTepvIOGRRMWSiieNEXf+ewMXLFbvCQGdIAmE2MmYOZfkytC8EdCkk5kZnHPBMT7GPjODYixJFavnlKX6BYLuffNSYiaAIkJHQAcMGyB2A4btDnHYotvskCFKGEEHnuiYxUcnkr1sXkP2qe8YjvX4UZ5D3cP+3HF4r+Bqm8oZXWqfTn3jrtWH1kkiCaMj+yoghCxePWSJpyUMmMCYeuA0eSpC2cvN9LCFNFJrwGThI2o/BYK0fyz40vZ6TgmcEjhPSDlpcuojpnHElEZkzdcRdG+BJTEzkSSkJFWcUAjOS6PmkSnhpAKKksDyWQA1mXlQ+CKy/C/2bu09G6PaKGJ0JRm1bUCVKJrkPSWM0yh7uDMFj3hCpcxIU8KkioA0TXj79h3u7+8xjSO6GPDy9lbDtAXxDmFGFyN+8uUXCIHwcNwDJOfAzc01fvbTr3B394CUEr7p3+Lj3Uf12ku4P4749sNHDDFg0xFuNle47jd4uD/geBwR+gHXVzv86u/+Fr/+u7/F17/8Ja5ubnF7dYu+67EZBsSQsYl/AGECOBUwXYT5Ige0P5Yfyw+2VBq5FKMTy9+ns5rz18UZjeU8nRLuv3uH+7s7pYEcHagEQ8Gq1GB71zGX4YEzkBOIIsyPsw5TvCCgnqBCP4kS2OQXlW7T+k3puyg8+0Q1vlE6IWfN9VAUy0IcZOd524TZY6B6BXCjbC5/AGB0bWYVCfhEa6Z0d4p2oORuWsgjiBbrS4v/10deaFtjr0q/as4Am/fyXjNGIHfAw09GUJ7w8p/fImahDVI+Yn94CxAhxAAGIQ4b5yFLRcEOAK9fd3hxG/GH7Ut86K8krxEINyHiigJirLRLS0KYZsJoCKeYcDyTvRMauGtmspy9j5XiTLi4M5P9lJ91rcqTAaAs3st9P6CLPcA9aLxB/3ELWhF3+a1uW9B4BXYXmNsXyt5xz5qeoOgOM6/tiNkF4/eUF2bjoLLb59DcjTyrqX6fSw+8QqjkH1tputyfzcPJQhKuLH9zD/xv/4CBIzabLQIl5J5wfPUGD1fXuH3R4XYbEDXqqoUNLk15Hn/ZSP18BHS4td45//Cpds51ofnpeJqL6j/TtzMVfK+2C77+NZh4bl2XPv/Mdj5LMRlA6clpeJlutng/fInhu4/Yfvu+8GNkyhgi8eizXBGUAa7RJ77afY3rAfiXu3/CkQ9NH078ON/xS946dUOH+nnhis/+fGp5Ymimx5bv8f5UFHOqFp49ibLwyydXlBGloQsOv0efMBnAc2f5WXpTAKuz8Ccvp2PXPqOuT7h/DgYZQqD1XYfQbXBztcPN9RZdBuIxg/cH5OOE/O4B/OGgJ3hzhDetP7p5TynAThFmNgJnXXt6Oi89ZNdnpBIcLfGytGA2juNMXwphPRcwuP6xWSATqsbfn3Zzois3tJVYKq+NpSUAimWRoyKrcxS7Oo2qnPXZfWstbNbn0Ii8xjvCCNIG51jzXJIK+nsmdC6EbTkg2BGavol5SkEURgpBXM6zPZAZHNr352YQBJfEuh0IvEKoCNhMZGiCNmfBBmgYYWfdVavkksNi1iGsFUL1MJgT6GUmPMeAdi0apseve9Ne4TDk0WJVr8p0jf8YwMhsi6VCRZY4xEQKMaThnEiYNguZUMMOMAJyEXbGLqLPPfrUIacR43FC7hl91gSCkerQSK2yubqQc1AFjCUSzkkVTbZ2xoRWp/icJPTB8XAAQBgPB3DssBkGEALyCBFobjaYxh4oDvUZRIzQBYkcr7kzcmYJOQNl5GMAqZCWdd8b35ALwTdfb4d7qD5PCEWJEJTJDf6dzMjEVbmg+TqEKVJtkwvfJttDY93HCMoBGRPIxBOqKAkkTGvsesR+gxB7FEtKrj32RdpQ3EasQgsTrXvG6czBYWMsoauWLs/WNoHWqyK3b9Zulm/rdFMVMkCtp+RPklHbPFpc5TbWbqt8cLU6nFgU35hDgWeZFTdnbyGrXg+WGL54RDj8RBJyCeASaiNYngoNF1U9GAy/K06zPQxTXFXPOAltxM3z3qOi1LUA7TmWdiNkTarKGSklTClhHCeEKIlXrQ85yXPjJNbQk4Zns6Tc4vkRMQw9+r7DZugxBYAzo+sitkMHooCUJaRa10d9bsA0JmyGHptelEtgYEJVjkjOGkJPIyIHHKcJU04I/QZxt8OLL7/Em59+jRev3mCz3WG73aELAR1lBEoIGBFoAnAu2e/69fNliT+e994FbzyTpL2UFi6K8iewEqeVOYvaL2q71nt5H86XHxJ38unFz/fjc/TEsesBSeW7o2/Y/xY8sE8j9mmak+6olGiLZ8ph2j6s31gTTBNMWCKEZ1YBi+DbkoPCtVPxZ+3/EtvZo57Wr31gttBzZgzARelhoZlChsQTheXiMgVD641pJZDmfXB0u+/xIh8EUATqoXyfKxwcbVI+5vO8LGUZCz0m/9lUNlbzdk+fY5233MmFkMwT8IgujwjpAZSU9koTMmehP6GkSggIXQQNm2LgYB2mXQR2HXizQe439RYRaipquLV1Z2W5XCHNexEa/UHUTFYB7QX/+xieLEcrNxdtv3B7BR7eK24lpCwerTFERIpgiggckVI3i5W5LM3ylQsnlBCo6wr33qKO8loLG2W/N/xONeLybOvSI2PO56Glz2af5Qcv3lzftmvPwGhfpdNTRvw4IgwE3gAhRoQYMPUdsOkRekLvogAX1sztp3UUO8cwZ8rKY6fQdgtVp99/UmOPlEWbC7qR/V25wvMva105TWe1Hai07PIcWZurE5XO4OPxtpfj+pSyVtuyD3Pe6VxN51siCN+YN4Tcx8UT1Hwz3K58IQRHDSzGRUt28PGFu4g8u5CGe0KzTyhrAPRpDTxZEWFNtvupMraXlcuRTdPWCkSW+4tOfZ7yebfUj+VzlVPLPWGLkXf4m59c49c/ucJu22PoI+Lfv0P45g5vf/t7HO4fkB+OWoEle3U1r2DahUBKmW5ag8VZaRAoUOpfR6bkn1zcOwnmKlw7FQrA998TVovnz+zj9bodSWEELJsInUsb3gMis7ic53l9DDBpLgBAhcMQBokIJvTOLiZnsYIGIGuZ9Tn9y5W4mxNTrSXr2pw5TEVUf6gJSVZlQyaxcAeZEFkFt5zF2pvca9p/UAKFCGSS+P6OKhUPAS4WNUU5Q5WxChSRo1l8a51pUmZBggOVlBO2GhRAITaslVnzFOttKk3JeCx/A1FNkA0uVr5m3QbmEn9dgaUymSqQF+EhmpjxlQMR5rTM/SzDbdVPmdImgIL6RzoLNoNGo/fnqysCbNm/QcfEjroSC2WBK86VYU7ThBBrboYQYoVlBCADKU9gZhzHIwIR+r4HBcJms0FMPf7i4xvc8xH/dfoDuCNQUGFhtwUhI0GTRBsKYghDFTpQnkBBYtannJGSCA8pSFKtrh/EOyKKQNIyBI/TiOPxiN3vvsNwfY2//NlXeBgn/Nf//bcI04DNizeYGAjd75HSAWl6AChgsxmEb0tJ4TkJ4xmBvo/o1SpxmpIITzlX7BSUCXfCblsVAhdPFREeE6IKlmPXSYgdjfNvjG9KU92/ChYSQolAMWrIoCh5A8zS3cCl68HMiOoim3IqeCCQeFeE2CH2G/XE6Gqs35xQYmV7yztTHrnfBbYYChPV4rKBY6qMfAOXqErNYh25quA2kYHMT4DMYWnTPABM6B7avi36YeNRHMbMkjtAwzHNOgkAJQAdirdAbh5KKVlXYa0QtcNhZnAS69hpSpDQTAmcxSti0sTU0zgiTaN6K0C8YWIudVvS8q7r9LN3VqFcFAs1LJMl2o5OEWHrRuW8EpwG967vu+HkOpa5m33W+cmsyepTxmE8YpoSDod96Yspd6ek+3qcMKWMLnYIIaILjO2mw243IISAm+uNhGbLO6TUgzkjhohNlHVPMYAiYXd9haurHbZdh9R3uNpscL/ZYLvZ4kgS6okoACFiPx7xMI04PBzxniK6bkCMHb78+id48xe/wF/+3b/Fz/7iL3F9dY2u69FJDDts+LcgPiJoeLgGSDzArpZTz/9YftiFzgiR/vwLF5rY/1lphaBLsfwF5cTjxhdwZkw54x+HCR9yxlTok0pbVwLN10ez+pxQMzOYEhgmxJZ+F5pczzmjz4MqLIKdIyGW88Yn/DWugjhLnYYvjdtgo/+NVhQ8l3Mu+M7orhiC6PUhBgdGO2Ql5Mywx/w87EyJSlznEITeDlV4HQOVPF8hUAm9Zx4R8zOpnlj194J3m/0S0lHHafMNr4SQc8u8BCts1VoyAQ9fTuA44uVvvkN3f8D0Xz6AOeE+S85C0pCRXT8ApImmKSDECHx5i/T1G82vUWHz20B4q3NjeZ3KCAsdYQNemiw0igcYnVN5pjnvVH6vREVt6/A7i5s5X/Jj8zWp/Z23fRw7vPtICN0GwzCgpw2Y4wxm5WwWz3rFZLpmxoaVNaq3tDgI4HVo4Nm1sq+rVsHBSa73svuEeUZUPgCOPvSjF/7QYyZb2/kMnsbZvPh2+swmQGl04V2mkDFixNAN6Pse29uI8RaIC9KxzlBrdLPg0GY/Z/fd4cNrDN4FxbGST3jHE8+XtbH2PinMLSDFxsnL1Vg06WFv3Sqofd9423J9BhEr82CXHlWCfR+UwIkqT7d0ftylLNaN4WfFo+bCs0BwS4MTSA9lYsmtF4CMrLwYQDnj5ndvMQRGd5NxmAHbpRTyAgAunOrPvyK8UqnH3p9eLldEnFA21E29fv/R8ugqrDzg4aegtvn1tpaz5QL1Ip8Z2yWjfrpVUrvQz/et+Pzl0bi3z4GDZ9TZvhHACOi7Dtt+g9tdj+tdB9ofMX2YwG8/gt4+IH3cI9/v0RDza4j4yTtMgG9JKpx4+mT9J4gdMkxEsycZSyVEW4ev5lLvnjneW3vr8TjI3hLIFBFVOXDe4m9pU22EPINdvgUljmfz0ljlLs7tU9zgCRxGtZVmZjKDyQjIFeEh1zF455AybvViKMny1nu17Iy2ExCQSZLMMpJMifYpFO2HvOOtiS+lJdamwhQXZS1Ual6MLzyROYM945MYzkKDWiJ1SRudJ47p5B1t350Tp4rRFWW+iIpDD2luj2yKIRd2TJ4LICQEELLuwayKs8gZgYWJjxSwCQNyZmxShzFljNMEEKEvChiDYq6/CMo4BwQ27wsTImRQ0klNCYEhlm5BiCRhGhkZAcfDHqGLCJwlHrNwFAj9gND1oNABSQSmFEjl+sLAS1h+I8S4CFFjNMVSDZ1k3WdyyaF1DBY6oDJNej24ZMjBhOKELhIioQihmVGJPZGy16TOppAMoXhOyP/yi2zuYih7OYQgSp4QQSFq6DKDcf1TYTuYK2P+yPn2lLOj4DOuL1Y0VPd6s2FgylcnFDi5Pwyi6h6jgpAqPityLRVYLAkWhUqup1zxYnJd9eMoniJrOFfnOWuCeAWy8sclX4QKoajCisfGwSWGNgZZpksEDcyyx8grksv4PCTqWeXmqswg+efqeCpqcWy1jdXhR8MJyHpO2PgsREmqgrk0SYiqTmNcd12ngjQJk9VFyREzdBEpyN6Q/BjSftC56DREX5okHJR5lQidXNciUEAGkFi8IxiMbtiiGwbcvn6Fr376M9zcvsBms0HX9YgUEDAh0ARK6glRxnwa8FdI8zPl1JOfhwa+hDw9tccfo30fu19ITl5O12P9avNsrHGmbQXPIcMfLeQ/HM31dIK5vvt9CDNWy+XcvOGCKpi4cDLPPLaqO2hoc8AElcfAOEZu6+Pm7TONVvpLPhQfs2FuI8QU2xn+Lfl8DFcaxUvqDenOjJbMBeaKWRsLt2dpzm1YpqL8ACQcYwY4EJhL1ggUsZ0+S0JBFrMjwf8AsnhxWpLpJpSW63s5MenEcs3xe5nSFnbKUaf3vEdEpSFq/9nVkTqAAyNOWRT56QDKIzA+ANMIjAc5Z0MwklTySG8jOESkYVPPw90GeejLuUagguKTzY/buHOlQIXHOuIKq1TnwwwTqJ2duVfEfDLJP+PmmADMY9mvvD7/smjXnWbIACKJIcXYdcihX5Xd+LUo66Nk+JxntKsXl5myqdZgNPS8vtKDyl81za7XB2C2FvP5+PyFKSMRg0n4BBBL3pHYYeolx1oMWJ49c36vbJWW1mofRoNXtAP1mbUpeWyZFJYLPsFyvs5VQfYAPd5UM7LS7oLB1d+8evlcn8i9d+7d5X1e+1g87ffIyZpOgSW1z9UXLoPOk+Nd3VfzCycGVmgvWcBFHw2P+6pixLTpQeNUc0UYg2ZwwFyVFSo7COOEEAkD9TjGgDEd2podQbw6hQv4WHvoSVjp+YUXXz5720/ziHCCOqE95HeZ00eVETT7/FxFLDII1CzwReXUTprjxyJpexo79ccisX9Q5blKqU8oCRuMfIW//uoKf/2zG2w3PYahw7v/x3/F+Pe/kxAjDORUhX7LYoT5/Oojq1jGex74CtlzCVAsOtHO6fIcs7bPHGjcVnuKeWzFM08v1gOL725JRpsQG0ZtkTukS2MlE5A8RlwS8Ur8fiPa1JIqVALc9BOs1vol/BOMcA2OKKhjzQ1RQnNeCybMMvmVWFeLsMwEmeSsubP1MDPQuSNUQ3QAYglOHJALUS6dr5ZFS5hiZonVT5ZMFiAKGDOAPGksfIC6IOFpgsYa1Wnwsd4BiFXaSjHGrWld18zWMqXJeTGQWmgFjYdLauHMzouAykFdZsTWKrMKHpeoQ8bMAhe2lva3gmfIhGKE4llhNJWcW3o9oChmiIQLzkZMkGagoCAJZEviaC4hl0IIBTcwMgILzE5KsIyj5LLoNFzMdrdDlzr8xfsRd+mAf7h7h2PfgQjou4jNsAGDkZOEOUGoIvUQgF6FsMyTzq0lt82YJhGYd+ZV0PUIFND1EcyEu3ffYtzfo9/2GCmAs3jPdLtrhP0e1F8hjSP2+xFdxxg24mkw9D0OU0LSXBFICUPXo4tRLLMZOASS5LY5i6yVja2S9e507YdO6uyCWCuKfEM8R0SI3Ck+INzsIl7fRuR0RJqmwotR14EoapzqIDkiXEgeU44I/yLWnHD71qIMlVA7FAGm0m+DacFVqQh6zftgzcvBYFTgy5P7NYSG30Jmk5cdPItg2gOxjs8QpAn9jfm2exWDlfqJSZyi4Prj+rYUgBpeVIG+hYwqfZb+GiyW97PzwgAWB0bNLzObq9yeCyh4WvG74RfFr1JXjYHt1c52veskzFmn6z9NI5gzEgNmZStKFhHQmwJLxsclIbZOiAFJwQ113dVCmCouzWbNqIM3ZU6eTJEiaxcg8N6FIGGapoTxeMTheFR8msrI4maDzRBxc7VFNM6egZTEe+T6aqNniXiHdNq/oZcQCUOMQMr47tvvcP+wx7t3HyVXxCihnpBrXxA6cMwYp4xDTnjz8iW+/Oon+Df/07/Dv/kP/w5f/eRrbDc7RIoIyNjgDwi8B0jCQC2ERY32+TSjO3vrx/KEYszvn6b8ua/Y+f7PrV/LUUHr9MbzWm7tgmu+NMChbEd7zb40Ap2Ke5r6UMWb8iVDE+TIn+E79YgooTtD1O+qSDbvsRBnSmpjKIIjrNhdh+D5JF6wyfKnKa6TkHX2fEDIJBb+mYBQjRvkyDRFCYO4ekQEOw84SmhSJabN+t/CPZbnlK6r9P3MhImwcmq3hWHDnBla6bgt/GMJxWT39OVMwP2bEWmT8Oqf36G/32P8r2+R84gHVRZTtPNO5jx2Ebtdh5/+fIv7YYt/ufoCmQiZJAi/0DmA5H9CpRMcIzNH03NBPq08WKsynoiadxcTRe2Z7+G9ecw/XmZ1rcwaWNHmVVogIvbiNdL1G7x9+RKHuAHUE9uH+7IWZVvIt1zBVp+et1DL6d7OpAXsPGEaoxPlEHOucGM88UxLXYzIYDiBCm3p0dFCsea13qV/a31vCM+TIyMCprjHuLlDwgdsTQEYCffXVzhc3+BVDNjB9sNKE6Uv9hlWHnJXWlQ879LslQtwMy+/LxRV5wwqypxe3uQjVa48vJyJkzDo+17g+nxj3jjpfL/m9y8fBLeEoa/x4jqW755t7OSDZbfPoizMQ21XUyQrhMOLKxyvNxj+8A67bz/U2spj1TAQACij2HhFivhq9zPc9Bn//OEfMebj6X6ub8zV8oRVcJU/syz261P7cFm5WBFR5PDCmbU3LlJG0Ozz4pblnZkiwJFC5dtjBMSyakfxrbRa2vE/FpiRTi/3/GDA2p5ZX9LPSur/KfiGp5p7XVLfCtI1q51NH3AzbHC7G3C17cB3Bxy++YD0/gH5YcSaQORTdpNBW9VBrMM9zd46rfh6Ono5dWf1Pp+8I+UEXelvN2f4rL8FEVtjjCbutwianWUTdA5LIno22fGi34Wp0u/zPdOwEtqeHLK5jLsmqlsZ3Jw4mfN4cNdo1laWxMY5J0QfKx5mmaRYiQiEmlDPiFAThtu8WOJA4YkqwVCwHvkumnANwihmFVRnm+P5elcYpXJ4nj4BWZm+xoMZ9t3WozLqKLXVF9ZqLsZ4rh1P9MzhQIQuXJhMYzRrRe2iEYzoB1YgSp8Wi+kiZADAfGIuHPHJAJAhXgfcjFYZA7XYZgsLk5CDKIUoEAJHbEKPBMZ26pAhQtMAgHsfo9kxe6gMZVAFlMgUMghJPbxlr5mgEkTgECT2MgETRtAYcLi/Q4odOE0AsySe7jp0wwbxOKCEqlMhBcWAkBlEuTAXWb2aQiAgQBIEI2JKEiosldQvsgdiQA2PEKnE9Rdhh4OfAFgi5BDEI2JiDdPAdSYkzEJQa/hQPCpMgQQiBAtlEWIJBeXhFESw3AiSfsMJx4vVulqoFcpCcZQTYC9ABYSFFVeBu8L54EyQPa3H6nJ0k+2xdnP4j1UlXtN2aaDSUbaH6xz5ifL999SOjEPwkSoqCi6voyhCDFcLN/jDCWxs385xPFW4IA23YcUUJ+YxEGK1TCp0Y1EiV/hYjG2FXikR8ULFswBpeKd2fyrCLlPbWAKbxTHMmrcKRIrHR2axpAqEGCTH1dB16DWvg1kQ5yTviLBJFCGBJYQbAHRkilLZw8fjHvcPD7i/v8f+cMCUUhFimyrLQpTZcLa3N7j54g1effkFXrx6hb4fpH90BNEEwgjCVM/yRjh06oClOQTWV/5I5Tkk6KdY+rf1XP7Mpf0sNJcXDMuV1frW+3CqY20n5vKXOQM2F9BfMm+fIpR4TvG4aNk9f/bT7PofB0q5fFYL6faO/3WKZrN71URCfrIzbGGUYLRe6Kn0lHnbmRcEmULZnlmUYkoOw+ENbjOaPFvuHwnlaHQEAPWgFJqMQUDWPFzwffZ/UGUwkFXRwGWMdpYFxW/af6KCotypOvuyNqnNbBYazb7XMDqVv6lKCAtkmORPj59uGkEhAdODeEOkEZQTtjvxgKNQcx0hBqR+C+wixs2ANGyRu65OgA7IzshCB/mh2dk1G6db2cVk+PdA5dRC8S6c1VTeam7P6z41xyceoNkPT1vot54YA2dsiEsoWTDEQ5kkTO0CfzXfudkGfofR4q3l77OoZP5cgYkWhko/Vl9Yq79tZCH5epa85cw7ClcMBgdTBNY+hAgEZR8yZw3vVu8bRmuODWOmLiyMGdwtpuY8TQ2sv05zWca597m2cWKZV+tp98MjJx/Pe7r+RpE7zV995Fhd1rXkIdb2wlPLnOJTrP2Mmrj5OHX7xE+sj6HNv7dUQmgJYigKF4q3UrP6P3MxbDQTWjCBmLEZGemyRXlkDE8pbr4+keb1+O9knz4DGff0ZNWs00+PsdKfr1zejnvypELk8Rr8r7ppjTGd1zlfhVME7Y/l+yw/e93hr35xi812wGazwdv/5X/D/j/+BpTnlmMra+IJsGcwnieVdJhBx4m6nwaqT991lYh2CGoBtisEI88fmeegsANMK1TCKrPlcjArcnPDNqtfT3ixECyF2NdEvRDiSug2IeyzKjJqOIpQmCNDmPZczhKOwltGNVJnwLWJag2rVt5QN3Yiif4XC9OPMuasSghKE3gkgIJaryqDpMyPxCMHsiYK5Cy5AHgcRaja9wAYeZLQGCYoitHCkJxiFgiBIki9EAhUwpkUQXKw8apA1cVLNRabaQlRGSIYy1mUAIxQ8kKwo9oLw0dAicOuQusKJZXQ8XLVBm5sLRhlTQEU63RZG1TG2DMWnmhyzCDg4vVbUmO9J8mnM0BR+SyS+pmcABpljMGE4SXmr/ZFYTQQSdifLDF5LeSKhUEOgdD3A0KMuL69Rj8OwPsJ9+OI34Y7pKFDDFQFrSSx3tn6CtkTYvFPiDrH5okgn4xpOgJghOkICgGcNaZ8BDIf8N3vR3A34IgdmDr0wxabqx1uXn8BEHD//h04jxj3R8S+k0TOTOgATKNYcYdxBJglXEuM6LYbMDPG6Vgs2XNWzx0AfewQSLw+QhC4Fst2WX9TPASqVvkxRg2dFIEQC0/TdT26LorgNASQfkLfFaVIzZ1AsVPGnCEHuCpT1Ptm0jwFKVli5KTAeJpBKsL9GT43ZdG69dJsP1iy6/KyzUet7VwRfoiLIMc8ukQh46LAFoGI7tdAhdEoW1GFDZbjxXsLnD8PHQOjOMbCiFm9Pg+P4HHrEwNsOTgYQC7CKfOcyxaSKZiigRr7OYA0tJbmYyGJA84soY6KEsLGZl4VJ4SmNtIgAFnCgIVoXhSh4DubH4MoUX5UVovByNNY8uiws+aN+h5lRsiMwBoaq4vYbjbohwG319fY7naIao182O9FiaD7vVOL2T7K/U0/AETouNepCTgeRnz37Tu8/3CH3/7u99gfR9wfDkXREUNAYIC6DgEdNldX6Ldb/Orf/R3+9n/+D/hX//Z/wE++/pnk8EgJHf0OHe1LfpSSy+SUEOQzCfF/LD+WP0YxwVolUSqOXuQI+tS2Tlzn2c1ihKLnHzf0DVWDYiccnxPupTon8LTfBECcQc0oQ6hCAqqQWz1AS/I269AKLwBVulrIPdawlnkSBURKCUlp8+zCq2aYIEdxtrVVBqjesuprTMQlIoOc7aQD0XkhqBccNeeQjOgEH+YmXo/XhnY1erXkrXD8DrjSmq0CQkrkd+jGdzCqe/c7gIlxf/8ex2kEYsAwdPj5L6+w2fizKuAQB/zm+kvch4h90CTdKnA3r7zq+UCVni0sg/IQM4XlHIoLnJULVfmAAhv1nntrxj7659o+rAL+CktbLjXXbWztjS94xM/pgH3Y4ND3CDkiH7ndBif48ho+y+0dNd4xkn99r3pFn80nl33qZ5qMPoAZJVQ+RfhOZzRne+qRs3Nh4OHaNFpsPt45briY2vQ07ZqcABk3O8bVDSME5f2bGZj3xtPQ5xpe6ciinKrgzIiohdlTNazYpjQ44hJRzLzus3h/5YlzJw2fav/COeXFl5WfdaNcVikAYzDW3rgwMtOJDj0GsTOYXyzg7GnP480GXcwYCRDDMaryL3fOVoohAyVfBEp+xevffYcuMOItY1zJnXO695/w5PxYptOA+mioURSU9r2WJygirCufSoI9p5z2dmgnyZC4HsKF2368z0u0vfaEcfDn6nOLztWWefnU4wAAfOJs/ymW6lR5qrnXhWXTB1xve1xvewx9AH/c4/5375He3gPH1BJQ7oyf0VFny6ezHbXxU/v+1PW50eVi/iodtA61Tzk/Hrs5R9bud6WfTNhUY8A+3oU6ALZP8sQbivDQ2gCM2J6vDpfDoh0TNahgvr+W+82tF2WwxTpZId5F6SIMVyixb90z6vUgIZvIegnOCeAA9Hq4sXhEsCZAXuAOB7QVDEzRIkmWkxG5qvghjmcXlsEnAEfWwBKPF2+O+SG9YoVVDre1E2wFWCuT53rFlXFiDY0EUibM1WN9auuzOPiuvRUrdXuXvCZGiW5TuJe3jLhSACVWbxd7XgmWkudAFRrIki8iMyGHpPMkcd433YAMwtV0QCZgHEfxUIhdScQ9J+NNKZJJslIEEgtCSe6sIeiheRs4I00EDhGEgMwd6CgK9WFzBSZCIkaMEZvdNcb9A4ZhhzQB4/6AHDIQpe0YIhKJsitnBo8JXTdJuBmVy3YhIOueDMEYdkIXQ5MoUnU+zULY+veRsNl0GLpqwR5MOQjxvhAlRVRFhCkhQpnbAEIkCclkVuOW8J0VYWYNB5bUUyu70A8ioLFznMq/Sw/UhYUyQeNzt5SKCVLW4FJtzxqwtZ1Y0/2ZFemiB5X2KPuE3ThQiNPVs42otLDo3yoRZoydw7YL5X/1HPLeAnNEUJSAZd8q7FgOiGaOSENYBKdEYVESkiWyRsFNa0oIE1K117RNU0SYYobKC67PzRTYMMCakJVVIJczq+ecWQJLKJRAEl5QFOuEvusl9Fmnoc9Q4TOXhK21Ye8JAgQ9pQhEEWOYkFLGmBIOx6PmgNA5NU8SAAgRMQbsbm9w/folvvjZT/Hlz36K7fW1hkDLyIJBQEiYq4NOlmfTenOAnp/Si4Yuq3Xl9VNdvNQTYqGMnJ+Bf4Sy9IyY31+9+nkaP7E0y3moByw/wQr2T1UauvFzsSyn5QHNIwCwS4Q0EfZO6GHUVyMI8c4IK2vqx8FUz7D6v54Mgd1VTwxR84acLSjnR6EFGbDkuzkzLNxeDU2XYHlxDJ9xUUQIy86ZkMkMagyGPKw4OsimkwCE6gFZHyCHrivep+btWdUL1sp4AONBKoNiNGu29VCeI3WM1GeEMSFoiE4Cg6cHTNO+KLMTC02z2RDCrgfFgK4j9EOH0AUchk2ha46xA3cdMgWhf5XmbMal5xMDy3OOmhWd/V8emf3w76OdP1NWEeo1/615lU7dauqXWV1cWtaxpgDJBM4RBAlLSOz6/xRG/ymFZ59r+JSgyixqXlg1DFyt/PyleVvLCw3xeEElF1SdMuL+KCElpyNyr0CHrDS25+eW+4xn3/hMv3jR+vn+t1Ng+Glt5Ws0i3PF0+v1+TneeASu5jiFVi4Cpw5p9Qo7U/mTz3ZCC7utfGaJGWrfLoEeKrzHiaefAYJN6yv0dnnu0QWdwyKdhK5mrQlIfYfxagM6jgjH1LxjvJgon2Ph2QgApbyglp82BXMIPoUzTrVwAm6f0P4lIHaJlO9cebJHhBzCar33TArteW8pwbTCvH/SEcPnlmgOuE8O/vRj+Z7L65sN/vqXX2PQOON3//k3OP7//lkYdgJAXnQxw0V/tKV8ziadd+5UZ1eI6qe21FCUjzH9etcR5HVuZ54QuTIjy4mvCJW1Qsv0klkYLI2iXsNSqNW/9DcW4Q3XDqlHQFYrJRZi0EJpOBEOm0CHFFFbd5rxyPfAYZUgsEObNV9CTB2SWsNzsfRVwVbQ+LcQkKSkgucQMGRBwzlPms80IQRNOK3JfU0AH9Q6zZQ91ocYOw3Zw8hkgitCP5g1mwjHiyXNuUPbMV1JVSekdVu8c2hfdIAwi6xGAQNCsMTZMHihmu+jidmoxKFPgAso05oARBBVwXtmtTooSgoNKVSs1pTJFqnkiXE6mFKX/hCCgA1nsHDHxTKNScMMaJ4TCtQQojEKc9mFDgmSdDZzzfmQOMl6dz36PuLm5hrbcUJ/l/FxPOK3/AHd0GO328lascVzJrFctnklIAaAmSRHCjNiiNqWjOk4HiXnQR5BRDj2ewSKSPEKmzTh1e4FuCe8YwaGHq+/+gp9jJg+3uPu/TfYf3wHTauDPvYY+gEpS16UaUyY8ij7s4/YbjeqIFA4VkYk6fqa5xJR9fQpbt2cFd5ldNe7Dj//6ho5T0hpQhe7Ji7rMAyaB0PyRFiOCLXtlPmggC5IknAN0qY4IoM5qefIhJQZ45gK42TsazCmiiQZfKCaRLt05RJBY0nwqRWjVZK2hG97MYMRPNNahI0BIsoT609v1UOo1p/WVvGMAgHVwaqGUfICBc+0F3y5cm6WBk3Y09ZVcXTzMAzZVyVEMwGyl7nd/+IVFtD1XcU3gOIOiZ0dyHKikKhvKSOGCM41lJkksV5ls5oxMCzvRFfgoQ5PrtSlmhOPwpLkNGGaJuz3+6LcKmHTzKtMFV8xROwGDY/WRWw2G/T9gKEb0FHAOI6Y0oTxcERKEwhAJJJ6AzB0vSSh1zwSgXpNJD8gqW5tnBLu9ntREoaI0EUM2w36EBEIElN7u8Ev//Vf41/9n/89/u2/+/f4xa//EjEBY87oQOh1H5hnmClhK5N4GTF1uVjhx/Jj+RMXFSR6JeYnKyVObBUmiTzJJJb8P98H3D8Q/p6BqbyYHSI2RfRqt/VT8V0wxbI133o2EDkCWDvDgEN8oeC+8ojRiFD8BqHXueRWMo+IDE7moZzES9TwoDNSqlEWIhKRGmJQoS2LYrycg9DzXVXz5r1hNH9RhKGsG9k0zuapXF45kkyoZjSCXMqaB8KuVeOrw1XCw5sJN394j903H0tdD4d3OEx7MaAAIQQJwfSrn+1wdRWLAUsMEWPs8LvrLzGqAQlIlEjBncsWPssUEFTmqkyOoxep/SyDKw+0A1/QA7X+esbrg6Xtdt4uUVLMS1mf5rydvVJgtsLjlAd8eBgQug6x70DohHa3ULlnN632fUGPnO+rPVRpy/p+6VnDHiitULYMo+TGal6vtNFsV9bhn7m+6HQhUeobDdtFFwzTPRH2I7r799h/8xbvHt5hwAabfit73nimeQdWepwrEbV6/zRtQLNftLzF9oPX3ynA+TQKpJX92So7j7W1cqKJRa6J+QtlLOs06/JlwrlZq884T605zFMNNdR2wrd1Hlq8B9l6F55B9a305yz/5Y8y92NNWN7MIC3n0Jo5vLzC/maD3e/fYfftXQO3TFQMNpsQTc8mcOcvGjJaYRwfeZfLu59QTszn4325vFyeI2KG6mrUZCw9PxbIhVAtKPTKM+eG9d3l9M478JwGzs/qUxD2JU9egjb+ZOUchftJ9T4fciu9wNj0Ede7Hi+udxg2G3QjI747Iu4TMOViCTmvYI3mWLRjZ8SzurrykhEWT6pvbVOtEBnntNXlokCbCdxtD9HaRjpF6cAfMiUVs2MOqpVr9YbIiwOjLonF8oZYjftmWcRwJSSPxZlNWYSPnuCuo6vtzw5osv+L8BOFeTK5V8FLTX+5EEyNxRWjEJD+YM05gSYCpwTOqTBXUAEQZVa5cgRR0u6boN1Vbt9UIQMngAPDhWKSBMv+LYkPrgJKRhX2c0voEzwTa8SvMtq2Lv7gz7OwWlRm9Twx6/agZ1BO0ikzzGjeJNbHzBkhQcMJBHCQEECkCXUL2Z3nlnQe8FEVUfUU852ASG0t8xRUMA0l1tRjg1lv+/0tzxVL/oziS5KTKDEmZSrNyruPPTYAdscjMoBjJwqqru9gSSMZKMyv7zERQEHyHQRA8kJAFFOZswjiGchTAogx5T2Igf3DO4R8je31S0yxA4gxbLbY3rzAOB0QP+yQkJHHjExJvCpIBMNTSqAsYY0YQOxknmIvluSW+8G2UkCu02rrYWsBe4aKZXjXRSTdEky5gf/Q9RKQVi3hSRn7IihpEi1XRjGrQHgRKsfDnsExBZvtwnxQ+TMrUGohx503nvxhnYs6egejtp5UrzMERohqfpl5LoJiCOL6ZwOQOS+RSmvfTVnYFG9RWX/b862g3cN4a21af1O7pualom+3mMraEHgRoZScK5m57B/ScGxRLf9Nqc0qXDNFQ1RFg/mLgAIoaL4ECk6R4/OZ1X41s6n43Z+sZXw2WXr2moDKr+A0jhLOaJqqwl40zHrg5LKXrN6u6xBjhy5EVbZm5CTKOPGkmERhF6POuylYREEgOSKq1bOd0SESuo4wdGpNGyOGvsOm69BTRAwRm6sddq9f4auf/Rw///kv8fL2BTZdj5wnIDMC7xFpBFFqZ4S45qdtweoiFvZycvIxwulUCxfU7I+zz1C+T0+IFbnBqSefUuui7mW9znr0DH24VuY4x/Yezy/+kctjNL5s2xXa4PTT59ubfal7qAdDrblZcR8DEQExG862PzmX1Azi0TYBfaWcjy1ZV2kxrb8SwSu1OwBozgSjL53BUWE0cvUAY8lNY4mxax40q8oE+qHwaPV0MLxW6Th5pobGMFq6Ih+9c4I2bWgRtPRw8TpxfJvRERYqE0ZXdYxxyIhjQjiO6KaEzf2EcDhgnPZFgcUEBDUWIgq4uuow9BHDpkPoAw79FpnEqGIKERNF/a3n6/x8tjU1Xig4SqWQGu21ht5tlAzzyaHmaqVPqqGBuzED7jm901TyKJ4tHjazB5fGcoQNMq6QsSs5jjpQjtjHgDEEpND2z6OusrNpdsEPZf59bZvzqRt117YPPyYOnV05gVoWONTfeLT6Jf19slD7NU8J03d3mO72SHlCzpJvLvM047lm768gWvbXT90/06liuOZfKBOzRoFc3MBqm74ttwtn1VyIl23YK7TLRUv4jCcwM/Irbxo68LKkFaH8kwVia0fnJaTavNnntt+8f3Lz1l+n9jILvW2hoZt3zeCRjDO0EE2ETCzhATNj9zABYcLDNq7P7aLNOUG25MVOvnq+5ic9vZiTRyt/3ho9wSNifnSjnGcMhfETh76945fwMeZkydvU02R+bjyLh5hZ3p0qdObX460vWf/5WXeqC5+JL3pe+RMwBo8VoTO54NIXVxv8zV/8BMOwQTds0X93h+6/vUP3bizWzacqqkTr91yeqIDwdMFJpChPot1FZ2sFoAL1NZCnOUwaMd8iP+tOG3LJCCsugj1JqGkeEcKMFKumMsDc1JmgTEkQJJ01OW4meZTzpNbYCTH2oBiF8A56OJgHQON9ocjI4saYVZhKc7MqP7K6SltEexHy6ZjVGp81yV8gOZC8xVdhZAhISa3gxwM4JbX8Vqv2EEFdAOWM0E2qRZ8AMMbjUXIDaJJRKkycCqshgoDMrHJWuZ5h85MLNFAMiAGQEOmMKYvQ2GKN2xpTiGqBrEKvzAAxIgVlxMRSzuIiWnz3CihULJRbkq+urSTQJphQtFqVrYVmIOMuAaoCOm/1xcjglJGJEFmtyDIhgkqrxriZcke8FqqnRCiCaoHewNWbwvVE4V+8IGR8QVwwJHGGwDfDKa68lXdACEDXdcX6PueENIltY54yYgwYhh4hdtjsdqCxw9f3Ge/HA36X7zAMg4Avka6J8Q5UlU2QZNOIBCTxJIohysi6DpwzDsejtH1MyJwAOmKiexwOd9jdvsBXrzbgeAU+Dsj5Fi/zz5G7gA/3d9jffcB0/w4BjBQYMRJi1yGpQugwMviQwJzQD8BNJzAes+SQCEF6XfRsJOFukFlTJLDOliSb7GPEEDt0pC72FMtaWcLgEt5J90pQnBGdAoLBmJzyQ7wzxBPCckEktb4Xbxh5suXLajiocrkQMZWZrwmQ65vmwVXe1/MmBMM1pPshF1gzxU3OjDSlUrcoq1r8SWhzQtCsbQBQ5ytY+OxoeLA5AFolR0nI7PJINIXL9tR3A0hzccALKHRuQoj1VU0CbmHTiiAlAYkzGAJHmbMoYIKFLIoFNgIFpCSWtJZHJUSJp92pRyTnDIQEHERJG4J5m4lnUw2zZHit4oKCHXNGZvNokhBKICBqHhILKZKTnX0yxhjk3cPhiJQTpuOIek6bkkPwR4xRlQ/6GbqSS4gA5DQiM2OcRKkxTQeklLHpNggxiAdojJLHJUT01AOQFNKZGdMk+70fAnabiJdXHQICun5A7Ab0ww6MAHDAq5//Er/+n/8n/Pv/8O/xt3/7b7HdbtGjw54TpjShp28R+a7dAgJ9BR4bUJkRuXTqnnvmx/LDKZ72bAS8cuUTajZmvTWDKO1+Qs1P6oUpjN3ZLdcBYK6AlT1ioTJFSFP+e0Kja28QMl2DaAfCBoEltGfKGYHF+KWGmdEwbaW/3PKw9pj9KMeX4jqq2LmeV3VNZVxamZ4hoVRuRigBNaSf9IOLcpXluYLnzfsrlVxqOWdwSk4h6yMMyJnBmJADQag6VF7O0eXGlzTK+Nm5fGYZ3Dy210rtxstoC6ZwXssFcdwk3H014urtHV58eIvNgUDvCHfHO7w/3kt+IxJv6NBti8L8q683uLmWsy1TxO+v3mAfhjqOQgNrzjk3xiqTp6JoquGYqIUDW2+/3G4m52OXEhq6AB52fP0ehqiuU9NCmP1+pFRd/7zPodAd1uMXyPg19hjDDsduAE8d0kR4fxvx7S5i0xE6Xo7Ww9ESs1FJxrzot/Ennue1zqCdRTNlaefX7V+uL7G7758p+xeGq6idcqwUh7t5frm9XfhkXqvPL7MRkQCmuyPu/tffY58ekMKEnAh5AvI4Aml0I+Z6bCwFG8u+uHaXB8E60VBx8dpd+7/BGu0zT0bhFdZ5XgH75y6r7VRnJMzP/LaH3WeewQ5OF6R9038h/teWbY13bzGzP5CgeNpdoRPrvtbdz00QnCRSz1xTICOgNQjVmQhglBynBN30ls+IkAmglPDmmwc8dBm//XqHFM+1tXL5kyeCV76db7N5YPWZz7s4zwjNhGYftIyJv3rq16WVX/7Weh/OvXAhED6zzLbi2XbO9XupxnhmRy5p7AdebI03Q8Tt1QYvbzYYhkGSqcaIaT9ievcB0/6I5UD/WCyOb5L9x4z0vXxtW8WozQKjPdDdDnCma2bJ07ZbcKu9POOrXD2eYNG6at6GGUFmygmzhgKK0M0TldK+HnQIKAoAQrVwUoJP4uzX5KXIAGIVZJH23+yemwRYqwRNHUOdl+pOyoBYubPanbEqG3KQ+P5MmsuaG+svIhmLzbb1WRIP25wGgHIRogbWsFI2zaoIAFfmyzwAyClzGmLVWfmahYYwTMuxV+UCqgVEAYgVWGQuLocFMqjObVFClASBc3i0BZ+Tw6oQcsRyaZ3duExY4GnJApJchL0hRLBJ79DGQzRhsChTxIOkxC41IlxhQMIgzeaArBslCmS5HixwjrcA9FM6qywQIVvMd2ZNMF0l9IEC+tihi8K+5JwxHo+iWNBkuTVnRksMipA66G7KIBbBfoZaikM9AjTUmSS5PoL2D/j49h2GK+D66guE1OO4GbDdbbG7vkaejjjcB3CWRNUhSoibLgTkGDUhNTClCTgyjgMBHBBDtUS0+RUYB5JeNwF6ICB0AUMf8OK6w3Yrwg42xKR73SdStlBZnskx8VYBJQ2fZRsspZpfhuvEOWJbSXwvpCJUIyJ1uW3CiVHLGJb6Z1ZeAmoqwC4Mu0GyEbLqFaAhK4Krn5yShRR3eUtJ20+n6dXaQfMIaPd8FWRYGI9FDeTtU6msSyuvMO7V5sWNdRXFSDi+oiTXrWnrKwqUiEgEUuvQoEjfEkijJKH24UZQ5svwZc62B5UTItJIJ+aNwZbLXIRnpojIudSRvMKSK34xnCNhBEXpxZk13JhjiQNpTjtVRPS9JHvXUGMhdKr8sKSuWZXyUAGWKGbMOyRQQCyhw1CMAFLOOI4jxuOEAMLQ9Xixu9FhB8R+QL8ZEDcb9Lsr/OxXP8cvf/UrvHz5ShTcOWOaJoR8j54OCBhBBY9XBnMdws5f/xNQYj+IMhd6tHTd52njVL6Kz1Q7/Ll5quqLcNDsdyty+/TyeceNOYGsbXymuln4Fc49EDelOcH7BHrVg48EvMvAREBQPK/0WaE03Dkm54R1co7nZ513QmYuHiD6Wwkui2tuXrblPOJ6pgriNEo8F9qVNQzdIl/c4kgoDSlOzRCjH4O3GSfjf/hut4Tt6vM8+1KOQuOXuHo/yPjKzQKruWNMW0aOR3TfvQPuDhjTQdZM5zFquEAKAddXPTabUAwL0tUVPm4kjF4GYQo92JKCE4SfoKqAaMImAsVTUIZclRDe0KHe82+ulcpZNOe2vkSr1x2V4NqoFbW7fC1nVEv8o851bbD2r3g3aL0MgCNy2oK5Vw9gCceIOEieNYS2nsVhpJQTkRpscEOq2Fbxr83RW8tLFmLgCefcqScJS2SqXIifN6OZztRXsev80D4BETSfKgdPQ8DwaovxbsLh4YichFaxUMi1W0Y4z8fR9mHR27XpWDtU/PhXbnkstlY9wfAdlnCx2lCZ/VrLCt+8rmJfK4uFW97DcphLrvlca+tSJj77rvP8OIEz6zxI/xc+PuzeIGr7fhKJr/f/VPG0zuXn/QwWLlqo+UOtkZbxRPKDAMUhrIewcVO7sBEFJ5+o9vzlz1tONrK2jo++9FnK8xQRp4rSEp+ZDPxey1OPjfUaPv+IP1kJ8d9hYQDXux7/+lc/ESVE36Pre/R9j493d7j/59/9qbsoZaaE+JzVns7NoiixIEiuL82KCVdRPmZcgfIVDDirj6pkyHoYmWWoWOQro5FNgG9thcIPkaufiQBlNoTc5iIkNeF3AgDORbBj3S1WuEpyFMvWXFlaguGiyozpsNy0cJlTUgIvcxZhUZbEnilnSeQneggJd5NTU5sa5wKqOEmaMwJFEGUCtIBMJlQCpikU6zBJaGw9Dc24CEkT86qFeIn7brSehPrJOgbP8BX1RWYwZRXoVlLNsbJLjMNQokQYAfMmEUtoaqzVimKh5JCohEipjp0AFSYWl5bLbDrCfhXKzSNH7Y0sWWt5WsdeYuMbv5MhYX6yWfWhwDQTIZCGYXLeVMIUyloEDibGL9b4OVW4RxlbLRZEIQRC5oCg7eWUJH67WmnHKIL2Ydhg6CV5dM4ZD/sRfddh6HrELiLGrrYFJcDUSjsEnTcVrgZE9UgAOAYcmcE5IEP20nQ8YEwZ0z/9E16+PuBXf/0aw1WH43GLdLzB/os3yGnE3Ye3yDlh2k/YbAd0kdB1kih6mkYkTjgej5gCEMOEqQu42g2Sq8EzIWxhzjLAAdLDqNbsHW6uevzi663kItGZA1mCaxO2huI1BF3zKiyoOIyAgjNSTlU54AQM1abTM+vt+jVKLYNtfYxoeUJX5Uf7XjN+z7R7mNZk96Zg8zlhJCSRPgOUtTclBIjACovltx4TRUlpfI9aWnrldQmD5JVdK5JSUqQaSgLwGbtalES0vMfaDzLrUl2Pcl7YnhdvIstH0MVY1xyiAAwAYhc1kbIlKbd+o9anCcm9B17jya/3TRlhHESypNJ5ApynncEDzf6ZpWwN/6QjCTWMUgnVpnMriohOc0N0CNQhUMD+sMd0HHE8jpJ3SMff9wMAUqVF0BjjoeQGEuaIMY0J4zjh7u4BKSX0iKB+h/71l5imjOM0Igw9uqsdXv7sS/z87/4Gf/Vv/k/4i3/1d5KbhgjTNGE8HrEN36HDx8Xp8Dwm8MfywytPJVC/H17nz6EsBXNPm4f1pxkh34NwD8IA8NC8QD2BfjGAxg58n4BkIfec0pkMk/u1VPwvCSdKf6vnmj1mZ6AJotcFNT6ptLVZn6k8gPeIME8Iy9dWwyHm8o7NQT2fGCVkptLiIbTjnc8jtbUs7i7GVPii5iK8It8SUNtxP/eEAIC0YTz8JCG++4j4v/43MAgPqsgHESj2GPpNOVe//GKDVy+E3gGAf7x6jbtuUwwqCOKtV6jjhk6gRvGwFPKHsq7k1hn+fnn+9B62kJrtNavL0QDlRCiNtm+Q76PnM1eeW1z27fhrVGkZGC8W8TCJEiJ2EUQRyAB1W2wwQAyvTu1TUW4V4SFQvEcr73qCB7Ecd3DGLucKtYqeljKcf7Z99Pea95rtOPMO8DQO2u+Lrq4MsJ369oFh12P4qy8w/VPGx4/vMU0JcZqQUwZZ7jzf7pMVM2ulxW2+3vNPr7zX3FF4FybggraXNOS8bs+5nlTWNz+o0NWrddLs90qbp2Hn1F4/txr1nbafK1BrhpMVEzX4tuH/1obwSLnUE+Byj4G1jXEKRpbrDizX1E4yDSAIVvkCqxyJAiEg4KZ/ia4HIn3ENAunfVl/l5O3UACtlBUu9dGmLrzxWeWbn1cR8QnlvOCdTnx/7B7avchrgHi+V09BoQVYy++nr9RiHi7Dj5eVCw6hcv00Dv+jFmZCwlDYf6YNuq5H7Dr0fY/p7R2O//JbjL97v/b2ha3MDvxnbjATas/fX4ODuQXvpe0WZcTa8946YwHqPCNOvcDJLThj9l3rNSWExgPySoj5M/M2vNKgqVjPKYlxPxMSKYFnCe/KC+7DqioJaZUmtHBCNlOyJmqroJZaNleUFUWUnOZyP6klrDBGEubDrFHMAwRFsOrm1QZlQjY9qupBJhZSlGuAAiFu9B0Sa3YbFyAC61iYRhurZ0al30b/l1BGzTJyoUSNIDWiaW7DYRbWQqc75kj9jUX+PWfNqSYg0xJmdIgMtDLT9Zq2yHUdi8JtBWWXtgp8KGwTW+jhtrBbAcou3AEK4+stGJpxGeMVGCGLlwGsjyRERibAJwGTLcQ2a7CVFotoLlvB9ktKluuDMKSIN9jhASPuaI+cGeM0qbU8Stx8aLimokRzc2P8IUMUFBlAFztkykgsfaUQQUxIxyP2Hz/iu9//FqHf4na7Rdr1+Ljb4XBzjd3tCxwf7pEe7pFSxjhOoBDRdQHDkBFIckUAksiaMhcFSxeU8SaX6wUAQkBUIerQR7y87nC1iyKgThZXmpGYESkiEIOjJP+y/AlU/d5X8WZKqSh9uDyzhPO1UnPd6B4re13fCwSQrQMV+CsC6RV8T/aeMtTyXC715wIPVITWFk5pfhzXfesZIK4wXPY5lUTxhuuM2644marCwit3S8dV3G57UR8pwhI/m8a5e2rd5hGGfmr+glbXoQoIaDxtVUSY5T/pwFmjPUmy8lYpwiwK4DQlCcVlySD9uWTrw1xDdakHmz0iSiwLL+KVWII0TZjU5tewOUBJjB2DKNmDCqd8sm0JyaThlboIcuuZi1JKwqFZPgjLJSHKS1FQdLFT7ycGFwWKCAUDZN93DPTDFlOcEAOhv7nC1Zev8NWvfoFf/dVf4dUXX2Cz2YCIkFJCxB4RR0SaEFWptcbsXaKE+JzMyg+p/DmM6xSDvrZsl+uTjPZ8KlNwesJWlZ/PKJ9DKTZXshWldaGDns4OnWezTPDOhW4gAMN2B4SAL/Ie99OEtwhIxCiKiBPxvhdMaAYQuLbFpPl1Vmj/ph4ueLOcgVpxs/TlXLWQTLkq040+c0pcAFXAy1KfnD/teSz0lVNM6H/z4ZW5PDGMQtutEJLFiME1ao96oys59xIiHoQ3SCNwyOi/zaD7O4TYy5lNNQzstL1C2u6w2QQMQ8DxtsP7rYUxJKTYl1C0Ogs6xMoz2XFs8OfH7T0kqkFCfb+cx35+XA1rMDlXdPj6V5+h2TVYf1vv4pMt1sHUS8xlrds+aCsuHCxxQOwGxChGOsgEDtnRWSuD9FXPwL+do2V4JoOWymsqjLi7Dphcg/Pv3F4v8HhiS5+4Xmuct/0YhqLmY3lrna7xz8g+SDh2HabtFbrYYaM8zGxXzfq6RFFPK3Ma/tQdf5cw1x6UNeX5l0t7MIPqZn4cT3myjvq+0e3LQvW5prITyM4/YbzRKm5fbWr+ZfkS1xoLPwCvfODZG7M+2347148nlOfBES+/lYr41KPQQwHjdgBeXaP7uAcdx7I5mSCyGzO0s7Ok5AXVWtwcrjSy7O0qPrnoVZ3yR5DHeqsn+nB5008tT1BEzDfCWvHA9rm7uiA9TvflMcic4+1H2/0z4Do+d/mBDDsj4pCuAGgiLwziBTH0GIYBx3/5Le7+r/8FhZr9E3OIlyghPncb2pA7VB2pM1MONEQdlNlqesuVWjAkW4T3KN4PXsDkJd721YRbEp7CQotkFRSTEv0arkgtV7IJiKCKArVmNst5KgJs12P7mXk2MU7xACrxbs261T5FlhhKtWbFlaYJRv9zhrrB2yAl2V4TgqUcZlTmgTMjwRixStxJkt0sCglm5DyVeQwqwGLO4CRzJlGbqOQzyJp/gzWcE8GHStL8Eaz91IGVuOaks6gHIgENYzkXbpJp9UPQPBIiJKyECJCNKfYwYcy7q1sOZoBCLuBV6N4VGqAc2u45C+dlgsScMnLIEteeqeT+KJ44DZwwjJG33BFFEBySMIOZGq8I2S8MEfyr1Y+63ksdJILyHNQaUJlvG5YykwCVcAli4Q7xmoFOCsT6f5d7bKZbfNfd474/IuWMcZrQxw7ciSV17DpJO0IWw7ha6nmrMQBAhO5BIOQMnghMGZ3mi5z2e9xNCcf9Hi9fv8ZP/+JXyFcR9y9ukdKE4zjh3Td/wOH+AdOYkVPG7jpiGHoAjLEj7PcjpkksyZEJ0yCeTqHXcDJRF9Tl7YhBmMjdtsfXb0S5LHlgMqZxkjwUmSWBb+wQcxYBr+Evg8Gyvtx8F0G0wIebHM0R4Fe30NdVMMHsFF3uT98JLEJz0oExUKzrXVMeghoGvQjsc4Dl0qmKBELQJMIhhkZ47SsvysAixJNBsFr45UaAA/WIknGK5aPhIyqeJvawJfYu82ViEuNfm5wVjqklwx8W/imX88/tiCLjKrMVxFtIhPZBwi1pteJZo3lFYB4y5AQ/dVoYwHgckdKIpHlZvCJCBHGsa5VLCCLzgLCRmiLM9qXHbbaeMv86JFWKCV4n9JqvoibQDpp3o3ryxdih69waM4qiLqswb0oZfU+IMdTwTSS5fswzou9FCHZME5iyjiWBmBEJ2HSd5CeKHcaUsB9H3HzxGr/4d3+Ln/6rv8av/oe/Q99do+824gkxjhi6d9iEO1EChlDCmrUg+Dwxwo/lT190a39KDSvXLq3wB8BUnCinlG0+vM1zxWftm41UwoVr0N8hYHd7i+20Q/j2W3w4MN4jIJGe9SR0X7XiN0lIobyKJ2ggxf2BETRcAWXWvGeV8DKavPajKmANe/MMDVSDHzsrW2VE8YoooVvbd/WL4t1q1a+dgLdWt3NrIRFtynz9uP1sWITan8LPwM4l84CoZkSECcP0LXh8wIeHd6BAGN52wjt01fNBE8lhf/MCH168wovbiHgV8DY4vktpNAvbulASFBqhCit9/ocq+fBnr6P6zANiUW/xJ8Cy0Oyd9TZmTy/fKd4X5B9ceXe+H7RndZj1uqctCv1GiIiI2JRcS8gAT1M5n43vXBupHdulH4VYL4wc5gZaLYOt/NQcrpt32H1IrqlKBfn6sFgSXr3MlW6a0bCtUU3LB5d3sXJ5pbQwQItnLfJBSgnjsEV6+QX6uMHgecqVeueyEEctP9qn1XJ6+mZXZ/y560sFz/XGTyvHK51Lc6Vw+XluQOz+b/vW7NuT4aPWYbvWfqLfJ49f23Fc2mzFabO1W1FinxztTEs8D1v87OK31yMgNB/G6rqeJU2k1+PtDsfrDXYpY3McnQxIcQoJZgkZggtj1nMzoFF8s507rvGCiM506Cnk0+qGv6wC9nP7RyjP84iouLq5VOyPFUYfA7dPB8eVGtYqXUH4PL9waTuXWIGdr+Fp5ZmQwA2CeGbrf0JekxEw8YCcIwDCbhPw09cbvL4d0A890tsHfPjNP2H8l/eVIKZHNnFTLhvcOUXCY/O6eLelxC9oe97eY89zxXKlufPzUPFguzEWiJpRBKxGhxkB37ThiMigwpfKeM0JrPYAD0Q14Q97Rqj4wygRpO7fbAJps6JWq1Zm1zcdWwhOmdCujQirQn03Mxi5CI6FBufS32LphawJnxmUcyGWJT+1KFYCpH8hJxVcVlbAaPvazazUsQpcAwOZkDlJWJ0sFujiocEAZ02YmiWxaxTVuzCfVOhqTxSJYgeIRoY7ZsgzPyiHZrWACAElZvkpYtOXJbya0Nb/pgIvIBPWt6Fz7LlQHosqsxNr98wZlNU50jMLfr2LkDihIeJ0jYtVe5C6vAC4Oe6Imr1BNn9BrwcAWRfVlHxusuRyZZQ4a44FoAlruOUBX47XuKcjPtIBmTOO04SOBUS6TpJSBy+Qp3lb6tUCUituQgxqgxkEXjMymBKmtMf9wwe8/eZ3yGHAq+sBedzhOL1Gnibk44hxfMA4HUUBlBO6KAJzYkLqMkKUccVuQOgiQt+r8FTIjK5oKYG+I9xe9bjadgAH0VFwRpqyKDxUGcBpAseMHCKCKe9gniEm3DUFou1NbjaW7TUwl3jAdp0BCeHjlBA+VFAb19pTDbrvuYUHMLd5FgglQbq/Xmotj1GBe1P8xaBJyk14zlwEHmx0lkse5/H9nKatcyBYqYRjMo8DIt1T3MI7nMCfKwPSelDAfSeHQlri1/lFOOQREIKMW2Q4wYW0Q/GIMOW0heqyNkxhNKkAfhyPSGmqyVFVMIbi4aaKaL2fplQUu5ZzArAuaGilmfV31PwUFnqprL+GEOu6DuQVEaQ5LKKGtFMPhxhNQU+iNMlJxklQb4eArgsali0W5Ya00evcSN9ySsiTjDMA2KiXRWcCygBQH0GbAS+/eIOf/fLXePH6K8RuByIJ+RZpjz7u0YUJFr4vZxsfu73GmNMHPyom/rzKSfnKBUWW2lewRg08HR6+bxiqodNqO6u2S4wFfMvD9esxM/6QMu7TWvrOtUKzz5VGYWdEDUW3ub5GCh3evEl42I/48O6gikGq59SC3i2YWGgKpSuyni0EEkEJjEbxRIN+uDkwz14f+tT+l99qOMTOu6zgXsP3XMiTQBqG1A4pMtquCuuL4nuNrSP/YzmVSwvxdjz1ttLzNoqigAE4MA7X4lm2vTsA0wHj8Q7MSTzYQgDFTpXPEWO/wXG3w2YbsN1EbLc7cN+hH4LyQaRD1VlwfBLIzYWVorSwudDz0NN6bh3q8y2cNSEkZ19O7bY15YPbMdY91EFQ+25YfaP2cbVNZ1RArg91osrcXQXGK8rYUo9IPcBAOmR8BOPDFjh2wDlBLSuPob9KH83LqEzhAgWw8nsCM6aE8LuCi6bAYMn2p8GbcVQzWhIzWtPa40qnNqy2h23yVNsMv60Nw8GBUaNz7OR/LdZMx8c5YTsEhOuIodOxKzw8zQDT78unnQGXt1OI0uX7ZJ5vix6tvjN/qtLL/lxZnfnyvGOF9Hm7SK65CoztaSvY/GxxL5wcl6/R2nZn++M0Qtur1qDRffN8k+NRLiuP9765dYqGcO0+ifRxayFVMIoiGbIKmbnIIAvqIAKx5R9VHJ8Ytx+O6GLGxyvzhuNZW59AmF02kPMt8IVPfgoBuVI+a2gmBWUI8NFpnHLm1nPKxXUt6JOnTuaPzNYfqzACjnkHIAIEXG0j/vZXV9huBwybAfff/R53/8+/d0T3U9b1snX8FG+G5t2Z1YT0gF0Og7X316+tP90Kw4ql1JxXROuuW3FsJXg8E+YFe5xzQcSVuSgvlO9KLovFsAlgjAZIJARgtvqV8PPELUOFp6y5GGSuKm0oVtmJEii0DFANE1X7ZcRRBpV6WyVEJQK8koNTkgOnmHP72c2O4ERpX4hpBhCKYDqzhP8IIYvQFp6grJArbUOSqepkSN4HeTZDBOQ1ATaXxKgpTUAnqDzGgEARmRKIAjKnhmYR6zgJc2PtSLSWavm3hANHannFEoy4rvPawK0yHst6UH4v4FkPec8LlDVyfQyBRNmilncC1zXkUyCrRWoygSWx5oNwiWdFp5OVYRfhPrvYyrMOKoDWsZigtlq3Vw5a/S8AApJ6pXglR+JUhKMixA7oYsQuddjxLb7p73HfjZK8djo2sxw7GXJA6x1gc+sZJAmRxOhyB0YGhSx2jiSKsuPxHswTeDri9uUrvP7qaxDdIoUBmDIwJbx79y32o3hpZM7o+x4xisA8J10kCoh9h9AFdMNGQ9BsUX2S5P/dEPD1qw4xBjATpgkAJIH3NKYauz9mpEAIIRVhrM9pYGFwTOicVPjRxQ4Is0RpttiOuG8Sac7+BByXGLfs/bJHLIRDfad4HKAKfxo5A1MNr6HSMAIVBYtYykfZ37nim+IJgJrf3vBHYXgZCNHDAJWhZ+Yi8C+5N8qedrkSgCIwL+xqSb6mQoXGI8HvFb97/cms0OthMxAIURSpAqjlfRtroACweMeFooTQujSU13g8Ik0Tjsej7JWUCh6Xs0G96zTsEnLWhNCprCMHSwov/TBFunnNmfClJo62eVWcEy1skobqUGVA0BAcVh+FWGDElOgpJ0zjUYR4BIQYQNTVPBIWikk9I/p+0GwZooRLY8Y0JnASy8vt0IMA8TRhlti1IWLoN3jzk6/xq7/61wjXtwjxWtEZY0MPGMK7khhezphc1q8Ky1hhDif3yI/lv9/iUKhdcd9/+LDAPM/nVGkwX5ZgTeXinhn/bZ8xLoSHT+iH7SPUGTRvWUAUjtcvX2FzPYER8PbjHh8/jsU7DFAPX/mCoozgKkIMQYRMxEAMJEYSgZCZyh4H/Ao6+h56PuYkod8K3V5nrb5r4e1Y6aDkaGo/p5pzqxGWuvPSeCJap74EWRcpw8p8ogVHxVN2flZ6tQ5E/dA8G4MUGPs3CV2esHn/HfJ4wMfxAQiE2PXqRdgJLg8Rh6sbfHj1Guk6orsN6AnoATcuKviz0LJwv2elPrt8/9QzVow+gHt+jc4+83NJ9c73i1uv2ZfmnXWPClr8b3VQ+Zy3V+9fh4xfB8YUIo6pRz4kTA9HvL8i/O4qoAOhS/MBo6X9bKFhnzU/xqqMreToYpg3vCkhOM+9ANyO9ooHg7+y753Bi4ddR0uWHnoksejbfJjlYDYCsT7ip7t5i1aApD608LhQvHCzC9i+6CEKTTXMmXeoRRSPFF7vx2rHXIXzr4s6eDEKv0aL9x7t67JtP8dnwwyudJuND5hjNq55LBZGTGtljV9xl1vZQ33CINjpSU91+VTDzezyyrf661IawfXpwt6cnna+ZBBPqXD2GBsbV6+RKXgAoow4TXj18YB+w7jf7pDjTC54Ygt+SqnwdengV557LoHzhPJsRcQ5xZOdfzOyDu00nzggZ/flGzWXGs3jYx2dI+nHnl/UeglCmSPe54PTc8naZ3s9/FCLIsvtEPCLLze43XXYbAbk9w949//9B6RvPi4PgAYLuO8LpmO1scVrz+v2gipYtEKoNJEcAZ8CL5fdWztYlmGbKsKqhNp5iKxyqzo6kbMGWCiKeszPyDW3f+odT6A17JHMkzFGOUhII1Ue5GJ9haKdFjd2EotWYnijm0BkDudCV5UO+TFzHaDeY26fA6oCg0Jd10ABySzFUkKiCSHWmLCgds4AC+2SkKYkwigl7gxgxLOCwKrQCIGQTGBrHhmBQPNYh56B0W6bZ0MrPFUBlGOuLd5/nVtUpqIsoG+vElJUXkBzvwh/9eng9ohU7XJI+LW3fkLGSEHqKF4atLQSKa2zWcxn9QhRYaAmQ4SGrmGGhDPKwTENbpRGFBYYQ32OVOjICYAIkRlcE32Tzb1GlVWBSAixCklZQxzp41epw9d0i3GaME0THnjCOKSyNl3fSX9NGcFwgvRK9kk6eALUI4JjBDgjQxJCDrFHIEKaRtzff0T+QwT6HV7fboDjjcS+7IDQB4BH8dIRyTb6LgKdWgiGiH4j8Y+7rYSfeXN9pQoHnUXOiEGF5SCkSa3VM8A5iz2owqzhAtvflrw5ZQ2lNU2GSAGw5nZRy0E263rUjTn/vgYvAkwCiyuhkbxiQUllEC2VzQVujBktelKu14sCQa5lZoQMZMogUMVr7OoqruAON7s9a9s9eKF+ER7IXwlv5BIol0bmSi0/O4pjTBgxp80qnvEMeJunQaaXrFeKL6mGGnPVlSUDl2ShBM0zwYzpOCLnhMN+j5Sm8jtN4jad06jnw6TwqoJ13beBgp4LVJOhu/wUhhdrSKjQhqYqoCo5T0CimKMQENR7IURbB32eQpnTDMaUNadFTgCxKPeiwHQ39BJ6IoiyputFEWGK7nEckVPGNB7BKaOPkkQjGl5TGEsE9Fc73HzxBV58/RNsb14Cww6gDQJ/QMQdOjoUgVOLQ7ywy6y//Dp+Wjm1b35I+o1PpQvXylPH9+cwH0J7zIREcmf2iZVn/rilWDE6Uua0J8RngPMTtTCA308T7sIePwk9dqaULc3LuRc3AeGnA/AwAb+bUGhPrgrDzOrJy4pnNBlqJEaGeVDp38xyve0UF0+IrOFYOTthPfwqVzxjConiNZzb5+1bSxtWetGfq6fnnN3/zSX3kwv5bnS7N6BiV0tric6I4R4RCTdvJ1CacDg8ADkh9Kpo7jpM3YD761sMQ8DVVYdhGPBi06HvqXht+uGVcdm5Nzsv53i0sAkzBcQp5cPc86Gey/69tVLxen233mu7Wc/s8t/qOBrghTf6ab0om4d85wv91VRUGu5w5Gs5u7oePAmdlkNEh4hoiaTWyjMQeaMssPxNhabz5lducxQ+muteslCVuRpjGElcXl1WodfbfvtfJ5fW6noEdVGp8dyDNaW9f8+M7YIiUcYKTcD+q/Ek1PyudRJw0RItec85Plg7gU7Oom0XnvXrUnChWvvZVAPnqqjEfPu+LiKXB87wLqdac8Nhnq8joclrwbM8QOV9hZH5PRv7BXvrKWGZFrlQL3q18ryPPfYp1MfhZoMUgf79PeJh1HmViskRFJzF6JFZ8kle9dfgDiqr4Bb+ZfM046hfT/e2MXIr6/zM0T3rtU+n456giFhZ2lM0zJw39b+cJQCwRqSUWtbbovmF86+tX7ps4qyfK6Dx2cpjdT6X/D0r3P5EmvpzJZc7WequxnYI+Fc/v8J202GzHbD/p+/w8P/5Bw2Fs+Z+eQ4hPjLwTxxPi1RaJMrNc4+R2J/Yi0pln37KEeW+cbteGTOri1bnpzAmDEcwV8ENVCvsD6CGsJoJ0DxhZj9kvuQgZlgoHonvbQyQ5XYwy9WSKNoEbs5V14RykiuhenrI+NWzQkOYsCapLrBerL5q/8gxXYDMAwUCJel9SgmggC5rXoEFNNS5z5kxpUkIOxUqieANYE7IHBDBQg84i9xijRZiIVhUTtYQh+zH6QgfUstnUdDA1csIgYvQfI5ZTBA/hzljNGk2XAaJFZ/NVWjPABOOVmWUPyeUYZkJUU1Z4v8we7MoIczzgQAKEcaysHHMlMHUgcOMSHAMVJkjU3aVkREQRMlRhQOm4MllLSyXgPUyquW77bGk45GcEQOuxw2O44hpHPEvdI+HcNAwPWptT6TCThQGx4S2Foe4qnYITAE5EIhVWQig07BbaRxxf59x/3DEizdf4PVXNyB+idANQGDEjnD/4R0O+ztRChJp0t0Ofb8FxQ5xM4hFf0foh4gvv7xF33WypzS/Sk4Zx+MROSXdx9JBm+WowDuhrhsgYXEyzxVONDuTSMI4kSY1RlU0ksJxg3+5XWfrQ1BF1YKxOiEMWOP2TSAC1PBRS6bSKzEysvMm9UoI90INQ7eYCesKFZRNxtgL0Du4CSqs4tJOI8BoiGIvCECjjCjt+Q7aJ1u/3DWSdgTGRR5m82z7puxl28WaEyeHrOGwkuZ4GDFNE46HB0yTKCByloSinFURoUmsBQlUZYbNkeXjoBKyquZusLBV4okW2/nRD1NedH1f5pk0GXsgCack55abIa55inLOElqJVRHRSbshEPqhLyHQAhG6LpYQf5wzxnHENE6YxhFgHzZK1jWp4jUB2F7v8PLXv8DLX/wCm5uXYOrBNCDwN+j42xL2ak4DiCeH9bvCV7vnZjA9R51nyycSpH9G5YekTJiXNXr+eYqmNa7OzvJzhOml1O+nT+JTeRff4lrYjUfr0+GvCQgYwO/ThJgOeLnpcKWGJiVMEWuotj6CfrYFfzgCv78HoEY4XI0YirKWRdjBFBBJHCEAwbOSwBpArol9mxEW2pBVaGohl07xNKa0qJ6dNR9cO4mG0YWlmEsIvJDLndFPWKpWAaFXuNJFZVzszEzcEUuU0acP6NKI7ZGQcsLHdAARSsg9ih3ydoePL15jcxXRvRR+50Z5jyZUpo7T1rOMzY19rpSwa48pIBo6d/Z9uW99PWvFhRFteuLfr94ca0+V8zrM7tt1slV1jTS0GM3ekVL7JfVkGnDkl4ihUw9SBsIExA5dGlZHNwehxzFIywAL/WG0GhtDAYMizw8277Hlw9P3zHDMyQeqUVaFycJXAZijlhVycDaH7s6JHAOtFO7SOZk958m8zJIHaxXDLUur+jPO5JG3VzvIax8r767VzYuvzxfg+vFcUk7wCmgwX3vX0V5rtXnwW77tSzWEIdcu2/72CNHXwYDPh1H6WRR1vjdrxXr5yAxZtbMLJ2Zl9irN3j1fLlrvdoMBAI7XGxy2PW4OI7rj1Jz/bEwXMzKhhGgiIlx1N+DIIHzUs/pCOuLEZTKaYo4jngnGT2p8/tQntPkZQzOdQWOzjbOyrs/d/pdO0TNr/7H8sQszYcxbDH2Hv/nqCrdXA3bbAXy3x/v/9/+O9O5e3J0KM/CpTEklHCqB/XR4YVdPufbY4ajj4GeOo9ABxS37TN8ZgLfaXRweszr1v9ZStn71YloT7BdL0eBcD4ygsr6xVuOXzyVrFefX+SjkdygnLSNzAmXA4n9LiAsXQ13rIpLcEMxB8wj4oQjhy0poFmVE067zrijEoc6JMQo6Vi8cFBo7QCylM3KakNMEsMYD5wRLikcEIACcpPE0TcghoNfQMhRILXFQw1KVw9lZEpsQzzyzZ9ZJZW0A6QNcQtuGaeIqqIPFQpXFmhuIVwLoHAFJZa3Jaa4YkPDCYfZuoBJypiT0Q12XuSW3/yvXFZKiDiyQpotTJltCrmSQCgkb+KQa2zhrv4P1n2R2AoAEE9ypEghorGFCIORMKvxGhUtOBc7mY5Ik5QKLmc1VthML507CtIQ46hoypmmSMEa9hq3x+QlKYUkSzoxJY9CjCwiQUE1UBPQZiNLHzBP29x/x7g8BcbPFl2+2IL4Vq+wQ8NB3QJoAzoixk+S7fY+u7/Hq1Q79EJFjlhBanDBNuQhLwEmsuEss/+RAkCrcEnT9Qs0DkzMCgoQrMk8oQIW+pCFtLIncaXgsSlJAcscoLp4z99SE8HIWoY5YtmsmzM+eIyh4UMKomULsVJE9KjjJLM3Im8cyNF+CYaelMKAw/iCFS9m3VRiiCaBhyhFN6h1q2CebC78zLdyZKS2hY15YZ8IRxyr8LxayqogSZTVgYTaQW4Zd5pihagpY+DLW8GZpHJFTwn5/jzQlHA975JwwjRNK0lRI22BWLxtTvgCgUOaDNL+OCVKieiAEC9WkoZRiFAWA94ggAmKnng9d38BVCJazh0o+CujcsJ1dimcoBETNpUKgEvKs6zuXB0YUoJQlJwbnhL2GpMqQUHzdMKCLEV2/xbDZ4PbL10hE2HPG9uULvPnlL7F7/QY5ECIeEPEdKNyppNKEVYIDLPSUCcGywq8Po1KAcrWwrt2Zvfhj+UGU78eoaE7XnmvjT8ej+aFX/FMvGi4lAsbM+M0h4SGzZqi6sI05rq6EuLTBDyAaARqA0MNC1DEAdISrFy+Rjg+g6QFBlYvIit+cx5d5BBaBv4XPC6SkttJITJIPJ0vuF0+vF/pMjXsK7lVBakYzYYX+8zzQEpy8QJQq3XmG7zkPLSvMlacrHT3XfnIJdwrINBxfZnDM2H7cI4wTjuMdRiThGwBQwe8R2PYIP3mJoRtwM0R0XQ1fSDrHJohvhLyNwp5W8GG99pgCQppoHl60d6ru+uC6MFNnxV2hkm6hUSIADW1UrpZrtX+FltIzuLluz1L7ftvd9j1QQEAPipKrAzHp/eWYWn6WC53X0IdOKWBfhBbRoF3Zkpcrb1qUWk65Veqo/A2QC72Sde8k4xXYnrW2uHTPuEwAiwTxa2V93d3IZ8qIpRLieYczAdp/oedqre3O5bUftLzJc1eCeXtnbvPii69X+vnoKFfYppP37P5Tpu7CieAiFDhRDbcNL2f8seLyyrnmCZbf90Tb3LZzWk62hlsKV3D+UXZ8YHnA7c+GnFi2z6WClTHMp/oTSY6qLNZeOr6vVF3y7lE5g4cE/OX9Dncx4Tebh+WsnIPD+a1njeHSdTtf+eckGZ+liLicqSinSzmM5uWURmt+LM7J2XNdOKv5bNo41d+zlT8Xb6/05I9cntjvx6yhvg/PCEbAlLfYxh6//skO11c9ttsNHn7/AYf//M/AmGZwNEfoT2tNPp6nhFg8u0KA8+LbqX4+E7AapmnWWlWhL3pUD27/jHIhhUiSJ9nuzwZX2m0EM1WQ6Og6x9yt7U1HrFVqzI1Da6uUowpsIbG/m9BMYrVa+waAVZBFodbph1TGWzXUpv23sEvsvA/qYWdEMqwSlbFljd0POYA4gzOpIsJZIOshJVMvFdocBEATKFci3YhfbzEs41DBJWp/rcwtkYIqNzjZG8pukHMnZzk0kSoc5JxVMPU44zinAzyPwMX11b1ncYsK/Ni8GdNGmJ8dJriv684KF3WdKHMNP0ABKFZ9jBCqRwg5wj9zRtCM6a5aZGLxqmks0qz/NiBVRtg4UC2TA1vS34zEKMqdynTaeAAVNQNcc3mQKgC6KIlrU0rILALJkMXbIsSADl3jEVPW15R9YJnWEEDM4nnAGUia4yRALckzDg/3SIcRr7/+Ci9f3GKabsRbJE0IBBwe7pGnsYRLin2Pfhjw6uUO222HERo+YkyYEiOlGkpN4vdPun7qDUIoQhECVCAv82YKh6zvp2lCUq8oZkbfSw6WIQyFcT6LyalaKRaBK6rQnwquqIvMTKIcQk1UWNYfij5gSjuDh4pPzGurKI7haBHd5yrSEEEwA6QW7r7UsDloNhsBiosNTmcsiio1SvJMOEWEJmsORYm8ZkFmSojTiSDJ/Zlyz0IisWPCxTU56HyhWBvW+WNNaGqJWQ0XCe6fxhEpTTgeDhKSabTcENU6iQpyV8GNrXmoCibzepGwebLusRPFmigiAogkFFKnuSFIEaUp/vquk/tdv07jaj9MENYoT5UpFAWqJT8lSVSt/apeCqbkErhPKeGgCpkARoxAP/SI3YDN5gY3r17gL//H/xEpRtxxQrfdYHN7i+3VDXIg9LzHwN8gIyG780RAhRxusnEIrracImYhraDlxtqMvrxr9T5WfkhKi89F2j5lTN+7x/EftZyie58+tjod6+9+rlwlRXDtSE77HAH85phxvESwVeqr+JBmKNlK4AMCHUHhlSa1r+FlAhG2Nzc4HIDwTlWzdga4/GiZzQsTBeexfEExT7AcDSGoYK+GcLO+MlgRjbWhZ5u2UULVNALcctKVfiv1Vn8UWrlcOLWS69cbjdHslq2Z3ShnTx1VntNpDHAAjjcZvEm4+fgR/XTAXdoLBaa5feQs0FB7V1sc37wAh4gbO1MUV9q50Hrk6oh0/KvWzCu4tlVGLGlf91DbVqmr3im/mzYegd5mvWaia/LwZP1w9c7OkfK+4x/I1d32bWWOHP9CekZLbg7xUEEYATU484X9p4VDhdEFp3D7XDHA5dwz4xAzJDDaAlxpllKnC7+qxF/ZO8zc0opWDSocuyoW5ezKncAvj5YTlc5Wti1lb9mO1TwRtrfPnV9rtx7p93x9tZGVJx3NUtZkDafM8g+caZ8WsYqk7ub6I0ecx011P6032oaLm/WF2tFcNC9nlAu1J3pAPXXdlj1Eg8vgxu6qoNX6qJ4nelgW+HPTdVZO51kevyjcwsVq8ycKcTXwa98hN2eOryswJ1cCWHLJhIA+AV/dBWwG4Lc9I80NMf9kZN9lDZ8Gj+d3/PkeEeX8OI0WGev47dw7J+vidi95hOevLXtwpiNnyg+IF/o/VNn0hL/4eovr3QZXuy3o7oC3/8t/RH73IMK0k8wGzz61tFTY8vlnKiFOlbXDbvnbAzKfOSQK936yVifzcofu7Fl1m7QDkN2LiyYM22tehdNIR8O9qFCrWMkWwTm5MEYmjHLKCCckMpdui6MJQJP+uoHq2WZHAbPFlZ+KIkIEI1mSDUPiHIYsxLAl2z4lELG8BeSZOSOKw/IAKjb6ZMRtDb1CWSfaLKRY+pXVijUjF8K2WO82xCxD8qmmkhQPQfJDgC3HgBDlYqVaiV5xodfwK7aeXglE1e1flCKqjNAk1iY8DCBJtmQCWUdok3HVZfIMHyvZYIyDCm9bSnYFSzNE6VPGgMIIg6r3A9XmUCyqlBEybxSCxta3EAU5FD5JmJgCQZXwL/3QhMcUEJPNqb7Lkkg8OO8dgwOCEIM5rWXIQ1kHE/JGjghq1VxhuY5QlBeAhUOYMMHyrdxOW3RTwPv+gPs4Iusz4zSCssS5EsVAXSIGiidLpBqH31qUvaJqswBEAJFkDfJ0wMd33+KYDui6Lb56ucFNvMVh3+N33wQ8PBxwe9Vh0wcMmx6xi+BxxCGPmFjD4SjTlZIp+mTfE8v8WVgps6nK8GiEihDA4CMbU1ehGkndX3vSfAOa3Ne8hUyYb7AfnODfhAde0WZhgrwA3JQgwpDW9c0OZ3ksoeqkgnMb5rZAYUW5xZqeqsKrrbFMXfPpeX8LL8QmKHNKscog8GJsM2CdQUedk1V6jghF+wNG8YDISeFT8F5SDxrOGZkIWdemHglZx+HORNu8eh7kaULmjONxj5QSjscHTJMoIozxDYp/fA4HW/ei1HTwEGKsfyEgdn3x8jFlhOypqCGa5H377GIAaMaocE2cnlPClBLG8ShtluERIkEUI2oFbcm4YxcVh+ueYIU5O8cgQrLN5goMIHZBlIA//Sk2mx2ubt/g+sULvPnlr4EY8YJYLHs3PXoaMeBfQHxE5kn2AVWlUAE1xcstXqr7JJ+SlPxYfixny5+M0z5RjBZm/3NRTnIeT1AYeXxfrnkSSRWfxucYaRCIMXDAzx8C3j8Av2M5A4khglX1jmBHg2RQpYU1iSwHBucAI1EFMYYmRGah29VLmI1+NUWwWXmXuTp1fqz8VnTC9Utza1Ef3O/F8nh8xYtXGbnBZ/bA4UVG3jCu3j+gHyfsfr9HognT/igGN714VyJE5Bjx8fYlYh/w4kUEDz0odjCBf1E6KE50R0udAi+Mt+lYKCsq31SUFitzSNTcWdTnXjirgJgrKzD/7Xug74fym5rKl4oDT69T6R/5dshb0LsOzeCFbD4oYIeIL8IVNqFHpB55mnC8e8A7jHi7Yxyi0Jq25BWeK5XPXK/7XrPdRFU0FA9Y9go45VPtpUKgGSxq2NliaMDFE4Kz0gRw/VwBdUbd94+WgkscobNmDFAQjzU636P61QMNze7PESAxNoeP+OLuD7jf3OKwuaotfh9K9Lmw4mQb7P5vr52q8tFixl2FxqsUfNkns2ltW7czRqs7cf9MB+qTPMcds3fXfhZ+YNmWGG6eeHnR/iWl3WHnV+lES0QAUwPeZ9dqfq8sSV0UOvHo+SJ7hwmtx47up4fbLY7bHtvvPiIeJFKByVAkjJV6ImoOT2Rjac4PaE2+/bnKqWbnaPyUovbyq5eXixURa7LS8xM1P2Bmh9uJUjRKZ58T4DqpeJj/9Jfp8TY+5/KfBP61VV6zcDhZ7wW9/H7g+JPKOWsvIkLfAT//YsD1boehi5j2E8b/+nvwcbKnTtTMyzk9qYSwV56nhJgfRm1dcxg81Sdj9E80spQInH6mIYRWfvtXTnSrWJHaoaRItLxlJ0K5RJX20eScVdjlCD+Y0MtyMTS90H4aw1PDcxTiaW0E2lcTyWROxco6U1dlYghgygBXRYS5lQfEwgcxcFao0h7U+js0kwETTkt8wEoT6gsyvjyBQSqgrMqIMgdlruQQy8yoynIVULIlZ3ZCTbeYnLMuW1RmSdYxZ+uXMBES7glIysyK+ypVobjmEAgi1SvrCLTgWIWZdageNxULH3JExfqqasWVCNefNaH0gthQhsgn71UiIDMDxCBWS3993s7/piq3j2T+ak4CUdjoEJglTwn7ztl4FSZzJfjIAYAlnASLQC+DEWYWhoXJDEGEASRnXEqMGGXNdqnDJgccu4w9qaCXGTkxKGdNUgth9BzKMGKO1BPCYtTaelXhfwBF2UJpnJDTEfsHxn464s2bL3BzfYWr7gY5bXC3P2DKhNvrgKtNkBjKFDBOE9KUkUwRYX3wnjpUmczK/LSJ0tkvsSo7eVLFI8w6TfdwZlHwaeXmpWFwR64fjRCgKCFCESwbTJg3U6OE4GoVZ6CTnZJu1RvCXyl9NjzGAEJd+zIfFYMUlDk7EsogyndbTXOx5hJOaU4xtJZ59joVXFerpzJH81BvtThY44oTcrHWTSUPAlyelqwI2M5NziwhpIgBmgn3dV9PaZJk1OOEKY04juIRkdUTooud9Frn0bw/yiyU2HLk9oSEYYpdh9B16LpekkPHvuR5oCC5XMSjpCrdpU4dfAmRKLCTM2vibPFeSFMCQazwTLkBkjBMIXTFwlNyvmjIvSLMUJgkXbsQAAT0g+D5bjNg2G3x4uuvsb26we2rr3F1c4vbN18BXcRVADjI+UfpO8TxPcyzx5Qf8ySGNu+VhPcKO3n+0wUOcwvex8sZkurprX/PNPL3Xf9auWRJ1oWlf4zyqfBypuZyjp7g687wHt5L6dQzKFjEnWmLihavLNtyl3n+nClnje6w4wgSZvKLMQAj8HslP+oByJrbzGgZ2biCPwI4EHIOIIh3L0G8dCkwQPK99KXMRQ3LVNrwAta1AS3GvrzhlQf24aetYRFmL/mztK1ifd1YJ9EMXQBg2mWkm4z48QGb6YB0/xHEGbkTBVDoJCk1QkTuB+yvbxC2HbYvhR4O1HoZ+FB1pvy2m1WJj8Wma+7pl/aaId72eX9tzuPS7FkFo8X95dpQ+41c/21IzflPbtwrHpJlHozWouZa4RVX5sX3VW6JAc+GOrzpXqpnMSEfMsb9AXebjG92CV0K6LWGSjO1tFr9XNvDXGC98BCFjgF8eN4Ks7oBGShKCPdu8VrKWULrFk+jMotNXbzo05lSyMQ5Mj9Rgdun5H+Uah4/A+bYrx8PuD18wNRtcMBOar6QJlgTiF/24gr+Xh0w1UdPVv3oA22TC2H0iepW+sY8f2x5fbV75GphVFxma3nCW2OtqjmuFUhg92u9+KDWp9B9acdgm048+cgyc6nE4dIy4FMv88rP1ofhuZQHg1fDgjED49UGR2b0Hx5EEcEoE8BqzAuCetIDYtwrXFY9Vtc36+Lq4vxYe+vkIB4tlyoeljTPp9N0nzFHxLKsuSh+cjm5Cxa7vP1u7z22i/4Y5ZGF+1N3709R+hjwy69ucbUbcLXbgfYTPvy//h58dwCShm5pjmtHDDYExoXM3zM3z+phyScQ3WPr/IkLbcIZ+b8lzNvtoIh0poVtDqDWLMuCZsAO87XDtHUppmaLgbV//uArjAwKcVZCtZhwVAk+Q9CEmieg9NmIS0Kxts05S8JfJVzJXM9ZiFixLq9jQlQFhbZvBCJpuzYWs2InnTvW+SEnMAVDLX+FcQsgcBBhU2EtCu5hwDxA9J1pEq+GbBbjRKU+ECGyWm6HUMNXaes5J0mGrSUG0oMOVbBIACNrngnx+uhiBAdGHpNjwIUhNYG9FxJzFiG8hYWqBKcHiHZ/FMtvG7uDI38yFNlvgRELtyQrUnJg6Csegg0O/fuk/c3qHdGE9dL8E1XAWTcMs8VYTkghlDkv920ohmfmYyJSHYLCqE9KTeKlAJaEsqQvUw5gnkr7bljNKMULoJp7vTwOuEodvu33uI9i2VxyRoSMDrEI2EHASLJDQ8pqRZlViF5knABIczIwAsQ7Ig2iOOPxiI9v3+N4f0TXdehixM2uR98zhg7gyDhOkyi3pqQbXzw+ECzpusx/8XAxJoqkTc4SAotViEIINnjBYQRT4YkgNwaEIPOYUrU+T4VBpiokXiXWofmG5FcuRKSEKrKQRVnXsuaIqOeQV0TMS227wpkpAL3SoSRDDqERUNu7lltApk+eNzxqxL7kxpF2LOgRSITnRcBRBHHt2SNL4JNyy1pQkHdqWCO/72vfTdhva5CmIzgzUpLE0YKfE6Zp1BAFEoor+DNHd6opKUQ4T2X+j+MRaUoYNSeCKDRGJHqPFA9ImERxSm8QKCKSw9sGezYOU6qol0PX9ej7HrHvRBkRO1VEdOIlQVHfCWXdgIrzU5pECVHis8t+HcdRrCAtBJmOjYLhVy54OsQOFIeCc+vyq8CQCF0XcPXyGt3QQeylAobNBjH26G5eIA4b7F69Qj9ssbt9iX4Y8JAzQhacw+kOcfoDgLGyn0GUkDX/ksEGNbgRMCGKjbDuseezeD+WH8sfvxj+XCve4MI/L1/Q8pHLl9evOZqF3G+aPZbB+Mf97/GH+B6/2P4Eu7CrglECqO9w9eIF7qZJvP6oBFaqMkm2Ubj+aF6HAKOjRBnBTMgZEnIS7lxjzWXUhNNztLvRyWWCmtmqY+J6ZS5W8f3j1Wu8Op8Wyu4ka+XeH28yppuM7ccDNveHev59c4/03Yi0n3BIDIoBXYgIsUOOEXcvX4G7Dje3AV0X8aIfxDO5q+fqTP7f4Ox6efmc52X8w8VYwPFgRZnQVgpTgNtF/4491tLXdmbN6kN73V9r9Ckweq0MVp+sBj5lHuqEtK21mht3LtOsjtkZ43gKct73Mm6F254RrxhhD6BxSl4K9nn2Xb5wAb5iLMI1fCor/VYUGIsKZm0aPeh4mZxRDTNWNs66IH2t2FzUtxfU58m9YRvyMWGyp5nsygyQMZuTZ9IAXmZz6RwsDN1O1NlgWV4+fQJtnS2FXfBNLDt4+t78PZ5fWKmowaMoAxRZ/YpB9mOyLZ9zbo6X2bU7e8r4i/p75TkvX2oOIQMkduM5A4HGE3L97eUNvunTw+UGiB+Dm1NVABBviMXclANW0RUV/tFmiRC0fyJvymBR/hejn5WE1f4/j/xNmTFr/fssizY+g9JhrTxPEXFu07qD+bIX1suatrRloFeplBO3ZtRfwU/n0fHpzs0314n7tBKX7mIlxMX64e+xPAZ0T+uhaf/te5lFAmJHeH17heurHYbQIR0OmP7hW/Bh1DjJZkH5CAWKS1bVIXI89wC0L21dT8cOK1yJKwXm9Yuv3lvcelmYCcgaQoxRZrwI0+YSKUCIRMWTxkAQsHAVrQITqkndMJ8X11tu77F12sJ4lAeMiRLhnxnheKK2Edjqc1kSRugfYKGl6tYXpC/pCBjMqmrJrSUcXD/8AWYJPOsoNBE1WJtlp0xhCaNUOQItLuF1cfe10CU6BihjyNDk2zqPZMlUZ8QIuIYhgmreM+sZRnXuVCkgcQqVmC8CRU9gqLu/KVGEQlQL9Axin7zXz8eZwjrnK49X8KOyFXJZ34pHBf9rGCnX1zLwUrXAVmD19MhZQkwZMwVRzDTnCKPAoFly55yBEBAbxoHBgoVqe25QVAgRnW8jHBpGTeBGclQEALnAFvt3Z1NVFVDCeG5SxDZH3PUjDiGqEks8JJCArAJiE74aTiBNvEcqVBRQoSK8duJmEY6DNGcE47h/wHgYsdnuMAwDhiGiGwaARZGWcgZPjKyKCMKksKfzHwDKqhxgXVcCQEqsBVahSUYRnCuO8MAiCTeFEe10nnI+6h5iBHdGVEa3PSEkDBspgdnubcvjYOFwcq5eEbY2IBRFk11rUSk5OOEKezqvBRpWFBHe+8DC+5SeGw4o8EJFqdWMwdYx1BX1pfHCoZpwE1Y3XMJ6Jziw+wAX5UUVwig+S1k9AZLDbxqajuXTzn8ClRjmdQKz1k8QnJ0xHkeM0yhJqVOSkEbIyPQApgMyTwiIknTdhU+al6r40bwmXYe+7zEMG1FE9L2GaIroYidKCPWEqAhd53iaZJ9OqSSjlM1FFY/oHxvDQaTKJpTweaKIEEFYAXs7e3ICE0uIqC7g6sUtNrsdQiehpG5vXqLrN+hefPH/Z+/PmiXJlTRB7FPA3P1sEZERud6lqm6tXdUzPdMiQ6HwhSKkUMgH/u6ZBz4MKUNp4UxPl3RP1VTdLdfYzjnuboDyQVUBBczM3c8SkZF5A/dmHHdzGKDYFLorKA5IISIMA9aXlwghYJ8TYpYcNZRvQelVUTT0TJUXkBRFiKEduL2lFsYe3Z1S5uOjGyy+3JmIund5R3zV3NY7uTxOWIvDbXgG/+dWluZvXnDSvWO08ez8yeGMEOOYk5epkJKObp2BkwF8P95inUZ8tdF8SvYbyf2wPjvDarVWxbN50hXoKqSGo+2HQndSpVlJDH24eF/KO1XpYDSqwtrTboVDsAdze6nlrnq+xE8Jz37vGI/y+wSY+ldhzeuM8UlGvLnFJl8X/pNv3mCfdkAckEMA1JMzDAMQV9ieXyJvVtg8JQyBsCm8Dhwv4vYTtXjMPreKCWe01bNcfVuKmxvU6BXqvr7+1qy9AlTfn9khBqPnEfrlswEXWOpfN+j6u9WZlf243F/NRIauX+rAVGMHhdU8Bplr3zkwaMWgHWbK3CF1zzzvZ3S3O58lZLDtyJlDbxRBOav6T2nL8RZs9KTyAXNnpgqD+77qHpib4ZPQUcFF9eXZG2DpWpABlHnzudImbXcQHYKvEfAfGdBcUuvJsvQI5kj/i8h8bn26n41WPtqR3bkHYJy+0Pbv1Q5ypcy/e2ysi7f+AcOStqu7esM6xG60pR2SORgKf2I8SbeXTpwyo1VLfx04M6/MValrR/1+0vuR0Ni6sV9r0mtMZTnFyAtwhgMLNHCHC+TrPWi2B5GU754ev4MiYmnw/eXWXEvzF5yW07XAUhtKSByssviwJQKrgIIrnN2n6bcFmBZ/PjK+BST3eKxBgzIfrdWjpVFX6j89ggBhl85BIeKvv1jhyWXE+eUVwj7j9f/7P4Jf3YLHVJES1eNIcG123ZbV7M1TPAE7wUfLl74vc3fd4SV2BGClMycMUZXZeyTXXW7dnHrGYO4SNnrcX1wTJgA1LrsEhdcJJFaZuYU04sIQNOE5TEhVnsi/NQGqaXtzBQg1sXROCWKpb4RNdYFtkDzXfmz9WZUKOSekXEPAGHEUNIdEMCE0p6J8ABM4SWxskeGJEJdZYs1T6UMFlmREMAEc1DK9XpSZJJwPYyz5G0BmpdztLQLUPKY+JwCBkUdjurLE+ycULw6z6q9sQQCrwDZQKAKvcdwjU0IIQAQjRrFGT+NYhYKoVkVDHDTJ4QiANOxT3XMxDiJwzUmXsCYrtfWpp6jb19C1CKF5btwzGRNiibLLiz3z2e7hJvZv+U32bkns644eCOIto9c9Gcjd8SrPjQlPDASzPmcQB1CORQnX7npZN2tLtpWIHwmyz4pFh+5JmZaAIdbQYEUpZltMGeASvszmXJUEn2zP8GS/xterN7jWdhInIAHEGnIpy0YiqDIXGXlMFReqd4HF+i+njwmMQc4oMqS1Ebvbt9hv3yKuoiY/N5hlfFXQPrjb13KwZIQxuASaEpqmLBVpkmZTpGjCchPIS3tBzjCAGIciJGYwQEGgLThQ5rvsC2MGnYSVKIOSCRrae8MsIFlxSV1zC89m46ukolmOZ8dZFd67wcEM896S7UsYLVeN7JBCQFHZBxJOzRRnVXnApS+AEIeVrg0BxdvBeRcVJYYqQWK1iiWSXCIlVQVJO8x2P0hbQ5T8CTDFzbhHziPyfoucE7J6CuSckDlpHgc7J7L2onyJ5ZzKOKPgjnHEdnuL3W6LV9e/x+3+NTiLkmu93uieZRBH2TMMjOF7RF5hhU9AHJCZxAIsyHzEID4/gSCeEGdnGDZnWJ1d4MmLF3jy2WeigIgSqkk8K9w62OoxsB8F3+92Owm7t7+WXBjjXr2T9kWgx6okty0RdM5jEGtcXl0C8ULONdma1WTVFCIoBpw/eYLVeo0wrBBCxOb8DHEYsD6/kNBlul9DjCDssOavRTmzIxD2Zf/CfXLovu5nbp8xT+mW+TJfZyqoe5zyM5SjP0J594zjT6VMhCWFHmvxZaDoPA4TMlK5D2F/AZwFxt+eR7xJjH/eZYy5UqR3LoVh6d/NCPkbxPAGoE9BGECJxcAAhKvNGr/6dI3X14yvv5VE9msiJAogUk9Hz/fqHco5Q2wfgghOcoY6wMJ7iYhHBFcFfKHjZZxEimd4ToDSDqdCwUXBXWj1mZGXO577FmYnEAQgnTO2n5ixAjC8eoPhux8QvwPO3hDG3R5vx6xK/gBerTCsV6AYwCHg1ZPnGNcrfPI0Ig4BT4cVOAQMg3kiG/qvimPrC/adpvQvWR4ER+tOsG+jzHBeBOVxjzOp+x0zfSt/0JIy7j1qYOnzAkwNFzrayNfX74Wc7rU1BpkpUmbebSGs59LujPMQ8VV8hg2tMNCAcbvH7voaaZ9ke4wD4ss1KFU+Q3dq932Og6+nt4TN9IoDKO1qtDLQhvksuzjDUtOS3vnG7/p9buFEhTZFI9gssBq9Pyn+maNDdd7KOMzQp8ct5Nfdfe6OcLO9uf0wXu9x/Y9f4+bVKwDA9vwJ/vjkS4xxU/ubk29MBjnz7NQynYaTSrsHHoFwcEqYGYfr5XdOrar1S6GZ3+9Tll7sr7G5hZvbMLN9tO9W/ND33+JSoJ6vVuKzDHi9TaipZv1VUJbDb5+6L3plDJQvvPnkEtvLM5x/9xrD7Qgqnnu5HAk2sY92sdkT/s3rK7weRvzT+fVC1zNw3UkB9K7KoU1093K6ImK2/clN11yI3VXWvDk5jrMEY190FRfmYO6IU3mvg4htd/RdHUoSsnQ53AUbHq872+Kd13fu0u0b6evcbxNNBOvH35D/aAWiNZ5enePp5YDNegPe3mD8/Svw9bZYNfr7tBIYM7BTR4A0cPUEbu/SdrexF4Fg+3C+HXc2+uUvF9nMrE2UEe4dx2bIv/5Bf5SstaUjpoyWFzo0jVXewVn1UDPU/qqocdOrV0OFXYUzyG1CPHafS2tu/cn1YsnEMjdEmxGCKsWtY8gEUHa1HLAlcTRLGBgCSjK1ZtJIBaWhJKItgy/EYwa4MmoCd4XFlqdZb/PcULhzIBEHcyhvNFBQbbYkX7V3VeiV84AQMkBRlDGBQIlEMVCyDKplcM7Fzt8ElEVIGwLMrbDHplz+1wGnY2+3W79DdP/QAWzrFBLlnHC73uVHd65BVM+NWVRYfoJi1cXde6UxHb9aCXJVRJRECkEs6IPGfyz4xp0RZi/wlZLtnOoZKqGcggRHEOF4niGXKr4rCglNQnmWAjgFrIaIgFE9HDQEVxZGJ0DyRzCzCCuZRVmhey4Em4dQrI2MFOQS/AHlSUqS1HFNayAOVYBhSfyCwUww5QnQ5jahLB4NoYszT3WKUXNH15BkdbfoIVDvnjDEcqUL/GrJFtQPwSFeVlitHmnMTjlKXUgfhSN7TGxK0Q6ZN0ymx8kez9raM6MkcnfbR/J9JBHOAyIDD9UzwXCew/yOqbVuqHiMuM4bXGF42ZJbSz4Cu3PQJN+se6G0hBKqKARwSmBOQB6BnCRhak5AShrWypSg5t2h6xgEv5GeI4CKJ15OCRmM/f4W+90W291r7PIrmJIyUgIgSsEA0vOQkWgLUSongMx/SUKhsc0LCJEIwzBgtVpjWJ9hfX6Ji+cv8MmXvxIFRIyImrx6yQV9v09VEZFG8O4lctpjt5PzkdRjAqRCCZdvxBQRQ4xYDyuk4QJ5uKyWziGCKGK1WSPGQcKbkSSkNk8OCgGrjXxfbVborceIRwz5Gk0Gz5mxzIxuWofma/YtHCNvW4HaYq1FOOb7uB/d+hjlfSpCpvTZh1d6BZb75cBbd+G37gJL+36lJtlfqRM4hO5QH0FqBxSJ8Dxqkvld/anEgz4GE/rRzp0+Rs434LQHDc/EAKKATVgNA56fDchpj28iiSMhiS0RgyS8oWtLPihNpx6iAKnCOwvGd/d0sQAvtJbnHRwHVi8Hd2T9HNT3cvlutLenM/yrlTZnQMJYYGlqpW6KGek8l/t1eHsD2n2PkAZgJ/keRiIEElqH4iBK7BCAGDCen2O/2WB3GbAegJXd/SWdUKuAaPgmaukCmQpG5adCUfT4iSo19f4vFGvXR1EKBP+9LebVUEuAe8H97d4ttLD94z0fqKnXtEF1DM60x9EyjvYuzYT6sfnQ3x3Wdm1jhYin8Qmi0kQ5M8bbHYoxXgoIuxUqpdJuy/lTOX1a9x3Xfez4S2ZPBdkbtc/aKje/2WZm/6hgI4af7TtjvDLAuhptO9TUbXef/2kZK/lVSmPG/ocbpO1epn61xs3qUttmzVfA5YXFu8rQ6sKQ2jEcaKKvNMvPTb9PZ2Cpk+79pUv4AZfyoTfZcYPkXfnv298hgmV2QltYakSE0/v3ZlfTfBZc/3QKXjk07b26pMbhOdiV1ylr3V8i3L/hTs2BefLyMau1P1uD1glnPyi+557+kJoiaZGIF0NiPNsSmAPihjFqyCYq/LN6TxT+6CHlvg0c2A8Ld/J9vGzvnSOCOgTXPHsH1Lln8GeFsw8kWttefqrlQ+VQnKs/gF06A2iFv/zqAk8vVvjk6TnW6wHr9RppNUps6ELwtOsxJV+nff1UyiElxLRyfccIpTyDCaaWFPOkWIMsVEgiDIl1Zhe2nboemJl1UcbFciVUxYKOUq1CTQkhsfQlhrggXZ6sbz3vyhzpvWzhc8wTYLLqunVMuSDy1FqLOZWKhelCjcNvkYsyB42nH6pVUFAvC1Tmrd6dNcQSESGyhNUgyshUGu3WRNdImTTWsEABNp8SyqcIwqGW/xQRQkZk4USTMRMEyXUwjgghAkESCXNk7Hfq8p8ZIJlbNkuxkpsha65kFThCvC7qvpF1M9BLiBsbDQmTSglTSxFCsZg3YWtZ6cIJHLj8MjceKUXRgPrdFC+WqLdhy3WPibA2I5UwMVLHvDdSyiX2vSyrrVkGsuxIs3iX8C3uPFv4I12/ksNDGVIjxsRijhEjl3nK2hcHUR74eSunkRk5qSJP8wm8uNngSVzh2/UNtjFV4i9lJDB4VK+hQuzpPod5FWURcEYReJrCgrN63VjYoEDFe2NUi/AQvMCbC8NlbvTDIGSGWMYDKY0CCsu7xeuowUnQ0GzCPVky6UABK92f4qnD6u0iQ7OEwmlM4rIfquW9g9ApphwDXIQAVIX0CEAU76KeruHuXzIBP3JVKukcSvPq+aNrltVEZkxj3WMqEApDRBzi5ApkzUVgio4YBUMOg4YaikETdccyDoDcvq64qawNtUfOvCfk7NeQTVnxn62DwJywH/fIacR+v9e9JHl79uoRkDkhZ5ZcCtpPUOUblbXWHD/qCnS9+wa36SX22x3GccR+vEbivYgziJBzqvjJCW8YGZlG3MYfZO0Ut8UhgImwGyLW4Qqb9ZeifHjyCZ7/4it89Zu/xnB5gZWGNLL/fJisOp8y9pxkfZMmUOed5ITY76viRWbfFBBZc0akggtiiBhiBAb5r4a7EriH9RpBzyRgng4ZK3yHQPvqTeKUqjXUhM7nx/KxfCyuzNDER4Qw77a08CQA/7hNOA+Mv9r8HpuwBocvgCGAVivQaoWwGjBcroC/2gCvAsK/JhFxBBMG5kJPFkGndZEZTBmZJayqv2NYBSg+zGg2+t1BPJkuo13dRWKW5ZZ7ia2VmWmeiAsZyANj+3lGyCOefPsG0dwcFdiUR+zTDvE1cH5baYiw32M4uxSDEYfHS+6lXzxDvjwDNBzhk2GFTAGrlXrYOTrAC91LmEJUutboY1Sw5HsR8hst0cpGJoqJQoO4NpwIuJAAM4xO3z8c3OV3mnu1VUSQe+5bb+mejk5qB+7+1t/I/+bG1Ix70rXrMxCKe6ayntb2Qd55nvWdrWNQsXunMbTqzgDVSpPmQPYrlXe4qeH526kvCwPV03jm+vbc90F5dDf+yfqfUiYv3UFWcZ/+3lNZkiMef9Gv3XJZavlOc7K0uA+xRGDZPY2cxeG4SfWZT/0oDkLD/gNpOMAjsNkGN7Ti9tNhWVnHn3XK7ubXxWZsfnp/qvm+Swhcw3kObROoyOiKcRAgfCGhRCxY3Y746naHN2eEH56sqvKhjGNmpHfYuiZXWXqHl5f2wEZemkA1LLzj0bqXIuLgAT6wqYFjG8lX7DG8j0N/l4P4cHT4ICXHiTvmKFKcPU0H6s3Wfc9XQweLWBcTQANCWOHp5YAXT1ZYRRUS7ROwHxfBPBX6Muz+0uiQwkMKMw4cxikwtr4TRfrSrT2zzl4J0aBYe3fShkmYKrXVED393lyYL99UkWXapWFtss1rtaaq7yspxioWYSOwlNAzhqdnUjy1RX6YZlklyg2LcSuE9RIS5PJuQxn6gekY5FGNNy+W1Y5BAYQ4NgQPgF3CvyIH4moBZheQTZZnyCb0clFWVNjbRE2VeSmCMvKW6+QUQqyErcbhp7HsoyoQrxept/7x+6V3Rz+GE+tM1VWrbsT6P2fdYbPYxyKe6MvARcBnDwtoHSPUl35Pi77HWQJ2h3OKJ3R/uyMl/TE6DgawMwDAQo4F9aQwiwdjfIiC/s0qgLQY+bBjo91ZH3YLVmutdYpY5YBXq4gRjMQZTPUsmtC7wBig62GW8DX0msWub46iKnf8PSU6PgmzY9G33Dat71o8TASEzBjd/M56uMycXwspFKN4aWgKbQnZhJapIFiulAQvSHeQy+9KDEr0npZB9i8UZnxyl9ez3rHXTUu2HcwzwycYLYoK1P1WrOQKQVv3ru1W5spOkO6hKjw3YbaDh6iZ6yK0CeSPhIO8CuDraZY5CKVt2dcpj6Jk0lwQpjwVRXFVTuds9pOk8+HOv+aQyHlEziNu92+wTa8xpj1SGpFY21blHVhwvygzbZIqw5Bop4ISCR+WVRDFtAYNjNXZGTaXlzh/+gxPXnyOz3/9Z0iBJEm9JcUk88qRds1DM0D6zFlCmKS8EqXYWsa6Uk+InC3MXw1VyJyrYhKipI4hgAYCRVTBlgrJBs1ZUbmbAKKEIe0RcFsSzeaiRO723YFSrlf4vXtamTd4uFML93zvT7c8Atn63krBiyctb78XThuoIx8Wfp/D5xNqqye+Tur7zsUNcY7EtSpyJwCvE7DjhG2+wUAjQhgBFqMSCgEUB0QMGNYD8phAK/UOy0GMA5QwN9l9xeJCC9QE1dqvI7uae1lp4sOz0iohPD3hE/5ah21rudkkjeFKYOR1QsgJK94i5uyShgaA9xjHG4RMCCmCQIiDKh02K2Qi5BjUMMX+RqTzDcaLM1iOjcEpGIoXIdl95/cRVZrbVo/q87qmpMZKtQ0A7j7t6empPXpRRFD/S/+lwlAf1fE0bzVwzLTZKEmoq+HGOFGitDBM2/Xf7B031umg3Ffx7ig5+gpfSUicMBKDS6awQ4VL66fci0azHWptQuPNtzJToZ3fti1v+ncKtAu3N83/NIeOT72BK3bmbmjK23HlkTs2rm3nSIcn33NLiHS26rTRU7pZarbnJSe/HxrkXS7yyUarPML9yswZVaHOYoteLkQuHOzM77Ovu7NXuZYlyCoPXfhdgv+lA2257xbPMXhiFbkMMWn/0kRVJk7v63Z0WcP9TeVfBi8BZDIEmcuYGRd7xhiprsVE9OCZNPc7nX5+F6eqUU61xUIJz752oK8TnEObcm+PiEPlnbAW7rD8ZFiXu6itHlQ+cA5Fie9dPgdjhd98scHzywGfPNlgFSNe/f4PGN/e4vxfr0E3I7AdXXJIKTzz6T7lUZQQ4KPIF8DiRm0ukdmDbijbjd+YATZPCLb/z7Tvm3LovWgRnJVKd6CMaTCrW4vt7sMllZAizPYH1nwvSK5tMlIWy1GxjDbhqHxvBtMRugV0ZljMzVSSoqr3hSX/Mpdkg7Wk4dUn6naezWpdu6hW9pZ/QJI+c9BEvixW2GIx7qfOBH/JzYG0nZMm7SVCDrEIljMspFR2XiAQS+mcp2tq662TnVljyAdIElPzIScC1OocSazsUxJBsYQZEQtoViFhtRQXC1xobg6J5Z8k+WsgNZtvZ7Va3R65kOZYLGVcQhAXRSYRkmeXI0TWhsqW5Vz7FUsh+RzIWfWhhl4R9BEmZ9WGYQmNU0oNmg5B8mTUGPpc9rXAmzXRN5Uk4xzNct+I8FzgtqnzChTzrqHiZSL9ajZnRISihzIrav0VDAIHqKCXkaEJznUOnr9d40kY8PX5DfaRZW+QJl1mljj9umgSJ38oQmkGI8FwpHcKVuJXpN8gkv2UdS92GUBgOTwoySTEzKAg652JEXIoOEEE1NkJxgPiENGXgoN0nBQIMQB5L2c6mekYQ0KbBRV6x1iE8DbXslP0rwl+Jx1C96YRwjO1/B3AFUYbV0omqFbcoJ4mwZQCrqmSQFnnwDwYKr6qSiUi9fwgwmo1SGie1aqz4q8gStxw73kiczyEQXLAOOt9AcaEVH5u7GyFEjJLciEk7La3SKpEQGbkJIqJUccPcNnDBEIMhBBJlErMSOMeu+0Ot9sttuP32PFLZN4jY1+9i8odI3CaMD8GyTcSObiE0bbC4iFCRBgiYRUucbn5Ck8+/QK//rf/HpfPP8XzL36Ns/NLrC+fIBEjuV0/pO8Q+A0qc0SKhmUkQTfJQAxE0jB2Lv+IKcbdfmGdC2Mnq9cZO6bGL0Uo/ZUtlzPAO8UrHz0ePpaP5aHFDEhapSzq+TScWu75e/IRd2Bg9wz8p9uM87DDX69+hzWtkeIz0GaNqxefIl6/Ab9M+CFk/O6vGPRyRPyt4PuAJIragmlctwwUOlfHY6PJSn8ZHVjZE0cs+2Zs3spf4xfcb9xTElWkGfEGId1U4beFpSCAEnD+tYSeimEQT7f9DQCopy9hvbos4RmvLiNePItqPB/ww+oCr1Zn2h4pLU/gtSp/LQyj/l5oyCJYr+GNCp2ge6DhULzg3n6jamjTUA7kP9R7uhWaUbmDJ4JD9/5kGxmd4mmcSbszoJS2p3xXZRS1LZuvpv85aZj7ldrnywrC+lfo0YgRVxhpBaII3u1w++q18FUAftgAL1crzc5w6FhVQWLd6PZC5Wup1DXiz/3ljm/v25vt1ZpgTN+eL0TuuAEa/mz6Zsk9VyGZacz/mXpeTKE1WqStZ+/XtXdvcfM6ilJicYQfSDm2eL7aSc3VmmJoM8WXUvGUPnsBint+4t3h31t+qD2pXOGwMXQhwJs9ebJChG1v9I/tRnB7prcwaP8ch9GdZF/uIo6thpFNC3W+uh6FoQbevLhCeJJw9fVLxN3op62tbSHAAQwY8Gz1CfLAAG7cjd11Zk+YF2A4Vrq22Pc034rh1dP7ONTacjlZEbG4SenI76U8Amq6lzLiAUTj0abnLtTmw/EmDl6fMy1NONWF5x9C6YCPMYJohacXKzy7GjCQCGv3r68xvnyL1Xc3CLfZxRiXcnhoJ851I0zXN70lzom/8QQ5ndj93CgccvIIeVKNraq/9WfmpdsLExrGE8xhfuMIzWShP7jEUi99MopUSO6vQqY0bREsdZdZVlWFhng+mOs4N3MqENadX2lUbcPmSsM62WXhie9251D3VydTY/EHuw1sLTpVs1RlcMhTAtrjlslv1RJMLmDNHUE2glzGXlojSKKxhMUigizhUziTRuxQa2jOyBxg/rzN/Jc+SIzJctc3oEb9dW8xV2vzShu4/WL7Eu2zgze+Y7xsO3L2jIyuZ9OXJUSucsayPw12B2M7YW6UDTFQczj4IYUwbaQImLMmYnZEt4XgsXTbFe66oY2vzUlgCUHCoAWYN0dlFQIknIBEgMo1RLVBXTiVdny2l1ccEAkY1kAioGTx1TNULKezhHUKOWsYq2CLjhKWQTqs/dleNga7E6ZP5g1cY2UyqXLZW005vKr92vhKPzo/c/iZ/QVpZ42ynAuFnQzHlD2lDFVj/ad1/XeHhdiN1Ss1OtrSEZ3+DHUzNDMOU2I1SgiyGbR9XvefKBBFoWAeED6ckO+GO5jMCyI4r4l5Z+m6z1H2tjtjmvg+5yRKiKQh39jC5ZmiFSjeNkCV4ylwOY0Y0w678Ra77RY7vsYeb91kyj+N7I/rfvHtBiLBf/VpUW4NNGAVNlgPT3Fx+QJPv/wKT55/jk++/JVONYEsE0hOYCQQdgh8086J+1sc3MvcigItgOuhL9Xt3mEXxo7Lvit3kxuz7Flq4uo6MUmt6iA7pdyJl50c8PsRmstXgj/E77/chTn9WO5e/DXiv/tnrvbBNpbem2u7L/6eXe5p+ZeKAWt7D947S0Bou5mBN8wYmbEdbkHIYHoGDAPiZoN1GnGFAWNMWK8Z6ZbBA4FGQmKhISRM4PSEFZq5KPjbu0JRlYKp+M0dVY9/Kk4yQxKjz4BMjBzk/qTcYStiIN0ippuicLWkzlYv7CKqUD+AVckQV6LUH2Isioj1ecBwsSphOcNqjXF1VlfN7n0Sr8RqPFKVTdDnQg+rp755sJJSeI6PqvNKrj2UduD2jD5sp6ASxMpyWO3Q/t604f/OmPpQV6+p5eGba3f2oc5d6J7Swjvup0l/HRz+npzUD1jRBkNYQeQ+jLTfF2OtMRBSUbW1XJ49KHdlYf2Mx+OZ82fP3W9e4NoI7lqwrY/2XKDQnncpSiW7f2eKkNTzcMy0OFmhu+Kug/e3+9YJSecaWZqPx7+LZzri9sv9qBkplXI70ko34JN6XaryEICXGtGDcwpcQsq6M3HH7maVLF3fk1QOd94YdnFR93TKe/XwLQJROcGF+gCIkDYDkoYEnIUJDGbJzGTBgokIK1pjhRFDZiTiEgZ3jj5mA28ROSyVKc475fVH2XJHysM8IuYu0/uUu2DqJU3jT7A8bBTvY3vcr/THx7SBv/ki4NmTMzy73GC1inj12z9i+/otNv/0Guu3e8RRhFUeYbyvUZ6aYKVaOMw1guN8daGK7noNtkTQMhOjuuVimaPPa65eVOsfI3UAE+TlLFb8EmLDhCyemOLy3JxIKz6UtsyiKEnAexVY5fJXrFydMJ4BUzJIM+LdYEJhf19wEXIllLBM/hIrvEDF1MzKCBXLr1ysVmt2iRoLV9phHZsK9XMQIacX6kOYI6LgdGd+YbLOqc6LxmSx8WebB7VGDkGSEnJmDf1UiV+iaq2fOIMlzDgiDYiREKNYRu+xB+XKAqSUiteFWM2LNX5jAQ0II6g5KNjBZJ4TlQGnQtB7JYd5DChvW/cKzK7aBNF+7mzncNl/Jsz0+iBLtGjWerYZMnMJ2VPSerNYbNjq19AAphDTX0JpRgTvKamQ2ceFr4VzBqusvvzOKtgfxS/B8hMUryDLhWHrqv1zFuvnbIkYfYKJQCVswsADEpLsKBdWyYSrhKDnoOITVgXdi1dr7EPG1xc3GAchekxozZywT0lyUHAWb5nVysWEDpLbJEbEGNp1yRIOh6IwgJYEWxJRhzoe3RsMxj6NCKogAcQLw4cOM+t2U4CknKVfOLaVUDxVGJWpFUFEwG40bys9S4XBVdsxXXeiaudvAnwQiWW97W8VCDh0oJ/ruTDvjJbZ1yUMBM5irc9EiIil7YlHBLv8GM4ajbNY5zdnAcCg+R8skbKPfx0c8VutUCUcouXyWK002XGIYDBG9doqiic2j5MAdqHbbHxEQFZPiO32BmkcsdveIueEGNUjQNch6foGnaagCJBzQk4J43aLm/EHXO+/wTjusdvtQTSCkRAtZJEKnnLOmiTe4WfOBT7bL6H4DREoMAIxVrTG0/WvsDp7iotnX+Hq01/j+Vd/i83lBYazS+y219jdvkEkndv0HWL+AdTkWJih+v0GASAItB7lUwStVbgnd4nUcgrsbPeQvdCKd44LIR6zfLg058fysUwMb9zzo+/6k2Q0fs/fLhTu8cAdSiVzqHzve9sy8L9sMy4o4c9XwBAjeL1BYML5ZxnDbovL2zfYDm/x9pM9Xm4JP7wWYQjnjGD3dx1c+Z8fg1dAtAJUx690shipm937Rs9LP9unGbfPGFffv8HZyxtY7huze9jn17jFHoEGuY/Vg83C4OUoNCtrnoCL86fYbAhfvIhSN1Z67c2wwW83l2XBU4gYNNRSQbFUqVmfQwlkNIN5SQCsSpFeoeAF8mXtnEGDPa1ikbn9Q6UKuboVv9uzKaaf++Sb6HdQ230PC80+mvs68ZiY0Qh6qr6MY45Iovqrf5yLMgg4DwG/Xl9iTQMigISSal4N0aanjt1fo508reU9+2ffcr+bJKLS7TWvmK0cIzs6wHgYFN6Ns3K59r20rvzzgjyrzCHNDFLHAqDhdfrR3LUs47l+/RiFLir0sYb6JdQ5Prjv3l/hCmT3/P2XBykhPoAydz/duYEjz5o5agUKR+/i2aKv1G2pd+3sPtWS6w8i8pBzSGHhtLEpjuu9Eshu2r7I08wkLEMQedfmdsQvr3d4dR7w/dOhqT8L5NI++fGO2r3LHRQRXjJ0qM7874tn667q4nsVOvDt+C+eSJytcmBKju+Jw+Pvf50cxHcwfY+h5/FNZBZicrOKeHIesd6sEImQrrfIr25ANyPCVkOeUMU9jkw+0sPhcnSKlgZ8H032seMxwwAsgbDY3zEwvORosoF60o8LHMX6ttBjlbjy1iB2DtjhBE9HM9dnhe1hRhPaf26kjJpzogI8HXgDY2WTyLlSl1aNzmNgLnBdO8c2ugp5RWmFwiwd2CcqxCDVKg4uqBDXiNemd7/HNDwS1Z/7D0aFF0ijtmsWYzFEnSK/rhCCmIA4jXpTpsxDl5jFCtySWnfMF4hKPPgyc0pUUzN+10H52M+Dn6v22JGumzESNjbbkqKzKWQ9bNACSt0n3alDvw4WYshbjtfmLByWAdruGYM3gxHKtmGTS8q+INduu3HRh1fxoSAoEAJPlWBST1r3zIC1vcqiWIqjrCUPNS+C1TXliAj43TnKYrXtLc5BpIoDKI42YX4Dkvvu842I0iHkmnyZyp61/CWuL1T8w1yVpkSkHlpqT0JcFKuBJA9A77FT/pazP8/0Wfvtc6pGNW4spcl+HxFALLBwEKG4X7HghBVkbToFhM1zBV/Pk7XiFA6mgKhwH2cii8LC9WEh6hqhE/V0hveE4OIJkVOq+SE4I2TXhuE2J9Czi12UFCPGcYddusaYbzDmEZlHtVRt18Q8QAoKBZwAX3G8eoowZblEzLCWgBAjzs6fYX35FOdPP8HZk2dYbS4wDBvFI1n6ZgLxiJBvQXnrxjJ3kTbTNWGYdKpmsdyEP3eXnrs+mn7rcLskeg+iPZfLlCw/RnQ8pLzLtj+WuXKq4c1jlcdk86Y0c6Vll5QR5d3uO9n1eQy+U+br1DHO1PM3ScUbcv4zgOucwYGxxR6ZGasQQKsB8ewMFAJiShg2CeFsi23eYVgJXsxZHGxHRMi9SaAxqbukp3+54J6eJl5CBezfC4wUWMIx5iT0TmYwJSBIKLmInSgbqIZFSgMBiAghyjg0lKL9N2xWcu8PQ7n/VmtCvFDPvhgAEm+KHDbYDWuYdyyByl3nFQ7ldrM8DqZosL+FjXAhT8uN2BrUNFSzMyRo9kuP8MkHi63venTe8zJtI/5On+2ku79nq8zc8/NlGkqpg4XKp7Z/6p/WdyejaepKHrBIAy7jgEgROdXLf4+MMTDGEkKy7b/fr8Y7eIMd4RcnleberLSfe2z+/v3rxXAPLZ9S7/WOC+lZET8pPKU8ptVnKdHHKYsNOgWN0nkW2pWcm0bDx1XmabGjQ7KQ+5ZeCbGIou96P9EsZjwNlg+xnASa8CMnj+PgPTz9cRYXcVPhHnNIE9bPtyHbcmnD6dnyB19zPEzg8wc5ACkG0BAljFIXVaQ2bcZuGcwRIQHnKeA2u4SLNIfVjpz3hy/Pey/38IiYY+jdKVehUaPrnnJkR9ruy+Nhpoe0VIjWj+WkYgd4n8+QsQFWF9icneH8/AyBgfM/bDH88RZhFGvHgii4v64fAEOBpW3Hh+R456Ucj9Zisi8Tq6wOB9XL/3S+yQgZz6BV4luJpaxxzJmV4BPhpAe2kF0zOFh+1bj8haBXeDOrwDoDaj1SiFQ+Ng5qlqe1ajeCrxXd1Clk/b8IMxGBkOukBBJfB/OoaGlrHx2dCxHLDLX8rsyLTXYoIUEUJs4iRIW+g4wYB2jIftnjlieCzYpb2wgaogdi0W8JgYnE+p3cXFhMcwoBMZAwpzwgpVET4TKSuk9YVHMvM8sav79Ya4dY90JmjGnUPAzcCj9R90+dN8fccv2txkGn7rwxJE2IehZkEZZ7gTrbgrHbfzZ/0CuZ7UJnZBIhNcCy3XL1fjGFmFI0gnICATkAGDXGvPwcQ9S1q9urWv4zWL0ZJByM9BGyxCE2QoG95o2AIUpSvazeNtUKfXoKgph5gzggk+QbyGTj8TU941z3DPIIYuCz1xvsQsLvz98gBcsLEjEMQ8NZmScBEaQfhTkn0rAJso7GfBS+cbL8lfEn1QBm5cbSmESxYt4HiisoqpOq2xtt+CbzGKK6RjkhgxAGEWqsVpL7xCz8jdw0j57i12MKHvViyk7oweB6BuuyNXdIO/XtWTABRdQQPSv3Xnlf/8sF19puKZW16aBxrC2MkvRnuSF8ycUTxD+v4wgq4KleE4Lvc8oYx7HMB0gTepb3ZC9bpChm8a7a7Xaa12GLlBNSGgHOSGbRn1m9fkhxqa5/zshpxO72Ftv0Grf5GyQNzVRhjRhi1P0GyF7TNiKVc89gzS8kocWGYS3rrHiHIM9jDNhcnONX/+4f8OTFL/Di1/8G68srnF2cg/OI3ZsfkPMekRhDfoVVegXwWPZc1WK7MndpMZyy1oDsKvpLuSxebbK/y0yYVl+ZYd4qOvtYPpaP5S7lA2PoepK/nnzhn7d5j/90+3tchjV+s/oSYdjIrTasQSFivd4AmzW+uLnBs6fXGNMeab/FH9cR355F4T9yRvhDQHyZC76xnFwTAym7z/t7r4FZ4BsvgNvPM85f3+Lq29fYj1ts99fYvBywuQ6ITEhryQ3EQfIDhRBwEZ6CYJ4Q+lc9N4cIfP4pIa0Cfrt6ipHEw/CGCL8tNKvR4XLHDy6OiG7FAAEAAElEQVTvQ6HRvYIAgCU5ctSGowtaun76fr3z7U5G91v5SH0/bTnKg/b9ds0vSzNmnjfvHuZ5l5Qb6J6XdiZwzTbWfF2CQeiwASM9w542AEXY2Flp5pcr4IdhJZSBu2e58JVqcZyN1lIjHkfvTgvXfc7uHi60W27o+Um4GKVTLZed98RWosSdL3/SlaapLLGbS/X2DlMjPvLDMFDd1m3mtP++tF4zy314p1QSxysjKpAtr7fc2qHfHqFw8+dj+RHLIUVCqyCY2Q+9oc+huqXGTI/kzl7T0nwbcg7rJvLhkc1gTp4zQOKJ+PqzK4R9wpM/SK6IidISADTvaFBP73VYYQjPsR8S/oAbFEHHwvCWT83xszQDjfs6w6e84/KA0EwL01AYoxq65TRO6X5o4rhGfyYC8qLw2URbLSyTPk5coIesYz8blUDl5vu9Gjn2mr73IBm9Q/6bdUSIK2zWa8TVgPR2i3Q7gm5HxF2ewDU5JDPCzrvBsrC3OuuMiiA8QX7ivjxqWmUEzSmNecpCvld6i2fhnBDbx3roAfGEUxH2d30rs2ICxxkRTTsGt3xFAExCdan9BCoeObZZnTAP3PxtX2nhkm5lPLmxWDJegcvY7OKaziR34FUSbX7JuVvnlvC08bKbW0Jd7uD7L4LLLEl+URURlfjVMRtzRgBzkMSxlOr4SBUfZWKgiaIDKCpkgWreDEDzY2Ay11OG2Y/9AGPVDg1F6TAn5G0m0eZsOt0Va5ugXMakYZIBoAr9yxuGRxXf6/m1kGMW65QMxuZdwIe+aX5hX7P5ovklSPYcqOZYmDPjLHwnqQCeQExtorCDuET2xMABnBjDXqz0UywHuUKpoXtkCpT9YYhFo8R1mLGgne/cKyv62iI8BnrPpIJPVJDvvXnsfNZ4nnWvVOaS9X1RNnpcWdaHASb1ArFVzxk5qEKCxZorBwljtWgkI6BWxZp7ZuOHCSlsBQ3HOEU0wc/ptDOfvLvmc3BKE+7qOrzS9+/bAyDKv5TVw0UUd8UOoLMgbRTazMUTIicfZs+Sm/aePQoOMzKPSGmLcRyxHa+xz7dIvEPW0GIidG8TbVthD7/LC1Ty7eRKE9W7iRAoYhUvsN5c4fKTz3D5/DNcPn+BOKx0/XfA+BYSaTohYAfCzg2g9D5Zn/nS0rrs/p1SkROqo/m8uDMalNjSCXO5Vz6U8jCa8j1yRB/LeyuPt01Pa+gxLVIbEnm2r/7bHH0+bcBTn9x8EAOGXR4xMOEGOwwIGIYob60Ep8U8YhMCYgTSuMe4H3AWEjarAM4JHAg0ZNDK5iOL0REnoUeUBqo0OzrYq/GPYUZiyXsVOSHSiFXIQMxCq0QCU0QYIgJFxKF6PoQQkMMKHCS8IggI64gQBdfHANAZA0NAjiswBSRVImSlF+zOMgiD/y4Erb8F9U/3pNyNVO72+it1d6LNBvkG2vatbncHNzPZMyLd8zmMR039pVrT3/paBznFmZ+8YVnz/nQ6ZxuYgkuLoNsdvoprnFluiJyR9nvkUWiFxKQhdVta065rb57medpqGIUynvn7deZgT5gO4xnslme1s3P9GZ1imKe04fZP18X8tBghNQWHDhKqC03d4+eCipix3e+QNCdYA1PHJ/Tfl/F0pVvlvcMwnlbm5wsOpz24+Z6EK/vKhd362RRH1M6Rro/e21LjvUzg1Hvd4cNCjM7/fgwWb8xY70Hho0lp8jzEoswnN19zkLLDCwMFrBm4TAP2lLELaQYx1A03117/dD4HoG9n7jndjfU5temF8rAcEUfKRBnxGOVUTsZfendCCI8I659qcUIuAvCXX63x5Wef4MmTC6xjxA//w3/A+LsfwPusNEm9gBpR4wMROWsbs94QJ+yjRYZ+wcpDu+sAAI55QtTqE2qnfY/rmE4t5VXunhkBpVb5OSX4+Pw+Fr8RdH6tClk8oZGqEJ45l9AfJhwSNJnkfSYxvyYRQjGyCqRQ227gt/lQRYTGCZVMvRUme6EwVNZ7yIUxsXAwnDOIuFjNV4qRAZIE0/0gxRIrakx6rev22YRA8++p5XG7x00wnUs9L7RPKSPkjB1lSVIbghK5GSlDwuiAQVwZPIpi6D+OQGZNtE1w66H9J0KgjBAGgIAhRIwQy2SbBzG2zlXB0U+1+9oKoVuFzNSIKKs3juUKkXcLPlDFUdHxKVPi95sNpSggWBlakhwKmbMoZNi8caDzwEAgDITiCWIJ1AGdM64wh1CZXbOyB6DeIqTETRWay5YRJYfUN4ZO9gAB1cKbGSDulCXaDhhgSdiYKWBMI8AJiYFsGU7ceub6sviFEGHIAV+8PcdtGPHbzSskknFa4nL4sE8EBIoYBo3ekMTOnYqVemVKzZvHwoLBzU9zXmbmrfwWUCz+y5l0ioiyJzw1BxRmLyd/rjQPATNSyvU8mzKDURKyZ7OmHEdRRrCsZeCATOa1kQvuAEGUdPBWmHUf+xLK+RW8Yd5lvfLAUjp45YUPE0FU8z/Uvth5P5CcdyL1nggVFgtboOs8DELqpTEh5YT9fu/2sIwxhiD1NExGIA1toblsxnGPNO6x391iHEfktJc7i3VOi7eYrGcMBM6ElBJ24zXejP+KlEbs0w7iMZbKfBleCypcYnahzkJVytg5trU1rxI1LarhNhCxGq7w+bP/Cs+++BU++/N/wObJMwyXVwAn5PEtaP8t1vvfgyiCKMq9ZEt74Ipd5v31HrCPTSMVmTSsuZKnhFYB7hUv3fV6Iiwfy8fysRwsTqBQvQOAIkAstKgeskMGbIv44u48jJLLrQBXlREg4JpH/OPud7gKZ/iz1ZeguBYkvl4B64iw3yNuz4G0B8YdPt+OeDomJOzBecT45AZ8vlccnpDSFjkrPjd6zHgAJgSsVbAGJCTs8rbHbDjPAH4guUefXOKcLnEZAjhG5FjDCcYwSB6eIEmm/7i5wLWGXaIAXJ0nDJHLdN+SGAUQBQwgvdaqosFCGDUCTyPyvMDX495+Ha2+/g2ljt7jXWVq6vtGprTNfKl1l9lQo8f8DpxRISw2cOhiOHxpTPton/dGDgfb6gXRjn6c3oby9SwQfrM5xzoOiCDs9yOuv/0eaRyREoNjNUTzzIfwQJVfFe9hM7ioPElvtlHBmzLvzRlsfkERaDIgPAYszKV5RHTv2MHuT880HnHt020DZcFPQzVL7S0Wa5kO1t2PO/zuu98ixIA4DEC/BuxzMbrvfGCrvqNi+6NMy2R9HwGghcWosk8Hy8+iGBN1nzcfew7KSTytrolcFH/RzHmfLVUAIcZPepi9p0T5N4fpu3PYhtVwEhkBhJwFu3MIeHpL+IfdOf54PuKfL67nwaO5h0dHcodyDJmc8Nodyv0VEYewitsfrTJCH85WfmBZAGeW8Dha2kXokcq7KLOz0NIiDUT+21KLdcYfBvuJ8vgqQEIEc8D5Wmjjq/M1Ls9XwJsb7G5H5De34JtdpdSofd8O+iEh5vK+qYTOnBJiWnO+paX37mvRdxCO7u6fEDD6oQg42NU/heDgFgE2lhycG9iKMsgvxcwMWd91j1l7VIjEZv1soMxq1e1/EwRf4qJOiHovyGP33XlF1MfNW94qRehgRjkRppBinhti25DxgSZktO7KHluCw9lPFaaCWi6ljMuYE/tbQyFlBggZOQcE1DBGQa3WTQDJXIWRJtgME6bJ+pX5y5AwVZaHiaAx2bk9B8emyJJHN6NfOC9OzyVr4+INtefBGE4lah0c5JQDViSXA6kQk8sYy9oQlbwTQE1QLomlnCDXD6zHc92jqnjj5fGWF/3b5h0BFEHDpOj4VVhr4Z+IbeyVO+HJ3rM+CANHrDJjM0aMMpnIxEhRFEySm0vbjJIUnXLW0EWao6IZs7M6c53bGZ0zPOrXipWozYySn8PWySuk5Yh6HNDBwawGlRWv9Yx7Pe/2YH6hCnp0OMaHIyMVinsi1PA7TRpS1FIW33ctWKHs9UYZUYUrk6TpbmLtfJtyU+apPetNGx6360BDCKoA0LwT1TWi9omqrE7qSZFzKvhvcmFZd1k8KPbpBvt8I8Iu3iPzXkZvzHWZ0/ZceTCCKfdIFEQhoNuPAqeMIWI1nONs/RRPXnyJJ8+/wOb8CsNqo7hmD+RrBN6CMILanXy0HKI8TNFlf91CtO+T28/qITUntypz3PTt6NGCU6Zn43HLEn6y304rhXZ5z0KJj+XnV+6z36d3d0v7zhb3QmLGdWJc53oWfduHel7iIg3rTO/HKQiGD3Zg3OY9rvkGxECmhBwSUhjBg4RvHMcBIwUkSuB9wjCuENOIFCJy2mPcb5HzCmmMyDkhjTs1rhHDEDNaIR5gGtOIiNnzTgQEQozAehWQQkCKERw0xKCFGQyD4PKgoQBXazECsfCDq30JewkAI9W7QbqZuRuNbmkmy98mHYPV06juHlZiq64HdSvj257wWfXBISVE2/0CIuxo4LvldOlv0sXmT/uxn9qFt6mdpIMNTz1DagkA1gSsSIxKOGfkMWGb9riOjF2o97Qnrch9Lzuo/2D0KYCJkqT8bQnpOizC9C6ewtE+4xm8Mtk4KFxpQVA8faUb5xRbuPdn+JaTy4H3MjSMcyAErrw1ObqTO63DYWXEMSBPQfLUVZt5510QR0eaXKQm5xD7iW3+SZTFOeDuIvTPj2/2cs8qrz0Jr7ZQSuQCe7eQ3nOAOvwQCON6AAMI233dgw1Oosr3Kt8ZmBATMPAB2fOhPXSwcjMy/fnApltSkpbf23eXvS8Ol/spIk69FAtufPeC/HdXdLOo0OTuw7gnZilnjvQz3/9iec9lzGvs+QJ//uIMf/HlBheXl9hs1nj5//r/Yfe/fwfsU6XUiCY4ZU5oP7nE5g4PtQlS58pDkvTNO1efwMi0rE/bYkPoilCn4FqPsDxtZKYRjvA4SgP6NrkKrn0sS/OIWFoDE8QFR6wbfAzUnAc6DgndYXNuceBZIueUJMuSNIHcgKnEJG/hthj9rLH/eWLpUqcqm0CTK2zmiCDgBBBnBEIRRldJbhXyMLdW3KQwU4w6jqTWZCqkcwqeQINYM4fg1kq8KSLEEjyb2b3TLplFMcEso2W+UmIQJeRc4dHlVK8FLkRfjJrcj4Ljj4wgZFVkADmnIuQGBYQYSxx/b51u+09islvOgACyxNkqTc7M1YK7WD/pmmukfjszOeWSG4L93JtQ0iUF5Cwhc5IK3UJnlV5jqFZvmRwycpI9Ip4EwLAadC1kf+aUpD8Xh1/Wj+ueaLdEI5Jj+585YzAjRq1lCgPdmCknHVdwTO6Ub5hDIyEQMqK0rQL1QJpAGlBPEa7jh99SYjl/xgG/vH0K81S6Dlv86/qlWnJxUbINw0r3lHhGSCNDwVUMaBIueS+Noy73WpQWPYem6KIKESrjxszglMQLoWp0YApEOT4uN0RpgJtxmyIg6FmzvWNrako9r0isoY7qeszyb6ReG+olUBIj60pxliSgbagoII0Z/n6oc+BgmxQqTJtMxfx9FtR7YKUeUNZmMM8wd3YohII/k+bQIBLvqWFYNTkkYoySgsP6BSOlPXJK2O93GPc7jOMeOY3we00hF5wDAnNGGkfs0zXepn/FmHfY77d6J7DmbxCLOgutBK5eQTWvDMpaBRJPL3Yi+0JZstBncb3GZn2FX//lf4enz7/En/3Nv8fm6hmePP8UmRnb7S3i+AOG/FsEMEJYSQhnzXE9f4VPqf75a1ZsnAq+nZCLPGFe6tzNt2c4uHoi1dwVS1TFx/KxfCzLhWHhLfW7kX7uvHkPCX+4thn4X7YjtixKibv3DHgcMhVmFKZ5+l5X9Yb3+C/bPwgFZkLBoN6lxNgPG+zGixJC78sMfMYSsimnpH9HpLxXWmgvdKYaJzEnPznF+3fd3F/U/L3YjHh2ucU3tMbvwkaHarQVihLfkNdG/S2sEG2m9yIZD2EGRJWPo4nEnxxM8r3g2KZhR3z1OL0bV1+WBO7TW2Ja+jBHc0RfyxOSfzgt3FfpYJrj496BFvioEoK6WV6uJv8xQNloefG8fR2B71crZLicCe4CNba4WilX2qkxBmHjqbj0Vxrjyq9Yg5JPMCCShBvLldmYnl7HSxsveqgUfoJ10Pqw0MhuXryt0hK9YOPzlTxNOzkBS3u8e1raYP/E5ZkBGiHtAiW9oIxYGMfJZQ6Husfv1kLjY/kgyvx+m6+pt/BkWxw8VfD0u/E6fSUG13MXCa8+u0TcJTz9/Uvhb7OjK4DCRUpoZMkMKrkmatSMWVlmdzjvJF8veOT4uSiGayfUfEi5uyLCTf5JQy901THPiLuX2cnvH50wPwuGa10jBDeY+b7eQWkTWc712QPzeEj3VPydmcAcy/ez9QpPVitcXaxxdnYGfn2L7TevkV7dgLfj9Ja7S2cLFkzkOIujTfXE4F3675uCtdVdfpj9Cj/waml7pFRewAlI66U/tS7RveoYrQZG1OfsGI3FQlQiH5kSogi0rc0sQpImtEpB3GSy077hInAHJvRTgy2aT8wlKem01HVof28PjxB2JsATKnbxeDXUm0AbiCR0jY69hKNhbqezaVC+SJJcF/dd2y3tF0Epyl+jQi00C5EIIhlG3BmzaAoeCZlTaTG9QM2yGAGBxHKObU6pehFYXbmvuBtHx/3o2FW3VARn7V1ZvRmMSM96Ifc5BQLVeagPURPgLjCHjeJO4WZwcc9uQGeAiTUEk1rooWXSWuYFmmOAClOVXT0LI8MmRHabWGCrLJJ9IrV4KEQJVcv6KYNj7QUQiSAZwZgDrnOUUAeoZ4u1bWJgIPFWSxix4gEXaYUdJ9zSDpZsK+csVk9u7qHKKm+RiBAAUwaWc1/PvleugVW5ZmuL7pz4cdhi6lnKukmNBKx9oeCboKF5zLLEX9Xk9m/BuaZMK0o1W6wWJFFg+NwFPSun+K3scFdHc1LY2Z63AuyoGKq40luXVMGL/I2RinJkApM/Oyb4KcoaCXURoygdY4xOIeP7k/UQr4asnhBJE0BmVR64O49QQ1axeEJs92+wz9cYs+SCMPiDKjpDoKJAbbluUsWDo2ncnBR8WZZLw37EAauzM6zPL3H1yee4fP4FNk+fYXN+oc3sEdJrEN+UMHi5o5uW7+I5us/fJ9P7pX3b4ZXaXVePmy6aXDsFTOeJQ/7NWYjvXXo6+CMv//jF5vhDmNvZ8KUz5aEyzIeM9ZBXMbAMMzs0hQNzLmQJd2ito5kB7BkYjw6kpz2twXq7T64/zBnseSanAFXuw70aEbCrzaT/BQbHDIQM5ITEkgGHIyFnQkoBmVfgbHd+QA0rwwBUEaGUjt3Z5ZYr+LfCnFcDthvCiBWAoaFrAZd7Se+lieOAoxubK8EMC6zHQkd0d275scI2f2+7R93v7eMDG777bYrz55/PIuZmLKc0AreflsF8TKXDZHxuL8vvelqO9TmzFICQmZdhg4uwkpCnOWPc7pDHPQBoCNpKSx8UdbQsxfRHpeObW3umPqFUBSu92zEbzYvN0xORndCoaOxcPY3QwDJ5MtPWCX0+aFsQYTjf4OzZBeLZpvCfRgkfK57M10/2i691CICj9XpDng+qTBfyJ1oeeRA9/959o5kuee753Hbyz8vPp9vvVxiolQW4tprf7Y6PETl4/qVtkVUpKuMQgzZDBHFknN9k7AfCOEyAb8a16H3j4Z57d/p1BomcsM4P3Ap3U0TcF3sVocCH7xmxrLG1QSxW+JMtidfY5cvy/ZfP1vjLLza4uDzH2dkZXv2P/xt2//mPTfiVcsMDlZAWKuOkPvtqZVkmh8whiBMbu//lddp7jcDnYL0WtD7+/gJF24E0M1HwnhBZQ+MzqhDdEZcqPQxOWOWRKTstbza3bm5hrR4RKiSHCNEQzNqzZczKPcK5wFQUJvZd+/KKDGvELOyNqWyZJSr/iZeRjG+O8HNNNoCJYDIWYX9msTROKaknRrVaDRQagTUxIcSIwBnjEIGRkZGai651RSeJp4uEnEUom8YRcRhKXgO5viIIhDGlOjdBYsOT20gUg7J/rJ4VCeCMlIDAjGTiPhWKW7x7s1quIWiqSiCzWVDL5dzGvtd1BJATFRQqXgRc19VKsPm1nAFGlLd5B8SDozJv4lmRtSkZgyVhziljvxer/WEYxEsEEOVZGkGBsKKVCD+jxHwxxQWXsaEIlQlUhfDeO0fDD5hFVbXKl/HkZEl9bS5zwy/N4wKrq/cnSf4OAiGHDNJkwUkZNzYcmlD2tVhvsMwZR2RkMAecY41f75/jFW7wz3Src08YeQQDCDQihIAhr7BaZ8QYEWPAMKxAIWBgUajt8s7F4bVzxxhTKvMWAhBVqF92epjJnaO4JjMho+ZgIUCE7roPiyeIy4lALB01ySbV0j2WewCAhSGyNssvvWChhisil0Le0hT4mgBVJwT9G5jEhd2UXHCKJ6/4LEoO16KGrqihp6QNE+APcSU4VIspQkWxYqEwoPOtOTMUtkiqgAgBQxxg+Req4ljb5AzkjHEcJfHpOEqSwqQJqo3ZU0+nGFcgAGm3x368xevxt8hphzFvAUjOCEDOWMkHkcTTS9pBCdsRYkCkUGAo3hbkxkXmgUVYr9ZYn53h2Vdf4uLp5/j0L/4OF08/xdmLF4ghIOUtsH+Fzf5fpCeK1ehR898EABNtuH9Wvve/6wtOA2nrOt+Wb8Du1CSeSe4F8a5wdyNJwnkvRHm/5WfDQX8sH4sUpS29N7A852USuxcn8KFTwc2fu/GPM636c89GYzmJqlz1yMQYOCOGG7DSeLcAfmcEByvNpHQSEMWgDNUrrYaptHu8498qQVx+ewWAcA4GFeFCKBYT3UBgtMmhGeDSR32TynevcJ/vwX6a3u+1Yn/5ats2D+W9XO/rpoel1ff3gdLCM1fCUmkVKDN9Ufuh/VrpxsPtz4B8pHI7kx3N5A15/PP+w0zfaxrwl+df4ow2AAjjdoub774XvipncFBHBT1w9WYk70xwpEh9MQSyJ0WFUmh3304gKnWy0f1YlhM0XPoxWQIDMCF+TXE3pTkmZfr7qTdzn2+th2VZGVrP6uUvP8eTv/mNRAaYtDHt03t1dtDMPDt1JN6Iy/d14uvLCP7u5b7NeBA+aNLK036PBejd2jmEZe2TKQLqE56reGIPU2RdvSlIDiycsab93luYEFTmkjExuoIp9xmMgKrpZ5xf7/CL1zt89yTi+6fzovp+vMsjO22uG9oC/u7zfc7UP/DklHK6IuKnInw/JNU5BUMRzSK32jhVYnJh37YESAvWYrddvcXZPtjnoZeObFhHvMxDMO04MyHzgMQRzITzTcCTs4AnlytsztfIb65x88fXyK9uwKOaSx/YRgSoRfFUzAMcXz5PAMj3U06oQ2P3VEB4q+a+FLGDo8SWp8AJHRxoHdvjWsaEvl7ab95CuQgr+wmbAE/FYrgg3AKbE6ipwqAqIqr1LVRoZMIjZhQhbtkPZmVdqEuzfBEAJx4WXV4Lm1wGq2W6hYfyk1Jt8lvyo5uEaubl6rW7StCz/ScMWy4hYoRZcZFRlBGjslZEBDZLaw3dRIXp49IzmQV6IKVQU50FzsgcqtWwzhupu2zmLPkEsoRBK0xlFgVQEVhGSSgroW8yQqz7xGvCqMxL79vmdzOVvVFc8MuoqmJIQa1r5GkcP9Pds8q06vw4fCL3e+uSX/5SdafmrJ4fVFeWWAWaqHRACEH2c4GFFfVnUHajL+PUe8MspkoVfziVYWdG3XVuDpZwLrvPNl1UvZMY4iWBQAobRCnCRih5fxTdVznAYuNvsMJTOod5qozIGDVcEjMjpIA01hA4QUMUNcfL8DapcgZclFdEXEMoIReGxHaRDS9zLiHC6u8Vj4uipd5jVLaqWOADANTCvyjQVHkKF3faFJrzwguFrQ/D6K9PBkz4Plk1kjBOINWZKN7z7TOy7gX9HW4+bD+TKEAyy54JqmAxD4YQI0yxUS8Ygk9w7c9oCW0RqAr7g+ElcvSM3WWiABAviISsCk7Wz1nDjIFMsSDrn3PC7f4lduON5IOAhEQzoYo615Rry3LYsIbnIyIXhbziIQl9ZV45FoIqSLLzELA5P8f6/AJXn/wKl8++wNnFE6w3Z7IPOAHpLYhvAGSF5Qh1cJRWWq63RDb2v8vjikWnd7b+4nzIZ9HEHByPTK5X3moeWfe816ll5hqfq2U17tb4I5a7jusUdundGWsuXKiP8M77sMN6p1as3H6Yo5NFUY9CqwEzdOAsiN3DpXE0j9t5l2unp/j7dmf612aMNrCbleolWWgZq5+VPinsAOsdUe4AO9QEmjvz/h/uYQbKLT6hyfT5pEV0m6vts6wE1bqTZ0s9lHt2ZiQ0/3XqwRhOgNmD7vbOlExehvXkQu2nuSb8ZWOPDnW12NDB7u/+M89VIAQaQGGQHFQsNN/ICa9jxo64Gc5y+3pn+jNR3vJ/K33Zc3iLA2raW3jBf28qT3FsUYjovBd6bQmGA2XpnenzhbN8oGRKyLTHmG+lPkkiepLkeoUErevSt0jtopV9dmjypk+WsAPPPXykMtfk0fVZAvpQQ2465igej2Hnmzxt15wK2mOVfsffrf5Spa7WknKtK8fG28NK5eH0jumNdhdhC4Tt+QpxAOLNbiYklONjOYu8KDMiR5xjjdUBqE9VMJxW5jiTKaHxLqiz+yer/pGLnyTqkdyDGu4p7R4ldJhiQqzU947QHrPlMRFD29YR9DPZXTKhTU7d7uAljtimq/L8sycRf/fLc2wu1hjON7j5D/+K3X/8fREwTC9vrrIG/YcwPceHeOxDBMHidX5PRqcN22I7sArkF99DL/xugGmQib9Q2+c8bcAStOq8NcwS+ykWZoTdZ8uLUCzOwc4Ig4TIDwQis3jQWmWspoAQt29OY1FEmDKCYhQL1iGKFbceU+aMbDHwOAO+D/Mo4KrQgHlGQL5ntY5vY2drCzmhBJWhKoCDErUWjqnGJbfx6AQSNfOYwSjpCMrmVCWEBDJF5lHi6+YRnJLEW6cggtLMiKtqoQyCKB4AhDCAQYgxIzMBKkxlZkn8ZwH61XtEYpXq/DGBUtI5JpmvovABOI9IELs0IRZlk4iCJCCuBxAzBgxIKWO/2yFTQAgJFVDPvdTpEra0pniV+a2zZuFbVoMQqhYuKrsM1ZbHgXWd5BIWeXE9LbV/ET4SxLC7rldQxJEJmlukPSQxCgKzsDJjSohghGGlPYjySlxCxBK7sRBXJU3OtubOW0WFupYLoijgQtA4+bJHajgBWYM0JsyVai1HNkn+VxQUQJrcGZrbw+bewWDn3yffFsNHAnFAGCDtZ+CSN/iL9BnsTH0X3uB3eInqAcXqnZCLQBxQzwyyEAtUFAXZlC1e4E+EnJIIyqN6vFDQW1LaHlOSxJZRZiDqPpNcJpZ/ReYk6DqQKv/2+1EE54PkZRmGqPMdbPPoNpWwZhlZlVHyH7m5FxVd0JwBtuMrrjeliilYWefA5ivEqBb2obufpLVqIRr0sUuITQILhQiioFb6loQ5iEePC8eUUgIjg3SfUxB8sIriAzKOsv7BPB/iAG9RKnMicJawYpxKgsicE/K4Rxr3SOMOOY2S6yGNJa/E6uwSIQTs9uIJ8er2XzDmLdK4AzhDM3AgljFqtC+dAQ4m4iFEkv/0hgEgyiTbB0MMiEQ1fFtcI65WePrZl7h69jn+4u//b7h48hmePH0m8GUA+RZx/K0o5gp6YARIxoUmf3x74sonfzUulhkacLn4QF520y9lODXkewe65Z1ym++Dff3Qyl1pxh97ju7T/5xg6OdTZHTTMRoFnmEewqI4V7Wp+98dZvW+yhSeWYEjTU2crGBKXeMBqBpauhI4ViYBghEF9J4BWwCgY74WwXyA5qp/s+JhmtTou6HZFu6whnOsPQEnnZGFTu4fKmlKix/pyv1Gj46OmHpK+9QXURZKBHLk5lkMtDgEpJyR9Ga8oYx/PRO+bm2RncuVuAQFoRhqQM++4x2ENnRzypVWnhMwKosiOQUDiffCPe9jrp2Ux2U2s4Qvu/s2mW6KRm3mt8CE3nFzslD22OI6fofr9IOE8zVDn7LDWvmOV67Mw2r188zvsyNykLYyjiWol1bnnZBGj0Ae2HGY7JVHL/edgWN1j11Ud2zuAygND+BkHJUZ78v0YR4iXn92hXg74tn2e1Ce8v9FEZEYHIAYgHVYYRPWeB1HANeu7nSeHycEHy98Lr1Mn/fV7rlh348i4uAc2Y8njsBZ61ZxlXPJmcVe95udYhUz/6v7TO2ju+yJD4Du78HlmadlCssYVSjDjItNxNOLiOdXAzbrFYZhJZabgFoILzDY3DWJ06bjvlPWH9a7EBIH488ebKefTb9JHZqbyBwPtUkVHiNaeIpGSiLRTglRCAD3rLQ8kbj0gKk1d84aez+BUwKnrEycC0sEtegv1vTKzIUAUqEmM4HM4ZZRPGKqQFU/G5zWv6fLCUVgWogTskrTsCd+TNnmRolQMuFoAXlmzxg8QGP5b4Su/18ByBFNRiBbsuceNmaIgFUTQ5ugG/oZius4c3Xl1bbtQrNQAzlkhBzKsEdkBGaEpFbZFCBG6EK2ZkiIJhv3nEuttxYkItWTkHPp5zK3oTfDQ13PQpA3FLL7WAc0cxq4VjKh5AwDYcooEd7mosQBi+JNEtYJXHnSlxNCGHLiOrfEEQgoYcZEAePPDdVzJzMyGcVkYktH9ZEbymR+iNWanESEbknGJeyZhaBSLwR9R/aeEb6qmFB3EEbGGa/wNJ9jhz1uw4iQE9IonQcOiEliP8coe6CGZTKYIEL8wtj5faEeE0QIwWJPVyG+zJmdLRunIjlTbNgU6FhKQsOsoaoA5ExNQnNLpm4wEAdkaIJs7WeZmFN1lW05vx5k4YIMz5DDR+0tWran5w/tDBFgST3NG8Ln4zAFkHijhIp/AFQPElRvFYWzJo6v9UzRaPDL2uhcZptLUUKMqmA2BXDxeAMkx0SQez7nEde332E/XmvyUxUjdHMqV0Fdk5p8GVUxFAxLkptjKsonHSgoENbnZ1ifnePZJ7/Ck0++xMXFM2zOzlUZzAj5NYhvIclTpoS2x53+w+RKX9oad6T/D/ELSyz7Q8tj8nvH+B1amr8PqBxcgxn472Oh73Myve9yny6ndN+7KYbGH9bGI8BY2Mh5rqPyJNJXYsYPY8ZNbiPMns6MHIJ5+d45ufTDsDsNmG4Iz3D1FxTP7B//wPNsTpDLC14T8wz0oblYaKP7OMHbS3XfwXa+pwj+QHv9h+MrPwtDw7LR/G+nlAOd96GXHjYT8jYx8HQ4x1lYgRCQU8J4fYNxu1MPZomvGQul7tafOnALH9wPov1uxjr+90KfecO0OZAXvALLz0eeLL2rHAOaZBG+Jar1Djbn6Dr/qPy9x6Lxdofd199h/+2rru2Zz2WBjnXUr8G0maXXJr/zTJXHJEL6obxL+qY5x++ym8dGjne4x94TWXTvm7XfO27Pl08HGpnoR9X6KihvWGRvpRmVHZD0LREaSMM7N8SoF4tU0Lgcug7IO9CiR67e2QrdQO+7ZX+yHhHvrSxcCq6C/p1WevhF/SOXwjTMYH42uRDj+WXAP/z6DGdnZ1ivN4jrFeJqUEHrgjurL4vCxscrD2FelhQYs8qCieRprjgCfuYGnWuXVLjUKCAwgwRsqZyAvVFCeIETLHwKlxbM1bI2mtv2NW67JLcbkcZRBFep5jmACYwCqSeAChlV0BQQi7CNOQN5hHk+FKtjJ/At1tVwVtalKxcTnjXurVNARM0lMHcWLZ+D5ckA9LjXmCk21TL4jCLMlFBMUEG81GXI80ChxPaWfjICQwTXDMBcjMsaEqpVu64ZGMhi/UsQYWcMQTxJ9G7KyBL7vsytrbPG0M+iiGC3VziJxwMFsWYeYkSmoK7QMreZqFhi216yPdiUIkQNAGURPHJdv6wJhPuJl7Gh4ejLDjRGoGN42nPhk2jL/ImVtykC6p4mhTuK1LzkFsgxAqyeMSSxX6PuPTf0sr6SWBqavFf2Dal3TfES4FHivLOIVy38U9Y9XAFCPSM2v24CuCM+qtDZrbFKdAw2kTGzbCW1Jiv5WoJuuyzJyQlBPEjIIt9ySTYPJlzhDBfjGt+EN7jGD9iPI4gzYoqS34SC7C21zjfhdIxRLdwFVyXdDzlp3odgOVX0b6aSZBiBisJMcp7YWFHGbnlLGKheF+pVY55YGEdwEMUKw4VoyjK2bOvpkyQHVSYg17NErnc9916PZPte4FfLWSMyFXfUHA6KOV3eEQAl+bclcLaky9pBs7diDKo0tD2lyjDLdaHvxDiAAKQ0ggCZW5iHAXV9GxGrYKoSQjwhRuz3O6RRcHxKEpJpTKnEFh+GlXg9ETDud3h5/S/Yp1uQCv0NtqKctpUMBGT1bDN4iIqHjcylKLCjKWBsv9qhCREhDnjy+ae4fPopfvO3/ydcPfsSZ5+8QBhWkhuHbzCk38u5ZIc9pmjsp1+WZSMfywPKB5ns8kcu3fX8Ey4qCKX5cLBelrZj4L9sM24ZE+XqB1MWcIDRQLCfHV3L7oEXaBze9SYM6YQzj3JU5oUpS1Xu1vLxF5cMwNp3+TQYjgp2lh/SDCyPLzhcKO/5LlmFiF9tvsBZ2ICIMO52uP3uB+QxATkjRcIqr8repQZAL6Szb/43o3zsSfW3LjWNzDNLE+Mf0RmxEQAmoUPUod8in/np8gY05OiOanzVNjktc9yqO6O+idk91u4UJzKY7ZAOQGIlvbzB7X//P2N3/aapvfTW3AjaCl7u8Lil8IYL5U+dVLo3HnmsiftAr8+DhVFkOofnT8zieyRTZWASRtmSXVecA5RcMSb/QjfdDq3R3PMOFyqw9dGMUenR9bRxzNVrZDJW7re4D1JEHBvDaSA9bGfXeeqS7HD7+yk9lberFKr5WupNu2nd+63vd3zgHosenp2Xvm2uFykjIOUVNpsVPjtf48XTFdabFYbVgNV6hd23r3D73Ruk79/OtjO3MZaTGT1iuYe53t1h8oQ0l00wJSq9qNRt1gNNtkmuyXXVpNqST4yJEkJqiEmXJebjLglwLQz3Gmz1pd2ElDJyGkWAnR0lZmAFbyksEq8SKz0EQGPtEyKYUh2+CnlLIm0TOIKLF4YpJZqktKhnNWcuxCAHlrj8XfwN28mWtFuEozbsamEM8MwcqGVwiTeuF83C8jVz6iY1EKnQmVSuLMJl1uDyptSwQkUo13kYOcmA5J9QGFUZIHlv1XKZZT5SSnrmQp1LE27b2Mm8CEwRpHvQlEG+rqawmDICFuKgvc+cTwTMp8QYDWvDbOwWhUHKMAQCMhGAAEsAXeZM/xYBb7ceInyf/laUQaUh0n0kXzMktIvMofzuczT4ovyL7m20CUR6QG1cOrFVWDCPQ+xDFQyocDuwhAaKkpiaGSpMFzF/CLqviTUijMDOZQ8QzniF53wJjARkYBtH7DFiHGORPGTzwACQOYJqtj0UAstOmyp9yK2FKa0A3W7wHgK6A5gA0vEENAJstzxlD9VQWgAoyZ5NpjhQxU0ECEEJQjT4QXZFDSMmB8fPu81zhTM0a1ph9uP0LYSSlD0UZUOrsNV6RLWeV84xt/nbyXlmuX7shNZq5nVhc4sSasqUOSmNSGlf8Htmh/uhYZ4gSaKZGde332K/v8F+3CLlnSgPbE5UKQc/PrRzKk9CHTuJd4/hOve4KG4orhFWa1w9/RWevfglzp49x+rqCiEOCMSg9BIBWzBLotal8qHKFO9TfgpjuZ8S6N0MzBvZ/BieC3+K5TH0Okv0wGOs4ZStrrRl1v+OC9jmgDul8/tNzqn87SwYjaAClY6cfVspMzZas3t+hKy5T1lmie7R8rFX+Ei7Pe460qA3Rjr6zgyffNDr4VC516S3Lx07Sqeh7eVaRq18MpxjE9aIapzWhOFFS4N7HoGgvJJ/7kvHn/S/c/PZeF0un4mqss0Po+c4K6/Stlm/Kx3oeEj/l3H3vdz0RbOjX3jxgadxZhJZeUdmo7c7hNIblM00NIHqhOE4ccP0+Ql49BCWe19laQynLuejldlJXKhDR+rdoZ/GsO4AOLOgvSt67YS90xsG1udH3ouE26szxN2I1fVtlQdomyX0E5UnADMux4hf3J7h1TDibRwXeppSLtNPJ746V+Xktb7f5v1ZeETUy4inSSa5Ivx30W8DQyvrfGf9AigCu/scx6PvzFTw2vzEEdt8gednK/zDn22wXq+xWq+x3myw3mzw9p+/xfX/9E+NcNbxfNO2O8vrxy73ZVAepIQo321sh6rWWeLpj/OvTT84+TADbDHV6w9i+ayC/JyFzMutkMYj1yI8tNVXgX1OKqzS8B3EFjLDLNNRwjKFoFa9ztqVWRLsmpQ1w5JXS685W4gQU0BY7oSqhGg2E7lhqicASIRwIQMcazUvbgTMgl/nhyGhjljCiUk0F9+f1cuNlbtZa5sVs5/LKqy016tNTghRaTUCuAoLMzMoZ/AogrdBJHkIKrS08DvFSwQV95j3hCx1Qs6CKCwxrWna9/t9aUtgCSpolGTb1aqnKiN88fuGSEnxqskpiqTMAVGnhXSOtQosAfTkQjf6lUvF2pGrxCp9ln0m1v5gtLETdP5jHECUkXKyZYTe8wCZWqF2wb5fZZuqR7aOMWcJMaTePSEEka3aQbRxg0AsHgIyUx1xPotnDuBCnvlZr71ApImszStnKIJ7dkrRnAOMUcvMCCxKBY2bBBBwxWe4SmcAMnhk/G54hRtcgwjInJDUq8Zy1YjV/lCYROgetf2ec1DBukGBUgdUlUVeGC/Cdi6/ZYZ4b+RcFHbykoTHsjZTyqpYkc0UNMxZgLQVMYh3U1GQ2nq1FnNyLt0+JaCGwao4rsXD5tEE97zWqcqLWM6gD03lSznzKpDPWb2+Ejdnsrxve58sP0XFdqaACGR+ilw8p7jk90maD2Iryubyu+RwYSYMwxoxCPzgEa9uf4/d/g12u7fgzAjrTUkiLR5vonsLRemqCbvd5iWbX6dsDTrH4g2h+R00V0ZYn2HYXOLzX/x7fP7rv8HF519iWK8xYADxFsP4R4DHd0ZTfCw/h/Jxb3wsrti9DaAQQYWsu4PA78csBPXePAbrVBQndNz0PXfLyDXpyTC7LXmZa7mvyGjC3z5Q9nRU4Lsw/oPvHhDMndLfwd/4hHo/wWLzEgPhy81nuIyX8gMLcUeWe9ARui3vJiSqGAehnFn5vfJ1WrNOZaMQsNecB7fjLZnVAML1at7Dwq+pZbNt/EMKSEa7nmDPWqDdOJVGP7R/GqOTjn/wVGS1+zh9Exn/NTl/mHtwYmPl+z3a6Js81t9PoPxoUJ4y9+/0qntY4z+RW7gtOud5NeDtZ1cYbnd4drtTmVcdjSlBAYjHfpTb6JNtwCfbNf75ivD2fHxc2I5MJp9Q5zHKyYqIO4pKZt7vW3jg6OaEU1AEPhu36lB/1NSoQoiFPg4h0+a2PNDlqeV9EiGLfXlJKnCxIXx5tcbzqzU2mzPwfo+3r7/Hbse4vWbs//hSq8/NPBdB111Kaxlxz0lxl9R9BRT3ihc892nBXWYJ0dLkQ23T809GS5lQtip5qtWr/fWW7q61+lcFwazvs+aEkNBM1dJUjME1/ah+pmAJmvU/VCUFQ2hCL9cFW4x9VUAwN/BZKBZ4mIugdzrfnhCjpR/1u3fXZQvDopbuBZ5oVsGaVNkE8Uow1ySzJJbxBT6z/XGCSk3ebEyuhKiy9K0+ITKheGuUsQRVYLAmB1YYzfvGWR4HEoVF1vj2VISBIsxMmTHu9xqP3oSE0geViePGGrzsJavfzb0R666yrgNpgrvp7rZ4+q1fgrEVrOGEUN6l4Jlog5Pa3HMed5MJjD3sqJuPyZ0TKIMhZyg7Cy1bU3O9ZIj3DaLkwhAr8KBnAwByWRMPr+17D6PNJrez184p+2ctnmjykxTlWp3f4DwX/F9mIEAVKsySzD3IOXN29GDKuMIZQgqIiAgp4O1qhzEm8WwKhJQygNElUxY3dmhiv5T3SIEQNVF0iAOIMzjrGlrYsV6BrdIPU7AREVLZ7jLOoAmwPYMna8iKWwAKLAmwowqzASCEolAyhQ0xIWsS8BK+imXfETQJoOetuIYMsjmt6+ot6gJMMUZBQq3BPCLcusqH9jTkbOGsVBlclF3uDOqc1HYsQTwVWMyrQnCH4HMoPs85IaWk4ZgSikedKoBNYTJEUWK93X6LMd1gu32LfdrpuHRN3A71StpGuU/m8SHeE6SKitDU07ZU2RdXZwjDgOef/waXTz/H08++xObyCmG9kr73P4B4C7YcFQ7/1PXCYvloGP9uyk9lXh9bjvHj5oqY7/NDVc49FK6TXn/IMiwQ5/eG+qHjPfbcwzshkpd+OMKnd7Rzoehopi7qPXS3wstw4wH83yFQCktxpO1DP98brIU5n7T34yHRO/fscM8pAnVAaJL99Vuk3R6cM7ac8P0a2M14ENetbYyv/8xo9qJVJmpCJTnm1j0h5f2M/2jHbrkIAwEcCJSOq/wevxzepbMnekZusPxGZZPt75gTfnj7Evu0ffhd1p3tKb+zDOlik+/7Tlu4C04q7On8rknuKk46vWO5I/7kRdxzoO0j89D215+o+7R3z+KsDHuI5ls/DAhPscNxAI0XovrR5GENPw9DY9JH+R9BDDDz0t5wMJ1yTo/s44ds87uUn4VHRF+m2uR3OZWEH5NAeF/FCE4G42pD+LtfnmGz2WCz2eD67Q2+/9ffYfPNHue/vy2HDPD0QbcG3PxZLEUwzu2zYkF5h/JwRmdOiFqJl5kX/Jf+R2uhfqfmT/PrMQIaqMLIIjxVgkxCJzlL/pxLnPsi6O/gbsZq7+YsIX2QS7xzi5UusfRFeBZiLJbCpDkavJWzWJdXUscEXdIHFxiLZwe4wDQXy7cDvf5mR1OxvRGuhtr7ObSZEKWAvkASyqYoJAKrxY4I+djNQwgBnDUQkVl+k/usfack4WJikHj7gQJAxRcBXnHBDA3RpPMcJN9BziV4jKwlJASTWU+HGBQ+FW2vZNRmWZ7GBM4ZuywhVtbrtV6MNaeDgG75BHJzr7EKqplcvoaZtWiNvBWLEIrSoHiN6Px78r9cxMzqjeDZWrL/l3YQACSbM2kt6r4LUT0+zD2mNl2YaM4e1+i+tPmzLsteYk2kl8RSXZPnEpOE9SHNx0AoeQqIOzWMNWu4TP/eGU8VeO0/e8x1jmMUAkwF7zLhWZUtEIWA2slTzhLqiuuKgIFP+AKf5AtQlj3yr/gBt7gVxWMmpDACHIA41DuAQsE3YxqFkeMVQghYESGjCvlFf9GHyWJl/NTrRMNoGf4BZF5jjEDJV6GTwrnMRS5eUoyYo1rzcz23urlLbo8s560yprZWNWm0netG+YD6ORSruqDvm8A9FE8HoBXOm3dIwZVk+5bByEVJa95uhmvKFatjoigeEVn3tOXKIe3DQupxzo0SIo+jeESkPex0WT6KGKPiLQLziLfX32A7vsLN7RvklDAMwYXdqjdYE3aqPq1rSi5HBlFV+PjzHSIoRAzrc6w25/jLv/s/4os/+3ucv/gMcbMRLwzsEbdfg/IebYg26nAXPpb3WH4qSoiP5WNpymTfqmJ9trw/pHK0J5M8moRjqU65NO4i1uTJTx6rPxpu/aBxRi+eeV/imp9IuSfCzzlj+/IVsuYd3EbC6zhUeq7vBtzut0L32Zf6o6almtDfjPY//2MJF90Nx/hXdbaV4fZtA1WwrP/1osL2+Pmn3gTocJmVFaB/cNf1mOKElBO+efk14jBgWP0sxYYnl0dFTX6quW17bj89tDxIibvc6LtHfw/tww/bpP9N03ONP+ZcOV5ceZ+SKxSkkXwrFNXo1WQYFRwRhSzBNrmUj4M1V/dUBOTrPqA8DkbpqY/3yXmotGtKFtjCL9wQbSNLP9wTpsdt7n5l2vnp4ExrMhjn64gXTze4Oj/Der0G7xNev/wW+29e4ezrHYbrVASPd9mbc8nirE/ALvNewnx6eWwFRI+0qjLiyPuz+3D+JVr8UoBo3rSw6T6RNgPFNSJbUuZkyZlbIWvREbM942bOLSeC1Q9FuKQKB8RiqV5CMVnonwK/raclpeYizLewIBYmxDwwqlC4utAWYd3k2laYuAoMRS1ADQxsgmSTRFc5c5kDoy6L9TszTG3NVAXRBqvNVcmHoTeH3R/UUasMaM4LFRyalb9X2qjgMEuMKB1JtSD2t1NmlkTUICCwJreOGDmp4JEhyopY+4Ek8c0gjGMSJUdQ4tvC5JiA3MLXOMxa5srtE3KPRKFEiHrZSUz5CGqSVHO5DJswVtqvtOPj+KPNMWDraG/pXFroGktwK9slgMgnDK5npSQZV4F1VaRWBYU0UdepDB/Q/BHSkTA99rsIcW1MEjBM9oIlZa4nkIowuYyPl4gkV4QyccrZjkFrp1TytyAAmcAREr6MI0pc3OBCpRVFUMdGEfA0nWGNAa+HLfZRwl5lVW4EVf7oZAHEyKnmghlCFME2VKjP6rVQF3IioO/XueRKIQAYIIqWXAX1snkc/uWy3wUWBhKVcxg03BBb+B+w7hk7B7r20XmosNZxXIQpHbwA3v9nuXM8/qoh52QthSupXholedlMvgM7Gkym9KotmxWNzZXkhpHQetBzJeGYRgm3N44lcX1RGipcMYqi6nr3HcZ0jZvbN9iPWwDQEEqhWbMyF91aFs48eFxm94h5nSh20zvk/OoJNucX+OTFX+Lyyed48eWf4+LpM6w2a1AkrPbfgbBDQFa8QQ4GP8/t3DkjqY/lEcv9WID3TTAvc7cfqtcAsLxX+zlf8sZYorcfA4b7tXXXxh53nzS4F57CoUL/LLzZN3Sok/sD+CAcdUCCc0gA4asVWqeXWkwrz577O8NN7t8HllMbuXNnp7xw10aPCip+GqXwT/MlEPBidYWzsMaKVvqK0pkAdmB8t0q4DYyMuNAKLxwIZzjUneujMDelw5nle8WppIln0f3WNrF89uZn6JS9357Dpbq0+MHePz43u3SL19c/4PUPX4OIcHW5wuefXmJ4su4d5TsQWT3gMb8fHrK1PX/0gGZOLjT78cM8njMwTZQPB6xy+ron+/uctp0WXqW2r6Mb+hHKwpFdfH6wEWq/HqpPhDQEvP3kAnG7x/r1rYThthplCiogdnw+2UdEXOK71Q6vh/0pAJ44BALGEdhv0eDPUuXdb/STFREPPfCeuLvbe22ZfbsTUjfv8Mw7ZdUP9zkhuY7g0iPN3rPcv7WT53qpGrcfN6uIX33+Kc42G6zXG9zcvMYPv/sjVt9tcfHHbXeFHtoxPUHbE7t1v0yUEI9Qjh20Hpb+vf5eNWFPEX417xwEZDr3Jy5ZadcE9DCZobOKZlUeZEZWBUTWJMWck4JqSNCEu86iuHTB8jy750qISVz4ACBqWA5qPSJU4OZDyzBMsCbPqhIilZjkNi54gZ/z9FhkEAmN1bJZ3NpoLO9DhoXcmZt2U3YEkAo1A0tU82AEM4tQUIR2Gp6pzAtpFJZeAKfrpZd2DZlkWnJN7RyCRi+TuRMheSwbL8aIlERXkHXxRZgKUMiyH4PkZkjqWSICSBG0FstyZuwTA4khIXUINAwyd4DEY2cZV1Brcwv1MsdnVFpEGQC1rGfOIMSyDhR0P6Ru3WYwqu1j23p90l7phsteM0GmKF9yEXJacl4uIYq8gFoTHJMKpIGq7Ch1ZW3r2aeyh9m8CWwMzvIc0OTpZXRTQo8yxM2bTyT8TMBU5hviSMA0zZFkfeheslBDCOZ3IorCoPCahX8IpIpKmX/AnVmds2f5Ak8y4zYk7OMO45hUCCxhfIaw0jBG8t+Y5MyFzMCQMYwDQowAZU1NIcJv228WsmtWCdEkvGbEGIugRNBV0nOaDVxZiyT7N+dU1jUTgXIWb6KBEVjyEwARANdznHVdVXECqIKmnAmbY4ORynMiKC6ycHX9PVOVR5655WxKZOg5MqK3P4P+Mqk7LSg+jHp+La/POI7QTD0SjintMY4j0n4EIwGqJhP6SYioGOTsbcfvcTO+xO32Dfb7HVaxenjIPVhhMlzU0FJsSSQtDFOoZ1f3ouliQ4wIccD5s+d4+uIz/M3f/p/x2Zd/jfWzJ4jrNRADwCOG8XsQ35bxN/fzCXeq7Pvj9X4OZW6c79N2SHt83x1OZSHGhL3TPn98acW8J+88jftjwPLeywwIRrofkkfOr+S7G8/jTdXpe7AxBEE7OgtLU384Ufr04x+Bn0m5y4Z43EmfY1UPv8CLlwqB8OnwDE9WT7Wq4xoyMDLj6/WIxMA6++gWfu/1xjZKQ1mI0szNK6eUupsJfrQN5U71sxg5qVfsscb5JMq+AtK/XvhnNxfkoXt46ZeMAWz3t/jdt/+C/fd/AIjw5HKDP//VE7y+WuMljt9vZd/4xo/I0WYBe2h5gMXJj4W+TlrZA2fslHqPWk7qwm+weTncKSfl3gqTRflk9/zoWI4SBr1UsXziYcD1J5dYXd9i83YHMQgzY79OfqgHiIjwbDvg2RbYP8mdIuIR1jaNwM1bgcX3f4+m7gPN+/GxuvMt9pC+li/AOzcFHNlky6Tpz4H2yiCM+UxDxgAjVlivxRtisznDuH2Nsz/cItyMTqA7x+UCLtPr0dIoIR65HENYi3F1J4SP1u+OrV/7d8KiVHl+DSWDKhyvHJWGO3JhmUw4W0OJuITDBV4RVpoOALDjJDH2K4lGTbJjM9m3bzYJZpWuEkolNtVKP40lLEhOSRUSFv9cE/k4xQqzn9NqgUsunIspKEoCWBMMcxWqFkEZm0fDzIm1CXD7oY6L233uw/cAFaYFQaHtmcwsS2A0cyGwta6LTWIW0SY8CSEgZS7x6tPoQmdlLiGxQggo3icq1Aw5IJIoO2IUIWdKCVlj+VMIGOIgShcKxXK53pNV+VVEnyZBdAl6LXxMCeM1aMgeNweikGEErl4hfsIL62sKqACAYp00YzpClHYt9j9GgKC5ATIiRRQBJRF8qghrQ/JmJCDE4n1iXAZzApWE1uTWWVkgzoCG9DKBalE4mQeQ9hbKPii9gzJLOKTJ+IvMG+U84EAhqEcQWWfQxTjwSkAIDGZSwbriCTIlSwSyy4NQlJWyPi/yJS73G3xHb7ELo24MVbIFCUEGZqzWg+Is1rVRpSjnmlPGEUJkZ007tjwJVnplRFFEwBIlAyNLUrCSCBvmZWT5IHTOckAOAZEZHAMYUcM01T4iGKweReY1IcdRQ9IhFFxkZ9nGwEwS/oqy4gZCoKlNWcFlivN8+DdXqSq9msLlt7q2umKq5E3jqMmu5c7O6h0x7iUuM3uEBKhCJWq+mYwxZey2W+zHLZhz8byy3DN2PiRVjuQGqve5wSdntIa3UjVZcEy/5hnaXF3i7OIKX/3y7/Hpl3+NZ5//GdaXz0BDBIMxpG9BvAPyrlLt/azMkIQz+uGP5WP5WH7uhfsPVHC1/U+v2Y8FQMvFfJyU08t9JAAfttTgseUaxWguZ2xfv0Ha78VIgjNCHqQ3Vrrh0IEsvylt2fBRWN62XiShdC/ZZ6Dyj/bI01Vcv5IR3f4ZOXKk6b8DxmgfD1NH23FRsNj7VHgD9+TRCwEI+4TNb79D/u618Jxn5/jh6nOM6/P7K9nft4Cst0q5C3J/r3DiRBRLB+F6Hxbs77J4nmHp91Oe+WKyrcmzCQu13M5UQD+/Dg0O6U9p4aGrAZZ53Rcj1QX4Tf5keVeLx6u223vAMrMIQHa3cAhkvqRxOkhgMbIj3BgfozyOIuIRAZpuQDudldHtf5020tY66Z1DZSofQrkxFgqjCjk+mHKPge/zBgwRCmRaY7XaYLVeY7XeYNgDq29uJcO7CeQOdnMEWbh1q7TF3YnfJRgaa547zkUR8gMzSKbdtw3pblLEjia681L001CsSIRIywqfxRL3Jl65KCVcgmpDTI5yItc0AZrHoY5Uhj1odQurYaGPqLZH7bXQu76LxFu9M3JShYR5RQhsxhxWjUg7jw4rN7RFE4e8CLk0JwWjhDqxuWMjdP1c+DlvMLEheq3KJhi2eW/AgicxPdjWTfZhY5ouuLsQufxriocSmkbhGwHxihgBDoyBBvUSkHAtsgd0oogldBaAGCJSrjk/mIEQWL0XVLmUAyiGssZFyGpTpPPsY6oS+0TB0mf0a9Jmlq6z0ghRTagqXik5ZxeWifS5m121Qhd8Bc0XIeGhEIwQCBpGSYXDJB4bGVm8XzJDwjfFMs+tYlTfCxVKsHUhmc5bS1vdsz4cVZcGwfYOmEs+CcflKI+Tm+0/KdzupRIKjMTTIjulI9dKZXziGaHWZ5rcohHWR6+IVcUey5o+y2dIOeNVvMat5tXQZROF4ErgicMgZ1u9EsaUEEhyslAICMOA4AZuqVqIKtNaFArUehsVphaGgmSv5zRKaK/gJz1AtkWue4+y5hFhRI6qzHDLCAb0bBEg26Psd/nLmSTOFcxlvypQK+4g3V8BXMKroSjIgq5BVjwuOSG81swpITyK0K+Bps/hFRHZklBXxXQeE8ZxDyWP/Q4BERBjxBAjdtst0n6H/W6H/X6n+1U9JdTjAgxQhLsbIMnKXZumQDblBbkxEcwjgkAh4uzyCk8/+xxf/vq/wi9//d9gdfkMYb1Gpj3AW4T0EgG3yJo00qcY8YS5KSOWSNWCuz6Wn1x5gLHjI/T9094zP5ZnxI9dymgLHd3/8P7LQ5fg4OtTcnLhLZp5PtPyXLWjnf+c99gHgAfuzVy+n8KFZ6DKM7F4a+/eiCKCOWMkQshRadEjArRO2VDb9VxT++9imRNSk6PN9FEJpOJ43mbK1QppapTZt10VHf7V48vHyiL2fXje92gjON4Tg8aE1R9/wP76LUBA2pzh9cVz8e49pYvlpt3Hd48XGgw0Nzl3BuHu4v4yzkMvtuT3/O8Hm7AKj4ME7uKl0L8zLd0pPEC4LcnW7qtk6ad1cTQLzZ/Sb6lRDGD9L41gA8L6mSJCZSYmRC213Tsl0kE13pr03z0rsovtDZDHDsqZ8RBNJ4YW6s6VB2y5n33WGSfi+lhOLMyEPZ8hcwQo4OJswG++PMeTixXOzzdI373F9//rP2L84a2EAul2r835oxP3xVJhGTEwHF5zuEBkQd1BPbFbE/Yf+n3u52lop4cVzzyJgEuItBKeR62Li0LCKyHY/B/MKtwEevKsSGmyeDDkEgbEhRxyCFVCbgBAa/lfhbUa1x8E6bkSeSlLMrKc9tULQvNDtBbAXgBscErfgSJCjIiEYkltFtFmxSteAaEIoqStOlcCp+uLax9FG0MB2owTjMtckcRS8gN3tKltPq6/UyXFPaGQYRbzAo/kjXBhWECwBLNQa2MA6kEgX0II4BBkL4yj/qaW1yEUOFmF+mrbXxLQWsiunCSkzUhqsRwjODLAGldawfcJeounjI4phijW9Il1f2YgATnkJsdCsHuPgUwSJmbCTJmAsgh2dW+VC9IEqsLeBCJwVCt8QPeS7QtR5LBuSfPUYdbcEKASzilrZruSvyPPXPyeSFNlIFFWQavtAZKwXgFFGeHRQiHNFGl6R/TSjxIgjDyxUGBtsOKaOaEBtYL4zBBfmuphwDYeBjhIP5Izwy1GUZjoHrXvYEQQPs9P8QwjbEd/i7fYhwwQI8aAzXoDICIHUTimUdzvmRkhRqxyRhgGDAOQkIRxDUFzi6CsP4AyHvN8Sikp/pKNHqN4zYRxAFEAguxrW1fbv5JwHbAzJhHLGCFnxMjgYApbKkpLU7qFaB5ZqtCJACXAvBpCcGGd3K6R5lQB45W5OscZpqRsmXDBuTRDG9b9bV8tXJyF17L2chr1bwbnhJRGDbfGRWkp2IERNdxSUAb97fZr3GxfIeUbMDKGWL2QoOhGxka6bvJ7QpLzozgtaCinaIjMoUNTUmyuLrG5usDnv/g7fPbLv8WzL/4cw9UVaIgAMsL4NQi3AI+lz6r0qfjd1vWQwPhPTAb7sfzEy5y87E+nPCY313GHnVBTepuIBObb+aksyFEwD1eYcHsNg9U9O6m/j+VPpQQQPltd4SKeY81rpHFUT4gd0n7ELY/4Zk3Yg2A5nuZkCBMRpRqDCY2DwksVgb3xDVjYjn5TF+E+VX6PPBbwxPsMUCcgZ5qh87Wb2REeao672v3709qH4bIPCXvs4hu8Td/hm5dfYxzHGmWADuPDRZmbWYPcAabHKB+y/K/n9hh8FOCj4/kRjSMOC+yrPKm9Qw6fGfOQuLMSohfM61/P6x5vw3308kPqq1H3vKMb+mgPDOTNCq8/e4rhdoezl9caLWA+B6A0Jmfv890Klyni95stXg/C/zAzcPsWsDyh9mZhik5UG/5Ie+d0RUSDdO8PrIkuPmT3oTnayj9/VNT2jhZ+YjF5h8IIGFk9ISjgfB3wF1+c4/xsjdUwYHxzi+3/+nuxbK2y0K6NxQ8FwvrxACKaaPnm+nICvsJL0IEbsUcT96ecq5cFN682gkG+a6sepl7y6IgtrkJQGXurhCgJwNTLoMwHV6FxsaC1kCJBq+U6NzZXoqtwEqfJXIgAzIKrkEvSK1JWVZxowlTxiKh5FrLBr611pGiBhlRAFimUvBRlqfUfi8cemjVmnYaS2bsKgt2MTzgt8m2jXAjzM9DhNpI1IlZhamCUpMuAhu8xAavbS9TuSUZGzmSqdH3fhaRSRVJJ9J0ZyYKqOcrRhK/WvwkRaw4I8ZxB0lrariV5NqIgc7V6F2GfgkwoChrxxFAhPWR9KZtCy895FQ4vafrJpseUbeb14J+DQRoOJmqi5DG7eTX4uF/QOt8WzsyEwAWeBTxtHhXWB3Ndv+rWTRq1yq2vLw2qWJgDAESijJi83u3jhnCxyjZZSpNQZmX2an+maDJoARS3AIOflK4JjCooV6XE03xW9vEOI77FW6QwajgtifcvS0BIGJGThRMTob/l/sghIKgyI9qm0oVuCFJVEhEFwTWZxUqsCPcld0QmUz4xwEla0n2R2SFFJlGMGOPKqDlwdMtkWMJnmfOSmyQEhJz1PKuCR5U4liDeL3bBv8G52FLdP5wZKWdVPEiemxLtrR483RtVJVb2gCrgzOsqGV5QPJs1v03Ko+BlKke9tBhC1LwQDOSM3fgKt+l7ZBZviBh17pt9KrAGtwaUCRQ0GXkgwdtUk40zuZwRIYBixObiAlfPX+DTr/4aX/zy3+Hyky8QzjaKJxJifo3AbxX3e1qnw6WHiAAc5H9+tuVH5FMxtxbvGp5T2j9gnLdQ/+FA37eNqoh/f+WYx8T79Azpu7rbGb6j/W1DJ/Sf79Lr45X3ibL60S5h0z6kxDz3QpMnH8sjlPcwpY9yuonwbLjC0+FZCRO5v75G2u6Qc8YYGDchIrPxak4IbzQSur3G3Xkusjf2VaQcCE9qbdunlhaaYoBjU97W4ckvXv7g2O9JWeznxAU5Vm3p90wJt+ENbsY3eHn9BpGAMIQjBh2neJUepseOl7kZWW5vYiV+QmsHSyEUTqhTOjki83TEx2lyUV4YspcNLL453/diV/eQ1y62WYRzU4nbrGCv5XFO66Or1vbcPBPZzPI7bV/U/HCodzNAnNZvH/BqwO3TiHUgnL+6BcxT3vh0V92+EhGuthGXiHi9znhDqfI7+538957LY9wNPwGPiIciroeWvm9aeP7TL+IJcY7MEczAZhXwN79UT4izDfKrG/zwH/4R+c1tJyydEayVm9iEYz1S4ebTKaWxNp/Abv94mKgFs22t+3s6EMXa2ff9qKUje4olcqd8aASPuSgeUOrmgqRUXqzhwmrYDBN0VccWsVrNRhgVQabB1FNMVKxtKzTthLSJw1QYpkmpq8dGFTQuXw9VGRJC0KTYAFGNbG5isVApSTcfItCHKiNsTv2UNwokZwnjLZ99cCAUqH1sdR0Lq/eBeUKw9J1BJSMrKdFchcl+yG6PZU2wrcqIEl9QSwgBwzBInxlIOSFkEuJRBXxQ4XHmoAmwNZk3AlarFVJOYlkOl9fB9UHdnJrnijhqULGYCURA1LnkXObYYvybt0IwDw438D7uIcEsyuueZTYvDCO81PNnZNAgAlsT/uYcVLgv9e2Sty5tfU0IbuFqUkq6h9yYDhz0eky4KlyIKvwEUUYBDUMkjJUevo7pOlRKVVsn968QWKr86jBvEYTDPJpUiZcNDmmdOaIVPpGEnmJRYDAYnM1LRvGOTREz1gj4RX6GLSd8m99IfhJdf3ZrzmAkzVcQxuA8Nwx/qwJuDicwl3NAFMBUFbH2/rCSvBQxReScsVelbM5y/huhXgbM2yNTRogMZsuBEMBBZ8spejMrrsnZ/L6Kh0VG9Z6wPWxFvDyozLHE85T2yh7kjMCxKItDJhmj2wA+f4bgYrGQyaPlbVJFRJL8D6zrMI4jwBIaL4SAQT1I2OYUAXGQJNdvr/+A2/EVtvs3SOMOICASgRTbljwaTrliniwEDbGl90oTTsvvRX28uTzD+dMrfPHVv8Hnv/p7fPKLv8P588+A9QoJI4b8NSjdgHBb1hiQ0HQQtCN9uu1S8tu0W8cpgHqvlZ9e+WlD/7F8LD9m4SrA/CgoP14eNEV34fg+lp9L+WL9BJfhHGd0DmbG9uUrpN1O8kIU44jq8co+756Ty5lIgZptZEoL4erYtVN+99WhfLRn/ZxQMhh3T20MgPp2+9daMRbBfCr6WoX/OCLGfFihmSaa2WvqLkHDNztc/+P/hpuvvwEx4+Lz53jxN7/GcHU54asPfn/UMscD4KdJ/DxkjuinikMV7g78O4+GJmJ9YKYNr3CQPsKkJgHomIX+7XkQ+t+9bHLyKrW/lxdYjbZEDkNMYrvGUOOsHhYqvEwx8TWFR644pzeqabfaHfbde9xi91NElIWbX4xSzT9eeOXufVo7NO1j6VX/Go7jruX5bzcG9Y/t/fYOnAfwkZD14uG7T6GAlNdgDAAlrFfAL16scXG+xipEbK/32P7TN8A+1QOwNFtKMVThtP9pWfO7xAicpoSwvo4gkZmFKyI4o3QWXpogP9d3IXYepJnokY+X0tZOG0sRrnCbcM17SjR4VhOsmlDZhFxFgGaOEypsLFRaP3qjEZV5yyb8c9NvxGDOGQXDAiIAgwrvizU5d2vY9Qeo0kGTxKpXhHkXOBtuvQycN0SRe8qHEi/fnjvaqRfb1s+OKCVUYsCEs/VmwHzhMgUESU4sSZdR1swP2xPA8rtYMIuFetCwLw7WYh2ueDGzJoE2a27Jk8EZAGUJURO4xGOPQ5T8zoEKUS+KLI39TtCktVWYD+jaBknUq+oWJxy2y1XaCzkr/FWAanA1c98vv7XVnQly+9b2vAjgUZVVgcQSuwiCp4RQ6UvPsnlF5OA8Kgu3UoWnsHUzqBxj5NddzhzJes0IO0rosCZvhpuGjs5fxDG6LwkAUgeJu/iICQh69MyiPYj3jB1jIjjFhJScgxBInGXSgyhcBE+weklII8SEp3yOLY/4ga8xMjQkmIzfdMYWPo5yknBB3M2B4VfD/w639EnDp0ePEMKg85q0bqj4yisBLE4Yl13cEI8U6tpX3Krh54z5Ys/wMjKrJwMIHPz+BdgSYMAx34xy7iRvi+61EOUsUnAbwCnxywe7F1iSrtdJFtwBLgqhzAnIEhKOiDQ/hub3UDwbFMdu8zVux+8xZk1QDYhSxp8NgnjR6bNgRDNE6QIOEprN6vtVKtNNWJ1tcPX8E3z65Z/jF7/4t1g9/xzDxSWYMjJGIL9GzG/KwIvevbSr5+wADeCVEA0MeODVfY+yREq/kz5myvvXv7y7AT9kDafsxRS/P3af9y290uw++R3edU6Id9n+ozS91MacQcgDm/ywywyfcajcodryCT+1zzlC7U+53GWtTpnb91MIwGU4x4v1C1j41/H2FuN2W0LCjjmJ5yoKVQQAhZ6xJ4ULL/e+0dRWzbgAe6Bllk6fwin0Q/0+y/X3bGp5fybJ7h22r++F+x/m+JW5U0ZLKzsHyNz78j3vEtJ//gPG168AAOvLM6y/+AwUI+5aZkFfhOkeDS6UBxuXeDnRKUdvqb8FImHS5MnwLsnPps/mwG2305HJnAi8Zh4eAbuT4qDKlWqbc03wnPFfL4dzL84mVnYMB7mH7fnqIZwDfArh8v6i5o99oeadwiiJTEQNRcmizHAHWnNUpa1IRWWqvHrbdpUP3fMczE/ECeXu5/pkRQS7ibgPWFOEfmQRjw3mnppXf+hnttb8E/Yf/IP5/vsRvHde71491k28XgX85VfnuLqIOL+4AL+5xff/038Av9mCcnbJVmfWqDsw8/A4QqHKg0oOAzUWnwrsfDvsEtWWarYn5K8J/uTlfgf6tnmyaAXCEiLcDnfpfiI0Kz/4cR68uPovB0gILnRWQ3gxQ6yinZWuWCuzOyJqMQy/Ij3FYtgvCJomTY6rIT5M/iW1FFZTeGRRKvR2IKzPJS67nwhNjJwtqbaEVQkUZE0tioxdeoQiZA8WezwEIDrBnOUY8FvEkaMlpwGjGHAD7IRgOkbLw6AS6EjVWt7mkTTWjBHNfg7NsyEDIM4IGchNCHUSAaCui4k9ZWKV2CaRgBdDY4ZEzM8SlscM6k0Z2OC0QCAONcmbbRTbtxCL9sBZPVlqkmKKAev1WoSgY2rxK0M7rh4OZaw5I1PGgAgmwjAQQIQ4BBFUj6p2YgZyRlCBpCnF2F8uZX+ziw5EAGsIGxU6Czisa1et7MdxhLewFi+N2n7QpMySrBp1h3RHObMI1u2HYsmP0pQTVtU3q0WUzE0o94zsnZInxG2eYtSgrWQVstMkriTXY+rwWYGLax3JhcEyXpjFPNe51Y7VERQWpkmpJT9MG5kCh4JbiYN69lT4GBK6CJlBOWMFwq/SC+yQ8O32psAUAKzXG4QQVeBOGPOIgVeqYIQq0kTxUfAwACbJQ2JrwpzVAj8g86j7UvZAKAdc8cc4yliSPDdPl4ojWAXq5JKcG5pxTK4qMrJ6UUxRt7SfSXOjgGqYpai5N0JATkmZcYD9IKHeNIavxoykuWQIEubKxsQFPisZnMfSZv2rnhGcFT8QYhjEo4ENO0nemBgDOGXsdyPGcY9xHMs5NSVFGantcYevKJtSkopyU/IPkeaGsHNMyCCcn5/h8tkVPvvVP+AXf/Xf4ZMXv8Lm2WeImw0CZ9D4LYjfIPAOJTaDKcshlkXkjsFSWRI4z/32vsvc7f+uQbonGf0nVD5Ozs+n+NPUrasqq6tnL4EQUXxse36ia20mVd79QXt4NSnU3uCPUeZkQ0ul5Qbm+e2p2qet9yOj5J9Geejem2nufi8elt2Yp6cYQkCNIoAtMr4+HzAGZTFMGchtW1MOXs6jeVKYZ0U11kH/YQEy82GobdeQrO37OUu/uYS6dEZ4qPRpOSjN2rDvYTo/7qnnxgF2MheDdzqG+VZd/z3Ka37s2iAUQ64QlReZyMzaOVvqeOn0z0EzBXrp9yNdn1AWj0xZ+vk1mu36PRJRx+fylDZq4ZlPp715fNXm35+7e30D7nuJv6zjnuGzqH6chaU9y/3Hu85lD3vfEpXz09bv5s3kGMzI5xu8/uI5hptbnP3wVmSsMGWTG5+wnBr2lvDVzQbPt2v8y/kNXsat8IJuvpb6fvfl7v3dzSPCGL3puja/z8PjBE1Eiwe6XmVW/8DWvi8X1WulTmlignPdCJbG7Rjjui/f9aa4w5j6NwmIkbBaBXz2yRqX5ysEIqSbPfa//QHYjkU4NrFe1sLsY3gfgNFboy7WWmjAhMpFgLjUBjkkN6dFXu7b0Ra1Nep+dx9K9UKpH1FCeBiP/m6Csg5qLvIwmCICQA2FpO8TifC57HpbnokmWK3TTU4JDWDEXELAlHNpAjwToDHXPWEEiIVdSrllOBxmrQJn+T0QkNkEtnoBafLfEKOG/YglNnudC7ukfD9un0zWuhKO9ZEKIh0JCCMq0fhEuLPN/vWWOWUUC3IRjDqqlHVvKnI4uAv0dwstJUJMy00gBKKtG+kllZncnmgvM5kXLhchIEoPUc6rl0bwIX/ce4bvDO05C8LMWT0joFbVqtBRzYFdrsxcYvlPV0TrMRX3RAvpUr2wlu8G1pA7FKKm03CW6AUv63oSl2S+fq4LTmGa9jFLh9gZs3mo5JZms6iVncDf5wZwE4oywbNw9UMhtzfaI2AKGbF6r0MxRYn8JvkVmHz/84UA8aRgrRvI4UQFkCF5KYiBFBBBeMIDtnnEN/trpJCLFcgQBoQo5zpnseLPQmnJ2GDKVSr4hXMwR6Iy2MwaFgyognk/r1BlFiyUUy5nSjwdCCgCe8dQFkbKn3HFh2R3ndsuzV7RfV+2nvtfUO+kRmmsoatKTohQE1NbHc/YETUJyJtQBuCKky0ElTL/zGNxQhNFjSlWAVIlnRG6+zEhjXvkNDqvNipwmRJAptnI8KK7KbBXPCpr6xW7hl+HzQZPPnmB55//Bp/+6t/h7OwMw2ajSg5G4BuE9EZfC25ddL14ep+VlZhBF23IudnX3mmZoK6ZI4/5Rx/LkfKY63m8rY7Yf4/lrnkbDtLa3TgPKeweAtPDy8JBuUPRm0Baa/A9UPKHFSGA17Rjstx3Ge0S1HcX7N+nLO3TU1ut799FGdH2M52BWZEq1bXpyJ73UKy3DxnzzvCxjwQudX9Pf9G/UT8HUDHG8WFPzVBunzPGCOxjkJC13NI5tcV5iIy/6//WBiqNcJi89fRAz5fU9wtNat+N6XM0T0cFHt2/S6i1vmuKkhZOX/Oud95ydVYP9azt1gTV/t1ehLbQVEGlVbBa59PN+IkQTnFYYyB2h+Jt3+a6qzwjdc8bInIWuklfC/XvWt4VRvK8zkPhOAXGuVsAcNduwz9QfYPuNgcTecEiPFTqexnE4dpdP+V4hv5H9xa7U0yFj+MVYfdEQhQQXbv6eu68sVRpk3A5Bpwz8PUmikMFERBCkdXddb7myvu6e3+cHBEfzbB+nOLu58n0E7AaCH/1xRoX52e4OF8D11u8+f/8J/DbLTCmo8xIifPPdkFg/iScoISYgl6BbyyA+6Nig+upgTuWObmcbVvufrjrYT1167cJjPsf57/y7NwaIcHuszyfa0gIRq6CrNzln3ATKjqEah3SE4FmSdwNTN61NgMBOVQrdvurXVkMeIqigAiaQFeQuXpsODc0I3oFTstB4fanGzsbPFwJTD/GYu0LoPf9MwVQVktm334VIAI5CBGWNUxSALn9ZcLWapXt3fdIYShG2pmReSzUYDD3IVVymCCTzNlEYaIQpTXS+coZGQE5JyU2Jbr6MESkTFM4yM2t50Sb8yGKq5ydx4OuX2DxYCLO4FCtDMtKnIALLLxSTxR7S6yiDMpZjN5NQN+9JEOQm5pUsCw/hZI7Aei8TzScUVWM6NgCNI+BwSBwBEsubDNny6QuP+YBYTCprFyi6c/hiEAI6l5jZ6eMXzbHZB7Z8LFRJQVMz/SptadT2tS9XZncQnDZ3lNCr7FUMRyZGbSpTELgiL9IL3Cdtvjn8RuEISBeXIIoYHO2wX4/Im3VIjWLh8MQYklqaN4zhalklpwKYIQg6h4QEGLQBN1ibRdCPY1EhNV6AI1Bzqy/nziAcgbG+jCEIN4BGpLMJiZl8XBgtfC3OZjcj5bHhWx9K2MHQMMnQfNVGL61vSWh5cyC0NYj+E3l7sIxjTL3wc0SA2PyOXgAUbO6u8vWR/FqjAPACcwJb2//iLe332G3e4uUEigQBgzWcVGElnB/MmgYdh5Tlj0lyACrYS11FDczAZuLC1y+eIHPv/gr/Plf/R9w9ekvcXFxgWEYak4Y85yzPWjTe08m9GP5WD6Wj6UWuwfvh0vMMvtj+TmVJeb1YzlUemHz56sneDZcYYU1Ukq4/eElxu0W426HbR7xh4uAkcQrslcitLPPLbkGFOMLsbnQHBNgl4OtPZTUPZ03UKg8WAGH7Y/SnMrziWcHV9644R+tfRK+0ccOtsedoLAZbw/stEZ59tBdWuEkZOxwM7zCDj9UuIs3hOdhlP7qV8nNXflFv3hlhHvcjab+dgRg9/VudGCtOz9zB2f0flrYD7gY1d6uy2LtXmR0381H5Z/6qFjKze/zpuPJHsBkL3qZxSKw3aGjyaf50oRY8hu509BVMM3YyxR8JqfSZ+Z9RCTykZL70TPtaKdAea3nr7YYeI9vr66wO2Pg+hWQxslAT10qL9k87a2Hn4cHKSKqSG8BWHfeWxGfHmai+w+BDm6vu5XDeOnepT+zP3pxOLTRBRFhCIT1QHh+NeDifMAwRIyJMf7xFbAdJRSDn5+DA+OqhFi49e+txT75taoIORIy2oN18He7g3zdeZLnAFQFjmWA6tzYXLWAeETRT8rhee2UEAQUCSzaM2qCJgvpkl3S4QmJmGsi1IOadbZepkJsCpWY8BbspBJaolhyFBAFB0EAIzsdQRVYVcUATxeuGacDxh0MMgFjAyyjeF+YIJBVMDzXNqHG0Q9i6S+eBZOJcWvpLh8yQKrixRJ9T0k7mz1738Y8JfdkyBk5hyrI1QsyUGttTTqfnrCexGNk9bqhKqS0dRKXQSp7dxYit16wkTmvCBvZ8rGxNWG73QsD4cdx+JxSM+0VtmPvGoHe7qUiw+8U7zJWAlniYcOX2llY6IkAsGnpMrcTyXUO53YFiFCdncwbovhGVCLQdVaHwuUZaTt12KTCb5s4Cb2UwbAMKBLminCVNjIXSRKvW6itEKLuQemq5CmwoTGrl8Xc4qvHBGyPCizMdj7qEQIIFCJiVM8fp2QxTyjyIYcguMb6laMksDBsv5MyXk4J6BVj/Rq4/gBlplUpwpgOUbZzLstAE2ZOcZwyxMH58DNXhVVDfRlT2OxJCXkXY8Q4jkjjiN3+BtvxNVIWj4gYNUeMeXgxwMji8VMUMijeCXKGASZJa20kBKvLEFHAsNrgyfPP8OzTX+PFV3+D1fmlKCFICHQLgYBFzOHnqt3D09BpS+8d/v0xys+Kd/1YftRyKu38PpV0HxWC7668m5m9a6tHKad7/zrp6UfZS3N9nsA43rdpzDQ9Ya/6F5deOOHxI8s2jpVAAYGBi3CGq/gEaRyRc5IE1dstdilhDIwxAIlIQ29OmIoDPXDzv0JAdbzzpI0ZQn6erORGPmXKxqy8sA/1e0ww4bixxT5p8cuhhwfEhPfcuhmM/fgW+/GmGMAMqxXCMCjQRud3AtIFEI7C457fFdyWRzvt7QmNONdrL+T27x/5fa44Fu3g7++i3Kfto+88RqOLygbMEMtU//rtt9BBzT8538/8mvsPS9z+wro3fVC/MZu6XELg1p+Fg8oABXDUiBI14em0az0zNs7NTkLGvYxr7NcM3AYg+evkbgvmZvJEKuHhO/hRPCImSoZphQbWIihZFC6cXu789j37KwKEe7394RSvD7Dpj4HwV798jsvzM5yfbzCsVlhvNgjrHXYxgjXG9axXApYugQXJyiHYZj5VIS1VBNVKdxZa003H9BjnRFos/VbBMfsf3FjnaOkiyD3YR0vUmCVs+duSRqhCTP1uOPSQ6prcPvC3pAq9MtcYmCUWZrbst1W6ywZvxbLNYE0AaIJCVo0QmeAwqBAxcLGkMABlqkQIGGLUxKkakikY4Qqx6AeXUCloJagajkSEfWWZbNzslBVsXgkiABdrbwmPghCcYN5gZUBjtleLY57eF2zhrcwOXpQq5Ce9K2bgTu6yCVCCnRk5j0g5gFJCBCZCfJt7huUGIFCUscQYZQyqcbffc2ax4Cdx84sxSsJmzg1gQYWtdhyTSDsVp8tezDmBIYwISPokImSNM885I+u6ksGPkhoExTukuBjaXaFrrnul3eG6jvDeLxaSxwmHs86TtkmuTwJAQcLihBhK17YXAzKybgMuXjBOgaaCZjHglnEmIlDOIFLFjFNy2WGt1yAV4TyYRSAfqLYNT9SS8wJqN04jqC6K3zypSwQQRxSrsrIf3HpHgoUtaogiI4ZkdksoT7YEzZEkhwuge4JBNOJ8BP4ifYob3uH721tQJMlHwIzVeo0QCCmJx0+MJHtFso0jLtwlzFys8CkOyMwYx3reQShW+wMRcghIOQNc2yaYV0vdVbYHwOK9QlmSdGck6U3BkZw1hICapF2mL5YzTNqOHNPc7m+baxXYxyBrkvKolnc134JsD00sTdWbwpJTVzrF4jEr7gm1D7CEUYshYrUaEOOA1WpVYL/efovXb3+Htzevsd3dFBAHGkp+C7kGGEAURbFfD81HFCyknv5uGDRTQBzWiOszPH3+F/j7//r/iYtPvsT6xVeISo+E9B3i+KrgIOJdWeuPnhAfy8fysTy0NDik0In1UcHbiyzGRxz0sbyDIozDjw3FPYvA/Xm8wrP4FCtaYRxH8YS4vcW422E37vGHi4gxRCRo/ijHVCpV7Ih7Y06ds4PyXaYUyJqP0BvxLR3bYqDQ/iPPvIihwQ+sHhcZ2XuZGk/eiCZc3yQyCAIXV/9ezrEoETiwBbyx3unv9f05+ZvS8ny7w/X/9x9x+8MP+Oab3+PsxSW++m//HYazdS9CkHe47e5eCaK9HNALqA6OAgcm7oTS8UlN3weanpFM/fTLCXN+/7a7v4cWrdSlmYeH324jV/h9Tk2d2RYmjxbqdXUa+UPpf2EPFZhYeW/FQWymtAHj5Rle/uJTrN5c4+K7N1WuMA8kQMJjPV09xRld4du4ww22DXzHxnC4nOIR8Th75nRFxCkIj6p4VL7SfF2tV5QRTRsPwS5HCi0u6Smv3aO/h+HKB5WZtZkrmQkRARdnG1xdnGNYDSIwuNmBb/dNO40y4tSumU+8nJZR/zTcyKlvs75/eA1nLYhn2/JfZ2aidDQvXIbXAFj9UndmnJX+KnAWUBoZNi/ggxkkTkB74bYeFlz+1nBLrELRxvLEn12vjKiDVaOJOrNeMGgfzIqcJpcPVeGcxjEPJdRP0DA52Sk6FvalKk7mjgNTW6evZNiiIT6KEsKUUHXu+vfKU/3H8jKU+jMX/+I+dJeXKFeqFbUpIRqvDF1sC11l4wsadiip5Ngsu+1vAwe5ueNKXJMKYU3IymSCbKvPkAcZIFFClMTUsGErEU/OTRGVBCjEPaGZp6J0Y5R91gsUJpdNI02Y3yeNoN1GWV7t56WDpX4p0FtPpEowIOhenfY/6frIcwNpTi/rn88V36Z4G9nD+RflnIhfeZkLO++9UoVMsaMJ7x2zFJDBOSAi4JI3AAMvx60oPdX8I6rCL3NGcFbwE7AWxiewEkJX1a9hCCokD6EOAyjCbQrZwe08yLSyKMlCgavkfeF2pXzornIvcNktsHjJViTkUvXoMHzBWc6S5fDwClMuIfEEPu8N4/jxslbm4cHECFnDTsUBMWqi75yQOWM/3mA3vkVKWwnJRFTCJLV7QOCsZ6LiCwK5HC1+DUzRt8L67AoXV5/hk8//AsPFE9BqA8p7gPcg3oLyDcCse8GtaTO4AtWkeAXhj1Uek7c71tbSMJf4zB9xWj4WzN8FDyk+tv77Kvfp677n8f7DOvRiRzsUmrzeXfduuq/6/pblzuXd4ob7DPxdI6dTYZrjHN514WYLLsNyt5/fSekul0CSF2xDG1zEC+SUkFNC2u0xbne4zXvsA2OkgITQGlCV4hk2rs27Z2ZwVGgicJNr0D4dWq3CAzo2dtKnPVElhOW2sAoFjtJXS5tUrkOVEU3v7pz5n05dx3tsxZbFaX1rM2XJB/bNa6TXb7Hd32I9XGF4+kQM2XplgTV4x33nJAIH4Zz79aGnbxo+1fN2d2zrHdd/1HKACCys30Q2NfP+XVfFu8+f+s5SU91b3MCFmbXs+NPJnU79a65xd5p1M05G0LU7OyJ3ZnpZgn1lCM+ahwHjOSFudyq2cDJBvzSuRyIgxhU2YKzziAjG6GCevNx0Pv/4DhUmfO99y+PmiOjw7KKAl4/8/gGVnyqzVmR4diHOeAYwgNt0gRErZLV2XK83yG+3ePnf/wfw2x2wH139JSHeqcqGWn+uLIgTWsEljokfUJFoUQosw+ZF75Mm7kPYcUuoVDjQXfwd7TGjhGhyYZjio3w2QVQPpNndz/ViMPSkgAmxtN8sguVsQlSu4TGatbDPJuTTOO3FQrpD/MEn8mF28fct+ahVVwhJvB9MCVGEdWVnB1FkUK4vF6KSMRVYaevk8lNArZM7Ib6FZCF3bKq+ghFybb+cMRNea7y/MkaLAR9UQGeCaT9ep2iwu21CM2mCbm1acjHkAA4KP9e/lrtgHHWucxar8WEl3h0p6XMZR0pJBJQh1HEVxrx6IbAKJSkERP1tNO8ASQJRFBpJ+xxCBAPIMWpcVQmlZWF9OAiRG1U4DCQgA8ksnPwRZsM39pWb5fXKO5GDyv4xTNDsBLJzBli8e2ZRcpnSq2mXSJVQFY5JUWGrKR3MMt2YkH5N2eG1aZFzaGHLmjpEmuQ5F48UsCZjLvuhqgRKgt9sYX5kNkoyuhAh4bSmfXHO5f1mEGSEPVWujqBzVLFMZmisWUYYIjbnZwh5wLANeBO2+MP4CsNmhYvzMzBnjOMIAjAG8S5phq3zUqaRARCX8xxCEKF9GaPAG9X7xpR1IQbkXIXkhlsahYwJ9lCF+/LICBgu5yKEDOagWKmeIXJzFILFB7UuuD33MLwla1S8kRwcmYUZzjtZK/OIsDuYssfuhGG1quPT9gMBcQhYDQPONhvknDGmPd7cfI3Xt7/H9uYNttsb8UxhFE8NzuILUphsqnjavsu0aL6OoKnrTeMDUUDEzSWePf81/u7f/9/x7LNf4Pz5F6poGRHSdxjSdwCPyJwwLfe5lD+Wj+Vj+VjmS0sruqKChp8oC/gTLx/x/E+xvIhX+Gx4jogIHhk3L19hf3ODcbfDfhzxx0vCnoaSW7AphbcsXyr9777LI+cJoV78hUHzoo5TZGnuH893VzaeC61nvFSrQHE0PKPQY2Yw1rbmwDoA23T3t3IMBs/KdPpXShVXdSKqISAj4W38Dnt6jeKVHYPEricU2rhLxavtkf8yaVv+UPO3/HggbnYjS12sdfdSeccDAuQ/heIMreZ43VM051N+ti+h2etL+o3azJHVKNuFJmecmoMPEe+7SmUPTrqYORA9XHNg2fYtvy8jnkPyUWGdCWRRKUJUmZgZXEq9Jt0723jNy53x/IctVtjh9xEYu7k4tfR46X3dwo8TmqnbXT6p5SnKiPIeTtv8DwAUoGqr6QWIBSbg4AL+lFDXRLzlDrFcowGr1YD1sEIIshXy9S3Sq1vklzfg620JSTMvKjthwu5cnMSx9Dp3lc9D0rTirDYPhWia3XIeA5xU+rmuwtxOvjwL7yI8KgyuAtcqaWX3X1t6YqA9YzRbt7YvtXPbd/ndhTzxz702emHamrETaaz1SnAUUqVR3JgXxOzIZsr8zPZETVubm3r1wvIrZi/oGyUXQttJfaf2WK2g26eHvK/bXh2ecjBl5lnCsAJT+++Z7UCWaMyF3KJ5htyIf4n1X3G6CLA74tLtx9KnEjxBFzJnE7QyQobmgYDgGhOoFuv6ZgqmZfLcMTC99UH3ebZJtjA4lbCZxhVFsWQ4dl/Z3KMI+D0BNWPtX8GQ/aXnZO5Qeev56TjN18nmkqo8eG7sJIQbI6NY8dv5nCNKda/bHBE0VBR3+8EAYg3PQwExREUba2x5VIUnYKGHijC+lcMrOuKSz8InxfP7u85vnZsSWi0l/S4WaoSaaNnyozCZJcq8N910DtWriDUpvaQbh3l7mdLBlMTBEkqzrY+BS6XdyTk0vJO5xDgyrwrGjCGAU3qLclR3hSq2YoxFOZHyiO3uGtvdW2z3b7HPO1FYuZBQ1fPDCQ86ZZ3Njp11w02mjKFhQFydYXPxDJfPPsenv/wbXDy9RIwM5iTKUt6CeDsvGFw+tQfLUu6ID6m8D5A+wGF/LI9YPuRwZe/3zN1vHtS8p314Mt15tPGfVFkSGC19/4C3npYjAC79/JCFf+icHIPpLu1PWPVH4t3LwgdkBAy0wnk4x7jfYxx3SLs9knlCEGOkAXkOF3D7pXjqs/u5KCGqwqB6RnBtw7H7C6Sza9P1YW2XoXmvc+u/GuAZTIXGLO87I73p4ArN3D2czMHcp2NqUX8OT1pZrZSRsRtvMe63HSBUaMlWSFllfEsTTP2n2Wr9Qy59Gi/WVqeu7t0KOfjnwTnxPHyoCO8Y/DNymtYvhqsOouefywZo94df535WJnKbWV6Kliv4wt3P1PXfjIfq7029uYN3vOtJsbnQ6WjCvc22f6BxE9UE4cEpBOTVAKQMcMIcLphy/Ix1IpxzQFwNSARwSpOazVsn7PWjHFcvxLrnsXhcjwgt3pLbQnccUkbUr+/BQ6JTRvyplCoMla21TZcArfD3v77A8ydrfPJkg7BLeP0//Efwqxvw7QifuLMpbnequKa7eO9apoe1XO9GAKBHf3NjbD/TQr2DZaIFmNu38+Msj3sB9R26NLqmKB7MEsPPMQuRVPIbGCFk/zQgE5aUMPa2B0CsP3K1NEEuiXEZeWZ+fH9i6S/CQoIkCRDk2tw1jmCTCu6SMKEVCCgx9UPppBCBGhN0YlWjY2iZchWkaQgha8jmuFkql5zWgC3JfNXyWghcTdDt5l6SPIvHQlBrbiOoRYCYkREQVJho1tkNkcczBJwrJZE0KaGMDCDCksPaOlEAAgdwCMgMDbvCCDkhgBFJckWEIMLWLK4bGMekQtoqQASg8eYzRh4RMcCyKUnuDgJnkmR0zFipF8s4jmotLkLPYbXSmO8akicnyRUBsWRfBc1jAbFe58hAlsTGUMajCEU9ynDHlGBhpuw/DSukmXIpEGzLy/iE8AqhCqStHfm/ERh1l5iHRdDFyoVTsb/qSQQlLEqjhoP9gXeJznUcgUxRDIAzkj9mJBZKQfNuAHK8x5QUBEkkrIAWIswSQMc4wHAJg0ueAptCE04bnCWEEBluQD2j9l85vXVd/NkSIosQhghkrRsJKScEGgQ+Eg8Am4tiraR5Wkjn1uAJdk4U1yYkMGf1ZDH8IVZpxCr8d3NNum9N4QUGQs56Ls0Tp8JiylDHkpU5s3nPufVqKpZkLHkoOJnHidUzD5vu3iu5Ueo2EU8iRggsXg+hnksAWA2r4jVmKpZ6ZwiQIQQMawnFtBoiUkq4vn6L1zd/xA9v/xUp75HSvuQDGmIER2nPvHKSO4NB94H1EfRcDkFz4HDWTRUxbNb45Ksv8PTZr/Gbv/2/4vzZZ/jki19goNcY9v8EQkJAEgXIHO6uw8CUzpiwP/hYPpaP5WOZKxW9GH434WHFl3aH9MYfH8vH8rFMy4gNRr7APp8j54zbV6+wffMGu90Ou/0eXz8ZsI8DGFTIgoYnLAKFwpWWUEtCp8qnrMqBbHwqV1pfmyz0HKOlT0oh1xWMza5tmNdwlWNVHk4+ZVWEFGay1imvcKWXXf+VrzBAvCdFnQdHfjbFBMVm61vbnhMZ0lSEMYvGCHmf8f03r5BfvsZ5FuI6qGe/4cDGY/9IaXjYU1DnXJ3KONXfH6AA8EqIB+PzOeOsn1CZU0LY90YZ0dWvtch/LSX0Dw8YA9afT1yLUreDuoeNfA0q7y33Nd8/z9aQlpuIRK7d0uukySN7ThnJEBj7JxfYnq2w+eEtLr97XeR09nYGI7jQUURApIinm09wxgl/fPIWY9giv/4enEZMwictHslTnk5xTCs/Wx7ioXI/RYSXoxw5jEfD9tjrXoBxoDyKoqJTRkw8Iw696v79EJ12G6G0f87BonyDiLBZRcRhhScXK1yeRSAnjNsd8psb8NstRHhMvuHFTSY/+ZmZq3QMaXuSpKEQFsUM5W6a68fW94BJxNRj5AiMXmDfPGsVD05eh+aFu24XE5aX3npB5tLM8Pzj2WqegGmJuuqFUeeqRTr1tvJdlD3YKUC4+31SqDKAHm/PIcJqCeN/qgzlbOMNBFUY6zuxbgvO0nVjVUQUL44ydFOeeoCP4buKeeqIMF3OhVJha1+Y4DKCCHFz0HBIWYlsEiF/D5oR1znUxGoUwJwKuEX54s6ZmkBrEttKgBssJsgOCNq0NGYC/Er4yySIoiFAEjxzlxBt5iB5osrvt6KsI6WQKhFhytPi2eGJXtjF3+7q4+dtYQEbkLl93nxm1KC1NsfFrwFmb88I5Q6T8VAhIHXgjRLZE5byl4qzAB8gqCtRSvUcgNEIaRZKA49/RgEUGIFFaL6iAWdYQ9RRUsvPptc52d6aoydEQaFjBAoDWqzxoblMXLst8ciy59n+WxpY3Se2UrOzIJeP2xp2D+ltydzA4AbS9GNnTfhuwUGNVZO708u6GL5y/QYK4o0SIwgZ+3SLcb/H7e0tbndvsR+vHe6v+MmUEOjanSVOtX/beUyQEG6rNdbnF3jy7Es8+/QXePHVn2N1do4hJgTeI+QtiDMISfGGm+NZXDr3jA/89uGWPz0vhR9vwD89K+6fZ1kgXxbLlJ5b2kOnL2gTfrJ5vT4wL7CbzNhhEoL+nZX3sy09PXy8dNfStLUl3vAeg3kv43/0Tk7do8dhmOEytUWaezzzvtvD98S3p9+m5gkxYKA1IgUxWNqPGHc73OQRuwEYiZARyhkz8miOlC+kMLyxmNLDjEKjsPEPjjRnBzQB8/RiQ673vLvnRbT97h3uGqnho+rcF2+NngqmyYfZcujcGEvTmtPecUNPumfkN1vw9Vb4B88XUQs2HUEdta69u4Q0/MfDiKV02fErd6efZl64QyPN3XVfZcR7JPoOdzX/o1dGTH+Za4JmmjrUMS3fI7PvzfP7/fPW8wEo4YTLg2XDagImrPlE+eIezrFuy4VOqmx8do5RWNAh+o3f1BUcZeHZhO8awgBQxCUxEgNvzYB3afrudTdM35n6wdy9PMgj4kN2BT5aOmXEkWo/yVKteYF9PsM+r1WgCvzbP7/AZ5+s8fTqHDEQvvvn32L/8i3Ok4SVMEFkacD+9o/dPC6V4zkkZgRLJoBBe+ctHelJ/8Zo0Dxq47banS4U7v8aEZJb5qbgLf3Abv5kXE7YVB/CqJ2ihvDP2Kwx2r5ax7NlSqGugwknGeLFMDrCTi26zSyDW3KK/JwW1Xo/y3WwhZh0Sg4PiwlN++91QBngoLkWfBc2YTyZj1ad76cji4NHbscUCgxQj4PqKUAQTTVyViG2WDW3TGuhu5YLA0wZjAi3sJoAzZG3JV+uIzIJIqN2B2DCphChhM4KKhCMETEA+3EEI5ewSJIAHHqJcdlTKWcEkjj3ADWx5ct8jAkjSJ1HCCGKt0EaR9mfWRKf2XnYAQgh4uzsDJEihtUKmTPG/R6ZNT8FM4j2YrU9DCBI8mJbyuqNo0lwu+vP8pNIjotsEXjEEyBK0uygVHRG9QSACsWLsJ0tjJGMN9gZabRegvOKUN/tpAITGSNkyyyeK/JDx7h0nE52Lcmc52JBL+sh4yO2/AQBrC4CYlGOasTJsl+9J0AlpkXpJMnGlQHTvowBCRTK/DdWXgo7sYQi0h04y3gYDgwxFAE8EbDKGc844Cyt8AY7fIMbOR8sXiY2Y4FC8VLo74OyN7N6HXBWZUdAYMuBEYtiwvaanBeXQ8P2UZha0JVzQqGEF5PJFhxSrWZninrBmILAklg76Mtf9t5drF4xavVnHkkxioeIeX6wep3FaEnhBa6ccpnrgIj1Zo0YAoYYcb39Hj9c/xN2u1vcXN9gHPfYj9uiqJBzRBrj2PaNjiK0q9sfCxADOclaxAHDZoPnv/4Vnj3/Jf7hv/l/4OLqE1w9+xSB32BI/wXgEZxH2YMHkOdPmtb8WD6Wj+XDLVxp96YQsEfAf95mXDOQHU90zGDup1GW+YSP5YHFM3v3a+CxIHmnJWGDEVf4LKzwi7gBUsbNboub3Ra73R7fXAbsVyvlawqzimLbYtNUaODqcQ5UPk08ti1Pg/eIkPekmY4HPKLxNBasKDYcDWy/w8NtxI7jZSvfWXl29HDYoA98ZveOlx9MIVb+U1niQyLOYkR0pBAAShln//sfgTdvEVFzMoaAwg9UT3R+2NbWTo8qybzQ1/0146nTwv35Wexbqn3cu9xVGTHT3ykgNOKMB4E8FWjPt2cHdKmZOpdVVHHKXuvlRTO84vJb83Dai9Q8gZ2O2ubiYCYHaR6MqSKj7smFls2gbMK0znTC0oXJomIQ47HcRyJh60/wT1SEGhAwgPGb1xvcEOF/zhFb7JdG84jl4e2froh41/diuTzu99qx8iCSgJcOyIdbqmyAwAjIHMGI2KyB9UC4OBtwvhnA44gxZeRXN+DXW3Caics327g/GMcn6FEFCY7AmBNMzV8+0yp1GCfA5gXF5TVPdHTEhylo2IguFXAe7KOFvoev9YRwbuTNZWDFCbFnS8eECAVWKKHFaVm0UHXPFVESlw9FqNafc58PovneFzZBlfe9ydqZW5tmSEs7oz4nd3uZ9W9oYODaEtussckhazt2Ec7BXwCj6fdCSDuBJHTu5hZA4WyUV82tprtMHxFp3P9A4ukAT3zTtAtWQbgmTvLj89ZJOWdEC3cEUXqYsJzBDWNvYZ8kp0WWMDlZBbsqxpbkbupx4t4tFjncrpr9Oxm+zYFbnwb1EBCYkGE5DabhccpLZKvdnjd7zxagnULHLKAq+4jJAVvfZPdMcAQqbnL7guvMat8ZnENZIyr7Yr7YfEy8FPT5IewtWzqg+tQfKEsEVmlLBfIqTAcTzpiQCLigjB322JEoFTKj5CQpe9bjp65bsMeJtnfcXphMju4grp8l7BbDQo8JzKKAsNBrNhoJ2VYmaH5quGXkaBbP9fgd5axlcGGEA9WwU43nWNNftRQkiPInBvkPnLHdXWO3f4Pd/hr7cYeUd+ASh1SUIeSg8DPlcdtSHakXEELEev0E64tLPPnkKzx98QtcPPsCm/UGIewQ8h7EOzkbtr5z09fceW3vlcg/4f7+kcpj0o0fNg16jN748cqHPW8/zfIuz9z7Ps9V8Fc97vyW2WXGDmSRRu/UppVTtuCk+VmN+APLRDhr9958l0sgvYsz9W5WnQ9+fZflmLKqF68dq994O5/Y37F3HlpWRFjTCmc0YE2E3Thiv90h7cVYhimAKcy4EzmIuju+UL1F0O/o78K7LMyVZ7PMqGiZpWzaYczgngn94XPXcfeLg2uObFkA1x+6ZSWEf0eNX1h5EccP3b0wEu2ReA/s9uB9whYjduPe0cWHyhxNeIdyBJFUGXJl6AgQZcTR0jMjRjfWX08AYR6uhnU4vYGpnMaeL7cx553wkPN8yrLKHM9Uo3Y+jS+YNtfJhCZ91ndnf56UA2HiqwinbZ+ma38YpkNQ0ORfX/XYFujlWgUvu+eGjghqEDdE7M83oP0etNuXOoXSVhFFeUYih1kzIeWIMKzFKOxIrohuiOVLj+cm5RHv0neSI+K9ljnKaWZXzMlH7tzNT5Ch2eczjPkMWeNS/+bLFb54NuDq8gwxBrz61z9g9/INNv/0FpvrEUgaT92XuiPfefHOjEp+tHDc97plNMR23TanD2xKW1QBmQl/WgLfvXAS2DNuoL5ttFYYTS/d3LRaYBN09XyI3aYZliyU9T/k3CgO/FUzKwCbDgWaklgE0R5uFQ6GEAHU+PxmadyINNTqmIlUNmgIsgrvuJl3R8x6CxbkNnSQEpRQ4WC02PIWksj6YQCZQWqxW6yW3UJRIBDbG4QqDGyJ3UIYo1f2OSlcUa4ZU2zr5ATClEuIqMwMMqWBWVuTtJlZc0pQQNRXTbtewiWR89QxeJmRKAEI5aIMmvQik8KWEygAkTWGP0WxpjYBKlcr/jwm5JAw7iNCiBhWQ/G0MEtvZvGoQIwgl69hwhhQt/f052w5GfT3QKHSLnZ+GqseQsgBCaOMjwIseXQlDiTnicxl5RA4A6DsmIgWRgoAMxX4zaqLk4JvMfQLeFNGpDwlQs0tAaDx5MkSw9/yRpCEPioJpBq+T3dezv6hzAMRoN4K3nupvqo7O4TmTMr/694tylan2fBn1fDGEAfkkEtdzhkrWuPp/hI/DDf47fqlGNZniQlMAQU3mXIBOYNDKOe5jiuDOeh6AoB8Ll5HXE4pAPEAKt4m9k5kiLmZhhoKJHvS+i7rxO1edLMqaEDGbd4Lcj7q/vJEqCjrkrbNbh9InRiDKhWi4kvxbCl3td0VFWEjhIDzzRlijFgNA6633+OPP/wn7Pdb3Ny8KRuESPJBIDNyGsUKJ1Bpz8I0mjeEbPnq8eT3H4WAENfYbK7wN//2/4KrT7/AZ3/5b7A+v8TZ888R8xvE/b+AOAE5acQ0zWPDc0YQbu/jEMH/EyTOPpaP5WN578UbDf3/2fuPLkmWJU0Q+0TNzN0jItnljxXvrgYwwDmYg91gAezxuwFssBjgYGa6expNqrrq9SP3XZIsItxNBQshKqqm5u4RGclehd4b6e5mSkS5cKnirFVnrqv3yP3X4Wbeg4T4RNMHJPAeUzd9rhY2zxPhF9MOyGLZfP3yFa5/foWba8JhfwHsGZgsN2lA1pgaui1YJZhyUsGh0cU7DQ1r96MpAC6H1nC4Qis6zsvNWVDR2ppfUfLYXh1TLPRuZWuVspHeC+8sQ8McrCpTui2unQWd3tTRnmIZM14N32OPVyBk3M57/PHln8DIoGlc4lsrWkvr7Nt+ZrMiPgtri8qKQRgRX0Xw1qDqMvPviTZS8wkcP0H7zZzXeBwlF0K9Q+rrki4fUvU9rqWFzXuZS2rf1LUsF3a9OLs9o5gv0qVrwom2lt5sxaqprVr3VfypOMFdh34JtsNIVQZd3gQQi8eN/bMnuL3aYfv9T7j408+ej1FXa2vCFe8AjGnC9ORL3OAa+afvgfkQmjo+18vnK287w3bfdLYg4r5aKueZT8WGrOCpfDU8FbNjRZMkTqDX8aHUpT60WhYbw5CQmXC5TdhNhCdqCTHdMlI+gH66Bl7eIN3MoMNihPr1thqpH0g9ppAGJUthBtY5HbEBPE7EQyhaRQSifsgNHM1Y2s8VGBZEzQJYXlZvyS6HBdJSw1Frfgfmp/1ja6YDQjXyLRawMrDmbzMKIQSCM9YZWuSS3RwNxuwMbXObt+plO1el9hKYOamrodotlDNXUdZRRADLUNS36GJ5dPtHbuXhzOPQGRMQFNZp+Vb0cuzPhBAE4YSbwKQQ00zswYIZ5lZnBbos0SBSpQYo1gMRcZZx0bdJmPuZc0GYjHPJhHk2RusgF2ZKPqbRPZTPXw9BCLDIv+EsiuMVPu0dExcXXDZyhlc7rlsjXFX7iy0fV1cNpODMQTDEuh84YUhB4MiLojK6jSCg0EblICmMFAmCXpYSFYHZXbR1rB2StVGEfaWagriRECsq4O4R0ovn1RFCLsCzuPYMxg4TnmKHW5pxoMCYt2DNuj4yZD+6IMJGzie17rfHl4DsnURQ10MypmYFRQp3dGG1hmR3xzBm0zOhtYRocSJxG9U/70nLpyRuk0Sokfz5MpCztDkOycuAM97c/Ii31y9xc/MWh/nWhTppICDrWFi75grPpyy0AVTCWAKQ1Jx42owY0ojd7ivsLl/gi29+hSdffIOLJy8wbLZg360zwL2TZw1r76e74qR3xkXvlU4irh8AhrXUwrZAIj5g2x8/RSH/55xWyJ1PMgVe0gOm8yuMgv5zajk9lmeeVbHOUzXc9Vy7EyRWqMXda+KkR1G9a1rHgz9eOiYAOI/hx0d/rj6jTttnDlBr5fAxhBiMBMYIYMIIoSNmFxrMuB0S9mkADwp8MpjhnzVWAcf73Q0ouHxaLzngzqdgbHD7CP0S2+r86OzDuEv8OwFL6YTlMRokllruWetThxTobhB/3Lyvfrb8gO5yZjDN4GABPOcZSLRgDhbFuKZe/3pkv7Sv1vK259JCehAuEDqd/ViTDWW7XnC1wljZCU8i517KVZ291w91Wq6th5WWqPsUNV+C6szh/aIiRDppWd/i8aLQ+rOqdNVGQ88vQO3VU37VYK4N3srN2S7jlfMr8ixoSGAawSktK0C79Rmg5PNAzNgegFtmXHv7yzp6c3ynxPcr1qb3ahHxYQi/Op2SGK6c63+2SaT7jN98OeDXX22w220wDgN2/+Ul6E/XuPjtS6S31xKF/cTArAdJbtHYuyQr2dymUbtTs60F6V3WZ59R+7e0EbXUT578vdRoVBXte6mid+GRFTi2JypGZ+BSOqONV7tuh2+pPo5DXagixpQZl+eMzKadzjV90o4RFZFQQcQq4IWdlVsuKzsDTZIwZkXIQO6OiPVALSlaIfjycG22jLWkY8esfPm4nvTIJtEIH8YE035moLgHYihjVmE01r0x+NUXfW419dGs3xYuvXDi6pehlhgHUlTGx2QLiZU/SGSDLGM8q19/qFb3wJgPWRiMlL2PAIGTxnCYZdSSMUtTKvBkxpxnJDAOs+QRBmiBTwQGGZxLv4eUQBMh39wiZ0Yag3AEwGF/kBgUylA1S5hxGJBzFv/9cS8BpZ0Ft6Ug4k6wZCCNCUl9nBYmtWrW56CVDg1ebBo2ATMwzQJfhc1RIkIc/ebrMICWFBnQANkGx36eQchIaVq9GzkwaMnnR8d8LuevNWnzOAyo1l9WywmLBbI8N/rtF5c/HGIEZOQMtwogQGIrUOMKys9F06SX/9p9wIq92FyAZa5yZjzHBZ4eLvDD9Ba/27xC3u9x2O+LMGLQ2AjzDIZo0dsnxbbtYCINlq7JLHFknZtrt7JOiUish0Zbe+ya/gK7dbU92+qxFSb/4EKEngDCxts+y1okHY/ssR82mw2mafI8drZ6rAgTtJAIeC52F0jq/ur65mf8/sd/j5ubN/j55U8gAgZKGMcBm3HEYZ6Rs8R3yfMsdSYbv+QWITYeZsFEVM6GcRzw7PkVri6f4+/+/v+GJy9+ie/+5m+QNhvk3QYZwO18AOcZU7X6imZQuFHCWMXA3i32tkZRPKbH9Jge0zlpBUtzPPXxXHlMd08nKcmjjIj7UdIfMmVscMBzzGruUGImyPu3zwg3g+DYkTHoO6qVJig+Y7RFjI3FXMI03C1FoUWfkSewN/hxA5vjJYpHG0ls8eEAAInAWayR65ZaPkPkc9giYPSI2D52U7EeF8zSNkXc6uhJRlAFF405F+g24z2IBfOShSHjcYTJSQ0bl2gJC9WKlEfZ+q40dP6iWPJF3oVntdLAKnPmxB2y9voerKmj9dnLI/CUYaL6d5WjPPWwSYu7MjVNtSs1rodOGz1W2Vpdi3ydvdaFsVf3eS/XhzDuGfl9Imv/lfJjiQiD0mDCFmp5eXLuZqjgUGnVgTO+/v4tLnCNf94w5sVYrLd9p/RA9Xx2rpnOkf5ze4w1J3olqlBN68plipnhUjjsO5tlIfL4WDhr5wDMPCBjxOVuwDgMuLoYMU0SKHYaRhze3gKv3oIPMyiXXb+GH0Ud86q13o6MmsKL9b82SFHrwR+tlKMChzOEmgM2NO7X/cmls3I1uaZGaa+VyaxpXyz402tNRUantdeA0kJm7bmZoz8w5paBSwgRkGGaG9oTONNcGeCuYUxWtqwPF0EE+Bmxk1a3jVhYUfGCaKbK3O7bjIUV5GNSvtfvfDX4oy5mGVBCchASDRKQy8eN4uqCnSbSCwZzhDBoSkfhgDJCvT0y90f9xUAaMwESh9jPHf9HXQZBNbVTEqZttAqxbSBQEAjJtVw4YI8FaSxjQoGnGmG2shw+bVxJgeT4mxIIWV0r2ZqKCKYyMlmEJIPBlBKIAaKs+7QNREYO8hp6JPVAx98EM2X52jlfAgIL3IlKPyiOEXPcMYja/bZ+FgSM1azrP7V9sPdZ5rSyvigDX5+fbP2qx9Flst6muZFqYLH9yP5Lm7T2Owihbv5K7uvunlj9s7IX6R2rXUSTyzuuHwAgjXdhfi5HPJk3uOaMazoIEBafwRn1peWkjP7IkI9N16OFcAQtzW3LnS/Clpogi2cRxdzw+BcKixF2BVdYQQZ9GZT1QDkhEUt8h3EIc2VjFtsUAjihuIFiAIfDATf7l7jZv8TtzVvsDzceSDqNJmZjnw3ZhNJCDmOqnbaF7TAmdRM17XaYNhs8e/ErPHn6FZ5+8wtcPvsKadqARhM2zRjzGwx8vdg0i3stTEgt5PtYCNZyn68TImtIxjmwNxvls0x378NCkHuKcP8zSMdw0Y/R/dO4seV7t7V5rPjdq75bgcWx7T9QcARuXdNSIB7s3m/PpCUc9c3Qh/Shdvk71VNd8gX9WLvXvc36Gnqn9H5Pu1M9OVH03MTxa5z588rcOR9FbO4OaXGdHr9f13qyIcLTNOJyUDej8wy+uUXiLPGoBgCpqKKUCgtd5Z/KYDM6I9tfzu6S6XRXuTPTd537Qg338caI80ZrZ1Y8PeCJTk81iHqsM9CMC1D7pGJ8vfhNqzmaWdR5P9ANMh2adaRKNJsRT755ge3zp4u2Czlp+OqZG+UYA3yBA5+eNwqDtsDhea25eiwezsIgAnEGzkr1u2NQmOLW2WCcyNyHriy4xTqiFs52LVH9PazdvpVE/Gl0TPPi6OI/0zqhpQEXAop6LZx1UvSEaN0nFYeoU8+pdrQsAXk34fbqAulmj3R7KNByoddie0TiMntLWxyIQPQWXUnnnYF6f+m9CiJOX8fHpv4hB4Xrr9QsEi6S+yXMMdiRLezl4v3gU3jidj7wDvt8gV8/n/DrL0dstxuM04Tt7gJTGvCnP/2Ew+9+AAC0vtaWY8B+MawRC9x+58IE80QE0RioL8nI34gNxFwLnGkl+RHTxUGaB7Eza1LUI0KIgiRFBpHVRcsqF+eg1hcYam6Gau8Mtqg90eu0qKfCLg4fL4LOnc6xtUU27vafWkTwLP7w9VJxhCMr8zMe+oaEWUPOQM3hPfxiWmgFO37HwR0MwhjXxJGvlaA5bMw/eF+yjlrWvPqpv4VZLq5ZCIQ0Dkgg1faWIYxzbQSquBJp0D2S+pIy8HK0FLB+a3uklhY2TJkAUi1uIhJ/95TAKetLmSoyxr2uqZQSMBFwIDAfyjpiQejd+iFlZE6i9c2QTxIBhYxnfTFVgcQhwZLAQJ4PoGGABSvOWZi8STvCc5ZBS6G/g/iMz6pxPqpWt/h/zTgcZgyJXTt9UMuIPMuQ5pxdC50UMRZGfBENtPGljemfNeD6MAxIamnhcUEySxwKyBglKSha9VnWVkq2mAgW5QQklhRmMWQCpconfzWY8pcNp1IJiW2HeT7AYwYQQKo9Yq6O2Ne5wGPrhxJrnJOMyCBmFrN48Fzyk7Ro7rBMc8VjXei6G3pmn6loqct5Qb5wZRckL+8WD9wdCa2lRi7NYiHHHEGYxww8nbe43E/4/ZRwPe4lPkwurtTA7O6FbCyJZL0fGJimMg7S8dnHVZ7JPhjMckbrtPHUaW+ENbXWn8xrOSPtLJJYEwkpjb5OZEmZtYlV2YwY2ZmWQOOMYQamzYhxnJDSoOeYCFtSSnrmyx4ZRml/O4m9wc3tHte3r/H7H/8dDodr3Fy/Bs8zkDOGIWFMhEE2m5/bVIDwdS97VLVusvhwMlNhGjdI04gnv/gFrp59gb/5+/8Lnj3/Bb741V9jmMQKgiFtpPwG2/xbkJ1ZNsD+PdyB92J2nkH8PaaV9DHH6z5z/eeS1k/Mx/SeExn6KriFoE+C/yaY4HfQv4DPrtS1hpafyPKJJYHyXGEEcIzh9ymlu4/+fRmU9xIOdFo/CW/v9V1BXhD6/TZ7DLXnifAX2wtXfTns9zj8/DOGnLEdE8aUsE8Bp9CKXDFGH1j8tKx4yIElNuF8KDEierA6HtWkai16O9TNUPO6WUljh0xL1mIl1VsSnTGCay4jgAnUrIX429/bsyDg7BZs+xe/BbSaHN76eSlQt5OR8Xr4ARl7IQ6M+CWNLfbFE7z4P/wr0DiKMk67Vk550LDGyWBa2VGmvNO8PW//rY/V8TPJyr2vg2ulXp8XWs9zrE+BDjnZ3mrXaoWoSAv1IHHapt584XtaPJJ6U2ygXrd9sJzHcQzyZaFOPgrvq60vP3gx/zWM/Rlo+rHGL/QUhZnVCXIE3lCaFV5iHJ4/w83VE1z8/nvsNFZEpbSd2TzpAhD6M6WEL7ZfYUN7/AO/BHjuwvip4Jrv3SLieFcfHj37WMMa7rD+IfiQKiRHkllCXGwHvNiMeLIbMI0SrHIYR9z+7kfs39wiv70BK2PnIZMxe+48r22Z3k3elTgfSUGTlXoYc+Fw9wpLSSIPDBzB6mvxFTNUQjn4zkrGSF9Tse6BZ20ZE689yOUcC0cie59bxRSOZZTZVa4fdk4mWfkIR/XDLiFhGkd8pY2jAHWXlDkXhK4dFCixiAAziuZxDXwBp9WPMWavzYv5WRemIdVDF4QQzjRlEZRQqi8V4ZFHRDurhk9GQhLmcoMZtuuiZqH1/e23FB8BEpOhuu5KXAaihISMTEliQ7Spd/TGZ9VWrNelMW6TLjDZXwEBNgGRVWMMe6siZ2SIwMEFNTon8PzqImux9gsS0YJbjWocK2OsmrY8bI1wlccqMMGVpeQIdXHtczR11Kf9PAhMb5f3Gc7GYsVCGiC7rH8uyDrxQnBsbdoRymSkY+EmuKexBjZfVu16CHNpe6A3E8stu0bMnj6zo9Y/cUICcJk3eIFLXNMet5tZtPDDWWfuopwx73MoK8gEVGYUNudZBRDhPANUMBfOUR1vMuEuUIJlO7xloIqQlQC3hJDk7qB8XxicugojamCEGYlWoQSCLlHXjXAHRPg2pKTCMwCc8fbmB8z5gLdv3uJ2/wb72zeY51vkeS4CDAsUzxoQPGc1hqPgfqtYc1TC5kQYVDDy5Nk32O6e4Ouv/wJXL77Ek+ffYPfkuQouMyi/QVIBMOEGied6Faxh4Gen8/CBT0PD/px+vSsufNd+tmv57ml9uj6FMbf0/mE5tcbexZIgyJyPvn/Xeh4y3WXPLeFZK9tBTjrlTzW9SnX6QewY/HGQ7kjnnD0iD31edRWuzgTlzOrPqbbN8gGW4cl0muH5Ac+x866zD5Z67FqJDbEBaIuBxEXmfLsH7/e+BhIl1UsiL+9a3ewPhIcGBkzgwCx4CkypC+o+MwCkOJTgpD2aMSQCghap4+Ft/6rs3RHo5VMsndR+wlE6wwdhvQ6IcsCj1cI5kw2G4PZtk93uEWHJtiEjL0s5/S6WD7PSINozMqW9jJtXM/Ir5QeVSRQcNNIudUtL6Krj8rx9c+ejLu4RPadP3a3Rur+q6K5t9xbMHVN3XPxRy4wJZahb4O5tVVWUteo5Gx5D9c3ok5V6lxb28QQ4cqs7Pddpsw9487F+T9erNtJ8FfUvcJxoubyJe3zt2I4xaev8x2r204WArGcEpQQapILoIpfBfhZaez4FREhpwMAHXOURiTa44X3DCzq+jo6tn2P0/H2E+J+Aa6ZVtPDDtf8p0Ux3SsstcOAN9vkCv3y6wV99M2EcR6RhwLTZYBpHvPq3/wH7//JHP9xc0f4BUnRnc2xXxyZN87fhfK6siDqP4BnkCMpx2NYv9fUUThpnxqBYQoRsTrhwrpCAupnwsMtr5urzdApMbbLf6/WHUoEZmlXrRBBFEyK0V0gEn7WfNfDwAxAMECcQZYgfTWu4RgOdGaxc0mR5FnPCoW/FhYu7YrHOilRgOQB2MIOciTmmwdui0I4Jg0zz2Uz1U84idWbTYl+uJ4tTkPPs4wlSdyn6ox4CLkIMFAT3nDOJUsLQe679kRgJgFiGNOOk+dzlE2zeuWiHK3w+lLE8A8wzsjGFWQgKY9iLRUYSSx+zIrCxZ2UGgzHwIO5kKMncJIs/IeNeL7F671cDafvG5rJhAjMDxDOYCHkuWvRl69TjvRC8WKA9i7eQLWaFMZLtfT0XrJKGgWStDWqhcZjFKoNzBlJyF1VMDF1kgohYYHE2AZNaRtg+ZIhGu+/H+twlLhYLYo0S5tSEIirzsHNE3IqF05JI6SP273Hcue1ze/CsnEM1GmiCwXKWJdXSeZF3eH7Y4A9Xb/Hj9qa0r/1IGpTZ4jGYBl3OGUi69xJJ3BPMyPtZWlTmfkoSXH0+aH0EF4qZkMzhHDR+C3rMF43PYp+GWBNhHMeQq9nbzMiYfaztfKIhARiQhlH2khLls/pMHscRKSVspgkpEfJ8wGHe46c3/4jbw2u8fvkzDoc9bm9vdJ1ABJfjiEQJTIMElzzMwcXVANm6ai2hY5Stv+qKabu7wLS9wL/53/0P+ObXf4evvv01NrsL7K6eIQ0DZkoA32LKvwfx/vRiwN2yPKbH9Jge0/tKrQXfx6dRH9MHT58tT+D9JqYJB5bYEESEw80trn/8yXHUlAYA7HiUFGLHQ20vGe0nLmYVr8kZh1ktIfIMsySVRL4NiUShwhWvjiSq9vDaOwVz0dlusVKWaXlW9Eh8NsoSjrea4IXVLW9CBpiQk+axwhZvrm0/PukdVwGKt+lnHNLbBQ+CCJj3GT/9/iXw81tczfUImP35Kb5JnIc4HquWEI4b9/sRKm7K1d9NFW3dlSdQKw4tR/FOp3pkLbT8nSPrsFjX1PyPs9vrPlgTkjWD1K2i8CJaenm5mPSn56HmeWozhlx0dP+Vpqh90GSLz9fHuRaWLV42T50LVpVphRMLYBe/et/6/ID11NnAXLwYcCKkbNbpgSdA7Xo3ZmqJd7qZB3x3s8WrlPDbzUEpzbW11yzwlplYsdQe9oL8BAQRD5PWhmVd/lMvzOYYPVHr8XRUAeWu6jtA/0CuziTdQmwfkiGlhGGQuBDz73/G/PM15p/euk9GqYOPMPLPP6bdEsKYgsHZfU87ao3Xfi90n/qz9jCkg23C4haoV68jWoEBVUBbw3i60ojVV7CqWFukoD0bGFx+uRgDsaksiAB0ztQtjyFWbtEQL/sAMgVND2uRota2tC9ebGqBhYxTLl0MTN+s7oAIdYAzmNaImxBa3+U5cxyYcsGIH8+kbnykLtGcFsZl5Oi6yXDm4qrHniEj0+DBtOs5bS8RHdvMyEmZ8wx1/Vb649ByjaDGcTp2MjgIEVdXBj4cOTCGKzuhEE2O+7XK2GeTAuidlPXiS0SYswQvTsjIUP/0RMipMKrjEWWCRnNuxVmtNeYs62aIjN0EZmEWs69fLc9F2NFNDXfYfsofwQScLvCLY+1rzNZlrFa0xs3tkUwpIQq9qjO/gqk8pKSaYtkYvIzEGTmHwF62rpmRUhCIweYsEj/WXxEoUDY3SRBNfgIISd171X02IZgJS2pxnLwnXbtVv5qzdnk1rVj0dPJ5dcEqxutILOfHADAlXPEWaR7xdtjjxmJGQMc0BoPmsl70MJG2EkBcI812dkbXePFsIZ8UG26GBA4vj9ubx4KwAwAGEWbY77od+Pks1SZ1kwUXeJG6eGJoUG4uQs1xHDCkEcwZh33G67d/wH6+xvXtGxwONzgcxAqiSPrLmcCwYOY5CCFSCbLuriv1jQptNxdbjJstXjz/JS4uXuCrX/wlXnz1HTZXTzFOG2R1H5XySxBuAYhA9v738DFK9JznWosLCt8deX6AKh7TY0J1VH2g9CHbW1emebcNdE4foqx98S58a50nWDLcqiWzegyoIw2cTA9Lp+B+g/NAi+LYmK+lB+//QzT6Ps73u7b5UQamNNnnBCQwbbGhDb4aN3gKwvz22i0hiIV+u0bG9cjYp2W99o1ZLSE0zl0JSm34rrm4rcsZy4JhMfdK/S0np9sjqvNxhSvG0kER6dieD8/nYY+cDuV5NXdFwcvRMcW/5iz02pA3IpAwWtU1bgIl3DBaD7THATcYscGIjb870A1mMgUQBqdD5zDT35kx/ukV8OoaNBe3s4IHa7GWmX9qkzsf4EwhREN/KNQLeJe1LSdnHbTOi5aU5CN5Y7aFe/HjRaiyyjladcjTr7+wGY412FIlVP0q8xPe+vroLZTwpM2zmLtA1/mXkmP1SAu0X91gC0GjQNgFcqWJtu4whvVuW6+h/kmLp9w+OZPf25GRaXFVYU1QWpJUeFva812gfCavIiUMPOJyfII53SDRG+Tg6aG1EKqFRvGsWZuTh0ufgCDiQ9+29cYoz3oH3eeT4pryuywliQux3eL1f/xPOPzHP6qvcXImSFVBZ2NZfcewo4UQQpkmy3gQa3AXJlnLtqhaZT4CxdoRep/U1OLazw2fS7PaoW5ukMjdfgC9ALJST6jPGVLhdDm6L2ohBBFKfIheV2JVDr9qSbtbjtAfJhgz26G3L6pZbb7sC8JiF1xpVA7NhLKC4gGtMKj2izShmsRsd4T2iUs8AQDOKExEYrvhwqHY2QSy2BhUEJ80DCqgGyW3auBnPuinaeRkX4tkauMJECuPhKhRH5Mg1YJMS7gHKnPUQTA4lLNdEIUtbfI1QoAEpDYNdinLTBrPozBUTXs/SwerdmU8RcDAYEC1x1tGPDQYsiwLtaTJwnYmEGZl0rtGNxGIZjCTz2/pzwzOBKK9B7wF5LyCm2IzYhyLrMIihaI7hoCGqjChQwfBrfskedkDR5PXYU5kXEimbqTSkICcQJwlDkaCul+UsY9TxoFaIiKMQ0JOErfBzCszgGT9pKRIBwGs2v05EmW19o8x2JHVaoGyn8Ok/w2pWEQEwMIxUPfTdpBUY3ARmo71v/fSAlc0pEYRLB331JxfJeC0uCh6kSe8uGH87uI19lNZx6Lh7wePM/ic4NNDKVGqQLWz0zTrWkQsWi4USw3yse0lE4ikJOdnGkcQJQxDUuJ7rs747AcvIUFiSlhTKQ1IaoExZz2rGdhsJozDiM20wTAk7G+ucXt7gx9f/1fcHl5jf3uLnGfMt7cyf7m4a/Pw1Ay1rCjmvYNajlgGEWiyrvkRaRzx/Otv8PSLF/j7f/N/xbff/R2uXnyNcdoiDwMYhP0BAN/gMv8BSQnhj8BLeUyP6TE9piOJyyWHggt4ImBVaPl4oD2mP/PULnH5PWLGM1yOW/zd7hLzm2tc//ADQCwuihKQMvByw/j9ZkaaB5CHgxKs0vFKwBW+ZrXIP2j8KRFIKM6bPUobHHNUtCyzuDA15RyjF5e7NjIuy79AwBWrpyh8DKf/lK4PmYoijQC0n/bYb14GPLlmT5rCh1t854wMxnyYgZxwef0VUhrR6H9VeHcFIxHmdI23ww+4mJ9jyluH/Sa9wk165fmcJqpGRT/njM1v/wR6fYs0CIZYXOUc56jYfBQ0W3kA1FJoBeZKABHGb1k3LRdil5boZzrN/+3zSlaP90g7YAnzUYuIlcDbR3ljAZbuCjhSFKZEFbNVA6BvA81VsSYad2axzRaW2iOH1b0CHK28o+UPByW0EYUnoRcr9ayC0OTXuowHt1au5eOtCRSONrhW95E9piQwIPRloiQKnaQnn/EGMiNTRuKh0NVEmIjwYvclEl0jzT+A1AVxGdcG8TnVn/eU3o8goh18Xm7Gh2f6r9V3fKDft4rbGp/Gm72PKklIOSfs8wjr29XFhO8uJ7x4MmGz2WD+3U9489Nb5B/fwjm8q0PFnZ16HPNuhRALAceyQNXc0Xydw7jHU2+KdNP5o1sjEEWL+rxK+9e91tZIMTiHseJysRpLkEPv5cxURrPfHxoNLAQGKstKUD53IePNmOsbaN+MvatIhMdSMIyI/QJibQONayoBIQbk1XXmpZp1xCjaL2fMYuQDkiOEAeEzjDJz6RsUIXINDBVe6GHuwoEsE8ERply75pGmikVMbL7A0q4bPfO435fYS7aAse3eWSWGO4vRp7heY4AJBSRixUw6Tr7KynkQbUnqqht/rCbgUARbZBMJCQmZAn5D4p7LXWg1DGyeMzID85C87aNnQmaTNEBib6TA2NUBGMKYNedZ+RphqZFmgiDi5s5HqpH1kRLAOfklztJjtSxYmy615FDXOIC4aGJm0YZCEXIIODrWvpdM01+EMYnNCqUB2n7b3swAJ4a5F0raps+DIyTs+1GIlngGxfW+7NwSUZZ8htRRvUm6eYHiaq2f6vvq8rCBWwCCcTsA81D2TiSKZN1J0PZBCR5xHdC2RxoYXc8xI8TcNVPcFeEwDESnCf6JtC49Y0BmzaACysL90nkviLwLAyF9MaskInWpBMI0TRiHAeCMw/6An1/9Hjf7V7i5eY3DfOsBpUEJHhgD8HY80Llp2sC3VDnriUBpwLjdYNxOuLr4Gtvtc3z1m1/i2Rdf4vlXv5ZYEOMWTAMovwIhYwIAOgA8n0MJfvB0H8uITwDsTzq96/ickmM+pj+3MTqGpX+g5v2rwFKUgCK+XXDpT/4IuM8CWZR5mEV2H1Da8f0gy/3sSe1iOViDcmFZeq8279TkPRNXH8cO8gW7qqBHFXlnO8gwS/L6Fe/JRqapooMqLJriU0sLdqgQ/y6Mai7uWHvABrqm/q21KM5uZJqRkeXL2mlVcNJ5uMWc9sjptlL+qvtgjUDxeK2XWdy+MmM/vgGxWJu3xLWfRU1/ZrpRS/Rb3NBL7xTTARTH5cxLmglhjJcpWkM4TUCBgqJ6/TeFK9gr8r1T5r4WEXVz7YY5PQ6hd3eE5VidR/Kuvuqs6wAfdyCl7hdaPm8DTOvi6gkVlmBR/PA2mtexsaZ8v96WQqRqnZV31ajYNnxnJJ3KGKznwJpS8amqARy/RnoTHQoZ32q+3OKan4FevsZwfRNyBVqbizW7jQ0RYeSEJ7zFNRPe0h4UAPrIGBmAT8Ii4uOnjz0JR9Oxs5SBQx5wM1/CmCG/vNrg73+1xWa7wzRt8Oaf/oT9v/+dM2C7dR5Ny41xEtxuNmOEtDtzrRI0m7RzOZxIhpOce/2sgdKN3XDWogkIiQsGUCNdzkDTy86ZbG01pMxgQ/fK4QlCCGha2GaOSrmWhbVftE44mHkBADl2mZwxhabm+JUAZ8DZcwJ7N0pgICp9NQGIab5U2Kz1sYNRCoBYMo8Lo5udeVe0k2Mg2SGpH3RFolgGDzyX4K0lBgCc4S79Ig3wXnvPXCwFY8Qygam4uPJrNHKtjUkZYLduEsqF3LoE47jRqjzivsi0wZO66ElDAljiM8gSKEzHmMzFEoKQTPoRUAtl1Ocs7pXYJTqDWMEkiflgzFnW4NTzLK5aZEwJhzwjMSMdCKAkjNiKkg27N1ywtk6kVttX5u6rRiac8WrrMQFKA2kyF3IM09gBi5/8DAThVsY8J4CyClqShpROoFSsUurTUgmsLEHDU9J1NwzOnDaBBBGLDCWTChB0rNXiQepi5ExIKcMEfaa4JLSTBEcXYlDWX3LhB1RWI8HUD/kgsDGDSZjeCUmC1EGECRlFYLPAn6IQsdWA6mnkVO8U5XMBREFuixBR1kK0hGIAT243uOJJMzH+uL3F9TBrMGb4Xki6/3POIDaXbCaQ0XVCSfY/JRVERCKyDCzHM9kIyiJtg1unJVn/lAYROqmFQc7Zg0JXq0OFZ6RnVBTimAadBaSexhHDMGAzThgHwu3NDQ63N/j59T/j7eEn7G9ukHMW905EAAYgcXVOKzB2sOgZKJYQSbuYmUFDAqUBu6dP8OSL5/jNr/97fPfdv8EX3/4Cl0+fYXP5FMO4wUHPk2n+EQNfh7Uxl7PjnYiEzl34mB7Tn0mixX33mN5n6vHeizVEeVm0dO0SBioE6HHKPsP04e8SUa75/BdLO3KCPgTEwpUaFN8N9K3ZQZirW3F7m53e4WgBoSW6STj3juOJ8MDcza7x8morClCdjyCwJlLdDe2LQ6AV1/U7YQYAOAx77Dc/F2tYWlrLM4DkincDEjOy4rqCf2cc6JVY08/qxV0VhXoM2aJCAgwgzHSDA27g/AUctxpvh6o4QGgGaJEzfIuCBbLPdZw/fIT8PkOd1s7BG0/t6SN1rCr53QOWU6Cu8PD6AphlfZHu9pKB1qnzhjuromeaGpt1FddU1ejiN9Wf1LbZK9zAtvJ7uUmpm6+2ollr68ykGc+INnNujf0ya8VjluXGCawiwv75U9w+vcJ2njHe7CslY1Z3uqJXy66ECBLadzsP+O56i5dDwj9Ph7AkG9Fje3C9C/l2h/TRBBGVRq4+KYm6PMhz6rsfLB9svEubNQ+xgyUfh0gsITa43I74xZMJgLgN+fLphGmzxfz7lzj84SXy9298jBdEz/lncQe+yNguWZa5moW93gJsU1X3iyMDnaOiO2RSmHCXee3lZGcSu6upY5eU3yCdcToqhOgOrTMxS79KeyIf0Is8MP0cjNKwtpG93aL1H31yhmC4pK0bY9e1wgV4cyEkI2bWE8VI1tmTgaFoP3wcDDE1Jqe5BDEtjnjhoqebJqvBETkXrBS7VmGuURFIOIJYLmdBDLMLH8TtlLqeqrQDqMwJCqLql0S4jMMSLD0wxHWxxIKGekyanxp3VBp0Q8eXq4VTzlMx3fNJIGigo8HXi8T4KHuNWRnXDUJCII8NYSMA7Y8HlnZmCiMzAZkwECl7X9dokmDfBfkGiNjNCeecZVQTlW6RMu0jg0BhyEo8tMdFJdPycUEYpzgBtifb++cYxiCxMZASwpKV9Z+i6x+LuaI1M7Qs+dwmADmJsI+yBUAWt18mHHGZIEjGi5Mz640QjMHgyeY37msSF2WuxcYJnIABYiGRvW0WwY4TlbRYg9WYNl9i0PU4Yg5YeGbroh3rxTZo6iR7RqWOJ/sNdsj4ebzBIYnjLsBiiZS9mvUsLBYRgGmLUEoYB7UqNKECALOIMEGhCcMMdhNcyFlTYlX4leAEdxG+WslmhGQvBEFFGmTPSiwIEXAkIlzffI8DX+P2+hr7wy3281sJwA5oHjmTWa0mZMH6KNh0AcGqJqn7pWEaMW4nXFx8hcvLr/Dsqy/w9Isv8c23f4vnX/4SuyfPMWx2YAw4zAzMP2LArQSkriPL3z8trtBzbvC74U6rtYQFWO4I+32vKh/TYzqaHoURvfQw43HusDp+D8AxILtn7rrv+yTAySK4e7EHSp/O2nu/kJyqvUP/nVP+SLUfUwhxF41tAM1mWdIquwS8mHZ4oi5t7c8Eea9wwMtpxsvtDGwycDMWnIdLvih4iEoujuorDZgZokiR5YWh6VFG6Fr/ho81OKXz1rWBPN6A04yKHjUcmAl0OwlO11qxx396w2rKXooLSnOpKs8Q2s1itSElZGYM6r6YSXA4KE3ATlvbWRToyzhtICDbXAAeW4JjnngstXROzT+YxoRffHuB8cU2nH1O5OpPqh83fa0Hj/yjFlq0+dqCHVC7RY6v87tYwR5h4awnH4oj9Rs90OL/9UdV4Di8hU6pHzt11TwO9EaH7mqFF4FwW+2Lj31Tnz3vQi8LfLVOSa1SW0tHdkZrdax6Z3qzaig8PTrv90EG3j1RgC8RiUKj0ppZ3fUaH0P4eOz/OdgpYcCAJ9vnmHGNRK/d9bQPQLfx9927kj6cIKK555bpSK8fhs5cqZt9gXWZ3e85xfu/XufNhWIv9ffMA27mHb7YjPibb0cMw4hhnMR1wzji7e9+wv5//me5ZpKLIkL9pb5V7cUGk48EUyuE6C3mvl5sxZ2r619WUV6s4InFl3ivfftCC8atP19rkMVhUfTpvVyGvZuE0HkY6uBqzLtCiFaiEy5vX6PxQm/64YgeohBF3Q8hq3AhWiQYshOPaZWwchkPIDLVIoOdgJRAHlchBO5WrrIfkAzVjgndswu0ueQiIkSLNWQIblaNY+sLhfLJBRApDZWmivXDNJWdaWj8NKrXrgh/ypjmzBgCT9PnyZGBHnpRz1UMIGzzVIQBTX5mQK0LKJSLQyK/VcPfxpgAUMIwqABBLzPG3JTV6As2BysMkpzZrUw4S7jqOK/imokluJJqjctnAmbyBmU7ziAi5IPW5+68aIkPEkoMbo6+Y32kqrqtDwhrNdIXUQNL2l7iaAIDKdNfhSRz1n0XrFfUgsSwGa4V32Guz3LOoCQa7pmgQatDHIzM/psoKRGmsLPBYfDb0ohMlHKGZ2VAW5DtFALai2Bi8HgoZhkl54sQTJQISS1hWmscE3SEEV9o6NTIYzwV7cyqKmwfeF8cddcFITEdyrH37CYh3zKun83Iw4ywRPSTlACW3+YWy1MSIWrqCFzEfEb6S470VQD62ZKI3OpChwgHNb2pLSEIPudha2dmYD6oMEMQzXEcMU0jpmEUM37O+Hn/J1zvf8DNzVsc9gfc7m/AeZa9DYlH4XVmAnDQpuweC8HKbL8nEUTsrq5w9dUL/OIX/x3+8q//T7h68hQXl0+wuXyCabcDaAIo4ZAz5nnGZv4RA79BcuK3MBbW7tYOJhAe1CTz+0rHcIa1PAFN/ITSJwfQZ5bedZ09zPjfx2roPm7GPmRq4TotbDlvLo5191QTRtT3mqvuOMfB7O8M2Apqc+8jbIXEeYB095oi2vk+03s+6d897z0BPErLxvQQ2/d9HAGBTwUAOyL8xWaLcRiWqBsyXo8zfruZwdsZtJ3B+0FowBzp0EBzOo0rn4WWtk+lcxNDfQY5vWnCiBjXLQoh/KmjmlL7fnMDnsSlCSvtCGbMcwZmwnb/wulZIngcMk+hUkN3rV1zfys0Vgr0o+ZlUVRKpNbM2QQPlitpHDcKe67uW+98IDDYnReYe1uuaB1CoV973fFRIsI0Jnz7iyscLnb4PijyFASe/HerJrhIJ4QQS4Z8U9PKz7I0T2/Oc+/HigKh87b9gru11pTRoy1xuZQkNFU04xMECutj1XO71LZNDaxhH7WwtzA2+8xrX9TXra1b5+o66A0s1XUf7eey4c7XwBv1e/s8uN93KoJa9UiRxBV0GoSeNysIOV/sW6Dnk/LDiDClDZ5tn2PGBnT4Q0UH9rt7fl8fYlQ+iCCix+Q5v/DKs3fs/VoVH0MY4W23xC7Hd8Z8HHCbN7jcTvjV1xOuLkaM44RhHDFNGxzeXuPtqx+Q31yrRji1VQHQvrOxm0sb9fW5bN/eVEKINtHiiK46GYvdZyoLE98ubg3Ou1ZTK1AxMLvcBUGScijHcZxOAByri8xOr8OYTr3BYxTNkcKCKxdemEsKjVVLxoNhNZYP2i9/b5ejcvhMs1dqy+BZQvbKfJWAuXC4ALh0NpzhiwGB4ZrarhwGxHBt6/4lxijBf4N4I2qvsTBc51yY6mL9IExB99Vu/EEyOMQENoPVpQs7OzilEly7Sq5Y7Bxnh7FaHzpf4nOUXMCzSHFN6tg6Xq19iPkiRBJgOY5VXR+B3K2OabrbuSbCmezzZXtIBieLlr4x5xHiYfT6kNTVzSzjIog9IZME3xVvBnamsOTNGXk+VP1xt0DsqDQ4ak6ENWTj7lpLCpuJumLKbGaHjKKJQU5ACH/Y9oQJYRokiaDvIjHFRbNJF5WcP7oeAsCssAYdhWr/iwyPHBZA4ErBPVPZq/C9K9+X69QsIEwoB4hghInh2lK+DgBOFsRc9vicZyekElSInakR/MAFVdV9Ge8IuwNs/ZKtgjh3kdpdHqzkw6jEaDjvKh+4iTEMI8YxuRXN4WBxCiTXrCbvwzAUCyzYGaSrJJ4t1hLJviAicEK17kpw6lSEJlxiQTgx6C4RZd5V5iPlUOoZhoRhGDGNowshwAzOB7x8+0fc7n/G29sfcJivMR/2QM4Qj2vxzNJ1llkDk9mCCYNKCWkYMGw22F5dYXf5BZ49+ws8/eJLfPndd/jiq9/gi69/jc12i3GaQOOEWV31cZ5B+SdMfI0B+0CXyj0hW+10YLfFyo2H+gdIfz7CiMf08dIDECL3aTWes2es408/fZg9v9663seO33bG83Mf4k8wfdxZPyM9NIDviZfRpvP4F6sUW5MGzLhApp3QFbd7HN6+Rb69BRS/EGtOjWnlfk81BoTSvvPmBjkdBA/LGTNnLWcuQrMqZMwuJKCcMOx3ij8r1ErnWyyvyOBe8EwVR5w3N8BwAIaD0yKk8RaZzAiBsd++AWdxN4kMt4KN4zTwhGm+cLpc8L8ypOIloNZoj6iXWDyzWH9ngEmifLMCkhAVPK1vKJ+aGPAg2v6E4GMVFR2ddu6uAYHrkGf89PZnbHeEb3BReNVV44bsUeE/rN09LjAq+HIljGgG56hAIw4iAtnQDkqbelLUNQWZKu95G5LWv6xkPAMOosV7Qm+cm7loGnJKiZrsXWKe6j4E0roelbJejpXvwbOA234tFne9NupV0XynZY+Pr4c+WHoidN49xMF8/zqM/pV9DYkNmYD9syeYxxHjj68wXJtLXOU3kNKxKqQgBsQFsXhHGNIG4+4F8uEa+fpNs0fueRk9wDC9H0HEGsXGqJgJ79bGkXf3qPzjkBTLdEoDJXPCPu8wTSP+8psNxmFAGkQYMU0Tbn78GT///g/Yvr3B7giBsmo22mi6rpU+Nv7VpVJz5g3lD+2Q37n3S2Xmum2GtnqsjlYY4ZpREQFpC2qTkQnXZ6ZLZmfAMzwAabcnDmdpW5rSE3dxMNdtCSPYkDpF9AS7g5trsTHcCiMUitgZ8iFmocJUZh2KHNYFAYHhr1cbIcSQrZE315iP7NiAmCzGwXtVLzI2NzKlw5jzLK5J3EenBqS2oNTJkFWBMyuzcea5uEPhgLr5+URh3QQ4ygIOgNb9NYSwiyjFqmw/aH3FMoT6RZSxzqTa8WyjFNsmrxsmGacCqzBUS57CNBfGaQqXNUECKiysUdRfssXgyJl8yjMyiLUcFyYvUhLlpgRIqIiyvoWxr7EXbK44w8yTF2eN3bBdpCaOV8A9FHs14wXLINYtwvjPTEH8IWPsVxYXF1RmEZMWa5fCHiqwMBiJA3Dm69ZTQkrquinuG4+XYrUvU1w7UUMr58KcZhTmt49TIhAnDcAtPv3NDZvQUgROCQMN4MRlXRiy4/BQBKQCzPYT2e8gjIiVkM9lqNXWQiC1yOsr56G9GMYR41iISo/JoGDNs1jfjOMA35dELnQByMs5oy9of4nJcC74bhBAWIwHMULRIOTMwGCBr8PYqTAYqj1HGp8iESHRgHEcsdluMY0DpmHAfr/H4bDHm+vv8eb2jzjsb5Hn2c9HIkIawn5m63MGkIOmjO1ZbW/cYNztcPXVl/jiy7/DX/3t/4DnX36Dr779JabNBtN240LUwyx9EgH3jC3/jIFfetfcN7RbfhTLEEtnX+8n8J+HTPdh4rbL/LPnAT+mzz59SOuI6NbynLSe7+E3eiu4PzsJ+hOUbdBlViwbREB6Hz4dQR0/m/TJwnxPwNZp4ja1yOgDwnLONn+wxTMg4wqZtgAI+XDAzc8vC82U2QhE2T9ZhBFkinCKj+TxFvN0IzHqcgbPs1qgzxVdmjWGXc4ZdBiE6V+p9xcayRndAQ+sVSAVh59ukaebJeVs8eIIwABkeovMwCEHS9ZItzIwHXaY8sVisEnjpJHSRWT0E3TNxGOCAMokaFI2pa3s+HI1VZEh7YR2dD1t3IIoaqBCoxYytoK3ZbjmPOOnNz/jikYAFwFvJdRDHL+tLMRmbroCiHr0vKnjyZDv4zRRhGMtLYekwVfP2S9Uf7nL/ct1BWVu66flWQgwHXvvTZYvDYjUedxGEEGnL/3alg87s+p7tH2xrLGqQ+ms9ezrliDra0sSrzW9AlV3jN8lBQBO4SnVPtYJ9+3ICfOTK+wvd0hvbzRodeAjGV/FeVRU9iMlTOOE8fIZ5v0Evn7T7IPObH8g+ub9WUQcUx9b8pAeuO1+/c44bmE7pepWMRyp1PMBEyPhNu9wsRnxm++2eLIbsZkmZcBMOPy3n/DqH7/HfH2Li+u3GK7v67OZw7+9tw0T7RTWXwk27H50/zfwMbWNg86h4jgde0WFwGm0zo8sufgZv1PQGLVqOWxoR5TW4OsBG1vwj8hkXEJo7cR6jrVlS1aUqRXhUx+cs1lCGKLoQMj3RCS+9t0qQS4PmZLIqoUruBhfOMZakCCvWr86tfcz0NaSaXs7oaeIiQW51fZczODZCvPXfNfXS489CBrZWLVaGspgN2Vdd0ejWjzOMPULh7vEJVH7xNpdrn9Zj2qJEeZPAqKVOWag9A9lXOLYex+Yq5YIBUwCaZDhGobIUJV9q8GLM2nchgZ2hgouWtGDBoVTxl2t0S8WFkypMEE1wHOGBYqOF7AIicxXrDH4SQeYyeZEGb8Md0kV+y5SE7STEoCOF7K5PVI/riCIG6rsbnNynpHAyKalTkCOCH1onZXwyo3RRll2VDBZBSCTnjPtyHrVCUm5/QISVfDX3SrlypmoQfu0+pSKELG0RV422fwlQUuHNCCTBh+HEmEqEPIOWtdsVWdbVwwnoBrhncjLdP6rNcxhU5V7AAiusjoER413y6+BEl5cD5hn4M0TxmGUvU1zFsJWz0KzWjCkX7TXyvknx1NGhNLOOGlN1ka5ekSjLms/zQrJhLYp1GH71wQBFoA66feUEoZhkL80IM8zbve3eHX9B7y9/Qlvr3/Afn+t+4A9CDkaWHMWAYfEXUkYJmlj2k0ShHqcsJ2e4sUXf43Lp8/wxa9+jafPvsXX3/0ldldPMF1cYUgEcPFnLPFzGGP+CQlvkfha5pUtno6cv0l91eUPjBu9S/rz0Ch/TI/pc0onaIYPkZrj83wGc0gL3OAxPaaQPvOlQUTYJsI30w4Xw4REXHyLKw3wajjgh2HG63HGsJvBSfH3zR45zeA5IyMjD3sQWHBsFKUnty8npWcgdAQRAQPjsHvdAGUKHIPTooAogwQqSp7Zk/EAs1gW2MsHqc6dVC3KUqO+M6v07ModDNCMm/TS2+HhEBqNChjJz5gEAnt8uKw0m7hlJY2UbXCwWTRHvC7gU4a7Gn7MQBUjgo2GtTxBaBEqbMZUW9GYaMW7ROAJIP4MNF1VT2HaUpgFL9Npf8koty/t5jEasriuIhnIe6VesUIrWZ+PbeACz53a8QGiJk/NtzD6powPLehyH70KhrZehClsqKg41LGORTt19TF+WqTDljAsa6mgC2Wp/mcJY1VHp49dWJt8q7zKkq86Q9ol+xB0Qn8bNFmoou9J2Qk27kldkNAgtKTRhMY/zKznbGbxrKB1EiXsMvB3b5/ix0z4RzKvJ52+f+D0wWJEtCyYk2ntPLpLg21dKEy1e9VH5cu5iOtDCSwyEw55i2Ec8ZsvJ0yTxIQYhgHjMODw8i0O/+H3AIDNUlX37HRWryxTZ2Pb9dUrInd5rphj8bPwd47s1ndA7iJjVxvq54v9CgdCYexCtDSWt8yitUqQ0UorqzahzPKmg7TcOzXYVjd0bC34ctT270BoCFI4flopuIEZp8sYyxYE2hjIUqq4SCoWFNbn0DPDyey0Vwap8eh9eGqJF+pfKMxplh1J2qclclDK5myMVq6ee1BtJmWGN1UozO3SdSk0x6wEJHOFVK8JDto9fTdcLejBDdBiLpdrsBJmNctR3PMUTe6lZr6tUTHjQ7sPSN9rOQuMW4+NakEpQcGsDHZlwCJnETGQmCYbw74SMgIgUnNlInUbJIzPImxiJyAWAkIbgrCGxE1TAgbH6cKcFEHF4LvNEKRotRIHNYNzAiW2ZWNUgGo6lTgcDKiPf+kXMCqTXeEOm1KERUvLn+o3HO1AKIlqwpWYqAVlWeOdxwWifm1TEnN0dcOWkUGZ1PqGUBMT1k+2alc1X1kPJ4ekVQAIPSixOJq4HdWtEhFYciuay5sBPBP2T2fwAKRhBiGrxl2AJdbnOH5ZU2VWHCpHvk3Ly+V3dqbpHjYBnbmxSla3frJZ5ajQwQJRj8MgRLA+JwLmwwHz7Q2ur3/Cm/0fcLu/xuFwQIK57BrEtVZzVJmbL1uOQ5qQxgHbJ1cYNhPG7QWePPsV/uZv/8+4fPoCz7/+DtvdJXa7K4ybDcbNRvZbVpd1FnuHM0a8xsA/246AWV1RApgsDkk/rV7bRxUZOodwN70bjnVMGLG2rh86mHWvmfU6Pwap8Jg+9fQhLCPe3RLiXdquf691s30ey5Vb3d9WH/cH7h3Ln5FWSeJTKpYfIb0bJA/Yj3tWdS/B1Il21+p8KB7B3esJ9ENLW+iamojw7bTBNIyKbBjdJIjHDRh/nGZgM4O2Sm9mII8H8MAee48C3S/Yl9QRPeGy0l6EhJwEicnDDQzlF7iSKLakBMEqBX81ZRfj75B/R/VX6Bh4w4UWVfUchSkno0uLUlcmxjy8dZiN5vSKFFjSMXSsNUl7WQUSpIG4pVkSTaWkJ5NZC4d5iE2wwavIqll2CF+CVYGKfZRjP3ukobVT/uC4bsUwaJN3jvwjChYWQgj/oG41dRvL9iIuXWq63z7tlarvjUhzHE+LXO0FtMzQ9NlojPKbtJ4q0DSWd3tZY2fu/UYQQvFZC1/LEAptCs7clGlh68LUW0fN/gn/3n1sV5JvmuMpgNB5c7z82vkrFlE1VSkf62vX9rcozkOXiPBvkNVtMiWkRJjFHxNqTwOBRtMKCcDICV+/HQAa8U8gOSuCG6cI3gLek+n+d+aHC1b9qSUuriL8ET49Es8sIXabAX//3QaX2wHTNGAYB0zThPl3P+H1f/gd8struYCPdMA11Dnu/bv12JXl74P08pLxWcNn2diZX0CBsTDyl9YeZ/ejA4AxCntZWyFCaBD1BbLSlNM5NRuxgBJJomIp4khAqJs7Z5nXrlrarL46RRPY2okatMEMjiBBtKyvrKgLo8qXoBrdROqGJGnAYtGgECYsR3ACJ7jqUeeoakjCOF5H1ov5p0+uISP1ZzCSWViwIVga3JjZtVtsPLJz8gxoC+DbsyiKJoTa54aZT4ZYc3MxuyBGL4vY93ABxDOIs7I0ubaIqNC1iCjKAFQMV3Mbw8zBX6AG/SWoBryidCr0MAGVMSJF26gESWfdD5zMJRDBtWHMnytn5KBp5OiUMltTJuxNEGNIvnFQFb1MjnWjwKJzkJL4SzRBEJ0hfGVkZHUXZaauUIFL1jgjOZcA56GgrIew1wWsKHBRDSpSg+zgVcqY4az1D6PNTVImvgWotjwAiLtnUu+cs3VvRCAIhSkcADZhDgDMswrudB8PwyjCH8CFmPJrdtdBvgaSCnV8NopKFpMsEEIRckaz4hrwglwbIQjo2grMYVkSYU3rp2xhOYvSkMCDuCkaBmAzMfKQpU85uxbJMI5hAqPrNrFgGgC3lIL6IRb3c2FNKHGdjcj27uj8WxR7DaxtB4RZP2w3WwxDwmaa4C6etI43Nz/g7e2fkA+34Ntb7PMbcJ6RCBgU1kSo4j+1xMQ4Jlw8u0IaB2x2l9hsn+DrX/5vMW0vMFw+wcXVC3z7q7/HNG2wu7jAlG6wS78HZQJdl5OQWElzWRQg3MDfMvt6t7vkvjaYn0J6H4zTx/SYHtPnlIxoD3cVNffWOcfE41HyaaSPOg8fkZuwxv87azxMI74UIyLM+wP2L18hH/ZqZQ+Ao/UoK+NMkkaag+BpxTWog8AFj2BVZiACkjHqORUAUHArhy8GhFYa0Oh1J5sLQ6HgzRo/rVBgRUnGmfDadtL6ONApEsOBXAmj8CgMTsVQHa+M70XJyCyTjW412sE/Y4UwoUZpoFh2FPqVErubKfPwYGSt0OhcwdnMePlOhtMr4U91PsM1AydhIYDwOtvGGIvx6nzppp5wvWC/pxb2EpD1Uufv2SonUfdFly+ldEvJGghLx+nLDvT9GPH9Zs6Owtm851g21rUQPHTG3OZ6Jc9CWW1J9HV/cdO3iqbpdq+3uI6ko0N03pwf5TEee8WN27SqUAt3u47Yszi1LcEdcfPFU9xebrH5448Yrm+VtSR8sczkFhFenTIYKCVM4xbD5ZfA4Rr59UtUh/f5vV7kve+V+9EEESev6Q+NRETufAvDAtDzDz4O/9Y5jk9vud4Jc95gSCO+ezFhMyV33zCAsH91jcN/+V5yHtVIrBmmve6+a1qrzvnSkel8bAiPHORHGQY9ADjoBKwJIbAyo4YrHbuy2japbqdvDWGf9XgstCu1gfOmyQ4gdkSxO1YdpEHaNx3rXm9JkQ9hyAGBMUdUuVwpc43wJNazNn+0mCsbo2IRsOwzyEzVCO4ayl0riS/2Imsog2yM6xRiT0fcspoev3zrg9byMJqxjgJOq9vWAUKh0K4UKw85bNAqbonBoP84SqhItHr7D6Na6wcZUivISYIzvE0En9m8cJWasggdrD7vj3dCYnPMNr8OLyBmC6ne0+bqZjbrE63N4160hAOcOV2mReIuuGBJ4yksdotSKHHfEQnh4/xzlMB0nBk5VaGyq3VhwoLwVudfYlpQQDLtLHCTyTxj8Fc6L4k12HeTbP+mzv43qgthWLluC0n3ZrPG7B5ITS/MRVvKCVlNTTx+BjI4FX+3SaI2l9bDAUpAJYxwkDtd9JEgYOEbVNsvBGizv3QykhJ8JhRNxEgDMPAgRN48IlOGRIYg7ye7wIbsCygnDTyY1ZTeBHmDl7NzCiq0szgrZU8Vk35HsgEXOKRBFAjEImKELRfOsj72h9d4fftH8GEP3t96DQQRROiI1cQJoQh7NBD11fPnmLZbXDx9hsvLr/Cbv/k/Yto+xXj1FNN2h4unzzEkwpAIE99gnF+qX2ez56ACfLynulNo59TqJB9Pq+VWb+b3kurA1Hdr98itdjTv/VCwu7R2Zo3vOMwPiUveVyi0TpDXuNfd6rwXKI/pE0rtHXhGiWbi9Rw6p3wnT7gpz0qndjedyHeX9FDy1/Oq+XBn+aeQzu3tUfoy1FPhevpgnTo8k1Hnj2uacLFm84z9mzewANWAKL+I110u+LHVwXU9im7DLCGcUnRtPcWdLH6d0WUVnqP0p+FaZHiQ0H+Ci2WHw1wCk+FsK6NQNO0BZsEnWWlLU9CS7S94oUBseFLRDHc3UfZvwAmh4yT4LhcU3khiI53sfY+O8VHSMSJX3QGYkBODs5QvNPCit51ncFiFFmqVSihMbphjf0X1d/954tRriORzLPn6Oc44XavNVOPnd0nVXmzhPdFv8oHTP2rGrYKqpiVqmtLqK+v2eG/qd+6GewF3XDHUnQ9rqu5j/7v3ZFFP/TueNV6v0zp1GR//dludMZtnzfdqppWxOCNV3hJQ+sgdzGC5dmQ/Ob+Q2L2xzE8ukXcbTD+9Aq6VVlQ+QLSIMEsJcxUudPCIafcUfANkerWg8+7ax/vmt/R+BRFcbVuLcVpddqfSQ9MBC8Z2bMM0OtG5CBaZT7VTGGb3Spxwky+wHUf8/a8vcLUdsd1sMG1GbLc7HP74M17/T/8R+dU1jDt2V4RXoOv3tTXzLoKMwHFaTWWCswJmmriuCNGMizBXAlQsWrcxX49ALQq/eskfgYiJqt8xFWsR/VTN8gWcrjEQ1vN6pQBKgGrmZgz9WSByQn+MgUwphfw6ltys4wx1ySQawIYw1uMKvdAI5p5F6sqCehlDmEXTlwFpmxmDXkyFcZfASAKHTqo0GwRegQL0ceRwESqylNlG2oJt285hryaOm69zksM1qda/YXTFHI1LAF4TpKRBh5nKcEDGDaYRDrKQG/JLMT4CYVBNnOSmDzJ+zgC2SaR6nsMbD4IWNcWNkRnXF4LrqTLPLHNLEVFQy4REICYMnGD67BHfEcZ2zZSvr3qqLAt87TBjnmekQYMXO2IOUGK3khE3LoSsaKysEHIf/WkQZjHGAcgJyZi5WYiHGAxafMQOSDRgGBJoFqkBz2oZQQAbdYPyTJj7ZbCzm2WUZzacDAINSXy0aqyR/eEgFhtqMUNDAniWGBLJBHFanuDxMHQlgDIXt1xpUA0nEgYvC6N3PhzcFQ81SD9BrBkYasqeWd3elPkmEld9lcDHgZKfFpw5qauflFIlzLH3NtZDsBigLD56bW5kCEu8DzG1Z7cmsHVr8Vpcyt1BQPvnZS2EqGL+OJZc9itZHqhANBnxKLBlZmCQNTlsN0iZQYdJji2VBJnxDWmFDAlYziwBnuXcSEAaPIaDCatmtSJKw6j7WOfEJ1IEBxNlF7KkYcC42WEYBmw2W4CBw5xBnEE842b/I97e/gG3+1eYb15DfHeWQPHEikxav2lEGgZcPL3EME0YdlukYYNnT/8C291TPPv2lxg3W2wvLrHZ7PD8i18hjRsM0wYj7bHBb2UOZ4Cw97XEaOesmqh+4ohc3zGdLPDQGOB5qUeE3YdBfnaJgjB+hPSuDX+cOfqXmh5qbd6z9djqB2rzoZPhn+Zb+QDQHhEJZ1eeKFRAQbcM18vL+zek5lo+a5csmNI9zsta+hynpoXzkzlK7nIgd/bjg8JS6nwfw1PVyRBGNgZkeopMm6BYobg5M14NM/4wHnCTNGYVW7w8ZZZprC2xGmYAGoMtzyCexVVTNnqLA10oyfC0gu/on1mPmkWEw6bCAzZlNBYts8BrYIWRuaHtXXGMUEhtwSehiiaCOyfROM4S8yEHzF3ccLIqORXFlKgIBiLH64Vh38G2jEGmk+3UYGBae1anHbKgqpmAZMpDSudp7D5CN5phVRcx4+b6gP/4jy+x+XLA5jkUj6YCSxirlrdQsRlQvyilmoz2vFHeKa+X/faky813G4XnvW5Sp57uRm3bpPbNCqy9BsM3/0cJhjAu8HUOUKeO6KKLOuPndfux1dRfzcf6KRIhXhMMmdVOzbI652TqwEBrJSmM2eJp/Wyh3HrWJHfyr6+18/vYNs1l/zZgtHvkJHhRSZMlNiINI1IaMFDCbApyyKAslhMECG8rAS7EHRKuMvBvXj/F93nGP4T+FQ7bh72KP5xFRGc/nJMe8vKtN/2pdgODPu64uJhWqjkX4ewKAOyTCIwNKE345ukW2+2AcZowDCMGJBxe3+LwTz8AM+vZVhgBy214fCP2YInxEO6XDDEIjGU9vSJT2towGCh0gl0tokDag/7UfNq0tbnKdMZj1Wqtf3fjVhBWD2uvw5m+vCAW3bzTCJsg9BFNjCNdi8ILAOYexvsTl0W8pEAqbY6LOYyECkvcCsGRPfHtL4zqBHHxo8iar57O/KgUoXQ9YANs+jEMjx0ShRa9bgfkUZS+Ewrj0maZ2+ERP54+XxSeA+Kb1JDW2IrOGQU0ToUQxsRljcuxZAS0h4V3oOwJMkajwRZwFV837X4x7SO2IayQjURCAoBIXTGVcavu6+ocq9CPCnwTAjGEOcupLsxWJumf96+8z0akaMwHIstfhBH1+rMDQMBImj9b/A6b3xxg0TXGqWgMWK0MW/JNQDvbIEkHEiI0NJ+wJnibyebgyHkNJzdKG2R7hSF+pGbZW5mRkAEVisUUZEtllMNBUAgzZaLEMWjhsrMlrP2UksdJEXdu9tzqLUILyrMHWG+vAwZknNSnrwiGWOJKKDzmcMh17Kl3nq0jYyao85F3GCVjsj41NuQuwExAwqDud1U4lpZCD4aayevJm7MRzwNAA1JSi4g861q19o0YllYTFWsCAjCoZhsNCSkN4oopjRjSiHmeRRiUZxDvcdi/wc3+Bxz2t+DDLaBac+EAVxjl7B2GCcM4YXf1HNvLCwyXlxi3l/jVb/577K6+wNMvvsUwTpimAYkSpmkSi4yUkPgW0/xK45ZE1DNORTgH7pDOzX4XxukpTbm2rhK/4XgbZ2ng2fnJ/fzlfL1fWjmGP7MU7/dPJz3EeAY0qPv8/jN/3vrrp4BPv3Nd75Lu0+a7jNe9i66CIXdFhsQ385tjmbV//Zc8D7D+l0KIHk659qs8MW3uUPGyrXvCG8/Dd04r5Nw7E/xVve+2xz5muvPwROTMca5IrK7fiRF7cryfNiDaFtIRZYXtwfh5yoovs+ap6QIohVhUHDIISi8ho2CGEFqQi4tVx/HcAsJiEhZLfIBcMaXQlOi4gYI/UOqh2WsBv1LCgBRiGzP7nrO4KQahoqeMdqv/SOnOanRRFLzsSXEVRKFCsop9PJpziYBEDGQRvmSz8iZzNXXsXi4zWqh4IM+MH3++xdVujwnGRNURceYxxY8AFXmN8VERpqxAEoUQlRJSU1e3C2XUuHq20t2jz9tMsYPt2dtrI8zR4uhu6I6qk1HA07gks9xlYXTaRZkMnae4J7qumSqafyV1+70sJ2v51Dm7OESOtbzo71E+WzPWi/6eOMqXa+xud8aCd4rmYFBhxLEhWlzX3TFSHgpMwTg5DwzDCDrs5TTJAFJGRlJVbvag9QbTmAnP94RrGuGHo55pxxyXva/0LzdGxJFU7q17BrbupFhPYHNiuYwTbuYLTMOIv/+VWEJcXEwYpxHb7RaHP73CT//jvwW/vnGTvnOIWd+MgbKqNuiayxxrg3F6RzcNlg3JbmHgdXaLBDahf22D4rSpQkM6r8NBsChl4BBcuxiI1qdHmu0dyUHY0L2nqEIEY15H3Fi1PsIlYNYA/pnLOLkAogoGpgxCb0rrNI1ukk6WuAOm5ctaJ7vlgyqYVGhL7LXFhyiBsUOAbJUGLJFfaSezOhKqApjH0Sx9l/9LnIJEcZwsI0FcAQWEyBAhv+wDMhUQQWOAs2pDF81ugyk5slYwdSuNst6rroZIbIAzjY3xXhi5UETc9m9hNCzqDEI903SxwNJDID5Eq6n01+ouFiJhD8S96sMjWvn9dZxqfFHnI1GI2+B7QS9PY/hTWQ+DMrxDh8BgzDwDzJjng1SvrremacKe98jzjDLypFs8zF3KIixCWEsMJ5gicp9INfzDechZLEAoMYydPqj2e+bse8gFMBqAO5aPCLFZRRiOaYGxSeNSkLsUi4OdkJIEns8aOFiCGcs+FmpIKI8ST6EgtGaBltW6IYnKFigJ4z5x0r0prrNyLj5rgcCwdwwh3FlC5WhMDyoMeL9aKkrCz5I+MlkjxZ23iIvVcH23zCqLGAyZH9G0M6uchIFUw46AlAZZW1XT5OtSxpIxg0GUBdHLs2rBydk2kFn3aMsmBNN+DBYjgjaglLDbbkEpYRy07du3uN2/xKvrfwLzDOQD5vkWh8O1xCrRs0zM9EUIkibRfLl89gSbiwt88fxvcXH5BZ5+9RU2lxfYXD3FuNni6tk3GKYtxnGHRDM2+B4JWc8IgA8MwgHFBVNInyI3+TE9psf0mN5LMvwkKq60OFzgx1S4KKo772FSy46glXfn1NNSO49n+2M6MxGwS4RfbS9wMW4wgDrxnxSHHQHazIF/wGFj2J8IH5AldmHOGTzPbnUPQOggIlAmd0dahA8EUQgBEg1une4InG0NxbsTZQmYbfSXWUYUfptCanSA/C54KpS+N74AiyUEm9WstBu9RawMI4qiCmnbpu7iI+jfQBRCoRlsyespB5FCzwx25SztKgEzrB6zzBDfnwXKgjsf557EPBXp5LR1ydpYbiDkq5po3leClvr1XXlvTtJTGNN7pwgPrcBS6M/FGPoz7V8KoxjelWkNMSOiYCaW6T7vigbkX2rbPNLPuuQyF53IcUaMxnPqXb4/Xe9dY2Ss5DojT69Up0+g+kyI87ZGYx0RDDkmENcUASln5JRw882XuHl2g83v/4ThWuL4cQhgbe6ZrB5R7EzgnDTOX79nHzK9X0HEp6Di1T0/ysEPNCifcuzs2aplxNnJAnuek1Pd5iQRPHzxZMTlTr4PKYEODLy+wfy7H4GDaUzeAZy4CZoN0XfJ0OAUZ/XB/iVnQkeGKlfX4RJ4Y+r6PcC17LnicTV316lxODlO3AzRu1xmjhv066gYsLEMLbdNYVCGsdSyUQixtGIpiIScN+USrHjb2gajlpoK4lT8wS/HLzAnEfVMjKEHfx6rRcjjQ1ANE3lfQzPNe0MEI1QR27TgX3XDFc7g+Ap7e1U8Bm8pVtEQiEGAEYo1sIY+O/Eb2qc6BzH5dzSlrcYqOLEGuoiM7MVliMVMBJR2+dT+7WrpOdJZv7LgtbmaY/L14/1rECWzVhFXRwF2RnHdNCQVdpSzWDTZayAkWHk8JODDbfBHZA/hu8osZYayEFA5MObF7ZkSTQEJLDERIjMjIiK2jjySubSTW2ZDGWIdUQCzy9jsLHWNqgCzl3BhB4U1Wda0uCJiH2NfhrbevV4T3mkAgwCnrFHpt8WHoTDmfeKjjPHixG62cJ30QCQOtdTFq7LcCL3dlZMUMA21nFRQQUXS6qSzzmuCmbiz140gpLX2c/RFDHMVlwAaxQXXuMGgAps5z5gPb3E4vMLt/BM4zxDXX1m/a/wSkLiFGkakNGHcbDCMIy6fv8DV82f47pd/h6fPfondUxFAbK+eIo0jxnGEIQYJM6b5BoRDuY94saMfJPm2XKn8XOuEXr41i4e136fq/Dja44/pQ6eHlKs9yug+fjo1B+ds665OzGqFp+vr1tl7QXcN5LhCGx0BqznlVt+8Szp3HxTc8oxM75r+Be/NLn8ivr/zwVVw8ufDgI0qbojSk8WFYMwa2w1DBo3WljWaHVdSJB4wd79simfsrpmkQbV+9fgIgUZwRZpUgkCDCp7kdUjTBFGgS7nE01uOQotDFPq4oispjq2OttEqivH3lnF3aSspxMcyBVoEjucHusdAAak1vBEHKHQ6B7y+geneWyUIQijAZcOwoKlC/6h5sMDfwpc14UMsUi3pbl09umqt5/3Z4/Cqbx1MK98VJg7zGAbJ5tGFYBW93Y5NWIMRBBOSVXnq2ur5OH7QLvDhoxfp+rvem3Z3LKvur4l3TQX3FyhO5D5VmZGIq69jMnrYeQHHMp8FS7j5SX4b/Z0AHC63yJsB0/c/Kp7BxdrdNr1+mgcNIoBSwqD/MYlisJ1RHzo9WkRoWju63m17RE5qfRyXw1SZpiDczhcYxgn/+hdbPNmNeHK5xTiN2O12mH98jdf/r3+L/ObW47+eB8GZq2qBsKwgN96VeMhxlYGNIcTGdKuZtYAhGJ26HRbS+7UwZtcu7u4luJaaG80YdEUucP4ujOxVIDL+9Bn3mSBmPeAauPLmaEsmcCgwktfPbTtEIAsoS+XQScWOFXlW/JCz+vZXpNH8vqekzDdDKgUNtUlyjVoGOM8eByDCnBfjUI+FIaV1Iu9vQf4C9kZmDVEu49y0C0h0kXqdyqbx9aQYYdYYGTmLmXFmBhRBdqZp7flFYIr5w/pp5w3g4jue68+sc18HSbV7r/S5u4eZkVmN7zIXdzr6XxAJoWj2SEBcwO9WX3t2adWaKdS9wwnwuCUMdgGEuKAhkdQjq+a/MbFljMWnv16GSdrNqtlDyK45kjnjMM/APGMPYMSocQwIKQ2y/jIr/RL8yWZGptnXPHQ0ss5p0pgncczNYkbGXuYkswg0eM6yJ6j4xRQ/s4rwB6SwtUIqewV2zPtYyzJTn7JU52XOTgyZOyWZOxM4lbgoSa2CZKwVLp3HorGFYr2gum0WT8RU3cxygpmqsnJOp7IwFUizGLLdRlCNNkOWnKgwM/Gwn+JmoiJUsWHr30Qt4m0rPZXviqQxZ8xmoUXSr2EYdErMUkLqikKFDHEfkEGlr7lAk4g8XgfCGVR5xyKxiCBKQJrkrAIjzwfsb9/i9vAKb27+K+Z8izzfyDhmaRlpFKuXlLB78gQXT5/hxZNf4cmTX2D35ArjxSUuXzzH9uoK26svMW52oHEC0YA0TEjIGPMfQLzX8WaIIOtMLKCVaj2ms1OLBT2mx/SYPvVULCFMczCef4WuKIhbQUsNr12rmpe/HwWgf2bp48yn4+1OBj6c54a6nYT5MOPmx5/AhwM4M16njN9tD9hPM9JuVm18tZwW7Rpd+0rjZrGGyLMoWuT5gJxnscDP7Axf0v3BQ9I4awWHFdp1AJLg/jBGWmRRaEWUGMxmAUAgYlcsMaUaCopDC7wScDqgPDPcGoCfE+X5sUSu9BOf+TfBGxxvjvwRwVBTdOljOHlFGxqFI/H43DloEqsIimVXDis/+zwrOV9F4Erlu4Fh7Bv/LHRjxVx3dL11TdT06cjZuMonb4/YqvY+FXE6UdOnzs7yOyHSLg1DTunY4pqr0GUAREFP64rrsI2PV1k1VCCGufD3/TrbDsT1SG0GanPeJS1zv6uAYSm0WtbXChsq2p5srNf2adj3/eHyemwPnUdL2SrUET5R6KjbJqb6jNc1kpSPkLT+pLEtZz1X5RhmZPUSQomddwYWXsiLfIn//fB3+BP9jH/c/9YaPKeHCvga0OdXAbwvQURn8a0tyJPabu8KS7xPzi7DBsw9m+zNTnUV6ZoOzCcQhjRiGiY8uxjw5GLANAljAjd78Otr5D++Qt4fyk2wsgrY+xwZYe9IJsfyhUu72OgNq9mZcFEQ0TIBNWf1Sa0woprEO87LsXkMDPKjbpXaNg1x4oaRGMofO7KaVV/PZrVmi2BH8A9uDt6wVithBCrmp8dIaPpR/PMXNqtcZCLIYE4AGXJpB3Fpx0GzuQ01RYZl3WMb76XBrzyvV4PGZu4nDuMOQ5xCX+ytxYEwFqTjcrnAaIh0TE3DJiDwOW/GA8vccSsuhDU9fZoyx3UfC0zwQc6KgBr4EdzFmHHYX2gy9s5hLprzZgHg7dv6clTG3BxB7YPDio77oUV4KxD06rbyzLoGSxwO0nJsewGo0CqbH28ldNMQ7qVGNXTNc0EQVUjGlDzmRD1VtSVAxAcpDhACosRBk0gXhTD+6/mOhJAjr7rOivVTCv2wqN2lnnbuSywJO7cliJ2BaS6aqDrT2kGqHoS9FxdecRPVQXMXqYv0LX6FtWQIoZ1TNj4Nws5swl6CaNIpjPGItLIQRFBGMQhiwpkW/7Xg7MXdm42s5EkqAAPJ2TLPM3g+YH/7Bof8Gvv5NZhnbQ0SK4UGEI0YxhHDOOHy6Qs8+/IbfPXVX+PLL/8Ku2fPsLm4wHh1ibTZAGkEm1ANxXoj5RsQbkHVJrCpeTe8ppdOVfU+guj28Ihj6bTpttW7fLb2+6HT6Z3ymB6TpFNbatUP/B0W8el9e6quh9/3p9J5R025Ax3dd9wv5qvpjbvaMxwH4Yy6jszV2ZBU7QRc+IzUnokFw1rJf16td4JhNT3AVLwfu8CS3rdMv6IrqO7POwkliDASYSRxL8mZMd/egucMAmMm4PWQgZSRRqV/AsnktKoqxhRFNrOCsL/cKJAB5sqWWyQNpApyBed1Bj0h0An6gAquzascPirLMXxVpF4QQmoWvxBcgZ49PsHUfG/XXI2xxlkzHD3SR+X7/ZfV+euC2i81gYPCJyjvFv1YfgmPqH1VPT4CUXhUn9lUZTve1979ZspmReDTB67QN5GeqtusaTMorYCQv7lfqKkn0jNUw7Icoyis6t3zdU9MMBeKLPvJzW8v7P80Zc7UjF40dQI3P/Kr1LH+7pz3QM0tqoU7Tft0qqZwyzFXy3GtXGy7+57sn1K7rz6SszCnDAwDeByB233gSzX/clHcJiJsaMIXAK5xG2vF2afMA5EsjxYR7zG1TPb4DIAz1G7mSxCN+PtfX+DpxYRnlxOmacTu4gL55zd4+f/8d+DXN+IDYk0cbE/5+O87p4bRa3DLJ/xz2W7R1M+dYL6mzxrXvDMKERGtsoNLe+USu/c+YFacQhrPecm4OYnQGRLYHeQyT4XgsUJ1G1WwJoOJC/JizNXsFhH1hUU+jMWPuV1IEkchIl2qkQ2Gaamb6xV3xeKXGYEog1niBbgwibMrCmetx1Z6PTyKqDpDj3W8jg+qjVPO7YQYAiBNydHaxDGgpC2pdrMiyUk9sBTTXxvrYg1RNF1MoSGOrVowKKJaNPk7DD/vSeD9IQYAt5dalzGpXbgVR3C9fuuGaO9ngEUjZhmcqlRgRIOZiIrlSyPp8bUl82UBjk0TvMeUFtyF1I9rUtworH1lyBIx0lD8vPaQoGRzqEz3nDPmOYNIrDnGccB+nzHP8puJMCTRBsga30P2QcGpRPOckTG7L39jJDvCEASKvr4YgPrYJ0D2h1p7JLCHv6DYG9WGKQQa+54jhlsxmJXQPAssKZW5z5nBfACRBDrOeYa0CMzZhBFlOoQnXawtrJ6UBgljkWQMsm0IBzWpmy89q9UywvJ1RWUd5LGKfZNFuFJhYVzWyaIcrZ20FMoURCwFAYQIBMQSx7ToQHALreQBwUnpSGvPzsXim5XJCNwE1+Dq7L2kLgJ8P8Q1o8R2zjd4u/8n5HyL/e2NagPuATBoYFAaMAwbTNsNds+e4OriG3zx/F9hurjE7vIKF8+e4eLZM2x2V5g2Fxi2GwzjBIwDmBLk2M7Y5T9g5LdIGJCYkfgAYuCQVoA/lh6Ac/K+GTCP6TE9psd0nxRdnCo26jRHdkE/3o2ueKjUapV8xPR4nLfp05gXTwtO1inWVp1izg0l/NX2W2yHLSYakXEIdUrw6Yox77iP0IXgDKiFvAgpJGZXzjPynJHnA+YsnzFGxJASOA2gPCgum1WIQAVfSwklWHUNf+Qb2D8uFIl9JcPUue4GNb9DP+vYgVnpgrbeFX6B8QhgSHmfnjP6SfoTNOFXcWMbc6Ov45+8C79ix3C2Ow2L1aEwGa8B6LJoK76MM0wb3kYbS6Cv2d/CvDYCpw7q9ZOrywCnwJMqj1BZ3Bs0nfKVsp498bEglNc+oqUfVbtRYS3wPFBYB1XeBp4CZWeyuuuJqn8rcqsdY/ve8rKi4ORIamfk9BXXW2n3TeuMlPudlr16ywBVa8zPi2aP8PEeeakw7tVeYXG3nMYJ17/4Gnx7i90//R7Dza0zMDipS+nMwBBwHErCj0kDLAZq6cmpEXlYrOC9CiJ6i+x9aMi979TVIn6IejmBQRiHEcMw4cluxFOzhCAC3t4gv7xG/uEN+OYQAt4Uxgd6a93f6dJqh7y3b47BuWzqdObCKV4kRyR6TKmT4C2O73sh7NVQZfaLu26pOYS5+mg2bqfi8LASQjg/OgSa6lTi/yqDS75aHeXSMziMmdbcVNXF0lozOCIT7hEKmtEVZ4khAcesXJjgczSM6iHo97u3Bpb9CPsgMF0L/MGGRvuQs2rTJ2tbBipXfpPaiiqRBaxmnTntRZzbc9ZhRHCPL93FXC1aiJtfBRKI9gERemNQGyP6aMPhvtQ+h7VmaBQvNFLMDU+LQJX148LGJqaA95UC8qvnlwSPF2FRImMSS3npcztKtiYy0DCU4z6sNP8bDqrSJrCb328AKvOd1Z0UUOIutONXkQdqLm5wRIFTQTwNTrPeiLPJvmehJvFiGRFh0zHzvoW9gGC6Xc1bf7/FvdhdLQXYetxQLD1KC+h894YWWjqOFpOtY4U7zpe997PLiEzq4MhN7fasg8CnwMTvGW1RSsU1HCn8DMz5VgWbM3Le43B4g5lvsM83GkgxI6VBAkmnAeM0YXt1gavnX+DZs9/g6+/+FbYXV9hdPsV0ucN0sQUNQoCnYQTSAKYDCLNaDM4Y+AaJbzHomV9iRq5guJ8Ic2st+b3zQdo6/vvMWupvK3V8jnjv55Lua/5/bE4+RByRh14T71Lfu8Pyea3vRX8X/SfcZhHovr+eHauZljCdWpNH5/BuvVir6n5jcc8RfMeBX6ck3n/6EMd9hV0dJ5rXU5M3IWGXdtgNu+oMZDAOxNhTFuU0x/0rDBdl1IVp7+8UHy+aucE1E4BMhOTCDONbhE4lUnSNVvonZVpcdnUaSBW/ULrBIRZipPai4l7rvq0aw5afgeCWqcKR41gF3Fb/XeiEKbxLBo8Brt/aaYj577ogO0CUoQ//tnMRHq5ZVS8w/VjRgnnbee7v6+a5hefcPnv7haYoKVg0dOBYCAqauvy5xjNpqehIZwOofPhXMIW2axBaqqmzeFqYVwRRVH1ZWdT9ZuF98UOpX25pWXjqsHo4PKzHv73LrlhXsuoSWuuVnJENQLW+na/n68XWu/G5AN5uwImAofA8NGa1fILdiEi9touSIhFGDNgMO8z5gAPv+zBy7+HDpEeLiBNplQnzAOk2X4Bpwt//aocXlyOeXG0xjQO2ux3y61u8/H/8L+BX18Bh1vUbGHrtXbYGfLWCebnzjpZn5DOyOp/aL/aiTRutIaLf8XLYtj7+EbrJer7ZgU2OiPgRfR+C0bWGVeteNaJi6kvMUXAuso6fbt+0lOMpZozcSis8IhQAoHEYsiFtxlwkACTXSdTqznbyNClDPJMUmCHCl1ysHGwsbV7s4rUYCBZMVWIMmIa3HYZFUya27oxpROTL1snyRC919pA9QrxKbP7kew4Igblf0jn2Na9rL9u6sRgH0dLDm8FiXl1Qpb0hwko3qv5Ta97LFpdCxpizzeeZa8nB09DHXJBluCuhTjkDQ130zDz7mBElcVvFsl+L9n9YazmHPaF7lx1VFz6r7k/T+Jf2svfXLQAOMzixB7mzG96071koDrUEyEgaWJjnDIzCBE5DQsoJOTPmbH0ZfI5sz6Xg4sgEMcI01tgBSfqatF3mudqrmYDEhcFLJO6nhK7SWCLJAnXb6NT70JaTBTXO1VjW8wOIdcM8SzyPIpCgBTIsFkMzAPIAySlJRYeZZb/q3h7GMawudosmIl1T0dQ9JBN/1HuWHAFyc+aqL7omNGq5hvY4M/XOXVmnboFglg86c7bmQECiAUNi0bBjRhpUqO+mw7q20wi3AAtN2zoCRuRs515wCwbGOEq8HXMZdnt7g3m+xav9P2PO13rmZHC+ATTI47CZcPniKS4vXuAX3/53mLaXuHjyDNP2ArtnX2DaXOLi6RcYhgnDuAGNBBrL+W5wTPMfMeRXOjOExAeUe11PB7Ix652hx4beNu25c7VMj/z2x/SYHtNnk5jdTYwxRgniGfIfbjPegHCoODTc+d5L70o1vk/K825QfOwaPp308efjQRN1ekT1VzFsZbxNGf+ssSHoIsODizldozSb0tP2XawhjHZUXErpSM5mX1BozZQGZAA5D8BAAaNXHFVxQKPewIzszDh23KsQ6uVDaG5tzVF0LuhTVnoQhWZlCA0DwOPMNVpEEDfGSfCxBZO3wFHoTHYehL1rmctF4SaVepyICUOelcbNItyJ55jDusb0CTSpc1QISv8ZZ2Jpt96Sx04rtrDHbKpEuyqE6PJbtL9rTG07gp3uqntYjR23BesOUZXfsgXBARUaqRSnqoJa4akuW54ZsIQIsY9OFNY4Hr/MiQUMdX9KW9HCIbZ9Oq0JLE4UKp/dK/IjnKHWZCccaReanjs3G9MggL3TzXZyzNfaLF9bJWMiUyI2vssAHkRZ07xYgIGchOcx6ImWs8SKkJixEmfza36Ki+Fv8bvhR/zj/rcIJ8gHSQ8viOgMeDxwT6Wuf+oHSu/LsuHOMHACI2EaR4zjiMvdiMvLCeMkzJH86hr552vkn9+Cr29j4fhRRrTlNywfdfMtnjsjIl7ioVCHeVYJsL1/K/dfC+RqOgcJXztFjjXWu5BRGLnAndYeA+fHdXGtinhFrcFl+RV5yVzVsbwQ4ZMuH7YCVCcjMHmLWLeIi6pEbcUKtwstDAHlcl47k56raiRYWBmnNs9JWi6AUvCVdn7WK6jacyGZBJwl9Y+/EIpQ96uuyFIH8TkTvzK/vo+j25sj9TXjdKzlNbytSPN1LagbH2pMZRdbrzdH4VLmTjmZowSiLBL6mcoCYCjCDDAPAWEhhZ+rSW/jDfhzCPM586xuaEWYWJDBIKBpMWcAnFnwzlNahK12FhmCV6wTiIWxn1Jcn825WaibQCDU67mA0sBq7ayeTUbolHHyE8Dc+TkxVk+n383tMojwcQfpCvNUArA1/T43BSKmeVHw2rAMCjJfFylB9gTJysRFCEGlPqJUAk5rBaa9VmK/iAjGzs7qQssZlFRQpG4G5sMBPIvGXxoIRAOILxSwhGkz4emzr3B19RW++PY32Oye4OLJMwzTDtPuCsM0YdxuQTSq9YNZwxzE7ZoS8UO+xcC3MIFKm3Ixibj7PABlq5xZfG37vIuGdVlPd6/j/Wu5n7p/Ph5u+ZjOS+esq1Ox6z7H9LAWGPer6xgIH36IA4a40OyiO52Di9Try0rnuzo3AT6v8M7zd+wsPArSZ50KtnLGgro3jfrppLa3gvIWfPWcRAC2BOzIvKoy8jyD573gQATcJMZMjCEp3eLaTS3OweHPnrB/VsGesz01t8OKa7HV2/SDAmNV4zjUhtkBJmf2L/taM/UKbA4tB9qQg21HzojYcO9eiHS90IplTLrLzeGIn2jmriLwK1pO4Ctj6nTP2am0Q0TYbRM2U4Nftkz5wH/pxfysao3M9UXXOvk1cVX2JOirj7nhFbUU2kKA4OSFlSt0wjK2g5aNZar2CLHnS8FLG8S7tFmqaetr+tcZywKLN1rwaixTbxXfK9Ud1d8f+5IxWNqLtpOV49x0qjFX8RXj41il5/Z9fbzrtVzDIuS5PlVlxLyZgDmDbm78DCSOHjHq8ysRYeIBT3iDH2gK/WsQoC4gD5MeVhDxQJhkFEa0fLHPKbk2dnNq3Mw7zDzh3/xmh6+ebnB1scE4jdjtLsBvD3j5f///gn9+C+xzqKute+3Nymq5I8ZZLrOA5hjzyZl7ERcpzBor64z3cBCWv4BncIx/UOoh8cIO08qNF8b6mmiQ985riQ2RHdmIQcMFTv1O77b2or92F9AoMlFp4hrC5HAUJmdmVl/4eqAkwoDlhRb7UY2EanEkNdcy7Y55nsGc6/5R0IOgsgaYM2ae1c/5IeS3f4omWbncg1a8jjV4rmELCGzps1UbtULgDEQAod7SflkX4SVBhTiRNKFymWh7xWpihVAMnxUaQoByJFU7Pa73gMRY4DNbc9qe3WuZs7pUshgUx1Zdi/z7CHpQZdszNnZVMW07qyAmccnmI6Vwusa4WuZEhDK6ULGA50kZvJSkz5w1iDJpcGlFBMQVWgYPQRCTAD5Y14r7KKsrEj2cGWlIoDSJ1jokXkTOGeMwgCgV0iKME/m+U+2hXBC1ROU7uRAQADIySVBgt3og0+Aq2vKSBrQWIURiLZFJzN6ZgTzPAAGDxi9IKgwSSwkdYa2H2Yifst4EhHoO5lm01IZBYBiGAcwJN7e3MrN27toOVwQxZ14sN9stRbOijGV1xpBVbed7XHAIz2QsU+sf1sbTkPXwmpoKqJtHf6diKTcM2vdpEtjUUgLqwoqSWDOMg4y9WcKRUXdz6Ws+7JH3+0Cmyn+HOWEG4bDfY+YDbm9uwczYDC8wjQO++vXX2FzssNk9RZombC6fYNps8eTFlxinHbZPvhS3TLuL4PcYRSjIezkqD4wN/wkjfpYzNAMEiQHhHsf0nM4Km2EMFqLjLgxUy/+5uhH6XOF+TI/pMX24FPmmTgP4W7lLpkT42ynhkAb8r7cZb9t4ZR88fc6U8GeaIp1wp9QwcD6DNBHwr7YJF0lw+HzY4/qHH8GHAzhnUArEuv+h080lZ4KVds0WN4IN/2bfjDkDCYz5sBeriGEAaHRWQ8F5A41HRkeZgpzFO8xhk2eDIJCK0bI+doAdnzc+RKRLLSJiPCsApVHIcNF2OJQOregXs1yIcGqNjv+n+EBadQv0Uo/TH8xOC7k70YavcE66vBjxr//6OfjqEj8RQjw9gyt0HSXWoOQp+6XQdTVdvhBAHBE01JT9/dOifKCx/FFQSoKvMVIWS6A9wtqJ/JeFcmmgawIxE2ikJT1TQRvHJa75AvCyf1yXLXXU1u5tk30SgTo5Y2rXVI94s2ypk79fy7G0qPau5ZqOdus4utgK3czGIDu1OjvWFXfvR1wLwdGyLo5CrwM8Ed7+6lvQzS0u/vG3SDd7MDIyi9Im8oBMGUjJVdlSSnqODufTi+dku8MkvRfXTH8W2hbHpGLnJu1/5gRwOQy2mwGURlxuB1xsB4wHxnCYcXjzGvzmBvz6Fny994N9oXjQNhC0U8vRHTIbg/sIqNQ0sGTOH7kSjHGHqEnQa6Nf3rUlVBOi9IBXy9wtLZGjd67p6A3JzSdgDG+fqjBnntvGPBfWFypGpyZndJfy3X5VOFYjIOJiaUEoCEcpaohYhrgvUlZXBUujFR/go7BuSdnsHtKai3Cpn6i6vytEwAA2uI8xQk0wVjFPA3qjGGbZLV0jVJRRNrgCwhWI2LI2Gp//DHRySY2dvVJkff0xqvZL3WOdZyoXVrNOqzo7C+fofqvOmZLbBTm+dzV+hCyspm3vucDql0XpneUOBcNRV+ZTfPWXKWVmOWYp1GNURFgjJY5CmQOGRRZZbBtQZiBxMeu2ijwPN59NF8gsaNra6xQFoT5iHpPC1oTEmVgGJIcTThHJthbFxVVyRFqeq6lpFxjUU9C2tyCgluNRYoUsU+3r1wjMKoO/O54CARFSoiSu75ozoUQX0cnPs85IEPqrO7G8P2A+7B0+3zd69NJIGHjASBuAGdvtDtNmwvMvv8Xu8hLj5QukaYPd5RXGaYPd1TPQOGLYXGAYRgzTBuAZhFuYIMRgMwE28Q0It/AHTeLO9zh1Ry1MlwtuNZ3D5H8XS4Zj9a3Bctd2WqvHO3Q/1mLQ3antkwj+R8WVewTxeekh5vpzsDb4c7SQ+NTS/fbjfduqkZ+FgB3AJhESnR3a9RNKp3GMDwpD2+ba/N4TtnU64mih814/yHh91MO9m9o9RkgY0wabYYMZBMqMfDhgzgfcUsYNGcMbjjpVEj3/l1DjxpYj3NlxEYY6LKBqJlNcQ2CH1vhg5HaUurR+UwpjY/RzeeelCy7AzXujMSrlSo69WCCr+l9waeswBquMKNjIpghptTYItzdT+s2URcGr5WdoHVGhroDerD1nVmORTDt6OyXMU9vHUqaHmcdYCQWtt98d+vyIAKLT5Pr7SO63L7vnTqRJIp+BnDbyJ1TWsnyN5UrfIj+gGp2KvqHwmOp8VfZALze0Szt2i+T5234dK7ZCn50xM1z96lVX2uaeu6NFLadSGJuVcv2rxgagvpNO9bDB+JrvZ1awlrVXltdexGLL984vsvU9je4JwRTLCMLv4xT5eMorsPWSCGNOmHjADMasbp/vfX/dAY97jBHRSw+MCe/zFvu8AyBSq3/93RbfvJhwud1ipITdf30N+vktXv6373G4uQYOQSPXbpq1VHGpqP/ueA2L987Uaqqqqm8ZsOYHXi/DEgQYRdocLlYXWHBz8Yc6C7LBody7ue4qSEdNfLQuUowBSEdvumXdNdKhhSoGJQOs8SEsr/rKdG0M1YCuBBN6ESaQ+ndbF+tU06T/ynyQCBRYzW71gLL+FysGPbQ4I+eD/PFBkSc9nAiK1KRw4MgFnYwBacrI5lsz6yAkm/POIadVE5FrCJNWVCGfDEHMIJdcwIN0rMvYVfOcMkwrvkYoTPOl3NoFD4imlQEbsz3QANYG3vU1l+s1V2DMyCkVv6cBcyCGxhIJSCsXKwSzTvD9ATNVlh4lldzL/lNXTFnWgcNgzGkyy6PUxYtZH1YMWVBBhMPlJkObkCi7D1dj9Bu+nJVosMuyCL9k/1GjSWGEwTzPGIYBiQhDGsADa4BgtSpADEJd3FAZ0DHgtFsbRG4D+fR6v3POSDT4e7FySNpvieFiYwhYzAaZF9a+UFJN+xzGHrJ+pWu5GvTKskatVCRmi5QXywtZ+/N+DozWjGkaQZQwDIMw1VULa1RzKkpJzTWrxVt9tfpSSv67Oqd13qPFW/xsU//sboQQkaAh+FrxOjTgjWvHJeg5IX9OwCaqrYs4g0CqoJWBOWOeMw57sRghJ94k2PQ8zzgcxOXSMA7iLkmBIgygRLj6+jmmyx02uwtM04QvvvoWu90Fnn/5AuO0xTxdAmnAtNmAhoRx3ACUkHV9pJRA8yuMh392GJzgyYBAXCz3bGoYUETT9jWJVUggQChoG55KZiXHcQ7vgkVaPR+Oy/WYHtNjekzvlAo+VS4ZAtx/cvER/pjunR6vhE86OfVDCQd8g1vsMCKDMIPAPUZZJwABAABJREFUuEHGf9ntcSDGzAxShTTbM5H5HVPhDRSc0eIXZObluuAM5oQ5H5AwCE4y5AIjNXhiaMjiHYqrzFlx3SxxE2B0i9ZEpT6L5EpKj4NZceU50OFcdFQo1KE0LiWxGvbzggzHrJPHyVM8vMR9LFbyUXnN3YxW/AexMLe4bDYPYgVR4kiKAXNQYFpOjzE5BFcuZPCC3Qob+1g20Ittbn+ysIQoNO2i/t6D3rnRvm8qiIz74pIXcE8KiJ20Tje0PcV8tdBCuhTcvLb9X6FtSqNWB1XFlp0rMDfVLTvdKVuEJ1S9r/t/LJ1365VcNhm9DdrkpWZq73Q/dFfnMq1oNJxaXue3LWN5tgDcmB7+vR2EI+UIIW9Q8GXjWZDyUBjiVyNjGEZgyBjSiJRmHHhG5hlzFj5ISgOQzAOD8f0kvuSz/YBfX1/hh80tfkxvu31/H+lsQUQct1NgfRB69ANgiPWy7x0enXcAmBMyJ78sttOIy2EA9JK6uhhxsR2Bl2+Rr2fMP74FvdmDb27BtyaFqlbgMvUGWS8X1z5oXx/vblUPh+9lQxsjsqmTi3YxAtMEwFII0YxdRFRajcV7Jw5fqou8gwCh9M03eYC9rTP6sG+hjEIIK3BqLzAMcSiMVnMXYkGnCjwoB5kiK1ErviB/NtZcww125q8jPz4KqTofncGqCBMqxlYHC9CLOAUkrcApZQyBKn73S1kZ+zj/xlwvJpGem1U73QQ6PiRWr3wWBl5ARGuIvTfC9OfGulF1XCgWDUx/Kqa1y/MxngrcfNpPEVqw9sn2mt9VvbUT91c1DWVvGYIqTPDl+aSehjwvMdSuTxCgVXzHN3gZCYR5M0FcIqCyhGj6IjiirC1zv7ZoSgZFwIgEhZ1xLgTSWBGZpU4dS4tPog9i75tPbc9cFFXIm7aqJvqZM5ITJUF44+st7B7u3BksQhCLQ9Bqdrea2j7kNtpxrPWcSPFdqEsUIliECJmQaQ51s1vitHPTJrekqODrzRcv3t853k73TYcZJBOv7yywXlyeel4BsMCFHtpGqzgwI88HHPa3INjyZ4Az8pyRDwcX1gEiXB02G3F9NYxI44irF19ge3WJrVo8PPnyG2y3O2yurjTOw0ZMYKcRCcCQ9rCxp6wnCb8F+IBWW6f4FtZ5JTnP26Evp4+OQYXvtpctL5+h3COfr5Z3ux7fvR/tOC+Hhju/lgTG5zqin3PqLfuHTsXy7L7lgTtg5N300BZI7zM9BIhrY/1eur+KBN0z+Z3V4iJL14gBgHumE7TjybdLLOn8IT4jZx8dv3N6P5YQ73qXxPyf3r5ctVAFAJLYlYfbG/B+r259GQdiHCCuVJGKEo+SdQAqkreb5L0qG/UyGp6eucKFegzyqk4o3WH/sbpnyuzM/2oxMwUmOSteZRbLBbcuf7nmCSBVY2iWEEaPF0az1aWdY0A8CwiOafSL06iu+Nh0slVqC0p31Rt2agVGJtVjFAe6N6KqPZ0IN+MWedgE7kAo0ZmI2iNB+bLA3I8JdjvshG4243kYWU5tIVOmo+pp/FL4UAZ3Ifopvjc+hGc32rgwBGJdUem/tnqwNqjTrzh2fdoUx95VryJcBsWRDbQ6yOefeo73Vu128jWkcHl+oqUFIo7u8WHPKdTZznsIanoCl+iMWafNU2oK1V3SNhhg5IpoqxqAT0Z7NsQ1Ed4zEogYGBLyxRY5Afz2rZy9dv4qDzAn5R9oE4kII014ki7wOhGAtxVYa8Ne9/l+6dEiQtOxJXW+JFHSnje4nS/896+/mfCrLwbxa06E3W6LAYS3/9N/Rv7dz9jTIDxjXmHHBMFAj6VWfV/Bys9aINy0Yu2uMCnkXbmohXHO1QZsLSGcUYT6wrffAB5WE8kl/2EMjwgkiquSlf7GOlfaK8iAoQb1uCqbtDxndm0GzhnzYfZ8QNGuTi65VOQHAQlAUm0VOZXksWhQMJMw2Bjql1MFDCyWGETq4gZJyrNpr5gm9ez5bS5dE9fGKhESolZI8EuYArJFCk/n1C2aJKSazlJH9N8PFsGNuUQqGufxuGQ10MlV/IJymus+I+17tT6Ctof1g/paLvNs+8Om1tZvijgBhC/aaJPbOmCG+P5sR8NoV9L15tUH5iN8vBfL0fZZRhV/yawdVO4gmjSk4yO34rKjBiuK5YJI1gui5gg1M3KID2LrxY1fGLKWQKCchTGfhnImxH7mspeqXme1smCFewBSNoFexpwlVoALIwCH29ZlramiPQw0Um/3cwYyhDGfUgL0PDeiIquWOmbVdk9J1xg5ocVMSGmAWRuxTg4BGIbk45hZrDzc4kU1F5DhFg6cM8ZxFFY8JSSCBE3WdZ5I4iUMA8AHO2/NMsp2j5zPFWPMj2pdrxmVMMIZYOEcJyLXsFizNOsMaagFvtYjUu7fqSlmRdSywNzM5SzxQijbGTfr+ar9TknG73DAYT7g9uYGQyJMwwhAhHKHeY/DYQ+aNhjGDTabDcZxwvNffI3LF8+xe/Ic03aHqxdfYdpdYHOhsSAurkBphHg7BhIOILC697jBNv83AAeJEVJGGC4QpoQMmV/rtk2L+SG2zptVja5yp92TCU+SBZGoz5w+PWLWO+3cPKbH9H7T5yv8ekyfa6qE78YQrJgGkbXy4K2f+P0+0uNh/pjOTPOMt3/6EXw4yN5ISssOwHA563IN3g801VRNeSY4JwpNyaw0qOUXhD8bosNKsJgZApHgPl3/aE5QCB0zZ3CeMStunLngpiCJ0VYpehmt5zUF5TtmzPNB6Q0usJDQo8RUYkMkodEHKjhyCWpd6HqGWEOzWSg3whJhogb+g+NlqmRCQjflnECUvV8w3oHHvTS8MRKMLY3JMMas0RgAkDdbfP/iO6RpgjPeQ2otHBZuk5sSUTixetKdeQTGNqPFw7K6zhlLka+kBLHBXp76mMvXFIoHCwgCZEE2fe0AtLQSp/CuwBKeLmFvU2qfR1rJM5Q897pizisUuClnlmvH7PjdVBnsL4ewWzVZfv1R+LfseyG00Cm8Uvc9r9HzcdxT82V7zYQKqHhVon3I4iViQ3j762+A6xts/vN/xXA4yNlDEh8WCUjuiUP2UqKEy80VprTBq/RH4PbHU0N99PldhusOgojIprtjqjgHnWfovH+n1FbSA+D0UNpE+x5YPGhaYcLMg8SEAHCxTdhtBlxtJ2w3A9IwgIYE/vEahzc3wJtb4JDBCcqK6MO0NlRxC62AVJc9Q3VoIcXj/glgF10rea8Bo3IQRC8rXqbPJDk2Qy6dXu3xcrw8+Gz1EM71dE19Z3rKd2PVWf7o6sP5dlQ0G4rGxwJqPQSlvYrpx4VJms28EoacFGsAF+iksE5i99Uvpt1thQMb2lRtDDddRTOW1SkSg3nHsQtBtFzKr/AlkveUase61UKVvMo+644XhcujFni0nV4+KUssN8guangdIS3vHCUhgIJQpfZnj4p49WGt+lGvzRzK9OCOTP4yrlpP2F+sGv/23OZncdFx2I9UXDV1cKHQJW7GOfalwCkdYo1ybXUGbX1WZHoxJr02pVaCuQiz1Vif14VxoESHCY5yWcMuR8l6UdteCO3I96x1kpdte+ktE2Cuixzx9X2ubpRIEAGxyrA9kyX4nlp82L6ULU1IiSVQdpGSAGTumazXZQ8U91ms5Qk5CC5D+CGH2d19OQ0V6ooHMVE0nDor+XrrzPEp7Vy/Qk0QEpacL8EwHvF9vOdcQKP7+bDJ2KcsLuRmMdEHswp71AoBhFnH7HA4qCl/BiMBA/t5O40Tpt2ItLvCsHuCzWaDabPB1Vdf4+qLF7i4fIppu8P2yTOM0wbjdidWEoO4bBKZa0biNwAyEgMJe4AOkJgQM1aT7SHoUVBfSXEWoLu6nZ16oHWsfD9UR9M6snVay/rU+/shcnzk10OlWuRct/Ig6OdnmE5N9xotdcwN28dOLQjvE6S71/3xx+d9puV48JlrjBb5TtHx8Ro9la+Xx7QEOZ6nPRyp+nK6Px8ztdrMDj3hrKX3Tl1r910nC628uFu7K505UQmfk+lkZWuL8p6D+4Eunnj9G774NBF2RBjsPswZ+zzjOjHeJmGWE2UlgNnXvxA2quwVN8OC1sno0nkI+KMRmQ6cMHpdVMDU3DUGi1hAmNJJNuW5EHSaksTopCEOMzmuWZj9QZ3NeBPMMC/TAlJQtXS6kFAsJSgg4gan/usCAy7wqWvYBKh1fKpwuqiIZEplCLRHHA2HG2WaZFrWLm/Jk8Hu8IA5gSkhUwlme2ppLsjzQL+Xh2uFe+87ayUcy0ZHnR1fwNsI8xPWlvMBKCghxnyRcA5zvhSuLHFxavrndS9gazra1FmfdE2rVf/W236wZPWGK8W/hWV51uysxI4oNeopQf2RWFRXwdj+4Pr5sb3ReSOWFucTy2cLIO6jjNMr4rS80tbDBAyzKhFaLBwViOopRpG5R6J4OwwjtnnEDhscaMbM82qTdwVxLd3JIuJjkW0V7bya1nK0G/RYG8t8XL1Hvfma7AeecDNf+gX07bMRf/XdDptpwjiOGDcTUkp49e//AfM//kkYFJRgpn2AXhzuEuKMFC59M0mK8lD2Svs9WxBroSxQNpNJh3tMkZa3ZckldeEc90uSufoDIH7LAY8NYBWuXoc9isXwmrZPju9o/IXmYvOMeti4FgdEaz6ZUMXxJWUYMVD87UsddtewdpjUIsCYVIKASGbBo8TFz3zYFx+aytwEEdKg0ncyjQ7VxvAdGZAyqOa0DVciQYBIEMo5H9SP5gwwtG6T7pPjd47FWNVqxeBTGubILm+iEUiDvksQNey4lkVD3EbcGHLGUJZtEBA5u/gxNLNp/tH1tx++Zf9kb8bqs8DGOoa2LqlGDhw50TyVZYdp9aCsWbEqMb+p8GemvSyynxDorZeyaB65kkfYx1nXomnJCwPeZp3BKHELfIQYYNMoyqqVj7KTqhSYyi2AUchBINdoSuQLX9cpmTBeaZNaEGDNENR6xZni5i9H1zTJ9znAQaECt8ZQyb4jPkSgbFY9qgmlc0Rqymxnt2jtA5QGmIskP3O4aJozoBYFCXOWeAJJ13XxrajWOkNCJmA2bSyJAoCUpB0PEt1YYyQn4GSOXcvd5l+FG3POGACwxoRIaQSzMLVNwyoNo55RFvuBwXPGjBlEhCGJuMdFWUaAkZyFwcuYj3xZGhKXo8SkKDMb90HU/qmQsFBPXId29nbPd11bmXPxzRrONsIoYwGxEnv59BbXwwHz7S2wPyDPByGo9wcAwJAGv4tynrG/3TvCBiRkJAwpIQ0Dnry4wouvn2P48pcYXvwKu4sdNtstdhc7TJsNdtsdxmnCMMoasn1BJG6g5J7YY5t/B+K9E7QdcXjpdbhH4rmmp1HRytOUQs6KcK3mpppNrKYWpTsT0f7c030w2eNM0nbgPgx+/DmnnsDi87GSiJTJv5BNc3Yq98L5ae3weY/rIeB1/SRYWEyBFXnH9C5r5Dwa9s5VvadlW8anD/fDNbs2LveboQ+VIrrtfIXIbe2XOJEiJsXt5VRVbN8mEP5mQ3iSEmYC5lkUuPYE/MPugD0xmGdgzmJlKkgygBKnrkBoTHAWGsCsUjPrnyCZEe9jSHVZ+RjEGZTV2ngcQMofSTY+DIjXAnPBdADyATwLzjcfZhzmg2j9Kr6XeAAoI9GkiJPGdPCBOIAyYU5DcZHLrDSyWnCAkDKBBzgdILhZQkqDx4godDcAzuBZe5ktjoP9zcjMmPPBC1BK4MTIJG0kSkI/kFg3MyWAZwBqSZGjtl9ekO1G/7Yrp/2dzco6kKiRTV9WFVV1kNPp3SVWHrQMe1vmDVO+PoIDDejbgtFguyErl3KBDik8hKK05AKHYNFfKO5YDqFMPQbk72y0CjxxK5spDzXjFwahfG3HrUmLfjeDWqaCFiX8jYMR9q1/DaI4uuMZvWh75fXi/fFWTJC2Ehr7SDudulr8go7nDwXrFhaF+OjPd0kOcTNnZaU1mVVgCRDSMADjiEQjEmWx8CLGnPUMyQSkATkTEskZBnEwgac3E3719hJ/3N3gJb3Faor7v8NDOjedLYg4ti3uJdF557TW5nFYVjW7Fps7Ehi15mFkHgiPIGHmAZtpwvOrwjR9djm6EGIYBsx/fInDy2vg1TUwZz8U/VIOExlJnPK0ST2VL6K6bIMsrB/8d0+VEkRgxPbOW6CsU2fGmwAiMDvb8bfLbu346k2ng8X1KLq2wJ3S8qI1YQSjZsTFi7/qBgOgFBiv7PmjKai7oqESkNr9Wbb3mPeVA5OKFuubF1/q3zkXLx4R3LWRKDMV9oMy96GBY0lNYO02Y4NT+15h4McmxPEGq+fEpdUr7zCW9VVwilS5g7JPbzM+9j6wCwWMCdzyFw0Z9FJs64Rti1pLDdQdLteJTVpvtdotjmL2cL+i3ZbCam2bosBIoHJGMYpQZPA9bNBwgXmBpGp/vNvSdhyTtk9VuW6qz+X6pGv7bUIkcZ4j7TboH5UxjNPa88cdhWZuos26VkkIsKyCALKDI5xriSzoXA1Dy7xp3YIZ3CluXC1n08BKsFUMgYLROP7ra9D71+AWcas2wgZpr3+h9ix1SuyXAlJr2k3hX1sr0o5Ywgjcsm8TEW53DJ4y9phxyAdBtuyPy8hW9xMS0jhiGAdsLncYxwnTdoshJQzThKtnV3jy1RcYX3yD8fkX2Gw3mEyZYBwx6H1uQe8HaJyHatpmEM8g5NL+GbdPJTyoEI0wLtV4rtWzbOssBi/3y75rupM/+4h6hXSq7N0Z2GVcW3zrYVBafqiKTjRz+mz8UOkh1k5bx7nzusx3alweHtb3kdp+ta5M/9xT3c+Id9b5KFwbD5paGua9p14ryz3wYWf/XVo7tX/vWPdZ2dfa/JCjtoIbBfqHeuDEy+gYoXu06SXd2ocFAHYAbcEc3RYo/pskECqGWvmKQ2mjZxmAcbNNEUhkEk4tL8lQtvLZgXSXR1D6N6HwACKS7wIDs4aYMWcRQuQ8Fxo0kTD5UfDjMkaKpyZVSKIw8EaTm9tPEuUhzqgdA0SaMSK3LMFjI7huvWGBqo12TzaGkRoI4gDSQNVsSnIJRBZPdG1i+zYDBHHRfHt9g/z6BuQmHyt1tY/X1mLk46xVZ3i+5y3g9si8kq/F0EKFLeG3Bmtsk2LdptxUaBv5UgJTI7yjTl1oZs3gKtROTYtyYE40WH0H8CN9ivDW1NMCrtXqfPy6AK033slHzfcGk1sUORojgmPc1pjvvmd4mccl1V1yVCAAMLq9q6he8RgDsbyW7gB6dyUcQV3LeMvFQpTAacDh6SXoegC9fCV0NIsgU87omj4lPWs24wZX0xVeEuMljggiFgAc24zr6V9AjIg+EovqabsBl0dDd0/r/XrghOvDFb54OuB/8+sNzO/8OG3FdYMyLl7+r/8/7P/T75GgTOZw6bX8wxbyZbeOTzZ3vsXfa8Uj46ra+sZY4iZ3l3Ehfau0MwEJkALAgjW1SZjY8LtFHhoTL0K4rt/ptXIcRSpCAMtjCJD/bliYAVmhUk3dRy1tblIKHhIRANP0LkicxWkwZm6eZ+TMmLMw3oZBECeLKSIITirImcLDxB5bAsqcjAxh76d9qta6jZ8MgbmR4QJrHGvTENFqq/eOhMnDBLGuME0Ds6IwOFj7LHOf7bw8gkOQ1GdtZos1cOQ01lSChhmSmJT5K8iFmasZM7eMVRnD5A2z4aWqOSLaMjJnjbWDZ89hXTVzEXpY0l2ZC1SNfZ0MXq7wtO6uUcAWAZ7ghby1IkyCrDtiv4ijTkhGM6kEQaDBgtxxLr5QbR/SCnzVOaJl9Xk9GvUWpjCPwjQvQkAAbtUgwBXtKHO/5kSXIukppUqYBAgSJTEACDwkJNVQmucZnIHDPCMxuaaB+xy13iQh/HIOBF4lOLY+JEXITIdfglAnDC7E9HGxsVFhGWWWthsjOyfy9EwhZZq6GzEu8NiW681PGxPC+uGCimqetIYUV0vQSOqtZS6aXhrBBoP65E0D4eWTjNvdAddv3uKw3+NwewPMs2jKETAkQXHEaknPkyFh2m5x8fQJvvu7v8b24gIXT54iDRPGaYdxM2GjQae3V088JoiNh1mG2KIb8/dI+c1ibHQoP3j6l8KgfEyP6TH9S0trDKn71bRAVY5xzz4oE/szTY9DdHYKpNoyNXT2Ay77BRQzf4kDXyoxti8x+cDC0LrMDoO49FViyBV2zFIZgq+Zi2EOVhGBHjeq22I4ZCjtC2CkBKRBrAySuCmy2IOL8VEhRM4Z80HcbR72exzmuVhEgDCOjMQDeJgUA4yWvSQKO9xSY7XCmQyV0o5RYGPKMUksI+x5BkBJaGujfRnFbVSeZ6Ul5zLUSWLdWcxDUW5KHgOOnBExIFFW90nBXot5df8tuEAz4+ffv8L88i0u51zotxbPp/7SWyzFrhDC6ItSKM5jq9zLpZqqhdqaoCEsm/bLz9A2UZWlWEKoG6zYZ4LTg24NYUQ06vqqfq6MUBFO1Xmq3I0goU1rY13eNzlWYYqPemXqH2vQrPNr+s/4xPs2LbiJpEfNGuzAWYTWkmNwblrP26N/T1b1Hu/IwscgZGLwZsT1L78G3l7j8u1bYBaXxMCAOWcgmdeB0sdEhMvpCbZpix8B4PantZbWAQDu1M97CiLueCOeuwLtVYfJdL9GzkvO2vbFXlY91Rmr89DG+WIiPH+S8PxqxDCMcokOCfzDW9z++AMOgzCV889vzbX64jApbdjlvoL+Vou+cygzuw/1bpEjTbdV1hdDC6a5I2qZaFgw3Fqcqk2VSw/nBgLep+YCsz765eWPW4avMQ3rRk+eBdVluZYYkXHInFEk6Izg1K4wzg13Y0XCFFmzwFXQdSgmmcldugAdjXYOzGYf95ip7SVXf8Ykd7SJFensCJsW4x9esbr9saDO7jIqkcU0g2m8uGshA+f0IFeZlIftjOWi5dxYHYRqHY+wHwQUNy/lsqb6H1jcEGLTohcpcp4lvkYxsW2Yx0xVjIQIV32R6u9qbXAxDV6Md0Qyy6oXZq+xp7U9W5tAVMJfpMpCaME07s4ATIdfiAtylwYuV00EmsmJEwc39lwvyqgfxWwWAsudWcrIDonj6BcvAsJypAdt/xea/YlAmesxpEIIReY6Q1w/ee0kezeT+afNYJbgyCmTB9wrMEZ4ej3nZX+q870QQ/XaKKNjFlM8lDO5muZ4T1gZMnRzeVKKv+AGyW2zBbx6sfxodTm2OfVRgdsV0QjY7wBsgX064GCE3Sxu51iDPRMINA5Iw4iLy51YMkxb0DBi3O5w8fQpvvj2lxi3W0y7C9AwgoaN5ttg3G4xDEMRPMyvAdyAsp4RFuyPD9UA+Pljy//IovyQMoPWArF93uRufrdzc39862S656Dc22LCca64l+8Fwsm0pu3/EMKjJcjHSMC7pR4e9aHS8bEpuNHp+bd8DwPXh0qPgsV+WqNr1ubZ1jC3d6Xi5EuG0NHL6gHSefN6LNextVEx/dYYJjUKcn46kdfwqXdauQ+y7D+9vRNjbMmDMwueupKrvD0aYr0IAzi8ucbhcIsf0gFvU0ZuyMlKmSfQWu5iGQyVRvizDBFQMITeNRJUyF1TolGrA7WoN+Ujx7vbbWmVMNeBmi02hLkeVsIv89CxPCkKTkJzmxVGeV9odcWbOCMTBWU6zUmBVa51JkgffR9wGKesymxmGQGAkgxSRrEyB0iFEKSKMMpi4KxWI70JPUrwGcD6M+CDREu8fjlkxx+cuY5rxrkzSaqxPwpEKbKaBSFLnJdogb0QQqQogLC2/Mmijqo5e+T0YLyMlnglV85Vu1/WulT/8uZ6Y3osLWm7zkY7A5ZTufqWB6dKMlD1iZRfsnqaV/zBEw3cAZ8653osd+ux3GHRNtnOGp9jBEn3nVLznMQtcRIFYefN2HmJBB6gfDn2cyAxIacBF4cRV9jhhg448Hw3fOgOee8hiHivmNk9hRBn1Xz0bV8Y0c3ob+zz+SXhL38xYRo3oGFy1w1v//m3OPzPv4W57bDLNbZZfrDX2da/Csjqq1JLb8+t7UO/XDmMR2fYirYwFKlYxrTww7kFN+RtfYqnRoBhFS39XpuWbtDsb9rpEyG9vjTwUflYuxg5/BMFCQkZGCzIVnswlWC07tZnFqbZPB8CjiAxIVJKGIZByqEgDH5I6xxnHw/RHZHU+rQNw2+IHxezrIRUQUvhz4eNrE/tAOq7ROJ3Pw0++baiXWDjSJ0FL5NTuGVKW8XFTLVoUEug37LExTVSid2AMI6OXInKiiCbkFgCSbUiumsudC1zYSqLv/7Z/Z3K92XgWUMujZntgiJHfHSUmbuWbAyIQGINqJLL20Em5Udn3782NwxWaxU0zHqFL8LUaW85M/o8S3yMRLZ+qCAQ3Cmoz4XZrUz8eOQaCBqvAQobCHIx2t7kJv6E1103JZ+GRKrukMIgFhGK3JfALzBGvNE5zNljPZiFjqcs/lwNqU1pAJP4uE00y9kwZ+QkAaWJB5j2VRkOqp6VHjVWcgan/sheR1jjsP1dpiBn1XaijqCJgUxLAsA1gYjVD20hNKu9WjDG5vBYtrNylYS+rbysGrJzELh+yjg8Y9y+vcV8fcBhf4N5Poj2msVaIAJNO2wud/jub36D3eUlnjz/EtN2h4tnzzFOW0wXT8E0IA8DMggzJ9AwiLBiYIypTELinzHkHwPgAbmM33QOzkd3P7X0+UL+mN5XelwTj+lzT0tEyxmoITnr6f2SundMLT0R6LUTyWNhndLe7PGmHtNnmHqTeIyaZXA+4Prnn3F9uMU/Xe1xS7kJVcnOmC/8BS6xDp2uzKrXVtwNu+KW5wNECGE0VrCiTgNSEmVOSkmFESHmobebxSqdRQFF4kIckPMBh4O4ZzKqK2mchUIcNmNgtIMzqQte50w7VnySk8R7MOlKrMOEJgQgJ9PFC6Arr4AFdhOcAMDMQlmkzODo9smUEilJ5DkCwCNymis4jV7ppcIv6KWilFe7lrp/ImP+RMEOGS32Pg7VmvCreE9UaG5ymh9QE/VCO5IIfWppdhRAUEU/LV03x99U/ZZvqcrSF8acmbz6mjsSU3+223zxTKDqMddfVlK1AVaa6fMUjqfoUteqWeVQLBOhw08KFfaITV586VW7mqPmUdpdbTnbuebVn3dOC+WJwg9JLHwHDCMwjBhIYuXM84yczNJrduXCBIsbmZASI3HG88MIvL3Af7u4xkta8roW4AQ4Vuegk+4oiFhZBo2k9b2kO9ZdtGLKTFdCsw7T6lgKji/ASDjkDS42hK+fJjy52GCz2WEYBgzTBvP3L3H4w0vwn97oGUd9X5ANMNz8PlKgyibwd7iZp5tsko7Vyuao3BtlWWgmhFi44ViRUPZcdpi7nP5OPzI5xuw5spmj4rALV5aNLFK5gEL2cFgJMqGb2Tiz1SaEz7mYZyoSZj4n3RqiIGdkfsedsai3GLf1WrCw0o+WTDG/nKKFEhBHGC7JjiXJswxzpRTbsuTye11rxVyVFJWJbqTqOkz4UpBVfdNolrTjZk8MsSG069YQsKCRg5LXv5O5QgtIUvhYJEeMyzxLcDFFIF2QE5jFEVG29dYK6BxBq7L5OK6lIiwrFg+xSfFZmgFOPh6Fka6M/7D2aVE5KeRR27/Os6KvD2Qgp75gIM6JEzH6jhjFPVPVSTi8vhbCXbtYG4bwupC3BI6vjiMAIowSFz2LubFxqBBLs2gpAxJPD4FPLRQQgvAJ1uuFrO9mIVEjKFzNryHH0rPswpBKgK3PMqNocpk2j8Li7tdcuKyCBBe+lD7XhIqe/4b4mVAoznDcpDonniUQG1xGqcy338f2KWsuM4kgt6eVFfasx8vgjDwDh1kIzwwRhA6bAUMiXD69xLTZYPPiG2wuLvHFL7/DZneBiyfPMEwjNtsLkAbzci0QqCuAISGNhCG/AR1eFzD4pgGrzG+5h8qZRk3uu2Kdp9CqT1NTuoVJ18IJWPlUZz9ICmdhA859h/rsfj+me6e1IVxbSj3a4DHdL91n/b5bzIvlnBWrIvt9LiR6P3HAF/yueYdz6GQ3Tp0JayXWyvXP3N6zggvy4h3b3X8aRKEbjuSp2CMnz9B324d3YXh8UqntdsWU8H/W04L2WKt4mYUAfDUAF4kwUXR+s4hYdqRWR3kED3ZEqNBjZrnOEc8NNRfaTfkkaQANwnj3gNIwjFa/MwvRo4KOoig2g+dZXR3PXsIECb3k2GocgxbOgkJLO1ArD6404qQ+JwAU1V0w3yPMXHBvzsiZSlBvHdxIUwt1k0CUg4JVp1MRr48dCOMOzhj/9BqHn17j5cufMB/2hZeDMNfcWzvksAGlv3dK1ZCcuX97i7jLyKuofyD8CcwWEwIwLxaufKX1dH/DrFCWmH2oMKKR+rxDebd12BlpD9q9zXG+F7U1afmmPu2PzBc1OY5k5cobwEqefvXrdQKI2plt1nNP+lXhTI8RWy14akt4jfaq5UEs+kjUWdLxYm3auA+qUQ04VY9s3wptrgqqw4CbL56Brq+RfnwJgllsqVCXEjIzEquHDRK+7Hbc4enmGX5IjJdK/zan2TqId+jYHQQRH5NAfPe0JoQ4O4VCMydczxd4ttngL39xgWkSCwhz6TD//rfY/7//EUBxWQPUE+MT2AghToMWmFsBtFWCmcOZFvMs8dDej367LPBn84+PQkR4nALbtFbSmTNBsuznPNXzY4d56J9DV/Wz50poCXbcLLUVSqcBS4sIsXX2LjO6bVrL2DjxrJr7OQY7Vh/xJP4xzRoiuoMpPj7kI690OMc+weaECyCK8IjWStBw1gs9uhjipq52LLx+ZmAA5JJObmFgsx0RtlK/EX/NQmTpq/OEw5ltyGItlGEwckB6y0Vna4pSEEJELQi0CGINhgUTE1dMswsgBME1BnUu66kZ97pvFhQ7rPOI1Yd9sHZ8s09jru4yEUKYpnpBJG1/tPNo1gj1kLPHO3B0n2MeXuwj6yfA6jOnbHoyt1y2N5oNQoC2R8t2oNMc4LZ5NRa9nw8MxSnN1LYe2CIk0nFnicsgwr/2XLBxsCIU1pX8lTXYlMsmjJDzPqUk8TNmM1PPQE7qfi1rcHiq9sPCZQsApgTmWQQOqIW3mcXagkmskUaCItVhXM3qJMxhceOl48UmnCzrlSCCA9FIkyeZwjniHS/A2tjEXVWyamZvY3m2ghhZ55WoCJhiSmF/ZM445Iz9fo/D4SDrI42YNhOmzRa/+Lu/wOXz57j69d9i2l7g8vISwzhiu93BFof4Ji5Eqgl1xpEwDIR0+xLD4fe+HtpUCNRyBizW1KLUY3pMn05qjrPPML3rLnvXHfpZD95nmN79VC34e4XtaiJDNjrtvMtc379sgfHcfp/Ku2RiyLcOfboCN1vR9vWi2ZpZ9b6EER8+PdDt/pG6nQD8aiI8HxIOSMg5LHsDjRxzAwccO1cwC05b6LqinAjDszNQYhkGuogVjw2CiJQGDBofwvAxy+w0gQd8liDV5oopZ9X2zQfMBxVEECmdndHStwV9JdTiF6NPCx0Vad4S98Ksb3sTSKisp0uHfZxEGTBbl0DIYmEeeCUFp04AiUMfbhX+Ii3NERpGV6zEAGbG9Lsfwd//hD++/B4zGJvNxjOUkgxmalHxqpf2hcKIFjobJ7bJuy3+BV7u/AIdH4MrBEB3yw8XQpjAK9Ic1PSjthjx3vUGhoBK2NHuLKrhrtUmw9na6VfvVe8prTxfT22JY+W4KnLsllyD6hgUbIyfztK464kb6bHVfgkhXJ3F3E5C/8oEQIE9F9oiVIKafuG1O+TYnmgvDPL2FjkpgSkjcULebnD73VfA6zfYvXyNZGdYJswmCOWs/ILiIv5qusJ2uMDvsAfd/nwErndLfwbBqs9Zmut5Ck+cutnkXCbczhtsRsJ3LxIojZixxZPdhM1mUkuICfMfX+H2t/+M/PufpMYFv6VZYD1JdfOtB39XY6a3drl+ztWrcNnZfqj2CHvfq/r0povumHqaTBXEKydTK4BYgl9u1dX54TXf9lzg7cGwttcr7ZAORAzVvuCA3HTahmhdZ4ZqamiQKm4QMoWfIExSN0dN7bhDBU7BL333BigWKqwWG2x+M3tCk2ThHMQUK7NSC6btEZmPsSkuzFPODAy6nig6pVJUplmHC5C9I9w5mw0hWABQQIwDlCLiYMGo4owaI5v9e6XBrf2y+Z3V5/ys/qAsloflDdxuxPURwRcefd0HR4m5uUTaPI54i9Al0ocWn4MzIScNmtwONMsWNquJvECOw5CHsW/3DYPVDNvWYXzNal0TzP91yBPICY3SoG1qshsbRfoARx59PvyIag9U7RyVgaYMEcpIMBFIvAAT7MkVmxJknVvPmCBum1JR9DcteT2jPAbMGVw7X0+J/PxklADZzAnU08zQPnGDpJoDLvM5SyQCDxqUyMqMGRmUGImGQBQQUspljmDnpfV8KfQyBg0Rg7KeSdB5JNT9X2gGnbiLK4SNYa7kzE2XrxsUrU3bq4lkHWUigFjiUWcgjRPGccLTL55js9vh4uIS026Lb37za2yunmB6/iWGccDFdI2UbpFwrfs4YwAHN1/l3zQTKBMovy5ra61LrTD1ZApn3Zmp7Ld41lQ5TrSlv05qrh2D6d0IxodIp+B/tC44Ly1o9y5e9WFgeZjUA7anldbJdVfK1lr0uu9OGn/o1MXP79vxI3V+uDrqc7CNfXO62pooajHBBlU7WUVd2RkMnPbp2cPwMGvHWA3ts9hK7fc6IuUFY+e24Dltr+QvjJ+IX+Bolz9bS4iHTGvjf2J/EwgznmDGDsDg697wcEoMTOwhurpTwUe+qxKPFO4RkPqh9Bsp7ZuGQf5IvQO0XVGaS+IszO7qyCwJhOY1S4zkRfpj0IBuikdVIfYzwmhDVmELqxClbSDuGGNet22ZNUSG/pPYvSVwKspB3nXTpGKhmZyp3u1ITV+i+d7SmJmBtBvw/G9+ic2zS8S4bHXOFUI1Pr3PtXLPq6hmEzTs/LKgq+DUVV57Hywfym/jTdl4A+4XIjRc7tHysAxzqDeWCTyHRWe4HY4j9MJisNcO136dvHxU0ULr6Uiuc+7OI6naSu+GokgVjeLqkZzlo+XJ6PP10ly1FRUqV0t0L881+m4F1lNZlF8AEtfWSd3cJSrulkUQPCNlAg/G09QVmtRTARE20xWGzXPkm7fI+1uHwLgT74qbfFKCiHdFjs9vp2am9bQvw+2DmRNu5h02mwHffbnFdhoxThsMw4BpmpCGEcM04fDDG+z/P/+oPLGVHXkK6zzC2L5Typ2lUTGCyveuRHalTMWADt+BZv44foY8oILcVNrz2srK+Lj2PpZTVcFgPQj4ATenWzQwIMCDv7YxK3r1uxDCECAv18w3W+yIjPkwO8NQkBnRpDD3VoawmDUEUrmqDKHgbMxvMlykmjcBMTvDKsY1yBqLQtrPFcJl4ZmQxZ8cs0SEzmqCWjCaZjbYELRijeCXdnf2OHwuXsfp6X/3jPHYYxe4xBUAIqREJS5LRCAYEKsLYUAnKjCZEMHiftj4Fe0bdiFDEUQU2DJbfAaFMCA8C01xRdYdsPjX9pnjJ6rDyzVXOEYGiesVytAVrXxKgbisENcOW1rfR2RbSmsd9qHryWI+FPwrwaw0Svl2r5amchDKVSBkrrVRdL9WDHsiZZYTPOZCgNkwdjObdGEBQ/MTLByy7f/i7ol9f9UpnBOLtoS2KJMuQj4xlQyD5PXYOSPrOfpsdaYAsyraJI1xAl+jc4YIDqYEQvKA6aTm7ZnnACZrm1xmgWz9s/c3JWX2q2WExOkoa/aY4GHtFrMvsgJ1HTd3RFnfNidQhEjd3CFhnoE5J6Rpg3EY8e1f/zWeffUlnj7/AtN2hyfPvkCaJszTBYhuscs/gHgPqEA28QyAxfIjHt2yEGE7gsN6pABeuRPqnr4vDCbiKx8+LbCC99wcncaT7lzlRxu8k+mk7/Z3q71p6z0188mle+DMd0j3X6IfeC89pipxwEPY8WRuJrO9n6sK+jhsRfB8Xpusx84SOqt3LpX1u7aS79P7sp/+Be8PZ0wA3VFsh+bMgV67+xhPkempusSctcrCkKOduungQN8dS45zc/XfshMlv9BaAI0EGiQuYkqjKuRRQ1YL/VqU6yzeQgl6bfEoxMuA+R52jbUCp+O+bIAE/NTOBlMAK8eD0YZGF1YCi5W931I0XqdZigBABlJSWpZDddWYCc7up1NcJ1x9FHgbOq8a/DAg02aLq7/+FdJ2AzXZXvan172GV2LPTqaHOCZ7NAgBbo3g9HSxIKHwvdBv5GMZ8wFQIUaq2/M12etAYwlS8WmaUtSppRnuOPeFX7Bsc/23E1v9RPEjlDvNRV82d2reI79j5b3waApv452TE22228+ocwW8UFXzon7TCiS6dXXxx/vdfYvtV9VS1veQBnAyQYRYXzmPkJTvBUbKrMZCkpeJsdk9wbhl7H/4A7C/7bT3bvf2AwoizjtVitbKEuh17fZjyeo5Xm6xdxbZI/NOLCBEcxWYxgF/9e0WV9sR2+0G0zhgmjaYf3yDN//5n5CIMAwD5h9eNQfPEoCj6Gq5PWp8g+ThaRlGcxsterZSrseENDiUoWVI+6It1IhOFfyX681YWzVUJ2Af0HCZ+gWwQNK4KcKGVwSmWlkjzvcKSaosmvQ1IljmzeosGhHWBhWFBWOqZXHjM8+zmInmoJls5pk+JkVqL0+kbXG1pJoe1hZJoGX7z4mpsGhkueghM88SDDtnWJBohlywwoSz+Bwq+HDN/6zfo+kpF/yFIYgaoIzQjGQBvGxq27leHOXeg2ZCSv98XkOW4tIq+3xExCKpW6tEJIKdeFGwIoD2m4IFCRvyCUdC3Rqh2loFOa/ipjS/PTi2rQ/PF84sQtPTiExaO6y4tGPDPnqSvwBXn2stEslxJs9KJoSISDpAyJw94Hfcp5nz0h2dra0gwCxiNt3fYXxbhME0g1plw0b8BJFwOpquWlIs8TPM/NasJijUsohbgCCIkPtA5jV5uSLAYCD4svU+A2AVYpR5CrAvGB9wIYmfWUEwCoj2ggWLTkospDQAkCOFWfYGiMs57Evf+tYKXSIMzVnKDECDFqZUzpiIr2I9UZuxxUM7QqcYzSTeS94NOz6TWCG++PYbXD57im9+85e4fPYUm4snGIYJ2F4IApX/AMItiG8BFv/BVlF1zFfIpGl5hHljF/mhUIq2Do4MwntJ90P4jjO77/vuZKv6uYrGd97T8UG9Iwf4bJwy4Cvna1e/W3ooAQkd+VXaepCmPqN0aq29//ldb/+jNOzpY1oPPVzb9dlyfr0Rjyq4nCVFh89r+rzHAcoPt+acnm7a65FZa90VC2duClH1jcM8vMsRUwsj1qD90OnUvfXQzTV0sY1HiMl1t+rquVq8139mMP44HfBm2Bdlk2p/hf779jEaCA0dGoR7UcjX/C60KJCGEeMwYhjEzTUFPL4CJWfArSDszxQDuYJNaFv7o8UARDorwstVPZbRhBOpCD2CiyYvr0PVwabrb16nFQsCCqM7bfSpz+Yrems1fRGoqkKv2rtDxs0/fI/Dj6/x/R/+gNvXb0WBrsOOWaRIxrck/SLT+0nRyqAmdRUon2ajO4syYhRCCF2qdJvTWcVVkxRvBRANj6hZUkU7fAGt/Vz8qOqztLbVT15K1Nmqpye2orDoDJw0vL/TqXhmvYX6uh8O3hUA+L686/psd1B/KOWYpuYMOC74WBdG9GFYq+Nk0nVLiYDNBm+//gLp+hrjDz8JzyZn5CQu7jhB4i3yUBR5E+HFfsSQn+K/5p/wM9ZwBlp5fjo9rEVES3P2stwXCzstSTia/WjeBtHKKojIPAKUMG4S/uKbC1xs1QIiJUzThPn1LeZ//9+QM2Mmgvmc6wFT7rPCjemDuHx6rC/VeNrlacvh2Ko4MVfcXMi99qLgaHF4cTOu5f4A/EIor9a6eK5UtFJMMDgNMWrgd5jbSggmTO9DUjGrw/hQPdDGAJ01cJYLAha4kB646g9zAYxWn3NASqoLA8IkjcifNmIImsFgwZdLKgHCxVzLxkf7ZhYBWq7gHubTs0Yui3VMs+hOIiotKVMuxqI4zt5UNoGKBUELjH8iZf4nFK2HqLFhCHNYl+ZiLIc4Fi54UNdaEbWLFxPD/Mt39ope6DWyyM0ZgIIIBe2fUmdE8s2SxYoyynRbAHhgLYCUuy+w3bayrY6ez0GQIMszWnlw0e5JWZG+IhDKTXkGV0JLmxNC8UFbzgVlSR87ChKB3JIgjls8g0i1+oFa26+sL8kWxzDBhFPU7nPWMWaurDMCnur/RtBbIa7Nm/EMxJ2UYSnBwsNrKohzShnA4FZP8ww1czcE3PLa2pCVK/VlMA0FViLvr88TM5AIKZd9diwtiKUyBA3Wbm7TYsFK/OSwV17qGCpcGpDGDb7+i9/g61/+Ak+/+hab7Q4YtuCUwJRAfINp/ydQvpFex0CA1l8Q6rvLRKN1o3a2UYDjbumeeM87pffX5qn+vxPT+xSut8A19Gz7jDjt7wfWfp2f0bA8pse0mtaPhe6tE0t6+YLbOeraSYYY11Xz4kuvbXtmTBTDux5Ev/MOSWCICg3124gPHr8pCKkDfcBh7sx66M8P0OKsOE4cvpf0iR2WdwSnwrdWqvE8BFg8rgzG99OM1zmDfM0uk9BDRX1M8NXy3veUCSksn+NQUijo4gEQRc40jkhpQEqFCeYFAMBjMrTWEGa1Lhq95v644LVw+qpKRk95vaUvtfIZl+aT0IoW69EEIIMLIqi7Xnu7x8auIkP0cHIqs4KZln+FtK2qsDFv2+accfPvf4vb3/2AH/70PfZ5xuZicnp1PRnfoTAbG0ofDQl0OkWi/2jLbcVRIEDxsVdWLB1UCKGfMmSpyR+sz514MyHE0hrCGbsdwOvpOt6xOlZqY0mB+9AYSyCKgl+zl4Al9N01sCx3h+a7pdZPf8tQ51jjlPYKK8XcycanAYvA8eqD1WJyNCrd7jyMwC/o1LG4744C1S9XpVhHtUlFQXfebLD/+gXSz68w/Piz8/pyJo8RwZy8GBGBOOHpDeMqj/gTBvzcaaoHwl3ojk/KNdOHTD38jJmwnzdIw4i/+maDcRwxThM204DLyx2mySwhXuHNv/sH5J/fqlZ5fSC2cqHqzo0ALKG6Z2fiR7zZaHlbVMWCO5VYB9fMMgF3/XdPGGGMxczZtXIqX3zxvuZlnYu2/DyI2uUBQYgdYGc3lw6B0AoMqrQQThjxIghJNgQhTibVWDIzQFmCyOY8I+/3OMwz8nxAzrOaOdUMQjkgCJRSNS7C2DWfl2JianEjatcuBU4EK405HySYbZ6VyZ7DUghWEB6PohBOVRBtF+g4aVPaBLy9OiB1vSYokQTMYfP7Hue2niKfBB9a8/nJ+l3Mbtt4F5Hx7Z9xPq0PCr7PZy71AoYgR7TOfoaJD8SsjbmvFZSgt2adAYtPkOv1TWRwt8xQE0IYgh2hsb7Ievb9a2vAAv064og6NZuuvZtXL/3CpQ/jIuiNjVlxTZXABAypHLKJSIS1YdLcMkLHwYURHZ63W0XEwdMO2PnCvqxLrzJLsCapmusygMb8sOqsX+InsYY1QyzkyPM7EaHm6zUCFKENiGtEPOK4hlJRvFNemCDGrKBUOEkJKQkhVMK7ZLfGMESadL3URGPRwnL8SZGW+ixWX7iO/pMG9mYPOl6fhCdShYDDaTdqTF58z3PJnBKARKI5t9ng8uopnjz/AtvtTtwjAkDeY8g/gnAD5L0fMvE8oJSqduKVGScpnld+z/ta5G6nuZ621XRvQuPPOR25oh/TY3pMj+n+iRe/XKv75O3VO+vXaKIeI+TjHWsV/dS+ezxwP256IBzgXGFQAvDdSHgyJFySYZt5ifcbXmi0CICCgVP4KzRSNloQxX0x5+A6CaG7hoqrC6ZxmjBOE4Zx0LhkRj9ZZsGxjf4TrwSswggTCjDyzAEvJ5hPdKe5o0BC6TqvSz0AVApKke6H9A2cVOmqWEKweg5wJa0g7TTqWUvAFLEEj2/G1JVj9JFaLleDViapIksLgQvE2HSmJPb6x2vMb27A+xmupJeoRlIrornQOjE5FRCLrS0/x/Hvd8ZUipdxjUcr9Mh/Cvh7ob11PSWjVEK+YBXhtGgQQkjVZk1fvju3qIVrvSP9x0fG5e5D1tJPzSOno5p7qpmjOP1lxTmTYdHi+q13CsL62epRGBRJz0vLjAvrhB7Buka+n5m8SCOMWIXhPaayb4rCKpTPNKQBNIh7Z9J4OjkTZvUWkGhAHjIyK+8gJSRmjWPzfuB9IEHEp4DI3GU7NCUDnrbnDUae8O3zCU8uR0zbS6QhWEJsNpivZxz+0x+A/VzxLWqhu16IFeOpXOcnu7EKaz+D3JPZv5N3jMKDkrm7IVosoWnvbGsWrb9yxdJcEnVTfKe6o2q0ExEcAmh7naXYKWF/w3+qESdHNgwxkcwE04TWE0eRCta4DHNWIcSswoBk11jyA4v04ivMaB0fDzQtjPjCtEZh/LExHgt8bjY6Z2nbmdk6NikJ0qkXsAshtAsRyavnJQgRWpzVP02XmPzOMzalMCyjlomjsKtrXqa6MF2tHzlnxXqzjxcljQtB5luUKmbjAlYbpyy+4rMLJErexZrh+JF9/IUJb4W8dJnTCrGLVzv55eCfsCUWEOqIbeocizygOnAcOKbC4G+AWjI/F9JYHE3SA1vv8DgiZnlgbsuSa9GVtbW42/11dWrqsbXcsO0Qt5oyxIpszsUqQvos6zktyhFKDItSRj5XzlnmBWyOc6yZbPjh0iD9XJ/CtUCXHRaHOdAjdt5bgHvZ+4JMsM0HqMheyc6M+kwuFkVlr1A80xDqIvsNH2+Z2ELGntK0bGc1yqars6Xaa+G817qHcQBtJuwuL3F59QTDZgtKCfOcwZgx5B+R+BrIc3XXLS3P1Npfx8VjOzVC5iXQ3JVrt8vm7Gutk7G3zlbBOauN8/K9n/QOjVdC0M7zTyCdJKYs38pkvZOFxEmccQ2W8/O+37Ry0f5ZpY/Xp2PucD/ntHYsrI11hXsao9BeHB2b5lLq1t3cVB91rJf7af0MsHuuKdMcaKfWUPv4XY6zRVo5XAuO8SHG+twT/g7pFHLUvDw5pGeMORHw1Uj4ckw4uDUsA0FJyvE7/d7rsbn9sb+is8bCrOIS0FncErPT6TU8BKSENA4YhhGJBhEctP21RpTuM8U3F36wKaeVuA4AiTltoLHqoVKozFLWhJJOWBflNR8HPyqyW15wzkAyukzNJoACR6zX29Vhcnio7jPB8e3Ta47rPGw9K3BnBt7+/Ba3P1/jYj9bA6X18L2bVtdWFEiQ0xlVDmdwn3coUPjXq3UmW4n3WCncpdCCCxUaxUSnayxfssrLZ2sJ4XkBjzXZ9LO2bHiXdJcKTh8eQlPp84oxTotia3E+FjdJBwcv078C/5mXAzX5Fqv+CEnGi4xrKeQ8NdzO5mhrb+iyiqdjQ0xlzEPTxywkzhm+ewmnXHlOlJ6HJAK65Ge4nGFzziBKyEniRHAqNDE7gU5F8fMB78J/sRYRMQ0J+PbFDttpRMYWwzDh6dUGm82IabfD/OYW1//jfwTtD7ihAfz2RiRJYVX0GBwAAkOlZaaELIbsnYCziwTagmiYWq5tvIZkVplRMdHaVtaQzz6zsBZArOUrDXG4sLXeziK3/jiTNdbBcKRHMy/6QaDuUASeZB+8zIZXFaEH7ECQOovAVm59C1A9Hw7ulkne2alvaBJ5XYVpTSJ8YJbYEorspGSaHbWf+kgkMbMIPfKMnA+uiWICBEOK4t0LqFaEz0Vt6tpNhMCEtFgINUwUQCvuefTgcwvb/lHmBIav6WihUdwy9ZNOMgdLEijDmYOgRU1qcz7A/XFWB35q7s+ypsvzuO+4ZEtFYFQQFvN+Xy7zOOdR6E9R8OICJsCEED7QteRzMQTySf5IKsnhgr1jqpCTArBbQnAQREXMPVbh8xEu7wWRK/1NFPW0GgFFwQKdZ8woY+6lAvXAut45DlCHm8E2ThFBJ3IXaUMaPICzNVLO23IOWNtJNswSi4j9jpKTwJVvhRFlJ9fzmlKyk8nngZmREIVxreVNRHKWAon1xE7gkJVdCFjq09c+2f9lAO0ei3lLCQ5jgZRBOSEzMDAhpQHDMMj7nIE8Azkj8QyCCSp9opzedu+54bdZUTkhSlArEw59LYWMuIzuwFC19pge02N6TI/pIVI8Yx8kRXyqSTMz/vlmxlsm3OSqyOmD/TM6+ItiRY84OpaOcIUe0yeSVhh+4Y9zxtuXL/H2cCt+wqH0Yo3ghcIpaMZSlUFIFBYrfLNcVxdKQioKHuxbjggDEZAGjOOIYRwxDkmVaxSP18Cqgrhl4P/P3p/3SpIk+YHgT9TM/R1xZGZVdVWzm0NyMBzOYIDFYr//B9hdLEDsLBazIMjmsNnVXWdWZsb1DjdT2T/kUFE1NXfzd8SRFVqV8dzd1FRFL1G5hecSNjiEZjJNSHa+RgTQAw2eAFtyBhqvVZgGU5KYh4UZU7miIfBglKx+WxQxuHFY4dPkCZf5QWHFojzBQgqL5X479bnux2jwwjKFJ3VNMIQm/v0PGP74E/78pz9gurvDnGdgt0P+zb/C4ZsX6kVtPFbhe8rany0FLa8+VEof+GhvxX4DaZ5CA1frGE8NlZekVH5HqB++x6gE5DkOtb+Qk1MrdOF88ADPfr6Gq9fb8lDEtWBG32r50hMg1Q2fdykf20MND9nlo+Lretw2F7YGfu73ViMjse2SAMqaN1VD4DFL+HZOYpSbEyluJVDOnmNVvCIy/i79Eq/31/iX6U94N797MoifSBHhN0v3a1cmcWbLi9dXtWzLzsrWK4DZPSdyQ8Lrq0u8vL4U98CUMI47DMOAIY3A/S3u/vv34NuDXxLS5bHBcHUhLODl6k93rFX1VSVEabvSnDkEx68AExxu7pfWW6y8J7Jdv808VcLTRgnRUSD0YI3COfu96r+zaXqWzFWF8Kfu0+BqORCZ4apJIzLUaj/njDxLTEsp6mZpF4JNhQujqaybEVnef7w32x0dBdUaFirPLrhvN5nhpfpSt3ZC/EtuiZ/F8IOU1M6+hIWptbimUa31wWZNb80ti82njE8UC4UwjO23RHFmgFjzJqB4eCwVEXOZlAqSXBMuNgNBKFoRlXFqgrC8EL3wS7sooGzd6zNlbUbFV5mNJXrt39hLYsV/OYKP27eczjCFSsSzDNkjPhfl/DE15PoC2NBXmJfjWnYbf49QXyEwFFkIY1XqFObbWpbnko8hnu2yPhkMnrPGByrrXKwhWzyk54eMQakxZzh1OmdlXNWR7aJ+FuW3js9wB9Q7Ys5zdzqMIC2JsbU1J9JydZ7YQus1O0O6tbkCKtf+gGOqu4+sX5u3jOIyH17utcPifUNZ95ZynERCWHneGhZmVbg8biALeJPrvmoMYvjl+L1Ync1j23bl/acqTyqcQx+2syz2af0O71S1Xru/NoAdbauF+zFeBieNKFbKSSvd1SH0Hmzt+9wNYOcv/LLKTz7x5uqWxY12ZulegGf02+t7ra2H76lPVcq6PnSePu+yygquPF+8v/LbXybGu8zoONaW97j57p+W++T5Z/1he7OrjOBlnX5/vbviZI9nw+jdhdefdj5PAf2UvbVtNXP+UBTTeV8MetqKFO4p4HB7i8P9Hfi6WPY70UX1ew1ltwDWDMbME9/zNfAKrlVBcaIBaRDBcVKacMFbZxbyjtn7iYoCD9fLQsmRCtAs/HDk54gina7MVg65H5u2TS9jRp89lriZiOU+tXa0v0B+O3Nfe4J08HXFGLQfo8zJYFTeZ85Ib96D/vwT3r19g/v5gN3+EmkYwd98i/zqGqwCe5ufGryeB0DZQ9VSYeMWPlbJWWjvVejz0HcqANVKBGW8E9UKiIqvCXy5JamWL0EJQdq2QVEZ4lnXkXfZMuoNdC4deeYVTrSzxvs1D9o3ly3VezDOgLfVIPwFDfwQOjy8Y7gjQgAIH7gVLTt7ew4aXyXhNzbSHt/m+xaPPkcNJ2AKx6T/TGVvTBqyLBEwJJAm5GRA5ZYFl4pXRDFNJAJ+ka/xOl/gL/QG73BcEXEOX7pZEbGNTdpwyHrtnLFRWyQXGdkoVvCzzOZESNV++B9+kfHdS8Lt9Aozdnj54iUu9hcY93uAM9798XvwzT0u/3wLuplAU5aknc1u4upbhMmIC/aeW8K1hn/Zjry+ftikvYxiuB6ELB2kuVb80rL+tKk1e/UFQRi0lwBUkJ2r0Di+xpxR4hcqauGVTRsZ5XhFOy3A6j1gLqAhJE28yKhYQSzi4JWK1e+scOW2HtqVLz+W0EETWC3tXVAIib1GbuWhF6LDR+pVw8jTrGGZpPeUkjBDLgyW9SLyj6VvTU5dkDZV50CdRtUpI8n+kU9qESIEWXEctcVRNRAF4oDkfR+H7gPiDFDSuSMwDSq8nUBV0tsi8GOyNZaQPrRYYy7us2H+CWpB0hKtMKIvV3vLckFICJuioIil2gMN5ScImzErLCbstLWpckM0RaJghd+duNPzEDO4yaK61UzxDomFsTQJ4Ob2UvgUSeRUxPj2L8d3Q9fyJVz/VFt+l9kqMIvqLHu77R3aWhNJXxyITMtPYGvTjE73fWmcjN6W8TV9RBxBGUiDKhEYup/re8Hf8q5lvwxDAk/SrnnapFRcf23DxnmT01as8BPnct51PgWKmLR7AUwtNNc+fAoaCzNJDSH3lBzlWYnygPEqHMh6duv1iD+4ArjZgayKG/scnvggqPpmgwkzzbxCUBqTIO1lQD2oJgAZd7fvcfcG+PDTG9y8eYeLF68wjCMOPIsHv+Gq6j6rZnhRzDKuGgcHpZcfjIJ7NvIAJ8rD6KYvrWydl6eagaWy+uOVz3sV25UgdFDtz74s8X7/uZXPe02/lu3F6MOMzOI9PM8zdrs9UhqURtPQpdRi50aA6B8XhNFHLscFVyf3Lh9rY3tg6KdEs6vK0bMESk8B0Fpngd9uez2r2yUvWRqqf6Ytg2887407tzdneo2JXoCwR4IYdxDrXyDkpCP/W9hFoQY5DWAkcJ5hwS9nnjEzYWbxKMrmVa/5GxxugtvjWZLqYRgxpB0GVUxQCjkAjNUC3Aglhk/Kyo/lIAsAAWkYMIyjejAPIJL/xDSYABZPefN+mJX1lQTUcNY3c3I+AkQYbAhuACT4QtpNZfHdWMW4EvnX+GxR0ECNaQhDIoyDhqhKo4aoSpUAWfJSmMAQysMKZ196sMkSGD78p3/G9Ke34B9vdE4GjMSS8/Ryh1/85grj9aV4o1DhYc1IyCIeCD5MvpuKREZ59lYw59+30beFJ4oYq8hHCKTeCYVXNJmOfzcZHVFZZ3sWE0+74gf+uytbXLkQx1j+JRRFhh+1OK5qiJEPD98ffVW080jLr84nBjq4XpjmneN3yHFo+s+fk2ZqcaHbuzWdRn55M1Rcz9kp3rGG60TNhlWuZTBbytqluNIdh5jOgrjAV5e4/ftfI737gPGP3wteyow0Z8yDyAwyMiiTSigIUA8KCeVnZyoIDhQMwvmk0KM8Io4T6twIxPrlPAaxbAdqt34t7XBoonDJ0EpKwHcvCL9+nfBuusKBX2C/lyTVA43I84T7N+8xvfmA8Z8/YDjMoqmvGlwnPLn3jc88lCZ4bNa5rpOrAxLBsanvLkGs1xuDdby634uix2PDu3AGHnKnXBjdDsplqV8qDWHou1rpKMcK1hFCK7PvDQf2mBKCUH+vPnGROVmfTqyvrHvIx1BCG6mg0c6tX4r1RRqFvBJiJPucJNIx6Su2piWEpFJMYrMN2xVhkapzUPZuBjDoPtLktlwiV9olxtqHzWM9C6k0y5D3zZ2WVEEB/d6GfXFNtymQyJfALE9EmGqeEHM1BFFCoMxhGCF0X8yV8gLeZrHWCR4jhkSpzJlZqZeGjb4re7QYadgakcNXl/BLZUnRQV/xycoRJTunrflKWzH+qBbl7VqWcdmXEzcJt1/Z1wxE5eyExkuTy7ZlT5MIjqlNltz0xGGuF60tAHM8RSH8XFQc2V5p57HsSwj+J1HacQYysgr3bQ6DiKL6Q7pEXAT3HPdV3AdxrQ0fxPG0I2W4F4eTMyqAN6WmuqyTh5IKhOgKsYp2nViRTYCt2rs6vjXc2J6fWMe3p1s01XW4+ZSZQXnGfH/AfHuL+5sPuL+9w8XVy3B/CJ2U7M5d7OnO3mrGU35amf+V7XnKKn+5r9fP2UOt8h9aniOG/KkWK7z3nHDwukekz/MCknVY6nw+y317BJKTsJ4uTz8/H7/EW2ft2Vpp3mkJuq0l4Oke89qv/tAz2XZw5utHy89hP2wrq8LpTlmvJ3QuK/0XPWwtsan2hnB5dKa5c2l80rK2J3lDnUf2/GxX1Ar/uM6GPXHpd3KSPF55fvY0RRoaNZ22xlkv2P3q7iNkXCLTCxWoz2CXI5Rpjb2YsJUZ4ETgmZzeF44zIUNoYzdhYxXqt+cn8LAgURYk84hQwXGxQC+AFCG7tSXxfUn5MNF3qJJC4TZvWbKwxinSxjVd6V4PzMoCm4GPjdWCtZaJCvLqZtaXK2PQO67R/1yUbzyGwuopkau27T1rMXsoqnrNrKok7z78/idM//g90pDAkHCmCQxKA3YXA1692GO43EnYquJmUMEv0BRepzKmasffsBhltjt3YGcTu7C8MtQrPLWFQhV5AhXkk5IrIeooCUn3nK1/mwcCRdHh+yNy7w0sheFfDiXwhPU01rzluvVtGC8YMR9qeb/pY60Qqj1mXbfgLF86XsIJ67/q/FNDS6/g0pOeAcYbhivY+W0XmjV8ZoCF/Kc4D6cuj3b/NzzrhrdXOWGHrQD3GNiO1wy4LkRmwH6H/O1rMAMj/SghjZkLTZQzcsqe09Zzyuo5GZKEvcs863aMPNT55flzRPAKtnlQqVnFLRuCAyokAL/+9gKvry8wXoz4kEek3QtcDhfY7S6AOePuP/4D5p9ucHl3B0wzhrmlBE5vyCJv4eMV19pp3lv0qM+zXkiFWT4+z+XwAsQrYVDsQu4Ka2r1T7xUIzMfZyzG3iv36LYJya0ljr3L1lY9QSTZoP1CAWidQG7uBZkWRWzgct/33mmwjHljcM6Y59mtFSSMlxAXAsuAIqTVSzEVYql2AVX4E4k3QbKLUi2weXlJWbLupH04okYCpezKGlkv88aYdV2XeRK6gw0/JyiR6oSdhDxKgRCgQVPisKUv1vAs3irDFBS+t8I2Lzkr+mC0xfajxA5FiSFqr+uesdA1vodUa1crFZaqBEuSFieL4dMMdy2mhGiJZB/ihdgT+jNs/cKZXlmCYu3R/NbBO8Zs1IRdrfyTOeZqnnpzEGGFk+lhLrEEy+g3I+4LcFwYJTuzcnjUI6goNUujhkgKtikK0RoOBoOY3BMmDUPVfwyvlDn7fJQ1CkycMjb6QBNgx+eW/klaSJbQXOc2KSEQw/vFmTR42uXuCUOjAljwiEJNNr/1PMsZUpwTdkIdVqoQSvIm+T7P2XB5CweCkqXps9m0RZlKPkDPBxQUWL5P9Iu1a/FgGcD1Twzc3uPt7/6C77/5E9L+Apd8jbQbsBsG8J0JmZLS42W/bS2tbir+/rV8LV/L1/JlljWC4q+kOHnEFTKnFX7hr3u2voSRfzkrFHnj52tLn5zqjBkTZ/zzxYR344R7ZHfih9HpZHIDpVkZYDK+vMhWGOqBy01+BTUWLDX1TRUCJ+V/h5QwqCC8kuUaLGxeTPZXfhcFRPbQnBns/Ke0O2BImneCBlRheJTfLrkhZvWGyCVXRFZjnjBnlRzKeN1qnhta02hZ5TdbT02iJJ4KQ5KcZynJvLRKUWbAIx+IVwRaQ7vSMN795T1u394hfZhARPj+7Q+4mw5iRLXbg//+X2N69QI8jLLOiRweU9gkC2nlxpL2OXRV9Rt46OpZfyP6TPo7xpsWnsvkIK6EQJGFmAeKPSsyKnsmnJhUN88H2wPka2D16rGQQxShs0dxzs860862EhbMRNz8lbyNqzqbeZDKuI4bPtpaPoMnWqtLzednRMeRR+/LKfs/fbIbgqA5VXFeTounBUFwuHswGN4hzS/JHiVknmbQSEickHPSaCUsMsiUMAL4t/nX+JvdN/hv8+/wLr9/NHxPqogIorO6HJn8c+P6blvHZS2R5xKuL3Z49eIaw7jDjAEjj0gzI1EGHw7If34H/vEdRoQLq9KgN/CvgWA35VImeLyYYKh6j+tnq72foDxOnMZi5e0SverSobauv1NfrtWlhSDUqySj8N+6a96RG7UCz7pP+xMUH9Q8XJSIpFEO3LHil4ciwcDLmIV9Ec0SzD3QiQpCwEZ2geqzZs+YAG4RR13/cjM35TvBhcy+Z+Q3D/Vjg87iwdAmWxcwm9u22l5k3YS5KEosY+qI4bDL3WuXe0OidM89+zY0b4+FCNcFodK2nxvdk1kpa27OTqx3HIYy9O6+q4panduZaS9n2FzVDcfzTKjXlfQSW3oJNc3G0hlHdZxY3es6UmX2vzovRjCVKlVr/nUDgiuEO7AM5RPPLFUwgFk8CBrJsK9ooxhajr3g1BZDLveTjlv3PpvyQAlzUTCx5yjo4a+FwoXjOGL/a0RdYPpQ9nc9pvAvAynCXbUl1TLLzrMzEr1Dyt7i0re9akNAq1Y7dhPLS+0+jk8dhwHF0iWur66/GQ5J8kIFEcDuXnDZ4cMtPnx4j8PhHrt5j2EnzKZHAqiYtPpu7cHWlrWj/hxW++sw1H09lYfEljGc3VdY1zOqfxbFbnUpxyFrvVWiPvtpIfq5ly0T9nOch483pp7y+OEn79OuxRa0u16H6zodHmOtLIUe4Qb+orbnGn77fAax9WoNpAL6zO1TIOOOIPBIOXWnniMQ23L3lu4KHdrSuF6x5ee07ruU8RZcDNUW0BptHgiwppqT4NqECfj9exGFhZ6lzeipQItxszfoIaOMrlPBvDSVy9ybcJ80P4R+TsqbVXMT5Bee9yt+j4Y63E5fDafQyB0ak72b+m0yeQWC8kSND43vr7QyNc9jipfIezvLBMb04R6HN7fYT5KL7e5wh9vpHrv9HmkcQC9fgl69ADTErPVTeB0bpa1LGTZVT8LvgY2LooL4wXiburHgcVDtNwrzJIadBZgoGyEgfnZ4y3zG55HfX0bKKKOLg3O+harai/eWD3rFzlJbKcLe7QUNS75aFqhowYQpCB1Az1FOdMfZHmH0+9nSV5EfLrtyVLQ2H+eh7+PvKWO/tcn2bNifre9tVbKcLLHvcP3LERqAcQAmBjSkewwdJ6gl5MvUf1/zJa6xx7/gT6DM7mjhXZ4J5/N7RDxJ2cYcludUEYgE4FffXOK7l1e4vLjAOO6x2+2QQDj8f/4J+S/vcJ8GmeYPd8Xq9Qgkx8G1y3NLZfjuWAqbuH7u1bn5W95Z4kJa/O1t8CpJU3hODbI2yKp3dONSeCf+F18zq4YFjL2l7cxfIRb85erAn0oe1EPsFXyFdvIfogXGsr5ZTmTMc8Y8yXcCgdKAlBhmYWC5Icx62ZJzWTIthngtUCIgJwxJ3hk8ZqagAbYk1ppQWvJJKFEGez8AaUJVEDLPDjdIYqmDMjjG5IRoPokZM4LguEfohkxombO4eHmMUd0LCo95QpBQXqCJupdIrdiRMcrvxaOCmCTEUMSyKGuVzbIlM4A6T0SLHFriJLX7VoHyLUeyhkYQF4URXKlE/g4BJFb50RKeAXcjZre4ke8F/QTPlrVi+713VrxNO3Pl0DBBpNPFwF//xsVrG2wRVCCIufFespetnQpH6T5iUyChnBl9taBQLpd/RwnhkcCMIM/F+qpa8sxAynJmUhlLxG+Gl1JlNWU4K4MguSLmWUOgsUZmZSOIIco72wvqhTArgyfTLeeUK2snhZ/LPiAloMX4LHh8cBm7Mx8AMmlwtbBGROq1ZHMNW9+gDOMCG/ntUDMhTLpNAvG/RJ9lLZ1cIXifRQkUcXV5e0FgJgKYCgfXmJKIMmjGhw/vgJ/+gtfvfgEk4GpISAOXcHb1QB9UPqbS4edQ/ppm61jIp6/la/laPr8ShYtmSf0wnBX50p8f1ivK1k8MyM+orO2So1Pco8U7jR0L5RibKCF9w38otHYthTM6jvx3pgRJuEYAEjjL7+I9oOGZOsZB5jVhv8nbwm8lImdlqJKdFAWB0HzKbytvKHkhZsyz8cFZBOspIQ1JclAMgyetLgZ3QodnzREB1vyKeVa+MQeBXKC5XYIXZ9bmLfBZrEqCwDe63MJYTyoeB6ReIfLdPDhMZhPmIWeVNcySS3KWfJLZe1AYmTH+8Q32//RnjHcZGAcMux1GZIzjiP3lDr/82xcYX1xjHEf1TDGZTSq8rA7XkkB7HgX7bNtCGbfAulZrvxBCt3KlShGi/EMyI02DpfAfnmvTclYEpY17bTgf0npGUIGo/FP+beRHFOo8tCwM3ixMTq9uFGmEFsqneKZ6fem/TcSMKITuNHv8ClsTMm6Zlqe6HtfkERFddUtv4A/sm6iei6coHQXx85QiyxMRXAK/uMLNv/1XoJ/eYveH7wGw4MCZMKeEhIScCOABSXmdYSAwJ9Cccf3mFtP9LT682mPeDXjoQB6niDjHtHB7o3johlnEiQcwEGFIwNV+xIurK4zjiGEYJPl0ZuQfPwDff5DYh1Qn9ezInfubsBK224W0EegVJcTi+bE6DsZ58xYVGnWIjkKPLM4+uIMPVEiGgESjVpnKu3U81gful4gT7eIpPwThdB1rvg4B02+00nfy8jmaeRKaw8ZlY4RfcCJQDKGHqAjfTQFRLsOCsSkROCthkkICLFuBoCApsW4DuB3kX6w1gjKnSP1F4NiYPRQL6vC7vtb8BIb4LSSnQWsAynUfbtqjl1+Y7yLJXP61umY57uNTiALhXU6TgRCIkGZrULN/wgOYAoLDT/XWskkpE1X+5c7QuWie3WzeiNoyxAJrS9jVDbL3YWcz7GdS5Q6l8tsacjlyRp2PWSgh6jq9MJfxPpcpWt8IRlwvIIkM1OK8ek+IDwSexcFQmOLqRYWtCtnj3gWUkZGQYzV5GFqhuNaitJC2ZF/E7VuURckF+k44wHyC7IWmN8c9TdK4diQ21+YqGvEj5PeSc0LnhJvvC8I84tgaL9R5qLmMvUPwL2ZPx25ra8eijI9xmO9xf3+LaTpgmifk+T4wtDbzx+/Y9d8fTx0ey3XyVG1uvUc/J4VKC3FUTj667Y88H0+tjNgK1lMKCK2tZd8nubxnLMf7XMWFD+npsTTpF1R6Q/yMUMPmshUPtjwAUO7KwPGEdgCAMBKwAyETIx+dn97Dz++8bGqhsxHWZFCP7+tkDet1Y4uncdWpnD+fqrSsG1Dmh1pmYQOozhpVBFmQp3HhxAYmDFkTTIeaXV6/cBUo9v+o/hqrZh4RZuCyGKkC0OO9ojWbU3Cci3CfizeAKCMipRcF1XDBtf2vwF9ecp44F+VBZg5ttguwlCMULqDQrAiygXrohSonkzuZJ4T30TRuMobMkNHn0HZRmHjYprsDxnd3Itti7WcYsLvYY391ieurHdLFWBm+AWZQF/4uIKqNkdrIF8a7LjzF2/H4PIa2DAafC3leQnklb60oHAyG8pt7Ttj7IA/bHeVDEf4ahlXI/fupY9ieukhjLVioLS05Yih4boVz0n/LUzHgRPi+8lr74AzCYLMl/wOvqboJncTqcooVetz4A7ruTfBTKSN8Q6x3TscrPLBblWsRgccd8ksC3d7575wZOWmIPajBpSMwO69yjnYTYz8BN48E8TP1iFgnQLj7a8eCWcsvX1/gV69f4uLiArv9BXa7HQYi3P3v/4j8ux9BNxPYhMG0KvJaQFETCeHywRl7tFFCLA5wt6Hmnd6ZD5KgdlqsjxytzE05YJfayvyzdlj61ne8X++17i/Uj8qPds2KEqRYcVeQ2AEIAqyirddfwgtrs0eLTaSMBht5JX218SidfPHLX/IPZIvZyFmdEgzOYF1gBxgm7Kdi9UCGWEXpkNIABsP0D6KIaOdcEMacJ43tVkJCBbbLiSh/T61GSp3ZvRpaGJnl4q8JKVujDE3D3dyqGmt/jtVrIo5IlH5LCrtdqWiNUn426xixeM4gFwXLdxaTHCcy4321ICEiMaXzT/Y9QhIOGsEIIiGCoyVJIaqOcw7WpixLIf99vPpPFWKqg/3Mk6DXwaqdnz3jHC6VphxBga7kCUR2e54NL3I8h0Ql/4MLzDk2XL65MgktL7Ucf/alXgzChO5+pXMGmrBQ9drK+olFfsCXmd1qK4AIQkZmyQdRGilWOgBhGKTunGfFF9L+gIIHci5JMxlZvaAElpQSZs7Fc4bhE2JCEz8rzNVakJ9nmyDD//294TiXWfGT4NfFlta2CSVXkeMGn3vpVEKLlTpZvTJSVkbRvYtKH9YvJ4CzJLsv3i+ApQ7M84TD4Q7zdI98uEM6vMUwzxhGqZwxd8f5tXwtX8vX8rU8d3kQ+/+spRgRsVpum/FQsaodCfj3lwNuAfzXuwkfXGnxeY3l51v+eud5mwyiLT0eoy+oVJEtiIGRE/717YgP04zf7hm3QzFhsjbZ/5Z/rX0urIDzBYVfhoeVtfHkcI6IA25wAlBdKswwQX8zTwDxiJhFWKa/Zf/MytJoQmblpSX2fxFgO1PBZsCneQQ5I2N2TwjJP1Ho2aR8gXn5u/FElogCyCyeyUQOa84ZPEvuicLckdCxuXiBiJw8tO2TzL4SRt97Uu4cxhHW990PH3Dz5gbDu3sMKeEv737A3XSPmYD95QX+9v/2H7B7/QLD1WXJUUmWgy16RBR4BMBgjGS7IygqUJbN57k8q/8KmqVC0Fs7UW5iPEQvCTVB+CzPEQGU0Mg1/1WUKcrbOdOva3GU+X38OVzUIIDj3j+30OLD8cK9uo/Dry1+OgtffX4kwYbSAv1FDiIU84oAkAbQOIocYgYyJsGn04wZExIlZBJ5iIWYT0kSVr+8/AY8Dng33mN6BK+9WRHxaaa97VFQ8lIcF2sQMhPGARgTcLkf8eLqGoN6QuAwg2cG3twCb0Rb3KJKbjbcsXEXhQRX36sKR0yQFkqIpoHjc35kVQzRIyCJTlUXwvllZhREv541QQHWGgrqLk7PKmmt1DZK9i95FKCSGFX6M3m249tF88eEwnH8vLDg9cedltgIFSfCrAu78EwJYZYZBm+4VDtzVdwfQ1inal5MACzCSVbhO4c6RYjKTmQ50QURzoLgY+5oZ8pFDiNG6/mgtmqYGFZBoVUmQHNOLKSZywmwZlafKChUhJweR599hqq56F0jAEK6jiNXaUPo2RZnJqRUz8SWC5lRiPdjo+RmHGsePT3meE0ZWIZkiAueB8IYILfU6TI38G2wBnn13hp6Mq18VbdXOZxPonqbOlNzYs4781UIfShf0rPgqcPYRYaqbrCGgaCw+g8JFBQVjmfsagiWPbI3JMmyTU947MOu8B/K+czMi3wv0Hkr7sC2evW+jeclDtOxES33kTZfLZ3D1+yxsneCEqpOmuH9V0ZKVN5tS+aMOc/O+FG+Q6IZQtqcy0ScU9Z3/8Pee3h5Dk+Hcy1ETxr3WL2V37uWuFv73ljvY5SnXIrnyg3ysFKo48e9v6V8fE7De964gE/iufPoFp6uRGvNEzWrb6f3qF0mx2jwWHe9VAZQ3een31/wWYxm0MozEeEqEQZU0Uf75bOQSXTo9+foxa70B3S1vjynJm9tvc9t50gPHfqvLtsWuTJgOkHfH4UHYTWdrzyjgVOiAZgQnHCVE3heihbX5z2cIV+EQOBFmMMQKrId3ESmcUIchTjWvpTHtb45F57G7c2iQF4NhixIbs0yBQMnBaZ4FnDxiGiGU2REUbAdnhhdy1QUBf5XhpNzMy2t4KmdsQBE4QvsPzNaKuORmoT59oD5zR2GaQZAmOYJ99MBFy+vcPHiGuOrFxheXDeRFnRXOL9RC/DJwawJ84XxWTW8/gDl1RT4Fjs3FpEklb4tJLXLSwqcxYjO/mq7gWHqeUAYA7+ugKC6elyV6qp4OL6Nc9nKG6n5XoN2Cg/1YApxPnw/9/o+szhoD5iHMIxTsER5xEl4z6XL2upnDOWhc9ilpD8aDaGnzuQvxmCnhLwbwTQB9wKdh63kjMypERGKgnI3XmFPMyjNwMdQRHzuxVxNDvMOd/Ml/vZlwr/51YjL/SX2lxKSaRwH3PzH/xOH334P3E+gwZCaLE5rT15KpNK5u9f7MrRwYbeSpPi4JY6t2qn2I4SNBWzdTnm58oBo++JCZIgVwbK4vUR43S1ffS4jMVYq5pybd+xLDUi0spa6Nn0UvvfRHzdz266n7RNH9mzJWYRKcKvjDvfBZtTQXWsBj4qfo1gQmHafqIzBlF96iZaQPLHBaB1RLIqN+CjWIGp1wTPA82LERqCZoG6e1VUhEYjFTsTvdH273kOkIA9AVq+LYNWSESxFNMalFYsTmpJ2kKlaN6IEcPHO4PC5rIVNeO/QQfNEsMQpJVlH3+PH/OnjJUq1pUecO65/qMCQfTh4Y5XCLyBs+24Jg4sVXq6q1kyMXgKZNc/FCaYg9g+Zl/IFi4tOhNwcYC3E2hphUViOgEP8jAbiLU7DCk5bhhAqzwwb188Kc0LCoZRk6oFWq4e5nLPCcGovXCt6GCzBlljwmXkEIdQh3e9QPJWZQZxrHAWGWfsYgZwoXOwg4UxSqhJNE6urOTJyniXJ3jiA84BhYORZlXyKxyyfSVYPJQCau2Jp6UN6liODZb+TzqXPRQ5MjuJbw83SDruipH8fsl971q+cV3geosxZ2zWrKDhw4mXCOm8EV4Qi4AsAM8+gw4SDhmZKSXJEFJzxUai7r+VredLy8cNoNUTY1/K1/FyLbu8caDAg8hlfS10iZfZcbTe/mpDqCbs8rajaoowAzsOPbXun3j3SPx9/vGipEvbVDySKAAMDg4YEmiXePkg8zD12U9W/0FXErBb+5bfyH5Sny4hOwsbPZ1UqeChWZmWszYNglr4V8AzI75a/YZ4xR953Lr8x4HkFhlTyQsiYA42v597zK8zZIwV47gmupUFEcCvgYdAcDmlwXsLGZ/KRrMYx8zxjzpOMK8fwyeRzUPE6przIkoNjzrMvQ84lF0ZuFSbGCjFj9+e3yP/we4wTQMOANI4YEvCb/+t/wMV332C4vlT4iydE7RER/jPegODPnAeLvPzp3aj/T+V9FWYCJHn5lN8CIHMrH+BKCMDXU+QsSWUpEe7Sx4IvjzxqF2KqnrV8cDGg6p3ixyCq9l2qf17gpJZWO9F3sBRrjca+6PJzGchC9vd0pWs8We0HkSHMr17g/b/7e4x/+Qn7P/xZ5KJ5xjwlxwWJgEyERJqDMQ349vqXuMqv8fv8j7id7+tL54xyliJicQ13Lu3no+PWxGMuPkXO4op3Oe5xdTHg+nKPgQbkwwH5fgIjAe9uwe/u/MJattVMYiu1acpJhpFtbRrBWvtaV5rTR3gxvNF6OS6oj5/LbycINYUzyjBtU7uwqemrxBhfgTIKE9mEnNqbK3DKRVNGh25/vXHUShMVkAWhnfXF/i6BTIhNZOK4E4UgKV3n5rf6YnfAq78B6s6a2q40waCFcYFbRWQXinZErzCBqyiC5DNxqvo2y5E+LKqLpgTiue6DSxqz5DXb94tAtry7gim4/lCsb2qCrWutH2SPCyXCWllR4FVWPw5RJb3t4I+q4bo9lDNjCpLjxAxXc8G2uN1DDSVE9XJxaXO/FME7hTtpnQnrNmW4I64JNevCjWeA/9xrsdTqPZUzqwOtUYbsQbeIacbuW5gRTbAs90n/xHCTDL3s3DLesJtZrbuCp5ajrjhCKneV98RZ7iV9HpUkOTNoKAJ/eV4zLYXGPo5nKzjsPLe/29SVIweb6UqZDYbnkuhvDh9D7b0W1wyqLIuKyfa6ZX/J+VZrISh2GYw5M2ZVdBNtsJzZUFrFYAXT2WXre8fPxvOWsreLEcC2vjkei1A+FuRPUSj8e245d77W3v9UZXv3C2x+Zv2jUNTfVpr+Kix++nLu9nva/frx934g+5uyfXN92hP72PIQ6AsB+rjl33bOn6Yfg/cpV2tp5OE9Ol0MBDKvendbD0fKBrzod1kj01x2UPhrpECjEoCsFPdQSM1ifNT8XSgjBFChpRHqZqdTTS4ij7OHLxIzHIXNPP5NQYD6u/XRCtaQGuM/mziDxRUSxRiJ9TnHuuHtRMbjqBAfRQge14XD/7JFLcjFAG1t/Ty4skctyOAcsmv4XGhIaOML7fndhHyYgJt7DLeTJA2HGQQRxqsLpCtRQphwv/AbxgejKCBs/9gf8l3ldeu9JbR5fTaWBKEpMeSRhVMKCoUU4GoNF1GUF7a2lSKieifKV+KZpeZv+9V4yfCMlzKHUxglckxicIqyHwMfd/SsN4imAenU23U7gbl6MH9EYV84HB/nJmwVdvLbSt3mweZbfa3BTgOPHXf3ethaziC7K7mQ/jV5he+icQSuLpD3I0woxJnBQ8C9DDEsVYEEETCmHTIRdjxgwIAZGQ8Z0ZN6RDyUPzj93poSopRp3uF2usKvv93h3//dFfYXIy4u97j5/ke8//MPuPrzHS5+uAfNWTXBK1DYBWqXUEw6sCCgOpfKElOcJqZWlBTHXlt4NHBxt+kywwHU6BFRrM4D/QAT76zM+5bx+NiXlWthZQEuO5Bx/k0AV1+ELRrqfTJQegOwGOlmbZ5zlljnLsyyOIP6T5fyJICS5cRCmmeASN1FS64JGpLEVgtCRh2ltKLEUfbvRbBaQqpALYnFIgLM4FksSZA150eeUS5f+SsxNTPyPEmM+lkUCRaf3ufX8lXA1ixsCFIigBg8JFDWeO3N7rB4kzkkznYUaMeLIJbsBqcTqfX+lL8xnM2pYu8EoX3Yzc2qyd+WUHVBsQNSwSMI3JRuHS+KNUE+y3nyPWfEuJ3VYPFRxgC3Hqo9O3gxnmM/L6vVOKsnMD/diM1xIIUonBmro4xGJCjJYPBiBHDECf3VNhslso0Tz1lDdLZtSaAw2flWg4iQEwEaVzYqZg37yfowoF4SAjohJSBn9eixPZxUwK9DzkEwDkDOWGDUJL8IMM/iTZEoiZFPEkZkmiYAA0qitkHWi+H9RvdKwRkBE8YzoDAlz8+RCqxhLZIJ8UlemjOQKIf1KYridpliIjnrP6oEKq8Zf99ydpCjWdbEIpkhoc+oMC4WczilBAwJKe2ANOLu7oCbm1swdiCYG/zHIZB/fmUjMvlavpav5Wv5iOWpFSCVFy4VD8OKjfMrNPInP7+7ZX1MS973azlRHiVletoSxa7GkzIKTYWBgEE9IlKGJOZi5PcJNDJwPSOR5sOzMElZ+E3Ks/CdWX+rwgYwkHPh63PwiNAcCTnPSDNhnmbQCMyz8sqaR8y8E+Y8e86FrJ4Lc86YshihZGbPCzGMI8ZhlPwQJuthO+sEVm8F87AoXhGmOCjD0OkSb4hhwJAGDKP8TfofWa4CSC4zACFawYxZeW/PA6er4ZwLk/B4JHAAhDRPkBxphX7POWOaJkxzxjRbXsoSnur2H/6A+//0L8DdDBDw/dsf8eH+Rrwi9jvxMkiF34xylZLnsAiao/eD0//Ga3hI81oovWQm7T3zhAgJxE1+YvxvCnKSkDvCGQOi8L4qgix0E4y/IFdsLE8AynM0bGaUSfRK7/czzrbxk8zBYG5LH0cePwgrMyGmpP8iywklxDN1+lF7A57u1o2y0aiM8D0PCec8JMNrlrNSPK/mafIzmojUK0K/p4TdnPDru0tc5wl/2N/i8ID99SBFxGYWNRy2p2Vrg9AOxRPi+nLEi8s9rq9UGHF/QP5wB3p7C7w/ALf3cA3syfZNKFUEJ/Zd/q5skTN3TissYe4L6srzjURwkDcWeS8XGgGRwO6/739X5J5VofrJ8bjtUcURRlsJj+H7p2i+S18imy8CyW4vJ6bJBWpurVC6Z4ggleSfSuju9sR6bxWChao8COT/ifeN3a0iaIvooV4QtyIhKoYkECWEC4CbwYUdW9ZMBZXucprrncUBSKNJq7Vo5k+eB2uJ2E41sb0vTga3W6UZCld/bd9C//bi+Jc34/+WsC+/FJgWSKG3eYh8XUyQvdZHFTLJ1tFGFNe+qzg0S528nFttYjko/X2DVmHt9ZPvmQWSWRSh4EffEVGZw3pC9bwKA7QsC2+U6kx3rmPd335OtgyGhRS00Gxt/7aPOJ7BeOYjqvHxCg6Ia8vqKYDgUeHhnECa54JcuWjrDGhyatbDGJUiOo+u8CRLEK1TofNBFSy9OQi4xhYGjQWTwbmY8iVGb63A26ld24qubNCFXKi8y9VQxujAmYJIrNLGcQCNO8eVzMHLzeHsw/1xytOSklKeipp6/nlYO5610vuJ+1xpc4GvqT3zshv1advqiV6flsLdUvr3ZikPzynxABZo0dWRvo8TDCfptq/lePmU87fNM+g4gNvhX6u47exWXFaQQZlRwk0G7j4Dsc3j56NDY529SdbWc+satM/WvCmPtX8uDOeXlm5fe9aWXmjkYtARSJozQF2i1IYw2v5meZcin2SbXoRKl5yATLijQMhp6G+he5WuUuKTgkESSbBRFMaRC73MUM8GuDGP0bTw31RJkTNyAhIngZEB85ZwAzxErwizwBUCWBQDQ0nAHOdAgbHwvabQkBjoxVCsZX0J0HTXIoBLlIrVvgnRjZX0AQOV54bxSzZmh9pmzRJkZ8kzkbPQ+baWLKFSOChiTGSRDxn3U8b8/g789g4zZ8xgTPmAzBkvLna4uBoxDGWtoxFeDMlkA655n/h72Eth/8D3R7P3qNQjkAZHKB4PlRICzZxG3ryjhIhhmco+buCLX4P8gesHVb3l6enTQxts56pis7OYpQ3nelE/yJjW+jqrrKLxlR4eKkSo2j7R95FJPWd8m9HmsR7ion1K+nRr3yvXZr33wm5U5QLvRuTLC/DhALqbXRHMipskDDVX541SwhX2yHyFhHusnZdj5aPkiHgKFm2J4uRb5hEf5hf49esd/pe/f4H9xYjLqwt8+MtPePuHP+HiTzd4/acbCXmoF8bxKVrfbYtzsXGut1pmLpUQ8Rkv/6rkJwqCHDCR2YRLtVzqAEJ4mPI3ym8yMZLXD1ZCJkyMk9FIwBiInmd1sXuViwiqXNyRCAT8YlECwIRt1sdDEEKtSGK1KmC3Urccyw0J4wKwRAlMjJTlb+UaCQaYQImBrBdlUmuDFC56I1CzEUFhTD5FwfJ4Fi22ESAWYolYBLEpAXkWcsnF8GxW9bN6RYS5VViJuLKG0GEq3ViAclc804jqRBohmDIjJ7WWISW4LMZ8tUYlFmSFHBvBYdmxcAIu1qUOxVCFcKo6LW6WdWivJeMQ++wV2/8LJpsi2bYsMdEaEOY2DKG4GQM8mzY6O06gDqwF3paI6kBje6k5tq23UR9+9ndNscU5xlYulvAUx8cMVmYgeAE6DEXBW/o24h0NnPVQWBWEAk8maJ6F/hhsPyIBST2IeFAvA0oi+zd8GBUAzfk2pFr2TrNVWJSXJmQnWzv9zaz7C9Mq6z0r05F0LcZhwDwDsyoeZ8t9kI1IV42EMmGZLaUNNUqvtdmwM11IY1OW2NlMlDQ/SUbWeMFirdS0xGWOkhjSqWdEYSSKotX2W9ysciGzxiau9nnFVOj7FlN2GJGGAVfXr7H75jvsdpegNGCaJgw0Iw3DacXM2eVTUqBfy9eyVn4++/KrEuJrWSuPV1ra3W60OlDTGaT3CzAR4R/uZrzLjGlxvs6Bo6bqvxYrcT7W53PL7B1bjcfM+pMpySPb9+Q0yfnFBdgkdHlOCQMN+Nd3wF1i/OPlhHtTv2UGvyUgMehavRmY3RuC5hnEMyhnyZOmZ0qoNOURM2t+BPb/hPoWvjvlhDlLSONMBMoJORg0CQ08gzl7fgjLlcDqDkCJMA4jxt0eu90O47jDMJhCwoYyC0+sXhDzNGHOGfNU54uQJovgWxxGEsYhYRwG+S+NGAb5L6Wh8MbGdyuflLPBzLUixbSbSdbA+OV5moRfVOMoSgOM9/KcE/YfC+3/7s0t3vz5PfY/3mBHhB/f/YS3t++RxgG73Yj/8d9+i2++u8S7qz3uNWqBWzgHT4hk+RfMMItqWjzylrUw056bgIbizwAIbS4IV4akQccp8gv3cEjWjkWmKEmrQUBC8jkymEufhT+rYAxFzMjCKJp3lyUwsL2nJ891zQsZ/7qlPPrm4PL3yVFPwx5/jHLOGI7tgcd0/DG87Z+ih14bHekTzLhvfv0S7y522P35L7j4wz0AVq+u5PJPclmAvDemhF9c/wrXfMA/5w+4m+/PhvN5FBELQV34fPbsrm+gzCNSGvHN9YiXVztcXQygw4z5T2/AP73H8PYe6WYGzXU4lQeBcQ6o1YFvpG9bi7cRWmqUEAyIVQLswrDnMk6xyI3dc/h8+jAtLFUByCXCHaTWzGwtbey33sQZb6FxwVh8qxG6tiLs06VgZScYwK6YMdkom4CUlnMgls1lAtpLWS7S4juwqNFcWi6oRiEATMgXyLESYxJl/XWhi5KN5Yo1Dw8TJpoweSHDr+mGZi6LG2lTvbqXMxiJJbSUWclExVbPmrrdlxXRXz9cQGbKiGhNYr8Xa/oAOaGqf7R0zimtURkmUK7g1olp93SjSOx2rfXMJS6HkEwt3WIi5DK/tjLUPXJPw/zIgvqZq5asmV1fCwbToDLv4xhnkQ/Ez9eJddO224Nlnku+VZVJkGoZVY6PcqzkXQr7KeChhRIi7A1TrjqeNaKcoXiOEX1CPK/DYm7U4p+KAqu4dNteLmOK8DWT0p2qOBrLncEaIikS5OVcWRfH28wsLp6s43UmJuTmkGfFa6Rqx1BuOFe86E7u8WkHYE+4uNhhv7/Cbr/HOO7BfCPMLUwZEts/dQhOH5K2iSP6u6Pvnft+05q9/ZCXsWWcXlMB32xdv0AMx9/rKletz9hk791tED2wnIswZfM+h4fHU+WdOK+drZTyiTZ7aKm5ydop2+rR8rXU5WMIOLk936v1zgdm+ysPGyjX/zT8D4X/pByYcehfeV9c+fihpNbvqIeAwuHfBR440t5Dx731teMoKdA9gPPNThZtBe1svLc+95mBm3yHt9M7XA9XGJEw7vfy8P4eM3f8fzR6JjlD14Zfst7Y/2sbCFRxMFIM8DFQjFrEQ9iqmSEdW4LmXHsZFKG9CLKTJqkmzYVgjJJ7Y7hXgeyPzBkZmssh8gFkr5MbCqXKsNDCAkUL/rK4Tp9HXqiaGvG2Smw0vnp+gDCnLIZJPgcckl+LQeJ0P+P+9oD57Q3op/eYPtxiur/FYZ6E77G5uLoCXb8AQnJtU0IU2MuS1EZ6FOQDMiFevUebR2GCvavtiDGprpV9duOm5HNt/IyPvlJCuLlSDWfgW3RLrAG5Wk7LBwpP1NY1g7O2rB3xyLIWprP0E9/uXkHnIpFjgJxZelw8KZ+rXx5XmjE9BINvRpknyNzHQ7JePsWNXE2LCxH0K0Fy6+xGYBBcYbJRMZg2ZTL8r8g/gJRGDMy4nEccMOKAqbtP1spH8Yh4itIe+znvcDO9wC9fjfjf/u01LvY7XF5d4f4ffo/D//u3GAC8JgCcwSSudbV1ZX+ayh0pq/S4M8Xe17bapX4USslP7H9rK3yo8BduzWMtEShsvvoSPLlJVE7Ubt4yKy2Ta++dnrEWJucNDEDThlfQmkBvpc0zCE5mBIv9csjAwABL4qxEi8Jh0e8pmbAhEAmNla8IGJVYWYxFr1ASr1ez0GBoDHiCx0EnmKJECaaYbDq0NSTxhMiatDpnkn3PJaamUViEpFmlnYQq8FUCd10YBoSQLAREIbpyIZ4og3KCZbowly4A4j2SdB07RCjnkh9D5rq3aOjeyCawji6/1U7Q9SgETv3Q981WZcNaoWUtI0Tzkb0ZyXaLyyfWP3IBCI1GxYIiaCRkyCvnsDk/ZpXfP7enFbR2+fh+ysawkBPtpXLx8pF3uTs/nV7KmNhPfXXouy0w69hsF5U1lctUf1MmBFDHJxJLJ2OAsiXMI4A0l8LMs1jx+D6KxYjeoEzlMoeS60W8QiQcmzhae+xVs/rS+aI8gyghDXYChuIWmfUe03i0KaUwrnAfODKVv0TqGaAeLJyVYI7Cfv0dCbrPzEtG/suckWcGMAjzorB7RNwQ+5ZJPD+ICMMwNleuHWJ1m08aVlhxr7JlmhSQnCny0TGEKUmEN6+Au5eMf/fdK3zz+jtcv/oGu11C5g+Y5gnjqDGPPza191dePoal0Odbuizj1/K1fC2fUXEBIYrBjl2J5HfP13P8qcvP7S4xuc2WYT1694WrqA0X9dvDj9gd3uB/vv5X+GZ8jatvv8E8z3j/5++B6b4cBidqNf+gCtUlz5l4QIA1LFMwsiEqPJwbpCmdamyAheEhKs+gdK6EODZ5h/Idc+E12fI7eCIHzd8wDBjHveSIGEcMKoh3WFi8FGbLDTFP+nd2DwvLYVEWC6p8SBiGpHHUR/lvsDwRUYw2u47Gck54wmpVSAjNK58pE3IyBQswzTNSzkWCo7w9Mop3BWfMmfH+zQ1+/P0bjL/7C67++Qf8+ac/4ad3bzDsdPzjDjQOuPn218jffQMMo8yHe0XA+fmiHIgbkIoeZ7Ej455q5AguK9A5NL4F6s2d1DOi7VsqlnrC/MIVFi7Do4qPQuj1ZPEqKuBaSLdsROeVaLi10mFVOMi00E57t/6pFje8+Iylb7T8tWwqz7pG9c5ZGnjGAyR4IbknWQKz4NmcZxAIeRAZBSe5A4wfT0zY5QG/ubvAdc74l4v3mDFvhnK7IuIMwqwnc/KD6pKPWLntYqUvAsaUcH0xgDHiat7jm5c7XF3uke4zpt/9CP7xBjTXSULhwuWVEtaqphN6wrx2oCfKZiXE8nNrfeThmGLbFJUNdSMuu/RWTOPfgcn7Cpa3odUo0AvOAAveWxVkEerYij/gempDqS8Gvxo4ClOBcJ6qvrpt6jzZR6AQSH4wHa46f0UhluCXIAgedsUgLhr7FKwpOmJLUvFdmMBaduhXlMemZU1SDY6CVru8w4WaEqCJb8tg42okPQombGx2Tbu5jUgksywpiEt6DsQIz2CWsE1uVGPKM2QwJxkrF2WKE2xRmKpnjGy+ebnKvpaAWtdwEGRWs90Mx95r22wPdpyTpu+mtIJ8G7Ycs1zttwac+j1XNOo5t0TVlJD8jEXCa12R2kDjPRJxUHLFs71spVXsFbdqwBSlS+uTaijx2J1RbC0VhhXhP/u+t07sew0IOyD9vhzjRcTPUIVFUlm2ql5ZZy4qHSMurCB0EABj0hLCzC8BEhyXxWde6xh5a0OInjGSK0LWJLO5u9sZbW8F8vH6IAHHIaSIO6unCJvCISVQBkDZlTWW8FpgkORVICqWayir1FdMZzBHRrQ+l/Y++d0W5ls/MBFoHDDsRmE8dwOG3aCMjXpDBLTCPTzy7ITz6bt/De2cPjePgb2mck633cntsvp6aNuIgXLtl/ULVVoGsCifmk6OLh11KjWvb6DFargeUuqRLn9fK8sOt3oAbGqZ1uv1M/ec6oW6H0++ZvXPMBxZNLk2xV9YefgMrBS7Bp+63U4fD6mzejKeDeC24UjXWP61DDFgCLFSuvRToc9Wm3+msmXKP145H5Ll+m7DN71xUweRRQqx8StV0n7Z31PtOaNxq5CxCkn/hfLxmFFzTb1tALaHC62RhhDPOWNKhU9BEjO7Yb/HPgEv5wm3NOMG2Xk0MEJiMmfcVClReGCCKBkYgFiyZzFYUb7WYBUjPUlObKGCjMd0mt3GwBmWH9HyOQQQnFd0ITtZkuoUjOZsGo2PsZwMlkBb+G3LOGFTGpWTEkooyXyRGrqooLy9lCrv/PJnwXkypNOsvHZiFgPFnGF+z6IXEcO0mTOm+wl3twdMb26RfnyP6c073N+8w2GegAFIgwgTr757gf2rl0iXe2QVLkLnSv4Ent6niYIyIGyuIPR3oz4qvEydI4XcKLYYcSle1VwQFnKJkOIka9s2t8p/BBis7+g5UZUezdSlEzbSL2eUpZfEqRKI44plO/3mFgren/tR4ur7SUh5GyzWo8vOjtHpJ2n4iPkegKR7BqXKh9Rnr5nBzoQ+551b1qbl01cgWF2i7euz3kfdBhEB+z2mly+A2xtglnvAFLUpmfExIalbjxkmXg6XmImw2zNmmjbCdqZHxCrvd/I9R1cNoWAfqPnem3d5erkf8G/+9pfYjTuM+yvsxh2ur65w/8c/4P7/9Q+SC8KRl77ZCu/RboQjwypSaMAsXFkW6yRjy9u2SVQ4FM8H+HfuwH8caG2vEpyZQKufei1algsRUc0gIpr1gxyoAXahkip9Qnx1BsTSFkEA2sU38bJb3jPZrHkDXJXltf0aiJSAhUu9rJc7s8eYLC3KwXRBmY3dEyMZUMVTwaeLyIm65RzaviRYlzHGJRhurewEFgVraLUCEZfQoVBJBlMiAAPAE5AlzqTkh5iBnJUwK4SHex0ogSlxKeM8qBBwGDS/1KDVC+IRyxcSQjFniDE5N/tDPyazXsmYzRIlxA11apcBz8rrh8B9fx1+EchGlUIR+tu+ISNYOogq3rFUPiwIV88lElbe5jFRr+1C5MY8CjDQQ/9FkWR70eZRlRDMYnWUxIqktchnMDy8ELVPwlz4Y1VGLA5ZPAJlPYwh8L9scMGU4QWmcJaFd7DTt5x73+Nse6l+ngOOEu+fAq/gknC2bVxYXqlRwTXonirrLm3OOfv3pO7g4pWSkRKLlxIHrxaS+KTWIyU5cszCOBRLIGCeZ50PzcVCAywEU3FPt33PisuSJ1uwZHXWtbhxq+eTEvc8i/UUz+IxIV4IdZ4IaZYgh2b2EG9E4k1FIFASPDPNs3iJkAj1h0Esp2aCWJPNGQNEATEMgzJ74sFjDJTtGbtLUmBSGJqPBwTkAZSAweY4MLpMwWOLZHXsF2ZgpBEY9hh3F9jtd9hf7DGOCTvsMChnJ54o8b57TtKyLU/RV9c37IzeayzQ3EYPbvt0WSAVL+znvUMHBJiMWvBKEWEDWMSq+1pWy6mpaihiAJHai7dJfN5+OAuilc+PaCaW5ZV8us6ZZUsXx95r76pjbZ9VFjT1M5QtADoRLOVjYt7ThQBOcs/nCZknME8AJxAGgJP8Fy36woIV3gJYjuyhq3d8hirPwC+qtFCfN4rezXW8fo/efEjIvO2nc2nssFr1jN4LHxW5zmMgdW97hodVYmpnp8BLRLj67ltcHA5IfzjgXWb8nxcTDk7QGz2dS85BzrBQTMIjCs1lBnkJjJkImewsGQ1NSMNOvAx2ewxpkFwIqXCmzObBa2GZ6r/Oj2QxnBlSEo8INUyR3A07zUlgfMCs72VkNk+IGeLgzZhzveqD0u0DEYZEJSfEsAelEcAI0ICEQfKoKTGTQa7gMI9ml5NkghvhAQA0HwQzEqtgjwDiWecBWst4BMb7nz7gxz+8xe4PP+Dyt9/j+7ff4/t3P4hBzuUOw7hDGgb84n/5N9j/zS/FM8IUKUTu1VwMDHW/mAIihV1CVNEPrbeYhVaKchLh6aInAyQslP8e+Ow0AIGHtfdivgrf0RHWuMfdMLHhRY8U1tdafvH0q3T0qzceHq9LAQOVyzqMDrFWfY1zz1htubQOGDbposAnswLgwuvGdYn0vXfVn7Sa5i/1yhxuhHVFGdWyEAsipVvn6cqi2a5xXO+NxxGrboB7Yq1JAxozgOmbb3B3fY3d7/+A/d2d8P7ImGbJh0MpIWVgZ/LElEC0w7eXv8JVYvz+9VtM4zMoImj1S//y39zO4nKsW7SpGxPh5dUO1xc77Hc77HZ77PY70N2M+z/9CflPb0C5jnNd7bOww4oM6Pwdxw2SWX/OK78v3gh1uKrb9YDolFVcyIYLToyzGpQhcxerdc51gxTihJP1qQg114et4KWVPcPNI/9e5sYPFvlElTFyhC5ganP1zAUOgaJWjq0qKJnVuLdGXnZ3tFMckbFZVIgCqwJwgZtlKXIZC7MoCrySCTojsaD/MC8uV3teYjKqYkoFkTKfgYiqmrW9EJLUxv3ddqTJqr2aCSR9UYriwQi0oghanpfuWJqhh0lrxluIo7ie9T6J60j12MK/XRg6v1VJqYMAv3sxxp64XLMNhnIceaqYRdb6SbdN2tmsAZpolR4VqYtZMNytTEf3DtgAd4R/9VkkblbIRRmZzvuGBauEoc16l/9MoM8VAWzeWbFtYmUwIHkSwHJ6mFg9mqChmsjfWRksXCnXH2QzLAmHVlVrJsBX3hkAuDLCQlVFRgUQJalbUOlz6V49H5J5ReiveswovOP4LgBd49vwjEQZsrgbpNFylgEQJYyXFxhfvxQaYEgeBo9yGO8TEpRr29P1Uw7yyh3drNsp0uME2thYHt1AKY+ZS9t89rUd26m220sSa98fueAdUuvha/BwWNY8IVZx5KlpaaDZNCSnRzb2eW6p6J3m0SM3/qZd8ej1Pd7npyjVOJ8VIDqNwLzakXv9JA5cq7AgRs8r3Pz1zXCs8kPLsYXY2PYKyfAUMqRNy/iIi7Ru/wkvZACnN3mg76v7pxPdYHNpXzoCwwoJd25/cl+uRD7olm38wpv5AzJnvBheYJd2+mrC/vIS+wMBuHf+s+Zb+eTkVTZaBBVIs3oTEMZxBKUBKe3ESE5jkpOG03TeCeWze5hn7V+fF/s6quhYF5qHifNwOAznRUsONjNQbGbSeLCkvI59Ng6ZCNX0qFuFx1RHIOtRi1SNLwCz8N5s/Dhhnmbc3xykHQB0P4Nu73H/wzvc/eF7TD9+wPThHQ7TJGGiXrwEXV/jxYtLXF7tMb64RtqNPq/Jx2BynTJH7p3sPAAV1ll56WLMFj4b7e9yo+jJQGJUBbjRXglLa4qGFH4nV4aUPuMm8hWBK2YrYV/YcydK5IZjsXVZowu6P1vlYKxWNbZavDd/3c/ZGgCrAqozygbE95gb1vn1s5gYWZHIltfnsB/66hwO4JjkY1nniXmLT1kW9A7Wt5Ce5ZQIeRwcL5vitOSyYZixeeHx1SuNWJTL1Dd675WPkiOi5y7peKU8aD/IN93Il/sB/+Y3v8DFXpJTpmHA/uIShz/8Cff/9/8MMKvLF8p/0nkDy6cs/d6rnA+ROA6CwIdTnQywbSRetGWby4oJ/NylLtUTabEMmet2XPDrlxWq8EWl20I8rJrqMUoy6EYaTSSWw9T8bu1T1UgYW/yjArToKuqRJHmG5XeIJTOHXK0BVZF35XNpl20dB9HaKQRQZIaFFgkH111QI8EVPDQCESRPxQU22J34O+Y+mjTBVkG38l9mW6xoqaGWDmYxre+IRTP7fmJYqC6xAhG3CL1YdYYzZyQmJSRLnM85z6qIKB4P1gshWnXH64H8l8hN9I9HJGRCaeaave+l5VTJ77Dcq4WhCWeDNdcAwz0iigC6tOEXNcq+MQ8ZD4GEQtC78g0LMKo2EqBJkmO9QqyJl03vStbV4viLD9THZzAVy/+oGAtKAIOhxcNUHluYtT7+642wtNnSYybsF8uPsFeayeopVh0HKuNgKVVyZlAqSkEEXCgpFcJdRqSxYOV5JNxlXBmMBDC5h0DxQotzwvUe9M9ln8c8LUnjdrkCKSo7sKQDU0rq2TA7LkwpYRx3IAu/lBnzNGEYJQauWYWBLU+NKCpAYsElCouEYajhlzOWOmg+jD8TeDBYa09GzgwaCp4DFE+nhJffvcb+f/gNrl6/QhqUYEoE0jn29v8Ky5c06mP4DKhxw8+3PJKx/Fq+lq/ldKlom/K/mr9Yf++vAhUtignCPzUcDyl90ZN5SDxcGfHcZQlUNDRaLMXaJdp5bC1nAP989wNGJPyHq78XD1NIWJ/LVy8xHwbgwxvEsEjJPxvnWDyFjZs0PpNzAlN22i0NI8BAGiVPwW5/gTSMGHYjiBKGcXAuE2DQPAsPnBmMWfhmTdjMyK6LkKKC9pSQaJAY554PYYB5l9ssuIJA+VBobj547oY4V8GTQOOhC50qCgky5QQYEp5Y5mTWvGpzZsnrkB3beOtGfwuPLHxipgxiAlHG/c0Bf/7tD87bjH95i/1/+wN+evsj/vyXP0oOjGFA2o3Y7y/Bf/O3yL/6Na5//QLfvroQA50Q+sqiIphSQhJ6o4qWICxLMTx0zjEoK2LdItnQdTaFgykiogykUjpAaHX1lLCQ0XW+CuNji0DPREJ1aXjNL7g4rg1I98TxPtoWTMH2kfFcbTz4sPLU+LknFl40z+tz/VleFRtKS+McLX7GkwTiUBw6e7SOjHmaMaRZ7qPEjltJZZ5iUEhn+fOfkSOi99PDN1p805N2Fimdl4EI37zY4epilHBM4x7jOAK3Ew7/9Dvkv7wTQd+G01ptvnN3OPtVGwHv1LGF7wvXjserbIROvQZ6/R4pIpxfUtIufKvaDX8orq8J0/Q/5M78kb/jOYCs22pofao22gkQm6se/KIuSuelIBF20JyIIBXwcVurgttgtb0j6+YdASTCdbG0TrUsmhy8oyXIIlHW1fZHlM4uhY9VaCu7+FMqocdSEDhzGF+ESd8zJYSH8tHrza27dbxOsJGnp3bio1hAN47Dvjgaq54hUUVscjKL66qFcApaVUsMRmFu+3ilVIgWE7o7EBMGh5mvP7ZHmOvn8fLksKfioreuqU64Mhcr82ovlnpt0rgIQ9mbOq8EFdQX8rzafzYPvfPU9FVImc5mZRSlX4DVJ7MlZILUnDSxcMQPDlsLkp/tehCxHleIogGyGWtNKAfkX81hnag6DHg5bd27Wj12SDtUwboPWfdgooScJPEcQ0KUWcLlak8zwxIy192YQISqRxVLFHBbFQ6utC6/2zLbNMfPNlskOMSTTJsSjLMyDGXPz/OkxEhhZsyLAiyjIQbMKqKPm9mZkS6B6s/LWGLxtTYmhwhpHLDf7TCMA4YhYYcbjJRBRxNknSRDHZxzS6U4/MJLdX08WaP1BJU9vO7Fda4S4gHLtijteB+7rmtDiGf3dBtnjszvtX7bzbX3UcpTKpQKLbjWV13vWP3HgvXgfXHGs8+KMX7ghFWU7okmnlP5GA0VjJ5dzDct53Y7RMdqnrlZuPvxScqS59xa/+yeHvpi00Zv7uqbqs+Or9C9R/uK768XcgJrtcYZ/Z4q5r1+Aj8UVqz8pKRlZUjHmhOBGD9Ob3CX7/B6eIWRBhABIxJ+iUvc8D1+4hlzZuQ7eZ9T3V9NTTlhrH+Th20iEIbdXkIyjRdi6KJhg8TgBXArx8SeSpFh+cfghjKFPzE4lFe13BDatyZ5g4xWAknZa3b6a3kNaY/NpBrtGSl6svbIvRYyQ8MyRaPD5Zr4SpIYPN2/uZVfU0KaMsYP95huD9j9+Q2mecbt/R2mtx9w+PAO0zRhv997qCi8fAF+8QIXv/gW47fXuLzcI43mCUG1IgIESkORJRDK72bgFPkWo8mVnwGRGmAZR2H8mL5hOSBcEWHPh8A7m/Fa8j4LT69KEDM8oqU4s+JlmnO/WLcHllW679iF3xAaJkivZAq9vqIsBSssPeJo1vDh05eWGzvHuCuimxOdaJ0F9b2ApR8PoW7qaJfl2JnkSOtz9fwpy0Obi8anT9ppbwKNVtaLQhSvwHx1gftvXwHvP4Bu7l1WkHMGJTUsZgr8P2EHxi+nC7yctqsXPopHRNlAEYXoM0VM9nub23K3S/hXv/oWVxcX2O0E+e73lzh8/wPu/uN/A825aFipdd/piZZwPlW1sX4rrAskjf7MdT2/DuO7qN890ffqoYxKByKxVNffM9fwSDsyh3bJiJUrNbi1CI41ynctaLPNHOBnH+ZyHAVpKEngtICE2HJMRoWoXNwD1cSVyeN2DUK9hcDUB0mSUDYIl8HZLXolpvpQ9lqrcXGxZ3Ex89wSFKzt1erdpkwuUxV6hrayh03RsZsSooqzGNaRzYOiKIr8glclhMFjlvdi8aKxPcO82bEMtAOcXtP/yN6L65iBnJTodbA0V4JbjGT5L8v3RCYYjjsqrJGOgTu/EYLyJNTw/dg5IK2FgHnuRPxRW6X327FH5vngrsNBKQHAY7Oy9hXftTrmZaLAyx+KhF6/f4Q2bI+Zt1D9TsQzAclQ/Mqyxg3eXCghYEox+yf20sFX2g/H9xfjiXu/wOn5DqgVYIfPQaDAzTyKAoDA5FwNTBkg7cZ2lhCZ5b+lLQFLWCJ/S/tIRMiYHQPMzEjQeIq6LqLUNPzQnBub9yzhnOxxONo6jRmcEyyYo/SN0nYQ8JZG4K7kgLw6poQMYJpnvRumgPeNmRKCYxyLdRlx9lwQhp/ECio5nqo9XNgVXcly5BCHcHOuSixz0pMc2jyrFdhut8fl5SX2+z12uxF7+hEj34Z9kOu2vrjypcL9tXwtZ5QHcVlfy5damD8HzGa0NtwZFyh0dq/+pyyFk3nszB0bx6kxntv3U89Zrz068pxcEPgQ6dIWlr8nMGxqOCwPK8v3uPN0wVdQ582V7TPxjN/e/4gLSvgPl3sM6RKUMy5Swr/fvcYP+QPe8C04A/NbBnYZwwsjpY1JhPKBzigXgXYSD1UJw5Qw7q+QxhG7iwukNIIGo5Etl4PwhDQRGDOYJjVeg+Z2VNoxBx7XhNnKG0sCbM07QZJ7ArnAyBYhIuS6iAvek1OVH4TWhdK8LqeANOO5IbLwAB5FKrZITXM546c/vUWeJKTJ8P4OV//wO9CUcQng/e17/Pj9HyQR9zggjQOuXr7EMIwYhx0Ov/41Dn/zN3j9yyt8+82F0MggzysodHdC8Yiw+SJAPSakusyPyAgUOAqUuRoLkecBdU4wKCworCdcVgH3IintSp+Dy1agbZc6NkFlJeI+b88eHfnWK+djhfNLwUHnFbknTyKYo++f9+AZCi153WN1l4ux/PFRN6ALYaC888r6rzwohq9ffjm6JqqEQEqYvv0Gh5dXGP/5j9jd3KtHGovcgAhzGgCVf4DE4HnkhH/9dkTO230izsgR8TgiqHp/jeDzC5SQEvDdyz0udiN2oyQHGoYdcDfh7r//C/KP78UTotMGgCg92wDcMSmjNVoLLxsZSfWKPY89R4GS1Yxhg7h6e1tpoe6H9Ai/ByXEamO0Zllilt4u6oFfVETdSeBja8AcBLTs1g4FGMMUBR4TirfW3iXOo3XVoItmzHI5EECsSbQVYZIRl1SEy+AStqkeQDOuIlazxNxQ4gkp2GHEfRHh5Wae/A4qRIN5QkSGqSxtVpdT/Wukj7eRiuXBYiht/6wEFpfPlBVO04JyISD8rSL4NPGizQm4WF174jGfBLOQoDC+OKtSCsHiWEKEyrKUSmiu7O/qaMR92SH2F9Y2LVCsipvm1DY4oa3TQlclsy6bN6xRT2Bf+rJ8HHFNKwE3Ny/o3zjq6JmxcOHj2pm4GhywaOeoC6BWNiUdVxpndnjZzoz1zCxW+B2a7IgOwYX/FbcGW9uQr2VxL5Wx27gs3E9mAMQYHBgq+58hVkCuDCyKByP8c4PnKjxGYhmVKIPZrImWhKwrZfRYOtwh3FYh/oLbpJvE2fyo66UqE+Y5y5AGiZMkihWA51wsIHQciSjkiFAvqIVquqyDr70qyQgETgTKYf7DAvu0KLMny0h+DomANA7Y7fcYh1GTZsvj41Epj9+vH5NGb8vyzn2cO3WFN1eQyJbmIwp8klIRTstQeOfkB3i2/AXdvrTpNVKxAeVc/vFReRH619hHKZ8idNbWLk+t2VOWrTA9BJYnn+FPieg+g+KUEDvV8pGm5EQnJ2FYUDlP1/ejy6fbU/0zVfiKooyw3wN9+MhyqgmBba3S2vptW9eGW0bVVZXXg+qfKdD9+nRi4I+HA67SgF+xGCQyJezSDn+DCxzyhOluxu1EeD+oF+2sxipzBgYAo1nHZIASkIR3zpwxjCOIBvCUkOcBmUbQMEoIpaGMOWel4mhWYBPMTdjOa5kA438A86oQzwpLgKwKA1bDHUpgsvTamsqBAxvezK78TjAvqswadldDVWXWcMhZDJYyz5hzllBMzGrsh6odqGzh9u0t8mFCevsBfD9h9/0NkCG5Hu4njJSQU8aHuxtMPOHy+hKUJIQVrq6A19/g+nKP1y/3uH/xEvfX17i+3mG0EFdEsBBLST1DROFgyaotPJMqi0BupBhzxZkiwp5D59o4cJPlkdUN/UbjJA8JbSGYrE2H1eoFYc+KjHD965H6vSNI9RtPdgf0DKnQ8OYPwJdn0+Kf+p4/pqm1ZY4yorYqt/xvWLATY+svu77febfrGRHgaOtVdR9bnnKZnqAtMTCWiyIRgYdBw94pjjZ8aOGaiCBhp8v7gpOfQRHxqNIy2f4TdZ7Ll3FI+M133+Dq8hI07JDSgGG3x/zjLe7/938EDrMjVqC98F3qVPX5mDVaU0LEXktH5MLXSPQifg7Pqs+hdI8w0fqzABw333Pbf7dp1XgnyyNQN8uatwDxsBKCNjscZvaXXMjpkEf5k4EYiAwTniVdU4k2tnIxIayHzaNj7F590jb1X++jXIBGdFhTGRlDHTNlsZlaetPmS1xDywsLgX/8a4m9/cLXRE+WYCrB58LuaYt1aR4GOc/gPJc5IXO/pMrNserZFqFSKpjSQYm9rOsfLFFA8MS8rIOTpoogVH5WJcY8axx9jc1ZmaPBEV090WW7VLEpA7EjqBGS9KuiLig2g8J2xhlYKZ3HFXTNGarye1QvhTnNGVGRUikF42VXCajj+wwTxPq60bJerWwqSibfk4Dolrwh+BmtYWmEodX+cNrRz/siv4GOxQXjxgQxYAkQLdRagTEHONi9uWIS5G7hJV6rlBGB4RBlgYVIWh7kMr9lnwv9oswF6Smk8oIQ/AASYZ5UCZElRm4a1CpoZsA8n1JZZ6JUzojmUgHEsqt3M3Bm5CRquGq/N5oZ102QhZcrz5Mqd1JKyDljmg7FhZskmeB0mHDIGZTJk1ebZwQgsW+j0kW8KdjnPoBSnRdVRSDrRNt+KOHLwp1uc2xwk8zXbrfDxeUFdvsdxkHImBJqI/b111eekq591tJhVDwW9oOYqC9m5J+8/DWei6/l05djtiIfszh/5mFeeCNcnwHwX8uGEujhSpj1ccsxWdxz9wsUWtbkb/G71wVwAPDbwz0uE/AqXeICCZkGXI6X+He7X+Iw3+DDhwN+SMBbYkw5Ic8z5gmYZyBdA7t9Uvo4lfDMA5AwII17DGkAfxgB3oPSJTCMGK4JNBR+RvjoBKTZvRg4rl+2HIVKZ4IA84CgJF4QaQClEUiikHC7QEpgpZo9bFLFtPs//lV4XrjCJQ+S74GQkYk1D4Z5+c+YZ1VGzFnCWbH2Ze3pWN798AHTTx9w9V/+BePdAdfDTkNWjcKr73e4vZ/xfvoAEOH61QtRtAwD5u9+gbu//TvsX+/x4rsLvDA+IoUcDRY1AeYpor95mNWSwxIajsvqxBx0RZFgOyZ4LNgG077lq7ZhjJQrMlB+88+o+iFvrz0w7W7t/X5m6bx6Ek884UHebF1/AoF8Tlb6LRSnZqs1oFyMgwBo2B9ukdbHROq+32v5yEJ58dwwPEU3zaKswk4EUvkAILjVZAXIjJxnEWkM4hnBmQUHJFlJkMkntpWnVUT05YjL74sdSv44EeEXry9wtRsx7nYgDcOAzLj54Ufg7QcVAjUMLPrntTsVpxBKpcAg/1Q9ascS6Nho673IUxCVEB0lQQGxIO0t1EyXcVcauxYw9jdHdG+shhUEhO371Fx4Vde59aAobRmCgcWmdwG2wYKqjwJjAcpm2OfTiAoub1YvLhauc7atHVccmAVwnbBZew4MTHgnsxNh4h2hv+thrfsx4SagekYAZo1CJbamh4Ipm03kiwSwWmBU/xWYTLiYaKi4QNubJd67xb4vPTGEAEsk58A8GmTIuVg5UJgZU+CE+TaFhiSnVoUJl1juVO2fMsZatK8EC1A0rbqulRVFWLvYJJtCLP61V0DLxOoGyeLYFSuX8lN7gepoGqWgzXmK8+Ov1m0U/EaIwnt5jVymLJbxDEI8KWEchmN0nSPaKgojSeBW9d8Z1mNKHCb5eOQHXzJevnMM61V6HBNC6zquvVeTtNZD6NyOtbeVJedJpYis8YQT6ympxRm5Z4REe2PFd+SwcmZXDFYKNdZE2NQI1JfICjFfjjxeUBmwiyl6NFTzob+ZUt/qWaMeqslCVPl5S0iSHGJxfy2su3WxzQuqMEvse7tdabn+DL/IHybg9pLA14SrawnTKC74ZvmGJym1IuNhzMfa2Ymo6pz3zilrNOsTHuenKx3cGT04u+VTSHbOLNvXUXBQm0NI2mgbab8387BxXp5i9p7ME+KpGKwjpQW1Ckn6yL107jTUiv1HdX1mZ5+2fBYnloRmjhxdZTDWsAxd5g7PsF1PNLg+d3yyxobmN5bPZy+1Zck3PnS3RT716Urniqv6Wy8PHEcwoGmVDxmSfmEZvolBuMHMB/yOEy55wLeUkAYCjwzsLzC+fInr6Ra/vL3BnIH5QJgmNby5y8gfZtwMGXdjBs8Zc56Vh03AHsBASLTDMOyR0og0WPLnQn8TqZe7829C/C1myre+WOonD1s8BENKMkISFo4pw5QDQt9nk1MARR4ROjFPBjf0m2fkeQIDGFQoT5Qw51kSuc6ijMjZIhRI+zdvbjHdTaCf3oPuJox/eY/h/oARCTQM+HD4ABBj5B0oDRiHERPNuLi+BPYXmL/5BhcXI169vsB8cY376ytcXg7iIaFzFRNFy9RQkB+UvzJXVCsiYB4P6jFh/HbREMAUCfWdab/ZcqjXhc2/rpHVrerZ6+jx/1s4uN7jlee9n9vfmI+TUPEgn0E3dOWS/HDeomrnXLy8Fe4VJPgQxYfVp7gnVtruvee8on4uXgtHxnIKiSvd2ZKf62sSRl0LER40Jw8q8d5Y6y4SN4v3StkCr8kUiBLyq2vcMYPevEO6uVUFrRkozsisIZqUkEpUjBK3lI/jEQH0YepI+hIBv3r9Ai+urpHGEWkYsN/vMd8d8OMf/4z05hYvo5B+rQtr+9FURS1MXHzpNO+Cx6jQiAoI+WE9TFJbTikhqi81xdx6ZvSbr49fa1EtPoytwoTCPR8RjNQv4+XFuSEV0AXZX2WdQDANua0zVVMQFQ4lLNOWuawFe9yso8OhxAMRSwxDInVjhL8kHgMcBJdFGOpcjY9J58TmIsAs76jyIMyiyCZLkqneUIRAUo+IecI8TcXbwAk7cktmFwZqTEx7HwwJrWLuV0EBxnkWhUAitx6rBEUtbM1cyBxpbghVlMzzDLPMJ9gSH7+kwqT4uGxfyFoRwCIsjQJZXvvke4+LDLNJUGPEe9x8TjIvFF8trEqwdfamn6MISPXqknDTLmGW48ZJWHiz6gSG/mIC7aJggwpvmwup/3EJF/vMVGVxBqnazbEmtHP9xtXfijhg9jHKM7Onj3iFHSyufjlSbO4j81E6dSWEH2kuBz0zJK+Cav2jZ0MaAMriyZCzKCLZLZCMqalzRbilgY4y5xnAIMoIwyWkJFi5XOp5WVx1Bmv5MSrwba1SEruFlAYhLubs1k2AuIpnVXYSiYKU1K0b6hnh+YcWpSbzLJybxQdwS6lmWxEYRIPMl55nq3v7gnD4NuFX1ztVRKiFFze9OqPd36tfy2daiobyZ1uWw/t4e/TnOLNL3Pe1fM7l1Ho9VdicIz3IHyH4I1dQCdn6AqRIu31Jpb6Ll2vQimT+OsuXiEdWbw+G8ny63kpJMQrZ63ucMxI+IPOAf572uKI9Xg0XorQYhbbdpQHXHz7g1z9MyFPC4cCYJ8I0MaZpwjRNOLzIuHtJ4JmQZxFqEyUMWRJTD1cXGMYdhnFEGggpiSWte0ITwSz5WsMaXnwwT2TxhCA3ShHLf+MFxX9BQo1mBmaN7GCmfxaqSfiB0r7zeeqBPOcZmGekPLk3sv1vzjPmPGOahA83g0DzvHj/0w3ufrrBxX/5HcZ3N7gYxPNhGAfMO+DD3Q2YGHuekThhpAukIeHq8hrTi1c4/ObvkF7scfnd3j0aCKQWyGpEavyxhT8iQpUQWj+XEE2moBh1LmveWpjKYqDoioi4LhRkNajrxzq2Q6n5XkkPNhEnPV7yAaXX16rGoHNhbaFTj1x0p+/A401/yrImeO/eIL152jg2Anl+wdj6owX/LjRCe+RPwgM0MhNv4zmVEZ127bitiaCa0HybS5yM0Mf0zSvML66xmw5It7fgzJiTRGCZZ8IwMFJmYNBzTR3l8ZHytIqItZ5bgRvLBiMLYQS5sH75ao+r3Q4X+0sM4w67iz34MOP+//gn5Jt7XL77ALqbNbZ0bLMI5lwkx0eEhFq6KI3btjsCN1+sFjkVy+JVJQSb9X/zHEVItAxRsyxGfESBXRQ6UahYjatSOlCpGH4vBAurAL2EZDK8kqhcgEYQmKwuKiE4zpPKq3Kikt+DygG2q6pKpoRILIXxR2F+yOdQYApjtlH1tkRULOQCtwnHPT+DWwZwhbwsZ0KezdqfJYRSEwPf157NQwCAexfYalhf6mVilg0pCA+jAFwVBfIfAzF/AyEQH8kJElZPBOle3pEyCIypEBqmbGFAE4QVJQ3AJQeCxKQBcQZMUA52ZUNmEVaKkmR2RUghniLREtY6HEFRlgW3UTKBo+69zJAQN0ZaNstcfYh4w85fuZVcsNwjhMM5eOi1Q9UHqs9IqGVzk9rBKDTM8XK0+7Xs58hkt6GjIvPiCrUWvh7stGQQVuuGeu0Zj9f5QpGo+6paBQZKBvSaIHAFRNtGKKfWymkdnXMBgQALR8caZimFeLWZkVMWK0siCUvLSS2Kku9zXyu1NJIzWsJGDZpQL1GILYuMTMtxxPG1T+J9EPG04eSsUxj3CaD3zZCQZ2DGrP1zYVq4KDQyi3IlO2ikYZ56M1zfa/aLrKCuYxT8oNl7EX/5PVavZXQj90MAqCdaDcdaeS7hwzmeFV+iAOTZyrmTUZ37pwVlraujQkrUe36tjbV2nrqc08VjPQQeUtouH3IWPhdlxLGwp03NdbT00DX4HCagKa3iu/xePvfAru6MJx+X0Q1uJtSsxTHaod1obd32gpJ/umz5kw3rFOW2tifbud8qkvlcSjPRPg31fHxux2LNXme5rVpK+8idgpVd4EYvZkhXkUmhT/uQQfiAie/x2xkYWIxk9iB8OwygywuMr15jnmbkwwE4TMiHewzThDxNuKJbfHdzAE8ZNKucIBHy1R7zfi/GpWlwWjjfE2hm0IggVWPEEbFPUqQVhQEU45rkMczlf/2cjjnwrxZhmIOnMhJJegsjJeHHF9PthNsfb3FxfQUaBgxplJxuEBrVckPM88E9/jkzbt7c4P7DHfD7H7H/6QbjnEFDwvvDDTJn7PY7IAHj1SUSEXa7HbDfIX/7K+RhwDAMGF9c4pe/uMZunzCOo5LNIf/CIreD8chFAQEqHhDGw5giAppwtsgLdNDWljHbZH4OzT50XE1FbtLjTiKvT1jUqOp2fzrKma6+2vt5M0o4dhdvRSwrCo6eXKs8t3dRM+v+eL3vTWCtTJcfvwpmXnyMcof4oOXfSndnrXbddudaolCpfrS4rY88PQ1DqaAyC7bbvOE5HnPHHNsH6PTXvEvYuOZnDN76tFxBAzF4EKVvIo2CkFkNKNUDjADiBFIhwzm8xMfziOgWE0nIZfndy2u8vL7G7uISwzBit7sA393g5j//Afhwj4shupyVyXfBRuVvGG7d8Mt2uMq/cZF5bdNxrYRwgWCjhNiSq8GFKRU0a1Au263f4RISCDpPUeONPvNZLItNaN7BBEEJUb8p1gZFclTPIWWUGJIB4RYL2XiRUdWy1XeBfi59FYuKFveb4DhsmHacmiDXxbUk7oWmGHCGKgLMZmlewiJJJYJnk3UsUazS5RDDv7siKhWiwZQfMZxKZvFO8GS+qoTJPLtCJIYcsrlMbhVhc04+Hway6j6KRwQL/Flj14PLnNcz66SKTgk5bK54ySW5Vw7eGKJw0/HGBuFOONUOcPuTiihVS/IEMXchUj6kPTXkq2feN7UCQBUjKiCOVuHtOTyqhDiD6yEKljgtYnGC7lQXZpHPItwO560Oj2V9Vq+Gc179fJzk6+EN1vEck9R12l7LK+EwcfgQ8bvjAfiebPdLv/f1n5yUoqae7mFKaqXPZumUgZzEaoMAi59qhP6s+zFnFgOtNOg5kt1teRekSxLX6SzJ8HJmEEn4M0oF14RZ2iivknqmQPB94nhCcMOgnpTzLIrKnDOGYVC8nDQZtc5FCMvmTApQnaeFUJZ07Rmw9BwVhq8ETw65K1EZ7MoFV47C7oremi8v6ocIJFoC8LEKhRPH40nKY2jitjwjmA8vH2MSPxIIpjCUz6dW7unH+/zW5yf6D/8+7c49Pp827seOfU3Q3oNlM2O2Jqk8Ve8jlFPjPFeRday559qXTk4AdY6ITeXEXm28aqtqZx7frRaWVMF0XiddIfhKL6WPz7EEmiCsAXc+rb3/JFB0JvLUmTh6BlBzwNri8fZi34vfVTHBEfPGNzIGfMCMEb+fL8CQXGKvkPB63IPSiN2wR5pm0OGAaZqAwwE0TcA04dX9B1websHTe9D9PUYNmfQ27fBhv0MaJM+B89UHAIcMvBAjNmKVDyyYrJof8yVW+pg0AXOx2gpUYWahOVmUEZZklat6Qi9SYjWYDPNDjMP9AW//9BYvvmVcvLpCThmDeUVTQs6SMy3PEyYLkcwzPry9xc0PH3D1h5+wf3ODNI7gccTN7RvMyLhgCfG0v7zCMIiiIV9e4cOvfg0MI+ZhwPVFwrff7IJhZsmNakZPxrfLH/mt8oSQyg4vUEIwiUeEtWs8AaSNOPculwq7isrv/oTiGiyvr1M0dKm4eLFXaVtbZ761OJLbEeUDINiAADbSm4Xlt9PeaZtWv0hHC9BotXqRqvQ4sC3rd7y4EH7BzpX7qMDw8LL2dguyicaexAOi3VNr88NlLrf3eYQO2fIqK3w69YkSxiT5Lj3ShypfATFwzhlIKYu8oFEcnyqfUBFBuJ/3YB7xd79IeHk14MXVNfb7C+wvLkET4/D//e/gtzegw4xoFlwE0sGqFjrs8EO5aE6vwvlbiv2PWY4DHUKEg/BzReDW+627hNwced0QOfTdCgetLY7vBOHR0eGxCfrYZ9rEPgS79Bw0tzbQLy4881VShQjbxchi7e2HjLxlt5iwth0ogwuqhAj9AAwkdpluBVvZEL1pXayNXOxpgUwJ4s3Dmi+B8yxJrPLs8DoxEKfZ+2DfM1KXMLiCTYXyTlAktzBwZRbMo0K8IXKeIZ4VWREGSa4vI0xCQnfArNkL4+VC5aSEia6NeCyJ1JB1vn1fCLWhsDA0qH2tbELZ86aIKBbiuuamHAGqMDO1JTFASIXgdCJJQeESi65cveXkA2YJFM7OKeGLjc+JumYPrNEk4YwfYwk9/4udE6DWQwThasEGdsbD/LA1o9ci6Zy7oiqAZnMShfk6vmNzwUpsO9wnSlGu9BqrGSn3uLGwZNH1g0v9MpfFe8TOc6WEaCa9IhZ0qqmzMGHalVAn5JSQcpaEyoAnmHbwHd9JIu3EuewVSqAEDInLGQgdUdjAcsRUMZdIGUR5npmRkEGcFsovCdMkgOj2Ls/ZZ8i96/xsLYQuho8M9HpybP0peIKYh5MpUVhfJp1cu4ckFFO5JCoPmYCf25izi31GtpYozFU1nuPn7XMoYmzxOUP4tXyqImfh0+zgT6mE+JTlU4z7LGXEX0H5ZFvPSALna04AYpf3F3FUPveb8PnLowVET1wecu6jbGqZz+GMdkKD7pcTBCW93SJ8VcaAtwAkH90BA37LL+W0UMblSPiGdsK7Dglp3mGYM4b9DofpCvPuEnx/jzEBIxF2vMe3NwlvXo64D4J0Nwr7ACHORwZjFuVBNKzTf7liqpeQe05GZmi2a2SNGpDzBJ5nFMWjS9xAZPMjns3z/Yz3P7wHmDESI09S7+7mHj/98Q2IkoQG1fo5A/PMGqpkBv3wFnh3g+HtLa5uJ+wnRtqN+HC4wcQzxos9dkPC/uICNO7Av/wlpt2IPAwYL/f4xS9egAZR4uxGwjCmwjeiyAgA84ioFQ8APFeGywKMFrecl85Pa04Na8d434pRRJAjlFIMkULdULXmPqoXV9bw+M8PKet092eCJ0wWsFYCsxT5prZK/eFheLBr7V911HlHBdZNQyf7eTBMT1GKRmEBe+TVHD9+ydfquVPnd49OjuEcMA7fvMJhHDD85ceQK8IMGAkpZ0ElaThrvjYrInob4WGMNfniT3kE4wKvri7xq2/22O0vkMZRklMf7nH/j9+D33zwiQjA9CFa/FAENf0xNa9toIyNMIh0aauE8L8WMigKKO1iXVFCLMWeNbwm1FqLP+9EjxPP4SJv7oxeP3UM1CBIy1wL1xcCWhN+ZkThogsKAzFPyGDXtltb4fLqxqJh6wLmpeEBmeLcmsBQBbSniitOIB4tfnGasGtBBMri21rEBNHFGgHVZ59OEw7bXHjb+m+q3SKjMqZwTwIvW+IsNvcoVpjZiRGKxIf1wx1BsRMdJQwQsXolGKFYedVQEECqR0LGol0ZZlFCuKIqCCDjNlpaH9efTQlBKTkx6bvbGl4o+8qH7m5wit8EqOUc9outb1mPRqy7+FyNI2rvlHDknCWXQKzZWJUYqMcUatBzd8zSc5nYOuCSRXPOsft4yv7WViqaxQPuHC2uUvN2SximpmKAuzBImu67KGCbugZL22cFm28Xrt9KAJCQmJETStJpU6R5jpKC05gzclCqJhIHd8nyLusbl81yRcha2nhkTlMizIZjsoWxszGWvQpmCY2GZgxc4AIDGFJFbLWeCksFbAg9pedV4vzW96SEeertcPteM98rvj31u41Cwv4Y+LbnhOkq7vfmfbVWzhV4HbM+eQxBXBG4z8gDtffq4vcvoPSmZwH/ZyBEr5TvR4RN20L21Odpq7X94nVvvNfqAgLta1sXjy2LOeoMbVXR/xmWcxUaT6KM+IwnpuVvevNzCvxnUxJxwd8lfCgvrqEjrz8NbKfG/9RCF9Skw+NKw498oeWp9tjWdo6F7Vu0US7wapaXS7fWd0v76i8meAMQzSK6rVDGiBvhOYgxYY8/5gs3ePkuDfgmiYcDDQNSZgyZMcw7jPMF5v0leJ4xEiOB8QoMmmbcYcBBSVLnpBnIdxLZYLieIeF9xbjOmX7nE6kLsfvpGz9vvKbR2Dy7JwQ0HwUBKssp9KoZz/Cc8eHHOxAzRsvpnAjz/YT3378DKCENCQlquKSRGeZZZAH7f/wTxj+9wY4IexDSOICHAff3Bxx4xuXVtUT92F8AF3vcfPdL5N1OZAD7Aa9e7aV9UyJUxmCmfADEcEroYVKeg2AGjKZUKFEELG8EUDy3SfNgRrlHxadWAqMlrb+0G1pBMrV2ItQvS3d+WaNqNiK6tlql+OrA9FTECYU+GJGh7JcVDURPAQF0ZCkNLbgAJwzrqOB/bVofcK+ceiWuwVMpIyrerjPnwdzX67uUYVXu8ligtu+pNd70Udvy2DsaFjkRIyMhv36B6WqP/Yf3GG7vJCJLYsktiRl5GFU2dmS+OuUjeUTUEB3mPWbe4Tff7vH6aodvXu2xG0fc/fgT5tsD5h8PSDcz6PZeb4Aes3Y8fuLZ61FO9Jmv1Tkh4l8THtW/LS0jPSfEMSqxES62DM2SIOoQNwvlwfKNEv6i9BmJ92KtX29+Ecpr8mQX2gW4giAsCusRNPvl83IMRWHA3p8J3QrBwRImxUJ/9LZNnI8GrmqqQD5fLUyc5eDN8xwSLxcBr1/+1pj3UTogLuO1i98sE9iFeAXIzDbujFktPGbLDaGBjGRNihsmgZo9okRYVCoY/ZHqumZnLkoITVYLE0gK8WOCSs/nEZk7FEGmW1GzpA1zYgcnik6gWXokJa4sia2EYjKBrpG17PS2XSAV4d/SsZVgHSXeZoKvJqgQ87KGrfBGiekguHfiPwpjW1wW5mUd65TzWOEYqomtwkuH87rANcWKvkyHvqVu0S1PXk1VQwy17W/FnDUeW63l80kEBL2PMhLHS3sxF/xhhDbCLOk7+q+cH0JiUXhxzpgV38xz1mRxRZkgHg0zEo1gUtjYzmKZM9Y8E5QSiFnPlLRJBAxpAIHUM8LOa8GlcWVkKSLDVegqBoKXSclhwXHutXL0zpC+NbeF7QvD/1y/GxU0xtDUc7883fZ79xqK90AsdrR1v1+8foGrv/sWFy+uypgUzmwTw1uzmHwtn2N5PLvx11g6O75zz30tn77Y/f21fKLSsHoVzUPyS7krWyrhr7F8qZu1pWabp5/rkjrYNfzHR3O6SQBVctPFleD03XJiEibs8AYgAg/AxMCftB4T4zDvccAVXtGA18MOGPbgPGMAg4ixHxISgF/nA779MIEIyAT8eTfjLonwnjPj8NMMpAzsZ4fD+GMTOkhuUaH9ssodOEuexjnPoFwPbJ4OwitPE3KWRNIaW7VJ9krIU8bbv9wgv7vDi3/5ESkz9qPYFImDATlvjSQGSwTGzGIYmTUM1HA3IV1c4N3te9zPB+ElKGG82GG/u8S3//O/xXh1iWEcwWnAy8sXYA1ZNQ4J424Uwyb1rjY+NJlgw+Uw0eshhFIi8xwO8Apj47IFD81kHhRWh8wW2t4pPHL5VuasW1ojmMj2nn7745THdH5KcfAcXSv/bWz4ViXEOgytHKO0GwX/NY//uSLN88pCDIQwtkog0Me67Twcm5e2ry+qkN0Z8iGlhGEcMKihc2YGZYgsg8ToUvJHDkide2StPIEiYsv1WPJAiPxwwMx7fPtij998M2K3H0GUcP/2He7fvMfuX+4w3GZNBNQTi4UBrmG4zlvbxtKRWTdCrW1N1W2tWU54TP4GCgqf17soQsqjJVwubT/2uP0NLBr+vnU1hf+8Olz4nLn6vj4Qu9hS21wNpwoR3Rrc55ZV8FSHZynIdKV0EG+FSFxg1kdAIuwOlv4m2Ce9rD3h8xKBey8mWFeCwAgGqVSEg/FdIAj2LVGMjl26JV/nktfCBIorE0FU4rn5vMk8i44jeriwEDXhPIggUtfAFoDDR/aKPp6OiHIFWRePDvmriYBNEEoUBNTlbfcagqxH2b9UtRvfqWDys0L+wOArW4JMrq2I2gBhH3u9z8o5t5/nYweXi8U7uOy7sv9JQzFJhSJoLvVrGJq+bK+2v53AJYUIephlJ1sjWyoG/MYDgRGSy8Qj0h7dWHz9DRdRVSlC4tNFipOQkShhNobLcY2eAZ3rzIzEpKGUKCAiacyUFmBh2hznZ31Xgiv6mlBKxYtCz6HsZYUwUKJxKv2IcbgbtO1EolRx5U4cLwxOe5J0rsvEVPhR92Zm9pwZZS8cu7nqtdtCjjNQFGBE2F9d4uK7b7C7vAjgsK5BrsbWgrC267r33zOVhSXLyhxwVWf527HStvgoZm/t5QfSWltgKXdBbxY2lOdexC0gPIGU66w2mvumLqS4Z/Hrw/pqul1rs/q9pXEDHlor514vD6LTn6z0qOkT1beOb21AjxnnKq29rdFTuLQyNtjy4qlnDyzL4ZjIwQnH8Hug2bfC8giYl8KLR2HqquVjX7/4chZa/FSDXz8h62cs0lhLOrW3O9qmNuFMIaoCj9xwX116esaYZu9vBvATQwxvGDgQcJf2uMAOIw8AJRCPSCSC+t1+j2EY8O37t5gP0sYBM34YQvcZ4NsZOc0SoskSioVBCtlM5SUOxo/ZQiXXPt+zhmWSEE3WXhyvGfqIgeHtmzukN7d49eMdRs64GAkpAcOgJD9R4efyDOJZFREobDAG0DiAKWPiSb4TY9xfYH91gYtffQd6cQVKI4gIe8vfoAaBZuxk+RxKfgjlf2OyauXfK4UCihzCcj8YfiueECUXhPMqKFVlhiPfGphhWwz092W/2Bh8uqsPp9rpn5rVk1H/3m28L3V4uvJU+DyUoIzw7/GxUc4NObJOlzUfmCtlhL/ra7Z9TKdm9pyZP+qhcdYSBlzSe9UZRwpbyLiRh++VTWC2yNsVwxG2re09kHdqQQIEPSiKTJTAmven5FkTT7Ps3+Eygq1lsyLiuKuTIfZWGCHlMO9xmHf4228TfvmKMOMCRDv88psLXFzucPPDWxw+3GD43Xu8eH+PNOnC07EpXCMYG6RGgkzLeV3b0Bafu/e8/04tyqyF7/KxFuS7hjFYYXdGtPitS7hYX903Akzx62Kj6x9mgGor0uzCu1KnjeXtf1XQXAvHLRtze/R1XSMCtBBEOv25IT7iZxN+u3A8xJH0PRjyCCymJOzkhbCDbc9RNVe2roAmXJ41MTWrF0RSwCkBSDCBY7y4ExOyCbjtZ7W692SuulgclAsMTa7FWeNbavgoh08EptA8Ciaw8/lU0iLYbzusKcaWVKsJs4A24q7k8mOYlUXyyZK/nGcE51jfD+apwSheEmUZCnzU29/2LAnyk3iZ5DCUNdF6RDIVs5FSGeYsUkIt1f1IiBwq0whzeU0hPBgF+CNoOqcc2Np46UfCLtX7Md4vZVbsx9oDx5RtDNbwV/K/pPHHZL/6xtXlJxl7gMfODdk+U7iLlUvBZoa7UDEqWOIP32OItQrOAKM9u+X3uqUFOUnaX0FA4KykMaFzOTR7wRpRRaE1k5FBmSQpHRfHSxkegchOiP7VZHAedIoFNw4cbkSW2LCWOE62dtJzy3q2FK+FuUhJ24MI0bNaciXFC7N6ZFgOlkh+yPJUq6MDzGX9gCosFAEYkuyNrFnqmSzBNgGW7JwQcmm0N3/B90hJ5iJFRsd3/eK+q9e44FgP86Su5KZsZH1KGBzXDLsRly9fYLi4AO92OMwzZhL3+RT2S1G41LD0yvqThxNwp1p+7vKo8C8tGdcbRkVmPP04l9AvMATW5/ex6/Yllt78xGfP3DWOdH/qVe5cLZ99+XRn+1OXc0b+sFk6thm2M9hLfk6+y12QVTg5BbpyRKIdSjKous+CDjn+fLJEmj/yix+t2H1+vIp/Wt6Vn99eX0DU5SHoZJXeK8+ryNzaOBWUzsev4qr1hi6urmmUJs0TgGHsYnOWXGZRt0QUjF8I4tmfGCMdkNJb3AH4PQHTfImZL/DrNOKbYSdEbSKML64xXl1gev8OPGX85kPCBMbhAPAMTO8n3NGM388ZE804HCZwnnC4v0fOM6b7ewx7wvhiBCDWuAQgTxk5TZgO90Lz5tkhz9MB8zwjz5ojAoAJITJnvPv+PeabA3Z//BG4m/Dyw4Q0ZVzsCQPtsNslsQQeEu7nAz4cPsCpcVJcgiw8s9L0xk+PL/a4xh73v/gV8uUVvv3FNS4uBqQXL0DjqDkcE0ZXRAhfN+h3y80W5QRVHggip5tjeCWnfKM8AMXYqKx5ocMXiobFb/Tge3qLwc3pNtbqr7USaaLe/j7voLdnqX//dNo8RprhFM5pH2jlxWQEc9XVtopqId5Ji/YVpt5Qgm3rUUTJHZzVYOPVd5e1gsCk96oN5iTi5uU3Asx41HhfJ0pRjE1X4X3iu6LaY5XFb7+ug9orTwkbSYSIDIYkox4wpBHgCZkZM8/gmTFOEzAoHswtHbVezvCIKElh12/GcHOaiIcJGSMyXeFiP+KbFwOGQf7bjzsMNODw4QZ3P77Fy7f32H2YYMLG2OI5BGhbyoarPtTPq7ZPrGCjoW9DJtnuaNQU2roddEMGQZjUk1YGIMvGM2FUOKZUQo4EwMKYekMo6DQiDqvQt9yIMJaxuYCb439AsaxVAmmhISgXpCdStkvC2g9giFDYqmTv14W7FNtewt723l/peOGKLw/BhPJmmc7KQOu5cMyu/zFQZcatMH8kEgLQrcIKcI2jJ+/KOc5a2GMES44hXRULa286tG8W9GYVUWLD13lNWo8Yl8/b/tH54Nz6gJRLZDnHxWKlOtuVBjjky0gI89Tuv4JvysyW8YrXxLoYsjRpOKckCF+9b00ZAoS2l/jJQkkJLZiq+V9eevZapFr0DOley1HZU7qpdgCRhNZJYU9FyEwZ0YJsSij/3RstORFsLk7QVQX1RPzkS7yOE1fbQX2cPLSFn/k2UTo1bXINi86/ef4YaorKDY5rYgxB5rDmYZKCssQ5fiq4IoY/itWlY/b8KjY3iRJyykjqQS7wN3PkcbTK7347RyJbcTAbriJy1aXUzb7GvTu9TtfT5JfRdxf7obprqxecuHLcZ79DvZtCXhzPJOSXEyENA8b9DjQMQEqYOQNzFobQcWwZP7tQacO93iVqzqM14lifqpzd0gO5Rd+nQWrVXcZYWsLhFDNwCrajr2+YCX7w8D9q6SuKtgG+8C4oJ7+teD5gT1xOxkOPqPOR4D6vAPFLKguC5fQbGyfvaaa4geeshTtnk7Q3UzknQudarHi1MIYaElU0+3kjPooqO5/Wamzr64y5OKtqpCm23pnljecubQ+re3dJuG9q/zxlRI9meMJyFC+uPTgGS6HhIuTLVVyOi/x3dtJV+CtCohmJZhzAuAdwnwZMecDrIeH1qPsoEYaLHYgHzLcJw5zwasrIc8J0GJAnxv0dY0AG7bJ4WxzEwHG+F+O/6T6DOWG8psIfZwbyLAaCaYYY8ZQR5GlCnmfwLHkiMGcx2MmMPDNu3t2D394i/fe/YDhMuBhHJCIM+x1SIqRxFKO9cQQou5GX+miDkZQvspCmYsyWErCjC4yUcHj9Dfj6Bei7S6SLAWkY4YoHIk3uSkg0SAtDSSjt/LLLxciNmwQOyxEBVIaI+uZCxhRp8IDrFvjE663tpON4Yq29UlZyAy5q1Xuw/H7sHau/YLo2l4qn3IzmIvJwBrWtsR2Gzi/Oq4Yahfc7AtcSlOUPUehxikRdUV62j1ax1Ikl2eIFUdU4Jj9dtN1vr/4uB32VNm3lJw+8A9bmh8Knvvckd0EHHkELd5Y0mm6blC8NahycE0ASIj5TRs4zKFkEpNy2vlrODM1EcBFGFKYAvR2Oad7hft7jV6/2+OXrHV5djkjjgHEnCP7wn36P+z+/w/5wwD5nDPdZBSXaluk+PjmHUYR0tSCmlkH5b+G9+ts6YjYBV+yDrF1W0Zkejn5Ips5pMWFq17XE2jCBlq6s9YEiJpSmWkTGvjTimbB9mYoyxi4KVuulXI3RcwzkTsNcw7c0+TFqofaAqGbY27YLQwXyJvsiI3IlBiQAzZ+l7abaolrAokgHVBx2agmAZJ/L2joCZMassS+58vpoL0gCYSgW/EewWiFpEswDxlxAY2gfZnFR9X7NurhFUnF4plU2Kl4JRN/LZM9QW3aAfH9XwAIgkpAyyZJu+Z713eeeO+XiKK6FVjn72EvrHL+AYLlPLExW7I9s8hYKx3bt47oAFrOzR7ARqMDufdHyLrVzAC4J44Gwd+JqlHlzBWBzU9W5R04UOm4BY0y8wdro0xyqQgueg8eN4C4J5AzsiCtrorqcXxv3sktVQYS9CYa6MQuTI+0VxTvZhonWYHZBU7REEe+l5IJ9Ea4XUC1JnCmxoHhvBkPeJRByKuHeUiJkv3JjTo4at9mM6VBgKFPSqDCYhFCQ3C6AuVXmnOEyfAg+yNWk6TooLqywLll4OUbOCDyOfagwtHtfhFbLUML69orniUlJjBj2e1xc7HE5vMVAd0i4lzHrmaJg1fqpqYev5Wv5Wr6Wr+VzKYW3MMKlGAXZPbaRRvpafnblYeKGrfslcvcb3+iw9o8tFYXHSlkafd3jt2H8XuGdj5WRbjGkA94RcMgJv07f4hVe6eFK2L98Bc4zpkm8FOjuDvPhgGm+x3464NfvbzDNwN39jHnOONxL/ofpMGPGPeY/fBAPh2nG9M0VPnz3AuMADOOMMQ0YhkL/TeoRMR3ukacJ+z/+BLq5Q84TODNevb8Dphnj/gppD6RBDFw+zLcgTjiweKAPxOAd4XL/WnEE4+biCjfXL8MMySR+83LA5YWEqAIBL4ZLzMOAi/0oSahN8eAeEBKiyfgXU1BQQUiCnjzMUgr0dlBEyIqG7UWFvgYKrot1/WO9yZYy6vVNuPrs2MY9T+P3oFJWpLNlz+j6Kc9gBRO3H2K9UwDW8sIH6l3/ussnly0/pgiP/RGOkQsXSJWmd7/6DvevrjH+7s9I729gxtlTzuBpktw3ZxyYzYqIMS0FvQwJ82BPEpkFpQAw8wCeL3B1MeIXL+VySClBvdmAHz+A//AGg4ZdccFkaWIhSDtaeof5yGQ8eO08Me6yW158kBI9IeT7aXjWUBNXnRy/HI6N0UKkmGAvuhwHketC2FcDp47OLhCOb3JnHlDkVNUwuBBAXATizjDENqhu1sRdsiODwM54C2rmLEpHA1xrJGJ3TU2YHtfehOwwTX+nRQWotgiGv8OwBLVAnjW0UbRwbiaiiJUbQW31IXRu/dtbHi8yvKz9RW+IBWMWJLKufLHfo8U427iKW6iDceKm9HBLgTEsse95ET4sCj5tH5Q92CbU7Z2NBvcspfhdOGtyoKlKWH2v2VArsxHHEMFcI/xKa/G9NSVA8ffpHLLuC7qpKHyFnfXyjmOTRf99rLZU0hYQekLqVXaOOjO5OMBcCduTIhS282x9i/YMRLO8SdQJI1b2iIWvK1aWeqqD0oQUPoIk6ysTpHNI8PvFENfa7un+Ht/XhiU0obTn6WyIwvnOkFQS0XsgNElrPEOLxOG4YHFttzi/+r1gsQKx/mbrojCbMsIUEmO6x0i3yCWG3BI8Xv2hO9663pdDqD5WeFZw/Vmd2stPAsNTlMfkZ/i08J+Cu74DV2E9MYZPv0L90uiWH9HOxzizn3AWV4e39uDxEorNLNimSsdrnWxj5f2188DhfjbaunrP/j13453Dm1bvNcTTpywrIGy37jxdb2Gg81mVGv51GudUvbX32ne3TMCyTi0IXeu88HBGMy1xaqA3oyELG/e8LE5JtoZXK9AQgIFmgGbcMXAA4TtMmNWIVbwNRiSMwJSQM2MgEnjGHQYGXhwOmGZgOEiI0/uD1JumhGnKuL+fMB8m0P09ZoyYLxmcJnACeJiRh0F50ZKs+jBN4OmAiz99wPD+Bnk+AGAksPdNREhjQp4nzJyQBkIeEnhI4HFASoRhHIQtTUC6eon55TcqByhyB345gK6MeQUu3ThpgIdCpgTzUqY0eHJq+HPlko0+JgkSGzQQymeE7xX/0/KzKXyOz8q7vRKVGE9ejkhRezhoYSO1oRw9qputZ2lZdTP+Vj48zF8lgmplZqe6IMCkF50mtpVW6eQSq1NE2Ce+s7Z2f8Yde/bcPXAKHnx6wpnu5+tdKiPq3KiPAS7IyZTeSQRMV5eY9jsMf/oRlAh5Vjlwllh5nDNySmuNLspmRcT/5e/vAmwibHhzS/ivfxyQVQD1zTXjf/xlVpou4cOB8GHa4/pqh2E/YrfbYRxHzP+/f0b+3Y+gD/cYRkXM7US4DGDjZJ6DFDa02ltEjv90Gui90yOOewmqm4YqYXLW/opQPgqIARPYOOWxkPL3pieOIQi7ubFNN6l/o0ApXhm5JItqhI1Lmq4om8q86HtsbQHMs8Z1z4iKCFdUkQn5EiQ8SBnfGjkVrcrb321c8p5YRadeI6RjYGDgwftzIYxNoY+rzK8OH4Ri9WAlW8LrPIkb6jyBmTFrPEsXXoZ1JQTBYRxS3Dio69soE7FYfhOXhPBkAVukMfGIqOeq1kPZQOt+5Il6Q9i+cBhIY2ra8S5CcK6xKBKJNbx7RASmT5QQuRE+NkQXhUcyItSFIg3mQs4qZBr3SCEbpnrr6B7NuZyzZPkmjLBsi47FFIWO6ttzW8EPJzjVadcTBfebl/5zyI9g00RxzM1pOetSZlaZt+/45nmLE2uCqyYqxfsHYR0QlEVFMbAO4HL6uKkfN3D5XTOsaBVJiB09wGrCXs8Hsz8rxKB6RKTkc0GkSloOZ1CRjWWe4ESueJX2T7s0LsOz1ONmuTi0MgMYZK9qTF1KkiMmqweI5Yzw3WOhqHyeCEiy99hdNDIyQrJ7BcCTxcd7LoDrHlExAZ/dYdArrHqnf68SCEMaNBG3uMWzh+v7Wr6Wr+Vr+Vq+lro4r1LxFkpjR8Hf1/LkZcGefkblc9ALPWlZG08hWCtDzRiRoXq1VUCEr1un7E/5J/zA75EyMBLwb8aEF2nETX4NYJR8CUQYvvsOOEwYb69A84zp7gbzPCPd3QI5I833GKYJ4/09+P4OdHuDlzTim58SBs5IuFejVqWnM2PWRNVzlpBM2F8Cww53t+9wyBOy0am0A1HCMACgPV4Or5AGwjiOmPY7vH/9Gpd7wuuXFvYY2KUB154kuvAK4yAJrgshq7xWsuTTGpJJk1GnNEqNEKHAlBKwdiMvUpg4S29oq1jxBg0HX9o4cgaXRmGfx4FdKgLwMDRdhEWP6PyB/dpcdryONikh7Pc+K9stxeg08rHL5/b5S+GfHgpn760vZcz9Ynx0LeutwrI/rmlvw6K6DBoaLg0in8vIKrOcwBhwmGek5wjN9PpyUsAMSQI5J+yG5Bm1r0bGN1cixGAk7HcDdtOAYTcgjQMoM3DIwJsb4Pv3EmNqoYQ4c9YqbWLvOYL8aEVAvqWbpr+F8LRTimjmnI7Mkrgj4HVBTRgzW8x3KohOX40eD90B2Zxwa3VdrNyPEY6WzNhEXx3Nw5FvNlYCkYRkysYcqBLCvwdpZBGoqxbQlTAMcEneaza1PkSY4PjEalhbx4ozKlzB48JHjqLEIsgLtIJDV7alWmlbBnr9CxdmN/OrBAiXVjYVm5OomFiUSnJtAtV6NzegdF7n8Hbbe2mKaR16s4r2/Q3bc8Wt3oXNa7QVAx4HP9RpIEG1PhtKNe8dKzsnPP0FDk8gAnxfjN4a1G05/Vk+dEv/57h3NozTFGtdbVwBj0LdHk246smzBiIpMxSIbDJlB7BZy3/qPBwbv48mevkQUJChoYglYjT8QuB67hT/UOlAm7V1LeSfN9sye05crMGMdQ7R+rfwd5QUd5gyq+DHtfUqwyW/atr6BXYO4zpVhOHaisEKDjXm0ZaneAB5r4tGT/XyZRGjz2W9vyA9Plk5e1d8NqX14Gt/L9/PabXQEk1v/Z/PbPWcJrauzEO8E352AsFnL+dOWI9eeVyLp7s0Wmm5w05i5WAstKXe6vMIRqDXrRxtf51IPf7cYVt7+TT13odrGet/Uzm57k+78s9xlltj11P3YH9fcFNn9e2zYNtS1vZpy2O1K7sGYxl+4M2aupWdV/UAi8jNfKSzPonJi19iZwzglmcAMxKAkQkH/TbjGgcQDgTklJD3F+BhlGTN84zdOIKmGfOwR84zMB9A8wzs7oH9HXjcYWTgggkpZySeIXGUizFcziJLkNCdhHncIQ8jiA9IvNNk9QmiiFAFQkoYxhGUgN1uAF/ukV9cgy8S8ovCwyUAV0qvO09NzQQAMG8E8YKw/oy3T6A0wBQRCeS50qoIGo0Bq3sNU6/bKJkIbzSwncQdz66E4MW/67WeojuOfza33Juprif/epeFN9pYv/PEoVnWOX4btMt4DO6PpYzoy422lZPwreGvh3a4eHlZFkadZ8nlyrtdT6BS8QgceuaJ6zvg6DunSjDtLsw3iBISGDQM4HEE5hlgVqN5kV8+S7Lqm5sbgFBi2g0DLkfC//qbyT0idgNwmAh38zVu52+B4QI0jhj2e+yvLjD9H7/F4b9/D7o9gIYUEGs7S+33DYd94zi2iLG635SK9SvXEVpQSLQbW09aTPNN4fdFz6FN6TJ8r4TDnSY0poiLfw2kqJTyC2tBdrhkKYYsYRYFvgiYylUhYZxyGDtrItcWGfYI/UJFSgZ29hjoZpU7zxMq4S5DY7ijOgxw8SejahoMYkl1arOYNTmVK0zK/R1AZZ/YIoRMzTnuIQmh5oq7XLNe2jar6YJ4I1jfqnTJGXmawHnG4XCAhVJJIKRU5swvNdRnxxHPkaPi2ygXpY+VNAT0R0X4T9VEkbdTf0C1LuSx9JdzFS85r9K0Y2dEBIwOvSircvb8FbMm7gZM8Ju8DwMpa/JtYk3YG9zFqBlX+RQmkTsXg64Daw4Pn0ubs2pTNYInUAgBlFSh22iOOc4Q1UGlLIeF79P6b93McYFDdfk57snVszWBWmRgFmzICSJv4Q3Bdtnp+TPBg90PzN3xRXxcElaHvBU4ImxouNkcznBREpa1POGMoU0FfJ1R521h8U4hiBUaETAk8apKiUTx6/s5zlUgBVg8imqixT7komhlNGuwpPhyziC9zxmMPAuunCdJNlVi1HLVTlH+2lilz0pZ6PMq85+UCas9J+w9s0OFKCU59maF5BSQWGAM6naf84x5ZiSyUFiErG5pyzwXf03lwVSnlr+2+fpavpav5XMvJ8jbsxuTuysXnoiM3vmY+M+ZFnTx9mdijfwll7PDVHxhpWMTc7y+/o1sCgMh/+0ZUpJGLtGtSOXsZgYmAv7bAUiUwfnPyDzghq+RMSBTxm4g/O3FFXYM7HbXmHPGfi/hlab5oHTfhHmeMB0OQJ5AeQbyAZQPbsg4a1Jq5AziXKQBnEFgvMzfiAxiUC8F2rlIahoSfrq6wrgH9i8m7IiwTwkDibeD8CrNPPq8UvNjYCKUmSZzl9DfEo3FE8L4u5oBRsWPx7YjCumVxkPCFRiLhfoIpdlbp4S1R5+eixpPKCGObXsGd8/YGvztr4RaefA4rN7IvU6Ur1dIpyz2wqcr55nAYsPSN/hJZTUPP+JLGUoCIacBd7/5FfDtKwy//T2Gm1tkZsw5Y55nUUZsLJsVEdM8ASCkxCoYFWR5vbcFJYhLRsJhHnHgS4wYRdgyZeDmXjwhfvxQ4t+ZkKsZ5OYSrHFXq6Cswqp8bCGnWQrdqr62LGhr+XaqfqOE6MLpTfd3lQjgpe+ivHCJeqDk27ngRvhZLqyihLB5LPCawD2G3+kA24VTLI5VoOvjDy7TlbDyxFEVKVaAXTw63LOBW3hNIF4Luq0tF3qSJGP1KSqdLZDBgrgDoOJNF26zr4f8rYk5VmFiBudZqgy1YD2Ia6vBuwKkpVHiBEUFE2yfiSCdCB6ixd9QC2OjnZY0apR2FvLG54Koxn6bEWHtOVIV65IFbuTsngUU13tRyirUa/6wUp+Tfp/UTlhlySJCV+IOSWFnqddsIFKpadPabaH0M3VuOTZJCmM/Z4xVKRf90fnmCGcQfMf5aohxw1dVG8GarDvaNU1C1XbxBLN2S6A3O/e1eLzGPaz/5/I8vJ1ZvDsSZ/UCKGOlLqFb1s7PvnuqBeUMRzzq/2BlE4XWZTjkuJjAyHKW/Hj3Fq8+zHH6I1zuhWGU0ImDZ/NZ71fZ83kAaCSQ5plCNXYuiuouojm1/+vnFcPwiYj4c+jGCu8+SYl0w1Ygynp8yeWxAqulx8PxeexcDxuK0g8Pe/kJ98n5jXHn29mMWNvm6pqdAu5TcuinvRLWCnU+ndfzw549rLN2xU/jlmNn8AGYadF/t/lj5M4DZmX5Tq8Drv5062yAdRN0K5U+huXrc5XzrpynOeuPuR5OUiEBn9eSkdOw9+Ba68/nTf9d9yDtt7esxiu/R2630ImZGR9UHsE8gznjFjNmZoAYGWJMS0wSxykTiBNSZqR5BOcEmkekPGMY92CeAZ6R5gOGfADnGTkz8jyLQUrWMMM6zAEzGBl7Nd6B5SelEQCBEosF5uUleGTwxQGJMi6o3FVEQMRGC5xsPLPS0MKnCrNKIIvf69+LTE2TTlvY0or/UDamAFBP9PEfTj6LuGDTnXwu/RF4mbrfjeWMI1xzdV1g6m8bgNh89rtonKvHqxTL4sEJ2mZhcLWyJmfSiGvr370vnojmPwefr3ptLOiN9vlZEFV/tla3fqLcrq72AHq9ZfKOylRi36U6m8BptZMT7TY7lwjAxR7zkDCOAzwGDUvodOJn8Ii4v78HKGEcE5ATBg9zXzwbbqc93h++w7i/wsXVJfa7HS4uLjD/l9/i/r/+EXSYJVl142J2asDHytZaXD5i46yXqux+BnChca8QVXEW4+8LwZn9jkKAtH9j/WWrVC670CaDgWywkgtn3WLVqQJ7TcaT3aLWLKKTxvNPKLFRJH+CX79cBGUL7KGXdiQAfLzmmbBQmAWlRgeDFEVLqNAeLh1HBiMZ3IwSzqdihah8dsvy5MlQZQxJm8jaVVx/DmNRzwZmABKLnXWAzm6nQZ8xkHJpQ9dhzrMQTxorfySxTC6Rmcr+snaFaEmVzgU+Ju0XKLH8mV3Z4XNNEKRB9VIlJLUw1pZ9OhnVTHBIDk5i7SEeCLLRiDUWvgokyd5e7Bmz+CAnXGWORaHDWfJCzHlWDxedQ/Fu9URe8VSfxCRBQGq6u4Ka4kExmAteYDsztsLFjaZen62lp9BzSr4sTrQ+rz/FpppzYWvjBLHA3V7oxy7JOFb5oeCg6ggqDjGPDN8bFcNTxPXxbT8rzf2wnJcGpwYYeyveWvInIj93jotsfuJLWhIRcqKQY6GMKRG7V2DpQnCDtJkEFwhSQBaXJLl9F0qWQjT4VZMltJjNWGb1VFvcoeVcLuZFE2EM+k5myYUBzqBEGJIkBZwZfrYsIbSVbGPy/W57XnKkmNu54dNsuDElhBTeHejKPBirVvFfBNy8Am5fE66/vcJ+f4lxGEGUJFcMMlKW+ShK8fOIvS+tfA5Job+WT1nOvl0+s7KNcv9aluVLX/lPX9jvfVYCuPWEqIW1/tbK7fq85dHr/fWofZJybNqP8yS84GOesrj4Qf8xjrjLR5z4HkjqIx0ieFvYO5HmZ+zSO+wSgCxxDP7Iwtpb6Od8IWc1Z8Yh73AzXcMM0iw6wy/mGd/Mytcy4/ec8ROV8NHClWS82N9gGGahGQF4HmlTAoBxAeBvlA61eOhlyEsK06hi480oPrB5ch7IeM5CD1NUTDgfvGiitL3Cp5wu/VVeKgeUp1+zJNsqfO4qouP3x5dTo3cOU3lG+XNSMvBsZQ2fb1dCnNtyXZ4PszxtWVU2bHy+KOdMp8tdznin9z4eAOdjS8C1LvsD1Ciwxr1ntdmK66C4cRgx6H95PiienoE20seRslkREZEisQwmI2HOqglJhCmPyLQHeMQ4MVKewIcMfncHvL0T4U1qhYVrk3IaUXDzN4DZrecSxNUKjyukwi0RzPabrWCNl/FJJQQWg2svOxeUquW9W6TqM0883YOLUSSxTV9yKempzKyXakywuhhZ+d5ezJUgsz6e8cLlwAksLvfVmeUyDgp6jgDn6lLbYVUB42IjqRCWudhIuxCTWYSLzPAQKUocNebCZW5USWTCUDBUqVGDRFQQ2RKhKQEZhNRuGu1CwnYQ8h8HWL2jOBEQ+Np58P7jslP4oK+VADfywzFlbBkvVf3Zfs5KQHDznyQMJk0SXhRMrYB2Keptp6VDbDXT3O4fg23Z8Jaba30vdvGGC2kbAa390TmvWm8vjSDo9Xp6TroJr6mpt7VUOO141d5Yj979j8LT0dtiDYjQe+P5UJRoDFeYhfdbaw5muNcLJeVC7BxnwI0Fmr3XObGh4bLQrpQ0pX61Pw0XxpBW7eRVC6wJ/gKGPbJ4y2cFKzn9xvVzwJTSDZMWwFhzWgGAPADznkBjCkIjgh1Dyy9yjODr6D2PPv9cS+8s90tclTPL2mScYnrXnn8pk/vIcjr+97P0ar08e0tbV/FjrPbDPSFivcfO2cNG+jTz02/lFJ7b3tIjSiuA4tN79KnD56zdBW5QEWjGZcgTLGjALrGysc/HznC1U49c5afbed6TeWwJnxIFPn6r1HTRGu3x0H6OvbapyYouPM05He+lP/HGJ5h1//lDPf2GUn4Og/QZvGYViKR5IkkZxXuI93BkM1nJ6IkYsxrUIRkPDXAiiSKgFjwMEgNEwHl1QkLeDaAU25azH0NoA8BIrLhhQCxU1eLwexEctOygz0Aw1AHFd0h/SovlWlB7Fb+O9umiPHQvVsqIBzyP9c7t+9SOXtQ7hlyiPM6UESf6/5ilO309udpHND76lJ5ykZfeLMRfKLxWK6690gGk+tNeGYt6a+8DcDnss5d68gS/2xw6c46n2fwMSHjxDOx2yBc78M0MIDehkU+XzYqI/f4CACGReEAkSriddvj+wytwGjGOO4zjBa5fvMCL9xmvf/cO9+/f4+7NG2CakYbkQlVDvafX8zhyQaeN9frbKlUCR73hnAY1E9UFoV/c5KMyogdCbQnQPO+9U01U+UKhDyeqmYNyQAVfVOJwd6CR/2UJCeQCahceBymbzkPW8XsegI7iwn4gf71+6MLkRmPmVgF6WVeW6XZp96RHHMev4/B3UqlmYJrwjqRPAjyeO1FCiv3GPoKAT6Y8I8/iWmrjEYthQNO2hJIwKEysIYVkWo0hKrXlrCSkYUCJfV9WTUCSw57SIIm9Aqx1qCzdv+qemllit2WeFV7xvjA/l3FUoos4KMqOcGAsyW8jcSlrR+CUkHJGbogVg85+KXExmx5ynG9VPmQLXcXSN8x7Itknf2bAmCa4Utg0sGyxErBzXSzpCvyAJjlDOkkvVOtTN2Qg67jDzeeXov1WbkkfN2yrBrwQ4DNviAjeAue0XgEBTMllwsUSvlXg2D7ecMGLl0y0Tinj6+eDMFgfcIPGC9gYIN8qBi/DY5sFNONCC329ytGh1ZlIheAS4qgGW/0ATNBv7eWSG4QoMk/1XiSS9u09ygROUveo94r+zWxK5EH6pOyeC8t5Es+IOWfwnDHr+MVDLO6yMmVFMSOVxfFCZ8znsMwfa1iqJaSCq03H4BhR91TMI5RzrvZ273Zboxn/Ogqh4274tfxcixM2n6rYvfrXedq+li+tGD2Jmk7s1it/2kdfy6cpH0un/al157UhSf27lWWY5p5k5fgF0bPD2gDdApbyawcazh1Dl/hd/5L856IBEkrX2gIzxjTj5fAOztsCADJmZvyAwusPYHybC79VQl+NqJUL2n7ABe0YurihmfdOOs6qtjwItKowFOGdgoR48WJstIYmyncWQtuF0H1prHNs6V3Z0Pn92PPHlKUoifq/r77fyJuMVTa+23i3HHnkJzrvTzEVq3KXjZ03RnSL5p9hzT5FeYyy5KPj9h5a/ij9kvLpRRlBbIaVnfrdqyLIPyJnTSJd5XHE7d/9Cnx3j/0//g7Dza3k5zmjbFZEzNhDxA4DRI4yINMOGC6R0ohhvJAwMvMM3E/gD7fAhzvgw50KPpaCZFsbDt83lQ1KiL4g4rwLeq3r3huryoiNO37Vkg66aQzcUF/mrxDVWQlr1yVoC+0ozQqh9NvOp/1WEwryTQTXlRICi+oF/srSXoVtLnyv3yOWECQlxrjNQPf+dYrDFRuIyhQNCUQZC7LAhI2GjoOXDlUdqUIjXt6maODsgvyiiFDPiGY2i2CoJM8WoVzY/aF6HeJE4WCDggs0hbrRurbW3DBP5kFgCcZNWWN9t9bTD8ObD5GHUIF+2Ri4CHnjOnMt3Ix/HYYG+IclISxXHcdf2rb9sBUh/oI/WDZ9vFgDfpaXsC8IXS57aqks6eGAgo7X0FQVei3W6Sz2Uv11vCysHex6aGHFEkO1INj+bcd1rJyzv4u+tQDX7yL82sxRTezq3UAEC2VVniw2r59XsUCKbaBzp9Yz6zgBACwPRKUMqNc/AaKEADypNYxxa/Z1YWKp+bH+jTnWrQZXf+TuFwxjwnhxgTQOjgf8hqgafVqK7zEEa7zFHmLNdK4V/XrtMymsY4j8nAMWy5fqfvJEpaXvlsYZD9oin740uPA5VnW7pfxDev84+3AxhGdY6/U7/An67hgsbKn3HEmC12iLVeGKX4SFVzIe6NlW/8icnz8lNfWzGOdngEqfG5237T9sX3U5d2vxAe0d74mrb6WP4g1wus9TdY4rJbaXLdf6Q6a8pdGt9GBtbsh+gwQQcodvEZrzoLQn68NhYIuI2vBEhXMsq6M5GRuSdPGZrOPI7xBSNaZmNH54W1mESWkKNGYPJXKcPiLpktFcRnMOZuuta20UeGIPVjudur9vKdWYFh4f59KbDkTFDbW77iHzdbS/pt31cmZ/awdzwfs8vkS5UL/PJ+kmtHc+b7AG4/NdQ2HnPBOdvk7X2HMEgQ3Cr9RUim/FduI5OEcZ0eMfy3wQCNjt5KxZ1KO5AuZk2ayIuMHfQQS3Zn09AsOA19/uMQwj9rsLHN6/x7vf/wH80wHpj3cgIMTaj7rf3nCKDV87hfWcRC34UxSb9Y3eEKjX6SmJirVitqimdDC4swrFMzNggnFAEhCnAQyxZF2X80p7Wa0GrO2y19nu9+KZYdK0aGVgVtQR6QelTK939yAAkHRCWXKxg2gA/GJv3+cAKwcLWfVGMEE7SGeOFD7xMqBBLJNTEgt6GrSOuUF4fg3rLysBo217Xxk5z8jTDPcqQS1QqKztifyZKJFUZcGyjp5wNSexrCcC0qDrC0A9IDjLmCNOJJtnE1hS0jmwuiyw5oycJ/nsnhwyVzEWvKx3AjgHsqcmuronkDNyTv5GfNXmlIPdiLmhLu8hjl98n2Vd25LHRNayhNMq3iC+Zg5MQOCxv4Bj67McPEkcDi5j0ZJMwh/6KLo3KmcmtOGy/RxziCyLN7mehVzh0f3HJy4zCt4GhusqAnmlC431n21eYkJna8MH1RCm4QgX4mG1qwJrGZ6uf0n8ThXgBYja06SzsZoeTIAu61pR3svmUUKyGSCL+3pDifWzzpttE2swVZyQ4ls/R6qM8PBOjEqdowpMVispV3IoU5PzDFDCUHubSz0i90qjQc5anjOAEcziqZWS5I3hXNwvhzRUYzCvucESSWXWs6nKWN/YhQkwwp0cD9c7+frb1/juf/pXuHr1EtM0YZwmgbWhYIrXyRo18bEK13vma/lavpav5YnKQ+6ev/ZSjFjMOxhOM7ihRkV8GL2jX5+Q6/xaTpeTxjGfoO/Puax5UJzXRp9sfur56HpSsOVzQBEWFdIXQMgRaaydeyYrnRyFbQThVYIHMTNKmJRGfsdt+JTI2gENbmiqUs0X1y3xcv4WTG+QKSGKWmj5ypqQfo0tX/zQW0xaVHnIVnoSHOnKmSe+4ZSX6k2TyGg667Ta1trPjQxAy6K/KmT62vkyoVrcGRtAe8S0nVRCfAblQUqIs4fzuVFXTSSLKLg6Vlo8hcawfQVnHH1m3YaIHQMlYBgwDAMSDWANtbe1bFZEDOOF9q4C3TSC0oBhlCQV+/0e/O4D0vsD0u3kQjZKVCPzqnAfcTpebaSY5S39EF4+dfp84tZm/fElekWc22T17okSpyPG+jeBrV3qR6fEiXAV9fFp5kZkWeyfY36IkhOgPCesEEdcryFTe8hMKGxIvQl3ZQLdrF4QqoSI1v42SayJnCnsKUlKpeFSnBpxUqc3UTAFh/er/1niWReyoZ1H+WZ6gq6Y1eGloK3r3GQ+PizKcu3YFTPZlB2a7Nm8R0xYH634PbySCj/LJdmcnUAtRWLO3Fs5/Fv9UUBt3skbq98qcThtV5Wx21gN3ri2lceC9dVYnTRgdUutlOwoIU6eVUIY4LL9Hsm2ZpZU4cO2nfK3F7v/WKkUBj7dRWFmIFVz2m0ozk9o8wgy6RGsi/HZHgs4rdcod75YfoaVBgFE74ka964JkAuGKPl3joZ+7DF0nYfrhieFqbKzw9Tpl8MbhsuO3idc4Yuiryvzm4iQWdzNpZ2MqlP30mhaC2giKhi64zt1ZzPDPOTSOODy6grjbqfeYgckngGeq7NUtdj8+EVZnHeA7dxM/VdXG+3OUr/myt75miT7acopD4l+2XBeHlo+w3V9Xk+I5y2fMR9flZNgfikD2VgqusOMpcK/mwQQ4X6zclJodoq5OqNUBk5nvvOxytL6fZ283drOE0CFTytgqom2c3j+rSVGZVipceTtep22lZp3W+vx5Kw7DRrbDdRv23xk2zn+yLBcbsqeChWqvInz4Q1Qxppz1UULdXxhCdCSly301inB9FrpexA3kJ2zpVflU80PRGftg3M8aQq/vrXx7XA8Z+mvxUqd48yv/VNWMipBKO6h+l7aijspSFD6IBx5WhmCLhru1/sYJcoXonzmCcraXcrVeT6vjVN37mPu5DX8vsXY0+UXoBP7oG2ogzSDDCVTQr68EHnohxmY59MD0bJZEXF5cS2gUAKlhHHYIw0D9hcXSMOI3f4Cuz+8wfC7O1AOlsLLkYWvvUmgZryEGO+4FgQGxnqzCrcRqPYgDMKvIGs/sW2OtwssBV6n6kaoOMJkVtrZhMkioHXrd2ax+F+VhQbLcY+hGARxXAS9y8JFbg551xVGjXfIaQKkrKEsnwoI9T0qyRqkBxZh+mzjNqv+PNfz4sJ6JUBIvAyICGkYkCiBzFpXqZlC3CMsY7HG55yRYeGYGHmeJN/CrEFMGCCqQ544vZOUeCCxKE4mvGe4oLdiLghlTnUGMyDjZvFyoCReHTJ3Geap5POgyhHzhJjnyb97OCmLtc7qWaDw2XrIscuwBGKN6AREhszg78RxmCU91AKtunyJNLdFmOv2/gv7Utagbt+UEKkNMwN4rg6HNbaLeizSBlX9ZlU+dZPuHBPw8jrB4MJ6rrXFnCtqOiD33gh63bIr4sIL59GnNq9+j1GZ/0gANO+cYoar56GdrTSMnT/7jFaxqXjf62i7Cf2QduW1cHeA/Y/FrnUFKgFRgc2ZwaTto1W/hnE7sV1gbddndcC9Zzp3xIRMWYK8ZcupY++owhMJTBk5EZKeYVlLco+BeZpl3ztuCrg2mecjg7Psg3nKwC5JLhmiEm8Vci5BWfPthI3H7HeJ/6jjM8bPrdTiGCMsREhpwOXlJV6/fo3x4hLDOOIivcEet0Am5LD+w6Bz8rGSg30tX8vX8rV8LZ99qehU9RiulBFk4VkJK8xPaOupRCBfy6cvZ1hCP1kxPsFolxqA07zz40p/uNLrR6WcjK80fj2CEvlJM4yrqMlAUwLIhEB72nM1tCNqEsZ2ZqCV7i9EStT/7ItV+IQlfF3Ts2MAtI23rW4upyVTvW6bwZ84IMI2fWE0d+OK0POKWNoENoLYXpu9n9sv5kLu98+y74Ijlm308QMtv63I8FZ30ZdgePDESoi/xmKeEZar8+z3G1kvQEhDwt3f/gq4v8P+v/0zhtvteSI2KyKYknY2iCJitwMfZsy//1Es2nd75B/fI8185ABgIeStS4vclxuO2x8aJL3oBj1E3IolUQ7gkibYXKKQM6K3PlTLsskqLggHnZDmekOQXr6egLmBwRUPCwIoCuda2KXksAAuiAIWG9rusYLynLJAP0eEUhGU+texW/LrSzmjO59RSwJvUoRrSYTtiALwRh5Zfjbljyo9bM4zA5XXRVAeGANjBBSpxwU0FFRK9dRG4alf/GEXMQHIRQkVlstb9n/gayr/y+oJYYnIVWHDElrKwnqJZ4jmpAhhvGL4OOm2TcVlkxvnO+xHX+/mnMvGVEVlKmJcJ9ZkzgFIkt5qTSNu0bk+aVWt7W4hELSv4lmD5cVsxO7iLqf2hy4sVZNxP6Oc4TLsYknDKNHD5LzpmLL5tjSwkin0CLHRklvmROEYkqpPn7TxNVuljRyFWlnh2njqt7kOD1dIxWEihKTqoTq4Yjw29VctX73AAnc5Axnsygh79WjzrEyntdvZKgvFju8zZaisITbE2iqCpO2CewJ0bhjA3rBMKRUFMEOVjlyfMb9rMjJr6KZEIE6OC93qjGReao6SCtyGLzrPfc2o4AQ7i7LWCcOww7jfY0iqCDVvJ6qba66A/pI88J4/VqKyKa11vK0hH9RaMw9iMKXxkzU6FFKzfdba6OzttbonwajxS7/GoyZ5tc9PUdYsB9dKxQw8Zi+3G+nUFCz6cqJk5fm28nDr4G0noXuHPXC5N23dY8sScOBWEKolWmm7N4fb+Ioznh09/239h2Opk4A0e7aLJ/Sn6KkutL3S9H6HCH9rhgU15g2Et3fX8DtbxvjE980zXF/rfT1hZ1+CrOtzKOdOU0UJRgEr1WeQT9ZbpZjqb2csZKACl81xrNHtyiDsP+6hmMpYpnndaWr7Huagpb/XQOjdl2uGT06PHmFCXFhyjNqLjxdEVlM78BpdYLfgqzN3oNU/ct+c5Q1l/NAxMDYMZxU3G4/TUUa0FRdgdw2tl2AVGI70Dzgz6+xWZxPFE7LM/LoBiAqY0P6nViCds8/O2ZJH6m6XP9R748EGCNx+fI5LMMhVtpBd9vxE3Xp3NPtO3zXPM+wG8DyKsXeqDYSPlTOSVe9AiTDudhiHAfvLS8w//QX3/4//DMwZB50BE2o40MwAlZA1a2Xp1gInGvsvExYTsla4Fthw9YGtSuxUSc/jDB63n0/wg6f2RmQYYtijOA4wiyeEWZlzIwAkQkqjbgKqkIwnVQY0Bndetg8IIqbk92IJUW9HSN5jH7RZoSZYGKW4x8scFyGv5TtgMBLMklaZgXqBXAmR8wyx/o7jZwgTYXkhuN4W6jmQhsGVaGQ5FML+Mqt6E3ot+zA4RBeRda4tETuIZBSUkDkrODKuYZT1SGlw5RDHMaqyI0igfW5ZFlgSTc9zTVJY3gtKXje7F8QM5BmsOSHmST0h8lQUH4DMCQ2gQfdMKsHjmVXIHYTAZT0pwBHGw7Z3izDfw2WB3CuFFFER4EqlrPvDchG0h8U9S3Se7eJenuG6lOS2WFq70ZJRt+nhnP09e8c8J3yfM7sXDLWN1JxBGZvue9Y4+KnZE9ZnSjZtVBRObg3AoGyeG1DvqLCfMyTniL2rxRRQqfI2aubElQ+aY8TqqYtVMtTb4Kt4VhRgBbmvjFgWmbSok6McFHCZgYRKJebKiEZoWby8zEtA/laOMjZjDBRCP8xXteetNnyMmQAwucA5dWhmOb/wCgkEi1W9GHskIJr7zObDxiW6guT7d5EPhUpbzMHjR9coI0P8G1jDwemk52JBhpQ0UbzioJyBaRJcmhIwiMfEnGfwnIEBgkMs706cAw6+U3YWwyKKU0UW/MDJ58e8/OZpxgxgvLzE9YuXGOYbDHzQ9esE1FsV4h+7gb+8UqGYzqfHttwlq442f4IIOqPv5fdlw+0vn5il+jLL4q56RDufrGzhvD5yOSUksXvn6KbtETTdK2K7YPCcaVq7pjcVetZVqWjh7oTon2peCMwz5jwBmAGSnHSJ9kg06P3vF7Y2Mq0aYnz1jDhVHouRN4n0HlHOa69X+2nunMeflN4RAIxHiZz4yvuBiVvwROcoHSKv1cC3qLuUovTrrsFP8S971WKkVPMFXjeSKZulkmfMweIXKn01dLAT692NFCjp9gPV9RYQcJycwKAv6n8cHPYQeXcxpXrYKTuJnyMfa/uWO2GNfCqp8+Np+FaxmAm7WlohGNGVuv22zvFc6ZZg9LQonwFB3ZjUlfl45LbdcuyXnMinuvOXnE59gstzV2a1Vwov66+Ppf+7vRWPgxkhgoBEIzhlpDRioGfwiBhGER6O4wiaMg7/9GfwX94Ch1kEiRYepRHc2IdyrrYt4kKoF79yc1EeQ8g9CyF0LtZOH8v3yqXWHUVc+DNNfqk3b9qoCXJdkG8hiEK3JvjztsgEcKimxC1NwWZ4Xnqs1GmIL4W8JGqtzvUOryKOrSA1Dv8KsQMVUPXeESGXCZpMCRMtZLkCm1wg6YJPkoTXRKmZCF5gtKKgyapsKHPeClcIFpqFSu5VlPYJCUgqoHbBd33ZtUVHWvVl3339252hTbuIj00ZoXvEEmrP2RUrWlEbSMKEpSQaTFWcANwR2KKhdJtx6Fo22M6/M+BKgOjN0SORTpZAX/mK2p4GPCxTw3+utEXVw2I556sh1aJ0PDbWCjw7/dh+NUWL7+WqzrbRO0wczrLDGjdpF5CNfRRcs0Q0TXtrBIw+syoLa/9TMISm+yxah6C2/bTA5WtgrjN/DiufrKrPKaAVUxTIe9W6BJxlsNWA1mMqKJlc+QVfl2ZgHMYamLCuRSxDXDMNzyb9TKlutrPl621Wty04hlR5vey37NOmQQ42Pjo28ZAAmAgzZ0zTpDluCt7zuawUMdZIHEQD+EcphDO2fOftJfG5Xj5WYuy1OVzZIKtlFSE/4J3Y7xak/+nK55pjYytUyyugpuoW9U9YeG7qc7NQbElDfj5lfbyFju3D/5yjWIPqKWPXd43AnqN0SILVepGBOLecogV6MPD6o1Nlvaut8H98nPNUeG7JRm9p99i8dCjJR27Kp8NGj6dTOty7/N4M8lQPp3NN9Ps+ZzKdLm7FDWev95GiZ3UhQGzP8NZxPoa04epPYALq32uOdGP5XK66FvAnQj3n8o/LBhrZSdW2/VjOX59drH99FDzeVS09Ep7syHIeEzQA2/dxWxqDyyMVT/f1RLRDl0d2KTt3znCEoddgU4lP5NHtFObT6/4xFBXHOcH+97K7j8NXjP/Pnx8AoIEwvbzCvNttfmezIuLiYo+UEna7HeY3b3D4f/4X4DCpJiTEql4rW2/rE6XEAu8kQT67FIFlZUn7hPsoElJrxH1qrLSL0DPAw2Yxnut2TOmggneXfRCF0BBF0O5x+03SHGgBBtSS1AIKZYi3gxDtUtWSEbeInarLQoYUCSsGYl4C7dSUJghTwDoHFgrFxuyJlnVO3BLWhFJkECRPRC1eCEXAbgN2nMRimZ49EbUKjd0S3OpTgDlawNfHmzPEC0PiQZV5MAlbtNBgmRPfIzmK6FRklzMyz6qAmkVZoAoWjTkFkO1hXd+ckedZPSEmZMulEZQZKQ2yR4YBaZCcGaaMQPQE8Smriaaw8NVHe2zeFL5vXDkmoaBcQQSAqCjWTAjubVZHvFi3L4hX6ytn3xu+Xr4nl/iisqS34arHThH4QgWrDDbL7hOop6yv7CUGdB0A1wDqJsytQrA8DBA2NbicY4PZJsxDhVVrVnTgYUBLuN2L5TQSdGt/4+kX78huLoY/G4hJBhhZ8EnAywBCzpiCo9sldTzQKMXy5ks1sHInXwieKiivWbfmrVLyjyxxZhsXlLmEfarAYEiuG+QmY1LwGPE/7HugpxCv7rrMQGJwTuoEkSUPlOJWa8fOsL1f1rTUybp3ZkiYt8G88nxsxXV0ObN6VoCQ+8jAZ8zzjLu7OxwO95jmCfshYUiD3ydtnGXLJzMQdff5c5enkcOcIil7df66Szi9X8vX8rX8lZRzzr3emkoWKX3fGKTUtb+Wn1t5Sh7/cyunzsJzDP3znE4lnJ08p4pOpkVM/k9ZHkC52CuLMZw7qKOi79OvVt+/POprMfqeEfFTKiFinxR+iXzRIjzU1+KTFhdsbRm2LM+ZxuIPfOXzKC7KquW+y2r2nBfVNkhDkIiQxx1uf/Orfn7VlbJZEXH/5q2EbfiQwT99AM0idGiUuh3o6DiO043VumD1tDZ1uKLjiKHv8tcRf9Tyi6Y+4EqW6oVlMat8QjuWKGI1YQyF92iJvBe7PVhS2/MwohKLq/7dxxIEi4wchseIM+rjI3sW4OIg9CpkfAEnCuEa4XQsFfEfJG01jtHnenhKaJ0CQxWKxPsuYVUSJBdEyQ1R4r/G5fWwTyaozy5VbcZQPDeYLSl1vcuIIeFwEoV1NStm/cfynjCKcmCxCXWc2WDSUFYqgkw0AiReGQJdAjDDvSG4hGiypNXWh6mYRFGVkIaElEZXnDTTU/ZNzvVcow6/Ul/mvU9hHluej31CgiIw7i9TJGBRfJe6ciriCWmGLan2MeWl77U6kfSiGoc9SvUc9OrK3wBbOH+babaglCx/eamEYMA8q6Kyxs94Na4O4WuKE9uTK7eQnWGCJDzKi/1bmqNuzITThas9FPF3YB50MWIuDZHtR+un8m5vXbmdHPXikK5kjU1JVdpb4tljpLypR9eUJ8feib0QmSKsvnfrHBkhtBXs+iW45U2ToEq8DgimvJHoV6WBaIACFiXJAN2D3kd9Z7uCKsUZ8oGFKbQP5I+I62w0IFEmD8OAcRxFsbwygcyWl4F039nvRw70xrLV+KdSvh9Z58cxMo8fz9P3ce45P9Z+S9s9DKLTpdfy1l6en+Fe4ouIB59mX5e+nmdPbWl37TxvNTRaJs7zJwaF1tvU3KPKxziZz1Eev/69ud+GE87t+yGgHucne/XLv+WXE7zsE5Wnt6h8PqDbOewa+3TIzE9Vnr7vtQY74V2evOuVHqju+1y0F0/tqbNZsxSP27lPuTZFhNIwmhT/0NMqI55rwY8tYMMr+88tXYqSO65vCdTKeo7B08qrjlfvVnnqy7gh5c7diQv+7Qh8JwWyW3mF+Mx/IN2fxznKXjtPsv1Orv2GNrquDI8rdXgm9bhv8E1X1ogT8/MAl4i14X0cT4ga3vP6rOmZDtao6zQTuKknkpWiISHl7bBtVkT89E//jOE+Y/ynW6RJBXrJYmiafPWBC3GMXjXEUikhTr3UaSD+EoTqvSRmm0AO1aq93MUfRUBs/Rer9pWQTLUrRVND5t2s7cXos8QIyvGeMcGOCViD0HBBbJvwkdldxET0VJ67R4KKiwi2D0w4b+CXEDzVXDcT5warKvGSTO52JIo3CHNWL4WexbwKnlgF/8Qgz0MgoYeiwoftwDHAeUbmjNms1ZFdYO5Cc/1bhJ2peC9wOK+a88CSP3M1/43LHQcFgedQUPLVn83ImTHPk8+7J5QmEqVHxBKqRMnzLP9Nkh/CwkzJaxIuKg0jiBJS2iGlAYkGF74KSIysVsWIEZ1MOJIq/5ciuLXZLVqBslC+3mU+fcv5O9I3wnNbg14xuOT94PXh3QYhZ7eF2E7Zb/0KcF40yte93Zay4KAYshj7Bpud2VM4LNKHKPOaNWl6dZysuu6RKiRCg5/bMUDnrQof1QMC5VFRVbKHw2or2q5v17B2lTa8SDBB+Tr1oKfIcWmHlggHrWy/IzsgjJWznLGeYvz43bCM2Rjd2yvF7Rmsoc9TIpAJ97P2wJAcGqlgLN9cPtyg+GOgShgN+HlJnEpI7GqtymSK0gKilEzlzklJcu7MFhJNz6815V1Lh9pWBnNaCim0jt1twzBgHEZc7Pe4vLyS0JAKqHn3RU8vGa/+59urvT+/lucpX+f3a/laqvJXeyS28mcfsQQexMN3+j2/8kphFb6Wn2HZokj54kpDFFdk/tYmHtLtA955zhKXslJKKK9alBGA0dNfVjkP4EoZ4U102jhm9r1BCbF6gp5L+fCEzZ2aUep8elBHx34ilFtpbRk6D7bAf17Fz6Mc3Y7H3ut8f/SwH+IS8RHnetlV+ws3v67xxuvyn+6c67zIEbf8r9sHvlkRcfnjQRQQzCIsCiaoa1qZNuyJwHv8AFdtBWFJ9cNKP1Ubq+/22+iPYQnrZg1UEI7ENxglVIcrIaKkyAXSPRmchMxAEtLC5EVFAVALjSwproLjCpg4Oo9gYnkX9HniLJd0EG9JkxouybQddqnbkExQXnUShMnVQe6QSJW1LsoYguDRSlKLW1IrZkpFGAUiVwhYH2TEhg7GlBsZ4nVgcBTipLRfebEAGrGKIAoYq2dJt4tATYgPzTcAAQAASURBVMaQbWhFBhiYompQDJRQVCW3QxT+2kQwAyDW0FImSC6hSmwWCeXcecJnE9apB0ctRTWFU9YoQgJPkU+a1TUvB2VjKN9QTmhZC99rqojxMXMQ1gNOvESxqDcAyLuAe41Y/1XRbea7rSu9jsLMfpH3a1v1LlZW8KMSopoRKjuyr10/IjBnlPa4eSPpvgeF5MS2Z+z8sJ8XC5XE4ZmdAwtltAxrxbHHxfbtwrxGvPJ6lbYcN7KIeKQPg1k/bSMgbV+XDhf92tmLGNJwDXON5poxLLlCrurEea/Ou76s0dPk3Nk+qF0kYBu+MoCyK6bBz1WoswX1VhPDbDCxKmzD3WN7yWfFYNF7jh0sBULHtBYWI97rEhZyxDAkpCT7N2tYOyIqeMhm06YlKpkijqqGuL4nHr4va7z1JZWHMOQVb/uIvh87X+e9X0O6xpMff/fMHlcEX92cZAGH17A8rO8jUD1ROw8ptKrgXYtTfsqD4pRnxCl4+mX57lPPWnceuuBwe/2f3+6Dy9O1dRquB/YV7yte0nXllqiFj+ecpu184DO0+RFLu0QnLeRXzmwsn9JD4pQcqYzvsbj1FK3ZIyifsFQb+/m9M7q2W829tTbvn0QBYIIz2Mx3JS4bCnc+rXT5Ee7rU3NZGac5z8LLG/IE4dvnBmOFlTt6wxys4cHWOOzRpYOITrYc+ayVZv7/7P1pgyQ7khiImXlkVtU7uqdnOCSHWkm7K/GL9P9/ivRtlzqW4nKG5Ex3s7vfURkwfQDshAEO94jIzKoue68yItwBgwEwGOzAsZR1r33Z7kySpfU/OojOCuFVE9qWsTtn5NlsfpHbdpj6lar7EPr3/c22Yzi8EyL4FO0XCr91cSD0eZL+HrJAW/xHUI+Wpi1LlMNyIOLHf/wZANiJ/grmddfOa2yTByE8Dl3lQvrpwDjfrIE9mUiHY4GaMky+FDkqaLMF+GHSXQQoTlnjoBEPU6SJfCBiQF4rqV0ZwY5IggJ8r4KduLQuzRMGRADb1lbrD72z3J6jNrQSxvRfYWOBusFjgxAVtzn6ROhuuzLCCgB2uPLZ43a3BQDf2XGpmw420waue6oTmXBzNGyAcjcCn3cuWXiHQXtPVPSujkBfafc8UNutwfjV2QfNeb9VhyiV2l5Fnfp8ZI/KdQ5AbG03RD2+yjJvDX5okMYe6yS9ibX+ThtBMGlsP5r2R/ZrFkDaal2hBYPa/SHNwwitI4xT1qxwNuVUFuE7HUCDO2Hs8jN7PFPlOCOMOzHg1+1rXSezcUNDph0JOKAjzQAA2HhL27TYNJF2qTXLsEDsVnmv3k+iPMtHQdkdCwQajEDzjI12WTVI2J1M5xvC0zcECQSAOL475wCN9YosfZdxUnZHg8WdyCQqBGVrk6nd8jQwtuolzyE4RR63vHUO27AKC1VmefYig6iOX4Iiu7KACKLhb0MkmwkmiL8+VXDX3OdUoN4rAQRYSqOJA8K1IAkoAmig3PQFAEIhaqc3kW2hOsRaRIZnBdwu8OHDB7hcnmo5hedH5ivmd57TQT5fQVvpYFU3/trgduX+1oY761D4Bm8DbzVCvwR4QwH2FcDQaU5VbyRZIAJ/vQL7rxD2ghH3g9VCHkzMEWfdXxOYYAQApE5fgZEouTdNrwiDszgW8uXfl4MPMdlbNGJG65Exckc1M20OuwAzcxR/xXBIXCU+UQD167jAG4IT/F9qUOIQdD6z8PsBvIUIdXHzVKB6WA5EqHPEGPwMJH8cROfR0rbHoaO6p8h+2KTWcVq/9pytDvqMxl5EzxQXTDma5MJb6+MUp/DUujBOQyq++tjnDH52kEuh+6V0SVHs5FLHKQDoKn65cLRJ3ta21T5SK2l6NuhIaHNwBsEfxyJktaBI8dnEr53WK+BpNFedg2TlfLnyMU9Xxy/iAEM9lsnyvdIQnGxNqZELmpnvmArnEPVCgNNAqfl5JwQHAhz3NAOKoEBB3Y3Bz3QoOqbRoBofzdRWz0u9LH0ShCD5B1AAcFPHIGfhAAQReFZFTYQ+pFXHQ0tMLQghwRNjeyf9a+Uq95u70yAbqBjyN8ft0MY3loprStzxCzQSSguoyE4WIcmc769e+ZRmEVlUndxMiN71Ydup3RfighDcnyDBxeqc3lpGHsHsDKd20bnWW1ShpMJnFmDMZJ6O6aSs2TRpg1xnVQvX3+rAr45yEwQJckwuXwYM9zRAHjzByTuYz4/Ct+CPs+MAtyWNWaoGnPiz8pAGoMyxioM+BlOmo4RFhnj82y9SngNs7SfzFUIXASHwd6Zbtm38X4hqcLVcJVi8r0eQjMXB8Lo75CSR6ZM1peweq77uWd/R2OsU/6jgPACiTrafcgQew6y9VlSoW2B6Tr01muxCC6HlFRr9HcCojVbvlhivcvY6UoYjlt2R8tU1/W3Co++qRLc5WXa3YCA4FaSXdwYrz6UEO+NviaqdzO8cVueK4/d4GHtqB/bM086+3cfIqYfPddHLYEfW+mTjYNZOb3rsU6RrIN/aS5vkAOQZZuP2NWBanKkkL3Q7IrGqUWiYtLO9k3LEh7YGI/rvx07WFjgBaL8OMMwQh7E2XXhmYWKM5zs/5ukOwzDrTM9YRztVNTqURwRWQrjw7wPGpsE9XBvgPEfHaMn6cMyH4TnlfP9ep+/ZuFBTfI96Y2TDQl0tPlTZhf7RWtEDWA9EsMfLAnVf8rwzR8cOHJm0tJNaA5PJT/YQDX5PEI29jNajjSuBB+fIBXU+chnpoDDMkTmyIwxo5SNhjJ8ud+xyYKHYo3F4atoAr+zs3qClHDZI9eEjex13oLr8uF/4QuH6qgVB6KpxklYJu9uhrweDnr1PAPVSm/b+apz8ugvCuIs4CNHOQBdHv6so/0FXZw4gZIGIWq3iVworlurAbs7g0hxvdScEiaKjgYEChRCglLojpnqsQXeq9IKD266SumldtQGh7oxpwQ92ABp8RKXuAIk9KTtXoLm7SYtGU6adkDgfFSjXFogYXG6jDt9WEQLggFnhldEJT47kjtNfRrzMtbaKpWTMkdoxz5/F1KnyFP9ndddaWlypJbs3eMIIEzm3b90JoceQsXFVqAXegMwuk2LGkJEX4cxk1xadYydtsjEMgsCD1ydgEUG0aiVvYnqUArhh2LA0MrQs3pW5ULcwdu+nRjlpEItXgtBINanMqqRh+5+Atra7SC6w5j+mDhTCD/LDah0ixU2ZgQQirrXkVU5rO6MsDe2OoFZh4IDeVQKzST3lmRqDPAe/oen/DQ4CqpCfp4P3ayg8CuxOvm/w9vDXxn/noJfAj2q3FVkvC46MbsRHjtqjLEOm+xP7DZYh6sTx9wFM4bu3+1/bOf6+4evRnI50a9wlDsA6un/iCwBgm9RgSgjJH8/gDEeOxsee6kAHVi97xEm17sA6y8GIrGyKj07ieiSktuhqXoBRI/fVN86zdwpZ3wybh12p0B2SzS+GA+dd8sGdQGq1I/DUJWn8zBlwO3bOPn0onDVgrSPsvRyIAFc0TKWk3y2xKIGjfA9OXA9mhbctszkoRd90gYnAhFFYOY99ID/9wfl8JSodZnW33KXAxwT1jr0IckxSGoDojxexDlAiPtKnOYf7oWpyNUewyctBgEIICFcA3JqryW9LYJzbJnfjgv/LdYauDkyv9ItcUG0c1fJP8yNhizHoKLG7GUqBeueBLYmag5+dsi1QUO8T4Dr5oAIfXyRO3dj+rpLNQczeL6FGeY/P9C90FYcvIjv3WhABSI9CsvcdcGIpsvVTASjteb2/tsgulspuCBu2lQ7i2Wv1Mj5HaneB1AYkoGu93Jp3RDhHn/W11o6VXT8y2sikZ37gtnTtxWPVH//USwv0vkZzxlEJfMW3mlhSW61d/wBiczQPzh0S+hpNzH924CFjNr+ZV9un5oOmsG26M0B9plIGkT7JZKarrvS9OqUZIwdA5J4RW/ey1TtmCIB39cgru6UFwfHJEJY1/V5jVaUZ5TeahtGAsatyh+MoxMUf1hDd3bUxMFrFgGE+AA0a1SnQ8CY2WRfGieCCcGG3yAhLS5MGG7rj3eJ8VMu3c0YbDVid/jMDiUek8A8HFW2G5KvqOvUIjK3NQ92YMWl7Omp9f/5I8Pk7gqdPCJ8/f27BY9BFA5Y+IACWb2DEXlcrC5iP7zvD3k6H6UqXxSF2T/IfpbDfq41z18DECnkY3FrexNoKadz9PmD7ezxnvBUc49lR4nl9RuP2FqfiQ2SAm9enhQ/yP4Knb8N5X5LmyGJZq/cUVMw8Ccf3cUeEzs17JGY4h7Q46fS64/NMHz3CIR9RHh1icXfS+uLd2XyAgEhOB7RwtBlW2m10P9BpGDXEjBRWOx8UeLkf/5zDs9AL7TNv+y7wxbajsJLnKd1Z07AfIHtB1JyCnK1mvEa36473EG3BgLgpGGGBXlv2LupjjXEmJlhDc4S51CrKaJi1Q7pz5B0EaEckjOzQ2cCKi9EPta3VKzJ9ICkv+TpKMoTe+j+Go9NX9oIQEXmTcexNRntc9WinEW6HeOdgIOIgnGDieQBikKd5Ku3REHF3xAoMB6l0nDrGRtE68cOyMwqMTw+bAwXBOUy0CCkBgB2T7JBvFIL71LqVhqSwE7vT/jyh7libUqDQtZZlnNnETnhipzZoxcX/ia4usnIPza3pZMqUchlNe4YACEVwEFA7bqhdSgqtzajlAQ1CVJLZuLAbH9udAABt1f0VypWd/JWATS5v5r5hr7G6tF3TBX8qGzNk68htLAxB4twXjyXVwco8QgX8kUygNHJ/iAgtpUYfrgXKhYvz/Y6I7Vit4muA6PaLEBVAQnOx8lWPZYIi9eK2ACK94By4ON45oS3PZelZ78qz1CpMciyT5XHNa7qx42cOQnAb21a39Q1hqfqMmiO2FMCLtga4+wDqd7ejIRwtg0ynM3y1jhJYQASETY7Dir7iIrsRNMhSq1wbul+xheYvuKAsTxi8E0J4QoYtARUE3PzuCheEAJVXGUzn7uRlh8fI521QiHXkT4k4CMM6tQuQo7Lh02t/9MCBOM07QCJ01ICUr6f6RWowgoPXV37vpgAEe0lzpFPxEsixSMj7r1q6kNcFVMwzqiQJr3VH85gZimmUgIq0geZCwFHTCMlEBD9/KPDT7y7w208ILy8vsitiazJFd1Kx3AP3uT/965jOVp2fdqJQ+MLOFGmnfUS9fyGvjMx4x9Wtu0HXLq+4ev+RJa1WY2gs7eZf6TQdr1/qzoixgyqXjS3XUp5159d+OhvcOOVU6/I8oK9Ol3G7gLifjBkjWi9j3g7RALc6BS/UqL/ZJtsrjjqxPgo0ZLI6PotzQOck+cLh3nJqfBn9KD1ALyvuRc09xtLj+nmoZ/ghMZ2fpvrZQ4Gk/EMQDXP3MyIb62FrwQjF4xb55Ktf1uhezNrbJAfKiNDV5yjQ4ey7cs60x10CCLm59j5gNRhxEM6029781RK9CWjg4D74ZjyY1vxoEGIPn32eCboFwetyLQejaf46y0GhnquZD0wejw1ELEA/GfeOEQZ1MuSTqzgA7WxrfbB2oKGuOiWaNDLVc/edUycZDeI8Z8eqcczoKnvj6B7UkYsg84KP0BEXK9o0oM5YE7yQVfTOCWzLbOfGl+qgh1J3UcgRLbzimgrAhq1sxsl+pepcRUuUtJCukGcDQBzOxnHE56vLkxYMkbbkOiKIA82Ky+rbNw5c0z1yRA4AlLbSn3HLEVKwAWzMGwjRjW0dvL6W/KwozzHblbqzpN61QMA7ZARJq48cRcT1l0Lq0Sm4XQCMg19oAaqroLdr3cWwtTbgxmIcfL9HdOJzv1Isu13eXQqU8hKCEFaD1ZUKfFk096C0nhgNxmfa2qgQ70qpOzu4bVSfQ19Xsj1uJwTbXhz0S5wU0gTMmXsKuAkIOkAZT7yzRHdbQNfOVaGtQQgOdHEgiAAkICYXSpvx3nzG+8acCdgQcrAPJCDJY24zvDxVzDjZQG7YtpjNSLjZvEpj/Qj5ggGxG4TgbNbQbPW34GM3uisAAbvdNOfByL1OjnvlBdsY0DECbQ6KSg6B28WArT1bMrl7YQO4EsIGdmePZkI08pzABNL4+K4+l9Bh6a/MCrARlILtknt0tbe7EzayOHlc9nvzPGtT9gFEVSZ9fnmBX3/9tconKtJ2stNCaCUnsaJrag/u6+i1egXFCu/k9O01XxEz3vf4Db7Be4b3Gli5m5OQcnvhrxvuNfeeKJn1TtDFWAAgupxZZ7WPK9qq3+SwwHsc0/cA1nIcGNvl7Tj7G4waP9WdxI69NdiiGrD/fQOqWRIT9JjmWa3TDeQeKifNurPjYY+2r1PE7MOtfbZUBAffev/Rw8p6A7ilnudpXshn7EXjmlnDQMnXRzVvs7ejDD0qU08FIkbR9t7B5B1QLq0uGc3LiK93KmZ3Q3i06jAZaQuy0iIpTP2LZGjJjQv2Nft7IeofCUK0nQUd34tDmB1x7KQ0dFrSEAAImxNTAyAWKeLmnXWhlvVy6ivI8TiFhA6AurWmbBtsBYA2Mv5hhG5ltzQRgcR3m1OUDH1EdrV/U+uMk1jr0s62F2LNhO+62lzKDeAvjeVABOM0dzQgXir9HIRwIweljl0VHe/oHQDEuzZqw4Jc+ByPxgltxQ4/cUACme6qTmyFIunrSuoCWOSpZ1F0jKKFCqrCNWiYm9OvvJg+gC6f0Ct9x8Gl0hytynPIAr7VDGQccR4Q/nXQjEKtVpQRtj5ospmx3iXvBUqoVV5EAhqIi3Ii9DNqWglCcIBQBYtxFuvRG0tBCCmbtL34wnOKO6PGUYjRqr49GM3d2Uo0dsIDaJ6jk1WfLzhqw9j0spB5Y1Roc9ynLvlZHgAS2TSarIzcSlCNHM4cMOUgqexKs3mTlbtZv3BAT8UCb7FE324ilq2QJahydnMrviJHUQugWhtJcYCI1QjVV9doCUl4Pi3Xa9sRcdWXbQ60FdCdUkeYq++3W/XvKDqR2/TAzojM4ZECDi4/v8FSW12d+z79TZHmSKRXBB9Zh0mX3Q33++yDPTDzsA3AH8ybPz8Ce2XeIASOwukOHbVHfH8cbvVB3NPBcHNwSPRPkONSFSUbN2M9aa2IV+SXd+r+fo9BiOOsM85Qp/L8/XvokahD9u8BmNK9+ek+Pshbx220D9f5q9eh9tFPIZ1yMv0iQ7ow16DhoWG10aPasSnmJdJZUTeBAzbkwPY5garDl+IcqYaZvXSopAzpTiFH4b6Dcr+4BwcjbHVeJYCfFUE79Qy/l5phJ81ySzpfUjwifhW58bsdApYx5NwBw2I7F96x/lwORJxXsDJnbnQK2neu0H0wFn91bGYGOQCviJUFSu2zrqqMeYxjWD7njgNxQiazh7t3YLd/VDkO7iXJS8JbRRw14vDYEID44lp7EShoZoC6kr4xKe9SqHjYQd0USiLgqxmAnzVH8UjhrH7y5mwGcvgLsVNMtzSKfcCBA3bey86JDdoWgebMakoU36ncVqS41UwS2Cm1rvYSZ5PQ1QM36aNNvM0NV8Kzeq8GSFnujgfefQFarF2NTc1pbPulOh5bfVvAQRzWZI67YoMKCmAJLnh2jmJrU0RwOyZIk0ILeBWqOxXK9aXWRc5iB7CoyeQh/lo4wIQAUNoK7VLbky+4Jr1sW9rGHAckJCUr8Z3SPxk/mPwQ53c75ksc/NwuNt9E3sixSiaYqPSB8IiMR1BZIZdIC2ksc/QuB+lVonBcEY+33vgh4It99Q4MPuqqGJ5l+1ovYffKX2dUMf+LsRJXrWI6Z0tjmGBr104zIO2vOfTWwFB/4AAEjmT3eQVLg0VGZhNAPMIrgzaEpL7TibsFsEo7PorHdA00XwG2TXd6geWvNtG1oB9sJGNsAwIirH58eySZp1Jp2zaZ3mSeCBfXM277wAb5p3WkRgfzO4tqaYK6E+PD9hf4AJ8Byi8aVG4JZRwyHSN78LXgprKPZM7Svj9n0OvAW3b4o6GOj/e6i+Ac7MvKb/AN7gmse7FtJ7pREoQgm94pwd8gg69HLv11w1vPMVNb4YuIwN9X+RwGIW7FC7euRj9ez5j6XtVJj9m6uX73h7c2S/4awLbvvfjrTCwmW9x+M9KTVNzSDm4cRQY2daCmVz1uR0SIzgCsDKb1IMQkNjGhaTGd8SmLDzIRUPkqB++kyRwqmo3Cb3Z0NyHZFN6uHIr5gnMw9Co7g9Xp6Zm9+hCToAeZvOygqp58cS6RCUQAbLJKGBX9gMvUiVQd28YJZv7F9tT6NicX6M4O7Z8CvDNgfD67d68qTqo4we824OOuzANpQj22qTkZpe20rTsaiXQHRLv7QCJGm6xplpWxBHyRsAd15iEAFqiewtJ4VnciQGsrBGxBB3Srzi1CaXaWI+T5i7ere5p4h0dYhS28yveHqNOb/YiF+4slUnMyyhFapYBc67GjJnAZfSPxS+gFo+UR65xszleABSW74bQ7E/i74xtuLVcGP8/KSGSirWMShMiBTPtyyaDjjHlP2Vp4UDEsCNCGI59cxipVdPzHshyuXTJmaoUJQgwmdSt/Pbp+0pwv/jBjH/r7LXy+/bbNxip2eOy7Jo/cvSX5WeZSD+EDAnvEGd/hgzwm4l0VQB0u/uT46FSzMWNlPwhBvhAwuFHH3bZt8LT9Ck/0k7mfW4UAYgvsAdUgDcQ0d4ARqlNa3uIqlz3w0795PMc+XFQxyXd65VI60b01JApS920n5ckOnKh3ezlhHIy4I5/fCp2sXYc920yrfa/6LsjqRGetE+M5lFMx4grLR+No5L42eOpmMr5Pdm8bPG0pUc957jb/5H3QuTijrC5I8D2srY/gXU3bS7N+ce3OXLHQZ2g/b5Hv6Vg7zt2qhzMcUjrTdMd4dk9JujPQ9OdxdJPK2rln73jtMf4zVE0QJE09nobu1C8jNJ1cOYKsUpvaW6kNdlttEHZOB0hyKNxPDu7uZjiQdxkeIsbvg3SmQo10xqNjammx4B0n6ozuI3XZk6gp+Tt5joKxjH2JnfwdtNtozp0phQf7gOKIvkMf2qMrbRnOz3OymANHM7ErCybjLDgRrB4XlGsLo50MghXtPQQ9pBNm8EWyU3EE0THLzssOtXFQ2vRkzmTXpKiOzI1X3re6NOeQxb8hQD1THqCuYk9cnkybKwubw4aHnKqE2HIS/7XHBlGBUvRoJrnLANh5V7V1PtNe0LMNJopeu8cASQ0p2YFA4pwncc6344C856v9LiZ9Q7s91VptF6kfmU7dcKttvbE/iwSp3pvBObmtAADYWcWri9nrxTg4L9fBBFOkRdtuACKgcpWV920JsjrSYJNTUMQJ3/QK3RkiN0+7DxCHIYA9iqr2SW0DQr4PgrNw3XUnRN1cwXeeFMFNAO1OiBqIAL40HBC2rbRyeiWBisFFUM/ol7FRAGjTNiradgV4fFErBUxDRIfxQFgb1q+fxoPMbWLxltrgG59tjwi4GWcltb65Nr5tlqqszG4r5nqHNlXcbVzKln+wzleUruH7ICpP1bGwAdRjbVo9tg1hY7dzo8PuVrJQWjnSBxwYkmZpVG8tCLY1ekrNV+SIrpmzuHd4EQ0u87QGChuQk8kplssB4nFAoOt46Ff06zyEgafkKLWibVnlDPNFxkpxbqh08E4sEkbT3VFGyBi6TT0xV55tgLwLkoDyNMtygLpb50rY31mtBQHLwiqq/eQo+yeincNzoKG9bgjyCV2PcNtx+yHABSDlLJ5TVG6YyaVh3C4bPH94hsvTU5sga5CXQ7tafsMRxjTLskNAZvXrSUAAuWdJn+zlSIk5XngmN9/F6sHXoIG1lTPlBcNiEVQhPwf1PpgT/fxOYER5JpLnL1awsly8Fy/tt3uch+ZHBN1G1xoXnOPTvzqQOZz1dP73AoV+BYDS5gveCa1zpWrqdT4icwTgo1v+TO8Gk7s+yx6GB5Fb1RYZv58HIxwFIwIOpAkU0PBHki++X2vVvWOjJzmXUj1i9CrFc8wr0mmFNj1G9jXk0GKLeRW7x7DLO+PWsXr5ys5qOq0MMB2Rvqic3+8wG1/SGaznKbldy3ZWVXgfpNg9Heo3I1jH8FazPS9Wvhtkk8dOJKSTZ+kY1zmke5VNRzHrdBoJE2I2LpM2WrMIFnmA6JDg7hZ9rpUyLT5+tzaPs9iRNadjFvR6ICKuMvZfOFHyWB03GVS/jtQuKTfj1dUJf23Foa6WMZ8E0uq9U1GbXhzixvki4hGBPTcuCDFzsGnAJXMMimbtvD2STpfBGkeNGRLGKQ/EDnT+R9pV0BRKim2v/UussNuJE0lbnB35ANV5VPiCOOsYInABH3H+X4GPceo3THeqsXc+2XbiTnHLD7m9/AWvLkgEepGrvQOBAOpdCA13/e8K7JSXXRDgXHe1rA0FH5Nld+lUgbZp2/MjJIBSlaB6wTW4FdHE9SHQy3q5LYmakzy2hQ9k1Xq1nSPmDPbqF0R1fNrR1MYtdY5s5Uk5+EjuyQAXABF8m+lh7MVHB8tzoyaMfBzvDGD6jKTtBip3k3KkaVvSNuwAjePEyDspE5RX6sFcXuipIR1oESyk/WHpbrSqL34z9QWHgT+z4wmUjvZGxn7fEUsrLCLeVNZlgELtbmp2KrgdLFYuhLKj118SqFOag8rU7t/YCmlgx1eoysLFXTf5C0uqYRIjXtEkRURTO8P37TgnMGMdXV1NWluokX8ARs6gT+3IHymImL2rUIAaVzJNrey2+OCybfD09AyXy0XqSIUAt+a8be3DegTv+CHzdxUciQPGlfmxY/QMH04YdWQ02feR03fqM3ud8PctK85u9gPPir55udecuDmWYxWL0kiOIjtowI3Ez2peC68ZcxrVUp4HedEJLgjz6Wq5pO3+iPoeCz4cwHs4R1Y5rvvtND3cj5jgP1tm3xJGdztATF2A9dKemWNs3SIKi3frntwVkqkg6919nYftPEGzn3HwbphlRU7J+5XWOtCiRofJivPPz/XU7okN45wpTa8BOcVzGNE35vDMHsiNs1eJTRyFwZg6AnvHpzpd+kRBVAuJX3Zp8ItiJ+SNynT48+dDMAHa46ERZ/wmj/fl+7xMc+rJpE2P45VEp2GetW8QoZxGtLU+uJPgediOv0UCMz5O1z26ttg5hmvPcUDMxzMusUa4faYPHir+dk3Ao/PWvCAXhEgK7zVR/XWk6FOXVY9hreg72ZNL5SFCGp3mRi18FJFxzEJw0lpkuaOaV/Pb7qjel018inZbC4JfxauMLQ7fLDJI/SRvnR0I0FZhorzjQAkVXpl+bRfZmp0HpV14DTVQUJXZSnh17jSH8wZQ2ip3LK3QrR3BA0Uc5tLwsc1lpTa1/4upKq+ab7s1gI/XaDseUgFmnN3cbjx5cb/w/RAsZNqS5/qxAbQLvWWnhORvZ+1fK40cSKmKVvsHGnxgPmq9DojtYmLc6gpi7ubm2K8O0roDgkMihc/W5x0JVO9YqBdJQw12tICH3mvBfFXbtLTgQ2k7OMActVTbOtkRQVAvgY08x/Xyg8D0n3nqoireAefGmvBwrsS6x0R5sgx6z0HHg9L3jU7+5GAYGFkgATIg2Kh2WyGo38FEe1ubC2+7RhnMu9To490z4lAx06rBqUE8Vxkw3Q6yg6eNgc3wOCLUezuQ5QiT0SuQuKH7nY9j6Nv7APCRRnZii4EWfmoIkU/vmo0C0TqnQlqWM5FVQIMRLo5v5gOLu8pyx6jmY6zt2ICLnS5cIOaAtcT5OACY63i8Ay8ZHy5VDhti2++mvDLUJXnsu2AjyofsTjEkxJXgUcn+8ON38Jv/8d/Bb//+7+DTp0+A22cg+c8uNbCf2k8PVgu/wTd4A9izqP5a4HXa4XVW/R6F90jT+4aq1qltZ22LjY9P/YqGlXUR3gfIo4os+JC2+zpl3ZenmXwd/fBq7X64ID3GVPNaO+yMo/8bfE3wmptmZQfQ3ha4ewL7XIN/4r5lwHwO+4rgXaqtA1gORKzI1ZHC3juDFpBNsQwQIPjLp3uf6BCF3w1B8fUkM9mR42lBqI7omfNmByINbrWrBBz4AdbVrkKAIZEdzuJI93cxUHuujk0APmqpbsOE5hwtpkQEKKUFI6pzTi5SNc45odi1rR4lI45tcVQbx19Yuc5o+LVtJOKXwqzswPVtxiubHQ7zjPPwcULEgRYA3QFABQoUs5OgtZEEOloQwtAvjl/k4I05lsj1Z74CS53dzd3smKp5y4md0WTa1gTWyPS11FX53rUVasDNlWM7wQJy+C1hdjdEjAPaBogmebq3yQ4tRxH5J9oPJm9AKi1ughBAVI9NKsRnpwHw6nMCAA7UcCAg8CZf7u4L4hFXkYwWVxOQ3t/i3rDKageAcbDLsLEBN5f0EMhmDqmnpVWN+lDFfbxtTIx4LIkl5SD1RqOwoxlXSpCtQ6roTAq1r/r6LjYqxZ+0W0/fxqQ8aOlBAAoRd9dvZ42YNqfINdgssLogX18G06eBljAWZGCnIxyIAJ6en+H7v/kNfPr+O3h6egKEl5aVj5qDhCcjIiZytdL7sNvfVt7kGDjhnShagG4VA+bP7bsdVMONIR1OnPzagZMa9blcxyDOWyO+iLImmyNHbTqC0dx5FM8jYKitz3huALFNR/WNRZyBPl57Gxc9igdziRnS3KHwkTPgrFNsRtL6TnfGdaCCorYGXUr0fj+n9aTcfzDpAoi8iOUSY0Kj692LatZA3JMU+YKdfrTsHb54DTn/CBjLsVtqVHXEo/2+NpZsmjt68ygMgJSfjxgCCSQ7gNNkI9J2wGp7zv+0AqYMdQBH/D2yI/PctB4JniOj+O4BkrWueht4BZ1qf35baZgRocFWmg0ZG4w4VHZOQW+X9biGQYhBsW4R3yokNvi0GCKYn7X2Coy6U0Rsr24uOaF3c7ajeuQZeXB8R8QNk6X6nI8wc1MScyKyDPU8+8yvacunukLbHVFjHbG9R9E5W+zqWnZbsp9IzmVvq5FnM4btaOeUSzjAqQEWJ7oXafrqvyptVf0VyrXeDVFKuxtCzkznQAPVha3YHLFQqqPr2uq/AQBsgNsGUEo9AqQQwMb5t4wKLaPRA0VX3cu9EK1S21bPbt2ag5F4ZXgMIrhqmgBCoVpXPspDmoqdarwqvh3nYfmglOagv1baSj2CqRjHc/1oOyE2XV2FjTjkgES7pJqg1KLbfQXch/XeAmwBHe0n4n5rbWRX3kvVG/8RIADyLheSO0Bs4KTyf6tXPEIoBCHs8xVghzvCxs3ZobHBjuh89Xe02Mq1PuExtUQNSNspffrFSRQz3m0eDkJAaytChK0UuKIZe8wHpdQAX7sfoqLT4KOuWa/p5R4JWTnu+Vnue5B2iY4YzcMyiJ9LMIt3QoRL6zkQ1Q1LVLm1Cpkcr/064hlV1PMgBLddxDemgPvABiwHcaauzmldT3qx9Lxc1B1QXKyLEDGfeChEVc5RPyfkTktyfGADnY4ubo9kTC7Vq1ZOPvfUDCaJyM9R5IRWewZewfPBZq3L5fkJPn78BN9/9wNcLp/bmGN503hG/qL5hJ7PXwuWo2h/LZAwwDe4Ab61571hPwjxnj0kXzs46+dgTtYr6v1nbOfVnRC6e3k6r2HUVe4DpxwpbwCiv06erOa8Bb6NvB5Y92S9EW9o8/VcecrbxsjrzGl567zfUfh+KbsV7isb3ktRXxOM7Mp7w5EAROc7umEOlfJoUEu3aDEe9TUg8K8M7qHDLAcioks8rpxex3Nrx2X5q5QRB07n8IC6rYm0/D6CRPksOpwbjXJrHZ7Wyc3OvZXmkeIPts8ebvbVgXUCmwAMWQWb5FOdhc3Z0xIVoOZMR9iwNMXnUnHJHRHWYMudlfXYIBK6vCMc9T/j9NV7KVgYNCdc52SrilkBc4E4gZNeNT7kpFlzoFl62WFbmtO0yHE6zpFvVlShJYYdd8wHyYV3NQUf37TJxa0tcgGydn7Amq5RoaXn4JK0k+5+sUct6RggucTXreQ/As0D2a0Yd17l/lEg3ycsvi+Iy5hnDmN7vx6yQ4Sd2n2C2nYbwmaDKEaeADv4d8vi5IHPwPMiSZq4y8KH0/ISzU6IkNLRaJlwRjPFLxM5TnanRqAqKA9R7mTlzIQnhf4axWaXoFvandWvnwzYodEXamSgaWeen/LdGJysBSzIPE8qFElMm2riO3PdL/zcZwWp3nqrorJpTmwkJPCGzYOIcLk8wdPTcwhWeCQqWQd07vB73N0zG8+rbRHXM4yJWn0+LiPCrgg/4DXY2/m0Nl1M+iZNvkbfQY3JoJ/0b1ytys9PlnUE9qrdiyodJ+8VOjFkg/mDVCN92Nc3k8kDGlZEfChjgGmcb5LrS4I9XWZX17lLQ+RIjtiQ/f1/IAthGPjITp60XqjAy7B0yTWl8Qjs7YwwCXMSRnBPcUBhOr97AUskLCZMJqXORgC4D/1jqrI3XiW6v7QQkbgIu+N8cS46VZVRpmAXHFv6v/Nid6eqH9dnptQ93XCvzY/qlrfCSmmuVXZF/9AqXSfqYN1GO05XdPkleISoG8jz1EYPD2Z9j6jphkUfaA5ncx2ZexcK3wtA9OUZvTGzGQ9AtDNHdHY0RvmU/vrrAhuMOCMzj+2IIAB/2fBBoPA5IxjZIcMZRjMsmk8TjOCiimfS2Q6IHjsK+nT1fZdBV8Hravg+Y6XRnAkon7zDwhd/eMLhuhAAQXOet3shCt/BQEVW+ZPrEFsYQXVib1A2UmpbkoL1EKGyAVyoVowKAGwEhGSOieJ6qxDhcqnw6v8iK4Vxe64XUIctYewsV6d7a90CciY+vy7mnoTqZK6X0dU8CFbvByoAuHF1oYVbWgk1CKF3QVy5MnUHxMY7X3T3A0ibbpIWENvuEbLXRNR/ra4EAEjY7oRo9Ld7IXing1gESC2ztg+18VnppcoH1HaRlKu8d1I8sOcZZwbz+eboiWn6Z/mi4SzwQsDHTtV6bx1v2dzxiZcRYNra9LQxTjMMAFDv6yhbW/GPwEG8lRAEAciOCb7zobTBtBnrgcCOd8XKwSwwwZ76GpWeVkfkDIImmeTDoyO7IUZK37A8S+4s2SFBt6NoJe+biAKSiACoYWL7INmxkOGvUxPvhIAqr1n2A/elwduCFlbmq7Mtb3tqjIqEehm9vJhm9RAdqy6o1CQ/et7Tq59BdtjIxZ3C+zpHIfZBKORxgnUuQtIdOtGxERVwIoBrAShXgG27wMePHwFeLhCSRTek+duX8w2+wdcDq4P/G9wG39r4iwYxG5rNQXVXeNMEoO663gAA4UoA/99fCP5EBX66wdQ9TuKXsTPii4LcwADqvj2y3b2MnnkyTpfwgIDGw2FI8xdYly8dDjT5q0ioR7EAGznvlcei0ZL4AQD2zeR3LQ5Gzn15b7/uVRTmDDnJvrwT4j235QTUD/6O+d3AeiDiXnUxDHhM8coI2MlPXFJLTTppdwGJCW6lc+ZwQ3EugzilDwbzxSkFqkQRcYhF32F04XgkjMY6unRnQPNC7l4czNgJEEp1uNkXyI620u7lgHqWONqLX1s99iKOfNcCUXPmuWK80w2a85gd7c0xWzaEC25SHMkuBt7dYfCNSdFCzAXX3Ga8k8Qdv9SOj8J2/BIiQimGZ1BLlTwmaMbBK9vi0PiUCukxUwMHW+qE4z5m917rCw1CBExNoDtcMaI3cmy34EO3UjbjqVMykXcgcF+wQ9aX6ByZjY/25IN2eda6eXoEEufycDLtMrJBRNI39sglM9QdZfxcm94EGXisEMsGTgFSbStjpX5a7BoMjLlAkc/i+LAdD8W4wNB7epa34zJ5u4LW7o4y7Stzgmmk0TylciU636EfPybXMOgwmBNnXRDp3OVFHoMdvnxwMk1d+Vn9ZNwpPTwfNmSVYYM0nuuTpDIXt3osnxzn5GXZu1O5dsbOYTi4/DDE2tbxnwAh6R7VXQxk7qM5zw3D+xdOY7wf+H6dyJNA7GtsmLhP+8TxPSgr6myce1DRGTuc4ZX3wAtfHBhbi/upb3uKWWp6fhC7N2a3qmpqH1kdDMM/gJ+I4E8FZKHIa4EuboB8SK+M329M6SHw1r6Gv4z4BDG35tzBa8bJ3krw+Py0Jr6ScVVfCb+F3Q8rMju0YFbW2pyzBEMnw85vmNuStx6b+6hA5+pq9H4Bm7y4G84R6H0HAP68/zcSmAPdpQJ27/u1hPv26TopJ3GtjOssEEzZvNzTkhYZbe5dEiZyLrNfk5+0Y6G+CQRxlcn7WTBiVdqlPq4hy7ZTdE4MqQM7Iui0Ycfd6Ff/mxcM0UmCx+ce8bO3MqoyyeficxofhMhazjqneiLIZ0GATRzPmzqiVmknUGdzUbZnJw5BvZiTCcvP8m90cZ2A2m6QAmDuCyjl2pzbQnotT2jd2vNKP7Xjk+LmDj6CSg5wYod/OwO93sfMK/K5zXz/yzFRxTjICaB58mtdEeVIpiL5AYDqb2yCCWkDoLqrQe5SIN9P3C98DJJvv+C0bfgL7xopdScEbnX3xbZdALcNLttTbQ3cuAtgu5i6aAe3dAAXd5aUtlFpuzGu5aXyQblC4T4jMvd4gAscbBvW3SLE/VX7G7j9iXdEaB/ICvs2KW9uZTiXYQ7aspIrPB/dC8HV7hQQ9qNj/2wEZPoe290ltlCSNo6gwgSx1dMUrHdxMA+PJ8OR+9inaP3M6Un5ifvGCSOpn+Li8tHRHpy6IRgh4icY9zxmXmMe5cBfrFuB4ndcmMCay2+cfz6t3fVBLq3PDxALd3K8TzycYIoZa9h2P2XZ7S6lDTYjuCWly0RQx6rldw20jTupSLsOBgkyGV4hkTb1wtu0r31cmUmVl7wYCGWY6kmlYrurfOyDLUTeAYNQZX6N3RG8vLy03XAIdY9Gdv9QbQBsM4KOoW/wqvAOdfavH77mRu+NqNct+xu8FzjK5VFHkPm27ZYGNHoa8mGwWyiFJO8Ncc11mrn0M0P6rYbJFw1Nf3sA1m/wPoHOjK299Dd2+IpDfdXpPsufO5opfBvZv4lT+SZ6oqR97KgR20gWNQK8nX4xKzOft/QtTX9buPWYsBWYzouZnd45P+5HS05D+3DMFjh9GoT4cqELRuw52m6EsYyZw/odERSF1Vg2Z++XO3ZSh7nvyNJnBQ25hZqdA2uvU2a7D1w6/ZAV8xmVCQqht9hQjcEhx4Zg3XUwQETmj/qtGLe9M6A5XcVH6U+By4Io1aHNzlD2gTYvqNDCn/U4JzkWyNAhNLIDL2kXdsyJgwrUWUzNs8uOZ8lWijqguPJG42CDQ6qGUUgH5xgQANNP6ji0jmwO1ljHKTl06jxUZ2NSljShv8uB5B/JzggNCoyUAhIi7OXQXI/90etfdfcOi8NT6fA7WFD7iPvJjceWjgMh0gZHhCMBZEfVRL/kQXAkmB8e1UHELHy4LYppF5kgk4k5BGn8l0X1icL3s36V1OnvjxniZ1GpyFf4K084zDavc5bbYETCK9lEIyiT1fwzMDJmWAa0+dwe3ZC0b8rSLQK3xu49Q2fTl/KHz+bSolcQ3AohU1x3P0Uoh6spYnA2JZrgWJSuvbMHhacAEXQDFLoAKuPLjpYCwP0xwRkAhuPhXqvSHM6p7pKXNG7c+i6+HbFsN1wiDQcGSL+q7XHO2lHt73cUxQwPj7e1slRE5/n2DUL9e/b+kRGtSlN8vlTMORi126lCjzkL3vNRJWfv1jsDw110C81z+mztneRexbqxn4YCIntkdQerS/NEFm2Bt+Mhmc/sNDnTbSn96uDenJaRlcMCcXcvUwt8V5LA8vsdxr7TgToTYq3mD22fThd/BRgwyXLZ9xgoUb9clYmPbiDM9DdLx5yA/D2epzuhJym0t72iryXNNnaI+t0RjRDGdlzInIYz099RifaQ9EHu3CRlg78gbZR7yMoEt467RfrfcjIZNUFiv48W/qrzTh4ssfsaTyiyM/xw7I4IONYXTqE6SJsIG6e5GrwYHgK4+yCi8yJjxFoQds+Ry9/b1WAcJpoTFiYzNjtbwIB49X6BQgCb6MXqRCf2AgEJvZ5sdqCREQ4Nb7nWXQLlau4a4DaU2vo5xTr9REZzUEGdgrVIbEGHDZBKO4avyD0FWmXfN37HhK3KFUppDqlWHgENVwVTawvGZUw9kHP1t601bL0rIt7hIc5Hokp72zlSpK0u4jyvnxtsW7snov1jNuedC9oHtT3IBHIAdNW1rr6ubVauL1BKgev1pe5iudY7NHhExaPCuqATcLsy/fXf1Lxix2/npMrT8gfbcXbFs9BkL8y22ZOJRZ2Le0YgAbVLNtA5vsckS5vHck1Qr2T3AkSksmukd4b2GVGVoYZbjtmSPhEPkiuOeb4uwse8X0xRBNQuQg/GCfBks+jYmihvLl1rdwLy7UDmvVTE428JRoiBM1ZHASmDEYkcSAiHIc9IEGO3WoJjHOhQxpc7G1o3IkK7LwZ9FocbB99tKt3eGOX7LfoYzwm884lXgDr5K9Uz7UWKoMqvdp8OINTdf6WTP35XFTg5y3WsOeyOJt9mW5sE8XKBy+UZCBE+lys8QZyy/diB5NeXC1Plo32qLvEN3g4i/74nCiTA90XDazqHv/S2+jrhbK+Q1YuB5P64bdtEN9xS5Inx+UrgbOcDeb7BY+DeC0lX7aI1XLdS86VArOj95PTZlbxnymlf4otprnWY1GGipJzXH2/QfHiRXobyDkUc69PX1C+Ojdl3ods/QsjIUNjxC9wKCMCmeij66wKOMxwMRhyCBzXc4UAEgwvEZBVqwkN9REmaI8IlbQDjdKOJkO/SRkdT0ik7tEmWReWhayLyL0geNfHZnKRz7NR/k3ZozkJzRI8cQxUDL0nAxV+pKujqEVTYnIISjPC7BuoEw+WbE+wJgI+miQ5TbYU6UPgehdrGGrARQlrkBE0+368owRQOHmxQnbsINhAhVfBt2bGIOqHX+pyknvZuBmkfANMfBSSEUsxOCLlsOzoLsR9/pGWyZ1Dbi5qAUiR9vKE5930N9iFrC7J9Gl6sgEuWKQjMd7FsO2K887Mvg6T91+uJ3aPoLI60WBMYTFDIpk/LV39xWg2Pt32iHRF2nARJ0jmZm9RZ4GvXWonMvYvSRHWi7OXfCm6lwO6o4HEzKS6fl4dNUoOxBHysGUI2rmQFZocqGR1MR6aYzXZR7E4U4wR2B1OahJuwfWUaLV2rCo2dB/bm1+sGUJ4Anp8ucLlcQuAPTbF2PDH6xxmUR4N7DwE3fjHhrnl/SJwQRw/WYbRKbg/TESkxD/hmkM0LR0F5bR3HODg9kov5cQc5j412o+iYjGVY/aaX73ez+24YCrNdVeM7BI4WulrR+4/pt9id8cU5OXagE0uHhIf9VF1JRrfgnuxi7/S6MyAWzUJarzt6LDkJlHyzud60l08WPuLjXXbQLWLnCh5ApurcUkJQ72Qh1q0xYzIa0E0tsND+aZK/nsjIHDpeofT5CoJZkx7b8c2Z7M8JUy8pcjf09yCrlZPIjsRHBCNGr95Avd/fHbLQzvdacLJQ1qsN88Q+OaK3rFhG+3XZZ8C7yNw9WNzm6s+4Icl6l2DECE6OUYCTgYjlskowkY/WeVIxs8hFHCklWV0vSiexIyV0GPLqW1McO5YWghEdPQsg592XonEB0uMwOmcP9Exe/dctoTHmhAwC4HNgSilA11JX3rcEsuJ082eiakCHAMncy8Dtx06rDQFLa6cNAcoVCmCjh6BtT2HdXxUt4mOH2EnPbVeMY2kDgivAlYS0YtoHoAUXNl1Ra890ByLYLhdAQNi2mm7bNvOJbTUUCv9g+yxk71KgFnjB1l7cV5XKWiTBthEA2nBKu3xbdqAUN+Fb3q11Kw3nCxARXK9Xuc+DAxXMBOKXbm1Vdwe0tgRpcjnaqa7GN/l5hwg7Mdquk0y+HQlKUKsY7/KpFbI7AEDaUA2FiNnm5/Kt5hQUs/0hKrsXPLGer7XVRkiMYM/wOdQkQR1xqEv/aluMSmP5o6cXD8oqJPikTAK9LF4IAj1vfwbUxufGdOQOsuwOiLwSYTI0gxf7pExCQpcKQ5qkFL6x7GL6rcpKgxP893h/jfQxQnc/BAh/6orKeo8EBFpJ5yfg+QUrLQDtrppFyCaFneSO2Fa6OCTDhMVyXQOuesE42TTQB4i05WqKC+4zHAeYsTGn0xEQ4OfvCf70twj/+l9/gh9//BGeLk96rjduQHRtGSaezL9a+NYmbwGvtaoyLfuYeHhncETTiOnfBr6NrvcPYSlV05ELAN9Lt12gzsjVJhC2wqi33C9ck61WjFT7T58714Zj3uz524+ZbzCGR8jvUzwbMu3aVzH7mwrGr1PvedU2fXBZXV26s59nmQGqmXtMz4rp3zT4/pWx501teXC4kvhTJkvNEiGqPp4U6ToBXyhYnaMLRkiaxa7YS3hS1TgciFgOkBrHKJDPlwmRoWAxFZPGpCBUaDIgnM8pT2ODEWAcUJa6DlmHY/q6I4j9eVO3JDsRcwzADnSjQRtcJP2QUCvOH3amRR8eZ5cC2SHFzj2i5sRWBxSKl76A7IiANhAYB6lgsH1m/ZsoFa8PC/cxOwDl+BPNITUXGlizY85S5y7WvRHaFIQAfPSRdfyLp9s4hF00pNWDSIJuzO9k2qUYnHaccvfYAA0Qya4ITWVIsX0iHcXRGpDgjvZ9XC+rx3ABBJwrkEanoe3gMYYf+eT8fRzQJZPP8+w4cNtqFseerWBSjjiZuX1cZCjPJ08HFZAgYsAwlUsBleXT1JdrGkHlLI8dajFJb+jqrgDwjBfo09W1evdDVN5WghCdHB/4mLJWJET3XuSxY5zBXpvkhLc+0Zh466ywRPigE81QJMWtJcaUX/u8cRzYlW+HIJlTpYkjX6LuztPMOVd3z2RFM4C9jNvjQsgCe2UDoCeE7ekJnp+fAbdNgo9Kxdu5V0ar098C+vbbH6cAiSj3kf6baBqKa5Y3K7uvhuNnr3IHBqkrT78reTRMYyEO4VUDbSXdMq5uanYaXZL+XDs5aBXvStjpX6ePhHPgxmQd5cl5/fpyWKLcfpTVQ3dCkPs4kf3QJJY/P9k+czPpgW0GrBLHOdyuQH+EDEfzV0r0fbBSbdb1248glea4cPTidWFvSAxtg1H6vfKGhaOYTPs9ftBbNkWV2JAnYEW2vHpvU/flMNx19AVbZ9+Ds4qWddi3H093hTPVSWz8czh6n4JP4m1UfTbhmOAPGMrb11LbZc7OdLKdBowNPBOIMe2uHubfd3wdy3o7M6fCZCEnmvcnUO4kyh7u2+yPgqE8WyDJ+RHMnHTHme4wnD6aKQOdi0iUPitGbgLTSlGo8E4IvfsgKWuH26qjQw0Qayjd2jludWpzHLJTXhz8phBZWcvelrAgV3BAc0aNvEJyxA/VFUC8Eheh3W1Q640IUKiKpFJ41ZBHRm1VPRY+kmmTIES9r5q/F6hO/QLiTtzapEEAfNcB9xXvdKj+91YGbgBIcC2h/bhTZIWy6aU2ukgyUHWitTpuvAtiw/YPAIAv1AaTrznOFLPSbo0YhNquUAClrmzKNjylQCkE15cXKMS7G6DtxtgYrRzBdL2+gBylZYrHDW2HA0ABwg3Ye4gA5kgnAj7aqRRmlCLlMX9vxkm45NZxbYvavsQ1tgbezlhLUmmspu5W6M23jCq2JhaPMmvBM9mlQdDuhlB+9MfOMHreJjC3lPYCGhx04hXxuhIc2/9sFOsno9O2Yh4lkX3sRK58i51DDLNoptBkegGh3n0A/iLqeAfEMgRdix3nlUbtO4ZNyqG+rUUBCapSE56+HmbHD+SrZ2JgpVN221iJu0tSaHXj3UUuGNi5DB68aprs/NgTXIdrpmySyIKN+ZHZD1FlPI+dFrVwPOLktDEa2v04l2QeE3bFmL4mfn5+gu+//x6enp666nDoN6r0C5LgK4djKuUsQHwK0vHLf77Ofvl6a7YDf7UV/wZfHIg9avW9usMO0ewMp/H8eS/Id0YEXcGrZmacDQbdI8iNOL+CsZ47AzNA83nnxn0ca32DE/CmR21WAr4snjhpEvZIXqHSb92uwcZ8GD1foi5mfA63gsWQNcOZEvZ3MH6lcO9jm3bgroGIKlfUmSvPAHrO6OzUcaWxOwse1PlDwQkF7DgLeRYEPUYvpFk1caZPvB/KOGrYS0XerVb7nj1ATLA6uJ3YtvWx2zGIX6mDXxwzos22Y43QrEbjSpqdDEy/cxg7ivijOo4QijjXASYysTnq1AncdgKA2TVAADUCQ6bx0ThvO6S2JaFepMpGBkpeDYgE+mjQvuhrzSn4OBwq7aiSdkSWjStS867zEUlux4AJ9vgLjA0gAEi7sqcZxZVpjxRjzEAEciVF4C+uw5HVfhR/cOd0c6o6fiPPZDid8zBcFI3DlAGP9XchgGwfkuNl9upq+yOBNl5GVJAbICZQg6jBLITd9jDxlCVgVuHjpSQ41Im8zBlof56daMx4PIBCgy6DwIiMuUlDdOUltbAyF3NFYm93RxeEWADmB+EL+dsksixZbgoO9VV1XSq10OAFsoyhcYBlQiFkDS9BRARRu8JMKPWwq+dtG9rAVV4MJZhD8hhRYDl+eQLcLm0sy6Rm0nlgUbALR9h/B1+2ausgiojwNEnkeO9cecPlF0tCal8uHFsxno3fSenRn7gD9wzC3C5T13Fl72X3KWSyJcO3q60twdFaa6lJLaIccLquJlBRFDGsU5OlZN0qhWXmWqDhaKPdyKdeVxsUnnRGf5wt9PV/rXPBJm02kyly9KLTixGcAilVEEXXlHl2XC+AdMeOkepU+TCXHp32R+n3ujHmO5p+ljRJu1et2RvXmmjnJM151K63R1usyfoDthYBIFL1ARxoOGNxLud5BDvfghLdl9TaSnNYsUPZGMp+isvjuMya24o5qdlq/B6PkT9R3gzYIW+qgzy5OABGpE2LS+meCvC81GHbJoLtUHscs19dGTO1aSjH0NQx0VnOCbtxunSe7r6cAGcRBtK0YfbsE5dcFhreB2Iz7Cbag8H8sULJ7erDsfngMIzavp14wwJT+m2PnBOkLgcidvWNtpq5/k+pgMNMsCxAtl2I7xkAsApoPzmZp4uTNXYOTFrlJKPIuizonrqVpVQrU0Uqr+B37aSra2XFO6Pd7BLTyh1W9rC6zat1Cbbq0AEEvFz8Fv7yAnK3A1RndqEWGihV4DM7Cm9SE6xUAOEFADeAFuAQZzCYMrAAEh+1VOq9EoWA2r0MhV5avZ56IdoMCMG7tSBFK0FOZmllb9sF8PIE2+UC2/YE2/Ykq54IfJ/W361tS61/DSyEGRdrW3A6VXK3uosF6pZfpqq4OyLqP+5/a+CVFjGS45i4aN41UVpd5XJwpVzHAJdVd144+kD7xF7SLfxnmtqtqCdXGFjnIwLUrTvICTHUTwNNHrCbc3kM8PFOfvhaZcMRZt4S8O4XKwPQGJnK6n5sxt0/4vTFngpo73RnTKlXoZC536TVjS8yxqJ5mRZxWrqjiGIdfd1Z9nM5Re7/CEmb/JA+7tQE5aG+7K5YoXPsxEqE+VC+N36xsnUgV31YEVVPD4rLoBQljzyvjPPYCoPwgBieZrLuqmeOFqlD2cyDkVzScbe144b8XRHUBeZygtG3QSsvNeZtX2/Q1UBet3kIeAcWhjbh8VXA8QNz6CYTncoQCR4ASOC0vzS3mFWpBittAPgE9PQB8PkZLs9PAFcCohdAaGFqaqMyzDfRT5PBir50i7p+G55Mdp4pcQ1Hl4rng3s1gEM8sdprqdP3r7hQZxlENxq8ua0v1+HYjqs70IQIPuq3ihObKqB8ntr0LD7QZz1c3AGYzxOrKW8t6dGwa9HVv8Rp/Vz2WnGHhKTTmQvpv7qrGKDOIlubvUrTTxpPEhq97sHjWJo4t/KH/qSvGPYd/ft94Y7SQX1208yKdlycRQIp+dYunY2x0at7cOcIx1TsovlycILG7su89FG72CPWlATStm7662uOnbUghHmZALtaUIxLfroDww470D876trM1NMhYm3OExxK3Zf2i0/ncNxxAO/+OJvT05G0wPpiyS+Uc+NottlvnbC76W/U4sd3EJxaOHUIf/JDWHIgiB2cabvH6XZ3lV9nA0AzIk5U/S47InTV/YLykFobyfuRTdc5eHxC7IT0OQWSle3zsoAzohPmJCvjM2GE+iGrP83HgBY9loikL1JFoR2/hBsHWzaogYfgGCQtVxwSSfXkGgfrr7ITl0xCKHmsJPDtEKV7LJHXMKGgcb3cnKUb7/TYELbB0SriLMT6Qy/N1sCQgFzeC92g5V9IpV3UDWCjh30Pe6dcJIyddtQceTqHs3s+6wxrMLa+k/bjFutBAlpxIuULZIF5AfR7xAE1LXXKxgGYMfYQmtMRITKBD+SZtLZFjpZj8zs4qVjpHQxcyp5U95pgJ/PanzWF3mGSz+iId+ko5wPfsj5vt1Ipe851IZ83pZNqZhKESgvf/RKIlqOShjil2KBK2VWvKwqc0GPlHL8a8we3uwt0h/TD+dQFWEZlBI6/RYMJ3Ry5cndscfXiZeopIGxPF/j44/fw/N1HwG2DC36GC/0CCJ99YGUYJINdvjo0dGdNPIHDTe54Zwf3pF5xlC4XGt/wlIOjB+G5E0ThlWTba/jblPij08moShkctefOaZ/3hjgQMmr2BssEtctiZGcGGISIzTIqY9Dou1y0QwLPHkcgnXuzMkb5DdVHeALFs7NSyrjMIyVy7vx3V8ichi5wPS7z/K6iAUoyvBCmQ9yhiFOi2Sl+tPgIuzudFgrxDuvB+LCOtlXCz+jvAJm5ZugYZc1fPMJVHM/2H3PzStnHLQkL0mQ7/oVdEerea70eNdfQsOwAA91gfS7MmeqcL7W1CBtJPdpTsHu2/uAZ553KgGQs9bZdapEen5BWYFDUHt6uv1PmxJDu4IiMJtoJ5vdm3kSQQa4rvvbCmFjcqhYATocgAPFDLHTi5NWo+jqK7zSvP6yd+0reRuvJvPeY9h7QRnIYy57ckgzH6TgViIhKXVxl2wcHmkP4hoZmZ5TFPQpCHN2abzD4Eg+ugukNbt82EoRgx7cpFlsmBFUsiarjpvqW+bwdTyufcuLMG14Rz3dCQBMGG8C2IQBiuyMCAVDvxmgLheqqIUgq04QZAbTF+QTVBb/VFe1bqRfOEteFZzCdYqQu1vlPfV+GlhVq+GJnhAJQsF2o0eq4bbBtG1y2DbbLE+ixTAD1+KhaP8StxV90V0q9U6HA9XoVmY0AgAUTKnhXBxsn7fm2wWZX9RI5pmjXEMeqhWZG3/9AdRUzAQBtjYqsrXxABRDMhg7hgNYHMlBlXFkaZ87Pfpom4IiUWzkuAZF1yMvNtIy2s0Net3s/JH0ybhuZ8TGCrqpYopF41Xm/+lxW7qORefY96wGkk7M9cmdarlSCx4CWyvm5xPnxMMdWLGSr+y1NGL4xLa5M89tdOFa4Vk1OmRsE/Y60XvYvEj8NRnSQJLQ87dMmk8xScMAkLwSEBJu5BOiokyI9hrCjlT/WJ2Ae19mO1KEinAxVLwc0cIkuoRkYjYOfv/sEP/4f/wF+83d/C9u2wTP+ET7SH6HAFQSjGAX3d1y8Ndx+2e0CXzwEeD5ovx5mPHyD9wEk+t5bFP128LqFH9vp8hbwVvJmAcxcFO+SArGDUBe2DPSdLxXebAcLfGnyf6WRWN/GZj/dWCLe3kZfE68+BjD9+pZw7uz5Ex6+9wa7gsgMiL2k1JIYf80k6V3hLWVqhJW6ZXY6V+J1dQtKv36DdbifpsXO4/19IYeDEQfhQCCikroXhOhy7QUhjNIXV/10x4o4J+cCxV3UkuS7FyIT4jzG4Xttlza4kzHPK4Ap5AW0TtQ5HdOVRa2MEtIQbrBtLbSAm1xUzM5r58SGAk4zMg7Oiq1IWT2NKPXXCUKdphxEUEdS+0ZysFLSAspzFTWJg7GiJ/b8ahBn8xczA9QicOPy9SLteoRRqccoEZ+jU50p1b/eegu1D93qz8ijrl7qhEuddR3wOOm1U1393xAUHR3SrtrUjbKxk1uc2c6pzT4knyEGK3xloQUhlGZ3qbcrs2Zy/dL+5CM6ayze9QB8qzufYCWNhFJW6B955ohnyebqiy4vGvo5BblnztnebdUINUAeLWtBCKFXZAgXXOms9UfLJF1Wr4tPJhMns2yZ+a6J0aToj5qybct/+ZuRD261fMXsgy5zuY9ottwnDFhl4QANO+u7XVTUJ+ujv/WoLENHzZrPjSPFT3aIhDr1Ccl/t3JBCtTfUwWdu2JnTu1eE2kp5lgkSZYWGmo+GSe4bfD8/AyXpyfYNj70ieU3wdolEHMYLViQlaQm0bBfvIg4DmuqTJ71hrwzfDOW63ZGxHT81/SPvRh2VsYeXY+GexqX79NpvNKQezrvKNtiJ/XR++TZYGDG9z3yJXLewjk6Nd72CGIZ5HDYmfJxFermsoPOsNsDqvPijuDnRTqsQ1V7AYwT6/5j9h59szcij7bBCoyG2HBNxlDfN78X2+Ke/LyHq69nPt/7Vkf5wDTtHOKYOrxwcpDukWLtnk7XIapOl8rtryM7F2Pc0WJ9NHQrwYPpeWiFseR7G73iFjE+u8vOvhM7HO2zHTu6GSHBo5DQkLzFrDVneu1KSp9C7d2cnnHWYw0+4yPedS+7kc2CPxuM6MreIaEzCTtfSy3jbvJ8RfWYvU8aPaJM63AjHNOYksQHh/zh9m4DKaUziZSv7AY7CueOZqK8wyJB7iLkBTzWTTEKQtjv1sA9CjowsZvYTiy8TZxD4m3Ulb9EEFflsAKcbw1bIITLEDrAtyvWE1ABL/WFWSHMjmEXjCjgnIMctNhEeWr5NoKlEdLS864DIN2twW3Buy+qYWCdU15E1PLbcGmridkHx3c08HFMCJvLS1CACsK2NUGMfFdEgUIciGhn7wNBazW9e4IsDTz7Zdp3MdNPvXeC+axvGh44tU7eQY8mMFJBz1tHgI3qRdnNsCpEPj3a9gThEQ48uHsNDGylkXOADSm0zapi7tMeGXS1w7fK3O3R5toZwQawzHgL3VDlbB6MMJQ6fuLxYUJqQpfIlCHluiJ8TWxZnvBBCH4td0KgpmtfDoG9W4Lzu3tEEuWRi/FPIgN5ZiK+pB5qXZRlDX93FaCkHFMCByJbLgqN68aWCY72OFasHO5HwwcU2j3VfH1t4lzXXaCNALxbrb7nPx6HBGhDCXP5vKMezbJPxreTOVB5/FqUbzo6LbsVEj6+bAjPz8/w/PQEl4teVO3b4G2MsvcOd9KfTxc+UkwjL7+XFWXf4A1hUY08hPJNB8BfMzygM+8KbOMYjQO3Xu/5Bocgk+XvYQw+mgTZ8y9O79ep9KO1n8OOsy8ARruyI7z27pKZk/5rhnRxMg36ZuI/TIMJWXrqvuwgHyJYTn+6F+8sR6ydyE/YIcQWaBe5O+oDtRmi2+6dT62pvPv6h2AKd5H9JxAcCEQMGHTg0AGYC/yRweqcgcmAfK3JPm/N3rvEjhFLd93ZwY62HhdHwhmbV+IG9WscoowSaWAHunEWIkG98NO6+rmUUh3tRABU2qXRzUFotauGS44Hgg0QCYouAO7pDNXgS5jl4uZC7bJxv/uCgxC9TRAjy+JuZBFbnclYAwcbVKc84qWVUfHWHLy6lkWwXlJdTF8hfxX5XPKeQYtN6867FNoPk9S4vO1FxgT+6CBZ/mHbksKjInkBoJu/NAhhkLQ6qv+fbAbzbMGyYB5v9doPQvidEhJQnOTw8yPy5pfK33zJbyJmtHqUVlF/Gwdny9ilF2awtPeEuyDEIJAjtA/h2MyNHNFg57hB08kkV0ruEI6rdKyTnJVHAr1HxObdAw3cxLWd9tM43Vs9ZuB3aVS5a4eMC4mgBvf6Y7MOaEvcRTLuaPhuBVyb27ysL7IDdzS2jCegXzXW16uOoXA3xQRvVh2y7YxzjrZ1kZ874wC3DZ6enmC7XOq9P05uaD1Wis3H6RqM5NnpRRDDLry3XnOb9j/SftbJjAmZP7OR//XDaIHNI8pgOMJSYzbeR9If2HgMfGwS/fdeqfEkTSo5autju1Xm9d9dcT21gRY7aCDwhmWP0O6pHROIq7j3ZPBQbh7h/3sMlTBH69RajamN9SeB9+OkHEEuWXfyHCT9HunH7XW0HROj8sEQ5/URP1cd6C7um3cFd4nL3U2nsdr8MRjWY+qsvi8Md0ZkQL0NtlDAeXjk0DpKVzTcFtK7O0lXcRs4vnqcM5KhdcFXsgOUfJs9OVpCb3Gz54zdG8GGTcsdDZtJBvecOn6725y6oAr199eO8x0q5NFg6WY9xi0YvQNdxtG2N5vNd/cupElgORBhHW97jLer6NM+oSuG+cwJMHM+Php0tasqv9H+ZkfeyhZYKzDqp12L3Rx7rU19OW0FKvGl1EJgo6ntAChFggSlOdCRHfZb22GATHc7+gm9E9xuZNCTS1qAhjgAUe9h4N0HZHYP1HxxJ4NvVWndtsug3oVAEmKohmupuzo2bKv+KyWyCKqUaoDwz4bzWvhuiBAI4R0bxqGt27ljWnZ8cZ1JHHbck7ZHuQ+kar6L0m/RZOJ27D237JyOODXgZPtP2padioeNZGvs2aO2IoPby2U5gEe7xTnHqqz+R8dz3tMJBq+2iV2VKxSKv6MPpMhuCestMROr+oBRcMFwklj1BGhgDbvXZrzIf6GdF+TrDJwibOXKwkXDe7sKqnjphbP9y+X2dPV0Mg5lD5TJVPJw9CrDizqPHHFQdTv2zFiyux1G0AVCoK7KVJkpiAEAoEBx98905R/tbg4EUMYpVV5uqHRyLJNllrUXqJ5753C7H9wuBN18FzbgSNYNET58+ABPT08tCFOD5uQa5pUn9r9yWGnxI2zYy+IvHb4+h9QeqA56D2+IQ7rw7hv8NcORnbf8Kff0QZvbcDMcli2CWqYm/P6a5NpxuF8Q4r1B36/i1sN1nvwG3yCFpkKsBiNiXP6Lh4nYTBfTfQViNvp69vrzXv3tdtQ/pIwEi3OjGMNwB+6hWTcXhiJ8RZitI9yHrB1fadSHhSePCEIAHNkRseDcUsfQIspuNXz/PC0HcZKmd2oS4aTf1Ol3FLLdEAZr+2SaQctxIwIguoujU5TYEc5OW+Mk7DCIB24DpLbKPxwhwh4lInB3DXB2Yvdmc4Qi6tZl3klR+wCrc7JzvtYyhe6246IY53xstQ3sRIMGkeEHXqnf7iRAghpYAATCUuu5XaAej1TDE+0UmObEMny2bYbm3LklGwq4rYQeEOc08jlGyA5bgrrLooC9E8M6yjkQwEGfCGIoSR7eXaO7MrQdfQ1c8zmcEUzl5Oc56eydy4Y30cuMuLbaOVwnuKUdxGncb6Wv6ezYNzt8jGP4qOMrBpq4rEi4xkbUET9ckZn2z2imMjzZdfJOnaJ/KGN3gK7bCdRg1+AmSVAm61fl8THYoJslTYIQkb5OMiXP91ajxC2nAZ27XH4HpLlYDlFog9Gl56Feq8c/uUKpBiM40DM0VFy0NDKACSy0t+ncRSY75E1HI+bpcJHrI2KqCNrRVmHubWN8uzzB8/MHuGwXne8nQb2luzUeBTcU9QjHRTeMVvMt1OM8tTm/ZPW/d98NV7Mm5dzSHfu73b5BBrHJj7Wgz71iMM1l1xEG2E/7KqvoV4s4QcqefOpf5+nvsRMi3SHPujJg9yzi0cVaVQ8RsyWyQaZuHSX2CFffyCIr2c9Kpfvw7604HjeGVvm3g7OT7DIdt8Gdyfv6oFeNAUDlyO5C2RMtu6IbiHOdkmBE8MbeS03KTP/X8nOutnfmW0TKbaDZ7v/qeB8d52GRPFaP68UODXWXu+uURv2RYATM5wirMw3TDaIF3myj9MUeu92LHaWebyAYd3fZzWgavVsU9OPxvI8g5cuRjjZyGuzA+o6IlZ4bcaijv/7YO/Jg9FuKCluF9XtPRD2Xel+h9nwyGFUxX6b0DtqhW7UNo/5ix7NJROCEFf+2BaP5W2eyDZCPHgIAPpbEXqJa2uXUfIQNUhNLLfjAF+H6QVSAj34i4xA1hLkgTd0FQVCu6qAnc5SUrknCvu2knvZBayOqBzGVcgXArR7hUerqXA1+1PqW0nYN4NbqcpE6uo5on9jdgdG2LLUoBDVFobQdGUgodYOiQQiv8VjeJ7CrkW0Ke4kZO7eB2j4D7kPTDozTXbKaQSYjkmNVlpUCjxYIzB0V/ALtT38uftUH4sDJ+to63BG2LashuU0/he8hEMdsXhNXlh0bUl4opQ1M3unCx9zwUVF2fR35Pw1nLdeKAjnmxlYfPd9wEJLJ5t04aFf7NwJXAjyziSTewRPfZ0eA2B0rmRTOelUhGfeBC6W9CKQwH8gAN57cc0sov0t2bqwqgASgl9gHJTcDDeLu94vbGWHKqLsXfKX8Lpg4b+a69LhGPjMRQWnylHepkSlnrrSG92bZlgS2sLZh7c7IMwgbbvD84SNcnlRFGQVuHwnzRQ/f4Bt8g/cCK0GIdwW3LZN7I9izlh/twBnYjYlekqYqfg62WkDuezL2zDf4yiHr5EyTvXeg/K7oHKx5Mf7aoPXh48XVGkSdnkDunxsFI271k2dW/2sDOo1/vANkuMAZQU4WyQLSHW4zGGJJb8oGzff2eosWPP+vBiNGMDxaeFp+eLRc2EBnOiDozg/7dyhNo+n+ajyUPc4cjGtw7rJqhpXeJO/cGq12O3sfRO8oyPDEPLtoB6CIZItvECDRYWRFrX4lgBbN9X5wQyiv5jYr3yUNwYAZeJYy74PSLbSW5tg29UAAoHpoqvsPUJ1FNdVWbzUuLL60rIqr7kgA0B0QfIdF5YV2JJNzEqPgsA5aW1lxYAGqwxXq8Uu4FShXqJdRb9URjbhVh5oEIqCdIILN69uCEsGXW8u3jczlN0e7BCNQfGzU6NX6tnpSpanuyql41Ele8224AR8JhUBQinVA82cBF4TgyYsIiIMs0nho6tDzinUaJ/5fNr3iG8mhExf5TElZrknRjgbUUqbDvPEj86UjWHlIxwfjI229TnELAYhYoiT2DvJujBr6hC8deWQ/elpERrQjo6pm5VEYBMUikmAE5rXJHNbJpBWPJeKLHONZ0B2uDMLK93UgAPK12MsfRYZlQR4H+ne/HjFAzsEAnzaE/0J/6ItBWchj1xUsOymmR1rxmKPBcTbJzo80GGGT2cD2oNQ6T7Wjl3hOSmqYZJN0CKBBNhmbbcwEZL88E/zyfYG//c0TPD8/1+Ayl2oCtLeATDuLeEbBCOzkWVbWsZFwBrpNQfWpsqQXjBmGnff3hD0a7ljSTtufvucjx2b+7sjJAewFRvcpOJZ+7wi99XL1762geuaYI3xJmWE6yNlPAh220zBqsD3eOhKMiIIrzuc7eOZH2T5m7N+yE2KJJsMsWVnuGNBmM4g9iiB65eOBdfPRuzHcw/2xvsgiK2ml9AN1W63MA32l6+w+kC2dafUac+dxOENVZuaMNha/DjxwfNrJ5s5+xsOO9T4hAAW/DfRTCpq/h8CpfQ/QAfcm8o6cmW3Zp5suAjtQnb7UJEzT4cHdei2x00IQYhZkOQ9tPppNS0Na8hbL59+s3PjtIISFl4aIXm6Zsmw77pY9nHvGvTrXdSaNfEhFutf4fF/z1W2BiD1oA6zfteCV4lWDMeazz15z1aIVHLLCU4iJK3N40rGDp6UbbC0T1bl5qv0RTeAGn7YHNcd4ywNQ732QwQdA0k5Ud0IUEGc5mHSK1zo6UXDUpFvdNVBMplZwAUt3dZRTaTsYig9CCO7MI87Gg2lvbB6t+sGeLQQo3JYXALjChhsg1vsiChkebJMuwaWu8+WV52bVrrdPuQy+TaLoo9bWmlKDEBxsAACgYhyirV+1C7GupEcOarBIJ9MvWqYGIUiCEIV3YIDB6dqRP/qx5yd1X58MYhBCeXIgaoMyEpUIFetZwW2yb8EjuxPCt6GdZvRRLhKMAkHQ85eJEtijNix23WXRQnUIgHzWcHAs9N90N8TWVpoXrEfu1CBA9CpyENKPebtLyU620a+Btr6ueeaKT+cwT8co0xM5boCbVO/RIUTt4qU9+c3jFKALnrCcsDSjnn+5CnGe6rZS1hfmB5fVPjh4MSiT+6Lb9VdIDSGb/pZ5TaIQCU+19zZQB+DHZJWpALTxfFZcWqkPxDlZy7Rt2PUwj982tpnKz88A//23BL/9zTM8Pz/D5XJxVarlmeolsOpYXvf/9QmlDPFLzJE98sieVT/sPuxYbwMRnaWRYfgaPr5IwsExc7e7KgZDrb46Po5Xjy3oC0vSL9TvjKjRufts+3lBavtilxwheMdjaXWt+PzWbj/aaE6AGtvgeOTHoFzLy217ZHyMeY/nirwBZzrAWehw0uB7lpPVW2sL8LlMcVdpzG1058UCMxI0TywqiN0usDzQrY/0Yv9kNfcNHXYrnGniW4sc9IEvxcqn20vdd/LnL1Y05nvB2wQgXhFC/U7PvXeCuIofew16D8GhZA+t5WiaXoXgO7iFDm/jZEWp/e+fB5ttVo4Z0NNeWwhCLJd5Cu6hADGmNxgnJ4VSvpTuSDu8yqh5EIz0sjvW5YQt9ZhAhBlc9piP/KiTwSR7RFmOjp1lOwzDuyo2ZnZB3AmROQh9HCKW0eO2v/lCNYB2cbQpS29cbqg34+SRdlZlmxWlhoVfAgja4HgC690xjljXdvZ3PRcdG25bDtMBxknIRQsdaAd07zzXHQbFPgWQA3D4zoQNqoN8g1JKc5tR4his4qb2U21joAvIJRDsRCEAkPsGWtmllkWlv/QbQG1JAu4/03f2aBbG3+qMCLBt1am84aY8VUq9SByKltnaobTLqUshE4QwhmHrIkTUO0K0AZN+bE0AbfXzIkwnnzgDT+e8AZ7GfwhbGD/MS55W2VWwAq0PpC9C27CN2lK5Y6R8IAfGglf6WTUxwWu99wP7VFEkE6fFE9+5jg34jAM6prfyzAd6YCALTCFu+Ib2nDhrK3uGgrqsKP4C5ogZcLDMlr2nM/hAZc0njhuQW3M6NATtnhjxKQWZc4Oed+T8fF0kO+IiDE/I8GfDkTj0qADQBrIFWvGlVKS+Pr6Fg1r/zcBi3ra6Y413RUgaM3Zje7zW/QLvGu5nX3ich5OuEnFvYo/D3YIR7xVmkTu4rx1yHirjrvTF7jGUXxIcbvzzA/w+8uxdMMsUoh5Td0Y3XZpUR9jaIqC6EAhB7uoigKWzxL/BVwlzcdkvDnpv8H4p+wbOPsnABB/ewsH7jtn6FKy2odqMSd8cXSywTxToNvH26Wzm19VsdnlyJ++rw9fGpO8Vmq/00c19KhAxjBbHn2cjVmFl6kkk+n1wPoUPQNjveZkSvSTQIMEU8lXEdlWSkmmCB9SCEOZy4ug0suGDjGw5sgc5Hzsg9dJo5zDEgDMJDHs5We9hYAFtV9XWHRCmXtDKArsbYu6pk7skWhsJH2zY2mUDXUdb2qTdjn8qHHDQyqCpW3TJ8TkizQwGcVBLf5gdCLKDxIOfpwj43H9tA9uAFb8GIBD4jotCBAjXSkWp9WFew9YuQHrclPQjdxrKImPgmlPS1tgaiNlDd5j043p6ZEQcBofmsgUBZxy8XV4JDmj9CPacGFxZ/uXvtbArnecTs+5sMB+2FOHdPqsPWOrOqGEoIpGDHRdrNUzf63vTt6R0qQNbZYFbNQjgAqzZtkYOxvjyuioMVhYG9smWpLn6TPqEet49BBS+m2BEX07MEOCETudWA4f+XlMS6444H9jOddoYaOoxtXTgAy1dneM8MTxaxUpgcERFzicgg26tIdNFDks5d3Ct6h+jZHZ8wWo/zvlrCceO49kRF0o9BMNpPFEg9qhZ2hk1IeVGbfmewYij/X2fQnfqn8nWs0V1HT/X5zIMOVlNCwvzT00X63dO2rsV8VGcnWyaSNrj/Qi9vjBqjb0j/26jwvP5PZwS9xjHlhZ7ZGopbFs1W6AFIPxKF+3PUzGiCKu8EIcSPw526rn22Zmg9vptL/stJByEZTQ3ljdu5jtVJEC/M2JczmMoeCdwdCpZ5eFHoDpM6wE6Fqdz9fGs6xt4zzbrwGuv411zcxhrpyQf/Q4HjImXYBqEkER4YkIYAIGh3Psk+P2rqY5JWae4I0l87/jNozzit+oxN1F1w1AcNceu/jnIeISE8a7X4xU5HIjQy32Dk1M+esfZrQGJYzspQBrCRvmiXW6Vu9zvQP43ryQW4UfBgArORcAFbohlVZxylFBz3PmYR38ki6JoF0BL/QFkFX1pF0UXXmFf6eOjl0iO3mguUQJnqPGZ33JcFNNc6rcNSOiuF8KRGWDaVxsQhyPasSwgxxJpXZT+6vjXlUlUoO4EoQLE55Y3aaeXnhLUoMfWXJf1qZzsQwWoIBCqc8wGgcjSYD87HgAV4iLMVYOQR5mgRzWCsN0RIX1qVssXDigB7yppwZDCOy8UtxyjhQj5LogHA4KpRwsMLZbf+0hQ2ideTi0BwaDwAPio/ngS7GWUqwME5Yl8KQDYLnGHE+2LLCkkbzcP2QfJUQrbyOnKPIyJ8tfazDqgMUmnRnsQXxi+TkQbBxz65j3DjPaIrOOaGQdRCCnt7zh/nYYFxbGbuI9WJ/SXX8Win5Xv7Txg5CtXl98Vq4B5HjeJu7lMHnXyz1CDnlreyRaPhnOpiIAIJci60Z/hI/wEL/AXR52pWddGtp6Pgq9+Bf0rw7e2/FLhNos5D5qu4LzDAF8K1n2DLxaI5zlrXxljCiHMPibjnem4Hd6QT1/ThngFGFXnQT6uw3B3591XBHNxnXnvFzz6A3iTld4ZnK/Cm8E9yGUcoy4/Z01mHOKDEN26M2cW3XdwnuOxvhbRcjuQ9Rt8gzeH5UBEavAHhrZHe8izYcBg/vzMkU2yisW5Jkmd6h2Mzz23SCO+bDWpc6ACAGwTxJlDjPVjKnq/AFlHbnDEOT8pgfhlO+W7vi82CEF8STavxsfaRlTgKjhBr0AQ2UvmrXcAl1YuFXPnBM0ijNbYDE4uTs1BD+P43xCA2grdunq6MqIGFQxeY2jqnXRtvS33QTufXXZfyDFIcfutOuUsPUC+HnFFsquugHWW1/bfNg36oAk2Sdu1PiWqd0LUy8Y11CIUoDp1hpOcCRj0ZJ6YpUzh/liglUnbtmdtA3Rs0TvKmbdW6B2NbxnDyQye7SSIOJEPnIl3wjDfDPLdCr63W3kLiPsA8UCWkH4hDgaBBpc0vc+fBTTOQy6rXbk7+CPN42OljtDacOyVnQSPXFkJHakjtptjTjKQlKlywQbsgV/FVTkpmN18WSAAfPVSvVe6AlX5d+RW2VZKgQv+Ak/0CxC8wOdBeUOwAXkYdn9CeTI/h2dCR5c0lNb9PDIucsqXMXQ8eLsAuj/GpIxA9+oxPQdKGDw/YWTuNMCR/j4tMZ1udh/I6V4ZfQfoSJJmwYhsJ8QdilIds0GV22v41vjeKjIzxPP3Y5rWiB3tzrmno20XU0iwMmbHK+5O4Gq2hLsvjndCoG8Zj20H95kmvO9Q3Uc+WXDzkPrdJ/MNxfbz5ltQMuap9j7fqnpfWk9PjWaMPIiEo5h7UgZ2QvpssSHu0fituHscrXQch9rRQssw3ZcBcfYi+4ZVAbEpErsbrF0b37FNi/YDrC0wdGOctXEH6ozVeQ6jM/09w7LHFrmeZPQtXNEbov5+JxX1Rn1vZSzN34+sn5MV67fApSX5vlqTZUdZc6xi6hgblnyHwNz6jghx5PZlq+MtqHAnCGQnjnPmNC4WWSLPzWQpSYORcnBc670Gih+JV8yTrpw39PKqdvH1GGFmO09XqapSDM3hAgRw5SCByVN9NZurrqO3vSCodwqUUoCgAF3N8U6sfBMAQFvKjXzuvjoX9XzUKnGIDUIKJRLVS6eJV+XzUUzh4ms70BothdsUsNJQE0LHXPLPCwcfndasrYUgHhBT02O9nJvduATAOwbk/gYuh++CIF8HezwAAbi7IuIOFe4/Xsntdo+0F4gI2+WpXardLi1uY6j24xVKudbAw/XaKq5BEtMbdWcJYH0vS/V5h05pfkjsxrD2lOFNHsZSmZH31vSB3NmRCKrNzOLtfpXWGs6h6RuQHeBb2w2Bkr5uryeXP/qYTfypvdPdFVxXO55rkVWGcF9IbUjT8wXuwnekRKsM5H6O8tAfD+ahPdlM+0v5cVJH1ydk/nJdI9jx013GbYJWLoTSdinpbpT+yB1vaFHrXwC508UpWDqm+Mz/nGf64LDrzwCF9MxnDmZhfO/JqF9xbUW7D8TUvzLX8VTDu49koxmmuHkMxp1M7j30ytDx4110XtSdENhIZB7T3sSWjgxtjlMHQRIbAKvKfuVXbDJIeznWx3/WGrc9L4iwXS4AgPD55QqfP1/h8+cXuL68iPwwNWxyHYDnNZ3SdKz7gjOuyxxRQZKRf+Z4zfCITzEa7wMQuav1PG6WHM+xCon68ZWBnfhG7/fgbPvP8q3gfO3euZHPlsidJ7p3jY/sclJxECUHmm/2XacdBox7BiaFX1na7JmXsveBrI322s2UfgfDdc+2zOpKcAWAz0D0AoVeYKMLbPgBNtiMpVZcDoW9/nk07JVN4XMh+eOminU6vlAYBWr1b/ZmfQap3IbDkhYIvCGJVZQnyvejwehDAHiOFAxfLN8/kkVZdaZcp+/FP3Y6Zi9y5jLIW4UDq2Fa5/gyWHy9krxC1o2wM9egFjwkwdGKmmWHl+wY7JGtV9j7Joxt1tCIn+0YWmv2T0qEdL7txD8ZO3ZSFpAtdMQQM4jUPoJxcpxnS1oJYCivHKHIZR6m6adqlmVHa8Q8drwlZBS0P/e+H+lYIKKB1b/JNuCEtiOrOfsVpWaQcqDAZoiNQpoiXbHZBlG+Bau5IZoDC/lCGXZAGyGGwO5FFJx9cUaQMV28Ght0VXY9+z/cPxAGe96E1kGrlxvXcq7OKcpO8OYtc/QSGYd5+4umb1VRJ7CBAnbI64XSJM6ZSKdvQBDHk6peJh1wEdmFcU16tyxyVA2S1kuSNqdOO8bJuBEFlX5yG5pdDc0xjfbC1HSFUSoqRDXlVchs7PLl1LjVY5m4zWsTtaOXSHew1Hbw0srvAdF33fSwMvGargVo83tU4roMABKEaMsGlEssoSjjR9s2FxYa2DNHMukQlN5zZ0gnkxuRP9Inyp+4qylTcgmo62rFmQDRgGeNrDGKtXmt90R4id+3EjuNzcsWN0zpogHP2LJtQcIqCBCIzkHym0Ctkb92oFEhVbiNbBspUiJLmpLk7yrQNrD9tKwfWRo5Tyd7+/YK3aNloP8+4hGn1PQaRkofBzCiQtS7z5vh6uoc+L7dq6L8jkmjcdnYiVNGSeR7z8/HgaTYOPw8mS7t5dTXcoWXlwLXlyuUwrLZg+NXnt/sWDYTdq0z+cfQnqFhALLtQ9Bl8AS7FvDFksj2ofFjhwmRfwg8zVlGmQnxMI/GQk5Ap1qFAH03j54At/svwTM7ovOt4f1RdBvsrxirMN7pulvA28NkJdoq5Lt2ogwdmANDrplMBuZdtuirERXQxUltr5xVyCaFHPodmI9lgGg7+sUnBYBeAKC0ttpggyfQRVkloY8Xxenve8Eq+43Ztac1fQx23IaHe9243G3H22U1xzK33ugcsdPLGNWsjJEral6DtImRdYam000x9HiWW2KlzVTZWwS8uS+0bMhtJnkJ7nnnO4rZFmza+m11cC68p4nNCOYdAgD1Tk/PHyrTZ+qQvBpUY1S/XM4lbZ/YBJrl6NKp/dRZF57mMJROGSKy2raYFXd1vpo+JNd0i1kHCVMSR3qAzYDzIbZe2H457tkRTpl0lHMAaFJKy7XZ53rsnJPvqAtM3yYODTM3HCpBFv+uZBkJj5Xcx9rm1GXVqwXb3Q03YyYAvii4W208Wn2aQv7cByHsc7dOWFBgKze97MzRrrsRCrECbMux7aZH+/COAVcXYoyGthYMKOXajkUq9Q6GUuSuBnFoYaMZUGgXKhtdRYIMpR135Ec2XyJ9Leost1RZ51SEzj2L/pOLISC508K0jAaQNj3+yh65EndDWDknARP+gwU6Orle7TtgvVei+raM8cVKIqLhAaYAXIRbViBzPuB2t144bdtS9B+ZFcCmIaZjnHfB6O92oTWvBOiqTG1s+R0Co/TSvzjr6QCmjGyMMa6ttYvflQCmvtTVXR0ARokk3k6ZBRs5WOAQ5w7XrhxfJYhZFuVzXXlAgLQpAlsFYSJj2HTB2ZWiSMaTgCFY5FYIDnYJu4qhPNVgZQhCuCz2OQHIsVZrdYhHUU1hqJ+ZCbyNQyCo981A/T1dEQIqy3X3hXup43s0x5xQXCQIgb2B0rUN5+A5ZKK9m2He2iFrWkrHkOTbgcofrPD7XQNddia41bUGfhF++vwBXn7+Di70B3iGn7u66txmd9kgiAiRwtqbKLc4kMBlg5kjpJRxBalRwTWsjznzVtsWQ+ND8pOof+ZkQtpqbwZjWaR6xeqOoy8HbjaB3wdkUfdv8A2+cBjJEo3v6sKvND9g+mq2cOZLgIdS/r6mpXcPR1xHj4cHUXJXh61DPNRHteikbGtXuYdjRCuroO8KqeDxP5V3buOiY0GIVt5Dxvi+8MBJstOLIQ6ALJ+UOeRhRZkC7t3Yr8DH70eoDeBcu+Y29h2BF1kl5t8dC3FlrWV53Q5dDkQkPgrzfUz0XQxNAqNEknd0oS0fc+dLT9WyHWYdyeRwsjPZOjZ0ZTuAOnnrEwq025S2LiirNtMJgHSKrJNuEbdYDEKkK7MBmoPdel6NsCV2RmM78kdtVnbE1QuUdSeGIzVxUBNA52cR/yvqp6Qx/CRBGaZfHEebOPW9oxLEO9o7RA1+dvQGH6c96qW2tHHWGocabXqUiKsRojkqyddD2glRHKD2vVyIbRy63IWZC2Tk7gRCzT+TJ8KfjYP4bpKkhOmwmmuGoN1A5pHnhOhA9CiNA1gcqIYnNgAqKOmOQ+50r07gqvzKRBYDGx2D8YQ30izHW4xlZEtna3loMq3YxWkQIpQ2BXbWZ7gN/dyvGuDpNTaWK5Y2Pe5oXxBzXfy9KVnddnBa0kySVVpEnptijxoss7sj7OpNC+o8Xy9rfdrVxmB/vS++yRPH+nVcePk3xu4JS0oP/bFtbTcTInwuF3j5/AwfAQG3a49IxEigp/g5PtIZneV8R49b0yi4eRBmFVTiKWiTXfwhiIXs7HsnFQ26aSsPX96uTIY4Zb/iMC2z34F2DDL843JH42YFr6+b9sCeLOiqN6rviKZXDAREErKijxrzj9wJMaJ3vECr9Vm3WGBc6K12yfIRTqO2n7THsg6zl46iIPp6YL39RUNxnxXJammZEbGaN6PptvS5zpnkmzzD4YMl1OM0K/y9gPJQeqdbxpzneP8Om6bGuPcKTgodWRQWjkrwhwClX6dJe3tynqsPRsz6WS1PXLkDzfDv3YIRWecZkvfLaMo39QcFjWC0c/p4EEIoCPgniXKzbAh5+LfP2NEgtjHbxffj6RQXKS/dGzyvnZdbPYypTUvZmw8m70a683FdcXHywD7t4bl1gbZ78FVuOnp7kdNl5Y1HSJBRQ1IP8C6t4OuT36JmntsRQbX0+tFcQkzMGXQ73MOr8Hm1fuFzrMU/yCvj7W4Cpgfre/UTB9xaKVkpzQLH1LODtoKyeT8g1pzaH7vKnO+EUAewQ6iOoPZkM4laKze6eJdFMfcJ1EuuiY9msmWg+URuAxZDbZeGXJDdyiqlZtvq4w1qEsZdylUoEjeWXV2qDShOZHv5NrXK6o4SbusW7LB93PDzUT1bWy0rfRDa3Q/N9t3tpuEuzlbMF+Gppr2ALQQdX0E9mEjo5+oJY4I84c6FutpX5+wCULZa73KFci1wvV51RwvvI2HHGc0FIxWCK6jDjh3E28bV0r4h4LEFJrBkdOG+eX3f2vZPrR4r/JLV8o0POaDE90FsXZCm5S19QZWEkcLI/Imh3wm0X3Ino1PkMElwAKzTvh6h1VSvFjDj+ykATF0a60jz4p5rLNAfndmAlh11rEp6TQlgjjsDkH7TXUlcGy2LZbMdLWTeZwwyq9HRyX9gvymuMG6OBEIMoqGCnxIk+Rrvlf06ZfVeo3HBA7D0ntN4uQfpkzkpHNAG0CkyrQvarwiIF7hsz7A9PUOBDa7XAlco5qJRlulGCQq103Gd9LkZ87JDzch16+Qa3feh71ouk67bdRHqiaPfDNTmR+TZZOd8ZGlmCg/vA1kwIiVD+pvnkX1uSYMx3Kfon7enexh3ytvJeoTB79jGbwHrMvZeRvH94exxCfc+4/YbvF9wF1XzAq3m1NvarmoOfH95MZtvfMzwpbeE6gXNXhEb4KBD/EtviF1YDUZY+1NtmCPw0GDEK+HYDz5oyrzQt4KZ0mtAVH1suah/P/JPBNt+rGd7Xrob0H1Y4y6E3NDXicft8bBD8n3pWMU1S/eYsbQvow7w7lAvpvC5k/wgrAciaPrzMMwMAX/GHzvdSb/rKwBgn7GeIc7dHYMQUeCYQtRBKU7z9jylcMZQ5LpdHaDRGWWcNB3WxJFtabY4CcwRTHycj5ZvUfJZ0xhwq1eHnXaKgYU7B1H4rFW7E4I/EMDcpUAch5A2ie4tu5lAqTF9YYjnY2SQS8LxHOWCS1wvAgngWJEJcZUEbyJJ/WVcWaYC2/FQ9S0hQX+lhelDRMWCKDxLrdDS+hCETu17M9vW7zvjp2/DvFI1HfcnybO0bU3AZdli4/7P5VhDK9yTo0jrAmAH+8wRzYrrENCl9HRiTGqdUL2zeYq8pwr4iCDG3a3YY5lmnPz8eE8IEzX8xgm8d/xQJNn1W1IVG7z1mBuBoe9mRxcJzg7T7kCv6e6glBxWXgb9MOdHk3cF/24aO1/4efE2qDirPGjfHWHjAvxxRE3WQTxyzQoaO/tV4b5tl3pqd5uX+EjAYu89KmZOB4DL5h3gsQ2cLmAXKLCUNUd16fu4+80D32khl7C3+SGVWKjiU7eWW7wsf1QAEbbdeUM5aOemIL/OwEm+yVakH125vE94L4hWncpLyXh63ZFB3RgzOschYt7K8xkb4950JM0wapn9nS5r6e8By/eRHKXBrkbgj1cJhpzs1z3dIo6P1V1JZL+ujpW1ZLPMsts4QeatsEe5C8YwtjJxJ91r8M9BmJD0ttQe188BzLA9pjZLiSjf1spzBZtgxHHYt/3c45Vp960grUoWjOgz9SOGbeqRTdE/umswwpYxsDGH6buX52myPpIxNMl4VCAeSj8wLFHfj/rKym1ZvAeQ7HyZ9F7XDiMfyX3A3Td0FvFS1/sEtMdrkgfX+68bXCsGr/Y32r47BTQs8ubxeheZG57elZGmRY5pWIRsgd8x8o8JjQOBCC/YreF4a/tmyqsqjtBWx5OemS8ODDSLslGcbRacewP9k6we6sb3q/p0HIvnIrzzf+vCej3mR4IpDpsZlKhOHpSVhXwRNO/WqA5jvoy63iNQd0VQoRbkYEOKz58nsGyI1plBugOBeDeFBBqYwiY82mp0vueCgC9dbs5FbCv9rf+xYjcrWbX5a/c1Z1aprvhCZjeH9BlKWr1DwBt1fphRGKQURlHrB/65ca+2TJvhK9xg27ZupZS44CYyOzNklUNq+cT3UQBCIYJyfWk7IV6grtiyRnF15dXqEVDwdNrggz0yi9tOhgy13zVT7fNkp8EUDk5UQpftG9BV97wimVelxTrlNOoxTlpGbHeU8edWF4NxkGV1CU2B2uMr1dV8wcmabUGdKsZWsVps81EghQMSnZImY8HICFNY3E2Q0dlP+lwW1DgKcZtvkAyLHVwNY3RyGrpWfHqrxkS3XVLklSpP9uLsuIIeRK6BmTNDYDEhNH3GuA2+tB7UQlpIbtcFEbQxgiYoXClitHY3QK9sqCAluzErmUc9zcmLJrfiTpyKkwdyJYoQYLts8Pz8DBsgXAHgiZ7hgk/wn/7L7+G//fefVMaJbAG4bAj/49//DXz/8VlwawA9VC4SSYY2p1OgTwPKc1tLvG0bACJctq1l2ZrE8IEXETltHGwi97zM8+ntbgtU2vid0Ol5q+zweqcnuXoyflftA3BMCX1rcMGEMO73wOqIXx/cVq87ml3vFI7UMMpsgJvad+WYEbixjFHRUUC8U3CL1podUu+egyrrcWt20lRx6O2Md8HY74KIb9BgxEE3jZQQjHCseG94KPI7gzRqDEbwi9WK2N55w8rvMYlUiY2q7sVaMam/ZFboXDTeA/Z2SJ9EqtDaje/N2wffGQ9dK2B8OM3rZPT2g4roKhwVSHeVC3nhdwv0vWd4s+rd1rK7ognvM0YO3xFB3ROFGcGj1XF7QQjxoLAjJxrqzkDX1eay4lCM+YxCrZVzVCTOGPQ/gzO8OYb5ATvu5NN6ZMe91l1I6sgpYFf1UCkAbfeDP/qEdzwEgkGdKHzPBAAEnGbHQDdpWcdPaB8OQiR1cv5/0ajEmwXiFG+JHeXsJDM7ITwLcR1sHjBGWkZvOGeRAOzxS3q8xibOunWvhH6ZOyhaeSQ9awJApflDGjLnqGor+5Gak7fiGAUh5K4PU79aXbLdCrEd95SPfnWo8rjQHgKXeX7u31wh6eJ2FoPJk4tadEJSWpBXF492BoTHvcMu8FuYRHtxhuFvkDF7rKWEQxbIYFQV846h7KOEwvqJuPPIXQbzyguKKbh2HNR5FETp04HICqXhjgobhe/YeFwMQl2l7iA4lQVFIjeHx/0EfsLAxxGvd2JPKtSV3wgG+7kHe6vQIPBHlfX2fpNAFQ9/l5Ha723bajsjAH0u8Pla4KdfX+BPP/8qbVrM3Pq0IfzycoWnp4upt5kjE34lINg4iEAkQ0T2NJh5vgbqQXAWAABE2Fo+oksLGpRKPyR3NGGVx4gItOkz02jKzcJPNei6QQ10EPBzktmMj7MzMfwpdPLPT7wdv6yuQj/jlB/fm3Jw/t2RRXPSJjoD9nOMDU4P2PuvA3amnGG2BX6KuxOyY7wqYJq+TwcufYbjCH19rgkcaKd10/GgXjo10I6h6p4Px3D//OxQGd2dxO/yuTfIfq+8TRYMjYhQvDMIaxEGqOZIxu+PjraFNl/VR98AvAX7uuD7b50C1lGdfZvAqLnFUmjKnyygmlFB3ZcDJRPMkd8fhqy2Kq+wfumDEcdhaDLJZ2JrUpLwUJms6fb6VodTGaLa86KmrHVaF4QYGvuPFwCZ3XR3nNDad6V5ggOpl9k5grNyyc0Nwbhbdso/RCii+Wb43bZh0lfqqxoYqpLOf8NQ3rTeISjr8b0S7PDS7Ts8YFzASZS3t9F+be5h+xy/rJp4lX4kxLjaAjPG44nic/lunZdEzslAxA4gU1Yz0uU8c3EitzTtMzNmu50QvOSTatOvGPQykETJ5by6A4IA2v0LGVOg+wBbR9tmVFeE606Iq5x1qgEU8sdKSLuRFwBEUMgU2XaZXK+llVNXySsWnSTVP4G8kQDk8mj5vQHfs1DPji9Cg1wsjQh6DYA6zku5aluCMni3E0L6h1fM6/n10VEm8stM5ID2kurmUDAshLABbrW8bTOrdVv7EaEEnjZG3pz9KotrvZzsYgdW8RKtcB+8vLhgBMr5tdqfuAEU2gDA3LdhgwBm3OgRXAYI2hiidsSJb6s+cfoihcqFYRybb8JRbTxuG4ILSllcIQphxzSvNN42lN1SHvqAlepdzNXmCLHdmW3H+WrKyRDh6D0ZpnOpE0Kwpo/TgmAMimYxbY4I7QgxlL5XntHyFn0vCWme03SnWGgHY/j3Oxz68tH8ZfwFqAVgCXInR99RdhfDbFpdVgDJ/7a7JSoiNhl5PChuBISt7QBguTUsZwL2Es5qyOS01x0SFtm4jnM9i0wKO45N/jaWJTjEndruGaoxVMoyunqVFmDfnp7g4+VP8OHyZ/j//P5f4B//+V/gl88v8HS5SBnFBXkI/uM//ykdq7xThOd5yVIIfvfjJ/g//f1vwbaTd3K1PAVkdx9x0AKqDNIAQ32WsIl8w3ac32Z23+m0R8IzTIf82xrvoN5NhK39NJ0vLdbHz3ugwX4w/BsacF/2+f6zNOwdz9TrhL7cOJ/PZVTOl6dAdIVW6CH5/xYwH73n8K3B29SawvcjnW5l2T3K/wZvASxbrH05W+zGujGn27DqoO7OIGOL9YgeUIlv8IXAyc7vDCwvq45KrlU4g/OLY29pvLZAD+4090+BdXz5E2g5DlM7IBZtfBhKxw3wFa+i0DbVHeMAPCTZn6NNiPzS6cjiZAm4HwdeM8mtiMeUOiliVV3aCUacAuvfDcGIVwM0nwfLbq6bQb5VReN437cleIfzpbgS38w9u+DgHRF+4AJYByHKi8ovqvztorZO+/qgr2SruTi9jGMSjOGrjgCU130nqkNQHfnrkBrWIq9CG0kQIi9DZZ4KRkHJvpzC7gmCdjKSrYEU7hwJVLT+ZLpP+oWfkxzpNBR5MpLULWgDQikQmLatdeuDEN6BAWCrnztFhHbQIARQo4d0slHGIJVfqC0VVwTwX+UbW65XHKF51fiIJDR1VAeMFUB+LEROcEduCe/78/2F6YnEQdNNV8Z5L3Kzqws4PhjDWLPqeJmYC0lp0MHMSQw05xIHpkCLcvwZwdTFsUWGm3F2CoQIjH0YJLPzYU/DXGFxSg/65/oz5Ir16HRQX2bfdtjzQJIXZQwNkqYggnn8zv22nzN6knEPoLwWJ8Y9eXQXUMUWu7rEMabBErfyyWGb0xtXyteSTQCmMU02t3jchlNSu0O5b1WPnFLuyRuUNMiGCJenJ9gudVfD9foZfr3+BX75/Av85dfPjf4NeCvP1owy5olfPl8DztZubR4usXJU4LvPV/jlpdT2zhqoOa8Ky+dCrs05CPDh6dIC1xTkMdet/sHCgQoNJCi/2HwEABvUk582wIJQtgIbbFC2NqpbIIGDW6NAn38nT0zwwswa6GXA7H4d3pnRp1/XqYZzER9JZ3c4mo+emO7LwfL2x+QY5/x9LlPR1+Vg0aLC7KRbkuejiWkvfft+2yqwnaK6xs3KmkmWFOvO7zVcR+tt+et0m+1kG+4cuEcXyRAkj3uHBotgud7DYarzaQzIx6MVrR3KNo9AXaHBP9ZIWiX9prY+x4t3gbH69Waw2pQjXfvNIMp2Zyfy8/mOichIa3WadF6YSp3+736dbb2d+sAB1lohQcR+/ZLbBeNS93clzbgKBcNNw4UC3iivoyuCzBd1MtxQvtV51wRAx0b3gIHYG9lPY59aovsC9+V4PCkrcXtkdpUhrI3pmNIfr7rHGb2/YNymCafd0BErPGuDOVFd7dO0PhF7JoOF0XKHwNjNetYBEtbxJ+lWZdygrLP2yh6Ytc+9LsN+SLjf+F8PRAA0gyNCM4D5jyHcf6ri2impIQhRjPLIeax9ZJ2R7NyW586IxoShwmr6/nbhrs69j6mtxGHlF5Re+w+a08Jd3JnxTeL4qPdPkx6XRASlAEC7zJihnjN9MbgYR92ZICtyebcDETREQhIBt3Wlr55/jq75dHs8St1qGzbBUwrAVlfq804IVbzYWbOBXF3hGL24laZSD0T95zqEHd+6K4ANnO5CVBku9ZN3z0QFQ53X6typxzNxvVsJssK4NNbfgLAez0HcYEQApu1Nt7o24Vpcr7XNrtcXRw/yillA1TUQ2sXFKO1PAK1PSQSEGREVg+gX1lAj6A6CCQIIWzsjbkFh8eCCEBOQLgWUVb3cFaXE/MoLUhNkXuQ+orxYp4Ba5WqizFhWgQNCfhY8GWUBbsrNiZgV4T5TfZkG5vMN0VyoDhoo5aZFT/do9XEdjtoHNi8HMCIOyZ+usD44gRrHfgl3BW2Brprefm11vse06VBga0td1e5XgwOLK0mO21q9ZfcYaDuW0s9VxNvbov2AY/7VYUxtjBvjUfqSCV/vp24HmGAwcrEZ3pigJiDYPn6AH/4Pfw8//KvfAQDAf/3jf4f/8i//GX759TNsuAmbRQcTS9SoAJvpEETikpXLF/jTr1f4X//xD2l9+rLsLkSFp8sG/5d/+7fww/NFWk7vWuLAhNYTAeTeJaEr7HKsugPfJ7GZHXLg9BxZfOGeba59VWcS4QYAGsCwMg8NYtW9DG6HGEOwu82NSUBkeBxZFjThz8An3VFyFo6xq2ZjPdOVbCkRLoK5dM6k9wmCDgKB3id1GxyVyZZ7Xwtes6z7g9oMXy68Je0zXov2mKW06g6lBpPZFoWwI8Lkel/9c1KwfYP3A5lSApAbDVGBZttztazjqnV8cgxBl/eVedXZtufLjir0NO2KoTYpJPamozwaZINqeVl3I3RG4DuQOSskJOpWt8MkGLmzxVZS5NDX4fXnvZVb8x3B43y4m+J9wi08eTTvavp3q2+9S6L2wBqd1HyRt8Phy6qPgg1C1N9BANvfwzJw8BW9oEIcCC5bfv2dOROGkDlNXF7vaJA87PzqZNpcuhL/FSdGoFPmCT8bWmcAQTEDUHGBXAatos5VBUGIVedj+9U8SLryqDkdCOpRRYUANrtKCeWvOjKQ/5d6FQ7aiO8LB5OApdUaGV4Hka/SPAhycy7nG3SB1tauFA1t2ErQYyPEtSQBHQICdww3AYCcGW52c4B1WPV0TFmlW/1ls9hdB5GOviyzhwK6to35Mfy2hR+FnfFak+xoI7Zbjd9oNFF1jnJTBp+d3q2+sPj504quhO5OaelIGTjmkud9PXqhNArI7K+8B6Cw6tjyp3CUG5ZB9kzG05QzVhX6NvxkhwFpOEZ0xqxj98pOypnRMELCNFj9VccVeX+moMu3ZHeKK+2YoVHOLNgPlk6h3VDdI7TyYXwEkNAprJPP3RVr1yCwbQjbp49weXoCAITPLwV++uVznSOaGI+4tDyURfSxUD5Xt87FFZFMiUTw868vMAK7q0LvUPL9cSWAX14ILp+vjk9lHJlPJgstfhNgo0LwfEF4Qg2qy9SDHHixOk0LhBF5+WRbIZlQEBEKmmMYzYIPvVjeByM4n8OUBSNMWps3bd+4sAJ41yvp3G7bagh2Dk7eTmiouOtfx5d2cDj+7cduCOmntE3LPjmFruZPxIp555SdV4SofI7e3bHETAfquudg2ctzDuskC0L6IBy6p2FnLNxa5qtDa1K7KExf1A8riwFAdaPFpvCz4kDGDJDNZUNWQviZ3Wm2qBLsJHUglC1m2Es2Ve9O2wyDyW2K7xi/e1TJ+Inp5whCyomsZYU2IF5qqVzVSilYfXoUcjuIYaUPjvRhHC/9WGY3RWpP09hGzMvLXqvOMdRNA7mdjgzpT3mKAACDXal3DUZIkdSPsa7gg7bWtDz7NchJN1z6Bhul9/rZMRqlyFRRkD+KdycY0eEfOXsYHfNUoDs7pYM0k8ORPLgTGIn+OuramIxJmZE9V90MHUzU09Pjbtme2U+3+/ykqjlanOrfq4eDizoLB+6IyCbjYIiR/JGVijPyuqNqushlcCkkBjDY7y45D9Q4tzfnwN5OCKXSfXSP7ezDnvS6nSEIHPQTosNF5kN3BsjCzeZA5xXUXN04SnSwUdw4AfX+hyJ3NninActXhA0uYHvbup8AEQohABTtKlHuqR5TdEWpQ82zgV78vBmJQAB0BTL1zb29kK60TYFYFzEOKRklCBKtyFbN2lXV6MsGaKuRCepOj+YR2wCbU4hXnxojqADwjg3e+VDfMaH1Jg7b16hkgHaKWcUr1Co+oChkLa+MPQ+Wplp9O7a4rXagjfcjAsjpOGb82gCOZb6p0RZW4ROhydNqIjsm8iOH4uSel6cERRYdg9nF5Zw8lCp62XyXteuegeTKb2NOOcbKZMtP9bg0Ed8RL5p7Woxc3QUE8MelJe+b3EaybWz4VPirjUORFU0ubLDSGSLRRo4HlkM2raQ3cwcIb5F5xmObea7l1IkK6pg0/M5yD0hXpRvo5lZzHJC8yxgFAdxuCtPPeSuFOXgK7HCeA4vyfvOH0Q5txNDi3y7w3XffwdPzB6fiiLnFVbeGGRohSAGfDaSb3VM6P9k+lRrIh5WYderI5R0CwP/23/7Y9zHXFwAypx2/r+9KazuCf/jdj/DvfvdjQ26CAX1uh1uLuAoNXa5+eLvq887SrUUeJcjQ6WP8aY+FQnP3BZrn0N3lxe94/q27TH1Z4wCnxyULAmLdTjhc+/FPPMG4drLG7uvuCnhj6Kq6KxEeRMhbw9dar/cLmeOtM7pFxvOnyt8iC7Ga7LG7zDgP1d0TVhViW+fNgOu2mPQb3AtepzVFtwsO50M7IRocn/HuCBNV/1UIWzfQQK1dvQg8vuvVwqbLwyM4I7ECWQcdLJB7NKzEJO5W1kSudzbPLD+ZecJ1VN9joxjCAXErZH1pcvdoHQEeW89H69Bv1UejMu8fQIy/g150R5BxczAIN4L1QIQpy69+i+/Z0V+/H0K8AGy09g8NSvsoOBM0WHIAUkEVFAfUFZDibMwyJv4OjzjLUzubz2Pm5dji+DKoR0JVHCKdoR7alC9dHioUPGW3C5NNmc3vaApsLuHmZGD/gjQRG/nZiq28+IOQOwmGagQ7RuV9yy/jmS/61r0eXXfaficum/Q78RMbrKs4QU7J8E6fuGton3uRsUzAYwk+0znw+8Rx6xCGx6MV4CBBN5Kho757r4B5xcg4ntDWundw7sNea7GiepAzm1M47zVDPPTzBdpUQeCv6dsHaEUwcTrTeUbWu6HR1cGWqX1GshMpnzc0HWfrxx3j451TlUdI0qoC2rdx1+7iVA3pGK8ZuwBQL7nueoVp1B6qfNnGg7lnQ7tNufPoaoXR+JJjDvfGrK+S4xkZT54Vx/yF3ZeWjvts7KjnT6m2yFtbPMLT0xNcNoINfwWEz74SM7Bsm+3EIB2JekQkdulVpljjVDsUvVIhcOWjD0OPuVW6A13C6iVEBL++FPjL5yvwLoVe72nl7OhZUhdSl8bTtsHH5yd9LpOy1rsGyrdWVx6fyTyNbe4CkGPHSqkTWb0vQ9u2uF0SalhqwAPNKAEJTGRjxAYiUBQPGC0cbFXd4aHQPbVZzGXwcZxh6Gnqn+/OwlGxPkM3RLUyzu1Rnp4r47xWNstHyfdROwSsA1l0ZpX+If/VhKhR0YKXAgOdAacYvA50i6reEKZjKugMrFfKQidTjxEWSr7dEzqdtleURxmPPDYJFuuBuIvr8PC4hZ4h0rX8lk/OlXgi1wptiV2UfXdJJ0pV1ie7vD2Yzx8Baq4NBfgizOcHZ2EGD3pve2aKbcAfdXhJUr8M1e49MocZ7DzUKRqiV0S+tvqPPg86gLNDfNuM+6XZV8ZOGfblAegWekhZ8zx+UdjALkrT9+27RqdC3pWPn4jzsY2GxcIcskDSitm5qr8ehxWDd70990SIZWW/R+aMbL/hNa0kup2G+0O/9HREQtcVB1jnwB0RiXSNXMCX7rbBv2BjpbA1hai79CVf0pwWoAOJ/zZcxiBPAQGQcsehOhRAB0vnGxivyvMXQ7a/lkHbKhxpww0AqTn8ceNE4gghf2YBQNvlUY+QaPQWYG28EUOygJTbFAEBNnK0Wuc7mPrKqkWsBNpVxHZXA+NHrA4J3HjVLwFAqdM4owbQU4u4SSNr9Y98+iVI7ieRV94JAkBtFXItnHeSlFKPvMIN6+n+TDxuiYLZeJj7hZ1UZINWANDuorhsPOT1SC0un+wT7tNWd7vZw7UJ5hNJdLZKBnaaI7n+mMFMLlpFTYIMXG/jWOerIXSTUnPs1gpIfh7LdkVbVqpb3bYLPY6Y39KOGXM6XKQ0bOpws6tuyDhf47dOnsgjlPItXSNFIYpLorY7p2sUDhZu1eleAOzKccXV6sJea8raF90ndk78+kqc9rgBtxACQuGghSufA9ukssg0TteGts9MUuvctJ+SVnjTVwoJB8GIhE+4vzBPJ5LFyuMmx2cKn5sH25iIlxOXNmCdk3cBoiPb7quLMBhufXki12rP8j9n3/BTrIYO21Hb0wbfffoBfvyO4IfLf4YL/AT1DiHIGK6jNd6BEGmVGkpgP6un5WNTOzd392VnQDw/kOVYi1BlsV6kTfCHn1/gDz//cTK5+XueUnrMeKdGDBHB3/7wCf7nf/gdiIMdgm5jiOe9KGjmK3eUoGF6bja+yoQXIMQdEWgCFFka3Z2HgtuCqnwmb2wnE9iwOPZ2SGymTPZlZPOlC95FmCkrDwF6/SK/wV8lLKlUbwzxbh9WoguR7qhsMJMHvNbB2XtfMwTn7Td4PMydqfHLHFaduhjKze/ZO8vvt/DPfcaYzIUH+Lm2STSgje7OqpLM+5rjXpLB9oG3JYxtg2r3HS23C0b0L3bb6/56BqVfO7DtsIzZ2jVz1H8F0l2Bzey3puM1AdHdLzdeHPpACMU9iu94wfN94SC1B5nr2GXVM/xtJWQWhKhPwE+TVvB1EYvGMWKQhrITIjB5bB0G7G/pjMqRwyIY2v6nwexmD/MOAZDNWlcB41ZMPKas/HrnUAtCcH4qhsbo3jAuayIg51FurYTshEHg45I6Bw57hUe85/iSulfseOILn/noFwA01e0dfxnY+X+Xv6VNWNKuKQvscrKRdHHe8CfJTRCtiEZ/OnmTpoPaK3ZlrIsNCX+Yi9+BV4Bzj5LhDcOPtgJ2hwxCStdeO/SrKWMCy2mJ0JuttMgocTw0p04UMHYQSTCGeZd/B5L4D5p+TmhTpVMllXUy2xWyRCpzCNFd2qPBCuXcfdNgztsrk6bvbv3R8cqO8aMxVouwp24+rmiYsPoN+T/QOSDOBSrJPOZkVSP3xwqMjkjKKkNALhgx1tMPTNJd0uhoDX1HPl16uS9fJt9htrtN9u2yfiibyQvtZ5Y3lt9kKc7KJeAaEwJssMHlcoHr9QX+8Odf4OfPvzq5dxc4suJm8GxVia0s3eZcAABCkQq2BEJzlBUBlNIqnSk2LY3Xs3J6XHAXatV/vRb4889XQCQNfpBPVymLOkH9+unDEzxtuluBAn9a2W4DyIX7ukUqOLC5tbmqLnLQo51UY4jqmvKg7Kawzy3Zw4BE31YIWLUlRAC5dyNpfvStHQNxiCiiX+eLvbkNpCFDK6a/hjgEQy/tV+Tj2ZVw47klr408H6gOmiZzktm0K3SOaEjgpJzxZoDtCXTvnXo0wBVrRPFdNk+dNDyP5KNDnJTktqryYrGdvZV8cz/bHBXloiwIIiN7YKv/cObUE2XI6OITeg8w0DDtisGyluQgjCZ2fT3kgCkx96H0OBY/0x7Ff//2PYl9kR9m2MetcA+5YbH3bZ6VgDeUPdR13F+zM6LpBazLZ0LU/8KUdWbBiLSPhtVTpclpOAkOKQ9Uf6wft3KnEcQxAoJJf5r22Ct5xGuzfL3pECbMZp5hXHy7QkRu2iVo1kfNMmBSNgJ0brk0K48SCkkjc97nnP6Mjluc9SOxddddFnsVj2N4pzozyXIznJDj5yDKkmQAONvepMuSuV/qT1XbFkD8pGm+fVgORDjEBMDb96E5QHils7rBTb4gwMi8rDbo1t43nGGyMGZmIiQN0sHKOQKeOMWla9KwM2wzxGlH2rRSs0ywdb3QDGRHErrvnIyPs+AdBa5Lm2FtDmgw1S2VEcgckdToL6UAlSvI/QsIANsGm0HMK/sBdBUiGwwVChMYa5tUWju1rlCsAQjcNtg27wyQI5naXRpVKAdhKwZIlCS29cZiMpoWvKJT4qDGia19xNzBxgsAtNWfJM4TX76j0c7tQHUlr6Qx78g4gJojBhEBtktF0lava9ktrQSHSJFxmDfwWhT2mqPRU6wSxC8T3kYdnxYK1P6TXjfsyatKy8blmDEFuoq1hFW9VnbOFWcNRqBLjYZ3DB6Eyo8AZrWtbQ89RkSEErB8NS1HnJ9aPVqZrb/dwhLJJQ29O6kL7WHCIm5rIxsqGVkroWkXlalEKgO7MtHIXouf08TgkpXfoy3BRnZmjroNt1ReU/vD49TvskKpg9w3gygrrXeVpkzR4guCJw4Zt/MkTIRZNoICaCQtj1HeBdZxeiLmtNrF8DpCH4SwcyOogmvGo9c5/Pyp9zh4IrpypK17WdDtzEHHICIPxOfd5py6+Ybg0oI8F0TYLht8/PgRfv+XP8D/+k//JDKwp537e0+7Ix0nU6db3ALWM8uaUt7rJ3zpMr+2u9fQ5QpybEhJLAH6JpC2tj/qePr5M8F/+Mc/JNqQzRv1HqXs3/+7v4Pf/fARdOWx3fEBoDyLvl5NJpSi9AD6dNtlg40Mj8lcSpGQ+uHkObLapcncrossjyHFyBJN7/PawuPiDbfrqsnGGlwxbWmDqP0lKr5yQhmkdZ8DdnkIImd5xGv8Td0v3cF5DGTkkt2dtF+5cRBib6SM634c+rm0Po3tk+92O1tyxgavcWG0r1eBUVvukcJrqHrAju3ZpjTofbTWfaLOr65rsMm9AoWuUOgFAAE2fIJte4INL8BnohIQEBbQIEURFDexyhm4a5lLAsNDVnY2hN497FsUoxypHL4L+BI8Jw/oXeCHV1/hm9Kwnu4WVsp6xssekkSqjra5eEiklS0oOs3apooDA7bZAGl/pRWzz4M+IMXecWBGIS7NslMGLlJB6Vf9FQMjANIJ3haYtPduV/B8tWM7mG/e5wMAvEAYwC32Ohxt3wFG7ZcwHcdtZ0rFzB9xRN5Iu9Wx6Z6S6QZMxiYGIrdDwiZxJWWJbgHDJ+fQBv/wTtrpq0lUplsTGnRuBFC/cuTJE012YEfEQMQ4x3mvjHbs7QTJvLTdyWrZOGvCgwBcKzlhHh/672S+UJcuEsAGafYbZY6kUNaeSMyryI71Ioq7PY6hv+S4fo62JNuVRGQe2PqrLKYO8x7wCifZIeDoy+vHf+1q+JHFgya1m/AMvU5zMRF3FciKXunN6DITk1xijSYg1NfDEdU5o+pMzgE9oZmDaG7FZM9/I+eVlkzDdotpux5d3OmwN6r3lLru9R577JU50FfIJVgF01NmQtNyFJesvpFkPRHDkoeKWsifIBAZE+mzPUsmnbwiyNnDKBSarE/Y2plDCDaY1/m09/xFIhsSekx/YshIO4qyddzoHQFZ+T4D75CqY1OPQIqXW4+cThZ3XOF5DEJfHMjTl2lkISbPIw6ncKyWieZfeMVv2u/yBPDy4wU+/fYDXC4XgIJwLSlDrhU9gVyW98/ObN/VTY4+n5PHGJ/1RLt5bFaefPHlDW+0aYHUYhZmRMgv1SbJ/udfPgPiBi6AZwKGhRcWmN0HHON8ftrg+4/PmsfIqra5YQJRMGr/yLgyuKT+aI57cmX4WRIBocjltZy+D/5ZXBZPH7zI88mxYCV/nmobPPeb3RaxSaYwYKVEw22/7AzpC+vpM++tfJOgPb/2z+P1oCm+BPycsiaTRmLkmCwdg+6eyS9TjjsjRmNP7kUJkMkT++SInDqyInGM9+wcZlU6zF/Eck8UJWwounSVT+TGAYJczDZSFF8VAt8fHeP3ABr/FPPI6QKvQ9zQLnlYORF26psJmCWD2NvPifqpzwb4oolE7inLJJs+yKe0SrGwtx4bHmp7rfGg2mJe33DIABI9GHVKG8LxcTCbK4Zg6EA7ECmqA2N8XaBmFdTpMknk9ZJ9tT3n2mHGzpDcSR8VyVSn5fJHWlDUEHubs/4dVXZBAGDyfSpKFuWfVEsM8wXqHjDGZ7bEGTl+JMssbePnURL2sUsTAuw2z3SE3KJeSF66AUkCqQKq79YCsBMcB2B9R8RwEmRDsK3YvUc7tYbfTI264o8UZPuPbN7uEAxRXN0qXCP0ZJIPkVqlsVm68pgkiexqMFE2vYcg1of8KDD4KhRpc2gr7Eupq/Cp1B0REac6H9F9r8UbwU6gijsE+kSxd81YV/9F+oM7RRx3BYRXyDRhFxwJ9Jv19/XXhAV03tKOZwd/hltSch8TmHzKQJmrUc8b5/7wq2uZjH5FetuP01Zi+msmCAhKa6uGr60kJdTWsH7w2fgXnh61GWkNl2EgXO2qeJuYV3Vz3mzrYaTJTQJZBUdyiUwCVo66v22oYmi9xgDSX4Y8JzFcV7K6r42yv1LR7k9ynGrKCmN4qLyiSRFAxmo/ZqRZU9YwO5lsP7jgs+9TSQNWZJgjemzCodJZP0o3XnhMb64slSELCqHQdnyissGleCRfGoxQr/RAxo9BVySoAbXvqLUI6p+pDkW6GQ0BAONFM65f5wXr6vgpJ9anXMxWfxMB/PqbC7z8334HP/7D38OnT5/g1/IEGyIUwEPtdhweiZvBj2M7BtKdJww2sLbb7z5B3KnEHaNUZKuaW1L5Y5+pgPjPv/8zAPzZOVVrEcoDAJ5XWf787Y/fwb//d39X7wGzOgdO2sNOJ4YXLE2qr+SA4YsZmprGyKcYVLB54/0s2ae792IzI8Li3aQ0yUd2ACVQj4esHekviO/l8d59GKtOkGk6AjDbK5OXSUNbpUW+DHjRLTVMUOy01ez3aUNLMTjaTjmYAqzOS141emxZrw0+uLgICLXVCbt8bK/Uq9XsXUpW/2tI4Hx7fu0wUsFfo1z/7f6UvFmPNxFitLy708I6aR/cu4e/5i04Yg2s75p1BaU2odtGKcWewIcy/i1zxRHChv18tzmg0tL7XVby3ZuWQ6VCr2Sax7F978ULp3EcyCjVilLFWGb34mtj6+szsq9MwleQGStFdMv+71Psu9AeHjyWyNpadyjr8B0RjhihIfViAYBOBCxwd/tetfm79Kg92kMc9/q2DouwklmSGAeTOnHV4LWTGjba44qm7uJFRxt/KdKY6qzmEoIa1hzdtVrk/vFl4SUcMxF3ReQGGLWqmbYC23Y2HYEeZREn+B4vN50GH4qpIxyWS5mBKUa5dQRKX3LgZHYDMwGf351OShBI7YImrkZAMX2Ch52zPSWNx1oQgo+yYOqmW8oWdi5ktAndJkvvmAwJbPdN+rDWc2e1+Aok5GTOlv780rEgkSBE0hgucAUgDiRPUqbSoHmj9U7P9o+02zEX6U6rwrjr947EoWhGo6SbxIY7nOPbCG4Wg8bj7PpW6SabQPh9iQukEG9QVLqialPH7tix1DNOpiIp7RiakMddMxowphgVawnPekEdcNEhyp9EKOPQ81/O49To3fjS7xGlVp6nKVp5e4N7AMo2PYcLz5qlBogI24dnePrwEZ6en+VCY4Ao0/WZoTQ35khbhVlmIgm6t3P1YyiB6y/jJM7e2zTTSeIsdHnR/CWwQdAOOmd46zPDemnbBF6XmvNqOkL4fC3w+z//0nh7IJkMzzh9hKxuZvi9fb8gwG++/wiXbRvgpun0yItCmLZsxwMAAGHpnxv5y783vn/r6vPjpscE2jFt6+2HjX3ueSYG80WnMO0rY2c01G8FyqcmPY9bi5d3Qo+miYGtkHqfjAcZX2M+BbCDQgPv9rl91mFmTEcp6nHOqh6mDJKjAk+012Ds2zkLYKh6BlR37K+EAWUZFesSTZfeNh0jOq/068YHU6y+HxKSQcf9O2nuAJO551hJPZ5sx0pewweMyZWmPzu0HgHDVZzGgDIy9CzJQ/ZEMOPgPqD6TStAi1ouZiWYPCw/1aeSOT2UwbaCNHiHs/WAdIT5vUDVMv3mgvBxm+XzIMdLMhslxTKcVw9AJtAHun3U0Q4Vkzw7NR6SskfUDPWG0WBsesv5+Ut7PNpHbiEK2fSRgPxdmpXcl4eJxGyR76yFdndGHFEDh+92ahsUlrlv2tO1HES8US991fUimRlNOa/6bJrxjJ/vdCDCBiBGK1j8TgD/PJVr3LE2GAFmPtghyBu+/rkNQlCT5EIHWvr77xUB67PezYZMH4b6CgnRicJGBIGoyjagAJQ0DikNLvhQHfp8znlhul2gQMEZvQY3AcmiNirtVgN3NrdR6AmAz4AeG37chgWgbABIUHBrOBvtxa7GyByoZDCFekgScun4WANWKHg1HQchbJdyF6liAoYPBpMume+MxCm8vm9Ng7k3jML5wBF0x0Mx/Sufpmk2bYXoLMnA7oaYDyOld4aTx0FMFp0i7k6DVlF77IWDIxrsQmYvYwy3kzeaMSwzl7tkOh7QMd078E2hYM8eTIWcQHQFltZPVkGNedIiwchYM1kKz5H99PkgpPGkItj7QepwUrkVHU0Oo2MP5lXL7F2OKQ5Ls961oPK5OldyYrSL1dWQ9q9yrqHaUth42dRbnB2xKiqkgM+379vf82VOM7RghE8/HpvMv43OrUrEmF6mCUewyrVTQQgyqRHDGfh+DkQwd3sQAGwX+PDhE3z49Ak+fPoOLj951WRP4ZsqhbtyL8f4SBgFIXZ3ia1h33k0F7bZPSTdWLBKUHw3KJYA4OeXAv+vf/p9w9FLyaFkaGOoyJi3jt/65ePTBf7v339Xj/aKgQq23iVHvyiGmi51FIZ3RcQdD3zsk7mXywaQXbsnc2W+8wIEV31mfjt0fd60DkehVwNcef4tpe9v4XS7COVesLwrwfFOfLmA4FayZShE3WcHMc+XZ4s15R1p+7ssQOyCpGkiTQskdkcRG7BOrmg+78xCXxGQ+866V68bvTZYeR4ePZSYBxXQ0N4Fe+eNH/64Ed5m0HT+JKP7qYzx9XS+Bl5gN2wmYlOuputk5aDexvZaqoUEI8RjsZPH8Dw1LXpP1Dsd/86QRpKMfjbIdjfZcWAyyVLedeHCUVQ42C+OgyODbygq6qUnDaLDcP8iXn+W2YPbdjS9f0iP6bVjmxL/B0B0MO3CqUCEdWwdDULE90OwCaxxOIm2YWLYshEbV/pXnxpPBn76j0EIbfgJyzXPDQKGExV6Ic1OfHuBtnlrHJG2riT1KKUGIEqxuxJI8vA3xqgX7ILHZ6pZWiRCzo62DEY2uw1CkJFpwcgkaI5LvrjS1JfsykMtQuf7gDHRA7rdLVJ/FNxetQDnZBADisjdjd4X1V7awFj1GrhAgrSW0BFL34FmHErQpAUhSqlGFONj1wbTkRqCpHTcLCKTJaQU+33ikDbkDmUBo9mnZSHNHgrTh8O2g1ye7RqsLtO4ts30VUcvmUJF9qRqihIY3D7dI0dSNpnEMULuee4nRSA0d19gqMtE88TmmM5bZZAxeO6d8wptW/WU7q62GOQbgQ0OpU6cgG6yF8E4Cz3uvt/jbog9+pskasKUAGRnxN4AtQFNG4RYdh451hcEg+LYCYvCnwgbPH/4CJ8+bPDx8he44K8gE89ZIbZr1ScTy2nI23jqqBvqCV+QgptULw4PbQPuS6/Z7KqCnAr1ekDb2txWBAj/8pef4cPlojob8cIKLc/pdqAv60eBHz5+kHss4g5a+TbpGum3En63gCIWFbA8r9TvaoTKhdfQBxUA/PFQ8SgoyR/ABilcQGLAh8MFA12FW7DaOCY40AO0M+9bNDsO9X6XUZ5vb6eNHgkGX8YYy2gUlcHoZNDGguWhkF0CN3vVvpu3yJbtP0/hiLQY3X1Go94RUQBg83Nwsyf+5aXAT0DwK59XqEUkqEeTy9HJ8niy3dyTBl5v+vuPi1WMN6n5w0L2dKDjYGa1QYKd8noFMMXbcdqproky8lw+BZ2/Yuqhxn0HluoWXPFzMq2GoD6dbvUPge4y9pgjrWIfdZd6UZLPBBNW2KzpQXZnRA+ZjOn7ccRm0/YevDzTRZjgmhZ9EL/w1D0DB/eEg2Tt6rusBw6mmF2zBlZk0w6CI7BafwpfWB+7aa5Zq8hue5wt0ui3vef1HORs/hjenwW99JQZSTxBxJnO0bEciPA0qDOZKLxEdWq4nQF3bseZCugEo4ne6I4DqA61RiXnlACLyauZo0HrJwDjuxGMqWuMdAeDHDUgn83J3yxYbGum3U4CKhqI6JzeY+HlWonrKcY6QGmr7nn1bnEdTpKPXH5+52oIwAGe4kWM+9VWJolNxMEJl6YfKOwYG58J3RxvhCZtEZoVt+XN1pZsnCdKlrtHAAHmI853gvStI8HkZ2OyFChAUFofcxCCmzzyW/8rKCnA/UXx1YTuHo+lkb8zv7Vu7FvDjhPjaDk9Ad5h4tQgBPYPBWyAiyfMngiNS6G2cUduOOpLilRHlAyZ9seOprRh2bljZSwAwOb5qYqVxgE7fT98H5V9prMp9PurIbXfeXcFosqYmZbVj2xtC5zRvENLhSjb+nrEQIKl5/DWw274GVni6KDkfTSa9iqucxki1Rg+oTmnPmnXPdhxKJZGOg9vvyOwZ+DNYKryH+FyeYJP3/0IP3x3gR+e/hme4Kcqkx+jf8EDEa/B+vRxZ3icMilZ7fzo5iw0vARGBi5U1oq38Mou6Pj//bc/gR1Lol8N6m2d0rwj7X/6N38Lv/3xO6N/kOocTleEbq6QX6Ir9TNA17yid3h9Jzu6yTqZ+d221fFTmzeXWTWlBoO3LQYyTKrwm9NlxNfyiu9C4iBEneckKGGTNPnK+sNb3FfAC5K+OAi8Z/t5FgC3i7HO7iJ5H/dKBP2sfR/1phuTotIh1JPT1Nj+T58J/qUUeOmv1/sG38CAn6CrqMOHMs1DVYLD8DpSc6hnZ49FvZ0s4TA2vomZ88sOuV284HdIzGlecqwafPNgxDl4TfkVW+5s0bOFCLmVdh7exzw2hr1gxDcAeC05tEvC2I3xRYPb+QChPtamukNFD+yI8AaYPDLGmWUM3BHY86LMLJE6m1cotSSaFf6GXD1qREWozj3eCSJVnVjrUVhGytV5TkKTPBfU6qQjPoiA7HFJbasx0wjYn0iCCOkxJa6Y1h4cLGif1HZZxPsUkOsjNPvfvtYFZA0/xXar2JzhCySKnLdn++OlKO0T9o3WspG21vab4JjfD+GRE3vVzPnsdgWjupmVDqRWY4QWB2nOxHTC0zastS9AhEBba4NS1LvXJiNxTTZng6egQz2EkTt2nGodfa4siGtyTK7wZXOycG2NP9a4LjVvy+w3bfRyqg8oWdrGtRk5n+1wRX4waJh0QgoaG3WltUQdeVb2mDY1ATRHM6ru3bcHK7/BqLIOqNDkEnSimnC0Osni4R0TuJkxH/p7FxacJt1uFeodYCzDnEMC9XNXN23dPCRnSqYdHSi7TlQ2kgQPfMPr70HYNXniz7c/5HPygkYfjnDY6d+imRoRLBsBXj5u8MvfPMOHf/09fPz+B/jlSvAf/8vv4fd//ks/H5zReLoslLw4o6hMVM09iwzjT0zfxZU27wYm5FhuVegqvI9sNGHwU+uwB4TMCSm0oGlLr02bVfIAW5tr//TLZ/jHP/zFsIpKZ5X9Xgm3hi3LGCCCj88X+N0Pn+oxZCsCJq2z6okl7OpEBCilnxutjhGDFzUgPN4ZIbswTDn5J5fpNCFtc2x3wHQrKIKL6eTOh6MwOo5vmmfwfFdixATTYhbqdUb0mX4fvYvQpR2WuyYzp112pj8pfEFeTDWfoKpNUprtxHpmT8pYW2/Frcrk7PVek70LMU/pV6W9jvFVUs9U6Z7NEOX91LbJTINd/g+K9QpPj9I4lGh+3q9Fbve/ntGV5tAHBUzth8Xl8+TI5nGFZfIw+WZmwKDX9PPsrF1iQGXUn8f1PZ7jD+xcfiCcLf6meX3PuOE5EI7T1+3IXCzzXiNkHIzA7lE3bSeV3efUCcwyN2LE/3BUDp5aFIFDcgD6vl7p+4zk2cKeZRi0Rxa0tMHPIbrpWw/R9zpagHJ6BN5J5hzcEUHut10hNs98nDAtBAYcsqoIN2EN1O5BaIKJ7w9ABLduOXEqKgnknhJH382KNnZWSTkIIA4VvsuhOZn9qv6qINdfbXcCsNOsvSstCEGKU6bIQXP4MdD6iwMzZHZnNAO3NJrshddRYWd6eyPcT+IS/DHtXh1jzWCVPjTbGrkNE4eytCfjtjqzaQaJLXEApyiujG26rgUAOeyBz8gXZ0a/WlCQcPkI6YXSNVlxv2o9aga6tnrxTgi5pFqLE+M+q4UZK/XrQvBlCpV5CFlotj4aWWuobclOboTW5tZx3fDIeIOBMmIcSHsQ+SGtTQxCdM4CEjyrk47uDXGYfbmiVKPwkCtTGox8DrNiOCod1tmzAmNxSR3BnVPfpuVyu+3KnIJ51ji2tljv+djW/Ji+4/fa8n7lcE3vV4ZKycRUGjpdqrPKhqVbH4tMN2h1QwyvhjI819rVy5hjNMUgxOFAxAEohja5yyLyRHuIUOXitlUiiQBePl3gp//rb+HTv/p7+PT9j/DT5/8O/9s//1coJciHmzWeRV3lENi+SRou67qEj0fvbJoj9fcquumfZQwTOIVkTzAvPnZDFV3TZybjaMVOdtySVZH+8Jdf4Pd//sW917wZDlea6GcAAL/9/iP8q7/5oR6lFAMagQ49IrQvk8vT4zhNbWW5pvY55+mOsASAbdvaDim7UwoFV9yFwa/l8m3W3cz8nB2j5HdbePyq2VQBlR8ldcZAPQo7ZVD8Eue9e8uUrOz28609TQCQaTdziJU4X3KflUL/dAoduPFk1aygL4xmmA69S3SDvvDeYVqtrK0VXmPUPgTm1foGr904w+LyF+qeZevggN6UOAEIWHeuejmhLcPTgrcyz0hXtEdOTeBdTA2vDQ/UDw4FIUbTwIi8A3012xmxNvvcmTFGbN6IOWqrfElw08KwA8GId6VTJDSP7Kou34HxeXhHBJfhHWc7cFRfI//VOiTqMR8edcjSNV5uNGI7y1gDCexlD6apm6T8KqOGp2XiOcOa/tJWzdHk7kkQrz5vbSfXVNaQrJet6fFJSqO65DoIzO8cO4KX73woTEpjNJvPlhADEGYYcTshgDhPSe+fUGx1x4INRFgJJ5dwUz/oSdHnQAAEBeRYAGlv7S0psstL2m7y2QxlOVc2Zp65yqUnte1NO7ji+BXzF/Uy3/H+ziDvhJu3uZIfaYPI8yX7ywgfhw15XXwo3oyLjJRsF0RW5L6BngSPEpQi1hyRPNatw4VkvPJQmaqLpj6s1zomDsFPtpHHk3rzvKVBCPbKNYHkCHOSCdhpHjk4OpmyIyB2dW7O7/Dbuvg6Z3TGwEQIGYf6gnN4jXlibSLyvJfkSRQyPYLKB90QUO60WJ+bbQGVhqGkSUnMnDL63QenV5xJfZoqWrVwDjj2NGSDjdrxiAifPn0PHz99Bx8+foJfPpuV6JDw3WA47NO/qoCQQYlT3NGh3TuEV2nLyuk5fQRJz0zSTQyFFd4Ug2OxRWOie9qOQ0NP+5CSdM7IJNS0rFzYPGGltWZlPcoVLH9Z73spBP/593+BrQXe4h4f+9Xt2g1J+B3fF/X3v/0OPjxdhFA+aon5qRRquyVqfWMAQ9+vcxgHLdDcT9GlNHMHX9a9mcUc9cMvQuFARBXf/nssp9crGEdGsX7r7ECZXwWVg376GDGb13fI/wlIF9CdgD3j/1QAI2Sh2HgJFTFdtqNF9J9lMo7QHvRrqPxNpS7uKc3eATA6net4SvtO9PSsvOTrjLwjcLjXXtUbObYbeipmNsYM95E8Myy2/EhLZPSVchfbebU/XrPbluCUknV/2FFNrdvmYSSM1DNNwdS0Xxn3LxIoulUmz5c1rsWyrA70eAacWSOrcFSK1MQ5k6xcCn0IhqaZvpA+PdiVLhgB4BriDUbl/fWY5X7w9tV96h7L7sddHCqrwRavEya+k0OqzX14dbZLdphHbOK1eotv6QDNhy+rZgNrjyCCdqlpcCbZFO2h4NWVwdpH9llNV705uBNxCW6XpmNah4QJRkRnfShTyg2/vTBDvprApDflNce8Cy4UTw+nQ6h4yOycICp6fJJd6W6cb0IHkPiHuD7d0QGt2j7YofW0/euvlgRBLH0TGY60pVmvt0kKFtjIG6fMHTbdaPV9WB9e/zY8peURtYBieldoDpa3mq0irGYv3A1dx1n9+DAtYRzPvm08z8vl7J1xPfS8gHQopE22ACygssdk7utqR94A1PETJ8PEasMR5WSbcET1pM5MwyAFAMiqzAyvGsXcLx53j2tEBjcCdTthxLli6QyBB19cw2WcLJHfK85trkva/tK522WwgTk0d0z0O1fcoLS6gLStO9tcxqRhDkRDYzJ/5ENdK9P8BtpVZF4hdFzmygtFTQbIiJs2RJEtUn/yeUaBHUklbdYIt/XrGCIO/kFnR0dKWuZsDM3H0ZosQffXH+sCoTpGLhIAbDUQ8enj9/Dx43fwcn12QzIS43dh+nbPwabfqUWn6E90DOrPva8Tj3d2rKl7PfOvSXJ0qXxZt61LmhqOYjCz+KQ0bSp3c2LTlup2LS1VyCeaLxNgRcHrEKzLZXSOjAirN9ksn68E/+lf/rQ7txQzf3e9b3SEQgWeLxf4u9/8AE9Pz8Oasc63bXWhybZtSqPTp30dsjQM9mimmSFjd0GMdkTI742PiUou32Z5Ghc3WDogzDctIclz6uYCN0Tbg3HcOryQ+a6rdcg3wGcT7Kk8gc7htnra04K4xH6OXgFvO+ynmf7u5NyilApTohXRfUL+bOMASIIQqp4e3C14izA9Aa9c3A3QabsLaWfp7l1zz7uYPD9balqbwcrXowWtjYsszfq4nuGMs+gIbi1tTAU7s8aFdW4HkakzBT/O9bFggi4BAbBzh7D3a2mJuYxbAXHyiW6lSpbW85bWntvRMdWZ8bBLnQkKOC35pp0NM/unT+mn/RPlusWWrH+v6Zy37BbwR91apSB8eYWgktPLB8Wlj48yV5o+6oJ5wVP7ZfAkE92RRfbE+7SUN5zU41y1G4RL/MBLvNsm2aN8fjgQEYMQU9XCOkGys2p25MDIET2nLRpapDqpIgZRUs1qZ3lJ5HzBdSWaIRtHQoza/5zf7wRgeuxlrc28dDRZGt2uBX7Rit6SlWlkjiThIKqo5tYYKATgLsG2CnxXK/3OjqDCKn7sI11pbR2PSgc6XNaJZGlw/qYhNeoID80sLTt20PpHBOCljjGI3bPAKxwh9WUFhST5mQdIPEGIKO1byfCq9AhEVGMy8R0KVgycQ82S743ANWD6pI+G1IyVJ6t0UqvrUbWiZo+CQQc+uzkAwBxhMQJlLMyi30uwVwce+P5pNqfIGAS9aI3s6nXpBXX6yFg0Y8juVpFo+l6ljCOlHueBZgInweBWiLj89e0G6ilQx1SQxeJQaLRrRBJGXM60iBurzVO4w9BRke1oH84LlZZ4/bXNPFdwWlq0iWFHI9pT0Nv8p3q1ydUbWlyDehmgSZ/86C5DlaHBfFCq4xEBLtsGP3z/I/zmx2f4zcc/w6+//KxzHe0vd7jdFGb+OprNZHgF5T8HPxc+koqO9/nBpO6HL8UNskfw3FSzlby381Gdq4NsbAoYq8FR/7FwEdnos9tnRAAbbYAbwn/908/wx58/m7bx5XLQlEoxY4n10whGphLB3/3mE/zw8UOnR2fHLwHU46JkLjWLhGY7dblNEDYnN/MghA3imskFaoBY9UAzX9i0Tv6YeZp/O1G1wAd7ziyb9Ba+eiuxYkm4s2yzI+1QEMJkthqsH7n1F0HbBUH1qFkqBUq5Qiml8WobiZYHnA6vC5h4YZEl49HwDrr9JNwqR2c1p/0ku7mjDnYTyjz/XYIQk2f9l3OFDOGYHvFIXu0cvLIaLpnzjD0I0M+dNfkOb/qovEsvnM1fuorfQYcAE4wAAD2m1dbp64G0GRcgb+lXbJxoNK1muxONfocExpfAi6TYxtXAwT1kndfLozS9Vx1T8OpcPtwGlewf77fGdLEN7AeVaPhjD27sqcHCMP5+q8X8CDh4R4RhNGvQYEgYVkTWvNWJ1GfKzKJ1ho6povHU7YYw+gwKvZ5+p+jKhOaN/owSdrcTVWdLLc8bkgAkd0XUn0Xy+0YlUYTjpCpGlijSjvxAo2Xqiqy2Sx+EMOv0k6FASoco6QSxjoIn7b7BELDzvzECjgCCbiQQXJ3ShuZvyB/luRGxiBs0ezkBcoOb7B+NHrmVhhoQMu0UVo8DEmBpDlvU/tHVoclkaLyZ2vtoer8bLWmNOtOO6xOCMl3+bIhMhLkdZ2fkrgt0LXkF4ljwBfer+nOHQ7etU/oOg8YKwMEr9AiEeL8KZkb78Mc0sbj8sUknSgoTJw7oPyvyyLfNvGRFrIFSk2AgRmWxDIBchi0YW9vihuJg6PIDgL8vo9ZxRPa6g2hSb/R44pFMLCOdPGQFsevPEyZyyvM4f52ClSw8r4xLT5q/FTZuVZmnAlHb9gTfff8DfP/dM3z//Gf4A/4i4zKK7+mdVJ0QXgfv22w1Z51ll08SORzIOgdHc+7pJ+sw7sMVqiJ3xBwrtJ1vtYfDpDpdzYLTfFrzrPvI87wdD//tTz/r807no6Zm1rzsTHWkm99x9+53H5/ht99fjM5ShtRTo5HMA/JEmTI8VHl5NfMyByEAOHjNwQUf12SLFGEDvbdilMemt+83o0MzPa4ZLa02DfVzSyf5BJevt93d0zna7CRoILbdnq7zCGdAGvDK0t3TW5aql5Pys3ajeidfKQWosE3GaFD6qbehfBBify6e0/LFQRTfe/WR+q9UfG+OyNIuoh7lDU9PqgoJ7sW59ox9M3wQ5f4RXW+vtHOIbqFlNb04VLuABDhbTsdv1ui+sD4J2/NBUVfDROS/lqh2VlbGkc5380jzl5HMPQN+vlXWJA6kozXgOXuJoNV0EGzy25n89Li3MmM/LbfhIMdi4TNa5SSCNGPl0VEwYomWmNASw32CfDpGSHzH/o+0YPiSBkKyZg+PtTV2dKvbJwqp58rOGecvnxQ6JGtlTO2mWITbh6PAsR0RGo2oRk5T5nJ3iBrxyncIw1t80/IYWViFaZEaKMbZW7NrWV23Wn3UvLErw8ikM2PPUZI52ajtNOApJCq2w90HnA4IqECNUZBRnqE5XNm5iSC/e7yUsrIeCwWQOnZsEAkSw4IMDpvfW2W2hbrHfrWbp60zmCdgffckf/spVPWJ9emEnZ8eU/sr1da6+5Y0K8lt0hAkizyIHTf2III/mygIIBPyc5EWYWboUTruGmEJqkco6dkuHEaSehD8Z8w1UFbR8Wfk06LPk36wsi+lDqG2jY2cJZ1kf8rr6Zw/UoRNQIvsE9AjmYTkVhK1luaL3q3CwR9NDhHEY+ps0XYeaMFaOae5T67UkeZFLYvp03IBbD94eVB3OZBjl5Zf6mDax3TCWN4PFB3QNmVId+PJOytjyHzG9+ZBNr5dIp5fmX8Zv/J51uaRNyt7opfFpLLJF4lJzWt5vVKn6T5fCvz5twCffrfB999/D79eX+B/+d//Gf7888/iQNV5b3aeK8v3s1pRHGXjnzkck67r0M9j67A/z52lej3fKDg8am8v07NyElVrSNtQUV8Bk2l2RNEeHFkNT8bJ4OQsj2HyY7TSZWWZytm6Wo7gQmbVVqiTr5Xf+faHnz7Dr9c/dYZTd2xnG6J8Yb29u+y7D8/wb/7me9jA7HwsmW5H4PZGGtqqqEUYThRmQoy7g+18NNoFkQUvanpO7st2QQ4IfIDab+lF3i5pk9MW0POa6oLZ5HGLvLsV1nXou5aaT8jj9I05C5Vqj5Vqk/GdKL7vh0i+wVcA9+1GAl5yKIbdHk+eIGAvS2eWL5CxVtrbjO8RZAEOsUXsnMZ9sgNGJZ6XK2UMGjax1e4vkqNV8ihd0xaJPXN9AwB4byNjBybBiLtBGxv5PrMhYfelYalEdL4PpsKNqVuGVpI3orqp7d9iPL6yHFgPRJgghDNEkIDIOORXpPFBXlQTa4E+/lktJPllP/wE1tsEsiWX8ZDB363UbbRJEIT1E2+0VR+7OaqJSlopDkLUhuYt777orX3RCwoxMWQAwPAShSbIRl0fXQRx5MkT6X92FFGPyihobGD7gESv/cvqJVNODtZxF5+NQfSJI7PJyI9iOsUed0WqnUqa3pjnulrh5Avy6kf9ZL8DxoTD3+aHHRuzpk3Q2K7vy+uFVd8zeWOLoyizs5eVai3NlRuds+4T/PjvyjfOg4jLDsaI3vzUOpP5a9N4J0N3GZXktgOfHIYecTKeOVlSRxMfOOQwc0docFtNlJxZP9rdOprer90Q54+UBU65smV07L/ku1irvYj/TEZ2hYe8UiPspxHwwyinVfmoWxTVrZa1n7OaoVC2P7eGOrvxaeZ+O79ioCEUcr0Q/Ol7gKcfn+Djp+/gp+sf4X//lz+6ozNqoA4D4nU4vzoXdzvVV3k0/9yiyGXCfYAv1nNHeCYS8e4ggf9Ii+tKknbOZ0KDL/md5TnQarsw4p+VI6di0NbSA4Gm2lRsEAVdgMJxDfzcBsm7KQmr/tDYOM4t0tpkJYsi+dMvn+FPv3yW36pDaueRy+91ZqACv/2B4N/+7W9gQ1afqQqvpuc5IC2EDGKSeva6jAQsSptx8Qo2SMBofbuACxJ0AQq+jJvnleR3ZdfNzEsAMZiRlmPmWgmguxW9A0ZJwB6/2jN3p+j3gFb31IfCK3sEJMWlBWb6kjxZH5WrcryfGhsfUT2SSQPcoCKe+yyoecMyV5XnAROenhEGbfla0K/mDN8y0o5OMNmAnSbbb4+OPYfkrvG9taMxPtwh63Dv7WbwNB+M1aWFLBd5JM1JRYNC55EcVZTJLztE8t0Qx9kxD0YMJZr4wQZ6wyo9VnawQ1nyq96eZo3q1m5/JRqSE4bWGtuBvbIW++Sgln+4zFtAWbLXyRZFyOGyRvpMVpRLE4IRN2nDo2ysj6H+frtZamzNLwcjLHi1+Djs8N4tLXViqJ2AwHlD/h6kOwDrRzOJ+hh6ErwSZ+2j6YRIHlc1KuwTNaTmdKnCCQAmEGAUXrP63NfG09FNfPwNIakMuUgjGUOqBkGCE5ocRlc327aS304AYhDV89Y5AKGBiHoZG24AWynteHQugGkoUAq1o02KWXnWVvk6zcqQTbqquGFpTVpptKvg5AOF2oafjcXWlBvXjNssuOQR5bkDyWKVgmzPhelpp5yNGUrSbc3wRT67uNVCFBxoPFOUd5gmnpxa2sJGd3EtBHz3g24xbQQ2g0jQ8NZMN+Sw3RFgK5J1XhQK7cum/gAPaP6mmPSIph0gk5aswd6ggPJOHIt+mA2Y0lFR0/CuWTEqKVDq+oZz5nWxvKLHJRBQyD8CVmC7pG0cW26wqyZnqBWj76duMoXotq9KbHe4hrBeu/Q6OHzirhPB2voTQ1oCqnwZukxXKqkRAVgvTmWnkx37cR+XLPwNraNHeNjW8JByNPrWsa/rcGtUTCceFHHe02AMBRH12dwRmanJ4Q70viKgKhPUrzVTQ/27XhlVrsHKBa5tiPq+sLjcl6igsPwW/KC72vnJ0wbf/9vfwY//+u/g43cf4PNPG8g2QJnEFwdcTGPE6qlgxJ7ScRZWaOmiOgfy2rSTcZGXa/PzgxNtB+guvs/BCmE/J/clemm5gw16ZpynznQGrvpwl9cIXSb3COKk1mXu5qkJtWMCrCDzGbdQvoxrJRCcIzyKzI6IXr+qT1k/usDLleA//tc/VdQswKKuCCyJjELCaZrz5R/+9kf44dOz5grprG85o5HMXUE1facYQJvoAa9a/06+oplz7FwGRkdk3UPmpirrNnmGZq61+LgMzYemADuU+QnB1dGX6jyGRscUMbjTXlP4LUDmgeGl4SiX+Uox+lE2GuUDQEWFcTxmUyDpFwlClCsAfAaAXwG2H2HDTwB4AdrqnFrA7pysul7nvFkUh8PRflakvhUE/WycSOd7BnSv9uaDjtki6qNdYNJi9jDHhGlC9whZxi2Xv/b0GOz0CGVTzqCN76TsPEJl6ilmJsC8QCf/+sEmtgTFhwMut84sQ8O4Jcdrw3PN3uadwEi4L8BKv8xlb4KhGwAxjW+hDP8qv4wWfBCA3EX1aBgG+KKKbr6IFRgW7LUvoKcq7EASFDoEJhgBE5vO58kf9/to7Y8lzOfqkICOstXRpnmCl7n75rTT+4vKV4RBW8+Gb6JedT37gDY5viPCfPU0oFGce0XX8R95ZqBmUWT1m5lwZoEWaOs0o4b0uzr3MyyQv99t4DqriRHFhlEppr6DyHxvA2h7kDGW0AswOYYJtnp5LurQ2qDU+6dbehv9I3aGU1XMwbVboyBpcNEBuzoYWvl7CY0ndkulc+OKixGmuEkbTIuPhlEkyvzQnNqfq8C8p0QZ2s0EYp3wNQihjlQwVLAhxHxhecsFFMwqOYbNtI0cfbbbCLb8XmsXJ3HIbg3qVQWHqzsbk0vUSsDR08krxtUXR54h2qcbL0lZsuOGA0HRYTohuLIouiEhLxYYS3vDTHaMc0eozEwF7FL493b0IBca3vZ91yppxuWYF1iqb2pbClrL2G28mAZkSelq2fonTAtDsMeCMO4jOzkMefolWT5Uu9kOvDAIO6cep9IwEZnn6szoc/E7bn6Kq2I5pff21XQYSSFl9UGzjI1TlntWnoJ/F3BEXhVMQYYSdnerV/zbBh9/+yN8/JvfwOV5g+0XAj2GkMNmQwGY1MvM35bIA3NBD1nmrI2yrHmKzo/WscZNBHs8w/4eP666A7QKZvwYuGNgCE6Plol4KT4atUGQIdP0k3aMyijAcODIWbwxQMD6yihwZOSB7QuXKiHx1CqphATXLaFaMktQ6++EV7LL5jPQuEBz0DS98+UK8M9/+kn02XGtmobiBaa03d//DQBuFxBD11zcWdvW6tsgBr7YFNzuVkcXXdPsbElkb9cOWVMgmqB4fswT/97MYpMq9+0iLk4f3ptylB6SDdUx6OdGCLYdeKjLIqSvY/+6oMFA10FMhqCm6/sw4Aywy+nSd3l58rOTHRS+FwBoRzRhgQ0QEJ8Atw10nJJL3YXMWEwM6pDOh+TTSMI7ifgxjGTSAXC0R220TxwPxpF2WTEKhi/IFR3Ya4+kSSEDomjyzqSJOt46rOWYyUqGPXNkrkYcZ8I7cNRSqXEcZc8rX/Q6aXGpO8HgIZFReXnYoenqQACAuru4fqJ5nQkCX5jLk6ZD0GPNo02S5Lm7jDEc4JzjK/n6RK53zGI/W9JSEaMowZ30aGd6DfQrfa5ts8N98wE8sDFjO6VZYx5T1tF41lyH72E31Y1dIjZmsEnHKXMiZic42Nyz0Eq/yHz4U/XsOwzKdQxW9zJPMwRLc8WgLZrsO0hcB8uBiHgRMIOuHjZKONO4SpgRQPsqTxj4I5QNrziCYTCgaG2gpazdlmMRgQQgigQiWp2WIrZWyLPhos81kro1Q2UzRgobGHVwikOLePdDfV+YJoIdw1BxclpTVc3POz5ah3jHaxMUNgixbSpIFqPYufFC6Tt3KWw6OcX08Ysv2cySpmyoxoxpl0J2DQS3Vfs0bZSH2SxmXU/Bd51EK2eDdmn2SBGwKzjJ714ZXsTIMj0J0C8P38GzOCl6484qgF7BnrOHlRVrfFQK1cBdhGQ+k+MVMsWGeZ+YDtw1CHraJ+q4UTTSmk0Ky9MPikIAdg+nvOS1GBVF3QpOkEk2yTHVB1CI21EKZo5OnKQb1lsy5O9lBxhKMt4V1lEg1RxV1O8mE9KEf6DhNUfsiQyBbiuprcRxvTuXhXuimNt5hn+Iwq4GQqjzFwAAbHC5PMGH776D33x/gd98+D18vvxlOjQeCRLAcVHQGxGuP34cdJYTj7dxn9H0bYCsv/ayjvr4QLEPgXv1fUQLrVoLfX8PQ+UMpDJ2lQW6OQBlwSo7ved7/Uy9yT9BAvinP/4E//KXX01a8Hxt9FOn5RvdXPQv0cNqyr/78Xv4+99873GDmd/JP49F8+4txojy3tdXVcneRuLn5kN0kBlsgGB1lS540f7whdyhQIff6eWGvu5oKnGyqO7jMVidDkAiCDIAbhfw0TmSNlMLmGSrJm3wf4MNNtza0ooNWAmu5GLbuav1GvZIS4ZJ9Wj4472CDOhUt8vTn+jZg20xNdfi3HHvdp716aPgoYW8HSOu8sl+IOU87l2s6OXdEGR+aKcbqIoltvwSGDxqOmFIktkCuygbrvcJb63y3RXUoST8U3WY/FSILw7eyDbLYLQhagkW/TVNTYDVine6e/ThfZFAg+/3hwOXVWeiLXFoTDnEGgPtiTE+Ztn7ZiAvwG0i81MVmHGZAsv2mCmbAAjaUUfmny0rXWEdFD7l/H4Cw3hMEBsbegCvaX/jzBLjybZEUu8lGJjJYVT7zevtczUIERytWdR5FpzgtnCZzKozV7TtI+G9iHsu7mTVXcadIQixqliRZSyXApMjmaCzxJSdWtk2QMN4MK/amER+g5N08SmKEUddu2t7HHPi8zeS8bSX367YBOj5z/Y5hifWvBZnRBQZwfrcr88ggVuhGGZLF0RCKWiqyI1ehGJ6siLfaeI0wICgR4zlGUcU7oLcR9E6O65KRudMScbQiASMPd3yYVMcwQYebP8qZ3ROI+6WpH/z1TP+NwfgagCkKEFJRRTfiNn229yx2IhA274DlGk3Z+2NOjMgAuCG8PT8DB+eN/iw/QzbZs6kb39XOaeLO4c5ZEnxZPthtMIqULdHzKpc2y3uBMSyfZClSg0nOyJ7ZzhPKqKzVVXuTitZbR11FUiUywEtacWT5yvQmuro+fRZE84w4EqqUb1WClh5H+EQL/ZWIbZ5Uo8bzBF6buRk7Ulj0D//8hkgua9CwY83d6F26D/RhVq2Hz99AmjHm9oFHGKstnEjaqXgbklL49Vk8CIvwDHprYOr430wrZQJA9alOAn/t7X7KlqQl48WZZtDNO8gy7NgiDxHXnMYdzba+qud0gfFrXLXGhLNroxYtcUx1ulqKVuh0hYTGdHS7zIHn04+E73WJrKvRaja0FuiDwzfTGBc4WRQhDm8V1sXCiNfXIpgX1BMddSzkMnDtAnuV3qP/vicEhesnS39tI0xyxH10va5RvF8hhMcifkQ0eSYBvPHmel9L/HANsj0GGerxwVdOOaR8W5+HOftTJowOGeN+ghw/hMPh53uO32yhG20+OcMrjlKeSe2RWbUBX54UC+8CvBqfl3Vb23iCYySrDaGsykHwuOgSCXOMzIhUhomBvxuYfeBfZF/trCVfMdwn6HkQCAiFmU6xzqpouIXHjksuxR7LtOgozE2XFktEAAA0O5BqMnjMTo3AtWy686AWk4pBNACEvwetw0QLqa11GnFv+vAqBNJ/bhAMRc8o6zORr2/wLROvEeAHeCya0EcvwTubohOmQtVFCPOB1hk63vT6rvt18gGkt+5kQUgxgZILymmDqXW3hwUICLYJGjTV26oINDM+aU8SKT3P1BMYoxd5btQu5ECNZiwNmiBKOYfgwNAJwri/JY/7VhJDNANttaLE2NmF2YzNnRKC49FIt8X2lf5pNOvnFynz65wl/J6D0qbdxJVivrOEYnHKyBunaSk2gjd6UDyfEerCYo0YVWKsIBbmZEdDSYM6LyjpGN6WOaEngPGoFX2cWIQjHiZ8077YYDXlwHgbrYIssc5cmQww+h0j6549XmFG25ae+v4CLLVgFOEIXSZT2lqFeqAAHW3BwJssxYJdYjfdCBMe7u+I0DcYNsu8N13P8CHj5+aEy3ry+OGwy0OfZf/DLKDQYhXh1kw4hS+u1BVUalyd9egzKtCE5/7Oz7tfKh7w47BAxvpEGOsU+6axYkOazNEy7KXW7PyKfky0v1///ML/PxPf5R3dtz6BUXUvbOfHW4C+M13H+B/+Fe/SV83jJ4uci+7dEqP+Q3QLtBWO0GPfwpSmnWa9tgfl9d6YbM6PDT7BfyciRAWRCV6RJzfEKALtkjRcf4Dn848s04QgmYvGZ0xjiPWLwkIChWxWYDbi+/YI5fBq6yODQMDk6WG06O+d3kWzwS/AWzdhdIHOChoIY2HBwt0iRreGe3weT/eU/hC57Eoio5VIzbG+22EfsGSl3PyOKuDlRmgsk5kXmy4vaHCtnAQYvdYSf+Y0fF1w1mxKXYY6xRhoeL5YOR7gcFkH2EsPE8U+QDuXV2htgeLU8E3mMPJQMQARoKXVMCqk9a820VmQQX/mI/IzBNe4ZcIplGO98BXq+EubBRw8IPvDTBqWpsBrFIt/j++2BUA4kWBvBi3Bh7acTxiIBhBNhzs1mipl1SLDp7lU601IhoEcSbDzTk7YShE1EE+QTR4ax141jnNlyADQb3U1Tn5kkk91dxzIKG5/bMr6Nw7ED6fBSHi9yFg+OxeD5Qksm2cbxM1a5TtiFE0NKJxRdzWUofEQaIIOtqGaA/6CG29ho1ovgeHL4Dpaw3YVOOfM1tFQ2sHmnJCVyTF9AlS95zpqBjY0A/4rS1MaHrCYBk5dLLVZjmhafbu2UI/9TvAOmrnZdsik4CRQdzhTXdPEPh2Snd8oEt/b2PYi6aRDPWfStAKsIweOIga4uG24o7nckGF9gkB0AZQNgS8IFyen+FyucDLtcC1sEy9TZXL2PfIyrkuGDGCfhnwNEvkszg3vRrMghFkv4T5dYiuycNObs51BP/ap41Bv6EcWTDu08eLIm6OrLVPhiyl16TzTGboWeT9O1s76U6zW8UZuo/u+W6+5UHRyxumnZpMrrvb+gOiPr9c4deXa8eLouuRfdK+R70v2jMNLpcLlBbk5UUyvhQMZQD0C1uUFr7PgoMQ17YgCEuVsNuGAIRA2wZA1F1QbptKDyFqj7nNCxobBQGpdPpFlacX2UlQVfxcZ2L9xAUYMOhDvOjKOgaM0I6XUxN3MAdiWEBQQkP7xtMz3xNiafayz+qKYT4KasVIHGF8YHO4XZa9XTkd12fH4mGHy468P0nGGbi1LKuH7zkAR2Wl81iaOJkfKP5kWlbLCjz9mo2/AyPx3NOoo2Jk0avz1uZJS3Vlx7KOcfnc/sp/e9nfoeB5B0wwYo2YDscenZ7G9SLOT+nr46ZbYBXSWTE/lanrTLZDZQ8Yvq208x4ZogsAyHykVaBumhrW950M9JFt7H8kfTQ2go5DsNmP8u/I7qpBP50b79riB/svT07ycoot6kfLZUfmHeQ7IlxugAOBiOgssoRQjfzRQUYZrSiSZ5XZ5X4K44DrnONuNYtdwa/pJAhxAPRQIbOTgPguiAKl1JU2VGxd1Mljt0pX/XrTRsJqHhHUMwY5esrbrGHjI5n8IGT9uO7GaP/KFcr1CqU0mkoNQJBcUj2pt20jrivvrCgEfC8CX+MWQSadrV1ly7shRsXt9oGfutT2s0aB8oJcflz02Vyh6GmYrTxQQ9LylPKa/tLfd5lLUL8gwNRjIrzdDMDeQdKwiIPAqn2mNe8rkZW29HcFvaS7jpXudluLkZhOdM1B7NyZBDYPL3BuBRKBuWA74AQAvtRINyvMldwR/y+tfmlZOehGcfeGky01mFFlSzPqZ41g+fqW2SUq1tsoFDY2ToY7Ifi39TADgBuUQ7pq/f0KRqMVW6JWwAhk62xq7hnI+H0Y10H9FPnu0ucZ/TzYp9HqjdPEC08Z414zKGl2/Nr36N4TEHy+APzx717g499d4H/44Uf4+eUK/4//9z/Cz58/Qylx+L4PhfyR8B5W/6/0dZchPjLjL+OnDkYDv8OLGoxYQrr6/HCt12BXxpL/BIDlxpC0jwW5UyqSNPagHUC+gO9WELGD7kFXHFX+qi/IPu7SZe+xMxJ1DPzyUuA//NMf3XOnBomeFt4bW4ed05cN4f/8r34LHz88yR10L83uEAOdd0aYex1SPdCRW98VR5iX62k8Y7sAAMK26a5jSzvPhXHe4yAEJnoa707YwmfcbWovh8eWrz4prdY1wFOI4FoKXF8Iri9XeLle4cq2UbvbA0qp9k0pVS8gkOBQrscNeMSqE0DCT6rD7DtRWJM8NeMZ29tJNdT3MaCTgfZ+PvD3qXusbNIqvM6kuR6EyHM7Oh803bwtrDSGF/iYPLUp9+4TeiiwEOPxhN1LJ5993qBf47jD3QizMtM8U935UA0Ow+NaO69/emz5NMeXBcIeaqgDgOlPaoL6NStqfFJfonn1WmPhCNiTGWw7IkDzhffv9iHxS0yTv0IHnijicLXhQCCiX3TLykkruBkvubsOmnJnHDNRjmdldh6tXDnwyjYFW8+WOW6e5eNVBGcNkHhlX/Na1VOOQZHtEAB6TqxOXNVXhCKo7I4CP4U3I4Z3YbSgQ5HgCx9L5dZyKZ2dNqBqt+ajJrlKe1vS5rPOJnSfvigpqQsAjJk2C0C492oxMMVaFzamowM6GeurKyIpluUsR+A4wCHodnYsguo95Maiw9Uat5l/XZlirHKuUB9jyZyjzT8Nv/IRn38f4Isr1dnRfFQKBh0yS5CbZvq9K7LRoi0YkeNuFbvg2cA8jkSNdxJMJvTO5raza2znAQ6Dx+4c6Wik/tHek5TG7vUgwRHtKxMGMmGZd7tDwsw7AdWpXaGm3XpnfeyQ3txT/6hN61erphD4uGYzmnTn9bBpAioguG4Anz9d4OMPT/D0/AGu8BP88S8/w7XonOWqtiB6xmGu4/AagYHpDpPXUC4FVPBlUn+WpdeTjBBd7Ld4Vv6wyKCnZHhymmbvjQFs1aKZp8RT1eE5Al4V25HrAdZ3C9wZsn69hV0X+eRhgFb+WafhXDdRkef3fKp+TXAlgj//XC/Zlt41Y8fr5bXMrFQigqfLBp8LwXMBIEIoVJqu3/AiAIrDQ/H6YIDl17rD4oIbbBt2ARVVLX0wwUkLJPb96wKM9qeIM9/aQ1Xf2bAuVlJbo8ImwQASuTDn8/p+kzpvrV5Vpy0tyCCf1xZ0YLMG1N5hM4wDEdNdlZ6E8XO081K0X2Qy7uCMER/z5y/25nkAtd6NEEyIGamGo+E8XZW6Cq80LR4PBc3Sh/mG9OM0ykGG5fn7HYLyPC1NCUsq0o4+lfPgfIJTNw917xhXuoPClGq/TWPEkOyquEPHDoscETPY+TvFJXkHCa2qGOS864HooKHY3sehz3OjYCHl3Ey9zDh6EqOaUnZL91Nk81kZY0G+Bou2zOjtqJ64+1KRjuT4bQss1/IigA9GGLrG6Mg97JIPyh7ZRsvWyZHxPICsikd59fDRTJkRLQ5hq6BsXrhwbq+C8xQ0MscYRxm2klca2dm+sxII1JjTT1+m3hdgpkhS/PFOiJrTr0iCDet00nyOsUxPS+KYdDshdEdGudZVPeX6Ulf/lCtAKVDKte6MKAWIrhqQCIq1Z5z2twUcpP1KaYp50XY2wCdL0abrf2Grd0JsuIHdXs0wXgluBq7Q1IIqVhm2hJsBW1c4xaabD4U8qNKlculrW7f24IsKDa5DdwR0ZbfV64422/851K4lQ0TAyzy0sbm2eaemq8PyTLOYNlHiBENwZGLC/5OS03myFYJuxmr1Xlmla3FVhBUnXzweaZe0oXJMB6fsxjX0zbdKXhLIs19skKmuJM6PeIorcBg3xXdcpthRE0JbttKWgXRhGBsIofb7jo7XI05NV4s7W25sRES5YJ1evMrb6mxOZO0OMQqfGVQkNvjRByNyrCtAaOYuV6wJfSICtDPFoRTYLhf4/h/+Hn77b/41/PDDj/DT56sJ4B7nBbsz7tZgxJsFIe5dxn2H1QJ4K6eKi0V5vhuMuEW9vQ2Ozud2wURf/3xA0/DNN3gr6HTHXc9YyBeFeWJcusVLBNDNx0bXRUT4j//yZ7hsmN9NZsl0up3R5wWl2mD/w9/9CH//2x8aPg2IKBlBf+t0D2v7gDjxqTRbopSQHqCg3svAi7jYGYWIcNmq7bBF+0HK5h3lpLssEIBDEohbq0+Bl5fP8PnzZ/j182d4+fwCn3/9DJ9f6r+Xl5f273OdrwihFLOjnEh2hW9MfeQDN42i/Zrqdy65dVIk0GU/IygOi87oUrA2fNQJ24dNauqoj2+UbF+NYGwtM1a92vvbKzwt4i7YbwflNLWVOIw4L/u+NZuehJCRQtSPhZipLYa7VZ/sbM5+WL4Z3IULeEjMghFfKnhh7wP6CLDxKQWvQAcRHw8ZXs18EJm4fyVZfPf+jwEtC81Y6qbWg3K4O7EBoJ1ws4LPT6ZdymkQIrcp7PeVtnzraXZ9R4StjtFXbESGgGT7bbaiJTZQfBbhcOPsRY1Gq1BS/gyOcVkdROkARkI5UsYGJNyZG4zXlHHsglterdOOYwINNPBxTFaBZuHTT5yT1mdnJAEQ2Iupe7AH0/CqWfH3hlW08U6IFd8sAdl945rLBiFCLuuIHfX3WJEYDFkZ8LYOZEkxOP3Qj7JotJqo2jm9MPN0jHklE2Hp8VTqCw1sMJuV/BNKfo0oAmBeUoVT8GXNPZOaFJPkYrY+3VtRNyojN7jSyQxNv3d8sAMj0mbNusO2NrizVPVDoie2Z9BaFo3kQ7Z06swZyaxe0eqSWZ4MoyMeVbZMIoy6KlMQ+ntr+A1AbNvZpb3z2TNbkLJsGMWEYf7KKMHx64S4DT58+gQfPn2Cy+UC20t/Dpu2aR5eONI/p+z62Yqek9blbgDijmUBDXhniI/CryPhkplRDnN5Lh29KhVy7WG6O6N7n5WDk9d7dN2uwh+TNn19Oz17cRHO6PcUUtQ3tEFmje900buDTplFeUz2N+tZBGYsmjucLNsGnL+8XAGA5AjYPQ1W1RZj5KK+JajHR32+8oKjoE2H+ZYDEU6PC/NzddojXKY6XKXDBiEsv5ZCgJtstnD0O3GCLRDRdFpZ7MUUUg0oXNuRtdfS/pnja6/XK7xcC2yXKwBt7Xm72LqABFKuWPGqrBq3u2v81n7Y8UP7Mx02iT6+r+KMaRsZXuMcgYYdGc28jfc7XOesT55S+kdpHwO5ndc4eLnQR1F3BtZoyaeSkSLQHICsYi7pAgcnh9W5bUVZProwoeOB8/3p/AKHPNjBTusRz+lK6rzOvgspeUjMghEuOP4+QEyESnyeiAY/6jnJ0GaV5XratIfEecByVK6+7qImD+LPW7YvwTfeGSOYdZ8b670+C5kyB8/znzft77gb3IOG+11WLfoi6UXBUbE2OvEUSfe7DVzyzlo9z5OWmUf9Kug+Y5l61j+vtrdKs9K1IZ9lusnCTxTPzKZO+jNOBXPnAQFJoOF61R0QVWl+aWedXtv2YwlDgO4mIfPPKvjgjILC90HQVdtWmwV0KS+3ALb68Vn/2NohCtWo1EIiFBrFfK8Fr0Rv7cDnyDIruWG4xRNZg50Ea/yhjdJWkjcjjVd6yY6IrG0CHBKei7A66He3t8u4MbzQ4Rjg3qXDt3UXLBoY7rJI7GC52XFfWeBvRmtXqJEriUmYohilG913MHX37eiP0REQd5jwnBsd9Ls823CVWQ93enAzPhMZrUlQ7gLxR8RNFDkDwyl3UVvoAqE47oGU/vD+lF9sZI8B95cqieMxRuHTULVjj+l745DiKSHklXkrxTsvKO4EqrvqEAA32HCDj9//AN999z08PX8A/Hwx01Kmuk0a7dHw+lsL3jcYHW8vYeVn3O8+diYCBt3qRiLl+44gtW9Jj4W5FfK595Bp8oXArX02YhCa/lRAcMJmP8OrgNNFWZjzj8CSvOgpnjQJJrlIfb7cuUuH3fOq9vftwHPbf/vTL/CHn341QQabyCytWZmf29j9zXcf4X/6N7+rM6jgNbZAk/O8u1h2RLDDgXdYhyBHkfm7WERGRF+19gQAVODlyjsifoVff/1VPn/55Vf4+edf4Keffobn57/A5+sHQNzg52uBXwpAub5AoWI24nNZQetB1gVqJyHqnRkR0GSS9LBmFyKC29Xq8WYTt39wfgZlu9scMNX69BCONxiLA61+J88j6Iwy/w31mZshseHvAJVD3nhO3NP1ZguhFmC4AJGf7dgcDlewXNY5al0XGpf9AGgV2DuO7z1rTUf6r+rHbfcP9vJZsCRMs1aCcQIkfp4UB/aSmlxiMkkfK7/sXHkPcHNBDEbENgl+5G5XEvTP9wABWuxpziPdm6E8OjYSvoQZ51wgwvqysg7jBmcjUwxYi+K8WCEuOBrG7Xm8s2HkSFlfNexxesqb624zOM1qJ3bSTyqyU74JLPA52qW0c2KLXrgmuyQAgPhSaW2X3hiwFeQyzLtOIoUfpk7svKz195XN+5lXNyUNw+0NGoTQtVAD9RLVNeiFGDs+ExJWgNQAsOf6rgQh1ouwdzz4gTKcoFaAx574p4+5T/fGxsi8iG09H+d5ITmddbzXclfqsW/k0WjlsC9V62D4zK16RBhrmqNdWHEAaWHyTJSbQWOzszjiwRnfWyZ2yKKR3TvkXN3DZC7t0Mq4h7ISbYOOl+wKkq4+Nl3Mf4Y2L9PPghvvwlYsY1Dntj5j90Pz75fbByEG+HvRal4cFXaeN7dtA3q+wPPzB9i2DX799c/w+fMvZtPbvIxHGauHuvNIo5+AB6Nfp2O5rcd9tn/Ou0dRZQ4M8XXZYmAzUJ2Zbv17+xQh6o7noM3cqQVwi2MuH6S5ozh7FtvrPDzknopTdFHeznuen5b1Jhg4h00CN23Y8uSnFZHUkxQp75zhSZFi3wxMUNYrXq4FPl/tBMu7CeQB2J+uewYBjo/PBX59qUEBkkVNftRZW0aPX2VbjRdvmYADIjxf6kKGXvcj1RNI7YS446IuJKpv3I6IlyvgdgW41CNvSwG4Xttu8xiIAHXIczPXYMTmVKLxAh4EvtOtBhc2vUR60q8E1abuXgD0POh4TJmOmODAg4Os+ZPd8YLdd0p7bERBKAT7R7NyZ5J7bz67mz3n8kc9T0tbx3EfOI/zXsSM5yOx6LDqwDHP3g7A0axe05pUR6rywAUoI9TpsblDJBCqGvKaqScvzw+ue9Z2qBlMAz3Q+l91xnvQNNZ15gu3XgWS6TlMvbo4syrICyhWKjXWgvPcJ3tCto0oT1p0mXjfM1OXi4be6S/aM/maZm0e6aq/76A3J3S9NdybmjOi8/SOiBZsE4WPgS+sRqpG3WglR85pE48bqYIJoKv3KzHQ5Rs3xojD/aTHRx7xHQm1zFBU0z432fFghBvzelQ+KGFo8s+lDKqXUdfVQHx2absLAgpQuyuC5FgmQ6siNZ9GMLfnpRkBBABQWPMuSkkiJbJVOGgMIK3WRLlDECOjEQZA9Xx5MjsiuK8BjG2yWTT2bFY0H2vKimzvZopJL7xDRNmVUXdplHY3yAzWJajyqO13zx1qWp2ArL8aIj7HvzRryyvLedvtHdlhnUguWCPkoMPvtjfy76yAEvF01elgT8nQfmy85bfPgN2J4+if4HRGKqDu0kk1wh0CG6LRxDXK3VFI+twa/HlmHYscxOod/EkbhIiB2/GBR0ZETlJGsldYjfItASLzDgHo6kcVEbYAQKbc9fxGkBlAefo9WFphuoujfzZ0gKRjevSMnSy6g0VVYZVEu31qA8FQ72j5+Dc/Av7uO/jxb/4GtmeA//Cf/p/wcn2R2SoFgokO8WB4oDH6RULr/j5IeXqGOoGC54p9qRJHd29Y9BrLWZjxbyIwbyrrBmpuyLcy89lHr2zlnx2rt4zxoWORj6epOu24JUy7DbxGlHxzGcT7nWEfT77TXZliNkRNNJQd3hEA/PTrFf6X//z7+jtbgWlMAhIdn5/19BQq8OHpAv/+H/4WPnx4BnVrN9uAj6EtJCZTCXfGVVOO75SoxsOVCrxcX+DXl8/1SN3rBX69ErwQwJV3lgM5nVaQSTOg4OQjibnJg2qvpmDTn+rOD5SFa3FHqxah8s5YLU4PS3umzfmePTxynPCOA2sTH4Uuy55C6GoJCQcdK24pz2vM81lvfSlwL5r37B+86ybUUwtM7g07C74yuLez8tEbe5eamX049F5GANuAd8N2MH2zi8SnZeQDiTtM0iKBv+R6hW6Zx0ED/iklmQ38+oDdl/vhHWky7iGpjRun/Vvoev22vBPhZ0qOis8inA9EtL9ROZHt7axUMp93c1B9MY8C+4ziqA+j1K666Ohpf5zASRyePeORL7mVIw8bDnsgkPheCEwZkR6jiQvN/rMt7wmXvrWgA1H+qSNJv3d/tey4+t4Ursr3Ci+5NrBVM2VlczFBPcIr0/HFGU+OscVMaQGMLgiR0OIoEj7Iha8tx9HRLJzoXJ+5peMElw9QHLzzaSwf2ucr7ozpTghlkyF4u2swaQX6XTsNmjoLSOQzUX9I0JoTNPndaWPkYmHTtoi7HNieYi2PnXSRxoOaDrebNzsHd4doJMc1CpN0SDnC8MME5CpO21eDDmWNiTz9OgUMHB+rmnJDFLdIDndugGk7HiyzoQ+JXDQkjkiyyafd3c05eql1PZaptVKgUSVSlBcDmpa6feSh2uNXnq8X1RtmUUQo31/g6ceP8PzxA8DTFT7/5Ve4ln58d3PxjgA4u/vmpp2KN8JQJBkS7nfatkGaEXEC3Hm+ZiVyexvK7R/lSNt4naxic2WzzI2BEUNGhylMv6stfKalJFhK8fkJZB7DhCqnfYVUMd89+AsBoOymmkLWd0dJyPLG5w/xBWbIRvrbSt4jZeCAMZ3SNnw9PGrA6jaSHt17j4t5vGL59eUaZLjVYH1aMsfPpjVpsuWnz1cgQLNiuuh7qsGHy7bBx6en+huoOvslWICwbVu9l+iywbZtgLjBhgi/wAZlQ6inrkrjAC9+M8S40VVVHaMl4f+fvT9tkiTHEURBQM3dwyPyquqq7jne230rI7L////sflh5b2V7Rmb6qM7KysiMCFPsBxInQSpVTc3dozKRGW5mqiQIkiCIg4eoPy4dq4dYcSIg4FrmfATWfVDyW+B+8DvO2cbmNm31H9bT7IWZmoPLKuXumQYy2YyWT9I+dxgOz9cNLeHbnmGdLga8hZYZ9fX+asUEjOfW14FjZbe8mMnDjtBPOmPGth/5qyRP44Ma4JUl7+hIvUcwIiGNi9sNsjh0l/CIX16Q57JKGrPziCpc3HR+3pwum83MyLJVhkY/obtHJS1nVAE/h1m9997HLPXIsBBdD2lW2tFHzhTp2RPZ+O+9MS+OsPuJIPP6zskkSqTs6VHww/oY7kOBCHZUqw/bCFrUs+mJe84SiDgYTBasS8+oHOS328pzk6OhL8HaKDFWOeYtxcDKm04Jsa4l+LDI/QWeZJEqpgwrZJTAWC7BCnjVQERZlc8X1vHW4bXsIKj3OUBYCWTLsMxinXcadCBT00kmavowbMQtaJsJlUiV5RDuCW3RVKaosaq3F34yjglnI1n5KwZPX/HWNloBYZGWIFrLrhQCXSWPqHeh2CbJ7L6hZLPfAsMi/wgGkS0veRMdsb5E0nYm3m1DNSXCXsMk1oVXn7V0mtVZrHjZSnToFaqdwtAnkFeOYd2ttEUv05wGWRDdNj4xzjG2ccVmHGNjKnNSbKAz46090FOUU+U27CIoClqQc8Dt2XN+uIJSOWRX1BdDWO9h2axPExhoiRA6G3L02VrbeEEoTg12HsSIqBuDPZq26e7mNTJX62Jp6JW9p9Be2k6l9rLbpGK24ALXJ4Rf/h8f4MOfv4dvf/gePl8/9senU2jG8KKK9O+Qgh6R9HJlddTD9jt23mXvT4KCtv4lgjZoc194gW7YhlnLcXOH6Z1h6TzPeMUCAiuyG5BZH33I7yhJ8skSyfo+m0KQ+TCjZAfjR7Uowed1Il71n4ty+4zsfXKU0FrnyP/zX340jj5NUfTzosP+8M0z/Lf/9A9wIYJ1XQCAYF2/wMPDAzw8PMDT0zt4Dx/g+f17eH73DO+en+Hx6Rn+5eEJ/gMW+PRwhQtdAQBgJd2twTvNiVbpdtcYyLxu7ESw+VWvF5uxHucUd5huzdhL1NVMeZoWzVHBxf5W3U6DFKLPmgIyrugtqhJdPKwk0vSlTW4SsU3mtrXehLz7Hd48nLrbYpKrW9/H2uYl6M9Dbx1m53lr474V2OXdPr1w8xf1iL4miTgEqo068p9mstEs5rU+P5lKq3zedQH6nWCy/HkO4kWIKHrELM4srXPHbYDLPyl0GrfJKQKL/XtbhXZrPIG/l38edgUiVOkrn/Z3k1ZWravwGVVLnWSZJ1f+5OXEpPrSrQjx5SV5mnI6nSNjduRwJGUi8WutvojQhnLHgxxJVFfhs1NenMbBYQXJo4Z0o7i7TKxVQlVYAUoUESA/A7fVWH2vURFqZMsiTw9WAbguoSNI+MoRlZCwpQjYVfqORapDNGcLEoHsgkVSBcOhZhVTgiV8CcQnNA2BFX5BOKcGZalsEEIuB02HXdv2yhNqikogC7ipIkNmNKijpi0zUEu+eQQrG3GrVSaydqTm8dAZZFHZMWHet9vo+Tf1z/JNx2PmYOAye87iweQUUabDN+TPqkKazjn30ePfWtXdrQJ47hj1B686cbvsummN088Ql69IQo4ptQVGfgm0u2eZBrPB1plKpDox+WdJ/h40chg29Oxk2JjWaRK2ilKGELMXALjAw/v3cHl+Bz9//gJfrp8HhM0oNXMyMNthJO946tvi41gy7kj8CtAjreGFoRwcDN5uwdER9QKQVsFOGBvE+OlMoZNt2OtGqNk5TneM7INY1h6z4IxUo1Ld0XiZirY1RgZMMkvdUDbGl/Y3B7+nuyQqAfbVLqERCUzLmpdHHVmrqFr2Z7X2RsPRkTB4HLshDrcy5emcrfJaBxMBwPUa7B6DkW2kT19W+OmXT/B4QXj3cIHLUnY+LEtp+2VZ4LI8wuPDO3h8eg+Pj0/w8PgIsFxghQUQCC4EQBeCZb0Cfvm1HlfLthNB5tBgm8mTVa/VrvoLw/XyBHR5kEu5fWvZpRrSUfYDVuC5TGly6Su+ZdU2bXZZiOKD0j86w7uEpn7QND/r4HyZNf9RcdfZtU0mONHIgWCbdVVdyt83ulaeO09wROKOVqe+lI7QrtPPSWo5peTmp7MC8awJfiQPDa1BII7bO+ogXp+ep4zlUKCtL7bTh7nUT9ra2Js2bcqejQAd0BvpGZiPR4GMIj1UD92vaHiG5y8F1fAaxv6T9trVhqYjrd3Yk3OUllkmc14wZ/0MvZE7b0UluQeZ53WHOGEYm0v+NAR1Xgxs7gFYv3K6DHP4gJo3zkRPDWLK+y+ma1Yz8LdAY9Qbd4/ddAZO8M3qpy1+9szccu7adCCiKFXlXgZ3NJIlaInEeydQdCPpdlP/uxYFujq/lNdcPlbpIMcZXJYfoL5cM3VLsKB+rvY3M5UqVLgoFr/q2h6foSto0jKA68JHK9W2YiWX67eu8rw2gNauPuMyiZmhvhc11Xu8hVkI690AZlt90U/rSqIq+Cw2mUaxZVPBQoUa5NFopIcM0Jp5RYJF+gHq3RCciFf/oC8dAfRCu4QQB+TOoNXHFJRmqnTXviMAwkV5gKD2hXI0QoliS8DNGOWN88sqDpEOAL3rxAAiymTjVxil1XS81VMHeJWWjh+Po6zCB9CzExH0Il2QtmgENNd5Y6Ygm8EK2DWOpfq49h23joxbSYuAC2kKMrtjhB5yuPpQeckYX0SgK1VWqnc+6HZ/ljHC1IQAi5V3AL6Rx+zqjhECAOd4R/NexADP6uqkJx63GdsLbj8RhgVt/rsZfPxoCf3EBnrmxLf5co2pP1HGsdvb+RTp1FV/TJYZj6zIYRgnaQCiM7GSykbGW45W8n0u85uYHwFZs4ODnPww2N37gAK4QXjGQsc3i9Jsyhlyomk/S4fON/6pyoqOQosLLMsDfPfDH2H55lv4v/71X4HWX+ER18KqpLh6vOBLnANf42352ObP87g43l3tptnl2kfTbOXtVS4aL5XfF//bfd1gOUlOUdto36MTvsYRl8xN23XZAyKYk3LaIqXktOixgdB/kxjNZs54SThld8eGnTTM6CaWgNN+pnlJ9LvXgV652fO2Ihhlwx50N8Ks9BmypO0+tI95jOmcWaaXWOoCzDw8HH/+9TP8v//5X+BP332A//af/lR1uCt8vCwAuMJyucDjw3v45v0P8Mfv/wzffvM9vHt+hnewwNNKcF2KU/lhuQBdv8D7//jvsHz+KAT6+yyg0e2i+kv2WNH65Zdv/wyf3v2x1NXowBysZP1azVCWbl4vlG/mjgwpyMzfbt7yf0Adh64DREUEUDur0T2xvl3MDmSHy8rdRb65Hc0Znax/80/yz7e4z24Sshp6m3CIZjLDxkhISN6wjKRvUSzjfaBFWquJeYwfRf3d5/dv7ZPeqJ6RCFFfyOfpfErp0ztOafJQ78cMTOgQg3kszxVb3doaCO03zRXWAu7g5ZzIw1MwpLVIEpE55c7LmjMUl1YT5WIna9UYVQFrKnq0v6ZKSRqnuKGqlzOtRDJGyFthzAtU5Z3K6YSquDsuQqxfJJa/huzDxYHxe2R1wQGpXd+quiwfe72en4nQd5K3frCSIw+3uJIyM4eShCn0xrxfvK8DfM8Izax0C6JcBKxHx6LqEexX3gvzOyIoKjwNLUmeznsz0Lv6S8DTi8Lx1qMyxvI0dt5NjcKBwMI6Oth3rXN54kSCwsB2npVLr01ZfBzOai5jtoqt7IwQNJZhfWjHk88URsZN6hfbNGRB0GNT1JGWYyx1ZilCYt8x7To4g+ReSFb4RKcPC1aAoFzaqDu2YodsO0VZCuqgKzxTe8zyDzv/JZikExppRuntlgO0ftPH66TdQ7ljT4Dr0Zl0Enw2gJgFFHYTaXDnk+dxJUNZRgdTrzWlT42T2eHaaJ9uM/sBL7JgF4TmsKzsvsgEaJVQ4xAmM0aSZS3e4BzUt/fKCUkQMYI8rm+ximzxByapiHPT+SuBrhEasYBzFHEsA69uQrDHeLVdsa+CW7s8lEgzqdwMjSbZyP5u2kmUIuoXgM/PBPAe4fHpCfDhAVb6FVagonxkOlZPx+QXtfmbsXQQMp50/R90iywokWzEmYK96c/jgXtArjBLP+mwyWFyTmoWV0xlG8xLE03qp7csw8AYy/Kku01vmDu32nYauq6cyXST4KJ5Lebyul9GepxdN3muNczcbTEal6cFIY9Oijf1+cn92SnhMNYqSvSoqihbWmObjxoligHzMnciIlwuF7g8PJR/l0v5tyIsC8lF1w9ffgX8/CssdIXF4HK3GVFPbBAAL0pIdOLH9TPg549tnppmrbJCTtnlxUpsC/GCp/qOgGBFhC8P7+pDVIcOL9RaM6sRykIqaejwkkrGov4twHa2tjbAFQjwygsQ2kUKaiGtSpcZNIXGGqQQdczqZWb/arpaxgPHp1k5KHpaR1bTCJPSr7gj71WbZGvoTg1tz9tz+uDouWpGh1fAZzqtscn9asS9BfSVPl7QE59v5T4DnLnXSzDKL7rcXuqqMBkF22wXlEJMgfqifO1J3j5dXZW7l14WXk7oa1khgmeisAPQ0JUJp71gcfDaR2jt7f7Cs0G5zfMxgXa5jiz6hSq2h0rL+DHFsnvB9glo+n00uHBG7tk5zMrLmMY/ieN6hmNjmuxOlC6e5sV+5vMnBLXp5QqEDWxNySh/NmnYprHivBnTnh0RvDpcpnpTxczhBO3rRnXc1i0qLp70u9rfjO8ppKf2M11VzgxY/gyjiUJebStZrVLveuCgBAd1an20VLuCRtvZbnth/K5NoG0WVg3jxO6GWFdglXwI5oYM6g9iGfpm3FBVpplWAnD3KwBCVfLNTg4z2ZZghMSLpe2tgt30hRXIIWDWiJaqhNtghCXC/iTiHSIkeR2zuYg/mHZFbTSEtAGldcKAQaPo7eVtC7LbgvvEGGsWsByUn4/lwZhj3OmIt8bFJP2Ccl1NgA428qOU49vJ7vzIJJJ/5J5i3fHCqwgQhOdkBXgyYQ1r5hTGwL2BpLYukd4trRgGSo+Rcx08YloiTSngMiU6ZaMJE9qX4dkx6MqkDto4b3nFgmScWNLkeQgs+p1Kybw4KNuOecbbW8RSjMmzzK++Jsq7kmy9eA6YU98suoJkvQD8x58Qnv74BM/ffwP0+Ai4fKwOjJrnSNU2ZcJxiP0fy5oLHp0BN14C/CKQax7Z21GX7bPdafD1hHFyDpFjuCP/7oNb2+vENjGAyXEJuy7GfAG4RS+bh7yA9CL0t9U8AHBPNo8Dn6DlxarnVjtkWS6wLAs8Pj3B49MTPD09wePjI1yuBJcrATwALF8Inn76X7D88jcgugIsC/B9cZcgjyn+cNOGX3zG8P7TT0Cf/jaoly6AKp9hLqqNyQELIIJP776Bn77/BhqXSzXKaCEA3tGtpmSgnxr6OzWVmrU+AGOwWHCLx/wuDN5FZ0IOjvxm54/R2cQWZAyNmYFugDKJ7Ki1dNgy9beZx7pibiD/Mn2um1ipOjpe/KKGJdFPO/ZrpCwL9DdfO3d/WD4Yzg2BV8H3o+S3PGmiKjMl7ILUXtmT+T7zIMAAdWcCymUuSZYWPP1HanNkbj5rPj99jmHZes/JfegS2Wp9Py6I/UUANbjM7+gAW96RjxPQkwkm/BmT0LXPqvxwsgOrhZs0VeNvRnB+s/TutxdsvtlgRJtR/kBa8VeAHXdEsFOvTgTmmIwyeQQni8uJ/oLhjek2XfA2cCxRELKqmzSaRVpOcwQIQF0YP68WsLMTQR2fGoTgoAQA0KqrXojbao4TYkDGOs+R31u9yvGY7lTolpdw9CyPinLKK7eNccABmUJ7UbmwHmNDYYeDLVAURat48iNmpqAclSLJPwMjKETwlXQajHAlGL6rDW2FkijJ4NMnTDpyWvlglFUEEjXCtgsaAjtldZ2pUSFVhDmNCb+0gS0bn9cvoupzc3fKaBQSCa7pBOFW01rjoq7G8u0zP2shDtLXYITaRhvBgREw/YnWlG4mdJMFtCuFZuhoxlM/dBLiakk5Og43HbFuakCHsOjOPVWZjYx9jcz3RzB/I6Ao6VuhItcmYRxG2vhy7RiM6K0K6rB1U4YdJ2NfZxtYnoc+j6e0RAmXddkgiMWvcVng3fffwvs/fAdP797B9XLxBjOGTEH+R03CJa75Y3Nscc+WTPZ0JIVgiyOK0l7f936ntEz2cyyry3c0l66I1NDWTXONiMtVY19e0uH1OXZxU/KtV36ez/9uBHHzlJovPZgdlKMxVdutw9A8K553OfiMnN3ui9tISGgQPuzJrM0HOcLXgJHCsNGBW7ulGqN4q5rDZrpfG914XfEYd8ee4ce66Ks8R0RYsNwdwd8BV69gEkHZkmB1crWy7DP3w4o0e35FI2Z68kiLV01L7RaHw4iKB7rC+08/1/sQk7Ywi9+sjuPaLrSjfMMFPj+9Bz5eqejiI55mYq2R4IMymh0BryD2lKmdvsc1KKfyprZDXNATbQOLVSfn9NBDhwsBls6QGaq+UaGZyuZ6jWAsNtqcjWLmdnDwQpZqKUGqNDUEbsiDIX3Zy9ln2ftg/I7kJuv9Lyryyfy9BU1fk83sErVzAOIiQq+fDqwgDF92BnpmbO2XWEDQtFynzMxWa1unjI++HtrLF7Ek/VdFo6duH+d4XweBnJYQh/UOtHs4eMJtlKbPYOtkgpgakmPMnQQ0PoocxYZSBQOdP9pwbo7L8NxBCDUDs2NrDbJ7U1ZPvhmX00L+KqdnC6YDEdaZ7IoN3Bgdq2WVZWGVbMosmbJHJC9EYWK8iUFdnOx+hOSGL9NZSzH1siu3+RZ7XgmtOKzzQc/DKnRxoKY8XNcV9B4IdTqvklZryzsufMWStjHL0G1ZW1B86XrnRHdLnZCwVNzca4Nh5cYjcWFlNT7xbhr9XIQXCHAFPQrbtnOYEJW+PDgUd7Q0AQibDo0AtP3Q+C/YiEkGakuAKbuiY09bxvSGH6QMISPkiXUAe2RPfMerqwNu8z2O5TKXoRmhyWTdG6O1aWglvSOmtu/cRIUN38t4WQ2VOFLxFUUrjwYlo6ZHiyRBjGRf9yrWKSyLlleE/XbS4K4LopkjmnpbQONKtdmVEaoUVC53LLBeAAD6kklEQVQiXffUDA3orToInzbPyuqOGkrWOW/r2dRjBjCMbx8xG2TbCFgQ9wEbc8w7JkkyJ4VBvKm4TNNjsVLOtpvBIlde/eS7d7p3E/hMnjP4V5kjS/sssFwu8Mf/7T/Dt//5T/Dt99/BL1++ADqnRsYqI2d0AK9V5YRm8mzUPo0mGgoh/nipnREvCz2e2gdek+0bo61q3BscXQPhRHj93pyhoKtJ/wbhgOHzsl6qFwF7eXg/EVS22dBTZmCXgNgU0gfA20+2DJHavKCFCIjWMr8hlkurHx5qMCJUhe0wsTPcidyDJjKpZFJTw2Jc68QtRX6MU+fWcSKC5foFHn/6XznqaiO6IIS1WQ0ubkbbmuvDI/z09L/DenlQHI1NZWhiHUxsRvKJZJFRh9zwuztrSB+Bsw08LGFMsF8gt8mq5gKsusU7L/3iS+3VxpmGAEhLe7/FDtbP2qcdcrb/cHvenglWAsDo0tHRRor2wWyFe7ztU0SSMhLZ/3B3vSwTBCc73LdsgEb/DGqBWm9wV53pawZKeE12QlEc/1n+HFpXnt7/c0Rl6UEMJo8WQI2tqpdnEOtPafwvG/PEGYXL7hH73cyrm3CUuNMrlTFULlNdatkh0glGHKIEjdSZR7hjR0RaqgN7H4LqJn0FOa4Q9Y41VpwmaHBCBJvXRnMwsjpfyy3OP4yNmdWBCy/1ZqWPncwlCFF3QIRVKWAESKoYucg/5+H8wZEMWi8/eZEEaLxSbnD6hnKwORap86NZfUPSBlI3Q7OvN7/oT+q66pmLU74rdTaKdcQ9rI+R5Ka9uB4avOjjsjxlV2a75lmVvugkboIQA1J9ueS/NzYGKYsaKOUl25SljAETOD7iRonO9VZI2vNem26WCSgGPqNqOaf0tQtoUJ7vwuWSVMW/0ps1kziTTfW5ZnFFfbewmlfPSeY82/S6JHTbRBOVhLgiwrVvHBt2jJqG0OPYrLHKH1xAYsJzNTCuT/RlRSPS4YWBa8CK+47C2DgvAv42ZGbrFxpohvWkqTxBKpOkUcIcN0JqKUVdWahnJfTlP4JvgOAIQMGNgPUojKend3C5PMBlvcICv8AFP+l82TDSronHP8aobPdxRUMuzp2OJKkb9yXrCUF3OTjGuiveZvLa+aPV5afy5e+MfuJE8RSHad7tVBAKAADP6e3XjPgwdw7r347Bdg40MuY043FrPh08R/vzFmLu7KTZA4nOVWAPjVnapH28ilpyZnp3Q8sB2IGnuyaI+TIuSOgottt3YeHG+JmjLR3Ss+11+urY8aBxjibWJzjIUFeZEQHASrD88lfAT78CXr9ofsOeYHWYaC827ZodmTDHp1HfcsmEFmEO2Fq2QMDu9XJXA7GOIKSqACT0+1cWIHj+9DdYlwewuj5BVmd+TW7+sLMb8+iXx/ewXh58bgJZAChldCtV2zco+D79Ndm9kdhXRhZo2yMghR0SLnuwXZw+BVDuGOxc0u2+5rM8JmtBiAbzqVnY0zGpvA7uiQgZ8sdzsDW+t973Cw/atI6vpEq9EZEvnoqYZyDXWTy+ASTycjiGezoe/0HjE8neb5RtsDuKjrRMr5izRP8M3raKmQ7ZS8vJYkI0C4brqR4j2RuU8SKqmG+mFdVNOmOakerR64K2uU5RdicAnT2p01v9HWV769Dx8MIBwlcJeBrg5ujRERfPNj69GIw4FebbZlcgYqTyuCAEV3aDAaKqEVeMyhnxRqmMDjk9KsqKTaU3FAgAehODXXGNAAALNgOiUURMfe2YYJHE90EAUA1CmGeioBkai85Tx6IaFGr8GsXMBROGapqZgfhy7EILb21qdjglAmzeZqHwUVezVyfjGjzg3HYR0kkvUxqp8grLdAl+kd5DsUlxZ9VE6+FP8zQ7K+p7ClkRYlmGlwM/A0CDMyfeaM7pa8MnQIZffP2Ko9Bwup83ldYNNnN1kCGEwwlR3schSnyHhfKojBHERhH38qBPZyYU0Q6+3UA6Tpv6ialSUso49uMkc5ZHA9fqu1nkOtsN0azGKBZbGozYWkk5ahoX/KIEN/+tY1J2RCXKhOOhOnCyMcbvi3w0/EmenpXWYb2IFclZu2lGrEi/AtgzelX5pKooRkV0xLvo3pMov7btgy3VZ6vkmRrLwDsikNtX6+SGSTeQiDL2y/ey+vTd8zO8e36Gh6cneKBf4Gn5K3xeP5dxDqAOEVMrNaj3KEdoM07BaFdDJrdU9PJY5jFe9ZCdwmTkQtpaEZfvDDxd725lRI/HDGX7+i3L31CxRyGZw98UE3ehVYPzhBJ/h5eGvsndvW/ndCf5W4VX5OabBNSekchzJEG54U33dqI5molJWWGFpx//BZaffwQic6cfWHso0+7tb/uZ0T7tBmpzLyG/iDBrIffKZR2p7HLv5mhVOAAA+Pbjv8vLRt+32Y3dkSG2WstPP/wX+Pzw7O4RlPKtzbvm9yQxHQhlbuLffad7gdSPJQ+sroWwLJfQZV43b1c9LyaZziXub6bPYqKzE4Y8FQfrGcFPIbpPrbU/v7w+bZqDhNa2nr0+tjbYPjnS1bOSb1uY9JsZo0fEShtNmoSZAgfv40LTrIROc3gRWvuKqJ7OhDm6jbL6BsLb0Xy0CtbfMLETCGBfNTpd620F1g0nd6/bMcN2552a9sViCCeDl5Z1XBsn0uEmyxhkYtFGXCQM0NpktywgOwu2YjNJDnAVqwtU9OnLM9B8IKJSGbcnCkgQgquilx0n5rIiJP/EPhZMVPGTKjRdMoU8M7ma5FGWiVhZeCV3cBCRzwe2jtaBYpQAPo5JgxDU3EPhS+d2NQqOwQekKhzBGpQs+0nmQ4+EAinfKGrSwqKe95kZAYC8yG1UcDI0swMcksYzzquWLwaiJpuEDHqqk7HWLQiEzYklf78FWzhcWkMfrV7ItcppToffihmEonEG20BHHiT252G1TtvI45yvPBP+6TTR9ELYtD4kPN9ZL5Si0/nGjquC76bJOZMBru4eOcYvZB9Uie9Wkc9PXDYYkU6CTeE5jZp+ouxuwCt88Q0EgPHBPkBeuSgPDJoe65Gde5IU9pFjPT9v9VfKjwiGPlH8t/Z9JMI3YUTCYzTwMYFedA1UF6pjq0jbMWEEuMx9COB2QozqlAYhWl4mJPjpwwr4DcAfHh9hhQX+57//BX79/DdYV557jB7Af23Amj8nmp/HeVuBUSYuJ84pE3Kf9YcdAYlNftwD2J97jsq6dN6sbeqdS1WzG8qOVq3tpS7jwjCa0c0ofDsNujpIfS6LXIxhhFZHOpmeGTjcrwVw8OS3A8xLiTHmku227jx0nbV5cWNUW/NoPl/08c2XfRcknTm4B+2OEM7Y0Wmy8ozBxwta+Hgfn5n88LBzaaILt5Ntj5Zxum3otfdcP9iFDN1DkjGnsOi6KP6zuKiKZw6+YL59jzJf8ePnz7/AI1CwWezf8rnyJduxugmtoj/UOfzz4zv48vAubxDJUUNUrkkKX6xE4ShUfl1pTBlNZwwBqyfFAIIENYLfwfgCJIdFWe0HXHjxCBrdt1NV8NzCC5S4TqI69liK+T15P8PZlO6kDIQ1YjexcbpvWrHU+B+jznQ0MHpr0Dr4KmbSWqWlkB0rZ4IRu8vq6a2j1n4DIHVL+mNjjhq2x9aUyjYVeVtzyxfkHNwyhWVzWdTBe2T6dzc7wUdtdgc1fKswbSLT1ghDOtOWTNLrnNJbUAr9Og9k5LS/4BYIq3x74ihdTDciXmzolx3v04EIOT4oWaDAOwv8ETkAYI1VjEOr3B9glUvimRAAzDJXYKdkb8UFhhm0d7xNRK2EoVdObYY6+TLvZ0YBrzhYzR0MUIMQRZFqV76X80pL+zSKBmF5J2f5F3wrrLX9t0aGoYHW4vghkhXJAKtJTuK76Tt9qX6wEpsUzYEoINe+Wm9r+dujQDrlxWr1DDtgRZlEEWv07AOyeY33f4B+51UHBP3V5M6VSYZGALmjYUtgZe/7zidy9OqF5okT3qzAWTAfKwWnpyGWK2PevOW/YwUGzcogbHCZqrT1Tds7U3BtlsJTKQv1q+94Lpuo8v7D+r8xQatxmxkUvdKJ2n5m30jXyY7Nl/uCtSFsoJXi+1b+7YXhyhNqyyiO+bZzdVeGppumwMz9XTukYwX66rfjyDKXW4HeFNTXBl0wwiR3pm/gveKLMbJ4pP+KrMBYRJP5igA/fkew/AFhef8OCBH+v//rf8Hnzx/hga5+/gG7+sQy1Txon4xlwRjJgSw1Ty8gcUYZXTxB6T1qhGSrfLJgRFM+dAaCkUMUZegQEOL51Mrt51tBGL6Jjit9aumvO4e8/n86Tb9pEOf/C81frwgsr/ZNi2+D14767nJkcLi72fFt2yWjq5on5f2i90QgYt0F73EILvmTle2Jj8dn5hBsIbbtpqGftqcV2/eqDjWTd59EqLoXmWYyX1xyUltyqwofPv0E9Omv+liaws9GzT2MGyA2CwH8/O0/wPrug6+X0cXKgkGsDvg6yzgGanVKodVXp1fNFNxiSX4QVNXF3NPFixQjby/LAku9m4+nLbb7et1qiVAVc5GpvGPhmyFSF7006oDRGDJVU/Ib4WEXW8Y0XUj0kp3Hzp4WjDgKe4IQcwiT37GN38bccTc4GHS42d9aB55bioXQ5SfkBGIukIyrVPjuhNmAyG64w/Aow46qzUThntIODUdstIAiPuuBzOnWJhj5IRjxG1Zf36ocOH5HhEzmJghRQVYlIxZHp3XKAeguAwla1MHjfBAkSiY7hWecWTYIIYoqgpM4fIE2KyHyrEVWy2V6lW4NuKymMaCudC80i2s+rhjmWZ23iCMWPOQnDz7SSHY2rKxkOVVNaeHARdW8V1oNPazpJW1Y24icYq0KqLaHmfCdcsg9xkqjOtlZAS7fjePL6gGiGMhoN+VMDJwQhMickHNnVVuctn6z0JGUQZm1gQLJlpSfr3hvE9t6d2lPl+L126RZWRIVYbJfUFI1RZhUWl0/9sgU2ATsoFXSAwGgq4AQ/LFfe/vcl211Yp3ATBs79C2RIlvqajLbAjk/ZlNmJltZjqKnqQuGZgoVYnqytjI0OqdJpvcOSna1ekmFfw8M6lB4P/BGMpwwjAM7bwi7YGtQUqOIhpf5wAOeQwiDvGvyYPhU2sUxUadpy/MNKQ2GhCqqfbwAvPv+PTz84Tt4rPdDbIvyTrBwEvJgRIYQ+6/OKnsa9975pZ/VBj9mDJF2J4gW43QBl8D8oiLL+8txLM2xngP6LB93E+Sy0pfdKTfK7TRffSursTuk3Ao34d3RphB7sFf4SCnJypqrQK/92jgrj82OPp5SMjsPvh6kK9M2yD3Oc3kf3roY4Aywu7kRgxz2CmGT187Bc1XRBVm8gq7M5QuwfWqt0451BGxS+Xp4XaZ3FFAiNV8c7OxPtrLo3ztxHZ7HrmJEmShth6kZn4KULT7mBWiah6qdYPmh5Wz074xz+/nLZ7h81GCH7UjisonLMYUjVlNXE6/LA3x6/hYAjaO+0hXN+0LV2j0lWNOrgmjXYHIaHxfX1uKWX5cVLg8PgNeyoIyPuqS1F7zRDrJ6nyxEqX8Xl9zaADa/jpzMh4LuRaAgMhrIw0lIOCxRuXpqyUsfnXIzZJUTaBS3yiNGVvL4CHJVzWRs0jaL4KBNk1EQMg0gLnXJsdw6ZWXBw7Og2MTFNhzhj5pSbFkKi5gOQfRdDNXrjr6UVWKCpMgze/Qw9t0QYLkwWoIRLQksNsSfQioZkxVCnfKSZzIttJSL/m/mDnsqxRGIJ4NuoUk0oXTsApi5JfqIb4QMQ8YaItp3FnnbZdVgJnFXsCp59as2HWlnW8UBAMyANKoF3zXQlAFNS+ybYBCaYzczJ69ZpW0VW0c76c6Fsm+hKr8rK8GkK0qsk4I7zEQFpVxbVg0krHxofqb0mjsZgAjWdS3pV70jwuieCYS3olwA8O1mRZHEdrAbpc3dR1DxWEUYgIMR9jxNFkiSovACny3vJs+8lwm0jyL0+pW3ybUr/Y1YSvS4LchoLPSZgJppsy7fdvi9P2mT+y67IaJzvw7MECNMit+QJrabF1ZqAwYdIp2yEqWm4W+TUQdS/bk2SXq4Z4HcF4pfTXsycxvnMiYGWnigZ8zqqqfsXN1Z54UGa6LK47D5PO2SdofPrbR2GmPAlPCXe8WyENjgOckIOIzGM2K24o2/+1UueYFpfE/KYUxVjghvmIFCBDBQZMuMQtDcXThI3x6UFL5Z+5AVrRjsyIbfZptr2+KC8PzDd/D8pz/Au/fvgeLFlKB81sjZG8AHBKZydN/sXbGcB0KOQZ+vRpnqJ7Z8MJUv+40btWHB6FcWJDBHi5c9I412Zs5U3W2mHceO2g0EM3xyiCVsW2wVOMesiYaUlHBDW+yFLHC6Q9c6jYaT4FynB4++RE/qAE6kunXlZPDbHoRoRyR6y0Y5/gi1Xn1VmCIugLDAgkte92BDDGaHJhjRKVW+z/RLH3pyYB9g88W/2ypF9dwh9hysd6wW5nc7h+QAALTOt5ZR3AkIlusv8O7nX/IkVeeIiyF9Yn32+fEZ1m9+AMLF2ZmNvVthXQEWVNpdoMp/tPoPlUvCnV3B5JiL8xbiXXoLrDWSs64r0LrCtXO3htj1RgfVXfGqn7qggn2nUQdvz4veZ4oJBqZf+DI/BuIulRHrbY2OrykI4XyrPXXH2FbueZwvrFyLun2CfzQ/bK4K34J2O02KUxe+bZd1cyAjCL4tDd7J0Un9skFAZjy4spN+2guDlR/pAtUWQYcGazsLypq003899Gxf1YV0hCDBiCnIV/QlZQ06qLO68qZFG+l4ClD7v3ddmcwvYoOG8d2pkqLq+4L2wGEreud42BWIEEe3+c1USNvjInYE37uQEsqKgPuN7h0fo9HwhJkYbQLf/zxxlu+F31uttrsjglid0e+suIB75ncjsON3JVn7Lsqt3JpRlQbZB8C4TH0KLr5roq5wkPaok4TpDw5arPJZFJLyc/WMMdLZTf1TZiIzqUWasgCJmcp0i2l9ll7Wa3CDtrHQ7b+YtFnZeR3sEV8xGMEBoLjLgI9jck6erdlKKQxfuJxKotPF50ZwDMzFy34H81BT5izYaGuziiik01UC5kgwsgVb5ys6hV51AoSgI5c01UPoA158fFrcFeFpl+RuFUjSjVFxyyMAIMZCXA2Ugsocu3NrW9qXBCvtcC5yzjjPJivlhwpXpqB2hhqEx7PKahpkBj8W9jqrNfCt+ck1hhm/AS8BK0axvVF4svDvVgeSEYk8SaK1yEC1MVNKtPbr1DjT81v84YuuhqLNYoK/MntvyDl9jTLvXy4LPLx7D+/ffwOPj09wRSxx+ZU8ujjOToBZx/NpBc5CmLb0YZ+O+boE3DfZ23YuQflQTW6gAWP7aC/4LdHGUmZlaQq87nioHRt8EcFOvp3tF4vPDZRzjItRsZPah0k5o0wOMIk6fKyDdgXcxGkwc4zODla7Mc8E1v6vhFeSodjBtLP9etTdPLb6ePeUkweOy3yzris8QOn7smjGKpZkZJu20f6u7I/Pluy9Y3n/ONuTw9ko86bNPnqiyZ7OhyY9QF0hO1uARYzpLgsLKwEghTsoHDoNUjzBCt9+/HeguHiIbUTyWKy+SRD0V7uYhwgIF/jl3bewXh4FB4alJwTV3id/ZJOcLrCAHJu9Mm1V/xypGghYgxj2GeOvv8ziKmcx1DHEQQ1kmpZ2PX38EPsH23RNf4cFTG5h6wRYW4ugtQ3LCwLAZrnPmwDxYQXhFhcejhdLZbpK5V+z4yK1904CGfIyLuzSuVg3TbeNt7+Qa5ow850AOjJQj6g7pVV4PHS6xn7p+nNgZ1Bo1FCiOOyr3e62DxNsMYuLkcs7HVJORvt1MqBiDYDeKx4H8rzb2DpOYGNXxE0TKI+PccN29SFqvtwVzihlOhDBly33haGZKICdKVbZkxym02NHahlFduoKfw8asY/OyzJhg/h3/MpfO5lhS5ojUXckVFJEgXCOeKGP5Ox/IPvPMhRzJ3OQIdS2ANUAAl907ehYpXzbNsWRq4GHEoQwzrc4MAbStFUENK3j8Yp75fs+6qM0P/cZ1j7JdimAuZwG6lpg8nS2DuaaYCAN0y1jRgjJBUKeGPcsBh8krBQq3Au8kalVu4pmXmLFY75cwMQ+48mZssZjhW+kuLTvHR8zD5Kx6Roc5PuvTjJl4umtZNPvsqAmrKyhZrVPmcScE2xWOkp/jnphwFuVviU4N5rAh/ueNNgWma5vW6TqINf06coKNDmMPRFFdFdZX5WHy+pCly0ZR1TLONOsPTDL90REGEf6WIMRgFCPwYrHKikf+qAiuWcN/5jut6fzUdhP213EsTX1D9oa3Xs040sJ1lFe2nlfS9dVp8sFHp/fwfPze3h8fKzt345z8R2cDKnYm0gbITTNZrp+Av6o84OzPmZNGytIj7yfhM7U1B11FFJgW5u9lHWdxam3MW+7vM/iXDHLfN3BuA+ahjAPevKp22iTOsSOKsakZ0rtHtzqyI7ysK+3gFG/efHD8XJdGQfwzMqWfqHhS5g/0uMZyGUUXbahbWfP+/nvNhj6SrJ36s2CyMHk5h29G2IJzs1iNKqymovlVk4rPa1xVf6OCM5x9mF/427lSFUUoxPH12fJA8RQdodXdwfJjNPcf9Gi+MuCBECX+KYDBA+//Nj0J6363r0xdrm8tfqlCUbQssD1+Vv4slw0QesyASB7zyOYgFrh5bU0GAAZv4FYg6DsbX02UYHnosVEj+1f29fqM6bNl2WBZVm6HeAu6w6Goz8gyhRS39nn+eK9sGyI5SvL/Jqmp1YMeeDegm0Cml0PmS8gL7jFZeWc8z/5/t2CYY2SScFrLDnF0W/hFoM25Z8ThGhQRIFnFuQoL3l7CWAHm7ixVetHkY5oR47wTSoTM69H8y9AKxJ66TfbQvWWFQiQjxgW7vR4YnwEO3NnfOp8IbdCRG5+N3x69qS5C26v7+FuPQDzgYhkxKpDSklb2LGBzbQCPKOK87QzaFg42sm6oGIh6SezuMI9AzY80OFAM35XwSGfZBXZIBTsJMABk5qB//PtRoVWsA5tXXnPSQhIVo3Culb02l6lWH8Xgz3CidPECUYbInwPinTP0aAroW09Aey9EKHBfZFV6VhgaXjDD2Cqq3LDauLGCahlz26jSqPHtW5dR6kRJjEYYfNznXN9ekL67xndFd1Ka/PMQlH2i+MGZfeJ30pr86vaKimTskmCXU15bmK1fUumG+tzKiqPVXbzVuqbInHnA5dl+7mu0+lguFWkFjm3OHnn+ZEsA/EHtkpl63jL2r7/uoxPDL8zilXRDCN0CGT4w8khE4zIg8ZnA7HonOo+bofVyPBDIO3llcdY3aFTjeccT2CDpzGysgxAvqzdrJxnWC1BaHnWb8XvYaQF4K/fEcA3C/zX776Bp3fv4H/85S/w+csnwPVHuMCnUgq1Op3g2FuVV4a9QQj+TtBphJuhHRyZnXLzFntXkv9mP8eU7Xs/TVdSeBybWVkZzb5Wc6vptwkEb1m9KtPXljir8Y9QQNX8tAt0foc+UPMFmnaLzfi1CVYDI2dUml7MFLWdoGIodtgGHsp+DNo6yewXMtnUb7kj2nrNUrtn1G7i9GrWJkS/XjDRGrTyRebfOBcaPYdI+KVZ63+JNHpeET60iRK/xne//hXWzx9l4pKrMWL6oChexOmP5VgmIljpCrQS/Pr0AT4/vi96u8m2RttNVD7jx4BqO5qRIlxNAO4CDBMYuMACdtdGbBXJYvI2XGPsI+cpMPqztRtlgWNMz7QZxG1xxi5eNuSL+I76SUxJ7vdxPSsq+AM8EwNwk3SyfT8LW/6N3LhJ9a9VuKzJyvrS2zhe61YZvlWH3L7MMRnZlS7UmYWZfPfQzXqKCrqffM/m4f4PaO3zIy3Ws5/oFhpPhiP1eg3tZD4QQV5AxHcues6+k+hA4QmZwEX2W3yrS2vB7WTooCg2XusRskEIRGxFu5mQuXwanlFJ8tcGKNT5KggzAkGirJKsOGjWdTW4wLQFCyfTFyYA4ZzEUdmBjviITi/z2AfczQoOuQtrtQlcPR2mOvkvsACI3mQ1rQg2QNNLFBS+Qb1cLonSeFQxGNFTHGwwQo5uMQzUvSTI9GWK06zSnDG6bD3irgyouSWB8Va6IESwWWcCJsTlNdBKd1XCHeFCE9XfGL1DPZQOjbYnz73qbFMkhGpCCNogq7KiZ0Cc+XZrQZST3fqg/3qi9O8FIWKR+1f5aOCzsBxftDVoxFPn4zl1HgM91rjaD1Eqamf1pjD7vFmta8afV7ZbLcmuNuuXp+1/XEELvKoTkhpfYvQN8CACIcIv3wDgDws8fniGy9MT/OuPf4XP11/hHfwNFljN/PXScJwZt4dKJ4GImfZ9psj6Pi5926gy3Tlmi8Yb7ZRBsdszp1AwK+LTvLep1kFOZSpIIr/S+Sv2206KMGQiN457sCFcYzVvaaqKZ1ucd/SkqHrMFE3MHZOZejreC0qWW8bS7eMwQ5B0YLTDpjBv66Bpvh11mk3r+5MrRP7RZr6Sa+FjY9DLIaVFl5BtFpCUuC/9y8KYqqyN23d9B6VttTknW5cgUacxTbcpk9A8o96sYWoiwyT4C+RLPnvbAig8Z/me3nsZa0MAz59+rr9iqpA/OHXtokxexLhWHR0enmB9eJCFlBw7wDX0dvUdAGJxS7DhZpvf+iJkIZInMVsUoyplNjYSPnGrcOpRqDY172RCgKXqx3Z3hl244xed1k/K+CXXn6P+DeznGt4EzIUnHDcpFvycGcuqPR11dikkJtd0Y70i6hIdYqNukQ/R9GFpO1PWRpHd36iLDe++7k1LB6/lQvPdyouY81CJSUZxm42QZkr+hgxtyh7N/3unw8m0BODGTVNyrXi8ami2SOuTmdJrZg2VZII5Foy4IzNP1mWLAjtndhMfGJS7AxHNbxmfVWjzvRBuMFKdwFa5w0AVFjNxR+tMkuiqW01ncDMX0wpES139Xf5RyGPvKQCE6ku3Sm2ldV0BWNDF1bQ8cUMNVBDpxdB1N4MkKYWCsL4Ibk0gTuX6idXBT0h1uxZxDmAFioBk5wDnE9pMqljvtN2YIhtxJqzNYy9YJl1Z7JdWAh93oC0eFQI0HeEtXJQa1TKA5AgYWwRTzWNArs4AD1Yh6QUX4sr/cgILNeyQTDP6TM6RB1MnapNJcAqappP6R/RjfV9/sHAmVrYYX3mGTiEqzwgIFns/B/evqSva7oKku/m7aWO7Kr/MhZVvmU+57xcAJNI7ZDrOnZLF9ngtxwTZiOubNE2tiTmJA2FZTKWS9CkdG94UWle3oyEVwwggBg16d4sd340cJBu0rSkSctLV1rH8+i6tTsaT/Er4Gk1b884E0j4I9ReZjSyL/YqrBczNdiyLKz/JmDBjqCXYGwn8WFeH2HGuPNSrvwRwut3t+VjvQeml9i2hl3Wz3IcwUYDwOyoS9xmnIkcaEkBtUz1jOFTG3SYYAEEuDRPDtBCeJFc+XIQAAlgQvv3HP8G7//JH+OEf/zMsT+8Af/pV8NWG0IpQVh37ZK8y11A56NNCh5Nn7vVtZYOUPXKvjjQ6AOUVlatd6EYreIAlcja9LW2LphVibch98e88NjKv88pIWrs63sggMLJWg8pkMvdoD3PJ5jwfUSXz06C0cRvOp+8sKEwhvt5LwVbmpHsHIzTRmboF8dzOv5tZpMWs4u5U6AUy3soqtwIzPTtIM1mVt7S6TyGrVzxyZYVytOuXskKceF5dAOFSPpEA4Br6W6wL4PlhTIeVKZEiTfXaLejF2AGpMMriDIUZZButMSPK2+Q3CrsZ6ChN8rfVue2iL6w8SG2i5Jz4ZK4Ov1pZX3S3pdqbH778Au/+9q8mgfomFBfV46W0vNyO4XSrs5E/PbyDX5+/l1QLLoDLIvqduibMkdLDDuOAR2wQ1burCqA2AvhdEq7NLWrhU90Z4awmXGSCRXlm80WbxqPWcn1wBFxOSeKey2zXLNDsKfv2l8qhyBMtxzbcB9rbGNLMSS3rGB7aQ1GPsWlDd4/xxI49F4YqtrQxOj8EgGm1qpfE1vRgG4N/6gLcxkeUEpXLiB7EIGcrPzp6j5kGT9UvI1BkicCr3O3GltwsX2yFsRbjx4EhqPnqeU/ktn0sQ2kgrU+IoG3ZArGEYfLax+qfKJ9DKmtSN5Str3MHHA5ElIeeJmylOyh31c/VuqJ0NbROPu3gwojSEyb08TRf+M7seKgRVJmorBNWWtFEWM0kCrwjIjqMQI9NKncykAZaZLLVSUgnJgB7nJE9VomrzCyAlfbiLAlihD9Gk3p1OuUM2w49tLisFCWSy7jNdghFw91OzMz8zK9o2J49mEc6b6v84VXZXRB9IDhObcDGlRp3NsxCnTQQwbmarPwicvSqod3SG1F3pb5x4slPuzKdBQQCtBfqZogjTW0aL546QCDBLK906qf6ljxnjPpTyt3q8+7rqjpYg8m/Uhk1RpHSBpE2q6Cg+8gfcvrR8IjBiAPQBCHs9w3e5+AG74KYVWJGBdlVFwQEGpdAlStU5aXNqYLAYbUrtRaEet5kqAVuqSR9yn1pO/rArbiyWjv/sRVJGIZ0PuAH46HA/B6MoFB8nrf8leBSc/Hg4vrN+QErTe//8B18+49/hvff/wCEi66E4vkXqF6Q50PDW/UZwwam2mUjlnelZG03A1nhteyMa8ocL382EM2Bby9s+YDxixJpeTIodQFEVxhUFBNh5pVVfk2pcuLaCXWZgmsjozcyz9qx1Nv5QWmRMWGv7ePYzVLO9Zu2Y/9dms92T2cqs5NaNi1GjcALhi36We6a8RbUaftN6Y2UaHmshebjPJe1Q7V3OI/2Hm/329txyu+UDSNBN9Xdt8rme0DgpShzsBgSxdbStAvq/RAl9Qp+NBo+Jf7dMUhSWlo4o4V8bcdjdUhNT3HoDRqn12b5wInx0bhM847g+BQ4jWy+CDR/x2naMvyclaZyakaReRR5eqN8Nm94Adjl+gng+qnpcrcoruoB+pzaLjfpSgq9FRuXRe+2qHyg93dWoogXLvCdj9RteEJzGgbjMHqi9TFZe46/4sSF07IIVZ9UuhfR0RFAdF/0ndMs6kRja+Ci+o8GRuynyeTqzV9YlIkm3uitADosfTOWdlL3FoYEW9wedWirGcYB3oFM4chK4iExeDeT/2zoqoaJGcDHXnsEdoxzm8U0ecH76jQ3J3XHPoi23sWAgcdLJpVQJc08tNUbGBjyw9JrbBmzUG6oL3MxBJu8iS59L2HSlxRQTzbKnVg4gTmFD20DyIk9G1TaJAeDEAA7AhFSrkwy5AVzrGs1NMXxGogsMjrvMX6n8rROLmSPAiJxPPFRRuyQ9VGdOqDKzNIwib0YWx3uq1yIq6u5bbSSTPn138oraygwsXX+2RUJJBPyKjsbhKjykd5erz3vJmtpKgRYEQDXjgmntOhfkMmesbtVESS1b/nSFoA66e4BUYDWnJEZ62KUDFldTSEd6if3WjZrx1XjVuSpohbXNE9VJtRLn+WyzQr7mcleeUgDZ4qmUXskMBCECllsgYd4UpTLg/SM/ayPUJRC5W0CHTvNZFjpjcezuXGo2Ofa3jE78wE4GZM6oXQAeEf2MlFqMiB6I9Z+WnqmAdF9zRSMWaXCZJpWHBkHQVUAOK/bumwkEyk/W2XWSh0bJLSBDvB6PpgsOibN/CNlu/7wCHQxfpwT7g99ZTsJKAxocvMn6pfYt2InVUNIhTqEcQLdvvdBK2zeNTIAAPCywPJwgefn9/Dh/Qd4eHgAois84o9Ayy+19zvzyAxg9sP092iCsm0Blld8iN/zxf0Z5JDaNp7YT4I9BfQk3Hkls47J812bpjaKkWe6K29LyDltup/sUGeN4ZyuVOPQB5qTiznnbJLDoPXZEjR7ar5PC8uDTQkJXyEcNfQCktPkx72DM1GHzvUCWbYlOgit9btZCISsr3SVwK223arn3wGDJRBn2t/h3lB1VOM3yN4reBsuLghtuNaZzSQP1Ez2by3y8lEXoywAH9Yv8PTxXxrqyGarizUFX0/3ldLJ0FKfrQSfH97Bx/d/6PqNjFErPhpXhwEUva/6lxK7xaWNxaMPWHBQQ18j6JHiSzWb3ERd/mcd1ZZocUc1qxFbVUdCtayc3djWpKaiVncIqLt7eglcA3fN604K8f2kGfLZDg1Vt4DnDv7V0Vmo2EMr2512wZixRcWLJpuGQw0GqyR6i2cczScK4d3+AqbhPBL2QWBBPn5/ND+dru6eqOqInGy/TEFXz83Kmi1DGhOVf2fUoipAUpf1BEwHIrLLVcfAFagznEwOMDb03Z4tL5RVZFgRYibI2DOoGNzAovarCsTVDHaSfzb4AKRHFq1yHwNVHyqNqyir2Wt6WB3eEcwIKgAAXABobYtu8jttwbSDMCyMC8w9Bh73FLABoW3QTEGu+4JxYtKoI9PQv5eW9PGOUe+weSWxh3/GmJP2qc56vXMsURJ4nqT+hTryPbwuVaUSvDggWQigCUI0FFJC87CjWMlTaVAwZDLES45uy1qeMkEI/p2vJG5hawIsDyL9PndawlbT2/fYU9saEibKaKd2H0Sud0NUJ7gvNxgYE2PGBSH2tHXDQxTS7hhrWMeK8LulJVN1xrsS2nL0ez9fr4NQyqMwkqzxA5AED8S46RgS0LBRoNouCOiZZgWWZQFYLvD4+AiPT0/A22If8BN8gU+DUusTa9CkTZfIOLccezCW2EiLec1dTWnmWRF1i4LaHYO9wgig2Z5+nICRIi9841WyxBRE9/w+DVXkZ7OgxRWJjoZWZyrzGm7cdn+fFXf9Fi4w7gmFDt3oRzklSVOWIfkzAUm6Zh6KxVKWDKKEpiQFuCdJn3Um3xinfmtwZJdBV+89RsDGg0k9PugdZwYlsvr2Fxuwnh1tGWu/efoIPO37mjWbGDaM/DvDsORbPVy0MSONCw+/u5NInvymNs0k0XHY4hbPX2fxwtaYsjrgHDoEMLY2us7VGdTKbSw+hZqR3yzwBR4/fTHpQPOSScnfN/ikmLfWNlU8lwXhMyKs6Mcwl8XzGJE50loWVA5kJ2od05dD53HQgOqCibKQh3XwciAcApRjq6DszPKLy4rmLVmkbABxtlJNF+sgO7fKi3I01yJ95ZI62v28PBzDUd2ELf5W23uE1y22bRYmhoyhC1Mf5K4hJ0zTIEisE5BV+GFRp5oPuqBOlBAw3bxzfFK3aRotbxOijplzemefc7fsrTJvl3+NRhj9cORr1k4dYVdwj/QZUqUfef6ar19DWzVM5Hn7ZQpGbsmGQ5J0UV+TPqtkiK8nxa9avJJ/TP/bsSPCMHBsqyJh5afoirxbgAcxBUyhP91l0ppQvtAVqjwg+SRa644CxYUucxXSoidag5kA6gXRtK6KjwhgXYGAdGeE1EPLLXTzdsP2Umt0k40qw9I8UO6VyC9ySpQeowwSt5uJ/Nu2WpYFiFa/g8XisyuL+ZMncvlrs2RC+3YgIIC1BHZoVaVFapLYnew0jgaQHiVizFxhOxIesLsGYj15h4xcAM74jwww6bbOQO7gbFcbo6kL910JmsmY6p2biJAEI9gZE/kiy+5dBlOTS+Wj1fAUQLnIlohgQQjOIOY5yay0A4giNtUHw1mfYK3KNIbJTAMmK6uMAzyhSE+1KqThWUN/r+23mjjVFsCTiv5ZnLsJqOrM+/m61K/dAi3iSFVFN1Py3zYgHemwynbeGFE2Zk4sO77jxXVngpTRacu4lZvbyN0ds1FCjpjxA+i5VtGgsfNd7fetM1bF+EFwzE1mhCKADR/RgvD47Xt4+uY9fP/DH+D5+T38n//9f8CvX36BT1+uUrbDs2s6wfyn07a8QTaFcqDIHYV9JgJDlto1fvkrd0UQtMGIDmYXVN1BqMiPKFwyJLMwwjUHUXYLHcX7oMEKYjmyT6D2+fJ22s+BOp8K70YZC/K9lYr994fIAAC3WIEAADlk0Giw3d/zhQH05vb4tVfGLXPAvXcAjMqtX07FegoKOxxPap+5+pJ/T9Y+KPbEunr7EI19gDYf5z23gS1pXy+8KvFvpeUso78Vmm6EamCLKiWOaZ43fegXLxCq3uqvTcuscUyN2866QlTbLPbZBQgef/n3MKfHBUHGHmA/gdVbbZro+CbJKcm+XJ7gpw9/BMDiT4mVZRyrsWDZx6BS0BzTVOWPBinKxyI/bC79ojZlO88T58Ny7BwndSdEBNBNMxgeRtoNMZI+oTHiljaOSEb9n2kofdhabBBL2jMrzehGjb8CAk8hPwPplz4y8rw/IWKaJM5UyBegTuGBVtPd0r7uAS1dBCvVsYLtspSbpPIsa0767ObKLP4RKfqgQp4HIzyy45aL3XEyII5l1EE1dX5HhHyxl12Se4t2N0MV0kW2B4WxCk3N68lWxw25vxbKDgS9ayHSUd0x5RkJOrfdkSBMPkQahOAgiqyoKenksm35x8dFqVTUY3HKhKPHA0jR4tePzplQSalbY9KlPe1ZzW8PtEIyBCHMd1HGzbw6KLAP3K5hsssmRefkJk2ZCRpNQ34Amoky4xZua7/6GuS30lBzNNF5kK1gntt61adQn3xaHBpttQGyIAD5o2+LQMMtqgL6HV3a242THQvj42pBs+zsCHBpDPYBRd23bZS3g607k4/AKhroJhP3PJRpV8dkFCv6lobsGLEpUqM8CtCPppNL4x6F+pJL6IXG8ckvFq4jujdXp7yMIEeLba3alMi/aASTJHY6wrfrpLrE8gtt2ko/zxXk07b4PRG7F29gzdfjGUtA6ODl3QM8fPMOnt+/h8vlAX76+Bf4+OkjPNIKrkrT9IT6Yf626bLmbpBBvlFf72HeI9PjbNogchyWZDeHl3elk9qAs81n+aoj6E2RDkfXwJqZJY+D6qMqEUTNYoZw4zmVGvptOBdk4/fEesk42sUVUPpVu2BjZkmeJpp1j4RG4JufkT9Fb0lIbvDuHDgO0VYf5DyfLb7Ys5J55Gw/ZxUg5fRsot5fdmwKP/dkkNQ7DJWjwYjeCtijwpXI22uFPJSFKHw0qBwa49WXDuL7yLN9cAOP7ejWLH2r923kl5e3jPNb4Awc87juFch6GUD5qyfP5PUxoynBADoGlzjHbOhm7E5Bq7+UjwVWePj80Tzl+d3TWIYxGTmwajLq9RAvbgQXcFiwBEB04alfoMjIEFbp+9J+ZeGd8H5deIer3xlhRXu/ZdR2XMKjkncB7ou1yjYE0ztqhNas6FQ38ZMhBbvCFFU7pKSkRiWy9u14IUd4cuNwieJnhI7SdH3B10otOyf3SuM3vOBrYr7Y2Qg9mnr6TvZursQ8/8vJOPKEGlu28GBPOt0GPH7byW9u7teF9TOFqT/FliY+v1jBVIcO6awNFHXHQNNWcKFbpsnrFivXIvdqSfOBiGVpkFOYpoiqo1eEPe8WCITF1cIsIBcWdDwLoUweq3H+ryuB7GQIVvoiuyl8GWyw+V0JJeAAVHY+rOta7npY13LkEkBdpa8TmQQm5PLmKBZQ6iSRbyx4dOuTzF66Wt04AHRFH5dV8nDZ68qr4WvjJrMYB4VaGWcujILQfgAS3JnSL3tQ40PIEzfmZom0fWoE8CpOlNuXyu4J0vsKZIKvlCYjn+RTB3YRNMFY0g6+Wbj5AMSOeYaCAmVWeGpF6liwl/AZ638lgnaktrTEoymsw/K8FcKe/wqZsQBURRHcY6NQGUWnB119QvmcgHcKbeELK1YSZdcnjzNBgc1VEBtwq5IG0CqVAJVcc93OiEy3q0joyQ3LLXrd62RFwxyyvOzSBSgrgeSieqdsd9BV4npbU88HNnrItWlHSsKglSQvf4yDvjaMgE0z8rxZxtuEsmrGCCHAx3+6AP3XD/D0hw/w+O65iPSVjTplItoaT/cAdB/N8zPJ2YVqd7ksz3BTTivn9HgIzaedgPMxdgwSS2JEEoDyR5J1blccF1uNa1HKR+XdGTrNcFszl0ZUneagvnYilLl1u81vKKF+HuHRufTZTtkW0/3vRrgX/vP4PSLCuenqjCITG1vrxY7D1dlyiFiOD6wy5J+/EPzlM8HP116DvPAcNQn3buL7wJHxeuY89FZ78x6wVdPTJqBxEcQ66A5J1rlrOngpqipJCfl2RwPrSkt808gO/U7u3QMSPH38t3pva1mR7XOoLm/x//z8A/z6+E2gzbRDs0LILozlL+0sdA3Fk/0Bav9I0KHb8FZ/vIjOL7av0yWMT0t8LcbXBdDWy9bW0NDqb+29rXaRqHuX1OWQHKxo9d7Mnm6sfSNpCJ1q43eUlPeaR0HWKQ90XmdrHwH0ZaPh43ZxZr+UuGPQ5r/JOzadtZOQ61N3g5+9kx1Adb/SlfudYnFt95QdPYFrnBDmB4JZMH83ODBt79gRkTi0ErZ0xwxlxGBfsmSCS3DyqpYqrUnKSpThDlh+0qh3nUJI72pw2/rABiRqerIDsuUCOZIJQXZECEOmbaJoomtAyyRQ+vRIHld6YohaH6kuWuYJOgq+VhAK/p7uktSHJ3QChHgUs1cGtBL5EUGB6yRIEAMsmKU29YzU5UJ1NHaoMs/0eDetsCe9/S6lxSaTfqvGahCUeZlzz3ry9qjx6l2fpe3To0I0mWe4hB4ywtQpK6j9igZnPBIN6zO3g8tQaX/1oL8ispOrqW9UVEID3zDfbxUdoRfBd+I1fjZI5miRoOsMQcDiSsdDdwcCFKejC2Kbt47IoBgLP5Epo3akONa2Rv4eZSChPudzbqq8zk7BVEvCf4/l2MwJZgx/k8VfHZwI1+cF6NtHuDw9wnJZAGEFXm96FHYdo9LjQSdKdMw7rtjddyOGH+ggzY9Mh+nkJWUyRIhiP+1MO9t5+jDUf6SgZDDZYMJAthMc57bJrQ4pL+IYRp8noY7SH5pnzFpb2nSo1xRUnCfKdid4CEwwYtJwOpMUxrkhtwrkmu6OUuDAoJ2GZq5Jx5YGC0410KU7z+mdPbrb9mq+rTHR04s03+E227A7bEniHHTOSuOoA4BfVoIf16Pj8R4j5zjcTM1OBEEaT+bvGRf7yj4Cb6u3XhvGrdGsrk2gJx5uYYPpLGQWmya+BdVbWakPM2LV90VaOXuj2BH1BxAQLOsnn8bobaKpsH+qvvlCK1wx7J4A4+IVfw4XRGwdF5yrliFIpfpLcZLKK6MvEbh32+qz2uW4sG5p5+bQzKiL9Piv26XR+Eg8TglkCK4V4g5msdHNfIKA7eZJBCBYAXGZHt9xhhppEbJOvSpVLi2Bb9xGnWmxpjrnxuTcnSPDRO1XpRvpTIakvAAPzlbal2cz3Y4ENPgmwYLYBwDD9hwuMBnZEFF+2Odb/ZdNkPeIoOyZ4Cbk+76iWe5aHtyHY/6OiHYEgQrU9s0Qwui3kVZvWJegwMr3NdTgwJoZqpzXSAqqOHR0GQd2DW6sVHZFrGtZQbOu11JOPZ4p1iau5kRcqvAtwoqDEAjme+fC4KZRRCeu5RLXWXd/kL1LoZltWq8E11d3kZCbNLVsMrnstwFHNXOkLXNwVFC1FFZTRymKeNLi/kQRIKUN4pmvjT4ieCH0lRYfzkknbctC2tyoHk1ih0G7AmzzCf8DmT4EgLizI6I7rIHfEHFOnerVbPczOagyFsoGr7QM+yTbCRNWy5AOBElPBPWkOc/rqIXPAfdFmGy6Z7NzITs6Z/PoiH3kOlxb4TWVo+6JUsGBAtOuliSV1vvmim49s0zVwSBy2FGQZ7a71lbpPyvNJlelTncj3zdU62bYDjvjrcsiPY064V01yqDq1XZ3npBQd561dBTU2ps85y0yPqusXy6wLBfAywK4EDwuf4Wn5W+A65FgxE7h0+2DjAfaeXIn0jy18H0iwG9DrUZukCmt0/fEGekmVHGgRvqM/mgZTvQQ30Cyl7Q6IQiibKX0621wB4NhbBYeBCMMCOo8m+nr4Um4dPF0sg7BPdr8GGwari9N6j1Y505w7x0jvTK93VTviJAdEWVHrI3Xa+aordgUtzf6PbvuK2GJ3+HF4A0IipOKTyUI9kwA1e1mVC+VF3mC7oK+xu/B+pn6Px6+fIRvf/7V+CE6NGR2B1l7d/X2GgH8+u4b+Pn9Hw2u4rtq6fcPeJHH2iSo8nFl+5d1icz+wm7bqry3zj3OpsGj4q8pOyEWuKT4NS26502gA6EEM1KStD5OU6zDo3U7hImBzCerq9bXRCYPf+8sKCRGvHJRpk+gx2sdOO7U8WV12NuOr4auO4qVadTWdBBba58/ZRZYko49Ceb5KWTYUwk8nxzB9epzwQTsuKw6hxlV0y08ZsPT9C6GTwYCkCOQxPE6jHgFcGWC6w8R9NbZX1fH2LshrP2sRXtDzwVRjHPLETS9R8dIPzu5gd8J0VZ+6I4GK1JU+NWBbB9MkpeYtQa3+V6dJG51v2n7ZtK3cwEHeITuUCqaL4KeBK8WpfQMV5AOIE5mFsWcuXVcIDhhlOs1wA62xKcDvm9OhuB85tLSWGGApu1C32fpY+a07XtBiARjfFNih7YRa7rgbLfaWKbHii7DPGcTib6GIn9ivkiTrRqCvc8ATLsxPW6AO74f8UBHh6o8py/bIYRgj0DB0bnfVp5ujYctuRQaTIMQ2SA/7hQp7dchovfYPN9q+1SB75habX143RC6VMILXbIDQ3bn4OBQwqyNbT0Qfv1yhevyCZC+AMK1U5c+NEMfhz87byy/jvq+/3bGOGjbt+2PQM4knoqLRvKrzZvt3vEcg83zMewbN9GG8xB4l0kN9esFLK10Q0juvaD0qykzlJNNKC59jmkMsb28XsMysnl/K2yIuc25vyNqG3SBdOwmnIBm3hom6z7RAPjxtpyZHzM4a9dCQFogVQZgmmXuou9NFQzD+X173t9XVO+N7G6vv+WoV3ZwJZmPN9l2zr2Bman5p/mRKB4vCpsS5Hf4isDaMRaGnHmj3Mlswoi/LwZ5Uunr66ptF3mgC/LrQqEwL9m8lqBCg7ULiw1ECLDQFeDLVf0RHeAh25zOwLKL2ve0XuEzn+BRsaymjHgCAKxyC05ZyGJtWgRY8QKAi+r6xh51C6bq05KGf+lklR1si+aP7EbjnRA9Ax61b9SnBs6nJuEKwZn0F995wTtouDwCUyc+Gh0AqF77He4VZM0Qqdrri2AD3qWMQY9tXFXIGI3uC22/3wrNgsVaX612VPRaeb07+LC7CpR82w9UB5tt+y2dZ0arjwtQejOYyKAgjHZs0thEKrs/Gpq3kJ4/7w4X5twI84GICaVNHXi8WtsnVN7nwdsazeV1Scm7FOyRTN0OaFaB2nRemBY0a73IrAQgeMcAX27GdVBBykX4aaxe4V7Ogzfbzyw1K2aXRQqaRiiw8Oe7EPhOCFpbHCLYLWlcZQKQ3RQr4+L7LnjgUodlo9sC2n5keiP99TfaLY6I5bJn8BOcncak5NqWfNeB0mtXnnOQwq7VJQAJXOU0yfNKW5y8ev3k20EqqL8b57V+apTUi5NdholVHoyB1QRXHInJxBhpT8FvYR+kaojkYKEEDm36MH5KPRqkys8Wp32/o902nRNhAhFjtcFjm0xX3pczLnn3lKkbiMoGs+e582dtAgPK4Spi0d1z0jhSoqKTXNqcNaNVLGV8kspzKxVkWkIEd2Zj4DEdiob/hxER/Zjtad0u7IWglQOtgmBKCOOlIWlm2HTzDnYEdPCVKa9hfIhB/G6ZrMRM6A1Y8baysEesn+CKglLyryvB/+ef/xm+AAGsn7cLjyWk9Uraoft76/kN0FXe2+f3WxHcylz7TINmIz7p0FXHMeBgwcM00ByOyUHeJIn5Gt1Ef2HyrUV2BM7o3xnTaBskPEMAbuevSZFkmgNsvpTM3JxNpP13+O3Cluy5H/AF1LzSueye5tXCJRBxuVwA8VKJK3xL5q+Ht83Tb5u6M+Dvv4a/g4fXiJ1pkUv43Um4Qxlp7uDMfiWqkvpHrGJTvl/oEzx//Jfy2PirHFZSHPyU3Uf2RIzr8gB//fbPsF5YJkrpXV9K1LWsBG3tTm9vik5cbfxrqs+aDKB+A+s/QADA5QKAl+BvQy2HnyPm9zUSmvQmLzps8g2rrw+vQd9B9UY5O80ioPCzFygzdeFFhyV7kj61edv3zGDBap+D1OY5Z5BuU9EbO3qiCfPnnK01X+9Zjbbc51tbpLHZOc3Y3dEvvHwRsUN2zM0CqcuM3JdDcK9gxHQgYqtwu1JYmo96bG+cYwji5BPHP0D1xNSW79q0mcAIArLpufKFAw5y6XTGQBFxVV7luex+KN8BARZ321LFO7kbwk06Vao3OzMcNT0vlqm2qbfdBeKitw3eHKdPSw1++9s6whBY8OqxCuqETkqPDkOelMNAb08fqD1pZ8SIR0qZF6Zy54fDBSWwErZYtLWpEU0RRhgTKMIM4sTe0Naj2vRUywy7oNtumDjYs+CCyV2yYU5OO+Aa1mdHS2rsHqkf45hoR0umKEXcr2a2wSa1krZP0db2Uqf5zjqKqA35enRQ+OF4B8OFqK1CliJvSG6ESSd5sro8mYlVBcwr1TiFKftKkrYia9LoXIb24RAsizbyzg+lkKspvMm3xUojTiFD2ZD9XXoAe15qyUsgK0yrsv7p0y/wma7weFl3qayY8g+BO0M2mUo1KFhzBPnfDS4PFy+M4SVXG+v4lycTuVoZyc2yEYOueXqJxmULjwu5WfoqS8CvrtMck8ruYBwrMqNYyvxr02yVszVBT0Ive6a4zpCzt8BNWTtXcDMXNWN2XzulM1pg9VYE+gTNoqMMWUaW4fFD47kV7n04YrvHir+gzLkNjOxh6ImBTTztrz1NyUEIqCo84qK6G9xqlrc0jlOy9rAlQ7dxUvMlh9vrt42/kHFDKV8df3/tMG7wV9lIMwm75fSL8FRsMOMLC42Jzp/jLz5mEJsHq8MVqKrARaZeiOBy/VzTGoOI0QabWfwinEOO9gZYVoAnusJ1NTo0L/qUvLzAUOmTv0R6CxyBy2fpuy4XAFiG9hA1voMqL4n1Dt9O4nZDleXlC0oKdt2s0C60ElNPfJdm54XBg/zuWukICy/Kr2iDotCuCdHVPzKnP/2DU5B/4OinijNf9LTfaXzrwL99sDldLtUZTJ2NMyINALiWnpgoXTknz50WWdKX/XJqxt2EJBl2dq+aTN64vkcwYj4QETUfHrR8670df5kjwK7mxwXAOqYNboKqPFK5v4FHLhKULVGEsPAWOnHyBYsUoQYYmJRV3kn0lgMQHB0mgxEXrYvQbIQbgGwTQ6iKLZ+vrRkAYAVar7ElQSmjIPTBCX4OlugujT4QgEbMZPdA3b638r0KvFKdFeLUOuviB56QwlMuUgM/5fkqrQBQduJRvUipowDVLW82mENQ+1Lo7gxinvjkM6Zxs+i0YdQ9kqkKRKRap6wsKYonNm2/nrKXh+1q/SVoFnAnBjXvTOgV1ttJ0dDcvMDsKzBvxEBRUxtjBPZKlbfEQ2L1aUQR2Jasell8VQyWJU8HrIBYoVs/Mg2ooXvM2yNQ8WeYU3Sh6ADiPFXxHNwRMmv4xvTuF5UzRcvED67T12SCNPqyl/lpeSaPeab1NMI/QqMlhDHo+q4q8oRgd+1JLVL0rdJKZrKamYw11No3/KYDomHARue7LYJck4VWDmN2awx1pJ/TjS7LAni5wMPzEzy9e4J1+RvAl0+g19jxzhmofVDKbZ3rLT26wr+m2RJcDh/XMYfhHS4joMixsczzQPzoHOjZVQQrQ+DGC5k2TNHxvHaU6B0Z+0bUmDtb6uzEB55HmmDErbCnE2YL7fFUAB8Jji9LawZ12H+bpx3DNzsXAdjpyupWNzZy1q1DkkdltfOTe2tWPt1n99LvcA9wLNHRcUWPIJtkgWVZ9J4IlqnANkTV/2iT6d4GnCLL9sD+Njm6+Ot3uBX26EgREj0VzZszp9JY8ilIX3xgKBi1M20j9J9ZD9h5lxcvpj01nPqosTt4gQ5d9DEhwNOv/+5KbXdjWH0/BBpcupim+i4Q4cdv/hG+PDwF2glQ7s0jZ+PaoAT7P5o6E0C5I7NtIZHgs34eKPOD75eia7G+s9T3fLdghnuR7RmY4hjp8R4nSht5KsNPknMXgj2Yj22mSY929ozYHm/FvWkFwH0gP2q1LVDNGZJjtLK+kMXQR4iuNsO95BxkeF9RbEXozh7SLucGI26+I6JKATfo2V8l/n2Iw4m9Oj6tGpOJMAQr2Ms3MVY7KxsLytULyOrU1yivb0wUo3XhHOCGJ1eU+V8qrkcFdSHaRbZxIl2SOO9s52Tk+hpHKMcurFNPlHNpC4/TNWNjF2c9CVqWoVftUwqX+1hviBbkfAZuQhSqzb+mdKHB0xNojTKO5vxZpXsxFUgSjBACkokikDoqszewXXS8N4lGCisvWf7o4XW4An2OH7cgRrMJugJrxmcvCo+tFgLYE92KLpJNYLYsXynMfrQVB5YXh5TjSuMeQyxyUO/CUUcPQRqMEF4JYyujxz5L5VNDhb3zxfZ5W7+8PFtAHg518oZi/7U8heZvk38AzcqTBnhc+fY8NAmb/LcY5ej/DMsRWTyHVVFY3kmGl029vlsAny9weXqEy8MFFlqrgdGbD3vqXU4l0yLriQKTevbALt0j3NsJey9GhU1aQV2oek63r2cJt23GFdaxh6EOvBrPkxvG4InLJkfBiInM7kuvO08zKEZi4lYQIm9DlmhopmFmGd7QBHl/64IAQ3aX/rGU9z/sU2xZ2PJpF7uddwYUmHl6KJN7SGaZakoQR2SZ8T8v0d8sNG02N0dvoo26IoR5GgFiMK0pvZF3Z0gNL316PXi4pIxtOguobobQLHv0oGaMfcUs/FuFqXk0U8NfDKLe8kqQNhRlDyV57jCYKwMhyMnMmYMAQN56QgBYVl3o59z/timDD0DfrY38dDKBCFZAeEdXWOgLNAh4PwUvGFu1bO/vSGxfND43LMdM0XLxiZw+Yhcn8x/VhxZXHuvBXBQC4SqnYyA/M2UhAKzVb8g6e8SRzT/S+842TDqejxN3UUGul6Yf+XykFVx/Wh3ryJGyc4NtekhuJXTkJTYh2rc3CIKDC0tT6ImlnbpQI1b22iMdFbOHIPXe3SEYsWNHhBlw3nPsBps3dAvD82pugaUOYk5JfHQNC5u6kr9GRWWhcl1NSTJwSHYBdPyI1Rm/CkPJKl7ydyXUqogSt3BNqNdTRSCV3R32jgij4LKAlx0eurLfnu3HK76t07e0Rb5a19fTC30SSWt2gdR2pDU7q9xOLggLe3kTPTw6+x0NtWy/tarwwQpylYZrT23vKrKDgJX7LRi3odrpOmQmrrxq8YdgoFEKM+kMV4lKVEMntaPQtOsAeFUXj6XSyaR5CdyRPOkEY9MDlFUBPGHbiS4hhasdnblY+5NdkVE5Ebo7eFV8lGDKSivwpN67V2YLXF9yIQhFhgym3sjztptXw/c2oVI4SSvzFfN4Flhg+WUGglUapC+CMqW1RfeZ0zF+3igpsV/tsT3JeIw7LvQzp4kXrG7ycJds5S/GY9tLaAr1LgpjySXpCMzK/AM8OJ11dmJPWkKZQAeeVTa3MGa6L78gEGUXbXoE+OX/9h4u/+U7+If/9AM8v3uGX3/9yeyGio2rj3bpeQQ14LCXF1KL0Lzr/b5NwTrPDdSj/yz8Gc7CQKOWy2Aq7fTQ2Sjdjd8gZxBgeprI1YIOPRt4hnknW3Jvo0umHNzURDrG93DPOUGnuf5s09SGdTJtK+vOBpQi7nWvy0bZ/stM4t88jFrCNqnuotazknWHcsilxlMH4rG7jGSUByfTnQFfEX+88DD7HWZhzEO7/XLnqVRzMFOGdTNQ8/iGotdqA1nfwuB+uE0oNvJGEv2K3VeGHgAiDPoRpulSqI1WPggALj69fQ/6/Y+ffgT4hD6ZSwVgfRHiL6SIzf6xzxH+9s0/wC+P34lNF0/QIILqLyzP13V170c9JUEEuyjVVNwtDK7fbLMu1V/IvhHkU1fMNGLvOfTHRak9qr4ycO+1SE2jxHcqJWVH2t82tLq95UBsfja/TwSna3RGTrOZp6Pz9fL3rhPZDZFp+edEmzRi/ORgxO4dEdaQkaNM6kelEMA6d8gIhThADKjDxwogLksNZEry8PdC2wpAi3P0i8MfoB4Xwhf38ADkhraXFdW81jZ3jcB156inYlFaiyNsFVvZBCBGNplxTPqKaiY3vsgmq3Wl2ha2TFdILDUXoNwPdlV84/SXNFHw+90OurI1FJnwhJ1wuLxmYo0TgUxk/Uk4Ly2H2KMjoPgtKTAdtCkfmNmp/hZWlgk42YzolAR+Zhvc7lZpn0nR4iAMAywClj7uaaeHTS/mJ0eC7k1K5yGeqMFlMsSEIET6PSLtADqyNmA/56WGshFn5SdpvV2f9ajwTpYmaStioKxm0XGVbdvs159lhZHiGN+xzLY9GhCGIl09jOLlE8cJHtKap0GbnLFitZo86Y4USR8b16fN2qUpC9MM5p2X2/b4nYZ+228DlkSbAJPuZnn+9ACPH57h6f0HeHz3XAwOE5SycvSQPLDlOeKY8fv1GClJ7Q6Llm+kqGGKHrH5ANm/yCZWbixHOICnSWMDGdlh5qQYZLwNeggiJ7C2NcGQvRLSZuY6buHbI/+3uBjHr0fFRNTJoofSXRm/DwYAmJ3Dw6Sd+rLutdGOc3N9d5AegjxbMt7ir4bVtE278uLm8TDCE3TGUVPvSTOVYH68edgaC4HQs9qvB06Gk9oixDoIQnEHPZiBYKHXDoe1WENPxJGXXVJNltVT4JJqIIDulr91Iqb065uHA1r+BqYza3/GePwK4N5VO9IlfeXuJDpulR8j2MeLTiesZFH7tj1hwADfVdHvSnLv2VXJcrlZNBI+rQ8HgHQRmssabLgKT+sVaP0kOovaUbwQl7GWU1JWuiYGTfm7LgtcL09aqPPvoUlbG5HpbpMAgFkAzbspOjah7KQwQYly+j1WG2wxPljOY/0F9UBcOSKK827ZgmWRJwLKfa6GLIEzhvBIW92bv5WcfdoDw0/YBjsIkgIpfdeybtVTIqrO0OtSikmmbr06NsVGabOtdEtAYkcgwgwYhHIngmF2fgWs67DgqJ54Oa8TCBa4AF4M43Bn1V0KZO+GAADApaKuAqTeu8Ar/LXdF3XA886DSgjfN7HW3QlSm4UDCYvIGpLqUhHKjKfSUj6WGiVdWiONV/Lz3QbrCuv1WlYzr9xUJFVXB3URBmttt+Lj1bJH7gg5cqrWv+wS0F0f6Rl7BpNEXBdfCsmuDLtVz04EoG0Mpa4s+BSVCnGxCfgDsUSLDW3MAyu3I9efj8tynhZpgHoPhirerluqQVK22JlqCrMC2Gvp5YLqpm8N75jdEqHRwDe0Vpi3zUUxlO8+sFp/vSvE8sKCMZWZ2bkiBGU7JjeMmUAFkxmDy1ojzuZoso5TpAlWpMBjUJuhdF+2G6K4mb0RCeA6mzSd79/FJEOAsGVURYThNS1G7icRdAQNfXqHRDFqFUlI52iND7PUflqVcySB+6DsCJEAJa8WQa9LWHNWKwKyE4AiQT5Zwzs8nk0DAFMGCG2kXi4R551Mdo0Jmb60fI+deTM+V+HAslKZ2n4yXiP/zXveURLPo8Qwl/kxSI4Wlqn2yJzRJNyUBZAep8XlqswGV0ZICYJBZGggkkj4mvsCIdyRQlRkZWEUnd/sgDWDBWGBhYMMVPpveXiGp+cf4Nvv/wzP75/hX/72P4HgVz9+esFKe0RGIg9yYFobbHna4aM4yGM52xKuD2vK8y0kY4DsWjgyn5owmZpakCx+HPgMaNKgy7ob/OoAD3aubQmEPbsK9ZTHaHSQ/EWmR4w6O3tSyDcDGy2yP8LUonaGeKcM3W7kESR1YfERtbpZkkS6EbR6rpYARTbsKYF8/3Xnyti/tu57+zC0rfmCkZ9SWu4ITYNtDO5GOWnzlCp1xuNL1ev0Qr2u1E7M9QuVVbXX9Vr4GBfA5REQn2FZLoDLFXBdVTdlZmc+cM3G8sOOiKx+vRpujQZ9vzVTlOSdFKIKddo5lRvQ7xZyHycB64ih/HMLOQTnD4m5ucwld7rt24U30F3HodfEG+Og/4LlQ3b/YGvfTSCefH8M7FSqQ4+SBJWK3qsqT5pnCcwHWINkjf6KgTr/8OVn+O7Lz8kC1fqN4u9Yc03z6fED/PjNN+29j7zbhVYoFnKxqwnBrjhu6lHMsTovFUSx5FAbtQl4N4YGJxaxxRmTZWh3/JNNJ32zgO21Bbk8bD69/dn2LbpXkaYWnIo1JeMSrTLyp/mU0dakSebpZmV0r3zF7E8Gimn9PC5PwgJtm5riPZpJdbn0HAMk9LfzTkYBAiRmdNRvxs2Tj+v989euHRG9NcWGqvqhAQDvDBrl4d9txyBCSFTTuWgliAPT+DGFBpnkbd+Z3QzLIk8BAWAVpxopASIjzEEnxk4SkUkAxYHPzvQV3A6NWEGDXGlvBWWvzbmNJQixWsFNEB1hQzYTQ5dYn5c61W8qyF227mzVL7t6EwgxjD9qmwmULLVdlXm8U1yxiZCStrclheMnJubKJkk68TYuX/dJqMc8dW2K0QAzyJKWM0itCEMjjbJCW+HFDdtLvQW7/TKBtjXUo78OI4zPDn0EELb1ZXXu4AYzkWPgRdfZY3xWnCjfDnOYdonjYjCjM3NZ2ZXOZkEAW8Vvb/8FlM13jA96mWpyU62snVQK93GMihnK1ZmMO7LcDWYnfCMC8ixBeYhRXPlYAXABAoRPjwBfLgTPDxdYlgU+fvoMn4HgaoNXBA2L6bwdKGj6O1e/bBq/o2ZmPDe10vLj01RW7uCWPRPLELev256FPJaOJpttOwI3PpXijHaUoL6kmhH23e6JutZYR3KPKX/f1pXx2zwT+pUl8RYYWmb8PbZ9m3Snfj8PnSbXMrdKb9tzb9GJmdt70ZT5qrBPidvOd6SjeyTA1tb5fbPgbRAr5unapy/6vm/tFNZhyoNmpemB6u7h7lGqWY2zjyPw/dDeOkjEfqJ2FBP44A0M4Xk4It0GNvCbgR5NBzv+teGmqSHIqE1cswK7MRb3k9aUe3+Ivnj/chJHOOI83YVr8MUWtbvg1ddj7T+7WBhE8VXzw8wVdS6wuy0A1J4veVZ4v36CNe18hHK0u/r1rP4bU1NFXsynsqzw08M7AFxM4rXNbMwamcsQa1qUFpT85O3huFBWAxkr2NZd6yI8ORIqLmwLp0m0c2c7r9r0IWmpD4Kj19rwY66ux/F3nAOE0mDCMxnGfBSGvhZ20kVh0Qcp1QhFMItO2UUxY8edUz5n8fkajoapL9La0to3+2qxX4GdDkTIERjBaVz73BBQGp/WeieCjRJWTCps7EizQsMlU7z8n0QWa2reZbBA2YXAqVeQIEDjGq4tLNHG4IhZQDnOr8AFLczRh7XMGoBYr+Xf9QrX61pXFrMw6XWushszMQux8rQ96oh3j5DcQ6EtxX3hACkruMo4Aj1qh8Aq994xyc+42opQV3NnwDSFehjGJWlD64g25BsBpsEuqG2+1h0qTZH2ixHU/BthBd6Nw4ZLWwPpnd3ChSCzfHI0ZVdMTLctgDgAZ3iIP1D7j0y/SonSDkaAMA9slHoO2KCMVw4qYc33sSGZjSxzcXccEhsy0703WzTZyC8suS14mQZax2WuRLBgHdMAMham+oJlXcZc5H+4oeEUqRjQmgQic3Ewmb/jaWmumNz43gzYpY9DEBUq76er7PvohrUyZVlFPt0hm4qHdoaIF5yhSdklwy8PahPXVS/5zgtyWRjTWmn58ZsrfPwG4H/77gkuD4/wz//2b/CJrvCAX2BZUC+e6/BjGlya1l9EsOkcdMS79Oow04v74b5yu44Y2j6y514go8PN9eXp18gFDNuz/NmcMlEaf5A3YC2w/PBS/zcAo8krE/qzc6pbRDDbni/LHcfgHjRGfZnE7lvNgjU9e/utt9EM3LkOdx/CXwOvvhZQaJ7f22kXWJVqmo9/b+O7QuOP9o7rJqEYjuG3PIryo+9NE/9Z4wtaWg9HHXoPcIXnX/61Jm2dEXahsPjDJC01+HRRMcEVH+Dfn/4TrJeH8F4XTROo7e9o5p3SZP1zNq2n1QcG2O8ZfWHVZ2d2UHifqHXVaxr3fEGHbwknDPBz9pPYIAmXV1N0h2xJX06ikCpgtHFJ6mnNefFnuOZhAWFPDMmFhvE4Nv65AtwHkRbNH3OhedGbDb2f4uikXPWftIBmYLlS1dO1s/yd9vj8joheK4lQUALUcS17Iwye3Nnj5A5HyqrOyOOLCErgj3GHlZXi+CBwwQpHQcXJSqm7hMbKPLtlxjFnrshqfXkXBMnRTNqF5S8ffoFxELmW4HqvvmhTtgqgEuSQIER0RhsogoRaAQcowYiCk3Fx3UxNCYLwswWY41tMERIBR8ZR+AC5HBG0WZt4fOLYEyG+NqvnLW27AgcYaM+SYHXCaBYHduLh9AkSrYQtPIMO/bpKAIXfS/lseBmC+A0FfDX41DoiE7GTCq3bQQJuGyA0DsvuYBInuZ1URzTFsuPUa19CeqGQG7Yb+Ec0yFF1se9mIcxyjb7ikpq+QPT1sgxFKYdMQFQeR2rHWNHs4zwPNKBbS8rYr1uklQHmcSJj+k55r+AZFAniDdgzZM2YzOMzBPjuAR6+eYDH53fw8HiBC34G/PIJEFdJI0K6yR2/eZmtPriRNVkZm/mbAqPvhHYXUFbuaFRv5Z1I3ijv5lfn1rJp32aKt5+u+9AYguPdljcQMYGzQeHUtLkCnKJPx7knPeqtV9AELceImEw3U0mn22P72xWIh6YlwUDme0beLM905XKfuONqTC7X8qRHG+f2uYxi4yaoM8dOK4ez9H0yG/Z3+Ch9tw+8jeNsnqonEa3VBtOy47i0qx2PlT/zdH+a2zIMIE6n56pLO+G2+XqElWFaVbsrFRspB+pN7nQ9E16VAc6FQ010VrvGdrxXf70sjHgTAMbV7L271WwEAKD4oC1MlkUYJ3dMm8l/dYZ39P/qupHFh6wiie8y7M4AADIbHhYE+Gb9DNd6hLzM0uyzlMWEmiezmKDm/IxPcL08bC86SzAobgKgRZTgsmQSkyZQA9iZtKv6bBGw7LKwaSQiws8LHnsslHPPBDuMAGqaeoymWRDf9B9ilZ0Y0fi5QezGno0bMoeycONpnGwzenlduCt7aC9vPUxgkw8Mo4VV3PEA6Vk6SOzxOdh9WXWPAnFYr6oArquNFAJzKcTdBzxshXVRksp7ALPKZV3BIo5GIJ8PznRx0bLlSJgffDCilmbZhwgddbFXrUN6pbIDYl1XoPUKV/5OpJKIR1stpIwZAmzOhCaA1Z9zr45rloSgQYiV24ia9pD6M2rAuvvBIXft5QMQZrjVMiW4mDC5hCLknV19zQKL1G9k5SeB3PXA7YUQHeU6gHjnjUSImwmLwBUgeBAsPl3dPhZHTK47fw/NEU8cCTSNe4sa2QaCChU2CCGFgGtpjwc0CGGj+Yypu7K1J0xMxFOn+TARCrWJ3uBos2iN4BaaOMJuJqwxFvemJ1p7/dJ1KoU2UrlAsZBDulakoQS8zD0pSSAoThIEUGQwJwuRaT2mLikz4569nppOUIlbyg7jE/ws0PRupjjdDHsI3Uo7OmLMJfPaUcb3zJZOliXk3NoErCzZOZsAnr55hsd/+g4+fP8dvHt+B+v6b3Clj6ZgnT/I4Mrq0CO0iNKeypmpSv7d1wGT/PDiQO7DPUb3pZt1X1knVPKr3BXzRoFVTYjd3WWI5N1WGSf1++/QQDcIEdOJijDXF7fM2zsXyk3jBGAdl2Rh0rqS2l8Aoj8ui9X/SfKqAvX3B8HMmob7N8fv438Ee8fm73AA0H0AgJVxt4yc30B/3VjNw3PJoEydX1AXl4gB0+oqzn4w+s00ac7t0ZlzL9VfV8t/+vQfQb1m/x2IjwaAfRGcNxZZ0v/12z/DL48fyv23NQ9polCfukC6oZOAoN69mzprOH2ZN6NtZQ6rF/dmeRBxVd9g3UGxLOx/WsSX5os0vgyTz/tsQwlmN4f1HVo9AQDEF4y41E9Th6b22maM0wai+h6n6KGxP8d6c/vE+vqODZyGGndCDitAev8pW9fBE93lywHxQ7gxEKGFuiCEDCR2eFbO7DgRG9+E+h9rAt3lUFYH62XU4vCuSFaT3gkdCUKUf4s89gytK8bDXQtCXFb3cukZrbwTYhUFWGkGiRbCwg7suhq97xsMrVMHk6yMtNuBOIqasK9rexZw3QJNaTYIYwVjELi9fqUqspBJrviqk02DIXGyN4aDCBLlC3J5fT2T7snrxmkxb4uGBeM7s8WM+RuJ2suNACRYFe/C8GkAsiOZWuJQdgrljvFJUOluUTevt8AGC5B6NGj/buksbnKpHcTb/HzUvHLzSCjbCyG4LRG7FwXn9OTPtVsGLRWXFXYLATn3kLvW404EBJFevJ1r0GYaaQiro3qbruwnmSd+941NkSnw/gpkR9FkUzlszkDLA6tTePgv+jZpA4Ax10Bqm1ftbiP7vB3imHyJwfsmSUuBpuAmwux8T5O02zu2wKXMCwiAywKXh0d4eHyEx8cn+OWT2cJpVqg2QyWTPbaI0F79ecKPllAZ2MMDt+U5ms+PmuRV5+HWHN6Ou/1A2YdiI/tlo/gBek8aiT5RfjaDaD/eOD80ctQ8HOphHsZHUuEheTYLo+Mj5xDsTIvj7u6/GBfem0O9880Usr+ITnk74Kg4eGXYG4QtbZ4Y4CmaRhpM5pumJvwe8DmZ5GSGs9heJYHdAX8OTS8M202+mUVmT/4iYq+t26x+vAe6oqPRO4619SjXy/XefEmzY+R1gxF3aLmjKI9UPWOrVsEewwS9FL6ZpYl//zA2+efz9BJGmZ05ZbKc0d6YnldYL9+aRa39bfsduvX3Xrj4rS5GZocmARDqcZitC6Ckeb9+hsv155Le7KZw1TbCZqWrvNBXvZoW2+vL5Qm+XJ6K/wRq21j1nGIuITJ5TrDUHRQrlKPUF1p1bjIIvJ8RAFZUP2qzu7F+1oUGTbpA41ozcRBET8cx2HjBtzE1S9rqrK9lGL98MEHrj+UkWTCNJvPW9NJFTYGAF5Sy/7YpX/zA58B8IMJwtXOoUmUWsxNCjyWqaaxvsXY0V8M5e9B2Mmdb62X01dFfnfzcWAAARHpfA68gZpJ1O25hSFzUuZ0r3lTKXMkW0ThHyorlOkzWenHNSrBev8Bad0PQqkcGlQGxyOCwR72scpRF0tz1l1PYiNuufsooaCSvNKpfQe9HDLXJlT93zKfoBrzpVB7IXA9SPVhdV0o7f1tAo5nOP42ZElfw8E6FMaG2ogB81FKoTJrN3gXgghBYzZ2wIlxWtkO/KTOFNFdSjXANpPa7yPZxjeuuWerWKbalKLPwbtKS7UWhHGRHQ3Q+dZBjnaTcTogwDktJSrub1pkP41JuAg0GHgIde8mryv5zg0YCfahjA8C0Kyg+G5GPZWrhJSwaPWE6odsW8oEK40auv1vg4KRgccwXJ7/9yrhfMcmjZjOXX+1AvvmzkWz3n+13UNh5wDydQSHiycqRGESZpGeqQDL4kvQ1eFqCpThublzMJWYID5cHuDy9g3fP7+Hp/XvAL6q8lYUDnQvYdlcpCzz3CD1LNbo3VGX5tckYAbkP9xjdlzbPzQVH+ZkOtMZqGdNBHbX7FJpv78lUD3kTwCZJp5azYtpm2ahmu3L+QCH3lgX7p7cXgJkQREZ4bNt8YPOCMEmVzGcvBqocmd8EskiNViC6AlC5c2tBti1zWqn5MteaXzO8dv10VB8Z378dsEFbu+L7d9gBmPzYbMJj42O0U/c3AWfpgUNkHTku80Ivb9QAezA6uG9rvvSP2lNgAj2NuqtesJLCzHHe/QEPXz4CfPkoU2G09cV/wD4gpy7rj2YuMEGNn59/gJ/efVPdJ2bRM+sDyOktyrb/2IOx8tHsa3LHJtNi8OmCaHYB6WkkEeR98Bll3omStOyIWJbS1vxZmsAuplf/G+IqOy8QF2mr6AdTmozcRkPJq+qQRgaGrmI3WWQ41y8D2Ful6UBEs4bWWKNUt8ACmGNyIlujZpNaRiaqONV5q4wul0BD+XSdjKuMZSeEUJ1MCxZNtOd0kkti1rq7gTxTIYTtO7XziEp6WKleUL3KP6LyXFYuV0wSddOtAto2sQ6NMCSTxia0A1etOB04lfa1TJHBXe4GJ8k3RU/+TwPu+BpDl/hDWd0UeczGrdX6jYEDyh4Nm/BqJ0sgahl+QaWnN5t2yHe0S2V7x01fXI9FXUpUlrX7MmtfZBd7lqaalETI5ej3SL9G2zMR4nHxy66yxJOWlHlcqZJ+7CWwZZmIdIlHGgobx0R9yBOujVCh1j+9VLX1dKR0p8cyEUDvvHbBHSjlzRmbIjzrk6CD5EruwdksrD6OWPJtik0iYF0EEOoxc/voaYOLWtsZ8LsXvBzhL7LDy3U9pow53g0RJ+dQFozqY3/zFkgtM2vv5qzLzKAK7eVkVV8SONAp3c/ePCa1yUpA/+HpCZ7ev4ePX77Ap5/+Br9+vpZakOHzoOD4imU/enRma8zmdljeB/ql7A5OAfhujM9uoKVXTCZUMyytdlLyGPUvorkRdNz1aoVGxmu2+/R6Kw+5uDrnbnbwbMMovrOCEXvwbNeD9bWaPnudvogJbFeN5VI7jg4NjjuxRjZgz4MZrLdpAHsGrNXlb69vWCNxLDP/TOgpppHdEcF24ALLstSjmXz6FsfOenaF1cb7I+iNrnUo/1T6MDYPNscMiZr2WCO9znx/2oS3G9R0mdPrZnFaOHUn31kddKgL9lWk0dk7uogO68jpalxHTfx+gYl5O2k3Zm8e+iLhbsWawkcFDPi/GP4htfeTTBJhyposewdW/kXBn4DxGy9LZ0cC108SkqG0+oHYByg+qLYGdbIEwHwm5Tn/HVwBP38EG4Qg8178B+SRyxLr6LxGBFou8OvTB9mRIOmk2/lLrbMbasbX2VANcsKEKTD0JJnnV4AFYFnLbv91CQvb1zDhsj8Zl/LZ8ddYWBztlqoNQACAZfc4c6erJM3nxRxKstQPxH2XjClXhvm6V3/aeTQT10g/hSnl/gbqEwtsHGHlFD+YnTFEXB0qOw6oXgK9rm5Fd2nU2pDuKCU+wqYwDCwIy8LrOVvhondKlGCKrOYEu13H0kjS4GWXRr0f4nqFdb0CrdfaDOhkB4hTB9sBR9Z4ZKFp3ttuCB3tjTv+rGVJ8KX+NmXEi4Jz/2ykrdIPpl5ctwa8gJJjPTzRrYlp2sljI/PJRoamQyNEejCeiPLy0nS8u0Z6qd0N4ZGljdvZ4aHFyIU2TV7WkgbjrUGnx2Opkx2UJyWf75u0xTBpK/Kv2/MGcx6J0/CCfBwNDnIBABnnrR07InyrAzMJRoxUiSm/TCSM2vZmusouMlti3mfxcKZmnEOfZoliT3heslZtnO8bbVDGf2XeZavBPJ1agJEpYRxsxYri6oOe483JB7ABQxC+7yrcBkco3awaGIMzHOtdQH5VW4/uQJfPmHRPsgCgphwFI0oebGSyIaR0LyEQj81lgXfP7+HDd9/DX3/9BB//9jM8P36BC88priOzyqU1Dgzeto2VUS7ZG4E7+cNPgba9rO5lWrqpRPZ7Nrx1DBIVR9/x0I1Ks+gYEL58XfDmdkZIR9/e462eujefkaV/p/AaNevPs15/fztsqZOv01l5AVmdg8oCOQCs9l9Z7dgeUfh26pVAQtuI3PPE3gnjHUYaTpsWbi7xtwE+GMHwe8vdArNBiD4wp39d/TA7Pu8OqavAUJc2baA8dZG0y277XoU9MHDa7IRmmVVYfKaOZXRp5ImxZyNlcmKKvGh9ZF6T9nM+AMADfYH3v/ylvjM+OGN3x8XBZNs+mWA/PzzD+vwt0HJRhZ8XELAOTFwpAnC74gsdPX3SoOtA3GEPsOAiixUYVqqLys3sZO8Vdid95NUUO57ZufFrIQZ/gM1r/KETIIuRoyzjdxhaKuh1sTn5JJsWZ4IDlA/2ws4dEYWyYrSajTfMPCvUIIEyq3f6VgOWGQyLl1VduQRy/n9BDEQE1xqIILn42Ss4fF6ZH7gA5WgXlFUwdnuUNFa9uIXqxdDrSkCwgoTyjIOtBDKY0vq3Kr5Uj6Za16sEZcStyIwoDIfO62bEhGknC5nzEmt71dyUMQBKGwDXPQqLBK9d+eSZy+PXxeI4PVB64HKjcUQbYMG3Mg/EI4Y2SSjtYGJJWr+u1yP+zI6zyUuy2TGkppAmNp8VTATgjnxySTXCU/7Y4A7l3eIu5ZF8UO5O4NXshjePnKtrd6cI3Qket7uF55tkF0JpA/1F/NfsKHEOHKzpUdWOKEm36tWjQ+vYh+bSbRuAjcjQP3KlEYAGfPuFOhVikG6Leg7AFoev0jsM3iXM278vZIOqA2LEBiVj/4i8BRW5EoyDvF7tbohM/rZSeitwornqJWo4nuCtDLBBzlTXVso9QuR5Amt5LYFR0rp+EyIWIChB+k/fXYC+f4Yf/vQDfPjwLfzyyyeAa70Taab/mjS9THnDYPdHq0gN0b8aJAQFsZD7GLxs311OasQZxTWqantgLNb2A3V/gFvB08natF+DKY7xQfGd50WdGjPa1s6JeMyNft8ORvRw3yWIEZSUrATX5ukYvwNdFhr04zLzLtlB45C/ThA7sR97PLQT7VxPnNFXPTumvk2LyB4G4RT0wBZZ1QiqblnMk3os7m5TZWsM6ve3Ms00bCN/4A5DcJubGq2pyxa5XH8r7ToHd2voBrzpt0+H2mrV0RQyrNn9q71dFsZEg7o2ryn76BTdWAAdYjh1n7P7XoRRg77cyMjYq9EZezDLE5kOiuBs/E1cBCUTgmHirB2zcdqmO9b6+wdBnmNH6XFHhatW8XtV4zfFjuYvt4P6yfi0Cn7Hl4CTNJnxyACb44SR5+PERPDd55+AcNF7cutdEewTEl9kWKDNdq7uyhBS3RdChI+PH0qww9LHvg0CXaSKoP9A9WgCqifc6H0d7PNcapvIMVANm3HLYmVL9SkhgPiXEew7k13KGyywNnjFp5cwp57mk9ufNhghvhM7XfcdD+bHsQngwGXVBPY4GQK+oBmqA17vO+CABbKjMyHSBweqc6YammV3xSpMUAIRisfzHHojiBmlroIRRgGTvwZNWGFdiczRTAXPpVaEo2R8aztUJ/gqbVDulVhprfdlkDkOqjKSiaQJoR1plrmLmHozhqQ+0aGOsIDyLrrsZP5znCYjidtSB2pkMK1CptmrcNjtWESQy4m1LA1eyaqnZHK3fVxeelGLDq9xUJuqsDMxBhxmnKq8EkuFqjZpqJJsCJpRW+0dE7NLt0Yr2LoHmsiROta1WwV1IaRblh33piD7UUoOSp+Uw/T2h4Sf0gxP2l0PoTqpb01ZgMqdMRj5YJJpnQGlDd4c68byDQBSX7B7phmzcZfVy5bt0jfL/iL9KZb6nfkYqziIoyWgGrwbw5ayPS5NV2VsjaFQ1ohgy5CxPDNZT1OLURQJx87k7r5pV4NkjVB341TZmV0G78dIZ46WUgh+/cM7wP/2D/DNf/kzfPPt9/Af1x8Bv3x2c7PRUPPqYPdBGA8hb94thj7Yz06vAh1Zaj6buczoSeeB6a9eux/A5mBmkpOEJPOm1/KyUgZjY1j8OQ14QnMN4eV2RszUYps/9rXHEbmf4ehRomka+Qs8H9xQfjstp0nuyR9nwY1riDpwpEVG/dHmbcezTs56aSdVm0JXO9o5sJnvvoq5A25nrFPrOTuWt9Jsy/XXA1vHt0bfOXP33w20ylN80KbnL5Q8HmfqPlEdf3t89CnM8p7f0YessGRenYMNJT4z2qN90CWqfvJNxLvG7B4N8bgAnc7ZS5hWBbs/xW8UF3YOUToHXGNb2ZXybC97/wGEsdRW5gIAT7/+FXTc2UBG8PAJweUY/pXrxCnIoDH+kOvyAJ+fPsD1cgGCtXAEL5YPu0j4uxyThQB0LWlXKqfd+CYqGRfrz4W2LWsq98DdfwrmUzLowvn2lIyos+lC9/LOetw4sdZV8Cb+IRu7I1igLEdlg2xrDE34Vjqw+7Lq0kkEQOV868IzBHJJtOFAEiOgDgLnqKgNwell5aYyFh9vJDshOB/E8/csQ2F1LtptuOq5k2Mj1nqpa926y8cxcRBC2nJRRvOhDPK4zG6Nmk2CDohL2RrMQQjxTBqHJQ9EHoSphGeGWrX+tc11ylNaEcx5qFZm2Iu4yYxxI22ErMwZKu2NrultVZqdAyFtRCWDOBkgbFRIm5tPrmuE1vDEapC0g9rzpOKzz6Nj2R1rFPtQBiQqa4tQqcl2zvzpXQUGRXNMhfyyx7sgtHcboMlX/wY9YXvHizJXtmNEaERDP6/mBCPjMPYMSNpM7VuJ600Ay9L0qjS02dYoU0anTukq0zSag83Aaduea9hkDmni1wxfDu3YVfrcuNhAlvI68oXflUewpTyr3bioIr/y5x5zynI7x42iFk5zxYjSIausM+TSysOiq+j2ek2ngdzxUJHcPZ4hM4Fkc2Ir7ezrdtcZP9XMqmQtVSF99/wOnr79Dt49v4fHp2cA/AnkeMS9fROr03wx5HYTm6ZsEOAEv9xIdAfybrSExlOxyb5qqdq9bcHzQuTN+cEbBx2avxuA4XuX5B62UaYohXKdyY0L/ugw6l5O6KWPtTkaUJjdGcEy43jgotW5PB38oknaISovQ4ya+lsWEVm0zcX0nveEj9Nuz+t/trM9LSWJdtxHstwOR9sj40detXifgIYrqTtnii1jAhBlTRjBBcDbX9OW8nzv3b3qo8K2yERI5o5ZGGl6/dSxePd+Q4d70bbs2bYpMOGjBp+n/rgj14Nd7MlPnOrfiiWwdTgl1v0qgm7Aba3y1Pgamve5OXYYoi1xnK9HulEp6Ra4JXd3p8QtJe0QOY0oofi8fOuhahajdolpSz6y4/8UIPlzPHu0DSDUfYO1WGNT9c0vV1MbhnthS66WTKzXyY6LxkKqF0pDxa2XUDSkEq2AsMAP149wXX+tT9ewg4J9rRoQYH8vAZX7j4ngIz7Cx8dH0yaksR2rjMri9loz1HK8fLkCDlbd6rFPTROYRL5drU/SeLqaMnh3KJ/ww/MQ+965Xs3CbsabDPqYjnYqg/t3RIjfpnIAdySVjq8ba4oPg0CIpkwRMo+0o7TV11Wd/c0WdmPAKGC9PFh3HiyLccRKORqE0MYvxzE5hzMgsHtTj1Ui+aercTlqZ5iNO7vuimAlGHExgkC3FhHwJotVcdmaSTtBA7ICX/gQoW7ACOAd+tbBm83bvSCEc8JvEccJ43gISoENALgVS2Tb2dA1oT860eTw2xQeVz+oEWZHO9iFH8nQyMlR+VFKOG8KUweE0tjrBg6IZO/d6mpyGfpg+b4pTHGonM7xSR0kKwtgO2XaMnRAc7VxJaDOPQVxFwIHIWT6u0UTt1lp3P4tYT4/tY+62XokFMY0x91tBVT6iOojMrEr3AyKc1/lHD7K3NM+o0bEsqQxbzulbJRZBWe8LAxAm4vlfiYHMn0tmemanUDZ1p+RsjbqOQlBhN2I0FEatLz4pZcCCwELwnJZ4OndE3z48E0NRLzTBQXRySMNOCDe1GJEw+aQot6PrDfOg9zI7wEG9kkHnHe0Ukx7RFZpoa41KHzhbpwYu/dr0bOBmq/k5pUC59TnNl6jIFsy7BmUqZKm0rnfO4wFF6AfVHN77mqEXoe23nQ1auPbtKqbHHI9pWq2jXuLHc6AbJLaKDqSYFV8G/RyfGfeKekbhSfvxv0w3pnpd/Sy7aiV0COazmnbXWhuVfrHit+g3DOsjQmDK4E4a8hsfuIEcp+56GibZfIpynUdE2cGIwpmazt30p5lfL447CO86YlGlzqKOYdsAeMY+3i+/83DRqfY0cQanV8EuYVmbBvRMM2ZdgW5j228+7mVHKtF+6i8yG2DMbRWuJ//xwGIvDAxJbO8UV7yRoNE/yVa4QIAj19+rn65ta0W+4KlGdTnC1DuiCAiwHc/wPXhQ9ErqPqLE7oLNgRcfRtndyZG32PfIonpbDLvh9DH2KRhni2n5SBcLhfxkxe7U+9H5qOgZOE2GrwI2kamn9RmRWgXPI9h/o4IFwhQg9re2VB7qWkVyWuCEQQAuKj40PcAUB0qfNyRnvteq49rcb5zLATYB1Idvktp4AUXKGdbgySk2uB8zJM+5LrVTyjOfMCyw0KNdMUBFs9KJj8PxsUwdut4Wmt7KT01Arf6FcN6pn9tL3c0lqRSwbxUZnNaMuc1uwogA04Xn6PBrc8ax6Q4p6Gpb61M89M69N1RXTyYyRsYWnpbgOoavgI9uTYSuAhY7qOI5Fshq11R0VGLVPJweh+M8JPEfmDhwIItU25VVBTlN16vwdQ3pIeoKPqXIXd11oojPF/V3rJWOTqms+kjyRGcwkSw4gJLI8erbDJ1wI7gdoGYDt0lnVl9aotKYfSGVxMkk0w7Zwk6hPHkXtgra3QvL2SMuAkLhH+68KK680QhQYeb7QsffKLQpn5FLjdToi457KJYYIsxpSFJpWMAocXfh+5F3TChDGayGv12TwCEz398B/CnD/Dtf/kTfPvt9/Djx4/wbx9/gc+f/gOe8CMsvPV1XFqgboOOXbBfQT83fwaJMB4UH9hSP19gvB1eNPtmYMB9rPd1cr521Yfya4OFXpJ2mf+OFhqUiWz6s3rKSznNXtU599KFmz7YW/RWn1j9qOnsdPSdJbPj7ExiW5XS9Y6IRsGh5gucu1zodSFY3a9U9m8JXo9vqHpTvt5gwzmQSQU2CYUhqU1zH2j9MH/P0NiPMmc0RtRN4GUL27fzEuft9MR9JaT3lYyLa63aLEUO+2y/fs4uedUmjju69F2lsPoLES9abSTgqEU8RlxiGUnZSAsQEXyAL/Dw+W/ARtqaLtLm+2utIad+V/VjFiK5W8j0DQHBp8s7+OXpQ20LBOJ7M6JjiBjPYEG5Ii7XBgDUxRgIDw8PsGC5doCo+J1XIliv3D51QXtZ3V9dmNWbzXdboP00i47vviMCqrI5TACy4JNqY/EVqNxU7LhBa2WZ1e9AJHdEMOiZWUvBt5TzwsTHyyteFoQFFsBlUdnHnUZr6RDDLHbSlnXrCwc1vCNHmMc49IHMrerB6cn3HTjHEhtfRBoYIQA+GkqZkwddpIDbzLcnSLRqqaPL91Jpz2z2DUp8z6llVvXzRxQ+2W4FyYetg7cJQgTQHRwNmV3IDVvGn3Ou293QINkuWIRBcHa4zSPJBL1XcmcruRDqeKMaGMqCMMqVYI38Pca+lNwEILrEZrk1H1nehfFq+56nprZ3G4ClXlc7mijtZ96eZie3tk2lv0fpEhr83hhw3piebMXILMOV7nPrEGIelsddAzwELu6pPjVyYsCnzfMwlCMOnbiVqbJV4Jblgl7hh5N9zt+RIAYTsgIIYzCC54uEkkR+6usdgqTBHVbDcBBC5GV1Y/zhHTz9P/8Rvvnzn+D5/Xv4H3/9G/zHx4/wfPkJLviporN8OhBwPXKzcSxa0CySg+nOsEwcDi9znaqbldWNBFCuJW/R0Emfv7bKcCqtx0hvhjMa/zaUZ1KwH5dKpNgvZY4YI51hj5kebI7dCe+xppkLRjhNyNMpK63WzuKpGeWoY3Y1+qenYUo+3Qp7DLGDEZfdOU4aunPk5lpMBtNVz0wX95rMZ/0nMlV3JueI78QH94IbZNs99bY5SI2sLrRiZlvS7Zku90BH1XxT8KKcPCzs1tbaW5NJ/AcaSHeczKDdx9927h/Bfqvu7YDMGXeYcrVnrJG2tw/2wx21hwHsK/HIaQ8tp5u2xFrrsyvOTixHRTTko53cGREIelR5Nd6L77g+o0tOQyKu2J/5vH6Bd18+aRKKPgR+XBfRr8qLxTw3q+ZB/dziQ+LfRPDzO4DP+I3oyOWwnhXs+cNcLwLtY3u5tq0T1eOoiBe4IxQ/OQCsC8KlBlvW6wrXleC6XlUp48X9rEM5fzbUo/+Nn7sGLfaKqt2BCIm417+N3xn1LSuCK4AswSYolSirlAnInBcuzVgd8mvd/hJte4QFFgQg8u6jEjioZxIh8DUWpVHrRdK0+iAEkBkD1SOqAQQsUTUEkaTEF2dfr+VeiPUqdALoaqAFAXC5lLPr63ZgqSddawTqWvCtXxSv3IfBg94bUojKUBq5Aul83VGAzoPGQZ24nbpR7skrcfJ9ATWIIV/va/uQ6bb3Y7TpLBinjdgQFZvwDnVthoaaKi9x4YbhFb5cPpm6s+jF5pk1Wtk5x/9JO4tgCfsh2FZHdC3GjtB2J4SfPHV1GZdt0jh+4jzsUEXHM+UDTWI/hepqb4NUisHQuH0Jw8J+U2FalcdsV8rOIa6XCOeeXW8mI/SSgq+yATmuybrn55QUv7qv5kwc8W7HF5HUazEjSeRhEf9CEWcTmm35gcTmOCIaJNZK+CTyPQSBgeUgysXGDZioWtodLEstzrTjuIXa/pA6BgaJ/Cn0s8yLYw9C9/O7wHSFt8o1VlENit9ZdkogSca/rZLWS4Z3DzF6rmDFY6nbInFBoNXXa7wa1YikOo/JXShk+oJsGtAxZEmznVzpenx+hm+//wO8/+Z7eH7/LVx+/hUAzSVcYLe+kuTb42TLkiLz+i7lphGu6c8mee93B0dvHLgvmL7slGEYPiLP0o9EGSXpeu0SMvarb/S4iqdNHQbduKid/boPsmOY3ibgiUSmHd+mcgpIKLwjs4oMRXey3Fz3sX7COTi0jp2Jr6RDNEfrRGyn8E5/kGV3lfXR3EjIrfnvBG6RFrKKo/wS33Pf1icZxvB7ThfrpeCFbnaxUjG6v8BKX4DgCwA8AeIDAD4AwANguTXC4A07IO8lLWqzDaeWDhs49f1GUNWqh2xmjoggo3mHSE/kTocSn+dMsHwwU87bnklm1IbuiGN1ZaOJ50fs68CIq0fWyC245yHjt42FvZKKrSDbA+eMB0p+zPDB7vZIM/QxqSQKdU1laa93h4Vvk3dC2n7uGSX/FpiZgzOw7d3Tz+axTYFlA+xhzvoT2xSo9rCoK8EcazBFXwFYHZAAL0vgOWp1QlrKOF2SiZ4DDrZmxrfJuswHIHj8/JPJpuXY3S1advUR8OlBBLAiwk/vvoe17nbgHQ+cFmvd+D9CqKfdlKO4eWE8UG0/sD5P09bOP2kWeuwUS/NHM3kXA0gIQIi25auaQwAA61rbm3Es1TdSO0s6W7eg0LoKBhHAssK0OFdK5W3BWF9h3RHAmilIEIKPPwomhnwTx/VlkXI4sbBMDUiABDZqIML2wbLUXRUXo6BrwKJ08tUEH9bKSJae0URD4ROEqeIMYoMQAKDBI+5C6Urvfm/8Vrb06B22TGAAEcwlcTqQkL8Lk5vPjDh+1FkxDgTV4c8//CBZTD8KLoh87elvVtZZ/gplC3nmkY4FcH4Grp4XSdHo1TRSXOIUd4Iwzufs0LTlckBNhg0aKiiQEVvaDYQW0CpJtRJbq8IT/MIb4RNN/XgTAQvUQlaUUZarvBOkH9zw5Y2d6qZHA2/alO3YceLKYYqYp8CMlz3mUzwaqExItVVltwrzr/JxqtpJU1B40QMdm+6ZzRfHKMWktm9S8ROQecpVBajBlxE/gK9ar9+8oRF2kIWvKXUyvRm54dokyKjQNgRQjzkz8yRAOg517CREoa8hIsLl4RGe33+Ap6dneHh8VwLtkQ7z3XLWPHip6Fo4iLq9mGRuyQZ+dyV4GAeCY1ioaYOgmFFMdyPkAzt/5oTTdrBhDOES6Dg4bZEBXZPycCNknRAnwRPa+DAtE68niOvLGo9otp5tukZbSfilJWg0DLbAot6iu+eE5Wlvvw+/bdF210SbtuhbrvQB7ggvw4V7oVFlB2R6FR/FcJb3gLpTJso9LRHytti+lD3Lk431ctbxFQjKvwILIFxggYuX5Tbj+MFtwPP4Bq+mLYP++znBiJmJI7dN+lD6Y99w3JO6x1MVBu0yJ0NnadiQxOG19t95PDXCtFVK+v4AaTOy+yUgnEFwCEfPspvP1S83yptbA51etyS4pReahcThXTcwaj5vq01UMnJsrGv6BVJ7C9cMr8u3iZELMCekdta546qag+hbypKkhR4pbFxOipB4QUynIGkrbbSempcWS5rd+0l4DBrHu0sLYBfYA4Esmmmsd2krXpy8whOt8Pj5o08XHWL6ppRNtUwq+s91ucCvC8KX5aEsfAeqi/eLL7yGH6pvgGApVyTDQiU2QkCyYFiWaVofai1HjmZaUHwMR9bUzO+IkIZQI1MawghDe7QHrxJf+ZeJ4MBalRbetZA4WZGqkwjFbaWrPEEjNJYBKhEVZz3eaeXdB5bWxWXQVa5mzbtlsrVexH0tRztxBEvZ2zDqwqtasVFC5Cyu9QrrdYWVyo6KdV0HirhVCE1bI5TVSYupgV2gSrX+QHJ2mT0Oh5V27itnUrjdGFq/kVNMgXcfLK5dlGaPoqx6A12ZT/kxR4ag8CgKCQzJ2cjeHiG+SrWDrSFgcR21wvOSoZllsA2i9Oog487Ut02jeMuwi4Z46CvolzurTHH/1kxdxWfkG1Rn63yDR3pP7SoGY5Q3jMKPNYrUZh2s1t3UN9qBMabVKa/ZW4/QpduKchdBkuLJaOi+pbYYu3OpQZU09/h4L2+wyExF5O5Xok1S6ypdhLIFtDPzlu4fGCjNOxRcSfX6SogbxyqrF1GgTP9tyhHVN2TWwTKnPT4+wocP38KPn36F//nzz/Dp07/B8/IzIHx2tOkspX13y7byXvcfwYMAQmsReZjPM0cgyitI+tGIiqHTb+f0MkU/K44pc90KlmN8/eOIdiQFBb9NdbBnTunQ3zbMOE6P4FR9D1VG3GWC/h3uDqzQozdAs92kJxcMo0FedkWQW03Y5v86wKoYx4IQm9rkm4Wml6LOd1O73AYZB70GHWfD37M4Plo369eaK2UPRV8vTLdIN6HtkUlsiavkNwMvVectV+Rdy6XBIG1H8PaYTuwx7wqYB7afjaOB/W4ezaJlqFkP4gQDACDVmfgeU6IwFkjzUSaBqu+l2Nta5gUA/vTlJ1hRb8Dg+275hBlcoeht12oDU72sut4VUWzU1TrixN9QHtWTeQDhr0/fwZfFhBN2ToQ7LqvWmmPznIwTuXTIat9bZZCNcODzyL1zIAK6v1gVXu7Z+lyWSgcjt5ZdjlAqn0L7khwhw44brDhREfHxUny/hDhaIqUoiIxTqDJAXYnOF12vdRfE6jq7bQdV6v0W4hI0IfW+LW0++az8z/0VUhp+V29gu9Xa5CWArgPODsrmyzaDWnfG9jEvfRAXcKzCNAXmp82faqChbPSfe8vN8uXBDwQbyPFntDdJXTExypt6dkO6kj1pn5Dd5rHxx/iwccWGBxrojIqgOmwB9HLsjP4exFaKyduh2F5ULT9SW9esiE9oaXD04IRlcCNHcLNdkMtM8dh8YCZCM9mnMmYMWfX8/qwRJfXJLdZTcEYXehqO6ObNiJmTV7kj1hWZeAQ1CKHlm1myaYxm50lSYCYDqMp5fEBYLhd4fHqCX//6E/zl57/BA32EC/4aHD2RD+oMGNpodOzJ/AyRVGJHzlrwsMxp7DItxokgUZSz4TyYHmdH0paI4H7QVcuDhHMP+2S7OYHa54JAEyaaTydPD1nI/aJeoY3ZZAcp51G9Z2zwHLtBTGGiaWHrVQNR/gHQ6rJGhx0Ufp5fe08L7+2NRBlKf+/Be0ve+4GoJVGWw2CI5heC7CvXloNF+2uFH68wJLE1JfPeYWELja97qvaojAOTTWeK3QHz9tdbhdamNO+M/8En8fWe7frx9DxhANo3HdvwbnCki20FW3Xz7wqOao/jYAQ3WqbFjPL43K8GG3LuEMpWJG8U3kJsUZHlX4MYG+mfiUvtpUkIKcPv4/rr3vrs533DrEalhCGe3L4U8wTblMNqGMbM/GPiOg1I3Yk1GNKvddetfekIpMacsnSsYO+hALisn0z5xmed6vScRhevl2xhgTwVHNafvwLCL0iw1kn4iP9nx9FMWknXUMFRTHY1O1GtSKmQItMDYYiwrpguGqKIetQOQ7Z7wjET/jyq8owjONyY1+sV1i+r0LKU26dhCQ4b0aflToGCEzmIsl5LtIgIYDWBA6ax1h8QYMEFlqXuiADpUulUWq+wXuu/ek9Ex1srDrH2sly+6FYehA7T1UAkOzjMYIzlheXIHITwF/YqTUQAGFY9ucuHky/8V9qjMhOFlpJB0wtOcZ9xeSMajs6sUXm0n8yuKxSDmtu2IfeMWR3r/zhEp75qBHv5cYtN8fA47RUr6W8B52BsZYYtK74iJ1gtf07QxPKip/WzrF38o1P0MLT8niCNsybFFxZX/vhW2tQBy5/nwPwklG3hC7TsIqq2uVTvmLlh48G45TTpOeS6Adq+F6RtCtJL0FO2MEaRKY/v4tFdVFFJKn8Xv3VO5nTHkrUxfvnDBei/fg8//N//DM/Pz/D+l3+Dn5cfgdbPZmyew0HbWFhBKr/aPtoabHvKyvO17we8RiaJHXtbhUdh1El/pNU3g/vyejTnDNqFOt97aRvteiP/DkF9puh8u3Ca9IbNhjVJ9syVBFC3p7N9UDVYdCn2EPuVw9kT++uA2RChz+5Z3lYCNqhXAAi7zHk3/bROe2L3nBYT/fpZ5hDcbIfcVLb//luQVDtizb+DwMzgfIMD+CVIaspgSyTYyl1wnjST53cmvQ+8jJRLj13ekbt8eJ8WhtcTGMCpoplqRvHneYPGnWZCWfEo6QCgHp/dvIYFLobWnt1LsHZJL47dxfnESJ7LbzZfzeLNP9GvQNcvwL6AaTdQhR1HM7mPRLMKzSdOcCiO8BWMkzthcrfq1+Pyp5uYIEQ2Tgj0gvK1bjPhSzrc6hhzb4GU0R94xdG86s3jlSAEkG01ACUIkTmc1ImvdJTABO+w2Hu2Zi1Ctvf4AyGKr0Md5GSYJu6+yAdVqAPTv2rPFLsyGzL+WxcMIjKXHBdbos/Fwg6JpmSPWNlypmf1RthpNPCIkz6NRlnfmXgu6JjRs/5BhEbTAhyvEGJ1VfvM6vnp+sjRJ40A2c7bdUJ1hKyzGEwt0AcdwUiBFH1TeH1S+xqzHQqRF3tRiK6TbqM9mq0ig/Qz+9VNHZpUTYAE+sPZ9O2RSHgXDJ/Yarhm6M210HGwZuDPk/AkUFLmJMQsepzgBDATskwBAHdZm3h/IDR3VVjKmUxtEDmxot2cgMrndm30+nwB+E/fweMP38DDwwNclitc8BOs4E7C9PjuApbPGrJNmoyBZ5g5L9E2cz6/taqjS88KBvXTZw0Xh++tbZsNl2ye3R47hq96hRwhrPc6WXAw7M4bGuo8B8w9R8K9cfdmRtB3taHsHCvPm6w6bnVletV4pW9tGbfBnv47tKJ9DnPEmJXSSdvDdX/HQFRtsgVQSlGRY9pWRjre/VimARhVUxYIVXMmXdCzrgDrdawv7VR7bwo83GV4390AOQE2xsyg27fbu6vATqbWsTqY/abgbhv1Tua57lxIs0XNTsyzcjBiu70hb5asXePEYr8PeIf8aUhhBumoZts7IVq7s6d1ePB6s9pFvbRjTClpbxDOpXEPtnGvUPJN4QQlLMXZ4Rqrs4zmiQRj867Lvx2JM6PqzcDkyRfuJKGMBBwRgWWtfVIOMV4T6ChY1MoXf7JrcIBn+gJAXyoh+yXz7suqxdkktLHTQ5VWghJ1kdX4a3mGzcHH7ES3DpYiXAjKqk4SDwrC0kS+jGORAIAvfF6v5R6G6wrXehcDK6Hl/gbUyzXSgAqjLYGCsmGheODlFChcikN01bX8suIGFTdBoaecv7UqbfUT+Dwuqg4k3+gAWdDGUtv4NErfENTVQFTP/aJSB3cOOkA9N4ykH5dKO7q+4d0LBM1KY3S/OuDr4JtdCRKWGuyEQKl0DhgHCfR4r/DDGsva2IXBtBLq4Fw7Z9E2F2Rvwu2KDC4ARJi2g5SBUNuj9imALNKdtR9HQQvExfWxBiHm1I0ynlnekHCPN27HTt2sJV3QDIvgjYG0w17ndFiE/u92ZzYpbOU5CEesIHQfBldEu0ehuBVmeYlTKz8JCbwql9N0FIE2IIGyQ28PSB4dGCOCDb154IxnHr1HCWGpO/raYPj2AM9KQQR4eHiEd998C4/Pz7BcHoC3b+qOjPqHfJB+cSb7vOn61oyDhtM6bUjh82wa3g50xt4JRB46TinJ4hZe7Kbh2DTw9wMjM4dA74kjcMGIETr+yoEHHumsz391bb5XUu2br74+uK1us+N+a7kWQbEjrivBda12KIDYNAWsLk/w8OO/wPLzj4CffzFY/p7ga61PGDO9aeeeEy9AKPQtaih3hN9QVRlepMod0/wl4W4BsYPw9z5Dfp2QM4nOwz0m4ue9HrU+oVvAOs19UEIoGJjbPSpb/wu5dEOqJ6vUWChpW5RRMaL9ECTKtro0bDsSECy+ndBSRJ6Wg0TN74gAcA4Udg9idXC48o1TKndQqYOOHcu96T1zv7hiQrl8GTTJvxIMQXs59WJXcuUFS+SnXA5h6qwklBjBAn43Q+sAoorP0qNBgk7FbZ0gv/itfUKeTrJskvWTPpcucUGIFr0iwc0gieQZJHEM3mkHuTg7Pk/wpAmFhi16cwKy8p3ymzo9fDnTjjhjmMf8udNf0/IWr/KMnZTgrXwEXZxbgxFI0KxsHpZLijIGJNy9E7lfl98qMosYjBPJNDKvnvQXk3f6csNR6NyjhsAjq/hEfKB/1gQhuhAEeftqP0xM7pYf03G0gcL2zDhDzrNHID/KCW/UYKciRS0d0QE3UykZg3VgbNi0NnjCF7u6FZ0st8mOBRHkHpddVW7aqyFBdgnqzsHlodwN8XB5AKz7Nnm3I6ukaTXMi62xZY/b6zdLefOqDksjRwGgUXrPU6vPxPISDbZBeUeDzxyQs9Rv3TvSYtxwYpL//tJ81hdj53DFPthQShudoJM+jI+Y3gZ3Z23Sl+iX3m64mc2GA6xwzlicMofvAlt67hBkXro/3X5/uJkfG9uAYPn8EZZPf/O203xBOXTtpwO4DhPxVnBsyd85fTXbXX471VtjadaWeEW443C6jz4yfv+abZtTGp/2tNNxPWfnjK10zeZ42N9W9w/eHcNt69K3ATR1X1fc6IsdT9tyT4DGv3MrvpcZqd2UZtDaN+3a/RyDz7OXulxi7NE0Rny3eVqNKSgr71bOeQ3tHwBEX0MAWdisu03QffYOKZmFfYEIgOJIBwB2YvOxRHyL+Fq9lNkKcUA9usgeYSS0y+pPTl97OOsJkj911wWV+xauq9y9sF6vQBXtstTdEJcLXC7l/oZlwRK0MG4EpBUAq1FEfJH0WlMgIC6eY2kt90hoCvOOd4RUeip9dL0C0RWg4ua2yZzXsuqVgqEdRhmVxgc+zGNd6y3pvNQ99MW6etezrqhdDEJFTrwC9h6joqLNzmR3QYAYEHBOaZOHqxwFCNWX5ukCnBY266Y5zXExPV7fQgTsj9SOXKwTcOjEN6iaIaY4GtpN1Resxzet5XORIMZoGuC61l86ULUr0O+kKUOYz8DDpI3b6YL7Ym2e5v09A3GikZ0QBpE6fHP8edMMrjCb0hA70+Vm3+836EVKsTxANH5VUwsrL5JKU0jT49ObjmcI1eujYppxs62LOLRIWzS7YaKOcZ4jzjcY4K6voMxxPM5keNWxBQCASwzLtczn7lRCpt3s6IsNiGW+e/f4BN9//wd4//4DPD6+A3exCqcDlWUOz0G/01Yw4iVBRdtEX8MrKo6vDTdU/ow2yy88j+bOvEx6G8GIW1pmX31346ayY7nZyWuL78g4oaz9sl3yK/TLeXDPPjkHZnXPfUg7P6SgWYewT88sZh1rZdFXtYHWupN9sfeFVb1FZ9kp+M3K9RRm+fiOrTalI98CIwfa79xwD9BWnem7e2tbUXfokPDCcOv897o7Id7S6NlDxf0ofhttcRQs9UFxEF9KdFTGfC3GKcd2SBMXzRr31HQjz/ZFo624MhLf26ygqHgUXX+R/stBcTqMdpaM7qWdgR2BiCCUTaNzMEKO75GXyinG7yH/jhxvERUgIgBaa7l1F4TdEaGFchCk0LNY46lxSAWHnPVZGucdO7rdGk7bLrUtePcDrWs5nqneNeFWY3drmx/KAc5Rpe2uwQKSf7ZK0mgJRi4GK9fF3Sw+WzVEE5qPTpK7TLTBkQCEfOSOD1yogGtX3WaDPTqevKw5ePSDsEk/tzqFUfPEygpb7qfC7l6wOObv0qC28bDk7/c9M1dSkSF4l9IQfa/wqrk1/TtI2y0m7sjozhKV2ubdYIZtmjk86KzG3gVVppXjygDskQWDkIovzuDow3gk5wEzHa9uxwba99RtlhGDuNXOeYrwHUPZkX7/eQtEsu1RZplKw+nLXTCWjqowJGPMH9WUUe3rSwRACwA8EFweH+Dp8QkACL58+aUE5zu0p+3RzK99aHdGpJJ5jMSlO5q3IWycXZWCKL2b/pg5mes2sPWeb6u7Onft+KPuq25WTPJN52f9bejwDp3S21XXKezWtttQz24oM6vv/gkk2JcOdxfLBp+3lO2hZ77BPb2cfzr7CDMcG8W7NN1XBSuPc8jlTHqvS5wIqD5zuLfbpSWFGhrlSEOmg3U1i4Rgu/ti9Wa7+37C/VAhbQvvIVD5dTZXz5IYluLk9ICUg6WfA2MCbtsxdQDSsfDasuVY5Y3G736Ph965ddWyxqWdpFU6aHhmUEhcTzW0xLJ8k100NSYTmjopporeJm3CRn0NODDod+U4Ab/3iPUoONqKUbH3fhc06WZ1/mTickURgAtatPayzbx9oFQv+7xUzZSKNqc/rnwbbp4SD8GeueSoLlxg146IqtrV762DnOofe1RMPTei/KorLBdcwLOlTj1OVIXV/CsAACIsomQWhXNdr0DrCtcv17L74HoFvgga8QLLZYHlcoHlUlb8l1X/QqTs5vCWE/EGDQAogYvi69QGJyxHK2E9iLQkX2VnAu+oWOWuiRXW9YujD9YVYFnqmO11PCbOJdN6q/YJ1DaRdgvGoFu972aZ2jfiXC19x/djrGSPp+pd9GuU/qQmXLuRTTOxsNlAUoIcexINnJYW93unkJfURO09E5KGDG8Z7k6Tm4oTO4XNDe9p+XVcEOkwaxJu1AsBkBZ358VesLshBGmvsO6z1pgcwayI5F0OsR34ku50yO1ecuKFsDfbDgrorsdrP6pCCR8Rt7pnU5H6UA3GoSSOJ97eLp0MlIPqjh3ZMbRFZ00zTKq8QP5xFfleieiygD1iaQqSVQ2kc4ahvlHeMtXKlrpAbaJh+yTveLIe5P35/Qp/+wHhn/7hHbx7/wF+/Pg/4b//2/8Lfvn1V4+K2qMJb1NLzoQ9ilQOPCfxggt5bv76b6Y1XPtqEG10ANU5sEcGn1XeYL6NNspEOmdAQ9b2I2jnWhXrXqDtNc7T0vZOGV1EJ+C4M/i6EtTNWjrPmnnh/kYSlzDf+K+7IvRrh94Eu8doNbl2dUbZ6cClscVV5GqRrSvvhqB6RG/FvywLoOzk87anISYW93cBja0DG0dNTOLZSrunjN/H5AFo2qzRJn+Hg5At/myPs31lpjW+nS1HJcYH7deNTDthumnGtuPfK7wW57TdGvX22yhrRZIqi0RxFB1Abv0Q4XFTejTyDcRa972rWljDqQ5J8F3nWMyjUIkmh/02HhM9baz9tZ1S04XWpVC7kyfs3UczKVSXNJ9Fn/oYsUarUAwVtzATIHG86HOvpFZT1DiRCABgJd0FUe9eKJ+1HLQXSNsASG3sunqe5JlFrs94RQ0uKHlpZYexYVbj5JeLoKtyXI5i4uOaSOriD4PxjNd1FHqfmQ6DsDOiOzhiqHsUAAhlzYA7BiSgmkHmV54n72domEgzoiRf1QVuEFL+GIpxhADhuKm4y6RP10CpNDio1zcn+7m6q+VR32fgndVtn+YCs0dDwM0ygce5wWJF7+geiNi6W8czbQLLbcnvOX4T54SAf1EnrwT12scjwIQvbEAi8hImDOGDEcDeYEDZrXUcsjbsOUHbnCaPeTJ9FNWQdtThnabLVUn+MqShjhPB0mFyqnP2egGgbx7g8v4dXB4e4PrpM/z8y88h8Mr8bcZYr/yJPssdU7m0aN/PFpRTmGLRzk0xNyU1qDF836+In7cKv1PvmV1qjdY+lpAZze2jbG4E1QkpBiM2aMxoCIPaByNCmVYTMzTcAtP5hwIp6GrmNXLeIeLsu/19oJLNxLmfs00sYx+kGUdy4zjsWRE6D71+AHipmX1LpsRVtIiYyOYcyUgypGy+gS/D309bJk4OTNj+Q7ZBQ451eQC8PAHAZ4D1Oir0hWFfoTF1RyM/SMsRGJfV48HemMsWzqS68CGxNpNpHuFdjjfbTcW9oSdzx3rOXm3tRevb90g63qNUyp1A6Tns1+Q7lNVUcdc8eJcOCxb0nLA7UMwe4k9VCg7BmU19OERA7qP7PiuBkmE0bNVOWd7fwv6KcX1u7b12IebW4A2DabK5A+ffAGObbQbu5Xs6GIigjRX8BZC1P7BnW+v50mvFgcYIFAe9W7XKqudanCdmB8O68p0QZbcB7w4oVx0ssDxcYFkeyq6IZQFYkFVVphJggbKrAcAwSVk1wpdzLpel1gmqYF8BsQQbCPgsUv0s9auBkZXpW2X3hlxYXelILyLm4EfiKBD3j1x+XWgCArkbwvkOomJkcC5Y7uzQTtKmsCuola7wOzgdkY/AQoSFg0CVXotbDWz3Kg9CbDiQA+IuqN+B0s9d59o3wTIlgZ0d+nrfECaqYwERVlihXiHepiHl5jQYEDueAAgJsI5DCS9MkCb8CIUmkP7mT1NIpQ8oHtWWta+mV1rO0TSiEN/Tz83ktlWKyBAACa6m2bzjQao74t07nZvCcmT6DMMUgnEY5MEtIAGwynccmOBgRLsbZ0xbSYqyip/7iKcy6ndaoYbvYjDlTU/vTl/x8sBdNg0gvEBkxu9mIdhNpCvzoxxFN9QsCz598w7e/x//BD/845/g6fEJEBaRS3a+mRIeb8d6Pg22VvOO+f8rbhBh+G3OjzpcNx2FL00wYra9/NyTFdJ1gIHqoTYYMQs7k39VkOta/NIaf/FlH9/9m6r255vol1kC7mXqHYfWqdqjT7UttdG37h3bwilovE3D807dlV50bb8rguodfMUMvRS7pPF6IHz6/h8BPvwR3v37/w+WX35KyXntHol67F3LCpUt61AmdeDu73EZ23hZE79VV52FURjntbnhLcBWG3gbJ3++F+fbgZYHb1vpfSh2diO8bGvPjpxM0kVh/PbmyJeFvg/lKNyjNTOPpvPqRreQn9yrmTyjOwRzJK7eT2np07yvLawNvzNvJ0OrEwW75CaIWCIRwQ8hj1GeIhGsJ0faDwciHCCqw0geqZNSnclLkC91kyhWFjU2KPGXpGQ52Z4TstHJ9z4bJ/iCKBeVqbCPeKsnyj62/VV3Umg9SJViY/AWBXg1dSvK8CqBFQp12+hIcR4ljcCKt/ld/idTQ64EM1EyQCVY1AHy7eUcZk1WNB/ecc7srsHAyEODn6NjqQa9muYPgQf33AZAkhVgBHwUSjsINS1m6CD29YxxXI52AnHIUNxdEXr5DOjvfIh1DsGHrDI2CBH0i6yvcqPUCEBz9BPy3zrWc0eJwWgEqYVuu816Lyh82uc9GX8U0LbGvErXRxed0vsnls0mGuwmyh5xLDSymrvHwgQjbKPqnSdt8RpgoPpcX5BNPGgCDaa3Rw/NmOlh+LZFYezdrJ+1lBh+3OqL7LWUwPxePxEBluUBnp7fwfPzAzxeVkBcQY74Yrq2WPGgrjKXrVfhYwNtWI2+97pPQrClwl7OeXo2FdYDNTa6RYO66hMYxoML4grDU8iX/bxNYe2J4qEenBgjd4EovJLHc3g6OH0HNOUcgrt4PXrI+vKrm222eka16DdJtRg2p/MNOrsw3xeb+p4b8GfA/d1bmdN6NBt6Nm91YsURh0GiNxiEbmFTUxLq5J1MlkhUdkLcXVjMQmt3ZN/P4JIZOeVWfmKY1AYZROXP+nMHbdEMHuupYx1uG462qh9rJ/poHMzhPYUzOriOVOwsWTpStmJKCily3M3T3jSwSdrIvzQPI3V65AXZO41OU9hjg11wRBdL5pAZO2PvlCfpj/TZtoV9LF8PnTpPWgz7O6jh0xtl1m0s0loLGJ7HxX+SD9XuH12ofMp4SFPPTKL7S2kRJPUPED06+2CyB+fcT7tgZyCiirwNbYj9GUvxZjRJHctROcJGnbt8rJDZs5Bo8MSrXvhSauPY53sglmUBvFxgWS7QBEEMTUXRWUrJspuAyuSyLH5VP3IwgQDk7ocrXK9fyhFRV10lutJaWoyuAMS7JVawIsC5lWT1UGE6WbVulTBSni5jdBW6V94ZUXcxuHbLdhkA91FR1JeOpdTIaG4KcUYvBj3qe4QaAPLKKyVs1KCfNrbNJCeBmf4oaURIDRxxPjR9HYMRUxRZgWos5CyA2HWwmHFGUPgccQFI7pvYkggIoGebV2bv7r4x34fBiMqiGHBZX6bQuCWwSGrbCGtLZe+orxFesOgq3dIWROX7CTq7ih4du1J2dEa6oMnkbogpiFPQWKNuj6jarz6P2g7Z+N+AXrVHAXcOQFFtX3tJem+OVHw+BQeoV4LA9YnBjejkgwtiDKDcVcQrGrBizHO6wJ5TwlqqfMbyJzY5mh2Iki4E5bgoK48QEB4fL/Dtt9/CH75H+OOHv8C//eVX2bHI44nli1cka8ecrKy8Odionx3+NODnKZQbyl9itvXTorDLsGA5pi44luROEMp1s5ay22FaPCYGze/w9wtuej/D/3YyvEWa7gnaD0UiiVxKdKGYb4jUZolqJekCL1nsJYu/CjhdFX3exx//F1z+9h8A65fJWv4WoGPkbw20O3jglZMCLd3UFs4agLE9Xn52ObtpUz25ebNHsxjj/h1eFo713MGyuu4Iyh/fVtqp2H5b0LE832CTtqxEhqGto8nPSUeq0vUb9HxhobRhmWQSbNhcXarYUTTKHwd7D39zklFHShANBMimY2/jvYfpQES7WicvyLvYc5en9ExVHovvPWvVThnivOQVmlomLvxvKf9waYMQjYRGUWDtM8vzUXktW385EEJy3NJKa1lhox7GqijXo5vknSeFACC4jEzZVT2wx0dx0GY1Sjc7NIV3x9uiC350jjyly46eQA+YHSa6TNgFKNB6vrXZDG7TAAAm7yRUR3LjeAjOQXY6azbSzy1Hop1ctwQIhYrY53VHQ+TxdmUpelQBD5/Nbp2FXTF4QBr3tj3LMxuUaYQeU5L0ieCxA14RoTM00X1zhTHvJVSSy2mFd5Jo45m94FoDByVg6oKCKcINDjaTZhA3g4mjh3ZcVq6ImoJ0yLa0DHCXQADp91lIGNsO4R6mvAwCDkK06SWFS96mMC+KR71sfjNiNuZq74sZEM75sJ0LbXdrQDeizhmCwwgYnvRHcJu7/a4OJMQyd8JygYfHJ7iuBH/9+Wf4fP0s5QRCU3zyumNBN8GwTUv7TmbVSKVpJpPac0e03Yk8Q+1qUP29LdNOaRTe1ppGJ2DIr4snjMozKvdQu8WBmNT2ZN+QTsvGyOmsznL5qPcjgFndVn53E0LChN2fUnR9ic1To3MIszUzZxGvPYE1DWYeRvtsa44MvycMLIzPXZ5SJtnKbULQXHplzqCZHJw9Vb0p2snbkdKQpDs4RnoLAwpm/0L1JG532rUbZSwjor6vVOhTDp7Wfwh1sRTbLWHeW6+A6xc3/wSKOOWIsJNgroMySuaom52/BthoB1PDVn/uhRGyLZrOImSsKNwhFrNTdm3gSr4VSO7qlKftTOLTjEvaKqOffh+0q7zLRNbTjNsSN+yauYqnMFpcNS7ouNwZF3eOXOsHIfbQwLDpaNkgZvy6SXwDy22rpQPkUzpOnl+18xnEG3CiXBkXctLcuUFva8XkWtKEShmN9K4itpfldjwuBcfFzQPc5/XirZj2GQzzOyLcVQEIS+as0qXBNRmv6qeS3Qgs8aWzomjQLbDU4zfI4DXOFna88zmgxUMEl+UBcFngsiDAssCyIAAusABKAIAnKqyry2mpn2uhndMtfCn1grACwkOtB+++WK9XoOsVrp8/lTsgrl9ALsoWjqiMyndCXFfgc0u5Hbk9xDCsdSkNUR5YxYGIYK2NycGQda3hGHM/hUpFRk7mP5D+S5VzAg1sVFRKQ905gaD5UNOpU00tXaf4EJh+BYN1HlQWFR6JsqJvUHA20jTBubCAVtZ2SylHBxea9xIgqrlQUvAjO3jsc68IrOvavhKsBLReS/vWo8YWRCAEWNfMICRp7qb+QLqFjTgpyTul1NPaHLNki8KkPaOCYtAVNq/1BhN3JpMQ27QWiR5dpXX1i8i3uWqt2duJyfSzCUasq9k1o0IMUg52OpWdTEjKBgDZOaQibkJV78h5e1xXBg1v9tJY31uTHJtjhoZgeSdH5+eGHppUBSsEdhfqbdJZMrFMWznAa50nuCgPWgWxfsQAsmtjtHyISbr8txw7GISRyqQScLftysZWGUL++KilPrMtaLuWNy7KLrZlgcvjO3j+5g/wl48f4f/6t7/Al+sX4PuI6qAP0oLxTvAv6Dg4272zZcochnQrQackVoXMmPazR8yTjcxTqYfIRHHHA8+lUXOIOIhltJER+9TOc8AHhYGFdSd129bt+07r2wD8kKLO/HgzZKXO7eaLpNgsNhDoHF1d+sOLbL6K4yPqAAAAyLrU7WO/O15GFd8N+UjYlT2DUwTfLJIwd2UpNlAtixnwVPZiAwIgxZnZ8hAvGGI9WkWjpJWv44EjMkYUfQBYl6CXlh3pRNdia0HZjbgsj7AsF5nnS0peygbyt77owI180OCag26JGYoNNbR9clRYbcnT84D5ZruYTBc/QxjP47hHEMJg3/htn2/rKN70tRZtnquV2Nko7g6eBNvGbDq5gCWjpyLQz0Ewopv/EHRo5k+MPDLDs2fKnayMCUEiOuMAza1k2Ad330q4j/CJNSidfFE3skUnetKLwEtr6nmZfizcbkFE26VfsqadKVEsaUcvdXHvhdxePo//V6OdZff1TkE0baayz9dhx9FMVmBmRpunDN08Yze48NZZxllWGheFlvN4VbVZPRboQSkPi7Jcj1Pi1f6cnGAVRnLHa6T4Q+2Ng4poBTCXobHTSB3cxAVKXr4jIi8DzT9xjUHbxgDsObY7IYpVII3a4LYDTnsCY7ETfGOOQHFBiMwojg/8wD0q2D3Kaj6YiMnWqloi0042iJEcVRMedJV8at5jpnEM6zHbCIWHuBPqR5CohR1NDdyqzkrqRnFb9wdMr4S/QVKr8rZRltE3y08CK3EcTgJ3PBMA6PhPymbE9o4Jddz5Lu9WYqMNmvoFPs4uq++Vsb2V0OQB7cduHs9qJW10NsmLPYNaJ8SjKsimK8uOib3KfDi+iB37gk/ae0xNdzdHU5ym2xIbvibYedqpayPnIuX1fghEwMsFHh4e4cv1I3y5XmFde/NXB4YdqzOSTTI9FZ1BQiwIAfqO7JDc2hAUEW3nJ/drlPpso4EtSkYfNUyfjsKzHm+2j1/D2PGw1db7+kLT2rnDPt9DUx8xmLm6hxXl9X7daSwHtzhuPC+BHdYbJLTBiK6OMcSZUBsfMZ/f5NyYqdhOjKq23h+sjmTKO6vsMZqqkVFj2SlNLvU23oZPCeDxgvDh6R08X64AgGCPZlJdme0hslkTqu4Jrygb71L068t6Dzt1vSZveDLyCwwwHR1bL7GDpF9GJjx7mJxGvIuq43n6eLw8OAH3obk16hU7yhlmGPH0Vkkb9uNseb8RERkhY6XZZxuYj5BzQt7bs5+P8tb6FP2uq5Wro2+7xAEpxa23MWA37ffZ8ffKkAz/e+lK04GINM6dOmb9KkkP7EDnXQPVEEE1epHsYUvI/9fcbVll10VdpbxA2YJ7WcAf4EIAUAMGXQeaDRTYksgkKfdB0Fo+13WVf9f1CnxPAy+60Z0bq+B39ib/4ahNXWnNK49WSz6tAOsK60qwrnznBAHBqhdkx/Zh5xlC2QGChSbd0bA0uxp8+/J0pO95Ja4cNzI1WZPxdwRjM3h2NvGRHwpu98NEEMIdzZRTmj7D0ngAnbZiKO0tVk+YnbCtoFu1Ye5TQRos7qTqS6qjpEYi3AL9iN/UBgglSsr8PgoszAnOeRC2rvWQXTTUljQKQtg3a6hnT20jKrsoVntam3VScFSn1441wMm/hwGZwSuhb9r5tFGGdS5Qa2wLLGrCNz7YhEZfVM9lxAkiv0OnPud7XkZyQ6mt0iw64xMa7TguIjo4xe4EZQxn7pomJfh2XHQaKfu6DgICwgLLUoIQz88f4NPHvyVlZxTlz+NdOy2ubWp790SdATnueUeCW5nPYuIEulpMJ8thns4ScbcPbnH83A5kv2x50k8qb9Ynfm/o8em4Gaq+TfnRnfkaikQvWreO3NmGs3WLcWE7BvXfE4iKaXS+E/y0wmN+y3Q3o1opxhlA/kumg2yaBFDsoG/ePcH//sf38Pnzz/DTTx/dPIpu3vcy9TfIEV8RiAfphfLV3G/AD/T3Da+rM7RwsMOp+fIG4ShtM2Mo+Df2ltlVVG4bv28DXosnXr7cIyWeLmN5a/ZMoT09MPrrNuAFzI2b4YwRdK8ABMP8jojINejfUarkmeTVSSpBhk6deH0sAujC74o7OpFFVPHuByxHQS2wqIN/rQ57AsOo4lW3BVfKqrpMxkJHcxxU3QFBtNYjl/w74AujQ7uRrCY1E7BsE2bawQUltJKFfntsCO+wqHdfg8NsnfvywHgdoAYhIHGkDnhNghBGqbf5OdTSc872F0znQYhmWjOO6lknFFlmM/5I+zyuRk4NcdRV9ihHdGSgdSlxi4DM7U7wDtKeJyWuWs/b2ORj+8sGaaCyM/JFo1yHOK69V617HJNW9TZg/ja1a5GPC9Jq+knEqroWKx/pVLpHZQuavup1MV/U6i+d3iCVtN98WlTZxUkR9QL16Dfp7bKJntDKCv3dET5c3JAbf2R1Sutpv1ve6zGP8vvMBiJMxga4foq9bZ7PKCmSPAlAHITM2deTgxqE0Lly5NkmYRAbEDYJbXNN1gMB4MsjwecPAN++v8DDwwMsgM3oBPm1gZd5sQYjcsVN8aSjX4KEJnnIHYsc/R6RCuhrNdv9Pf22e7zADC2MY46EY5CpdVKZo4N/T/mDfL3gMq9+SrMGwX2w/bdgUvvol5ouqYvJG2bynzJ37eBTpkKmdUorcyvfNwM5lsEKSfKqW/QWzq188ccdgxJbO0i15j0+NuT1+Dxguwek6kaWcESO9FumkWkhvVpEKZSmq/ruwjzFO9UBwB4/izEP9PSTe8CJ5SS0T59rD/vr3Et9vxEU8Q90jZuJC/PMSd30usGMsZLUir5M80oyngqnCPQcNieR2yDdbX8K5n1lvgyc2C8NVH3t5MEy01bCdZtjI+BuUG+VVWXXgSrepc9vRHkaRbkx+DKQKc2TPBh3RZxZDTrEK5N0T6FJtHFUyuaK2t8aOwIR9bOnEQ4NSvNZl23zGdzsiPNQnVP8Vd6v4oDn/irZ68r+SzkD1F6euAKXZxXTggtgqXSXnQze0b0CwgJlCweTvpa7IdYVrvxJKxBdy04JIpD7AIQ7SyAEjFOJQIMO7NwveZbaHotr0xLEqPdMrOUeCyICMIEQqRc70RZZZy70FDtgMW2QO3ic8DNOTUCj1G+uENYXzhnTpMcaj9mexinisu+M0VF+y4ualySdC05AkEnWLo9kYwlCUP3cAnWuMjNkyrS6+KKjVdrEemmp5FjXdbCbZTB91fxoitoUG6QYp49kCuAcrhBZTgaYyTAwPDxp4By29k2zVc+IIjIr4ZLdCAhg7/BMCqZyoa+FgX+OQp9YJ7d1VPOuEObReEF2U5FYNNd5II9ZLsxNTMdgrECh+ST5nAlG+Dx9DrGLP4HHYIel7Ip9NM9mQORoNgxbqrr1U7lGbRDCltf8RpkjxdGCbQYr73tNvJQthfDrO4K//Rng+R/ewdPTE+AF6/SV5ZwYpzLN7N8ZcWsgKFWssteZCvIC4IPgL6uV68ibBSOnXqh9GKwKWfTixJA4CPexh/Kxsn2Z/MHSkubo1au0YY/xT6FmDi8LZ5287kBLVqb5cQMPTdZyg5CoFbx1mBgpA8ZrjzwVDXBnqao1M17Wi9f1CtfV2HuAsOClXRCgxefdsVmhV4LMTtuV/by63DYGxqAa3kF6CUAvM+tqiv7XG+rm02Bkfv8GYKz15ql/hxeGrvF3PwkT3ED63KgFt8kDCt/n6nHXgNNbEwAIryd0Nzt6RkeemJ82X2c6UesnPAoOU69KY4fh3bto/mgmMo5PA617LTgdiY2e+s9pf6pqoPXpmWTij7QrbBldLYxX6OfsUi8kE6mT9EAtjIDKXQsAQAsC1SCEJjW7IYraCxxUKQnXepmtMZYbaWcDBKiNVZ1Anj6SIMRKJJdT22BOxh/qoNb+oLrDo3sMg1FuyXSVkMp4xeFVp3e5KFidbL2xnRy841qkdQZ5RFtBiNKHxnFrV/TXOgofOBYkcDsEyPeB5kWAZWtHBEmNCLjtyRRnG5ZsltLXvaMSAKU+7pJRDC5lNvao3Z0yMnkl0EDh2aAPm2BM6uQVdm2CEeUL16li53Q9B3wGm073Nslo941xt4WAifnh/eE5P3TI8i50O+aZH7LJzaY3/bKh39hdEZnk1t02HZp5UuyUkYyUF4AjXmNtqN6RJILNBobMjhkpispxgNvlefpmJ/PuLhbMuTQt2rJUM6+0oMf1ISwPF3j67gM8vX8PiPWuIpnjbjEWKHz23ne4yn4181UPS78MO8L12UgVjVRF6AYLEdN5Oks+PsIqoN6QZxu5zbeB0N4oc1eJB/KOuET0K34mKkTrbGyxiUIjxJ3rahxhItfmQdszzzt9UP82780OkRle0DbcTjvGUqjNVgmWHYadnCHor8ToTsZ81anHeQr5A+ivHN5XfirTG5b0D/orL485ZnSBVp/qbJxGmTRVehhQHkU+KlMCNpm5zkl2wRGBW6BV5k5e5NXHN2iVqVSz0MOQ6pr23UbRslt7I81eeDm9TsF3U6dOG0PKPhjpa19P8CHOUhOzFutJG4qMvr+9MfbHds/pgIFGv6ucoWk/eDhbi3Oc3F8zJMw4bIyZeW+yH7ovw9w7l2kn5PXY1A0YMjbuNcmdeIu2cG+I6ladOpnQGUPrhPJ1V4Rqq9ukzcnqHS9uh0Qvm6nJ2bDjsmqoq4i9UyreCp85lb3hSPJadgUs/IS1BtIJFABwLSfa02qdlsahhwgAi3O+S5Ou9V+9qFqNHgB28ItTn0o6LK9i7csOhHpPA62rBAYkbx2l7Hhtzfx6JAo79OsxR7Cog99ut5cgxLUEPmTXRt1h4RzFUrGKAzuOXNR2y7Z+i0M4vLA7ITjw4+9nSMpiLASeVlN+NwgxgNRZ00Q9/LFC3tmtPLTUBlnZGWHYuzmWCKlc3LGAf94BJ54sKiSITa+BMh4fwVkSYF2p8NJSDUy7tMsqn5ivwbRBCktn7tjTfozPl95WhxGkq7/1ngcirFvsZzwqga8MO8XcbqgQaMDQZ03zR1xDyghcY61Jm6L522K1dcd2rpMqt31b2MiXF4/2GtKd5NdXvrymDZBp65djQnRjWu4CWm7/fPS9dKGRqbcCB4FD+4ncBYBFb4BAXIRR+0fs4WZz+6MNAR7ePcHDP/0JPvzhB8m4qYBu9imFzwxhlIqJ3JpcQTsGxV9FJAj9gyrM6P8O5vTTIVD2rTP9HVvc3em3yE531IUz2CrOUk3ugXnTLHfuwNxWrEmYwWPkEDCbUEjR6gi994poHwOUsu1Ym22DmC7noa2Ar6azerlSleW0esusU3Ustqq+9VpbfOzvtkM3Mh+jeVdPD3SB/QU1XGsLSjHiULD58c02mCzWgjIv4oJl9youHTytnp68+Srg1p3LOwrycGJxt2+CpAbR1+70bXfXyxvY4tGvve5HITu+eGvOaETwIN05zfoadtBbAjpVxJ6DqtEup/Ce1pNvfrwO9I9EbelPqW++ohVGdBZJcJ48eC3I+fyl5o5dgQiBkYBGMAqAHhPiAxYbQ5b4X3HhrfUZ8f0LXd20OF1KoKocYVSOMTI7G2QFf52oyBzbVKMPbrKSi6B9sIKJJCXWN479YOfoYt2bGnhghxIbQ2u1rPkOirXSZhVsDXyAOKIkuGEdV0r9uM0b0PS6E6bdEaOOR+syQccjm+tBJ9jB1zuvS2rCcj9wm5ogBNOGdbdIadJ9IiXYWd27BbgsoNKKli88oVjZuBNA4KZGs+MhkMucOQdmwu1k0aCI3VlU3rSrOGO9lCYgcCuTmM+VhzLa9k3vMrqabfheeR/tiPBBvJE7qAM2QBfkwdhpnBv+ZwECX1LOxuqevJ5uK8UAbpMv8kSaqn0X22w8hWyPYeeztEnN5MIyz/YnAs8vfQKimTgHJijnCLVHLhn527AQ32ETsm+Uipj17AKXiznKwrXPCFlII0jrGN/kbRUeLMvXTbbqyY0ZMDMGt/0suglvSSK95Y2wnnHW5kGW8IvilzlaxjCudFNmZ/X9pn2xW7aNma15u0lAQs+9HNCb42RbSsyMFo+SXN/E1C492nE2U9pWimbQl6dTfU5AlBwr1089SZPPlYMfe/J0dlvJXvBKuX/e0Z0GA+oYLYmO6nTiKTk9UWTUvSdytWmwBiNiOp/S2mG8a1gxLOXIXij9+uN1hY8rwM9rWdjVDpj76GB7xnPv5XzwbVYGJs+2WD+xN7q2w6R4PUMM309zfhvggxEMmRLr347UYcf6tzSg1QPeQEeoRuuV0tsDdMcaLBPtvZ0Rx22qtw4H56vbMk2CHSTWp9IbPIn9OuEryHQtKeHIBBHVrnuzTObbMBB9QC6F6/4dhB4zqBMC7gXsL6COvH25fYhjLZdTRJ9h0KVmFJGTG/ZYIKJC7mBOnIcEYIMR7FQBRLOi2jB4dQrYwAM7MrSxUO9BYH+RZjb5KTQsARCyugp87wLV3Qaq8WkAQgZVvQ+i7FTg+midRDmu78XpiLwOuDIsglmFukjgQIUJ77y4AlHZgVF2QqyVRLPGupaBCBKE4PLsgJhZ9CfKvEknOyDCJdVjRCT+u55zR3ZD7BAsHITI5NKoaitpvQoKu91lAV6nVRx5q2IVh6QpBNlo3qeQEBcO9aP2jVWM2DG/bLSLOB2Zt1GGmJTDK6vdUVUGxMkaGtDuOALQI1sAoNyP0dTbirje7gvzSfZ76RfeCeEn1Z0zTiWTHatSNrdJN1+g2P22b3QwmTir5IlSfIVQp6RcBWpfEXRaM1ATWSXuEIlgFYnZ4Xeqry6bM7aTkdnZsxnHdjwWkEWLIBvGpGUE9bSFZKpr6emvDLaBPSsjFD2PX5ZQ9SnvhjBENMG2Do0ON+PnIEcNsCzLYna9kZt7u0C+fNfsjZN9RmbenmKcXr1/OSbLSBjesCw4Mji4LapeQFmreIrSnTI97CHZLU6eNPDh6M0GwBlKaiLHMLxPXtjh3afCzFSv4TUJRMrIuqWfOHsWXElXtc/yr9FZJoMKJ08YgZITcjqBPpTu82hvNZCNTviaxvZM4GiqOBadE4k1UNHj07AAyuo48tUEINg2IwCs85i9O/BfrwT//csKX6KIOU12nQymji9VXsODdyz6bpuR7ieKXg0wDAMvNG7opDfI9m8Lgj72e4MdhzfbdCNrG+AMwnsiqe8N+LrALY5tKvr7qMmgeBOTltmpX863baZn1c/mFZm37RyT6XdH5vObAhG7gb3hlVLr5BQwOxjYAb82yyIX58wv+YqzirU2orUeZbRWx3N1uKwItOgOCQ1CWOe0cY4Cp60OmZWA6jFP/FhVaNJ0sALSIs4+veBZPVyIixzLJNlBd0LEf3yMVOOsqri4PbLgTgvFoc5H9/REBAcLJGiwQyZrEGLoUeiUO6dapePGKmvGmdQEWlAzsMN6ISh9VpqmZG0CEgTEKw+JpMfTY3ICjeowgNAMCNvnzktK9+kaKpVnVO9aadtdHK613po/MdB7HWL9KIyoydYe65MGqWad4222ll5HIxPZvh/ZKxrAC2OuUR20cbKjmJqYRlKgW8VX0fkdZv4lMqNuQey3pMIIpv8zPum0kJMbUzJB07VG1QhiA3bwi1OjjybnAM2/1aTSVikGSIcOgOWlFrIgRIx4aUDCPMX8cnKZU9A7u1WWLV0+RES4XB5gWS5ljpJKJTS2uVXOmskimnFx6GvVzlBVu40cCtw24LUWIU1lAFlckY1nQJkfemW0FHhejD/SmTRbCT8KFtj8vVfS1bbcpHTiPYQ3OkJc2W1rDFkDm47t4PVJtnv/jpDOozsoaTqOpJ8x4Ml4y87R0g7mNZoGj2T1tDlfzuaM3NIvuyKY2wbMmULbJsOflUwd32je5ULcr2KtY58N7y0IzJbuJrVpo9R0Ot4xrpV7O5K56KbdmJneGeVHQ3eiuGYkhKN64w5sL2OrvWQvq8ZyNBNKpUnnTGtPba/UOg5HlFqAOZmQttmBPHvedxOGcZ/omvLuaJtMQ7Vxd8JLn9J2FIo+GcbCBDTD8I4q1244qe3V3pwlLM5icQ59AS2hnUj//uC163ZTG2/x07bdkaht58DJ7XoLOtFE07suD4DM/68vmMfTcae+M6vAB9lLwdvZBcdG9qyYOdWvTZTaDZ05fwQ37oiIJE2kt87y6DAns+KfAGC9luOV5HikokziQu2CYoS6pLyEBda6q0B2JwABwQKABLiiaEkasChpBC0HAFztahCi3jmh/9hgM4otWVsPgc8n1XO99UxuFY52Rc8KKwckWKleWemwBky5TJQdlkuiRcVV7u5NDUbU4iutqvgDguzWGG9r9O9WboOMSxhXBx072Pj7XjWLeMcL7wwAkjag9KwPtXLKMWAEy1J2SiwheCY5BA9Jl8iq7RqoqKhcMi0vGLjmr6lJ7QoVZLr43jonfTU8kv6uCNenuABSuyqNFToOVi2IeqRSQ79WTVio/uHxY3mo4Un1naoVI3w4dqbFnRCW/r6Uzft2D5CpeOu4U5KceZaN0SjNifIghIUlGZF9uzB/L8nKSMvstpnWmRmjuo+I5U0P86iv83dp22c6wUQZzMRclr+DZQM2kmWoekEItOPW1Lsc8bcNLv/K20aVIdGksyLJByKc520TvARJrF3+yIIuW0UcduYkPw2TxABP5nht2c5rBjntFPjdv0UM/GrLT3dJZCWwqDRyjLwUj45pnz+ZG0j7h0K/NQnRj+mbO7FT75Fua33GUyzCDNCw3BEG25qAZ2Fn3nTe4p6YEfpFQaU6z8Q8zfiM/NDDHoUv+t1G2Qwdi5E0aDr2jqC81XKZdWYzff6Lb5Ohjkz2a65nSTpDiha5NblvA5Hv6f3Bh8l5wNXV/WlxTQQAyI7XVNQof4r9x7orIixYF6+JTlkbeSNQHN+cNAVNZrpBnpw0dI5S0DE3XhTiCBuDn/9fPxgxolf9JtOqac+QvmXKugeMJvrdqEZ7yi3007xEAGKPefE7fL3ALo3fQsBpa07dg4V19WrA3oizYhz5hKCV/3MLJan7czt31S+t7zWB1p+qmussOLtqM+OQmKbKR+X3dCAiOrhXvk/BruI1fxtiqpFIBP7oGe4w4p0PJJdAr7xbgZ2+uEJx6BcjylZ8tTsaeCcEX/ZMKyy4lGeRMLcaRrtZVho4O7zsriiKLqjBvpYydXGN6SHe9YEA/hgm45CkEsxYmd7V3AchSEOv1zZErI6pLAjh9Hyy1TFYZJN+22Hm0xpJ4qQgdfA3xZoyI8oRnzpHNRNPuhtE7dxQaGelO1T6yj9dq+5TI9h7RMSxA1CDSYEmb1F64UAAfHyT0JmO5cLDlF0mfVTWbgk/brPOzggC1OOXDN8HP51RnNyIH0Kq3Kf0omAseYKxGlaJ3wrF8dEj7iDOLqYcZzopjiyh4Kwb6jWONc2EziL4gKM5lrsF7e6R7HuTydNpAgNRFjZOD/lC7r1v0hlDj/G3aZs2z7qwhz02+TAIocf2TQ2fhnYe20kqlm12gCPAguWOiHcPV3i+/Adc8JMgW03P93q1KY3yNvR0TvCfVXpMZ956r0qWPU5bRNCMSbdqfAJ/1JXsUY02+NDF2BEsMn+7ilDyLUI5f72pm3U6O/0ngcm2jzPoDPgdYu3xWRQGNlbWnC6hEWJ7pNr9YdS0yEyJjgnqywmGloe8k4ba143Z09NlBhD6KOpfEX+pFoaVVbnWlhS2k7gZHKyL7Jsf95Vh8xrZ2ow9IxnqasMth2mrd3n9bou2LFkvsNkuLOCdB/V7L1+PlPjefbF2B5WKrlTu9Fv9fXqIKEcNZiWyNtHRzsLvg/JhpCg0OI/x8ZDSDsrjI6aX01rYidJyJkh3nj/ut3ZSvGSgor2/pv9uCH2F7ZUhnZy6Q2W2ykXvzTRkdL9iYbcGH1JzDpLxmdrUbwVOknuvDcNGPVKnLScLl7v97kYug8yz0OKcmW/2pbDa2H1Z1iqBdBoLqszsU5/pMi1sCNQXkLd+2Z8aPzvdOoJh/DuHplsO1HU6EIELHwEBao9Qq1yuWI63cQ5DRIB6rj4iACz8XCkXRzOZo4nkiKK1Yrr4WhKAXqBrHhKZIEQhdoW1rm6PnWf/kMPDddTnVbklAg5KlHcr2O3CggVLO5RdEEs9r5SDEVqKxhlWCcLQau+siIZDyVz3h0B+d0PJ4B349a9R0NmoiccCSe+xs4qxpkGIzFCsLeKcL6bP0TyLBZeMQvG22LAoUcuU7io8xN+5Ys6dZrsYSrstfNwFUnJ0UVq4ghF2cSu5TiEFKaE+SYVtaEM3vCztnD+hcWt1SOkbkl08fDSZTgWGPuoRmoPyyL6ZxLCBYRtyzpdRl1jn3qgUIu/olUXjE+Q2sidAVBU2cQ6CRTaJOKLSUpkaCr8bogKtmOTyuLyE7CjYE/08GkYZi2HC8GkAVL7ovKCruq3c7ZQfjDx7qaulsS04pMBe6r7KmFATvjFe3QE3yiPkUfhh5ma3G6DKREIogYjHzzUQ8WsgufR8h7uq3O2+TYhK6hKdzE32/drOOEf/rbhWKK4mhokBDX7+VVZU+aXTlU+zibd8CIfu9WehWYQQgxizNGRF7Q2s2mRSfOCfUX+XaDLode075hmb3JR77O6PcTEZoH2ZOCN6jhQ/B8SxM0EM2h8T2SeMN0vhFqTTppO9XL8pdIeg18VekrezWz/1AKx47GSRwCa2WO0Uw/qUdn9HdsaftUHRMV2XTPfA3u83kpQz81v3zbhhJLeXlxDeeRuSd8sWGyzqEHFhE/rX0O4Qvc8K6Z049yTfKcdvLdQ3V2nT7vBNxn2ebkNX6CLfIzj2tdAoUHGeU7kzRm9Bfg/2DbDDMsx/jWjcQb8d0k6vH9jCt4zvtxVIYBhqHhPptvG8VrXH7b1hf1SY5VU/q+2x4bZp2A9WF+vV4KzS9gy4+nlQX4smc+lfqwTizWVsByG29L1R2n5bjXwicUet/Aon00T0Yd879PmBhrTthqYJkzbbWdx8IAIRkEqggR18ZdfCWn0j9eghgvYSVNOIjQ2E5i6IuvuBL2imlR394by/ajCWQMASRCHf32COOYJynjrvh0D2tohCXvLH1UO+783xPqzw1jxEoEdAEbeHx1P+1eOYFgSEBco9EmVwrFV5Lp/lSCq7cgnDGBSnfr1jQt01ugrJ1t8pL9a4QNMege5SBLs5vEarFwxT26GNpTApPYJxLPy+NcNbz7Ez1gwEWjadpURA7JhjvrDWIGD40AvQ9RcIew3NMjkeC7f15zC2aCWgS63TrAIcGR2840X63NSXTKCKa7fXVyNBHalBbdTG+W7bRH9yzW3MzPOIcRx32tyuNPdYrMOzc5SVqcdM3TF8mw5CjAqpcmfyOpGSJcHvZIhJlKHl1um9uwc4MSTH2mmQcRyEsM87CukuhYa2xyUkbHxQW7JHKkWHqBwX5fBv9cLovfLmr48EP79f4fnbC/zhssCPH3+Fn/75L/Djx0/buBzrJm2+JZh677m/OwGJDgnz+AGilZq8p/Daph/dwGDzBIFUBzHZPjRjcI+zgaDyBW1zHFXrHO2AtoHw8WR1GEYXtvt0h20MaObSG2CW3i70BGZTjmn5Ddlln+d3FO2APVk6vJjz6HjuTOloyKp/J+fZM6GrNgI3VxgrM0j4cW+Siu9twFxkQpsnuxNkSwYKW860q7UT3KNJHbqPMqWtn8mXn88vYBYdVXuqPkeIOyIiLffSYv5e4BXbR0462MGwrDvdNJXlss2/z2l6mw7p3yiwWT0xl3y9QYgjhZ9F8FE87cz6GnC7pnhvuMW228rTq/mNvHGga8djk7WWSFfP6d7Ho4stJxX0abijAMjcQLvKO5E26QbqctEROTp/R0Q9HqKcNc2OeLPWm1ZYYNGVM+Lot07ihEBZ1ctHMq36aY9bSjujlKtmGdX/y24Cr2gahzrvAMgMA6PLkPmmQYFVHbR8ybUcU+UNqaoCAyD/43sh+OK0EozgeqxUgzAc3QiwhOgGD6t2dSzTS9KuXaDaJhzM6CV1TUSc0b9L/TmTTBn6V7um8kfTHjEQAIbHlDDHBdY7zW0WfOKOBnYyIZrLy7mpzYU8zvFI0jTKM7qKK67IVr7dDkZIACC8tKvVTAhkCgQfljErARUxQkH5wrJf0tdRTZ8iA4Ev5oBKBFAzPkHbxwYokkay97q089bASTKhqTrnVGcHUkuVD0KoMRw8DZYMfh1pIt2BRG1rp44BSspwcnkSNruym2DWWa6plLKdhl634/lpveDbpfEyVS4hhiLHXVkDrbW/mLPPJ0xTyNDQJYGz+mkDaepYwrzaExYSF/nlQvDXDytcPpQ56m+//gL/8R8/CtU2MB4bY3jsRhIE18IHhNkiQkAiT39Q4XL5TJ34SfM69mEGYXyST6to2pny0G4P0aNUL2jS2HmRQOR+KqxlDqv0xvm5148jVWOGF8GXOw126pQ/O/ImZR4LRviGyHDG1E2a/bW/HwQBGJ3pLRvw/B3xSAL/O6bB9EdTSh/JAFJ0fpz2hoNXywbyjB+nz0ObZWmwnXdcD5A2JO8O7bZCM+/bXe1Wn+3zeDpmRRZnOkePmoHhvxmktl/7acUuJXs0E+8YXxzXbMuiNzQGOzBTg/PcLVsDODNYjoSqRuUH42kLXOV7fLqndaIi0BnA3TwvD/O7MxJ9+CCMRuirAOsGwZzSlxt5LWzpqzOQm34H4U5t2tGJGLZ2lneB7VpXVtd46uOh7o8dwFZev1vHmFsbfJ6cnTTnJspRbPtz9boofWVkyahxDY70uZNd4igaljxmXLWtZbHL1Cw6etbai9u4dshYjD8n/Xv3EAtVb2ztldthOhCxViZYV75/oR4dtK4AVdErZzIVJ5koqQsArNV5WC/EZWexrNhfrxVX+aR6ebSoMctSL2ZdqtMdqlOSma66801QI4J14PJROEN2YCVqASBYSgBGjoGqdae4Q2KV0m0wAnCBBS+yKqc4ABCIrkBQ7oZYV90R4umAlH8RUO6G4DawyhWtvD3ZtwfvnmCHLe90Achm6baFVum7UaqCjo9Dyn2vxcgnMMY++ffOYNictb2JyLtq7PvSlKZB7fbajqAngMKzpm2IByQiLGYLELsGxdys9bBkZAEJv0NACxbn9YJa/WY1mAvDtbyP9l3lSDM/2GNHXJ+aSYCg8CaSHgHGolyCcqBNuAwmHzJ1LyvcuX6uQRIburQz8afUaIdYN40vvUSedgznQZD0obr+RQaBHZ6ZgabO4tKf6BsAfJaGwzvpmmrJZ7s6Gysee1xZTq6tie4/E+ezEWcp2MZRghKyZyZSHk++MOuEsVhbbL4u8jSjvcerxOKBmgJ07JgSkcsV8rug8o1cfyDwzo9eTqv0lOPi5NYbbI/ny4KWcqm7cRIQBwIvC7z74wd4/8N38Pz8DJ/oc6WXajOYOdeSNJDNWOeBLrRMn7y3g22n2rNbS4rylYesyqc5edPnTzv3xufmh37f6Qz34wuTZyZdqE8+ll4OdndXzNyzfW5CvFXoZMqEd1tuu5WOk/rLzQvZy4xr1CluA+q7KBJ1SudfnsMs1INewRuneyHXd93163Yus7xl1cgJmVRw1RmVdYGsZdrpJuAwvxF0N0TcQgHmJ/dBJ6rOssFoK+55Y3xykTyHiZ0zQXT6foZDEhzEc+gKZUN64YmVCNb1E6x0BYRyUfUFHmDBi9dheDqjELq1eks22d8KrXjel6f9eSMhkYhmxtqP6+hWpm6Ee4QPDR9WWoRHkyKOUbaBJdP/R3m22ufsCaun6B5Nt7fsl4BeOcEmQah3MzaphlhG0BcRZi4xj7ZCdMccpEmqMD3E5wAvpOFl5G5WkTo2sJ2vMnRRrvXGnZ3rPGy3SWMBhmcn8nwmjl9QLd+qidRa7LPQBnFROiTkdwrxPbilTJL76L53+Hv+iNFotvnJfB/ljrrXAeCpVRZLZjgz5rhFsmVEZGXdhnt3IELuRlivheeu1VJYSBQ76+hsABH0Yue1Xi6mwQf9NDJo0d0EjAKFFu2Q5uJst0pUD83hX8NuFG8pFFunemZlnMkXvuQ4GACgK1cRyv0QgHxWqZYlK3iAAFZ19HPR8ZsQtXRGJNUAz2rv3VBHmQ2TaJthlBPyo9ELM3vANJfWS+9kkBX3nsykTO4Xcn05Ph8aRM9Yan6QPrL0o88gnBAICEQSEcCy+GCEC4ChdoUtovJlE0DoKeid1UOorysedMckMWob2FglYyu4/WRtDjyrf9QoReD7V7ivdPOHGuxZz5QD00qybte5+mpZpT5k6NaKuWCEyRvVjp5SyCPfM2ycvKLkoi7/1bV24FsVQxpNu61AxJrYV14S8M4uTzLJcWJSJqf1kSXlD1e10CcyuKrUiAO9B9K0LgQa6riVvy2nK4p6SkyDomOW2l1Nh3XJKOPydnJnVBr82NBb5TSRmfe8TC79yvm9PBsZMhIMF1yFo/ACcPnmGZ6+eQ+Pj4/w6bPKOwKQ3ZCuhrET0rHSp8W9Se4q8ri7aDpwq7ZuDJUw/jTJuIzR3NXdRbKqcxV53CaWpL3rKdJCyTeb16YfN6uZYL8CkPFiZe0k7WlPSlsNUyX5cjTjDLONvEFDmEa6s8qGWjUqPwt2xe8sWnjamB6NQSQL/4k+rSVlOwP3tWKbv/1p5Y/ZVTBZUklqd01Tyg/7nFNld59MyVmQq5bF6TxFVeYjhsYmnwx4kVVCj0w/9ZjOwbn52dGwze9h9Xk3cKfV3fAhWOkLANsesEC5X9AX0AztjLY9zxpkeTo3cjZ1wvmiIwm5RLm1gltAwMc0d/H05sw0UDvbONbYiEpcq5N3a9dVMk3m9Pco4W3tuzWNbU9z/s0WZefCTAljjj2XBtVl3FN0Kfrz9eB5O/RHPWL16G2dfVx4krKTdO86nrZsb4PchGoqrdF9pwql9HvbN1tz7QxkOGb1EZPO2Bbly07FdQC3YqLwaXHGcqg7flkJ3NZxesC6Wn+MxEEd5nrWdw6WvyUOsmnh3rJ1HERptdtx+00VmFSqj29PS88fzbSWjlzXFehaVvDLyj5Dy2bha9m9UJzlegxTcerqjgLrjCp3KningAxxskquEkKgK/0VFTOrpVIDCdx9VnVBgOJVvZbfC+oaLDG0qO5AAJabfGQSwrLU/IJ1Lac5AQBdV1jpWtqU1rIjwkLdrUAL08wCK1Ooa5tUB4UNQrDTEhOt17ikjB5XV4yTZVwvVPt2OW+P5n5hHknO/LVSEjcmYjk6yvCHqY4668pxV5aewrfcVoZH7BECZpA1k5Y4N2oF5Lst40anF5EeO1LLKX53s+NhUobk23Fb+ohWQGc0VOGG5NsDoU4iklO+LWacrna8MTbuV2kidIYK1t4iHjyW1qkmzaeCrQk4iurseILp9t4Q8N3Jb+UxlYwtsk/0q65SDEQ6fhyUafWfZGL2oYhaL2fXxUF8LvRWinZbd9e8OjFOd+DrKxt+rorI95B89qW5Eq4I+nKNXcO6rmXXI+g8RoAguxqs/ETDI51VsxmkrwwbC603i9QbVcGJoyWOldHJQ9S8kuMBrXISpI2mMWMzmZdbO2FEuxX6PXW7zQHp3HMMdh8ZA8qzjtRsoLaW6STMzPU94+BcyONTfs6I0mfuno4RrQ0TwSZf3HhESzwia8r0mWHCDaKiHmWl92x9NLtlwv2t0dvRhIDdqqpesWWAV10f91MmRZO9M6x1xuSZlMaZhRoIqDsAO/iLGmlaHRGW/397V9okR25cX6Kqu2dIammuJIci7P//r/zFYa0sWRK53CWnjwLSH3AlgERV9cxQtMJ4u8PursKRuBJ54KCVIzljCit88fmtpuSjPHuFK22eidfnSd/HJFODq88Wu6jqNtjK79XI3wfybrX/75D6U2lTwrpM8F3Gp8Q/vv1Y+fYqtg45sa5t1ajf64aNOnF897GXSIjak4fWnXbJZN+x7yUz24ZBZVeNv9B2sN+IvqI3CFmoTu9ZLDKa7NBOC/qPf3JQsOW+cqF2OyLiiv20gt9FwzfCcSm+KWKD9OfmEJajI0N+VuEpC5KSweQLS12jbAFIZwTHFTTFxogYgTI5qPOuiPfG2fxC2AMQ14hK9azolFIJYw5GHR/ahSOuoiNDVFLW6gW9aq3G+k/pl/VZGoEzcYVikt6JSghH1GRFQ6kfikJODhQNytI7mviPYEQNP1rp140SumeVYq705KiRRzWp5xi/AHHlWWZMym4IGV6bhwutN69uL5XhbQZQGJDl8z0CtJjsSwM7FQnkpqQUj7hVEyVVstelbEj0cUncc7RikbZMqgeuAlNVPj1yZ+ZpEl+ZdNWVX/I7Z8W8eq6lE/lcprCTbzWO7qleMZwAiEvBexGaMu7ot83RQk2ivcy01DrPtySpDe1jpyyVdy+UfH0tm1U5rfe805BlH4jjGX6cxkkxZhpDMecjF2MZKHjhWel/iPNLlgXq+u22mDbZVwak7GP7PpKc5riPaChqeD2HBQh7ItfPBc9FbOLMI3u9mor8++kn45+ygjkL6mH+CHw4S3eZrvIbimd9vrASUaaxMcg048pup91z5pV6furmpc31W/03yEpbwUSWa0botWS6d23t4M+llLsPTZu8eCj3Zakq531JNWNcJ7Aemj3xRI3tBQ2l7stJ4P4VsfsVwsLgL+KsO3n6u0FrATbK5fXRlg31Yh7RZoqCJ+0cYnKxVFoEFfgXRblTJhtYsyHfn6OmQ2WiFQ2i4dewJV503qlTTVPOEi9TX+4diPfwiTJGm/U9eYuKebYcoMl0G2ltNZhMbkNkfCnu5QoaSj19Lc6361X9lL+PfNfsStjT5ivV81zj3Hq8wCuVIJoIssWuezn0Wc+aDvWCvrJyMkTXSfEKWC9XQcjLMkp8oZWGqfPdkyVly1VJehf+oSNrB3/WdgLtDb83j9X4vWerou0GV6PtUHtTi0murC6pgm7oSUmH/BY9Yb1/3pPj/h0R1hvL3RIvghbMgsgvjY52i8JmKWc/f14+h2ODkhEeXFQ8GROSrY8+kcbdcCFZcVxECF0f+xIk4IIJJSYR4lEKHYoVxNPgNAF7YTH2V46OFJdeh3jhHggTj2OKeed0UlwbLqZ2uSq5EHQ9U6KqGlNdiLIUuyBinXAVujK+y+9F8kGYL5V9DvUUVxxS2G5PSMfqcJVSyMAg9g0q842yfSrJdteNxy4UDE3s+493Q7iw08aF88/rYyworZJKRHTUpxX0ZnBecUJU1kYOWkixOgPREJ3MDbtJijtCKCm+oQ1iHcm66wk3lbJFlSIXFT3mcEdGaSFJm3d6hrxkCBVtQgZwciMLoYnLMU2u3jV9+nkTOMcGFav7ykvKe0bJaIjV8yxWJFZjUo1H+qXk67R7/lTIMFV+PdqKrF9Dk5J1JkhYW8WcQ6sJpvi0Gq5JGb0KKGXd3sgPz4u6LEy1eq6Vc6u4h6TgkSSSN82KUiPOfCudZNt9sqLI78yLJhemYjdOHI6TIUzzDOMD42oPOC/vYPgJBuc22cDLauG+ae9dQ7FsA20nyT8a7MKkX6O3iqsqLjX8DGUA+a6aC+uA+rqqigyRUavgtOnXPCZLUnn+SRFTO2s9n6KoAiRxpg5TyiO+ubW+GwTnykCaoq0oIvWF3Rp0WUr2Pm6eq3W64Uxuae3RLTqNYAvdoKIALKjOeA7/fun4koSXhdDvYEJ6F3nPZg6cj/gssXOi61Cd7kdT0uj7DTj8v0V4nrfK6KwU+m7pEyW9++I2BneNhNgla7pTOG6/R/7QGbdaVlrW63G4iRh3x0fe5ZzfWe4cw0R9hQA/v/ocfj8TfpgmXJcFN2L8lRhXtaCQnUTM3a8gI2lY6cLfZwZ8DmpOKhnbc/CN6hrKTKazAQVcfe3QqLGmb1ecF+C1Za2envR/tPgoZaF7jaV1nFejaEt3++5M4RVadNVDsl5ATVJrn9dBNJq1AcqqDWI7nnys0BQXbVVzJBU6YlkClYKeuroWZqu/bDQl8yuMX7nwLSkN++PszASvx2n0XpZSjza2VdNFVeYCOxqy+fm8gf9qPIqQbOE+3ZfX9v4dEU6sdo/G+dgAaceCEYJfIFGU3QmRMa9cQVXRecWmN1xXCnFIyX9wos2TElaRZ60HRfU78Z2E0ZJ6E04UVcTZpIKUbNAV3ZP8PRDReJuN7mLdTthRgnhHRqgnb1APhiLRvARk23BiWIXGII5ialcx1av1U9UUScrJF6Ha71EXSqXLJ0G5WlI8Su8Ko8jGGIkOEBeUOD8QekwgKIqhXLGvybRqA2Oqg2cyRtVdUDDdrSmtqgvK5k5G1T83BNssUIXfVIbbFK6kV07Wm8w+0KjvLCnFuo3MckaajUvmKb7ks+Rz5sUODZFYG7IMURqYwljrCAOl864vPPRQuUPVeLqoVI7PtENr1yqEFi/VkfrCHm8E6EFbw9/yFF832mTey7B9V9tR7l54E/tIJjHl9LwpWY6hkEpDVMOw7yS85JNFP6QwrVFweKTdHDMYJzBu/n0MKJPsGOH3OSHqnr41+Nex1s+fBXFvTdm2Sk5xrhE/Zek8u+ooujVzU7F3QMV61zlIPd71FUeCH6e04m8GYFLhivGoDYq6Y2i0fgPzRNeRoeTGyrcIWUdrruE6jZIt1zX/AmgTVkI7PvcleA9WxkBBnC7xqBd2d3hwwx24bYFdQ2cF9ytnUr6u+5gyg2lOiPhAk1sLrDRg085bEuZWLmJAi1C7a0c4pffJfT3a9EUb+xPg9MlRtCwWTQFviPAIxpUJVwd8BmMR2WWJlJXyrMkaEuIePuWt6b7ppbb+tB322u0pMozK/VeoUnhjZ9yStFhphPM+jpjVlvs6wnqZ6t3DdRhB+4bGpn/v6GnpWZbDevPQWq4Osl72UVdQloYWF4Fey0iV+1Wth/EuugWleLU5cy9iu8QJqdqdtdobFJ2xTV/yNa31az1nL6p8Uzaen9MO2voy0Xbeud9Sd1zfs5jyfjo45IHis5eQa+QULeB27avl5PhGkSoLliGYJ6+Pvl0UNZnQ/cNH6XRpDltJ60Wj9FkK+I5k7+nBjazeS7P9TikB2u5Su2jqzb68+rvGc3ZC1IvS1kkTclCYSl7SjLsdEXbxlyQ4GwdZMFiElf80G5i4CyAR7u+D8NsgsgPDyymUdy5QLlSarIQwEF/76Y3TjgqXjmZywdBOIn5VrelYqSBckj8Ln8wkaJA9iZNMwshxbbjPwYbdDH4FThxPIQ1CuGAbiEdExfTYMZyzgAMWuwQHggMTMAkHBsDi4mppCEiVkUgN13ekT88LXfZgErq9RMjtALxiFcsLhJX0qR0ibfqxRipjjgSEukkKgUJDHaelIdYxh/btKKUhy3vgN1oUKlmvMNoLQUR2Cql0rSDrt0GQo+xA2rtCXmw0aEgu7s/YlHRKhUs6krzDTyaznlhUAEtHAbyjMXZaQBDe0V7Sv0LAqqiT4ZlLgdsLiwSSO1AEP/BfGPI4km55dkDWmFoabXZPPKyMUzvuevtkUkuEL42ztNeHmcMdJS8QK57hhIg8s1ejquHqbsL2luuOlGXQYq6qeZvv3wzknWoB8X6VMk4YUY0hNT8vEHh7U39CyN3qrpfZ4tPbG+gd4RSUFmbGh3fv8OH9j/jLx//BXz5RdqAHnOYLZnOLnTnPG5vVWIt0KwTy6s+2f9fvXyLjcjXHUBpULZEMcTNRpokD48t8skK142KPPrsPteC63SyRJzGF2UayDIaozPIuK06ykyoBIMsuGu5roO9x3rWUI1cVjpfwzpfqYn7wCRqoHFrfQNlrQZ3v22jXvDCoHmqh7WuuWEW8K9+uRFeIdHGnta9QIcHsSFmOC0ZbqO8P/Y699DIHTAtUqP9uB5rjobDdWxKf7zS+XPYS7x0kmmDI66VmmlrHZGiOHw3jh4nxd0u4MvBbAo4mO5yYsmLlU4huBC7ylvgCxs/OdJv6B3J48+Ih6cfCGYSPLs8uj8R4X80rrbiS5RIJx4S/M+G2kfMRwI/GNeyF4r/pgTLzMPCJDb5ujIOJCL8lxpTi7dakil8/M+GLEAT+xTAeC31CxEx8dH/6KjZZQ9trMkWtbgsAFwY+ssERwAdyq0NOpTB147Lsr7+an3CxJyzukHI5mTPmaWlFAV3RFgSvoH69hx3vKSoBjg3Oy0OyCczG4jRfVBlO5U1qsnHkEc7LCZY9HzHkcJrOMGELbeLHd/GHtjIu9gTrZpymMyZju1RpWSkzQTe+kDjwmQ2+NLor4wM5HLforrI6g/Cpe76pnFm9NvwbMB6LG1ypCWwBfMSEZaNU96OexSR14VuwP3w7AaDWq2Km/+SojVobuLt2ufmyO71N2WX3XCL6RTNdlnaD5+DFPL5SLVRNnNHKWDux3xERVgcyBX9iWDk5G78LIl8IVhmpaydEIT2KDkakshySX5xolCAwcKqAMlKpPIZ47AVUZngHSqEsZPE4uTMIfuW1MwA5n0YiWQpyHJMIRgfyRiYy+TniBOPrwSXa844IDlESTTZPSGmlAUXx04U7O1DQwfDOHxfayYAwVQy5ritmhjWuMH7FOqUgBvoFApx2bWRx1udnY/3AG3lTkFyVPh6ZRKvvU6VkQkSYKmbNqfxIdVWA4mO56yS2VTkEYxs6sjlN8pNl73xaBmMJFzgnQ0hI1BiCCyuJiUu7koUL7VUqLGRkAwgBJdaHqAsSDZbyFtENEYxYKRjb3qV7W4C0IoysH8MijUNY+WHTOSIEUNjezgAbB0fxaJfwPqQRz9q1BIAs2HBxlFG620UMMwIHZ2XoBRNgmQEXaBZ1r51dTOx7pI3LsYirfDIzbxg4ATP82XHWlEIfpXqi/Fm0EdLYiX1ZPS5HzEy5mXWlUD/jXLjD2m1LRSqlvyuUw4QVH9Vqi3oVp5TLc3/YOA5FkqCVPzPQprSRZTarwYnROrI4F5nKOLIe5FEd7UTbv5RK5R/diVo4rRItVbvFEHG+EKTKlVKRJ8csXehPTo69mA4AZ8JMFNKkwM8cxzYMbWACXSTrpCpP3SaCBy0H4HxiHI7ASYQ6TjMe3r7Fpy+/gugE6xZYlwX9Axs4NmEOo4I1526p1asmrOwXYMoLeWMbd+Kz05/vQHTKx89cKD2vOC+UqwGh+i/kPNvDmsF9S+BrRkPH6Vm/Z84OCE7dscorMQ/S31e/146wad4UNKkhdqMtcuKsWmg50tUwpHzb037NWtDEnose8Sw7W2bzkrMoYcvOp4Vsoq3XfNV/qQ5f/eoNzyKR6h1XEcUUk59TG2cnap9AbpOVC6AZAN+5vjNNn1WdrSSi15fe7+qa6CWr9d8Uvpp+o77U9lsZMDsFk2wLgs5xfWW7xEhLaoUUFltAhJBhwrPAe1z49McJGlgHLI5xWxjGOBAYzhGAGUwTGHPQWAgMP3+dphmTOWB2DpaBIxgPYaGaXO/bELEyQq7s9dleWxxAeFhZFLILFOvAy+Gx3mcQHmJSsa5b8Qoa/RbABEqqZw8zGEfka5DyAjoScrI+Rh2ACYBRVgnIKplAeKBspEiLnzarRyRCjIOjpNsRgAPgF1wUk7Joa9LGf8mrdewJs4+v5l9izAMwDMzk5TSjpKSNlfpBWM5Z/H5NMAjsJjgbW87hYAwOXJau3A0KTRjo/K71qcA9upMWrVeIAssGNzcjGmQOXMrGZVIr9ae8YgALzyAOthW2OE1+LNUyz5oBUUor7aG1BOsmsJtwnAjzXb1O1s5+OZPgdfP6NFMDwpHjmKuT1NrGl8h2cxelFG1+AOMhSAhqnyZgYW8PEy7UlF8ZlCohqCbepblHBlQlK0Y14uq5ZB9jK5y9Wp1xnQsV8Xh1rGVa1bxX3tdyxT0LhSjYn/ZgT7pdFrAmayHKO3rEVeqiLN2aBao+JXgUgNZozcVHxbDVE4J1epT4yH2mq9dQ/SzUSkFWqcgSuF6Tlk9IaChYx25HxE/vF99YzlegMTMeHOH3XyZMIJhpAsLqE09CNPxH4/96T0hiLJUdzjsd/J9z3tjtrEurnQn+CCdTGQ/j6lNvHHDhzoDcOQzD0wskw1zMm0EwjyfvR+CwA+JGgLNwVwt2gDXGn6w0cRLc470QxkygKcwswXjMDnB2gbMO6T924MlhYgPDAB8JbAgcnAzkgOhBZSLwzHAEgBm8AGRdEO698XkxLtSRw0fzhF+mC36/vMMH95h2M9SCzUIWN2Px0+lnPJlbsavjgQ/498sPmDH5MoHgxD0PsZ1+Ppzxl+OX1NYfLo/4cHnwDioYbxylUolxBPzp4Que5iWlYwzh4Cb84etbHFxWbJiy4heaM/WblB4z2DksvMDyAhvaPLZ4jG/IgAn48+MXPE3eLz6zwb9d3uHopnIVaMjgabrhz49fwMbTyOzvoKBgoDfGgMjgw+UB/3J5BBY/IP92+IrP0wXLZGGJ05nvpnZERIXClY4IY7xEn1ZzBcedDPNhecTvLm8BJhgHfDye8Wk+42aWZOD0dE6hL+bLaCc2+PfLe0xk8Ke3X7AYByKCcwy7+PFu7ZLageDL6evb4YfLEb89P+Lj6YxPD5dQL07Qb5IzJbW9NPYbL/C76wXOOSxh11V0iNFk0u/Y9u+XB/zr9S1+Ppzx19NXv9rNmDKPQF+kh2V5b+9xYIP/fvuEq7H+cl4g3Evj8yTNEUEo8jLGFEJjNjpxoiXfcYP0LoZNZRT5RKcTRWYkIeogJJZ+eyeA7+WGTE6jCF/x32QILWeSzt6Soow+OhXhs+GiJpuL9/KulqZviDh1+PQuOLa1Nsr9RH8PoOgPdVk0yHTkBdQyjelGIBvHNSX67YHhhMNG5m2YMC9elTRmQmJmMwEnP97JkMg/71Rj5jy2rgy4eNa6Ab09wkzZyR7zNqbsP8mpbAwwGRwPB8zHE6bAa7zDw8Faix/fvcPb4wk//e2v+Nvnz7FmcF6OMHREdO7L+l9Dt/61y5OlI7lON/Wt8LMRfe4RhVqE3hmJzEJnL5cgp3CKHxC8uI1aLXhiTkzwiC5dVfwNbDk0yjtMONdzQx/l3MVXI8LRHXR1CEJ9y/eqP/Y5yaOWg8JiFnAh19Tt2PCbxPvjk9YEq42JUgKLbSCfFAkUaTV1Wxnq6xxaRVo2a+ZXUumokbLgUtuqg7d8Un9fjoSqzjrzVNsG2tjR6e+j1h7r+a0d6YVuIqJ256Iq4L27ebr3UilzsW5xKBKLsVFXViOnJPlCyaeiIelUQTaU/aAOEzax14Up6CMwHuYnzGQVnu5XK3+9PoAdsLgbHg5H/O7tGzh7w3/9z8/49GnBf/7xZxwOBzweH8DHA377h3+FPf0GjB/8Yh1YnN1XXOwV/OYdeL7g4dMfcTr/CgvCU9xBD8CFPhrWIqFj6ijrkxnvZRGVOE+9tt1Mva4PxnvKRijDwFdR96qlIfaBZkplPALJkVHHlEbfc8Vmalkp7V5XeMaJGQetMCz6DwMXC9zIVOPujhoixsyMD/KZA55Qju+inyZefGeeze5GvX21Zm+TL+VrTzbjHfue9BRXLJaNkz+KOVMmTllH47J1ttjHfhBcMYf7HQBXOvr2TY/bilgdWRWBUu5Kdr1OAj3e1UNcHhV1jcVN+HJ92w9/V6URbFxsGexNX65voI7HndygnuaJCNb5Nni6PYBWLJk9qXZXztXiTQPGb5oyAFeg2GUVd/ir1RYeOgDv0Jczclz/ZQHwOf1m1GWKwY9oHTOrOqEi+0dbpCwRIFmAeJfkJikLltIl1XFS+bINpy1J+VN1pmhoHvd3nYilveFDl4tk363nfI3kmpZaX9XgpPCg8dD42TLAbpqpJXr6ViHkaQGoKUNOu5Itk5Av+r2UZ6t2FMGDLXMbW/Jir5/r9hQkG1qhs8R5nRHsZ74WG/12F8Ueux0R1we/kp2DAXaaJ9hlAt9mv3JzngEisPFrM9gxnCW4yV+D4OMF8qLiA4Y8Yz7cdy2UcM9M2PrB6Bx5J0AScLLgy2SSgTdWoDemwG8eIIZsy2kimImAycdLxqKwutMdg1HSMdgRbkRwlrAwYF3YdcAMFktHXDBUmwmYTCCPGNZ5B453PlhYZ8FkgxODMTt4p8dsQFOgwSE5GgCAieHmsMLe+X0IZJ03ypPDAoebsWB4A/zZLPg63XDmBTdYUFw5TvkiXgawGIsrLfgyX3EOhnlvKDZwDrgsfvWQmSgYzSLTyszmerD4erylTvtoj7gtzjtlyBu3vaMorxGy5HA+Lnia8/RkjMFiGberBbkp5VMYAMHpeJD0HMEZYy1ubsGNbnlXgOxyIBjydfjFXHE+eMP37AzOwfBukk6Uh9FlWvD1cAMbYJqmPDiJQt/x3x/tjNtig2GQcJ4snuYFt3mBM9k4Gv+kUdb373KVvjHeqGxmLuJIZvKABTdrMYVxeZkWn6dZsBib4k2Tfy+NobMjXJ3DBOB8tLBzZlbWuuQcyHQaGJoSDUdrcJ0snqYFX+ZbQZs0lsbP2BYknjMzFniHwGKWXP74PvaCkO6JFizW4Wle8PWwZOeAZszm2hFBuDq/K+TpsOA62VTn3vBrMM1TQZuEMYxpikw78KZq8pXtmcdKS1fKU9Bd9o82XvGZ/UlI0ykBJJxP2o6NXp+rae/RvGbkX3VEVP02juueQ0H+Fe8UR0Rh8Ejhy3JG9BwRMg3tnUyrCMcMQ4CxlHY6eSEVWA4OmNo2AAByjJmyMzMZvmYDeuTghMgycBTaM29AstnSEsvKMCfAHE1DtyeDYTkqWZEvGBgiHAylvo9UTp/fcT5gIoOHwxGHecplCOJDup8oKhYdwS+1UdV1kii+0fca5ZpCf/RPguxQpb17KYkGSnRFQ0tItNX/Iz1CIKcUjsL/VJSBqk8AYtWn7tir++Je+KSaykl5M0fay3FeIhs/WNBgjKSp5V33wMsIlRKoF+Y5iYcPRQkN7Ufymf+G2A8anryq7GQZNqXVkM0iTbkKt+J5qU3a6ijLQmXU2E6V0X4v7y7yAVAcPqYFT9n4+ip0uEqRL1Ed9aXMpYlLpDLEZ7Xydw+SuamKLfOQdOVwnkZtBMvwjKL9m3TWsdbWa3W0rxb6vGVLaY3QZIcef5K8vy1/lQ8Yh8nCkHZAEMM6A0NHOEMwbGDMAfP0iMtCOF8JXy+MX58WHBeCcxaXK2FxR1h+gONHrxvAwsLBguAmAz4sMNNn0OTHrWWkHRHxbsPSEbHN5KRyrbVIPB5ElSvuRC1pWoh6btlCnLQQLWcyrKnDKmD2K5ZTODH2oxwUd7y2/MyHn9Ci7DZ+5bLjWIad9VPJC4QyLwYy7VxGiXJFHLeyXjYyRZTBM/VKpMS36ue1UVY3I0ZxcoHCx6PsUFAVaBLlZFPyssZ9/oL5u4g8RWoYDoeUT+JWuwUFrZyCRyV5pBN0R5I5xTJMrDpGmKUkzZtGypX0K1nW4ZBkkC49dXpJlxPR5Pw4+SR7hzLFTLpjfA8Vpq30Yp1loLFHg5Q5E0ivWq27y5gOUZKIO881OaeUQ4rhLab0YjcXGWUudmkRo6Sy4K0F5JFRpUwga7Dk04J3NvXRyohaO6pjrFnwtd55S2ssUJ9dkxwrle4tjDdNWj7XPHDj+F2dAlmm1ZG5ZL4NjZ1k413Dnd3zaU5Q6lIupFSu5ZOEw+vIQt+I5QhzQlYTQlgxJ60tTNOgSoKKThn1fULbV6L9zHXrLiw8ju3/Aux2RNCP79OAMWbC6fSAycx4Oj7CTBPm08kfuWIIbC2W24LltsBer7hdr7guV0xmCisuM/+iKPikEczg5RYMy37tyu22lEZFa304ht8NYaZkkGTnDajWObB1uC1X2NsNzhl/pEUIdzyeMM8Tjo8PmKc5bXO0boFzHFZUO1wvV1hrsVyfYK3F9fIEZgtnr77jsjT8eUPtNPk8HHuBdrHOG8kvFyzTDYuxYGsTBzrOPs7hOMFMJnVUtjasIAr1Ev51zsE5C/tw86voncuOEWfhrMNiGDDAnw+/4u/4ChNoikbb2LkXZ+HAuFF5ap4xhMUw/uvdL/74n3QEV3D+mDy4rxAGZAAfj0/49XBNBl0T4kVFxTnvDLhWeTIzFuPw07tfi22nkl7vXOKSAQCwzsJai/PTGWc8wZm8a8Gn4Q0csRxu4sRQb7D4z8NH0AGYqWWyjgAfOju+fDrlGPl4eMLn6eL7rXW4GReOrMrlkJ/NGNOM0sWq6BafDxecj9bXLwgXXmAp7Abh3CbRcSKVxxsYP735BUQEa/LkqzlMfHwUzPjnwwW/0AULOe9sXDFAJsMWA4AL54oD0agMysb/ZAwNDDI+Y2b8Ml/wH29ucKbNQ6sj+cwB+OPjLzAwWODSzCGN/7VxvF6JJQ350RjRGhoyvWs09QxC9xoZ98SX9NRGzrrf1elp358Dzfkm09WcAT0HQU1vXT6Z9t763MqrEwl8BJhMGhvsytUbmiODJoDfBKOr924BMF6JV4VHNG1GRKA3Ux63IGCibtv6vP0ckmXEWPcmzKUm7y4M495am3ZGvHs4NWln3qz3l7q/6XVM8Pe3KP1PGV9aHlraLxpLQgOKgpoU3BTLNKSoTZSPNcwE1bkIkZGFIM3liqvaidGgoiU5toAkALfWqAoxUKrznIa2ezr16yDMxd1YxujOiJ4htQxk0ry81na9+FvtveW8JMVwnATV8D3oDV2DKhf9gBsFh6rw8qk2l2jP67LE5LhqqMbpp3TGOPetwb+Wjggxtnv01DtbNMMAsgyt5hvTrGST+J1VpXgf4g6YSIlsjzVnTf2ph/Vp+vrh9FvmvmUAqNPVdlfK5/sN2pzMj9r8uJeX1u/jwot6Z0QMG/uKjNbr14YWtA4qIO5uv1k/fpfF78Rla9ux4zjNXdZaYXDgturJgH/zb8CbPyQ+6AIPdnG3aRpf988pq8fT7W63O/OM7UhVzwvFlyboNTOHL7EuD6cwUZdPO3Ip87/OYV0qzU3e2TG9t37ywgUxvjmWRPxU+mFejcorq1BX6CD16y54mhI39f/unM+adNLUn+ek0rCFIG9wjvMqEDKDYqAyMrOdFdTlO1X7kTY075H/njH+ijlgK68V/Vh+1s+3845/rR63OWYUVhgeh8/1+M3CkRU6tfJp9O3mg6Gjl/YxwK/ijWJF0yGyjNSpo1K+oLSjWb53zvq7XkW6AAlntXQ8AMw2/dbKbUgTKNvxI0pRhrxHHm6e9dsvaiGJpQLJDlbmzW07K+0uF35qn6tjqLK/FK8gaytPeJKmeuFEfL4mY6f8Onr5nsUXiTLObR9tR6VukXkzw2V+LRZP7h0b7aKSmqaMfFJLbtcYLi5IrhF1mryw090930nsdkSYQ95IaaYJ0+mIaT4Abx+BeQYeHsKWBu+I4NsCd7nCXgxuV2C5ATxN4GnC5CWWYHuJ3jBfGGaGXbxDwVq/Ynm5xQIHI72wQhL5XRhsDBxlo2mMe71Y3GgJjUugyTst6DQBhwOmxyNontPF2XahkKc/Ruli/f0HN+uPP7pa7wllslEyjk0Ti49p8rzLMmFxDAuLhRdczYKFFlha4IxLE4ibCdMEuEM+i5+ZwVPZAeNfdEQssKkjpE/rd0VEY/mNLGxYye1X0ZYr452rPbupZr2zIKyqN2lFvwuTLlLZneNCZ3CGcQ3h4k6MGB8A2LSMODMi4DrpF3Hl8pcrohnwygYszuaGJ7rBGQ79KoZz3tgW6DqQuDmDgIvxzq2ZTDGIo6I2V0NFYzrWEBayfsWVyes/aCVenWarGK4Pb2sYF2NT/bqw+0YTIBomFNrXGx/bybahNSjV8bklxm0Sl18r+dUG4qigkKDHG3Y6zBxlvTgCrma/YlOX92ZcGgPU5Fcp/rTuZIDihHgJ7jGavxY04fW5ivEeQ+M9xkVtPBQGmH9wXXVhKM19AAJTD3+Ij3KdJroNJed90qI6ZdLKTRQclenon3uMJKL/Vsa+VjDyf/M0YVrZ5fN8JwSE9lz2QSkEbRlpn2uc7kHqMbWDclv4BIimbrgabVnilteM+4wSphnHuw2LziFfr021DadJI/0h7Cab+rRu8hbKx//10tjiS/cab3J6xTYzGQOgtt+v0VZ+tvOVqvxv9O8mjYZfo7BCpVikx8u/827iLqpyFOO7S1PLj5q6dxZ1P69R8Dspl1R53D1f3eGI2OI1a+F1g8s2r27bSS/nvfM2h0VWa2lv9TntfcELFJq87C7pWMvj1ITzadgwF4Udu8Y7Gy62XXPLyegT+2mWi+t+CwCYjrlJUn9n5Etz0uykswlo/UAPV0W6I/B+pKIUFlv5TD7fypvEv6FNZJyoE0ZZJulm7Tx2DxjiLse99RPDZatgI180aWVLTf5U1Yyq3iq8SCbVDGEbaXbfF/0YwhZW/o5fX2RFkvQUidV9LEqdFambMkGrh2rhGdwkvlcW6BnFt5DiaPpyL+zG863fbd7wxxxDlGdn3r024fS5USdCXuvR15tTenW+ux040im5GWeq8wpnkXb8rddTfJYcqXGBWaGD+jtGubBDEPKqjzTYRHkyH9TK3Wnhzpv+EaANen2ysXv09U4u0u8t/sgLbtbaO9+H2MotW7pSoUc2dBbSm2DjmRaZt0xzbewnG5XiiEi2rE1dMPcHmVdIGbLuk6wiwjm0pzjs1YH26MjxjlsneFgMZ9mmoymLvMN9tmxiP2/b9R4Qv6YlbWBgYGBgYGBgYGBgYGBgYGBgYGBgYGBgQGDfMq+BgYGBgYGBgYGBgYGBgYGBgYGBgYGBgYFnYDgiBgYGBgYGBgYGBgYGBgYGBgYGBgYGBga+GYYjYmBgYGBgYGBgYGBgYGBgYGBgYGBgYGDgm2E4IgYGBgYGBgYGBgYGBgYGBgYGBgYGBgYGvhmGI2JgYGBgYGBgYGBgYGBgYGBgYGBgYGBg4JthOCIGBgYGBgYGBgYGBgYGBgYGBgYGBgYGBr4ZhiNiYGBgYGBgYGBgYGBgYGBgYGBgYGBgYOCbYTgiBgYGBgYGBgYGBgYGBgYGBgYGBgYGBga+GYYjYmBgYGBgYGBgYGBgYGBgYGBgYGBgYGDgm+F/AZ9zqfaLDub0AAAAAElFTkSuQmCC\n",
+ "text/plain": [
+ ""
+ ]
+ },
+ "metadata": {},
+ "output_type": "display_data"
+ }
+ ],
+ "source": [
+ "plt.figure(figsize=(20,20))\n",
+ "plt.imshow(image)\n",
+ "show_anns(masks2)\n",
+ "plt.axis('off')\n",
+ "plt.show() "
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "id": "8c937160",
+ "metadata": {},
+ "outputs": [],
+ "source": []
+ }
+ ],
+ "metadata": {
+ "kernelspec": {
+ "display_name": "Python 3 (ipykernel)",
+ "language": "python",
+ "name": "python3"
+ },
+ "language_info": {
+ "codemirror_mode": {
+ "name": "ipython",
+ "version": 3
+ },
+ "file_extension": ".py",
+ "mimetype": "text/x-python",
+ "name": "python",
+ "nbconvert_exporter": "python",
+ "pygments_lexer": "ipython3",
+ "version": "3.10.10"
+ }
+ },
+ "nbformat": 4,
+ "nbformat_minor": 5
+}
diff --git a/VISAM/thirdparty/segment_anything/notebooks/images/dog.jpg b/VISAM/thirdparty/segment_anything/notebooks/images/dog.jpg
new file mode 100644
index 0000000000000000000000000000000000000000..26d6454d626bfd71b386ca1ba032836ea12f8a35
Binary files /dev/null and b/VISAM/thirdparty/segment_anything/notebooks/images/dog.jpg differ
diff --git a/VISAM/thirdparty/segment_anything/notebooks/images/groceries.jpg b/VISAM/thirdparty/segment_anything/notebooks/images/groceries.jpg
new file mode 100644
index 0000000000000000000000000000000000000000..85f791c45610e5a3c230fddb1e712dbc602f79d0
Binary files /dev/null and b/VISAM/thirdparty/segment_anything/notebooks/images/groceries.jpg differ
diff --git a/VISAM/thirdparty/segment_anything/notebooks/images/truck.jpg b/VISAM/thirdparty/segment_anything/notebooks/images/truck.jpg
new file mode 100644
index 0000000000000000000000000000000000000000..6b98688c3c84981200c06259b8d54820ebf85660
Binary files /dev/null and b/VISAM/thirdparty/segment_anything/notebooks/images/truck.jpg differ
diff --git a/VISAM/thirdparty/segment_anything/notebooks/onnx_model_example.ipynb b/VISAM/thirdparty/segment_anything/notebooks/onnx_model_example.ipynb
new file mode 100644
index 0000000000000000000000000000000000000000..155dd27c957a5941505a0c805f2405e0cd094f4b
--- /dev/null
+++ b/VISAM/thirdparty/segment_anything/notebooks/onnx_model_example.ipynb
@@ -0,0 +1,774 @@
+{
+ "cells": [
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "id": "901c8ef3",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "# Copyright (c) Meta Platforms, Inc. and affiliates."
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "1662bb7c",
+ "metadata": {},
+ "source": [
+ "# Produces masks from prompts using an ONNX model"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "7fcc21a0",
+ "metadata": {},
+ "source": [
+ "SAM's prompt encoder and mask decoder are very lightweight, which allows for efficient computation of a mask given user input. This notebook shows an example of how to export and use this lightweight component of the model in ONNX format, allowing it to run on a variety of platforms that support an ONNX runtime."
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 4,
+ "id": "86daff77",
+ "metadata": {},
+ "outputs": [
+ {
+ "data": {
+ "text/html": [
+ "\n",
+ "\n",
+ " \n",
+ "\n"
+ ],
+ "text/plain": [
+ ""
+ ]
+ },
+ "metadata": {},
+ "output_type": "display_data"
+ }
+ ],
+ "source": [
+ "from IPython.display import display, HTML\n",
+ "display(HTML(\n",
+ "\"\"\"\n",
+ "\n",
+ " \n",
+ "\n",
+ "\"\"\"\n",
+ "))"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "55ae4e00",
+ "metadata": {},
+ "source": [
+ "## Environment Set-up"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "109a5cc2",
+ "metadata": {},
+ "source": [
+ "If running locally using jupyter, first install `segment_anything` in your environment using the [installation instructions](https://github.com/facebookresearch/segment-anything#installation) in the repository. The latest stable versions of PyTorch and ONNX are recommended for this notebook. If running from Google Colab, set `using_collab=True` below and run the cell. In Colab, be sure to select 'GPU' under 'Edit'->'Notebook Settings'->'Hardware accelerator'."
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 5,
+ "id": "39b99fc4",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "using_colab = False"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 6,
+ "id": "296a69be",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "if using_colab:\n",
+ " import torch\n",
+ " import torchvision\n",
+ " print(\"PyTorch version:\", torch.__version__)\n",
+ " print(\"Torchvision version:\", torchvision.__version__)\n",
+ " print(\"CUDA is available:\", torch.cuda.is_available())\n",
+ " import sys\n",
+ " !{sys.executable} -m pip install opencv-python matplotlib onnx onnxruntime\n",
+ " !{sys.executable} -m pip install 'git+https://github.com/facebookresearch/segment-anything.git'\n",
+ " \n",
+ " !mkdir images\n",
+ " !wget -P images https://raw.githubusercontent.com/facebookresearch/segment-anything/main/notebooks/images/truck.jpg\n",
+ " \n",
+ " !wget https://dl.fbaipublicfiles.com/segment_anything/sam_vit_h_4b8939.pth"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "dc4a58be",
+ "metadata": {},
+ "source": [
+ "## Set-up"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "42396e8d",
+ "metadata": {},
+ "source": [
+ "Note that this notebook requires both the `onnx` and `onnxruntime` optional dependencies, in addition to `opencv-python` and `matplotlib` for visualization."
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "id": "2c712610",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "import torch\n",
+ "import numpy as np\n",
+ "import cv2\n",
+ "import matplotlib.pyplot as plt\n",
+ "from segment_anything import sam_model_registry, SamPredictor\n",
+ "from segment_anything.utils.onnx import SamOnnxModel\n",
+ "\n",
+ "import onnxruntime\n",
+ "from onnxruntime.quantization import QuantType\n",
+ "from onnxruntime.quantization.quantize import quantize_dynamic"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "id": "f29441b9",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "def show_mask(mask, ax):\n",
+ " color = np.array([30/255, 144/255, 255/255, 0.6])\n",
+ " h, w = mask.shape[-2:]\n",
+ " mask_image = mask.reshape(h, w, 1) * color.reshape(1, 1, -1)\n",
+ " ax.imshow(mask_image)\n",
+ " \n",
+ "def show_points(coords, labels, ax, marker_size=375):\n",
+ " pos_points = coords[labels==1]\n",
+ " neg_points = coords[labels==0]\n",
+ " ax.scatter(pos_points[:, 0], pos_points[:, 1], color='green', marker='*', s=marker_size, edgecolor='white', linewidth=1.25)\n",
+ " ax.scatter(neg_points[:, 0], neg_points[:, 1], color='red', marker='*', s=marker_size, edgecolor='white', linewidth=1.25) \n",
+ " \n",
+ "def show_box(box, ax):\n",
+ " x0, y0 = box[0], box[1]\n",
+ " w, h = box[2] - box[0], box[3] - box[1]\n",
+ " ax.add_patch(plt.Rectangle((x0, y0), w, h, edgecolor='green', facecolor=(0,0,0,0), lw=2)) "
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "bd0f6b2b",
+ "metadata": {},
+ "source": [
+ "## Export an ONNX model"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "1540f719",
+ "metadata": {},
+ "source": [
+ "Set the path below to a SAM model checkpoint, then load the model. This will be needed to both export the model and to calculate embeddings for the model."
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "id": "76fc53f4",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "checkpoint = \"sam_vit_h_4b8939.pth\"\n",
+ "model_type = \"default\""
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "id": "11bfc8aa",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "sam = sam_model_registry[model_type](checkpoint=checkpoint)"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "450c089c",
+ "metadata": {},
+ "source": [
+ "The script `segment-anything/scripts/export_onnx_model.py` can be used to export the necessary portion of SAM. Alternatively, run the following code to export an ONNX model. If you have already exported a model, set the path below and skip to the next section. Assure that the exported ONNX model aligns with the checkpoint and model type set above. This notebook expects the model was exported with the parameter `return_single_mask=True`."
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "id": "38a8add8",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "onnx_model_path = None # Set to use an already exported model, then skip to the next section."
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "id": "7da638ba",
+ "metadata": {
+ "scrolled": false
+ },
+ "outputs": [],
+ "source": [
+ "import warnings\n",
+ "\n",
+ "onnx_model_path = \"sam_onnx_example.onnx\"\n",
+ "\n",
+ "onnx_model = SamOnnxModel(sam, return_single_mask=True)\n",
+ "\n",
+ "dynamic_axes = {\n",
+ " \"point_coords\": {1: \"num_points\"},\n",
+ " \"point_labels\": {1: \"num_points\"},\n",
+ "}\n",
+ "\n",
+ "embed_dim = sam.prompt_encoder.embed_dim\n",
+ "embed_size = sam.prompt_encoder.image_embedding_size\n",
+ "mask_input_size = [4 * x for x in embed_size]\n",
+ "dummy_inputs = {\n",
+ " \"image_embeddings\": torch.randn(1, embed_dim, *embed_size, dtype=torch.float),\n",
+ " \"point_coords\": torch.randint(low=0, high=1024, size=(1, 5, 2), dtype=torch.float),\n",
+ " \"point_labels\": torch.randint(low=0, high=4, size=(1, 5), dtype=torch.float),\n",
+ " \"mask_input\": torch.randn(1, 1, *mask_input_size, dtype=torch.float),\n",
+ " \"has_mask_input\": torch.tensor([1], dtype=torch.float),\n",
+ " \"orig_im_size\": torch.tensor([1500, 2250], dtype=torch.float),\n",
+ "}\n",
+ "output_names = [\"masks\", \"iou_predictions\", \"low_res_masks\"]\n",
+ "\n",
+ "with warnings.catch_warnings():\n",
+ " warnings.filterwarnings(\"ignore\", category=torch.jit.TracerWarning)\n",
+ " warnings.filterwarnings(\"ignore\", category=UserWarning)\n",
+ " with open(onnx_model_path, \"wb\") as f:\n",
+ " torch.onnx.export(\n",
+ " onnx_model,\n",
+ " tuple(dummy_inputs.values()),\n",
+ " f,\n",
+ " export_params=True,\n",
+ " verbose=False,\n",
+ " opset_version=17,\n",
+ " do_constant_folding=True,\n",
+ " input_names=list(dummy_inputs.keys()),\n",
+ " output_names=output_names,\n",
+ " dynamic_axes=dynamic_axes,\n",
+ " ) "
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "c450cf1a",
+ "metadata": {},
+ "source": [
+ "If desired, the model can additionally be quantized and optimized. We find this improves web runtime significantly for negligible change in qualitative performance. Run the next cell to quantize the model, or skip to the next section otherwise."
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "id": "235d39fe",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "onnx_model_quantized_path = \"sam_onnx_quantized_example.onnx\"\n",
+ "quantize_dynamic(\n",
+ " model_input=onnx_model_path,\n",
+ " model_output=onnx_model_quantized_path,\n",
+ " optimize_model=True,\n",
+ " per_channel=False,\n",
+ " reduce_range=False,\n",
+ " weight_type=QuantType.QUInt8,\n",
+ ")\n",
+ "onnx_model_path = onnx_model_quantized_path"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "927a928b",
+ "metadata": {},
+ "source": [
+ "## Example Image"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "id": "6be6eb55",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "image = cv2.imread('images/truck.jpg')\n",
+ "image = cv2.cvtColor(image, cv2.COLOR_BGR2RGB)"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "id": "b7e9a27a",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "plt.figure(figsize=(10,10))\n",
+ "plt.imshow(image)\n",
+ "plt.axis('on')\n",
+ "plt.show()"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "027b177b",
+ "metadata": {},
+ "source": [
+ "## Using an ONNX model"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "778d4593",
+ "metadata": {},
+ "source": [
+ "Here as an example, we use `onnxruntime` in python on CPU to execute the ONNX model. However, any platform that supports an ONNX runtime could be used in principle. Launch the runtime session below:"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "id": "9689b1bf",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "ort_session = onnxruntime.InferenceSession(onnx_model_path)"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "7708ead6",
+ "metadata": {},
+ "source": [
+ "To use the ONNX model, the image must first be pre-processed using the SAM image encoder. This is a heavier weight process best performed on GPU. SamPredictor can be used as normal, then `.get_image_embedding()` will retreive the intermediate features."
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "id": "26e067b4",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "sam.to(device='cuda')\n",
+ "predictor = SamPredictor(sam)"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "id": "7ad3f0d6",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "predictor.set_image(image)"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "id": "8a6f0f07",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "image_embedding = predictor.get_image_embedding().cpu().numpy()"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "id": "5e112f33",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "image_embedding.shape"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "6337b654",
+ "metadata": {},
+ "source": [
+ "The ONNX model has a different input signature than `SamPredictor.predict`. The following inputs must all be supplied. Note the special cases for both point and mask inputs. All inputs are `np.float32`.\n",
+ "* `image_embeddings`: The image embedding from `predictor.get_image_embedding()`. Has a batch index of length 1.\n",
+ "* `point_coords`: Coordinates of sparse input prompts, corresponding to both point inputs and box inputs. Boxes are encoded using two points, one for the top-left corner and one for the bottom-right corner. *Coordinates must already be transformed to long-side 1024.* Has a batch index of length 1.\n",
+ "* `point_labels`: Labels for the sparse input prompts. 0 is a negative input point, 1 is a positive input point, 2 is a top-left box corner, 3 is a bottom-right box corner, and -1 is a padding point. *If there is no box input, a single padding point with label -1 and coordinates (0.0, 0.0) should be concatenated.*\n",
+ "* `mask_input`: A mask input to the model with shape 1x1x256x256. This must be supplied even if there is no mask input. In this case, it can just be zeros.\n",
+ "* `has_mask_input`: An indicator for the mask input. 1 indicates a mask input, 0 indicates no mask input.\n",
+ "* `orig_im_size`: The size of the input image in (H,W) format, before any transformation. \n",
+ "\n",
+ "Additionally, the ONNX model does not threshold the output mask logits. To obtain a binary mask, threshold at `sam.mask_threshold` (equal to 0.0)."
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "bf5a9f55",
+ "metadata": {},
+ "source": [
+ "### Example point input"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "id": "1c0deef0",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "input_point = np.array([[500, 375]])\n",
+ "input_label = np.array([1])"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "7256394c",
+ "metadata": {},
+ "source": [
+ "Add a batch index, concatenate a padding point, and transform."
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "id": "4f69903e",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "onnx_coord = np.concatenate([input_point, np.array([[0.0, 0.0]])], axis=0)[None, :, :]\n",
+ "onnx_label = np.concatenate([input_label, np.array([-1])], axis=0)[None, :].astype(np.float32)\n",
+ "\n",
+ "onnx_coord = predictor.transform.apply_coords(onnx_coord, image.shape[:2]).astype(np.float32)\n"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "b188dc53",
+ "metadata": {},
+ "source": [
+ "Create an empty mask input and an indicator for no mask."
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "id": "5cb52bcf",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "onnx_mask_input = np.zeros((1, 1, 256, 256), dtype=np.float32)\n",
+ "onnx_has_mask_input = np.zeros(1, dtype=np.float32)"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "a99c2cc5",
+ "metadata": {},
+ "source": [
+ "Package the inputs to run in the onnx model"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "id": "b1d7ea11",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "ort_inputs = {\n",
+ " \"image_embeddings\": image_embedding,\n",
+ " \"point_coords\": onnx_coord,\n",
+ " \"point_labels\": onnx_label,\n",
+ " \"mask_input\": onnx_mask_input,\n",
+ " \"has_mask_input\": onnx_has_mask_input,\n",
+ " \"orig_im_size\": np.array(image.shape[:2], dtype=np.float32)\n",
+ "}"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "4b6409c9",
+ "metadata": {},
+ "source": [
+ "Predict a mask and threshold it."
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "id": "dc4cc082",
+ "metadata": {
+ "scrolled": false
+ },
+ "outputs": [],
+ "source": [
+ "masks, _, low_res_logits = ort_session.run(None, ort_inputs)\n",
+ "masks = masks > predictor.model.mask_threshold"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "id": "d778a8fb",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "masks.shape"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "id": "badb1175",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "plt.figure(figsize=(10,10))\n",
+ "plt.imshow(image)\n",
+ "show_mask(masks, plt.gca())\n",
+ "show_points(input_point, input_label, plt.gca())\n",
+ "plt.axis('off')\n",
+ "plt.show() "
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "1f1d4d15",
+ "metadata": {},
+ "source": [
+ "### Example mask input"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "id": "b319da82",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "input_point = np.array([[500, 375], [1125, 625]])\n",
+ "input_label = np.array([1, 1])\n",
+ "\n",
+ "# Use the mask output from the previous run. It is already in the correct form for input to the ONNX model.\n",
+ "onnx_mask_input = low_res_logits"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "b1823b37",
+ "metadata": {},
+ "source": [
+ "Transform the points as in the previous example."
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "id": "8885130f",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "onnx_coord = np.concatenate([input_point, np.array([[0.0, 0.0]])], axis=0)[None, :, :]\n",
+ "onnx_label = np.concatenate([input_label, np.array([-1])], axis=0)[None, :].astype(np.float32)\n",
+ "\n",
+ "onnx_coord = predictor.transform.apply_coords(onnx_coord, image.shape[:2]).astype(np.float32)"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "28e47b69",
+ "metadata": {},
+ "source": [
+ "The `has_mask_input` indicator is now 1."
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "id": "3ab4483a",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "onnx_has_mask_input = np.ones(1, dtype=np.float32)"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "d3781955",
+ "metadata": {},
+ "source": [
+ "Package inputs, then predict and threshold the mask."
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "id": "0c1ec096",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "ort_inputs = {\n",
+ " \"image_embeddings\": image_embedding,\n",
+ " \"point_coords\": onnx_coord,\n",
+ " \"point_labels\": onnx_label,\n",
+ " \"mask_input\": onnx_mask_input,\n",
+ " \"has_mask_input\": onnx_has_mask_input,\n",
+ " \"orig_im_size\": np.array(image.shape[:2], dtype=np.float32)\n",
+ "}\n",
+ "\n",
+ "masks, _, _ = ort_session.run(None, ort_inputs)\n",
+ "masks = masks > predictor.model.mask_threshold"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "id": "1e36554b",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "plt.figure(figsize=(10,10))\n",
+ "plt.imshow(image)\n",
+ "show_mask(masks, plt.gca())\n",
+ "show_points(input_point, input_label, plt.gca())\n",
+ "plt.axis('off')\n",
+ "plt.show() "
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "2ef211d0",
+ "metadata": {},
+ "source": [
+ "### Example box and point input"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "id": "51e58d2e",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "input_box = np.array([425, 600, 700, 875])\n",
+ "input_point = np.array([[575, 750]])\n",
+ "input_label = np.array([0])"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "6e119dcb",
+ "metadata": {},
+ "source": [
+ "Add a batch index, concatenate a box and point inputs, add the appropriate labels for the box corners, and transform. There is no padding point since the input includes a box input."
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "id": "bfbe4911",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "onnx_box_coords = input_box.reshape(2, 2)\n",
+ "onnx_box_labels = np.array([2,3])\n",
+ "\n",
+ "onnx_coord = np.concatenate([input_point, onnx_box_coords], axis=0)[None, :, :]\n",
+ "onnx_label = np.concatenate([input_label, onnx_box_labels], axis=0)[None, :].astype(np.float32)\n",
+ "\n",
+ "onnx_coord = predictor.transform.apply_coords(onnx_coord, image.shape[:2]).astype(np.float32)"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "65edabd2",
+ "metadata": {},
+ "source": [
+ "Package inputs, then predict and threshold the mask."
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "id": "2abfba56",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "onnx_mask_input = np.zeros((1, 1, 256, 256), dtype=np.float32)\n",
+ "onnx_has_mask_input = np.zeros(1, dtype=np.float32)\n",
+ "\n",
+ "ort_inputs = {\n",
+ " \"image_embeddings\": image_embedding,\n",
+ " \"point_coords\": onnx_coord,\n",
+ " \"point_labels\": onnx_label,\n",
+ " \"mask_input\": onnx_mask_input,\n",
+ " \"has_mask_input\": onnx_has_mask_input,\n",
+ " \"orig_im_size\": np.array(image.shape[:2], dtype=np.float32)\n",
+ "}\n",
+ "\n",
+ "masks, _, _ = ort_session.run(None, ort_inputs)\n",
+ "masks = masks > predictor.model.mask_threshold"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "id": "8301bf33",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "plt.figure(figsize=(10, 10))\n",
+ "plt.imshow(image)\n",
+ "show_mask(masks[0], plt.gca())\n",
+ "show_box(input_box, plt.gca())\n",
+ "show_points(input_point, input_label, plt.gca())\n",
+ "plt.axis('off')\n",
+ "plt.show()"
+ ]
+ }
+ ],
+ "metadata": {
+ "kernelspec": {
+ "display_name": "Python 3 (ipykernel)",
+ "language": "python",
+ "name": "python3"
+ },
+ "language_info": {
+ "codemirror_mode": {
+ "name": "ipython",
+ "version": 3
+ },
+ "file_extension": ".py",
+ "mimetype": "text/x-python",
+ "name": "python",
+ "nbconvert_exporter": "python",
+ "pygments_lexer": "ipython3",
+ "version": "3.10.10"
+ }
+ },
+ "nbformat": 4,
+ "nbformat_minor": 5
+}
diff --git a/VISAM/thirdparty/segment_anything/notebooks/predictor_example.ipynb b/VISAM/thirdparty/segment_anything/notebooks/predictor_example.ipynb
new file mode 100644
index 0000000000000000000000000000000000000000..8374c4de0e95b99d2ed515efaa873bc8cd3cafda
--- /dev/null
+++ b/VISAM/thirdparty/segment_anything/notebooks/predictor_example.ipynb
@@ -0,0 +1,1023 @@
+{
+ "cells": [
+ {
+ "cell_type": "code",
+ "execution_count": 1,
+ "id": "f400486b",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "# Copyright (c) Meta Platforms, Inc. and affiliates."
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "a1ae39ff",
+ "metadata": {},
+ "source": [
+ "# Object masks from prompts with SAM"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "b4a4b25c",
+ "metadata": {},
+ "source": [
+ "The Segment Anything Model (SAM) predicts object masks given prompts that indicate the desired object. The model first converts the image into an image embedding that allows high quality masks to be efficiently produced from a prompt. \n",
+ "\n",
+ "The `SamPredictor` class provides an easy interface to the model for prompting the model. It allows the user to first set an image using the `set_image` method, which calculates the necessary image embeddings. Then, prompts can be provided via the `predict` method to efficiently predict masks from those prompts. The model can take as input both point and box prompts, as well as masks from the previous iteration of prediction."
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 2,
+ "id": "18ab8c70",
+ "metadata": {},
+ "outputs": [
+ {
+ "data": {
+ "text/html": [
+ "\n",
+ "\n",
+ " \n",
+ "\n"
+ ],
+ "text/plain": [
+ ""
+ ]
+ },
+ "metadata": {},
+ "output_type": "display_data"
+ }
+ ],
+ "source": [
+ "from IPython.display import display, HTML\n",
+ "display(HTML(\n",
+ "\"\"\"\n",
+ "\n",
+ " \n",
+ "\n",
+ "\"\"\"\n",
+ "))"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "644532a8",
+ "metadata": {},
+ "source": [
+ "## Environment Set-up"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "07fabfee",
+ "metadata": {},
+ "source": [
+ "If running locally using jupyter, first install `segment_anything` in your environment using the [installation instructions](https://github.com/facebookresearch/segment-anything#installation) in the repository. If running from Google Colab, set `using_collab=True` below and run the cell. In Colab, be sure to select 'GPU' under 'Edit'->'Notebook Settings'->'Hardware accelerator'."
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 1,
+ "id": "5ea65efc",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "using_colab = False"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 4,
+ "id": "91dd9a89",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "if using_colab:\n",
+ " import torch\n",
+ " import torchvision\n",
+ " print(\"PyTorch version:\", torch.__version__)\n",
+ " print(\"Torchvision version:\", torchvision.__version__)\n",
+ " print(\"CUDA is available:\", torch.cuda.is_available())\n",
+ " import sys\n",
+ " !{sys.executable} -m pip install opencv-python matplotlib\n",
+ " !{sys.executable} -m pip install 'git+https://github.com/facebookresearch/segment-anything.git'\n",
+ " \n",
+ " !mkdir images\n",
+ " !wget -P images https://raw.githubusercontent.com/facebookresearch/segment-anything/main/notebooks/images/truck.jpg\n",
+ " !wget -P images https://raw.githubusercontent.com/facebookresearch/segment-anything/main/notebooks/images/groceries.jpg\n",
+ " \n",
+ " !wget https://dl.fbaipublicfiles.com/segment_anything/sam_vit_h_4b8939.pth"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "0be845da",
+ "metadata": {},
+ "source": [
+ "## Set-up"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "33681dd1",
+ "metadata": {},
+ "source": [
+ "Necessary imports and helper functions for displaying points, boxes, and masks."
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 5,
+ "id": "69b28288",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "import numpy as np\n",
+ "import torch\n",
+ "import matplotlib.pyplot as plt\n",
+ "import cv2"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 6,
+ "id": "29bc90d5",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "def show_mask(mask, ax, random_color=False):\n",
+ " if random_color:\n",
+ " color = np.concatenate([np.random.random(3), np.array([0.6])], axis=0)\n",
+ " else:\n",
+ " color = np.array([30/255, 144/255, 255/255, 0.6])\n",
+ " h, w = mask.shape[-2:]\n",
+ " mask_image = mask.reshape(h, w, 1) * color.reshape(1, 1, -1)\n",
+ " ax.imshow(mask_image)\n",
+ " \n",
+ "def show_points(coords, labels, ax, marker_size=375):\n",
+ " pos_points = coords[labels==1]\n",
+ " neg_points = coords[labels==0]\n",
+ " ax.scatter(pos_points[:, 0], pos_points[:, 1], color='green', marker='*', s=marker_size, edgecolor='white', linewidth=1.25)\n",
+ " ax.scatter(neg_points[:, 0], neg_points[:, 1], color='red', marker='*', s=marker_size, edgecolor='white', linewidth=1.25) \n",
+ " \n",
+ "def show_box(box, ax):\n",
+ " x0, y0 = box[0], box[1]\n",
+ " w, h = box[2] - box[0], box[3] - box[1]\n",
+ " ax.add_patch(plt.Rectangle((x0, y0), w, h, edgecolor='green', facecolor=(0,0,0,0), lw=2)) \n"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "23842fb2",
+ "metadata": {},
+ "source": [
+ "## Example image"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 7,
+ "id": "3c2e4f6b",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "image = cv2.imread('images/truck.jpg')\n",
+ "image = cv2.cvtColor(image, cv2.COLOR_BGR2RGB)"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 8,
+ "id": "e30125fd",
+ "metadata": {
+ "scrolled": false
+ },
+ "outputs": [
+ {
+ "data": {
+ "image/png": "iVBORw0KGgoAAAANSUhEUgAAA0gAAAI1CAYAAADsLNpwAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjcuMSwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/bCgiHAAAACXBIWXMAAA9hAAAPYQGoP6dpAAEAAElEQVR4nOz9WbNsSZbfh/2W+94Rcc659+Y8VGWN3V3VXdXVU1X1jAYaUwugjEbCZCIk0UjpkYYnGp5I4xP4gm9AmvGJZjJKBpOJb6LJCJlIEEB3o4eah66uOatyzrw37z1TROztvvSw3H379thx8hZICa3s42k3zzkRe/vsa63/mlxUVbktt+W23Jbbcltuy225LbflttyW24L7N92B23JbbsttuS235bbclttyW27LbfmLUm4B0m25LbflttyW23JbbsttuS235bakcguQbsttuS235bbclttyW27LbbkttyWVW4B0W27Lbbktt+W23Jbbcltuy225LancAqTbcltuy225LbflttyW23JbbsttSeUWIN2W23JbbsttuS235bbclttyW25LKrcA6bbclttyW27Lbbktt+W23JbbcltSuQVIt+W23Jbbcltuy225LbflttyW25LKLUC6LbflttyW23JbbsttuS235bbcllRuAdJtuS235bbclttyW27Lbbktt+W2pPIXHiD9F//Ff8HHP/5xNpsNn/vc5/jn//yf/5vu0m25LbflttyW23JbbsttuS235X1a/kIDpH/yT/4J//F//B/zn/1n/xlf/OIX+Z3f+R3+7t/9u7z88sv/prt2W27Lbbktt+W23Jbbcltuy215HxZRVf033Ylj5dd//df57Gc/y3/5X/6X5bNPfepT/Lv/7r/LP/7H//jfYM9uy225LbflttyW23JbbsttuS3vx9L9m+7AsbLf7/nTP/1T/pP/5D+Zff57v/d7/P7v//7B87vdjt1uV/6OMXL//n2eeeYZROT/6/29LbflttyW23JbbsttuS235bb8xSyqyvn5OR/84Adx7mYnur+wAOntt98mhMALL7ww+/yFF17g9ddfP3j+H//jf8w/+kf/6P9X3bstt+W23Jbbcltuy225Lbfltvz/WfnRj37Ehz70oRuf+QsLkHJprT+qumgR+k//0/+Uf/gP/2H5++HDh3zkIx/hP/w//R/5+C98GhB8EBRQ7xGNpR4RQUQYx5ExRLy4gixVFe89YFap3L6IoKrlOREp3zvnyJ6L3vvyTv48hDD7W1WJMRJjLPWMIbDb7yD10XvPer1mGEf6riPEwNXlFSEExjBy5+wOIQRW6w0ahTCG0tZ+2DOOI13XsV6tSx8vLi8IY8B7h3hh1Xfs9jvCOCIi7Pd7NpuNjVenMYZxxDlHv+q5uLrkubMzfudzn2fzxAm8/S4P/+Ar9PsBOsF7V8ZVl3EcyxzZT63Wdno2z1M93845xtSHGONsDfPf3vupTRHESZnrti/Dbk8II8MwsF5vSpvtvsv9ze/ndavXUURwIrQ7VFURYCWeq5XQj8q9J+/ynT/4Al2InN47w3cOFHoUpxCcMnawk8DP/ZVfYRsG1usT8B3ar3AnGwaAaOvz6Mdv8uoXvsHdQdL74GNE0VLXeNbzi7/9qwxekd4h4gkKSId0HRHH1nk++Klf4Mmnn+fBuxc8vLxkN2yJRLaXVzzz/PM8+4HnWKvy8Ac/4LVvfYOOCCESiMROIUa89lwFx8d+5Vd49oMvERCCCBHBRfAjvPzn30HPH/Ct//v/g/GHr3LlBmIMrEYhOIcSZ3Od1zloZCTSiePUr7izOrEzKhF1DvUeVbj2kY//6i/gP/Ak1zKy3mwQPNI5nO9AIQ6Rte9569XX2V9clvNZznSMaI+NeX2COIc4AecBQRF0GCEqWyJPPvcM3/x//z7xmz9mvR8ZRNNagAd2olythU/+9d+kf+KO7enO9nVE2e8H4jiy3e+Q64Hv/qsvsXm4o48QUcQL3nVst9eMYyBGZRwj4zgwDtFowjiWvXfv3hOcnZ2gxHKW2n3clvKd/YWis/OqqgwK+xB45ZVX6bqO1arHeW+/uw5B6Zzjzt1T8kyB4pxwTWT1wWd59lM/TffkHQLQiQffsXYdnQgqwKi8/KWv8+g7P+Y0gGokagQiew/rDz3Lxz/3GWS1gUS3a7ocBIZxgLfP+da//BPc9Z5OoQ/gVImijKLsPKyfe5Jf/N3fZtsB3tP7Lq2/jXccR0IYefjy67z+5W+x3o50MTJKRJ1w0q0Y9gPXu4FxtD3U9900lzKnJTWvqGl/jIr3jq7r7BnfsfWB7vm73PvIi5w8+xS+P6Hre1znWKmj8x3BgY4j12/c55u//yestop3jugE/+QZeM/w8Jz9fsuzH/8gv/Brn+Mi7qHzqBO8CiKOqIoTQJVhP/A//Y//kkfvXvDD195gP47EELm8vOKlF5+jX8Hduyf8nb/zv2K9WeO9x4mf7amgCiq89dZb/LP/4Z8x7AZW3QoQZLvjydM7/MLPfZpf/Y3f4IMf+zBjJ+iqox8hjoHXfvwKf/blr/Da91/m4VvvIEOYaGo6p857BAgxQsWzgRk/XqLh9b+at7dnoablS/yg/n46O/PPqhN2wEeW+pX7ojqXfdrxIBCb7+t+5b3Wjk1VQGX2bGmTtGdrvikC9VjS3zfSkPRdjDrJEDHMzqkqKHO6tESfZv3E+KyqFjlp1DidM5b7lZ+/qf52ffPnrbyR+6HYfMVCMeWg/VJHCEVWVLV1a/deTRvyZ20fahml7s9S/8tzTohM+yGEMJ+Xhd+tsflc5TqNV3rQw3m0R6IdhOhAQCXy8Z/5GB/9+IeJQ+SV11/j/OKS3fUVF++8S7zc4oJyud1xHUb2GL3vxHN3veZ0fYKXubxV+mwTPxvD0l7ax8D/9eWvcvfuXd6r/IUFSM8++yze+wNr0ZtvvnlgVQJYr9es1+uDz09OTjg5O0Uj+CA45wluyk6RNxvAerOxv3USkGvhPsZYAA8wY241Ea5BU11HEe4qgJSBUS6ZEbtxJIoJ+vnfer1mv9/T9z3jOBKjtdd1xoS994QQ0OgQsT70gO+6UreIsFqtTCjznv1+j4gwjHvWmzXDOLA6PbXn1mu6rgNV4hjYbDYMw8A4jnjviTGmZ3runN5hfXaCXA9su45T8QSv9J0/GJ+qQmL+9ZzkeannrgaoNWjt03jz/DnnynMHhC0LuzoB2EyoRYRtCARg0/VlLvMzNUOpiWNLDDKh8YlRU/WhHmcXQXrovfLUvXuceM/K92y6DkRwAmsRHDC6yNgJp6endCj3zk5Zrdao6wldh2zWnPgOjSakn3y44+EPfsz6fKAbIqoR5xQcjB6u3cgHXvogp5s1oRdwIM4TxaHiEd8Tcaxcx/7RQzbPv8hTTz3B5u4dzs7OCGHknfvvsD7d8PST9+h2Ox5urznte8QpLioqEDogKr309NERrq+4e3ZGlI7ghSgOCcpKPQ+ffpoh7jlZrRicRztQ9ayAwaS0Ms/1/EeNBBnxvqfza9xqTeeAMBgTkBWjF4IbefqJJwjdCrdeQ+9ZS490Htf3hAj+xCMRnn/+eR7qm4VxaFJUxBgJErhzesf2h7PzqM4DDnXgQiAOAQ17ri4vcE7wfccmCr1TgoCLJgJoD098+AWefe4ZYm91Oe+LQLLv94T9SL9eEdcjn/z5T/HGl79Fvx3RGHFe8L5DnafzQkDpfCAo7MNIUPBuYrInXcem6xHRGR2qy1EBJ/3LdK4WDr2CE8em6/Des/IdXZf+icdh5//E9zgB0QgoQSL37tzlznPP8MyzTzOubU77rkNdR6dC5xwhCWe//Ju/yo/XZ7z1re/ix4gD9gQ46/jYJ36K09MT+tM7gMxoQQbSwUF3dpe7/W/xZ7//J7jzLSsRiJHoFNcJewl8/BM/Td95+tMV0nVFcMzjNZobufczH+ee63n1i9+g3430okQHm1WPBCVIwDub+953hWeoLM9zLSBrtW6ZBgWE05Oep194nrPnnkHunCLdGtf1dJ1jg8eJY3DKMA489fGPcILjW//yC6zFM4gab/MC1yuQyEd/6mMokTsnJ9B7IuBEiEoCaCb4btZrfuVXfpk/+P0/pu88OGHYj7Y+48i9e3f4wIsvcufsrNC/TKcn/mhC4AdeeIHPf+5zfPkLX0JUiFF59oMf4N/6u/8Wn/vs51h1HSpCdIAI47vnfO2LX+FP//CPuH73EW4I3FE7K8F0STNaXfOXGgzUyrUW3Mx4UrXvl9apPSs1Xa/rWQJIh3Uw6w9+zrdaAbAFcktALwuxdd/aZ2seap95YmgE/iy3oEV4z+/UfPHY/LVyUN7fUWKq15QTiuLElX6FOJ//JVmg/kxE0BhnAMWrTMCuKTNFbT3Hbr4/2jmcFednf87mQST1goO5n/VDJrkxxkhsHqn38NL41emBTFnPy2Kb+XnnCBoLkPC+O2ij/SkiB7Sr7BFxoO6gzQyQVANOHBpN8a2M+KB8+ytfJ+4CF5cXjCEQxkAflX61gTHSdSvuCgSMbjq1fx4BBecOZT1bg2kOkXlfwQBiO683lb+wAGm1WvG5z32Of/pP/yl/7+/9vfL5P/2n/5R/59/5dx67nnL4goGbcTRBIhNXmITwjOiH/Z7ValWYbGa6+XeYDn8IYYb0i3CV6szP19YnVaXrugIIhmEADOjEaBrgGCObzaYwnPrAZQ2x957NZlP6kNuox54tR+M4zqwuuV9936c6hWEYy7iZzQ+l3dyP3W5n7fn0gEDUyKpLwmMYTHuZ2qrH3mrL6v62xKDV2NTzXK9FTdzqd5xzdk6c6ZtqAqKadFY6Zx5LTC+3c4xBtYzHNQyknc8QYxK2HXEMqIIX0zyFxOz2MRB9x4c/+mFOzk6h8ziXBHPvwHlc50E9uxDYPHGHT332l/jW//ivCkgLYQRxjE7o757x0k99FNd3RImId6Z1F4e4DrzH4VDg4p23+fr5BS9+/BNov2a727LuenrXsVlv8KpcP7jP9f132DjP6KLxZ3G43kFUZISVd7z1yo/w6xM+8omfQ5y3CXeCRpIFdNJi1ftNcAXUtmshYsQyuI549w53P/ABzt95m81O6McRUeGKyAc//Un6e3dwveN07dHe00WH6zroepym7gRY33uC64tzwjASNRBU2ceRECIvffiDrNdJQ+47RDwqNn/RKc55hJHQOwZRPvnpT/HtH7zFuBvMAiFJ8Ow7ZN3x8U99kvXJCTGf76TZQxJodSOigaEfuPPhl5CHW974xnfoMHAoMRJCnptlbWFtlTCGewiM6rNXv1POG41gUe3nmgEdgi4tAmLUWLR+CLDueO6jL+GffZLVyYZ+1eN9RyfOQB8O7xw7DYwoKpGP/PzP8sq3v8MJIAqDi3zq879M9+wTdKsV6/Ua5/yMVoOds5GInnruffhFPvazn+B7f/RlXLQ9NKJchZGP/dKneOpDLyLrnn69RpwvSqY83r7vjTafKB/81E9z8cobXLz8mrWjylisW/N5KvO1IGAsCRb1+yqgfcczH3iBJ59/js1TT8JmDa7He7Mg9UHpfIeuPAGF3cjHf/aT3P/+q7z149dwfZfm3rGPgQ989EOcPf0Eq80G6T1u1RMFE7DV9qGIYsgGPvqxj/Lw4SU/eu11Ql7vRAvX6zWf/vSnTekmvnxXK7U0/Rz3I5/5+c9wuj7hC3/yBX77t3+b3/0bf4O7d+8imGVZFIZHV/zwu9/jW1/+Kt/75rcIu71ZycQUQc4nQVRBxCVaOwlI2uzFvH9bgDETnBZ40cF+b36/6Z2ltZ0/+17fH57TFvAtKQLrUitw23rKOa/aynJE++zSPLXzt8SX6+dbhXNtvViiXUtr1LYrkvZq9V1blj7Le7L9rqZzN4HkJdkAWLQQt2CvXbO8Bm1/l+a2BYe1vNKC66X3l+bj2D6v5wqY8eE8V6WO6rl5UUTTAyKMIdA5Qfcjw8UVYRfwQZEIHc4Iuyp4R5dAr08sI2KWYbWOLoPX6s9jfC5bLx+3/IUFSAD/8B/+Q/6D/+A/4POf/zy/+Zu/yX/1X/1XvPzyy/xH/9F/9Nh1ZME+qrIf9njfGR3RuSVhsg4Fuq6bgZ5cDzBzv1FVhmGg7/vZwW+F5fxedntpD2EGRebCYeBqtVqZ5ac5FF2yBmWAtNvtCsgZhiG1be/kz2twA5bQYrPZlGeGYWC1XqM60nXr8nz+SQKNIQRWqxVd17Hf7xnDSBwV1ie4xKjy+J2YhSqEsYyzNufm+aotcrX2cbfbzcZbH8AWsLbgNT9fz3MNZGvi1Vrw6rWtP2v3VE38cns1wWyJ4/SsWUXKevoOxsSs7PQTiezHQFh7nvvwB3nqQy8S+4g4oe/XjDg0MURBwDm63jMMI3effZrNvTvogwtr0zuCU3ZEfv6XPkN3dsLYKSIe58TACKZZEeeIOFxUNl549+qSMezZh8huv2fz1DM4cZydnhKur3n75ZfpxhEPIB6XNL/B96gki1Ic2XSOV17+IS9+5OOsVuYKOuwHXH9iYC2aGV7cfA0RMFtanM0zGC3tpeOh95x+5CV+6z/89/nj//6/592vfQN/fo2MwlMf/RA//duf58HDB6yAtQoxOjxm+TFLsU8ARokE/HrFEAPPPvcBHrzzDk8++wxXV1c88fTT7Iddmjc/A0jiU9+iZ+08UUfWJxs2d88Yz68TQTfQPMbA6RNPsbp7RlBwxVFEUDX3qmEY0TEwSmQXI2hgQE04DdFYhygxhmRFdkUwkYpJ1/vWieOYTrtlwO13+Yy1ZUmpUOiljYioSUtqlSEinDz1BM999EM8cgF1QhhHfDBhN3pFVcxNUhT1pig4f3SffQxsos1Wf7Lh+Y9+mCsf2A8D4zDi/FxoVFViCCjKNYFdGHl3d4V6IToDmlHA3znhE7/8GfabjiAG3qNGkmrlQPG0F0U7YXCgTpDkhhc0ENHZnOXfDWxOoHFJ0F1aE1U4e/YpPvzJn+bCDezHgT72OJQw7tHg2PgVLqgp/5zN/l5tvFloCzGiKkQPn/rFX8A/eWLa1MRjtHPpWUka7Yh4D1GJCC+8+MJEY026BIHf+q3f4qWXPkjne0Qmyx1Mbs55TnrfE1eRX/jML/DXfuev8dKHPmR9iskVcDfw9o9e5btf+hrf/to3eHTxCBcCfXQ4wDlhdBCdIEkydpDoZtmUUIGPWnF2TGj6X6q0e2/pu6qjMzyzKPDd0M503hOPc4cA6Vh/5nINs2fmZ/hQmF8CXEtC94FygDmPrOnJ/AxMPLsdb9tm3oua/zMii0zVzM7YzO3+CM2r52BJFmjHOQ+TsH68F3Buv2u/vam9Y8CrLcdAvVVkP+o9dAyQTpXM/5ytx3Gcb+Amz4tzCJHeezqSJ1WIuCSDRDBFDcYXUcElx8uIIyZ3u2Ng73HKT0oD/kIDpL//9/8+77zzDv/5f/6f89prr/GZz3yG/+6/++/46Ec/+th17HY7E4BipO9WyYUg4hvmlAGGCenzg9NaXbLAHUJgu90W68x6vabv+/JMTUhq95QMPrIrSAZI2ZUuAwdjqukgihA1a81gs16z3e3wyed/2Bs4CuOIakxudII4iGOk7w3U7HZ7vPdst9sCTrquA7E4BhFhu92yT1a0ruuISVNdg4wi1AqmTXRC1/WoCNfjng4lDhHn5360bTEQ5IvveJ6zrnILbDVhS+4TNeFtTfvW0ETo83zbuh4XAFuw0+6Huv26DidiglnTH7K1AvDeAOUQAx2gIRIdeGcis3cdewIn9+4QO8d2f0Xf9TjfE6KiviNGkAhCJKi5sQwi7DXSixDDSOjMKoVCf3ZGdGZVxGdtsRCJqFNElCi2z4NaH5+4c5e9eHzX40R56qkncaoM19fsry7RcTDf925l+xM1i1Byq1Fg2G9x697AYKKmq83aXNiGHb0Txjgmlb7F2KjIxPwS8zmgbRGieHarjv75Z/gr/97/hn95fc31N7+LC4HBA3dOuHjnDe6owyfqGyT1QjFwk6izqvLo0Tmu83TrFXeeehLVyDNnzzKG0cYlDhWz+ChKNkFpGJEYDDSpMhC42F6zEi0MW0NExTHEwC4MiK7o8KARjXmP2h6w9QDpPLGLDM6E3r5YYkx4DjHia9cakeTqMddktlx4SQHQMsulZ+vikOLV0wpOPtEeoqJRiWLPK/Du+SPeuP823D3lRARvUWF0YjFx3glOnLlMOtBOefKZZ9jcOSO8fUHnHFfXV7zxzhvo2Zq+7+iyQORcYsQkUOrwQOhs3br1ikGjVSxCFNjFwFYDl7s94j1rWeHU3EqcmO+8k+QZgLlLRg10pxuCKitxOIusM6tnVrgl8GExPTkCa7YIRUGR92P1lc2pwOXuiocX5+zXcHLHFFgSzWrkOqPhIQZQb4KFc+DBnaxs3qMSx0h3sjHXwc4xhBEdFR8jQRXpPOogxLzeSucdGkHU8eDBA4ZhZBwnjwCA5557FlCur6/wvp8L2Kp0fZdcoKDvVrzwwgs889QzdL5HQ8Q7s1lfvPOA177/Mt/96jf48Z99h3C1BQmmdCOdiQQySZ/ZscoKhmkf1sK/2v9KfI6UL5IVZ3FnH5b3EkaXBG3SOYVDkPKvi9VqvldkhMynFvrVtt2CxYlGGL2nWKMnoNmCmna8NZA4Vn8uS/HZEx+d89iWt7dzYH/kdS5/UhO7zD/aenSproW5Xir1+PNZiDFCpZStn12qawZy7IHZ80ulljlqT6UW6B2TV0SkKBDq72vl/tK6lTZYPi9Gu45bqYz/aFIDghfzjx2H0XhCkhMKds1tKkje64mvzUyGSx25gc/ZXL+PABLAP/gH/4B/8A/+wb/2+/urrfktip2kOAZc3+H9XLNUL64kZpg/yy5vrjkAqlqsNHDoZpV/z3/nDZ5jgLJLXf49g4KimVVSQoZIGAPD3sBN1/cgysl6Y1q1/YCGADHS+w68Yxh2dNLRdbYtx3FEnG227NKXwVGMEXEUV7yY3L9yn8GIWY4/GlMSB3NfS0KwCESP35ywv7shvHvJBkcUodVUiAi+cwYSnEMEOufY7/fG/CRJRgtzmP+u3QHymrSxRbPvpTELF8Kos/dz/eaOOSWSyNat1gWprq+udykOLX1Qgu2Jyk4iIklQsUh2+uhNYFS4PD/nbnzKLIrOI1Ho/Apcj/gN0vV0qgaSfEQU3Mma+OAKr8JeIk/sHbLuOH90wVObp9jgid6ZNcX5JJX30FXkYAyMuy3XD+7jNidcDQOXGvH9ms3JCScyonFgXEEnHZotlyL0AnRCcBFV6FyPRojDDokrduNAGEdOnWN/+S4nV5eMcc+ogTW9uSs5U2rY/DkKxswMVZVRAl1UNsFxstogd075lf/13+F/+PF/zXp3yaOLc8IwcOIcZ9Ix9jCsHA5zbZTOm+CkZu3oVAiXAzvZ88Snn+aHP/oyn/jpn+L+a2/y9LNPE/qObtUbCHIW5yfi8HFk38HYe/rR3ALixnP23BNcPbpAx4DPYqLC2ekJqpFu5YkupvGZoBc10nkh4llpsmSsek6eusdARNVEccVcLOM4JREIJDcvZzGxIURW2e1J5hrrurSCzVwAMeVMK2BBAkjR9rF2mDUlW49ROjHlj4mzk1vL6eaUlXOEqHSKuVSIxdFEDMBGb25rRrsdfr2i69cEf0VAOdmsePbJu7w9XpplzXclPkDEJ+uC4jCpf6VCiHB29x7adcR9RJLLY+eEEAZGHeh7o6mddEaDpKJEIohGNmLB4Peee463vv0y3SA4dXjt2Udz4Q7JXSwLPyHP7yKDztalvAYmqOZ4oJUoVxfnrE+fwrnOQJ+H3gt4T0y8zTkDg+oE7eDJF5/h7ZdfRUeh1xWdX9OfnnE9jsTtjtVqQ+ccvXOI7xBxxB7Ee+MnamscQ+C5558yK7NOPMt7xxtvvILqk9w5e9JAbYpHc9nFrvN00XN25y7PvPA8/WadUZgJedsdP/72d/nKH/wxb/3wx+yvtgxhJIpaYg+18QQj4XRiSq0s5KlN36TJD9GsS0nwNEuTFPflyZKXhP4kNEbVEmB/sDoVT3kvgbq1ruTPl9a8/v6mevMzS4AH5sJ2/rsux/pkz5lnQqqpKF9sWuxMtvXNZaUphrgWzNtY7Xr+sgJhCTTmP1uFSz3WNgFHUVwnRSCS9k3+s2p31v/FmZ7aWSp5rG28knOOtre1F9IxkKdp4EsKq2Njr4FSW5ase/Ox6GyO674cG3tpS8Ro/SIYmu/nYkHHI8kK5FUhBi7Oz1Es7jnEtGAak6tdqlcMjinMPI98PvNL89P8PZMFRRoQ/XjlLzxA+p9bzA0lmn/6GOm6PhHbvEEnxiVJSEEr/920KV0+2A0RAFuI2nK0RKzyxs7P1pqTkq2oEtDzeyEEhmGYgZZsveq6rsQCQTqkqiaQ5SDlEIgxGPhQS2ZxfX0NkPz2J2tICFOcUgYHqiao5v7s9/smg5yyT+53JuAIT734PPtH32fj3az+maYpmntLtqLl8YsIGufB1jVBLcHM1eGuiW9rQSr/yn6IxYVSxCwo9VrWdbYas5owLDGJXHLc0xLDimp7EY1cX10RYjAioUDUpFVWgpj2+MlnnmY/Dpz2PZ0rDmf4JLiZAJb2bwCJyrrr2YdIF5T1aIGrofc88+GX2F1dcCoCY7QsbpJBZRImnCDiUIn0ODqFte/pEIb9jv12y27Ys7t+yHB5wUoDnXNJM+UTczXte0AYgwKe/TDy5o9fZfXUU6zu3OHi3Qdszs7Q7cBwec24H8xKFGOyahlwKa4TzBmHAF1QuiFw1q0Q9bh+zdMf+RjP/swnOD//Bnfu3MXhkVGRlDhCotJTaex1IpgOcEPk6v59vvXP/4hHb7/Nn3z/x7z0kQ/jn32aDqFPYnd2yxMUr2IuQkT8qHi14OOV77iOmekbmxhCYLXaENW0YdkKU1yGUpBxVIUQkTHihogM0RJ8jBb3F0JM/0J1RuYaa6mZuOpRzrC0T2shomWG5Twk1zJN1ceo4KWAvQPBLT0XogUADePIPowWOEzEk3zOc+A2tp81gTCSompELVFJMHdEL544jojHAL9qWdsoMHphn1wSu9XK6sf2N0PkrDvj7mrDxdU10Q1E6YneAEDNdQUmN1hV+s2aQSP7kCw6oSfEyJDi6sR7fCXM1zThmBBU1qRam5NuhYwKuwBjTFHu9r3X5CarFkKU6+1Q1uLwQe1fcuZc9T2rvmc7Dkhn2TJFBZcy2HnM5S2M0cBDBqkh4tNe7dIZkDHy9Nk9ZD8SVyPST0o1SaDj5OSED7zwEqdnZ0Q1JYQGRXYj7771Dl/70pf55he/zPb+I7qgCcRgvPhQPqZok5t5rBV57X6urQrvBULe65mj67UgYNpWWRY8a54xxQi6xWfb/uV3Dp6Vx+t7y8Nm9Yj1XJPcWve1dunLIQkzYfgIGKjbumn/1688Th3t7+U5bgY/N5Wlfi1ZZxZBaWbGVf/zc63XS1G6i/GFGhAeow1L7b5Xf9uS6Xmr1G+tUUsgyayuU91TuImb0auDObMv0BgQMI8kMvzRxCuY2YIz/ZjJjmTg9HjjnQE5ezB98fgQ6X0PkCzmyJh2lzJFZRc7XwkQUY3ZI5JiDJJVgbSh8gZP77cakQxygIMARFUtmrUly0O78fO/OkFDPmRZINona1ILsK6vr/E5riP1dRKirI0WGMUYGcMAhGJB2u12E4BLTCfGyHa7LWMehoG+cwV8KaDiiF1PWK8YgwmLeZy1q5zvLFi/1g7k5zIoVdUSt1UTmvx3/c4Sc2nn2fbD3KwvYp9l0JqtY1r1YUn7lOevjVWrS91O/e44jvi+Z7Vem3AY94zDaOfXQUQYsRTKQQ3ChXHE9xajEcQyuMGIYFmuAsnNZm8C54gBATdEhr5nuHuCPHOP3dU562ixHZokK0uabMI+IqaxBTRZIvrNGokdvvf4EIj7nfkDxz2qEbzDibmP6cRVcd7hpMMxovvIer3B4bg+v+LRO+8i51cM2x3DxQXD9RaXzlXAZMDs/daejUwsLYY+0jlTL7+72/Ho4pwPfvaX+dKffZuu82hyFxxQs2biSsxCIeoYzRxVGcaRR6+/zRPB0Z1f8WB/yfjiCwzjwBiD0RNXEWpJoMQZsM+C+RjMkkBUkpHIQI9zXO92nIVAV+2pYp1O/6JYzFGMCqNl+RGxLGLJo5thtPibk65LzEQJaQ5tb4rRtOYMtOen3qvtc6gm18n5e/Y8tv6aQYC5l2pU2ztZ0QSlDoudUoYhsB32DLsBEFwvdM4XjX4oezLN5TjSeUtGEhNuudruuN7tWOMJG1M0dJ3iZbLEq9jaDxqJwbIA6jgm1z/rY68wbPeM+4EgDicDoxczqmZrSFKyxDQ+Eo2M2BnpcAkcjeyDpfl2nbeU/bUj2Gxql8W4ei0UNbfMcYT9nn4MEAJk5VxMiqXklpjpawgRhrRvcJYZzjtiStRwvd2Zxc17uk7wojixOVFHscaVuLgQiF4IEswNN/Vvt9sjCPvdQE+Pd53x2lXHiy+8yL1793DdCsQs4rIbuXr7AV//ky/w7a99k/tvvU2nghuCWfscE/iGA4vbTYopOHRDWprX9wKnP2k5dnYeF2gtjePYd7Wrfv7ehPPjY2r71M5BzZ9mMkhUkMOA/yUhveXH9Xe1nFSDrEUhfOH3ttTKy7q+xbEXH5f/5UoNCo8BwrbM6eYciFgChMdrN8t5P8neqvug1eetUrdWtC/JZe06F2VEBi+V/FsDPgNHqW7JV7/k1ODQwtlasfCTnVU9mMeWXtiHj1/j+x4gTRshmUZ9Mhsna5BL8QQ+x6OEADgkx86ACTlJcMwCW6679gPOG2a/3x8ApmEYyvMZeWerU70xlzZ+G6cUQiipvvP3uc6T01O2+13pS3ans/gmQejK5s0/c/+6Tkof636t+hUhzDNi5e9DsABbJ2Jax64nrlZsuw6/27KRaQ3ywRMxzaTzh3ey2DzIAeGrNYRLzK8NFm81JAKTH7rIjABkkFlbl2qNSu5LnUZ8yUVgtueaMRVGgeB6z5hjFNIeVNQyuShFAFbjT8T9wKDeDDQeRlFGHekkgAoDWQiNjMOerY7sneKcaY6vXcS/+DS7dcf1OLJWBd8hYtJ8AJBkTVWz4qxGZbsd6QbFb0c0Brwqvu8JpzCGHt95wn7AayRqQMUTZdKYK6BeGKMwinJxdcFTd+6wUnjp+efx48j9GHj09jsMV1v6cTShu1ozq+yQeY4aCU4ZHJxfPGTYX9Pduce7+x0f/tQn6F56jsFZBr99CGw7S8rQCQxqiTAQR0gCQBwjUSzF8KPzR1z2a4b9DpxyPey5CoPd3RHsDjUDSgmsi7DDYlMCBrS2IbAXtXvVorWn0e60ubi85Mn9wNX1ln6zoetTeuMMUDHQqs4sstvdnodXV2xFbaVVuLi44PzqCo2R9YkwRi0uHhPDNvEgW5ecn87akga6FmbKPtcpfqMVBFSx+CJVXGovhGCZCsXbOASGaMkYsoVbQuDRg4eMnUO3I6hH4wi9I/aKakTUUnSLwm7Yo9db1n3HlUazMAfl8t1LLi7PiXeh77eIc3R9z9oJ4n1K32vzHvcDcbtH9qNZpUIkuI7QOcYwcnF9zeX11rInOXNN7iCB6gnoBVXG7Z79w0uuzy/KHAVVu4No2HOxvUZjZLVeTUKJxmLRO0YzatfgSXFnd2gNMbK7viZeXtGjdBpZA/Qp5YiInUGMVo7jwPWwZ3RK0Ei/7pBeUO3YxsDlbkdwjug9Pgprl10co6Wcl+Rep8puu+Xd83PGOLKLexRlJLKNgYvdjn0UzvwOHwzQf/TDH+YDL77IerVOWl+HDpH95TXf+fLX+OaffomHb77DcHXNKpq7rBdfzpJojleYC+4tPV3S5k/KAbcIkOqf7WdLIudNmvpa0G15QZYdjoux7+3q1PLGuq8HvMV+Ofiu3W+tErae18Mx6mxPtv2q+5RLy7dbPlz3/1B5eBww1YrJtv91KWcn0SOV+Zq39K2u+73Wui7HeH/dxk2Ar17LrLh+L+BzbP+2c3mTEiAr4WoZpl2vFhzV3y3tGyUryw73ZQHvYq66zrmStdbqMt5ksUZT/Gh9N9TSnNRrVYfDtMahsr+cFKXOMVfapfK+B0gac3a6KUYlDAPifQoat2JJB9TiPLBnYrQg0yl1q5Q86nnia4JcE6MaENVarfx5bRnK9eTNmbUEefFrQT0/mwlO7VKw3xvzEpHiIpcBxTiOiWBrcaGr381t5f5lNzr7fbD7VxaInADOKeMwMIyB07MNq3tPcO8DHyD++BVkP8ysNplx5ZCVvLlzsonahW5JmKjnuv18idAVbQaHgYs1UKo1M3mcddZB5xyr1aoQlmwiPyAWR4SfMm/ZdUwTsHSOqOluKefBpXTMgA8Rvdzy4J1zfNfzzAsv4E8V1mt81xMv9/Q9+G7FGAL73Z54tSNc72xODKUxOOHnfv7TrILAo2vGJEytfDRNtHOE3cjqzDMOA9swcLHfcaWRcGfNhY9EC+vAASvtLBZhN8J+ZBwEv/JoFyy5gEtJKoAxWmxcF0bO33id3aNz9vuRO+sN9zZrrt98kwevvk7Y7fEZhGc7VJqn+g6GSeumDKKoRN59/TWuX3+Nk5OOe07oRPj0b/wq3/rSF9ndP2e83HG9H1ifrAhB0dWaiNBFn7JgRXQ/EneR09WGcT9wcXnJMOy5ksHiIi6vGWPABfBdD70izoBSQNAeJCgyKHEY2Y97vLOkJaOmeBpJ7kXbgfFiy3pzCjpAENxKLO26s2BlFyJhO7J9dMmD19/k4YOHjAo7VTrg+nrH+fklq1VK2oEjRnORzdo641qJRqkpM1qGuLRP67PX7uZl0A9U4mCmM7kP+S4p773FWO087/zodQaUNSv60xP8ek236rnzxF3OnrhLv7FU7Ofn52zvP2D38ILri8syHgbl7Vfe4MGjdxnvXhMvA64zK+fq5IQnnnmak9MTet9xfX7N/bffYv/uOfLOBT6kuEkig8JaPO++/YCHj+6zuXeHcDrg/Yqu7+n7njt37uBXKzrf8e7DR2zffcT12w948OobMAYUISY6ebm95tHlBQ7h7OxO0uwfRh7VdKYWVuAwa972es91CIRHgpOO4WpHd7pBzkbWJ8LJ2RkiDlWjS7urK67Oz3n08GFyffZ03puSKwSu7r/LxYMHxLM97BTfbYkndolyt+otztGJXVZ8ccnFo3P2j67xY6RL9YWo7Lc7Hp1fIIyE6Pjpn3mJn/3EJ7lzcop3Do9DQ4TdwBsv/5g/+mf/grd+9ApX754j0ehgn+egSjTiROjFz7TIx2jsDODozfu7LXM+cigA123MlAbVWrUAramkrPshCJpiAmvQ0irh2jG2pQbSGo5fn3Fs3K1wXQubuf4lcLBUFoXn9Fm7p9vP7Z0pA2/bzuOAmBb86QJCXQIRN/FumCevacdbW5FCM74lANKOXx+j/aX+P+5zh+CYIiO+1z6Zv3cIMKd3lucxy6yqWpIt5DPRdX3622HRs0zvLgDsMo6mj/Weq98t56LIraZ4FOeguorhvcr7HyCpJuEg4qMzYa3v6RE0VKbaYPE0Pt2e7hC65FONmquFuR7VyH9uhakTB9TuWbnk7/O/dvEzQKoPen2IaxN1BjgwbYIMfPZhKC5jtekUoQR0t0kErO2x1J9Tl1vGs86C4tt7lFQZ8+9potYnp3SnJ+w3a1ZnZ/hwPjsoBZjEsVhZasvSxDwOCVl+riaqs9SdHBKZvP4iUgKHW0Ka685zWX9ef5/nJrtLtgS+ZWp1PaWPmmKIvJu585mlL+0PiXaZnBt58OPXeXj5iO3DHd8d/4znP/ohPvKJnyE64Xq7487pGSenp1ydP+L6esv+4pLhzXdxV3ucpsDRCHdCx8W3X+Hdr36Xbed4O1zSBXjmuee49/TT9KcncGmWonfuv8WjsOc6wPmH3mRzejelT1WcOlDP/sFDtq88IFxfsupWnJzeY3X3LqvNyoBvmvdxv2cc9vh9oNeeZ1dnxCDouxfst2/y6M+/y6M33rRYCIx458QJGrH7npgzHjDXKFRgOyAPHvKV/+f/i49+/pcR1/HGxXdZiyO+c8HbX/0Ob735GneevIN3cOfJe2yef5rTO3cIFzt679lfXnP11jtcPbzk7R+8itsO7LstIvDMvbs87ddc/uhNdvsd450zC25fr+lXa/x6w8nZKS5Y/NDujXd5883X2XewffMBRNLluOBwhGFEr3bcf+UN+nceWRzhOHJy55SzJ+7x5DNPs16vefjGA17+7vd4+PAhD+8/YHh0ySYIqLBL1u+u7/F9z34c0WhAJIQwCWXVPiSdq6WyxEwnmnHoAnysZGavmMDmkutjiMEsptGUTcOjwJhij37w4OvgvN3VI4L3wsnphvWdMxDh+vKS/fUWHUd0u2UTPYTI/vySH33zu4SoXIxv0vc/IGKA3K1XdOue9ekJTz/1NJePznnn4bvofuBkhFWw58YQ8a5j+85DvvWHX2SUgOt6QkzW23TmTzYbnn76Gbz3vPrqK+gwWGa43YCMgX3ItDCAE+499SSd87OLy6WZ31YYaed1GIYiQA1vvGMAQoTr1+7j1j3amZeDl467d+/y5JNPoqqcn59zdXVF5x3Xjx6wCSaQXL3xDu5sDQTevvgeFxePOO867j7xJFEF33V03gDqnSfuMQx7Hrxzn3feepthby7AL8qGh6p437PbeKIOXL7+gBdeeo7f/PXf5IMf/gheHL04nMK4G7g6v+Bbf/ol/vzLX+P+62+hw4hEc8tVJ4yqxfqRS44Gje5mLf2xvXtMk/64wmX9bsuH4bi3QtvGErC4CVzUv9d8aMmtfGk8S2f0vc7ssb5O9R+31rTlWD/bvtXfzxI43VD3Es/On9cgpbUaxqb/pR6OUcP3BiqPs4/qtmp3vGPlJtpw0ztLe/A93uK9+MCxfh3vx/F3sgJNMNkzhkCIkfV6bf2WSj6S6n2Zn4Omo7O2itwlS6qo9AymJHckOv2Y5X0PkLbbPcmHKGmmBVKcg6j5t4tkjeeUiKFc8poWawwjYTSsmwlHFtj7vpuEArEtuM9Wl5DShjs3rWsRHNK9JarmM645O9ukk5UKALhkvep8xzYE0wrGyJisPpLSk1tohqVQ3e/3KYAc80dPAfWZMO32+xSroXjXAfmwWZ/GMQB2s33WyNi3Nl7vBOd6YlBEnR0W59DO4Vc9eCGEaIQK0yQoE+HPoLC2JMUYiSETFZIm3IKsi5ZaUiyGRiRlNmqTKkBKaBFDcZGxeZwnj8gAxXcd4uxCs1gDVUzIU7Iri6U4z5kHQ4zmshnT7ZMZXBVnuaS9SItqa+WJwW6Zt2xfI8N+TP0OiDhGBt74wSuIE9ZhRRc8599/g6/+6C3wjjDafIikpBqYS50PkS5AcJ7ohLDb8c/+z/83VJWzix1KYLuGTuH8R29aooquQ7wnCuhuYBXtTqQ/+sPvgu/NuoGyFWHfO/q4R6/O6dTc/PAdbmWCGyIlvft+HBj2AwJsVif03crScw8jcb9jd31l8VchmvVEksYOCGqxCK2LXS4umBuQ7Ea+9T/8T3zzD/4V+I5hH8B3+N2ed9XO7psdxDDiVz3xzprnnn+edx88sKxYu4H95RU6RJx4nj27h4ZglrDLLT/44jcYCOm8CiGaJkp8R98nS8PdM8b9nv1b73I97Nk75c4e+piyEzohxoBXYXt+yfmffx+iWAiTsyQF4j2nd+9wdnbG+VsPGIaBYRzoFVbB44PigCDCer0x61UIdr7SXW/edyVxAuZIeOB3fhNDzXs8vTABpOqZcvYIREJKqJFdhhL9SX/nc+hzYhQVvDg6b5Z6J44xRCS5oPl9RLeXXL5znlzSIn1MZ6nrGUfbS6IOlzIGdurpri0b16jAMKDXI/F8zztvPgKBtRjg9iFpfjuPjJb4YuU6xquBzinKYDExKZGDOIdeXXPx8FViVE7I/MD2vbgOlUiIdr/HnbXF24haFr9iSEtzYvMzF+qdmAUq8wOfsocNcUQBv9c0X6D7iG53Brg7S4pyfv+CRz94za4ISGu7jyPeKyvpiEEZL6+J+x0SI5dxRFBGhYf3r4gxgUFVXhfB9x1hGC3WKRrd8iJ8/M7TDGdK9J7Yee4+8wR/9Xf/Gj//K7+AnK4tE16IhGHk+vyK7//5t/mzr36d1/78u8je7jzxYNkXJd2PlMEMKVZLs1AlILqY1bcADaWirTWNXXZvWrJslOcauXFJGC97v/rumOuZZD5QrbFLvLettxZ061jX9wI7s77JlGgoe0XUILJ9bwlowNwjBShx2tnCk3m3MBdoW6vasTmpXXsPxnmD0qBVZr7XumS+XfOOY4D3QMLncM8cA3htP+tSuycugQ9JdKK2nvzrAtx2ntsx1ms4AyJH3m2LzTlQuYamWgq/yWCIvJb5jIhDk/uviLAfRlYrk8tMYW9yk5Z4MSULm1kWnQ/W2qhmjiJckc9PedDkPBFzhY+RB9ur95zPXN73AOnOyR3L7rXqLFOSWvpQl9I4g2U+iok55TjrGmXm70FT8qC8sSBfBBJQxLspBgO7hG/SboBPQETVYihMYMjuRCas5ztNxmGfiK8leHCdZxhMEB914ORkg6qy3e4IYTRBfTR3vM5ZutVxGCDanUjEmEBNgonOsd/vCtEOIdD7zlwfgGEYIQi9W9F3HVECMdj9H5aFSu3ujBgR8enZzgLKhz2dd7iVZxQYifS9Jw5jciHSFKM1EcvaqiYoaADV6v6naExQbAw+CQzprk6cUIKUWw2idz4J+JPGKX/vnCNIKKA1+wOLT5aybDFMc+eSUCpil366DJjLpatKSuBfNBfBkv6iSroADTR6Npu7CD0iAUPxOXV0miM6fOxwapc3ikAXFd0HYKRPcxdiTAfZYi6ykDAQC3DcXFwbI0vPrfYmFBEtK1QcRkQCXZkfZ0LrsIPRXDdR2GDZsUSUMIJzFkcVh0i8vi4+wDG5o64R1omX6vaaoFemSUqg0mmkU4v12FfWWQVGJyix0EchWyZSymgco1oShG6vyLhH2afkByZkWfwMuGQVIEb63ZZ333nZQDKYG246H65TiLb3NJjUpDEiIbJKls0xWJ49xNrbq7J//X5STggbVdbpHI2qBoSc6dGGbKENOvlLiwmOEiLxwQWP7p/jcaw0JoEeY2ydravXAGJpUWM689ltwkXPoKPtOOdBxySozRlw68uf704SsdvpSWfEeaMPPq0LtWJDA+otRiYCBKUjsHIuMbspq2TNeEPIGkNLfy2SgvJjZJSJHbrCOE0gi2MwxVZSUBHsUARRSyxQOLdaVrYQC/gstEQgWs5nfOdKDJXgIU4ychHbk9VcK8scqummd3swqpR4nS5MArFVmGiWtZDfmvZnjKiYe07IFpOoSMRc2XoH6ggiRffiXAISERDbICLm/prv/BMUJz10grpInxKaqKhZp6NdrWCyhYGT3FcJkTUuXeCoRFGiE3xMqcXP1vz8r32OX/vdv8LpE/fwnbOzGgLxes/Fm+/wtT/6An/+pa+yv7iyRL9JaMrr7jTHGWWhLO8Jypkl08s0W4UOSLVJNN8xZWNI9vsZGLqpTM9MtKf+/Jhl5aYY1PIcUzdLffHmCIhc37H4kPxZe2F93ks3WbCWxtHWO38nlvXJa1XS9Sc5J79bu8dnHtsCp7rd1lOj7fPS5zVAWgKSNQBrR16vGWQZe+LtmbbN/l4oS3M1yRzzeCI3A5eNUqSynB3bpe9l0WnrbPdubcEqfT5Sx3tbj+pYNZqx66QMqOeXBKoVLPuKB0dyOU/WPSLqQImMpH4qxV10AkN1T7RcGgtiSZPyE633XOmPZ1Tl2gs/OH/3YKzHyvseIG02J2hUhp0lTrCLAx3jMBTGHUOw+5G8CajZSjBL4JBcuywVuCubRJIQoDE0yQUkZZCakK5EI/cuJVXQfPFkNJQdogkzXQreX683AOkCW4dPvpSSwMAw7guDEIS+6wlhRMRZDFUCPeNg7mwuMZYcC7BK/dhvt4RxpHfWRo45sjEZEPGYtoMUUAeARrw4nDNL1m6/hyuld54xRPbbPRoCq76HaClfURj3++RCcninkFlXmLIGVhqEQogWNDkuaZvzQW6DdWdkv3KLa10N2wQVtWZvRtQq4lTXpaqM497mu3ZvtMoKu7esY1P8U16fOaFKgkAivqbAaRkHMwJba86yIqZodWaEJoGHel4z0YuKSiyCd86Elol51gahlg64nqesNTKh1hF1fsFy7mPRriWNlmXFm981otW6U3ZBXj8D67leVUVTvJ7qBHQVU3qITJY/wRg6sUqtWmlEc5kx+fxMEtpaTWie96wRzxcFl/kOAdK5PVivND7v/TTXjtn7Wp6NKWNhLBfxIqRMaxCDrVeIEdWIT1n22rmc7V8Oy3Qu3UwQqgUN7zxdqscurM0JC3L2z5S9TifFTxl3+n4SHE24qGc11PskWTg0bfj6fhZVuzNoVrlqUqroLL7FMLLtGydu/l49/jJfTDFdZW4muq6GodPZnrSrWcg38pXiJuPBFrNnYwpQTm6SaQAG2NOFtZkUWMarDG6tzVxp0OrM6nR5Zf697LUksNTzV/ZgtOyRWbgfRYm9YxSgX/HBj3+U3/m9v8XzH/oA0aczFRQ/COfv3Ofb3/gzvvYnX+Tq/rvIPtg9WTIP0p/muNkTFW1bcktqaW7+7HFjQdsyeyavY9VOS4/q99o4nvzzJsH6cfrTjuNYPTXfrN1hcx2tu9ux+pbmdPZ9aReyt4ZWc5VLuwat4F3XX7tNtcAH3jvd9ePOcQtO2zEv/d2uwU1xRMc+q/fB0t6p27mprpveb59vlV71e7PY8Rvg+Xvt0WNtt2d0Nq7S7rS+inlgDNE8aDJJkvSCqZamOmMlC9jDSRn9Hum6a0WKI2WBVdI9m49X3vcACTH3gJXriCHadRrEdEO3JDclMyV758tm6mQSlMMwGoASgRTXLukSwaxZ75LGtHOdbQExtyzPJFT7BJrCOBRgE8JAHO1OI5ekHUluV0VrGSwYfBj3FtyGafzDfrQLFlc9fdcxDCMinv1+R9f1OEdykbNb18UJzveowjhGeucIux2rFKgvYC4sqqw6zz6GFFgeEAe98+n28+nS1M1qVS7hurq+5t3zB5x5gTGyv75mBWkcwjgM9N7c0kRgv7dU4gdJHESKI3qtKXPOsQ/jLN6qEJyYXXqWXehYIIIwabtq7VIdJ9Ym4chJMywroD8gclmo1HT/1gz4ZeJZLChahE/ThMzTht6kDWxBA8w1WnnvZ8tBW1STabxhZiZgWV7qFgTEYoWcMzvnXBHuawKcx9HO96ytSnhrGVGel0xm6zazEgIml5J63orLZUuwEyjL61j3JaHaWb9Kn3XO2I9p3Oo5ywCtFiZCsoQa2DpkkPkM5Dkuonjuk0bGGBlTvGANoSwzp0BK+TwMo1kVJAs4cwEUDtNw18XOxmTzWBJAOmcXqipCUNMOjii95MDYLNjX9SYtJPN9LE6KpTu3XwurBRSki6SFLPBLcUtOb5p7ZLIkGkhJ49BEu6HQi6WS+2bKi8M9JNWcqhrImc5sel61gMCoFIVZbiDXE5ObiaIQYezMoioh0odI9C6BNC1jsHbddA2Faklfn4WOELJ3QoWwSGB5gb4IgqSrGaJzBG8JXnZeuffcM/zG7/1NPvnzP2fWf2fzL1HZXV7z6je/yxd//w9567U3kBBxSrJASXI9l9mZr+dyOrMTKFpSQLSAoKWT5R0ns3eW6sltTztGZ7RiCWTUvy+N5b1KS7fyj2N13KTVP6CV6AxwtnTqvYBSfqZNxFR9m8iV0eSl+muFY03327lqQVz7/U19bMtNoDQf8FphWssS+d3WyrXEg5eAaTtHqpQwhzY2uZ3T+fws3yF17N16vus+H1Pq1oo+hIP3DvtzCAgznbtpHW4qkhT7WdnU9yu2Y0yKvAkhlbMMswyENZ+Y9vqk+Ftuc/q/JwIDVyOEx8dH73+ApICGiAYLGtZo96EIlIXxyY1EILmMSUG8Of13l+4kajMP1ZeodqQsTd4zpmw/XoQoVk/nOqIGc+MTZRxGPJR034rDC/Rdb4xTDdhsVuuUNGEzYyarfMeTd8QQWfcrG99mw34YGAdhc7Ky2+2TD+l2u2M/7BnTBbNeoe/MAuS9J9taxmHE9ZbKebvd4lzHGM2Noe86i+sRSRczWpzH1fU1l9eP8OsVst3ZrcghprTNdgKCjsRg9y7ljT+OY7kEV9VSIXs3JUGoE154dWVtDGjVqdPdjDhARWQyZqgAUU0UljLoZcG/9u2uid8SA5a8j5gzjUIAY0wCEZxfnFusFaAaiSG7Ys0JaS3MlzYqgSMqB/3JAMiSAzCrs5yN+hxUddu8h1ldtcASm79LH6upuIk53DS+mkBbu3OANfUxa9N1xgCM2blJeKWWgm3tAoeXMquqpYWu9s0MuDEXwpbeL/NTNLoZHJhAmp9wmJAv1Z7M7xUtICnFdpjMDqrRzrXGWZ01YDX5SwijjTukZ/O+yucpxljOT067Wvcl/y7icE5K0oDZftYUj5XiiJxP2dyi4qLinGUP1UixrOV7jvI+KtaZhDjaRCp5DTLYyf/FkNyw0u6eWYIktWmmyWledHIvzGsX6z1b72kqoYjMwMtCIJoZNIXJq2JrKpneSOqzddAs+BNtyhb9ktJWBfGea6fsNLJWoQtCJJRMjga2tPTX0nF7A41ZwEqOwTGYK7fNZd7LuV96EKsSNVpMngiDU64l4u+d8Wu/9et8/rd/E3+2SfenGfgZr/c8ePsd/uhf/j6vf/O7xIstq1RfGEZLhe/NtaWllbUCqgZJrUKpfn7prM33ah5/XqZlIX65HF5C/jhl6dl6LEuCpqHjyZLcWtdqWlj3P9OkfAbrpE81vV1qu61zyQKWvz8AOwlwpyeAxGMr+pvfrbPf1mVpLdvf85m7yb2wnZfZule8wA5j5fbezHM7X0vz0JYD/to8I7L83tKeK/2GdDYX+HOzX28Eg3AwjpqvzEDXDfW1c7wkVyyNqVZuTGtq/NusNund1Obl1RW7MJgyxyqewI7IjC4f9EfsDs3y9w0gaRqXElxkF5VR3vv5XN73AOl//+//Hzi7c8eCxtOm7PquaHCzBQimDenTHRoF1SZG2BUXmLLFyqE0zYHdcH99dW3WowyqRFit11xdXaFq1odxHOn7vmje+74rmsQskDvnae8E2u93XF/vcE64vt4S0+WVPgEGRbm+viZGZbNe22WkMgmV4hzjMKaLcaesbOK8ZZsKgf1+b5akpGkPceTqesurr75aCJgBQJvDtbckFUMY7W6fqIyXW1YhacvV4rhynAGV0JkPacnapIq6MDvceW1yKnCTVSYCXgRjZMZIoTrIMmmO8nuhuGTZ3VX5gC8xjGIl0bnFK7fRMvbWApX76crZFE42J/SrnvHi0uJwNCLxkEDVP8vbM/Ciy8+JIIe0uXyX71/KIKUwOgA5okkUmY0pf1+IfUWs6nla6l89t3U6+3LLuLOMeSYd1u2lsTPtjXzBsdUxaeUy07UgTXs3Wx5uEpjq/pa9xaHGc0mYKeAqarnUdMbAJWEeyYB54Z6tBGxCnCyoMYm+ivlvW5DrPKZB1NzrxhhQjXTJmp0THrRjy8oJbQBhNRPG5Kp1rveCWWSkWOcjYvdBJaEcha5zxa1NRBJATHOYXbCSO/MYxhldmCsjshXXms5JXGKaL6O1+S6xKbOmuUTa7yKU7JHiLDFCXfLoVM0Vb05r0j15kq1YVmIDZqc5kglcgcUMUSBTcfmMGgkInSpBhR89eJsfvP06n37xI2y6OwwaZsKDNFZK76Y+KmqxqDG7P5vCYAJJGedVFvvKFXjoHFuJxHXPz/7KL/Nrv/s7PPXCs3Z+Ulwm+5GHbz/gq3/8Bb7xla+yu97itwNrUkKhaEDXeKtZ92K172q6fUxArfdbrQCpAUH93LRbdVHYbJ9dEsKXhMNj5ZigmOe0tYDVdKEWUh+ntHXV9dV9rMd0E0DJ/cz11nSn3hM1cLE6mj7JMi1s212ik3ltZ6D0CMCo36vHXNPw9jNVLXHFx3hPDZhmHiILbc8F/+Xxqcw/X9rfBwooJuvzsT3VrvNNZwaW90v9bqZp7ZzQfH6Mx7Vz3Y55sV0m2mrzEglxLMrWzGNctsC1/UqydlClTgue5chjY80luGh3J4rS8/gmpPc9QPrWt77F2elpudRxTAd7yX0oH4IlgmGMyG56d2LuUDnFtGACiHcO33WcnZ5ydXVVLnbt+p6TkxNiCDx89Mhc6xJQ8MlycpUufay3RRjHygSZmI5OAKsW1vu+L1aQYRgIIbBarVivVvSrVbGG5cN2dnbGbr8njCPOe1arlWV2QojjwMlqzZ07d0qK9Ifn52xW65RVrDJZYwHFEmEfRsYR3DDQdX0KcmdyJ8pMLm3orG0CDohVFmLadNr4aQz1Jb22bh2T+8m0btaJuc92AcKVIJYteVlIr+tYEqZbolW7m2UXtZphxhjpu45xtMyJV9fXDMNI1u66pAVu21hieDXzOsbYzQpxpJ4MHlgghPX/Fwh3zVxrRiMpFXF+vgag9fv1GBYZG5S9XJHf3O3SN6DcUTZnlqFMoyYjgojYZaUy1dXOserkTnWwf3Te33a+l/zmFct2pmluymV10fK/dcy1uDPmJAlFabZSVFZEMwAk0ER531zsKBajGG3sYwgGIJgLEzO3k8a1qYB8cQSd34FWVkRzEL0rlvGgWqzu2ZWtzqoqDmIcD/ZsXadW/Zz2WV77uv+UsyPOWRKZgyhd0h1o83dFDEwih+tZr18u2doSYwSdFA+qlfufNVa9ueCyJNMR16RdDRot42RUBpQ3Lh7x6uVDPhxH9iGgbkoWc3iGhOCWrAaWPVTVIVJbkUgKhKlPtfZ3S+ClT/40v/O3/wYv/NRHzWKUxuDFEbdbvvPlr/PVP/wT7r/6OhKULoHGUXIsZYqnzPNjjR64rOW2l+jbv34R5ivXfCuTAuuYMH4TnW8F/veiafXntVBbN32w7xbAwLEy0YT5uI/VCdPF8zfN+4weZxfNpuT3j10s2tazNC8zILbAZ9q2lgT4JaWm/Zx3u6bn7fxkWaSA8Wa+Wtp/ZLDlcEu135fWse5/beGpx9+WJTBf11e304LGuostkDtWWhB2bPjHABNUClpN162gxCj0fceq98mLQIqc65xLnlw6KZaSkcHmSolMCgYnx9OnzwASWHIaYNXf4c948+i46/K+B0ji0w3ooxHxEC29YPleLF4huxRZdrXs9mOTbO5fk3Df9/0Emryf1aUK5+fnE7JNms6HDx9Wz0yXjcJ8g83djSCEsTxfLCjNIYghcj1ep/5OsS1GvCLh4oLNZmNJErD+vHP/fnFHAgNqggV7e++4vrrm/NGjksXKOU/vPQETFsb9PgEKE/y6rkNHhxclXFzRhWDxSimlbxF0sANqSXCSBjpzUtWkUZmsaDWYqWOQ8nzVzN2AqhFzkUrQT/UrFWGKJiyMYUqM4Zy5KqJTetM8X/WlsUWAzm1i857TkGdeVVur8nshEVGNEWdpyGwM3lv/GssMIskF7whDjhGt4ivSTkzCcnIhSgTfBF7KOoQkqEqaLE2JDSJ1wHeuMTEpk8CTi5EWl6dpYecMjKTRhcpiUzMgTSnuEWqrVf7MGPSM9ZON6iMpmLNQS4cUomyZbtAUSC5mMSvEtcpZX+bWe3wS+W1+JsblJd/wHevOpHFmFy/bwxPDq+Yj5sBS64sAoxiQk0S4xxRzqLYBidHmIe8L2z8wxGRHEiljzm5lQUNywbP1d5iVKISI+GnvZLdU731JpZxvMRco8Vu2Vw8FxLwpolqmu6B2JYBX8FHZOcF0P7ZnJF1+LNGsKl5Il/bZeGNWGHmf5jDMBRy1pBy2X0kgJZY5DcNY+lwnOzGaOk7WpbyPJTFhV+2sOI0rv1s+0OSmqJK0nRMIgsntNIOgUmcYp98rgSNrPZM+t7hNDlHBOUJUrrY7rtYbOm/Ww8mIVAlKCvi5MJP3pGDWphyfZaKFpFjalHikM2ATUZ584Vn+9r/1e3zys79AEKAzmitj4Pz+u3zjT7/E6z/8EQ9ef4vx4ho/WsIeh6S03dmK79OoxDKMVouYabLRgrlg1wp4Na+sQU0bazGbk3rNKiVPWYMFofGgzInpwbs3AZdWmXa0bV1q4bCu9t261K7ilslvOUhfZF5Xba1v664ViNNnU8xe3tzFWlkpEutSz1UNgjIfbefF/slkWc/vp3a1WssWEBWVQN4LOW6yYg1LAKWMv+5HVdcx4HZsnCyMaenZ2ZhjxPvKJbx6b0nxubR/b3rupmeWSrvnlp5bAta1sm3aP1m4g+wBknlz5z1Pnt2Z6teKvtkjlA8SH8hzVKvA5r2YgPxEnXXaP4km7vsI7ywO/6C87wGScx68x3eJcVie2Mp1w57zvpsJtD7F9+QFz5mGohoDkySwhzgPtrf3fZWeei7w28FNRDTf+aOTJiG7fOSNE9M74j3iPYrFDGgCFFo9mxlvTCmmI2ay3F7v6dfrklI3xlhS+Za2R3Nx21/uidFSg5+cnNClLeJc7eoCq5XdhCyuw4vH48EJ+zAQ9gPjpSVokNS/4maWfvdOWHWdaW6SW4wTxxLz0arfwOwg5pJjmESYJW+QJECWDFJxEmJFkrsPwri3BBLZygaCis1vfbv45PplZmIDYyZ8Sbr7Z5b1rQJUuY9jGAhh5OriIeuVZ+clXVo53ZWVlteC1hOItXnIYDBbOyBBTZRk+aLaG5KFdBOuS/wCTEBVsvY7xe8kd9RInAuN0dLcuxT1rwmIuSQ8at3vQu+k/D+fj2z1yf2IasDUeSkCs0YTiE15mYXiymKEMJBAJU18g4Iwltu71V4s5yFMdNTmzk37LAwhAW43iwdTFNFoKY9TCu9sfYsqqFpSgpiAd1FSpD6WwWLuu845iy3RdAeQWt8KbUjKljHKpNBJMT+h0ugaOM7zJQQnxOhK7JHGSMj3IskUW4nYxcl2hi2OMe8kkck33jtfrHn5zOX9HJO9ptv0hMsLnEZCsGQNiieOmlwmSIKzQARHusA45J2RFkPE7r5K8zTNWQahEZU462eeF8WTyUFmwmWFxacEElp4tuTsfhW3jRmnF5BdovfQbIoky0GJPid6YGRlEsyykmIiZUYnNPGDrHDIdYWUxW8vysZv2ATP5eU1F6t79KM1p5osNN6BmqWuE4E4Wdo13QeQMwJKsuqoRuz2P0sA5KN5ROz3gc1Td/jV3/1tfuV3fp07Tz+BSrK0RmV/ccnL3/w2X/wXf8D5m+/AEMpkFYFSBC+mRADLEF8L7zOBSrN6Y1KgtHFIwMHP/HtWLBbvjG5BhNGK6mgjxLrDevOS+Qa0ln1RxPPq+QVwkT+veVhrQSz/kHm/qlJ7TeTv67/r+qZ3bR8ILnmi2J6d3FBDAaStoN6231r6irBbzVbUaVaW1qouLeBaejZb7mtlHSQlSi1oV33Oz9qHtk6kY5rvvDwm5JNHlOuVyu1RpJzP2fPaAs/KnVqnXXNUmbkAGo3WGr1pXfLqcS7VWYOdpbbqNvL3TszK/7hlknumM7EExGpDwXz/JIWxo3hIiSgnmzUrzPDg0nobJ7C5DzFU+GgCTyqAm5Qr8+KQJK+qZNnCvDXyZzbfw2OP/30PkBCPk0kQ8M6E8igxBQRrYt6uxB5pnPxwRYRxHNnutslf3+oq8UUVIwBbtDpQcablqUy47eZtD0d+PyPzshkds3pijNN9Tkng8Ux9FBFz74uR7XZb+p1jTnK8B8Aw7Evb19fXDMPAyckJ6/XahMcqo9x0cCMqnqgWkzSOA2Hc0xPT81OMCVRZ6aLivZsxuCVze23eFie46EpwaO0mkBlmfjfPZck657qigSjgs5rz7XZL3/eoKuv1egJjzIlUXtOgdjln7nMGZXn98ni7bro3qUuAUMRA7tXlJcN+bwTZmdUmg8VY9RHSRWeqOJeJiJCuWpwxvkIMshhS8c8sZKKTlk0q+dTmJdiFpOpwTNafonV3wuhTCmZVnJeUmc0V96hWEwYkkOcY0t1CJZ4kGgiK+f66RMQsrsOyf5H/2S6hKDaywKtagZxpPHlwJdtgtLtlWu3bxJDEAGVMoClObY9EosQKBGo11smCFyNFmZJhayUjl/5a0L59mEG8U9O+F9dElBApgn+uX3O/8l6vvhsVQoQQxe7n0XThbgpszee/PmOWiGGuAa7PTiuklpUQj3eOzWoD4hkjSLJmrMUh6ojBJtA57F4mEYbi1pbAU512tQDsad7yXEzJD9I+qRmkGi2SJo260ff6L5286nTuSpM+oix69ZU4i7PKFuo6OY+kejQpM0RThtM4n9NhDAZkYyhJccy6bi6CGoVdDGzWd/jwSx9npY7toJZiOw+aCbY5hd5B5x1xDOlcO4b9YJbBEHCS1y+muRZUIoNz+JXwM5/5DH/z3/47PP/BF5BVh0SLWxv2ex689Q5/9qWv8PU//iJuNyLxUEifJkhK/MDjlJqW5hiMJTfOpefbpDm1cFY/n3/OeAiP1795ZYdKmGNC8E39n9HEBYE2z0HtWVLLAMfaKjwpTn/ns1VAs5s/X9d/bEyTYF5ZeGReR/vu0nc1jW0F/gkkQAbLdZ0/iQumQEk8tPR0bd2Y2vyfV2bjbj5fAp6tfJOVJC3oys8UpWIjH75XeS/Q2j7XjmXpOXPZnVzPH6cveQzeOZwnMa+kkEsySVGCMlmb8/UfB/UxyTiFoVKPwaAxSrnTtN5ftVXxccr7HiCt+jXr9aYcSlWl71fARFhqwtxuTlWl63pOxARz7yfBoY7DqDMC5UMYQijueLnULmG1IJ+zpe12u/J7LcgsaaWyNi0L9jVgy23kvo7jWALZRaSAgP1+X8CSiDGd/d6A0m63Y7fbsdls6Pu+1HF2dmYxS8kaMA4j1xdXjGHE6cCm8+XmcI3jzG1wAn6jWSKquc5jrC024zgWoGeB4FqE6HZeWxA6MZocCDkR3+yHnX/v+56rqytWq1UBjZLcCGYWwKreNj6qJmIZMNWumHWK8FXf8+TZPV5xPySGwBiUmouFUAkiYnEGJtypWY+0BtZhAjlM1o0IhDD33Q4JVLgEr4qrI0lTGsGrWYWyYIDm4ElHUGWnoWjB0ZTOPo3L7nXVGdEHu0gZ5whjSEJmYv5qSMRciJLkn4TdGBWVCdhKmgst8zyBQbsLdNpHxaYm5JtJzUJX1Hx5bqGwSiHFCoHL8S1k4Amk9Z7cRAxU1YQ8qgEBWxuF+vZRpvkkzbsCLlslUbtBD02gwUBOiFIAQ4wQKv/sotXDHKhGlXIRn6ogwT7LiC8LmDV9C6HaP3n+Ktp4jHEKdk3Cut+gozGunLEyBtsThYmGQNelfZitjcklK6+jLW9NF60VzVNW90MaYVdBcAU018/VkClqnt9pz9d15PXOfSlfjUlADTbTdsFsUmiIlr9n+2HOuxmNcBFQhhAgjvi0PSSAiykjpcDp6gwZAvshMMiUBMhwYkxChzKqoxOXrnOAEPb2XYx4yRZyRUPAebsUmk546ac+wt/6t/8uH//Mz+JXtl87tfHdf/1Nvv2Nb/Ktr36di7fvswqCGyPqpot9DwQwjWWwjwMeMp8yRcm4+MzSvmuVkze1Uax72RLj5KDOxxLyGpGqVf7cVFcr+JZzd+SZ3OeaH9a8rW570u5nS/9c2C1yggZatUH9XAtYct31Z+VeOc0zokVR2Y770EVv/nsLkvLnzsksWdC0bq4A1EVapDoBzub4t2OtZaqbBOXHAmRtf94DQNfrVX8m1WdLz7dZbB+nry2AKWt5w7COgd48zvq81Qrj9+pbTc/tapG8V2sFoibPg7SWNWkvSqucnKi5pLmmt4m+x6wcmLaFvefcT2RBe98DpGkhHF03Cbm52O81im8JkGnfnOtwRMRpRdznueaXCEHtBlBn52o1KPnf6enpTHNQb8ia8BRBe7WauZTVfauJan4nC3e5LxafkNOFSqkjuzHkZ/reXOq22y0hBO7evYuIsB8Hht2QANJAJ5ET59JFo7HEA7SaMe/mF7Lm0mq3cykxW27SD9UgqQZU9RyZBWcCQjWYqYFqnqf9fo+IpPFCfVLremMMJXVlG/y5pAXKfc1As+s61ut1mX+vjjGMjDFmkabMU9SY4k4AQiGqaeuW8cjU0amfTJqYmbUzmOVnOgdTBpldhGySUTVG6DVpbdWsPlE1XVxs7e3DSBenGCNkcocREdR1lnoaEM1WFpJLkMVu5YB7hSphSUo2EDMoNbP8GALRxQJ2JjKbgZ1p0CvaWuLMakFjxhIEXOfNDJOHkcYnCD5IAdrZla68WBhB7VZjlpNpjhsNvCadmQBMmk3nBNVxBmJiMLAWYmQvWtbU6Jb1xYlZZsdxZAgjThWnybqRtHa5b/nnMAxlglolRnsWa+VFjJaqfwzmnutUS4bKUQNRA951yb/eBKwO289eBS+ugGCX4o4ORJYENgr4qOKF5skQBFGZXR47A61McV95HCJSBOa8boUJZ/pfQHZe3zQXaU6zoqfMD0CUMg5B5vvTGX/xDuiSIgu7niCOg7nKqbJylq/QqbJSCISEs62+OKT6O49qYIyT9XrVeZz3OBJA8KbEkq4DB3eeepLf/b2/yWd/69foztbEXhAv6H5k3I18+wtf4at/+kXuv/EmDIFVFMuwGSNBQfyhNaDWxj8OOKq/ry3vLS1dKvVevCkIvu7f9DKLWumlNma8PK9j9d0xxUENYFoBs1UE5u9qRV1ttV0CV0t9tPlPIQCNN0v+Pvc/19XKIfWctQBwnsUyzUiiifWY2nlo+WL9r+5ffjZGPYg9Bko6+xpglLWtlV0k2VqrM1yNt10f3mOP1nOS320tWvNxT+Op52TJKngMqC/JebmOti8tWFka72Ef526fS+C4/b1+dql/7bN137SaLxGmi9TjPGbJ3K9zWvAEbHRyW5z4q6I5+671qqy/YO7ozi4qNRpNUnKrWtt6MzBuy18CgAQmZE1muSJQuEykY0VY8onLlw9OiyviEWf11JaaY0Sz/qwlDK3ZvNVu1HXUB01E2O8tTqjv+5k1o36uPli1G1h9p5CqFuuTyJwoDcNQBNx8X0qMdnfKMAzcv3+/3H2jIVomOzFhDRE05hvh5wSjEDmNxUWmtsTUBDoDmpro12WJyOQMf/X9RXl8S8ynXrtMyDLIWq1XpX+5H3lOUTXhpMrEB7DZTHdV7Xa74vrXAjhxjnfffUAII8M4EvbBYlmSi5BzzoSblGo434PSAkoRIar1QSFZ2aZgjMDkfpLfD0nYbrVJmelFgVhbOWNK4iEUQJf3q/cp86Eqo0sJRfJ6kwGwJKJmgmbea2EMibFTLtjL7cXstucsLq8AQNlbkLkTdmGwk1oYQLW/UpC/yDQnY9JUF1FZsil/UkFJnPZVTGMQMfc3AlWMWpW9TDLgM9pie8SSnYSQQYwJx9Na5H4ky0AS4J2ze2g0XT6i6eESmxgNKBycBo2MQ0x3jwVcDFgyBKUX8I6ZUmKW1r0CdVlgncUa1S6+5PMcGeOIODhZdzx5dsqj7TVOnbn4OnMBdQl8SJpbSVYycZ4u7QXXWNmmOYpopitZCK+zzpVVz3Ry+nDOwKdn8tlI0BR1OSazUpikC499sQTGtB9ldpmz1deAbBWmg1ULSgI+lssPRboSp2pKAUcXBImRUWD0hqdW0WLmMtjJcZrZ4i8uA+hQ7s0zS6hnVMH1jiDgNh0/94s/z+/+rb/Bk08/BasO7yx2KF7vef0HL/OFP/xDXv/hK4TLrbnZRksQEx3E3hVQmOd3Jmg1a7dEp+qfUx3CMEzeF0vgYKke56bEOa0g3q7/bHmauuZA4CdzY2r7dOzzJVDQKt6y8uGYDNDWk/tbnjmK/EyWseyzkzzRepjMeHPthlZ9l/Qfic8fxsfUfWzX+ZgQPefDzHh9O69ZOVOHF8jByOeIqZW9Sp0/wRrftCeOAcT673Z+l2SZ9h2Ye8UsvZvnr5bb6j2xBLTacR+bn7b/7e9zXjAff2vpbOcB4Pr6qij8LGGVs2Q+TDSbqm/5XISYUsGIGPipAI+gxRNFNXsHpP/r5CtQx0C/V/lLAJBy8HTRcZHXTTUfUEnPNQFtM8CTgFXjI1sziRYg1RYKmBO62pe63jhLxCm/W2/Chw8f8swzzxw1ey5pPdq4p/xMthR5P23IDL6KEJyIaQ7YntJwO3AOL54YzU/dZpmyeXPbtaUrR0e3BL+O0cqfHSMoS+8X4bZZp+wq1xKcds7BwOEwDHR9Vy6uzOMuKU3FLtNdrVZTG4nJZReQvL713Jef4vBeODk5ZTy/xsLhKhCRAvZjCvZPPlOg5lpUM7p6b1FlkPK+M7eeuohpXHJmt1xCJRyIOGKVMCODa1Wl7zpiN1/jQtScue25iqjl3+3vvK8BbwkFQHGuIyefaBmkWbl8ESSdm9LVn8ZVAZtSjy+tT7Y+lHOR4kj0iNUXMaVJsUZV/bA4nSm9fv0vYoHzlr69Pu8geGDuHpvBdp6PSWmQMw0KPmd9M1SIlgs/M5BNezdlrTRgmmLVkptg54QeswA4NcAYo5TzWzTW6QyM48gwDIjIwTmv56OMz6JrWfcdH//QBzi/urZsbKKsxKVMhxzQqBgsHsY5N4k3wsziUu/pvB6ROS0oOsRkPSpz35KLlNZ6oo8uHwOypVDRWR0FEKXv6/64nK4d0lgqYbAFTGVrCc4vA0GAATVXtggDkeAtfsyHyV1EMihK+9GsrJbcJc+f7zpQJTrP4HpGp3zwpz/Kr//13+GFj7xEcBFWnYG4UXnww1f4zte+wZf+5I+5urpk5Ve4YEov57zhPe8YRGAMxSX3QICS+dBuEihrRVgIcfb3kmC1VEcrtC3xzNK3/Hvz98EaPabQXPfzcd9pBcj6+oX8fQ3QbgIg9fOl7kTrlsYhCbO3MV7HBNgDcBPrZ6szqYeCdAsGF+tbkIfss0kGm/VrJrPNla0xxpIcpC31nqrbsvn6ydb6gM8ujFcmgr0IIN5rX+f66zZqGbGWJ2vvjKU92HoSlXHrHCAcs8K2fW3XrZVLjwHC2nJnjyQ+6L3dybnbgaopLzVL68zuTQOg0NksEx3udZM1TZETmeJLi2pSlsd2U/lLAJAAlgM5y7cLm2zJJxQEEUuHHWJOmeoTE1VEDjdVXf8S+oY5kGrThh/2AdbrNS88/3wZlznQpAv5orlA1WCoHk9utyXYIjLTyDnny4bMj3o3xe2sVzmRQRqDOKI6S+O72+OwmA/S8/WdOFmodm467G3fJGm9tKQIzvoBmRMsrAsmpKdkDc4nbW+6oyFh4AzyckzRsQtfCxEKMd2tpCVoMGKXMI7DaAKEYpnCgqXrjEGJccA5V1Kyz+ZaIWLZ/p649wQf+sAHeGeIuKCmoWNa8xCDZXdzU/rqAjDQYmVSmiQRMgEPy4lgUl7Mc1mDCEwArP2cDZg0TMVtzFKULE/Wv1SfS+5SykzDnlONa9LeZJc8u/zUFeFTY8ruVaWotz0lIBHf+cnqkQARiqXkluwa2sSuJIEx+8mP41gsA9kdpbbs5fkoSg6xPe0qoDrGAKzIPv82XynWq2KCBTSWSZ5bdCfaks+VKwKH87bW3iWQJFIJkWleYiW414DCCdFRrtETlD6BVIcQx8p3W024d2KAbL/bTQqM9Izd+VZptPO+SxPsnOAwN9pN37PpPPthT0BZ4RBN1pskOGSXnNj7ch5hArGWRruioRVD1zzYnIQhjTs7YWSgVS5NFvtkijlKmDndR2XfpXuBfKbjybU1nUMbs0I5M2k8WrkDOqYFsB5M9AYp66oonU4pyKWskNW0dt4SKgTFqzCmNXOijHYYktervZvThzsMVIkzS2jnjB8MzvHkB57hV//Kb/HRT30CWXWoF0Q8u6sr3n39Lb71ha/w6JXXefDam+hux8bcAfBiGUkjmupNYN9JyWCZzxiaxY+8GTNNmQvJtpyHwqUp2fwB7c3Pt8J0XUrylYU2H0f7Xn9WywAHPKlZ4aWxtGMsQNC5RB8nPmOWuMPLbmth9Rjwavl2+Xyhj/mbVuGzNA9LY7GlNTBe9n5muGlPixx6ydSAoOWvNxZJZzWfi1hOGcqcdtZ7Z8rkU1HdRoivxzvxv4oB1nNQd2mhz4cAtKmvaqeseYxH57ptYum9Y/NZ11uPzdyqKWufhAc7w8zn5Rg4mgPcTP/yv/z+8t6a3pvqnZScHYpjHwO7cUxYR8tBE5F0zUpWFEwx2SZzZR41gSYBi21NYwlZjpDMtsRy/KgSHt+A9P4HSHXWuRbVL7nE1YCiRuFtQoCcHagskIuITPcr1RaDvAGXiPKSgF73J/+szcqaCOz0TtVGZQWrN36dlCDX0wKErFEmaQj7fjW5NmmKPUl3tThn2sostCogzuO9wm5fLG2zCxapD+OcodbuBSRCHEJKh1sIcx4jkPyVsxCc56Hz/cTcUsYv5yZLTv0vP5c1+jU4LVazFC80DpYaMobkduiTRWmsXTeTVUcmTW9hlEnYI1hCgkEjrvPosOfOepXiOCofcknAwU8Att4HZY8BQ1TLGJbWyjTcQErekBlb17Vie9rrKFEmsBsFsw4wuWjmhZnu2IIgJgC4DhQHQQvoRTW5BYKIT3Waa2LaYmWtszOmyLSeZR2cgBgQo6RyT4CoEPrpvKiakByjxdBpTriRQK5LKcwFcH5B9MltKwgRQiLYapYxEbH079m1KRowzEoKKXOfBXUHMqXcdjg00Q7LWKgGO9WEUZ8EEBE1QVUUdMRlYZ7MELKIzZSOnIgPiqeybGffd1OhTIKjuOLKGMPcxYxy5ibmLRX9KbRGs5VIEUa8RjoNaZ4mEGhnNm0aFJ/7n6c+/xoORTxVnd17rmluW/pG3ncxpBlK1zXM6CEJuExudjgLa5S0xzSqXZMwc7cy5p2TixQhIe/FWrggn4/p2QL4ERyuCAFQWHtKfW7WN0HwqUpNygBNYypTJi4BKJ9C2TzaCTsR1nfu8Lnf+Dyf+PVfYXV2gnR215VXuHzwkG9/5au8+fKPef3HrxCud4Rhh1foNK1/vkeGtH1R+iSsipvuKCuZprTMZik1r2sBxMQPHd4fegksCbbtnjgm5C8BnfJ3ZiwL77T1zgDQMejRgKT295hoRv6sjgHNMZU1Lc91LskmSzLDfH4Ohe/irscNWcGqulr5xEmXLF2t9SMBSGH2fB5H2+866VI7bwfnGJhiUesxHwHOaXwTeEvnvNkj9XwU0HE4HYulnpdj4KgAuZo3P8aetnHO571+573AZS3PlDqhZIaDij80+7sGsm177bgLLWOayzrp1WH/JgVi6VM681GEd88vCENEUgbYonxFEYUxauF1AOJTHD+YsgjJuvcCmKjOlX2e3KihuIeqwnALkKbSdZ6+7wrDmgTjWkiuN2FiWM6MfRPhmurMGpX8Tt5TSwJ4K9TmumsTaWv6zu/X3+cN6Nx003ALhEo7Oq+rLktEt/19qS9UMThthj3T9AuqIWmpmV2omUFSrWmylODz+J05eJp/Vvonh4e7AB0U53xpp2S/qxhwnvthGIrwn4FRbUHLWfpUld1uV2K1hmGg7/uDTGAzTSWHa5C/894zxgwqLbZntVqxCyk2SSti5w3GtAysXtNoZieEKT6mrIktUInnybu2CHf57ptqDfMcdynTjHOS0UuypqT3Rezi0Qz8xBIciMLQ3kpexc+I5CQEE+F0ngIuwSxDqfOmS0zg4TCouJ6HCYi31rC8xnnNgtbxJrM8Zgdzu3SGD5UaCbLkM0ol+6dLAFlwc6Xak+1eSQYBRITOe9S5g0ukDxQqCM4vK2PasbXnyvlll9+alrWxSPmZAzdYrTS/1ZzlUsdBlr4suNLWZ6u0l+pe6sd8fqdZaV38pjmYz3kWtpwIkqy/k5CddltFb0v7jfKsLnV7rUvnTcJP/iQdLUQpoAk1gdeyewl0jr0X4qbjk7/4GT7/V3+bu08/SXC2/xywPb/im1/4Et/4wpdgP3J1fp5TItqZQMGZxdSnM1/v1SXB75hg1Qrwx3iLCdrzNc6KyZr/tfu8fu69yvxs5dTCc0FvkgOm/h+UI9J0PfZ2Dup9MqcXUsadP8vvtO7eNa9ry2yeE71eavO9SitHtEJ/28fSv6pLdZvH1qyWU5ZA8U20ygTiOKMFIsLRndXswVpWWAJlszYr+rVUb1uOgZelZ9ox1ndg3gjAFtqt91j9nGHa431aGvvj7JUlGtrWV8/tsfHk+Pl+vaLrOwqoJbFEEfbk9PzG29szEaPFt+ZLu51z5moZLDmY0Y9MS+xS+UCS1cPtPUil2GTljXSIuKXWOsx+ZkawwLwk11Np1pXivlQTghuFksoyMPU3aZ8qi0b7vdov5e/MTPLzNbM51m4+lDXQOSBKWeCTrHOlZLObMX5J6H80XYiIXfwZYjhwbWwPksjk2lcY5Q3EQJhcEWtmGqPdx1TPQxbqasGunftWcJu1VX2f06HnjITDMB2ypT1VC19lDEkgcM4harEDV5eXxOtrE6qbNV1ioAdCISCoYSlJaxHzhawKKniZXzzoZE5027U3NyAKGC2ssjo/mQhb2swIUTEx65CROucYYzhg/mWuiqbIztGMPcl0d0+9hrWQXJ+ZPDc5hmYpLs2nO4py/Ei2gKI6c/EThS4H6jfCz2yMOvk7t2eonYuZ4GKDmNYlCQ71/p0FJDfC1U1nt7UOo/P5qvdDfrdVyNTP1HUttdcK0zcx9OlageOuRO38LQk7pb20drnUQvzSOWrrb/tX17EktLVCYEtDjo0/qlnD6vdqS/7iHGD70GWAZEysxJqNTgi944Wf+Rif/+u/w4sf+zCjg713KWFH5J3X3uTLf/jHvP79HzI8vIAxEPc7S7yCIM4TnQEkqvNb78ultblJqHo8AWy6O2m2ns25XtojXQVgDwRE1QOlXBlHI9TD5F58qIB5r/4f8rP6M9/QjTLqTF855M11Pa1bVuZzuY35mFNSG5krBMv32ZXghpL7MSlaD+Wfae9PLlPzz+Xgs/rd1ovl2Pmf0xtmigmY8++6hskdd/ns1/tm6fzDBAyPjWOpr8ikYKnHt+TiWc8VlbK+7nO9Frm0Z64AhcrTqTxXtXPTOTomc7Sl7VfdVu7HTfyu7oNzjieffopf+2t/hfXJhtVqZXOX5tF5T7fe4JJHU76fE4SYsh7VbYQMilSJ48huv0uJpbwperzD9yvE25UhV9sr/tt/9EdH17MufwkAkt1Wr5o30nSHCUxgJz1d/XSIZF/LI1q+WaCYI+qhi521daipqjd1XXerSVgCLarmDpLjAzKBz1aRbFJt45DaTV2nHc+AI1tdZkSmaj+PR1VLdrt8j4qqphiR6V6nmrXWd0Ut9a8QFSz+pp67PFf54tb60GUwkNc0z3EtiNWuQe18thaHlhDXddbPLMVOWV+meKtZfVrNg4Ptblf+FicQmbkjLBG4WrCaBMSYXGEES0mvkC6GdPlKaVIMUOJ5NcDIbZU2itFbEmBIxD8LaGUiQO0CotTvKcg2W5BmWZKadih1xlm1M91l2ld1DFsGNWOcskHmz2sw1QotRfhPVc8EAaW4auYU0jOXy0q4qvdMaWOB0VjbNdusE6IUR7MDBpznMp/pFsjkhDPLcZJLczw9X1vEyh5WZhbpXOrn67rbPdi2uxRH2VpW6ufrtViyDBwTaGb1N/M/szo1bbVjab9v6cSx/VQ/W/9d07nZcyESq7k/WIeqvfnfktwSQUWInWP0wijKveef5df/1t/go5/6GVj3sPKIKp049g8v+LOvfI1vf+XrPPjx66xx9KOd7X2IiJgm11I9mJXWLjB2B2NrM3nWe+oYgMo/H2cNHtfNruWPx/ZFK1gea3+pjZa+S0pBXH9/E28vY1oACHkul/rantvHmbvpeSkKrCWPFBNkFoc/63PbVr0H5nVPngBLVq+6tHuk5q01Pal5fd2f2uOnnscy/hpgcAhwDuaCOR2rx1nXUa9tO0cH86YKkq9smM/d0v6qaV04klyjpmEtTWjHsHQG8jNL9LSdn5bm1Z8tgbQlQFTXWa9py6e6ruP5D77I3/3f/T1iijvN4EjSuHMSZKtPzStFLEGTT3JGTFnvinwiaooe6wmqlZyt2B12qpxfXMI/Wpyug/KXACCZdkXBtNyqM5eI9ND8bxE0hnQRYBZylsz82ZXjUIA4RmxaZtj2tX5uqRRwkbIY1ULhOI4H1qX6MORnl7TqLSFoBfyWgeX2uq4raZedcynsRRDvilBcW4hKHWLxPPkA5oO0pIHN7wPmMlIxlDK+5CPfumrUWvEloakdZ3uwa6Kf26oFoJYBxmietCKHDC7GiARz8Qqz9iMhgMfP+tWuebsPpj7qnMiIkXiLeZ2SWRiY0hRzMp2Dw3EbABdvF/5WS2Y7Pe8dFI0ZTxghqznELF5FzFUsu8BN47K+y9HxHjIXW4P63qDDrIRL82X7cQIzwrRvVLW42xW3S60E8OLsNO+H+eIf7oNjzGMGgFN7dV15n06xCrEIVXYOzHKd5zArKVqml7PRle90EiRyP8p6hwjukEm2wnD9e312WgCzJOgdcyNu6z9WjglfS88dAzJL7x87Z63Q19LRm85k/d1M2G3oz008ou2jilg6ee/YdiD3NvzKX/lNfvGzn2V97y7RY/WPkdUY+dF3vsMX/uBf8dYrrxEut/QqIIrzHSGMrNfr6kJssYQnKc4jW3BrhVnb31p4rBVRS3N8U6nPr6oWt+saRNwEDpbqa/lV6TeTEi1/XtdTW5Jma48cPN+u9bH+1Hw2113H+d70Tjvf7ThzMSWHIjJZIluX75xevn23PbuzsegU03EgQDdyD0zKvVqwrgX7lqfWzxf5ZUHAhhusIErht0sIsF2f3GYbk57nTHW646w9/0vnoPRHKGenHlPL79p3210zo9nMAU5Le46eM2P2P9G5WSo1bV+qo5av2nmuz18d/w6UOzZHp4yiST2TPaMsCZEGnd2hKc5zvd3io2OdvEOkAqR57qMqiBa+6kSIokXBZLEIjz8H73uAZNHGOkP4zjX59huEnIVbp3MBElqtZ+NmocuEFOaar7zoOpcnZ0ShPhi55OdFxIZVfV9brMYYGuKk1GmU21iCpdiCmpj5RLxqAa4GHGTBU6DO0qRRLS6lOtA3CV3tgZ/maa4pqYnszDIk8yQL9bzUdbcuPnmseUz5rp9MSIHCuJfM2a3Wq45Ra8cjTiAYQ+v7vrjdwSEYrRlNOz+T4OxQzdYMyj+sxsp9bU58m4SL830tYgJ11mylNW5eQDUi3uMdiFq6d9U50y3zw9ziR8ZTUwOlrdk4F+Zw+iaf58O7iZbmPjeglTbYJ+ujQEnpDlTxUulcRdte+c0Z41+Yx3KWmc5p6//uvc1DbdXJ/1Sn+83yXM61t4dxS6kHqM7byQCp7mi9Ppbyffl8HmPC9XlstcM/CRN+3NLOK1RucGmnHyv1/N5Ujgm7S7TxJhDQ0qayj5IyINc5O48t7WNaLnEGjoIqoYOf/uwv8Lnf+13uPv8MuJSCG+iC8vC1N/nWv/oiP/izP+fq8grdDfQKq64D79jHEd97XJysbplKxComtBXMWmEp9/e95vS9yhKALa6wDUjK81iuWjhSWiGz+maBjFW0oFLOzXiim/P/dq2W9qa1RqGbNV3PvP/YfBwDLEt8DDL9M/fImm+UvggznnRMcD5weVOlTgZVl0illGN5znOdbf0ZCKtqcVk3ejhdJ1LXkce25HFjYocUJVUa4cH42jmprRrtdzU4anlyW+dszEn3Vvczv7tkQROR2bUx9fftPN5Ebw7fn1J5L5+Dqf9tn5aeWZqf+ozU9dTnZMkFPPPqYb+HYcR3yVMlg+DEM6OXopgYkjlptVmbbJJzcKldRQDJWKGKr/aO987CPmLEO4+6pBDVm+lHXd73AKkTh3fmdxqzhlscfZeIlCkoEsHK4GhiwDFOWdyceJzzCaWC5kQE4nApG1J6lBAmq0lMRNZlYVUc0CUBKaT2Ju2dqmWVIt8OT2aYk7Y797ElbMZEVikeylLF2oaoXIxkugslb/bazax+RlWJzhVXnxgjp6en1fwEywLlbJ4lRIh7u6xSKHE77Y3pkrQc9QGuNQ3RfJ7IaZY1jT+Mwe76yAJ1ITxaiGsNjkSmGKeauM6EFzG/1yKMQkpxfKiZz6XW7LfCQ56XJcYWBFyAblTLfqZCHyJITK6ROe+KprieSSuVrSZ5jrquS20ta7VN+MUu7RVJxNvuw/HOW7auDHQSwC31pP1dfHlNVWesJwVxayClh5nimjJksHms0lcXDRupL7FYO41AThawIuvqlGkvrXDhfV11Dm1fV3ediZBTL6hqyoSXgfuhgFrD2bHSmOaVyF0oGfw0xZOIVFbkac41facY4XakM6oWK5b3HFnoS9ZW73PqcYAphipDXJ8AQc4cGWMgBhD8TAtf96NkY6sEjJJApQJVJfUraU3zeeFwbLVgVJf8XX5Hqn+z0vSz7Xf9M/++KByVhrOgrtPc5/Ut9JYy55NAc6iNrWlUGVPTn8mrIDVeNggFAOV5kPR5DDGlPbe08MhkZQc7N6KWvc7lD5wjqOJ9x5bAUx//EL/6t/86H/65TxBcGp83sDM8vOTNH/6YP/4f/wX3X30DF5Ww3U4Xy3pnbWRQWblpaszXHnSzONp2bZdcKut5q/9u61jeLxmEpHmtLFKzrKZVmZQSk1CKkC6ASECgbDypn7Tfq24c9DEpavL5mIGdSsCrx7MECspPKYLFgbC8RKvr35f4TjvXc/fv9HfFK+1ZG5NL5z2pLpsz1yiM8/6WCnhUe8aqmOa15n1131pAUuhPBYDrecnvt+BlGuMyvQhiZ9K8yWcC3dH92ipNCl1t6OhNa9I+F+PEq+vnblIg2e9zENLKEjfV07ZV+pv+5/J+tlZmeyOPof7ZzlPdnxb41Tz0GMDKPJLcbrrDaHe9JUbBR8+439N5z34YWK1WJlOJMCaZc5WSNYibQJH3nckMITKGka7r0SRPFT7kOnQMXLx7YYrcVc+du3fx3W2ShlK8OHrviRrtNvqaaCkFgWZCrargLGZpEiCSMJMhTmaiLm/qdBMwFM1z53JcjNL1KRWr2uWd4EET06/FhyRoqvOEIaIExFsfs+Cu2e2vbFqzdMRktnfJNciEXor52S7OCqbp55Dwtgeldr1zMgGr2oIiImTFlIKl2B4G4hhwIRijTxq/ljH0fUdIlprcTjmMuR9JHs4CZIyCqgn9rl4b6/jMLalMqc5d+MqY8mdV4oX9bjfNRUPwMxiqS34vl2KVatwnaiISROlxdCrshgDOceI6Bt0xxBFhrsWEifhPdU1Msb4LYLlYhEFh+GKWT8jAxoY6dbfy603t5u8y80nwrQIDKRVxiDMmnIFXfkZEys3Z9Rzn9N8lo5ymcbo5Yz7QVGWA4bKWHiJzRuOkGpMmW4NL7qnOlbHk8fgUxGtxdToDVPUedoCZlELZp2XG01gMCOWsdgkoqeJEy51QWo+B1F4WGEXqhSEDHmECYN5ZG1nfJjK5bWSwkAGJSgJ45O0yCUiQaBdT2wdCXLXms3WoSqZTNSPNn087bHo3KzRaoa+uuwYtS65vqjkVeGLalSYdsWD5+gwWAaf873hpBQdNe8iVj1uBc+pDHqwWAaVKeCMkF9gyG3Nnh65jTyQ6z/rOGb/6V3+Dn/2tz+PvnjCKsBaPR9hf7Xjl29/nu1/6Gq99+/vsLq5QgX2+WBhFuo4x96GcjYkWhhDos5t2cs2sLeqtILS0B2qa2655zVta4TArd+pnWzfpA0tWmtcMgsp+tz/Lpdfa7G/m3LZd6KKMyr+3Z+9xygGwqfZevf+WgH49v3n8+fPZ+Ks6pn9urvPIGnnJ85wVXzmJj5RnSl/U3JbK3WdADmFVKEonYcq+lkvLc48Bu9qNsf7u2NxkelYnUJrNt2CWgewinJVYFejI77XrUPd1Bpaqtpcs6otjY2q3ba/td7u+7WdtW+2+aL9vzxlUiZgqmj6JCdNz+YwdgjZmf98EpGrLYL22MVZyceELJie8e/8B/+1//d+wHwfOzs544YUXSgz9vXv3GGMwBX7i1ZeXl1xfXzOOAcfk0dT3PcN+b2C789BZWEDnHKfrE0iyxxBGdsOeu/fu8fDRIx63vO8BEs6CUT1K33lLmZsIR9HOiiC9B7X4EBUBSTeSV5vDiyAaTLOfFVVJOIthLFpeEXtv03XTRYUpKDtUt1S5VVf6AnXWGrP6jOOeEEeQrhKKwfkOienyxwSexhBNuAsDfZLjhxBYrdYMYwJRCjGBlZaI5U2dYx1qYNECnPbAWKBhcsWLKc4ikdVaW1Qf5HEMxbxcM8LWX7cWirKgXR/fGrR16V6mrAmq45CAktksx2cA7IeB3XZb+piz9NWlJgQtEa+FiFxiJXwsEtNEqJxPaWczM9bpuZpghxCIYWq37/tiPWrXsS2tcDmlPp+7TxwIsKoHwok9a5qyNgVv0drkfUHSWCWhT5hkGg72UCUnMifI9bzN5rARJFqXSSeu+N239WkllM2YDROgbhl2vd9bJjuNbio148nPtXEa9Vmq+18LRvXnec5zffV+zZ/Ve3RR2FgQcOvyuHtpqRybp/x3LllRlfdk/v5Y3Emt7a0BUiuU5Tle6tdPWuq+18UE70h9O9OSgLI4VyKoSLktvnZz7dTAXBQIvXAtkbhe8clf/Ay//jd/l7PnnmbvzZq/Fo9eD7z6o1f43rf+nO985Rtcvf2Adb5HLVlM67M7vwRcgLk7cqj4Qj0H9dja9XycPVQLTEt70qxIciA0Z1pdC12PC1J+kvWer8/j13HTGSh78YiLYPv+Er851oelZzXJGG3/l3h1TTPrZ9p1BgrAfK8xt/26aW5aOeCmsS4J6ofgUiYBvKHLtZdHew9k3WZ+ZsllGg75x+OUln4svV+AhM4tmze905blOXn8MotV0zkAvykjZ93+sc9rnpr/zrKZU3j049cJ48ijEPnRV75pz8ZI1/e4kzVg1/R0fc9qteLs9IzNas39199IsrfjR2+8wbsPHhQAPyaDAZruEVRls14zjiN+1XN6csJwsMLHy/seIJmFI0CMdF3P2pv7U3Qe6TpA2Q87s6yIQoyMY6TruxJUDnnBA85hl0QmEdAufXRcnZ+z6TpOTk6wG+YxgBNGVv2KDof3jt04MuxHoionJydEHMMQ2O/37NJt9hMzCoxhIITAnTt3GIbBEjIMjlW3Qrzd8QSw2fSImFOQhh27/Z7Ow253xfV2j1utCxFos8nB/KDUzKjVsOR/EzFKt4Uzpf3MbhuShP6lQ7TEiFvhtNVMqCoqh5nKgAPhsY4RySBpu90yDDaffd8bgaqIQS2AFSBRCXEZgNXt1kJeLjOXBypmZS+U/nZ9zxhCskRCDIowD2LNoGZufeuLy0I9nzcx2lpgK4xa3GL/M5Sp52++ZnNBqfgiOzcT+orbHCkhB4dMzOqZAEbLaFsGUL9/k6UwyrQ2M+2j5uQqy8y5HnO7n1qhY2IChxrTnE621RK2a1TXW1tp2zVsBayltWkF03aMS8zuGIhaEiJueq9+f6nfM1qT6FCep7rNdi1qMLQUE/M4gkg7L9PDB48uvlu349o9/piCbqZdDnN7cSY5GGhKnwWEwcOuE57+2Ef4td/7XT780z9F6IR9uji4VyG+e8H3vvZnfOWP/pT7b78NQ6APkB1cQ3Kp7WQem1crPNq7RYpyzk0a3yW3xpmyqrH2Lc1Fy0cO5xfy2W/frzPnzdaYZDlo6PCSoHdsTQ76WGnWj4OQ9y4zT4jmnXm9RV10tNRz2v6snxGRZB447HNNv+rfMx/LfC7zvppm1ZeN5vdym49jMboJRNfPHaNBbVkGl1DiV46UFvjXezjz1pliFopgX49viX6Xfiwoydox5lKvTYzZOXR5Dy/NxU17+xi9nh46BL7H+nxTPW18Uc2fZu9Ue6NWhg37PZfvPuSdt96qxpQ6KGL8O68Tk7LQLuiwKzrW6xX7/VAU3r6zDJ6ojXCIdpXK9W4LIuy3wvXDh+zGWxe7UnbDnmeefYZ1v6J3Zn67vtqy24/0fc9ud83V9RXOweXlBbv9jt1u4GRzwt27d01ITbfNKwHv4eLyit2w52RzBq7j7Owud05POVn1bDYbus6Q9zCOtiFD4PzROaBst9vU7pZHj+6DdAQ1Ld6w33NxeVFZmQIhBtarFZcX56xWKy4vLzk5OWW9PuXs9A6bTRIy8Mk0rqh3+NWKd+8/4MHDc/p+zZ3Vurh3LG3umftQRTCKcM6U5Qcma0xUsxYpXfE1BYqwnB0gDrTAUDZ+dlWrD3cNRvL7zvniQ18LTLle7z27lDo7Ez+wjF77/R7nXLG85Itfo8zvjGmBz9gEjNalFr4nUFvFrqQyS/Cgigr4vuPk9ASK4OWRGBCV0tfcT5dcwZxfTsqRNTP1mpZ1qJjVQfrlBeYXYyxEdJkwT+vWMuECdaq/Kc8b0VryL6/7dJQBNeCkHlu9RyZCfaj9nuqa6mwFwXwGaqBcz2stsNd1tG3U85KFvPqC5XrOl97JdbcCV7tPs1vCEjNvP6v/1W23gvCxNch1LQG4us9L52Q2t1W/6nbbsd3Up3bt62fbeW0B2Gydjoy3nqcDS20lC900V3VxzllCSRWcCp0Txhjtktdgrraxc2yefZLf+N3f5hOf/SV05VDv6cQSL+0fXvL2j1/n21/8Kq9974dsLy7pNBLHlMUsKXzyBs9W9VaTDkrOeJZpR5mbal1qq367Nq2wurRPlwSmlm5IAiaZfuc6c/25/dblLwt5tUB/zGJf/75E00q/qs/e6932HLRFRIqg1p7D9MQM0zyOQNzO8wEdXHj+cXhB++wxQXvpHM3mb6FNOKT5La9qx9y2n92JRWSe0bahE7Uyu92HdRv13l1y2T0GEI7Na+lPkoTa+ViikbmYPDTfJ+263uQG1/a95QW5jVKXzpWhLe2t669lwGNjaufhIGSieq/mt1Ej22HLoOOBAoQIThUvUwy+xoiGkUGVkBS0u6t9ebfvekYNNvti8kt09s9IjBa5Zq8jj1ve9wBpux344cuv4L1n1a/wnUejJTIYx0uUQN97tvstD84f8e67D3jmiafYXl+icWSz2bDb7Tg/P2ezWSHe4sw637PdDoiDvhs51y0XV1cM+7cYx5FhHNHkisQYGbY7LDA9Mgx7vIfnn3+efqXcOT2zRAZrT9/Bbrfn9PSUECL73d4AWlQcjjBEdrLn/HLPW+88BEwANzcJs0xdD1cosOp6Tk9P6foNcRzQRqMIHMQA5FITHO8cWmmYsrXGrFED9J6u6xiGPdm33Q4BZGtDfr5YdmLA+yoWqBKiYFmbKJJcVJwroCOPPRPe+h6nYRiKu+BqtSrjzT/LmCtmnouqElLa9JaIHBMAJwFKZkBh9lMy04/sx4FhHFOSSwyMJRN0LUyragnobplj3X7dxzxvS8W+t381s6xdDPKaHAjfMPM/b7XIMmvDKhOUEJRYdWfOgA8tYUvuUy0DbAlvO8a8X7NV1vo6Z4QzAcvPM0HVbbZMa/ZTJ4m5FUhaK2L+u3Z5ms1X9e4x5lzX13537Gd+p03z37ZbP3usP0u+8+/Vdn5PRIpSoP7s2Pzmetq9f6zfS+ezFTDrMUgjcN4kGE99zv7083HcOJcCFt9hCpQYFfXCNYF40sFmw8//+q/yS7/5a5w9dc/iPZxpS/124NHrb/GFf/EHvPH9HxGvtoz7ARR8J6hLlzXn++9qHLcg/MJ038wwDHNhXwRNgL620i/RnXpe21Tfx4Toej7ts8MsaUvnOu9dVZ0JebVSJJ+vOgvagfWp6f+0H3SWabN9dnFN3+u5hh4eA2ktjVnav+14awUhTOBoqU9L7bWgvz7b0742urYkcLcgpK0/15Fp+VF+cYTOzGlU5knzayOm/ZGE32Z/5j7XNH6Jl9fA+6a5XDoDbbkJXC3zaAccXmpc11N7txyjMTeVJb5Rt1PPxdJ6PE6p6XYtzy3RcREDutKnRFEp+QLpWcekiM1nve5jsvXZ2nlTOod072MeacTclaPaHZPOOSTlJlL3eGOCvwQA6f/y3/wTnnj6KU5OTzg5O6NfrzjZnLLqTglhpOuEEPac3dnwxBN36VYrvHfcu3vXgr36HtXIk0/cY7Xu2e53IJ5xtIP16PyKb33ruwxxZD9szVVuvyeMFmR2fv6I4WrH9vKK66tLEMU5+JlP/BR//9/733KSLE7jOCbg5Lh394y+XxGDo/cb0xJ7z+XlJcMu8NWvfJmx6/HdqoAnUNbrNfthYPApKF4Dzz/zNL/06WfxzuGIqLgZ0TgmZC4R5cyAJrcHQ+SWXc2yo4k0cSsy1yLWpuy63vaQtn2riUsGNzXzy/VmYXi73eK9L/d95HHUrne5H8eItGICVAuAaiLT1mUE91BoKv3H0vVGVZz3iHcMwwidaXsVPbCo2e9zl6+W4LYgKb00G9ecCB4yvvIMZBxx6NqEacpYElJjBKQkBjBrVFrX6m6C8i/NR3Z5q9vLgvw0p4eCbA2uZ/MllPi2VggwoXHO7JcAw+KFyRXjngMfq7PdBzXQK8S9ugepbm+JsbfrXddzTFitz1Jb7xLoPNb+UmlBTf1+/n6JMbbfLZUlAbJd82Pjeq9x3CQMtPSlHevyPFAEsvY8HtDR/E7bJyeMDnTd89Inf4bP/62/xQsf/hCDBoJ3lvEwwoM33+LN7/2A7339z3j1ez+gs4zsBGc+907BUiN6NFmQfAJw2Q3twPqSLk7P1xmoTjSn3tfH5qae07q0gnE9L4dzmJQFahRlyash1wlzvqHRrPC163Pd57rUoK2ur+Zl9rvQDmlpjO1eyr8vlZtAX0svjs1XfRZq2rE01sdxGc2lpUvHQEz9TH3+68/bUs95BratS3g9tnY8bb0hBkTmVowCvjQW4tvOXV7jY8Cz7mOtoC08sHrmGO2Z1Snlf0fnph1v4alH+ljm4D1S299U5vydEpv7Xnu4Vib9pEBporOHc2F8WNh0nksBJScsm0qUZCXWScGU7cY+yRiaBjTRBodPnztRxpgyA6vCGEsstL9hXdryvgdIL//gx3xgVJ598QWi23PiOoLs6UMK6lePF7sk70PPv8C4u4f3U7rRu0/cZX2yBjXf+e2bb9P7jr4TNpszdruBV157FRCG3Z7tdsvV1RXXV9dcX1+z3W7BK5uzDU+8+Dz37t3j3t0zPvjCc6w2J4j3XG93XF9vWa9WOO94+tlnWa3WvPvogrjbc7W7whPo1h17lJ1z4Du2KSZJga7r2SsE5xhDwIndpj7sRvpuhSTBOw6H8Ud1StX8+YywNAJRFmCnuJ/sQuSII+BcyX4jzDVWhYmqaYRyGvCaWOX2c1sTQbb/xeRbKpp8iNOFphcp08l6vWaz2cy15dHmIx9OSP1znpxuliSo+3QRp6L4rivplTUJ/KgW7aCk32Oai67rUmp17OLFmNpLvEE0EoaRUQ1YrsSzcp7RJ8LvHJ0zNxhNwoO4lPkq1zVjroeELhMkIyJzLV95Ni3OlAUvEbKUqjRn5MnZjrIgU+rPaxLMXO6dR8VXnvVaLGMIRXNucyBlLD61YRA/AWrJmelck+hBDLDmNWj2cSHC6XnUMsiJ8xWIMdO9JqQkAt6BRvs7g9uc0YmS6CFM65HmLe8tTam+XTX3Bf6lCclMuBXmWjDQCkBLgkP9d6vlj2HKmIZI2rNpnjSd5bSmkhh6tgjmM38TY2/7UAvELSM8ZJaHwK5tT+qfaoK+a/b3MYG7FeByqRl8+51EZvczKBVwQkr2yDoboGkv27i99FyiJQGKS50ktzofHOKEQWBYec5eeo7f+b2/zoc++dPIqmdPxCn4ELi+/5CXv/M9vv31b/DgldcYtztcFmStWqJaCnDLgOgqQWKunOm67DptgxmGULLVdd4TYiSGlDSncr2qXfNs/mrak/Ypmdb4so+EnGk07wEtC9sC81aqb89zqwSr+VR2H6zLMVDT8pfDZ6XQ0rbO9r1jn7UgPyuA2jHnPVR/Vitgap7XAif7OaW0R11Zm7qttu789wEowRR2WfgUsb1V0ptWz7YCc5aR2nPdKg2W+tOu0zGaI2JuVtnSC4eulPm5tq0lWtPyyqU+w3zdanfPJeCT57GciYZm13W062PAQIpckeWlqc75HC1Zmdr2WuA37+cy35zvr/mcLc3P0vfLoN3GVn+vqgn0bjDDkdGv2Wuzcad6mM6OrU+Ov1NUBXVCyHJNtDPhxVKExxjMkPATKBHgLwFAikH58Y9eYT8GXvjQBy3IfzfQb3rWJyf4GHEhwjhYoOxg9+xE4PTOXTYnp5yc3sE5x3q9QdyKq4tzwjhwcf6Qcdjx5ltvcHF+zfZyy9XVNSLCycmGJ+49ycc+9jTre2tk5VAcXd/jVXF9zxACTz31NPvdnovL1xDfcXJ6yiuvvs6LH3gR1/XE/Y4XPvA8zglvvPk2J3fv4Ncb9lHBOwK22ZyY9QHn8JjgPu53JZe8TxvDLBH5XqS8f02azOnEa21j7d9da88LeFGzGoQYGUNmCkqIkRCVzs+JyuTOd0iwal/43F7LLJybwFQBXonBhxBYr9ezJA75vd5PcWEWUyXl0EWdE4SZZlJyCnVMeD+IR5AizFm9TPdFaAYZKQ12FvicM8FdsHujxkAUy+bkkxtOEj2SO2LqagIPpa+pDZIQM4slkHRPTjWuGdNIwvJUkfU7p9rOqdWTmqY8ZgJaih1I9VnmxrSPKkFIS92Z2SrZD7gQawHBl0dMiNMCyjPQqAn0gUtjUzQxG/tHer96QKpuFStXNN9ZyUlIOBCC58wia+K1gK8Y5lkO6/moBYxcR3uTfN1G216ttW3HegDKqjnIQnPNKGOoshmm6wBkgYEfm9ta41r3sxY4loSPMsZmbK2gma8VmASI6exQ0YyaDrQAqK3zJuEo128dYvop03e2jZaFo3qMwSUXMBU8Ho2RlUtxQM4x9h7/5B1+5bd/jU//+mdxJ2vcyr53MbJ/dMHr3/8R3/36N3n5299D9wNdiLhUf2SKFfLO4d3kWlzHbGb6ngUK0+Abjdzv9yXNfJ5vcfPLv3PcTz3XwiS0SWml2hckupUBef69CdWp1yYbkWq6m89DPh91v9IDs3O1tBePtdeuFyR3cEw51e6T+tmahtaW9VZQrYXsto78fbZY1cCobbPd5xNdN3rmpMuMIYGbZdBxDKSUvzMxTAoqJCusjoOIm7xPjpX6OVfNdV1nPUel3zKfp/x7tkAeAzxLoO1YaWMyyz6/YV/Ny6TQzGOrLZRLYHqpT/m92V5aWL/6+Xrs9f5dUh5klt4Cnvc6NzM+08hBN83NEkAUsSQLGnOaf9Jl7XU9c16SabBzQlSZZAsxRWq+7F1FLElNeS+36ZBu+cLfm8r7HiB1nV229+6D+4xx5OnnnuXOvbsEOSOoo+9XBliiENSxObtD13vefPNN7t27x9nZHdbrNVdXV4h4nn76WZ5+8kkuLx5xeXXNxfXAa6++TsDx5JNP8YGPfoQnn3xidllpYACnjEHxruNk1bO93hYGcOfOHV566SUATk9PGYaBN15/g+g6Tk5WKWhfWK1WadOnBASJSOfMbDkI19C5bYyctKDrOhP0G27VHqz6gBaBO42j7/uDAMuJ4GfAlZitd+gwXZZbCBpJEyiHQa5ZaGzvF6oJTLY21dn+Yozs93tEpCRfaN/LMR/7lDO/ZLFbKCJTFrIQ46GgUI07C5o5s1w9lpqZls+SgGOX6Fq/T53DdM7LBAns4BdBsWHiceEzSAJ7dfHjYezInHmIJHeIqr4WFGeG2s4HmJaGysWyFUxa5mW/A5rj1ZYY2ZwBzlzi9DhgaD87JiTUe76sjXMH84XMyXfNYLJbaRugWv9e931JQ93O0VyInIOXg73xHkyqLW09S3vncQSLPKb8+7FnH1dIgWm+amG/7MVEi469t9SPVoBr12PpmaW+10JZLci3e3yfGPgqQB+Fzq3Zx4Cs1wwbz4d/4ef47N/8a5w+9yTSebsYdlTkasebr77GN7/yNV79/g+5evCILig6hpQp9ZA+1zSxHlvuZ+2KrGoJgkTMajSn3fOg9TyW9t63mwT+FkTM5oXJkn1sfuvf6z7XGTyXgEfbn8ctB/RggZbcVH+7p+v5nNW90F77/tKeXWpj+qxWzglaxUAu9XfJLbg8I1gg/MIaHqMr9dlZomdLwOlxaFQNKI6Vw3UwZRYNOFg6z/V+v4nmJeHp4HzfXGwNMnA+4MUL47LxZmXbvA9ljWZjfe91aXls3Y8MGDL/ruu76fzWdbfztcRv66Jxrsx0LsWNn53S9X35rFUeHls7qeLo637kZ1zncd4V+bCdU+PrtwCplH7Vo8PA9fUVu/3WtnGIdNvA+vSU1WrEizI4uLje8sHnnyGMA889+zznjy75+MfOcN7Td4HVasOWPb1fc3pywt3dnuu98qlPfZr13buIm0DR5AohdH5FjIG+M0AGwm63QyOMgyVzqIWyp556Cu89F9sdYDcKX11f8eTTz7BarTF6bps4p6xerVaFKWZT4uQakTaPd2iYC5v597bUhC+3Ux+S3JZ3HjQWtw4qK0buYx5XJhLee2JKX94KQW3CiJq4hxAYkkUsxlhAyW63sxTo6cDVwm3LiJaIQv6+HWsGNFkAyWnWlw5vHlubQr0VQiGb0c3y1/c9cD1ZtHR6ZxajFXUmKNVt123MhPAFUFCIn1AsXYcxVtMeOJwfprVm/lytA1oSANq1NsEk9f/IPqzbz+9l15qg057Ka35MCKvbbGNoSt+qua1BbTuWdk6MKc5BaP7pxSFVEox6TQ804ywDjbqP7Z5tGVvN2Fsh+BgwyBfy1vUcY3o1A20ZUN2vOu6lFZTqeWzbqxUws7rF3AWXzvHiWlZ9WerrEsNvx3lsfEvP2AfgVfBB6KIl/Ng55XrT8ezHXuKv/s2/xos//RHCSc/gwUfo98r9H77C2z96la9+4UtcnV8wXF3TB4sl0gjaGW2o3Z4zba/noeu6kpSmPe95LbLWPSe5yXO+RFfq8ccYzQ0VWZy7+vy1+6uusy2qy+uW26jPR9l7HAqO7bos0fZj6+e9pQcOVYKhds+2fKPdn3nPz/owG2e9/xe7c2N/6/ftLFMuh7f4nOwkNz2/xPvqubL1isSq/iWl5VIfjlm067K0R24aY/397F3Vxjpav5O815vvalmirm+JB7X79Cb6slTK58ktseYB7R5q10AEjgHcTM+RZfpT11tbNGvZpwVmmdfm0noItaWdt3YfvtfctN/nfl5fXaN37874yU3zWzwKynrM+bS9v5BFb0H+uGnPtuV9D5B+9dc+x5/+6RcYLweG3Y7XX/kx796/zwsf+ijXl1f06zUQ2Xjb3GdnZ2haxNVqRdetGMeR/X7A+xV9v0biiHcdm7Xn7p27nJ6eEXD4vrN4mGqzjcMAki4iw6ERAhEfoetWdF03E8Cfe+45ALa7HRsVus7x3DPPc//+OyCOZ555xoTbdHCyVSeDB9sQEMbAyju8z37aHhFzyYD5hp2BqGpjlQ21wBDz91kDkn08c1xQiBb7YLFJU4DlMFgO+jAGvJPiGpKZd4nraDZxm30uxljGrar0q1UxHdfjgCkLTP4996Weh3pc5RlncTM18GmFvzyHcOgbfaDVFjMtR/NKLBeW1taLXF8rUGYXtLbfWWCohfsiXIgQmNfTMoLWBeCYcFzaYyJS9bsiKcboBmJe9620lbVnx4RRYWZ6z+te96nMw8IY2jmpGUn9nsjU97xn67WmEZBaAbpes5lwVz3TJp5o16FNN3/szLVrmffikqB7IMQ3awGTsuUYE2zfOSZ8HQOVB+3pXNNaj22JUebvWuXEewk/bbtt3/NeqgXxdk3rdbhJ8BaTdFhFQYMjiBBPV8jT9/i13/1tPvG5X2Ldd+V+rn6E/cMLvvedH/L1P/wT3nz5FUu4ECwOKWeiM4ELxB2Clnou83ft1QgwF3qdc4SkXW2F+ra07YmbXFaWhI3W/bi0oQDz59u9d3ROm74s7dO6LNG3lu6183fs8/wva6PbKx3afi29Xyf5Ofz+ZsHypvFlfmIWpP8Pe/8aY1tynIeCX2SuvXc9zjl9Hv0k2aRIig9RoiiSIilREtmkJAoee3Q9NmAMbAzGuB7A15aEESTDgKEZQAYMCfAP24B++JcheSwI/uULW8Bcje3rudKV5esH9eSrSTb73X26T59HnTpVtfdeKzPmR2bkioyVa1e1JAOD9s3G6arae618REZGfBEZGckAtZ+z/bXfRzkshnpdSmnRR9PVZsXU75y3G2SLXZuWt1p3EJLzOUxzfh51HRbbXLRfrd8tXTXtbLu79KyVOWVNKp0k9et+WCNusraM/J5gCtQYpbUOW7KzJW+1Y1bzCJGr5kzXL1hQdJ+ttzUHaQ5rvTc6HiNydF0V5qjnS5yZFy1veQPpk5/8BB555BH8+q//OjwRQhgQNhvcff01PHTtOobtBtvtGvfjFoSAvVUygmTStts+Cw7GMKQ7kTwYkRggh9VqH3v7BwjOJcPH5QQG0KmkMxORByMZCV3n0HULHB5eQtd5HBwcFIZOExngO48nn3wHPCKeffZbODldgxZ7KUxsuVcuMa0EUj7cvlg4eGKTzSsC5KuFohed97WgrBQMpkIq7VLE5DjByODeeWyGMXOclCq1dgbGGqRI27qIYhLPKNG4IPq+x2azgcs0h43dzSXGWBIEaA+DNmiknUoxMcA09lsvOk0jeV+8slaJt4AKgbBaLRsgb+xzURacjCodplILnOmCJyJYMVOH0qTBNUEpYzTCZ0obhEos/LxCnigIbnY/PRMZkXU8cRtk2e+B2sjR71jArzMspTNH9WWIhWayI2xAuFWe2jiS34PyrFtPnQZf8rlOWtLaFdPgXfMb0XQHr0lXWx9qXpl7V/Nyaz5bn8nfc0ZR67nW+pLn5pSnnQftvJgDEC0D6CI0q+W0AZRECCuPcGkf3/bx78ZHP/sD2Lt6BS5f6N2FCDpZ4/VnX8TNbz2Pr/7eH6I/PQO2Q76kNXmTA8eUnCKvQ+98xSNaNusdb+vZ106nAiZ2gETNV5YmGtS/GYA5VxK//snrkaIdBUDbUNf8N+1L7ZUW+aF36+x8S2kaYW4u2cIff4wVQC+fpfMc+py7nR/dZwnHl0pawHqu7RZN7dqwzqIWvVpz0KrPvmMBv+yiWbkyt6a1g0rLa110FlZrlEwMNP3uDrmpZc5c0e1R7sOc4WdLyzmh29d91N/VBsbUANrVX9v3yfwxUvZazbNqXg729/F65sWWI6PFj0k61vq38IU0q/qud8rl82G4eEbAt7yBdP/+fTz++GN473vejW9+45vYWx1g6HuE9SluvXqGbQhI4W8MRxHeIV9SGvPEjUT1foDvFvDOw1E6071a7WFvtYeT7QaLrgNAGLbj/TsOhM51YMrJDELIuxIOQz9gvV7j2rWrAEaBnM4ceVy7ciUxBwFnZ2cIIeLo/m0MfY8+ANuhx3K5RDoDkRdTBJzPnjmkXPBJwLv0j6cCERDBMe72iCKwW7d6oYuBRM7BO4cwBIDH8A3GkA+BU1E04jlwGBe/9qxLv6aGw2hYyXPDMGC1WpXvRLAB0yx8WnBb8DXn+W4BYnm2UjKqzPVbFrGnFM7BnOi63W4RYkxxs3E0kCqlk9Pa1nPVVjx6XksSBjl8Wz0DMI9KpwI96jNNn9Svup3aM5b+aeFlt7r1HMv7wYAkLWhLdi5VzotVJxrPkLWUoVUkQoPIXJIVaAA8DAN8vmC43tLX66jtWbTt2rFbBW0NqBZYkPG12tEZ33YBDVu08a3HZxWWve/G1tsCUFKsA6I1L3qN2TbmAJo8Oyc/9Ls2hHcWSACV4W7rB/T6Ss9GEPqFx2MfeC8+9qNP4eq73gbyHRbUwQ8Rfdji9N59PPe7X8LT//H3gPUWi8iIQ7qwOsmcTBtCuQeJMMovoY8GetZrbccMmDWsAJGVYVbW13KsXv+tNdjiezTW99x3trTmaa5o+a4NyBZN7LrTgUfWyWXXgOUTayDo3zWNbZ92jVe3p7+reL8Yq/lsyUw/LO30Od4YIphq/raOjFb/Kn2xo1hda8fWoqWtO41tuqMEyLzV82NlyZw80H2osFBmdCtHm3yj6eyma8GOx+qC1NS4NrXeHZMoTXXHlEb1XZJzOkBwTRnrjKzV38/NnW1bPi94CsKbU7703oMcTZw+5afi57r9EV/o9VTkkzpHrMeg5eT/nuZblV/+5V/GdrtBGAZsN1tcvnI5p3HeoO8jQoy4dPkSHnn0OrrFAtQ5pHCxgBQhk1JqHhzso+s8QAGEnNY0JAMBNMAvPOA7bDabJBB9ymDkfcrQJQCscw7DZgtggf39A1y6dBnL5bJi8L29PTx84zqYgH57Bloucf3hR3B09ACv3z5C2G4RwdhsN9hstgW8OUoHcB0DiEnwefYgEJz3SaBGBlS2ssxV6eCuqw+RF4UcQsk8JYtPwtucKHGiNM7Og0MAuVXOOpIXZeQUbsgpzTI4JUAARoUk4Xa2aI8eUbpkVV8KW4QcY+wn0uHT5DGtlZUsGOsdmYBNR4hhDHEDSUKE5GXSisReUqvpJ3WHEOBiBIMQCOg2ASvfYXBpHjryJeucc77Un7aEa0+49vCGGArOsMaOI5RUmsi7dvlSaZCX6U+JPyRCTu9CTBQnAYxRCNqt7KSuRMFILGHa+bPKQdrwZRpS45xGW51Lsj+LQQP1rlF6ZSTSnhGMLe8uGnPXdV2ZW5l3UV76lndtVMkcpTC7RJjIyXsvzoFkzJTew5GDZKvgfKJL6g+Zv5EVKpXdhmKWTpR9pfTVfLV2GTwonVHUiljkn9JPWtFYr2Nrfm2ZW3Na4UnRQJXzXJdU6gCse8ClitLc5OfkXgxKFaafun/CQ0K73JcIRqQIDwJydsmInG4fjAUcPCe69wDOOuDS2x7FD/7I5/GuD34AYeHAPl8h0Qf0J2d49vf/EDefex6vvfASwnqD0A8IMZQdHT1HXQYQkrZd6wdW/Kz7zEDJTkdqt18+J0U7TfMWqG8ZPkle6IuVEy0y96V0zMgAE0VkZlcdgQj5Qsj0RhYTSOqgBkO2b9ZIkQsk5/jNgtq57+2454C/BaUtkDox0jE9qzk+n+jRqlevY1a8keRTDtvlei2Sm9+L07vZum65IkScjumKhzybCRwAZkxaVrbOmllwqsdhwXY9x+MOHoirnUVyQOA60kTacUQIDQDe6tccL1jAnSJx2udrLG9oBwNjNFqp1JvwY6Sp4yf1qR0hUPgXlfhtOs/02Frrp6pfSNzQq5YHpQ3Li7Z+a5RVkTnp4arfUrcc/5g4PJlLiHEU7IXkNEqXvhZqJN7ICbiICF6opiJPHKUrR8b2ceHyljeQ+n47Zl8j4Pj4GIeHh/DOI3Lagdjf28eiW+Dk5BT3ju7DI51ZSWeQugxuB4S4BRDgyaNzS4RIePDgATbbLTaRwTQARNhstyO4Rc4eDAIoGTWIA0IgLHL96/UaAEoGN+89lqsV+mGDEALW6zWuXr2OS5ev40tf+TqWiyVOTrcoZ3yywnA553u/HQBOindBK4jwEdVYmD+mrfkRcIxZ4ESgxZjTIMdYMr/p+yg4hAz4RRknL3zXrdAtIoABoQ/iKskApT5LIn1iTpfd9n3agdOe0tHTwCUFbZXtjsv/ACRhP4SUVEHH3Gsgq9sVo68Ce6CJIJE02wXGGsGkvbzaiCntR0aPCHjC+sEpFj6fSxgCXL6vR7wksivIzIiYxrEXpak8V1ZhZ3Ik4BLr+R/MpaVjHSkjnRWUMcYyvzYEp/xUfRCAlM7fyV+mbxCDCuMuGVH1tH52DsRQ0kiFn6HeF/Aryitivg5Zg62dnAkgAipQYulVfvJIv7GzySAKCNk2TcCexeBU2SaLYVZAPBXNqemtFXArfHRXuAQllDrKLUrZ2MTA00bfnAGk6aMVa4tXLN+1vP2NBkbAZvuQv5PdYqf50hgUdtzNNZAdBogM4sSP+VojgNIZI3aEniO6a5fwic98Pz7wqY9heXAIRrrLjEPEcHaGmy++jD/4T/8Fx8+/BGy32Gb9oB1R2vvrXAqxRqwNb00b5nQWUK4gkOdaZ0LAyRklZzGd9xhmDIhdhoP+W9MPQLoPDdPPgeyUK/0uD8zyke6HBmcWXMvPXeBX86EF77aI3G61dRGAbduEek+PaVf7mr76PFmZh5hC4esLzOMESbf4pdWeFznHeRzyHWrZputqtWGNOvvMLoNV5iXmBFKOXNnRLrxMdTh00WHZERxjrI0V9W6Lb2yp6JzHPzcm/Y4Ob22GEgLZ1TV9f1zz7d3O80qLJ60hMqU/JjuG+ns7PtuOXiOt96ysED1meTtyxDD0RTdMzroyMs5IfMgQ2SttjhE+Yx+mu+nAiENG43COotPy34SBdOXKFVy7fh3ee9y8eRNEhD4EgAh9H3Dnzl14D9x54w6ufPSjJd4bqL0L5DIWjQChAxyle5WWS/ghIOZwoK7rSrY1ZnXRHhEWC6QLrSLj9r27uPrQJVy7egXAGGIHAJ7lkkqC8wu4LuD0dIObN1/DSy+9hH4A3HKJ/cuHcHknJ8Z0WzCTU4uW0rkk51KoBtVjKvH+itE0M3M2bHQ8p14kkiIUMQLE6nMqQK/rOhCnkLg4DAV8a8UvmcmswWE9FkQ5TaT3NRgwTK+Fd0tw2md0e3OKUozDItC5Ds2zfbdCQX533qGPAXt7q7TjGGMJuxOP06ie8k5Mca6kNspcGM+hCJu5cxxzRQuU9OsUIACoztNoGurx6n6Wd3djA1WyZ5XbgszSU3+u+bkFhMt7JpxGty2eJ12n/V1/Ngd6rCHRoouuS36fA3EXmcMWELBgRfdZPyOyx/JxshGmddi6WwC6ZXzYv/Wzc0Zpq8zN7y5F32q/1Td5PiVLoHSxcRKcIHKIDtg4Bh0s8e0f/TA+9tQP4vDGQ4iOgEjoGIibDU6PjvHV3/0DPPNHX8GD23exZMai8yWZjtDcnk0TYKyTy2h6auNK85nN9NUybnSWzRYvzNFkF33Lc1zPxVyx9bzZeY4ZFAPTUMBWv1p8eF6xIcYtMNmSP7bvmqfqc0BTIKvnSz87gr5at9cDbc/hnKE3R7eL0mlux0CPXerTY9JzoaMvEj+r+/RQO3q48XmRGaR2603bLcOjJZO0kVOFzu4oF+etFLmxKxS2hXla7dm/55xerb4JTrJh77b+8/hbYwvLO606dBtiyHJk7O8fTOonkmRPZqdM61wzVh3R8Kdd3vIGUoyMj3zP9+Dylcs4PTvDg/UpFt0CD+4/wHC6RhzSrsaD+ye4fes2whDgFlPhlBZkMpDIOwAerlvgm88+h/snpwhECEPEcrmsDomm9xxiCNj2W5B3WHgP5wkv33wNH//oR0Bch2d577Fer7HdbJO3bwjwrsODB3fwta89jbt3j3D/wQmuPfwwLmfjijmdSXJZiHae4LJCjDkkLQ2l7cXVwkovHhEYWjHL5977HMqWQk+SEZmsfudzWlmk3Y/IsYTYOecRwnh3k96V0oveKo50ZieBC32LellcqIWBjKe1oHX4TutchTxv49HF2GK0wWKJc1XnqsrCzQtdQh6dSgs/+uxGTw+QwvlKv5QQr/ofQyW85koloLnOCjYVdO0U8IKDWgaD/G4Ffsxhhfp7/a94eBQV5BereuaAihbMLcHdqsMCBKJxfjWfnwcS5zytGoToflrDRH6XedXzpPmqpQDsPGh+04rQgmXdV9nNtWuAqN511nPbDhfhyfwWpacATWtudH2tPu6ad01Pq5Btny4KlgkAmBLfEqUwXecQHSEsPB559zvwfX/mh3Ht296OwRPWADoQliD0D07x/Ne/id//D/8ZJ2/cAZ9ssBcZ7BibUB8a1v3UTgf5F0LIzq3xOXvWQNPD8r6Vd/ZzSye7fi3PtOZQPp8zdJIo46rvrf7qudllbMh45PNdxph+xu5ktowa3Q9LWysrzwOydh7OO+8h31k+HtsDkhPNJBNKb07e30WL1tqZzP0FvVotfrNGgB6f7of+XBIw7ZJTmv+ICJ13GGI7+Ys8O9lRbfSrko887k682aL7XugY59eaXQ/n0czKZzvf1hiZyGRKnGLlga6zpVdb/W45tKu6jJNVnhW8d3Z2Budc5Xgf60k7ozGHfabY/hxaa66l0LSbm2fBFamNSVdny1veQLpy5Qre8fa349LVh/CNZ74Jv1xgsbeHq4sVyN3H0Z0jOBDWZ2v8+9/69/jcU5/FtRvXSvptZh7PIAAAp/sgyDs8eHCKP/rKlzEgxVMuOle8g8IEadckgMiBnAMToY8McoSnn3kGt964hccfvoHtdlsSDsSYMrSFGDGEMbPW7//+H2AYQonpXq6WyaPf93A+nSOIMYU6hCFgJQA4e18cpUQAwjQSxlYMiAySNONLiJ2UGKcHOFNoGCFCUnunUDKCZtAc85zr6xaLIoC1EbPdbidgzgoAu5jK4jNKU4wvu+2sPbZE47064t3Y5ZEo/XAa1k/BttBPvGMJCBMgBzIZ8D5n38v8otPhElnPZfppUx1bUKPnSL7XNCqfZQUon9egbdyVku9a5000jTTAngMAWlhrWurvJcBBK2fdrvaAz9WlDeJSr3xP6X9W0QjldQpQG2NvAZ7un8yPpqUtlnaWVueBd+Fd+5nuh6Wx/nxOAVugXfFMI4y0xQcybvnbnheoadUe265x62IdKJM+m7nXdNN83PLoytqIHEHOIzKBvMcAwuAJB9ev4lM/9Gm8/3s/Apb7jJyDD0A8XePWzVv4xh99Cd/66tPo75+AtgEY0gXKUd1lpvtqx2JlSGvemLkkW2jxsh1rq/7z6K770OpPNQZue8SJqNIfrXmb29HXc2jXYqFBoy+WftqgOw/0WjljdYduv8Xfmm7699baan0PtHdk0nMRzLU+K3OcKq36rJ1oWjbotUBU3z2on0Pksv5b49Nrze5K7ALuuj5tEBGm60LwC2IN9MvYzDi13rNyS4+7hQ1Kf5CbjNOwdl2ER+13ds2W+aTxez32Fm3luV3rU9OoFbHQ6hc5Knxin7FySeqzclLe0yGPtr6iC8IUe4UQsOg8Npt8cbWKHgKQzzMmp5T3DiFGhBzCy2AQamyjz6631mcZyzmyrlXe8gbSdrvF//rb/yt6ZhyfnWDvcB9+0cF3HR7u9uBogeO794AY8Pprr+M//of/DT/+f/pxhDzxsohiTCm8iQmUz/p8+atfxRt372HISmDot9huNui6lKxBGGdvsUKMjJ4DlvtL9EOPuFiCY8Tv/f7v4wufe6oSygVsInkwYwTOzk7x9NNfx4PjE3DMdw0NAf12C8pncURROd+h65ZwWbi5fNt0CBHMU3ApCz1yLdwK06qFYbfmIzPYRTi/SOeRYgBlg4ycA3K62j4McHIolDmnI58uSGFwq5hijNlQdRiGlCpdklvIM/p5LYR2CTo9JrtbpMGePcMhcfUtZWkVUwG1NLbZDz2AFAOOCnTIzxSbPI5jZnHTmLHNCjD5vfVdmpt5L4xTYYka7IiAtcpH03Omo03gKmRJxjRGhUzJ06MS/EzGtato5Vf1k1AZ0rbYT4T3rAGwq7QUnAWWc++1HBAtQHue8rTv6Xdb37V2NfR7LVDbmvsWELwIzfT7dh1qwNcC/S2APVe3BRFzzzvnMcScXc47YH+J7/zU9+IjP/D92H/oEkI2jPYiQJuAzb1jvPD1Z/CNL30Jr73wAtAHuHwvXHTA4Bo7jwagzAEcy/MjL7cPxNvxXgRktUDQrnebBoD4INScMyfHmxx6t+Bc/5s63nafF5oD4FK/Ngi0x1vXMQ4CRSfp0Hg71lY//jTKeeu9GBIY3XJ6vYQYq/MewEg/G1Z5kX6ktmrHjy67eKNlnNgx6v6X7ziFomnjKz2nBm1pQgDMGpBn7Hht9AswOhwnO1cWXDfGrPlZ/808Xmxb5OQONpmTSUQ0JjxpzN15xpulY3m2MTZLMz1mG/asn7U00HKDqHXySp4Dttv6GMpobFE65kKUEo15n/ocA4LiD22Yt9rW4xFahhBKcrCLlLe8gbS/v4+zzQbUeVy7fj3HLhNiSFmbrl27BgwBx0d3EQLjN37j/4MffOqHcO3aNTjnS9KCGCOGfkDYDgA5bAPjt//976QEDcxYhJg8hYC6sFV7wTJT9Olg2hAiOAR8+Stfxcc+/GFcu3YVYiTJApPQPEcd/tN//i84OrqPGBmbzaYcRu6HAYgBy+UKC+chZ5HONmdYdh6He8vcF5cPw9eepCFnAPHeAznURhit5JBnLtuy8o6EBPocQgikLfIQImIkhO0Gm6HHohsXZAwh15Uy4+kFbAWqCH75PISAxWJR+i27czo7U0vptoSELXqBayGq29dAgrMgH3FKDQa1ENELeBQajK7zYDCGEOA4AamsI3J9IqQo2zFzYIHFzqkAoxYalp4xRp3XYRYsW8FLlMIDRdBYALMbjE0vISzfxJR1TDKzBY4jCFDj0/2wwt32g5kn59pSfW3DoXwm2phGWgi/ybPtWOfRsNW00Px8EYNG5qn13aSv59Rlx5hyYczT7CJhWFLXXJiYli2ye6rXQQs06TpsWKA8Y40Eu0u4iw5WxhR6lIdkLScagZBSzy86BEd45we/HZ/8kc/hxjvfhu3CYe0Ynhy6TUS89wC3n38Ff/Sffxc3X3oJYbsG9T18Tm8biMGeEBxAQ87geYHSMpQ1jezY7By0DAJrTGh+0/N2Hj1nf+epzGBOzhbLV5rfiOo76OaMntIOoSSnaI3NGhXjHXpT3VAKTY3oXWGfLRqc9+xF3t/1bh569Ww5x9aQM/W9g/P9mzNcque0wpspc4aRfLdL/qXv5Pwtyk9OArsC21bPF6eryLiZPtjxaYBd8Y2h1645bRlh+r3iqJt43lo2U72eItc6o2XsVMZIY3235laeae1UtuSulRe76pZ/JeEV5m1DiWASDOqcw6JbJDpE5IuplU7J0TaMMUJLt5lE+Pn69jw9rMtb3kBaXrqKvcPDJKTFe8XpoteBA6hzuProwwjEOD66h1ffuId/8T/+K/zFv/gXwcy4cuVK3qlw6IcBm+0WgTr8f3/7P+Dm3aOUvjEMONv06Pwig7IA5uTYIEoxsgyg61Jq8GHbI7qUKerWvRP8z7/1O/jxP/tnsN2ewTlCiEAkAnEAhx53Hhzj9/7wj7ANjNX+Hk7PTsFxQNiuEbdroOsQncOAAA4RDI/OeXTwCP2QlUmHMQlAw3sAAR0xp18MWfhmD4gRAiXN96JLl+ZySClr84pw3oOGHhTHxRKRvPchxmT4gdLWOZBkQ1SeARDiEMpOGTMjDEO6KZmBzvlkbC4WySgMEV6dS2oBIb3gBeCPB0TruFwNrPVh6rEe5F2Oemtf6mkBsvQvguMAt/BYLjs4BzgST+WYrrIG9gxQgBwUHw/pENJlrylDox2zBUC1wlcTrwoRVXXZnQIB2NJHO765osGcnRN0dRINDjGfZaOc/a7tGbKlBRYnihq1rtLKJaXwToYqGDldfgbkRNXOk6alq4zUlBiFWUAjV3zSmqOKFqrfcwpoFuQ13i3ryTlwUIpa+ouRneaAgKT8JQl9ZBQgImGaesdul2LW47SlBfjtd/J+a23NGQPZNZTTxLpKnlEO2PDIa9Y7RE/oVw77b3scn37qM/i2D74P3aJLu0bM6CJjOHmAOy/exAt/9DW88PQ3cf/eEeSkHYMxgFOadJfOD3FI/GXvmdP9nTVANQgCzP1L82O3tJ4DDTpSwia0sSFL1gAufUcaawHRAlxn+Fj3T8tQLVdmeeYcQ9+unbJWk7BN6zef7yzLQdU5Z6RJH23/dIiPpZOU1s6ZBpu6LQt6R5oTHI3RApNw2xyaJE7McpUHUHbHWoBet6eNagdFIOU8AFCybeqxye9NGTIz3mpeiZESEok8ZVC+u4PcmDyhaoO59FNuJCA4cEh1aX5tGTJS9HOE0fjUz+7iYz0feu5H+mIkXu43INcHsEpbr+iT/y9GRtLNNK43NWctfWHXrtTJqu+6r3PyU/PFnJyRZyfRFjHpct2e/L5cLLC32kNP27Sr5wjESW6Qr52WLstsAmGIiUfSdT0ZEMaU/Er3qFpXnJzQnuq08OeVt7yBtFitwM6DieAkdhGMGHtEZMI7wtVr1xBixNnpA3zxi7+Hv/AX/mI2FDjdNZQvjQWlOzJefPllgHwKlwspRbMU51KmIiCBvF4OoQXCdrtNjBQyw3nCS6+8gs12i7SnEBEiwOTRcYAjj6P7D7Beb8EMrJYrrJZLnJz2eaGkTHF9PwCuA5gw8LjLtYo+3b1CBJBD5KnAL+CGUIyi9L1s6ydm1J4BOSu06OqD/loODP0AuNqjCWSBY8CU1G09OrruzXoDIpcxp7qThsc2gOmFlEBtHOl/spDFGzG3XSx/S10ySPlMAx4NFHXbQMGWiR6IWO6tsL1/WtJa6kvj5N0CBijTQsBqAxzPKd2JcDdt1KUeW9WOUpLyndDbKp3asJruHMwB5aJoIpcdK/1eSwHPtTvphxHyrfNaEs6pdxFZQLbikToMdKy/usuLpnNlDVjNi02aN/6ee2YOfJ1Xdhm3BaiJcZz/hSwz7C7pHLDdZdS2+jsHSOx6tHNq3y+AQv7lRai/jw4IncPgCThc4Xt+8PvwoU9/H/YODwCXDZYQQcOA26/exMvf/Ba+9sU/wHB0grjepHHQ2NYYM5r61Vkwq9tuGEu61NcZ8ITWFkxbAF07dnYbk1ZmtcB+NECV2QiFbBzNzbe9rNf24yI8q8dun2+dLUnPRXC0NBhlqqVFq29zO5YXWj/GEDnvXUt7LZ9knPK5lXHl+cyPu9aHXYMtB195B9IHBlOtd+fWemvsGkiPz6VrPNL7mIDdlmyg0iNMMp8SOXRuTBmuy5zs0DRpzbXV85VuN/xr9abtm0jUKE4n1HNRzi2jwZdqjWv80lrfFQ3zkfa5Plue0MXOrzWu9XyWOUcbDzHn6KeMOSnTCPmdEKf3YcpMe+crvgPaIeK6b9XYJjXPl7e8geQ6D+czQ2cuFGvdOQfidDA7EuHatWvwHths1ogx4vLly3AuJV7YbDbovE+eGb9IO0niSULaMWFOSQa0JwxAYWCd3nUERBHDkHZjDg/3AQCn6w0CM9LOI4HgEYaI0AesT86wOV2nO4/y5YVhSHGbrkuLMHrGQLHc2xFiwBAiOjdVpDrMQZ+RkZ/e+9GYUwxXey9SSvKWWtMCSGd2Y6JyyFiKPS+kFd146JvRdYvyrMQT6zuMWgJb6tXpjO3Cld+18GgJwDmA2zKI9N9pZywboY6xzaGSzhEQxRPZApqUsVamJSuFDs5uoalHSOqZ84DtKnOKb+65io8ahUYd0KyjelbqEIDJU4/XnMKzczXpB1G5TBNAbcxgakjLZ5q7z2ur4gO0U8br9uyZtTm+K32ZAXG23/JZVHJKf17qzl6NFlBujVX63Cm6tM4k/XHK3Nj0d7u+t7whhksOAobjOhsWiBAdYeuB7YLwbd/9Hfi+H/08Dh6+AXQdiADPBGwDTm7fxavPvYiv/P7v4/6tN4B1D2x6ODgMnMNEicouVWuuWuMTQ1wXG/evZeIcTWxpAdYW3ca7/sLkGb2+5Xc7tpR8p4igC5Vd6/NPWmy687HvXDzTcwByDvQCiU72MHjLsCjvYgrGWnrB9qd1HizpOwZ4DFttyZQ5w8bKrxYQnjNw2qUenV17c7y3i1912FQlf9PLAFxzbPM9rK8vmSu2X5x3PVoh4S3AXd4zOEK/86dRrFFH5jP93VyfxVjWuECeOU+WtLCFrd/2t3Uvm+hT59KF2Jt+vKdSsI3FUhV/ESowIWfE07nwNs3+uOUtbyC1QsoKEM/UDJHLQfdLh5ew8CmL3Ha7LZ/3fY+D/X3EGNBjNJqc7KBwOuejQ7Z8NqhSP8aZK6CMGavFaA1vNlukO4JShpU+bhHjgDCkyyR5COmm4BCwf+kQne9SWJqn/DtAnpDOtKXU2tt+gxhDjlGmkpLbhgnEmNInirEhn0uacMIYgiaKIP1MsaTkHIYwVOFGzrt8v8+4IAsIjOMC16BL7zQRpft+ZJEkujkwj5kCZW5FydtFa+uXelpGjhWGerxTY6Fe8HoRW4VglW3aPWIMQz687FIyC/1epQTTh8lWYPGGU+kG5fTtVlja8U36bwWP+r4loHSdeuya3+cV2DxAtHUW2jsqBmNrbLoPFy0MrtKuameG5YNK6QCAa4PeOfoR0USY69LyIst82V2tOUCn22rRoaw5Fb46mVOenxe7s1GPbwTFOhNkq7/W+GoZchZ0zq2fVv3ybAvgMpB22rNyZQLYAdETonOIC49rTz6BT/zwZ/H2978HceHALodr9AGbB6d4+ZvP4eu//0e4+cJL6c67zRYduZTpi5KsY3FU8NhH6YeVHxbIzIFkPU+WL1tGWGsXeyJPDN/aDJS6j86lC9M3m82kP/JM0qVyFnWcj7ky5zCwNNBtaZ7Rz82tCy3rx/oweccag7ot3d9JqHGDL1t9t3Mq9GLFIxdZ2yPdUJIx6Dv55uaFmVO4sp+eK7VrTf/d2tGs+0qTsbVoJ/2wu8w2sZBupznHb0LGl/dzFj4dPmznyPJY+Wloossuh5ctcyGHRS6bzy1fWVlZ8JN6Xj/T2vUq7zDnKP1p1lKLEzR9WjSysqJVdL0TGihbpmAaEZ08deiUvqn69HhLHQ3+btHiouUtbyBFTtnZhFH14X7vfI7THQVWt+hwsLeodiaYGYt81mUYBvjVPpaLRboJOMcyR47gWHvT1+v15H4jET5lmzmODND3PYZhC9+tAMn4RmmHi+MA7yIcBixcAA8buLCH2G/R5Wc8AB4GOArjDkPnC8BOOz1tUBJCCucTA0/i0UMISbjGxFiSuEEYLcq5pkrgo4S/EbgYinXMOhd0ZYWzVebjgsipctV86mekbgvC7ELRn+udJ/lOPweMCnKxWFRjlPCi1vtW+ADIWRAZ3EcEjugWnbh0Mm3re5qk7aQgbOhfhKRXt8banMKuivHU1IJW7mVqKP0cDjAnPC0dRnpU3TRjaRuRnsbLmlvG6y7h1wI+rVIBCRrPiOj2St9U29orZuufA3ZSWvHvu/pn65xr04KAigYYlb59PymlqaPgPMNEHyK2oa6WfnY96vpaa29ubdvnWuOvAEX+zkksf+cREREWDkNHOLxxHR/+vk/iQ9/7USwPVogCpoYIXvd47YWX8NUv/j5uPf8yzo7uY9Utge2ABaf6mAjkHUKmYb6Ou9BE6NniV2vcyN/VDpd6dlexXlpdrEyxMlLe1eePpM3kuNtM6pL+lHHxdL21gJ0diwV49vcWSLxIsXIl/aQS9WHD8FqyRNPBOslaPGu/t/Nr69V6rNUH3Xb6PaQQqRky6LVoqNFsQ+vZOlxyuoNpxyo6XH/XesfOod4tnQtXtPqAiACqs5btkpljP0cnlawr+5zFG3r8FpO0aDCn7ywN7HfqoWY42Ti+Wr7aMVr6zrVT1jy4Wu8tvdKSuZbmLVlmacIZJNkz0ACK44U5Amfr9J4wNo11WhxIROVcsNVVMj7Nay0eezNy5C1vIDEIcGnXhAEETjsrFJEAAwjOecQg23xAjKEAZxEe6/UaIaSLYFndlZOAqsPQD+WchRgDIjREyeg7dhKwBjZbvVszwPsO3aLDEBlpSwjYP1hib+VBkXD1yj6W9BDYdTi8cgm0XAKdh/cdMKRUn77LWYFA2FvtIWajx/nx0tcW48UYq92j8nmI5b1690i8yNy8fTrGCEfTBRZjLDtLZZ54KsTtgvc+7VgxT+PMdQidXeD2911AUj+nhXl1DgDZzjSKsDUGLTBCiHAhpDM1BDx4cFKEt17c+p1SV6wvWyUS0FUrK+1NJJoagHNlTvFocEVEE2Fu+3peaQEF+XyivA1A1O3Y522Y2pzybfVHK3fNH5NwppmtoNb4x/5Mn51T7rsUnB37RfoAGGC6o315zqY2tnTX/EQz4KhVLC11u7bvLcXWWhf6OxsPr0uCxgTK2eTCwiMerPAd3/tRfOypz2D/8LAYOZ4BbCPO3riD55/+Jp758tfwxkuvYjhbY+E7hLBFl0FXRPLIxhxe1zVAdEuWzQG8OcMCmIYw2nnUcyBAskXDOT5pATugnotdAMn2v/X3rj7YiIbz5ErLyLKfT99B00nTGs8cANxVNGDbVecuGaCfsz+dcwBPs6JKsU618+Za66w5IDmRyeWz+f7bOmS3qBVKfF4pWMPQYU6na8yV2kdlXLXql58W5Gv6vhkd16r/vNJa81Z/aOAvY9LvA+MxhrniKO10a3q0HDK6zovOle7nLh2jNxDKVSbnrIciB9MnlY4eQ4On7+r5uygm0OW/AQMpwZowDMkwAlJ8aZCzM+mMTowBHBl9vwUxYbFYIISUPvvs7ExRn0ra0L7v4ZHSEo4GkitGU4yMGAeVStthGMZdFOccAuIYsw5KIXx9D9ct4L3DZrvBjetX8TM/83/H8b176E+PsfQO+wdXsA0RN9+4hYdu3MByscSyWyIOA8ABzPmSWedwfHycaADO6aTbilYWjTCdLJy0E4TJM+l75DjfWA5Bi5OLQAhhqAyvIshkfpL7uvRHh2lJOKAGq0JX/awVkHNgpKWAtREhn9vFPbdN3gIV5TlmQLXv8qFMcgRPHkMc0hkkziEQkTFEzrtCDjEGiCvFOYcgyRuyMBFPEIB8aa3qB49gXpSTHrNQfBewaPHFXNml8EvbkZFynDQArBJeWvDFmC5F1nPc8nrptuY86WXsyak16Z/+u02veYBu69GKmkHN56aAnzPLWIU8Pi8Z9oimIOxcBcZp4HO0E9qeB15asoORdoxZP2Ne1/3UGQGdBgE01ilY1q5T3a68SDK+3Bc915SC6wBHCN5hWDo8/r5343t/9Ck88u53YuMIwXl0RHB9xPboAW4++wLuvnIT3/jyV3H75uvgTY9ltwAQgc4jMMO7nA1JXbyoedieQ9XzbY1yIIddcwrVswbJHOiu8L7inZZH3M5Bax6Fvlre2TMhdq225ljLYtvnuZ3flizdtYNmbZ1z5U+Wx1Udjf7Njaf1bEse6PXDgFqzWicBAvJaxdJo7Mf0nj7rvNDjkhLVWmmNz/Jtayz6b2v8S2kZE015saOO+aKysXKdNtsaMyP9k0yVq0CatRrsIPNG6ns7xl19vihv6+LIpQgk1YdWqeZb1WvpOqenBBOQ2tXR2KrV7zldsGtMml/kDJhe0yJDztZrHB7sj+8RktON8xySoocWdHkMUE7hoh8VFnozoZBz5S1vIAFcUl0nRQqQAP4YMYSA9XqD7WaDs/UZwrDFIzceAsilS4AHRmSHrlvh6P4pwBF7hwe4/tAVIAwIYPQhXzpGcmYlhWJR2R0I8EXxJWE0DCFZz95j//AwPx+BGABOO1qMDt4xYmAc37+Ny4d72NAezk5P8Z53vh17+/s4/i/3ce+N1xPAyZn0hhiTp5/TjtliscDBwUHmrcRM3vsCNkUwxjjuOghTpz5zMUomi4mRszcBq4ExOGC9Iiw4YB8Ezs+HvGskQAbKmEwMLMItpyrNTO1So0ogpMbCMKRdHWaAY0qS4agy4Ky3Sm/12nh+KbKYdHx3E2gwILeYknMp1WimhygjRymkgzmllffOIUoy4EhYLPYQuw6Di1jGAGIPonTYMPUXxchy7EHwY9uUPfja4CyGUaIfYQRvkzHGODWsoDzf+vdKyFGl8HeF9tR1yzO5f04Euaij1s5APScyL3pnrwKMqr+zIZjgysCYKy2Fq5OYtIxv+76MWzITCr+PzzNCGEo4b/oc5acAqZbRwlwbD3NKoHynFI+U4kHMOyCttdFSMIXOkSGx5CkrE8AY66rWRB6UPEt5nci9dOOglFe0fDO24+QcpRqLA8FxkqzBAXC55RCx8B2YHdYLh+6JG/jkF57Ct3/3d8J3HQZEOE9wwwDqI45vvoHXvvUCXnnmObz83PPotyl8OS5dUtaeAJf4hwnQN7oLGJBsn5TPWKbwYwUQZN6cXAQudM5jjgw/jjrrKS4MQUJ/EwLLnN4jIlDXlbnhTGdyqbeU6TQX5tkCuS2QZGWDgK6K50xpOUK0MWnXm901qzusJAZDEnzmsMdpu0mmZUcVTx0pc0bdeeDKPm/XaFq/2kiYvmdpWQ1Tg17UdG+C4BYAV0a87bvIysLD5rzQHG1iZs45x1kLQGtH5FxfLQ2KHCUAJWveaHQSuTKn8vwo81DwjPCe5c3WDmlrxlvn/yZ9R87MRwTKV4/IKk4HIJqEAsDljKges+jbYhRkJa+NjZHHUpYUlmsqaOSrGCMij/cSgRMW4eR+zE4qBnmPEOKEJ+b4rLXOrQGvI4s0ZnCO4Lt09Q47pGsQlNxjFhknilDJ+oyh4TwGwapCI3mvyAOjg95kecsbSP16C+c8wEg38+Z7edZnZ+j7Huv1GoDERK6wPDzA9WvXcHa2xunpGtevP4zlcoUQGCFEnJ4cY+/gEMSEe3fu4fDKQ2BiLJYLlPz9OUGCADHv/CgYM4j3JOkNGZcOD8EAfLfENmxEFmDoA5xLmZQIhLt37wFI9w196/nn8OST78SNRx7BydkLAICIvFXaecSBy11Fkn1nuUhpI0Ug2LMGwJgRRH7XHkQp9cG4DNIBdJSABLskIAijV0vXCea82yY1TpWxPjcGJRDAo0EnC1kSOcCNgKPl5dTGk/1OF60gWl4IKyTt9xqcT0A6Ja9i4se81CmFrhHGCxUJKuU3YzJvBWwwV+PO1RVjSYwtHTol/bBKz9KjbTyOYK7+vK5D99W5dOGx9w61wcmzdaSfsjvZnKbqPf1uC+QVxYlpaJL+fXanjOo+zhlH1iCryxT8MHNljMc4nlG0/Ux+gpoeNkxibmy5waptKTEyGHUI7XllDsjNhWrqOXG2X6ZQ6w8CuqzAE/BQ80GErUvK0XEyQjw50MIjOkI8OMB3fN/H8JGnPo3ltcuATxc+dOzBmwGnd4/wyreew4tffwavfusFoB+wXaespb7zcBLWVIQ4irGnadGSJ7KzJuu10MbMr147ZR5zm9ppId/PAfP0Xk3z9AVGi4vr/pR5UbxfQmpDI93uzPztMiY02NLGjwb8b+Zs3lzbLcBW9UF9Z+W0bjfGWBKP6M9ahlzLwBnXKZl60++t8CgpdWIJ1Z6xc1oGnf5O180zz2jgP+cMtLotjarOENcG93XZpUOFJpqm9csj2CVSdTOX3Re745iTw1bjsP1sJdHCDj62fa/GmeeHxaEjuh6AOIKn81UbdtOxZwNL7ARVLD+29Le0IxhQ7zISTRiq2Zeap0csdq4cYC53IE3mNbcRYkBJeZ5lHnM+38q1M5alTkWbES+NY9b9qN79Y5S3vIEU+wByAIeAzbbH6ekJNpstXOexWq1w6dIhFoslYgyIkeEdcPnKZUSOuHzpSrn/iAgg53C2WeP05BQPXb6Cu2/cgUOHxXIfPueXlyLCOJ39ES9A8pyLoUYAHDH2FgvEEBFchwiHpV8icsR6s8Hh4SGcIzjfYbFcAQjAlnDv6AjHD76KGEMOV0n1S5sAqox6qT91wE8Fhozg1aFMITOuVWgj6E9hYxTHbW2rGMp8NA5KFrCfi3ceIQzVYhwFXJ1JT0oCmcn3ahWH/LMCdAJITLH9ap0DkL9t3dpAKEZfjAgcELLwlMv7GAIuczgEdIhR/qfIZvshym8i0FB7bexc2DnXNGrNtRZGWkloGsxta+tLVuXnOEc1zav3UJc5A2CnYaA+d3DlEL1+T94RB8G0H0mZWMOoBQgqsHcOaJSwNnlPz58Nd5HQV6ug9VzNglTmyX1S1olg359bF7sA0Bh6S5P52dm/C5W2ARuJ0DtGF5NxBFC602jh8OSHPoiP/cjncO3tj6WdIEfo4IDtgLM37uLWCy/im09/HW+88hpOju7DRwYPIe20qHX2x+23NWDkdwsY7K6dfce+a+db5nOO7nbOWsB6FvipcpFD8rbe1jqVNaKBljUS7fdzpQa39efVWIgqQbpr97sFDFs6ZRiGyT1w5V2u5Z6do5bBMmf0pHe4Anr2fbt2yzMNOSVr1bav+2XHW+uWum09V5UjQBV9oa7tb+vv0q/UiWadzGL5T9daqo8nvGSB/pvh5TkDUrCV1iOj/NjhFOKpY1HmZtc6nOsPkJeAeVdjpjk+Sbs9u3WAXcvnhd/btnUfnfNYLBYNeZeiZ8g4JcFcjE+pl5AdB819vz95ecsbSKFf5zuAPDwY+8sOD106gFt0OTsPY316nL1FjMgB+/sHCEPIoS8OIfTJE0DAtevX4bzDI488jEv7ewjrNeJ6C14tsB3SbhQI2XMfM8DlclmrCFPZ2TnYX+LS/h7ABCaPS1euwTuPkwcP4PwCnDPPkfcgdIhDBHkPz/kMlE/3PFUCrHGXTmLiWtlXAFgtDPGelcI1GKuUuSS7ECOQkb3gVBhZFlIFNngE7faAfGlWvVcWI7mqLgGOkvhBdp5kbDYu2yohXWw/rWKwYVs21t8CFl1noXc2jkJkbDfbyugAGCHme7RKgJGTaNu2wFTtTcAVjaE4kx0Js4Veg/QpUCv1l2bnt9/1+KVIuKEVqOM81buaAEpWSMZUMFswVcasnmkpPxGqQhPdB12X3kkFRq9gW0HPA9dc6QR07KKfXSva6Ezf+QlQ3QUidZ+1ApadK+/9eMbNjGlundi/54CG3SmYVc6VEm6NARAvrKZzkgmEZUiXQsIBQ+ew9/ZH8AP/xy/gHe97D7rlEn2OyeoiI56d4e5Lr+HVb3wLN7/1HF556SU4ELqYQk7Ipcu1xZC+KJArvNXgVf2e3bmYrr82zVuGhv17AtIbz5OrQ2gtONOypNVOEzQ1cFyLH2x7rWLXxpsDiaPDSdeVeLTeQW7JbT1Xk9ArI2PlO60HKtpQG2Banmg5KuzZtfH3qQ7XfdG/F2CKenemkmtmbHO0mPSDah1i6Wn7o/s0BcT1POp2iShnGp6W8hxqvio0odFe1jynadOa04xkilyT0tpxLXWRA2M0/uqz3AGuSuxlDF/Fk/p8d4tGrTKVnzXPWRksbVj+jxkztHSVLTvDX3XfUGNL3V/nKO9sDfDIOJeTnB775gw/5RB5mW/DS5aHdU90+xctb3kD6e7rr2K1XKHzPudZZ/RnyGmWF/DOwTEjbrYp9M13eOihK7hx4wZiTGF1Y6YMh7PNFmFgPPbow9hfEGJYg0PAEJNgDvnOIVlc280GISeEIHJYhyFvuzK87zCcLXDj6lWAHMgtAFrkaAiC9x2c60rce2SAyYmvAs77lEkpK3/xpch2pVaaOrZY/lkgJswlXu0qY1Wm5wQE0ihMxpIuc5U2gBEU6F0G26ex/rEt6X/pM4xRpBce6sWsvThzglloA2BCixYosX2SsemtegsydJtDGBA47RSdnJ5UwpAonzsSYAadHrOtGDXVbb/T/UrT77VAtJ61GOUMSbv/wl8tmljANSdA54CTfDeObV6QtZS3NXhs3zRwER6y3q9dYHUCCs3nrRCcFlhu0cnynn6nNiqswqjntdXHokhMX4rCBk/mZNfcWQVqaWO/m+tXu672nBOlsdu163PYnXMeAwirG1fw4U9/Ah/6zKcQL+9h8AQfCR059GdrHN2+h+3dY3ztd/8A9159DWdH9+EjwJKdkajwnZ4n6zjR32vaM2sA0M44ZgHwLtBoP5tN2GDmy/KQpfPcPLZkoK1XaDFn4Oix2z7qHeqL7prpz+04W+ultTMu/daGYSVrbB2Y8reWL1pvyPdV3zLwtfRuAcu5uWvxmx3z3K7hHD3suHXRc9OaO/lJROncMdpz15rLi+zUXARwT+YtphA7m6JesJDVeeettV2ltaaqOgydgXHcrVBV3a+WPpubJ/vupG+qD0S7k1CdR4PWWtb90vPakhcVUUx7m80Gi0WXj8CwOS9UgiNr5y5zkc/pnqtxwC1Z+yctb3kD6Sf+xv8Nly9dwmqxROc7HB7s4+DgEIuuw4MHD7BcLrFcLsv9PpevXsPRelNAg4TeJeITNpsBbuVw4/pD+H/+P/42Hr56BYQBIAfOh8a8TxN+fHyMe/eOsO0HLBcrDCFgs16j324RYkzpwIcBb3v8sXTHDqUQOwLBuQ6LlQdnIAvnkbqQgC8T8sWEo6AiaoPKmllG74kIVzEkmMfQOsnUV943QlruNposPJfiXWVni2LtAR8XURsIpGfGi/msEosxVEZWtWi5jnkF6sv5rEDR7wrYahWrhKVeICkonRLejkf/HmNMZ7RoNDi9c2VXjMshASR+ikJv8WmdXyZgW21Jt5SUBVzMuRc0nlmy/DP3fqsvpU5D+6khMpM0AyNgtbxgFYwViq1wjph3dWUNWE+a3llp9aPVjua1ufASO/YWv8hzdoetHm/63K6pXcCHOfGArrtyHMTz+6TrmlOqc0C7RStd13khGmOdgKwPkVUAQJ3HZrXAt3/0w/jeH/scDh+5huCABQguENxmwGa9wf3X38B/+q3fRn//FKsI9CdrDBwxcMrG6XKIspO2FKiy68R+pvtIZp21QIzmk/Z6MIC0QSdtuOlnLLiyjgMiGg9mG3Bm67dFz3/FFzNA6CJApbWud71/UX7U/QAyHUxIn5aJFuzZ9WDP+bXW6dgwKk+47f8cf1h+qN+lSsbIM3OpnW09u+aipbs0v9gzU9YJa9+d+3xOzmi6X6R/0o90pnvUr1VIZtZlc3hA/m7Wr/ppnaGWR8srasvKhpq3ZEKZy8ZO9UXXjfysnieq6mydLbRyY8QZdd2WPnbc5/HVXBHcmXQtgOyQletfiMQpxhjPbwERhJwHKP2vsY50f8fPEoZ6s8bTW95A+uD7341l1yEMAxZdBw4R2819DGeMYb3B5b1reHB0C6enp1gsFthuzrD/8BPwvkO/XSNGxrbvEQNjsVqBnIfvOgCMEDa4detFHCwdfLfANiSrVjKYdF2Hhy4tEWOH/b0D7O3tZVDm4ZzHcrmEW+xhG9JdTK7z5SI7BqFbdAXc+HxxLOWwqyR9qew2iSWd+MJ6vmRBIwOl9N2o/D2cj0CoPWV6UUgMrRaaQIojhScQXDp4HBkeDtt+i84w7y5lVoP3mol1mFyM9UWKNgQPAHye75QpSi1iTiF4BKrCi3yuJ4ZQpVyXsc/1ue/7agdIh/bpUikExwhDRIgR634L9NuUmh0p05/3KdQTeb687wA4xDhAGydVnxpGQowRHEJKQ2zeGY2W2pvdmhOrGLUN92aKFlhTEEAVT44vYRSO8m6jTj2mVtFjFKWqQ111ae1qphdRyG8Br+bFVr9g+IFjRDAgUMBay5DSdbXA9lhPpS80oYrsSGNLO5IxxkKL1D5lWVFehJ3sUWHa8KNEJAvG9BhqcGSNjNSuzHByANGYnYzT/6Q3ruvQxwj2Do+++1348Bc+h7d/8NsxrBzOwNiDx2oT0d+7j5dffgnPP/sczh6cYH37CCd3j+ADw3mHbehLPzgmOeecz46Fdhhn+V14KvcpyRpMJsHKvhbAl+8E7Gp+mANktmjwPIb3jPyswcIuQKp5b26HdXL2gGkiF3YBkV36QH8uY3kzxdK5gOK8FgnpOo0CFE1/ZPxarovDUHSG7ft0XXLycDcMFCtvJ2C6YUTUoBGF1qLXW8B1Spj0HqUHJtEHk/7z1HAZAf/o5CNKTpZZg7D8TAJKOzHnjPJdvC5htcgREqOIHftexLWAHlOsUdogU6VTW7J3Im9pVBIaJ2kHatOg0JXwaNRJbXPraEJn6Z+KCGgZ9bYfdZ/GsYneZePMkbZaPLfLYJLvXZ63q1ev4saN6zg5fqD0ifRhdJoK7ogxgiNSVJXQd4aPdZtiXInc+98NJFWe/9qXsd2s8cwz38AwbMEccXp2iqEfcHBwiIODA9y/fx9DP+DSpUvw+1fw3/2V/wGr/Q7UpTNAvluhH9ZwkbGfkyZQ1+Ghq1cxnN7BAlscrBz6AJydnuLywWVst1ucnh7j9MEDbDYPsF51CIFx//gEd+4eI0YCOY/lQ0/gqR/5s2lDcUhnisg5pGCyruw2ON+VwKsQIxx7AC7f7UQInM7nDGFIggoRkSn/SyJDzi6MIVsCiBiAywxJGZQHMKc7jMD12R59V1EA54PRjI1LUbhdH8AABocKZACJYb33iEP7zgZRBOPvU0GWBOLI7HJwfdV1aSH16eAsh6CezQqduSzGJKgDkFPrMjN4CIDPB0pjKEBWAxbdZxue11LoGjxHAMtI2AbG3rUrCZS+8joiEQAPsE/Ai0QAh6IUK7yulK0IkvMOdtpwOhv2KPUKgLWgvXyvRFIrhFGKpORWk9acc6Ja2Gvh22X1GpTxyqoH2jjRdcyFRNkwCH1w2IZEVX1ESrAidUu9WoFKHZMQJOFdZegRpXt0dvGT7NLanS5AeIIKL8t6rsCAooejERRy/i+Hcmcek/4yus4pwzE5WKyxnKrPOy/FaAoFPCcnh4xJG1Cpj+PalgQzyZZfMNBzwOAc2CdvYRcJjhngkECW77BxhP7KZXz8C5/Dd3zyE9jbX2HoCG7p4YYAOh3w6le/hZe++nXceu0V3L5zGzEkJwg4h+rGiC47mTpyYJejBjiWM2h67Zf1A4yGGxEiYgFq88CjbSzqZDjOOdy4cQNHR0fYbreFH3YBjl1AT3uLzYsgTnK74BHhHkIJvS0GBE1D4zQAS+2M1etnLKCS3+1n2ijT7WpjbBddS93jcCZGR1ZHIDDklOf4bL7414zL0lLqnZuPidFk5GIrJG6unpbRFGOfdjkzyEw8ChB5MA9V21U7IrOiRAik8UdmUM6ym85Mp/v3nEt1ytUfrHgi6dbROUAsjgsqjhglocf1QqPB2Bq/Bd1apiKO55C6fJ0J5wxxGbYkmei0UycDbaSxJedqMTtw3nUP1rgAgMih8ogUhxPJWqv5uYxVyQs79s55iAHP2Tk6mjq7HQ1Cn7kdRP3TfjfdcYtjmBtSArEs1HIdU/3d1LEz/bDP99ttmku5EiE9gLSblOSzGNWgtMMf5RA3o9xrKhd0DzECvk0rqYcjg6bkmC1veQPp5PQ+Ll86xHd993fi+PgYwzBgtdrDwf5B2q0BYQjpTh1HhNOBcPny5XKmRINI5ojlcgmOKdU2yOP4wSmuX1om5gZj02/g1x6bzRZn6zO8dus1xLDB/mqJ9WYLIF0EerY+wzAw3vW2y0DZ9g3ouhzmpUCn3FPiXLofCRDhBxCn3Sa5C0CAmPCkNipiBt4tMAq1mGyYEGV0rgFz7TnIwsmnLPUuSysGV9lbKi+KI3TUTcBkWkBTxVCAosr6JUUEhAauLQUnn+vQQi3IrEAZQkiGp6sPTlqgI/UDdchdqwzDgAWnsDo4SU4g4ZFFTJi5m3qfS7veFX7Rz47epPr9Mgbjna7aVLwnBm0xyFrPowY4+rvyffqgemcsI9CfnFGoBP/Iy1maNses6aP/FsDi/KgUND/oYuk96bF6X/62/WiFNGrwaekldUjomFXQLYBm+WGkCipwpgGOnVe5SNLuNug1ZA1BIB96byjIaTha/bsdu4AK2dECEbooRkhaE+wIwQOx8wiLDu/88IfxqS/8MK48+gjYOywA+BDBpz3uvPo6nv2jr+DFr34Tm/vHCNs1Yhyz/8W8PruuK0DRzoEev/6sgDaaT4PdKvV4p5dCSnuvv/76zndtsTJiTjbNgXph7PJudgTYOube13IBaiz6vjLhPb07NjW222u4tUZs+9ZQbNGnPI+al6s5Qf23Xg+tfuo2rYMmd65yUow4Ygombf9ba7weU0rWAm4bx7oO6et0DWs5ltZzMrhicbxWHqVcivyafKOG3tBjteE0LXM78JZf3OTKirotLW90eyMds0xRmEYXjjEZjlQ/Q0Q5wqd6Orc57rjZM71pzmfopOddz4tQTLU1twZbn8+tB4tX7HdWf9s6WjRpOSNbfbTf3bt3hIO9vXrs+Xz+2KBUYOprRNM45ya80BrjmylveQNpy1s8WLuU2tt1OLp/BnIbAEcAUkrprutwcHCAvf09XHnoOhaLBfphUwl35pQ1znXJc9P3EUweL778Gu7vd3AuAg7poi28AdkS7FYrUFyCCNg72MfBwWX4+yfYhruImx6PP/H4RFATUVqklBdq9hR57xFDnzKCEVVgQ8IAgNoDBWjvUwIgc6DWApvyLqYMLm1Wsa7eIQzJ2t/2PRYzc8LM2aMdi5dWpzt25Er4ivSpKJaG+S/GiyhlHZMt456EhKjv7EIqoIdQgVVddP0tQ0zTVtpPdx3lNjMdTk9PIaFkoJqeeh7tXOnwj7n4f1Dd7xpIRJDKS6+VqPYUnSdQrEe0xXMAwDvqkWyPwPxt8OlB1LtHqAGnLhbYjAZSvT6EB1uAcNfYW23q8Wpa6L+1oUJE5UyEBYMaZNq1rOubAOIG+NEKxPJVoiNGrzTqtb6/v594FNMzVhMPpKG1lRkaIDaNPe/QE6Njh0XIZ4Kcx9YDvSf0nvDIe96Jj3/hR/DE+98D6jpEcvCRgH7A5s4RXvrqN/DC15/B8dERTo+PQczYbrcF9Mt6lX+27xKaZg1DPf4Wj8waIGb+NY0sbaxBdpHSAr26vvNKi8d39XO27WLM1vOs+bZVr/68Bcik6DXzZkLu5kBSEziq9m36ff2cXYNzY9Tvtna5W6UFUCeytPRr9PinZ8ZdTvvsHM8yUHBEena+f601cd4Y9GcFS8y00TIE54w/4QNxTOt31B+ltTbdZ/Qb1Tv91fybR+f0QEV3C+7NvALzu0Da2LNttHTBeWWOpq1353avrXw/r+1mm0UPZ12dQ11z/Oe547D1A0jROOc8+2ZkK/DfgIH0la9+A6vVHrbbAS+88DLWZxsMfcBjjz2Ga9evI8ZQvDDkCD/wmc+j5cUnIgXck5dzuTzAiy+/jmce3ANowHbYZCGQgJjsDvAQUwgXCL5bgInwxu076BZL/Nh/93C1k1E8FSGik80Bl874LBYL9NsNyDm4CIScVlKSJZSsbd54RIQ5qS3sW0IUqHdF9PMV+MmkSmkulUdbaOZ8BsC2DVRhLHIpXzKe6hAqDQQphxVapaQX6FSRTD1F8rwOsbJzIL3Q8fzWGGj9Ls/oVNECIiKnOFom4OTkJIVtZd3s1M12rbqbChjjuSo95jQH00O9Mh5mrry8WtCz7GU1DJ8Y5RLktqDRNNf0YPNMDcan75ZwxrzWiEZvofOupNGPcVqn7Y/mEeccguIPy1+7jBFQW1nMAbwJGLHtACl0LJfWjo1ty46rRXuocTXbVW2OIGnK18xcLtKeG58OwWr1zxoVrbrKdwSwSyHBKXzYIXqHTUdYXX8I3/fZH8AHPvkxxMsrbIjROQKve2zvn+KVbzyDW996AfHeCejBKc5u3QE8YaBx10poKHdvyGfWmWLBh55n0QOE2vmwa64m84MGbwEVvc4rdg51vdZRdlGDQq9/+btpyKq+F5o1dKatY+48hC3aILA8aS+8nhgrDbBs22uCTaBEYcyNszU2G2Kt2xDHz5xcsfTVDlmra/VuXKINJ0ThHFAcXbW+s3xs5yE518Q5ksOaNGlo1CFS9A6g1KHbnNLAGJmOJnSWvk3kkhqDzcQmnztgcp5zpASKsTOVl2OIndWPumhZCCCH5avdLMXDWkfqsaTdOF/1z45bv1Pjq6nM1rJIy1nb79bvF9Hb9p1dpSVfyjpHCu0GTcN801pOobnVWiYqyamcm+4Oa0yj5YPodX01g52bi45Jl7e8gfTarWOAHiCECL/YRxc7nG6O8eqtO3j9zn04ohJudHCwj0ceexv6oc+HMgFHPguOFLMfY0r3zUxg3yFigT/40tcR4xaRdAz+GIbBQ4DLWTpCjOhDwGp/D+9+73uxWK7KZXO6kDOCjYHFYlEEmRZ+smNSFKwSTtXicGK8TD1guxYNMN2SHb9jOEq7Nj2Hklq67NqoG6R1fZ33YyivYvIYY+XJAzSASXVrBSrFhjq1BMGckNVtaUWFmWd13QJqW7tvk79F6TkgDD0evnoVJ/dPwc6B2aUwh4bSbIGmImh5BDQtECpzbgFphsVNRaVprPuS+sBVqIy806JN63drBKT+uDavqTnQSoMyEEphIVNQYIWiFuLSjA2f0c9OhHIDzOo+VX2bUUC6jUJn1Ubdx+l8Wj5ttZMUSN1P69yYAyEwbdlxaVroud51NmMXCGoZUyn+HmDnsek8gncYOo/v/P5P4mM/9GlcunENwQNwDisAtO5x8uobePnpZ/DKs8/itedfxB47DGcbDBwR2SGA4dUu9Jwhoz9vnXmRfuudBTFGLF01/fT7c59pQNziN/3ZXFstmurPhL9afKPbHS8dn85ha50XWiHJL8uzLZ6r5rzRd/2+ddIxj9dPiIPnPJpow8zusJR2CUXu7QJT9ru5+Urh7ARgum7t+O0/6Z8dm6UtM4pMTo/Eipd0mQsFlXqYx99bbWlQ2pIJLVrIuxV9GvS0v0/kJKZGl37WFq1v5TrGVqik9Mbqo6ZclblCez3Y9TXhIxpxl8UPLR1padXU07NlDM2z4f5zc6R/bz1jy645qORJEumz9SVMO2JWsDi0Zow5quepheHI1XJnyku7x6bLW95A2gzLrCBTCBw7YGDAuyVO1ls89NAVdF2Hvu9x6aEbeOSxJxCG8f4fZqWkGEgHkYHNdgD29vDEE+/E2fq34LzHdgjYbFNmsy4bPEMYsCIPTwTyhM2wRT9ERNfjkUcfR4xApDE+u4QYSSgWIYVCUfJ8pm30lIjBKqsinHOabP0vgaeaMay3msx3FVCdE/AwhgSUR0aBey1YbX810Ch9ijx5BiVGfPSqWWBpwYQUmc+WsaGFZ8sQkTr1oW3bln0HqMPzhDby92KxwGpvD3x4gPshAJCwu92e9qYCp7Fe/V6METHU/axC2Hw7Ht3GEVjDUs5w6H+6XUsT5tETpj8bAcHYaPUup//Je77zOaRCDIw2ILeKthKgPGNoKpq1jJHd0fMXKy3gU9wMM4CsVZqKIxfrfdZnuqrxaD5qzJcFsPo7q0Tnwlfn6tmlfJfUYXCEswXw+Afeg09+7rN4+3veDXiHsFgghgB3FrC5d4TXnnked198BS8/8xzuH91Ft+iwCQMGl51FPp1ha+1U6J0tKy9afa5CZ5GdNRgNppZMawIlU7RcsTS+SLHPze3WXZS/iAhe7WTscvzodyifI7S0awF8vQtxXl/kHbm43K7xyTmhHWDd1r2LJnbcmoYayLbAocxpPlrXpIVdi3Ptap1lx+OKM1KGXa/3XeNRPYZA8YpmBCRHcHvereyfkxe7SlNPmO8t79hiwbddR5HmjKj0tpVTziWZEVW7NT7g6j39/lxIGiARNufLAz1WAmZDxiw/VmM32PCiZba+C7zXmsu5+WPmdH8VjbqwfM/ybDsclVDjsQrz2GffJD+2ylveQPrWsy9juezyvwW8d+iW+4jssNrbx72jY1y+fBnOeRwcXMJiuUKMDI6A965Ym4nYKTzKdx6dT5P8nve8F3uHl7E+O4FfrOAjEEPE8clZin0nh5MYcbDaw8GlA4TACIHhI/Dkk+9C3/dgGndhZJaTVS23Io3eS+8dhqG4uwBk0Cv8RyiXp8mBcL1wUsKlqSczcn2Jnl7sMcZyb4YF7MhxvJJRROrw3gMkmbrSwcqYQwmZuZy9kN0zadN7n7yR0GGHOctLFGA+zu8wDONulRh1lIeqwDAxoet8Cc8bBVybb4rxx3nHJMSS2jQB7fqi0TlFmcInJdQC4JCM3iEErE9O0W8HBAAeydWlDT49PwlMq1A605buwwi+eQIORZD7roN8PBpfKHPKPBWyCRxStStllWRFPx49dJG5+Vz6u91Won9WSi6H23Es6XPzJpipa2q46t1ZQuJVHa5i+6X5o+wkcG5fGqWRHtZ0aglmq1DtWB21aWpLC2TZ8du13VJg2iPPMZaDz6265gCIrNm+77G/v1/PeVZkMZOL9WTJM5RixiknLInM6DuPw8cexqd+5Cm893u+E4v9PQwxwnce/WaL07tHOHn9Dbz41W+gv3eMWy+8jO3ZGbxL4xg4grsxnKXLqfo4faDFJOQcnlP99s4BkvqfU3a6CJRQbLhUX0r6IMBTPPiFSmW9SwKKmics4Ib6qelbfpvMjS52vlsGyhzfTSur/5wDGBoQpnbrC7f1+rJ8tAsktuRAq20g38UXQpmntE4T4XfdDSQJf6oxc02r+bOb9c6fHs+UlLRTTtt1KfpP5I7oNWtAS5GIbKIWj0373vqMCKNcS8pbscAo22T+tJNH17fLQLIyo5hkWY8CI9fPGkJzukYW2sz45/go6brRWHc5dI4ZxbCVIvyFHHrOaJ/ttbJWtz0mianxi+637mPhrXxcgvJQ9fq0fGnHqedrV7mIEVHaV38jf0aNZD1l/c1ggkTLhJ985xGGAY4kSislwmj3S+PA0biX70D1Om2N7wLDLeUtbyBdyTtEQI6zBdB1iwSUQoD3C2w2GxweHuDhRx7GcrFEP6SoXk8enhycYwQCNn2GskxYOgdHwI2HH8alyw/h5PQBMAwgMPp+izD02KzPAAAL73HjxlWEOGAIPQDGlctX8I4n3o6lXyKSBwdOQCIwFssFeNjAu5TKiZAu9nPksFyusNlsUrxljrlkSuedxCgawCkuF1mIRwaHZGxF1AdoK6CEKUCvvjdKIdHU5/NDAhwT0xJRkuCOAHLonMcmC1bvXDI4lCITpTQMQ+pnADin4JUdBo6ESHV/9vf304W7YUgpPuV7oFpkjCT4iAjOJ2M37VpJeMg0FJAobRFTZHiicqEmA2ByORylYZioM1LWW9oxI3pgiBHUJwEyeAffp3TjpNJUVgvbUbo0OM93KUraWkFbYsyVIE27kGIEjYI87bKquHeqw4kKX9DY5q7QP2uUkXPlPgX9rDgegHoHovAbc5HOctZB0spaOWcFYkuhitHcEp42y1bTgBHrGynFPWeQIlSoge/Mjl/d6fq8lzxnlH1lfFAyJiTRiVXKlh/LHBjNrPtHQEmMkkan+lfGjkIH6QMZ/pN3HCfgFQilryn8NsIhpdunmORH7DzWYHSXD/GBz3wa3/ODn8bq0gHIJRmAAVjfPUJ/9y5efuZbOHrjDt545SbWR8eImz6BcwbQMzxGfiainLo7wlG1VACO6dkMepLBm4BQ5wgcA0jomB1EkSMosggkpHujBkVbhvdpHWnjZwROQkUBtdpgsfxIEOSe5mjKz7sMaV2X5o0WWE5jaSes2GXI2PuAqkQ7andf6w4NtFvrVd6xbVs+k4vSnZd6sv5CQrhWlossYZfOnkhIT9KrVChetWGAv9QpMs+GW2qaJlky0qJVdkUraP0h38lZ5cQTAOd0/3DJIA+h4WSambvST0pOp9FAlEEkOafPfMmcW0OkkiMNftSfOdKAn8uOgIDblhyzdUzCI9Xn091ErmRpTZsUnigOi6otSuubaIygoHx5+7jLUc9Zi6dtiGjiUFbMRlV9ds5ETBCPsjeGnLzL13VXuI13R7noPlqZ0qK53sqS1TKuunb9Wq6JfNE8LxgWiACNjmQUP8fcDmJIuI0IRKKvpR+jo681vjdb3vIGkvbCkFqcSY4mhuj7dObo4Ycfzm9x9S8tkiELJYAc4F2+jJSBw8MDbDYb9P0ZNptNafvSpUvo+x5XH7oC5z1Oz87SHUbOYbVa4fKVy1juLRHiKBicjp+MEc4nAS7fL5dLAHXoH1ADrJgTCmjFNB5qG9PT6uQQ4o0DWhY3V89JSW2igDrKBIoxjheuuuShdd5h0XWlb9KHOYW9XC7BzNWB41YYz3a7zbHoHs5N+6oBpFa849mBKBxRFFs9vjrTXaEzoVrwtUEwPbxtvSfee5weH2PBSbnJIcMWaKjoM1aMVtH9deRKQgUtvFP/U0L2cedt9LoLAJHfq/h1JQ9bAmdOqVnjSD/PnDzyQB32OVe3GKl6u90aIhbcjHWM/dd1tgBia0wWuOixtp47DzDYdqSekL3cEyMHKEbvHPjRZzNabVoes4BjDnjrT8qaoBT6a0MdAqW0ydLnJHOT1zDEfN2Ad4idx7Ds8K7v/hA+9fmncPnxR0HegxzBMaE/OcX63jFuPvcCbr30Io5u38bZgxNsz9ZYb9bonM9nYIwhq2lmhkKVHTp/TkbPiaXhXCjTnBK2bchntQd7Gsa1qy+yrkfgPC3aMLGAvtWn80BTq35mzoJpCmLle8tzE3mqntW6S/pcnV1sdUT6yPU4dF9I6Q+7rlrj0s+2wunmSpm7Rp26TdFtk/PHRp7pOZjj09aY5uZY85A2Wq2zxRZ5tpWEQSeYaI1FnGkXpfkuWlc88ybe0+vM0qFuAMWo0nxHNDXU9c9d5z3l/dSPyYigjTQ91/rYhfRD5J0kJNBzXXQj757Li5RJ/9Eee7gAT7bnO2KzUYnNUiMzC7zW+9JWXe+bN4DOK295A0nSY1cAAcCi60COsNkM8L7Lu0iHKJ7EbBjFKIAe8NkNyRyLocMx4qGHruDk5AEWC5fqwAggrly5gtVyidPTBwgxIjCnHSCO6JbL/Fy6nLXrutzXdC6DnIf3taC052VaRpBY5oV5qFZcIrDkIkogMd0uZi60M8I63WwszVDZtfKgMUkFM2IYU1uHEODdGFZn6w0zysiCZy1A0i7WeL7GAgIAKU272R2TBAHSF/2M9pbpn845xFArg7q/o8CbeE0DJ695BpfyuZyVANWLfxdwnytFYPNoJE2A0QxNy3ia48IYGtH6rvG37XtLeThHCIGbvEeGd4Um2jM4p7Rbyiw26p+lwQw4mSjOHIqi264A3TlrSrenaaTXowYEjqahExqoaFCpxzmngC2Pyne7DDkBgE71M6izaVE8/JzC7RxTlhUegycEBwwLjxvvfAc+8aOfxxMfeC9o0YHIwRMhbHsc3bqDzb37uPXCy3jhmWfhYsDm5ASbszOcnZ4CROg5onOuXPRs6Zd7PKFna+5bOyZ27Z83n3q+LPhvPdeae0v/OQCo5UurDanPOooseJ6sE7M+dwHxsc9q9wFTB0Jr7C2a6vHsND4bvGnrsyFwMcYUqtvgBd2HVj+1jtg1RyKvQwgpIHqmn1q2z/GGlm1C03meqR0gut3WDpYOj2y90yq7eNk6Ee33+uyrXSPpIQAcmxB3p55hLs5KXf9c/+fmW+vZIQSQm2ao27Vmd/FRqx/mk4lcEh6Svk3WqamnNuSmToc/jWLHO9JmvKbDjm/XfDADp2enWeZAwIW8OdeJiXwd6//jG4Nz5S1vILWAAZDOroAk1jfdHi2XxQIAc0DMOzvD0GMYevhlMqqGfkiZ6Ryh8x0ef+JRXLlyGcxpV0bO1RweHmK5XOLk5AG2fY8hBqw362TAMGO1twIQ05kk74phxCz3cKQ4d6mvFtjtVNbMrFwUmZEVCJo8i1qZaLoVrw9QDu5KHaPQTV7bfgiIbqS3pHDUymlcuLXw7vt+BFYxwjGKAWoVnjWqKsXlauFgt9zrPgiFCCHW9NBx31ZoyfdczhkkvrFCXyvBcQs8h4YghZyFEFSYXky7OMpgkx2vJCwH4AJKrAYeaTt/F+DQ9C0HJl2dnUzTXPOHVbC63ppHxnf0762QmxZwkecrAEs5Xaw5xqqBru0PkBWL8WYCNWCwOzBzwLOsI6o/s+Nr0bw1zkroqzVrwaNOU25pO1enbtvy9dRpcL6iIUrbMHNhUx0DjimF0UUC2KEHEMlh3QGHj17Hxz/9ffiu7/sk3P4SQ+cwEEDbgPX9B9jcO8arz76A2y++gge372L94AQnpw/SHXCcd4q8nC+yMknTejwHpNekPN+aD00/m8xhFxBqAdl6PdalBbBbv5PiL/19qz/2fV1ErulinQOEqb5sgWjLSyn8uM7ipeV0y/Bp0dLKjjlZwkCzn3aMei60Q2xuTlpGo+YZPXYrw+z3UCHLeidAxjPHE5pu0xCtqREOoIR/t8bRmr9dc2H7o5+zRqeMxdap59PS1AL7EkniWjSc9kHTgM1Y7S6YyOaWs0rLgzmc2DIuW3JX3pcd3ZYztyVD9DM2hb2WPUKrMudEOcR3es2CvRtqjqZ2zC39UPo9Y3xYunvvdzoGi47glIHWkUvn1JGwkc1KMbdGNd1GuqIatcUBc9hiV3nLG0gaVI/hROlsBuJoIBGlSxE32w1CqBdKSq0tB87SjdPsKSVDyLsWIQyQg6rL5bIcWj45OcHZ+gwxBmz7LfowwDuHbtEhlEQKASEOYJazUg5dl87MyA6WnKMSgaJ3jPROkj4sWxIYzDBFtVgpxba2Frf83gLEMUYMOcTDkS8XgjJS7G6n3nN5bN54v8XAGAuX3SddWkrNboHLc1q4iNLRYQBlsRh6CK1jjCUFpeYFobfQzCq0VO8YE1z1Ia9gZkbgAYEc4MY5T+w1FZZ6/FbIiVCyC7/ME2pFapWorksr8OXeqqLz+FyEPnhu29N/V7w0I+gSzdu7R5qmk3HFCHbjZ9XuhVLik/4RiqEp89L3fbkPSxulQG0wzHnFxYkgbVpFcx4IqcYl76Y/JuPYVSwQuagyOG+dzSl0EFXnpzQI8DHCM0BMCCBsCQirJeLeEh/4/g/jez/3Q7h8/RqYCAGAC0DYbPHg1m0c33oDzz/9Tbz2wkuIZ1tszs4ABkgBAu99cTgSULzIGlSO4596/HcZPBYo2efsGgLaRpGmlV1rLXq2AGYLfM+B+1abrXFLfwVYVeA7MiKm9VuemrTfAKdEdbinBlKtOuXdlrOkogOV/+2koaal1AujD/S7dse1RVcLKHf1QX+ux2VLC+RqvTJX6vmdhnzOyY0WX83xU4t3WuOcWx/n1U+UHYyYhozN8VoF7Bt1F34iAjdIoA2Q1ru2f/bvOZmqZUpLrug6RloCQPv58/RFDLUhXWWbnZxprB1wwNQZZrFRkeXeI4TROLOGfgBP6hA9GsKQkgApOcOcXFpy9KLjDsN2Czn3ZsdezRFhEmI3Yh1qJpC6iA6cK295A0kTUf7FmBMXcMweaBYski+2Shd8+i4ZT8tuCVBacEMIKaSMHGII6HxKIS4Tslwu006Uc1iv11iv14iRMYSAbrFIYXYhlB2Sbb+B910OqWOAGOQ45e8PU8/NGG8+FW4CrGJmwCjnjM4RtLmWCtDX4XfzNC2XrXEERWDos1EWQj6vNR7OH0KAI4LvPCjUuxLVTgtR5cncNbfjuNvKSuZ7TikQycWUYz9EcLZ2QKptdxVGJ+F4aUES0OpP5CLQHRGWiyUWlLK4UAw5DJFKPyQ0pu97BEyVbEtxT3Z6HE3GPUfL9XoN7z0W+fyXbSPXCKIa8GngcxFhZEGG9jy3AIhWzDInIUo2u7FOnQ1xFuAzEDlU/deK2AJa3aYdQ6mXR0N0F4hq9cuub1nDu8DIRcsuw+zN1DcHBMFcvBJCJ+dyAgbnEDggEhCWC2xXS1z/9nfjkz/2I3j0vU8AjjF4DwQGtgFnt49w//U7uP3iC3jxm8/g+M499GdrcGQERPjFImebS333+SSvGElpUG+OHnPhUq15rMM7284a/VkrfGrOsHkzZboeL1akXTFY7PsVbahtXM3yAdA8OqDpqGkpsl4DptY7LbCZXsAkmc0u2oo+I45J2zf61ALDc+tmTo/YMicHCgaZeV/z4YX5hVAuYD2PN1pzq/tb/kZKgmHPD9m+Wp3TAuW7+qJl9nlzeV6ZtDdjAFljpuIJM8cXMVikThu1ottqgXUigJyHTmvd0nvyt8iV5Gwdnx+GoUqFT67t1LF6u9WGnhMg66YaclZ0AWo9putwRIiNdtLxlBS5VfSr9As6+cq83LRzSKBKBs3R8c2U/wYMpHTGJwGP0fsNABwjtv0mH4gm3L59G0SERT635Cl58perJeLQIzBjf5UudnUERJLscgwixnK5Qtd1CCHg9PQUp6enhdG870AAFosliAbcvXMX67M1mB0O9n06bAwAMQAxGxUxZU/yLmV/YgAxDJDFpA2+AlAzCD89PS2GCWPek1nClvJOmOxcSBIHIKXohqSqzuewBMgBaXGGIQDsEGJI33uPxXIB128Rojj9xHvHJeX3Ip/DyvZ/SmhCKcRI1iTnf7sAECkVrRdTy6vZEnbagJI0sNojI3/Ls1HytzQEvHS1KHkBApGLN8U7QnfpAJduPIx7R/cRX78Fx2PoXrZC4LxHkDNrXVf1fxSWcdxx0EilIdA0xcRbA6TzWQ8ePMDBwUG6n8ko9CKsUINiPWYrkFshT9WcmbmwytECjKpPOVwmhsRvLtNZhLLwfAsA6PUgTDYMQ0k2YL1oFsxYham9dXMKfpdwntAFM4CzQbvzynlK5rxCyWdTsvXlxpMRlOlMmRe98ymjJpIBS8sFNgRcevxRfPJzn8F7PvrdwMEKkQYQM2I/IJyscffFm7j5zedx9Not3Ll5E8Nmg+FsXTyFRK7IAO88skWaMmJxveNB1AqlrWmgQUyTtzitQfko1dOakVTs7pH+Kb/rHYsJjXcYUun3aX1zxtmuespPQrkQNhRaAVkgjEmBSl25XpH/QEUzohSmLGtefyc7s3aNA7VTrNVXO48Vvzd4vwWIKoOGx939OaNIz4mla0teJepQ+b82GWmsuPyUKzjmjCBLVzuO1vyWzxVLXHRs58kFjTHs+xUNaMoX9llbdPhgjBGsQuz03AuP5hbrZUjTsRW9CMbQMMKn68sYfCy7M/VuJlRYfUv22siFGhOQWsd5vRW2mBppLYyisYxgEL1bI79771PWW4kwYi74yxqhdt6kDqJpUpfW7zHGktBJ03Dsb53Ft24b6LdbeE/VewDKPZhzpdX/lKaY83UsyZnWwowX0ZtS2hL7T1B+8Rd/EZ/4xCdw+fJlPProo/jzf/7P4+mnn5508Od//ufxtre9Dfv7+3jqqafw5S9/uXpms9ngp37qp/Dwww/j8PAQP/7jP46XXnrpTfcnZTkbEGMyLEARfdhg059hvT3FdrvBMPQAM5755jfB/ZAMIwK6/I+HHnvLBfYWHRyAjggdEVZLj+WCcOvmy7h8sA8AxeMv2exCCOh8B+86EHksFysc7B9is+nx1a8+jWXXgYcAHhJo4BBAHOEpAQ/vHJaLDt4THAVsNg9AGKCtdi2wdSghkLZDo1JQLUEmyk8XDfxjDMVAiZwYMOXNRUqb6imDlVyvIwwuGZAhqIQRJGcV0vvk810juV5koRY4lu3xSCiprVkAmVpI+iyUpoUeq4zFnuPS4YpStIDYpTxIxZdPv0MxbCkjrZxEG6AFFuzQRcYxB9z4xPfgPZ//DE4cECilZyef74VBEoJ+0Y3eeTM2uTi1NEyk0qvvCOvBKOAEwKxWKywWiwl/SFzxHC0sb8nvc4K+ZQDZ74D6suLWeQYC5wP6aa1QjECMJQ14q05mTndRhbSLDGZ4cvCKf+cUoF07lZGF2vvWalu/b0N/9Xvlp/qnQZamhy4TQIh6R9SujUrJqbmojHAAHSjdx+YcqMu7q2Jg5ztYfCRQABwtwPAIqC4rlAABAABJREFU3QrDwSV85Ec/jx//m/89vv37vge079EhYLUNcPdOcP9bL+Jb//F38a3//Ht4+Stfw+vPPof+7Az9dotIAHySEZ1zWCDtGhEzHPLayjIk7ZImJ1WSi/J7UtA2dMkCXjvH4/PpXxJNDkQeyCtZ84Gmmy56l6TF83a+9feWZ6S+Fn9pud8Oux7/iV5IMsIVWREy4EqhBwyEWIxj5HXlGsaR/l232wL3ejytnzKOOaC4S/60DBdNZ83jc3SUfzokUNO+Dfzz2YeYHVsMyJ1pjqikaU6yJpHX05jy2Nar+6LHZ/vXMrbn6ttlsOwylnadzZnTK7pNrWfn+qbra/Uz7V5wEYR5VY8OU0OT0q9US0n3r2mn9Zn+vTxDPksbB3D6O+XtmmbAs3/Pyf4EczwcdblehzS06Xuahq26NZ3suEvbme8IiQfHn+05I6IS+WQ/nystfaf7Lriytc7yX9j22/z3GHY3/3x6RxfNW2BOuoozHmBOY96BRc4rf+o7SL/5m7+Jn/iJn8AnPvEJDMOAn/u5n8MXvvAFfOUrXykZ3v7+3//7+Af/4B/gV37lV/D+978ff+/v/T386I/+KJ5++mlcvnwZAPDTP/3T+PVf/3X883/+z3Hjxg387M/+LP7cn/tz+OIXvzg5aLqrxBjw4MEGfb8FI8L7tEDIe/i8QPxigaHv8eUvfQmvvPoKrl6/WsCicw63bt7C9evXEWKE9yn86M69e/CO8MpLL+JrX/saAGBvbw8nJydYr9cVc0dOOwd6Z8I5h1/7tV/D4cEB3ve+94PyxarL1QrrzRbMjLP1GsvlApFjNuS2WK83sEwiC5+Zc6iPy0o9Ce8YI4YhYBgCui4xS5W6GUihcKzTgdeC0oZD6JC/mBVAQBpn0gUppG6RGZezsUeUzm51XX1WRO/YsPpcFEnpS95GnShioCwG3U+9wKwSLWOKtWIUINFKv9ry6giNbPjbVLGkuQn9FuRRklucnZ0lmifrr6Kx1KsTQUzOWIhhpL2WFyi6f7I7lX5iMo5x3G2h2BpvpSBM2zVIfXNeHd13a0AVgJ/9ua16tTdf+ljOtJzTZmt9EFHaOVX9scJ4F6Cw39mxtMBDC7icpwBsmNjcGHX9A3O50JUZoJjWmWNgACN6AsFhG4EuOzyic3jsQ+/D9/3ZL+DGozcQVl0yrBgYzjbY3LmLO6++hme/8QxeeuY5UB8QN1vwECDhihPAwzzhbT1+nbSmZRBaWuux6s/Hn4Dm2hqk1u3bOZgDFa0dES1brTE1VyxwH2kwz28VbzEDbtzhFQeJc66A94usYW3QgMd3JOS41WdpR+S9BtH2OTtXFb8zrBqctKVpkt6PkyyW1iFmx6f7Z+cOQHGUzRU7Bl20DLJ91ZkHq/aImnOe7uh5c7vEmk67zh3bcdj+yHc64uI8A2oyN5gH7+khVBe/5y2RicwrczkzVtunliyXcy7y3BNPPIHXX38d6/Uai4Wv+4G2wW2N2tg4Z2R/13xQYRu1PmojcOoQkL/1v4pPGotGH6uo1vSOMpULbbxFVLeo++Nd4tn0ucjc80uLxwRHXKS/b2aN/KkbSL/xG79R/f3Lv/zLePTRR/HFL34Rn/nMZ8DM+Ef/6B/h537u5/AX/sJfAAD803/6T/HYY4/h137t1/DX//pfx9HREf7JP/kn+Gf/7J/hR37kRwAAv/qrv4onn3wS//bf/lv82I/92IX7c3a2hvcOq9USi2VXBM8QY7okLY7C786dO/jVX/1V/PW/8Tfgu4ghbLFcLnDt+o0EXCPjbHsGZsb+3j4ePDjGP/t//So2mx6+63D/wYMU2paVgFjkIpSlbRFGb7zxBv7f/9Nv4Gc/9J3YbJNRRM6n7HbM2ZtP8K7D0J/i9OxsdpwFMJJkw/PJKOoHRCU4RYjpOHABH9p71xLa+meQM0Y0hhZ4RxhCMkqTETbAK+CivQrAKOxtOkth9KmBMS5wWcga7DG4XESn69f16EQN43mW2sM6d+ZEl5iTFWgjrqSTnxgVejHn92PE3v4eOufB/YAFORBCZSDJcy0Bqv8W4auNjnNL1kha2BRQwwC5MT1wbYxK+FFbgNvx7uyCqlPT+M0IMFm7Ok6eY0DMOx425AcYlYxdE9wwkSYKRvGQGuzsAewW0LP9aIGglmE0NtcGjruUmlaA5xUNdCKlf7k1ePLZuGcsOBtOziN0Hv3C46FHH8UnPvuDePIjH4I7XCHmjOybkzPQNuD2qzfxypefxqvPv4j7R0fpUuh+SJk6ncsXIk7P+bSMQU3HCYA2Y5Z7zzQAmayjKgykTXMrG1uAsgUm5/qnw3bPM7JafGRljAUPlXNJnd+TbG62DoZcujh/wakdVxqDK1c3zPGt7qMGfNb5ZsfYogHbUCv1jq1vpAUX41vL+9Y86vFJHXq9nidnW7LfjmOOXwBMwhL12GIckzaNdxnOdmVn/6xsM09l4LpbFllaii68iDwvdTKXsDDbr9yTyhDRtJsN5TbN2jWh/677WK+jvu+xXq+TUR9jobV+Rr/fNGzhJ3S5CM/pvlbRQcYQmaOrfmZu/mQNalnU4s0LqI5S5zju6XdA3vmhdNYo4Y6LVS5o4c1gBNv2m3n3Tz3EzpajoyMAwPXr1wEAzz77LG7evIkvfOEL5ZnVaoXPfvaz+J3f+R0AwBe/+EX0fV8987a3vQ3f9V3fVZ6xZbPZ4P79+9U/ALh06RAHBwdYLlNWrmEYErjNuyXaW8kAvv6Nb+L3fv8PsN0OAAjL5QrL5R4YySu9XO4hhIjNeouvP/0NPHhwgq5b4MHxCc5Ozypr3AJW/bukA//KV76Cr371awAchhDRDwEhJENpf/8QRA7b7RZ7e3tw1CHFUddeagviUlgd52x8hJQ6mrBeb7HZbLDZbMqCkBAzRl0XoGNoUf6WdmNMiRjEGJDwizlLPYRQLqJN79RCRId6tUBRibOdMT4cuco40vTWXhd7Mzg1PKbyT9/dMFEQXAvGViY53T9mLuEBlIVC6Ad0zqfN/HQMqyk8bYibnp8WqJf354Bg+qOeoyoxBU09fJpmes6k2G1+274O89R0kc5IfVZpWGEtfNACbxXvNTyiuq+6flE+Ra/OAJo5sE6o32vNla5D3m+F7ehxWjCgdzV1HXMhLK25b/XNGg0Vrb1LIbTeocuXCTOAHoylX2CFBUAe7qFDfPePfAY//hP/PZ78/u8BX15hoJS58ez+MY5eeR1f+8+/h+f/6Gt45RvP4vSNu6DNAN70KSySkkGrk53MgbepIcAVjXTRoMLOuzPt6frnAH56v46rt2vCzs0c8G/JHTsvMr5pH6b3/LTmvjXvdregalvtEFu+kGftrq33vlyPIfW31vocWLP8DqDaXZrMremX7aP8tAaN7ct5O6n62RafMHM559Hqh52bypmn+jgvF9sOEH0WVepohSO36DsB7kbW6bmf+9eilZUru+bHtpX/SOGHWdfZCJHJ86pY+o/9GkF90UOGNnqnetx9GtdxjBGvv/76KIdN260+ad4q/VIh7fJ5S6cUbKUMFtvn9OzUIWrr0u231pjlcbvOK9rOjFnoZdssv5t3yhxQem7oh/w8lfPt+lhGi05VWB0wGb8Vl7aOBgvNlv+qSRqYGT/zMz+DH/zBH8R3fdd3AQBu3rwJAHjssceqZx977DE8//zz5Znlcolr165NnpH3bfnFX/xF/N2/+3dn+6HvS+HI6Lwf44KJCtUiR/zBH/4hPvih78BytcJ2GAAGhjBgGALCsEWMDO87/If/8L9hGCKcS+CqH3p0XYfFYlExAzOX7HXMjG3eLUqfA6+9/gbe974I3y0BpLCr9WYD77qcaIGwWHTZs5cOpjMlY++VV17Bo48+ahhIFmMykoYhIOQU3n0/lJ2tamHEOpQgvT8yoV7YlYeZU5xn5vECOpaLJZzzSUhlhifkg94sc9IWnHZhVAoHKHOllYssVH3wsbxjBNYuQNTyLkk7ti/MXIWSjEIuJnPaCqJSb0qscHL/PmLfJ89rzHe7uKlXSwvCicJhTFa8FrZzYCzdJzMdXwhh4uWqgIqjqj1LZ/v7LuA2/o3J9636d7VXtZkeLEBq9jmrsNOXsyBAfmpeijE2Qy6A6UWDuu25HSctN2zYpu2XVpytPuvnNIhp1WdBWfk8x64LAA4cQZ1H8A5nDnDdEu/6rg/iI5/7DK4++QS2HWHrHRaR4bcDjt64g+3RA3zrS1/D8994BvFsA8ohxIkOyYHj5MwcprzcAhFzxpCsSaJ691jes+C5OeYdgEOoIvOjZaS8Y0HtRIHvKO0+tQGzjF+Hyuk+zxklRFSSLWggysyIiCVUeTIu1PyinUIpa9aUlucVcdBZ2lgwZ+lD+QycjKEVgmT74tw0nHd+jqelJVehONYaIC1Dp7xn5saC3V19sEB/UvfMeHTd5+lDABXwlfVmnZjV86ZNKydb+rKsZaIqXXSla2ke9M8abeo3K4N30Wisf/y7NuTq2ufqmfAg13RqyQW7FnXd075jNjux7q9eWzIua2zsoqNu0M6z3v2dPi79zcDQ9g8JRkiWxLI1xHk3VK0HG3KOGXpz/cEsbd5M+a9qIP3kT/4k/vAP/xC//du/PfnOdvSiwmHumb/zd/4OfuZnfqb8ff/+fTz55JPVO2nBMkIOAWvVRCBcuXIVznXYbHow0tmcvu8Rh4gwpMOqQwz46Ec/hme+8Y3CZHrbG5CzPwP6YSh3EglQ8d5jsVjgxsOP4f0f+CDW2x7LvX30Q8CmH5LiGAL291bw3qHvh8IsaQFFrFYrPPLII3DOYRgGnJ6eolssQeTR9xuEkAy3YRsAJnTdAs4t0HV+Ah70vFgwbedML9oYYz4w7XIyjJRRLRmJhajwXZeSUDCPWcbijKBzAIfRYBGB4pwrQE0Edm3QTGd01+JP77bfk2IVjxThpZbhZGurgAmyxyVGPHLj4RTi2Q9wmApmrVhsPwpPkyv3R8z1u6msMcoZO9/SPw3Wi4EcUS7k1WNrjVf3w3qg9DM6VHFO0c+d75pRcYimn7q8WSFp+2yVm45Xbz1rizXCmyMwIEDXJXx/EZByblGg1s4LgHKw14sh3nUYPGHwwEPvegc+8fnP4p0feD/QeQQieHbw64Dh6BgP3riNmy+8hFeffQEPbt+FX/cIZ1u4bvT0ifq04EEbdHO0aoEIy0O79IwOs9X8J3/r9VG/P+2HljO6DnvWs9X/3WMDiMycNIww/fmu+sbfacJbRFSdY5n2rwY71ZyZ9ubrqOfA7qqUqyXy9zZ1v3MuEwXNvtixml5By+wWb7RKi87jHLSfb8lAC/Q0r8/JCxl7MSRmwr+TAzLpMssH5/GD9GfsnzyDiXHyZsouGajbTX8k7GV3RWXeI0932/+kZVd9rTNZSR7xrIPQlrk+VrqjwnTTtdI6o5gbRuTppeit8dX11deazI3DyhTtCLDPOCIw1Q6por+MfaR5U9dHpT4u0VzNnTP6k829lusXKf/VDKSf+qmfwr/6V/8Kv/Vbv4V3vOMd5fPHH38cQNoleuKJJ8rnr7/+etlVevzxx7HdbnH37t1qF+n111/Hpz/96WZ7q9UKq9Vq8jkjxVuDFTBBUgQy7SLgvfM4vHQZH/3ej6OPDBcCNqcnWC6X2PYD1qdrePJYbzdYdB2+/QMfxMOPPY6jO3ewXK1wQMDJyQk2m026u0YrR0oGStf5IvSXqxX+D3/2z6JbLrEdBtw7OsJqtcJytQKI4BdLRDiEPiCEHs55xBiS9y8Q+m2P5XKJvu8Tw2UPT4xpETOAPgzohz7TAaV9vSitICUaUzSO8ei1Ui7GHiWLvgBqULr7BABFBoVQspNIusl0MG/qiZffdZafMo+mXf2vAqSYCj1dv/5ZhED5n/Z6YOKF0O0BgCfCeGlq5qws6OVES3o+79DAFSNxy4zh+Bgu9HjjlZdSalGOYK49oBOwnQWLnGuLM0JDGyZpZ21cBwkkEMj5dHcGMKZVp9EI0vRqlZbxyOo7/RkzCugd3UWjkdYyiixorp5ToE0OeorEZSAhe3mOxhZFLLcMCr0DuQtk2P55ciVWOY0zlnuadNGgsAWm7XPz63N65qnwZiEqQfZjKlCViANWu16eAQ+Xsk66lEkxpW4FuggsODlABu/QdwR3/Qo++dlP472f+B74S3voQfBMWEZgc+8Yx7du4/VnX8Dz3/wmXnv5VVCIKQNdTBukoujgKGV5FF6IebpoHJNzaU1pw0SeGQ2dGvBbcDVqaFZ/c54r61yRuuq51r/LO9rA0vOlL1J2TjzmYwjn2FYjdFdNVFkb6lPKcj1lr+Q0w5wdPTQaAFz4YKZw4nXOshugvOappO0dx5t5hdxIpYYRIGvL8ub8GPUcjs5DLdMtjaWtjNwTjSmDvguAp11Gw1h3+/uWEXzBoxNV3SNfTyMSdu06y2fyr6aLRMlk3iWAkPVF4eW8i+OS0xdioJC42KIaEgE03XFgRo4MmeoFLa9axoc1xivaxCQTnDgQs1gQeZbUa5Heef27yoDTmKGch2Jk5yPKnXm7+JGzUGC05W7kOEkiNVeq8do2MO7uSNIunZjDGtC636Nc40KbDA1SdlFGSSWv15DoXqK6f3YXvD1nY5KM8h6PVwSIfC6SjXLW7ZK6XWER9VeIWVfmz5zmX6Mfk6zipDfaFE//z99HRes/bvlTP4PEzPjJn/xJ/It/8S/w7/7dv8O73/3u6vt3v/vdePzxx/Fv/s2/KZ9tt1v85m/+ZjF+Pv7xj2OxWFTPvPrqq/jSl740ayDt6BGSYhwZ2jmfPi7nPgDvO/iuw//5r/xlfPv7PoDVag9O0nPDJTDpO0QQ9g4OsTo4xP7ly/gr/5f/Kx66ej0LjgR8zs7OUnrvrsNyucRytcJyKVnxfGZmh8899Tl8//d/Ggf7h9hb7WO12sdisQKYcHa2wdHxCc42W/QhMZHL8bnM6exPDAEcxMPCcJ0Hu3RwOoIKeI4peTZC7CuQBqTF0fd9Dvsb89aP634EMNbzBeTbkCnf1UQEch2YOvRMYEqJKiSu2MsZCiVI5TupX3bdrALWh2n1ZYfVQqYpSGqBeD0W5yjvNDBAjMgBIQ6IHDLwqBVbESTM4BBTmmkieErpiJ0AU/Jw+V/OUZ74DCkkK/gFlosFVjHg6PWbadesAYClzcCxpFaXdLzklERS4yrjK2mQHZDPb5WrkQlpHigJOs71CfBK4Zh9FVIhXh9N18prZP4hg7n0u0t3geUMiym9qQjsdoz7RDja9lxKIBCIEYgz38vYINoVommJRsNPj0mLipahYs+STAw3ToopsRCX37u842nbsUp1bvxVGxjli43Pr/oVE1+mfuh+5d+F6jz+G/thYvIpp+/3Hn3n0R/s4z3f/yn8+b/5P+CDn/0huMMDuMhYBIY/3eDBq6/j5jefwdd+93fx9B/8AW69+DJ4uwU4YogDgovgjuA8wTuCAyuZk2Yv/RSu0d9x9Z3+XMBmy+gVj6HwHBfmcAlggcpP5HWrmGdSny6yRvWB+hiTbB8ziaa6YxR7hcpP3a79x4qJs/hId0xxkgXl9KGjlAHVUf5erj6veUjzHSEb9TLHoCLDigGGZCSP6cDrO2s0fUUutOjVWs/yu5aruo+y3rUjwYaHQgy7vP4II487qs/jhMb5x5bTRfO+LrvWprWQ5LldZ+laRpC0b/tn13nLwBvbYRCJhI8ARQABzAOYA4ginGOAIpwHiERiRsTYI+WhDQlfIACIIDcmJYglDF/+Tc9f2XLeLnBFg3yHY5JhocgvOQohulUukpc5t3qhciRl+Qfmshve6kvV/wa9ZZ2jpTcwNbrs3Fk9J0U7qicOB0M3y5uenJLtSr4r48KGqkoCLbvbo/vT1u+j3NWYmrPBWPQNZdkuP/M/rYs5YyAG52teRpzANK6oln4jkvlMRnUMsfyTez/F8UNAuprCYMEZNmyWP/UdpJ/4iZ/Ar/3ar+Ff/st/icuXL5czQw899BD29/dBRPjpn/5p/MIv/ALe97734X3vex9+4Rd+AQcHB/jLf/kvl2f/2l/7a/jZn/1Z3LhxA9evX8ff+lt/Cx/+8IdLVrs3U7QABDCJ3ZRY6ieeeAIf/q7vwmqxwOHBQbHq+75PgvYwwPtFUlIxot+u8a53vRMf//jH8b/8L/8zmBh7+ZJN7SUIZifEe4/lcomPfuxj6LoFlstl2jlaLsv5Je89jo9PAEoHpMktAB6w3aRdnWHIGUeQE09ABBZDYodDvkQTSCm3BxPvrUGi8w5DGGCFTAuIWYXm8uJ37JLQZcZi0eXvAYAKzcct9DHjjcxBaVctTO39CCGAYltpcAb2sryssNZGmBVG+jNRYGMd4+d6l0u3e54naQTSSUJ7cnAR2Byf4PiNO9jcf4DLPG5V63fSuHaXOeUvFLHCe66/8oze+ayFfP7MPG8NJGlDF1JCu+UV3jUmbSwWWmahCpruplg6aIAFHkGT5glAe7um4xZlY7/XY5oIcsqodmYGW2ur1X9tGNm2q/f1em543eeAayCgd4QFCItAWDGVO8j6zmGz6vD4+9+Dj/3w53Djne9AcElJLSKwJI/To2O88fKruPnsC7j5wku4ffN1xE0Pn/vRdV2RO957OIjXs71WgWkiDesw0A4SfTZCQlJGMJHob4GqpkHrDIylkf1cXzjaAtVSJvHzZj7maFCBqJl5k7937fLqfrQA2oQHZ4wB+7ztt9C6NZf2fb2W7JrR56nmZKsFdLtk78XOSbTXx9zcWNnQMoRa/SjPu+mat/qk1a6uy+qk+rNQ5mOsGxCQbnX8bFFfi/yW9+z6tDxlf2+FrLVobPlBGrc7VqWejF10O0Uex4i8IawuD8+g3g7VzKc2aCojpibLBBNpGlU7NzPLQvON5UFbLD5pYbS5MrdO7OeChVtr7jycc5FSv592Cr0X/ZbDBjFaSeethV2l6ANMefSi5U/dQPrH//gfAwCeeuqp6vNf/uVfxl/9q38VAPC3//bfxtnZGf7m3/ybuHv3Lj71qU/hX//rf13uQAKAf/gP/yG6rsNf+kt/CWdnZ/jhH/5h/Mqv/MqbugMJmCpYYdpV3tERwwQADg4OcOv1W7jxsMNqtYLzHotFh853WO7v4QwbhCgZ1wYMYQCGId1VpJSyKOzi6QU1gePpyUmVKQ1AARQhBOzt7aPr0qazc0AIhL5P7cYYcXa2BpAPTusc9hFlF0CMDTkDpUGB/tsKK71Y7YFOayBp40iY23cdooBHuXSQkqFEIqhht38zHWhkbp16UtOpeYaK5gWMHqu+HNZ6Da2SY64FiBYSWgja/s2B0Rhz5rohYuUWuPdqApMuJO9MNAZS/qOWyo1i56YYVlTTbPQouUnojhzytnxRtZNVREugi4E06QeLs6BNI+FbOx7m8T4Q/V7iERrbPEepaPoIuBUAVsuTdljD3Jzqfs+B39TV9t1IlhYaIFnvuVbALQNpHMF8mVMS4o/1kdBFAjmHrQfWHXD4tsfwPZ//LL7tIx9Cv+exphRy5/sIPj7BnTdu45UXXsSz33gGd1+7heFsk0LqHFWXDttQNOmFNeQ06JPftYy0Y9fGrmTlrNox/G/nSvo3R69dhov+bHzOQqhpGvJdxpHQ6qLAYFxb80ZSCxRrPtO8FcHlHJKVhbZPQv9kWI0gsGVAtEKHbJIJ5no3Ts91y6FieaXQREIPJ3RKAKxF2zcDAGXdixzd9Z6lXwgBDmlXX4cstQB2y/Gj+95ydrbkqAXhll7zA0Xx/MuFpqon0Kh/Dtzb9m3Rn9tMsOO7KJhBl7JOGgZG/TPVEWLKngYaIyHmip1TMbTn3JW6/ZYjTfdp7l1LD1vmwuCa4dZI9Jzed0nFqSh1zvHvHO/N4UZLhxYmkXcksiIlHxsNVo4RnGVJS/dqfGJlDLPRiSJ3yMiHN2Fr/akbSOcJdCB19ud//ufx8z//87PP7O3t4Zd+6ZfwS7/0S3+i/ly5cgWHh4fw3pczSl3XYeG7Kl0mEeV04MtiMG03GxCAhe8wDAOGvsemH7AdejBSikJQCqk7Pj7GwaXDkqih7HhQMo68UgJiBO3t7WF9dgbnF1XmsO12mxYD+ZTcALGE0i0WHfphDYDw3HPP4f7xfbzv/e/HYrXMI+ZkxIWY+8Doc9IHrWi0wZgAS3vrX8Yhu2lN8MijUkoKIxmQactTFk0dzxliKOB04mV1gJzq0HG5SYHarCxTga+Viw1H0otcwiBs3PtY/5i9S4pdnC0goH+fKCgi9CGAmLA9PcODe0fwuZ0hMNiEgO1S4i1hWrUn4XQKDKknAdS7EkB9T1YLVNmxzoLuCQit+2j7PFesYKy+U2B0TglZQSq7qzLG+pB+MmYEaLfCQ6zCaykAeV6Us+6H0Ne+p+fSAgQ77pbxVJSMqc/yp6UtEaFjgg8pPJSXHg8oID50gO/8oU/hw5/+NBb7+xiWDrwgYAiIZ2uc3XuAZ37vj/DSM9/C0e072JytEx/HdIbQ5bWtQ6NKn1V8vAbEWjbpneUWr1me1rStw2/TvNo51HPV2qGbA3yp3zWw1fSUOH/7uf7dznutvBu7K0C+yHvqqW8BK2ZGCTsztNe816Krrb81/hYtYxggxkKrWLDZAvYtI2GuDxocVmM3BmpNbxSAaw12zXOtObCltBunzjvdrl7nFd1Qz4mWC/KcDmfU89Yqmm6WJprWE73f4IlSpxjLIKTwvC6/K66wkX6t3W09brve9JmzlizTelpetWNKhgCDuJ5LXSQMvTjSGCC/e5fUfmrluh67fK/HYt+xz2p+07tTQkfpm93dkefk3WEYxrsXqzbTmOV97RhNj7SNyQnt1Lt2rC1+nMxNQxfzOJmIMWC7HY99EBGQdbLQxm6IWBlR7xArOuShxJiOJsyFtZ5X/qtmsfv/h/Lkk0+WsDW9MDnUCxpIhtPjjz+OGAjL5RK02kPf9+h8Sovde4/T9QbOewxDj+VqibDZ4B3veEe6SKxzWCwW2NvbKwJvu92mg/BGoa9WKzz22GM4vHQZq/2D6ixO13U4ODgAUQciBnNKzLDdhrLIYwx4+9vfjhubh7FarRDy2aEh36Mk3qmUtjk9D6TzJva+IKGD/GwxkBbUE9AuEcGUDMF0s0+Pfhiw5OSl51AndWjF3hYjca4vnPuPltduXJwiNPRdGnbx2xCBi3iXnXPlfJQUK5ws7axBFR1SvCwcVosFOt+BgHRH1JxTj0aQZ/vWmqu6f+0qRWHYeW3Rqvn+BYVMC6Drdlt12rltKf5oxt7qd2sumWseqQAIU0mzLs4TW5/dDWiBlqovVKtTC4AsXayi1O9ZAGZ3UcnwSWseW/0lAM51WHtge9DhsQ9+AJ/40c/i2tsfB5MH3AIdM+i0x/rkFK988xncffkmXn/2Rdy7dRsc084x5fN8IAJ1fhaMcWK+CkBautl1tQss23VQz89oKGmwrNuzYUq6Lg3k6jkav7dgoQVM5W9Nk5ZHuDbu9AzVczq3Rvu+B7O6xgK157kFWmq6AWx4qLUWNf3S59Nxl7XaCDO0MsCCLk2HFk/Myp9sH83xihiNtv+27Ardq/ohbeouzMjkij6KNm05VTtyNJ9KHS1dI+/ryIw5Op4X5izPSu9S/ZrXa92o267eN/zTjAgwdKtwgUtJJazDMde4Yx6TPBTTuYldWrRPtTbHIIat/q4lf+x4hIqtfrbwxGQkhvdb7akaBUIVXTfWMbcHNu23fm/Cv+o5HeIs8zu3Pu34hqFPTm+UpVvYak7PtowzGXeM41n9CCRHHdX1XQTfSHnLG0jL5RIHB8kAkZ2ZdDYnCZ2uSyF0oHSWJ4QA75bVrskwDNjf38eQD64v9/awWCzQbzdYLBZ429vejsPDQ2z7bTlHVN8lg5KSUYTdYrFI9xGpXYwQQroPIANx50SgDBi2axzdu4O+38Bli3h/fx/7Bwd44aUX8fTXn8bHv/d7ISFhHDnveg1wjNFQiwx2bUaXohlcA0kRuq2wMsrCyKVYwJLG3IWhuiS0MLYRClpZSPpvKUX4EsOhm/Gq1aBGPtfATLcn5yJk/Hbx66Lf1zHy9jJgmUftDdWLkojQI4KJ4X0eEzgduiakM7U71u6c4rRzWIGY+cog6bVbwHBOkBDR6I2boddcf+aASQtY2jlr9SMnbbqQ0NNtxFjTsFXsuRLdxk6ANu1pBR51ERnRAhRase1SNtX8i4ZpGB/jvKE4M+Tz4D1OXMSld70N3/9nPo+3f+A98MtFSjRBHUIfgE2Po5dfxXNf/Rpee+lFhO0W27NN6udikZLIEJWdcsL8DmNa4+2Ux7NUbPCENphteOj47G6jWX8mfdAh0i1vfDo/OT38n94fF3Fr3Pr3VghV6zP7PYBKHluPq/A4mTU4JysqQHNB8CB8aw3O1rjte7v42Y7frsPz6pc27JwBoyy0MrkFknf9XX3Ouz3pus9aVyCvQfm8lQ5ey2U9R+fJRT0fdq4vYiCML6D0VaJD0tfCR+02ddstvpszEnR/bJ3yd2t39aI865wr5/mszq9kUIPfSp93iH0tP/R7Sd7NA/uWEWC/k+91O3N0TaqgXkNFFrvda0m313L+2LG2dPtF+NR+T85BUtaI/tL0bPH0XNhteS7Xx5geKbloecsbSFev5h2WEAB0iXEY6IctHAj7qz1453D3zp2c6ADYbM9wenqKGCOuX7+OCEa3XOBsfZazfoW845OMAN8t8M53vRt92GJ9doaTkxMQp8P4jzz6GJZ7e3jxxRfT4uS0LbztN+hDj4eWHcLQgzji5OQE222Pa9eu4sGDBwA57O3toes6rM+2eHByhsUiMcUQQ/oXApgIq/0D9JHBERg2W2w3W2y2AX1ILHJy1iPGnKpReJ3yQqIxZaMUUbxyHkrup7CCnCNAXfKPeKKU3psI8B5+uQRvNiBSHkaidDapUhbGU5sengjdGCNi6NMOWOZ86b+9t6clUK3g0vW2BE6arvH+DS2opR29BWzDRKzgJSIgAJRiCJMBHAKIU9ZByqmARX8WXcS14pkYNS6DX3DKAiNtiXTgERyPJXuTmHcKwjLPZT5qcK37Yw+T132uwX4l+OUZXX2eWwKNwl4+IwmHo3LmqRrZTiGYxq1DLMs3jtLZgB27pfLuRYylSqlqaQ2ksboaDOifln80zVwOhxXjMGXwSbIlnQGUMaW8VEwEdol2HRxoYBAceqKUnOHGVXz8cz+ED3zv98AdrhAJ8Ozh+4h4doaz+/fx3NNfx8kbd/Hqc8/j+N49LLoO3jssuzSv3tVZu2IIkIs5U98lVIYgmTKLN9bRyONq/NbTHDKPlDUV005O4XtCyeZW6OESxUBqfUOA0Mh35eA8MIYrUs4OSuP6Sv1TU+oldxSS0yF/QZT6UUI1hY95ylcobcUc0pvu2SNKu3KWJhZQtcJ6gZz8K6/Z9IxyChCXLKchamO1wb8zf2sjLdGvvQ7OC2+xILBlMEzpNf6S1UX6SfXzus/nGgSqDxqg2c/rv0fdUhtA0zZqOsQyNyBGMeW5fs/qj1af7O/Mkoobmd9SxS0D2Zaq/yKzitBKcibJv3bY1a75bdFB972cRKEkhwEGB64ccrpOCb93qOVmeZb0+PPu4Y4dFOkHc8pm6zJwkagXsOwYzuw8NQyG8jvx2DJlOeCSLA8x32FFnHbgM0+RgyTSNaFkdf3TcHguU6blQ/oA43pBvd7FcWix0BzPzX1mQ/LmSmRG551K6EUlJfsuHa4dVwV7ZPnGCACSflPKp9S5C+O0ylveQAJ5gDqQc1jtpeEyGDR0wBARh4jNZo03Xr+N1cE+bt++i3sP7pdsdMuzU/T3e7xjfw/UeSy8LzLDkUcMAPkFrjx0HdvtGpcvPYTOv4HjoyMsuwWOj47wbTdu4D3f9m587RtPY9v3GMIA8oT1+gwxDLj12m3EGHFwcIDj42MsFx3u3buLyBHXrz8M3y0QQsT+4WUw99hsThFiwDYMCDHi+iMPg7oFNtsBznmEvHPUB0YfknJfb/qcb34MvxNaFKCA0Wutd7uAFHKkDYOykPzoMXYAtsMAFyP6MGDZLRCYQJGwIA8QY+CAAC4x9cA0BCRhhGkMswDUftjC+3SfkywCVkKh8vhgXLRakVnvpwZkMn75XEorxMH23Roy8rv89EhZVUIMcI6xdA6OUZIzZMiv2h0FXtPgAhIAVvf+RI6jXiuHmqSuEUxoYd5S7lPjQANd+3mbjmOdRdtOBVUU4yhLbrWD6LyDzsxY3supnVs7bnPj0IaVDqGrAAHQnDcZQ/poqjBa4VJpTaH8zCawdKqgOc1LWtG3xiKKOv1LwxcAD0oOCpezzHHWhpzzevuQ++Q7bAjo95b4wMc/io/+6Gdx8OiNlAY+RqzIIxyvcXznCDefew4vfuubeHB0jON790AhogPBB4AQ09UCeXyOxp0hn+dGsm2mro9nEvXcFDkj4wcm9E0GFQnjFmeTnn4GilwRoFxuduHUvqZtMXQpgRTncuISMdjiKHOQWTPI2koKoCwrMbgENEN4PIRiXHluAzkiQpC5yvXJ77IzpumgaSc/bax+ZOFVKoaWnOdI9M4JC0CjDBeeM+dDdLH9tudSW0V/p3fAWk4BnY3QJtyo5rm25DIAHcWBBasF6Jm+WSArgCs0oh5acoXBcOQmcyNjbBtVXIVcMY+6Swx5kQfSngXBNnR7bFOBX1BC4Yhg7hFjvWM2JyPL2EjMCi7OAUZUtJ6e/bHzaeuf7ABRWU2jEyL/lGspQALm2w4kvSvUOpOjZXHlcFOl1tdxlCucnB6lPTVVLdrNAvsk1IpTSC6+dV5yeqZRE2Vq8yibxBHRwhatuYQxfCzNhBaF8LmII6cV/l5qnsEMltb2Hf15+T7/XK5WACdMxFmHiGxpyR+bO6AYSERIl2qb3SLmfL/WFNOdV97yBpIOp0n3EDmEGECesH9pieFsg9u33sBmu8WDs1O8fusW4BzOTtd5Yj3WZ2s8+sjjYKSwtr7fIuSzKCfrU8TIWO7tIcaAEAZcuXIVZ6eniDFg4Ig3bt/Gd3/PR/DI44/i3/zbfwvnO4A8Hpyu8eIrr+LsZIODgwMwOQQG7p+cIETgZL3B3maLPfZppwiEW7dv4/Bwf0zzHYHNZgPfLbDZbBFDj2Gb7q/ptz2GIYDgsF4HhCFMBNRisUAIAev1upyDijE2L92V98SCT+GILjG075IBxqOnhfJu0AicuHhfGJzDCEclrHdFivBrGDKtxakViDZutHdVwuKkWEGa+KXO0CKKrLU9a8NatAAoCTqsQGcxMgPWZ2vg0kPjGHasW91Xe3BSl9aBylZdpa8ArJCzNKnqAyqj5CIHU/V3eu7GuUYxjhjq8lskG4JdDrtUnlAxuXaV9pZ6vpdB0aI8kwFu67CwpU09r5iMqUUP2xcbBiF17M7UOYbsWcUTCdg6wHG6/FUADIFBgbDPHmcOODtc4vp734VP/shTeOSd74BfLIAwoCOH2A9YH93D3Vdfw8vPPIdXX3oJDx4coV9vwPnCV1dAxtSJIT/tOtXFhnQWhU8JvrTOKGi5IkXmx9ZXh9kBcqWA7aPIjUm4sKbpOcBEnmnNY+tvqWcXCKnBWh1qMuEhMx4plDo56ccI/GvjRNdlx7erLZGxeuds7j1b5sYCTNOSz8kj/fsuvhNeiKaeFuBuAV1bf6FFjEk+Gfpr8DZHA91OayyaDtqxN9e/XKupk8sa0HKqRQPp01xobLV7ORnN1OiZ9m2sx37HqNe2Xa8tvioGqHGeFZqbi7pF1+mWdtHCzjeLXpoxAmyRz+ZCu3T9tj8Jh42/S/uts9KWRlQM2/NLvUama3uW741c2jVPmh563YgjLBYnkBuxALXxmaVb5YTY0fYft7zlDSRhKlEMe3t7ODg4QETE5uQUJycnuHv3LtZnZwhg3L59B4888TYE7rFcrXB6toFzHvcfnGC92WBgIAwB2/UGjoDbb9yBI8Kly1cAACEMuHfnDIvlHvp+gPfAvaMjHB0d4d3veQ+uXb+ON27fQWTCvXv34dweVvsHuHXnLpb7B7jxyKO4e/cuAghDiBgC4+7xA7z22us4Pr6Hq1cvYZHPB4Qhot+mZAjb7YBhSJlNQt+XtN4C1vvtFuv1GtvtXsk7L/QB0lmt9XpdzlBpT5+lpTYAIkdEdpnZk8EQYr60K6ZbuyMPBao5l+5bcs4nFIda+TDzePmtCuGQQnBwLi3KYRgqJWSVkV64Mv/CCxag2DCzccHXhlbpB1HZxZqAEyX0rCEnnznn4HwyuMHzAm1OWNV0G+lThb0QNZVOqc98bttqGk07lDOnP2aEJTX6PSfQlAAsikm8YlTAHxqK7rw2BCxoGlka2N1GC2h1vZpvLJjWP1vgFjyqak3zXUqmmFVqYqt55bwrwEBH6ULsgOSsOHWEw3c8jo9+/tP4to98CG7ZAeRAgUGbIWVVvH0Pf/Rfvoi7r97C6dF99EMPdClcODoAMV3MOmed2vAZTRv52/a7Wis7aJZMsimYnCuJpkkutfqizxNaY0E/bwEkURsMj8+jWUdGIBfg/3qXQPNVa2e7SQdKF6ZKRsYic4pDq214tACi/V73RXZ50kH63fNh+9kyYoAxhEavv2oOTF+0Q6EFascxTN0qdr215LzVDZXMUPJhLsxOvm/RsmUoa0CsnTV6PVg9NfY3jXOcC/1vd5kDxDXvy9hrGWD123l8IM+V383ejrTVMjA1JpAdGVsf8rdCi1zJxDg6r69tHmqPY66euTVm7xxqzedceKrm/WnIYr2DdNEikRot3bZLVlXz0ZBvVqZynocURknYbDYyqsJTrXVnadKi9065Sm0a7ypveQOp77c4OTnB9evXU2KFvsfewX7eXRlw+/ZtbDYbrDcbXH7oCjabLV69eQtdt4Dv1iWV4p17x+iHPm2JxmSIIEScPHgAjhGPPvY4QgzYrNe4/vAj6IeQzizFgBAjnn/hBbz7ve/FZ556Cv/Tb/wbxAi89PJNvP7GMVy3gHcet+/eL0rHOYdu2eGNO/dxcnKGvh+w3Z7hwdkDHF5+Lzwi+n7AZtNjO6Q2hiHg9PQUJ/fuwfklBnYYhoCeAxB6nK3PsF6vcHBwUOgjyrfve5ycnFTGUUswysKuAE9+nyl7Poa+1E0SuiJ3MuVL2rTwF4Yt55CM8B+VA0A8ZrSR3S6bwlz6JYtFFppOKy7vWG99LRxc8WS0Upwzj7tgFtwSUbVDZoG3qATJikckHv9aCM6FaWhwp0MMdN/S79MLQwGB2VMBZoWbnmciKvcojDRSY0bbIzu20VbqjBRKB87GsRNAmc0hUtCGkW/bTnzknYc1XqRoPi7jypXpBAjj/E0Bsy0WOCT+4kohWYBphXxpMxFsMne675M6gSp2vOJJBpacdpCIE88OlML63KUDfOAzn8KHfuCTWF6/jB4BLgKrQAhHJ7h3+za+8eWv4tXnXsDRG3ewJA/0PTpK5zKBmA7RZiNGQhwtiLHzK2v03AO1DaCs6SX2haWRBv6yliQcOFMIkoxkTmFrZ5A+0GzX0zifKWxJr2spIUyzQsp7cr7yPAVtwab1IFu6WbBMlHbs7T07FnDoy5K1Eab/ntup1n0t8f8GMEu5iNGl52FcV3XIaWvcc3Xa/ltDRNNqzjDQz+n3qh1DahusmsZzdGvRaYzAnba7a4205FX6LDkIiMRYmDqSbBsVPzXAbdL5NDG5WnrEft9ylAAy7LYBOweEAYk2GHGCJF8a+4kKkFMYjSQrB3QfWwC/zD1NDWtgmhm31d8WjSx+kGfL2UWeXldif99lGFh+bmGKFn1ba2OubhnHzjmuaJDjEHJSGx3WGmOE49owbI1V3mlFeljsqpbWmypveQPp7OwMq9UeiAgnJyfoug79dovFYoFbx8e4f/9+InIIeM973oO7d+/ipL8LZuDwMN1rdOnwEERrbIctumWH7WaLB8fHWJ+dYbtOdyW9653vwJPvfCe+9a1voes6XL12HTEGvP7aTSyWC9y5dwfHJyf4wAc/hKP7Z/jDP/oyju6f4NKVJcJpj67rcP/4PmIIOLx0CZcuXcKSk1U/JASJSB4npxvcuXcf1y7tI4RsJPU9QmQMIeLmq6/hpWefxXu+/X3olvtpJyn0WHYux0onxjs9PcX+/j6YuVwodnp6iqtXr1YZ+ICaKeU7rbTlv8hInsn8zhAGLPOCoRDSbhNidZO4XgRFYSvmnoYbcSUIW4rYLn4b5tIydqRUXhPUqVOtwNRKsKVwZnfhQkQEY3AooZqRGV0DVJ2neGNDqY7v7BJogPNTYW0Vru1DS+mV39MHkzbTewCUYiIa7/4AoYRYcLa/tEEAiDJmNaRkmOv50XXP9dEqN/3TZWOiRQf9bMurp5WEpVPrd/tTGxtWcU8UE49+0Ao0McPFCHIesXM4IwYO9vHOD30HPvr5z+LwbQ8jOAYzYRkAv+6xPT7D3VdexZf/4A9w88WXEdYbLOEQwxa+cxhCBMUUlugclXNKXdflGPFpP/RY7dhbCrQ801iPqraKh+r6R2Pf0lZ4HZiGurQBZfvSYkCnvQWAqdEx1rEDJDXk6tiB+lkx2Ow61PSb9fIqrGkNKBmDlpWtNTMHOlq00XRuvdeSj/b91g7sXCFQdZZ2rl9j3xKf2PFa8Dg3Vquraj3TDk8+D4C2+gmgZH1t9Uc/r/l5wrMxu1LIgciDMYaDzxkAlh67+1xHLrSek9+tTm7KtJkQu4uWti7O9xhSXnaN3cE/admlD/VOdYsfd+kC+V6uZ9m1Flv1REwNHP1ey2klutg6S1qGZOt7faH3XNHYphLnWZY5VX/1rPpdirSnd1nny3mRGe3yljeQLl26hCtXHkoXxe6tSrrvPb/C3t4e3va2J7A+u4ZLly7hnd/2LsAvcMmtAIjyAYYsiBbLJUAM33lcunQJ+/t76WxNZCyWK3jf4YnHn8Dx8X3srVa4fu0qHnroIaw3Jwixx917d/H4ZoOPffzjuHL1Bvb2DuEXK/iug/cdLl2+DALQLRaJWTqHPkQs/TIxR+cADLhz7y7i+hSd9xiGCIIDxxRu9thjj+FwtcLe/gHIL3BweAnggM4xusWY2np/f7+AVCBdzPvkk0/COVflv9fKWAu78bvklXfkECS8CymLTgjp/iYGwXcdFo6wHbaIxOAhVmBBwCFQZ9rTiyPdp5QNAxWbrXPw2yQMWiC0Fjpg0mBqAUB14Nt0KxsTA04vZAukrRfE5Qs1R2MsVPXoNq1AKu1g6hkZn2WA2557wlSRWYGk2y/CVgwZI+Qh/ZgBoOk+mnpHJx2KT3SOYmZTqqMtFI3HTrWljfpdBpIFldLPGGvDXZ61QrjQzygKTa+5HS0AFeiNje/tPJe2iMr5tZyebDr3RBgcwB0hLDyuv/vb8NEffgqPv+/bgS5lteqYgc2AcLbGG6++iq9/6St4cPs27t+8BRcAigTiCO8dgiM48iVzHIHG5AcxImbDSdPD7nZYBafnv0WfXUXXVc/dCPgtIEu7R/NtCWi0INmCh8IjRGCTbGE6f7U3ukrnztw0sO26seeadN/teUsLQHOFFY1qXsoZNGfAkwUic0XXydwGevpZ+5n8LWumBfib/aD0j2O7n/P9z0Z+bJ+x2ZVwYnZHLa8L6evc+63SepaZq3NSmudbAHAKVPM/AjhtUYM55jl3E15orcld/a2Grn9XY7e8WvcPbX5layK1jQBbCEg7Q03gn/lRQlVLf9q7W7odS5uLlqlsmuoaoH0O0+re9NmFm945Hu24axuobcOtLVvabc2Nw35fZGKMkPPAlYanWqe08ByQ5noYhtFZ59L52FafieR/b24+3/IG0g98+lM4ODzM25XKgkbOacGMmJMXpIxMDgFUPPMyKUMYig6TLGExh1N0XQfkrCSPPnwVzhHCMMC5lHFjGHqEOKSECc4DcPjEx787MX/28BAlo0IWVBCwTMn4iJEBYgxDDyKGRzYwOO/cOIf1ZgNcvQT/tkfTDouE2Qw9Qhhw6fAA3qdQlNVqVRhIvC5ywa1dJClELln3RKOAcRL7BMopi1O4kU+VAkMPigHMPSI5eNeBmBGHAT4dHQdzBPF4KDFGuaMKpX19xwkMkLdnQFqApWmcZKXcUha6tM6pAEn0kktIg8RDlY1FAbC2DzEmvvGZTp1zWHaLPM0OhHaWPDFI9O4JldTIU+9hXUbAVkILMl9p2ljgGcuzPAHhVmpXQrdp2AjtJHQtKW6iNIbIddhDC7y0DJJdh0O1gBXwBWAMc5KU6nl3ilymI41mhwCOVFcathXard2QlvJtgsbc/kgkFMPHceKvZJSiZIcDMzinBfZMcPkelgDGQIQT53HpsUfwic9/Fu/+7u+EWy0xUIQDg2KA6yPObt3Bq88+j29+7Wu4+eqrKePcdoADoevSOvQLPyZWAYo88p3PRhGaRe/ozYGvltE//j6G7mQuSbweE//od8a2Ioh8kSHpjKXIEAZz/V7LAdACBXp+dR+TgSRzKWGxY3is5l8dVhtDHJ0B4qmVdUD1ey1+t8DGyjV5r4AJA9zHeud3qFvPS/+n4E39w3QH1Hp228ZkGzDvksscuZyhskaYSBK5tkIcQaM8q+u1P63skp/6vEg1puw0YM7nbWXN8Cg7rOHYooVu3/nakWSjGFqGw/h+Cg0Xx5NeS1ZG1e8mvpaQLjkOMsJXKvKAqJ0sRPMeGu21dtdbf0uxO4otB2XBBcCUNrnnzmXnrcyfwha6n3Nrq1oP+XvBQuMr446mxiFzYLySf6zbFYObIW7Dlv5o6VdmlcVPyRMr3yZjKvW0+bOlz1uYSMvNXXWIDNKyV3Y2C9127PhoPhPjqLSh2puTbW5XNixT3vIG0kMPXcLe3t5EwAM1cAWmHg5A0tQygIVa6ItSl8RAMhOc84ohO/R9MoxAwGKxRNdxuSC2JaAllj4p5vECWWC0loGVEjRj+sfFYoEQD7DdbNIdTCpFYoypL4vOgfKOy3a7BTOXxAxakUvyA02bcpaAErgf19LoqZV7SIiyMI0JmIkXK+S7PTwcXM5MFmJeZMmdXmK6rdBrCUc7l3OLswU2ZEytcMLSLqZCtxL6aWQQo7GoExovI5V3Stv5kLsnB/D5F0PqduQxAesWZLbAhEay9X5Y2xjhhPzGv4FyJkgUZ6u9Fqio6T7SZ6wknd0h1Te9JqQOC5Tk53g2rQGijFKoFW1W+MzZts/GPY+GraaNlrPa2z2OeUrXOVCoxzMR05QVg4A4MbYJEmafxhA5v5vunoreoSfAXzrERz/9SXz409+H1aU9BJ8YZY8J25MzHB3fxb2XXsUbz7yIF5/+JtYnpylVtdCQgEAAPKU7h6CM16xw+74HEeVzPmkXqQW0W0rZ0sECUsqArjyuPgtcG17aG56eJ4QQ1Y5RW0HKjqAoZbt7MQckNOiXyZJ+xshwbmp0aBpoYyiKIpf+Nd5pgekWPa0RYoGvtK3nRZqdgpbx81b/W7tqYx+Ss0PT0Ibq6M91/+047Zgt0COiIjsnhZFh5VgPq/M3bPo0p/vngN9UvqZG1VRiNIxGoKfnSNOjBTxb3n47ly0ZO9JJnlE04N2gUdwRDMri2eVs91rvCKBVxMaUz+YMDTt223/RM009BjR5Sc9XU9aCCu7QZ5vPe78F7kv7nJzjRHp+pnMB1OH9Ld5Kz+t/I49IFjtLy4pmRmaVtt04J7sMjYquSte1jNNd82r7VNVrxuBcOm8sd6ctlgssvMPJyXF2NU133FrYQuNo5uwQagxV0McufTRX3vIGkgbXdlHo70MIKdEAp0x3gDDcCMJka1AmRpiv7/tJvGkLMDJz2RKUv4mm+d6FiVqHn6X+vt8WZV8OJuazAcjMIu93XZfSdhMwZINuu91O6pfx6YXMzIXnrOKWsQmEJ3Jw2TPgiNDHCObUryiANC88ju0F3wLIlRJFezG2PrN9tu3Z8MFdCsQqKsRYvJItgTfXF0+EYQhgArbbLe7fP8oAjbMx2SjMxTPaKnNjz19W7Vu6aL4t75Y5rd+bU876uZ19Mf0tf2OUa3PgZErjaahIC+RJHTZhQwvUk4y9oYg1DwrdxjU6HwLTosWcQVH9nS8IRcxrWfty2YG8w+AI/crjrCM8+R3vx6ee+iyuPvoI2AGRGB0DvB2wuf8Ax3fv4ZVXXsTv/c5/RLcNCKebMaQwg4c5A2FuLrRMEhrb+W+CSvWulcsaFOgwWp0YpjUnuh0dcqufZx49rHLxtQUuuxws+meLR214pR2rljP2b/3srh1hK5s17eq6p7ur9lk9/rm2dJutcdm1p8c2B84mdzaZUEzbB+bxfGp5hqYOn1a/W0X3sSX77XitDmnRoHVWzDqTbLY9PT7dho5saK0T3W5r7JY3bZs7S8Uz9ZiboaGY8oGVD/Lurp0FLrtudV9bddXdZYDaDlQ9JCIxAQGrSO3at6UlCzTPlrVvDEb5vcXXc/XPfd563+o1WSNy1KGlFy3eqp8ZjV/Ly5YfL1rOw1wAcHR0BE+A992IgeL4PoDKca/HXs0ZzUc2JONpt1xolbe8gSSlJXRE6ep00WIkaaWvY5OtEk0hbPWOizCrpIHWbeit+pYC10wvReqWPukU3lrhd12XDKQ4Ahd9cE4uJ9MeUzGuAJSxS/a1smuVzO+qr+V3TkkHBmaw9+XCUrmwMcaU9tuB4NVuGBmBZgWppk21Nd9Y4JZ2tt4pCKtD2WaL+a7qF+YVOkyMs57rkMPsOFe/v3+QQxiHpvejjEONx45zVgDvGJt9pwJXM+Nr0R1QToEZes2FRpTfU6VNJVvRYEbxt+KTLwIMJu0YoKydBS2QOdeW8GzLOLBKpwWUQGmXwQHoOOU2lMzaKXqTAeew9oTFo9fwA5/7QbznI98F9oTAmd79gM3pGus7R7j90qt4/pln8Pyz3wINEUM/oHMekVDi9+34pE86Zt+eE7FGp35f12OB8tzcJlmlzeWapvp3K8/1bqLQ3c4VUXJmybxqvtHvWGBh58kWZ2ho53puJ6Vac4rPdsmkOaCu+ylGewijEW8BoAU7u0CPXse2PfkeObRLf67HM9fOLvC4c1cPM/KAJBx2vj09v60+zvFrE5Q1xlH/3G2k6bECo96ck5ctntSfa5rN8XOr3tEYqvsooYpVHxuyQvjO8rMd8+xaYqDaJsd0fsUAsI7d0lclE6ROzg7bdB1JinIhR8W41utiTtfptlrzVsakhtOSBfp3Oze75nxufWhdo+slGkNLm7uspo6Cb1E74ltrt2XgtOrUv1usINi4yG0iHOzv495mU8IUJYud1qO2Pav3OUqIfE0/MIPpYrLOlre8gaQNnLmFLYaChFyIINTGhXwu4WmaKeV9ANXukDyjGUIznWVweU8DEWECMYBkPItFV87m6JTVFtAwp7CYRU78ABo9rMvlsrQrxpB8Z2OutaLVAi6N3SFsAxjjQWR5xjmfd7WyMDE00PXL30L7ETSplL5wiLT7vJHum1WGel71/EsbUrSQsQrRe5++o6nQSLQc6ad5qIzPu3I5mvCLpA62xlX6svaWWuGkFUbVV+Y6PM4UoYcGBs65yV6VBQtW+bXAn+Vz6af9LOFhlw9sTu/QsbTTY9b1WiUzB3Dsdxr4hUy78+6n0IAhjam9YzynJM8DjUIX4ryzwwAToUdE8ECAgztY4v0f/Qg+8plPY3ntCraeQN6BhoD+9BRn949x55XX8PxXv45bL7yC+3fvwjsHYk7ZL2MEdT6lA1drUPcrrXlCjNMLpu1YNK1bQKwVlz+VhTK307lrgXv5XXvmbUZJOy9WQY/jnHq4pR0boqY/a+3yy7stsKrHYH8/75ldAE7a0/1s1UskntQpyGvVKbpgl1GQvk9V/v/Y+9NnyY4sPxD7Hfd7b0S8NfcVQGZiLwC1dXc1qjdWN3vYs8gkmg1FjY3+ttEHmaQxmT5IMqMZOU0jWc1e2OyuFahCYd8yE8hErm+NiLu4H304fvz69bjxMtGc0QeQDku89yLu9d2Pn99Z19EFfT6l83k9uSZpbD5yJnyMCTyJQcvHlp7BfD+O3S9jdQ7NPdO2hzKqXPCX101EcneeKHxb/X2M5o2dwbwu/SdrqwATQAhCchIbOUbf8/XSNVUeJV/LnK57lnQP6dqna5ze27HvyR2X0yhjDGIGY3lp+G7GQ6xb+5ze6zO55Y9akedrM7aXcuZ+HW86dqfldY7xQk/aCzndDp8i/yjtw7p9vq7kZ3nwmffB1y4VbgFqOus7CdSV74HIQyX0Os6PocGejW1LRSfY4Kwv33iA5H2f8ybfuKqJ8QljpAyrSxjY/DJ1zg3UfQDis7qQZVkO6hljRNddBPmGVI1OGqIz8pfUm+gpQfKdmAs2TTN41xiD1nXxvZxByyX+YwdT/46MJUlYUmONJKQk+V8kaCbU50SCk5vy5PXmEjolZNF8h/0KIVy37inYHWNG8/Ho/KXzmRKMoaTGD9YgrUvNHHVvpdKSwvTJG+vaYblcgEgj9w1zZkTiCYI1hC4wdmn/1xH6/tJZf8lqHem6x/oyc6l1768Q+JE+6NwN+jVguIbr8CQNn36Wm3TlY8rnaay/6buGKCSvO1lqpz/TvFrMq/0f6/uYtG+s/5IQ2YAdh/D4QGOBtiCcf+kF/O4f/wjnn7kqIMcYTDzB1x2OHz/Egzt3ce/2l7j54Sc4frwPVzewEE2UA8OJSz2qQBNMYJpzgJTSIe1z+vvTzFO63nqu0vw76/ZjnIcRuq1nO+3TSSFmc8YnF27l2v6UHqZM0VjJaWXazlhfxujP2FifNK/5+MZ/798ZMFXcS4vzd/I7IGVOcjqXzpMGJVhX1EQmFwaO9X2sjbF9ovVmM7Ty/Lp5XmcOmfbnpPnWOnLwP/bOyhqMjHddP572mbT9fPxj5yjtl0YZzat8Ir1fc59qGVvvMQAEoBewYvVOTs9tCuiJTliz7HNDq5riJ5V0vHn+x5V9mo0tFbycxHekZsXr7sB8rU+icyc9c9I4WSNzZPWlc/VEaxAaAt+xZ3WuRMNNaNsObdtC6Yd3Pgpb0nOe09mRUSAdQJxnkPjW/QPKNx4g5UyvlrHLcQAykkt47NJIGdWqqiIQy8FNfojyS1B/V6Z5TCWaHs5UW0REEajpT+8l7LjWp22oFgnAijYrn69VIs4Rza879NYYcaTWg0SmB1DBrIziXALrwHzuG6BF19CQPZEBTecs/3sMEOnvymQNDuWaPA/ee7iQ8DYl3IO1dyOSKAyJe9e1aJs20nH5OXKZhZ9lWY5enDlR1D4REeDXEZNh37Uu+XyYsX1sT461mdedn7ecydJJceiJb17HWFv6WX7Zjr2b92VszwwkuyNgM60jl3L3oLLvx4pkaw2zRkA0qVHTSw0UEUN6E8Ebg9YCs/Nn8OaPfh/XvvcG7HSKLkRCRONQ7x3h6OFj3L/zBT7+4AMsj45xvHcA30p0OibAS4MwZS90KKyFMXZgfpuCIi25D8iTLuwxwDIGfsbqGWtD5z4/t8y9ljY9b/lZ18+Udo0xemNM27rSM2jjzIzu9xyop7+n7Y3t/bH983WYnryvPTMPIAl9PnYfjTHyuQZkVZCxCrRShiaNNpXPQ3ofDwRiTxjTKhjAigYm1fatW9ux+V5nTnQSYB5jKodztB50pPVr+2PCLxnnen+5Mbqp9eb0S4v0WVKG6DKedAJOMrcbq1uFtOmz6RlgZsDQyr7J79e0xHnOtIr99/2OPGksY+AlbT/fB/mY4/s0MqaR+UjnTdZ4/R0B9EL5k0p+1rCmvq9DP/LzoGd4/Oyvji3fZ/q5MRpRWv4VRc97G6J4fvWd/D5I1yH9nIGBjCauFUFjqXzt8p8FQEqJbyrJVpO1IUMjs9gDJrEdiBvCyyJaY6J03ncdkFyY+QYCsKJiHrtscumyggV9XwuRoO4hE2uhzLVEnKVoa+sD8QERrCmgEZes7Q+eNT2A7LpWIonE9sTsKtXExXk0QNcy2GtuZMBYC2c5hFI3YiLEouDUcVsy0YRNx5eOP5XWKCgDACaCZ8AHXwu1WWUgmO+NE+28rpxo61ynF4wP+4FItAueEhkFUQwYsXJ4Abg452GfEMDGxLm1HpLclxiOGCUDIBMSpabAPBB6NvHy0nWJY6dgIkH9ehFJxMI08EPX6foFwgwxuaQQVhbMIeoSJCxAHFuYE+YoKOYwvwPSSL2zf7pX9Ts2FC6REJxNCZ0BLEw8a9YK4NBoc1rSM5RfKKsXW8LEhDXRtVNCbDQqU3BO1TECytzqpQtA52WEKcv7kTPx6XfaJ0MGRQjMUXsHbwJjZyR0t+0MvDVoZiWaWYE33vxtvPG7v4PN07to4cHOw3qg2zvA4uEeju4/xqcffIiHD+/j8PBABBrOwRZ2wJyqb5MJtA+BxqWMQKpRRzj3OQMSx2FN7w/CXoQKRCjKKtAeD88dQtBGmUdQpCkMApEFiAWcor9Qx0wntQ8qMIkSYWRBG9L94PtQ+ZzSeu5zzhAEHOs+ibQo3d7oz3fck94P2kr3hZpsxrshGQcw3EvpuJQ2pftGf8+1pvn7fT8A7iddpMPU8wiRWVEuRV7sf08+jz0mAmBkrVgSEovgTDTOKkTTfubat5yJS89ITkN1DXv6If/zSuORjpUG9J0x7McYs6XPpv1K2183x2n/0v7nNC9tP9/PYwxzDtzTutYxtU8SXKWf5cLetH55BgB8oMGpdpfCd6p91Bf7utfRuHQu0vGnQGnAA9E4WFm3HvLBuCAq9pFIkuZqH9DTofQsjGmpxtYqn7sBkF/T3zG+MNbLkpMsMEPqCRYakPt4zAQ2FeLnfZRofcOpiHe1CXOSn7XYr35O431EcjdHOp+McZ0AaOxv/Uz/eXgUIV+m3MkIvGLS5+xs6tjTMz1oS6MpQ3jFoBeLwmypa6Vba8s3HiDlWpn0IKRMsU68Xi49I9l/7kMuIPY+TP4Qred27JR9rv/GLjztU8qkqGaLeagRUiY/BX56WKpqAu+dOCRaCxPMBjUYgzXpkgdGhSWQgk0ObS51GzuMwkyQJDuFXJRMDO86mGC+w24YGAJEK5epzlMEawnjkyat5cC8krEgyKVs1F7ar5qnpYdZ+z6mJk/XJi0MAYClLSOTo2szxpjomoapBZEBXFiL+DmJdknim4fkwwR2kqjUM8Mjlb6r6lt8RyhhXGIeBh4yPhHms0SGSQmz9FE6OHbBxoWFEv7wbhii97LGkTANdtP6MgBW2d8qTZK2+j0gl/JqGOD80skZnzjPCfM7JKQ6r8qE5f418hZR/7z+nmuH+vqGfXxSYTBaSzH4AjqPwtoePEwquKrAhW+9gN/6x3+EM5cvwLOHY0bpCe28xv7jPezfvY87n3yO+1/cwfzwEMtmGYU7qdY8Xv5jmp0wgpQ5H1yYWMOo6cKxMN/ee8mfFObUOdWqI/ztYK3pme/kMlRahBEmK2WCdVzpuUvNIlMtcKSr4cyvSD1D3weAMGfAkj7Ec4UE3CS/63PQM5gyIeHznNHTMsYEIa8j30Mn3PTMGDjYa//7M+9X1/SJe1eZSjk/QmtkXJoTcPB0xsSM9T0/T+nzyi7mf+fnbTCPYS+O7Z+V+kdoeH7G9buUuR/t6whjn/6eM3n5nZHOhwg7V+cvZS5zxlGfG6WFwODOS8s4IAnj9wQVjik40te9ph+gVQ1qPi59JuddUmY3BQbpuFYZ+DVml4NtPHIfyx99fczDuyuZz3zede1zofaq9QXFORlb75P7zYnmM/mMsTKH+bqvjHM4Hdm89GPL+YLQZFYPRcFRfq5Sax+dp7HzkLYX5ze277CxeQpbW1s4PjrQFsMVMe73mo55QMOyNQUFIZWR3Ee8SqKeWL7xAClnanMJwZi5WHpZeS/BC8qyFGmpk7/FZlLqr6pqcAGlBydlVvQC1zYUdKQajTyAQGrKl4Ii7330edJ+qEaEaNhuWtfYRZGW9ELQNvN8IbE/SpCBIPk28FBptIP3ww08WIsg1XkaYpT+TMerzxljYKwF+17jlj6Tjym9jNJLJf9etW/5JTdGnHKziAiqk5+A0B+jF27HmM/n6DqHSeivMqr5+uRtDiNxYeU5GRvHy1b7GMdmxOxqjMUiIhDTYE16IoQ+UuHIRbyunDSWlbYpbZviJWGtfaKvSfhtwIzmz67rd854pL/r4+leGjJVCdP8NPNCQFdI+G7jCBNYsGOYqkBjCZMrZ/DDP/4Rnn31RdCkBHtGaS3cssH80QEe3X+Am598iju3vsDj+w9g1Nwu6aP+ngOl9GfOII3tdaLhHojzmTBjurfato1+nGPmiGMXp+5j59yoj2J6PvVzpWuRXmb0I21P686lxGn9K8KRESZ27PO0/zltGtujeRspc5H//tR7aaQQiVXAmOBnrB9pv9PP9PMnlVRMMFbfSSAp3Wsp/dKcevpMziyn/UtBVMpUnlRyWpP2JWXi9XcVUg7pwpA5TO+usfHnZzPvy5PWKu9//nfefj4/J/mQ5Cah8t64r2Banmau17032ANYtQRIn/1PqT8vwqQP/04ByNh66XP5HRDnnftgF/m5PWld15/zXmj+pPnPx5bTkNinTOCVmjTm+zHlW8j0oCZ9hogGlk4nlXRO5VyJdu/w4ACuaQAE7dcaX7iTaMmgjYiXOPJbhHFe50nlGw+Q1G8jJ0A6yan5SMoQpJKiQZAHHqrtIzMMMS0DsLIptfRR5voDoxqu9CLTy1/DbqfBI3KCrJHnenMx+b4oikEEuHUXXmQ4gl1oLp3VPuaSvggEDcAdC3NnbdB3iGqWSBzu0rntmZNV4qXjIeoBZaq5MsZEYJr2JV4KzCthi9cxPqmGLJ+X2C8Sc6Dc/C+/VPXzdZK0MSmp5ipQQBvBFK0ysWMXnRJz5xzGTGd0nK1zsg4I5lAhqg8ZA47ePxiVHI3Nc3qp5AAzH/eQMA8J7EngBUDCiPTjzZn0XKIWmRnTS+HG9no6RylTkJ6T/AwI2B/a8ef9fhqGrO8HwXoTgyeAGF1pYE5v4Y0/fBMv/fb3Uc6mcESwYHDnMN87wP69B9i7dRe3P7+JW7duBa126CMPBSppmPJ1fR0zPU2ZwjBz8b2u63oGIctnk54tCs8Pspxzr+FJ+zG2J/Lzpn1ct+ZILvu0PymTkEv/0z5rbrv8u5OYv5P2fdpOHN9oLavM/9iezdt4chnO5bA/Yso6Vl/KAK72YfVs93frUCCV15mPJW1r7DMGx7tDP8uFiencR2sQY6IWeqzNsc/WM6jDPo6ZfOZjG3yX1TMGovX3tdp8DPdHTqPSMkaP83rWzceTGHCd8x4cUDQtzaMcpvyW/j0wkw/1De7FsOZa8nGuo7tymzFEuzXcu2NrGuvE8MpL+5cKdtJ5zS1oVugF+jU/aQ2e9FnaxpjFQk5bngQenkS/BkBohH4WRSF3d6Lh0/s4fWfdeHO6EPdoUEm2XTcEWcIQrfQ/5yHXzZuCoWFQsGGfnrZ84wFSfgkD/eFTxl8XXH4XaaMCEj048WJ2Q82G95J0tZpMYEPEu7H2078BRGl4Svx7hnnVJjaNqpceGu2fJrpNGe50vH1/h5t0zOQs3/jalrY/UJODYYsCzH3iVEMGzjWDA5Fq0LRttTHPmTRtL+17al6TMhGx70hCgWcgNN0D+v7Ys+n4mUUi5PwqAcgvrJxAab1pkIxI4IJfiyXRPM42ZkD4vWmbaC60rqSEMhJy05smDZ4FwD4Ne9z7LRn0/hfp2jOzaI8SADu4vAkxwWg6FznQ1P6RcE4AM9SnJx1HOmdpffm5GQOy+VrEz7wHaDy/z0mMbPr96qUzXN9VIrvKBOZjSfejDeahBANXGrSVwTPffhXf/tHvYevSObALF67zWO4fYbF/iEd37+H2x5/izsefo14u4ZlRWAtQcKwO//KzkNK7VJuURtjM50CfTx1ocwZPhRzp2HQP2excpOs40GRma5czUWvBRrZO6ThSJnaMuU33uvY71cbn/RpjdnLGPT8rY/ss3+OphitlOPK1GJunsbM5ZL6HzJUKnnTdjBn3nUn/zhnFvN0hw8pB+LIqhBo/LxjdV4NxZ7Qiv3fT/vbr61fGkI8nrWuMwcz3wbq9ODauwZmHmECnws+UHqSC0YE2YmSO8vkfKycxqk8qY3QqbS+v04/06UnzkQOnwb3IAbKM0NfcvHGw9t5H07S8P+tKCpLG+pGDkHStUv4ozsUJ5yStc+x8r6M54ctwd46PYx3NSPksfS6tEmb8TKX9yPlANV1N52PsPI7N3Rh/BMg9zexhvIb2dvCcWAQltFFLrlEb229AmDKdv/BJShOftnzjAVLbtphMJgCGF4YCinwji3O4GTDyKjU1YbOmktmU4ciZ7FRiuUJgMnVuysykkerGJLx52HGtp23b8N4w2EFqIrCuP2mfciKm9ejfA7M29mDDgBWbVLKBQ2MBTtR2Q2Y5tGN4SJTzC3/sAKf9Si+cfq0yCR4NJdhpGRuf9jHOwxMUs3lbY33PLwgmBjofpTGuE7OisSg1J110g/lJxpYSTYlMRsGvJUhRqJeuiHImaPqUsIS1k7DjT75s1wGXAQHzHrDKwT95bP27QD7/6wiivhfPlBmaJ6xjcE/qy7Ct9XtB+5mu80lSLiBErbQWrjDYfuYCfv9P/xHOX38WZlqKJqj14LrG8f4h5vuHuHPzFr64eQuP7z+Ea4RulUURTQgYchdYQ4M9MMaUax/1bKSXf8oMKC1SZlrH0gslaMW/K79Y0zkYaqWGc5yvRyqtTucuBz1pf9L1ztsaMK7J5+vozZBxG/Y37+sYEBhlukbGPEZv8z6P9Su9M1KgN5ivpN85iCM6Cez3Zdj++BkSjWGgIyPMYj4/ukdSoZear2n/rLHRjyvtX1pXep9HgEvDc5rPjz4/tr/Skmtj1s1ROqbBfKyhhWP7SvuXCh3XlXX05GnK2LPa/5z5Z2aAhz6gg/eCJGYMvI0xxGMgYeVsyYcr/R3jk+L74f4b44fG6ggfpi0Ovs//jc1XTlP1n0+SJadt5/ORz9XY5/18jM/Vuneepoy9N0Z31rW5rr2xvTm2FmOlLEs0vgNxoOOOR2lJvi5j54iMkQBZnLaX7sGnPzPfeIBU18tIjPNIZenkpoxDzigIE2DiuUqfUQAixNyj63hFC6TvpG3pIU8v8l6L1Us3cx+kvKQMmbar9TdNE6XGzjmwH6pGtQ0doxlhHMbMj7qu65OlqrI6zEVHLCG+rY3akpQw6pyChwQ0NwccI0JaYp/TZ2L9qyYRudQgBy656YQyhs5Jxph8zccYnJw5yyWDkUiAQtQ5AAQ418F7CfOc6OeF6K+sdigZ0fFYvaBlAoKWDlp1kNABUdtHATBx6I9uU+/DyEmBp9Lq+Mtgn1B04I5D6+cV/fucgIkThpf+1fd+jGBn3xEo+ld5ndPINIUdO5i/rCWipK8cJZq00n4q2ev7mO+nfm7kGTIhchwYdGoLb/ze7+L5334DmFVojUFRd7BNh2Zvjr37D7H38CFuffo5Ht27L/QrJCH2RHDMfWCHpF9WI9TF+eydXimsJzBkMIkonFkfx22tRdf5yExrMUZzoJHMjxHzXOc1FD/pSoAIcI6TduNUxfmKzBY4XpAM9H0JC5XS7VT7pc+nIFXPXs68Dn33Ejqr+zihtynzkl/2OY2SeTF95Dogmnr2248kujbJ+WJwnAuCaPd1nZLTFunyGEOTtp3+TbR6NtKxA/1d0O9eDH6PPSOK/WIeCvdi/elZGWGMcuFbKoxKz4yWVNiYA8ExwUfMS0gAU0+LdO70/FImhAQhrskKAEz6sa6kd0va3/S7/L7Q33PmON7NT8+/PXVZBwbHGE6lgeGD0ff03uj/lkvCjzyfrvtJzHx6v54EsvRZIFnX0KEc2I5pDJ52evP9mAp+0r0YzyL0uhnyfvl+yOcnn5t+nFJjZPyzOUBs9eSRDdaXEFNZKK+T81f5O8mHwzbCnyet7bo16Hss9UX+kNTkfdUdJt8PY/2Mc+SCu0KkgVKnMX3k46cp33iAJImoWnjvkgzqqxeLrEUIrW0lNLUNDENhLGwIS9txD2JSMzmQJL6aTKrYhhRd1FXTEV3kMRMNcVgWSRoiwKDINAggCO+QhF6V0MVCKAJ7AvaMLmhxwJDw3YFTJRIncb3EU6YqJTQpyCASc7CeWEgUPGOEDTQEGJQorIU1BTy3K6BHDiWDA5gRE7Hg61NY8aswEmicWcLoEgsDZdATm/SAMzOgEbI8B+0JwCxhwQHAkoEX47IwZgJxGL8pIgfvnQOMhYGJYYGHe8oE5iYw4uAguRepPhHBokCngSogzBIYMI7BxgCWYOBRmkLC/4Ys0EEmH8zY1hC8yHEFgsfCcKstNgJYYUhi0FQUZclEn7bOdeicC+A4rKeGDi8oEnw2SmSEmYgsOQGGkz0ThDbxQtD+MktY7wiMQthQVtAQGCBlGtNC2nfuARyLupwcoaAQEEBWNTBIgCfRZsq+S3JrMIO8MutK4ft57ULob0PUM8vGgJhguACBYGgIEpmcRB5knXkRYHkGYAp4BxREMJbgSoO6Mnj2Wy/it/7o97F9+hQ614mmtWnhljUe3nuAh1/s4c7tO3j04CG6upaohz7QDGJY2Hh+EbWAHp4dLBWAQWKSwqHfCTMLhqFAw5jh9JCEcOPWyjm0pdIZ+SfbRPogF1B/wQq4Cdp1ZoGFDBQ20VAZwMHBg6NmU8ckHI6J6+4NgZEIPEKQXpEwis8hvPhDgEJEpTAfDAPvesZNHXUVpckuJFgieD2bxsQws0IfeqGY7GMft4wJ+1wFRQLGAz0IQUzA/W727ENwlrBDDIG9CjDEHEtAooJ4QHXYJuIoSRiNMCZmCZWbmhgRCS0QsCXRQo3E0R8yjmBJmRDuLh/omQHDEgtNCfsexsqcEuSUhTZiEIUEIDEzKIZ+D9MwYl6WMnopLR8DEek/rSetj5kTf10jdI0IXFgAHQr2KNjBegOiKTp2cEb2ooGH9ZKQgkMUxTQqogL19I4e9C/Zn0iEJinflgPbdSBA9m/PFKdMa8oQpoK89Jl14CMHHuOMOgUeJRBQvTNyYYa+z8r8cjgj/bkC50z88P10LAPBC50MDlNQMjCZhZAPvRa1SpZ8IP0+imvVg3ntVzqvaV+1XaWlOS+00v+RceVrnIOJ3Fw17YexwQDD9PdXvP+Gk4ueTq/yDrE/pGxOBjRHQI4KEoZCAOFRfGAGLFnJf5mMW8ejvHEqBEnnhIKJObNH58SdIR6gTDCR76d1+0u+S3wX0YNovZucGz8nY+UbD5AmkykAoK77xQL6gAkpWvfeR4IIz6hdLVutAIxBvBDGEDEzw9heOjWZTHrTPDMMbZmbE6QEL+1bx21grhMHQgpAAhhsRGAIiuQSN5FpZq8+BcXAljeXIui/ddHCUqLhvUQa8t7HNmM/KEh1M+JcFEWcF6DnM4koJnzT+vXij3Pke41XGtq8N2dEUqcSCYbmxOkJA0U/Gue95GoKRF6lF0Si6dG2U5NJDsxAUdioqdPoXYOAHlglQNYaOABsENXIUHDnh4QbNH5bRFLIwZE53YfaVpzXvh6dY1sU2NjcBFkJelEvlujaVtaKlcz2tVpK6g4XqDC1GKwjs4AiSvdNIFLgIeEe5BjySLRgw7EapMyUEvFwIVoDDsRawFkYJwNTniQh4EP/2cMD0DAf2nNl1A0IhWpMtW8ALAMdAa31gzOVrocJIBVEsT5SiGiBzgCd8Tj9zEX80R/+EBeuXIYDoz0+BpxHW7dYHh3j7hd38NXdr3Dn3j0sl7WkrSgAsjIXMATHLjByABsTmG4CsUHFfYLgwpSyRiaMJebNkm45djBMKEiiTyrDBxDQAdaWaFwHb3oGMNUTFmxQkIUJObqYfAAxJPs7nGFmD0M2AuGCXdAu++FeImH4lYbZsHUV/Dv2MmbPooUlAofnlU4Si6CKjBVppHOhD7JOVpmRsLEl4XPYWzbwH7qfKRk3AT4iaQ8YgMiHvjA8ybel97I3416Q4pnArYn7X3e3nAWP2FTksCn+kJxyYc1kIwuTRICHCQIkCli/ZwJLBE0lITK9ejYpAB6QzJv+bsEogkrFdYzOM8gLnEXIY0ZG7xgBV2Sol4akRYeanel1gCGNNEiGAtM7zlTmRX1zPQBvCRduPIcLL1zHr957B1sbU1zY2sLh3Uf46tZDodtMIBfyzMEKOKA+aukAnGTaKx0DRdrWj2vMWiGucXKXDcBqrqXKwEzOuKfzkc/luvIkTVisI5xfwb2rAY5WSqTrHPZXb+67+uh60Cf33urzY7+nmrn4OSFa3GjI+XUMdjyVoevp3K4D6Sf1P23jpPVYtwapdjV/P7eW6b/La8n6lgB3Tvd0xpuMCSOARKOTWVaNjY1o6HuZgqR8ztJ2TTzfpucZ2Uf+Zmze8z04yp8GH2ofnhfrKcCY9aaD68o3HiCpX04fwIAGyDbdmPrPcZ/ACkFCgSJIMDMgAfSmPN4jhgRPwVF+qNYx0PozSiqYwc6hLMsBMNAx5Or9ngm3g42fa6hy8xJ9XxF2LiFJ+5jOl4IJ57zkVzEGVPQmKhqFKP6dqokzVXh+WQwONRIH2yDp1uiE+nmuWk/nNC05IUpNCfM5S8fcz9HQbMeF9dE60jDHuhZp255DW8G0pe060R45HgCLky6ztP28pONXXlf7nfZ/uVyKFFvngdKL7QTzPiBIyREZ275tRPvedfs77X/8PFuP+B1Eeg4meI5scAS7oGCSxBwY0kBY2YBQhmfCeDjoHz0wyRClMmSwDG8Dw0yI5iJcCMNLzIBJmVkp1hOM7xNUqvbPBGfYjjzM9gzff/N3cOP1b8Eyw82P0TqHrvFoli32Hu1h/9EBvrz1JebHc7h2gUkQqBa2EL/CsM9d0EIYMrCFXmCAIQuLKZiD5hVB82UMyBJaDlELdY+xmHYasrCUnAdmNG0LYyuUlUFnxL5eTWazHQeyKgAKYI2BziKacygDBIhZoHWyrjkDxORAppFFcQzLDAsjGlYwGtMKoJGbNWhPOTDthewNjyBQsgLCSbRa/Znu8yI57+BJxmStAdvUTI0GJseS9yUwESxzZ0iEJF3nIjCWDdtrgEV4FMCc6QESK2fNIvQy+aYaFO6PWcIQEonWw4SDSwh+hyBYEu2I7n1FMBEAB0zDDBD3ZuQmnGEiA+86WKNnWjVfq6ZusqWo7xuG554TjWvOtKU0XumT/u7ZDb4fzEi2D6PlhfcoqgLHrsWLv/t93PjRD3B0uAdbL3H/45v4/MFfYoOBsmEYB3gycFY0k5RZTWhJ7z0dbwRLCYgbY97ye12tWPI5ysc2Bory+XvSnDwNIFp9T+vX/q+e09wcMi/S7Dg4GWs7mkI/5TtjTLHyRPl+ytcmujEkScvTetYBgRyk5Cat+fPr7ucnzcU/5Luxko8l7usTnh+7o3N+ZAzAjXEL68FUqE+eCu0k/Ga4u540trF2+u+lhcgGkdw7/bk6sfpB+cYDJJ1MBUdpcquIZBOfEWZGWzdoWNT2m5ubgYEycRukRLQ3HTEwlPj0ZJeroldtWz7vTfVyBM/cM8wpql+n/RnduNkB0cSzao6QatPk39AMUEt6aaV/GyPOcGUhKjbHfTZsZWLJmIHNa3wvXKjppZGuRxpQYgB+zKrJXzp3oxKFkb7ngTDSyz73JdL26rpGVVUyR4nmISUmKsk0xgwiY+m+sGTAJpjmWIOiEkbec/iO10s50r0RwXGYx9Hxkwh9QUMCJfvDwfsEABIFMyQld6uSVPlU4VNYv6R6zyLdHwN5eT0DwIahBCvOJwDycpHp3IBZtBUsDA4RxFSIuQ8lDgabFrFz4T0AgAVcMKVRprI3UfLBxEyl6wQyFrAGxgMz7p8PMyD1B9MQDwYb2fPCfFsUBeGVl5/Hi7/zXdCswmJxDK5bcNNh0Xnce7iHvUd7eHR/D8t5i3rZojAFZuUuqsJE2mIDAAEYLbl4toya2jLgjcHcFOCoOaABQ8BB42mM6XNxMaMhBVIUTVvJGLTGwBGBbR+5EhHriDmWMQhaaSO+h0bCrMOYaJqpezZmeHehX04SVCuIatsGXX0IuE4CmbQOrnNA52CZULRzcNsG4Cn1Ou+Exhihs54EFIi2iWDIigAHDKY+n5tjhjEFjO/A7FFCNGECskXrrD43AHpTNkgEQnYOcIzSGlgCNE9qXRbwNs+RlUq8e1qYCmUMbAQRpM8CIAaqjgScM6Lm2yBofbjXulhrw94UwZXgPDG/jrSVCIZkjXR1TGGDaazsMxPorPcGvu3EcqI/yCt0wRgTbNTXSWeH2oGxuyr/TmionOd19FCfTwVrlTXoOo/D+w/xi5/8FC/8zvcw3d3F0Z7H7o0r+NE//a/wi3/3N+BHS5ATEx/PBsYCJjGfz2lYyoSn66p3gPZZn03v0PT3Ff/EjEbqug94i4xvyJnXdXOSPj/wlVnzLhElkQj7z9atWzov+ruamj5tiXXyk8RySR+TcaV9SIPOAEmONIwE3SCgS+64dSA3bXfsXhusDzjOX9rPsb00BsDztvN9kj+T17+uvbT/sr9Wn8vnYB1QzMeV7td1fc/7C4jw0UL3+UhYfubBPho7L2O8kvIyzHK3EBHIUiZ8xlOXbzxAcq6DtUU0W0sZYmXOI7Ejwvz4GM2ywf7BPjY3N9G2LbZ3dtC6DltbW+L8lSxINJWjVelSTtzSCzE90F3XwXuPqqp6Z1MEBoh6lWV6saaXQm4frf1IQ4KnzLvm/FCwWJZlaHPV8TA9WDmRsNYGswthGJg9yBpYMND0kf+6jPlNL5QUnOQgScczjAYIwK8S61FmfuSApyZz6TNFUURtYzrXKbDUPqv/jk+kgXl7qyBZ1qH1DsyA61oYgtSjDBuGF+nYhbZCFJPx5WMU5gJRMKf7nUgkSR4c/S4CNxVAA2PsrtI9AvRAlcN7+t0YQB0j7rlZ59pig8lWTrAZKJR5jcyjARmDjj1q22kHhCFUQuoB40RimUazMZZAnUWBCUAkvltEsDaAf+Ig6e+lcN57CWwAiy60xQQx3fKM3dOn8Orrr2L77C722hqH88eSt6xpcfjwMe4dHuG4bnGwfwTvCNONDZS7p1BUE7RVCV8UKKsSRVkC1gYwBpQloSgLVFWFqiwjfbOFBRU25CDrzXqtNTBlgWJWBQBjIg0gCmDG9vbhZVHAmiA0MRaWiqhVUDMuIsAbhjfBET5oj3QPRZ+fsP3EVDLk7mIxPmQFbwC8c2jqGt3yCN1yifrwCPXRHEeP9rD/4BEW+wewh0fwyyV828G1HdA5GFOGfcFgOBhrAA4BedShCARbWBhjZRzGAGRgAYCN+G2hgG/7NAtkbADKIehMkSSwBsOxnNvOE8S8QMBUBQN2SjsEdDB7eM8g08GzA0HTLQRA5hnwFspbanJnoRkiXIPSRY2aSgQihuUmAFr5W7ReVjTVsL2AwBSADwaMYQ8YgtQXBFZkDcqiCucF6PwchlpYBXx+9e6LZzdjoAY+ImHPAOPMeQ4aIt3ItPVpyelGpOfeY2osuAM++uuf4f4X9/GP/+l/i3Onz+Ng/wGKSw5v/pMf4Wd//ldoHi9gSTSCvd/qKtOsaCHte39X9YBW+5Waz+vPdWPUevWe08/H8hHmYDKtQ0sOHvJnU6CQfZvMua7jMDy5/kz7lZsMMg8DNazrT363MXMvtFpzn68DMV3XRd4ufW7MfUHf98zhzIyDlXw+c8Z8lPmn9eAprTdfw3X3ez53+t6YBu8ksJT2V4U/Y++mZR3vkVvQkJ4fGgKrdft8sDbiJApjLMqyRF0vwT7wVAnPktd10hkgCib3XgRkyqfovsqff1L5zwAgOehsp34reqA1CWjXdajrGgTCv//xj/HFl1/g2o0b+MEPfoCj4yNs7+6gaVtUdpglXhfdewdDdrCZ08OZEoL0mdTXZ7FYRGKq2oY0Ml1alNBpXiKtN60zSn1DSfuggATotWvKFecHW59JD2gELdwjfUMGHhQ1RsYYMR1LLk0FgCYbU9qeEry0L5GoJ478+l36bEpUxohy/ozOY5oTKwWu+py1Npo6GmNg2PQHMQFV6fqk+y0t1lo0voPzDm3XBY9+Aq/SqdF+D+YLokHJ18s5F4IMrF6gcf8FQCPZqymCIm1mjNgKuApO3sEUjdQHJpjujF1keR3pv3TYK8yJKcCJdJEVzBGh8UHSzWEsQeJsGNh1moA1MOsqVbRAU8rMGWuiaRER0IHQ2BJUWHgCYAitFS1pawiuEP8tPXdVVaEsS5iiQFFVsGUhgK6w2D1zGmfPn0PLHo9YaNCmanC9w6brcLmcoJzMYMsKZTVBVVZi5lpYoJJ+GGtkHTWTOUGAgGqCQoABkGgVCs9xASkwxxw2SvSp0TXiXlPBgz2aXIhgULyPOJqrMQtg5OHWTmqg/pID0CVnzlBYG3027O9NAMznhEFkgmXANx3ausHDe/ew/8UdfPnZ5zh48Ag0X8LNl3B1CzQdTFPDUgfnO0nCzD44fcveBBnxS7IhdLkNIGFSAJ2TufY+JBpl0bhZC2MtWqV74XL28DESkk+YFe89jDcwYV9GJhfBfwwMCtJSdqIhYQhTT0zxMlaJrIWcrRaSHwREcBS0mHpW/aynQVYD27DkPwvrprTIFARrgqAwgCwTNNkm7LGinGA62YAtDLzdQ9vWcsZcJ5o912GMxsqPNT4aa+jaSYX7SuMdPUb/Vt4joCMP2xJ2WoPFh1/i4JM72H7hMqabWziqj1Gc2cHLf/Bb+Ns//0tULaNiG5i8XtM1oF2hL2P0LNV8pHdAeq/nGo2c6VwHHtLv9f4cA1pj7+b0Nh9T/g5zCLiA4Xqm/TiJsRwyzavfjfUv3Udfh2nNQUyadiWfm9QKZKwOHqlv3fjyu3wACtVMcGQcAzARvs+1jflzaf/1+RzondDZFW1cnBdDgz20bh/mWt20n/kYMhZjhRcZA42GSL1No2+qCRYL6byMtZmfwwEvwTwUUJAA/bS+J611Wr7xAAlYnVwOphgp+CjLEm3bom1bfPLxx7h2/ToePXwIYwy2NrcA9IdE38uRPbP4dkwmkxUtRMp9qtYqXdyyLKNE1SUbLyeQOp40Yat+lh7g3D9JS94v7zma1gE9yEoJe2rCkQI4AMJ4+hClzCg40s2JpJ1E+hEYmD5CnPg4qH+RmqaN+SNRdDamlT4Gji/Oc34xM1YPR9T6OScR3RTsBRDowp5xnkHOwdoixFIwiOYthmBgogTSkIEhK3kRQDEaoUT8kWhrZA1c02rHJKJWiFgYxPQi7eFeEu9jqMqcIvU0ygeTI2G+PAgSITB9Ll4MwV9EAlWEB8KPXuuiZh69RkINzXwwp1NggiQ0OMKe59jFXqsB6v175FLpzVcV1AAiLW/JAIGhYyBazXkmdLYQ8EAUDYtAhM5aHNkCJgQkKSKoKVFsTOE2KlSTCabTKYqiwGQyQVmWKKcT2EmFyXQKOylBRQFTWhRVhbKsUBYljA2aFwBFWYrDN3QYBmwp+AgxYC1aMCwIJRtYLyNoDaElDpHxZK08+kuSiFF5cWKVwAWIUceIxAxG7uIgvtZ9TR7eakASjiZx+jdTcpno2rD0ww4unWEIfSYf7n2CJ9XMhWiGnDAaYf4JEI1btkf1h+UQgY6Hkj3PjNaKuZdngmPATEsUkxIXtq/j3IvX8fwfvInueIHl4wPs3b2Peze/wP2bt4AHD9HVSyyXC7CzYN9BMX9BJdQc2ATaYo2FMwa+KAEwqCijeZnzDmwNvBGTNRPAtAk00FvxwVMhD5EJOVAIXJYB1Pf0qygK2YM8ES2R6RN2Axzo4RImWEuqfxQHhnXTObggrIkBbpgBNkBbwXVuYObCzCDXougWMXKhggwFxioYMEbAkWoqJ9UM08kmrCWgmqGu5/C+xXK5AJoF0AUWOlg9hO0nke2Yh8BY15f15CYl9GE9q8ISbIOGPrX9GVk19QEAtoQlHCZUoOoY7Dv8/K/+Fm9e+K8xKafY3N7G8f4hFgXAWyXa/RoTJpAHGGa0HW0jjin5XnFEyqDlQrscGOl9uA68pHd+/k76fd7m2O/5fKXtpc+YIBgQIKjfrzK3YyW/ozl7Pm83mrmGeemFrVhhtp8GuORzOGbquCKo1L0Zfk+bTVvM687nLV+3kwDsmOZo7Gf+TsqTpLzYWO7EsfrTv9kxQOMBuHIANljTNeMdqyctOe8Z10J5YuoVFRw+Z6+hnjDY+2NAOu2D5xCBOOVfCMGQoH/Odf8lzHdfGCiMjTmBZNI8yArTVhaiCTAEGGJMJyVeevEl3PnyDl56+SVsTTcwtaUwunIrhskWhk+Zx6IMl6Jz8J14IdvgrM9OghBHMAOgSH2JvIfvuijN0E1COoAIXHRjpyZK6UbWjdBnSgdyKdIQoRdFMJ2BhwvSwZTAatQ779HXGdo1huCdmI84ZpBnVIZguIOZWHEKtwW8c2Lr7RgFWbTMABw8C0AgY8LGFvt+8WUJy8cqDQnScEcgNgF09AeOnYSn1YhryrQACL4pIckuJSZxUIZeHNBNYFYcexRVFULglvBwEoUKFraaCI5zDQy3UO7YB78QXTEDC0JvmsMIJjGGUXcNbCVmeiCDCRWYOi9hqSHS65oAbyxKB0ydRFDTPRSBRTj4NoBFH52tE/MBslF74p3vE6gCIo3OQKYwOSyWbWAwiuDIJBvPhv9gEDQIQathxI+FPESLYkIIYUvB/MgCxsAXBbgwAiIMgS3BGwEjstcKlGWBoihhygLTrQ2YSYViOoGtStiyQDERbQ1Zg2pSYTKZoKoqFMEkzRSFSP9Dnam/k/irUDxn8ZKMQwy+FBF46L1tEjMhxHMsYC+hN4EpRzg/IUAyHBzY9jbgFhoUTMKDW+jFLA06QgwXnVxJcplrOFkg2rz3DQfwNOgYh8ACyryyPhF/pno8ZRr6avvwu8M7l5BOHiutCt+ZwbODUUR/sbRNJiNAjfvnOT4fmisNqlObmOxu4NS1S7j2O6+jOTrGgw9v4r2338HizlcSFp1Y/MksoZhtY2Njium0xHRjhmpzA9VsA1QWqKYTWGsxmQgILgrZf1TIfkU4WyIcCuZpBKhdSRyCIndDMZpi/3m4wF3ky8I8KtOh+65/SaZB1s30L8T3dB3YIwbPcE4y03vvAefBdYOubdG0DZjFp7Ze1qjbDk3rwc7D1y1c3YA7B+MYpd3EbPMMSkvgg0dYzvfhmjnoaB/N/AhuuQAvlyjaDqZegoKPmONO/LC85B+R9eXA7PSaiXTXec9gDVXoOUi3g6UCI+amShm1OEMjf3Ng7q21YEPorIc3wP79O/jyrXdw9tkzmDd7KIoKO5MJ/ugP/wDv/uRt7H/5AFMqgUQwmDKzqbVFej+qyWHOPKY0NQVDca/rPgHknjdCWzRNQXrITgJoY+AlZ2jT53KQkD4rQhGomCmAIzvqU5PXu8I0J31O53HUPCs9KymwXlPifT/yfj4fKaAYmzuD4ZppCR6Lo/VqPfovFRirkEKfHwglgJU9Aazu48E8Yrj3UwAz5oOddHiI8rKS9yvuYUKMJivBXsJ8sGrQDXxaccIXaLJ7rTcdXzqmyFsCfZoXAHVdhzDpfqXr+Vr38l5hgnzgfTUoWMrjcKDLRBJpVfv4tOUbD5CKJDme+o+kWhQgmE4g5ATpHP7kv/pTIRCBAXDBLtJ5B3IMZgUnfT6Xrh2aZqUL2qlZVvYvlW5EyRMRyqoaSFjkma5n8rIDr2PJJRRahgcBACTCloI8/S7XGMXDzxDb/nDNERCZbrV9Rwhz7NnJ3BUWxaxCc3AYgJ1o7qyRiFreS7JLZhaHYxPAJBlULJI/F3xFxGxE3KQ7K/PpXMghpNIFI0erIxe1S2pSRED074lSdNAgka0P4X6VGLgANC06ia5FBtPCorIenXeA8yAqpQ0KFzskKhhbEgaXGWAXgJCMo/IWU0zg2QKTAtXpM6jPncKybjE9WqJiwhwek6sXwVsztEzwS4flwQEW8+O4LrpexECZaJmEQAh49AQ0hYRO7vdBAAdBqxEv4F6nINqwYIpD1grQVxOvskA7qURzU0jUQgEtE9jpFLaqUE4q2EmFajZFNZ2gmE5gphXMREzRTFUI6JlUKKsKFRcoSSKPGTX3CX0tIeYvPgAGBwQGDDHyV34OTpIyrTsb4UmFzPGCCXw5IqeLAV/fP5T/ydnHFC7dgCkoYZDHqokgIisrl8fKE6slleqPFUYPxvJao3AhfjN8bh0vMzLTJ30Zax3t5qD7Yc3DHoAxKE9t45nf/jbOv/IC9u4/AnvGxtam7FlbwFZTVKWBLViYdmPhgqlgZSiiFmZG2zTYPziAB2NrextVVQ19bWIfViWpwPgee5rvVubjKevU71eYHQYs2QhH0uKNmOpZhOAKzsOCgNbBdQRjSvjOoZkvsL/3EPODx9h7/BBHB4c4eLyHZr7AYv8A7eGx+Jq2HWhxBDQNuG0lZxcziBmWDWC6yHiLWbJo0GFNtJqgIBzLtQDpXIwxzmPMr95FKg+oQPjN3/8M5dsGTXMAhoE1BbYmO6gP5qi8hXNi6qyS+dwMKZVia7tjWz9lnIHerF+12JHnSMzNRwHUyBjXaX/GPh8DMwMQkDDYqwxjKurr30ktZ8Y0Cenv68azbmwILQ2oy0g7ysflJe1XqqlYezeooCGxUontEAZEPt8DufYvpvYYmYNcSH0S+DuprANSqcvI16l7bI/0wpfej0ytbpR3YqwHprkgY2Ve8zZJlQF63jyauhv4def1D36i3++aOseSms33u4lOuvyeUL7xACkFIVpygqIEoqoqWFtgjkWMrFapb4G8CEDQqjHid6R1pGZzekDruo4hn11mvpXaVKf9SJ9JkXgeoSUlhrphc4lNOtZ0LuQzsedIBD7x+VTiJHUC6oSdtikATjQunliSQDoBTx0RbFXFBJ7WGjHbiPlvLNReHqyXIwAQfOHRwcGrqRj3AAxgEHsUBWALMY0jYsAEoAWGavaihENEI7p8AfyqhJIEfIZ8Tsb2ZiiWCDASQY2MQWkQcoSwaExQSLwoQ8HfJzBg6MQBPJjMORQxb4g1UwCEjj2c8TBnzmH7e69jwR0Of/YeNlpgUVqcef01NGd30BYF6sMFzm1uYWd7G4vFQpzxlWv0jK5tJd9LkDaTMejaFnW9xI4RXwdjgv8MSDQ0pWhtCITOdVgul7DGYDKZoqqmqKoNTKYTTKYTVNMpbFmgLEvYogg+NyWKSrQ8IAKHKGaE4BcUGFgPiKO7D2ZVEXFQlFbpUMRMLmhvRBwHE8KfCxOPmMOQla8dORP6+9h5l7+HUtTV0rPr/dn4hxPZk8o/7LpMS85WnPTk+Bg4nNG0ynjZx/+l7aVfPqlvT/3wP7gwAU1JMKc2cGZriseP9nHgfPAdIkzhsWktplUBY2SPORKzWPiQ44cZ88Ucjx49wunTpzGdzoJQqPe/7GmpSNyBkxm+VQbkZKn0uvK0wGooaSUw9REiB89Jtmc4dHI2CxKz7lLAsAOD2KLc3cT5SxsozHNCZ5jRth3aZYPjvSMcPd7Ho68e4P6dr7C4cxvLh/fRHh6BGgdfN/B1CziP0hCATpIRkwes+gwi0OMhg5Uz2WNO6U+aB11T30mCWLQMs2RscLBQgEeDQxgHVFShpTTf16rPR3p3ppqYnLbkn6d/D0Hcqvnef0rJgcDY9zm/8J/S9kkgTpNA5/1ZB+xiH7P+pu+lIG7MDCwd8zqfo6cZh3aEsf7s5msavzNDX5ixeX5Sv8bAxtiZeNK41hUi6gMXrJTevDLtQw588nfzwF5j85/3dbC2SAIt5UA2eTZq6bBKJ+KasPAF4hN2smDwacp/FgAJGAYZcM7BJhHeNHoZkeRLKkoLY4OfjzViqsEsWcy9mOOBJZqRgiUwR4mQRj3z3kdH/1QyZUwfAjq1w82lVilxzgM9pGXM92jscPY/U8KlqmiOvg3gXj0NVmLHYHbwLoBAa4JmyMO5Njr8O9cCVIBNAQMD6wjkCSVCBEHu4B3DkIclB8nWIhGV1I7fgdCBYAorocM1ZC8IlRPtkbUW1lsxfQu+HZHxVTDFCCYMFigkjK4CIIYAWrFVlbUg0/sQUYjO53SurYErC8CWYMthHkwIjxvMagLzTk4YM51vy4zOOTjn8bi0aCsCnEfjHe7OF5hdvQpbEWjusbz/GGYyRbd7CsvJBL6sUFZbWPoaTTMHG4bvWhRFiUlVoShKwMxgg/RzUk0wm81QTSoB+NMpNre2JMhE0J5aa1FYC4teatsbRoVxsACS8GE0O1ACBcj3nY6ZgNJ5lE54oP6iRKzEcH+xDNO+ONFNBmDKAbUTEToKoeNDP5BesCPnfEx6NbxEKHtzjIlfZR6Yh8+exAinz6y9KE4g3P34Vt9fkaJlP9PnBkyTl7DaSkeUFnnvRTJIQ8loL2kNwpSEAWT0TCsl7fXBXoZzlEsc0+9XGbVV04zh96tFzrPsUFsSYIEf//ivcXDcYOfUGZw/dxovv3ANF8+ewqQysIZC7qxwMctk4/DoCDu7u5htbEAj8o1J93Op6JP2wpMY1ieVPJLY09QPCmOjXgAWdzd7FK6XwoIM2HA48yFnE0N85GDQeAkywiUDFaGYTnDm1AwXrl/C8+5VuNajOzrA43t38dWtL3Dnk8/x4PaXOHq4B25aFPNjmK4BuIOFj+G0pRFpO89hk8/RSQzXAHiGv32g/4UxcJ3D1BbSHpeikQbgPEsyZC/RVwG3oh3Ihal539L1UUHsOu1TWi+HuseC+KTjGxv7mNAz/fyk85b2/aRnYieTcpKma7gG48+c2FagUevo3RigG5uXFbq35qwy9yZxKQAT4ejTn+HB356RRp/J12MMeKQ83lif141Ny6jwgBMz7IzOKF+Uz0doRZ7IPs/v0rE7J93HacLnfL7yeiRYzbCdlJfNTV01+bjy2Pp8BFaDSZMRedWExrZXpndt+cYDpKqaDDQ2KZFIQZMSK/F/EHM6ayTcoNXEj7qovovfydQzbGFhi3LFHENAgxssvGqV9O91ieO0j9rvgSleGI+GCC+KYpA7KK0jRfgmai89iiIEFoAHh/CzYHFKFhN+gu86OWykGjIJBGBRhohMHkUAiU3Xh7B1zLDlBMaWMBAA0tQSNKAwBTyaEKErDWkKAIyqKzBxZXAAR7hIARBhyY04VIfQ5OT7YA9kJSO65BQKCSGd5ICpLcXgBUQmvuMDOBSTu95niQF0MKgh2iN18BawZkDEIGIJBFBY2LIMTvsFXFEARYnJZBIDANgQEQsTC1NYVEySW2dnG3ZnAzSrgO/+ACUKlMai2tlGU1owDAoG3MyBSl1TDa2MkCclrFlgbKCqZzLoKCTU5aGUx3iAsmTD8qZo6EwALaG6yNAzDR4e3CVEgCsGX8f3HEoEQ57InJ5wdcYaVgxZmOMdlGqCTrqIU4ZA9tOaC5wAIh7M4aCePqbIsI5sJP0FEkagF4NeVgFmei+aCOZEKqaSr2D775wTcwckQWaAgWmIStbiBaWO/IHpUNpRZJqzyLiZXpuXCpEoAFZpm0O4ZwFLDAmiUU4qFLYIZ6KLyVVFiGKjsCW2m7StQQ70n9iOjwOGcbDb/22dk7xMZHB6ZwfNosGDrx7j6MhhcTTHzmSK7aJAuT3DpCzF1MsQXFAtGyI5v6XkJeu6Yb6bYRmXkI719SQGP302L2OS5LSudQxurBcAUx8uN33eAqg8RY0tQkJdANGMRpkl2YehL64DafIxSPJmGIKZGBTTLZw/+wIuf+slfHtRY753gC8/v4UP3vkNDj/6HMf3HqBT/yXvUQZBjzOr65r/ngOhMUZ48A7E1BkkjtsGJJYGxqAzRkyrvYcnwHEHtiQWxL6vKz1baXs5DwEeStDXMZZpXQASX+ZVCXy6vqmZPTDUlqdzkDPa+R7Ky5PAdk+vzMrnY+NMJn+0vrztfA0Z4uPCNGb6xZm7wSpQW/f3WiFE2NZRSJSBghwAp3/ndce/kzXNQe86wL0O7I7Vv7L3ss/ysY4BNB8EkamFUt8PtShaD4L1nfy7dWUMJOnn4r4h9Ga5XGJS9C4TqljIx0DhXhutV2VdRBrtKQpzB/fv08do+OYDJGMMJpMJiAh1XYcF4oE2J3XmK2wJYg+dGg7qYl2QchoiXpVlPLTOOTStQ9N5TCaTnmlJiJi2p33JCWqqlkwJ8Zh0KSWs+reOLTIb2SbqCb0fHJZInIFo/oakfec8DDnAtaCQFJYKwqQyoBDwoPMO86ZG6zzAgemBwez0ORw+3BdTNs/o2g7edTJHZibaEOcgeT8Sxq+zMGRhqM/XAghPuoCDnUzARQHvXR/pqDAwts93Yq3BdDIVJs0a+KqACSClUsBiDKwtUFhx/idjRLNixbkf1sJR8IcxgLEFGEAxrVAWFgURYIWxs0Uh5mfWwFvRfCjTOpAoBmZXI4Ah/M0GaMmgIAvbOXgDkBGwUnmATQnvAiIhCkyqSEeWBUWiIXtDTMMMMwrfKbYEsYtExBFjWa3xWQPDJBdX1CARUHhC4XpXa5vssY4YXaIaSkGQdUA5clExAZ3hXluVlcJjAJLiaeCe+MX2Rgj7irSL015lwkIWf62c+dDnUsI6dunquU/PvtpG5/QgPX/9WXMRiCBzvNc1TS/NVPihNEz/ds4FJr8PBGO4j4LmnIuBa1znsVw2kpQVjLpu0LYtptMpDBhdV8N1YnK8tbWFixcvwjmHeVujCfbjV65cwe7u7kCLRG7cTCndo0rj5Cwa2KJPWKv/nqowgvmlhykKXLx8Be9+dBcLt0BHHb64fx+XLp3FbFZJuwiR8kgvVIOPP/4Yly5dwqVLlyIdzPeVlHFJ97o9cRKjmj6nJW9vnc/Fk+pEEpAmrdMB6HTeE0BAFEKRUC+a4Bg8giU4jgvnTo+RYQBOgoDYQujxrMLW9BxevXIBL/72d3B47zHe/dlbuP3Bh7j38afoDo9gmhZEFuRrMPdal9z5fJ1f7UnFil00HCS6qtjwAA6Sb45YIkQWBDh28NAkzH1Z9Tvr53HgH+V73+O8rNsTpMAtuRfWCQCets78s6dhXsfKgMn+h1WxUk7a24Pn0NO1HLDouylfk9OGJwkbBsApzYG3xoQzp9cngRF9PtVmjPFzOQBP6xob89j41423/57iPT/2DGNVG5jPRa69UcsTYGiNpXXmdeQWTfpcOteGxMeZvAs8itSTpnlZETjIqAbtpSH1+6+EyItrQz8XawHzmvKNB0g725uYVBMslxbTqpSEhG0rzvrhmaqqUDcNZpubwsx3LWazWZxwZpGGeu8x3ZjBdR26Tpzvp5MpmBnHiwUOjxcorMFsNoNzDoeHhyGbr7jDVGWB6XSCwhbJIoVDki49S1Q1SjZrPFjhaaD3UzLGoG3byByJv4/EzxIQ0efjmUwrATl6AQVGoGskozzreEmkqtubmygMY1JwLx0O//demR+Lrm1x1LQASbSnpm6wdA26U1sobYHpdIpZyCHFzDBVBYSIRerrBUACAmxP4S1hNpuJOaItUE0kNDOVE5TVBJNJFZhJG5NkwoTkYCTaBc0sTzDwkTBlTDEgQE/H5oeXg4QFCAIna+A0BDJDAA4Q/WK6MKclO0w0bDmz5A+J/LkJDAoDIcKdhZgJOhM0W5bgjYOzHmAn7fgSIc6edC9EQQIzJm0feKIfVLiIyQVaoURev2ZMXEbgw7CJCYW38TMdnwAlC09JUHAiIASJsJ4lhHM6t4E+OcNg03u6cELLKhf4LJVax7kiuODzFduLFTA6Tv/MGAfu7anVnEIH5L0yl/JB+p1GAWPuCWt65rDye5gjFs2qdx5t22K5XKKul2ibFuqvwqGfOm+Sw4kHl4/W7tpeYupChEsfzOR0rG3bous6tF2Hrm3RBT807xzqpoH3HlUQ5LjOSaTMAI6891gul3DOoW06uMbjeD7H0eERmrbBYrEQoYvvQOhBWFVVeOmll/DMM8/AW8LWqR0wM+7e+Qqz2QxXr17B5cuXYa0IC+RS8gMwq8FRdPtQCMkquYMAaw2KwgYhho3CDGBcmgqIgAEhma9j4Mpzz6Dmn6LtWtgWuLe/h8fzY2xvzwADkAHIG7iwqcgTGtfh/Q8/xPmLF0HMvWY6u1RVyDaUQnP8fMAvsDJ+QXPRb7x+vZVBivt2oMOJezUyURHEhN3LurvUZ07vivCZ7jeSv1oCakiwSWsMEHJGGaLobykgSIPWhJacAbEBwwPEoEJMlUGMiizQdgBRtMp0cOCKMHn2Ir5z6U9x8dUXcfOtX+POb97HwZd3gfkCVBuYrgOck8SRYDgEMxoQHPPAaV6iMWqPEE3qBkw4ADYUfGOFjkRhBBjGMywD8IzSSvRPsSJc9QtGUv8YOCHqAzukzFtqHtvfl2lidx/8VscZ6H6fDUvevxUBULanvm4ZgAGdzDXPjUnxhYl9unZzAKzm6vl3OTBJhcrAKlBKyzqNjd6VY0yzmvOvm7/1wKT/Ts+c0jqPoZYwrWsdKMr7lgrM8z0zBrBZutAHkQjgiUzsYdracDwY14KtmIpm7a4Devn86z1kwppPJhNxszjB5DQCq2wex7SnSPvAQ2D4dco3HiCdmU2wMZuiqcTco3Md6qZFFxByUzeYVCVmxqCqSmxubmJ+dAhLwMaGJOFbLBawxDiul2gLg8ViCSKgLEtMpxJxrmsb8KRAWVhszip45zE1siCP9/dRTWeYTCcoDYG9qA+jrwvkArRGcuc4CDNOVAIgOATJsrHo15yVu4iAo2kaAAxDDIKP0mICMKkkXLclibxclgKS2rZF0zQwLNK1oirQ+A6ePSorYQg2CoNKbpTYrodDB4nqZ6lCBXHEb8NYClPh6huv4MK5M9jZ3cXGxkaQVuqYKTmjFIkxgWLo6AhQoWB2xeAqKbzymzKkwntTvFR7Bxid+ySfwMrZ7AkehwNtdP41OlzSYGCR4GD6uvQmD/2IP3wYb2ihYAEziqts10cORJDa9nQhsbc1CCxFz3wj9rHfXwO6HiIhKNEU07rwKhGcEp3s/4YIRSLxirmsSMJ6p5HXBhKo0IFU5a1AxHcEWQKZQM0Bw8xwIbogGCF3VjCPYUZHiOFIvU/MBYPvhBBJ9TtDFB7ozRGnQ89gmKhUuqbAU7MRGWNBmhA6hMlyTOicx+HBIfYeP0Y9XwjDCUDCN/u4KWN+Gwo29159dyCam66F6xwWyxbipuExny8i8a/rGm3jUdcN6rpGXS/RdSIEOT4+xmJRo207uK5D0zRY1jXatgEAtF6AU9u0Il0L6+dYmFI1+ev3i6wZJfuIiPCTdz5CWZaojMXlC+fx7e+8jm996xVUpsRH73+AD997D89du4ErV5/BxtZMmNOAlOVSpJA4NVCUEKGTWMy2nGO0HcMYF8Jui+mdNUmqAaTMoockXzeClNjg1NYmrG8AB3DLaBZLHB0t0J4jlB4olFEIwJwJuPbMNfzLf/kv8fs//P1g/tFfsN4nLHlA98zAfH4sQNW1IhRaHAJetHdd18Xop855NEuHzgXhFyGY/A61COzFx1Kl6c55OFj5mZgT6/lmdqIZp6HWzYBi+H9QCNHrxTy4CFp2Y0SYpwmPq7LEdCrCp6oqo5BNTB8pmsN4drAW4LYVv02I5phsGYGsMRQihkok0LIkXH/5Op597ioe/eC38PEHH+PT9z/C8Se34R/tozg6RuGWcLxEYxw6tCgbEdIt2cORgLnCE8gzaiOAxCWgWSNvKfOrJqUchApF8J/z7IJptdJvEsScWIqYYIuu+ap65k7WKZpmQWgUTO9Do3guRtUP9UgzercN8+WsY5JTjXFc9wwwrIJ3rP0710KMtRfrZFqp/2kKoQdJqUZinUYo7n0Mmfl1wPEkLU4+7vz9fM7HtVFDTaacQzcACEBqlaP7DnpNi0ACAaBwb9kzNt+5tmlFa5KBi3Re0+cG8x+kCHLvBR7KyP0DnwS/Sui6CWdABOQmBjpIeYq8/Rykj/Up38MR6HDIkhIsq7quhUfw6U/eM3pXM0B+uN6rc5p870XIEnkq3QdfYz9/4wFSVVhsbWyAZxwkpgW2NjfhWCQ/i+UCANC1HYrCYjqdYnM6wb1793B4cABmYWA2ZjOUVYX5ssbx0aHkXilFI7W/f4CmrrG7vY3OOVRFAVMSrCG0TYNT29uYbmyEHgUzMJKLikhM/8SsS4myXJIeRkzcXO9/FJkr8vH3PuKObJiiKIPpmRyEKjjzEyFoMxhF8KHqpMEA+Ao49jBgtG0jzGlRwpoJIhjQf57ATpgqbxh126JpOky2tvHCiy/i4sXzsAXBWoOt06cGpmZjKD7dspRKklZY9CeX9CiPXwZ04p9jX0aJGp/8CmW/jPV4tE80/L2/5k/sHNTcJRImopyWrW2fua+fyEDhC/OQHiqTwMxwal7EQUODAFg8h2SR6lwpDGVvcib/lMnTZ+QzQhfMyxSgiEOmj5cth47FfcDCCzuXhgPunYQMB3OAsAfLshBG0FtUpgCCrxEZ09cbGJpcGqYzTSRzoTlr2DM653FwdIybt27j0cNHKKzFtJqAGJhUFdq6Rr1cYlkv0bYCWvTCbUOOmrqusVgs0DQNDg8P0dQNWgccHx1HTU7d1IHpdnAdo+tcZKhpcK7EjDZuvOQcOXBictDvLo00mTMiWgwSqaX3aF2D+bJGaSz29g/x0Wc38Rd//Tf4wQ9+C7/9O9/D7s42Pvz4U3z0yae4fuMGnnnuKqazaYw8COrPNdD3RaSKAqYoSBK952h2KNayw1QJcT/rOjEAJuxsb6MsDToWzUTXddg/OMCybjApBEDIoya+t7u7A+c6PH78GDs7O4N56GkWA97iwf1HePfd90RDFSSaV65cxqTcxKJeom0a2GKCspjCOAf4FmXBAHdRmizCARFktW0b9riot4xwNWhdBwdC2zowk4Dz0J+udXCeYYzmP+s1fTEPWWDom6YFkVhLVLZA4YDDwwM5K9ZgMV8kCbodNjY2AjgVX8rt7W1MNqbY2tnE9tYmprMS1USEbMYSHBPQORA5AVMBDBgLELUCQMigmpa4fO0ZXHr2Kt74re/i1gcf45Nf/QYPPvoM7YOHoONjmHoJ0xo0xsU9w97BGRc1hSntWomaRejptArGMqZYEi/nO/DJJWdox8qwLwSVZqdmsCljOWbiNcZopmMYa/8kELVOMzUGoOLvhqDuBWN+OnkdPWhEf/8lIGesv2quJfeCi7Qs73cKUk4q6/q3YuaLcW2gdH11zOvqHQuKFb7sNYbC0MRnxxIfa8mFc2OaopNAtY4t/BX5gyFPNHgDffP9PZ+OA5GO9AA2HcO6sYwB+QFgVQsWBubzuYC5EPp/AMDS7mZjXjkHIyA8zNY/COx/4wFSb54BTKdTLBYCiAgMsEcVAiZsTKfxnePjY5QhCIBIaWtsb29HcwRLYnq2tbUFIsJsUmFrNsXGxgaYGfP5HJubm6jKAmCPoixRVZPBgTNGctVYa2Mf9FA6AFVRomOgacXswFrNmxCiUHUu+ASVMIaCuY2AuaZuxXEaNtwuktCVICYFxhi4TiL3ubYVMyDvMa2mmFQVmq4BWoDYobAVVEWimhLyAMGgRIkGHq0HyBZ4/qUX8ez152FLi65t4BqP0xk4Ap4ubOvY4dPyJCL5v0VRTQuAEwmUFJU2h/OaMKTDKAf/6/WLkgtpIPVUbiF0SUBNjOsSpdvabwUuPShCCP7h40Xm9ZJhjhmwPfMwue/gH9Bx4ocTKvaB4QbZWKc2qqtuAnAD50y1gDoFLeqnA8jZ9q5D07ZYLudwrkXXtSgKi52tbZzZOYXtnR3YkNxZ/JkQJW6ppDBnhuR3H+f5yy/u4O1fvwsGYVpW8OSw//gAtz6/iS/vfInHD/cwny8wP56j6zp0rosmbp5D/q3k4pE50jxcqsXjIN0LPhU8NDEg7p2YiUTYQfGC6S+Jjhmw1M+pvh+0DcMx6v7psYdeMvId4CBRHJvGYX7vEe7963+Hv/3pz/GHf/gH+J3f+h4MMd597318/MmneP6F67hy9QqmG7O4bn3JmZV+7yhDWRQW3hF8ML9TBlmjzYXXgAD0yrLEdDLB/nwh8wyhy3VTo5uVISR9/yogWoPnn38e7777Lt58881Bpvp0vtuuw7/78V/h6PAQx8dzNI2YN29tfYhLFy4DTDg6OsLB4WEwdxSt3vx4js45dEFL2HYtulZypDVNK6bbzsF7F8UjnXNofQsEpkTD+FP4rmm6KGFViwRDooWnshj4pVlrURQFKrKYWfGjnc5mmFQVmBmzjQ1sbW5jNttA5wt4v0TXdfHOREjlUFUltrY2cOr0Ls6dP4OzZ07j1O42NjdmKIsCDk4CehgNze+iX5kjA2ssClvg1LldbJ79Pq5991Xc/fwWPnnrHXzxq/fQ3XkIv38Iz0ugbVG0jBIMTx6tcZLI25dxjtKSS7bHImGNMZm9qeJqGWOkc+ZP29bnxwBPev/pZwONzQntDfq6BqDl99GY1P5p3snbOun9sXfTudS+5kGy8jqNkSSk+dyk764LqLCujIGKk56NNAcI5r69r81Y2087JyJcpV5YlYwJGA+LnYOJVFOS+jnl/U/rHxujgjVtX+8deXcc3OidrcLD9fdi306qZVP6Mx5cQ6ZF8pMS2nq5sgfyMXxdkCPvyT33NHshLd94gGSSBU0Z9dIaGGtQFiFAQNgs+/v7ICM+McwCOA4ODqJkxFoCs0PTLOG6Chubm6hrWfyDgz0YI8EBvOvA3qEoJJiBtGP7aCxACM0sm2G5XEqH4wIyOseJdFEv/io4XYvpg5pzeOdQhmzvRSWBIIoQVKBtm2D/LuGmO9eFAws0dRNNl7quhiGHrckEpzfPoK6XImn1IdEfEQimZ4aZ4DwBkwqvvvEyJls7WLYduqZF1zbYmE1ixL60fJ0N+g89EKtlKJmKBHzQ1upbJxFjZdJWCQuQ+fz2BIh7U46nBYnp73rpp++ngQH0mfhu4u+RMgz6mZphpoBHhqPmfSx+LwgBB7zvTdI4mANxP5mUMNF9/0Vi23kv0R+DNErNC60nFEhNToJ2igX4qMZJXuqFFgrYe/87YZabpoWFaEgp+DCVpcXy+Bgf3fwSTdfh7LlzuPH88zhz9gyKsoQNkSvHJFBa5LKUq8J74O6dr/D3f/9TnDt/CcdHC+zvHeLdd9/Fr371Kzx6/DjMtfhtxPlPtGI+iXoUJdtezFA1kiJY/FfE980giNkAFlME56Q+WAVTLgF5YT5Zc0IEEyPZgf0YIVENtY+pMEDDu/fP9v2CMWCQOMSzR7PsML/7AP+ff/Gv8JOf/gz/5E//BC+/+ALqpsZbv/w1Pv3kc7z40ou4euUSJpOJ1GcIfeAMMcnKmbLI1FoCs4CjotB3wn5LBA/i9M8oSovOtei8aCeXdY1l0wjINxKlM11t5xxefvll/Nt/++/w5ptvDvZBeqaOjuZ48OARptMpPv/8C3zw4UfoWklsXVYWXdeic92Kz1jT1lKXV6ZR8g/F85gylWCoaSebhPEMcy9HgQC2QYvbM9+RgU/X14hvkfqRKtMlPp42mvtZU6AoKuzunhJfsOD/OZ3OMJ3McO7cBezu7GD/4B5uf3EXzOLntrlR4uL5czh//hyuXr2C06d3sbm1CRt8gagwaLkDg1EUBXwh2gJbVNjY2cJz334VF164jse/+9v49Gfv4NO33sHRFzfhDw5hmGDbBq5rwYUBWRNMaPv7YcxpPL33072dA40497T6TLr+af3p96lZ2JgWZx2YSYMp5X3O28z7ko5hnWboJPCTMuCpmWc6fzIvwz6kflT5fEQGOJ3XkbbzuyttM60zZ/TTucqtUNK5HpubnDHP5yH2N/Q/Z+a1v6nmJAcCebAOBQWA8nv9WPL+65ymIbLz/qUWOGNAMp3zXBgf1yLb+ym41zs3X4O0nXwe1+1RfTaNPriyT5P3O+ews7GF5fw47rkngaMxM8N8vnQ/eqw/TyeVbz5ASswwmBllWQYJnWhEVI3c+Q5d3WBSVoAxqCYTNE2D/f39mE29qiTAwdkzZyTgwWQC9h5FyDfjO4f5fI7SmCjxK8sSjiHgggBmQl2Lc3RnLcqygrWi0XGuC0jaBjbEC4NHHNTPFp1rUBQlNqpZOMgMsAQZ0EMnob+BlrtgrudC2ESGDX5EJpgWee9Q2AK2LDCZVJiWFaqg5iwgDF3XhUATtghvS66i1nXYPXsO565chbclGhf8GboOhoDZbDrqQPc00h8tJwGU/Lm8DN5LIw0gExZGItBL25UZN6QJbBM2kQkaXT+0lNj0BpO0lP7FSwPiY+CFaPgQll0ApwArRsKMsUrRlbHGqqYlJYhhYArSjDHgrs/35HwfBj5lKlYlUsp0BmkUiQbSkvjwqP+eah6UyQMTuuAjpPPovYfrOrTOgUHo2hZt1wZgHsbYCKg2xqAsJSx513Vx3+rfbduKprRt4ZzDclnj+OgIyxDBcX9/D6w41PUXSVkVOHv2FL7z3e/g4rkL8Mbgq/v38Zd/+Vd47tpzuPH88zh79ixM0UsJ08stWUhdbTR1g9/85j0888xzuHvnPh493Mfbb7+N9957H3VTi8dSUGqJJoaC85oZGECkyg/BpTZsU5tpOBJTg8D8+mAul5pUxK2b1ikPoTfbRJx7baL/hvr9zopdEkZhsKc9NOg6kUERhDd17fDZ57fxf/u//894/bVv4R//8Y/w8kuv4tHDB/jlz9/CF7dv49q153D58uWoqRfGXQwBdX/2w9X9bkCaM81B2teomUQxLzRDcmsQeXjvopO++J/WYd4pjHVIN06fPoPFYoGjoyNsRLPoTEDBHpPZBOcvXMTss1v44ss76FpZbE8NPDej5kBRSKJMCVEwLZK8ckjmfUChkkAlw1UgpE6TCr6JxM6+yMLZR2aO5B8RRWAUOijrWJTYP34UIyjGKINUwVKJza1NzGYb2N3dwekzp7G7swPXbWB+/AU+/ewW7M/fwvbOFq5dexZXLl/GhfNnsLO7BTIGHmo+Lmbe1DSgsgBVFtXmDJdevoFL15/Fq7/3fXz+H3+Gj37+Fg6/vIvu8BC8XMISS9QryUOxwujlIGAMDKVMtjK2EZBmjPYYE8jcpwjJv3saJ/AhU5pqf1dBUt7uunt0jHlM52PMuV/vgDFAASiQf/J4csZcw13nQRRyYJaOQe6P4Tk7aZxjzLuW1JQtBzn9u6sR1oZAafVzrSPVuqQgN+9P+p0HI/evGrOkGUs9o+3n2tCx/TL2e97GGFjU38cAPoCQgLUfXw6m83nM60z7YkwQTYX9ZazBbDrFzs4O9h4+WOnL0+yJvIyde8//RYO0Upz3g80ljKdI+L3vYNiK3WPr0HY1ZhubgBHb6o2NDbRtG0NzE0Gi1O1sASAU1gAEbG1KAAJnWsyPQ+JU7yUHE4mNt/PBTMYy5uq824ompzATeNdhWoUQ4cEso/YAE4lvUtFHvGnbBtwi1m2thTUWnRNzvKowUdJR1zVQFQAKIXhOHJ9V6liUBbzz6FwHY0hM8MBhbnx/OYfL3QNoAfjC4sIz17F7+gxaByybDkyS2NWxx8bGNDK7GuJ8TDL3v2XpDwcAXnV27Z8Z/q2O4EQIzuvDEM3qnMvs+gPHwqC44ISdHsIIBEJbYtLGK8Qv75cClfSSSqV360BhvBTJgDVQRwA56tsT2w1r33VdDK8pod0tvOfoKyNAu4MLzuddJ4EAQBR+d4CRsJ0uRIokiHbHeY+mbnF8JNIhz4y2abBcLnF4eIi6lYhry+USy+UyaEgZzjvUdY2maeIY6roRplcGOJBCaTTEqqwkySURirKAsYRbD+7gZ7/5FbzzuHHtOn7vD/4AV65cxScff4rbX3yJN974Np699gw2ZhJNMc0ppvMqDLX8PDw8xJUrV3F4eIjbN2/js09u4bNPPkfbdvCQcymhUij2kyBMhw+gU7U2CiYHDvgmCRwii933JWh/88/lT+rNOVK+moBUy2Kpr2MIkIaOryKm4cHfzMoYOpCElIltW6N5ZhzqusMvfvE2PvroY/zB7/0QP/qjP8Lz127gqwdf4Ze/fBu3bn2B5wM47TVKISZzKHouvHOA18TOHuIHJvnIGBK9TmlVcJPHxUsXcfurewDJPdB5j8VyKdH+qiIwh6sS6kuXLuHWrVt45ZVXVrS1zIzpbIpqWmJrewPPXXsWZSU+bUQWHhZM1WAu+30kjIFozRA1FqoNTIHoYF1NgpMHa80rtEFfJSBqi+LCQcE0Bd8eDvdAuCOZg48Zwzdi6tdHZwMMLwDvsX8o+eaIJKrhZDLBztYOLpw7j0uXL+Hs2TPoDo7w8Je/wlu/egdnd3Zw9colXH32GVy6fBEb2zMQAx06eGIY74DOgA2hmJTggnD+2mVcuvzf4aU3fxu/+fkv8Onb72Dvsy+B/TlsU8PzkYxmDSBK50PnKl3jlX/9FI2WHHxoUvhc+5I+G++KNQzZGDA6SSqfj+l/7bLCsNOQLowKLZK/I0jqfEz6vg6gjBX9OAd1Y4xyCpLGGOc80ln+nPr4pXevahtW+7XqP6P81boQ77kWKJ/bARjL5jMHj2l9aX/Gfh97L697DNyMrcvgWTM8V/ne1d9zU8qx8xjnpXNRGH10fIyyLOI9ua4fad1jezB9Z9h/A8MnJ2YeK994gKQalDEU7pnBrhMzMUPY3NyCLQo47iVMZVUGrY4RDU+w41YmhVnssq2R8M1EYn8OiM9T4KvQtg3KUnJwTKcTUbkGsxjPDhuzWQwJXliLpq1hqZCEq0bMAQkUzOEM4LsgJRUwQ8TY2pyhqsootQaArptib28vgKgCrpMoWhubIh31zmOxXKAyJSZVIfbrXdeHubWyYUUrxfCmQLW1g0vPXUNZzTBftlgualBRAJbhuhbWGsw2ZnH+pfTmhHnRfd0TyPTbDNAEsLZCxriXxMmfvT8Ns0icmVcvmEioEuk769jRS3GU0MSAA0Gro6Ytaorm2avYPYwnly75mLQVEZwlZh7gPnBAGKdKnpzTfvT7uutc0EhxD1ycl4gwnYNru6idQhhL0zSSk0r9ipwLmp0OZVHAe0bXyXOaX8t7iabWBLPLtmuxWCxweHgYAdSirlGH3wVcidZHdRfcpZI5g8mkAhmDhjxsWaKaTGLgElsV2JjtYDP4WxBJrqkyOJJXkwmWrURtdMklQKSSKbnsyBCqssDuqV3MZlMcHxzik/fex//0P/1f8I9+9CN87/vfx63bt/Gzn/8Cy6bGSy/ewGRSJXtApf4GiGY9QNt2OH36NP7D3/xH3LlzBweH+8J4g8CQCGgcLmGVL3DYD2Ejyq+eo/nrYG9mxD/dteljQ4aKYG0RNE80OCeUvShMYQBJDKQnKmcYrZ5L6Fh073dAkluLSPpNRBLCmMXP6vDwGP/m3/wYb/3yLfzpn/wJfufN30bTNvjyyy/w4MEDXL58GdeuXcP58+cCcCNAoCWsIfhkDiXCWydjLfqZUZxDYYGMMdje2gz1+HDuGIvlEm0XghuA+7ElDMurr76Kd955By+//EoUapCCGbD44GxvYLFc4tLVqzh97jwODo5CtKrZEHQBAw0rqakvJf51OrkZQzq2+AOmBgqQhsIUDh1OwyZ7rwlxw3kKgS9itLYY3l6iLqokWxORe+9B3KCp51i2i0D3CMdzSc3w8OEj3Lr9Bap3S+xsb+P8hXO4dOkinr9xA23n8d77H+GDjz7G6TOncfmZK3ju2nM4e/4s/MTCwMF2DgUBXVvLMasKtFWFzRuX8LvP/td49c3fwcd//zY++fu3sHf7DvwRg9sahl1cX0dhH3vd1sNQvzrHut56BnxQ9aZM4LqyjqnN/x6TtudM/Zjm4Wna13ISWEoZ9OF7qV+hAcEPmO9hY4mmOQdLQjRWGGG9DVUblxa9SzWlRzQ/S9YiUiJWqwoa0KZ8HtQsLZ3bXGORz0fkAalvW/unZ3xcJIHYZq6hyD/X7yJggDDpIvwLqTA4OfvJmJQej+2nXCumoE7PPAXBmOeh71R8ligKQgYBiuI6rMx0+NxE0KsAI/fRHANFY4G59G4V+i71No2kliCifn4SQWB6H607N1HQiMSUPeHPOJ/npyjfeICUIt1I6EnNVQxc8F0gIpRVISDFCCPLEKn5wnWSNNEYVMVsUB8AkCeYwqIsJ9je3oFzDtPpFHVdw/kGnfNYNg02N01g9Mq4wEVgaETV3+cJmlRTEEl0r7KQJKeAABWyhDagYWsMLAHTaYWNWSUbEn0gBwuLel6jKEvs7sxgQ96msizjOKbTCVzXogjSxI7FYdIBgAtEyFosHbC5u4tnbrwIMhUWxzUOD4+FCTUGcA4WPuROKpLxUGRuUqldWmTTrmpM5FeV3DM630l+Cy8+Kb7f9fCdSyuMIZUBEjeMwLBGkKOPGplnJAfZCwqJPjxKeLQQKF4QCpa8U4Kvhog9ke5cF6KeSc4aF5iPJiTldK6Dcw045NIBxLSubmrR6JgKIBMimXnR5AQTmM530SRNzdKWy6UkAoWPeXDquo42zuJ8XeP4+Dhqgupa/hZmoQhrJsC4rEqURQmGk/wpRRGJVlEUmE4mKDY2sR00SNPZDIXmB2FGWU1QlmKSWjeN+D4UBbxzcCHcOZGY/GgeH9fKhFdVieWyRl3PRdoNYDadYn50HOe17booCW+7VoIccG8CceP557FYLHDxwjm8+sa3cffuXfyLf/XnOFw0+P3f/z189ulNvP32u7C2xI3nr0s4fvZg7qCmZGQKEIWcZlWJe189wueff4n9w0OUGwXKaQm3rOFhRZlhGAWF3DHhwgcAE6JwsTVpLs8eOAWhyIAxTv7Qy69nKpIqAuMyAEbycGwj7ns9ixg0FbREQ7ZkKIEHLCw45DFLNaEaKlYprAyHULcdvvzqAf5f/+//L/7upz/Bn/7pn+L111/D471H+Pzzm7h//z6uX7+GZ69fw/bOBrzvUNogfWUr598wXABkne9AQVtmyEStnAxTdHfnz55CYQgFHAzEHG9Rd2hawHUEW4wzcRcvXsRf/MW/R71sMZlW4SyKibIskcMzVy7jrbc/xIXL1/DMjZfx6/d/DaADswVBNfQCStiLMSp80PqH6KJImDg1E1S/sZRZdzz0OdBFYgCcmoIm6ylMRh+u13APHDXfkQ2m4N45sHMgjbtrQl3Oo7BetHfMsDTBrJpFWuPZo2u7GOa8bWosl8Dx4R4ePLiDjz96D2+/9XNcuHgBN248jxs3nsfe4QJf/vTXePuXH+C5557D9eefwTPPXMbW1gY6cmDfwVjAgkHsQGRQ2grnrlzEmf/2T/HKm7+FX/79z/Hp3/8Ch7fvwOwfwC4XYG7gqYUnoCALBPPKcNBguAyno4ugSKZEAesqcwf0SS9TQWuqVeSExqQMW8qQp7xCf4bGpeD6/UmalrE6UoCQlqHEXfkWgEgCfjA5qCVE/o4k8UT0c2Rw9GUDA0z9/Ttg2jH0zRnSjn4ucq2Ihdy7mhMvpUsua0c1NzkwWhlD8nyuRUr/HtTB43Ob9n0M1KZ16XmNz6dSHp0LHaMZzlWk4QpME0Cg1jjGSCROgbipYE3+l74zXJtglBvAUfq50n1KZHgqgCEa+vxJFX3wjHxu8/HHdhIgrSyV0u2yLNEs5omwqL/3OPRbNd9jc89E6uItfDzEkkPmv59HegozWC3/WQCk9BC5YGKWHjAgO8jGxC23sbkJ7xzarsO0qtC2bUxOqptA1bVEkvBqsVhgMplgMplguVyCqUMJxvF8Lsxy14UQqgVKW0RpnbWSSLZtO2zvbMdIR+oIX1iLcjoVppQ8PAuzVliDqrCJBCNsLSMHsqyqkExVmFoxsUsOHiAAzDt0LMCo9R7lZCrST+ewbD3OXLiEq9efh4PFweER9h8diA8BCLdu3sSzzz4La2zQnA1Vubkz5hhI0iJ5iVjwiWewV5tm0Uqoz458pv48vpekBOau1/hwjLAWnRf14BFA1ohTtfMD4u2dC0EqGE0rZl7e+bgmbefgXCcRqAI40f2mTIS1JpqqqTSmDUyFmpM55wTMOEkqqsBpWS+D702H+aLG8fECAMF1Dsu6Rr0UPx7nWzRRc5NIecL4y6pEWVYxYEZZFJhOZ6iqKWazTRBR9LcQbRCjmoogQHJrAdvb22jbFovFHGQ4rml6vvS8dc7j+HgezfNE+yVEK9Xm6jyxw0BanTIf+nfqdBqFHn5VChvfNUNb9cePfw4AePddxgsvXMNLL72E1157HT/+8Y+xu7uLl19+Gbdv38Zv3n0PZ86ewZnTu7IXvGoXPQiiyStLgzNnzuCnP3kL9+89gCmAK89cwuHhEovawbEm2vQCjpTpRXLBAqKayS7idBxpSS9sin4/qyYs3q2atqT1K4Osn8W+jDybt53XSySmVsb0ayXaTgRmPSTEJIKxFuw9FssGH338GW7e/L/itddexZ/92T/Biy++hFu3buI3v3kPd+7dx2uvv4qLF89IXhtQ0MoNHcTTve69DwEjdEwMkMFsY0O073E/ieZvWdfgzRkkbPZwjr33mEwm2NzcxN7eHi5cPD+YIQpLduP5G/jX/+avwXaGF158EXcefIXW1/CtByK9GuZJUcZmdR5JEnWMrHUcE/V7W+uQcRdrzbhM8K3JTZwNqeYkBPjxHhTOVFEWsDZERa0bOEjeKtJ9RwbGFDGXiK0cSu9BXqLzNU2NrmvRLmvMl0vsHx7i7v2v8NEnH2N7cwvPPvMcrj93A5cuXsb777+HDz/6AJcvX8QLL9zAc9eu4vRpSTzctR1M4+VeKjy48CjKCtsXTuMP/7t/jO/+4Pt45+9+ig/+7qc4vv0lzPEcRV3DeofOuAD0TABJwszDC6Oq8zE4a2sAUs4frDCcI8/rWudn6KQ7Ly8pDczb0+++jr/ToI+AwB2OcvoA1vtvEe49HYL6amkZCGm0ryP9B1Zz1eQ0bkC/A1Ob0qD0eb0jxhjwXGu2bvwCTlY1CvF8GBG4RO3FCNgYA7hjn6VjSPuW9nVdxDkiCXCi8577i4H60OeDe2CkrrQ/K/MvfyT9pgCOEiCU1Tq2dutA/Trwnorl2DOauhYhjiVFayt15dq1YXs9nye+qgqOel4xv9ueVL7xAKnzHdoQUUiSInoQe1HDh8nVCB6eOSZ3Sw+8qkbnCzEt2NralNwhIbpXQQVclxAMK3kouq6T4AeFRUXTAdJug6N5vazBQbJvjBEnYmZMp+LDQ8aAWGxdi1KS95EhsDVR/T2tJJy4MsSAEDvdCLu7u3Gc3vtokmSMgQt9KcsSrZcgC3UAgQxC3cim3dw+hUtXnoHzwLyucXw0x2QyxWRS4S/+/V/g+vXn4L3H1tb2gAisC9KQS5b6Z4QZ7QGR+Bp4F0zYOtHUqPO+akQUGKnZWzSJC35BPkQEbJoGTSNhn9Xpv2UfE2sqyNGcPK5tY1ve+xhREMZg2TSol0s0bRvt0pfLJbrwTN00mM/n8M7BM2N/fx+dApkw72rLLvtNNFkSTcpGyVJZligCyBFJGGG6tY3t0xVc52AKCURAZATAGwNbFLH/hkzILyDmaGVRYDKdwnX9Gihgk9w8HXjvIGqjiAhffPFlnNPOdWgDcEo1ZwBiniNmkYI7JyGLyfShvPvQ3Qxj1NlZpVhDCVu8SMzwYiCIRkHPQH5xMALPGS6YeJEw8NGHn2C5bPDKKy/j3Llz+PGP/x0uXbqI7Z0t7B/s4d333sebv/s7IvXjROqH3mG9MBXu3buHpqmxNd3A2bPncPfOQ0wPF5gvW+lL0h+ZK44RAPV7ZOdC6UBexhiB/FzpGR8rA0aGV6XeeVv58+vaSy9KnRuNhKgJMT37ZA8KsFnWLX751q/x4cef4I/+6PfxJ3/yxzg6OsZXD+7h7/7up/jed9/Ac89dhTUEEAdzjF6opWAMQIzOxixSbgpn8dTuKTGHNv042raLZqO5GVA696+88go++eQTXLx0ITyjMlaRqu7ubuPZZ5/Fl3cfYLKxIybFNYuWq+1D2w6YREOAJspWgMNiJmeFI4Em0lZAx+wlQqGIWmHJBhOSkLtKJh9pAl2EnnoDMAjGloNooqTrxRZFIWbdCpSCWy3KqkJVlmAntDEKNjzDsKYCcCAn4Ip8h9JYFNUEAEeNUt0sJUfe/h6Ojo7w8NEjvP/ee9jd2cW1567juWvPY/HpTbz/wUe4cvUSXvvWK3ju2rM4f/4MDIuZcNMxusKBbCPCzbLE5pWz+OE//TO8/IPv4Df/4af46D/+HPWdh8BiDvgjgF2kS3Lug0lVAlTyPb2OsR5jjNOSM9hj50Q/Wwca0rLW5A39OdN7L213AKyTc7sCzLiX4Cc6BfTgKHxOIkYcRGNjjr6q6+hH3t98Xk9ipPN342eBYU/nLRWSPAl4pky88ArDtVwBcRg+s05gNVbyPZCuw9h86R2b91cFIzm4UiHHOkHWP7Qozzu2lyQgUC+cyoFWDpTyesfCfKclaiaRwKax+SIa+lYO2uv5XuXpVZspcxjmKDENfFL5xgMkUxhAgrxJ9B7n4MlElZshsXnUSEcyyT5okQiFlUADG9YKAvVyAXsWKTWB4AHJzQHEUMh1YJJteNbY0IlgG1lZyYukpntKm1znwGAcHR1hyxoUZQHngyYpbLDpbApjxUTJOYfWORgwkDCrzktUGOcdbFHAhzo8cwADLYpSNEpt22LiJ6gXS4CAd999F9PpFDvbOyiKAsu6wQ/e/BaMnaD1QF03IDJwrcPte7dxdHSEyURCeldVb7qnJSXkY5dRenA0wahzGvAAcL5DUwsDvzxa4vDgMAKcZV1HRrttGzHNCoCmDYBFmHSLrutQ10ssl7UEzug6HM/nmC+XwdTLo2vFt6brOlhjUC+XODw6ggsMRNu1WC6WkogxSKFkfCz+HxRMkIKWUcZqwvxUsFbMKycTATuikSxQViUYEiHOOR+TBnedSORtIZyLcxwTRPpGgH/XtsAymM+5HsR458Gh3+pTJRoeIRCu64LPFKJ0Ja7BSBb13gGz12CoZkxKSrhIJLYs/WYvUkkRPiguMHBOdDMpkUO8nCAMJSVNgGCMjSp08TNAIN42mDUFplk1GwTAqBbCwZLF3Ttf4cyZM7h69Qp+/vOf4f3338V3v/c9LJsN3L79BV5//TVsbkyQJp9lz7C2vzyWyyXqusau3Y7rKRiI0DoHjUPOKpk1FBjiQAqS2dLxrzMFOekyz8s6qebYmcyf09/Tc7qOCcqZMO2bviNmWA7EBAfx+RFaJ+vWeYeDw2P8qz//N/jgo0/wz//5/xEXL13Fw4cP8Pc/+QVms01cOH9GMCUN52MQSMJzjGgme02enc2mApBIgkcoQ7VcLmXvF0VMA6FgSy//q1efwa/e/nP88PfeDMBJ50c0itYSvvWtV/Cb9/8cp+wU21u7aLoWrmtX5jVKUInC2xQ1+b0WNo4GLmhGNbgPA/FoeSSaxlhfAFMpnTUkea9AUD/V0CMURDH5L1kTTMeLEGylBbwmnhXTcWMMpsYCxqALQhXnXQzYwuxBXYuuWYZoqR4GwGyzQjWdoeuWkhev63B0fIz58RxHx0d48PABfvPuB7h06TJu3LiOum5w8+ZtXLlyGS+99DxevvEsLl06D0sWXcvwrkXrWhSuwbSYobMWO89exg//+/8dXvnt7+PXf/UTfPbW26B7X6BbLmGaAhYeBXt434r5TeLDkQoslXlax3AqMDmJ6X0aZjUVGp5U8vOf/p5bY6R1p31bB9IAdVZPmH/dZDoujJutpePL5zF/Jn0uBYY5cz32Mx0HSCCcH5nzFACO/cv7pZ/7rA/aVvTVy313RuY7/y6fn7Exr6sr1wKLcLfv03ik2TV9Uvu0pOS0emxvjK3FANDS0JJj3fykZyWtQwVog74EemYKCbBUL+bi9pIFzznpPlwZvTAEgTdLNbrjgouTyjceIL3zzjt47rlnURQFiqJA0zTB/G0WbMEN6rpG5xymEwmewGAUZYm9x4/x2eefY3trC6dOncLm5iZc22E+n+PRo0cipTx1CoAsYjWpMJvORMKTqKSr2VRoD/pNr1KYlLh4F71LYYzBV/fu4fz58yiqEuwZx8fHODg4QN00qDamwSxOQoGLGYQwwk3r8fDBQ1y/fl2YQudQluXAntqzl3EHMHHv/n0UtkDTtrjz1T2cPnUKDx/v4fz583j+hZcx3dxFyx51Jz4jDx8+xu3PbuJv/+Pf4p//D/8MV69eDcyIWbt5xyQL+WfCzEt+Je8I8/kSjx4+wsOHj7C/f4DlYonFfI75fIHDo0MsFgvsPX6MphFzs845zI+PsVgu5IA4Cb2uFixNXQsoKYoY+tp5cRxVvyxmluhMwZmUjcVsWzLLG5JgHdVkAmPtwJTOGIu6rtG2DayVYAJqoibhvTn6+yzrRuY+EGQiQtP1IY49czTtZO/ho+exSMpd0KiBxAY5OkNyHy6VmUPkryTynWpogCTSkD6PuJdNAoLEjJECeO0dH6WkEc844fq1PgEmlPhcIFoUaxUEjVyWXgTMCGH4+6JJRg0RSiMmXhzNPeR3hjB+KSGODLvsMngP3L37FV544Rqm0wk+/uQjfOuN11FUFY6Oj3FwcIiNjVkw7xrawxtj0NRtiK6HmAJApPQcHkyluFbmQS/rgaR2eB7GLlP9Lr+McyZjjDlJ30/fzX0k8udSze/XkUzGC5EIMBa+E7NRAwNmF3MwEYVEjCxmXh98+DH+H//z/xP/w//4P2JjcxdHh4f49a/fxx//8R/AWAbggkpwRNIKYdgNQrj9YD4kApsK1tjow+m8Q71cou1aTLzF2NCICDvb2wCAxXyOKgTtiJubJAjKiy/eABFhPl9gZ+cUvrr3Vd8n5sE6ynyL6XYvrAj7FhAAHyTWqoUVAX9qfoTIwCIwASGeJsAcGQtSkKiblhFgWS900KJ3ggp0OkPo1Jw4gC4DgNnBeMAWNpqE67icc+CmxZIMPC8AYrDrBBzbEqUxKIup9DGY4dVNjaZ1WCwdjpdLfHHnS5w6fQrXr1/HfFnj85u38N6li3j99W/h2vVncOHSORSlaCNd59ECwKSELwtQYXHmxefwj569jNd++D28/1d/g49//R7mD/bgjuewbQNrRdDWCy1yMLO6r9btex23PpOaPK57L2U01525/L38nI/Vmfd57PsVpjhIqVb6yQrAGMwOMP29kdODFHjk//L+p7/noa5z5l/7tBJUAetp3bp5WAeSVKCZ1jXo50gdYyUHqzkwG6tjjL6uZ9o5MvgpgBLT2oHMKLZjMt/VfK7yPesybcrYHgy/QYnluj2c/p373A3nHj0tCsJSdc04eKwavv79Aag+4SrSCLPye752ovhYZ468rnzjAdKHH3+A2cYE165fw+bmJpbLJTY2NmGo13QUVYmmaeJGLAKzY8oCddvg8u4Obt/5ErPJFJcuXoRjj9nmBo6OjtA6AUyTyQSmsCiCBmWxXEZbyaprUU2n0cxBfZAYQOuEARbzukZMpozkGLJViZtf3EbbNGiCOdi5c+dw+uwZbGxvoXMOVVkE/tJjf/8x9h4/xukz57G5tYXj5QJN04hPUGFBTqS4bdMCJP04ODjA0dERiqLAxsYmvrx7B1u7O6hdh7IssXv6FJ5/6SU0jsULwxPu3L0HA+DMmXN46cWXcOHCRTRNg62trRVTDy0nbcpVCZlBs3S4f/8BPv3kUxweHmNZL/HVV/fw3nvv4vObn2O5XApTWpawxkhQgDD31lqcuXAR1gpguTKbwdqy9yXyHCPp1E0doo+JRqXn74OZnutN9RZtG/3C+OAQ3nVoQ7hrNV30avpAIr1Qk7qYkFW1TsGUb4xhjYSXe0DDJITv6tVn4R1j3oRIUhS0Mpp8khLCCwasEPwk3kxgsASQB14eSKROQziAwe/qhzBWKHlUeLhECmRsGNsIULZAyF8uQN/0z6VbKQVwMj4K0j4bzUbJiGkhB+0SiKVtACALQw5wLQCPx4/3sFxewmxjhsePH+Lo8BDTzR2UZYWDoyNcxAUBVCz/UyBpjEHTLIOtug8gOA2/noC1hKePFy/3pgyD+RuRyo2Vky7Vk0DS/z+LmmQU1QTE4qvHGv432IeLBDFc1gA+/ewWfvzjv8Sf/dmfoSyn2Ns/xnxeY2u7hDGquRxeynEuolAAYU+YAFpL2LIQX6RAm5qmiZoP5tXwu95LmPtLly7hzt27uHHjehASKMMjKSI2t3bw0osv4P2PbmFjYxOT6Qz1fL7Sv+jMHOVfcrYRJMAEAqu2Exgy30Rxn3kfgr8EAQYREKPQeQ/fdejYxXfUnCwgJmnP2BCHQcCkCvFEuWJhzST6APiui76dgAgrrAFCkzBGtFzGAJ33KCZTzIpS/u5aNM0SXdcCzoKJQRRynswqTCcztE2DtutweLSP+cLiaH6Ehw8fYnd3F1evXsXhwRKf37qL69eu4tVvvYjnbzyDS5fPg4nRUAPjO9hWtO+tbVAWJS6+egMXrj+La+9/grf+8u9w990P0D16AD5mWG9AXbNGoKCa3XFhQ7qmY/svZ45ln6zXOKTv6+f571rf0zDTY+BkXR9WS/qMAcCwtgxa2VXQp3RqzDn/iS3R0BdPz9vKnZCBC5OAhJPaG2Pe0xLbGvla7g8TBRFPU/K1yUFXDvyepsS1C/4eadS4OHbuLTnS9pQGpj5io+MMn6vFwpP82cR1oe9fLtz/OuOK7SevMlj8oINwh5J5TceX8in52IWejodd1/a/7n34jQdIf/SjP8GVy5fAjBDeleCZUFVVVKdaC0yLss9ZFBbw3PkL+L1TZ9C2DR48eAQPYLoxA1mDLSIwAcdHxzh15jTOB4ZctRBdMHdaLheY1zVgC3gQyrKALau46SnYpXtmdJ5higJVNcFscwvee5w+czYwg8LAGyPJND2JaVJZTUFgeNfh3IVLmG5sY3O2ibppMNvcCn4SLYwRUwnvnJh7Wcmb5CH+IXt7e1guH+Gre/fw+PEeZtMprl27jitXnsVXX93HmfPP4OjoEMfzBS5euABLFv/65/8Lnn/+BorCwhjJ10Q5QIqHIFeT+sGBFiZH3qsbh08+u4lPPvkUTd3g8WNJwvmrX/0anjxeeuVlXLp4EVVVoalrCVntHRw4+Bg1qNsO3LSo6xqHx3N0nUPT1CHstByWrnMhB5AwH03TSMhsVlM0YRDEFG2Yt0jjhveHkyKoioQAKqyT/ZQ6WyoTZ4hEUmeD632Yo6KgAH76uWzaDqd2T+PcuQv44MMPsZgvIH4XIdCGimQQuqO/hN4IQZVeSbMmMlDKuAOBeSLTr12gOfKsiaAMQNybAAaf5cWYYnChRoJMAAdficg+yvQEbWfO8CM+p6BqY2sbV65cQRt8wR49fITH+/vRTIRZdECShyxctF40cPWyQWELLOsWd+9+hevP78IYI8FVkjkJPHhYX4nut7Exkwh6TYd6uYAtRNIe2P44zznjk+6LtIwxS09TnvTs2AU9ZhaTMlX5ZydJbMfaIuiFBIAJZVHBkennnr04/hsTAIdELPvNO7/Ba6+9hovnL2DpOhwczrG5dRqS92hN28w62whcnVziAHzXoJoKvQtyAdRNg2XTYqNzIEPRzG5wGcPj+o1r+PDDD3D9+rVBc845QQns8Z1vfwu/+OU72KnOYXO2iWaxCD1JpMYavVAQsqSEUJNWZRKDIANEUShDwQxY76NegguwCVGamKQvpcWk2oTrnITLdT6AQoBYfc5MJAcyU/3YVbBirUVRTEFMIphrGukPGIYZXdMEbXif7kB8dKVjRSk+X5PpBBt+hrZtUR8v0DUdOEQgZO9gbQU7LTEhoct13WJZL1E3NY4Xczx6/BjbW6dw6eIlLOoFPvvsM9y49hxee+1lvPDSC9i+cArGeRSuga9rlJUFCgM3m6KpClz5zst45qXr+OQX7+JXf/03uPPRB2j29lHMDdC0MPCivYSTuWeOOm2luiZsecn73Z+HXIihYCHVrK0DPrq/0rvkJJO7MW3NOvqQM+hjWqogpgl7Kc9wBhhLMSiUQRr4ZJiXKAciY7RjbCxpf5i13UAnMKQx+owIm/poxOvayOdqTJMTfxL6CLhpHYDcx57gRt4dG48+k4KMnLaeBKLTfqZ91M+dc/1drbxG1t4AqIFXPhubp3xfpUK7npMI9YPSNHoAOEYPTW40RIFPGItj7i0vdN6d3vYU++o6F4EXez+ITswY9j9RFMV+c/zbxy8ZYj3DCAJk9Dkgn7Z84wHSdOMU2MxQFgVKANVMzJzmjYsJVsEMDw8mi67zvcQZBFMYVKbEt7/7fRwc7GHv6EgiizUNWu/x/CsvYWd7BzAWxlbg4MBaQTbobGc3hrdu2xamCOY2oX+61t57bO5MExM4DsRKCIMlQhFCf/eJJgXsGWMBY9F6RjHZgmODstqA9R5XrkjwhLppUE0qOfRBElkUFWzncfr8FqrpBhbHkvzyxvUXUFYTnD93Ae+88z5eff3b2N/fBxmDzdkM8/kci8UCy3aJ85cuwHuHra1tkTyCoZGrJHCnRhLxiPRQnoogSYzDNYAEcPP2HXx26zbqrsPtO1/i7bffxueff46ds7t49Y03wMx4uLeP+/fuYXm8QLNYoG0bNK5B17WD3B0xiEPQ5fa/6+EK/Uz6FcvKJSArRkQgUw4kOL2PQvLM4AIlxJCyrN8PidCg6dCgEgvyHmSB2jPs5gZmu6dQOwBMMLZIAJyP9RCAAn0jK0Q+/TNdnJUvkRCksHbUmz/k3U/nkOJzLKGERy430QQNCbwIhGjYIyV2UQLlYQxwfHyA/f0pJpOJMF4FgUJoedLxR8ZQ/Ao7BgAP5wBrJ/BugePDOSwzSiL4pg2Ruvo+eAcIxvWQXDElwAauE2n76VMbIHIwVMGzgXjeDC/NdeBi7MJc98zXeTdn5saATspMPK2PRPp+PiYOIADhnCEw97YoUYQ9I9ESJd+aNYTCWLiuQz2v8enHH+DyxdOwxuBwf47Ll8/BcyeBDLJ24j8vEd0YYd29x6wssD2t4JlQGiOxDsijcR3qzsPruadUQhnqBuPixfP4u7/72wDeAviCXsYOcDVevvEcTm1OUC8WmJZTwMveEyueoakqB7qtdCmlDxykxYyQxNcQYp5umAjQQQSyAeyAYYjhqIOZzABbYGonqDa2cXRwhGW7wMQUoEDzTNDUuiBlTUESWCwXSlsG4QijqAi+7bBsa0k4zojAN2XoDDP01HvPQOtBtkBZlphMK5yabaKpFzH1wGKxCOBQ6phMNlCWvg+aE/4tF3McHDzC3bs7uHT+Eg4Panz88R288PzneOX1G3jl1Zewu7MFFISublB6KwEjSoO2rFDOJnjp97+La2+8iF//5C289Rd/g+VnX8AcHKFYLEHUgtDBWycmjTFwU0/JKKGLul65w7kKG9RsfigIzARCGAcY60DQcI+sZ3Qjc/kUdEOZSM9eBJohcbFX5tLIXe3YIg15nfo46c91dCU/T0mvZdcl9F7BEVFILsIhDL7GnCcMhV1Jm33k3tWSgk9dgyFI8yvzHMdCNACE+nm+timtTP2W0ijJ66LrpaBJ3x+bLYQ7NxIB5pjjbIwGE4R+ENEgamx+X+dBZLwPQqtB2/K3F4le3/dg5ic+9YiIKnUZAIvFUrwCwCJQCWNhNr0MtihEsBPmLKY5CHd+NCUmAGRAtvcp7YGbgqlkjUjnhgAOJs70X4I0xGKDKRsr40CEcjJB27Y4Oj7G5uZm2MwiGTeFhk2FqPk80PkW+/v7+OreXRBJqOkXX3wxBlhouw6VLQfMSM+0iBQPwCCSENCj35SxGRDeENhBP1MJlQ/RlspS8ykhOh0yMxz7EH5bEnG1y6VIao0FeTeIgU/BD2t7ZxfTqsTp02dAZLFY1DBFgc55bG5twZZlTAzadR3eeustbG1vY2Nzo+9LNvfM/WZdvTTClg/MjYAHYDFf4Pbt29jY2MC7776L999/H/fv38fu7i5eefUV3Lv/AO+//z4e3L8v+Ts6OaDie+AHbRL1ZjWGRJVcFMrp67wHg5NEQhN7moEYlYwjkXwg+W6s5ETcGBuJvdSUVrL6ru4PYwzYISZT67wDSEJ+k9FgEHKpaN+iLKgf8sj6pP0fH4OCSS155Li8ztG5ILmQ4YX49RIi6eM6Rj69bHMpHEECWlhrcfeu+H/IGWGwt0nTvSaOKM1tIuC5Kkt4zzg8PARY6miaNtbVdZ0wvgDUjtlai+l0AmMMuhAZbVJV8UJDsgK5FPMkCei6ffR1ytMCrPxyHWPMTpKgjrU1JuHO2zFGgpZ4ZyShsZcgMyIt9bjz5Zc4OjzExmwXR0eal8uA/El7tN8jqd+ERIO0QVMlUn724n8pe85EO/98jNOpgO6DgwPs7u4mYxK60HUdtrZ28Pzz1/DWOx9ha3MDZVHCd21gZjgyNwIeXIzApFGoXIhwCSBe9MO+CLhUJsR7icRqIBYBnXNgY2GNBFRonQTl2T57GmUzxfzgAJ4ZhfcgbyKg6TVHkiZCBAcG02qCvb19HB4eRv9JtYxwnYv3Rsr0d10HY/uom8zB95IZVFWwluJcdp3kFGyaBsvlAs7J7BARyrKUdkJ6gLZZommX6LoG86Mj3L/3Fc6dO4+j4318dutjfPThx3jttVfw/AvXcerUFpqaYYyD6VrAMVAyqJigmE3w5h//Pl59/VX87K/+A979yc9x/OVXsIfHKOsGG00DXwBLakAmROI00bgZhg1sEOClEcdS2p6aRY5pDfLoX2nI7LEz9XXN18bO6Rh46f8Owh+faTtT4ZZU8rXaf4onwz+V9PPgc2kz9dtcvWu1rTxVi3R3CHTGtDoiaOvXZiXYwMj9DgxB6jqwmu8NfU8TvJ4EkgYCn7ExjaxtPrYwgJU7W9/J38uButaVfs7MIB7OiM7bSj+y93sAPMIrxPWmwAMGOj+yJlrEdNuDXa/1inOGk/0G07P4tOUbD5BMYSW5FHpm07FHNZlgvlzgiztfYjKZYGd7B2USgY2Z8ejRI8yP52jbBkVZ4vz58zg43MfZM1cwmcxiNLuiqEDUX7S5alOJXUoU9fDq5zkDmEoZcwlGRM7MmEwmsR3N77RYLGGLUrQjBJTVBG65xLKuY3Q0rbMsy2BzL8DRdR7GFHi8dx8///kv8M/+2T9DWZY4PD7G8fFxyIWzwBdffIEf/vCHsNb20aLWZCLPpWLqJKmaAi3OOXz55Ze4cOEC/uqv/wNu3ryJg4MDeO9x7do1PHz4CD//2S9weHgEawyqogIKikxvfziE+BNU8tIzG/lFQjDQHG4Agokg4vPhrfCOSMWZGYgZ7PsW+7eSy4YRk2em36X7I75Hq98paAMAaw3qehl8z6pg3hKkRNl8a3nalGhf9yLWdTyJ2IwCA/BAei4C2v4iGwQtyS+u7CKxRCiKEtEBnght24Vw0LIHVvqE5JwZg6ZpUVUSoXIZnPclHHwdzemIRCKHkBfEe4lYuLW1jbIs0TmJsLh7ajs7A8Ox53OSz/vYpbDuWS1jF97XYawGczMCjMbaWPf5uos9B1760wazt7YRExIO5nbHx3Mcz+fY3DiFecgdJ5JJOzxoseF+XdP2jTE4e/Ys7u0doSzKmLuOXSemuV0HrsrBnsvH/8wzz+D27dvY2dmJjRETfCf7z7sG3//eG/jZW+9gY2ML00kF19Rg8r0fQNiHkrPMwxqLpm2GmgiS/aXS2VRwpoZQDMRgDq514ILhjSQDl+AxHmRLdMGkz25MsVUWWBwcoF4sYbxBASNWskalugLWqqJAURi0XYs7d+5gY2MDk8kEAKLpKtDvUb2DtDgv0QrD5IECSCqKAlT0CdCNMdjc3MRsNgs5A49RN7Ukow3CKGNsCLBhUddLLOo56maJxfIYB0f7ePhoFxcuXsR8vsBnn9/CSy89jze+/RquXXsOmxsV4Bw618I1Hq1tMZ1N4b3DxsXT+MP//n+Pl373t/CTH/97fPqzt+C+2kN5sEDBLQoSmm4M0HEHbxieWM69G95heTCVNGpXun/Ssx8FnN6PMpfp82nd68pJzPQ6cLTyTPb8kAbR+HkbKScx7KvgTWnzuI9pLzATgd9YW+lcPqkPOQjIQY7WF3ky089Lvg4pAE55NX03nccx8JHXme+l9Jlc0JSOcey7vOQav3Xv5YBGP1u529e8l5eT9t6wAqj8ZxTgpzxdfyb8SgTC2Jfs/bF7MAfNTyrfeIAUCRJz2PRqzw1UVYWrV6/COYeDgwPQgmK0t6ZpMJlOcebMGQDA473H2N/bw+kzZ3Hq9Okw8RphxQUwMp68LJUypSh27KDpu6oajZd6Aox047ZtO5DyKVHxXgx7jAk5SchgMp0G05YaQK/OLcsyMPyMthF78moyxZmzZ/G9738f585dwOHRMY6Ol9EvQ4NFXLlyBWVZYjqdBfCnBGJ40NNDF5nfIFlQ/t97Cb/bdR2Ol0t8+umnODw8BDPj9OnTKIoCH3/0Eer5ApvTWZwbHyUbJJqxyCgBPSFWQks9zxwPFhBVfByssjNhTCTrjOQvYAA/EgPdnp0RCVha+rDRqwRmLUEhCmaYjLoWH4CqKqEGgrzmXY7/OCFuFH+IuQ+HuyqTEK0xsQsdDd2iwd7Uz1b6wVE8gR6vDgHMky7YFaLLGo5cwJHYFgu4V0GF1juoO7wumh8fzKf6cMt67lTDYEwAbaJsAId2VBtclAXqeom6bjCbTWNkTLgQr43SgBMnSP3WzN2TytgFoOPL68yZoLF3xvZRqsFOn3+ai3AtcwCEy1GizSEm8fNomhqHh4c4e9rFXGHi35WexaQPcjMOLnn9fTabAntHIfpa0CxZi7pu0HUOzEWsZ1Va6XH16lW89dZbeOONNxInaQMK5p1EHi+8eB3bmzMs6yW2NjYxPziEjf5+iBLSwmiqB0ZpZc8REMCB0P+yLIO2qQ+OwAi5k4z4BUZBk3Pw7FF4hm87UFHAwYONgSlLMAmQ3y5L1EdHqA+PQvJdg9IWKIyBIQaF1BMGBt51QzqdACIVFqgmRedN1lP6x8yA86Cw58XE2QwEEwoMJ5MJqqpE13VYLJbRR5QD4SJbYLaxibINOZXaJTrXoq4XODw6xldf3cOlS5dwcHCIzz+/jRdefAHf+fa3cO3KBUymFrAMmBZHzqGYWEzYo6IZzj97Ff/N//n/hJvf/y5++W//Gl+9+yF4bx9mziDvQN7BeAlq0XIHCr44ad8HY08Y3fTzVOij8wYMgVI6J/lZyoVRab25BmodvVwrdIufCZ0azb/GPY0eMxNL61zn07gqSNPvhoxx/BAUgwHIOHjlfkv3Zw4o1/nd5ICDgZgfT8fXP9wHOcjfywGGfp+CkRxsjPUp7XM+h2ldORAfm+PVv8f3Zdp23scU3I2BJYzcX2N/n8TP5HdRP3YR9CpIzec4n39jel55sO+k0cF6pP3KAfXTlG88QBKeTJLqmXAqyRgxU7Biy0hg7J46JRF5SBjODd7oTR884+zZsyirShiFskLbNmAyYAobcORyHYYsHoa4zJGxXjj6riYkTZkarS+VPOaMCxHQOY/j4wW2t7dBRgmKxIU0xkJ9f9KgAWLLSbBlgZ3dU/jFL9/GD37wuzg8PkJdd2ha6Z8yLNeuXcPW1hbKkLx2MOVrGL3UxACJEluSDjIWiwXOnj2Dv/oX/wvm83kc2+nTpzGfz7G/f4CqnMDGqGXogQ4I6r2nxyU7nv2vyRdy+N3wMcUQvPJ4Vk5iaHV9889XpX3aj5wo5PNojGYSZxRFKUxJwKPrmFTHiaQyJVBATIwc2xvt5eqo0n6la5pfVIPxaZ2BM471Mw/ChqcXTF4GDEcCQhDWXnwpTgZbynSqM2jbttje2QQgpkI++As2TYO2bTGbiVkQGMEURaqoqhLb21uYTqfY39/DfD4Pod9NZG6pt2QdEO2nkf49qawDoid9NpC2PcVllz67Fvgmaz9Wz7o+cdhvBAFI7AjeenSdaB4ODg4kKqT3mM/nmM6m4i0/Vr/SkxGm6NSp07h973H0BTLGAN6haRs418H58sT9dvr0aRwFv9PIcASzXGYG+w5bG1O88MJz+Okv3kMVtPjxIs7miJL9YIwRR/iQ8FjvCLXjD0+KBkN6hJjJPABveI9usQR3DFNVoAnBFwVgAxNt5L7bPX8OxbmzeHT3KzTLGkUDEDxsWQCW4Dqhg7r/U6l4BEkasMYP/WGYGa7zsEXY5wEkiRlhb/ac1qf3V1GUMMbC2hJdN0Ndi59S3TTRsqEoDcqyQtcKOFo0NeqOsaiX2D86wKndXVw+vIK9w0PcvHkLb7zyCl771su4cvUSyHo47uDg4BsPYz1QFrCTCi989zU89+INvPvzt/HWX/w1Hn/wKfzREYqmhmkBeIeCGd70grX0vs1DJKclvefHmOH0fOVnKGey0/l+Ul3pmpxEI9Yzq9lzI++n9H2s/3lJAYLkkQPI9AI6HyKw2kKEmH4w1v5eynmmfOxjQud1wCYfe/LB4Lt1747Ry/yZFNRqH59Ud5oA+CQhl9aXtjEEgONAO30up9npXlMz9LExj+2hsTK2L9N1SU0ZNX+jCD5Xfd3SM7H2HuXezC4fo9LWQSTApyjfeICkjFmcKCDaOJdVlYQHDugdYUGAeLk552CLCTY2NiQUt/fonEcRGD1htobqYiKKoZ1V2rxOrZ6a2uniq3mDLqZqelTSDYgGTC/afjMBOzu7mM/n2Nvfl/w+RRHENRSSy3bxIPb9kWAPs+kMy2WNnZ0dVFWFo6M5vJcDoxqrrutw/vx5MDNm02k0leETAUN2uNUAjiXfho5rvlji008+QdM00cdqMpng7t278N6jICtmcfCSYBQ9M8+BAyetf0D40mACPYO2YmucAAUGAL/uMFFPTEceWU87KL5w0jEdJ+YGbSuBKHSviJldCpAzwp1JNbUoQxb3zhOI3dP08aTL6D8NDvRleFmInbr+0zZWtF+Dvo5cYlHT49G5DkVBwUdiiY2NadZ2CHFb2eCHNAUHP6WqLMNZD9oQz2BinAyk8/6Nj/cfAqjGLvExGpQycmMSNqUxTwJ2TwOO0u9Us0kk5qPOGJDx6JzDYj5H2zSgTcLh4SFOn52OTmNkEszQLEl/njlzBq77ULRHYQwUEjS3bQv2U1AxzmBqZLLNzU3s7e1hd3c3ahOJCQQnfpCw+O533sDf/O0vsDHbxsZshoO2hU1NZ4hAvs+/olSASEzovO9EwwSIiY/OUaCPCMmbPYBgFweioPz2Dt418B2D2ICngLEFwAa2srATC1uW2N7YwKVLl3Fw7x7ufPop2raGn5QwJJFZNdUUM/epKCJjItGnYtCbnGEHQxRhMjZrbcgtV4VxDKO2UQB4zmmuFwFBVSX+wfPFAvPlIjA0DoBHURpYU8BVHZqmwXxxhGVt0TQ1Dg4Pcf/BAzy6cAkPHxzgk09u4juvv4pXX3sRu+e24YnRUCvAzRmUrkRZin/Sd/7Rm7j26ov49d/8FL/+6/+I+s5XcAf7oK4GyMR1y+lrqk1K943IgGhFSHTSmVkniNDPU5AxBgTy/bvu73wMGjhoFARk/UzNCNcJRMbG1wOp3ljUexaNIzhKItUPWZ5V/iAZRwJS07l/Eu3MwZKWlBaO3p0nANwnlfy9k+Zp3Xo+ifbn9afvprsyB2p5O2PjTWnok9b465QB3chA3DL4V6ef5SBHSOFwHP3+GM5Xbrqo+8b8F4DUF6fMH5EkL2Q5nNVkGsEPIK7tRCShr5lRFgWc92jqRph/H8xudNNAzRw8vNUQoSaiYgEVRcgH0aIsJaN7Cpbyg5MurPytTKAQDP1bLyE1G5PP+jo67zGbzeDZ4+BgHwTCxuYmCithvq01KAoTLzsTE8J5zGYb+Mu//Cu88MILklDVEtq2Qb2sQ24noK4XmEwKVJMCk2klARKYo3ZA930OmFKCxmr8xWK60XUtirLEe7/8FebLOvhGiQS46zweP94PDr0IM9ybxfUT2H+Qw5DBYQyMWao90SJAj2NdAwC1hlDQyO/p2AfEDwrUe3aeg0QY8bJdhW4+ADIJS96iKI3EoeV+CtYRs1TStI7YpdKatJ/JE/2PhIDnkp2cuA6IXMAKK0uGpwMCK2eFEOcph2NjICltU01u27aLUqe6bdC6FmRLOM9o6g6AJABm+DBsisIMhsf29kYIcyyDs0bXTk3JKAhaELXTK/1Zc4muW6t1krwx5iq/FMf2wZgkcqwveV1lWUYhUPg06de41HTIWIfHOESqIgvXtTA0wWIhud+MNZjPlwCXSK/9waVJ4bSH/QD0Wv3t7S10XdvnXWKGsQZd06LuOnTew3gOmIOgSlkiMTsqigJXr17FrVu3cPr02Rhyl+EhaW8dLHm89OLzOLO7jeOjBhvTKY4PD8N94gGNLEkco6JRnCIOkfykv+m5GeY9AXTCRHCjHUXoj4NzwezEd7AAuKpAJGklqtkUmzsbOLUxxXOXTuFbLz6Ln/zd3+HRgwdo6gW2NrYxLaewRYFJyP/XtdT7ZBJAJP45zrn+LDNQlSWYgUlVwRYWpS365QCHxLirDCDAIcG2mr/oOQA2NzZgixJNW0v6BSfBPMjK+9OiRDmZYLFY4HhxjKZrsGzmePT4Ac6dvoTDgz3cvXsHH3/6Kb79vW/jueefw9bODHXRgBpG2zaoygZFVcGWJTbPn8Lv/R/+DC9/93X85N/8GJ/84m20j/fBiyVsW8O0TVwvzyyBV4P1CSB3SVwSFk4gZVJzQeaYz2VexgB/fg7z+tLPB3Q4oZP97UIxaIg+O9QaiFA1bSMFuGlZ9/eQ8bfBLDUHaaqZD8ApeU8EBBzMm1fpXWq2ODZ/Y7RO3pXJWKFrOkfJOwO+5SnupwhSRsy88t+V9qZ9U1OzJxWl2foz8o06kGwO0vv46xQF/YzhuoyBuifWk8xNyuUwgEVdwxPBJ6AdEOEJAs/oPUfht7Ii6hsuFjUmJskOsx3rZyIRJv8XH6S+WFJTDgBh0j17GBRwvkPXyCVc2ELyMwTnf0ME3zm0dY2ubdEtxal2OpvChRDA7AKb7iSsKXvAhdClhmy4vCyYZAN3Xdf7/ISSH/pUiyTSE6DrHKzto2+JvziHRGI08Llgzygk4Qa2NiaoCoPDwwMcHTzG6VOnURZV3HimtNGcD2BU1SSAuRI7OztYLheow/jZeRjy+PzmTezs7GBrewOTafH/Y+/PYy1J8rxO9GNm7n62u8WNuLFHZOQSuWdWZlYv0N1M780OQ/NALMM8jUbvoQGNpjU9AiH+aSQEgj8ACfT+GIQEgmFa89jewEB3VdfSXXtlZm25r5EZGZGx3+1svpnZ+8PM3P349XPjZlH93lPNs6rIiHOOu7mZudnv9/v+VqxoHLiQoL5CayzMc0GosRZ8GmQrINc5SMVrb7yFtYI4dokvlEqYTcfs702BCBP6bmkgsNalwm4RqUrrsDCccHTEQYHdr7nrQ1Y1gOoLwl/1he6QOvcZgXs3xnYIcwHWWXdYm4K99c8TcGCdhBBoK7w1wpJnM4arq1jpNL51DZjlAGOZtqj9WxDqG9/Uc66I0iJT7eqzPRbp9RTWBmK1uO7tvrrGf0ADGNa/+k814uq1tc+Xm06dMafQrjiwjBTaaGb5DBmvYVGkeYk1ArfCwZ1GeBdHRa8XMxz1fS0kJ3AMRwO2d1K/HxzoreLEFiD7QQa+wDw65ns/cNu+tguodqaSbey3LmbXBlB1/GLiyiKI9vkOyp/uMQu/EZwV16+vFZ7G5VgjyHNXl0xKmE0zsD0gxXJQ6AjvXwgLwjlUO7BhGAwHlEUJ1iKtcLFBUqKxFMZQWIm0LpsbgPR7vDp3WnPu3HleevFlV/rMCIwIsREGi8HojLWVDS4/eJGXX36Nfn9ELCMKXTgdhhcyK/WZBwJ4kK+kJIoTCl0eEKpkAzhZawkFKJwbp+cXAkcbjMXmuStgXeSwOkQoQeyt/P1EsbmeMIgk8foGv/gHf5bXvvcKr3/3DXZ3LeujiOFQsbG+yt27d9Fl7sCLPy9KKPqjAcb02NvbQ8mIKFKcPXOG/d1d1kYrrn5cWTqlgdbeUuD4QphDE6TrVsyTm7fbQ/0kIo4EcazIMkleFJRG+2LQEiU1KyrxBWlTsnRKWaQUWc7+eIczp86wN5ny3gcf8+zTz/DUM49y9oENkiQGZcnLgtJqVJnRt31EnLD14Gl+6b/+U7z/3DN8+3Nf4fY7VzE798BMiaTBFDngMglqq1ECCPtNWA8M3V6r42Prc3SAHi05w82z204A0bZ8NBNodAqtgZYEElh/7QXJRevDsjG2x3uAb3TQsuacpWzE5bX6D/vCGIuStRIZGrytoXRpAoJlY22vRROM0AIM1bXe9bpZqLQJxLqe1bXmTbp7mPW9TZPba98cXxOYNte/6YpX0UNZPy/Mexmgac6va25u73TLD11KuK61aT+rVqI5vmmFqErVaNzZUSIAnqoKmd+8AeYHcFTLFlVWzFrqd+MgyFzWGU2O2H7oAVLb73B3d5fRcIRRrkCdNpo4cWb6KFJeO+eSOkwmE6y1HNs45ov7OWE+9Lf4sj0TMHUQpfKpTyMVo3Xp6if5jEBdGzZ8Xwc1BguXxRiNC6isLUjGaoSpM7qEcTmeKqp7V1dXuXXrFnfu3ub48ZO1YC/rA6a1YWN9g+l0ysWLF5n5ivBRFGG05vbtO1z7+DrjyYTHH3+cXq9HHMXIzsx1taDUbAc1NW7DG2soS82duzvcuHHTA0LDaDTEGMt4MmE6nSKFQNM4q7b5NA8W/ffN76wfS3h6rbHCz7+tLZLVNQuz6jj8IaZA4n2r/XWVgA6NFJY1iLIijM1WGh8HnhbBczuw0FrIsozR6lr13uxSN8Dvv1VL3ABHbQbaZAJwcH0WrBUW73LWpHHdYKrdlgkWn4ShNycmKuIqfJppH2NhfeatNYUGZjNX9DNg4WAVMl4jHilFEgpDl5qxtxooKdHSCcYYQdfUmlq9Lre2tgDSvq/Ll7pLyFnWT/tZzetDX10t0CgppauN03rWgob2kOchfGHkcJ0AgctiVxQlWZpWMZvz+ZyyKIl7h6U+XhQkwt6Lo4h5mgK1QBUEjSzPXU05GeLXDsbWAIxGI6bTme/TWdprYY3KxfJHf/QFvvrVbxF5d+zd3d06UY5fk6bqoSnguMRAroRDtTf8UIKrnjF1BqcACh0YDQoH4V3uLCYvyMdTylIgRMSoH2N0H6kcqI+FoIwlP/JjL/DgA5f4+pdf5N7t26TZgJWVEWdOnXE8SQiEksQ+tkoI2L63TZamnD51muls6ly4rSX2LqZBGdicZ5cQ1U5U0D7b1jpLbU+5JEPWWtIsYzqboQsNCJ9UqEeSRBS5V+jpKXmRMZ2MuXPnFufPnGdn5y7vffAWz3/6GR5//DJbJ49jtAFREscKXUzoJwkoRb8/4Kkf/RSPPPIwr3zlJV796je4++E1iskEawXKlEhdEBuX5MJ6fmElFfgNoBKx7HwszrWLrrUF68PWqUv5UdFnltOAw867Nb4+FwctXu3kAc2+mtc3+w78sf3scE0URc6i3wBL4R23XeGPEs/ZHF/4UyVmsLUiJPQT5KplYKsLvCxbuzZtbydqOIzftZ+57No2wKyu8/z1k/DFwyyZn6Tdr4+FvcziugghSJKkivc0trZcAZUMtbC35GIm0EAPwcVf160BOD/BfH7oAdKtWze5cOE887n2ACVDqhWyLCUg2DzPmM0m3Lp1iw+vXmWe5nz6+ecZ9Aasr69hrMZqXQEkAAQuMNUHjGvrgueD650uS5RxptK8tOhSY7BkRe5dInwtCikR1rrqwkYjlfIv1ltIhEVFIQWldpYcGYqq+nTJpZP2w+YxhabIc7RxGryyLEizObdv32Y2m7KyskoURfR6g8o0nSQ9H5+kq9imPM+5ceMGH1+/zmwyZTydMByNOH36NEmSIFUoYHh/AnxQCAvE3Lh1VBFvvvEmRVG2hLCUe3fv+vsPMeUKEEI1xQ9HkD1VXnRucsduUbPlvq9KVdmgsWoQ9y6ABD4egepPAGUL1wUQ7MFC5Y3tb3Ir4iTx5riMd/PUwVSES5ShIuVi6HTui68dZFLVbJcAkcPATXuey75rajrb1y4whQpohYcvjq+L+befdyQABI13V/df/ZsAjh1R1aVzMw2xecHFFgRzryQInVrr7nOFn51gNlpZcRnxSpf+fjQagtitBOcFdFRvp2pOzT9N7WubMTbXO8SGtNek63N7/oe1wNCXMfzQZzNIvVlDaHFMTdZ2yDPDOEU4r7ViSGvt061Hrs5U7NyND5xDDgoTYRwrKyuu5pLRSNmrzyCQpSllUWB6sQdslZ6ymrP7I1lbW2N3d4fjx7fQOiRgEFikT7GteeTyQ6ytrTCZzOn1HD1dcEG0i9mxQjPGYssSaxw/aSZ4wFqsaKT9DvPz9+pK0PMKicglGqK0SFti9JRJURLZkmPDhPk0ZbWXIIR18XO64PTZE/zBP/qLvPa9N/jut1+h3M1ZGa0yGAzACoR24EsbZ/FfWVlhNBohhIsPi6Koyt4Y4rZCkpNQtLu5j7rAexCKg6IwXBfHMaU1aP/bibVVop1d0jQjS1NH+6wD17IvieM+M586vCgKSp0zm004vnmcNJtz89Yd3nv3Ks+/8CwPPXSR1bUheaaJpCXN54gkQltL2TMkG30+/Qd/H4889zTf/NxXeePll5ncuImYz1CZILICaX00rCdxtmHB9OiomvvSmKUO2hlASJM2hkxzzbMWfmuf20WrRK0MbdPyLjrSbO3vtdbV+W8qdNu0u8nDFubF4vkKf4c5OGVinTwKJJGsrXPN+5bRqi6614y5ljJkJVx0U6vHeNBFu7rPHj1NdJOntS007XU5DOg1AV5zfssfXPO/o4Ce5jottSTdt5ejtUUgt+gyKlqfuwCptXYhBslqXecPsNbLVR0gqCGDHPX9wf8JANK3v/0tvvvd76CUIooUg8GQfr+PQCGVYDIZs7e3i7EarUuGwxEWpx2NlGJ3d9eBHZ9uW0Sq0iTnuQc71qVTjePEaQyNrszWLo7HARzpixQ200s2M+G46vLu5eV5jqVO3GCNA0rpPCXLnV92KFQbNJhOq+zSEDv3Pm96twZdasbjfa5cec+Bo6TP5uYJV7uj3+f5514gTZ1rUJZl3Llzhxs3brC7u8t8OkOXJcOVEU8//TRCSldzSS4vdhdaW/PSJOgOxCjSdEpeWN57731AVGsNtipO62o8xaBqLfCCgAlgJZaQIQWf+tkFgIsOK0tIceoOoBPSfEdYEaxCB4mHm4yLWXAaJ+oMata7Di0Iwq5PAGu8VlbUwNLYwGC8606DadVaSMc8pJSkaYYuNb0kIZ3nB7TS348maJEYLUryXUzofu4NYRyVNt/3aPyln2SEB5jsf6amKwjwQlAnaRFunOl87jRYngYEICWlc380PhmL8fEpUeSKkAaBfjAY1M+REqvNAiAWctGdoutsLAM5y4SRrvkFgWoZAzqKVrL9jLZgIvw+DhbzRcHNLFhmD0tjDA5MujghRxOzLPf0zNFCB5T6yM5YhEVh6yDYDJYf1xytjisrnNYGGerDNeZbn0M4ffo0H3/8MSdOnPQCVnCTA20sVuSsrKzy+BOP8bWvvlx5EDj3ZdeMrzof+q1omDEVPQlnJYAjghImvINgFffr5KyxtqIlQlusL0grjPWfDfu3Cq6WOX0B670BxDDsJahejzhWWGF5/see5dJDl/jmV1/i5o2bFDpnNFhlkPQxpfNQkJGzaAUtbxhriK0N+yJ8Dsl9wlofZd+F+7T22Qa98COlJEkSVtdW6Q+GGKvZ29klz1NMWSJFhFSKwYrElCV5lpJmKXmRk+Up++MJmxsnmU6nXL16lSeefIznn3+GCxfOIXoKITQ6KykQFNYQxTFJFDM6e5Kf/VN/lIeefYyXPv9Frr36Bnp3DzFLwWqXxMGUDmALiw2FsG23Uq0937ag3NzHTQvbYTS3Kx10zRstwnueLItvaQul9TMWBfo2QFs2l7YwX11jrVdm1sBhwaW4cX7dWNtxiwdpZtc8mp+7YoiC8rPdh5MdDtLALuG9C7QsAzJd/YSxdRW8bY6ny1rXvmYZT2iOpZ39+MCadNDmxfe2uDe7nrOsde1X0XqPWZYtyMNdZ6dyWxXU76kCXFTy+LI980nbDz1A2to6zmw24/jx44BbSykFzsrq/OcnkzG9fsJwOGA0GqKihPfff9e/RBiPx7zz1tsUuuTxp59kOBpVm1pJ5bT5scvY45h5Xgt1FpeSWcgq/ihkCALvwtbUGIpm9jsHtsLGTtOULM2IYndPL+05zZ1ywlwozBfHEYNB36WP1Y75WmnRViOlxVqNNgWTyRiQbKwfo9cbsL19jytXrnDt2jXu3r3LfD4nTVPWVlc5ffoUcZJw/vx5VxW9siAtHhw3jeUEuP63E66KwpCmOXv7U+7cues0lh6A5XnO3t4eUrmCjxZBaep6NcHKFAQpY0Mwn2sCBaJ+1uJ43BU1kXQHriKcC9dR9dj8V+0bjbMqOCehBdN9uLqbgDjttBLe4mT1AQtDWFfHIBXGuoKmxhoHuBuakarX+xCrrrYgSB8Cjrre7WHPW7jeC1RW2MZXi3un694uRnNoE+GvbiGk/qcDEdpookhRaE3mz65EMZ/P0doQxQLh91ZYp6IsWV9fZ211jchrzNM0ZTRaqRKeHJgP+ID1+pV1nZn7nZ92UG9bQDkM5CwDWO33cJgA1Hwv1tYZy7Isq4SeJshextybMNwGBYW/PvTltObCucnZHgsH5AgtiiRrq6tVrIubkBtzWZae1hqslV4zWWtQm2tx9twZvvbVb1QCa6B7AlWVUgDNpz/9HF/6nW+gtabX61U0OaSKr4AViwoXq41LW99ySw1Z5ap1xCt2Ah9ruBYKUVuohJJoAyqOkaXzgBjfusdbsxQ9zbh46Sz9Xp++VAih6A365HnB6uYKP/cHf5b3373CK995hcl8H4shUT2MNZjSVBY47ecUhLzSKxKbAfNBsA/u5c26M10Cb3jnlWbfC/hBMBfAYDggNoY4ihj0++zu7DKbTl2srI/NiuKYKErI0pQiT5mnKWVpmc9Sdvfusrd3gp2dHa59dJ0XXniep55+nBMn1tyu1IJsXlIWhjIqMYkgiWMeeOYy5x48zxsvfpuXPv873PrwIxiPUVmGkjHSlK4+lgCkxdSlrKo5BuVoG/Qs02q3aWAXTWz33+W2aOxBmtJ8R52fG7c4RYKurIRd97XH0vxc87Du6yrrWOOxR6H1hwHF+wnGXWDnMLBwP97XtZfb4+pa6wAS28kWmr8vA0BNWlKdkVbYw2H88zBecVRe31T4tO/r2gu1nLHY72I25nod2wDXBrpMnfQm/DcA6loGxMmE1laH0dj/vwWpakmS+IDq3oL2RAiF1iVCWPoDl1J7dXWFKIpBSJSIGA1H3nIhSZIYaRS9fo/N48ddvJLXAEQq8qnAI5IkRohVLHUWIoFECoVUkiIviJO4tr4IF6gqhYtxCloyC2hTkMgErUsQEVJJer0E5X2+tTGVJnQYDRkMB1XtieDqIGRtmu8P+gx6J1wih8hZ0QaDAY88cpn9/T2+8pWvcPfuXSaTCXmes7a2xqVLlxj0+wgL/eGAzc1NktgBPikVxtSI/yjanPqAOIiRpilRFPPee+9TaudKoSKqGIeiKBgOR07YtYum6qbJ2+EEiUuDUNcVAYH2YOjg2ZaNv8OY6oPUJg9NLfTC9xYI7n0N4bu7NfTB1oJPtEElOC0S9lpTL7CYSiMrhIuvEGLR/eD7bU13BWONL3T5n9ea2vxPDtl+cG2RqNfCZLAuBKtuVuQutbTfW2ma+tg/V6BTLmg9NYNBn9jHIAnhrMX9wQgpFaAPOJkJd2G9046oheticF2gYxG4LAdZXcCnPY5lgkUbHIU0wcH1JiiH6rPlWh1XeXgT3l0tz7PKKh5FCel8DmLjvvcfHK9AqajK8BbGrpQi9UolY1zhaSdXNJUj9RoMByPSNPUeAc61GBviywxSCYoy4/LlBzl27Bjj8ZjBYLCgtQVX78PNs+UW1XifC0IL+BTmXpDza2Rx9D/UOVKeDkrftzXWJQcsi3rPFJp5YXnze29x9949nnr6Uc6eP0FvECOkIOn3ICrJs5yLly9w+uxJ3n79Hd57+31WBtCLImzpQH4VG2kMtnQxHUVROLe9hrAUnt2M/+pKQtIW1Ko/fg2sMSivYNTGUmoX4+RcXCOSuMdsOvMxSBprXPH2Xn/okg+lKXk+x+iMvJgxm0/Z3d1lOp1z9+4ub195n+c//QyXH3mYleGASIIpDaU0pMU+Zc+7pK/2ePbnfpIHnnyMr3/xy7zztW8yv3ETm2VQWKTfDzWPqyYF4R0d4RzU+3fxHN4vvXUnD27QrcOsDEcdT5cSpsmP2/Sn3gNtilj/ftTMbUcZWxcdPAgwap7b3qvNOJbm912f27FQC4rGQ8BHe0whvKEdW3pYQeBlY2pvvaO2NmD8flr73TfXpK10qi9aHK/Rplb0NBR3gR5YFvdhraiuE181f7fgspeGvj7B4vyfAiDleU6WZa4YbIVSBUUpSKxh8/gJdne3SXp9hsMRCMntW7dJen1W19aIooiHLj/C3njM6tpGFTAKnmkYS9L36YBNfUhlVZ8GDyhk5SoQmHQAVlJKaPgYg08VajRKxh7kKGTiXPyMsQjlsn/ESeL8L717hpJ1lXalIhASow39wRCBRgiFJCJRCRvrJ1gdrfKv/82/5epHH5LnOSsrKzxy+SKnTm5RlDlGG/K85Pz585W2WLpUeshQuLDRljG+xcPtUP48zZEq5t33PmA+nyOjxBF0qciygjTLkCqiLL3A6bVyLruY8NTAE2bRJI6LTEp44ace18KAEUEbYYMm2/u2N7UxLRwiGv+QBxh+95ossggXV1YREOo5Cf8wp3GmmrsQUBYFGIuSyrtwLTKnZe+hi3A3CVcQbvIsZ1m7H+E8TLg+0Jqanv9Mxu26a70dUX9fz93lTgwJAtxecmuJMeg8p8gLSBSzNCMvS+IkrvaPE1RdAHESJyS9hDhxAniWlvSHCiFc+ufKOUo4Al0R7tZ428w7vJPF5BzdgkWXoNJev/ZzjgK4uvZLl/AlvDWw9IK4S/l/uDa8ejbU2kAhXJrkhvA/mU3JioK432c8TXHGcEHA7vVcl+8TAZw7c4q72ztEas2dLQvSF5suSu2sNDhrhVOV1Aqc0IuSitX1dXb39zh+/Jij86axp4zBliUbx45x+dGLvPjiy0g5IOklTujBVC4l7XdhPfMOjNuBZ+pPFkefKkHDPVQYQRm2uXDW6BD3JqR0bnjGgnftcxanAisEV69cY7y3x+XHLvHw5Uusbay6vawEogeCHEmPT336WS5eusBL33iJ/emY0WCEsGAyQ1kWFWABqhptlSZbhGeCUBFRAqJ0taNcbJJPXkG9jg5I1O9ABJ0VTohECDCujEVZupjBXr/nCrbHimieeCCbo0u3F42FeDAkGfQoc+eFUc6n5GXBLJ2zs7/Dznib23fv8tGHN3j+mWc4f/Y0SlmILAWa0maUJkfFCb24z+qZE/zin/oTPPXME3z9M5/j+lvvUu7sIdMUkc+JdMjR6tyKHR03SIQDUdIpxoK1p0t73j47TeDY/K65p5rWhoruWbuQ1azL1arZX2XJEE2BebH8SBdtOAy4LZzJxjwCKAB3Buti755eiiYvP5y/hP6a40KI6ijXY/V7zgqfxr4dobxI75rAsitxRrOFd7lwtuViUq72ei9TcoV5tJUszfk2n9nomTZN7HrGgX3SMZ/WgBtrVPcrlaoUAE52WZR3qIBMfU9F9338tESAcZ44xoK0Cmvr+nYa7fexD6OoeHGYL1gMRlTRV3W+ANzeEsbtq8IuL/Dcbj/0AEnKiLW1IfP53AmSQoGE0pREsbPKbIrjjCcTL6wnDAZDRiurJP0BMk6IpOLigw9RakOc1JYoIYL7XH1gjHAxQO79d6fgDOCoeTjCQWgSDgCBf5afjyNcAuM3jJARQilX/Er4THbaIkWENS49tBARUoZrnXYxEhFKJjz4wMNcu/oxL37jJWQEzz3/HCdPbiEkZPkcrQuEcC6Ex0+cII5jNydLFRPTJch2aSEWPgvr0rZqy2wy4+OPb5MVBZH3mJalZp5lTigSApAYC0KENOg1EHL+1XVq30Vi0o55agmIBAYtCO41SvjD10ZEHBTFAjEIIU6VwH/gSj/eptxF0GoEBOTjIHw672YVeiEcYzW4WDWMpRfHXvBenqZzWWsSxuaeq9LQfx8apB88yFneR5dmtdbGH/YEl7bYMRV3vUvS4OLUrC5RUiJFRGEy8rJgSKidoDyNFlhj6PVd/Ea/H7O7Oyadl5wZjJwwLDSCCJ+2pVrPgNOb56Pr313azzaACX8vaMs6QHDXunWBoS6QfVgfTlbVrfEdemvrVfg542O0LF5odO7A0/mUQpcIGTGdFxgtsEJ6xUXooh3v1xq7tayvrnDj5k3vfqUw2iIjhRA+dbQ2xOG92kAHXPL80LS1bJ08ya3bt9g4tu5GLWvAa631WRpLnnvhCb7y1S8xS2PiOCaTzrXI6G5BRIjg4uuH3FCygduxsLh3rAdz0uGJml/IYNWyiMpt0LuqWYNAYnUJRrC/s893Xn6V7bs7PPr4ZU6fPUmv5+KzUJZCOT6zurHCL/6hX+Dtt97j9VffZJT0ULFyihoEWV64JArUdMspBN1YjJAI4UGgUJQUSGMpSw1WV7zSk7rwnwrcBJEnKBSlqsshlNqVzoiT2MV4KUHUU+R5zHw+d7TSsSusFiS9EVIlpOmcNE/RtmReTJhM95hOpsz251z/8AY/8unnePTRS6yvD1GV6qoEbSi0hsgSR33OP/04f/zBB3j1ay/z7c9/mf0Pr8FkH8EMZdz8rDBo2zp7BFp/UCHRdrVq3teM0eiyRLUVHmE1m/JDkzY0LVIHaBAWawtXvkS7OM1aSeSxRwdgaaetbtIa59XCwnMgxIIqD2QaJRwOoeldyp2FNVkQkBfHE1gugX56kGQ8rRaN69sgsMkzm89uAsTDeGG4p7luTbfSZmsCzy7l1jJ6Hohi8952vFcbbC+sN4t7swmODii6/O9NOfXA3DkoOxkcXRAeCRsLMkkgSgGFwIWjWBHW3SAMSBH5Z5rFhA1AlSa4uYaE4btn6G79XWf7oQdISjk3suAnHdzOhF3U0EZRxOrqKtbC3t4e8/mc48ePVz63xrhK3nHSqzYz1L6zobU3WFPoCH2Fz8E3vbkR76chEa2N39Y0ANiyFlq6fF+lryOxsrLKyuoKn//s55nPU7ZOb3Lhwnlv3jRo7bIIZVnOqVMn6ff73np0eIXw9qHrErosLvg6iWO++73Xmc1mldth+DtNM6+ldIKLS6He3R+IKr6jmWWrvXad4w74pPr7oKbkfq1NuLrasudXBGbJPVI6C6Dxn3WpfRKRyAX9m+XuE0dtxtBqndwAAQAASURBVJgq61S7m7b2aRkD6NIqdrYg9IiDMLJ93/3m1EXkIby3jjF6sEnjTJZFSRwnVQ2XcJ1L+10gxIBKfvfP1MaQJC4LZLAAl2VJkvQA6wRV7fnUfZh7+LuL4bfXov1dO0NYMwahvT7L0om3tbNd73tZa56r+wGrruc27zVQZSTSWjObTsnzHITwSRoCcOkeR/Pv0Iy1HDu26TMS1gJo5GlxludVVrogOHmWStOl1hjD2bNneemll3jsscdoiJyEnWGtK0D6+BOPMhoNSecpo1HiBUKnrZbIA+t92HyaQnKn8qASVOvMXEI6jW5pghukTxpgrEsjbq231rnCvO+/d4W79+7y+BOP8cAD59k8vo5A0e+5OFAh3N5+7MnHuXjhEi9//RvcvXGHfJ5hLMzmU8oiZ3V1ROmtQgrvFSG8a5VHd1YIIhRFkeHqBzWVSsub8i7j1lqfBbam84G3DwYDoshlPAyf5/M5s9mMoiicAG4MUkX0+kPyIiMrUudaW2jmacbu7i63b93k5o1rPP3U4zz3/DNcuHiewbCH9UXhdVlQRlMKVRAlffrDET/+sz/Do5ef5Ftf/DKvfP3rTLfvwWwfVeRE2pAYg0GgpUWHtfDeELWrON41vhaMl9HeLsF2AXA04pzc7lyURZo0oW11OkBPRYgdqsXco575RdmmfsmL7vG2EsC7wEP7+ma/XetUL1gNrpvzqRUP9T3GJ0pp87D2PLvoavustq9bBj6anxdiG1t93k/ZFWSEBbAtOubbGnPX85rrv1ReWjKOw34/0I+nsyp4DGDJhOFTP/IjZGXBnd0d9vf2yLOU+XSKKTJsWWK0xRTOhmSwHfFEqiIozX0hhESICExJJJP7zim0H3qAFOJY2imHAxOez+dMp9Pq+ihSpKllOBxWqFsI536U53WQaW1FOqjpkQ0mHz43iU+dWKAWgprZTJrAJvRbCcr+IMVRVLnrhWtCP7Kx+RcIHlAWGiWdKfPc2fPs7u7zzW++SFkWPPboo0glkDZYayKshSTpc/78hSqOq21mbrYugr7suvl8ThwPeeWVV0jTFBn5VLFKMZ1OXbFDQlpjQZZmhLoM7bVxtPegH3CzNb+riSSV5jqMq4ugfb/tKMSj/jtof+sWBPJAy4VwQDDPc3p9Z80rtVnYB9/PuJvvKdRd6epnmSvI0Z67fC2Ocv8yAHbgc/jvfZfBAyRdAgnWZ3ssigJEUgm8UkiQFuuLPxqv4U+ShDiOWRmtsH1vh6IoKIrcz2WxKGL9xFqYXsY428y1Sei71qlrX3cBr2XrGdr90uZ2jbX9XfP6ru/b9KHZVxCUXDY3y3Q2cwAJyHMH3uPIx7IgEKoJUpYrQEajAfv7+z5b3aK22WVOKn1sCBXjFuLguq6urpKmqU9G0BSGmsJmyfHjx3j4kUt89ztvOromgzXKgak2TewSwLre6TILn/Dgy/gEBVXNNyGdG274HovVPr5CCcrCFUnHCPZ29vn2t77Dvbv3uHz5IU6cOMFwNCRyfnEIv1ZRT/GTP/X7+Jf/7H+hSEukFCT9hP6wz2Q2Q3qFgdUl0mdOs35ZhXSF07UuQYKIFKY0tba+8bdtfgEon8woeGw0eV9zjYKHgxAu2dFwOPRKvox0OsWUJQJQQjKII+IyJsvmZLnLWFkUruTH7u42e3t7XLt+g0+/8DxPPvkEJ7Y2IDJYbbE6x0QluSkodYlNBqxe2ORn/swf4YFPPcpXPv9Fbrz2GmJnHzFNicoCIwRauLimyNSuqD7nRpWBq7mFm2emLcQeRvOXxQO1r++iQ21QIIXACG/l9OCufY6XKVUWz6RPsd/I1Frvd6pQ4Pbeb861SxnWxQe66IBYXFj/NzTd7w7I8YeAiGa/y85v+K0dY9WlIOuSFdrufV2tC+xYcRCEtYHPsmc2r+tay2V0vUsR10XPfC+uiLb/nxZgMDzy9BM8++M/SnxslXQ2pUgzpuMxH1+/xp1rH3H7xm32dyZs39v2NN3x6yxLsVYCwboEwjoAhnXFYVXcQ0GlxDlK+6EHSNevXyeOY2azGRcvXqTf7zMYDpilM6y1pGkKOAvSnTt3EEKiVESv12M8HjMajej1erWfrK21kG10H0BR+C18FkLUmYxY1PQ2QY9uxSA1N/HC5vd/08gI1LzGpZMVVf8hU54QkihKMKVhfXWdtbV1vvGVb3D37j02TxzjwsVzhLTGwVpjtGV9fb3SzjXT+d7v4HQdpDBG7etj7O7scOfOXad9Vy4ToBQu1fh8Pq8IVii064hzlx/womUgfN+ltTkMtNwP0Cxry4TF5lodJqgKUbvGhD9Nwai0rj6UtqW3vhUMh2oBPLWf355r19jCfmsCn67xdf276xnQXSQQP7WqXG9LCFg2xq6xNMfbBBDVH/+s9jjDc603GdaAShDHLo4vZI2M4qjKGIjAp+wOA18UWqJIUZZO4RFFEUmSUBSpE4CsrUBuE8C1V7q9R+4HStpza4Kpo7TDntP1jrtakwY2U4p3nbu2a0dz3OCZv7UgJQgXe5mmqU+i4MocuGfUz0aIRpynwZjFPe32gmB9fcOXUNALeydJYnTuYizduL07pO+vjbCttd4qkbKyMqK5TAEUa1PSUwlPPfUEr7/6NnhLlBQKKw/Gn1X03ZgqBXzzHTZdeprv182PynVOyjobpkuiYLENV6aQQtzJoa7uXojZVEphrGE+zXj/nQ/Z397joUce5uKDF1lZHSGUJOrFaCHI5xmvvPYmk2mKNAIZQV7kbB07wezWrHI3NIJK8rcYB5qsj1kTzoXSWFcbUEpXu8niLR/+fDnrWJ2oQQjhlBWiBprNNWzupcFgQJ7nFd+Oooh+nDCfzsiy1D3baFSU0BMukUdRFJTeUpllKfP5jNlsxnhvwrWPbvDc88/y8MMX6Q9dxjprXTr1uZmgTUY/Thj2+1z61GVOX77I977wVb73xa+ye+UqdjIBXaIpPXkXlUIvuEE6zxaLtXUcTXtuy87XMv6yDCx0CfTLrjWmAWII5+v+PLQLsDR5dTiLjo7UcSnNfpYBjrZM1EX3nMV2Gb9vyG3hWQ1X6OqqJfy8XhuzAN66wMoC7b8PjXfFcouW9eNgH+37FsCOB7FddLytZOni3117qQtQtWWern7bCvy6X1spBAwWjXMX/tf/7t/y29/6Jj/9R/8A5y+c5969W4y3twHN2Ycf4FO/58dY3zqJ0ZrZbMb+/phCl1x5/31u396m1IpbN24wGU8o0ozJeIzVPh7fJ80p0zlHbT/0AGk0GlEUBXEc0+v1XOG5ovSRAfVBG41GAPT7fdI05969e9y8eZOVlRVOnTrF5uamL9hab4am+9oi43LXBJ/pIDyE75vCRHvjNwWlNiirmvVJGkSN2Bc2r3GCXtBalGXpLTMSg0QpyYULFynyki9/6asYbXn66WeI4jqBhfEFa8qy4OTJU5V74mF+z/XwDtdMBM1tr9fju995jfF43Fgzl9rcgSMnAJWlpsiLRp+LAoMjbp4gSnnAta49hoXvO8Z5PyH9k7ajAJXlrRbiK8AkhLOuCbfHilwvuBJ0Pf9oz1oygg6C3+6/6wwcBjYDSOi65rAxfr/vpiLiYZ3CUTGGvMhdwLilqimWeKHApZcOvdQ+1lprD6xiBsMhYCm1Jo6TqpCrEzx1Q1tpO8Fsl7CyDHAfZY7L7jsK+DyMCXd9bgLU9u9t2njYc4PlWyqFFM6FMZ07Rma0weJSf6+M+v4hzn0sCFzt/pqt3x9UMYjud+Mt9hG5nlOUvv6clI14jYMAz1rL6dOnuXXrFsPhQxWNDsK9tRZbFpQ64tlPPc2/+df/Hl1qsEGptEQBY51g1rX27eub/MGBSu8iZSEojkoLRmhfcsAL3wKE9JlXtXExrIBVijwrnAUKN/47N3cYj1/l3vYODz/6EBsnNogSRa8X8+I3vsmrL78OSF/FviArU2ddimOSXuJS5VtBUZb0ej3W1tcw1jKfzzx4clmqnGFWEicxUeRiH/Mso/AJP4QQ9XkNdEd48Hof8BCSCQWlpEtaJFiREUmvx3Q2ocgzhLBIFZHImDi2FHlKnk3RpsCONfN0zmQ8YW9vl5s3bvLss0/z3PNPc+r0MZfUJRPM5nOkmNPrR8z7PYb9EVGS8OO//xe4/NTTfOnf/yde/fJXYDqBwrh44epIBEoowKcoXlbUNbSjpFNuJisQHTSn3drCfZvOO77tYjBD6n3RYaVoPiPQhbqwrLvH0lWbKDz7oLJo2XibyoMuC5O1LCRZWuyvPuntrw7jSW0+3vT6abs2H9aWKaFCVuKupA7LxhG+r/lHmEx3a7/Xplwafu8CRF33wEHX7U/Ks6QQRFIwGo4Yra5x/cOrfPmLX+TU6VPs7e0wG+9jjSaSkhOnTrFx+gyPPvooL770EsPhkCRJeOKFT/GTW6eIeiMm+2Mm+2PKLOfWxze4e/s2MorQ1nlp7e7t8r99/j8caXw/9ADp9OnTCCG4c+cOpSfYcRxjS/fie72eLwjpKosrpRgOXQ2L/f19sizjgw8+YH9/nzNnzpL0HIOuhNWGBr4ZXBk2TdslqZm1JnzXTIEavmsSqtBf6NMx8yWuYNZWfvzBtbDa8Maxm5XRCpubm1x59wM++PADhsMRF85fcH6d1gWjS6EwaJKkz/r6OpFPKd1lOasfvaiN6votrIfzE495+5130LqsBEtjLFmaMR6PfY0SH4NEKB5YC0QLz/EE8UBwZ+v5P2jwc9TWBIefrHkGKpzwjrDe3cWlo3bCeFZffR/G8v20w4TlZZqyw8DRD6L9oPoXwrlulmXp6nrhCkAnPSekpfPUaXZ1Uxihuj6KIp/9zykT0nROHDk3H1tWD8G5PS0y5a71ut+8frfW9X6A9rDWVvTAQXeQw/quQFZIaeuXKC8Kp021BikkRWVBDtcEOskBWafZkiRiOBziUrbbCq8GBZIuQ2rd2rbXBF7h3Bpj2Nra4rVXX+fhhy67eSMrl0snl5SUZcG5s2c4c+YMV96/RhT1XV23Mq/6WxQyvLruCOsfzllbUFoQbvFFwoV0xbKdGce7NwlKU6cSli4JplO4SQHCZb+bTVPeeftd7u7c5fITl9k6vcXx4xucPnOab5evgJAIoegPEp7/9NNcvnyZz/zGZxFKMhwOnWukMZRlyXg6ccpF98aIorgqSSGlIlJOoRASMJAGd0Fn6UI2rcOiSmEe5t8W5poKSlcg3qVQzrMcI1xmLCEFaarIcl+c0rhUGEkPVGSZzyak2RxjDLfvFEz29tm+s8Nkf0ISx9y6tcYzzzzGB1c+5ne+8FWyfIyQJXGsiJMe/d6Q46e3OHvmNJf/i99LtNLnxd/8DHKvpFc4a4VUzrPDaCrLhYUFF/mOHVDty+Zc20JrUNI4eeOAYeTA/V1/L9L2xaQlTYCxjHYczPjmrVGN7HiLwnU3mGuD4C6FY5cCUrTuXVBKhyksaV3rsOy6prx2lNYEgGENwjqkadr5LrrG0Z5zkM+cAemTgZT2urbBd1uu+M/hF65T503iSLlzt0snU4arK6wmfSZ37lFMJqyvr2HygjPnzrCxvk5W5MRC8P7b75BPZ9y6fp3hcMjV998nGgw5fuYc6WzOxuoap45vUeRzIgXr6yucu3Ce8WTC5njtyMP8oQdIQkpWVleJk4RSl0RxzDxLUZGq02yrUPVbIVWEKA3D0YjRygp5njMej9nb2+PKBx9w6dKD9Pv9A5rRdr56aFiZgNK7PYRaR/jAe0cQXTCr9Ro/ISUC0apFIyoCI6VyKUS933zQ7LiaLhbtGbEjUI6wGeOIj6bkzOnTWG355tdfZDqZ8OSPPcFwpUdezP3G10jhqsCfOXOWOI4rN71Q4Pb7ehcNggARe3szrl+7CThNTEhXnmYz8mLOyZNbXLr0EK+//iaT/RlZofEJIV0/1noBICx4N0EM/66Ot7ULAZq/m61JfJqfuwBb5d7jPyGc24FzcRA+o5NE4OrNKCWIomYNp+UapjYDbf+2cG/VY03AhBCBrx1wE2rOsUvzZK0btWg+Q1AR8i4G2DWH9nodOpfGf0NzCgx8vRt3nQaQLoDTGkmWFlhbemuqJEsN1kh3pY+Itz6jjtY5K6t9+n1XwNT4+j2j0YB723vueVJirPZCfL2+YaxdAu4Pui17T+22TChYtnfagvoy9437aa0X+sE6NztbgtbkPkYoSnqkuUYLibElStRv1927ZN2ERQpLkvQoSuhhkUIjhEGJGK0NeVG6M2ZDX2EfL66hEILV1VX2x/tYa6sEO809Z61ClzAaDnjssUe58v5HhGQE7XexrB22F5prpY2zTlrj6aCtM3Uq4SxCoXB17doqkEoSm8i75+HcuoyPsZOWwloX32Us23f2+N70NS49+AA8cpFzp87y8MMP8fp334Skxyjpsbe/T241Fy8/yGw8IZ3OWFkZMs1Szl+4wKlzp5FSUOQF+/v73Ll9GyaON0vr6ZuVrgahKugJyNLUgTb/Zqt9i7tPC1O9X+PyYdE4YgvCd1AkSSl9jKFEKOEKvOc95umcItNEUuEMjYbVtYj5bMI8naKjgrLMmGdjtndvkmZjfs9P/F6m84IP3vuQ9WNr/NIv/THyYoaxBcY6d/Cd/Qm7k32298YUMmLlgQfJrl0j39lBOW0esZCuiLuAzJZoaX1R6rrYtPQ0y1oXzF6WxmXa9HKC84Rxtbis9WcI7zImD3K6BTAd3DrD+Q3W4LCQQuCwah0vBcLX2+qmDV1Z10IcnnuuIGg1rBFgZcVjmorlpkWjfRaaoQkWJwu4uEC375v7oGldqvrx54OwUo45LQCEpcCrdT7btHIZD2vHzDX763JFW6Y0ux84kVIuZLPU2vG9Jn8P/bTfURPsLUsQ06WcactaXevXbNbLFqFaizAWPcvY393DjnqI0rDWG7J14iTGam7fukWazpBScOvWbYyFQmvSrGA6zZjOUz71wvMo3Bn/rc9+nrXVVay2mFITqYitE8fRWjNu5By4X/uhB0hWuJicrHC+7BvHjqHiyLt49THGHDiIKoqQ1rnIBHCQJAm3bt3mxo0bXLp0aeEZ4WC3iXK12RCujo9wGjqn2QPrNTPCEwMhqH3q8Ro/GzZi7aIhhHSFrzw4qgUECcIQxXFFgFwqVYFLoyhIejHHj59gvDvhWy+9xHDU5/GnLiMiizKR17IaMm99OnHiRAX+ukDgfde/ceDCocvzAiUT3n/vbaaTOULIygVCa1dx/fTpLZ548gnOnj0L1vK1r71UMXOkqJlA87AuIVjQyAbj16XOBikWCMb30w677wD4sLbKBBji36p+mv8SgFAYaxFCAWXjCreGYIliSWVkaml4ms9vjucwgbW6RzRFTosIRQVqLHZgjvcV7r2AYw/xX+8azye9xp2E+vuFOVuLq1NkqxoYxnhyLRQgXXarfEa/t0FZOIbuUhQvMl5jS0YrPTY21nCZvgrm6ZSklzghVSlKo9E2bLblGrijauQOAzZHae1YswVhqSF8fz/jaf77MKbeZr71cy1WWoQv0qnLgiJLMbpEyAFpVqINqCA/epp4mCYY61yNjx/fYp4WDNctVmqwBimc9aIsSrQ2rp6Pf89ubI1u/JijKCJSEdPptKobtiBACEVRGIpC8+yzz/Kf/tNnMKZEqYgoduy2XQyyUonch44cONPWa18rWXYxEVEAFEb4WAwRjq/0dZdslV5dWO96ZwVIg/C11WQB6Tjj/TevsLe9zeVHH3TxIhhULBASRqMV8rIgNwWfev5ZKDQvvvQSST9m6+xJdvd2uHLlfXq9HqPRiAuXLqC15qOPPiLPUoSVWCN9+vUIhaYvepTKkGfFgsuRtYEWBZ7nrEoeRTlhXtSxvM01DRYlFSm0jh3AVQoZReRRQZEX6DJCiB5WFwyGK8RRTJrOKYqcvo3J92d879XvsD+b8yM//pPcuP4hJ7fWOXX2BFZY+v2YKBIgLEVmuH1vn9ffusIbH95kVyvkcAWdZaytDSmmM+wsR+U50kJivKCu/VyErOiN9hkcBaGEksDV/6NaC799a3dscRActQX7CoCG39q70gba6OUP3z9iuQDcpgOLipTalc61eo7Ng7wstXVz/1dZDLEufMDaCsgF0CEac27SPkNDadDqu+0h05W8Zpk1pUtRuIxGtr87ivLksHIe1ZyFWKzHGfo3DkiKpkW2gw8dWQm5RAHWBLnh+oMAy91jvLJSWZejQyrJznxGv5/QSzNSrSmtRUSKNE/9MwV5odEIkv6Qu9t73Nnd5zuvvF4V8R5P58S9AadOnXHPyUt296ZYa7l7d/vQ+TXbDz1Aarq+xXGMMaZys6sAkXe1CABH+gQK4cX3+31/uODOnbtcu3aNEydOOGbpNVNtIWPRHU5VY4FauxWuC/cc5n7V/l36lLFdlZZNkVcETSmFKyTqCiNeeuASEsEr3/su4/E+Dz38IFtbJ0AaIqkoy5rIrK2tsbIyQilZMZf7tWWaleZBzLIUpYa89tprFKWrYxFc40J81oWLF4gixb1791B+nXXpajw5ot0ksgcJxuHCXYeU/wNuXQJi+L7p+ti8VjT+GxhWMJlLWfvgCyDPMx/zErsAbLv8mc0xfVIB+JO0LjAYPi+MpNJy+jfR0j79rrYKJFNZEcuyDorVpSbPcw+IBFmeU5YlUbwIHsKf0WjF0QAfPC6lZHNzk3feueqUF/eJvwlzP2pyha77my69zda1podZJz5p6wJWy65rjqNL2G8K/Qin0S6KgjRNKwVWcIeSDaOpED5QWnU/P8z31Kkt3r96C61XiWxNR5VS5D6+sUvT3v636+sUd+7c4fz58wfmIoCiKNFGc/nRhzlxYpN7d/eIosTtkU/Y2mvXVMZ1nZtqPRvfOftntyAbBORwbxtwhmdlmeXmjZtMpvvs7zlwGMcxW1tbPPXUk9hI0O/1uPLhBzxw4SI/9/t/ka9+7Wt8ePUqTz75OGk6ZzKZAHDt2jV6vR4PPfQg89mYqx9d84Kp8lbmCJRECueEY/PcDcm7xtmgsLEC4QtNBuVXkL2W0ZMgAAfXuxDzUQ5LdGGc1Wg+ocwtCpf4IkkS5rMZushRQjKfz7i3fY8vfem3saXmnbdKHnrwNxkMBpw4cZw4jnySkTk379zjzXc/5OPrNzCzKf1sTlQYfulP/gmSSPKNz/82k2s3iPbnDGYFUa7JowItDNr6QrMITBBqTXf2PikkdawzQHCL80mbWkqpGti7HRLIoq0UbcGCtagsEMIlyhAsp1eHKU0OpT2NPX2YIm+Bj/mC9W26Fj6HxFdt67ZlEQwuE/bD847S2nSwzS/az1o2t2Z81lFdldvXLgOpojHr9hlpyqKHPSu0pmzdRZPa2Vebz5JCVMWswVedky5Zii2d/Oq8iXKkivHJS52hQQqipOeUOJFTNispFsaytrbKdDpFKcXKaIVslmILTV4Uh+zcg+2HHiBFKloAIO1/h/TaVW0jsWjuFEJUliQXixMzmUy4fv06p0+fru49dMPrEiEO1r9ob+qDwW61Hjwc9ioblBeWw28LmVRUhHMB0p4wuAt7SY+TJ06STlO+/tVvgIUnnnyCNE9RsSD21ihnxSodcIKF5AzLhKFlWp7F+dSVs/f2tvn444+refUHA0pdMp1OvcDp1ihNU8bjsc+eF9xI8HNfdME4rFWH1dqgc2wM7CCYO2wOzd/ahKhrDbqY9IGK34tXVL+pBlgXog66Ln0WwDhUl68Y2eIe+yTtqNcvm1eXxqi+pnvPWJatQfeY7nete8ccqI9QMQkPrIMg5WiAO1dxHFOUhU9qosBayqLAaAOJrATHsI/dPRH9/qB6T9PpFClj8K4NlvtrWttAoy0gHHbvwtzE8oQI4fogRN1vjT/JXugKGj+sBYEFFuuw+B4JYru1rph0oK/GVY2Gyr3Yx0XcZ09IqVhdXWV39y22zm4SMoi5GLKYsqytFKJCX92aUmstJ0+d5L133+fixYsLngPuejeXIk9ZW1/jwsVz3Lp1F1kmmIYlpLnG1X/twf3dBkFNQNn1Hut9LjjwNqwlWDIDLXEWKFH9XHo37a5SFNpqdnfGGAOnz5zj0gMXwJZcufI+aZFiJYxWV5llcyY3p/zUz/wUr776Km+8/jqPPvooV69eZTKZUJalz1I64+LF0zzzzFO89ca75KlLLBGKgQspSZIEY02V2WuhMKR1roHalD5e1b2H/mhQKUDvF0AeeLuONPRg2E9I0z77e3vM51OU7AGG0UiSjscYr0DJ8xSZxmTzjMn+hP/9f/9PHDu2ydaJU8RxQppmTMa77M8m3N0bk+U5EYbVWDGKEl5+7Q3+8q/8dzzw9JN87TOf58Nvfhd9/R5iMgNVOg8Rr/G3QqCFxFpDsmBxaZ59ifSJS0JMnNNnWuc2pw66erudQHV+6vO7/DxV/N92X9PFD7u+O6AYgSo1dfO7ZkbgZe8wvGchRBV71Rxr81xUQMnYzmkeRYHUfF4XjWh/bspM7TEt63/Z2jXpZvP3Jvhsr214ZjNDZNfzmkCpTV/afTWf3czGDByoxQeLngsiMN+Gntoa5xCc5xlREoOSjGcz3n3/CtYa1tZXGY36LrREg9Wa8XTGZDYnSwuSpIegPs+F0AghuXPnNuvr6yS9HuvnzlGWJds7O0vfbbt9cpXWJ2x/+2//bYQQ/Mqv/Er1nbWWX/u1X+Ps2bMMBgN+5md+htdee23hvizL+O//+/+eEydOMBqN+GN/7I9x7dq1T/x8IRY3ZdNUHxhAE6wIFpFvk4FLKVlZWWFra4skSbh7965/xkFf+vB9l9DYJQy1N3dTA9IEKNU1DXAEi24bwdpQud/5e06dOkUkIj58/0OuXPmA02fOcPLUFmmRkuYpmdfWGqOJo5iNjWN+4y8Sp65D0m5d83LpU11Cgffee4/ZbOZT0tYHLM9zV2/JE7p0nrK7u1sFa4sFoCYXAkGbz2kf6IX38ol30dFa+x02v6+efYgwJyrRsPV9ICiN/rQ2GG2IE6eZbgL/ZZkGDwNzzfEftTX3d9f9h83VXwCw8L66zsKR+6N2pVx2JpvytLX1OQuZHq11SRrm6dztSet1jUuYbr/fp5ck9PvOXTdNM1ZGI39mRaXdXnZe2mDosGvut75d4Kh9PkJ/7XXtWts2k172Ptp09SjvqQI9DdrqsrItPn82m1HkBQBplnoLw2IBRdGghe2MnuGa48ePM5/PK71xSAKQJK5AsHMvqzOIda1FWN/19XV2d3erZzTX3frPRZlhTMEzzzxJ5EsjKJ/optmntW5v2QaNbb/jplAU+NRh1vwm76gUf4FnLLxLUY25cj/z3hThWeF+54oOWguwir3dfa5f/5i7d+/y7jvv8N4773Dz+sdsbZ1gZX2VeJDw3odXePSJx3nwoYf49re/zenTpzlz5gz9ft+X2xhy+/ZtjDE8/dTTKBlRFIbpJCPPDXGvh4wj4n4foVzcbWkNuS6Z5zPSfEZWzhis9Hjy6cf51PPPIJSzCDfXouucNIXNkIkQ76rV7w/Z2jrJ8c0tkriPQKFkzNBnunX7curcwcuCrMi4dv0a7733Hi+9/C1efOlbfO+V13jrnff48Oo1tne2mczGTNIZ9yb7jIucD9/9gLs377F19jx/5L/6M/zS//XPcOyFJ5if2WDWT8jiGJMkIJ11WoGPO1oucEsZoVTkaY/y79fFIS87k46f1nW6QlH2NikJchS2PjtN8HwoX2vR+aYA3ryvmfAqfN+MNWr21UXPus598xltJW9z7dr3NMd+FHmnee1BMHBQBg0gq2s87Xk259ZM6NCWaRfoUOOdNBXrQhy0SB3Ga9vjF0IcKPXSpSBr0vTwJ9znn7ywB0J/ReFqlyElmdbk2lBawe17O+zsz5ikBZN5zs7ehCx32ahHKyP6vR5xHDVCYmLiOCb1CZh6/T69wZDR6hrHt7aWvsN2+121IL344ov8z//z/8yzzz678P3f/bt/l7/39/4e//Sf/lMeffRR/ubf/Jv84i/+Im+99Rarq6sA/Mqv/Ar//t//e37913+d48eP86u/+qv8kT/yR3j55Zc/USyM1oYodoejKBzhbG+08LlLmGh+r5TLoqaUot/vs7+/X6UQbx/2EMArhBd7W8KEEKJRn2hR6AqgSIm6xkgYTwBLVi5qx5pEpX2AAli6cP4CZaF58ZsvURYlDz/8MDu72/TXekgRYYwgm2eA4OTJU57oOkHvfkJcmFvz9+bnMLcsy5BS8uqrrzCbzUDURFCXzqoyHA4Y9PuECuyz6czNISSzCMSH2nrU9byjCGo/iNZ8d11ELhDDLmZ9YJy2/n4BvDcYVLi+KAt6vf4Boav9jPutQxfzWXZPEDDb6921Jq0bGz/i4whsdS7aY2n2s0xA73xO8xmtmB/hhSCsd0Op1tddkyQJaTplPptXcWK6dJZYIaOq7lgYR1mW9PsDkp6/1tbZ7apxdSHexly7mHrXGixb66MIJp/k9+Z4lrn8djHvrnHfrx283tNL785sjCFLU/LCJZ0pi7JhcTx871VjdA9ifX2dsiwaMRfu/jiOGJeaLM8YDXoVEG7Osz3eXtIDoCiKBWHBXeRpsC0pypRnP/UU/UGP2aQgVtESd0jhaB1HO4PtuXaOV1C59OkGXXJOU4t1ygIwlEISSwVSVBabZqkIhCBOEkLmvrt373H+3EniOObMmS16w75LftBTJNEAqwQ3bl7n2OoxfvRHf5QvfOELnDx5kkceeYQ0Tdkf71MWkrt37vH4Y+e4c2eb7TtOGTYc9Nk4sc7a2hpIgTY9irL0RR4tItKsr6/z+OOPs7KyAgIm4wmbJ4+xtz1e0GYHTwpjTMWXgwW+AkuIuqCuMWAsSsWMRmtk2ZyimGF8muCiLJnNJiSDIQZNaTOm2R65Tj2/jMCCNhZtDUa69bWRQqmI0pbM5jPefvNtjp3aQiaKJ37vpzl/+RLf/OKXeOWLX2F2+x56MiO2BVJr527Y2vaL77upRAtCuvH/VlhbLuFPDkC5/WtxrnhBaAXnZlfHP7vNSZ1kx7fDFDdHpQ+f5LrqT+u3sGeD3AQN+aLxOdCQBbbUcfaa8loXnw+8vTmmAzShMbYuwLYMpDR/C+Nrjqudlrt5fVuOPWwtuwBo8/euZzSvXQYsu56/sH7NtbFOOZGXJZGA/nBUfSelwqYp87T0SnIP5pFI5WTvfuxqlyJr67OLGRXs7u5yfHPLnwPL8RMnDl2TZvtdA0iTyYQ//+f/PP/4H/9j/ubf/JvV99Za/sE/+Af89b/+1/nlX/5lAP7ZP/tnnDp1in/5L/8lf/Ev/kX29vb4J//kn/DP//k/5xd+4RcA+Bf/4l9w4cIFfuu3fovf//t//5HH4bL7uAKO0+mUPM8rQBNalyDQJdA6TUwdzzQYDKo5LaJjqmxv1rqg46aLXROIdTHBcOiUci851HIAKt9pVP19sx/hHuAzbQWCA6dOnUJJxd2b93j1ldfY3NxkMBxw685t2DGsrA7ZHG3Q7w0oipJTp04hPK5TajHO6jCAugwkCQ9siqJgZ2eXjz++4YVJRRLHvhpyhlIRg8GQwWBAlrmq9ZPpBGO0cwhpCdrNZ3aBJFqXV+v9yWS5Q1tzXbrM02Fs4dqjAbfAoML9XhOI8VZOl7Z2OBgd0Hp/P+DQgeHFWLruCyG4pjUVC6GPIzcPYMJe/91sC3tyweWtZnRaa5SPR7A4IN9PSiSyKiTafIdhrZIkZnV1ldFoxJ17e2jtkmm4NdFtZ84jjfV+QcFHbYvn7wcfc/b9tiZDPTBPKVGN/ZRlma9bB6Uuce9MYheSlnQ/w1oL1sWUrqy4ehnNvaa1RvmzUxZBYHbJb9p9Nxm+tYb19XXu3r3LyZMnO9bVuTWVZc7p0yc5e/Y0b7/5Eaia9i/seeH/Y7//WLQwxupv70JkjCvSKiMn2Ici4qGWkFM8Cc+f3LMjpVBSos1iAiO3ZtbRIK9kSNM5Kyt9tk6cYG+yT1GWSGtQsaIv+0RKMZmM6cUJf+gP/UE++9nf4nOf+xxnzpzh5MmTrK8doywM/+r/+W+4df0eRgsEkpnJQe2xsrLCxsYG29vbDIcDTp48xcraiKjvrOcbG+soJRkOhuxNdtg4sc69O7vExlQxRs4lLq+8I6ylAk2VAsqvvxTOiql9rcQoSogiRZ5JCgF5klBqjdYleZ4SxRIhS4zNKI12/MkXlC5LZ4FGuj0ltEsBHkUjGETc3LlNXmRILaAXMzq+wc/9iT/Cw5ef4PP/5j9w7533EPv7RHmKNTnWGDSyZl2BhoJPVhT2rC8bIkLCp9odVQin6HVeIcGdNbiV2opPiypBRG1pdBZe/xxbxyfBQVDR3DNHpTttwX4ZzQvvLViyhOz2Ymhe1wQ4lVfQIdbiJvhpJ/xoW6nbc20rqMM9TVAVeEib1h91rYRY7p3Unsthrcso0BxPFz1quheWZVnF4bfvXfb+umQwpXwZAGMoipIoeF/4zNJJr49AYEyJiARJr0dZFC7DI/hsvo35+DqgIX7eGkuhnauu/QSOc79rAOkv/+W/zB/+w3+YX/iFX1gASFeuXOHmzZv80i/9UvVdr9fjp3/6p/nqV7/KX/yLf5GXX36ZoigWrjl79ixPP/00X/3qVzsBUpZllfsWwP7+PlBbcgJIms1mrKysIKQiZE9zAWOq2rTCWsB4Yto0m4ZC74LhcMh4PCZNU3q9nic8teYggAhrLRhXi6AOTLcVMQ6Cb9CGhPSM1tpKUGimvARXTCyOY2baVy4nbFj/PCGCd7nfVJozJ8+BFnz7W99id2+bF154AW2LCmlP9+cU4wIVJWxuHCeOh0RxH4RAqppYNOd1Xw21czjB4uIeSl1gEbz9zvuMZ3Osz1+qVEyRZYz3J0jlYjr6/QGzWcpskmJNIGwlEtWwOjhG3x5Llzbl0HEeQsiXaca6tOj1Pum2dBzKRHAZXUIGVPe71+4KFy9ghPXZjJwgmecZcRyhlCC3umKCrusw1uUEs2s+TQIu/HPa1p/QT5sot7Vr1TPx8yK4FFG/wzaIbQHJ7wfo3e974YUJawVxHIRmiYpihFIUWU4/ToiEO/PaGrdXnbztzoLWWK2RQBwLkkSiREQ+LxgNErA5kc9CKN3BXoiLsq01bK5/0No3v2/Ooc0cw3fh2uCHXxTFQr/3OwvLfu9SOjSFkOa9yzSRy5huoLnh305wkwirsFqiC4PVGmGdW2lZamzSxBRBgFvcL03BBgy9SNGPILKCyESEKJ0ojhAS8iJ3tL5yN6ICDO29LoXi1KlT3Lp1i9OnT7dctR2tR0ZobRn0JY9cfph33rqBtiBUXR9LCKfwOagHP/jel7235p3V/jIW66uMWGFdmnnt/jau6I7XWJWe1wmEdvwQXYI0JHHMgw89ytWPPmJvbx9dGqQUGFtW1lJrLbt7hrLs8+1X9rj00CXu3LrDpj7OysoKSZxAL6YUirzI2Rvv8Af+0C/y2c98nrffeJd7N3exaD788COsBluCsQKpIkoLWeqsQo899ihFmfH8p5/jgUsXSHox83SMMZrTZ8543mk5e/4077/zATc+uOWFT01ZFpRlTllqd2Z9yv3gSoZ/50EZKKzL+lWYgmw+ZzQccvbsWcbjCeO9CK0N01mKsJYindHvrWEtGO1Srgda7Qi6ctlSPei2RkMc0R8krKwNEQKXxU+67K29fo8kibn8qUfZOPZn+faXvsHrX3uR7ONbxLMpqizITUkuLDmaKI4RpUFpXIayWNT01FLFlvn8YARrkPHmH+GFUiHC9QEwBvIsECKqzrWTQZylTTb2Y5Me+S8qK60bTpB7wu9+m+JAfPi+rczp+txMqFXxioUQgPCg8C4OgreKx4XVkYsuiFV2vFb80zIQ0f7cRaeb1zRBU7PfJg3t8ggK/zZmsdxK0wW3Ceza/YT1CWvSBlhN3g+1EiEoELvWqj2/Np1fxsOdnArBicQIVwrHWoFNcyIEBRYVK6IkRmiJLkpHu5XLeClEBMJWmSilVMSxyyA7NylSuv1SFBlRrJBKUswLr2g7WvtdAUi//uu/zre+9S1efPHFA7/dvHkTcBaNZjt16hQffvhhdU2SJBw7duzANeH+dvvbf/tv8zf+xt848H0TtQ8GA6bTqXvxOI2Z+y1sMF0JlzW6d58D3Wki5SRJ2N7eZjAYsLGxUbnlNDem1hoBRJHCGLdxQ6CpbGweIZwwLIWsNBvNvkJwddOXU4igdbQLvvXGB2sKK7DGcmx9k5XhGjvb27z04ov0+z3OnjvNdD6tgvyVitBliUJy/sIllEpQKnKb1xhEtDzLXhcxcz/gNU0GY5220SJ5/Y13XNp1a1FCoqIIPZsxnc6ZzeY89fRT3Lp1h/k85fbtexgTiLMrYhuoqqV2kTiSQP0Jhe0wn6Ned78x3K8vw+JaGq3p911h4ixPqzS9oWVZhjaaKFII2SQ4y5+/DLx1fg5gpvmbU1suve8wQS78CX039/6y8R72ufM5YR8eep+o/9jFLHLau95YbcizjCTpuc+t25wW1hBFitGwz8rKwCtVneAdx4oiByUE+GKcQhxYzoXxdTGp8PsyYNvVAjBqM/dPCja7WlcGrWZrCwrLBIrm9Qv3CKf5VjJCWIkuNHmaOVptBbossVaxaEru1uRCUDgZkiTixLE1KDVWu3iO0IdsuJSFPdG0krbHa63l5MmTvPvuuwvuKe55Fqsl1kBZOJr17DNP85nf+Jqrw6fcRhDC6/5lA3x1rNuhTbQ/eoHK+gxo1ruRa19RRwoH0AArBb1ezGhlwNmzZ9kfz7h+7RZSCo6tj5BKIaRzdwbB/nhMkRcof160cMkAekmfiw88xK27t3nvg+sYY9g8dowHH3yQ7Z0d0nTOs88+yWA4QGPY2d/nZ37u5/h69E3efPUdxxNKV8XIgQiDlJrRaAVrNGVRcOLEJqVO+fjGR1y8dAapIkCwvb3LyVOnnRJPKgZDxSOPPsqr336bGzduonwMoYoTkBptSozxtQGtpSw0VnuLGpJYRTz88EPcuHGN8WSHvJiTbo/Zn+wgpXLWRiURymXNKouCMi+QBtAhRkS7LWQsDvV5tqMEQikipVhfX+X01hYCl4RIRcq9K9w7K5Rm/fwWP/lf/gGeeOFTfOn/9R+5+fob6L0x0TxFlzmxV9haAUReDqCscidYQFu3I5SQlSwglNubTmnlFQvechSOYX0eRSdt0hXoOUifrfVKvIW+Ap1vKjQa+52D9GkZzeuyaCxctzDmxeva3h2H0ao2HV5GB5pAo/l9l8Kxa9yBRjfXOYRRhMQj7Wct45vN75v9LioruxWSbbrZvrcLCDXHHd5LlwtxW8Em/GazXiEB7t9G4PZxUSKsU/SVxmDKwllPdenCMLSTf7MsoygKkiRx2epWVlhb3/DhNGU1rv39fc6fewCEcxEuvfHkKO0HDpA++ugj/of/4X/gM5/5TCXcdbX2yz0KAz/smr/21/4a/+P/+D9Wn/f397lw4cLCizTGVCm7w+dm321Bu/mym78HN7eNjQ16vR55njOdThFCVP23XeOam7tLo9EeRxeBqOKPrHM96RI+3L+N84UWktIYzp07h7WW969c4aNr13jwoQeJ4hiZK4z1LhS4zR3HMefPn3drICVSNTT/rfHdvzlTvQRKrTEGbt+6zbVr18jSDKVi+v0e1rrA+CiKSOdzdnZ2OXnqJF/96tfBulpOWnvhpbUfutYq/BbW437CRvvdH6W11/5IAk3HfY1f3P8b67yQXbHlzgCQ+5g6B8x9seDKbeL7b9XeD1ms3LdHvveoa9HVut7bJwap7lMnkBPU2lG8dRWLP6ui8lXXXlliCYCjzg6FdVqrML7+oE+/16/GHycxSRyTCldTTEhvCUR0Wgvac2+O+SgAp71WTeZ4lHdxvzX/foBqk4l2CfxdNC8kyanos6cLk+nEazOjql5cOCsWg7XyEOWHcPE1RnDq1En2pnP6Ptg+rFUv6blUz1pjrEE2XI6WtcFg4ITBVlZAa4Mg6FLSFmXJQw9fYmNjlTt3twGfNU7KBc33Yet7v0xs7RYAvw41YaR0riZxRK/fp9AaLaA/6vPAIw9w4dJF8tKQHFvn4w+vkhYlZ0+c5OatO2xv7+AsLRKlYqwFbYNTlmEyzfjww+toLGP/nvb3Zty5s+vS5StJmmf8vp/9KZSw9BNBUVqeePppvvedNzAFSCJKXSAVJL2IC+fOsnlsk5s3b1IWGadPnqTXU3z2t36Ts2dPc+r0KTJTcv6BS5S4chdY5zUxHk/JspLpZI4xrqTH6uoKKyur9EZ9tHKWnDzLiIRw53Q2Y3d7l+l4QtRT/PFf/qOsrazyzttvURQ5K2tDxuM99nb3mOyN+c3f+E0Qkiwv6BV5JUuIsMctWGvACA8jLBKFtU6hsnFsnWMnTvji9ZrSaEpjUNoB26SnyFWJ7CnssRF/+P/25/nOl7/Gtz7/25hr91DzFPIMazTaQhGBthpldHCUw+D4N8KBSambLp1iwQK7jEZ08fxKNvIAv1spFqxQB/dpF11ZBkKa4ziMzy49D9YpjtvuX8LPf0HFYhdlnObz2jJhe2xHGsshTQix4CHUtpK1XQWDK3+4ty27dMlFn2Rc7T2xrO+jzAuW1JFCHKCu7hxpyiwjTVOS1RXyPGP79g55nlOkGVmakfissXme+zgjB2OOH3eW65BvoGnBmk4nKOUSgCXJ0WHPDxwgvfzyy9y+fZtPf/rT1Xdaa37nd36Hf/SP/hFvvfUW4KxEZ86cqa65fft2ZVU6ffo0eZ6zs7OzYEW6ffs2P/ETP9H53F6v54K0Wi0wsUpDrDXGWiIhFgBLGzF3aQHC/eG3EMsUxzGz2YzpdFox+vByytKlIA3gJo7jlply0V2mnbWlvVG1dmlGu8YX5ujcBt0zhsMB6+vrpOmcr3/96wgheOzxxxhPJ3jnZcAV6JJCsHVii14vqVJtSylRso6vaptYD2vBPdGlHHcA58UXX2I6nTntCC5RRZrOmc9TD/rgS7/zJYSUDAYD4jjBWqdVNrahtfJjr8zLrXVq7wERpJaOsR8mRLaF1k8KhJr33u/aSvvXeLfOehFAT0ND5AmE1t6CFMYWQFJrb9Q1Mu4/h+o6AqAQC9xkGdFt+3pXY2j8p72fl63PJwVai1qyxbZ4ttvvs97TUaRA4N2QXL2uXi8UA8XtHz8mo011DkejEaOVESBYW1tj0B8QJwnGTv383Rlog4ajtvutU7s1fcTbfRy2D7vWvE0Tm1k1D9PmtoWr9rPboKz63Mj8h9cazmdz58IUR97FNLgxuZPhO1rou3qWf3fWQr8/5INrN9g8caICJ9a6wuDpfO5pO1XfiO4kGuCEmF6vx2QyqRILOcFQ4+CDU1hkWcb6+hrnz5/k9p3bQOKSUPiC3KGgY9fafD+tyjjnhWUVRag4xgqLVAqpFGiNkBIjDJsnj1NKg03g0mMP0B/EXHvvCmlZopKEotRg/L41LvEAWKx0lrfZdE6aZq56qXQ8xGjDuJwipCSK4NbNO9y5dZcTJ13RcW0Nn/nN32Q+mxKbBCHcOC0lFy6e49TxY0QqYjhImEwyVgYxkdqkyHKuvPMujz/2OKVS3Lx5k4sXLqCUA8jXr17l1//l/8bt63fR2sVqxnHM3u4Og8GA9RObnLp0nhObJ0FYdJ4x2d+lN1zlzIVT5GnOeH/MF778O6ytjPhTf/JP8sDFSyAy9ifbjPcmzKZzXnntFW5cuwEStC6dqFe9d7+vTJ38xb0Xt0X7/R5bW1usjFZQcQwItDEunsJnUsTExIlAxJISw04+4yf+6B/g/KOX+eZ//BxXvvsq5d0dojxHAaV21lWFQRjnpiiQWAyEWlJBtggKCwCf6KkZitOmD23huPLYoI6RXTgfIiSFOJzOt3lE87cuhU0Yf7u/Zf2HOXbRXOsuoEuJ1jXX5vcHLMaNeSyjn+1xNoFm+D6Anuaf0G+g503FV1N52uXW3zYCNOce5IPmmnT1sWwNwjq059T8vt0qBVjzuUtksaIsyfMc8ozJdMLde/fQRYEtHX3OipIkSYjjuLIeWesynu7u7jIcDqtnhPG9/c7blIXl2OaxT0Rff+AA6ed//ud55ZVXFr77b/6b/4bHH3+cv/pX/yoPPfQQp0+f5rOf/SzPP/88AHme89u//dv8nb/zdwD49Kc/TRzHfPazn+VP/+k/DcCNGzd49dVX+bt/9+9+ovE0AzErTaVY3Axdm6Sd5a6pPQibJiDX4PJWaZ87Nm4ze05Ip+qy2FmsLSvg1G5hQzXTr4bvI582NhQeDddpDL2khyLizKkzWAs3btzkrbffYuP4MeJej7TMEcLWGElKhDU8+NCDVXYuJwgtEo8un9r7NWsFaZozm8556613sMYJK7WWA4oirwInpVVEcVyBI1dPRoAVVUCm0wy5AqlNDUXX5l8WF1TNAypi2rX+B4S41ndhXbqCN4+6Tl1CffNXV0RNobVjwkq6cwMOoDcJYNPiI2VNTNvjb7YmQV7YZz67lQuIbSxWR2v3uzCHBsA+CkBojqXrOYe/z+VMPgDIuh9RubQ6QdqS597dymhXob0R9yWVcoJHA4QkSUKv10NKwf7+PtPplJWVFbbvpT41ss9+5y2qB9amY/3aTLjrnS1bt+bfRwXER923y4SULsHqsH7a9y4wX+tcGkOMZpqlFGVJX/a9i53xrp5BSFtcn4XniRqcnjl7hu++9nqldAgMO4ljJuMxuixrJYpYvnYWd15OnjzJvXv3WF1dpQLRQUC2TpNflgVCWp751BN857uv1bRKCD/ug1rq9vrdz62x/Vt1jZRESeJ89v2aOouFK6xrjXaJBkpJ3O8jLZw/d5r1/oC9nT2kNUgswjoFjTElKhx+40FkSGjhXdeEdH+QznVdWJdy+tq7VzixsUaUxHztS1/izrWr9IjA5KCcckJEkvlsn0kiePThhynSGeO9e0RSEUnJqNenpxLu3rzNsbOnuHXzBlubm8SjFbJ5yr/6X3+da1c+QNnYn3PIiwwElOmUNB2zv3+P+YXzPPbEYwzWR2weW+Xezl329vc4fmyTza0N9+604bNf/AJKSi5dPMOzzzzGcDAgkhFPP/0UV6986HhvniFw1uWQuygkSHJkw2UodLxZMFrps7GxRn84ZGVlDStcDG54LxQlUQlSg9CGY2urvPH6G6yvbHDxicc4/sA5vvflb/C9z32J8QfXMfszImOwJkcYgRSOL5aFdorNsIdCxlxvUdUhdpcWfew4l920pOY04Teqb0TlddIGEM3rlwGbw37vasvGXlP6RRlGCAfmjVg8M+G3wAu7stE1+eQyftc1nuYZD61p2WrLEW0625RxmgqwLutY85kHaJi11Ws7bK3b8k277+bz7/ceF5KhBJAE3lWzMRbhFAt57lznImPYWF+n0KWTca3j7VGc0Ov3iaKIwWBQvaeQMKJtYYvjmCwrmKcT5B4ue/IR2w8cIK2urvL0008vfDcajTh+/Hj1/a/8yq/wt/7W3+Ly5ctcvnyZv/W3/hbD4ZA/9+f+HODqTPy3/+1/y6/+6q9y/PhxNjc3+Z/+p/+JZ555pspqd9TWBCxFUXizvyJJ+hXAaSYfaGtfw4FpWmegRtdhAzQz2oWN0AzebaeCNMaQpilCOOBTFEV1KMG5cLTH0kyQEFz4umJwEpU4ZE3E+sYGxmhefvllppMpzz73LNPZlLIsUHHk/EClRCrJIOlxzNc+qpto0sFDiekBLYaQXuMrKUvDtWvXmYwnSKXQxjAaDSmKgslk4nyxPXA0WjMYDLwmyvl6V77c1lZakECEa43QwTGFMbd+OfD5KFiv2V/Xv9vXHdZH52/ugvuMgYqxhb0dx0k9lgWmVV/T9nUOY2lriJp7VwrBcDRyxVJzrxmy3USweX+7WfBFPrsJeXt9mpqvhX7souarCzTcTxgPNodwWbh+Pp9z4sQJ4ijGWpdyXknhhZ/AFBceBP63ldEKq6trKKXI8ow8z0ni+IBr5LL5NucW/n2/65trcr95H1WRcb97F0BMgwF1jWcZAGx/7hqbUq5Ib/AKsA65Imi4ogSMQb1mi3hc1N9ZEBK2TmzWMWa2VopFcQw4JVY4K20gvTBuaoD0xhtv8NBDD9UJMSoFggNARZGjTcETTzxKkkTkmbPAGbsoQIQ1XRAiDlnLZS3wOmtBRQqhXEyrEgptLaVxiRqEgUgoNkZDdra32RvvMxyt0E8GJJGiyKbMx7tEtvQHGHrCuDgX6yxl1jjwhAFrfYIYD5CsEBghKKVE5oqb773P1VGfosh45etfx8wLl4hDgJQJf/SP/zLj2YTf+eIXmGzfYefmDRCK6WTM3s42O7u7zGczyjznu9/+Nj996uexZc5k5x6rccSXPv9bvPf6az4ZhfLvye8BLKWQ5BNFvnePYvceH7//Ds//2I/yyBOPsX5sg7zMuHX7BqUsOba+ibCCIi945613+PxvfQbyjNOnTvPE448xTHoIDNIGC4wHBBWo9nWnbAAK3p1IWDY21llfX2M4GqGimPFkymh1FStcjFBRGubSoIuSGE1sJBfOneeN19/kuRdeIBn1+T2/9NM88uijfOsLX+HNF7/L7N6+S+CQ7WONRhiDjAy6LBHWECm54A6n8bHOyrlRC3GQhzX3XhusCyFqd0Jaip1WH13uVaGf5nUHZIfGmWi6nzV/a8pTzdZU8oUkR83EN5XM0Bgj1K5t4UweBhrb3zWfG/4d5MYw3qbr3LIkO+H6wIObsT1d4KftfheubfP06rN3925f15xH8xld8+zq+zAQ1QUifQ+L6+q/LQoHiPoW4iTh7Nmzzi3Z+MRDMqoy5w0GAwpfTDxJkmodA98IY9jYWKffH+Cw8dH54e9qHaRl7a/8lb/CfD7nL/2lv8TOzg4//uM/zmc+85mGqwL8/b//94miiD/9p/808/mcn//5n+ef/tN/+olqIEFtCQqpPkOab6XiaiOG65r3hNYllLWRc/MQNL9vjrV5OJva/ChymXECSArjDQF6IfFDePHN57QJBzimKLEUecHasXXnYnBvjxdffJHhcMipU6fY3dtxQbs+gYL0sRfnL13AWksUxVUyCKUOpkFvC6ddRAqozPnaOMHjrbfeJggOzt0wIc8LxuMxZamRUtFLeiTSof48KynLhiDmtYLYAI8Wn/39CYKVjmnhPd2vNQnZMrPy0ie2CMwy7c/y+90hL8sSozWxF/DqPsOFi9qgoLkJnSxbt2o/W2e2Vo3ict5xYSkYao6j+jeOMDefvTCf1po0BcWDc7ftL5oPrTvs2gqNM+jWpa3pWrTKirhWcHRtrfBbv99jZWVEkvSwxrqaOqMRcRSjddG6qV6TGtiL1udDWmDuC3qL5h5uDvTgOnc10f7Q1OzVTmzh8TVIbwoEHHyPB59Yj7NJz6q9IqhKlw9HI9ZHI6TEu+O6VmfSwudpM67YtKiT7SycIw9SrbWMRisYa71bVH3+HD9QlcJpWWsLimtra8zn8+rzwb3p/srzjLPnTrO1dYKPr90mUhFGFNA4S00X2Obz3Dlofke9R0RzTcP2D/d4XqDcuXOpbrUDS1KggFgIdm7fQQrD2WPHuHXzFpPSUBqYz2bk8ymxMEwmY//iDcYWLhueNRhT+jlbQCKFrFy7ER58qogcRba/y7cnO9y9e5vZeEIkXFFY25P87M/9Ii98+ml6oyEPXjrHv/2X/xs3b9wA4YKq79y+xfWPP2Z3e5sbvR69YZ/t27c4u3WC8c42fSH49je/QTmfu6xx+HILwT3ZgzVtDKU1zLbv0Vtb5UvjMbfv3OH3/L7fx/HjJzh2Yp1bN2+ys7fDubPn6ZeWp555mrvXbvD6t77LtSsf861vvszKcABliYpj5xESRQhrUUK4NOrWYq3Bepc75+LmErtsbm462hAnCCH59ne+y/PPv0DS74GQWCxTU5JrQyygj6LX71May+2btzhzcgOiiK0Hz/OzZ3+ZM08/yZd+4wtcf/cKBTlnTp3k3KkTvPXK97BFhrIaaQVKK6RP7Q6+rpV0rngSGvTQW8Cq7w5al4XAafMFlSWXBh3QWJRUDjhaZzVfBAa2cX3g68vdTF3GvCUW9DCGamxecRUARAu0LIArOty+OlwHFx53ACTI6unN+NKary8q++r7O6bSAXiC98eB+bUU9l3Kqy65bJlisfl7V2vf0x5H+/5lwGnhuS2FlsDJwyJ3rslrODf30lqvpHWeVqU27Ozs0Ov1eOihhxbWoHaXjyrLUlEURKpW2Id6qEdp/x8BSF/84hcXPgsh+LVf+zV+7dd+bek9/X6ff/gP/yH/8B/+w/+sZ1c+2V4zGOKUpADrs/w4BtUEPfWhartvHRA4W0JXmF/Txc5aqniloigJsTlR5DKyBUAUhO1gIgwazYCQwVnooihCWFBSVRKLNc6XPpYR2rgaDsfWNzFa8Oqrr3Pv7l2eeuoJNAWoCg64uRqNFZKLFx4EBEoJpAIhfZIF6bL2CEFL27SYOOGAFlyAkJL5tGQ6KXj/ynUMEq0LRisrSBlhTEGea7AKayRR1EOoCOur4jn3mGCW9RqjQBStRVhcMnOB08K1x+CbFGIx8RX1+VwmTzfnFd5re28ta58ErIUxG8+YDvbh5iqFQnqLI8ZCYTCFJhn0vGzpwTsC6cGkET6daiWZN4icXXxOtb9ZFOBD+mDb+O5+2qWOSfrClRZjF7U4xi6C3UDo2uDzgOauOoPuswwM3j+r2qU2zNWfVSGcMCLc2ZFCYUqNKTWRFEhrneuRcql4S+tiNpxbUTBdCDRQWkuURIxWB6hIYK3GlJa1lTVfW8WNOzi7WGucoIKlyvotam23MQ0aU3NeN7/wT+HPXQAhC2seVXDLVm/M0whqLWXT510Iv0CVrBOEFxtyRvrHuGe57ENhRA1KEvaOWLTIVozaz7NZY0VKixAhdgeElgwGQy5eOMd4b8+5SGFZWxm5PV1arPaxLtbdr61BWYVAVu+/AgvYan6j0Yhh0kMXBUJrpNFIq4hVRCQj8qxAG432ebibgtfCvjYuZXZQgGVZVru5BuuFdMVGrVHoUrC2OuKJxx/j+tXbYPzelikupXmMkLhFtS4LmPD7ImTvq/eyu6Y6b6IEUSujoEDgeF0/ibHCWXpM4dxCjbVILDov0WLA+PZNbt26weOPXmZ29zZFXmDAZawrckQ5psi2fXY5Zx0JNZRkBY4cjTEAPlMbFoSVYEsQEWWRcfv6DlqXJLGzHJUSLj31CJ/+6d+LFpq8SHnqmSd58K/9Kv/uX/0bXvzaN1CJ4Oq1K9z4+AZFMWNv7y4jvcLnfvO3KPOCfhwTK8nHH10DU3hhXKMi5bK12UbdGyEwuHTc0/GYotS898rr5OM5/8Uv/hzHT5/gwbMPkx3P+OjDq5w6eZqkpzi2uobQGlMWFLpgPh1jbcgeKimNc3mOhPC1pF0q7Uq945dJqYT1jeP0+iOEkPR6A1773hv04xWeevpJ4iRy1j0Z3OklWQkklgsPPMgbb77OieOfxpoMhSXuRTz/E8/w8BOXeOVb3+Wrn/8KH334ERGnePznfz/CapJEoNOUbDzzsWkl0+mEwWDAaGXIjXevkN/ddbTUgjAW4d0nrc+OG3afU+x6i4YB5RWd1tO1QKdi6U+eXXTbttaifG/CCrSP9VReICmFrnmxQ2pEUmGlckpk7eQJ6/eb9cAs1AYUQWksnRuhsC4OMETxIqUvkezokxIhdjkA2oqQNc6+41dKuXsd+BUIYb1CQFRrJYQD4O4YOMW3O6cuVIGKNnoro6eFgfY1+V9T7uwq+9BW7C9LHnHQ6uRqZDqFpa3BJ4tspH1/U9ZtW7+WAckuhU+zyRDb7vm/kA6sR1LBLIfMJSF5/Z232dvZQ1k4trpBL44YTyesra+Tn0pdunvhMpwWuiQDkn4fz35BCBQSUxoipejJ/y8mafj/tVYWBf1+vwJGVSyQdv7UgckJEYQ2SchWFbR6XVYKZ2k5uHxN9N+83vVpKnQbgBMNzUlI4hD66fV6lTY9uOQd2JReAEM4EOA0Z5bBYEgS90hnGd/42jeIlOKhhx5kf7zvN7jwz3LCyfrqOmurG2gdtII+J71tuKoQDnVby1KPv3kIjHevKwrN9Y9vMR7PKEtHiOIkwVrB/v4YQahH42qdGO1AEdQamC5NVmjhiAchbWF9qt9bAnY1/gPdLW3NPo9qaTpqv8YLkBxCUIQn3EFgFUCR5/QGI++2qA/goBoXBGG62V/4vu4fKln5IMirUNMnn19jNAi8y11oUiwQyuZY2k3UG496NRpnIVxn62tVIw4rWCmscIxRCIGSkrJ0Reci6YBVWeSUSVnjEIJw72mEZ4TGWpLEFyLtJ8znM2azGZvHTgAGFUkXN+aDtq2t0/yHfVsxYxGUAtZrd4MQ7GlEoBMiqpQFVeHGaoECyA7ufQEdCox2Ak0UKZIk9ooXd86dYN+O3gq3126swtrGcovWpY1iw0YghKr7aM03CAkSZ9kAhRSghOW5Z55ESsl0vIfRms2NTdZW1tjb23WxlTLCVeNsAHcrKnBUb1QnBCjvMhfHEWtrK6TTGebYGkoKl1tACJIocbSnAa4q8NfWwuLepZSSY8eOsbOzw9bWlp9T0MT7VMdWkucl2hiefOIxvvi5r2KNJZIuVtRJ8QphQ7A/9bysdXFAHhQZ660iJrgPaTQeIPnv8jx3cU9KUppZxWsqF1c/MymgzC3FfMb+9javfOfbnDtzFhl5oVbC3v4u6WxKHOHiZApXx86a4DJW7z3hgZMwGovxBVfdHiylBWMpS59ZColVEtmPeOLZZyiLkmw2x8aaF7/7Cjvb2xzfOs5oZYg1lusfXeXevXuYsuCF557l5KnTvPrmO+zcvYfu9Tm5ddwJfV6RVGpdxUrZsG4VSHdWBaUkptTsbe8SyWt89v/4TZ781NMMBwOmkym3bt7kt69/nv39fe59/DFlkaPLwvFHtD/HBiEix0OEi4cNZ9QpVBpxm57HbWwcq3hOWZbMZxnf/MaLnD93jq2tTWIpnR5GO6BsJVhToJQi6fW4cvUjzp49QywKrCmxRjFcSfjJn/kJnn/uOa5fu8nbb77H3u4e/VGfa9c+oCxyBv0eo9EaP/FjP8LZs2fJ8pTx/h7bt26zc/M2ZVZgigJTaGxeUBYFeV74OlLau2o716fZbI4qDT2fOTVcExTOkTUI4/aD1YZSawLvWUjko5UD3cb69xfVFMUYv2ddXUppPcwJwMCrf4S1CF8nUVhBJCOvzHEZATW+GqT19DSwD2Gw0o/TJ7MQQWmGV7YEGiescx21tlLCBtpSBlouHaCr5Q+vePJgzBWgDnUKa9rS1ZoyZPPfba+Nw+SRttKzoifCu8EKUbEHFlRpi6577XEtWgK7+XTzeW0XwUUrvKj2BJ5GI5wxoShyJvv7qLUR1jrLkiwtWZoiRY84jijLgjTPGPVijNWM9/e5c/2WC9eII6I4pjfo+7NpGQ6HnDh+/BN5/PzQA6TYZ7lo1hFqmjGbGefcZ9XQQh58+e1g9rYpEaieU29qaDLb9sYPwOh+m01K6dIf+orwRuuF3ypkj2Bj4xhSSK5d/YD333+PM2dO0+snJDqi0AVxHDPs98DCZDLl0gMPUZYFURRVwC9Ybo5qDek6pGXpUia/9957lKUzbfZ6CXGcMB5PSNPMr7uruSSEc4UI/w7vpav/A2tFLb/LhkAJOO3/EVp7rouuBYvveNlvh7U2waotJqKypBy1HxDkWY4QEClFmYe08vVYZJChobJSOAHpaONtt09iGWuekeZ6HdAs+f+KlhYMaw+MswJQHf24W9piO4uutFhfe8b73gNIQZLEDa0XNaCyIQlLPaemBVlrTdKLGa0M6ff67O7sUpYF6xtrRJEg9YqRYB2s9J0OAx2AJCHTlC+p1FjMBi0QsmJmB/msF0YCQApA0Nd5AYswGmE0MljQnd6uslTUoBovtBvfTet5zQtpKyWctRNqpitEUGQ4t158PRrpAVOcRPyeH3uOJx5/jG9+8yUnkJYljz/2uK9Jpdg4tkZDJ3zg2bUSpZKEsFaEJGucOHGCax/f4JT2cTpSVZ4F0+nUuzYnLnHHksMYFFJaa7a2trh16xanTp1qeA0sMuDgBfDI5QdZWekz3k/p9xVFaV2ksi3ApFhTVllPHXD179AUhJif2hKHY/x+tQMIQGuUNUQyphc54drt1drlCOEKKwrh3P/iSCIRzq2uyEkairnwJ7g5BmDUVkAFhQUWrPaCvf8sFAeE41JrVtZW+PiDD4mt4NixY3z5d36He3fu8rM/+7NMxxPm0xnDwYDt7W2yNGV1ZYW/8F/9Bd56+x3+429+jtFoyNmzZzi2tlbVGww8MXhcNBWVwmkRnbClIlyheMt4f0rc3+O3/tNvkqUpZe74lC4Kl+2wSroULET1e41UtwhVe5vgClkqSRRHIAWpTw0eRYYsS7lx4ybvvfc+a2sjev0EgrLI1u74WmvOnz/P6698hxNbW1hriWKFMZZeP8Fay2h1xGNPXubRxx+lKAqKomCezijyjNw/89ixdaQSUEBvtcfquRNcjJ51dM46aCAqadmBS601RptGLHdOVFqUdsmV8jwnLwqKvKAsckSh0XlOlqZuHGVJlmXkWUZRuL/T6Yw8TRHGUmY52TxDGoEpXe0ra4LFM5Ri0N4i78C2DHzFOkdGow3CODdHYRxtMEDecBdsakONsNQU2VYeMlhX58kiPH12/3ZKQ+mUEsEDQEiEckDJAJS2yggYyjsQLONCHUjK0KXwbco7TdexZbJhkx8tk4+CfNjkW22g0+73fq3LCNCp0O0AeeCVpNaikE7mFrU1TwpBMuihbYktMga9iPnEuUbPy5ySgv5wwHB9hWk2QyaKeZoyG0+IZUQ0WHHu11KSzzOEkPRXhqh+wr3xHsPh8L7zC+2HHiCFTVCBCuPcA7pimdyGrNNUdlmOQmtvrCbYCZu83oB1ny4tc1T10QYBTfReBQw3nl9lxGoAteZGlUpitGR1ZR1rLC9980WsMTz2xKOMp2Of6UOxtjZi0B+Q55o805w/e5E8d0W33NgUSsmFeXYd1MoHGRbWKlyXZRlZmvLhhx9SFs46tbl5nLwomc1mZFmKEKFmlD/wjTVtAoo2KDn4smv5rapoH4QJu/zgLwPDhxGdMJ725/uCuA4g7YZ38L6Dwn8QzmpXJmcRdQJekZeuwnRDdAyAocr+50FH5Zvttap+EOGuJi/pnGfoq2vMhxHKxflUUviiJag5lkUp2L/HxR8OjKfjrAZNOhIKk6F9YcdISXpxTK+XIJXwiQEUZakRQi+8o/ZaBI29kJa1tRGbm5tcvXqV+Tzl2LENVlaGTLZ3nIbf1pkYnUDLQnrdMP4gxOpKR+rmKoRzufM8xF9X+/ZXTI/Ia+I8Q8JbrhFIG7mMhNZgSoEwkXPHDP140CH9obHWumx91DpGJVxRS6wv7GnbdYBCpqwCpbz7svEV2fFrKQxR5IBE0os5vnmMhx95mBeef4F+EvHNb3yTvZ07jPd3ePbZ5/iRF57j2vVrPPf8syS9CFFZ/+q9EixqwooD6xkyFVqrefDBC3z40VV0aRFCVcAzSRL29/frMg5LrEfttrW1VZWuMMZlh+tqZVmwdeo4p86cYH/vA+KozyTPyNM5ZWYwegZ2MdOkU2SAEtqBermoxbWAEs7yJz3xE8agrasMK7TL6mSNpdQ+pbhw2u4sLbBR5CxEKuLxxx5lZWXId777PTKfvr4ZIF+WJVaIyjWnWm9Pi6ypC59bh6lx7jx4hUSDLwhBHMWc3NpCasvHH1zlS5/7ApP9fU5sHueDt94lTecuzXtZMtnfJ01T+v0+/49/9I94970rlAZsadjb2WX3zh0HjDxta7tahyalREYRkUpAKkDh4Tm793aYz6cVTVRCogzeWhcUJiFeTnhwZRBRLXc3ebdSqgKxQkpUpBiujNDGuHIgpaYsLRcuXODq1Wu8+eYbPPb4I8SJtw5T9xnegZSC/mCFDz64yoUL55Fl6TTp2gn4iYyd270AFPTihN7IAS63d0Lhe0NCH4slshYdst1pT3/cDN179TQ3HLTgCSOF9K6mtXK54peldy+19UzCfjKmdC79pcHkBZQanRVkaYYxUOYFeZa7P6kr/ZGnKfPpPpP9MWVeeEA1J5un6LJElwW2LLGldue/1BD2u0/3Dg64Y50roSJGWo3BKSKUd8m2OJdqIxytc965Foz3kBGS0uqgoUMbgzbBA6Sunyakc8OzIQzBqgUZsa1cbX8OSbiEqBNMNPlcWPM2SKneVGv/t61NTYVS9VwZXP7sgWuaYKzZR9ua1OZHbf7ZbAJRybEI4dwQjUWXBel0TCI0w0iynvTII0WWlcgoQirJ6ZNbnDx1CiWks7DnORGCZDgg7iWVK2ZISvHYk09wbOs4X/rKV/jw2ked4+lq/6cASCG+JyQe6NLgty07TdNge8OEF94sEli76i0y1uBmZq2ufP9Da/pyNsfQfHZIxuA0ThErKys+S1aC8AH64RAJ4QSvtfU1hIy4d/Mur373e6yujjh+fIO7u9soKVlfGXFsbcXVxDA5p7ZOszJcI51PqueEw1DNv7Gei4fRoZDwXVNTYIzTkH300TXnImFc4T6lIopZyng8JmRcqtcYrF18P8132W4LgGPxF0RT605D8Gj10w7UXNA6HkGb0hzHMkC9rFVEqKOPpc+iBksuxbuoMnE1AY+1zlWmqT1TTWHfqYMry1I9psPn1v6+/V1boxWuW5Yiugl66nvq35oz71rWrqw9zQsXzqIHK8YYlHSa94cfeYidnXsURcGxY8cwNmc2m7JxbB0VKdbW1lxskF18pjGGUpcYXbKyOuSRyw/x6quvce/eDkLCCy98it/43OeR1hDyarkimxIlgo7THtyTXtCrrDjShVJXgBaNqwEmvN99YJQSQc8DGN+3X8RKSWCdUG0Kd08sY7TOkdJpyN28tD/HoCIHsmpLXnA7drGKIZuQUqpKdx7HMaNRwuqas6r1+n021tcZjkZEUeRrwRx3RTM3jhHFgt2dXW7cvMm3vvceb775Jrs723zqU0/zJ3/5j/PwIxd57PFLJIMek+kEsL6OkfB7BqwIWspFmupWXVYA79TpLZxsZ32tHHdNkiQVr9DGuAxwYjF1/4KixgOE4XBIWTrXI5d9b9EdJtDysiwZDC2PPHaJt998D6s1+XxGkc3ACJTQLm4pwNGGFcpZj7z7H+E8OcHVNAChO+cGa93+cEl/dOXeo4LnhNbu30ZjjWZ9bYVTJ09w6+ZN5tMpveGoinsNllRXv6hWQAQAYK2LfbWRcaBMBBrg+JaKlC++axFBMRgpzl96gIsPXUIKxRuvvU5PRYjBiGw259bHH9Pv9ynzgkgpMj/m/f19vvmNb4BQ9EZrzGczIuDWjY8RxiUXsta56wRa0ywYqaLY/ZERQkZu7USERVBkRRWP4RbWWTktAiudi1Ycx859Ubgz4o9UI6FRnV447EGpHGCJkpg4SciLglJr8qLAWkGv1yeOY65du8b+/j4rKwOEihf2XK0ctZw+c47XXnuV4ydOIoQTxKX0boNCue+Ez2DotfOu5pX178bJ8cIDamkFkkYyKawrMivEgqt1OCcy0DEFSOkBugPdBLA8qIKcoaJAtfVTCp/kwVikAbTGIiiFcGqhkELeWKzW3q3UWZZMqRHWOqCUFxhryNM5+TylzHPSyYzZZMJkf0wxS5nuTxnv7aHzkjxNsdpgytJlZS2ca5/RDqRJH2dqKRCULnlVqT3NdC6TQloiYZyXi3Vjl9btt1JYT4dKB45sg75DpYhqgh5HIxYTtAS60aXEb/KJw5IYLSjNG15SzWuasiV4ltFgck2+1JaZm3Jx8/dl/26DOxuAZ+B1QlSxrcLCfHcPk2X0jGAlTlg9fpJyTZMVBZktSXJNemebXpwQRxHRPCObz6DXY31jlUKXpFlGnhZsnTrJ4w8+SGHgp3/y9/EfP/MbB9ZtWfuhB0jt1NhOgykWrDPNFt5tU8gPn5vfh383s8o10zqGz/P5nF6vjxBq4d52qsomKAutC5xFUURRFGRZRi9JqvTgoWAWQrCxeRxj4Dvf+g6T/X2efe5pZukcIWF1uOJ8nROJ0RarLQ9cusR0PKfXjxZissJzlQpJGo4m9DeFgizLeP31uv6HS8uYV6b5siy9sOcqfmvddPvpBjSdrWE9AiqC7gRKJ0g217JLu3LYc+4Hzpbde5SxB4EnKOu6tEHh7wAihXBzyrLMEdxgjQyFNnGJGowXbl0XtrLCQBAvG89qaEI7kcgnaEfZK9U5svWzwzgqxrzwUmutprXOHxwWmUKltWrcGCw91jqNohGlD5q1nD9/npMnT3D37i2Ob25y+tQWt25dpyicNfXkyZM+5X7p6ow0rL5CCHSpSbMZp06d4OzZc5w9e473r7zFR1ev8jM/+1/w3vtXePudd915txItIMQtaEIms9Z6COEB1OKahB0uhPEM2L3LSLr3JQQYnTtLkAzCqltgAdjI+PgLR4v6/b5PjWqJYsFgOCRJEpLYZc4crQxZHQ1JotgXbY5ZWVlhZWXFn+WY0XCIkjEW6PcH9Pt9ny10Rq8XUxTaZ6iU9HoJRVGS585aPJ1OePP1t9jZucfVq1e5evUq2/fGJEnCT/3UT/FLv/QLPP7EI5w+vUGpC3b2x2hdePrql8XjJGssGu3Aj3E7W0oHjqjiGQ2bm8dYW111rj95CSNHZ5NejFSKLMs8/anfSZMPuP20+M5GoxHz+ZzRaORrah0UMpyLWsmTTz7Kb/6Hz5GlMwb9hHy+h3JOQphG7FELLxNcBS0+mF5IBwSEaliHjSumKJym21ootbc0qTqrk1OcyKqmVBxFnDi+yZuvv0ZR5JA5a2tIPBFAIt5txYHcPoPBoEqtO53OCeAiy7LKcyJN56TTiUv24RVhp7dO8MADD4CQ3Lxxgxsff4xSithbMozW7O/t+zgmH6/oBSejDUkvwWpNmRekMmV/b59Brw/eGmBaQmHg00oplIwq0KBEjEW5YHvp3Ew96qxiIgwuiUCSxJRlTp5nVYY0cF4eceTA0Wg0Yjab1bTPA+m4l3Bsc5NHH3uMzePHEcoJpvPZPlqX9Ho99vfH7Gxvs7V1nETFB2h+aFJFJL0Bt+/cY2NjHWOdS61AuNg8TxtUJBEopIwRQmHRFT1whXWda5m0AmVrEiO8ZcQBJK8UEnXcYLUnJRWBEdRZ4wRgpaxUMyHup1LuhGRPfj8oqap9lWMgAD6ks8ZGwl8niD1Rc7KcqJL+CGN8tkoHZKx3B8Q4i7LRmjLLKdKcPM2Y7u0xm8yYT1N2t3cY7+4z3R9TpClFlpNlKVmeYUrnKii0xZauv9LkWNw5QxsoNdLYyu3PrWsJ0mBtibUuIY1lkW80m1IH5TyoZcqmrNpWqtc0YhG0NHlh+75mq2U8tZhptvGMNrgJrcs61PyurdxeVJ4G2lzzeut507DfJ4qcd0x5b4fCCr9PXDyZwjDdnzO1lkhFxD5ZmRVgE8XtO/dQkXKxb1Jw+942X59krJ88w4/9zE/xxKOPctT2Qw+Q2lmwKuuMqn1Cm6ZPtylrFN+FgMPntqYwbNLmpnQWE4VS0YLL2DKzY3NTNdOHN5+VJAnz6axKMauUcv7G8zlJr49SEfks51svv0ykIi5dusQ43yfpxWxsrLMyGmEpKIQmiRNOnTzNbJaR2Kgag7VUmmlH0GrB6sCYqYXucL8QboPnecG7777vNPBKIqUgz3Om0xll6YrZGeO1K7jAbafxPAIoOqRVBgjrtVem27LTefhto4PWde2ZN5+4CKYDkGndEcBA4KEH+mnMIOw1T0WEwAlgnuFIIciyzAk5SeyBbMggJVCJrK9VsgJfwRVGCUFRaN9Hc04HJr9gVrJek70wOWtrcFcx3OXv8KBPcpB063URrX0VngGN9yHckw68n8ZH6d+HG5p7AaPRiCefeJxnnnqKL37h88xmU55+8kmUkhRFQWkKTp86xcWLF2qQLULsYo3orLVMpzOOHzvB8ePH+JEf+RHu3bvB73zpSzz44MP8pf/u/87/8R/+I6++8hp5pplOUrK8xCIxUrgEDI05GW8pUA0RA5x7TRTFREoipRPKRqMR/X6/ciFcXV2l1+uRJDFJL2Zzc4N+v+eqjicRK+sDhsNh5eI7HDoB1xqBMU7giOIYY51iJ88zBAasIMtyH4xdVgL/7s4ut2/cJkkSsixjMhk7lyRr2dnepyhKylK7YPT5nNlshpSSorCMxxOMcYHfWpcoJRmtjPj0Cz/OC59+nieeuMzpM5ucPnMSawsm0z3yvHAabmudMGjrc2bBWX5MnTk07KKwG8ESJzFnzp7h7t198jyvaHJIXBFSfbt3fDCY19rF82GMYWtri7t37zrg6J1q/AtdAPplkXLp0kXW1lbYvXOH0XDEZO+OS3Ag/SnwjL65ka2V1VREo++gdQVLkvRcAVDv9iSVQlSFyC1SRa42EdYrU1w38+nMFWCNe0wnU5SKqoKL7jzWiXpcBr2gcRY89tjjPPjgJT7/hS8gI8X6xjHiOGY6nVZn+/r1a6hIoWwNkAaDAbdv36bE8PH1G2S+KGRuXP0w6d0c48SlwnZTFQv13rRxMR7b2/cwVlNaiJUkimKM8NTEx/NJ4wTAOOkRqb4DlyiEVCCUB48CK0L9Igc4rAkKBWf1mE4nJFHk1lg611Hrs072+wNOnz7NrVu3EMK59A9HQ1bXVtk6fYrTZ85w9uxZVtdWHd2eztne3nZZbY0lTVPu3LnDQw9foieGncrRQCUvXLzIW2+9xQuffh4TEloisNrLJNK4rIUIpDCVMsj9Zr3LnqdhwusP6m88rxEViAnvu7EjkWWdPRbPtwOQklYQNnF4d9V5saGOWeBpzrorhMBILx9Z7z0TrHlegWp8YgwrhA/gdGOMEFUfzrXKun0TS5f+n5homJBYGCDY5BxGgZHWJ3kAW5SUeY4uNUVqyOYlOs8p5hmzyZTJ3j7T8YTxeJvpdEyZ5sx29ihmqbs3LbBZjik1RZEBJaDR2sUPGh0UlR7I+AyBBEVXQxET6I+xBqFceIYgACZvdXH+zQu0KfDeylLXEaoR3DWDIjwKBYSrd3zQ/a6tpG4bC9pAqA2kmr/V91HvkXCfdl4MifDvXka+SHSEEJGz+ltL6ZUYAlzcmfUysrWIrERIg7U5Vng6oRQfv/4ms0mG/T0/Rj9KDoxtWfuhB0ihNYmNlBIlnG+2Nsa5lIFLS2oWNYChNZM8QL1pwnfNz81N4lw3WHDzW0D3oZiqR8jB498RDkcQpHSmfo11/vxCECcOFI2GK74Argss3VjfoGfhlbfe4ur1a1x64CIyUURacmJjnTObG6hYkOYl0kpW19YptPFKM1f1HITzKVchye9BcNhaXQ+SnIHe4tzmirJgb2/Gzs6cKEkYjCQqgdwKsqwAq4jjGF06gqC1xeiDWrMjNb+W+Hvr/FaV+Lkw9uodVTNsCufe7YwQyFk9pLEGhjpTmCf2Pre2qIJL3G8LsSRWUlnHwrphfaYwhUux5kfbqD/kslU5Rq/L3AXyW0upC5SC4SDhoYfO88LzzzHo98Gnnl1ZWXEFTIuCf/fv/h2T2RwVRayujhDKMJ+V3L1dQClAGIwpfByF8loevFBqqmJtygsgmFBXAz/mEAMAAR3WYKrB7AWoYOHAubwJL7RVrz0wXO8a0gSfzs/eIpVYOH/9fh8lFVEcoYRkOBwyHA4q7flwOGQ46LG2NuD45ia379zht37jP7Gzs8N8NmdzY4P33nuH+TTl8mOP8cxTj3D8+MhLdpKQnl/JkJLdCdHpXFOsah6+fI7pbI+dvR/hK1/+Gv/L//K/8sv/lz/GX/iv/yQi/y/Z397l7bff4c0r77GfzjHExHGf0WhEksT0e/3KFWp9tc9g0CeKI5I4IUliRiP3LnuxJInrZCrau2hYY8kLTZqlTnDzLvFZljGfp+RFwWzfZcKcz2dVghRhJOlMsz8ZkxfOQpMXOZPplHQ6R1m3xmmICcgzoigiz0vyLK+YsNsSTjiPvZuutQalIuI4ckkbNKyNBmxtHSPp9VhdXWU0GrK1teX+nFjn2OYGZ86dZnV1hdksZTqdkmYFunIRM+BjFsEBYC1deunSSEQJKlZInxzJCSs+FsRKzp49y80b91xWNe2zx6GJezHzeUppfZrmLp1IeKqoLUNbW1u8+eabriaH1a2LXSfGWnQuObm5xcULZ9i+dQsheyB7CKGJI0FWZFWR3IUujK0f7IFRyGinvYUozzx/EoY4kkSRJI6cMaQsNUU+cRp3IbAiQtgYUOhCMOivMZtqpuOSIgOtXEFZUGgrfeFVhcJlThPaYkrD5UceY388YTYvSeKE6f64OqPgii+XWYESiR+2pN9LMDZib2fC5cuXyWaG6X6GEN4SGmrzCV/yQQYXLkHP89KscHF/hS6YZylxnBAhfQbKmqJLGaFxsWZxFJNEfXpiiArFc5UraiuF8JkUHR2ScYSRgtK4xBTzfAa2RGQGyChRFFKTK01RCJdJbjDk/LmzPs5WIaOEpKdIegOsgSItsBp6qocQgp10l7t3t8nmJdk8Yz6dMZlO0BjP47uzhFmrGQ4GGKOZTab0B32wQdGkHb7TATxYrPBlRaTnay3ML7z7oAiAJViMAlm3XdKQQFuNCIqpinC7+8JbABYUk0KImi9bnIAsTK04lhUnRgjT6AVESD4T+Hf9A7rB24OyttaPBG5eg776LFEpDJ11C0SikEnMaH3g5LXW/QFAW23IfeKJ+WzO/t4ek7u7jLf3mI0nzHbHTHb3yOcpOssp51OKLMMUJbbQSG0wpfa58uaONxrt3FitUxaXAuZKu2LKVlbZfSUhuU1JkGAEEmmD1VNgRL3uXaEcXbWD2u+5y9oEB7MVi8YLEc1NY+v4JNNxLaKhDLKu/ECATFImGIw7oz45Bni5IbiUizAmXb1Ha31NOSld3BjSxdbZEq2nmMgQDXsctf3QA6QQ7BaQcmDmSpoWHwoHrxbOm+55zY0VfI2bFqi2xqf5OVikmsJ55QIglQ92tt6vuXGv3zDWCxohi5EF4ihy7j3pHKWc1u7YsU1WV1YRxvLlL30JpSQPPfwQaZYyGg05tr5Gr+d9opUiL2Bzc4vpbIZSsdeQOxcSpQSLVPIQacGbRSyL846TmNt37pCmBaOkx+rqCju720TxoApAdH2IStMpfLHBLpNz5+MXGEiAG7B4YmsCHTQkthozFQH8ZE00/uCYlF8D42tqVT7Hjd6d5icE1BuCq0M91AaYasykgu3NbFS4zC5YS68XI6zlF3/h5+n3E4osI4ljVkerGGsoTcGVD97j1u1bSCXZOnWCNJ9z49o97t2dUBdFcsDEpWkO/MAHxAtLCJCXUKeiFo0zYkoXGyPwftpNJQI0i3n2er2FuMB+v0+/368E/ziOGQ6dj34cx1W6fuWtvyqS9fL755SFL/apDXmeuVgKH+w9m+xx786UdD5hOp2yt7fvkohkGU888QT37t3j5s2brK2t8mf/zJ9hbWONSAnyoqx3ifA6FKQToIXLsrS3u8/WieOcO3capX6cOOrxta99nX/+T/4F7333Lf7sn/iTPPf48zzx4JP8UpmTYrAiJcvnFV0pihCsbMkyyTzNvZCpmeztc+vje8znc9Js5tPu6sp9cD6fu3tL55KRZRmFt5CU2mm6tV505a1iG5VywrbRIAQqipDebUggiYWq4hL7/V5llVIRDId9ksSlXe31+wwHQ6cF9Br0OI6JopjBoM9wOCTpJchIMlodeTetPlGkiKLY9yMxRjCbp1y/cYfZbE5ptFMICB9vFFKlW+eaozw46vdiRJKgpHcpDYKfpKIrQirOnj3Dyy9/jyxLG7VdLL1+r7JsLwqJB11WmtLExsYG0+nUn58mym8q0txnpQRPPvko3/v2txxdXlmlzGdIbelbifDWdNOIQVKiplUY/y+viCjUogBr0FhTgFFglavrFUVIL3wGgSLqOW15r9fj3IVj5MUOQs6Ikow4llDVlCoBl1VP2QhhYgceteJrX/oG++MJiegjS4X0qdaFcApBMy8ZyA3vLuWSh6wMVlA6IRISPYuJZorT/S3nwo0TrqX0FoS4V7kPKqXo9Xr0+32sEUR2gNCCcjNHWUEkXLKVJFKgQApFpGKkd6nr9fpEvQTZT3ymVkmSxERJ5KyyuJiRKIkRUUSmC3b290jzjJnJULGgmMwY39smzVImxZxbu9tcv/UBpUnZODFkuNpjZWOVLANjJAUle/Mpc12QlgWFsBAr1tfWGI5GjFZGfPdbX2M+m6J1wWQ6doV9jQHVUXiYuibOAxcvcvXqVR5//PGO60RDN+j5XaO+2sKVdjEJQE3rD+eIQQYWQUbx/NQZfBoc7//N3p89e5Jk953Yx91j+S13zT0rqyqztq6lF/QGNMANBAhSRhk5IkUJs2geZDZ/i/SgRz3JbJ5HD2NjQ4myGco4MxwCINCNBtAbuqu6lq7Kyqwl15t3/S0R4e56OO4eHnF/md0NvRUZZVn33t8vFg9fjp/vWb4nnhcMYz67b7om7KM+88zHZ4S3GRgrxu+QYz65ZgjKBv3Snzl4lug+LgMOOq0ZIO1dkeBIrHyg5xPm8wm71y8LqNeFbKHW4xvHerHi7PiEs5MnPPz8HidPDjk+eMLZkyNOD49ZLRb4Zo3rOtp1I6QVbYe3FuUdcxv2B4RoBaPEaOAtVpEAIQqpwWRCvqrreNaxycsT5Wrst425vaPr0+fpfvncO9/zg7BAGMhYCPOEnkTNOS+1y9J9eoKp5IULh/W9fuxHKTTeW/b2dynqcgPgf/rxhQdI0YtznipaFMxxIpyEkumkfIxD6nLv0JixLg+xU6pnn4l02TAEU9ADsvh3Tk+qUnFWlRLqYqiDc1CWkoOklObixUtUZU1dT/j0k894//332dnZ5sLFXcBy8eIe29vbUi/HWlAFKKlYv1pbiizePAoHRQh586Rq208LDcyPeE5VVSGMoE3UimdnZ8y3ypCXIAukrkpstw597pNlJ+/bX3YkwJP1ZQ9IQawMktAO2Wbh6SVxfzf6Je1Hn+fzJ+8LNfheZEaw7mTCwgdPi2Q05/eFWGdqeM/4q0dHqxBhE/PQuaDclSX37n3Ov/4f/0eU8qwWC7q2o9ATlqsF62ZFZxvq0mBKzcnRE7a2dii0RuMwEQD5EL1gekuRUjqBkiLUjqmriqquqCuxiE6mAm7KskIBdV1LTkaYM6bQEj4TlXFrh/VJPCm3ziOsX+vVms62LJcrzhaO7lGXwrxE0bcJ/LgwdyPNr+t6ABHjuBOosI62kVyduq556603uXTpEj/5yY/Y29vlD//wD3nhheexzrFq1kHp7edZvrkIWC3oWsuTJ8e88cbrKAp+8zcLrl65yo++/xPe/elH/N8//q+5deMFVus1h4sTVl1D153RtmuclXdJ9M5AS0FrQ0K96a3oCgXFcPcpyzKsOU+B5KNNpxMm9TzN9aIomEynRA9nYQyTySSE3CmMttRT8WapIihMhSiZ4sGKimURrptSVgpTyL3rumJST0I7JdRJh1yEwhi0MTI2ymM9dNalcVw2a5qzE6m70oLtPK3tgodUikda54iZQT6MQ9TGjdGUhWE2rbFTh3NCXKMrYe3LyTU8nv29XWazCetmHXLTesBOUO5j2Esc4379Dnd/Cf2S5y2XSybTeqBcJhkEWN+iCsdXv/4m//K/Nyjn2Nra5ejAotcOp3uFschEi87CMHNx4Qj5C9lX1lq0alDGUBnxSDrlg9Eiego0pqzQlaJrWtZnJe1WTV1cYjIxYKRwelGULBdLulpygGb1lMrUuECIMKvmzPf3qaqawliKYkQCo2JYtoS31XXF9tY2860tsQwrhfrmmxRFwXw6Y1rPKIuSMhApFFrCxaMRRYwnhrIqoHQURgBlYQxGaSpTUFRCGCHXCJW3d1Luw3lCfkxg3NPC+qqjJVr5oJB51t2ag8NjOtuhlWdiNKrz2FWLc7Bo1ty9f4//6//t/8Kjw0d8/OHHfPbJPYqypq63mM620LUBLXO5s5bTxYInh0/4rd/6LbZmW9y/f58HD+7J+igUFy/uY4oi7Pub81XicfnyZT744IMBK+7f9BjnWefK79OOuGbiMsy30GTMY6Q3hb7tF+T5EK3RU8Kzzivy58/qn9f/7jN7Rb/PAClHM76v1mPdwRGzM/L25eQ5/TzSuOVSQr+0yBvbOYwuqKc1072rbBdXeeHbX0ZZMd51yzWnR8ccPHjM4YMnPLr3gMPHTzh69JjV6YKz4xPccsl0UeNsJ8XKfRtY94RIw+tQDDnoHU4pqX7rGXgKozH+lxmcBQAO9d1fRf/KjcDPHs+nH4OcfEgeOx9IvJTugWkkSHlaW8YhgiB9VJXlr922LzxAigpSVDLyCvL5kSs9eU5SBCU5KIJ+IvSgYjN9Y5xkURjkoKqfAMOJG1mDFL3XKhFMkAs0TVnWeAfrpuHSxSsopfnud7/HarXgq199E2sb9i/sCjgK8bmd93g0RTGhc0DYNIbU5P2Re0DOg4/z1tK+nz3L5RLnHFVV8uDBPdq2DSeL8CoKCRV0XkLItJY406iUe+9pmubcOG16fm85ikI7ZxSKydVREKpgIerBnyheQ9e+nC8/1ciqDGMFqrc25VZj53rrXKxggyJ5DoEQTTf0QMozNUIXKudpLQAmWdu8xXUd+xcvcvzkkO//+Z8HamB5XqlnEk5SKrZ3ZmxtbeOVZWtri66Fl158kZdvvoK1okSVVcF0OsGYErx4W6uqEmDdWdpmheuE4aqzUrPFWSeAZr2mbTussxwfn/Lk4D5tF8+xNE1D23bE0KtIMBIV5dxIEA0F1nUDj0cu6G2gjc+tn/EeuYc3jpGsTyhMxfbOLjs7W2xvb3F4eMjBwWNu3brFH/zBP+A73/kOdT3hbHFG23ZCnR+ZlbL7xXHXSvJ1l8sVcMxrX3qNCxf2mc1mvPj8TR58/oC7H33Mw/sPWK5WHJ2dSLE+W2H0nKIUD01kgSsKjderRJwwnUySx6SaTJhtzykSKJK6YnU9oSwMhRKlua5rCiOApixLtNHMZlOm00lSlotCwvrKokACeEEbDUbY0Vy0KIZaQWKs9GEtxXHox8Y6AT3duqGzazrrE3jt2i7VVOmsh0CrK3V/rCQIOx/qzIh3JNWOUqSQ0lw5iQBJKTAGmq6jaVuaSS2AytVMlRZFWukQdmIlD+n6Fe5+8hmrUKslspBp1ct8kQzDMc/lSTystezs7HBycsJ0NknyYTD/kPyLtmt47bWX+c//T39IoTRXLl3m/Z+/zzs//SnHh0f9XqViAjtEr7GJlvnASlcUpdTYCSUZjDGYoqBrO1G0y0JyE4MlqigKJnVNWU2YzbfT2O/t7jGpKr725a9Q1JVUoUdRlbXUZnMiK+vaUJXy3LIqxeAR2miUotQGo8UAorUOMqPDerF6e++lrwuDKQw46LTDdg6pdS+kE5oiePF0ukYiQSxE76G1+E76edWIIUF5S6GFBrpr26S4r1crAeZrj11FI6TMzahJdp0Nc9TTuo626zhbiKe2o5P8pM5Lrok3WKU5PjvjhekbcHyXs3bB2eExS0458o+ZTEq2L1yimkg+UaeWrIuCxcEhi4NjZtvbvPvOO6xWC7bmM3Z39/j6178uHnLymmzDvTfVZwOuX7/O3bt3uXXr1jkwkxtw4t616ft43/hZrlw+GySNPKrZEdXlXjaHPEHv+1IF9Pvk0JOUty9ALe+xbrNy74n6wgbFXPXtGH+mrERuJNCkop4TZUrflhgJggpeitA+hRLSnViEWXmpnQUsFkush6KsqJuaojIUod5YqQxlpZlc2efm9Su8rMQNbJuGs8MTnjx6zMPP7/Ho8/s8/vAuRwcHLI6PUIszjO2wqxUFjs6D9l5CcAWtYW3ULXrAket18e9NcyHWfhsbAfP5EI9BdBXPBvPj56T7m9zD4wffeaUCi2KInrIBADKcr/Fn/vvYgCnvJqQxzrne2/8rHF94gJTn/URL6nrdCPtMWQ7ADZC069zNOEbRcRBTbZXsszgRN7F7jJW2iJahB3KDQUcUg7Gwku8ywoSgbM/nWyyXa37wwx9RVgU3nr+GNp7ZrKYoJO3betl4nFNMptu0rSSxKaOSfBouqgjqzntmxu+XgyNZQKJsxOKHkksgORD7e3ucnp6hUCyXLVqLkiP1SVQauxh+Fa26OS1l3o9D704vfIfnxPtG0NpTmKuQvyS39uTO21yQ933ueytHNDYrJbUWgofHhNw25xAWNB0qfROBWshjUr1wAkkYh9wzQKBpVVRFAbsO27UYBVVd8cLzL/Dqq69y5dIlLl+6yGwyoW3EI6epAc/Z4oRlcwbKsW5WrFZrbOtCQUoR6G3ThMJ+bQI+Nnhl2iD4u7aREJAw3tZ2tE2bAHb07MSQyUi6IXPKJ7ahmIQqcdXZGMV5H8lUQjJuHIeYtO2dD+xfffhemptKhY04hmyqsEZEmSyKSQhRdZydLbh27Spf+cpbfPVrX+XLb32FK1cuc3gs4XdCUTxk5RmDsTizvBfygaZp2d/f4xsXL3B4fMjFG3vcfOM5sdY3DZ21YbyFVUspqQujTaxw7qkKKEwkjlEhj6eSOVEYirKkSsqvpjAmJLX3ycBxUxegG2oSBSDjAghY2gWLBmxnsWG8rbfi4bFSFNH5OLa+z73yAAZ8QQxNyf91LgYIE8Y7j0KXmHlPvkYDsPXCrOa9x4exlwLKvl+v2SYe7o7RniYVWbX9fANmk1rmDj55DF5++RYffnQ70Vk775O3IlJD67JIz+rlSmi/Hs6Ha9eu8fjxY65evwr+PPMpeCETcI7t+ZxXXn2FJ48P2d+/yh/8w9f45/+H/yNNs2KxWMjaL8TbqhR9PoEXemQRKFKrp1Am5av0nlUJ3Y65GVGex35Zty2dixWACDk4nvl0i1WzCoUwFYuzRVi70Kwb8BrltJATWItRsj7bpmV1Bl2rWK9WrFarJDubpmHVtmhtsM6yXociqcaIh7sRqmlnvVjdlSRld60Vhr4AWJXu989CFZS2SF5tHxK2tVLpu+iMj2WByrKgnBaYqWI6m1BXFZNpjSlCnomSfCQV1qAtLI0Rg86ZbzluFrRdS2EsShVY75ntXuHKt25weHbI2x//nLc//GtO149ouzXd6oyjhx5TTJJBKOoAd9SHuKpEAZWGnd05/9V/9X/mlVdepnXg7RAsjNdQVE5v3brF9773PV555ZWBfBK5mekfShED0caKbq60jj1J43vmR+89ykKr+m/TOh3/PQyH8+euyb7t91xCPmC2FntFOgx1MkZuVv7z+wKhwOxQP+j7wg2uywmjbKrzpnpZoETnK0EiMrRBVZbFcoXuOpQpQtFTHWrcKVoluaZar3Emejw15aUJ16+8wI03XwQUq7Xj+OCAh3c+4ZN33+fhx3c5/Pw+xwePoVXoVgp+F4C3jk5ZnCaBxuF4nQc++ftrVKbznAecm4zS3vf7TV6eJjdUbrwHIs/ylJZNYxYpwPPnPe33sVEhvWswonVdG6JOnu6BGh9feIC0iYmuLAuc7V2PWusElvAbPCgZgNqEXuN9xucOQZE6dx2ItSWTJGmAxYro+wTd8bND+JZ4dTWz2RZVVfOn//7PePToEV/60stUdcmly3vM5xOMiTTkLd4XrBvPbHuCQ4mFVQ8nVk8mEanLn20dGLe/KAqclwRmgMPDI2bTGXc/ucPO7kWef+F5fvbTn0n17a5LY+W8h2CxlvwFUVoiU1a+8M4vdk903+fgUxomm44KyrLSoHQIKUOsP/G+ucLuIuA1fX8QBHa0nhvT0+wWpWy2cfMWS6+hqiR3pjRCoyzXiGdtOpuilLD7GVMwn81o2gatNJOp0CafnJ3huk7CebxjvVrinYDGux/f4eOPbgMebzvwLuUmudbRdi3Wi2JrnaVz4bvOJRYxUaCG+Sm9pzX3zPRgM9+soscr9nHeV3G+SjXxWBHIU5oCVQxrk0VrZx8XH5TaUaIp3qNtKD6afR8FIloJU6WSnJoINouioqon7O/vcunSBW48f40XXrjB1WuXufnii1y9eo2zsyWnJ6fCcoYPXk9R6vN1GH9qNbSYnp2dsFwuJMxtNuGlm88LWQuermujkRLnO1HglKYoi8zaqcEVKPpkfBfY4cTLYkMBS0/bWaxtEoBpnBVAG4BCWieIFyWuC7GchhXihJRFih46oVnxMldc+NwFK6mQPwSFEqEul3nhU96M92KFd6q3Lo6VoRTqcm6zDuCG8K5Ze7XqrZbyM8gBJ8n1RRZWGd9NKRXYsApMUGyss1y5ehlT6OBBaqhsHUBoSdM0QpzDefme2p8dzjmuXr3KnTt3kuI4mI/hGq0K2k4KS9586SV+8Ff/b77773/A8rRld3uX7a0t6btGPCYuANwu9IkOoEgYt9pAbxtYrpS0Y7FcJsNGZ1UysDkra915T9uCpQozWgWxKfPK+haHDeOm6broUdd4JihfiwLpLUXwZkdihaH620dJqLKUXLFAJRz3LAVMLBhEsTRag5b1NKk1ha4wRoyQRWGCgUNjSg0TS1FK7a2yKKnqiqquKVRBXUyYTCqKQvplMimZzCbUexV6B2ZbU6qqpK7LYIBJavMQMNhg3LGObtXhnE1GHB+IUQo9wWnDT957l//m//Xf8+4v3uHRg7s0y2PaztO4NhnQiqLAVGLo2N7b59rVy7z1pZf5J//kf8sbb77Bqumgc6kgcD5/BgaZ8LOqKqbTKScnJ+zu7p4D8rlMzQl/8uM8+N/83fkLJSGeEA0xPNMPPuiNx4glVw0/33CJfJR7jZKRsteXvQ8kJMHgKPpWb9pU2f/Trz6CAT9QfqPxaAwCZF0NXlt0CUsARqHIrgenAymMUezs7LC9s0PbtLRdKEgbiuwGOhCsCmFjSYzKXDSxXpgx+FKxc+Mil5+/wle/802a0wWPPrvHn/67f8f7P/ox7eER5brFNR3Y0DZ62b4JGOVgIv/OZi86ZpmN98qvj5/FiMl4rzH78mBM03gP94v8e62HYdHREB26eQO3KIP3GevYsS9OTiSM+9fJOP/CA6Qc/PQbdVgp9Fa3qJBp3XPtQ58UuYmLPl9Q+eSJnw9dgP01A0uQJymEWqleeeH8xBHPUZwo0ZEtG/L21g5dY/mTP/kTAN5443Wm05r9/V3qusZZhFIUZMF6k2LJnXWpeKZnGLPae8POicDh31lbY18XpuDGczfY3d3hyZMn3HjhCoeHR5yeHLG/u88rr7zE22+/gzZKwicQ5q0YctxZAU5N24TNKqMdV32hNULYj4pChuHCzDebqPCksQ7yJB/bIlLAhxh1yb8okzdtMplS10Wg8BTa2vl8HkLDHFVZYIxmsVjQdh1GCw3zar3GtZ7ClFIHY7kIrGArrO2B4oOgBOfeGOvEWyP6iKXrWrztQjHGGucczXpFBElJSQzjal0Mb1DJqyBWVwF2kaUuuqKHeDj+rYLw1ln4T9+nIDkISkdPCCF2OCrnKnhDDN71wFOr6CkxCYhH61wZqMpjzkCkzDdKU+pSLM4BSEegpY1UrtdaM51O2dqas7Ozw3xri53dPfb299nZ3WF7e8JkWrK9M2dra4738OTwiIODJ6ybdQrvkk1Zo2Jgd7B8xUWgk/IRk0Q9XdewPlqjnxxKaJSRdpqgGCpUoF3uwwEToCGQxAZZEoGmj94Bp9JzBOj0YN6qPowiV+oF3JkUmhblnApzgaggO5dC61wExTbQpQblP7K+aWWTYcUH71LMK3O67wt83kcRHCaVdNBO70nXubB2XbpHDOtLZ/dKk5MaObZrA11vG4CkA9vh/ZSpqlHaoZUYJp67fo3Tk7O+9poVRtP1cjEAcBsVhTD80YI6nU1o2ybkWWWGsLgZB5nlnKfrHBcvXuL3fu/3+e6//wse3jvk8Z1jjj9vWK1XIfdOZIF1Dh+Wmvbyrwij6ZyDQge2UZJRKxnklBAUyJqUNVwWmqK0qDLkBirJWcNDaQxFpSkr8Uaa4MGJeWROg9IGY4TJsS4NdVlSFoayNCIry5KiLCkLAQJFWYgbR/dlNGKEQVEW6LmUI6hKE4gaPIVRlKZAKyEOSvtJYQZkA0UlebRGhxqDYU5jCAyXEGsjaROKkCJ1d3xQtWScQrFyetZNpRTGawrAUONsyGdRcp2zTVAOPZ1zHH/4hBe+8iLzFy5ycnTI4uSIzq6DzJY8taqSXL7t+TaXdvd5/ZWX+b3f/R20kr1OPKeBSS/tY3ltG53NfTnefPMNfv7uz/nt7/z24LsB+FC9viPfbQL7oxtvACzDr33GUDfcY+N1A/0l3DDmiG685+jleuImArvbeZ0oepA8OQDo32icr9S3l77wcfjMWtfLs/g+EZBlunbeSik9qdDeY7WjVFq8RT6QwhRa0oKc6kN3vbQr5jMJL5KSVAetcOsmEKtYpsazXi7oTCl5g1s1e6/d5NuzP+Drf/u3ePevfsR7f/kjzu4/QDUSGYX1IQpD5qrvm5/GKAcU8TNcZBLsz4uItDe09XJvPN55CF/UV58azhcNmaOxT06FCLx8ZEWUc3NvIT7LVxrdH0QXiftpLC68Xq2fOa/HxxceIMWcI+99otpu2xZlCimiWYhV3xEmh+5RdW61jptP/HswQTYo4FHZ6ZVxlcIcnHOUZSmKorVohKrXJOYaEdpdG/ICVFAkgwXbeUfnLUZJPRBDwc5sm49/cYe7H9zhyrVdLl/aZ293m9LUeAsKhzHQYXCdMDZZ7yi1xF/bztCWnlIrqc8SLD06FA8T3jKdWIXSoWRTy/ss9ltRlFy6dJGvf/1r/Lv/9U9pzjwvPf8Kn925Q10UvPTSy/yDf/D3eeedn/PZ5/dZrtZAUNpxNN2a1jayEJSnqEq012IxjpbpMN211qiCAdDtN2MhFzDGJI9UXMhVPaEoJ2kclZIEdwkLFDrZOIds17FuGgqjcF0LIWRscXLG4viUup5wfHyMbVdY20j8fQhnstnYy71ssNC7ZAVP1t4Uota7rG1QWOPydyEMoNC6pyklCo+o0HlQHmUUZRnAQ7DCCi1oT4EVWcqihddoASJaiScGHxjDIjVuZiHKlbJe+ErYm4QtKXCKQosSVRRFUtKLwDxVlWWo4VMlRdwYxWQu1uGd3W3m8zllUUnOzWTCZDalrCpmU2FHm0wk/6OuK8q6SO2syiJ5P0QBV5Kw7RzWdayXLSdH91muG5ZtKzkxsS/SNPfCMeql73NtZGy4SJsgAQh1Dt9a1LpN8w7Aogkh48mC14cvEsKKfAK7KdwWfW6co+XUepvWRJxD6bpszPK4+ji2+RyMhweUEYDnw2aTQIxSom5Gg44KQBLJtxHgFICa7g0ZPrM4J9AX3sfZtNUNfio8OJUURwFRYRNVXiy0eDobPWsL1o2nbT1Yh/MK6xUTXzPRHmU8N2+9yPf+7C+YTrcxRcUEIRPoTk6E/lv5QOluM4AXFOoQwJYbSKezivV6xXy2hXNZJEI4R2PRKJrVitmk5rU3X+LytX3e/fn7LB959rYvcvjkiNu3P6ZpG6LqIQaAQN1dGqqqkDBc5VHGBVBShPDRgrqqKKoSFwg0EsFK8KQWZUFZFSFHzfSGhSQzo1c3hlbn+0CukIR9UY+yNn1uMOTphwIbw5cCQUy/fnrvI9nnSQEKmlKch6S9wIf1EH5zgSnUBdkXtF25TTCQYYQ9K2ury7wXHSuR4WkNEphlRXk/ODrjvQ/uotyE+bSiKCbMd3fxvoNgfC1MybSeUBYVW7MptWu5dfMFOuto2ybkWnqKpDdGRdL27+1FR/FhEXrgyuV9fvrXC2y3oqynQbnUqZ39GIS5GIw98nlmmEhuIJEncs1QDgw1y6FHKx+bLpW/GF4j93iKR2H0d+7dIMi1/Jz+O4U3Y89yf90QGPa/uzQH5BCDVTDuMlS0Izm5QkUrbJiPBM+6QjtF4Tu0N6hC0fk26XPWO5w1eKuxnchphcbGOR3kqdR+lmdEWbvSPnmTrWtBSQ6fLhTFzpw3fvfv8qXf+Tv8+3/9b/jor76POXxErRwuePa7AHBkfROF9MAAHscuAgp510HPiOc69F9OVKFCv8bxijJk7AEdj3EyTqcnZGMU5Yc6f52ir3vl6QvCC2CXRZ8uc07CBr3HONgqZyHF4XybnnZ84QFSHnudu+BydJsz2Y2R7HiAc2tiLhjypLX8GdESHmmtI2hyziWPQZzA0fsUKckhs0CGTSL97sWrYIxiPpszqSf88R/9Ec52vPHG64Bne3snKJQlHsfp2SkKQ9us2N2b4elZ86QWzeZEO6V6S4G1bgAWx3amPIm+qjTz7Zpvffs3+NnP3uHBg/u8/NIrONfw8YcfgrW8+upr/It/9p/w4OEjbn/8McenZ6xWbWC5U4kVLXnenAsCvs9FiONb1FJMLvZ1tE475yB49WJOlCiklkXbgDokKZneBTIByauxXtoSQw2bpg33873VOhQMLMuS1WolFio3tKRkGnOvUKsopDOrSvhZhvylOAB15uHK57ExBu3FQ9PH0sfNNHrD+mrlRcwPC8I43iMHOkYZypAbYwoTzikk56Uw+MCkY0xBFSyjk+k0UDyLp6QM3pLpbMrO9hazaU09qanKkslkynQ2FatqWVKWhul0QlkVwVYULN7a4DzJAirgIno6LOtOCCG6rqNtO1adhJqdrhZgVK8g0YeKRhAc+zWSpMjaFa+OWDtVMkjILHfgbLrngP3SQ7RCp3lJUPJ8bxiJVlQbQnW8khwXFzfzCL4QYET8LgMtnn7+jD0bzof6X2m9RsbLnlAhXmOxSb7l4RTn13+2efUfhb+FkS4/t5+yvfEiV3a894EmneG5mcIz3sAiREo6HCM5jAffgur7vnOWs+UiUafvNR271rLrHSjHhIqrly+zWEjBTusc+xc1xpTByyNrGh29/+f3AeiVAwmzu8zjx4+Zz7aTtzlXyrQyaCVe4dPTU7a3t9nd2+F3/vZ3KJzk3ljrsPa3iWqDWMZDdkCg2VdG8h5kjvRAPoIJED3IRgBM3JcGozjq8+F38nohDEaF6J3U3/IvylWsyLH8GcMxHR75R1497Xs/0G/V4D3GSvWw7flYjb0lG7a3jffN9xWyvDjrCTIpFN4uCt597zbrtQdVUFeGsi6xCLunIQBTU1AYyTtS3mGUZX9/n9VqTdzZte71hdRi1Yds9u3zcTkAips3X+T2xx/xpde/nAxdGTOy7Gt5CiCMxj2bAU8BPfl3T+u7Qfvy8cim13lGus0AJs4f50Jo7wZPUPaCWT2ddLcI9c41Q/4Yvn+c51rFVRdkV5Q7PhRuDdfFtrpQR8oikRveOlzBIJ/UuRjiOtQJ8j7LwUWMVFBKhdxj0J0Sz63RdG3LhQsXefz4Ed///g/Zv3CF3/5H/4jnrlzhz//1/8Dq8IDaWymiqkIfKAGFOuhAm0DMeHzz2ZEMF9n542M8fpvumfrtGZ6lp90/v16pXOY8pW2+z2F2ztGsVtTlr14kFv4DAEj5ZIgLLke7sDlPKX4eKTTHCYy5i3ITKMo9Kt73xAApsTQ7P0fyMRxQgMuQiaS31McYbgk5mM1mPHr8iB/96IfMZzNeefVVZrMZZVnRdUKnfOHCHicnp8IghcSuF2VFzPuJ7dqM+Pmli6M/V9676zqU9ly5us+jh0/4x//4H/Lf/Xf/ko9v3+Fb3/gtbn/4c37xwbscPLjPndsfMZ3NqOopzXpF2wjdse06zoJlPM+N8d4PQnqikl/W0nfHx8esVqukSDvr8db3+RuZ0mhtC16KRcZ8o5jT4AgufNcz0iUgQbBmZ8pq06woCo2zkpekir6WQlzQ4S5ZOEz/vRTVNEmBj+GhAlp0qOrej5MpDIUp8HZIaBHnUNwsYw5XWRbCQFWWmEJhalII2mwmxUqrqqYqK4qQsD6bzZjP59S1hIeo4PWZTqfBCxrzrMSC7WLCtNEhJEa8CagOhcvINvqaZJ3rOFofYRd9+Kn3BMYzI8DFyybjvUvA3mbbXwQASaGPNb28S5tmT9ZiAwDrwaYAkQDPghd5nMwZN2EJWcw+z8BbbEMESoKr+o1eESzASuMjDS09w2L8Capvu4pgWgVv8/lY8TA5Ac8YRMffo3c89le+Xp91PGtDHCggA+VuCD6H52x+Xv+YpyhieTMG95GxIynK8p3DsepaFkeWJ2dLdg6PuHxplyuXdtndnjObTpnPZzw5OAjzumIyE2r6po25I7GAsRs8L75W3jeXL1/mww/v8NKtVwYRBPm7R4DedZbFYkFVyYZt/Zo2WHe98QlFRCCilAo1Qjy+zedZ1ddbGwFNH8col9/pf7lcT7Cz/93H7hTlKoZT5QjDR/Ae+2Pj7+cVJJfn1arhd9FKjFIBiZzvZ8b39YxmTK50x/Pl76fm0o7uEb2fHh/63QWVW6G0kaLgSmOt5oPbd3CEnBGlQRkKM6EoKjRSbF0hIMU5qQ139bmrlGUR1r8bhaBuzhfK+yFf26+88gr/y7/9t7z51tdSH+aRM7mx4tc9ngZgNrWrlykQJ9n58c/Dac+D0vH90rzVnDsvN9KmMn5JP+tzncbtHP8+lonjC31YAyLTeg8nAJa0zhwe21oanZd7IYDTzQxyY5A0Nlb5YKjQDqxTaKtSuP50a4ubL93k9sef0zWOV3/jmyxaz1/9T/9fiqMH+M5iUptDOHfWx7GN+Tx5pqzP2pmfl98nB7bjXP78GZv6YTw+m45f9v2mdoOswOViGUDrM8D26PjCA6Q8pAr6DaPr7DnK7xy4AINB32RlzYFN/ns+6SQfSQ+E3hhk5ZMptqUsS2znBpvJIKdACUucBybTCX/2x3/K0dETvv3tb1MWJVtb23z3u3/OZFLz1ltvIIZ0w3KxoKrndJ2jrAydc/hQsTg/olUyF3qbFpCiXzx5H7VtC8qxvT3j0qVd/Ou3+Gf/7J/yr/7V/4cf/vBHfOs33uAf/f7f5Sc/+Rk/fftnnJwt8V68OtZJ/RMXwtPiRq1UCEPyfrAopaDoDF0VrFdrFstF8oxpLWFkhSrTGMewMQGZVShmSsiVkWdopVJxyiFBgBSUU4S8mA3zwQT2KaV0b9ELczEWPIzMZFVVUpZV6uetrXkAtmK1rCoJO9MeSlNQT2om9STUsikoSsNsVrG1PWc+m2NiiE0p4TSTWmrb1JMaHWL1q6qimlR47UM71WDORsWw92jIIUnzks/krKVxLa7NwgadDYpRP8+jyhXv7YJHJ1emokch5q9E27nED+sU7pKsT17CECPrVPTKyHUOYU/0mZInIEaFUC6tCUm2Q2+kQkhRVNgMh8YolfZEaU+XFEwXLO15zHxaM3k8mdw1gDMlRSGVVAm3bqRQevBOrJfKR+XDZ0prAAXhJaNXCXV+A1ERYOnNm2G+kY03v/hZuk+23s8pTAMF57zyk64Zdkm6d7SWBwQ5sjzn9+6vSYYj1VvbsRJaIYqhAl2watasVwuOnjzm8GCX61cv8tz162xtbXP3zqdU9YR6OkNp2RKbdSvFktEMMoYHYKI/jDHs7u5ydHSUDDbnIxDkvWIY4mq1pmlaISAownioMXjtlfoIwAcgyDf9uIUnJDDjVJr7CfdEWe19kl9xHUbltQ8Xlf8r1GDs8nDS/P5pbpK9wy9RzL2K4zxUXJVCcjNG58daYIO5p0Yhftkzdcihim/j8svyq6LxIryI1OOLgEhkjBAnCQBSWqN0wQd37vL44JSymknUX2QqVR7vCjwSCukz2WY7y61btzBG8lglHzCs7w3ddW7PHa3DqqrY3d3j/v37XLlyZeN5+c9B/48+6w1Uvx6gGl+XXx4NTvm/X+aZGuo6m4HNwOgYZVlmTJKPIlEQo2fml0WDVmb4oJ/XLnO/eeclPDuuo6wMDC6ENnaRsOQ8YcAm+RrfNTfCpxB2HQqs+5CDqDWOFmXFQHrjuedwquCjD+/yow8+5NZXvsmtJ0d8/Kf/E2pxRuUsGo+Vqmk4xSBcbpMcz8Fu3v68oHB+jMd0DG6ftg+Mdaf8+WOSiE33z88fr4m87XE826YNLKC/+tz+wgMkGDKe5XUE8o7cNOhPEzBj1B2BkPfiAco/jx6kTc+IwGiTsNikhOQWSKE/9UwnU4w2fPe7f8ZsPuOtL7+FUpp7n9/nvffe55vf/DqTyZS26fBOcXq65MWLz7FctIiVvaMoJQQrT/IVpH3eqjJmKMmn2niSrlYtRVlw66WbWPsxX/3a60xnFf/L//Jv+euf/pTP7t7hy1/9Ki++9DLLVcPBkyecnJ6yWq9ZLpc064b1ep3CqCL1tPc+/R3b17UdrmnRxjCfzAdgpiwrcGQV6vuxkMKoYuWLIQ6SByNAp6qk1ocw1JXUlTAroTxlWUiF9iynZjqbUk9KnOtAqeB5qSlCkv5kMmFrawutxRI0n89Dbk1JVUkxz7KU59d1lYDapKqY1CFPSBm0KVJMvVMrIOSPZBtVX38p0nVHCuYl68UCa0N9iWApjXMaRHGPSnm/gcjG4iDdK1be1j0Paz+Xo8LvwVPgnEreuFxIxgKgqCJZj72LZAEdDjdQxCKQ0oBKTDhkyqPDBcttfihPqLczWIVpbSqkrkTOyNavSyVFhpVKnshIbNJ5JyyBEY1lzzWJTLlfRulvjdAMhxoxwwTmQKIQwGR/LZnV3afHiSrXx7Ofk1kMw1/HG894E0vNjZbTkYITk1/Himrf1z374XhD3BSu0YPn7NyBIiz9oJUSGuSoRHgXclfEqKFRUrYA8bhY51Gqwwe2QIXn0cPHHB0ccPTkGBvqcy0WC+bLJaYQxrXlYhm8nCF2P/Z3AjnD/nPOUddSmLVpmgFFf5I1UdmmXzvOSZ6i6gzoUUkJH9eQXO2sS1NBfjpQHefhZugvYblI89Inee4zUKGGyyTN4fNjymDMnmbJzcEV587rFdL4w/fPCG2Ka3EMpGVLCiBybOUfnNcDftd/yLl+GuzHEZyGdqm+dACmxnZw78EjPr93n5OzZUh91zw6PEaXU9Ax5zE3mklpDRUEp9bgnGU6rdnd3duobI7tG88COTHX2VrL61/6Ej/56Ttcu3ZtQAS1aZ2N77MJoIxlwvgYr+vhuSGHUsV1nbOfOjYZaTY9v/8nUQh9CNoQIBUxCkMeTQ+IIsbNvOgZMsrl/uBNve9lW/Z+nhgNEN7dObosT7RDIk69t5lh+7wi/yzZmxvrwy8yp5xEpThvcT5GEGmmdc2NK5dYnC74/P4x7396j1e+9dssnzzg83d+hj49ZqJDiHcEiSMdc6irDveO/PvxfB3/vglYbTr3adeOnxn/zs/fBOh+2ZHG2Fq6tqX6NcLs/oMASHlSvoSvDQvHPm2RxmM8ieL9ItDKQUUs8jq8ps9XGE+kMegae6RyhaFvj8O2kmi+t7fP8fExjx8/4oUXbnDt6mVUYfijP/pjLl28xMsvv8rVq9cAz/HJGUoJB5IxId9DqQEwShPQ+4zBa6TQZpYO2XeGbvP+MJydrpnNDK++9hK3b9/lVXWT52785/zg+3/FX//4x3z3z/+Ss+USrSVBuqxqtNE0ncdrgy5rumYdaKolf8ZZR1kYqnLSP8kUQiagFCYSEWhFXdcoxMIcWc1i/arJZMLW9hYquMTnsznTmXzfti2F1synNXVVizdmOmFST6SYX6Gp6orZbJZq0kgYW4nSJrEWxXErqwKjI9AQYFkYjdZlUMTEuyFzNAhjJyxc1gqAaboYHtj0eSze45Wl7YQAIIbbRBAxNngnBcyBwmTzMD7XC3AOSe/993EOiAEmUk4754Q1LoadjJWrcJ11Hdb17YntT8GKwXsXN6sIkLwSD2f+LsliHcLtQIBP8rR4sZLlc1Jq6TjwOtFFx/5wRE+aBNLI2u4SCJB7aDob5n/yFslP612oOyEdrTKPgx+ocn34nvR1B41oZDExvg+PUygfPZeZwUaP1xgJNIIw/oxjzMMp/ZzgvIKTH8O/BWBH+Tn2xuchG2S/jwFSlHku5AvE3KixhTVek8sipSS0ULmQgG7Fe+it6wttO0sTahopL/mB0j7LYrUIYaYlrutYr1bcvfsJH398m7ou+I2vf4O2a2nalrrtKOuKpm2JRuwhCMzWVG5oCbJwf3+fo6OjVN5g82YeQmiV3C8ZJ+xwfIbdKl4Mb+N86Ik8NoOVHISGcSQ2XfXeEvoK9fH9hqruENzn9386UMr76Pwx2MsUA4+PT60briOVAZjUNRseLfJDPaVZ4w9HIMuTQJo2BmctWhvufvqAn/38Qx49fizt0waPRpkCbQpMCjVWAe/l/eL7f8qjlOXG889TVYWUZCDKs2x0Bnv9cL1u6kfvPXt7e6xWK87OzmTPewbA2XTP/Pen6UNDr85QYR3v+3Gv8L43iMXzcyNAH4qWryM1/FyJPI/RGUOCIDCql70R3MTvepn8dCAYZ038WqfoGYhjEn/3Bdm7Oaw1aS9oOmGo7DqVGDRtjFAKZVnyd9sUZhb7wVoLYQyVD2G+cW4ihrxCQbtasTMVkFTX23z8+REPTpd89e//Y44PT2nufIhfn2GUS6ygvwxkjPXcvK82eXw2Xf+0PeVp1+Xn54zRm+73NHC/ycnR/yEepKPDo/8IkMbHuINN0ec1jCcBDK0n44kc84P6YqibOePH94qCIYKoHgCdF4hJmIT/94pCpqiiKIqS2WzOg3uf853f/g7XLl9ld3+XDz/6iLfeepNXX32Frm159933uH/vHvfuP+A3vvXbrJsWbaQuS6wzES3V3kW+ftlo4oY0FqZ9u/Md63y/4x0nJ6fMZlNefPEGFy7s8vDBY37vH/x9vvnNb/LJp5/x6WefcnBwyOHRcSiiKQUGYxiIsLg4tDJUxrC9tcVkMg1jJ0rbfL5FPZngvbBOxVC2yWTCZDIRRrS6Zj6fUxQFRVEwm8+ZTCowlqqW/Jvooi8Duxq2EyrcLBctt2rlwj4CcI+Rf9mmt16vSOx0DDeK+C+vWyPaTz/3olIJhCrzUWlQWK9J6SoCa8LleqDUyvk6bcZDb0MfQoYn5d8MBKqXADbre+DjvEN7Ug2IgInC97bfSLxNtKoJcAcPl1YmvmBcNX24nerbNVynPr6w/GWDxdBHQbyJ9cih0OKRYqj82ZhvQP9cAXRhbMNIet8zXPVrkXN1xHow169jIK2tNFpp7kibY9FBnEdCAEeKCA6fAdHxMzUxqTsqwX1/jQGNbNzh+b5XMsbyMHazB5Ttw1rOKVTRYILCBGHlfQxy8Sk/LczEYNWT+jxN24oX2Fmcs9iuk6LFbct6vebs9JTl8SkurBFrrRSeDrmGeCv02G0bvMKBtbI0NM0Sj6eeTJG8EcdqvaZtG6bTgr2P93jhxZs0TSOGiLZFo1iu1kxnE0odlfghdBgf1jquX5eCsdeuXcv2jX5eD7tWB5nbEcOw0uIJ49OzCkq4XwJHgeqdFApGkhl4H+iPw/yJH4d38Mg6iSHFLjxzU4jmICQte4wAq1FYdv79s2yOA+tx7Jd8PW8AXiqESwb5NgBuOR5LuGQzcHPO9dfmACzs35KDr3EOrNf81Q9/zAcffU7rStCVzPFQcNoUBSiN0UJ77ulr6A3Fkxex6zo0nlsvXg9AfpjXllrpNwGRODX69xIvhU7r+sUXX+TTTz/hpZdeTv0p39EbEtJj/GAuRmNY9PDGeeizn3k+Z27wkPblE4VkM01rIM6NsAfKNivgR0BD6P/IpKhNBpII9eKiB6YHTwoXalLFNpG8kLEve5A01LN6UNYvneHRg7jYdzFnWN5XJ0It7z1F6UOkhpTxaLsO23WSLmB7T5PzTogdAnGPVn3R7NgWkAgYYduzKeVBayUFtDU0tqUynpVdcuXiPrpsWDTw+f0jDouKb//eH/Dd//7/ietWFMhabq0bjHUOTPPP8v7Jx3aci591aN9n+b4Ql1oCmkMZGk9J9P1hqmwC688CZU/7vtelheTCuY66Lp95n/z4wgOkqHgq1Se4N22LGhUdjAPxNMAUf+bAJreC5PlHEQHn4KrPT9icxJaTB/QT10sid6BCtXkIjodpNWVSldRlxT/5J/872qbl/v17PP/iDX7/7/8eH330EW//7G0++vAjClNw5dJ1dvYvcHq2ZFrr4LYu0GiUKzBoSlMGhVVLmBUBnNC3bVN8qM82apFH4btw7mKxwhjDdDrjpZe3cZ1UVX/jy6+wWq1omoZm3bJYLumahi5Us4/5RaYIBUaVFornWgqveoTvvqprjIkbKMLWFkLflDYDQR9/WidEECL8faIc9l4489v1OsTz9wA39r1YwIfAKAoGHwR1ruTHwxEBc2wp6R6xH6PXIdvLsLkSkG9gMjOy+R7fb7gBbmYe7BWRIRByCJFOr9THcDJHZCETSS7FLKWPnNM9IUHWhuiBIApA1W8yDliHUn8wtFIBGK97RV/14+A9aN8THwxZiTw29+Lk74ZDyKmzeHXAqwjY+tCanPZUqz5ULioRCeD5CEp9psTEDVWAT8y9SrJFxXcKFsOkSHhU16GcDwpsn3sCoLSm1WGTC0OkFKl2SoHM9c72dK1xbkevwdjQAZGuVs634Vwp7OnxoXBolH1tCG1tlku69Zqu61iv11LTq21ZLhZo2+FCna6maei6jtVqFeaBeAzbrg11wBqatTBH2kZCxppmLZXPbc4gZtM7DJPaRWmKdbTKQmrxdK3H6Bl7uxdE6SoMRVUGymDPhf1dmmaBdQ1Nt6ZzHa0TFtFV17FwLTvKUmqNdqJ5OQzDxcmgHZcuXeT99z/A84aMZabwOH8+VEXkQBG8R8FbF+aF9dHy3FPiRiWKQnISRCGMwFfa6OOkQNE5J/lZ+KC1+uCd6ZU+pQKLZfRSDXSfsULT53PkBiA54pj0oYCb+mjwXVRokwadnsQQJGUgPJy46RmbPuuBmwqkCVEGZffw8pnR8uzOaf7ihz/h/Y8foHSNLkNdG517N/q1AZLbGsEsCkmQB3z0GHrYm0+4tDXH+y55q9NwZe+aJJkffo43mZzJL/TcuPEc3//+97l16yVc8jR6JPQ2yOQM6seSeEEaZ1T8Qw/DJq9Dfv/x4Vwffpwr3WKEjXNA8p610RgTPSsm6GhmEKoo3/XPUSrOL5XKUuSK/bit2ewYgsJ88NO947zowWuvI4YxIOZVKWKxWO+l8GzsE+dFt+g6IZxK3qUYmeBlj3fWCS162A96bCyhmVoFbcB6iabwUk/QOYvX0CqDVgW2ha3tLeriEbMSTs5WFHs73Ppbv8mH//P/TLXS0NpU2Dmu4Xy/HaeN5B7+MXjK+0t5mxoeu0ihkjEi6zYMsVyJQqkidb/KxizVA81HbgNgytu16fe8jZ3t6Kzj3v3PMHu7G+bG5uMLD5CiWzZXcPO8IDifHJdvYoOYcIaKZq5o5Ity0ySKgicHW2PAkYe6jfOk8mukfhLs7u7gnOPtt9/m6PAIZ2F7a87v/4O/K0qENnzr279J1zratuPajRtobWjblu3tgqZp0aqnOY9Ju7GmTWTUEuTt0mY/FEAqfdZbD6JZILyz1mjlhYp5tQ5eIalALSxqW0n58p5QG6pPHjZG44lhSbJwRPD01uTleinPS+AhLviQK0FeZ0ZuEmsUEYrOpraPAYaKr9aHXAUtJoAlFxSVfuMZzAty1T1nlxrPlxjOFK1afQNcprWMPQFk70w2RlEZ8tnPXMnJJVAq3Bnf1eZWzKhkgyVQSdO3XSyUXhTiziZlPwdk3vcW6pwqNfhEMprWMaDM1IUEZlQK/5R+dGmTTONFTs3sklrgUT2ATd/HvgmCOmuHj6DGu9Q5LjwzBy55n8d144G265IXIFKNp40mvlucLwGIKgR0pTHzcVxljkYK6WE8vg+KjotwMuRJ9aHFEXznsi1+bp2lWTc0bZPy+1bLFe1yQbtaslguaJuW5XLJ2dkZzlnOTk9pm3Vai10n3h+AznepT+M7S/HTmJ8gLFP5WGul0V6ldds2a5wTgLS/v8/+pYtMplMmkwnb29tE9sTJZMJsOpcwurpmFsJoQfL8JvWMojBEtm6h2T7h9u0PWK8biiALtIk1TmTlnC0WOL8XwKXMqWQCSmtcrojvMZ3OUvHx8fwP7Pvn9h3Zm+Je0q8LfLCWh7W5Wi1DQe2w7kL+SVWWFCYUTTUG11maroNICKNUKFjah84qJeRBvbwLc2cUsjdWNHMF6vznbnDOpuNpxsfhSWGl/hrW42cd+aXjPb1/hkrbl8fz8d273P3kM0xRUZY1sJkdcqyY521OcwXJW8R7nrt+FaOVsMkmzdFzjv46tT3XPxScA9nxO0ddVxRFwenpKXU1IWfBFRAdfOdRf4kyJTGzxeb0hsR4fdpzfN+nTwNIsdh0rh8loKOi51EHgKQoikhsZM7Jtay52Xj27bMWCadNRroBvWi4QfZu/U0Ge3k0ShL3RnpjmbW9F0rrnvSh/0m6uVLyrkYVFMZQVcIUXDtF11natg3y1WJtR9dpOtclg6uzcV5KOIZ1Q6U/9o/WCoyK1SmlhAAdL77wPJ/e/QGznR0OV6fcePPrHN7+jKOfvU1VeLCWDMpsBEHn5vEYRDkHSqf5p9gMXGJNv9jHOoSY5H7n3tyRD4/q//Zx/orM9c7Ty97zc+9pcsIoJTlITYt6RrHi8fGFB0hwXmDLwJlzoW45iIodbUeduWkijGNJ8+tjzaPovRooSCMBkuoi0Qvy/F7xp3ifRDHQWnHlyhWWiyVtY/nS669zdrbAaENZVlR1zbUbN7DWsbWzy6rrEsNSvGdMOB8Dvf7vPgTnPEgSoR3fKyqJ8TtZ+G1SlvB9aE8vW1SyvnkQ0OIzz4ycIn0U8kJifK/3rlcso7IYLoihkIAUvo1tDop2zPcZ0KqGF4zPiJ8phhSZESBF5Sanj43q8eD0CCCDUjIESH3hvn5DHCIYn4mV3AuQz4u8AYP55yPJQWo4Q+EehJfPrEjZ7VKB2hww9Lpf+DugOq37r7L3S9gl/JLo2vHYfLNS4zU22tnybvF2cF5ufRvS+fahosIvlM+rfnOISszY8ikAzBF5KFw256KHNM2bpEBIeJQN8w3o86o8af5HpSF/vbYVtp2u7Vgul3RtC0Ee2K6jW62kCLG1tG1H2za0ITzNtusQ1tHRNK1swq2EsMU8tdhOWftxs7Zi3bQuJX5b24F1GO8G1xgjcqwIBXgBYWM0GqcUVV3hzIRiUmK0oSgL6rpOtcLKekpV14lhNMpGYwzKw3K55OjwCbd/8QuOnhzgreP6jet87Te/w3xnW/IITQFKihuKQhULFQtzZdrUPZS6FC+KloLJdVUxnU354P33WC7XTJTUH4oUvpFA5exsge0sqqzI1w2DLX44P733bG3NOT4+Zm9vj/x4unwN6ydZVlSYV5rT4xMOHj7i7PSU1WrFcrkI7HdrVssVtm1TQefZfM7e3p4UkdWGxsHe3i7PP3+DyWwS5qRCQjltstL3SpIKIDpbORtAyiYAlCvtvwzM/E2Az68ErH7pTcAxvE9/Xw9aIiaazvHuBx9S1hO0LnGB4GdMELDp56CN8b5IiJ1WiqvXrtJ2DX34epwPwz3+ae+Nt4O+7l/N4buOGzducPv2bV579fUwzgGABZkWjVFiKCKwo/WAwycyBT+YnzmIj6/lR/tYPJzrCzCMIwIUKin4ZVmgjYQ+xTU8pjgf90/8LIHSWBYhgJz0M42Az/aoflTGoxW/T8ZDeZPBO4jhOjKhngfLZO88vk6HQullMNZbZ1O9xaZTdNbRYekysh+f9XcO7GUsRO/SXmG8RfuWSkudw7fefI2/fuc221cuc2w7Xv9b/4C/+PwB/sk9jHMDXSI/8rU7HjdC96mwjw51k95QOAZWT3vGL1u/+bdJo/ChH4h9cL5OKbBxfeA82ige3X/Apf/oQRoecVByhTmCFqWGIXH5Ys/D4HIAkIfs5Z6f8WCNvUU5kNoEeiJYi/cfKG8Dhc1T1zWHR0fU1YSbN29y6eJljBaLhbdrvIf5fAvrPNeeu8HZYslytcJaR13XSUGVsDShnM7bnAM/HZRej0oscnm7fKQbRurbQGQC83TBOp1f46woXHGZek8SMHGjjp6h1D/Bsj6ghM7pnxWkUKwIcLzHuJjoKXk7sillIWBONpfMLBEHr/89HMOaWoR2brBiBHtUnA6R6l3c8kNGNg8pfGC42QRBFSwnbgQGBs/L/ow0uC4IWBfygPLrooDTgUJUlO+4scTnZfeP/eZkg419LePg+5MI7vPMAwoqGPB8UlgjeIAQPpavu+xcsVoO10xUYOXifkxldsb1AZ2LFN4hnyrcN4KWOH9iTLnEhUsoSlyr/XoDRR9GkPp6ZOTw3ifvQQQZzWJF1zQp1GwgUzrL4vSU1WqNtZbFcsFqueT4+Jj1ak2zXtOsmzSn4nPEq9J7pHwGbKELFtowRxXJ4heN1rmiZ4yhrErKUCeLwmCMMDOawlAUBXVdUkdyEmOYTGrKsqKsS/kXCgOXhcR2l1UJCkwAQHEMxJAg9MhqRJzjCXWugNVyydnJMV55fvLDI/Fg49m9fJmimlBWpYyNaDQil3wvuwhKiAlsdrqqMUpIUYpCwne2t3fwaJxVdK2Tf4EExWiN0pr1umG9bnB1RaGDQkseQdDPy3yOXrt2ncePH7O3tzcEQX4oV/N540L4oAsFqDWKT+5+yg//8gd8/skd3v35zzk6OmK5XCYrtJIFmOZpUsa0xitFOZnzpde/xLd+81t857d/i939PVTwIvbjYUKIkCi22phMwXz68TRgs+nzoRI5PGfTZ7/KfTfd41dodCbeh4qaePccXhs++fwBy3WH1QV4Cdcee4vGiuC4TEdso9aaQH7J1nzO1tYcvMVal+ii8/bE63qRnSl7SX5u6Csl82p3d493332PV15+FWt742+UzSiwYc9L3unR/JTPg0GE/jvoyWAkB24IpqKM1cH0P/AOZ7lFMX/bFJH1Lwc0fd8NjQnu3OfJiKwyoJb21tCHGWDqoyjk89wYN/guXhf6Il9XBjC6D/lL8yJYz55WZ0trFfIii3BvQ10WWOdYtw1N29KsWzpr6VpL1wXWWYZ6KJD0Q68MJoSzFii6pqEoCi5f3uPC/TknyyXTrV38nuH5r3+d23/0b6TgvN0MVJ65Bn30jKnAxEmcEJIGkt0j31vGDoahHjs2FA8BWvosts17YfULOvtYdoyvzZ+plcZ3LYePDygeHzz9PUfHFx4gjQcgdayXiVaWJUVRDAZyLNDjMbYaxOOZyFs+JRcYOQDKmfByQdt1XaqhM57E0dr6J3/8J/zdv/N3+cZvfJ2qrPn0k8+5f/8edaH54L0PcCg6B43t6JzDIiE/ZSgQGy3rcfHC+XjUCAglaX+TBTS+H+ncyIZmPVIzJ+VhuaT0Kp+Lwz7mOloIXFgQ8acskt5la2N4UxTSYUxTLlESopHkoHcsp4WFgDvFMNQkvksS/OEQhSJ+Lhac3quUbSK5JSn0qw6go7df9cKhp+PO8Vmw7sb+Vj6VvRkf/dwD5VTgYVCJ5CLHfmm4vKfpugAqYp+EflHnlb70L1wfldP+3eMYycfOR6NCNj8iUFZ9Xk0MGcr7fiAcvZMwAi2JrFJYVgr5qozJL64brXUA4P2Ydp0lssd1XZdyWQAaa2nbBuc8XbOmbVas1ytZm84J3bOzIR/JEj2WpjAYUwRviuTMnJ6ecXR0xOnpqVgGm4b2bEG7apJHJnkLQ6iChEmJ5zCGsKS+djmToIRUoRW+kDpeUvi3wJgi/V7VJUUIrSqKgnoyoSpLyrKmnM4S3XxRFJRFITW2igJdmAE1dfI8Go0yRvIQg9xJE0rHVdQbOCB4dVCSx6bE+m58T27jRx5bRZANSDadric4pbn5ymu8994HNIsFnVVsbe9jfValfiBB5P9RfpiiJBZ+7vDEkBDJF9NoU1AUFV3nMR006y6wRUY5b2hWDcvlGjufSXqGGi6/sRIXP9vf3+ftt9/mlVdeGa6dAZDtzxcK3gDIQy7LydEp/+Z/+J/4+dvv8MnHH3J2dprCGOMa0gMjjhqsNVEsjjh8/IjPP71L0yz5+re+wYWL+/Ieyob5KyqA7SxKGbquHSpA2fHreG02KV6brt+U8/vrPm98/TOvGylTcS+PSphTnk8+v483FblXcpOnaOwpOPc9BAVbxur6dWGTFSISTcYBQ763bjKkyr2fDhQlH8qJV0Zrjk9OmM+2aFsZz5gD7SAQePSAIifriSHe4zkq7Y4hwEAiDMkBlcxxo0TuRyAU+8cYIx7lYDjJleq8GPvY6BS6J8nC2EexbIdP5/ZAKsqVQW9tWK+blOlo+Eznhf1OKTAKSmMkZFcN0yKUFkrzTQZzHdZmXKJKSVicMZqiNNRtSVu2tK1lvWppdEvTdrSdhElHY3GvIyqs0mFv6kPI8R1eed566xX+/Z/9gEldcbA44dobr3P/vZ/T3L2DZn1unm3qj0E/ZefHNvRAfhiNkq/3mN6Sg9r+Ob3BYewNGjCc0gOlOCBPM6xs1r9lqyq8wneWrdn83PdPO/6DAEgRgRtjaJoGkBwYGA7EOBQuV7ziveDpg/CsjSB+H9uTQr9GYKvruj7cZCR0Y5vipPvd3/17HB+d0DQNW/M5Dx8+pCxKrly+yGw+42y1pvPQLRa4tsEpnxQdURrF0lwURVJ2x5M15iiQcfv39WZgqOz3Xh/vkWf7PqSu3wvUCCAhVqCQH2SzXJ8cNDjnEwNZHwvbh7lFZqce3EEUkT4wweiQ+xAtEuJ3GCkECXTl0E0OGz05gWY3gpvh5RmQULENYaP1uidPiiAoAYkeJAigjvcOpd687yt5D/ouzElxFyTOhtgvsadzFiJPoKn3UcWNQlv6Z8x2lgu4sbAbA5suEF8o1Ycx5mAzWf4G9yadI+tLNlDjY87TcONsmwbbNokJSCE5LtZKLs16uUrkAE3TJBIBby3tepW8PLEGTtM0rJYLnG3pYigaveKeweA0TmkO0ofSxry4nLRFBWWgjx+X9V1O6lTQtyxLod4Pc0I8HaLYrNYrPrn7CScnJzjvuHr5Gt/69re4sL/Pzs4OJoAdUxRsbe+wtbXFYrHg5OQkKeDaFHSRGjq8RzSKODzeZJuTD3mD4WcYyKAEDMk+BOuIop4X8dTK9JTkWqORNaiNwWWbXTwfFWocaShNRdVYdrzh+Rde4vYvPsAUtcyjkL8QUFkvi32UySJHbCdzqfUtre0otKbQiroo6FTL1nTGhf2LfPLxZzjnk7fIdsIoVxiD0QVnp2d0ezvo0D8uyYTNCeFaw/b2toRGdt3gHO8g9zgnWYWn61oJiWw6Tp6c8hff+0tu/+I29z69x9lySRfkpyokd5OojOreAJLnsymgKkS+Pzl4yC8+eJebLz3Pzu6MS5cv0dqOo6OTkBfaMJvNqKtpAua/yqGfAqTiuonHWJkZK0J/k+NZSu7TzpMHngdjKhiRFIrD02MOj09BhfDRGF5KL3vGe3a+52RPBnpjqMOyf2FPiEdcg7UFKVw5uy9s7pP+3psBkhCCyFq/evUqn3/2Gc8//2JveEMFA0SQZ9keiOuBTnqPCDgSkJIeSEpyDpAynUEBTklkSh46G3/PjczWhhpmkTxEmUE/9L+raIMbAiQdIgIicKIPA4xt6VEYQ09E+tL1skQu7EtrhHZ0XZfkTKkVvrBYWySgEENVYx3hAWhKumL0AvbAELK876oMdRcdVVnRth3LdcOq6VLkQZQnYlBRKGsC8nJoK+DNe40rGnSh+cbrt/j+j37MV779be68/wFv/vbf4wcP/iXGNufXxS85FL0xRisVeZk2ztPc0B/n/5jYLD/GbM7e+0w/7EuXiAHc4fUwRSW1Md8Pxu33DoNie77F9tZ/BEjpUOG/uMgie08eygZD0DMWgOMjX+T9II3R71CRiKEkUcBYa5OHKD4/HtGrFPNCopIePV/GFNx47gbKw52PPuadd97G6JKf/PgnvPrqq1y8sId1np3dXXRRst11vPf++0znW6yX6/SuzjlMUYRQFGnn2LIGge0tLz6XeWgiQErvl+VYuBDW01tjonrJqDh9b/2JZ+UKs/RJCIsL6zQmcscNQGhTw2YQgFM/RiHZX4OOuTI+U9KyJM58PGOfxN89pA2233gIlv50ah/nni/W8G4qhHvlYz5OlEw5KVEIeMBwjhkont95mW/xuojJUu2f8AZ+JNEGylsu2BSJkju2D0L4nEdiNBiug/gMRZ/TEOs3+ZA745yj7dpA5GD7e4eNz2V5MJ21rJYL/HpNu16zWEqIaNM2tE0j4WeNsKY578B5bGtxndSEsq6l7TKvp4vt95KoOgh59QHQSX9F6ngVWKuUUmGdiOelKEuqskQbTVEIuKnqmsIU1JOaqqqYTqeUZQmFDnVSCin8G/JjilK8NjqsPQlD7ZnzPB6vNW3b8fjggHJnmx/85V+gvGayNefWK6+wt78X6HCVFBguSrSpKMoS3TmcXoohxtmQ7CsKcwLT4d210mBMkI8qyUfvo/lAgckU4ig/MqOJGG1kHnpcCnnzSJitUhISYn1WNsEP10nXWbw2iFOxAFPylW98i6vPvcD1a9dYrhpMYRIzFMQQMY33vTIS5XrbtOjCSA15JZbtSWHY255jCsXLL9/k9ocfslw1LBdrViux2lpnKUuFKTSnZ6dSFmFShXmS0UTnCmRYdzaEqiqlWC6XEvIclTobDAEeDp8ccnJygu1aTKHBSN9NypqtrZoXXrzO1UsX+fij2/zgx3/F48ePaDNmz6IoqMqKKngOxXtYM51OqaqKqjBcv3KRK9eucvX6df7W3/3bVNOah48fs7e7j3OaqtxivVrz6OFtPvrwDl/5yleiON9wROWj/0T2KZWd38vOPNTI2ZBvl0K187sylNWjvIv+8Nn/h98lZTie6ftzo3Kanja6f7xWDAaGzz6/T2ct3kTinuAG9T2hEt6HmjRq2Fe+NzbFD1yIvNiaV0zqmqZZo5yEzUZyG5GRm3WJdLe432aYtLfgh2dZyS/e2trh7TvvcOXqdUBCUG24ZTJMxX7yQpMd94vUrrjvZM+Runw+7XW9YYs0N7TWgZI7Kr0wZqSL8o3gje8lUc/wlp6bNtlhSF/UsRzCAud6pSHcywfd6emHyt5NwmrDDqY0JkQsKKUoQs62GOA8DR5tHdFDksCQ9akPevAU/hEif3QsAJ4BAy3PjCRVReGobEVRlRTrjvW6EOblNYEy3Ik89xaMKDfWO1o8Xiv02lECly9sc+3iDh/8/KdcuniNstzmws2XOHnvBG2lpIQNdc+0V+eMB5FNTvrJpvlunQ3U5AFsan+un3OZmNZ1NC6pOH+C/AgfJH1LATr33IbnhJ/eB7r1zJA7xl25vwkkBNI5x3RSc2l//xmzYnh88QGSkppHOkgWRU/VGb0xuYWgt2D3Sv8YPOVenNHT6DeSzLMxAFK9EpIruvmz46ISy47cV7w4ApCm9ZRJUYKHL7/1JoeHh1y8ss/Xv/EVAExtOFsvefjkQGKdHajOYlcrTJYfEhd49CBZ79DeDRG7cwEghbh1GznMotVGpxwSa2MOkhzOdz35g1zUL6q0UIYbn/wx7GuffheQEcPoxPIcQYbH+LjZ6VAPJniVFDikPy29wCa9SWxBWHQuboy9skMAp30bHbEGRVTWBkfaX3o2snzTSRuB6sGLDjS/Wpu+bkVob+e6XljRb0xeQeN9AkjKy310sI5Z+vAtH0PTsrk2bLPv+zbLG4tewa7rsE2LawTkrJt1SDTtaJsG13W4RohGVqvgpeksTdtguwZrhQ7a+8CoZB2pGG4ENp3NGAotqm1xrqP1FkuwOkr8Hs5ofABzhSrQDgovb95WWYiHVpRVkcLOjNFUVc1kUofwtFLya6oSXwgddCz6a7Tk6BTGhNAKIUdJ3xtJiF81bSYTfGAza1mv2zA/BBT5YAkEMJVJ9S1yA0S0KnpT0mE4swU3bmre/9l72NUC0ExmW6AK6umUuqpTGM1i2dKeLCSfR5WgJRHadR1KiYe2l28B3OgC0ANFVxGTYcOaUYoubqBePEvOK7SRmh/OKrQuQvFgjZBaSF0QpaJRJeQReqHyjgq2czb0icLZQsKC24bWOtpiws7zN1kXhoPjM7z3ybDknZPftUZpCf0zprdGamNwTmN8gTZQaEuhPc9dv8S3v/k1jPK88dot/tv/9l9xeNqwWLSsW0djO7YqjVl7lu2a02aFmZREb4JRGeELDPYI72Qu7uzucvDkCZcvX+6NYs6DU9z+xcf85Ic/4StffotbLz7P7s6camYwpUkEOg8ffcY/+k//E2zbcfj4iMPHT2g7yT2K0QdSEDSKI5GNdV1Lm2yH9y2rdcvJyYKf/PCnnJytePDoEQ8ePEHpKZ1tJUdROVrbsrN7ieeffw7vuyTz+v2QlMOSiQtRYlB4enkhcys/UZRbNnhGYhTDOfkZHzD8ICnlQ+/VEJTEcgA50Jd2Rbr02LYAdpUiEBDz6OAJ2iis7yScVYdC1i5a0eX6HiT3Cl/elPgYeWbHpf19XGCH1IBzbTL0RZDoU9i7TnIk7wKvxIM53ktCz2DQrBpLUc1ZrC2nizWmKHBAF0KMk2EyhMIrb9HKCohy4LzCwgCo9jpMH34XFV9pukpKf1lqSsOg8HXsIOccHVl+qYsGzuCxSQVaxVjmwxxwTva0CMr6w2HxNNgeAgeqSOe9lEoIG3HupYheJJ2mmMcbA05Y44zRwZgqpR200eiywHuTdJwuRGN0PuSvh+h/AdziWTeBgAI8hbIY4/CZUVwTGIRjSQbVRw8Y4yVHq6oo6gKzWqELxWq1om0dtLIPKgQ0OyWkPr7QGAVad6x0yatvvMEf//Gf0W01rL3nhW99jR/dfY/J8RnGO1rjsFozsRpsH+aYDb5EMqBDNIHDO/GIxrWWHBBxLkAKgRSNm4HcIMgNHQxOeEWEYtG460OH+qjxqOjF9SHv0qB9z9ia60QRY6U5oRTWKDoP7XKJalp+1eMLD5DyBZWAAcOwoU3X5BbmXBj37uHe+7TpEItoNxDQ+fPy2My4KY7d9jFsJG+Hc46qLFmv12glNLdXrlwRdDydijXEFMznU7GEmIKjw+NAw2wT+BKhJ8LPWhfaSrDmxfovIpyEtlMUGZcKjQFIbZIoNHNSBe/lOuuH3pHxmGx2iQ4ZfnLQmq4dAVaxJgRFRatg8YoLq08uBVL9mryvc8AQE9+Vis8JC3nU9lxByg/rfYrxzjeTqF/0m00PeWRRq6RMRhrkZHlRmQChB18gW3t4SfAe6zxt2Iybdp0Kbsbk7vh7dN3Hf7Eop21bCB6fGDYWz++ahm4dXP7JmmWxnU1FPLUK+Tr0iluHlRDPUCE8jX14CwHrfc2jaG0rJyVal1ShL2zXsTg6wTYtnfbsX7zI9edfYD7fYlpP2JlvM53OULWmCKFrYnSQBNk+7EEs2tEiFfGvVaMaO1phO6FSns1mzGfzPjcw3LOsKprOhto9ouyX9URyAJctHqnNIyAGTFnhrEMFhrfCFGijJR8peNs6K2xDnfNUdc3e/gWuXLvOpx/fxirDqnVY1bJsLXAaOxF0mcgnvDa0kW3Pg1JF0kUleTwnLukZNOMaiet8QNiR1gp4F7xG9GYGG1jwtHKSTOuGybTeQ+sALeBFK0lix4u3rLUNVVXTOY0yE8qQm1MWBbPCSA6VKYKRoyddUEpAlwqJ4ARFzOhCvHY4KgOzScGsrjHA1nTO7/zOd5jOtvl//Nf/DavlkvVqlYxAk8mU1WrJYrlkPp0K+ArgPhqPeiURegW+4+LFS9y7d4/Ll68kWdZ1LVoV/NGf/Ak/+P5f8b0/+zPm04q6LtnZu8CFS5fY3d2lLAo+/OgjPr1zAB4KCjE0NGuaRtYuwHK5oOuEqVDWtk01qYyWldQ0Heu2AyUgct00PHr4mGpSSQ2asqCe1tSTkudvXOP6tSui8yvo6ZF9Wh/5bqkyA9fw2wxIeRASH5Vd1/8ePcmDe/Z/MTx6gKQ2hMr17XDpUmtd1hZHTqedFFol+83J6QnL5ZJo5CQp/r01e5NhKVrFB/taaIlCSAt2d3ZYrpZ414pi6GQPHuQbpXfKvCXxvh7QKoWfD8BJeJ5GpfDeuq55cnjIzs4OrXOJuATCsMbwYNf3qScwigbM6v15PWmTsTcadY2RGmEeJQYLpVLerXh4IovicP8TfUvCxiL4i2RQ0bumvN4AkCRao8Ey2hgFMHpSpEsyOsc+kJFJO2rn8vklURxO+SzqxBLrHUXDd3yY/B6L1fZ9Ym3XR1loj7PCgpe8SsqHvxkYxlMYrlKUpUbrmrIwVGVBWRhWqxUr1rguEPbg8SicUrJWw57V0DCZzHjjjdd5970PuHLlOvPLF7j0pVd4/KOfMms0tVO0PqyRVIw201mzvvbeZev92UeMHlDZHB2PXR6GPgzJJRvr889TkMKAh55k0r0GxhEvc0grxdHREW3T/ErvAP8BAKSceSyG1UWX31gxhqcPZuz4OJHHgiIJ7kxgDND0BpAVn51PkkHYlRerbH691mL9VlkoTqSMlFwDw8GTJyh9JELPwWrVoIy4jGOCc5xMgORcIMJLGHdUmpwuxOM639cNipYd70PSp+9BZbRMe+8SfXMemnG+z/tNYXzkfZz3S9aR8UQRxlGq+/76nuUmW4DJEih/RTYVpXqglzViANYGSkAs8BYXYfaNKPl9TgbeB5Y0yatJgtb7VM/EO5/CaNpGaJnbtpXk7GYtdM5Nmzws4nHpUF4ATBtyKKx1dG0roWjNSsBSpIG2Ngn3Ljwzzynz0UKTwiD60D5FmPthPmpjQk0rEexFqVG6Sl7Juq5D0rDBGSindci3qVKYUBEIAoqMcECU3lBJ3ZjAPOewbcfZkyN+8fN3ee/td8DDhUuX+dZ3fotiUqNNiQm1NJJDZGDxTrsnDt+HCcT5p8AQALQWsoGyLFmt1lTTKaaaoIoKFxR/HLj1iu5kyXK9ZrlcSlgdipOzVZh/cm/XWXwrNX1imJ1tHU3X4n3T09Tn81IJ0YnRBZQ1N1/5Ek8OT9i/fJ21UzSrLnjDY5iZw9MSFbwo8+R3BZZs3tneju47fFZsGJWFEiFAJIWtogJA8GgcrmsoCpM2flmnwQoecv6ibDNBhgmDVQXeJ6UKL6x3aIfSogAbpcM/RVUUlIVPY2KMkEpMpzXTSY1BlBEJc5yksGGPxxsotGE+m7C7vcW0qsBD2zg8ji+98TrPv3CDO59+znJxhusk9KeuJxhTslgsabc7lCrD+PRW0/OGFug6y87OLu+9935QMoMcDSDp9u3b3H/wAKMUk1Kzu7vNO+99iNaG6XQKKE5PT/jz7/2lKJ5ROXQ+5dnFcYhUztErG+WN1JQyMoecE9CjFdZb2qahMApTGGEhrEp293Z5+OCehLmGOdC/mkrGosGuGGWej7logynUn+bOy/a/ybHJc7LprOgUGuypYWsYNzQpcMrx6OCxhM6lotB9gD7xvOzn4Jmjc+R36Z+6qlBK0TQtzoonXasyOCR7kB2Jk2L4d9w3oiDz+EH9t8FzIXgxhFxmZ3uXx48OqKoJSiuR9b7P7XA2lCjwBu+0FCVWDo/FqhB14Hwi7hyDpHjkOZVFUQSPi0F8N+IB6LKoEq1N5i3v90Ebw9QjQEpg0fcRHX7oUQOCVy2fl/G34MVGPEG2E6+PDYVacUo8IZmRQ4gjFNqIQS3uUX1OuAVc2A+jsV3FVqO1I+UNBz0whtS5YPBTXcxZirlZUgsqEttIKF4fZm+iobAwA5BklGa16pLe573cV3h8LFZptHa4ruP5G8/xySefcHz8hEUFz/3GV3jwi4/wR2dUtkMp6IzkfxrX66TjQ3JAHZH59WlH700/H301vN/Qc5YfEpR43oGRnzvWw8fG9MFzvceHnLexUeZZxxceIOXCJ+/QmKSYK+s5iMkHL94nv9cY9cpXPdhpW0n0zllc4jPyhLV8MubIXUfX/ghsiSIq9JBkCraHYIGBddeA0njraTuLtVJ/JMWAD0BHABEdoCTMIH+3WDTSeTeYWNHaJRuzvHtuZXNhU44AIs7zvj8zADPq502HbHL+XN0DUQhCCNmG+4gHRyXLhw9givQTBA/1XrHoJZOQtT5pFUJiu1JI/GyfY+OstKHrOnwroWi261ivG9quZblYcHJ6Srda0zVtcJW3iUTAWUuTish1g1Az7x0+EAd414c5eATMtSGmHRU8A4EVTfZWlRRQneYixNpExohVXqt+k9Ol/Isgpwh5amVVUddVoIQuU2haUUiYmo55NcGCrwNrUcxHEG9BBGMuDmOMHJVXSIyKEpLUeQmEKRGr0XS6he3g9u27dO2asqqoplN8UUBR4HWBRVGYIQOVhCYVYWOLQY2h/hZZXk6wNMmmbfEWdFGzah2LZsHhyVIUzWh4cRIPjtJoXbLuhIDF2UD5GgwGJPkgoQwgXsbcWJKUARR4g3WW1nVSq6hpuXjtBr/7D69iZjWHJ6tsGvfMRhGQhEUTQG1S8dI1cX2UZYEYkvuE6jhWBEtyaQyqUIn+2gU2usJ4iIqCVhidE8sEuuzMoASy4dfGoLyEylWVAOq6rqmqElMitOJlSV1WbE3nVGXJpDa4QtZ8UUTFJUxs59EpvycLa0ZAQ+eb8J1idbbg7PgUvBIDhG2Zzra4cvUS77z3HouzRchl86hSPPDr1Zq2ldA2TQzM6uVUr+z1/WpMEeoVtUnOuSBz4nxfN2tm0y3eePMNfvSTH/Po0UOOT+SdFsslVVnhnMVgEmNXDOOLyoN0d2aIkh5BeQUueKERAOO1SgpiaQpoFGqlUUZzcnbC7//B7+MIOWNh/sSw3HhEB4yIdp1qgaFU8rxG0LT58OTfqOz/6du4BAb5QgmbJut0umYEmnx2x/x3uU+fw5nu4WVJHp4ciycXhcHglYCV1BcjY5384dPYqxRulLXZeWbTaahXZlFeSm37rhnoFPl7eFSKHIggNEqsCCM2ETno7KO6nnD37ifs7e1jygKrIVLCY0Ooq7VyV1/QuQ5wWN/ilEv5hYqesCoHnLkBpqqqtEdoo0X+qyC/XdvLVqXwjU05TrlhMTLf5iy08TufpTr4oK/0XjvwyiSZbDvLer0S0pXFgtXZGYvlgvVqzbpZp3O6tsPboZG817FUSsOIIKksSyaTCdNpzWw2YWtri+l0ymw2C0YNMX4oJfueePE1NqydTguA0cHDrY1GO4dxGm0FVBbOh/7TSY4X2R5WGo2pa0ww3hmzRmvPauUAh/cSidR2Ml80Bms6qqLgrTdf58+++z2m+9tU+/tcfO1Vjn/4U0zTYbSmK4OhsxvmOecG/Jj3M5j+G8BUbuiP+uamtXPOE5vpbhIqma0LNgOiPF1kTBoziAALcmo2ndK0/zHELh25wh5zEpzvNxgYduQmRBrvE4+nKfH554nQwA8XYZ7YnnuFYigT9PzxhdEDAJFbhFEiVLpgjZFJJQpMl+iICfeXwoeycfYbedx0kiejtTgXlWy5b9dJ0rILbti4UUcQEfOkYptEuQz9ocg48nMvTU9pnDbMvJ/jpr+hn1NoRXpG8Aa6Ph4VJeEG6V5+GDMd87BiSJiy0o+xqGYXQ8rWK9r1QkBOCEuLwrezbRLcXdeyWCxZLhcslytUZ/GdTXk1MXzNdh2+c+m5OTiPY4Dq6yYVxmCdWGyMHgqWWAelaVta1+IQUo7JdEo9qZlMpyFxexKUT8m5icK+KEqxIAeSgaIwwlymNV5rXBlyOsKcIq4FFZXsOKdlPhqjUaaQEJCQrN91HS4I2VJpvDI4F0gVMElziUA6974676kKg0FLLYgwdqvujJ2Ll5ju7HJ2cogqS6rJFGc0yoj3RiEJ1/m6Ec2qT5CNc8H6aCWNAMUlgIRSBHb4sKnL3JYQFfEKydjFsYneud6QkPdVrmQ411e1d84lr5V4Dzu0qkIYYyO5fNbjnUKpApZdouSWOH9DrDEkYbnBqluYxEqogDJ4j621VMGqrbUKA9Bbgr0XFjdtJM67MrF+iQ4evoKqKqknCoWEnpSlhBqmmjEgRVnriqKIIcSG6WTCtAj1RAq5Z7LYKw9eFLWuE7IOrTXYFm9buhAS2K59UqSTnLMMEt19cBk4PF5JHqbYlLQYo2PoMJbOKy5dvshqfcZ6KbTsXWPxEyiKina1ZLlciVdGETIch5v7eK8ojKEqa05PFlRVJQYmJfPjYmCRwzsOnjzhzid3aNozmvY0s35KsV+lNF47OsC6Ls3V/nnuXDui9y/OXa/AFCWmLOX3UvJSlJIcioKCF19+hS9//Zs0nczLKJOdd0Hx9mnfTOI3E8+RACQ8MfMAhGXHeVk+PpLhJ5OL/f1VGvNx9MF4m/DnsUO4B0h+UrbPhGuXTSNFyBXBMBkJSUIOjVcb7yn78TjKIFzqLFrBpK5o2nUwzojhSjvVy1Q5O5MTQT4pkkcw6Sr+vFGxf14OKFUoFC2gx4e8LB08sl0npQvabo3zDVJHydI5SxfyyQQgnVeAc2V0rJjG6zrrBYw62fNjqJuzMl4RCPXX9MRPedi3D3PQ4tJw+bCfd13HumlZLtacnp6m8gqxBp3vOsjosXOFGi8BdjmhQt8Oh3JieI2MpvH6tpVaQ865ZOCZTCbs7Oywv7/DhQv7zLe2qCopTu2JaQ3CthrlY8ydFDmrMMZijREyoBiCpzUqGEWiYbbQCl2WoR6RwhQKbWC1bEK6hAevcMrhTQjXVmsuXbzAc89d5c79+3itefFrX+UH733ApHMUgXxj7BQakJglfSr3LA9l3tP04nzebDKEb1rv+fwef59/Hufe03T4dL6FyhQprPRXPf6DAEjRe5RbQPIuyjsaztOXJo/I6LzxkdM6xkHqaa/HOS49/Xh8Rn7/qMhEq2z8PnqkYiFWFwSId56qqkCpQMxg6WO/tfDPJlAih7WOqB+pYLlqu0gD3tG2jdSpUeBVoCbP3O8qKAuphhIxHje3VJMtKjWgz4zvqZUK5AHResCgT/Lzje5pMq21tMFC673H4GnW65R/Y7uO07NTnhw84eTomOVqye7OLpcuXWLdiFBdLVc07ZrVaslyuUyFGNfrhq5d49p1oouO+RXRYhrbmOde5QAWeqpTAF1oiioIQGMG4ULGGHTV58xEtjStlHhJ6jJYzGRzWDcNZ6en/PVP/pruTIqDvvmVr/Lc888z254znc0wZYmKFO4ZuMnDnpx3SZkJTcY5KFTv+cxD0aISquLUCtYtowshNFCyjYlBohcvkuCpAzuNWMqyBRbmTG/B0z6EYnkBMVYF5p6ioNqac/HadU5Oj6kmE2IEhvMdOLFWdmSWzjAvXaAEd7anTFc6knk4vFIpV00pNciXcg6s740tcewFDPR1RlIIGoS1mimV2WailMTny3wpQMtZpijRusKYabDutgI4tQZdoVRBqXQASBJeF8M4jNFh3EaWOi0BC0b3OYh5O0oDpe43/Ol0gjGF5FzVBfOJEFMYIwBH3kvmc7L+ZmtU5Jsgkt4YImPsvafzrbAkth7fZMqRc5jQxzZ4QG3oS2EgjCF+AmZVMsaIcjf2VkULNVoF8giS1dmFe1tr8es1169fwXvH2ekZy7MlbSNgpCxLVoszlosVZVHK2lWur+6epvB5g85sNufJkydcvHhRgC8dy+WKN998i+/96fc4OzlB4fn5u++CtxSBylzy5XqinHXThX2LQW6YGCIGKCWjKLaYkLfokRCqUoHWBVt7F9i/sM/e/j7XnrvBCy++xIs3b1HUMzHoxJDbsMdEuex878HoHxkAuSLJkXwMRGaEhO5f5fAkj+74Eh8A2hCMbbi1f8oenVgqc4+BKMJny4W8m9YZAFbiiVNCRJS/c/+HC+uNcK/+K6OFKl9DyBuL+5ko4PFd8/fDx5BMn93Th2tJe286P7veMGyjMYb1ei3kMBHEKQdaU2jNfD5nuV6wWi9xPsVDpHDvSLg01l+iISXubbl+4rzU17O2641REACPD2FtPSMekOr82IxMKP600QjpmlSEex1YTVchX9B1osvE/hLyJIfWBUppqsQiWjOdTijLitm0RiuyKAiTPDfaKJSW97ddh/MCbM7OzlgsVpyennJ2dsbZ2Rld13F4eMjBwQEffyz79nQ6ZXt7m8uXL3Pp0iVmsxlFLfdtukYM1k487F3hKZxCO0PhQYXivkUIv1NG5hFRfw0yrqxK5hqqKoSkqwWrlUSgSL65tF10CU3Xrnnj9df4/OEjVos1ly/ts3frBRY/fZeZUxhUml/n5jiE6KPeeC0RFH10Qi5zc7CU4P8GAJQfTwNJ42vHe2ju4cr1xXOgHjGat03DfDZ7Zlvy4wsPkKJQTYDEDL01cVPNF/omMDQW+mN2u/is+DMpQRvOi0cU0HFxF6ZIgmIMtOJ9dVCGuqDs+VBA1GnwhYAgLUVHgqcHWfBEBa4XWCIwg5EsABfb2SS0Yz6MdICShM64eQVQo5G6Ptr0FK4J9AXhZrsuCbqmaeisZb1qUjhZ13WsVgJSJHm0xXbREtRlwtfhOiELaNbiLl+t1ukedJb1ao3zTjwrbctyLfVwXNuds3ak+O+Bd6YfF8khsinfwRQFRTGRHBKtKYuKqq4pg1cmMptRGkwlXppJXaONpq4k/0YXIewsxh8HC39RlOJWDsrcwCKjYpy1D8xv4pE6PTvlk8ePWXzwC5QpuHD5MvuXLwVgZFCmEIBEto0q8EoUW6/EKmdgENKgtaKgr9MlrIbh8lgoN5/zYWP3tp+n3oNRprcKepmHUrDTk7wuYRKmeYmn6xxKK5rO9hSmTrxuTdvSrNa89uabvPD88+zt73NwcExRVtLGoARbfAopzcGsksU7MEhIaIQCrWlsl2RCXrzQeYVX4q2JfSG5RAatYhihANCus0wmE7QWKmySjAnWuOh10yYQCsT7BTkEGKUwWl5IKS9Jz7rAe8VE9XXSygCitZE8lelUPDZx/lal0H4XRmO0S9fE0EitNXUJpfHJo6iC/PDeo32Hcm2yfrfrNW2QbxL+2HsXk5XbieGFaFV30eMjCmir9IBGvrdeKrBBkfJize9Zr8BYUV1dds+4aVs8KI+ykXI/PlMMMJGUhgAaYmhY13R0nWNSz9FKsViccro4DZ47G/rZsFy3VOuOwoTQVN0r6TlTqSJ6UxS7u3scPD5gZ3ePtutQhWaxXLN/8SL/4j/9T/mTP/4jTk+OWC7PcE2TrOIAyjgWiwV4j20F9EynE9CKroshIjEHKXYkKGWCx06BC+FMGIyu8Lrmq9/4Fv/sf//PmWyJHLPW0baW2c4Oy6YNMrG33udjmgRkL0qCSu1AxQLh+V7pMxDwFECj8r/7JH0FieExXRbl9/CiIH4yoxt9qJ/qPwznppCH8AyN7TpW6ybJfaVUAONyXd7+XJ7EFkewPgRq8kdVV7L3NcEbGPfyWIMuAz/xOnEA5rK0Vx6jVT/qKUmv8BKOHA8xrNUcHZ2wvbOVFNuy0Lz44k2uXbnMtasXOTo+ZrE6Y9W0rFYdv7h9h4ePn+B9zDXsxySF6CF5MrmSmrepc2Hd0nu8khzwvZE0zqno8XEBEHnEu9uFnNmu61g1EiLnIjFQrK+jikCWE2aPt0wnNYUxTKpKPC3SwxJaZ1sUmtOTBU27wAfwU9eS1y3gTEY2PqOuJKx8UtdcvLjPCy88z3w+pyhKwLNcLnny5JDPP/+cR48ecnpywr17p9y/fw+tNVtbW1y8coHnX3ie7e1tkZ2dGBAL67CFpjDB6Kz7CIrCCzuehNP1Ml/q1EXSoQIw4A1KSQSLty55yJWztK2A1dlkyovP3eCDu59wuDjjta/9Bj9+/2Nst8RKgiombfQqGaO9D+HmCGGFSvuN6+dtWCLRbpov7PRZHIsRyDkHruLK7dWffj2r4epPhmkVGO8yfWRoYJDco3lVUU9rftXjCw+Q0BLfCaEAaSZwxuAm5hVArkQPBzOeO/b4jABrOnc8CfLv5PfIrBIGOFivTGBMEcHbu4aLsgxeo5B3FP5DIcqYBy0xJKG8KBhvMd4G3UBiq72ydM7ROUdpKmzToqxFQ0r8i27u9Xqd8pBW68CKZm2o3eITfelyuUznNk1Du1xh25bVao21XQg5C6Co7cQlHISg7WwCRMp1oU/iqvNh07YSGx2VH0gWUwBaiXvWpcGUBboo0vhXtU75NnleTVGWVLN5sobVdc1kMpFQtDrUIgjEAWVZirJZxCJxfRiXeNfCWAegk8+BfqLFcZZjHO+b1A4fcmGCFVdc7BqlHFjLtJzhfMHNW69w/6PbGAPz+YyiLFFFiS5LUDqFmhHmSp527IJyqVDiSUxzVEXVUza50M86hG9Ksdy4NiSp1fsOb3vCi3xTj5srPqMRj0IxhIY5etZD573Q2XqPsgpvpQaFhBAEgorWQTXnZGUpuhalemCDVriQ/xNJEZIXDwGEWoXQQS1EEGVZ4FAURSgWnZL8A+22NkHxjbmB8s+YAqOygoDeY+L8CKArgqNEsR6AV6U9JnCgyqmi3JZFwVYN82mdyCsi0FHeUxsElFclZVH0bfUeZcQD0bUtbdelBPE41/JDxknotb3zdI3FNs1AedFRuHkG8hCEWjb3KPjsnGiH7w1UpLltlUt1WKLVPB65jI5rx+GIbJqDtkdPrlL0Zh3w+cYdP/X9fI2Kt7de2MQ6x/72nK3pFovVgsXqlHW3pOuWFMUEpQtaC6vGYgohkSiMCeupDxdyTowJhQLvOna29vj49ic0naNzHr92LFcdrYdbX3qV5199mXXbiLK8Xktae3CfL5cL/t2/+3f88Ac/wHiPMZ5/8S/+BR9//DHvf/ABy8WCtmsQD+N4L/JoXUoerJh4wBRce+EF/tkf/iFFXdG4PtS3KAuh0G9X2bwYGua8Dwn+G8CN91JPJXEx2PP753je9X/0XpdkkPRhLJUbX/rUIxpqohIV/44e5NxgOT4kb6NDB6MQAUjLdQP7Gf0JoQt8P7+gN7B5L3LVQZbz0IfePi0EP29jTiCQX5fkKsO10wNIT6EMk2nN8eER8/kMr0S5rUzB/s6Mzz/5Beuzh0wmNRrFvTt3MPWEa1cv8ujxI1wgWSC8S1y+SutEZDGoAZS122bgzYaYukhUMgZG3vvkGdJelFiLZ921rNtWSkRYl1jttBKygrqssK3kleJkjKrS4OlQWJSy1IVhNpkym82p65qtrbnQ8BcFs/mEw6MDmqZhPp+xNd8CJVEDXQfrteXgsXw/m884OT7h8OCQx4+esFguBVglb9EWe3v7fPWrbzKffwutNQ8fPuTOnTt8+umnHB0d8uTkkNt37rK1tcWNGze4evUqs9mMrrMUKoQbFxKmjHZYD9YZCYnVjqIQD5MQSGiU0wIOUdSlQc0kkkcrWC3XAkJDBIQKeoDTntdeeZlP79+jbTr2L11ltnuRrrmHcw1GS6REmuPRQhCN48EQIdMveuxIhtEEjDyDqKK4fMR4pAbG2E0OhvTocAefXZ8bOwfXJL2pvz7qORIpYsTIpyUq41c9vvgAiR78xCOPW8yFeJ4TNPY2xPuMj16I9QrzpnPziZB7lZx1g81EjSZAfqS6Lt5TaEPXtiigNJJfpL24EE9PTunaltPTU54cHHF8fMJkMmU6mXLw+DHL5YrVak1rHSjNYrlitVgmoLMKVeClnVpYDNqQkxQsPF0IzxLlKiMocELmEAvA+ax/IvuVKE2WSCMbk5zLUmL10SIsmqYJblwkR8YojK6ZVFUYqz4n6/TklJMnh4BnPpvx6utfYra1RT2dMJnNmE4kmXIymaT8DRW9YKYPO4qW9/i7itSeDBUGF4L4x/MjWj88AhZkw9TZ5jfMXjDaDGLK+xCiwBpmoMg2HyExkGvKwvDc9eeoJjM8UNRTinKCNxqUCe04z54YQzR6YZgRP/hemc2VjljF2+Ok7oJzKYY8JaB7ARADxcgHq2dg9IthfWLhiX0XayqoVNdIBYtQ6WUTUKrAGI/k2BQUZY0vBAQXpgeqOuTkoEqx2BIBTj++KqP7zn8655mE4rCRtKKXDSYBoSiMTcjpKVxDEYoclmXRk12E8FgBtzLW0cs4nU2ZTWFSmZTkHOdhYQqMkxj5SGohGpcC71AuEnZInaWklAEx5EopsYCuMkVsePRAnDBXeyUvk0EjJTk/vFK9UkxmKfagI5XBWNmG3oPpI5jpv3MDgNQbGWS+9c/ON1kgq4Ryvq1jZT3Jf+uxjQVn6azl4oULHN85Znm2oFmvWDcNZSkFf7tg3HGIPIoUvvn7SX8pnDZ0rmM+nXJ0chyuk++sk0KvNuwBk8lEFIp6EuaKtG17/yL//A//M7wu+Mn3v4u3lkcHB/wX/+V/Sds23LlzlwcPH7BanSWDVte2LJYLtNasVmt+8YtfcPDkkMKUXLp6nf/sv/gvqOoq5RjFeV+W5UAZH49Z+sz182FwHuBVLEk9mj+juTeOpPBOnRuXfkbZc3PuWce59mb76bOOmLMFv/zcc4caZ6OFj8P/IiB4GlB8Wl/n3+dHnheyyeABwagRgMBisQi5ewrJM3L89Mc/4ejxAx49uMdkWnHp6iXOlg17l66wf+kaRiua1Rqnini3wTM2MfLGduX5Q1EG5cBoE0ByTgAQYW9orWXVrCW81ssOZoogS4OXQPngnbMdpgrU5pVhd2ef3Z1ttuZz5pMtJuU0eeS6tqGzHYvFirPTI9ZrS9d5Dh89wdpHCSBJiQpHzFtfr9ZMp1Oeu/YcZVWJ8VVp2q5juVxwfHzMLz74kLfbFWVVsr+/x4ULF3njrS/zzW//JmeLBXfu3OW999/n6OiQd09O+MUHH3D16lVeeP4F9na20NZgQoF0E3KcXDC0WR371QbWOyHC0ONIgpTioWnWbe+Vs70nbjqpeeXWLd758H0OJ1Ne/vpXeOd/fUDVCIGSDWzHIEbEqiqZTqesjs/o1k1PDa8cw2KuwzkY5wYb5n1yGmQG5LGRYHz+pnn+6xxx3jovBsxf9fjCA6SxhV7cm136bpzUFRf1WBDEI79XPqg6FCrM7zP2OuWf50qADkpyJGvIz4+HUsKMd3BwwPb2Nq7tWJ6ccffuXT759BPu37vPwcEBzXrNum2oygqArnMUZcXuzh7TumYSlLpPPv2Mw+NjiW/3SEJn0xFZvmIeEiCsN65/V68C5bf3oMXSFK2yWvUeO210AjtFUGSrqqKsSqqqoK4r6uCtsV0nljbvsUpjCinMWJQFShGKp0lhyrKUZHAdcnmstTx68IC/+vM/wznHzsU93vraV5htbVFNa3RRopR4fuKGHjoZj09u46yzQ20qiPHsKo57HBsP3qtBPau0sYU+SmOY6icgub45FRSId0JnXkbvUT4L+YyLO1NAo/Arq5qvfOO38B6KyRZn6w5dFCLgvYQ05O8V83C0yu4XFGXxVrnIqCpWP9+TFoiAccFrEDdxUg6crAGTFFdpsxgmdKiLoYKnLdKDx3toeqDqg6VSkvczym8VgYmRMIhCwivI1ppWkhOkfKS+Hi1gcdKmeaDo8+N0aIvJAFcc10IbCgw+sFBF4F5Vhq16ysXtCbNgiazqSvJVjEmeM9Kz+rH3fhGUQIv3HcoqsNCsHcr2uYdST8j1U0b19dxiO2M/RoXGBwCqsnoi5zuil0ExpI7snjL3ItBx6Z7xsIwUu2TB6y15uRLdn6eGn2f3sOnzHBRm7H7xHoN7+1EO/VhlHa7P6KVxwYjjOst6vWZ3Z1dCd9uO05NTtrZ3mc92QkmFNiRsK0wRi4wXfb5VeqYoEDEfxHknBV59X3XFq8ieSIoCwJQQCEliHxVVwT//F3/IC9eu8r0/+1P+9Ht/zl/84IepGKwol10qv+C8k3AapFBnWQk1/Kuvvc5v/fbvsLt3QcghdB8+G8e5aZrB2A7kmY8GFTcYKxGDMk5OzMPn5s8vVWa8Ht6fbD7n1PO/5Bjv4U/7e0wo0D/3bwCO5CbnrNopcoDeOPs0gLTpZ64DjEFQ3kdPA0jOg1eiT0hhbhfyHSV0cDaZszQVW/UWx8dPuLtacOnKdWzTSEiaC8VrnccxTBHo9Z3eqNiFXJe8jb8uQPLehyiSLsgEKJQwLKKi8RCZ513Mr9Hs7Wxz9eoF9vf2mc/m4jlftxwdHvHos0PWizUnp6c0TcNqtWK9XrNeSQ5T10qoemc72qbtjXd0QcZLOK3WhqoqqcqKejoJxAxChrS9tcX+/gVevnkTPak4Wy54/PiAn7/3Pu/8/D12dne4ePEi168/x1tvvsnR0RE//dnPuHvnLp9+8imfffoZly9c4OatW+zu70ueclFgupKy6PAhFN86TWuFrMkUUguuLMxgPCIbqPegWLFarZKhO45RURheuXWT2/c+4ag546U3Xuad73+XomlQvqMLRlox6EmERFVWLLtjtIueXYIXUULtPD7lk+XOB+ccRhBUmhtjPWsQJjqay08DTJuOXw6aZJ+oQtTFr3p84QFSvgnAcPHGv/NQqPz3TSAl/04FRTp8m2LR82vVaBJE4JErh2PhkwvMeG1s949//GMePnyI9vDo4UM+uXOXDz/4AAXMpjN2d3a4du06W9tbVFVF21qc9VI8EzCu4/T0hAsX9igqqfGhi5LDw2OWSsLjykqKTVYBvEymU3ShMSGcp4osaWVBNZlS1eKZqSqh6p1MpmIVr0pMGSigU2K5DvlKBcL6L52wXK04OTlhtVwKe1zbJAaZrmuwrssYaKAsK4wO11vL3pVrVLMtzhZneF1STGeoqkKVNaooUboSJvOw+NOY4vFZnoh3MfwHhH6pSECKqEyr3n1rg5KgTXRDe7GMZHLBDwyvKgCQuJm5iDVSiKfNE1hdDC10g6RVay3r1Yqmbbn6/Et4D4+PlmizJpau1iYQI8hbirdq5L2Jnh0vUhVSWxUq5Nao6GJXMWStr+UQ57iOSZz0gMXkBgajQ7hZ5oGJwMfX4PWAgCOGubVaLE1j1iTvPXqgNOdWfI/BJYAmIZjRuurQdp28PJGuvCxLCq1TEcW0ZlUIf/MK18i63dreZr41ZXtrzmRaUWgB2f267aDrsB3CLOXjyBMMCWHuDOoxBIU5AJaoHLps8iR5ZMI40QOvfux64NoDIEKowuZNxGdhTrGPE7iRVpCMAvTv48YAKQKj7D36z3vvpMcTY7XGSrSLrcyU7/gGyQCVyczoccpf7dx7pneRNunAhxy9c64Tz8u1q9c4eHxA17aslyua9VoMV2GtiNwu6Dqb3iXWFEv9o8BiMShWTYMpSk5OT5nMZ4kq3IXEb2XyulGGxPcZwZNXmGrC3/u9P+C3vvM7fH7vcw4ODjg6Ok4We6UEqG1tzZlMJiitmU2n7O3tU01qqnqCNlJo1nqPDtEGsctzRXsMLDb+ngm1HPiOQfB4TxvOkXywzs/JaAiJPqlfpiCN9+mnAYdNe3pSwn5JbZenPvsZV3mGYOdpbX4aUMqVRBi+VyKb2ghCe6r7s7Mzud5ZnBOvx8XnnuPmjRusFwvOFscUUwPK0HpFG2ohQmT87N8ugqIiGKZycAMM2pmDoTxSZ/xZ/nvqT6Woy1IMCiFHtLOd5Bc7y8X9C7z80stcungBZx0nx8ccPDzi4+PPODk84vTkjOOjY06Ojzg5PeL09CSBo7YJdQVtA/Ternwf7vtTpb1eiFNM2rPi3pGovmdTqvmcy9evcvXqVV575RXA8/jggE/ufMwnH3/Mzs42168/x29+69v89m99h/ffe4+3336bR48e8/jgCTt7u7z8ysvs7O5i2o6uLLBGyroUVgcjscZ4S2EdzqrkQYopAsZILbVYIma1Wg36uW0aprMJr926xUd3bqN351y49QJPnhxRONn/4vrDgTKwOpXiyV6LdVEouPswe5FXQ501zodNa7c3EsbIjZ6B7lnHLwdBQx09XhP3ce36EOZf9fjCA6Q8XC7SV487MSLstm0T/e34HvlGkgOXHHhFsPM0z1FuTUrCL1jzxnSF0aMUrTBRMfzGN76Rrt27sM+NGzfw3nNyeIRtWj7/9DP8/XtcvXaNrrN8+unnbM23eOmll2mahgf3P+PBg4e89vrrfOM3v009mTGbzyX0S1copUOYUJEKmamiwBmVlJdorZWESgmriopMVIyD2tADD0jhIwDeFXj6uilVOefi9iWaZs3y9IQ2FEaVKvHrUCCxo+uaVOSuCYDJa4WupmzvXWLZWIp6hi6neFNhVQGEOOXgxRhsTohFWaikQw5N3PZC2FFUroKjIbTfJ2s3PtsIoxWd4QbYzxmhGXYhVDElpPtYVVsNNo+oKFon+VXO9cmsQtig6TqZP2UhBfp0EJhFYfApV6b3lMa5FOedNmZgCZXoPpMUh8hiZ7SRt4renQAe8KL4J8AkEz7VM5IHZV4ORVI6ldZoX4IN67OVugwmFWt0OCTvKglhpcSjFwq/pXXjfYjD9igC+xuKWVWmjWNvZ87+dsl8a05ZFBRFmUIqNfQ5BeFFotdHLKpZgUAVvCt2jfKqnwuMBHmujQ6+U4RsqPS5y2LIvLK9Uu/7ORTQQQYLs8NLfw09Lf01MSRSXsWn95Y6TUPLug+D5bxL63r8bk9TpiE6zpIWnqzpPvlN8u7p/7bDNxo8U2ToZiU7r5nzrI1Ua00Xw5oVtNbiuo7jkxP29nd58vgxjx485Mq1K6zWolQZLd74phEmMllLpHU8sOYryc3yKFbNGqXlZzmdiOwnI7RRUf4gpiKfbhGWonzQeU8xmfHiS69w8+VXB0aCWJcqeYFT3yjx7ntorRPpNTDeng8dH17P4LM0VlkjnX96nw/mwgiwDI+Y7Xj+Ws95cLXxDhtBwjOeOAJtsR05aPxVrNbPPFepc+BvEyja9Hsuo8fheblxdtyOXLaI5yN4eXyg7UeYMz+8e4eyMEyqErzFrzoWq4Z15wXaFxO6di13GiVg9YRWQ11laATp97uxjNgElvL3LcsSvBSJBlicnXF8dMT+hV2+9NYbXL9+na5pOHxyxLtvv8Phk0OeHBzx+NEjDp884ejwkNPTU5ZnC9brMzq7SuFlfSi4B9Whjey9XWd7GQ9AAd7ErhzslUbJ/poM3rHga1FAVVC9M2EymbC9vc3e3h4vvfQSL916ibKa8OjRI9595x0+vXuXS5cu8fyNG7zx+ut88IsP+fFPfsLBwSFHxz/h0qVLvHjrJtvbc6zRmLaVHKTCUBSaojQU2uELUi61937AKlhVVerfJssr9crTtmteuv4cj+7f59HxIc+9+Rqfv/1zpsYLwUM21l5rqumMxXqFN6G+oZcIF0SDC0yXQyCde1HHa2DTXhLncP77IN8um0fj8/L5FcFiPq/kO2mM9z5FOP0qxxceIOUCZdyR8fDep8T7ZwnbKAyT1WlgMRnaksaKaC4Ycm8S9EUn43XAwC2f38taK4XIlCg29WzKp59/RoHGdx337t+nnNRcu3aN46MjFqen/OP/zT/m8pWrHB8fcfuTO9x6/XX+zu/9Pq++9iVJ5gfaDryug8vZRoM0JoRVed9v6KKwOwqtwIWk9eA5cNm7EO7BuYkt1ojocVAKfFFI9fqiYFLPWK9bVuslTbOm6poMIC1xtqMLYTE+hJV0neXy1RssVh27F66wbsFqL8URnce7FmNcT1mdbfrWk0KJcksSgHL0ykemhDkEsOTjlc+3bLcdWKBVzA2KhVIjSEiWZJkTxgRmHiXAw+oyxexGUCYARktVdi9JuMYojO4VLB+oTsfWmaEHKI5NRH/xu/C80F/i3QrzPE11lcBJcDwQlY18FXkbPFdyiYTRKSO1t/wpOKnrZJQGJ7lfJZq5RjaFIuTfJQY4TVUVacM+/0/WZyTXKMvI7uZRPjIjWmxriaVjRanIFJsMIEn8ncUhQNvFehMhJFUAiLxgrhCOwbjLvFnQbjwPAlgfX5/Pq/RZvPOmI/dkR29Hf68h8DiviApoO68wD57QOxQSGPMAGVOdDuxdcR0xqN0zfu/z7xcNCD2DoM+6Ifz+VIAk36sw8cR7pFIoZyzeenp6ynQyxXaWzz/7jBdfvkmzFqbNajpNstfaDgG2aqTEyrMiyPUo1us12zvbnC0WTObzlPSnVXh25hvTvmdMJANLEMhUtBhyCHuBDYxXOHmWOLJ6UgxUyHcM1lMfMo9ErvcsreM9aRNASkZF1SdMbzrvacezvhsYnUbnpZDeUejdr3P/jc8cGUjDH2h+Pesy9GJwY9vyfSTTBaDfL57Vvvh7fL9xeOD4vHhohTDLhjHr2pa6rmUO40PuoGLVttA1wmJKgdPQWkWHwlQF1jYohrnbvcFZDfIFxyB7HFYXv98E+BLoCvug7ToODg5Yni14+aVb/M5v/hZFXfDo0UN++uO/5uDRIx4/eszDhw85PHjMkycHnJ2dsl6e0TQrbLeGQOrUOSH3GXtJ5bkqGaAH+6Nve28usu7SNfS0AdHwqEJ0jF0p1IlEJjz8HOq65oOfv8329g6Xrj7H62+8yQsvvADAvXv3uHfvHpcuXeLGjRf4p//0P+Gnb/+M9957j88++4yDJ0+4desmV69eCntYQVEWmE5TWUNhLL5zqZBt9GrFunhaG8lvDEfbSjRO6zoKCqYonr9wmZ/ffp/XXr5JdfUC/mSB8Yq2bZIxudGaYmJQOzOwnRSs7yzKQeGFWr7LcpgjqIkg5WlGgjEA2nQ8Uxfn/K63ySkxvCESYtk0T33m+PjCA6Su65JXaNNmMAY92sQwpOiO8yEURjjubbD4q2BJEOAglnZRaGTjiyx0MXcg0bcS3Pneo1RkQXJBKY01VOReEZjomDinEBaZsHyb9ZpPP75Ds17TOM/y9AwA4z2lLjh49IhvfvObfPVrX6WaTGjahpuvvcTV525gqpqT0wWlLihUId4MFFZpSl2gi1IYpZRY1Y3vrYcOj1YuUA8jtSLCoUzV9202DtH626vQ8v9Ug0cpVCGafaEMZT2hXJesVitW6yUmACRjK9bNGqVblDfBKt7iWrj03C0uXHuB+dacJ8cLyrrElKugmcaCpkWyFsWwChsFaFAI4xip3pSbvCJReRFhHljNwrjEc0z8LgPCSSAEaugooNMWqyJtdLifiiQUJnngSECnF9ACkoIXUokHQeFRWhRiH+m685o/CQD0oRha6Yh+g64ZCtcGCxEq0Csrh1TViQDPheLDPtX8SFS0MhHw3lOqFq08ZVkEUoKSyaRmOp0ynSkmtaEua7a35pRFSV1V1GVFqZz4KAebcxCwDGPaZb3ZkDtFooOVkESHtY3Qx5J5c0fKaMxbinx/REOIckQyCwJ7Y8TSEehHADOwrJMxvZ3bLCx4l6zN+ddeGVF4yTYKH3yb+XlRIfZ9++NKHQKq8yF2zvbEHwPIkis8RANBaP9gz5H1EDfHwWamVEiyPr9xRUV90xE9VnL3eF0PQIb36d/x/P1y5ZEgXz1dG0JEndT0sYHdc9127O/vMd+ac/T4gMXxKevlmq5t8ROp+WGKYOzyPTFJbyQLPRVlOrBuW4qq5vHDB+xfvEgR9gQXxivmIUUzxEijPvdGqUYJsgcIwY8OHsAYKiYgyrlA7UUETMTJGvq1D1k9TyKQGxPj33Jtj0PFSBLbr0bjko/TOKzlaeedf9+wup6hRMV3kAvy99t0IvRGKTX6Kll3evAof/TXDm8zWM/9/Iwn+rSu8/eJq6rvkziHhgaK3LCRK+jRCJHPlT5kKWt/mFvz+YzFYin14kKzOivcht57lFcYTyBf6o0aSnkpTp7t7dFD4b3knCn6yBmpQxYBdwibi/T+aR1H/Uv2Ou9cYuA0haFpGu4/eozrOl595VVeffkV2tWajz68zb3PP+Phg/s8fHCPR4/uc3h0wNnpCavVgq5taJsG5zrwktMZPek2WxthQ88iOXpPh7MumzvZmCkgAUHR9XzunQhp2kUnOpNQ50u4uO3WrFaa4+MnfP7557z383fY3t7m5Zde4a0vv8WF/Qs8efSIBw8ecfHyJV669RIvvfwyP/3pT7l952Pef/8Dnjx5ws1bL0qR966lLAusLSgKS6NaaiukP4UpKL2ncA6jHWUhtdQmdQXesVShtI1XtM7TOc9zzz3Hh3c+QumCr/6tv8XDD2/TnJ4KOVDbhNpd4IxiuneFup6hnMcu1yweH9CdHFEohe4aXDCqR3mfth7vB+ulL8CcMaTGXTTb25VSKKOHxb/D/qPp98Uke+gPYdwdredgxm+WS5bHJ/yqxxceIA3CEbKNOlr+zsUsOpeoZo3pw4BAFkesrOrSYg9DpHplRTbI/ndFZBWTMbM2FF0NyqfUChClsgttUjrb7ILQ0VpjCkPXdVy/cpVLFy7w5P5DPr37Cdvb26xOF1hrmc/mLBcLnPf85nd+k1uvvUxRTSS0w3Usmo6T1RpdFhhTYihQ3kpVdaVRRYXzWtimYkJ7ZqE1SqG1T/vBmOgCRnpUHIcMpCarmAmbSDYO2nvKErSuqErNbFpJuEvTsHZAOUG3LaqUPCXWDU5V+Gob5R1eOXyh6LynazsBmWqCUiYUeAw5MoRirYUZbD4pJE2p4DGI4CovnpoRA2TWJ/mu93TEDS55HE0fVhX7Ll2re2Y9iOE7IrTLwCCQh9LEIzKJyefZhqZVYonyOlNOw77ncBAUOqJAs+KGj8DAR4FHsA7hET51iUFWToBDoRQTo5jXJdvb+8znc2azGbPZlMmkYrtW1KVK+WjRgyVAtKP3KqhMxwh0EM6jlEsGhfR+/YsmoF0GkdZbL6UWk4tMPs7TOkPbdSn0IoZf2M6hvQ41p2K4JUHYRwt8mCNBIZI+771t49wArxVO5QrPUBHKyVkGiqK32Xnxf30XDQ5Pmhf9s8MXTzn6gqOiwjiTtcsNy4E+zVOQy9Nn5X2MFdz/f7wNG8EYY66tDEyo6Kn2/eaND4qggk7ReYfXEkp86fIVPn7/XU4Pj1kv1ti2FYu89ngrssHjQ0mFGAba93/EqjE/q5zULFfBSBMNIjEJPsObDv/0YqTZeT7M5f49o7c/aQMplFL5nswjGSzojS/xfpvj8jMZHQwwUqSyPyOSXMgzhkVr87moIsCK45G/2mgch2A6etZ/+TEwFGyYc/mzxoaW8GWS6ek7Ui+d38/I+px+vo2PHIgNgY9KMjdfI73RNm9zD4iUikaJMaFF3LuEpEYmoaMoS9ZdKzJSThSZk72ZDd3mQ56rQhRDofHv9+W8T12q1TckuYh5fT4NRV+Tyof+0FrIBsqqDpEFnnuf3ePo5IhvfOMb3HzxJgePHvOTH/2QTz/5hIf3H3D0+AkPH9zj5PSQ5eqIpl3iXIvtOjSFhFyH/U8h5CmCeUPQru+BPJFFMzBt9gPEYPxlnEcjnxaRXB8Vf2fFFKm1RTtNF/QCbUPelupYtmtWJ4c8eXifv/7hX3Ht2nW+9htf5/pl6SWUAAEAAElEQVTNWzx5/JiDg8dcuXqVr371y7z6pVf56KOP+PjOJ3zw4W2ef/459va28XQ0XSdpEFrRekvZtVRlxQSPc4bSlCEMrkBrxXRSoChpWo9VClRBoxV1XXPt8hWWZ0t2rlzlL773l/izM+gkh7Ywwhxcz6fMrlzn0pfeYnfnIpU3nD14wOfv/YzTe5+inhxgbANY0TmUEjOtkkLJKvRRUvO8J5DhhjnOYNuPeqJB9V5+mYRBFxVducj2WTJ9XEHKBw9DJTnwStM2Lc1yza96fOEBUq6AOueSqzH/LP+pjRl85lwEM9FKMqTyHgvacahCDsyitS5ZYUbxuOMwuzGYSJbykH+yt7fPzZs3mW9vM5vN6ZoOrxTHZ6dc6FouXLpENZliTJlIFI6Pj1CqQKsOUyjQBdZLOIZT4AsFSiOpFtHTosnN1pu8cfm7P+3v/Pzo/s89eOmeAB5KYyiNwYcibdY5Fm3HqhHrRtO0dG1LUzcisH1Myg/vpoQW0ztHaWrxxqjepR+JBYzqyTZy2mdUprbHtsZrsw0jB9vyTycihnOJh6Oq7CkvRIFXke465Fal/CTwqgh7Xm8pTnMjYMweksfNz2e/yU+XXePiDi0PCJJK6FZ9KBynvEv/DI5CG8qqYLo1YTqp2dmas7u7w97ONttbFXXtKUyR3inKQ+P7PAt5vkesfXH99HNkAAYG1uwRCB+BjcE4jZQOH+K0rYfKaSJDn7WWtpEk4KZpsZ0Uzmy6js6GmkyOvn5TLFCaQkRllUTB77xUSLfxXE2q6bRpvQwtw/li2axY5e86OH302aa/n3aOw4PVAwv00+71LGv/Jlnw7PyTzfd5+peb30MMUk+/37hdaW743osYPTEXLlzg/abl6OiY9XrNarXC2T4fVO6hiYUyx3J8rEgqpUIocO8t3/SeQUfY+J3K/v+sY2ygUpnsGRsIB/d/BoAdvAvDpRnldPyj9/iFvCIV57gaXPgsj9B4H/1Vj1/n/E3rzbN5nkdAMv48f+bT+uuZbcg1wl/zyI2+47vGvUlLDDPz+ZzTszMRsEHu50r/+BZjY+ezEuc35RiN+yI3TkfZXoQ6RjjP0dExd+/c5ZVXXuF3f/d3OTw85K/+4i+4/eEvePjgHgePH3J4cMDp8THrVcb6ScwH7cfSZLpb3OOeZiMa62W5/rHJmDXu/9h36d2dw/suy9Hq5UwRWGWNCZ6rBmxnuX37Nnfu3mX34kW+9o1v8Mqrr3D/3mc8fHifvf19rl+7yuWrV/k0hNwVpWE6m6T2FjroGYXHdR6sx5UVqlZ9yK7SFIVmMq3RRtE6cEoIYZQ23Lx1i7d/+lNefP4GLZ6TxQLXNAEgaabzKc5VzGZ7sHUVu3WB2d4Frr/6Za6/9jqf/vxnfP7dn9A8fgT+CPxSCDC8pkAIrhTn9y8f28dmI9qm/s7H6lljuHG8nUS6tKs1n3/yyVOfNT6+8AAp1m+BfiC8l5yjmMAWfwcBSNFTEK+J8ecuWLLHgCaeB33uUC4YFJs3p01AKLYvhgblEyKnHz588oRP7tylqmr+4B/+Qz65+wlXvn2Fv/j+92nXa64//zyXr1zFWce7772H80oY65RmMp1x4cpVirIEF4q44QIDk1iSUthWbNsz+nhs/XraMRCWIyA5BpFRcU8ED0VBARRVzXw6xXmP7Tq6VIXbS2G1YL9VOuSTICxUhlhILXot+uT7WNAyp+xWAcDl9MFD618fxpQruqFHSPkA4/FWDC2teehz0lDTXoYPlGU+WuR0b5GLYCfWJzkvHCL4CXdXQmDQM3+Fd/U+O1esixrHpC7Zns/Ynk3YmddszWfM51tMJ1OqqqSuSvGoeE+hwfkmgLxQsFjlm7jCuWyO+L5Pxjr0JgX9WRbhTZ+NAVI8FBEci+enDIVZvRea2ba1NE3DumlZrhuaNoDwzgpgCutFGXHaoyXgSYc+lLb27+1NFmp4rrVBcG9UdobvNFZ+h98HCByfEX4ONh4/6ocQ5us9UsPGPh3IPBO0/A3O+5sc0r12oJT01vPzHqSntWsIkMIaClTGbdty7dpV2rbl5OSYxWLBerVOOQrRYp7f95fNQWNMClV56ub9TOl6/p5P+24ga/j/kfensbZl+UEn+Ftr7X3OufN9c0S8GDMyIkcPie3EQxeIoTBNuVrVVJUlKMnqLlRCQq0SBahKwBegkRF8qEJCVUjutoCiBKhVyA0u2QbjIW0wVGKnc4rMiMyYX8Sb353PsIe1Vn/4r7X32vvsc+59kWGqFazMF/fevdde8/rPA52gHOm3F92nvgBCQceSIC06mDCGL5GwEEF3pzROD+PAofk87jhTYr7BH2vm03f+bqTOLOOjOJ8+pX0ReDQkMBzax8e9N4OCIVQjYZfE4hJQZzQaURwcLOGoVeu0BCNWaJD6Y4mCgvR5+i8SxONsjFbiq/zGt18nz3L+z3/4D1OWJb/5v3+Rt956k3v3bvPo4V1Ojw85OzumWMxwNgTdSXLRWeuCaXj3/DeMGcvCp76gYJVwYNX+DDHX7Vo6vG+F4PHboigwSofw0gqtarJsRJZBXVse3LvHF375l/jSb36Rz/2u38WLL7/Eowf3ODk+Qo/HGAXjPOfk6JhMG7a2NoLJvGgKXe3wxmFrS01NbQxKeZREixF/tCyTBNa1p7bBfNvB3qXLbG5v45TmhU99gre0opjO2cgyRnnGaDJiViw4mc05nRX4UcnYOrY2Nth//ln2r1/ixb2XeOdLX+bBva9zdvIuuizxVlJ3eGMa+ncoomNHiHkO/dgvfeZ7SDgVlRwa8W/2tePk8OjCfXzkGSTv2nj8QMP8NOEdnUiRsywLvhO04uzYRiCe+85+8Wf6rM80KaUa1X/srz+OPqMUpQ79A9UwTM5RlCUPHxyglGFnZ5+T6beo791H5yOevHaNyeYmJhtxfDrl8GQq2aidw2Q5m5NNnrr+JCPEEc8qR+VgXom62oXABnEmGtUz41omQvu/rwL6HcDT+zt+pxMGKurmpf0ovQ0EZdZmPvcoahdN16IEUz5WiF+WTsbVl+ANhU1dAp6JmYP1rgHA/fMQIhAsrUEzbp+shaJx7vc+E+d/aEJkR6bK+ypIz1piWEfGBy9mcbRAX4iFmMeh78sS/WyCpBlPlinJUD7K2dnaYntzg93tTbbGObn2jIyS5VZiLqrwaF8GBslB7WlbDGuqEolcDxDG+UeiMyV8O2vuh4m8Zm0Gfk/XYRngtv4HKkhTlZFVyIxmlGdMJjmLomQyGbEoKxZFSVFUzBfCODnnqSor/ivagLeSGFVF88tkni49734Fgek6deS8X5xo6tTsEMm+81KYDNkL5VqiL56FVcTB0DqfJ/VbRYj0f+/3t6otMe80zdnufE/35A0RNH2BFwRTI6UaM6KiKNjc3ERrzenpGdPplLIqQx9tMuHYzrrgAVGoZpKISUGuslRSWJQSlEPrkM6p3/d569pnpPprs4rA7xO+zRwTeKmgc9aWzNV6cHLdmNcxDOcxWSnBtO6bwbkOnG2p5wPu6forr8KDQwxrfN9qaFqztFX79DjrQoqLfLsOm5ubS330aZc+rExxpEoFvWvm1tdope3Vdc14PBZzdq04Ojzgjdff4LOf/gwvPP88r736Km+88Qa337vFw4f3OTx4wMnJAVU5B1fjsThfyYi84DXx/TXNvV91dlvBxnLk4fTZylVdgVeG1jKt32c+lYKqKpHUGRKF1toaYyTZuas9h48e8iu/9It8/Wtf4fs//wN87MWPM5vN2N3bpyxKnPfMT84wXhJMOxy2rNFKUeuKSpcYbVjMF+TjnCyTQA3GQB4CGqEyTIi8h9LkowlPPfMsd+/c4ebzL/BzP/cLlPMFvqrY2pjw4ksfZ2t3m73tDezsCDfJsOUGZanZ39tgf/8yk/wGeaY5+Tf38fmC2dED9LzCVjFlyjLO79PB6fshxr2PP867F32YH30MtVJsb22v3O9++cgzSDpoBfqq4vgsz/OGeYrO3DpbNqOTSCGqgyDTd6sYB2mjlealphp9rjl+F/0iUkIgMnI6SA2Myqiqmi9/5cs89fRNPv+DP4g2mpc++Uk0nlE+QuuMspKEakIXaVxdszXKOb5zh9/8N/878+mMzc1NXv70p3nyhY9R4KmMxypABY+dDpE1zKnHd+mzVcg3EsyrvuuYAHTkq+L7YwJF1ITkDtWNbuvJxwoar6MQuUklxFWArkOMWttKwxk29TUquIB2may0rEJmWvmWSvLtOGTWiR1/ouVRCoyuiX4wPozDZCEvg5JoNqM8ZzQek2cZJssk63YTyrnN3dIyStEe3DPKNXmuGWUZ41FOpoRZMFqjsaiGmA6MYdC6acA7CTZgvcInsvwm4EFg6rz34Wfkl3xcxQ4Dl65dvLbriI7z1ryztwTzk/iNCmakwUzOKY/JNFqPcZMxk2jSWdYs5gum84LZomRe1vjKNtEVGw8PFYmtpkPSQ7IKF/vI7Db3ohsJb928VyL4geWIRpj07mN6r1dF4Vse8/K7xyE2+t+sak8I8OV2m74uQFDH3/tRRdO9KcuS3d1dvPeiPSoKFvMFs9mMje2tJgBGKuhK2x7qSykVkjf64L86jCNcb7M6bYX7k+KcVQxqQ8jCEmyK36c4qB+mvA+3O8K/HjESGUzCHWrPvMzTh1DyXulONMRh87DlskoY0n93Xolz7Psdr+svfSb/lts8L2/LqvEPneWhb89bo5QxEbPf2D5oT2MaOp/PiULGOJY+TOm3q5SCJNCQ975Dk/RLeib7zNTGxoYQ5N7z9ltvcnJ8zA/94A9RlyW/9oUv8O4773L3zvscHd7l8PAR89mUupIIekYpREkU8/nFtQs+oQrR5CdjT0tqMth3bUjH/jhlCBbLfJe1VbEY7UN+qWiua3HOousaXUmUVm0kTcf9u7f5Zz//c9y8eZPLl6/jnCfLcurKMp3OsdZx7cY1Ll+/gkJJCHclgvONyQRlBP87Lz7M1tXUVUk+ytnfu4TRGfP5nI3NCVtbm2xtbWEyzQsff4n/4Pf9fk4PjihnUx4+fMCr334dbxSXr9zhR37PH4BqE20XbGQ73Liyw6XtMewZrrun+Wz+Q3z5V2eokxlGnYEvJArlikiUKYM6xHyvu/9pKO9V+5f699qQx9Fpxe7l/Qvv9UeeQbIhg3CfA1VKTCqstYzHY8qybBYzlfqmSCl+H0sEFv2QnX3gFhFxKs2IJnSxfvp83SVuc+PAnTt3+Z7v+Rx7l/YFXGiF947cGEkkOi8xOmuIWe89owxM5fkX/+R/481XvsHJwSHeOf7tL/8qL37v7+IP/sf/CdmlK9QKvHI4VMff5nEQU39N4jwaBqn3ri2+Qbbp2ogE3iZAmBZgei/hm+WrpKkeER2I+4b5pCU4+tIhaJlD3zawkilqqvhkFE17rd2t0A9SxwRfJ61F9W5M6geVoY0Wnx5rJRJLCG5gjCTuzYwhN21fXSYdrKvAS7SuzjutyHQmIbSNZpTDaCQ+X3kWnc8tMb6Za2Yh/mp4L+9ixEfAeYv3dTN350N+LC+/RybA+64kNYZxXgJ0imAKFzS3qktarDuLQ/c93cK0XoeRDyZvOgbWGIkkzo8d1Shna2PCdF5yOi84nc6Zzgtq3yYXbvY4mLyIk/lq5qY/4XaNxM6+3cuL3bvHYUL6v6cEbH991rV50XE9LuzoEB9xTT9g6cCRBAalh8Fay2g0QmvFfD5jenZGURSUVcnYbXTvLN1cG31knhJjeZaJmc1GtnINmvQDQ2PvtbtuTs14WOaP+3gsHfcQ8zUkcU9H3wZQiDgijivORwZvoUlAGdvr+m2t5XG/ozI0z/RnCquHdkY193e9kOIipWXO1p/kDuPTW5jUh3klYR+EUgohJCXoyrKWKP5LaY3OWY57ODDnofmn+YLiuud5jlJiwfPbX/oS1y7t8/kf+AHeffsd3n3nHe7eucPt929zcnzI2dkdFvMpOIJlAhIJU6SBjeVEDFkP0VKkm9emoQ/6kQpXzH9o/VeV85mpYf9siWbsUejASAUXCiyZCRH1tEIZg9Kaqip5843XufXWLfBiTmh0hveiOXv/3fcY7U7Y2d5mMh4zmUzYGI25tH+JvctX2N+5xO7uLhubE7KQbFYpGI9GbIwnCOXjKOsSFZLgKm3Y2t7l/XffZ6wNzz//MZ68eZOvfO2rvP3OLbIv/lt+/x/+I3JenLSFV1Sbjo1ntpk8uozZugTqEZoFMMcqCfSx7rycV4bWPE2rsqpuCruUVlRO6NnReHyhfuHfAwZJmwznJLkfyKIZo6mdJctHeCWBDUaTidiKu5hvo+uEq0M0N+UJ9vuAa/0plNZ4G6CS63HBqQS9dzHFuS8MNhABqT1xA+C9ADvrLFppKlsx3hhz7cY1UCGcpQpJPb0jMxmjbNwQehBoe+W5981vc3jrFmo2ZTuXLOv16ZTX/vW/5cHte/yRP/bHuPrC8yycx2uN81qiHJNEHgn/Wye9WUvA9g79Ut2hT30iyYvfpwxrh0jpXSyVmrj1ch012hHfSETDJON/UCqJpuLFKCcdskqqK5xEYOkRxipoazKjyLIcY7Imd0GWGZSx6MAgRWZAgLpG1XQ1ecT5eVQTXQ58kNjEudeBCSEwmEaL+abRmo2RYpRnIQGdmJgJcS/FxYAEKpXc+dC3a30c4jmFlhnH423drLPDN4ErpLQhtpufQwhLXLDC2qdS2JDvo/k7kWQrhVfde5YiR63aZy2QTpha5yVqmRd/oiwz6AzyLGe0YZhs5EzmGZuTjNMzw+F0zrSocNYKk2hdGJ/ChXxS5wkYus99Z7NXAf2h96uk832E3a+zRDD2GMxV411FNJ73+0UZpnbPaExpVGRuVjEUqXykifZFIPptQjSLUEkClGisr8lHI7QxlOWCYjFlsVhQFCWbIdqW9p7ReEJZVZS2bLWPzR77RpggoX4t43yEq2r0BoNwrTHd7RDhfa3FMpGeChriHBshHKl0NmarF41OPPPL0txW0h5NyuWbmABaxiTwKs1BJlYP1taJ2bprxl95F8ItIwSi82gdI41VOG8xJlhnqLAiDawP36kgmUqibgpMG9r/sLeJQEr+dg1MTeF6A7tW3A+fwJ54dlpcsiwx66OouH1d2wiZ06rAHfF5ykC2QlK7VD8KnogSvPCd1qqlV9Qwsbnq7vfP6nL0v2FTRmlLBANaw+zslN/6zd/k05/6FJd2LvG1r3yd99+7xZ33b0nI7sMD5tNTrJsG3Nr19VOhvcZkuIkKKufFuiSqY2CalA55rdTy2PpCgVUROIfm1S/Lddv7m76zYV5KCT5WSgcKQXxb8RJV17s64JwMrRRVWYIHrTOqqsB7hVYZVV2yqGfMz06ZTCZMRmOMMTy4d4+N7V02dvbY29vj8uXL7O3tsru7y87ONrnJKYpScgJqxTjfkLUymrNZwae+67s5nc341je/yc3nnwFX86nyk3zxt7/Mt9/8Fle+8gR7l/bw/jpvv/U+z9y4xmh7RG0yshvX2Hn+Ge688W1ybyXZuTLikjywpg0jna6nc03495amWF7zeA9dqCNHP9yZFftjFNiqZJR1Gep15SPPIOX5KIQp7UkPkEOhvQ9J9uSnR9TT1qaqeEEyPhCi8WgLoPYtUYVq4ul7L35LCoUN5l1NfpiEOJBDkJi2JABbK90kMBXtiWvMLbx37Oxvk49F9ZqZGGpY5uW9b/xSGnpfgclG3L9zF+YFmffC8RiD9uCt5fDdd/n//L//X/zoj/9nvPjd383Ciepe+ZDnB99IxT0EQq7PGC3vQwfgpVKqtkbbimr+06xRbHclME/alvcDphQBQXZvpG8IL033QvqkbkRU8Y1ukK5v9zC81cozzhRaG4yRvD8mEBNGWYxuc0qkY6yVD4xEQIrEVXY0QrNkTUQCpTAxfivgvaX2tRCCKCwh47WSpKmjPGM8GpFlmnEGozwJSqKEzbJeVqENZd8Smi2SHvKdE81TJLRahA3O1x0zmy5SajVNHWIEwLb+U519RvzKWkInMJKRc1V95N2eS6OTs2OXtTTxuTyT0N8Y0LliREY+yiV0+dYG2xsjJpsTDs/mTKdT5vMa6yVVQDCqpU3Iq5akZqlUvek7Mn4XFDisej7EWD0eo7aeOICLSwGHxrOuDAlMVLrfvXfn9ykwq6H9VJuHSCTlCu80m1vbbGxtcnx8wHx2SlkW4nfmPd46xpnh+tUrvPve+5JEO5qZxWEo3ZjRiqbaMMlHVIsCtSuM3VBicK1Vc/7bfWr3Kv1b6rfRNtO7GBmXtO2499E6IQ1CFOvFv61tTcFTuFvXkltG8onVVFXZ9BvxFqoHF4LWtxFOWYeQrRrlFZkSQaXWweHcGJyH2llJDxb87xsGMoHFROZvYM91usntLDvwOy0pHO8+j6RXV6DSF34ul2gW2nuajicZS3v/lzUP3TEvj7H5ewlPBU29UhSlpMPQyb6nsHtpbOHvmJOsQ8x2kXRTUmsapWBzMsEYw8HDh/zr3/gNfvfv/jyusnzpN3+Lu7dv8/DhfR49usP09IjF4hTnoplyYh4amTo8eNucsRSORmFcZ03COjnrOnVT2NdnmPr73787FyspLdT7JvhLeQhnN4larOSuuCCM8K7GOkuee4wegYI6ME4ocNQCR0qHqyuUc/hg/lgYw8nZGTy4j9aSJH00GrG1tcX29jb7+/tc2t9nd2+XS5cus7u7y+bmpgQqMgrynO/9/PfzxDNP8eSVy7z83HP8zz/90zz/zJO89tbbHB3cZz495eTohIUy+Mqwv7XNo3LO9o3r7Dz7FHpng+rMY3G4yuFsK3hJ1zfGB5C96lphxVxT9Pe6f15Dnea4JDAhvYOKkIzbOo4fPrrgfv57wCClCKeRqofQrmVZLhF6WmuqqupcpgYJ4UNSRbmSOlXhyu4QhWCeBFCxDIDiuMQ0x6GCxKx2tmGItNJyaQKx6pwNiMaCkwg1zjlhiBw0EKQPMNKL7xxnJ8dsTSYsvNjda2VwXvK15E5hHx3yc3//H/L7/+icT/3g5ym9F0lAbCP4JmkC/ksjsa2IchS4kKR+r57vV75YuYgUul/vPMKxrbvOrMIHri9cQiW+aKM8Z5wrJiO5WlHKGotWptkhkX60obetsNLDE/BdZNwACw9FHV/IeBy+kf4qJdrTPJcADONckrAaoxiZFPhEJjbOOTI6jpg3pSXgXPMuJeqi1iO+AzkP8b6kd63LIEUENUCoqBjkpAWEsRhSAkIFWkxF6rezfC0zGhnhZcZEmKjAZNGaM2rtUbVokWU/hfGdTOTneHOTra0Fxycjjk9yzuYLZouC2tomX9KQxiUtFz3H55VVEbyWCa8P1t+QL+eHVdZpuOKZfNy20vudwvLYppzJ1mRpY3ODyeYGxyeK6XRGsVhQlgVlWTamy9PptGM739eKqcB4+ZAnKB+NAlNkQvyWZUY5JbxTLUUaubQj4OvVjQK2qqqWHNPT9ts5d+GaCoxbX3g3BCvT9Yv9NhYFHSZA2jXeo60lM4bNjQk7W9vs7u5IsCHrKKuasqooyopFWTKbz6mjadU5W/5h3ZuLMOzfSV9D+P9xx7B2TJGRCM+N0Y0ATaLSJoFJBhjoPiOglBKTLlqfuz6BC+35j/dKa804z8i04eH9B3zhV36NH/mRH+H44JQ3Xn+DRw/u8OiRBGI4PTmgrgugFve8HuhatR79KISr6sbzmxLnQwxT32SxL/i7aFktqIIhTrrvlxPdLvI8B6AsCzJDCBMOBM1g/BnTVMS7G+lB5wrJ66Y1i4V88uCBrEGWjVCI7/04mObt7Oxw6dIlLl29wt6lXXZ2ttjYmFAWBccnJ1y9cpU7t++wYTJ8UVDMFxSV4/17B0znmrM9ixtlnN45Ymv7MpeffIa7d29LwC8rETw7SYYD/KlrS57nS4xpn/bu+42mOK7PPA2d5X45PT07byub8pFnkKArBWhCSKsWWMSDGSV7KYKJpcmNRHuBDG3yV9Ee2UaGYAai0PVLutnRkU2AW5toVCaA+IwoaVMZg3dyIQRBtcCqP++0L7xHO4srS+r5nMx7NkxGZnKq2mFzg7EKW3mq0ym//L/+DKWt+J7/0w9TOAkDHrkhjRLJugsJR5fWPPabPkzHmV6K+C7+3ZUCPE75IARbSkQNRZ/ptxiJ6dbEJCSDyzLyPEMrh24SszpsEyBBmN0umyVMjoeY0i55HgA1gfBvxIQkZnQK2/jMebyzgamBTGvyTDMa5WxMRozyXMJaG9PwDyJZDiEnVGRuPB7RXoo2qx2/JzBTThg7ogTPg/USbj22ASFyo49nvGWqWjMRgkAgkeKlAJN2nNA1o1R0JZotwUpDnIljOck7H8K9y4dt8t/YTtVB+kpFnyThuYRJCvl+Ea3chlZkCia5EIAHJ2eo4zOmswW2qjrEdJ/g7RO+xL0+J4rdkLSzWYkVxNxFCbA+kZyWdXmNPggB2RdefZiE5HnwUAEGhQ2EuDEGDexfvsz7t99jOp0ym82oKwmakxuBv7PpbInZHCKqVGAYNiYT7t27x1NPPw2Khijo7z+wRLyl92jVvvSJuzr43aZEQ4qLVjE+bfGNpD4SyDI202S27wc70ElI6EjEKa3ITMaG0extb3H1yiWuXb3C5cu7KDzz+ZzDk4L7Dw/AeRa2wNcW4xXaZFSqPWtLxHsSGKm/r0P34bxy3jdDzuS0M14qj6N56DPY59Vb+Vy1f8d8eVppJpNJh0lIGYIhRnlVwI7us26un3g+J5MJGfDw/n1+/dd+nc9//w9w//Y93nn7HR48eMDx8W0Ojx4wOzvBuRKtHHgbBKuG1Svane86xqg/H8FxtvNtCuP7dWNZF00tlvP2LKlJOrd+f6nwITI9xhjKssDamvF4A0JoKMFngoeUMsG0VXIo5nku/JOr0V5hvW9woLVQlwVZNqYqFsynpyileHjf8G6WMdnYxOQZm5tj9vZ3uLK/x/vXr7OxuQHWcvPqNe7eusWtt97G+QnzyjB3Exa1YmdvB6cchpy9J57ilskYYZAk8CvguqdjVdW/Y33GMYVp/T1Jz/MgHedCuC7n+7LTteUjzyCllz3ltr3uXhDvRQNQ17KhkeONiWXj+6puNzwmj1RaY0wm0u4grXHBxKssSzYnG9R13Ymq0UgyFSitsXUNWomDnhUEl2WZ5CYKbXl8yOfpKIuC8XjSjsWlF7WVmsS+GkBRlhSzGb4qmWjDSGsyk1P6GqcVxilqb6msoppO+bX/78+ived7fuSHqIDSuZB5O9jd66ABWwLyy1qYyBgN4Y1IxEbNzHmoZR0h1Qc66bMhpDVELPjARDdzCD9bZsiQGY02msbmWSnA4V1NZetO+7GL7tqkBFCs0K6HvAuXXmcNIxXXJ46z8kKMee/BibllroI53dgwHo0YZRm5MRglojqP+K31iavIdDnlqa0NAwr1XNTy9Jh7FzVK4HySQBDEdCAyRbjwrquJikBfnIlDj4Hx6rCTfcCID4xQZCpUs4SpCVL6UykxgWwSA9uUUI02+9KU8pJnw9uaTGuMUmjt0drhXKirZByjTKH1mCzLyfIReT7m4OiI09MpVVV3xtCeg+Wz10hpewTu0JntE9dDxHYqsUufrSPeIuy4yF1Z1feq8Xrfrv15tv9p21opGiPfc8bfh0Xpusf7a60F5zEhL1pRVeAdxij2Ll8CRROgoaol0IlWAvOKsljqqw36QkuoasiUZnNzU4I0GI31XQ3M0FoOrcUq+JWeg5RIWKdJXLVmEcfIeslzCVUuWlObmCzFKFIm5A0UAYJCh4haxoh5T2YMmYKR0dS15c7duzx8eB+N5+T0mKOzium8pKprgUlx/F7hdQuDO+vjW7Oq/roNaeIep6y6l0NMrFRkCS6l36UM7rr+Vt3L9N6m7QwF67A+MAFSE40O+yNkXszzNzTP9Aylfpl9Ir4lXrtztNYKc2QMh/cf8Gu/8gU++9nPcPu9W7z37rscPDrk+OiA49M7TGcniEOqmG1GjOjpCiPXMa0XZUCH1jONahj/7jNKFwqGkdQfOjdJLfqMX7/dPmMWaTeTiZ1pXRdk2YgYWVi+iVFtBWvWdUVjuieya8kXGc+QEpFQXZaBXolRCgWpz+2ULDNUixnz6RkP797h6P59/vAf+AM88/QzvPf+e5BlvPrK13jv/iFPPvdpKr0JWU6tM7Y3J1in2Llxg/H+PtXZUYPLI6zoCm7oPO+7HAAdc+ShO5QKalIzz2Uc5sm0CMBOj09X7me/fOQZJFvXjclcA0isBXRn40AQYlzwuq4xxjSMTYN4vJjZeR8j5EGGpigLjMmjSByNpqprDo8OGV8fdcaUHhJrHd5KuGCFIsvzoFL1IUSiHN7YpwtBGkyWNarYFiFEQii23fV5UkrhncWWBVjLSCkCB4bxCHWrFXacQeXYdFBM5/z6z/wsBsV3/eAP4I2mtDVWGZRyqMYMKwW6zUxRHby2WuodpVIRRKqonVuBMIbKEDO0CiGsG0f6u/cOcWxWGJMR8zAZLYS2Dtozb0PYAaH00xY7+DMS/rGk43I988T0nLhGetRjaPCSbNZLStlMK8ZGMxllbExG5CMhVPJMmCPVEMziGJoyWj6cNRek6rGed62WSDQ9SjRIicrbOYf1Xphn1yajbd77cJ7DeYnChahxikviib4SMqfgIBjWow1bLnVdYIwiQ5QEmYgMTNTwhW+VljDxjQ+YDgmEtQ6aIdUwXVqbJsogIZeUUmJjbzLVnIsoqdVGM9YSen2UacYGcpPx8OCog5SHzln/fKb5n7pES/fcrDq70M10P4To10mk1xHvQ6VPjKbILGX0WvjbfbdqDk2bKvXyWx5Tn3haVVKY6G3w0PPSduUstq7Y29/DeU+xWFAsCol2Ghh9TQjUo7qEeJyzSpG891hnmzQQ1tqOrn2dNm6orIJ96+BdLH1TlCxrUX9Hkq7b0Prxu0hoaJ2RBuXJsqyZW6ZlTauyagR/ZVEwt06cy53FaIm4ohM4VHkvCZjxxKhpIb9lZ3yd+fmQrqFZ5i4BH5+tE0asKx1BxcB3nXVOTuUqgcJFmPlUej70PpaOuXayp9FXOVCkGG0awQJIUnWCxUm/vUgDpUIM4uwSvN5nsHwQdFVVxWQyIc9zTo5P+NVf+lVeevEl7r5/m3t3bnN09IiT40OOjh4xW5xIJFoi2xDXLxg+P8ZePQ7z26/btxhKCe10//vmqENtnT9mYWAuMt64/rHfyDQIzKzERE63/urtHXA4V1PXEmQsy3JQksTcNnOLY4i434ck8xqnaoxy4DKsBWsrxqOMw6ND3nn3XT7+8su8+fZbPH3zCY5nBXduv4Oa7DLeucTxYow5yxllGdevXOLSk1u89hv7HL3fPf91XTdnzAQrqLjG6xjNdXAyttdnjtJ3IMyhdRKca3tr69x9iOUjzyClRFpMBmuyjNq1Yba16Cob+20TbM2j9igCBuc9la3JVBbatBiTBdMz1WiNrHPUXhDx/qVLlGUlZzkgmriJkQlSRqOCHXxt6xASuUc0BZrCBVM30XS1iLksKryPYTWXkaSKgNJayXpuHXtb2xRFgbceXytyoMCDUWTKkBc1I6eYTRf86j/531DAZ37kBymdk9wWSqJ9xVDQnuXwpN6vlsr1dgrViTzmmu9TdNmHQT3BIkrFfnxS3xNzQfUZFHx/XBABiVZpBz60IyaaEuoy2niHviIz5OkQcx0CsPHI6c3eCxCNEK9PFDjfao3Sb4R1EhvuLBMfo8nYMMkzJnmGChJdFc4rPjJH4JxuNFIdIQBy3CKzAjRMkIT41g3TU9d1o/mpnaN2LQMWNUvRzM4R1y0yS25JK9Vl1gDXrlfXOBEktGKr/ZGfgeHxLaJrzGYDM2SCL1GW58IIRabXKEyW+hnpVuqlPQ7TmNg5H7VJgDJok6GDT3pmYGucke9tYfIxOst5+PBRa2OeZWS5CFNcPI/J/PvS4eVz0iWsOkvSu/N9xDPEoPVLX2q8qlxUeJG20WekVtVZN67zvu8/788nrlme5Yx0BjpjrKGoDLOzI3Z2d9FaU5QlRSkMkmvMPGiYtQjvO3fVWWJqAeVBOcEfVSW2+KkP1DoifN16DEnSUwa0v9+tg31qOqo6ktvo+1BVJVkeIy+2Ety6rokJpq21WGtZLBYNbtW+DXYTfSO00pIQU8sNNt6jMYQkewI/TY03HhUIZN/AOSLIlTUgmoyJAEMPHJHzhGEXLeuECecx9P1yUaI4bWvVN+ke9v1XBIT42CCgAnxxOOsa4nTIh3B7exulFLPZrPtetZFY03skAuU2J9h4PGY0GrFYLPjlX/5lrl69xoN7D7hz513OTg84PTng+Oghi8VUcKPS+CDo7USzXSFMveg6fpDS92cZunfn9Z0yUavh0Orvh85TS/DXRJ9XpYKAXAdGNghNA8GBJ+T78RL1rr3vGZFJExop4tjIWAT6xVnwQbtvLc5q6qrm7r17fPqTn8JkGUVZ8JnPfILjL32dLHMU5RS/GDHOcqbTjOOJp5qfcumJq5y+aqjm3Zxx7fm1mJ6VwioYljKvq7RIfbwQ6b5GixRgiYlCzwuWjzyDVNWWsQ0cbCVMCzqQ9ErjlaayFjxYL6ZOBkXtQZlM/Io6xL7BBcsjpQzeQVWKZFD8ThKtVPxOCVGpvRZpmReJs9IafCVBI7wQdyJZl3EbnWG0aYhR7xzGZFgnUgHBw566Ljk9OUYrzcbGBkVVoNAhQSFsbm0RtQVFVVGWCzLv2RnlmKqkdh5rAO8YoTDOkXkxnVhYyxiFO53xK//kZ7FG8ckf/DylcnisSNC9EmKAKPoLUniCQ3y4w50ABN43jqNyuKX/GKkqSiqVSgA/oOiyFyn70nQfNCre+7ZCCH/eCtl80kAKpFUCWMIoGiG2RJOLWsSIgGJWdKGdomStNTPrFCVzaHpNzpY8880fKfGD6pqmdaQjWnIXjUcjJpMRozwjzzXKEKLjQO1ViAwTmCPvm/bkbCXaHsCFELQxqpW1QdsZAHAk9uM31lqRwIdIV95JtnAXBBHepcyPo65teOepLc2apQEewON96/+0tJTNvnQlvkaJOZzRcoaJDE+WC9OjBAGZokQbLcl2jcZoFcKgC0ISBslhtKE2HqOqEI0wJOdrNEgW42O+BzBGo7zkibhiMkaZwlczHh2d4hFhiK4VOkfyXjTCi4BMvA/EIo2k3HuRmivTiteds7RatTbqVLs+Paml90EjF05f/DU02ScCzyMMUoalz4ikddruh/Zw2Q9nsF7v+aq20jZX1Y3MQW5C8m+gtjW1q3Fesbd7hUzlUNWUswXlohACU4UAPU60yv010lqC6jRzcgInTIgsp1Sr0YzjSsecli7RlZxx1cIZFE3o/FQK29X6LPvUdoR0XjQAdV1TFMIMelwIxa0bhke+k52IMMr59gypDoyW82idSAxiMmbnJVeaUmKS51U4jqoVQMZUCkYZlArrE2RHzboG4l9gqQqCR9fAJJfsd4f58D1511LxbV9Db300+RW43mqx2ouUfqd7fXf2t4NzYgfStglzXhLkNfNVTd0oUvORpiEw5qHhGChEezA+Rm70bf8Btszn846ZWTo4E3J0KVSTNsR5sM5jdMbGaIyrav7Nr/86vihY6Bnv3XqH6dkjptNDTk8PmS9OZd18O8+E/w1TXF6n/vo3o/qADFNfmJDiln4givP6Su/T+WN0+F5ORnmtSK0FosBP8F70HQrapFEYr5MAGiZExkukCELHCkQjzzPEUsqGdqOGMI4t7oCMy2LBlRhnMEjgr9p6jo7PUJlm98oOZ2enbG9v8WP/0X/E67ceofG42jIvKuZjz6PDOfdP76N1zqIq0d4GfOZbHBaYsjrmZvQtc6oCjDENHeUbtxLvCS4drSCgEXg7OaHOR/94hclygY9K4Y0TLbaHYjYb3M+h8pFnkDSt5kApBLg4AcwqqPS9l2huWZ5TlCWuEBvzPM9B6+B3JARmbrJANLYXKyKuNIyxDRorpRS1JUjhWg2DdRbnKpT2QEsQxp/eS0JOrY0wRDY4wMtkJHR0luG9o1gsWMynGK3JDJyeio3lzs4e3sPW1jbOWpRWoqGqazKlUHWNCTlywGO9w3iNsZ48zIlRhq0qNrVhuljwy//kn7J9aY+nP/kJnBFNlvESNScySPHKRbt0kKZ0Eu7OJeCxQ8MRkW1rhpOCFU8burEDjKDJCRvBb7ddR+r43oFdSTut/X0EmokmL47dOZSXkLQtgPUJ0Fke3yoiv1uWAW78OwXmfSCfqYxRljPKR2RZjjYKjGj4vPN467G2S3RJWpfWubbRHjknTI4XH6TIFDknZzr6FNnaSvCJoCWyzkqQhpRQCYxTba1oKaM2yUm0LQKj4rxKAj40MrFmSRr6or98Pl3zJEyorzBILgWTSYRGgtmBMZpcK/I8a5lgHTVI4leWBb8KqS85qkzQHGXGkGlDZhxZkEZFIZxSrS9B3JuRVuxtjFBP3cDiOTw8k3XGo4zHZMLoZFkW8oboRtobz15fcxIlyHUkXkPfTcT9nrRNa7mbOrlJDaEFrRard97WaWWGzmnft6bPMK1iBlZJbTvfR8Q+8M3Qt6uIlvScx5xIlbPUzko+OGu5cuU6k9EGtpxLxKb5grqqW2RN9y53pdBiJj0ajdAe6rJiYzJpBC95nncECylTk5ZGawNy/jLT5EyLTE2aUqIvcU0FF/HODZUULvW/j0maWyHNAOcQ/o7an/hX+86LRQ8khKBtbmvDACFn0gTmVQJmrGZyO4RtEmQpWlik9dLzoKOJoBrAH3HsHrQxy20Qz2XWMJ/rmPZoPuaTdZIeWt/K7v2IX3UG1AywYb+8OJo39yE81oGzU9BoZpQSBicPAh3lg7l+GEkMVd/XSjbzDgNTgf6BkI+xckEIO0IrxSuvfJ23X3+DJ25c59a7b3NyekixOOHk7Ij57BQfLGraeQaGqD/P3hhWlXW49DwN4tBch9odYoCGvhkSDA333/+764IgbUm9lmYNlkUBJzRh/D1NrqQ+PJLvXRDUq+RZv6/U+gVQwlyJwFtRVTVaaU6nc86mp1y/dpX79+9x9959/sjnfw8PD7+EyzIWQbg3W5RkesS7b7zDM5mhdI7cexGpBHLPK98I8hzCvECM6EsjlHbWd+algpAlZbAb653kggkeDMGZrEPnIyyeOliiKODRvYdLe7WqfOQZJKckg65SCoJ01mRZkGA7TBZyFdXhQOksZD2GsqyoqiqYIkBV1cG3wVBVdYOsbGA+VADskRmrgsZKIURQBODQmlrEvEaNxMeL5N3WFokAUmCtEFARCZTFgt2tiXwfDslisWCU52IaUhQYE7K3GzEjanLw1U4ODuJDpYPEQiOWD2K1pLAeRkFQZY1i5gomLoPpnF/6h/8r/9f/8v/G/rPPtNw9rYQr+tbGf0PiuCYHSf95YoJyXkmJgi4CHq4L5zMqFwF+cd1Tl6G0Xp/g6zsOrytDBEufOYrPlFLkWUY+yhiPR+S5JJ9VeFzt8UoyXncZOcBHaW3XhygSRtY50QZZSWLnnDA3tpZ3QpAE7U8k5r2j9rXkYLKueR8j4Wk0+LgOSpI0++AnhMf0BA4xEp7xecMk9RGMTSXbgYBTBCk1JR6RgMnc5forDTWOqjIdMzoTTBGrhEEyWY3RkUFSZEbMsmyWhdxjRpga5bG1MBx5lgVTPo02IrUzSrM5mfDc008zn7/FfFFRuZqRVbjScenSfscHoArEeOpsCoRknF2Tx5RZbojYgTOldNeHJy09vr5zr9YRKv0z3T+f5xEW/XaasUZNwQrCY9330GZZX9VvKzEGEtbQIwTI3t4u4/GY09kZRbFoNCzOOZQJ5nXOLRHI0rYI26y1jEwuZ6oSzWNRlKKdHYBvfZiRrqPzFqru+KNWVs5Nd15DcKIPU1ata4fx6JkfLRH6A4znurIKPqZr0JHss+xHN9RfyvR671FmhRbALxPHzZiSwBRDY+yfxaG9XzrfzjdMVbeuEMZDwoO206UpdMYz+E3ve0W7ps65IL0XLWjjr5Qw2P05Dd2bCKfqWvyOjFbcv3eXX/u1X+OpJ57g9vvvcXpyymIxZTo9ZT47oyFmnY9EQres54VWzn+orGN41gl90jO27o5cVHN13l1Yx1T172saTCL6UIogshYXj964Qe5NXQ9HkBuEzfKiGYN3Dh+ENGVR8PDeI555+nle+dqrGKc4OzqiXpzy0mde5I2Hc3KTUc5OOThd8PD+XW5c28TrDIsw5fE+S77QMFbVASbCEGktGp+A8324s9HaCN/iczEVTOcVPNmioE5DWRWoXHCyc9LuyeHR2r1Jy0eeQbLeUdU1o9GIKiC5HAnIkGUZdVUnSWEFmVnvGxOKqqqbw5aZPEh1fePPJFmPRdVZVpWotHU8gOLHIv4WtgFU0Np2x7aVCmFUfRuBKEa/ghYpdtTg0gXOiT24VqrJ0zEeT9jc3IJAeIrdsJOkYkHKZn00BRTHWIJpFB60cijryLxirB21tpRlybaZMH90wC/8w3/E/+X//hNMrlzBaRWcmL0Qlwp0wK1+FUBRKlK9zYVNEeRQ6QOB3tsW6A98N4Tk2qEsA9UomYiSuCXiw9NhkIYi3sTfI6DqPx/qv0909qW6kWCOGo/ReMx4lJMH5jiOS2IbOAlhHLqzsQ0XGSTbmG5GAtA50STWrqa2rhEcOCvf24Y5EgItEvHOexw11tdLBKA2GuPFzA2yBnG3xIPF0yX241h0yKPQN78Q6ZJ4SqFUiCYYFxSBjgTNVAS6eAHWWOrao5TFWoPWkqNGAnEYrHFoY1FljTESvj0zEjK9rj1G1xgljFSe54F5Cr4cPgZ7kBDSUXOZZTkbI83zzz3Nt998m9r6Zj9OTk5DpKnWBEJr1RGodM7einOrtOrct2GTmfVlnXR1qKR3cp1W56L+NmuJkxV9r9MYDfXR1hNLgBQOKaUYj8fs7u1yfPCAoiiYz+fUtsZ7hyJrQFfst+PgHY5pXdf4WgRRWovpc1VVqMSvLdW4LTNaLRwYmndkhtPALv316MPLVQxU+qzfRjq3deNcXtvVsH1or9LnUehiVJsEdx3sjuMTJi4ISgbwiHd+8KzJH7CKK/ngOKnbxkWYfVYPY2U7chZotOytzqCbFsEjyVOJuRy94EynZI+zLGt85Vb1nec5s9mMPDeMRjnlYsGv/PIvs725ydHBI85OT5jPz1gUU+bTEJAhCsmUwQ8s1UWYiccpF23vvLP7Qdv/oHWhKwyFGEWyjf7WJHvWGc6JZdMQc+1pGSqTaEPTfpbG6aOWpvURrp2nrEru3bvP937Pd+MdnB2fSQgtV/Lk9V3eeDjFVgtuv/kmb736VfziEZ+5/v2Mt3eYn00FJvr2VHoPRosJcsrIo5RYuuCC9jgyQF5ilJOYrUb9bEIWKLyYNeMDbabwueHStSvs7+3zxre+jXUaMyBAWVU+8gxSWVqMGeG9oq6FIagriWJXVWk0JSESq7puGQdiZnFxdHPOB1+jCPRNE8VHDm3eaJa01k3Qh2gDGu0sUxMIKTFCnQ+XgOa7KEGIQDomHJTnIpWp65rLly+zs71NbS3PPPNMY2YXL5XEwg9OfSo44RuNdR7tPbaq2+h8tqZ2XjKaG4XSnkw7bF3hasdYb3By+xa/8I/+Af/pf/kn8OOxmOvkBq91kBK1x7ZfInHcrv0y4r5I6TMPUV21Tgr0eMBxmUDo1utqdvrALa37OMA4JRpSs7g+oSFRpEy48OHs1JEzFTV7GaSY+K6mSMyqlJh62va5MEHijyFnK2ihXGsLHbWc0qZvGCSlxe8nCz49OrFdz5RqIldp1SZeds7jbEUMXR+j73jnkCPlyY3cs3wUojYGP6XJZNSYylVVTV1XWOuoyor5PJgAokIEQBMYNBEGBHIWEP8qhQoBJmqs86haNeGKa+sx2lPnJjBHMs/cGKo6aJLyDGPAeslobrQhyxVGO4wBbUXruL+zw5M3rvHe7TsoZfBeUZY1xsQzRGCQuue1f1YGn3sas7nISKfv+9+3bUjgiouUc8fQK33C+CIMzSBB1Gt+HZxYR8wuj7vVoEVEbUzG3t4e7ylNVVYURUEdBGUoQs4WNbjGUTvQ9OBb34b5fMZkc6OBB6s05anU2Pcn3pljIBBWMBxDzE+/7hCDkr7rPl8+P30GflW56H6lZ9k621mLdcx7M1fooJw+E7Sa1F610sPM/YWIdkWzZEvz9wPjC889q8e5iln0yUfey39EN9/uo1Yar8RMNApTUW3ghbinQxHc4ruyLFFKMcpzlHe88rWvcff2bfZ2tjl49JByMaeuFixmZ1hboXDgnQTnWE0SrIUfHwYD1b8PQ/33YdNF4NtFS58mWQWL+z99736nggutfWNd1L8b8btIv/ThVEo7NfN2YgnlvJj2xdxvZVlydHrMaGOEyXPefOttpmdn2LpkczJCG7BVya23XuPg3rts5DUHhwdYZai9CtL3Ljyx1mFiTs04/4D8vI+5ilRQAIQxxwVpV7U5vwK7kcAvSqGyHPIMxmM+9fkfYHd7h1t37nFWPQrjuVj5yDNIRVEynkwoykrU6NpQFIvgX9EySAKEhQi0XhzNI3KrlW3MWzbGGyFSXCCuakdZlaAUJjOcnp41UV0kvDgoZTpAvosYVeucTeooqJuEgjYZq3wfbOfrGhXCJEcthXcOE8J/S1um0TjgFV6DN4bty3tc2dvj5OEBi8VZ823tnTBGykOwR80sbGiDymFaV9RWVKp3Xv0a/+YXfo7f+5/8Z0xthc8N1otWTcUDvqacR8hcpH5Tt0OVrP4uJdTO6y+VziwzOb4DvPpEyCpCcnDsK34fImgiMIuZsCPRb634UIh5owAa5z1F+JlqoECe1dY2JnPxnNV13fgWxfuAVzjXMvAxyasANQkSIEyDkyS5CfHUnN+6xNViqqS1knxBWcaV/X0yrbl0aZ/RaMzW1iaTyaSxSVZJrgeTRSQrmspxHnKboUK+iEgoKGE86prTk1MeHhxycHjE4dExi7KUaHqhDa0MzqnArLjgYxLuthdi2NUWp1tp3ijPRbtmHZl1GGWoKhtyv8TcMI7Mesgt2sHYeIwyaO154uplTo4OOT0rkYhOos31+MbUr/VLHD6jg0x375x3zt06JqRPo13g7A6VVXeqTxykSLlfN5YhxB5jNq0a66qxrCz9TwOnVJUlly9dxnvHfDGnrivKqmwQdfys73MV75YKAi+CAEAh/qxRM9KHP0vD6jG0Keneh0GK9WZRw98Nl1Xfpox090i187ioWXS/9LWcTV8eYkCZWG8Vg9QPaNH9JZ0HjZnp8nos+4PEMiRgiGNYua5+fZvpHNad4XVRKgf7HHjd3rXElyx+4hyj0bi5l6mP3BDTXJZlk9/q5OiIf/Uvf53JZMSDB/ewZUFVlSzmM4rFDGMQjZUPgNkr6Ali1gkPP4zyOEzOEIwdauei/V5kXkNCilSolN6LFHZK4JQ2ZUHXh7HVBA3B21X9emgi0urg5Oa10AmHZwcUvuB7v+9zvPbqG3zhX/5LJtublLYKYccrqsUZxhVshoiGTmVUzjf7L3NLmDRC6H8f/cUD/FQ6CKGkREur9vvOAiY0ICidBYY/46nnX+CFT38SdfkSamOL7/3hH+bXfumXODk9ufA+fuQZpHmxgFPdyRnUSFQCcdmaRznGo7EwGF4cYUfjMVtbWyJh8YCXHElVVUl+mcDEoBT5eNRkMU+jCHWcpZOD772ovPPRSBieoN7Oc7FdH41HjZmN1mLSQ+D0tavZ3NgE7ykWBcp7JpMN8nwEWrGxsYnWhtFoIjkvvGgLvFJs7m7zQ7/rd3Hw7rvM5zOKWUFVLsRkSoPPtZhReVFX4kBXYr/sc83CFRhbk9UVv/WFX+GFT38vT37iRRbe4bzGEpMq0miShv0fIuJZtXtrRE4sAzClYnS2ngQoIg6f9jkg0et1I+NXHUAT200NX/rS1nWAtv98FbHUZ5LS0LxZyIHVSmNi3w5lITiG4YBKRb+hNJdXCJRg60Z7FOfnXBt8QRgjT4ymE3GryfIwFt2YNSoU2pUYwNaW+WIe/OgUOzs7XLmyz97OFts722xsbGC0oaorikVBXVaUi4JyOuXs8EAiaYWADlXtcVbC38c10GGvM28xSjRpo9GILMvY2tpie3uL0aZma3ubvSev8dzTT+G8Yjafc3h6xu3DAx4dHHJ8dMpiURNDmzbIKBrnh7+8Dwn3bB00XqIFs9pSh0ANuRPGKAZnib97Hcz6nGeiM5Q2ZErx3M2bvPb6u1jXSvtEigdOR0lY7zz2EOYSgRU/6CHX+MysuEdKddmxdcTAUJjgodJHwOndWC10WPbtSH/XvfEv9SG/Ef0qwl/Qu6tJC81vKvnTeceVK1cAqKqKsqqoyqqVTiZMdKyfOtA3XXhP1PCIiV3dmeNFmaTY59Achgidde01831Mgm+ovZQw6zMv6X6vy+GVEoSdcSqJZHcRhrL/rmVjh8yPVjxfo0FK5xv7G1znc+jhdG7yIN3U3uibK73aJLHT5jljSOv3cfHGxgaz2awx34p+LvFOxSZjYB1jxHj4X/2rf8lsNqXUiqoo8LairkoW8ylgW4I2RFqMaz80nyWc3StDDK3Uf5yzvY5hVZ175pt7HMdM8i7tax39sroMjXkILirF0vPI7FrbvT/NvFXznw6DlJraDTFlQhsIZIvfxPNwNjvh6OyAo+kxX/vmK3y8qnn2heeZLwrp11nyDLSybIwztNHkGxsUtYPExaBzDrVGBfeWNDqd0bQRMhX46EvF8r2T+cUAbAbvFE/cvMnLn/40V24+hdnZ4qwuMc5zWhTMqor6MTbsI88gfe+nPsvG5ibxYkbTntZWX4I2SOKqNuCC0aax44yJJm1I5tqormkERU3pHLzwSjawyxylgK9PNMSfXknIYA0NwyHjzMDmjLMNADY3Ld5p8vEm2koI2slEmD2UJs/HMmqfU+mM0ln+9de/wtNXr1DtbFLUNW5vm3lVkY9GjALTt5nnnJ2csDg9ZX52RqY1ea2ZWChdBZmCxZTf+Lmf4T99+f+B9Tm5M3KojMclAiMfJAPxr7T0YZYQIG21LnHQrSvtym8q2NA28fXjWiZ8kvfQYW/8Em5qxuTpAqtUiin3Nx1gkKR6+tNbJmjw3c/CM09LLPdLZLqzLCfPx2id450GpbFKxuKdZN1ukrgCta+CNsg35nTWSsS5ysf42jIGW0sCPx+jGQRALAENVYjgCFrnaAUSNlS0Q7PZlHqxYGQy9vf2eO6Zm0EbNKYsC2azOfP5nKPje1RVSVVJABRbW+xiTlkUTahhW9fB5wPKoqKs6kZrlTKLuTYSnCLLGU8mjEcj8lEu515DPsrZ2NhkY2ODnZ1ddnZ22N7d4ZPPbpO9+DGm0xn3Hzzk6PiUBw8fsChrLBmZzkGL6Z0cC9Euawwa0+Q5q7VHGzDeUePJfEbmHTpEpTPOYghhuE2Ny8BoR5ZnjDcn7O/t8OjwOJxfBSqEifbxWCwjvxRuLEndIZjYpYyeHDRFNA0OtyY9kywJdleX9Gz2iZpem/3vYsYNlTzr19NhvM24wu9ODl5LW3qSPGXBAVypznvE5jBhdVXPB0JgtGlgiETXLJ1j9/JlCZZbFdSLGdV8iqtKsONgiaCayWRaook6l0QUjPMJ/pnKKKanZ0hyY42n1T6lCbKToTXtr+dlLuYDs5yfbsV3SX8SjMJ3ibTOAHuCryWeQ7F8EmI7Ap/TxM/Qn2sbRa1ffArDVft7IGeHv08YlCWGs7/8A0zQEiMWiMn06YVIL9+b0jDPPtjvKtygInKL9YMgKSV+G8EtLT7RSgs1Y+sGNxmlePLJJ7l35x7WAUZRe4vTYu6slOPh/Yd89cu/jbc1pa1RylLVCxbFKdYWKOVDvvQkuEcqhRia48Bx9M37vmBG3gqq6jLn3Yaiyav4qcY0Em24aWknMo6pRtQjRLx3MXR8QxWkI+uMJz4/706e977d5+izHgVmrX873ocIyxato+WCwTnQKmthXdTEysYHgWo84+2aaa0lwIESOGiUkSyLzlPMaqYnc248cY1ZcUpRz6jqkvdv3WZ7dJlaL7BK47WhKGrKqsIaxdRZMa9PVkuirYo1V20dEqRJM9nY4ObNm8xnC04OjiSKXnBVyYPSYl4ssEFzJpqruBYSJfnjL3+Kre1tpouKnXkF1RlVWfD+0bu88sUvYmcFvrq4tvsjzyApJf4AUcujEGdzE7QxKtRRkTD1QmgDeOvkSliP1xJxjuCnoYwRP3A6cLfxj4hACpD2wj4675roYYqY2yIMtkccOx3DuNKmBIsqSwuRrFHKoHTGbF6IirxyaJXJRQm4NyKkWinY2iDf30ZfvcIzLzzHdLrAebj2xBNsbG5y6dI+09Mztja3uHv3Ltpbvvmbv8XBe7c5unMfFJSLKT7T4Gvee+NV3nnjW9z41HfJuBQ4HZmTFIX69r8+ARLDeHoFKE1Q9FKlFlF2tDm+SyjRGdGyE3RnBAkz27dFjz4JadErpBzp7509djE3k8InyWxj3S5BrIP/WTAHDcxeV8MV/HqcQ8CcMBdpuF/xQXI4HYJyOB8QrGuQZ5zYaJRLXgGtyZTGGQfKUZUF09kZZTFje3ODZ566xuW9yxiVMV/MmJ6d8uDBHRaLOWVZUi4KinnB2dkZpycnTKczzs7OODs7YzE9oZjPGzPWGDAC6JiXNgxqRHg6YzTKyXPRtOYhvPJkMmEyFqZod2+Xvb099vf32drcYmt7k/FGztb2Jnv7++ztik/Q8888yf1HB9x9cMRsNsf7gFC9+FYp78NaiwDCKY9TgjidFe2dBLcwaKvJXDC5cxKW1efib5Rl4FSNcorLl/Y5Pj2VYCzaNESEJ/oMLJtaxLM9pElqztPAzRHQ1fWXazVmFy/p2VUN/IzCgfadTuBfrNuXFjeMUP+75F3zXOuOw3lbTRatDYwzzESuKjEfjEKBCb6Z3nP56hXyLKe2NWWxoCzmuJAUuQN4fDBHCXdEx7ak0WYcWZZR11UQnPUZ3FA5lPYuhzGutZlfb8bVqbmCue7Aqx4Ra8yyac669jt1evPqlIQn6e7RchvnTi/huiM+X1VtJcOpeswew+u1xDTRfrcalwwPZmgcQ6s7qP1pliclHuKdbM8YdP1M4pbEu5qHUNFaS9JWYwzj8ZiiWLT+t0rhbDR5Fbj0hV/5Vcr5nCzTOFuhsJTlnMViRlcAs34Dlxjvobq+K5dptLjNGq724VE+hXOazLSm3ynZngoB5HvpWCuND/Af6Gg6Wlwe/24tTNaViwg02jqtJmt5DYJPrbdUdQkqx2QxL1409fWNoDfVCsWFTmFQzEMoGkLps66rEEEZHj045OVPvIwx4uZRFAWHB0dsXr8mtGaeS05N6zg7m5KFdCNRaAu0wRdC+9qEs6phtphxeHzI/u4+5WSMtZbJZCQJ3E2GcxZT6yadiEajjA4afKE17z64h717G+ccm6+9GhhGRzE7w5VzJjubGGfh/XO3APj3gEGqnadyqeRMpPy2dkL4KEXModKo67zDIL5BOiSh0+hGQ+GVoEFQbXK7hpgFgsS5YQI8EHPS+FRyGC5VxLW+vWRNnZB0MsRqxoawwbasGlW4957xeMzJyQnGGMqF5HFqIowlNtq1ydl76iYvvvAMWUDWk9Ly4MFDbr3xKleuXOGHnnsKZxx2c5Ot0Q12NjZYuIoXPv5x/vk//hmMz/ELj/IWo6GoCr76m7/Ff/zp76HwDhsyAGrTl/p0iauLliGV/Hn1vlMTkrSdSFCuswfv971qnH2Ctluvi0zSviFoE4MkWPbWtWfLp35s0U/IY23ZiYbWMFNIxBfxoQ3AK/SXaQPBF0aCLuiQT8kxmx4xn58xynOevXmTne1tvHOcnpxw6513mJ3NKMsFJyfHHJ8c8ejhQ46ODzk7OmYxmzGbzYKJakldW2xdY23ZrEMEaG10vFYqn0oSBDnqJvx9NCFQIUCC0YY8F41Snom/1mg8Ynd3j0uXLnPjxg32L19m/9I+27vCRF27cZ0bN57i6PiU23fuMJsXIeS/XGaVJIbMjIk6gEbzHMcdx6SD9FEENIk/lg3mkjpna2uLs7OzkDAzho5vgMeak5kwJhfw/4hERf9MDZ3DdXdnncP6ULSktO5QEsaheqv61QPjarS7SvzOUubvvD49vokl00jXA5G4t7fHeDJhOp+LmV1ZUQUfoj7zF7+PkvxUSBPHvrW1hbvfwpE4rlXholeZpfXrOrsaHg59P2Sp0O2rq9Xr13884u6Dl3Xn84P290HmMlQ6319s+R+rvw8yLgGPy9YpXfyVHM62M5RSbGxI8JDRaIRzjpOTk4bvdCEgT57l5Ebz/ju3+Nar38RohasrvLM4V1MUC3zAO78TuLg77CSYhPed+5sKlZRfxsXR3zxdjBi+XMpywtjmveozRwlOdS0T023/MQ5JUobgQl8YltIDMXdaZvKV7UVmKW1zSAiglOrQl1VZcjadMdnYYDQeg4KyKHn06BB2CrzS5KMxJs8YjUcU5YKtvV02djbJosl/SC9jgk+89RUEhlsSuRswjuPpEWrk2R5tYoxhQ0+aMe2aPXwQSEWzehMEpxYPIcm7957JZMK169fY2txkc3uTza0Ntre3UUbzD37iX19oDz7yDFJRV5iqbCQmipYRikkiI2PSXgrV1PfBR0OHuNUqxPF3dU00lrJNGEvVAVRRe+ERbt9Z244jed8/+BAkvsqhnQoaKC+RvRApTl2WTY6meFHKsmQ0GlGWJePxuBP4IZoDjLMx1649STbeJMs180WBH2dkmxvoPOP9O7c5OjtFG03pakocM2/Jr+yztX8JvbWBcxZtxOxF8oI43v7mN6hOTvHjTaw2NPlvtU+0Eo9fhhDjkiQ67lpywbtAQDeAYQg5pgTjKuR5niRxSHq9avyr+vWDUqKueUSqGfNeTIs8NmGC22h1kl2+GhxDvAdaKTAG5b3kxEKFBKuZhNm1lrooOD48wjnH9etX+cwnXqZYFDx88JCHtx8xO5tycnzC8fEBd+++x9HhAScnx5xNT1kshCGqiznKe+qqWtof622TXVvVcX5RqtUsViP5agl9RRGiKnkv3zZ75FUTCl3yE+UorRhlEzIzIc9zJpsb7F+6xPUbN7jx1BM8ffNp9i9f4srVq3z8+efwyvP227d4dHiMCQn6lBYzOILUChW0F64VRESiUykRFMgdFaYpywzeS+RBbTImk0mIOBm1wbI7PtEMpsTAqvOXnpmh39eVwfNxTj/9d49zv1N4l0o2h97BxXx20qS68dvzxiTgd3juk8mGMK+zGYvFgqoqsTEQTsPEtvU7c+s9917SQkzPzhoGLCXk+m2sW/OhsaZzPQ8+XbTNVd+uWtPHaf+8tlbVHYL7Q/O+yN4PlSHC8SL37CLlovu7jpGFYQVL+LKBi/H7uA5pWPkotIz16rqiqkzDGEUtvrW2UdHE4DRaKagd//u/+g2qomA0EnMuhxdLgcUi0DsfjCFYV5buWHp36Ao4Gpiplv3jWn9wQ9TAyLpp0rw6KkkqH+G5tN1ajfTPZGZGeIQRaLXpYvuTtreunAdv2/fLPktx/7TK6MuFVrWb+lV3AuL0AjvY2nFyfIKznr3dfYzOKMqK+/fvYy6dkGVjlAprqhUq0/z4H/txyrOz4CIimiTlooDJo7Tg0CzLmGwITkaphs5tBG6qtVQQIaVYf+XBF1v2x4QAZGJgq4MwM8vFAsa6ujnLh8dHF9oL+PeBQapqdNlGD4oR3Zx1YMHakjzP8J6QddgHzVHQEKXIGxr1tY0hX5VqAgOkwKuvVVJB66RUDFvYHmq50LqRklon/XsNlAHIad0keFVK4apWg5RKr+u6pqxKNjc3m7E0F8vDGAOVZZyPuHRlH1CcHJ+gihqzN+eNR4cc3XvAjSefkDxISmO9x08m5Cpjc2+P09lMMnCH/DWZgvnDRxy8f4f9j72I1QoDrdliKI8jFTyvpPsJdPZpqW5qz/EYpc/s9IF0+m5IEtz/ZtV8W8C3DPRS6XxEcj5IpxrnV+Vwru4Ayv73Q0RDk1XeezKTYQJSyXLJyTM7m3Lw6BFGaz7+4ovsbO9w7849Xvva6xwdHXJydMzDBw85fPSIhw8ecnzygNn8SHyMyhLrarwPQUaCnUTKSHaJAZlXZPbboQZtSvNN97kKGp34M0wHcQeRMwpQVaX8zCtGpuTMOvRJxqODB9x6720m39jg6tVrPHH9Bs88+yxPPPUUV69d58knnuCZmzd599b7PDw4YDKZkOWZJPz00ZZb41U3eWu8mxUayQFhiT6NkUgmqyRvWEhc7QNBopQK+dRaLDdESA+dsaG/+2d4SJBwEe1O/CZ+rwfGN9Rn2u/QHej69i2fj/h3lGj328WD0ELds34eERuRblpfax2IQ8fu7i53H9ynKAqKoqAsy+Ysp9PoBm9ZlsRGIlWH9A/pu8eBGctCGrgoYBsUwiWE30W+vUi988f8wWH+RcZw0XbWlXVCuSUG3q+/m+vaXDWeIcYszl2EsANrqbrf9u+O0D2BsdBtJFznPEVRdMyvm/5VEP56sSowSnH/zh3eev11jAJvLd6LFYAwRw6jxPSbc9Z41fjXsYBDRRih9psoMI4Cx9SvKD0/8qzv36kTRqZlfDr7OwD7mvuPMAE6mmQrCeglUxo2fb7oHFeVOJ+4d5EeVCprtqDzve/ilbR0TDHDN7HdurYURcVsNifLJB9oXVmOjk64tCjZ2p6AFh9PIXUdH/v4C03ezXhuNUIXCtiugZD2w7sGnjWCW5L1VyrQDxCFidZa8tGo8RPzAtClP6ODwasT+tXWaOfIlSLrJRJfVz7yDFJZ16iygmDXXxelLL6X4Ax4j3ZyiMqQ66KRQES1arQtDf8IF80rRRUSWfYJjFZSIV9Fcz18l5DKsgwXJDYGwEjS2aKsILFYMdHjLjBPecJ8xOSw3guwU7TmYBH4AYHognk5R+ea/cvia5QbzUaWU48n+Npy+OiAp55+msrWZCajtJYsH6G95vLVK5zduyeEoZcoXQYF8wX3332Xyy9+nCphSLz/YIjtPKDwQSSE5/XVZyjizyHJ5dCY0voXHV9KRKXWMkNEljDW4uQl/Lf4vnhfNSZpbf9wHrKJb/MsFwSoNUZpzqanHDx6RGYyvuvTn6EsCx7cvcfX7n6FRw8e8uj+Aw4PHnF48IizM8mWXiwW1HWBczXW1oD47mgNyluiO3NYpYbYVeFZ1JIS5tUuUDpS1X28BuFEfin245F7V/oSpyRfElrBXKGMZjKZcHJ8wJ1b7/LNb3ydJ558iueee4Fnn3+eq9eu89TTz/DEkzd48623OTo8YG9/n8zokDfKYULY8tScFULuKCdwJXMGZ8RcMR8F8y6tGY1G1PUiORPLdyY1y/qwykXO6FCdOK4o4VtF5K8iivsE9Id5l4fGsarv5mD03jvnwFouXdoHQiS7sqSsSjFhyUdLV6vZrwHmJjLEWRBywHLY6iGCuD+udczxEIxdKTBKiMSLwOUUBv5O7tVFS3/dlgnf9l3/Wf/dqvZ+J8u6vV21hyKAVS0NMlBS5jxtt6rEj0Q3fo5KAo24NoVCZP67Y2n9tTOTkSvNb//mlyjnC7IsMFnOUZcFVVlIEBZ/vrlvf+5hpvH/g+s05B+m4jyStuJd8z4kxU1Kk+4EUMqgIoEVGboG13ia6Lt94RN6aQMaoYdrv1eqNeVzLuK/D+8epcxEZIAj7BJzO4sx2dId9+HjdcKZlI5o2vViUjebztjc3IJAY9aLgvmiZLIJ48mGBMxQkg/w4cP7jCuP9sHayIN3ku9wNpuBVuRaYZSmduLXPMpHAE3C+ToGc3IuMLtw8+ZNJpMJv/qrvwrA5tYWtq4xSnIwWiu5HKuqbtZkb2eLJ65d4fT0lG+89tqF1/kjzyDVzqFCFvQ8z/EaTJ7jqpqyFN8HFUxxbOSgtcbWdSdkNCDMVGCcoDVdc8gB8B11pQmMUE3keMuy7Gg8+oR3SuSKViioq73HBCf5GFmorCuq4EBnjGE6m6KUpihLtIfDw8NGcxKBn9EapS0FFQU1ZjOnPpOcR9545mWBHuU8PD7EGUVlZc2qeUWmM6pFwbVr13lPfbORtHjvxU/Fw+133uXTCmpnybzq2PVGSW8q6bqoxG0dAlndwEXeL0s6+2Po71HqkLtqrGu77UkiO9GlvFoCvnHukamGaGYX/N28xyPmdK32JQK5/t/tnBWgA+LLjEEDtrK8//57KAUf/9iLlEXJK1//Onfv3Ob+vXs8evCQ6dkxp8ePODk9pq4WlIsZ+BqlvPjWkAMOY8K8Qh4Yr1QrQ/OtFFSEPKqDQFTCIKXMUpfp82HuA+coILq4PijVMEx4HzRbHlywW7ZQ1wVGZ1T5nMV8zPT0lFvvvsu1117lpZdf5mOPDrj25FM89+yzWGd57VvfQhnNxtYWOuRIShFw1CB7F3wUiVGIQjRB7/CZDwl1u5plpQSRONVqDh+L8fY+SnI6j1cRHxdh/NNv0jM51N66dhXdYA4fbhm4w6TO2Mv10rWNf2ut0VnG9es3UEBRLIRBKsWfz6eAjKG5d+FBvONV0Pr3maPzprK0juHPKKxbNY5hYnt47l0p88BwPmTGYRWD8kFKOo9+tL7Q24XbCYN7jK+6NftbtW5qjdhHqQYdKRVhY9zktIHoM9fC8BYPDTNdkUHqaC4RixQC8e4Sv+j0ewFhDmMkbPPhowO++Y1XyExGDOPtnGU+n4cxRc2TGryJa0sULsRpp9E4G5Cf4AzowNr0TnXzYrU4FlJfoxDM4jFhUZqIe/lb1btjku/PWgXKilVDw3z0vlyB988dj2q1u60rRY3WOUH+H1skLtwQXOgLGlK4EDVIi0XBfL5ga2uL2awMaEYzm03Z3b8sgcsQv/mqtvz6F36V+199jZ18QrEosHWFt17M9utacmxmGUVZLB136yzGSCRdZ9sYAcZobly/yuc//3kO33iX9957r8G72mu01W0wisDca63Z2Bzz9oawO+/evn3uusbykWeQcE6cCK2lEoqJaVGiETO7jcmEYlFy6dIlxiPJIaSN5vjkmOl0mhCdIRqHdyhnu/auWgdzp5jkURJrlkWN0hqtgl9IlHCEqHp1bXFYkaEH4FAVRciNlMsV9p6qrHFaYyYT0Wo5h9eGRV1jbI1TnulijlMSKWtzlLGYzRiNJb/S8fSU09NTtPdc3ttilBlU7VClJ9cjrPdU3lEBu5cuMxpvSOjaesFEjzgtTtHbI85sxfaNq4y2t+BhRm0rrFXkiBbp/vu38MWUbDzGKYNVNGpnEQ+dL9HsP4slMlgRuDVEto9IQpEKrzpf+6SP+J8IqKSzpGpwZIzAJvrG+PZ9Mz4Vj9hqqVmfweqXrjlc18ldgB0o77F1HXpuAzH4Bqj4DoCLyMJ5jw9JextGxUu4ZW1AZ1qiGDnFwcOHHDw84MXnP4b3jle+8grvv38raIoecHT4kNn0jPn8lLKYU5ZFiwzi3dAKkOAnHtoov6mEN/5Hddcx+pCIqd2Kc0LCWEGD2FesPClCiPtnvQ2K965JrLUOZyvwnnm1wOiMfJ4zm5/w4MFtXn/tW3z2M5/j7OWPc/XGdb7nM5/i7sP7vH/nNru7l8h1Tu2stGsMDoVXCqNAB7ghZnQCsGskp1KW581IZNVss3Bxf4dyAw0jzxYxp2z8Eq+UIL+hVrrR4lTnZ3O+5GG32aXhDBF53fb7bXwYJLgn2rnHv+Iq+CWtkcKLs7nzjQDZaAUm49qTT+HxVMUcW86pyjkSpjsNi+7BWVAq2Nq3566dpmj9bV1JSHHEn7RZQxWDcyRr0KEFu8xLB1qF+7zE6KFCKHLfAb+CAl3AZw7dax6W97EdwxDhm3zXY3r6RNfvRBnStMoMImwYPlEdfjDksRINSDwtwQ9wacYt3FK+vW/9Og293xHwtMKdjktKChvpRqCjEZrEyG3J7qv0MAS8FQQzSkneQ4XgabFeCW2FgE/atWcjHV+zb1iMgjw3gOXVV1/h7OyEiZHknjjxKa3qQlAyWv5JSNTu0vjlcxW1WW1JNORJ9LnIzAR0H3U0IWePkgBakTkJ9EDfVGwZXjrSTVAqnqXwrtma7qh9zzqrPQE6MfOVEbZwO/pAS1RhF6wOWjg+fD/6cL4vJE7nlz63zqJdgfdtMLGkUvtdnFtCo0SNnA4CzcAl45GAZ7P5PPj9iEklrkIXpzilIBuTKQs6Z2Ez/Lzk9P5dFlGYS0tXuXAGY0Rd71php9amzTJCa1avlMbW8P67U372zvvi61VVeK1FAOtAuZZB0lpj66Ahrc44PBGmvqrLwfUeKh99Bkln8g9NFTQ0mc7waHSuKGohlR4eHoP3wlRoUSd6wJicOgZHMAa82OWiJGGnaHtq5kUJSFQtkQY70DllVQEheWQm0UUsoDPJt1LZMpEcK4qQXFM5cK6W/EtoauuhrMlyFRLGWsqqYjIZY23NyckJTmVMNjapNcKVa+G+y7LEhjwyzklyTVvWEr7cOqZnU07PzihtjVOiVrdJgAetxPTK4ti5vM9kc5PReMLZQtSkCkOWGY6PDpifnqCyS6gsC4Ew4mUO+7EKp6wpDRBI73QfqPjusz5gS5mYJa1QIoVJ3znnEiTYZ+BcQILL38b+Uolm2ndfIxb/NYlXaZmjZHqdsaUIcxWgjEAu4EXpQ6lwFhVokY6//fpbXN2/zCdfeok3X3+Dt956k0eP7nN0dMDR4SOmZ8cUixlVtaAsFsSIbN01DusQCQiS9ymuXLnv7XerJWfL5Mr6klKdyXpDo+FNq0bfQuccFRVVXVIUC3FAnpccPDjg9Tde5bPf/d08+8Lz3Lj5FJ986ZO8+eZbZPmIydYWZS2aZGUMoNA+ECSxG++p61oYpTCuNtpk1EKJRi2ewcjwxnDn50sWEyK9+Q/J38uItvP1AEG7RCj02up109RZer5q7Cvu2YXKUsc+MB5ps30OZLnPjtQ5y7h6/TrGZNR1SVUVVFWZ+Bt1m1DJuNt3vlNnMh43hHWToyZUWDIhSn/r8Ee+867fV8fROvjBhZqhH5q1aTtKYcfQFW2J0w9S1u3nkglTDy72363TVLbEZof74ELIxvs2MFNCKLadt301MHcwAqFU1rol1pPPu3WTj+J56MP9iPPU0kcDU4uAXqVwtKtdiULFoD/BKIXrMV6xOGslkBVihfLlL/82xohZd5xbUYj2yAfBlvcKnzIfSbOr4E2ruUuft4R9ZFyUUk3EsrTNxi8r4uP0hgyclyF87aN0hGXGZHUJur4OHGnbS+frk6BBAu/rJViSjm2orBO2djU/YmJW2woTaF/VvfAd2Jf2nWqj4uC8F7xYVRWLomA0krQatarBe2w1x2QGrxTeWRZFSW7EnQVnsa61jmq1fq2fmMdjvW1hGBatJEeXT2CjdzUKyJTBleLb5EFcPcJ5UV7Smygl4eejAKCsPJWrQIll1EXLR55BOpmVmLJVvysFCycba0wmjIMXxOK8g3mBMio5vKo1iwhAb7FYMJlI1I2qqijKgmJRYUxOnucoYD6fs729jbWW+WLBKM8xWchhk/gTWG+FofKSqNMYYbym8ykmmD/FsVSupp4u8NYy1p4r+3vYuiY3hk994hPMSnGiG2m4d/s9tjYmFLZmd3uLupTkbRHALBat2YiEGfaYzLCxucn+/n6QpipqawU/KpHYbG1ukI1yJpMJ6hi8FyJ8Z3uLg2LB7OyUvStXxTHOtRm5YQiQDAOhPiI8D2kOPe8zJUNllU9H7G8obHFKiLjk935/qcNjX7LaJ8Yep7S+bSHYSM/nZbkErSeQZYbcZCHMpuLu/bvcvX2Hl158kenJKf/qX36BB/cecPDoPgdH9zk6OmQxn1IWc/ASytW7NqDIujUf+vvDMNHpr2X6bOicrep3aM1SaWNkZOI/W1mKYs6sOOXu/bs8/7GP85nv+h6eee55XnzhY7x3+zYnR0fs7l+ijsRp0DxrvXxG67omUwqrYsb5NkphX/oeo0jFcX/YvkgXKRdlph53j38nzsjj9JEKGOI/rTXGw/7eHvkox1YFVRWSGAd42G9riHhP/9Zak+d5Zy8/7NKHmas08hcJzDBUfKLVHOrzwu0kBOjvxH5/0HIRbdcqJq1fRBgVJfhSGtPSASZ0Xb8fRAuXCudEaLuMi7SW4DLRPDvOK+IV5z2jLEcpxb07d7h7+w5jbSQXZF1RW6F9oom3CHV01GUtjb/PeCxrQoaZmf5Z6Wu6PmhZRUs8Tlk1t34dYaTk78gotWO4eJ+p0KXfXX/sAmuyQSqrpYeX4fkq2sk6x2KxYGNj0tI4aGwIMNSaL3rKSoTySomvWpx3l5FLBFLhzMlLmufpz2bike5SvdQrYVHEClIYJWMEB0vaX2F33AUjCsK/BwxSUcMoMBmubhdTpLF1+3sQN8qFFKDiibHtPVC3kgllmJU1xob3GMxIDkcVtEHZZINFLRKY8eYmVVVTVRZjhMB0ddDoWAn9q5TGOk9tReWIGrEoKnwYo5jxSUAIhceWC4qyJM/20FjyfJNtFFy9gq8rrlzaxzvHdDpld3eH8XiEd5ZcC+FfVRVFUZCFUIm2rnFAZWu8Ej8ir6C2wkyqAGgn+YhsNCLLM7x1eK1xhOh6rubo4UP2nnk+BreUsJNJmN4IUDSqo1GHFuCtkpT7KEobkEoNlQ/yLgV2KdBbAigqGGH41k63r+Hp/57WSwHEKgKu822Y9hBx1/cF6XyvaXLx5MaQZxl1VfGtV7+FNpqPPfccb3z7W9y5dYujg0c8evCAg8MHHJ8+oljMsXUVJM8OMc0xHQbwgxBa/fUeeraK2UnXp//+ImMZWtt+G0PMzMyeUVZzJnVBURecTafcvXOXT3zqM3zik5/gmeee4bLe56133+XK9RttH8h9T/uMyMA6i6u69v+RIYpjTSV6k8mExWLxoREG/bC4/TVat37ntX3R8X3YZ2iVQOaipV1zx3g8Zm9vj4MH9ynLQsJ9hyTG0cduSJjTlRy3+xphbiSOhsKXP+7e9uFq2u/FTTPXw8N2chf/Lh3Huvfr2vtgZ7yLIFbBinR8zRomGot+nfTv/r6umoONqQDOmU9nDD1cch5DtmpOq+5zRwiUaLciXEq/lWimoJ3na7/9FXQI8hTxcFkusFYilbYdLCdPv8gZkHEvP5NxLZueN98PaIuG7l9/HVbh6qE+1uGYdekX0j3NTLbEhDZ4wFZLZ+Ci/afPU3og0lHeOUlCzrLSqI/n0jVL74aYVCtsbQP8CuP2ddOPC4nRvQdjJAS4Vpq6tmQ9nBv7HMorma5jxHvpO63EoDImNyZYaiglmk7jo/BWKNAsk/fWO3TwIbV9wnNN+cgzSNPpjKIK6rt4FhSNCjq9TEKYiE16TAoomxo3TH5Gor9D8Dd/t/4U8TlIJKRoLhOjXUnIWC0x3JMwjWUhoZZra6ltO/amDzzOi7owywzaiQO4NpLxWJsRkyxDacWVS5eaCHnZKMeoNsEWQJ4HrVe4WHWIiDdfLJrAFRIWvdWijTcn1NaSGUPlEMaurNjaHPPw7m2ec5bKSu6Zrvlr76IP3PXzgKlCSebkBBDEd+sYjaG2hvoeQiYNwkvDQyrVzK3P7PQveb+P/vP2HAGJ7XJ/LLrXT6zTRO1JgEm07VXOMxnljHJJmDo9PeXrX/0aT9+8SVXX/OYXv8jhowccPnzA4cP7nBwfMZufsSinOG8lXGlLOsgdoB3DeeUiRM55hNsQo9wn/vpEy3n9nscQ9PfeeTE7LcoFzkuCzgf3as5Ojjk5esjRwSd47oUXePnFj/HG2+9w+do1PEoSUptle3hjJF9EJJyj6cWqMULXfOo7ZVRW3ZVV5SJr1G9/VZv9598Js9f/ft04L/qtViqYYWq2t7Z5cO8O1jqqkHvOWddEGE339Lz+4h3tawBl/S7OUK76u0+0D8GQIZi0aszr6p1391ft/zqC/3HGdR6s7+/LOkZGfodoKbGK4Y7fnBecRAnBQF9TFH8fWrk+fFiFQ4bwydA4AWJenLStLtwUekUpjenh0VjXZIbZ2ZS3vvVtMpREJFNiRrdYzEMQKmGKJMJbJ8TE4Bqtgz39fYs0VVy9lOZq5s7w2g2Vded2iFka2v+Lttf9btliJbbdmt35JaZhdfvL57R/772PKWuGx7WO2erDKVEWiJnd5uYuSqlAA2ZUdY0wI1kTSj76B8tdaNtug00t95nOY+hnlmVkSjNCmCCjTWMVpo1EsNMdWlxhMtGg1XXNoiwlynNRrFjT5fKRZ5DmZ2fk41oc15RceKMNLjqTh83K8xytJKygDb4ARsuF9wSfEhfU1UbUhuKbI4ROZgyLIkh3IeRJCo7axpAbhUX8imxlgxTShMh0MhYVwjKORjmgsEZTlN1DLNJHT4YEYMjzHONAeWnDBa2XCdp9hUTSm05PwXtGedb4TjknUlKtNePxmLquyfOc+XzO6ekpV65coa5rCSpRy3i9Vowmk8ZR2xixPS2LAjJ4eO9ucMRTwkSwAhieQw+kF2NduQiR/mGUPvGx6v0HBc7x20ZSMhA2PgWgQ2ZWS4hDwWQ0YpTJnj96+IBXv/kqzz/7HPfu3OXdd97m6NEjDh7d5+jgIacnh1SLuYTYDNKhJhBGDIoRp6cuTtB8J6WP+PoauBTYDxGr68oQgukD6rZonCMEWijkjNcltl7w6jdKHj16xMOHD/nEpz/FSy+9zLvvvc/W9naT1TsiwjokG41SuZi4saqqtYSj915Co35IpS8c+iDlcb5fRWR8WOflQz93gMky9kOob2tFelqV5VrYtYrIAsQsWXUFZ90ev7OSmqmsW+8+wR3HfC5zKaqGle38uyyPe8fPFQCsaHvo+yFYMdRi18COBhUqFENxaB6HIU19E1eNQWtNXdeMx+MO7OyOUvylhiwbtBFh7tvvvcfxwaHkYgya76quQ6CedHLRN6kVop0nnOjCb915njJDKZO01O4Fj94QczMEB5v59zTsq/b7vDs0NI60LR2CdvXx2ncC04Q5slhtybI2+m1aLiqoaMcrwrzt7S1J5eFFsG6DMiGachpjJOiCj/5hUvo0TAorIzyMwl6v2pyl8X2WZWTaMA5aothXNFnUiib/VMt8yrs8N4zGhnojw0wvvq4feQbp+tXLTDY2KYui0YaI7a1NDr1k4q2rCptpcV40hlGeo41pNjhKeG3Q7JhgVy4bkFFWY/Dt+xhmcGNjg9F4jHeOxaIIpm1BBOkU3nlRHYZs1ePJmKqqcTiqOqoQRdKTZVnINCwRZkw4BNhW26UUjQOpcPISAACEk55MJk3yw93dXbI8DwDXsLUlRF1RFBhtKK3EpndVjTJQW8vu7i7GCKNZ1466FsbLVjUHDx9iqxqVTbDOkWVqCXGfi4iT0pHWpQR6r5wvxU7Uh/16Eao3/Nzqug0QXdHnUP0+Ql1dutqhtH6UMPXbjuvjnA0J4lqAMh6NGeXi7Hjr1i1uv/c+Tz95k2+88g3u3rnN2fERJ8eHPHpwj/n0lKqYgRcHW6UVWplOoAq/elnOLRdlplYB8RSQRiCbru26NtdJnNOSIsRhKVfQoHlPXZfiBEpNbR1VZTk7m3Jydsp8UfCZ7/5u3r11i63tPYzOBHaYFuBba8lMG4K9g4DpRrJKz8+q+cl38YPuu+43LbHRRfgflMAd2sPkrKwsvTPV+/6DjKEvHEi6WTOMZJ2T6h7Jxn7jxhNoJftUliXz+Vw0SPmKkfQIqXT98zxvUj1E4qE3hWYUvjeui5So9ZJp+WZuQxJ930h4ITUBje/jO3lO53nsqzOu3hnr7uvjnK0+kFnxbf/gRLlbMh/o4Y/0YPYJbu87XS2d4WRtGrgbK6w47CoSh021VqUkd7yttwo3xDYc3bschZxpPe/a/XahblmW5Hne9t9OSNbHewnWlM4jnJ0Y+e6b3/gG3gotE10AimIezlBidhfw8zrGWatuHqGl4CQDQsI4r7RqG9J6WcOzknH1fiVwUSrh/z1NOO8Uz6Rj7M+v2Zs1ffiEtlBKh4AXnpgyJWqShnB9v++LyiNiQCXVRBZUzc9VODHFNakJoTx3jEZjMpNRV/K9ddEHSfBcXVWk5wsnOami5Y+skyyTDv7MxpiQN9HgnKWykkQ90sQEOxbvHJVzKCd/Z+LgEiytHDqZk47MUZaTZ5pMK/LxCGX+Dzaxe//99/nv/rv/jp//+Z9nPp/z8ssv89M//dN83/d9HyAb8Jf/8l/mp37qpzg8POR3/+7fzf/4P/6PfOYzn2naKIqCP/fn/hz/8B/+Q+bzOX/gD/wB/qf/6X/i6aeffqyx7G3AZOxgMmpBbjjEkVmKWe+NGYfzrUKkqTTxliafRKyYB9V1ZJA0zlXokUEpMNkYkCgwzgWbXFcw2hhTZRnVOPja1JaNjY3OBRQEWpFv5nhnMTojC4Efamsbe2FszVbu0b4CFGiDt/HydZGCMYbRaCRzUTAejykXC8pFSVXVjCYb1NYxtgZtxih1hq0943xMVZRsjMYUtmI8GVOfnbGzuUWGZnu0SeZLCi92yLZyLI6PoJihRmNQGd6bzkWMACfT7cFvkblcXudb8lDwlg+AtUUC5zEbS8ijAUwBOaVAPIT4bXBmxBONLKwNQRmhdBrdroPDPX3M2khTvPcS9a8HiFpJoA+Sn+WIexoVnP6TbwPz4r0NR0AcZBWKfJwxnuQYV/Ptb32Ls5M5e9uX+c0v/janp0ccH95nenyPg4NHLOYz6qqS+QYsEdcoZQgbwP/BBVuDZR3yiX/3EVXfwfQ8BHZev7HuKmbLezkDzoOP8EJrqGq0m2O9p/YV9lsVdV1S1yWf/a7v4vbte+ztXsIYSYaH1qAlgWBVVuRZxvbmlgRmmU4piiI5a91xxTNibY1S2dI4W6K1+21rVpPOLcXjj0PA9je/224zgiXapM9wXpSDWdd3O4aWKBpgxNMzkJ6TBM6EQUqoZyVmRBjDlevXqKxFeUVdVNhFjassTNozuMxYLJ8rAI2hmBWC3BUBTvh2/DEkf3+vEjKyP7s+gRnXWbctyxkItTvMV8NUtGZM/b5b6T0d4k/5KFgKZ1O3B6q9Q4/HdEu6gqbncEZTWK2aemv9rJN3OgL0SJymoZ1DZYGZ3TMrxHdy4qIQI0bOgkaM0eBkIvgP66JMFANIvRh2PbTXnXvLjXZ2NIw7RsL0YeBLcK3znaRAddZRF6WYzyknBDmJWXpsseXbkIhijkwrMg1lMePtt99AZwqvxdfE+op5MQUdNAGNrmz4/HeL7oyzZRhBBSuFyPSoTt4jhfJtL2LZEM7qKqFaWJdmvVXQ6jURCuO962msdLuHOjNh7+U7AnHvwjloAlqEs9G009vCljlqNWJamyQkujzLMh3yJcW8hl3GpdvqKmavrR99nLIsD9+0es2LCChbYaHcHWtrRqNcmGIcHhuiroZ8oE5RlrXMRTt0OLsKJGS9khNgtCJDGKQsKCJ0SGZc1hUqUzz11FPcv3cPW1Wi6QzjLlSEex7KKg5Umo8wOQhGjDYYY5hozfZoHLT4K6RbA+VDZ5AODw/5kR/5EX7f7/t9/PzP/zzXr1/njTfeYH9/v6nzN/7G3+C//+//e/7u3/27vPzyy/zVv/pX+Q//w/+Q1157jZ2dHQD+9J/+0/zsz/4s/+gf/SOuXLnCn/2zf5Yf+7Ef47d+67ceKwrQzkbOxta4+UYkD+KzEx3LtBmjEDtGZz0KTVVX1FWN8w6txg2Hm0qtbWCAskyj9YjMtMSbHMYRtZXIX7a2aFUzmhj01qiRQmVZFiQGDue85KVRCu8t+UiyrzdSc2MaTZDyhjyTXBYR/bkgBRPpR1eyMWnM4jzVQhJzXdrbA+8ZjXLKxYJpuWAxn3F6dszW5ga1cqhcY0eKBYrRWDE9mEuo6Nqzo3PQFmckcS1eU8xmuFpCm0cANCSFEcAckVcXofoe4aJVm1wXzgPAwyXu2VAbIilJtDwpQQADY0fYkISRSkFiis67tJnqzKvf9jot2BDB3PzDN/mavJNQ9Xmeg4dvvvIqZ6dTNBn/9otf5Oz0mNOTA44P7zE7echsNmuJ7z5Ubwc5sKIX24fzGNlVTMrgmg+01ZE0+va8XSTS2+MwT6vG6DxgHTWSdNp5h31dTFC8c3zf9/0Ar7/+FpevXpWQ/ZFYDuHxXQikEs2vAIkUaFY5grdE7ge5B6vmc/H5n9dvSwSsKx9s6BeZc1+j2MIP6M61T2I0hFQg+J1zXLlyNSR7tHjnKYuyEZ4NMkQ92KWahmUc3rXEugovG39YYn6Q5Xl3r+PwRU3hW3P+E8I50HaNIKiBuiFlwWDpTSYlpCOWGYZr3Z8XKQn/Fb7tm2AlY+qBq8HxNoxRQmh34HEqiEvxUNv/cLNdJqsDqxrmM2E6Q71GQz2gnU467TAsve4Gqnf7Ve0LtNaUZcnm5oY8SlwKOvNO+wqasSi5v3/vHocHB4yMFoI4EMlpGOjOT/pj769pt0YaGMNo0xGApXX6QtZ+nb7WKmWStJIULSleicKmvmVLw9wMHFwf6Ku+xl5FxivR6vWtAqJGT+v+mRZ/ndSPuMljuO6cnFMa5khZrLNkKksIkmGGsi8g7DXY0LzGGMajEcViHnydRUBrtDBfzgkdMt7YwJugNFAKX9eNFZYOYcGtUlTao8cGMx7htKIuPb60vHP7jvjm13ImI4Os6Znbh/E5F+BnKDFKI96TKcVZlrO5uYEZTy68jh86g/TX//pf55lnnuHv/J2/0zx7/vnnm9+99/zNv/k3+Yt/8S/yR//oHwXg7/29v8eNGzf4B//gH/An/+Sf5Pj4mJ/+6Z/m7//9v88f/IN/EID/5X/5X3jmmWf4F//iX/CjP/qjFx7P5lbO1tYoISg1HmFAtB6FDY8+AgqrRY2YZRlurKnKiiwXRy9rHdqIclwOlTioZcEsTxPyH8S6WpzErK0Y55kALaUbBkqC51m0iRHButGHFFoutwo2y9410gytI9oU8zlrXZCerj/8Hs/Ozg7vv3OLrY0NrLcY5clw2GLG/PQYW8zZv3aFcjbFVSWVdlTVAmzNw/duow+OYVFgrEO7XhbrqmZ2esb25RvYFBAuEbst2r+INmiIYF5XukzHcLCE9GerQv7OokqtGkfTFgkDpboM95DKOzIAMeHgUB0fgIUCxqORmIYqxStf+Rpnhycs5gVvv/kms9kpZ6eHHJ884uTwIbYqloD1UB/9eVykfNA2hhikPvLrt7eu/uOMfaheK20PMqveebHW4lVYu9pTLDwnXvHG698WLTOKlz/xad6/c4cbTzwFeOqQWDQmn3YhfGqTO8uYIMTpEuDtWXEf6E4MzosPvl79su78/LssHeEHDDAcy/WGinOOvb29xj8T6ORCGgqXLZLvbjvRhDdLo9cRJccMEl2pkGVVWQXT4u+DEmLAh7OsBr4b7GfNu3gGXcLEnSfY6MPEoedD/Tx28T2eKEGPKnm/doIXGMsQo9wSyMME6NAaLTFZ32FRSjGdTtne2e48W3f3oxP9aCRC3DfeeENgXGSufDDLu+CiLa/VsO9s9MnsMCpr4H/6foiRUIFuwnd9Wfp10nDbKS6Ov0froVjfBwZjFe7pf9+aArbjjzRelmWMxyMWxaJZ964gP1iHfIBy3vqs+iYtnTWhZbq0FjcQdzQNAh8nQcCCCbnSYi2R5SN0lqNdEA4pjTYSPt46h1PgFJR4PvGpl3nhU5+kMoqHd+/zrV//Iov5DFsHKywneQJxnkwlvknN2AjuKpIE3odk9daLRlTjOLMVmS1Qi/8DNUj/9J/+U370R3+U//w//8/5whe+wM2bN/lTf+pP8V/9V/8VAG+99RZ3797lD/2hP9R8Mx6P+b2/9/fyG7/xG/zJP/kn+a3f+i2qqurUeeqpp/jsZz/Lb/zGbwwySNGnJpaTkxMAtHIoggmSjkSqwjmFUmI/q6IWw1uMjgdKSdbzXKG0HFZjPJIKqb2kuQGlXMiiLsSLBEnQjRBCZwYIYX29pU0aFqUYgixb6UKQLFSuUf1rpSQZl4/MXPSXcIHZE5TnfZeL7ktetJaQkw/v3+PrX/otrly5zNnZKbOzKfb+EZydcW13G3X/EQcPHuGsZZQZ5mdTirLg21/9OvbuAXY2F58kRNVsjMF6R1VWHDx4xM4zH0PpVhSWXr4UGA6N8zwEO/RsFYMT3kKyZ6sYoaG+47slQC+VO232x9IfHxDyTrShnFeF4u0jCWHy2jotwyvn0XuP0YZxNsKg+cZXX+H+7ftUs5I333yDYnHG2dkB07NDzs6OqIoFWrW5nM4jQFYxJisl6QNzv0ibq8rQmvYJjn7I1VVtX4hI6X3fIbRCaZBYuP8x5GjJHOcd77z1Jlgxmfyu7/4ebt2+zfUbTwYzlQAnjOkg0sZfb8WZkjqrx91hDjq/L03rscq6+9EvaxnNNe1dRBjRl8yee+bOITaHCB3vveRx855RMMuoKgnFWxQFZVl2ojF1xtDrTqCyCLhigsUouVYqfht8OVAtTHlMeBjrXfTsR4a/X6ffcpe448KE8Qcp/T1No5R2x5maKPbgCKr1mSSu/6qiGnpAtCtdHDH4RW88Q+dwiGCOpeMjlsy7Pa+hrUH80V39Tt9KdU1Jw/uyLBmNxmthW3+ukaGoa8tbb71FlonTPUq0nFGDOlRWwfT+PUt/j2OImpSh+Q0FIOmvYWwvCmxjIKm0r/iN1m2bQ2sz1LbAXnNhWJp+F33CY1+RGbp8+QpVXXJ4eCgR1lSr+cvzjLr2jQtId4zDexl/pnUjrJLUNdCPELIO7nb3ucW30W2gqitcXaGVb/zqrfMUlaWyHmoHVvJ9OmspyrI52zUOlxn8ZMSNp55m79o1Fsoznmwxe+MuX/vtL4dzIQImZy3CB1kJCBEDqfkwpUxhlUZnBj3OUXnGaDLGes9kYrhySaLv3XjiCfiNX7nQHn7oDNKbb77J3/7bf5s/82f+DH/hL/wFvvjFL/Jf/9f/NePxmJ/4iZ/g7t27ANy4caPz3Y0bN3jnnXcAuHv3LqPRiEuXLi3Vid/3y1/7a3+Nv/yX//LSc+WdMEAxXLUXDYxRIsXLdLTJ9PiYfyQlvIAs+L+ImUXrB6SgMWfTSjc27UoJV62bCxk47+Y7saf0IRx4RFWNM1o4rMbo5l1MtqWU+D5EW3PnLYYUqNAwaUuAGo9F7DLrecG/+dVf4/reHhvjEa+/8k04LcDKeik8ykto26yGvPK4TFHXJSPr0c5SaI/NFC4EiHA4vLUcPnzEiyic7xP5hLlIQIhmjwYQdEvfLBNE6ximiIBWSU36CK2jyh8YawrkOsndPKRAal3oyqXxRsa550fTJlrr9h0/ShmkTj+A0prRaIRWije//Tqvv/YaOMU7b77LbHZCWZwymx0xmx5jy7I7nDVE1XnM6SpTtlWExNDfq/qJzy9ClMe66Zr3z/+q9lYxqKv67u5LJGgs3imcsmDBl57pmee9926R5yO2t7e5ev0GJydHbO/uobzH2laamLattZYcKsn40z77ZgSdcfR+T4nKVaLydeu7itAbKquEAunvq4UY68dzXt+ri4r/P7ffNLdXJACyzLC/v08Z8k+lDBL0zr9vGaLYtW8vLePxmOPj4wY2twSHWBbE78QXcDXB0hei9AUFsd4qB3OBXz5hktK+ztnjlW9UM+R156A/l3XPhhiQyLBFZnIZFvoW7zb4OApPEvO23pC00jg1bMLdhyX9sQ4JitJhnXd3OncjWKIwMPf+sLuM4XI/kUHa3Nzs1F8llIhnxgSzqOnZGXfu3EEpsZDxSCRfFzRJj1sETnb/7sBoVo9raG79NYCWuVsHt2S/WsYhxesR/vZ/bxnbZC4D/ad9tudONBn9PEhZljGbz9jb22VnZ4cHDx5wdHTUfBdpjqGob0NXKo4lZagiM1bXtcxzKHxiMu51sDeuWVwbmY+XXIlOgg5FF5DKOs7mc+ZliV1IhFZrLbauRXvkHF5prAZXVnzjq99gYT2lgte+8U0evfomRVVjvQUUaCVMllb4kUEpz3gsUfOKouT69Ws8++KLXLn5JDefeYYrN64x2dxAGY0DNjdG5MFs/Ww6hf/nX1m5Dmn50Bkk5xzf//3fz0/+5E8C8LnPfY5XXnmFv/23/zY/8RM/0dRbBYTWlXV1/vyf//P8mT/zZ5q/T05OeOaZZ4QZUQofI2U4h1IaZ1uONF6A1vShlZBEGUSfaIoHL3Wwh6jyU8nv4VJ53WT1bYh472R8iUS4ixSkDaUITFCQNDsXnPugrqvG3wSi+V1ABkuAASyQKdjIch4envDO27fQdc3s4Ii8RBhJJepShSdTkHlN7jPKyrFhNNQSNt1qmYP4W1i0keAL9+7cQXtxOER1gVz83fuLyyLTby+Sg2IIoQ1J3i7adwQG6d9C/az/dvkbhCjRrenc0DzS8S3lI+gRSJFRHuU5+Sjn4Z37/PoXvsDlvX3efP0NFrM5VTmjKE6Znh1RFgsxBfWG9Z7Oq9cjLUMS0X7d5TGvJxZWIb/HJaofp16fwBkiPlcV7xzOx7zH4qwKUFeK2fSMd955i/F4zA/80A+SjzcoFgvGGxOEhvONGUcT4tR7lNLNu6Fxr0JmH7Sct7aPe2cuynRdpP6/q9IlegQnjEYjbt68yZuvv85isWCxKBptEqyIchV/BiGKh0Y6PpvNBCT25p6KGVSPencs34O+cCUdf/w9Fbh0hBpqNezq951WcyqZXFrHB85wrUHg+WWImWva7/TX7arPPAn2k2eSbkMEWp3l8u1P1TRK584vCxno1OmP7Ts9x51vL3Dd+uuT7l0k/NPExEt9xK566ysMkub+/fvMZjMmIckpiDQ/Rlm7yEz7MBX6f7fnWaM7lhVpGYrsljIxsa2okQca2m74TLVapD6MT/PR9Rl2sfLpRlIdElD0f0Y8ntITdV1L8umq5OrVqzz11FMYYzg4OEgsS3TDJK2CwUPrEtdQKdWJeCiBQtTKb1eVRqgS5iJMmOC+uiqoq5IsWD6ZLBNmCs1BVYRkwkFzppwIIozARA/YsuRLX/kqX33tNSoXMGhdMtrM0WbM5tYWzzz/LM9/7GNcvX6N3cuX0Fqzu7uL1prjoyOefe45xptbmMmkIc2UUljnKMuCs9MTFotKtPiPQfZ86AzSk08+yac//enOs0996lP843/8jwF44oknANESPfnkk02d+/fvN1qlJ554grIUtWOqRbp//z4//MM/PNjveDxmPB4vPVcYbO0kAIMD74JEUWmcs8ml1fLPO7TKQIXIHYiGRMwgFEbLYfOhLZHex0tgG+aEQLyKA71hZOTQVFVFnsdEVq0qGOJlpvu7ClHdwt+NBiy0117mFuJHX6Yl6RsCRBWwt7fH0WiMGm/y9LPXeOXoy0AAQk60R97Z4EwHUypQwpBlwe9Ie8lJbLQBDXVITLqYzkL8++i8G3sGVFf1nRYfmLzuS5/MrWVEW6DX/Tv64nQBbGue1lmPAeI3Dd/avIl/u2B77dPxtHX6TFj0PQBC2GyFdRFZ9+yYg4xOC4fbANE8y2T/XSvhayVMDmcdZpQxHo2Yn834hZ//eTSKN19/g9nZGc6WLBanzOenOFuHGDbDTM3jEMGxRGnVqtIgqbT99pADXU1ah5Em3fHHI79aKW50gG+/7yO9pfErlUjXo+xh9dq44Bvow5lX1EGAYikWcxSat958g2yc88P/we/h8PAhT0xuNmPxIJruHpHtaYUsIn31zXo2BMoAoUxnthcrq4nRZa3ceW10oub1Nq/9vMssq/i9iuOn82GYfmsypdotSQncWLljogbgEzPJgb1UyX6jlMBZIMtyrl27xrdefZXpdIqtK6qywNY1jMZtqO5wh2V87fpHIZdWGZkxWFsHgqfNh+US39LOYnVKC+fifCW4g+58kYJF3zgxt+Z78fv2Pg6vRVymZnpp2+moQhsq3ZAVa7zUD73zpuIe+Qg4QNFoVPA+MIsehekQbXJlw/w8xAhzWRPSV4XvVp+tOHfvXaPLS7/1YUyND5dKzlTaYoR3/bnGPYyjS/qM2saEdGVpb/qM4XKNZi6NH7OSxPDL9dTgvVZKNfmO3n3nHVlza8N98nhn8TZGNWNN6TIlQ8xRXAcfopt5/CDj3x93HHMHdqTmdMFEWeD+MuPirDAro/GIyWTC9vY2m5ubjMfjJiqxUoqqqiiKAmsdp6enHB8fs1gU1LZufcnDersQ6joVBKbMUxp4IT4rSwnsY43i3r173Lx5k6eefApnHUfHRwHXS6TkmKRVvk1XZPX9Tdcp9YVah+f7NGPyQu6ilrQhNlg0ee+oaou1FQpH7eHa/iUePDrEaQ37Wzx54wbj8ZinnnoKrSQ3V1mWPHz4iLIo0SZjMtlgPNnkypUrjDcn7F7dZefSHpcuXWKyuYnJM6xvI9PJWAxGa8ZXdjmrK2bzU8aukgSyYdh1LUHSdiabYrVRW47OjlbOv18+dAbpR37kR3jttdc6z771rW/x3HPPAfDCCy/wxBNP8Iu/+It87nOfAyS09Re+8AX++l//6wB83/d9H3me84u/+Iv8+I//OAB37tzh61//On/jb/yNxxpP7S05oi3SWqIIKa3ItML7GkmgFaX98nttq6WL2EphxO8HYDTKgg+HF6IWjU8DFnhBYC0Yjf4DrmGOpGqbkyL20TBDDRxVGCOMm1w0OcR17ZDhpFqGrmNfCkyMVWTWsXftKhOTsbO7x+a1S+hxRj0vw8H3KDK0zmROSoF2aI+EdzQa0b1pJgRJt9YoVwGa4uQYj0Vlo8BsgVYBmXlCbqluGr0uMGkBN779DiXRUNp1i/Mj7GF0HlXgumuQXvcYqhV8ExElApFo5hjHBIi2zkdEosVe3XdV5iTnxcX5kIzTEwiaqBXUDaCOtu8mapS0pq4qNOIvVluLVRataIAmOJyz5JlhYzTCWM8v/8K/oJ5VnB4eUMzOoJ5T12eU5RnOVUGtHbROS/BvGWj2GYml9/0NGCjNuq5AfB4aYjTpbLitwafdsXaRsfjjaUVDIEpJghwk0b76801t3lPCuk9ceBQoCf6ikTNqncXXHjLNfDHFH3neeesttra2+N7PfY7DB/fZv/6kCEBcmzi68XGM50nrRsPsVEsjNZql5F+XqEoZrsCIrly9izFT67RW/ec6jCUlCrt1w1gVzV1smKgVQ0vhY7tTPpl/fNQ9KTJueeZ8209CFaPwjaZGK4/GgZZIxtevXMNWNc5WWDvH1QuUrVG2bvN0RJgUmbjQR/RnBYVW4iysvA3rIxM0xNwwfdO7uJbpcqRMCHhXN9PRStNKh337P5/6rcV1TxiynnAn6azzq+73Hf/2YRdSmJzUXdofhutFs8bmO5USvQFGxilQ9xtqOAbx+fJxYL35pOfQJ0r0kO/NOcG5ASY1+wEEN99kjLLZ7bHsrmPnvnVgD8tpIiJDSECyDbjy7TS8x6R4vncPGkohjNFaFyL1KupeeowOfRNWpa5rlPNoD9rDvffeZ6RUgEniQ21dja3LZr2XBSvBhUCb5uxHZihednmvO78rupYffc3cOsENPvh8xxWO+ESBzoKJm7PgJVnzE1ef4Pr162xtbgZTNwMqaLEapkraj0ECrj91FYWiqhwnx6fcvXOXg8ODdj2NRntPZjRlWeF9xCvh7iPBCUyAFZG2qcsSk+d4B3du3+Xq1as8+eRTFEXJfDHv0J/WRouC1dqkWFIBcUdLFs5VmpS3n1MwZfSabxPYb53FVhXis5/hzAQDVLVlkW/zzEsv8d57b3Dz4y/we/7w72H/8j7OucBsWjY3N1FK6OXYbxYEwQrR+lhnhbkhgduy1VhPoItqnEdyhjqH0VBOz3DWUpYlWZaFYCOavc1d8jwn83DpMbieD51B+m/+m/+GH/7hH+Ynf/In+fEf/3G++MUv8lM/9VP81E/9FCAb8qf/9J/mJ3/yJ3nppZd46aWX+Mmf/Ek2Nzf543/8jwOi3fgTf+JP8Gf/7J/lypUrXL58mT/35/4c3/Vd39VEtbtoiaG4Y9/OS5KpOtiBR4meAJXWfCslflMVdRP33ssmijSwe5lT4irPc+qygiBFiMEVZDx0oqRESUMca/wZL35VVYm9bGSQaiAe7HYMQxqkQI1iTMbmzjbaZPi6DFqtnFoLYlE+mHWE+kIwEGLagzIKBxhCpBglRLvRBo/h9OgYW1dotUG7onTHwjLAk/ctkdDW70pEJGqfhEZPNUfdbNEDEpD4ZoXfzErpVcQgK+YyKH1XvU8S5J3WbcwVEkDlemGE8fGs2sSBVuqMR2MypfnqV77KN195hUxpFmdnaGWp6pL5fEpZFl3H2g7h83jmUynzchGyOgLZIeI67XWIGbsY2X5+3/1n0USij4xXSVX7pb9eSrXMV2QI4z2t6woVklIfHjzijddfZ3t7h2efexZblZh8hLeCR51PGHQBSB1ecSjvTl/rtGqccUUH56TavVgnveUCdfrav6EyuH7yYmlgqQ66c716xO7yX50OE3YkqZ/A3a70Pomq5R2XLl8GJXtZ16X4INmgZfCeqJ1av3KSTkGk092R9Ge9tD5rWh3WHnbfdWCuDz/VGljVDmTlOIJYIHnR7nh3LbsM0mPNDd9hrAc/WgLzwuj2pfnpyGNJ8Xa3qUggh+fhLkYibZXfZf/Md+fql571Jf3t2IaZgyigWxqzCsewx1TUdcV4POr0tYSrwtzS+WulKYuSu3fuNPwaaLyvmkSmXQHlefhDToBSCh3TlCSHrg9rz2sv3Vcd6aMgpOvseWB2rLVcvnyZmzdvcuXKFUajEcZkGGPIsoyqEuFhXVUUtkYpoTEkytxEfHsDzl3MS/JM/OOrquLBgwfcunWLxWLBOMsaX5/+2eqvffq7BNIYURQFp6enaK155plnePfdd1kU8yXzOvl1PQxOz0wUUFprMTpvvl2GDww+j+df2lRY66isResMZTImG9t47ykWC0CxuTnBGMjHYyzw9rvvglJcvXqVzW2JqFgHhung8JA6hP9eLBaSB9B7rl69ypUrV6iqqtHyZVmGUhrnhSZfLBbM53Mmk0kz38Y/VCnKqmJzawuA45OThmFaVNXa85WWD51B+oEf+AF+5md+hj//5/88f+Wv/BVeeOEF/ubf/Jv8F//Ff9HU+W//2/+W+XzOn/pTf6pJFPvP//k/b3IgAfwP/8P/QJZl/PiP/3iTKPbv/t2/+1g5kKAlIqJDnmgJdIgi5Zq47umBjdLZaLuZEj0pwRdVnzEDcqwHLYMVoxalas4sy5q+4s8hIrsP3PtSgTgXGWP8vnvgl4hSJaZwo60NssmIajbjySef5PUsY6GjyaAWLY+PCMpLsi8vEnKR5gWzIsJaeofRCh1Ck5eLgvHWGiABXWkoAVajGpg9qHHwy86OINKvvi9XWs4LddlltAbGO7BHQ2F+zytRupfOpz/eVOMSmWYJDhIj70hOlvFYQnqfHB3xz37uF/DWsagKvLdUdsF8MWVRLBoE8H9UWTqDA3P+d9l3GiZ7iIFKiatV7aR730fuESaIlNChtMLWFbPplIOHD3nj29/m0v4+J9M5L378ZXSmKcpKQpMas5JgHRJ6rGPk1jFPnTEPfv0dFh9NwIaR8PC9WSaHO2EE0rvjE179sfj75bUaklpHRsI5y9bWFnkmycHrun6s+9QnVsqyXIIjj0scrprPkJQ9xX/dya1u56L9fZBy3jn4nYQJjwOr47oNCSRWrfkqfDX0bt1YVq2JV+v9Ift9FEVBlmWBOF7WEkAPLijB9SA+3Gdn08aUOxLHkZFTSoNa1mQIX6KXBL1xXi4JPrM0losIXpL+TMgRyQq/ZGst21vbvPDCC1y/cZ08z8nznLIsmZ5NqWuh/yQHXTQX1yjlqaqSojhlPptTVqKN2NnZ5erlK1y5cgWA09NTAK5evcqDBw+4fetWMLVzQYOWrLHSaN0ViMYSUwiMRiNOT08ZjUbs7Oxw5cplHj56SFVVg+HGL3KGUnrJOdcRbKzDJenP9szL+ahqsRTKxxtoM0IZSaZbFXMmI0MWtNN7+/u89PInKKqigZnR17aqKsYTz+7eXidCoZg4moYOj2MvyxJrLVmmQtJb2f88zxGhuSSE3djYaEwR0+AbWuvmeepjdl750BkkgB/7sR/jx37sx1a+V0rxl/7SX+Iv/aW/tLLOZDLhb/2tv8Xf+lt/6zsaS1zkuDDxwpNIXFItkwyQ9kAlSKaPaNJIRkqpRkrfP7xt8IfWiTAyT0qJM60Q+LplfBIb4thXN8pZK1mtKsmUHKVIKTPWAegKCAkQJ1ubmPGIaVHw8P4DsGGE4R7Eb7tSfnFG9yr8QySJPgRrUE4kk3VVcfjogKeuXqNOHBn7fkE9EWTnt1XAckjDFi9De4njeFdrA1YBlz5CXFU+OCIXINPvY4gY7zjoW49BST6AypJpxchkaOCX/tkvUkznkqkaR1UXVNWc2fysk7flOynNWaJLWq0j0Nat0SotSNpXv82LEldBmLgCCcv7dcEloGuW0Ecc6d0dGk+ENaPRCFsJM4vWVFXBfHbGvbt3eO3Vb/KZ7/5uHty7zZWr1zBaHMq9UqgQ4bE/9iHhSRfWBGFG7yz5sCCdHPZ9AYK/WBLmi577QSnkmnbEd1C1YCEQa35AEpu8HmT8Vq3TRYv34gtow3eTyYTJZMKiEhORuqrEHGmAYB4aQ2yzLEX71Mw3wSerzlu/jeV1WM3YDAWQaAnc4TZX7dPQGez0Jy8H3w3NYWhfzjtbq+oOrfVFxr6KUV21BkMO/f16QwKW+GwIxl8Evi21s0J70ODssPenp6dsbW0tnYM0vLUPfxO+yYJP3J07d4Qg1algJqYQaRmlVeudBigaml8qcF535letVWqV0FBEvhVcAnzshY9x85ln2NnZwRjDdDrl0cMDqqpuGMa6thweHoXIkkKfjccjRqOc8XjC9rVdvIf5fMbx0Qnv33qfPM+5ceMGTz75JJcuXeLw8JA8z3nyxnXefeedsHbpmis8tsE76b1XKpiXBR+jLMs4PDzEWsvu3i671S4PHjwAupZMKU5fdd77760VM8PoM78OLqb0mpw5MdP1HuaLgnyygdJjnMuYbG5jjObk6ICtcQ62ZmdrC20yyrpmvliEQGKilV2EdDzOukaLp5RqGPq4h1EYlec5k8kk+HyJ+WZ6Vqqqaujv+XzezK0sy4auzvOcLMvIsozJQKyCVeV3hEH6/6cyBEg94u+RHrKoBUK1gDCqS+NBiQcYugRW3KB4yVs1tFyQ3GThcHWBRQRUsd34fRMaMrSRArT4rUhp2ouWZRl1bemH907nDQrrHVaBHo8wo5x8NOKtN9+kLkvQSrIbB18cpcQ2t0GqmsYyw4sJsZjQeR1CHAUnQOs4PTmhrmpJPpWUlFCNY2rN6pb3bN1+pkXWbJlBugiR3m9/HfIdGsN5kpwOg+LVEqBPpRp9BByZYhX6leSjMBmNybOcN994g1e+8jUybXDeU9sa72tm8xOcr78j5mgQgCrVkUBdlMDpt3NeBL8U2a9DnMNr35qipO/l9/VEUxRSDI0tRUCrkFGsF9fdaOHInK1R3jE9O0OheO/Wu9y4cR1lMq5dvUJmDN5bSTCthnNtDK3DEIExRISuIqpWlfOIlQs0sMbcaHmMjS9e5G7j+5T3S78PueNI57hibIPRJFm+62kdT7vPWrW+alVVUSUZ4ftt9GFH2udisWA0Gi3lkRkad3pvh7ScQ3+vumOxzjpYtupspWXt9345SE1TRyqubee89tc9X77jF6t7kZLCiYiDV5nYXaSsYnzPY3Sbb3333arzrJRisViwvb0tNIHRne+aMxPMkWIr0Qn/7t072LrG5K0UXgTJYl7nXOvnszTHNXNKhcBD4+60k5zrPvOTwrY0JHYUTH3yk5/k+o0bZGPRyhwdHVGWJaenp5ydnTGfFyH4VhB8h4jCzlmyzDRRJzc3N9nf3+fq1atcvnyVra1N7t65wyuvvMLrr7/Os88+y0svvSSM0sOHPPfcc1y6dJnXXvsWRVGGwCwObbrza9YgwBdow44XRdHAikuXLjGdTpnP50tCuXU4KH3fX8Ohe71uD5SSvJuuFnriwYNHbG7voPSEslZcvnIVUJwcPiJTjldf+Sq2rphsbDJbFMyLirPZgrIsG2GT5C+qOtZUSklgDGi1g5Hm8d6HNCbCOEUGezQakWVZQydF+FoFIdbR0RHHx8dcv369qbtYLAbXa6h85BmkdQTiIFDybaLVdOHjBUwlNJ28OLTEbt9Eqtt8lzCLDFJfHdjXVPUl3k1iWNcCUAFgvtN3B3koiMEhMJ7dy/vM3r5FXdXi5Bg0Xd47vMoa4sMBFeK8GYGf8/KsRhECszVIUCnF4aODZrx9wC2/t4zSusg15yG0LmHYfZ72fRHE2CdoVgGNdFznSb+gS6i4sFj979M2IoHdN6nEe7xz5HnOaDTCWcsv/rN/hvbClNra4nFMp6fUtqSqy3PH9jtZVhEuqwj6Vd/C+YRSKljo73f3W98goqG+ognAeWuW9tGfS/y7LArGWR7giQ37WlGWBYePHvHGt1/lmeee45233uL5Fz+O84JMJTjLd75n6dkS85xVk+nO50M5L77rQr5ujEATESoG1FCBSWpCXPsIZGjGqCIT5qE+B86ed8aGiAYXHPZjQkLvJQO8tbX4oPbMs4dKei7quu6E3E3n0X/WJ8Ifl7DvjynFHxKkZfluXhRODpXIUD7WNxe84xd9v6rOkGDjcUqKEy6Cjz7oGg6V5T1Zzeyl+MoYw+npKVevXu0IW/p3XAXmyCfRUZVSHB0dd5lafNfS5sJykh7eH/guMk1D8LQ/t1QY0rQd5uucY3d3l89+9rPs7+9TWcfdu/c5PDzk8PCQ6XTaEODj8Qbj0QitTUNvxTadq5v7v5gXvH92m/ffu8PW1ib7+ztkWcZ8Pufo6IjT01MePHjAyy+/zNNPPclxyGP0uc99jldffY3joxOhIZe8sZO1SYQvkiA2DwxSzmicc/XqVe7du9eMsc+0n3emO3ggWbv02yEmqWWOJMXMaJQDnoPDQ5792MscHM7IKtje3cM6y/TslC1TclaWbG1scuXyZfJ8hMmFzei7mGjakPHxHMRSlmVjWpjneeNDVVuLc+1+K6WaNlLf7DzPUUpx/fp1bty40bQdTfEuWj7yDFJMGheTssbSOSgB8YEwECgfQqRCXVti7HshrLrRc9I2U8Ir3WzrbBuqFJpkdZ72EEZHvXRscSOj5CAFvqLClfEWZcHGxmbDbMSLIxmIW4lsBKfeBPvNrU3G+7vsjS5x+3SKn89EEWQ0dUg2CxKwwasQ5QeFw1MHoqQiRshxOC1R/Mq65vLlSxgldVTYh45aPERSi+HAu8QPrEIEaSCNdP1blquPnGTMq5FWH8l0+04ZucamWKXvfK+uSOt9+FN+93EYaKVwQRMn2xMi/eh2DdqzmSSvJGiHgPFohFLw5S99ifffe48JWQASNYvijKKcByDflQ4uUcgqkdTHsxlfNVWWIwqlv69iNIb+Xi4tszxEnPefDTNWEQHTmD2hFHmWdxA+wTwkEqqrwpNHIiCmDBiag6wJnXGn7+KeVXWNURqNau6idp6yXFCUGffv3+fS5St8+cu/zdPPPofORmgPtbUSyrRdiaV1W7uqCaJrxud77EpYOhF4DPST3sfOd769bIGZ6Rbf3sMV+7+07t6HiI5R20V7Z5KBLElPVYt0ac4RjR7Zhz/kO8XSOvp41/rjC0SXNmAgH+VsbG1ycnaKt56qrEIkTIHBS/nEwrhVZDzDsumQVDwmU+wTO7HvGH0uGRENrOkvt0rn1T+Lbbh1uae+ObdKsXSvVhGmqwRGHYK2N6aB1W7a7xPD/Tpp30O/D33XH3MsfVOvdUKZdIxD7a369rw2Q63QQfNR+kf3rqiIG9LxqAZXDM0zHX8sRVGwsbER9ic5Xz4ZQoobFWgjUVoPDh6SZ4b0bC25IjTzWWq0O/MUHjmPU27wvK3CNUqpoHFIgq30zmJtLfv7+3z2s59lb2+f6dmU23fv8ujggMPDI7SSaHUbO1sYM8JkE4zJyTJNVZW8d+tdaluyt7vL9RtPSBLTqsLamqosWCxmzGZTTk8OxYemrJqoi9PplC9/+cscHjzik5/4BKPxmLt37/PJT32KN998kwf3H0JqJdPAzUBP9QQUta1RlaIIvlKXLl9ib2+vEaZL9dY65DzBRrOOkRZJ9rT9tqU52v2IuaIUeZaRj8YopXniiSf52IsvcfClb7B39TLj8YRqfkYxP8OYkqdvXGVjMmJnd5OaEMjM2qBNs8HUT4KBWRsjQo9YLBacnp5SBD/NaApnrQ34kwDz5VlkdrXWwY9McG+e540wamNjo2OdM3iG15SPPIPkrGvwl1YqhJzWEjXKOtAtI+K8RGvLdEZlqxCHwGNrx2hkGuSSBmLoJ+NLL30TwME5XGAEIqcbkbsN6sLoQDYejztmff8/9v6jyZYkTdPEHlUjh/pxfjmLuBGRNJJVZlVWdTVBD2ZE8AcArOYHAFgNfgqwgQgE2GAxgEAgWPQWMt3TnVNZVV3JMyMzMujl17kfP8yIqmKhxNTMj/u9UYURANmtITf8nGNmampqSr73I+8X36vtMqHwxAxKVWhdOwFDUCmnr3DConELi3ExQqXW5EoidyZsffNdbm5MmJUr8oM+r16+ZLksKGvrr2qXVmGppg0oAaUx1FJQG0MiDCmGLMnRIqWQEtXvcffhHaSwcTOJsNoCSQOWhEyiidveTEUkGHWP+a3YPxNucpvwvNGZwr8X3amlEap9XfF3u4l4ocH/JkJ9gHNvNJGbY1OHFxq1dzk0zfvTzkLnm9ESUvACXdxM+3ulDbWu6eU5aSooljP+/b/9f5FJg9GgqVEsWRZnGAqU9m48kUsc7RL/LprOCJ0QxjXtDNpvo4W9BHiEIdDb+xwmWMXDZQF1PTiGywQW8Xl2IbRW1aIogsLAa/m7sYixpt7fs0u20hzrCk24+bdeIPCl0ooszVwuMyvgGFWxWi04P095+fI1q7Lmkz9+yvtf/6a10rpzvUB9WSCTrXfRFRa6bWg+R2AWNzJEw8DmBV0pRBOTBC1KYhPFRxp37poOaACKu7+O6hAB0BBcR8GAdpauCPhIz9rlgIMfzYF63wUE+yS9MbNlACghr03TvnBzj7HdOhKSe2uNwKC0QiQJo40J4vUhEkvBX6vS1iv9PeP649tYSdeORRBohE/rQKMEub501oVorYnfaZQTwvdG+xh2DdNa03X1XVe62v83WUfiZettrVFXxQJeB4iuGutdS088N64Tvrtz5br4xJbl5ToB3wEHgaezJrwb44U9P/Na7WrOC0J0+N4iWr8EzLrP793NEHEssWnGpWuBBCufJAISqOoV84tzK04bBcKvXRqfQqSlGGk9C5dAUgtgOtDXdWW+9v0CUrl2C4FJmvXP76mjyQbf/PBDJpvbnJye8+TJUw6OXlPVNXnSZ3u8gUwMRqT0hjcQ2QZJP2fQz0hEzcn5jJOjl5xPz7nzztcZT25QlyVGrTh8/YzTV88ZDhIG+QitQJiUREi0gv29GxgMXz59xnQ25zvf+Q537t/j6dOnPHr8DkbavJ9SSNIkoa6Vpfs29oULH8MtCaBL6ZrVaonRhn5/wHAwYj5bUJU2BxMyRevyUl+t6z9fkjTBxhL5ceJp2Ju1JB7yWitAIqVBpCM2t/a5dfsm//yf/3MOL1aM9m4w2LhJT2YcP/8cKUpGoz5pmnL33g1qPWNVKLRu4nY92YK3JGVZRk/2OD45cy6HCWmas1gsAElRFIxGI6p6SZ7n9Ho9hDCBXMMTpRljWK1WrVAUb4GKE+1WVRXINd6m/MkDJLi8CPriBSG/KMbWF2iC5IPGy5iQICs+N4CeNfe6ahHzjEgSERJngWXxgDYgapMz+HYbpEyDsG19aC+bDtsLD9TaAjJdGsYbE1589jmTwQiTZyzKCiUSSFK0UajaCXRSUiUZNYZ5WVJoTS0kNZBKSSogTxLyvM94e4d/9tf/jJfHJ3xw8w6JuUzzvFZLd8W7u3aTjTRKQSMXuSa1gr7bF4Y7Xqvz67SxG0h99XV2o2vJTFcsWl0Kz3UbeiP8Q5YkCOA//v1/5Pj4iDxNqWsLkJfLOXVduoXNCtJXPWDXYtQtMVB4Ow3pVUK5eyYJQjT5rxqAlERAYP1m2cxRa7nxGi9f1ikm/O3jeEBfYnC0TthSSoX4w1jYDmOmI1xdJdw1GkHVIl/x9yhWBUdHh2S9AX/3dz/l8QdfI5GSStVWefMGS9FVJX5vzXs2V9YW4QNfgZ03Iog9od5WP16xrq7tkzX3XNuW6FpvJbryQtEIaqJz8G0F71iql7JtsbfCiyW32NnZ4XM+pSorG4dUVTRsiJefqNE3XFaerdsTHKq4tm/WFxPdrHtxdIxoXeoAnqv2rHXlKuAi3A26a+ObgLw/p+t50a2nC4LeRiHwprnZbYNfE7rKnfh+3fquO9Y977rv0Sy71N7m3LaGv1tPvD/5uGivnPCB+W/CrEKKQJ/slQ0G3dqn4vb4Nnf7tfu+tdY2GF9ePq/7vP4eoQ7XLQGH+fOEJbbp9Xt8+9sfsrm5xeHhMV988SXHxyeQGIYbI8a9CcVqyeuXT6i1YfdGybd/8M+RvREYhapWfO3D73P4+ia6rsgHG5RKkaQZWZ6xf+suR8evmC3OSGSfjdGmVRprq9SeTqfcuXOHre0tnjx5wj/8wz/wve99jzt37vDy5Uveeecd6rrm6OiIGifPxTGGQqKcosML80opS3mtLaPgeDxmPB5TliVFUbTk1evGa7do04SAxCln/DuKizF2TG1tbXHv4Xv84Ic/5L3332X3xg2e/+oj9vb3MMkAuap48exLEmG4f+8u58cnfP/7P0CpmrrWJEkW2pfneZBn/N/ZbAZAr9cL+/XW1lZ4ltVqxXA4JEkSlstlsBjFpZsuxXuAeFe9ONbJswa+TflPAiB1B5KJfo/jfeJN4xLNcmcQ+r8xMGoFU9Je+OO645dZV427T/c+lxckwjHZWWgW8wXD4SiwzMQlTBghyBKJVgpTV+S9PmfTGb85nzIcjhCbGwzzHLFYMkwzpJDkeZ/eaEg67NPf2CDp9TB5huz3yIYDxhsTBoMB/bRHP+szmkzQacrxxQyZpG6PXh8Mva68eSNp90Ncr7EXrKmzo/FqHbweJK1rQ3dDvE6g8OetE4q6wlJsIezeUytNL7cUmMvFgr/96U+tNqqqEUjqumSxmFktlDEkMrFJhIMAd307YwtRV6i7irTgTaW1SQovcHtQIoA4K3cDWKqqCpYf2zbjjqfhuDGQpgnG0fUL0bAB+azmXatr/L783F/3LrXWASA110I8UtrrwNWA2QI6RRdcWxBWspjNyJVmejHjy88/553H75MISW1q0OvzR71NWQdQvHCyrkQ4wbojY+dMDKMvgd4rhN03CbDXtXWdUPs2xV/XXZ+7bXnTHOgW6cbDZDIJ7fIAet1a3b23/2vfeX1pfvniV+3r1pQ3rUPt864Xpv31V/XHV30H3f1qHQBb92xdS+26flzXnqvOi7+ve75431437rpr9VUKgC5g65bwyxXv7KpnWfdsV/XDde+oLEt6vZ4jP7k8rhtg2x0ksFguUHEuPnN5f4jn27r+7rbbxtBaRU1sRer2yVXPZ3B7CG6uOGVZmiV885vfYmdnh+PjEz755FNOT88YDIbkgz7ZcMygP8HICwrzDCM1Zxen1NSOVXRBVSwxdcVgsocwBoVE1SVGGYxWGFVx+8E7nJ8esDEYkicZSZZRVQVFseTo6AQhJA8e3efdd9/liy++4Je//CU/+MEPuHfvHk+ePOGDDz6gqipms9nl983l8WitvKBkY3UZj8fBKhKTgH0Vl7H4ba9bD7qAezAYIKVkPp/x8tVL7jy4S7ZY0Bv0GUooK8XZ2SHHB895eG+Hrc0N9jY3uXHzJq9eHzCdLplMthgMBoxdDqR4DxRCBJc4P568B1WSJPT7fUsJ7sayz2V0enrK2dkZ4/E4yPBxTJI3OOzs7LBYLEK+pOvi3deVP3mAFHec/w6Q5lnQtLTyIOkmMNgLUuARqkbpOnCvrwNF/h5+8HoTnz/HU3r772makkTCWnxtvGj7BSWeSN6lDuDk9ISTkzPu3Lkb2nFpoZUSH/30+WefcXNvn2985zuMBgPyJMH8+Z9RlRVZljMajUmSFClTZJLYXEcIakBJicgydCItLXGSkssUoUFpg9Yw2drCYLNwx214U7luk+w+03W/tepcd05nUb5qI3yb+q86t7t52s3GL/G2rAPFzft1geG1QoD1A05T/v5vfs7p8Ql5miAkqLqmrJYgGgun6WiK15V401v3POu0fNf1SaxY6Fpm2/c1SJmQJhlCyOCHbMGTNelbamwvpts8C1o7VjgkOBc0rde1p1EgrLP6rduQuwKSXzca8hTrHvim0h1Lvn5PN+rvobWmrkqqsrBaPZHw61//gnfefde6relG67ruHt3naL5fIfByNUmDENZKYnDynBd0hb9PXH9b8F/3e7s9lz9fdW1X4FrXzu73N7Vl3RxYd8+r2m+EAGPYGNtkiCrEptaX7n3VOuKLqpuUE5eUbl8dA7/hfgZjLoMkX7rB3VfN9S7Ii8tVgu06MLQWFK4BAt35eJWSo1v3JeGSy+/lqrEW77ldENAt68bX+rbB277Uq8Djuvtd1574HM9gp5Ry5EtXtJ9m7Pljs4sZRVmSJo7dTdj1L963rgPr3ecJspfRSC6z6a3r65agHgfVewujECAM9x884M6du5ydnvPHjz/h9PScwWBoc5f1J/TGNxmPd7l1b8B45yZHRy8YjbY4v1iyUAsm4xE72zcZ9HpkiSSVEoMCNLo2qLqmrlacnx8x3hhSzGZIYHM4oK5KZtMpi8Wc05MzDJr3P3ifx48f88knn/DLX/6SH/7wh9y+fZsnT57w/vvv86tf/QpV15b8RTTKtW5IBa63vTKmqirG4zGTyYTVasViuXDdcZl6vrvexXuOugJMXaVMKMuS+XyOFid8/tnnDDfG/ODP/5zRcERZLygXS/7wu58jKPnG1x4z6uXcvnGXra1tKr1gMskcw7L1mPJAx+9tXvb2MrX/5/Mh+fXSz9Fer4cxhq2tLbIs4/j4OLDZ5XnObDYLCs79/X2yLGNnZ6eV7uc/A6SoxFrg2C0udp/zJQhHkUtOiB3RmrquSLOkdX48uONFYZ2GytcZU3oLJ5AYY8KmGzPnxRtXs6jjtORelhEMhyNmFzNrWk/aiWjDhqE1aS/DKKth2t+/wZ07d1muVmg0ta5QygoARgi0SFAGmpgHXBSAjSFKhUQLG6OkncZSpjZxW2Is80lwgbli4b/q+7py3YLaLQJom4Yua8quu/c64aGrqekKFd2Ndx3QtbLQW2jMTMO2prQiSxKyJEXXir//278lTRKEsZalWtkgUoNl2GrqcvEXkSDg6+0KLG/SrLzNsbiOLjCyYxrAgQ8FJlhBbTCwMWCUpVu108JuINb1yTTKi9BN6+MirCKicWWL52P8b108k9dc+eNtGlKiz/G8XK9Bj8u6+xpjUKqyifYEfPrHP3J6esLGZNNaLrgKNFwnNF2nXGjpBdogOLpcRO/NynlXA8x139/0+1Xlurm9TghoHefSDP/KpSvkCQgEPgPn4oExLQvSdWtRV1CsO2Mx3A+vGb96LVjXzrit8XnN8befz+uA5lUgyp+3bvxdJ+i+6dyrzllX59uA7249V+3H68q6Pfi6cum8BpFcatN1/XZdf8XnxSVmYfPnzOdzhsPhWuDrvxtj3MBrr9mrYuX2DSunGPye0Vzbvd+1fUEkZ3Xk87cB6saYAPIMIBJJrRTD8YhH77zDfLbk008/5+TEWo42xhuMxxPy0Tb9zTtMNm9RacXunYxstEW1qhgPN7m9M2E86pNKqIolq8U5q7KkKK2yMZU9mwtpNGCycZ+y2mM2Pef06ITlYkaW5QiZcH52zuZkg+OjY4QUfPOb3+Sdd97hk08+4Ve/+hXf//73uXHjBq9fv+b999/no9/9zkpG7hmV0UiS1trQkKqYwG7n32m/32e5XDSpaTp9t24MNfP18jre2gfWvIuyLKlPz6gKa70iSfng/W+gVys+++g3TI9f8Y0PHvHw/m3KxZL333vM9vY2MttCiISDg0OOj4+ZTCaBPCFu1zo3/i4wSpLEuhxG8nGv1+PevXuUZZPrcTKxHk15ngeAJ4RoETr8fz1R7P8vlTgrr09KlSQJRVVeou32AyWmYo0FJ5toqrEGxdd2LUnXLSC+vkboEgEgeTehGHjFdXa1XVK2SSKklGFBW8ebrxxD1uZkk2fPnvPw0TuQZShH8oDU1LVCyAQpLapHJmhpBYbMCIwCoWm0QX5wO42zpeo1EXC6Wot71fe4vElbF951B3iEM95gAHpTvW8q3bGybgEK90IgRXuRukrY8O9ba82wNyRLU373m99yfHSMNAaNHSdFubI5j1SFDaIVrU2vy9wSj9X437r+uOpZu+d3rUTeTN5oc+3TW1pVLEAyfjNtKyma34S7JtauiTBn/ELn50xch+83v1nHG08XzHSfJ1Z4xIQO6/rBX3uVIBX/5udkEL60oi4rkjTHAPPZBb/77a/5F//yf4IqDVorlz38+mW6Hex87amtdjXgqPHzB5BxHeKN0+efXL6qVu//k+WqdUl0OnI0GoXxXFUNBe11wLFbTOQbf+15/4g16KuUbjvXKX7eBhxcBzjetk+69cXKnHhtunZNfUug9VUATyywXXdNt13/1Hd3FSDstuuq67wMMJ/PuXv3rj1f0NKMrHseu0badXKxWLg1z67RWptg5f+nlqv2/Te9E393IWzckZCCD772NdIs58snT3j9+oB+f8Dm5iZGw/HxMbdGm2zvTag0XCyXnJ0fkSWauw8eMOoP0Lrg5PVLTo5eMb84QZVLBDbXE0KitSTNBuR5j43JiBs39tja3mZnb4/TwyMOXr4kz3tIkTCbztjYHnN8fMznn3/Oe++9x7179/j888/59NNP+drXvsZisSBNU27cuMHhwQEOryBoj/fGC6NRqFVVxXJpiQosOUEe5Lw39V177MtLBBndMRfvd34f78mMRCbMzi/45KM/sj3e4emXT3ny8R+4d3uf7333W0ihGY+GPH78LkmaYWRNVVYMh0MODg44OztjNBq17unXnlgh4S1Avg1dUOM9sLwb3Wg0Ctamoiha+UuFaGL8vRdH/Z8BUrvEPo6+XNJQRAucp1yO0aoXuIM7kBCWFcQlbFXKukElLmGnMbjfNXmeNcwdgeJV4m4CwmptU8fdrpyGeZ1DT+Ny0GwaljZRMJlsUFUlWa9vJ44hJFR0+ggSpxXa2d7hp3/zU+7dv08vz6DQnB4csr27R5JkGGHzIqFNADmWslgiJQhlEEYihNUwIUB59G9sDINlcfPxDG3tdduE09F1RmxMJvzf6lkbi5Q7FqMg4Xh/vKarof/hKrRksCw+Jq6su8l5kBxuinNZMk31xoS/VjMXP5EX9L1W2j2RMWCsr7HPQ4GI2u3unQhBnmUIBH/3tz+14yyRqFrZQMiqDODX4KmSraOoqi5bNdpsiNcTDVwF3hqgYseyPd/nb0qCksEKlSoAJBvf0rjA2eub+qzVyJMoNKQMXovkzzdGIEPyQ6+Dt5u6b5fNuC3dFJNBQ5/IxL2/mJbfKyFM1JZG0dG1CMfCnHdluk44ijVjvj5tDLVW5FojEolRit/+6lf81V/+lV3cTQMC22tUDBSb735wSuFnXPip1S+4o97NQ8Q/xoqFqN3/YwGYLsBYJ3A2G/jlMeNqiR5AYDpzvImksmOveU3RHhACzf25bgBgOy7NMwsWjWMeVcqlgmjf27a5ffe40f3BwFXbZjwz4uqx4/ujK+THf7t91n7ydnG3j86Nzo/qkLL5HOoUtP9Gzxb3f9wtsXqITtCnCeu6/6GpJ36m7ni4qhjAdBUuOGWM21GF8eusm/PNruJaZOyybAQY2cyL1lhs7hfqDPe53P/GD6ewo5nwIvy+0fRSe06E+7U3vGYOCBzza7O+a60Zj8cNQIptrCL6apq1IZGSRArKomy933UgsfkYP60/dvn9hNAG2bYevAlQSildKpBGCgDY293nxv5Nzs/OefbsGUmSMhpvUNWap0+eYgwcnJ4zvnEHZYacnc0YjgfcvbVLajQnB8949fwJi/kUUEhTkUhtP7vhZyQIXVGtKg4uzjh6/YLRxoQHDx5y48YNNgYDXj5/TrFaspjPGY0HFOWKV69esb21zc0bN5nP53z66afs7++zv7/PF198wf379zk5OUFV9l5ezgrjK8zDRsntSTcuLi4c+1tKWRVhX4zzCV1X/Plx3k07xqyTtRCW6j2RCULK4Lp2++Zd7t59wObOLuPNLT779DM++s1veXj7Dt/6zvvs7W4ymx7xvR/9OTIV1KoGY8FmURTcuLHPalUwn89aStM8zymKAqUUw+GQPM+pXFx+kvjQEytDWBDUPKNPi7NarSyI6/UYDAZorZlOp+G3NE3p9/uhf6bT6Rv7yZf/JACSX2S2trZYLpdrWSzCQiwdJa2T6LUT/pECYaRb04Tb4OxfbQxCJDbZqhCIQJGbkKUpArvwtIRO5TY3TKDUlWniAJq9T1XbBK7QdhW0mnG/QXr3F43S8OLVM4pKsbezz6g3RiKpVIlRFWkvRasaISSDYZ/ZxTn/h//9/447N2/x/MlTTg6P+Gf/xf+Uv/wv/kvmVU1iHC+e0qAFRkJtrEZbpHbJkpEAGzTQzqolMCQYAs/62u2aLlZq9lq6G47fXN278gt3uDY6r/VuY4Eguq0xVlNsmpZ5mt9WDilXZ+tajM0Z5dpkgnBpf/eyVesKL2O4uk1s4fBgOTyCfa6qrhj0B6SJ5Oj1a55++QWJFGij0EaxKgtqx3hT13YcIDRCOKHZtLVSTZ+030UXJF292Lbri8d0IlO00WhlUAI8+bJvg+9/D36CQN9pW3NvL6RdPmY3kkgT5nWMIvoMbm7Zl2GMRgprGQVDXVcIoQIQg27QcbOQa90VENrCqB8ub1OCxVlKjNEUVckwTcFozo4OefLZJ9x7/4MQrxi75Nn2dd+PE+yMQWiDSJKOMiJ0gRM9BcJYoSNxv5tI0RGEN1/1mrJOY34VA1mrGW/bSZfvSHscxCDJgxrfbNG6Thk/vr3rZgdQuPM8GG/uJ9FCoxNBbzSgN+xTlyXoGlQNTgklXAIDDaD9GtaSMBECtLYWVIN0iivfh7F2/qr3a3+zADt26RattS3uk/XwyD5xA9jVpbnXBk9Nz5oWyjYQAREbC9jMY+1Ucg3Nta+rM9e99aoFFIRNxUEEQI0Hvm2gZDrrtEagWwDJJVtw+0ZQlOjI5d4NHCllGDpe2YcwDvK5erRpD69OL/sl3Dapsw/54y2A3AXtLh2G62orH/h1sgFKHuxbBaX9Ll2uRmMabxQrVNr46ZYyTNoWadcWqQyZEKSAcZ4I2nRjYuO1sbMv+x+jd9y1AK6zCPp3ea0iRgjnciyww0Vw//4jdC14+uQFxapgPNmmP9xEIyA5AFUjREoxK7hYLtja3OXWrX10ecGTJx9x9PIpOKW5VppKq1a7pFSkaUaSQJok9Po5dV2zODvjo9NT7ty9yzuPHvHg4UOElJyenZKkgmQx4+LsjC8//4LJeIM7d+5wMj3j93/4A3/1l3/Fzs4ux8fH3L5zlydfPkF6Rjvh12ThxpyLCnVrQbwPWJCTBsZjIWysWF3VwZUs7s9470gSGcJEhBAYbcGRjQmGfi9jMBiS5j3SLEdpw1/91T/jr/7Fv+L49IyXz57zD3/3H3nx5Albk00+/MYH7GwPWcynbG7tMt7c5vj8BCEsY12WZUwmY4qiCHFFi8WC+XwBCLIsZ3NzMxAvLZcr562VBeNE401ilfOePdTvN96DpCzLkA9pe3sbIIAvDzKTJKH6zyx2TfGDa2trK/jkXlxchAETu+ForQOvur92HQlDXII2vrPv+2tj82CbNtgt6OYykYS/NonuqVvaSr+oEDQLQGA6+fTXv+UPv/uYTOQ8fPCIew/uAoaqqkHaQEShNO+99x7/l3//E377i185oV3y73/yU77+g79A9PrUGKQxYDRGCNI0IUlTpPHB9BIpIBENM18r8F/Yye65/ddZLt5UOnKG/c33yRVave51b7xH9Dm2CsWVeMwcXyVi0NRGT62ybjOIF7BYAI5/9xM7TROkEPzut7+xC00i0I4RqygKtzhUPn4Vn1vIgog29ft1ff4mq1GzwbXZ34SwQZY2v5FwrmS6BaK6IKjrkndVeRuBukte0rL6RgKv18zZOeksysL3l2mBoHXrw9uV688L874Vh6Ss2wjWfeDXv/4Nj77xTeqqcbntChbrtbkiULdebrO5RmCmdb7pDPbrwPRV/fJVLE5tUHoZeNnfw6crfn/jXQhQ6A1zoKXNd+Ol1+uRZSmrYkVV1WHj9RaK7j269Vk3JXWJnhZ/RfO/qK5u+4nAUXxOGxCKVjMuP6sAZ9GwIEd31lAng0ZwxMObWMnRuM/aIzIS+nGf42eMxmt8QIgg4IOw7GQ0ICOqoNU7foh2118DGKG7S3CoROMJkjyIA6/A05FipbGsidA/ECnOQvNFp10m/L00B/257ifhEiPrKHeXt6AF3EeTQywI03F9rsLECY7e1cgLo0opklSybhyAz3nmKfvtb17IpvMs3XLlNOqsHd6iZeeKfZEN2F8Pmq4r440Ndnd3OT+f8vL1Ab3+iHy0SX+yw9buPnu3HzGbnjEab7CqDZubm9y6fYNydcEnv/8l58dPEbpGVdYqYef2oBWO4em0jTHBAtHr9ehJm5vn5YsXLBcL3n33XR48eICUguOzE3q9AfWgYrmY8fLlS+49vG9JGj5/wrNnz7hz5w7T6ZSbN2/y6tUrq6x3ChxEszZdJjayfeVBQK/XY1UsSdOU7e1t/vW//tf8t//tfxs8pdoKtfa+65ngbLxtGsm5hkoplmfnKG0VIrdu3eHew4cslgs++u1v+Pk//AN1seLdx/f42vvvs7u9gabEGLh9+w5nZ+ctuTnLMra3txmPx2xsWLKG0WiMUq+YzRZIqYIFyLufx+PFy0EAi8WC1WqFEMblQxIu7CUNz3h+fs5wOKSqKiuTCOti5+WkJEmo/fh+i/KfBEDK8zz4PqZp2vLB7L6M2PcRmg0u/hcf9+DGa2/8C44Ftvivj2lorq1p3Dts8aBHyqQFjOIB79nrYmBlY6wybt68zR9P/8jzZ0/4u5/+R3b2dvgv/2f/BVv728gsJU8zciG5//ABN2/e5NmXT6gqBWnKj/7iLxmOJqwqRyOJdbHTxlBUCqkMSkOWZuR5YrUd4moQ2bUyvOldfZXSJce4qr43CWvrBOC3WbDjsXGpzmhHX2cdWScod8/140lIm+37l7/8OVmaWOpRDFVVIgRRnIwhSTL7Pvxiay6z3MTt6D7Pdc/qNzsQrfY39bcJS2Jg9FUAUVdAvardMYDpAiQ/L7oAwwofpnWNbdt6Ao74nte1622fLZ6vbQKYmjSxrriff/YZFxczesNhS1nzVe77JgVEGzq9ed5dpYh4m+veuk3XrBNe3/Kme3yVOt+mCCGQSLIsI8tyVojgNqKVemPPNRrpJulhy/oB14IZ14hIJm+sJtYtRrSub7UnAl2xFt+49TwoBNxvCNG6xn6yaMsDJD/fkiQhtiAF8HTF87eUL2sfseNhESk2CC1oAJoHD/E9/P2veifW0VyHPiBK2N05kcbrwfaz0f4+3XhEvzbY7mvWoXb77SWuL93xJkl2DHoA3bgWCSFsvKm2lnmMlVHqqg5WpLquqOoKsMKxT4Tp5RC77HUVRk37LU5uEmpXVR0/Gd4V+W3X8Fbt0fuXUgbU3ZZlrlbIrSt37twB4NmzZ2gD+WiTfLzFYGuf/mSP7ZtDbmrFq1evSWrD3Xt3WM6nfPLRrzk7eg710gGFxCZhHTbgyO65MsSr17V19/KeR/3BIFBPn52d8fHHH/PBBx9w+/YdFqsVy8Wcfq9PtVrx6tVr9m/dZHdnj4MXr/n8889tvqStLQ4PD7lz5w5ffvllK9l2ty9i2aQFnoS1nFRVxcnJCR9//HEAEvFc95/TNGUymTCZTBBCMJvNHH14HY1XQZpmDIYjNiYTNiZbDMcb/OHjj/nbv/1bjg5fszUZ8PVvfJd+nnD/zi1u3brJ8xcvefDgm0wmEwe4ohxPUgLWzV0pQ5ZZF7qbN2+TZaecn50zu1iwKlZIIdnYGIf+9YpXmST08pzRULKxsUGaysi6JJxbXkVd1yyXSy4uLlBK0ev1GA6HgarcGGssKVzs0tuUP3mAlKYpRVHw/PlzxuOxJWgoyzBJY6DkAUxX4+2Bk//sS1vwahaguK44yWsw8Tl06zeLGDDF90xkWxsco+kkaWgRvRCltSbPe+xs79DrDej3BpRlxaeffsb7X7zHzbpgY2vCxmgMIiHLc777/e9x8Po127u7/MU//1f89b/6Fxig3+u5vdJquDTNxNXaUFYVQkpkanO2rBOEukteF3heBUIua4+9HpOwKb9JKOouMuvqf5Pw1LUm+M/GGNcflzWG9lhbYxrX1XVD6goG8Wf7PnOkEDx//oyj40O7yRsb/1CWBX4Dy7KUBpE5WSdq3zqmxe6zX9UP69zzYuATW0ClSFtj2J/zVQT87r26x7rjHmhtDl1mH//sjd+1bxNBe2tMA1hi4AXt369qb/x83bkQf+9aC+0zWICUZ5bCdL5Y8OWXX/D1b337Ut1v239XnycufzK0ciRdde1XBWlvamO33qsAaPPO119/Xekql950fZiX8VQQNonheDzi7OgQpZTbkAPTyCX01n0mPy6vcidtE5VALHjb/zUa/iZOx47l5pnCZeGeXQ8I49qqDdZlLgYZuomBiJ7EWT1cbBH2OmVMK9atwWixpch3X/ObFzzjDPe+b8J87gjOLVIZX7dsxoQFijZ4XyayNU5afaE0SdoIVgGfOgp/+5t2FiMsa6bxcZSx8sc+sVVACdcFDkgZgzHr3MhsOobasYx62mP/3KvViqIorMWosp4By+UyWIHm8zlpkiBpEl3muQXteZ4jE0GW2eSfz58/5/bt20EWsX3VrI9x3/p4UIuTbfuLoojOsx4DlpwqWuPWWEubd9R2r4vX0kTYNbgLtvw76RKG+GNWhDckScqN/X2KouDk5CTEnYxGI0bjDQajDdI85/T4hPmy5L1330Xomi8//R1nR08x9ZLRoIfWhsViRVkW1HXBYDAI46koShe/6nPu2X4syxKlbU40n1PHxxh9/etf5979e3zx2WdczOdMpxcMRgMOD4+4/+gBe/v7PH/2jFevXrG/v8/R0RG7u7s8ffrUhlxfJfOs+ZskCVmWoVTNdDpFa83PfvazMJa6e7sHBqenp5ycnLr90YZnbG9vkuUZQkCe9+hlA7JeDylhNjtnuVrwe12zu7PJ195/yI0b+4zHI8aDHkW54PD4NQ8fPmR//2YYU3VtglXI7nUl0+mFk0lsH0spWK1KksTKC6PhyM0LxcXFLOyRy+XKyux5Tpqm9Po5WhvStB1L5deV4XCIMYbFYsHR0RGvX78OADHPcwaDAadnZ5fG2FXlTx4geZo/KSVHR0fW7CbtpG9rvy8LqP7vOmE2Ll1gtI4xzAtGnklj7cblSp7nIRlYt23+Wi8ExhpmIQTzxYIk7TMabQAHbmJXlEWNxLrW6aqmkhplav78n/0l9x494Nbt22zv3wQyhOihIn99gwrubP75jDEYXaOUcFqIyxNTSHGl2vdtNMmXD/gOb/d9/PzryrrFp/ue4nPXCYLdceJBUve4ccLMGzytQv1dDZr/G5OKJGnK73//O6qqtOQMqraWR6NRuuq09Xqd9jrhrPs5Pi8GGM0zXnb58uf69xArBuL6rhKCr2pf/K7WgaXrgPbV92kAklHtsRCDv3iurgOW8b2vGntvM8a8gGjjBjLqquLjjz/mG9/+MLgevC04Wv+8604CTFuJ8abrrgN+/ngX8F/Xvrdpp383Nq5xfXuu6//rnuEtzrbtdEJknlvBqnKsSFVV2bHhTrUa/auBXBwfsG5MxgvcumbGYMh+b4+vOF7PCiNt93F/T6V1AEdeQRcDwkYDfHn9FtHSFgdMmy5/c3xNZFDx4xwI9LxWI27BiYgAl+ce8cml/ZornSBPBJgQzj3PiHAvb2HxzyJEQsOWICwglILEufVhDMY05EjGKOqqQlAjZcKqKCx7oVZopYMbln+ui4sLalVb52ujWSyWgGea1W49sTlbvKeJd5ey1hXBcDSil/VIZBIEYbBJsYUQJMKyW2JsMH2zBtp4sjS1LmMHBwdXKsXiPccgbBydaSxFy+WyvR8ZPx4bWcN6vcTjIv7S/v2qNfI6xVL3PIQl+JlMJgyHQ54+f06tajY2RozyhHEvZWOQM+rnLIuS2fSMvZ1tRr2MZ5//npPXTxB6yWCY0x+MOD05ZblaAlDXZWCIk4l0CghLK+0Tu3prRFXXXFxcsL29HZTc5+fnPHnyhHffe8ze7j6zsymroqQ/HHJ4eMSNO3fY3t7m5YsXPH36lNu3b7OxscF0OmVzc5Ozk9NW36xTLMbyhU8CnOc54/GYs7OzS/Ji9500+5u14mljQUaapWxtTUhTwSDvM+wPyXo98l6f4WjMzu4+t27dYtBPMKpia2uMlAnn5xaY3b59j15vwPnZhevLOqw1/p79fh+jbUy9NtaVXMoEKdIQ/2sZ++yE9ylBFoslRVEwHo8wBpbLgvPpOaAYDPoMh8Ng9OiOocFgwN27d0PfxZ5bX2UH+JMHSNBYh7zQlojkkpYK2sJgd/L6v91JHgakMWFhaJix2sJVHJPR1CNcEGXjb+lpCrXbMPxgi0GRlGkLkPlBUlc1CZrhYEiW9xAicTSHFWjDMO8zzHssFguEFCgM3/3zH7oNCoxJ0LUiE5lLl2bACFKnKLWaI6cp09aa8eTJl84Pt2OCF19tMH7V0l08Lh9bDwDWAqYrXOLi+t9eEF8DDE1z6E0lBPFjfXi1Uvz+979vuW8Yo5GJQBdXCCadZ1kH+ta3vf1bvLk11hXTstg0x5wA0qlvrUAookayvr+vEsDj9xG3tQtarir2HK9pToKqu/2MbSr0LqD5x5S47bElSWuX+8k4bTXw5MlTFotF8BWP6/gfo3StZPGbue6e3Td4Za+L9rkxm9+b6gxVrBEirnrPb6rjKoWA/2zBhZvGwrqk7e7u8LHW1C4vSVEWjYLKW5R113bclHXpI0J7Pcpi/XrWfqr17QbReY4r+klEYEy0YznbbWsDtQh7XG7ZNfNNxtYvW6sd+9q4JKANUVErosu7PXkB3v0eiJO8LsrFUXmXdP8cWmnKqnK54ezeulpZtyKlNGVRcDGbuTFoXIxDEWIabAyKZaG1soPdyz2zV5LYtB/D4ZBer8dkMiFNM0eOICN3/sQB1jYjo/QxSCFW2bp3odrKGq+oAYNE4Uk+pLSg0FvytCOe2Nvb4+XLl2tlmGYIRMAR8MyxBlgulwF0Ac4dU4fx9D9GWaeYDLISTd9tbm4BcHR4hEAwHPRQqym/++VzNp4+57s//Cs0ElWuuHHnDuV8yqtnn0G9YDzKSTOr/C2VJTkSAsqqpqwKZLLBIB/S7w1JkiyAEO+ylec5/cGA2WzGxcUFGxsb5HmO1pqDgwO2dnbY3d3l7PiEo4MDMILlYsX52Tk39nbY3Nzk5OSE+XzO1tYW5+dTbty4wcnR8RpWufZc9kK+EILVakV/YGMZu4q960CmEM7lXBjKcoVSmqos+PDDbzGZjBhmOZPRmNF4g/5ggJApRgj6/QFGl5SV4fz0GGMkk80dHj18l7zXZ7WsArixpC8yspYTLKGWSY5wTmO1NeH3WK6wbH05o9Ew1J2mfZLUKglCeIuzVMV9GMtQMRMsQO6UDm9T/uQBkpSWEU4531LjNIAyLHgO2wgPRKwA2nULCuDGaYd8MsUQNGna7jOx9iZNUwtGlGPUMgTTuQ1K9UKJcG2xcR517YQW596mnJlfJilatQFT4vxRQaLLgtFowHDUJ8msyq+qKoyCXtZD1ZqirOymklScX8y4deMmAsFqVUGeUCtNSM1mDCifUdv7rVt9klaGW7dutQSdljB5zbsJ2im6+lM6n+xu2IAe7+7RbOQ4jWmzE3eFjPW1hvOdVqylgXHHvYFfaxM0jQi3MfnzhddCWiYlr3v29Yb6THvRs5TokdbdWxyNIUtTMplwdnzCwatX9qm1AqNRjmnIJ4ZtFxH1WiRJxL0RAaiuQBZv4s1mJaOgR0d1rCFNLB28Hacy9Ges2TZuDAmBtd4SgVuwzxTd2xjLLKSNxrJj4e7htd7+Xblx41nyhOg+ZutZo18QwoE+l/zTSLCsUwJVK2pl3W5sklpt57xog/K2sLB+rNlTLltV/IZn1worLGldU6sKEFycHHH6+hV37t9z+a6wmnSrr7h+XnHFcdMAd0/G5UeHdlpF2RGynVRk36FojWSM0O05a19sc38nUDftsVcr4+4fHW9uJ6I6mnfqiQPCk3WARlhzLvWFf2Y3dkxs8cHNPbf2hkByh5mFwCBBGLRS7OzsY7BuIMvFisViSa0UubFxmg5N2mfy7XLkGwhBfzREGWsFCXtB3M+hzV5D314r1gq7ov3sAhmElY4I7PY6u3fpqP6WhVTa+dxc2wZvth7t+rK5r7zU8826Y7S9p98Xa1U765C9MswlN1B84LrWdSDE0I7IpCgKVqsVtdEorVksFlSVzeFX14rVakGaSsseKyV1VZGkKf1+j1RmGC3o5T3yXo8kSdicbDEYDi0BUZQn0YOaRCakqUQbvxeD0m13e6MhTknQ7EPGjUARgJzw/RIUOp4dDrLUunFJDEmahLUnzfx6btn9oEkM26z0nt7fKi6lA/l+DBII+tz66S2fTtmmagUmxWjNbDFzY1hjUBhH15ymMWvoNSVagC4J7DFQXiPMrwVJ3o3bGHb3dinKktlsRpampEJw+OoFZ9MFh0enTDa3uX33AdsbG4wHOZ89+ZjZ7Jw87zEeb7BYFcxm89B/Xq5K0wxDAjJha2+fGzdvs7O7C8Ywm8/58osvODs7I5MJGxs2hidNE0ajEb0sY1ZUvHj+nG988xvs3bzBbLFA1RWzxQUnh8fs7+6xtb3H0fE5rw+Oeeedd0jSnNF4QpKmbfINGpmzG4Na15apbrlY0uv3EcJSciupSJMEo1RgYb68Xrh9VbsYQmryNGNva4t79+4gjaaf5WR5Rq8/ZDAcsFiuOD09ZlWsEFKQ9wbcuXWHW7fvURbKUsIjAluil5Pz3ILLmDG6LJWL/cpJEklV1bT3U2nnmpOjbc44ESkZMjsGE8VqpVrPp7UOcUixgSJWEPnz13l1XFX+5AGS1zZ5dhwEjukJTNB2S7Rb0/xmEMcPeeuNlJLEmSi9v7YHV14rFiPaoM0SEXU4flJqaqVIAsuY3SC0sQtaJhMHQNouemVVh8lTOUtTludW0HYB9CjNeNRnOOpjhKN9BktxnPVIpKBXKxaLBcWq4vWL19zYvkEmMwZZQlnXKOEXUe3xh+urtkbSuwn4QRprhdv0tWuKA0hx3fav21oMYROxp/vPbuPp7OLe4mbPiAEUrYW5AxWiv223gfh3O3ZMkNFEs700fSEERthEm9oJvp71yNfr81UYYhdG28HSgHL9oLSil2ZkMuGLjz9BlxVZmlg/+2hBaPrD1dvdjwLQ6W5IJozd7vltlzr/t46sRBKfRFgIm2vIu2uF54y1lwiEtKCk8fFvAKHNAeUVEM7/X2jLdiWMAyrud6ODJje8Sf+MOBcbITAmCcfbi6QmJNMNo8GB3aiPrHeoQJAghUSZKlwfW6vaY2hdaYBRvC74dcW2TwESbWqMsZowWRU8/eRjHj28jzFYwGasq5mO5tVli5aDHJGA4e9vA8xj9153XEgQdq2riUVrJ5QFkNF9WmHXF39X3SgxPJnHup4xRmCcsslSCTfHJCLKI9duS0A2dBgsvdgZaV8v3c9rwjwAFM46Eik2TCNF2nVP23gSZQSm1uzu3UQmKUppVksraFW1plIGvy00414EgAh2/d7Y3GJ6fk7tFS1dUGTa7twuU97lDd27tgmcvqWZC9KzMUoPloy1agnHguZydllttH//OOWbnQtaWzc2IZq4qY6zmpvDDjAoha4tURFuXNdKOVdgQ1VXzGYzcOculku7diGoa8NsNkdK6dzJbAxMnufkaRbc0yzTWEaSpiRJTprnpFnG7n5jrUlkQppJ0lSH+euBCcZYIGMaD5FYAL00RvGKK/tNAkbVdn0XOGWKBiQkIihQbB96OlEPgi/vK94iAw19tzGQ59aVLElACN1qXxjC7m0bra284Oeco0VfLi6oyiWqsu5/QoLRKgB1IRplgBBgVIWqavJ0yGK1ZDo9s+uTURjj3bmVk5EaYNctjfW5GS3+txCzuja7Y6fvu4K9EIhEkgrJaDRiuVhQrAqGwxFJmiPTPoYlaZIwGvRYLebcvHOf1WrO0fFLaqXY2NgkzYao2QpVlQx6PYYDJ7cgSLOM/mDEN771LR5/8HWQSWCx62/tcO/x+5ydnfHRz3/BYnpGWRaslgv6eUYqc/IkZ3p2xvl0ymRnl97hMcVyTl4VzKdTqtqwsblLkj7j8PicR++m9IcTVssFw+GQuXPl63pCXN5r7BxarlakeS8ogPzeidF2DY36r6UIEQqjIZWSNMkZ9fqM8j45Vt4sa8ViVcD5rIkLFILBaMKjx+9x585djDGcnZ2xWCyZTDZYLlZIaV07PYtqVZXWFRRLNpYkjRXVWnB9AlgdzrN5j3wORZs70RLiLMmyjNevD9jf32OyOWJ7ezvsoavVKuyvfqz5forl1G5IzduUP32A1In1saURGmIEG098L/DHnWlBij3B0/LGAzhG+35wSSmt9cZtgN4MGAelxkKM35DOz89ZzBfs7e6GiSKlZLVaBaIHf2/v226DPjWDfEhdK7a2Np3/pmG1KkDYwTocDVkVFaNREkyVp+fn3Llx29FFS6ixm0ok5Hb71DUeLwb8U8zv8QAWSXsRjUFnDMR8n8V1+HJZw0/rWLe86VzhkVH4nbWTzZ8mRaNta52zFsDghHMrZFTOJSRJErTSfPzHj612yAnGypmP6/qqmIav/h66bg3+cxyP0yViEEK0qOvjdsTzwRdv9o4XM601GIMLQ2j1lcU9DXX15QUuAkk0goIxAqOb35PEal0bYaUN8OO+68b0+c/2e9y2WCv19jEwMUGDr9v3S0wugTF8+cUX/AvfRu0E3US05uLbl8vz5fIposWo5Iu+8hrTGc9t1+Grb+Pfhf/eBl/+uDFBNXH5ztc8R3ysUbJcfv7u/O1aj0OrnFJjZ3eHPO+h6oqyKplOp6yWK4bjjYg0oL1mxu95a2uH589fUdV2H7BC7uV4jvi2sab7UhyeEWjl3UWtkkUrA0IitXRWOhmAglY+ebIdQVo7UOMAU1nWCJR1Pysr6trmJqnrKqTG0NoKP/P5POxnda2oy4osycjyzArxxpD3cvr9AUlqQf1gMCTr99gdb5BluXNBEy6+xrYzTa1IIoUIcVFBcPTvRAhMZx41RAoghWpeogcQAmQqMMGFB5IUjJGX9nl73Nt6PCrxLmZeAREaF25kPzXJq42pw/j11Yf3Hd/MrUEWtFhgrmnee6xB6FKRa68saskORwz6KRgbI5cI7/rk1i270Lr9XVCsVpRlhQBevHjO+elpcH9UkSLH94sfm2+zCsVCf3gnb1Ha1lMrpMd5dIzRluI57/GN7/2IsqoZjibcvHmb5y9eMRkPODx4ycV0SpalDIcDlKqZz+YIIJEpaWbd6GSW0+sP+Na3P+TBo3dQBqpakcrMJV83rBYFo8GIH//lX/Lz//i3KF1yenLMcrlkY5yTpClqueT169d8/Rv71p2usu6a5aqkLArGk016/T5nZ2dUVc1gMOBies5kY8J8Nlu7h6z7zRiDqlWgrjbG5cDC5wTya6c/n/BFCEMibT4hKQW9PGc+X3B2dm7X/ySlqmq0VvT7A+7cuc/Dhw+5fe8+aZ6HvXt3dzfIZEbD8fEJL1++dFYfqzyxLLuSwWCIUnVLpvayhY/j8vu2/WtJJJJEOrc7O/5u3brJZHODPE9CjsDpdGoV/UURWPo8c60xJsSKlmVpGfGk5Oj4+O0GIf8pAKQIiDST1Wl+aDbJxvrRmKahjb6FECh/zFgVp3KamTTLqau6AQzG2TBq60bn/Y09aUTjP+k3h0ZYMsZSIs7mM8YbYytMGlgWKxejYCgq+8Ixwmo6sUu0xrAqSzCC7d1dbty+xR8++YSiLMM62+v1SZI0PF+eJ8xmc1ZbpXWvcFpsgwG1BgTEmgkDyi3anpUoLl3h/SrB5pLWaM39/HuI31tXS9J+z5cF16vA0VfRKnTrWveMXri5SjhrC4ix9plgvcyyjFrVvHzxMhIAJEWxarvF/BOAadOGy3X4BXCdb3MMWONn6/ZlEGKMZWvzx2LBT665xtflkw7HbVzfn9G1xsdO2POCq2r0jF2hMwY8MTD0dXrhzWrF18UnNWPhqv6M64rv59eC+J1qrTk8OmI+n5OPhs69xwo2/9j3fdWc8GAkbl/3umtqddfZehqQ5K+5vH40GvP1a0sbfF79LNAA7ESs97/38uWVY+XK7wafnNTOTRiNRty4sc/L58+p65rz6ZTZfMZke5s8bdbT+L3G40kmGQ8ePOKjjz7ma1/7GmmaBF27d/1r3oMfnw0AFyIJbbPCsXUPAhGCtK1QYq1A8/kynLtyQrDfh4pi6QB5w9CaZZmLt0kDQ1S/33cUwZvBiuOf07uk+fftc+N5+duf11g8nQCkjQ2GB6C2ydm9e7oDEMYvir5PXSJPIZ2FxSc2dtVKCcooa/GM9CceHNopqhFCWasStk6f/8cQu2c312NiDwf7T+vaH7TvSUereQvA+vOa8dUGXu53HSkhjBsRyiWrNSaq02B0RFHs9hnTDHKUMrx4/iV7e/usVhcuhskALiGwEGilLMjUGq1hOr1AayiWS/7h7/+esliRphlVpalr1VL2rosZbD2fs5xe+t29z+ut37SOhZQpwjr7+8Sj1mLgvvf6bNy4zd7uPlJI5hdT8jwlSwTz6RlFsWQ8HCCM5vz8DFVV9ro0Jc1c/qMs59HDd3n08F0QLuZLSDTaxauDkSa4eX7v+9/nb3/6P3B+fkpRlgy1Js1Skirh7MxalzY3Nzk6fE2apBTGuultbu8wGo04ODhgNpvR6/WsZXky4eXLF1f2q++P1n7hCDWsnJBTmYI0yxiPx44h0VC7vcqvId6xQGBIpGBvb4cPv/sdtnd3GA6HpFmf0XCD8XjMZHNimeUE9Ht95vMFysXrKaU4Pj7GGEtesbu7y2Qy5sbN7zCfzzk6OqQsSwbDIVma0+v1OD09wxjDcrlAKcVgMHBhJnaO5HnP5nuUwpEVSWSSkKSCjfEGQ7cH2uevw/q0v7+PMZbafjabMZvNGI/HAIFEp9fruXgmGx/4nxPFdorf+BpqUasR8sGPbXe6tiY7FmBkkqCieAnpgImUklorSG1cUVmUYYIrpUiFpC7tAqWUCgjXmgDBaEXey1HKLkhZZoWxnb09aqORVgFGbTSJcZtFYoGSVrVb7KwWUrnfkiQlkYL7Dx7w6J132NzZZmNzE60sRfjuzp61ChhNltrkuBeLBZubE1RVkyaJW0gtCIwJlLqWkZixrM280lxzFQhZJ4zFjHnxOW3rwtUCaFe4+qoAaJ0gfZUwd9UzeKHskvDtBKIYRnpA5ePboLFsTKfToL0FXFJR1WrTeqH3q5fYuuHHKhAWI+1c4aRowFE8T7qbpzHOkmo09pBujRl/T/QVwrDvNyfkxeOuC3jidts4J+FoehsXsMbtI6b6bd87do31feCBmo0VSFsMg5eb3B1rjStj1wLg+ztWmHgtcCpSZrMZx8fH3BmPbLuU679/xLvuXtEeL+tcML96rf45m+/r32vbbaiZ45csJJ16rgPjXV/9drk8Lq+qO342IUQA78oYUiG4ffsOz588cQH/NgD75u3bBOF/zVoRxnyasrmzgxaC3//xY/b39ywtrTbg4gmLogy+/FppVk4Z4tfYsiijbhfgiAm8a4oF8lbp5mlt/VyxcTY2T4kQBJcWiP31CX3bvK+2hSvI8pElxLs0B9fjaA4l3TmW+dw84Q5IYYV4UjdPbeIhJ9c5QgIhgrXNXm6sy5u0gDBx8Y0BghjrshmuEQajoySodvO2BBBeYUNbwaaVcu2x7fVuwkL4cZM4lj7rNo9onK89+VLcn16Z4t0T7V6ng4LBaBcHGI1NHQhDbPtjcge/RillAfZyueSLLz7j1q19Dg9eoY22LLPa5uzy1OJ1ZWOQy7KiKCqSJOXg9SG//OUvXDsURpigELo09zqzJfQZxsXvtX/3n7tAa91c9MCoGX8aIywgAlitVm4sS7IsJ8l6iCRFYKjrin4/RwrFfDZFaIXRirPTE+YXFxitSRM7PrLUWhQmkw3ee//90Og0TazrlxAY6fYeIUALRJKQJYJH7zzixcun1jpUVeSZTVzqY+RGozFpkjBfrdDa0rQLIRgMBiGvks/Naa1bKnhjxGtSvJa0lC0OyCWJTQNiMNy5c4f/7X/z33B6csLBwQHPnz/n6OiIw8NDy7BY19Zt3Sh2dnf4X/1v/td8+OG3+Ozzz0jTlL2dmyRpHt5RlqbUbp1blCsQBJCxtbXVek9FWaCNJk0T7ty5Q+EZH2vL9jgc9tHaMBj08CkNPICxIL6i18sdAUpGmrXZHhsPC6+YMGEsGGOJU3Z2dsJ5WjfJkuMEwEopsvTtYc9/EgCpYYmJE2mJloDii5QiAi/tjdhP1CDQSOvbXKsajCSRmbvW+3zbWBOt7Ebi3ZSSJKEsS/I8pyhqMMJqtgCMoCwshbNNdyFCzgQAk1rzqtaavNezi6wTmm1CO4M0KdrULKuCGzdvcv/+fd57/z3GG2NrftXQ7w8QQjQZozFM5xf0Bj3yNEPVNamUKGMwUl5D4noZUMDVmuh1IOc6YXPd37hcd+06oLOunuu01euOXVVPc7z9bDF4JIrN9puxm/LNd2PIsxSZSJ4+fYpSNVK0KePthL/MLNQVUN+mxNfEwMWPeT/2pJQkMsVrsq8DoX7+GC+I0IDF+H1agb/pk8ttajYFf89142Y9wGqEJSH8fcS1YzR+V80GpZ0LlQ5zON7AbRVtsBhbD7wL1DoLTnecBDdCbGzWy5cvuffOwxB2YoxpxQS9jdLB90V8LAaB6657O8B9eX77302j1I6O+0/r51P3c/zbVUoAq5n+qsDucpsvrVV+XDqNuJQSVVXcv3+ff/j7vwsuLufTcxaLJXl/GFlF2nX7Oa5MjTKanb0tNrcnXFxMOTk7QamaxAgyz4DmCAPyUc5uthfGWiyQ+HhLLXEa9mZNssI1eHY348ZrzPKEs5jYR2zmWhBAmqcgSeP0FaYZS9H7T0T0so0hdIXwSp/GSil0pHSiurSGGfccRtl4CimsFUqbhohAmYb63igRQKVVQkXrkPEKPacscVad9pjyNh37Vzv6b6Nt/phESMfYatyebiygE9bTwytVtbaWr2Yuq0tjW5vGYh7HIsb/6qoKiec9q23l2Ph0VYZcSsY0LkQGmC9WnJ6e0ssyPv3jJ60xqI2iruzaVZQFp6enFKvCJQu18aynp+eUlc3HhgNmHlB5pdR1FqQwYkT3u5sHnT1g3by/av8SQgTrZe2USFImYDSpqMkTgzAaVRcM+zlaVZTFEiEMAktdXqxWYBSrhWGwsYFB0eul7O5tMxz2XFqSxI0tHLGIt2gk6FRQVyVplnHn3l36gwHL5YqiLEhT6zJaqtrF5mySphkHRwdMRkMW87nNdefc1GazGfv7+w4UpW/Vr75PhBCB4h3g4aOHvHjxnLIo2N7e5v69O0hhiT6EEJRFyfRiahOpzucIYxiNR7z7+DHDjTHf/d73+Pjjj/nk80+5ffMOm1ubNjF2mpEDWZayKlYorUI+odVqRVVVTq6uKctVeE+j0cjRog8QDsjF+008jrpsuH7egEGpCqWqcI0HOd4tr6oqzs/P6ff7AWzG1PheqesBk7d4+5CUtyl/8gCpEVJEcBkYDAacnU2pyiokSPS+z/ZFNgtoHPeitUakVr9TqxpTR9pfJUiSxrqUJilF6V6EsBtGWZbBdxIcglZ2Qa7r2mmDnHYvTTHSBrgqpayFSApUVbkXbjex2mVCNsZYljEk2jimM21ItOLBO4/Yu7FPrTUSHcgdFotFoPQs64rK1BwcHnL75i0XKJpY7b78x2iXWbsQfpVr/ynlTeDrH1tnIwT/oxT57f4IQgIg2tYvL8x88cUXwZIChCzqPsHpP6Wb4rnhv3vh3y9Kfnw37V9vJXGP03qGK337hQiyWCygXQc812liY3eOWPC3i6Fvq8/X4vW6DUV58/z+Hu12ggeKAsvm1AhVXitl/7maIzDctBOMuZyFviv0++sa9z0blPXs2TN+5Cw8XpseKWi/wjxZD4ZsAH5bJL6q+Ods1xqxWvk2Gq/5J/z179w9ZbuOCDiuU6A0979qfFw3D7wAfMXRK+59qRi74d66ddO6xrjNejFfsFwuGNebZLJxP1t/L4OQhlrZfWBjMmKyObZWZSWQwYWuaZuvy+Y/a0B35tJAIBRQuxhFPwatNUGK1BIKJH6SWGuIkLFrqe+j6EFb79i6kYElfmgOmeAWJsACCN2QCrQUGjpGyyIAM4EJ7mp+jAgRHTfeQtVE9nhdijQqtEVIgTQaoS2Dn9aNAGSModmVDUY1AKmrrfel6+qqQ+4YjSmUJVNx1h6f8sACm9rmmHIuUMbYtBtFWQSrs6oVVV2BwSlWbT/WVR3ox41SgURBOWDm2yp9zxlrVSsKC5AOj4548eo177zzDjs7Oyzmi6BB9yRURkvmF3OePH3K8+fPnXXcgr5EJiAkCTahrRbCpYxqWzAay/1160VbERb96nJQtpUSXUX0JblBNPc2xlr1jFNCSmGgXKCKC7I0Q6iKtJejtaIsCxJplQplscIYhVY1y0WFwliPnFSwu7uNMTXDwQBlDFWl0EIgtbUIFaslF2XJ+fkZvXxgGd+kpVM/OTm17zxq53w+w7K+pmBw71W19o2iKILFyNPBX6eo7faXVhrhrFsHBwfUVc1kvEmxWtHLE9JEoWpDmmVkmWRvd9PKnkVFVVYMR0OWywUiTcj7fd7/+td4+Kjk5YsXLFczsnxCpZxiJRP0RO5o6K1b3ObmZgR0rOXIWrCb2GI7t+UlK5CPo49/89aixojgE8FaYiG/rmVZ6mRk2xd7e3uh72JA5FMqxLKUMYblcsn5+fk1Y7dd/uQBUlkbksoSL+9s7zDZ2EBVNWqgOS1OQYERAq2dtcdYWkvjGKPq2pqmy6JEI0hU2liXIkmlrhVQkbgFpKxqBJY5qDYagaaoKjLvI208+LFaKKUUaZLa5U8IqEuQGiGj+KfSAisLmKAsFF5daM3lmkQmGGHZ9qpKUSnF/o09sjyhKFaQ9SmqiuWqClSfVVXaBV0ZlvWSw4NDNjc2kJkNohXKuSoERWOk+fGauXCoEUS9NjO+pNk47VlAoEz3G4Ho+KzHCQllKxi6ec/XARZjohcVfffCc1foD/iFtgAshGjEh+heLXHCNI4n64Q974qCaZjEgvDghOkE6CWSBM3LF08R2PEohB0zBrv4CBHfY/3De/cN32/xoO1aUnwfKKXxlNBCCBKZOS26ZcFqhHho8mdYLbF3AxNS2s1XRAK9G2+iGw+EvV14/wGwOOHMrNHw0wVuTuA3gkApFveM/26MY4tzi6eLAWysTc34iq1Ill3SudTYme3Gj9V2xVbnLvCMx8KbhIuwSRoNWnD8+jU4n3ifB9S+93YclHu0dh+1AFFbAGm7uMQCahiKbmzKprWXmi7CWG8ftnX6777/o1ncVORviLW0CXE5hjE8JzSg2ESgTvjG0qrTYIenXPMeogubut38JprDQggr4EvACMZb25b+9uKC2fkZi/mU5WLu5mOGEElw7ez2hRS+zwAXPO8tYEL69yvCAhMESbdeSAz49U9bpVsiXO1a2XoQYc4LU9l1288f03SVcK7iQorWq7AtbgRiy43llRFWSPH7jfBKGm89dYDGfm7WdEuaELGxBqQlENLHXkVrb/RavXLDK5Ka+ziFSJgvDaBB6LCWNvNRgtFoVQUlCjSJa70SUmuNcvlYvOeGUhqlNEWxoihXgKXk19qg6hqjPGlOHdpQVRUiSagjZYxfU6xrvwhWvVjZorVG1yq4S/r4LIG1oqVJGpRWRalZLOZ88smnnJ9P2dvdI88yjg+PSLOUyWSCFAKZCKqqoqoqirJACkHirWrarvU+L01ZV0jp9mThxwCh78M+cXkxiI5H34n2mbDGdtfD9toUZmf4zeWsM9aVstnrDdPTE37761/Q7w/40V/8mCTr46nshZQkie1jZTTK1aWMplKKtKq5mF7YuSXsOy1LS75SVSXn59PAvlZVNaquGE42SYVA5D0G/aGVHx0zqm97XSvSNKPfH7K9tYOqCxtPJqySRUirYE/ShDTLLLOflBjHLBmen7YCra1Q06i6wiQJq6KkqisePLjPvQd3qMoVdbWycYd1zXg8Rib2XmmakQ+0fZ6qQq5WJGlKmloii3v37jGbzRgMBmEM+nEppCRxY9a3xc4jm9jVKnDs2F2tVhSFJWkYjUatHHDe7df2WRrcCwGyLMEYycXFOcVqxebWlpWpHZjCQJr2ABsbZcebI4RIRLCmV2Xp4uhK50a6Cuvg9HzK25Y/eYBkTXyKu7duM+wNyERCkgi2RmM2hiMqpbhYLJjOFtRaOfFVWVYXIQL7hjEGREJRN36TPnDaLogWhOnEd6n1KfcTQnmOeCNQlfUBBqhqTe0AUp5C6oQXrSwlY5r6wQh+Q7eLsXWp8656VtA3VKYGx/olEdRFjT5VbE4mVHWJQbAoSvr5EK1rlLZ7mdGQpjlVWfDi2XPE3TuMBn16vRwvk4TNj87CSbPYxVofLxTZ/avtbmTTd693SRFRzEAX+JgInbS1n37xiHbY9SMi9GcAQmsEcP+7CVaKBhwFSBIBO98nLfFrjVbaYDCRhdLDJtc0jFakQpBgUMWKs5MDtLEMQ9rlPxLCaqV8PhJa/WXad2uBPv/dv692ngD/2Sot7dj2Obnsf5K474XwcM9nd/f+9JYWVwiC9bH1qsIzOwDsBAeZOpKPIFlbJqtLmwOWtSdNUje2vCDUxMMZX4+7lRDN18BEhQHhtL0aR23cDrYPljTjhG43/oz2mmbhcpw1Se68IOTraZ63NVwuAdTgXuffmao5PTpidTFjuDGx7q4Y7Oi4PMbtO0ku/Q6NYLLOKqg98JKNwB7aZ9pg8woc3mqDHchhpFw6pzVGndDUPE8H3PqFB6zbm6+DRkgGbFB/OGYvDE2JFCwirtBe2L6X8YIcbuzb+DlLmiDojUaMxiNmp4ccHpzR62U8fu9dqnJJr2dpqI0QQbli41eMG4MGiRPwXEuFX3uEwqZjEBZJWf9ql2vNgR9XVRhR2o7fqCvtPT3oVdEocQBJY5DGIExD++yvFdFngwHHZGYFpK7/v7dmNO/DeOWC1uC0uVopFDXCsbJprRxAIkxKa42zzJ1hbBjbN8pRAFvLkPW00Eq5YzrMu/if1oq6Vi4GwoIcA1YhqGpngbAuOrWyRA2rorDX13UAUAbHNmusS5+34HlrUJqmmFrRAHzbc6kTOLVDo3meI4QI8RvG5MG6E7sbeQuDJcnwWvEUrRvAVNcVSSJZrQoWixXbuzucTS+YXlywu7dDlqUMBv1gnRgM+gxHI6YXFyyXoKY1o40hG5tjDg+PbEwaCYgEpW2snQlxz37NM80YiWbPVbuscO/PuM07KJtYD5C6iqRLVj0DRguqSrmcU03C9IODV8zPT5menvKLn/2MP/vzH9v3rg1JavsuSRJGozEX+sK+W5dOASNI05y6tO8zkQnz2Yy6KlnO5qRCMB6NGI9HpC5Oe9Dro2tF5qi9BcLtG4S5YULqgoStrV2K5YzKGGqlqHXtF2o7twQgEyxJu3b7pgkkiessm9ZyJkilsFZWY3fmP378B16+esbtWzfROiNJndIOiTaCs/MLer0eo/GYyfawFfOklbXI9vsDBoNhUPg1sYlNjFmzt/rUANZC2ZwrkDKlrpckCcFClGVZ+AxYS532JGrWXTRNM9IkYXNjk5NKcfj6kK2tLfr9PsdHxwyHI9JUM51O2dzcZLWyrn2DgXXnOz46ZLFYUNc1WZYFqnb8XNaak5OTK0bu5fInD5Ay4PHDh+zv7XFydIyqLNLPEonQGikz8q0tLi5mXJyf0hsOMAjKygk8kYSeZhIjJGAtS8K5zUEjDHjaTW/10di9TxmfDNLmiChW9jqZJC5TNfa3LAOX60VKqFQFQgTttFbKavIRqLq0+SaqFTJxdOLGoIUNaEyThKooKUVJVdW8+867nJ1fsFoukKTOlxcQ0goFRrBcrvjlr39tg/DcgE/ShHVCeNc0vk6QxTTnxcxlyNi6dB2gaRcv3PnFokssEAuY19XxVe7pS+wH262vcwcaICbWntt1L/DF+8oKYZPRrVarhsigkxy4qQs35i5rnOK+v6od/l8Tf2Q3pJiprnu+yzDmNEdWQxwLrPF97MLa5DqybREtIOQT425MJozHYzY2Nlym8qwBbkqzXC2ZzWYsFgum5zPLruOYFmUiULoOAkfchga4R9aCqG/8mJRc7W5lA9pFGAPBHZE2uUO3j325bF1qb36+TmNcnAJ2fTk+PmE02bRClwObIaGr6PT6NfcXiNZ8Ce8nuq4ruDhc/ZWLFIRN3t28eVY/cOJivIa9A2CaEyxIjZ6lOYI3ZIZbCQhkHQ2t2aUq2430Q9KPBZ8Y1zGraTfGd3d3eP30S4aDPtPpGcvFjGq1QPV7ZIldKwUK6XJ+oT1RiM0rFyuMCP8aJVgAmQJ8LqM13ejeW8PIFCs/MLr9bJoA2rQxiGgt7lo3vcVerznHHxeiTd7giR8srnKA38XGJhhHFGAakhlnZascIPEB27UDKZ5IwAOZqqzCvqqNcvExVWvexP3g69KqiX+qqtIJoN5i4tYvB3jKqsIDHOvyY2N5tQNDvZ5NfDkcWma/fr9PKi0Rk3QACEGgEzYI0iwlz3t+sIX2SZlG/W7bErsKZVkW9nPLOGvp1ZNEMhwO6PcrRiMrR2xtbXHr1m22t7cBgvuWt1YtFjbXzqtXr1itVlHemDgeqL2vX46zbK8r2meaXlOMWzSusn5cVbpAKf4upQyxIz6ORynFcDji0BiMkIw3NkizlLJcIRNBr5cH0OzJEYqiIMsy+r0+o9GY4WjI4eEhDx4+RAC72zu27r2afr/vrHc27kkI4eKzLfieTqdBgWbbY8dgmiZu/lgF98oYF7vrgZN9Bps3KLXW37co8VxUWpFoD6xtf9WqJs9ytra2vIMK0MT5jMdjOzYT374mDY19DoBGDvB/7TERQjuSRHbepUQGnYftj9FoxGAwCFbV1aph3q1cmIh1PbTz38bjF0ynrxkMBgz7A4qi5OXLV8znC7a2tlBKc3x8zGKxCvWtVisWi0W4R6+XsVwugxJjuVwymUwoy5LDw0NOTk6CVfdtyp88QNrZmiC04uzkGIE1n+d5D1VZjZXWGpllDEdDTs5OWRUlWqQIkaK8AO4Wc11b/3Gv8dTa8qv7pHraNIw6fqETWEtPwzhjwY+PNTJU+BgFoa0QIJyGvCwra0Y1liXEDy6wbnmeGcUPhhD0iWY4HLAx3iBNElKZ8Mfff8ytG7cYDga8nh6hlCTLcyt0uM0uwXB6PgUhOTs/J+/ZZHxGSJKkLcyHTbOzqMWlaz6PfzNrzr8KtKy9b6fedefF97uujVfVEf8WW1quukdzr0bIu+qZuptB/DeRNij48PCwJXTrsHG1BesGIF0WEnxi0zg2wPulN9c37bebYhNM2dXwNX3m0Y23GmnntnHVszqXDftDONYfDNja2uLevXvs7+8zGo0cBWtGv98jSa3AaOP+FHVd2bwrdU1VahaLJSfHxzx/8YLXr15RlGUAEXG5NP46gF7KxnIRv+erxosH50liaWAz2YCKlnWmA0zjjX+thdGDr9SCSGMMrw9e8+jxY/s+o5iE8G4iZBA+dt6bZR9saPjbAfteWxw9r9MQtiq9VK7RJRsfLRVqDyXGQFYw04172eU311wn18+rcGnHomG9ujpjIe5vYWi79NkxbRwNl3RuWUJoal2RSuuGs7ExIutldiMfj1kuLiiWM8x4gDCZS/6tbM4aryEV4WEta5p/h16zLnV4hmYaGZenKOm00T+HwZiq6SNXv/F/I8GrGe/2PO3iYDwZgYnO83V464m3BBmDczezQo/NleQIhHzca3BLUyGzPcYEsON/h0YpAA3NtY3faZ6hViq0JxYOSew7blj5vHeCdTMXkQtbXVsLfC4zRkMnJArBYDhsetXto1JK55HRuOBJYROJesVc5j7bMdm2/vh1QQjBYrGweaASSVXVjkLduiNJkeIT1ceEOHaOGxKZITLbdlUrVquCqi7BebcURUlZ1sxnS5bLghs3bvLq1QFGG87Pz0OAfJK8pKxKKqU4PT11Cl1vBWuvVbHirzW/rgEu60ps3Y3XIW8piHMEtq6L1rUuSyk0jGUe7JRlye7uLj/8i79kMBjx4OFDNIKL2SlCwGRjHMCqBzteAdnv9UkTSSKEy2c0p9/PGY4t+5zx78K9m56zAnodxPn5OUdHR633h3v3PuFxUFhryxRs3bMlAslwMEJg8xxKceUCe+ldeKVl8ARwBBveJfTo+Ihbt28ikU1OMdfX/X7fXtfZ15v6/L+Gdt+/Q+8tYYmKvDuh25uFDPO61+sF4pDlchlZi6oAZsqytAqJsuD8fOpyJ1lgX5Yli/mcXt6jqiqOjo4wxrC7u8PFhU02/fDhQwaDAf/u3/07R6CRhvrSNAnrS5radAUnJyeMRiPyPA+Wpbctf/IAye5RBiNttvCy1mgqtNLUtSbJUqpak/eHiDRnvlgi8wS7+ST4NaOqDPVyaScxbsPBBldaoc9uZNp42kKFFLV1w3KDN89zyqJw7CgWiVt6V0WWpWilmFcLSjdQajfQBCCdyd0z2lSVNX+OhqOWJgpn9lwuCopFSZ6mSCG4yC/47W9+x7vvPaYoCo5Ppow3tpBZ4oI0JZlQvDo4ZDgacz69YDgc0u/3nS/vZeYysFqSqxJJep/RWCD0wYrrrogF1qvA05tAVRMfc1mQWlfHVfWuqz9mNvTHrmvrm0q8SPm6lFKQ2cX44ODAbqbORdO7CnmhJBYaOq12da5/Vunig3zeEm/98AKMEEkAO/Hm3d60vMp+PQj2G1F4tsS5WriEt9vb27z3+D329/fpDwZMNjYYDAeBHrVWNapWKF3i4wGHaZOfRcoErWE+n7O4e5vH7z/m4uKCVy9f8emnn3J8dGwFv+gdGWNIhAgyZtcydhWojZ+ra22z9bfra1xA1pe3GeMhNs4YDg8OwvlCiHZcjY6UFA7PrLdiNaCu2w5EBGAEIeahUWZ0BaTL/WXCePD3NbRyA3Q2+eYl2PiuqJWtazo91NTRrbrTl1YZ6oP9I8VBp/4uYYQVdNzzafe8GPJUYIwCU5OmgtF4RJJIRqMB6JrF7IxqY4DJU5KshxQGhUILRW08Q2kzZbybKMbGsth3agELysbRSAmmNkC61jqstQJRB8HTx//596G1CkKa3TtUELjrum7ypCjtLDL2uK9HKUVRFkH4UbUDSc5NTkhhr6kq0LUDk1aIjON8MAShysSuO9IKeFLKEKgez2+ZJIHCOM8ayt+yqkh6lgbYUx5Ld8zW7TX1dkLUdU2vl9t1zbvAGytAFWWBVj5Q3DJ/eRdA22+6BcL8SLX9ap9vNBoBVslYVqUjVrD511Yr2//L5cIG1gthcxJqe77NT1VQ14qisLmqrABpY5p8/ERZ2jgTG+smSdMMoyPLjwGJtWJorTg+Fs08FTZ/o9YehHlXYG/ANJf2tnVKTfuM+tJ5Yd68RYld7GKFUrfOSwpEYQVoa8EbBkBbK8X+zh43b95kMBoFIKnrks3NDfLcWpG8R8KTJ08oigKMdbes6xJZCj75+A/84M/+DOFSqBggS20eQhun6uUrULXis88+Y+byAnn3R58CZjwe41O22PGnGGZ5GBNSJuR5j9WqQGmDpkmG2sKEplmvusDU5/L08mYmM9555x3ee/wew+GA1aJgsbBEHZ7hTQhBkjZJ3r284fs/Te3zedmidmReNrGtBR1Z5l3l/NgsXHyek1kd2dhwOOTk5ISqqkiShKIomM1mzOfzyBXWWoQSmTC9uGA2u2AxX4CA0WDkANWcsqzIspSbN2/y/vvv8+WXX4acRz6VgXWjHNLv95hMJhhjgoLGGMPx8TFVVZFlGaenp281VuE/BYAkMi5mS0RSkKQJtdZU8xV2ORHoQjFbLPjy6VMqx32fGGtdUsoyzlhtgsHmZmi0XgEIuYBG7Yaz1pWl25bSmnxXK4yqKZ1PdOLyICVJEupczJfUVWXZiRwJg0CQiMS5JdjFNUtzEpHRy9yCXNQURRHcArTRGGHjoWqtKRYrMIZUJvzuN79lsjnBGMnLFy/pDS/IBwOyfk6aSgZJyqtXB+zubPP68Ig87zEcjhiNLICyiTIb16JgpYi7+wrtUmPRcJaOSFC9qnSF+zctwusW1qtA13VasK8KeNbV5S9ZZ8G6SiPnAWWS2A3/+PgYaDYvL1iUTmgJAnXE0ySEaPT13sgTH+sIz7FGKmh0jQ7MV3H/hTbiA8ENNgaicyNoCeLhfolkc2uTb33rW9y6dYt+v8/Ozg69Xo/lcsl0OuXw6MhRz6qQmNW6i6YIKcIxu6Cn7O3tsru3Q5qmLBYLtrY3efDwPscHJ/zud7/j9cFr16eNW4Gn6r9urF5XYhBksIHa61z7rrrWj8XYEujvW1WV0/wZpLSZ7L0WzcYmNvTGHaMJxj/TmmeLAc+lv8GtyxbZ7ZcIfzWvuUE1PoKoPb8cSGIdUFehUuvTHsfKXOP+EGMbTDPHuGIpcQ02Zn2dojtsRbAhucfz1kvr8lhrhVIF/V7O7du3ubg4J8+sl8B8espRYpBGsTGaWMHPzRERXOyEjeuR0sbPRK5sXjMNToGnK0cY5Al4GsuMdiQC1oJTOqG3sRh7cFLXFVXtrDhYlzeb+87e1yurgju4Nvi4WiaXlQABAABJREFURjvHbL3KMaUinHXbrQc+z58FKQKZWGVckiZWYE9s7rA0s+7eSZRM14+xLGkLbNbrwlE5ZzbYW4DVMgtBXdVs93KUatyrLy4uyEXKYDiyHh3BcmT7a75akmc9+sMhSZI1a5qUpFqghEKbiqosQQiMW2e01k4AVBTLVRAClVLMF3PLJurGfuV+L4oC5UBnWVQY3cQ+xDGGHtT6gerfHzQafRs4PwxCpdYKgyMUUFiLRIgR9XuO1+w3ZEgW1EYWREeSItwCcp2S8BJQce3TpokbXAekfImfaZ0nQve6q5Q7vq7lcmkpqLMsAKRlUVDWNUMnb6VpQlEsmUw2GI1GTKdT5vM5u7u77Ozs8Pr1a+tuaXx8oebp0yfs7GzbnJGb287iI+hleXhGIWys2ueff85HH31E5ZLOernIkzMMBgOKomCxXHB6dIhAMxwMARFcwkejDUsRvioQ1G6/83Mr7qX1ylzpYrnrqg572+Zkk+2d7cCAuFwuubi4AAiJUpXrQ+++P51OGQwG3Lx5k8ViiTEwm80oyzK4yc1mM5cwWPPq1avwTr3FyNefpqkFn+Dc5aacnZ1R1zWz2YylMzD4ZL+CJLj3ZVlGmuSkac3p6SlG4cBWQlkuqGvFalXy61//ltVqwWQywVN+B1dIIcgy6566sbERjk+nlmxjNpuRpja/4NuWP3mApI2NGSqWJVpUFJWNx8nSPmVdc35xwcuDA4qqJst7Vp+4qh2tqrJsH4G1zoKk2JwKdnAooylr6/fcJOyTqNJdX1fWBJil6LqidoKQUYrRaMhoNOLifEpdlvZ3bTBIEhSVqVBaoWvLcOM1WdK5LfVzm3xLGIE0wlJ0GhuzopWiKkpWxlAUK/7Nv/k33Lx9l15/wrw4o1/VDNSQLJXUwMHhAVJC5rT14/HIugZ0zLJ+M46F46sWwHgB9YJ4G1a1r/HCVhdMIERLU2zln/YC0rUgtT67602kmRZc3gQa4LEemL1Ja7YOFMXuW63fXQlWHOc2kkjJ2dkZ1j1TBY1OsDIRMQJe5QNl2vfrmudjAOn7OnPWK39t15XECk32r3EB7OGYY5zy3/2iJaUk7/f4+je/wbvvvstkc8L29jaqVpycnnB0eMRoNAqJi6WQrIoVorSbf62g1xP0+30mm2N6vR5CgFIVh0eHfPHll+S9nAcPHnD3/j1WyxUbowk3b97kyZMn/PrXvw4bRfc9t6x49kDnXfrzm/fXev+GAEi86003Ru2q4tnGLrUjHnPGcHJygjHWZVdp646WrAPlQmDCPKWxWNBobmOAFl0Ja+J7TJDaPZBq+sFr15s6Qw9GHdY8Q0sxqjt9HLeDhvGsaUP3PPc9+iFZA5F8+6WM6osVOqYDrXRn3QnabW0PCljOpvR6GXfu3OHFC8ssqVXFajnnqFoxPTlhPN5gNLSZ3y9mM06Oj5lOL1guSytgO6pnrTWVd5cqHLAxNQjF5taYmzf3SFKJSBrXyJh1U9UKohillgIKsGyXzRz0fRK2Mny8jI15zPOENM2Ce1qWpg0RDZCmkl4vC+A0kTKsV9pAkqQhN4oH9MYYqroIoKyJz7DjOXXu54v5HG00g2RAmqUkiYtylFBUFQkZUkiU8GxkCXVtny9Ne2Aki3nBcrmkrCxIqquaxXLBcrHg+fNXGGMD/YvSvgfvCqTqmlVhLUk+bUYgXNF27How2Yw7RxzhtQZ+X/QxT4A0lvWTAObteFNK4bLLhr3cgkPZsT6LwKCntQkxkH6N8X3sk3en0rK2WZejaH3BWKdPZz0yppnjCBFikbqWcv+5mW+Xf39bpWV8/jpF3bUKSxoGyNPTU27dusV4PGY6nVKWFcuiYFkUTIwmTVNGoyHnZ6fcv3uPmzdvMp1OmU6nLjePdassViu0FI79TJIsU/7+7/+OVbHkvccfsLW14/YZ4ZSSJavVik8/+5yf/exnHB8fWwDlAIK3VIw3xoxGI05Pzzk8OODi7IztyQbj8RgQLBdL0jRlMBw6YhBNXa2CYkDEi+xV/WGMI2yy56ciwxjFF19+wevXr9nanFAUBf1+n+VyyenpKXVdM5lMWCwWKOe+PxgM2Nzc5OTkxIGlC4yxFtH5fM4nn9hcWv1+n62tHZ4+fYoxhtPTU+7fvx+AhjHWrdNTdfd6PabTKcfHx1xcXCCEYD6fh37yCvblYuXGg01hYK1BQzvWhaAsKvKeJSDTSjF3KRXS1LpM+nqrqnJulzVVZdvrwRAQ+sLvzzdu3Li2f+PyJw+Qfv/kBePJBK01ZeUY34xBLeeUZcl8uaT0JArG0YbqxlRtF8saYxyilSkCuznZzVGRpQaZSPIspd/LsSQKlhXOqr8yZGIsU1ySIEUS/HDtHq7ZnIyYTCZcnJ8xn82pigojJCJ1lJwuG3ZVlQgJqRYuAaBACE8TajfDhBSEQUnLmKexGaYNBrWCL778gizrMxxvsC9ukskakhSRpsxmF5TbW9RVwauXS7YmI7YmG+RJghaSLM/QwrpZGCcMX474sMWA9eePhExjDFqY8NmXlhnfaeZt13gdHQ7cXPe2I9rhRiUd/hhHEWoQkQLca2wut8lLmML/FYQJrV0FRjTac7+YCkPD8OSFVPe1eRoT1ecFHGWF39SOjfPplIYSWaFczpCg0Y20+FcXe07sX+z/NlY9b42wlithLwguKxC52ik77o2zfDasQlhGHe+3LB3rnYD9mzf4wQ9/yM7ODjs72+RZzu9//3vOp3OyPCcBjhcnHB4ccjGdcjGbUtWl7Z/aIJPUzTtJL88ZDfvsbG+yd+cm+zf22dvbp65rvvj8S1arP/DwwX3u3rvNfDYj6yfs3djl17/6DZ999hkike5dG0fbTcAAlrNMBQ1de9NuM/1BFMejRXALavr1MsCPQWnX2tQSzL3Q5ZJ5LpYz5osLNra2MLXGIEFcjgEEAvWyDOe0nsC1Qbc24QATOsoHnyxVBCp3Zy2yA94dd+QJpqmrNe7cj7HSIShU4nuF73X4xVswbN/ZZ/PxDXFfxsKX31y9EkTg51wEFZ2eJbbcaOOBkF0roYn5qx2BQFWXnJ+dkaUJ+UbG7du3eP36FYvFygpxUiLMlCfPvmSxWHF4eMTBwTGrZeH2C8L7NS4WAXDuNbVd11PJ7u6OdZNeWvKdrG+12FImLjeNXSv6/b7tJydwyMS6xsokIU0ThDTheb3worUmkWlQyARlhjFBKaa0Du41CBEAgvdk0ErRy3ukIc+L4uz0lH6/T7/ft94TkctblvYpCht3UGk/BgHtmL2qGqUSlsuS89MTBBYUnZ6fBcuLd9+xMU1QlSpQV8cWGq1sHJQfc16Jod26TTRu4qK1dlp5HcCxHzLSkX14kpCgLPWWdKwbJnjrq1MsCft7yBfl4r2EY85srw3NjPCKqThBvL+vCfe1M8cYSyKgjaZGkDiLnN9BvQXSU1Hbf81NJZBKy4rp94bQJhevEluOwvpn2m1uffJzzz1frDDzx7xSycTnR8/vn7dRAiqEFJxPT7h//y47O9ucnZ2xWs6pV3NWsyknWIvBIE94/foYc/smN2/e4OnTJ0ynU05PTxiNhi6cQTCdnaO0W+ulpD8YMJ1OefLFU7729W+wu7sb4lZev37N06dPefX6kMVyxWpVkKYZvXwIRqJqgZZ99m7eI00zzo4PqQobg5MNBgw2N6mVZjGbMRgOSfs9js/OkSJjNp1Z0h3XB94zwfeqV0T5Pmn631pKb97a5+zsBK0tiCiLkmJVUJWVdfmsFYvFIuRv29nd5cGDh1RVFUiATk5OWC6XLJcr3n33XZRSTKc2uawHN728x97ePu88fEiv32PQ71MUK87Oznn98qUb05Lj46MQIyalzWXU6/WsDF2VGG33yn7fuhmmmd1H+/2cXr9PrSryJLUW8LIky1LqyrL33rp1k6oukYkgy3NSZeuq6tLmZhIiuGL6dcFbjYbDYXA5ftvyJw+Q/vD0OcPhGYmwGrEsyyyKzzPyXg+lDBpJkibOrS0Jgn9D89qY/2ViAVLiNT/GWlswdgIbrJ+nBmrnX21EhkxB1zbngMRSFDdCmELVJcvFBVLC3u4u5ydT5vOFnSjCkPYyhJaIzFJ96tIGr9oFsYkhsTmJXJIsBGmeU6kaZUqXzM+QpxKtK2bTE6pizuPHj9nY2mE6vWAxn6KV9YFeLJc8f/aU3a1N+tltEmEQWULMuATYOAjTsZwIK5iokCvDKmyN3zBE4z8tvMQi7GbvQUTr/6ahmWwVE38UxGx7cVtsc71Q2RXkHDjqBksaETRXuDYYx2hlhAlJhv2Cb7BauhTZJsdq9loboO1/i7XsbrOTidUC1rVd7PwD+GvCk74hsLN5NvtJBk1hE4xp5XsnmoZcGKl7j7olQPnnx2Umx9jgZeHeGViNsvYbINbV5vF7j/nWt7/NxmTC3t4ur1684ODVgdOa1xy8OOTw6ICyKDFaWIKG3oDRaIiU0JMSrQWKBK3t2D8/m3N6fMbHn35Cb9Dn/v37PLh/n0cPHqKU5tmzJzx7+jnf+MY3eOedh7x+fUCSJOzu7fHzX/yCZbF0uRX8uLIKXeEEfytgq7awICR+bF3Wdto+bFxYPOqKx0BbS+uBdmOhioK0A4CxjSrLFdPpGaPNMQanNpQEoNAuLn4ojBMakI5GGEsAEl8lhSAJa8flJwuw3s9BN4+bdcDdw82tRp/RCKgetPjnavqKILRqDMLUoYKW645w8Y66obqFiGktWE/sPPICvQX1DUuafwdKq/C7wSZuXK1WzGYXVGVNVVekaRK5slqFwc2bN+n3B6RJRpZZbfXh4QHn5+fWzUatqKqSV68OODw8wWhJWdQoZeOYfD4yKwRXSJGQZSl5X9If5Ozt7bGzs8NkMglu08PxOLiNrdvcY0+GwDwlrUudVwx5Rr+qruz+5RM1Ope8VFjhvXJxSx5QGWPdPpM0QSQpplTUqqQoa+ZLm1NntSpYLUsuplbp2AgoNatVQVnYeCejDYvFIowLG2frYqCimCVvSbcYyrRiJH3pKtda7qL4OOF4jFslzroxboyjLHfzogHrrjjQ7c+NgX1DLuLHe5yAV7u9xoOVZt74+uL539o+BcQW2mbctFMz2D3f0ZbXGijCOO/2U/y9ASSSxO0L3rvA3xNpAXKwSEZKwNDX1yjo/L28GyZgx5FvW1CXNGAgLi1LtyNOmU7PqeqSjcnYMf2VlMsZL5+t+O//+DFaaz744AMeP37M0eEBt2/d5fbtWyyXC87Pzyxhh4A0s8qGJJV2zfDMikrz8tUrjo5PyHNrcVitVpydnVnwNRpzMV+RJCkD5zZXV5q6Noy3ttnc2mG1XLJcXLCzvcnFbE5vNCYbDJgenlCXNbs3b6KlZLFakWcZs/OptV67tBlhTER97veHZj8W7t41L168QOsSmYz5+A9/YNAfMJ8tmM/nwSWxKApr3U0Sxhtjbt++Hfr57OwcISRbW9sMBgXPnz8PbIfz+ZyLiwuM1ty5fYeT4+NgwfRMct6dtbFoChcmop2az+YlSpKEzLkjZnkPIwR5Lw1EDovlnDRLGA56TKcXZFlCng+p6pK6LqmqAq2HbG5NWC6XgI0Z9MqcoliRZ3mIPer3+2GdEcKSpggh/jPNd1yGwy16/QG6rsnyPlmaMtiZIBLruqSNoZePSHwOFmN91q2yyccEWNIGjCYTkKVJoNnt5z370rUlfDg9Pcc6ZAh6WQZCkmeColyQ9lIbrKqtr3qWSobDHKUKa4ka5HZgn50xyPsIozk7P0cmEmFsbhmJJEtykj6W9tkHwjpGlkQIlHbMskKjam1BSiptPUjQBH/wclXxxz98ghCC6XSKqio++fgP3NjbpSwL8izh1YsJw75gd3cPRI1Me/iEmV6T1Wh9vXRkhSIhEyegGcfvC4kTNCPFs1dhYzX5jeuYEcaxCNqYjXA7fzxeXHV0MC4BXVjAc+mM2B081ojF+AVwiA5jnDYxbMqNAOi1P917tLFjI/h13apSpwVezBeslsuAcfwG6hPldZq6tviF1QuYomUVcRpVPPuTCFZNe59mcW5bmxoBN3bbEUIEYQYhSLKUb3/727z3wfvs37iBEYbf//4jsiRjPl/w8vlLzo5PULUmHQ3ob0zIsiFJ2ifJMnq9jFcvn/H65DVZnnHn/mOywQa1Mui6pioWmPqMqlzyyR//yB8//pi7d+/yrW99i3feeZeyXPCb33zEjRs3+doHX6ffG5HnfUYbY/79f/j3ViOFI7/wnRkJ5F0tcyzIdF1R4ni8OBfSunPX1R0XL+Q3TF6gVU1VrpBo8sRa5lJnySbSUNt36tnQmnb4oeKfIXEcCUFji7UG+ViZTossMMIpN7SJxnlr4gSQ5K03ETJzAKdx+WqdG/eVssHvNpjfso7itOBlVTs3IR0Ee08dHVinvNDocuFYrar1txdCMBgOyJ2rhY/P0coCpKKoePniNaenU5SqeO/9d9jc3GQwGDAej5lMJmRZbuNq0oRMS5IUsvwWWZ64WIeKXm/Azs4eeTbk5OSc5fI0UPc3c0cxGvUZb4zY3t5ia3vM5uaENE0sfXRqGc9sEkcbbzEeDwNgienajTGBrcu7A6lSk+fWRUhjY1ptfhjQSqF1iYGgRV6tbDxEmqfM53PmiwVaKcrKBmJXZYVShrKsWK3sfuU1tEp7dsUG6MfrjI+L8vMgdsETuiE7uWQR9Ba3aBx3hfTLo9XQrMqX51gXWP1TioCQUNUXP//jed5dA+K+uMq1LV57gaAJ74KVeG3ugkhfpz8Wu1Y3xxvX65je2Sp2LVlBPK/+Kf3miTiuKl2rcOtZnAJ2tVpxcXHBZLIZxRctEcJaXBGCL754wje+8U1OT8/Y2d7j0aNHHB8fU5Yls9mMfr9Pr9en3+tTVhX9Xkae98nzvgPjhvl8wWqVcHFxQV1XljREGhbzJShDfzSi3x+gtaGoKtIs4+7dO/TynIOXzzDG0Ov3WaxKdnb3kFLa2Bpgd3+fpQMfAwTz2dx5XlxWAsTjPi52LdYIifMO0nz44YdcXFwwPZ9SlZbdbWdnh4uLC0YjS+a1coqgw8NDxuNxABCLxYKiKDg/Pw+AyscMgXUd/eyzz6x74GDQGpttIhjLEpfnOZubmyGm1gPNjY0NFy+8DOMtXs+Oj4/p5Tl1VTGfz+n1eoEC3K/7UspQz2q1CrTv2ilgPBulD0kYjUaMRiPOzs6A9fHRV47Ztz7z/0/LeLyBlBlJz2YBlkK4fCK1dXWTdgNRtSZLU3zfKUeDOuhlFMUKMOQJfPDwPu+99x4bozF9x6DR7/VBSEqt+clP/geePnuOTFOS1AKkXibBDNne3mFjtEGxKDDacOf2bW7f3iPvJWhdM5/N+elP/54vPnvK558/4fjkhMOTI955913LviMEeZI6QToFY6gcjWrsCpX1MpSuqCqodUnez0l0YgPdK4M0NiGtUhqjFFWtSBLJeNijn+9QlQWnx4dUZUFiap4/yxkMIE0Mm1t79JMUn4vJCl5OEKdhcoEmkqDRJEfOeB4QhXJ5AfC/CWFIEr/hGdYCAwdMHE5bi5NiF4BLR7yiqm1eIjZve4DhmZWaapzg2Gp9qDDktAn/M81zeeuVTQ5nc1wJYLVaUJdFaK/NF3CZbehNpe0D7rSYxlqgtFbOBO6T3bVjk/yi1drs3aIc+8r7Bcc/p5SCH/3oRzx8+JC9G/ucnp0xW8xYFQV/fPIFz5+9INGCcX/MIM8os4RstEnamyCzMf3BmCxL+PTLl0yXFWJVsS9y7j54j6LSrFYF9WrO68+OmF/YgE0h4Pnz17x6dcSjRw/5/vc/5Dsffo9PPvmU//AffsIPfvADHj58QJan/Mt/+S/5H37yE5aLpete4wCk1T+3BTxbtPPn9+d7IS1JJMIk+CSSXcGlK+i0N34/WNuCYNCee1iiDcoFFRtjSFNBJv3Y9NZsP458jI377saPtSTUTRu0cfoE6wbkKZ39eHMnhnnVAjLOSqMdkPFtjoU07+7kY22gCVa3Y7CxGsTX5MKPdwdcjXXD0lqjnMDmSwCldR2ClmOttQ9sny9mLleGoSgH0bswzioFUmRoZfjkk8+ZXcxJEsHt27e4c/sek8nE5iyRWUgKaambS2wicdjd3WE0GnJ2ds5yWaBqwXJRtrTySlsq/F6/x2g04P6DO2yMR5RVyXg8otfrOS+HPGz6aZKS532EqKkq7aw6kqq04GW1WlFX1uLlAc18NmNVlKyWpYuhrVmtViE/SJswgOg9NHEtceyhNh7oCkIW3Wj4+piyAE6E9cYwbofoiOxWeYdA1ZokWnO6c64by+jHbld4jhU1mDbFdGushAmxpjiFQSyQ/mMAgbe6rQNI3fU0rvuqNX04HPKd73yHn//850EDHgONuP4YIHWBYKuPOg/edWnz9QuZYISI5tJ6K96b+id+f92Y1k5TWiDbn2eVb03ewxcvXrC1tc2tW7eYTqcsl0s2NzfZ2dmlKEru3bvH1uY2Val4+vQpjx8/5v333w+kBKvVitFowMbGhKIo6bmcSGmag7EyTOlcN71blo3/soyb4/HYpooxhlVZoDDcunmT7e1NimLJ0dEBQlsLi0wzdvf2KRZLTk9O6fWH7O7fZLZYUJZLTFU7q1ZMetHuFh//1nbJFMFTwACJTDg/P3d5nvIABqfTKUVRIISN1xkMB2hjgcTBwUEANLPZLPT7crkMwMP3f7kqwvgtXZy8J0Hw48UTVsRjpNfrBQCUplb54slHNALh2Z0dKcRyuaQsqxAz5Nu3ubnJeDxGJpKyKgKIi4FQlmcY1eT/8nTeQjSkK1mW0ev3rx2vcfmTB0j9zE14txAMej2rQTM2k3Gv10MKQeU6uVwtMFrRH/cRUpBIweDmDpubG0xGA0RdUs7OMZmkUgUvvvyMsiy5d/8+t+/d54N37qPKJcuiIM/7DIZDJhsjMIrVYsn/8//2f+WzTz5DK8Puzi7/1X/1r/nrv/4Lev2M7Y0N8kTyy1/8jC8+f8rh0WuQgtn5Gd/89ocMhhtoZTM+IyDNMtLcZieuytIm3cMgdG2DlhOJTlNWyro4VFWF1NDP+/TSBJMmlKVl6qlqG+OyWCxYzmcUyyV5nlIMepwcH/I00whjyPMevV4fIROkTx3jLERKa+t2Zkz4q/2mZQh+1w2gwinudWtRED6uxwEeL6C50zulgVI+saNfUNva7UZ7296xG32jcPcm8jWPXTKajci1Wzc5hqSUkdwQATlDYPzxG3jT8uaDMTY3icws+cDJ0SFa1Y5uu62FXYv+1pR4Yw4ezqJxr/GxTB4geFa1Nihs97jXKMbPHd9PCMGf/eDPePz4Mbu7u7w+POBiNmMxn/OrX/+Ws4sV/cEGk/EmmVA8/eJzLqqSmw8e890ffZ/Bxg2SrI9E86Osx6///r9Dac073/iQnf27GJGgakW5vOCT3/yUs9MZ05n1mxZJn7Ks+OTTLzk8PODP//xHvPfe+7x69ZKf/OQn/PjHP+b+/ftUSvHXf/3X/Pf/7r+ncpm2ff4VIRPWFZ8LLXZBiYGVf/4494TV9otLcQTN+bbPuy5EdtzFFkADRiF0ha4sW1YvGUUWxYjBDJsXx4NpaIQSbSq8W55yEb7K0amDccKzBUqqtsk4q7IKYze8d9VYEpWuXVxLEuZd/CyqVqGP1gmfXkBPEqu8WtQ1Alp9Zi2g0iZrjPo/jL80QRhC/IWPfUkcpfxyteDo6IjpdMqjR4/44IMPHHDxlPkKQcpyUWKMct4EytVhXZgbV2ZAK2opESJxVhWbGy/P+/R7NVUJg4Gh11si5TQQ/ggEk8kGe3u7pJmkLEpO6xqtalarkjQ5D/1c17Vdz5WmUiKKt9Esl9b1tgt2YuRic5a4/rMdhlY2n04s+ATBzIR8tmAEgiSMw1Cvu0UjmMVKIjr02G6txCckTYIF0wJ5dw2yNX/C3IrquUrpsK7E1sm4rBPmY2AmhXWX7wKvq+4VBHd042rdAUb++tiqHFtjut9bz+BKWZYsl8tAs+zHvRcK4+s8OFsHttYBMXuubo0Fb+mULv5Iu2t9/FqzB71dCXV1LGddoCilbO+NxhDP8eYaycnJCdPpBZPJBpubm5ydnVH0Ku7fe8jW1hYPHjwgy3rs7u7x5MkTXrx4wa1bt1gul/zhD3/g4uKC+Xxu430Tm8g3gCOlqJWNy7XNlaRpjlJWCTMaWA8HgLIqKaqKnd09bt69Q5IInnz+xK5jyyVFWbKzf5skzTg8PKRYFjx4+A794ZiXzw9JE8Hhsxf+iTs9F5GtuH6JXWztmHUETpgAoi4uLiy7ompc8vw1GxsbVLUFK4vFIlgNp9NpS0klpSVB8HFEvu+9K5yP7/HHPZW6d3XzQMSPWf9+/T63XC4ta5+zcHuXOB9nqLWmcDmvAJe7y1qa0izFYOvf29vj6Ogo7MmVy0nq50Ds2gkWrPV6vRBT9TblTx4gZdT0s5REWIrcQZYhMjsXlarIsJv4luPW37hxi+3JiM2tCZubE3Z3t13GbsX56QmJEHz26aecHB2QJSmZQ8ynhwdcnJ8xnmzwtcePOD45Ict7zOcLEmFIZcb/49/83/m7v/lbQKCV4fjwmC8//ZSjV6/58x//GUmW8KMf/Rkf//ETalWT5bggQc3nn3zCnbsP2Nrecb7SadDWSyRJlmLcJqiKAq3sApoYyICqrimLFaqsmGnFyxe1W3hLN0BdhnNHTiGFdSXcnozZmmzw47/4S37xi1+wtbXLcDgCdBAmvaudcQDJGINRoiFbiMCN8NYa7SEJTuvXFO/QExbMAGoub3rGNAJ9LCSYS3Xa/68HSLGmkfDd6cVb54a9yziJQrj4hyA20JBjufs0LlA2KLa73XqLgVI1g36fPE0oVkv7XEbYTO+eHliploDxphJrXptEm/ZfkzC2a2Va18+RgGHWa3yFEDx+7z0eP37M1uYWL1+9Yr6Y8/rggI9+/RGalPFkj8Fkl+HGmONXzzlZrsCAqmGyuc9FCRfnJ5SrC1Q548H738AgODiZ8vrU+n6nScJkkHP/0fssFjbx4ebubZTSzOczFvMZi/kF//bf/nu+971zvv3tb5EkKX/zN3/DX/zlX/Do0SOkEPzlj3/MT37yE+tuJyWoazSiwlvZOnE/DiQ1LlTNhmapT5MQdxELMF5waAmqlwQoggUySySr+QVlVWCMIJFNrgpjHNW4UlSqtO5Q2ga/+9gbv/HULgu8zS9RYrRhMBxY7Vv0nv3zeEHPx2P5MWLHkAtQF4Ja1M5aYMFmk0zQ5nDz1yYywQjjYu2SkNTT39PGtTWbWuIIB0BQ1lUYsz5PjAd7AkjTDOV+C/2iNKtlwe8/+ti5UEs+/PZ3ybKM+XxOsapJkgwhJXkvI8sSlsslQkBRVJydnVOWFeNxFTZ/26eW0rkoS1aONnfpgrcX86Wl8a4ti5p/p1VdcXx8xMXF1C1pJiiTvJJIYIOMZWI1sgIBSRqAMDTrlw2g1y7wPx6zAu8O2fxix5tngPTzPJ7qdr1x1mzRrHWmqYSGBseOAz8ajIjOjJoiECEGqrFW+PxIjeJoLfDpyIzXAYnwvbN2tQERINe711iNfHOf2OoS1+PnQ0i9YCy7bPwM6/75a+O/8eeutcuX5XLJz372s6Ctl1KGhKmXLArRWv9VS/d662Jn3593kfLzzY+NNTjs2tJVkMTgye7L7ee5qiilODh4zfvvfc2x1F2wXK5I0zlZlnN6auOFer0++/v7vHz5kjRNefToEQAff/wxy8UcpWqKoqRYVcyyJY0HBVS1CgDFruO5tSKn1qJalCsUgp39XR48fMRwPOLZF1/w8sUzu5kJMEZw+849KmV4/uwZaZpx5+59FquS07NzNrKE4+NXQSrw66fto3ZOx1ZsGDjFqw7nykQymUxCf6Zp0lK8eQCSZlkrDsy70XkyCm9p8eDUWyyNsxR7S5Ffdz1NtydS8QrCeB/z1iYPdPz7joGREJYF1p8jpWwpBcqyDFajJJPBZTp22/ZtyrIsACQP+Pz4jRUWb1P+5AHSg3u7jEdjMBZhpknKZDwmkcb5ew9CRw4GfaqypJclPLxzg+VqwbMv/sh0ek6WJgiZcHx8hlaW7x68Rt1wdn7KxnhIIjVVrZmMhxSurovzKQcHR/zhD39EJhlVUVFXtaUhVZqf/s1/5Fsffpu0l/Cb3/6W7Z0tKlXS6+XW7U9oFos5z589o1hV3Lp9G4PdcKHR6B+fHDM9O6OeLyhXLrlcVaBUZTXF2mY8N45txMfNaOOSDOJWPffPKEOepfwv/+f/C3b3dlHa8Pnnn7G1vcVmJkhl6tiZHDsQBh1l5/bAQBvtQJQFFBYkpQiSxkWjtS9GLmxhFW7cw3yxFh/3FgwgrFZDJglCmEsb0boNKgYM7mC0L7fhEZ17m+i5jGncf9owSESbigDVaNfj342xcSBpIsnShPPzMzCWccrIJkjXGG+du2bQ+zsL0bmHeyZtLQa+79I0xTNq+dcfSCCinTDUo731w8eK2bK3t8eHH37I3t4exyfHzGYzXr56yUcf/Z5eMqA/3KK/fYt8ssPmzha37t4l6/dYnp7x8OF7fPHFM2aVIO/nbE567N/dZtDrkaQ5tUlYFRV1WTI7P+Pi/IR8sMHXv/19NiYTbt28RVGWHB8dkeYnqLlksbjgFz//JavVij//8x9ijObv/+7v+NFf/Jh79+5RlSXf+973+PnPfuYsHVdvysKbOyPhMj5mNxxBTMluA90b6t5Yqxxb8vxC3xKqnLuPVoq0l7CYX3B6Ilku55RVyXw2CZuS9xcvVivLWqQahYHNr2FdAAUW6Hgtns+fpuqa3iC3a4K0G2KSZQggSTPSNG/GnGg0ygI7t23wbdYEkscul6aJS7PyqTuWJGHuCKc9NvYivI6iqhpCAe3iP70bpzHtOQGWzMK4tcxaXxRFUWFMws0bd8h7OQ8fPmQ+W6H0nNnFLFiqVsWKly9ecDGbIqRBa8Enn3zK06fPAnD1c8DSzjo3wgi0NK5E9rlsu517oFIIrdDCB8Sn4JnstCUF8c+TpX3X30lg12usKLIBFart8nR5zLbHqMEQG0h9vwXwCyGWSAi3NpuGoS12r7PsbNYJVArRRKPZhbE9lVyfNDqvtxOEPbFEvF5eZSGJrmqAXRdwCdGiLe+CLRHdIz7HKzdigSwIW8ZZ+rRuXbsO8F0FgtZ9j3/3MRUx8I/XlO71sdXgbUsMVpp/EiIrWFs5FGkAv8I9rvr9khLumiKl5PXr1zx88Ijt7W12d/c4PDxkuVzR6y05Ozsny3J2dxOGwyH7+/s8e/YUpRUPHz4kz3M+++xTzk5PkdJS5dvwAG2xu0gaN0MnuPs2WeuJXeP29/e59+ghg9GYp8+f8eTLz3n+9Cmj0YBBf8DNO/fIez1evHrNYrHg/u2HbG/v8eXhS2qlOD4/Rtc1QubuyRqrmVJtC3psSQM3vrx1Frh9+zZbW1uWOU5IjDZNfiA3j05OTlBak5ksgHwPKlarVRg3vV4vrHdeqSeFCPGeHnAIIRgMBsFi5MelV8bF7nZtK6BwcYsmWLH8GunrydMs0Kz7OZdlGePxmM2tCUmahFxO3qPKE0EYp7j2feWt95ZQZhUprN9c/uQB0r/4iz+jl+ecnZ3Zxaaqg3tFWZakiWQwHLNyfpd3b98Eofnd73/j0LVPilUiE5tfwAoJtn4j7UKepRmPHj8mz3Pm8wVHJyeOr33I3o09Xr58Ti+3wWtVacFKVVtT4ydf/pHXx6+4d+8Op0cnnBwfkSVpGJyr5QJMhVFwcvwcrRds7d6gPxyiaut//sUXX3JwcECaJPTSFLR1zRFYBhGtayfQNJpdb9cRbmL6wGiMwSRWMP7iyVP+j/+n/zPf+MZ7vPvuuxwfHfLi2VPyVDIYDO2GI92mCpa8QFmzr5cppbMueauOFf6qoJkWGEwgWHCm4wgcBWuQMYH0OghUptFiCqORxiB99IaJXO68G0oLAOGEgWiBdoDAM7D4nCCXrSiOici1U0ZZ5KVwA8PdwFvNhEN0UjSCRqMRNoCml6VgNOenZ1aYNYSAfU+v7VmRmg0qAniXihXCPDgSArSugSRs+t5cH85BO6HICWHROwh3EeGM4Kr6/R/+kNu371CWFWen5xwcHPL7jz6mnw+YbGwy2Ngh39ln8/YjNrd2kfWK9z+QnJ2fUSO5ub/Fd+/dY3dni15q0KqgqCqqusYgkKJHnmUk8jaqrji/OOfF85c8e/aSL569YHtzl70bDxn2J3zy22fUlWIw7POb3/6GJEv47ne/y6os+fuf/i3/8l/9K+7evYdWmuOjIz777HMsQ9/lfvTCkyGOM5KBtheTACkYv6nFrm0mjP04izlEyRON1x8C0uY0EfiYHUVRKn7969+wMRmiVO3SDXSJMyzLW10Xzm0vCRu71fhJ0jSzY09Kikrxi19+xPb2Du8+fsjmziTEweR5TpbnGK1tTi6nFfSbWxD8YjcuGcU5eMuFIayfBpviQEiJ0SI8t1eeJKlNjaCNdol3Naa26QQqlHUPWxZOYFQsFnOmFxesliuWLsC4KFbB9WPpWJjKomK5XIVN+8XT1/zNf/jbYF2xMUgGrW2MnxDWvc66z2nm80VrfRBCBLZDPy+li20V6GAcSaTE6Dpwagoh0J4uWnStNG7cOSFEpJ7Exo0zY4KFxjIQujhIo4PSvTtq7UoabCKIKMGAX+/xehY/noVECYFCYpB4lY8fjwhp8/xYVEQiDAiNoUaQAykG5Z6NAOykG91SWvfMrgDcrK8RaEOE781SaZp9RojAfmccIJPSCkfKeKWFDOPToT1MJHjG/ebPi2UnqwRyCXSVQSQ+/lTTQMLL68XbCvrXFX9trM0vy/ISAIvPXXesW9+b7tka54lN4eH72AvVUjqQHu9hrX5wKk7jLVLeNayxDsfgsXHb8+dffh571B+3MeJffP4pX//6N7l16xaLhWVts+6c9pzlcsaTp19SVSW3bt3i5ctnlOWKO3duMxwNefnyNc+fP3eMaJDgXHQdARXSCecolLLjU5IwGE3Yu32TnZs3SbKEz7/4gtl0Cs59Le2NyMdb3LjzkLquefX8KUl/yK1H77CsKqaHJ2zmfT5++gopU3RI9O7HfeRK78Zb+ItXklgCG20EQhhGo4ENiSiWDEdDBv0Bp6dnLQXcYjVHyoRefztYjrwFxysBYmtLDJIkPnm0Pc9be8qytLFq7r1pIUAm9Hp9vOsuuKTnUS6xWikSaRNm9wcDwFqzhLRkY3mSkiYptaoRiUD3aqrlimS8wfT03IbGGEFKgqkN8/kcIQWLcoGqbUhJExNv577Wdu0qi/KNc8GXP3mA9OzLz3n33XcZD/s2y3WlWC7mgfd9OBxy69Yt9vf3yfOcl69ecnh0EBC61zglLrNyzFhlV2W3bgvB2XTKZDJhtDFmPNlgMBhQ1zUX87kVbl0W7CSRCGHpOWtVsiqXlNUKhObw8LVDxdZHXQio6gpjbDCxqWrOz+ymvrm1zWg44sXLVyzOzxn3etZvWLtAepGQDYdIAfP5BRjtgg3bxeZvaYQf5XxwhUy4mC/47/7dv+Vvfvof2N/f57/+r/9rnj17xng85MaNm2RZikzamrFm04oCQHWTA8EvAnZyu39O7LcuGcIFgkcAyYES3Vo044XZLmBOgRlttjjBo62hj0t3Y2i0+AatCIl3fRusa0tDHWuMQbqkih4kmqjupOXWIdr9YowVzEVCKoUlozCGs7NTvNbX0MRUGez57dLe/GIzvHALqv8tZkKKTffN+/N1+L7S4YBfBIN2wGu8jObbH36bh48ekuc9njx5xtnZBR999Ad6+ZCtrS1WiwVKzPnggxts7O5zPl1wevCCen7B3QcPefe9dxn1exTLOYfPPuHg1XOm52esilVgyfEMOpuTTfZu7LNzY49vfvN93n3nEU+fvuKLL55xMV+ytTHi9PSM+fycW7dv0e+P+OUvfkWa9Xn//cdMz874+c9+xo9//GPOTk/5zne/y+HREbOLWcCcXa21ffdx/iDr/ui7QgjLcmRcEl0/z3TEauX7u9XnYdxZkIGWzurUaL9kIvns888ZjfvkeU6eZyEzum9nnuf0en3GG0OXH4fgkuODVQf9kW2nSLm4WDGdzjg9m7FcLbl1+6/p9QbWjSRJwAikTEkjdwq7FlqoaK20CarWjdbQzYWyKILLn3KuKlVdNblsKsto5JmTlFKBZrt2FjFPSxvnuakrQxFtbt69o2uR9f3W1bR316S2tcAqanDzmgi42qXGW77dxMIL6gS6e4kFzcJrhtw4khiMFKD9GPBU+gZj3PhwQmdjofFKLE1TWyzomgDc15bIUuPXw6D1FwkC7x5NtJZZa1WaZU7Jo0k8GYhf55y2VitL8CJlgjGJzSMoBJA4K5Vdm5NE0ksH1LXLi5ImwSXQehxAXasApmJXQr+2XrL0iMtKK4ybPx44hrkZW3HifarVUUCbTKK5pyBLEx4+vM/m5ia/+93vUApMklmCDqPCmhoz2L2pvC14Wmd1us4S027729y362UQzZWov9rWo4aKvTnmFYdx3d6Fc317uooircylY1FV4YPfU1+/fsWtW7fZ3Nrj7t27fPnll8zncxKXKuOPn/yB169tjM90es5f/dVfcXp6zGw25c7dB7z3/vvs7e9zfHzMyckJFxcX1u1LW4IuraziwAhBkmWMxxvsbe+zubNLPhwwXy357PNP0KUN1UilZGtzG9I+j979gCwf8OXnn6CV5s6Dh+zs7fP8y6egai6OzijmcxKpW/u533O9stXvvz7VjD3HB0F7BY1h9P9m78+CbcnS+z7st3LOPe8zn3vuPFTXXKjqobrRIwE0CBACOIKEJDMsipKCerHDIT/afvKDIvygN4cf/GIGGXZYkgmCJjgBAYgAuhvdXdXd1V1VXVV3Hs589rx3zrn8sNbKnfvcW90FChLJtrLi1D3DnjJzDd/3//+//9dsAhI/8HUzalUqEccxruvQarXZ3t5mNBqTJMq1UpayktvJUtWdWvayPsncG8Ve2RUrZNgss78kaQZS9ZOyNHAopNp/VKPjAiE1QKaTNUebXji2MqVxHQcLSOKEPMsRtgLo8iyjLErSWKkkPNdjsVjoulW7avZs2jUYwNswZwaQMYmdlLKSfH+S42c+QVos5hwcHOD7Ho1Gk3a7je/7dLvdqsNuu93m7OyM4XCgOmrrTcvIZExwZoL/Oh1tjqLIOT4+5vHjx9i2onYN4lJIWek1y3KpGbcti9K2KaUkjlMdFORkaU6aZqRpUg1IQ3NLqYqC00wShiG+59JuNpiHAWmWrhRRqqJtdGdyG5VMry5W52sgjKe9er6sdPvzeUqWHfN7v/cHNBo+kgLHs+m0W6opoVgiFTqP0Kie7j/xrKRJSr2RiXN/Xy02NYu11AiiSV6gHkgs/4/az6vFxTy3/t8K+WK08CjpjHntUioHLXNtqgJ8aWlkqYaACQcbw8i4gK6nsCwQNdMDrGpDAV2fUbslyvpSMp1OdJCsggUj3apeZ2UD+ZjNVqw+rp4Qnd9Dlwju8uPUE8Znv7567Y2NDV544QXa7Q4P7z0iywref/8DEDbtbo/RdMbho8fgBOzceBkr7HJ4eERgw2fffIOdzTVmswk/fPt73L97m2g2Vei0LCuWTgCFEMSjIcODJzz4UGAHHtsX9nj+hZd4/rmr7O5u88N33+d4cMDa5jqTyYjhYMLlK5fIsoLvv/192q0GN27c4Hvf+x53797l0qVLxHHMa6+9xp/88Z88dU3MdTt/DerSAXP9leOXMXLQ9602hovaWFoGgXLlXpj5UxRLvX+z2SIIQu2e5OE4tpr7vk8cxyv1CQoRVAmFkrCqJF9KyPOFSuBKpenevXCBwdkQEJwcDxDC0a5NiqVSNYUWcbJ0QFOba6RtVyFNFIMdLaJqk0oTZSRR1pyv6sCJMRypm4FUaKVlaQbKXDczzARIS7M9q3Km+vd1Rm31Wi/nwOqYXwbQK3/DwrDAtXxHfUaNEZxPuqSsscrm/WoF/KWlWemqxurfnGH4ZIcBkMyXfk9pg3RRwaZEUGhmKsexJZalmOwwCGg1QwLPJUlT5rNIAUalxLI8pIQwbNJqtXE9l7X1Pu12m/X1Pmvrazowa3L92i3uP3jI7/zO7/Do0SMWi0W1l+WFkntLKXTCu7pXmHm0RMIVml/ky3lX7ceovj2WVQ/MzWuwch3MmFrWL7BSswXL2ptOr8l/9V/9b1jf2OT/+H/4P/HgwWMFekmLkhQjZawbi/zbPP5MzJWel+drKKv5Ck/NEamBygqHk/Invmd9/hngx7xW/evjEqnzR90V78MPP+TTn1mj1+uSprs8efKE+TxC9XdS9t1FUdBqdeh2e4Rhk5OTYz744AN6vXU2NpQN+IULF6q+QUmilD0lAmErNsTzA/wgxLOVtfSjB7eZTCbKlVLYTAZDkiSntGxuXL9Os6VAuuPTAb3uGjev32I0GDIeDWmFLrd/fBcs1U5mNXE/J5sUPLWGoZ9iABrbttnc3GA6ndJohkgptckBNMJQybDjmNM0I0szFouIXDvLZalurKyvflGWBL6P0H1DTX3QeYmplFInQAWuZVctQsqypJAFjrCQWQGlVvXo21uWxUqLAMuyyOKkijszXQM1zadVzKwYIQWwHBwdAks7/boRSrPZpNVq0ev28Hyvshjv9Xp0Oh3CMKTRaOC6Ln/89nc+0Vj7mU+QlL5SNQmrO4GZBSAMw6ogTDmpLO0lzQCoU8FmETSFamAmukWSGAlIXhWsWZbS8TabzeUN11bYpmu5LCXj0RgpLdqtDnGUIyXasWha2TSaz51nOXac80TCpcuXtSSEqm9PxbZomZ1jO7iOS1I7l2cFBmajMcngcpEUgENeCL7z1tt0u02miylu4HDzxnUaQaBsyPWhtPTL7821U+9h0PHVjao+4GFJ76rPCvXF8/zP5xfvp6h5say/qQdq9eeao/6+pVQsnxbGUErt+sayjkR9fOXgJ9FF9/oxlrCwpLp2poZDpXpWVfBv2w4CSLOMUubYtmARLXQtBFWwWH2u2n37uMTlPKK+msgvkfXV55jniRoL9/TrrwSESKQQvPbaazRbLcbjCYso4sPbt5ktIvobW/itHkdnY6TlIoRNGkfsP35Af63HG6+9TODCnR+/w49+8H0mk7EW90hljFIo0xCjU7YtG8vW47MsyRcz7n/4Yx4/uM+NW8/z4quv8ek3XuSDH/8Y4jM8PyQMFINaFJLFfMz3v/c9Nn7xF7hx4wbvvPMO29vb7O7uIoTg3oV7PHn85GPP+eOu8/LQLENtvagzUsoxLa8lqUWVIBkE1sjqfD/Acz06nS5BoLqQx3Gm/4U0LXHdRDXYRWpHo5I8T0FohzNts51ps4Y8L8gzbS6QKBAGBHES8a/+1VGV2NV7HanAlGVioueFYUKUc5msQJDzSLQQQmvg1aVQtY6FDirrAZm6fiqBM4nReeRfvYrZsCsARx/1968fRuMOdTnXsrakfo+ruaPn6XKZ0Uwius5frK4/5j1t21YyYw2z2FatNtFS2vvzn8HSZgtluWQoLbF8jZ807n5aYLr8bPp8UOoFixwoQOQgcppNjwt7u7zw4nNcubJHs9ng2tUr7O5skyYRjx8/xhKu+rIV6NUMO3S7G7Savar420jBYu1UdXJ6ynB4Srfb4rd+6zcJw5DZfEaapIxGI45PTnn06DH7B/sMBgPiOCZLM/JCta/I82JFTmpZqs+fLK0KMNMji4qNE+bcQReV6GummX8dyJnGw3VW93zC22w2+bt/9+/wuTffAGz+8//8P+O//q//L4xHcyxhY1sOucyeGj8/je35d+UwwWXdMAbMXCowEru66gBWU/unYopqTft4putZrNX5z3V+nNevsZlDi8Wcjz76MbduPcfGxhpZlnF0dMRsNicMA/Yu7OF6Hru7u8xnC8IwZGdnl+l0wcnpGaenpzQaSuXQbrdptVogSiwb8qIkzZSMLctLRuMJ0+EZSbQgzRNGgwFrvTWmUU60iElyyeWrN+ivb7BYLLj/4CF+2OTW8y9R5gWHT57QDD0e3PuAPI8RFGBZer1YvT6qvnHZ0Lt+PeqGDZYlaLfbWJZFmkYUpTJ0soWrajCFWnPm00WtLqj2ZqWaQ4p1czQrqllxlPNbp91WzL2gktWZ2lfXdSlTHSOJpWNrimpRYhIhowQw52EeVzW21vc1z3Mc18Eysm4kru/T9Dwc26bRbOA4Dhcu7BGGAXmW42oXvStXrrC5uUmj0cDU2buuMu5BCBxb1ZYNhsOPnQ/nj5/5BElYqoeMUH24lsFDWZJlaVVEreIaC9Xl+mm3KpMoGV/385uxaWhYn7xLtwxRWataTxVmC8BiPJ6yWESkWc7t23c4OjpRP6dxNZjMe2VZhsgUtX96ckQYNsjzFClztdFKG0sYe2dZNbNbDW6etlc1v6sXeRqWRz+bUpZMplN+/MGHSvOflWysr9NqtZTcztRQWFa18ZvC8HowY4JekywZRN2xneoeVaiW1EIzsQzghLlf6lOuvPbHHfWgrSyXDmD1BWclMUP7dGnK27UsLSkxKLZ6nGIa3SqpRUgsS7sKSgtZFNjUdNgIwNaIjZIMKVlSRpalzOdTJpOJvpfqU1SoOc9iNFaDzWrsn9uE6lpy9W9tY1uBvc1rrvZgqAcPpVQa9K3NTTY2NvA9j/tPHjIajXnyZJ9Gu4MbNmn11vm57QucHRwShA0QsLPZ49XXXqXIYr79jW/x8MP3Ic8QhSp4lqVqtWzmiy0sZFmSZJlm9MDzfFzPxhEWRRzx3g+/z9HhAV/40pd4+cVbhC48uPuIZthGSMjTnDxPGQ5GvPfe+7z22qt0Oh2+//3v88UvfpHhcMhrr73G/pP9j02Izo+RJWNaAmaBURewKFT/GcG5BqnUHX6K6jqbBEFo9mg2m+D7AVAwHBbV/FCPPQ8ElHojOlccr8fGMgmrMwlLxHwJIFSwhXodISjzp2sW1f8tZYtcGzfWElLWwIH5eZlnGMOG5bmo86obBRik51n34Hxif36dfio5q/3tPOv/rOdWv5MGoRW66LcWHFqq0fbqGq+kyjYC17aX19PUHVkCaRkJ3jIYMGOhzJc6/aWRh06kxDngpvZ9Hfk319MkAGDV1jbI8xTLsumvtbh4YY2yzOh0G3i+xZe/8ia9fhvPswlCR62vcsjJyUC76Z2xd+EapbSYzaY6CFkgGWFZLkgfpJLmOXZJGDqkiWRzo0+z1aLRaq0EtVKiXcFchLAqN1UlVSs5PT1hNlOI/nw+YzAYEkUR4/GIH/7wRxwdnmn5jton8qLAcvSYKsGya0oFvYYrmZKlAUUl/1PrjBrvBtgTQuA4ykb4b/3W3+Kv/rXfoCxLPN/n61//Jb739g/4R7/9O+RZgY1FWSz3TWBlTPy7ftRt+ZWhy6oLGbWaoafUMx/HID0jq6/iJD2+68BE9XexahV/ft+CZbPZ+nseHh3Qaje5sLvH1tYmIDg9HTCfLSgbPpblMB5NyDPV16jVaqk6xSjSkjybw8NDHj9+DIBtlyi81yJOckppkxcSYdkEtoVtwZP794iiOeQFRekghcul67fYvbBHEsc8fPgQKeDqzVs0Oj32790lTyLGiwVnZ4fYlkRgKza2fumeCX48fUHNGmVZFtdv3CCKIoLAJUljbfqiXstYczu6dYHn+1Bft2zIQIH7TlmxLkURKwC/KFhMZ2RFTlKrgUvTtIoNbOzKMCaOYyxdo+Q6TrXeOfp7Y8Nt1q1Op8PW9jbtdoutrW2CIGBrewvsZX8jUHI9Vzf4NuoJIZTjp7kexuXOiD8DX5EYio+QZGVBWYDre3zS42c+QVI7nSrCBXAc5SCkJl2BpMQyLhplroLGWs3GszZcExjVrXCVbGsVPaqeh3JWiqKIPMuXkx414cNGg29+81t84xtK4pMkOWVBpdmv+8nbOgu2LYc8S5lNp3iui2NZZFUwCyrIkRUSadzdTBD3LHbhWd+rc1NHWQod1EMUpbz/4zs8eXyE7zq6NsKrEkHTNMxxHBxXFdyhNemmGNCcj+/71WPV8zTSZyua13YcbWygZIkV2mVZlUSgjgbXz69+GFOISuKjTlDdI8uq6pRqI0fZW+p77zhuhTpKk7jUGtiZonghLCx7iciZz6vO29afxSAnagyMRiPSOGc6nXByckyaJpjmo3lherJYy6DtE6gRDKpjUNI6WqPuZ6nrCCxkee6Z55Kr+jUtigLbcSiRPP/883Q6HSbTKWmScv/+fSzbodnu0u72affWuHTlGlev3+TBg/vYjscbr79KGi345r/+A473HyGKVBmRAL4fKBcdWbK2to7tujrAkUiNRI1GI8ajMSwK1dsgCHEtwfD4iP/hX/5Lfv7LX+LWc8+RZfD4/iHdVodud408i8gzjw8//ICLF/e4evUq3/3ud5lMJqyvrzOfzdnb2+PJkycfy0Z83LEEGURVi2NZqjl1UTybjRPnNkbTE0kFzym2LRiNktrrm4hEMSjoTdLIMGp5cu0+14PnenK9yi6YASCr/xt2VJuOsGRhNaShv1aGTXWUq++8GsSzus7Ur4OCdFbBjvPj0FyPepL40+7TefCnDgqddxaUUlamCwKQctWO3Q10c0S9lpnN2/M8NvtrtFttbK0aaLZauHptC1pN+utrBEFAnuccHR3x6NEjhsMRP373A06OTvAcV/cqUQGNFIJSLJH++rg0c7GeNK5cF6msGRRTVOC4cPXaJf7Lv/d3eOFTl9nff0y31yQvEgbDYx49us/Dh/cJA49r167hWIIkiWi3mri2QyPwKUobx5JMZ2PGoxn93g5FUiCEiwR6vT5B0IBS0u+1cWyX0nawjOurvu6mZifLjfTcNdQPlm2zvb1RTZCiyGmEDdDnfP/efX70o/d48OBB1d8qiiParTZ37txlMBhWTK1t29pNUpnS+J5fqT+CICAIAnq9HmEjxLEd1tbXaLfbXLhwgRdffJHd3V0W8wnD2RQhBFla8Ou/8Wu89fZ3efjwEbIAUa72+jkPiPxPdfx5vL4ZQ/WeaSYQlQjFcNRigY9zyDN7jJk75vFPf8alimP1PFQLAPM65wG5Z+1DQijgIS8yHjy4RyNs0m532dnewXUCTs9OmM3GZFlGmmbM5wuazSbT6YwHDx5ycHSIZVncvHmTW7duVfUssohohA5ho01ewOnpGMtyKUuLNIl4+OAhSRTT63ZJ8hw7aHDp6qform0xixLu3b5NkWfcuHmLre0L7B+fMp+Psa2E+3c/QogctToamWi5cl3qCeEKMFNLToUGsWzbphGGhGGIbYPEQxaSMpHkWYEsVbNqZYsN08kMhVEtjT/iJCHVKqVqPRFq/a+UPXofNvOp3VY19q1Wi067SxzFjCdjLMum2+1y9eoVLl68pE1NJK1Wi1KrQYqywHVcgjCoYj7Tb8/zPBCC8WSsATyJ7we61QMMBkMc12ERLXAch2arSZpmxHFEEIYU0YJ+f40kibEdVVpiObbqDVUWulHuJ+/l9TOfIBWFofdylVjYS0QtDINqczEWq9S0lOeTIFguBIYurNDgUlbFunWkRVGlUtGGQpDnGUWujBAsYeG4Ps1GkySJSZJIS64s8mK5idQnjGWpXha+6wOQJDGDs1PVCdoETSgXFksnSHG8qOQbJqP/acFfXXIgpZKaKTMGpRdXdYIWs2nMTDvjCZ5ODi3bVptefRNHW8PWkHjDjJiFAlRA7Dhu1WB2GbxYK8GY+Z0qODS/FSvfu65q9GgSLWHQqmcsvhViox9rFmqzcQghcFwb17Wr2g9TNO+6LrZjaQRT9ySwbTzfx7Ys7Qi2LMJXiJjNdDrF9wIeP3rCnTt3kdL0DRBVkuw4QQ0dXj2etWnVUft6grR8zvK5skbzL1mE1XFikmWzkDZaTS5dvkwYNrh37x7j6YSj42O6/XXCRoN2p8vW7gUcz2f/+IhFlvOVz3+eMk/57rf+hKPHDyFPmS0meJ5LI2xgWTZRHJNmGVJYdNfX8YMAR2uUbdthY6eB44fMRiNkUTCfzWk1WziWTTJb8I0//Nd88Zd/kec+9TyTYcxsPKPbajMZebiOx3wR8dFHH/HZz36Wzc1NfvjDH/Lmm2/iBz5Xr13lyf7+ny05qn2nXBlNkKGlr+U5c5dzVxqWiYsyQxBV4m7bBsxZ3i80U2kCBMq6BKP+ms8GCgzyuIQ+luyUAGQlfxPVvDas4pLJMsnX04nZU0cNtFH/F9R7nlT6O4FiC2uJX/0zi1WodQlyoA1ezgVV9WShLvs1AI2asw6u59Fpt7l+/TpBEOJ5Hp12g167xdpaH9d1Kye8RiOk2W3TX+vjuk61T6jeSRavv/KqQmhzFVgU5VK+hGMrsMcSZHrDFsIiTVPee+cD3n/3fe7evce9e3cZj8fEcUwUx5TCBEeiGgvm/pp1tWKiSqkfp0x6HEuoRM4RvPn5N/jbf/s/ZGO9w6NH93n8+CEbizX29naxsPjC57/EfBpR5AWnRxN+/gtvgpQ8fviQxSIlmQsajRYnZ6dqPRIe928/pNXa4MLeBYSQPLx/F88PiKOU4+NTrl+/SbO/Rre/jus6LBYKCGk0mmo9sixcz11JUi1rafvuOA6llqbnRcHpyTFbW5t89atfJEk+UxXXP/epTxH4PkdHxzx6eACoXjDNZpP19XU8z6coMmXB3GhUclHTU0gidW1UqUA42+bs7JjZbEzgBwzOBsxmM6aTCSUlX/jCZxkMjxlPFji2Q102VGeTPmkC/2/zqJQUtlJ/GBZB2Kq1yXng0fSqeVYC4zoOyCXLeX5fqhsGmUO9zjIBq79X/d96bLF8rjGJyXjv/fd4+aXX8L1QmRYIaDYDzs7OmEymJEnKYhGpoL7b4Wx4hlnjhsOh3iNVM9jPvP4KeSE4PDzh8PERWR4TxzlJHOPaHv1enzhL6G702bnyHH5rneki4cnDBwBcv3GDrZ1dTodDBoMBXd/izge3KYsEIUpUHaANWCAyliYlywTJsozaBINurSSdQihlUpIkzA8n2DZkeUoWZ6AblNdBFVXSUSBlUQHtvV4PK10a3ziOw+XLl2m127iOQ6PZJPB9bE/1iut0Oly5coWLFy/i+z5SSvwgxA/DCsREGDmbMjLJ8ryqI5JSEkdx1R6iLBTInCZKWpuWBY0wpNFsVqUqcRLjFCqRaraaZHlO2Ghg2zaZdqwbjccIyyJsNDBV5FGs6mLNel8UBSwW5J9AbVRdj0/8yH9PD8cxE1LVexgUtNqshaWLnJfN+Op9YpR7nEmOlr7xClFVG5yUpbItFMvFxBg8mACm0vJL5f4jUC5QlhC0Wg3mM0k0j0iiGM8LlFyG1UViudha2I6HsGysUrKIY+bJGMf18H0PS6LskG3BbDYlimMdjwhs6yckRyuqrWUwI4QOMKDauKrPI0GgGAgTrOi8Qr2MltWXpdF+q/NP63bjElUkrJMmWdTleHW5wlJeV193TfAlhZFT1IKksnxKemTpHi5VwK+n1NLMQb+u/qrOs1ZPpRYnR9lZmsJ8HdiZz2DQUMdx8FxXfa+1+rZmkCRSM4IqER+PJ2xsbCpWZvKkuia2DcrsoX6T6nKjpwvObUsxTrYJzouiQoYsy8G2HT0WBYVcWo2ar/rrVd8bpsK2uXj5CmGzTZIWpEnBo8ePsD1Bs+HTCjy21nv0uk2GsylHx2d8+rXXaQch77z1pzy+/yHInHk8o9npsbm5xWQ8YjYeM52OkWVBFkcsophmq4UlLALfJ9MGAPFigSwKWq2W2iAWc9qtNsISRIsZb/3Jv+arv/grfOrFW3z7T79DnJccPHlEli3Y2N7m8aMjbt6Ycenidd566y1ef12ytrbFaDIhbDZY6G7bZoOqbN/FM2zfzcjXlahVLaAEISW2EOS6EaiyhjauRI5ea3Qyo/zw1Z21HPLcyCCt5RysATVSKsMQUY3gc4lOJedcdegSGtWrRlEJTmFRWJDr+hopdXcQgRob8hwibFGtKcqdEz2HNJtrGWBJG80LC0u4lCXYQmI5ZkKqT6qs/VXdg2kGazsKXDHjNMtKirysGgwqCau6L6W5VwZ4Ecv8SmiTFNuxcWyLVqvF8y+8wFe+8iWuXrtCEAR0Oh263a5eM6Riscql5MSww0VRMJlOODw64vDwgI5GUgPfp9vrMZyM8VyPoiyJo4g8L7SM20aietd5nk9ZFhrVnlOWJZvba9z61K9Vev3FYsHZ2Rn37t3j8ZPHHB0dMZ1Omc3mTCYT0iQhy1WfKIPydjod/CAgiWPKPOPizhaf/8Kb9HpNXM/ixRefYxFNiWYDvMChv9YHCSdHp6yvbfPk/iE//+bXQCjpyv7BiDxNuXTxOX7wzjtM5gleAIOBkiVtb++yu9uC0iKXMBiO8b0G3V4fy5qxteMQNhu4Xohle0gpaHf62j1LjX3HUSqBxWJB4CkHrsf3HxItFgSBcp71PE+fc8r2zjbRdMbBwQGTyRTP81jM5/y//+H/k263y6uvvMb923fY27tAd2ODwHVZTKfYLSXtG5woa+fNzU1u3brF8eFhJdtJkpS33vouGxsb3Lt7j26vy3w+Zzad0+v1K2WEENBr9/j1X/0P+Mf/5J8xnUVqvFmQyRwcBYqYJPnf5UPNHR3zGAt0k/SgkmvXdVWDbscmjnOyPFWrh1CxAYAlSjzP4803P8f9+4949Hhfz0G9i+rtvBRPm1xVa4p2+j0PyimCe1m7slRjmDYJah/M05z33v0RN27cIIpikiTFD3x2dnaZzaaVS10cx7iex+bmVmUOcHp6WvV2K3ptTgczhsMxH314m9F4Sp6X5FlBWkjSoiBsdLh27QIb27uUwuVkMODg8QFB2ODy9Zv019Y4HZwyHpzQskvufvguSaT2lGUSKAFdFlFLjOpJp62xIiml3ktMGwj9XDL2Dx6j+qhZSkqXlzgoENlxHEI/oBE26Pf7ZEVOu9uh0+ngui5f+9rXmEwmPHz4kE6nw9raGltbW0iprLODIFD3y7YrB1HLspjOF8x1a5xOp4sznSpQU0oajQaObZOkKXmmamSbzSZ5lmlVjDL/yTRjZ8zShC/Is6xi8kxS0263n6phiuMYx3GU3bdlsb29TZIkVWlGpl+nLhmtGsj+GcxUfuYTpKIocd3loKw7zdQ1jqvuSHW99xKFXNWHLl/DDGqDABh00qoKdFVBqNTLkbDU38pCuXQ1dLGZZdkEgYdtOcRxtFIjUKfs8zwnK3JCz8WzPRw/IM0yilISpxkOEEcRUhaq43Ohiv+NBe3HJUjPICGqkzXBsayduwmADN370w4j6TLXq6yCQUtXPsvawruUkCyvwXnK3iBK6ORz+fOKREos0wr1mvWCU1mZZlB7TPW9frKUUvXC0EmQEErbmmdF5RAoxLLexKA3TzEwonY9a+9XZxAGg+GKbLAsSyVTrFl0m0T0PEK3EsSKpTTHjF8lDVKBp9AdSlbOnWcPgmoz0wCDBC5fuUIQNjjYPyDPS0ZnQ5qNEMqS2x/8mCjJ2bl4keHghF6nxaW9Cxw+vsd7P/oBZZGzWCzo9Prs7l7Eti1OT08YjUcUeYYAHDdnMZ8Thg1KWRJlBUkck6WpQnul0pHv7u6SpinT2ZRut4tnO5ydHPHO99/m05//ChcvXeDhnY+I4gVJNGNtc5s0zbl37wGf/vSnCcMmD+4/4lPP36J11ubS5Uv8+P33zd2vzv+ZLJ0eeyaZNmPDuDPKQjHIah1R/aWEpa1GywJLKDtS33dpNEP6vQ57Fy9xuD/kzp17WlqpLcNra0D985jEyDAKhnm2LAuhzVOqRL+eOVTnViCtAilcBMriW1DiiBJLCqR0l+i+rie0UWNe9Z5RSbPFktUQVoHjCi3FaBL6Ia7tE4YNet0WrVYL27GVhNZ2tEOfi+crICkIA1rNFmEY0u/38f2As9Mx9+8/4P6D+9y7d4+D/X2GwxFplpJpi2oV1IkqyXIcG8dViOaVK1f53Juf4/NvvsmFCxdwPZcojiqGpyzzSgJSliWObSvpla43siwLP/DpdDtcunQJKSVRFJGmKZPJhCzLODg8ZDyeAMrIRwWXRlZrVZu/uUe+7yvJXZFxNjjBdV0GgwFBEHD5ykVu3LyGYa+B6rkmsDCWvGVZslgsqiCySFNkHnH50h55kbJYzPj93/t9vvLVr1DInMl4wfr6NlevXOH+3XuUuc1oMGdzY4/RZIJlWXzquZfxg4DvvfU2+wdn3HoO4qzk8rVbNJttZAmtVptmo4UUDv31Ga1Wi/l8QaPVB6Dd7mD7DWzH03teoUR/hQIXs1S5VLmOQ1EUnJ2cMjg9ZTQcMZ1OSXUz5yxJKYuCNFZ28L1Oj1ajRRAohuCB+5CjgyN+/+j3+NGP3qPf77O3t8ejR49UjaTvY9sWGxvrbG9vc3p8QhKpZupPnigg6otf/CL9bo+To2OuXrnCcDgk9APGwzF5lhEEAZPxmHa7TRLHbG5s8pk3XuePv/FNxYxYLhJBIUtkmevk4ZOj1f82jpX9tPa9Uo2oXjtG4l+xYmWpjTrUnLMEuI7L59/8LC++8DzbO7uc/u4/J5pHaARVA5HLfbBuymTkj/VjFYBiZc9cjcUUgGRYqCxL+eijD7l8+TKOazObzRUj3OnSarWZz+farS5+6v0NgzaeTNg/PFZOwokK6hXQ4RK0O2xvbbG+vonjekwXCadnx0ymM9bX1rmwdwk/DDk8PCCajnBkyoPbH5AsZrUaTX3dxRKIXJHVnb9H+vwNqKqAV8HGprI3D4KAVqvFtWvX2N3dZTQc0mt3aDaaFWjiaaVLgcQLlPtpWZb0+33CZoNOr1uVRQB4rocX+LUWGy5ho4nQ4IkQQrdpSJnP51UvJSEEo+GQIAiItAwOJKcnJ5UCp9/v4zsOBSqpNqYPUsoqiTGJq6NlcqtxoIqxZ7MZlqXM0cwablxdHd1zcDKZVK8RhuFKa4xPcvzMJ0hCiAp1MC4epjjWBB9mAzQ/1yerSaLMDTA3ygxqEwRbNVTE3FiTzaK1m61Wk7OTM3zPwbKVo5OwLFzXIQg8Go2QojAyCWtF27x6TlAWSnbluR5r6+vKpStOiBYLijTFcx3N1giSNNZs109OkFhZK8XK7+s/fvIBVi4DSFHxMaAlSOsb69y8eZOTk2Pu33+gdbIqeKzQaWmCP4EQtZovWWJyheq8jPTEyDX032QtwVSaWB3Y6pOr9ylaMowm8VvdNMy1qyfc9d/XZYPnUTIjCaov8PXk2zzWTHwTQHmeh+Uo7W/dKvqnH8+uJdJ/+jc6TMIZBiGtZos8V4nOcDAkyzK6nTaj0YjT0zMGoxlXb9xkPJnyxmc+S5ZO+dE7b5PEEVmSEQQtdrYv0ev1GAxOmU5nVc2RYztYtovj+3hBQOj7CASNrMFoOGIwHFLKvDJN2d7eZv/ggMViQavVxLE97t69y7WbL3DtymUOH91ja2eH/ccPlYzGtnn48CHPPfcc6+vr3L9/nxdeel67HO3w/nvvVwmoGUfLJOMnXR9z3UFKQYmtxqkqZsOySxxH0Gz5XNjd5NKlPfYu7LK+sc7aep/A95lMpvw//v7vrIyrQtucGhTbHOclPHW3tvPAytNyFw24iBJpFwhcLGxsUWKVMS1PKimvVNuEYzsqeSgEaZbR6AmEHVPkUicCKqlxXZ+w1eWv/ebfUnKNZptWu41aBy1CP8ASogKRTk5OmE6nuK5Llqe4rkuj0VC6eg0yZVnGzoVdfu6NV9SmmKacHB9zcHjI+++/z3g6UTJWvRGur61hOw5hGNBoqFqTfq9H2Gjo66dYskajUc1V4zLoum4VFJqAwCQjsNTlG5TTIJZJkpAXZVVAbOZ15ZAKVYsJ8xqm/tISsgpQer1e9fzT01OGwyGLxYKNjQ1arVal//d9v3o983gDzi3mU5Joqly5gPF4SHftIVnhcunydS5efo5GEGLbNp3WHCEln/3Ml0mzlCdPTnnuU89hYdMIOrz++ueYTRNu3HiJra1tBURJget4GliULKKI9c0dbNthPI348MM7pGnKZz/zWTy7IEsjyrKoaucWiwWz2ZQ4UYXy/V6PrY0NyjxnfW2d7a1tNjY2KsDJ7KcbGxvaIGLpTnjx0iVeevll5rMZb731Ft1uj+PjEzY3N7h+/Rq27XDt2jW++91v0+l0uH79Onfu3GE4HNJsNrl27RqWZTEej+l0OgDM53PyPGc8HuM4Nvv7T/S8sjk7O8N1Xfb392k0PK5f2+P+w0eUcYnn2mS5oKREWhbLvk7//h/1tUbt5Arg9VybG9eucu3qFcLAZ3tzg6uXLnL79h0yzaI96wpU0lOebgPyVPzBas++1TVtFTgtioJ79+6xubVFr9dnPFZ1SKbebG1tTZk0JIluMp2SZTlFoj+rZTFeJHiej+OFNIOQTqdHq9XC8UMs22WWJIyPB0xnc/wg5OqNG6z11oijiMP9RxRZTB5PePjgNnm6qGKNZ13TehnFU3GZvtbnr4kQgt/8zb/Jiy++gBBC1yCpWLbIc2bTGRsbGwRBQBzHzGYzsjij2WoymUwqu2vDnpo1yrIsgiBgNpsBEIahBmZVrBPHMScnJ9oUIqgkfiamNvuTsgc3Pf2WPZWyLGMymRDHSikVBAGNRqMiLtTv1fPN92VZMhqNCIIAKdU6GUURrutWAFGV5FpKIbBYLKr6UONUXblK/xmOn/kEybZtkiSh2WyuBKvnC9ZN1mprJMv83mSy9QzfbHr1oKSQJa4tqgFiepMkaUIpYTqbqkQo9HAdm7LMtf2gRdgIlU6zyLBtU+iv6oVs7IoBMJ/XdV1sS9GvWZZSZBndfl81+ZrP9EBXmnXXtbEdiyiaf/wCBHXVYXUsH/Ms5LyG7iCePbmRSJlj2Q7IkiAIuHT5Ms899xw3b91ge3dHTTA96e7fv893v/sWJ0enqmhPSpQcfXnd6wyQbRs0Qd8raiYGJhcDhSzrhMhSEDdGJ61kQVTyKaoAdzXhqd5f64LryU+9ULp+bZ+J9mtk7lnXsh7cLtlMLcHTDNJ5pO3jDsOOmTq6FUMRuSykfdbnsKzlNXjm5i6h3WkTJzEfffQRslSBnI2N74WMizlCqBqANIoIHZsLW2vcu/sR+4/vQ1lQFiXb27t0e+tImTMcDLBtm7X1TWVGIQSu6/Hciy9w8+ZNOp0Onu2QJAlPHj3im9/4Bh9+8GPlmON5dLpdojhW6HsY4DguizTjh+/8gK9+7WtcurhHFk3Z3d1hPJ4wnU6JoojpdEq73ebBgweVO1ej0dCGGIoB+qlHbe4YQMAkSUJYOK4DQtU2uK7ky1/6HL/6l75Oq+3TaPjkeVE1TM3znD986zs8fviIetf5ypjk3CZZv2/Pup/Pmpd1xhuglDbScrGkhS1SXBa88Hyf3/qbX6PZkpRSGUX4vl8BAmdnZ3T6HdI8ZzScUBYW3c46srS5cuUmvbVX2Lv4CtEixnZ9hK2YnVIW5GWKYztM5wtOTo6REtbW1qpGwKpxtWbv9fz0bRvl1pdTloK8SFjb6LO1u8nzLzyH46n6v9lsxng8JtCtB5IkrmTWUkpGowGNRgPf91WDQs+vGg+GYagQ0NGI09NTslpCaua1YYYN2hkEQa3+p6TZbBLoxKPVatHtdqvAZbFYsL+/r1tPxCRJwnQ6pdfrKhdM7cgUx3GV9Fy4cIHd3d1q/pqkwKwPqkEkFZhiDsfzaLa3Mc0Udy5e4zf+6iWVzKUpnuNgW5YCIoRKRMvcocgL7tx5xAsvvEa/30eWJbc/fJ9HDw9ZzFM8r0kUJ5yenBFFMe1WRwU4heBf/dN/hhCCz372swSNFt/60z8gbLbJ8wypkeOzszNOTk64deuWTihVnUE0m+MgaLc7LDRAZBq5LxYLNjc3lZFNmuqk0uXu3bsqwet0yPOcx48fc+PGDaSUXLt2Fc/zePvtt2m320iZ80u/9Is8fPiAb3/nT0FKJtMJG+sblYHRk8ePmc/nOI5Du91mvlgQLRbkeUGW5RoVj/F9nzRVDazLNGNvb4ter8P7P/6I6SymLKS6nqV4au2vH88EKf8dOs6DgysMNmoPcR2bn3v1VW5cv0ZZFIyGA+bzBW9+5g2ODw6YzuYUUsl90XvSeVVFfZ88D0Au91+58pjl3wRLw6PV63l0eMh8HrG9vUWWZUTRgjRN8DwX1w9otDv01taxbBtZlhSlqhMoLRvhuPh+oNdcu0oQRrOI8fSENE1pNJtcvXadTqeNlHB2ckQSLbAoGJ0ecnr4GIoEiwLE0wxZ/bqej3Gqe8DqOm/2gCtXr/K5z322AoQMq2ySm2arRaPZxPNcojgGIWg0m7iuS6fbrZKKPM+rhMUwLFEUVczRfD7X61GPslRrXr/fp9vtVooWk5AYBtusUYpBtxmPx5Wxg2HUlVGNSkjH4zGz2awCjoRQPdGaTVWneD5Zg6VZmZSyYp9s2+b09LRaN8zebiTxRpr9SWMo+P+DBKnQdQr1xclQdmbyrTRJqy0C5kbXTRvMBTYXuUqmJCs3YtmnQ0m4+v0u/9F//FsMB0NkUfLtb3+HH7/7PkVZ0miEVQ8lZQ9ckOXp0p6cJdpi9PD9bk85c0hJmsaMBgMm0xllkSOkSSJUIYRK2LKqEd+zEqRn5Ecrf+OZ8iJdVClXk4DlIifo9jrs7e3xyiuvcPPmTdbX13VxrnrDLMsJQo+Ll3bZ2l7n5VdeZDGLOTo85tHDRwyGA+bzOUVeKB16lpKlKjlNs1TZRqKLoku1eBTl0pff2N1K61zTU4F29QPVl+VZjNrSrbBaqKVqvFs/z/MbXz2hNT+bhNmxLYpymVjVr+X5gPdZ5hx1uVz9sc9isKRUtSB1B676c8z3zwqwFQPyjE1Sy5gajQZxFDNbKPeo6WyK5wc4jscLL73MIk24cvU6ZQlbm1uQ5zy8d48iy8iSiHa7S7/fAyE52N9nPB7RbDaVi10YcmHvIl/4whdY215X0s5S9QtrScnG5iafevFF/vD3/xXf+fZ3KMqSJE1Z21hnPFG9mDqtDq4Nh08eMR6csXdxj4cP7uEGPi3jKJnnDAYDrl1TMqajo2M2t9dwXVed02S6Sp0+dY309UTbpMul3M0U3Sp3xALXs1nrtvkbf+3X+cxnXiEMHEpUPZUsCiwJtu3iOx6vv/Zz/P7vf484WbXFNwja+bHyrKSpngw/6+fVw0FIF9dKaLkzvv4LL/Mf/NortFsJZZlQSuX+KCzVNLosSzrNDmlZcjIYIUTM+toGUTQmz+D46B7jiUWvv0ueWWRRRNBs0Gw3EAI820NIxRI3Wi0cx6HT6+rztKu1Lk3TStJn+og52jnOD4OqiHcwGjIajXAcpyanUi5wrVYLIZQjqArwLB49esze3h5RlCKsBQ8fPmR9fb26zo7jqASw5tRk1ALm+hn5XJ3NAxiNJxX7axghE7zYts3u7m41R02wIKVq1mhuY93Fy6w/dftvs1+ZhM2sw0mSaHZFMbCzWVR91vlcdaFXP/vIoiSKUlyn5MLuRf7FP/9nrPXXiJOYF194hR++8x67u7uMx2O+973v0Wr1SJOMO3fuspgrM6HFPOLb3/oOV69do9EIuXb1Gvfu3eMP/+APFTNz9Rp3b9+hLHKazQbHh4ekaUq73ebb3/qWlm8pdcf25hZFmnH50iWKPOfJkyeKAWw0mM/nbG9vs7e3x3A45N1332VnZ7e6Vu+++27FBGZZxksvvch3vvMdjSY3+bmfew0pJe+88wMODg9YLOZYlqX7LkXVPT89OyHLMtbW1hiNh7qWTUm32u0W4/FYzy+PsiwIQx/L8iiKHKTgtVdf5qPb9zg4OkFYDjItkbZVySL/fT9M4iKlBFniOhbP3bzBzRvXEQJcxyJLEmxKQtfm9dde5o+/8ac68bBUTaT19DpUxRE8HZtUQGHt8q2uYRpMfhYIZFnMZhPm8ymbm5sEgc9sNqMoMhZxgu2FKy6H1eEJyjwjyVWMmCZFxZQ6fsDW9g6tpgJZ8ixlcHpMEsW4FuTRlMMnD4jnEyxRKCaRVTVKfX9f1qCu/s0YldQPsxb0ej1+6Rd/USdwiuE2Mel8Pqe/tgZAnCWMZxMEgt56XzHgllUxL77vM50qd8b19XXd/FsB2fVYVrG3S1DIxKBmTTRsTrfbJdRmDVmWaRZe0m63q3XKkBVqLaVKeIz0zczFy5cvM51OK+DQ9/1KRmzGoWH3TaK0WCzodruUZUkcx1WCVZeIJkmy4gr9046f+QTJtm02NjaQUjIej1cSHoMM1iUQ55ukmoFrNj0zEM+7tNQlfPXJ1mm36fZ7HB4d0W636He7CAFXrlwk+ku/zP37j7l85Rr/8l/+K4oypyhKykIVTZqib/N65r3zPMe1Hf7Dv/VbREnMH/zB/8BoMiFLU9WktJKJGcMJq5IomATpz+NQVLtKhAy7Yls26+vrXLx4kZdeeo7LV/doNlT/GyXRyZGyAEtQlEtmrihLsjRVjFuRc/PmDZ577hZRFFXJpilonkwmDAaDSnOqUNKMaBoz1ZrTs7OB1vunzGbzlcXdvKe61yWSeiKydLuSKGWU0ci6rkucxNVzzydHZoL7vl8FKkqnm1TnkGU5pngSahvAMwLXuhmAQV3MGKxbs54PkM3ridqG9JOkVucPKakC/KfOT1+ZtbW1CoUqioI4imm1WviNBuu723zplVfJ85y3vvNdXnv1VebTKY8fPEb5EEh6vbayCj7YZ3R2rNzEXIXsXbp8ja/9wl9QC6lVkGepvlaqCZ6Spgr+4q/+Ku1Oh3feeQdpqRq0ZqfN4OyMwG/guA7xbMbD+3d5+ZVXCZpNMn0fja38cDjk2rVrNBoNzs7OuHLtIs1mk72LF3n/vfdWdPP1ZOPcTMAwRmbkqHsAUuZglVy8uMt/+V/8p1y6sAVlimfbRElOkZdYeMzGc1SjPkmvtcmli5e5fffBSi2d+fqz9Fn5OMZ4VS6T41op22uCv/lXv8znP7OHLSZIzX5bTgAyR+ZLZ80kiiitkPlU4Npd8sxDljaz6YxWA2aLQ777nX9Nf+0i40nK3uUrXPD3KMiRtsBzPOVEpO9BFMU0Go3qs2V5TlEqpzFXJyF5roCRKIqZL+Y8fvyYvb2LdHs9tra2sCy76s+xBLUkSZzguC6e52MJB2vTodtd05K+jOeff75a9w1D/+bnPlc5nBkXySAIVqTTJlAwQYHneWxubSNlDThjtebCrOHm+pv1y9JrQp7nVVBgnud5XiVBMUGSkf0BtFotxcJEUQW0GR1xURTMJzNcz2F/NNDOmx7xQjV6zNOM4WDIRx99SLvV4qM7t0nShK9+9WucnZ1yfHzCnTt3uHnzBvfu3WF//wlxnPDSS69Q5AXtVsDp8T5pljEaj2k2Gsgi53D/CRsbG/Q7bQVgFTlhq8kiWiCQbG6sK1Q/jun315hPZ/z4/feZT6d0O11u3rzJd777XeaLBdPpVNszT3nw4AHf/e5bdLsqof7yl7/MSy+9VDGA0+mEosx549Ovc/v2bS5e2uPwcJ/hcMjxyTG2bVEUOfN5TLMZEkUq4ArDkOef/5RugBlXAeFiscBr+fh+QCkL9bPvAgppbwQBru+q+pSwwcWLF/nw9ke888N3KXFIs6VE//w68u/bsUzYLcIg4MUXPsW1q1fR/BBpEhPN57i2YDoecOXSRR5cfMy9B/tKWF+W2JVeYzUZOn9N6vuV6hVkPfNx5nfP3D8FKCxScnx8BEIF4q1mCzf0iNMU27aJklSVSNgWnucTBgFh2ABUaw/P9bFtF8dRzc6zLCNaLJiNBhR5iufYiDLhyYP7xLMRFCm+kBRICqAUDjZLANoAmR+3f9e/Nww6LEHyv/JX/gq/9mu/xngywNYmGvXzn81nlDoWyfTaNVvM2draYjQcVnugkac1m03CMASo+kKZNc6wM74fVIy1kb+Z84iiCMdxFGgax0ynUyzLfC7Flhv1gWlpotgqv4rHG41GtZ5ZlsX+/v6KRM5IzE3C4ziOYsqaTaSUVU2VictMvG6+hFCy3oZ2sPykx898gmRQYljau5rJZ3SUJljN83ylmB+WFG/dNcVkoGazUuhuyHp/ndPT0+pvxgbx7OxMaek1IpWmKbZlce36NV56+VXyXBU7bm5u8u6P3uXx4ydYFppBEitW0iZQth04OTniv/h7f49f+vrX+ft//x/wB3/4h+RFqehcuTyPUi6d56idX7WR6kWEeom+QaZryYJ+JmpBFNUEdl2PjY0NXn75JW7dvMXGxga7u7sUMmEwPNF2tVF1vVQg7BEnqkg2SzPSLKXIc84GA9JFzvb2LgIYaV14nucVspFlGa7r0uv1qnqBOI4pOgXu1asAZDqpiaJIaWbjCNdR1xEhSHRgYts2YTNQSHGzSRCGrK+v0+m0cT2fza0t3n77bf7BP/gHfPaznyXPc/70T/+0moRmfHieR6/XZW1tXRkFeB5SSo6Pj7l//z6+73N2dlbJ+sw9MEnQsxD/+pfr2LSaTQQC13ExxhE/6ZBoxkeu2h8DSEtWj3rmM88lRku2RCW6m5ubTDWlrqh1NacKAc1OBy/wmQ7mSAHNdoOH9x4RLyKKrCAMAsqiYDYbMxgOSeOYRtjTxbQdfv6LP0+z2dLuSiXCtlQjOiGQQlnm52nKIlrwuc+/yenZKcPhCCkLur0ug7OBMmdx1CZ5eHDAaz/3Gmvr6zx88ICu71ddtYfDYTW2zs7OsCwb23HpdDrL8z53nVcTWuP4BMb/oP5wSUGRpwSBy2BwxmRwQryYEUdzRqMxaZozncw4PR0QxwlloYxWjsYzjERSWKK6hx93z88zSec/Z120IYXyvRMCbAtcO+fGlRb/0d/8ItcvO1jyFFFK8sxGODa5VJukGbez+YyykKSlakA4Hg0o5ZAwaJJmEccnj9nde4nR6ISf/+Iv0OnuUuBQCokUJZa0KLKSLCvwvJC1NdXBfTSeMJtNASo5xnw+1wFyqwKm1AadsLGxjW0r+37bcrEdhyzNsS2BHwTVek1bOZiCSlx6PW1cou3RDdNjmJmyLEnimI21dYQlqtork7RU8hQNdhiQQBqVQVGQFwW+57HQ9t95nuN6Sr6daidGiQ5i0ozZdEJZFtV6lmUZYRAy12yH4zgV6wkqKTIIq+d57O/v4/s+URSxtraGQDAbz3AcC893kTInTubs7z+h2WohpVCfIy+I5nNOTg7wvD2iaM58EfO9771Np9NhOBzSbiskdjGf0m2FrPc6jAfHrPXXuXDlIg8fPuJ4cMpoMuHo4AnNZpNWq00aLzidTEBAUZYMBmd6zVPXWcnlQhazhUL285z5dMbnPvtZDvcP2NreZjqdcnp6yu/+7u/y6quv8v777xOGITdv3qDZbHF8fISUsLu7Q1Eot7v5YspwOCDLUv70T79JmqZauilUnW+eVy5ep6enNBoNJpOJ6p2ig8MszSpToyxT96vf7yGEaqrZ7XYwe2Ycp3i+p5q15wm3bl5jY6PHd97+Efv7x1jWstjdmLUob/7lxHx6lv7bP+r7Up2Z7nQ6vPm5N+i0mkTRgrJwCDwPx3Xo9bqMzgYUtmQ0OaLTbuN6LmVWVn0Gz+NLz2LFV2pFpPyJF2S17leBVYbXV/trqTYCKcmylLPBGY4fsbaxQ6/fo8gLkjQhiRPSNEHOLFrtNo7jAoKyyBQgJCV5miMluLaFzGKi2YSHx0dEizmeTLHKDCGN+ZdAYlMq6xtzMpWTW/XZoNo7VsaAZSH044zFf6fT5tZzNxmOBmRZzHg8rlQ5rusosN+2SHSMNJ/NdeLncXp6iussWxMYkmA0HJFluWKf+j2dgLh4nlvVMAlhcXY2qGJnx1HvZUgGy7KquWTbdlUbnGVptT5OJpOq7s/3fZIk0fJXRV7M53NlO67Xu/O9ucyYMOCUAajq9UuNRoPZbEaSJBXLlaZp1fPMME6f9PiZT5DMpndeziRLKHLVzVgtAiWO7SGwqhoRY+ENFnlubKgLikIixJJJEkJZJZ+dnVU3yRS0pWla1SRZlqXeU1hkeYHtehQUnA1PaXcbfOGLn+GNz7zKdDrh8PCQwXDAtWtXKx0lUDXWkjLj9OSU//Yf/UN+7S/9Bn/7P/kP+dPvfJPFIiY3rASCpV23jXaG0KuxYn+k0NIgSRWIGmbItm0sqWxAbcfB9Vwc28a2Va2AsATrvS6XL+6yvbVNt6uCyrOTI6L5hKzMmUUKGZ/NZ0iNNgRhSDMMsSxlVGGuk+3YNIMWLV+QxhHtTodrVy5rqYOg2+3SaLaqbthAVYBnWRaeZRNHyrUvSRIi/f1kMmE6nbFYLGpUcKDYxc0NglZAu91WLlqeX+l+0yQjjTKGpyfsbm3yW7/5N0jTjLsffkjYamDrmoe19XVdOB3gOq6SFKBqTsJGgOc7hA0fd2qTFhlFvmR/DNJS34gMS2QCPNu28G2LXrOBK2wcbHJylO+fbuhXW1grNkxo+aO1rLmDZa1VWWZLFu1cXdSzJFwqwbKQlk2UZuQSpBREiwRZSCzLxrddAmHhIyjjmHYjBCEZD0+hyCjLHN9vk2U5Z2cDovlcW3PPCcOQl158jvW1FlgZlCWOZSGlhbQFWVlSoOQdjmNrSSW89nM/x+/93u/hur6SYTkeSbIgCJS1+mSqGkmur/d5ePcOFA5ZmmFbNosoIity3MDn8OSIrBSUwiZKc4pSMYpI5URX39mXCSeAAj6WdUeCstTJSSnwLJ8H957wf/u//t+hLLGFTZErdsS2bRqNBs1mi253k+3tLVzXI+iGPD54wh/90R+TZjGWH2i5nsRiySzWE9/zcsj6zxYSIQoy6VNKH9sGT0Q0vYgvvLHLr//qC7SaGUU0p5CZ6oIuJDLPKYscaZUUFCRZzmQekSQlaZIzGqYsFjlxkuK6JWGjBV4TWfZ46cXXiRYlQZjjeA4CG9vyEGWJ7S1d3UzxrAIXeitF+ULY9PtrSKnqB2WppDN5nlVj2rIsLAG5lnKZ5s2OY6lgRECJGjO2ozZNWyrAKggV+yKAssb6eLZLPE9wHZtcpDi2TVnkpGmiVlNbOUFGNXTUsiymkyl5UTCfKzvuixcvkufKTCSxqFDS2WxWBYKDwaD6XtVZqfk4kOrxo9GAoiiYzWZVoKCCBJvRYMTm5ga9Xp/9/Scq0YgXhEFAt9vD81zmsxllWdBv93D3bE7PVB3W7uYuWZ7z+NEjHM8nLyVvvPEZJtMpm5sbzOdzskxJUnzfxrYEeSkZjYdEi5g7d+6ws7NLluU8ePgQVYta0u12yPNEry8wnc20cUaP+XzOeDyugDJkwenJEUJYTCZjms0m33n7O3zhCz/PCy++iOO6bGxt8kd/9Ef0N/p8/Vd+iVazxXwyZTYdc3h4yP7+Pq+88gp5nnN4uM88mpLqQMgSJc2Gz2Ixo91u4zgWjbClZHFIOh0ln1zr9cmSnEUW0V9bYzFX6Hoe5Ahh4bk+o9GIbrtHKUtcxyGNM9bXuyDKyhJ5NpsSzye0GwG/8OUvcPveA955510WsiTLjVS0BBmjbK2tc8nRkmH5d+Gor/2u69Jut3nh+edpBAFpvCCNY2aTlCxNyQsVWyRZSZoVlCgX4WarTabVO6auEp4G+J6VJNm2jbCX18QoPIzCASmQMtOvKyiKmpmDtKC0sHA0WKh2SkeAzHLODh4xOt4nDPX6GzYUUxQGxFp6ZtsO6MQ2zVKKOCGaTXVCHenPUWBLkEJQ4IAwTr0WtgBLghBLJqMo8nP7R4VmY9QH6hqUWFj63CS2A5/+zKs899xlJtMJRZHT6bRZLGY8ePCAbrdLr9fXTEkTy7UI/RAEzCYztre3KfQeLAREUcx4NMN1fXxfYNseWZbrnmElUiowoygkUBCGYWUUJISokhyTlGxvb1dsu4lnFouYxWLBzs4OnmfT768ThmEFSiwWC+a6pcbm5iZ5njMcDqvExhASJrlRc9ipGKwoimi3lTGU+TxA1YzbMFSTyYTA1wqA9H+R2FVHnj/dfbwsVEGeQQ4VsgNmcNZRfYMoGqmFmbj1pMtQfFLbUJsBUq8XqTveqQzc5ejomP5aj/5aj8l0jEQSNnx6/YtsbW9WmXddaymE0EWvsLWxxWIR849/+7d59ZXX+fTrn+ab3/yWQhukSXRsSinJClWYixRVLYsJwj3PIwgCEKp/UrPRoNfpKjRAWLieh+WpoNJxnerzF0VOp9kgi2PKImc0GlVN9vLcpZAlDW3Furt7oXJ3chyHZiOgEYbKWabfx6t1oxdCKFo2CNTrWUsnFCVfKVfuiZGkeJbF2lpfoSh6kVGNWx19/XNcx6WUkmixQAK261Q9WQyNa4q1ETlxkrC2vk4Qhty6dYvNrS3u3L3DV772VdrdDv/Nf/PfMJlMqs+da3fBNE3pdru6Qa2oFnslFVjWvwEVI2mQkfqYE0K57DUbPu1mE99rVP2NKslV+ewalLqhhEFN6oyCIkdMcvQsk43lsVy0VfPLKIrorq0RxynzqUK5bUs14hUSyjxnPp3iaRRnPp9BTco4Go4Yj0ZqLkm10OVZyvXr16iaZ2EaMFuUQOB55LmlmmcWBZYQpHHM3u4uvusxn89ptzs4tkWWxEtqXUuPmrpO4aPbtzk+PmZ37wJlos5FWBaLRURWlDiOR7fb00Hw8vwrzu08wlkxbnWpnb53wsFxLNqtBp//3BsqubMcGqFyI3vppRe5cfOm0sj7PrbjMJ/PSWTCw4cP+cEPvs9gqLqKO5aqV8nyHMsSK2tVvai5Ls2s7p0QyMJC9b8CIRas90v+0i+9wZuvb2NxQpordFuZn9gIoeSMeZ5TSMhyi9lCMhxJ9g8mzKeSyTjB9QJcL6DV7rG5dZUvfOGLXL76Eklm68B3iuXE2K5HEDQQWnIFCiDxfK/67JUTk16ffF8BFpZlY2GMVUDYCkHM8lzVjTo2nkYTDaNX5EvHR8demt0Ym9o0SXBdu3qc53kMR8qitkgyitS41SnZmmUv55zjuDSbTcoiZzZNdCF/xsH+PsISBEHAcHAGsqTRaGgpFywWc4bDId1ul8UiIgyDSi6nrIeVdbiUkna7QxxHeJ7LYj4jSxMcWzVWTdKE2TRmrd/DtmA6GbGzvUXUaVfOUvtPHlGWJd1ulzRNGY/HRFHE6ekZzXabaKH6NKk6BGWbm6Y59+8/4OjoiJs3r1f9R07PTsmzhG63Xa1lSZLw9ttvqz0WWwdXDtPphAsXdkEoibeUkkYjJMuUfG1zc0MjxjMaoajQXc9zGY1GHB4e8id/8sfkpSTPCy5dushf/+t/jQ8/+oCDgxHDwYA0SlgsImazGb7v88MfvoPnuUynE5qtQO2ROllTCZml3q/RZDadVkm5EIL5TAWJ85lSlOw/2a/Wc+OgJWVJqgMr13VpNpUE6+DgCb1+D8tSgW+v19OycIfpbMYrz9/EpuDe/cecnY1YRAm2LSgKtLuqpJT8xFrHf1uHOX8TDK+vrxMEAccnJ5ydHChWRGg3XqOAQEnKSkRVs23Zym4/z5fOkB/3fs8Ceup/P/8zQkm2q7YGQrce0cnGsi5UAY1UwFKBZannLmYzZpNplbxJS1BqZYBtW1oRoJgfqzR7ExoMU6+ltRXIClQ3ALXElDso513DIH6SG6CNaooC2xZ86Ytf5C//5V8nSRQIf7YY0m6HmlG9qUAkS+D7AUVRaj1QSeAH2FYbVaslyXWde6/XVeqlEgaDU93cvsXJyWmlrGo0GjiOw3Q6reLYOI4rNY+p95RSMplMqvg3TdPKEXRvb0/LX6dVzaaUklarVbHlvV6vOm1jsGDk0p1Oh6IoqjpDk6wbUxwTl/u+X5lNAFX9ZxzHtNvtytAm/V9qkJaHCTSllMxms+oiA1VviRXpUama+Zmg3NR/mO7R55MmcxSFMgZQhXuZomOzTLMJUGj5XqfTYWNjg+PjY8IgoMhzHh0dEoYhmxsbLBYLTrUUK02UTrzVbitXt1JWaGOv2WY8mTAaTTg7G/E7/93/mZ2dXXrNDvN4jqkWcRybjY1NWs0mEgibQTXoTYA1Go3odTs0Qo80UWhp4Pk0GiGu7dDstGn2unR7XQI/INDsiyUsmmEDz3FXeoUYTb7juUixZC8Mymop6gjbVjVEpgbMJEb6QlfNwOIooigLgiDEdbxqUtbvsRCqKW6z2cRy7FoymYNUsjbLcUhy5WQidBNKyzaOfxa27ZCmytdfFX17NFttclly7eYNjs5O2dzd4W/81t8kWqj+O91ul9lstpLwGF2uSTxNIur7PosoXha6stR1mzFVLwQ3NQiu69Hv99naWmcR53ozVhKd8xtKPUFSDeXEyjWqgmbrJ7jU/ZRDCIt+v4/tusRRoueXSvCOj4+5e/cuX/zKlwmbjeq84nh53iYhdF13pV7E8zzCUGmdSz1nizyv5JxprhD8NM0oy4JoPtWJjMX62hoPHzwgTdIKg1XMo9og0zSl0WohkUxnM5IsJdXF03EUg4BcOye6NcdAWWv2WAUB55DOj79OwohR6ff7/MZf+XUu7e2wsb5OI2hguS5IwSJakOc500VMlqsNYzaf0mw0+Atf/Sr/n9/+J5SFRNoWFhZ5qSxUz0s86yx5fYypQMLGshws28J2Crptm7/+l7/Ai7c6lHKEFK5OSlxyXStgzE/m85TRKGaxsFgsfB48GHN2mmA7Pq7fJs4suu4GFy+/zq1bL9Lu3iRobBAgyfIC1/MoSollOxhr4FJ/Ls/3dJKv2EI9WBVbJCW53iRd18WSSqqVpim+5yGF0F4vguHZGWEYrtTqWJal1uGiJIqOVc1Is4nU4zFJYvI0IY4TTk9P2dzcYDabY9sWgR8SuD5RpGoIkzRWvw/U2mMKk401+FImMqvYkSAIuHv3DJAkSYqUReWg9+TJYy1DUYXRxiq30+mQZalOeEvyPCPNImUqJAvyIiVJFWjgeQ7vvPMDtre3q3YAxvXJ7FmdToejo4PKEOLRowdMpjMuuKo/iZIrRti2oNfrcnx8ysWLFwnDgHfffQ/Lgv5av9o/p9MxaZrSanY0Ehwyn0dQCr3Wqd5Xi8WCZqtR1QYdHx/T7/d10KkKzRuNBkUOvh9UJhuTyaRq/vyPf/u3kVIZJLz5+c9x+/aHJEkEqIaSruMihMT3Xc1MDen1uyuNJk3QZsC08Xhc7fuLxYIsy5hOp7RaHdIkr6yFTb2y2o9K8iLH0Um5lDlRpPrruPqxSwmQoNPpEkcRm2s9FvM5t65fYXdrk/ki5qPbd3n48BFRapMVBpz6dy85gmWs0263abfbgLpmeZ5DoRopG8m42cfKsiQvpe5qsFrLrdakn/6+JuZ62snu6TIBA1zVH7Nck0sQdXcH/Vyh2GghpAbRFNtjZOKK5dcam3y57tsGBBOKKS11DyiT8EhRViyQfsPq2ijWqFz5/B93zVfWbdRnazQa/MZv/GWuX7/F2dkJQeAThk2EUE18fR8Gg6GS1woBlFXMenp6WrnCxfECP/DIsoxGmCElrK9vsIimlQsoLOudnjx5Uil2TNJi1qnRaMR4PK5kcaa2yDh9mv6EpjdRr9erwC9TK2nus+mlFARBBcoEQVAlQpalbPiNhM913ao2XAjBzs4Os9mMfr9fmanUjRoc12WhY7Ljo6OfPgj18TOfIDmOqtk5PT1lNpsppqQmPYPlZlqXPZnJbgI8ow03m5kJfs1gyLIM3/V093S1ac7nc1qtFgVUMot2q0WR56yvrdFutzk6OmBne0chcnHCdDKl1KyX6/pMJzNSN+Xo8Ljyf59NZ+zHT1jMItI0Q2DRDEMaQcinf/ENFumCOIoIwoC1/hqdbgdLWORFTikkm1tb7O3t4Xle5dD08ME9ornSs1oI5SqU5zTDBrbvkdtozadHmqpmfa7r4jk+tnCwtIxL0ZraWMJS/VJMolOv4SqyFFCuKK1Wq0IhxuMxzY7aYOM4BksQNJfIgSjFSjGe6QVSliWNUPXKiZOYNFN2sLbj6DoBpZlFQKvd0vdV1egYqY+yzGzoZCaklOp5J4Mz0iJnHi1wPJd2t0u701nRuZpxY/71fZ/Dw0M2NzfxPI8XX3yRjz76iPF0hq2bEpuxZw4zbtS4dSrWp91usbm5xsbWGotFjue7iBk1hGopT6jrsRWDsSxWNIvesxbp8wH/UwF29TfFkJRFSZGk1b02stQnT54QxRH//J//c37hl36RQLNxtmOvsK/G0jNJEqRQ3bd7vR5IdU2SLOXk5IQyz2no10izTBmRCFW/UGQJa70ejiXwPZfxcEi8iJTs0pyjVNIpAN/zsGybje1N0jyrzi/X9QFIqTu2K7mWZVmUQslG6gxSfRM7f43M7+rXMc8LGo2Q5z/1HIFvE8dzRsMzbNdXyYhe8KWUFLIgaAQEgY9E8Df++m/y+7//R4wnCyVjtI3Edrk+tVoter1exRKYsVxnIRES2wVLSELfptdq8K0/+QF333NYX2vQWVMIWxD6GjVVzk1RJJlNPU5PIgaDuTYuaOB5a9i+heMJSmkzTyTf/PYPePudO7SaHS5d2eXXfu0vsre3hxRCy93U2C70OatxpACLXN+jJElAo4tpppqITiYTfD/A0euyKc6tHJaKgjRJGA2HPHz4kJ2d3Spws22bJE2qYuOjw33yoqDb7TIejXAdWwfRkiLP8DyHJE44m86ghCDwORuc0Wo1GI0mlYtSmqa0Wq0KrTRAj+s6NJqhbiwpCBuqp8eFjR3VJFVKzS53FGs5nxPFUcViHR4eKHe+LNUJACRpoqSDpXLDU8YvMZ12R9uVu9X4MedpgrbJZML+/r6u2VG9pVzPU58xyzkbnNIIGzQaIa12kzt37lIUCiRQhdMxlhCsr/fJ05SyzDk7PWMxj7lwYY/NzS3i+DHjyQTH9Wi3lbVwGAb4gUdZBlVyZvpbpWnK1taWkj5PVIH33t4ejx8/Zm1tjTiOK4l6lqWkacSPfvgDPF+1yACwLbWXnpycECcRtm3R7XYoi4KiKOn1ehwfH1e1oI7jaClksVJ/YQx1wMJ18srd1gRyvV6Pg4MnpFmsndCCSlJp7MaN41hDF4wncYrjuNiUuJYgbDZJo4jmep+Lez/P4dEJH9y+z72Hj5lpG2zda/nPpK77aeDWTwvGP8nrW5ayWzcWzub3olQSbrOPmvcTAkohK5nr+c8hhP2xn7uu2jnfb9LsG886p7oD3tOvrRJQlffUmsfrHo1GsicsJYcuyxJLlFhCLmNECUKq2ikpbKRUkjfFHkn9vUmUnt4HzDkYVcFT51D78TxDZqSg169f51/883/BgwcPGJyd0el0eOGFl8jzKe12R39uh8VcMZSOq6T7YRDy6NFjbc3dIwwVwD0ejfQ6ljAYnALL/cQoebIsq8o7zFw4PDysmBpTD392dobjOFy5cqUCIqbTKaPRqKolFUKwv79Pp9NhfX1dKVC6XbIs4+LFi5ydndFsNivpsWGXTOsCwwyFYUgcK9meadJtzKsWi0WVWJnHmeuf53klk+/U2KqfdvzMJ0hAteDt7u5qVqGoPNHPu3uZYDlN08rxwiRMJuiou3uYwLPf69NptnS9y4ROv0+33SYMG7TbbSbTCd1OV+mXXZdOu8P+wT7TyRTPcUiSlOl0qhzBkpg0SXj8+IDHT57w5PETXNdlbW2NGzdvsL62zubaJlub2wqNbjRwHKUPdj1XlRrVAmVzbkJryCVUzkgG2dnYWMOi4OT4mJZ2++p0O5R5oWyzNUNk0M2qQ7wlSHTQOp1O1aBEMWZpmpLo69hqtSovfMdxcGyLJI44Pj7mwoULKhnQkzNNUsJGQ5tRaAMNjSoUeVHdN7P5maQCS90/LwhUb6ksI8sU61DmWVUXEEURtmXTbDWVcYOwSdME1/UqlCeKYpTcyGE8UEYCmxsbLGZzdY0tC7fRYH19nbt3767IJ82GbFxdwjDk7/29v8fv/u7vcnh8wnQ6W9HHmqO+cNbZJIW0W3iehcRTQi5LICpZF0+9RsV0yrIK8OuHkkM83ZPi447636RUNH2eS8JGyHw6rxI1z/OqRc6gOI5tEwbhSnK2tbWF4zgcHh4SNpUmWbnuZPgEmslxkQI8HRQ1w85KY15blLiug+c5pInq2i5L9TuDUJnEzXEcXbuSc+nKFVzXYzwa6aJ5VWdhoeSDZVmymKv+J5ZmrxDP7vX1rA37KW09Stb1ZH+feDHD91xazTZObhE2mti2RRqnlb47S3KyOGc8mXJ0dEKz0WIynlHmqUI2xVJGYta2egGr+Qxm3VLXXdJoWLzy8sus9/oIWeDbkMVzZouEpHA4PbMoy5xSZqpdgAWytJFlD9vepL/mkKSZlrjmYBVkMkeUkOs6wTidM1tM8Rs2nd4aaV7w4x/9iE6rxfqaktI6jkusNzelU182+zOIvuu6Va+goijwdb8ic7WjKKLZbFbr2GQyrc7/3t27lcxjNpsxnU8rKYYJAAzj7HtuVbD/4IGSd/V6PQI/pMgKAxgjRINer8vW1oZOZI5Un7skrvUQccjyhONj1fdjOlWgR7/f5/T0iKIotZQuYmdnm7JcylIM4NPpKnDIdqwKwFK1DpIwVAF+u91kPp/jug4X9nYI/IAoVsBAHMX4gelGrxygFtGM/f3HtFrP0em2GE+mDIdntNsdtre3KIpCBx8BnU6H8XjG2lpf742qHYKUsLW9jW3Bzs4Ox0enZFnOeDypwKzR0TH9fpc8z9na2iCKFrieU/VSMc1/fd/n4OCgMskxRgynp6dVrcFHH36EAIIgJJcFi9mUJFIMXp7neEHA2eCUsBFULncIqZ8fV/UKJplWyWVeJUrnJfNFLun3+wyHwyogNCDoCy+8yHwxxXVc8qIgDIOqjjTwwyoOOD46qZhAIQSuQgCYzubYrsPJ6T1sxyXNVQH9hQsXGI8nTGZz0iwjzZSrJU8v63/uxydNnlb21/rvMeshUDlSlytZ3setjT/pvetrp4lhlgnG0/sbUMnIzWNX5cWr6+VSCi1BmKxUqKRHoGRmctmgfuUopbbt1gCENtswe6lKqJ4tDzTX6imJYPX98nEGnFSxpfrDe++9z+3bt/nGN76FlBLP97l54/v0el06nS5BoJwWXddhfX2dNFUyuLwoCHyfshDcv/8Y3/Po9gSe18S2BFGUMJ9HBIGvAYl8pdGqEIL5fI7v+zx+/Jh2u70S46yvr1e1SaanknHCM6DNaDSi0WjQ6XR0D7G0YqSGw2EFrCsFSchisWA8HtPV/ZqMqsiAUyZmt22btbW1ygAlCIIqkTcywCRJquvpuC5YgjhNPnb8nT9+5hOkLM0qtw1AWy47CiXOswqpMJIa44gGS+e6pdRJbTiGQUrTlGazqRKAsMFsPGGt3+fS3h5plnFycsLZ6anqNu24+Po5s8mU48Mjjo6O8H2PR7NZ1URwNpup7D3NEJbDa6+8xq/88q/w6quv0u/3CQIlQfI8n7xQMrW8yBBa81uWOUiJEErvmheFalDpuYpGLpb++67rVBPWth0kFruXLivHMM2UCcem1QiRuv+IZVmUuseSuY6yoRakRrO5YjpgJpJJwgw6ZyR2jTCoNssrV65U90Faokog5jWnNCEEeaLcnQxzU0cCpbVkKMqyxPU8HNdlvphXDSSLogAhyIqc8WSCJSyKrKg2TljWQrSbbWxh0fADiiRlo7fGYjJlfX0d1/UoZMnm1lat+HJZ5G1YJGOXGUURX/rSl/jv/9FvE8dJFRT+JDTNbOBZpuQ5rmupAlBdwyRBOd08A3a0tZmGLCTGacu8LqhN5SdtwnX071lsSbPR5Gw8IgwtXMfRxZwFFy5cYHNzk5/79Bs02y0Oj46UzKYRrgSntm2zubmpDDqytJKzTCZTmq0Wvu+rBpmypNTSzLpEQUqpbFzLAsexOTw4wHVsms0Q21p21RayxHHciu3NtUQrL5XTmBCCyXjCYjbTHSsUEqjcx9R1KgsV/NcZpE9+yMrYpNPu0W/3mE5ndNqbOLZiiZIoZjiY8ejRY+7du8e9e/c4ODhiNBoxHA2Jkgjf9yjKAs+3yUtlAmEkq0mSMJ/PqzFj5ptJOjzPY2Otz5W9HTzHYTafkmc5UgqyVFmnSyKQSkokkNiO6iNkepg0m21cxyfPU4QosGzVd8wWPqVGyi3HIU5ifN/l1379P8D1QxbRnDt37tDvtGkEL3A2n6Ga57qcnJ4wOBvQbDWxNdOW5xmWZTOdKmMVKaXuOeQQLyJmMyVtarVbnJ2eqF46aY7jeESLBaBq+vpr/WqsddoKjex228RRTBD69Lo9Rr6relAhWcwVaLGxvkaRFyzmM4Sw8TQYcnZ2iuupOTSfL3TyZTT1QjmYAUGgWBTVBFGqzxXN9VhPGI9Hld2tlJLd3Z2KMWnq9TMI1Do0m821KYTEslTdUxjaOtkIcR0HR68taZownyszhGazWQU1o7EycUjTtGpWfuvWDYoSFouIJ0+e4HkuWWYjpWIux+MZjx49oixVMqYs1FVDxzRRdT+XLl7Bth0OD48Yjcb0+n36a+tMJmOkLJUUnJJer1ut36aYWskIM123u3S4Koqicpy1bIsizUAWCOGoxuiWxWQ8Js1SAi2Vdxy7khyb4neQWikCzWaT4+NjNjc3df3HMiE36+94PMYSNnmugnCDUHuex0iDKKZWwgTcpmYriqKV4F2BajaylFAoU5FSSrAgSmIsHXQmRU6SFdVaaJcSqyiV0+MnpJH+xzJEP+34qfJrsay7VN//9Nf5pB+5nuSYfw0jXneblBJsa1V2t5okLc0QjHuiepy+ziprQdUR6eaMoL8//3lYJkfoLwFSsy9alKcfT+291bgwSdpKcifqkrzl5zdJqekLZ5IA9TuLLCu4/dEdtf7oc1AOdirZKLQ03HZsbMuumBspJZcvX+Tq1atsbW/SbrcQlsD3Q9J0xmAwqFhxQxRMp9OqbMK4BxvTGGUiM1KSe+MKrGvLTZ86A4rbtl2tdaDAo0ePHrG9vV0lMyYZNnWJQoiqP5Pv+1V83Ol06Ha7HBwo+bAxfjFMkpRKldJut9XaUJbkcllP90mPn/kECVCONBrFjuOEWDurmf40jUajqouI4wSh3b/m8wWNsEGWZsznC5I4rah1M2h9P2A8mnB2dIIlIYli4kXE+++/T5KkNJsNRsMRsHRtsixl7ZqkCY6jJCCe57G5ucnzn3qeXq/HhQsXaDTbbKxvKlYlU179png5yRMQkCQ5pVSbg+d52I6FLAW2sBFlieO5WLY6HynBtpdUte97VK4yqhJafS8lthAEjaYqjNbUpGkS6jjLhaYuSzQoqEomHYz7nBr0SzakLAsV1OvB2mg0ePzkCXsXLmDZNiVSO1YtbdSr+oJcLRLm5yRJGA6Hqj8REs9XLNXa2hq2ZVPIgm6nS7vdZmdnhyIvcFxHB72QxAnRPKp0qycnJzx69EihovMFVqk0vPPJjD/4vd9nfX1NmXv4Pn4jZDwagZ7UsigRloVlr8rTfN9nOBzy5ufe5MXnX+Db3/lOZZ9Z7R3n8pW63KDq7WLbeJaH4ygHq1wnsroEtHquCZBtW9VgmN+d/3eFXaztXD9NNiZLVUhuNik/8LFsJeF0PY9PPf8pbty4wWA0rJiCXq9XMX5msXcch06nw/7hPrajir7v37vH1tYGlpZGquROXRzToT4vCoUB6ut+enpKmiVsb2/juC7DwRjHdgDVMNkLfFqtFmeDAWiTA5V8qhqPu/fuKLOHy1dwbMXmRos5ZVkoU42fcm3OH6tSD5N2CdVwMC+YjGPef/db3P7oLg8fPuT05ITxZKw2jywjL1QTPbX5FgS+R7ff5cata3zuzTf5B//w/8XpqWodUJQleZYxGU+UOUuR47kOzz//PF/92ld5/733+PKXv8IXPv8mk8GAd997hz/5439NnC1IshTXD5QRRllq4wcq2bAQkkymCCGZxTmNoKUlgxmuJRDSQUolA8sLJb9yhM3uzg62ELz37o8QSK5evsw73/8+FuA6NoPhkDBssIgWTMYTWq0msUnytFuUWUtMg9WyKCvDljiOePToITdv3CDwPMIgYD6LaLWaWj6nCvMHwyGu61BIhWyWRclkMsbTktzA80iSiGazxebmJuPRiCRNWV9bU253haozcByLsBEicStpcbPZqBKZJI6r5tHT6Zhms1EhmEZ377o2zcYaslQGQb7vEem6PGMKY8CdRtjg0eNHSv5cFCBK4lgxpHES0el2VK2o42AZJB/YPzjQTFlWrRHdbkeDSKq+YDgccTYY0Gx1iKKIOI7odNoV2+i6qklukijpW3+ty+DslFKW5FlKQ9cIDoZDWk2VeOY6sQnCEFD96jzPRVgQx6q4f2N9Q1nqZzmj4YgoiphMJsjSotVq0+v26HY6xHHCycmxchtzLbI8ZWNzXcspbdrtDsKCJMtotVpMxsqhMoqiFaCq2+kynU4opSQMQu7fu09e5KRpRpKkS3OfPKfT7TKZzPR6KkmSWCew6FomG1lS7X9FWdQkrMZYxCXXdU/T2VTJzkpH9TmzLfKyYDqbkJcFZVGQ5CmFVnPkpoWBBIH1ZyKPPgmD/T/NYaThhjUxyQycf/tnqRc+7lg+Vj61L5nDAK3LFzzHKFmicvpUMYhaTJcSOFPjqhNbhI6DjLlCPVGi2l/LiiUz8sFSP2zZEuU8a7TKZn3Mniuefp4BaQHdD07ovVxQZCVCSKbTWfV3x7Y1WApCWJSlqOTdRZEyGs04ODhBCMH7P/4Iz1XmQRsb61y/cY1ms8HFSxfo97sVO99oNCr5rgJSPO1sqdRX7XZ72Zha1w/Ccv8wIIMBf0wc02q1GI1GlaOwabdjQO0kjrH16xkGyKyRfhAwmUyq+K/T6ag1U6uejLlKr9fTxi/KiA1LmYcpZn/ysePv/PEznyDlqSTUrm29zhpJnENhMRwOmM1UMf76+nrl275YLHBcvzICmAiFEhV5odG9Bq4VUsiSNC14/+GHqo+K59JvtzjNT3Ecm8VUyQ5mkxnSEkhhVXrJZrNJs93hQq9Pr99lba3PzvYO7U4b3/MBZas9Hk9Iy5w8k5XHvaJAmwiNDrvu0hXE0oPArpiJZRPXQltwWlIzD6Juhyn1IqDrYqQkL/VvqgmtFy+x3CiMbE9NSnRZd4mkoNA9RpYmAWAW0aJcNk3Etuj0e/z4xz/m3oP7XL1yhYt7F9ViElAF1KqTdUaUxIDg6OiIKFKd4o3cz7ZsbGySRcJIjhSK7Lg4fs3739ad6S3d18SRuB2bMFRdpZ9//lNcvnyR09NTTg6PODs4psgS3njtVU6PDnnxU8+xt7dHAZyOR3iWg2spJyw1RlQdC5ZycxMSVQeU5VhC8Cu/8su8++6PSJOE3HHI8kJfW1X3cT5JsiyLNMsQwkEWYLkWri6wVpu4oJD5ykJsnqvOeVkkWze2UNIha2XBNov2szawuoTBBEhXblwnLQqSNMNrhCRFTi5zojQhTmM8zwUk0XxOp9fFawTEWUIhC8aTEVubW7RaTdWF3HZIogUfvv8e169eZGtrE0qb0lEaJ0tYYEkymYFQxf82qgfOd9/6HhKLtY1NJuMpSZrRanYQlkNBxnqvRxCGzEZjAmHTcl2GSAQlnmfjei65TAnaTYTlkcQJzTBAoI0thB7F5za6nxaISKlqiiglDx494n/7v/vfU+YFWZKRpRl5WZIVua5NKav5J4Tk4sUdPv3p1xmNx/zWb/0trl+/TrvdwvcDdne2SZOMf/w7/4Qf/fA9iqLE9wN836PVdnnppZf4T//u32Fvb49cN6osy5Jed4+rNy6RpBHffeu7MJ0pVjZXBehKuuni+a6Wg8XYeCrADn0cSyWdjquLZJMMaemmqbrI2bYd2s0Wg5Njms2mQuctwXvvvsdsMuWll1/GczxGupFzmWUUaYaDYL3bx3XtKrDNsoxus8dkOiFNIvxmk8l0jG1ZNEKfo8ODinlMk5Rev1c1Ec6yjDxJmE9VobIsJZ7jsLm2wcOHDxVI5TlASZbEzKeq31oczTk9ySo5MICFhyVLyiwji2Pl2qnrUoMgUMXqWUa/3+fwyRPyRPdskw6itHAtH88JCAOfmzeukeU5k+kU11eSrSzN6IQdBJYGwTJuXL3Kk/3HCgG2IQxcXZgsSaO5Mq3xWjiWT54VrPX7NBohR0f7hEEPWao+Y+12h/l8rm3TU05ODlks2goxTtIKrU7imH6vX5lDzOczdna3sCyJ5zvkRYZt+5QImu0ei/mCu/ceEseq1rPVbhLHCgwpS580Va6rnusTuAsiodhhM96klJSpJIpmzCdTfM342JZF6AcVIZFmKWdnQxzbxg8CHEepPDzf4XD/kCxNkVLVadmWbsadZxyIA5Cql2Ch5cpZXiKxKlDJJFPj8YKCUjX11MF31YNFSspCgLQpS6mDPOVWd3Z2huN5qg2GRseBqvYBI9Wq4mBRFe1j2AtAtQmharnxP/b480qaflJiY4DVslxlafQjf8Kr/iQHN5VoLd+m/v2ydqmu1lBGLAVCCr2naRZHxyqWLap6RHTtuTTnIoUGhazq/dC1RYZtNEmHAnWhshevnWoVG50795X9GNUuxjCQ6kSMNO/ZyZRlacWIic9qboGW0KCRbSMsW8Vp+u1kWeq2G5ZqDSHVu2e6HIRSjb0ky1k8PuTRE7VW21bO+kabzc1NwjDka1/7Gtvb25WpimLy3Uq+bD6LUfMYSbBhiQyIasorBoMBe3t7LBYL5ZLnefR0fGNr4xRP140bMxtjxmAStSrWM0yZJgyM8YqpUTUyWmHblKAMgMqCxWzGWBMWn+T4mU+Q1tbWUFadY37wg3cqdzHXdXnhhRe4fv16VQ+hFnc1kYzczjjiKHldQxULa3RTSsnDhw85OTkhz1JcR1Q0oeu4BKFyjBuOxrTaHd3vpFk5cSgkpKisoKWUpFnG/v4+g8GAn3vj9ZVifVii03UGp07x1+sOVJC8tCAWFshCk0WalgWV8SMEJdphTCg5A+jAWJgkp6zQA1P3YNv2SlBvgkcjLTOJSZ0RqdPg5j0uX77Mo0ePQAj2959wenLK5uZmxaAsHQWVc5TptLy9vV31hqqbJSRJwnymeut4nlc9X6GmcYU4FkWB4yxZtTRVrOLFixe5deMmQluKO7aSD1W9VyRsbGzwy1//Ovfv3uPO7dvY+prmaapc8sxiZlkVBf35N9/k2rWrRNH7avOVaWVbbsEKjWTucUVJFwXNhoPt2GRZSimVjTLW6oZ0fqE1yVJd7ihZJk719zrvznj+MEnV6dkpt158HlvCfLogCEOmkzFpkrKYz4kXqj9BIwg5PDjg5q1b9Pp95tph6+xsQK+rjAWMM1KSBJSy5Bt/8if80i/9okK2C2t5TaRU8k8pNSgo+eCD2zx+/IRms41t2ToYVDR/psfexYuXFNN0fKKsgGcjkAVZnrK2tsbFS1e4c+cum5s75EXBdDYljZPqWiKlYlc/ho07f73qc8A8fT6LiOYxlFLVNSEoKCoE0nZsLAGe57J7YYe/+PVf4O/+Z/8p0WKB66rxmxc5k/GQN954DYHgU8/d4uGjx8SRkg13Om02t3sK4SwLTo6OsLRT5GI+p9lskaQJr7zyCuvr63z3u9/h0ePHWJq9VDbtOvApMhzbIU0Vgu57PmVR0miEGqEs8QOPPC9Q8k9VvBwEIVevXCFazJXdepqwiCJGoyEvvPACg8EZZZ4hi4I4Wqhi3DRlMBySZSntdqvafJVENcXRNsFpmuDYdlVYrW6J6mVjdOe27eiaoAAplfObEDYNLY0WQuC5qkUBskRYVPJpU38ifF/XRaq5boAY85mSJMH3/UpG4rpu1Tjx5ZdfJs1SHj18yOHhAdevX9drvE1R2MRxqQICx8GxXFrttuo8X1p4jkukXabKMuf69avK1fT0eOlIKalqtI4mR1y9coP5yQxZqgT5wu4FxpMxIPC8gMFgqFwRZzPW19d5/fU3lCxuoBoTb21tkiwWynQly1hfW2P3wi7NZoO19R6O43J6ekZR5mRZQRwlhGHIwf4hRalk1kUpEWhJS6dDHMU6Sc3ZPzhgcDqsrMejKKLf6zObq+TcdT3KQrVTMGY+ZakkrpZtKzBN719KTqeCPqSSrimXUlmh2HlRLBF5qeXkOqhN0owkLSrzj7Isl/XIpXKZXTE2MWtpKRDCWdm3pnMl45FxrPbOWo3yeXlXtS4blkWNpgo8rP9G/erPXzr3byLHe9Y+8JNfRyU4dfCozpp8gndkhblZef+nm6mbx5h7b679swyGVj6ifiu1L4IQq+5yK2NA98CrnOp+SqL5caoMIZQpzdKKfDUhqv9cOSLWGKk6w1yvTS7Nv0U98dS9ospSSYhrsVy33+TSpW1arRZXrlwhipT5iO8HuI5Fr9vRNUxpFafmec7a2tpKDbFxTXUcpypdMK6QJt4wMY+JG/f29pBS1fr1ej3QNcFBEFRrvhCiUpoYmbAx4TJ1SkVRVPLySLfwMLVKjm6TIcSyrjOO42p/8zyPOPlfapCqIwgC5vM5u7u7tFotdnd3cV23kuNEunloPQu1LNOx3cF1lXbS8z0dPFiVnExKyXPP3eLmzRsURYZS4+heMLU6mjxTLIEJyIGVyWySCfM51tfXARgNh2xubipGQi8etqNkNabPkSUUpaxQBlM8KLVzl1SPLcpqclpS1SWZTNugeUEY4gV+VSDX6XQq33gppdJOw9KmMY4ppcTXFKaZuAZJMKh1feKbryqxEktP+263S6fTUdcmy2m32pWNZFO7A5nnAVy5cqWaoAYtMBPHBP4mWZVSVkmScWcx3vqqqDatJrVpXGk08hYCYakAzfd8CqmMAHLtyx90O/yv/vZ/zD/7p7+rFoI0JZclqW5WO5vN6Ha7XL58SdUIBD5f+8pXePjgAXlekCQp5cdIuCs9cqYCbROM+b6vki/D8ukxZa6nSUqN9OC8A9B5Y4h60m1qWMzPxl3QHFKf/3g8psgLAi0D6nTaDE5PlXxEB+TtVot+v8/x8TGfeuF5dna2OXiiDEdm0xnDoQqc+v0+s9mU4XDAdDpmMhkRRQt+4Rf+ArsXdnURdVk5Dko9pt99/8e8/fb3CIKQNC2I40TJYhsNNYc1sHHr1i2SOGYwGPDw4X2Ojx6zvbODlCXtTp8gbCGFy/bORbI007V7ivEzFQHWEqD7RMdyg7QwPYvKTPXsMUIP27Not1u4nkOaJvztv/0f8+prr9Lvd+m0GowGZ8zn86pg3DhoFoUa48PhGMcW+B7MZmNcp+T2h0esr68xHivJnuldMp1OOTs9odPpKJ144JFnKWmsDEssi0oGa+aVbXsYC3zznkVhHNMKPM12q9/nevPrYlmQFxknp8eVQcT6xhpFmTEaD7GlVE5njQBJySKa02gE+H6XxWKGZcH29lZlua/qahrV3B4Oh1XTSjPHlWZdbaTNppJjRNFC1+7Y5IViHoUl6HRb3Lhxg93dHQaDM+7du8fp6Wk1zn3fZz6fVWudWaNME0TznqY2ZTweVyBNEHpKUra5RrfXppQFrmcTxQvyItdrFdieMqVJsww/CCjijDRPyIuMEpW8ReMFZVmwubnFnTt39B6h6v1AqDXbc7FtwXg8Ura4nsP+/gGLxQI/aBCGDebzOc1mkyhKVJsEL0DmBZaUOELgasen4ekJw8mc45MTVdeUZ1y8uIeUgsk0AimZTKbM5hF+2CRNMzzXoyy1fDwryCMVrBSZYkURNnGWM48ShCVwvICTwRAjbwblGFkP8lJtBCRqrLWpGVJ7p2IWLJ2om1oHYSm7+DhTTUtNXZJZC/OiBGw9n881j1erIVKqOWt+K6Vhj2vAkVCMpAKaFOtk9vFPsi6cD57/vI8/e2Lz53/8j32/p8/haXDK7NkGFDbPexbw91SiJmrp6TOSLnOY16+/xyc96u9n2U8rNernUT2uPs5lCXIVVF4mb6vnunJuOvEzdT914Nj3HV56+Tl+5Vf+IrZts1gsCMOQ2WxGHKW0Girums1UY2VTe2T2IGMdrsiEJaNl2B6zNhoJnGFzdnZ26Pf7y3gzCCikpNlsamOzadXzyCRaw+GwSnxNTGZiSxPnwLKPpDGbMXGgkja7umG0IEtTDZzPPvE9/JlPkF577TVarRaO41T1KqAGT6qLv8ygXTZ2zXQw7eD7rpanqVDJECqFbrZlKD6JQrVz3dfCLNyq2aRgNp1V9TT1ZEgVnttVMFqWqrGfbSs0fK6LkuvJh9o86nR3HXVZneC+51bPlVJW1tSO49Dr9aqMfzqdkpcq6DfIgXldEySbAenYtrJMrjaspVOYKagzwYX5fHV51/kJXQ/Ei0L1TTG1YYYBHAwGjMdjFosj3Xh2t2KXTINXYOU9zb0BqsAmiqLKHrjVatFsNpb2w/rxZoJ5vkeukZHJdMpY9wS4c+cOs+mUbrvD8889x+bmBr/8F7+uLDERFEjQtV5mDCi3qwhZlnzus5/mn/7T/68qOHQdZKqS6/ObglmczfgDsC2lo9XL7TPHgDlUsfDydZes5dI2tf788+ibGk9PsyMSKkfARruD7Th0ul1s2yKJY7I05Zvf+AZxHHPr1i0s22Y0HHLl8hXu3b3H8eEhnu9xcHDA7u5uVTyq7J5zFosF7733HnEc8dxzn+Ly5Sv0et2K1b1//z7vvPNDTk6HXLp0ifk8whIWx8cnuK5Hs9mGUoEDFy5doNfr8fjhA+aLuWJ7tfmA43qsb2xSStVFfHtnl0W0wHUcZrP5chH+mA30JwUBK4XbqIBMCrAdgW2p+rp+r8l/8nf+15RFwSKa8+lPv8alS3uMRiPOTk+YTqea6cyZTmdMJqo3y2Ix1z0tIr3pBXiuh5QpO9s7BL6Hu75GnuVKnolkfa3PdDLl9OSEPFftCibjMb7natWLAlfU/TcNEiW27WspQ66LW6Ve+3LSdGloAsodtNNpMxoNQQhm8xlhGNBstvB9j7U1JeGajUd0ux2klLTbbaJI1ZD4vk+3264CgCxLWVtTneGVnbxK1Pr9vl6Pimod7vW6em6n2o1Ssrm5oSVUU1WDVJa0Wi2uX7/GfD7jyZPHXLp0iVu3bvHuu+/yzjvvVL2E4jhBq74oikK5LepEwhhfGBvadrvNyckJ169fZzqbsL//pHJAqzPgjbCFwCIIA/yGcn4qzbpqW6RpjLAtLMdCCJsiLZnPpkzHM55//gVu377NYqF6isznytL2ws4ug8EZcRyrBsOaJRuPJ5RySrerHPoeDfZJ4oRWu8ViPkcWubLDHo+5ceMmg7MBrusyWcQMh2OyPKPZbHHv/iNlG2/ZvP7660hZ8tZbb+O6HkIoy3rfD8nzRJvJSM2IF9qlEEBUzTyFUPKnLE3RUR5lDdwy80sxPwqcMPd4GViqREaW0pAWut+geq1Sj10jXxLCrG9C7+NKDm6erj6Hmdf1wFqz6lVRvlkAlIlEKc3rL521zq+Z/3MlK89apz/J484/tv73869xXpnwrMf8+SdGy9+f/5z1L+MmDEs7b5PUPOu+VDK8Z7znx51TPZn5aXvA+c/6cZ+jfm71z1/t2dpYog4uL78Xz/xswrIQtXul5LWq7vbsdMg/+93f5/RkzF/6S79KmsY4Wx5BEBJ4DWzLqSR2YRhWILVlWZWix3wOMDV6VvWZDZBk9nOzZt6/f5+DgwN2dnYqBj4y7rFa8WPmUdXIWydhJgHyfb9y16vX85u4zZynMQpLNFPk6fYerVaLKIpWAOKfdvzMJ0jmwhlDhgsXLlSNqA4PD4miiMuXL3N8fMxsNmNzc4OwEYKQFGVeoQy2o9glWSVUSo9aFJlOmgRZmpEm6RLBB8bDEc1Wu/o8ZhCoQlZlK50kcZV1R1FUBYyWEKpJqi5URghiw3g5ogpcTNBrGBiDQggERaaoSxtVLm7YHvNZTMLWX+tDbUExi44QKphT8g71meyqgDpXTFYNYTFFcWbSn18Mzg/OZyEqtmYJhBCVs5M5t/k84s6dOxweHlbWvfP5vPLiB+VcZBKr+XxeyemUC9FSPnl4eKgZwmXfKzOxh8OhQqHjiMPDI65cucylS5cIw1A1RkMFcMki4vadj4gXC0ajAbKU5LIkTpPKPQWo2Koiy7hx7Tpf/MLnOTo+1hMa4iSlKKgWbVgulKluampQUrd2D/WoWrme1XN1KFAxURqBr/ekOs8g1Re7+ustx696vzzLODk9YWNnh0YYksWxquFYRMSLiHt375GmKWcnp7z5+c/zwY9/zOc//wVu3LjB8OwMgSCNE46Pj9nY2NDMmEccF8SxckIbDAa89d23+NE7P6o+4+nZqXa8KtnZvUhZKjnr48dPyLKCdrujjBayBNd1eOONNyjLkg8++IBms0m73SHNXCTK5r3V7nByOqDVadPtdbh7/y5FWTIaDdW565jp4zbun3SojTEDBI7t4PlK49ps+Kz1u6xvrHPnzgd8/eu/hONY7O5s8OD+bfK8IPQDbAvaraauEbLZ2d5CCMG9e/dZX1/j8eNHTCZjosWcvb090jTiwYN7WJaSlKVaDmvqI4wVq9mAjHOb67gobf2y03uWpSvn4WhXuzw3a6pK+l0tV1NztYFtqx4heZ5VfXccx6bVagKSZrNBFi+WSdpkrF3NFDOG0I1kpaSUBbPZBGEJJpMZjm1TlCVhGGDZitF1HCWzODk9BsDzHBrNgCRJCUIfISyazRY7O9vV+t/udDg7PeXg4KByTfvSl77ElStX+OY3v8l4PGZ9fa0CrCzLot1u43kezWaT0WhElmUEQUCr1aLT6bCzs6OandoOwjHtAhweP9rn2rUAKUt8T61ltuPiS1RPuZozmmV7yLIkWkTM5lNmM2VdLoqSJ0/22d29wHvvvcd4PGE2m7G7u03Y8JkvZqyvrdPv93n//R/juh6OExDFKaPRVDsDWmxtbbG/v68leoqRLLHIPrxDp9PhbDhkMl+QF4qNPT0bIktotdr8/M9/kfF4xLf+9JvMZnOQAtt2aDSaHB8Pqr0wz+vMjVZIlCVFsQoynJeynV+/YGlvov4AslrnSkzvnafmHLovj5GqaeZXmv/J6uWW7yf14+sgfP29nyF7K6Vc+fOzwKZPenxcgvJnOf5NE5M6WPmTkqd/m6yUeuufDFLVk7dn/Vvf69SrsQJ8fdy51PfDepJT/xwflyyuXDNJrf5MHXUV0fn7UN+Xn3W+5qgnT9X3paoFNeBwHRAtCsF8lvOtb36PvQtX+LnXXyOOCjxPsSyz2WzFjtsAQXXFTxRFtFqql+R8Pq9kcmVZ0m63K1meiamM6sXzPN3TzsdxHGZnZ5UsriiKKgECpfwyPdMAGo1GxWCZGK7T6VSNbU2dUhAEVbmMuXdBECCASDtp/lnG7c98ggRqQze2nyYIFEJw5coVrfE+rew6ozgmiheVhbdin0xwUGDpRmFFUVTa9CRJcG1b9WCxbQoJUZpwcnLC3bt3ePHlV7h16zkGwyEPHjyg0+lUcqnNzQ2ybFmHYVkWh4eHChn2POxapmx070o/L3EsAVIVET588oQkjllfWyPRSJyxmZ5OJ6huywGO41aJj2FSVJf2kul8XvWjMQtCZYkoJXmaqYL21FhQWkpqYOtO03pCnkcZ6r+rB+Ifh0YZ+WB9gtfv5ZUrV/B8XwVMGjnK8pxosagsXOuJoEEf64V9vu+ztrZGUeRkWVolTY7jqIaZQcB4NMYWFns7u9hYjM4GjFCTd31jjUZjg6ODQ77znW8jpOoPstbrs761SamTZpMsmolbpClCQqfb4YMPP+S99z9gEcUV2lE/6ihNlmXEUYQQFmGj8bFj3Vxfw2BanNfFPxv9q//tKcq+dpSlRNgKgTs6POLGrefodrsMz87Y3trm9ocfEkURa1paV8qSrc1NjgdnDAYDbt68yfHhIbc/ul0BAtPplHa7TVnmBIGP6znKxth1kIUgSdS5l1KymEWUBVjCJghCokXMyckJi0VEp9Ol0WiSxAqZev7ll9jZ2eHR40eMxyO21ta5eu0Gw9GI4XDIpSsX8Xyf4XjApcuXKUrlBjebqY7htlCbmiquVnOgriH/SffAXEvbUe5JvX6L/+i3fpPvf/8t/sJXv8zW5gaO7RBo+cFiMWM8OsP3lXzt5OQY27KUo160AARnZ6cEQcjpyYj5dMF4PGIRzQkbgepf1m5rRNsiWqi5PBmPOTo+otft4Qc+WZoQLebM5wvl12QBFMr5SaDXOhVkCo3Oo+er6zgaEAFJge0ILBscR/UDunTpOmFDScg8R/XAmM0muru7JIrm2LZyz3RqzO50OqlqQ0upbNttWyVVZnM3/XOOj4+reRwnmqkvcixtzJAkMUma0Gq1dJ8jn06nx+XLl2k0GvzoR+/y1lvfVU5n3S5JotbeyWTCc889xy/+4i/y7W9/m8ViQbNpVcx2mqaqf5ptV5t9mqacnp7SarUYDod6zbMZDlUfpPx4QJ7nvPPOu1VzWFAOS3uXL2HZNmvra2xubeO6Pkhod1rkecbBwWMePnzAdDKh02mz1u+ztrbOr//6zUo+GYYBZZHwy7/8S3S7fTY3tvgX/+Jfcf/+Q87OhownSqriOi5f+crPK3ve/Ls0GnOysuTg4IDT4QFl+YS9vT0cx+GjO/dIspQsLxhNZghswnDOf/vf/2Mm0xFlkVGWakwo0uZU5RfW031eyrLULI9dJTf1dcjSBj/mKer3OiBUE+hjZa2yrkmWzzDG/pgn1uG51YCbeu/4p4+P+9snzGc+KcPz53V83Pv9tPf9SX//nysh+rjjWQmKOerjyvxcV5MAq4mIlHqN+/jXOx+jmLXgJ7Fc9aMOPBZFsZIgmdeux6P15y2Z0qWj3ep5LKV49XhLCFXbJoRuqFxLbFQvQIHr2ly+vEe/38OyIMsjPL+BEDZbW1vVZzTKJdMA1vQTE0JUyYiRfpuEyjA/RgpnesSZcg1zT87OziojHMMAGXtwBcg51XkbcNn8zSRe9bjefF5DDhhmypQMIOVKicgnPX7mE6R6gRpQScBM0agJpj3PUzUlQUApM1QvhzMcx67cOMKgieO41SCZzWaVDKYZhHRabVqtJo7rEi8WPH70iCLLmY4nTHXPhI2NdTzP1zdedRxOkrjSt5veHVJKpZksFLKb5wWJl2gKM0OQ4Xsevu8R+D7Xr1wCJEWWMDw7U6iwHtBlljEdDQmDBh3dfGsexzx48IiLly4rzX0U4fleFRh5nhrwSZKSJilZnJDnGdPJhJPjY46PD3nxhRe48dxzlGWhkNNKF1tUQTqozUc1PNNslKUc25610EgpQRf9Gv2E1DIJy1Juc41GyGIRUZaFdrgrMJSzsd5V11C9b1Ho3ku1hEUIwSKKdNBLRQvXTQMs2yLwAxWcFwVlrmysBaq/Fo2Qbr/LX/1rf5WTo2MODg5Y39pAWIIgUDVrRVlgWTZJHBOVJZPRmNFgSJQkvPrKq9y9e5/5ItKL2up+u1zM1eeL4pg8y1UBurpata9ns0j1hLhOf0upak4qhoml4+AqKkdtsdZqlLJECIuT42Mmowk72xdotDpYWIRBSLSI6Hd79Pt9Ll2+xN6ViyRFxve+9z2++tWv8uqrrzKejDk6PML1Vf+aOIr4/7H3p7G2ZdlZKPjNufrdn/7cc9vIyIjIzIjI3oDTBptMY6CeMVXlKtNIlOlKFv6DhQ0GCRCWnLYM0jPvIRBCj5JdpnmUnwA9qqgSfo8njDONjbNzRmRGH7e/9zT77H71a876MeaYa+59z71xE7LKKMWSIs49Z++11lxzzWZ8Y3zjG1IKHF2+jK2tITqdhHITtIfVckkV52sF3wsxm8/M+Kxw+/YdKKVNlfAOVKNQNwo7h4f48Mc+hqIs8epXX0G300WeFSjyEnlWIghiHB5ewnK5RFlV+MAHP4hVuoIQGicPj8GbE7+QpxeYcow1QVHmJA7x+77nuzEcdvFd3/UpaF3i4cM7gCIP1/37d+AHvonoVEizDHXZ2MLFaZpZ/jUZ/AOijGmFo6MjxHGIXo8U48IwMjlEHsoyx8HBPiaTcwSBB19KKN/HpcND3L5zx9QPkQhNQT+IVlo/CCiXUillo5pCCvjCN17BEFIISM8DtELHFBrlPE7bXuMVpKjslLyHQqBsGirgrDSu37iB5uQUSRwjiDyShq9KSEVrdpZlSNMVhJCoq9pucGEQwZOkZJgkEebz2hYXBIxxIAWmkwnqqoIf+KjrCsMheR6zNLNFrt955x0TUQ6xv7+PN954g+r7jEbIDeAWQuD8fILSlGXIsswmEgdBYLypwNbWLsbjE1pLJRkJUkisVhn8wEdZVbhy/To+85nPYLS9RZS0mpwORVnA8yQO9w/x3LPPAwDqvMD+/j7Oz2ldv3L5BqqqwvHxQyhV4pVXXkVVSVQl8MEPvozT0ymKQuG54S4838d0MsHn/sNv4I033kAnSbDMCqycZ1KqwYPTMYkiNMSukIYarrVAVlRE1UUDKYzssJAmKiPANdDWwI9dQ8jhZZUgBc+S1otv3Osbs4jmjrMatiuc0AYgOWBqLaKz4WWHGyRyQ0iOQX3hXHauYNHT5jcfT7HSa8CNvQ3tcbGdbfY891ZPg0sueh6zLbgglNsm1t4DL3L0P/dJ27VMPLYpj+07vqx4j+/xLfi0C774JCDDV2/r5K2LOWxGZgicGBAEx+EluB3rOS7vBQzdKM8ajc9xCis7ll0nsUdlV+yopBfWUueIBsj7bgvS2J5tBbk27VxWfex1u+gPBsSMihNcvnIJ73vfdezt7SAIPXS7MQnhBBICga03yc/PFGjKM21MQWxa67jQtyuQxc5ggGj4ACwlme2QoigwGo3QHw7tNWxuNdiGVBbocH+x7caf8bVdcQjOuwJaMFZVFTpJAt/zyPHpPz3s+ZYHSNyhbqEtRqU8eIfDof2dvJg+trdiDIfbaOoa3e6Acgg0G52+pSwcHh7Sy/M8s6kQ9Wq4u4OPf9sn7b3yPEWSxKY4bY2mofZwuxgY8Qvm8KDSJZKkZ+UOVdOg2+/B1xXGZyc4Wa0A1aCpK4zPTrG9tY1f/43fxCpN8Xu/+/diZ2cHYRRiGMdYLmeYplNESQdFpbHd76PKK0RhD/1+giD0UdU1pJAoygZSBEQh9GJ0B13k6QphEKIThbjz7lt47atfQpYu8PInPommLuD7AYQmaUxWw6pqbfOw6BBUUwLEGd+keGlN8ss06T37d6AVucjzDPM5JfXFcQwpKf+BF37+SZOaCrQ1WmKxoMgAF0IjjmwMmIJ9PFbYMyKEgGoaXL56GWEYUQ6aEEZinSQ7I1Do1otCbO3vQZrCkp7wbBRQCIlFOcdsOkOjFPYuHWE2neG7P/09ePXrbyD7yldRFg10maN26kXZxVUCZdWgbBSKqoLwPYrimF1QbLg+2ZvUNAraaz1LQEsZEEKgNhQYT3rWoAFAXl9jHLFXnLkqGlSDwYOELhqc3T/F1ugAw+195FmFS4dXcfPtt1CFJYa7I/hJgMprsHe4i7vv3sZXvvIlfOKTn8CHP/YR/Iff+HUymnWIpqpQlSUe3n+A5XKB0fYQURxBaQFIgXgwQFk06MoQYXcLeV5gPp9DCInBoI9Ot4eqrpAXBeJeFx/9zu9A0O/hi7/2OdRFgZ3RFsbjKVH4qhrPvu996PWGeP3NN7G3f4St3UO889ab8KFw/+5den7jbxaONP5FB+9lZnhDAGg00V49AN0kxqCXYD45QbebIApDhFFi6tKcY7Wc4fLly4DWCMOI5p9H6oa+H6DbJalUXqO6vRCDYWydO7xhEDih3BvO21OqwYsvfginp6fY39nFbDajjUQIREFgNxFJE4dki50NiH8GYQiYdaqqKvieh9qMM/YEDvp9EukoCxRlSTWHwpBykIIQZV4iXWaII4l0tcTOzh4+8Ylvgx9G+NBLH8Wd27dx//gW8tpwxwMfi+mMRBbKiqLgYQBAoqpqzGcLQAv0+l2oRiGOI1PDxgNJn0eYzaZoygZ5uqLaY0WBJI7RjWNIz0d6nCFPSbxgfHYOpRQe3H9IY0t6OD2dQCmFsqI8HIryCzRqASkkNARJXccJrly9hgfHZzgZnyHpJEgXSzSqsRFNjiJfuXYDH3rxZcRxF+OTCbVZeFjOFzg9PcVqtcTe/j4W8wXu3LmDqtKYTqYYjUa4dfMWlkZAoqwq3Hv4EKenp6SM53mGnreEBlCJltZjo8iTRTtoLVYwAKVpAEH5T3WjjdOERBQs7UebQc7Gv9BoWMDA2oZcM4YOpRub88FS17ROtcbwewcn1qM9drLx/zcusBaZghN9sOvqxuWfNjpykZUvnMm/9lUHYgishageDxbaxYT7aR3w6Y3vXnhriwjbNctBW+Ix13vkGu4f3qt/Hm2Xdu954ffcYz3CuEntc8HyJh2NHLLrf2+v+ShNbS2yJDXN47XxuzGWjIQ4AEcw64Ie0NROpXjuCGMzGEU6tADNVaVsTNkUu+auRX8C1HWD0JRzUVrZ8hnCRPyDIMRwOESSJLh8+TK2tga4dLRnlef29/etkBU7e6syRycZoi4VgiCBbpRR/27thKqqbKFkVpZj1lRZljZPnB0tTInjHCOec71eq0za6/Wwvb1NTCjjjGM2lXuwneKKLTAQZCcvABtUYJDGUSU3gsj2T1mWkL4P4f3XHCR7MACJomgtzGyT383vDKJcaeoAgIjFGkIH2vCoyxXl6wgpEIgQI6MNz/KHaZraRGQLfgw/k9vJSaq+71v1ENHtIs8pMTcIAiSDASlh1QJRp4/z6QJJHGM6maNsgJt37uPZ557DbDbH537t13B0dIQXXniBJGu1xnK5xG6UoCgLNPAReh6yPIPKyDiiEGSF5XJhk51934fs+IDvIwxJ2e/7vv8PY3x2in//+c8h7g1wdPkylFphOBwCijwmSrfgx02ypY2KFho37G09K4Lkq5tGPdLPvh+i1w0Rhh0cHx/jwQPKYVmtqFp9mqaIIlowlKJ8hkYp1IrEL/j98eRt6hq+J+wkszQ/h3esNdcKKVAUhQkhB1CqMblewGA4RH8wsOC5MkCMvNgSQRRitL0N3ydDc7mzwv37D/An/sSfwH93/ndQ1TehoNCYfDTX+6UUSRgXRYEsz8iIlh6AGhd5Jq1HTK8nsrq5cW6fuuP3YvrAugGgAVtL5K0338C1Z96HpD+AgsBgexvJSR+z5RJe5CM4O8OD2108c+0ZlPv7uHP3Ll599VW88IEPAAL4whe+iMnJFIHfgWxq1E2Jyfkc08kM0pPwAt/41ajootYelAI8z0ecJIiiEF4QYFXkqJsGvVEfv+vbP4X9vW288fWv4u7tm4g9D8vFDPPZBGmWI4y7uPH+F1ADmCxW+I6PfRxpVpIQwniMLE1JIUvX1rvHxtXjQVL7d+5noq7W2N3ZxpXLR9C6ROT7aOoacUxj4/LlI9y6dQtCCAwGA8v5LgranLgKubs2LJdLlGVpKKKNBS29Xo+M5Cxbk+KPYxJxqKoKw+HwEan+FozDCg/QOBDg5HRWSgRg18jWYVHg+vXrSIwoQVf3oKCwWC5RlhXlW0YxTk/GODy8hDzLsFyl6PdrHF2+gvsPj5Gen+PKlSvY2h3gS1/6IvI0Q6krSM9HUVQmZ6ZGXpQIgwgsLR7HHdR1hbokUZUo8lFXRAObTGbQSkMr4Hx6Ciq2qNBJOlitlqhqhbyoUNcV4jgBNOX7EQ+ewA/PHa4lJMx60thiukSfuX98hn6/j93dfTz77AvQWmMcjnHz3ZtYrVakFtVJEAYhfuurX8fdew8RBiEBoLqCL8m7maWZNSwpb6wCtBEBkCRSIUyejYZGZWhCjVmL7HwH0IiLDE7zEp15vub1dvJ2nHiL/d4TowDikX+s3XvzXjRvnuJyF/79vQGNEK2D1D6/+W8tnGWv+97XfPT5HUDzxLXzqZpMX3M6ZXO92YwEvdc1NoGG84W2SY+9jHj0gS+6p10rLm7D09ILH/e9x1HanDPxuHfwuLHn2iVPolxd1NYntWctisS2hGaxqNaWdJ2WntlXmA7n5pD7foQgoFy/OI6xt7eL7e1tbG1tIY5DDEdD3Lhxw6q/jUYjZFkKIcjJtVwubYoIAGJmmOg+5w6xbcZAhOlyAGyOupuPKYSwdDteA5m6xuIITLNjKjLnvlZVhd3dXaK+meflqBQLbjFVjvNnWcGuY1ILeH/dfId8X6bVsU3H74WL2r5XRNA9vuUBkjVSHWNwU3GD81h4A+QQ3WaI1jUugUcFB2zexwaA4orEnEjG92RJaQ5L8mZrJaaNV9g3hbN4UIRxDCE7CDsD7OxfApTGlevPYDIeoywLVEWB3YMSl65cQ7/fQ6M0oCU8CXhRgrPJFF4QIYwDpFkGP9QAJIQXoMgzQABh2LEVjYX0sUwzipIFAbwwgi+Bw04Xv3+4hf/4m/8RUZzg0qVLYJY3hYW5snPbp7wAQLS1BYQgwQmWl4QCmrpBr9c1Sd4+VWqPY0CTwhRTEqtS4ex0giiO8OD+iTUkF/OU6EdJBxAatart+3IXxKIooJvK1rxKksS+Pw7/Mp2SFw3P82wi+Wq5RK/Xw/jsDJ7nYTgcIopjhHFMct8lKbkkvS7KooCAwGq5gtYK73//s5DSQ5b9X/G3/tbfQqMblHVlx0ELHBuUZYU0zZGuMiNc4UHrRxd2F+Qw6OdCbq66D49j14B4qoVDECBThraYrpa4e+cm3vf8Czi6fAl3bt/F0Y3reONrr2K5WiGcBTi+cx+JF6Hb7aHX7eLdt9+BUgovvvQSOp0ufuu3vo47N+9ASIkojBCpBtrkxammgVYNhKfgCaqbIj2iVYmA6jmlZQ4tBA6OLuFjn/w4dnd28O4br+HNV76KuzffRrZa4cb1Z5GmGdI8w4sf+zZ0Btv4yqtfRX97D5cuX8OD+/cBCLzx+uvkTTMeyTWTULdKjo9TwnHnved5CATwwvPPYms0gBANhCLpVm1U2bIsw40bN+wGRBXGQ1uPi8ccRx+EoFo8S1NPit+t3WxN9JkdQFwXYv9gH0VKhTy5thvPSd68W69cbTclXjttwn3dWC8hF/yjauYSi8XSbnKdXheZya2bTueoqwbT6RSvv/4m9va2EEUdzBdL/LP/8X/Exz/xSTz3/Afw+mtfx43338D3fu8fwP/6y7+MPKV8M2hymlSqgBBAlqdmLtD6xLXbmkbZ9udFDtU0iKIYeV6YOUXiE0ppFGWBulaI4gSqUTgbk3Ibv7+6bkxQpbFrBjltajSNBle215qSokn05xxvvXUXda3gm9p26YqSjpVWWK1Kype6d/zIXIVs5zwzFdiRY+JAxF7wqGApgRUNLdpxWKvGCRQ8GlV2f76Xkbq5511krD4J+PyXcrCBx0JN36iBtHk8DSj5zz1cZ+Hmuuzm4z5pzXa/957HY5Kv2rpM793ex/39GxkX7r70pOtecCcTvSGg1J72pGjPBVDXntiet9mNT2pT22763fNaOh+PQQYYDDoYHIxGIxtdOTo6wvn5ObrdLj74wQ8ijilfuq6pQHFZloiiEEWZI89yeL6HolwhjDxMZ2foJB3AUAellPacsiwRhSGSODbKoMq0kyhwy+XSUuHcekPMbuIo0mKxsJEjpRSSJLHsHK7zyTY2521xoCLLMpyenqLX71NRWJPT6QJLlzbIY4j3I57PAOzex33v5pizuBdHvPjdCSEs9e9pjm95gMSKdUCbrM8KGwCsscBo19WN35wMDFY2NwZGu9PpdM3TKISwilGDwcAWLXUXDncQ8e+bk5fDkxxtEkKigQcFDelH8KRAJ4zQG4xocioCCUwxK8vC1hSZTsfYO9hDnHRRN0AQxFAakNIHYAxPB0hKKaGFRgO6picFFUQFUQ0HIw/f/u2fQqfTsfRA6h/jcTd8WbfSMT2DXlt8eeI1TYPQCzFdTA3P/sQm80dRhOUit7Qeoq0kJmTtIc0z+57m8wVms9dMXlkE4bdGJk8e8nj4UKKdmDw+eCJyPwwGgzWQIaBRFTkFwpTGoNdHv9+3xpUf+oAGyoKoOb7vkTdb0z1Jr58A1O/6Xb8Df/AP/gH8s1/6JaMK1sqy81igPIgGWZZDygACEgIS5OVdB0o8vpRWa+Fxfh53fDFAchNSW2O5jexJKvIFrUmumgIqREJ767Wv48qVy+ht7aK/NYTwBA6vXsWDO7cQzJbwhcQb2Wt49Wtfg9Ia125ch5ACWZ7jox/9KL7td34bLl+7ite//jomp2MoLeB7AQKf6vNoUzlIm43ck1QQsqhK1KrBaGsLz77wHN7//PPwAh+vvvIK7rz+GjytMJuc4yMf/jDSvMYqz3B4+Qqefe6DmCwXOJvO8Xt+z+9G2TQYn42RTqc4PzmDlJx7Y8aoMJ50dbFxaL2xzk8aJ0AY+bhy+RKWixlGwx6pG5YKYRijVjXm87mt48LlCMqyQKdDNWzm8zmCIMDJCVU773a7duNjED+dTtHr9azTJ89zxHEMz/Osyk9VlugmHaRpitVqtfa+y7ICJfVqCMGFWCkJn+oI+aiq2iqTLRZLTKczk/sH7O7uQwgPWgtEUYzJZILFaoU4iXE+nuLBg4fY2trGbLbA4eERZnNzf9Xg61/7Gr70xa/g09/93fg9n/40Pvcrv4pLly/jgx94Eb/2+c/j+MFDZGlK+UqSqBVFUUJDoK7IcdA0Chr0PFzjTRmvIj0iycjCiYCQpHyDppnQ3NcaVckAiegmtdJmzmpUNdXH0oqrWLFRxkpUXMaA6DQqL+zewIprjVmXa0WUGnIQaUAI1FrZenYMknTTGGq3svOxMTXteExqKOOMEuSVMgW7tFYX1la76HhaL/nm357G+P1mgYanPS5qIzvgNtvzOLD0tBGPx523Gb15NAr0dP120fcucsxsRpzaMdS25/Fgto2Arbf5YlvEvb57raeJrF90POkZ3c82nc7rF5F2TijV1v/DRh+6wgibe97mc7Xtb+mZ9B8AQTW46LN1Fozv+/B93ziO+uj3B9ZBniRUny1JEjz33HPomTqBnU7HKvL6vo80pVp+abqClCTolGUZqjxHmi2MOm6JIPAxGPaQ5zm63Z6xZzzzNqXd+5lWLYRAVdcIjcOd+4RLBPT7/bU6kBx9aR21bdF7jtYkSQJl2Dmcq8TKdBylWhnxLz6/aRos5nN0er01B99qtbK2MDOt+GBhLbePz8/PTV3AFtApRcrFvO/x31iAS0qJvMifOCbd41seILHy0OZE4N8Z2fOkAWAKIXIBRDI+N18Y0HY+hw45ZMnX5cgQyxpuLlrudfjY9Bqx0eNOUqUVGgVo4SQYarLfqFaTea0e4PsCwg/hRw26wy3sXTokTmsYoaqoynyjFKTwobU0qkO09bJalRCAZ6g2nvFqUvEtGqjDQZ/2ZidsLARQ1Y11wbASGwMQDYUg8K3SHgPJPM9RoYaAhyhKEEcJtAZ8r0bgR9jdpYkdhiGm0ykATVK/+Qp5QbVBAj8wnhmiC2ZZDRl4a5PfrUMVeG0YufXituox7Ml1Q+BCa8gwQhzR+95MHKR3B0S+D6E0yoyAHfPSOWJVFhV8P8Af++N/FG+89RY+92u/ZqOHDOilFFitUhRFYXOvyKA1Y+gChgMZTHikTW5Ymp9585BCQEtD42HPnLk+Ve6WVPiuIRnrdDHHW2+8hudf+igO9g6xmC+we3iIosgwOT6GBEXqspQkhO/cvo2XXnoJ49Mz/G//9t/igy+/jOeffxaHh3s4vn+Ce3fv4fT4FHlRQNVt7mCbv1Ah6XRwsLOPq9eu4fr16+h2SaTgN3/9NzCbnGNvNEJdFrh+/QaCKMHJvVuQcYKXP/YJ+H6Ir3/9dVy7cQP7l/bx8M5teFB49ctfhoQwXGy6I8Sajt3aHOX5yYe7rtB60qDf6+OZG1fQ6UTIsxWiIIL2BLK0wCJdWPpcmqY2ehxFEbIsR103lm/Nz0cS6JF1GvBmzOsY0+u01phMJnaulmWJLEqhtcbrr7+J0Whg6b/umOCxzGtfXdfIc1pH8zw3AKWwToTpdIY4PkWe54AGgjCg7xYFFDQ86WM+X2J//xLqusbx8QlWaYqXP/IyTo9PkGUF3v/sczg7PUW+WOAP/sHvw3y5gITAd31XjFvvvotf+n/8EuaLGbIyg/TIKeBJHwcHh+j3d/Duu+9imWamoDLNLxaYoRo75ChSDRUb5vekzXjmf68Za6YoOB+uR35dPIAOXjckYOeM1nqNmuhSuBSMwpsZZhAt/nbbQbV2HBoXtFlStaVHCTrJgHinnXjUQP1GDdanjTx9M44nefX/U0GLa9x9I+c87edrQ+aCvVtvnPc07XjayJz7bJvXddvy3gCt/XzdUebUctMXS0/ztZ8UUX9StHKtzRe0zwVLFwFOBkL2d+neSzv06NYZbWtXOs5p1+kkhEYQsC0gIT2JbqdjVIB9DAYDjEZD9Ho99Ho9hCEVhwaA4XBkPx8Yyn1dN9YOJWq+K0LAxbAjLJdz9Ho99Ps9Qy+TiBMS6smyFHEcIctSk9/ToCyUra85q2fodcnBJiCR54UFKXme2xxWGLsmTVOj4llYIMNrXJZlVrbb1i4zB4OUMAytneyyFdwxxI59DjzUdb0m6FAWhS2/w++B6zUtl0trI7HTmK/TNI3tb6J45zYixlEjpum5bAneC5v6v6rY2YPDgK73wF1Q2LDgv21KJzJAYS88AyK3tg6r4jHlhelfAKyQwOMWK77XJn3P/Tffl9srpYRUhgLRUNV11dSIQlPTB9KJmht+q8+0MA8yIM8HJFnWvu/Dkx4BJk+YWiZu7hWBJCmJ3kEVzo1RVSvkeWEBBBtaZVkCpi/rusZsNrOUtbIskXRi7O7SIJ/P50iSBIeHh8jSDKoGppMpsjRHq1SnDPWH8rxWKbXd8yTCyEOnO8T+/o6pLO8bUOpZ76pyNgG3HhBMJIgTDQHYdy2EsCAYaBfrPM+h6wahxxWvNQojZ1k3NSVzV7VJGA9Qo0CRUyX5BgpaanieD98PUTeVLaj4Z//sn8Xx6SnefvvttQULABbzBbI0w2w6R1lrQ7F77/HPtE+3YC6Pcx5fj2xuQhjRBgZIwtb9sJsUXd36H996/es4vHQdgd/FlctXcOfebVy6ehWqrmyi/Y3rN3A+PcdotIWd7R2MRiPcuXMHv/kb/wHbuzt47rkXcOPZa7j+7HWkWY7ZdI7VYmXr9fi+jygK0e/3MBgOkQxGpKizXOKrX/kt3H73XYR+gIPRDnRT4vx8Cggfb7z9LmoR4GMf+zZ0BiO8+tVXEIcBPvaxj2C5mGF6PsbxzZtYziZg2Mldq0H26aY3fn0dgZ0PHPmjDdfDCy+8H1EYQAqg1+lACg9NDVR+g6ZurLoR5xFxrZ3T07Hlc08mEwwGA+v1KwqqH8V/Yy9dt9uF1iQ0c3x8DK21FQeI4xhSkCPg4x//KN4wcuyLxQJ1rdDUNCaLskBjaHRtMqy2tC56PqZPAMKXaGqNs9NzO17rukbSTbBKV8iyAoDE/fsPMJ8tkK4yLLIMWVHixrWr+J7P/D7cuHYN/+Hzn8P/7X/4H/Dt3/1pfOo7vxO+7yPP7+He3Qd4/rkP4OatmyhVDc/3URQlFvMF5oscD48nePfmPaLUGWDH74CFXspGbbw382YF17NxDUw2btfJOdpZP4gevL5O03QRkFDmRAY/jrGLjWNt2mk4wmwbg03adhkk55zjAPe1q2384Rs4nibC8dt9PI5q9iTw8Z8D7h5/7qMA9EmA5D+1DY+zHR53XdfeWQc9m+dJsCQ0n9euYevP4LZhk2XzpAjSkwDS2nexbvO4131cdI4+dNvvRsSoJIHrJFRKWdVJLhYfxzG2t7ctRWx/fxfdbofEgkYj7O7u4uDgwEZBuCaa+xxJkuDevXtr6sgsdCCEwGJBTIHd3V0URWGjGZ7nYWtrC57nmVIXyoKmbreLoigwGAxsjk2n0zERMgnPC+B5oRHz8UC+GIGqKozt4RsmQmKdwnmWwXMYOPxMw+GQnFzmYFDCwMZVkGN7jPbjyAJNN10liiJbVJvfF0ebuD1LU5IFgAVXDJa4SOxoNLKqea4dNpvN7NhiW5sd2CxcxE7wOI5txIvTV572+JYHSJtqTGzwbnrU+Tuu4cMDIM+p1oqLpl2PBkeNmqbBKiUvbdcYLgCsFjwnsrkRLXfx4p8ulct96fwZFBksTVMTzz4MEEckuyvoomAFMiEE7a/2fk4dAC8gj7kBkH7gOdEoBSk1pNCoqwp1kUGDap4oEI1ssSD55cV8YYvdNo2CVgphFCI1cr0cReskHfT6PUQRyRJ3Ox1ACHSSxEifSwR+gLpUNqmcE/+CMKQ6LQFJWGqtKYlfStQbXg6WJybvq5GqhmeiHxQN4GK0dVVifHqKsixtEbEmTpDnGWC+KwRNeGpPDSk9+J7EIiVgSBQlIM+pVk9dVgg834SbqRaKFBJZniHpdZAWqZGbJ9BJFLwAgSfwZ37o/4K//d//dyiNt76uKYo0W6wwmSwQxXP4QWQBzJoxv+nlFfQe64Yky8EbpomYQbfKgAy82/nQ8qdpw4TNJ9NaodEUTdRNQyS/usaXvvAFfOendxB1E2zv7uPk4QNcvvYM7jZvYzqfY9Dv4dKlIwyGI9y+dRv7B4e4fu0GZvNznE3O8R8+/zn0BkMcHB5h92Afuwe7OLp0REmsls+tLCB4eO8u7ty+g+l4jOVsjl63i62dbSyWS0zGZ5gvFlimGZSM8KGXP4rdgyPcunsPp9Mxfu/v+zSgGty9dRNVusTbr78KX8J69TlaJeDYo+Z4xCtveO/MmIIm6mEQ+HjhuefsG9IQWK5W8EQA3zO5h2FEc6DTwWQyQVmVRtY6tdQE5pB3OkS5ExAYDgYI/ABlXkAKgTiM4EsPeVFiOpnh9PQEi+XSGgPS5AMWJQGu1XKFNMtAhaorlHkNPwjIuyaoH4Q06w9MziCMXLPwDZ1LolIaZ+fn0Bqoa8oFCoMAlWqgBUlCa60QxSEODg9w9959LFcZJm+8hddffwODXhdXDg/R1BWybIXXb9/H/+eX/1f0uj28/dZbePONNwHjVCmaCrWhzQkQ+GEQp2DobxbkkFpmrZoW3Ahh36/WmtYHaehshrTKhwYVqnXfsWsLKyg7nxSUUbpiFU57klXzdOcnX98FQ0IIk2n0iMlNwEmsf9feQG/Sa9t/fzNgjhCbkQEXGG5+eeMrF/z+CIhbv5lzWtsf9JFr+BrMiHWj2ro27H056tZG78zW51xzc910og72qo8HPRt3Nti4Bcem0tMGSHo0KsKtZIcErz12KRdiw/jnKCWDAlhnoDADhoMrQsg1D4/7JPxsWvN3he0HymNpHbgXgZ2LwY94zOemnUZYxKr08Xe0thEgyUpjZp56bMd5tCdJJ5rlOp85ouMHPgb9PpJObPN6ONLe6XSwvb2FMIwgBDAaba3Vf6zrEsvlgupbBoEFKkEQYHd3F8vlkpguhjU0HA5xenqKKIrQ7XatgptruPd6PURRZGlsQgi7pud5vuaM7ff7jkBBB6tlBil8CBCLhot7C+EBukEQR4ABKcvl0q5bSRyjqWsESUK5+JJsACmEzS1i+2o+n9voSxzH1mbl9+PmzjNYKsvS1jBkIG7FiYxjlkvkkI1BAjoCAnXTwGfWg6GE11UFz4hehUGIs9kZyrLEaDgiMCnXa0E1TYO6qZ1anSAbK6G80qqke+UZUQg5WqbV06+M3/IAiWkkQAuS3IJSACyncXMhqGvKEeD8Fz6PqShujkqckISsFrAvrNMjj25VVtZr4FKx3EiWe00OXXKbXQBlf28qSICiPeYeDPpqRZ5oT1JSMYctsyyDkCYvyokQcYRsvpihaWrrHSGAGKPKC6zmK2NUpTZxHGBPJVVVhwaSJES308FgMMAqXSLLVtYT0DOcU55MUMT3T6LYAj9fSvixRBzT0KT+JW9WXdfgdZPzvkpj4HOfcfSKQ8HsiWBaSl03ADR8z0ejGkBpxL6PxXSKJAyRrlY4LUuq1aQotM2GKcvBL5dLUk/zpfWepGmKsijhBxTCXS2pavN4PLYAhBbUCuMxCTp4voc8y+EHAcqihIBGnCT4HR/9MMo8x/HpOTQoVyIrNG7fPUanN0KSkGCBpxUgAbbLLzo0KJ8CggClbhqzoWqb1A60oHydcsdCGtpulJrpPsLcV0pKWpcSk+kZfuu3voAXP/pxDEe7KGuN2fgUN174EB7cfAfnpydIKoWqAfK8QppRQc9OFOHeO/cwXy5w9fo1FMscb379daKPhaEBkDQ/q5o8QGVRQkKgl3RQnJ/jra99HRUafPAjL6HRCvkixXxVQIRdvPixT+Dg8DIeHB/jndu38OHf8XFE/Q4e3L4JlWb4ym/8OlSZ02ZsokE09swctAMdduy6dDoydqlfhAaEAoRosD0cYG93G5PzKdKU6uWEUYhuIjGfTxCGAUbDEaq6JvnWOEbd1CjqyuT0BZhMzpFlOUajIc7Pz1GVFbJViqYm1Tb2hGZpijTLobWH8/Nzom9WFarqHNAaURxjka7Mpq0t7QNaU/4OPKhaASCarYCA0ILsb9snRtnNDAFlIlJlQzW1iP6vUVQ5lG4QRiEK461T0BhPz5HmK6R5BmUi4OV0ibPZW3bEiQfn8F/5OgASamkUOVyICqfagS40oOq19wADAteMVH4/zt/WPNfKfcebSNj90QKaNYPcgDX+CtbImECjGd08Dk04p7Z3WgMXGpuZ4o5xr9avrTeu+40fokUf5sqtjbtunHNB7/ZTbr9e+91tkgs+1sGN8282eDdb9phogpRifS7anEwzJ4X7kwCIS5leG0NOc10gqtHuv/wkQghIZw8HX8ca7E7kz4G+2uk3uiZ9l9qgaAHRZg4yZUwzYGkpYUKsy5VLQ7nn+7d9fnEuEX3IzBWubaVaUGWcg9TH6/R5ITznHi24E0LAk4F1Tgpj8CqTuye0ALy2OKot1ioM4URTeymvWBinJuD7EmEYwDf0eSkldnZ2cHR0iL39LRwc7JtC4Yll9PiejzAK4ZkajUVRGhtOYD5f4N69u7h69SqKIkVVEUhhahnbE/1+H0VRoN/vY7Eg2X0W9ALaiAerujGwmM/ntlYa2z2r1cralZx3xKDi9PQU/X5/TWWUoy2+72OxWNhoVFmWCPoBmproabohG0eKAMNBd40VVVUV2TGrFZhdwJEVFi6RUtr8KNcOZqcpjx22s9ipyiklzJiSUtq+YiAVBpEdG1JKlAUptJKNrJGaOnJQyjqtIci4EFpAVQpQgIRcU7rr9XpY5qbcQdYCTiEEQi/EfDW39DylFEI/RBySo34ymeBpj295gDQcEle0KAosl0tbNZ3BDtOpiqKwincMVsqyRJ7n2N/fR7fbtRENN7yqlMJsNoM04VvmWXLSGA3KAJ5sOZDt4qBslIknBQOxliLCSkatx0lKicCEKymS4qHmAVqWmM3npmhhbe8Rx7HNA2JlD54kQRBQPlBMk2exWNh2LpdLVEUF3ShEnRj90cCc49tFtM1lIa8Vh7K3t4domlaKug2Rtou81srI8hKFLgwDkzPQoN3IqMAjQFtVVZYIwsAuAtDAKqeaI1lKiYIPHtyHHwTomfo4nOQ3n89RFgW6vZ5RzKOIT6fTwb27d7FYLHBwcIA333wTh4cHkJ7A8QkBzLv37kAIgfF4jNVqaaiINMYmkwmyLKO+9AIjwFDaBYmBIUDjod/v29w0zikZ9Hsoqwbf9ju/HR988SX8w1/4v+P+wxOonDwy5+djvPnmm3jmmRvkSUe7kT3qzqWDx5lLKeWFE1qs/a0F74/WjmiNCHmBV9l8rmrcevt19Ho9XHnm/TjY34MEMJuMcfXZ5xF3Brh75zayckqS6XmGVaeD8dkp3n33XShBG/V3f/rTZGgXBfI0RV3VOH1IuStXr1zFVr8PMfKgAg+qrHDvqw9R1hVGgwHUMscyyzAvKmztX8IHXvoYuqNtHJ+NcfPmLXz4Ix/GtauXcfudd5BOz/Hmq69gMZ8hAOX2wXhb6U2Jtm+duef2y0X9oJoG0DUuHR7i7OQEvlRYLpcYDofQmiJLWgPbo22cn55jOpshLwsUVYnCUttAfVSWaOoa77zzrjVIVN1YRS5eg4IgwGy+gFLCiA80xlMLMlIEPR/PQaW1kTJXJvHfpxwdIwfrRiXdZ6XrKmswKjNHtdLWc8jeYfYUSiHwK//+16xBVDXs+V4vn2DuYNdEvvfmWDS/PPIOnpYatkl52jTU+fk3DXL3cM33p4MkF3zryc73x/7+iEF/oRf/P/EQ68/mHhcZ2Zte/M3P+afb5jVQ5RryF3x+0fUu+psLXCyi00yndMEKOXxYYawFry1lzGWV0MG0+/ZzVwGM107XuUTfaSOIBJzoM0/6FKE0ghsCwojgUPs1GhvRaVE6gRUBuR7hWusSeeF7oP5p/+1GrqjoNz2/lPKRd89gV0oBz+zb/Cz2GtDr4wDCFKGmZ9PQCLzA7vfcJ6EpKyINMur1ujYKs7u7i62tLYxGIzRNjavXrkAbR2un20XT1Nja2kZR5Fit5taW48hN0zSYrWbY2tqyJVY4kkPvpqFipf2+pVwRG6S0JVaiKLIAgvJCM3s+M4wKk0fDtDMWKmBnLVPQBoPBmsgAgymOzoxGIyvg5YI0yk+iSA7nFHU6HQgApXF89/t9TKdTS6fjVAaO8gwGA8xmM6sulySJVXJjBxvngLuCB/fv38dwOLRgEMCa2AHbNNxffA1rY5QV8rJAknQghLCCCkyhk56w/c55QpaeKHxLOVwulxaUuiwu7ne+Z1VVNjeXwSD3N+faPi7v+nHHtzxA4iToxWKB6XRqUSYndbla6S7HkV8yyx+maWqjO/xdXhAODg6gtUagibKmlcZyvkBtkuIAWG4mnzcajex1OLzbNA1msxniOLaDjhdfd5PRmihNngmJcpSkqiqkWWqkbKlgmYChuSgKaSZxiL0dKiAG0SqCkBcLNm/H9XhRYcQ238LzfDswfeGhqWsKZxqvj9YesjQlAGMWTxIkKBDFsQ3XUp5BDt/zACGQZRmyjBS3tPE+FQUVjdSawuylqQm1XC6MYiCHvRdQSmE8HuP09BQAjOz2CEWRQwgqeNjr9bBcLFHXlaEfhZAgJZc7d27j7t17+PKXv4SPfvSjODk9ge9L9Ho9HB8fY26AZ5IkiGOiBHJOxtbWCKPRkBI2t3cR+IENsfM45PA9c5N5svo+KYidTyaUBzKb4+rVy/g//8D/Af/TP/8XuHPnLpSJmE3OzyCEpuiXJ00Oy+MNGncxWaPQCdq8N2ml7NFUThjaNVCFeNRI4s89kDz3669+mRZPKbC9swPp+ZiMx9i/ch1Jf4C7t97FZD5FWRbI88x8bxtZnqHX62I2ObcbRSeJcfeMCsxqTflizz//PIpVhbSqUBQl+v0B4og8baeTOWQQ4vmXPo4rz7wf8EPcuvsAZ6en+OjHP45rV45w/84tZPMpbr37No4f3Ae0QmOe22AhawwxVRWGyrJp0NM8omKFTUP0BaqQLjAYDrCaLxF4wEde/giUUjg5OcGdO3ewWCzQTfoIgghlVUIBmC8XmM1nqOrGqLFpKtws24rp2uZetM4Iz/NQ1hoQAWpVoaqVeX+0SVmFNdFSKt18Ia0pEqFMRJcplUz3cd42hDHQlaJSzyx6IKUkb68dF8bDKgPyaAMoq5KMPJNsw9e5aDy9F/hx11/XYHWvc9HxtCCKgcjjjvcy5p90bJ77NG3avI97jSed/4237/Hf3wQzrjH+ONDjtu9JIOqif2/mGT3p32vRHmdN5EgO0UTX18R1MCTXrsvjCwBcp1GbzyKt0eZGV3hMk6MEa9dgQ5PnYBi0kvzMRCC2R2OjYu1//IzGdSMuGhMAR802+3itELjgiBcAj9d7jiC1c972nYCN9PDytxkFW49YNfB92tc8j1Rj2RDv9zrY3d1FHEW4ceMGLh0dYdDvo1ENdra30ChmaMTwPAnfp7o8abqwz1jVFeIkwHxxbg3m1gFFzj8GWVyOgJXk2EBnKhkb0xzVYbuPjeo0TRGGoVXYZSZOXdfodrsoy9K0N7LPyfcQQlgn6GKxQBAEtpiqEMLalgDQ6/UAAIsFPSfbh11TB5NV4myOe1nCk9IKQTAtjkEKqwpzHqubK8Sqdq6Dim1MFs0CgJ2dHUsXdOcFzxtuDz8DzyUGqHlRkF1omAauYFqjGqSL5ZrEN7dVa0D6rdODadSr1cr2C78/njsscsQKei4NMI5jy/7hPKSnPYR+6h3j6Y66rvE3/sbfwD/+x/8YDx8+xKVLl/An/+SfxF/9q391zfv6kz/5k/gH/+AfYDKZ4Hf+zt+Jv/t3/y5efPFFe52iKPDjP/7j+Kf/9J8iyzJ85jOfwd/7e38PV65ceap2MCXq3p27iOMY9+7ds5OJETkb34w0GVmyMeIajzzY2Ivsem95wFCBx8K+UL4+I3oANmF6Z2fHeg9cgQCW/AVadM/3YBpUWZYojKdCSmlFIKwyizAgz/esR4efQxnvrwABBimpgKyGRt2UNn+naRoIKVFXNYIwQGWoekIIeE5kS0JAVaaIZRBgMplAa22RPOdnsZxklmUITVVkpTWmkwlGoxFm87kFUr7nYTKZUEFGI4QhhMDuzg4ePniALEvh+R6SOMFiMUdRlghMaPj+/Qe4fv0aXn75w7h37y4WiyV5yesKSivsbG+Ddf9nszmyPMP7n30eX/ziF/GFL3wBQgDXr13H+559FsvlAmEYoCwL4wEprRINKYalCMPALgCLBUkya0Xy3lyvyPMo6lJVFcIogBDAeHyGvb19BIGPMCRVGikIMGoAZVVDSA8PHh7jX/zLf4l3b95EWVYoK3ovjRbQwnhIdRthBPDIxsV/j6LI5lIJIYlCpVuKCG/itHm244WvRd/z4NIrXENJ6Ia8n8KHF8T40Ec+gb3LVxElfVSNxsnxMUJPIPQExif38fDeHWTpEqEfIDGUMu7byFDrBCgaeO/+PXiehyuXr1BCbVFCFQp5VSFrGqyqCkpK7F8+wjPvez8GowMs0xxv37wNDeATH/sItgc9nD64g/nkBHdu3sSbr30dQjUwsibG29nKLwvJxg5FQRhQun1NyoQKTVOjqZUVXx8MOjjc38Hh3gh/4Pd9Bq+88io6hi6xs7ODt995B6fH5/iO7/jdODy6hE63i0W6wv/0S7+E2WyOtMiN46O9jzUwBdHPqqpC3dREFzUbUt2sFzhu1ykCP9p5l+1zCEe+Gq1TnVcK11m9AaaVA6DWDGZ4YC4eR5PseJHrkaEngZnHbU+PAxkXXWv9WR9vbLuHaol5a+duXue3EyBtGqZPc957H+KJNL3HtXltfGJdmdU1xt7rnX4j0SP+uwt0WvEAbo8EdBspcksi8JpH97atsJ8ztRuQzh7afoeKasbk0Rd0fXZEMVipawILXO+mqiqcnp5BKWXzZdjumM1m1ginIu3kqKD9/1FQzNQ8tgPoedYBkq2n5zzZ2tplKHX8u3U8SLIbfN+H9CSaurEG/uXLl6FUg8l0jF6PaGH7+/sYDgYQUsLzgN3dXctQeeaZZ0wud4blYmYEATLrFKYIxxxCmLVLUzTO93wqsu4THZ6dwcvlEnEcG2nsBlEYr6mjZRldezQaWYq7SwVzRblYFKcsS+zs7ODOnTsAYAtvu2wednLzOGP61sOHD7G7u2sNfLYv+J2wPcc2mi04ba7npnowwGCFUregNz9fGIYm2EgqyXxfPsfzPCvyAGAtn8iqbZoggJTSqvuy+ptLt98EHWVZ2j4YDoeYz+c2ssPiC6yKR7nXvmUUKaVsdKyqKhRlZiN/PIepEPoKURhbxhWDV0514f7n/mU2hWu3R1FkHYFM9+Pvn5yc4Pt/4A9jNpthMBhcuK7YNeKbDZA++9nP4ud+7ufwC7/wC3jxxRfxm7/5m/hTf+pP4ad+6qfw5//8nwcA/OzP/iw++9nP4ud//ufx/PPP46d+6qfwK7/yK3j99dfR7/cBAH/uz/05/Kt/9a/w8z//89jZ2cGP/diP4fz8HF/4wheeKkTmAqQkSdaiRzywefDx4ssDwhV2cCcTD3DXy8kvXwCUgCaovkuR5yhM1GRrexu9ft8OBjcszxOCOa88UHiD4Xu5GwE0J4+3oX0GUUQMokWvqc1kMJGOIi8sN9j3fePRpYhXWZGuPgAT3ZDIstz0i4Ayg4wBHCuqpKuV5Z/2+32kaYqqrFBVJbKsQG0MOZJXrFE3tZGxJhDUejak8Y6Qdy0KQyxMMUwpJSaTc3Q6HfR7XcRRhMgALw4HV1WF4XAIz/Nw//49ikalGZJOB8PhAFrXyLMcdUPJiWdnZwZcJuj1BsiyHMfHx5DGK5MkCaIoxGDQx2q1xGw2w9nZ2PKG45iijhxRXK2W4I0pDEJoBcvR7/V6KAviw4ZRAKUau7D0zbgoywJC+hAQSLMMnU7HTuy33noLv/LvP4evfPUVLFcZtJAgaq7Z+HXzVDQfl2sMTbjKLb7GG4HnUTt4fK17qVv5481xSYVrNZViERJK+Hj2Ay9h9/AKRJAgzXOoukTgCfS7HQitcPLwIc7GZ5jNZoBSCPwAge/D9zx4QgKigYRTONO0qalq6AKoAYheB6PDQ1x53/vRHQwACJw8OMXJeIJLh5fw/PufhYcaZw/uIluc4/Y7b+DtN98080hDMCCCACAtQAKUidARP9py/NEaqNSmhiJINamKhX6AnZ0BPvLyh/Cdn/pd+H//P/9fODk5wWg0wnd8x3fg9u3b+OQnP4kwTBDHCU7OzhDFEaTv4xd+4ecxmUypvo+hrpEyIhld2lCIqrqCJynySpQ3oziI1oGjtLJ1fACsjRGtHQCwYbSuRcnEOuVqDXQxiBDOl90THzMqhaa8Iu6/zcjEN3pcdM7mNd3vPA0wIWz33t97WgByETB4L7rmN3qPb+R4PCjFGkB6lAL5+Ou5AGkz+vO4iJe7F75XG5/UD+6eLOw8FQTUzbymEbspauFQ89Y/ITYENFTjXpPOaaNJ/Bls1BbgKDTXFHPvR59xtIhtDPba83d43WUQRNfkfFBh93zuuzAKoVTttNEkxnNiu7NeMdULINED6VE04/DwkjFgG2xtbWF3dxfdLokqCSGxvb2FTqdrKOEh0rRVzgSA6WyGOIqQ5Sl8z0MQhgYcUJmCIi/gO3nbHLHo9/u4d++urRPGTl/f9/Hw4UNUVYW9vX1oTbUSozCksiueh/v3HwAalsJGjkqKwrD6mzZAgull/Dn3BUdNWF6a9n6yS1hIgR3gDH44GsGGP++rDDg4rYFtRFuDxyi7sUiCC7hctVmm+nHNofl8/giF0zPvkIV4+L6uI53by3ZinufWxnbTOvhZpZSWXeUWi2V6HwMgtv/42bhoOEer+HmqkmrnZVlmbR2rqFsXFnQxE4JF0epKWXEvdsxz3jkHLNwghNYtJZKvxREupZQVaOh0Olgul/jMH/ie3x6A9H3f9304ODjAP/yH/9D+7Qd+4AfQ6XTwi7/4i9Ba4+joCD/6oz+Kn/iJnwBAkZyDgwP87M/+LH74h38Ys9kMe3t7+MVf/EX8kT/yRwAA9+/fx9WrV/Gv//W/xu///b//PdvBAOn+3XtWZaOua9y+fdtS5vb29hBFkU3q53yRNE1t1IcRKUeQpENr45fN+vJNXcPzfGitEEcxojhCr9uF8DxS7TDRIBcc8WLhSYnKGQjuxsHfWYtaOee24AikJleXCIMAdV3ZyIUQpEBXViWikKIIi8WC0LskAMTRjfPzCRrVYLVcUhSpLFEXpNg2mU7heXTN2WxuPOi0+CZJgmeffRZnZ2emRpFAmmZmEBJ4c/OquLbU7t6ezZmo6wplWRkuLQ3+PM/tZF0tFwh8H3lRUJ8ZA78sS/iBqcGS5ZhOJ1RYs9eD70kkncguBtRvtMAVZYUk6dkF8MGDB7h06QieJ5EkMZqGvE6TyQSLxRJSClPHiTbDJElw7eo1SyWkqJrxlBrjlkEUALMpCuvlSZLEbI4CnqETzGcz9Hrk/dFaYzadomoafOW3XsH/8r/9CmarFI2WqBrj41fNI0pX7Ya/biiyxwkAmkrZxccVBvGkZ2lZm953QEJK/4K/A5odDUJBCo1GA0qEuHT1GVx99gWUDRXDrKsG0LQAd7odeJ5AlqZYzOaYT6dYzhcoUlJNlKKxhgTQFh3udLro7uxhe/8Ava0dJJ0eyrzG9HSC44cniIcJnn3uOexsb2G1mOHBnXcgigxf/+qXcH76kOMZaM1B04GaKWAwuQDkbJCC6aOPRhIeBUg+kiTA5aMDnJ9PkGeFiczy+BfodLrkSKhrurMUKCrzu9bQTftC3Tw+z/Mo8d+4hF3DUENDeO17W3tHGiZ7gdu+Plae1gYnZxBFlbRoo0uuZx1gg9k90zG6gTXg9p97XASAvpkA6f8fbXzS8c0ASE9/jfUI0jfSxov62P3son7fBGBPQ6t73P05wkM/nUimk0O0CYTWgdWjgIwFWPi6azRl51ncKNb62Fu/j1t/h735rl1A4Ki29HTPMhAEIISlaA+HQ3NNZYqSDjAc9q0Y1M7Ojr3utWvXoE1eb7fbsXk0nu8jTiIbIRptjZAkiRVxyvMc88Uco9EIy+VyjbY0GvXhecKKqJRG2Mj3fCwWSyQJlSTgqAbnd0NppGmGMGxznYfDEabTCeq6wnA0xGw2s85aKT00jUISd1CaQs7Hx8cIggBXrlyBUgp3795Gv9/HYDCw75JzaZSiwqGDwcCKEzAQYao723VCCFszyGUBcduZSsbglAEQU8pY7Y4/y/PcAhIGUdwnDJQYALh5ysvlEvP5HHt7e2tjiiMl/X6fBLfMOHKd6/z8XFycpb4ZGLhpJLzvb84vfk5W3OO+sIqoBqi40TUGu4sFpT4wuCmLFvgzuOI+K8scURzZ9nMulCc9ZFlhFQH52XKTXsH9rrW2fcft5KgZy4Jz5Ivz7rvdLqbTKf7Q//H7nwogfdNzkL7zO78Tf//v/3288cYbeP755/GVr3wFv/qrv4q//bf/NgDg3XffxcOHD/G93/u99pwoivBd3/Vd+PznP48f/uEfxhe+8AVUVbX2naOjI7z00kv4/Oc/fyFA4mQ5PubzOQAYDzCH3wQOLx0izzJUZYmqrlFVJbRSlKcCyjMYbY0onVMpChk79AGtNXrdDqRsI0lSCuiGahGNx2N8/vO/jmeeeR8uXTpEHAYQihTLyjyDZBpfQ9z/pqkACGjPo4RJKVEWOZqGlMrcwcFh3izL0TWTrSwLUOGxBlEUQ+kGiykViOSiYtQvJL87nc0gJenIR1GM5XKJvd1dnE/OkRcZyoKkG4uyQBKT8S6gbcmONowaoKlqDHd2EEYhVmmKQb+P44fHiKIIVy5fsZtAUZaIzUBvlELHJAlWdQ1AY3x2gizNaELEEdLVAlm6xGhrhOlkirKqUBSZERZQyLIV0jTF1miEuqkglYCGwunJQ+v90EqjKDJo1SAIA3S7Mbod6jOlFMIggGoaVKjQNBXCMMb9+w9oQqoGD08ewvc9RHGEPC9MYr3CapUb8JRguVxAQOD+/fvwfQ/9/gBRHKFRDaqyRlkUaJTC+OyMai70++h0EgCUtNntdm14P01T+J5Elq4w2hpitVwiCkNURYmqKtBohU98/CM4PDzEv/13v4p3b97DKi2JEgZNUsMwdV2sIcARxXbxc4E9gw1gnY7XGD46G7lKaQuCyRPpLqgOEGOpY5gcJq0hpcL92+9iMpvhxQ9/FJ24hzoCAA95WeJ0soAnBaIoxM7hFRxdfQZCG6ppUaAxCm+e58EPfHjGkxXGMZoggtLAdDrH3Xs3sZossdUd4sMf+jCGhyM0TYVbb7+J43u3MT19gLN7t6GqHB7YG2uaDY4gSUAo+1xkk0gDkNjgcthn9mAjiX42WiEvCrz1zrsAJCBaYwiawNA85cTgBsJEeOndGZDNBp5YzzNr6gqaQnTQer0aPH3ByHQbUMTvrW39xYebc+YarZuGvWniow53h8ZL31fOea1hTIYeed6fDh49gvwfPTYMW41NAGgAnWl7K/v9pGte9Pt6L3LUbv1veLRvzDhqpZuFM5D4ERyjemPO8r3dU3g8kgG/cR3ni9QeVhNrn1s4n2nd/u3JAEmY1yFcy990v1lrhKQyDKCxTeNBWSOfjZr2uuugqY3oiDZ3zj6907kO2NEa1vGgtZkb4PHmwRWycQuJskoazyFWiLPvQSsSVLAvtS01wKJE7RwkMaGmqQ0waYGTe7RULSpGGgShpW1fuXIV29tbABQ8n6IoR0dH2NnZwXK5RL/fp30hitDr9ZAXuQVC0LQLdLtdm+PUKMpp7sQJQj+whZ5ZdbVpKqyWJfzQRxLHqMoCdUX7f6fbQVWW5jsLKlKaZkizlCL8vsTZ2Sk834cy0ZRutwtPCoyGQyRJgkYplEUOrtNITuSGqOJlicGAxI2IQtXF1tYIQgjcu3sfvV4P3W7XrJkVzs8nBlDEuHr1KgCB+XyOTifBjRs30DSNFRQ4OzsDQI5VztFhB7kbXdna2rKUNAYtrjHNEt+TycRGOTiniK/P35nP59ZAT9PU1p8je63NHdKaommcf82RPgae7MBkYTEAVvaba97xeXu7u9C6zb8BYOluRVHY/uPIDzukue0MPhgoMugh6iLlWu3s7GA+n9tzWYmPrwnAUhcZhLJN4RaG5aindhZM6VGaRKMMY4OmKNV6EqTAnBf0xzCKEMcRirK0y73WGlVdAYLkvaFhC+PyfstRraYhUQ7O+X/a45sOkH7iJ34Cs9kMH/jAB6yB/NnPfhZ/7I/9MQDAw4cPAQAHBwdr5x0cHODWrVv2O2EYYmtr65Hv8Pmbx8/8zM/gJ3/yJx/5e11XaBRNjPl8jpOTEwrhGclHomAN0e/1yGj0PCiOdHAdBSOBWVUlPM4lMbxJt5hiXZXo9Tv49Ge+G7PZDLduv4u9vX2MRkNUFYExzsmxtDhJofy8aAuD8qRZZTkkBFarFfFDowhJHGMxn2MlgDRdgZVTAApxB35gRAmEDRv7hsM7m84wny9t5IxVUkoToQm9EJ1BB0eHR3YiCSGwWi1RloWNvjDNrtsbYLVaIQwjxGGMplaYzeakDJMVEEIjCCkE++67b9moXT0Y0KZjvF9FQTWXiiJF05TQuoYQEufjU5yfn5MHBhJa1cZgb9DrdVBWBcIwsGomUA08QSphcZzA9ymkHAU+oqCVt2RA0uv2UOYlAl+iqUpsDbcwmUxwUh4Dgp4lSCmcn5YFPCkQ+BT5WRgAnme5pVbu7e7B93ycjE/R7w8wmUzRqAZxkiBNqfbR3t4uGLAz8OVFkzbpELVZXCkfSWO0tY3p7AxhKHDj2hF+4Pu/D6989XV87nO/jul0jkpK1MbAlsLUaLHH+gbN/N/AD9CgpWe6lE4phQENhjZj7As6NIRYV1Vkaid9ylQwaQ0piQb5YoIv/tq/x7X3PYsb73sOfhwijELEiUIYkudpfD4lr5YfIAgDRGGMKKE6QRCCnAd1hWVWIT0fo8xLNFWFOOlgb3cPH/zAh9Dr9JBnKU4e3EW2XOD47i3ceus15KsZpK5N/3A0x7Rbk/iElCZPh401rNOGCN04trJ2CyYCnm+ADhSKmt6H5wkINNAg0E4DeGORatiQbI2zhgHcRp0bDaydTwp0DKZM/hQbx/Y5zLu3BuUFnn5nmPD4sefbOiva2Mh8fmucUz+1Sd4ERtaBFve5WjNyH3+0RrP75cec5Lb/QsEG4dj3F0eQ3GgAIZnNaCGP8Ufv68DLx7TPZLg578pt8xrQ3WiXdNTDNqlsWjX2OhzhaNv7OD062LmpeUzbawozJTgvsX2vAh6CILIUGabXMOUagGVaVFWFBsYg1exFJjAl26Vh7VkUG0oQEJCQImg7mB004DybtriBBkd4WYjhUYDHTgIp2/estbY19SAklIah5PAYlmZ9bEEUFeSkqHIYRqjq3FxTwvMEAh0giluvd1M36HS72N7eRidJID0Pu7s72NsdYm9vB0dHR/A83zJkWKY6jmMsFgtrjDIlPIl9DIdDir54Alm6JFthRRGevb09a0Dzvlgb8FJWpVXjDaIAuqRoN9P+V8ulNdSVMSjLokRdVfA9D9PJBNvbJPBU5jX2dg6srZLlOaqyRJnXKHQN1ZjIAqh+DbQw9RILS4U7Px+bJH+KJN29exdhGGJ/f99Gq5qG6H5M2yJAKQ04IobHYLBj99HVamUdf8wscaMqWmsrisUGPke5GBwxQGADnwFIr9cDM2UYHJVlaeWkOTrFAlur1cqyX4QQxindjo1Op4Pz83MLKLgmEtuUTDVM03RNMY72b986zZm+xwCQ93QGdJzDzXk5/Hscx2uAgtvPqrpsJ7GQmVsjiWXP3TqKzPTQWtv6R51ErIE3brMnPcxXc0ALAnIQqKoGeVagqRXCyEcQGnpcWaBRbTqMH5BdR+PBQ56nCAKap9wmXqPSNG2jl2aNWSwXj1sVHzm+6QDpn/2zf4Z/9I/+Ef7JP/knePHFF/HlL38ZP/qjP4qjoyP80A/9kP3epmflohD35vGk7/yVv/JX8Bf+wl+wv8/nc1y9etVOYKWoAFe/3zdGmzDS282697xpIHzPSjRz6DvPcywXSwzMJCmKwoZjlVLwPQlPCEwnU4xGI6wWS3zuV38Vvufjk9/2SWyNtiyvNE5iVGWJXq+PxXKB8fgM9+7ehef56PW6CIIQDx8+hFBkSE+nUwyHQ5uIp5RCv0eTvNPpWIQcRRE8411SSlk+LQPNdJXC9z3cuHEdvu+hrhskSWwXBuKSrlCWOdHxzManNUlwugsQe6F4AjJPl1E66eF3oRSBqb29Pfzqr/6q9cQopexk4YWLvTtME4jjGFtbW9Z7liQJJpNzSz9zF9vVaoXhcGgTXQlIqbWwcFVVNpTLi0W320XZ1CirCqvVCqvVCvsHe1it5hBCYjKZYjgcIEk6lhLAvOWicKmZIe7cuYvRaATPk1gu5xgM+2aRixBFl+F50gBkgaLIAdCiubOzjSTpmFwtz1Ifu90u7ty5Y5LxG2RpYYQiAnz0oy/i0qV9fOnLX8Grb7yO2bwgg11Tcq3m/CToNUNMCGEXdAnPjnk3eXOTcnLRXL3o78Cmj935uyK62s23Xsf9e3fxzLPP4fDoCnzhQTQSh3uU1JtnGdIsQ5ZlmC4XaBqgUeQBV6Awf5TE2N0ZIeoNKeoY+qjKAlm6wtu37qDJczSLKSZnJ3j37bfQVAV8QXWfhOHAEy0AAIx33RjDboLq2jOze8vpR+ZZt7VDWkPP0u+cHC6OwD3uWPdeP/57F/X75jtznS1POv+i+7gG5JOoYJvnus990ffWjNX3WOv/c46LqFLf+Pc4VPYNHBoAnNo1DsDm8dJCqUcpiNI5z42cSdkmOW8CJAYbLsWsfW9Pzh+6+PEocuP7PmJD/ynLEhoaQRDB9wMbhW/pe7sAAQAASURBVODx7441dti1ubwC0vMhTRsNxDGKh07USLe1b6SUpg5d234aW8rsPW0e5Prz8HqFR/qd5zx3sVIN1nJ72JOPCkIKm0NTVTWGvT6iKMS2EfgJghA729uYLxY4OtrH5ctHa/kYu3u7qCoy6MZnZ+SQjGMUeY6eofsX2cqwP2iPOjw8AKCtYc6Gd1mWOD8/t9GOsizx4MED9Ho9NE0NrX2EYYA43rFKZwwm9vb2bAFQ3mdZrpptB9/3qfi0aBXIRqMR1Zpz8m+WyyWuXr2KKIpwfn5uDX/KR1nC93wggI0QsuovA+blcmkjI57nIY5j+3y813OEgoGBm+fT5g7pNeGCXq+HNE1t/pCbc5Nlmc0N4rQJrmvEhbmZrsgKawxWuJ6P1hq7u7sWaHEZFJaVdvN/eG/lCBVTzfj5uaYRR9tYbIIFHziPez6f25Is/C6Xy6WVRec+9mWr8tbr9ey1GQSFYWjlvAeDAabTKZRSNo+awRgHDzgCxGMQgAVK7ABhYMd1mXj8cm4+U+AAmNzr2vYD0wrZHt/Z2bG2NNsf/X4fGhqdTmzXEZ7/PI+zLLN5ZCx6xqCR9222LTmdg6NXRVGgk/w2RpD+4l/8i/jLf/kv44/+0T8KAHj55Zdx69Yt/MzP/Ax+6Id+CIeHhwBgFe74ODk5sVGlw8NDlGWJyWSyFkU6OTnBpz71qQvvy0br5lFmGWqD4LVu63ioel3dhYvCbm1vQRUKTV2jyGiSQ5NE7f17d/BuXuJ973sfHjx4gN3dXczncwIkdYV0sUSapcjSFNPJBM9cv4FXX30Vqm5QVxW0arCYz3B6cmwT8FerFTqdDnZ3djGZTHDn9h2sVitcv34dUOTt2N/fp+rAZiOazWYYDfs2VLg0nh/W8+eEutFohLOzMws4XnrpJRRFgYcPH9pFh+kBwyFxMVlelCllUgrrQajrGsfHx8iyDM8++6zl1vKCxAsFAAyHA4zHZ6jqwvKDP/ShD+H111+HlBIHBwcWyGmtraeEEwAZyDB4Yk9HFMXWqGfpzizLMJlMEEjPTkRe3LnGAMtl8uRnzX0/8OEBmM/OoZSG5wXI0sws1AT4aHFMbWjd98lbNByObE0BVnEBgO3tbRRFhuFwZBM7pZSYTqem/QpRlEAI4Pz83PCsCaTkWQ6tgfl8gdlsbvLABM7OTtHr9bFjJNopghfgk598GVdvXMbDhyf48ldewWKVoao0RXIgANGsGaQuZTMOE/tMvMDxd1xjDHjUqN40nt3Qufs7fc9QgpSGlB7qdInXfutLeOeN1zDa3oYXJBgMt9Hv92wfxh5FH7O8QuAJKN1AC6AXBzg6OoD0A6waYDI+Qb5aoikzBEIjW87x8O5tTO7dRlNXEErD44iGlNbs5HEPazC1NYJcL7x9TrQGpQvmeSwC+pE+WuuXb+LxpGtuvrf/lIONpScBo8eB5sf9zXVC8c/Nez7NcWH06z3a9qTjcdegiE/7mZTuu928hnvuY66HR0UZLgJoF7ddQAgPXHdt81yWn2c6G4F/+Ug7Lzo2xywpNfqAJtVOvj9fn/cY912yIeKuG26UyRUXgNbw/MAaSZvrTtuYdaqnG2FrnRvtM/Bc9TwJ33OjToAMjOfZlLOoa8o77XQ6Nrc1DANs72zh4OAA/cEAg34f+/v7qKoK29vb0JpyP1y6VtM08ANhDdkoomjDYrFE4EsANY6O9pEksaGSNYgiibpusFws7Z7O+T1cy4YNyU6ng8PDQ1y5cgVpmlr6HO+LrLLGnv3z83McHBxYg9HzPPT7ffR6PczncxRFgd3dXQyHQwCtQE8YhjavhdkM8/kcp6enuHLlirUhuK2smssRGEvpM6CY83Ymk4mNaA0Gg7X3PJlM0Ol01vZ+Bk8sUMSSzOz87ff71oDnfcLNM+KxyAp0HIlh2hfXwgyCwAIwBnPj8dgqDXLkLggCC5LiOLbMJs6B4TYXRWGBGgNKBgkcsev1elZZjgEB0//u37+PwCgAcw4NCyr5vm8du8z+EEIgzzJS9zO5VlVVWbU6pRSGw6EFLxxtYXEGADbKxfYQ0/FcW4vtJH4Xm2IiPCddsQfO+2G7zfM8bG9v272SWUhpmlrwApD9Ph6PnXzjVoWVndm8znA0j4MY/K4AgbKoTF4b5eitViu7FhVFYSl3T3t80wESP7h7sLcJAJ555hkcHh7il3/5l/Gxj30MAOVF/Lt/9+/wsz/7swCAT3ziEwiCAL/8y7+MH/zBHwQAPHjwAK+88gr+5t/8m99Qe4osx1wDgUlYZM9DU9XQSmE6m2LQH1CoUnoo8xy1qjAej633gI+jw0O88+4tnJ6eoixLTKdTnJyc4OrVq/AF5aIEvo/FbI5LR0cI/ADdpINb776Ly1cuYX//ABUUAl+i1+1Q9KppEHg+4jBC4Pm4dHiI5YKS6TifpmkaLBYLG3YtihxK1RYY8QJZFIXV4efFgeUmGSQBGvv7u9AaODs7NYO+hNbK8HGpwF3T1JASCIIQtSlMCZDxzxOXN/Rut2sXV046DMMIBwcHaFSNLEuxXC7xiU9+EnEcYzqd2na5gIaTRzmMz0YoAzFa5CjywkXP2HtSVRWOHzzA8mSJy5cv2wLBvLi6YWRXRr1RCqpRAIjzeuvmbVy9dhmeR/eq64xECwIu9BsgjsmT2ukkCMMQUZjYhSLwI9RVg9FoG1mWGk9ORAp8/QGKokTgh2i0gic9bG/tIs9KzOdnSNOV2dh8kidVDYqcAKZqJKbTBVarFFIKLBZzHB4eII5D9DsJ+s8+g6PDIzw8PsObb72L07MJ8rJEIyRUUz8CZlTTFmfjBcSNol5kzLEH2AUDa9ERm7fzaLFFrRUENJraiB5Aos4Vxg8zNNrDiU8y3oeHh7h8+TLRPoQAPFJayk0+V7Y4x92bKQFNBMiWS4xPjzE7P0OZLZCvFiTdLSoIrSE10JjcKGGLMbaGNOVXqbVI8kXqYgQ52+iM6zWnTaS2338SONo0SDf7cfP3pzk2QcF/boRm876Pi2y5bfxG7vek9l303O3vj4+G8droRuw2v+Pe+6L7u9FT2PgGRyTaMeGCpU3Qx1GTzbbT7YTz70efo30WknduHXgECNy4kv2uBfh8Hc/eS0A6gJkl6UEFhKXAesIU17ih9d9gGe4ZcKFVd3y6/cxOIDa42fNLBm5t9qXWC0y139gxw8+wXlbAFSty1xl6FrpvGIXo91qFWEBj0O/h+vVrAIBn3/cs/ID2/tFoiKouURTE5HjmmRvw/QCTyTniKIIfEE2prsjrHYQBtre3sVgsoZXCYj6FH1DSe+AHIFlqhd2dbSwWC5wcPzQG4QhNXWO5XKGpK9y5fYLtnW0MBhS9iKMIZRHa8dbr9eyz7u3todfrWUoVUdhDW9NnNptRBMpR72KVWP5vYkpnMFOA7R4GU2xX9Pt9bG9vW3C0t7eH8/Nzyh9qqB7R7du30e12sbOzs2ZHMPuCo0scnRJC2JozV69eXavh45ZKYYDC+08cx48IJ3AUqK5r7O/vW9DB+TOuw5NBFdMFmXrGQM7zPBwcHFhjniM63W7XRsL4uzzWdnd3rcx1XdfY3t62torv+9ja2rJjc7FYWJU2BqS8N/B77Pf7ODs7Q6fTsYa7W3qD5xIDDXdtZaBG80Qh6vehjW1j2UNmrjDoYyDP4IrHR1VV1nbk+cZ5UAAsrY6paeyM5sgmO2h5nDI4coEc5+HVTYOqrOyeyf3J/cb2mOd5lvFFEcHSvkN2lrOdwsCNI2Y8llSjrPOanS+hUTzkecKCEk97fNMB0h/6Q38In/3sZ3Ht2jW8+OKL+NKXvoT/9r/9b/Gn//SfBkAv+0d/9Efx0z/903juuefw3HPP4ad/+qfR6XTwx//4HwcADIdD/Jk/82fwYz/2Y9jZ2cH29jZ+/Md/HC+//DK+53u+5xtqz62bt+D5HpRBnXGSoNftoTLSiYvFAtlWhv39faSrFW7efAdBRIPotddfw5UrV7CzQ+Hr1YpC0+PxGFevXsXXvvY1zOdzPPPMM8hXqZWw3NnZwb/45/8cV65cwUsvvoj9/V1keYrx+JQmy5IW326na+vx8AK5OCP559jUEWI+Mqt10MZDmxvnEPFCwGFrXsh4wnCUgBZSibqpIUDt5GiN1pQYKhqNpjEJexEtGkkSo6oa9Pt9vO9978NkMiFZZrS6+oPBwC5WpPJXoCwL+EErBHDn9m3s7+9b4MIJh+xJAmCL5AJEk2yaxikgpu0kZa+bVYDxfbz/2fevafWzrn+apvb5eRFkr1WaZTgdTzCfreDJALPZDP1pD1tbA0Qh0eiKvLDF64AMeR5BSoHT08ZOujwv7GavtUank6CsKnhSmjHXNdxwohFQvQzP0iw6nQ7SNAOgwQm+VVUCICXAqmqMhygGQFzbW7fuET9ceoCQkJ6P4WgHH3ju/Rj2j7FYrbAsCyyMeg2Hp3mBaGtutMWPeUHd9BADrfIN594wmOINadN7zt4erTk9nXIeyABrIJQCtITQCkrV0ELg3s23cXz3ltlMQ8RJB2FENAQZ+NAASlMnQpcNiixDU1UQugF0A9+T0E0D5QNaCM6moQYJFjsQpm21EUAAmPLkLp4XRUl4A2g91p6hQDXWKHS/e9FifBEYuui40LP+mLa9198fdzwNEHvS5xdFQS46Z9OwdgGBmzO0HnncVKNbfzcXg3Q6Np10F533xGcS6xEk/juNc/6dQISbp7PZVY9rxybFrs3zAYT0nPEhINzntucaAZULollCUM0upeC0V5tcJkAJBdj+bUUR+H6bQNQFQ54nnH5Y73M2SlyKDvWBh7rmyNK6yUH9xzlWzdqzAe3+wnONzmng+Rrvf/+z+G++7/tw48YNAkhBgKqqEXltEv14fIY4jrG/fwAhAeEJHB8/NPkhqYnEcOkDjcCIJe3ubGO5XJJQgcndqasSeZoChn3heR48KVGXFaaTKQLfR1mUKFLKAYqCENLzsL+7RypbooKuFWarGcI4Nmt+aulN73//+yl/19QLnM/n1hnJRiX3La/VLHgxHo+R5zkODg4wm80sRYyBg5TSRqGYTaGUwmw2Q57nqKoK8/nc0q20JrXhe/fuGdq4h/F4bJP/2eZgmjt77JnW5cpS8z6xXC5xeHhojWBmeXA0iWmA/EysvsZ9wdQ0dh7z/OL9y81/0bqtxcjGPhvbq9UKZVlif3/fgiW+Lxvx3G8cnQIoGsRUtZ2dHUynU2uXcKpDr9cjkStTD+v8/NzSL916Qxx9c8t5cFRqNBoZu3BGghmdDqIoWlNm47IrTHNj9g3PSY4CDQYDa2MxOOR9nOcr0/e4D3jf5vYK0eYRcQ4UO63Z/uH781hjqmcUhjaXV2tt6Y3dbhee59lyJ+69lWoskGb1PXaY8H244C4AS7msVLVGjXe/x1E7APa8pzm+6QDp7/ydv4O/9tf+Gn7kR34EJycnODo6wg//8A/jr//1v26/85f+0l9ClmX4kR/5EVso9t/8m3+zFgL8uZ/7Ofi+jx/8wR+0hWJ//ud//pHcgPc65tMp4jgmcBRG0HUDKIXlYoHZdEoemiBA1uuhqWuEQYAo8rE1GuB8vINeJ4EvBW6+8za08BBGCWazGebzOWazGU5PT81LT3DzzTG2trbwxmuv43d88tvwta99Dffu3sMqXaDTiQAQ2NgakYelrkoIodDv9WiyKYXj42Ps7e0hSRIcHh5iPp/bEOXBwQEWi4XhkjZWZQRoi6MxaGJvxsrUKeLoUaNqUEK6QNPUEFIjMTUHyrJEr9+1izFAg68oC3Q7fSt3zaFNVuw5Pz+31YqZm/zgwQOUZY6Dwz0L/nhR5mgQh5nZ6OTvMGWNF0hWhSHvVrxWsXqxWKCua6yWS6iajPWtrS0bEmepzOVySc/ieMAAElk4H59DwEd/NILWwPHDE0gJRFGAulYmikYeQQKhS+utIs9Ebhbm3ExwjSwtkRlVHOgJhOH8CqGtJCX3L9DWA2FvFwDkRWEKeAJVRVLPdU2eEmUS/pu6RiAF4iTGwaVtXDrYx2hrC1Vd4eHpGe6dnmOVpjg5OYEQAjdv3my97AprCybQ1htyDd212mCiVXTko+X4c6HVCwxqIQF4IImENhlda0X0Ow14gjzcTVlBVQJVLpEuF2hMmxpNnm9W6pNaGcEEDUgBpYFCNxAeIIz6FNHoWD3MeOH1OqcZogV/jwM2wihWWcDnGId13W4ULm3AnvsYkHQRQHpc5OP/l8d73eeiNj0pEvONXHPd2AY4Ovko0BKP9NlmBONJoPSi9l/0WXsPV7tz/SBAxNHW2jhGTE2cDYDxpHe7CcZZ/ILHpP37BbQ9GxVy2ug6NNhh4Yqv0E8CJO/17Bd9zvRrvgePc8rnMWDOXCOMQrS11FrHwkV98mgbHwXT7u9RHOG7vvvb8JnPfBpxEmOxmBh5agUowE/I8TgYdKGaCkVZYDY9x+7+Lm7fu4OqLLG/v4f+YIAHDx5QlN8PAK3RSchTvlosMV8sAAiohqL9gR+g8ogdIYTEdDqDJz0sZIpBl+jUCDyURQMpJPKCcpSrUkE1Aot5asdo3JHWucnF1e/evWtzcXgf5YgPA4Pt7W3LGGGDnvNXmF7F0YS6rnFycmINd6UU7t+/byWYp9Oppfnz3stGLOfjMBBjw5bzuKfTKSaTibUtZrOZNfJdMBuaWkhsEJ+enqJpGit8cHBwYD385+fnYGcrAwpXQpuBHDvkGFhwP/EaztEGfj6OMrCQwWg0snlLfHBOFgAsFgvEcWzFr7ivmf4/GAxs3jWzYDiqQhLlgbXF3LQPHv8Mivi+VVXh4ODA9mNZlhZEMeWOgeja81eVjfax45dzrniessIc0fsjO4/cXCA++F0yhZLFPtghyGDMjRYDsGVyhCCqGzvkhRBYrVI7ljhfmx3bbg1G/p37u1G1iQjDKjHzGsLj092zaf1sbREeOzxvmALKwhNPe3zT6yD9l3JwHaRf/pf/MxmMVQWttOHtBhgbetlyRclejaZFDQDKqi12xbS1sizJSx9GODsbW83227dv46Mf/Siee/ZZ3Ln5LiX6L5a4efMmoijCxz/+cRAXurabCOc7cWHTPG+jI1/96lfxwgsvoK5rUj9brXDp0iWsVik6XQILTV1DeuQxY28JANvOTiduDQEAnpTI8gyqUYiiNmnS9wNT4IsGLhWMJQlvN6EuCEKEQVuESwhpBmCJRmlEcYR+f4CqIvoChVxD1HWJui7XuKIcGvX9AMfHJ1bUod/rE1iNwrXaRsyVnc/naOoavt/yUHkRPT09xWw6Q1M3lgZ3eEgKO/fu3UcUhQhjCmUncUwTyUyY8fgc52czrFYZRqMtfPkrX4HWisQywgBJnEA5Hpm6ogKeZUlUiUY1kKZWhdZAWRSoFZBlBSDakL2AoMidsT9cQ833PPh+QIBVkFqbahoo3YKpwGzKZVmbSZ6hLGvUVUWRk4DEIyBpMS2rEo1SqJRA3bS0Fa2Vc2/OrRF2UWcw5LbPzStYK5hoxpdqWKTASN8689AuXoLrkRihAtdYhKEtOUYynWtMTgOcINrEefJKGaqbIHAEl8Zk7qW1kasQsPdmgMSUQAhQ8rYwUS52y3OIQND9OEqktLbAlaJj5JF38yT4s81j3Thc/zsv8nRPR9hYa0c5jtryeHky954b4si6/bekF9Y2Qjx6lm3L+gOAczv4NPHItcR6U4TbkvZ3CwQ04MpVXwyQnOvC6UdDRaNkYvKQCjuWNI1xIe3dXUU+pmtxd1o5aMpSg9bStpVyMvmGgOeREpPW2sxrmuNV05jhvZ5PI3iyrHWl+xK5Rg5v8tweQJt8Im6vjVpBQIKlpj37WRxTDb4sXaGuSRylRVxtn0kpUDeNycnzzFd0K3/N79W+EwXf9xBFoc1h9f0Ag+EAZVHi4GAfBweHiOMIW1tbuHbtGqbTGV555XX8m3/zvzhroTs0BFyVPuo3U3wVggokQ0EImmdXrlzG93//f4MPf+R5rNKVdVgMBn2iwjUah/uHOD8f2+vWVYWyqjAYDkimOgwsJScIKT9FNxrQJM6wWCxQGdpQXddYLBY4ODhAGAQ4G49NPm5FUQIh0e2R8FNdN4jiCKvlCmEYQAOIjGe+MmULCmNMDoY9CCnx4MEDS8ty84lYCIAFipihwewQNtgBWANQeh7gOBs9z8PMRIU2i4kyg4IT5ZmtwmpsWre5QW5OFOf/MCDhNrCHn6MHDPCY8SEE5fOenJxiOp3i8PDQGsacR8z1MBmwdbtdnJycULt8D51u10iM+/ZZOAepqmtURoSB858oX05Yo7zb6aIoCzsOO53Egg4WVQBgbT5OA+AoyipN0TF1C12wY9crIWytIXZqs4Oa89TciAznRo3HY+zu7iLP8zXlQiEEiV9oWLp9FEcWFKq6IRVk0+91VZNqrkM5s+U5zDipyhJCCgtWmIbJbawrquU5HA0tQIqiCKvlEr1eH2lGKTSe9ExNzRBaA3VD4zuOY9RNgziK4fkeqrJVUmZQw/l7HDXiPuExpLVGWVE9pEY16HW7pBNQ1Sircs2hznshjQONwjB5ANh7uHTfKIpQViU+/b2f+e2pg/Rf2tHp9gAt0NQKp6enOD09w872FjwJzOcUiYHQWGUrxHGEwA/gCQ91SYtRNyEEuipWCOMEnudjMBhYb8JkMgFAIg7dYR9REiMvclR1he3tLfR65PmI455F+nQQr9vzfAQBGfbT6QRVVaLbpZAqJURGqKoSWbZCEHiAqSmRpikmeW7zdYqisEbsfD5DGAV2APIkCAIfRZYDSiMKaHL0TPhXK/KyxyYq0k06NnS9Wq3gSZAcdlMDQkCrClWZQ0OgqT3UVQmqdUE1mcqiQKcTIdc1/DhGEAbWowhjYCZRAqEFJCSyNENTNxAB0Eu6SLMMUMBiRhGz27dvAwCOjg4hQPWfZrM5goC8LnXNqkQCda3w8OGJ9WRNp3OsshRxEhthCg/jszNaQLVAlRs52kZB1TW2tkbY2d3F+fk5zs9J+SXPc0RxDE9KJJ0Elw4vY3t7C3ES4+joMrqdDoTZHGqlEcVdywUuyxLz+Rx3797FV175KkVJbGJrbRfMtjK3Nt4tAxQAKBA4YYPAghPj3RF1A+QlbZDcx+CoiWtYbhSANf+um4ZKKjq0CBcctQZMmyxpowAS9jNr+Nr7GeNXuUYvAEMx0hoGcDjec8eYY1PdXlFr2yuEXSRFn+x1zVMZeWwy/lpKgVIKWrHynLCGmNtHbe0glwbWUL0GBi7Gg94oiojRs1xMK9s8qD/5MVsw0p5u2mPPXweUeMx12Xjf+Et7zTUal7TPekEDzcn6kXu5kYj2/bf920Z26NpuhMi9hnCe3cV7j0aA3iOiZoBtWdUmsmhygEQ7noSzzbUgCBDCRBc3HBYAoBWJFfDYr2vdPpemouBCNLYR1J1US8eGKTfaLJ/giqSu5nwc5YzZxjgJWpU7IQTVBpMepAFJUkoISe2rq5rq8ukGgU+RJKqDZChr5n1IKRFHIRpLGZMYjYbo9ohxEfhETeoP+hgNRxgMe9jZ2UK/37MJ+FJSTb0kIWMz5Xp2UYQkiTEed/Hrv/6b8KSHSpPjy/YPA2JTR5A80sZIUhpoNDxB9Y129kb4xMc/gk99x+9Cr9dFVVRoysbWnZmdz63HeDqbUn0epZAXuc3RYOqTl3vWQBQQULWyiqzj8zPzzKRWG4Q+wihAWRVIsxWC0EevTzm3aZZiuD209KowovIEVV3g8PAAeZ5jNpuhaiiCEYoARVVAo7FRoigMMRgMDKOkArRGZeoGVlWFLaMoNzX1gvio6xorUDpCXddW7CkMQ6ovaMZoaOj6MyPSwKwMpvFx0Xs3F4ZB0NnZmVVvo7p/SysUwRFEKSUmkwkZnsbO4CgOU7S01hgOhyaS1LMROPaTsR3U64WYTKbG8VkhSTro9ahYaRwGaOoaXhhCCoG6qiCFQBSGtuYly5GvlktAa+zt7FpqutAC89ncrlEHB/uAMOwIQcBYKxKcis3YYJuqMYCyZ1IBpKAiu0VRYHx2ZvfGOEngmwjKZDJBv9+344wjYUz753cIwPYtiyWw7RdFEZKQCvdqpREGIXRDNQ9nq5kFSkWR2hwuT/qoq8bmBRE4lWu5X1zKwq23RGkHCfyuKZtS1sizgkB7k0NrgcViaR0cja0RRmtPICSgKX/R90gqfzmdPzKuGHRydNLdNxgoEVjmHKcQk8nM5Ol50AqIonWFw263S/duWmoevzv3Hu5a+7THtzxAeuHFD2EwGGCxWuHLX/wieRaaCrJW0ELAs0mMAbhqs++FmEyo2Con6lVVhVWWY8dMoG6ni9VyiUuHhxj2B/B9KjbWVISYuQAaqb2xJKc2+TEekiQGqw8VBVGxPvCBDwCABTyskMaH+5KZ18p/5whHWZbI8hX6sg+lAE96iOOO4Rgvkafk+RkOB6DaTg08L4AytaLyvIBSjRlYnHBb2ygXSTaSB2k2mwEa6HS6UBVR4jxIJAF53mbjGbqdGHVdITCRqyInDnNeFGjKErMsNcl1Pjzfw/jkBGdnpOyWZRmKskBZlLhz5zZOT0/R6STY3dvFoD+w3gxoYJWuEPg+KuPZC8MQvmdylMIQQRDhcP8SXnrpJSilcD6ZoCpLTCYzfOlLXyHFnzjGyx/5CI4uX0ZdVbh87Qau37iBy0eXIT2JwWCAjvFCdeIE8/nCSoWOx2NMp1OkaYaz83OcTyc4PT3FdDZDXdWYzabIsgyrnCJ+JA7RhtnZsHQ3QaAFKhASWrS0MAY2m3QVa4iahczNFVgzMF2PP7CWP8OhcwZjvHA9jjrmevMvOkzMAYCyv61fZ/1673UIPDk6s/mRC/ZaSe5HhRjch3BD90op1A4dwRW1EBeFBp7yIVw61nsF8jfpWI+/qBvBat+XELARjyfT0FoAdJFM9Bqw2WgPU8/oV2nvw3353u0HOILT9uvF57mRTADQioCQFJzcLG2UZVMSmov/cn9xFMxGlCAAj94Nzx82BpVSBmB6a+PfbsbkBjJADc7zbxa/aqM41oVh5iQndnP/+SbvhyNRjVIg7U0NX8II69D89TyJOAihVIPYo+jF9vY2ut0uRqORNVKuXbuGnZ0dHBweoKkbK3Tj+RJh5CGOKJ+1bmpkaWboNQ0GA6Jub21toSgKHB8f4+joyPbPbDZFt9vBdDrB+bnCfL7Aw4f34fkCYeRbzy8/P+Ud1Sa3yajRxjF63S6SIMaNG9fxwgvP4fqNK4jjALP5BNPZuaUBFUWB4XCIhw8fWrEgzjthytTOzg48z8PZ2ZlVbGPaDkfOmQbEogjswed9mNdmpj4ppTAYDKCUssCAqVaLxQKvvfYa9vf313JZeN9lhxmLE7DiF+eYMHuF80I4isSOKR5TLAfNSmFu3UOOsPi+b5gXlMc0nU6pyKypZcP34bwMlrtmI5YZH1JK22fs6F0sFlgul9je3gYAmyvsUt9YLZblu30/tFLQTIXiNpOQxmhNXY6pg4EnUJY0H1gNzo3GcMSJn5nGAuX8sqofvx+mFRZlWxiWVGmHkFLa3GcuJsu1ddzIj0tF4zwjhTbv1lXJ4/flUgNZSIAjbZ7nodfr2dxqzr0q0mLtnTO4Yoo/R2b4+1pr+/c0Ta0wA/c1BNXyYtok0willPC9VsiM16A0Te3anSSJnRcMqpl655Zq4ftR3v5qTXSDKbXszOC5xLQ7Bkr8XZ7L3Je8BnPkkfvT3WcY1ANtsVo+qqpCs2FjPen4lgdItQC0L9Hpd/Gx3/FJvPHmm0iXS8i6NhSmHFopeDKA79GCkGeFDe0y7/b69evwggB5VaFRDYLQw9ZoiPPzc/R6HfgmpF3mBXZ2duzEeeWVV/DBD34AYRjYwcA1jeq6AiXql9Yr44Z8eSAy95bVPpjqxrk6vOksFgtTWyDH1tYWOp0O5V6ZgmCdUQcTdQ4hgDTNEMcJiiJHmpLKXGVqATF/0/M8NHUDPwhQVQTs6rqyfOVut4vlYgmpJe5HEXlZjLLNfD6HamoEoY8ojDAYDsDJ/avVCmVdYjqbYrVckVEihN0M6gooywp5lqOsSgRBiEFviDKv0B8MMJ8uMRnPoQEkZpESUqBUNaIoRhJ34fkepJBIkhhhFOPbP/W78bu/+/diNj7HeHyGD3ygg9HWFt55+x0cXb0BrYG9vT3j6agMdW+M115/G1995esYnxEAUlqRsEeaI8tyy5vld6u0htINFNSaEc75K5BGSUoT7UwIQUVBFXn/6YewlCOOnWilLHBxIzqbBuim0cb33zzY/GwjJE5ODloTmBd1oE2YdiMFa0aq/R8uuK92frIhSgafUhdLZF90PMm43qS38e/ryjVizQB11Xu4fe49XJ622+dreRN6HSRtvosLn8P831KNnvTdCz676G/a8crTd7z1yNgTQcp73WMDDF8AChl4cGROqRakSeHkvdgA1UX95ER+NgCaSy1sI40EqLTi/Lk2Atp+51FA196zHctujowQno0WuXOAyz7A1BtznQOeoMgOpLC5evae8uKtliNsvpTWs+vSzyAENGr4ARmpAkAUR+h0uuj3utjdHSHLMlw+OkKcJNjf34cUAgeHB7bA87Vr15Aauh3Tq9j4aZoGXhIgijxoVLhz513s7G7hnfEYSRxDaW2TvA/2D9uItWPc3r17F9vbJGrAkRGAwM5oJPGZ7/m9ePjwFNPpBEEQYmkSz/f29xAEAnEUQUiB7a1t9Ho9okQHEQa9PgCNNF0hL1JaG4UG0FiDXymFu3fvAiBq4dnZmc2x6ff7mM1ma7Se4XBopZxZwIfzcdgA7fV6NpeEjWc2+lnu2i3dwCCH+4ZpVxyJcRW33JqFbLizsclSz/xu2NC9fPkyJpOJXbe4hg6DhKZpbI6GqyDIeSuNUlaunK/LgNjNVZlMJhaUse3DhVNZWMjN5eF5Mx6PLUWQ5wuLAbU0fZbn7qyp7DKFnpP/2QA+Pz+3fRkEAaois8/GOUHclyxLzlETVsZVSkNAWrsJgK0PBGgb3eL1nMctR4+AVjGN37mbY8PgitV3tWpFSpj2yG1lWh+PBS40y2kCnCfmOjTDIIQM5FrefRsVEhbAu7lL/M54fDDw5v4Po8DWh2KKoqt2mOeFjcJwwVwGPiyexX3C4IojZHwNFm9gEMfjgil7LtWObQlXepvHgMu4chXoWACCz+cxB8DSQN178z0Y0P22ijT8F3d4ZIBqAcTdDj780Y8gTzNkiyXOTo7x8MF9qLoiYzpOIACslqSLf3h4iN3dXTuIp7MZBqMh5vM5wu1tNHUFCY3z8RnOTk+QFTniMKKaR1ojzzI8ePAA29sjDId9M3EzrFYLy++dz9vq1Z7n4eTkxOrx8wJ+6dIlW+TLVV2pqsp6wXiR42ul6YM12c08z+m/VVvPJ89znJ2dYWtrhKRDIE+p1mjkQRqGpDHfqAacrF4UJaaTOaSQ0A2Fndlb0SiF05MTxFEIT0pDwSEPtjBGRKMV0jwDVyUHiAfv+x6SuAfZCESJh95ghCiKsLU1wksvfxSVUgijCL7nYW93D5FR2ut0OpA+bba8GCyXSywWC6yyHF/68qv4/K99AbM5CWvkWY5ev4fpdIaiKrFapXbR1VpDaYWqqqGxrtakTY6KVoYeIKm4oRu5gWAzr7F0NwgBIT0CUJxvYQEM2u851CulW1PJ9SK5huVa1Mg5LkqIdo/Nc1wQRJxv/5G/MS3Hva8L0qzP/0KAo0EqcvzvFrwxQHKf74ngbuOZuB3cXv7OJuhq/3YxuKT31H63jTpRMVl34Xav6bZps+3vBVTd9nH7L4rwXHT9i/tlM1qyDmg2gS09J9bOc8ea+77dDat992t3a6+tBTzpUOk2cJULzC/AYfYf0pNGht+0zdIEuR0UlSRgdHENqMf1JwMhfk5+1+2zrPeHHRdKmXQ4YZ0M/P40hDGmN+v2EFDTJseH+g/wfTIW+r0E2tBFev0+dnd3rTpYnIS4dHSJPM2SVDGDIMDe7g6qKoPSJPRzYgSDSJSIkrtnsxnOxscYDIaQnsB8MYH0aFyHUYA0LYzDLwFEiGvXr2A2m2Jvb9d6crvdIwghkMRdLBYrCxLCMMT+/j6WyyVGo5GNinieh+PjY+zs7GC5XGI47OP555+D7xM9/c6dO4iiiAzv5RSj0cB6s2fzOXZ2r6AsCixXU4qwGVCkVG2KokY2P5XV2uI4tjQzBjpnZ2fY2dmxFLR+v7+mtuX7PhaLhTWqee9tS1WEFri4ip8MtNxiqQCsiqwQAltbWxiPx5jNZrYkBXvHl8ulpeUlSWJV49ykfo56sfHIktqsUMeGONficY1tm5NkxvRoawu+cabyPOBcGTb62eZgO4QLmJ6dndm8orOzMwwGA/te+TscueN5NZ1OMRgMrPoY50yRklpbd4eNWn42ltPmCAYb6Gmaot9N1sSVmKrFEYTRaLS2P81mM2RZjiKnIvVsKDPTBkKjKeleHBlhw5rHMBvebEcxyGEDmw1/uyfIVjmX1xQ3qsNgk/PLGJhxbhKPTY6ASE8i8iN7Tx6X3A8ccQJgbUAGBkydY7uQn1NIII4jax9wZJPonrFds1wBBe4zBj8MTNwomOd5SNPUqgUy4E2SBHmeW6YNAzyWabc5ZFVbFJcVADdziLifOWrlOjr5P5awZ4eE1tqOU3ZmP8kZuXl8y4s03HtwH6PRaA1AeFLCMwbBrXfexr3bt1EVOaIwwGqxxNvvvoOiKHD16lU7eUajEc7GZ8jMQFmuVphOJrh27RpOTk+wu7ePpNvBsD/AarnEl77wRbz11lvwPQ/PPfc+CKGNkkyrfFTXDZTSSFOaRJygx8mSvFgx2ufJu1qtbKSJBy0P5sViYQuuSenZSSKlQLpKERh+72AwcJIwM2PDC+R5Zidrq6gmNjwq0nif2GtMeRxSSni+hySmPivyzBaIi8IIo9EQfhDAkxLbu3tIej07gIeDgQmnd0wODhWl00ohTmL77uZZhvH5OcqiwHw2Q5pmKIocp6dnWC4WmC8WWK2WJvJW2PM0XMlpzl8x1DI2+oA1uk1jlOLYaLbABK2B04ID+p4QAloom9vxaA7Po1kf657r1jBfOxwjb/MzC97eA1hsnuNGkNaiL2bxc1WJeHN11Wv4PP6bNPkfF91bQzgJ8rbLQQpXhChd4OcapZvP+TgQdZFxvPa8mqJXUrT9t9aXgiNaam0DAYxKGmDH0+bTcWkc7g/X035hm4zB7FLF3LGyFn1wxs9mPo8bHaN+88B5bPY2tg8uBhDUBtdX1tLcmPqlNeUNCve9XDTGGFg5Y0HrTblr6wXAo3TL9edenzt8HTehn56Zn/tiUPpofzp3fKRPhIlqcv9uvg8JTQw84xJQygG3QgFSIwojdDpEzfJNGQLPFJ68fv26pXnt7uygP+ijl8TIsxRJp4Ner4tBn5S8JpMJ8qpYk6klA47oz0VJHmyuLTcej9Hv9y1QYlqU6+xg2hfnRLC3mM4/AwCijzUKjaFbh2GEqqyhFBnybDCxUyyKIpyekvDR7u4uxuOxNehWhiazvb2NpmkwnU5NMe0CTUGlC5IkwenpKXZ2djCZTDAYDDAejzEYDKw6G0c8iP4VWYOWaVici8Lzj0HX5cuXrZPHZWiwITsajbBcLq3Rzx5utiHcMhNstLHRzweDJFY36/V6Vt2VbQ/+nNvLFKjT01ObD8JAx6UY1TXV4AmCwILQ8/NzDIdDG7VjI55BLUd4lFLoDwYoytJSxShKR1EzFlvgtYedslzQ1HXa7OzsQCliUDC9cLVaWSlppsRJKS1AYioaR7PqWtkyHBytYrvGXcfYCSylJPYKtC3QykDALSLvRqSKojBRkRDQYo3uxrZNEAbI89RSvaSUhn1TWpDMESWmGHItxTwndUIGtQwSF6uVjQpy3arKlKTg/ZTfv+vYZiDBc7uua0ynUxLxMiwANyrHhj7PQwbziRGQsGIo5n1qrW3kmHIalbX9mG5I78BHGET2XXB7XUogj0umH7r9whEzHkvcDj44yuR5nrVdOfrEY4YprEyJ5P5wmRxuVJJtOgZX7n14nLAdY3PKmgZ/8Pv/d08l0vAtD5Bu37mNra0tSkrWmqICWiEMYrCQ6+x8jHu3buHBvXtYLhbYO9zHrVs3cenwEo4fPgTMIjo+H+NsfIq6rvHqq68iTVO8+OKL6HSIrhV3e4iCENPJBFop/Kv/+V/h2tWrOLy0h243thscJ+HVdY2mJgORB8tqtWpDtgYpCyFs+J0XI6rKHWK1So0UJBvVlExHEayclETMYKyqCh6EBVskWCDtwsbt401Paw3P9yEFSW9ubW3ZTXE4HML3ffT6fewdHKLT7SJJEiRJjMD3UVc1oIGqrrFcrVAbOoYQFCKdrzIs0wyL+QLT6QTjszFxquvKJtPmWWbpAQBQ1w0qTVGc1ggkQ4m41iQ2YMxxAIYTrIj24n6flcikkIBWaxuBa5BZw96yl1jBy6kOj0fpQiZOcSF9bH3CMdBy7c0LpuRGhMG9lxvpWLvPBVPbnuN876J78fhjoQ42RFwKgOshZ4DkGvxr7QHWFMT4WZRSgG7pTNxGjjy413CjHwx0XWC1TqVbeyCw1DDJiqvH9I+2Y4s/48VeSknRvwsjcxoC67WjXEBzUUSDLrJeVJSv+6QoEZ0m185aB0j+I31J91TQuuVqrx8tQGojM+2zboLVzUjdZvvpuxdHwDb7YB04PQqQ3O+7IN3tJ/r3k+7Tjjf63FHhE+tgf61/zMTkc2jsAx4aRKFP0eowwKVLRxj0+9DQeOGD74f0JHZ3d03SfAAhDHVaNej1uvD9AHfu3LHrKbRG4JGyYFPXWKUrxBGBm+Uqxfh8jKPLV7BYLCzFJ88zxFEM6fuoyhIQAoFvqtf7VJ9nYQz+xXyOPC9w9eoVkvuNY8r7DHyq3xMSgPODAGVR2iT/breH3b1dvPP2O9bJyIY9CzNwPgEbOOzxj+PYeo1393YwnU2R5zmuXbtma7torZEtloij2BouMIZVXVXY29+zoIiMJFK3K4sCVU1AxI0qMPjh/BGOLrGxx0ZvmqbY29vDeDzGyqjEAi39ivdd9pLz+SxcwLQ5N8/HlSEGWtoRy0UzOONxyDSnXq+H8XiMqqqwt7eHuq5xfHyM2WyG7e1tW2+Qi5S6lCUuBuo6UDmXg4GZUgoaQGE+d2lTDBqiKLKRLrYv2OnqSl+7NsNsNluru9jv9+17YCOYaVRpmtpcMRZS4sgMpw8wwOUxxMDP8zwkcYww8FGWhW0zAy4A1pBm8MP/LvICvh/adnBqADl9NTyfbB+OOvL64D43jyegLSUAtOJIHGXyPA9lVSE30VXOv2EQ51Lj+HwGHm7OGD9fWZbodrqoygrQsJEWPo9ZMrwvc3+7DksGEPxTKYWyKmzUmseq3ePrNi0gjmMsl0s7pjbzfHh88Hjmccff53HBQIXtPgC2NhEDWrbv2GnB6zu3mecz/53XBAbYPG/5OXlOctu4f7jmUlmWTw2QvuUpdk1dozKSgdKT8CSgNRWj8k2Id3vvAMOtHVx/9jm8/sbrePft11A3FV7/+qsQWhlrt8CDBw8wmy1Q1w1CP4BIOiiLAqpuUJQFKVsZPnDg+ahVhel8gjgOoNUAQgrUVY35fIVBvw/AQ1XkaGozyKWPYX+IoiwtuKDq4g0ylPC9EHfvPkBVVtCNgGpooJblsZk8jaF5kBdBg9WWDF3LGOJRFFovRpIkuHTpEg6PjnD1+jUordHv921F7263iyRK4EvyTM3mc8xnc4zHZ+TpSTOcnE6wunkP9+7ds96b6WSC8WSCpeEuc1i64TCpkKiaxkpEk1HX0ri0Jm91UzfQBvBorQHZChRYT71SqBplrH4yrpWpRg82do2kNXl7jaFtlGs0qDhuax4aQ0oAWjXgCIeUbIgpyjXQDJnQohsh4AkJGJUezrtyDS+6tFko2cNtJbABTvBe89BLsREOoGdlAWjpeaYvTT8JDd0QiLNGHgMbMIvvUdrWpoHqRifdxZGfiTcNpRRgBKo4mrjWWK0pkd7QrrQy8woaQiii0lgQ6kbIWhCx2YcAz03u+zY0tQZf+EUYUNuC1LYv+D00HIVoO4HOVMpSHh8FGMJ+zzwRUfL4NUGs9TVfXAppx7JrxNN3lc1Bacc1beyb5XlcmKf1ej+1j+FBwVs7Rxjw7wkP0JvUTYDyPeibnrcOijh6sx4J4uiRMHIcbo0K+tz3PGgwvxyG7ku0XTZOqqqGFS8Q3N9tXo80tFblyFfz/CW5/dZBQtcwwMf0rSDZRQgBeL60nmr2xHe7HYRhZGu0BIGPvb09O9aPLh2g10lItcpvwX1T1+j0YgiPaueUhgJd1Tk8X6CpG5S5Bx3UeOb6VUwmU6yWSwInSYwgCgGt4Xk+IEiCezDoo2kUJAQCz8elg0OKOHgBqdXVNBeXyyWuXbuGJEnw9ttvY2trC4cHl3B8fIw47mB7exerVYaiqDAYjEzEKYLvBwh8IxfdaARBiKZRKCsqxs10mKIokK5Wlsq0t7uL6XQKKaUpU+Bjcn5uhHhyeFLi8tER0cDzAlvDEbpH5PirwgrL+ZLyVSFtpD+KYnS7CXrdPsbnYwhBn41GI5RlhbKs7EhjAMNFLtm4Amiucl4Qe/RXqxVOTk6ssbdcLi19iD3teZ5bgR/eWx48eIDFYoGrV6/a5Hl2Wk4mE4yMyhx786uqshEprddZIa5HnQ3a8Xhsozh37tyxjhg/CLBcrQDJgLCGHwSYzRdYLlfodkmkaTaf45IpvpoXFRLpIc1yZDmBw9PTU/T7fWR5hq2tLZRliZOTE2usclt57eEIVa/Xw2q1shSx4XBoRIhSC0x5T+D9gSMRo9EIVUV2RxzHmM8X6Hb7iGOS4ueIGhu8HO0r8wJNUiEMQgSejySJqZxFUaLIcwwHA0xnMwgIdJKuoT3TulhXDTpJF9Nihkbl6CQdBEEIKb01KpeU0jiA6e9RFCMMY2RpCiHJyaA0kJtyJQzOu90esjyzY6XRlDKglEJVNyhKI+UdM9uF1x6JPKeSHFK2oiJpmjulAwTNcenB90OU5RxRFGOVpshXmRUJ2drasv1cVRWGoxEgCGwzg6WqKrvfc44gM4EIjAU2As0RFa0JJEmhLAUSgAVuDEgA2N8ZvHDRWAZD3F9AK1jhCknwuex0YKe5lG09KXa6uMrM7LBnSiKPV/fZOHLKgNgFo1w7k6ONT3t8y0eQ3n7rdRuRIaU0HxISZVGhqSvytvmUYxPFEQCN44f38fpvfRW/8bnPYdBNoIVGVuZYpilWCxJN4PoRjF79wIf0PJRlgTyjZLTxeAzP87CzvQ3VVGazpUWcojYCuiFk3dSNATUE6iAApQgkAa1KUdMY+o9m40PCY88+YBRRAN/z0R/0EYYhup0uer0e9g/2sXewh8FwiDiigqvD0QidbgfS83E2m2AymWCxWOJ8co4sy3Dv3j2cPDhBusgwmUwoGbAobVgVXNxTNdZSqxuKHikB1Lr1xvPgbxrS7+eBx4ZUo1pviBtKdwGGEI9GPdhgk1iPbrgTxEY+oG29K/5dO23c9PpvRmb4OxcdbdTAs7kSmxEQpdeV6/g81wjk+67Rv+S6wetGMty2c35Z+531aI9rBLv9ytez7XX6b7Otbj6S27+buSt8n4uibJv98rj+1ZrrJ20Y/iYv4cJoG/jPj3r7Looc8ThjR4IbOdlsj3vORZGyzc85osbfdcUdLuqX9iBvOgFn+k+AJKS1UPbZNqNn0gFBrqgBACgnqmPflZQQGraukxshpDaRs4Lr7FBElK7Od7HfBUxdDgJy5M+Qlm4KA940SE3QpdW0VDbGu9rS5vh+nhRms+vYTa4F6BW2trZIptdQavqDAaQA9nd30O8PIAStn1euXAY0MBj2IaSinIrVCp2E6G3stR8OR2YfGWAymazVPAnD0K6H+/v7bV6IqhFGoa0FQ1H1BCcnJ+jEHWO4BTZpfjKZYDqd4sqVy7h79571hnNdltFoBIDyRQeDgTUaODohzHc5QZvr9iRJYotMskeVox7z+dwWGXdzcNw1l0EHRxeyLEPg+5aCzIaLO5Zdw4RKW1AUgxPHucAm07Q494JpNCxTPZ1O7fvlc/keTB1k4COlxOnpKba2tuD7PubzOYIgsMJDzz//vKWLc1t3d3dxdnZmRRw4b4RBVpIkmE6neO655+znLFTgerg5wsQCBiwlzkps8/ncFi2fTCaYz+e4dOkShBA2X4qFMjgHg8bQOkXOjQ6EYWy96kx7T9PUFlcdj8c2WsYAcTqd4uBgz8qOM4Vrd3fXCj70ej1kWWbbtL29bfcTvv/x8TGapsH+/r4Vp+j1epYiyDlUi8USTaPs++R5ykCo3+9b8M37SBzHeHj/AcIgsJE0VndjYOm+Q5Ys5+tyNMbNXdFa24R+lttmChdHlLjfV6uVjdJlRQ7pcb1G30aJCFC1RXgBWJEJZv5wfg5HoLhILe+bvM+wEBY/PwsI8PsOwxBlUVhVZO4LBiJ5nqNBW4bDjRJJIeEZEMqfscIht8WNyLt7Fke5WIkOaJXgOCrKOYjcN+7ez1RFHn+szMjzlSNpbDfzuwJgRbrctjCLhe/LkSKOfHKfc+6du5fwv5n6B5BwyXQ6xR/+P/3v/yvFbjgc4o1XX7WbDBnflPQ7m88RBJ6hPEgUVY6mrpAkPQgRQ1cN/uPnP4fXvv41eJ5AUZU4P5+iKSkEWtU1VssVqrpqw/o5bURhFAIa2NmhDTDNlijKvEXPUpiirREEJLRZED3PBxsWSit4HhVUDYIAw+EQSaeDMAgxGPYhgxZZd3s99Ho9dJIE21s7SJI+oAVGW1vwfA9FnqMsSmR5jrPpBNPJFCenpzg7O8NsNqOq2LMppiaxsWka1E1NHkreNOu2pkltvEMU0ZFoNPFApWgLK5IxpVA37TUAxxg0gA7gPBRlFwGWROcNdzMpng0pNkDthLigYrtrFLsTxwVAEOsAYpNu57bd/dtF0Rb2XnPNGfdeHD0QYj0Rno+mbsCG5yOgbCNo4YIU61WXbVG7tg9aehL/dI30i9qo1ToF7aKIxGY7No0lPtzFc+15ngCQ3N+1Y/BzRMG5Ox4HkPRjQNFFAImfg4x3PAIANwHdZhsZ3G5+zn93+6QVpGifib6PtWvYfCFIkJAA1bMBACE1WM7bzZURQkBoN9Kzfk04dLJHqG0bf2fQuzZG0Pa2+ww2AmbAEPUx1WvzPGmjZ+RxbcC4zfP5uTTiKEIUR4giEhgIggBbW9vo9/vQ2ogXdBJcu34dO8Z4q+oaSRxTEWzVYGd7G4vlwtRaoU1XKwXdtOtVaYzq5WKBKI6swQ2Qc2k2m1ng5lKu2FicTqe2OjsXpHSNm6SbYJWurFd+MBhAa03yyp0ePOlZw4VVylypY462M32J6Vycl8rKaGzwKMDSyS5duoTJZGJVUplyxAYcR092dnasepv7c39/f01oYbFYYG9vD8fHx+j1evCNIcuGCxs3bOhEUWSNLgZ3/F1O4ub8pyRJbG0cLmURhqEFTkxBZ8U5pva5ERs2fs7OzmyhTVeYiKWl2cvM4IwB4Xw+t/PSBQLcz9yH/X7fRqH4Ovy8/Dzs2OP283rCYgxN01jPP9duyvPc5uhMp1NrbMdMP8wyq3gWRRG2t3cwm82tOtlsNrNGKxvw7PXnvB+SCKf5cHZ2huPjYzz33HNYLEgoihXgODeN8z/Y0B2NRmsiFRwx4IhMlmV2nDBo8v0AZUlt4jwp19PPxjaDFwYcddGqs7n7PgALeLj/3YgQgxKm/7EqG4thKKVs3hADKR5TbKyzwyEIAmhBTBde51i0gs/jccR5Y+wM53HCxjuPCQBW9ZdzfthZ4VLCeN3lc7XW8NA6ibmtW1tbBK6kWJOAtyIXnocooHWLwYwr2c45UQyEXMeGO182f+c1it+Da1PwO2PqLL8v16HjCl+4e6wbaWLgyWsLvxseD64qJM8xzvXifYrHBgALCLk9VVVhNps9NUD6lqfY1UWFKivhBz7yknjC0pMo8hy+l6DIVliUGYJAoq4L1EWKbncXcZTg23/Pp7B/aRdvv/02NIC9/RQP7z3AarXC+fk5IBpAKEAoKpTqSyhVo6nJS3XlymWqzxNtozHGMQ8wANjf28fOzg72d3YhfR+x8V41hjcsJNWj6HS78IMASitMJxOs0hTL1RzzxRx5nuN0PMVrb7xNXOdGoSw1zk7PiKZR18gMB7hqGmQm/NtY8QIyVppm3SAmQ0eYSBVRdCjSI1Br1VLBtKYoktColILQxnDSRE+z19PaThACGK3RLJldpgCy74hyw0aJuwhyocfWXuWQroDYMLrXIxGPRk7obFN01QE9m9EW95ruvzejKvQsEm5ejAuw3LZsRsbo+2ItutU+4cVt4UWUvXfrhjiDh9ZDvxkxcoHkWm5N68Z/tC0OKNsEUJuAxL3uZoRpsz/WQJH7rKJ9BphcorZXHq0tY6+h2oRS97qbwM9tp312PAognpQrY/5if7b1gDgXp82pktKQz3iSuDQy57EVPJvTRfdu+9eqQSoFKdu22PkkmIsu7HkQgGc24U2AL4ShxSlTx0cIwIMFO55PwIYpgazCJkwNnjiOkXQShEFoDYLtnSHiOLRUtTAMMBgO4Xs+ur2uWX+Y7uthNBohjiNDJ5HWwUKGKKl/AiafIi/Q73WNzH4OIRpsbfdRVCm2tvq4eesWDg4OaOMGMJucIwh8RFFs3o1EFPuo69IakmzIJUlCeTsm34cTtQEqmM2JySwLHcexNcbTNMVisYDS5EFerVZIkgR37tyxm3on6dg8FqaodDr0NzZieNNm2pfrde33+9YA1FojdOqP8HtlT+3JyckaXYoNjrt371qD9vDw0IKkPKfyEByd2Nvbs0Y4G7cADIWqspETBhYcZWEQwMqp/Fx8/nA4xNnZGU5PT20eyfb2NlarFe7fv4/hcGhBV7dL7AdWx+IaNxx5YUM/NAVD+bPFggqMsyef10mO7HHUhB1GLHzEkQYGbVJKGznixHqu8cMiFGycugnqrKq3WCzW6jJxtI9BHBt2XCA0iiJUpk1MbQRgc5zsfJUSvV4Pi8XCGpg8xhig8rsiOhlF8HrGmcqGP+8DrtIeg3r2zrMRymCYwRhHJ/b392ksmj5ZrVKUZZtTxWOADzaCmRLl5kT1+30LDBnQc1SFr8PCWe474v2PDWd+HzwmANj8I+5/3psYrDMtUshWrZRtEK1JcpzfEdskrkhCVVU2eufKw/M7Y0eIEMKCau5zjo6xI4HndhLFts94XOV5Ds+0iZ07DFKIKtfuazxGAKyBN3Z0MIDZrCnE74gpqLxX8nzhtvPn3A98PY768jPxOsvnubliHM3j+7rvie0/Fg3hd+G+QxbO6Pf7FmjyGslz32XjPM7Ze9HxLR9BeuULX0Kv24MUEmVFi1MUR+j0e4DQ6MQhmirDfDZBVWYmNBhT7R+DWNmTqxqFPM0RhgEapZClqQnZ1sjyAlIEiLtd4saB8hqkkOh0+qhqM7jqGqtVSgVQywrz2Qx5mqJuGkzPz3F+fo6zszMsFgvMFius0hRNU1vlHRp4EkpI1E0DrbSpoN6GW4mO1xLYrLErJGrtggs6rNGoW9uYc3Og6TmsESvaGjCelIAEGkWTaR00KEA1kKItrMmDvWkaKM0SuxxBcqJDkox7TszjiUkRktAsmg2aZp0WJtDmjlwEkFzw4AI2rqjNG89FifiPAzpu/7Wfbxi7DsUPAjZPYjPxkcNE7kJl7wUSlnBBGZ+7CdxaIHCx2t3FbXb78eJIyyYgcg/3vm7f8e8uONo0zh+3YDlw1/5kw5navg7O1s51Njj3eS96hrW/SzcCsxklgn2W9esYCtxF/bKRQ+UeLuhynQfmU3BNH3q+Bp4n0TRcl2cdyPMckxo2CuZ7HpShx9VNDYg20kgUCY94+kLAk9J63g4PL1nqzaWjA3iewM72DgCqwXN4cGiUJSuk6RKXLl2yRj1velHkQ4NU0rhGDhvTaZohXRGNB8aokYLU3s5OT9HpdG3kmz3ORVEg7kTW4EySBJ2kg6IsrEHoGp2cYBwEAQLTV+zNZ5pGnhfwvNB6pKuqskI4bkI0b/rs7Y6iCMfHx1aemI26oihQVAWEFDYBXwiBs7MzjEYjDLoDPHjwwBr/TB1iugrfs9vt4t69e1aeeHt7Gzdv3rTFWTnaAQDT+dyCDI5osRHLx2g0wsOHD61hx/RANoIpWrdl5Yfn87mlrOzt7dk+K4sCUgjbfm43J9lzhI3pg0IIG53gGjxSSisuwIYaAxQ2vpRSVomVAQLnJ4RhiOVyCfbas2efvfKs9saROKYSsnHt9r2rZsdjl41sVvgCYOlcfC7vE9xepqU9zlHElEV2LrExDLTFuF21rpUBCPxeObJIY7bEwCi+8n7P0R2ttQVV8/kc/X7fUuB8fz2hnoHzcrnEeDyGUgpbW1s4PT1Fr9ezrBtWBGMA5iqRuZ5/rbWNbi6XqQW3HDHhfmH1NHcsWqebavNbObLLhjI7CkYjqvvFEVHX4ccgiT8D4NhEZJTzGGDlOo4k8fpAOUU1tGil0Nu8Jd+ub26uDI8Hfq8usON2uHQ3fte8fjMYcSMqVVVBCoEkii2w9zzPRo+V1hCetNFm7h8GVlDaRmz53bhUcwY23C5XIIFtLR7fLsBhkMORT567DFh4n2cgxn3BDgo3d4mdJhzl4vHAeyOf59qG7Bhy5xK3kaNvvM9yJJjfEUd2z8/P/2sEiQ/ph/AjSpzzoxhBkmBrawtpWSJNV+gPOojCDjrxCA/u3UW6SLFa3cdodxf9rS2UDSUNl3mGIiswmc6wWq2wXK0I3OQ5hoMhaiWwWBV2cJ2bhNU0SwHlIU1bit1ivsDrb7xOC3SRo67awlVu6LGxkQgBFghoGlN9XAgABDBQcz4Ncf9dO2w9WqGtTC8vsHx9ANAgQQKtjQgBWiqNUHRLAQPIFAEgq1ZlLqNFC8wETETNmXAAjMGmoXVtr9961WGuyzlXje0PAGais+fdUKBMAzz5qMHNnjK+Fk8WF1BuAgV3k3ucAf84Y9uN0mxej9vqggb+nPvM9QSv3c+5L78/PtyFj4826rAOkp7kPbGfbYCcpzncRYzfl/ssrjHvfv9xIG/zuc0n9q9as/rfOkCynqINr9Fm/7jv3wVr7nfdfK7Ndq0DPidPCsB6gVP3udoo2vq7oryd9T7xzMJv8u6g4HkCviZRBcr/M5tGGIDy3gBPEHWt3+8DWlNNnZ0dQAhs7+6gaRq879n3YTqZotfv4bnnngOURidJUJUVqv8ve3/yLFuWpfdh396n8/a63+Z1EVnZVJWVRjBNpIkagEARIAVQlEx/nBozGTgSBzJxSEogRVFiFVCQSIGSYOhRlVWZGRkR773b+vXmtFuDfX77LPcIshLTsHSziPfeve7Hz9l77bW+9a2ua/X+/ftkxMuy0PEY051It/ln//yf63p7rdl8Ju9jRCfOFnFq616L5VKnY63N5kqZc3q8v1cIQfXpJO+91su1cp9pGIHd57F7VVVVWq9WcQ/6Xocx6pFnmWazSvUp6lda6EaSKaZwLZdreef166++Vt/HOTW3t2/U1LX2u5dxHkczRoco0K/SQNGnp6eUkgMI3mw2KZIEg393d5c6jCEPOH4wqtvrbQJlnz9/1ps3bxJQuLm5SelFzrnklFgyyDmnDx8+6HQ6abfbKc/zcSD5KoHl/X6fUv1oh01NEQD093//9/Xnf/7n+vnPf56KlCH89vu93rx5k0A1z2xn7ljwstvtYnfSka0lkkNrbUC6c1M6DUAKQATAwREhMobjBPO+3W4Ti050yHufIm+wydQ5dF2XHGMiQURY3r17l2T5+fk52QDSBpnHE0JI7a2zLDtr/QxgZ0+J+gHmiWahf9AdNg1MUtoXwC6O3mazSQDWe6+f/OQnafgqoz5wQne7fWLZaWnNGBKcQpz6KdLRqmn6BOxfXl7OHN/YXS7K8u3tbapRsy2ZWSPW1cojUQBq5Ij4EDFh/2hZzv0D6J2LrOysrJLTQrSTaBL1TtSoEOnlHJGq5pxLUUPS0ti7xWKRuqbxO+6faNbxeFSW5+rDcJbqaYF/COFsMK+k1PQCEgX7h/ODXmc9iTbhuDMfiTohmglwr5wxaWwVn8WmXsgb8ojDspjFtuG2DTwpcuga5JdoC9fH4bBpdESweQbkHjtmU4WZS2ajnomMHm0nZ5/o0aXdxWGjWyLRIJxO6zRSg8R3oGu4T7AnsnLZR/i/6/WDjyD98he/1s3Njbxz6rqxEFtBbRjUd4PUB3WnRs3xqF/++S/09/6T/1j3n77V/GqtcrnSoW70uttr//yq/eGoQ91q9/qqru3GvNVKv/u7v6sPX/5UxzaCruNhCi9G1mevvq1TqJdUgof7e/VDq8EUZDrnxogQ4DAWjufZxIgMQy+FTt4pFZWfRyJsepYB+SHmsXGoziMlMZLCz89CkiHImdqJ+J6xoFpeQ7iIsCSnp9cQJgVhwWE/eHk/MTH2IGV50DAQirbttEenUC4xCdOzS2HoJE3PxXNYcMzvJqA+JAx7Ge2wDtDlMbEOkU3Zizt2no5l7zOu87lTlRyLgVD599TsuPCd+/m+KNDl/f23OUjf57CYGz57/39XNOny2vYerYNkoy7f51h+rxP6nZ9893XJ2qbPXjia9vf2Xi6vI3M/35dml3LDR5CXHKQwGQB+F69DyiTXnMiJuEZBSh3snHmPGwvGK8kFLZdzyQWtVkutFxtlPtPd3Z36vtfPfvYzbTYbSUFXq4XqptH79+8TO7q52uj55Und0I2gcJHYwCh3QfkIhmF96TpZVYVeXuKQap/Fs7parvS6f9XL804//vFP1LaNJKfD4TACgqA8L1RVM202V2MntbnatlFZVsqyXPP5Qv/yX/5LXV9vzQT4UxogGkJI3adi2s6rsjI22anKUl999ZWurq708PigxXyh5XKTCr8x8M455ZnXrCpU1yeFoMSoeu/1zTffpM5QWZbp+fk5AVuiTwxvpC6DVB9m5gCQ0mDE5Vy0iielBVBxeD2oKqchp3bYad/3urq6Sml5gHlmGcH0f/nllwkQhhCUjfWppI4BnGmIcDqdEnigkByH7+rq6swBiDKkBHDZT5yZfmTIQwhpUGrTNGlQqK29gbUmkkBKIX/SAQ/QzL0wV2Zqx3wOLkMIqQ6kbVt9+PAh7TlE4HK5TBHQvu91f3+fom/z+TxFqyyLTl3M6XRKtTgWZBFlJJqBo0kEDWfNrjdDMjlLyHXTNMn56fs+pTI6FyOP7XjPNA9gRk50wGMERprqcoiusVesP40g+r5T00Tmn0gfNTfUB9Ga3Y91ZpCaFNcjS+gInBv2i/WMEcJT0pPUjNg6M54FZ8P72P23yCIeWCwWMVV1mBpUWAIC2QCEW4dEUpJpgDhOMWsmKT0X38GrrmsVValsdPpwYGzkxabeAtixNbvdTpvNJj0XQB8ZIxJoa+K4JxwYbGfXdfLhnEhNmM17NV2bIlrWQSHyxBBhSBVq+tAf0tQFjhRV6/DgJCML19fXSU7tvQzDkNJQF4tFIlggAHC0iD7Sjh8dz/5yFvksTXG4Z7vH5+UaLjnm9nsgbaqqSnqHtfzDf/ff/m0ESZL+wd//r1UUcx3rRvvdQbuXF73u9jq2sTanaWodXvd6vL/X89OzDvtXZQpq+l4+z+VcnKPjFduu0pUtgqlC+0Onf/4v/kyfH0/64sc/k3Ne3eBU1ycVZak+dGq7Xk1d63A8yo0pBrPFQtXxqN3zY0ylGYKk2DLWazzwYzvpzMfmB4mlCoNiV2QL+sbGAMOQohTexaQzN0ZoaPvtPTVGY4vtQYrDa2N9jw8JJ0ZDrCkylFj7TKMj5OTD5CzE79R4n0prGEKs/YpCHpS5XHlRJuWIYfVZJo33RVRqGGIrb2YoWHALAB1Sg4Yuph6OHiZpghS9ky5IMwkZgxKsI+b8NPwz/X+6Zoq8uZH9p56E23bx78Mw/sb78fpTlzDqPbhXOR/bYMuN7bBdeh/rwP3yPTGdcmzvHszdhu+mUvLz73tZ5ZOchGmR0/dZx+PScbz8u40afq8jpvNBrdZhOnN4iEpaR9xxX7FuawjWqXejHzq2ZR+5gSFuu7y8htAnI47SDHLybqrlOo8SxZRSn/mY1uqc8jwOUfZZlvb68rN57sZanTy116ddcFlGxX17c6MszxLY+clPfqLFYq7b2ztVVTmyXr0WI9ioj0RNItv99PwshaB3796paU46Ho/6+PGjtuOcna6vtVot1LS1qjLX8RCNWShytW2nzfVGnz5/0qk+qWlq5UWu4+Go7fVWzWutajZLc0qGPlbtbTfXyvMIJA4je3p9HaMqu9edFOIz102rxTJOde+H2FjB+0y7153Kqoxrh5w7qW0bnU4+tasdTr185tV2XayF6no1oYmDVH2mm010cL79+qs4i66MzD9OQNd3KSVvv4/NEzCY1B0AIiw4BwRdXV3p5eUlGf/dbqe3b98mUHA6nXRzc6OnpydJEeTsD3ut12vN53Otl+sEXGbVLDlbYdyvp6cnXV9fJweDNB5Syyg8n4+ZD5yTRLi4ODupyHMtx7k5zjl1bZwlVBaF9q+vqpZLLWazaEtCTMM5HY8xtbIoFIZBjakXyrM4fwbCbX84qBijYG/evEld4uguBYtNilfTNAl8NE2jr7/++gyQk2p1d3en19fXlBaFM4EzZQvBATh3d3ephgHGmfPAWSY9qq5jm3CK4kkDo7AbxwidQ1oXwC06O7mcvLq2V9t0ms9im+tZFd9b+/j8eVZoMc9S2+iXsZX5fLZIzmDf9+k6mc/VNp0+fbpXP6ZNDX1Q8E7z+SJ9d5bl6rqYUu5CnN2IM51nudq61vF4ks+z5Kj0fRzIu9vt9P79+9ERyFXXrXa711HnR6LCuVqLxVJxCHCewG6MQGXqunpM9/XabLYqy2rc80F5XipmPgSdxtbiVVWO3xVlmOgkoJ/6JaK/d3d3yc6FMGh/PEgGNAcFyTs1Taunl5fYxbLt1fZjKcHoaHrv07nz3mOxdaxPqmZVAv2n00ndEGsbu65VP2I69nxQkDed44hSZFmWzjmRIimS8aS+QXxQC0fNGumenBfSyayDORtbhDMTKYQgl2UaQqw7HcKgpmuTbexH58ySeXzX/eOj6vo0dr+N1tv7TGXm5eX06dMnbTablKb2/PyciFyic9aWr1arlEZqHUp+D9GE/kQfUJNItA77Tt0QnyEajbO0WCxSDRkRSs460XjqJiGzcHaXy2V6psVika6FU2vrSv+y1w8+gvRv/dV/Xy6fawiZvMvlhihscpmOdZzXMIRuZHZO0YFwIc6saOM8IjduWtu16oY2KepZVUXnyXtVs6WyYmrBiULI81xNfVDXRqUAqwjQy5yT12TwALbOeQ3qUltogKYUD0GZxwOBsNpwbOjicLFoP8fOUsNYUzS22B1GwzeY7U+jdlwEmLTu7odewcHyX3avcsp8bv49RUyyPDNtf6fZD/Hz0VEC1AIovffSMLW7hIlMDpQ/b8HNf947DaHRMEx5q5f/2c9ZZ+K/LUrC7+x77HPGv8frXNaQXEZS4uen7yRtkrlM3ns5xZkw9nWZBnb5/P3QaRhaUZNiv/8yumSdEXtvf9ka2FeMOHx/wePlZ7+vlupybYhgED1xBDqJfMqsmZuCWyGENHg2fYg3fc938Tvv3NgXL87MsfVxQV5ZVgrvPMvyZBAyHykGogbz2VxlVWpWzVSUud69e6uqqlI6VdM0+uKLL1QUmdZXEbhdXV0l5pnzijEFbMPiw9Ba4AjD/OnTp3Q+bm9v41DlMe3J5soDPO/u7pLxhj2H2WUUwWq1SikNpIW8ffs2gUSKwdu2TS2FAZa0VraGarfbpQL73W6XUmMYKEmRMGAUlt4aSGkqLJais2AZzWEYEjjZ7/d69+5ddOKGqeMThfjL5fKsnoh9wPmhPTNpR23b6vPnz/rZz36W5t08PDyktt7b7VbffvttYjzt2cGZYk9sugrnlyjFt99+qy+++CIx7Lz34eEhySaA/s2bN4nxpaZru92myIZNqwJsABZgrjl3DC+l8QMRtHfv3iWwBMizUTCcvdVqlUAQ7DxpPDC39/f3ur29TeuMA0Wd02w209XVVWqrzvN77xP7nOrPZrN0DmCJAaU8E+sLYw/Qx1GiEB2AZZ8JcMre46jFLliSd+fpRqRE0WqaqAwAl2ch6mDT6qgtsmmVsOrrqyvVbZP2BjA3m8UB7EWWnzmL7I1c7LTLtQCXdAFEn+CEA07ZC1h6nCvWSVKKzNJenbUchkFXV1d6fX1N12BektVPtiuerWfC9rB22Cv0AhEp3osuhPwgalv4KW3NRkTkYraQBfW2HoYoDr93ziVwj1M0DENaOyI81F3R0IP0La7L8xDJIJJ1OBySk4gdsR3a0CG2Yx/6HFsWQkjXxQGz7ydNEKeCe0cPhSHo5ekpOT1lWaaIJBE6XjbbJsumwb7oV+TSkg+sH/vG6wzzmnMBtrERW5tRxHOw3jbdkPWZSjf82VnDQbf6QYpDj39bgzS+fvKz39XzvlXdSHXdqW8bBefU9p18WUYnwOURfA2d5suFmvokl8XFpN21GxsfDHKSz2KkoyiVKXZ1qrtO/Wl3loaDYBZlGR0d5zR0vZTlkQnyPg4m63oVRWyJ2w9dOiRd16jvJ0ZBOhdaAC4GYPrOMadziCzDMMRmDjHyFCM8kRVzCn03NXpI4x2d+qFX3wNCo1HPfDYyFdGJi5GYEfgHKYLOKZ80L8cBjGP3KzdGbYY0FPK7KVB938vrPB3PpjPZl416xPWINVjDuIbcI47cxPBfdorD6Qvnzzb+jj9TQIMok20jwBDPFMGhliwb71/pus44m95TmBmHdV4CfJSJTeWztQqZz0S7axwMu57WQTivjdHZ+5MzHQZNneLs85rV8OdRsOmX4SwvLoQx3RDH0NnfGUdurFdjjdmveL+mjmiwn6VD3Hhp52NQKaXFxQiqHI0J4vXyLFPu3DggsEwg76c//anartPqaq35LDoPV5urJHvr5VKr5UI//vGPY8ShyKf0iBC0vlopDEH7MTpz2I/pZmPkj+5gzrnU0ldSyh233aEAIIAZCwzI3bdRDlIpqHtcr9cppWK9XifDDyv88vKiT58+6erqSuv1Os7+OB7TfxQyPzw8JEcKQErKA12kAHbOudTljfa31PPQ9IDnAWSyBhRxE1mD6QWw7nY7ffHFFwohpJk26/VaklItxWaz0TAMyfHquk7X19fJGXh8fPxOehD3RAtgUkIB8TCsrLFzLrXUJZWGehQ6uuHEsD8AHOoq7u/v1fe93r9/r9lspi+++CI5ZwAM6hNoKhFCSEAU8IVDRGvdh4eH9CzL5TLdm6Q05wcHFhCD8wB7XhSFvv32W7Vtm6IukhJgvrq6Skws4IPapqenpzSPiDO6Wq0SCAGA4+AAcn/961/LOad3797p8+fP6XmRlaenp/TMNERA91H3AWBFRm3aIB3PqFsi8gKAxxnH0YDUBGjzsh3luq5LoBLAKCnVeKGnSf+yheR1XafmHYBnaQKnz09PCt6laBg2kefCIeQ88ydOP/fHfkIO8H3DMCQAyRqs1+sEenGysbc4RoB5W1/mvU/vv7u7S/Vk7BFpmtwL/+EsI0uAfq7Jz3H8beMO9hbCSJKKsX7TtrKOFiCoHUeVcN98Dqckz/PU/ez5+TntCRFduwc4w5A9RKOurq7Sd0JSI0vIGHrbOkdER3DosfHIHfYJp8q22baNMnAoId3YP74b2aqqSvWo65Bpez9EZW302hJ5PBOROsg0voP7sngBHMc99X2f9BgOHGePGjmuxzrigIGnbVqjxRHUiiH3OE84XRAT1nH6y14/eAfpd3//9/T/+yc/V5XPlFWxsUCWOZWzSiEMapoYKvaZ1/39Zw19r2qsFSq7VnRKi6+gYejTINRJwYVYnDwvzyINbHBeVPKZ1zDAnIRksBazhfIsTnZu20ZD6JXnmbquVdvUaupTai3JIYmFyxGakquLspJILQpnXjspZcFJeV5oNpur61qpc2cdTjJP+pJXXmQKYVBe5mcHrutiFznvvZyP/y7KMbe16xO7n/lC1NMMo6PmfCwu9D6MEYFp8rIVdpQiSoKXVY6WbYhrPagf+pRux1qQSieNkZwx14q6Dzwf59zYKW5sPR633BT1uXRNPIuY/ejOa73Ga4l0RDe9XyE2ygghaOjjeoRB6oZefuzqZ9eCtePflmmK3+/T95+/pnqx9JPkjOIQXTqdbtyvy7qm7zpMYXR6+DO+zaU9dWNap/Nja243PY99vvgun5y32MjAjdeeHNpocKcoI/du/5uMcK7laq7ZbK7Vaqnt9lp5nunDhw/68osvY03dCMritbx++tOf6Hg6qgudymIEk2WhzGcjwx3kRfOJTnleKITYtrvvOz0+fk6gf78/jnUlg7puUFGUqbsX6V2kwmB8rDHFoaAQlTSgxWKhl5cXrVarBCBgBouiSKlHODJfffVVcjYAWLvdLhXRYngxOERtrq6u1Pdxvgw1Kxgw2hRzNp+enr7TYIBOYwB4SWkQJcYY0IRzBfjBuQNodl2nv/JX/oo+ffqU2jbjwKDvGHBJ1IqIGPVDGGfmlHCmuq5LQ0Pn87nW67V2u116DrpbxTbl5Rn51XVxICtzfHgu1oZ9sBkFpIcBsAGJRNWIbjFgFRnhGfnuPM/TAFpSSQBMpPJISqCNa6EnYVpZ776P7ZUpdgaMSEqOIraERgjr9VoPDw8JINHunPe9vr5quVwmJ9nOQwKIPz4+6t27d5rP5/rmm2+02Wx0fX2tz58/nzkdsMecH/QgwJPoINEsyygjAzjG3scmAziP3Ct6iX2GuMiySFwBqIkK0rLb1rhwNnAaAGzsxTDEocTsgxSjrziDwzComs3UdG1yqHHMvv32W0nSdn2V5Ik/m6ZR3TTK6yIRGujDw+GQ9hRnY7/fJ4ebvbZkEWc2y7Kzph44w1yTDAGuYfUyTjXPTqG9cy6lqFpdzrmkg+B2uz1z0iAqbDoaUba+ac+cjJSSpalg39ZXJawzOiKsC7oUnAWBQIQIeeBn7BtRIPQwzv9isUiRFb6TZ7WpkDg6nFWelwYL0tTFEbm294e+QH7RF3aYLvJZjA4ZWQesOfdviQLb/Y11jHPpwlndHXaIdeIeWQ8iWryo0WI9kSPkFpIOZ4f1Rs5o4W73EPmt6zrpXtYTW8F3EeH9TV4/eAfpv/cHv6d/8i9+oa6TlGVymTSEXvvDUXLR2HRtp6HvVIyGdFbGCcDzaipWjA7ISfN5Jee8Tqej+n5QWRYKQ9B8LmXBn21aUsKK9TcojlRg67yaLujU1Oq7VrHddKu2qyO4bRsNfZ/SJTDMXdcpczFKwYEAjIQQ1LVDmnkiTdGm4GK6W9v1Go7HGCnqh1j7MkYQNALSLBuFPM+kEZBnWT5GRLyGIXajk/Pjs41KuZxCnjiUUQlS0NkrjPNM+m5KlcEhGoZBZV6k9WO9pAlc8z6YYJzUvo9RBu+yM4cBRQw4GNxw9rOz9MXsfEisUrnL98/9if/WWSRlGGIdGD+iED9Fr4IbfYrx7+NbuT+ucfm6jLYhE1TW2Bcpd1zPvux9T9dATrzy/DyKdebUhGkOjr1WcsTNd0zK36nvO/nsfN2mGqBMYYjd18IQI6ARCBbRAfWxzqisylRkPJvNdHtzq+12ozwv9P79O1Vlpd/9vd8dwW2l+XymoiiVF7m6th3n6ZxUFYWysTOYUwRhHz99VJ57LdYLnerYVev4sk+AdVZVeryPLfg/fPigPM+02x1Gdnemw2Gv+XyhPM+037+Ohq5WVS2SQcdJwPB03TQ3AsP6PHbGBOhjtB8fHxODTGqLcy4xtIBD0j6en591e3ubQBzrHkJI6TBZFhs9ACQBk5AQNzc3yWkABFtw9+tf/1rb7TbNvOEePn36lMAIc3uoWQEoY8BZF6JKdV2nZgmkSfV9r+vr65Qy9fz8fBb54Tts9zWiZ4AN7h9wbI03zXO6rksNBzDQzrkEhiGn+Pl2u9Xr62tyVj99+pScX9uhCkYTkEEaJt3Pnp6eUloQ6wBYAACh756fn1MXP84mOgzb8PDwkJxlHD3uiX23UUlkHKBHU4jVapXADPcKmKaxBqCFCBpRBhwHnu/u7u47RfF3d3dnTitpSrPZLDlWRAQ5L5KSM0TKDc/D9xIVpR1213XJEbEOK2l7pGhyX9gXGPvYDj5PNSN0PZzP5+lPHHHIDEApupBnZP0Bp6RiEnFy3qsPQ3IqIRycc6pGYAthSlZJanSxjem5yDxnTTqfZ4PjxXPa9tUAf+sEAZrRVdgUsBE6wToUyDNzqgD+DFq2HfgAtDjP6B/0FPfIrB2+83Q6SSOOOh6Pur6+vmisMNXwoWttuhpplTwH+0UtEl3PkLGmaZKDa/UAZ4Yzy7VZU9bMdu7DXuI44cRiQwHz6DPex/UYaG0j3+AHHHwcl4QLxwYO2Uha00ACZ40IErqAtYeUgNDCdpO+zLnnvewfziFkgcUINqrKfqK3kVUre+gBdBQdISEVOV/IFQTj5f4QQf1NXz94B+knv/NBb29v9c3nfUwzG3rV9VF5VkVQVmaqx9kiRVaobmqFLNditpDzTl0bi4O991GwQixwbdVoPo8OVBjTs/quTwWodV1PbQXdFCVp2lbDaDiyPJdCLPTOxyGzQb18lqmuj1LbKHM+ARwEqW1bHV5fzvI2JQPiYXGMArRg2vt8jLLEwk0OgDQko4aXXRSFmtH7dm4SWIyFz3LVJg98GAYVY1v1MHSazYoJ2LWDhj5GeaQpXIuiTlGSdhocZwG+jc4g+BPgnlKpQjivqSFNbYpA2JbKUp5/dx7N2Xrqu93vWK/xzs5kzqayWaVwGWFybnqm+LMoR9JF04S/5OW8T3eAExMbPWis7zlfPxpX2FtPzqC5xxDCNLiWei0pNZeQdLZHyKjd06g0S8XW9JNTZw1Ilnl98cUH5VmuahbreH70ox9ptVqpqqKSXa3Xut5u44BO77RarnQ1tuk9HmF152rqRvvDQS8vzwpDryL36rtWfdfq5RSjMUPw6upWee5TyoT3Xk3bqWiL5ETAJg/DoDBI2+2N2rbXt998VJ4XutpcKXZizJXnpfK80PPzTn0fVJaFqmo+1oBEYP3111+n9KztdptSuGyeOU4DDgFGAyPDsMdf/vKXCWDe39+n9CKAHUyvrQsC9BAVOBwOKSpjHRpktiiKNMC06zo9PT2lupFhGPTFF1+cAQ+AFmlnpNhIOmtvXRSFttvtWTSDrkUhhNRJjxoYdClAiyGn3BfGmecnbYf0IsAODCcAm/2lTTapirbYH+C/Wq3S7CCMtZ0/RHSIc7HdbpNB//jxo25vb9PevLy8nBlzSSky8fT0lEivzWaTgAY6wUbt0OuSEhhCPqhDgTm1banzPNc1DTxG3c26wMLSge10Oukv/uIv9Ad/8AdnqUKkz2HviFDc3t4mEAzgwoFerVb69ttvVZalVqtVatrAkFgAkbVz6CMcA5xRQBiMMM8nTXNlWDc6tKGviATh3N7c3KS0Rph2vr9tW5VFlaJDAGnWh3vZ7/cJpJIuBpnDPQF2Aas4OJYwCZJ8nqW0TfvZu7s32j0/JzlnzWezOLeRyCxnHOcah5afcT2iA3wG0IvTiLPDuVmtVslJQj90XZdqyDhPXIvvx3HAiWRPOHuz2SyRIkQkLssUcEpIvyPNq22a1P2OtSRavr66Uh+m2iU6d9o1sQ4E+8Ue23Q57oE6IvaF9WEfpMnBti+bMsgLPY0eZH/AUTadDEcEuwxpgqxy/cusGhyyFHEf4qxIvq9t29RdEQcf+WX92UdLjvGc2C9LGtsa0Uuyx9abEfWzBBIvzqNdP84vug5CCRsH8UGHTQgOcAlr/28SQfrBN2n4l//sT/Vf/oN/qv/ij/+Rmm7Q4/Nn5blTVawlhdGY9iqKMQzZNqqKmEoy9EOql9nv9+raVkPXKkgq8nzsIjaoLOIckrZtlOfFmLYXU4vKslBwTmUVI095kSf2oet6Zb6U97mcH5Rl0uGwU9Me9fj4oNA0csOUzyxJQx+7ymmYnAPSJBCyoopgpW1aOR8PN53QQvAqCpR2rzAMyot8jBKNzNlY96Qw5jMfj5F5SI7GlCPq80LdELureaPk26bR0DfKM6kjAiSK62PkJAQbzZhAeTbOSMHxwZmAUeFl2RY+Sx1NzPw6b40NW+Kco0FeilzZa9rDno6HU5SH5MhNDS5ihMlPzsYwRZ9sdpp1ci+fO/59csSsczZe9Uy+bXRo9InTzyWZ3333eF9GwlBerO+lg0gELc7QOo+WhTA52ig8ij9vbm70/Pyk6+sb/exnv6N3799qu93o4eFRP/rRjzSbzcbC+L0Wy3naG9I/qrJUWZX6+O23Wq3XqutTKji/Wq913B80qyrlo+GUlAYxr1ZX8j46YE+PjxoCNTCFqlmVADaGomkabbYbPb+8JHbranOlWTXT88uLqrzU626KsFgmuqpynepTUv48/263083NjR4fH+WcS787HA56fn7W9fW18jzXy8tLmqsDUIC13Gw2+tWvfpUiHuwRXeU2m41ms1kq6idFBuNBagyperDSOAnr9Vo///nP073wDJLG1ttTMT/GG9BCZIJ8feQOp8am52F4iXptNpszUGxnweAM2rQUQAzPiOy9vLykiBuRD1o6Y3wBgXwex5NoEkwqIIj302bZsuboPq7H3B6AFwM6bXrkbrc7I0ZwDPq+1+3tbSLSAOG0yoXpbNuYQjSbzVIUjWgfewlgon5tuVzq/v7+OyCLf+OEAVYAhkSh2GvSB6mFYyiqPetE4HHCIUlID7POu2XRbZev5+dnbbfbcU5VbCpArQwpPtRL2BomnpvvJwLC+cFZIgLR971Wq5UoZrfNTwD9rCOpP+v1lerTNJdFUpI1q6+JgkhKzrGNzgBmLeCliQaMfZ7n2p+O6R4tCVjkuYau/07q4jDEjJGmm2bm2GGp7ANnabVanZ0B0jdh2XGWcQzyPNe3336bzoFNUyWCgWPP+cGx996nFu6kyMH6W9tn6+FwAKg3tHVnOIbIUV3X2qzW6b5xpA6Hg5yPHemIFFk7j/xCPqNPkOWiKFL0mjVI+2BSg3HcbZ0Wuge9CXgHpDvndHt7e/YeS3bY82FtNKmdrDWOKBEfnoHntGnYOILDiPm4f5wqzgzyyfUtCc85xAHDFhG95uxgT7EhpPRxX0R/kA90hq1t42WdPTIUbBogeoyzyp+sRVlWsVzF1M4dDgf9zb/9t36jJg0/eAfpX/+rP9Ovv97pf/8f/B/1/HJU07Xqh05t3arvp8hHrCsKquujuvYUQTb1JyGo6/oYzvWacujzInaxc7EFZZ7HQXowIAqRdw8h02Z7o9Vmo/l6LRWZisVMfQjKBq/cZTqdjnp+fhoHLg7qu06hftXzw2fVx5My7+RDUN/G++41jJEtUjMG9X3sUFcWuWZVpbbrztpBR2EekrPU97F5g8/GEPSplpNLz5FlmfqRoSWDi+hDlmeJWR/dGPksFuT3Qx/bjw6turFhgvOmuQAl+aMjg+MUX04hxLoQ52JDh9gyODZByHxIxfgpcjH+f+hjrU/fxy59eVmOrUAH5W5SvoCcIo+Krh9ipCQagFiHFBW41PftWSg9Hr6gvu/GltzTKzkWPpNXrqCgoR+Ss+S9lw/fnz7HszvToIIugrFRxpAiTnz+LEVtHPCLgklh/BDks2nIH45QlO9hnLkVGxpkeT62gY/t4os8VzGmkK7Xay2WC93ebOUzaTFfqJpVCkPQT376k9Q2eblcalbNVM3i1HM6rq2v1jrVJ9P15ySNNT2ZmfvDeQxDbLu+e31VCEHb6612L3Guz/39fRwYuVjo9fU1Gde6Pmm1WqtrO9WnU2QQRzmWpKqMnY3IOccASEozF06nk+qm0ayqtFguzzoqnQ6nSB6MKaD52BI3hEGvr69pcj0zcmwkzaYTfPz4MXZkGwFF13UqmSsyGrL5yLxifADMj4+PZyADIAW4onmCpDSvhd/jMF1fXydD75w7mx+02WxEUwEiGBYQsRbSBDJ4Nq5nga+VOdvQAFBBDQ/5/DgQzrnUJQyZ4blgH6VpngogxNZpAsyRKYw9IBrQ9fnz5wQ4+RPQAvM8n8/1+vqa0oFCmJrHvLy8aLlcpvskPQ3AzVrbmgLSszD6RBZtpz57zqUI8h8eHlLEhvUGFNioii10tzVfNvUKRxrwFNnklZq6HSNVj3LOq6rKUa5eVZRFigLiuMXPxrq8qozObd3UGIbogI4OTVlW8n5sYJDnWo8Ave9Js+61XK7knPT8/JIc9+PxoKZpVYzk5WK5HAmuWEeMXB4phm9bzWZzubHEtCwjaCYdbTabqQAkj2dmvb4adXavfhi0f33Vah0HENu5N7ZjJGuBjAGacUpxjGy9yTAMKfeg7zstlkvlWabD8agwBF2tV7G5wDDIjw79drtR3/c6HE/K8iyBztk478Y5KfeZ+qFXkUfZ0Eg2ffPNN+rDkNJOObM2vZLnI9JAtBc2vm2nuiicoLMaqLGjIhEWHENkEzkF6NtUS2SX9bIAl1Tfz58/JwfONu2YzWYawCrjzMS8KOQkHcZ05jzPdXd3l1JZLRlI1IhIOA4YBAH3gR5jvWgeQrQU+4HDajMsaLZCpJz75vk5h9ga6yhYYgiHALICfYns8b3sL2tN9L2qKvVdr8xRP+0TgUB02pIdNipDBIkIr9XxdoYWz0NNExFsCBLsrdVdiWwfnaQYvZ3KHjgnVTVTXZ/k/dS0CxtJSYFzftQHuWJqv2nn3sf69Kap9bf+zm/mIP3gU+zarlZVZcr9oKY+qOl6DWFQfZpaG3JYQwg6HvbqmsOZ0eGAeO/VNZ26dmw12kx9/iWnpokgtT4dkvF1zqssZtq9xNqXbF7FduBdL5dnyvI4J8jluZZXGy2vNmPu/avqvpV8rrrrlYUgH4LCEB21LgzqQ5DU6VTXY81LBJpd12p/PGrqSBaS1526qom0KqdQj3U4wwgkTvV48OJ/5Ww2tgGIA2s5sJLUh6AQYg0QazEvSjknZc1JnghFGFnoMSIXxyhN9SvDGJXh/95LeRbbscf3xH/H752UQVJ2chpCr6AwTsKOTklR5LEZQohtzIOTMp/JaYgd4HKnPIzNCXwE5tXYoSwW5ruxwUaQd6Py9V4h9Gq7JjV4sANtc19EbBAkl8UOfhmsCLVbinVCGhtqIIPxe+PBz900HDiE6JhRn0P0DRmLGzqlujkXm4IUY6tqP9YCxVREp6LIdXd3q5uba5VlpaoqdffmjV53O/34x7+jqzEFJjJLvebzOE/g+martq1jTdGYV03ed2Rb12Mq16BvvtmPoMzp6elBZRXZnFhr8zgZp9ExKIsx6nHYT8XrQwS0T4/Po2I+6nd+58fR0AxBcl7VbJ7SeKJR3WkIU4oMyv04pgxRrE3HNFhhSBXA++l00mq51DAMyempfJn0Qd/3evv2jR4fH1MkgFoIm3OO7iAaROtbSVquVvrzP/9zdV2n3/u939Pj46Pu7u50GoH4fh/X8PHxUT/+8Y+TnsLBgwGktmk53i/pTtTYwJYiTzzP9fV1Ylhvbm5SG2Jm82y3W0nTGAFJZ47s1dWV7u/vU2SBYn3rrEhKqTtN06TBpqTtbLfbsy5PzCuiu9bHjx/P6rVwACSlZyJKRyTA1o5aIMHePT4+pkgRTg7OG+kyOFUAn77vtd1uz6KOpFpZAMHaVFWVutZtt9vkoLA/pALZOgsiIzDYpMsB9EjLtIXXthbIOjvICXOJ+Pl2u00sPT9nXfevsZYuMudELL3aNjrxce7aNNRyqh0NOh1PCsM0CJXztxh1B6lozjm9efNW9/f32u8Pqbvc09PTCBbjmuPIPz8/p/Ss+L2F/JjuPQyDrq9vUvrUfDYfn3siLfq+0/PzcaxdnE/OZ5Bm1WxcCztI0qltWhVFqf3rPjn9ZGoQuUNnX2YdQGZAWCB3OMz7/V6+iM4A83lsG3LnvPpxT/qu0+bqKpI+da0hDCqzqXV56vLW9yrzIjX+IPL3+PAQO/iNLcC5b9YAUojINo4vuIgU2RBCGj7MmZpS86eGVUSw0UmWOCFicYmt7NohV5wvziRnmHNAUxaNyGM/RiGQEwgB1p9oDDrKOZccF86sJSRwfG39HgQN9WycJSLPnCGuJ8UILU1A0EGMPnDOnenrhEFNkxWcUewUhBX6D7IDZ4HvsY0VsOPee5XzQhpCykiyjhgROZx8ojesO84a+y/pO/VHOM6SUtQJnURKqK1PtEOJp8yk84ZUcQ/zFBGyUS06UlpnLsoZw4PD2ecsYfqbvH7wDtLXv/5a0ky/8zvv9a//7OcKigDXZ5makTFgwaNBb78zDJODHH8XW2eHEKfPS9J8sdBAx6q8iHODxlk+fd+p6Y7qD41O/UG1Wr3/0U80n88kn0cQjdFnYvZ4IA/qVZ9OCi7T4eUlRpXCIMl/Jx1qenn1ilGWvJylmTU+m+bRFGWpPIsDyPIsS8lboY/RiLGH2CiwIc4aC7HxgK13kmIVTh9CUrbSFOYt8kI+TE0FWhfnM7VdK6dBeR6/i2hVGGJKYxibvvksU5FPToLzXl2bKWgc2BmCnBviAFAnZUWMhg0hSH0fo2TDOGh3JCScgjQ4eZdJwY/fGa/jwhg9a7tkKDNfahjzdmdlJec0Rpi8vKvVjfVSLgup3ifzmZw7bxfuR+eLBhFZlo0zuOJcocHHRhZ5lqeozlQPNTqrLjZIyItCQ99rnmpHKi2XESTd3Nzq+nqrzMc21atlNALv3r6dwu1FoSzzur7eqO8ZyBgV2OPTk6qi0GoZAcPLS+wMVpWldq+ven5+OGOjLeNki54xMLDnck7tCHK9j/NZ6ITVd51WY93J4+OjpGnuF0oSsAFbi+Ik3Qrg2bZxwOhms0nGFaaLSIDNA0e5ct+SEqtPzYU1BhghGMNhGBJzCsimxXLXdam+p+s6PT4+JjZtPp/rMDqXNzc3CVDO53O1Y1RFisDj3bt3qus6MbgwsIAXog6wae/fv09MJgDTppl47/XmzZuzVAaAAKlufPclQQTwkZSACLNsSGmC5YXlxiCy93zf8XjU6+urdrtdMm5Eb2gXjQMBGJ/P59rtdnp5edHV1VX6PlhOABxM6svLSwJdluXEOZCUIl3U7Nze3mq326XUQSJGj4+PaT+dc8kpJUqHwbc1nzinNveerm04Dcga70HmPnz4oOPxqIeHB93c3KS1sMDsq6++Sh3xLAP7+PiYnEVknO/mO4jOeO/T/CjJSWPqGd3hcKaLIk+sNGCJ9X56fNTd3Zuz+hbeR1E1NpaoJWuO7NJCHftBTZiNAhIBsqDq+fk5tX3/9ttvk5NOYxMAHfLM+bY1SjjB6DWAG04QoJp1BB9wrjiTNgpA+h+OAZ9ZLBZyWaauj88B0LdplO3oQKNHVquVDsejsjxLAJ3vpjsZehCygX93XSQ20A+XZxJbg4NEtNfeM46hff5hGJKeJ+oBEAbA44BAJPDd6HR0MHVFgF4p1vER6WI/cAptU5YQQkqrJdJsxxOwtzi21B79+te/Tg4cZAz6jsYbyJ2NXl9iINsMA0eE82Hrc9hf9DHrjF5A19gUMuwfjoVtSmDrpfm79z7VhLI2IYQkE0Weq2mbMznl2vyMM83vcWYsIc1aEaGGfLHRQGQT/cw9W8eY6CNyx3yurpuuz3lHf3B9dAy/Q4eiQziXNmUYfPCbvn7wDtJyMdfN7Qf9W3/tf6Q/+uN/oN1+p7Yb1DZdEi4WD6YgK2N6HF7plFcdgR7pDXXdTKx8FlTNovB1XSuaIAyS3NCpqY/yfaNquVBX16quSykrx5S0TsGwgv0wqAuDivlCN2/e6/ZN0PPDgz5/+428k4osS9GXvo9F8Cho7726oRvbRw9jW+0YxcitcPrYkjsbHSXv3Oi5E4XqlWU+sVOh70fnY1zYsT6p7XuFFIIdRhCZK4wtxYexriYoaMgLVdVMapvYuGI8TL4o1Y/tnV2IM5q4j+DifKjQj1OSF2vlBcXRMxV5MaYxhvjZPJfzUp5nenp61DD0ao4HvX7+pMNY85AOeYiNNcbHGdcuPmA0lqVcXij0DOOLdVt0+yuySkU25e7CmrtxraNyiqCD78yzMfql6Lhlzsu7sduND1qtlqOjc6Plcpk6ic3nM+VFrt/92c/GFMJBeZarrAqVZZ5ywYehH5V0jBjtXl/0utvp9u5O3sUZPMMYsXl6vh9rOkrlhdPr/lnODXp8/KSmXmi3exmVe6+uK5VlLoXYYf9ZK4aHEn6HlUxrMsp2URS6vr5O4OXt27eqx25EsPnU49Aq2vtYkLvf71MHMwvKMUQPDw8KIWi9WullTAshfYthrDB2gC/uBUeuKIo06JBZNRb8YxR5zpubG/3yl79UWZap2NWmoPD8OKd3d3fKskxff/218hGgURwLeIpO+mSkjsdjGohK/c7pdNKXX36Z0sUA/qTL8e/tdntWFEt3vKg7+vTMFM5Tf2DrJjgzIcS8+DyPs0NI57PRXJ53Npul5gXWoYDdxBDS4Q5Ax70ChDF4z2NxOs9BuiARFfQ3bC3AmkgRMzswqgAsGFAAGA7109NTWn8c49vb29RwgXQd7tumEyIvb0dSgnWzDicpedTRvI6ppEURh22WZanPnz/r7u5OkhLoYY1pkGBrvLz3qa7r5uYmAU90D/ttWVwAJCmA1RhRgTDgWZqmUdCgopgiBzhIIYTk4BPR5Izwb1vvQa0WzpFNAQToUMuBE0vqFlEcQCNgdr/fp1RUgLOVDWQLgEbExIJD0pxsZzAcLwgWnGCilbbWyD4z+yJpWr9RL5BRMQxxoDKOPnqpzPKk75DBmJrV6dTUyZHnOWnL3zdtkidSn0irOpmI5WKxSLoEhzulHY6YB8IE5xq9ybpzX5Yoy/Nc2+1W+/0+nSPOlY1y2JQxromzij5izXGceI9NKeaMIoucJ5sCBsC30VtqsLgW8oVDCrjmHBD1Q0cTMaFJBdGTZOvc1OES3WhBO10zccC4xiXpaJ+b9xERsmm+OC+2MyLnl/NvnQmyGWwNlK0LslEr1pHaKZsyanULdWyWTGBvrGPFM4C9+ZP3xOeO+NbWTuHs2Xop7snWkUFqIsPsOWu0GNPyf9PXD95BcpKa+qir9Vz/w//Bf1//6X/2/1DXuzHNaarVYPGdU8z99X4qgByB3xCCun5QNzQ6nGjEMG6qi62vEQSfTZ075LyGLg4yPR5O+vqrr7W6utZmM5cvcgU3TSDPy3FK9HIhDYPaulF9PEguU5aXOh0OKvNcYYizmFDOsTFBnOeUZ0Ws3RmdKPlMQ9dHJyQrFIbY6MFlmYax29kQJPnYvCB4L2W9BjllZSXX9xq6NjoUQ58M87GJQCrLMwXnFeSUl3N575TnRcz4ymKXMiIh2dhG2/mxI0lVqior5aPhPR6OCkOu+WyR8v6HEGL9iKTZsorPNs7g4UAPfVDbOuVZIedDjFCdWklROR4fP2k+GwGKMlFLVJWxViiCwolc8N7JaQzxFtm4P61iE4hWXRvT1iIYQAkyKLdX5mO64GKxmrpyLRYqi0zzeaV3797ryy+/UAjSYjHXT3/6U+1eX8ZoQJ4+U+SFDsdDAivORVnbbDdp4NrT04MO+10CGUPfpSLnal6p7RoNQ6enlxdJMUXg3bt3cqcIHuqmNukQRJhiMXxspzvT62ts1xoLm6coAawPCpJIEsq/KGLax26sywAsYrSen5/15vb2rCCVVs+21fW/+Bf/Qnd3dyn/uyiKlJaz2+309u3bBBTmi4Uexpx1Om599dVXaf5GVcX6qF/84hcJSNHmmvkQm80mzccB5EpKwATm6+HhIQEiOqHRnhaDOtVI1cmhuLq6Utf3ato2paSVZamrqyudTidtr6+1ubpKbCuDRN+8eZMANQACQw34scw36V10goPNxfDi2DNbyXY1whm2qUOAPRhVjI9l6YlQ7Ha7BMCRib7v9fDwkOqRMKTMarJOEy2mbToPbPHHjx/P2HsLwGy3LAsKiebYlERbQA1IrOs6Re0kJcY5hKD379+nSBuOKd3aAH0MVLWRBSJayA0MO4CH+R2ky+EQWFafTn+AFGRLUnJcLehE/qhDoXkIjG7q3jhGTubz+dixrU0RS1tP5+RSyiZrxnPMZwu1bZeiMxZI41RQh8F+QHKQAkT6HdERnOpIEEUniIYcfM46PHQHtBEzXoB57KwFr5aNJ1rAM+OII+tErIkuch1b74bMkv6GHpQiyM3yXPvXnarZTG/fvk2Af7fbRV2SFwlXWLlar6/UD4PKKuob1mIYBg0mrYkzzeeKIjaKgnXnfulKZ1M4bYoY0W5SSG1tHjJESijySB0P+gOijIYY8/k8pXKhOzivtsifNebcETV4fn5Oss3ncXDRNURlrBzwTJx/nCn0D7oJvchZpfGCzSgiWoJzDfkFGQQxYcki5ID1Z284L4w9YFyCJQqwqTRoIJJG9IZnQDaRNzukV4p4a1ZVcqPOwoHg95CINMhA9rAbOCLWiQI7cy/sg40SYkdsfZnV27Z7XtRhU5t4SakpDWcQ+UIGkVn+xJEjJRx5T2mI/jePIP3gmzT8f/7r/0rzxVIuq/Qn/8//Rv/r/83f1eu+UZbP02IDAtq2lXdBfVendALek2WZ2q5TH6IT4Z1PrY9DCCryMqVllWVM4xv6QcfjQfP5bOwMVyorKg3Oa3tzpw9ffqlqtZLLY4Ghd7HSp2nisL/MF+qaVkPXqTke9PT4oNN+Ly/FmiRv5tOMEZdhCArjENaoJGPhPd0E4mGnNmdIzQOyLNbtcFgyP7WG7fouppSNEaWr9VUs3g+xCUBTn8YDQLHq6Mm3rQbF7nbOe+Uj2B2GQW3NJPCj8pGhOB4OknN6fXlVVZRn3U+Wy6W6vtPp9Krjceos5VxsZx4jgsU418brdHjV6biTd9LQNcrGZhF04+uHXlVZyXmnYehGZTDlVhdFqTgna2yjW5RjKttKdVMrzwrtdnv5LCrX+Ww+MhRzLZdz3d7daLvd6s2bN3pz90bOO+1f9yryONa16zrN5qT5UExYJnA5pQm1kpyK8ftfXnZqmno0NDNRnLhcLhN7btscZ2WWQtmwrTG9L9MwxH2Kc7YyNU091jyUOh32o1FrlefTJOrTqdZisTxLo3l4eEiMaZZliZkHWDvntBxnh6DU+N7NZqPMOX399dfJKcTQlGWp0wgyZrOZ7u/v9eHDh1QYe3d3p91ulxwu2KHb21sdxkGVFjha8ERNC4wTHfVeXl4S+GvbNnXUg6FHX1CYT6tmUkNWq1UycACv6+vrs1Q91qobhmSwh/HvgO76dNK333yjL774Iukgy4rCnoYQzup/AOCss6TkEFkml7Q1DLBluPu+Tx3Y0AdEDEm/YFgoTgYgz7mY54/BwkHGgSbvv+97PT4+po5v0sSYkpIFU0jdD1FHGHBm0JDO9zISAKSZYJRZC4yzpNTKG4NKCqSNGDA0lmfEOeGM4rxzDtBJ7DVOAmAAUCtNc04sUOVn/B0QxHkBkAHeqJODaT0cDqk9PPsO+KI2kDUFrLBPUgQS8/lC3mXpTNlmFd47td2UnvMw1rdEgFjqdDylNFZkAl3G2QHYWrnBSYMBh9jAXpFaZJ0NIkykEfKyaaOAdpv6aR16gBcpWXwf94guot5PUpJ59pnrpcjvmFJozzKg0zoOfQiaL+ZnkakQYkOoqpg6DPI8TdPIZ5n6MDljOP9hzAgI/XcbC0Q7M9eg6WzbOjkiPzhUAEmejTlNRJd4Xtsxzjo6nGEb/cZpI5LOWtjmLxaD2ei1dX4gE9DdpF+Remydf7t/7KFNF0Tf8uyQa9wT0XGeG2fUpnih0zj7kAD8brPZpO/hu9EtNt3Z6iH2APkngsuaQFKiT+wZZu3tWtmGIWVZqsjymNo/2hTeixPGdSELcWaxwegDnGFsGvoDh4mhwgQZkAfWH53Lelh5J4PIyiZnzKYzIufYdGlKyZeUyBscJfb7VJ/0h//O3/htkwZJ2r++xm5jea8fffFeN9db7XZfx8J9d1lj1EkKyrNxJkpRqG4aZVmuIst0u72Ry6Yls2xACHEgaBhikwA2LKZTOWU+l0ZQ1AdpaHt9/PprFauVyuUisalSrL3phzHX1Q1yPigrKq2vtiryUkPXyYdBbfLWZ6OQ5JKT2jAe9NyrD0HVGNJVkMpZ0Hw2k8+8ZtUsDbDNslxN08ZGDHlx1vmk6zvNl/PEKry8vOg4GpK+qeUVC+Drplbf9elwu0Fq60Y0JYiGKTKXfdPEnvzJCe0npalGeT4dJO+87hWUeS83dj7Ls0y+iF2TyrJUto5dwbyT3r97o7Y+qCozba7GKES1kFwctjebzXR3d6eyqnR1tY7RtxDT24ZhGDvHeRV5JpdNLY5xLuLgzFxFXqpt6QJDimJQ09ai1fvtzVZdf5QPXs/Pn7S5WinPvOrmJLlYe3M6nVTNIxPnnddyHtNc9odDqhHzLqg5HeU0qMiy2CBkGMZ6skJd28u7TN55LebRMXAKynysN9q/HvXu3VsdjkcNfRjr3Cp13aCqWqShmnVd6/X1oJenp3Gy/a1++ctfar1eazabqyiqBCBIM3l+ftaPfvSjBI4PI7tq0zdOo6GkeQDT0jebjbqm0U9+8hN9/PgxpW8BLJxzuru7O0s12Gw2iX2GESZiRuc1zifRHj7/8vKiLIv1DhTR8zyAURQzxn+z2aiu69QWm9RAdMa7d+/SWYf5gkGMsuGTg2INfGNSHAAkGKG2adJgSNJVvPeJaV+tVgn4cV0YOyJCgAhSyFiHqZlFk6JQMJ2wn0QbcJ6sEYMxlJTAOiklgEIMepbFIbdXV1ejbL0mEAC4xljiaEhK+/P4+JicNWSK6IpNgba1aOgfgAmAiM5crBMOCunQyB2zv3h+2FB0mKQEONANGF/ea51pvg/CAKDz8vIy7ketOJ+vTpHC2L2vUt93ST9bkEd663q9Vp7nen19jVHJtosNDPqJtYX5JYLLegN85vN5/Fzm1bWdnp7uz2btkIa4XC0SYAdUcs5wmhjOil6fzWYp4mn1Z9NMg0DX63WKnFkHnagWDpQ0ASLrNJ5OJ63Xaz0/P6dIIYxznuepHgvn1J4TvhMH/HQ6pbRGngvwyTkEyGETiLzaLmjID9E5QDYyXuRZiprz/rZtY2r/ODLB1oCkaIKc1ut1Ol+73S7eS99rvVwlQqiqKtNePqTIvQXqAFZAbN/3qfMlOoz3g5EAqziUl3U9RCZ4TpuiyrngbFJ7ArHAviJfeZ6fDfC1YJxIufc+zdTiPFpyxjpc1kEkumf3FgcPXUxkn++2IJzaS+SQ9cH5IevARnAgP/q+T1FY5BoyGlsG4USqJUSLJZGkKTLJfeA88aJhSMKXY9MC1oZzy3lAlyEfVtbByzwLZ9aSDlP63FQfjwxbwsrevyXv4vp2CsElMgfbha7lZW0SMoVza2u7rMyT7fKbvn7wEaQ/+i//75rNF/K+0GHf6j/8P/xH+n//o3+sboj1NMMQFJyXz/LRIXHyRWwVnWWTAc3H1prehbFj2qC+i13Tuq7TrJorz0aA1Q3K83Jsge1U1yfNlzP1XZ9aLkvSfLlUrUHFYqEvvvhCRZHrQNvQIDXHTrNyrvv7T2rqk8qyUFHketm9aPCxDmW5Wo4RqhG4FIVy+VS0WY8FnHVTx05ufRTc3cuLyip2L3t6fNJhv1dGMwbnlOeZDse9hqHT0AdpGAvk+kGn+pTWQEOncnRmsjwC9FhP41TlXpmPnYIwcrP5TMvFQmHoVc1KzefzxAysV3FIZTXz2lytNB+V4GazUea95ouFymLqiBNC0O3traSxNbTCOJPKaf/6Kjr6rdZrvexeNZvFAu/Me7mRQYyHJ85t8iZfeWKhxg5O46GLCimobSMwXa/X2u12STFiBNo21jDN5/MxwpIrhHj4j8fDeP8ao2vRCTgcTvI+OoRx8F+hwyHOoTns96pSQXO8p35M16CeIoLOlXa7F7VNq+VqUsJ10+j25kZ104xt6eP91XWj2WyafxFB5BReR/kDVsuyTPnptrPXbDbTy26n15GNBTy0o2IP4x7BrEpKgAPQTwSDFKSiKDQrp9lVzchewWjO5nN9/PgxyQiGerFY6GVsw2pZPpQ5fwcgPD4+pnqvoqpSasJsDP0XZRm7FYapgw8RHPKZbVEyLDQOGUYAIGe78FgQhoHd7/ejg56npgQwgoAF5iABPDBs1E/g6GF8LtvI2sgQ77ORHlsjgAFi7XECuG+enb9DpGDMABR2CK0tkuc9OJik4th5IjhsXdclVpq0GKJrDGclz5/a0aqqUiok4D3K+UmZz5SNA4rbJoKpro9t1g+H47gvg5xjrEBQVZXave6S02cdMBuRgY2WovPc1GMx9myWZuzNqpn6vtNqtY7OY56pbSaHdjar1PcxrWr/uk+ArihydV1/Vr/QddNgVed8AiKxrXajtp2cmP3+oMVirrpupJEUg0EHFMEWoxNDiJkJzrmU3k29qq3rsk7FYrEYU4PdWZcsACW1T9I0/8UWVaOjba0HABaZJ/2I9bZninNgCUsA+/PzcyIaAE443ZwxdBHyautEbIQQp8U6eLbwHVkkCjsMQcdjdEbIZuj6aF/zPEbzAfmAPBylMA6ld86p6/to651L+gkdQTOD2TyOFKG+imeytWist635QG+wfgBUHBqblkc6qo1gWTtNFggOCzVokAhSrJ9kjdGR3vtkb5Bn8BM2GQCOfNhoPnqWc4kusoQLshVJ0lUavC1NkWaikehhIug4B0T1uB46zTrI6DfWCFIFJwmnEPuI423TDyWlpiSW2EcHY19tGh/7EMlnKXM+EYr39/epqdBqtVZZVmqaWqdTfeZ8xZEcU6QcJzNG7mam7jWMZE43ZiplZ3V6dFaN53ca01CWxYi5p3vm78gge28xCfoXmePnkx481wWQkf/Ov/fbOUjabDb6J//kH48pL14KpX7+p7/S//Z/9x/oed+pHzRGdXrNF3P5LI9d34ZBh+PItijWaDhFsE39DoJZFIWaulavQa7I5F2msqyUZbmGQapPjfIyU1kVkdVzXtVsptPxqJubW62v71TOFlotV3IeJi7mYfqsUJAbha3XbFbpVI/tQ4tYRNe0TXRqvNR1rbq2UbOPxadt06rt2tQ9Zug6dcd9GhRmlU3oe6mPcyZiOp1TlrkxJ9pr6FptNxt9+eWXiT3Nskw3NxtJvRaL6Khdb6+1GYFK3za6u75R0zYpDWi72aodu+pUs1Jt057l1s/nMz08fFbTxlqPX//613rz5k0Cghw2JrlTE4CipCbApmi0bfyOt2/fpo5BNkf7dDol5vbbb7+N9TnOnTF+doo4ihbl3jSNHh4e9O7dO/V9LKDmu3ivNB1g0pVIYyG1jHQUWFdSlSxbzp5R8wKg5X6YvwLQbNs25SwT8UHposBR2Az0I6UM0EGjA8CBc07ffvvtWc7zcrkc8+OrFH4nLQ5wyz5wDcADwHU2iwNPbbrDYqw5ev/+vX7xi1+kGqT5YqHf/b3f0/Pzc0qXeXp60svLiz58+KBujPIkx9wUIF+mJ1Hv0A+DuvF7cViOx2OspWkaBcOI4yzmea5Pnz7pzZs3iYnl53yXbVZA6gLgj3W4ublR27apYxl5/RTkDsOQ6o7QPXa/cHr4flJCYrQzSxEmZB5QgbHi97CX1CxVVZXS4mC7cVhxqEgptCACIEChuU25oXkHIAoDRh0GoAhAwH7Q5QmHEWaTZwFE4nTjYLEX1FqkiOMh1tMBNuq6Tg4s5xWwyTNHvRIUNKQaBdhRuovZqAJnJr4vjO2jizNHASBLxMQy1aSH8qw8L2lcRGR5r00Benh4SE4LkUvAJ89oc/9h+2HR0SsAC6JG9vyi24h6EUlAVqitQieRNo39sZFI0q9CiAOAITJs6pU0RXbQG3bGCrJEExZJaeAoZ51nsQ6ANHXiJLWIeVYQOUQUsZmcBQgRrsEZsNCKlMyp49dECNjrRgc23rcdRIs88l3IO04GqXo2fY50rCzP5fMpvZA9JgLCtZEx+302BYzzautyGKYKQIeAwdkhNYraTYYNPz4+JtnG9vN5mrnYaC/3g/0i6oHsWGITnY882We2+jiEkHSq/X6ccnQnTio67VJ/s+/sLfJJVJF0M8g1m1qH3rEOp6Rk19GpRGuI6nDeQ4gtu9GpZHGw7kkGiER6r3Kc/yhNnVmjrK81ny8SdrDRvDie43yQODIn+dTUwaZTxhTYKQqEXE5E8jQ8metBcti9RXdNZ2eqGbTOtDQNRWadiWry/afTSYfDQX/7f/E/+62DtNls9Kd/+q9GAJQpDLm+/vW9/u7f/Q/1z//sW3XjkFSXxUGxs0WloeuVB6f6FGe9AJKzLFM/DDqOYXqEG8asd72yWSFpnN8Qux7EQ7qYabGYjcp8bBNLFzlX6XUXC5Q5zNQ9dE7qhl5t2+h0OupweNXh8BrDtn1svHA8HTQMvfq+lRTUd51yJw39FG48nU6xaUToVfhGeZHr5uZGb9+8kXNxqnNVlsozp/VqpR/9zpdjBzzpiy/e67h/1dDH1APLuGy2m1i/kkcA9vj0qKGfCggX1VJdE7vfHQ8RaK6vrmKryaZVnHI8pZZEZrCXc3EILgdpvV7r8+fPCfhYRkjSWbtTgFhRFHp4eEjgCLBiDYBNFwghtkO2nY9Qshxi2yYatnG/3+v29jYZ1sVioV/96lep8BCFhiEhrcjmGu92uwTSN5tNAomfPn3Szc2NFouFvvrqq5H5jcwYTQSocdnv9ynVCAONsiYdgiiNZdcBn6SjWXCcZVmq8YCNsfUeKPCbm5s4q2RMpbm7u0u1DwDnm5ub5DCQhgH4JpWOtBgiJV3bqhnTMABDOG2z2UxXY8ckCqphlkMIenl6SmAIp4Y5EjwXMiBFxfnp82dpNEYY1TikcavT8aj16HyyHpZptmwejjtODikrKHee1cod+1ZVlV5eXpKjC5iHqR6GmAp2f3+fzgYGAtmp6zrNNLq6ulJRFGmwoaTElA7DkGbMWKBkO/ddFrunGkWTOoNzb1NaAPOk49naGWRpGIYEPm9ubvTp06cEqnD+ARPINOuI8QPE8591xmzKBZ/hvwgsg9pmYnHRI6w7TihgBAd4GHoV5ZQyx3pgxJF7Uspw3OpTM2Yj5Gc1OIDpPM/T2WTdbR6/1V3YH9aE75GmomRki0YlANmPHz+qbVvd3Nyk5wJAQQzZtEGAHfvPWSONlL0FWAKgJKWzAmNt0124R+SBqAaAXFIq/sYhYF3YLyIX7D33bOt3+CxA0BbNQz5BXvGd6ATkyzpDdk+RTesAIrdWLwBmp+9zZ7qXe4lrNnXe4juJruHUSVOKv3XSOcNnaWveK7ip9oX9RnaIYOCQ8n2n0+ksBQt9gC4i/Y19I70LkGobcmCvcS64P/bMphRie3DA+U5sGY0pcKIgE+1IBfQp9gHCghRCu3/ILZEXHBAiV8gUugQZsbVQyDNz8GwkiM5+RPhZJyJRdNnE+SISvtvttF6vz84L68TzW8cafMKLM4wuCiEoczEzgTNq092GIc4LuoxYRn3YpnMOUQHh8vz8osVi6o5q5ayqor2wzVumc3newc6ee54ZGeZ3Vu/xjMiK1YM2Qs2ZsDLwP/9f/Xu/rUGSaNecK8+9stxJrpd8r2Nd6+n5RfPlPLbm7jvJSyEMMU3LeRVlofl2rcViqTzPdKprfdhsJMXBcrGWJ87qKcpSQwdwOCmEeIjqppY06HDY63RsNfTx8O92u9ih7Hmn0A1yLk5+7tpOeR7nD+33O7Vto65v5Z1T18e24pl3mleFlou5vrhZKYRMm82dbm+v1TS15mVsFXu9vdb1zbVmVaXZfK4sc8r9lLrgvdOsmsXW2JIUBrVtNMZFmel0OqrIO/X5oM3NGxXjAFUXBnVNreeHh9jJzWc6Ho7q216H/UHb7UZt1+l4OihzXvtdfObNdi3vpaL0CiEf09AKzWZr9X0r7xVretygZhzGi8FBcTP8b71eJ5aRblk4UAwclJQM0GaziTN3RpBAtAVDCWAgHI5i7ftY40A0gvkrKHhAMUr78+fPSXFQNF0URXIuHx8fU6SA6BczHLz3ur+/T/eH07zb7dJcmNPppLdv36ZIzGazSSkqhJe5J2voSQOhbgcnnIYKks7WmrXBMOLcABCs8cdIUGf09PSUhjy+vLwkhY/RsA4XgD+EoHfv3qlpmlTcOgyDujFC0nXdWQektm1TDQfdrXBqjsejVqYT0G63S+9BwbK/KNMUfTNpGHme6927dxFgLpdjK/wpnatt28TWXV1dpWYVt7e3KbIF6O77qXPWarVK854k6c2bNynf/+XlJbGHNkWIfSHKYlPYAGA4vaR+EVH9+PFjGtRKjQJRBAvqYN0ABTCQ3Ptms0lGkHRM1sqCHlhT28qbveY/ojm8IDOIRrHfvMeCHBjf5HiMjCFrxs+5Hp2vcJy8H9thO6/5PEbZLJDFEFtDT1rn6XRSWRUJTEJmSJrSWEbjDlsO0Mjz8xRP6by2AXaV9EzrFPFspI8Q3WPd0R82iiYptYJm3SArqOOSlKLJpAkhAzggOIIA1RBCAjxErtEfOC5Ec3COLHmBLoAksmCP1CWeGRsO6LfReOsIWJDFObCRHhvRsjUNFnQBBr33qWaKz+OkWseCe0A/Wj0K8LSfQQbjGkyst9Wx8Z6GlP5nr8fnWb/r6+skIzhwnAVkzvs4RLw1GRMQBE0zdaPkvTiTRD9wjlgr6qxw4q0jwHWs44jcEjmEJFytVinKZAE3zwh5BtH28vKSatXABWm2T1GkNDHOrU23JCKIA0ZEhlQ79oQatTyfZuIh9zgG1oHnrBHRxpm3JDK6FWAOAcO1cWK45ps3b9J52m63Sa45pyHEWjKyFIhacyafn5+T7YXkRYarqpIL57PlbApkTLWf5rVRmxefs01rah0Q7BL4A92N4xznQTJjtDOOc6s8LxLxAllr9YiN4NvsBEuKcc7Q/1zLnjX0OM1frLz+Za8ffATpH/2jf6TNZqWiLNW1g16eD/o//Uf/sf6//+yX6rqg9XajxWKptuvU9p2KqlJWFfKZT/Uxr6+vUohdZ5RJr7vXBLz6ITo34RT08vFZQ4jO0OvrbjRy0eA9Pj1OYU7SXLyX62rlPh5C2io7F5sJvN1utVktVc0qzeczLZcLZZnXhy/ea7WdaVCvxSKm6+Vl7MLmndN8NJyZz0ZFxfwep64bEgO03W4VmzM0Oh2PKvJcp9NRq9VSXd+q66hZKFSfpvzQEOLU9GEY5LNMxyYWaSsEPb+8aOh7LZZLZT6o76dBfXj5Eej0KvJSeZErzzI1bWz7W59qveyeU1oIRlg6ZwtQ5FdXV6nOgwP/6dMn1XWtL7/8Mikea4xhibIsS9Ep21rTKrpPnz4lxUs0QJqKH6XJwHVdHEwJI0+aE22TSTNkHUg9IYIEoI6szHMCUxgEAAwGAGBhUwWZ0s1cIoyZNcIYPXKZbfTl+vr6zHCh0Pk7n0fxWIP9stvpbkw1s3VKzGRBwZGChHIFLMO8VmMd0OFw0Kyq4rwoAyBSM4G6VmZSgwASfd+rHMG+fYbD4ZAc2ePxmFqmXl9fx9qArlNvIhMAsjzPUw2SpOTcXBpFDJZluzHI7Nn9/X1yQJFJVDDRSRxbgDnXtg6RpDPjYHPCuWbXdbq+vk5GEmMtKa3xMAwpvY+XTWkiYjkMg25vbxOguL+/T84wKSs4NdZpghEmlx/jzt5bFlSaUl8BcIAM62jZNIssm7omEsni5zwzDh/3U9exgUpZxO5rpGChD0gxtSQL6xLvJ4/1Q6McDsOQ1h6QDslCxKXrOi3mS51OdWLobbSb1F8bqSXyh25g/7kvXhZ8E41lbdFpsM+AG9ou27Q8IrXsu02HIxJpU5JYV6sPrOOCo2VTdfg+9oUzDSjFNqG70Fvof9YTeUXWeU5bW0dnT9u0A7COAwSI5CyhP9lzXhZwsy7cE5F3nhHdbBlxy2THtdEZqANsx2fMkjxjj5AVQCnptcgF+41tJEI9m8UOuq8jkWNlBZ0URznE6AnylmVZckBYY1ufZAlCnhvnp+u6RGSilyFO+Ltl/FlfbATRG+QN55/9tftpoyncG7qXPUAHceY4V6SL2lQ39oEzZAkHIu6S0gwlSy5kWXZ2b+hsZMAOw+VPXqQqc7ZsJ1KbGst70ZN3d3fJ+UBXsb+sy1mksevUnKa6Or4vEhuLM7kDb0D6O6ck9+iRmB4a5NwU4UEGI+7pz1IwOd8R0/lkQ3lGaxNsOp6NZlldwL4hSzhXNvUVso6zdzjs9Yf/7h/+NsVus9noz/7sz7S9XqssC4XBqW2D/vW//oX+6E/+G73sDtofazV1r7aXiqLSV7/+tQ711CVqv9/r9fV1NPhBcq26ttOprjX0vU4c3l6a+UJxMOigq6sYLZGLgyvXY6eVqir14x//RG/fvo1GMA/KfFSWb9680bt37yKo3e+1LCtpCKrro4YQB7eGcb5RH3p1favlYq66OakoC7Vto1k1U+inidqzWaW27RRT1zLV7XRosiwOie3Gwz0BklzSMNYKBVXVXId9nUBj244Fj12nclSsfpxvNPSD5otxCF2eq64jEA6SVsulmrbVrKp0qk8pNxkFRrTkdDrpw4cPCWwBHnBU5vN56ljGz3E2AIowSmVZJmNvWTXqsvg3SsU6HFmWabVa6R//43+s29vbBDgZskd6EylnfNZ7r4eHh5TahVIfhkEPDw8pVI0iBFhst9sEXGy6IPuF4aDmBKOFw8P1cMYsI23n5mAcSbchymXZW5QYDokdoocCgsVCUTnvtRwjFTZPGjaIfWJ9LZhhDWezWYoOtm2rqzGSRU0BStk5p7ppUrMNZBf2zpkoGmkMOLeAWpQ9gCtIqQMfBhLA3TaN5qaOx6ZksXZ5nqdhtACum5ublI7E7zGMRAZxSCy7aI0yLC1zUmAM2Rv2HKPY97F5yOPjY0qzs+Ci7/vU4AHnHcKHdD5k4M2bN2eMPOCdwabDMKQUGs6rNU5lWWq326X0l6enpzNwxH+cbfu8yLlNYaFw3tbk2bQ/9oZ5IrDCyBQMdFyvTHk21aVhmPkOy4ITPYoA3el4OiQASQ2TBdrIJGxnnuUqiirJHWceQEDbeJj72DUy1rpRm8R6A9ZtuhLODu9BX/Ansk4Nl3U+uEdeFhwCiu3v+M+mOfN5nof9YA+RD64hTcNvuU/2DxlGJgD1AFx+D3Th9/xnU2BtWin6nwgtMtT3fepYBsnBZzgHkABEXiF6qJchnQuQx32zV5w7UhLhW1gbSUnvYOetQwOgBQyTkk3kg6gLZxWdOp/PNYSgtp+aFEDeEVHbbrdp7zhT7Cl2mTPH2vNZZA7wbh0v1os9vrq6SuuHo2qbRHDGLUmCTWOPiKxdpnqxBzh0Vq/wbJxp1plaZevIEm2y5BrZBikiJyU9fhltYb2wM9wjsoXOJgsAco3nQOYA/dSnQRwS3eR+IJfo4sfYCwYq2/TX0+mkvu1U5FPdLfIZ1z82d0GXoG/j+sZ5jTbtmc923RQFs+mAEWNMza2Q1+nsTsSTjTZaUtvKliVIrJ2ccOlUw2XJEPaJzzw+Pv62SQMO0r/6V/9KZRk7Ezl59Z00m6/087/4pf78z3+lX331rT5/ftbnz8/69PlRr7udQheNZTGCzv1+r6IsVRZeVRUB+of377Ver/Xp82d98eGDbm+3Wi5KzeYzHQ47/fSnP1EIsVPb1Wql+lQrDFPnDYBzGnqqOKoIoFYWhboubn7dRDa2LDK97F6isc1nyrNCr6875Xkm7xUVqyQfiljflMU0Nue88mIMO+dTpGO1WiXBbbvo9G02V2OXuqAs9zoeDprNZxqGXrFr0tRS8XQ66f3bt+r7Vk4usVX1qY41T8rVtuFMyU0HulDd1AlcStFYkPpFK2gULnNyAOWWmcNA4HTAGtp0OhSLTZEg9QPliTJyLtZlffPNN2f5zoAx27qTVCTSkIgSAX72+72G0RqStoaBgTnBgdtsNqlWCbb97u7uLMXMzvZB8Xkf970Z1xglwpqiYEhTwMnh+6hXIZpE7QxgmOdFwUmTU4Hiz/NcXd9rICwegvKRAQR0E72wjh37htN6dXWV9rAYjW85gjUYYQDQ3szq6brurJ1pOQIdlCf3TlodTvf19bWOx2NimHID6mdVpc/39/KjPIQxGkfhNilcsK44iwBe773evHmjp6enxPzSFr0Zo644EkQAYagx4qwzzhjgaDab6/npKZ1riINf//rXuru7S4aMM9L3/TjLK57RlHpSxu9p2tjh6ptvvpFzTsvFUnkRn4dUVu6jLCsdDvsxQpar69oUFTodT8ryTNvttbquTS2sq2qmEIaUogO7HKemT8NY8zzOZ8vyLIGdCOziGAMiWnGaGHV2XnU9TYynPTYv23VvcrDH3HY3da6k5oKiars3WRZnp4UhqJrF9GT2NL4mIx9BZDfKZS/n4h7sXvZn4Jnzi/EmEgb5YFNx0D1EdCzzjo60ToIUGev9fq/9fp9aV8OCX11dpXPIucJZtgAFXWTrlGwxunWaLyNcNhpnswBs1BBAhG2waVASzhTfMzU7YM1wSCZWenLAuFdJaX04QxZI2XWmoBtgZiM73OtisUhZC0Qk0V/cO6mpyAMkBH8OQ0yz47zneW5qdqaueewxf1rdicMyAWuntm1i46muUzXahn4Y1I7nATCPc00WAbOySI2krgc7Zh0H9tx2+OM1n81Tp8OqqhSGEM9pG6MtbdcmPRiGkCKxVVWpazt1/ZRmhy51LtZrIz/VrEr3MJEdk570owMoSbkhT2wNTJQfL2b8cZ4iDqgUxnlTNlJKM6X7+9iVFieUvbKkZd8PCmFK23TOpwgMqXDUpnJ9zoZtopH5LNkFSXEmpY+dDNlLzmUYgrq+mwjE0am1pFeZx1mR6FPwCPdo23NPz9Irz/2IDRpV1TSfMt5z/Jx15NirYeg1n8/S2lhntu9DcmIghTkfkMM2o8I6nPaFHkKPWNKGM8Ln8jzX0/OT/tof/tXfOkibzUZ/7z/5P2u73SjPC9X1SV3baXt9rRDi4Vmt1qpPjT6NTQD6rtfjw0MKOzvndH9/ryEMurm+VjYyEEMYEihbLpdjB5/TeGCikvKjkJLrCqPD4YVNvLq6OmMgMTZNMw19jHOLqnHWEBseO+vlWa7d6y5FVJq6TUxGNAyD6nrMOy1IqejlfRTaw36v+XyhIYTx4E8pWeS4LlfL6Ph4p+PpJD8eeNvJTIoCmGexXXrfD8qzXG40uE9PsZ1409KpJEtRAVv/YDui0ALapkpwAD5//pycPBwimFJAISlmt7e3Z0W3rD/KkrVGaXFAAQoYdQwszhrpKgCfw+GgYTSqdHSzKWTr1Ur1KA8wzLYZALnxfN/NzU1SngCr0+mkzWaTGOfHkVUDZCUmu22V+WnCNkCCiBJKBYPIIE5AOOl8tjMUaSk2zcum3bFGQwiqyjJ1fGzGKEfX96rKMrWltSAsgtCYeno8HlU3jfox7YV7ZL9gEanF6rrYSpz23DhZpC1gzDA+OISz2UzL5TKl281mM1WzmZ6fniYgMTofr6NTxTMCMg+Hg15fX78zD6nvY0dDjDhpo+xDnudpyCHRakln9ULUP7B/bdtqVs1VFKV85vX8FNNRF8uFjoejXvevWi6WCTRjAL33enl5Vtf1KqvSRMPys3oDG0llLo6ctJgvxnvNR8ehUp7HFtmn+qTFfJGisn3fp6G7tNrtula73auaptZsNtdqvZJ35JJ3yvORec+83Dj0ekrbGFvie1uo26sopvlVQxhiBHJk59kj59zIgrbyPlPbMtPJpTW1dTasm/NOzmcqijw6/d5rGEIkqLyPXUfdNOzQtpvNMgg5jTq6Uz4O5kan2TQgAJKth+Ce2BfAmk17k84L8q2DwHPc398nQGKHi3Jd6voua1FYO0CPdSqInPD9Vtb4GddCb3EGuL6NeloQSnpuBGfRAW+aemzqU44pbQsdj4ekQwGpOEk4apadp57FkktEqS6jZ9yXTTeyETPrMEIg4ThcXV2lNFIcWZwLzm90oKZOak9Pj2kuTlGUCkFnkV3vvXa7FxN5L5NjjL4/no4aNEXHi6LQMEZGF4uF5MKZDSOqGzFIqxDideNzn+Sc12wWB6bTPGkY5xaGEIv9q/HcdW2XoiHOOZVVGceADENqYX6qY0t9HNq6rtUPEcDmWa6gSDaslqtk44ZhOEsvZT+KolDTNirSYPoob00ba7WzMXWxbRo5H2ukT/VJeTamXecxpb8fZZPOmshEjKptVBSFHh4e03lcrVbJDrL3Vi4gv9hXcAz2qu871fUUqU7NiLruzM7aFuV9w/DUMTJdlUmPDGFIA+r7vlfbtbH9u3eaz+bJccvzqKPDOK4GvYrDy5m1aX3Iub3X6MDESBPOTMq+CJN8WcJGkpbLhZpmigZH2Y06nXpVCCwIEhtJshFhq+dweqxjZKNR2E3ubTpLO/3VP/yf/rZJgyQNfa+hH7Q7vCTvdj8Wtc/ncz3WkTlezkdmr3BafPl2BKxR+fz4xx9GoFOr76UhtCPrttfNzfW4+FJRxGnjknQclWTf97q5uUksdVEUiZmxHUlgxmFiqX9COaR0kTAp8BhWjKyBNE3GLspcp1rqh05lVmg+X8n5OGysPTbJWdvv97q6utJyuUh1FWWZnwERlPrpeEogGseLTlMIZVS+vV5f9ykCQUvPWHAaYjQqDIkxv76+TmF351wcdmjYFEAWih/F1LatttttUlYYVyJGtFMmbYy1xxmjSwzgdLlcpuLGz58/p0P5+PiYutRxIHk20lC4LtcrRsfAptyQNjOMBpwoDUAdx4N9J9oBaJ3C4LEd92azSUb4ars9q3WgcUOeZbG+a1QUgIHdbpfqnjDil2kntoW0zYEGcLAHrIXNy5ekvusUiiK1/u3aKfLId81ms+SA4xCEEFIKQVVVWo5EBTVbnBkcI1IOcSyHYUifYY9Q8LQQJ+2ACEDTNKnb13q91i/+4i/SZ9iTfnTGrq+v9fj4mFhXAC7pIxhMDO56vU5pldwTsoW84wR9+PBBj4+PyTgQ0eMeSKXqu2hkKh8JA+q1FouF1qt1MvT8ud/v9ebNG83niySLtWvO0mQsW4tTzz7Vda2+jCzj8XhKPyuK6CQ4uSTPGPMQwlldH6lrpK3adt95Pg0Unu4ljjrg/NjUMQwwcoszMZ/NzxhlSzZlWZ5qPgABpOJh1JHPPI9OUXM6quuLBHZwxqhOscCF/em6WB81n8V0suR4DlO9mmVtYVXRW13XpcYfAAxSfAAlRDWI3rLXdEBEpzJAE2LDgkzSgNAZNrIlTdEXm9InKRFC/FyaGmjYdEvsFueD95OGiQ7hT4gnzmy0AUFdVyeSir08neqzJjFWBnAObPoc0R2i88mBGM+4bUU/sdt9Ams4Qcic3TvsSRgzBLhH1pm15oxz9qWgpqkTKWNTlcuySsw66x2jokRiJ+Yde9TUjXpN6YUQhlmeKx9HdxwOh9QhTpLu7+91dbVJKV9VNdn7KIdHFUWXIuWW/S/zQpWJVPCd2CjWxwJl0qA4v92pi5GhMIJYTZE/GyGy6ei242u+JCo4pXAjj9EueRWFS99h96oqK52aOskf54pnOJ1qhTB1KPV+GkBt6zdxmnBEID8A5FwfHbTdLlLqotUXNuoJ2VmVlXo/6Rf2JaUmaxo2zOexlZw7okjookiIRBmx6fboeknJWeG882ciMcczBZFh64Z4HggfIlPgA/Aaume5XCbZ4L45V7zHpl8nQsw4dqQ7WtsqTS3bwTjomH+T1w/eQeJg29bGKJcsy1LbR4ylnRD9i1/8QtfX1+lg3NzcJGVLkaftV4/y4aDA1FgDb4txMWoUEPb91D0LxYNygOGzE5+lKATr9TqliFDXwGfLskzgj5Qyvhfh+fjxY0pNIvLEoeu6Tre3t4nZALRnWZaaG1A0aOthbOoCLGXbtme1C3me69tvv9UwDKl7C4w84MeCRNg5gB9RJYwzoJ0ce76fzxNFYN1gaWzzBAy0cy4BdZzW29vbxHgQXQPcPD4+6u7uLnZLq2sRlv3222+12Wz0/v376MSNbGLf97q7u0udwTCiGAX2B8UDmEBOU5vurtNx3FPqSqRoJA77vfLx2qwthdowm7Aqs7FFN/JEy21qd1CKnCcMKYbLFn1bpXk8HlN7X9YfYIIjTHQN8HJ3d6fPnz9rGAZ9/PhRv/M7vyOKiT9//vydOim+C2WbZZk+ffqkPM/Te2G8v/76a11fX+vm5ka73U4fP35M8hkZwwet1+ukM56enhKoZQ82m006tzg4nHVSJekQ9fbt20QGOOeSU2Bz5TnLACvOn20CQov2uq41ny0TAw+wpTsibBr3yuvz589njUAA2egUgBzRCYw8L0DvYrFIxgiH+HA4pIgm8modemSSKBr6F0Bu5RywwXPwPu6Ja9MUgc/ZyAQpkmdpN6OOBmzwd4ApoAz5jQ7V1HDAgtswhJQiw9rY5+Flo4WX5IIFSegd9oLnB7zjfFunF6fEtvYtRkICooA0T84Aa0cqGHrTsq42fY2zBRHEuefnyBHPTUoMDjG6185B4gWAhjCEBGDPANOW6ADIxfvIzogZOovyWew0KZOcNew+ctf30xw6m9Lz8PCQon3YO9YQIA4BwBBkG31arVZJRwBWbfoiESP2i/PRNK2yrEg60UbD7DgDC5q9j91Me03OLYRFdBy8TqdjIgaRFfYb8L9cLlNjB/aGPwG9RJ28prlMnEubamezOjh7yPSlbsLhtPPWsEf8ju+xdY2cgyw7T2NkzVhTdAm/y7JMx9NJWTFFBwHXRDAB8+AmnFfk+O7uLp0D9CBkIt0HcaT4jAX1ltBE7jmTfd+nAcI8P2fMtii3mTDILvgI+4JzS3Cg7/uzpjTgRnABdhri2Opi9hVHg/fZ7o02MsazWvlHZ6e0/G6aU8eaYef4rhS1NOfQEhmsnaREkqNHLY5FRqxd+8teP/gUu3/4x39f2+02Cedut0udVmDQAW4YRw5CiggURRIG60zhHGC0APZZlqU5KLZIVZrYNoAxB186zw+2oXnYcRS9BaGAL5wwHCNJqU0vTgN5/4CUx8fHxPxgVInK7Ha7NLCSVKG7uzv94he/0I9+9KP0TBg0QB+RML4fR4dBq4CYKV2gSH9KE2PAYeYAb7dbffr0Ka3Tzc2Nnp6e0iH45ptv1Pe9vvjii5RCJk0tWnGMUOqWZWTPbW7942NMe6iqaUYBwA4ZCCHo+vpaDw8Pqb0maWIPj49p+CzpapI0Hw1uURQJfFv54HuIqpHDD2i+v79PhbVVValpW2WjPBCNAbyGELQyjC7poEQs7+7ukkKE/UXBAIjW63Vy6lGAtntSCCGBUT6PsbUDGvM8Dq60qYUYHogBDAoKlnOHPKEE6UYn6awFvDQVugKGUMA2KgkYglGGeWdAMGQEipb1wNBdX1+nLoMA7fV6raenpzQAmKYAT09PevPmTQLfKH3ABw0kANgUiKMjHh8fzzojLZdL9V1IHRLZryyLTRZI88Dp43O2BsOmTli2jXNia3Vs+gNGFsBvo0WWgb900DBwOPUAW9tdkQivBWx8B+QTZAZMoo38AHaRN+QIuebZ+W6eH0fL7kkIsSa0G/oUdUJ3xBqpXs0YxUB+0V3SeRtdDDjd5bBDyKMFJra2yIJOdBhgzkaELPPKs9u0V0v6SBPAhym/lAWiuZAVvOeSveZzvFhb5IH7R0+QFcE6Az7tmvDcyMtstkikowWy8YwEXV2tE4kAWLZRN3TRpa6nyQ5Ak59Z9honEhKUCCiglm6lFjcg65A/9lk4d4BLyEn7Xuy35DSfL84yRSAebedBQHNRFOqHXt0wtfCGcIr3FbTdbhRC0P39vfJ8amPdtp36Pq4/jam4R863JbESEdD38s6f2Qrkiz2GvLSOEjJjiQ3rBLHXYB50BGvNZ9nzsiwkTZkA7CER3WGImRPMM0vErXcaDGnHtW3dM3bEAnCrz9g3MIKNxNsIJvcPTrQRH/ABto5zWBSFwjCorZukgzh/vNA7/Ikd5v7atk0EM8+CHrjUWdwfWIz94OzguNlILnadlF3q7uyaWcKCveE7+RnENucFEmDKVJi6a/IsyJvVN1yT72Xt0dvsR13Xv3GK3Q/eQfp//YM/SYvIBiGkGGTmtgAqqS2Qpm5wVtkBFJirgxABLpiTgiGA7Vgul7q9vdWf/dmf6cOHD0lJHo/HlHdqO5WwufwOR4gIFYwzStJGxWyKBEqOQjicrd0u1i3ZuTU2jMm1iBIwzNXmcFNvQLclWFZYaQDp4+NjAq2wZhgqC7QwPJLSAQf4WMPM/hVFbMXNIQAUAvwxBBxm7g2HAeUFW8hsnZeXl8SmAdZgS7z3qasdB5Zrt6PDko0HEtBF5zdnDDggF5bJOoo2BYwakQ8fPqT9YY7EYrHQbnwe6+AT6Rm6qXuRjQwSKUH5SVONC9G0EOLwURoTXJ4dmKM8z1MHNPbbMqPsHcoSAMleZVmWBpNeRh4tyy8pse6wUkSO6rpOkSzWgogGa4kxApxhFHDiLWAjHWy/3585Vsg877eRWtbdOhv7/V6bzSbtDREazhBG0RoXmy5g2UIY1MP+dGaEm6ZJabzoK3SLBfhEpVhLnBn0FmeE/wCnpAdTn8fesy4YPZwiS3xIk8PAfiEzrL2NpsHIAzSJnqFvMfKsCeCL61r9jKxbA8resE+sFbYBne+8l/y0B3y273uFftBg0qwuWUmMPUCDtEZerDtMsT3vNjqL08maEClgje1zsx88i2V6uS46Cn2L48V1cNYAs+gve3ZZCxsxg5DhupxDIu3sNfeJ42LTdXC6aVAS12kazcC94iQ3zVRPakEXtoLfWV1SFEXSU9hOG90gehlCSKnP2FxsKJ1JuW/khe/lXLLvloDc7XYpQjGlC56SLHLmmqbVbDZPth2ZsU7+arVKupp21V2Y5uBB3MSUraVoKnLZja6qZsrzSQ4ssXQZNYOw9d5raLuUpmkxEPuI7uEMXqaJQmjYqA5rwhm2IBjbb9M3I2G0SE0DLFaLe1mqbaczYKM2bd+l+liemXPLfzh4NjXXRsWtrWL9wDfcn3WIbLqbxTyM57B4BR3RnupEykIGcK+2CyQOjz3n3Dt4iu9kby05wpljHXkvMmDTHrk/dD5ktCUSuQaOCnoJhwinH90CBrLnyUaNuFf2HrlkL2y2FWfF6i8bhGiaRv+Tv/4//m0NkqR0YMjLJvTGBiwWiwT8LejAueGwYijZ6Evmznq46/U6ecUoRCmCO+aHdF2X2GFSvGhGsNlsvpP2Rd0DgMiyIQB7BrBRx4PCt7NKAMTW0wZgAh66rksgAsFEEQPeMDKs02KxODOwsLYYDhSODasy44B1BMBalth2npuaToRkPCiyhxlg0KpNdbLMjk3b4F42m006sKztH/zBH6isqtQCXZpmH2FQYSgo0mdf86KInes0OdjIx+ePH1OEBbCOoZCUwENd1+m+rMMNYIBZ2+126g1by70hN/24R/f39woh6O7uLjlEDN4ktYpoKANlUco4yIvF4oxlt+FyjCrDCwFCrPFsNtNms9HXX3/9ncgg193tdqrrOjnryAhRVFpWY0RJr4H5QrnjfFm54wxjDAE/pCghI5ARbdumCB/PSHoKBo/vJzVFmtLhUOY8p3MufY+NsFBjZ2WKOVSS0nmj5gnnhWgyRonIE2k4FuxYIoXaKEnpLAAoLEOIw4ITgpG1ezuxtOcGC+OO7khpOX7KJ+f5pKlLmwWAyDoGtmmas6ny6C5AC+tpHSXLTluyAvBqa4IAu4C8LMs0W8zPPp8AknG8bKQAgIcRJ12IaMxlNID7I32S+wCw2GgtcohNsqyyNKWmXAIY62ABaC1AJXJHNoQtHJemSBeyQvqOdQ6tI4JuRw+gr5EvouHodxw1y4xzzaY5qqpmZ1FNe/44jxaM2UgLdoP7RbfiHJCuhBzb1EJqQYnMeh/rJYjq4iCyn5z51Wql5+fnFHnFOeaccP65F5rITGn8t2rbya5L0+wZonhkJGDTy7KU807D6JSwp5wxaqPRJXY/0EvoJEt0WPkiqpvqe8bf2fRtQDufs89LBgkvrmtHCBCNY005CzimtogfOez7IUXLcK7ZX+4L54P9aJpGPsvUduezl7BxOILIJvYP/cA5t2tkHT7rhGKvq6pK6dWQIMgyOsdmufCsrBVYiSwL9skSRdaZCyEkfQkxRtQe2bJkh43OYM/BZFzDRrc5W3y3fVkdhB6y9ZNcAxtq74d1tSSDdSatLUNnY+fBzJfONPvOXpMR85u8fvARpH/4x38/RT8A409PT0m4NpvNWeFq13X6/PlzavWKZw54RJmSpgdzzeHmYFjAAxNO2B+FsVgskkJ1zqXwt3UIbC4m7Vgv8905NJdA/pK1LopCy+Uy5aYfTyctF4s4ILM7LwTkeV5eXvT27Vvtdq/JEev7KSwc25VOHZEiAMrk/cRMMPtks9mcsbEYSIwQ6RD8juYOXdelgbCSErAhfI9RxAhGoxjbCscuevEAPj4+JqfPKkPWF8VKAwDWCuUHaLPFsziJRP2ci/N5ZvO5VstlNJxjtKqqKr2OdUKAa1uvgmzxd7sPVjHQrKAsS/XDoK7v5Z2LQ3tN62vnnDQMZ4qG61FHR1tt5vfYTjbWieQ5UbKcDRtFIN8fgE2tVJbFlFMIA/aQ6AEOnwUUpDHSuht2je+FTcOpxQnF4KOUqd/gOVh3C6gun5W/U/yJ8yZNLBm6gMgwyrupm9gm353PRQGkUmQtTQp+GIZ0tqn/on6CGjDvp84+r7u9rq+vz4wH6YwW+FtnFgBHR0PW2Ps4mwhCAxkBwGAAibpy1pB1a9RtGhc/4xmlCTxbcMb1kTE+Q7TTpl9JUz2hZXCJ+AE+LPMdjbUTnfJCmACRXR9ryJ1zcpmX95nqpk6tip1zGvpBTV2rTFGeqSV11EHn80z4nXUisSkAEbIIeC6ce9YfXX/piCLvyIFlsXkfYIZzbdfQRts5B/ybdbVRNe4bXcB5mQBhbMXN/bdtJ5nGAZxV9oVaD2wlewEY7vugLPNi3AXrFQLNH7pEEpzLR+zAFoLGYvop2occskboMBt9J7JIFBlC6VKP8H3IOGvIftrUX5s6H/HDaozwtUneX152I4lYnO0HkWGyBpyPA+GR9dPppOPpqHJ0ViSlOph4P00CvnkeZWC/Pyh2dCzU9+esvnNxyHw/9HKSfJapPtXK80xhXIdMUzol+Ik9gkTEaVqv1ylVG+cA/YgcQLgkMKwg76KOposk18uyLM6/G/VN0Hgu+mnWkJxTnsV223KS00gW5rm6vtPpVKuopvbzyAK2lrNCpgv6G9sACEcP4SzYaNrz87OKojhrhc7nIH+wx/wcPYs+autGeTY1lfHeq+v7pH+yPFc16vqX3U7ex6Y5YNTD4aD5IrZUR5eABcFeyAZnwzrSfAbMhCzz3JYQ4nyxhuwrjiP181YnYnvRYTZKBLmMrb2MBEE0WNnFocbW8CyWpN697vQ3/tZf/22K3Waz0Z/80R8rz/MUubHggY1H8L33aVglCsYWIXJAL4UL44aQ4SSh9AHclrXCANnaAwuUACr2BZNmmTEGagLkEAIOH4Xj3377rW5ubiQ/TbG2qShVWepldNReXl50dXWVhHIYgnxe6Hg8yPssXXO/32s5X6jIc7Vda9pu0j0szjVgThBOnk1ZgDk4nU5n6XVcA6NJPQQHjwPLs+R5rpfn16SoUdaPj4+Sk7JsSrWgkBHgC8NCOt3r62vaZ8tskMZiwQGdzZqmGZ3HPhXnfvmjH+nh/l5SNKQ4QGUZG2dcRrNQ1oBE2z4cJor1YW0AmigKQDmyZBke3ku0b7fbJSMlKbGBtq4F4EVkk32nkQH3SKG+ZbOcc4lAID0LcIocEwnhvnl+1JJNwQHE4yRaZo/nssrWXssy3NwHoN5GNnAUbY3NZXolzghDXiUn7zI1baO+m1oHLxaLFB2IMpqpqib2nJot9nu320kuzhKByBmGQZvNJp1J1gVgyHO1bXuW1sizY4SsrsG5uazNARggS+iZbHS8rYFCFxGZQF8hw0TopckQcubZU2Qe3WtTWax+Zf8wtOyXNZYYV0AOchANcJbugZ91HSm75626uY+2jQ6VjZQgEzYaxjmbGPNMcYTCBBpsFONyXSyxwzMg09gPnom/W9vCmlvGHJmwqVSsE9+H7rVMMJ+zNamQR3YfWQdkLgKSOHePiDy1q/F5p/RQ7hs2vK5jp1GIK2wkuoD0TM7URFRN78MeWZ1oQStR19iquk+2gzlwZJngZGNj0CucZdh3W6vHdZB59o3oinVaIYGiEzRFLlkPZI1zYPenaRoNYVAY3zOfz1ODGc4tcmE7KkY9GESdkTQ1CelHYi1z/iz62UNUGCeZM4quwT5DVE1khFLEn3T+9Xr9HeeYs8y5KqtKzRjRmc1maQh9MzY84mxA3hDh2+/36X5YP1KordOL7kfObI3KJZGAjKErOGN8D5ky2Eb7b+4PjINTzfkCd6H32Q/knLXhWsMwqO96+WwakAwGAPRbO4ccWKIvG50qKc7X9HIpZdWSdPY+WTvOOjrDkmKcM551sVikWnerc/jPRuqliSRHpnBK2UvOv402QRJbu2ZtPbYV+cTu2Nr4uq71t/7O3/xtip2kBGZub28lTbm8bJYNu3vv02GWpgKwuq5TtAKmA+fEpnYw4wiDwjXwtu0AQpQwtS620xuTrVHyOG0oKX5OOhrPwQFGqAm5kkZXlKWyMcpF9IT6o/2ovAGDklIHpVNdq91PxfOkhtzc3CjzXm7sZz9bzZJAStKnT4/K8nhwKJK0zhxMNIzL9fW1vPepWx3FyDwbM2V4LgZwVlWlvutV11MLUTo0lWUZ13gR09q++uqrs9QCDJkkPTw8JCeMNdjtdik0vlwu9fDwcGZ4b25u0uGlk1KWxQ559ZhbLOks3YZoJK3Ief6rq6vEsrGPHHQAq03dfPv2rY7HYxryyPth5HFEcFBZDyJz/Ltt23SfttAV8IwzSVc3GDEUUAghRQdxDrkW6wxIAWjzvbBs3J/NZQeYW8CLUUa5YkQABZzFy26Q5IbbyKUF3OzRMAzJ8NDwoOu6s3auRMEw5i/PO223UXZDGVKBN6CwKIrElvNzziwOGU0nKHb13qdOeyGElHYIuKMOAp1gjQUpO+yDTc2zaYi0qsUYsn48G9fkuqw/TgxNTFhzjDyOpwXzAEHul78jq9YxsgZYmnLnrTNgU8ysTrcOH3/2/VQoTBpQfNYYybNOGEa2KMqzawB0OIc4aDZqFWVqmpXzfaDSRgbsOtv3WLDHz1ljmzYKGAPsWbDD86AvuJ5lcFlbQAoyZdlczgh2UlKqcbXnCVvX970eHh6SDEfZOk/B4/6Rk5ubm/R86EM6iNqGLNjArutVFNPwS1vbwhqzNiGERJzECGv8bvQVDgnPaaNRyBpAkr1D1/BdfI6mTnSTBaiTDobejPcRHUrrOF5Gs9hr9rcoCg1uqq/98OGDsixLdbOWtLARAQsg7VkESPt8Igr5bt6PPOHMIvNkcPB71s/KmSV0rb3leqzv8XiMXeXyTPORtNF4dkqTCmZJHBpgWUKU90EM8jxEuLDpEKs2HQ7iC5mnLoi1hDRCJ1mcZdeZ96L3IB2Rf+4RjMR9Wj2K3Uo6TZOuxKZi86yd5ro411b/LMczUuSFvCFqSD1kDSCbLVZjj/m5zRqx9oxoGzoE/WJr/KxTmOfTrD97nijzQAdZ0oj1Ym3YSzJFrE7lLFonDDv1m75+8A7SfD7Xmzdv9PDwcCY4gOjlcplydi9DptZwohQXi0WKMMBg2XA6118ul3p8fEwHk+9EYKwhpOsMgoZw8PfVanXGTEyD9CL78fz8nIwV0SdbxMlB7dpWxeiF4xy1bZtSrU6jM/j27duUVrNcLlVWlYpylpQNDEGWZSryXBqmAXkYMSIO1axKBZoMLSTciuIk8sWewAoBtl5fX1O9CkruV7/6lSSlFLWmabR/PWq73aa6FdZpsVwohF4///nPtdlsEntvGdD5fK5vvvnmDFSgHD5//qy7uzs9PT2dGUppyhe2tQBEZWyakHUa6D5WlmXqeoYzCPNlIxuANEkprS/LMn38+DGBRpTQu3fvEqMKuCWqg7NPuifKfrvdJlnjP65pWdWPHz+eMWsYSudcamZgZR2WGGUI80ndFfvLulnlj9KnKJo8cwtGAXcWrPJv5GpibPNUc4RBIGWH1vMYQ54dIA4IOR6PqT6Qta3rWll+7shh7GAsyXtHrmzaIoXssNg4s+geGk1gzO2ATgtGADzcN6QOBnK/3ye9Bqi2jKN1XmwKGJ+3IMv+HifR6lDWH8AgTalMFiyg/9gLZAT9hzzxXBaM8Lzc92X0ZJKhXs5NaVAYS54pyyawyLPHQvRMISjtJc/Bnid21kTVJnAzzQ2xzC7Xt0ytjf6QFgL4ApQArCmQBwhY4Exqnq2ltaCDtWEdISJYXwgbnBxbryXpbG8tGYFjEtPBm3SfyE58/qnbJPfEM+NAWHmw0W8YXgvUiiLX4XAUAy9ZW5vmBSEJuRafZQKoPAtkEwQYNpi15/qWFLNngCjG8/OzJKUUYwgV21kvy7JkZ5bLddKjOLt2xAbAHSc9OVHjcFUpOqqQbdyr1WHsGc/Luls929SNvKYoCe+3ZxxZ5Xutfur7PrXktpE3K8/YIKt37XnabrfxfW5K97SONGeB+7PPdXmev3v+p/2zaVcWqGPvwFzYX0sUIssQZJaMurRlpKrb7ABLZIHdvJ9S7+3zWZKHM4hd5jmRDyv7nHU+a/Ulr67rlPkpYwL7Dn6159M6y5wX6yixNtyHjeBYB9zqLp4ZGYTIB0+S1cCaYHPAcjwvY0hIYcRht3ibDI1LB5Vn+k1eP3gH6TiyuZbVs54rRgY22rJ3AMrLVAjS2Cww5eDaz3z+/DnVXsQc4ymFjHtZr9dJSVsjBgMjnTM0ePZ3d3cJ0JO+RJoSUaX5fJ4K7gGa9cig3t7epu9GOS7nc71//z4Zs3fv3kmSyn5QcNNwRpohfP78WV98+KDmVCcgR51QdOSqBGyJFHFYr6+vU3SPNXt6ejoDthxiDHDf96NxicZzvV6nIZifPn3SZhO7+eA0Aayu1lc61Yc0v0Y6Z2sJDW+32+QUYHjqutbd3d3ZPhPlwzHD4cPZYc9wWJfLpW5ublJkoutiMwMYNlJSLMsCKEJpYmj4DP+2MoWzDtjn+15fX1MTENKBkJvX19eUcgXIshEAnApkhue3kVFJKboFg7nZbNL5sgypVVgYOoyNTWfkOXFGWBPqc4ZhOGthiuPHOgCMbF0MhglnBKID1gpgQqSUM8fz0SACUEN00zmvtpmK9S245yzjTOJQ28JWIjPfZ8htkwy+F8NjgZt1pHlOa9y4LztzzebB4/izzry4T/TTZQQMR88aZNbu+wzsZQqspCSvyJQ9m+wr/7bGnnMMyOG7WdNomGfKsimKwlpQy+LcBMwvAYn3WbINyBU6he/icxOhMqXy2XRh9p/7tE6VZYB5L2cHPYg8WAYbkge9CpAgiwEZQXdyDRxa22mUiC7XZs85XzZFirPO4NH4nNNsE84jZ965kAgjC94AXMgDABuQZR0UzkJ0JE6K9WSTM8MLmcTmWGDU911qd41NhLSwZ9R7f1Yfw/nEUaAekWe9jDxZgIceQt4fHh7GtagU63ebM8dGUuoayVnlnuSmAbCk/AIQ0d+k8qEjrG5GxyIbZVlqXs3kzH0jc+gVCANL0tn0KdaAzAvOHnvKe+257vupeyPp3H0/1tHmPkXepJjVARFtIwHTnk4OI+uMLpXO6yHtec3zPNl57DRELSQ0csE+IsMW76HzWBebHsu68/2sL2eM+4FAA1ei//kcsoduyvM82XHs5WV6mr02ZzfPc5WzSkM3NdBBd6MDiOjx3Twn17Z639oVqydZd84tdhBdZ8tUsMu2FpPPWr0M2bpcLlPDKYtHq6pKzdGo30WO7JDjS/vxl71+8DVI//nf+0/T3B+ULkp/vV6nhWzbNrXKRRhtqhZML6F/BFJSMggYFAAN70HQYAOJ+hAW5H02D51tgVW2yiXP8+QdYzRtKgJCicL/5S9/qZ/97GcxJG6YYAA1DL0f74FDjFJr2lZBXtvtVn/6p3+qzWYzdd5yTm3dJCbJKtYs86qbU7qvFMkaHQ8MDweCVARC4hwc5vsQhbJgDodyPp/rdJzAKMMRHx4eIgjw4cxRtSCV1LntdpuM9mKxSGzs6XTS+/fv9fLykoroAdg3NzcpF50UQRxVvgtZALzY5hIWWAKoAJ0YQIyATa1EGbPXpDtIU+oXsr7f75PjtNls0nOh/Jmfw5wsa/gtm88LR8jeF0qd+0Uh8TnAvSUlUL48L8YYpW1BngWYgDqUOUqPbooYiEvG3rJbyA/nHCOAbPEn+2JBMc8znVOnvhvOnpUzD7ixBAhraO+BNbMRB9aYPbU1JdbxsOwduo21t8woQNs2AUAXYLTQNQy/tKAHEMhnkRMAhE17swaS/bOso40CWlaP+7UOrk3ltDrWDjgE8KVUJBOt6vuJwefMxYjHSVnmv3O+oryHFKGw10TWbLTLpiDleaY8n9q0s76WSc3zPDXsYY1xgC+ZXCJz9jklpbRN3msdVYr6AcSWqaWWxkY2kT+7V4+Pj5rNZimCw/4iW1aOox7Kx6hbODvL8fljbRZnEcccG4SsWDCIzoEIQY9O9R55qklAbzJ/jI6iVsbj/ntdX2/TeaJ9PN8DM48MW3A4DEOKNEtKxA33i960+txGbey6RRJmkdYV1pz6FwvJcMhWq5Wc98qKPNkOG1mxURH7/eyPvR7PE0KIDQDCVO+GHOK0gZmQcSsHOLBEB7gHvhM7ZFOa+H5JqQkV665sAu1WFpAZ9Dp/t1iOfUKWrS609oM/bVMrdKN16CAAiLCw1jbihz6w94zOR6exljbbgvu0WA/ZYH3Pz9aEI3kf98J1LLFo9ZJNSXPOqchzFdl0jvmTNUIHXt6XXZtLl4Hn4l55L+cIW8Zn7Xey/pwhu2foarvn0hSNJhqJPrH44zIybZ3/IQz6a3/4V39bgyRNPfptGNSGpGGtmFeEMcawWEXrvU+1NChmwAaGzzJxfAahtcoS40Fxu609QNEC/mDObM43AB/AbFlCy/gAxokEnEZBtSk+p9NJXdtqMACGAzifz1U3jbLRwH3xxRcpX9l7Lw0hMZLee33+/DkB4aIolBfT/SL8gCXuGUePNAOUsjSFV733aTgn7AOHmjbtrClKjZQ/771m8zIpRhuWhS358ssvEzCECaWbHDnxGFNYPJQoA/Z4LvYTI8E+UAtGa1e66nH46VCInFplPZvNUttp2zZamlqD43gA6HFGLcCyABrW6s2bN8mg4HBZJ90C3uPxqKurqzNgglK0TRhs7ZW9J5tegYGjxguDg+Jj/1F+kAncG4YRJ8TOzOIMWAadNbUMtk3RQaFSn8VaPD09nUV3LGsY9zfT0E/MOrIN8LLpGKw/34ex4z02r92CRIyGdR45C8ipXRPeZ6Pi7JGVYZwQG+kiWkZdhXTeFOT7HCFSA3mv/dOCd2TG6lQcbtu9EL18GR1jjXByYCZtdAV5mfTtFK1Et0fd2sq5CQxxpiJD2qssq7TuyLmNflrw6JwbI9dTxgL3xfPYyCZni7/j4HE2WRcbPcNusF44QtYJz7IspSLj3KKb6WBoQb80sdnWiSYiYGskAWDIJHsbZWlq3sE5vdTjVqeh5ySlOYFd16UoN7pDUiLFLGMdm2jkSWc0TaPHx8ekr9F/FiwSwUFukDnGV6AjqA3FJqGbLDAlLYjzRudY7s/KinWwiVhIpH9OKU3Yc5xpzq6NVAQ/1aHZKIGN2NiMAtKZeeFY2GiuhildldpkUgVZI6uHLdGBjkL2rP6xOgG9zh5K59iMf2OvcUgsiYhjaJ0AnhvnDhln36zOx9ZDTrFP1E4C6u294WRAoPA+MCBEg01xs06Njehx39yXdRBwMLCPlkSgIZHNOrgk31kvayt4Rs56lmUq8kKDyTSwesBG8e3aWVtk14514Axah8zWdoUQ6+ghkMHUdq2tfkXHECXlXq3cIkOXZDl7xPXQK/ZeBtOw5C97/eAdJKIQUx4yaRZeu92ryrKQ06SECN0XRTmCgcnA1XWjLIvs4mKxlBRZRicn77yK2Xl7zniYhhSpaZpGZVFqtV6NEZhWb9+8VTY6Vs45zaqZirLQ0I/DPttOQwhykrI8ArG+H3Q8HJVluU7Ho4YQYhe63YuqcuxYltIU4kE67A/K8lwvz7HNdJZn6tpOZVGq7VopSMfDQYvFUm07Dajbv+5VN42c7zT0vXa7ndq20/UYbblar3U6HBMAtor18fFRV1drDWFQVc3UjAaPIXiAH1oYW4Ma05Zqvb7uNZ/PtN8fFMIwHq5pVkpZVsq81zGcdDoeFAff5YlNvL+/V1HECBLf9/btW7VjqiFtxLMsO4sUxfqkGMZer1ejLI1za5YrObkxHSSoaVqtVkt98/U3yfB3XaftdpsUHM4thxYGmFdZlsmgExq2CpF6NgwQqR84yHHNXHquoihSGoll3lHiKNi4rtP8l6Ef9Lp71WxOF7tM3g9yLnZDigNjpdVypbbrNAxT+9MQdKbInIvKq6qi0VsuV1IIOp6OyjMG93pJU3E8tQzSeStQG8my0RLOeAhKyrUqKw1hUJbFzlWSNPSDinKKRvT9ELsuulis773Xy8tO3vkxyldrVlXah4OaplWeTznr1tHsul5lkZ3Vm8GI8l3SxJJZoA/AtcDLgj7r2EA6EMnhd5AyOGcYSdt4Bv2FAZOmtBucEIAJYBMjZ5lDHHBLalhG00bsrLFkHQCl3LOkFCFBro/HY2rpTl0boIznBfSxD+gM28hmelHQO0XTIuAbRt0zpYbZqBtG16ZEW0YyrqEf15fofifnfAKVs9l8dATD2bVYf8sAk+VQVZV2u116Jpx15N5mHFiQbK9pCam2jcAlOoBey+VCsaPZVNCMvOA80uKa77Pr0nVditDQGCbKRUikgHWOok7qlGU+2cN4TqtR7+S6u3uj0+mYIoJ9H/dmvz9otYqNjWhWEh3XQiFMTjbAdzabpbRBUmsgcshoiPI66ZzZbK7j8aSiyNV108BNq3ujDo2RsCj/g47Hk2Kb8W7sClrIOZzVqbkHuqmuGw1Dr9hWO14DAssSC6R3WZ1g05GavlPBeRjvrygihsFJQDY4x5wvexYnZ8DJuXFIeNepHwb57LwRVFEUZ7O/IsgcmwfIKctHtt87DUNQUZY6jBFS9ANns+9jRzbJxWHMGsF8nqvIszOCjPdfZgBwbzbjgLOA/iLKQJQVvY1zfHkWkVtLYJPmyDmBTGJvyCiy+tfqSnR8tIGTPkafkLlhSXjOrrXZ6Bye0xJCNpJkdS7nDzs11SrXcc8yL4XJLp3qOmYDmUiZ/c+TpRAG9d1IrEhyfpqf1w+my2U2jV5hkKyNmtmoEFgTu8C+2houGwW0n0E+eH7W0OpGZB37UTdTRPUve/3gHSS6oCAs8b9MXdsrDJJTVNxX67G7XB9UFjMdD6cpjN1LRV4kZmroe+1e4sHo84kxebh/UJ5HNqksZqk26Hg8qiql25s36RD3fa8iH8OtQ1DXDiOw7HU81mdGESGXpqnB8/lSTd2qquajkeq1Wl4ltiHzufJM6vtBp2NsYLBYLFQVVToUoQ9q68lxzLNSZVHpdKyjQ9M0CnLKsyKlrC1msfPecX9Q7rwOr7Fvv+0zT+50UFCWFcqd5H2mshhZ66aTk1d9moZ8RtagO2MNvPdy8nLKtFqu054yD6I+tcqXpeq6VVlUqspZirhxaCRpPl/oVB++07r10hja0PswDFrM59rvj2rqyJIqSEVeqSjiTCUiDFVVqWsHbbc3yTEgBVGaQDWsk01JiPc3T79HsQFSbPqaTXnjvTa0DmjFwNI5zbLJltnqu6Dbm+ggNnVzlpqj4NV3QXHmyNRCs2snIJwUWzblbjvn1dS0Bu01ny/Ud72UOXWKyqzIq2Q8LDOeea+m7uRdpjAQYXJyrkg1AQCeKCOZunZsDCE/Kn2vxkSaFLyOhzHaFbxeX2PDkDjjw51FUCKQabVcrhUGF/VE06jIy2So8myMQreR8V/MpzoTaUoRgw2G6bTROGkCMEQTIWgAODYVDMOH0kef2cgU175kDZEJy4YiO5dOFffLXl+ynTiwkzM0KM+LM1mWosMQGfLT996rreeQlNJDWQ9bZwHQTHUKY8TRsqQwtnadAUDM0cJnKss8gdayPE/fg0DhDJdllYy/1Rl5nqXrRdKGLnSNvM/VdYO8jylnZemTI0YEzUZxIxjx4zM4NU2nLCvUdUNaz9g6fGrTbmtTsQ82ShD3NyjPC51OdSIHy7LU8/NuvO98BD84WDQtiLOLkBXsJvqnbWPHS4AQjm2WTTUK1BLYSCNMfYzs9mrbw7iuC7Vtrbpu1XWDnOuTfVyt1iNhdFIITlmWaz5fJIaZ6PCnT5+SDseZCGGqMez72OyhadpR7ryY/xNrpwrleaHd7nF0CKYMDIAa84qqaibJqSjKM4Igyn83XitXlvUGmE3nL4LzqYNb27apOY/tPGkjCfYcuiGoGx3ytmvSvtZ1rUFTVMJGsjjTFthbwD4Mg45NPT3LSFQMCirLQqWfaQhDSsfnjHG20cnDMKjwsastkRz0Bk5aVhajw0I65tgVbzYN8+baluxAn8ZzNmUISNMsKiJvIUwt260+HYYhRVOpo8Gp4f6xY6TRWz3DmbOzBiGfSJPkfqwzSUTDNtBglAyZJkTHuBciyqwFf9qIHXvJs9toNu+zTgiRsqAgIQ9h0OCkoirVnOqURcQzYCuKqlQfBuUuVz+MOhGSsO+lodcwzpgLfty3zKtvuxSBvsQuU7DCJWcavIPdsljDEkG20YhNxbdRJL7DZkv8m75+8DVI/9Wf/MPUQMCGEmfV1C1KmuajIGiWhWRDCZEimGwSygwjZZldivZRVAg2CpiDi5MxDNOALRQfIIvUAwuabW4mh/ESpPV9n7rGcX8oLIr4pSksPYEdjUxerKnZbrdJQXAomepNlyyUD/nFKD263/E5ADLPyLRrm9MMs4nRJT1lu92mHH6cC5sTjDHnkDVNo+NpL1K/bOoQ98S9xsjRIkVEmrpNTRxglTDCNtVnNpvp4eFhrOOY61Qfz6IFgBnrRLL3pDTA3lBkTXQrz/PUDp7mDdYA8oyw65YxxIihnHn/4XBU20ztlZ+fn5MTbBWXTUNARm1kBBm2UQMUkx3uZotXbeceziRniO/BqDTtKckZcp9YOBeNKZ8h+lAZUqTvp3o0Umfs5HjOF2ceoIKTbovgrdHA6WAdADoYbYyRPfc2wmKBC98BcEaZc57tXrK2nHfW1EbTLlPcOJPcp9Vr9u/oBfaEn6N3eE0pJHEGlHW8uDdpYvP4HiJWnAt+z/mzdV42EkkaJaws+ol9sGkVGEjWlutZXYvRtLqzKIo00ynqjVzD8P3rS+0SMmDTQCSXIuIAfdY1Oh5TWhXXjnI9nLGrVrc7F1LDAVLsLHE2RV76pMfiM1VJvvgMTVToXMn+8ruua8chqxMDi0653AfWOM7o2ijWbblEUrEv1LOQni4pRb2p0+T8vLy8JJmnzucyK8OeGUgTnpl1Yd9tvZzNUrAs+aUzbhl4dNQleLbp7lzLpkzxurTPFjtwzzYNGgcY3WML4qfsiim6lGTEu1RfTGodqdngAUsK2nNhoxK21gddxN95HgvecVYsMHUmZY/vBQ+0w3mzAe7NkkmsYXKqjK60GRiSUp2mJWFstBNSwq4Za8mzIINEHu1sQBt5Y+1IRYu2fpHWDb3DIHfsN99b13WKACO/EE72PNvnteQUv7eNNpDtS/m3to0zgPzaNYRYrapKXdMqXBAjXLMPQ3KIkFObUcDPkYlk47o+7ZPNmrF2gSgTGI4zaNfCG9nmhXzyLJakZJ1YF+wp+/M3//a//dsaJF5WEeJ4cOBhnqy3ihBbAMpmSBNTy4ECiAOw+TttoUlVyfNcz8/PSTkCrElNQ5gtuMM4A6BtiowFbLwPb5x7RiGgKO19v76+JgPJfZGPjWKWpJubG1VVpaenp7MQOB3rUA4wwXRsy7IszZWCVbQs9OWfsDCsod0TW7di88M5UJZxuAQNeZ5rvV4nAEQBOkyFrZ2xILxrOx2PdVpXnBUMnR0Eikx0Xae6qdMa8X5bd4A8IJd5Ps2D4nDf3t7q+fk5KTMcRRvCZ02GYUg58Db/fEqzOW+7DKCz5wIQbBUx30Oomxcsly3a5z6RTfbARm4BVqw3yrkoilSHhJPIPfbDVLtxqVSHMLFH7Imt48DAPj09pfXBWePebaoCe2MjEbwfw2sdFBqjkJ5mzzlGy6ZFIkM4wVyfPUG+2auu61JeumVJMVDIg91LC3ZYE4wIeskCLZ4Z4DsMgx4fH9PwS0lnBAp6IT6P13w+DV6kvXy8x8m02GenToR74L5ogsNakabGfVq9zHPZfbFMIZ9B11lGF1AIALM57RBT8fXdomfkJf5sqi+xoLMozlN+MOxRxs4bjACaYi3D8nvPd/zZNKjYOn4MD7ZpkdP9Sa+v+3QfAMLlcpnIrDwfB2lrirjFOr7pWe3aSlOXOGTeOTcSkF7D0Kbnwp6xdhAPyAGRiGEY0ryZEGLjJPYHZxp9Y0Ef62RtI3WalkiwaTfsJ3LCOlq9y3m1csI6cLboVmrXm7OMPrNnks/yHsAkawORgm6wNtbuTZ5PXf2oReVn3mXyY2TI2n874PlSVq1tugThl86RtY+cOUsacW7quo6DSE16F7qS9bJNIyCl0ImMBEE/Q9jYtDobZUIfQgLaCAvvs4CdNbBdB3mxbuAQUkkvnWlsNqScldG+Px90vN/vk77GocI5stF8ZNTayUtixhLLZB5Q23yug6ZZm5x968yzJ6x5cupGEsTWM6UMhm5y7LEX7L0lbNBvyQ6N/0bGydBhnyxhzt8tQW/PMPYc22nXiD21zib7Rb2gxci/6esH7yBZpWMZG+90tpEIOUJAgaFlPzmkMLJZlmm32yUwD2NBpMNGoxBkhsLaYZQ2jEgnMcui21CwdN6GFa8cQIlQo9h5LhSLZaSlKRxs855Jj4ApOxwOKVpTlmWK3lDcj0G6u7s7uyb36r1PheS2nSkCi/G3ESznpgYT0lRLJulsXyhmxaDSjMIyjc45LZbTmvB+DjbggdQdDOR8vtB83n8nxc1GH2hGYB2g6CifpyixDrYLF8qQ53Mutu61c08uIwa2QNd2ubPGwSoJq7DIqY5dGL18NQ0+lmI60nK5PBtgixK1jpdl0rgvWDMb6mafeRElYT25N5wlrgHYkyYWGADPfRZ5oTyfjB8sErKIcQYg7Pd7SUqpDDDG/N1GMtgL63SwnqSnhBBSow+egxf/Rt+w77CdGC0bLYNQYD1xGgC/FnRZhwsHn3tD7/B9l44pZ9KmdVjndhiGsW6vSPoJEALBQfRlsZhq5tBDWZYl+XLjPKDFYpEY2ssp6+wr64J8sLYUQjMkmn0GYJPiiiPIOlhwBqjBOWTd7D5f3sMwhAQWLIMfr6XURRQwy3dTb8TnWN+4jlFecdCRnUh+TCDDgn/2C3Bpzx8gGTCN/FPvil1YrVapu1tRFNpsNun8XV1dpagUEVjvJ3IBAMs64rwirzwjDiv3xT2TKowMogcBhvwM3WAdZyvvgDZklDOJU2sjBugx9ChEA93H0C/2O6wzy35jG/g+0t9wGnByLqMzNoIJcMbWIafWubLn2Dod2HR0ZwghyR06AaevbqZME9YVGeJerD7musMwDUVHT1kyzK4BehqyAIcXzJFs7mkiNs5soPfqTO0iaw5eQh4tMWpn25D+WhRTyjX6nv+sPbUEh3UWQgiJ3CV7gnuy+pOza6P76DPk3jou6Ma+71MdJal4YDocDEhJzs79/X0aX8JesCact/V6rWJMfwQvsQY2io5M2qg616QuDzxDvXMIsXlBH5SyXNCJcV06HUwTEs6zrQGzRMN0hqcaJfaGa7Jm3NswTNlT2ECex+o8S9TZbAMysGwzDLse1jH7TV8/+BS7P/mjPz4L1eIsVeU0Dfv5+Vk3NzdnTIp1RqzXnmVxaCQgGYWBEOCRS1PeLBGAS2aRg4WiQ+g4YAy649oAS9s60w5mzfP8jIFBkXGwMcZEGiyrBQO33+9TKgTOBQcVBUD0ifQ2BqNdrp9NU2C9Lg8Q34dzhDKyrAgGh7zmYRjO5iph8DD0OLkYaO+9ymrqnoYRtSwz9yNNbayd8+q74Uzx0JAAEGcdAQpDs9wrhCmljnvGEJKqZ1MBbETJtrtEfi5TH1De9tqXzhTyyf5LmkCNz9T353UcNlTOc1oHxUaguK69R1g5y/Rh2FgzFCmG3IbQbfgfOZIb0rqyzsk4KDtzTNlTaQrFs74ofZ6fe7LG7xKQAgAsmOC8cr+ccwCXZZptxMn+js+yR9yHdb7ZB4yZBfkWyJPCy33yLBaQ8p32P9YB2bAMMWSQBf48Eyx5jALFYnnWE3mMOuYgKSSAYBl6zuVltNJGRJGdvu+/kwaJfFkGkzOFzrXkAS/2w66/ddZZU4CMc1PkxbK5w9CrqqaoAfsaz8Y0i4VhzACqYYjywvUgsqJ8Vwn0njOkcWYOJIUFhawN9g2Hl1fTTDM/+B26xkbcWZvo9FexkNvoGs4KtojGEVZOnPMxbdek89k1s3qZbANSkC7BrNUPnGX0pt1HzjP3ZaMZrAOOH+vDulpdaHWWJRqsk8HfL2WJ31vwR5aCjcpwvqytsc4XMsPIERh37seSbJfErqTYWGGYuhLaNEjLnlsCCZ1BUwOiEpYsgYixWMGCUfCKdQK9nOqRtXdumn8VQtCpqaWRCLR6i+ex0U7sbdfF8gIcjaurqzR0HqfNksycqWEYvuN04MgC7ne73VlEEwDNOnFu0BU2KwI5t/YBYhlchB0ljY99J5UfJ95iUPbpn/7Tf6osy/T+/ft0BjhH6NXLwdAWtzKq5HA4pL0h8wM9YOVFISj3U3tt9OQwDBoUkoNk8QBnkOtbWev7XkWWq6X2aVxDq5NZN/tZacJ8XJ81RB4gXS7tgH0ui3vQ8845NW2jv/G3/vpvU+wk6TTWHKBI+JNDgCcP+4RRtUpBmupz2Dh7cCzoJ0XAOkPS5MWzUWwcRpIaFwskAEKSkoNF6gLOxGVkjKnUpG5giC3rxfPPZrOU247xtfdg3w9ARcABviGENEXbPjdrxXpbkM+6UA8C0ONZ+RwHD6eQ70OhASissuf7LQOEwiFX3TrMl0D9THFoYtX4LEaceiBYepSpc05lket1/5ocDb4LkEzKkgXmNiUAhWGBHPeHLLH+1lHiPux7pUlRWHa6aZvY5MKATpvGRqoABgEH2jpSvJ89tTPEIAtIg8R4sIfsDzKBU2ojGsMwyPkpl5jvAhhk/rwxgs1DtgCKPbfPYYtynXOJWLCgxbLMGEPLFtp6Hhu5Y0+tU4Hxtw4hRsgaIqvUeZ+NQl461RhM+x3fF33kDEMQQRxYFo7oDyDVAldYPcieyGSeVBRTeqr3Uy1RYea1AGKtwwcQYh2IelD/Z2umLHCyzhP3A0DGeFtZtyCGNeYMFEWR0rMsUI4yNn0eMH8eYTqvGyAVtapifRsNAgBr0/1kaa6PHR3Q91OqkCWT2D/abrM30gTwvY8ZCkR/JeokinQucLpskwj0Go5D1O2dDod9apZhdRH7Zm0ZozHm8+VZZIB9wX7gMNjoCbrTAn1rU3mx7tY2cvasc8p5uoyq27ETnGXbRRVbhOyji5AXG2GGhKQ+ivPDs1oik/MHGLbPwM8t2QTRANFEpBadj+xaUgc58T5TMdoBzgC1wPbc2/XlDM1ms7MumTZzwHZhswSejUbj0HFPmXNnz2RxzNWsUtNOw52tTbVygE5BL1VVlaIdpIpeptxanQ14t2tnO4uyFovFIhHG7CvRKXQ6vyNazbpL04gA0i6JkkPq2MgbWA/8cDwez2qRLPbw3uv3f//30/VwDHByeF6yXuwZ53yQ1oi+JE2f/UcmeJ4izxX6qdspeo4zSgQWG27JLT4D+TWbzdS1rdxYl0h02cqhxSask42CE31Gr1xGma1dYj1YO6s7WH+rf37T1w/eQVIYU0pOsUlAExplhqG1QKqu6zTjB1bS1ouQ32uNuBV6NvL19TU1hrgEqhhYhr89PDyc/RzFLZ23n0QB39/fqyxLrdfrszSOBM5HRw5gAeiD2drtdil9EOXIvVhWy3ZJ4bn6vk/D02xOMEqN74Gx4PltjimKClBh5wDxvRhihLnrurMhfbApvPisjV5NhmNM5xiZ7sx7nU4oSq+yzBSGoCwbgUmWq65j9KmclToejsmQAy4okmS9OfTcx+trrSHETmfDMChI6vs4c6VtO4UhphvkeaEwDBpC7KrV973GBjNiRobklPlMQwjqu07SWA8QYpcqhaB8HPzWD7EFvPeZYjvcUn2H8+50OBxHZXuUba1uU0FhQ7NxHUKQhiEoy7y6rlfTtJKT9oeDYlF23APvvUICNU5d148AOZdzg4rCKbZDjq2HeR8AW5pSOTCoeZ5rCLGd7fF0TAAyy8Z012Fi/zkvFnwgA7GL2eQ8AtA4GzCUOKo24mujtzg/NvXFFlFbcJhl2VnkkTUiPYYIp2VsLSnC+eAM2LNpjQXOhU1TZU0gXayxv4zsAQBtOi8GzUbykA2buhrvBaY5dhykjXSWTXVDVk/ZveE+LOMPG80LJl2a0vUw/rHN/pD2wTqxOIk8E4DAe3/WPIT1tENXeS4cHByYeN3GOLR9Ip/6Pn7m8fExOYa2SBg9RboXjiyAtCynGlHAGMRdCFOEI4zn/tOnT+N+5Lq5uZH3mXa7V9X1SbTXRz5wxJAVG0FiUG0q1O66sYa0VtO0Y17/FFnE8ei6fiTf5mqaWnV9EiMtkHfINvbcOkbsrXMuzavDHtnaM86sjaDarArkwkZzbNTKOmEWRAOgOes2rcqeQeQ/hCmDgZ/ZlDWuAdgkgmCjCnxWUuy0mWfKh0I+88qyeK+z+Vz9eC+W+AOLWEeC38V/twqG4ATMAiitQ49MWxK367pkt/f7fSIFyEaBELKRAM6M3XPvvTIfbSryaqMaQZPjh63BQUlr00yzGtFLp9MppeJZkM8ZviRNrC2xaYHsO+uL3LNvz8/PkpRSe6VYg8mZhDQke4ZzCuF8mR6GM2drwUiTJF3O2iSL54gO4STblF+b4sa5tHtjyUHuFf1qMamVr7ZpIl5WbN8t5yQndX0nn01NTuy9cn/2mTmT2D7rAGFDuBc7L8lGIdfrdZqbxLmCPLAZCxCf2GWe//K7WIt/09cPPsXuP/+//F+TM4Hz4L1PoAmjYZlpjAlOk2WuWWj+jQCgBDigpCHApLHMMAnkwOIUoWxtpAsAxaHkuwiFIyTWkFujQRE5EQFAnVVGWTZ1VGONUIYoHZ7TCiGfhQVCadmDggLk7xgRa9zYDwv+LCPL97CuaS6DJodzvV6rLEs9PDyk/WJvrXKxbDsKkfux7BN7YJ0fFI5VAqwD6YWsrw3pSxMbZlkza7S7rksplawj+w/Q4ZqXUSOANs+KsSFyaFOmANYYW9YYsMr3RPb8uzMFsixTN/SqxhalKKzPnz9Ho1yUaTYH8mbPDS++Z2L4p4iIDc/DClt2yO4fBsoCfxtp4T5sdEqa0lIt62X31MomAMA2MYDhpfgTJsumeFqninW0bLCNWFgV3HXd2ewby9IhsxbcYPAvGTRrKDGg/AxyyEb4WDeeH8Nl5d6yutwP1+GsA3C5lmXz7BmjWN4CB5y1EMJZpyjAjD3/IUxF1LxsNIG95U/bEIboiS10t/rPXsMSQegdKc7RQj+hF3E2OFeW+aSxAzVKl0NMs6w4q/cklQgwaR0Um8bDvVM3at/Ttm0CR1Yem6bRZrM5qwvF7lnQIymx4fZah8MhgVfWtSiKRGJRW8F1bEoOxCJn0uoGgBZtr5umOUsP4jlsC3GAkJV1SAsc7f1+r6qqUi0cxCHOANEg1hT7j8zFFuGTY8yZtXqGs8A6sWez2SzpZOvkdUOvbNwv7jWx4W131mzBRpc5E8MwZZPwuf3peJbZgnywruhHnMDvy+rgPIAlbHMMa99Ye57dRhviZMhzO4Buy8qpbsraH65pnSf2dBgGPT8/Jyz0+fNnbTabhBMgQsgMYO1t9I97ITvFNgBBbrIsSzLM77BfVgb5O1gOfR5COEsHZ515Puvgcj/oPYsreRZr3/b7fcJJ3IOtgbMYweIu/m0Ja9aH885z8f3sDzrVEv18nhQ/zhpYFecT3ELDDur3WCtLUEhTJz7Ie3v+7PpIUxdVHCur++3ZvJRPdM/z87P+zv/yb/82xY4XXjQHw4IMydRlZNPkbBQdzKwVapS6BRW2iBmlhWK6ZG5g8UhvIIRqHQUEFDCLogKkDcOQBJwDyDNiKAETCD0NDIjiSOfzW6xnfwmKrCHg4BJB4Vo4olzTgisLwiyrbYXX7gPg7NIZlXSm8Jum0dPTUzLGKFzW1wJeWp3T5pnDjfFDsdiDxh7YaJidrWAdPIAU94KCZg2tIrXrYg+6NSiE4LnfS6fKGjyUCN0KL1MgpHPHhL2wAHZiy3vFAYLnco6MDEPs0CjpO4wZ38n+UKxqwQFGY1JuUw0KYMGG0wGi1giw1vZcYQCtw2jTUDG67A0gnXXnWtaxYS94P+t7mVJjhz5eOoN8HlnHQNnPW6MLMcEzkf6HTFvgggzbs8n6X54pzrBNWbRnnWtYQGtTmXjfZdoof6JXeA/NP9q2PWstzX7alE7LDlrGEzmwBg5mlcgP0S5IJkA2wB9550xYsEAdDGuL/kAv2PPEmsUIxpA6HhZFkVKrARo2Bfj5+VkfPnxQXZ9UlkVqafvy8jKy1FOUnCGxOInIICw38pjneQITgESbRsoZsgCYs0C2AI4mwNQ6GLYdr/f+jGjLskxXV1fJUcJm2s52NqLDWUe3ct4suMX+2cga68iZZV1s9sDV1dXZObd6HJm1s7VYF8Aw1ySVCVmxJB9Dui0BY4lF5JS9wsZCNFzqgrIs5YdeMsTjfr9Pe1XlRdIXrOMwDGnMBvL/+vqa1tuSAhbMShOgtDbc2lZL5FEvZ4lRHFmrA5AnSWf6sm1baYiD662TY2WNc8y6sX/YR2tL+35qeEA9jZVfrsF+koq/2+0SWYMOKMtSu90u1T3Xda2bm5t0pnGcsTHoIXR93/cpWmTJZhvVtDW/6CPvfRpubRtxcO/OudSR0u4le4KulyImAC9aWwgZbqM16H70EDqXyAqybAl29Axnsa7rhFetsw6W5GWxKa8wDHLZVCJisTPYkme0GC/P80SQUevGfWGfLIFou9dxj5YQRtaxUbPZNAT6L3v94B0klDLOCPmRHF5e1tvn7zZUZ5s0AJRtZMWmkFyyPtKUo8l7AFzOueRYWTbDMpir1SoxdCgRHLI8n6YPo5ylKLDb7TYpBwRcmqIOKC7bpcyykigHG23i8AA4uAbfw2EEIFz2ogfkcl2rzBFwFKY1lhh/7t0yeewFL9ZeUlonmEHy063jhdKyio9DhvKDEWGf6KYC42QPu2XCLx0iG83h+y4BBAoUJpWDbtdeUgLUVtYBlCgFG4niT1sHwns4D/HPPhlA65SUZRwWZ4EOTmhRFKrbVt6dAyK73siQdcrKstThcF4QjTPGXnMPyJytIQOMYDAvowHspTSRAJwf7vFSQV/+HYMHG26ZVwsu2Hd7ViyosEaJc8se2PNuI862RsKmjnCOeWYLUuz9oheQWau/LAiyjqWN0Nq6BHLaMU7oDstmst+kv4UQUmSENaNrFA5q3/eJKOJ9fCd1beyV1Z/MJ8NhIxIAaWPPoY1GIoM4btwv17a1jVmWJUcAu3E61am9dtvGAmt0JQDNpiFvt9vR0YznlzEIpGrH+23OopBEENDndgwE5+sysm3JPBsJt2mcnEVbS2DlCtnks/b8ca74/WWkzgIRm+6IjB0OBw3DEFPdTeTb6jLAqG0khJPO+d9ut0nv2PbRfKd1iHhZXYzusHuMjed3rKHNmOB8QkySmspeXNoVS97wHMhRr/NOsgDgoijUNxOBwnownJf7Zd8gGXw2db200R8L2i25xtpwTe4F2839sud2LZFN67xZwi3PphQ41pa1GUYC5DIdysqmfQYbzbOAHnCMLuI6lERgJ/q+P6tdorOcJTwkpbPIv8EvyBb6zBJJOKnIp3XAeVl7j46IOuSUzhr4AseD9Eh75tDV2DNsAnoMZxIbbiOE1Cfa2lurG2wGBGfE1qhyptAZyA24GgIH+8o+xMR+d4YXrINkI2rWNiIX1i6yPpwpHGt7j9ZpsutlbWxRFOr6Cff/Za8ffIrdf/Gf/d+0Xk0DSiWdOSBVVenx8TExB6nvez+1/OagoTQRQASD4XY4RrZGxjpe0nnLWQTFMuSXIMqmeFiHjE23QmPDmwBKlIgFfLCkVsgsuOH5MDj2O7/vHqwx5fO8bEiY57cOhWXk7PrwdxwUwBRGxjL1lpng3m3UxIIi7rltp/onqxj4LPfNMxCdso7lMEyhb+l8nsbV1ZWGYUiMsHQ+u4j7t5EFux58t2X/AXqsPz9D6VkDYY2Hdaq4BoARQwzIjIC4lx2SybM653SqT8rGND3ASQLf3mu/e00GxYJ2wBuAwjI+cXjmlAZ5aXitU21Thmx9CmfPrqVlr3lW2z2Qs8B68zkr59wvTgsG+tI5ArQARm1UxuoL9oN7ob0+YJs1Yp9ZC1tvY8+YVd+WtecMYRgAtJxVwI8FI1yXtSBqQI0IxtqumU2btSkWOKCcX2Yk3dzcJGePVGMKrllfAJoFQwA+1o7nGIZBLy8vur29PYtwAjB4H8/F3vBznDJSodgzjDbnIoSgzWaj5+dndV2vrptq2w6HQxpGTPobTpo1/nG+0FTgbeVjGIL6/rwtMTNULJC0kdUEOg1jbIkBiB/73HzGdl604AIdAiD+vtRkzgWyYMkJGxWSlAhJwBARIQv22DMcQ/QKe4bsNk2Tanthtu16AA4tsYODj86AVOz7PkXgLOPM2UGP7vf7FK3DCbMEAfIOiOUZiO5Yu80zl2Wpups6w1pskXkvF6bB09hX9tSeQZ43kTFuGlJvcQFny94j1wXkIsucDYsbLJFk99uSFlbXhH6QN+AUAN/1vfLyfMi4dXQsEUP2C5Flfm8BOnqIMwL24eekh1pMZu0Z98v6cR3OiF0P61BZhwi7htxYwhg5s8Qm98LnWSPkE1mwGPGSxLL2k7VAvtBrluCGdAHL2nujrTbPiQ6kHTivLMvSPvCdpN7a7rXIHHugIaThs2Awq1tt6jq/s07TpZxYktqSkOgq+7L6jr3p+17Pz8+/HRTLK8/yxA7SPSx5uOE8XA6os0BEOs+dR+lhfJIg6LvddlCiGEQE7rIIke+zQIOXVbKXjgvKgQJQO7hTOndOOOyWhZLOp9bDGlj22gqunXMBwOazGA8UKECGg2wPLvdgQ/d2DhLrh9Kw9QrSeVtI1o71txEP9oW/42hIOovMoHgA00T2LHCw942TxjpZp4trEFLnfjmkds0tg8U64WRZB88aPQtSUKRWoVvmy7LEyJm9HkYBmSJ9KabbnD8nRiJoioby8/T8Jt0OY3bpyJBuZ2s/vHfyfmqXbp06GwGjqYK9pgW0yBvn2A6jJErLmiF3l04LZ4O9u2Q4YTUBvyh9nILL/bREApES7od1sM5+VVUJUNqoE/9Z54h9s3IWwtRelvXk3nA4bEqn1W+88jxPKSgwq+gC5Gq73er5+Tn9jv/oSonz9PLyohDi4GOb7oFOhr208mr336ZmEBUCaDdNkwZRc230CKCM/WFvAEoMJwXQ45jC7JJyZnUve+6cO0vVZv/n8/l32Gpkknvo+4ncCSGmAsZmGnOFYEDm+Dtk2xJTlzJhdQpOJAy/7T6GfCcwnn23ppL/OO9t2+rx8THJAQDTgifu0zq13KeN4GGrbDQAxh3bY3UeYIi9A/xaMGzTKi1RAQhk/XgufpbnedpzG8m09UqsLfbTnjMYcEvKcd2Xl5fkJFtdFUJI530w9smmynvvFVKDmyylWV6OXfDep7QjSQqaWoVjD6hrtftkyUQbPWHNLQBm3dA5yDFrYh0pdNHxeFRVlKlTndVXs6rSoJBsiHUqeE6ijKTShRBS6hx4CWCNLQb3QHLjWNpGM1aPY8stgWj1u03xQxfYdSATiZQ2K8/oJ0gC6tuxRfa82Qwba2M4q5bI4SzZaB5rbu2axWX256wH+oU/7XlzLg5Btj+HfLh00pB17oN75Jwlx70flBsC10bTiMhzLxbHcD/YB9bVyq/FPrZmyjrsvM4J4992sUsvm0NpwZz3/qz1qA1xk4Jk2ySyQQibTfXCs74EpSgsGCq+m4N16TRI58qc30mTdw7Lwb9tfqk9+DbnVDrv9MPPES4L4qzikCalwb3xd5u2xEFiPS+dSMuaWOYKBWcBEN9hIxz2M3y3jarYA4uDZdktG9HjXpAHDLr9Lvbc1hFdMvHWGbaOmd1Xe7/WcbBGyCrvS5bJGher6KzTzB5YcGP3iP2wa7jdbs+An1VCfHddt2ddefj70A8qTT4wIMt7L5fnWs4XyTni99wvAAfgTYtVK6c8c57nqQCWtcTI2GiMPZvWecWQck1pqgFAJq1CZk8wLNwPYJjvunQwuTagxYJRDD9rBFttnQS+zypw5AYnB1mEbIHls6y5BTG0m7VnJoSQfm4dB+6dM8E6AkpgSSETXl5e0rnmM7ZVsXMuTZd/fHw8q4XjfmB2kVvAD/dHy+Xn5+dUB4ozw/kAgNsRA6wzenu5XKbWtjatiC5SVt9aHS7FzlWAXFv4XpalFovYARMDzf0RnQTMWD0X9VmQlCWGFgfZAivAv3VYAVzIIM4o9oaf2zPEC93C/tHZ0KZX/v/Z+7dQ27b1rhf9l3pp134ZY8y55ppZGmOydyLeThTBGM+Dur1ENjEIQoRAEBENCEowovimIJHkQV988S0ggm8K2XjcxvOgQoxiwO1RouBJlJWYlZU5xxi999Zab63VSzkPpf5K+dc6RlxzneM5bOZJgzn76K23VmuppXyX//f/vvIV9yUuC9ixV69eZXkHzLO/i6AD2eb76D6VHB40AhqXpA/P5BUbyKiz+6yX2090E13CryAn2F2YceSRgBZ5BoRCAiKPMZYSTghqm38RAAEAAElEQVQs1xm3c1VV5ZI4z2LybCEEqUod3Za+t+97VbGUiXNd7AnzjTwzd6fnZw1xzF3nWCvsoQdW7uf8HsMw5OoSfAEBAr8vATw21Evqu8tFTV1KnXl2SeqHciQDsspZRGTqsEmUWRLIMm7PghFAAZLRDw/OKHslqPf2+k5GgSFYU7J03M8zpcgm4wZHoAM0XPJsjxNUDvClshcLPUaOkQ0nz8EljKdt21zJwr23223uvOdBBVUBl8sl7+Va4lonJXhOlzXsjZMfy2wYdovvc33f/+oBnPsxro9NZb6W5LePk/uxFktf6gRKZUHq13p97gOkqq5mhtIBNUoHyyaVSfZsAC8EnA2DOBo3IJ4Vom041+DavngYa/rov3z5MgcLrnwoitedeuSNAUDgckecsZTXOePACwPJvRBwLw1wFhTn4SAf0IeRcQDrzLcru7N5S8G+dL0u57N2TauoUZfYaxyldbNSmOaum+pIq0TFaVBqc93YGOq61v39vSTlMx0AKzitvu/zvDkATiC0UddRhsDJ5VF9X86ZScFFN2VAWqVOVUFtyzkmGNF5FzAPPN0oj+OYO8Qx/zyPG00PlH3NPcW/BAjUX7MO6b+o5+djXvsU4PfvOEAA0m6307W7qm1X2qzWippK/cZRVSjygQzzwll6oFoCuBLEkYEYx3G2P8idI85LUiYznAhIhvUy090kc2ltSolcrRhT63WYpeW8cm30zM/D8g39PC/Ms5cfse44VC8BItsIy+jZQ4Arelb0bVDTtEqNNEpQtt/fqOsK8UGGx8+Bqyoy3L1CKAERjofnP51OeU9GKoHrlVrHr6cxP1vJUxrj4XCcgp0ht8qn6iFlkpQdNxkXGHzuv15vJpu80atXja7Xi4Zh1Ha703o9Tt+rcpCWjygYRykE9cOgm9s7DeOgYYwaxihVyn8PVaWu79Wu1grTWiQbcJ3Gsp6ylXEqx2p1vXaq6zTndd1M75XSa2STJjVOlnmWKZWSkhmJ6rp+OmQ7tdN3dtb3JWCDvWGEZzodiCIj/A1AR3kRpZIEkk7i4Qs8w4X88QyUtZH5wY5Qukawy3uMmc+xvwKZxQYC1hwAMVdUdzi7DMBEl7kHvoxxexkb4A97xl4UAuGqqrKuUFWCb4JoxZYR6PhzYb8JevjJczlgHPppjsdR1/MlkyExRlUG/jwj5v4c/8uzVVWl1XRkwvn0rLqp1XUpC7hqV3o+P+f18oCM+cFWeQk75VfIkY/fbSDjg4yoFNRP8uglshAMZAsd5xDQEayQxVvKpJdyks1ZEsOMDRuKTpFB4/Pcnwwoz+2EGYEAcsacc3/PoCEbAHvWz2057y3JdPTCcRjyjs9g/dEx7ufv3d/fZ9KK9fU95pI0DqmU8/l00vn5LAVps9mqu3aKKs1sICE8c+Ql8k4Mgw3dX43jqFXbKlRh8lUpQA4hkQNch3GyRsXPlXuyHgS7bj/c/jn554kG1sDJo8/y+twHSN2107Upm72ZUM/8SMUhsWeEBXZ2yll8jIGXYUhlgahZxsAsgwMHxGx6/OIXv5iDIEATi+rMjxtH3wOAMKC40rw80JlEd358nvcwNFKp48TpOIMgFUXwPQ2esl6yVc4mMDbPDCgE9dWo1TjqRoNqjdK6VYxBGqTrID2Ogy5VVIhBdWgkVYrVlHI24+OOO4TSoccdGfMB8MU5JuUbJ+CSgHVqfR1U180UKA1TJqC1MoFKVRU0DFEh4IgqhVCMgTO3zBNzwzriBHgWxtz3fT6BGyYXWcB4ELD6xklKeUIIeV/F+Vy6953Pl3zyNg1NYPQBQ9frVUPfK0Spn4IDxXT6dpLxKq+5B8BSAX84r3R/SjpHNU09c6bMi++BYGyZhVXpyuPynda1ykA2yVylOJ01RQtzSYs2/s2sA5Wz6+iBO3aCUgdmADnIE1hq9rvhpL20gn0wOEKvu0c/eY6Ugbmb1lCSgsZRWq1SYILOE2xig1IQX+t67WfPlZz0VU1Tyq08yE1ZhbQnbRyjLpdzlokYpTdv3uqTTz7RN37jN+r+/sXEUt7ocDhkZ5Rkc5cdYV0XOaB0FjB5PJ6m9ygpaid5rHW9duLcrK5LTO39/YukR1Wtpk3r16xW2bGFENT1g0I9EU2T7OBQr9dEhG237ZS5qabAOc1zmv9hFujUdZ2737HOXsfvPsYddYxSCLU4YyxlJgpZgM6THUSOAB5OKDnwIkuJncNuO6m23F/l+ymRX/QHe+SlmAAWQDHz4MwswASiBb0nkHQygWDAnwmZYz64Nvv0loSQZyLcV6Izznj7mBzYSpoFIjD8zp57iRHr6oSjZ0O4JuPwEiiv2NhuJ0Aao6o2qK4qKUZtpiABPfRMFTYOwIt9rOta3fGo8yll5m5ubvT09JSeve91ilGqSrUA4NrH7YQh9gk75Jl4Z/m7rstt0r16YuxK1YeTkXVdS7GUZS8DWTLRrA84BRuC7V9mupBV1gn/4LbZsx10uIOIROe4lh8VwhidKPCxIGfMIUE3uMeDG3z78XjMDTXQA8cfjJ0ACtlzws/lDDnwhiJ8FhuF3A19L41RIUrX80UVpO0waLVq1U3P64SjB9K+P9sDJ8eV+OWmaez8RqtGClIMMv8fZ3ZLUi5R5NoeqC0rIJbzg64h326Hu65Tdy1k0td6fe4DJEnZmABSfCMrgsyke+QOqIbllUrtLQYVoeQ7Umlr64AK4+YbZzGuANavfOUrGYjhcMl6eOc9rpuA7XnmMLifB3QejS8NO07YI2uEFePGmNyhoXCwFVJRVrIWGEGCOLJfnqmSCqBjTOtLr/jpW30hrHVXr1Q1UfV2p8vTSf/P7qKbD+7UDxet1xvVsdJlGLRaN9o0jeJQ6oi5N3PJhmFn9jF4zkwyB2k9393Az7hhLhw84Qz4jgeQ6b3iPLmHywJlHQAN7utNP67Xa2Yz3fD6WAiSnPV1p325XPIBdre3t3p8fMxzAnNEILM0zLxHSRHr6cE/z8fYHFz6XpU05irfj88TSLgxRi69Rb0bcgdbIczPcGKePAPla9o0zVRbfpoBPZdVngc7AKFyc3OTnwVnixP2IB2Webvd5hbP6OTNzU1mUL38w4MkB6jDMOSsM+vNXi4yXd51c73eiAN6uRZzLLW6Xi+5pAR7mJ69mekpjO3xeMys/6tXr/I8UxIBSHE7wzq1bemo6CRRsr1lfyDAjC6ennl4/fq17u7uih3srrN9Q4wZgO02nsxGd+1UV6W7FO23sRnIm2cscNLYu3mwVc5FgqigRIhsEt/zgAAfhQw52EHPveSY9fOS3yVhhY9w0I9/c3kuMlBeBNc8C+85WHLfQrDr6wMByXEA2Di/joP+ui57evwa2FDXV18X9NBBknfb8swN90dG0H1knhfPtLwXmRZfewdsTtIw98v2xp51Y33xjdgbbB5y5rrDNbEznGWFvnkmzcmWa1/kivESiDJWAkXkkGuhPxCZAFvGg67kew2jNqv5+WruQ1gLD/JYC+QEG0/zFCdxkWcIQb/PMmj3rBEZMrL8jtEcz7HmzLkTAMgAvhG/7uPAVjk29C0ZXqIMucJzM5/YdPZIInPIuttUt81uC1xOwTVN00hVuoZ39x2GQe16pdECHObc78m9+M+xipMaXpbId1zv8AueaXXMhJxwb373BkFul3zduQ54dGWy2DSN6uZXS+zyC0AGsHTnxiSz8JyDUVVVBnCkgFkojIdUDLQLhoNfhBiggyPB2PrGVFdMFtKNu7N2vACV7hwRMK/TlTSxyMXJONviAuVgxZ2xO0YcPkbCGVMUmzpfjBqliDw7gJXn4XPXy0XN81U/+2/+H/o3P/V/6IMxaN2utH9xr/uPvqjx23+jNq/u1Fa1Vk2rOETFvtN6tdZm1eowbQpnTp114r2lUjnD4/JSVUExlsDTN0jiCH2jrDPmvMfaYEiHoWzYRvaQG9bSs3YezMEUu1Ojnv/m5iaPnftivHw/EHOSsmBJHjk80dkgZ+ZwAO7oIAz2+32WK4w+zgEH5qxWVVV5D0gpRyrGEeaQ+xMAMGeezXSH7oaR7/r8L9lP5JE9CazZarWaOVUvdXL2lXkgCPGyI8ZWVWkvz6tXr7It8uADWUHvvSsgY2YcMcY8nylrNOZzsshUJfuQ1oj9NzQLiTGVynm77ZK5KY1ZnDFOzn3Qer2dBQ9sZAcEA8Q8iwkL3TTpdPr7+3sNw6AXL14ohJhPrHcAkYBfeWYO3KQcDx3gvg6WXM55oU9OVD09PZnNC+qnclKACPMKkMG28WJNmFfW3sE7QBQ99q5uyKhni5wgAhjTCplxIbuQex6AAigdZFyv17x53SscWHdIN2TA/YfrOjLvMun2Ou9NHEujISd1isyWPZHot/soLxF0QoWxYxuwk74fDb/kBIyXYXE9z2QgD6yzZ1EcNDM21zP2TtK9FhvIdSmXYy4cIDsZtgwckBMqA5ArPzT56ekpB8339/e6u7vLe3D8rCzwy2qVQO+2LYe9+vlknsVwv8L8oH8eRPB97L8HhufzOR0UG+YtzDOgnRpQxBjzvhkH4ugi9pGDkz1wZi6QMc/SOUjGllFiugxK8VdLYhO5ZI48u+j22T/vsukENtUb+JbT6ZQDI+z/kqzHboJJ0A3adGPPWScPYJygpLzOye26rhWqUhnk+sb9xnHM3d3QU8cFnuXCNi2xsf/b5Qn5CpJCVZpJuE1xn8h9uJcHwW47+Tyy4KQeZfiONz/r63MfIOHQvBXjEii54US5UCgEQyr7dWA/+J6DMBaQRcLAYqyOx2O+FmwUL4wU4MONh0fT3oocR+f34zoYfRQSA4QiueD4vXCgGHVnP5gnB48+x9K8XbM7cRTMnb7X6oYQ9Hw+69is9On+Rt23fJO+ej4rbFb6lt/ym7T/n/9n9aHSpe801FGX61VVDKpCpcv5rP78rLAIVMm8YWgAXct59ewLgcU4lsyFy4YzTKvVSt/yLd+iX/iFX9Dr169nhsflhsA47VWqcycc5AgWB8MNiPaugMwfgbs3D1g268DY+HcBUoBDrsX3Mb7IOWN3p8H1KC3yzMhut9PLly+12+30+vXrfN6NZ79YGw+afI4x+B5EIHvIk5dhMFacOYxYjGWzt5cqknFl7ARIBVzPD/elNtznyPWMACHGmIMPZ13JRiD/vA+rVcodz7NyKrcrZZ/MZQa4mCPuKUnn8ynrGyWS7DU5n+dML+vadVedTqd8vgy60LatjseTLpdu1pLVASx7igAByDxt7gF9TdPkgG4YurwXZkkyOePuLL+3nuY9bK5CUAyF2USGliWeDu4vl4s0Rq0mu+hBzvV6zfsfWJPr9ZqzhVI5bNdtN//BijOPyyyqpBnY4j0vPeIay30oLufYN78+36N0MYQwa9mL7mJrAPJ8n7lA5gCxnoXlc2SmnfTy5+ffDnaYT+bA7RNr5gE6QAh9xz6iw+6LxrEcgM54sP2e4QH0uj1drgOAdrPZ5JbdbdtmGYZIcRKO+aWsFjl1ID6OqS09beGdpHl4eMg2B5/kJfQExszNkgTieXgPX9uuWlVGvGFjvDwZOcPG+bwu8RHzzwtdyPplMops4u/6qZEE+xAhQs7ncyZCHD+5TXE9wN8wHs9WQKD4XhX/nvt77AjELwEgfgmb5xjP18KzGcgeAY7rDDLpVTnYGtbA5dmboPgaO3Hp5eH4BD7n+NTncRxSt1nPzIAd+mF4R2ccBziZDZ7l+TyzSnDnhL1jovQMUXGM0/6kIs+zICqUPYbL4Mgz5HzfSWwnTV0O3Yd8ltfnPkDyPQsYel80ByMoE5Po+wg8FepMEwK5Xq/18PAwY648WEKxcEzcC2Hzkg7uw1jJ1ngGyBlHV1oPABEOr5mG/aI8yrs5IbxuaLiPKwjGBGPMWHle2N5lqtgF1cuxyBRsNhvFMaquNvq//M7/q/a/Y1DXX/TcRGmz1qcxqLleFZugoQ7q+07D6aL1Zqt2u9ZwvWocy5p6CQuBwJIN4XfWCTnAUfR92TfG55hv5vl6veobvuHj7Cw9Cwdzw1ytVk12oF1Xzr1Zlgo4CPbsyJJFpWwUWXcAA9jBaPA3ZzZxMDh2ro8cZ9YplFIgZ2SXrN2bN2/01a9+ddagwcsRWAcvH2vbOavDswEQMOAe1CKjOEnfU7HZbHQ6nbMeScplKJ6Nulwuea9M0e+y78mzvASPkAesK89V13XO0Cx1GnCFY+R8G67N39HrcUyNOnDYAKSu63R3d6cY+xmgdwaN8kieEzlO9ioFdAAaAMpqtcplgjSVYdz39/dTk4IkS4+Pj3neCTZZC+yTB8yw313XGdtcmswwxiLf81Is7AvAEVvC+K7Xq243Gw2xNLABHDBvrBUy7wG6+wE+wz37vp+Vp9J2GDkCRDD3yBBrwnV4Ts8W8B10wtcNUL0MrtwuIy/OcHtAfzqdcsABOeA+x5noFy9e5HX1LALr4nsteIbj8Zj31i2DDcAbAVrbtrq9vc02w0Gvbx7nnjwPn/Msgdst5sP3DTqhyfNwbV4uE/g4D9KXGYOmaXKpoJe1juOYS/AhOCBB9vt9ti3YXzKwjimotkAf8CHMs+vP6XTK8+LkDwE/RwTgV6RyTIiqkhl0otVL6RynME/8nYAX4I6PdxCb9UxBimWfNQcpt22rpkr+Zr/f54YCS5JL0kwHnFhFT7HFBDHoAmtNpoaz5pz0gtiikgFfBJnqz4z8utyRmSXjjz1omiZXcnCMA+QafpbgXypVHo4HwCjYEydXIbVZL7LGEIasD/dzu0YX0LEaFC2I9iCoDSvVfVlL5soJEPTbS4E9M4MNdUzAT89yjuMoVWnfnScrvGzY9daJU/cJ+GC3Fx5ge1CVg2izBV/r9bk/KPZ//9/+sfb7fZ4kBNqNkANPd2TOfjHpTDwsHMyyCwJOCyfkgrZM23vmBuXE+KGQd3d3s98ZF0zhOI7ZWDgD4MaO7znj5w6BMXoK0hlSjKFv3kbgPEPkgQYsJiUBvFyAYWclFXYxrBS6XmP3rLGJ0qZRpUZtL41xUL+q1TeVmkFaD5XqutFz32nsO202hb3xUq3l5nvW3VkpFLswvUExzgNWlwk+72VozLcDEGf7Q5BiLHuenDlaBp7IBGvqByiSgcCwEHj78y1L7Dy4ilFKjSZKqQEGGvmnlBLDhaPwbCxyzJwxT15SeTqdcskIQR36k8bUa7tN5T4Aen92gJ4/CzLoWQaeOclfCeTcMTIPLsOAoBAksBWAlQD2er3m5/YDKtEN78DkOuNg+unpKf9tGFKLZ+rhvU0uMsbvBFMEiqtVcdB8nszo6XSYPSM62/eD6qlRAXuikJ+mqTUMfV5bnOZ6vdZ6vdHzc+kACfAmy+CBBRlKnDpyTSkPhM/5/KxhKLLqDOrp9KzVap0zbQ68cLCn0ylnqLIM1PPqAAfBTnwxH8MwaL1aqbuUjdyu2y7PngniBWBC9hi/k2Pc06/lgRty4HbEA3kPAtB3zxgiz8wLfgU77LrsWQCu7/ubuN4yI+NA1cv2uKaTY87m+vc90GOuWHtn+rkHY/LAkN+v1+vsmAwvo3NgyHedBANMo8fIJj8Zvweg7ivJeqI/yK7rG0H7suSO4NXBoJfQ8YzYcbfhzBH+EVKOMT49PenFixc5m7sMMBWkapIFDxipICHYcWLVM4tLUsAJAc9i0AGwu1xVT/ciEytNfrTyRjoh21Yn5bgfmW7GCyhmPZg/ZMcJaOywl3WiN+5fzufzrIOikxSeRUFvkRVshAcvPJNXgDB2fkJSO0lLYMPYh2HI/sB1GLvD3DMmWqM7dllm4PK6jVHjZFPI1mX9l6SqZAjdxjlx5OQ/c8p1GL9jQeYKP8n165BKnJ3o45q858S7Y1b0F5/DnPByzOP3H4Z01tmvHhQ7vbbbbWahMQA4fzeKKKs0PwhzCeYxPrA5LnxuLDFi0vwgLkm5dAIBlpQNN04uKXjQ9drp+fk8lcqcJxCH43zOCuydoGgpLb17+Kw7DsbG8xPoYHy5hn8fAfcAEYfKfDirBGPC+w4OWAfPzDVtqz5EdRqktlFoKl2HTvXU6nuz3kh10NAP6q69KqV50jiqXaUW1depSwnMUnFk0vlcDvejFbdUWj3ztxhLVyI3nG5AubZnxwogLRtvCRbS3A+iux0d8c7nyxRklc6EGGWc2jCMWq3WeY1Ty+XV5IxL2+qqKoY9yc+cfS3GtqSbuQ4Oh8CGNd7tdu/sXYGBY45TEHq2kqpal0vKUqaDJveiNBXHimOpqhJoAXIwzjC8gGGv9x6GUU0DmKSMsp8BPC9lw5nRQYi5yO1pq0rPz6cJPKZn2W559l5Nkzq+tW05WBLggF5juNMcNJMsBl0u1xyQJvKgnFcC2065zeFw0OvXr/XixYscmJSAZa3D4ZTLA30PxWrVqqpu8nNTYkdgs16XTmg4VuYcFvXt2wfd3t4qdXdr9ebtW4VQpc27Meru/l6X60W73V6n4zGXePmxB5SIYE9hcxlrlNSsUvvhuqkVJjmNiqrbVrtpTwfPN46jQl0pjqP6MW0mHsZR124qUQ7zTf0Eaw7wPDAg6M3sZ1Wn8hJFVQoaxqk0uZmYY0VVTZ3OrVFqw8yYl6V26C42zdlVD1zQLw9MlmQK34HJd/3w4NKJNuSpruusYx6k4JMySKnL5nMHem4zuJZn4DwTz4uggOudTifd3t7OnoHyIw86kR/PciG7vPzznI9FpgQw62VNheQq5UlkfghWlmX0hTyat9PGBgJg8WuQG+gf5ayUqBGM+CGh6IAHsr5Xt2kaXa4XXaZgtK6SLFV1Or+lDUH1OKpdr9RPtu727k5VUytUlbb7pNOrps1yHELQ2A8KtdL+oCqormppjKqbsv9oWU3R933uiAc+yWsyRl3Pl9TVNARVTaXj4aC+6xPx0JUzlzzQHYaS8cF/kunx/Z4eQKBDYCN0BlkmM836ODlJEIQMoSfeEASb7PgQ+YEkQxd9iwLPh1wug2X8GP6RLJUT3D4HEJ3ouB/6zrrwXMgqtgU8m/3xMKgKlcY4YdmJXFGMClNQ6jpf11N3uSj1Y1Sog4Kkukot6Yc437/zPjKdtV76RD6P3SkVLKUc1zN3zDW2xbEVMuH3RHed3HN76AkKDzY/y+tzHyB1fa+VMUqSct0/TlQqNcsYchYHR4ZAwxD5IuFMnPn1TjpuwKXSscgjbXeAXDv9O7WTvl67mVGtKoxYAoqpPW1QjKV0BoWGsXJnjrB40OaZFWfYnPXy7AGBAsEV3+fzzLPfh8+R8sWpuXLUVaWgSuMo9adebZhKlNTr9DwFHVWlUVUCTlVQFSuNwyjOX0lOSdkZJ4DbaLUqzNLp9JzngnmOUaprqe+HXPbnwQXy4sqL7PAsKCSGwoMpgiKpnLdAC2qcZZqzWlUFY0bXvCZ/PpWlcQ5OCfCTAeeclPQf8oq8J6M43zvHieuJxS8bSd3YHQ6HWWkPWVqukzb7j1NweM7G7/b2Ruv1NstJ13W6ubnRw8ODVqvVFEDtcunZ3d3djLn1LJszxTEWuUvAEqBa9hmwhwKZ9I3MBLY4/3T9NM/DMOj5OZ2nBOjpe8qnUsvrdP5PKR8AUOCsk/4j++mcIkpUxjFqtWpmZwJBvPR9nzu0eeYaw//y5ctcluG6lXRR2anu9/sc/G63O202pXseQAAb9fR0mIDSoKqq9fLlXWLK21ZVXWuz22bHtmv3GmPU/uYmbbadZO9wOGS5hzhgjIDHuq4VFbTepDr/vH8pJFm+ndZ+vd0oBk3tiVNwUreNotKZRs8Xsy11CRIAOl6y7MQNz5035g+DRqVa+Ktlk86Xi6pJHhSCOiv3qSbA6eUk6J5UMq8AIgdJEFB811l7t6Oe+fGgCLn1vTye7WAsBIQEScjjMpsDMPHvoysE2jxXuwBWHoQwfogMSbmNMj6PcjT3G551870s3tCHeaHcjHFeLpdsR9jT48BqmRFH9/u+z80OPKiPMeb9RsgIfpz5IItABrOQPGUdHVBzLc/0McfoMLorSU3bSCFotV5rjFGXczks9fj2TR5TVVXqhl5VU6tdr2ZHPIQQJpmu1K5WCkrNEbD1GiTVUW3TKFSVagvGkS8IZQJVl7kQgkKU4pjOv6ubRrtNOgC4DiV7IZXN+uhd05Rz+rDb+E0CZNbfMwmMnQDeM1BsF+CF3LBeyDwBiJd/E+T6XjuugXxgVyTN9mQRFDkhBv5D1yGL0F9sI+XTjIuX6z/3xMYjhxDU+C6wXdaNcVQ/lkB0GAZpjOq7EghS4eNJAQKq9WS74jj52lrqDR8jr2RKGRvX9eAJHWTOmZMQghSLnLBOJTlQuigjO45LHXf5uhe/O6/wcYK+qj97kPS5D5DOz88pag5hJnAov6cEpXc7bjCpzkC60XXWDeXw1K+kd8pF/CcLSiDjzDYOyA/98iBEUj5EzzM/XXeZsaY8L+V73NcdMQIPCwHb5UEMz+vsGMbPnauzoZ5hwHnipNwB+nVTdifNNewQQUMIZbOmP4sHlcw7a+sMEZ/z1D2KxsF4nBnCfL+PvSFg5O/MDQyTM628x5oxd4xjmT6GscUo8LxulAjcuJfPvaff7+5uVde13r59mzsypm44rUKoZ2VmyC+pd4wVz8Lc3N7e6u7uTq9fvxZndiWQUen+/k6Pj4+zzePpmTt99NEX9ebNmyy/OAq6xr18+VJt2+buQy6LOIKu63K2wveaMP+S3unyRakGawBbTcYU/auqanZoIECbjO/xeJwBcPSObJk7YBxPXVc5AywVh5zGm2SOvS2+pwNZJdvFd67Xq+7udu+QMMWxlPanOOfEuO+y7cKx87whBB0OBzVNkwMzwH3dNmqmeQeYQX6EKgUKAGfmBllyNpoxdV2n29tbRaX9are3t4oxzlhg7E1hGufnh3kNPOvO97AxkCTMHX9j/hkTshdjzJ93W0emDpCDrYzDmMfO9wtRkPT39vY22yAP3tj7wHxQhuSVCOgyfqGu65yJcKIDm4NNdV+EXhwOhyyvzlD7fjonQ/gMttNJCWzWMmh3v8U8snZt22abynfIvqFfPDtyxpyyud/BJPPG9whwPIjC1u33+5xxAtx65oHn5Sfr5PPKvZummZW/exCL3WGPLyBwmfUA3GJ3HDA3TaM4RnVj8Rf4f+5NUMBze9WHB/8pCz51K1yvFa17qpMHUikvd3uLrEmlnBRZmb6Wn/P5+XkWyJLdYE43m00mVmM1b7jgQQz7LllP5ozn9rMheQ4vaUVvS6fWOlc0eIdAqmDcVnjmAd1w/073S+Z7WWaOfXDiAfzkJB/r5KWhTl6T4XZZRs48I+rBTyLznguulHInQcc2PDN2HxlkHiElHH8iE2PfaRjLnmVv5oH8ozesuwdUjN/tVlPNbYf7cSdeliQ07zFGfmf98W0ut+5bvp7X5z5AYuIclNd1nZkbBM0VFiWQChvhTBGg1YWBBXaB5jvOZGEsJW/9XDb7UrpThKB6r8MOIeh4PBZha8p+oKp6t1sRYGLJWjI+HBUAEYflZw1gEHAQGBU38ii1VFoGA2iXzCM/GR/XYwweVKTnVM6cOehxJ8fcw3SxZjhWgofD4TBbq+NULsRG1+PxOGMGHSwjV8tMEfddpsudFcrsiUqZC/PNXLi8eZaR+Yf5YW68Jh+jmwzZmDfI4qi4fzoMU7Mua878Hw6HGSglI+EAn0zPixcvpj045wxqkI8CeBI7S9vWqqp0e3urX/qlX9Jq1Wi/3+fn/MpXvpLXjPXiO5nBDEHH4yk7V5yMO0zmkbXj5UGmA0r2ZLgeY1jRNUl5QzT7ksic8XnKdFKXq3LmkwfTaV010yfPaLuMMf40Vunh4WHWRdDXqapSy3cHzy9fvlTTtOqnFrsAfuQV9pH5uL29zY5dUt4b1jTN7MDRsR+0muQQ0PH4+JjlfUno4FBPzydtt1u9ePEiz7/rG3rmjKIDYUCOVAJBgArPAWh0NtltBX8HWKM7qcHHKa+BB+D4ifP5rFVTDiFc+gcAHSzxsvSL0j4CeTZWMz6+Q9kRxIU0z/qi/06mYOP4G9d0AIYP8IMysd8QFNzXyUM+F2OcAUZ/bmTcsw74WX821nm/3+fvOhvPmgM83S+7bXeg6J9br9ezTDRyCLFCQOxr4QSX2xkPKsmq8VkPzAnkHIwzRmTA92bxE3sDiG2nNX5+ftb9/f0sIHIil3XgOd2WOEFxvV5Vh3kWImOGcVRUyeT43g3uy72RszSf5fBdz1w56++AOPvgRbdJvo88MAaXVfzs8jwzZM+DaGx/Ia/m5zZ6gBhjzKXAZIo86HISG5lAf7neixcvss4xBp4Xn4zvdSIVYsrHhty7LrCO6D7+DlsC7vDgoK5qhVj2sLFmHkgTvDEn2ATsgAcc6bO9QlWSDARpToYxNp7Rq7NK1UfJGNVNaSThMkEnVd+r5aQN8s99PJjixeecsPNs+Gd9fe4DJIQII8Zi+B4aqUykM2UYEq+RBMQvr83iI7BS6d6FMKLszrbxb3cMZaN6mDk/rs8p2Sy8MyFpjKV1M8+2BOBuRLkG45Te7R6CU2Mvio+JLBKGBOPgJYFuADyjJZX+/j7nfG+1Wunp6WnGSHj6FmfE9Zxx9nVt21bH43EGlPgsgBcZwYD5eByI8zy8z+8ES8yFZ19Yb6mUIHI/jFRd1++k+gHXfd/PShC43uVy0ePjY+6e4/OdnG8yiJRVleA97bvq+163t7e5mYaXHwBSnN3DIFGDLym3vt1s1tkZeIYIUHE6Pc8Yc4KUpikH8DEv9/f3+X5+QKGDQmfcASNkpHy/CU7HAyiXX+YUsOJt9Ns2dW7zpgOMH0Yz7f2ZZzGKTlYzxwFDnT43ZKDBOsRYzrZi3viZ5lSiCxxr5Czb9VoADvKdApuTQkgBK80iIFEul4tevnyZZRHAvlqt1Fn2fJlF7i5XXSf7BtD1jlAeDHI/gA4BFQSKj8ezJqwPdjTGsk+HNURHfL8dZW5N0+QMiu8VYU08U+WBqH/fx/D8/JzOX5vmifc9Q+2Ela+DZwKdZUVmKUGEEfZrUEaEXEAosBfWCSZAwN3dXSYWmJvlWKsqdSqUEkmEbfJ7MV+AyGEY3gnC8QFc2xuZnE6nnL1aMsMeHAJOAW6ekSTrxrpj6xyEebaSYMOBHvd1gEmQ56Qm33NChvvgb5Br9NozS+7fWU++/z5fAREEiFOVusXs9/vs87BnDiYhNuiG6T6+2JhRQfOD4nmluYrqupLtc8LB/SQ+P89b3ajelKyLk31OsvJ5sibteqVo91/6TJ7BCcElZsLOYAuwqb6+7g+c7OUzvLBXnvFc3heZYu7RSyduxrFklLk+ft1tGdfhWssMEf4MzOLBE9fx+VkGkbxYj2X5nqSsRzwXOiDpHZyaO+QpaujLAdfDUPYz8kIOGOuc3H6XGOd5kBVe6ILrDDaV6/mc+Jw53nI9d3y9asseuK/1+twHSNSAO7MHc4GDW0agLogufHzWAw2+h8IgkAigs56uaHzGMwXOjqXPFsDhTP6SReJ3wEXfd2IviBtOz6I4I4Xw+PUAMq7UMH6MEUeGkfK9VTwrjB2Hs3nNsZd8wEzzOyyCsyRpLIUl9Xvz8n1WvgbH4zE/P8YSIwgQ8rVhLhykcU1kxA2IVParSWXD8tJgLtt8YiwogaHjooMtSryQy7ZtcybGMxm+JgmclIM1yWx5eU5VlTajnEUBC8ac+PX5PgEX7DoALgVdJfXuBhrnR/DC/Lx48UJt2yjGMe9BArTz8iwC60jDAlgh9I/9OQBd5tL3YnjJK+sJmDufz7PSI54PvTsej7N2z0neUjYIcgOAkvQ47elB7hlvuncJrpdrCAhkfDCfwzBmmeWwSjJ4fd/r5maXQQHrvt1udTgc1barDCIB5Xx2WTbiQUm7Liy9Z252u60OT4dZhpx9JqmZxCEDOXRovV5riGPOJt7c3Oj+/j4DAQcGkD7MF/eB3HIgh/1hbIAjylW87bGXdHBtb9NMMOyOnLGlowgKi833HVQ/Pz/PGsTwfWeFPQBHpzzgZz6x3YBh5AB7Dgjgu3y/6zp98sknWS74DPPj5TvYEbInjBe7EELZqI7eIJ9k+0IIWefu7u5mJBp2nsDOzyLzJgsOpJYNdngGsuBv376dEUGScoB5uVyyHiKvTuwswZuTTein23xsH/KBbniQBlkHYebr5lkd7IoTnm7n+77X8/N5FljxDOAQ1reU8dYZsIJ3rtdrLiWuwrwbKM/edZ26vlcM8yMxPHvGfPJvxtg0tZq66BUkBT6q69KRBARvzOc4VfY5kYBtdJ1+X4bE5ZvndTvhxIQHSWAAJzQISr1Z0JIY4DrIOeTf0iZAIuz3+9n5Tk6eOCnDWjqZ5rqOzCH/XlbmwTzryfOVSp+gMPkavofsID/MlesCc80zM55xHNU2rfphjieRT56NdXe/xTzzzOCYEIJiXwh1yBHk1AND7uE21+fMcbeTzk6Ue/neMH72s5A+9wFS3TQZDGN0HShhmCkzQxh9oyVGQZpPtINYZ5u4Zl3X+ZRr3pPKhlZnF10gSslHAQUIBILobBKvsjmtBFPuKHhOAADPwZjcUXuWpmmavF9reQq3Bzo8B9fGmcHgSsqOxhUXZXKlzKUBkxFgDqRibD1Y9BdGgOfB4Xp6mgDLSzRYP/8dEO5K5wan68pZRn7/pTHn8wRUDmyQRX73gxId3NV1nQ007Dty5k6PALjrUmkNDDFGEdASY5KP169fTyD6MCuHHMdSx45zkMo5Rcgfa1rXQddrmgs/N+R8Pmu/v8kZJ56Fezw+PqqqiiEDDLIOkjIjTWCWgp7re7M+Tig4K+fsL8/JtZkXJwm4N9ksAKnvR0nXiLpei73wE89pDuKZAAkQP2q1ajOwY+1oPco8xBizDiWdIkDZzUokn59Pulye32E5z+fzBESbvMcpBVM3enx8zAy/Pz/gYbvdqlnNS6eQhcv5rA8++CBn0rBdkAceiLJ/rW2To5WUyRbAPiSKb6Yfx3GWRXWQyFgB6XVd5w6LlAXyvNhJgkAAlgM/ngGggC3zeydA16ltSjMdfAvZHCcIPLvuwApbyJwRUGPz3K+gr+v1OpdX4m8ygLEqB67t48amLtlw9ud55oB5xe45meAEIXKHrcLHIONeMoXdICBHvj0oXJb7YntYi2EYMnHmcsYaemc65phgEpvhz5TZccvGQM4g/16h4PeSlBsYsB5gA7Lk7oeYA3y7rwNrxFixYYBFAh3sMhlm5g0fT1dRxnh7e5vmV0H9MORmMx7cVdXU6CiWMxM9oHHCimBgu92qDqmrpLP5/PTAh99zEF/XinrXxrpvBnN50M37Dp7BBo7PXB+cuGBsBPYEE1wDmXK/jKwzBsgffAp+xMkWxuAEAfK7tF/4NyeoWRPHZzyTZ1ncRjBPvEIICu+5L2PzQNiDLmw79/QsXKhLlst9LGvhuAI7yYu591K+NM6S9fHAz2XI5RGd8TV1m+VkpicfXF5CCLqcC/n6tV6f+wCpu3Ya1qOGYTq9N7KZtjBP3mEjKWGjEFLHlfS91CkOYIHyeWbJFc7ZDRyVOxY3KIAivsdCpntUihEhHFXXjfo+quuu8r042dCZQGDccQqexVkGFyiPgw0YF2eTpHTmAmDegTmKhJB7vToOh4wLc3A6nTKLyvwQwAHGAcQ+X3SqS6+opmF/Vfq9beetcNPaFrbIjY8bBYy/s0mwgzhR1sjZJHeaMLCezvfSBIxx26auX8iTp8QxDAShlDCNYyqvxDgCcFNb5qvevn2rDz/8cNadZhh63d7eabvd6vHxSafTUddrl3QhpDOIQl3r2ne6ubvV/vZW3fWqoDlwcwMGuCCAZE/LGKXNbquqrnV7f6enpyc9HY96+/aNYgy6v7/PTuPt27fGsLVqW85ZYf/ZqgDqvp/kPWq93mq/rycAt8nOhDl2Zg4ddJYYp8nzAFac6WPd3DE7s06Wz9nAzYaT6VML9r4/a7Vqc9aGltpt2+bDWFMmrdNqRVamdMdL9uSs9XqjqgrT+UArnc/l8FsAlcsqIC/ZoE7DcFZVlXNAAOzb7VYPDw/a7/fvdDPiyIDdbqfT80nn6yUDX/ahobfYFD9PgnsQKJAluLlJLcjHWMoeACtPT0+z87EAZw4OPGPgQGYcRylGdZdr6q41DFo1rZ5PJ8VhVNOutN3fJKDQ9boau386naQmapDUqXQCDCEoxKjuelXbNGrrtGfv+XjS4+Ojouk4Z6kg28iKZ6AkzQAULC0NTtAp1gnZxS951pVrUgWxXq9nmU3kFz+FzCPvywYH2CVn2AlEeIUQsj/xc4Cwm9zDCQzXOe5BpjyaDHhmhfv7XhjWHlnxMeHfHEDxk+DYyyWZm2WwStbP/RZ2GDnk3wRq6I0DMIg37LlXEvhcPF/OUpxKvBRVqWR2kRvmlIBzaasA7rzne9ZY28vlos16o6aqZsRN9ottmzNIXkrM/ZgD5CUz/MOoru9UN7UqpS6TCkFjjBrGFJQRdHigJJV1Ym2d6HBMMY7jTA6QS6/MQJc8CCPYdV3ETnvg46Q1z+eyhWyyzsyrX88zFo4HXQaQcw9OsA/gBtbcAxBpXqLJ8y4z18xlGceopprv6+FvjBN9wr5cLhellqSVNI6qm1oxaDrioFFUVFOXsnTWyv0Gsuc4wYksfgfjjHHQECFfxtRSfCx40jP8zKMHRy6n6AbP5TaJuXTy6rO+vr6m4JL++T//5/ojf+SP6Etf+pJCCPqH//Afzv4eY9Rf/at/VV/60pe03W71e3/v79V/+A//YfaZy+WiP/fn/pw+/PBD7fd7fc/3fI9+/ud/fvaZN2/e6Pu///t1f3+v+/t7ff/3f39mpb+eV4ypZXNiArr83zCkMo/j8ajHx8fZeT3p76nNL/sI2OSMY0MRpJK5geHZ7/e6vb2dsZfuJHA0bdvOMgK++EmgqMtNB2kOQ6/VqtV6nVoh393d5Xt4xgfg5Gnap6enXF7QdV0uJaIMhcwFwR0lP86y4GQIoGhosATSPCcG5/b2Ngc93IuAY7vd5q5pXuKDUfaSMcoGuu6qGEe1LV2FenXddQKIlaQ4gRxJShvX+76UmJEuXyr7zc1NNiYYq9VqlTuNUeKyXq91c5MyInR02263s2wUrL3LhjMbACMAJwbag0HGQ5kLii7NT7x/fn7WbrfTl770pTxPgIy6bvT8fNann77WMAza7dL9FCpVdaVQVbq9u9VqvU7nbKxa7W+S/NLCmwDEgwIMNd3dACkKQUMc9XQ46O3Dg9abtb7lf/qf9OEXPszfAaDf399npi3pVqvUqjsZzBDSWQkpyGjUNJw/Uauum2zsXP5wMDi0XIc/AXw/b4N59O496DTP65lHdN+DWDIVHMSagpHVJAsh6/XpdJrpWgmuRnVdajm/XqfW9MfjSc/PZ71581aPj496ejootfEv98bZUz4qSa9efaDNZqtxjHkc63XSz5ubW202m1ziyPedFcex7ff7PL7tdpdLPDmMku+Ow5hlGIfP3PnBh9icTBo15eDhTz/9NDtx7I6zwqwdgNwBMTasbVptVmut2lbrVTofpqlrffDyleqqUne96vD0lM5tWq+13+203WxUV5Ve3N8rSFqvVlKMU+viKEWlc5pCOj7g9aev9ckv/7KeHh+13Wz04YcfZvvKQd6cZ3W5XPT27dsZq8yaewaZ+WCuCDarCcw6qwv4cBvKXlRKGSG0kAcylvgVZNUzNsj88XjM4/XgDD3xQAt7jV3woICDSocpY+E2zWUB/fSAkLJhNolji7kepIZnBiRlW8vYsTP4C/epzAt6QMYF+4188dweoPt8SvO9HOfzOes4LcRPp5Oen5/18PCg4/GY5eJyueRW9YfTUdeu0+n5WV3fqzWWnTHiIzzj5U1UPGuEHmOvbm9vs92iooO/VVWlpm1yxvbm5mZWys1eUq8qgeAbxkGhqvL5TClAki7Xi87ny6wRgtvVvisHi9PUiWdwQoTuqIwDDOUYhH3DyCedSqWSOfHAm/swHwUjlkZLyDGAH6zCdT3IcOCPDPseOu7tJCognfnHvjlu8Awi2R98kZPVvDw4Sc9V9n0xZh+LZy29uqFtVxrjqFFRwzhOeGClzbYcVeAyx3phn7HRnhHy/5aZ8kt3lULIstMNvbq+T2fS2bOj18g942W+CJyX68bcQho6WfVZX193Bul4POrbv/3b9Sf/5J/UH/tjf+ydv//oj/6o/ubf/Jv6sR/7MX3bt32b/vpf/+v6g3/wD+o//af/lM8q+MEf/EH9+I//uP7+3//7+uCDD/RDP/RD+u7v/m799E//dBbc7/u+79PP//zP6x//438sSfozf+bP6Pu///v14z/+41/XeJ1ZgD1JE1zKy3zTeDKwxWj4HpPVqlWMYz7bw9N5CAUCQj2yf87LkhAwBMBBHQCAa/N9nAmgzZkLBzswm3TlApTDMNMxymtQEXyP+nGkCCEChxHAYHJtxgXY4b4+NpQ8lQQ9zz6L4cKRe+qZz5DhovTBgZ1UAkQCGxSraVZarcqBfCgg33ejTZ2/G1aenSwUa3Q4HLLDB3h6uRY/uVcpvSpnPNAxDgcGSOz7Ph+06AwS80cGwFl6Or8smRcMRWYFpzHAkrGuu91OVQjarEqXNJdbjDVOlCxp13Xa7rYaxtJO8+bmJm/mdkdAqRigiDG4PCPvgBqpnGmF7IYQ8rk+ziSyjsjOMgvha+RBLfd1hhJQ67rgLYuxK86GAjh5LvR7HMfcypsx9n2v+/t7VVWVy3IYH40PnIXGRmFDhmHIG/ZZk+PxmINuAmbXF/YlScpzwByVfRBpf1M/Dno6HPTq1avM/FMqVVUhH6GAXDEGOqSx0RydOZ1OGmKUQnK2H374oSTlvSkuj6w/euLZaeSB7LOTPzwjsuMBIeVKkvJ+tvexttwP3aYMrWlS04f9fq+PPvooly35fRy4kW1x2ceh47SRJS8JdlAqabYvL8aY7wtgSP6pZFJonMK1fXzYPOwyAQEBA8w/r+UcYb/Yw4bdXoIQDyzQH2T/+fl5xvYvmyY5ScbzYaN5Ri8rwm8wBicdvRwPv8y9sKXemWxZ1sMaMG8FD8xLEFlD96Fc1zNu1+tVVdtk4O+Eo1eUOLFKG37Wg/Fgr1gjz1wQBPddpxA1CyJZs+F81ma3nc2jg34PUJEBfnoGXbLDh6vUSY2/MU5JGqPU2Pqwro5/8IFc0zMVnnFxjAIewt4xxiUGqap5AxF8IrjBS/OYA/dfyDJywzMjs9g4z8i6fwOb8cxc1301tsHJIR8zfsn1wef4ermqDmVLCbYMueI5mTd8XdeXcmA6+oL1/Dm9WmNJmrq++nryfYgkdImx8x2fS/83tgRs7djM9doxLdh/GSx+Pa8Qv95v+JdD0D/4B/9Af/SP/tF88y996Uv6wR/8Qf3lv/yXJSWl/OIXv6gf+ZEf0Q/8wA/o4eFBX/jCF/R3/+7f1R//439ckvTf/tt/0zd+4zfqH/2jf6Tv+q7v0s/8zM/oN/2m36Sf+qmf0nd8x3dIkn7qp35K3/md36n/+B//o37Db/gN74wFdpbX4+OjvvEbv1H/+//2T3INu6f/2nYO7pzFjLEsjJdXJeNfSqFYII9sm6bJqWxaA2MkcewImF/DmRRXWi9JQ5iSsNUzYfNmDlWlGaj19eJ+KCGGycEjJXHuAHwDKA4QYfS5ciOEY4B1pLMQAu0O14MylAnA6JkBNyawPs/Pz7kbEkqKcYDdb9vCHHEPHAZAk7Vxw49yAtYYM3KEw/dsVN/32RAC1hzwwWxyxg3r62wOWaHSeKOf1cQjdxhUQAaORJK+/OUvz0ruPM3dD4Pqdr7nDFlZtSsFc7QAieW+Bj7Pv5tVo+vUpAEgD/i+nq86P5/18uXL2UZOL7dwBwRQQP5wGM5Q8T2cBQ4XHUFfHPQwb0vD7cCJ+QBM08GPMSEzDsiZVx+HM+DYmaUOcj2ej+8gQwS/5/NZH3/8sY7Ho7785S/r5cuXOfPFc+L8np+fdXNzMzsjDdvEfGKzvC6cdUSGx3FUu06d7LgXYzoej9I4qqlLnbg7ecZN5hh7cDwetb+91W6/y3aash7WgtJNnk0qBAXzCsjLNm6Yl1/wHewnoP9yueTgzZl3bLDLHa/9fp/nxAkhZAsdX5ZnOplEYMkzxRhzqSJjwfGTecFHAISwnwS16D46CQFDII484P8cpFdVlTO/TnY46ENWvIQJmY8xzroHIuPYIieWmJOlXmIDWC8PTBm7B4nIE3rEuuI38dPYJObKAT73pb3zEmzy8nkmo3a5XGb2HpDn/gAZkZT3p3rwlIPlKqiq65y5evv2bQ7gyRqRTcAPsYa+0Z15cjLVxxRjVBWC6lBlWcN3V4kllqpSgul2wAk+D/KcwGLMPPP1etWqLg0CfCwhBMUq2QieDblDLh1HSJoFMk5yLf0FGMWJSXCHBxIe9MZYuih6NoVAB0KWlwei+ADW2XWfcXFfx4uOdXwu/bl4dnSIeWfNWB/u4cFG27bTobDdzE9CNnBd5JQxxBhVNbUG03fu5U06sAmegfPglfGzjj63ntV1DIfueBATxvkeNfebPOvycGSXV3SN9XOfcD6f9Qf/1z+gh4eHWWn4+17/Q/cg/dzP/Zy+8pWv6A/9oT+U31uv1/o9v+f36Cd/8if1Az/wA/rpn/5pdV03+8yXvvQl/Zbf8lv0kz/5k/qu7/ou/ct/+S91f3+fgyNJ+l2/63fp/v5eP/mTP/neAOlv/I2/ob/21/7aO+8zyUw0Ctt1YdbxjHruZAzLYX8ERrACfX+dRbDOLjj7QBkEDoOxoHwEMJwVBKMuKbej7roul2LhtHHgOIkl0EwCP86AMqwVCr/b7bLALg0HgrVkVF++fCmpsP8wtnwfYUXRKQ/zzIc7W2cxAB9dlzrf+KbXJVuAsZQKQ0lA6vPBuqcywKDz+aqnp6f8OeaSBh6uwNnQTC9S4mzIxAl78wYPnACQgDwUlTlGL5hDjDzs3n6/193d3UxuuJ8DGQwVMoWTQB4/+uij7DwxiBij9WqlMajUqVtbZsWotm4ya+mBEHLLHCLDgLymLaw+7DAgDrlBzhkPY/MN0b6ZuJAabQajrBWd0Jx1xJF5+ZiDBw8qMKju9MlMILfelAG5e35+zsAZAgSn6fPMePyZsA0AdXTbGTXGiQzs93s9Pj4qhKBv+IZvyPOLbSOrE2PMJW/Mt88xGSvu6wDSM8mwh0Nf9hLhMFnrOI4KsdiYvk/ni93e3magRzkvzU5S2dFJ2902A2bGCCGA3WNsyCBzjg3x9sa1tTL2QAabCFsPYHKm3IkXAkYHHs5iI0c4ZtbdiR4HKwRojGUJ4B2ok0kGxDN/ZOE8yMfukMVBtrgXLYcB1Mw1NoLAFRDnjDvyyJyULHzKarKHjnFI84CCABfbjw0EsCKngFPug/3DV0DIOSvvOkLXz2WA4mvuARjy4rYBP+B64MCSsXMPvu/XwJ54qSFzfnt7m/3kzH9VQd20/pQWDsOQCY2np6c8N657yJkHre4rwTncK8a0jy5W8/bQh8MhzW9T63KeV3B4VtDvSTZU0ix7iM7gm8geOUGErPT9IE3g2UldB7nIv8+5ZxCWRAwBO4E64J4gp6qq2TOhs3wO2fYg0BsjMcfYPtYTAsbLydBt/y7P5Rlg5gd9czzpJYDch+f14AjZ8OCh73vVVSErsF0uS742kIMxRsUg1Zpn3LGN/j3mjfewU9g05tztI41F+A56Ao5d2msN85bg6CLPjyz49ZhntyeMlXlw8uazvP6HBkhf+cpXJElf/OIXZ+9/8Ytf1H/9r/81f2a1WmXA7Z/h+1/5ylf00UcfvXP9jz76KH9m+forf+Wv6C/8hb+QfyeDtGTWChNTBNAj5iSsaQIB+RKs4HxB/Ltt22Zn546BUrq2La2Z+77PB+0hWCzoarXS7e1tDqy8ZrakfXu1bTW7J8FZUvhhdio8QkuWQZqf+0TWC4X14IX/YF9h2zC0CB2GjeAL58s9AJpE8AgqAU6MUa9evZploWDYGZOzpl7yslqtdDgcZs8llU4vqelGYds44d7L12BY3DBxHd9HxHM66+WfDSFkltoNGnPkxpgAgutXVTq8EQPjcsm1YUkBF57B4D7Iwmaz0eFwmJVasV51XauaMkgAMEDMMAxSXQ6RfR84Zp48gN1uthpVWFic6Ha71fV81TgkcHZzc5NlGcfB3Hv2YVlS4llPNsYz397xzQPkQoh0WWd3u51evHgx6zBJIOlZHA+2WTOCIQfL6LE/B/XonrV0uYJhQ7+W2TrkhvlzR4ldIBhmvMgQ9gaHDGDlbw60cTTYCnQ6xrQnYRhHhbq8R2DS9700plPbnX1+9epVtkv+HAQDq9VKzTrp8SeffJIBsYMcHKpnRJFr9vg4219XlUIswT6ZFq/ZZ+zINHPOT4ICL29ysDUMaU8NzD5zvmwNvV6v89ixWVIKcNFh1g9QimzzWebY5QGSoWmadyoTuL6DZ2ek+a4DTnwYtnRpNxlHVZVsdowxn6ElKeuMVAITwB4kn+8fQa/dDzNPyCL2kO9BRjAuyADP0rI+HiQQaGNn0WPISHwzYJbrMUeshWelCRZpuEJWcGlDvHnD0pYPw6CoUvrL/EHKIKtkah0Eetk56+7jxY/wAhuMY9S1v84YdvBHVNkfx3iofvCKBn53f+RZJge7YSI9PTtNUJB+FMKUtcFWYocYE/ac53Pbhf+j3JTPe2aPtWM9lwRr9oVV6ULs2Qb+7nOEz/S9zG6bnTRlvFxbmjd3cNDuPnpJaPI9npuyO/fF+TshSGPMGM59ogd7Ph5JufSZdeVe6JuTB/x7eW3sLTpb1r0Ehfz0bQbL8dV1rTiWboRc41fKOvId/6zjV+QgxqjTczkI/Gu9/r/SxW4ZoXkG4Fd6LT/zvs//966zXq9n5Ue8dvud1qv1TLn7vlNVFceXQaEw8IU1Y0HS96XUJa1kFzxgQsAdOJNFcDYb44ziIZA8g5f1kX1wQJ2cT5ojTqP3fTySchCCYPrJzRgcgJEHdAgWxgoHgTNxw8x1y96tkh7+9NNPZ8yhVJRis9noeDzOmBeYZphtADtZOGqEd7vdrOU433Oj5QaQ7202ycETwPHssHaMg3kjqKiqSg8PD+9kYrg+cpVZ9QlYekke8oyMnE6nWUchgB3ZOS/xk5SDZUAfQRHy7hlM5hmZurm5yeVInvEa46ixf7cDjrNovknX2Saeh3kjO9CPvRRKaRPydj6fNfajFAuAcpYdcMe+ibu7u3fKetAf9s/FWEqRJM2CDeaOz9V1KUFlDh4eHrJ8M3cw8ksji37gkNl4fXNzo/1+n+XRWbb37fdwZhqbQqAIePJMFuABOSXAqOs6AxxAkL/odIj+QNIgwwA8qdT4L1su52xd32mIpYQYnWiaRkPXqa5KwE0w/vDwoO12q81mo/1+r9evX8/ud3N3p8v1ktcdGfDxkFEEPLE+gC70NIMilYN6vQzOMys8n2dt0R/sawGVYwZtyBSEGbrY933eGF5V1YyUYq09i7FkmLHZ2BrWyuXR542g4fb2NttRZGxJviwZVJ7Xs1nYb38x3w6AkF+em838h8MhP6sH6Myjz7UHIIyJv3MPgJiXIjrITscBVNl/ck0HolLpyuXkAePygMwJDA9EeE7ui665ni7BmDP5ns3g/l5yFmPUoFJyyFrzdy8J4774V2yQZ68cqDPHTiqR6cWmd12nL37xi8nn15X2q6J7y/IubBJr4ZUu/N1BbJKD0iGY98EwY1BqgqLip7zKxkEtJBlj9uwSfkCaV1Y4GYwOewDia4zceECCjjgeJOBmjhkDeo8cIwuMC1l0u4RsePaeuXcizgM1nmW5Jn5f5q5pGg39oKGfnxXksrkkd3PQEqTe/IyTZXzeZd+DN66LvBLwe8ZtSVY58c89uMaqbnLGGvLRq1ec9HW593lajtOzlJ/19T80QPr4448lpQzQN3zDN+T3v/rVr+as0scff6zr9ao3b97Mskhf/epX9bt/9+/On/mlX/qld67/y7/8y+9kp77W6/B0UL+Zs7MI68PDg9p23m2j70vJmTNWSbAvqqpaIfhGuX5yZFdJMTtuLzWgHpw6cyJ/77jDQs5LkFp13aBxjKrrdO7L9dppvV6paarJcMIw12qaSm1basgZN4wnARpGFoF15oPP8X0H/kvgLmkm7M6goSRuBB2EYwCdKcRQpmdca7/fTfPRa7PZKsZRVVXrxYuXurm5nZ5BmbE8Hk9TJ7Covh+ntaVDWqlJxajDOKa5bmbtYD0L4eN1xfcsG3OBI8ago5AelBJQsD8BcAAw8OABR8v3GBvgCUAPa8Mce22+B0C+dnWVziKIw6CxH1J9eJSqqVzJz7fx9XbHDnN6uVy03qzzZ4ZhUNu0CjEoxKA4lj0YODgMNJkuDPzhcMiMn5c2+r4T5sn3BUlzB4vBJL3vMo9jYTyScrANsHGmzPWUcQCY0WvuuSwZZC2c+QI0ImfYBe6LrPo+BuQCp4P8OuMJ0CNLii0D8HmmDTIHGUMvuq7T4XBIzS8mRn+9WkkhqlJQVFBTVRqrStdhGsM4arPbKoag1Wat/TYdWPv4+Jj1gMwKhwmzpwObEkJQlXrNarVeq64b1Qpq62nNJ9lKbbwbhVCpvyaQ2/Vddq7Ipu+vodPZMvCG5ee5WTfPIGCPvYRnvV7nc2bIeiBXNHEg+8J9yCz7nDuJ4Nlk11/sUNM0+awlbKyXjhBse+YXwEDWz7vjeYaHZ+QZfN4AWexnotseHfWcEPEsBrqG7LssMk50HBlAj5BnvoMfomzU/ZEzxOiUZ/F4XsaEnjKmZZDiIBaSCXDsDDdj9ud3oMw9GI+DYDp11XWtbih7pwelLqBc0wMD5NFBLddzHeKZctlSVSl14m00KqaziFKSQbHvVZmcMK+sOTZ+qTOenZ35lDrtY+m6Xq2iNCQf0w+DQlVKxZkLD1CWQSf7sxw/Mf9UPXgFBTbOfYRnh/BLntlzktzJbj9w1/Hg+0hP8BR66XuPXFbARx7oOMHl2IjPvO+n668H9jxnx560cVCIoxSC9rtyltwoKVZB175XCKnL8zCk0kcfrxOTLnuMGbljHZxI9IydY0wCbSfjHaOMY2r3Dd7iGv5ZbK7bFdbQ55zxYEf+33n9Dw2Qvvmbv1kff/yxfuInfkK//bf/dklJKP7ZP/tn+pEf+RFJ0u/4Hb9DbdvqJ37iJ/S93/u9kqRf/MVf1L//9/9eP/qjPypJ+s7v/E49PDzoX//rf63f+Tt/pyTpX/2rf6WHh4ccRH3WFyVrRLbU0SKIgPHLpWxMlkrnNGelUtve1M43galLXrwEJktaFsXFmMO40RqbDAoAmfINAotUQtUqtetNpUqp3ed+UuYwOdVqChJKhzkibIQZwcIA4YwZj5fd4fjcsWLIJGXF4G/cDyF3Z4OSwEg4yOfsHDdmZIFCqKeg6qrVaq31epOzLAA8gEsIIe8t2m53MwObWiMHPT+fc0DqDphAg2cFmOIAMKawxM5yA+wc7Dpjw/tuKGHRAHEYfcCMg2IC23Ec833RJ8aKYXBndjqdZs+IoQFg4BSQu6gpg9VfCsNlWVN/Dnc6sJp8TpKqUOWTxNu21ePDYzL+ljlCdlzmyJx99atfzQHq8XjMwR9zAqjmfd8E6oCFvznbTIDKPZE3/s2+CKkwT86Mu4Fd7nsgI8M6ME7WmjnjugTGMGQEmL53a7nWPmYPiNBXDkjFkWPnPKDm3k6YrFYrPT09zbLI7HshQG/qcgBrHEcFSZfzRf04qJ+AO2Vcq/VaUeksFGfm67rWr/21vzbZjHGQFiVZ6Ml2u1Vnm60zkJnkwHVqjH3aS7cgdli7GOPsEGCyJR6s4Uyd5HCAjTwxj6xbjDGX9dJhDttB6Sd2HMfN+66bjBHZdCCOfcCeu3/ius5Ee5mVgz3+5lldvst+OGSNck7WBpl2YElzCYK/5TMxToCkZ1c8u+Egh3VB/vy6jIfSST6PDnjGgVJAXwPmAZ/sjLpn25xsQWa8TNmvxwtd9PJl5sqBK3JCCWmeMyPCuG9UqZ5gfpZ+hZ8eECxfiWwsbd1jjBr6ksnu+mveH8j1+CyfZ72w68gqhJYHDl410bSNxmnOM0BWCZJ9Pby82kls7CIEkZfCSqX8C30kI8FcYs+4nu/R8oDQ5dfJamy6B9eMD38LpuR6Xs7qWIrgzbOQzFlVlYNhPWhzEo/n9Qol3meN3K/Uda1mmuOqqnScgkzk3H170zSqm1LyR9aG6yLj+G3XSS+9w3a4LfbAh2fweUd+HM+EkJqKuM8l8GSNPOhZ9gTg+anKcRvwK+nKr/T6ugOkw+Gg//yf/3P+/ed+7uf0b//tv9WrV6/0637dr9MP/uAP6od/+If1rd/6rfrWb/1W/fAP/7B2u52+7/u+T1I6lf5P/ak/pR/6oR/SBx98oFevXukv/sW/qN/6W3+r/sAf+AOSpN/4G3+j/vAf/sP603/6T+vv/J2/Iym1+f7u7/7u9zZo+O+9HOijJAgJTIsvjNcOu1AjzEw8ZV0oaV03Wq9T8EAbYGe/vXuSd50BINPljaxT2kewUlXV+T0vM7tcnrNBRmmcPcdpwyR7IIOgL5lWNwAYeg+kYG0oqWNeGFsIITMvMKXOHNLalXtRZ817AMO+77Tb7XOA58bPDQuKcX9/P7uXMyA86+VyyeeVsL4eCDrz5rXpvi/A5cRBnVTABPeFJfPPOEDGWVLvnZ67nxllBz4w0O5MMLwwr0sH4wGvO1aeAfn2FsmUk8DWeR2zs1YOqjCmj4+PWQ7cqWM0kV/mgfnhjC4yYhg+gnLGwd6a7ITNcXE9jDRrhJ4jP/zOy8GAlxE547UMvigh4vkJrrxUChlYrVaz88V4dvZBPDw8zECld9ODLccpMT6ePcaoN2/eaLPZ6O7uLoMXnof7nU4n3d3dzRwzugtAAZBhOxxgAFDQI/5W140UyjkTyFzbthqnMg/mYrfbZaDJC3niPtdrOui1NxlyB+wZByewnMVF1/ibM5U8L5lqJw0cDBD8I09eRsT1yPZ59sj3PwGUHMQid9wXPaIMGz+B7lRVldvFL8EwsogNcwYbeXObxE8PCgAcMObYumU2iTWjgYCTCS43rBMAjGtgSx2YcA0HXV4mhx92goK5YS49e7UkjLiWBxmeacDWYxcg9FhT13knHtznLkE2fti/iw/xscK2U5JJ0IeN2EyVE14Szdw6+FvaSCdPKH13omcZLCRScTuzPS6jyIJ/T9I7+1+XNhGZ9PlD1j3gxx9wTy8TnIHlurSgx68+Pj5m7OUYDdnhGfg+GNDl0EH6+3yd23xsFWQBsoQtxge6ffKgz4NaJwyQTdaJ390++7ryQoaXmUtsHnqLHXLc5YHV+wJtDzCZA+SeueL7bj/4nXE4yeHYwYk798eZCFRQtbiGj9vLj9F1ZAHc7uPGdrs9+ayvrztA+jf/5t/o9/2+35d/pzHCn/gTf0I/9mM/pr/0l/6Snp+f9Wf/7J/Vmzdv9B3f8R36J//kn+QzkCTpb/2tv6WmafS93/u9en5+1u///b9fP/ZjPzZjhv7e3/t7+vN//s/nbnff8z3fo7/9t//21ztctaukLBgfACagHgfnTC8Oi03cXtKy3W5ngAWntt1udHt7k7sv8T0AwzAMufuPp2Sl0iUNw1n64EfFqMw+Ho/HfL++H0RJnwuhND8vBmfn4AZjA3tIpzwU09tJU9ZAsMIz48CW8+fAlzki6Hjx4kU2+pxBguPA8aVxNMIeNE2TmV+c0rK0YxgGvXz5Up9++ums7I3ro5Bt2+ZyK3c+Xi6HM2TNWRMCMjfEGH+ppLfJjmGcHaBgXJdBOeDKy2UwBpJmbTEZD87GHb+DFTcsGArGyDNgHB2Y+KG0yBrBi2fNfM6QI6kYbmfm3TC6jjNHu90uA32u4SUilLigTy7rPAcOgW5XOEn0FkfswbnLpu/RYS7cqQCKqqrKe3zcITq76SDNGcbr9ar7+/vZeJx59VbiACDfO8XLyQLafXtTl8fHxxyAAcSYO5pb4HSRWWSKElQCO2TSgxDO5Njstplx3+12uSyTAGmc9MN13EkngjH0erVapUNbF7YHmYBI8iwLh/9y/hdr7oEmgJB9C8w3MuCy6SViUinBLEFhyUAwL07A/fIv//IsM+Vlk4APbCy2iTnh7zwD8oXNoy03z+7gED1HRvkPucPeO1NOEOX7tDzrhyz6fDug4n4AQs9QefbE7Y2DohjLHkkPohy0okd+vWUg5VkPnpG1weezlnwHEIWeO+nk7D32we2e+yKAmdtbbAWBMMEOssJ8OekgKTP3/lwOTB2QM0+M20kp/Ba+g2vFGLMMua1G1zwIZb4IoJADdAD/SsYOvd/tdrN9yX7GJEERfguZ8TIuSB6eB1lizVkD39vnJI7LHLYS2eK7S9uNLfIgAxngb+5nXO/5fRmAcw3mlfvyu5MK6LgHYqwJZdTu+9yWLjMkrBtr7RVFrmNuz7geL95nDZeBK/fDvvp10EXIOebNyyOxAYzT7QVjXDelLTr3crvoJKrrhRMKjJM1RO+Op6M+6+v/o3OQ/s/8enx81P39vX7iH/1T3d/fz8CQL4YHMQ7qATZN0+SzOgicWBCEIS30qNVqftqylBbnzZs3GeSzwAhMXZcTq5dGP4RSVw47jaA0TZVZOGclEIrn5+fcScRLq3huZwvZCySVs1mYD9hl76IEkHSmEaMp6Z39OYwZ0OKsOgYMZi3NTamLZ44JhLyTGfMMQKPbkpdXUVbngNDZW4z2kmF1lhWZYfweHHvgOAzlTAifQwyFs33I2s3NTb4vBh65cHDqBo7n8kwXgIeXOxNnYGD4PDAGMPqzA94wbt5m1x28P49UjKbXVTNmdwr8pEU33zudTvr00091f3+v3W6XS704kDfJfknTA9qZA2fsfDMx6+36sGT5WFtn2VljiA8PunkmD2gIQh3cOABG9x2EopOsKXODvhO0+vqj9x588owOcpBZgBE2wh0IY0cOlowmOs81MxiuKzXTd8hCsg5xGBTH0r2MZxzHUXXbaGW6BLiJMWrVtBr60hEOu00mrKqqWWMBD0i5FyXErKETIzy7s8XoLmN3VtszsoyD7yHvMUa9fv0622GCkaVtdrbZGxkgNy5vzA22B58A2AY4OZMMycIhj6wtAQA6y78ZD8+MbLEXE/vvZAcEjesb9hzZ8DIoz7A4ObMEOqzTcpxu1wh80Rmu7QHEr2RLHfD635yk4DP4RvSeygleyIIDfJc31wNfT7fBw1CaAznj33WdVJcMMH9zm+tBsVSyPdgnD0bdjjmILDiiyT5uGIZMfjCP+/0+V5AQ6HjQ4JilrutZS3rvZMb4nZxFnz0QZiuBywS2g2u53cXW4sNZB2yAn1vFvLutd5nAtzmx6ADdA1J0AXzkWbinp6dMUHk2y3WGZ1kGYFQguT32LBGf5+XzgT1nvK4ny2AE/7N8Jg8Cl0Qu30dmHW/wcqzhcod+IbP8HdmmzDTG1Bl11bQzPXIfgny5P3T8ucQg/I31fnh80O//rv/l//fnIP2f8VXVtvmrnu+rcOYe5WIyr9fUDppMh1RAJ4yKG9i6LmUP3Afl/eZv/ma9fft2VmfuwooSSAWgp3GURgsOpBJrM6/xdxYZp7Df7/N7/Af70ratXr9+nQUUYyWV2l5p3l0F5eEZMVAOHpyNcRaFjZaA8/eV2pT5DxpHzYAGTAlguW3bDBYADlIpDwE0AabISuz3+xnocvAg6Z1n9GwFCusZAjZN8zcCDj7vrCQGY7vdzgwlsuWBAsYLp+KywZxizL2UD6PB2iCLnq1yUMl9kFUHLiGU07jRF88CuWPGkCLTDhTcCDq7S8c+gADf/fDDDzMAZC6QMT7HMzFnTiQAuD2Vz/eYN2+4sQzgPcjCSbqjZh1dV7oudf5izMhj2lM33zP29u3bvJeOa6IbdImCzfW9c+4gV6tVBv3MNesNSPGglMw3z0m2KoRS7lfXqTueZ0CcGefl7LxCKTkD8A3DoKEf8v4gxkXQ06xaPU/z4xlH5jNoHvgwB5RYYn9Zd8bkJT+FbCktuHlWZyOx3zyjs+1Lx8wcuf2QUpaPoxk8AHGSwvczIQdexRBjzA0QOEPNxwiAoIR0ud8IMEig6kEjY0IexrFk4ZFbJz7QUwdyzBlzhC4uCQ+CI//80v7wvmdPlntEPSDxjBVA2EGv2wYCRCc6l2Nw0s79GrYN8OuEHzLi9yLY8UDf7TbPsvQfDqqXQDKEoOsUhNZ1Pduftmy0gX46cHXAj41AX5AV3wLg8sOYwTbML/PFs/C7+wlsOONDvtFR5MyrHyA1WQuCLB+v23ieFzng/qyX7xH2cXqwiGwx5iUxvpxTdNxx3VI2Gb8TqawFGWQPbL0BiAdj2Eqen897ILDMfHrwQ4AlFRy0xBkun7wP+b3EtE7a+1zwctlFT7AX/N2JJLd9/t1lKWm6yHR8Q5h3wuQajNcz/kvsubQBWRb6dwO7X+n1uQ+QZMYPA8dmNva3YLBwZm7gq6rS3d2duq6bMXRVVWXhH8dR2+2tQlB2hLAJUulQ5FkSZ06cVY4xlR0cDgddr2U/CsYDIe37ktp0II/AeL0292NsrnD7/V7b7XbWrYhNuF7uUVWltS7GkWwJLCXjcUeTliDOhHkZALhTSn8rrbMJ6GA5yYD0fT+L/h18eP26Z1F8Lw711iUYLRk25ALA7Wwd84CCct6RG6K6LocMcy3uu9vtMjhxUMJ1MZru2J1p8WyEGwdnSCVlkA3wwNg5sMRJMGYHU4BR1orsKffxAALD7CCaZ0YHuBYBDN9hXBhAZHMYBn3yySe5rM/30ME0cn2yLgTUXgLggMxLiUJIG/Vx7G3bzlrHrtfrWYdAZGMY5nvXnPH2joyUdSGz+/0+O3B0Enll/JSLsReL94telANk0T+avgB6HExgD9AfL+0DpKBXbrNYO9/j46VUzEmS4VrH0zGDfeQmxDkIRr4ul4uGBavPPdq2VRWC+lj2hxBsegmwB/msyfPzc9Z15JxsmrO5yzJKzjXCfjAe5JR5R4a8HNBZaWeO67rOpYBcl4DYsyDoN/4G/d/v9zPZBTRha9FDb1jjGR/mEhICgMp7nCXlIA25AJh5JsGZaGwFYNcDWx+r21lJMxlH1yHZ0BP0jflGV3l2J3CWQSry5WSN20zmeRzH3KHR78WYPUhrmkYvX76cET3oq/tH1sPJNpdDby7k1RfIBaX8ZFfcllL9gtw7WetzTyk09sIJKsgDDxh4dq7LGrNOyL4TY8gH2Ojm5iYTOnVd5y0ABI1eucG9l4Sm67KvkYNlwC2NYtwGuL31/VLL4AJ/48QavzNPKyN0mFu3o+gO8wI57MCc4G1Z9usBNe8xnz7PXjWCfi0rEPx5HMMwdn53stevwws75KXhXJsxc09kBnvr9sDJWbeVfNaDTq4ZQpCm1vPYmkwEK3XSrepaivPss+MixuxYknsjZ8if//x6Xp/7Ert/+n/7icXBgamzWXoF0bM/gb1x+lsqmUuCT9Sc6mwBHAghKeGqqjUMxfjg0DEEACsHlLCHjA1DUtf11I1so64rZT8OQAE4XrbF9Z+fj9ng8exL5h9FdsEEjGL4fVO5G2k3ZtK8+xBgBAcGQPKsWQLXtVKXvkqXS+rYV9cocWFgAUfMi7PqDrAA385a4YD8OdyB4CwI0hxAZyWWZo64qtLG6fv7+wxQCXacdXEHxO/O6uPUynwU9s/T+a7UjM3Lgzz4hKl2RnKZZUEOmF83MKwna4XhdDac8UuFUfIAkmv7vCLv7vg8eEZ+cF44EZo+AAo/+OCDnDUEeNH4BODpmUHkjzUD3DBPznL7cyBLjPl0OmkcU6OBh4cH3d7ezvbOeHmHOyVOq2dN/YwlXg46AKzONDsDx78ZnwfJSyac75AtcDvh8kng49lGBynYMN/rwVwpJBvaXa9ardca+l6hSufMjTGZ19VqlZxcVfbYhBh1vXZq6lqhomY9nX91nEopAWoOJjwLwDoTLFNay1wDNJ0cQyb59zILgtw4aeOy4XrBfGED+IwTAdhY1gH9cxvOfwS6zsQ7sHFdYbwAcCfjPAO2JKh4BtcVB1eMnz1jy+wr98YWeAbZN+I74+vz7TYMnedZ0TeX5WXHWWQWe8XfvCTSWW6XVWQAv+H21e3Y+9bY/Rv/dsYfucOG0uYdAme/3+f756C7bRSqipNTJz84ERKKM/8aY5wdhopdcz/mmRIn2SCO8DG+D833KTrA5Rpcx6sIJOVnXgZP/nIZQK6Y88PhkG0hWXD8FvODXHrWBhIIG57s5qAqzEv5SwYhaIzjO/rgOoIv9my0Ez3IV/ZxUbpcrtO9OzXTXpmuu04Bfyl7T41r0rElHtxXdWpEkA7MrdUPfToSg7WogsZhXoo6x1qacGylcRwQIYVqqiYYrLFBFVSFKZBuG/Xd1ECmLtUjfd9Pnyl73qXUBTgE5fe6vlPbUM2S/pfGOSqEKo89temu85o0Ta0YU6fl0dahrmqFIKU951PWaqScdlBQ8XX9MEwB1ai2LuXtvJAVdNj3BSbZLTp+PB71B//X3/+rJXaSsuMp9d7Jcy8NQnpFpcYIZQ/R6XTMTsHbJ3tJh7NZ9/f3ObOEs0OpPSLnGlIJMJw5SwY2zBbW77vMNBTQW07yJqAAvHk5B86bsZ3P51y6BuOIkXIARfDHPR2ouHFdZkd4Thxr25YzQgrAV2bbmBOyAs5G4RDZfM68sE6U45CR8HEtwZKz+c5MEkjgvN3gM0deiw4Q8lJJB1rOUGOUeI9siDN7yJ8HQs5OEtgSzPGe7zFy1ol1Q768JhgZQT6d8XPQ5qww10d3fB49K8VnHHQzPwAXD4KlxJoShDL+vu9zo5KvfOUrijHqm77pm6ZM61U3Nze5HIXsCoAApg8ZYI2QEZw4c8OGfnTI5873fXjZm5+1BAvNuuLQCezZd8VzOQhFz5g7n0v2jDHHXjaDfjur6tkZ7uf2zgNy9BwyAfDlcsFaZOZZZQ1pza0YVYVKTdvo2pUDpOX2pm7UTuu+2+00DqNWbavT1LHNA03Gjt5ht31ct7e3+bMxxszccj/Whky5lxQ6GHQmGP3HHjjxtQSQ3Jt9nMwpGXeA3e3t7UyHCRaQC18fJzGwvzw/ekkgMwzD7DBTz/yi65xphk32zCnPzVrx7K6zBWjMz/pCJn2/HzIn6Z3Mo/tR7LsTVR4AEjQRQOKXPCvKOnpGzEvaCC52u91sTiE+hmGY7TFagivWiBfvYe9YE9+Dtdvt3lsaP9u/IymOpXwyxpjAbF2y8j7P/O4dGJf2FF/O706ssfbMO1kez6owZgeWBIF+gLr7CGyW+3gni5yQQXa9pJ6APNuJ6eVlnB68eBAkSUEpCMCGcs9MRoR5tzUPKt3fMT73D94AgTVMxC5Be9mPCNmLvWKur9cuB2Gs1eVcOlWGUKkKpZlVCEEaynExzB2/O8HmcpmJgbggKYcoTdM69CVz5p8dA1UnBUOkz1UaRwu2Q6l2SmteEg0Qce7HGDMBVoxB4xTohBBUt3XWXScnQggaY2kM0xvpUoX5MQLYkKWcuYy6L3Fs/1len/sAaRiHWRcwqRy+h3FnwpdMEYaSvzvDDgtHWhnhcCbf0/sImVTqQl2hpFKWxDidOXTWA6PibZ/n351/35kjNxLcx7tyOUiHPaFECIdwPB71/Pysly9fzp7Rx3A4HLIAcz1+ptKz6wzk7/f7WSMAad7ZBSPszgIlwSDjOABzHrgx7wRjHvAQUHE/bwjhAQSpYEotGRvztAzKHMwChHCU7qi99IcyLak4OUATf+eZAHLsg2E9HQDz7BgRBys8g2cHfA1ht3m5YXJwgHwjB8g+8s5aIMvujJZz1TSlTb4Dctby5cuXur291b/7d/9ODw8Pur+/1+Vy0f39vZqm0UcffZQDFHeUq9Uql5QBNCTl4Il1Anh6WYWDMMBb0zT5LDP0n6DpcDgohJADITbNO4DxwNIBemrhf5kx3TwDLdBZN8ASRIHrGEz2brfL+sB8OpjgubFd6DP7WQjs+LuDa3QI+0MQMwyDLl2ndtXOnBbPgiz5d92OkbFjbgEt2DFn45Ez9u04aHMdcBvppcE4dr8fdhVdRoZ5RmTTmXlICiczYCcZO+NGlg+HQ74m/1G+7UAQucJm8H30iedz8LwkWTyY5lnQAdaFtfM9dU7yuJx6QOkZLWwMGT2CLcoYvYTTiSVePJ8DU2wudhBbdjwe8/iReWne4p17hhByGSafb5rS7ZK5omTaS1G9eYp3UiRo5dm95NH9Buu62+3KRvSqlHO3bdlPi29mbRibVwZwRhf2w8u1GRelx57RQ35Op1O2mS7TkC4+J+iAl4h6Rg7AjE0DL+FXmA8PRLwEHn/rBA7PS+kwNssJVw92kWXmh8/1fa8xFjsrlQ6Z6DfPjIz7WPnplRTXSylV9QwZNsqxG7YIHeGzXjrN+nMNtz8+Z/hIbALz4RiLOcUeeKaU6yNfjMuDaObIfe+SHHHCwLGCVy24jciBm70Yo9tL9xFp7MoHC7u9CGEuR8vqmqVNcsxOoOZB5td6ff4DpH7Qzb6U4UjKG+ulYqCkd1kXGB93El53ilJwanrf93nTIcLJdxAUFpAXQAUGCuVLjFzQalX2Dbky+AZfroHBSZ97fztH7okguvIA8F2hAUsIG2DM2UwMMkYKFn0JCmj7mRzmNRtmQBFK4OPg2ZzZdMaRlysmLYdRXEA4xpt54xk9YF06WeSB58cQYcSlwuA7e8a4vXTJ9wwhe/4ZMjPOyPqa8dMdFNdhjGRLAezIjAc6S2bPAxh3XMw1LCK/EwQ5IHLgyBjdsS5LIpkT7kfAz8ZimmlICWBSroa8/Obf/JuzngCWHh4edDwe8yGRBGo8F4G4y/j7mEP0kLNhaDDiQSmNNujwxBzg8FPr/3LQLbqCY1h+nvk6Ho85APd9EoAdB4/IKE6XkiTYSHSVefTMp2cqIA0c3DsjDnjjfowFUMj8QkR1XadRUa0KePQsGZk1Mi6+Rr6PwB2/yzKfRWYZk5Mh2Ch0DlvBc6M/XlLFM7jdZN1oR+32l/GQufQ5wV65XrpPgTDhc9hP7+75PlLNHT6fQz/5CeDj5bLoQAxSD/nhefy8GOadQNB9maQZa4wd9mfAJr+P8PDMlmedeAayyw7efF8UhAbXdvuFXCHPT09P+ZnwCw68fG8jgTfjdT9EJotxcE/WARvne92wb56ZqWOl67RmHMLqe5p4ZoIyyLFhGHLZPHaElxPB6KHLqusQ1+BeyAxZZLII3iAGOURvcsZDmh3IzBp4i3sn3bwjphOLTto5XvOgyMnPhLUGBaX1pClVIU6D2madwTSyCMkLceBVL8wPcs6aIUfbba0Qyl46xwzLvXoO2LkHPs6rE1wOl/7R7TDryU8nMFgb7uvBGXrl9tHHhj1CZ7Av+EPHWjybdzXk88xV35fSdvCMkyqM1QltSKtkeztV9bsl+OmZ+1yW6rryPp1xcqvr+pkd+ayvz32ARNmYR/iwBp7KRgg8tS/NuylJ5UBQHByC4EJJ8CCVA8+kwuJL8177sEUOXNNn5vsBpNJBbcncInjJeKe0JgENTkaaCzhnGPDMlC7AGgNiPFtwPB6zsNIxKYSgt2/fZvCBw+DfGDPmNDnntch0OVODQSWb5IEdzBn3dAfMOAEhOI8Y57XsBGiAPRweCubsujM1DiwcuGFg/Hn5O3KBPPFdnoXvcRgk3QUBPwAo3vOygPexxAALGE7AMLLm68MzSpoFbn4P5NA32S+75zmrxPy40/Bzupzx4W/uLHECPhYP1L3jlWfGVquV7u7uMjB78+ZNPnML4Md8eXDi6+q6yjydz+fcyMHLGclyuUMABOOMmQd3pMgjAZbPmTu9Fy9eZOCI/vh1mA+Cbge4nglBV1hHD4g8YFiv17M9KYwDmVyykcgbgQ42DOfdNI2GaQ8nh9gyl1I648IzqoA91z8yo96UgL/zjEvb50wmgTBAxB0mvzuYhlQAhC0BFUDAASAyeT6f8yGqrIkTNE4AedkOQQrPAevPPbFbgCDsBLrBT2QIeWeePCBZthRfstOuy8gowTVjmrOxpcyMEkbmzQN41wcvK/R1A0CxXm6LkV38Nlkf/yyMOzrs9oOfHgw6scL1WS+3B9hX9weM3efW54U9NP5cHmjmOZ5iSu7J+AtILAfIYq/QTbrZ8T3sPv6KbCL20XXH5cKBMc1M8LF0S/QMCddl3j377sQFY+F5WDvXLTAHdtGDPebCMdVyjyTjauoml4aRkeVzDuyx0bznmUxklXnBxiyzx8OQji5I+81Lo4KlzfR18qwXmM2zX+iF7yVFl7xxissnc+eY0Alv9MCxrftz5MB11ckYr+JB/j1b5d/hfk4G+HseRLkML2039xqGQWOMGs0e+f1CCFpvCjnlcre8xzJ7Oo5xJvOf5fW5D5AAnbxijLmbFGwDgkZ6GSAoaSaMLKwz7nzXAykXXAfVDr5h2gCeHtFLlEWUunDu4Uy/g3IMQxp/aTSAMb25ucnMNK2v3clxTQwWDqiqqhwUuUJzfUAYLX4BkyGUg3YpMcLop0Bsq/O5lKq5MhEcwS64oQIkeN2pMwYOPB0seQCMkT8ejxkU8eKQO0A4QNjBHEZLKnvCYNIPh4MkZUfuZTg8/+3t7axkgyCWkibkgQ3gyI2DAHfaGAnOfHAmxeXOgzvKMth/5uVj/B3ZZO694QCZIQAs8uOlYS5X6BPBN2w3IBAgS3nd8/NzdooOxJGBrut0e3ubdUMqrYJ/4Rd+QV/4wheyE2QtAYI8jwNhnNFSv1lLfkem2JvlpRsAaQIgdLeqqlyiyvocDodZ1o2gSyptamOMs/PT6JLG33FQBNmA7Tdv3szaiANMAS9eIsE6eLDN+jmh48E0z+RgnIwfJUjPl3Me9+vXr2eBcRinWvzJHo3jmLNwfn6QA1B0zwEfvzOPXkbK39AVnsu7SK1WKx2PR+12uwzaXFel+b5JdJA5YO69+cYyA5aBXFM6ZqGHyAOfXWYQPGsIqMPeY2OdxGF9sJ2UbDFXyDE2gXshEzyz6y+AyJlfJ4aGYciNUpbAiDVwEsRBZN6DZs/A3HirfuwNJMTxeMzXJ8PBdXktmX2uRWDv1QsEecggcuN7CD0Q9YyMA1fXC/wj43Od4yf/xod6hcTy3xwiG0LI7eCRE/SeEj4nxDyQ4XqsvWexmReyuvh81sxLIX3c2C3HDW4/fP8q64KdpArGA2HkGH3xLBXYAz8TQlA/zPejpCzPtuzRUmmi4zjOSVH02GWT9XQ8k75bxuBEOOvnOgMWYR08iMDGOOGNfKHj+BjfEuENSZxYRu88+PXx+HMh04zBg0Hmh/XAV7t/cJzq9sJlA5znc1Pw6bwk0Nc9hKA61Lp2l9k1MzbX1OHOCEfH3azNMpuZxlv2p33W1+c+QNrv97NOVw5+lmwbCoIxgF3lvSUgdcAmlfS9lFKBHlTEKI1jlDRfUOqPk2NvtVq105ka15mTYNG5L0ru+zUkatLDNObUQYTvoKipEUVhXZMQFXDEy4G5GxaMTdd1eb8AY+CZPUDjPgBVGAzYNspL7u/vc3mSs8QY9hBCDkS4JobSHQBgyQ2Cs9SSZqdMc1YNQNnlg3nw8iJnbMexlPThwJfNI3wdCRzdaSAHzC/KTYmVGz6cGMbbARHMHZlA5oJ9NWT8YJqdfe37Xk9PTzNHBWDFsHF/nmnJLHZdl5lHZ+t4Hp6h67p8HeYe546z4j1n4lxnfY/Rkt2WpNevX6ttW7148SLLzjLA86Ac2XLHyXsO5ngG7stcX6/XWSD38PCQSyS86xJjxWGh2172y7NyPYAzpa4e9LJXiIwDJb/X63VW8oZ9QtYAGzyrl9hgj9BTnpe1XpbISMpglcDwcrkoVO8ejBtCUKgqRQPFfJ5reVmV2xQPJsZx1M3NTZ5vD8DdPkFeQHSxFsz/3d3djPX1rLUHCg64fTxO/EjljBvmz8GGr7czvMy7s7Tu6JcVAPy3JLgYk6/TkjHHJrFmdC4FXPjzOZPP9/kM514xnw72nJhy4OVAGFt9Op3yPZ0kxC844AKMewCMn8Gv+5phr3y+WCd8DvOHblLKy3phU/gc44YQORwOhaG2oDbGqNPzs+qqyoQfoNf1cRmEYKf4mwdSyKekvB8Re+EBKcES+utkFWvKmDmonGdzEtAzNp7xuXZdPuOMAI3vscbMOYE664495JqsNXaGufDMEo2zAv70OifM6npe4o29VpDquhDOjt3c/nmWDN+OzFEOl8kLlWxKmjPvJjev5uDfHhRhG7ifj8d9rwez4ArkDn1ijRy3uo1wX8Oa+vc8OPGMm2O5aHrAvZzA8uDKbVP6Pc1Yfs4gtatWilLXXTUOo9pJnge7B3YNPUe3MyERNVsDXnyWNQPflOC5BN+f9fW5D5CcLXS2xB0pC0wNKyVKsMFMfPpcpWGIqqqyB2S93hpoePegQN9clwx9rXEc1DStpEqr1UZ1TaZq1PF4UgiV6LZHEASIYXwARxf+NM6oYaDGPShGyvXY+JuCseS0ouq6VVXVqutWIdSi9XlS0KgYafxQSapypqPrShthqVLXDdO4rtNcF5YKxQYc39w0GdgAWDCyfEean6CNgrijZU4cSGKQmX8H+dSusybe8Q8mkRfGRZLu7u5m2Tp3GjGWEpqmafT4+JhlD0Xl+Z3p4nnP57Nub28lFSPkIN2BLHOI0wa0cB3e4/XJJ5/ogw8+0Js3b3R3d5c7eeGk/ADfu7s77fd7PTw85MwSxhdDDdChRMlZQwJj5pLDh5F7giFJOePIWKQkK8wzc8WceoBGcMc8oaf8/tt+229TjFE/8zM/o/P5rLu7u0x0wBT7hm1adiM7DgS9fGfpAHxvngNi5BKAz9gAZHRdo3mHM5d93+f6+BBCbk/ussh6kK1zZ79k8txeYMeYOwCQb0gnq+1BEU4HGXSiyfUVAqTrOq3blfqhVxVTxiiMUTEOClWlzW6vvusyeeLsoQMKD7DdJjRNMzV6KXtlWCvPPsBSI6vOBjt7ih0i0PHnRkac1PLafHQcUMGYIYSQYddf1hLAiS3xDIdn0HwN8EPIDaBvGcy5/UCenR1Gx7x5jwfgvtaScuaea3gmE513ueE5na1Hv7w0i3WHYMEn80ww8U6CsJ5cj387IUbpO39Dvn1dXe48O8/YeC58FrYe4uj5+Vn9OKiZxtvWKfAPTa2mqtTHZK/Wq5V2t6mCYwxSaFJHyuv1ms9ZchIJP+fAmkCyu3bq+2G2Ft21V93UM912n8HauM9wH7H0S9gr5ONyvaqaZKInoynN7L8D5SpMjXDOVykGKQZdL6UqY1kyXtZNqaPlqlXdNIpjaoqAvAZaTqtSXVcaQ8lkoIP4xhRQBY1DVNf1UpxsXlMrTBitu/Zq2kZt0+pyuSqOKUM0DqmMTiEojkrPMcmJqqgxjqrqRILXzUpjTGVhiukMx9W6zeRU27Qax6gQwzs6uQxWsO/IqgdRjgkck/J3x0Bui3hBTjkB69iqrmt1fa+oqDgOGvtpm8UYpUDDhJieux9U1UkWxjhKgT7jqSlaXdWpvbpSgFXVQQpTg5znZ/XDoDim4GgchyRbcUoAxDH9rW5Sx7thlBR07c75mb3xkJ8zyRw4FkQ+sH9pHvSZX5/7AMmNvKcZcaBSadSAEwXUeFZJIsBJSundxniFUBy7l1YsAW9h+UqNPcaj78umO4y/7yMCaHEdDJpna3AwhfVqsnF0RtgNKGw1ztHZHS97KY62ysEFbF8I6ewajOBqVc42AmAXFrcwA6TaHUC4kHtNM3OCU3XmyDvU0NWq70utOuCXTArz490AYRb5LNdu29K9ztlezx6SVUFRHQRVVZUPmcNQJZkJmbHk2TF4rEXTNHp6esrMEuMjq0GAhGNnTTabjT766CON46gvfOELmbFt2zbL1DLj8/j4ODPAlCAuxzUMQ96D51kUZyL9UFyptP50BgdW2A9ZZX4w4GRqWDvfEI/DwBDy3ev1OuvSBKjhO4AIL3FgrpsmdeF6enp6B2QQOAGofb1dxrA37shevXqVsyWMyTcjM9/MFePxYwq6rrTcRQZYH4B7Xdc5u+KkAmsn6Z1za5aO1jNL2EzWBtLBgwzmz/cl9l2vpi5BIuN5fHjIa+WBndvbGGMuUfH5cZsE0PYAEZuBHcjsvjGpHnR4lsYDccpsycwt19/9grOp7qQpIaXM1sksnzPGuMwUoUdeLsna+R4qbJH7LWyFl+hKygEgz4Nsu36iS/hPnhd5ZJ5ZG0hF9Ik9bQQ8jBM75RkaJykYD1k/JxeYs3Ec89/qus4kDP4Qv+ZygHx4+Zc/G/PEdwCZ7gcdjGJzYozSELIdk6QRH1qFbP+GYcgyxHzf3NzMro2MM3bmknXKm9hDOabDg9jn52e1q2ZWwoRue9may6jbfeYQf8lYNMkhWxUuh8M0jqBuWlMnHEIIs6Y2HrAcj0fVzZwAwF6O46i+G8pexNPzrJkB64VOuExiE/w58Ivn8zlnffDh6IEkVSFloGK85Hll7bEFXDfds08Bg80xMp2etdflMt/nKBHU1ZlgwZ47oYJtWAZSTny4TPM7usB/vM/6OiZwH+Bzd71e1Q9DPpcOG8jnhqFXY5koMv4+P7N7dyXrnkj3CYvHlHWr20brdvWOfrldQDdd97EHTgg5+QRudDLTiUC++1lf/38RILmAO3uC8lHfSwc679CFECXFLd/3TX2e2mXhUFjYWYyUByEIArW6zibAgkml+wgGCKVcMsIEU56F4H3SxO6YmQNPizNPKAJgcTmmtm213+91OBzyeRL8vTCj5cA0qWSDEpArh4n5f4yB+XKGnDno+35Wnse8Nk0zq4e/XC46Ho/64IMPZs9LFskdBgw5c8XeLQydl9I4CPKgBIfgbM6yPlgqgN+dCGVuGM+qqmYyxvV9szHZAdaQ4CEzQgayAWqw0IAXD5r9b+58ME6sK0anqqp8XlDf97P9X3SAY75YSzfO4zjmoP7169ez85Uk5b1rZPXats2BOGM9HA6z4N4BwKtXr7Tf7zNo//KXv5yDRQ+o3BkRcCBjyIbvb/H5IEBmvik9wunwNwy0f1fSDNASNPEdX0dJ7+iIM/g4cxwt98Amucx65oGMFjaSIJ7vcG9JMwIAG7bMTnmmaSmrkBrcG1ljbgnmeFYvj8CW+fpwbS8F9ewEwNT3SXqWCJCLQ8U+IdvYD3S2qqrcjIE5XGZJkA/IImSaMXjQ4E0M3P67zVgCAA/qPQDCRnmLYM90sf6eQUOW3F8RWGE7eN/3KeEbYyyHp3tDGS/Nwxe5vLkuvA/gbjabWdkYgRtjZa2d7IDkZE2ZO58/JzrROV9L9MWzOPhU34/k4KsJjQazY4Wlfjcgxb5jv5BV7gMOkJT1Cv31FuFONrCOm81GTVtshgdcDoyxRfg3x0Q+p8zr+wi9ruskI7O87LyuaymGmd3h/RR4FlDPsyfdqbKP84AY3Wa+ncBmfkuGKWQdIAvPmFkDD5IIxp0wZX54XsdjTdPofDlrtSqkJ+v2voCaMsiqqjQOoy6XeaWDZ0wdI/jcYaeQS+bGgzkfJ3Po5bXYGv8+c1ICv+m64/za2VaEMsdcZ1nW7NUrjit5MYdZXkJZH/6TlKs7mAtk0ufGAyXG4/jYSSPWdGlLP8vrcx8g+V4DaS7wrvy+aZ6/LcGiM50o8rLky9kN7yzlzgJBWWahMAa+x8QDIEp0pHcPEuO+7lR9MzFjR2kwiA40fJ78szgpZypgDp1JcBCT9o9ETTI/YzjSMxdnjVMnm+FMJo4Z59c0zeyAP54fUMCaANDoZsVnCEYcnAFQeC4HpBhVDCHzSiaL9aPJwvL7rBPAgTWWUtkKZW/LciuA5NIZuJOs61qvX7/O90SWyY4QrLKWvgkXZ+MBaQghN4YAhCyzCw4mXDYkZYLB5xSZ6LpO+/1+JnNdlxotLPfCsJeFeeXZn56esqFsmtL9z4ODw+Ggm5ub7HTIpA3DoLu7O/2Lf/Ev9K3f+q36+OOPcztwZIH5Xjp+9K3rusxM+h4zd1KencAm4LAYtxMqrK07XLdDzAn2gXv4/PpmXkCcEwqMgzV21tKdjAccgDXGhQ10MEBARctzB/8u+w5oq6qaHaKLHDHnrjdus5AZJ1vc4ZGxQEewrdhySvIAzQ4sPVNJtodAzMkmroX++fuSso4NQ2oWQ9msB2HYFK7F+mCT3Iew3ozN15K1ZTxesso9l8GpByB8l0wZNkEqLbT5ngdGdAH1vYuQcp7N45rIPPIMKcL4IaqQTV9T7nG9Xmf7mdyWL0tEmXu3HcwHGVtsomcY3f4wZwRH7gsAXxlDxFHBAk0AHOvE2qKbzDegHyDu+/pYA67ppFdTl/GxDqvVKrdFRh7Yq+X7frmPN0fw58bG45u6rkslUpOueOOe0QArpdhOWHJ99AkZjZpXrzD/0qgxzvd+Ivf8ZN6pfPAAAJ80DKUjL2vlussz+po7OOeayBnzln26zZHbUcbJmvvajuMoxdIkBP3FDnnQvSSw+L7jPb8vz0L22UkRnt0rFbi2yxnPGkJIJXZmz3xeQphny5Ebb4Lkdtvl0UmD7C81bx7BevlzgpvRGbelZITwIcv5x/ZwLeyVP//Xen3uAyQvwXID5c4AwCpp9jcm3Y1djIWRcECwVEiplGGw6LCYHjwhhAgxwkMKFsPgrCcL7OlCBB/hcVbHjQOpYAQcwcYAunPwwMDBsZeKYPgys6SidGmPVWnrSiYqXbt0USFIYv6kYhh9DwFKhPEnq4ORZI3c4GBA+BxG/B1lreeNGVgXzwhIxTlzcj2gHGfL3Hjp2jJ7iMI70+rO2QEcjtVB1DJAAGCQYUI2YZNYd9YGw09gBqAhEAUYl2B2fp4CsuBzQpYKGcGZMi7fN4SD9lI71msJlHgWnA0btx8fH7Xb7fImc57Ts65+/cvlotPppC984Qt5rmk9vd1ucxkbgSzg1c8ywk44WPVAyMuPeB7mw+eOZ5uVsqi05GXszD8lKawpZMkyoEeuAYwhhFyvzZ4H7ueBJuvoAMiBpKTcOYtgyZlSAmACM88oOBPKevqcOcvMnLgNQn/4vIMhgBefQ86xGS67y2yBs+PYcf5NkO/klxMofI9rO3nmoN+/M45jXh/G7DLqwYzbBc+yuP1xJw9A8Gyc6yX2xYNwl09k12262xTu4d9lnmlAQFc1xgqYIUjxwJb78D7y4WQOQa8TXw7mfF6RB9aRe1ANgp/1jLzvSVgGph6Q+xlz7jeYM42DBiOy0D8nQyEF0Enkw5sAQeT52vl6DUPa2xHCvJU5sh76oM12nbvPIUesH7qPz/RGCcwt8pBl1ID4EoPU1fwgUf59uVzUNu2s2sDLUtmL4iA8y7aCmrZk1Hwt0N1lBYfbMicC+C4y6WvvpIHr1DJD8z5Coh96tWOb7yfNy6HRRSdR1uu1gkrQ5AGLE1Gu8z4G5JS/8T38AH9fkkbII/LA8zn288C+qmsNYyGAeO70/SpnDX1enWB3DOOkE9jBqy9CCHRxyL4dOQWTOunLM/ATe+H2kmvjL3we0U9sxWd9heja9jl6PT4+6v7+Xv/3f/xPM8MJMJPmB3C6AwW0X6/XzOpjOJLT63OnMsovpKLoCLqkXGKF8Dpz7IbdBd8DHZhwxkjE7HW/fn2uw3MgaL6hHqX2zAQvhNH3eEjv1tujmFIpU6QkybMuXXdV1yXDTLkNtdQ0oUBRnbHEMDgLKZXAC9bSQTnBFwZoyer48+HAMWZkGSTlki7WktI0wBJGD4AP2CEz5ECCOWSsvJApgDRyQXDibKJnFJdZCzc+zjyx/g5geVYC0bJGJRviJAINFcgoefclPuNlSs5+xRjzmRowTMy/Ozb+zt/8Gi5r7DNgLp2x3O/3eX3QOQfYOD9ambdtq4eHhyxz5/NZ3/RN3zRjtGGg0bMlewe4wOA68+tlBuz3ctIE5wZI8xIbtyPICTqBnXDdxf74vAFKPABfsqBkwVx+nAn2/SAuTw5OeBZAqAdaBBketL99+3bWqZD5Ry8ADR40YNeYL4JlntPPRMMe8kzIPHPrLKNnaj248bIut6fIsOusZx58jvl8XZezhzz7wvp6yYvrItd1gM0aO/BwG+eZHs9ucC8nS7BhnLNFwO1rzfsEmYA0sgEuh8wnv3uA4vuQ3LY7Aen+ljV1cOSBnANrJwmxuQRpEDPoF9fa7XazA8k9yPUyN3SI63tggG3Le2tCAvU8HwGGl3F58M97bp9YT/wn12HeXd7qar6XkrFvtxtV9byEijmFuCDAc3DOui+JBknqh3crYzL4tiyKk7B93yuoBIR8j9dUVZWvO/9MkGLZh4ssezmV20nm3LtkortccwmGczBQlay4l185YQJhPf9srdV6NbuWZz7QdQ/sQkjNHpA7/LCv/TDMjyBwrOiY0c97ZB4ZG3LiQZUTx+iC4wW3rakZQzVb0+zflToCopuMj+flGbDdPB/+wkvecil9LL5i+TweFBIMYYPbts0YjTVAtp3kQMbQA2ThcDzo93/X/6KHhwfd3d3pv/f63GeQuq7XZlOaGyRwWqlpilNyZ5NqUi+6XsumvSR4qW027/mZJTh8B0eS8nlLxUimRg4IKMLjrKZnTjDWnoHBES6/g7D4YYMYaoJD7stzo3CPj49arVYZiPs9UQQXNmne8MJZXhQcwUcp3OENw6iqSsbGGVJXOJSBgMrBgm8wR+EYE/MtFUPr3at47iVgYv8OmQLkgZplnwMPCLxUgWvyNw+WmBMMslTAtDspQJ2zQC6jDkKcVcaROPPEXjpYJt4nS+KZGZ6BNV/OrW++dwftDFQu97DgzJk41pf7IT+uD/yOLAEsCcioLffGHgAjDLczZzBaBNCr1Uoffvhhlu/7+3ut12t9+umnevHihYZhyCUcvgYeGHlmjmdALiBapNKpj4YC6LqXnEF6OGBiLiRlR8Cz4cxWq9WspNHBngdTfN4zY9hB3gfwkX3kP2dJkS+eEzmhlM337C3HwueWDD3OFhkH2KBH3qEIHWH+HeQ4o0x2t65T+dGyxBq55nquTwRsbtPJwLF23hQF+eS62EG3x8gvL8CRg1HWysERP50w8WwxIM7b3aMfZNcZs++JQ389CMPv+R5EJ0DwE+ha1/VqW9jgqLou+50c9KeAPMzmvwR1xR544MM9lySX65mTfc5ew+D7GNoVB0X3Ok/kUMlupyZCyELbAhaHyT81OUioqkpVXaXOaNEa1tS1QjXt+xvG3E3Ou+uljEvqEtZdr6rqEgSnDFWQdJ6u2UiKmehxAFtVpdsZmaBiO6JCVZj/JXnVTDYBu5NkuHQeHYZBVV2Lw9ufJ91z8sUb9owTaI5pUVVZ4FFVJdvhATWBQt+z92aV/VSSy+ssS45ujGNq6d/1vc5mD7t+solx1DDOsymsD7qJjXAfCjZwu8Dcua452K7rKlcaOJmBbrufhUhM902y46TDatVKmh/DwLWattE4TD5dUes2kVBjHFXHOpO0Luv4As8w08VYKoGClLrSMRf8rJvUnZBtExAiBEdOlPseIz8T0TEgn+PlwW6ap/LMTnD54dlcY4lBPTDC9jqJ2TTliA3WkIBwmRj4770+9wFSCJVSi+tRwxB1PlPzXNgHL1dKRmktOtJ13VV13SgEqW1LbT8ArLQTLSxC112zg6LeGiMcgqZ7F1Dse45KN7s+M9wEPZIz0H0yisEFr1XTpJbdziDCYvd9nw8+JaDxc1qcIQ4hZFCDEXWmledZpqHdQCRFqXS5dJJQ/sJwO2hEkRy8ZEbKmEeCRAzAdrudAQ6uS8ZqMAcnaTZ29iV4PTPle0uGkn8vHTkKmmStlH44A+SMJddjXE3T5M5xrC9GiPnmnjB+GEYvPXJn6MbZsxyerXEmFfDsgQn35d6+58gzezgrPoPBZk8Whs/3rjC3jInPe7dEAh4c5s3NTS4fQWYcjHtmmPmj4QVjRyePx6M+/vhjvX37VnVd682bN9put7nhA05mCcTRVf5NgMHfkVfAKDJCkIRO+YZviA+pkA9edoV96bruHTkJIeQM2pKBBAiTNfMgGl1hbednRZTMJLqNXeCFnDE/BEe+j8HlnT2D7sBcbnkWWEKXd5d/10sAopdrepDigQuBAHODjHjGDV300mcPNHmhW870V1WlL3zhC3p8fMx/c2aVz/n6cC0vdXK9I2vqwaXbFkl53p1oANSx18SrIBygQGiwHrCy6LFfh2unMbHhOWoYCikzDGMOTp08Wq9XSjC6nKuT9AVyT9k28LweDCPLXmJFIMR9eJa6rnU4HhWq1N1uvV7r2j0mYH0+a31dKU6NlkaNimFQNwxTlUPQtR9msrmKUl03qutKoa5UW2Aax6g4LWUcosYhAb7u2musS4lVKbmS4hjV94PqKA0a1YVedVXK78dxnD7TaxyiVqt1ahuudMhlXZXKAZqPkPHt+159N0gaNIwT2I/SarWWFNT3aR3PF9ofBz1PzYDSHFfq+0JaVdW8XK1tV5PUhowv8riHUf0wSIoKVa1+GlMYRo2KUlWyqE1VS6HSMEZpspWbKfCLYyGhCl6a9OH5lNpuB+nad1OwmiSr68rh5E1TCN3umgJ013l0zUG5k18QEcihB1lJbsv5mI5zlkSnl1mXIFDq+qkNd532+xCgxyg1bZ0D8GGYskBVrRBT5q1pa53PvWh+VTclKxRCOkA1fVil9TavEDXGQR17/upGzSrZ76bGBic5W69atU2ag6B39x+D+zyI5XkdI/B5bMEyMPHsFj7dkwzo/ZKYWwb/+EfWi7Vb2k389Nfz+twHSC7Efc+G0sIgSPPT4RMjVoCcgxcvXXJgT0Zpt9uKA8Mo/ZJKpxVeIXjNbNnXhGAwJgAk95AKKxtjqctGiIrjGY0lKi2Oj8dj/p0XYABHDhi6ubnJAuwgwQU/PUvIQRtsuAdP6/U673VB4FerlU6nk47Ho168eKHT6aTD4ZDZWgwLwBpgzzUAzije27dvc6c6AK47e56T53PDCCvmWQ9nZdgc7J3l+J4rMNdlgzgO24NpxkFde13Xuf2ryytjc6PDGqL8UgHJzJlnanwfRAhlLxVg3cs9JOn+/l4PDw/5d2eYXU48KPK6ehhogi/2DzA/jNWDXQCP799j7J6NKGCrlFThzAiO2QdGkOz75siQdF062Bj5cMD55s2bTB7sdju9fPkykyeMx7OOyJODbamcm+RZgGVJggeykBReYgPgozQTQsH3V3Ff7BABIH9nzpAx7A8ZGGQXEI/zcHvi2UwHK+iVNzLwazpwdedG5qqqqtyGnPtS/oQNoW008+gkB8QTzwPBhPPmnnze7TVy7dlWnh/ny/vIjMsAoNSzT+g7c8S+VoiuZWZTKg0EnEBjngEVPB+gzoNaB2BeqotNdl1FJgjmCboYmxM6+BdpfgBp+n4J5vwncwyBQaY8yc+gdFh5acjhe+HGUbnUlmuWPaxlL8Eya8f69H2fGe/0vlLZm9m+nO2ZACDPis6u14Wxbtt2ti8qhKDL9arNZp3nybOMwzCqbdqZXWZOXe5ZJ4D4OI65Mxi+jM8zhx6kEsSWAGZ+xlPTNNnnQf6FarKxQ6/nRfMODwi8acqSSHNZZ66Dze98TVIb7JzBCFLbtHPfUddaVWUvTAjF/rEmEEOeKe2Hedm1Ez0ccu96G0JQUzfyih1srss3ANoz+JA0Tqg4JiFjyDOxJg7Cff+mzyGVCVy3kG+jwO6Ut/o9S+Z/TtBzLZcfrst8YfP9OdDpOXFWMm3YCuYJ3OgBCTaJLBLPWvSt+HuwAGMc+l7bddqm4oQptg+/hH3nXozHM1GOaZ3MdAIL+8+e68/6+twHSG3bzEBTifKLMLkAr1ZtVlgWDoOOgSDjwIGpACLqjilVcOaSBfW/J6Uqh7ayqH4AoiszwpvAy0Z9370DPqXiaPmuAzTGwfe6rpvtufASDgdFgHC+w/sOxAloPDiCwYcp9zIegk83yMyhgxZnBgAtgIHrNR22B2PKGgHEcHbLkjqUnxI6BwjO7DoIDCHkuVqtVjocDrPAGefpMkGZDNkDZACj5KCJ+WWdCMqc8fe14PkA2QTqyIpUarw9yPb3cfRv377Nxsm7ojkz72V5ziTxHvu3nFXjnu64mGsMmN8Hxpq18CDMWUvkE5Z8t9tpv9/P2GRJOajiPwJ/NpcDhBj3fr/X4+Ojnp6e8lklGGBk2efRA1Sex6+LvLJG7richXOQihwxv56x4/o+rz6OpmnyoZIuB56VcpYNO+bdxNzZut74fbCNHrhDfpCRKux5OXjXy3S4JzYP++FO2J0cYyIY9CDCAxv0yYHPUg4dRLDGyBdr4IQENmRJaPA5r3NHtwFj3M+JCdYbW+b7N93u8ixkxskesBaScjBZsgGlUYKvAWPwNXIQ41lvB0jIalrzAsqwpTwzdt3PbUpzUavvO1HaHkLJuKa1LOf8+T2X43PyiCAUm+H7napJ1nkf/UQHPMBzXaJDH8FMbmywmVcaeDBaG/GAvmBTx3GcnZPHf5AWXnngYBj5cT+NnjlhRjk49sFlvQS1rbp+3gzEwTe/Ix+sPfLYNM2swQ+yIGmGLxg7OobOejDsAJh7od8hBA2WGUCeMpFhwJk1TL+n02M9e80c9f2QTpZV8a0O1JF3wP5yfua4aprfOEpDKcPzkn1/fj/ri/s5GYHucF1fD9d/xwvYCuaWsbuNciKPNfHSOjKO2Cfu7/qKjGKXuB9EOLaFOeC+krJc+hjcVmXyJ5QSOeSKz4AHHLe5fYJAIEDHb4AduA8vny/G91lfn/sAqWlbbTcJ1M7ZxdJy1WtzL5eLzueLPvjgA/V9nzezYsAdUOPc00GXKYUKW41z8v0BOBJf9MrYCKlsMnf2OsaY91DwGSmq68qGdHdUdT3vpIKxgU3HWVC+JxUDRtmP77sBzLjAElgx7qenp8zkwsL0fekCBmvPIXKMAfaMYMlZMRdsnpPvEZzhSFH6tm11OBxytiSt9fwgPgejGGNpfvCcByp08IKt8HLEZb00mQteGC8HfBg/Zw7dIMYYc6aDv+92uyyDnrFi/xjXpeQQQ/b09KS+73Vzc5PH40wtc0CppW/axvggS9frNZf+rFarvNfj5uYmp9m5B6QEDCrz7M9EmQjP7w6AtUY3PGilRpn5RPYd3AMwghli9OTm5iaPifH+ml/za3Q6nbLsPz4+StKsLbqzxB6AetDqjhHnz2e8Rbgf9sp1cR7eVZPvepDmewUd/Do5gNx7VsBlj3klYJHmHTz5HM/iWQ7uu9vtMiBGf7wbpTN3BE+sB7aIZ3aQ5Swm9paxeNkjYNT1lrE7yMGOcF3GwXdZPydCkCkAOM+CLXPw7qXCUin3RGdw+NhRJ8iQF/TaATJyxpq4HeMn4I4Mq5+3RGbAgZeTGuixpGw/PVuAPs+BYin79GuTQeacKAfbXddpv7+dsm99LnOv63KQOOSGE074IHyOB7XeTprPhxDU9aXjle8/c5vsmQnmC7/Es3pVCXNPyTDB3TAMaupGXed7gcq6lP0nIevfct+Iy6PLlGf4nblHXv3aXOvt27fabreZPMAGViGotfJsAmTPgridcrkDqHpHRq7rpATz4bbMq1OkeStz5sCJQo1xJuPY/Mv0rG7L8M0pACrgGTlIvmWlcZiX8JfM1XyNvQTM58HJoXEcU01fKESLBzdOFPPsYAdkm3vjW92eul77e+XYlHmJPuvE/Zy8dnvhZAk6wfWdlFqSY8gquAC7RgbaMzE8DzYVP04VBDKCrQTDeGmcB0Lu9zyQ5T7YzoeHh6wfBKyeTMBnYAuTnS/VXF/r9bkPkHC0bnySUeyzwuJAvXTlcDhkJV+tVvkwRUm5RAwlTQuUamFZQAC6d2ryLAhK0nW91utSAgTIQqEoP+n7PrOsSeArxVjqagmgqqrO5WrH4zFfyxUEhcGxsMk9twy1aP9yuejly5cZPC6ZLgJIb6fqSoYzYp6leRc3/oayOZB14AP4kt5lwQEtkqZgdZMdn9fZw4hgaBgLxsXZF2du+Az3oKTm5cuXsyDEgyF/RoJFxoBhxjng7JxpcvkNIeQDGSXpcDjo9vY2l/U8PDxk9tPLIVkXjOuyTIVMUWJx17Nx8fKNl3zH18kNqWddmTd/ORN1vV51d3c3Cyoxms4UoovogOvUMnBGFiE0HNjhCBwwo+/+XI+Pj/rwww9nQZhvfPWMsK+1rxeZJj6HMwH4+HziUD2b4IAQGV2CcGQWEFrIkToHDgBAHDQyICmPC6fqwYzLot8PMOf6DFPNfVk35I9rOXvszCIZGeYEp8izeLOWuq5zGZdnthyM8R7j8GwmeoxD9cAIWSLgIDBzwsaZfECqrxXXdLs0DOVcHg98WAMP6D3rKSmTZJAz7sN8jj0Y97njWbH9PBs2n0OUuQalPWTipbJBupTolf0yzCPjYj6d0HA5SUFDpxinQLFd6XzuFYJmNph7QwT4vlDm05luX6OgeYc8bJtXifBc+BTe5zkAsrmMR3MZ4JUqBVZSLFUayDgy6hkTSTM8AAZgPIA7l1UvjWKcvk+Hz0O6eKaRoPdyvSpOWIJ19gyeB/AuP9gnLxkFTzF2PutjhLBc+hPsNFgHmz6Oo7rrVd21nN3nJF1dVVqty+Z6DwzHIZVwMh+A80x2qFRE+Hxid309sclLMhO9TLKQsoZcy+2/ByfoO/IFDnDCyGXKgzvsbMmwJh/uxzA4SYOOMe/u85wg4Hmd1MM+eCWLf94rgpZZM7Yf4GfwO/gqD/Ld72YbFsu8M3/8fVn9wLx4wIpv9gwqfs9tK3qXsUL1qwFSfp2fz2qbsqETYWrbBMgOh8Mse5QYisKAE/WGkMq/PJODICRhnCuSs/w4EW/9iZFJHYbS9WAKUCwcpCs0p8GP4/zgWTbdowAEfygKgHJZWkSUfz6f8x4UnNvhcMjOhawMETvPgKI5aEJpAd+Mi9bP0pyhXio6Y0XpnTlZAhYPfNwpMx8YWwfsOHjWzteJeaFshfcdXGLkfvEXfzEfNrrb7XItPWCC+1Fn60rPWjsgYC54JpyHs+EOgPnc3d3dLLh+eHjIQZRnB5hXnmMJcsguIvdSKSVgHpe64uwVATjzQ4kloCDG0gQDRtbZUQc16B9y44adNfBUOcBgCRK8uYkHN8wvMsCzQyp88skn+vjjj7NMMG8YcUooHVwyj8tWxS5nrLEzeW4zeAGwuq6bdasDMDIHPB+6VuzbvGyXtWaNAK1+Tw9c3JnhwN0JOoPqHbWKPSxA2R12jDEHOZ49lMqRAZ5ZPRwOGShLJTPIs7mzR2Y9cObzrAWNOxwgMHfMI7qPDeY5pFJStyRoKKt19pb7ZTA36bLvqUQXvPSY77D2vib8ROfwM6wtc+NrCOOLPmLfnM0fhmG2P8+v7SBxmeXh7wATAi5k8/HxUddLlxoOxKhh6NW0bdpAH4O6vmRLmTMnlxiDB8x+KCbgnHW6Xp/1PAE+ACy661kOnhm56/s+H+kA8EI2h37InecYF2O9nM8KYV7+6bKBXmO/HDQiz24jePGsy4ALotTnDN3gWBCClYw3FDXG4n8YB4QAOsdYGbcHiU6KOiG2zIJ45on5hmD1hioAaeY/XaPch2twz1HzfbfjWJrDbDfrbDuQ+yQLnYLCzA6zFxeZ5n5ObvJyf1uyJ6VbsJM/kma2jhdzd3t7Oxu3Z35Yb9eBYRjyURueVWJe/IV98wCIayJ7+PRlJYCTiMij4yqqEvArPscu5wTSjLfv+0wyLvFW0zSKY1RdzbOi2GOuiwxij5ygYu1YByd/+M/97mzP5uVXS+zy63g6TlmToPV6o9RC86KuU2ZeHQRIIUfUXddlo/PmzZus1B5pA5bYnIhww9ZLyteNsbC1HrHDEnjWwxlcBN2BqaSJFWEMjaSpT/9k3D2KpiROKsyVM8YuQF6CgIDGGHW5nPM1z+dnhZAOg3WgjGBKys6W9z2Iu7u7U4yl0whOkGAPY+ClEW6wKWHwIM3BDEbPz2tylg/DgBHwroPMiQOuZcDE2UBc73g8zhSVdeV3wEmMKe3uZTZuOB0044j4DlkRntnBqQcaAAPkgDVn3nh+xuiGNRswYz2dWUQmkT+/ljPc7M/DkHmw63OCjjhI5t6sMbLl2ZdhmLfj9nV041icb9EdALjPPU0ePvzwQ1VVpRcvXujTTz/NuohRBqQwJ4Ai5pX58pKapf7yGXfSrPeyzI31dMDHs2EbWFdn/fg+ukigC3Bi3ckY4Iw8UPOgknV2wI4DREcJElxWWDsIGxwg7zOn3MOJCu7PPQGG/hnPGmKPKUUE8Prf0G3sAYSRl2m4zcGOQHqcTqfpudP+1nGM6vsu+xJ0CVvkGQsvMXKb5pkxSbMAMnUPixPx8ZjfX7Zqz2eLVLXqupps40qpQcK8fTYvJ58KuKtUVZRiplL0ZBukGNMepOQLSnmdkwVuI7F3IYTUknnqfnY+n3ODgnEc1bStGss0bSYS8HI+T+eylEPaIRqrKrXIjpK2m03qnlelDfSsJfLk42AtsXP8XHZMZL5ijApV0GiBImta17XGYZzp5Ps6L7qfR37J4JJh8L0x2CdsFGW1+FG3uW6DIDAul4uGsVRABAWtNqWMj897uXNVVaqrKlWQAZ6HecDieklb77ZptJ1IXXSxrqvZHrfn00nN5IubutYgb92cZA6dwU66b2qa1OraSYqUHdLUCKJk5DxApYtdM7WvDtO/saVjnHzgOGoc382E1nVq2kWH46pOe9SXttoJAtYDmeJ3z15DZDjBTqDB+LmWlx4jT8iv+10nvGgU5b7A192DJMaD7XZMwmc4xBic55Ue3kDkfZnkKqQDZrlWmNahqis1VTnmgvVn7ZwYdtzgmUBejmEI/L0UD7lx2fqsr899gLRqGzUNCkdr5dJ5yZ3Efr/X9UoZQGEGff8RC+M/EzBbKR2MWtgnFut8viiEalKYi6oqKgTOmChd33gROCxLOGCVkiKs1LbF4KU0c1TflxpylBAHyj1QOE/p4khQVgKG5NQrVVUqE7q9vZ2CJ01OuTBxkjJThNByfS+dIiPgrA2Bj7Ncnk1h3M4mOkNC1y8HlxiY5RksGCCe++bmZgbIKDX0TBZn2TCPDtolzcqovC6ev0nKBgvwTzDG3FMOxfxwfklVVbPSIk8lO9B2x8c8YEyPx+MsuAZYeaqfOfdAEkDtWUj0xQkCWmTv93u1bZuDcTIPy/1Gvr+DbCNgYr/fz2rCHcy4s2YPHMDd1xfZgZGXCkuHDPk1eXlm6YMPPtDbt29nes69PXgGRDMfHmwSRHhAgMF2ps+BJdddGnepbHKF0eRZnPTwfzN2Jz9cF7xUw4MZ9DCDpbGUifA3JxNYQ1hdAALjQbeYI8bG2P15vcTKiRsft29YR44d6Hs2iyzkkvRATlk75spJJYJuX5vNZqvr9aLrlU3rgJ10hAMkjwNQ1spZ41KmWYvWyVwvlU8PZh+8Nfyg1FEuqqrS95McxOlvqRSOQBHAFqN0uVxntpUgmTVc7lnCLvDyLOyS+HBb7UxuuwqZEPLy4aZpdDpPOl3XUpQ2u4k0CZW2+9QkZdVaRnscFepGCvTYjhqidL5OgLWq1VTzMixfOx87fgO/0zRNJrJ4Juwqsnrti21UTC2vXYcgFyF/kCuIG+RcKmecsQaOARx4e3MpJ/i8rL3rOo0a9XxJVQyxt4CiqTVMBEldhSQ3k74i72ktxwRgQ1Db1OriqKAoxdRtLog9zSVDKElxTPucdtvN5C9GqQrqrv201SAFTTTMWq9ajeO85KtuajV1OVQb/DKOo9ab1O5cink8VajTHiPLBPpa9X2fAtspuB/6QdtdIjn7oZsRSlWoVNVBVQwahl790GcfFELQepNkV7Hsb/TqAc+4YNvwf9gq96X4P2TSCSOvinD77/stPdPi2Uzk5O7uboZvwEoeXCNPBCWeRSPTdzgcZhltHyc2BIzr2NJ9zjjJXRXTdrEQgvpp/o6Gkxir+zjWEWLMfTsEvttv35uFDeJa+E/3i5/l9bkPkG5ub2YND5gwggicX+5Ys15rHN898RgH644ZI8iisfcAJ4Ag73b7HHQB6gD2KJqz0K7oAEEYQy+5805OMZZNkBhmwIiDC3d63BMjSUmWfyYpZqdxHPThhx9mwby7u7NsTul371kqns3n2TMKDmyqqpRcsVYO0h3EuDJiVGDOnJEfxzEf1osTdCe23+9nZ7Q48+esnxtCby/MTwIzT/MCHLyEoq7rnC7mtXTEu91u1gVRKq2jM/M1lgMEPVjD4S+zNsypO3oME+CcTAlzsewmhxzS3YmxwCbtdrtZetwDBqkwhugNYMybhvh8Mz6607hcAqhd1xwEoXt8nwARO+B7sQisPGPL3x4eHvTlL39ZVVXp/v5eUqmTHse078/Hw9/5HSfiwBMb42tBsOz731wuPHjg/qXko9gKX2cCGGSPNfe1cRnn2k6m4MjJIPNZbB1yzPc9S4R8ojvMjwfFXN/ljH2W2CbG7xkunhv5RW7Rh8vlMjvni+wrJXMOZLC3AJCnpyft93vVda37+/s8Ru+yR1k2BBIkgFSyqk3T5P1V6JjXxzvje7mUoLKA1WHGliI/XubLnKW5Ki13IfKwR/iL99lAZ1/56eDebZXbLK7lTUZYF/SPcldIvaqqcmdI7s04vLTLgzfWkH9zfb6LbDrB5kGRgzrPnnmnWHSNIIb3nXTi+t7gAxlnPOxV5PtLm4JvRIaZB9Yb3+74gnEA7JxgYI2qKh3y6evgASr2kXlkvNhknt/XFzsFqPfSQPQFuUZOXK+kVPLH795JjXE4cQIZgh44ruqunbq+YDd0lUoTGgEwT6fTKT+br7nvo0LeYozqx5KZattWzdDke3vwPwyDQh+ybcV3IQO+X8f9JM/Lvb3cjfnwefQqJfSftfYggJ8eBPEftkAq3fJyVqcqDVa8IsDxqJOxrg/uJ1xuHV974qFtmilDV+TaCRquhR133LJarWZdIJ1YcszA+D348UCWz3nzo8/6+twHSKu2bO57H5hg0tgfs1qVDAGdbdgXVNd1zgZQpoLTWq3aHPygmH4uhHdCIjhbBjQOilAsbze6DPSkwsZjtN3wOOvM3zHCziqjhMuNlVwnAbp5iQ2Gc7UqzBhlJMwxQg645D03jCUDVp7Xy5VwoMy5G33m01PdGAYCl+VzYoT6vtfhcMjjguXBMPs+HAAv9e9k2N6+fZvXGUUng+gZODcabsDc0bZtq91up4eHh1mKnVpenpefHrBRZuZBAqWNBKfc0/e1IRswpxgh72wlFSb9crlkuSeFT8ZgGZjiSD1gcPbUWSx0SypGjrnhs8gC43AH4jXxvEcQ4AaY7zKPsPzOluPUmqbR3d2dvv3bv13jOOr169fZSez3+zx2ZHiz2czaa3uAezqdcjaQeUFXGS8lts4YYoecFMEJ+z1ctj0ThVw4QcF+OM8OuV1yHfGABfsJyMAmucP14J6/Y9vYo4c9ARS7rHgDCMBKCKVBCTrN/LAnzEkIgIuX22JfkAOfV7LD2N2bm5u8Di6HdP5KDn5UVbWzOfTyP+w3GQIP7MlaQeow33VdzQIJn2Ou5+ARWULenGRhPMsSHmSLeWb9uAc2gvlwUMTvjMHJL2d8sR+ug76HwIPzGKP6IW18xw876PcsMGSEs9wOxp1UW+4dpiIAYol1XJYNMSZkxbO37puxd+AHggcnIQGSfB+b7DaQOUfHPMAjQGaumH8PdDzQVXg3u+wyE+x3txvO3Lt/8bVn7dq2zWXzkFu8sIc8v5eQO7nitt9LHa/XTorzc8F8Lrg/WWrHOanz8DnLFrbD783v/BucQQCP7cf3+T1cVnxfrAdcrDff920S+EHHLh4MO7AngHCyljLg5TiZZ6+IgGxb4hfP+vCTkkwCJWQQLLdcO89+YX/dj/OakcRx7sMdo7m9cDKRl2eJCg4tJAnyzHtLDOzEJfrr8/pZXp/7AGkYBr19+zZvUmXyADZsygVQnk5HSSVa3W63MzaOkg/S2zAffmKzf1eSrtcuOzyUBuPtgA1Aw+9eo+zOeLvdarvd6nA4zMAIBgUmBiXhmbmuAwDAsbfqdWeTDGU6QTqEoLu7u+lQ3N2kGPw35uCIkjYEmBeOhZIr5tOfgbEyR85w8nKWTJozNxghV4hlSRPlZYzHDTmtmBk/xmoJEFivqqr08PCQjSfX9GYUHuzgEHhOB86AGtL7MNM8H4YPQ4iB5NkwHBgxGC6eYblnSCqML9kgnKJ30fH1cMfH53D0rAdyhNyiD8u19f14ywwW13AGmPljjvmczwMygH4hq4AbrstPyAH+RrA6jmPWx9PppA8++EDn81mvX7/W3d2dpALqIEF8/hmX2wqAn4PK5XwzL3yP4JQSTMa82+1mIBn5Y06Zd88UuW0C1C3nnOcgi+RdLfleCCEHyHVd9gFxfX46IYU+eCaZsRF4+XwSBLhDd6CKveB4AM8MhRByAxRntQEq3M/ZXf/e5XLJ2R/IBXRvHEd98MGHWQaOx2MuY2NvzDiW0mYH3dhwWFHWLa1dKZfy8aBnfB9dR+YBTMy1M9+Z9V6QJ97Qhs+6TfB1cbvqmUEHz4zTAYiTeqyDZwUym6x5AOIEI++TrfTAWWIP7pDBEz5p6QcgKrEDZf9LaeaBzKJHDlTf51f4LvrK2ngg5vZoSYg48OfazA/y5AQRv7POfjYR8zHq3c342deolBd62b7bZeyOz6NfwwlWJy7d1yMHXddlG+UElWexyPLyjIqlg6+TNARH2Dbk2M+4W1YaQJz4HkuXbw/mGBuNUpbBjYNuDz58jhgrmOV9mR+3kdgk1zMCfwf8PCN2DPkETzJm10PGgCwu59QDFMbMGjthxjjQWX6id3Vdzzp08tyO50Ioe32ZT7fH7oPQF88C+dmG2D7+5jrp9pS5c510gsH92dd6fe4DJACnO2vP4iBgIQQ7GLJ0zAC8ucCQEZpH/4UNx5khLOlexVERyPj9ySD4YtNaG9DujHgIQff393lvDPfE6fO7AzHG5hE+z8V1LpfLO0EhGxPdoQD4Y5Q4YR3jiwJ5+ZNUuja5I11ubCZo9HlCuB2Mk7lgnign2u/3s82qHmSxdtxrCVy99ModPutKMOsHCc83VLe580xVVXp8fMxZLDJvHkQyDhxT35fzQFg/jBwbs5E93/PkTKLLj7O47oTdOHk56DLw5HME0b72dV3PgskMeGLp1ATIhY1blgehk86sMs8OMDzI5js4OBgoAB8BHOuKPrhuSnODjjNjngDHHiygozc3NzP2H13j+s44AnTGcdSrV69yaVZdl3MkyBADMqqqyuW8ZJmrqspnN+HwkCN39O4AcZBkVJAP5vl4POYgwstsHZQ7eATQoT/uTPk7z8L6Esy7rjrB4L87ieDZWA/quBeyCgBhHtB15A9ZwVl7JprveBaHsQLIWUPWF3mW0sbt5+dnXa9XPT4+ZjmIsWyeh0BDt52AoIFEYejL3Dt4cZaU5+Z9d/TIvK+XE0se5Cyfx0GzA2VkhvVx+8C9sT8AH8C1zzPrx7NDVKZ9M5qtpeuPywb2z4Nlxrv0fciiEwmeIS9rVTqwOhHg3fMYNzLksu/k3ft8Hd9dkj6OC9x+cx3k1oEsoI9n9X2y0pQV6UsZ2zKzGqSZr/N55LmQV7cj+CjKVNFvlz10iYAE++UyC8HFWniWLgetoYBxJ3BijBrjkG2m7wkkAPaSTeSd77M2TqqgFx7k+NlQ7lv5nJPa/ITg9PPvvETO7ZHb6mFImdqbm5uZPDr2YO7RTf6OrWR9+Bvy5b4YvUffwZvole/xdEJkmYn14B67CWnneHoZeMdx3tUUOSbgSUmJcmQOpBxy4OeTub4s14h7+75X5hDbwNywHp/l9bkPkDxrsGQSECBAOo5xHJXZW0CzMx8sAEAlLV6px+RaGAMyLM6KOSsglTplD4I4q8KDu2EYMhvrQBlBx8DhDDA2Xuvs7BUAgrkIIejp6WlRAjNqs0kZptPplM/gSYamlCWhcBixpmnyHh9ePB9Ow1khZ9nIVnhZgAPfZSkPDhSldqeOgZQ0c27OTJJ186AAZ8V6woQ5k3O5XGYKDfgFcPs+K+rlu657B7T6ng3WhOzF+XzWhx9+mFtkhxByBs4NkqQsN8yJyxwyBEjnHtwbMI5BdgYcmWENkS3G7zXmUmlt7gwPAJ8xIdd8j05yyLnrqF/bmSFkxzOCvibMlwcx0rzDG5laZOl8Puvu7m42fgLwruv0sz/7s/roo49yJ0bfi+RgnXsS7BEUFr2KM8OPTm02m9xiH13wQNYznPyOE4H9xNHxrD73vEdwvgRmHgQtbSky7aAQ4sKBMPdHxvi7Oy/mCOCFHZZKCYoHFc7AOmhFDp099jXHvvmeEewi5StVVQ5TpHTG18kzwJ988olCqGaZmFLm3GVCwe0R+s8YGT+2CBvqgMf9Dr6L73h1wHa7zX4Am3k8HjNwc/DljDAglfmGAPKyUw8IGLvvs/GA2hls7IVnVJBD5KKua1UGfnw+XFZ9T4Prmm9c9+w6c+ZlmIBa972eOeKaPMeSLEMPeXYnG/ick0cEBcug122aZzwdPPIZD5pYKx+L2+bL5aK6LXqH7PR9r+1mo/UkH0uCibWHiPXxEPBgE5k//Aky03VdDqDQZ2yXE1Muex584FevlxKMo4fMrULJzkH6YL99HxxzhQ4eDodckkZg4CXa2Ez+5mQZa8y6+6HOPo+uV4yJwAl58/1Vt7e3GY/yE7yIrCMfZOeZJ+TJbQQyz7x6+Z3bTsb/PtIQHXLf4XgRmXJSCTuK/eV+yEvbtgrjfJ+n6y6+wtcSkgWyzZ+PdUW/sX+Mj8CZa3mQz+eqqlL1qwfFlldVz5lOFjRldDQ5mtRpLgU5qWPL4+Oj7u7uZsrsTJeDJpQIJ+ZgLBnGKKmZKdSSAUToHBgS7aM4GA6p7B3x+nkUFIGRStkdwoQRxpg404NgImzX6zWXnKRxV3r16gON46BxjPrkk09VValuH0ODg4MVQHF94zfPh0PEKDqTy2cc2DvDIpV0LAbez8vxoA1HyPp7iQbz484O5pjrSQlQst5S2bMWY8xnU/EsLjPIBoq92Wwyq+yg21l4wJnv80AeHXQ6G8kahpAyoT5/zs4wH8iQgwTkx+vqvTTCU9cuyw4K+P6S3XZAgKEkc8T8+ufQEe9g43Lv7KoHA9Sioy/IOWvl+jeOZX+EAzPKBpiDEEqjlHFM2aD7+/v8vfV6rTdv3mi/3+vNmze5NI+/k1XlGbEdPmcw3t5gwOfay208s7okA3ife/nZRYAUZPLp6WlG0jh58fLly0wgOKvsGR7WgRcy4mdhLUGfOzKAAWsCKYVco9usJ3ohlRb42DjPKjgocMCPPHtQ74EPL8CVA3bmqWR0W8XYTnPPwbWjYizdrfyA5iVZ5XpV7B3Z/kpVReXCqO32NtsUQBWAB53x+bhcLvkYArqbXq8X9f0w2e5yvozrOADHS7BS57ExZ2D4jm/uRkcIAl1uY0wd02IMulyuClWlrktd6qKCFOZlR9wDGe/7tD+rBARSCOmQdOya27BCcpYxw1Z72biDJ4AnlQnuK3kGtxHL4NUDnSUp5P6L97wSom0bRWnqpJZaa9OxUNLUfCEdE5L96VjGXYiHUVVoFCffjuzhv7FnVVXNDo7GXzq54Y2IGCfjR/cduJLd9kYm2Erm0mXWMQglrOM4KiqqqitdOzot9mrbrUIVtN0mf3s4HGZEB/fw/ckERE9PT5LKlgIP0pwI5bvIDWQNdgO76naDuXLCFbmgEsnxz+Y9ASq2B7LES2aZb9bIs+XIPfdzG+xElb/AFkssIOmdOXXCgPuhk8gl2NGJO+6LTvR9rxBjPoeUOfEMjhP1ni2XlPf0e1DNd5bkp2Nz941um9zXfdbX5z5A4sWkYwyriqg7Shp0vRIBN7P0IsDXWVEcr1SYnKZpctmEZznSYs1PUXf2E4MCsHSGWColDL4fwUEuSs93OMwVVseBNKwOAuf1ox7Vo0QYYGduxzHNWdO0Wq83ur29nRkNzgNCucimeMbAAaoHFTyPKy9sKPMwc7zmID0d7IqI4rOBXtI768OL65OZ2+12OhwOOQjyTA/f9+CC9ZGS0WHuyaLt9/ssA2R5fJzOMMOgOCu7dGrIBJkArg0Q43m4nu9JorkDWSzWm2fwTlZLgOvsH+vAmpAd44VD8vM++D5BIPrE/jY3hIBA1sHZL2TEQTHPjhxJyqCpaZqc9SGj4NdkHpEf1tezfJSbrNdrPT4+6uHhQW/evNGLFy9yYOmECsQJwYgH5Mi9lwU4aGOdCdCc/PDzf9zpL7MTIZRs4+3t7SxI9KwlMs1cHo/HWakRn+P+3lIfx+9AyokMd1a+IRf5J9PCnPA+jhrQ4N3/+CyNUzwgwz5i9zxIYx1dBz2jScbBS5TcPixZy/ScQdfrJV8fG+2+wUE04/GuaYUNp0tlq9QyvGxShj13Mq1UMJRMFH6qriv1vXdCLI0zmqbYB3QwyZfU9zDnNANKZ+DFWHyF+y8PTpcZjhCCuj7qcHzSdrtRHKQYK8selQwcABsw2/eF4Uc/z+dOw9ArRlqhl/OX0H/Kpylxnvvi0kSDYIHxU87jGTOAIDLNuqIn7h89kGbd+bez7qxzVCnZH+OgcSrD3+42s4C3tioAhUpNqGfPXdWVqrrNdnYzVQ4gu009P1oAv04wCEhnDpgnnzPWBB/hBKuXgUulgQr66UQfe0LRc/QvBQitzuekk+dL8oWX63kK9MqxEZ7d8zV1EO3Nt3y9pfkeJNaez5BFqeu0v+bp6WkW/GLjfF2xf+gFY0BXPEhfViRRAroktRwjup7hXzxzAymFnUYP+bwH+dgGxs84l36b97F7S5/CWJc+2Am93W4njWM+84zvLYNyZNIzbh7IuWzxefSccTqZ6T6Cz+M7+cxnfX3uA6RprmYMed8P4sA7nCv/7ff73LTB2WyplH1JZWM4SlXXlbbbmxkzjMI8P5+12+3f6XiDknhNqI9FKuUxHs1jsAh6AFNN0+jh4SEfbMYz0ISBjIUzQwg9QQ6GwR2hGxEMCA4LJUIRPROFkyGF7SAKoUaZvHPSMhuFsQfsA5Qw8L45nTkLIeT9BL6GzuYz7xh61pOfzs57hskVGOPnzpQ5YT8RbLQzbxhGbw1PEHW9XnU4HHK3NA/ICTS8BaxnZWCiALY8N3LLODzbxrW53pKB9yDGAYKDTQezgCOuAwiRSnDujROYL2SEsbD+yAYlgzCkzCvAivG4o3TWyJkrDDpyAPOHs+CZnAkMIeiLX/yiPv30U0nS7e2tNpuN/st/+S95H8qrV68kSS9fvsz6gawwfimxYx604wwJCI/HYyYwsCde8umlU75WOEoCEewUn+P7w5Bq9ylvKJtq52cl+bo+Pj7OynB4eftiHJw7Z2d7fX8ajtr3IUpzxtdLKvi7gxN3zHyH5/BSnKenJ2sskw4GZg7JbhMwLdlUbBHB+zAMOhwO2S7xvE6k4MSxK5AfPItn4JakF/f1xjlOILkeuwwwD0muUtUCIBqdSLayBBKetU+6VMp4PdBP46t0uQyZkEIuGCe/+3glaYwcYrrKQD0B0lrDMOayUuwK/sOBGNdPALNTCDGvWxpbOudpu92Jw22xyf4MkEWeFXB2nnlkTbFRzjyjI24TwRceYHE/Z9Tx1X2fzunx7zB3/Bu9QI4YEz4LPfJn8et4mS/fAQh78wzI1IeHhzxXBDZkWHy/rqS8f5F9qOAg9Bu/EELI5/LgJxk3c+QHw0ulnA856fter1+/nvle9AIbjjw7gPfSLIgiD3b8HhAtvicdm4gvdazAM7M2XAPswr/BccumGh4weGbG5Z3rOzZijll3J9PBp06KcQ/kinlym0xXTfe9TrrzWf4GcYmv5Pvcw8laRWkYyx48ZN/1iN9ZU7f7rB/6z/3RpWXQJWnmT5b2+et9fe4DpL4rXWYwKontK8w9AgnbgHDhFBFujEdmdiZDStnU+XyaZZkwxLC/OH4vLSJI8ZpmB5EEJBi2ZbYHx877GAzG6t19/IXgeN0/RsxZiiUrRqAVY8wbDJdn+7CnwAMWD6Q83b0sqfLre/DmLAA/mX9/dhQUJWeuWH/WhOfFAHjHHZyLAxlnqJwpb5omZ+pevXqVD2T1khQPDH1tpMJeM7+wcRyA5nJG8IZsEigRYGL8kA0HYzwT7CrAgeDMD0dkTigddGfCc/v9MZRe4gSobNs2y5OXNrJXxrv4uaHzbNZ2u9Xt7W2eby8xdCDlMth1nV6+fJnv406DAMPZcw8o3fEsA0j00MsBfv2v//V5f9jP/uzP5oYMjBGQAnDh2Rgvsu77h3jf5cWD0cwOT88GgHGmUSrNAqRSF+/Bq9eOO2kBqeIycXt7m/XBGXEcOQGAg0VnL6XSuQqnxVx60MLJ7cwZ7KsDlWEYcpOEpmlmAT965MCWvyP7r1690jAMeU6en5/zvgcHygAOz4pBXDDfOHD8C89DkAM7jT3yOXH7i81hXZJuD7Nru13HLiKH+KLb29vJx4TZGB1oS5rNK/bAwacD8fQsm2y/nZzxLAr3w17Wda2oUU1bDmtGhy+XXtKoN2/eKMZUlo3PS90Jy7w7A57s06CmYU9DVIxS3w9qmtSG3Vl6bOby5UGI+04PyPjd9c2JJ2fCeT7sp5Op2LIM/lSagOA/HKcgd8usAHbJM0LIJEShZz+XgJixPT09ZYLEgwc+zxEWAFHAOZ85nU557yaEzM3NTf6OA1T3304i+meYawJvcJn7BXyIZ2nQUS9x92ywZyYINiCh+M/vj/6zbozRfSB7z9FzxsT8IhMeXLKG/M0DEvTb/RRzgQ75entwiT6CGzi6wvXY8Y5jMvy1/xsZZR6cwOQ6jNsDFl6Om3e7nYaudKp1n8oYPVgEKyFz7nvdPlVVyqoTxPvfyKY5RncyYYkTvtbrcx8gwU4BQnCKMRbQ4ZkMZ2SZSO8Wg+DAmCDYVVWUDEVy4a7rZgZWnGHAOGP4/KdUBBElJIhZMhEAEhhdDIVH1s4Iu+HhuaXC7rjQYdgASAR9Xddl0MO9mCM+wzXdMPZ9n9l2B9pv375VXac6+Jubm1mq2ffnHI/HDHRh3AGGS+bRSxOlApZwtre3t9n4EqDBjHn3Oa613JPBGp3PZz0+Puasns8b8uDgtjC6Bfws533J5LoDZq4Jut3Z8Txci3n3dXbDTzYGY8n7niVzWXUWmcwFgImsJdksnIizQzh+Ain+htyzNsi7M7sexCHDgITNZqM3b95oGIYcqPPszjB6NsCzLc5Y8Xfkmq6SBNSeieP5v+3bvi3PAeOnPKyq0t5GDmTGDsAKegmkO31IkrZtZ50t0T8CUtdtlzMHVegwztebuiArHmz40QPoD3uInM3jXg44HJDjyOggtSQpkCEvc/RnGMdxVmoLoKTskef2jnm+qR2w6SUzTdPo8fExz5ETBssN//yOLPs5MEsd5T0vu/GsDAAE+8Fzodu8kHlIHQAfssG9POihhXgCs8UG8PfkE+bnoLFnhHv5ZmvaqCMjLmOwx8iej99lL1St7WMtVQmbDSRSyBkxv8/lMuRAEf+XbM9aw9BrGMbpP8imVsMwqm3n2R73s8jc8u/4HNbHCRC3/w7a3Iai8+47eV5kz8kDxoGdc1vPNZFtz4I5+GOuWSPAse8LAZw+PT3l8mAIAUCmk6CQcAQ/BK2Oe2h8AK5aBhLI3+3tbZ4z911ch4AefXMZ8Lb62N+bm5v8jMw9QQ9zCubxfztx6rLJNSTlknbWkXnCZzrZKpXKBKp10KHlsSwxRj08PGTZQne5N7oAdnES2OfN/w0GWmbguSZE8HIPtY/JiSauKxV/tAz0WEcPeHmPgGaZCT8/P6sKhVzgmtgxx63YVHQH/+7ksBMVPCcy6+V/kI/MC3OVA7vxV89Byi8HJ6XOvdXj49OMQXaGl/88uwEAdePmrPvlctU4nciMIYe1r+tW41iiWIwS3V48SMFoSEUJvbuIpAyk3DBI8843bqwOh8Ns4/7SiB+Px1kKuaqqfAo2DkNKBhjwL827a6HEACHKiY7H46wsBOMmKQdDbhycfZ3XxpefAHA+ixI4o+EMESl8HzfZKtaaNcXZe0YGuWBuaCtaVVUuhWPMGHg2lHoJAAHN4+Njdn4EnFzPx8m4PAOE8jvrw7WYG4IzZBqAxRpR7oP84zw8mF2y4qwx43KGCucPiHBgyrgZK3OLI3J20ctv3HBT+rTf77MMu9xh6I/HYy518z2EUgHIBBToh5MFS8JB0qzzJQG03zfGmJ183/d6+fKl6rq0oSdwYiz39/fZPjgrzbi4D68QymZ8AjHkHJnx84OYH54X50CXKQIkAkpnj5EHX1PkjOst2XickDOOzOMyAKcjJ7pFgOC6TfdDXxeeHfvgxy7A5jL+ZRkOOuPOFSDGgZdL5+ug1oNDz4wwB86m8qzMI4yuB438jb0erKcz1B6opfu+e3AmQABd93WnuUOMpfaf5yZYi1E5GEYGExgqxBv2j79LQXVd1szLxbDtbkvzOg6SQilF41mSLevVNHUO/Fjb9LN+x6aVciRK0gelPUlRdVVLISqEkrnw/SEeZOBTPXvk/gCb6f4I/+8YAZvJfVwuvHTbbVDf92rakt30ZiBuf52E83FiWxmvk2a8z9+wyzwr5AOyRDkYGXDsNbb89vY2y6tUzomjeoTzJdE7z3o4uEYmQgi5JAsdcbuO7hK88fzImAc/71vD9+3bcVvrdtF9jpNN/j0PBADirqtOrrOGy+yL66hnL1gf7Ipnr9z+uA3muuAAD158jiGXkSe3gTwDMux2hGZGTiizLh5E8/2lvWVOsFNtXauuyp5L38Pm/o9nQYYgDT2w9aCR+QHXu+92fWG+PItn8fHXfH3uAySMBR2LChAse0pYUBQRw+Q19Hd3d7kUCaGF9UxKkfYheXmTpEmB65kiwODAlAAWnT1C0Zwx9HIAqQBnvovR8GDLDbQzRVJSwqenp5wBuru7y/PlaVyu7+wVgNDLtpzRwHkyP85ewEA7oIEV903GrEHf97mMEQBG8OTMh2euAPHMixt+vgdwd4P28PCQn9PbLDvz4mATZl8qzRG8jI81RqlRVtaVcbMeDoJ8fQku3PEDTJlrN8TPz8+zUkOMsc+Zs1KsE0EtIIHreumCkwnICPLjmUapbKb3jI8bU67nAY8zbA6Sn5+fc5DuxhUZ5VkgDpaZYO7rBp65Zow+L+6wZwzUpJueCVnqHACysOWbvC5kzlhrL6/gHu9bO+Tc5c0Dc8aIjHINGGG+x5yxbr4fgXGiO7Tx5Tv8jefCFros+Lx70EaJI3YV8Ea21su5nPFE/xyAsabMJ+tOxov/AFkOiPhs27Z5LwXzK6X9Y1VV5WwT+owsINMEPwAqZADiDN2hfNKZYQfc+B4HUcjQkn31jINU9q45u419CEG5oQjnXpXgqs9EDs/jnft4kQkdhlRix734nOuW38ODixhSJzyXqzQ/qZOskwPjOGZ5kEppoq/POI4ah8QEx1Fq6pJBlLwD3nzPD3bMfRs64jLloNvXjqoF1sRtyjKrhw5g3yBNkElpfk6Nlzk6Icn8M3aye8yhZzYIigCYjIvx+LMhX5AvYAeusd/vc9DkWTz8ogNa5NltLofFQ5AuMzNLf+WH+S7lD/vjZIrvUyI49z1QrLn7D89aMNc82/sa1qDvzDHNllhrJ7p83w17uL0U0AOb5f49l0X000lRdMkbXiAPTjb49VerVW46sgyiHY8hW8w58kr1z5Locv3FXyTbsJ5VgFCFM/aD4oSBWHsCMR8L6+F7kx3vYHeQMc/ugaE9A+cl4MXejBPWKHuevtbrcx8gXS5XDcODMQzJcVRVk0sECJ6cnZHKxDrTwouAB8CSBNlPLa8UQqcYpRCkcSyd16TSJhGjsUwjYrT4LEw0wMrLzjBYDlhItSNAGHfGDLCnZt0jb2eYJM2AlzucJYjBCDuA9VIhF1oHG+78KN9zNs4NW4wxKz7Px74CB7Pu+JhzN7bMx/l8zhmNu7u7DBC9Tpn5ZzwYfWcGAZoOMDBcXhqIY2C+MRLOPo3jmBsGLNl8AgWMke9J8rnF0S5LcfjJmjqgBcS6/BMk4jgYJ/MN8AZEejMI/5wH8O5M2EfiYNbL/Rgvuuny62QCayXNz+FZllz4dyhNeXp6MoA1bzmOM/MMmN8L/fQgi2dDTz1z6aDSQbdUAh5knjHhpHkmdBGZBGg8PT3N2PbdbjdzhIyJNe370g0PRth1x9k6QB6NX5BfqZTyEEzw3jg93/lyVlPXqWtX06gfSnc5SQpVraqOGi6XqSSj0n6/m7JwMPKURqbSsTSPqeFO19k9x1Ep00Ewm/4rxFix6VIQRxYkn5AO9B6Gt0oNBQYNwzVfZ7fba7tNZ1SVaxcZR34Jftx+uWw62VFYYz/fRFNWZMxj67pC5LEu3nzDQXsIpeuhM/9jPrSxVtOU854oZ0rdHtNBuOjw9UrwMs31dSIRY1Tb1BrHKftX1aqblfo+qu9HVZXU91NToUqiTXV3vaqqa4VQqW0bxdip70spGjYr6aokpXbPTUO54iXNVYyK4zjN1RSMxVF1VUrxmGMHvK6Hvj8kB6NBGschV0I0baPtbqvj4aimmRqBQIKOUf3Qa9W26vtBoQpa1Sn4GcZRbdNqtWr1PDUKappaVTU9Q3jXx3iwie1Fjhw0vo+Evb291dPTU7ZT6LxnQZHRpb2B0MJ2b7fbXP2ALeMa2CP8GNfALq/X61w9gY3yoN5JOt+jjQ/hPe7lWV4nrJERB8ZO0HgA5jqzJN3o7Elp6uPjo+7v7zMmcELQMzLYTScN0SfKxXgf2fJgknl2/4qfcbllPQmA+N3nCP+DnXGyDFniP3Dl0oe5HfcMOFUG4BJJs3E5qcs1qFBZr9eK7ajues22n0BYoZDU3Mv3vHrJnJOfPldODHoJrM8J4/J14Dqf5fW5D5C6Lu3/SWzZOQNwsiZexyiV1sLOZEuFNXOGZ8nMt+16Ut6rmqZS35dD8zzCRlEwIARYDnD5HJkTMg1e3oEjdJb+crlkAZWUjRYGygGjM3conBtUnlkqmYC6rmeb9z3NylwQzDEvBBhuKBzw0W6aYM833nvKm2dm3Two4bowPV465swX64chYDMha73ZbPL3KVujhArH9D6mmjFSr80GWM9ELdkQ1hLGwxWd+m+pNHLAUJCh88Dey/R4Ri9tc+aTdXEZwPh5ap259rk4nU55nh3sAbTcSXEtHChr5gDAHSyGGYML4+Tyydx41pS189S6M4asHdfyrAiMG/Phhh4ddyfjXYR8DrmPs6joBfLpY2O+/XcnKXB+BGQ4paWj8/M/7u/vZ2wcwQ62x0sQuA4Ahiwmjog15HlijLq/v9d2u9VXv/rVbKewYx70S1I/Dhpt/JdpTFWIigparTd5nA+Pj0kGo1RVQeMw6HQq5+kUsoQMdNI9yvEA/lIqdU6yUE2fOc1kBdshSet1IWpSIJbk43zuRac3nhGbwTEGZc1SsJH+Xalpam23mwKwjbFfyijPloBbVFXVM30chqjNhr1izWyOsc3OBvNv2tonOU7nIA1DWhfIFansrWVOWLthoLQ5kXvIb99J4xgUQqOh71QFqWmmBgBVUBMmoFpT8iyt1ytdLlfVFeW8Tcr8xHRG4RBLSamX9iVZHPKcte1WUgoW6zoFeehcWp9aTayUWpTXsznBtrgtcsJjGAa1q1bny3O2r1VVSSGKAG2332Yipaqn6zVVDqqatp6yC1PFwyQD1+6qpkmlf+vNOtucYUidECFHkTEn05xw4qwasgppnUqwhG77fjZsI/6YOXBSkWswjw70Q0gVJgB5zwxgE7Cd+HJKtJwUYB0SwfE861LJ8yJj+BB/Bscsy8AAf8k4HBj3fT9rmOR7UygNfH5+zjqNr0ZXPYDwgNuzSOiqk6WScpWJE6w8gwciT09PGWM43iylpKVk3TM5+FeCQ64NLuE+jNufxfEKdpz1JrPu2SP3XW6f2OcEjkKumK8Yo/ph0HmyM0McdZ2OEKjMdzI3YD9IfUgeZIfxebWA+1Tmz4NQ/B5r1zTNrx4U6y8HzqT/JeUsBULMZ6TSXKGqqllaUFJWOthSmFfKFfq+n20wZIEBvGR2CH4wmCgZoMoVquu6DOoQPMaAYvK+75lxAPXy5Us1TTMrvXJFxbA4E+4Am3rfYRhmThbDdL1e85lIzCHGiK5ULuyMEZYTBouAizH5RlBvltF1XT5P4Xq9ZgV9fHzM89c0jV68eKGnp6fsVMh4YKAJYm5ubmZBKYaQNuEoIAabgPByueju7u7/1d7Zx9qW1vX9u972y3m/M9c7lyuKkGpoBZGC1VZamr4gKmI1aSviSNJ/SiPK2IZCYo1Nkxa0qX2RKqExJsY2+M9ItE3BscUpRBQzwyiKFtIiqHUY5t57ztn7vOy9Xp7+sfbnWd+17oU7M85l8LKe5OTec/baaz3P7/m9fn+/57d6jjApatAkFL/Utel1BIR7Y1hCCFoul/G7HjB7iQX8wjpYFwrPHTTPhgz3AWfOmxWAgsHDnvWo61o7OzuR96ATssW9+Awlxry8tMyDfMAJD2I9cMFQOAII/YZoEWtkTvAa/Lm9vR0DWubi2a7Oce2/OdyzmdPpNJbfuLNLIM69hlkgnBocA/jC0VCeQTkBsgwPsFbXc0OUGEewLSto+d/PLToI5IER70DiGuh3fHzcC8q9gyKOVZd56s7QYeg73drNybMiRVEoCUHZhseZs+u9myGKvQyAunNxw/3yv6OzkEF3NrkWXmEPPLPGvZFx1pqm3QugHaBxp8SRcPaprlvdPZ1s3ttTbJDyum4zMkmiRJv5J1KiRHXTqKlrrUPZ5nxCUF7kbWatrKNuOFmeqtjIY7lea510pVyhkdIkU1M34qWsbRZJUc9A40nRvrS03Y/2/X5luVaWpQqhRYW1edlnXdfK8kyr9UpVXSlPciVJUJanG0RZ8YWnbRDSb7riGYd+mVjHS8OXjrZ6rithd2ABHZqmaXRG/SwmfNEFp60TfHJyEsuZHLSjbNUDYXes4QvPfCOP7D8lmnzHZRdwA926s7MTg1h0mzdL8WCZ6gacXWjkQQL8h2yxLu/iCHhLGSzrdhniXthgfz7BT8fjXRtoryLwUir2gvvyXewPc3WgyO2Zl1Byb2jjNgBaDhuMeFDpvM/+E8jiN0IHrmX+Q3CQvXVdgQ715g7wugNWHsxjQ/mhFNL1Ojzjfq3rYHjSM2P4KO5TsGYP4PFzqqqKvhnrpxqLe3oGE57yDCZrIVinkyhVJTs7Oz1/1enu7zaEd4d8Ai286mMymej0rHu9xq3GHR8ghdAd5CVIgokhGEyE8vLoHOUD82DUyXzgQOMscz2d5FxweAaIvJfsuVFGUWFMyax4xssRmhC60iiPlt2gD4UQI8C6mIMrNK9tZX4owCE6BPPjHLiBoeOWO8c4fEdHRz3nkcwPaXWyBQRQ5+fnsVsZCp4yJp7BfpLmlxTRIkfhEPibBcoYZ69p5v6uANzZhf7QBVrAM54RwAH12mHoLilmiQgaPEPENRgwL7mE3zCk7Jk72zjp0Js993U4X+KQoyyZgweEOB1e+uDIE/dm/R40+NvrMWI4NPARa/DMmWdeMZLIsDtcblQl9eTOgynOPjjSyo9n2QiOcN787AdGFuXta2L+/M3lnd+hPyAE9D4/P4+NYhw1Rk5Zp2cP3Hn0bK8jjMMMEIaTdeJIuFHy1w144M33Wse7Vqasx29cnySJEnXdwlhLkiSbcqWqx2vQzsEhXxs6kOvZVwJQnDX2OGYNiqJHK0cdkS+cQ3gLHoeeBFrwvdQ1heE+Dkat12udnJxEvsGRLctaddV1cIMvmdP5uuvwBU86KtxmPFLVVWMOYrKpt0/a95HUdcx2tTRuM2cRrc/ytoys7oJaaNxm+NrzBO3ZoTZAKor2LNZk1gcF2iCJcy+ZQmiUpImk9t80STYldt05NH9JqYNQzMH1MWVO7Cl0dXDGnUCXT886RFAw6TIU8DyglvM5tgMdgC1GD8Hr6MZhaT56hPu5zJycnGh7ezvafkkRmITn+PHSX55LFgh7slgsYpMFbAR77brAzwZSAcE+Qn+AIAe6uAfyiU6ET5njbDaLr7/wQIn9pZRQau0elRPYHvwU5IkzsugPP9/nuteDIHQ62SPkWFKsiOHv0JF9Z63oZgfn3J/y7IvzMK3rQwhR9qG7g5gExgRwnv3A54Svq6qKjbTIQjIP9IqDX1QKoCNZgzfMwY7w+RBMIrih4ofjCdDUm5ZhuwmqAaOkrvw+SxKlSRq7zeIfZlmmvb29aKec/2mI5WX2rqcYPnfACnTmEFz8XOOOD5C8Gw2OE8TkXSVsotQFG66UEViyOqS7V6tVr7MKjI+C4rkgrRhxf7GiO+I4wKRJSZdTq1wURXyBpCNWCDGKDKfCHQYvbyIIIThyRMNLLlBI7lhi+N3p8gAOpcoPgRlZJJw4jCIZOowdguhBGUqZlrKsG4R5iCTwd5Q9ypH3l4BaoGQZjqxDGxANslJuOKTuxbPDTAUOoZ/FcaeOQ/ReUuYoCGuGf1CWnSOmXjkDvMteDR1b9tF5Lk3TWC7BAV3ow1xw6tkbR2Sdz/ylph5c+HAaMdzYouwwFsiEl3FAc3iQ9TtS5Sipl2d4kITz6eWW7jw4+sc8/e9DBNOzBd6ulHtzDfzBcNDDD3pXVRV5Z3t7W3me99qD8x3AFM9GuSOD3ENfX5PPg79zf3gMfsPgsy88g73EeGEci3SioK780NedbM6j+HqhQ53n8e3ewyy8y6kjvOhJeMXX54AOOonnDgM91yWSonPrzonvpZcmeVA/BN7YT+TTy1XLsmx1+mxHZ+ereM+2nIw2wujhpqcPJ5N8w5OJeFFq+91ESZLJ/YAQpLabaqMsy5WmgIHtOdmmaX+qqlJVt80TsBXYzdC02b8sw3Fpg7CdnS0pTbUu15rN2rNOvl9pSha4PYMTQrMJztaSujIt7BwyDu958wgv8UHOvauhZ43QdR44oFs8axQDKXX76pkfl08HqNAvlPvAA+wzVQ5eeuvlwcgRre/J2sOj6Hf0Po6yn10iW+ZNFJgHvAQQBi3RGWsLut3fIahBl7juw4l3HQHokySJjo+Po53n+zQ34BoAa1qIS4oggwdggCHoH+wPaxxWpXCG2F87gq1yPeKNXdxhJuBy+82a0WHQi/Uxx8lkEl/94JUITdNEsMt1Ajob3xAnHp5zmjI/dAf75zZ+CNTCX638pdGeSP2qDuy+PwM765UQXroHjZumia3cyaQSbKLvveSRRAPrVpCa0IGYnv1zIJrfPYBzgB6Az8Fp1un7JPVfRv9Exh0fIHmkiVDBwH4GR+qEFEcYgfVUYpq2tf44/97i0ttgI2ikHY+Pj3tlUDjxnrr1QInn8kxak3JvInip65iDMwjDMS8cXHegEXJHZt1xdcdNUsxigEJRwuD3ZF1Z1nU38egdBVMURSxB8wyRpIgQIFCS4j1Q6lK/GxJC5UaR77lTOxxDREXqZ/wQWDe+BNYe7KD8WCPPh1fcaXZHCcXj2SGMMG2i2Ud/+a6XBPi9HJV09M2zIl7SJHUOLGfVoKWj02QO2EdKJDyQcqQWmjrC44rKz5jxfGgHPxK4YfhRliH0m2HwjJsBEzzP94o9YM0e7DgfefDBvQjmPSgYKmOAE3cQeTaOBvNyx4S/OeKFTvJ7OpLsxt/LUhx95x5u/Jm7z4/1IgvQyv+OfmLu0ITS4R4ynWVK0i6jAN1CCLG0ChlnXlmWKTRdeRMBrDu+yJXz2M0CcbL9knplkI7yIpPoYHSsOxPwFHvCs5EjHFoAuNWqe7E3Toojq0M9y3fLqlII0npdqmm6LOt8vtXj2xhkbvh1Pt9S21TAX92AXKWaTMg6tRVwRTFR0/QzDlJbGkeglKg7fwFoMpvNVOR076I5QNtsoWkaTeczpatEdd1oPp8phGZTMjNR23Jc4gzR9vbWZj6JmqbTccg3/IU8sT+8swr5dCd0Mploe3s7nulAJztYggM6PAfjOsp1JPoZHeqBcl3X8R04N8s8l2Wp7e3tXutweAgZGTp9yL87xZKibAHEYS/RAQ4KoFPRedyfcnUAXX++8zO0RJ84PVgvvO7IP3IEnbBn+EUenMLH0AYfwBscuaM+zCY6cOsAo5dJMx9suAdY7B+yRIn3zXxCfAoHyoa2A7uNPqDZBMCWz9kri5ivd7F10BaeGWbJHIxxWrBOD55Zgzdz8gqig4ODnj1Hv7IeMm3T6VSLxSLuO2eHACich31ei8VCs9ksvmYmz/Mu2Ko7G8WcAKLd90SOnSf8efC6A5DD6gn3U4f24nONOz5AwiHDcXBHzB2jq1evxgCD8jc/H4CxRUniqGF4XcCuXr0aDzQjqBcuXOg5VNxXUk/4HcllPtT3np6eand3NypsFCaKwAXWzzm5IuF5KHEEDueQ80AYd5QwCAFBEAf0PMCgBMgdFNqGe82uOz0YGNK1WZbp8PBQSZLc0GGG/eRlrDA/5Qk7OztRyTZNE9Epd34RHE9vMyeEDyEFpcEx4noQP1ekwyDLAzcPauA5R7jquu6VDDq6iNIYOvJS51wRqDAfP1vhxo51MSilwDHBueDHFZ4bcBTtEFzwgMXRHFfoZDLcGG5tbcVAiMOZjvSwD8iunyXkX673QAzeYA5uJNx5gIeZG8bLh+9B54j2O2P5Z/ALOgMegZ7Q3IMTBkp+Op1qZ2cnGlXuBx+xTne4+Iw1kX3kM2QfvsRh8fcB4Ui4U8Ce4pw5oOM6hucU04kSQ995/9N6vdZ61RlX5hYDvrruldvwwkquA5GE3pSzIU/QyF/HAB/6v74XBKEOhnj2ta7rXmMa10VuV3AmCL4cAYUfXQexd2maSYGyXJylNlvT6gJeyNxmYTpgp23AUJZdk5R2vzNVVRsgJQlBR6Msm2yeC5reNrbo+KlWkjRKN6+r8Ixk0zQ6PTuJc57NZkqzRFW1caySNvhJkqC65vB/rrqutF53vNV1DqRUM+85VOgF9Bz2SOpeYol+4zoCc+brY3t7W3t7e70sDHtF84FIE3WBf5Z1rYiTpMvyePDGDwABNpZnnJ6exo6nrpd4PutF17MPnqVwfekywJ5g5yXFZk4uT/C723Lk30ET5oc+9bNzZGTYs/Pz8wgkUKWRmqwje/P5PFaOeJaPIJHvECDAI17x4DwBPZBraOL0wvYPgyKyFtDTAVa35ciz63d40Z/NtQwPKDnXyvCsM3rUfUz0NHzNHqA3HMyBdp758ywi93OwjawZMubt3B0sJBHgr4qBFu63QC+ns1cVUElQ13V8dQxBFtdKUqMq+lkOajsINASykHH+dXvE9U57p6Hz1BMdd3yARPRMkOSpS3dQQwg6ODjolddxLQLsTpqjvI7kz+fzqJBhQA8GQOMcSXAEgQ2V+u9jqeu6F2ggjAguCACBD4xQ192BPTIMp6enUTFyHconz/OYwh+iPNDM3zeAA8O1jopxHY6T12anaRrbknqmI03T2PbTHVlHKhigU/v7+711+XtV3PCgPKqqe3s96JundPl/URS9NqUeBOFIkg2TOqFFgfk8CXRdyaOM3EHIsiwqGO7PfhOoE+TwbA9APFAhmIWGw6yFK23/jhuAoVNIKQEy4IEbQQbPJNBwYIBGJtPpNLaXd7TInVw3Ou7cuyPrBsHLMZB9N07oAD93B295iYBnSJgHqKvvHbRDuWMUPHDlGb43ngnzvfAgxnnn8PCwNyfowL0xsMjR0FnAEXIj5/vDvRyxc1qzL+7U4zwAGni562q1UhmD+EpbO7vKklRJkCbFRNNioizLVVWlZtOJQuCcSpACh9zb8zHtS0R3IlCRJNJ6HdQ0BOqUjeY93h4GgO580lgHXsAhwdHFIYb/2Hvu66AbjhR/q+sum9nmYqQkSbW1NYvdsvK8EG3LW/Scxg3SZNKdF5QAzrpMd1BQkgSlmZQXqcryfPNZUDHJ1AY5qYqCOVdqmlJ10ygp+y+9dAeolUFJCj1aOX96CVAIHahXlqXqplZZVmpCo9C0HQf39/d1cnKi87pWFbr6/2STrVrRzKiutbbSM3RkahlJ+BIZmU5bXp9ugummaRtWFJO2JHpruwXHzk7PlGZpdO7rs0o7O12VwtnZadultKqUpklcN8+B1wmYeRbyTsbFwQFstdQFGugfnEX0utsUdACVLN37oPrnqfgODjH3QlcBZHrpNXtFUIJPwF7jFCPLDqii18hk8x1/ybCDXQ6Aeetr7Cg0Adxwmyt1zTfQefgM7ow76MN6CdxdB8NPzHk6nep40zXTr3c6cxaO+dzMlnvA5hUF6BtkB33iWWPPlFJRgz1Fl2fG+wRGbmf4cbASHvTAjf12/9DBNC+XpNzXwR72wunD85iX20D375qmaWt7m/YnSVtARc2Ghzf382APeWJtHsAzJ6eD2znoyX1Y/9DGpsnYxS6OyXTSK2GSuppZJzyOsjOi1B2idyZ3h5MNotwO5bO7u9urvZU6h9MVG8zk7aZxPFC8lGFRHuJlOgjSML2MUif4Iu1NihNkxR0mmI/sj5fMuRIEbXUkm99xZBwBwxC4ELizgfHCADqaWxRFr8sdtOe5lGCwdmgHbRyxc6dve3u7h9zzr6d63fH3TA5rKooivgUcRSN1HRIR8KbpOhyyZhQpdCWoYL89UHHnzAOdYYDljp2jTJ7Fkjql6U7kUNHjALLeoih6L/FDCWN43RiD9PBd9gIe29/f1/b2dq+c1L+LQYd2npXxOUFz6HIzB9mRWgIFP2NAcO9omwej3IvnuF5wWnDAF0OHnvDAamhUPNAB5fNA1ensQIlnruFrHFV42QEOPyPnmSHXZwSG8CiGyw0qOnBIK/YXh8oDiDRNtV6tVFeVFEIs3wpNrTzrOoM2tXo82CG6zQYI6NrgIjPox27OXfkJOs8dQ/aQTpdevnV6ehrLiLkWeiKX6B7u44G67+96XfaylXVd6+TkVHXdARHIS/tep1RZ1vLo+aptJBPUqK43OrRpaRmaTYYyItErNaGhB8NmT2oFbQKqLFETSuVFoklabEoACdIT1XVQmgbVTaXpjHLi7swh9AOYyvNMdd21Nm6aTkck1cYRTbsg//RkqUTS9ta8Jytu96qq5YPzTQerqqq0piGABRCAQbw8dV22qPnyZNnL7iDPRbHpdlqtFUoAgERlVaoJ1lWuyFXVlaqqjNkQKiGw1e48At6hM9Bv6KshUOmd4NA72ECqK0IIunr1apQFbKDrJsA6gpkhCAOvub1zHeg2hs58fIdgzrOxfi6FZ2NnHFxDBrARlGNj/1wOp9NpLE8n6wGgXBRF7MbG9a5rsKvoebcVkuL5YuQNX2xoawFION+FTvGAyB3vuq5jx1P4C1/RART/l++j59l7B1DxdQhC0DFu95AX/o9P4DotTdMIUntFiNsM9sDBN2ycB03YJvwe51WCS/cXoRFzZ47Y9bqu2zK6NGuLeJtGSWhho2LwbIb76B44Q38+d4DH/TMHxBzIY95VVamqxxfFxgGD8i4bH2w+ymPI7FwPAzvaikLwmnyCGAy3O2V8n6AJ4eGe3umD55HaZpB6ltRT0C4YIMnL5TIi4hh1siEoPLJnCA3ZHHf+YCwYztFFDlrO5/MopCh8XqYIk/PD/WkJ6uiMO4ZDIXWUxGuLXZkQmEAbAlcEDENAgwSnLULtddYumE53D+pw1L1Zh6NsKPos6zrlsffwp2cMCJZROBhcT++jAFAMHuy6U+col2cNnM+H2UevKZcUz1aBhvEdZIB/4WFo7tk79jk6JVYq4uUZHni6A45Mwdc4szisBAzuhPk++dp5Dtc7fzsi6DTDmebgNHztCDByBB3cecbR4JkELQAW7mi40XEdBe9jpB0dZQ8cQeTvdKhiL3mOlx66w8P3cCYcxfOAiQDF0Tp04LBkyA2g86+jjkOj6yAP92bv4KfVarXRif3mI369Owz8n7W6fsUBx+lhjfAN1xEoeRDswNSQ7+AV153n5+cx240cDBFQL1Ul2+n7leedferKphKt1x0g4d9j72az9nB03QTlWaq8KJQFmmSsYiCaJF1lA+vCLrgddYfFs/HIMuCjyyXrcNuDDFHmk2WZEpPHpml09erVuB/rsmtm4Ly/s7MT7STVIOw9++0BNnvJO7WwXzQQoAID2+q2BV7xzNZisYhZdgcZXEdwPolAB1uEPcZu46B7oE8Agn1wvkE2sXXeIMiBTgA7t6nT6TSe/93Z2Yk+BbzAM/gdmkBrnucZBgcYkWfsdpa1lRKTyUSHh4c9e07gQKafsj74jL31lzHDq2SBkV+uh1cdUGJenoHzMklsHs+A7x3IcdDMgSN4kmso42XvCEaxr/4eIfwoOt8RmLhc8Qzmw/5gK/kc/e2+nusp5BJdh4/kILwPXx+8AB29IVYEspv+eWD4EL3u9/GA1xMLrtfxDZy2PjwodhAR3vFM3hMZd3yAVJWVNO13U/L6Ws9swMRe8oVycicLAWfDYRiCHwwCBtfPMrmiQBiXy2VUfLzFuq7rXucQMkqgUsxnvV7rwoULUSAJrDzi90OWe3t7vcDCHSM3YAQAN3MqXWgQKEcQcAZAE1AKnm3gmbTfZn0uuFIrAAQ0PA+F746I0woDi9HxWmufH79jtPi+K1KE2wM39tcdO2jj95G6cow0TXstKrk/ThA8BgrJPQkg/N5etujZJYJsd0odWXHl5iVXHlh4AMzfhsGiZ4a4xuUKunhA65m6qqp0fHwc6Q8vOkLJte7AU7K5v78fgznW5ZkRd9qRQQ++3Xi7AwwvITcebLqz7kYHxwgnFyPkWU13bCXFM3XIBkGVzwEnBzp3JWadQXLZJcBHr7nj6bqAv/v5QQ9McXwwLt4e1oEYD9j9b6ydMhGcMUc1PcPF2pk/us3vT6YHXcwa0Jmsz5/vax/K4zBz50BHNOwWULNXPl8v9WAfmYOXxXqACe856IMTzXXcAz7jXr4mAmR3WN0x4Xp3HuCZuq7b7lHNpjV+070PR4Gum80N/NPyX38d8IwDDENwgrIYyqJwBruKg6qXycMGJmmqcmM73aFlD28GmLF3s9ksngNBT2DTXX8PnTEyRs4n7lC73ubMpDdOgF4OgHgwk6ZpfHcfACKlbZ4xBmjl/zjPw9I3qfUpcKShse/JEKjA/mAvWJvzPzbSwRsGtgqZXS6XUSbYh6bpzv/SxAQH2gEpaMwZZOenEIL29vbiWre3tyOwCi2pKhk2gXA/wgM8+NDBbT4jKKGRBToNsA9dTzAMuOedF6ETusxBc96VeHJy0gPmQmjP/i6Xy/hOI5cxMonwnldVsDaX1dlsFoNHl3+vSIGv4HMH1dA97An2B3l2YBn9hx7DVriPgS5x3eDA2DDTib4hmGeOyPHe3l60e0Mwyu0R9MAmePbM7cGtxh0fIHmGCAPkqU4cTCJ3BAQhcSEmcEGJEJFi1Nk4V6juOGRZ292NVphHR0exSw6ZH4wf5R5N00QlyrsAYB5HQ1E+KHmUIQyOsyN1Bt1T5+4c4GQPEVicBRcQz+AQ1HkJkTtyCA33457Mb5hqZT2LxaKX1fCsC4rYUW0XYnc46L7i6DXz428Im2do3BFlHV624CUzUofUOzKI4YTO7DuKZVi+MFRCKHTui/HCcfASUebryB175YoSPneHCiWIAeQ7OBkoMoI0jF9d17FTowfTOMqufD0QHZbG8Uz4yVFYrh+eaxqiQtDaA0r2edgwBIXqZ2nY6+HBa38XCM/14Ar+QaewRgAGmi7g6HANe+qZBC/XYX+RPYLjg4ODWGJ5cnLSa9N+9913x78fHx/H/fKAl7m7TDnPuHPjewV9XLexH44qQh8cJ4YHfc7v3N8zYcyFMlt0GjLR6akuOMJA+1qGZYmeLWc+fsZx6JCz7/A3qDvXuv7g7+hyd8Sd5wBqXPa4FucV/eUggNsa9tXljTk73wEwtOtLlOeTTYBZbXiwbb2tcGPzCfQQcg8NvMvqEN3GIcU5dz2KTLJfvuec5zw7PdXZ+bkSCw65x2w2UxO6IBJZJQuEPeT/p6en0dlGh/p7W+BtB55ohuSBlfMrzh17B7jAZ95x1ZsFwZPoJ0lRHxBkeIkQ9tJBrOl02qtEwZl10MwDx8lkEkuakySJZ3/9XIlngx3YdR+GrKcHV16Gia6vqqp3LfbSdQbXIxNDeYcP4DnPGtR13WsPjr80bGTBvrh+Rw6GfgLXe5UJALTzGfztGSHmiENOUITd9zPKAFXYBWzHsNLHwXlvRoFu8+eyj+wLc3W9zt+wjTzfgyM/lxblbPN9gDMCdmjCnN2/82REnnX+sPt3BPbYe7fHTnMP3snQ+jNdn3rwzf/dXkPr9erGZi6fbdzxAVJe9JsAIAiO4IMGSOopVldWtBj1TeF3FDKCiSIAiSnLMh52k7rD47PZLDZscJQYRYdjRvce0Cc/xEYqn+yEBzQoUxw2T52788O/ICaugDCwjkrkeR5TxI6aOyI+dDD4l3UisARp0G8+n+vo6KiHOt3MmUPIvWabfcTZ8fU5OjEsUXOHlmc5Ss5wNIV997e5+8vshigH/3eE2x0qSkuGjgQK0TMwPNvLfXBIhsrDnXb+zn5IrfFG0btjwTNRVh4AMjc/rzWfz3Xt2jWFEHoOgae1fW4+B+hHEODdfRxxYi2sl+vhzWFWiGdkWRbf0t00TaQ1mQ2UK3LnNGXfXQH7/jhK58EY62T+fAcnyp1h9geDDu1dLj3zyTN4F4Wvl+c99thjcf04BY5wSv13HK3X7TsqdnZ2Ikrs90buudblhPV5JhQnBMQUneXgkhtpL/3zjL2j4/A7a3VdE0I/Y4SMDAEDl3MvM3Ln3jOsvicOXEBDP8vBNZ6V9vIoD9ycT9BVDgIQNLvMcS3rZj890OPsjAfB3LtbY6K6ouPYSm1zgvQG3h5mBYtirrYzXZftYm6eyXJwAF7HmXee77KB3bsI/WWiQdKFTeMkXjjeOqLSat3OiUYvzBE5gu+KotDFixfjGRfnAwePkqRtKnF2dqbj4+NeUMZ1yJM3NHBfAn2I3mRNnPlFLuq61s7OTty/nZ2dnn/A/IalqeynlzKxbn6QF+aH7sO2I6/Dc8ToFp7rneTQHU3T6OjoKHaLZa7Qy1/t4bae9XhFCrJBtoc9J/DwcyzYA2wlQIXbCOdbr+qBJ1mLpPi6FQJZbImD3twTQI2GFPhinklCn/AMfCHnIeYKjxOwIUv+fPSKg6PsNfqBs1rsnWdLsHPOl1IXBKIbuC+leQz8Q7djbssdnHVdjL3onW+bTHu2xPUDPMy+uN/h93NQzrNmDogN/TLXSV550dJ4fA9SHNPJNJ79QTG4o+NZGoxalmXRccRQ1XUd6/lpvYuwSB0Kg6Ig9SwpBgA4SAjYXXfdpfW6fUfSer3WwcFBvJcL2TA4ccfCmQ5UzLviuSG+fv16RJVR9jAYjheBG/ekkw4CgtJG2SGcfhaLf708hECraZrYkAIFg6JmbgQeVVVFRcTeICgMEEEEzZ1IF2ifA/uKgLvzhjAyPMPgAaAj6p6lY288y3EzIyR1ZQK+BmjnTpDTGQXLGpkfvO3lTMzfgyp3BqELz2F+3ItAQuqcOM8O+hxCCDF7yL7AX37gl3VCN0f63dFk3l5+hGxwX5dX6MZeUqrggaakKMdSa+wItLMs06OPPqrFYqFLly5FJ8f3xxU498IZcd6E1/jc5QYn30tlfH9wAtxZAo2GJsgRGVHQR67FePIMN2CSegggKCGoJQfRPQvogT1OAygwa0Z+HCUGGPJA0g0zDhz6yjMJlAkzHNSA3i4XONm+PwRBQ8CD/2MDKO1D1/KMLjAoenzvgaikuE74niAG2cDBQ648o4mO43k4M8guAaWf6cMRxWY5qsv8PIjlOZ2zmird3LeVkVxJkkqbDnlBtWo7yOzgiGc3oBXvSIEvXN7cWUeOAazaubTvZ4KfoHOWZdraBDWerUc/Y28cZXc+dSceWV4ul70OYegOeA0+3d3djd/1oNxtoAf58DH6McsyXbx4MX7Xs3ieHfUy1zxvX1Wxvb3dA1TIOriT7Y0MkiSJ5XpDXUKQzzto0GfwAhUBbsPquo4Z56ZptFgsos6AT5EXKm6wqa6bGfAEnVmxT4DCrMGrd+B5Sb2GCgSa6CEHSOFH7A1OPvs2n8/jOpFZtw/utwAqE2gj//hWQz0A3wwzKgRB7jM4UO/8w9560Au/s9fsl6RIP57tATTPRD9RVeSgItdiQ7G9bmPdnqID/DP0G/djrx0oqJt+VtyDOebG3pK1dN3qvh22lH33PXRa+L6wRuZZ17WStH9u6XONOz5AOjw87KUvUTheCiT1o2SpQ6vZDJiHrA9MgEC60mXDYPyTk5Ne6nNnZ0fb29sRwciyTHfddVc0gNSrwozu7IcQ4rsVeD6/e82oMzvBFc4bgij1D9hzL5xlnk3ACALCd2FIGjRAkxBCr1GBKw3ugYHjOp6JwXXnGYMKYklg5SgGa4FWw8wTpQjc1506rx/HiHnQ4PzhhpTPWTN10kNDwb1YC8/i/7xvw1FNX78jo14WgeATyNAOGhqAInmZhqOhjhjCS0PUzQMPlKQj6cyVeWG8PQB1J8MDJxwd9pS6fWQPo8k+Mk/4GOOIAWHu0ApHxhEr6OBZKWRge3s7Ps/lCF7BEaFM140DNIaXWQ+0wVl59NFHtV6vtbu72ytf8TmimzCSOPkejOLUAWY4qOJ742UTLmfuZDviLbVAihtgN1ZeGjU0QPw7zCDwuw/20uXJ98x5s9VB+UY2S0PrccYV9wEZ83btOAFDtBE+5PkOBEGfNOW9PUESDlW6OdS+pcPDI81m07hfBLCOdrKvPMsDQc5Xsr9k6+EJ5AoelDrnDv44OVnGIG29Xqmuu3NtreNFGSgl5VKe1arrRkWRq2m6Zg9NqJUkXcnxZFLE7CK6n1ckOMoNv3lW0hF/dKoHsC1fts9aLBZK0/alsicnS6VpqsPj49ZBw3YlmU5OT1TkufK637UTXQvghk4nAHfZuBlo5YG6H8x3GWc//JnYPOcd5uHPITgZglfcB57jpak7Ozs9sMFlCB2Ok4hddMCWLMnBwYGWy6WuX78e13szkClN29duuK5l7/ANJMWurX6+mXPbyB42/ezsTAcHB1HukEvOXO/t7cXzx9gsP0+NnkHe3f45YOGBuQOZ8KHznWfRCbYIGjxIQnaRIQI7B3o8MEOXM9h3B+KxZ15B5GABAAo2A5uEDYN/mRtzYM5Sd57O7QV7Psywua1Al3jA4QCwlzMz/xBCfKcSQSl2meBfTadrWatn5H1OAAlDAMJtugM+8GpRtJ2OfV/8mb6+Jzvu+ACJYIjyp6qq9Oijj8YXuaJkJcVUsmcCcHLyPNfBwYG2t7djTSkvNPXucmmaarlcKkkSHR0dReWAMJ+fn2t/fz+m/ImeUXoo1uHZHBwbhIMaaEpipC4Vi9PJGvxgozM+zsnW1lZEW93xYW0oEBh/mNpGKKGVR+x+iHV3d7dX14oQVFXVy1RJ/Re2EWiCtrIWAiWunUwmsVUrzj7CyHfcgWNNfN+DBZQje4dC885IbrgQYtLxjlijeN04DdFPqQv8HHXkuyBAfrbGFRjBMYi9r9fPlHmGxrNT7KXzFxkClLYHKDwXnoUG7C1KVOrOcLixB2mn8+DR0VGkB993XgTJx3AOkUMyxO64MW9XwrPZTKenp72SWA+SUaTwSdM0unbtmpqmiVlj6ucPDg60WCzinJyfCDzcaUiSRPfcc0+UHzLbjojyXQwafE7gjqPiHZwccYMGACMOsqzX617A6S+dRv/gDHvm2YNd+BWd6c/3kkv4nft4ps/3gvvfTE7hue68QBJlojXURZy/z5c5QU/PPPE3+ND5BB6WpMXiuBdwwfPOx1VVqq4rVRWyUypNs4hWwwtecrparbSzs3ND5pY9Wi6XUYcDfLkMsUcdeMcZyFzr9arnpK3X3buFuEcLuLQvkm3bgydqwgYsUa22YXjbxEEKOjvrO2fsj6TeO/ncyfFg0Q+lo1ORdTL5krS7uxt1Cvs1mbb6V6FRmuZqQqOzs1MVm/cM+vUOBLFHDqR41o79QSb9PJDrRr6PboR/uMaDepB2dPne3p5OT09jZs0dTew5wC20AahIkkTHx8eRDxzAIJPB91ivZx7Q0ev1WoeHh1FvE0w0TRM7gWKzyFwRoGO3ObtF9oa99HJydLODPGVZ6sKFC9FeQrM8z+MrNtDB7MNqteodFXBQiucdHR3p7rvvjvPzMk8vT+b+W1tbEYz2c17IEICmA+jwjDeMwZ9gvfA5sjEMxDwbyv19Dg7oMSeCewJ65sTz3YflefP5PJaPE+C7nDoYvre3F/mTwX3cz+L7XAsd4B94jizk0H4hh2dnZ0qVKLMkg/uzBEDD0j9sFvdz8ArdK6lX+cNauqx4p+c9UJXad/E90XHHB0goOknRsbl06VL83Wvbd3d3Y5AE48McUnteg7p/HFIvj3JmdCbDGCBQKCUUpDuSUoc2IhjuqEjqBSyU2Ph6PEBiDigqlNMwa4DCdkdP6oIursOpQ1jW63UsZ4AWrqQRPBwM0BbPzg3X7sLkSmmIuEnqKUhowP55wMPzXDn5gWYCPIwQc5G6bM/wvjg/8/lcx8fHcS8ckUI4MSB8l0FmBuHP8zyiatDRFQ8BAOvlmul0Gjs3OU09w+KBjKToWKLIGe5QobAc8UGJE5wiY5SreYp7mOXjvsgcJTQYY5xo+AAexeBR/898UdgABTwLBN1pl6aprl+/HoNdABAyrMwVeWIe7nh50N29+LOfKfTyHwwa5XCSemcBcf6REw+4oQH6g6yof45xge6cQfDSDjfu8AwG2ev907QtLwIlZj04QJRZss/whGf+HM1noD88yAihzYJ5wONr4X7d3BMlSYfkwyc45Y6Qore8I58bVYYHE/Aazw5BPT529HOoIx0kwMEDXIBuyAJl1EMUGJnmOjIKON/r9Tpmmwgs2/1vnRjWyn084PeMbEu/rpEJjiDgyunpiabTWZQf9BxZbuTR9Rk87HRFV8EjZHCWy2V0bDzwTpKkd26obupe4Mq+eLUG4B17V9d1bEaADh3KY1V1DQyQOeaMY+uBkesB5w/mQAkafAe/Hh8faz6f92TF70VAAD29zNSzEwxkERvm96JJA/xNCT3gkQM2yAp0kBS7gmKH0jTV/v6+tra2omwDNLEHBG7sI74Ssgco69lU797J3jqQ5DyKX+bBZ13Xunz5ctTZ2HFsN0ArPIt8n5+fa7lc9vwS9tzBK/jIKxCQdQea4A9sMPaMfcFGOHhMIIQdcCfeg7shSMTrWtzm+3P9zDC8FkLonSmCvxyMZX3YEQ9uHWhyMBIZ5rvIzhAEdt8kTzMVm+AO3kWXQV+vJiLLOHylDXbhZnI5pLcDIg7qxT1vnnir7zs+QMJB8HMQnk4HSUF5egTsDjbGWFLMtBAlsxlsKmiYo9weUHEtAQtoBsqSUjCYp2ma6Iyh9KSuPpMMkM/b33+SpmksOeEeOJOSYnmcpIgUofykrlsUzo1noBw1xnB4GZ7UtSjHaPtBY7pTsR4UN44TqJwbXc8eIXDQwg0y9HPUxZF5RySgxxApc6Pqz3aknoYVUj+T5MbRUTEyQR70Sf3DnJzn8dQxtHfnZxj4+aFRzz5IinREibK30J77ISPsHTXp3sGL5zt/hBB6JWrcE8cXXnQUVlKkBQjZEF2TFLs0cQ++C+KFwXLZcsQ/hKDj42OtVivt7u7Gd2+g0L0NNj/sJ8obWqPsWZPLOHoCo4XziFFh7R6geJbDkVicT2iODDi44I6o750H1NBM6soc/FrK9Tzjghy5Awo9QdzhL+7r+wAv4OQPAxvoAM3IdkEvd7i5vi1zU9x3Sb2D/X6+w9fLPXBufP1DcACwoa4rlWW/HfGwJGUYyLWASXvWAucSHoYnhiAFNHM746VY8CQOoweNIfQbAiAn+/v7EeV3xJfS7RZY64IT6EBwwPo8cwYfelnozbIrgHZD+jM3D/y5Pzp2Op323p+HnLuzKylmXQEyuGb4jjJsHnrKgSmXcS9RczvsgbWj6+gDdBZ0zPM8zm1rays2dirLstdYAR6iuoV1uy5jTzzDKHXv+0GuVquVjo6OIkAFzY+Pj+PvBIT8HblkHuwra9/d3Y1njJgPNsv3kHJDD8BcvggC4R3AQzJbyANnHgmSHGTGB3Pbt7u7G/cTPeuBvgO47Bs8AhiFHPh9fV+Q7abpOswRXGFH8NPwu9hbD+5w1rFtgBv4Zw4iwCvIE7w9mUwiqObBRJIk8T2UVK546TfDwUjnf7dtDqh58Ma9CFTJMDrwgF1DTlzXp+o3F0G3OfiEzLI3ZKdc/t0Xd97ADmMHWBtBpX/fs/ZPdNzxARLIMxuC887GQFgYDGEBfZK69K47HAg+6DPM4lHu0FkGrSdYAu0py1K7u7uxpMI3FEF1R84P+GHgYShHpKUuPYvykTr0GQc8TdMoXAQXjkpDP4IWziNRvucKDSXlDIlC4u8u/GmaRvS/qqrY1c8dMITGG2wQOCH8rsC4zxClxfF2FNnRQb7L36EfygR6u+C6o+9O+vCgPTR1p2PYKYbnubPhjoorCBSrB0BSdyiWHwwzNHOEyJ0Q6IfDniRJD6VDabkyZx7MH+WDwkV2WDvGyvfeDaIHuN59ET4Ynv3hnvAHskV2lswI6wHRZT/JmKIjPKB0R45AHjnxFrRkpSX1ZNH30PmH0hD2z/VFCN0hbg+wPKPpWT0PNpkLdPKyB+gOeJHnbTmqo5M4N94Faxi8ecDKZ8zLMwHIJmvwsg13yHHuQU/hB8+EoEfae/Qdbq7nmczDnSr2Cj3ooInvC/yK/iyKInZIA9lExqEJcoPT1z63zT4R/O7s7ETewXHiDA+H22nC4ToaG0RWBNohh/CL1DlkXIvDxtmQPM9jpzE/u0bVgCOwp6cnke7oehp3oKfZe5r+sM6zs7NeG30vq/SABH6ijBeaTyaTWHJbN43yLFdQ6O2vv/DdQUsPXof3dLDKy6y8Y547l95lDIcXfuN5fgYHPg4hxJemE6D6fOAXL5EjuMF2IKfQme84Mo/dYR589/T0tFea72fb0Df86zba+c1BEgIfmlaQufGMFwEO8gZgTICFD+SAs4OY8LxnWii99owdNh2bwj09EwZfoTOxBQTTR0dHMcMELTyb5HaNShmyYV5CCQCCT3h0dBRtE7qE/UEumTv76RlCaM98CNA9g3pychJ9Tewj+gg9h5w4aAG/wOe+PsBgz1B5hs1BM3SoN2tC/jhbxX54BUGQevZwtVppuVz2GgtJ/W6RBLvIn3/m88L/QRdjN+An9834fghBsn2+1bjjAyRXPM407ryfnJxof3+/p2h4I/PW1pYODg560TWbwL1gaIywG32MEYoRh2l3dzeelwGVQRF7ly2YAuNBw4csy2JnGJT5MIUstcKxu7urqqpiMOPBG/fwjkhD5x8kBEFDINxhckXL/1GqON5Sl5kgWHVl4SWNHtzw3KFz7J30oAGf+V7zOQKFQmC/PFBhTR6YSl3XPuiCQvVMm39OoOIGx4MslCnPvRlPOYriRglH3uvmPePiwTJBAvfGOKGEXCnyLHgdmYEPPUBzlJg5DQNfDwZ9bey/Z1X4jjvZKLohUs0zWBvfZezs7MTPlsul9vf3e8EVBgajg4PDfkAnnEmCDngGJxsHgGtxOpEjr9FGNpjn3t6eVquVTk9PewE8dfge+EG7mwWTXhZCFga+wHh4hoTr/b1CyBbPQS/wDOhCwIxh9FIflzUHEqQuKw1NnIeRC0cjKSPz0j32AZ5ibvC9B/cu/66XfX/RF05fAKy2nKzWtWunsfqA9TDPoUPVZak7J7Zp2i5g8CdlX77fBBM4mTjePAuj76WorLOlaUcbzrJ6IBhCuEkZWFcuOdSdOKjQ3ME2zvqhWxxU8k5qXjLsTo//nf3xAByEGt2WFp0dGQJV6FfXuwcHB9GJdb4gCETu0QUuH15utLe31ztPRTaAPUY2ABOcl6GLg4HYavjbbSygRJa1ZcIAQ9DVQRXojcPt2VGXKfcbvNrFMxrwyPAH2YMu2CrPzkyn06g/CO6hYV3XsRyzrmtduHAhXnd2dtbLFpFVckBm6OSz53TiI/OEj3V0dBTPUuKbOTiKLR+CkQ4CIGfQEb3jGTnWBe08uIZn3e9iH9Cbi8UiZu2887Fntdl7lxFoihw5yADvYYNc77j9dHDI1++VN0OAyzNzzNtBRAJQeJI5ADBzXR0aletO5/k5WuaDnkKvIXPMy203NoT1EDy7fucz7oGe7bLCnT281bjjAyScQy9bcAShrtuzD8P3/nhXFjfQKFYM3c7OTmQe7o2Sltqa9KOjo5ihwuBLXetkzxLALF0ZRZf2JXUPg5RlGV886c4Ac5vP5/E9SRhWPsM5GgoR6/QSF5wPMk7utLhwwayOAEBjFK47OtCKUgSCS4/8UQRON+bEPUExHBHCyHiJGvuLECL87ty7AzdEmXxe3NNRH+gBfw1RPz9j4UaKLGMPeQldBs6DLngGI+SO89CZhk44qCgv7sUaQcAl9ZQQa0HRwDMoYZ+vf9eDYf5/cnISDa0rYGiNwee+BOSeUmfuzItnehmKB3c4HU3TvWyZa9zoguDiSJAx5doOXT+N4ARlIjTu4DwTSp57+7x5Pk6HlwziJLqDz7yGGRjWN0RY4VM3PDgHfm4R+YdfoZkH/azHnUh3AtA1yDe0k7pSKngdveYON5+5buiyIt1b4ZGPlq6d7BPQuJz5fciOOKjjDg/OiDudq9UqdvHEUfa9Q9c4kNQ0TTzXhqxn2Y0v4cRGkNVhnp4dZG+yLItnRulshoPg17dnOYobaO06E96BVtPpVIeHR3Ee7mC1clT1zvngiHrQ7UGzBztknKqqfVEodkBSrxuX2wwcRmyul1eGNIl6En6Dt3Gu5/N5bG1flmV8X5KDQ7TPPjs7i8GP+wTIEIGKBx/8i8x6trWqqlhiNuRpdAABFXzgttYzi+h0ZJ/9HsqXVzi4HvGgC77GEUc/8i5Ft2luu53W7B+fIfPcH/7iuWTm2UPWQsMHzp3Aw8gw2SKyicyLNeE4w/e7u7tRL/L6k6rqd/3b2tqKzyUAcJAKMBZa81y39+h81gYPQzNkgd/JBPN96EaJsjfH4Wd/fz/Oz/WvB6w8xwExeIr9YV1Sl610ANL3z6s4vFwPGrOv8CPyzH24twdHTdN1EvRul0mSqFp3mTEHhB0shO6sHX5ndMBOV8GF/nQwh2u9+ggb6RVgQWMGKQ4Iw4aSpZAUEQFQPBwjkDg+ZwM8tYkx52wEyg/ml7paVkkxg1PXXRmEH5y8dOlSLL9omiYeZpW6tzg7Ac5SXQAATXBJREFUuooTMjRcHiihqGESR6b4f8eIQW2L2M6BwnGeTieS1ZJ69o3noHgxFOv1OiJtBALD8kAcfxArlKCf90AZ41h7cwBS5zhfXoqAAPkL+DCY7nygrKGJ1DqsvKm8Q4a79Tu659/xVLwrLM+CoHwcKca5cOMPbTEo7K/zNfRjj91ZgWck9WjO8x1Zd3rD2xjLYeaFeXgq2xFLeBEnkn8pwfHMiBtq1uQolwerGFTvwuRZIzcuknq8yHWgSl7a5MFnURQ6Pj7uodS0yF0ulzo4OOih9wcHB9rd3dX169cjuk6HyqIoYgkbZxIdEZQUgy3fG7LW6CQAA3QBNHH5xTHxTI87GgR07AU8De+QfWCvvYRpmC2Cjh7sEERjTB1w8GCOd4p4qSwOogfErGN/fz8i9S39pDRNtF5XyrK23XYIjfK8y36SwQHHgA+m08nGoeRQc3sOhxbdVUWmJGhrq3Xkzs9Xaju+1VqtOBuTqq6bCIwliZQk6QawoENaiDoKu9KBPKmkXCFwdrDl58PDQ+3v78c9Gmb/cGzc8XJABFCOf1sHs4iH08uSM06NJECXSlk21XQ60dnZuTjThHwge/AtjiC65eDgIPJL0zS9V2fA24A6rrPgBbIqQ8ADG1etS+Vpe46hKAo1WaPlcqFE6mVLkZH5fB5pCB05uwsP+YuakyTpNZ+At9mr2WwWz5IBOKL7k6Qts/IMNGActgYZZZ9omIBzi5PuNHYgAVsAvR1AQueia3zugAwOeGJnkTuXZXjNSwy91Ppm4BufF0Wh7e3tmAlHHzBH1r+1taXlchmPEng20Z1X/BH4CP/Bqxew6wSgbvuw4545cpvgHQXdT6AyxwN2dCn2Bd/DdRagGc/wZzsw4ZkgAm30uQdADgJgg+BTrnHgkn0GVPGMDr6DJwfc3njgAu9BPz+3JklZmimkjZIghbp9uXOqVq9W61JJkIos1858S/nmPk3ZvfwcvuBfeB/aMD8HBtF/2A/WynVeVuu+IjrFAWgAsclkMjZp8JEXHfKEMoKYHDhDAN25xWFCCbMRKHeQEldeCBVCQ0QNk4IkcJ0fBjw6Oood2EDucJJgdjJC7sDQGcYZA+EEZcFBZD0ECty7VWypdna2ewY3hEZJQtZF0YnCmHmJDjRmTcwdZcgc/GAthhUhAMXFcSMdz/o8S5BlWUytY3gwZDS+cMXjCCEK3MvsmA/3aZ2XtuRjsVjEtUEvBNSDVVfu7oDCV47SSN3L95y3UNismf1wBAfF5gfV3UiglDD0jtZiJNgvgnsyaXTZcYXqhgenAbmAF+AreM+dDhwk0F5XzqyX+WEA2BOUK3SALhgB+IYA5cqVK/E73I/9RzZYN/cB5cPAkO3a39+X1KKWe3t7vQASlJ3Suul0Gg/S4uwSxPmLWUFLodd6vY5ZYM/eoNxx6KA/Rttlzh0tD06Ojo7i33BOpe5MJXrw5OTkhkPE8Lc/E+fJgSD20bNPPB9ewNFxQ42MSYp0crQ8SboWvx44tXqtAws8k81ABrIsVZp2DSza9xl1raGzLI3n5cgGoJtOT8/iWTZ3MtM0U103EbmE/7e3dyIA5s4sAUJbaplFVBb97OCGOw6UGEpdG/Td3d04X/b17Oy0l6kG8ON7ZDIdAOF9bS1INN1k19p3EIGSU2KE7LFvPHe9XseXoaPjABSROa7Psiyeu0JXIU/DbmcEJtjF1ea8brXhxUSJkg1v7+7uRsDLHUN4Df3KvdCjjpq7THbvvkojHXBm4U1sJw7ktWvXok7hftADOrlsoKuYK2e2XD/CFy6zs9ksNpbheR6weAYTurvd9ew26/dMmWew/awLe+MlSg5EYUcd0OJdRwCsbv8ODw/j9egWOv4BWiFDnH1z59erE7ytNXxJ6bQ7/pSvemBBNQ/zYp34Bp4Fcjl1+gJ2838HaZkT+4NsIsseMKMj0T3DTJLrRObuACDfIUvFvnlmnfvjY3qpI3LEPJF792snea71qpXPuqrUbEC7qqy0u7OjRFIDKBu6cz7QEFtHkyQHKJFLeJX1Q0f3X7BL0HUIEMPP7isM5cP38Vbjjg+Q1qu18qx7qSQOMIJARghHKU3bVsCOsnhJniMXroCG2RycPzZXatuE++azuVJXiuPOxZC5CZxwePgem48SxzBL6qEZOKPUYfP9Lprvt5+UEk0mvLirjgrdD8oSSHiaH0VD4EDJg6dq2QdHchwJZK4wPUoLYZNaI8n6mAt0omU0z4SG0BgHn+sRIndUHe1gH5kLyvbo6Cje05+BYvcSl2HQ6oaT/Rlm26CPB8DM03nP+QG+8oASZeIO7Ww2i01C6G5E0OcZKmgIz7JOyihxEh2ZAqkDwfFshStrDBB7FUJ7Zs4zeM7/jpJSBiJJx8fHMaBxAwXteK4jVdBnuVz2eODChQu6fv16fMfR5cuXYxADPUCO2VOQdHfE0BfsE/SFP3CAH3/88Wj82e/pdBoP1nNWaWdnJ55pIuDH+fCgF3q7bkPfwSceYDEP3pPBMzxjLXUlGQQCXtILX3oW1ANKD9xZE/IOz5NFdn3rKCDPd9DIDZ/rbDpZeZYc58i7OaHLPKsWnfPVKpZogkS7HsBBIXO2u7sbz1sQmKCv4AVQdcAFzyg7YIEzASjF+VUcGehQlmXUNTiWrHe1WvccK88WOJrr82Qfpa51OI4o9w4hRJkJIUTABNoCHgI60FVvWJbpOgTdkue5rl+/rr29vVheyP56edBk0jU4grbOd35mwXU7DqYHZJxFxL5yPUElASWAn2czAATR6fAEpbee6WFf3TFHBml8hF1B3tDvTjd0DnNYr9cxM+MAE2vwgAc9OHTguR8gBvOE9vC4ZzeQJ+wDvIZMsB72Fhlm/6TuvDX6nACb7KODEO5s+zkn9NowgHFeJygh88/a0C18n8ABWniw70EMvIXNcrDZs62u+5yX0c0tGHMaM1cE2l7t41UX6GZ0nTfycMDRgw/4AbDNwU/nKaor0HXcu65rrepGMr5zv8/LpqEXtHU7k6ZpzMI6WIs9dV+N9XniAvlGv3lmFFAXHeZHBtw/zLJMWdpVrdxq3PEBEsw5nU5vOFzpQuWZAwQL48OmIDB815sEkDHBiA8RHhQUGSupq8OEOfwchtQdfIdxMKI43FK/Bz1KC0PmzgfMDOMiVDBeGyykm+wLPfSTTY17qqo6uwHpcKXtjoOXUrnj4VG9Z1ZQvB6MoCQJYhxZAfUGzcM4IqzuVKH8/Tn+bDfOfE72kAwMwuoGxYMNeIcg27Mn7my5YzdUKuybo8nsE3QnjQ5fOrrCZ/Am8/YgCWUCbd1w0KzDf9xh8EAbg8V9maMrQuetLMsGhyTrG57lmSQ/oOlyArrK/h4fH2traysab+Qb58ibS7gDj1zgMLnjiCzs7e3F+RRF0Ttsj2PgQR2OLd9DXqXuVQI4WMzDy3JBbrMs0+HhYcwWegmvZ0Ql6eDgIGb8/D6grxcvXox75I43tEYu/f1nBHl13R7IJku7XC5jZhaZ9NLPJOnKlXB+oF2SdGU7/p4Tz+pRquNlKzgHgAzOU+ixIcBEgIWT7rLxB3/wB/rkJz+pNE317Gc/WwcHB8qyLJ4h4p1mLZ2T3vlN+MltStO0pZ6UWgFq4Nh7FtTny2H1JEl6Hbk4u7RcLqPegpfZdxwTMtdtqWHSow/flbqAgXm4HsCBQ1fw404IjoYHICGE+GJR5yXWzfmmomhfdosTvLW11ctw+dxYozc+4cdfVl7XtYrJRKtN8IZDR6bH5+mBKHRDN+MAo5/gOeiEHKAvh1UmgEHIlwMm7Ks7tTiC0Am7s1gsYnk6PAyiz954UwkPAnAIr1+/Hl8s663NqV7xID1J2swsYIhnZXgWtHMAAueZzIfTBJ8KGkud445+cOQfupPxYD+QefQE8/E94xq3BeghbBE+Gxke1ghvs26nOcANwJW/BNn32GUFveXBPWt3wJf98ODIs7J+Vol/4WHnFQfG3bdwsN7tqGezaK7hr6hw4Nz1OFVKPX9N0qQobtAPXOMZXAcN0UXoBebopeLuE7hOgcbcnyAQueZ6D3bhVy/t9XvWda2y6s7X32rc8QHSZDqJ5QpExmwwxiqE0OslTyc1XjCGILM5MBZOh0fbfpBe6loc1nXdS+sXRRHr2BeLRWRwhJ6MDEgowViet2+ipgwIp9QNuaNBXu8/7LKFo45T25aP1CrLVkCzLNNyeaLptHOOUQqu+Pi+BwgoT+YoKZYaulPKHFE8ILAoURzQYcYMYXPFCJrNvCT1sjiSogPuwS/f9/Q9//fzNyikIYrtyt+zN65gPFjE2LBG5gdf+Psn/ACr1G9zDC1PT097SJtnp9y55Ic9g5aO9vC7o2vDA6ZeVsd5B/jaD4jCX3meR2ez47W0p1R9bjzDQYuiKKLxht449kmS6ODgIBpqd6a8NA0DxD564OYI/NnZmXZ2duJhX65FrnDkMVohdGcTHe12Hve1g8q7zLtO4R0qzPfixYvRcXSUmv3gvFNd1zEo2tnZiRkAzyo5P0IvL9tlHU3Tdtr0YJuOm5SjYXQdFGIPkSH/vjsdfO5lrvAqsooe5r0nOOLogmH20Q2v04l9vXz5si5duhT3jezQfD7X1atX9fGPf1xf8RVfEV+SmaZJr1OZlxTzHHSqdz51cAYHv5WhPvCV53msRmhfhNsvX0KGXV7Ym64cu4r87kCZZ/TZJ56NM4h8MGcPWJAfd7wcVccGENy5boX3y7JrIoTDi0OEjHNvdCMZJUmxHJF7u65HH/A85klAgBOKzcHOIf/Hx8e9wG54jofnOD2QZfyIIXgHX/MZwTpBK74AOgr6ux1tmrbzIfoQm+Iygy/hQCI62v0Hn7vra/iD7A/0RxcNM1Huw2C/CMbgxa2trV7ZsfMi8u0Ao8/dsy4Eha6LXPbYA+7H3+Bx5BEdOwTZ0FeAEEM+R8+QRYMGXvnC8OwS9n9oO10uHFDl2Q6M7ezsRDvFvfCz8Fe8NJxnoQucR5kv13nmB9nyJjYOfrsM8Jk2+h+gd8hjrpsckGHuXOM2HB5wPh8CX05XaO7gMrrC9xIwge+zF9iWZuxi1x84zTAYDEQduaPHOAyeDpY6hkIw/eAtJRU4OAgjCBroL8gaCgCHwTMcGC6ejSOF45GmaURwUDTDF5ViFBx5GAoeStIZ6+TkTOW6VFVXUpCa0ChRorqptLu703N8PXPg2Q8P1iT1lK9ncBDG4ZkGhIjrcYDcoJ6fn8caas8YOPKF4fFAwJ01P3SOg8B18AvKDGFF4XhQgbCnaZsJJF3O/kv9dyyAcDFv0E//m/Otl2250uIgKQ6FK4HhWSvmzBxQ+PAKSnhYyuBBI99jfwEXeNeEI5LsgdS1R+d7gATDQAkegMZSl6HwZ/u9QLFBepfLpaqq0t7enqqqaz2c53kECjxIcYcJZwt+cGfPUSroulgsNJ1O47ty+K7zN86QB1cYiGh4Nt8h60oWgvmwh/yN5/srAigboeSIe7jBdweQv0ut80E3JZ/XMAvNfZB/rkcO2WsCTOcpd5rduea9OgQLODTw3PC5HiyzjmHQzTO9dKssy5jlkdqSRv9+kiR61rOepa2tLV28eHGzh115B84WJW+elUDvMM/lchnn6I4kMieF6JCj90OQmqaOugZ9yT55CRDraWU6VZL0D0BLnPPs2nXzLJdtdL6jscP7+DPdWYuORtNlueq6jtlc9p/AGafKzz+g47Fv0NDBKM+COPI/nU51etK9DBQdQVYNe+BnUeF95AM5xEnknArzWy6XPd1a192rG5znmC92sGmaCCIwt5OTkwhgwHNkftHl/n1JPVCAecM3gGUu22TmsG+U97lMsx/IiIMzrIMGRvhAkmIHyLruOpsxb9dzHvjAx2TMvWzXg2q3Py43rk/9rJjbAfiBs0roSfczepkDC1A5Z+MyzjPTNI3Ze/cLHCQgMHPAcQgYIFusAX8P+kM710PYTujr9EI/ejDiPgnPcTsOkOW2Hnnk+9Be6s6GwtMxsEtSpUnXih3ZRV87rd2PcVADf5k1+L3gf87xMifsg8/F/Qb4AV5wUMD9017wm48ldnE0db+jzTAd6WnOLMtuOP+C4+lte51pUTpE7Hme99Ki1LuSLsXhQJgRVo/GESSQR0dopX4dJo4izCB1Z50Q+qOjo/g82mQ60nB4eKjr1w8VQiIFAspKed5mufZ29xTUIWYwpdTVeDqigJBjRBBaRwwcMXPnxoMOD6QciRtmPtinYXtahMIzWyhLF1boyPNRyJ5d83320jR4AufI0SdHxaTuxabcA+H3zJUrPwY0RUHATyg43w94iD0AyeTe0NnX7y3uh4EYzrYHvq64sqw9swMvYBRwyPmup/CHdf5DI+EoEkYM+aRcDcCC605PT2PXOErkJMVsEPfkfRwXLlyIzxuiV8MyHfbIZX5vb6+nrOErN6Ae0DgN4AecQ/iprtuyNg8EcGBw5OANmrMQDPKSTn8GqD087dlZAhIye46MQg/P5EIHSsOGZwC8eYtnAwmQpO68j3fLgweQHYLeIR9CP6oBaAgA/yIbZA5wFNkjZAbn5Eu+5Es0mUzi2bWqqnTp0qUY0E+ns4gyeyDEXjp45h2SHLEnowrft/PtzgRSvdA6G33j76WtOGI4+zyvDSy7skt3bMpyHekv9Q/pO786su2OG79jK9M0jWf+4AH0GMCMywKOtjsz8CDNkbC9ZNTJhC8WC5Vlqe3t7QhEAqxMp1Oty3WUQ+7NvnvmZWgvCK48k+llUQQslE26nnWgCJvmYCFlUvCGg57Ox54lJTuKLBNEuM3HbvMM5J/sKjR2xxYZc10PcHFychJ9Eu7B56wNXUBJLgEYrbOhrQeQ8DJr9v1yoAv9StDP/LkngS38hN6AzoeHh1GmJPWCZ2TOgS7PtKF33HY5uItOYt3sHTLnvOzzRpbILFJCyrUEiVVV6eLFi7FhCXuGXE4mE5VVpdD0AWYPIny/yJphKzqd0AW96HMPXFzvu05Dx6DH8E1bW3Wu7a3tyE/oIvgNnmHeDuqipxtbl+sePsdnZnBv94uwzR50eeAIsO46EzmKc6jGLnZxgOSgcJMkiQfAQTYxsJS0IdAY+WE7YI/i2WCMMELhpUfn5+e99KkrEIIpR/XzPI9ZIp7vKPbOzk4PueR3Doo6Y2RZ+5K6um7rcVEai8UiBhkHBwebcpO29askpWm2QTVbdDPLJtERIkvBvBkoPpxJnBjW3N63M+ZDw4xBd+WDULF+qTtvgACB/uFEoTT8/o540RrcAxw35h64uHIBfZEUyySGjoVnyzCMKACJTN1JDGIdufXzIR4o8Qxo4QGOlxk5As264EtHx+A/nACyWO7UQpOhAfXUPv9n/Y5WE8i4Y+FOL7zjTiu84vvbOXxlPMuA4+6Oy3q9ji9axKFIkkQXLlzoBRZpmvY6GOHoDp0Z1gFNGMg3ZTs4EMwzTdNYogJPMT+MJPqFMkH0iwdowwwQcucGBh3gJZDsJ3tG+ZGjxwQ1zu+erZhM2lbjyB1zQi9xP3QY88GIe9ApdfX9AD44DQA2SdKWSOLAODjg+znUHe6E4sx6pozvOKCSJIm+5Eu+JAYZTiMHDdp1tG3F2/VPzXEsoo6cTltdR+aiLCtNJmT8G61WVAlMJSUqilzHx4vIS1mW93REmqYx+KS5jWeSWTM826HUQSHwAuN1fEcMXTi5P9fneVdxwE+7ti7Ic8f1ZkEBgAN6DB2E/Hvw4oEXe4e8k+nFET44OIiod1W1ZwsJGpIkUTEp1Jh+YL+RGQfjyGzxO+VrnP1Br167di0izVVVRf3l9s3tBzzveg3Zhj7wFkAFAKzrdWjigQmy6DoQUJM5IuPsA3vE85FjSm1xyH1+8D/PZ27IkgeaZHB4nxRrx87jd7i8D6sXCKo63s9iVpHneyttl030HToavey2Ap4hIwd4cnJyEp/jwDclsdg+L3skQGLu7qSv1+t4zIHAkT0jg4WOR5d6Nn5nZyc2BsnzXKnJhNR2gztfrTS3ZkleVoYMe4dNBwEcqPPsr9u27e1tHR8fR38Jmp5vuka635OmqbLpLOqFoZ12W8ReAuhyD3S0Z+uYD6+9IbhELvBz8BcIQB3A9OARXweZgH8dBGJdT3Tc8QGSO49uZCXFlsUQjr+hWHGqYQgnMIbC0T5HdlE6KArSmicnJ1FIYGZ3bFBy/MAQ3IsAB8cEheelPKSGWSdzJVBx5NwVS2sAi55RaLMB87hW7osyQUlRfiIpOgzePcfpBCPjZKIQ2SN3jLkeZYojI3UCAq3JyqCwoJ8HQDjFCDK0QEB5P4fUZXEcYXfB43wK8/eDz/CdfxfDDc95Ktlre/2QJ8HRkJ9CCBGZcjoRHLrRJJiFf1HY8J0HosgH5aCgMx5IuAGHx1B8nt6Hno7eOJCAIcbxc1ST70mKMoix9P3yEhro4qAF/M8+4Oi5HLM37Bdzkvod2FgD9ASJZjB3d9CQswsXLkTd4IEPYI3vGXINbdlfHBzojfyx1hBC7HwHj8NL8Ik7aOipJEluCNI8mJK6lvRDhxknAAfAA3z4Hl3mMsjZFAc04BtoADLp80cWKJPyQIjhfAZtQYcJPnGKLl68GDNFvDPHnwW9HC3GAfI98sP729vbEUXe2trSYrHY8FSl8/OubbfUdl/jRdnevteda4AAz6b5Wbr1ut+YBgeRYJS5n56exo5sRdEGyMvlMtoiZIeySeZzdHTUA0aYI3KLvvMzH5S3wQNkMHCQPSjd3d2Nuu309FR5nuvg4EBSlyF1oKXVWV0DCc9yeuc99gTHbTabxbPGu7u70WlDhthnb4HsTZWgPc4h/OetubkGu+0y7dkC9zF8TwFoKa/ysjL0CnxM5g19ynMc6PGzX8g6PgC62sFF1uy0xrbCb/wfWdzb24s0YJ95Nh0M4Y1hB1wHQw4PD3v2Cf7heu5zcnISm25BSxqESG3zGuy0Z1z9/w4UOdgCoE2G5WaZLvgeGUcPZFm/bBiaDitDAA3YL0rs+TxsaFPV/fNNw6yNyxD634NsAoNOZrqzvqwN38pLgrkfwJu0aSyxoTP081JDD77Qe9gl+KwouvPmgNroYs9Cu77FlrtP6L4kcj/cU/YNOXUedp671bjjAySEP4QQ64pJ/WJ8HPWEuEVRxHpyLwl77LHHoqD7AXlnJBzlyaR9NwR9/hEMDwZ8czkjRabKgwQU69nZWW9NknoOnSMvMBeKBaGCLtTuuoJwBwehdwffkYwQQi8z4UoapeBK3Y2BI3133XWXJpOJjo6OooGQulbM7vz7WRHWyjXM0b/Lcz3tLvXbqXuA6458mqbx5X+O3nhG0b9HWQlIWV3XvSYAUoccSuopGC+n8s8xRK4coIGj+jdDH9lLbyDCulCIHvhCN/bV0WVHuXE8yRTiHCNHdHLzMkdQTHgTxcg9cFIWi0UPxKiqtrwVZ4MzXtCd4Jw22N40YIh2O09CKwwr10EnHCscEIwT8uyt0AnmmDc6BHo2TdPrTMY1nunxkiGv7XdZ4Rmgk/Dw6enpDfoFpBsdxd88A8P8HDH2rCDzcvTWkTh0EvNEF7n8oAvQo4A5ZKJw/CVFOrP36E3PnnFP+B7+9TJkQBIP2jw7wFooU/HzE04TnCmfu+s+aIGMwzfIEBl7HP+q6gJa5OX4+Djum9SdAXDZdSdisVjE5hLMm4G9kboOYdCefUCukQf0FCVCXIdD5iUvBMNkpJqmiVkYgkLoyrlEAjYvgYOneB4VHMgMdgq+9feu1XWt6WyqZPM9Bhm8LMtiY6WbgWEEc/An80YPwff8y3B+Rdd6AEjg7B3K4D0Hp5gjvIP+yrIsnlcmuOJaAiEHrtxRRNfDe87vnAmD53mXFnaG7/h5OT8DCO/AC/Av9ODsLM8nSEBfedbLyzyZY1mWMcszpAE/ONRN074/6+LFizGLhe/CWqEL4BX+Cq/9kLqsNECly4ZnrKQOsIFv4HnsL/aCQBsQij2Fzz0Y8ixqlmWqN7IM3QGP1+t1+36hpt91lIDQM/S+Vmz00NdwvYN+ouQOeUDXuh/IOior8UQ+ACSGMuOgt9sqfudzaArdkXl+PNvDGVd4DV7insMyb3Sng8WtnX3iYc8dHyBNpp1Abm9v9zYcplkul/H/tNidz+e9Q8fuRC4WC52cnERHg82QugCJzeX/CBmGxVFaz0rgQIB4gahhtL0mkzW48oVh+A7MyNycIWE+kGCpK1Vww+vMDePSZQuakqqGaVEK3oUIRc3zHJ1yJJ014YTg1DBcEKLwmgMJfXFOnNbcl+e6wLlzzXoxzqyB+0MvP8DKPkBD9iGmzpt+lyN4h33i/yhC1oyhRyES0MFTGCTPOKBIcWrcQWbPmaMjixgzFC5r4AwMoAJleuyBB0447O5IUpLFmSDWQKmBlzi5o8leLxaLiFKyhqZpokHP81yPPfaY7rnnnp5R5dmusDE+Hhz4/nn5BjTzYG9rays6p7ybyIN05B5+hK44q/zrXYTQQV7m4aVx8CR0IXuJ/HlQ6YFBlmXx3KGDKPCpB7jwm2e04AFHy0HC3eDyHYAnlyHkzxFonCnmiHMCP0mKmQXm6OCOB7DD4MwDOgduHDiClt5+nvviACInXiLL/g1RdEeiHRRi71pHveMxdx7QO/CJl7gAbEGXpmkiQu+IL/KAPmB9ZC09AC7LMqLfkiIvQ6eqqnqBm5/zYC4ObrAvrEtSPGxNkAfAgh4oiiI6ec6Xe3t7Oj09jV3m0rR9LyFZfQLjfNK1Rea52OCDg4OezeJ7OGToMPbR990zSjhtZG6xTZ5pdCeRs5Hssb+Ly2XXQUL8CHdMsVnsBTwtKZZOIm8ehMBz2Ej2mrW400+WBh0I/7EWQEruR4kacyuKInYOhYbQWVJPZiTFVzKwFi+D44XM2IHh2gAPmDs/XO+y6FmH+Xwe98p1AEGKg8wOaLF2byiE38UaCYYdSAToAzBjXvv7+1FeCXaRc+aAH+Py5fff39+Pgaxn3JHtIcjnFSy+PmSFazwAdD3j9CjLUut6pSLPewEefOA2i+9AH2yr6zzXby5H0N5/514+F/aatTqYiB7hb8N9DiFIxpe3Gnd8gFSuy2gkCE4wFjAZxKQ8AmTD2+Qi+DhdkrS/v98z0DApDIRDCJrmbUkRGIw8Gw6Tkj52RYZTRZ3osAyK98AMUWqUsdR/aSidajxL5MgBAZALP04OB2iZP44RncQ8GPOuKV4Lz/y4j9MAJwVaswaEhmtx/jFE7ujwN3fAPJsg9d82jQJy1BzhR5m4sWR/PKCEd7g3RtsRNkd3MBQe6LoyIyjAqBEko8QxehgqR9lRQo78YfChnSsgD16HJZQ81w08z/KzERgGnsE17vBfv349zvnxxx/XPffcI6k7a+PlfOydo1Oc3YM25+fn8VwJfAxiCZ95bb7UGXJfu9eTu3MCWuqgBwivl+s5Ou0lk6CJKHZ4i2wkTryvD76dz+exIYXTdDqdxrIMz3J5aSHzcmPGHkIDP1zt54lwbF2WQEcJjtl3HHWQTZ5BkOg6gACYtbqhd8PnJS8OfnjpBJUADogAPDhtna+gib/c1EsH4QuCMww4/Mm/0MTlCJ3p2WqXT4JZ5xMHnXAG0R9eyuJ7KKnXmQpexF4tl8t4r7vuuis2tWAerAPE3lF0HE/4zMuvvDyMeWP3vEENPMk+uH4l4PTsBfoFR5vujPALTmpVVTFj5WW3rl89QOWspwOGHry7TWceDjTAQ95ow/0HBz3ZLwdg9/b2YqbDnVXkJs/zeJ6C/wOOOnLO+pgj2Wj2ybuyeSYMcAXaO2DEnvAy7CRJomwjU/AyFTEOmjrwCVDWNI0+85nPxHJijg3gEzzrWc/StWvXIuCGTcNGOE85sOH6ks+Yk2c4kWFk72bVLugB7/QKv7BG1sOz4S13znkW84Xu2Av2188Vw4eeKY/BW9qvyEHPQAMqJyj/RKfBz84zgPLusyGHLvueAfXA3INB6L1al0qT/msTHHjmOp4JYO7ln+4PDPcMPxS9AN2d53gWNID+Q/92GIzxOT9PZtzxARJdftg0hCLLsujkewld0zSxOwiGnyCF7+GopmmqxWIRU5UgQSAH7fNz7e7uRqUDM3nEjUEk4HG0Gsb26J46V9AWdyAk9Up+PBCBuTlciIPkSKGnQ92JdCfBsw9eSuYZC6l/9sMR6vPz81iaiGGEDlxDrTFZApQNBhPF711qEAyUE8I+RO1ZszspHgT6QfSbodHQgXsPM0wYSH7cYcaoMjCQXraHIvUyBT77bMiJOxvsg6e+h8oCmg1L7fhBsXvGje8NMwes3Q2A0xx6gQTefffdOjk50fn5uS5duhTPozjNHJ3iuTjllJm6cwE/eUbADS775ZkASbGM1hE1p1WSJDEDgzGtqkpHR0cxICMAcpmjVpsD6DhF8Is7IQAbOGPIKUbXsz/IJ8gpew69HABhjx1EwJlzGeDMiesnSTF7zdwAVTxwxlHH4MIn7sijd3m+G37uhYw5iMEeu3HFGcB5gw4MDzYcHUUOhqgnAQ7ZCPQpuhiegS6OpHu5LjoaucGZ92xZCIrygc5gDXXdnZ10WlG6x7U4cMwZHvSyK3Tz0dHRDaU1nVx22TNkwfnbUVfW741QKM3xkjkqARywQo+B9mN70HcE7Y6+hxBicwF4A1CgLEttbW9L52c92uNYuh50sIf7AIJ44IA8UnblJYHYkPl8HjNC0Nidef7updKABLxkWuoyKwSKZNOQcQ8Y4UdsCLYNsIn94J57e3sx4BlmOYdnuNhfsnVN08SGKXQrpPQdmSMoAywjI7K3t9eztZKintja2orvU2uaRgcHB9HBhU4O2nh5Mz80FMKulWUZ9RU6mvWwXkBE9gb+cjs8DHD53V/Nwr7ClwR16Abmx76jOwBkHRQbNsmIPmcIClXXMMaDW7dLUvcuK3jHdRP85991wB47CH9BP89CDgFk9mU+n6upu7J3ZN5lHZ2GLYDXHLTj/vgK/gzmjOx4gIRPx96madrzQ9k/Bza5h9v7LMukAfjwucYdHyBlGyYly4EiR6liOByNgcCkNclkOCOBdCVJe4iVTjmHh4cRIUEYQPQ8YEBxD1O+blTceEmdEz2srfRAxtfi2RicpKOjox6SBnLkxgIj7uczPEjAgUTJUyYg9V+yVhSFjo+Pe7Wiknp10XRZWq/XsSbYUVhfN4oDhcGcUZqepnVBZE2SeuuTuoPgHlhJ/XewoIT4m6ReFo/98sCHufrhas96kGlCEd19990ROeVZZEe8/AJ0EN5whwDliOMkdVkYV35uHHgOn/OOKUkRoWf9OPN++JNyDIyXO+w8mzXyXBAuMgm+Vw4IlGWp4+PjuF4vV8WpcIO0WCwifxHw40jCQzwDWfYA1A28O1bwgZcT0RralTGGlv3HqYPPPAOCo+v0h87Oi2SAnd9BKX3v4Ukv7x0G0fA6zjf6yEEZnHDQZDdk3MvLPXG44TtH/N14E7Bh2IfyheH3oNvLW5kje4bz7MEoZWOcAUC3O/I8dDjYC/SMl1gR/DlqjA5BFh3F9jU6Io4MlGX/fXGto9706EW2E/3uARTOAfKN3sbGYD88aPCsIs9ZLhfxc+f/JGk7yCELHgAN9Ts2iOGH2ls6pAqhc4T4ngOF/n/2xGmLzoRncOIVukYorovYL/Z1Pp9LoV8qBbjidtl1XJqmEbAg85EkXdk7fOSOFzqGtXMt1RdkK6TuvT/uvCG/8Cd21fnLs3zXrl2LGU4aXzhYioNMAFyWbbfIuq57pfFHR0eazWba3d1VWZaxcx8d/hww8YoFBwt5LnzL8wEf4Efoj2y5PcYvgybIDjrXM2Fuaz2zNLQfN9On/O46Cvn3+/lZXQcsHRBGRoZZGOZT13UE2rHzXsUAbdI0jSVf2MSoq5tGhWWm3D900AC+cFAM2fSSRQdLAX6gM/YmhBCzrlxTlqUmebf/wyDE/RCAI+RA6vxSbAh7DO08sw8dh/zjAC3XEaC67mCvWSd05b4tr4wBUhx1XSudplHhofQ9G0EmAgWIMnJki+vJJrFZlC7glGM8YDapK4FBKaB0nCldsOkY5YaLe2MQMJjUm3upDMEFmS6EH4WG4T07O4stwB2J4R5VVcX3hIA47+zsRIWEYZDUE14OmS+Xy2jEoR2C5WUp+/v7PSQSxcI13NPRYacLQg1Kw3wQLJSlZ/c8mGEvUMg4syBHfIaid0cQxMmRXp6JY+LBHvtMNykCWlAZFDDXglYNy3ZwIoZd0PK8a1vvCJTUOTeOyHtJEvf3ttGsJ4Sbd0DzgJJ7QQf22hF7dy7yPNejjz6q3d3daIDZT3iQFvYEbxhi+J6OQ/CapIhuQ2t37D3gCSFEZwh+9yABg+gpfWg8m8107dq1SM+qqnqd93DuPMB24+8OKxkcnMDhdY6koVu8wQPrw1EC0UTnYUjIBKF3kA9ejIl+4O/oFeQVxx059cwLz3cQAR5xY+XtiT1bgmyhO5A/+AhecpCEsxjcG8PogJY7ja6T3WkmgMH5gj8cGGIvcKahrwNG8Br77wYb5Lqq2g5yrROUSUolBUn9Nu3QhhJq50myW+g7QBWehQx4gMra2/0vFEKj7e2djV5p24/Xtb//LyjLajVNUFV1543qulFZds5nlrXvSJnPt9S2RA/KsrznAKHbvXwZx9T1pNtP9KGDfsg7++MOOpmU1flKdVkqSxKpbmI25NrZ41KaKDeE3UvM2XfOY1Fa5g1w0JHMG5rWdR3fbeNAAW2U4aOyLLWzsxP5cr1ex+yK+xeS9OlPfzoG6dgB7k+mkbMtBPaABtgfsq+TyUSf/vSntbW1FbP16Db2Y3d3V5cvX44ZEvi6qroX+/qxA892TKfT+JJaglCucd5kXughD3oYDv6ha+EPD+bdtjlY7NlkgFa3AV7+Dm+675PnuaaTqaqqVl01StNMidqXOadJqiRJleWp6iaoboLyYqK6rhSUqKw273isGwUlStNMTZDWZaVCXUfldVkq2QRG0B/+cuA6SbsOcOhCdDf2QOqAK8/qAIgzptNp70XiDvzwvFA3qlZrZdrot3wTENeN1nVXJeGBp78EG11+s5Jy/CXWgr3wANP9XGwdf2c/AYEZDojD6/jr8IkDD25Ln8i44wOkIi9iZgJjL3VOngdBbDrvj2BjME6Ui+DEomC5liDIEXuemWVdvbejKY5c4wSiKP0zR55gAC8v6Qxbo+Pj42gEPCCEmVF8ZNWSpE2r89wsy+KZBwwPTCvphqwG93ek0x1HBIQ1oSRhVlCHo6MjNU0TW7wOs2C+b1J3foQ1S13w6Q6Ro1VJksSMlxtlT+syd5SHZ/NQ8mRS2B8/K1QURXzhJVkNjIU7hp6qxvGka563I/Z1o0TIikBvSVEpwicoSM+4uAPuvMDwDlkYIM/ooIzdGYwKNnR13vx/2FACWeO7AA6SopMBn9IFDFQtSZJITxxzsqIYcjcofvidPfWAG5nFuHj5l+sJAheMNbJCYAONeSFzlrUvz0WfsGacm6Lo3n9E2Q76hdp80GEvufPyAs9qOKqLHgBB5tm7u7vR6UM+2F83aPAqMry/vx/bQ3MvaAmd26zEMpblOBKI3mN+AB+eLYBOnnV11BTaIF/sMfvJc9g/BzNcJ3tgNkSlXZdhF7x+Htqjq7iPB77uaPGZy9aNwVT7LqXWNp33qhg8S47+Qc4dRPBqA87SoI/5fpr2u3r5HsNLs9k8BgYhdJnhIXKNvDtIMp3O4jMdlXcwznkWWqRpekMZIrrNS8w8YGLeTbmO90fvt2vPNN3I6HK17GXa8qJQVnQOMaAEssUcsH9eXeDnwuAHdDR+gdtZ9xPQFcyXzFWStBUngJV5nus5z3lOlD3+5T2FZVlqsVjEFuUAAf4uNUfVKcObTCbRnsOngEPwL3rBMwvoYd7b4/oOOknqNb1wveDBvn+OLoDuQ0CIvcSGIMvoTkk9IAWeYm88K4S9ct/AgeCb/VtXLTDgAE5d1Uo2wVhuJaItDfpl28yfILjVF3UMHNkfBs9Ftrjv2jK47lPyLOTN9YuDNq4HJUX9D9964FJVlZpNsMs1lBVON0EHABlBGnvHGpwGLjvIGvLlpaToFQe0XRZd1wz1PbaVzzyodwCc78BPrpNvNe74AAlGQuETtRJJ016RulMYJITQa5lKEOHBgZeKoDBPT0+jUHu0S/aKbjwYbxTv9evXeyled0hdaTh6jDEBMXDEBwcaBnTnnbn7oVtHfECM+c7NSnPcwHp6nPtAQ+7tzS2kLpPiZzncwfU0tGc9vJYaunM/hIzndAa/O6TtDQr4Tp53h9UpO8GBpOMaJTwogKZpIgLn6JSXRAxLIxxRdbQQReTnHnDOHLEj6ANBRGlxSNsRMe+05qgZc8JJZbB/XnbqwRPGF9oMkRjmggH0sgJXlPAQzyMYBk1FCYNMQj+uxwCSpWK98CoOLHPBeLN+1kSmAScBenIf1k+5oQc6yDKOF/Qm0+e081IkV9oe6HjWxjMRQ9SdAAujiZFyGtFVkT1A3+BoepDMfIeOOPOkEyFnHr2UwXkE+QINx3nx4NT3BMfOgQnXE8g08wA9966JriN87wBTHLByJ59nQTscL2SYH+cD7o/cswZkBZ3tmXj2DeeD+3nmyufIPJkb90bmOQODTfDW1H5+lL2mLTIIPvdumiZmBPidZ6HnXJbZX/gFMMgrEwiCoacH6W2Dkc45gv/W63U8Y4psFUURX+TKoEMn82Hfpc6xJIuGnE3zLvhlf1oaZ2pCiM0b3Nbh0DNv7n3XXXcpSZLY2h++/sxnPtOzE+z5dDqN57Amk/a9Ro8//ngvQ0FQc/XqVU2nU+3v72t7ezu2RQco8XNl7BEZb+ZIcAQvEdRAUwKrJEkiSIJdgW9c5vBXmKc3DUGGuc6DLDJ1Pm94ne+FEHrvmXRwmX1ELtC53B9fjPmzRjKKHpyzh9wDPuZ3/oV/8aHQOaEJbeYoSXo6xveZ+7m/4tkg7FjnryQ9fYZ9GIKVDh6GzX2xC/h+LksEhV6hAS+7/GKLAFTgDw/oq7JUEjo/wUFh1u0+JPrDG17gV7gP5NlAD3wcWMUvcBq6vUTvu2y67u+CVUX9yT3QfehG91tuNe74AGm17nehcQFzZ8Y7vCyXy1i6g4KiAxFG39PFODs4thh+P0xLWRDXeXresykEaZzTIStDup7SLIwm65L66BbMCBrAywr53AM8zwYQQNZ1d/jQFTIBBHNAwUA/d+wcAcZZkDp0QeoyPT5vkA1Hg3D43ChJ/U5dOOSUWPGsuq57LxD0oII9xumndAdFxJmO09PTeC3GiDWCekNTDz79TIO/UZs14LC4g8Q+wUuUNly8eDHydYvc9oMEnBxXiARIXnONAwKP8p2hQ+HOkztMPMeHKzh+R85wijxI8n1DfrhO6gdz/LB3vv8+N/gf3mItGDFHtZqmPc/AHkE/eMNLbv29TiG0B8j39/cldYEhvEmwz5o484AMYdDZB5wHWt06TzdN1xGJYM75nz3zoJ1nosvQC54lGToNDjI4v6IrnXfQca6vPFOCDnBwiOyy6xCcK8/6ID9u7BwlZK7c52bGFr4AAAM5dOPJ/VivO1as2eXKs7LwlAfDDrx4GQhz8dIOtz1k8IeoqINFrjfhb8/eOGJb121VA41o6PTmTil7BF09cCTbwjrdyYU26C/XEcgB+pfvYjcnkyLqB5dbdIuDfgQu0GyxWPQyDwQp6C5Jca1lWWprPleYTHt2jbkWRaFGiqCMO3GsMU3bV1igl9Cx2DfoWNe1Dg8PYyUB9wFEvXDhgqTWvhFk4dCjj7/sy74sPpfAHuCDubj+wvn0BgDsvQf67Al2FRlm/h4kYAuQD0f3h62j0Wsue8gPZ5zIhnEG2+k7BKoI0pEH9hddRQbKr/cspvtaDmDhKwA++V67c+w2q6cXrOLEy8bX67VC0jUtcV2D/YjBTegaz7T6IJcUon9BVzoPGqigYOR5rsYAM/SUZ5jZR2yal62hS9AN8KrzDj7k+fm5sqTfvIJ7ux9CkgE+ch0yBBlZg/MhdtJ9CdYPLX1PnZ890HGfjwCee1KS7b6rZ6kdgLnVuOMDpHJd9qJcGAdhQbFDaDbQS0pQJKS2JfWUDYgeAsd9QPE4SOnlDefn5xHFkRSZHuVw9erVHhIJikughNPuaDzKgDVx4B4mRlBA0GP6uO4O2MPIIEsIOQKDYwyTITCsTeoO5XnQwX0828SzEBKcREcRPFjihXKOsiDg3l6Y/fVyA57vCBt05DoUORlGRl3X8SyM16STHSBoxnFiD0DzJcV3RrCfQ+SE/fH3a0Fn9pNWupx14YyZO2UhhOi0skcE6Tg/yIKXQKBgMVKs2zOT0BY+wwgRTLPuIZIHX6O4PWXuSKU7Zjh3yCjDlV1VVbrnnnu0WCx6wVGSJDGY8kP0OLLwijvClD+cnJzE1wKA1sK3UneesGma6NQh+zi8nuFxJQ/94HP0B0ETewBtQFwdQMHgedbBMzogZDybeYL+gTh7qR0OEbSADxx4IUBkzzBkfIYDAy+iK1zemY9nQ+APdLCjn362YThX529Hg+EZ9N+wXh36uiH2UihHsNEJ7mShs6Cfr92DBbq1ObJblmU8O0eppsuBlxXC3+7sAYp4wxF0CvrGwSn4HR3B3uD4wnue3SKr7c4qNMW2oXcdlOEegEr9IGutLEt7INV0OtXFixdjtoXnSDcGfvAjAXme58pCUF7k8XfOcaZJqvkmM+LfZb6VyQp628tk0ZfwFBktgtU8z7VcLjWZTG4ALPb29uJeSoolt6zPg3D0BE4cOoJ7YwO9gyFz2NvbiyBg0zRxn7wk1AEJZBsbg40FzONaaODgr2ec0SvIkWdt/NwcmQmvNoEP0WEEugx/bYGDcMinB+PwGSAl9PWAl71y8AX95qXCrIV1IONN3TW1cTtd1bWa0AHl8Cv3Qsbcp2zluZ+Bwm/wzJWfoyY4mmyalCAnDqgzfB4Acm6zPZBzPYvMRPuadO+rZP/QQ/gIgADwE2vC/rFPHkQ6DYfBtfs5+EXQg2cw2GtfE7LsWUP238ERz647391q3PEBEhvmyDnODqiKBy7ujPl3/LAhBKZmnDpTqetqg8HNsixmcVBIPMdbn5JqRrk5qvX444/He4IEMC9HLnm+MyiC6EptmPb2g20MjC/ZC66TuuAQp5ffUQ5eiuHzcsTQEQA3kDhMGF8MI512KIEkwBwillJnvEHOOZ+0t7cX780c+f+1a9eiMGF8cBYQZi9lGTYBQNk4usoeg+A+/vjj8XwbfEK5CjXenDtBEcGPOMoE6vCgOzwoeFdm8BHBFXyMcsYAExjibPF8lAvKDB7yEk6yraDdGEnPMAAaePbDkST4w5199hanH1oTRFIa6+e24Cno6nsNwoojQVktCnZrayvyrB9kxaFBFtyIsA7KY6Ar94cnkW0HBXA8uT+85kEo+49csTani2cjcZhcfpx+ziNurJiTzxVZcXSbz3G+3agxh7puS2IIEuAL1gxgxHOYH+v1wCw6LE2/TA4njkATGqJ3uIcHZp7F4TOe6U6GB0JuWNEByARZBDKHOAk84+TkJJaIsRZALQ+EWnmpe04u/IgcobcJmNBvVVX1XmQOUOHBBqVsw+AyhBDPSkL3xWIRgTECGewAc8CWeKAFjcj44LS3fFqprju7wbx8nltbW1H/k4kCXCzLsgdqJEmiybR7ubnUARdKu9dcEFCu122Hy2vXrysr8hsyx0mSxGYm/nJiQMgLFy70bB+VIHt7e7H0DscT3icohc+h8c7OTtRt6HxviuAZkCzL4v29ZAp6o7OxPd5wBh52PgZ0AGyEt7A5jtDD515+6j6OBzDIJ5ksz4D1g4T+OyI9O+qAtWcNHLxzB5/1w+/oJMBOl8MhYASPOT/y/VZOK9VVF6hgz1hTVXfHGtgXlyGeB387OAZvUSWU53ksT3XfYTOpXoCLDqL0Gb/VaeOZH2jEvZF9L/llPh6YeNDjmRfP0vFdv8b1vwPVzN3p7iC9B0Out7EL7CO85uAYgBt75DzmwDU0GQKutxpJeDJX/xkaR0dHOjg40Ht+6b3RkM+35qqrTbp21iF+61X3DoU0TZUX3YtZy/UmfZd2Dk5d1dFhTdNU56tzrVdrFZMibmBdbRzVbKPQi4mqutLqfKUsb3uxr1agLG3HkjRNlaUderYu12rqWutNFmw2m6quGy1PlppOuhbJjtQniZTASFVXjuKZAnfOnPlihmDSBR1N3ZX5OPNlefvvyfIkBpp50aIerbFvjT6GyNtdeiYlIo9pIoWgENRD5ctyrbwotDVvg5U0TZWkiULjZTXSel1qMu3eqr5edV3csiyNc1qvy03JR1CaJlqvS83msyg0Z6dn0VBPZ1NVZVsTvi7X2t7ajs+oyioisNs726qrOho20KCoYDfv4jo/O+8OSs5nSpREdL+sSlVlqaZpkdFyXSovcs2mLbo5m89U5IWa0CjP2vf+tPTuzqHF81MbPmzqDn0pJkXk5aqqVEwKFZvWndwThyBJW4WyXCzjOaBY7jOdKM9ylVWp9Wqt07O2ycD+3n7MAqHU62ZzxmG1jn9rFVeu2axFC8/Pz5RmWZSP2XSmw8PDuG9plilLM1V1Fff2U5/8lFbrlYq80Gq90t13362qrDSdTZUmqba3t6TN+uHV1fmq5etq09Wr2PBzmqluap2fda14QfkI0Fypl2WpuqlV5MUN/BuaoCzv5ts+v+VNL1FAR6Cwi0nnzDZNo3Jdajqbar1aKy9yrVdrna/ONd8cpMcQeXYkyzOdLE/a0pZJJ9tVWcVyy5h52ui30ASlWRr3U2HzlvEQonwUxURN6IKTNOk6YbZO0irukWc2Qgg6X51rUkw2QEGruwgY6qZu36uRdNmTaEyrSmXZ8ujZ6Vnk6UnBYeP2mSEETYqJ6qZWoqSn33yQXfFOgeh5PnfHwgPILN2gzKEfoE2Kic7OTjfZkSzKInshKcobzgzGuW5qzWfzGxqhYPSrqlYxKRSaRnXdxAAporHaINp5ofPzM52fr2IwWxRFm1kpJppvzXV6croJoJK4p0oShaZpO7rlHXiWJInKqit/NgJqIxgt/2S5VuuVdne6sqokSSKNQggq8u5sTtO09FyX7XV7u7uaTmcxcMNhm2/NI8/mRa6z067BkZc7Jmmquqk13ezn7//+78f3Jm1tbenihbskKQZzZIKCguoQNJ1OtLe3HwGSFvAptV6350Lrpm7XuOEZQDOXXcnLh7QBXqqeE+eOMrbGAVYyyczRSzZbxzyNe8tcsqxD0MuyUlHkqqpaWbbxGdZdudF0SjOoG98/kxe5VucrnZ2fRZkGXCjLdeTbLMtjwNrStFBtdoXAue3O2AVHHuwgU/BZnuc6Oz/TfDaPQZXLqoOv8DQ8CS/g+J6enihNu0DL9aqDLb4vUtekBtvJdW2QkkbbwTXYyLqpdb4pO4XOyGRVtg0csrQ7d4ztXK3OlGV5y4MVHWtncd0EZmSaIjCWt7o5SzNVVbmhxySCJW5vAdDICjMH9h6eRaa8dDlN07b7XtP5E5JUN3XUJZLaZhUb/wAfjH3zIx4t+DpRXXdligBaaZa29zGat509Q9Sd7f0bNU23vhCCikkRAzWFoLpuur+VZWyZ3mz+HkJQnuVar1exdHKxWOjbvuNVOjw8jKXyn23csRmkq1evSpJe+W3f9AzPZBzjGMc4xjGOcYxjHOMYxxfCWCwWX7wB0l13tSjSpz71qVsSYRxPbhwfH+vLvuzL9Id/+Ifa29t7pqdzx4yRrrdnjHS9PWOk6+0ZI11vzxjpenvGSNfbM0a63p5BRvnKlSu3vPaODZBIEe7v74/MdZvG3t7eSNvbMEa63p4x0vX2jJGut2eMdL09Y6Tr7RkjXW/PGOn69I8nmjRJb33JOMYxjnGMYxzjGMc4xjGOcXxxjDFAGsc4xjGOcYxjHOMYxzjGMY7NuGMDpOl0qh/5kR+J7XPH8fSNkba3Z4x0vT1jpOvtGSNdb88Y6Xp7xkjX2zNGut6eMdL1mR93bJvvcYxjHOMYxzjGMY5xjGMc43iy447NII1jHOMYxzjGMY5xjGMc4xjHkx1jgDSOcYxjHOMYxzjGMY5xjGMcmzEGSOMYxzjGMY5xjGMc4xjHOMaxGWOANI5xjGMc4xjHOMYxjnGMYxybMQZI4xjHOMYxjnGMYxzjGMc4xrEZd2yA9JM/+ZN67nOfq9lsppe85CV6//vf/0xP6Qt2vPWtb9XXfd3XaXd3V5cuXdLf+Tt/R//7f//v3jUhBP3zf/7PdeXKFc3nc/31v/7X9bu/+7u9a1arlb7/+79fFy9e1Pb2tl796lfrj/7ojz6fS/mCHm9961uVJInuu++++LeRrk9t/PEf/7G+53u+R3fffbe2trb0tV/7tXrooYfi5yNdn9qoqkr/7J/9Mz33uc/VfD7X8573PP2Lf/Ev1DRNvGak7a3H//pf/0vf9m3fpitXrihJEr373e/uff500fD69eu69957tb+/r/39fd177706PDy8zat75sbnomtZlnrzm9+sF77whdre3taVK1f0vd/7vfp//+//9e4x0vXGcSt+9fEP/+E/VJIk+nf/7t/1/j7S9cbxROj6e7/3e3r1q1+t/f197e7u6hu+4Rv0qU99Kn4+0vWZG3dkgPTzP//zuu+++/RDP/RD+vCHP6y/+lf/qr75m7+5x3Tj6MaDDz6o7/u+79Ov//qv64EHHlBVVXrFK16hk5OTeM2P/diP6cd//Mf19re/Xb/5m7+py5cv62//7b+txWIRr7nvvvv0C7/wC3rXu96lD3zgA1oul3rVq16luq6fiWV9QY3f/M3f1Dvf+U59zdd8Te/vI12f/Lh+/bq+8Ru/UUVR6L//9/+uj370o/o3/+bf6ODgIF4z0vWpjR/90R/VO97xDr397W/X7/3e7+nHfuzH9K//9b/WT/zET8RrRtreepycnOhFL3qR3v72t9/086eLht/93d+tRx55RO95z3v0nve8R4888ojuvffe276+Z2p8Lrqenp7q4Ycf1g//8A/r4Ycf1v3336+PfexjevWrX927bqTrjeNW/Mp497vfrd/4jd/QlStXbvhspOuN41Z0/T//5//oZS97mZ7//OfrV3/1V/Vbv/Vb+uEf/mHNZrN4zUjXZ3CEO3D8pb/0l8LrX//63t+e//znh7e85S3P0Iz+bI3HHnssSAoPPvhgCCGEpmnC5cuXw9ve9rZ4zfn5edjf3w/veMc7QgghHB4ehqIowrve9a54zR//8R+HNE3De97zns/vAr7AxmKxCF/5lV8ZHnjggfDyl788vPGNbwwhjHR9quPNb35zeNnLXvZZPx/p+tTHt37rt4Z/8A/+Qe9v3/md3xm+53u+J4Qw0vapDEnhF37hF+LvTxcNP/rRjwZJ4dd//dfjNR/84AeDpPD7v//7t3lVz/wY0vVm40Mf+lCQFD75yU+GEEa6PpHx2ej6R3/0R+FLv/RLw+/8zu+E5zznOeHf/tt/Gz8b6XrrcTO6/v2///ejbr3ZGOn6zI47LoO0Xq/10EMP6RWveEXv7694xSv0a7/2a8/QrP5sjaOjI0nSXXfdJUn6xCc+oUcffbRH0+l0qpe//OWRpg899JDKsuxdc+XKFb3gBS/4oqf7933f9+lbv/Vb9bf+1t/q/X2k61Mbv/iLv6iXvvSl+rt/9+/q0qVLevGLX6z/9J/+U/x8pOtTHy972cv0P/7H/9DHPvYxSdJv/dZv6QMf+IC+5Vu+RdJI26djPF00/OAHP6j9/X19/dd/fbzmG77hG7S/vz/SeTOOjo6UJEnMLo90fWqjaRrde++9etOb3qSv/uqvvuHzka5PfjRNo//23/6bvuqrvkrf9E3fpEuXLunrv/7re2V4I12f2XHHBUiPP/646rrWPffc0/v7Pffco0cfffQZmtWfnRFC0D/+x/9YL3vZy/SCF7xAkiLdPhdNH330UU0mE124cOGzXvPFON71rnfp4Ycf1lvf+tYbPhvp+tTG//2//1c/9VM/pa/8yq/Ue9/7Xr3+9a/XD/zAD+hnf/ZnJY10/dOMN7/5zXrNa16j5z//+SqKQi9+8Yt133336TWveY2kkbZPx3i6aPjoo4/q0qVLN9z/0qVLI50lnZ+f6y1veYu++7u/W3t7e5JGuj7V8aM/+qPK81w/8AM/cNPPR7o++fHYY49puVzqbW97m175ylfql3/5l/Ud3/Ed+s7v/E49+OCDkka6PtMjf6YncLtGkiS930MIN/xtHDeON7zhDfrt3/5tfeADH7jhs6dC0y9muv/hH/6h3vjGN+qXf/mXezXFwzHS9cmNpmn00pe+VP/qX/0rSdKLX/xi/e7v/q5+6qd+St/7vd8brxvp+uTHz//8z+vnfu7n9F/+y3/RV3/1V+uRRx7RfffdpytXruh1r3tdvG6k7Z9+PB00vNn1I53bhg3f9V3fpaZp9JM/+ZO3vH6k62cfDz30kP79v//3evjhh5/0+ke6fvZB45tv//Zv1w/+4A9Kkr72a79Wv/Zrv6Z3vOMdevnLX/5ZvzvS9fMz7rgM0sWLF5Vl2Q2R82OPPXYDYjeO/vj+7/9+/eIv/qLe97736dnPfnb8++XLlyXpc9L08uXLWq/Xun79+me95ottPPTQQ3rsscf0kpe8RHmeK89zPfjgg/oP/+E/KM/zSJeRrk9uPOtZz9Jf+At/ofe3P//n/3xswjLy61Mfb3rTm/SWt7xF3/Vd36UXvvCFuvfee/WDP/iDMQM60vZPP54uGl6+fFmf/vSnb7j/Zz7zmS9qOpdlqb/39/6ePvGJT+iBBx6I2SNppOtTGe9///v12GOP6cu//MujHfvkJz+pf/JP/om+4iu+QtJI16cyLl68qDzPb2nLRro+c+OOC5Amk4le8pKX6IEHHuj9/YEHHtBf+St/5Rma1Rf2CCHoDW94g+6//379z//5P/Xc5z639/lzn/tcXb58uUfT9XqtBx98MNL0JS95iYqi6F3zJ3/yJ/qd3/mdL1q6/82/+Tf1kY98RI888kj8eelLX6rXvva1euSRR/S85z1vpOtTGN/4jd94Qxv6j33sY3rOc54jaeTXP804PT1VmvbNQpZlEe0cafunH08XDf/yX/7LOjo60oc+9KF4zW/8xm/o6Ojoi5bOBEcf//jH9Su/8iu6++67e5+PdH3y495779Vv//Zv9+zYlStX9KY3vUnvfe97JY10fSpjMpno677u6z6nLRvp+gyPz29PiM/PeNe73hWKogg//dM/HT760Y+G++67L2xvb4c/+IM/eKan9gU5/tE/+kdhf38//Oqv/mr4kz/5k/hzenoar3nb294W9vf3w/333x8+8pGPhNe85jXhWc96Vjg+Po7XvP71rw/Pfvazw6/8yq+Ehx9+OPyNv/E3wote9KJQVdUzsawvyOFd7EIY6fpUxoc+9KGQ53n4l//yX4aPf/zj4T//5/8ctra2ws/93M/Fa0a6PrXxute9Lnzpl35p+K//9b+GT3ziE+H+++8PFy9eDP/0n/7TeM1I21uPxWIRPvzhD4cPf/jDQVL48R//8fDhD384dlN7umj4yle+MnzN13xN+OAHPxg++MEPhhe+8IXhVa961ed9vZ+v8bnoWpZlePWrXx2e/exnh0ceeaRny1arVbzHSNcbx634dTiGXexCGOl6s3Erut5///2hKIrwzne+M3z84x8PP/ETPxGyLAvvf//74z1Guj5z444MkEII4T/+x/8YnvOc54TJZBL+4l/8i7Fl9ThuHJJu+vMzP/Mz8ZqmacKP/MiPhMuXL4fpdBr+2l/7a+EjH/lI7z5nZ2fhDW94Q7jrrrvCfD4Pr3rVq8KnPvWpz/NqvrDHMEAa6frUxi/90i+FF7zgBWE6nYbnP//54Z3vfGfv85GuT20cHx+HN77xjeHLv/zLw2w2C8973vPCD/3QD/UczJG2tx7ve9/7bqpTX/e614UQnj4aXr16Nbz2ta8Nu7u7YXd3N7z2ta8N169f/zyt8vM/PhddP/GJT3xWW/a+970v3mOk643jVvw6HDcLkEa63jieCF1/+qd/Ovy5P/fnwmw2Cy960YvCu9/97t49Rro+cyMJIYTbm6MaxzjGMY5xjGMc4xjHOMYxjj8b4447gzSOcYxjHOMYxzjGMY5xjGMcT3WMAdI4xjGOcYxjHOMYxzjGMY5xbMYYII1jHOMYxzjGMY5xjGMc4xjHZowB0jjGMY5xjGMc4xjHOMYxjnFsxhggjWMc4xjHOMYxjnGMYxzjGMdmjAHSOMYxjnGMYxzjGMc4xjGOcWzGGCCNYxzjGMc4xjGOcYxjHOMYx2aMAdI4xjGOcYxjHOMYxzjGMY5xbMYYII1jHOMYxzjGMY5xjGMc4xjHZowB0jjGMY5xjGMc4xjHOMYxjnFsxhggjWMc4xjHOMYxjnGMYxzjGMdm/H9vvZfimEsBUwAAAABJRU5ErkJggg==\n",
+ "text/plain": [
+ ""
+ ]
+ },
+ "metadata": {},
+ "output_type": "display_data"
+ }
+ ],
+ "source": [
+ "plt.figure(figsize=(10,10))\n",
+ "plt.imshow(image)\n",
+ "plt.axis('on')\n",
+ "plt.show()"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "98b228b8",
+ "metadata": {},
+ "source": [
+ "## Selecting objects with SAM"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "0bb1927b",
+ "metadata": {},
+ "source": [
+ "First, load the SAM model and predictor. Change the path below to point to the SAM checkpoint. Running on CUDA and using the default model are recommended for best results."
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 9,
+ "id": "17ccff22",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "sam_checkpoint = \"sam_vit_h_4b8939.pth\"\n",
+ "device = \"cuda\"\n",
+ "model_type = \"default\""
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 10,
+ "id": "7e28150b",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "import sys\n",
+ "sys.path.append(\"..\")\n",
+ "from segment_anything import sam_model_registry, SamPredictor\n",
+ "\n",
+ "sam = sam_model_registry[model_type](checkpoint=sam_checkpoint)\n",
+ "sam.to(device=device)\n",
+ "\n",
+ "predictor = SamPredictor(sam)"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "c925e829",
+ "metadata": {},
+ "source": [
+ "Process the image to produce an image embedding by calling `SamPredictor.set_image`. `SamPredictor` remembers this embedding and will use it for subsequent mask prediction."
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 11,
+ "id": "d95d48dd",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "predictor.set_image(image)"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "d8fc7a46",
+ "metadata": {},
+ "source": [
+ "To select the truck, choose a point on it. Points are input to the model in (x,y) format and come with labels 1 (foreground point) or 0 (background point). Multiple points can be input; here we use only one. The chosen point will be shown as a star on the image."
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 12,
+ "id": "5c69570c",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "input_point = np.array([[500, 375]])\n",
+ "input_label = np.array([1])"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 14,
+ "id": "a91ba973",
+ "metadata": {},
+ "outputs": [
+ {
+ "data": {
+ "image/png": "iVBORw0KGgoAAAANSUhEUgAAA0gAAAI1CAYAAADsLNpwAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjcuMSwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/bCgiHAAAACXBIWXMAAA9hAAAPYQGoP6dpAAEAAElEQVR4nOz9WbNsSZbfh/2W+94Rcc659+Y8VGWN3V3VXdXVU1X1jAYaUwugjEbCZCIk0UjpkYYnGp5I4xP4gm9AmvGJZjJKBpOJb6LJCJlIEEB3o4eah66uOatyzrw37z1TROztvvSw3H379thx8hZICa3s42k3zzkRe/vsa63/mlxUVbktt+W23Jbbcltuy225LbflttyW24L7N92B23JbbsttuS235bbclttyW27LbfmLUm4B0m25LbflttyW23JbbsttuS235bakcguQbsttuS235bbclttyW27LbbkttyWVW4B0W27Lbbktt+W23Jbbcltuy225LancAqTbcltuy225LbflttyW23JbbsttSeUWIN2W23JbbsttuS235bbclttyW25LKrcA6bbclttyW27Lbbktt+W23JbbcltSuQVIt+W23Jbbcltuy225LbflttyW25LKLUC6LbflttyW23JbbsttuS235bbcllRuAdJtuS235bbclttyW27Lbbktt+W2pPIXHiD9F//Ff8HHP/5xNpsNn/vc5/jn//yf/5vu0m25LbflttyW23JbbsttuS235X1a/kIDpH/yT/4J//F//B/zn/1n/xlf/OIX+Z3f+R3+7t/9u7z88sv/prt2W27Lbbktt+W23Jbbcltuy215HxZRVf033Ylj5dd//df57Gc/y3/5X/6X5bNPfepT/Lv/7r/LP/7H//jfYM9uy225LbflttyW23JbbsttuS3vx9L9m+7AsbLf7/nTP/1T/pP/5D+Zff57v/d7/P7v//7B87vdjt1uV/6OMXL//n2eeeYZROT/6/29LbflttyW23JbbsttuS235bb8xSyqyvn5OR/84Adx7mYnur+wAOntt98mhMALL7ww+/yFF17g9ddfP3j+H//jf8w/+kf/6P9X3bstt+W23Jbbcltuy225Lbfltvz/WfnRj37Ehz70oRuf+QsLkHJprT+qumgR+k//0/+Uf/gP/2H5++HDh3zkIx/hP/w//R/5+C98GhB8EBRQ7xGNpR4RQUQYx5ExRLy4gixVFe89YFap3L6IoKrlOREp3zvnyJ6L3vvyTv48hDD7W1WJMRJjLPWMIbDb7yD10XvPer1mGEf6riPEwNXlFSEExjBy5+wOIQRW6w0ahTCG0tZ+2DOOI13XsV6tSx8vLi8IY8B7h3hh1Xfs9jvCOCIi7Pd7NpuNjVenMYZxxDlHv+q5uLrkubMzfudzn2fzxAm8/S4P/+Ar9PsBOsF7V8ZVl3EcyxzZT63Wdno2z1M93845xtSHGONsDfPf3vupTRHESZnrti/Dbk8II8MwsF5vSpvtvsv9ze/ndavXUURwIrQ7VFURYCWeq5XQj8q9J+/ynT/4Al2InN47w3cOFHoUpxCcMnawk8DP/ZVfYRsG1usT8B3ar3AnGwaAaOvz6Mdv8uoXvsHdQdL74GNE0VLXeNbzi7/9qwxekd4h4gkKSId0HRHH1nk++Klf4Mmnn+fBuxc8vLxkN2yJRLaXVzzz/PM8+4HnWKvy8Ac/4LVvfYOOCCESiMROIUa89lwFx8d+5Vd49oMvERCCCBHBRfAjvPzn30HPH/Ct//v/g/GHr3LlBmIMrEYhOIcSZ3Od1zloZCTSiePUr7izOrEzKhF1DvUeVbj2kY//6i/gP/Ak1zKy3mwQPNI5nO9AIQ6Rte9569XX2V9clvNZznSMaI+NeX2COIc4AecBQRF0GCEqWyJPPvcM3/x//z7xmz9mvR8ZRNNagAd2olythU/+9d+kf+KO7enO9nVE2e8H4jiy3e+Q64Hv/qsvsXm4o48QUcQL3nVst9eMYyBGZRwj4zgwDtFowjiWvXfv3hOcnZ2gxHKW2n3clvKd/YWis/OqqgwK+xB45ZVX6bqO1arHeW+/uw5B6Zzjzt1T8kyB4pxwTWT1wWd59lM/TffkHQLQiQffsXYdnQgqwKi8/KWv8+g7P+Y0gGokagQiew/rDz3Lxz/3GWS1gUS3a7ocBIZxgLfP+da//BPc9Z5OoQ/gVImijKLsPKyfe5Jf/N3fZtsB3tP7Lq2/jXccR0IYefjy67z+5W+x3o50MTJKRJ1w0q0Y9gPXu4FxtD3U9900lzKnJTWvqGl/jIr3jq7r7BnfsfWB7vm73PvIi5w8+xS+P6Hre1znWKmj8x3BgY4j12/c55u//yestop3jugE/+QZeM/w8Jz9fsuzH/8gv/Brn+Mi7qHzqBO8CiKOqIoTQJVhP/A//Y//kkfvXvDD195gP47EELm8vOKlF5+jX8Hduyf8nb/zv2K9WeO9x4mf7amgCiq89dZb/LP/4Z8x7AZW3QoQZLvjydM7/MLPfZpf/Y3f4IMf+zBjJ+iqox8hjoHXfvwKf/blr/Da91/m4VvvIEOYaGo6p857BAgxQsWzgRk/XqLh9b+at7dnoablS/yg/n46O/PPqhN2wEeW+pX7ojqXfdrxIBCb7+t+5b3Wjk1VQGX2bGmTtGdrvikC9VjS3zfSkPRdjDrJEDHMzqkqKHO6tESfZv3E+KyqFjlp1DidM5b7lZ+/qf52ffPnrbyR+6HYfMVCMeWg/VJHCEVWVLV1a/deTRvyZ20fahml7s9S/8tzTohM+yGEMJ+Xhd+tsflc5TqNV3rQw3m0R6IdhOhAQCXy8Z/5GB/9+IeJQ+SV11/j/OKS3fUVF++8S7zc4oJyud1xHUb2GL3vxHN3veZ0fYKXubxV+mwTPxvD0l7ax8D/9eWvcvfuXd6r/IUFSM8++yze+wNr0ZtvvnlgVQJYr9es1+uDz09OTjg5O0Uj+CA45wluyk6RNxvAerOxv3USkGvhPsZYAA8wY241Ea5BU11HEe4qgJSBUS6ZEbtxJIoJ+vnfer1mv9/T9z3jOBKjtdd1xoS994QQ0OgQsT70gO+6UreIsFqtTCjznv1+j4gwjHvWmzXDOLA6PbXn1mu6rgNV4hjYbDYMw8A4jnjviTGmZ3runN5hfXaCXA9su45T8QSv9J0/GJ+qQmL+9ZzkeannrgaoNWjt03jz/DnnynMHhC0LuzoB2EyoRYRtCARg0/VlLvMzNUOpiWNLDDKh8YlRU/WhHmcXQXrovfLUvXuceM/K92y6DkRwAmsRHDC6yNgJp6endCj3zk5Zrdao6wldh2zWnPgOjSakn3y44+EPfsz6fKAbIqoR5xQcjB6u3cgHXvogp5s1oRdwIM4TxaHiEd8Tcaxcx/7RQzbPv8hTTz3B5u4dzs7OCGHknfvvsD7d8PST9+h2Ox5urznte8QpLioqEDogKr309NERrq+4e3ZGlI7ghSgOCcpKPQ+ffpoh7jlZrRicRztQ9ayAwaS0Ms/1/EeNBBnxvqfza9xqTeeAMBgTkBWjF4IbefqJJwjdCrdeQ+9ZS490Htf3hAj+xCMRnn/+eR7qm4VxaFJUxBgJErhzesf2h7PzqM4DDnXgQiAOAQ17ri4vcE7wfccmCr1TgoCLJgJoD098+AWefe4ZYm91Oe+LQLLv94T9SL9eEdcjn/z5T/HGl79Fvx3RGHFe8L5DnafzQkDpfCAo7MNIUPBuYrInXcem6xHRGR2qy1EBJ/3LdK4WDr2CE8em6/Des/IdXZf+icdh5//E9zgB0QgoQSL37tzlznPP8MyzTzOubU77rkNdR6dC5xwhCWe//Ju/yo/XZ7z1re/ix4gD9gQ46/jYJ36K09MT+tM7gMxoQQbSwUF3dpe7/W/xZ7//J7jzLSsRiJHoFNcJewl8/BM/Td95+tMV0nVFcMzjNZobufczH+ee63n1i9+g3430okQHm1WPBCVIwDub+953hWeoLM9zLSBrtW6ZBgWE05Oep194nrPnnkHunCLdGtf1dJ1jg8eJY3DKMA489fGPcILjW//yC6zFM4gab/MC1yuQyEd/6mMokTsnJ9B7IuBEiEoCaCb4btZrfuVXfpk/+P0/pu88OGHYj7Y+48i9e3f4wIsvcufsrNC/TKcn/mhC4AdeeIHPf+5zfPkLX0JUiFF59oMf4N/6u/8Wn/vs51h1HSpCdIAI47vnfO2LX+FP//CPuH73EW4I3FE7K8F0STNaXfOXGgzUyrUW3Mx4UrXvl9apPSs1Xa/rWQJIh3Uw6w9+zrdaAbAFcktALwuxdd/aZ2seap95YmgE/iy3oEV4z+/UfPHY/LVyUN7fUWKq15QTiuLElX6FOJ//JVmg/kxE0BhnAMWrTMCuKTNFbT3Hbr4/2jmcFednf87mQST1goO5n/VDJrkxxkhsHqn38NL41emBTFnPy2Kb+XnnCBoLkPC+O2ij/SkiB7Sr7BFxoO6gzQyQVANOHBpN8a2M+KB8+ytfJ+4CF5cXjCEQxkAflX61gTHSdSvuCgSMbjq1fx4BBecOZT1bg2kOkXlfwQBiO683lb+wAGm1WvG5z32Of/pP/yl/7+/9vfL5P/2n/5R/59/5dx67nnL4goGbcTRBIhNXmITwjOiH/Z7ValWYbGa6+XeYDn8IYYb0i3CV6szP19YnVaXrugIIhmEADOjEaBrgGCObzaYwnPrAZQ2x957NZlP6kNuox54tR+M4zqwuuV9936c6hWEYy7iZzQ+l3dyP3W5n7fn0gEDUyKpLwmMYTHuZ2qrH3mrL6v62xKDV2NTzXK9FTdzqd5xzdk6c6ZtqAqKadFY6Zx5LTC+3c4xBtYzHNQyknc8QYxK2HXEMqIIX0zyFxOz2MRB9x4c/+mFOzk6h8ziXBHPvwHlc50E9uxDYPHGHT332l/jW//ivCkgLYQRxjE7o757x0k99FNd3RImId6Z1F4e4DrzH4VDg4p23+fr5BS9+/BNov2a727LuenrXsVlv8KpcP7jP9f132DjP6KLxZ3G43kFUZISVd7z1yo/w6xM+8omfQ5y3CXeCRpIFdNJi1ftNcAXUtmshYsQyuI549w53P/ABzt95m81O6McRUeGKyAc//Un6e3dwveN07dHe00WH6zroepym7gRY33uC64tzwjASNRBU2ceRECIvffiDrNdJQ+47RDwqNn/RKc55hJHQOwZRPvnpT/HtH7zFuBvMAiFJ8Ow7ZN3x8U99kvXJCTGf76TZQxJodSOigaEfuPPhl5CHW974xnfoMHAoMRJCnptlbWFtlTCGewiM6rNXv1POG41gUe3nmgEdgi4tAmLUWLR+CLDueO6jL+GffZLVyYZ+1eN9RyfOQB8O7xw7DYwoKpGP/PzP8sq3v8MJIAqDi3zq879M9+wTdKsV6/Ua5/yMVoOds5GInnruffhFPvazn+B7f/RlXLQ9NKJchZGP/dKneOpDLyLrnn69RpwvSqY83r7vjTafKB/81E9z8cobXLz8mrWjylisW/N5KvO1IGAsCRb1+yqgfcczH3iBJ59/js1TT8JmDa7He7Mg9UHpfIeuPAGF3cjHf/aT3P/+q7z149dwfZfm3rGPgQ989EOcPf0Eq80G6T1u1RMFE7DV9qGIYsgGPvqxj/Lw4SU/eu11Ql7vRAvX6zWf/vSnTekmvnxXK7U0/Rz3I5/5+c9wuj7hC3/yBX77t3+b3/0bf4O7d+8imGVZFIZHV/zwu9/jW1/+Kt/75rcIu71ZycQUQc4nQVRBxCVaOwlI2uzFvH9bgDETnBZ40cF+b36/6Z2ltZ0/+17fH57TFvAtKQLrUitw23rKOa/aynJE++zSPLXzt8SX6+dbhXNtvViiXUtr1LYrkvZq9V1blj7Le7L9rqZzN4HkJdkAWLQQt2CvXbO8Bm1/l+a2BYe1vNKC66X3l+bj2D6v5wqY8eE8V6WO6rl5UUTTAyKMIdA5Qfcjw8UVYRfwQZEIHc4Iuyp4R5dAr08sI2KWYbWOLoPX6s9jfC5bLx+3/IUFSAD/8B/+Q/6D/+A/4POf/zy/+Zu/yX/1X/1XvPzyy/xH/9F/9Nh1ZME+qrIf9njfGR3RuSVhsg4Fuq6bgZ5cDzBzv1FVhmGg7/vZwW+F5fxedntpD2EGRebCYeBqtVqZ5ac5FF2yBmWAtNvtCsgZhiG1be/kz2twA5bQYrPZlGeGYWC1XqM60nXr8nz+SQKNIQRWqxVd17Hf7xnDSBwV1ie4xKjy+J2YhSqEsYyzNufm+aotcrX2cbfbzcZbH8AWsLbgNT9fz3MNZGvi1Vrw6rWtP2v3VE38cns1wWyJ4/SsWUXKevoOxsSs7PQTiezHQFh7nvvwB3nqQy8S+4g4oe/XjDg0MURBwDm63jMMI3effZrNvTvogwtr0zuCU3ZEfv6XPkN3dsLYKSIe58TACKZZEeeIOFxUNl549+qSMezZh8huv2fz1DM4cZydnhKur3n75ZfpxhEPIB6XNL/B96gki1Ic2XSOV17+IS9+5OOsVuYKOuwHXH9iYC2aGV7cfA0RMFtanM0zGC3tpeOh95x+5CV+6z/89/nj//6/592vfQN/fo2MwlMf/RA//duf58HDB6yAtQoxOjxm+TFLsU8ARokE/HrFEAPPPvcBHrzzDk8++wxXV1c88fTT7Iddmjc/A0jiU9+iZ+08UUfWJxs2d88Yz68TQTfQPMbA6RNPsbp7RlBwxVFEUDX3qmEY0TEwSmQXI2hgQE04DdFYhygxhmRFdkUwkYpJ1/vWieOYTrtlwO13+Yy1ZUmpUOiljYioSUtqlSEinDz1BM999EM8cgF1QhhHfDBhN3pFVcxNUhT1pig4f3SffQxsos1Wf7Lh+Y9+mCsf2A8D4zDi/FxoVFViCCjKNYFdGHl3d4V6IToDmlHA3znhE7/8GfabjiAG3qNGkmrlQPG0F0U7YXCgTpDkhhc0ENHZnOXfDWxOoHFJ0F1aE1U4e/YpPvzJn+bCDezHgT72OJQw7tHg2PgVLqgp/5zN/l5tvFloCzGiKkQPn/rFX8A/eWLa1MRjtHPpWUka7Yh4D1GJCC+8+MJEY026BIHf+q3f4qWXPkjne0Qmyx1Mbs55TnrfE1eRX/jML/DXfuev8dKHPmR9iskVcDfw9o9e5btf+hrf/to3eHTxCBcCfXQ4wDlhdBCdIEkydpDoZtmUUIGPWnF2TGj6X6q0e2/pu6qjMzyzKPDd0M503hOPc4cA6Vh/5nINs2fmZ/hQmF8CXEtC94FygDmPrOnJ/AxMPLsdb9tm3oua/zMii0zVzM7YzO3+CM2r52BJFmjHOQ+TsH68F3Buv2u/vam9Y8CrLcdAvVVkP+o9dAyQTpXM/5ytx3Gcb+Amz4tzCJHeezqSJ1WIuCSDRDBFDcYXUcElx8uIIyZ3u2Ng73HKT0oD/kIDpL//9/8+77zzDv/5f/6f89prr/GZz3yG/+6/++/46Ec/+th17HY7E4BipO9WyYUg4hvmlAGGCenzg9NaXbLAHUJgu90W68x6vabv+/JMTUhq95QMPrIrSAZI2ZUuAwdjqukgihA1a81gs16z3e3wyed/2Bs4CuOIakxudII4iGOk7w3U7HZ7vPdst9sCTrquA7E4BhFhu92yT1a0ruuISVNdg4wi1AqmTXRC1/WoCNfjng4lDhHn5360bTEQ5IvveJ6zrnILbDVhS+4TNeFtTfvW0ETo83zbuh4XAFuw0+6Huv26DidiglnTH7K1AvDeAOUQAx2gIRIdeGcis3cdewIn9+4QO8d2f0Xf9TjfE6KiviNGkAhCJKi5sQwi7DXSixDDSOjMKoVCf3ZGdGZVxGdtsRCJqFNElCi2z4NaH5+4c5e9eHzX40R56qkncaoM19fsry7RcTDf925l+xM1i1Byq1Fg2G9x697AYKKmq83aXNiGHb0Txjgmlb7F2KjIxPwS8zmgbRGieHarjv75Z/gr/97/hn95fc31N7+LC4HBA3dOuHjnDe6owyfqGyT1QjFwk6izqvLo0Tmu83TrFXeeehLVyDNnzzKG0cYlDhWz+ChKNkFpGJEYDDSpMhC42F6zEi0MW0NExTHEwC4MiK7o8KARjXmP2h6w9QDpPLGLDM6E3r5YYkx4DjHia9cakeTqMddktlx4SQHQMsulZ+vikOLV0wpOPtEeoqJRiWLPK/Du+SPeuP823D3lRARvUWF0YjFx3glOnLlMOtBOefKZZ9jcOSO8fUHnHFfXV7zxzhvo2Zq+7+iyQORcYsQkUOrwQOhs3br1ikGjVSxCFNjFwFYDl7s94j1rWeHU3EqcmO+8k+QZgLlLRg10pxuCKitxOIusM6tnVrgl8GExPTkCa7YIRUGR92P1lc2pwOXuiocX5+zXcHLHFFgSzWrkOqPhIQZQb4KFc+DBnaxs3qMSx0h3sjHXwc4xhBEdFR8jQRXpPOogxLzeSucdGkHU8eDBA4ZhZBwnjwCA5557FlCur6/wvp8L2Kp0fZdcoKDvVrzwwgs889QzdL5HQ8Q7s1lfvPOA177/Mt/96jf48Z99h3C1BQmmdCOdiQQySZ/ZscoKhmkf1sK/2v9KfI6UL5IVZ3FnH5b3EkaXBG3SOYVDkPKvi9VqvldkhMynFvrVtt2CxYlGGL2nWKMnoNmCmna8NZA4Vn8uS/HZEx+d89iWt7dzYH/kdS5/UhO7zD/aenSproW5Xir1+PNZiDFCpZStn12qawZy7IHZ80ulljlqT6UW6B2TV0SkKBDq72vl/tK6lTZYPi9Gu45bqYz/aFIDghfzjx2H0XhCkhMKds1tKkje64mvzUyGSx25gc/ZXL+PABLAP/gH/4B/8A/+wb/2+/urrfktip2kOAZc3+H9XLNUL64kZpg/yy5vrjkAqlqsNHDoZpV/z3/nDZ5jgLJLXf49g4KimVVSQoZIGAPD3sBN1/cgysl6Y1q1/YCGADHS+w68Yxh2dNLRdbYtx3FEnG227NKXwVGMEXEUV7yY3L9yn8GIWY4/GlMSB3NfS0KwCESP35ywv7shvHvJBkcUodVUiAi+cwYSnEMEOufY7/fG/CRJRgtzmP+u3QHymrSxRbPvpTELF8Kos/dz/eaOOSWSyNat1gWprq+udykOLX1Qgu2Jyk4iIklQsUh2+uhNYFS4PD/nbnzKLIrOI1Ho/Apcj/gN0vV0qgaSfEQU3Mma+OAKr8JeIk/sHbLuOH90wVObp9jgid6ZNcX5JJX30FXkYAyMuy3XD+7jNidcDQOXGvH9ms3JCScyonFgXEEnHZotlyL0AnRCcBFV6FyPRojDDokrduNAGEdOnWN/+S4nV5eMcc+ogTW9uSs5U2rY/DkKxswMVZVRAl1UNsFxstogd075lf/13+F/+PF/zXp3yaOLc8IwcOIcZ9Ix9jCsHA5zbZTOm+CkZu3oVAiXAzvZ88Snn+aHP/oyn/jpn+L+a2/y9LNPE/qObtUbCHIW5yfi8HFk38HYe/rR3ALixnP23BNcPbpAx4DPYqLC2ekJqpFu5YkupvGZoBc10nkh4llpsmSsek6eusdARNVEccVcLOM4JREIJDcvZzGxIURW2e1J5hrrurSCzVwAMeVMK2BBAkjR9rF2mDUlW49ROjHlj4mzk1vL6eaUlXOEqHSKuVSIxdFEDMBGb25rRrsdfr2i69cEf0VAOdmsePbJu7w9XpplzXclPkDEJ+uC4jCpf6VCiHB29x7adcR9RJLLY+eEEAZGHeh7o6mddEaDpKJEIohGNmLB4Peee463vv0y3SA4dXjt2Udz4Q7JXSwLPyHP7yKDztalvAYmqOZ4oJUoVxfnrE+fwrnOQJ+H3gt4T0y8zTkDg+oE7eDJF5/h7ZdfRUeh1xWdX9OfnnE9jsTtjtVqQ+ccvXOI7xBxxB7Ee+MnamscQ+C5558yK7NOPMt7xxtvvILqk9w5e9JAbYpHc9nFrvN00XN25y7PvPA8/WadUZgJedsdP/72d/nKH/wxb/3wx+yvtgxhJIpaYg+18QQj4XRiSq0s5KlN36TJD9GsS0nwNEuTFPflyZKXhP4kNEbVEmB/sDoVT3kvgbq1ruTPl9a8/v6mevMzS4AH5sJ2/rsux/pkz5lnQqqpKF9sWuxMtvXNZaUphrgWzNtY7Xr+sgJhCTTmP1uFSz3WNgFHUVwnRSCS9k3+s2p31v/FmZ7aWSp5rG28knOOtre1F9IxkKdp4EsKq2Njr4FSW5ase/Ox6GyO674cG3tpS8Ro/SIYmu/nYkHHI8kK5FUhBi7Oz1Es7jnEtGAak6tdqlcMjinMPI98PvNL89P8PZMFRRoQ/XjlLzxA+p9bzA0lmn/6GOm6PhHbvEEnxiVJSEEr/920KV0+2A0RAFuI2nK0RKzyxs7P1pqTkq2oEtDzeyEEhmGYgZZsveq6rsQCQTqkqiaQ5SDlEIgxGPhQS2ZxfX0NkPz2J2tICFOcUgYHqiao5v7s9/smg5yyT+53JuAIT734PPtH32fj3az+maYpmntLtqLl8YsIGufB1jVBLcHM1eGuiW9rQSr/yn6IxYVSxCwo9VrWdbYas5owLDGJXHLc0xLDimp7EY1cX10RYjAioUDUpFVWgpj2+MlnnmY/Dpz2PZ0rDmf4JLiZAJb2bwCJyrrr2YdIF5T1aIGrofc88+GX2F1dcCoCY7QsbpJBZRImnCDiUIn0ODqFte/pEIb9jv12y27Ys7t+yHB5wUoDnXNJM+UTczXte0AYgwKe/TDy5o9fZfXUU6zu3OHi3Qdszs7Q7cBwec24H8xKFGOyahlwKa4TzBmHAF1QuiFw1q0Q9bh+zdMf+RjP/swnOD//Bnfu3MXhkVGRlDhCotJTaex1IpgOcEPk6v59vvXP/4hHb7/Nn3z/x7z0kQ/jn32aDqFPYnd2yxMUr2IuQkT8qHi14OOV77iOmekbmxhCYLXaENW0YdkKU1yGUpBxVIUQkTHihogM0RJ8jBb3F0JM/0J1RuYaa6mZuOpRzrC0T2shomWG5Twk1zJN1ceo4KWAvQPBLT0XogUADePIPowWOEzEk3zOc+A2tp81gTCSompELVFJMHdEL544jojHAL9qWdsoMHphn1wSu9XK6sf2N0PkrDvj7mrDxdU10Q1E6YneAEDNdQUmN1hV+s2aQSP7kCw6oSfEyJDi6sR7fCXM1zThmBBU1qRam5NuhYwKuwBjTFHu9r3X5CarFkKU6+1Q1uLwQe1fcuZc9T2rvmc7Dkhn2TJFBZcy2HnM5S2M0cBDBqkh4tNe7dIZkDHy9Nk9ZD8SVyPST0o1SaDj5OSED7zwEqdnZ0Q1JYQGRXYj7771Dl/70pf55he/zPb+I7qgCcRgvPhQPqZok5t5rBV57X6urQrvBULe65mj67UgYNpWWRY8a54xxQi6xWfb/uV3Dp6Vx+t7y8Nm9Yj1XJPcWve1dunLIQkzYfgIGKjbumn/1688Th3t7+U5bgY/N5Wlfi1ZZxZBaWbGVf/zc63XS1G6i/GFGhAeow1L7b5Xf9uS6Xmr1G+tUUsgyayuU91TuImb0auDObMv0BgQMI8kMvzRxCuY2YIz/ZjJjmTg9HjjnQE5ezB98fgQ6X0PkCzmyJh2lzJFZRc7XwkQUY3ZI5JiDJJVgbSh8gZP77cakQxygIMARFUtmrUly0O78fO/OkFDPmRZINona1ILsK6vr/E5riP1dRKirI0WGMUYGcMAhGJB2u12E4BLTCfGyHa7LWMehoG+cwV8KaDiiF1PWK8YgwmLeZy1q5zvLFi/1g7k5zIoVdUSt1UTmvx3/c4Sc2nn2fbD3KwvYp9l0JqtY1r1YUn7lOevjVWrS91O/e44jvi+Z7Vem3AY94zDaOfXQUQYsRTKQQ3ChXHE9xajEcQyuMGIYFmuAsnNZm8C54gBATdEhr5nuHuCPHOP3dU562ixHZokK0uabMI+IqaxBTRZIvrNGokdvvf4EIj7nfkDxz2qEbzDibmP6cRVcd7hpMMxovvIer3B4bg+v+LRO+8i51cM2x3DxQXD9RaXzlXAZMDs/daejUwsLYY+0jlTL7+72/Ho4pwPfvaX+dKffZuu82hyFxxQs2biSsxCIeoYzRxVGcaRR6+/zRPB0Z1f8WB/yfjiCwzjwBiD0RNXEWpJoMQZsM+C+RjMkkBUkpHIQI9zXO92nIVAV+2pYp1O/6JYzFGMCqNl+RGxLGLJo5thtPibk65LzEQJaQ5tb4rRtOYMtOen3qvtc6gm18n5e/Y8tv6aQYC5l2pU2ztZ0QSlDoudUoYhsB32DLsBEFwvdM4XjX4oezLN5TjSeUtGEhNuudruuN7tWOMJG1M0dJ3iZbLEq9jaDxqJwbIA6jgm1z/rY68wbPeM+4EgDicDoxczqmZrSFKyxDQ+Eo2M2BnpcAkcjeyDpfl2nbeU/bUj2Gxql8W4ei0UNbfMcYT9nn4MEAJk5VxMiqXklpjpawgRhrRvcJYZzjtiStRwvd2Zxc17uk7wojixOVFHscaVuLgQiF4IEswNN/Vvt9sjCPvdQE+Pd53x2lXHiy+8yL1793DdCsQs4rIbuXr7AV//ky/w7a99k/tvvU2nghuCWfscE/iGA4vbTYopOHRDWprX9wKnP2k5dnYeF2gtjePYd7Wrfv7ehPPjY2r71M5BzZ9mMkhUkMOA/yUhveXH9Xe1nFSDrEUhfOH3ttTKy7q+xbEXH5f/5UoNCo8BwrbM6eYciFgChMdrN8t5P8neqvug1eetUrdWtC/JZe06F2VEBi+V/FsDPgNHqW7JV7/k1ODQwtlasfCTnVU9mMeWXtiHj1/j+x4gTRshmUZ9Mhsna5BL8QQ+x6OEADgkx86ACTlJcMwCW6679gPOG2a/3x8ApmEYyvMZeWerU70xlzZ+G6cUQiipvvP3uc6T01O2+13pS3ans/gmQejK5s0/c/+6Tkof636t+hUhzDNi5e9DsABbJ2Jax64nrlZsuw6/27KRaQ3ywRMxzaTzh3ey2DzIAeGrNYRLzK8NFm81JAKTH7rIjABkkFlbl2qNSu5LnUZ8yUVgtueaMRVGgeB6z5hjFNIeVNQyuShFAFbjT8T9wKDeDDQeRlFGHekkgAoDWQiNjMOerY7sneKcaY6vXcS/+DS7dcf1OLJWBd8hYtJ8AJBkTVWz4qxGZbsd6QbFb0c0Brwqvu8JpzCGHt95wn7AayRqQMUTZdKYK6BeGKMwinJxdcFTd+6wUnjp+efx48j9GHj09jsMV1v6cTShu1ozq+yQeY4aCU4ZHJxfPGTYX9Pduce7+x0f/tQn6F56jsFZBr99CGw7S8rQCQxqiTAQR0gCQBwjUSzF8KPzR1z2a4b9DpxyPey5CoPd3RHsDjUDSgmsi7DDYlMCBrS2IbAXtXvVorWn0e60ubi85Mn9wNX1ln6zoetTeuMMUDHQqs4sstvdnodXV2xFbaVVuLi44PzqCo2R9YkwRi0uHhPDNvEgW5ecn87akga6FmbKPtcpfqMVBFSx+CJVXGovhGCZCsXbOASGaMkYsoVbQuDRg4eMnUO3I6hH4wi9I/aKakTUUnSLwm7Yo9db1n3HlUazMAfl8t1LLi7PiXeh77eIc3R9z9oJ4n1K32vzHvcDcbtH9qNZpUIkuI7QOcYwcnF9zeX11rInOXNN7iCB6gnoBVXG7Z79w0uuzy/KHAVVu4No2HOxvUZjZLVeTUKJxmLRO0YzatfgSXFnd2gNMbK7viZeXtGjdBpZA/Qp5YiInUGMVo7jwPWwZ3RK0Ei/7pBeUO3YxsDlbkdwjug9Pgprl10co6Wcl+Rep8puu+Xd83PGOLKLexRlJLKNgYvdjn0UzvwOHwzQf/TDH+YDL77IerVOWl+HDpH95TXf+fLX+OaffomHb77DcHXNKpq7rBdfzpJojleYC+4tPV3S5k/KAbcIkOqf7WdLIudNmvpa0G15QZYdjoux7+3q1PLGuq8HvMV+Ofiu3W+tErae18Mx6mxPtv2q+5RLy7dbPlz3/1B5eBww1YrJtv91KWcn0SOV+Zq39K2u+73Wui7HeH/dxk2Ar17LrLh+L+BzbP+2c3mTEiAr4WoZpl2vFhzV3y3tGyUryw73ZQHvYq66zrmStdbqMt5ksUZT/Gh9N9TSnNRrVYfDtMahsr+cFKXOMVfapfK+B0gac3a6KUYlDAPifQoat2JJB9TiPLBnYrQg0yl1q5Q86nnia4JcE6MaENVarfx5bRnK9eTNmbUEefFrQT0/mwlO7VKw3xvzEpHiIpcBxTiOiWBrcaGr381t5f5lNzr7fbD7VxaInADOKeMwMIyB07MNq3tPcO8DHyD++BVkP8ysNplx5ZCVvLlzsonahW5JmKjnuv18idAVbQaHgYs1UKo1M3mcddZB5xyr1aoQlmwiPyAWR4SfMm/ZdUwTsHSOqOluKefBpXTMgA8Rvdzy4J1zfNfzzAsv4E8V1mt81xMv9/Q9+G7FGAL73Z54tSNc72xODKUxOOHnfv7TrILAo2vGJEytfDRNtHOE3cjqzDMOA9swcLHfcaWRcGfNhY9EC+vAASvtLBZhN8J+ZBwEv/JoFyy5gEtJKoAxWmxcF0bO33id3aNz9vuRO+sN9zZrrt98kwevvk7Y7fEZhGc7VJqn+g6GSeumDKKoRN59/TWuX3+Nk5OOe07oRPj0b/wq3/rSF9ndP2e83HG9H1ifrAhB0dWaiNBFn7JgRXQ/EneR09WGcT9wcXnJMOy5ksHiIi6vGWPABfBdD70izoBSQNAeJCgyKHEY2Y97vLOkJaOmeBpJ7kXbgfFiy3pzCjpAENxKLO26s2BlFyJhO7J9dMmD19/k4YOHjAo7VTrg+nrH+fklq1VK2oEjRnORzdo641qJRqkpM1qGuLRP67PX7uZl0A9U4mCmM7kP+S4p773FWO087/zodQaUNSv60xP8ek236rnzxF3OnrhLv7FU7Ofn52zvP2D38ILri8syHgbl7Vfe4MGjdxnvXhMvA64zK+fq5IQnnnmak9MTet9xfX7N/bffYv/uOfLOBT6kuEkig8JaPO++/YCHj+6zuXeHcDrg/Yqu7+n7njt37uBXKzrf8e7DR2zffcT12w948OobMAYUISY6ebm95tHlBQ7h7OxO0uwfRh7VdKYWVuAwa972es91CIRHgpOO4WpHd7pBzkbWJ8LJ2RkiDlWjS7urK67Oz3n08GFyffZ03puSKwSu7r/LxYMHxLM97BTfbYkndolyt+otztGJXVZ8ccnFo3P2j67xY6RL9YWo7Lc7Hp1fIIyE6Pjpn3mJn/3EJ7lzcop3Do9DQ4TdwBsv/5g/+mf/grd+9ApX754j0ehgn+egSjTiROjFz7TIx2jsDODozfu7LXM+cigA123MlAbVWrUAramkrPshCJpiAmvQ0irh2jG2pQbSGo5fn3Fs3K1wXQubuf4lcLBUFoXn9Fm7p9vP7Z0pA2/bzuOAmBb86QJCXQIRN/FumCevacdbW5FCM74lANKOXx+j/aX+P+5zh+CYIiO+1z6Zv3cIMKd3lucxy6yqWpIt5DPRdX3622HRs0zvLgDsMo6mj/Weq98t56LIraZ4FOeguorhvcr7HyCpJuEg4qMzYa3v6RE0VKbaYPE0Pt2e7hC65FONmquFuR7VyH9uhakTB9TuWbnk7/O/dvEzQKoPen2IaxN1BjgwbYIMfPZhKC5jtekUoQR0t0kErO2x1J9Tl1vGs86C4tt7lFQZ8+9potYnp3SnJ+w3a1ZnZ/hwPjsoBZjEsVhZasvSxDwOCVl+riaqs9SdHBKZvP4iUgKHW0Ka685zWX9ef5/nJrtLtgS+ZWp1PaWPmmKIvJu585mlL+0PiXaZnBt58OPXeXj5iO3DHd8d/4znP/ohPvKJnyE64Xq7487pGSenp1ydP+L6esv+4pLhzXdxV3ucpsDRCHdCx8W3X+Hdr36Xbed4O1zSBXjmuee49/TT9KcncGmWonfuv8WjsOc6wPmH3mRzejelT1WcOlDP/sFDtq88IFxfsupWnJzeY3X3LqvNyoBvmvdxv2cc9vh9oNeeZ1dnxCDouxfst2/y6M+/y6M33rRYCIx458QJGrH7npgzHjDXKFRgOyAPHvKV/+f/i49+/pcR1/HGxXdZiyO+c8HbX/0Ob735GneevIN3cOfJe2yef5rTO3cIFzt679lfXnP11jtcPbzk7R+8itsO7LstIvDMvbs87ddc/uhNdvsd450zC25fr+lXa/x6w8nZKS5Y/NDujXd5883X2XewffMBRNLluOBwhGFEr3bcf+UN+nceWRzhOHJy55SzJ+7x5DNPs16vefjGA17+7vd4+PAhD+8/YHh0ySYIqLBL1u+u7/F9z34c0WhAJIQwCWXVPiSdq6WyxEwnmnHoAnysZGavmMDmkutjiMEsptGUTcOjwJhij37w4OvgvN3VI4L3wsnphvWdMxDh+vKS/fUWHUd0u2UTPYTI/vySH33zu4SoXIxv0vc/IGKA3K1XdOue9ekJTz/1NJePznnn4bvofuBkhFWw58YQ8a5j+85DvvWHX2SUgOt6QkzW23TmTzYbnn76Gbz3vPrqK+gwWGa43YCMgX3ItDCAE+499SSd87OLy6WZ31YYaed1GIYiQA1vvGMAQoTr1+7j1j3amZeDl467d+/y5JNPoqqcn59zdXVF5x3Xjx6wCSaQXL3xDu5sDQTevvgeFxePOO867j7xJFEF33V03gDqnSfuMQx7Hrxzn3feepthby7AL8qGh6p437PbeKIOXL7+gBdeeo7f/PXf5IMf/gheHL04nMK4G7g6v+Bbf/ol/vzLX+P+62+hw4hEc8tVJ4yqxfqRS44Gje5mLf2xvXtMk/64wmX9bsuH4bi3QtvGErC4CVzUv9d8aMmtfGk8S2f0vc7ssb5O9R+31rTlWD/bvtXfzxI43VD3Es/On9cgpbUaxqb/pR6OUcP3BiqPs4/qtmp3vGPlJtpw0ztLe/A93uK9+MCxfh3vx/F3sgJNMNkzhkCIkfV6bf2WSj6S6n2Zn4Omo7O2itwlS6qo9AymJHckOv2Y5X0PkLbbPcmHKGmmBVKcg6j5t4tkjeeUiKFc8poWawwjYTSsmwlHFtj7vpuEArEtuM9Wl5DShjs3rWsRHNK9JarmM645O9ukk5UKALhkvep8xzYE0wrGyJisPpLSk1tohqVQ3e/3KYAc80dPAfWZMO32+xSroXjXAfmwWZ/GMQB2s33WyNi3Nl7vBOd6YlBEnR0W59DO4Vc9eCGEaIQK0yQoE+HPoLC2JMUYiSETFZIm3IKsi5ZaUiyGRiRlNmqTKkBKaBFDcZGxeZwnj8gAxXcd4uxCs1gDVUzIU7Iri6U4z5kHQ4zmshnT7ZMZXBVnuaS9SItqa+WJwW6Zt2xfI8N+TP0OiDhGBt74wSuIE9ZhRRc8599/g6/+6C3wjjDafIikpBqYS50PkS5AcJ7ohLDb8c/+z/83VJWzix1KYLuGTuH8R29aooquQ7wnCuhuYBXtTqQ/+sPvgu/NuoGyFWHfO/q4R6/O6dTc/PAdbmWCGyIlvft+HBj2AwJsVif03crScw8jcb9jd31l8VchmvVEksYOCGqxCK2LXS4umBuQ7Ea+9T/8T3zzD/4V+I5hH8B3+N2ed9XO7psdxDDiVz3xzprnnn+edx88sKxYu4H95RU6RJx4nj27h4ZglrDLLT/44jcYCOm8CiGaJkp8R98nS8PdM8b9nv1b73I97Nk75c4e+piyEzohxoBXYXt+yfmffx+iWAiTsyQF4j2nd+9wdnbG+VsPGIaBYRzoFVbB44PigCDCer0x61UIdr7SXW/edyVxAuZIeOB3fhNDzXs8vTABpOqZcvYIREJKqJFdhhL9SX/nc+hzYhQVvDg6b5Z6J44xRCS5oPl9RLeXXL5znlzSIn1MZ6nrGUfbS6IOlzIGdurpri0b16jAMKDXI/F8zztvPgKBtRjg9iFpfjuPjJb4YuU6xquBzinKYDExKZGDOIdeXXPx8FViVE7I/MD2vbgOlUiIdr/HnbXF24haFr9iSEtzYvMzF+qdmAUq8wOfsocNcUQBv9c0X6D7iG53Brg7S4pyfv+CRz94za4ISGu7jyPeKyvpiEEZL6+J+x0SI5dxRFBGhYf3r4gxgUFVXhfB9x1hGC3WKRrd8iJ8/M7TDGdK9J7Yee4+8wR/9Xf/Gj//K7+AnK4tE16IhGHk+vyK7//5t/mzr36d1/78u8je7jzxYNkXJd2PlMEMKVZLs1AlILqY1bcADaWirTWNXXZvWrJslOcauXFJGC97v/rumOuZZD5QrbFLvLettxZ061jX9wI7s77JlGgoe0XUILJ9bwlowNwjBShx2tnCk3m3MBdoW6vasTmpXXsPxnmD0qBVZr7XumS+XfOOY4D3QMLncM8cA3htP+tSuycugQ9JdKK2nvzrAtx2ntsx1ms4AyJH3m2LzTlQuYamWgq/yWCIvJb5jIhDk/uviLAfRlYrk8tMYW9yk5Z4MSULm1kWnQ/W2qhmjiJckc9PedDkPBFzhY+RB9ur95zPXN73AOnOyR3L7rXqLFOSWvpQl9I4g2U+iok55TjrGmXm70FT8qC8sSBfBBJQxLspBgO7hG/SboBPQETVYihMYMjuRCas5ztNxmGfiK8leHCdZxhMEB914ORkg6qy3e4IYTRBfTR3vM5ZutVxGCDanUjEmEBNgonOsd/vCtEOIdD7zlwfgGEYIQi9W9F3HVECMdj9H5aFSu3ujBgR8enZzgLKhz2dd7iVZxQYifS9Jw5jciHSFKM1EcvaqiYoaADV6v6naExQbAw+CQzprk6cUIKUWw2idz4J+JPGKX/vnCNIKKA1+wOLT5aybDFMc+eSUCpil366DJjLpatKSuBfNBfBkv6iSroADTR6Npu7CD0iAUPxOXV0miM6fOxwapc3ikAXFd0HYKRPcxdiTAfZYi6ykDAQC3DcXFwbI0vPrfYmFBEtK1QcRkQCXZkfZ0LrsIPRXDdR2GDZsUSUMIJzFkcVh0i8vi4+wDG5o64R1omX6vaaoFemSUqg0mmkU4v12FfWWQVGJyix0EchWyZSymgco1oShG6vyLhH2afkByZkWfwMuGQVIEb63ZZ333nZQDKYG246H65TiLb3NJjUpDEiIbJKls0xWJ49xNrbq7J//X5STggbVdbpHI2qBoSc6dGGbKENOvlLiwmOEiLxwQWP7p/jcaw0JoEeY2ydravXAGJpUWM689ltwkXPoKPtOOdBxySozRlw68uf704SsdvpSWfEeaMPPq0LtWJDA+otRiYCBKUjsHIuMbspq2TNeEPIGkNLfy2SgvJjZJSJHbrCOE0gi2MwxVZSUBHsUARRSyxQOLdaVrYQC/gstEQgWs5nfOdKDJXgIU4ychHbk9VcK8scqummd3swqpR4nS5MArFVmGiWtZDfmvZnjKiYe07IFpOoSMRc2XoH6ggiRffiXAISERDbICLm/prv/BMUJz10grpInxKaqKhZp6NdrWCyhYGT3FcJkTUuXeCoRFGiE3xMqcXP1vz8r32OX/vdv8LpE/fwnbOzGgLxes/Fm+/wtT/6An/+pa+yv7iyRL9JaMrr7jTHGWWhLO8Jypkl08s0W4UOSLVJNN8xZWNI9vsZGLqpTM9MtKf+/Jhl5aYY1PIcUzdLffHmCIhc37H4kPxZe2F93ks3WbCWxtHWO38nlvXJa1XS9Sc5J79bu8dnHtsCp7rd1lOj7fPS5zVAWgKSNQBrR16vGWQZe+LtmbbN/l4oS3M1yRzzeCI3A5eNUqSynB3bpe9l0WnrbPdubcEqfT5Sx3tbj+pYNZqx66QMqOeXBKoVLPuKB0dyOU/WPSLqQImMpH4qxV10AkN1T7RcGgtiSZPyE633XOmPZ1Tl2gs/OH/3YKzHyvseIG02J2hUhp0lTrCLAx3jMBTGHUOw+5G8CajZSjBL4JBcuywVuCubRJIQoDE0yQUkZZCakK5EI/cuJVXQfPFkNJQdogkzXQreX683AOkCW4dPvpSSwMAw7guDEIS+6wlhRMRZDFUCPeNg7mwuMZYcC7BK/dhvt4RxpHfWRo45sjEZEPGYtoMUUAeARrw4nDNL1m6/hyuld54xRPbbPRoCq76HaClfURj3++RCcninkFlXmLIGVhqEQogWNDkuaZvzQW6DdWdkv3KLa10N2wQVtWZvRtQq4lTXpaqM497mu3ZvtMoKu7esY1P8U16fOaFKgkAivqbAaRkHMwJba86yIqZodWaEJoGHel4z0YuKSiyCd86Elol51gahlg64nqesNTKh1hF1fsFy7mPRriWNlmXFm981otW6U3ZBXj8D67leVUVTvJ7qBHQVU3qITJY/wRg6sUqtWmlEc5kx+fxMEtpaTWie96wRzxcFl/kOAdK5PVivND7v/TTXjtn7Wp6NKWNhLBfxIqRMaxCDrVeIEdWIT1n22rmc7V8Oy3Qu3UwQqgUN7zxdqscurM0JC3L2z5S9TifFTxl3+n4SHE24qGc11PskWTg0bfj6fhZVuzNoVrlqUqroLL7FMLLtGydu/l49/jJfTDFdZW4muq6GodPZnrSrWcg38pXiJuPBFrNnYwpQTm6SaQAG2NOFtZkUWMarDG6tzVxp0OrM6nR5Zf697LUksNTzV/ZgtOyRWbgfRYm9YxSgX/HBj3+U3/m9v8XzH/oA0aczFRQ/COfv3Ofb3/gzvvYnX+Tq/rvIPtg9WTIP0p/muNkTFW1bcktqaW7+7HFjQdsyeyavY9VOS4/q99o4nvzzJsH6cfrTjuNYPTXfrN1hcx2tu9ux+pbmdPZ9aReyt4ZWc5VLuwat4F3XX7tNtcAH3jvd9ePOcQtO2zEv/d2uwU1xRMc+q/fB0t6p27mprpveb59vlV71e7PY8Rvg+Xvt0WNtt2d0Nq7S7rS+inlgDNE8aDJJkvSCqZamOmMlC9jDSRn9Hum6a0WKI2WBVdI9m49X3vcACTH3gJXriCHadRrEdEO3JDclMyV758tm6mQSlMMwGoASgRTXLukSwaxZ75LGtHOdbQExtyzPJFT7BJrCOBRgE8JAHO1OI5ekHUluV0VrGSwYfBj3FtyGafzDfrQLFlc9fdcxDCMinv1+R9f1OEdykbNb18UJzveowjhGeucIux2rFKgvYC4sqqw6zz6GFFgeEAe98+n28+nS1M1qVS7hurq+5t3zB5x5gTGyv75mBWkcwjgM9N7c0kRgv7dU4gdJHESKI3qtKXPOsQ/jLN6qEJyYXXqWXehYIIIwabtq7VIdJ9Ym4chJMywroD8gclmo1HT/1gz4ZeJZLChahE/ThMzTht6kDWxBA8w1WnnvZ8tBW1STabxhZiZgWV7qFgTEYoWcMzvnXBHuawKcx9HO96ytSnhrGVGel0xm6zazEgIml5J63orLZUuwEyjL61j3JaHaWb9Kn3XO2I9p3Oo5ywCtFiZCsoQa2DpkkPkM5Dkuonjuk0bGGBlTvGANoSwzp0BK+TwMo1kVJAs4cwEUDtNw18XOxmTzWBJAOmcXqipCUNMOjii95MDYLNjX9SYtJPN9LE6KpTu3XwurBRSki6SFLPBLcUtOb5p7ZLIkGkhJ49BEu6HQi6WS+2bKi8M9JNWcqhrImc5sel61gMCoFIVZbiDXE5ObiaIQYezMoioh0odI9C6BNC1jsHbddA2Faklfn4WOELJ3QoWwSGB5gb4IgqSrGaJzBG8JXnZeuffcM/zG7/1NPvnzP2fWf2fzL1HZXV7z6je/yxd//w9567U3kBBxSrJASXI9l9mZr+dyOrMTKFpSQLSAoKWT5R0ns3eW6sltTztGZ7RiCWTUvy+N5b1KS7fyj2N13KTVP6CV6AxwtnTqvYBSfqZNxFR9m8iV0eSl+muFY03327lqQVz7/U19bMtNoDQf8FphWssS+d3WyrXEg5eAaTtHqpQwhzY2uZ3T+fws3yF17N16vus+H1Pq1oo+hIP3DvtzCAgznbtpHW4qkhT7WdnU9yu2Y0yKvAkhlbMMswyENZ+Y9vqk+Ftuc/q/JwIDVyOEx8dH73+ApICGiAYLGtZo96EIlIXxyY1EILmMSUG8Of13l+4kajMP1ZeodqQsTd4zpmw/XoQoVk/nOqIGc+MTZRxGPJR034rDC/Rdb4xTDdhsVuuUNGEzYyarfMeTd8QQWfcrG99mw34YGAdhc7Ky2+2TD+l2u2M/7BnTBbNeoe/MAuS9J9taxmHE9ZbKebvd4lzHGM2Noe86i+sRSRczWpzH1fU1l9eP8OsVst3ZrcghprTNdgKCjsRg9y7ljT+OY7kEV9VSIXs3JUGoE154dWVtDGjVqdPdjDhARWQyZqgAUU0UljLoZcG/9u2uid8SA5a8j5gzjUIAY0wCEZxfnFusFaAaiSG7Ys0JaS3MlzYqgSMqB/3JAMiSAzCrs5yN+hxUddu8h1ldtcASm79LH6upuIk53DS+mkBbu3OANfUxa9N1xgCM2blJeKWWgm3tAoeXMquqpYWu9s0MuDEXwpbeL/NTNLoZHJhAmp9wmJAv1Z7M7xUtICnFdpjMDqrRzrXGWZ01YDX5SwijjTukZ/O+yucpxljOT067Wvcl/y7icE5K0oDZftYUj5XiiJxP2dyi4qLinGUP1UixrOV7jvI+KtaZhDjaRCp5DTLYyf/FkNyw0u6eWYIktWmmyWledHIvzGsX6z1b72kqoYjMwMtCIJoZNIXJq2JrKpneSOqzddAs+BNtyhb9ktJWBfGea6fsNLJWoQtCJJRMjga2tPTX0nF7A41ZwEqOwTGYK7fNZd7LuV96EKsSNVpMngiDU64l4u+d8Wu/9et8/rd/E3+2SfenGfgZr/c8ePsd/uhf/j6vf/O7xIstq1RfGEZLhe/NtaWllbUCqgZJrUKpfn7prM33ah5/XqZlIX65HF5C/jhl6dl6LEuCpqHjyZLcWtdqWlj3P9OkfAbrpE81vV1qu61zyQKWvz8AOwlwpyeAxGMr+pvfrbPf1mVpLdvf85m7yb2wnZfZule8wA5j5fbezHM7X0vz0JYD/to8I7L83tKeK/2GdDYX+HOzX28Eg3AwjpqvzEDXDfW1c7wkVyyNqVZuTGtq/NusNund1Obl1RW7MJgyxyqewI7IjC4f9EfsDs3y9w0gaRqXElxkF5VR3vv5XN73AOl//+//Hzi7c8eCxtOm7PquaHCzBQimDenTHRoF1SZG2BUXmLLFyqE0zYHdcH99dW3WowyqRFit11xdXaFq1odxHOn7vmje+74rmsQskDvnae8E2u93XF/vcE64vt4S0+WVPgEGRbm+viZGZbNe22WkMgmV4hzjMKaLcaesbOK8ZZsKgf1+b5akpGkPceTqesurr75aCJgBQJvDtbckFUMY7W6fqIyXW1YhacvV4rhynAGV0JkPacnapIq6MDvceW1yKnCTVSYCXgRjZMZIoTrIMmmO8nuhuGTZ3VX5gC8xjGIl0bnFK7fRMvbWApX76crZFE42J/SrnvHi0uJwNCLxkEDVP8vbM/Ciy8+JIIe0uXyX71/KIKUwOgA5okkUmY0pf1+IfUWs6nla6l89t3U6+3LLuLOMeSYd1u2lsTPtjXzBsdUxaeUy07UgTXs3Wx5uEpjq/pa9xaHGc0mYKeAqarnUdMbAJWEeyYB54Z6tBGxCnCyoMYm+ivlvW5DrPKZB1NzrxhhQjXTJmp0THrRjy8oJbQBhNRPG5Kp1rveCWWSkWOcjYvdBJaEcha5zxa1NRBJATHOYXbCSO/MYxhldmCsjshXXms5JXGKaL6O1+S6xKbOmuUTa7yKU7JHiLDFCXfLoVM0Vb05r0j15kq1YVmIDZqc5kglcgcUMUSBTcfmMGgkInSpBhR89eJsfvP06n37xI2y6OwwaZsKDNFZK76Y+KmqxqDG7P5vCYAJJGedVFvvKFXjoHFuJxHXPz/7KL/Nrv/s7PPXCs3Z+Ulwm+5GHbz/gq3/8Bb7xla+yu97itwNrUkKhaEDXeKtZ92K172q6fUxArfdbrQCpAUH93LRbdVHYbJ9dEsKXhMNj5ZigmOe0tYDVdKEWUh+ntHXV9dV9rMd0E0DJ/cz11nSn3hM1cLE6mj7JMi1s212ik3ltZ6D0CMCo36vHXNPw9jNVLXHFx3hPDZhmHiILbc8F/+Xxqcw/X9rfBwooJuvzsT3VrvNNZwaW90v9bqZp7ZzQfH6Mx7Vz3Y55sV0m2mrzEglxLMrWzGNctsC1/UqydlClTgue5chjY80luGh3J4rS8/gmpPc9QPrWt77F2elpudRxTAd7yX0oH4IlgmGMyG56d2LuUDnFtGACiHcO33WcnZ5ydXVVLnbt+p6TkxNiCDx89Mhc6xJQ8MlycpUufay3RRjHygSZmI5OAKsW1vu+L1aQYRgIIbBarVivVvSrVbGG5cN2dnbGbr8njCPOe1arlWV2QojjwMlqzZ07d0qK9Ifn52xW65RVrDJZYwHFEmEfRsYR3DDQdX0KcmdyJ8pMLm3orG0CDohVFmLadNr4aQz1Jb22bh2T+8m0btaJuc92AcKVIJYteVlIr+tYEqZbolW7m2UXtZphxhjpu45xtMyJV9fXDMNI1u66pAVu21hieDXzOsbYzQpxpJ4MHlgghPX/Fwh3zVxrRiMpFXF+vgag9fv1GBYZG5S9XJHf3O3SN6DcUTZnlqFMoyYjgojYZaUy1dXOserkTnWwf3Te33a+l/zmFct2pmluymV10fK/dcy1uDPmJAlFabZSVFZEMwAk0ER531zsKBajGG3sYwgGIJgLEzO3k8a1qYB8cQSd34FWVkRzEL0rlvGgWqzu2ZWtzqoqDmIcD/ZsXadW/Zz2WV77uv+UsyPOWRKZgyhd0h1o83dFDEwih+tZr18u2doSYwSdFA+qlfufNVa9ueCyJNMR16RdDRot42RUBpQ3Lh7x6uVDPhxH9iGgbkoWc3iGhOCWrAaWPVTVIVJbkUgKhKlPtfZ3S+ClT/40v/O3/wYv/NRHzWKUxuDFEbdbvvPlr/PVP/wT7r/6OhKULoHGUXIsZYqnzPNjjR64rOW2l+jbv34R5ivXfCuTAuuYMH4TnW8F/veiafXntVBbN32w7xbAwLEy0YT5uI/VCdPF8zfN+4weZxfNpuT3j10s2tazNC8zILbAZ9q2lgT4JaWm/Zx3u6bn7fxkWaSA8Wa+Wtp/ZLDlcEu135fWse5/beGpx9+WJTBf11e304LGuostkDtWWhB2bPjHABNUClpN162gxCj0fceq98mLQIqc65xLnlw6KZaSkcHmSolMCgYnx9OnzwASWHIaYNXf4c948+i46/K+B0ji0w3ooxHxEC29YPleLF4huxRZdrXs9mOTbO5fk3Df9/0Emryf1aUK5+fnE7JNms6HDx9Wz0yXjcJ8g83djSCEsTxfLCjNIYghcj1ep/5OsS1GvCLh4oLNZmNJErD+vHP/fnFHAgNqggV7e++4vrrm/NGjksXKOU/vPQETFsb9PgEKE/y6rkNHhxclXFzRhWDxSimlbxF0sANqSXCSBjpzUtWkUZmsaDWYqWOQ8nzVzN2AqhFzkUrQT/UrFWGKJiyMYUqM4Zy5KqJTetM8X/WlsUWAzm1i857TkGdeVVur8nshEVGNEWdpyGwM3lv/GssMIskF7whDjhGt4ivSTkzCcnIhSgTfBF7KOoQkqEqaLE2JDSJ1wHeuMTEpk8CTi5EWl6dpYecMjKTRhcpiUzMgTSnuEWqrVf7MGPSM9ZON6iMpmLNQS4cUomyZbtAUSC5mMSvEtcpZX+bWe3wS+W1+JsblJd/wHevOpHFmFy/bwxPDq+Yj5sBS64sAoxiQk0S4xxRzqLYBidHmIe8L2z8wxGRHEiljzm5lQUNywbP1d5iVKISI+GnvZLdU731JpZxvMRco8Vu2Vw8FxLwpolqmu6B2JYBX8FHZOcF0P7ZnJF1+LNGsKl5Il/bZeGNWGHmf5jDMBRy1pBy2X0kgJZY5DcNY+lwnOzGaOk7WpbyPJTFhV+2sOI0rv1s+0OSmqJK0nRMIgsntNIOgUmcYp98rgSNrPZM+t7hNDlHBOUJUrrY7rtYbOm/Ww8mIVAlKCvi5MJP3pGDWphyfZaKFpFjalHikM2ATUZ584Vn+9r/1e3zys79AEKAzmitj4Pz+u3zjT7/E6z/8EQ9ef4vx4ho/WsIeh6S03dmK79OoxDKMVouYabLRgrlg1wp4Na+sQU0bazGbk3rNKiVPWYMFofGgzInpwbs3AZdWmXa0bV1q4bCu9t261K7ilslvOUhfZF5Xba1v664ViNNnU8xe3tzFWlkpEutSz1UNgjIfbefF/slkWc/vp3a1WssWEBWVQN4LOW6yYg1LAKWMv+5HVdcx4HZsnCyMaenZ2ZhjxPvKJbx6b0nxubR/b3rupmeWSrvnlp5bAta1sm3aP1m4g+wBknlz5z1Pnt2Z6teKvtkjlA8SH8hzVKvA5r2YgPxEnXXaP4km7vsI7ywO/6C87wGScx68x3eJcVie2Mp1w57zvpsJtD7F9+QFz5mGohoDkySwhzgPtrf3fZWeei7w28FNRDTf+aOTJiG7fOSNE9M74j3iPYrFDGgCFFo9mxlvTCmmI2ay3F7v6dfrklI3xlhS+Za2R3Nx21/uidFSg5+cnNClLeJc7eoCq5XdhCyuw4vH48EJ+zAQ9gPjpSVokNS/4maWfvdOWHWdaW6SW4wTxxLz0arfwOwg5pJjmESYJW+QJECWDFJxEmJFkrsPwri3BBLZygaCis1vfbv45PplZmIDYyZ8Sbr7Z5b1rQJUuY9jGAhh5OriIeuVZ+clXVo53ZWVlteC1hOItXnIYDBbOyBBTZRk+aLaG5KFdBOuS/wCTEBVsvY7xe8kd9RInAuN0dLcuxT1rwmIuSQ8at3vQu+k/D+fj2z1yf2IasDUeSkCs0YTiE15mYXiymKEMJBAJU18g4Iwltu71V4s5yFMdNTmzk37LAwhAW43iwdTFNFoKY9TCu9sfYsqqFpSgpiAd1FSpD6WwWLuu845iy3RdAeQWt8KbUjKljHKpNBJMT+h0ugaOM7zJQQnxOhK7JHGSMj3IskUW4nYxcl2hi2OMe8kkck33jtfrHn5zOX9HJO9ptv0hMsLnEZCsGQNiieOmlwmSIKzQARHusA45J2RFkPE7r5K8zTNWQahEZU462eeF8WTyUFmwmWFxacEElp4tuTsfhW3jRmnF5BdovfQbIoky0GJPid6YGRlEsyykmIiZUYnNPGDrHDIdYWUxW8vysZv2ATP5eU1F6t79KM1p5osNN6BmqWuE4E4Wdo13QeQMwJKsuqoRuz2P0sA5KN5ROz3gc1Td/jV3/1tfuV3fp07Tz+BSrK0RmV/ccnL3/w2X/wXf8D5m+/AEMpkFYFSBC+mRADLEF8L7zOBSrN6Y1KgtHFIwMHP/HtWLBbvjG5BhNGK6mgjxLrDevOS+Qa0ln1RxPPq+QVwkT+veVhrQSz/kHm/qlJ7TeTv67/r+qZ3bR8ILnmi2J6d3FBDAaStoN6231r6irBbzVbUaVaW1qouLeBaejZb7mtlHSQlSi1oV33Oz9qHtk6kY5rvvDwm5JNHlOuVyu1RpJzP2fPaAs/KnVqnXXNUmbkAGo3WGr1pXfLqcS7VWYOdpbbqNvL3TszK/7hlknumM7EExGpDwXz/JIWxo3hIiSgnmzUrzPDg0nobJ7C5DzFU+GgCTyqAm5Qr8+KQJK+qZNnCvDXyZzbfw2OP/30PkBCPk0kQ8M6E8igxBQRrYt6uxB5pnPxwRYRxHNnutslf3+oq8UUVIwBbtDpQcablqUy47eZtD0d+PyPzshkds3pijNN9Tkng8Ux9FBFz74uR7XZb+p1jTnK8B8Aw7Evb19fXDMPAyckJ6/XahMcqo9x0cCMqnqgWkzSOA2Hc0xPT81OMCVRZ6aLivZsxuCVze23eFie46EpwaO0mkBlmfjfPZck657qigSjgs5rz7XZL3/eoKuv1egJjzIlUXtOgdjln7nMGZXn98ni7bro3qUuAUMRA7tXlJcN+bwTZmdUmg8VY9RHSRWeqOJeJiJCuWpwxvkIMshhS8c8sZKKTlk0q+dTmJdiFpOpwTNafonV3wuhTCmZVnJeUmc0V96hWEwYkkOcY0t1CJZ4kGgiK+f66RMQsrsOyf5H/2S6hKDaywKtagZxpPHlwJdtgtLtlWu3bxJDEAGVMoClObY9EosQKBGo11smCFyNFmZJhayUjl/5a0L59mEG8U9O+F9dElBApgn+uX3O/8l6vvhsVQoQQxe7n0XThbgpszee/PmOWiGGuAa7PTiuklpUQj3eOzWoD4hkjSLJmrMUh6ojBJtA57F4mEYbi1pbAU512tQDsad7yXEzJD9I+qRmkGi2SJo260ff6L5286nTuSpM+oix69ZU4i7PKFuo6OY+kejQpM0RThtM4n9NhDAZkYyhJccy6bi6CGoVdDGzWd/jwSx9npY7toJZiOw+aCbY5hd5B5x1xDOlcO4b9YJbBEHCS1y+muRZUIoNz+JXwM5/5DH/z3/47PP/BF5BVh0SLWxv2ex689Q5/9qWv8PU//iJuNyLxUEifJkhK/MDjlJqW5hiMJTfOpefbpDm1cFY/n3/OeAiP1795ZYdKmGNC8E39n9HEBYE2z0HtWVLLAMfaKjwpTn/ns1VAs5s/X9d/bEyTYF5ZeGReR/vu0nc1jW0F/gkkQAbLdZ0/iQumQEk8tPR0bd2Y2vyfV2bjbj5fAp6tfJOVJC3oys8UpWIjH75XeS/Q2j7XjmXpOXPZnVzPH6cveQzeOZwnMa+kkEsySVGCMlmb8/UfB/UxyTiFoVKPwaAxSrnTtN5ftVXxccr7HiCt+jXr9aYcSlWl71fARFhqwtxuTlWl63pOxARz7yfBoY7DqDMC5UMYQijueLnULmG1IJ+zpe12u/J7LcgsaaWyNi0L9jVgy23kvo7jWALZRaSAgP1+X8CSiDGd/d6A0m63Y7fbsdls6Pu+1HF2dmYxS8kaMA4j1xdXjGHE6cCm8+XmcI3jzG1wAn6jWSKquc5jrC024zgWoGeB4FqE6HZeWxA6MZocCDkR3+yHnX/v+56rqytWq1UBjZLcCGYWwKreNj6qJmIZMNWumHWK8FXf8+TZPV5xPySGwBiUmouFUAkiYnEGJtypWY+0BtZhAjlM1o0IhDD33Q4JVLgEr4qrI0lTGsGrWYWyYIDm4ElHUGWnoWjB0ZTOPo3L7nXVGdEHu0gZ5whjSEJmYv5qSMRciJLkn4TdGBWVCdhKmgst8zyBQbsLdNpHxaYm5JtJzUJX1Hx5bqGwSiHFCoHL8S1k4Amk9Z7cRAxU1YQ8qgEBWxuF+vZRpvkkzbsCLlslUbtBD02gwUBOiFIAQ4wQKv/sotXDHKhGlXIRn6ogwT7LiC8LmDV9C6HaP3n+Ktp4jHEKdk3Cut+gozGunLEyBtsThYmGQNelfZitjcklK6+jLW9NF60VzVNW90MaYVdBcAU018/VkClqnt9pz9d15PXOfSlfjUlADTbTdsFsUmiIlr9n+2HOuxmNcBFQhhAgjvi0PSSAiykjpcDp6gwZAvshMMiUBMhwYkxChzKqoxOXrnOAEPb2XYx4yRZyRUPAebsUmk546ac+wt/6t/8uH//Mz+JXtl87tfHdf/1Nvv2Nb/Ktr36di7fvswqCGyPqpot9DwQwjWWwjwMeMp8yRcm4+MzSvmuVkze1Uax72RLj5KDOxxLyGpGqVf7cVFcr+JZzd+SZ3OeaH9a8rW570u5nS/9c2C1yggZatUH9XAtYct31Z+VeOc0zokVR2Y770EVv/nsLkvLnzsksWdC0bq4A1EVapDoBzub4t2OtZaqbBOXHAmRtf94DQNfrVX8m1WdLz7dZbB+nry2AKWt5w7COgd48zvq81Qrj9+pbTc/tapG8V2sFoibPg7SWNWkvSqucnKi5pLmmt4m+x6wcmLaFvefcT2RBe98DpGkhHF03Cbm52O81im8JkGnfnOtwRMRpRdznueaXCEHtBlBn52o1KPnf6enpTHNQb8ia8BRBe7WauZTVfauJan4nC3e5LxafkNOFSqkjuzHkZ/reXOq22y0hBO7evYuIsB8Hht2QANJAJ5ET59JFo7HEA7SaMe/mF7Lm0mq3cykxW27SD9UgqQZU9RyZBWcCQjWYqYFqnqf9fo+IpPFCfVLremMMJXVlG/y5pAXKfc1As+s61ut1mX+vjjGMjDFmkabMU9SY4k4AQiGqaeuW8cjU0amfTJqYmbUzmOVnOgdTBpldhGySUTVG6DVpbdWsPlE1XVxs7e3DSBenGCNkcocREdR1lnoaEM1WFpJLkMVu5YB7hSphSUo2EDMoNbP8GALRxQJ2JjKbgZ1p0CvaWuLMakFjxhIEXOfNDJOHkcYnCD5IAdrZla68WBhB7VZjlpNpjhsNvCadmQBMmk3nBNVxBmJiMLAWYmQvWtbU6Jb1xYlZZsdxZAgjThWnybqRtHa5b/nnMAxlglolRnsWa+VFjJaqfwzmnutUS4bKUQNRA951yb/eBKwO289eBS+ugGCX4o4ORJYENgr4qOKF5skQBFGZXR47A61McV95HCJSBOa8boUJZ/pfQHZe3zQXaU6zoqfMD0CUMg5B5vvTGX/xDuiSIgu7niCOg7nKqbJylq/QqbJSCISEs62+OKT6O49qYIyT9XrVeZz3OBJA8KbEkq4DB3eeepLf/b2/yWd/69foztbEXhAv6H5k3I18+wtf4at/+kXuv/EmDIFVFMuwGSNBQfyhNaDWxj8OOKq/ry3vLS1dKvVevCkIvu7f9DKLWumlNma8PK9j9d0xxUENYFoBs1UE5u9qRV1ttV0CV0t9tPlPIQCNN0v+Pvc/19XKIfWctQBwnsUyzUiiifWY2nlo+WL9r+5ffjZGPYg9Bko6+xpglLWtlV0k2VqrM1yNt10f3mOP1nOS320tWvNxT+Op52TJKngMqC/JebmOti8tWFka72Ef526fS+C4/b1+dql/7bN137SaLxGmi9TjPGbJ3K9zWvAEbHRyW5z4q6I5+671qqy/YO7ozi4qNRpNUnKrWtt6MzBuy18CgAQmZE1muSJQuEykY0VY8onLlw9OiyviEWf11JaaY0Sz/qwlDK3ZvNVu1HXUB01E2O8tTqjv+5k1o36uPli1G1h9p5CqFuuTyJwoDcNQBNx8X0qMdnfKMAzcv3+/3H2jIVomOzFhDRE05hvh5wSjEDmNxUWmtsTUBDoDmpro12WJyOQMf/X9RXl8S8ynXrtMyDLIWq1XpX+5H3lOUTXhpMrEB7DZTHdV7Xa74vrXAjhxjnfffUAII8M4EvbBYlmSi5BzzoSblGo434PSAkoRIar1QSFZ2aZgjMDkfpLfD0nYbrVJmelFgVhbOWNK4iEUQJf3q/cp86Eqo0sJRfJ6kwGwJKJmgmbea2EMibFTLtjL7cXstucsLq8AQNlbkLkTdmGwk1oYQLW/UpC/yDQnY9JUF1FZsil/UkFJnPZVTGMQMfc3AlWMWpW9TDLgM9pie8SSnYSQQYwJx9Na5H4ky0AS4J2ze2g0XT6i6eESmxgNKBycBo2MQ0x3jwVcDFgyBKUX8I6ZUmKW1r0CdVlgncUa1S6+5PMcGeOIODhZdzx5dsqj7TVOnbn4OnMBdQl8SJpbSVYycZ4u7QXXWNmmOYpopitZCK+zzpVVz3Ry+nDOwKdn8tlI0BR1OSazUpikC499sQTGtB9ldpmz1deAbBWmg1ULSgI+lssPRboSp2pKAUcXBImRUWD0hqdW0WLmMtjJcZrZ4i8uA+hQ7s0zS6hnVMH1jiDgNh0/94s/z+/+rb/Bk08/BasO7yx2KF7vef0HL/OFP/xDXv/hK4TLrbnZRksQEx3E3hVQmOd3Jmg1a7dEp+qfUx3CMEzeF0vgYKke56bEOa0g3q7/bHmauuZA4CdzY2r7dOzzJVDQKt6y8uGYDNDWk/tbnjmK/EyWseyzkzzRepjMeHPthlZ9l/Qfic8fxsfUfWzX+ZgQPefDzHh9O69ZOVOHF8jByOeIqZW9Sp0/wRrftCeOAcT673Z+l2SZ9h2Ye8UsvZvnr5bb6j2xBLTacR+bn7b/7e9zXjAff2vpbOcB4Pr6qij8LGGVs2Q+TDSbqm/5XISYUsGIGPipAI+gxRNFNXsHpP/r5CtQx0C/V/lLAJBy8HTRcZHXTTUfUEnPNQFtM8CTgFXjI1sziRYg1RYKmBO62pe63jhLxCm/W2/Chw8f8swzzxw1ey5pPdq4p/xMthR5P23IDL6KEJyIaQ7YntJwO3AOL54YzU/dZpmyeXPbtaUrR0e3BL+O0cqfHSMoS+8X4bZZp+wq1xKcds7BwOEwDHR9Vy6uzOMuKU3FLtNdrVZTG4nJZReQvL713Jef4vBeODk5ZTy/xsLhKhCRAvZjCvZPPlOg5lpUM7p6b1FlkPK+M7eeuohpXHJmt1xCJRyIOGKVMCODa1Wl7zpiN1/jQtScue25iqjl3+3vvK8BbwkFQHGuIyefaBmkWbl8ESSdm9LVn8ZVAZtSjy+tT7Y+lHOR4kj0iNUXMaVJsUZV/bA4nSm9fv0vYoHzlr69Pu8geGDuHpvBdp6PSWmQMw0KPmd9M1SIlgs/M5BNezdlrTRgmmLVkptg54QeswA4NcAYo5TzWzTW6QyM48gwDIjIwTmv56OMz6JrWfcdH//QBzi/urZsbKKsxKVMhxzQqBgsHsY5N4k3wsziUu/pvB6ROS0oOsRkPSpz35KLlNZ6oo8uHwOypVDRWR0FEKXv6/64nK4d0lgqYbAFTGVrCc4vA0GAATVXtggDkeAtfsyHyV1EMihK+9GsrJbcJc+f7zpQJTrP4HpGp3zwpz/Kr//13+GFj7xEcBFWnYG4UXnww1f4zte+wZf+5I+5urpk5Ve4YEov57zhPe8YRGAMxSX3QICS+dBuEihrRVgIcfb3kmC1VEcrtC3xzNK3/Hvz98EaPabQXPfzcd9pBcj6+oX8fQ3QbgIg9fOl7kTrlsYhCbO3MV7HBNgDcBPrZ6szqYeCdAsGF+tbkIfss0kGm/VrJrPNla0xxpIcpC31nqrbsvn6ydb6gM8ujFcmgr0IIN5rX+f66zZqGbGWJ2vvjKU92HoSlXHrHCAcs8K2fW3XrZVLjwHC2nJnjyQ+6L3dybnbgaopLzVL68zuTQOg0NksEx3udZM1TZETmeJLi2pSlsd2U/lLAJAAlgM5y7cLm2zJJxQEEUuHHWJOmeoTE1VEDjdVXf8S+oY5kGrThh/2AdbrNS88/3wZlznQpAv5orlA1WCoHk9utyXYIjLTyDnny4bMj3o3xe2sVzmRQRqDOKI6S+O72+OwmA/S8/WdOFmodm467G3fJGm9tKQIzvoBmRMsrAsmpKdkDc4nbW+6oyFh4AzyckzRsQtfCxEKMd2tpCVoMGKXMI7DaAKEYpnCgqXrjEGJccA5V1Kyz+ZaIWLZ/p649wQf+sAHeGeIuKCmoWNa8xCDZXdzU/rqAjDQYmVSmiQRMgEPy4lgUl7Mc1mDCEwArP2cDZg0TMVtzFKULE/Wv1SfS+5SykzDnlONa9LeZJc8u/zUFeFTY8ruVaWotz0lIBHf+cnqkQARiqXkluwa2sSuJIEx+8mP41gsA9kdpbbs5fkoSg6xPe0qoDrGAKzIPv82XynWq2KCBTSWSZ5bdCfaks+VKwKH87bW3iWQJFIJkWleYiW414DCCdFRrtETlD6BVIcQx8p3W024d2KAbL/bTQqM9Izd+VZptPO+SxPsnOAwN9pN37PpPPthT0BZ4RBN1pskOGSXnNj7ch5hArGWRruioRVD1zzYnIQhjTs7YWSgVS5NFvtkijlKmDndR2XfpXuBfKbjybU1nUMbs0I5M2k8WrkDOqYFsB5M9AYp66oonU4pyKWskNW0dt4SKgTFqzCmNXOijHYYktervZvThzsMVIkzS2jnjB8MzvHkB57hV//Kb/HRT30CWXWoF0Q8u6sr3n39Lb71ha/w6JXXefDam+hux8bcAfBiGUkjmupNYN9JyWCZzxiaxY+8GTNNmQvJtpyHwqUp2fwB7c3Pt8J0XUrylYU2H0f7Xn9WywAHPKlZ4aWxtGMsQNC5RB8nPmOWuMPLbmth9Rjwavl2+Xyhj/mbVuGzNA9LY7GlNTBe9n5muGlPixx6ydSAoOWvNxZJZzWfi1hOGcqcdtZ7Z8rkU1HdRoivxzvxv4oB1nNQd2mhz4cAtKmvaqeseYxH57ptYum9Y/NZ11uPzdyqKWufhAc7w8zn5Rg4mgPcTP/yv/z+8t6a3pvqnZScHYpjHwO7cUxYR8tBE5F0zUpWFEwx2SZzZR41gSYBi21NYwlZjpDMtsRy/KgSHt+A9P4HSHXWuRbVL7nE1YCiRuFtQoCcHagskIuITPcr1RaDvAGXiPKSgF73J/+szcqaCOz0TtVGZQWrN36dlCDX0wKErFEmaQj7fjW5NmmKPUl3tThn2sostCogzuO9wm5fLG2zCxapD+OcodbuBSRCHEJKh1sIcx4jkPyVsxCc56Hz/cTcUsYv5yZLTv0vP5c1+jU4LVazFC80DpYaMobkduiTRWmsXTeTVUcmTW9hlEnYI1hCgkEjrvPosOfOepXiOCofcknAwU8Att4HZY8BQ1TLGJbWyjTcQErekBlb17Vie9rrKFEmsBsFsw4wuWjmhZnu2IIgJgC4DhQHQQvoRTW5BYKIT3Waa2LaYmWtszOmyLSeZR2cgBgQo6RyT4CoEPrpvKiakByjxdBpTriRQK5LKcwFcH5B9MltKwgRQiLYapYxEbH079m1KRowzEoKKXOfBXUHMqXcdjg00Q7LWKgGO9WEUZ8EEBE1QVUUdMRlYZ7MELKIzZSOnIgPiqeybGffd1OhTIKjuOLKGMPcxYxy5ibmLRX9KbRGs5VIEUa8RjoNaZ4mEGhnNm0aFJ/7n6c+/xoORTxVnd17rmluW/pG3ncxpBlK1zXM6CEJuExudjgLa5S0xzSqXZMwc7cy5p2TixQhIe/FWrggn4/p2QL4ERyuCAFQWHtKfW7WN0HwqUpNygBNYypTJi4BKJ9C2TzaCTsR1nfu8Lnf+Dyf+PVfYXV2gnR215VXuHzwkG9/5au8+fKPef3HrxCud4Rhh1foNK1/vkeGtH1R+iSsipvuKCuZprTMZik1r2sBxMQPHd4fegksCbbtnjgm5C8BnfJ3ZiwL77T1zgDQMejRgKT295hoRv6sjgHNMZU1Lc91LskmSzLDfH4Ohe/irscNWcGqulr5xEmXLF2t9SMBSGH2fB5H2+866VI7bwfnGJhiUesxHwHOaXwTeEvnvNkj9XwU0HE4HYulnpdj4KgAuZo3P8aetnHO571+573AZS3PlDqhZIaDij80+7sGsm177bgLLWOayzrp1WH/JgVi6VM681GEd88vCENEUgbYonxFEYUxauF1AOJTHD+YsgjJuvcCmKjOlX2e3KihuIeqwnALkKbSdZ6+7wrDmgTjWkiuN2FiWM6MfRPhmurMGpX8Tt5TSwJ4K9TmumsTaWv6zu/X3+cN6Nx003ALhEo7Oq+rLktEt/19qS9UMThthj3T9AuqIWmpmV2omUFSrWmylODz+J05eJp/Vvonh4e7AB0U53xpp2S/qxhwnvthGIrwn4FRbUHLWfpUld1uV2K1hmGg7/uDTGAzTSWHa5C/894zxgwqLbZntVqxCyk2SSti5w3GtAysXtNoZieEKT6mrIktUInnybu2CHf57ptqDfMcdynTjHOS0UuypqT3Rezi0Qz8xBIciMLQ3kpexc+I5CQEE+F0ngIuwSxDqfOmS0zg4TCouJ6HCYi31rC8xnnNgtbxJrM8Zgdzu3SGD5UaCbLkM0ol+6dLAFlwc6Xak+1eSQYBRITOe9S5g0ukDxQqCM4vK2PasbXnyvlll9+alrWxSPmZAzdYrTS/1ZzlUsdBlr4suNLWZ6u0l+pe6sd8fqdZaV38pjmYz3kWtpwIkqy/k5CddltFb0v7jfKsLnV7rUvnTcJP/iQdLUQpoAk1gdeyewl0jr0X4qbjk7/4GT7/V3+bu08/SXC2/xywPb/im1/4Et/4wpdgP3J1fp5TItqZQMGZxdSnM1/v1SXB75hg1Qrwx3iLCdrzNc6KyZr/tfu8fu69yvxs5dTCc0FvkgOm/h+UI9J0PfZ2Dup9MqcXUsadP8vvtO7eNa9ry2yeE71eavO9SitHtEJ/28fSv6pLdZvH1qyWU5ZA8U20ygTiOKMFIsLRndXswVpWWAJlszYr+rVUb1uOgZelZ9ox1ndg3gjAFtqt91j9nGHa431aGvvj7JUlGtrWV8/tsfHk+Pl+vaLrOwqoJbFEEfbk9PzG29szEaPFt+ZLu51z5moZLDmY0Y9MS+xS+UCS1cPtPUil2GTljXSIuKXWOsx+ZkawwLwk11Np1pXivlQTghuFksoyMPU3aZ8qi0b7vdov5e/MTPLzNbM51m4+lDXQOSBKWeCTrHOlZLObMX5J6H80XYiIXfwZYjhwbWwPksjk2lcY5Q3EQJhcEWtmGqPdx1TPQxbqasGunftWcJu1VX2f06HnjITDMB2ypT1VC19lDEkgcM4harEDV5eXxOtrE6qbNV1ioAdCISCoYSlJaxHzhawKKniZXzzoZE5027U3NyAKGC2ssjo/mQhb2swIUTEx65CROucYYzhg/mWuiqbIztGMPcl0d0+9hrWQXJ+ZPDc5hmYpLs2nO4py/Ei2gKI6c/EThS4H6jfCz2yMOvk7t2eonYuZ4GKDmNYlCQ71/p0FJDfC1U1nt7UOo/P5qvdDfrdVyNTP1HUttdcK0zcx9OlageOuRO38LQk7pb20drnUQvzSOWrrb/tX17EktLVCYEtDjo0/qlnD6vdqS/7iHGD70GWAZEysxJqNTgi944Wf+Rif/+u/w4sf+zCjg713KWFH5J3X3uTLf/jHvP79HzI8vIAxEPc7S7yCIM4TnQEkqvNb78ultblJqHo8AWy6O2m2ns25XtojXQVgDwRE1QOlXBlHI9TD5F58qIB5r/4f8rP6M9/QjTLqTF855M11Pa1bVuZzuY35mFNSG5krBMv32ZXghpL7MSlaD+Wfae9PLlPzz+Xgs/rd1ovl2Pmf0xtmigmY8++6hskdd/ns1/tm6fzDBAyPjWOpr8ikYKnHt+TiWc8VlbK+7nO9Frm0Z64AhcrTqTxXtXPTOTomc7Sl7VfdVu7HTfyu7oNzjieffopf+2t/hfXJhtVqZXOX5tF5T7fe4JJHU76fE4SYsh7VbYQMilSJ48huv0uJpbwperzD9yvE25UhV9sr/tt/9EdH17MufwkAkt1Wr5o30nSHCUxgJz1d/XSIZF/LI1q+WaCYI+qhi521daipqjd1XXerSVgCLarmDpLjAzKBz1aRbFJt45DaTV2nHc+AI1tdZkSmaj+PR1VLdrt8j4qqphiR6V6nmrXWd0Ut9a8QFSz+pp67PFf54tb60GUwkNc0z3EtiNWuQe18thaHlhDXddbPLMVOWV+meKtZfVrNg4Ptblf+FicQmbkjLBG4WrCaBMSYXGEES0mvkC6GdPlKaVIMUOJ5NcDIbZU2itFbEmBIxD8LaGUiQO0CotTvKcg2W5BmWZKadih1xlm1M91l2ld1DFsGNWOcskHmz2sw1QotRfhPVc8EAaW4auYU0jOXy0q4qvdMaWOB0VjbNdusE6IUR7MDBpznMp/pFsjkhDPLcZJLczw9X1vEyh5WZhbpXOrn67rbPdi2uxRH2VpW6ufrtViyDBwTaGb1N/M/szo1bbVjab9v6cSx/VQ/W/9d07nZcyESq7k/WIeqvfnfktwSQUWInWP0wijKveef5df/1t/go5/6GVj3sPKIKp049g8v+LOvfI1vf+XrPPjx66xx9KOd7X2IiJgm11I9mJXWLjB2B2NrM3nWe+oYgMo/H2cNHtfNruWPx/ZFK1gea3+pjZa+S0pBXH9/E28vY1oACHkul/rantvHmbvpeSkKrCWPFBNkFoc/63PbVr0H5nVPngBLVq+6tHuk5q01Pal5fd2f2uOnnscy/hpgcAhwDuaCOR2rx1nXUa9tO0cH86YKkq9smM/d0v6qaV04klyjpmEtTWjHsHQG8jNL9LSdn5bm1Z8tgbQlQFTXWa9py6e6ruP5D77I3/3f/T1iijvN4EjSuHMSZKtPzStFLEGTT3JGTFnvinwiaooe6wmqlZyt2B12qpxfXMI/Wpyug/KXACCZdkXBtNyqM5eI9ND8bxE0hnQRYBZylsz82ZXjUIA4RmxaZtj2tX5uqRRwkbIY1ULhOI4H1qX6MORnl7TqLSFoBfyWgeX2uq4raZedcynsRRDvilBcW4hKHWLxPPkA5oO0pIHN7wPmMlIxlDK+5CPfumrUWvEloakdZ3uwa6Kf26oFoJYBxmietCKHDC7GiARz8Qqz9iMhgMfP+tWuebsPpj7qnMiIkXiLeZ2SWRiY0hRzMp2Dw3EbABdvF/5WS2Y7Pe8dFI0ZTxghqznELF5FzFUsu8BN47K+y9HxHjIXW4P63qDDrIRL82X7cQIzwrRvVLW42xW3S60E8OLsNO+H+eIf7oNjzGMGgFN7dV15n06xCrEIVXYOzHKd5zArKVqml7PRle90EiRyP8p6hwjukEm2wnD9e312WgCzJOgdcyNu6z9WjglfS88dAzJL7x87Z63Q19LRm85k/d1M2G3oz008ou2jilg6ee/YdiD3NvzKX/lNfvGzn2V97y7RY/WPkdUY+dF3vsMX/uBf8dYrrxEut/QqIIrzHSGMrNfr6kJssYQnKc4jW3BrhVnb31p4rBVRS3N8U6nPr6oWt+saRNwEDpbqa/lV6TeTEi1/XtdTW5Jma48cPN+u9bH+1Hw2113H+d70Tjvf7ThzMSWHIjJZIluX75xevn23PbuzsegU03EgQDdyD0zKvVqwrgX7lqfWzxf5ZUHAhhusIErht0sIsF2f3GYbk57nTHW646w9/0vnoPRHKGenHlPL79p3210zo9nMAU5Le46eM2P2P9G5WSo1bV+qo5av2nmuz18d/w6UOzZHp4yiST2TPaMsCZEGnd2hKc5zvd3io2OdvEOkAqR57qMqiBa+6kSIokXBZLEIjz8H73uAZNHGOkP4zjX59huEnIVbp3MBElqtZ+NmocuEFOaar7zoOpcnZ0ShPhi55OdFxIZVfV9brMYYGuKk1GmU21iCpdiCmpj5RLxqAa4GHGTBU6DO0qRRLS6lOtA3CV3tgZ/maa4pqYnszDIk8yQL9bzUdbcuPnmseUz5rp9MSIHCuJfM2a3Wq45Ra8cjTiAYQ+v7vrjdwSEYrRlNOz+T4OxQzdYMyj+sxsp9bU58m4SL830tYgJ11mylNW5eQDUi3uMdiFq6d9U50y3zw9ziR8ZTUwOlrdk4F+Zw+iaf58O7iZbmPjeglTbYJ+ujQEnpDlTxUulcRdte+c0Z41+Yx3KWmc5p6//uvc1DbdXJ/1Sn+83yXM61t4dxS6kHqM7byQCp7mi9Ppbyffl8HmPC9XlstcM/CRN+3NLOK1RucGmnHyv1/N5Ujgm7S7TxJhDQ0qayj5IyINc5O48t7WNaLnEGjoIqoYOf/uwv8Lnf+13uPv8MuJSCG+iC8vC1N/nWv/oiP/izP+fq8grdDfQKq64D79jHEd97XJysbplKxComtBXMWmEp9/e95vS9yhKALa6wDUjK81iuWjhSWiGz+maBjFW0oFLOzXiim/P/dq2W9qa1RqGbNV3PvP/YfBwDLEt8DDL9M/fImm+UvggznnRMcD5weVOlTgZVl0illGN5znOdbf0ZCKtqcVk3ejhdJ1LXkce25HFjYocUJVUa4cH42jmprRrtdzU4anlyW+dszEn3Vvczv7tkQROR2bUx9fftPN5Ebw7fn1J5L5+Dqf9tn5aeWZqf+ozU9dTnZMkFPPPqYb+HYcR3yVMlg+DEM6OXopgYkjlptVmbbJJzcKldRQDJWKGKr/aO987CPmLEO4+6pBDVm+lHXd73AKkTh3fmdxqzhlscfZeIlCkoEsHK4GhiwDFOWdyceJzzCaWC5kQE4nApG1J6lBAmq0lMRNZlYVUc0CUBKaT2Ju2dqmWVIt8OT2aYk7Y797ElbMZEVikeylLF2oaoXIxkugslb/bazax+RlWJzhVXnxgjp6en1fwEywLlbJ4lRIh7u6xSKHE77Y3pkrQc9QGuNQ3RfJ7IaZY1jT+Mwe76yAJ1ITxaiGsNjkSmGKeauM6EFzG/1yKMQkpxfKiZz6XW7LfCQ56XJcYWBFyAblTLfqZCHyJITK6ROe+KprieSSuVrSZ5jrquS20ta7VN+MUu7RVJxNvuw/HOW7auDHQSwC31pP1dfHlNVWesJwVxayClh5nimjJksHms0lcXDRupL7FYO41AThawIuvqlGkvrXDhfV11Dm1fV3ediZBTL6hqyoSXgfuhgFrD2bHSmOaVyF0oGfw0xZOIVFbkac41facY4XakM6oWK5b3HFnoS9ZW73PqcYAphipDXJ8AQc4cGWMgBhD8TAtf96NkY6sEjJJApQJVJfUraU3zeeFwbLVgVJf8XX5Hqn+z0vSz7Xf9M/++KByVhrOgrtPc5/Ut9JYy55NAc6iNrWlUGVPTn8mrIDVeNggFAOV5kPR5DDGlPbe08MhkZQc7N6KWvc7lD5wjqOJ9x5bAUx//EL/6t/86H/65TxBcGp83sDM8vOTNH/6YP/4f/wX3X30DF5Ww3U4Xy3pnbWRQWblpaszXHnSzONp2bZdcKut5q/9u61jeLxmEpHmtLFKzrKZVmZQSk1CKkC6ASECgbDypn7Tfq24c9DEpavL5mIGdSsCrx7MECspPKYLFgbC8RKvr35f4TjvXc/fv9HfFK+1ZG5NL5z2pLpsz1yiM8/6WCnhUe8aqmOa15n1131pAUuhPBYDrecnvt+BlGuMyvQhiZ9K8yWcC3dH92ipNCl1t6OhNa9I+F+PEq+vnblIg2e9zENLKEjfV07ZV+pv+5/J+tlZmeyOPof7ZzlPdnxb41Tz0GMDKPJLcbrrDaHe9JUbBR8+439N5z34YWK1WJlOJMCaZc5WSNYibQJH3nckMITKGka7r0SRPFT7kOnQMXLx7YYrcVc+du3fx3W2ShlK8OHrviRrtNvqaaCkFgWZCrargLGZpEiCSMJMhTmaiLm/qdBMwFM1z53JcjNL1KRWr2uWd4EET06/FhyRoqvOEIaIExFsfs+Cu2e2vbFqzdMRktnfJNciEXor52S7OCqbp55Dwtgeldr1zMgGr2oIiImTFlIKl2B4G4hhwIRijTxq/ljH0fUdIlprcTjmMuR9JHs4CZIyCqgn9rl4b6/jMLalMqc5d+MqY8mdV4oX9bjfNRUPwMxiqS34vl2KVatwnaiISROlxdCrshgDOceI6Bt0xxBFhrsWEifhPdU1Msb4LYLlYhEFh+GKWT8jAxoY6dbfy603t5u8y80nwrQIDKRVxiDMmnIFXfkZEys3Z9Rzn9N8lo5ymcbo5Yz7QVGWA4bKWHiJzRuOkGpMmW4NL7qnOlbHk8fgUxGtxdToDVPUedoCZlELZp2XG01gMCOWsdgkoqeJEy51QWo+B1F4WGEXqhSEDHmECYN5ZG1nfJjK5bWSwkAGJSgJ45O0yCUiQaBdT2wdCXLXms3WoSqZTNSPNn087bHo3KzRaoa+uuwYtS65vqjkVeGLalSYdsWD5+gwWAaf873hpBQdNe8iVj1uBc+pDHqwWAaVKeCMkF9gyG3Nnh65jTyQ6z/rOGb/6V3+Dn/2tz+PvnjCKsBaPR9hf7Xjl29/nu1/6Gq99+/vsLq5QgX2+WBhFuo4x96GcjYkWhhDos5t2cs2sLeqtILS0B2qa2655zVta4TArd+pnWzfpA0tWmtcMgsp+tz/Lpdfa7G/m3LZd6KKMyr+3Z+9xygGwqfZevf+WgH49v3n8+fPZ+Ks6pn9urvPIGnnJ85wVXzmJj5RnSl/U3JbK3WdADmFVKEonYcq+lkvLc48Bu9qNsf7u2NxkelYnUJrNt2CWgewinJVYFejI77XrUPd1Bpaqtpcs6otjY2q3ba/td7u+7WdtW+2+aL9vzxlUiZgqmj6JCdNz+YwdgjZmf98EpGrLYL22MVZyceELJie8e/8B/+1//d+wHwfOzs544YUXSgz9vXv3GGMwBX7i1ZeXl1xfXzOOAcfk0dT3PcN+b2C789BZWEDnHKfrE0iyxxBGdsOeu/fu8fDRIx63vO8BEs6CUT1K33lLmZsIR9HOiiC9B7X4EBUBSTeSV5vDiyAaTLOfFVVJOIthLFpeEXtv03XTRYUpKDtUt1S5VVf6AnXWGrP6jOOeEEeQrhKKwfkOienyxwSexhBNuAsDfZLjhxBYrdYMYwJRCjGBlZaI5U2dYx1qYNECnPbAWKBhcsWLKc4ikdVaW1Qf5HEMxbxcM8LWX7cWirKgXR/fGrR16V6mrAmq45CAktksx2cA7IeB3XZb+piz9NWlJgQtEa+FiFxiJXwsEtNEqJxPaWczM9bpuZpghxCIYWq37/tiPWrXsS2tcDmlPp+7TxwIsKoHwok9a5qyNgVv0drkfUHSWCWhT5hkGg72UCUnMifI9bzN5rARJFqXSSeu+N239WkllM2YDROgbhl2vd9bJjuNbio148nPtXEa9Vmq+18LRvXnec5zffV+zZ/Ve3RR2FgQcOvyuHtpqRybp/x3LllRlfdk/v5Y3Emt7a0BUiuU5Tle6tdPWuq+18UE70h9O9OSgLI4VyKoSLktvnZz7dTAXBQIvXAtkbhe8clf/Ay//jd/l7PnnmbvzZq/Fo9eD7z6o1f43rf+nO985Rtcvf2Adb5HLVlM67M7vwRcgLk7cqj4Qj0H9dja9XycPVQLTEt70qxIciA0Z1pdC12PC1J+kvWer8/j13HTGSh78YiLYPv+Er851oelZzXJGG3/l3h1TTPrZ9p1BgrAfK8xt/26aW5aOeCmsS4J6ofgUiYBvKHLtZdHew9k3WZ+ZsllGg75x+OUln4svV+AhM4tmze905blOXn8MotV0zkAvykjZ93+sc9rnpr/zrKZU3j049cJ48ijEPnRV75pz8ZI1/e4kzVg1/R0fc9qteLs9IzNas39199IsrfjR2+8wbsPHhQAPyaDAZruEVRls14zjiN+1XN6csJwsMLHy/seIJmFI0CMdF3P2pv7U3Qe6TpA2Q87s6yIQoyMY6TruxJUDnnBA85hl0QmEdAufXRcnZ+z6TpOTk6wG+YxgBNGVv2KDof3jt04MuxHoionJydEHMMQ2O/37NJt9hMzCoxhIITAnTt3GIbBEjIMjlW3Qrzd8QSw2fSImFOQhh27/Z7Ow253xfV2j1utCxFos8nB/KDUzKjVsOR/EzFKt4Uzpf3MbhuShP6lQ7TEiFvhtNVMqCoqh5nKgAPhsY4RySBpu90yDDaffd8bgaqIQS2AFSBRCXEZgNXt1kJeLjOXBypmZS+U/nZ9zxhCskRCDIowD2LNoGZufeuLy0I9nzcx2lpgK4xa3GL/M5Sp52++ZnNBqfgiOzcT+orbHCkhB4dMzOqZAEbLaFsGUL9/k6UwyrQ2M+2j5uQqy8y5HnO7n1qhY2IChxrTnE621RK2a1TXW1tp2zVsBayltWkF03aMS8zuGIhaEiJueq9+f6nfM1qT6FCep7rNdi1qMLQUE/M4gkg7L9PDB48uvlu349o9/piCbqZdDnN7cSY5GGhKnwWEwcOuE57+2Ef4td/7XT780z9F6IR9uji4VyG+e8H3vvZnfOWP/pT7b78NQ6APkB1cQ3Kp7WQem1crPNq7RYpyzk0a3yW3xpmyqrH2Lc1Fy0cO5xfy2W/frzPnzdaYZDlo6PCSoHdsTQ76WGnWj4OQ9y4zT4jmnXm9RV10tNRz2v6snxGRZB447HNNv+rfMx/LfC7zvppm1ZeN5vdym49jMboJRNfPHaNBbVkGl1DiV46UFvjXezjz1pliFopgX49viX6Xfiwoydox5lKvTYzZOXR5Dy/NxU17+xi9nh46BL7H+nxTPW18Uc2fZu9Ue6NWhg37PZfvPuSdt96qxpQ6KGL8O68Tk7LQLuiwKzrW6xX7/VAU3r6zDJ6ojXCIdpXK9W4LIuy3wvXDh+zGWxe7UnbDnmeefYZ1v6J3Zn67vtqy24/0fc9ud83V9RXOweXlBbv9jt1u4GRzwt27d01ITbfNKwHv4eLyit2w52RzBq7j7Owud05POVn1bDYbus6Q9zCOtiFD4PzROaBst9vU7pZHj+6DdAQ1Ld6w33NxeVFZmQIhBtarFZcX56xWKy4vLzk5OWW9PuXs9A6bTRIy8Mk0rqh3+NWKd+8/4MHDc/p+zZ3Vurh3LG3umftQRTCKcM6U5Qcma0xUsxYpXfE1BYqwnB0gDrTAUDZ+dlWrD3cNRvL7zvniQ18LTLle7z27lDo7Ez+wjF77/R7nXLG85Itfo8zvjGmBz9gEjNalFr4nUFvFrqQyS/Cgigr4vuPk9ASK4OWRGBCV0tfcT5dcwZxfTsqRNTP1mpZ1qJjVQfrlBeYXYyxEdJkwT+vWMuECdaq/Kc8b0VryL6/7dJQBNeCkHlu9RyZCfaj9nuqa6mwFwXwGaqBcz2stsNd1tG3U85KFvPqC5XrOl97JdbcCV7tPs1vCEjNvP6v/1W23gvCxNch1LQG4us9L52Q2t1W/6nbbsd3Up3bt62fbeW0B2Gydjoy3nqcDS20lC900V3VxzllCSRWcCp0Txhjtktdgrraxc2yefZLf+N3f5hOf/SV05VDv6cQSL+0fXvL2j1/n21/8Kq9974dsLy7pNBLHlMUsKXzyBs9W9VaTDkrOeJZpR5mbal1qq367Nq2wurRPlwSmlm5IAiaZfuc6c/25/dblLwt5tUB/zGJf/75E00q/qs/e6932HLRFRIqg1p7D9MQM0zyOQNzO8wEdXHj+cXhB++wxQXvpHM3mb6FNOKT5La9qx9y2n92JRWSe0bahE7Uyu92HdRv13l1y2T0GEI7Na+lPkoTa+ViikbmYPDTfJ+263uQG1/a95QW5jVKXzpWhLe2t669lwGNjaufhIGSieq/mt1Ej22HLoOOBAoQIThUvUwy+xoiGkUGVkBS0u6t9ebfvekYNNvti8kt09s9IjBa5Zq8jj1ve9wBpux344cuv4L1n1a/wnUejJTIYx0uUQN97tvstD84f8e67D3jmiafYXl+icWSz2bDb7Tg/P2ezWSHe4sw637PdDoiDvhs51y0XV1cM+7cYx5FhHNHkisQYGbY7LDA9Mgx7vIfnn3+efqXcOT2zRAZrT9/Bbrfn9PSUECL73d4AWlQcjjBEdrLn/HLPW+88BEwANzcJs0xdD1cosOp6Tk9P6foNcRzQRqMIHMQA5FITHO8cWmmYsrXGrFED9J6u6xiGPdm33Q4BZGtDfr5YdmLA+yoWqBKiYFmbKJJcVJwroCOPPRPe+h6nYRiKu+BqtSrjzT/LmCtmnouqElLa9JaIHBMAJwFKZkBh9lMy04/sx4FhHFOSSwyMJRN0LUyragnobplj3X7dxzxvS8W+t381s6xdDPKaHAjfMPM/b7XIMmvDKhOUEJRYdWfOgA8tYUvuUy0DbAlvO8a8X7NV1vo6Z4QzAcvPM0HVbbZMa/ZTJ4m5FUhaK2L+u3Z5ms1X9e4x5lzX13537Gd+p03z37ZbP3usP0u+8+/Vdn5PRIpSoP7s2Pzmetq9f6zfS+ezFTDrMUgjcN4kGE99zv7083HcOJcCFt9hCpQYFfXCNYF40sFmw8//+q/yS7/5a5w9dc/iPZxpS/124NHrb/GFf/EHvPH9HxGvtoz7ARR8J6hLlzXn++9qHLcg/MJ038wwDHNhXwRNgL620i/RnXpe21Tfx4Toej7ts8MsaUvnOu9dVZ0JebVSJJ+vOgvagfWp6f+0H3SWabN9dnFN3+u5hh4eA2ktjVnav+14awUhTOBoqU9L7bWgvz7b0742urYkcLcgpK0/15Fp+VF+cYTOzGlU5knzayOm/ZGE32Z/5j7XNH6Jl9fA+6a5XDoDbbkJXC3zaAccXmpc11N7txyjMTeVJb5Rt1PPxdJ6PE6p6XYtzy3RcREDutKnRFEp+QLpWcekiM1nve5jsvXZ2nlTOod072MeacTclaPaHZPOOSTlJlL3eGOCvwQA6f/y3/wTnnj6KU5OTzg5O6NfrzjZnLLqTglhpOuEEPac3dnwxBN36VYrvHfcu3vXgr36HtXIk0/cY7Xu2e53IJ5xtIP16PyKb33ruwxxZD9szVVuvyeMFmR2fv6I4WrH9vKK66tLEMU5+JlP/BR//9/733KSLE7jOCbg5Lh394y+XxGDo/cb0xJ7z+XlJcMu8NWvfJmx6/HdqoAnUNbrNfthYPApKF4Dzz/zNL/06WfxzuGIqLgZ0TgmZC4R5cyAJrcHQ+SWXc2yo4k0cSsy1yLWpuy63vaQtn2riUsGNzXzy/VmYXi73eK9L/d95HHUrne5H8eItGICVAuAaiLT1mUE91BoKv3H0vVGVZz3iHcMwwidaXsVPbCo2e9zl6+W4LYgKb00G9ecCB4yvvIMZBxx6NqEacpYElJjBKQkBjBrVFrX6m6C8i/NR3Z5q9vLgvw0p4eCbA2uZ/MllPi2VggwoXHO7JcAw+KFyRXjngMfq7PdBzXQK8S9ugepbm+JsbfrXddzTFitz1Jb7xLoPNb+UmlBTf1+/n6JMbbfLZUlAbJd82Pjeq9x3CQMtPSlHevyPFAEsvY8HtDR/E7bJyeMDnTd89Inf4bP/62/xQsf/hCDBoJ3lvEwwoM33+LN7/2A7339z3j1ez+gs4zsBGc+907BUiN6NFmQfAJw2Q3twPqSLk7P1xmoTjSn3tfH5qae07q0gnE9L4dzmJQFahRlyash1wlzvqHRrPC163Pd57rUoK2ur+Zl9rvQDmlpjO1eyr8vlZtAX0svjs1XfRZq2rE01sdxGc2lpUvHQEz9TH3+68/bUs95BratS3g9tnY8bb0hBkTmVowCvjQW4tvOXV7jY8Cz7mOtoC08sHrmGO2Z1Snlf0fnph1v4alH+ljm4D1S299U5vydEpv7Xnu4Vib9pEBporOHc2F8WNh0nksBJScsm0qUZCXWScGU7cY+yRiaBjTRBodPnztRxpgyA6vCGEsstL9hXdryvgdIL//gx3xgVJ598QWi23PiOoLs6UMK6lePF7sk70PPv8C4u4f3U7rRu0/cZX2yBjXf+e2bb9P7jr4TNpszdruBV157FRCG3Z7tdsvV1RXXV9dcX1+z3W7BK5uzDU+8+Dz37t3j3t0zPvjCc6w2J4j3XG93XF9vWa9WOO94+tlnWa3WvPvogrjbc7W7whPo1h17lJ1z4Du2KSZJga7r2SsE5xhDwIndpj7sRvpuhSTBOw6H8Ud1StX8+YywNAJRFmCnuJ/sQuSII+BcyX4jzDVWhYmqaYRyGvCaWOX2c1sTQbb/xeRbKpp8iNOFphcp08l6vWaz2cy15dHmIx9OSP1znpxuliSo+3QRp6L4rivplTUJ/KgW7aCk32Oai67rUmp17OLFmNpLvEE0EoaRUQ1YrsSzcp7RJ8LvHJ0zNxhNwoO4lPkq1zVjroeELhMkIyJzLV95Ni3OlAUvEbKUqjRn5MnZjrIgU+rPaxLMXO6dR8VXnvVaLGMIRXNucyBlLD61YRA/AWrJmelck+hBDLDmNWj2cSHC6XnUMsiJ8xWIMdO9JqQkAt6BRvs7g9uc0YmS6CFM65HmLe8tTam+XTX3Bf6lCclMuBXmWjDQCkBLgkP9d6vlj2HKmIZI2rNpnjSd5bSmkhh6tgjmM38TY2/7UAvELSM8ZJaHwK5tT+qfaoK+a/b3MYG7FeByqRl8+51EZvczKBVwQkr2yDoboGkv27i99FyiJQGKS50ktzofHOKEQWBYec5eeo7f+b2/zoc++dPIqmdPxCn4ELi+/5CXv/M9vv31b/DgldcYtztcFmStWqJaCnDLgOgqQWKunOm67DptgxmGULLVdd4TYiSGlDSncr2qXfNs/mrak/Ypmdb4so+EnGk07wEtC9sC81aqb89zqwSr+VR2H6zLMVDT8pfDZ6XQ0rbO9r1jn7UgPyuA2jHnPVR/Vitgap7XAif7OaW0R11Zm7qttu789wEowRR2WfgUsb1V0ptWz7YCc5aR2nPdKg2W+tOu0zGaI2JuVtnSC4eulPm5tq0lWtPyyqU+w3zdanfPJeCT57GciYZm13W062PAQIpckeWlqc75HC1Zmdr2WuA37+cy35zvr/mcLc3P0vfLoN3GVn+vqgn0bjDDkdGv2Wuzcad6mM6OrU+Ov1NUBXVCyHJNtDPhxVKExxjMkPATKBHgLwFAikH58Y9eYT8GXvjQBy3IfzfQb3rWJyf4GHEhwjhYoOxg9+xE4PTOXTYnp5yc3sE5x3q9QdyKq4tzwjhwcf6Qcdjx5ltvcHF+zfZyy9XVNSLCycmGJ+49ycc+9jTre2tk5VAcXd/jVXF9zxACTz31NPvdnovL1xDfcXJ6yiuvvs6LH3gR1/XE/Y4XPvA8zglvvPk2J3fv4Ncb9lHBOwK22ZyY9QHn8JjgPu53JZe8TxvDLBH5XqS8f02azOnEa21j7d9da88LeFGzGoQYGUNmCkqIkRCVzs+JyuTOd0iwal/43F7LLJybwFQBXonBhxBYr9ezJA75vd5PcWEWUyXl0EWdE4SZZlJyCnVMeD+IR5AizFm9TPdFaAYZKQ12FvicM8FdsHujxkAUy+bkkxtOEj2SO2LqagIPpa+pDZIQM4slkHRPTjWuGdNIwvJUkfU7p9rOqdWTmqY8ZgJaih1I9VnmxrSPKkFIS92Z2SrZD7gQawHBl0dMiNMCyjPQqAn0gUtjUzQxG/tHer96QKpuFStXNN9ZyUlIOBCC58wia+K1gK8Y5lkO6/moBYxcR3uTfN1G216ttW3HegDKqjnIQnPNKGOoshmm6wBkgYEfm9ta41r3sxY4loSPMsZmbK2gma8VmASI6exQ0YyaDrQAqK3zJuEo128dYvop03e2jZaFo3qMwSUXMBU8Ho2RlUtxQM4x9h7/5B1+5bd/jU//+mdxJ2vcyr53MbJ/dMHr3/8R3/36N3n5299D9wNdiLhUf2SKFfLO4d3kWlzHbGb6ngUK0+Abjdzv9yXNfJ5vcfPLv3PcTz3XwiS0SWml2hckupUBef69CdWp1yYbkWq6m89DPh91v9IDs3O1tBePtdeuFyR3cEw51e6T+tmahtaW9VZQrYXsto78fbZY1cCobbPd5xNdN3rmpMuMIYGbZdBxDKSUvzMxTAoqJCusjoOIm7xPjpX6OVfNdV1nPUel3zKfp/x7tkAeAzxLoO1YaWMyyz6/YV/Ny6TQzGOrLZRLYHqpT/m92V5aWL/6+Xrs9f5dUh5klt4Cnvc6NzM+08hBN83NEkAUsSQLGnOaf9Jl7XU9c16SabBzQlSZZAsxRWq+7F1FLElNeS+36ZBu+cLfm8r7HiB1nV229+6D+4xx5OnnnuXOvbsEOSOoo+9XBliiENSxObtD13vefPNN7t27x9nZHdbrNVdXV4h4nn76WZ5+8kkuLx5xeXXNxfXAa6++TsDx5JNP8YGPfoQnn3xidllpYACnjEHxruNk1bO93hYGcOfOHV566SUATk9PGYaBN15/g+g6Tk5WKWhfWK1WadOnBASJSOfMbDkI19C5bYyctKDrOhP0G27VHqz6gBaBO42j7/uDAMuJ4GfAlZitd+gwXZZbCBpJEyiHQa5ZaGzvF6oJTLY21dn+Yozs93tEpCRfaN/LMR/7lDO/ZLFbKCJTFrIQ46GgUI07C5o5s1w9lpqZls+SgGOX6Fq/T53DdM7LBAns4BdBsWHiceEzSAJ7dfHjYezInHmIJHeIqr4WFGeG2s4HmJaGysWyFUxa5mW/A5rj1ZYY2ZwBzlzi9DhgaD87JiTUe76sjXMH84XMyXfNYLJbaRugWv9e931JQ93O0VyInIOXg73xHkyqLW09S3vncQSLPKb8+7FnH1dIgWm+amG/7MVEi469t9SPVoBr12PpmaW+10JZLci3e3yfGPgqQB+Fzq3Zx4Cs1wwbz4d/4ef47N/8a5w+9yTSebsYdlTkasebr77GN7/yNV79/g+5evCILig6hpQp9ZA+1zSxHlvuZ+2KrGoJgkTMajSn3fOg9TyW9t63mwT+FkTM5oXJkn1sfuvf6z7XGTyXgEfbn8ctB/RggZbcVH+7p+v5nNW90F77/tKeXWpj+qxWzglaxUAu9XfJLbg8I1gg/MIaHqMr9dlZomdLwOlxaFQNKI6Vw3UwZRYNOFg6z/V+v4nmJeHp4HzfXGwNMnA+4MUL47LxZmXbvA9ljWZjfe91aXls3Y8MGDL/ruu76fzWdbfztcRv66Jxrsx0LsWNn53S9X35rFUeHls7qeLo637kZ1zncd4V+bCdU+PrtwCplH7Vo8PA9fUVu/3WtnGIdNvA+vSU1WrEizI4uLje8sHnnyGMA889+zznjy75+MfOcN7Td4HVasOWPb1fc3pywt3dnuu98qlPfZr13buIm0DR5AohdH5FjIG+M0AGwm63QyOMgyVzqIWyp556Cu89F9sdYDcKX11f8eTTz7BarTF6bps4p6xerVaFKWZT4uQakTaPd2iYC5v597bUhC+3Ux+S3JZ3HjQWtw4qK0buYx5XJhLee2JKX94KQW3CiJq4hxAYkkUsxlhAyW63sxTo6cDVwm3LiJaIQv6+HWsGNFkAyWnWlw5vHlubQr0VQiGb0c3y1/c9cD1ZtHR6ZxajFXUmKNVt123MhPAFUFCIn1AsXYcxVtMeOJwfprVm/lytA1oSANq1NsEk9f/IPqzbz+9l15qg057Ka35MCKvbbGNoSt+qua1BbTuWdk6MKc5BaP7pxSFVEox6TQ804ywDjbqP7Z5tGVvN2Fsh+BgwyBfy1vUcY3o1A20ZUN2vOu6lFZTqeWzbqxUws7rF3AWXzvHiWlZ9WerrEsNvx3lsfEvP2AfgVfBB6KIl/Ng55XrT8ezHXuKv/s2/xos//RHCSc/gwUfo98r9H77C2z96la9+4UtcnV8wXF3TB4sl0gjaGW2o3Z4zba/noeu6kpSmPe95LbLWPSe5yXO+RFfq8ccYzQ0VWZy7+vy1+6uusy2qy+uW26jPR9l7HAqO7bos0fZj6+e9pQcOVYKhds+2fKPdn3nPz/owG2e9/xe7c2N/6/ftLFMuh7f4nOwkNz2/xPvqubL1isSq/iWl5VIfjlm067K0R24aY/397F3Vxjpav5O815vvalmirm+JB7X79Cb6slTK58ktseYB7R5q10AEjgHcTM+RZfpT11tbNGvZpwVmmdfm0noItaWdt3YfvtfctN/nfl5fXaN37874yU3zWzwKynrM+bS9v5BFb0H+uGnPtuV9D5B+9dc+x5/+6RcYLweG3Y7XX/kx796/zwsf+ijXl1f06zUQ2Xjb3GdnZ2haxNVqRdetGMeR/X7A+xV9v0biiHcdm7Xn7p27nJ6eEXD4vrN4mGqzjcMAki4iw6ERAhEfoetWdF03E8Cfe+45ALa7HRsVus7x3DPPc//+OyCOZ555xoTbdHCyVSeDB9sQEMbAyju8z37aHhFzyYD5hp2BqGpjlQ21wBDz91kDkn08c1xQiBb7YLFJU4DlMFgO+jAGvJPiGpKZd4nraDZxm30uxljGrar0q1UxHdfjgCkLTP4996Weh3pc5RlncTM18GmFvzyHcOgbfaDVFjMtR/NKLBeW1taLXF8rUGYXtLbfWWCohfsiXIgQmNfTMoLWBeCYcFzaYyJS9bsiKcboBmJe9620lbVnx4RRYWZ6z+te96nMw8IY2jmpGUn9nsjU97xn67WmEZBaAbpes5lwVz3TJp5o16FNN3/szLVrmffikqB7IMQ3awGTsuUYE2zfOSZ8HQOVB+3pXNNaj22JUebvWuXEewk/bbtt3/NeqgXxdk3rdbhJ8BaTdFhFQYMjiBBPV8jT9/i13/1tPvG5X2Ldd+V+rn6E/cMLvvedH/L1P/wT3nz5FUu4ECwOKWeiM4ELxB2Clnou83ft1QgwF3qdc4SkXW2F+ra07YmbXFaWhI3W/bi0oQDz59u9d3ROm74s7dO6LNG3lu6183fs8/wva6PbKx3afi29Xyf5Ofz+ZsHypvFlfmIWpP8Pe/8aY1tynIeCX2SuvXc9zjl9Hv0k2aRIig9RoiiSIilREtmkJAoee3Q9NmAMbAzGuB7A15aEESTDgKEZQAYMCfAP24B++JcheSwI/uULW8Bcje3rudKV5esH9eSrSTb73X26T59HnTpVtfdeKzPmR2bkioyVa1e1JAOD9s3G6arae618REZGfBEZGckAtZ+z/bXfRzkshnpdSmnRR9PVZsXU75y3G2SLXZuWt1p3EJLzOUxzfh51HRbbXLRfrd8tXTXtbLu79KyVOWVNKp0k9et+WCNusraM/J5gCtQYpbUOW7KzJW+1Y1bzCJGr5kzXL1hQdJ+ttzUHaQ5rvTc6HiNydF0V5qjnS5yZFy1veQPpk5/8BB555BH8+q//OjwRQhgQNhvcff01PHTtOobtBtvtGvfjFoSAvVUygmTStts+Cw7GMKQ7kTwYkRggh9VqH3v7BwjOJcPH5QQG0KmkMxORByMZCV3n0HULHB5eQtd5HBwcFIZOExngO48nn3wHPCKeffZbODldgxZ7KUxsuVcuMa0EUj7cvlg4eGKTzSsC5KuFohed97WgrBQMpkIq7VLE5DjByODeeWyGMXOclCq1dgbGGqRI27qIYhLPKNG4IPq+x2azgcs0h43dzSXGWBIEaA+DNmiknUoxMcA09lsvOk0jeV+8slaJt4AKgbBaLRsgb+xzURacjCodplILnOmCJyJYMVOH0qTBNUEpYzTCZ0obhEos/LxCnigIbnY/PRMZkXU8cRtk2e+B2sjR71jArzMspTNH9WWIhWayI2xAuFWe2jiS34PyrFtPnQZf8rlOWtLaFdPgXfMb0XQHr0lXWx9qXpl7V/Nyaz5bn8nfc0ZR67nW+pLn5pSnnQftvJgDEC0D6CI0q+W0AZRECCuPcGkf3/bx78ZHP/sD2Lt6BS5f6N2FCDpZ4/VnX8TNbz2Pr/7eH6I/PQO2Q76kNXmTA8eUnCKvQ+98xSNaNusdb+vZ106nAiZ2gETNV5YmGtS/GYA5VxK//snrkaIdBUDbUNf8N+1L7ZUW+aF36+x8S2kaYW4u2cIff4wVQC+fpfMc+py7nR/dZwnHl0pawHqu7RZN7dqwzqIWvVpz0KrPvmMBv+yiWbkyt6a1g0rLa110FlZrlEwMNP3uDrmpZc5c0e1R7sOc4WdLyzmh29d91N/VBsbUANrVX9v3yfwxUvZazbNqXg729/F65sWWI6PFj0k61vq38IU0q/qud8rl82G4eEbAt7yBdP/+fTz++GN473vejW9+45vYWx1g6HuE9SluvXqGbQhI4W8MRxHeIV9SGvPEjUT1foDvFvDOw1E6071a7WFvtYeT7QaLrgNAGLbj/TsOhM51YMrJDELIuxIOQz9gvV7j2rWrAEaBnM4ceVy7ciUxBwFnZ2cIIeLo/m0MfY8+ANuhx3K5RDoDkRdTBJzPnjmkXPBJwLv0j6cCERDBMe72iCKwW7d6oYuBRM7BO4cwBIDH8A3GkA+BU1E04jlwGBe/9qxLv6aGw2hYyXPDMGC1WpXvRLAB0yx8WnBb8DXn+W4BYnm2UjKqzPVbFrGnFM7BnOi63W4RYkxxs3E0kCqlk9Pa1nPVVjx6XksSBjl8Wz0DMI9KpwI96jNNn9Svup3aM5b+aeFlt7r1HMv7wYAkLWhLdi5VzotVJxrPkLWUoVUkQoPIXJIVaAA8DAN8vmC43tLX66jtWbTt2rFbBW0NqBZYkPG12tEZ33YBDVu08a3HZxWWve/G1tsCUFKsA6I1L3qN2TbmAJo8Oyc/9Ls2hHcWSACV4W7rB/T6Ss9GEPqFx2MfeC8+9qNP4eq73gbyHRbUwQ8Rfdji9N59PPe7X8LT//H3gPUWi8iIQ7qwOsmcTBtCuQeJMMovoY8GetZrbccMmDWsAJGVYVbW13KsXv+tNdjiezTW99x3trTmaa5o+a4NyBZN7LrTgUfWyWXXgOUTayDo3zWNbZ92jVe3p7+reL8Yq/lsyUw/LO30Od4YIphq/raOjFb/Kn2xo1hda8fWoqWtO41tuqMEyLzV82NlyZw80H2osFBmdCtHm3yj6eyma8GOx+qC1NS4NrXeHZMoTXXHlEb1XZJzOkBwTRnrjKzV38/NnW1bPi94CsKbU7703oMcTZw+5afi57r9EV/o9VTkkzpHrMeg5eT/nuZblV/+5V/GdrtBGAZsN1tcvnI5p3HeoO8jQoy4dPkSHnn0OrrFAtQ5pHCxgBQhk1JqHhzso+s8QAGEnNY0JAMBNMAvPOA7bDabJBB9ymDkfcrQJQCscw7DZgtggf39A1y6dBnL5bJi8L29PTx84zqYgH57Bloucf3hR3B09ACv3z5C2G4RwdhsN9hstgW8OUoHcB0DiEnwefYgEJz3SaBGBlS2ssxV6eCuqw+RF4UcQsk8JYtPwtucKHGiNM7Og0MAuVXOOpIXZeQUbsgpzTI4JUAARoUk4Xa2aI8eUbpkVV8KW4QcY+wn0uHT5DGtlZUsGOsdmYBNR4hhDHEDSUKE5GXSisReUqvpJ3WHEOBiBIMQCOg2ASvfYXBpHjryJeucc77Un7aEa0+49vCGGArOsMaOI5RUmsi7dvlSaZCX6U+JPyRCTu9CTBQnAYxRCNqt7KSuRMFILGHa+bPKQdrwZRpS45xGW51Lsj+LQQP1rlF6ZSTSnhGMLe8uGnPXdV2ZW5l3UV76lndtVMkcpTC7RJjIyXsvzoFkzJTew5GDZKvgfKJL6g+Zv5EVKpXdhmKWTpR9pfTVfLV2GTwonVHUiljkn9JPWtFYr2Nrfm2ZW3Na4UnRQJXzXJdU6gCse8ClitLc5OfkXgxKFaafun/CQ0K73JcIRqQIDwJydsmInG4fjAUcPCe69wDOOuDS2x7FD/7I5/GuD34AYeHAPl8h0Qf0J2d49vf/EDefex6vvfASwnqD0A8IMZQdHT1HXQYQkrZd6wdW/Kz7zEDJTkdqt18+J0U7TfMWqG8ZPkle6IuVEy0y96V0zMgAE0VkZlcdgQj5Qsj0RhYTSOqgBkO2b9ZIkQsk5/jNgtq57+2454C/BaUtkDox0jE9qzk+n+jRqlevY1a8keRTDtvlei2Sm9+L07vZum65IkScjumKhzybCRwAZkxaVrbOmllwqsdhwXY9x+MOHoirnUVyQOA60kTacUQIDQDe6tccL1jAnSJx2udrLG9oBwNjNFqp1JvwY6Sp4yf1qR0hUPgXlfhtOs/02Frrp6pfSNzQq5YHpQ3Li7Z+a5RVkTnp4arfUrcc/5g4PJlLiHEU7IXkNEqXvhZqJN7ICbiICF6opiJPHKUrR8b2ceHyljeQ+n47Zl8j4Pj4GIeHh/DOI3Lagdjf28eiW+Dk5BT3ju7DI51ZSWeQugxuB4S4BRDgyaNzS4RIePDgATbbLTaRwTQARNhstyO4Rc4eDAIoGTWIA0IgLHL96/UaAEoGN+89lqsV+mGDEALW6zWuXr2OS5ev40tf+TqWiyVOTrcoZ3yywnA553u/HQBOindBK4jwEdVYmD+mrfkRcIxZ4ESgxZjTIMdYMr/p+yg4hAz4RRknL3zXrdAtIoABoQ/iKskApT5LIn1iTpfd9n3agdOe0tHTwCUFbZXtjsv/ACRhP4SUVEHH3Gsgq9sVo68Ce6CJIJE02wXGGsGkvbzaiCntR0aPCHjC+sEpFj6fSxgCXL6vR7wksivIzIiYxrEXpak8V1ZhZ3Ik4BLr+R/MpaVjHSkjnRWUMcYyvzYEp/xUfRCAlM7fyV+mbxCDCuMuGVH1tH52DsRQ0kiFn6HeF/Aryitivg5Zg62dnAkgAipQYulVfvJIv7GzySAKCNk2TcCexeBU2SaLYVZAPBXNqemtFXArfHRXuAQllDrKLUrZ2MTA00bfnAGk6aMVa4tXLN+1vP2NBkbAZvuQv5PdYqf50hgUdtzNNZAdBogM4sSP+VojgNIZI3aEniO6a5fwic98Pz7wqY9heXAIRrrLjEPEcHaGmy++jD/4T/8Fx8+/BGy32Gb9oB1R2vvrXAqxRqwNb00b5nQWUK4gkOdaZ0LAyRklZzGd9xhmDIhdhoP+W9MPQLoPDdPPgeyUK/0uD8zyke6HBmcWXMvPXeBX86EF77aI3G61dRGAbduEek+PaVf7mr76PFmZh5hC4esLzOMESbf4pdWeFznHeRzyHWrZputqtWGNOvvMLoNV5iXmBFKOXNnRLrxMdTh00WHZERxjrI0V9W6Lb2yp6JzHPzcm/Y4Ob22GEgLZ1TV9f1zz7d3O80qLJ60hMqU/JjuG+ns7PtuOXiOt96ysED1meTtyxDD0RTdMzroyMs5IfMgQ2SttjhE+Yx+mu+nAiENG43COotPy34SBdOXKFVy7fh3ee9y8eRNEhD4EgAh9H3Dnzl14D9x54w6ufPSjJd4bqL0L5DIWjQChAxyle5WWS/ghIOZwoK7rSrY1ZnXRHhEWC6QLrSLj9r27uPrQJVy7egXAGGIHAJ7lkkqC8wu4LuD0dIObN1/DSy+9hH4A3HKJ/cuHcHknJ8Z0WzCTU4uW0rkk51KoBtVjKvH+itE0M3M2bHQ8p14kkiIUMQLE6nMqQK/rOhCnkLg4DAV8a8UvmcmswWE9FkQ5TaT3NRgwTK+Fd0tw2md0e3OKUozDItC5Ds2zfbdCQX533qGPAXt7q7TjGGMJuxOP06ie8k5Mca6kNspcGM+hCJu5cxxzRQuU9OsUIACoztNoGurx6n6Wd3djA1WyZ5XbgszSU3+u+bkFhMt7JpxGty2eJ12n/V1/Ngd6rCHRoouuS36fA3EXmcMWELBgRfdZPyOyx/JxshGmddi6WwC6ZXzYv/Wzc0Zpq8zN7y5F32q/1Td5PiVLoHSxcRKcIHKIDtg4Bh0s8e0f/TA+9tQP4vDGQ4iOgEjoGIibDU6PjvHV3/0DPPNHX8GD23exZMai8yWZjtDcnk0TYKyTy2h6auNK85nN9NUybnSWzRYvzNFkF33Lc1zPxVyx9bzZeY4ZFAPTUMBWv1p8eF6xIcYtMNmSP7bvmqfqc0BTIKvnSz87gr5at9cDbc/hnKE3R7eL0mlux0CPXerTY9JzoaMvEj+r+/RQO3q48XmRGaR2603bLcOjJZO0kVOFzu4oF+etFLmxKxS2hXla7dm/55xerb4JTrJh77b+8/hbYwvLO606dBtiyHJk7O8fTOonkmRPZqdM61wzVh3R8Kdd3vIGUoyMj3zP9+Dylcs4PTvDg/UpFt0CD+4/wHC6RhzSrsaD+ye4fes2whDgFlPhlBZkMpDIOwAerlvgm88+h/snpwhECEPEcrmsDomm9xxiCNj2W5B3WHgP5wkv33wNH//oR0Bch2d577Fer7HdbJO3bwjwrsODB3fwta89jbt3j3D/wQmuPfwwLmfjijmdSXJZiHae4LJCjDkkLQ2l7cXVwkovHhEYWjHL5977HMqWQk+SEZmsfudzWlmk3Y/IsYTYOecRwnh3k96V0oveKo50ZieBC32LellcqIWBjKe1oHX4TutchTxv49HF2GK0wWKJc1XnqsrCzQtdQh6dSgs/+uxGTw+QwvlKv5QQr/ofQyW85koloLnOCjYVdO0U8IKDWgaD/G4Ffsxhhfp7/a94eBQV5BereuaAihbMLcHdqsMCBKJxfjWfnwcS5zytGoToflrDRH6XedXzpPmqpQDsPGh+04rQgmXdV9nNtWuAqN511nPbDhfhyfwWpacATWtudH2tPu6ad01Pq5Btny4KlgkAmBLfEqUwXecQHSEsPB559zvwfX/mh3Ht296OwRPWADoQliD0D07x/Ne/id//D/8ZJ2/cAZ9ssBcZ7BibUB8a1v3UTgf5F0LIzq3xOXvWQNPD8r6Vd/ZzSye7fi3PtOZQPp8zdJIo46rvrf7qudllbMh45PNdxph+xu5ktowa3Q9LWysrzwOydh7OO+8h31k+HtsDkhPNJBNKb07e30WL1tqZzP0FvVotfrNGgB6f7of+XBIw7ZJTmv+ICJ13GGI7+Ys8O9lRbfSrko887k682aL7XugY59eaXQ/n0czKZzvf1hiZyGRKnGLlga6zpVdb/W45tKu6jJNVnhW8d3Z2Budc5Xgf60k7ozGHfabY/hxaa66l0LSbm2fBFamNSVdny1veQLpy5Qre8fa349LVh/CNZ74Jv1xgsbeHq4sVyN3H0Z0jOBDWZ2v8+9/69/jcU5/FtRvXSvptZh7PIAAAp/sgyDs8eHCKP/rKlzEgxVMuOle8g8IEadckgMiBnAMToY8McoSnn3kGt964hccfvoHtdlsSDsSYMrSFGDGEMbPW7//+H2AYQonpXq6WyaPf93A+nSOIMYU6hCFgJQA4e18cpUQAwjQSxlYMiAySNONLiJ2UGKcHOFNoGCFCUnunUDKCZtAc85zr6xaLIoC1EbPdbidgzgoAu5jK4jNKU4wvu+2sPbZE47064t3Y5ZEo/XAa1k/BttBPvGMJCBMgBzIZ8D5n38v8otPhElnPZfppUx1bUKPnSL7XNCqfZQUon9egbdyVku9a5000jTTAngMAWlhrWurvJcBBK2fdrvaAz9WlDeJSr3xP6X9W0QjldQpQG2NvAZ7un8yPpqUtlnaWVueBd+Fd+5nuh6Wx/nxOAVugXfFMI4y0xQcybvnbnheoadUe265x62IdKJM+m7nXdNN83PLoytqIHEHOIzKBvMcAwuAJB9ev4lM/9Gm8/3s/Apb7jJyDD0A8XePWzVv4xh99Cd/66tPo75+AtgEY0gXKUd1lpvtqx2JlSGvemLkkW2jxsh1rq/7z6K770OpPNQZue8SJqNIfrXmb29HXc2jXYqFBoy+WftqgOw/0WjljdYduv8Xfmm7699baan0PtHdk0nMRzLU+K3OcKq36rJ1oWjbotUBU3z2on0Pksv5b49Nrze5K7ALuuj5tEBGm60LwC2IN9MvYzDi13rNyS4+7hQ1Kf5CbjNOwdl2ER+13ds2W+aTxez32Fm3luV3rU9OoFbHQ6hc5Knxin7FySeqzclLe0yGPtr6iC8IUe4UQsOg8Npt8cbWKHgKQzzMmp5T3DiFGhBzCy2AQamyjz6631mcZyzmyrlXe8gbSdrvF//rb/yt6ZhyfnWDvcB9+0cF3HR7u9uBogeO794AY8Pprr+M//of/DT/+f/pxhDzxsohiTCm8iQmUz/p8+atfxRt372HISmDot9huNui6lKxBGGdvsUKMjJ4DlvtL9EOPuFiCY8Tv/f7v4wufe6oSygVsInkwYwTOzk7x9NNfx4PjE3DMdw0NAf12C8pncURROd+h65ZwWbi5fNt0CBHMU3ApCz1yLdwK06qFYbfmIzPYRTi/SOeRYgBlg4ycA3K62j4McHIolDmnI58uSGFwq5hijNlQdRiGlCpdklvIM/p5LYR2CTo9JrtbpMGePcMhcfUtZWkVUwG1NLbZDz2AFAOOCnTIzxSbPI5jZnHTmLHNCjD5vfVdmpt5L4xTYYka7IiAtcpH03Omo03gKmRJxjRGhUzJ06MS/EzGtato5Vf1k1AZ0rbYT4T3rAGwq7QUnAWWc++1HBAtQHue8rTv6Xdb37V2NfR7LVDbmvsWELwIzfT7dh1qwNcC/S2APVe3BRFzzzvnMcScXc47YH+J7/zU9+IjP/D92H/oEkI2jPYiQJuAzb1jvPD1Z/CNL30Jr73wAtAHuHwvXHTA4Bo7jwagzAEcy/MjL7cPxNvxXgRktUDQrnebBoD4INScMyfHmxx6t+Bc/5s63nafF5oD4FK/Ngi0x1vXMQ4CRSfp0Hg71lY//jTKeeu9GBIY3XJ6vYQYq/MewEg/G1Z5kX6ktmrHjy67eKNlnNgx6v6X7ziFomnjKz2nBm1pQgDMGpBn7Hht9AswOhwnO1cWXDfGrPlZ/808Xmxb5OQONpmTSUQ0JjxpzN15xpulY3m2MTZLMz1mG/asn7U00HKDqHXySp4Dttv6GMpobFE65kKUEo15n/ocA4LiD22Yt9rW4xFahhBKcrCLlLe8gbS/v4+zzQbUeVy7fj3HLhNiSFmbrl27BgwBx0d3EQLjN37j/4MffOqHcO3aNTjnS9KCGCOGfkDYDgA5bAPjt//976QEDcxYhJg8hYC6sFV7wTJT9Olg2hAiOAR8+Stfxcc+/GFcu3YVYiTJApPQPEcd/tN//i84OrqPGBmbzaYcRu6HAYgBy+UKC+chZ5HONmdYdh6He8vcF5cPw9eepCFnAPHeAznURhit5JBnLtuy8o6EBPocQgikLfIQImIkhO0Gm6HHohsXZAwh15Uy4+kFbAWqCH75PISAxWJR+i27czo7U0vptoSELXqBayGq29dAgrMgH3FKDQa1ENELeBQajK7zYDCGEOA4AamsI3J9IqQo2zFzYIHFzqkAoxYalp4xRp3XYRYsW8FLlMIDRdBYALMbjE0vISzfxJR1TDKzBY4jCFDj0/2wwt32g5kn59pSfW3DoXwm2phGWgi/ybPtWOfRsNW00Px8EYNG5qn13aSv59Rlx5hyYczT7CJhWFLXXJiYli2ye6rXQQs06TpsWKA8Y40Eu0u4iw5WxhR6lIdkLScagZBSzy86BEd45we/HZ/8kc/hxjvfhu3CYe0Ynhy6TUS89wC3n38Ff/Sffxc3X3oJYbsG9T18Tm8biMGeEBxAQ87geYHSMpQ1jezY7By0DAJrTGh+0/N2Hj1nf+epzGBOzhbLV5rfiOo76OaMntIOoSSnaI3NGhXjHXpT3VAKTY3oXWGfLRqc9+xF3t/1bh569Ww5x9aQM/W9g/P9mzNcque0wpspc4aRfLdL/qXv5Pwtyk9OArsC21bPF6eryLiZPtjxaYBd8Y2h1645bRlh+r3iqJt43lo2U72eItc6o2XsVMZIY3235laeae1UtuSulRe76pZ/JeEV5m1DiWASDOqcw6JbJDpE5IuplU7J0TaMMUJLt5lE+Pn69jw9rMtb3kBaXrqKvcPDJKTFe8XpoteBA6hzuProwwjEOD66h1ffuId/8T/+K/zFv/gXwcy4cuVK3qlw6IcBm+0WgTr8f3/7P+Dm3aOUvjEMONv06Pwig7IA5uTYIEoxsgyg61Jq8GHbI7qUKerWvRP8z7/1O/jxP/tnsN2ewTlCiEAkAnEAhx53Hhzj9/7wj7ANjNX+Hk7PTsFxQNiuEbdroOsQncOAAA4RDI/OeXTwCP2QlUmHMQlAw3sAAR0xp18MWfhmD4gRAiXN96JLl+ZySClr84pw3oOGHhTHxRKRvPchxmT4gdLWOZBkQ1SeARDiEMpOGTMjDEO6KZmBzvlkbC4WySgMEV6dS2oBIb3gBeCPB0TruFwNrPVh6rEe5F2Oemtf6mkBsvQvguMAt/BYLjs4BzgST+WYrrIG9gxQgBwUHw/pENJlrylDox2zBUC1wlcTrwoRVXXZnQIB2NJHO765osGcnRN0dRINDjGfZaOc/a7tGbKlBRYnihq1rtLKJaXwToYqGDldfgbkRNXOk6alq4zUlBiFWUAjV3zSmqOKFqrfcwpoFuQ13i3ryTlwUIpa+ouRneaAgKT8JQl9ZBQgImGaesdul2LW47SlBfjtd/J+a23NGQPZNZTTxLpKnlEO2PDIa9Y7RE/oVw77b3scn37qM/i2D74P3aJLu0bM6CJjOHmAOy/exAt/9DW88PQ3cf/eEeSkHYMxgFOadJfOD3FI/GXvmdP9nTVANQgCzP1L82O3tJ4DDTpSwia0sSFL1gAufUcaawHRAlxn+Fj3T8tQLVdmeeYcQ9+unbJWk7BN6zef7yzLQdU5Z6RJH23/dIiPpZOU1s6ZBpu6LQt6R5oTHI3RApNw2xyaJE7McpUHUHbHWoBet6eNagdFIOU8AFCybeqxye9NGTIz3mpeiZESEok8ZVC+u4PcmDyhaoO59FNuJCA4cEh1aX5tGTJS9HOE0fjUz+7iYz0feu5H+mIkXu43INcHsEpbr+iT/y9GRtLNNK43NWctfWHXrtTJqu+6r3PyU/PFnJyRZyfRFjHpct2e/L5cLLC32kNP27Sr5wjESW6Qr52WLstsAmGIiUfSdT0ZEMaU/Er3qFpXnJzQnuq08OeVt7yBtFitwM6DieAkdhGMGHtEZMI7wtVr1xBixNnpA3zxi7+Hv/AX/mI2FDjdNZQvjQWlOzJefPllgHwKlwspRbMU51KmIiCBvF4OoQXCdrtNjBQyw3nCS6+8gs12i7SnEBEiwOTRcYAjj6P7D7Beb8EMrJYrrJZLnJz2eaGkTHF9PwCuA5gw8LjLtYo+3b1CBJBD5KnAL+CGUIyi9L1s6ydm1J4BOSu06OqD/loODP0AuNqjCWSBY8CU1G09OrruzXoDIpcxp7qThsc2gOmFlEBtHOl/spDFGzG3XSx/S10ySPlMAx4NFHXbQMGWiR6IWO6tsL1/WtJa6kvj5N0CBijTQsBqAxzPKd2JcDdt1KUeW9WOUpLyndDbKp3asJruHMwB5aJoIpcdK/1eSwHPtTvphxHyrfNaEs6pdxFZQLbikToMdKy/usuLpnNlDVjNi02aN/6ee2YOfJ1Xdhm3BaiJcZz/hSwz7C7pHLDdZdS2+jsHSOx6tHNq3y+AQv7lRai/jw4IncPgCThc4Xt+8PvwoU9/H/YODwCXDZYQQcOA26/exMvf/Ba+9sU/wHB0grjepHHQ2NYYM5r61Vkwq9tuGEu61NcZ8ITWFkxbAF07dnYbk1ZmtcB+NECV2QiFbBzNzbe9rNf24yI8q8dun2+dLUnPRXC0NBhlqqVFq29zO5YXWj/GEDnvXUt7LZ9knPK5lXHl+cyPu9aHXYMtB195B9IHBlOtd+fWemvsGkiPz6VrPNL7mIDdlmyg0iNMMp8SOXRuTBmuy5zs0DRpzbXV85VuN/xr9abtm0jUKE4n1HNRzi2jwZdqjWv80lrfFQ3zkfa5Plue0MXOrzWu9XyWOUcbDzHn6KeMOSnTCPmdEKf3YcpMe+crvgPaIeK6b9XYJjXPl7e8geQ6D+czQ2cuFGvdOQfidDA7EuHatWvwHths1ogx4vLly3AuJV7YbDbovE+eGb9IO0niSULaMWFOSQa0JwxAYWCd3nUERBHDkHZjDg/3AQCn6w0CM9LOI4HgEYaI0AesT86wOV2nO4/y5YVhSHGbrkuLMHrGQLHc2xFiwBAiOjdVpDrMQZ+RkZ/e+9GYUwxXey9SSvKWWtMCSGd2Y6JyyFiKPS+kFd146JvRdYvyrMQT6zuMWgJb6tXpjO3Cld+18GgJwDmA2zKI9N9pZywboY6xzaGSzhEQxRPZApqUsVamJSuFDs5uoalHSOqZ84DtKnOKb+65io8ahUYd0KyjelbqEIDJU4/XnMKzczXpB1G5TBNAbcxgakjLZ5q7z2ur4gO0U8br9uyZtTm+K32ZAXG23/JZVHJKf17qzl6NFlBujVX63Cm6tM4k/XHK3Nj0d7u+t7whhksOAobjOhsWiBAdYeuB7YLwbd/9Hfi+H/08Dh6+AXQdiADPBGwDTm7fxavPvYiv/P7v4/6tN4B1D2x6ODgMnMNEicouVWuuWuMTQ1wXG/evZeIcTWxpAdYW3ca7/sLkGb2+5Xc7tpR8p4igC5Vd6/NPWmy687HvXDzTcwByDvQCiU72MHjLsCjvYgrGWnrB9qd1HizpOwZ4DFttyZQ5w8bKrxYQnjNw2qUenV17c7y3i1912FQlf9PLAFxzbPM9rK8vmSu2X5x3PVoh4S3AXd4zOEK/86dRrFFH5jP93VyfxVjWuECeOU+WtLCFrd/2t3Uvm+hT59KF2Jt+vKdSsI3FUhV/ESowIWfE07nwNs3+uOUtbyC1QsoKEM/UDJHLQfdLh5ew8CmL3Ha7LZ/3fY+D/X3EGNBjNJqc7KBwOuejQ7Z8NqhSP8aZK6CMGavFaA1vNlukO4JShpU+bhHjgDCkyyR5COmm4BCwf+kQne9SWJqn/DtAnpDOtKXU2tt+gxhDjlGmkpLbhgnEmNInirEhn0uacMIYgiaKIP1MsaTkHIYwVOFGzrt8v8+4IAsIjOMC16BL7zQRpft+ZJEkujkwj5kCZW5FydtFa+uXelpGjhWGerxTY6Fe8HoRW4VglW3aPWIMQz687FIyC/1epQTTh8lWYPGGU+kG5fTtVlja8U36bwWP+r4loHSdeuya3+cV2DxAtHUW2jsqBmNrbLoPFy0MrtKuameG5YNK6QCAa4PeOfoR0USY69LyIst82V2tOUCn22rRoaw5Fb46mVOenxe7s1GPbwTFOhNkq7/W+GoZchZ0zq2fVv3ybAvgMpB22rNyZQLYAdETonOIC49rTz6BT/zwZ/H2978HceHALodr9AGbB6d4+ZvP4eu//0e4+cJL6c67zRYduZTpi5KsY3FU8NhH6YeVHxbIzIFkPU+WL1tGWGsXeyJPDN/aDJS6j86lC9M3m82kP/JM0qVyFnWcj7ky5zCwNNBtaZ7Rz82tCy3rx/oweccag7ot3d9JqHGDL1t9t3Mq9GLFIxdZ2yPdUJIx6Dv55uaFmVO4sp+eK7VrTf/d2tGs+0qTsbVoJ/2wu8w2sZBupznHb0LGl/dzFj4dPmznyPJY+Wloossuh5ctcyGHRS6bzy1fWVlZ8JN6Xj/T2vUq7zDnKP1p1lKLEzR9WjSysqJVdL0TGihbpmAaEZ08deiUvqn69HhLHQ3+btHiouUtbyBFTtnZhFH14X7vfI7THQVWt+hwsLeodiaYGYt81mUYBvjVPpaLRboJOMcyR47gWHvT1+v15H4jET5lmzmODND3PYZhC9+tAMn4RmmHi+MA7yIcBixcAA8buLCH2G/R5Wc8AB4GOArjDkPnC8BOOz1tUBJCCucTA0/i0UMISbjGxFiSuEEYLcq5pkrgo4S/EbgYinXMOhd0ZYWzVebjgsipctV86mekbgvC7ELRn+udJ/lOPweMCnKxWFRjlPCi1vtW+ADIWRAZ3EcEjugWnbh0Mm3re5qk7aQgbOhfhKRXt8banMKuivHU1IJW7mVqKP0cDjAnPC0dRnpU3TRjaRuRnsbLmlvG6y7h1wI+rVIBCRrPiOj2St9U29orZuufA3ZSWvHvu/pn65xr04KAigYYlb59PymlqaPgPMNEHyK2oa6WfnY96vpaa29ubdvnWuOvAEX+zkksf+cREREWDkNHOLxxHR/+vk/iQ9/7USwPVogCpoYIXvd47YWX8NUv/j5uPf8yzo7uY9Utge2ABaf6mAjkHUKmYb6Ou9BE6NniV2vcyN/VDpd6dlexXlpdrEyxMlLe1eePpM3kuNtM6pL+lHHxdL21gJ0diwV49vcWSLxIsXIl/aQS9WHD8FqyRNPBOslaPGu/t/Nr69V6rNUH3Xb6PaQQqRky6LVoqNFsQ+vZOlxyuoNpxyo6XH/XesfOod4tnQtXtPqAiACqs5btkpljP0cnlawr+5zFG3r8FpO0aDCn7ywN7HfqoWY42Ti+Wr7aMVr6zrVT1jy4Wu8tvdKSuZbmLVlmacIZJNkz0ACK44U5Amfr9J4wNo11WhxIROVcsNVVMj7Nay0eezNy5C1vIDEIcGnXhAEETjsrFJEAAwjOecQg23xAjKEAZxEe6/UaIaSLYFndlZOAqsPQD+WchRgDIjREyeg7dhKwBjZbvVszwPsO3aLDEBlpSwjYP1hib+VBkXD1yj6W9BDYdTi8cgm0XAKdh/cdMKRUn77LWYFA2FvtIWajx/nx0tcW48UYq92j8nmI5b1690i8yNy8fTrGCEfTBRZjLDtLZZ54KsTtgvc+7VgxT+PMdQidXeD2911AUj+nhXl1DgDZzjSKsDUGLTBCiHAhpDM1BDx4cFKEt17c+p1SV6wvWyUS0FUrK+1NJJoagHNlTvFocEVEE2Fu+3peaQEF+XyivA1A1O3Y522Y2pzybfVHK3fNH5NwppmtoNb4x/5Mn51T7rsUnB37RfoAGGC6o315zqY2tnTX/EQz4KhVLC11u7bvLcXWWhf6OxsPr0uCxgTK2eTCwiMerPAd3/tRfOypz2D/8LAYOZ4BbCPO3riD55/+Jp758tfwxkuvYjhbY+E7hLBFl0FXRPLIxhxe1zVAdEuWzQG8OcMCmIYw2nnUcyBAskXDOT5pATugnotdAMn2v/X3rj7YiIbz5ErLyLKfT99B00nTGs8cANxVNGDbVecuGaCfsz+dcwBPs6JKsU618+Za66w5IDmRyeWz+f7bOmS3qBVKfF4pWMPQYU6na8yV2kdlXLXql58W5Gv6vhkd16r/vNJa81Z/aOAvY9LvA+MxhrniKO10a3q0HDK6zovOle7nLh2jNxDKVSbnrIciB9MnlY4eQ4On7+r5uygm0OW/AQMpwZowDMkwAlJ8aZCzM+mMTowBHBl9vwUxYbFYIISUPvvs7ExRn0ra0L7v4ZHSEo4GkitGU4yMGAeVStthGMZdFOccAuIYsw5KIXx9D9ct4L3DZrvBjetX8TM/83/H8b176E+PsfQO+wdXsA0RN9+4hYdu3MByscSyWyIOA8ABzPmSWedwfHycaADO6aTbilYWjTCdLJy0E4TJM+l75DjfWA5Bi5OLQAhhqAyvIshkfpL7uvRHh2lJOKAGq0JX/awVkHNgpKWAtREhn9vFPbdN3gIV5TlmQLXv8qFMcgRPHkMc0hkkziEQkTFEzrtCDjEGiCvFOYcgyRuyMBFPEIB8aa3qB49gXpSTHrNQfBewaPHFXNml8EvbkZFynDQArBJeWvDFmC5F1nPc8nrptuY86WXsyak16Z/+u02veYBu69GKmkHN56aAnzPLWIU8Pi8Z9oimIOxcBcZp4HO0E9qeB15asoORdoxZP2Ne1/3UGQGdBgE01ilY1q5T3a68SDK+3Bc915SC6wBHCN5hWDo8/r5343t/9Ck88u53YuMIwXl0RHB9xPboAW4++wLuvnIT3/jyV3H75uvgTY9ltwAQgc4jMMO7nA1JXbyoedieQ9XzbY1yIIddcwrVswbJHOiu8L7inZZH3M5Bax6Fvlre2TMhdq225ljLYtvnuZ3flizdtYNmbZ1z5U+Wx1Udjf7Njaf1bEse6PXDgFqzWicBAvJaxdJo7Mf0nj7rvNDjkhLVWmmNz/Jtayz6b2v8S2kZE015saOO+aKysXKdNtsaMyP9k0yVq0CatRrsIPNG6ns7xl19vihv6+LIpQgk1YdWqeZb1WvpOqenBBOQ2tXR2KrV7zldsGtMml/kDJhe0yJDztZrHB7sj+8RktON8xySoocWdHkMUE7hoh8VFnozoZBz5S1vIAFcUl0nRQqQAP4YMYSA9XqD7WaDs/UZwrDFIzceAsilS4AHRmSHrlvh6P4pwBF7hwe4/tAVIAwIYPQhXzpGcmYlhWJR2R0I8EXxJWE0DCFZz95j//AwPx+BGABOO1qMDt4xYmAc37+Ny4d72NAezk5P8Z53vh17+/s4/i/3ce+N1xPAyZn0hhiTp5/TjtliscDBwUHmrcRM3vsCNkUwxjjuOghTpz5zMUomi4mRszcBq4ExOGC9Iiw4YB8Ezs+HvGskQAbKmEwMLMItpyrNTO1So0ogpMbCMKRdHWaAY0qS4agy4Ky3Sm/12nh+KbKYdHx3E2gwILeYknMp1WimhygjRymkgzmllffOIUoy4EhYLPYQuw6Di1jGAGIPonTYMPUXxchy7EHwY9uUPfja4CyGUaIfYQRvkzHGODWsoDzf+vdKyFGl8HeF9tR1yzO5f04Euaij1s5APScyL3pnrwKMqr+zIZjgysCYKy2Fq5OYtIxv+76MWzITCr+PzzNCGEo4b/oc5acAqZbRwlwbD3NKoHynFI+U4kHMOyCttdFSMIXOkSGx5CkrE8AY66rWRB6UPEt5nci9dOOglFe0fDO24+QcpRqLA8FxkqzBAXC55RCx8B2YHdYLh+6JG/jkF57Ct3/3d8J3HQZEOE9wwwDqI45vvoHXvvUCXnnmObz83PPotyl8OS5dUtaeAJf4hwnQN7oLGJBsn5TPWKbwYwUQZN6cXAQudM5jjgw/jjrrKS4MQUJ/EwLLnN4jIlDXlbnhTGdyqbeU6TQX5tkCuS2QZGWDgK6K50xpOUK0MWnXm901qzusJAZDEnzmsMdpu0mmZUcVTx0pc0bdeeDKPm/XaFq/2kiYvmdpWQ1Tg17UdG+C4BYAV0a87bvIysLD5rzQHG1iZs45x1kLQGtH5FxfLQ2KHCUAJWveaHQSuTKn8vwo81DwjPCe5c3WDmlrxlvn/yZ9R87MRwTKV4/IKk4HIJqEAsDljKges+jbYhRkJa+NjZHHUpYUlmsqaOSrGCMij/cSgRMW4eR+zE4qBnmPEOKEJ+b4rLXOrQGvI4s0ZnCO4Lt09Q47pGsQlNxjFhknilDJ+oyh4TwGwapCI3mvyAOjg95kecsbSP16C+c8wEg38+Z7edZnZ+j7Huv1GoDERK6wPDzA9WvXcHa2xunpGtevP4zlcoUQGCFEnJ4cY+/gEMSEe3fu4fDKQ2BiLJYLlPz9OUGCADHv/CgYM4j3JOkNGZcOD8EAfLfENmxEFmDoA5xLmZQIhLt37wFI9w196/nn8OST78SNRx7BydkLAICIvFXaecSBy11Fkn1nuUhpI0Ug2LMGwJgRRH7XHkQp9cG4DNIBdJSABLskIAijV0vXCea82yY1TpWxPjcGJRDAo0EnC1kSOcCNgKPl5dTGk/1OF60gWl4IKyTt9xqcT0A6Ja9i4se81CmFrhHGCxUJKuU3YzJvBWwwV+PO1RVjSYwtHTol/bBKz9KjbTyOYK7+vK5D99W5dOGx9w61wcmzdaSfsjvZnKbqPf1uC+QVxYlpaJL+fXanjOo+zhlH1iCryxT8MHNljMc4nlG0/Ux+gpoeNkxibmy5waptKTEyGHUI7XllDsjNhWrqOXG2X6ZQ6w8CuqzAE/BQ80GErUvK0XEyQjw50MIjOkI8OMB3fN/H8JGnPo3ltcuATxc+dOzBmwGnd4/wyreew4tffwavfusFoB+wXaespb7zcBLWVIQ4irGnadGSJ7KzJuu10MbMr147ZR5zm9ppId/PAfP0Xk3z9AVGi4vr/pR5UbxfQmpDI93uzPztMiY02NLGjwb8b+Zs3lzbLcBW9UF9Z+W0bjfGWBKP6M9ahlzLwBnXKZl60++t8CgpdWIJ1Z6xc1oGnf5O180zz2jgP+cMtLotjarOENcG93XZpUOFJpqm9csj2CVSdTOX3Re745iTw1bjsP1sJdHCDj62fa/GmeeHxaEjuh6AOIKn81UbdtOxZwNL7ARVLD+29Le0IxhQ7zISTRiq2Zeap0csdq4cYC53IE3mNbcRYkBJeZ5lHnM+38q1M5alTkWbES+NY9b9qN79Y5S3vIEU+wByAIeAzbbH6ekJNpstXOexWq1w6dIhFoslYgyIkeEdcPnKZUSOuHzpSrn/iAgg53C2WeP05BQPXb6Cu2/cgUOHxXIfPueXlyLCOJ39ES9A8pyLoUYAHDH2FgvEEBFchwiHpV8icsR6s8Hh4SGcIzjfYbFcAQjAlnDv6AjHD76KGEMOV0n1S5sAqox6qT91wE8Fhozg1aFMITOuVWgj6E9hYxTHbW2rGMp8NA5KFrCfi3ceIQzVYhwFXJ1JT0oCmcn3ahWH/LMCdAJITLH9ap0DkL9t3dpAKEZfjAgcELLwlMv7GAIuczgEdIhR/qfIZvshym8i0FB7bexc2DnXNGrNtRZGWkloGsxta+tLVuXnOEc1zav3UJc5A2CnYaA+d3DlEL1+T94RB8G0H0mZWMOoBQgqsHcOaJSwNnlPz58Nd5HQV6ug9VzNglTmyX1S1olg359bF7sA0Bh6S5P52dm/C5W2ARuJ0DtGF5NxBFC602jh8OSHPoiP/cjncO3tj6WdIEfo4IDtgLM37uLWCy/im09/HW+88hpOju7DRwYPIe20qHX2x+23NWDkdwsY7K6dfce+a+db5nOO7nbOWsB6FvipcpFD8rbe1jqVNaKBljUS7fdzpQa39efVWIgqQbpr97sFDFs6ZRiGyT1w5V2u5Z6do5bBMmf0pHe4Anr2fbt2yzMNOSVr1bav+2XHW+uWum09V5UjQBV9oa7tb+vv0q/UiWadzGL5T9daqo8nvGSB/pvh5TkDUrCV1iOj/NjhFOKpY1HmZtc6nOsPkJeAeVdjpjk+Sbs9u3WAXcvnhd/btnUfnfNYLBYNeZeiZ8g4JcFcjE+pl5AdB819vz95ecsbSKFf5zuAPDwY+8sOD106gFt0OTsPY316nL1FjMgB+/sHCEPIoS8OIfTJE0DAtevX4bzDI488jEv7ewjrNeJ6C14tsB3SbhQI2XMfM8DlclmrCFPZ2TnYX+LS/h7ABCaPS1euwTuPkwcP4PwCnDPPkfcgdIhDBHkPz/kMlE/3PFUCrHGXTmLiWtlXAFgtDPGelcI1GKuUuSS7ECOQkb3gVBhZFlIFNngE7faAfGlWvVcWI7mqLgGOkvhBdp5kbDYu2yohXWw/rWKwYVs21t8CFl1noXc2jkJkbDfbyugAGCHme7RKgJGTaNu2wFTtTcAVjaE4kx0Js4Veg/QpUCv1l2bnt9/1+KVIuKEVqOM81buaAEpWSMZUMFswVcasnmkpPxGqQhPdB12X3kkFRq9gW0HPA9dc6QR07KKfXSva6Ezf+QlQ3QUidZ+1ApadK+/9eMbNjGlundi/54CG3SmYVc6VEm6NARAvrKZzkgmEZUiXQsIBQ+ew9/ZH8AP/xy/gHe97D7rlEn2OyeoiI56d4e5Lr+HVb3wLN7/1HF556SU4ELqYQk7Ipcu1xZC+KJArvNXgVf2e3bmYrr82zVuGhv17AtIbz5OrQ2gtONOypNVOEzQ1cFyLH2x7rWLXxpsDiaPDSdeVeLTeQW7JbT1Xk9ArI2PlO60HKtpQG2Banmg5KuzZtfH3qQ7XfdG/F2CKenemkmtmbHO0mPSDah1i6Wn7o/s0BcT1POp2iShnGp6W8hxqvio0odFe1jynadOa04xkilyT0tpxLXWRA2M0/uqz3AGuSuxlDF/Fk/p8d4tGrTKVnzXPWRksbVj+jxkztHSVLTvDX3XfUGNL3V/nKO9sDfDIOJeTnB775gw/5RB5mW/DS5aHdU90+xctb3kD6e7rr2K1XKHzPudZZ/RnyGmWF/DOwTEjbrYp9M13eOihK7hx4wZiTGF1Y6YMh7PNFmFgPPbow9hfEGJYg0PAEJNgDvnOIVlc280GISeEIHJYhyFvuzK87zCcLXDj6lWAHMgtAFrkaAiC9x2c60rce2SAyYmvAs77lEkpK3/xpch2pVaaOrZY/lkgJswlXu0qY1Wm5wQE0ihMxpIuc5U2gBEU6F0G26ex/rEt6X/pM4xRpBce6sWsvThzglloA2BCixYosX2SsemtegsydJtDGBA47RSdnJ5UwpAonzsSYAadHrOtGDXVbb/T/UrT77VAtJ61GOUMSbv/wl8tmljANSdA54CTfDeObV6QtZS3NXhs3zRwER6y3q9dYHUCCs3nrRCcFlhu0cnynn6nNiqswqjntdXHokhMX4rCBk/mZNfcWQVqaWO/m+tXu672nBOlsdu163PYnXMeAwirG1fw4U9/Ah/6zKcQL+9h8AQfCR059GdrHN2+h+3dY3ztd/8A9159DWdH9+EjwJKdkajwnZ4n6zjR32vaM2sA0M44ZgHwLtBoP5tN2GDmy/KQpfPcPLZkoK1XaDFn4Oix2z7qHeqL7prpz+04W+ultTMu/daGYSVrbB2Y8reWL1pvyPdV3zLwtfRuAcu5uWvxmx3z3K7hHD3suHXRc9OaO/lJROncMdpz15rLi+zUXARwT+YtphA7m6JesJDVeeettV2ltaaqOgydgXHcrVBV3a+WPpubJ/vupG+qD0S7k1CdR4PWWtb90vPakhcVUUx7m80Gi0WXj8CwOS9UgiNr5y5zkc/pnqtxwC1Z+yctb3kD6Sf+xv8Nly9dwmqxROc7HB7s4+DgEIuuw4MHD7BcLrFcLsv9PpevXsPRelNAg4TeJeITNpsBbuVw4/pD+H/+P/42Hr56BYQBIAfOh8a8TxN+fHyMe/eOsO0HLBcrDCFgs16j324RYkzpwIcBb3v8sXTHDqUQOwLBuQ6LlQdnIAvnkbqQgC8T8sWEo6AiaoPKmllG74kIVzEkmMfQOsnUV943QlruNposPJfiXWVni2LtAR8XURsIpGfGi/msEosxVEZWtWi5jnkF6sv5rEDR7wrYahWrhKVeICkonRLejkf/HmNMZ7RoNDi9c2VXjMshASR+ikJv8WmdXyZgW21Jt5SUBVzMuRc0nlmy/DP3fqsvpU5D+6khMpM0AyNgtbxgFYwViq1wjph3dWUNWE+a3llp9aPVjua1ufASO/YWv8hzdoetHm/63K6pXcCHOfGArrtyHMTz+6TrmlOqc0C7RStd13khGmOdgKwPkVUAQJ3HZrXAt3/0w/jeH/scDh+5huCABQguENxmwGa9wf3X38B/+q3fRn//FKsI9CdrDBwxcMrG6XKIspO2FKiy68R+pvtIZp21QIzmk/Z6MIC0QSdtuOlnLLiyjgMiGg9mG3Bm67dFz3/FFzNA6CJApbWud71/UX7U/QAyHUxIn5aJFuzZ9WDP+bXW6dgwKk+47f8cf1h+qN+lSsbIM3OpnW09u+aipbs0v9gzU9YJa9+d+3xOzmi6X6R/0o90pnvUr1VIZtZlc3hA/m7Wr/ppnaGWR8srasvKhpq3ZEKZy8ZO9UXXjfysnieq6mydLbRyY8QZdd2WPnbc5/HVXBHcmXQtgOyQletfiMQpxhjPbwERhJwHKP2vsY50f8fPEoZ6s8bTW95A+uD7341l1yEMAxZdBw4R2819DGeMYb3B5b1reHB0C6enp1gsFthuzrD/8BPwvkO/XSNGxrbvEQNjsVqBnIfvOgCMEDa4detFHCwdfLfANiSrVjKYdF2Hhy4tEWOH/b0D7O3tZVDm4ZzHcrmEW+xhG9JdTK7z5SI7BqFbdAXc+HxxLOWwqyR9qew2iSWd+MJ6vmRBIwOl9N2o/D2cj0CoPWV6UUgMrRaaQIojhScQXDp4HBkeDtt+i84w7y5lVoP3mol1mFyM9UWKNgQPAHye75QpSi1iTiF4BKrCi3yuJ4ZQpVyXsc/1ue/7agdIh/bpUikExwhDRIgR634L9NuUmh0p05/3KdQTeb687wA4xDhAGydVnxpGQowRHEJKQ2zeGY2W2pvdmhOrGLUN92aKFlhTEEAVT44vYRSO8m6jTj2mVtFjFKWqQ111ae1qphdRyG8Br+bFVr9g+IFjRDAgUMBay5DSdbXA9lhPpS80oYrsSGNLO5IxxkKL1D5lWVFehJ3sUWHa8KNEJAvG9BhqcGSNjNSuzHByANGYnYzT/6Q3ruvQxwj2Do+++1348Bc+h7d/8NsxrBzOwNiDx2oT0d+7j5dffgnPP/sczh6cYH37CCd3j+ADw3mHbehLPzgmOeecz46Fdhhn+V14KvcpyRpMJsHKvhbAl+8E7Gp+mANktmjwPIb3jPyswcIuQKp5b26HdXL2gGkiF3YBkV36QH8uY3kzxdK5gOK8FgnpOo0CFE1/ZPxarovDUHSG7ft0XXLycDcMFCtvJ2C6YUTUoBGF1qLXW8B1Spj0HqUHJtEHk/7z1HAZAf/o5CNKTpZZg7D8TAJKOzHnjPJdvC5htcgREqOIHftexLWAHlOsUdogU6VTW7J3Im9pVBIaJ2kHatOg0JXwaNRJbXPraEJn6Z+KCGgZ9bYfdZ/GsYneZePMkbZaPLfLYJLvXZ63q1ev4saN6zg5fqD0ifRhdJoK7ogxgiNSVJXQd4aPdZtiXInc+98NJFWe/9qXsd2s8cwz38AwbMEccXp2iqEfcHBwiIODA9y/fx9DP+DSpUvw+1fw3/2V/wGr/Q7UpTNAvluhH9ZwkbGfkyZQ1+Ghq1cxnN7BAlscrBz6AJydnuLywWVst1ucnh7j9MEDbDYPsF51CIFx//gEd+4eI0YCOY/lQ0/gqR/5s2lDcUhnisg5pGCyruw2ON+VwKsQIxx7AC7f7UQInM7nDGFIggoRkSn/SyJDzi6MIVsCiBiAywxJGZQHMKc7jMD12R59V1EA54PRjI1LUbhdH8AABocKZACJYb33iEP7zgZRBOPvU0GWBOLI7HJwfdV1aSH16eAsh6CezQqduSzGJKgDkFPrMjN4CIDPB0pjKEBWAxbdZxue11LoGjxHAMtI2AbG3rUrCZS+8joiEQAPsE/Ai0QAh6IUK7yulK0IkvMOdtpwOhv2KPUKgLWgvXyvRFIrhFGKpORWk9acc6Ja2Gvh22X1GpTxyqoH2jjRdcyFRNkwCH1w2IZEVX1ESrAidUu9WoFKHZMQJOFdZegRpXt0dvGT7NLanS5AeIIKL8t6rsCAooejERRy/i+Hcmcek/4yus4pwzE5WKyxnKrPOy/FaAoFPCcnh4xJG1Cpj+PalgQzyZZfMNBzwOAc2CdvYRcJjhngkECW77BxhP7KZXz8C5/Dd3zyE9jbX2HoCG7p4YYAOh3w6le/hZe++nXceu0V3L5zGzEkJwg4h+rGiC47mTpyYJejBjiWM2h67Zf1A4yGGxEiYgFq88CjbSzqZDjOOdy4cQNHR0fYbreFH3YBjl1AT3uLzYsgTnK74BHhHkIJvS0GBE1D4zQAS+2M1etnLKCS3+1n2ijT7WpjbBddS93jcCZGR1ZHIDDklOf4bL7414zL0lLqnZuPidFk5GIrJG6unpbRFGOfdjkzyEw8ChB5MA9V21U7IrOiRAik8UdmUM6ym85Mp/v3nEt1ytUfrHgi6dbROUAsjgsqjhglocf1QqPB2Bq/Bd1apiKO55C6fJ0J5wxxGbYkmei0UycDbaSxJedqMTtw3nUP1rgAgMih8ogUhxPJWqv5uYxVyQs79s55iAHP2Tk6mjq7HQ1Cn7kdRP3TfjfdcYtjmBtSArEs1HIdU/3d1LEz/bDP99ttmku5EiE9gLSblOSzGNWgtMMf5RA3o9xrKhd0DzECvk0rqYcjg6bkmC1veQPp5PQ+Ll86xHd993fi+PgYwzBgtdrDwf5B2q0BYQjpTh1HhNOBcPny5XKmRINI5ojlcgmOKdU2yOP4wSmuX1om5gZj02/g1x6bzRZn6zO8dus1xLDB/mqJ9WYLIF0EerY+wzAw3vW2y0DZ9g3ouhzmpUCn3FPiXLofCRDhBxCn3Sa5C0CAmPCkNipiBt4tMAq1mGyYEGV0rgFz7TnIwsmnLPUuSysGV9lbKi+KI3TUTcBkWkBTxVCAosr6JUUEhAauLQUnn+vQQi3IrEAZQkiGp6sPTlqgI/UDdchdqwzDgAWnsDo4SU4g4ZFFTJi5m3qfS7veFX7Rz47epPr9Mgbjna7aVLwnBm0xyFrPowY4+rvyffqgemcsI9CfnFGoBP/Iy1maNses6aP/FsDi/KgUND/oYuk96bF6X/62/WiFNGrwaekldUjomFXQLYBm+WGkCipwpgGOnVe5SNLuNug1ZA1BIB96byjIaTha/bsdu4AK2dECEbooRkhaE+wIwQOx8wiLDu/88IfxqS/8MK48+gjYOywA+BDBpz3uvPo6nv2jr+DFr34Tm/vHCNs1Yhyz/8W8PruuK0DRzoEev/6sgDaaT4PdKvV4p5dCSnuvv/76zndtsTJiTjbNgXph7PJudgTYOube13IBaiz6vjLhPb07NjW222u4tUZs+9ZQbNGnPI+al6s5Qf23Xg+tfuo2rYMmd65yUow4Ygombf9ba7weU0rWAm4bx7oO6et0DWs5ltZzMrhicbxWHqVcivyafKOG3tBjteE0LXM78JZf3OTKirotLW90eyMds0xRmEYXjjEZjlQ/Q0Q5wqd6Orc57rjZM71pzmfopOddz4tQTLU1twZbn8+tB4tX7HdWf9s6WjRpOSNbfbTf3bt3hIO9vXrs+Xz+2KBUYOprRNM45ya80BrjmylveQNpy1s8WLuU2tt1OLp/BnIbAEcAUkrprutwcHCAvf09XHnoOhaLBfphUwl35pQ1znXJc9P3EUweL778Gu7vd3AuAg7poi28AdkS7FYrUFyCCNg72MfBwWX4+yfYhruImx6PP/H4RFATUVqklBdq9hR57xFDnzKCEVVgQ8IAgNoDBWjvUwIgc6DWApvyLqYMLm1Wsa7eIQzJ2t/2PRYzc8LM2aMdi5dWpzt25Er4ivSpKJaG+S/GiyhlHZMt456EhKjv7EIqoIdQgVVddP0tQ0zTVtpPdx3lNjMdTk9PIaFkoJqeeh7tXOnwj7n4f1Dd7xpIRJDKS6+VqPYUnSdQrEe0xXMAwDvqkWyPwPxt8OlB1LtHqAGnLhbYjAZSvT6EB1uAcNfYW23q8Wpa6L+1oUJE5UyEBYMaZNq1rOubAOIG+NEKxPJVoiNGrzTqtb6/v594FNMzVhMPpKG1lRkaIDaNPe/QE6Njh0XIZ4Kcx9YDvSf0nvDIe96Jj3/hR/DE+98D6jpEcvCRgH7A5s4RXvrqN/DC15/B8dERTo+PQczYbrcF9Mt6lX+27xKaZg1DPf4Wj8waIGb+NY0sbaxBdpHSAr26vvNKi8d39XO27WLM1vOs+bZVr/68Bcik6DXzZkLu5kBSEziq9m36ff2cXYNzY9Tvtna5W6UFUCeytPRr9PinZ8ZdTvvsHM8yUHBEena+f601cd4Y9GcFS8y00TIE54w/4QNxTOt31B+ltTbdZ/Qb1Tv91fybR+f0QEV3C+7NvALzu0Da2LNttHTBeWWOpq1353avrXw/r+1mm0UPZ12dQ11z/Oe547D1A0jROOc8+2ZkK/DfgIH0la9+A6vVHrbbAS+88DLWZxsMfcBjjz2Ga9evI8ZQvDDkCD/wmc+j5cUnIgXck5dzuTzAiy+/jmce3ANowHbYZCGQgJjsDvAQUwgXCL5bgInwxu076BZL/Nh/93C1k1E8FSGik80Bl874LBYL9NsNyDm4CIScVlKSJZSsbd54RIQ5qS3sW0IUqHdF9PMV+MmkSmkulUdbaOZ8BsC2DVRhLHIpXzKe6hAqDQQphxVapaQX6FSRTD1F8rwOsbJzIL3Q8fzWGGj9Ls/oVNECIiKnOFom4OTkJIVtZd3s1M12rbqbChjjuSo95jQH00O9Mh5mrry8WtCz7GU1DJ8Y5RLktqDRNNf0YPNMDcan75ZwxrzWiEZvofOupNGPcVqn7Y/mEeccguIPy1+7jBFQW1nMAbwJGLHtACl0LJfWjo1ty46rRXuocTXbVW2OIGnK18xcLtKeG58OwWr1zxoVrbrKdwSwSyHBKXzYIXqHTUdYXX8I3/fZH8AHPvkxxMsrbIjROQKve2zvn+KVbzyDW996AfHeCejBKc5u3QE8YaBx10poKHdvyGfWmWLBh55n0QOE2vmwa64m84MGbwEVvc4rdg51vdZRdlGDQq9/+btpyKq+F5o1dKatY+48hC3aILA8aS+8nhgrDbBs22uCTaBEYcyNszU2G2Kt2xDHz5xcsfTVDlmra/VuXKINJ0ThHFAcXbW+s3xs5yE518Q5ksOaNGlo1CFS9A6g1KHbnNLAGJmOJnSWvk3kkhqDzcQmnztgcp5zpASKsTOVl2OIndWPumhZCCCH5avdLMXDWkfqsaTdOF/1z45bv1Pjq6nM1rJIy1nb79bvF9Hb9p1dpSVfyjpHCu0GTcN801pOobnVWiYqyamcm+4Oa0yj5YPodX01g52bi45Jl7e8gfTarWOAHiCECL/YRxc7nG6O8eqtO3j9zn04ohJudHCwj0ceexv6oc+HMgFHPguOFLMfY0r3zUxg3yFigT/40tcR4xaRdAz+GIbBQ4DLWTpCjOhDwGp/D+9+73uxWK7KZXO6kDOCjYHFYlEEmRZ+smNSFKwSTtXicGK8TD1guxYNMN2SHb9jOEq7Nj2Hklq67NqoG6R1fZ33YyivYvIYY+XJAzSASXVrBSrFhjq1BMGckNVtaUWFmWd13QJqW7tvk79F6TkgDD0evnoVJ/dPwc6B2aUwh4bSbIGmImh5BDQtECpzbgFphsVNRaVprPuS+sBVqIy806JN63drBKT+uDavqTnQSoMyEEphIVNQYIWiFuLSjA2f0c9OhHIDzOo+VX2bUUC6jUJn1Ubdx+l8Wj5ttZMUSN1P69yYAyEwbdlxaVroud51NmMXCGoZUyn+HmDnsek8gncYOo/v/P5P4mM/9GlcunENwQNwDisAtO5x8uobePnpZ/DKs8/itedfxB47DGcbDBwR2SGA4dUu9Jwhoz9vnXmRfuudBTFGLF01/fT7c59pQNziN/3ZXFstmurPhL9afKPbHS8dn85ha50XWiHJL8uzLZ6r5rzRd/2+ddIxj9dPiIPnPJpow8zusJR2CUXu7QJT9ru5+Urh7ARgum7t+O0/6Z8dm6UtM4pMTo/Eipd0mQsFlXqYx99bbWlQ2pIJLVrIuxV9GvS0v0/kJKZGl37WFq1v5TrGVqik9Mbqo6ZclblCez3Y9TXhIxpxl8UPLR1padXU07NlDM2z4f5zc6R/bz1jy645qORJEumz9SVMO2JWsDi0Zow5quepheHI1XJnyku7x6bLW95A2gzLrCBTCBw7YGDAuyVO1ls89NAVdF2Hvu9x6aEbeOSxJxCG8f4fZqWkGEgHkYHNdgD29vDEE+/E2fq34LzHdgjYbFNmsy4bPEMYsCIPTwTyhM2wRT9ERNfjkUcfR4xApDE+u4QYSSgWIYVCUfJ8pm30lIjBKqsinHOabP0vgaeaMay3msx3FVCdE/AwhgSUR0aBey1YbX810Ch9ijx5BiVGfPSqWWBpwYQUmc+WsaGFZ8sQkTr1oW3bln0HqMPzhDby92KxwGpvD3x4gPshAJCwu92e9qYCp7Fe/V6METHU/axC2Hw7Ht3GEVjDUs5w6H+6XUsT5tETpj8bAcHYaPUup//Je77zOaRCDIw2ILeKthKgPGNoKpq1jJHd0fMXKy3gU9wMM4CsVZqKIxfrfdZnuqrxaD5qzJcFsPo7q0Tnwlfn6tmlfJfUYXCEswXw+Afeg09+7rN4+3veDXiHsFgghgB3FrC5d4TXnnked198BS8/8xzuH91Ft+iwCQMGl51FPp1ha+1U6J0tKy9afa5CZ5GdNRgNppZMawIlU7RcsTS+SLHPze3WXZS/iAhe7WTscvzodyifI7S0awF8vQtxXl/kHbm43K7xyTmhHWDd1r2LJnbcmoYayLbAocxpPlrXpIVdi3Ptap1lx+OKM1KGXa/3XeNRPYZA8YpmBCRHcHvereyfkxe7SlNPmO8t79hiwbddR5HmjKj0tpVTziWZEVW7NT7g6j39/lxIGiARNufLAz1WAmZDxiw/VmM32PCiZba+C7zXmsu5+WPmdH8VjbqwfM/ybDsclVDjsQrz2GffJD+2ylveQPrWsy9juezyvwW8d+iW+4jssNrbx72jY1y+fBnOeRwcXMJiuUKMDI6A965Ym4nYKTzKdx6dT5P8nve8F3uHl7E+O4FfrOAjEEPE8clZin0nh5MYcbDaw8GlA4TACIHhI/Dkk+9C3/dgGndhZJaTVS23Io3eS+8dhqG4uwBk0Cv8RyiXp8mBcL1wUsKlqSczcn2Jnl7sMcZyb4YF7MhxvJJRROrw3gMkmbrSwcqYQwmZuZy9kN0zadN7n7yR0GGHOctLFGA+zu8wDONulRh1lIeqwDAxoet8Cc8bBVybb4rxx3nHJMSS2jQB7fqi0TlFmcInJdQC4JCM3iEErE9O0W8HBAAeydWlDT49PwlMq1A605buwwi+eQIORZD7roN8PBpfKHPKPBWyCRxStStllWRFPx49dJG5+Vz6u91Won9WSi6H23Es6XPzJpipa2q46t1ZQuJVHa5i+6X5o+wkcG5fGqWRHtZ0aglmq1DtWB21aWpLC2TZ8du13VJg2iPPMZaDz6265gCIrNm+77G/v1/PeVZkMZOL9WTJM5RixiknLInM6DuPw8cexqd+5Cm893u+E4v9PQwxwnce/WaL07tHOHn9Dbz41W+gv3eMWy+8jO3ZGbxL4xg4grsxnKXLqfo4faDFJOQcnlP99s4BkvqfU3a6CJRQbLhUX0r6IMBTPPiFSmW9SwKKmics4Ib6qelbfpvMjS52vlsGyhzfTSur/5wDGBoQpnbrC7f1+rJ8tAsktuRAq20g38UXQpmntE4T4XfdDSQJf6oxc02r+bOb9c6fHs+UlLRTTtt1KfpP5I7oNWtAS5GIbKIWj0373vqMCKNcS8pbscAo22T+tJNH17fLQLIyo5hkWY8CI9fPGkJzukYW2sz45/go6brRWHc5dI4ZxbCVIvyFHHrOaJ/ttbJWtz0mianxi+637mPhrXxcgvJQ9fq0fGnHqedrV7mIEVHaV38jf0aNZD1l/c1ggkTLhJ985xGGAY4kSislwmj3S+PA0biX70D1Om2N7wLDLeUtbyBdyTtEQI6zBdB1iwSUQoD3C2w2GxweHuDhRx7GcrFEP6SoXk8enhycYwQCNn2GskxYOgdHwI2HH8alyw/h5PQBMAwgMPp+izD02KzPAAAL73HjxlWEOGAIPQDGlctX8I4n3o6lXyKSBwdOQCIwFssFeNjAu5TKiZAu9nPksFyusNlsUrxljrlkSuedxCgawCkuF1mIRwaHZGxF1AdoK6CEKUCvvjdKIdHU5/NDAhwT0xJRkuCOAHLonMcmC1bvXDI4lCITpTQMQ+pnADin4JUdBo6ESHV/9vf304W7YUgpPuV7oFpkjCT4iAjOJ2M37VpJeMg0FJAobRFTZHiicqEmA2ByORylYZioM1LWW9oxI3pgiBHUJwEyeAffp3TjpNJUVgvbUbo0OM93KUraWkFbYsyVIE27kGIEjYI87bKquHeqw4kKX9DY5q7QP2uUkXPlPgX9rDgegHoHovAbc5HOctZB0spaOWcFYkuhitHcEp42y1bTgBHrGynFPWeQIlSoge/Mjl/d6fq8lzxnlH1lfFAyJiTRiVXKlh/LHBjNrPtHQEmMkkan+lfGjkIH6QMZ/pN3HCfgFQilryn8NsIhpdunmORH7DzWYHSXD/GBz3wa3/ODn8bq0gHIJRmAAVjfPUJ/9y5efuZbOHrjDt545SbWR8eImz6BcwbQMzxGfiainLo7wlG1VACO6dkMepLBm4BQ5wgcA0jomB1EkSMosggkpHujBkVbhvdpHWnjZwROQkUBtdpgsfxIEOSe5mjKz7sMaV2X5o0WWE5jaSes2GXI2PuAqkQ7andf6w4NtFvrVd6xbVs+k4vSnZd6sv5CQrhWlossYZfOnkhIT9KrVChetWGAv9QpMs+GW2qaJlky0qJVdkUraP0h38lZ5cQTAOd0/3DJIA+h4WSambvST0pOp9FAlEEkOafPfMmcW0OkkiMNftSfOdKAn8uOgIDblhyzdUzCI9Xn091ErmRpTZsUnigOi6otSuubaIygoHx5+7jLUc9Zi6dtiGjiUFbMRlV9ds5ETBCPsjeGnLzL13VXuI13R7noPlqZ0qK53sqS1TKuunb9Wq6JfNE8LxgWiACNjmQUP8fcDmJIuI0IRKKvpR+jo681vjdb3vIGkvbCkFqcSY4mhuj7dObo4Ycfzm9x9S8tkiELJYAc4F2+jJSBw8MDbDYb9P0ZNptNafvSpUvo+x5XH7oC5z1Oz87SHUbOYbVa4fKVy1juLRHiKBicjp+MEc4nAS7fL5dLAHXoH1ADrJgTCmjFNB5qG9PT6uQQ4o0DWhY3V89JSW2igDrKBIoxjheuuuShdd5h0XWlb9KHOYW9XC7BzNWB41YYz3a7zbHoHs5N+6oBpFa849mBKBxRFFs9vjrTXaEzoVrwtUEwPbxtvSfee5weH2PBSbnJIcMWaKjoM1aMVtH9deRKQgUtvFP/U0L2cedt9LoLAJHfq/h1JQ9bAmdOqVnjSD/PnDzyQB32OVe3GKl6u90aIhbcjHWM/dd1tgBia0wWuOixtp47DzDYdqSekL3cEyMHKEbvHPjRZzNabVoes4BjDnjrT8qaoBT6a0MdAqW0ydLnJHOT1zDEfN2Ad4idx7Ds8K7v/hA+9fmncPnxR0HegxzBMaE/OcX63jFuPvcCbr30Io5u38bZgxNsz9ZYb9bonM9nYIwhq2lmhkKVHTp/TkbPiaXhXCjTnBK2bchntQd7Gsa1qy+yrkfgPC3aMLGAvtWn80BTq35mzoJpCmLle8tzE3mqntW6S/pcnV1sdUT6yPU4dF9I6Q+7rlrj0s+2wunmSpm7Rp26TdFtk/PHRp7pOZjj09aY5uZY85A2Wq2zxRZ5tpWEQSeYaI1FnGkXpfkuWlc88ybe0+vM0qFuAMWo0nxHNDXU9c9d5z3l/dSPyYigjTQ91/rYhfRD5J0kJNBzXXQj757Li5RJ/9Eee7gAT7bnO2KzUYnNUiMzC7zW+9JWXe+bN4DOK295A0nSY1cAAcCi60COsNkM8L7Lu0iHKJ7EbBjFKIAe8NkNyRyLocMx4qGHruDk5AEWC5fqwAggrly5gtVyidPTBwgxIjCnHSCO6JbL/Fy6nLXrutzXdC6DnIf3taC052VaRpBY5oV5qFZcIrDkIkogMd0uZi60M8I63WwszVDZtfKgMUkFM2IYU1uHEODdGFZn6w0zysiCZy1A0i7WeL7GAgIAKU272R2TBAHSF/2M9pbpn845xFArg7q/o8CbeE0DJ695BpfyuZyVANWLfxdwnytFYPNoJE2A0QxNy3ia48IYGtH6rvG37XtLeThHCIGbvEeGd4Um2jM4p7Rbyiw26p+lwQw4mSjOHIqi264A3TlrSrenaaTXowYEjqahExqoaFCpxzmngC2Pyne7DDkBgE71M6izaVE8/JzC7RxTlhUegycEBwwLjxvvfAc+8aOfxxMfeC9o0YHIwRMhbHsc3bqDzb37uPXCy3jhmWfhYsDm5ASbszOcnZ4CROg5onOuXPRs6Zd7PKFna+5bOyZ27Z83n3q+LPhvPdeae0v/OQCo5UurDanPOooseJ6sE7M+dwHxsc9q9wFTB0Jr7C2a6vHsND4bvGnrsyFwMcYUqtvgBd2HVj+1jtg1RyKvQwgpIHqmn1q2z/GGlm1C03meqR0gut3WDpYOj2y90yq7eNk6Ee33+uyrXSPpIQAcmxB3p55hLs5KXf9c/+fmW+vZIQSQm2ao27Vmd/FRqx/mk4lcEh6Svk3WqamnNuSmToc/jWLHO9JmvKbDjm/XfDADp2enWeZAwIW8OdeJiXwd6//jG4Nz5S1vILWAAZDOroAk1jfdHi2XxQIAc0DMOzvD0GMYevhlMqqGfkiZ6Ryh8x0ef+JRXLlyGcxpV0bO1RweHmK5XOLk5AG2fY8hBqw362TAMGO1twIQ05kk74phxCz3cKQ4d6mvFtjtVNbMrFwUmZEVCJo8i1qZaLoVrw9QDu5KHaPQTV7bfgiIbqS3pHDUymlcuLXw7vt+BFYxwjGKAWoVnjWqKsXlauFgt9zrPgiFCCHW9NBx31ZoyfdczhkkvrFCXyvBcQs8h4YghZyFEFSYXky7OMpgkx2vJCwH4AJKrAYeaTt/F+DQ9C0HJl2dnUzTXPOHVbC63ppHxnf0762QmxZwkecrAEs5Xaw5xqqBru0PkBWL8WYCNWCwOzBzwLOsI6o/s+Nr0bw1zkroqzVrwaNOU25pO1enbtvy9dRpcL6iIUrbMHNhUx0DjimF0UUC2KEHEMlh3QGHj17Hxz/9ffiu7/sk3P4SQ+cwEEDbgPX9B9jcO8arz76A2y++gge372L94AQnpw/SHXCcd4q8nC+yMknTejwHpNekPN+aD00/m8xhFxBqAdl6PdalBbBbv5PiL/19qz/2fV1ErulinQOEqb5sgWjLSyn8uM7ipeV0y/Bp0dLKjjlZwkCzn3aMei60Q2xuTlpGo+YZPXYrw+z3UCHLeidAxjPHE5pu0xCtqREOoIR/t8bRmr9dc2H7o5+zRqeMxdap59PS1AL7EkniWjSc9kHTgM1Y7S6YyOaWs0rLgzmc2DIuW3JX3pcd3ZYztyVD9DM2hb2WPUKrMudEOcR3es2CvRtqjqZ2zC39UPo9Y3xYunvvdzoGi47glIHWkUvn1JGwkc1KMbdGNd1GuqIatcUBc9hiV3nLG0gaVI/hROlsBuJoIBGlSxE32w1CqBdKSq0tB87SjdPsKSVDyLsWIQyQg6rL5bIcWj45OcHZ+gwxBmz7LfowwDuHbtEhlEQKASEOYJazUg5dl87MyA6WnKMSgaJ3jPROkj4sWxIYzDBFtVgpxba2Frf83gLEMUYMOcTDkS8XgjJS7G6n3nN5bN54v8XAGAuX3SddWkrNboHLc1q4iNLRYQBlsRh6CK1jjCUFpeYFobfQzCq0VO8YE1z1Ia9gZkbgAYEc4MY5T+w1FZZ6/FbIiVCyC7/ME2pFapWorksr8OXeqqLz+FyEPnhu29N/V7w0I+gSzdu7R5qmk3HFCHbjZ9XuhVLik/4RiqEp89L3fbkPSxulQG0wzHnFxYkgbVpFcx4IqcYl76Y/JuPYVSwQuagyOG+dzSl0EFXnpzQI8DHCM0BMCCBsCQirJeLeEh/4/g/jez/3Q7h8/RqYCAGAC0DYbPHg1m0c33oDzz/9Tbz2wkuIZ1tszs4ABkgBAu99cTgSULzIGlSO4596/HcZPBYo2efsGgLaRpGmlV1rLXq2AGYLfM+B+1abrXFLfwVYVeA7MiKm9VuemrTfAKdEdbinBlKtOuXdlrOkogOV/+2koaal1AujD/S7dse1RVcLKHf1QX+ux2VLC+RqvTJX6vmdhnzOyY0WX83xU4t3WuOcWx/n1U+UHYyYhozN8VoF7Bt1F34iAjdIoA2Q1ru2f/bvOZmqZUpLrug6RloCQPv58/RFDLUhXWWbnZxprB1wwNQZZrFRkeXeI4TROLOGfgBP6hA9GsKQkgApOcOcXFpy9KLjDsN2Czn3ZsdezRFhEmI3Yh1qJpC6iA6cK295A0kTUf7FmBMXcMweaBYski+2Shd8+i4ZT8tuCVBacEMIKaSMHGII6HxKIS4Tslwu006Uc1iv11iv14iRMYSAbrFIYXYhlB2Sbb+B910OqWOAGOQ45e8PU8/NGG8+FW4CrGJmwCjnjM4RtLmWCtDX4XfzNC2XrXEERWDos1EWQj6vNR7OH0KAI4LvPCjUuxLVTgtR5cncNbfjuNvKSuZ7TikQycWUYz9EcLZ2QKptdxVGJ+F4aUES0OpP5CLQHRGWiyUWlLK4UAw5DJFKPyQ0pu97BEyVbEtxT3Z6HE3GPUfL9XoN7z0W+fyXbSPXCKIa8GngcxFhZEGG9jy3AIhWzDInIUo2u7FOnQ1xFuAzEDlU/deK2AJa3aYdQ6mXR0N0F4hq9cuub1nDu8DIRcsuw+zN1DcHBMFcvBJCJ+dyAgbnEDggEhCWC2xXS1z/9nfjkz/2I3j0vU8AjjF4DwQGtgFnt49w//U7uP3iC3jxm8/g+M499GdrcGQERPjFImebS333+SSvGElpUG+OHnPhUq15rMM7284a/VkrfGrOsHkzZboeL1akXTFY7PsVbahtXM3yAdA8OqDpqGkpsl4DptY7LbCZXsAkmc0u2oo+I45J2zf61ALDc+tmTo/YMicHCgaZeV/z4YX5hVAuYD2PN1pzq/tb/kZKgmHPD9m+Wp3TAuW7+qJl9nlzeV6ZtDdjAFljpuIJM8cXMVikThu1ottqgXUigJyHTmvd0nvyt8iV5Gwdnx+GoUqFT67t1LF6u9WGnhMg66YaclZ0AWo9putwRIiNdtLxlBS5VfSr9As6+cq83LRzSKBKBs3R8c2U/wYMpHTGJwGP0fsNABwjtv0mH4gm3L59G0SERT635Cl58perJeLQIzBjf5UudnUERJLscgwixnK5Qtd1CCHg9PQUp6enhdG870AAFosliAbcvXMX67M1mB0O9n06bAwAMQAxGxUxZU/yLmV/YgAxDJDFpA2+AlAzCD89PS2GCWPek1nClvJOmOxcSBIHIKXohqSqzuewBMgBaXGGIQDsEGJI33uPxXIB128Rojj9xHvHJeX3Ip/DyvZ/SmhCKcRI1iTnf7sAECkVrRdTy6vZEnbagJI0sNojI3/Ls1HytzQEvHS1KHkBApGLN8U7QnfpAJduPIx7R/cRX78Fx2PoXrZC4LxHkDNrXVf1fxSWcdxx0EilIdA0xcRbA6TzWQ8ePMDBwUG6n8ko9CKsUINiPWYrkFshT9WcmbmwytECjKpPOVwmhsRvLtNZhLLwfAsA6PUgTDYMQ0k2YL1oFsxYham9dXMKfpdwntAFM4CzQbvzynlK5rxCyWdTsvXlxpMRlOlMmRe98ymjJpIBS8sFNgRcevxRfPJzn8F7PvrdwMEKkQYQM2I/IJyscffFm7j5zedx9Not3Ll5E8Nmg+FsXTyFRK7IAO88skWaMmJxveNB1AqlrWmgQUyTtzitQfko1dOakVTs7pH+Kb/rHYsJjXcYUun3aX1zxtmuespPQrkQNhRaAVkgjEmBSl25XpH/QEUzohSmLGtefyc7s3aNA7VTrNVXO48Vvzd4vwWIKoOGx939OaNIz4mla0teJepQ+b82GWmsuPyUKzjmjCBLVzuO1vyWzxVLXHRs58kFjTHs+xUNaMoX9llbdPhgjBGsQuz03AuP5hbrZUjTsRW9CMbQMMKn68sYfCy7M/VuJlRYfUv22siFGhOQWsd5vRW2mBppLYyisYxgEL1bI79771PWW4kwYi74yxqhdt6kDqJpUpfW7zHGktBJ03Dsb53Ft24b6LdbeE/VewDKPZhzpdX/lKaY83UsyZnWwowX0ZtS2hL7T1B+8Rd/EZ/4xCdw+fJlPProo/jzf/7P4+mnn5508Od//ufxtre9Dfv7+3jqqafw5S9/uXpms9ngp37qp/Dwww/j8PAQP/7jP46XXnrpTfcnZTkbEGMyLEARfdhg059hvT3FdrvBMPQAM5755jfB/ZAMIwK6/I+HHnvLBfYWHRyAjggdEVZLj+WCcOvmy7h8sA8AxeMv2exCCOh8B+86EHksFysc7B9is+nx1a8+jWXXgYcAHhJo4BBAHOEpAQ/vHJaLDt4THAVsNg9AGKCtdi2wdSghkLZDo1JQLUEmyk8XDfxjDMVAiZwYMOXNRUqb6imDlVyvIwwuGZAhqIQRJGcV0vvk810juV5koRY4lu3xSCiprVkAmVpI+iyUpoUeq4zFnuPS4YpStIDYpTxIxZdPv0MxbCkjrZxEG6AFFuzQRcYxB9z4xPfgPZ//DE4cECilZyef74VBEoJ+0Y3eeTM2uTi1NEyk0qvvCOvBKOAEwKxWKywWiwl/SFzxHC0sb8nvc4K+ZQDZ74D6suLWeQYC5wP6aa1QjECMJQ14q05mTndRhbSLDGZ4cvCKf+cUoF07lZGF2vvWalu/b0N/9Xvlp/qnQZamhy4TQIh6R9SujUrJqbmojHAAHSjdx+YcqMu7q2Jg5ztYfCRQABwtwPAIqC4rlAABAABJREFU3QrDwSV85Ec/jx//m/89vv37vge079EhYLUNcPdOcP9bL+Jb//F38a3//Ht4+Stfw+vPPof+7Az9dotIAHySEZ1zWCDtGhEzHPLayjIk7ZImJ1WSi/J7UtA2dMkCXjvH4/PpXxJNDkQeyCtZ84Gmmy56l6TF83a+9feWZ6S+Fn9pud8Oux7/iV5IMsIVWREy4EqhBwyEWIxj5HXlGsaR/l232wL3ejytnzKOOaC4S/60DBdNZ83jc3SUfzokUNO+Dfzz2YeYHVsMyJ1pjqikaU6yJpHX05jy2Nar+6LHZ/vXMrbn6ttlsOwylnadzZnTK7pNrWfn+qbra/Uz7V5wEYR5VY8OU0OT0q9US0n3r2mn9Zn+vTxDPksbB3D6O+XtmmbAs3/Pyf4EczwcdblehzS06Xuahq26NZ3suEvbme8IiQfHn+05I6IS+WQ/nystfaf7Lriytc7yX9j22/z3GHY3/3x6RxfNW2BOuoozHmBOY96BRc4rf+o7SL/5m7+Jn/iJn8AnPvEJDMOAn/u5n8MXvvAFfOUrXykZ3v7+3//7+Af/4B/gV37lV/D+978ff+/v/T386I/+KJ5++mlcvnwZAPDTP/3T+PVf/3X883/+z3Hjxg387M/+LP7cn/tz+OIXvzg5aLqrxBjw4MEGfb8FI8L7tEDIe/i8QPxigaHv8eUvfQmvvPoKrl6/WsCicw63bt7C9evXEWKE9yn86M69e/CO8MpLL+JrX/saAGBvbw8nJydYr9cVc0dOOwd6Z8I5h1/7tV/D4cEB3ve+94PyxarL1QrrzRbMjLP1GsvlApFjNuS2WK83sEwiC5+Zc6iPy0o9Ce8YI4YhYBgCui4xS5W6GUihcKzTgdeC0oZD6JC/mBVAQBpn0gUppG6RGZezsUeUzm51XX1WRO/YsPpcFEnpS95GnShioCwG3U+9wKwSLWOKtWIUINFKv9ry6giNbPjbVLGkuQn9FuRRklucnZ0lmifrr6Kx1KsTQUzOWIhhpL2WFyi6f7I7lX5iMo5x3G2h2BpvpSBM2zVIfXNeHd13a0AVgJ/9ua16tTdf+ljOtJzTZmt9EFHaOVX9scJ4F6Cw39mxtMBDC7icpwBsmNjcGHX9A3O50JUZoJjWmWNgACN6AsFhG4EuOzyic3jsQ+/D9/3ZL+DGozcQVl0yrBgYzjbY3LmLO6++hme/8QxeeuY5UB8QN1vwECDhihPAwzzhbT1+nbSmZRBaWuux6s/Hn4Dm2hqk1u3bOZgDFa0dES1brTE1VyxwH2kwz28VbzEDbtzhFQeJc66A94usYW3QgMd3JOS41WdpR+S9BtH2OTtXFb8zrBqctKVpkt6PkyyW1iFmx6f7Z+cOQHGUzRU7Bl20DLJ91ZkHq/aImnOe7uh5c7vEmk67zh3bcdj+yHc64uI8A2oyN5gH7+khVBe/5y2RicwrczkzVtunliyXcy7y3BNPPIHXX38d6/Uai4Wv+4G2wW2N2tg4Z2R/13xQYRu1PmojcOoQkL/1v4pPGotGH6uo1vSOMpULbbxFVLeo++Nd4tn0ucjc80uLxwRHXKS/b2aN/KkbSL/xG79R/f3Lv/zLePTRR/HFL34Rn/nMZ8DM+Ef/6B/h537u5/AX/sJfAAD803/6T/HYY4/h137t1/DX//pfx9HREf7JP/kn+Gf/7J/hR37kRwAAv/qrv4onn3wS//bf/lv82I/92IX7c3a2hvcOq9USi2VXBM8QY7okLY7C786dO/jVX/1V/PW/8Tfgu4ghbLFcLnDt+o0EXCPjbHsGZsb+3j4ePDjGP/t//So2mx6+63D/wYMU2paVgFjkIpSlbRFGb7zxBv7f/9Nv4Gc/9J3YbJNRRM6n7HbM2ZtP8K7D0J/i9OxsdpwFMJJkw/PJKOoHRCU4RYjpOHABH9p71xLa+meQM0Y0hhZ4RxhCMkqTETbAK+CivQrAKOxtOkth9KmBMS5wWcga7DG4XESn69f16EQN43mW2sM6d+ZEl5iTFWgjrqSTnxgVejHn92PE3v4eOufB/YAFORBCZSDJcy0Bqv8W4auNjnNL1kha2BRQwwC5MT1wbYxK+FFbgNvx7uyCqlPT+M0IMFm7Ok6eY0DMOx425AcYlYxdE9wwkSYKRvGQGuzsAewW0LP9aIGglmE0NtcGjruUmlaA5xUNdCKlf7k1ePLZuGcsOBtOziN0Hv3C46FHH8UnPvuDePIjH4I7XCHmjOybkzPQNuD2qzfxypefxqvPv4j7R0fpUuh+SJk6ncsXIk7P+bSMQU3HCYA2Y5Z7zzQAmayjKgykTXMrG1uAsgUm5/qnw3bPM7JafGRljAUPlXNJnd+TbG62DoZcujh/wakdVxqDK1c3zPGt7qMGfNb5ZsfYogHbUCv1jq1vpAUX41vL+9Y86vFJHXq9nidnW7LfjmOOXwBMwhL12GIckzaNdxnOdmVn/6xsM09l4LpbFllaii68iDwvdTKXsDDbr9yTyhDRtJsN5TbN2jWh/677WK+jvu+xXq+TUR9jobV+Rr/fNGzhJ3S5CM/pvlbRQcYQmaOrfmZu/mQNalnU4s0LqI5S5zju6XdA3vmhdNYo4Y6LVS5o4c1gBNv2m3n3Tz3EzpajoyMAwPXr1wEAzz77LG7evIkvfOEL5ZnVaoXPfvaz+J3f+R0AwBe/+EX0fV8987a3vQ3f9V3fVZ6xZbPZ4P79+9U/ALh06RAHBwdYLlNWrmEYErjNuyXaW8kAvv6Nb+L3fv8PsN0OAAjL5QrL5R4YySu9XO4hhIjNeouvP/0NPHhwgq5b4MHxCc5Ozypr3AJW/bukA//KV76Cr371awAchhDRDwEhJENpf/8QRA7b7RZ7e3tw1CHFUddeagviUlgd52x8hJQ6mrBeb7HZbLDZbMqCkBAzRl0XoGNoUf6WdmNMiRjEGJDwizlLPYRQLqJN79RCRId6tUBRibOdMT4cuco40vTWXhd7Mzg1PKbyT9/dMFEQXAvGViY53T9mLuEBlIVC6Ad0zqfN/HQMqyk8bYibnp8WqJf354Bg+qOeoyoxBU09fJpmes6k2G1+274O89R0kc5IfVZpWGEtfNACbxXvNTyiuq+6flE+Ra/OAJo5sE6o32vNla5D3m+F7ehxWjCgdzV1HXMhLK25b/XNGg0Vrb1LIbTeocuXCTOAHoylX2CFBUAe7qFDfPePfAY//hP/PZ78/u8BX15hoJS58ez+MY5eeR1f+8+/h+f/6Gt45RvP4vSNu6DNAN70KSySkkGrk53MgbepIcAVjXTRoMLOuzPt6frnAH56v46rt2vCzs0c8G/JHTsvMr5pH6b3/LTmvjXvdregalvtEFu+kGftrq33vlyPIfW31vocWLP8DqDaXZrMremX7aP8tAaN7ct5O6n62RafMHM559Hqh52bypmn+jgvF9sOEH0WVepohSO36DsB7kbW6bmf+9eilZUru+bHtpX/SOGHWdfZCJHJ86pY+o/9GkF90UOGNnqnetx9GtdxjBGvv/76KIdN260+ad4q/VIh7fJ5S6cUbKUMFtvn9OzUIWrr0u231pjlcbvOK9rOjFnoZdssv5t3yhxQem7oh/w8lfPt+lhGi05VWB0wGb8Vl7aOBgvNlv+qSRqYGT/zMz+DH/zBH8R3fdd3AQBu3rwJAHjssceqZx977DE8//zz5Znlcolr165NnpH3bfnFX/xF/N2/+3dn+6HvS+HI6Lwf44KJCtUiR/zBH/4hPvih78BytcJ2GAAGhjBgGALCsEWMDO87/If/8L9hGCKcS+CqH3p0XYfFYlExAzOX7HXMjG3eLUqfA6+9/gbe974I3y0BpLCr9WYD77qcaIGwWHTZs5cOpjMlY++VV17Bo48+ahhIFmMykoYhIOQU3n0/lJ2tamHEOpQgvT8yoV7YlYeZU5xn5vECOpaLJZzzSUhlhifkg94sc9IWnHZhVAoHKHOllYssVH3wsbxjBNYuQNTyLkk7ti/MXIWSjEIuJnPaCqJSb0qscHL/PmLfJ89rzHe7uKlXSwvCicJhTFa8FrZzYCzdJzMdXwhh4uWqgIqjqj1LZ/v7LuA2/o3J9636d7VXtZkeLEBq9jmrsNOXsyBAfmpeijE2Qy6A6UWDuu25HSctN2zYpu2XVpytPuvnNIhp1WdBWfk8x64LAA4cQZ1H8A5nDnDdEu/6rg/iI5/7DK4++QS2HWHrHRaR4bcDjt64g+3RA3zrS1/D8994BvFsA8ohxIkOyYHj5MwcprzcAhFzxpCsSaJ691jes+C5OeYdgEOoIvOjZaS8Y0HtRIHvKO0+tQGzjF+Hyuk+zxklRFSSLWggysyIiCVUeTIu1PyinUIpa9aUlucVcdBZ2lgwZ+lD+QycjKEVgmT74tw0nHd+jqelJVehONYaIC1Dp7xn5saC3V19sEB/UvfMeHTd5+lDABXwlfVmnZjV86ZNKydb+rKsZaIqXXSla2ke9M8abeo3K4N30Wisf/y7NuTq2ufqmfAg13RqyQW7FnXd075jNjux7q9eWzIua2zsoqNu0M6z3v2dPi79zcDQ9g8JRkiWxLI1xHk3VK0HG3KOGXpz/cEsbd5M+a9qIP3kT/4k/vAP/xC//du/PfnOdvSiwmHumb/zd/4OfuZnfqb8ff/+fTz55JPVO2nBMkIOAWvVRCBcuXIVznXYbHow0tmcvu8Rh4gwpMOqQwz46Ec/hme+8Y3CZHrbG5CzPwP6YSh3EglQ8d5jsVjgxsOP4f0f+CDW2x7LvX30Q8CmH5LiGAL291bw3qHvh8IsaQFFrFYrPPLII3DOYRgGnJ6eolssQeTR9xuEkAy3YRsAJnTdAs4t0HV+Ah70vFgwbedML9oYYz4w7XIyjJRRLRmJhajwXZeSUDCPWcbijKBzAIfRYBGB4pwrQE0Edm3QTGd01+JP77bfk2IVjxThpZbhZGurgAmyxyVGPHLj4RTi2Q9wmApmrVhsPwpPkyv3R8z1u6msMcoZO9/SPw3Wi4EcUS7k1WNrjVf3w3qg9DM6VHFO0c+d75pRcYimn7q8WSFp+2yVm45Xbz1rizXCmyMwIEDXJXx/EZByblGg1s4LgHKw14sh3nUYPGHwwEPvegc+8fnP4p0feD/QeQQieHbw64Dh6BgP3riNmy+8hFeffQEPbt+FX/cIZ1u4bvT0ifq04EEbdHO0aoEIy0O79IwOs9X8J3/r9VG/P+2HljO6DnvWs9X/3WMDiMycNIww/fmu+sbfacJbRFSdY5n2rwY71ZyZ9ubrqOfA7qqUqyXy9zZ1v3MuEwXNvtixml5By+wWb7RKi87jHLSfb8lAC/Q0r8/JCxl7MSRmwr+TAzLpMssH5/GD9GfsnzyDiXHyZsouGajbTX8k7GV3RWXeI0932/+kZVd9rTNZSR7xrIPQlrk+VrqjwnTTtdI6o5gbRuTppeit8dX11deazI3DyhTtCLDPOCIw1Q6por+MfaR5U9dHpT4u0VzNnTP6k829lusXKf/VDKSf+qmfwr/6V/8Kv/Vbv4V3vOMd5fPHH38cQNoleuKJJ8rnr7/+etlVevzxx7HdbnH37t1qF+n111/Hpz/96WZ7q9UKq9Vq8jkjxVuDFTBBUgQy7SLgvfM4vHQZH/3ej6OPDBcCNqcnWC6X2PYD1qdrePJYbzdYdB2+/QMfxMOPPY6jO3ewXK1wQMDJyQk2m026u0YrR0oGStf5IvSXqxX+D3/2z6JbLrEdBtw7OsJqtcJytQKI4BdLRDiEPiCEHs55xBiS9y8Q+m2P5XKJvu8Tw2UPT4xpETOAPgzohz7TAaV9vSitICUaUzSO8ei1Ui7GHiWLvgBqULr7BABFBoVQspNIusl0MG/qiZffdZafMo+mXf2vAqSYCj1dv/5ZhED5n/Z6YOKF0O0BgCfCeGlq5qws6OVES3o+79DAFSNxy4zh+Bgu9HjjlZdSalGOYK49oBOwnQWLnGuLM0JDGyZpZ21cBwkkEMj5dHcGMKZVp9EI0vRqlZbxyOo7/RkzCugd3UWjkdYyiixorp5ToE0OeorEZSAhe3mOxhZFLLcMCr0DuQtk2P55ciVWOY0zlnuadNGgsAWm7XPz63N65qnwZiEqQfZjKlCViANWu16eAQ+Xsk66lEkxpW4FuggsODlABu/QdwR3/Qo++dlP472f+B74S3voQfBMWEZgc+8Yx7du4/VnX8Dz3/wmXnv5VVCIKQNdTBukoujgKGV5FF6IebpoHJNzaU1pw0SeGQ2dGvBbcDVqaFZ/c54r61yRuuq51r/LO9rA0vOlL1J2TjzmYwjn2FYjdFdNVFkb6lPKcj1lr+Q0w5wdPTQaAFz4YKZw4nXOshugvOappO0dx5t5hdxIpYYRIGvL8ub8GPUcjs5DLdMtjaWtjNwTjSmDvguAp11Gw1h3+/uWEXzBoxNV3SNfTyMSdu06y2fyr6aLRMlk3iWAkPVF4eW8i+OS0xdioJC42KIaEgE03XFgRo4MmeoFLa9axoc1xivaxCQTnDgQs1gQeZbUa5Heef27yoDTmKGch2Jk5yPKnXm7+JGzUGC05W7kOEkiNVeq8do2MO7uSNIunZjDGtC636Nc40KbDA1SdlFGSSWv15DoXqK6f3YXvD1nY5KM8h6PVwSIfC6SjXLW7ZK6XWER9VeIWVfmz5zmX6Mfk6zipDfaFE//z99HRes/bvlTP4PEzPjJn/xJ/It/8S/w7/7dv8O73/3u6vt3v/vdePzxx/Fv/s2/KZ9tt1v85m/+ZjF+Pv7xj2OxWFTPvPrqq/jSl740ayDt6BGSYhwZ2jmfPi7nPgDvO/iuw//5r/xlfPv7PoDVag9O0nPDJTDpO0QQ9g4OsTo4xP7ly/gr/5f/Kx66ej0LjgR8zs7OUnrvrsNyucRytcJyKVnxfGZmh8899Tl8//d/Ggf7h9hb7WO12sdisQKYcHa2wdHxCc42W/QhMZHL8bnM6exPDAEcxMPCcJ0Hu3RwOoIKeI4peTZC7CuQBqTF0fd9Dvsb89aP634EMNbzBeTbkCnf1UQEch2YOvRMYEqJKiSu2MsZCiVI5TupX3bdrALWh2n1ZYfVQqYpSGqBeD0W5yjvNDBAjMgBIQ6IHDLwqBVbESTM4BBTmmkieErpiJ0AU/Jw+V/OUZ74DCkkK/gFlosFVjHg6PWbadesAYClzcCxpFaXdLzklERS4yrjK2mQHZDPb5WrkQlpHigJOs71CfBK4Zh9FVIhXh9N18prZP4hg7n0u0t3geUMiym9qQjsdoz7RDja9lxKIBCIEYgz38vYINoVommJRsNPj0mLipahYs+STAw3ToopsRCX37u842nbsUp1bvxVGxjli43Pr/oVE1+mfuh+5d+F6jz+G/thYvIpp+/3Hn3n0R/s4z3f/yn8+b/5P+CDn/0huMMDuMhYBIY/3eDBq6/j5jefwdd+93fx9B/8AW69+DJ4uwU4YogDgovgjuA8wTuCAyuZk2Yv/RSu0d9x9Z3+XMBmy+gVj6HwHBfmcAlggcpP5HWrmGdSny6yRvWB+hiTbB8ziaa6YxR7hcpP3a79x4qJs/hId0xxkgXl9KGjlAHVUf5erj6veUjzHSEb9TLHoCLDigGGZCSP6cDrO2s0fUUutOjVWs/yu5aruo+y3rUjwYaHQgy7vP4II487qs/jhMb5x5bTRfO+LrvWprWQ5LldZ+laRpC0b/tn13nLwBvbYRCJhI8ARQABzAOYA4ginGOAIpwHiERiRsTYI+WhDQlfIACIIDcmJYglDF/+Tc9f2XLeLnBFg3yHY5JhocgvOQohulUukpc5t3qhciRl+Qfmshve6kvV/wa9ZZ2jpTcwNbrs3Fk9J0U7qicOB0M3y5uenJLtSr4r48KGqkoCLbvbo/vT1u+j3NWYmrPBWPQNZdkuP/M/rYs5YyAG52teRpzANK6oln4jkvlMRnUMsfyTez/F8UNAuprCYMEZNmyWP/UdpJ/4iZ/Ar/3ar+Ff/st/icuXL5czQw899BD29/dBRPjpn/5p/MIv/ALe97734X3vex9+4Rd+AQcHB/jLf/kvl2f/2l/7a/jZn/1Z3LhxA9evX8ff+lt/Cx/+8IdLVrs3U7QABDCJ3ZRY6ieeeAIf/q7vwmqxwOHBQbHq+75PgvYwwPtFUlIxot+u8a53vRMf//jH8b/8L/8zmBh7+ZJN7SUIZifEe4/lcomPfuxj6LoFlstl2jlaLsv5Je89jo9PAEoHpMktAB6w3aRdnWHIGUeQE09ABBZDYodDvkQTSCm3BxPvrUGi8w5DGGCFTAuIWYXm8uJ37JLQZcZi0eXvAYAKzcct9DHjjcxBaVctTO39CCGAYltpcAb2sryssNZGmBVG+jNRYGMd4+d6l0u3e54naQTSSUJ7cnAR2Byf4PiNO9jcf4DLPG5V63fSuHaXOeUvFLHCe66/8oze+ayFfP7MPG8NJGlDF1JCu+UV3jUmbSwWWmahCpruplg6aIAFHkGT5glAe7um4xZlY7/XY5oIcsqodmYGW2ur1X9tGNm2q/f1em543eeAayCgd4QFCItAWDGVO8j6zmGz6vD4+9+Dj/3w53Djne9AcElJLSKwJI/To2O88fKruPnsC7j5wku4ffN1xE0Pn/vRdV2RO957OIjXs71WgWkiDesw0A4SfTZCQlJGMJHob4GqpkHrDIylkf1cXzjaAtVSJvHzZj7maFCBqJl5k7937fLqfrQA2oQHZ4wB+7ztt9C6NZf2fb2W7JrR56nmZKsFdLtk78XOSbTXx9zcWNnQMoRa/SjPu+mat/qk1a6uy+qk+rNQ5mOsGxCQbnX8bFFfi/yW9+z6tDxlf2+FrLVobPlBGrc7VqWejF10O0Uex4i8IawuD8+g3g7VzKc2aCojpibLBBNpGlU7NzPLQvON5UFbLD5pYbS5MrdO7OeChVtr7jycc5FSv592Cr0X/ZbDBjFaSeethV2l6ANMefSi5U/dQPrH//gfAwCeeuqp6vNf/uVfxl/9q38VAPC3//bfxtnZGf7m3/ybuHv3Lj71qU/hX//rf13uQAKAf/gP/yG6rsNf+kt/CWdnZ/jhH/5h/Mqv/MqbugMJmCpYYdpV3tERwwQADg4OcOv1W7jxsMNqtYLzHotFh853WO7v4QwbhCgZ1wYMYQCGId1VpJSyKOzi6QU1gePpyUmVKQ1AARQhBOzt7aPr0qazc0AIhL5P7cYYcXa2BpAPTusc9hFlF0CMDTkDpUGB/tsKK71Y7YFOayBp40iY23cdooBHuXSQkqFEIqhht38zHWhkbp16UtOpeYaK5gWMHqu+HNZ6Da2SY64FiBYSWgja/s2B0Rhz5rohYuUWuPdqApMuJO9MNAZS/qOWyo1i56YYVlTTbPQouUnojhzytnxRtZNVREugi4E06QeLs6BNI+FbOx7m8T4Q/V7iERrbPEepaPoIuBUAVsuTdljD3Jzqfs+B39TV9t1IlhYaIFnvuVbALQNpHMF8mVMS4o/1kdBFAjmHrQfWHXD4tsfwPZ//LL7tIx9Cv+exphRy5/sIPj7BnTdu45UXXsSz33gGd1+7heFsk0LqHFWXDttQNOmFNeQ06JPftYy0Y9fGrmTlrNox/G/nSvo3R69dhov+bHzOQqhpGvJdxpHQ6qLAYFxb80ZSCxRrPtO8FcHlHJKVhbZPQv9kWI0gsGVAtEKHbJIJ5no3Ts91y6FieaXQREIPJ3RKAKxF2zcDAGXdixzd9Z6lXwgBDmlXX4cstQB2y/Gj+95ydrbkqAXhll7zA0Xx/MuFpqon0Kh/Dtzb9m3Rn9tMsOO7KJhBl7JOGgZG/TPVEWLKngYaIyHmip1TMbTn3JW6/ZYjTfdp7l1LD1vmwuCa4dZI9Jzed0nFqSh1zvHvHO/N4UZLhxYmkXcksiIlHxsNVo4RnGVJS/dqfGJlDLPRiSJ3yMiHN2Fr/akbSOcJdCB19ud//ufx8z//87PP7O3t4Zd+6ZfwS7/0S3+i/ly5cgWHh4fw3pczSl3XYeG7Kl0mEeV04MtiMG03GxCAhe8wDAOGvsemH7AdejBSikJQCqk7Pj7GwaXDkqih7HhQMo68UgJiBO3t7WF9dgbnF1XmsO12mxYD+ZTcALGE0i0WHfphDYDw3HPP4f7xfbzv/e/HYrXMI+ZkxIWY+8Doc9IHrWi0wZgAS3vrX8Yhu2lN8MijUkoKIxmQactTFk0dzxliKOB04mV1gJzq0HG5SYHarCxTga+Viw1H0otcwiBs3PtY/5i9S4pdnC0goH+fKCgi9CGAmLA9PcODe0fwuZ0hMNiEgO1S4i1hWrUn4XQKDKknAdS7EkB9T1YLVNmxzoLuCQit+2j7PFesYKy+U2B0TglZQSq7qzLG+pB+MmYEaLfCQ6zCaykAeV6Us+6H0Ne+p+fSAgQ77pbxVJSMqc/yp6UtEaFjgg8pPJSXHg8oID50gO/8oU/hw5/+NBb7+xiWDrwgYAiIZ2uc3XuAZ37vj/DSM9/C0e072JytEx/HdIbQ5bWtQ6NKn1V8vAbEWjbpneUWr1me1rStw2/TvNo51HPV2qGbA3yp3zWw1fSUOH/7uf7dznutvBu7K0C+yHvqqW8BK2ZGCTsztNe816Krrb81/hYtYxggxkKrWLDZAvYtI2GuDxocVmM3BmpNbxSAaw12zXOtObCltBunzjvdrl7nFd1Qz4mWC/KcDmfU89Yqmm6WJprWE73f4IlSpxjLIKTwvC6/K66wkX6t3W09brve9JmzlizTelpetWNKhgCDuJ5LXSQMvTjSGCC/e5fUfmrluh67fK/HYt+xz2p+07tTQkfpm93dkefk3WEYxrsXqzbTmOV97RhNj7SNyQnt1Lt2rC1+nMxNQxfzOJmIMWC7HY99EBGQdbLQxm6IWBlR7xArOuShxJiOJsyFtZ5X/qtmsfv/h/Lkk0+WsDW9MDnUCxpIhtPjjz+OGAjL5RK02kPf9+h8Sovde4/T9QbOewxDj+VqibDZ4B3veEe6SKxzWCwW2NvbKwJvu92mg/BGoa9WKzz22GM4vHQZq/2D6ixO13U4ODgAUQciBnNKzLDdhrLIYwx4+9vfjhubh7FarRDy2aEh36Mk3qmUtjk9D6TzJva+IKGD/GwxkBbUE9AuEcGUDMF0s0+Pfhiw5OSl51AndWjF3hYjca4vnPuPltduXJwiNPRdGnbx2xCBi3iXnXPlfJQUK5ws7axBFR1SvCwcVosFOt+BgHRH1JxTj0aQZ/vWmqu6f+0qRWHYeW3Rqvn+BYVMC6Drdlt12rltKf5oxt7qd2sumWseqQAIU0mzLs4TW5/dDWiBlqovVKtTC4AsXayi1O9ZAGZ3UcnwSWseW/0lAM51WHtge9DhsQ9+AJ/40c/i2tsfB5MH3AIdM+i0x/rkFK988xncffkmXn/2Rdy7dRsc084x5fN8IAJ1fhaMcWK+CkBautl1tQss23VQz89oKGmwrNuzYUq6Lg3k6jkav7dgoQVM5W9Nk5ZHuDbu9AzVczq3Rvu+B7O6xgK157kFWmq6AWx4qLUWNf3S59Nxl7XaCDO0MsCCLk2HFk/Myp9sH83xihiNtv+27Ardq/ohbeouzMjkij6KNm05VTtyNJ9KHS1dI+/ryIw5Op4X5izPSu9S/ZrXa92o267eN/zTjAgwdKtwgUtJJazDMde4Yx6TPBTTuYldWrRPtTbHIIat/q4lf+x4hIqtfrbwxGQkhvdb7akaBUIVXTfWMbcHNu23fm/Cv+o5HeIs8zu3Pu34hqFPTm+UpVvYak7PtowzGXeM41n9CCRHHdX1XQTfSHnLG0jL5RIHB8kAkZ2ZdDYnCZ2uSyF0oHSWJ4QA75bVrskwDNjf38eQD64v9/awWCzQbzdYLBZ429vejsPDQ2z7bTlHVN8lg5KSUYTdYrFI9xGpXYwQQroPIANx50SgDBi2axzdu4O+38Bli3h/fx/7Bwd44aUX8fTXn8bHv/d7ISFhHDnveg1wjNFQiwx2bUaXohlcA0kRuq2wMsrCyKVYwJLG3IWhuiS0MLYRClpZSPpvKUX4EsOhm/Gq1aBGPtfATLcn5yJk/Hbx66Lf1zHy9jJgmUftDdWLkojQI4KJ4X0eEzgduiakM7U71u6c4rRzWIGY+cog6bVbwHBOkBDR6I2boddcf+aASQtY2jlr9SMnbbqQ0NNtxFjTsFXsuRLdxk6ANu1pBR51ERnRAhRase1SNtX8i4ZpGB/jvKE4M+Tz4D1OXMSld70N3/9nPo+3f+A98MtFSjRBHUIfgE2Po5dfxXNf/Rpee+lFhO0W27NN6udikZLIEJWdcsL8DmNa4+2Ux7NUbPCENphteOj47G6jWX8mfdAh0i1vfDo/OT38n94fF3Fr3Pr3VghV6zP7PYBKHluPq/A4mTU4JysqQHNB8CB8aw3O1rjte7v42Y7frsPz6pc27JwBoyy0MrkFknf9XX3Ouz3pus9aVyCvQfm8lQ5ey2U9R+fJRT0fdq4vYiCML6D0VaJD0tfCR+02ddstvpszEnR/bJ3yd2t39aI865wr5/mszq9kUIPfSp93iH0tP/R7Sd7NA/uWEWC/k+91O3N0TaqgXkNFFrvda0m313L+2LG2dPtF+NR+T85BUtaI/tL0bPH0XNhteS7Xx5geKbloecsbSFev5h2WEAB0iXEY6IctHAj7qz1453D3zp2c6ADYbM9wenqKGCOuX7+OCEa3XOBsfZazfoW845OMAN8t8M53vRt92GJ9doaTkxMQp8P4jzz6GJZ7e3jxxRfT4uS0LbztN+hDj4eWHcLQgzji5OQE222Pa9eu4sGDBwA57O3toes6rM+2eHByhsUiMcUQQ/oXApgIq/0D9JHBERg2W2w3W2y2AX1ILHJy1iPGnKpReJ3yQqIxZaMUUbxyHkrup7CCnCNAXfKPeKKU3psI8B5+uQRvNiBSHkaidDapUhbGU5sengjdGCNi6NMOWOZ86b+9t6clUK3g0vW2BE6arvH+DS2opR29BWzDRKzgJSIgAJRiCJMBHAKIU9ZByqmARX8WXcS14pkYNS6DX3DKAiNtiXTgERyPJXuTmHcKwjLPZT5qcK37Yw+T132uwX4l+OUZXX2eWwKNwl4+IwmHo3LmqRrZTiGYxq1DLMs3jtLZgB27pfLuRYylSqlqaQ2ksboaDOifln80zVwOhxXjMGXwSbIlnQGUMaW8VEwEdol2HRxoYBAceqKUnOHGVXz8cz+ED3zv98AdrhAJ8Ozh+4h4doaz+/fx3NNfx8kbd/Hqc8/j+N49LLoO3jssuzSv3tVZu2IIkIs5U98lVIYgmTKLN9bRyONq/NbTHDKPlDUV005O4XtCyeZW6OESxUBqfUOA0Mh35eA8MIYrUs4OSuP6Sv1TU+oldxSS0yF/QZT6UUI1hY95ylcobcUc0pvu2SNKu3KWJhZQtcJ6gZz8K6/Z9IxyChCXLKchamO1wb8zf2sjLdGvvQ7OC2+xILBlMEzpNf6S1UX6SfXzus/nGgSqDxqg2c/rv0fdUhtA0zZqOsQyNyBGMeW5fs/qj1af7O/Mkoobmd9SxS0D2Zaq/yKzitBKcibJv3bY1a75bdFB972cRKEkhwEGB64ccrpOCb93qOVmeZb0+PPu4Y4dFOkHc8pm6zJwkagXsOwYzuw8NQyG8jvx2DJlOeCSLA8x32FFnHbgM0+RgyTSNaFkdf3TcHguU6blQ/oA43pBvd7FcWix0BzPzX1mQ/LmSmRG551K6EUlJfsuHa4dVwV7ZPnGCACSflPKp9S5C+O0ylveQAJ5gDqQc1jtpeEyGDR0wBARh4jNZo03Xr+N1cE+bt++i3sP7pdsdMuzU/T3e7xjfw/UeSy8LzLDkUcMAPkFrjx0HdvtGpcvPYTOv4HjoyMsuwWOj47wbTdu4D3f9m587RtPY9v3GMIA8oT1+gwxDLj12m3EGHFwcIDj42MsFx3u3buLyBHXrz8M3y0QQsT+4WUw99hsThFiwDYMCDHi+iMPg7oFNtsBznmEvHPUB0YfknJfb/qcb34MvxNaFKCA0Wutd7uAFHKkDYOykPzoMXYAtsMAFyP6MGDZLRCYQJGwIA8QY+CAAC4x9cA0BCRhhGkMswDUftjC+3SfkywCVkKh8vhgXLRakVnvpwZkMn75XEorxMH23Roy8rv89EhZVUIMcI6xdA6OUZIzZMiv2h0FXtPgAhIAVvf+RI6jXiuHmqSuEUxoYd5S7lPjQANd+3mbjmOdRdtOBVUU4yhLbrWD6LyDzsxY3supnVs7bnPj0IaVDqGrAAHQnDcZQ/poqjBa4VJpTaH8zCawdKqgOc1LWtG3xiKKOv1LwxcAD0oOCpezzHHWhpzzevuQ++Q7bAjo95b4wMc/io/+6Gdx8OiNlAY+RqzIIxyvcXznCDefew4vfuubeHB0jON790AhogPBB4AQ09UCeXyOxp0hn+dGsm2mro9nEvXcFDkj4wcm9E0GFQnjFmeTnn4GilwRoFxuduHUvqZtMXQpgRTncuISMdjiKHOQWTPI2koKoCwrMbgENEN4PIRiXHluAzkiQpC5yvXJ77IzpumgaSc/bax+ZOFVKoaWnOdI9M4JC0CjDBeeM+dDdLH9tudSW0V/p3fAWk4BnY3QJtyo5rm25DIAHcWBBasF6Jm+WSArgCs0oh5acoXBcOQmcyNjbBtVXIVcMY+6Swx5kQfSngXBNnR7bFOBX1BC4Yhg7hFjvWM2JyPL2EjMCi7OAUZUtJ6e/bHzaeuf7ABRWU2jEyL/lGspQALm2w4kvSvUOpOjZXHlcFOl1tdxlCucnB6lPTVVLdrNAvsk1IpTSC6+dV5yeqZRE2Vq8yibxBHRwhatuYQxfCzNhBaF8LmII6cV/l5qnsEMltb2Hf15+T7/XK5WACdMxFmHiGxpyR+bO6AYSERIl2qb3SLmfL/WFNOdV97yBpIOp0n3EDmEGECesH9pieFsg9u33sBmu8WDs1O8fusW4BzOTtd5Yj3WZ2s8+sjjYKSwtr7fIuSzKCfrU8TIWO7tIcaAEAZcuXIVZ6eniDFg4Ig3bt/Gd3/PR/DI44/i3/zbfwvnO4A8Hpyu8eIrr+LsZIODgwMwOQQG7p+cIETgZL3B3maLPfZppwiEW7dv4/Bwf0zzHYHNZgPfLbDZbBFDj2Gb7q/ptz2GIYDgsF4HhCFMBNRisUAIAev1upyDijE2L92V98SCT+GILjG075IBxqOnhfJu0AicuHhfGJzDCEclrHdFivBrGDKtxakViDZutHdVwuKkWEGa+KXO0CKKrLU9a8NatAAoCTqsQGcxMgPWZ2vg0kPjGHasW91Xe3BSl9aBylZdpa8ArJCzNKnqAyqj5CIHU/V3eu7GuUYxjhjq8lskG4JdDrtUnlAxuXaV9pZ6vpdB0aI8kwFu67CwpU09r5iMqUUP2xcbBiF17M7UOYbsWcUTCdg6wHG6/FUADIFBgbDPHmcOODtc4vp734VP/shTeOSd74BfLIAwoCOH2A9YH93D3Vdfw8vPPIdXX3oJDx4coV9vwPnCV1dAxtSJIT/tOtXFhnQWhU8JvrTOKGi5IkXmx9ZXh9kBcqWA7aPIjUm4sKbpOcBEnmnNY+tvqWcXCKnBWh1qMuEhMx4plDo56ccI/GvjRNdlx7erLZGxeuds7j1b5sYCTNOSz8kj/fsuvhNeiKaeFuBuAV1bf6FFjEk+Gfpr8DZHA91OayyaDtqxN9e/XKupk8sa0HKqRQPp01xobLV7ORnN1OiZ9m2sx37HqNe2Xa8tvioGqHGeFZqbi7pF1+mWdtHCzjeLXpoxAmyRz+ZCu3T9tj8Jh42/S/uts9KWRlQM2/NLvUama3uW741c2jVPmh563YgjLBYnkBuxALXxmaVb5YTY0fYft7zlDSRhKlEMe3t7ODg4QETE5uQUJycnuHv3LtZnZwhg3L59B4888TYE7rFcrXB6toFzHvcfnGC92WBgIAwB2/UGjoDbb9yBI8Kly1cAACEMuHfnDIvlHvp+gPfAvaMjHB0d4d3veQ+uXb+ON27fQWTCvXv34dweVvsHuHXnLpb7B7jxyKO4e/cuAghDiBgC4+7xA7z22us4Pr6Hq1cvYZHPB4Qhot+mZAjb7YBhSJlNQt+XtN4C1vvtFuv1GtvtXsk7L/QB0lmt9XpdzlBpT5+lpTYAIkdEdpnZk8EQYr60K6ZbuyMPBao5l+5bcs4nFIda+TDzePmtCuGQQnBwLi3KYRgqJWSVkV64Mv/CCxag2DCzccHXhlbpB1HZxZqAEyX0rCEnnznn4HwyuMHzAm1OWNV0G+lThb0QNZVOqc98bttqGk07lDOnP2aEJTX6PSfQlAAsikm8YlTAHxqK7rw2BCxoGlka2N1GC2h1vZpvLJjWP1vgFjyqak3zXUqmmFVqYqt55bwrwEBH6ULsgOSsOHWEw3c8jo9+/tP4to98CG7ZAeRAgUGbIWVVvH0Pf/Rfvoi7r97C6dF99EMPdClcODoAMV3MOmed2vAZTRv52/a7Wis7aJZMsimYnCuJpkkutfqizxNaY0E/bwEkURsMj8+jWUdGIBfg/3qXQPNVa2e7SQdKF6ZKRsYic4pDq214tACi/V73RXZ50kH63fNh+9kyYoAxhEavv2oOTF+0Q6EFascxTN0qdr215LzVDZXMUPJhLsxOvm/RsmUoa0CsnTV6PVg9NfY3jXOcC/1vd5kDxDXvy9hrGWD123l8IM+V383ejrTVMjA1JpAdGVsf8rdCi1zJxDg6r69tHmqPY66euTVm7xxqzedceKrm/WnIYr2DdNEikRot3bZLVlXz0ZBvVqZynocURknYbDYyqsJTrXVnadKi9065Sm0a7ypveQOp77c4OTnB9evXU2KFvsfewX7eXRlw+/ZtbDYbrDcbXH7oCjabLV69eQtdt4Dv1iWV4p17x+iHPm2JxmSIIEScPHgAjhGPPvY4QgzYrNe4/vAj6IeQzizFgBAjnn/hBbz7ve/FZ556Cv/Tb/wbxAi89PJNvP7GMVy3gHcet+/eL0rHOYdu2eGNO/dxcnKGvh+w3Z7hwdkDHF5+Lzwi+n7AZtNjO6Q2hiHg9PQUJ/fuwfklBnYYhoCeAxB6nK3PsF6vcHBwUOgjyrfve5ycnFTGUUswysKuAE9+nyl7Poa+1E0SuiJ3MuVL2rTwF4Yt55CM8B+VA0A8ZrSR3S6bwlz6JYtFFppOKy7vWG99LRxc8WS0Upwzj7tgFtwSUbVDZoG3qATJikckHv9aCM6FaWhwp0MMdN/S79MLQwGB2VMBZoWbnmciKvcojDRSY0bbIzu20VbqjBRKB87GsRNAmc0hUtCGkW/bTnzknYc1XqRoPi7jypXpBAjj/E0Bsy0WOCT+4kohWYBphXxpMxFsMne675M6gSp2vOJJBpacdpCIE88OlML63KUDfOAzn8KHfuCTWF6/jB4BLgKrQAhHJ7h3+za+8eWv4tXnXsDRG3ewJA/0PTpK5zKBmA7RZiNGQhwtiLHzK2v03AO1DaCs6SX2haWRBv6yliQcOFMIkoxkTmFrZ5A+0GzX0zifKWxJr2spIUyzQsp7cr7yPAVtwab1IFu6WbBMlHbs7T07FnDoy5K1Eab/ntup1n0t8f8GMEu5iNGl52FcV3XIaWvcc3Xa/ltDRNNqzjDQz+n3qh1DahusmsZzdGvRaYzAnba7a4205FX6LDkIiMRYmDqSbBsVPzXAbdL5NDG5WnrEft9ylAAy7LYBOweEAYk2GHGCJF8a+4kKkFMYjSQrB3QfWwC/zD1NDWtgmhm31d8WjSx+kGfL2UWeXldif99lGFh+bmGKFn1ba2OubhnHzjmuaJDjEHJSGx3WGmOE49owbI1V3mlFeljsqpbWmypveQPp7OwMq9UeiAgnJyfoug79dovFYoFbx8e4f/9+InIIeM973oO7d+/ipL8LZuDwMN1rdOnwEERrbIctumWH7WaLB8fHWJ+dYbtOdyW9653vwJPvfCe+9a1voes6XL12HTEGvP7aTSyWC9y5dwfHJyf4wAc/hKP7Z/jDP/oyju6f4NKVJcJpj67rcP/4PmIIOLx0CZcuXcKSk1U/JASJSB4npxvcuXcf1y7tI4RsJPU9QmQMIeLmq6/hpWefxXu+/X3olvtpJyn0WHYux0onxjs9PcX+/j6YuVwodnp6iqtXr1YZ+ICaKeU7rbTlv8hInsn8zhAGLPOCoRDSbhNidZO4XgRFYSvmnoYbcSUIW4rYLn4b5tIydqRUXhPUqVOtwNRKsKVwZnfhQkQEY3AooZqRGV0DVJ2neGNDqY7v7BJogPNTYW0Vru1DS+mV39MHkzbTewCUYiIa7/4AoYRYcLa/tEEAiDJmNaRkmOv50XXP9dEqN/3TZWOiRQf9bMurp5WEpVPrd/tTGxtWcU8UE49+0Ao0McPFCHIesXM4IwYO9vHOD30HPvr5z+LwbQ8jOAYzYRkAv+6xPT7D3VdexZf/4A9w88WXEdYbLOEQwxa+cxhCBMUUlugclXNKXdflGPFpP/RY7dhbCrQ801iPqraKh+r6R2Pf0lZ4HZiGurQBZfvSYkCnvQWAqdEx1rEDJDXk6tiB+lkx2Ow61PSb9fIqrGkNKBmDlpWtNTMHOlq00XRuvdeSj/b91g7sXCFQdZZ2rl9j3xKf2PFa8Dg3Vquraj3TDk8+D4C2+gmgZH1t9Uc/r/l5wrMxu1LIgciDMYaDzxkAlh67+1xHLrSek9+tTm7KtJkQu4uWti7O9xhSXnaN3cE/admlD/VOdYsfd+kC+V6uZ9m1Flv1REwNHP1ey2klutg6S1qGZOt7faH3XNHYphLnWZY5VX/1rPpdirSnd1nny3mRGe3yljeQLl26hCtXHkoXxe6tSrrvPb/C3t4e3va2J7A+u4ZLly7hnd/2LsAvcMmtAIjyAYYsiBbLJUAM33lcunQJ+/t76WxNZCyWK3jf4YnHn8Dx8X3srVa4fu0qHnroIaw3Jwixx917d/H4ZoOPffzjuHL1Bvb2DuEXK/iug/cdLl2+DALQLRaJWTqHPkQs/TIxR+cADLhz7y7i+hSd9xiGCIIDxxRu9thjj+FwtcLe/gHIL3BweAnggM4xusWY2np/f7+AVCBdzPvkk0/COVflv9fKWAu78bvklXfkECS8CymLTgjp/iYGwXcdFo6wHbaIxOAhVmBBwCFQZ9rTiyPdp5QNAxWbrXPw2yQMWiC0Fjpg0mBqAUB14Nt0KxsTA04vZAukrRfE5Qs1R2MsVPXoNq1AKu1g6hkZn2WA2557wlSRWYGk2y/CVgwZI+Qh/ZgBoOk+mnpHJx2KT3SOYmZTqqMtFI3HTrWljfpdBpIFldLPGGvDXZ61QrjQzygKTa+5HS0AFeiNje/tPJe2iMr5tZyebDr3RBgcwB0hLDyuv/vb8NEffgqPv+/bgS5lteqYgc2AcLbGG6++iq9/6St4cPs27t+8BRcAigTiCO8dgiM48iVzHIHG5AcxImbDSdPD7nZYBafnv0WfXUXXVc/dCPgtIEu7R/NtCWi0INmCh8IjRGCTbGE6f7U3ukrnztw0sO26seeadN/teUsLQHOFFY1qXsoZNGfAkwUic0XXydwGevpZ+5n8LWumBfib/aD0j2O7n/P9z0Z+bJ+x2ZVwYnZHLa8L6evc+63SepaZq3NSmudbAHAKVPM/AjhtUYM55jl3E15orcld/a2Grn9XY7e8WvcPbX5layK1jQBbCEg7Q03gn/lRQlVLf9q7W7odS5uLlqlsmuoaoH0O0+re9NmFm945Hu24axuobcOtLVvabc2Nw35fZGKMkPPAlYanWqe08ByQ5noYhtFZ59L52FafieR/b24+3/IG0g98+lM4ODzM25XKgkbOacGMmJMXpIxMDgFUPPMyKUMYig6TLGExh1N0XQfkrCSPPnwVzhHCMMC5lHFjGHqEOKSECc4DcPjEx787MX/28BAlo0IWVBCwTMn4iJEBYgxDDyKGRzYwOO/cOIf1ZgNcvQT/tkfTDouE2Qw9Qhhw6fAA3qdQlNVqVRhIvC5ywa1dJClELln3RKOAcRL7BMopi1O4kU+VAkMPigHMPSI5eNeBmBGHAT4dHQdzBPF4KDFGuaMKpX19xwkMkLdnQFqApWmcZKXcUha6tM6pAEn0kktIg8RDlY1FAbC2DzEmvvGZTp1zWHaLPM0OhHaWPDFI9O4JldTIU+9hXUbAVkILMl9p2ljgGcuzPAHhVmpXQrdp2AjtJHQtKW6iNIbIddhDC7y0DJJdh0O1gBXwBWAMc5KU6nl3ilymI41mhwCOVFcathXard2QlvJtgsbc/kgkFMPHceKvZJSiZIcDMzinBfZMcPkelgDGQIQT53HpsUfwic9/Fu/+7u+EWy0xUIQDg2KA6yPObt3Bq88+j29+7Wu4+eqrKePcdoADoevSOvQLPyZWAYo88p3PRhGaRe/ozYGvltE//j6G7mQuSbweE//od8a2Ioh8kSHpjKXIEAZz/V7LAdACBXp+dR+TgSRzKWGxY3is5l8dVhtDHJ0B4qmVdUD1ey1+t8DGyjV5r4AJA9zHeud3qFvPS/+n4E39w3QH1Hp228ZkGzDvksscuZyhskaYSBK5tkIcQaM8q+u1P63skp/6vEg1puw0YM7nbWXN8Cg7rOHYooVu3/nakWSjGFqGw/h+Cg0Xx5NeS1ZG1e8mvpaQLjkOMsJXKvKAqJ0sRPMeGu21dtdbf0uxO4otB2XBBcCUNrnnzmXnrcyfwha6n3Nrq1oP+XvBQuMr446mxiFzYLySf6zbFYObIW7Dlv5o6VdmlcVPyRMr3yZjKvW0+bOlz1uYSMvNXXWIDNKyV3Y2C9127PhoPhPjqLSh2puTbW5XNixT3vIG0kMPXcLe3t5EwAM1cAWmHg5A0tQygIVa6ItSl8RAMhOc84ohO/R9MoxAwGKxRNdxuSC2JaAllj4p5vECWWC0loGVEjRj+sfFYoEQD7DdbNIdTCpFYoypL4vOgfKOy3a7BTOXxAxakUvyA02bcpaAErgf19LoqZV7SIiyMI0JmIkXK+S7PTwcXM5MFmJeZMmdXmK6rdBrCUc7l3OLswU2ZEytcMLSLqZCtxL6aWQQo7GoExovI5V3Stv5kLsnB/D5F0PqduQxAesWZLbAhEay9X5Y2xjhhPzGv4FyJkgUZ6u9Fqio6T7SZ6wknd0h1Te9JqQOC5Tk53g2rQGijFKoFW1W+MzZts/GPY+GraaNlrPa2z2OeUrXOVCoxzMR05QVg4A4MbYJEmafxhA5v5vunoreoSfAXzrERz/9SXz409+H1aU9BJ8YZY8J25MzHB3fxb2XXsUbz7yIF5/+JtYnpylVtdCQgEAAPKU7h6CM16xw+74HEeVzPmkXqQW0W0rZ0sECUsqArjyuPgtcG17aG56eJ4QQ1Y5RW0HKjqAoZbt7MQckNOiXyZJ+xshwbmp0aBpoYyiKIpf+Nd5pgekWPa0RYoGvtK3nRZqdgpbx81b/W7tqYx+Ss0PT0Ibq6M91/+047Zgt0COiIjsnhZFh5VgPq/M3bPo0p/vngN9UvqZG1VRiNIxGoKfnSNOjBTxb3n47ly0ZO9JJnlE04N2gUdwRDMri2eVs91rvCKBVxMaUz+YMDTt223/RM009BjR5Sc9XU9aCCu7QZ5vPe78F7kv7nJzjRHp+pnMB1OH9Ld5Kz+t/I49IFjtLy4pmRmaVtt04J7sMjYquSte1jNNd82r7VNVrxuBcOm8sd6ctlgssvMPJyXF2NU133FrYQuNo5uwQagxV0McufTRX3vIGkgbXdlHo70MIKdEAp0x3gDDcCMJka1AmRpiv7/tJvGkLMDJz2RKUv4mm+d6FiVqHn6X+vt8WZV8OJuazAcjMIu93XZfSdhMwZINuu91O6pfx6YXMzIXnrOKWsQmEJ3Jw2TPgiNDHCObUryiANC88ju0F3wLIlRJFezG2PrN9tu3Z8MFdCsQqKsRYvJItgTfXF0+EYQhgArbbLe7fP8oAjbMx2SjMxTPaKnNjz19W7Vu6aL4t75Y5rd+bU876uZ19Mf0tf2OUa3PgZErjaahIC+RJHTZhQwvUk4y9oYg1DwrdxjU6HwLTosWcQVH9nS8IRcxrWfty2YG8w+AI/crjrCM8+R3vx6ee+iyuPvoI2AGRGB0DvB2wuf8Ax3fv4ZVXXsTv/c5/RLcNCKebMaQwg4c5A2FuLrRMEhrb+W+CSvWulcsaFOgwWp0YpjUnuh0dcqufZx49rHLxtQUuuxws+meLR214pR2rljP2b/3srh1hK5s17eq6p7ur9lk9/rm2dJutcdm1p8c2B84mdzaZUEzbB+bxfGp5hqYOn1a/W0X3sSX77XitDmnRoHVWzDqTbLY9PT7dho5saK0T3W5r7JY3bZs7S8Uz9ZiboaGY8oGVD/Lurp0FLrtudV9bddXdZYDaDlQ9JCIxAQGrSO3at6UlCzTPlrVvDEb5vcXXc/XPfd563+o1WSNy1KGlFy3eqp8ZjV/Ly5YfL1rOw1wAcHR0BE+A992IgeL4PoDKca/HXs0ZzUc2JONpt1xolbe8gSSlJXRE6ep00WIkaaWvY5OtEk0hbPWOizCrpIHWbeit+pYC10wvReqWPukU3lrhd12XDKQ4Ahd9cE4uJ9MeUzGuAJSxS/a1smuVzO+qr+V3TkkHBmaw9+XCUrmwMcaU9tuB4NVuGBmBZgWppk21Nd9Y4JZ2tt4pCKtD2WaL+a7qF+YVOkyMs57rkMPsOFe/v3+QQxiHpvejjEONx45zVgDvGJt9pwJXM+Nr0R1QToEZes2FRpTfU6VNJVvRYEbxt+KTLwIMJu0YoKydBS2QOdeW8GzLOLBKpwWUQGmXwQHoOOU2lMzaKXqTAeew9oTFo9fwA5/7QbznI98F9oTAmd79gM3pGus7R7j90qt4/pln8Pyz3wINEUM/oHMekVDi9+34pE86Zt+eE7FGp35f12OB8tzcJlmlzeWapvp3K8/1bqLQ3c4VUXJmybxqvtHvWGBh58kWZ2ho53puJ6Vac4rPdsmkOaCu+ylGewijEW8BoAU7u0CPXse2PfkeObRLf67HM9fOLvC4c1cPM/KAJBx2vj09v60+zvFrE5Q1xlH/3G2k6bECo96ck5ctntSfa5rN8XOr3tEYqvsooYpVHxuyQvjO8rMd8+xaYqDaJsd0fsUAsI7d0lclE6ROzg7bdB1JinIhR8W41utiTtfptlrzVsakhtOSBfp3Oze75nxufWhdo+slGkNLm7uspo6Cb1E74ltrt2XgtOrUv1usINi4yG0iHOzv495mU8IUJYud1qO2Pav3OUqIfE0/MIPpYrLOlre8gaQNnLmFLYaChFyIINTGhXwu4WmaKeV9ANXukDyjGUIznWVweU8DEWECMYBkPItFV87m6JTVFtAwp7CYRU78ABo9rMvlsrQrxpB8Z2OutaLVAi6N3SFsAxjjQWR5xjmfd7WyMDE00PXL30L7ETSplL5wiLT7vJHum1WGel71/EsbUrSQsQrRe5++o6nQSLQc6ad5qIzPu3I5mvCLpA62xlX6svaWWuGkFUbVV+Y6PM4UoYcGBs65yV6VBQtW+bXAn+Vz6af9LOFhlw9sTu/QsbTTY9b1WiUzB3Dsdxr4hUy78+6n0IAhjam9YzynJM8DjUIX4ryzwwAToUdE8ECAgztY4v0f/Qg+8plPY3ntCraeQN6BhoD+9BRn949x55XX8PxXv45bL7yC+3fvwjsHYk7ZL2MEdT6lA1drUPcrrXlCjNMLpu1YNK1bQKwVlz+VhTK307lrgXv5XXvmbUZJOy9WQY/jnHq4pR0boqY/a+3yy7stsKrHYH8/75ldAE7a0/1s1UskntQpyGvVKbpgl1GQvk9V/v/Y+7NmSZIsPRD7jqqZuftdY18zMyJyr8ysrburs3pDdaMHPcCMkBAZDGZkRoTkf+AfoBCU+QEUmcfhA4XkCIUPJEUgAkxDGqhGL2h015pZlZX7GpEZkbHe1d1tUT18OHrU1NTNb0Q2ZviQaE2JvPe6m+muR8931nV0QZ9P6XxeT65JGpuPnAkfYwJPYtDysaVnMN+PY/fLWJ1Dc8+07aGMKhf85XUTkdydJwrfVn8fo3ljZzCvS//J2irABBCCkJzERo7R93y9dE2VR8nXMqfrniXdQ7r26Rqn93bse3LH5TTKGIOYwVheGr6b8RDr1j6n9/pMbvmjVuT52oztpZy5X8ebjt1peZ1jvNDj9kJOt8OnyD9K+7Bun68r+VkefOZ98LVLhVuAms76TgJ15Xsg8lAJvY7zY2iwZ2PbUtEJNjjry9ceIHnf57zJN65qYnzCGCnD6hIGNr9MnXMDdR+A+KwuZFmWg3rGGNF1F0G+IVWjk4bojPwl9SZ6SpB8J+aCTdMM3jXGoHVdfC9n0HKJ/9jB1L8jY0kSltRYIwkpSf4XCZoJ9TmR4OSmPHm9uYROCVk032G/QgjXrXsKdseY0Xw8On/pfKYEYyip8YM1SOtSM0fdW6m0pDB98sa6dlguFyDSyH3DnBmReIJgDaELjF3a/3WEvr901l+yWke67rG+zFxq3fsrBH6kDzp3g34NGK7hOjxOw6ef5SZd+ZjyeRrrb/quIQrJ606W2unPNK8W82r/x/o+Ju0b678kRDZgxyE8PtBYoC0I5194Dr/5+z/A+aeuCsgxBhNP8HWH40cPcP/2Hdy99QU+e/8jHD/ah6sbWIgmyoHhxKUeVaAJJjDNOUBK6ZD2Of39SeYpXW89V2n+nXX7Mc7DCN3Ws5326aQQsznjkwu3cm1/Sg9Tpmis5LQybWesL2P0Z2ysj5vXfHzjv/fvDJgq7qXF+Tv5HZAyJzmdS+dJgxKsK2oikwsDx/o+1sbYPtF6sxlaeX7dPK8zh0z7c9J8ax05+B97Z2UNRsa7rh9P+kzafj7+sXOU9kujjOZVPpber7lPtYyt9xgAAtALWLF6J6fnNgX0RCesWfa5oVVN8eNKOt48/+PKPs3GlgpeTuI7UrPidXdgvtYn0bmTnjlpnKyRObL60rl6rDUIDYHv2LM6V6LhJrRth7ZtofTDOx+FLek5z+nsyCiQDiDOM0h86/4W5WsPkHKmV8vY5TgAGcklPHZppIxqVVURiOXgJj9E+SWovyvTPKYSTQ9nqi0iogjU9Kf3EnZc69M2VIsEYEWblc/XKhHniObXHXprjDhS60Ei0wOoYFZGcS6BdWA+9w3QomtoyJ7IgKZzlv89Boj0d2WyBodyTZ4H7z1cSHibEu7B2rsRSRSGxL3rWrRNG+m4/By5zMLPsixHL86cKGqfiAjw64jJsO9al3w+zNg+tifH2szrzs9bzmTppDj0xDevY6wt/Sy/bMfezfsytmcGkt0RsJnWkUu5e1DZ92NFsrWGWSMgmtSo6aUGioghvYngjUFrgdn5M3j9B7+Na995DXY6RRciIaJxqPeOcPTgEe7d/hwfvvcelkfHON47gG8lOh0T4KVBmLIXOhTWwhg7ML9NQZGW3AfkcRf2GGAZAz9j9Yy1oXOfn1vmXkubnrf8rOtnSrvGGL0xpm1d6Rm0cWZG93sO1NPf0/bG9v7Y/vkqTE/e156ZB5CEPh+7j8YY+VwDsirIWAVaKUOTRpvK5yG9jwcCsceMaRUMYEUDk2r71q3t2HyvMyc6CTCPMZXDOVoPOtL6tf0x4ZeMc72/3Bjd1Hpz+qVF+iwpQ3QZTzoBJ5nbjdWtQtr02fQMMDNgaGXf5PdrWuI8Z1rF/vt+R540ljHwkraf74N8zPF9GhnTyHyk8yZrvP6OAHqh/EklP2tYU99XoR/5edAzPH72V8eW7zP93BiNKC3/iqLnvQ1RPL/6Tn4fpOuQfs7AQEYT14qgsVS+cvmPAiClxDeVZKvJ2pChkVnsAZPYDsQN4WURrTFROu+7DkguzHwDAVhRMY9dNrl0WcGCvq+FSFD3kIm1UOZaIs5StLX1gfiACNYU0IhL1vYHz5oeQHZdK5FEYntidpVq4uI8GqBrGew1NzJgrIWzHEKpGzERYlFw6rgtmWjCpuNLx59KaxSUAQATwTPgg6+F2qwyEMz3xol2XldOtHWu0wvGh/1AJNoFT4mMgigGjFg5vABcnPOwTwhgY+LcWg9J7ksMR4ySAZAJiVJTYB4IPZt4eem6xLFTMJGgfr2IJGJhGvih63T9AmGGmFxSCCsL5hB1CRIWII4tzAlzFBRzmN8BaaTe2T/dq/odGwqXSAjOpoTOABYmnjVrBXBotDkt6RnKL5TViy1hYsKa6NopITYalSk4p+oYAWVu9dIFoPMywpTl/ciZ+PQ77ZMhgyIE5qi9gzeBsTMSutt2Bt4aNLMSzazAa6//Ol77zd/A5uldtPBg52E90O0dYPFgD0f3HuHj997Hgwf3cHh4IAIN52ALO2BO1bfJBNqHQONSRiDVqCOc+5wBieOwpvcHYS9CBSIUZRVoj4fnDiFoo8wjKNIUBoHIAsQCTtFfqGOmk9oHFZhEiTCyoA3pfvB9qHxOaT33OWcIAo51n0RalG5v9Oc77knvB22l+0JNNuPdkIwDGO6ldFxKm9J9o7/nWtP8/b4fAPeTLtJh6nmEyKwolyIv9r8nn8ceEwEwslYsCYlFcCYaZxWiaT9z7VvOxKVnJKehuoY9/ZD/eaXxSMdKA/rOGPZjjNnSZ9N+pe2vm+O0f2n/c5qXtp/v5zGGOQfuaV3rmNrHCa7Sz3Jhb1q/PAMAPtDgVLtL4TvVPuqLfd3raFw6F+n4U6A04IFoHKysWw/5YFwQFftIJElztQ/o6VB6Fsa0VGNrlc/dAMiv6e8YXxjrZclJFpgh9QQLDch9PGYCmwrx8z5KtL7hVMS72oQ5yc9a7Fc/p/E+IrmbI51PxrhOADT2t36m/zw8ipAvU+5kBF4x6XN2NnXs6ZketKXRlCG8YtCLRWG21LXSrbXlaw+Qcq1MehBSplgnXi+XnpHsP/chFxB7HyZ/iNZzO3bKPtd/Yxee9illUlSzxTzUCCmTnwI/PSxVNYH3ThwSrYUJZoMajMGadMkDo8ISSMEmhzaXuo0dRmEmSJKdQi5KJoZ3HUww32E3DAwBopXLVOcpgrWE8UmT1nJgXslYEORSNmov7VfN09LDrH0fU5Ona5MWhgDA0paRydG1GWNMdE3D1ILIAC6sRfycRLsk8c1D8mECO0lU6pnhkUrfVfUtviOUMC4xDwMPGZ8I81kiw6SEWfooHRy7YOPCQgl/eDcM0XtZ40iYBrtpfRkAq+xvlSZJW/0ekEt5NQxwfunkjE+c54T5HRJSnVdlwnL/GnmLqH9ef8+1Q319wz4+rjAYraUYfAGdR2FtDx4mFVxV4MI3nsOv/f3fw5nLF+DZwzGj9IR2XmP/0R7279zD7Y8+xb3Pb2N+eIhls4zCnVRrHi//Mc1OGEHKnA8uTKxh1HThWJhv773kTwpz6pxq1RH+drDW9Mx3chkqLcIIk5UywTqu9NylZpGpFjjS1XDmV6Seoe8DQJgzYEkf4rlCAm6S3/U56BlMmZDwec7oaRljgpDXke+hE256Zgwc7LX//Zn3q2v62L2rTKWcH6E1Mi7NCTh4OmNixvqen6f0eWUX87/z8zaYx7AXx/bPSv0jNDw/4/pdytyP9nWEsU9/z5m8/M5I50OEnavzlzKXOeOoz43SQmBw56VlHJCE8XuCCscUHOnrXtMP0KoGNR+XPpPzLimzmwKDdFyrDPwas8vBNh65j+WPvj7m4d2VzGc+77r2uVB71fqC4pyMrffJ/eZE85l8xliZw3zdV8Y5nI5sXvqx5XxBaDKrh6LgKD9XqbWPztPYeUjbi/Mb23fY2DyFra0tHB8daIvhihj3e03HPKBh2ZqCgpDKSO4jXiVRjy1fe4CUM7W5hGDMXCy9rLyX4AVlWYq01MnfYjMp9VdVNbiA0oOTMit6gWsbCjpSjUYeQCA15UtBkfc++jxpP1QjQjRsN61r7KJIS3ohaJt5vpDYHyXIQJB8G3ioNNrB++EGHqxFkOo8CTFKf6bj1eeMMTDWgn2vcUufyceUXkbppZJ/r9q3/JIbI065WUQE1clPQOiP0Qu3Y8znc3SdwyT0VxnVfH3yNoeRuLDynIyN42WrfYxjM2J2NcZiERGIabAmPRFCH6lw5CJeV04ay0rblLZN8ZKw1j7W1yT8NmBG82fX9TtnPNLf9fF0Lw2ZqoRpfpJ5IaArJHy3cYQJLNgxTFWgsYTJlTP4/u//AE+//DxoUoI9o7QWbtlg/vAAD+/dx2cffYzbNz/Ho3v3YdTcLumj/p4DpfRnziCN7XWi4R6I85kwY7q32raNfpxj5ohjF6fuY+fcqI9iej71c6VrkV5m9CNtT+vOpcRp/SvCkREmduzztP85bRrbo3kbKXOR//7Ee2mkEIlVwJjgZ6wfab/Tz/Tzx5VUTDBW30kgKd1rKf3SnHr6TM4sp/1LQVTKVJ5UclqT9iVl4vV3FVIO6cKQOUzvrrHx52cz78vj1irvf/533n4+Pyf5kOQmofLeuK9gWp5krte9N9gDWLUESJ/9D6k/L8KkD/9OAcjYeulz+R0Q5537YBf5uT1pXdef815o/rj5z8eW05DYp0zglZo05vsx5VvI9KAmfYaIBpZOJ5V0TuVciXbv8OAArmkABO3XGl+4k2jJoI2IlzjyW4RxXudx5WsPkNRvIydAOsmp+UjKEKSSokGQBx6q7SMzDDEtA7CyKbX0Ueb6A6MarvQi08tfw26nwSNygqyR53pzMfm+KIpBBLh1F15kOIJdaC6d1T7mkr4IBA3AHQtzZ23Qd4hqlkgc7tK57ZmTVeKl4yHqAWWquTLGRGCa9iVeCswrYYvXMT6phiyfl9gvEnOg3Pwvv1T183WStDEpqeYqUEAbwRStMrFjF50Sc+ccxkxndJytc7IOCOZQIaoPGQOO3j8YlRyNzXN6qeQAMx/3kDAPCexJ4AVAwoj0482Z9FyiFpkZ00vhxvZ6OkcpU5Cek/wMCNgf2vHn/X4ShqzvB8F6E4MngBhdaWBOb+G1330dL/z6d1HOpnBEsGBw5zDfO8D+3fvYu3kHtz79DDdv3gxa7dBHHgpU0jDl6/o6ZnqaMoVh5uJ7Xdf1DEKWzyY9WxSeH2Q5517Dk/ZjbE/k5037uG7NkVz2aX9SJiGX/qd91tx2+XcnMX8n7fu0nTi+0VpWmf+xPZu38fgynMthf8SUday+lAFc7cPq2e7v1qFAKq8zH0va1thnDI53h36WCxPTuY/WIMZELfRYm2OfrWdQh30cM/nMxzb4LqtnDETr72u1+Rjuj5xGpWWMHuf1rJuPxzHgOuc9OKBoWppHOUz5Lf17YCYf6hvci2HNteTjXEd35TZjiHZruHfH1jTWieGVl/YvFeyk85pb0KzQC/RrftIaPO6ztI0xi4WctjwOPDyOfg2A0Aj9LIpC7u5Ew6f3cfrOuvHmdCHu0aCSbLtuCLKEIVrpf85Drps3BUPDoGDDPj1p+doDpPwSBvrDp4y/Lrj8LtJGBSR6cOLF7IaaDe8l6Wo1mcCGiHdj7ad/A4jS8JT49wzzqk1sGlUvPTTaP010mzLc6Xj7/g436ZjJWb7xtS1tf6AmB8MWBZj7xKmGDJxrBgci1aBp22pjnjNp2l7a99S8JmUiYt+RhALPQGi6B/T9sWfT8TOLRMj5VQKQX1g5gdJ60yAZkcAFvxZLonmcbcyA8HvTNtFcaF1JCWUk5KY3TRo8C4B9Gva491sy6P0v0rVnZtEeJQB2cHkTYoLRdC5yoKn9I+GcAGaoT086jnTO0vryczMGZPO1iJ95D9B4fp+TGNn0+9VLZ7i+q0R2lQnMx5LuRxvMQwkGrjRoK4OnvvkyvvmD38LWpXNgFy5c57HcP8Ji/xAP79zFrQ8/xu0PP0W9XMIzo7AWoOBYHf7lZyGld6k2KY2wmc+BPp860OYMngo50rHpHrLZuUjXcaDJzNYuZ6LWgo1sndJxpEzsGHOb7nXtd6qNz/s1xuzkjHt+Vsb2Wb7HUw1XynDkazE2T2Nnc8h8D5krFTzpuhkz7juT/p0zinm7Q4aVg/BlVQg1fl4wuq8G485oRX7vpv3t19evjCEfT1rXGIOZ74N1e3FsXIMzDzGBToWfKT1IBaMDbcTIHOXzP1ZOYlQfV8boVNpeXqcf6dPj5iMHToN7kQNkGaGvuXnjYO29j6ZpeX/WlRQkjfUjByHpWqX8UZyLE85JWufY+V5Hc8KX4e4cH8c6mpHyWfpcWiXM+JlK+5HzgWq6ms7H2Hkcm7sx/giQe5rZw3gN7e3gObEISmijllyjNrbfgDBlOn/hk5QmPmn52gOktm0xmUwADC8MBRT5RhbncDNg5FVqasJmTSWzKcORM9mpxHKFwGTq3JSZSSPVjUl487DjWk/btuG9YbCD1ERgXX/SPuVETOvRvwdmbezBhgErNqlkA4fGApyo7YbMcmjH8JAo5xf+2AFO+5VeOP1aZRI8Gkqw0zI2Pu1jnIfHKGbztsb6nl8QTAx0PkpjXCdmRWNRak666Abzk4wtJZoSmYyCX0uQolAvXRHlTND0KWEJaydhxx9/2a4DLgMC5j1glYN//Nj6d4F8/tcRRH0vnikzNE9Yx+Ce1JdhW+v3gvYzXeeTpFxAiFppLVxhsP3UBfz2H/49nL/+NMy0FE1Q68F1jeP9Q8z3D3H7s5v4/LObeHTvAVwjdKssimhCwJC7wBoa7IExplz7qGcjvfxTZkBpkTLTOpZeKEEr/l35xZrOwVArNZzjfD1SaXU6dznoSfuTrnfe1oBxTT5fR2+GjNuwv3lfx4DAKNM1MuYxepv3eaxf6Z2RAr3BfCX9zkEc0Ulgvy/D9sfPkGgMAx0ZYRbz+dE9kgq91HxN+2eNjX5caf/SutL7PAJcGp7TfH70+bH9lZZcG7NujtIxDeZjDS0c21fav1TouK6soydPUsae1f7nzD8zAzz0AR28FyQxY+BtjCEeAwkrZ0s+XOnvGJ8U3w/33xg/NFZH+DBtcfB9/m9svnKaqv98kiw5bTufj3yuxj7v52N8rta98yRl7L0xurOuzXXtje3NsbUYK2VZovEdiAMddzxKS/J1GTtHZIwEyOK0vXQPPvmZ+doDpLpeRmKcRypLJzdlHHJGQZgAE89V+owCECHmHl3HK1ogfSdtSw95epH3Wqxeupn7IOUlZci0Xa2/aZooNXbOgf1QNapt6BjNCOMwZn7UdV2fLFWV1WEuOmIJ8W1t1JakhFHnFDwkoLk54BgR0hL7nD4T6181icilBjlwyU0nlDF0TjLG5Gs+xuDkzFkuGYxEAhSizgEgwLkO3kuY50Q/L0R/ZbVDyYiOx+oFLRMQtHTQqoOEDojaPgqAiUN/dJt6H0ZOCjyVVsdfBvuEogN3HFo/r+jf5wRMnDC89K++92MEO/uOQNG/yuucRqYp7NjB/GUtESV95SjRpJX2U8le38d8P/VzI8+QCZHjwKBTW3jtt34Tz/76a8CsQmsMirqDbTo0e3Ps3XuAvQcPcPPjT/Hw7j2hXyEJsSeCY+4DOyT9shqhLs5n7/RKYT2BIYNJROHM+jhuay26zkdmWosxmgONZH6MmOc6r6H4SVcCRIBznLQbpyrOV2S2wPGCZKDvS1iolG6n2i99PgWpevZy5nXou5fQWd3HCb1NmZf8ss9plMyL6SPXAdHUs99+JNG1Sc4Xg+NcEES7r+uUnLZIl8cYmrTt9G+i1bORjh3o74J+92Lwe+wZUewX81C4F+tPz8oIY5QL31JhVHpmtKTCxhwIjgk+Yl5CAph6WqRzp+eXMiEkCHFNVgBg0o91Jb1b0v6m3+X3hf6eM8fxbn5y/u2JyzowOMZwKg0MH4y+p/dG/7dcEn7k+XTdT2Lm0/v1JJClzwLJuoYO5cB2TGPwpNOb78dU8JPuxXgWodfNkPfL90M+P/nc9OOUGiPjn80BYqsnj2ywvoSYykJ5nZy/yt9JPhy2Ef48aW3XrUHfY6kv8oekJu+r7jD5fhjrZ5wjF9wVIg2UOo3pIx8/SfnaAyRJRNXCe5dkUF+9WGQtQmhtK6GpbWAYCmNhQ1jajnsQk5rJgSTx1WRSxTak6KKumo7oIo+ZaIjDskjSEAEGRaZBAEF4hyT0qoQuFkIR2BOwZ3RBiwOGhO8OnCqROInrJZ4yVSmhSUEGkZiD9cRCouAZI2ygIcCgRGEtrCnguV0BPXIoGRzAjJiIBV+fwopfhZFA48wSRpdYGCiDntikB5yZAY2Q5TloTwBmCQsOAJYMvBiXhTETiMP4TRE5eO8cYCwMTAwLPNxTJjA3gREHB8m9SPWJCBYFOg1UAWGWwIBxDDYGsAQDj9IUEv43ZIEOMvlgxraG4EWOKxA8FoZbbbERwApDEoOmoihLJvq0da5D51wAx2E9NXR4QZHgs1EiI8xEZMkJMJzsmSC0iReC9pdZwnpHYBTChrKChsAAKdOYFtK+cw/gWNTl5AgFhYAAsqqBQQI8iTZT9l2SW4MZ5JVZVwrfz2sXQn8bop5ZNgbEBMMFCARDQ5DI5CTyIOvMiwDLMwBTwDugIIKxBFca1JXB0994Hr/2e7+N7dOn0LlONK1NC7es8eDufTz4fA+3b93Gw/sP0NW1RD30gWYQw8LG84uoBfTw7GCpAAwSkxQO/U6YWTAMBRrGDKeHJIQbt1bOoS2Vzsg/2SbSB7mA+gtWwE3QrjMLLGSgsImGygAODh4cNZs6JuFwTFx3bwiMROARgvSKhFF8DuHFHwIUIiqF+WAYeNczbuqoqyhNdiHBEsHr2TQmhpkV+tALxWQf+7hlTNjnKigSMB7oQQhiAu53s2cfgrOEHWII7FWAIeZYAhIVxAOqwzYRR0nCaIQxMUuo3NTEiEhogYAtiRZqJI7+kHEES8qEcHf5QM8MGJZYaErY9zBW5pQgpyy0EYMoJACJmUEx9HuYhhHzspTRS2n5GIhI/2k9aX3MnPjrGqFrRODCAuhQsEfBDtYbEE3RsYMzshcNPKyXhBQcoiimUREVqKd39KB/yf5EIjRJ+bYc2K4DAbJ/e6Y4ZVpThjAV5KXPrAMfOfAYZ9Qp8CiBgOqdkQsz9H1W5pfDGenPFThn4ofvp2MZCF7oZHCYgpKBySyEfOi1qFWy5APp91Fcqx7Ma7/SeU37qu0qLc15oZX+j4wrX+McTOTmqmk/jA0GGKa/v+L9N5xc9HR6lXeI/SFlczKgOQJyVJAwFAIIj+IDM2DJSv7LZNw6HuWNUyFIOicUTMyZPTon7gzxAGWCiXw/rdtf8l3iu4geROvd5Nz4ORkrX3uANJlMAQB13S8W0AdMSNG69z4SRHhG7WrZagVgDOKFMIaImRnG9tKpyWTSm+aZYWjL3JwgJXhp3zpuA3OdOBBSABLAYCMCQ1Akl7iJTDN79SkoBra8uRRB/62LFpYSDe8l0pD3PrYZ+0FBqpsR56Io4rwAPZ9JRDHhm9avF3+cI99rvNLQ5r05I5I6lUgwNCdOTxgo+tE47yVXUyDyKr0gEk2Ptp2aTHJgBorCRk2dRu8aBPTAKgGy1sABYIOoRoaCOz8k3KDx2yKSQg6OzOk+1LbivPb16BzbosDG5ibIStCLerFE17ayVqxktq/VUlJ3uECFqcVgHZkFFFG6bwKRAg8J9yDHkEeiBRuO1SBlppSIhwvRGnAg1gLOwjgZmPIkCQEf+s8eHoCG+dCeK6NuQChUY6p9A2AZ6AhorR+cqXQ9TACpIIr1kUJEC3QG6IzH6acu4vd+9/u4cOUyHBjt8THgPNq6xfLoGHc+v40v73yJ23fvYrmsJW1FAZCVuYAhOHaBkQPYmMB0E4gNKu4TBBemlDUyYSwxb5Z0y7GDYUJBEn1SGT6AgA6wtkTjOnjTM4CpnrBgg4IsTMjRxeQDiCHZ3+EMM3sYshEIF+yCdtkP9xIJw680zIatq+DfsZcxexYtLBE4PK90klgEVWSsSCOdC32QdbLKjISNLQmfw96ygf/Q/UzJuAnwEUl7wABEPvSF4Um+Lb2XvRn3ghTPBG5N3P+6u+UseMSmIodN8YfklAtrJhtZmCQCPEwQIFHA+j0TWCJoKgmR6dWzSQHwgGTe9HcLRhFUKq5jdJ5BXuAsQh4zMnrHCLgiQ700JC061OxMrwMMaaRBMhSY3nGmMi/qm+sBeEu4cOMZXHjuOn7xzlvY2pjiwtYWDu88xJc3HwjdZgK5kGcOVsAB9VFLB+Ak017pGCjStn5cY9YKcY2Tu2wAVnMtVQZmcsY9nY98LteVx2nCYh3h/AruXQ1wtFIiXeewv3pz39VH14M+ufdWnx/7PdXMxc8J0eJGQ86vY7DjqQxdT+d2HUg/qf9pGyetx7o1SLWr+fu5tUz/XV5L1rcEuHO6pzPeZEwYASQancyyamxsREPfyxQk5XOWtmvi+TY9z8g+8jdj857vwVH+NPhQ+/C8WE8Bxqw3HVxXvvYASf1y+gAGNEC26cbUf477BFYIEgoUQYKZAQmgN+XxHjEkeAqO8kO1joHWn1FSwQx2DmVZDoCBjiFX7/dMuB1s/FxDlZuX6PuKsHMJSdrHdL4UTDjnJb+KMaCiN1HRKETx71RNnKnC88ticKiRONgGSbdGJ9TPc9V6OqdpyQlRakqYz1k65n6OhmY7LqyP1pGGOda1SNv2HNoKpi1t14n2yPEAWJx0maXt5yUdv/K62u+0/8vlUqTYOg+UXmwnmPcBQUqOyNj2bSPa967b32n/4+fZesTvINJzMMFzZIMj2AUFkyTmwJAGwsoGhDI8E8bDQf/ogUmGKJUhg2V4GxhmQjQX4UIYXmIGTMrMSrGeYHyfoFK1fyY4w3bkYbZn+O7rv4Ebr34DlhlufozWOXSNR7NssfdwD/sPD/DFzS8wP57DtQtMgkC1sIX4FYZ97oIWwpCBLfQCAwxZWEzBHDSvCJovY0CW0HKIWqh7jMW005CFpeQ8MKNpWxhboawMOiP29Woym+04kFUBUABrDHQW0ZxDGSBAzAKtk3XNGSAmBzKNLIpjWGZYGNGwgtGYVgCN3KxBe8qBaS9kb3gEgZIVEE6i1erPdJ8XyXkHTzImaw3YpmZqNDA5lrwvgYlgmTtDIiTpOheBsWzYXgMswqMA5kwPkFg5axahl8k31aBwf8wShpBItB4mHFxC8DsEwZJoR3TvK4KJADhgGmaAuDcjN+EMExl418EaPdOq+Vo1dZMtRX3fMDz3nGhcc6YtpfFKn/R3z27w/WBGsn0YLS+8R1EVOHYtnv/N7+LGD76Ho8M92HqJex9+hk/v/xk2GCgbhnGAJwNnRTNJmdWElvTe0/FGsJSAuDHmLb/X1Yoln6N8bGOgKJ+/x83JkwCi1fe0fu3/6jnNzSHzIs2Og5OxtqMp9BO+M8YUK0+U76d8baIbQ5K0PK1nHRDIQUpu0po/v+5+ftxc/G2+Gyv5WOK+PuH5sTs650fGANwYt7AeTIX65KnQTsJvhrvrcWMba6f/XlqIbBDJvdOfqxOrH5SvPUDSyVRwlCa3ikg28RlhZrR1g4ZFbb+5uRkYKBO3QUpEe9MRA0OJT092uSp61bbl895UL0fwzD3DnKL6ddqf0Y2bHRBNPKvmCKk2Tf4NzQC1pJdW+rcx4gxXFqJic9xnw1YmlowZ2LzG98KFml4a6XqkASUG4MesmvylczcqURjpex4II73sc18iba+ua1RVJXOUaB5SYqKSTGPMIDKW7gtLBmyCaY41KCph5D2H73i9lCPdGxEch3kcHT+J0Bc0JFCyPxy8TwAgUTBDUnK3KkmVTxU+hfVLqvcs0v0xkJfXMwBsGEqw4nwCIC8Xmc4NmEVbwcLgEEFMhZj7UOJgsGkROxfeAwBYwAVTGmUqexMlH0zMVLpOIGMBa2A8MOP++TADUn8wDfFgsJE9L8y3RVEQXnrxWTz/G98GzSosFsfgugU3HRadx90He9h7uIeH9/awnLeoly0KU2BW7qIqTKQtNgAQgNGSi2fLqKktA94YzE0BjpoDGjAEHDSexpg+FxczGlIgRdG0lYxBawwcEdj2kSsRsY6YYxmDoJU24ntoJMw6jImmmbpnY4Z3F/rlJEG1gqi2bdDVh4DrJJBJ6+A6B3QOlglFOwe3bQCeUq/zTmiMETrrSUCBaJsIhqwIcMBg6vO5OWYYU8D4DsweJUQTJiBbtM7qcwOgN2WDRCBk5wDHKK2BJUDzpNZlAW/zHFmpxLunhalQxsBGEEH6LABioOpIwDkjar4NgtaHe62LtTbsTRFcCc4T8+tIW4lgSNZIV8cUNpjGyj4zgc56b+DbTiwn+oO8QheMMcFGfZ10dqgdGLur8u+Ehsp5XkcP9flUsFZZg67zOLz3AD/70Y/x3G98B9PdXRzteezeuIIf/OP/BD/7N38JfrgEOTHx8WxgLGAS8/mchqVMeLquegdon/XZ9A5Nf1/xT8xopK77gLfI+IaceV03J+nzA1+ZNe8SURKJsP9s3bql86K/q6npk5ZYJz9OLJf0MRlX2oc06AyQ5EjDSNANArrkjlsHctN2x+61wfqA4/yl/RzbS2MAPG873yf5M3n969pL+y/7a/W5fA7WAcV8XOl+Xdf3vL+ACB8tdJ+PhOVnHuyjsfMyxispL8MsdwsRgSxlwmc8cfnaAyTnOlhbRLO1lCFW5jwSOyLMj4/RLBvsH+xjc3MTbdtie2cHreuwtbUlzl/JgkRTOVqVLuXELb0Q0wPddR2896iqqnc2RWCAqFdZphdreink9tHajzQkeMq8a84PBYtlWYY2Vx0P04OVEwlrbTC7EIaB2YOsgQUDTR/5r8uY3/RCScFJDpJ0PMNogAD8KrEeZeZHDnhqMpc+UxRF1Damc50CS+2z+u/4RBqYt7cKkmUdWu/ADLiuhSFIPcqwYXiRjl1oK0QxGV8+RmEuEAVzut+JRJLkwdHvInBTATQwxu4q3SNAD1Q5vKffjQHUMeKem3WuLTaYbOUEm4FCmdfIPBqQMejYo7addkAYQiWkHjBOJJZpNBtjCdRZFJgAROK7RQRrA/gnDpL+XgrnvZfABrDoQltMENMtz9g9fQovv/oyts/uYq+tcTh/JHnLmhaHDx7h7uERjusWB/tH8I4w3dhAuXsKRTVBW5XwRYGyKlGUJWBtAGNAWRKKskBVVajKMtI3W1hQYUMOst6s11oDUxYoZlUAMCbSAKIAZmxvH14WBawJQhNjYamIWgU14yICvGF4Exzhg/ZI91D0+QnbT0wlQ+4uFuNDVvAGwDuHpq7RLY/QLZeoD49QH81x9HAP+/cfYrF/AHt4BL9cwrcdXNsBnYMxZdgXDIaDsQbgEJBHHYpAsIWFMVbGYQxABhYA2IjfFgr4tk+zQMYGoByCzhRJAmswHMu57TxBzAsETFUwYKe0Q0AHs4f3DDIdPDsQNN1CAGSeAW+hvKUmdxaaIcI1KF3UqKlEIGJYbgKglb9F62VFUw3bCwhMAfhgwBj2gCFIfUFgRdagLKpwXoDOz2GohVXA51fvvnh2MwZq4CMS9gwwzpznoCHSjUxbn5acbkR67j2mxoI74IO/+AnufX4Pf/8f/yOcO30eB/v3UVxyeP0f/AA/+eM/R/NoAUuiEez9VleZZkULad/7u6oHtNqv1Hxef64bo9ar95x+PpaPMAeTaR1acvCQP5sChezbZM51HYfhyfVn2q/cZJB5GKhhXX/yu42Ze6HVmvt8HYjpui7ydulzY+4L+r5nDmdmHKzk85kz5qPMP60HT2m9+Rquu9/zudP3xjR4J4GltL8q/Bl7Ny3reI/cgob0/NAQWK3b54O1ESdRGGNRliXqegn2gadKeJa8rpPOAFEwufciIFM+RfdV/vzjyn8EAMlBZzv1W9EDrUlAu65DXdcgEP7tD3+Iz7/4HNdu3MD3vvc9HB0fYXt3B03borLDLPG66N47GLKDzZwezpQQpM+kvj6LxSISU9U2pJHp0qKETvMSab1pnVHqG0raBwUkQK9dU644P9j6THpAI2jhHukbMvCgqDEyxojpWHJpKgA02ZjS9pTgpX2JRD1x5Nfv0mdTojJGlPNndB7TnFgpcNXnrLXR1NEYA8OmP4gJqErXJ91vabHWovEdnHdouy549BN4lU6N9nswXxANSr5ezrkQZGD1Ao37LwAayV5NERRpM2PEVsBVcPIOpmikPjDBdGfsIsvrSP+lw15hTkwBTqSLrGCOCI0Pkm4OYwkSZ8PArtMErIFZV6miBZpSZs5YE02LiIAOhMaWoMLCEwBDaK1oSVtDcIX4b+m5q6oKZVnCFAWKqoItCwF0hcXumdM4e/4cWvZ4yEKDNlWD6x02XYfL5QTlZAZbViirCaqyEjPXwgKV9MNYI+uomcwJAgRUExQCDIBEq1B4jgtIgTnmsFGiT42uEfeaCh7s0eRCBIPifcTRXI1ZACMPt3ZSA/WXHIAuOXOGwtros2F/bwJgPicMIhMsA77p0NYNHty9i/3Pb+OLTz7Fwf2HoPkSbr6Eq1ug6WCaGpY6ON9JEmb2welb9ibIiF+SDaHLbQAJkwLonMy19yHRKIvGzVoYa9Eq3QuXs4ePkZB8wqx472G8gQn7MjK5CP5jYFCQlrITDQlDmHpiipexSmQt5Gy1kPwgIIKjoMXUs+pnPQ2yGtiGJf9ZWDelRaYgWBMEhQFkmaDJNmGPFeUE08kGbGHg7R7atpYz5jrR7LkOYzRWfqzx0VhD104q3Fca7+gx+rfyHgEdediWsNMaLN7/Agcf3cb2c5cx3dzCUX2M4swOXvydX8Nf/fGfoWoZFdvA5PWargHtCn0Zo2ep5iO9A9J7Pddo5EznOvCQfq/35xjQGns3p7f5mPJ3mEPABQzXM+3HSYzlkGle/W6sf+k++ipMaw5i0rQr+dykViBjdfBIfevGl9/lA1CoZoIj4xiAifB9rm3Mn0v7r8/nQO+Ezq5o4+K8GBrsoXX7MNfqpv3Mx5CxGCu8yBhoNETqbRp9U02wWEjnZazN/BwOeAnmoYCCBOin9T1urdPytQdIwOrkcjDFSMFHWZZo2xZt2+KjDz/EtevX8fDBAxhjsLW5BaA/JPpejuyZxbdjMpmsaCFS7lO1VunilmUZJaou2Xg5gdTxpAlb9bP0AOf+SVryfnnP0bQO6EFWSthTE44UwAEQxtOHKGVGwZFuTiTtJNKPwMD0EeLEx0H9i9Q0bcwfiaKzMa30MXB8cZ7zi5mxejii1s85ieimYC+AQBf2jPMMcg7WFiGWgkE0bzEEAxMlkIYMDFnJiwCK0Qgl4o9EWyNr4JpWOyYRtULEwiCmF2kP95J4H0NV5hSpp1E+mBwJ8+VBkAiB6XPxYgj+IhKoIjwQfvRaFzXz6DUSamjmgzmdAhMkocER9jzHLvZaDVDv3yOXSm++qqAGEGl5SwYIDB0D0WrOM6GzhYAHomhYBCJ01uLIFjAhIEkRQU2JYmMKt1GhmkwwnU5RFAUmkwnKskQ5ncBOKkymU9hJCSoKmNKiqCqUZYWyKGFs0LwAKMpSHL6hwzBgS8FHiAFr0YJhQSjZwHoZQWsILXGIjCdr5dFfkkSMyosTqwQuQIw6RiRmMHIXB/G17mvy8FYDknA0idO/mZLLRNeGpR92cOkMQ+gz+XDvEzypZi5EM+SE0QjzT4Bo3LI9qj8shwh0PJTseWa0Vsy9PBMcA2ZaopiUuLB9Heeev45nf+d1dMcLLB8dYO/OPdz97HPc++wmcP8BunqJ5XIBdhbsOyjmL6iEmgObQFussXDGwBclAAYVZTQvc96BrYE3YrJmApg2gQZ6Kz54KuQhMiEHCoHLMoD6nn4VRSF7kCeiJTJ9wm6AAz1cwgRrSfWP4sCwbjoHF4Q1McANM8AGaCu4zg3MXJgZ5FoU3SJGLlSQocBYBQPGCDhSTeWkmmE62YS1BFQz1PUc3rdYLhdAswC6wEIHq4ew/SSyHfMQGOv6sp7cpIQ+rGdVWIJt0NCntj8jq6Y+AMCWsITDhApUHYN9h5/++V/h9Qv/KSblFJvb2zjeP8SiAHirRLtfY8IE8gDDjLajbcQxJd8rjkgZtFxolwMjvQ/XgZf0zs/fSb/P2xz7PZ+vtL30GRMEAwIE9ftV5nas5Hc0Z8/n7UYz1zAvvbAVK8z2kwCXfA7HTB1XBJW6N8PvabNpi3nd+bzl63YSgB3THI39zN9JeZKUFxvLnThWf/o3OwZoPABXDsAGa7pmvGP1pCXnPeNaKE9MvaKCw+fsNdQTBnt/DEinffAcIhCn/AshGBL0z7nu78J894WBwtiYE0gmzYOsMG1lIZoAQ4AhxnRS4oXnX8DtL27jhRdfwNZ0A1NbCqMrt2KYbGH4lHksynApOgffiReyDc767CQIcQQzAIrUl8h7+K6L0gzdJKQDiMBFN3ZqopRuZN0IfaZ0IJciDRF6UQTTGXi4IB1MCaxGvfMefZ2hXWMI3on5iGMGeUZlCIY7mIkVp3BbwDsntt6OUZBFywzAwbMABDImbGyx7xdflrB8rNKQIA13BGITQEd/4NhJeFqNuKZMC4DgmxKS7FJiEgdl6MUB3QRmxbFHUVUhBG4JDydRqGBhq4ngONfAcAvljn3wC9EVM7Ag9KY5jGASYxh118BWYqYHMphQganzEpYaIr2uCfDGonTA1EkENd1DEViEg28DWPTR2ToxHyAbtSfe+T6BKiDS6AxkCpPDYtkGBqMIjkyy8Wz4DwZBgxC0Gkb8WMhDtCgmhBC2FMyPLGAMfFGACyMgwhDYErwRMCJ7rUBZFiiKEqYsMN3agJlUKKYT2KqELQsUE9HWkDWoJhUmkwmqqkIRTNJMUYj0P9SZ+juJvwrFcxYvyTjE4EsRgYfe2yYxE0I8xwL2EnoTmHKE8xMCJMPBgW1vA26hQcEkPLiFXszSoCPEcNHJlSSXuYaTBaLNe99wAE+DjnEILKDMK+sT8Weqx1Omoa+2D787vHMJ6eSx0qrwnRk8OxhF9BdL22QyAtS4f57j86G50qA6tYnJ7gZOXbuEa7/xKpqjY9x//zO88+ZbWNz+UsKiE4s/mSUUs21sbEwxnZaYbsxQbW6gmm2AygLVdAJrLSYTAcFFIfuPCtmvCGdLhEPBPI0AtSuJQ1DkbihGU+w/Dxe4i3xZmEdlOnTf9S/JNMi6mf6F+J6uA3vE4BnOSWZ67z3gPLhu0LUtmrYBs/jU1ssadduhaT3Yefi6hasbcOdgHKO0m5htnkFpCXzwEMv5PlwzBx3to5kfwS0X4OUSRdvB1EtQ8BFz3Ikflpf8I7K+HJidXjOR7jrvGayhCj0H6XawVGDE3FQpoxZnaORvDsy9tRZsCJ318AbYv3cbX7zxFs4+fQbzZg9FUWFnMsHv/e7v4O0fvYn9L+5jSiWQCAZTZja1tkjvRzU5zJnHlKamYCjudd0ngNzzRmiLpilID9lJAG0MvOQMbfpcDhLSZ0UoAhUzBXBkR31q8npXmOakz+k8jppnpWclBdZrSrzvR97P5yMFFGNzZzBcMy3BY3G0Xq1H/6UCYxVS6PMDoQSwsieA1X08mEcM934KYMZ8sJMOD1FeVvJ+xT1MiNFkJdhLmA9WDbqBTytO+AJNdq/1puNLxxR5S6BP8wKgrusQJt2vdD1f617eK0yQD7yvBgVLeRwOdJlIIq1qH5+0fO0BUpEkx1P/kVSLAgTTCYScIJ3DH/wnfygEIjAALthFOu9AjsGs4KTP59K1Q9OsdEE7NcvK/qXSjSh5IkJZVQMJizzT9UxeduB1LLmEQsvwIACARNhSkKff5RqjePgZYtsfrjkCItOttu8IYY49O5m7wqKYVWgODgOwE82dNRJRy3tJdsnM4nBsApgkg4pF8ueCr4iYjYibdGdlPp0LOYRUumDkaHXkonZJTYoIiP49UYoOGiSy9SHcrxIDF4CmRSfRtchgWlhU1qPzDnAeRKW0QeFih0QFY0vC4DID7AIQknFU3mKKCTxbYFKgOn0G9blTWNYtpkdLVEyYw2Ny9SJ4a4aWCX7psDw4wGJ+HNdF14sYKBMtkxAIAY+egKaQ0Mn9PgjgIGg14gXc6xREGxZMcchaAfpq4lUWaCeVaG4KiVoooGUCO53CVhXKSQU7qVDNpqimExTTCcy0gpmIKZqpCgE9kwplVaHiAiVJ5DGj5j6hryXE/MUHwOCAwIAhRv7Kz8FJUqZ1ZyM8qZA5XjCBL0fkdDHg6/uH8j85+5jCpRswBSUM8lg1EURkZeXyWHlitaRS/bHC6MFYXmsULsRvhs+t42VGZvqkL2Oto90cdD+sedgDMAblqW089evfxPmXnsPevYdgz9jY2pQ9awvYaoqqNLAFC9NuLFwwFawMRdTCzGibBvsHB/BgbG1vo6qqoa9N7MOqJBUY32NP8t3KfDxhnfr9CrPDgCUb4UhavBFTPYsQXMF5WBDQOriOYEwJ3zk08wX29x5gfvAIe48e4OjgEAeP9tDMF1jsH6A9PBZf07YDLY6ApgG3reTsYgYxw7IBTBcZbzFLFg06rIlWExSEY7kWIJ2LMcZ5jPnVu0jlARUIv/qbn6B806BpDsAwsKbA1mQH9cEclbdwTkydVTKfmyGlUmxtd2zrp4wz0Jv1qxY78hyJufkogBoZ4zrtz9jnY2BmAAISBnuVYUxFff07qeXMmCYh/X3deNaNDaGlAXUZaUf5uLyk/Uo1FWvvBhU0JFYqsR3CgMjneyDX/sXUHiNzkAupTwJ/J5V1QCp1GfkqdY/tkV740vuRqdWN8k6M9cA0F2SszGveJqkyQM+bR1N3A7/uvP7BT/T7XVPnWFKz+X430UmX32PK1x4gpSBES05QlEBUVQVrC8yxiJHVKvUtkBcBCFo1RvyOtI7UbE4PaF3XMeSzy8y3UpvqtB/pMykSzyO0pMRQN2wusUnHms6FfCb2HInAJz6fSpykTkCdsNM2BcCJxsUTSxJIJ+CpI4KtqpjA01ojZhsx/42F2suD9XIEAIIvPDo4eDUV4x6AAQxij6IAbCGmcUQMmAC0wFDNXpRwiGhEly+AX5VQkoDPkM/J2N4MxRIBRiKokTEoDUKOEBaNCQqJF2Uo+PsEBgydOIAHkzmHIuYNsWYKgNCxhzMe5sw5bH/nVSy4w+FP3sFGCyxKizOvvoLm7A7aokB9uMC5zS3sbG9jsViIM75yjZ7Rta3kewnSZjIGXduirpfYMeLrYEzwnwGJhqYUrQ2B0LkOy+US1hhMJlNU1RRVtYHJdILJdIJqOoUtC5RlCVsUweemRFGJlgdE4BDFjBD8ggID6wFxdPfBrCoiDorSKh2KmMkF7Y2I42BC+HNh4hFzGLLytSNnQn8fO+/y91CKulp6dr0/G397IntS+dtdl2nJ2YqTnhwfA4czmlYZL/v4v7S99MvH9e2JH/5bFyagKQnm1AbObE3x6OE+DpwPvkOEKTw2rcW0KmCM7DFHYhYLH3L8MGO+mOPhw4c4ffo0ptNZEAr1/pc9LRWJO3Ayw7fKgJwslV5XnhRYDSWtBKY+QuTgOcn2DIdOzmZBYtZdChh2YBBblLubOH9pA4V5RugMM9q2Q7tscLx3hKNH+3j45X3cu/0lFrdvYfngHtrDI1Dj4OsGvm4B51EaAtBJMmLygFWfQQR6PGSwciZ7zCn9cfOga+o7SRCLlmGWjA0OFgrwaHAI44CKKrSU5vta9flI785UE5PTlvzz9O8hiFs13/sPKTkQGPs+5xf+Q9o+CcRpEui8P+uAXexj1t/0vRTEjZmBpWNe53P0JOPQjjDWn918TeN3ZugLMzbPj+vXGNgYOxOPG9e6QkR94IKV0ptXpn3IgU/+bh7Ya2z+874O1hZJoKUcyCbPRi0dVulEXBMWvkB8wk4WDD5J+Y8CIAHDIAPOOdgkwptGLyOSfElFaWFs8POxRkw1mCWLuRdzPLBEM1KwBOYoEdKoZ9776OifSqaM6UNAp3a4udQqJc55oIe0jPkejR3O/mdKuFQVzdG3Adyrp8FK7BjMDt4FEGhN0Ax5ONdGh3/nWoAKsClgYGAdgTyhRIggyB28YxjysOQg2VokopLa8TsQOhBMYSV0uIbsBaFyoj2y1sJ6K6ZvwbcjMr4KphjBhMEChYTRVQDEEEArtqqyFmR6HyIK0fmczrU1cGUB2BJsOcyDCeFxg1lNYN7JCWOm822Z0TkH5zwelRZtRYDzaLzDnfkCs6tXYSsCzT2W9x7BTKbodk9hOZnAlxXKagtLX6Np5mDD8F2LoigxqSoURQmYGWyQfk6qCWazGapJJQB/OsXm1pYEmQjaU2stCmth0Utte8OoMA4WQBI+jGYHSqAA+b7TMRNQOo/SCQ/UX5SIlRjuL5Zh2hcnuskATDmgdiJCRyF0fOgH0gt25JyPSa+Glwhlb44x8avMA/Pw2ZMY4fSZtRfFCYS7H9/q+ytStOxn+tyAafISVlvpiNIi771IBmkoGe0lrUGYkjCAjJ5ppaS9PtjLcI5yiWP6/SqjtmqaMfx+tch5lh1qSwIs8MMf/gUOjhvsnDqD8+dO48XnruHi2VOYVAbWUMidFS5mmWwcHh1hZ3cXs40NaES+Mel+LhV93F54HMP6uJJHEnuS+kFhbNQLwOLuZo/C9VJYkAEbDmc+5GxiiI8cDBovQUa4ZKAiFNMJzpya4cL1S3jWvQzXenRHB3h09w6+vPk5bn/0Ke7f+gJHD/bATYtifgzTNQB3sPAxnLY0Im3nOWzyOTqJ4RoAz/C3D/S/MAauc5jaQtrjUjTSAJxnSYbsJfoq4Fa0A7kwNe9buj4qiF2nfUrr5VD3WBCfdHxjYx8Teqafn3Te0r6f9EzsZFJO0nQN12D8mRPbCjRqHb0bA3Rj87JC99acVebeJC4FYCIcffIzPPjbM9LoM/l6jAGPlMcb6/O6sWkZFR5wYoad0Rnli/L5CK3IE9nn+V06duek+zhN+JzPV16PBKsZtpPysrmpqyYfVx5bn4/AajBpMiKvmtDY9sr0ri1fe4BUVZOBxiYlEiloUmIl/g9iTmeNhBu0mvhRF9V38TuZeoYtLGxRrphjCGhwg4VXrZL+vS5xnPZR+z0wxQvj0RDhRVEMcgeldaQI30TtpUdRhMAC8OAQfhYsTsliwk/wXSeHjVRDJoEALMoQkcmjCCCx6foQto4ZtpzA2BIGAkCaWoIGFKaARxMidKUhTQGAUXUFJq4MDuAIFykAIiy5EYfqEJqcfB/sgaxkRJecQiEhpJMcMLWlGLyAyMR3fACHYnLX+ywxgA4GNUR7pA7eAtYMiBhELIEACgtblsFpv4ArCqAoMZlMYgAAGyJiYWJhCouKSXLr7GzD7myAZhXw7e+hRIHSWFQ722hKC4ZBwYCbOVCpa6qhlRHypIQ1C4wNVPVMBh2FhLo8lPIYD1CWbFjeFA2dCaAlVBcZeqbBw4O7hAhwxeDr+J5DiWDIE5nTE67OWMOKIQtzvINSTdBJF3HKEMh+WnOBE0DEgzkc1NPHFBnWkY2kv0DCCPRi0MsqwEzvRRPBnEjFVPIVbP+dc2LugCTIDDAwDVHJWryg1JE/MB1KO4pMcxYZN9Nr81IhEgXAKm1zCPcsYIkhQTTKSYXCFuFMdDG5qghRbBS2xHaTtjXIgf4T2/FxwDAOdvu/rXOSl4kMTu/soFk0uP/lIxwdOSyO5tiZTLFdFCi3Z5iUpZh6GYILqmVDJOe3lLxkXTfMdzMs4xLSsb6exOCnz+ZlTJKc1rWOwY31AmDqw+Wmz1sAlaeosUVIqAsgmtEosyT7MPTFdSBNPgZJ3gxDMBODYrqF82efw+VvvIBvLmrM9w7wxac38d5bv8LhB5/i+O59dOq/5D3KIOhxZnVd899zIDTGCA/egZg6g8Rx24DE0sAYdMaIabX38AQ47sCWxILY93WlZyttL+chwEMJ+jrGMq0LQOLLvCqBT9c3NbMHhtrydA5yRjvfQ3l5HNju6ZVZ+XxsnMnkj9aXt52vIUN8XJjGTL84czdYBWrr/l4rhAjbOgqJMlCQA+D077zu+HeypjnoXQe414HdsfpX9l72WT7WMYDmgyAytVDq+6EWRetBsL6Tf7eujIEk/VzcN4TeLJdLTIreZUIVC/kYKNxro/WqrItIoz1FYe7g/n3yGA1ff4BkjMFkMgERoa7rsEA80OakznyFLUHsoVPDQV2sC1JOQ8SrsoyH1jmHpnVoOo/JZNIzLQkR0/a0LzlBTdWSKSEeky6lhFX/1rFFZiPbRD2h94PDEokzEM3fkLTvnIchB7gWFJLCUkGYVAYUAh503mHe1GidBzgwPTCYnT6Hwwf7YsrmGV3bwbtO5sjMRBviHCTvR8L4dRaGLAz1+VoA4UkXcLCTCbgo4L3rIx0VBsb2+U6sNZhOpsKkWQNfFTABpFQKWIyBtQUKK87/ZIxoVqw498NaOAr+MAYwtgADKKYVysKiIAKsMHa2KMT8zBp4K5oPZVoHEsXA7GoEMIS/2QAtGRRkYTsHbwAyAlYqD7Ap4V1AJESBSRXpyLKgSDRkb4hpmGFG4TvFliB2kYg4YiyrNT5rYJjk4ooaJAIKTyhc72ptkz3WEaNLVEMpCLIOKEcuKiagM9xrq7JSeAxAUjwN3BO/2N4IYV+RdnHaq0xYyOKvlTMf+lxKWMcuXT336dlX2+icHqTnrz9rLgIRZI73uqbppZkKP5SG6d/OucDk94FgDPdR0JxzMXCN6zyWy0aSsoJR1w3atsV0OoUBo+tquE5Mjre2tnDx4kU45zBvazTBfvzKlSvY3d0daJHIjZsppXtUaZycRQNb9Alr9d8TFUYwv/QwRYGLl6/g7Q/uYOEW6KjD5/fu4dKls5jNKmkXIVIe6YVq8OGHH+LSpUu4dOlSpIP5vpIyLuletydOYlTT57Tk7a3zuXhcnUgC0qR1OgCdznsCCIhCKBLqRRMcg0ewBMdx4dzpMTIMwEkQEFsIPZ5V2Jqew8tXLuD5X/8WDu8+wts/eQO33nsfdz/8GN3hEUzTgsiCfA3mXuuSO5+v86s9qVixi4aDRFcVGx7AQfLNEUuEyIIAxw4emoS5L6t+Z/08DvyjfO97nJd1e4IUuCX3wjoBwJPWmX/2JMzrWBkw2X+7KlbKSXt78Bx6upYDFn035Wty2vA4YcMAOKU58NaYcOb0+iQwos+n2owxfi4H4GldY2MeG/+68fbfU7znx55hrGoD87nItTdqeQIMrbG0zryO3KJJn0vn2pD4OJN3gUeRetI0LysCBxnVoL00pH7/lRB5cW3o52ItYF5TvvYAaWd7E5NqguXSYlqVkpCwbcVZPzxTVRXqpsFsc1OY+a7FbDaLE84s0lDvPaYbM7iuQ9eJ8/10MgUz43ixwOHxAoU1mM1mcM7h8PAwZPMVd5iqLDCdTlDYIlmkcEjSpWeJqkbJZo0HKzwN9H5Kxhi0bRuZI/H3kfhZAiL6fDyTaSUgRy+gwAh0jWSUZx0viVR1e3MThWFMCu6lw+H/3ivzY9G1LY6aFiCJ9tTUDZauQXdqC6UtMJ1OMQs5pJgZpqqAELFIfb0ASECA7Sm8JcxmMzFHtAWqiYRmpnKCsppgMqkCM2ljkkyYkByMRLugmeUJBj4SpowpBgTo6dj88HKQsABB4GQNnIZAZgjAAaJfTBfmtGSHiYYtZ5b8IZE/N4FBYSBEuLMQM0FngmbLErxxcNYD7KQdXyLE2ZPuhShIYMak7QNP9IMKFzG5QCuUyOvXjInLCHwYNjGh8DZ+puMToGThKQkKTgSEIBHWs4RwTuc20CdnGGx6TxdOaFnlAp+lUus4VwQXfL5ie7ECRsfpnxnjwL09tZpT6IC8V+ZSPki/0yhgzD1hTc8cVn4Pc8SiWfXOo21bLJdL1PUSbdNC/VU49FPnTXI48eDy0dpd20tMXYhw6YOZnI61bVt0XYe269C1Lbrgh+adQ9008N6jCoIc1zmJlBnAkfcey+USzjm0TQfXeBzP5zg6PELTNlgsFiJ08R0IPQirqgovvPACnnrqKXhL2Dq1A2bGndtfYjab4erVK7h8+TKsFWGBXEp+AGY1OIpuHwohWSV3EGCtQVHYIMSwUZgBjEtTAREwICTzdQxceeYp1PxjtF0L2wJ39/fwaH6M7e0ZYAAyAHkDFzYVeULjOrz7/vs4f/EiiLnXTGeXqgrZhlJojp8P+AVWxi9oLvqN16+3Mkhx3w50OHGvRiYqgpiwe1l3l/rM6V0RPtP9RvJXS0ANCTZpjQFCzihDFP0tBQRp0JrQkjMgNmB4gBhUiKkyiFGRBdoOIIpWmQ4OXBEmT1/Ety79IS6+/Dw+e+OXuP2rd3HwxR1gvgDVBqbrAOckcSQYDsGMBgTHPHCal2iM2iNEk7oBEw6ADQXfWKEjURgBhvEMywA8o7QS/VOsCFf9gpHUPwZOiPrADinzlprH9vdlmtjdB7/VcQa632fDkvdvRQCU7amvWgZgQCdzzXNjUnxhYp+s3RwAq7l6/l0OTFKhMrAKlNKyTmOjd+UY06zm/Ovmbz0w6b/TM6e0zmOoJUzrWgeK8r6lAvN8z4wBbJYu9EEkAngiE3uYtjYcD8a1YCumolm764BePv96D5mw5pPJRNwsTjA5jcAqm8cx7SnSPvAQGH6V8rUHSGdmE2zMpmgqMffoXIe6adEFhNzUDSZViZkxqKoSm5ubmB8dwhKwsSFJ+BaLBSwxjusl2sJgsViCCCjLEtOpRJzr2gY8KVAWFpuzCt55TI0syKP9fVTTGSbTCUpDYC/qw+jrArkArZHcOQ7CjBOVAAgOQbJsLPo1Z+UuIuBomgYAwxCD4KO0mABMKgnXbUkiL5elgKS2bdE0DQyLdK2oCjS+g2ePykoYgo3CoJIbJbbr4dBBovpZqlBBHPHbMJbCVLj62ku4cO4MdnZ3sbGxEaSVOmZKzihFYkygGDo6AlQomF0xuEoKr/ymDKnw3hQv1d4BRuc+ySewcjZ7gsfhQBudf40OlzQYWCQ4mL4uvclDP+IPH8YbWihYwIziKtv1kQMRpLY9XUjsbQ0CS9Ez34h97PfXgK6HSAhKNMW0LrxKBKdEJ/u/IUKRSLxiLiuSsN5p5LWBBCp0IFV5KxDxHUGWQCZQc8AwM1yILghGyJ0VzGOY0RFiOFLvE3PB4DshRFL9zhCFB3pzxOnQMxgmKpWuKfDUbETGWJAmhA5hshwTOudxeHCIvUePUM8XwnACkPDNPm7KmN+Ggs29V98diOama+E6h8WyhbhpeMzni0j867pG23jUdYO6rlHXS3SdCEGOj4+xWNRo2w6u69A0DZZ1jbZtAACtF+DUNq1I18L6ORamVE3++v0ia0bJPiIi/OitD1CWJSpjcfnCeXzzW6/iG994CZUp8cG77+H9d97BM9du4MrVp7CxNRPmNCBluRQpJE4NFCVE6CQWsy3nGG3HMMaFsNtiemdNkmoAKbPoIcnXjSAlNji1tQnrG8AB3DKaxRJHRwu05wilBwplFAIwZwKuPXUN/+Jf/Av89vd/O5h/9Bes9wlLHtA9MzCfHwtQda0IhRaHgBftXdd1Mfqpcx7N0qFzQfhFCCa/Qy0Ce/GxVGm6cx4OVn4m5sR6vpmdaMZpqHUzoBj+HxRC9HoxDy6Clt0YEeZpwuOqLDGdivCpqsooZBPTR4rmMJ4drAW4bcVvE6I5JltGIGsMhYihEgm0LAnXX7yOp5+5ioff+zV8+N6H+PjdD3D80S34h/sojo5RuCUcL9EYhw4tykaEdEv2cCRgrvAE8ozaCCBxCWjWyFvK/KpJKQehQhH85zy7YFqt9JsEMSeWIibYomu+qp65k3WKplkQGgXT+9AonotR9UM90ozebcN8OeuY5FRjHNc9Awyr4B1r/861EGPtxTqZVup/kkLoQVKqkVinEYp7H0Nmfh1wPEmLk487fz+f83Ft1FCTKefQDQACkFrl6L6DXtMikEAAKNxb9ozNd65tWtGaZOAindf0ucH8BymC3HuBhzJy/8Anwa8Sum7CGRABuYmBDlKeIm8/B+ljfcr3cAQ6HLKkBMuqrmvhEXz6k/eM3tUMkB+u9+qcJt97EbJEnkr3wVfYz197gFQVFlsbG+AZB4lpga3NTTgWyc9iuQAAdG2HorCYTqfYnE5w9+5dHB4cgFkYmI3ZDGVVYb6scXx0KLlXStFI7e8foKlr7G5vo3MOVVHAlARrCG3T4NT2NqYbG6FHwQyM5KIiEtM/MetSoiyXpIcREzfX+x9F5op8/L2PuCMbpijKYHomB6EKzvxECNoMRhF8qDppMAC+Ao49DBht2whzWpSwZoIIBvSfJ7ATpsobRt22aJoOk61tPPf887h48TxsQbDWYOv0qYGp2RiKT7cspZKkFRb98SU9yuOXAZ3459iXUaLGJ79C2S9jPR7tEw1/76/5EzsHNXeJhIkop2Vr22fu6ycyUPjCPKSHyiQwM5yaF3HQ0CAAFs8hWaQ6VwpD2ZucyT9l8vQZ+YzQBfMyBSjikOnjZcuhY3EfsPDCzqXhgHsnIcPBHCDswbIshBH0FpUpgOBrRMb09QaGJpeG6UwTyVxozhr2jM55HBwd47Obt/DwwUMU1mJaTUAMTKoKbV2jXi6xrJdoWwEteuG2IUdNXddYLBZomgaHh4do6gatA46PjqMmp27qwHQ7uI7RdS4y1DQ4V2JGGzdeco4cODE56HeXRprMGREtBonU0nu0rsF8WaM0Fnv7h/jgk8/wp3/xl/je934Nv/4b38Huzjbe//BjfPDRx7h+4waeeuYqprNpjDwI6s810PdFpIoCpihIEr3naHYo1rLDVAlxP+s6MQAm7GxvoywNOhbNRNd12D84wLJuMCkEQMijJr63u7sD5zo8evQIOzs7g3noaRYD3uL+vYd4++13REMVJJpXrlzGpNzEol6ibRrYYoKymMI4B/gWZcEAd1GaLMIBEWS1bRv2uKi3jHA1aF0HB0LbOjCTgPPQn651cJ5hjOY/6zV9MQ9ZYOibpgWRWEtUtkDhgMPDAzkr1mAxXyQJuh02NjYCOBVfyu3tbUw2ptja2cT21iamsxLVRIRsxhIcE9A5EDkBUwEMGAsQtQJAyKCalrh87SlcevoqXvu1b+Pmex/io1/8Cvc/+ATt/Qeg42OYegnTGjTGxT3D3sEZFzWFKe1aiZpF6Om0CsYyplgSL+c78PElZ2jHyrAvBJVmp2awKWM5ZuI1xmimYxhr/yQQtU4zNQag4u+GoO4FY346eR09aER//yUgZ6y/aq4l94KLtCzvdwpSTirr+rdi5otxbaB0fXXM6+odC4oVvuw1hsLQxGfHEh9ryYVzY5qik0C1ji38FfmDIU80eAN98/09n44DkY70ADYdw7qxjAH5AWBVCxYG5vO5gLkQ+n8AwNLuZmNeOQcjIDzM1t8K7H/tAVJvngFMp1MsFgKICAywRxUCJmxMp/Gd4+NjlCEIgEhpa2xvb0dzBEtiera1tQUiwmxSYWs2xcbGBpgZ8/kcm5ubqMoCYI+iLFFVk8GBM0Zy1VhrYx/0UDoAVVGiY6BpxezAWs2bEKJQdS74BJUwhoK5jYC5pm7FcRo23C6S0JUgJgXGGLhOIve5thUzIO8xraaYVBWargFagNihsBVURaKaEvIAwaBEiQYerQfIFnj2hefx9PVnYUuLrm3gGo/TGTgCnixs69jh0/I4Ivm/RFFNC4ATCZQUlTaH85owpMMoB//z9YuSC2kg9VRuIXRJQE2M6xKl29pvBS49KEII/uHjReb1kmGOGbA98zC57+Af0HHihxMq9oHhBtlYpzaqq24CcAPnTLWAOgUt6qcDyNn2rkPTtlgu53CuRde1KAqLna1tnNk5he2dHdiQ3Fn8mRAlbqmkMGeG5Hcf5/mLz2/jzV++DQZhWlbw5LD/6AA3P/0MX9z+Ao8e7GE+X2B+PEfXdehcF03cPIf8W8nFI3OkebhUi8dBuhd8KnhoYkDcOzETibCD4gXTXxIdM2Cpn1N9P2gbhmPU/dNjD71k5DvAQaI4No3D/O5D3P1X/wZ/9eOf4nd/93fwG7/2HRhivP3Ou/jwo4/x7HPXceXqFUw3ZnHd+pIzK/3eUYayKCy8I/hgfqcMskabC68BAeiVZYnpZIL9+ULmGUKX66ZGNytDSPr+VUC0Bs8++yzefvttvP7664NM9el8t12Hf/PDP8fR4SGOj+doGjFv3tp6H5cuXAaYcHR0hIPDw2DuKFq9+fEcnXPogpaw7Vp0reRIa5pWTLedg/cuikc659D6FghMiYbxp/Bd03RRwqoWCYZEC09lMfBLs9aiKApUZDGz4kc7nc0wqSowM2YbG9ja3MZstoHOF/B+ia7r4p2JkMqhqkpsbW3g1OldnDt/BmfPnMap3W1sbsxQFgUcnAT0MBqa30W/MkcG1lgUtsCpc7vYPPtdXPv2y7jz6U189MZb+PwX76C7/QB+/xCel0DbomgZJRiePFrjJJG3L+McpSWXbI9FwhpjMntTxdUyxkjnzJ+2rc+PAZ70/tPPBhqbE9ob9HUNQMvvozGp/ZO8k7d10vtj76ZzqX3Ng2TldRojSUjzuUnfXRdQYV0ZAxUnPRtpDhDMfXtfm7G2n3RORLhKvbAqGRMwHhY7BxOppiT1c8r7n9Y/NkYFa9q+3jvy7ji40TtbhYfr78W+nVTLpvRnPLiGTIvkJyW09XJlD+Rj+KogR96Te+5J9kJavvYAySQLmjLqpTUw1qAsQoCAsFn29/dBRnximAVwHBwcRMmItQRmh6ZZwnUVNjY3Udey+AcHezBGggN414G9Q1FIMANpx/bRWIAQmlk2w3K5lA7HBWR0jhPpol78VXC6FtMHNefwzqEM2d6LSgJBFCGoQNs2wf5dwk13rgsHFmjqJpoudV0NQw5bkwlOb55BXS9F0upDoj8iEEzPDDPBeQImFV5+7UVMtnawbDt0TYuubbAxm8SIfWn5Khv0b3sgVstQMhUJ+KCt1bdOIsbKpK0SFiDz+e0JEPemHE8KEtPf9dJP308DA+gz8d3E3yNlGPQzNcNMAY8MR837WPxeEAIOeN+bpHEwB+J+Milhovv+i8S2816iPwZplJoXWk8okJqcBO0UC/BRjZO81AstFLD3/nfCLDdNCwvRkFLwYSpLi+XxMT747As0XYez587hxrPP4szZMyjKEjZErhyTQGmRy1KuCu+BO7e/xN/8zY9x7vwlHB8tsL93iLfffhu/+MUv8PDRozDX4rcR5z/Rivkk6lGUbHsxQ9VIimDxXxHfN4MgZgNYTBGck/pgFUy5BOSF+WTNCRFMjGQH9mOERDXUPqbCAA3v3j/b9wvGgEHiEM8ezbLD/M59/H/++b/Ej378E/yDP/wDvPj8c6ibGm/8/Jf4+KNP8fwLz+PqlUuYTCZSnyH0gTPEJCtnyiJTawnMAo6KQt8J+y0RPIjTP6MoLTrXovOinVzWNZZNIyDfSJTOdLWdc3jxxRfxr//1v8Hrr78+2AfpmTo6muP+/YeYTqf49NPP8d77H6BrJbF1WVl0XYvOdSs+Y01bS11emUbJPxTPY8pUgqGmnWwSxjPMvRwFAtgGLW7PfEcGPl1fI75F6keqTJf4eNpo7mdNgaKosLt7SnzBgv/ndDrDdDLDuXMXsLuzg/2Du7j1+R0wi5/b5kaJi+fP4fz5c7h69QpOn97F5tYmbPAFosKg5Q4MRlEU8IVoC2xRYWNnC89882VceO46Hv3mr+Pjn7yFj994C0effwZ/cAjDBNs2cF0LLgzImmBC298PY07j6b2f7u0caMS5p9Vn0vVP60+/T83CxrQ468BMGkwp73PeZt6XdAzrNEMngZ+UAU/NPNP5k3kZ9iH1o8rnIzLA6byOtJ3fXWmbaZ05o5/OVW6Fks712NzkjHk+D7G/of85M6/9TTUnORDIg3UoKACU3+vHkvdf5zQNkZ33L7XAGQOS6Zznwvi4FtneT8G93rn5GqTt5PO4bo/qs2n0wZV9mrzfOYedjS0s58dxzz0OHI2ZGebzpfvRY/15Oql8/QFSYobBzCjLMkjoRCOiauTOd+jqBpOyAoxBNZmgaRrs7+/HbOpVJQEOzp45IwEPJhOw9yhCvhnfOcznc5TGRIlfWZZwDAEXBDAT6lqcoztrUZYVrBWNjnNdQNI2sCFeGDzioH626FyDoiixUc3CQWaAJciAHjoJ/Q203AVzPRfCJjJs8CMywbTIe4fCFrBlgcmkwrSsUAU1ZwFh6LouBJqwRXhbchW1rsPu2XM4d+UqvC3RuODP0HUwBMxm01EHuieR/mg5CaDkz+Vl8F4aaQCZsDASgV7arsy4IU1gm7CJTNDo+qGlxKY3mKSl9C9eGhAfAy9Ew4ew7AI4BVgxEmaMVYqujDVWNS0pQQwDU5BmjAF3fb4n5/sw8ClTsSqRUqYzSKNINJCWxIdH/fdU86BMHpjQBR8hnUfvPVzXoXUODELXtmi7NgDzMMZGQLUxBmUpYcm7rov7Vv9u21Y0pW0L5xyWyxrHR0dYhgiO+/t7YMWhrr9IyqrA2bOn8K1vfwsXz12ANwZf3ruHP/uzP8cz157BjWefxdmzZ2GKXkqYXm7JQupqo6kb/OpX7+Cpp57Bndv38PDBPt5880288867qJtaPJaCUks0MRSc18zAACJVfggutWGb2kzDkZgaBObXB3O51KQibt20TnkIvdkm4txrE/031O93VuySMAqDPe2hQdeJDIogvKlrh08+vYX/2//9f8Srr3wDf//3f4AXX3gZDx/cx89/+gY+v3UL1649g8uXL0dNvTDuYgio+7Mfru53A9KcaQ7SvkbNJIp5oRmSW4PIw3sXnfTF/7QO805hrEO6cfr0GSwWCxwdHWEjmkVnAgr2mMwmOH/hImaf3MTnX9xG18pie2rguRk1B4pCEmVKiIJpkeSVQzLvAwqVBCoZrgIhdZpU8E0kdvZFFs4+MnMk/4goAqPQQVnHosT+8cMYQTFGGaQKlkpsbm1iNtvA7u4OTp85jd2dHbhuA/Pjz/HxJzdhf/oGtne2cO3a07hy+TIunD+Dnd0tkDHwUPNxMfOmpgGVBaiyqDZnuPTiDVy6/jRe/q3v4tN//xN88NM3cPjFHXSHh+DlEpZYol5JHooVRi8HAWNgKGWylbGNgDRjtMeYQOY+RUj+3ZM4gQ+Z0lT7uwqS8nbX3aNjzGM6H2PO/XoHjAEKQIH848eTM+Ya7joPopADs3QMcn8Mz9lJ4xxj3rWkpmw5yOnfXY2wNgRKq59rHanWJQW5eX/S7zwYuX/VmCXNWOoZbT/Xho7tl7Hf8zbGwKL+PgbwAYQErP34cjCdz2NeZ9oXY4JoKuwvYw1m0yl2dnaw9+D+Sl+eZE/kZezce/47DdJKcd4PNpcwniLh976DYSt2j61D29WYbWwCRmyrNzY20LZtDM1NBIlSt7MFgFBYAxCwtSkBCJxpMT8OiVO9lxxMJDbezgczGcuYq/NuK5qcwkzgXYdpFUKEB7OM2gNMJL5JRR/xpm0bcItYt7UW1lh0TszxqsJESUdd10BVACiE4DlxfFapY1EW8M6jcx2MITHBA4e58f3lHC53D6AF4AuLC09dx+7pM2gdsGw6MEliV8ceGxvTyOxqiPMxydz/kqU/HAB41dm1f2b4tzqCEyE4rw9DNKtzLrPrDxwLg+KCE3Z6CCMQCG2JSRuvEL+8XwpU0ksqld6tA4XxUiQD1kAdAeSob09sN6x913UxvKaEdrfwnqOvjADtDi44n3edBAIAUfjdAUbCdroQKZIg2h3nPZq6xfGRSIc8M9qmwXK5xOHhIepWIq4tl0ssl8ugIWU471DXNZqmiWOo60aYXhngQAql0RCrspIkl0QoygLGEm7ev42f/OoX8M7jxrXr+K3f+R1cuXIVH334MW59/gVee+2bePraU9iYSTTFNKeYzqsw1PLz8PAQV65cxeHhIW59dguffHQTn3z0Kdq2g4ecSwmVQrGfBGE6fACdqrVRMDlwwDdJ4BBZ7L4vQfubfy5/Um/OkfLVBKRaFkt9HUOANHR8FTEND/5mVsbQgSSkTGzbGs0z41DXHX72szfxwQcf4nd+6/v4we/9Hp69dgNf3v8SP//5m7h583M8G8Bpr1EKMZlD0XPhnQO8Jnb2ED8wyUfGkOh1SquCmzwuXrqIW1/eBUjugc57LJZLifZXFYE5XJVQX7p0CTdv3sRLL720oq1lZkxnU1TTElvbG3jm2tMoK/FpI7LwsGCqBnPZ7yNhDERrhqixUG1gCkQH62oSnDxYa16hDfoqAVFbFBcOCqYp+PZwuAfCHckcfMwYvhFTvz46G2B4AXiP/UPJN0ckUQ0nkwl2tnZw4dx5XLp8CWfPnkF3cIQHP/8F3vjFWzi7s4OrVy7h6tNP4dLli9jYnoEY6NDBE8N4B3QGbAjFpAQXhPPXLuPS5f8ML7z+6/jVT3+Gj998C3uffAHsz2GbGp6PZDRrAFE6HzpX6Rqv/OunaLTk4EOTwufal/TZeFesYcjGgNFJUvl8TP9zlxWGnYZ0YVRokfwdQVLnY9L3dQBlrOjHOagbY5RTkDTGOOeRzvLn1McvvXtV27Dar1X/GeWv1oV4z7VA+dwOwFg2nzl4TOtL+zP2+9h7ed1j4GZsXQbPmuG5yveu/p6bUo6dxzgvnYvC6KPjY5RlEe/Jdf1I6x7bg+k7w/4bGD45MfNY+doDJNWgjKFwzwx2nZiJGcLm5hZsUcBxL2EqqzJodYxoeIIdtzIpzGKXbY2EbyYS+3NAfJ4CX4W2bVCWkoNjOp2IyjWYxXh22JjNYkjwwlo0bQ1LhSRcNWIOSKBgDmcA3wUpqYAZIsbW5gxVVUapNQB03RR7e3sBRBVwnUTR2tgU6ah3HovlApUpMakKsV/vuj7MrZUNK1ophjcFqq0dXHrmGspqhvmyxXJRg4oCsAzXtbDWYLYxi/MvpTcnzIvu655Apt9mgCaAtRUyxr0kTv7s/WmYReLMvHrBREKVSN9Zx45eiqOEJgYcCFodNW1RUzTPXsXuYTy5dMnHpK2I4Cwx8wD3gQPCOFXy5Jz2o9/XXeeCRop74OK8RITpHFzbRe0UwliappGcVOpX5FzQ7HQoiwLeM7pOntP8Wt5LNLUmmF22XYvFYoHDw8MIoBZ1jTr8LuBKtD6qu+AulcwZTCYVyBg05GHLEtVkEgOX2KrAxmwHm8HfgkhyTZXBkbyaTLBsJWqjSy4BIpVMyWVHhlCVBXZP7WI2m+L44BAfvfMu/of/4f+Cv/eDH+A73/0ubt66hZ/89GdYNjVeeP4GJpMq2QMq9TdANOsB2rbD6dOn8e/+8t/j9u3bODjcF8YbBIZEQONwCat8gcN+CBtRfvUczV8HezMj/umuTR8bMlQEa4ugeaLBOaHsRWEKA0hiID1ROcNo9VxCx6J7vwOS3FpE0m8ikhDGLH5Wh4fH+JM/+SHe+Pkb+MM/+AP8xuu/jqZt8MUXn+P+/fu4fPkyrl27hvPnzwXgRoBAS1hD8MkcSoS3TsZa9DOjOIfCAhljsL21Gerx4dwxFssl2i4ENwD3Y0sYlpdffhlvvfUWXnzxpSjUIAUzYPHB2d7AYrnEpatXcfrceRwcHIVoVbMh6AIGGlZSU19K/Ot0cjOGdGzxB0wNFCANhSkcOpyGTfZeE+KG8xQCX8RobTG8vURdVEm2JiL33oO4QVPPsWwXge4RjueSmuHBg4e4eetzVG+X2NnexvkL53Dp0kU8e+MG2s7jnXc/wHsffIjTZ07j8lNX8My1Z3D2/Fn4iYWBg+0cCgK6tpZjVhVoqwqbNy7hN5/+T/Hy67+BD//mTXz0N29g79Zt+CMGtzUMu7i+jsI+9rqth6F+dY51vfUM+KDqTZnAdWUdU5v/PSZtz5n6Mc3Dk7Sv5SSwlDLow/dSv0IDgh8w38PGEk1zDpaEaKwwwnobqjYuLXqXakqPaH6WrEWkRKxWFTSgTfk8qFlaOre5xiKfj8gDUt+29k/P+LhIArHNXEORf67fRcAAYdJF+BdSYXBy9pMxKT0e20+5VkxBnZ55CoIxz0PfqfgsURSEDAIUxXVYmenwuYmgVwFG7qM5BorGAnPp3Sr0XeptGkktQUT9/CSCwPQ+WnduoqARiSl7wp9xPs9PUL72AClFupHQk5qrGLjgu0BEKKtCQIoRRpYhUvOF6yRpojGoitmgPgAgTzCFRVlOsL29A+ccptMp6rqG8w0657FsGmxumsDolXGBi8DQiKq/zxM0qaYgkuheZSFJTgEBKmQJbUDD1hhYAqbTChuzSjYk+kAOFhb1vEZRltjdmcGGvE1lWcZxTKcTuK5FEaSJHYvDpAMAF4iQtVg6YHN3F0/deB5kKiyOaxweHgsTagzgHCx8yJ1UJOOhyNykUru0yKZd1ZjIryq5Z3S+k/wWXnxSfL/r4TuXVhhDKgMkbhiBYY0gRx81Ms9IDrIXFBJ9eJTwaCFQvCAULHmnBF8NEXsi3bkuRD2TnDUuMB9NSMrpXAfnGnDIpQOIaV3d1KLRMRVAJkQy86LJCSYwne+iSZqapS2XS0kECh/z4NR1HW2cxfm6xvHxcdQE1bX8LcxCEdZMgHFZlSiLEgwn+VOKIhKtoigwnUxQbGxiO2iQprMZCs0PwoyymqAsxSS1bhrxfSgKeOfgQrhzIjH50Tw+rpUJr6oSy2WNup6LtBvAbDrF/Og4zmvbdVES3natBDng3gTixrPPYrFY4OKFc3j5tW/izp07+Of/8o9xuGjw27/9W/jk48/w5ptvw9oSN569LuH42YO5g5qSkSlAFHKaVSXufvkQn376BfYPD1FuFCinJdyyhocVZYZhFBRyx4QLHwBMiMLF1qS5PHvgFIQiA8Y4+UMvv56pSKoIjMsAGMnDsY247/UsYtBU0BIN2ZKhBB6wsOCQxyzVhGqoWKWwMhxC3Xb44sv7+H/9v/+/+Osf/wh/+Id/iFdffQWP9h7i008/w71793D9+jU8ff0atnc24H2H0gbpK1s5/4bhAiDrfAcK2jJDJmrlZJiiuzt/9hQKQyjgYCDmeIu6Q9MCriPYYpyJu3jxIv70T/8t6mWLybQKZ1FMlGWJHJ66chlvvPk+Lly+hqduvIhfvvtLAB2YLQiqoRdQwl6MUeGD1j9EF0XCxKmZoPqNpcy646HPgS4SA+DUFDRZT2Ey+nC9hnvgqPmObDAF986BnQNp3F0T6nIehfWivWOGpQlm1SzSGs8eXdvFMOdtU2O5BI4P93D//m18+ME7ePONn+LCxQu4ceNZ3LjxLPYOF/jix7/Emz9/D8888wyuP/sUnnrqMra2NtCRA/sOxgIWDGIHIoPSVjh35SLO/KM/xEuv/xp+/jc/xcd/8zMc3roNs38Au1yAuYGnFp6AgiwQzCvDQYPhMpyOLoIimRIFrKvMHdAnvUwFralWkRMakzJsKUOe8gr9GRqXguv3J2laxupIAUJahhJ35VsAIgn4weSglhD5O5LEE9HPkcHRlw0MMPX374Bpx9A3Z0g7+rnItSIWcu9qTryULrmsHdXc5MBoZQzJ87kWKf17UAePz23a9zFQm9al5zU+n0p5dC50jGY4V5GGKzBNAIFa4xgjkTgF4qaCNflf+s5wbYJRbgBH6edK9ymR4akAhmjo8ydV9MEz8rnNxx/bSYC0slRKt8uyRLOYJ8Ki/t7j0G/VfI/NPROpi7fw8RBLDpn/fh7pCcxgtfxHAZDSQ+SCiVl6wIDsIBsTt9zG5ia8c2i7DtOqQtu2MTmpbgJV1xJJwqvFYoHJZILJZILlcgmmDiUYx/O5MMtdF0KoFihtEaV11koi2bbtsL2zHSMdqSN8YS3K6VSYUvLwLMxaYQ2qwiYSjLC1jBzIsqpCMlVhasXELjl4gAAw79CxAKPWe5STqUg/ncOy9Thz4RKuXn8WDhYHh0fYf3ggPgQg3PzsMzz99NOwxgbN2VCVmztjjoEkLZKXiAWfeAZ7tWkWrYT67Mhn6s/je0lKYO56jQ/HCGvReVEPHgFkjThVOz8g3t65EKSC0bRi5uWdj2vSdg7OdRKBKoAT3W/KRFhroqmaSmPawFSoOZlzTsCMk6SiCpyW9TL43nSYL2ocHy8AEFznsKxr1Evx43G+RRM1N4mUJ4y/rEqUZRUDZpRFgel0hqqaYjbbBBFFfwvRBjGqqQgCJLcWsL29jbZtsVjMQYbjmqbnS89b5zyOj+fRPE+0X0K0Um2uzhM7DKTVKfOhf6dOp1Ho4VelsPFdM7RVf/TopwCAt99mPPfcNbzwwgt45ZVX8cMf/hC7u7t48cUXcevWLfzq7Xdw5uwZnDm9K3vBq3bRgyCavLI0OHPmDH78ozdw7+59mAK48tQlHB4usagdHGuiTS/gSJleJBcsIKqZ7CJOx5GW9MKm6PezasLi3appS1q/Msj6WezLyLN523m9RGJqZUy/VqLtRGDWQ0JMIhhrwd5jsWzwwYef4LPP/q945ZWX8Ud/9A/w/PMv4ObNz/CrX72D23fv4ZVXX8bFi2ckrw0oaOWGDuLpXvfeh4AROiYGyGC2sSHa97ifRPO3rGvw5gwSNns4x957TCYTbG5uYm9vDxcunh/MEIUlu/HsDfyrP/kLsJ3hueefx+37X6L1NXzrgUivhnlSlLFZnUeSRB0jax3HRP3e1jpk3MVaMy4TfGtyE2dDqjkJAX68B4UzVZQFrA1RUesGDpK3inTfkYExRcwlYiuH0nuQl+h8TVOj61q0yxrz5RL7h4e4c+9LfPDRh9je3MLTTz2D68/cwKWLl/Huu+/g/Q/ew+XLF/HcczfwzLWrOH1aEg93bQfTeLmXCg8uPIqywvaF0/jd/+zv49vf+y7e+usf472//jGOb30BczxHUdew3qEzLgA9E0CSMPPwwqjqfAzO2hqAlPMHKwznyPO61vkZOunOy0tKA/P29Luv4u806CMgcIejnD6A9f5bhHtPh6C+WloGQhrt60j/gdVcNTmNG9DvwNSmNCh9Xu+IMQY815qtG7+Ak1WNQjwfRgQuUXsxAjbGAO7YZ+kY0r6lfV0XcY5IApzovOf+YqA+9PngHhipK+3PyvzLH0m/KYCjBAhltY6t3TpQvw68p2I59oymrkWIY0nR2kpduXZt2F7P54mvqoKjnlfM77bHla89QOp8hzZEFJKkiB7EXtTwYXI1godnjsnd0gOvqtH5QkwLtrY2JXdIiO5VUAHXJQTDSh6Krusk+EFhUdF0gLTb4GheL2twkOwbY8SJmBnTqfjwkDEgFlvXopTkfWQIbE1Uf08rCSeuDDEgxE43wu7ubhyn9z6aJBlj4EJfyrJE6yXIQh1AIINQN7JpN7dP4dKVp+A8MK9rHB/NMZlMMZlU+NN/+6e4fv0ZeO+xtbU9IALrgjTkkqX+GWFGe0AkvgbeBRO2TjQ16ryvGhEFRmr2Fk3igl+QDxEBm6ZB00jYZ3X6b9nHxJoKcjQnj2vb2Jb3PkYUhDFYNg3q5RJN20a79OVyiS48UzcN5vM5vHPwzNjf30enQCbMu9qyy34TTZZEk7JRslSWJYoAckQSRphubWP7dAXXOZhCAhEQGQHwxsAWRey/IRPyC4g5WlkUmEyncF2/BgrYJDdPB947iNooIsLnn38R57RzHdoAnFLNGYCY54hZpODOSchiMn0o7z50N8MYdXZWKdZQwhYvEjO8GAiiUdAzkF8cjMBzhgsmXiQMfPD+R1guG7z00os4d+4cfvjDf4NLly5ie2cL+wd7ePudd/H6b/6GSP04kfqhd1gvTIW7d++iaWpsTTdw9uw53Ln9ANPDBebLVvqS9EfmimMEQP0e2blQOpCXMUYgP1d6xsfKgJHhVal33lb+/Lr20otS50YjIWpCTM8+2YMCbJZ1i5+/8Uu8/+FH+L3f+238wR/8Po6OjvHl/bv467/+Mb7z7dfwzDNXYQ0BxMEcoxdqKRgDEKOzMYuUm8JZPLV7SsyhTT+Otu2i2WhuBpTO/UsvvYSPPvoIFy9dCM+ojFWkqru723j66afxxZ37mGzsiElxzaLlavvQtgMm0RCgibIV4LCYyVnhSKCJtBXQMXuJUCiiVliywYQk5K6SyUeaQBehp94ADIKx5SCaKOl6sUVRiFm3AqXgVouyqlCVJdgJbYyCDc8wrKkAHMgJuCLfoTQWRTUBwFGjVDdLyZG3v4ejoyM8ePgQ777zDnZ3dnHtmet45tqzWHz8Gd597wNcuXoJr3zjJTxz7WmcP38GhsVMuOkYXeFAthHhZlli88pZfP8f/xFe/N638Kt/92N88O9/ivr2A2AxB/wRwC7SJTn3waQqASr5nl7HWI8xxmnJGeyxc6KfrQMNaVlr8ob+nOm9l7Y7ANbJuV0BZtxL8BOdAnpwFD4nESMOorExR1/VdfQj728+rycx0vm78bPAsKfzlgpJHgc8UyZeeIXhWq6AOAyfWSewGiv5HkjXYWy+9I7N+6uCkRxcqZBjnSDrb1uU5x3bSxIQqBdO5UArB0p5vWNhvtMSNZNIYNPYfBENfSsH7fV8r/L0qs2UOQxzlJgGPq587QGSKQwgQd4keo9z8GSiys2Q2DxqpCOZZB+0SITCSqCBDWsFgXq5gD2LlJpA8IDk5gBiKOQ6MMk2PGts6ESwjays5EVS0z2lTa5zYDCOjo6wZQ2KsoDzQZMUNth0NoWxYqLknEPrHAwYSJhV5yUqjPMOtijgQx2eOYCBFkUpGqW2bTHxE9SLJUDA22+/jel0ip3tHRRFgWXd4HuvfwPGTtB6oK4bEBm41uHW3Vs4OjrCZCIhvauqN93TkhLyscsoPTiaYNQ5DXgAON+hqYWBXx4tcXhwGAHOsq4jo922jZhmBUDTBsAiTLpF13Wo6yWWy1oCZ3QdjudzzJfLYOrl0bXiW9N1HawxqJdLHB4dwQUGou1aLBdLScQYpFAyPhb/DwomSEHLKGM1YX4qWCvmlZOJgB3RSBYoqxIMiRDnnI9Jg7tOJPK2EM7FOY4JIn0jwL9rW2AZzOdcD2K88+DQb/WpEg2PEAjXdcFnClG6EtdgJIt674DZazBUMyYlJVwkEluWfrMXqaQIHxQXGDgnupmUyCFeThCGkpImQDDGRhW6+BkgEG8bzJoC06yaDQJgVAvhYMnizu0vcebMGVy9egU//elP8O67b+Pb3/kOls0Gbt36HK+++go2NyZIk8+yZ1jbXx7L5RJ1XWPXbsf1FAxEaJ2DxiFnlcwaCgxxIAXJbOn415mCnHSZ52WdVHPsTObP6e/pOV3HBOVMmPZN3xEzLAdigoP4/Aitk3XrvMPB4TH+5R//Cd774CP803/6X+Lipat48OA+/uZHP8NstokL588IpqThfAwCSXiOEc1kr8mzs9lUABJJ8AhlqJbLpez9oohpIBRs6eV/9epT+MWbf4zv/9brATjp/IhG0VrCN77xEn717h/jlJ1ie2sXTdfCde3KvEYJKlF4m6Imv9fCxtHABc2oBvdhIB4tj0TTGOsLYCqls4Yk7xUI6qcaeoSCKCb/JWuC6XgRgq20gNfEs2I6bozB1FjAGHRBqOK8iwFbmD2oa9E1yxAt1cMAmG1WqKYzdN1S8uJ1HY6OjzE/nuPo+Aj3H9zHr95+D5cuXcaNG9dR1w0+++wWrly5jBdeeBYv3ngaly6dhyWLrmV416J1LQrXYFrM0FmLnacv4/v/xX+Ol379u/jln/8In7zxJuju5+iWS5imgIVHwR7et2J+k/hwpAJLZZ7WMZwKTE5iep+EWU2FhieV/Pynv+fWGGndad/WgTRAndUT5l83mY4L42Zr6fjyecyfSZ9LgWHOXI/9TMcBEgjnR+Y8BYBj//J+6ec+64O2FX31ct+dkfnOv8vnZ2zM6+rKtcAi3O37NB5pdk2f1D4tKTmtHtsbY2sxALQ0tORYNz/pWUnrUAHaoC+BnplCAizVi7m4vWTBc066D1dGLwxB4M1Sje644OKk8rUHSG+99RaeeeZpFEWBoijQNE0wf5sFW3CDuq7ROYfpRIInMBhFWWLv0SN88umn2N7awqlTp7C5uQnXdpjP53j48KFIKU+dAiCLWE0qzKYzkfAkKulqNhXag37TqxQmJS7eRe9SGGPw5d27OH/+PIqqBHvG8fExDg4OUDcNqo1pMIuTUOBiBiGMcNN6PLj/ANevXxem0DmUZTmwp/bsZdwBTNy9dw+FLdC0LW5/eRenT53Cg0d7OH/+PJ597kVMN3fRskfdic/IgwePcOuTz/BX//6v8E//63+Cq1evBmbErN28Y5KF/DNh5iW/kneE+XyJhw8e4sGDh9jfP8ByscRiPsd8vsDh0SEWiwX2Hj1C04i5Wecc5sfHWCwXckCchF5XC5amrgWUFEUMfe28OI6qXxYzS3Sm4EzKxmK2LZnlDUmwjmoygbF2YEpnjEVd12jbBtZKMAE1UZPw3hz9fZZ1I3MfCDIRoen6EMeeOZp2svfw0fNYJOUuaNRAYoMcnSG5D5fKzCHyVxL5TjU0QBJpSJ9H3MsmAUFixkgBvPaOj1LSiGeccP1anwATSnwuEC2KtQqCRi5LLwJmhDD8fdEko4YIpRETL47mHvI7Qxi/lBBHhl12GbwH7tz5Es89dw3T6QQffvQBvvHaqyiqCkfHxzg4OMTGxiyYdw3t4Y0xaOo2RNdDTAEgUnoOD6ZSXCvzoJf1QFI7PA9jl6l+l1/GOZMxxpyk76fv5j4S+XOp5verSCbjhUgEGAvfidmogQGzizmYiEIiRhYzr/fe/xD/j//x/4n/+r/5b7CxuYujw0P88pfv4vd//3dgLANwQSU4ImmFMOwGIdx+MB8SgU0Fa2z04XTeoV4u0XYtJt5ibGhEhJ3tbQDAYj5HFYJ2xM1NEgTl+edvgIgwny+ws3MKX979su8T82AdZb7FdLsXVoR9CwiADxJr1cKKgD81P0JkYBGYgBBPE2COjAUpSNRNywiwrBc6aNE7QQU6nSF0ak4cQJcBwOxgPGALG03CdVzOOXDTYkkGnhcAMdh1Ao5tidIYlMVU+hjM8OqmRtM6LJYOx8slPr/9BU6dPoXr169jvqzx6Wc38c6li3j11W/g2vWncOHSORSlaCNd59ECwKSELwtQYXHm+Wfw956+jFe+/x28++d/iQ9/+Q7m9/fgjuewbQNrRdDWCy1yMLO6r9btex23PpOaPK57L2U01525/L38nI/Vmfd57PsVpjhIqVb6yQrAGMwOMP29kdODFHjk//L+p7/noa5z5l/7tBJUAetp3bp5WAeSVKCZ1jXo50gdYyUHqzkwG6tjjL6uZ9o5MvgpgBLT2oHMKLZjMt/VfK7yPesybcrYHgy/QYnluj2c/p373A3nHj0tCsJSdc04eKQavv79Aag+4SrSCLPye752ovhYZ468rnztAdL7H76H2cYE165fw+bmJpbLJTY2NmGo13QUVYmmaeJGLAKzY8oCddvg8u4Obt3+ArPJFJcuXoRjj9nmBo6OjtA6AUyTyQSmsCiCBmWxXEZbyaprUU2n0cxBfZAYQOuEARbzukZMpozkGLJVic8+v4W2adAEc7Bz587h9Nkz2NjeQuccqrII/KXH/v4j7D16hNNnzmNzawvHywWaphGfoMKCnEhx26YFSPpxcHCAo6MjFEWBjY1NfHHnNrZ2d1C7DmVZYvf0KTz7wgtoHIsXhifcvnMXBsCZM+fwwvMv4MKFi2iaBltbWyumHlpO2pSrEjKDZulw7959fPzRxzg8PMayXuLLL+/inXfexqeffYrlcilMaVnCGiNBAcLcW2tx5sJFWCuA5cpsBmvL3pfIc4ykUzd1iD4mGpWevw9meq431Vu0bfQL44NDeNehDeGu1XTRq+kDifRCTepiQlbVOgVTvjGGNRJe7gENkxC+q1efhneMeRMiSVHQymjySUoILxiwQvCTeDOBwRJAHnh5IJE6DeEABr+rH8JYoeRR4eESKZCxYWwjQNkCIX+5AH3TP5dupRTAyfgoSPtsNBslI6aFHLRLIJa2AYAsDDnAtQA8Hj3aw3J5CbONGR49eoCjw0NMN3dQlhUOjo5wERcEULH8T4GkMQZNswy26j6A4DT8egLWEp4+XrzcmzIM5m9EKjdWTrpUTwJJ//8sapJRVBMQi68ea/jfYB8uEsRwWQP4+JOb+OEP/wx/9Ed/hLKcYm//GPN5ja3tEsao5nJ4Kce5iEIBhD1hAmgtYctCfJECbWqaJmo+mFfD73ovYe4vXbqE23fu4MaN60FIoAyPpIjY3NrBC88/h3c/uImNjU1MpjPU8/lK/6Izc5R/ydlGkAATCKzaTmDIfBPFfeZ9CP4SBBhEQIxC5z1816FjF99Rc7KAmKQ9Y0McBgGTKsQT5YqFNZPoA+C7Lvp2AiKssAYITcIY0XIZA3Teo5hMMStK+btr0TRLdF0LOAsmBlHIeTKrMJ3M0DYN2q7D4dE+5guLo/kRHjx4gN3dXVy9ehWHB0t8evMOrl+7ipe/8TyevfEULl0+DyZGQw2M72Bb0b63tkFZlLj48g1cuP40rr37Ed74s7/GnbffQ/fwPviYYb0Bdc0agYJqdseFDemaju2/nDmWfbJe45C+r5/nv2t9T8JMj4GTdX1YLekzBgDD2jJoZVdBn9KpMef8x7ZEQ188PW8rd0IGLkwCEk5qb4x5T0tsa+RruT9MFEQ8ScnXJgddOfB7khLXLvh7pFHj4ti5t+RI21MamPqIjY4zfK4WC4/zZxPXhb5/uXD/q4wrtp+8ymDxgw7CHUrmNR1fyqfkYxd6Oh52Xdv/qvfh1x4g/d4P/gBXLl8CM0J4V4JnQlVVUZ1qLTAtyj5nUVjAc+cv4LdOnUHbNrh//yE8gOnGDGQNtojABBwfHePUmdM4Hxhy1UJ0wdxpuVxgXteALeBBKMsCtqzipqdgl+6Z0XmGKQpU1QSzzS1473H6zNnADAoDb4wk0/QkpkllNQWB4V2HcxcuYbqxjc3ZJuqmwWxzK/hJtDBGTCW8c2LuZSVvkof4h+zt7WG5fIgv797Fo0d7mE2nuHbtOq5ceRpffnkPZ84/haOjQxzPF7h44QIsWfyrn/5PePbZGygKC2MkXxPlACkeglxN6gcHWpgcea9uHD765DN89NHHaOoGjx5JEs5f/OKX8OTxwksv4tLFi6iqCk1dS8hq7+DAwceoQd124KZFXdc4PJ6j6xyapg5hp+WwdJ0LOYCE+WiaRkJms5qiCYMgpmjDvEUaN7w/nBRBVSQEUGGd7KfU2VKZOEMkkjobXO/DHBUFBfDTz2XTdji1exrnzl3Ae++/j8V8AfG7CIE2VCSD0B39JfRGCKr0Spo1kYFSxh0IzBOZfu0CzZFnTQRlAOLeBDD4LC/GFIMLNRJkAjj4SkT2UaYnaDtzhh/xOQVVG1vbuHLlCtrgC/bwwUM82t+PZiLMogOSPGThovWigauXDQpbYFm3uHPnS1x/dhfGGAmuksxJ4MHD+kp0v42NmUTQazrUywVsIZL2wPbHec4Zn3RfpGWMWXqS8rhnxy7oMbOYlKnKPztJYjvWFkEvJABMKIsKjkw/9+zF8d+YADgkYtmv3voVXnnlFVw8fwFL1+HgcI7NrdOQvEdr2mbW2Ubg6uQSB+C7BtVU6F2QC6BuGiybFhudAxmKZnaDyxge129cw/vvv4fr168NmnPOCUpgj2998xv42c/fwk51DpuzTTSLRehJIjXW6IWCkCUlhJq0KpMYBBkgikIZCmbAeh/1ElyATYjSxCR9KS0m1SZc5yRcrvMBFALE6nNmIjmQmerHroIVay2KYgpiEsFc00h/wDDM6JomaMP7dAfioysdK0rx+ZpMJ9jwM7Rti/p4ga7pwCECIXsHayvYaYkJCV2u6xbLeom6qXG8mOPho0fY3jqFSxcvYVEv8Mknn+DGtWfwyisv4rkXnsP2hVMwzqNwDXxdo6wsUBi42RRNVeDKt17EUy9cx0c/exu/+Iu/xO0P3kOzt49iboCmhYEX7SWczD1z1Gkr1TVhy0ve7/485EIMBQupZm0d8NH9ld4lJ5ncjWlr1tGHnEEf01IFMU3YS3mGM8BYikGhDNLAJ8O8RDkQGaMdY2NJ+8Os7QY6gSGN0WdE2NRHI17XRj5XY5qc+JPQR8BN6wDkPvYEN/Lu2Hj0mRRk5LT1JBCd9jPto37unOvvauU1svYGQA288tnYPOX7KhXa9ZxEqB+UptEDwDF6aHKjIQp8wlgcc295ofPu9Lan2FfXuQi82PtBdGLGsP+Joij2m+PfPn7JEOsZRhAgo88B+aTlaw+QphunwGaGsihQAqhmYuY0b1xMsApmeHgwWXSd7yXOIJjCoDIlvvnt7+LgYA97R0cSWaxp0HqPZ196ATvbO4CxMLYCBwfWCrJBZzu7Mbx127YwRTC3Cf3TtfbeY3NnmpjAcSBWQhgsEYoQ+rtPNClgzxgLGIvWM4rJFhwblNUGrPe4ckWCJ9RNg2pSyaEPksiiqGA7j9Pnt1BNN7A4luSXN64/h7Ka4Py5C3jrrXfx8qvfxP7+PsgYbM5mmM/nWCwWWLZLnL90Ad47bG1ti+QRDI1cJYE7NZKIR6SH8lQESWIcrgEkgM9u3cYnN2+h7jrcuv0F3nzzTXz66afYObuLl197DcyMB3v7uHf3LpbHCzSLBdq2QeMadF07yN0RgzgEXW7/ux6u0M+kX7GsXAKyYkQEMuVAgtP7KCTPDC5QQgwpy/r9kAgNmg4NKrEg70EWqD3Dbm5gtnsKtQPABGOLBMD5WA8BKNA3skLk0z/TxVn5EglBCmtHvflD3v10Dik+xxJKeORyE03QkMCLQIiGPVJiFyVQHsYAx8cH2N+fYjKZCONVECiElicdf2QMxa+wYwDwcA6wdgLvFjg+nMMyoySCb9oQqavvg3eAYFwPyRVTAmzgOpG2nz61ASIHQxU8G4jnzfDSXAcuxi7Mdc98lXdzZm4M6KTMxJP6SKTv52PiAAIQzhkCc2+LEkXYMxItUfKtWUMojIXrOtTzGh9/+B4uXzwNawwO9+e4fPkcPHcSyCBrJ/7zEtGNEdbde8zKAtvTCp4JpTES64A8Gteh7jy8nntKJZShbjAuXjyPv/7rvwrgLYAv6GXsAFfjxRvP4NTmBPVigWk5BbzsPbHiGZqqcqDbSpdS+sBBWswISXwNIebphokAHUQgG8AOGIYYjjqYyQywBaZ2gmpjG0cHR1i2C0xMAQo0zwRNrQtS1hQkgcVyobRlEI4wiorg2w7LtpaE44wIfFOGzjBDT733DLQeZAuUZYnJtMKp2SaaehFTDywWiwAOpY7JZANl6fugOeHfcjHHwcFD3Lmzg0vnL+HwoMaHH97Gc89+ipdevYGXXn4BuztbQEHo6galtxIwojRoywrlbIIXfvvbuPba8/jlj97AG3/6l1h+8jnMwRGKxRJELQgdvHVi0hgDN/WUjBK6qOuVO5yrsEHN5oeCwEwghHGAsQ4EDffIekY3MpdPQDeUifTsRaAZEhd7ZS6N3NWOLdKQ16mPk/5cR1fy85T0WnZdQu8VHBGF5CIcwuBrzHnCUNiVtNlH7l0tKfjUNRiCNL8yz3EsRANAqJ/na5vSytRvKY2SvC66Xgqa9P2x2UK4cyMRYI45zsZoMEHoBxENosbm93UeRMb7ILQatC1/e5Ho9X0PZn7iU4+IqFKXAbBYLMUrACwClTAWZtPLYItCBDthzmKag3DnR1NiAkAGZHuf0h64KZhK1oh0bgjgYOJMfxekIRYbTNlYGQcilJMJ2rbF0fExNjc3w2YWybgpNGwqRM3ngc632N/fx5d374BIQk0///zzMcBC23WobDlgRnqmRaR4AAaRhIAe/aaMzYDwhsAO+plKqHyItlSWmk8J0emQmeHYh/DbkoirXS5FUmssyLtBDHwKfljbO7uYViVOnz4DIovFooYpCnTOY3NrC7YsY2LQruvwxhtvYGt7GxubG31fsrln7jfr6qURtnxgbgQ8AIv5Ardu3cLGxgbefvttvPvuu7h37x52d3fx0ssv4e69+3j33Xdx/949yd/RyQEV3wM/aJOoN6sxJKrkolBOX+c9GJwkEprY0wzEqGQcieQDyXdjJSfixthI7KWmtJLVd3V/GGPADjGZWucdQBLym4wGg5BLRfsWZUH9kEfWJ+3/+BgUTGrJI8fldY7OBcmFDC/Er5cQSR/XMfLpZZtL4QgS0MJaizt3xP9DzgiDvU2a7jVxRGluEwHPVVnCe8bh4SHAUkfTtLGuruuE8QWgdszWWkynExhj0IXIaJOqihcakhXIpZgnSUDX7aOvUp4UYOWX6xhjdpIEdaytMQl33o4xErTEOyMJjb0EmRFpqcftL77A0eEhNma7ODrSvFwG5E/ao/0eSf0mJBqkDZoqkfKzF/9L2XMm2vnnY5xOBXQfHBxgd3c3GZPQha7rsLW1g2efvYY33voAW5sbKIsSvmsDM8ORuRHw4GIEJo1C5UKESwDxoh/2RcClMiHeSyRWA7EI6JwDGwtrJKBC6yQoz/bZ0yibKeYHB/DMKLwHeRMBTa85kjQRIjgwmFYT7O3t4/DwMPpPqmWE61y8N1Kmv+s6GNtH3WQOvpfMoKqCtRTnsuskp2DTNFguF3BOZoeIUJaltBPSA7TNEk27RNc1mB8d4d7dL3Hu3HkcHe/jk5sf4oP3P8Qrr7yEZ5+7jlOnttDUDGMcTNcCjoGSQcUExWyC13//t/Hyqy/jJ3/+7/D2j36K4y++hD08Rlk32Gga+AJYUgMyIRKnicbNMGxggwAvjTiW0vbULHJMa5BH/0pDZo+dqa9qvjZ2TsfAS/93EP74TNuZCrekkq/U/hM8Gf6ppJ8Hn0ubqd/m6l2rbeWpWqS7Q6AzptURQVu/NivBBkbud2AIUteB1Xxv6Hua4PUkkDQQ+IyNaWRt87GFAazc2fpO/l4O1LWu9HNmBvFwRnTeVvqRvd8D4BFeIa43BR4w0PmRNdEiptse7HqtV5wznOw3mJ7FJy1fe4BkCivJpdAzm449qskE8+UCn9/+ApPJBDvbOyiTCGzMjIcPH2J+PEfbNijKEufPn8fB4T7OnrmCyWQWo9kVRQWi/qLNVZtK7FKiqIdXP88ZwFTKmEswInJmxmQyie1ofqfFYglblKIdIaCsJnDLJZZ1HaOjaZ1lWQabewGOrvMwpsCjvXv46U9/hn/yT/4JyrLE4fExjo+PQy6cBT7//HN8//vfh7W2jxa1JhN5LhVTJ0nVFGhxzuGLL77AhQsX8Od/8e/w2Wef4eDgAN57XLt2DQ8ePMRPf/IzHB4ewRqDqqiAgiLT2x8OIf4Elbz0zEZ+kRAMNIcbgGAiiPh8eCu8I1JxZgZiBvu+xf6t5LJhxOSZ6Xfp/ojv0ep3CtoAwFqDul4G37MqmLcEKVE231qeNCXaV72IdR1PIjajwAA8kJ6LgLa/yAZBS/KLK7tILBGKokR0gCdC23YhHLTsgZU+ITlnxqBpWlSVRKhcBud9CQdfR3M6IpHIIeQF8V4iFm5tbaMsS3ROIizuntrOzsBw7Pmc5PM+dimse1bL2IX3VRirwdyMAKOxNtZ9vu5iz4GX/rTB7K1txISEg7nd8fEcx/M5NjdOYR5yx4lk0g4PWmy4X9e0fWMMzp49i7t7RyiLMuauY9eJaW7XgatysOfy8T/11FO4desWdnZ2YmPEBN/J/vOuwXe/8xp+8sZb2NjYwnRSwTU1mHzvBxD2oeQs87DGommboSaCZH+pdDYVnKkhFAMxmINrHbhgeCPJwCV4jAfZEl0w6bMbU2yVBRYHB6gXSxhvUMCIlaxRqa6AtaooUBQGbdfi9u3b2NjYwGQyAYBougr0e1TvIC3OS7TCMHmgAJKKogAVfQJ0Yww2Nzcxm81CzsBj1E0tyWiDMMoYGwJsWNT1Eot6jrpZYrE8xsHRPh483MWFixcxny/wyac38cILz+K1b76Ca9eeweZGBTiHzrVwjUdrW0xnU3jvsHHxNH73v/hf4YXf/DX86If/Fh//5A24L/dQHixQcIuChKYbA3TcwRuGJ5Zz74Z3WB5MJY3ale6f9OxHAaf3o8xl+nxa97pyEjO9DhytPJM9P6RBNH7eRspJDPsqeFPaPO5j2gvMROA31lY6l4/rQw4CcpCj9UWezPTzkq9DCoBTXk3fTedxDHzkdeZ7KX0mFzSlYxz7Li+5xm/dezmg0c9W7vY17+XlpL03rAAq/xkF+ClP158JvxKBMPYle3/sHsxB8+PK1x4gRYLEHDa92nMDVVXh6tWrcM7h4OAAtKAY7a1pGkymU5w5cwYA8GjvEfb39nD6zFmcOn06TLxGWHEBjIwnL0ulTCmKHTto+q6qRuOlngAj3bht2w6kfEpUvBfDHmNCThIymEynwbSlBtCrc8uyDAw/o23EnryaTHHm7Fl857vfxblzF3B4dIyj42X0y9BgEVeuXEFZlphOZwH8KYEYHvT00EXmN0gWlP/3XsLvdl2H4+USH3/8MQ4PD8HMOH36NIqiwIcffIB6vsDmdBbnxkfJBolmLDJKQE+IldBSzzPHgwVEFR8Hq+xMGBPJOiP5CxjAj8RAt2dnRAKWlj5s9CqBWUtQiIIZJqOuxQegqkqogSCveZfjP06IG8UfYu7D4a7KJERrTOxCR3HtmSv4P/0f//f4P/yz/zM+/fTztRIfHRfrWkS8OgQwj7tgV4guazhyAUdiWyzgXgUVWu+g7vC6aH58MJ/qwy3ruVMNgzEBtImyARzaUW1wURao6yXqusFsNo2RMeFCvDZKA06cIPVbM3ePK2MXgI4vrzNngsbeGdtHqQY7ff5JLsK1zAEQLkeJNoeYxM+jaWocHh7i7GkXc4WJf1d6FpM+yM04uOT199lsCuwdhehrQbNkLeq6Qdc5MBexnlVppcfVq1fxxhtv4LXXXkucpA0omHcSeTz3/HVsb86wrJfY2tjE/OAQNvr7IUpIC6OpHhillT1HQAAHQv/Lsgzapj44AiPkTjLiFxgFTc7Bs0fhGb7tQEUBBw82BqYswSRAfrssUR8doT48Csl3DUpboDAGhhgUUk8YGHjXDel0AohUWKCaFJ03WU/pHzMDzoPCnhcTZzMQTCgwnEwmqKoSXddhsVhGH1EOhItsgdnGJso25FRql+hci7pe4PDoGF9+eReXLl3CwcEhPv30Fp57/jl865vfwLUrFzCZWsAyYFocOYdiYjFhj4pmOP/0VfzD//a/wmff/TZ+/q//Al++/T54bx9mziDvQN7BeAlq0XIHCr44ad8HY08Y3fTzVOiTSsVT5j6dk/ws5cKotN5cA7WOXq4VusXPhE6N5l/jnkaPmYmlda7zaVwVpOl3Q8Y4fgiKwQBkHLxyv6X7MweU6/xucsDBQMyPp+PrH+6DHOTv5QBDv0/BSA42xvqU9jmfw7SuHIiPzfHq3+P7Mm0772MK7sbAEkbur7G/T+Jn8ruoH7sIehWk5nOcz78xPa882HfS6GA90n7lgPpJytceIAlPJkn1TDiVZIyYKVixZSQwdk+dkog8JAznBm/0pg+ecfbsWZRVJYxCWaFtGzAZMIUNOHK5DkMWD0Nc5shYLxx9VxOSpkyN1pdKHnPGhQjonMfx8QLb29sgowRF4kIaY6G+P2nQALHlJNiywM7uKfzs52/ie9/7TRweH6GuOzSt9E8ZlmvXrmFrawtlSF47mPI1jF5qYoBEiS1JBxmLxQJnz57Bn//z/wnz+TyO7fTp05jP59jfP0BVTmBj1DL0QAcE9d7T45Idz/7X5As5/G74mGIIXnk8KycxtLq++eer0j7tR04U8nk0RjOJM4qiFKYk4NF1TKrjRFKZEiggJkaO7Y32cnVURIT/3f/2n+D3f/A6/jf/7T/GP/vv/vsBYVOiPBif1hk441g/8yBseHrB5GXAcCQgBGHtxZfiZLClTKc6g7Zti+2dTQBiKuSDv2DTNGjbFrOZmAWBEUxRpIqqKrG9vYXpdIr9/T3M5/MQ+t1E5pZ6S9YB0X4S6d/jyjogetJnA2nbE1x26bNrgW9yeY/Vs65PHPYbQQASO4K3Hl0nmoeDgwOJCuk95vM5prOpeMuP1a/0ZIQpOnXqNG7dfRR9gYwxgHdo2gbOdXC+PHG/nT59GkfB7zQyHMEsl5nBvsPWxhTPPfcMfvyzd1AFLX68iLM5omQ/GGPEET4kPNY7Qu34w5OiwZAeIWYyD8Ab3qNbLMEdw1QVaELwRQHYwEQbue92z59Dce4sHt75Es2yRtEABA9bFoAluE7ooO7/VCoeQZIGrPFDfxhmhus8bBH2eQBJYkbYmz2n9en9VRQljLGwtkTXzVDX4qdUN020bChKg7Ks0LUCjhZNjbpjLOol9o8OcGp3F5cPr2Dv8BCffXYTr730El75xou4cvUSyHo47uDg4BsPYz1QFrCTCs99+xU88/wNvP3TN/HGn/4FHr33MfzREYqmhmkBeIeCGd70grX0vs1DJKclvefHmOH0fOVnKGey0/l+XF3pmpxEI9Yzq9lzI++n9H2s/3lJAYLkkQPI9AI6HyKw2kKEmH4w1v5eynmmfOxjQud1wCYfe/LB4Lt1747Ry/yZFNRqHx9Xd5oA+CQhl9aXtjEEgONAO30up9npXlMz9LExj+2hsTK2L9N1SU0ZNX+jCD5Xfd3SM7H2HuXezC4fo9LWQSTAJyhfe4CkjFmcKCDaOJdVlYQHDugdYUGAeLk552CLCTY2NiQUt/fonEcRGD1htobqYiKKoZ1V2rxOrZ6a2uniq3mDLqZqelTSDYgGTC/afjMBOzu7mM/n2Nvfl/w+RRHENRSSy3bxIPb9kWAPs+kMy2WNnZ0dVFWFo6M5vJcDoxqrrutw/vx5MDNm02k0leETAUN2uNUAjiXfho5rvlji448+QtM00cdqMpngzp078N6jICtmcfCSYBQ9M8+BAyetf0D40mACPYO2YmucAAUGAL/uMFFPTEceWU87KL5w0jEdJ+YGbSuBKHSviJldCpAzwp1JNbUoQxb3zmOIXV7+0T/8AQDgH/7DH+Cf/Xf//aDPY5fFfxgc6MvwshA7df2nbaxov5DO58glFjU9Hp3rUBQUfCSW2NiYZm2HELeVDX5IU3DwU6rKMpz1oA3xDCbGyUA679/4eP82gGrsEh+jQSkjNyZhUxrzOGD3JOAo/U41m0RiPuqMARmPzjks5nO0TQPaJBweHuL02enoNEYmwQzNkvTnmTNn4Lr3RXsUxkAhQXPbtmA/BRXjDKZGJtvc3MTe3h52d3ejNpGYQHDiBwmLb3/rNfzlX/0MG7NtbMxmOGhb2NR0hgjk+/wrSgWIxITO+040TICY+OgcBfqIkLzZAwh2caCgVIJ38K6B7xjEBjwFjC0ANrCVhZ1Y2LLE9sYGLl26jIO7d3H744/RtjX8pIQhicyqqaaYuU9FERkTiT4Vg97kDDsYogiTsVlrQ265KoxjGLWNAsBzTnO9CAiqKvEPni8WmC8XgaFxADyK0sCaAq7q0DQN5osjLGuLpqlxcHiIe/fv4+GFS3hw/wAfffQZvvXqy3j5leexe24bnhgNtQLcnEHpSpSl+Cd96++9jmsvP49f/uWP8cu/+Peob38Jd7AP6mqATFy3nL6m2qR034gMiFaERCedmXWCCP08BRljQCDfv+v+zseggYNGQUDWz9SMcJ1AZGx8PZDqjUW9Z9E4gqMkUv2Q5VnlD5JxJCA1nfvH0c4cLGlJaeHo3XkCwH1cyd87aZ7WrefjaH9ef/puuitzoJa3MzbelIY+bo2/ShnQjQzELYN/dfpZDnKEFA7H0e+P4Xzlpou6b8zfAaS+OGX+iCR5IcvhrCbTCH4AcW0nIgl9zYyyKOC8R1M3wvz7YHajmwZq5uDhrYYINREVC6goQj6IFmUpGd1TsJQfnHRh5W9lAoVg6N96CanZmHzW19F5j9lsBs8eBwf7IBA2NjdRWAnzba1BUZh42ZmYEM5jNtvAn/3Zn+O5556ThKqW0LYN6mUdcjsBdb3AZFKgmhSYTCsJkMActQO673PAlBI0VuMvFtONrmtRlCXe+fkvMF/WwTdKJMBd5/Ho0X5w6EWY4d4srp/A/oMchgwOY2DMUu2JFgF6HOsaAKg1hIJGfk/HPiB+UKDes/McJMKIl+0qdPMBkElY8hZFaSQOLfdTsI6YpZKmdcQuldak/UyeiD++/e1XcPXKRQDAU1cv4dvf+gbe/MU7gzbSSzfu84AVVpYMTwYEVs4KIc5TDsfGQFLapprctm0XpU5126B1LciWcJ7R1B0ASQDM8GH5KQozGB7b2xshzLEMzhpdOzUloyBoQdROr/RnzSW6bq3WSfLGmKv8UhzbB2OSyLG+5HWVZRmFQOHTpF/jUtMhYx0e4xCpiixc18LQBIuF5H4z1mA+XwJcIr32B5cmhdMe9gPQa/W3t7fQdW2fd4kZxhp0TYu669B5D+M5YA6CKmWJxOyoKApcvXoVN2/exOnTZ2PIXYaHpL11sOTxwvPP4szuNo6PGmxMpzg+PAz3iQc0siRxjIpGcYo4RPKT/qbnZpj3BNAJE8GNdhShPw7OBbMT38EC4KoCkaSVqGZTbO5s4NTGFM9cOoVvPP80fvTXf42H9++jqRfY2tjGtJzCFgUmIf9f11Lvk0kAkfjnOOf6s8xAVZZgBiZVBVtYlLbolwMcEuOuMoAAhwTbav6i5wDY3NiALUo0bS3pF5wE8yAr70+LEuVkgsVigePFMZquwbKZ4+Gj+zh3+hIOD/Zw585tfPjxx/jmd76JZ559Bls7M9RFA2oYbdugKhsUVQVbltg8fwq/9b/+I7z47Vfxoz/5IT762ZtoH+2DF0vYtoZpm7henlkCrwbrE0DukrgkLJxAyqTmgswxn8u8jAH+/Bzm9aWfD+hwQif724Vi0BB9dqg1EKFq2kYKcNOy7u8h42+DWWoO0lQzH4BT8p4ICDiYN6/Su9RscWz+xmidvCuTsULXdI6SdwZ8yxPcTxGkjJh55b8r7U37pqZmjytKs/Vn5Bt1INkcpPfxVykK+hnDdRkDdY+tJ5mblMthAIu6hieCT0A7IMITBJ7Re47Cb1knAdbxzicTk2SH2Y71M5EIk//OB6kvltSUA0CYdM8eBgWc79A1cgkXtpD8DMH53xDBdw5tXaNrW3RLcaqdzqZwIQQwu8CmOwlryh5wIXSpIRsuLwsm2cBd1/U+P6Hkhz7VIon0BOg6B2v76FviL84hkRgNfC7YMwpJuIGtjcn/j70/j7Ysuet7wU/EHs5058ybc2ZlZVVW1qwaJIFBIAkkITHZBkPTBtyLZz/TD0+0oT0uvye7eYDpZ2Mbllcvs/yM2wbzbGPwwwyahYaSSlWlqeYxq7Jynu5wpj1FRP8REXvvs+8+NzNl6H5L7qi6ee/ZZ++YdsQvft/fSBxKhsNtRtsbrK6sEoVxufBkFJTmfGCI444DcxFLS0skyZTUjd8ojRSaN86cYWlpiYXFPp1uiBG1DecD1JdojZlxzjA1xoALg2wEZCoDGfDs8y9ijCCKbOCLIIiZjIdsb42BEO3rbkggMMaGwm4QqVLqMNMdv3XETobdzbmtQ5Y5gKob/K/qRrtJrfmMwL4bbVqYOQ/rjN2sdcbeuPYE7JgnIQTKCKeNMGTphP7iIkZaiW+VA2Y+wJgnLWp+55n62pVqzG4uvfbonz/xz/mJt/0EH3j/O/nq0y/MPYzAYjknn3DEanbe2yR8zf7ukAD6+S//KXtcvrbm/rLDqSLm5MomB5ZhgNKKSTZBRksYApKswGiBnWFvTiOciWNApxPRH3RdLiTLcPQHPa5vJG49WNBb+onNQPadB/jM4dEy3huB2+a9bUC1NZRsbb21HXZNAFX5L8Y2LYJo7m8v/Gnvs3ALwWpx3fwa4WhchtGCLLN5yaSEyTgF0wESDDuZDv/+hTAgrEG1BRuaXr9HkRdgDNII6xskJQpDrjW5kUhjo7kBSLfGy32nFIcPH+HJJ56yqc+0QAvvG6ExaLRKWVpY4eTtx3jqqWfpdgdEMiRXuZVhOCazFJ85IIAD+YGUhFFMroodTJWsASdjDD4BhTXjdOeFwNIGbTBZZhNY5xks9hGBIHJa/m4csLYc0wsl0fIK7/3Au3n2q0/z3FeeZ3PTsDwI6fcDVpYXuXr1KqrILHhx+yUQAd1BD607bG1tEciQMAw4dPAg25ubLA0WbP64orBCA6WcpsCeC34MdZCuGj5Pdtx2DXXjkCgURFFAmkqyPKfQyiWDlgRSsRDELiFtQpqMKfKEPM3YHm5wcP9BtkZjXn39PA/e/wD3PXAXh25bIY4jCAxZkVMYRVCkdE0XEcWs336A9/25H+C1hx7gSx/7LJdfPoPeuAZ6TCg1Os8AG0lQGUUgAL/ehHHA0K61yj+22kc76NGcPVzfu80AEE3NRz2ARivT6mmJJ4HVZcdIzmof5vWx2d8d50YLLauPWcqaX16jfr8utDYEshIiQ+1sqwld6oBgXl+bc1EHIzQAQ3mvM72uJyqtA7G2ttrmvE53d9O+N2lyc+7r/asD0/r8103xSnooq/b8uOcBmvr42sZm1047/9AmhGubm2ZblRDNnptGiDJVjcLunUB4wFNmIXOL18N8D44q3qKMillx/bYfeJ7LWKXJTZave4DUtDvc3Nxk0B+gA5ugTmlFFFs1fRgGTjpngzqMRiOMMayurLrkfpaZ9/XNvmx3COjKiTJwoU/DIEKpwuZPchGB2hasv145NXoNl0FrhXWorDRI2iiEriK6+H7ZM1WUzy4uLnLp0iWuXL3Mnj37KsZeVhtMKc3K8grj8Zhjx44xcRnhwzBEK8Xly1c4e/4cw9GIu+++m06nQxRGyNbIdRWjVC87JTV2wWujKQrFlasbXLhw0QFCzWDQR2vDcDRiPB4jhUBR26um3poDi+56/ZpxffGtVxIr3Pib0iJZ3jMzqpbN730KJM622t1XMuhQC2FZgSgjfN9MKfGx4GkWPDcdC42BNE0ZLC6V783MNQP82ks5xTVw5Mf/gfd/K1vJFn/ro3+LH3ngR/jA+7+Vn/+F/9eO+ZnRVhicyVmdxrWDqWaZx1jcyoFeH5goiatwYaadj4VxkbeWAhQwmdiknx4Le62QdhLxMAiIfWLoQjF0WoNASpS0jDFa0Da0ulSvzaytyYA0n2uzpW5jcubV02yrfr+vq614GiWltLlxGm3NSGh3aQ/hEiP7+wQIbBS7PC9Ik6T02ZxOpxR5QdTZLfTxLCPh114UhkyTBKgYKs9opFlmc8pJ77+207cGYDAYMB5PXJ1W014xa5Qmlm972yM89tgXCZ059ubmZhUox81JXfRQZ3BsYCCbwqFcG64r3lRP6yqCkweFFox6gYNwJncGneVkwzFFIRAiZNCN0KqLDCyoj4SgiCRvffsj3H7bcT7/mSe4dvkySdpjYWHAwf0H7ZkkBCKQRM63Sgi4fu06aZJwYP8BxpOxNeE2hsiZmHphYH2cbUxUM1BBc28bYzW1ncAGGTLGkKQp48kElStAuKBCHeI4JM+cQE+NyfKU8WjIlSuXOHLwCBsbV3n19Rd5+NEHuPvuk6zv24NWGkRBFAWofEQ3jiEI6HZ73Pe2t3DnnXfw9Gef5JnHHufqG2fJRyOMEQS6QKqcSNsgF8adF0ZSgl8PKhHz9sfsWNvoWpOx3m2e2oQfJZPOfBqw23432uXnYqfGqxk8oF5X/f563f58bLbt7wnD0Gr0a2DJv+OmKfzN+HPW++d/ysAMNUGIr8fzVfPAVht4mTd3TdreDNSw23nXbHPevU2AWd7nztdbORd302TeSrlRHTNrmdl5EUIQx3Hp76lNpbkCSh5qZm3J2Uignh6C9b+uSg1w3sJ4vu4B0qVLFzl69AjTqXIAJUUGC6RpgkewWZYymYy4dOkSb5w5wzTJePThh+l1eiwvL6GNwihVAiQABNYx1TmMK2Od573pnSoKAm1VpVlhUIVCY0jzzJlEuFwUUiKMsdmFtUIGgXuxTkMiDEHoQ1Aqq8mRPqmqC5dcWG7fLx6dK/IsQ2krwSuKnCSdcvnyZSaTMQsLi4RhSKfTK1XTcdxx/kmq9G3KsowLFy5w/tw5JqMxw/GI/mDAgQMHiOMYGfgEhjcmwDuZME/MtZ3HIOSF518gz4sGE5Zw7epV9/wuqlwBQgR19sMSZEeVZ42b7LablWzZ62WqKuMlVjXi3gaQwPkjUP54UDZznwfBDiyU1tjuITsjlhOv90s7M0/lVUXYQBlBGFgfOpW55Gs7D6lytHOASP1wuZG00Jd77r6D47cd4d9+9d8yzIb8zku/ww8/+MPcffcdvPjiazP3zhwKJdDyjc/2r+3wb/bhpgAQ1N5dVX/5Nx4cW6KqCmtm6n3zvIktCKZOSOArNcY+ZxM/W8ZssLBgI+IVNvz9YNAHsVkyzjPoqFpO5ZjqP3Xpa/NgrL8n7xvSnJO2z83x71b8gT7vwPd11p3U6zmEZvtUP9p2adP3U/j9WgmGlFIu3Hpo80xF1tx4xz5kJzPh+7GwsGBzLmmFlJ1qDwJpklDkOboTOcBWyinLMdsfydLSEpubG+zZs45SPgCDwCBdiG3FnSdPsLS0wGg0pdOx9HTGBNHMRsfyRWuDKQqMtudJPcADxmBELey3H597VpWMnhNIhDbQEIVBmgKtxozygtAUrPZjpuOExU6MEMb6z6mcA4f28oHveS/PfvV5vvKlpyk2MxYGi/R6PTACoSz4Utpq/BcWFhgMBghh/cPCMCyjN3q/LR/kxCftrq+jNvDumWIvKPT3RVFEYTTKfbd3aZFwY5MkSUmTxNI+Y8G17EqiqMvEhQ7P85xCZUwmI/as7SFJp1y8dIVXXznDw488yIkTx1hc6pOlilAakmyKiEOUMRQdTbzS5dEPfAt3PnQ/X/jYYzz/1FOMLlxETCcEqSA0AmmcN6wjcaamwXToqBz7XJ+lFoDhQUidNvpIc/W9VhfU1vfFrFaiEoY2z4c2OlIvzetKqXL/1wW6TdpdP8NmxsXs/vK/S2Gz1ghRBY8CSSgr7Vz9uXm0qo3u1X2upfRRCWfN1Ko+7jTRLp8zNx8mun6mNTU0zXnZDejVAV59fPMbrs6/mwE99Xmaq0m6YS03V2aB3KzJqGh8bgOkxpgZHySjVBU/wBjHV7WAoBoPcrPvD/4bAEhf+tIX+cpXvkwQBIRhQK/Xp9vtIgiQgWA0GrK1tYk2CqUK+v0BBisdDYOAzc1NC3ZcuG0RBqUkOcsc2DE2nGoUxVZiqFWptrZ+PBbgSJeksB5esh4Jx2aXty8vyzIMVeAGoy1QSqYJaWbtsn2iWi/BtFJlG4bYmvc51bvRqEIxHG5z+vSrFhzFXdbW9trcHd0uDz/0CEliTYPSNOXKlStcuHCBzc1NpuMJqijoLwy4//77EVLanEtyfrI7X5qSlzpBtyAmIEnGZLnh1VdfA0Q512DK5LQ2x1MEQSUFnmEwAYzE4COk4EI/Wwdw0aJl8SFO7Qa0TJqrCCO8Vmgn8bCDsT4LVuJEFUHNONOhGUbY1glgtJPKigpYauMPGGe605B8lZJiBxqTJEUVik4ck0yzHVLpr0USNEuMZjn5+hx84P3vAuA3n//N8vcPP/jDfOf738mLL762ox+lNN/VqF1Vt9LDHYfsf6WkyzPwQlAFaRG2n8l0aiVYjgZ4ICWlNX/ULhiLdv4pYWiTkHqGvtfrVe1IiVF6BhALOWtO0bY35oGcecxI2/g8QzXvALoZqWSzjSZjItw69hrzWcZNz2hmdwtjDBZMWj8hSxPTNHP0zNJCC5S6yFZfhFlmayfY9JofWyytjkotnFIa6fPD1cZb7UM4cOAA58+fZ+/efY7B8mZyoLTBiIyFhUXuvucUn3vsqdKCwJov26Jd1nlfb0nDtC7pid8rHhzhhTD+HXituJsnq401JS0RymBcQlqhjfus2b6Uc6bI6ApY7vQggn4nJuh0iKIAIwwPv/1Bjp84zhcee5KLFy6Sq4xBb5Fe3EUX1kJBhlaj5aW8vq/et9avC//ZB/fxc30z684/p5SLNuiYHyklcRyzuLRIt9dHG8XWxiZZlqCLAilCZBDQW5DooiBLE5I0Icsz0ixhezhibWUf4/GYM2fOcM+9p3j44Qc4evQwohMghEKlBTmC3GjCKCIOIwaH9vHuH/geTjx4iic//knOPvM8anMLMUnAKBvEQRcWYAuD8YmwTbtQrTneJqNcX8d1DdtuJmVt4aCrs9EgnOXJPP+WJlNatTHL0DcB2ryxNJn58h5jnDCzAg4zJsW1/Wv72vRb3Ekz28ZR/9zmQ+SFn806LO+wkwa2Me9toGUekGmrx/etLeFtvT9t2rrmPfPOhHpfmtGPd8xJC22efW+za7OtnXmlbb2KxntM03SGH27bO6XZqqB6TyXgouTH562ZWy1f9wBpfX0Pk8mEPXv2AHYupRRYLau1nx+NhnS6Mf1+j8GgTxDGvPbaK+4lwnA45OUXXyJXBXfffy/9waBc1IEMrDQ/shF77GGeVUydwYZkFrL0P/IRgsCZsNUlhqIe/c6CLb+wkyQhTVLCyD7TSTpWchdYZs4n5ouikF6va8PHKnv4GmlQRiGlwRiF0jmj0RCQrCyv0un0uH79GqdPn+bs2bNcvXqV6XRKkiQsLS5y4MB+ojjmyJEjNit6qUGa3Th2GPMJcPW3Za7yXJMkGVvbY65cuWollg6AZVnG1tYWMrAJHw2CQlf5aryWyTNS2nhnPlsEAYiqrdn+2DsqImk3XEk4Z+6jrLH+V2UbjdUqWCOhGdW9v7udgFjpdCCcxsmoHRoGP6/2gAzQxiY01UZbwF2TjJS13oBYtZUZRnoOOAL4zg+8k3E25kOvfAiAP3jlDxhnY77z/e/iF//pv9pR78w8OIbKCFO7NLt22p5tO2h2H4z/1c6EVH9aEKG0IgwDcqVI3d6VBEynU5TShJFAuLXl5ykvCpaXl1laXCJ0EvMkSRgMFsqAJzvGA85hvXplbXvmRvun6dTbZFB2AznzAFbzPezGANXfizFVxLI0TUumpw6y5x3udRhuvIDC3e/rslJzYc3kTIeZDXITJQwlS4uLpa+LHZDtc1EUjtZqjJFOMllJUOtzcejwQT732OMlw+rpniAoUymA4tFHH+LTn3ocpRSdTqekyT5UfAmsmBW4GKVt2PqGWaqPKlfOI06w48+xmmmhEJWGSgQSpSGIImRhLSCGl67x4iRBjVOOHT9Et9OlKwOECOj0umRZzuLaAt/2gXfz2iunefrLTzOabmPQxEEHbTS60KUGTrkxeSavcILEusO8Z+y9eXk970wbw+vfeSnZdwy+Z8wF0Ov3iLQmCkN63S6bG5tMxmPrK+t8s8IoIgxj0iQhzxKmSUJRGKaThM2tq2xt7WVjY4Ozb57jkUce5r7772bv3iW7KpUgnRYUuaYIC3QsiKOI2x44yeHbj/D8E1/iyY9/iktvvAnDIUGaEsgIqQubH0sA0qCrVFblGL1wtAl65km1mzSwjSY2628zW9RmJ02pv6PWz7VHrCBBlVrCtueafal/rs6w9vtK7Vit2Zuh9bsBxRsxxm1gZzew0FbXPNrYpLFNP7L68x4kNoMt1L+fB4DqtKTcIw23h93Oz93OihuNtznuGwnB6vfCLCX3427OdXWeVM8aT5epgt74fz2grnhALE9oTLkZtfn/a5DKEsexc6juzEhPhAhQqkAIQ7dnQ2ovLi4QhhEISSBCBv2B01xI4jhC6oBOt8Panj3WX8lJAMIgdKHAQ+I4QohFDFUUIoFEigAZSPIsJ4qjSvsirKOqFNbHyUvJDKB0TixjlCpAhMhA0unEBM7mW2ldSkL7YZ9ev1fmnvCmDkJWqvlur0uvs9cGcgitFq3X63HnnSfZ3t7is5/9LFevXmU0GpFlGUtLSxw/fpxet4sw0O33WFtbI44s4JMyQOsK8d+MNKfaIBZiJElCGEa8+uprFMqaUgQhpY9Dnuf0+wPL7JpZVXVd5W1xgsSGQajyioBAOTC0c2/L2m/fp2ojNclDXQo9c90A3ryvxny3l5o82BhwgTYoGadZwl5J6gUGXUpkhbD+FULMmh98reWHf+h7OHzogPvUHgWu2+1w18nb+Q/P/gemxRSAaTHl91/5ff7MvX+Gv/d3/zJJks4dNcC585f4t//uP//XdfYWyyxRr5hJr13wWt00z2xoabe2kiRxvn82QaeckXoqer0ukfNBEsJqi7u9AVIGgNphZCbsjdVKu0kpXNsB1wY6ZoHLfJDVBnya/ZjHWDTBkQ8T7E1vvHCo2lu2VH6VuxfhzNWyLC214mEYk0ynIFZu+PzO/gqCICwjvPm+B0FA4oRKWtvE05avqAtHqjno9wYkSeIsAqxpMcb7l2lkIMiLlJMnb2d1dZXhcEiv15uR2oLN92HH2TCLqr3PGaYFXAhzx8i5OTJY+u/zHAWODkpXt9HGBgcs8mrN5Ippbnjhqy9y9do17rv/Lg4d2UunFyGkIO52ICzI0oxjJ49y4NA+XnruZV596TUWetAJQ0xhQX7pG6k1prA+HXmeW7O9GrPk2677f7UFIWkyauWPmwOjNYETMCptKJT1cbImriFx1GEynjgfJIXRNnl7p9u3wYeShCybolVKlk+YTMdsbm4yHk+5enWTl06/xsOPPsDJO+9god8jlKALTSE1Sb5N0XEm6YsdHvy2b+a2e0/x+U9+hpc/9wWmFy5i0hRyg3TroTrjykGBf0c3sQ+q9Tu7D28U3rr1DK7Rrd20DDfbnzYhTP08btKfag00KWL1/c1GbruZvrXRwZ0Aozpzm2u17sdSv972uekLNSNo3AV8NPvk3RuavqW7JQSe16fm0rvZ0gSMX0tpvvv6nDSFTtVNs/3VSleCnprgztMDw+w6rATVVeCr+vcGbPRSX9ctTM5/EwApyzLSNLXJYEuUKsgLQWw0a3v2srl5nbjTpd8fgJBcvnSZuNNlcWmJMAw5cfJOtoZDFpdWSodRcIeGNsRdFw5YV5tUlvlpcIBClqYC/pD2wEpKCTUbY3ChQrUikJEDOQEytiZ+WhtEYKN/RHFs7S+deUYgqyztQRCCkGil6fb6CBRCBEhC4iBmZXkvi4NFfvM//RZn3nyDLMtYWFjgzpPH2L9vnbzI0EqTZQVHjhwppcXShtJD+sSFtTLv4Jvd3BblT5MMGUS88urrTKdTZBhbgi4D0jQnSVNkEFIUjuF0UjkbXUw4auAIs6gTx9lDSjjmp+rXTIcRXhphvCTb2bbXpTENHCJqf8gdB377nMweEdavrCQgVGMSrjErcaYcuxBQ5DloQyADZ8I1ezjNew9thNsYw9LiAv/gf/xJG93pJsqvPf1rOz7/mXv/DH/hv/vBGz6bZTm//TsfYTiaWKaw1r9muVUiPbu+qnU5e1Da2Ik+QIBdS3Yu0RqVZeRZDnHAJEnJioIojsr1YxlV60AcRzFxJyaKLQOeJgXdfoAQNvxzaRwlLIEuCXejv83D2xP22eAc7YxFG6PSnL9mOzcDuNrWS7tk2F4rHCNuQ/7vLg0v24ZKGiiEDZNcY/5HkzFpnhN1uwzHCVYZLvByimqs89eJAA4f3M/V6xuEwZLdWwakSzadF8pqabDaCisqqQQ4vpZABiwuL7O5vcWePauWzuvamtIaUxSsrK5y8q5jPPHEU0jZI+7ElulBlyYlzXdh3OHtD24Lnqk+GSx9KhkN26jQgsIvc2G10d7vTUhpzfC0AWfaZzVOOUYIzpw+y3Bri5OnjnPHyeMsrSzatRwIRAcEGZIOb3n0QY4dP8qTjz/J9njIoDdAGNCppijyErAAZY62UpItfJsggpAwBlHY3FHWN8kFr6CaRwskqncgvMwKy0QiBGibxqIorM9gp9uxCdujgHAaOyCboQq7FrWBqNcn7nUoMmuFUUzHZEXOJJmysb3BxvA6l69e5c03LvDwAw9w5NABgsBAaMhRFCal0BlBFNOJuiwe3Mt7f+BPc98D9/D5D3+Mcy++QrGxhUwSRDYlVD5GqzUrtnRcIxEWREkrGPPanjbpeXPv1IFj/Vp9TdW1DSXdM2YmqlmbqVW9vlKTIeoM82z6kTbasBtwm9mTtXF4UAB2D1bJ3h29FPWzfHfhja+v3i8rCcPS4LKvbs0Z4cLYNz2UZ+ldHVi2Bc6oF/8uZ/a2nA3K1ZzveUIuP46mkKU+3nqbtZpp0sS2Nnask5bxNDpcm6OqXhkEpQDA8i6z/A4lkKmeKem+85+WCNDWEkcbkCbAmCq/nUK5dezcKMqz2I8XDBotSu+rKl4Adm0JbddVbuYneG6Wr3uAJGXI0lKf6XRqGUkRgIRCF4SR1cqsiT0MRyPHrMf0en0GC4vE3R4yigllwLHbT1AoTRRXmighvPlctWG0sD5A9v23h+D04Ki+OfxGqBMOAIFry43HEi6BdgtGyBARBDb5lXCR7JRBihCjbXhoIUKk9Pda6WIoQgIZc/ttd3D2zHmeePxJZAgPPfwQ+/atIySk2RSlcoSwJoR79u4liiI7JkPpE9PGyLZJIWY+C2PDtirDZDTh/PnLpHlO6CymZaGYpqllioQAJNqAED4MegWErH11Fdp3lpg0fZ4aDCL+gBZ485pAuM3XRETsZMU8MfAuTiXDv+NO198634WXangE5PwgXDjvehZ6IezBqrG+amhDJ4oc4z0/TOe8UieMw9GYH/uLf4tf/F/+Dvv27uHV66/yV//gr3JlfGXHc+N8zHNXnpu59tsv/Db3/fP7GESDHfevD9b5Z+//Z9yxdgeXr1zjr//UzzIaTXbcV87IHCBwo/tm1uGu57MNW2wPFXu/DdJg/dSMKgikRIqQXKdkRU4fnzshcDRaYLSm07X+G91uxObmkGRacLA3sMywUAhCp4vzoNszs7P7o+3vNulnE8D43zPSshYQ3DZvbWCoDWTvVoflVVWjf7s+2ngVbsw4Hy2DYxqtOfB4OiZXBUKGjKc5WgmMkE5w4ato+vs1+m4My4sLXLh40ZlfBWhlkGGAEC50tNJE/r0aTwds8HxflDGs79vHpcuXWFldtr2WFeA1xrgojQUPPXIPn33s00ySiCiKSKU1LdKqnRERwpv4ui7XhGxgVyzMrh3jwJy0eKI6L6TXahlEaTboTNWMRiAxqgAt2N7Y5stPPcP1qxvcdfdJDhzaR6dj/bMIDHlgz5nFlQXe+53v4aUXX+W5Z15gEHcIosAKahCkWW6DKFDRLSsQtH3RQiKEA4EioCBHakNRKDCqPCsdqfP/lODGszxeoCiDKh1CoWzqjCiOrI9XIAg7AVkWMZ1OLa20xxVGCeLOABnEJMmUJEtQpmCajxiNtxiPxky2p5x74wJvffQh7rrrOMvLfYJSdFWA0uRKQWiIwi5H7r+bP3n7bTzzuaf40sc/w/YbZ2G0jWBCoO34jNAo09h7eFq/UyDRNLWqP1f30WjTRDUFHn426/xDnTbUNVI7aBAGY3KbvkRZP81KSOSwRwtgaYatrtMaa9XCTDvgfTdQNvMAAQAASURBVEEDB2RqKRx2oeltwp2ZOZlhkGf7449cPP10IEk7Wi1q9zdBYB3Y1NuuA8TdBH7+mfq81c1K66UOPNuEW/PouSeK9Web/l5NsD0z38yuzTo42iHoct/X+dQdY2cn76SxdEE4JKwNyDiGMAECBNYdxQg/7xqhQYrQtalnAzYAZZjg+hziu2/bUO3yu9bydQ+QgsCakXk7aW92JsyshDYMQxYXFzEGtra2mE6n7Nmzp7S51dpm8o7iTrmYobKd9aW5wOpMh6/Lf/a26fWFeCMJiWgs/KakAcAUFdPSZvsqXR6JhYVFFhYX+PhHPs50mrB+YI2jR4849aZGKRtFKE0z9u/fR7fbddqj3TOENzddG9NlsM7XcRTxla8+x2QyKc0O/e8kSZ2U0jIuNoR6e30gSv+OepSt5ty19tvjk/L3TknJjUqTcLWVee2XBGbOM1JaDaB2n1WhXBCR0Dr96/nmEzdbPvmpx3nfd/4Yv/j//Du8+53fyK9896/wI7/1I3zi9U/c1PNN0ATwbbd/G7/y3b/CoaVDfPKTn+en/u8/y9Vrm4BjesROGAk3N5f175vrDfx7awFWDmxS25NFXhBFcZnDxd9nw37nCNGj5N9dm0pr4thGgfQa4KIoiOMOYCyjqtw5dYPD3f9uO/Cbc9G81owQVvdBaM7PvHDiTelsU9q4G2Cq76sbAau2duvPaigjEimlmIzHZFkGQrggDR64tPej/tsXbQyrq2suImHFgIaOFqdZVkal84yTO1Kpm9RqrTl06BBPPvkkp06dosZy4leGMTYB6d333MVg0CeZJgwGsWMIrbRaInfM927jqTPJrcKDklGtInMJaSW6hfZmkC5ogDY2jLgxTltnE/O+9upprl67yt33nOK2246wtmcZQUC3Y/1AhbBr+9S9d3Ps6HGe+vzjXL1whWyaog1MpmOKPGNxcUDhtEIBzipCONMqh+6MEIQE5HmKzR9UFyrNL4EzGTfGuCiwFZ33Z3uv1yMMbcRD/3k6nTKZTMjz3DLgWiODkE63T5anpHliTWtzxTRJ2dzc5PKli1y8cJb777ubhx5+gKPHjtDrdzAuKbwqcopwTB7khHGXbn/AN7z7Xdx18l6++MnP8PTnP8/4+jWYbBPkGaHSxFqjEShpUH4utBeKe1NxnGl8xRi37cV5jO0M4Kj5OdnVOcuL1GlCU+u0g54K7ztUsbk3u+dneZvqJc+ax5uSAW8DD8376/W2zVM1YRW4ro+nEjxUz2gXKKUJFJrjbKOrzb3avG8e+Kh/nvFtbNR5I2GX5xFmwLZoGW+jz23t1ed/Lr80px+7fb+jHkdnA28xgCEVmre89a2kRc6VzQ22t7bI0oTpeIzOU0xRoJVB51aHpDEt/kRBSVDq60IIiRAh6IJQxjccky9f9wDJ+7E0Qw77Q3g6nTIej8v7wzAgSQz9fr9E3UIIul3rxOqZ7kqLtFPSI2uHvP9cJz5VYIGKCapHM6kDG19vySi7jRSFYWmu5+/x9cja4p8heECRKwJpVZmHDx1hc3ObL3zhCYoi59RddyEDgTReWxNiDMRxlyNHjpZ+XE01c720EfR5902nU6Koz9NPP02SJMjQhYoNAsbjsU12iA9rLEiTFJ+XoTk3lvbutAOul/q1ikhSSq59v9oI2tdaboZ4VL+99LcqniH3tFwICwSzLKPTtdq8QumZdfC19NsYw+Ur1/iRH/tpfvzP/xB/62/8OB/90Y/y85/9ef6nT/5PFLq4cSWuhDLk77/r7/O3vvlvUSjFP/iZX+Jf/av/yDzTq5vtdxsxb/3s/73hNDiApAogxrhoj3meg4hLhlcKCdJgXPJH7ST8cRwTRRELgwWuX9sgz3PyPHNjmU2KWLVYMdPzDs7m4Von9G3z1Lau24DXvPn05UZhc9v62rxWv7/tepM+1OvyjJKN5mYYTyYWIGFNM4uiIAqdLwsCEdRBynwByGDQY3t720Wrm5U228hJhfMNoTy4hdg5r4uLiyRJ4oIR1JmhOrNZsGfPKnfceZyvfPkFS9ek10ZZMNWkiW0MWNs7nafhEw58aRegoMz5JqQ1w/XXMRjl/CsCQZHbJOlowdbGNl/64pe5dvUaJ0+eYO/evfQHfUJrF4dwcxV2Ar75Hd/Cr//rXyNPCqQUxN2Ybr/LaDJBOoGBUQXSRU4zblqFtInTlSpAgggDdKEraX3tt6lfAAIXzMhbbNTPvvoceQsHIWywo36/74R8Kcl4jC4KBBAISS8KiYqINJ2SZjZiZZ7blB+bm9fZ2tri7LkLPPrIw9x77z3sXV+BUGOUwagMHRZkOqdQBSbusXh0jXf90Hdz21vu4rMf/yQXnn0WsbGNGCeERY4WAiWsX1OoK1NUF3OjjMBVX8L1PdNkYnej+fP8gZr3t9GhJiiQQqCF03I6cNfcx/OEKrN70oXYr0VqrdY7pStwc+3Xx9omDGs7B+YKIquH3G+om9/t4ON3ARH1euftX/9d08eqTUDWxis0zfvaShvYMWInCGsCn3lt1u9rm8t5dL1NENdGz1wtNom2+08J0GjuvP8eHvyGtxGtLpJMxuRJyng45Py5s1w5+yaXL1xme2PE9WvXHU2353WaJhgjAa9dAmEsAMPY5LBB1CGAUohzM+XrHiCdO3eOKIqYTCYcO3aMbrdLr99jkkwwxpAkCWA1SFeuXEEISRCEdDodhsMhg8GATqdT2cmaSgrZRPceFPnv/GchRBXJiFlJbx30qIYPUn0Rzyx+95taRKD6PTacrCjr95HyhJCEYYwuNMuLyywtLfP4Zx/n6tVrrO1d5eixw/iwxl5bo5VheXm5lM7Vw/neaOO0bSTfR+XyY2xubHDlylUrfQ9sJEApbKjx6XRaEiyfaNcS5zY74FnNgL/eJrXZDbTcCNDMK/OYxfpc7caoClGZxvifOmNUGJsfSpnCad9y+v1gBjw122+Ota1vfr3VAfmv/K//G48//iV+6Z9+kL/zLX+Hdx9/N3/2P/1ZXt98/YbzcHzlOP/u+/8d33jkG3nt9Bn+yl/7Bzzz7EtOjV6Fu54xf9ilj/Pmqs4AzIadFhXobYzVt2ucyrACVIIosn58PmpkGIVlxEAELmS37/gs0xKGAUVhBR5hGBLHMXmeWAbImBLk1gFcc5U118iNQElzbHUwdTNlt3Z2MOBz3kmdBtZDirftu6ZpR73f4A5/Y0BKENb3MkkSF0TBpjmwbVRtI0TNz1Oj9eyatmtBsLy84lIoqJm1E8cRKrM+lrbfzhzS1ddE2MYYp5VIWFgYUJ8mD4qVLugEMffddw/PPfMSOE2UFAFG7vQ/K+m71mUI+Po7rJv01N+vHR+l6ZyUVTRMG0TBYGqmTD6EuOVDbd4977MZBAHaaKbjlNdefoPt61ucuPMOjt1+jIXFASKQhJ0IJQTZNOXpZ19gNE6QWiBDyPKM9dW9TC5NSnNDLSg5f4O2oMk4nzVhTSi1sbkBpbS5mwxO8+H2l9WOVYEahBBWWCEqoFmfw/pa6vV6ZFlWntthGNKNYqbjCWma2La1IghjOsIG8sjznMJpKtM0YTqdMJlMGG6NOPvmBR56+EHuuOMY3b6NWGeMDac+1SOUTulGMf1ul+NvOcmBk8f46ice46uffIzN02cwoxGoAkXhyLsoBXreDNJathiMqfxommObt7/mnS/zwEIbQz/vXq1rIAa/v258hrYBlvpZ7feipSOVX0q9nnmAo8kTtdE9q7Gdd97X+DbfVs0UurxrznlezY2eAW9tYGWG9t+AxttkuXlD+7GzjuZzM2DHgdg2Ot4UsrTxQ21rqQ1QNXmetnqbAvyqXlMKBDQGhTUX/s3f/i3+8Itf4J3f836OHD3CtWuXGF6/DigO3XEbb/nGt7O8vg+tFJPJhO3tIbkqOP3aa1y+fJ1CBVy6cIHRcESepIyGQ4xy/vguaE6RTLnZ8nUPkAaDAXmeE0URnU7HJp7LC+cZUG20wcD6T3S7XZIk49q1a1y8eJGFhQX279/P2tqaS9haLYa6+drswWXv8TbTnnnw1+vMRHPh1xmlJigri3FBGkSF2GcWr7aMnpdaFEXhNDMSjSQIJEePHiPPCj7z6cfQynD//Q8QRlUAC+0S1hRFzr59+0vzxN3snqvu7S6Z8JLbTqfDV778LMPhsDZnNrS5BUeWASoKRZ7ltTpnGQZL3BxBlHKHaV2zDzPXW/p5Iyb9VsvNAJX5pWLiS8AkhNWuCbvG8kzNmBK0tX9zbVXl6Wde4ru+9y/wDz74k/zA93+AL//4l3nvv3kvT5x/Yu4zbzv0Nj7yox9hubvMf/iPv8//+Pf/CZNJOzHyIKFtnezWx6/13ZRE3M+T3ypak+WZdRg3lDnFYscU2PDSvpbKxlop5YBVRK/fBwyFUkRRXCZytYynqkkrTSuYbWNW5gHumxnjvOduBnzudgi3fa4D1Ob3Tdq4W7te8y2DACmsCWMytWtHK43Bhv5eGHRdI9Z8zDNczfrqpdvtlT6I9nvtNPYhmZqSFy7/nJQ1f42dAM8Yw4EDB7h06RL9/omSRnvm3hiDKXIKFfLgW+7nP/3m76AKBcYLleYIYIxlzNrmvnl//XywoNKZSBnwgqPCgBbKpRxwzLcAIV3kVaWtDytggoAsza0GCtv/Kxc3GA6f4dr1De646wQre1cI44BOJ+KJx7/AM089B0iXxT4nLRKrXYoi4k5sQ+UbQV4UdDodlpaX0MYwnU4ceLJRqqxiVhLFEWFoI9RlaUruAn4IIar96s9P4cDrDcCDDybkhZI2aJFgQYbEnQ7jyYg8SxHCIIOQWEZEkSHPErJ0jNI5ZqiYJlNGwxFbW5tcvHCRBx+8n4cevp/9B1ZtUJdUMJlOkWJKpxsy7XbodweEccw3fMd7OHnf/Xz6d36fZz7zWRiPINfWX7jcEp4SCnAhiucldfXlZsIp14MViBaa0yxN5r7JJNtz2/pg+tD7okVLUW/D04Uqsax9xtCWm8i3vVNYNK+/deFBm4bJGGaCLM3WV+305qXdzqTmOV63+mmaNu9W5gmhfFTitqAO8/rhr1fnhx9Me2m+1zpf6r9vA0Rtz8BO0+1bPbOkEIRSMOgPGCwuce6NM3zmk59k/4H9bG1tMBluY7QilJK9+/ezcuAgd911F088+ST9fp84jrnnkbfwzev7CTsDRttDRttDijTj0vkLXL18GRmGKGOttDa3Nvn3H/8vN9W/r3uAdODAAYQQXLlyhcIR7CiKMIV98Z1OxyWEtJnFgyCg37c5LLa3t0nTlNdff53t7W0OHjxE3LEHdMms1iTwdedKv2iapnL1qDX+Wj0Eqr9WJ1S+Pl+nPcznmIIZU9rxe9PCcsFre9wsDBZYW1vj9Cuv8/obr9PvDzh65Ki16zTWGV2KAI0ijrssLy8TupDSbZqzqulZaVTbd34+rJ14xEsvv4xSRclYam1Ik5ThcOhylDgfJHzywIohmmnHEcQdzp2N9v+owc/Nljo4vLXiDlBhmXeEceYuNhy1Zcar0No3OlhupUwmU376b/wcyTThR3/kT3Pv+r27AqR71+9lubvM//vf/BZ/74O/+EfSh3llHvNwq0UIa7pZFIXN64VNAB13LJOWTBMr2VV1ZoTy/jAMXWhjK0xIkilRaM18TFE2gjV7mj2UZw+12d9/3ONuljZJ4s2WpqAHdpqD7FZ3CbJ8SFs3RVmeW2mq0UghyUsNsr/H00l28Dr1Esch/X4fG7LdlHjVC5BU4UPrVrq9OvDy+1Zrzfr6Os8+8xx3nDhpx40sTS4tX1JQFDmHDx3k4MGDnH7tLGHYtXndiqysb5bJcOK6m5h/v7+bjNIMc4tLEi6kTZZt1TjOvElQ6CqUsLRBMK3ATQoQNvrdZJzw8kuvcHXjKifvOcn6gXX27FnhwMEDfKl4GoREiIBuL+bhR+/n5MmTfPgPPoIIJP1+35pGak1RFAzHIytctG+MMIzKlBRSBoSBFSj4AAwk3lzQarqQde2wKEOY+/G3Se39+7UJ4m0I5SzN0MJGxhJSkCQBaeaSU2obCiPuQBAappMRSTpFa83lKzmjrW2uX9lgtD0ijiIuXVrigQdO8frp83zqE4+RZkOELIiigCju0O302XNgnUMHD3DyW/8E4UKXJz70YeRWQSe32goZWMsOrSg1FwZmTORbVkC5LutjbTKtXkhj+Y0dipEdz7f9rs+nD9BQlZooYQ7t2BnxzWmjatHxZpnrdjDXBMFtAsc2AaRoPDsjlPZDmFPa5mHefXV+7WZKHQD6OfDzkCRJ67to60dzzJ4/swqkWwMpzXltgu8mX/Ffc17YSq01iSXl1twuGY3pLy6wGHcZXblGPhqxvLyEznIOHj7IyvIyaZ4RCcFrL71MNp5w6dw5+v0+Z157jbDXZ8/BwySTKSuLS+zfs06eTQkDWF5e4PDRIwxHI9aGSzfdza97gCSkZGFxkSiOKVRBGEVM04QgDKow24HP+h0ggxBRaPqDAYOFBbIsYzgcsrW1xenXX+f48dvpdrs7JKPNePVQ0zIBhTN78LmOcI73liBaZ1bjJH5CSgTC2k9WIykJjJSBDSHq7Oa9ZMfmdDEodxBbAmUJm9aW+CgKDh44gFGGL3z+CcajEfe+/R76Cx2yfOoWvkIKmwX+4MFDRFFUmun5BLdf07uoEQQI2dqacO7sRcBKYny48iSdkOVT9u1b5/jxEzz33AuMtiekucIFhLT1GOMYAD/h7QTR/11ub2NmHDT/OEud+NQ/t0rqPUPmPiGs2YE1cRAuopNEYPPNBIEgDOs5nOZLmJoHaPO7mWfLGi0BO3XqBEorfvfl3911rL/38u+htOLUqRM7CKx0M162ISgJedsB2DaG5nztOpbav75YAQYu3429TwFI68BptCRNcowpnDZVkiYao6W903nEGxdRR6mMhcUu3a5NYKpd/p7BoMe161u2PSnRRjkmvppf39c2BvePujTbmAei5zEF89ZOk1GfZ75xI6n1TD0Ya2ZnClCKzPkIhXGHJFMoIdGmIBDV27XPzpk3YZDCEMcd8gI6GKRQCKEJRIRSmiwv7B4zvi7PkMzOoRCCxcVFtofbGGPKADv1NWdMgCpg0O9x6tRdnH7tTXwwgua7mFd2Wwv1uVLaaieNdnTQVJE6A2E1Qj5xdWXaKpCBJNKhM8/DmnVp52MnDbkx1r9LG65f2eKr42c5fvttcOcxDu8/xB13nOC5r7wAcYdB3GFre5vMKI6dvJ3JcEQynrCw0GecJhw5epT9hw8gpSDPcra3t7ly+TKM7NksjaNvRtochEFOR0CaJBa0uTdbrlvsc0ro8v1qGw+L2habYb69IElK6XwMJSIQNsF71mGaTMlTRSgDrKJRs7gUMp2MmCZjVJhTFCnTdMj1zYsk6ZBv/KY/wXia8/qrb7C8usT73ve9ZPkEbXK0sebgG9sjNkfbXN8aksuQhdtuJz17lmxjg8BK84iEtEncBaSmQEnjklJXyaalo1nGWGf2otA20qbjE6wljM3FZYzbQziTMbnzpJsB096s0+9frw32EymEC4xU+UuBcPm22mlDW9Q174dn2xV4qYbRAowdR52nqluCtDHjddcEg+UFrF+gXff1dVDXLpX1uP2Bnyl7OM0AhLnAq7E/m7Ry3hnW9Jmr19dmijZPaHYjcCKlnIlmqZQ99+rnu6+n+Y7qYG9egJg24UyT12qbv3oxjrfw2VqENqhJyvbmFmbQQRSapU6f9b370EZx+dIlkmSClIJLly6jDeRKkaQ543HKeJrwlkceJsDu8Y9+5OMsLS5ilEEXijAIWd+7B6UUw1rMgRuVr3uAZIT1yUlza8u+srpKEIXOxKuL1nrHRgzCEGmsiYwHB3Ecc+nSZS5cuMDx48dn2vAbu0mUy8WGsHl8hJXQWckeGCeZEY4YCEFlU4+T+Bm/ECsTDSGkTXzlwFHFIEgQmjCKSgJkQ6kKbBhFQdyJ2LNnL8PNEV988kn6gy5333cSERoCHTopqyZ12qe9e/eW4K8NBN5w/msbzm+6LMsJZMxrr77EeDRFCFmaQChlM64fOLDOPffew6FDh8AYPve5J8vDHCmqQ6C+WecQLKhFg3HzUkWDFDME42spuz23A3wYU0YC9P5vZT31vwQgArQxCBEARe0OO4dgCCNZChWbEp56+/X+7Mawls/Ypcf63jXe+ugDfPKNT3J1crXWQ8HJPSd56dpL5bUrkyt86o1P8c63vpP1vWtcuXq92YDt6i726239udV77E6ors+M2RhsniJT5sDQ2pFrEQDSRrfKJnQ7KxS5PdBtiOLZg1ebgsFCh5WVJWykr5xpMibuxJZJDQIKrVDGL7b5EriblcjtBmxuptQ12vV2m8Dpa+lP/e/dDvXm4Vu1azDSIFySTlXk5GmCVgVC9kjSAqUh8Pyjo4m7SYIx1tR4z551pklOf9lgpAKjkcJqL4q8QClt8/m492z7VqvG9TkMQ8IgZDwel0lRZxgIEZDnmjxXPPjgg/z+738YrQuCICSM7HHbTAZZikRuQEd27GnjpK8lLzsbiMgDCi2cL4bwgg/p8i6ZMry6MM70zgiQGuFyq8kckmHKay+cZuv6dU7edbv1F0ETRAIhYTBYICtyMp3zlocfhFzxxJNPEncj1g/tY3Nrg9OnX6PT6TAYDDh6/ChKKd58802yNEEYidHShV8PCVB0RYci0GRpPmNyZIxBlLkSHC33xMq4KKei8uWtz6nXKAVhgFKRBbhBgAxDsjAnz3JUESJEB6Nyev0FojAiSabkeUbXRGTbE776zJfZnkx56zd8MxfOvcG+9WX2H9qLEYZuNyIMBQhDnmouX9vmuRdP8/wbF9lUAbK/gEpTlpb65OMJZpIRZBnSQKwdo67cWIQs6Y1yERwFPoWSwOb/o5wLt3wrc2yxExw1GfsSgPrvmqvSeNro+A9XP2I+A9ykA7OClMqUzpZqjPWNPC+0dX39l1EMMdZ9wJgSyHnQ4YWpdQGOfaYmNGjU3bSQ2S0HUbOP9fE2wVLzuea1mxGe7JbOoxyzELP5OH392gJJUdfItpxDNy2EnCMAq4Ncf/9OgGWf0U5YGRgbo0MGko3phG43ppOkJEpRGIMIA5IscW0KslyhEMTdPlevb3Flc5svP/1cmcR7OJ4SdXrs33/QtpMVbG6NMcZwtcmX7FK+7gFS3fQtiiK01qWZXQmInKmFBzjSBVDwL77b7brNBVeuXOXs2bPs3bvXHpZOMtVkMmbN4YKyL1BJt/x9/pndzK+a30sXMrYt07LOs5KgBUGATSRqEyMev+04EsHTX/0Kw+E2J+64nfX1vSA1oQwoiorILC0tsbAwIAhkebjcqMyTrNQ3YpomBEGfZ599lryweSy8aZz3zzp67ChhGHDt2jUCN8+qsDmeLNGuE9mdBGN35s4erH+cpY1B9Nfrpo/1e+taD39geZW5lJUNvgCyLHU+L5F1wDbz26z36VYZ4Pe/71uRUvKbz/9meW29v86v/qlf5TtPfie/+9Lv8mP/+ce4MrE5k37z+d/k3be/m+9437fwb37tt8u2ZnpSSjndm2hIn/5YSwmSKbWIRVE5xapCkWWZA0SCNMsoioIwmgUP/mcwWLA0wDmPSylZW1vj5ZfPWOHFDfxv/NhvNrhC2/N1k956aZvT3bQTt1ragNW8++r9aGP260w/wkq08zwnSZJSgOXNoWRNaSqEc5QO2tv3492/f53XzlxCqUVCU9HRIAjInH9jm6S9+betaz9XrlzhyJEjO8YigDwvUFpx8q472Lt3jWtXtwjD2K6RWyzNuasL49r2TTmftWtW/9nOyHoG2T/bBJy+rTQ1XLxwkdF4m+0tCw6jKGJ9fZ377rsXEwq6nQ6n33id244e49u+47089rnP8caZM9x7790kyZTRaATA2bNn6XQ6nDhxO9PJkDNvnnWMaeC0zCEEEimsEY7JMtslZxpncCDJCIRLNOmFX573mkdPPAPsTe+8z0fRL1C5tlqj6YgiMwTYwBdxHDOdTFB5RiAk0+mEa9ev8elP/yGmULz8YsGJ2z9Er9dj7949RFHogoxMuXjlGi+88gbnz11AT8Z00ylhrnnf9/9p4lDy+Mf/kNHZC4TbU3qTnDBTZGGOEhplXKJZBNoztbo9ep8UksrXGcCbxbmgTQ2hVAXs7QrxZNGUgjavwZoVFghhA2UI5tOr3YQmu9Ke2preTZA3c465hPVNuuY/+8BXTe22YRYMzmP2fXs3U5p0sHleNNuaN7a6f9bNmio3750HUkVt1M09UudFd2vLlzpv3UaTmtFX621JIcpk1uCyzkkbLMUUln+11kQZMohwwUutokEKwrhjhTihFTYHUsz0ZWlpkfF4TBAELAwWSCcJJldkeb7Lyt1Zvu4BUhiEMwCk+bcPr13mNhKz6k4hRKlJsr44EaPRiHPnznHgwIHy2V0XvCoQYmf+i+ai3unsVsnB/WYvo0E5Ztl/NxNJJQixJkDKEQZ7YyfusG/vPpJxwucfexwM3HPvPSRZQhAJIqeNslqswgInmAnOMI8ZmiflmR1PlTl7a+s658+fL8fV7fUoVMF4PHYMp52jJEkYDocuep43I8GNfdYEY7dSblZjvMyx1rGdYG63MdS/axKitjloO6R3ZPyevaP8LqiBdSEqp+vCRQGMfHb5mr+Ef/ZWmeC2+z/w/ncC8FvP/xYA7znxHv7Nn/o3HFg8wPkLl/muu76Lr/xfv8Kf++0/x0df+yi/9cJv8cvf+ct84P3v5N/82m/Xxte+ZuqM3M306Ub32nfMjvwI5SHhgLVnpCwNsPsqiiLyIndBTQIwhiLP0UpDLEvG0a9j+0xIt9sr39N4PEbKCJxpg+HGktYm0GgyCLcipZ0HtPz9nom60Rzf7Nqp056bfcYzLDCbh8XViGfbjbHJpD191TZrNJTmxc4v4gZrQsqAxcVFNjdfZP3QGj6CmPUhiyiKSkshSvTVLik1xrBv/z5efeU1jh07NmM5YO+3Y8mzhKXlJY4eO8ylS1eRRYyuaULqc1z+a3au7yYIqgPKtvdYrXPBjrdhDF6T6WmJ1UCJ8uvCmWm3paJQRrG5MURrOHDwMMdvOwqm4PTp10jyBCNhsLjIJJ0yujjmHe96B8888wzPP/ccd911F2fOnGE0GlEUhYtSOuHYsQM88MB9vPj8K2SJDSzhk4ELKYnjGG10GdlrJjGksaaBShfOX9W+h+6gVwpAb+RA7s92FSroQL8bkyRdtre2mE7HBLIDaAYDSTIcop0AJcsSZBKRTlNG2yP+9//991ldXWN9736iKCZJUkbDTbYnI65uDUmzjBDNYhQwCGOeevZ5/tJP/g/cdv+9fO7DH+eNL3wFde4aYjSBoLAWIk7ib4RACYkxmnhG41Lf+xLpApd4nzgrzzTWbC7YaeptVwLl/qn27/z9VJ7/pv2etvOw7VqbENWHpq5fq0cEnvcO/XsWQpS+V/W+1vdFCZS0aR3mzQiQ6u210Yjm5zrP1OzTvPrnzV2dbta/r4PP5tz6NusRItvaqwOlJn1p1lVvux6NGdiRiw9mLReEP3xrcmqjrUFwlqWEcQSBZDiZ8MprpzFGs7S8yGDQta4lCoxSDMcTRpMpaZITxx0E1X7OhUIIyZUrl1leXibudFg+fJiiKLi+sTH33TbLrYu0brH83M/9HEIIfvInf7K8Zozhgx/8IIcOHaLX6/Gud72LZ599dua5NE35K3/lr7B3714GgwHf+73fy9mzZ2+5fSFmF2VdVe8PgDpYEcwi3/oBLqVkYWGB9fV14jjm6tWrro2dtvT+epuasY0Zai7uugSkDlDKe2rgCGbNNry2oTS/c8/s37+fUIS88dobnD79OgcOHmTf/nWSPCHJElInrdVaEYURKyurbuHPEqe2TdIsbeOy4VNtQIFXX32VyWTiQtJWGyzLMptvyRG6ZJqwublZOmuLGaAmZxxB6+00N/TMe7nlVXRzpfkO69fLtndh5kTJGjaue4JSq08pjVaaKLaS6TrwnxdpcDcwV++/L6ury/yJb3iIz575LFcnV/n59/w8H/nRj7DaWeOD/+Cf8s3f+oP8g//5l9nT3ctHfvQj/Px7fp7L48s89uZj/IlvfJjV1eW5Y3WdAph5X217YXYedi8zIZ5b3n2dnzam2mc+0qMxNkjDNJnaNWmcrHHOodvtdunEMd2uNddNkpSFwcDtWVFKt+ftlyYY2u2e5pw072sDR8394etrzmvb3DYP6Xnvo0lXb+Y9laCnRlttVLbZ9ieTCXmWA5CkidMwzCZQFDVa2Izo6e/Zs2cP0+m0lBv7IABxbBMEW/OyKoJY21z4+V1eXmZzc7Nsoz7vxn3OixStcx544F5ClxohcIFu6nUaY9eWqdHY5juuM0X+nNpNm18/O0rBnz8zZt6lKPtcmp85awrfln/emqKDUgJMwNbmNufOnefq1au88vLLvPryy1w8d5719b0sLC8S9WJefeM0d91zN7efOMGXvvQlDhw4wMGDB+l2uy7dRp/Lly+jteb+++4nkCF5rhmPUrJME3U6yCgk6nYRgfW7LYwmUwXTbEKSTUiLCb2FDvfefzdvefgBRGA1wvW5aNsndWbTRyLEmWp1u33W1/exZ22dOOoiCAhkRN9FurXrcmzNwYucNE85e+4sr776Kk8+9UWeePKLfPXpZ3nx5Vd548xZrm9cZzQZMkomXBttM8wz3njlda5evMb6oSN894/8EO/7v/wQq4/cw/TgCpNuTBpF6DgGabXTATi/o/kMt5QhQRA62hO492v9kOftSXueVnm6fFL2JinxfBSm2jt18Lzrudag83UGvP5cPeCVv173NarX1UbP2vZ9vY2mkLc+d81n6n2/GX6nfu9OMLCTB/Ugq60/zXHWx1YP6NDkaWfoUO2d1AXrQuzUSO121jb7L4TYkeqlTUBWp+n+xz/nWp5ZA76+PLe5y5CSVCkypSmM4PK1DTa2J4ySnNE0Y2NrRJrZaNSDhQHdTocoCmsuMRFRFJG4AEydbpdOr89gcYk96+tz32Gz/LFqkJ544gn+xb/4Fzz44IMz13/hF36Bf/yP/zG/+qu/yl133cXP/MzP8N73vpcXX3yRxcVFAH7yJ3+S3/md3+E3fuM32LNnDz/1Uz/Fd3/3d/PUU0/dki+MUpowspsjzy3hbC40/7mNmahfDwIbRS0IArrdLtvb22UI8eZm9w68Qji2t8FMCCFq+YlmmS4PigJR5Rjx/fFgychZ6VidqDQ3kAdLR48cpcgVT3zhSYq84I477mBj8zrdpQ5ShGgtSKcpINi3b78jupbRuxET58dW/77+2Y8tTVOklDzzzNNMJhMQFRFUhdWq9Ps9et0uPgP7ZDyxY/DBLDzxodIetbV3M4zaH0Wpv7s2IueJYdthvaOfpro+A95rB5S/Py9yOp3uDqar2caN5qHt8BFC8B3veQdhGPKli1/iM//dZ3j74bfz6mtn+Mt/9YM89/wrAPyv/+o/8PjjX+af/ZP/kb/5zX+Td932Lp688CTfdPSb+I73fgv//j/+3sy4bEM4PwJT7otmX+p9n8eg7zo2wYyesKrHWA2CoDzkfbVxHJMkY6aTaeknpgqriRUyLPOO+X4URUG32yPuuHtNFd2u7Fcb4q2Nte1Qb5uDtrHvOv4bfDfv+3p/5pn8th3ebf2+Udl5v6OXzpxZa02aJGS5DTpT5EVN47i7hLfso22I5eVliiKv+VzY56MoZFgo0ixl0OuUQLg+zmZ/O3EHgDzPZ5gFe5OjwaYgLxIefMt9dHsdJqOcKAjnmEMKS+vYuQdvVObSZEFp0qdqdMkaTemZZzwwlEISyQCkKDU29VQRCEEUx/jIfVevXuPI4X1EUcTBg+t0+l0b/KATEIc9TCC4cPEcq4urvO1tb+MTn/gE+/bt48477yRJEraH2xS55OqVa9x96jBXrlzn+hUrDOv3uqzsXWZpaQmkQOkOeVG4JI8GESqWl5e5++67WVhYAAGj4Yi1fatsXR/OSLO9JYXWujyXvQa+BEuIKqGu1qANQRAxGCyRplPyfIJ2YYLzomAyGRH3+mgUhUkZp1tkKnHnZQgGlDYoo9HSzq8JA4IgpDAFk+mEl154idX968g44J4/8ShHTh7nC5/8NE9/8rNMLl9DjSZEJkcqZc0NG8t+9n3XhWieSdfu7wBjijnnkwVQdv0arCmeZ1rBmtlV/s92cVIF2XFlN8HNzdKHW7mv/Gl859es55ugxl/UPnsaMnMstey9Or/Wds77s73epx00oda3NsA2D6TUv/P9q/erGZa7fn+Tj91tLtsAaP37tjbq984Dlm3tz8xffW6MFU5kRUEooNsflNekDDBJwjQpnJDcgXkkMrC8dzeyuUuRlfbZ+owKNjc32bO27vaBYc/evbvOSb38sWmQRqMRP/zDP8yv/MqvsLq6Wl43xvBP/sk/4e/+3b/L933f93H//ffzr//1v2YymfDrv/7rAGxtbfEv/+W/5B/9o3/Ee97zHh5++GH+7b/9tzz99NN89KMfvaV+2Og+NoGjVY1XyeN8aZO6tznDeUmMlNLmP+n1yjE10XI9qarPz1OXMHgpQ9shWJcueFOHOsGPoog4jkv/pxmiB6WWpSI4sH//fgIZcP3KdZ55+lnW1tbo9XtcunKZN954gwsXLjAajbDO5or9+/cjHK4LgsrP6ka+EvMIpXDAJs9zrly5yvnzF5xZhI39b7MhpwRBSK/Xt3PrGM7ReITWakaSXw6WnRu23pcZ4uPn+48YN9UJY3MOmnNx80xkQwsiK0mgEKC1DVsbyGCH1LtJwG92DM0+fqczr/vLb//LvP3w2/nf/v3v8t3f8xd49rmXZ8D4s8+9zPf8qb/Iv/8Pv8s3HPkG/tLb/hJQmefNGV65F/64S9sa8Ae+nyNveubNENLUSp4ElIlEmweoMYYoilhcXGQwGJC6iGueQaE0F7u1vrbtsVt9n/6Z+oH0f5Qys66bYF5Kghr9StPU5a2DQhVYJk6ykzXa2YYxpozKtbBg82XU57ZubljknmH29bYLGfz7WV5e5urVq3OYENtuUWQcOLCPQ4cOzNDzHcyToBQUNE1TbqXMzKmrwjOMYRRZ7ZbxDG9FM6top7aEQUC30ykFeLNzVmmvjTEkyZS4E7O+dy9Ga/KisPlGooBuv0t/MGA0GpLnGd/5nR9gY2ODj33sY7z22mtIIVleWmXQX+I//of/xPmzl5hMMopcMBlnbG7YSJArKyvEcczS0iJ33HEHb3n4LTzytoe4+/5TrOxdpjOIWN2zjBI5K3uXKWrJ2r2PUZIkTKdTkmTKZDJhPB6TpmnJE2RZRp57U0srydbKEIYxg8EC/d4CnbhDHMeOThRkWQJCIWSBNimFnpCrIWm+QVpskmRD0mxEno0osiF5OkQVE8IQ6IVc3LhMlqdkU5uLa7BnhW/709/Nn/rv/wIH7rmPaGUNEfcIg5AQCLXeYRpuBYd+H/kfqxGSInAg2fMcAUJ4Sb697oxNyx8prM+yoH7eVJqDQAYNTYBb8Q3hZJ223gyjXq/jRvd7/skz2U3eqxQq1two6rSmuabn9cP3vVl/E4z4e0VjD9fHXu9DEyB9rbS9zrfW29nB9+xS2sZV70/b83XFgjdtnQeS2n6aQTDAB9ywQoo8L2wgiUAiXGTpuNMlCKxGVYQhncGAsNOh0+vS6XSIO1E5niAISnO7OI6tkEcbcqWZphnmFmDPH5sG6S/9pb/Ed33Xd/Ge97yHn/mZnymvnz59mosXL/K+972vvNbpdHjnO9/JY489xo//+I/z1FNPkef5zD2HDh3i/vvv57HHHuM7vuM7drSXpmlpvgWwvb0NVJocD5ImkwkLCwsIRyy01s5hLKg2lTGAtky5qatNfaJ3Qb/fZzgckiQJnU6nJCC+rRlmWdtcBP5Q94y+NY2qJDgGyvCMxpiSUfAgyZcosurDiXKZy/H2sK49Ibx1OQLrY3Fw32FQgi998Ytsbl3nkUceQZm8RNrj7Sn5MCcIY9ZW9hBFfcKoC0Igg0pSUh/XjTa0tYK3eZKFEBQqxyB46eXXGE6mGBe/NAgi8jRluD1CBtano9vtMZkkTEYJRntVcoEkqGkdBMbstJdtk6bs2s9dwMt8wLdTil6tk3aA1AZCys/YiC4+Aqr93kl3hfUX0MK4aEaWkcyylCgKCQJBZlTpk2Gr9n3dKcHZbTyeiC0uDHjHN78VgO3hiL/zd/8X/st/+Xi1hmvE1xjDeDzhp//mz/OpTz/Bz/7PP83S4gLveMdbWVwYsD0auwhaHqRQvcPGXDVByK0y9vMOhJ3jtqYkUeSZZkkQRoggIE8zulFMKOyeV0bbtWrA5qi0Ib2NUkggigRxLAlESDbNGfRiMBmhi0Io7cae8Yvyms82aZyX2jffUZOpbV7z93o7/DzPZ+q90V6Y932T+an/bvprzhNW1D83TUFmg9cYQCJMgFESlWuMUghjGfOiUJgY70pT7hOYXS91zT9oOmFAN4TQCEIdOsbQEEYhQkKWZ5bWl+ZGUIY2bqx1KQL279/PpUuXOHDgQMNU29J6ZIhShl5XcufJO3j5xQsoAyKo8mMJIRC1c2HefO323upPlutLG4zLMmKEsWHmlf2tbdIdJ7Eq3FknEMoxzaoAqYmjiNtP3MWZN99ka2sbVWikFGhTlNpSYwybW5qi6PKlp7c4fuI4Vy5dYU3tYWFhgTiKoRNRiIAsz9gabvD+73wvH/nwx3np+Ve4dnETg+KNN97EKDAFaCOQQUhhIE2sVujUqbvIi5SHH32I244fJe5ETJMhWisOHDzozk7DoSMHeO3l17nw+iWnNVAURU5RZBSFsnvWhdz3pmQVGLBTIoyN+pXrnHQ6ZdDvc+jQIYbDEcOtEKU040mCMIY8mdDtLGEMaKUq4YvzJ0MHNlqqthFnjVYQhXR7MQtLfYTARvGTFnB1uh3iOOLkW+5iZfX/zJc+/TjPfe4J0vOXiCZjgiIn0wWZMGQowihCFJpAYSOURaKip4bSt8zFB8Nrg7RT/4ggqEixsRpHu4Y9eRYIEZb72vIglomVtfW4Q9AlRKmltd3xfI//3i1TDN4Vxa9zX1+TNtaFkM1z3cy4APiG/LvYKfwrmX8/Ow2GvYyO1/B/aqPX9TnwpY1O1+/x39eBRn1MdXBXv8//rfVsupW6Ca4fW92MdPacr86eJrhqgiKvebUCgab2bbZtP74mnZ93hls+FbwRiRY2FY4xApNkhAhyDEEUEMYRQklUXljaHdiIl0KEIEwZiVLKgCiyAoypTpDSrpc8TwmjABlI8mnuBG03V/5YANJv/MZv8MUvfpEnntiZVPLixYuA1WjUy/79+3njjTfKe+I4ntE8+Xv8883ycz/3c/z9v//3d1yvI9der8d4PLYvHquCtt/5BaZK5rKK0GE/e7pTR/1xHHP9+nV6vV4p5fIbqr6wBBCGAVrbhesdTWVt8QhhmWEpZKkRqNflpZ11W04rKbRMRd22XjtnTWFsuMfV5TUW+ktsXL/Ok088Qbfb4dDhA4yn49LJPwhCVFEQIDly9DhBEBMEoV28WiPC+dL+NmJmv8BylGi0gSSZYpA89/zLNuy6MQRCEoQhajJhPJ4ymUy57/77uHTpCtNpwuXL19DaE2ebxNZTVYOekZjckKG+RWbbj+dm77tRH25Ul2Z2LrVSdLs2MXGaJWWYXl/SNEVpRRgGCFknOPPbnwfemp8PHdpHHEU89cVn+Kv/t/8HZ9+84OSTlQau7bnf+d2P8+WvPM8//cW/x6OP3M+Bg+tsvzx2B2at/3OkTjfq141KuQ53fa4mbTWzUeSUM70xSpOlKXHcsZ8bjwWBdAdVwKDfZWGhZ5e6sYx3FAXkGQRCgEvGKRrvr9m/tkPKfz8P2LYVD4yah/utgs22UqcBN1pLuzEU9ftnnhEgRUAgQ4SRqFyRJaml1UagigJjApiJyrVzbsp2pRWixHHI3tUlKBRGWX8OX4esmZT5NeGl880x+mv79u3jlVde2aHxEdJglMRoKHJLsx584H4+/Aefs3n4ArsQhHCm17IGvlrmbdcimh8dQ2VcBDTjJOXKZdRxUlkDGCnodCIGCz0OHTrE9nDCubOXkFKwujxABgFCWnNnEGwPh+RZTuD2ixI2GEAn7nLsthNcunqZV18/h9aatdVVbr/9dq5vbJAkUx588F56/R4Kzcb2Nu/6tm/j8+EXeOGZl+2ZUNgsRhZEaKRUDAYLGK0o8py9e9coVML5C29y7PhBZBACguvXN9m3/4AV4smAXj/gzrvu4pkvvcSFCxcJnA9hEMUgFUoXaO20ZcZQ5AqjtIPKkigIueOOE1y4cJbhaIMsn5JcH7I92kDKgEAKCCQisFGzijynyHKkBpSX4Cu7hLTBoj537AQCEQSEQcDy8iIH1tcR2CBEQRjYd4V9Z3mgWD6yzjf/qfdzzyNv4dP/+fe4+NzzqK0h4TRBFRmRE9gaAYSOD6AoYycYQBm7IgIhS15ABHZtGnApMgwCUwLE+h4C0UqbVAl6dtJnY5wQb6YuT+frAo3aemcnfZpH89o0PzP3zfR59r5m8IHdaFWTDs+jA3WgUb/eFDjOE742LYk8CJRSzmhn6m3NOzfr1+v1zoyTneOo/26eF/56GxCq97uuIW++o6aATbjFZpxAAuzfWmDXcV4gjBX0FVqjixyjNUoV1g1DWf43TVPyPC+1RAsLCywtrzh3mqLs1/b2NkcO3wbCmggXTnlyM+WPHCC9+eab/LW/9tf48Ic/XDJ3baX5cm/mAN/tnr/9t/82f/2v//Xy8/b2NkePHp15kVrrMmS3/1yvu8lo1192/XsfInRlZYVOp0OWZYzHY4QQZf1+gdfrr5tXNAlPsx9tBKL0PzLW9KSN+bB/a2sLLSSF1hw+fBhjDK+dPs2bZ89y+4nbCaMImQVo4+xYoTRJOHLkiJ0DKZFBTfLf6N+NizWHkeDMHuDypcucPXuWNEkJgohut4Mx1jE+DEOS6ZSNjU327d/HY499HozN5aSUY14a66Ftrvx3fj5uxGw03/3NlObc3xRD0/Jc7Rv7f22eZ6IrYnbUkTmfOgvMXbLgr8Gsq1mEELzy6hne8e7/E2fPXkIrddN1CiF48+wFfuCH/gqHD+/nzJnzt9R223u7ZZBqP7UCOUElHcVpV70pp/1sbdWVE5YYPOCookNhrNTK96/b69LtdMv+R3FEHEUkwuYUE9JpAhG7moa1MQQ3A3Cac1U/HG9mXd5ozr8WoFo/RNsY/jaaJ6Us6ZAXGGVZxmg8ctLMsMwX5/eKQWOM3EX44UyctWD//n1sjad0nbO9n6tO3LGhnpVCG42lWDNwfkfp9XqWGWxEBTTGM4I2JG1eFJy44zgrK4suL5iLGifljOR7t/m9USS2ZvGAX/mcMFLaVA1RSKfbJVcKJaA76HLbnbdx9PgxskITry5z/o0zJHnBob37uHjpCtevb2A1LZIgiDAGlMHNkGY0TnnjjXMoDEP3nra3Jly5smnD5QeSJEv5lne/g0AYurEgLwz33H8/X/3y8+gcJCGFypEBxJ2Qo4cPsba6xsWLFynylAP79tHpBHzkox/i0KED7D+wn1QXHLntOIU1DLOCDgTD4Zg0LRiPpmhtU3osLi6wsLBIZ9BFBVaTk6UpoRB2n04mbF7fZDwcEXYC/uT3fQ9LC4u8/NKL5HnGwlKf4XCLrc0tRltDPvQHHwIhSbOcTp6VvITwa9yAMRq0cDDCIAkwxgpUVlaXWd271yWvVxRaUWhNoCywjTsBWVAgOwFmdcB3/fc/zJc/8zm++PE/RJ+9RjBNIEsxWqEM5CEoowi0cqtWoLHnN8KCSalqa0iIGQ3sPBrRduaXvJED+O0CQa+F2rlO2+jKPBBS78du5+zc/WCs4Lgu1Pa/HQmZaaON1rbxhM2+3VRfdilCiBkLoaaWrO7e4PnApp/5vD7f6hlaf77+ua3umxkXzMkjhdhBXe0+UhRpSpIkxIsLZFnK9csb1gQ2SUmTlNhFjc2yrHRnARuIZ2FhAR9voK7BGo9HBIENABbHNw97/sgB0lNPPcXly5d59NFHy2tKKT71qU/xy7/8y7z44ouA1RIdPHiwvOfy5culVunAgQNkWcbGxsaMFuny5ct80zd9U2u7nU7HOmk1ij/ESgmxUmhjCIWYASxNxNwmBfDP++98cIYoikq7Zn/Q+5dTFDYEqQc3URQ11JSz5jLNqC3NhaqUDTPa1j8/Rms2aNvo93ssLy+TJFM+//nPI4Tg1N2nGI5Hlkd0IicZ2OSB63vX6XTiMtS2lNL6udQkCTcPIjyTpEuA88QTTzIeT6x0BBuoIkmmTKeJA33w6U99GiElvV6PKIoxxkqVtalJrVzfS/VyY56aa0B4rqWl77sxkU2m9VaBUP3ZG91bSv8akpkK9NQkRI5AKOU0SL5vHiQ11kaVI+PGY/D3vX7mPMJUCYub/W1j5PyzRVGU4EjU/mmu53nzcytz3Xy++dTs3m6+z2pNh2EAAmeGZPN1dTo+GSh2/bg+aaXLfTgYDBgsDADB0tISvW6PKI7RZuzGb/dAEzTcbLnRPDWLfw9tc73bOmyb8yZNrEfV3E2a22Summ03QVn5uRb5Dyc1nE6m1oQpCp2JqTdjsjvDVTRTd9mWe3fGQLfb5/WzF1jbu7cEJ8bYxODJdOpoO2XdiPYgGmCZmE6nw2g0KgMLWcZQYeGDFVikacry8hJHjuzj8pXLQGyDULiE3D6hY9vcfC2ljDjnmOUgDAmiCCMMMgiQQQBKIaREC83avj0UUmNiOH7qNrq9iLOvniYpCoI4Ji8UaLdutQ08AAYjreZtMp6SJKnNXirtGaKVZliMEVIShnDp4hWuXLrK3n026bgymg9/6ENMJ2MiHSOE7aeh4Oixw+zfs0oYhPR7MaNRykIvIgzWyNOM0y+/wt2n7qYIAi5evMixo0cJAguQz505w2/8+r/n8rmrKGX9daIoYmtzg16vx/LeNfYfP8LetX0gDCpLGW1v0ukvcvDofrIkY7g95BOf+RRLCwN+4Pu/n9uOHQeRsj26znBrxGQ85elnn+bC2QsgQanCsnrle3frSnvzMv9e7BLtdjusr6+zMFggiCJAoLSmyHOki6SIjohigYgkBZqNbMI3fc/7OXLXSb7wex/j9Feeobi6QZhlBEChrHY1QCO0NVMUSAwafC4pz1t4gQWAC/RUd2Ft0ocmc1xabCAQtfOqfFb4oBC70/lSmLULYKrTI9//Zn3z6vdjbKO5xt5AmxCtbaz16zs0xrVxzKOfzX7Wgaa/7kFP/cfX6+l5XfBVF562mfU3lQD1sXv+oD4nbXXMmwM/D80x1a83SykAq7c7hxfLi4IsyyBLGY1HXL12DZXnmMLS5zQviOO49MX3gHIymbC5uUm/3y/b8P176eWXKHLD6trqLdHXP3KA9O3f/u08/fTTM9d+7Md+jLvvvpu/+Tf/JidOnODAgQN85CMf4eGHHwYgyzL+8A//kH/4D/8hAI8++ihRFPGRj3yEH/zBHwTgwoULPPPMM/zCL/zCLfWn7rRXSirF7GJoWyTNKHd16YFfNB65epO3UvrcsnDr0XN8OFXrBGswpiiBU7P4BVUPv+qvhy5srE886u9TaDpxh4CQg/sPYgxcuHCRF196kZU9q0SdDkmRIYSpMJKUCKO5/cTtZXQuywjNEo82m9obFWMESZIxGU958cWXMdoyK5WUA/I8c9FHBNJYp2IPjmw+GQFGVAEoMM4mvj0hWdsamFc82zxP4rWDiWtc8/NSN/dr1nHDOdoxZzPyLZdELUApewgH0u4bsAC9TgBLDQqWiWnm6qoTZ1+ajqXlOnPRrbTWVeVzprJZ78wYagD7ZgBCUwLWbGf39zn/kPcAsqpHlCatlpE2ZJkzt9LKZmiv+X3JILCMRw2ExHFMp9NBSsH29jbj8ZiFhQWuX0tcaGQX/c5pVHfMTcv8NQ/htnc2b97qv28WEN/sup3HpLQxVrvV03x25vA11qTR+2gmaUJeFHRl15nYaWfq6Zm02fmZaU9U4PTgoYN85dnnSqGDP7DjKGI0HKKKohKiiPlzZ7D7Zd++fVy7do3FxUVKEO0ZZGMl+UWRI6Thgbfcw5e/8mxFq4Rw/d4ppW7O343MGpvflfdISRjH1mbfzanVWNjEukYrsiwhLCRRt4s0cOTwAZa7PbY2tpBGIzEIYwU0WhcEfvNrByKlnX+c6ZqQ9gdpTdeFsSGnz75ymr0rS4RxxOc+/WmunD1DhxB0BoEVTohQMp1sM4oFd91xB3kyYbh1jVAGhFIy6HTpBDFXL15m9dB+Ll28wPraGtFggXSa8B//3W9w9vTrBCZy+xyyPAUBRTImSYZsb19jevQIp+45RW95wNrqItc2rrK1vcWe1TXW1lfsu1Oaj3zyEwRScvzYQR584BT9Xo9Qhtx//32cOf2GPXuzFIHVLvvgukb7sMt2bnwU2CAQDBa6rKws0e33WVhYwgjrg+vfC3lBWIBUIJRmdWmR5597nuWFFY7dc4o9tx3mq595nK9+7NMMXz+H3p4Qao3RGUILpLDnYpErK9j0a8hHzHUaVeV9d2nQx5Z92U5LqpPGf0d5RZRWJ00AUb9/HrDZ7fu2Mq/vFaVvaI+EBfNazO4Z/50/C9ui0dXPyXnnXVt/6nvcl7pmq8lHNOlsncepC8DatGP1NnfQMGPK17bbXDf5m2bd9fZv9B7bAmcYcKaatb4IK1jIMms6F2rNyvIyuSosj2vs2R5GMZ1ulzAM6fV65XsqiqIMjlbnk6MoIk1zpskIuYWNnnyT5Y8cIC0uLnL//ffPXBsMBuzZs6e8/pM/+ZP87M/+LCdPnuTkyZP87M/+LP1+nz/7Z/8sYPNM/Pk//+f5qZ/6Kfbs2cPa2ho//dM/zQMPPMB73vOeW+pPHbDkee7U/gFx3C0BTj34QFP66jdMXTsDFbr2C6Ae0c4vhLrzbjO6iNaaJEkQwgKfPM/LTQnWhKPZl3qABG/C1+aDEwexRdaELK+soLXiqaeeYjwa8+BDDzKejCmKnCAKrR2olMhA0os7rLrcR1URdTq4KzHdIcUQ0kl8JUWhOXv2HKPhCBkEKK0ZDPrkec5oNLK22A44aqXo9XpOEmVtvUtbbmNKKYgnwpVEaGeffJ8b3+z4fDNYr15f29/N+3aro/U7e8MN+kB5sPm1HUVx1ZeZQ6u6py1qYv0w8J/ra1cKQX8wsMlSMycZMu1EsP58sxhwST7bCXlzfuqSr5l6zKzkqw003IgZ9zoHf5u/fzqdsnfvXqIwwhgbcj6QwjE//lCcaQjcdwuDBRYXlwiCgDSzkbHiKNphGjlvvPWx+b9vdH99Tm407psVZNzo2RkQUzuA2vozDwA2P7f1LQhskl5vFWAsckVQM0XxGINqzmbxuKiuGRAS1veuVT5mphKKhZGNgFQURblXmkB6pt9UAOn555/nxIkTVUCMUoBgAVCeZyidc889dxHHIVlqNXDazDIQfk5nmIhd5nJe8WedMRCEgYsEJQhEgDKGQttADUJDKAJWBn02rl9na7hNf7BAN+4RhwF5OmY63CQ0hdvA0BHa+rkYqykz2oInNBjjAsQ4gGSEQAtBISUyC7j46mucGXTJ85SnP/959DS3gTgESBnzPX/y+xhORnzqk59gdP0KGxcvgAgYj4ZsbVxnY3OT6WRCkWV85Utf4p37vx1TZIw2rrEYhXz64x/l1eeedcEoAvee3BrAUAhJNgrItq6Rb17j/Gsv8/Db38ad95xieXWFrEi5dPkChSxYXV5DGEGe5bz84st8/KMfhizlwP4D3HP3KfpxB4FGGq+BcYCgBNUu75TxQMGZEwnDysoyy8tL9AcDgjBiOBozWFzECOsjlBeaqdSovCBCEWnJ0cNHeP65F3jokUeIB12+8X3v5M677uKLn/gsLzzxFSbXtm0Ah3QboxVCa2SoUUWBMJowkDPmcArn6xxIaz4tdp5h9bXXBOtCiMqckIZgp1FHm3mVr6d+3w7eobYn2qIO159rE9b4tn2Qo3rgm5JnqPURKtM2vyd3A43Na/V2/d+eb/T9rZvOzQuy4+/3Z3Ddt6cN/DTN7/y9zTO9/OzMvZv31cdRb6NtnG117wai2kCkq2F2Xt3VPLeAqGsgimMOHTpkrVi0CzwkwzKCc6/XK6NP+giTQojy3PB9WFlZptvtYbHxzZ+Hf6x5kOaVv/E3/gbT6ZSf+ImfYGNjg2/4hm/gwx/+cM1UAX7xF3+RMAz5wR/8QabTKd/+7d/Or/7qr95SDiSoNEH1cJ5RFBEEUbkQ/X31Z3xpY8qayLm+CerX632tb866ND8MbWQcD5J8f72Dng/84F98vZ0m4QB7KEoMeZaztLpsTQyubfHEE0/Q7/fZv38/m1sb1mnXBVCQzvfiyPGjGGMIw6gMBhEEO/OhNJnTNiIFlOp8pS3j8eKLL+EZB2tuGJNlOcPhkKJQSBnYUKrSov4sLSiKGiPmpIIYD49m2/7aGMFSxjTznm5U6oRsnlp5bosNAjNP+jP/ebvJi6JAK0XkGLyqTn/jrDTIS258JfPmrVzPxqqtg1oIYGe4MBcM1ftR/o0lzPW2Z8bTmJM6o7hz7KZ5od5oVWHbUqjtQTsvTUnXrFZWRJWAo21p+e+63Q4LCwPiuIPRxubUGQyIwgil8sZD1ZxUwF40Pu9S/OE+I7eor+F6R3fOc1sRzQ91yV5lxOabr0B6nSFg53vc2WLVzzo9K9eKoEw80R8MWB4MkBJnjmtLFUkLF6dN22TTogq2M7OPHEg1xjAYLKCNcWZR1f6z50FQCpzmlSajuLS0xHQ6LT/vXJv2V5alHDp8gPX1vZw/e5kwCNEih9peqpvA1tuz+6B+jWqNiPqc+uXvn3FnQWD3nQ11qyxYkoIAiIRg4/IVpNAcWl3l0sVLjApNoWE6mZBNx0RCMxoN3YvXaJPbaHhGo3XhxmwAiRSyNO1GOPAZhGQEpNubfGm0wdWrl5kMR4TCJoU1Hcm7v+29PPLo/XQGfW4/fpjf+vV/z8ULF0BYp+orly9x7vx5Nq9f50KnQ6ff5frlSxxa38tw4zpdIfjSFx6nmE5t1DisBNl482QH1pTWFEYzuX6NztIinx4OuXzlCt/4Ld/Cnj17Wd27zKWLF9nY2uDwoSN0C8N9D9zP1bMXeO6LX+Hs6fN88QtPsdDvQVEQRJG1CAlDhDEEQtg8LcZgjMY4kztr4mYDu6ytrVnaEMUIIfnSl7/Cww8/QtztgAtfP9YFmdJEAroEdLpdCm24fPESB/etQBiyfvsR3n3o+zh4/718+g8+wblXTpOTcXD/Pg7v38uLT38Vk6cERiGNIFAB0mgvZbQ+l1J4D64aPXQasPLaTu2yEFhpvqDU5FKjAwpDIAMLHI3Vms8CA1O735/r881MbcS8ORp034eyb05w5QFEA7TMgCtazL5aTAdnmtsBEmTZet2/tDrXZ4V91fMtQ2kBPN76Y8f4GgL7NuFVG182T7BY/76tNJ9p9qP5/DzgNNNuQ6AlsPywyKxp8hLWzL0wxglpraVVoTQbGxt0Oh1OnDgxMweVuXyVZifPc8KgEtj7fKg3U/6/ApA++clPznwWQvDBD36QD37wg3Of6Xa7/NIv/RK/9Eu/9F/VdmmT7SSD3k9JCjAuyo89oOqgp9pUTfOtHQxng+ny46ub2BlD6a+U5wXeNycMbUQ2D4g8s+1VhF6i6REyWA1dGIYIA4EMSo7FaGtLH8kQpW2G4dXlNbQSPPPMc1y7epX77rsHRQ5BCQfsWLXCCMmxo7cDgiAQyACEdEEWpI3aIwQNadNs4IQdUnABQkqm44LxKOe10+fQSJTKGSwsIGWI1jlZpsAEGC0Jww4iCDEuK541j/FqWScx8kTRGOsj401VGoCjSWRFY+/XcEQrP10fl3+vzbU1r9wKWPN91u5g2lmHHavNa+EkYdpArtG5Iu51HG/pwDsC6cCkFi6casmZ14icmW2nXN/MMvA+fLCpXbuRdKllkC4nh0GbWSmONrNg1xO6JvjcIbkr96D9LP0B79oqV6nxY3V7VQjLjAi7d6QI0IVCF4pQCqQx1vQosKF4C2N9NqxZkVddCBRQGEMYhwwWewShwBiFLgxLC0tId/gLIfDGLsZoy6hgKKN+i0rarXWNxlQnrx2f/1O4fedByMychyXcMuUbczSCSkpZt3kXwk1Qyet45sX4mJGuGduWjT7ke1SjJH7tiFmNbHlQu3Ha/WyfktIghPfdAaEkvV6fY0cPM9zasiZSGJYWBnZNFwajnK+Lsc8rowlMgECW778EC5hyfIPBgH7cQeU5QimkVkgTEAUhoQzJ0hylFcrF4a4zXjPrWtuQ2V4AlqZpZebqtRfSJhs1OkAVgqXFAffcfYpzZy6DdmtbJtiQ5hE2LY2dX6Vdvht3RgkjamvZ3lPuN1GAqIRRkCOwZ103jjDCanp0bs1CtTFIDCorUKLH8PJFLl26wN13nWRy9TJ5lqPBRqzLM0QxJE+vu+hyVjtiHKMtS3BkaYwGcJHaMCCMBFOACCnylMvnNlCqII6s5qiQcPy+O3n0nX8CJRRZnnDfA/dy+9/+KX77P/4nnvjc4wSx4MzZ01w4f4E8n7C1dZWBWuBjH/ooRZbTjSKiQHL+zbOgc8eMK4IwsNHajKmtc4HGhuMeD4fkheLVp58jG0751vd+G3sO7OX2Q3eQ7kl5840z7N93gLgTsLq4hFAKXeTkKmc6HmKMjx4qKbQ1eQ6FcLmkbSjtUrzjpikIYpZX9tDpDhBC0un0eParz9ONFrjv/nuJ4tBq96Q3p5ekBRAbjt52O8+/8Bx79zyK0SkBhqgT8vA3PcAd9xzn6S9+hcc+/lnefONNQvZz97d/B8Io4ligkoR0OHG+aQXj8Yher8dgoc+FV06TXd20tNSA0AbhzCeNi47rV58V7DqNhobACTqNo2ueTkXS7Twza7ZtjCFwtQkjUM7XM3AMSSFUdRZbpEYoA4wMrBBZWX7CuPVmHDCzISnsd0opC/yksBpK4+61iN2lSLb0KRDed9kD2pKQ1fa+Pa+CwD5rwa9ACOMEAqKcKyEsALfbwAq+7T61rgqUtNFpGR0t9LSvfv7V+c62tA9Nwf684BE7tU7S5oaTlp8qwSezx0jz+Tqv29R+zQOSbQKfepHet92d/0JasB7KACYZpDYIyXMvv8TWxhaBgdXFFTpRyHA8Yml5mWx/YsPdCxvhNFcFKRB3u7jjF4QgQKILTRgEdOT/D4M0/B+tFHlOt9stgVHpC6SsPbU/5ITwTJvER6vyUr02LYXVtOycvjr6r99v69QluvXAiZrkxAdx8PV0Op1Smu5N8nYsSseAISwIsJIzQ6/XJ446JJOUxz/3OGEQcOLE7WwPt90CF64ty5wsLy6ztLiCUl4q6GLSm5qpCn5TN6UsVf/rm0A787o8V5w7f4nhcEJRWEIUxTHGCLa3hwh8PpoqCaFPZOcBZJskyxe/xT2TNjM/5fcNBrvs/47q5pZ6nTerabrZerVjINmFoAhHuD3DKoA8y+j0Bs5sUe3AQRUu8Mx0vT5/vaofSl55J8grUdOtj6/WGwTO5M4XKWYIZb0vzSKqhUc1G7W94O8z1b1BzQ/LaymMsAejEIJASooiRwoIpQVWRZ5RxEWFQ/DMvaMR7iDUxhDHgU1E2o2ZTidMJhPWVvcCmiCU1m/MOW0bU4X59+u2PIyFFwoYJ931TLCjEZ5OiLAUFlgUVV/XHmR78z6PDgVaWYYmDAPiOHKCF7vPLWPf9N7yj1dmrMKY2nSLxq2VkMlogRBBVUdjvJ5JkFjNBgRIAYEwPPTAvUgpGQ+30EqxtrLG0sISW1ub1rdShoAP++9GaUQJjqqFapmAwJnMRVHI0tICyXiCXl0ikMLGFhCCOIwt7amBqxL8NaWw2HcppWR1dZWNjQ3W19fdmLwk3oU6NpIsK1Bac+89p/jkxx7DaEMora+o5eIDhPHO/lTjMsb6ATlQpI3TimhvPqRQOIDkrmVZZv2eAkmhJ+VZU5q4upFJAUVmyKcTtq9f5+kvf4nDBw8hQ8fUStja3iSZjIlCrJ9MbvPYGe1Nxqq1JxxwElphsEGCXNx7CmlAG4rCRZZCYgKJ7Ibc8+ADFHlBOpliIsUTX3majevX2bO+h8FCH6MN5948w7Vr19BFziMPPci+/Qd45oWX2bh6DdXpsm99j2X6nCCpUKr0lTJ+3kqQbrUKQSDRhWLr+iahPMtHfvdD3PuW++n3eoxHYy5dvMgfnvs429vbXDt/niLPUEVuz0eU28caIUJ7hgjrD+v3qBWo1Pw23Rm3srJanjlFUTCdpHzh8Sc4cvgw6+trRFJaOYyyQNlIMDq3SS87HU6feZNDhw4SiRyjC4wO6C/EfPO7vomHH3qIc2cv8tILr7K1uUV30OXs2dcp8oxet8NgsMQ3vf2tHDp0iDRLGG5vcf3SZTYuXqZIc3Seo3OFyXKKPCfLcpdHSjlTbWv6NJlMCQpNx0VO9fd4gXNoNELb9WCUplAKf/bUA/kYFVjQrY17f2FFUbR2a9bmpZTGwRwPDJz4RxiDcHkShRGEMnTCHBsRUOGyQRpHT/3xITRGun66YBbCC81wwhZP44SxpqPGlEJYT1sKT8ulBXQV/+EETw6MaW1KvqvOM7WVOg9Z/7tptbEbP9IUepb0RDgzWCHK44EZUdqs6V6zX7OawPZzut5e00RwVgsvyjWBo9EIq0zI84zR9jbB0gBjrGZJFoY0SZCiQxSFFEVOkqUMOhHaKIbb21w5d8m6a0QhYRTR6XXd3jT0+3327tlzSxY/X/cAKXJRLup5hOpqzHrEOfs5qEkhd778pjN7U5UIlO1Uixrqh21z4XtgdKPFJqW04Q9dRnit1Mx3JbJHsLKyihSSs2de57XXXuXgwQN0ujGxCslVThRF9LsdMDAajTl+2wmKIicMwxL41TNp30xp26RFYUMmv/rqqxSFVW12OjFRFDMcjkiS1M27zbkkhDWF8H/799JW/465ouLfZY2hBKz0/yZKc6yzpgWz73jed7uVJsGqNCai1KTcbD0gyNIMISAMAorMh5Wv+iI9Dw2llsIySDfX32a5Fc1YfY/U52uHZMn9KxpSMIzZ0c8SQLXUYx9psu3M7A2NcblnnO09gBTEcVSTelEBKuODsFRjqmuQlVLEnYjBQp9up8vmxiZFkbO8skQYChInGPHawVLeaTHQDkjiI025lEq1yazRAiHLw2znOeuYEQ+QPBB0eV7AILRCaIX0GnQrtys1FRWoxjHt2lXTaK9+I02hhNV2QnXoCuEFGdasF5ePRjrAFMUh3/j2h7jn7lN84QtPWoa0KLj71N0uJ1XAyuoSNZnwjrYrIUrJCWGM8EHW2Lt3L2fPX2C/cn46MigtC8bjsTNtjm3gjjmb0QuklFKsr69z6dIl9u/fX7MamD2AvRXAnSdvZ2Ghy3A7odsNyAtjPZVNDjrB6KKMemqBq3uHOsf7/FSaOOzB72bbgwCUIjCaUEZ0Qstc27VamRwhbGJFIaz5XxRKJMKa1eUZcU0w53+8maMHRk0BlBdYYMAox9i7zyJgB3NcKMXC0gLnX3+DyAhWV1f5zKc+xbUrV3n3u9/NeDhiOp7Q7/W4fv06aZKwuLDAj/7Ij/LiSy/zex/6GINBn0OHDrK6tFTmG/Rnore4qAsqhZUiWmYrCLGJ4g3D7TFRd4uP/v6HSJOEIrPnlMpzG+2wDLrkNUTVew2DdhaqsjbBJrIMJGEUghQkLjR4GGrSNOHChYu8+uprLC0N6HRj8MIiU5njK6U4cuQIzz39Zfaur2OMIYwCtDZ0ujHGGAaLA07de5K77r6LPM/J85xpMiHPUjLX5urqMjIQkENnscPi4b0cCx+0dM5YaCBKbtmCS6UUWumaL3dGWBgCZYMrZVlGlufkWU6RZ4hcobKMNElsP4qCNE3J0pQ8t7+T8YQsSRDaUKQZ6TRFaoEubO4ro73G06diUE4jb8G29OeKsYaMWmmEtmaOQlvaoIGsZi5Yl4ZqYagosiktZDA2z5NBOPps/7ZCQ2mFEt4CQEhEYIGSBihMGRHQp3fAa8ZFsCMoQ5vAt87v1E3H5vGG9fNoHn/k+cP6udUEOs16b1TalACtAt0WkAdOSGoMAdLy3KLS5kkhiHsdlCkweUqvEzIdWdPoaZFRkNPt9+gvLzBOJ8g4YJokTIYjIhkS9has+bWUZNMUISTdhT5BN+bacIt+v3/D8fnydQ+Q/CIoQYW25gFtvkx2QVZhKts0R740F1Yd7PhFXi3Aqk4bljks62iCgDp6Lx2Ga+2XEbFqQK2+UGUg0UqyuLCM0YYnv/AERmtO3XMXw/HQRfoIWFoa0Ov2yDJFliqOHDpGltmkW7ZvAUEgZ8bZtlFLG2SYmSt/X5qmpEnCG2+8QZFb7dTa2h6yvGAymZCmCUL4nFFuw9fmtA4omqBk58uu+Lcyo71nJsz8jT8PDO9GdHx/mp9vCOJagLTt3s7ndjL/njmrTJmsRtQyeHlW2AzTNdbRA4Yy+p8DHaVttpOquk74p+pnSes4fV1tfd6NUM6Op+TCZzVB9b7McsHuPc5+saM/LXvVS9KRkOsU5RI7hoGkE0V0OjEyEC4wQEBRKIRQM++oORdeYi+kYWlpwNraGmfOnGE6TVhdXWFhoc/o+oaV8JsqEqNlaJkJr+v775lYVcpI7ViFsCZ37gxx91W2/eWhR+gkce5AwmmuEUgT2oiERqMLgdChNcf09TjQId2mMcbYaH1UMsZA2KSWGJfY0zTzAPlIWTlB4MyXtcvIjptLoQlDCyTiTsSetVXuuPMOHnn4EbpxyBce/wJbG1cYbm/w4IMP8dZHHuLsubM89PCDxJ0QUWr/qrXiNWrCiB3z6SMVGqO4/fajvPHmGVRhECIogWccx2xvb1dpHOZoj5plfX29TF2htY0O11aKImd9/x72H9zL9tbrRGGXUZaSJVOKVKPVBMxspEkryIBAKAvq5awU1wCBsJo/6Yif0BplbGZYoWxUJ6MNhXIhxYWVdqdJjglDqyEKQu4+dRcLC32+/JWvkrrw9XUH+aIoMEKUpjnlfDtaZHSV+NxYTI0158EJJGrnghBEYcS+9XWkMpx//Qyf/tgnGG1vs3dtD6+/+ApJMrVh3ouC0fY2SZLQ7Xb557/8y7zy6mkKDabQbG1ssnnligVGjrY1Ta19kVIiw5AwiEEGQICD52xe22A6HZc0MRCSQOO0dV5g4v3lhANXGhFWfHf97A6CoASxQkqCMKC/MEBpbdOBFIqiMBw9epQzZ87ywgvPc+ruO4lipx2mqtO/AykF3d4Cr79+hqNHjyCLwkrSlWXwYxlZs3sBBNCJYjoDC7js2vGJ7zUxXQyG0BiUj3anHP2xI7Tv1dFcv9G8JYwU0pmaVsLl8rwsnHmpqUbi15PWhTXpLzQ6y6FQqDQnTVK0hiLLydLM/iQ29UeWJEzH24y2hxRZ7gDVlHSaoIoCVeSYosAUyu7/QoFf7y7cO1jgjrGmhAER0ig0VhAROJNsgzWp1sLSOmuda0A7CxkhKYzyEjqU1ijtLUCq/GlCWjM8490QTDDDIzaFq83PPgiXEFWAifo55+e8CVLKN9VY/01tU12gVLYrvcmf2XFPHYzV62hqk5rnUfP8rBeBKPlYhLBmiNqgipxkPCQWin4oWY47ZGFAmhbIMEQGkgP71tm3fz+BkFbDnmWECOJ+j6gTl6aYPijFqXvvYXV9D5/+7Gd54+ybrf1pK/9NACTv3+MDD7RJ8JuanbpqsLlg/AuvJwmsTPVmD1ZvZmaMKm3/fanbctb7UG/bB2OwEqeQhYUFFyUrRjgHfb+JhLCM19LyEkKGXLt4lWe+8lUWFwfs2bPC1c3rBFKyvDBgdWnB5sTQGfvXD7DQXyKZjsp2/GYox1+bz9nNaFGIv1aXFGhtJWRvvnnWmkhom7gvCELyScJwOMRHXKrmGIyZfT/1d9ksM4Bj9htEXepOjfFo1NN01JyROt6ENKXej3mAel4piVBLHXPbogJLNsS7KCNx1QGPMdZUpi49C+rMvhUHl5qlqk+7j615vXmtKdHy980LEV0HPdUz1Xf1kbdNa1vUnvqNM3vRgRWtNYG0kvc77jzBxsY18jxndXUVbTImkzErq8sEYcDS0pL1DTKzbWqtKVSBVgULi33uPHmCZ555lmvXNhASHnnkLfzBxz6ONBofV8sm2ZQEwss4zc416Ri9UosjrSt1CWhR2Bxgwtnd+4NSIug4AOPqdpNYCgmMZap1bp+JZIRSGVJaCbkdl3L7GILQgqxKk+fNjq2voo8mFARBGe48iiIGg5jFJatV63S7rCwv0x8MCMPQ5YLZY5NmrqwSRoLNjU0uXLzIF7/6Ki+88AKbG9d5y1vu5/u/709yx53HOHX3ceJeh9F4BBiXx0i4NQNGeCnlLE21sy5LgLf/wDqWtzMuV469J47j8qxQWtsIcGI2dP+MoMYBhH6/T1FY0yMbfW/WHMbT8qIo6PUNd546zksvvIpRimw6IU8noAWBUNZvycPRmhbKao+c+R9+P1nGVdcAod3nGmPs+rBBf1Rp3hN4ywml7N9aYbRieWmB/fv2cuniRabjMZ3+oPR79ZpUm7+oEkB4AGCM9X01obagTHgaYM+tIAxc8l2D8ILBMODI8ds4duI4UgQ8/+xzdIIQ0RuQTqZcOn+ebrdLkeWEQUDq+ry9vc0XHn8cREBnsMR0MiEELl04j9A2uJAx1lzH05p6wsggjOyPDBEytHMnQgyCPM1Lfww7sVbLaRAYaU20oiiy5ovC7hG3pWoBjarwwn4NysACljCOiOKYLM8plCLLc4wRdDpdoiji7NmzbG9vs7DQQwTRzJqrhKOGAwcP8+yzz7Bn7z6EsIy4lM5sUAT2mnARDJ103ua8Mu7dWD5eOEAtjUBSCyaFsUlmhZgxtfb7RHo6FgBSOoBuQTceLPdKJ2coKVCl/ZTCBXnQBqkBpTAICiGsWMiHkNcGo5QzK7WaJV0ohDEWKGU52miyZEo2TSiyjGQ0YTIaMdoekk8SxttjhltbqKwgSxKM0uiisFFZc2vap5UFadL5mRpyBIUNXlUoRzOtyaSQhlBoa+VibN+lseutEMbRocKCI1Oj71AKouqgx9KI2QAtnm60CfHr58RuQYxmhOY1K6n6PXXeEtyRUTvk6udSk2eu88X17+f93QR3xgNPf9YJUfq2CgPTzS10mtLRgoUoZnHPPoolRZrnpKYgzhTJlet0opgoDAmnKel0Ap0OyyuL5KogSVOyJGd9/z7uvv12cg3v/OZv4fc+/Ac75m1e+boHSM3Q2FaCKWa0M/Xi322dyfef69f93/WocvWwjv7zdDql0+kiRDDzbDNUZR2U+dIGzsIwJM9z0jSlE8dleHCfMAshWFnbg9bw5S9+mdH2Ng8+dD+TZIqQsNhfsLbOsUQrg1GG244fZzyc0umGMz5Zvt0g8EEabo7przMFaZry3HNV/g8bljErVfNFUThmz2b8Vqpu9tMOaFpLTXsElATdMpSWkazPZZt0Zbd2bgTO5j17M333DI8X1rVJg/xvDyKFsGNK09QSXK+N9Ik2sYEatGNubRWm1MKAZy9rbdUkoa1I5BbKzayVch+Zqm3fj/JgnnmplVTTGGsPDrOHQim1qj3oNT3GWImiFoVzmjUcOXKEffv2cvXqJfasrXFg/zqXLp0jz602dd++fS7kfmHzjNS0vkIIVKFI0gn79+/l0KHDHDp0mNdOv8ibZ87wrnd/K6++dpqXXn7F7ncjUQK834LCRzJrzIcQDkDNzolf4UJodwDbdxlK+76EAK0yqwmSnlm1EywAE2rnf2FpUbfbdaFRDWEk6PX7xHFMHNnImYOFPouDPnEYuaTNEQsLCywsLLi9HDHo9wlkhAG63R7dbtdFC53Q6UTkuXIRKiWdTkyeF2SZ1RaPxyNeeO5FNjaucebMGc6cOcP1a0PiOOYd73gH73vfe7j7njs5cGCFQuVsbA9RKnf01U2Lw0lGGxTKgh9tV7aUFhxR+jNq1tZWWVpctKY/WQEDS2fjToQMAtI0dfSneif1c8Cup9l3NhgMmE6nDAYDl1NrJ5NhTdQK7r33Lj70Xz5GmkzodWOy6RaBNRJC13yPGngZbypocM70QlogIIKadljbZIrCSrqNgUI5TVNQRXWyghNZ5pSKwpC9e9Z44blnyfMMUqtt9YEnPEjEma1YkNul1+uVoXXH4ykeXKRpWlpOJMmUZDyywT6cIOzA+l5uu+02EJKLFy5w4fx5giAgcpoMrRTbW9vOj8n5KzrGSStN3IkxSlFkOYlM2N7aptfpgtMG6AZT6M/pIAgIZFiChkBEGALrbC+tmalDnaVPhMYGEYjjiKLIyLK0jJAG1sojCi04GgwGTCaTivY5IB11YlbX1rjr1CnW9uxBBJYxnU62Uaqg0+mwvT1k4/p11tf3EAfRDprviwxC4k6Py1eusbKyjDbWpFYgrG+eow1BKBEESBkhRIBBlfTAJta1pmXSCAJTkRjhNCMWIDmhkKj8Bss1KSkJjKCKGicAI2UpmvF+P6Vwxwd7cushkEG5rjI0eMCHtNrYULj7BJEjapaXE2XQH6G1i1ZpgYxx5oBoq1HWSlGkGXmSkSUp460tJqMJ03HC5vUNhpvbjLeH5ElCnmakaUKapejCmgoKZTCFra/QGQa7z1AaCoXUpjT7s/NagNQYU2CMDUhjmD036iUIdvJ5UPGUdV61KVSvaMQsaKmfhc3n6qXi8YLZSLO1Nprgxpc27VD9WlO4PSs89bS5OuuNO5v63S5haK1jimsb5Ea4dWL9yQI04+0pY2MIg5DIBSszAkwccPnKNYIwsL5vUnD52nU+P0pZ3neQt7/rHdxz113cbPm6B0jNKFildiaobELrqk+7KCsU34aA/eempNAv0vqitBqTgCAIZ0zG5qkd64uqHj683lYcx0zHkzLEbBAE1t54OiXudAmCkGyS8cWnniIMQo4fP84w2ybuRKysLLMwGGDIyYUijmL27zvAZJISm7DsgzGUkmlL0CrGakefqZhu/7wQdoFnWc4rr7xmJfCBREpBlmWMxxOKwiaz09pJV7CO21bieROgaJdSKiCMk17pds1O6+Y3tQoa9zVHXm9xFkx7INN4woMBf4buqKc2Ar/WHBURAsuAuQNHCkGappbJiSMHZH0EKUEQy+reQJbgy5vCBEKQ58rVUR/TjsHPqJWMk2TPDM6YCtyVB+78d7jTJtlzutW8iMa68m1A7X0I29KO91P7KN37sF2zL2AwGHDvPXfzwH338clPfJzJZMz9995LEEjyPKfQOQf27+fYsaMVyBbed7FCdMYYxuMJe1b3smfPKm9961u5du0Cn/r0p7n99jv4if/hL/K7/+X3eObpZ8lSxXiUkGYFBomWwgZgqI1JO01BUGMxwJrXhGFEGEiktEzZYDCg2+2WJoSLi4t0Oh3iOCLuRKytrdDtdmzW8ThkYblHv98vTXz7fcvgGi3Q2jIcYRShjRXsZFmKQIMRpGnmnLGLkuHf3Njk8oXLxHFMmqaMRkNrkmQMG9e3yfOColDWGX06ZTKZIKUkzw3D4QitreO3UgVBIBksDHj0kW/gkUcf5p57TnLg4BoHDu7DmJzReIssy62E2xjLDJpqnxmwmh9dRQ71q8ivRjBEccTBQwe5enWbLMtKmuwDV/hQ3/Yd73TmNWZ2f2itWV9f5+rVqxY4OqMa90JngH6RJxw/foylpQU2r1xh0B8w2rpiAxxItwvcQV9fyMbIciiiVreXuoIhjjs2Aagze5JBgCgTkRtkENrcRBgnTLHVTMcTm4A16jAejQmCsEy4aPdjFajHRtDzEmfBqVN3c/vtx/n4Jz6BDAOWV1aJoojxeFzu7XPnzhKEAYGpAFKv1+Py5csUaM6fu0DqkkJm2uYPk87MMYptKGw7VDGT701p6+Nx/fo1tFEUBqJAEoYRWjhq4vz5pLYMYBR3CIOuBZcECBmACBx4FBjh8xdZwGG0FyhYrcd4PCIOQzvH0pqOGhd1stvtceDAAS5duoQQ1qS/P+izuLTI+oH9HDh4kEOHDrG4tGjp9njK9evXbVRbbUiShCtXrnDijuN0RL9VOOqp5NFjx3jxxRd55NGH0T6gJQKjHE8itY1aiEAKXQqD7HfGmew5Giac/KC64s4aUYIY/75rKxJZVNFjcee2B1LSCPwi9u+u3C/G5zHzZ5rV7goh0NLxR8ZZz3htnhOgahcYwwjhHDhtH0NEWYc1rTJ23UTShv8nIuzHxAZ6CNY4jA5AS+OCPIDJC4osQxWKPNGk0wKVZeTTlMlozGhrm/FwxHB4nfF4SJFkTDa2yCeJfTbJMWmGLhR5ngIFoFDK+g9q5QWVDsi4CIF4QVdNEOPpjzYaEVj3DIEHTE7rYu2bZ2iTP3tLTV2Lq4Y31/SC8NAnEC7f8U7zu6aQuqksaAKhJpCqf1c9R7VG/HPKWjHEwr17Gbok0SFChFbrbwyFE2IIsH5nxvHIxiDSAiE1xmQY4ehEEHD+uReYjFLMN76dbhjv6Nu88nUPkHypExspJYGwttlKa2tSBjYsqZ6VAPpSD/IA1aLx1+qf64vEmm4wY+Y3g+59MlWHkL3FvyUcliBIaVX9CmPt+YUgii0oGvQXXAJc61i6srxCx8DTL77ImXNnOX7bMWQcECrJ3pVlDq6tEESCJCuQRrK4tEyutBOa2aznIKxNeeCD/O4Eh43ZdSDJKugN1mwuL3K2tiZsbEwJ45jeQBLEkBlBmuZgAqIoQhWWIChl0Gqn1OymiptL3LNVfKuS/Zzpe/mOyhHWmXNndoZ35Cwbqc2BpooU5oi9i60tSucS+92ML4mRlNoxP28YFykswIZYc72t5R+y0arsQa+KzDryG0OhcoIA+r2YEyeO8MjDD9HrdsGFnl1YWLAJTPOc3/7t32Y0mRKEIYuLA0SgmU4Krl7OoRAgNFrnzo8icFIeHFOqy2RtgWNA0D6vBq7P3gcAPDqswFTtsBcQeA0H1uRNOKatfO3+wHWmIXXwae3sDTIQM/uv2+0SyIAwCgmEpN/v0+/3Sul5v9+n3+uwtNRjz9oal69c4aN/8PtsbGwwnUxZW1nh1VdfZjpOOHnqFA/cdyd79gwcZyfx4fkD6UOyWyY6mSryRcUdJw8znmyxsfVWPvuZz/Frv/bv+L4/87386J/7fkT2p9i+vslLL73MC6dfZTuZoomIoi6DwYA4juh2uqUp1PJil16vSxiFxFFMHEcMBvZddiJJHFXBVJQz0TDakOWKJE0s4+ZM4tM0ZTpNyPKcybaNhDmdTsoAKUJLkoliezQky62GJsszRuMxyXhKYOwcJ94nIEsJw5AsK8jSrDyE7ZKwzHnkzHSN0QRBSBSFNmiDgqVBj/X1VeJOh8XFRQaDPuvr6/Zn7zKrayscPHyAxcUFJpOE8XhMkuao0kRMg/NZBAuAlbThpQstEQUEUYB0wZEss+J8QYzk0KFDXLxwzUZVUy56HIqoEzGdJhTGhWluk4n4VkWlGVpfX+eFF16wOTmMatxsK9HGoDLJvrV1jh09yPVLlxCyA7KDEIooFKR5WibJnalCm6phB4x8RDvlNERZ6s4noYlCSRhKotAqQ4pCkWcjK3EXAiNChImAAJULet0lJmPFeFiQp6ACm1AWApSRLvFqQICNnCaUQReak3eeYns4YjItiKOY8faw3KNgky8XaU4gYtdtSbcTo03I1saIkydPkk404+0UIZwm1OfmEy7lg/QmXIKOO0vT3Pr95SpnmiZEUUyIdBEoK4ouZYjC+ppFYUQcdumIPoFPnhvYpLZSCBdJ0dIhGYVoKSi0DUwxzSZgCkSqgZSCgFwqskCR58JGkuv1OXL4kPOzDZBhTNwJiDs9jIY8yTEKOkEHIQQbySZXr14nnRak05TpeMJoPEKh3RnfHiXMGEW/10NrxWQ0ptvrgvGCJmXxnfLgwWCESysi3bnWwPzCmQ8KD1i8xsiTddPGDQmUUQgvmCoJt33OvwVgRjAphKjOZYNlkIWuBMeyPIkRQtdqAeGDz/jzu/oCVTvbvbC2ko/407wCfdVeohQYWu0WiDhAxhGD5Z7l1xrPewBtlCZzgSemkynbW1uMrm4yvL7FZDhisjlktLlFNk1QaUYxHZOnKTovMLlCKo0ulIuVN7Vno1bWjNVYYXEhYBoom0zZyDK6r8QHtynwHIxAIo3Xegq0qOa9zZWjLXdQ8z23aZtgZ7RiUXshor5oTOWfpFvuRdSEQcamH/CQScoYjbZ71AXHAMc3eJNy4fukyvdojMspJ6X1G0Na3zpToNQYHWrCfoebLV/3AMk7u3mk7A/zQOrGOeQ3XsWc183z6gvL2xrXNVBNiU/9s9dI1Znz0gRABs7Z2Ti75tqzbsEYx2j4KEYGiMLQmvckU4LASu1WV9dYXFhEaMNnPv1pgkBy4o4TJGnCYNDn/8Penz1bkuT5fdjHl4g459w996ysqszaupZepreZngEIArMANMgACtBIQ4Dig8z4t0gPetSTzGh6kqgHGo2UKCMhA0kQM4OZ7umZ6W26q7qWrsrK2nLPu54lItxdDz93D49zT1Z3Q28FRFnWvfecWDx8+fnv+1u+v4O9XZomxkQbQ9vBhQuXOZvPMaaKFnIJITFGMZaSn6MtRLdIYPzeVV1x/8EDlsuOrbphZ2ebJ4ePsdU0JyDKPVS2dKpYbHCTy3nj40cbSIIbMF6xg4BOFpKQ20wWgL/eoYp/yCYV+8DHmlo55ri4u1h+UkK9J4U6DE0twFTxJhm2l2xUCLMLIdA0FSoE/v4f/D6TSU23WlFXFTtbO/jg6X3HB7d/wb3799BGc/nqJZbtgs8+fsSjh6cMRZEEmAhNc9oPYkK8CqQEeQ0DFbUq1ojvJTdGEeO0SyMClMU8m6YZ5QVOJhMmk0lW/KuqYjaTGP2qqjJdv4neX2P10P3xOX0Xi306T9uuJJciJnvPT4949OCM5eKUs7Mzjo6OhURkteL111/n0aNH3L17l93dHf75P/tn7O7vYo2i7fphlqhoQ0GLAq2EZeno8JjLly5y48Y1jPkOlW347ne/x//9//b/4Bc/fpt//k//kK+/9g1ef+EN/kHfssQT1JJVu8hypetSsnJgtdIslm1UMh2nR8fc+/QRi8WC5WoeaXddDh9cLBZybS8hGavVii56SHonlm7nxqG8ObfRGFG2vQOlMNaiY9iQQlMpk/MSJ5Mme6WMhdlsQl0L7WozmTCbzsQKGC3oVVVhbcV0OmE2m1E3Ndpqtna2YpjWBGsN1lbxPhrvFfPFkk8+e8B8vqD3TgwCKuYbJar0IKE5JoKjSVOh6hqjY0hpUvw0Wa4obXjmmev89V//hNVqWdR2CTSTJnu2x0ri+ZCVUpvY39/n7Owsrp8S5ZeGNPnbGMUbb3yJn/zwByKXt3fo2znaBSZBo6I33Rc5SEYNsgoff4uGiM6MFViPI/gOvIFgpK6XteiofCaFwjZiLW+ahhvPHdB2T1B6jq1XVJWGXFOqB4RVzwSL8pWAR2f47p/+Bccnp9Rqgu4NOlKtKyUGQb/omer9GC4l5CHb022Mq7FK4+YVdm64NrksIdyIcq119CBUTQ4fNMbQNA2TyYTgFTZMUU7RX2gxQWGVkK3U1oABrQzWVOgYUtc0E2xToyd1ZGrV1HWFra14ZZGcEVtXKGtZuY4nx0cs2xVzv8JUiu50zsmjxyxXS067BfcOH/PJvdv0fsn+pRmznYbt/R1WK/Be09FztDhj4TqWfUenAlSGvd1dZltbbG1v8eMffJfF/AznOk7PTqSwr/dgNhQeZqiJc/P557lz5w6vvfbahvNUYRuM+11RX210ZhiTAAyy/vN3xKQDq6SjxP1UHD7FjpfOi4axUNw3XxP30VB45tMz4tuMjBXr71BiPrlmDMpG/TKcOXqW6D6+AA46rxkg712J4EisfKC3JmxtTdi7fllAvbayhbpAaD2r+ZKz4xPOTp7w4LO7nDw55PjxE86eHHF6eMxyPie0K3zf061aIa3oeoJzqODZcnF/QIhWMEqMBsHhFBkQopAaTCbmq/qezzs2eXmSXE39tjG3d+36/Hm+Xzn3zvf8KCwQRjIW4jxhIFHzPkjtsnyfgWAqe+Hi4cKgH4e1FJoQHPsHe9im2gD4n3584QFS8uKcp4oWBXM9EU5CyXRWPtZD6krv0DpjXRlip9TAPpPosmEMpmAAZOnvkp5U5eKsKifUpVAH76GqJAdJKc3Fi5eoq4ammfDJx5/y7rvvsru7w4WLe4Dj4sV9dnZ2pF6Oc6AsKKlYv1w5bBFvnoSDIoa8BXK17aeFBpZHOqeu6xhG0GVqxbOzM7a2q5iXIAukqStcv4p9HrJlp+zbX3ZkwFP05QBIQawMktAOxWYRGCTxcDeGJR3WPi/nT9kXavS9yIxo3SmERYieFsloLu8Lqc7U+J7p14BOViHiJhag91G5qyru3v2Mf/E//A8oFVjO5/Rdj9UTFss5q3ZJ71qaymAqzcnRE7a3d7Fao/GYBIBCjF4wg6VIKZ1BiY21Y5q6pm5qmlosopOpgJuqqlFA0zSSkxHnjLFawmeSMu7cuD5JIOfWBYT1a7Vc0buOxWLJ2dzTP+xzmJco+i6DHx/nbqL59f0AIFIcdwYVztO1kqvTNA1vvPE6ly5d4ic/+RH7+3v80R/9Ec899yzOe5btKiq9wzwrNxcBq5a+czx5csxrr72KwvKbv2m5euUqP/r+T3j7px/wf/nwv+DWjedYrlYczk9Y9i19f0bXrfBO3iXTOwMdls7FhHozWNEVCux496mqKq65gEXy0abTCZNmK891ay2T6ZTk4bTGMJlMYsidwmhHMxVvlrJRYbKiZIoHKymWNl43paoVxsq9m6Zm0kxiOyXUScdcBGsM2hgZGxVwAXrn8zgu2hXt2YnUXenA9YHO9dFDKsUjnfekzKAQxyFp48ZoKmuYTRvc1OO9ENfoWlj7SnKNQOBgf4/ZbMKqXcXctAGwE5X7FPaSxnhYv+PdX0K/5HmLxYLJtBkpl1kGAS50KOv56tdf57/9bwzKe7a39zh67NArj9eDwmgL0aKLMMxSXHhi/kLxlXMOrVqUMdRGPJJehWi0SJ4CjalqdK3o247VWUW33dDYS0wmBowUTre2YjFf0DeSAzRrptSmwUdChFm9xdbBAXXdYI3D2jUSGJXCsiW8rWlqdrZ32NreFsuwUqhvvo61lq3pjGkzo7IVVSRSsFrCxZMRRYwnhqq2UHmsEUBpjcEoTW0sthbCCLlGqLyDl3IfPhDzYyLjnhbWV50s0SpEhSyw6lc8Pjymdz1aBSZGo/qAW3Z4D/N2xUf37vJ/+j//H3l4+JAP3/+QTz++i60ammab6Wwb3RjQMpd75zidz3ly+ITf+q3fYnu2zb1797h//66sD6u4ePEAY23c9zfnq6Tj8uXLvPfeeyNW3H/bYz3PulR+n3akNZOWYbmFZmMea3pT7NthQZ4P0Vp7SnzWeUX+/FnD84bfQ2GvGPYZIOdopvfVel138KTsjLJ9JXnOMI80frGQ0C8t8sb1HqMtzbRhun+VHXuV5779ZZQT412/WHF6dMzj+484vP+Eh3fvc/joCUcPH7E8nXN2fIJfLJjOG7zrpVh56CLrnhBpBB2LIUe9wysl1W8DI09hMsb/MoOzAMCxvvur6F+lEfjzx/PpxygnH7LHLkQSL6UHYJoIUp7WlvUQQZA+qqvq127bFx4gJQUpKRllBfnyKJWeMicpgZISFMEwEQZQsZm+MU2yJAxKUDVMgPHETaxBisFrlQkmKAWapqoagodV23Lp4hWU0nz3u99juZzz1a++jnMtBxf2BBzF+Nw+BAIaayf0HoibxpiafDhKD8h58HHeWjr0c2CxWOC9p64r7t+/S9d18WQRXtZKqKAPEkKmtcSZJqU8hEDbtufGadPzB8tREtolo1BKrk6CUEUL0QD+RPEau/blfPmp1qzKsK5ADdam0mrs/WCdSxVsUGTPIRCj6cYeSHmmRuhC5TytBcBka1tw+L7n4OJFjp8c8v2/+ItIDSzPq/RMwkkqxc7ujO3tHYJybG9v03fwwvPP8+LNl3BOlKiqtkynE4ypIIi3ta5rAda9o2uX+F4YrnonNVu88wJoViu6rsd5x/HxKU8e36Pr0zmOtm3pup4UepUIRpKiXBoJkqHA+X7k8SgFvYu08aX1M92j9PCmMZL1CdbU7Ozusbu7zc7ONoeHhzx+/Ihbt27xB3/w+3znO9+haSaczc/oul6o8xOzUnG/NO5aSb7uYrEEjnnlS69w4cIBs9mM55+9yf3P7vPRBx/y4N59FsslR2cnUqzP1Ri9ha3EQ5NY4KzVBL3MxAnTySR7TOrJhNnOFjaDIqkr1jQTKmuwSpTmpmmwRgBNVVVoo5nNpkynk6wsWythfZW1SAAvaKPBCDuaTxbFWCtIjJUhrqU0DsPYOC+gp1+19G5F70IGr33X55oqvQsQaXWl7o+TBGEfYp0Z8Y7k2lGKHFJaKicJICkFxkDb97RdRztpBFD5hqnSokgrHcNOnOQhXb/CRx9/yjLWakksZFoNMl8kw3jMS3mSDuccu7u7nJycMJ1NsnwYzT8k/6LrW1555UX++f/+j7BKc+XSZd79+bu89dOfcnx4NOxVKiWwQ/Iam2SZj6x01lZSYyeWZDDGYKyl73pRtCsruYnREmWtZdI0VPWE2dZOHvv9vX0mdc3XvvwVbFNLFXoUddVIbTYvsrJpDHUlz63qSgwesY1GKSptMFoMIFrrKDN6XBCrdwhB+toajDXgodce13uk1r2QTmhs9OLpfI1EgjhI3kPnCL3087IVQ4IKDquFBrrvuqy4r5ZLAeargFsmI6TMzaRJ9r2LczTQ+Z6u7zmbi6e2p5f8pD5IrkkwOKU5PjvjuelrcPwRZ92cs8NjFpxyFB4xmVTsXLhEPZF8ol4tWFnL/PEh88fHzHZ2ePutt1gu52xvzdjb2+frX/+6eMgpa7KN995cnw24fv06H330Ebdu3ToHZkoDTtq7Nn2f7ps+K5XLzwdJax7V4kjq8iCbY55gCEOpAoZ9cuxJKtsXoVYIOL9ZuQ8kfWGDYq6Gdqx/ppxEbmTQpJKek2TK0JYUCYKKXorYPoUS0p1UhFkFqZ0FzOcLXABb1TRtg60NNtYbq5ShqjWTKwfcvH6FF5W4gV3bcnZ4wpOHj3jw2V0efnaPR+9/xNHjx8yPj1DzM4zrccslFk8fQIcgIbiC1nAu6RYD4Cj1uvT3prmQar+tGwHL+ZCOUXQVnw/m15+T729KD08YfReUiiyKMXrKRQDIeL6mn+Xv6wZMeTchjfHeD97+X+H4wgOkMu8nWVJXq1bYZ6pqBG6ArF2XbsZ1FJ0GMddWKT5LE3ETu8e60pbQMgxAbjToiGKwLqzku4IwISrbW1vbLBYrfvDDH1HVlhvPXkObwGzWYK2kfbsgG4/3isl0h66TJDZlVJZP40WVQN15z8z6+5XgSBaQKBup+KHkEkgOxMH+PqenZygUi0WH1qLkSH0SlccuhV8lq25JS1n249i7Mwjf8Tnpvgm0DhTmKuYvya0DpfO2FORDn4fBypGMzUpJrYXo4TExt817hAVNx0rfJKAW85jUIJxAEsah9AwQaVoVtbWw53F9h1FQNzXPPfscL7/8MlcuXeLypYvMJhO6VjxymgYInM1PWLRnoDyrdslyucJ1PhakFIHetW0s7Ndl4OOiV6aLgr/vWgkBiePtXE/XdhlgJ89OCplMpBsyp0JmG0pJqBJXXYxRmveJTCUm46ZxSEnbwYfI/jWE7+W5qVTciFPIpoprRJRJaycxRNVzdjbn2rWrfOUrb/DVr32VL7/xFa5cuczhsYTfCUXxmJVnHYylmRWCkA+0bcfBwT7fuHiBw+NDLt7Y5+Zrz4i1vm3pnYvjLaxaSkldGG1ShfNAbcGaRByjYh5PLXPCGmxVUWflV2ONiUntQzJw2tQF6MaaRBHI+AgCFm7OvAXXO1wcbxeceHicFEX0IY1tGHKvAoCBYEmhKeW/3qcAYeJ4l1HoEjMfKNdoBLZBmNVCCIQ49lJAOQzrtdjE490xOtDmIqtumG/AbNLI3CFkj8GLL97i/Q9uZzprH0L2ViRqaF3Z/KxBrsT26/F8uHbtGo8ePeLq9asQzjOfQhAyAe/Z2dripZdf4smjQw4OrvIHf/8V/un/9n9H2y6Zz+ey9q14W5ViyCcIQo8sAkVq9Vhlcr7K4FmV0O2Um5HkeeqXVdfR+1QBiJiDE9iabrNsl7EQpmJ+No9rF9pVC0GjvBZyAucwStZn13Ysz6DvFKvlkuVymWVn27Ysuw6tDc47VqtYJNUY8XC3QjXtXRCru5Kk7L5zwtAXAavSw/5plaVyNnu1Q0zY1krl75IzPpUFqipLNbWYqWI6m9DUNZNpg7Exz0RJPpKKa9BZR2vEoHMWOo7bOV3fYY1DKYsLgdneFa586waHZ4e8+eHPefP9v+F09ZCuX9Evzzh6EDB2kg1CSQe4o97H1xUKqDXs7m3xn//n/wdeeulFOg/BjcHC+hpKyumtW7f43ve+x0svvTSSTyI3C/1DKVIg2rqiWyqt656k9XuWx+A9KkKrhm/zOl3/exwOF85dU3w77LnEfMBiLQ6KdBzqbIzcrPyX9wVigdmxfjD0hR9dVxJGuVznTQ2yQInOV4FEZGiDqh3zxRLd9yhjY9FTHWvcKToluaZar/AmeTw11aUJ1688x43XnwcUy5Xn+PFjHtz5mI/ffpcHH37E4Wf3OH78CDqF7qTgtwWC8/TK4TUZNI7H6zzwKd9fowqd5zzg3GSUDmHYb8ryNKWhcuM9EHlWprRsGrNEAV4+72m/rxsV8rtGI1rfdzHq5OkeqPXjCw+QNjHRVZXFu8H1qLXOYImwwYNSAKhN6DXdZ/3cMShS564DsbYUkiQPsFgRw5Cgu/7sGL4lXl3NbLZNXTf82b/5cx4+fMiXvvQidVNx6fI+W1sTjEk05B0hWFZtYLYzwaPEwqrHE2sgk0jU5Z9vHVhvv7UWHySBGeDw8IjZdMZHH99hd+8izz73LD/76c+k+nbf57HyIUC0WEv+gigtiSmrXHjnF3sgue9L8CkNk01HRWVZaVA6hpQh1p9031Jh9wnwmqE/iAI7Wc+NGWh2bSWbbdq8xdJrqGvJnamM0CjLNeJZm86mKCXsfsZYtmYz2q5FK81kKrTJJ2dn+L6XcJ7gWS0XBC+g8aMP7/DhB7eBQHA9BJ9zk3zn6foOF0Sxdd7R+/hd7zOLmChQ4/yUwdNaemYGsFluVsnjlfq47Ks0X6WaeKoIFKiMRdlxbbJk7Rzi4qNSu5ZoSghoF4uPFt8ngYhWwlSpJKcmgU1ra+pmwsHBHpcuXeDGs9d47rkbXL12mZvPP8/Vq9c4O1twenIqLGeE6PUUpb5ch+mnVmOL6dnZCYvFXMLcZhNeuPmskLUQ6PsuGSnxoRcFTmlsZQtrpwZvUQzJ+D6yw4mXxcUCloGudzjXZgDTeieANgKFvE4QL0paF2I5jSvECymLFD30QrMSZK74+LmPVlIhf4gKJUJdLvMi5LyZEMQK79VgXVxXhnKoy7nNOoIb4rsW7dVqsFrKzygHvCTX2yKsMr2bUiqyYVlMVGycd1y5ehljdfQgtdSuiSC0om1bIc7hvHzP7S8O7z1Xr17lzp07WXEczcd4jVaWrpfCkjdfeIEf/PX/m+/+mx+wOO3Y29ljZ3tb+q4Vj4mPALePfaIjKBLGrS7S20aWKyXtmC8W2bDRO5UNbN7JWvch0HXgqOOMVlFsyrxyocPj4rhp+j551DWBCSo0okAGh43e7ESsMFZ/hygJVVWSKxaphNOepYCJA4MolkZr0LKeJo3G6hpjxAhprYkGDo2pNEwctpLaW5WtqJuaummwytLYCZNJjbXSL5NJxWQ2odmv0bsw255S1xVNU0UDTFabx4DBReOO8/TLHu9dNuKESIxi9QSvDT95523+y//Xf8Pbv3iLh/c/ol0c0/WB1nfZgGatxdRi6NjZP+Da1cu88aUX+Uf/6H/Fa6+/xrLtofe5IHA5f0YGmfizrmum0yknJyfs7e2dA/KlTC0Jf8rjPPjf/N35CyUhnhgNMT4zjD4YjMeIJVeNP99wiXxUeo2ykXLQl0OIJCTR4Cj61mDaVMX/868hgYEwUn6T8WgdBMi6Gr226BKOCIxikd0AXkdSGKPY3d1lZ3eXru3o+liQNhbZjXQgOBXDxrIYlbloUr0wYwiVYvfGRS4/e4WvfuebtKdzHn56lz/71/+ad3/0Y7rDI6pVh297cLFtDLJ9EzAqwUT5nStedJ1lNt2rvD59liIm073W2ZdHY5rHe7xflN9rPQ6LTobo2M0buEUZvc+6jp364uREwrh/nYzzLzxAKsHPsFHHlcJgdUsKmdYD1z4MSZGbuOjLBVVOnvT52AU4XDOyBAWyQqiVGpQXzk8c8RyliZIc2bIh72zv0reOP/3TPwXgtddeZTptODjYo2kavEMoRUEWbDA5ltw7n4tnBsYxq4M37JwIHP9dtDX1tTWWG8/cYG9vlydPnnDjuSscHh5xenLEwd4BL730Am+++RbaKAmfQJi3Ushx7wQ4tV0bN6uCdlwNhdaIYT8qCRnGC7PcbJLCk8c6ypNybG2igI8x6pJ/UWVv2mQypWlspPAU2tqtra0YGuapK4sxmvl8Ttf3GC00zMvVCt8FrKmkDsZiHlnBljg3AMX7UQkuvTHOi7dG9BFH33cE18dijA3ee9rVkgSSspIYx9X5FN6gsldBrK4C7BJLXXJFj/Fw+ltF4a2L8J+hT0FyEJROnhBi7HBSzlX0hhiCH4CnVslTYjIQT9a5KlKVp5yBRJlvlKbSlVicI5BOQEsbqVyvtWY6nbK9vcXu7i5b29vs7u2zf3DA7t4uOzsTJtOKnd0ttre3CAGeHB7x+PETVu0qh3fJpqxRKbA7Wr7SItBZ+UhJooG+b1kdrdBPDiU0ykg7TVQMFSrSLg/hgBnQEElioyxJQDMk74BX+TkCdAYw79QQRlEq9QLuTA5NS3JOxblAUpC9z6F1PoFiF+lSo/KfWN+0ctmwEqJ3KeWVeT30BaHsowQOs0o6amcI5Ot8XLs+3yOF9eWzB6XJS40c13eRrreLQNKD6wlhylQ1KO3RSgwTz1y/xunJ2VB7zQmj6WoxHwG4jYpCHP5kQZ3OJnRdG/OsCkNY2oyjzPI+0Peeixcv8bu/+3t899/8JQ/uHvLozjHHn7UsV8uYeyeywHlPiEtNB/ln42h678HqyDZKNmplg5wSggJZk7KGK6uxlUNVMTdQSc4aASpjsLWmqsUbaaIHJ+WReQ1KG4wRJsemMjRVRWUNVWVEVlYVtqqorAABW1lx4+ihjEaKMLCVRW9JOYK6MpGoIWCNojIWrYQ4KO8n1ozIBmwtebRGxxqDcU5jiAyXkGojaROLkCJ1d0JUtWScYrFyBtZNpRQmaCxgaPAu5rMouc67NiqHgd57jt9/wnNfeZ6t5y5ycnTI/OSI3q2izJY8tbqWXL6drR0u7R3w6ksv8rt/93fQSvY68ZxGJr28j5W1bXQx9+V4/fXX+PnbP+e3v/Pbo+9G4EMN+o58twnsr914A2AZfx0KhrrxHpuuG+kv8YYpR3TjPddebiBuIrK7ndeJkgcpUAKA4Y3W85WG9jIUPo6fOecHeZbeJwGyQtcuWymlJxU6BJz2VEqLtyhEUhirJS3IqyF0N0i7Uj6T8CIpSXXQCr9qI7GKY2oCq8Wc3lSSN7jdsP/KTb49+wO+/rd/i7f/+ke881c/4uzefVQrkVG4EKMwZK6Gofl5jEpAkT7DJybB4byESAdD2yD31se7DOFL+upTw/mSIXNt7LNTIQGvkFgR5dzSW0go8pXW7g+ii6T9NBUXXi1Xnzuv148vPEBKOUchhEy13XUdylgpomnFqu+Jk0MPqLq0WqfNJ/09miAbFPCk7AzKuMphDt57qqoSRdE5NELVazJzjQjtvot5ASoqktGC7YOnDw6jpB6IwbI72+HDX9zho/fucOXaHpcvHbC/t0NlGoIDhccY6DH4XhibXPBUWuKvXW/oqkClldRniZYeHYuHCW+ZzqxC+VCyqZV9lvrN2opLly7y9a9/jX/9v/wZ7VnghWdf4tM7d2is5YUXXuT3f//v8dZbP+fTz+6xWK6AqLTjafsVnWtlIaiArSt00GIxTpbpON211ijLCOgOm7GQCxhjskcqLeS6mWCrSR5HpSTBXcIChU42zSHX96zaFmsUvu8ghozNT86YH5/SNBOOj49x3RLnWom/j+FMrhh7uZeLFnqfreDZ2ptD1AaXtYsKa1r+PoYBWK0HmlKS8EgKXQAVUEZRVRE8RCus0IIOFFiJpSxZeI0WIKKVeGIIkTEsUeMWFqJSKRuEr4S9SdiSAq+wWpQoa21W0m1knqqrKtbwqbMiboxisiXW4d29Hba2tqhsLTk3kwmT2ZSqrplNhR1tMpH8j6apqRqb21lXNns/RAFXkrDtPc73rBYdJ0f3WKxaFl0nOTGpL/I0D8IxGqTvS21k3XCRN0EiEOo9oXOoVZfnHYBDE0PGswVvCF8khhWFDHZzuC363Dgny6kLLq+JNIfydcWYlXH1aWzLOZiOACgjAC/EzSaDGKVE3UwGHRWBJJJvI8ApAjU9GDJCYXHOoC++j3d5qxv9VATwKiuOAqLiJqqCWGgJ9C551uas2kDXBXAeHxQuKCahYaIDygRu3nqe7/35XzKd7mBszQQhE+hPToT+W4VI6e4KgBcV6hjAVhpIp7Oa1WrJ1mwb74tIhHiOxqFRtMsls0nDK6+/wOVrB7z983dZPAzs71zk8MkRt29/SNu1JNVDDACRursy1LWVMFwVUMZHUGJj+KilqWtsXeEjgUYmWImeVFtZqtrGHDUzGBayzExe3RRaXe4DpUIS90W9lrUZSoMhTz8UuBS+FAlihvUzeB8pPs8KUNSU0jwk7wUhrof4m49MoT7Kvqjtym2igQwj7FlFW33hvehZigzPa5DILCvK++OjM9557yOUn7A1rbF2wtbeHiH0EI2v1lRMmwmVrdmeTWl8x62bz9E7T9e1MdcyYLPemBRJN7x3EB0lxEUYgCuXD/jp38xx/ZKqmUblUud2DmMQ52I09sjnhWEiu4FEnsg1Yzkw1izHHq1ybPpc/mJ8jdzjKR6Ftb9L7wZRrpXnDN8pgln3LA/XjYHh8LvPc0AOMVhF4y5jRTuRkytUssLG+Uj0rCu0V9jQo4NBWUUfuqzPueDxzhCcxvUipxUal+Z0lKdS+1mekWTtUofsTXa+AyU5fNoq7O4Wr/3dv8OXfuc/4N/8i3/JB3/9fczhQxrl8dGz30eAI+ubJKRHBvA0dglQyLuOekY817H/SqIKFfs1jVeSIese0PUxzsbp/IRijJL8UOevUwx1rwJDQXgB7LLo82XeS9hgCBgP29Uspjicb9PTji88QCpjr0sXXIluSya7dSS7PsClNbEUDGXSWvmMZAlPtNYJNHnvs8cgTeDkfUqU5FBYIOMmkX8P4lUwRrE122LSTPiTP/5jvOt57bVXgcDOzm5UKCsCntOzUxSGrl2ytz8jMLDmSS2azYl2Sg2WAuf8CCyu25nKJPq61mztNHzr27/Bz372Fvfv3+PFF17C+5YP338fnOPll1/hD//Jf8z9Bw+5/eGHHJ+esVx2keVOZVa07HnzPgr4IRchja9tpJhc6utknfbeQ/TqpZwoUUgd864FdUhWMoOPZAKSV+OCtCWFGrZtF+8XBqt1LBhYVRXL5VIsVH5sSSk05kGhVklIF1aV+LOK+UtpAJrCw1XOY2MMOoiHZoilT5tp8oYN1cptyg+LwjjdowQ6RhmqmBtjrInnWMl5sYYQmXSMsdTRMjqZTiPFs3hKqugtmc6m7O5sM5s2NJOGuqqYTKZMZ1OxqlYVVWWYTidUtY22omjx1gYfyBZQARfJ0+FY9UII0fc9Xdez7CXU7HQ5B6MGBYkhVDSB4NSviSRF1q54dcTaqbJBQma5B+/yPUfslwGSFTrPS6KSFwbDSLKiuhiqE5TkuPi0mSfwhQAj0ncFaAkM82fds+FDrP+V12tivBwIFdI1DpflWxlOcX79F5vX8FH8WxjpynOHKTsYL0plJ4QQadIZn1soPOsbWIJIWYdjTQ4TIHSghr7vveNsMc/U6fttz55z7AUPyjOh5urly8znUrDTec/BRY0xVfTyyJpGJ+//+X0ABuVAwuwu8+jRI7ZmO9nbXCplWhm0Eq/w6ekpOzs77O3v8jt/+ztYL7k3znmc+22S2iCW8ZgdEGn2lZG8B5kjA5BPYAJED3IJAJP2pdEorvX5+Dt5vRgGo2L0Tu5v+ZfkKk7kWPmM8ZiOj/KjoJ72fRjpt2r0HutK9bjt5Vite0s2bG8b71vuKxR5cS4QZVIsvG0tb79zm9UqgLI0taFqKhzC7mmIwNRYrJG8IxU8RjkODg5YLleknV3rQV/ILVZDyObQvpCWA6C4efN5bn/4AV969cvZ0FUwI8u+VqYAwtq4FzPgKaCn/O5pfTdqXzkexfQ6z0i3GcCk+eN9DO3d4AkqXrCop5PvlqDeuWbIH+P3T/Ncq7TqouxKcifEwq3xutRWH+tIOSRyIziPt4zySb1PIa5jnaDssxJcpEgFpVTMPQbdK/HcGk3fdVy4cJFHjx7y/e//kIMLV/jtf/APeObKFf7iX/z3LA8f0wQnRVRV7AMloFBHHWgTiFkf33J2ZMNFcf76sT5+m+6Z++1zPEtPu395vVKlzHlK28KQw+y9p10uaapfvUgs/DsAkMrJkBZciXZhc55S+jxRaK4nMJYuyk2gqPSohDAQA+TE0uL8EsmncEABLmMmksFSn2K4JeRgNpvx8NFDfvSjH7I1m/HSyy8zm82oqpq+FzrlCxf2OTk5FQYpJHbdVjUp7ye1azPi55cujuFcee++71E6cOXqAQ8fPOEf/sO/z3/9X/+3fHj7Dt/6xm9x+/2f84v33ubx/Xvcuf0B09mMupnSrpZ0rdAdu77nLFrGy9yYEMIopCcp+VUjfXd8fMxyucyKtHeB4MKQv1Eojc51EKRYZMo3SjkNnujC9wMjXQYSRGt2oay27RJrNd5JXpKyQy2FtKDjXYpwmOF7KappsgKfwkMFtOhY1X0YJ2MN1liCGxNapDmUNsuUw1VVVhioqgpjFaYhh6DNZlKstK4b6qrGxoT12WzG1tYWTSPhISp6fabTafSCpjwrsWD7lDBtdAyJEW8CqkfhC7KNoSZZ73uOVke4+RB+GgKR8cwIcAmyyYTgM7B3xfaXAEBW6FNNr+DzpjmQtbgIwAawKUAkwrPoRV5P5kybsIQsFp8X4C21IQElwVXDRq+IFmClCYmGloFhMf0ENbRdJTCtorf5fKx4nJxAYB1Ep9+Tdzz1V7leP+/4vA1xpICMlLsx+Byfs/l5w2OeooiVzRjdR8aOrCjLdx7Psu+YHzmenC3YPTzi8qU9rlzaY29ni9l0ytbWjCePH8d5XTOZCTV926XckVTA2I+el16r7JvLly/z/vt3eOHWS6MIgvLdE0Dve8d8PqeuZcN2YUUXrbvBhIwiEhBRSsUaIYHQlfOsHuqtrQHNkMaolN/5f6Vcz7Bz+D2k7hTlKoVTlQgjJPCe+mPj7+cVJF/m1arxd8lKjFIRiZzvZ9bvG1ibMaXSnc6Xv5+aS7t2j+T9DITY7z6q3AqljRQFVxrnNO/dvoMn5owoDcpgzQRrazRSbF0hIMV7qQ139ZmrVJWN69+vhaBuzhcq+6Fc2y+99BL/87/6V7z+xtdyH5aRM6Wx4tc9ngZgNrVrkCmQJtn58S/Dac+D0vX75XmrOXdeaaTNZfyyfjbkOq23c/33dZm4fmGIa0Bk2uDhBMCR15kn4DpHq8tyL0RwuplBbh0krRurQjRUaA/OK7RTOVx/ur3NzRducvvDz+hbz8u/8U3mXeCv/8f/L/boPqF3mNzmGM5d9HFqYzlPPlfWF+0szyvvUwLb9Vz+8hmb+mF9fDYdv+z7Te0GWYGL+SKC1s8B22vHFx4glSFVMGwYfe/OUX6XwAUYDfomK2sJbMrfy0kn+Uh6JPTWQVY5mVJbqqrC9X60mYxyCpSwxAVgMp3w53/yZxwdPeHb3/42la3Y3t7hu9/9CyaThjfeeA0xpBsW8zl1s0Xfe6ra0HtPiBWLyyNZJUuht2kBKYbFU/ZR13WgPDs7My5d2iO8eot/8k/+Mf/df/f/4Yc//BHf+o3X+Ae/93f4yU9+xk/f/BknZwtCEK+O81L/xMfwtLRRKxXDkEIYLUopKDpD15bVcsV8Mc+eMa0ljMyqKo9xChsTkFnHYqbEXBl5hlYqF6ccEwRIQTlFzIvZMB9MZJ9SSg8WvTgXU8HDxExW1xVVVed+3t7eisBWrJZ1LWFnOkBlLM2kYdJMYi0bi60Ms1nN9s4WW7MtTAqxqSScZtJIbZtm0qBjrH5d19STmqBDbKcazdmkGA4eDTkkaV7ymbxztL7Dd0XYoHdRMRrmeVK50r199OiUylTyKKT8lWQ7l/hhncNdsvUpSBhiYp1KXhm5ziPsiaFQ8gTEqBjKpTUxyXbsjVQIKYqKm+HYGKXynijt6bOC6aOlvYyZz2umjCeTu0ZwpqQopJIq4c6vKZQBghfrpQpJ+QiF0hpBQXzJ5FVCnd9AVAJYevNmWG5k65tf+izfp1jv5xSmkYJzXvnJ14y7JN87WcsjglyzPJf3Hq7JhiM1WNtxElohiqECbVm2K1bLOUdPHnH4eI/rVy/yzPXrbG/v8NGdT6ibCc10htKyJbarTooloxllDI/AxHAYY9jb2+Po6CgbbM5HIMh7pTDE5XJF23ZCQGDjeKh18Doo9QmAj0BQaIdxi0/IYMarPPcz7kmyOoQsv9I6TMrrEC4q/1eo0diV4aTl/fPcpHiHX6KYB5XGeay4KoXkZqydn2qBjeaeWgvxK56pYw5VehtfXlZelYwX8UWkHl8CRCJjhDhJAJDSGqUt7935iEePT6nqmUT9JaZSFQjeEpBQyFDINtc7bt26hTGSxyr5gHF9b+iuc3vu2jqs65q9vX3u3bvHlStXNp5X/hz1/9png4Hq1wNU69eVlyeDU/nvl3mmxrrOZmAzMjomWVYYk+SjRBTE2jPLy5JBqzB8MMxrX7jfgg8Snp3WUVEGBh9DG/tEWHKeMGCTfE3vWhrhcwi7jgXWQ8xB1BpPh3JiIL3xzDN4Zfng/Y/40Xvvc+sr3+TWkyM+/LP/ETU/o/YOTcBJ1TS8YhQut0mOl2C3bH9ZULg81sd0Hdw+bR9Y153K56+TRGy6f3n++poo257Gs2u7yAL6q8/tLzxAgjHjWVlHoOzITYP+NAGzjroTEApBPEDl58mDtOkZCRhtEhablJDSAin0p4HpZIrRhu9+98+Zbc1448tvoJTm7mf3eOedd/nmN7/OZDKla3uCV5yeLnj+4jMs5h1iZe+xlYRglUm+grTPW1XWGUrKqbY+SZfLDltZbr1wE+c+5Ktfe5XprOZ//p//FX/z05/y6Ud3+PJXv8rzL7zIYtny+MkTTk5PWa5WLBYL2lXLarXKYVSJejqEkP9O7eu7Ht92aGPYmmyNwExV1eApKtQPYyGFUcXKl0IcJA9GgE5dS60PYairaGphVkIFqspKhfYip2Y6m9JMKrzvQanoeWmwMUl/Mpmwvb2N1mIJ2trairk1FXUtxTyrSp7fNHUGapO6ZtLEPCFl0MbmmHqvlkDMHyk2qqH+UqLrThTMC1bzOc7F+hLRUprmNIjinpTyYQORjcVDvleqvK0HHtZhLieFP0DA4r3K3rhSSKYCoCibrcfBJ7KAHo8fKWIJSGlAZSYcCuXR46PltjxUINbbGa3CvDYVUleiZGQb1qWSIsNKZU9kIjbpgxeWwITGiueaTKY8LKP8t0ZohmONmHECcyRRiGByuJbC6h7y40SVG+LZz8ksxuGv6xvP+iaWm5ssp2sKTkp+XVdUh74e2A/XN8RN4RoDeC7OHSnC0g9aKaFBTkpE8DF3RYwaGiVlCxCPi/MBpXpCZAtUBB4+eMTR48ccPTnGxfpc8/mcrcUCY4VxbTFfRC9njN1P/Z1Bzrj/vPc0jRRmbdt2RNGfZU1SthnWjveSp6h6A3qtpERIa0iu9s7nqSA/Paie83Az9pewXOR5GbI8DwWoUONlkufw+TFlNGZPs+SW4Ipz5w0KafoRhmfENqW1uA6kZUuKIHLdyj86bwD8fviQc/002o8TOI3tUkPpAEyD6+Hu/Yd8dvceJ2eLmPqueXh4jK6moFPOY2k0k9IaKgpOrcF7x3TasLe3v1HZXLdvfB7ISbnOzjle/dKX+MlP3+LatWsjIqhN62z9PpsAyrpMWD/W1/X43JhDqdK6LtlPPZuMNJueP/yTKIQhBG0MkGyKwpBHMwCihHELL3qBjEq5P3rTEAbZVrxfIEUDxHf3nr7IE+2RiNMQXGHYPq/If57sLY318ReZU16iUnxw+JAiiDTTpuHGlUvMT+d8du+Ydz+5y0vf+m0WT+7z2Vs/Q58eM9ExxDuBxDUdc6yrjveO8vv1+br++yZgtencp127/sz0d3n+JkD3y448xs7Rdx31rxFm9+8EQCqT8iV8bVw49mmLNB3rkyjdLwGtElSkIq/ja4Z8hfWJtA661j1SpcIwtMfjOkk0398/4Pj4mEePHvLccze4dvUyyhr++I//hEsXL/Hiiy9z9eo1IHB8coZSwoFkTMz3UGoEjPIEDKFg8FpTaAtLh+w7Y7f5cBjOTlfMZoaXX3mB27c/4mV1k2du/HN+8P2/5m9+/GO++xd/xdligdaSIF3VDdpo2j4QtEFXDX27ijTVkj/jnaeyhrqaDE8yVsgElMIkIgKtaJoGhViYE6tZql81mUzY3tlGRZf41myL6Uy+77oOqzVb04ambsQbM50waSZSzM9q6qZmNpvlmjQSxlahtMmsRWncqtpidAIaAiyt0WhdRUVMvBsyR6Mw9sLC5ZwAmLZP4YHtkMcSAkE5ul4IAFK4TQIR6wbvrIB5UJhiHqbnBgHOMel9+D7NATHAJMpp772wxqWwk3XlKl7nfI/zQ3tS+3OwYvTepc0qAaSgxMNZvku2WMdwOxDgkz0tQaxk5ZyUWjoegs500ak/PMmTJoE0srb7DALkHprexfmfvUXy0wUf605IR6vC4xBGqtwQvid93UMrGllKjB/C4xQqJM9lYbDR62uMDBpBGH/WY8zjKcOc4LyCUx7jvwVgJ/m57o0vQzYofl8HSEnm+ZgvkHKj1i2s6ZpSFikloYXKxwR0J97D4PxQaNs72ljTSAXJD5T2OebLeQwzrfB9z2q55KOPPubDD2/TNJbf+Po36PqOtutoup6qqWm7jmTEHoPAYk2VhpYoCw8ODjg6OsrlDTZv5jGEVsn9snHCjcdn3K3ixQguzYeByGMzWClBaBxHUtPV4C1hqFCf3m+s6o7BfXn/pwOlso/OH6O9TDHy+ITcuvE6UgWAyV2z4dEiP9RTmrX+4RrICmSQpo3BO4fWho8+uc/Pfv4+Dx89kvZpQ0CjjEUbi8mhxirivbJfwvBPBZRy3Hj2WeraSkkGkjwrRme014/X66Z+DCGwv7/Pcrnk7OxM9rzPATib7ln+/jR9aOzVGSus6/t+2itCGAxi6fzSCDCEopXrSI0/VyLPU3TGmCAIjBpkbwI36btBJj8dCKZZk77WOXoG0pik34OleDePcybvBW0vDJV9rzKDpksRSrEsS/lum8LMUj845yCOoQoxzDfNTcSQZxV0yyW7UwFJTbPDh58dcf90wVf/3j/k+PCU9s77hNUZRvnMCvrLQMa6nlv21SaPz6brn7anPO268vySMXrT/Z4G7jc5OYY/xIN0dHj07wHS+rHewcYOeQ3rkwDG1pP1iZzyg4ZiqJs549fvlQRDAlEDADovELMwif8fFIVCUUVhbcVstsX9u5/xnd/+DtcuX2XvYI/3P/iAN954nZdffom+63j77Xe4d/cud+/d5ze+9dus2g5tpC5LqjORLNXBJ75+2WjShrQuTId2lzvW+X4neE5OTpnNpjz//A0uXNjjwf1H/O7v/z2++c1v8vEnn/LJp5/w+PEhh0fHsYimFBhMYSDC4uLRylAbw872NpPJNI6dKG1bW9s0kwkhCOtUCmWbTCZMJhNhRGsatra2sNZirWW2tcVkUoNx1I3k3yQXfRXZ1XC9UOEWuWilVasU9gmAB4z8Kza91WpJZqdjvFGkf2XdGtF+hrmXlEogVplPSoPCBU1OVxFYEy/XI6VWztd5Mx57G4YQMgI5/2YkUIMEsLkwAB8fPDqQa0BETBS/d8NGElymVc2AO3q4tDLpBdOqGcLt1NCu8ToN6YXlLxcthiEJ4k2sRx6FFo8UY+XPpXwDhucKoItjG0cyhIHhaliLnKsjNoC5YR0DeW3l0cpzR9qcig7iAxICuKaI4AkFEF1/piYldScleOivdUAjG3d8fhiUjHV5mLo5AMoNYS3nFKpkMEFhorAKIQW5hJyfFmditOpJfZ6268QL7B3eO1zfS9HirmO1WnF2esri+BQf14hzTgpPx1xDghN67K6LXuHIWlkZ2nZBINBMpkjeiGe5WtF1LdOpZf/DfZ57/iZt24ohouvQKBbLFdPZhEonJX4MHdYP5zzXr0vB2GvXrhX7xjCvx12ro8ztSWFYefHE8RlYBSXcL4OjSPVODgUjywxCiPTHcf6kj+M7BGSdpJBiH5+5KURzFJJWPEaA1VpYdvn959kcR9bj1C/let4AvFQMl4zybQTcSjyWcclm4Oa9H64tAVjcvyUHX+M9uKD56x/+mPc++IzOV6BrmeOx4LSxFpTGaKE9Dww19MbiKYjY9T2awK3nr0cgP85ry60Mm4BImhrDe4mXQud1/fzzz/PJJx/zwgsv5v6U7xgMCfkxYTQXkzEseXjTPAzFzzKfszR4SPvKiUK2meY1kOZG3ANlmxXwI6Ah9n9iUtSmAEnEenHJAzOAJ4WPNalSm8heyNSXA0ga61kDKBuWzvgYQFzqu5QzLO+rM6FWCAFbhRipIWU8ur7H9b2kC7jB0+SDF2KHSNyj1VA0O7UFJAJG2PZcTnnQWkkBbQ2t66hNYOkWXLl4gK5a5i18du+IQ1vz7d/9A7773/w/8f0Si6zlzvnRWJfAtPys7J9ybNdz8YsOHfqs3BfSUstAcyxD0ymZvj9OlU1g/fNA2dO+H3RpIbnwvqdpqs+9T3l84QFSUjyVGhLc265DrRUdTAPxNMCUfpbAprSClPlHCQGX4GrIT9icxFaSBwwTN0gid6RCdWUIToBpPWVSVzRVzT/6R/9rurbj3r27PPv8DX7v7/0uH3zwAW/+7E0+eP8DrLFcuXSd3YMLnJ4tmDY6uq0tGo3yFoOmMlVUWLWEWRHBCUPbNsWHhmKjFnkUv4vnzudLjDFMpzNeeHEH30tV9de+/BLL5ZK2bWlXHfPFgr5t6WM1+5RfZGwsMKq0UDw3Ung1IHz3ddNgTNpAEba2GPqmtBkJ+vTTeSGCEOEfMuVwCMKZ361WMZ5/ALip78UCPgZGSTCEKKhLJT8dngSYU0vJ90j9mLwOxV6GK5WAcgOTmVHM9/R+4w1wM/PgoIiMgZBHiHQGpT6Fk3kSC5lIcilmKX3kvR4ICYo2JA8ESQCqYZPxwCqW+oOxlQrABD0o+moYhxBAh4H4YMxKFHClF6d8NzxCTl3EqwNBJcA2hNaUtKdaDaFySYnIAC8kUBoKJSZtqAJ8Uu5Vli0qvVO0GGZFIqD6HuVDVGCH3BMApTWdjptcHCKlyLVTLDLXezfQtaa5nbwG64YOSHS1cr6L50phz0CIhUOT7OtiaGu7WNCvVvR9z2q1kppeXcdiPke7Hh/rdLVtS9/3LJfLOA/EY9j1XawD1tKuhDnStRIy1rYrqXzuSgYxl99hnNQuSlOqo1VZqcXTdwGjZ+zvXRClyxpsXUXK4MCFgz3ado7zLW2/ovc9nRcW0WXfM/cdu8pRaY32onl5DOPFyagdly5d5N133yPwmoxlofD4cD5UReSAjd6j6K2L88KFZHkeKHGTEoWVnARRCBPwlTaGNClQ9N5LfhYhaq0hemcGpU+pyGKZvFQj3WddoRnyOUoDkBxpTIZQwE19NPouKbRZg85PYgySChAeT9z0jE2fDcBNRdKEJIOKewT5zGh5du81f/nDn/Duh/dRukFXsa6NLr0bw9oAyW1NYBaFJMgDIXkMA+xvTbi0vUUIffZW5+Eq3jVLsjD+nGAKOVNeGLhx4xm+//3vc+vWC/jsaQxI6G2UyQXUTyXxojQuqPjHHoZNXofy/uuH90P4cal0ixE2zQHJe9ZGY0zyrJioo5lRqKJ8NzxHqTS/VC5LUSr2620tZscYFJaDn++d5sUAXgcdMY4BKa9KkYrFhiCFZ1Of+CC6Rd8L4VT2LqXIhCB7vHdeaNHjfjBgYwnN1CpqAy5INEWQeoLeO4KGThm0srgOtne2aexDZhWcnC2x+7vc+lu/yfv/0/9EvdTQuVzYOa3hcr9dTxspPfzr4KnsLxVcbnjqIoXKxoii2zCkciUKpWzuflWMWa4HWo7cBsBUtmvT72Ube9fTO8/de59i9vc2zI3NxxceICW3bKnglnlBcD45rtzERjHhjBXNUtEoF+WmSZQETwm21gFHGeq2nidVXiP1k2BvbxfvPW+++SZHh0d4BzvbW/ze7/8dUSK04Vvf/k36ztN1Pddu3EBrQ9d17OxY2rZDq4HmPCXtppo2iVFLkLfPm/1YAKn82WA9SGaB+M5ao1UQKublKnqFpAK1sKhtZ+UrBGJtqCF52BhNIIUlycIRwTNYkxerhTwvg4e04GOuBGWdGblJqlFELDqb274OMFR6tSHkKmoxESz5qKgMG89oXlCq7iW71Pp8SeFMyao1NMAXWsu6J4DinSnGKClDofhZKjmlBMqFO9O7utKKmZRscEQqaYa2i4UyiELcu6zsl4AshMFCXVKlRp9IQdO6DigLdSGDGZXDP6Uffd4k83hRUjP7rBYE1ABg8/epb6KgLtoREqgJPneOj88sgUvZ52ndBKDr++wFSFTjeaNJ75bmSwSiCgFdecxCGleZo4lCehyPH6Ki4xOcjHlSQ2hxAt+lbEufO+9oVy1t1+b8vuViSbeY0y0XzBdzurZjsVhwdnaG946z01O6dpXXYt+L9wegD33u0/TOUvw05ScIy1Q51lppdFB53XbtCu8FIB0cHHBw6SKT6ZTJZMLOzg6JPXEymTCbbkkYXdMwi2G0IHl+k2aGtYbE1i002yfcvv0eq1WLjbJAm1TjRFbO2XyOD/sRXMqcyiagvMblivQe0+ksFx9fn/+Rff/cviN7U9pLhnVBiNbyuDaXy0UsqB3XXcw/qasKa2LRVGPwvaPte0iEMErFgqVD6KxSQh40yLs4d9ZC9tYVzVKBOv+5H52z6Xia8XF8Ulypv4b1+POO8tL1PX14hsrbVyDw4Ucf8dHHn2JsTVU1wGZ2yHXFvGxznitI3iIh8Mz1qxithE02a46Bc/TXue2l/qHgHMhO33mapsZay+npKU09oWTBFRAdfedJf0kyJTOzpeYMhsR0fd5zwtCnTwNIqdh0qR9loKOS51FHgKSwNhEbmXNyrWhuMZ5D+5xDwmmzkW5ELxpvULzbcJPRXp6MkqS9kcFY5tzghdJ6IH0YfpJvrpS8q1EWawx1LUzBjVf0vaPruihfHc719L2m9302uHqX5qWEYzg/VvpT/2itwKhUnVJKCNDz/HPP8slHP2C2u8vh8pQbr3+dw9ufcvSzN6ltAOcooMxGEHRuHq+DKO9B6Tz/FJuBS6rpl/pYxxCT0u88mDvK4VHD3yHNX5G5wQcG2Xt+7j1NThilJAep7VCfU6x4/fjCAyQ4L7Bl4My5ULcSRKWOdmuduWkirMeSltenmkfJezVSkNYESK6LxCDIy3uln+J9EsVAa8WVK1dYzBd0reNLr77K2dkcow1VVVM3Dddu3MA5z/buHsu+zwxL6Z4p4Xwd6A1/DyE450GSCO30XklJTN/Jwu+yskQYQnsG2aKy9S2AgJZQeGbkFOmjmBeS4ntD8INimZTFeEEKhQSk8G1qc1S0U77PiFY1vmB6RvpMMabITAApKTclfWxSj0enJwAZlZIxQBoK9w0b4hjBhEKslF6Acl6UDRjNv5BIDnLDGQv3KLxCYUUqbpcL1JaAYdD94t8R1Wk9fFW8X8Yu8ZdM107AlZuVWl9jaztb2S3Bjc4rrW9jOt8hVFT4hcp5NWwOSYlZt3wKAPMkHgpfzLnkIc3zJisQEh7l4nwDhryqQJ7/SWkoX6/rhG2n73oWiwV910GUB67v6ZdLKULsHF3X03UtXQxPc90qhnX0tG0nm3AnIWwpTy21U9Z+2qydWDedz4nfzvXgPCb40TXGiByzsQAvIGyMRuOVom5qvJlgJxVGG2xlaZom1wqrmil102SG0SQbjTGoAIvFgqPDJ9z+xS84evKY4DzXb1zna7/5HbZ2dySP0FhQUtxQFKpUqFiYK/OmHqDSlXhRtBRMbuqa6WzKe+++w2KxYqKk/lCi8E0EKmdnc1zvUFVNuW4YbfHj+RlCYHt7i+PjY/b39ymPp8vXuH6yZUXFeaU5PT7h8YOHnJ2eslwuWSzmkf1uxXKxxHVdLug829pif39fishqQ+thf3+PZ5+9wWQ2iXNSIaGcLlvpByVJRRBdrJwNIGUTACqV9l8GZv5tgM+vBKx+6U3AM77PcN8AWiIm2t7z9nvvUzUTtK7wkeBnnSBg089RG9N9kRA7rRRXr12l61uG8PU0H8Z7/NPem+BGfT28mif0PTdu3OD27du88vKrcZwjAIsyLRmjxFBEZEcbAEfIZAphND9LEJ9eK6ztY+nwfijAsB4RoFBZwa8qizYS+pTW8DrF+Xr/pM8yKE1lESLIyT/zCIRijxpGZX200vfZeChvMnoHMVwnJtTzYJnindev07FQehWN9c67XG+x7RW98/Q4+oLsJxT9XQJ7GQvRu3RQmODQoaPWUufwjddf4W/eus3Olcscu55X/9bv85ef3Sc8uYvxfqRLlEe5dtfHjdh9Ku6jY91kMBSuA6unPeOXrd/y26xRhNgPpD44X6cU2Lg+8AFtFA/v3efSv/cgjY80KKXCnECLUuOQuHKxl2FwJQAoQ/ZKz8/6YK17i0ogtQn0JLCW7j9S3kYKW6BpGg6PjmjqCTdv3uTSxcsYLRaL4FaEAFtb2zgfuPbMDc7mCxbLJc55mqbJCqqEpQnldNnmEvjpqPQGVGaRK9sVEt0wUt8GEhNYoI/W6fIa70ThSss0BLKASRt18gzl/omW9REldEn/rCCHYiWAEwLGp0RPyduRTakIAfOyuRRmiTR4w+/xGNfUIrZzgxUj2qPSdEhU7+KWHzOyBcjhA+PNJgqqaDnxa2Bg9Lziz0SD66OA9TEPqLwuCTgdKURF+U4bS3pecf/Ub1422NTXMg5hOInoPi88oKCiAS9khTWBB4jhY+W6K84Vq+V4zSQFVi4exlRmZ1of0PtE4R3zqeJ9E2hJ8yfFlEtcuISipLU6rDdQDGEEua/XjBwhhOw9SCCjnS/p2zaHmo1kSu+Yn56yXK5wzjFfzFkuFhwfH7NarmhXK9pVm+dUeo54VQaPVCiALfTRQhvnqCJb/JLRulT0jDFUdUUV62RhDcYIM6OxBmstTVPRJHISY5hMGqqqpmoq+RcLA1dWYrurugIFJgKgNAZiSBB6ZLVGnBOIda6A5WLB2ckxQQV+8sMj8WAT2Lt8GVtPqOpKxkY0GpFLYZBdRCXERDY7XTcYJaQo1kr4zs7OLgGNd4q+8/IvkqAYrVFas1q1rFYtvqmxOiq0lBEEw7ws5+i1a9d59OgR+/v7YxAUxnK1nDc+hg/6WIBao/j4o0/44V/9gM8+vsPbP/85R0dHLBaLbIVWsgDzPM3KmNYEpagmW3zp1S/xrd/8Ft/57d9i72AfFb2Iw3iYGCIkiq02plAwn348Ddhs+nysRI7P2fTZr3LfTff4FRpdiPexoibePU/Qho8/u89i1eO0hSDh2uveonVFcL1MR2qj1ppIfsn21hbb21sQHM75TBddtiddN4jsQtnL8nNDXymZV3t7+7z99ju89OLLODcYf5NsRoGLe172Tq/NT/k8GkQYvoOBDEZy4MZgKslYHU3/I+9wkVuU8reNTax/JaAZ+m5sTPDnPs9GZFUAtby3xj4sANMQRSGfl8a40XfputgX5boygNFDyF+eF9F69rQ6W1qrmBdp470NTWVx3rPqWtquo1119M7Rd46+j6yzjPVQIOuHQRlMDGe1KPq2xVrL5cv7XLi3xcliwXR7j7BvePbrX+f2H/9LKTjvNgOVz12DIXnGVGTiJE0ISQMp7lHuLesOhrEeu24oHgO0/FlqWwjC6hd19nXZsX5t+UytNKHvOHz0GPvo8dPfc+34wgOk9QHIHRtkolVVhbV2NJDrAj0d61aDdHwu8pZPKQVGCYBKJrxS0PZ9n2vorE/iZG390z/5U/7Of/B3+MZvfJ26avjk48+4d+8ujdW89857eBS9h9b19N7jkJCfKhaITZb1tHjhfDxqAoSStL/JAprej3xuYkNzAamZk/OwfFZ6VSjF4RBznSwEPi6I9FMWyeCydSm8KQnpOKY5lygL0URyMDiW88JCwJ1iHGqS3iUL/niIQpE+FwvO4FUqNpHSkhT7VUfQMdivBuEw0HGX+Cxad1N/q5DL3qwfw9wD5VXkYVCZ5KLEfnm4QqDt+wgqUp/EflHnlb78L16flNPh3dMYycc+JKNCMT8SUFZDXk0KGSr7fiQcg5cwAi2JrFJYVgr5qoLJL60brXUE4MOY9r0jscf1fZ9zWQBa5+i6Fu8Dfbuia5esVktZm94L3bN3MR/JkTyWxhqMsdGbIjkzp6dnHB0dcXp6KpbBtqU7m9Mt2+yRyd7CGKogYVLiOUwhLLmvfckkKCFVaEWwUsdLCv9ajLH597qpsDG0ylpLM5lQVxVV1VBNZ5lu3lpLZa3U2LIWbc2Imjp7Ho1GGSN5iFHu5Aml0yoaDBwQvTooyWNTYn03YSC3CWseW0WUDUg2nW4meKW5+dIrvPPOe7TzOb1TbO8c4EJRpX4kQeT/SX4YW5EKP/cEUkiI5ItptLFYW9P3AdNDu+ojW2SS84Z22bJYrHBbM0nPUOPlt67Epc8ODg548803eemll8ZrZwRkh/OFgjcC8pjLcnJ0yr/87/9Hfv7mW3z84fucnZ3mMMa0hvTIiKNGa00UiyMOHz3ks08+om0XfP1b3+DCxQN5D+Xi/BUVwPUOpQx9340VoOL4dbw2mxSvTddvyvn9dZ+3fv3nXremTKW9PClhXgU+/uwewdSUXslNnqJ1T8G57yEq2DJW168Lm6wQkWgKDhjKvXWTIVXu/XSgKPlQXrwyWnN8csLWbJuuk/FMOdAeIoHHAChKsp4U4r0+R6XdKQQYyIQhJaCSOW6UyP0EhFL/GGPEoxwNJ6VSXRZjXzc6xe7JsjD1USrbEfK5A5BKcmXUWxvW6yZlOhk+83lxv1MKjILKGAnZVeO0CKWF0nyTwVzHtZmWqFISFmeMxlaGpqvoqo6uc6yWHa3uaLuerpcw6WQsHnREhVM67k1DCDmhJ6jAG2+8xL/58x8waWoez0+49tqr3Hvn57Qf3UGzOjfPNvXHqJ+K81MbBiA/jkYp13tKbylB7fCcweCw7g0aMZwyAKU0IE8zrGzWv2WrskEResf2bOvc9087/p0ASAmBG2No2xaQHBgYD8R6KFypeKV7wdMH4fM2gvR9ak8O/VoDW33fD+Ema0I3tSlNur/7d/9Djo9OaNuW7a0tHjx4QGUrrly+yGxrxtlyRR+gn8/xXYtXISs6ojSKpdlam5Xd9cmachQouP2HejMwVvYHr08IyLPDEFI37AVqDSAhVqCYH+SKXJ8SNHgfMgPZEAs7hLklZqcB3EESkSEyweiY+5AsEuJ3WFMIMugqoZscLnlyIs1uAjfjywsgoVIb4kYb9ECelEBQBhIDSBBAne4dS72FMFTyHvVdnJPiLsicDalfUk+XLESBSFMfkoqbhLb0zzrbWSng1oXdOrDpI/GFUkMYYwk2s+VvdG/yObK+ZAM1IeU8jTfOrm1xXZuZgBSS4+Kc5NKsFstMDtC2bSYRCM7RrZbZy5Nq4LRty3Ixx7uOPoWiMSjuBQzO45TnIEMobcqLK0lbVFQGhvhxWd/VpMkFfauqEur9OCfE0yGKzXK15OOPPubk5AQfPFcvX+Nb3/4WFw4O2N3dxUSwY6xle2eX7e1t5vM5JycnWQHXxtInauj4Hsko4gkEU2xOIeYNxp9xIKMSMCb7EKwjinpZxFMrM1CSa41G1qA2Bl9sdul8VKxxpKEyNXXr2A2GZ597gdu/eA9jG5lHMX8horJBFockk0WOuF7mUhc6OtdjtcZqRWMtverYns64cHCRjz/8FO9D9ha5XhjlrDEYbTk7PaPf30XH/vFZJmxOCNcadnZ2JDSy70fnBA+lxznLKgJ930lIZNtz8uSUv/zeX3H7F7e5+8ldzhYL+ig/lZXcTZIyqgcDSJnPpoDainx/8vgBv3jvbW6+8Cy7ezMuXb5E53qOjk5iXmjLbDajqacZmP8qh34KkErrJh3rysy6IvRvc3yekvu08+SB58GYikYkheLw9JjD41NQMXw0hZcyyJ71Pbvcc4onA4Mx1OM4uLAvxCO+xTlLDlcu7gub+2S492aAJIQgstavXr3KZ59+yrPPPj8Y3lDRABHlWbEH4gegk98jAY4MpKQHspJcAqRCZ1CAVxKZUobOpt9LI7NzsYZZIg9RZtQPw+8q2eDGAEnHiIAEnBjCAFNbBhTG2BORv/SDLJELh9IasR1932c5U2lFsA7nbAYKKVQ11REegaasKyYv4AAMocj7rqtYd9FTVzVd17NYtSzbPkceJHkiBhWFciYiL492At5C0Hjboq3mG6/e4vs/+jFf+fa3ufPue7z+2/8hP7j/32Jce35d/JJDMRhjtFKJl2njPC0N/Wn+rxOblcc6m3MIodAPh9IlYgD3BD1OUcltLPeD9fYHj0Gxs7XNzva/B0j5UPG/tMgSe08ZygZj0LMuANePcpEPg7SOfseKRAolSQLGOZc9ROn56UhepZQXkpT05PkyxnLjmRuoAHc++JC33noToyt+8uOf8PLLL3Pxwj7OB3b39tC2Yqfveefdd5lubbNarPK7eu8x1sZQFGnnumUNIttbWXyu8NAkgJTfr8ix8DGsZ7DGJPWSteL0g/UnnVUqzNInMSwurtOUyJ02AKFNjZtBBE7DGMVkfw065cqEQkkrkjjL8Ux9kn4PkDfYYeMhWvrzqUOce7lY47upGO5Vjvl6omTOSUlCIACGc8xA6fw+yHxL1yVMlmv/xDcIaxJtpLyVgk2RKblT+yCGzwUkRoPxOkjPUAw5Dal+U4i5M957ur6LRA5uuHfc+HyRB9M7x3IxJ6xWdKsV84WEiLZdS9e2En7WCmuaDx58wHUO30tNKOc7ur7wevrU/iCJqqOQ1xABnfRXoo5XkbVKKRXXiXhebFVRVxXaaKwVcFM3DdZYmklDXddMp1OqqgKrY50UK4V/Y36MrcRro+PakzDUgTkvEAha03U9jx4/ptrd4Qd/9ZeooJlsb3HrpZfYP9iPdLhKCgzbCm1qbFWhe4/XCzHEeBeTfUVhzmA6vrtWGoyJ8lFl+RhCMh8oMIVCnORHYTQRo43Mw4DPIW8BCbNVSkJCXCjKJoTxOul7R9AGcSpaMBVf+ca3uPrMc1y/do3FssVYk5mhIIWIaUIYlJEk17u2Q1sjNeSVWLYn1rC/s4WxihdfvMnt999nsWxZzFcsl2K1dd5RVQpjNadnp1IWYVLHeVLQRJcKZFx3LoaqKqVYLBYS8pyUOhcNAQEOnxxycnKC6zuM1WCk7yZVw/Z2w3PPX+fqpYt8+MFtfvDjv+bRo4d0BbOntZa6qqmj51C8hw3T6ZS6rqmt4fqVi1y5dpWr16/zt/7O36aeNjx49Ij9vQO819TVNqvliocPbvPB+3f4yle+ksT5hiMpH8Mnsk+p4vxBdpahRt7FfLscql3elbGsXsu7GI5Q/H/8XVaG05lhODcpp/lpa/dP14rBwPDpZ/fonSOYRNwT3aBhIFQihFiTRo37KgzGpvSBj5EX21s1k6ahbVcoL2GzidxGZORmXSLfLe23BSYdLPjxWU7yi7e3d3nzzltcuXodkBBUF2+ZDVOpn4LQZKf9Ircr7TvFc6QuX8h73WDYIs8NrXWk5E5KL6wz0iX5RvTGD5JoYHjLz82b7DikL+lYHmGB84PSEO8Vou709EMV7yZhtXEHUxoTIxaUUtiYsy0GuEBLQDtP8pBkMORC7oMBPMV/xMgfnQqAF8BAyzMTSZW1ntrV2LrCrnpWKyvMyysiZbgXeR4cGFFuXPB0BIJW6JWnAi5f2OHaxV3e+/lPuXTxGlW1w4WbL3DyzgnaSUkJF+ue6aDOGQ8Sm5z0k8vz3XkXqckj2NThXD+XMjGv62RcUmn+RPkRP8j6lgJ06bmNz4k/Q4h064Uhdx13lf4mkBBI7z3TScOlg4PPmRXj44sPkJTUPNJRsigGqs7kjSktBIMFe1D618FT6cVZexrDRlJ4NkZAalBCSkW3fHZaVGLZkfuKF0cA0rSZMrEVBPjyG69zeHjIxSsHfP0bXwHANIaz1YIHTx5LrLMH1Tvccokp8kPSAk8eJBc8OvgxYvc+AqQYt+4Sh1my2uicQ+JcykGSw4d+IH+Qi4ZFlRfKeOOTP8Z9HfLvAjJSGJ1YnhPICJiQNjsd68FEr5ICj/SnYxDY5DdJLYiLzqeNcVB2iOB0aKMn1aBIytroyPvLwEZWbjp5I1ADeNGR5ldrM9StiO3tfT8IK4aNKShoQ8gASQW5j47WMccQvhVSaFox18ZtDkPfFnljySvY9z2u7fCtgJxVu4qJpj1d2+L7Ht8K0chyGb00vaPtWlzf4pzQQYcQGZWcJxfDTcCmdwVDoUN1Hd73dMHhiFZHid/DG02IYM4qi/Zgg7x5VxchHlpR1TaHnRmjqeuGyaSJ4WmV5NfUFcEKHXQq+mu05OhYY2JohZCj5O+NJMQv266QCSGymXWsVl2cHwKKQrQEApja5PoWpQEiWRWDqegxnDnLjZuad3/2Dm45BzST2TYoSzOd0tRNDqOZLzq6k7nk86gKtCRC+75HKfHQDvItghttAT1SdBUpGTauGaXo0wYaxLPkg0IbqfnhnUJrG4sHa4TUQuqCKJWMKjGPMAiVd1KwvXexTxTeWQkL7lo65+nshN1nb7KyhsfHZ4QQsmEpeC+/a43SEvpnzGCN1MbgvcYEizZgtcPqwDPXL/Htb34NowKvvXKL/+q/+u84PG2ZzztWnad1Pdu1xqwCi27FabvETCqSN8GogvAFRntE8DIXd/f2ePzkCZcvXx6MYj6AV9z+xYf85Ic/4StffoNbzz/L3u4W9cxgKpMJdB48/JR/8J/8x7iu5/DREYePntD1knuUog+kIGgSRyIbm6aRNrmeEDqWq46Tkzk/+eFPOTlbcv/hQ+7ff4LSU3rXSY6i8nSuY3fvEs8++wwh9FnmDfshOYelEBeixKAIDPJC5lZ5oii3bPCMpCiGc/IzPWD8QVbKx96rMShJ5QBKoC/tSnTpqW0R7CpFJCDm4eMnaKNwoZdwVh0LWftkRZfrB5A8KHxlU9Jj5Jk9lw4O8JEdUgPed9nQl0BiyGHvOsuRsguCEg/m+l4SewaDZtk6bL3FfOU4na8w1uKBPoYYZ8NkDIVXwaGVExDlwQeFgxFQHXSYIfwuKb7SdJWV/qrSVIZR4evUQd57eor8Up8MnNFjkwu0irEsxDngvexpCZQNh8cRaHEDBI5UkT4EKZUQN+LSS5G8SDpPsUAwBrywxhmjozFVSjtoo9GVJQSTdZw+RmP0Ieavx+h/AdziWTeRgAICVjmM8YTCKK6JDMKpJIMaogeMCZKjVdfYxmKWS7RVLJdLus5DJ/ugQkCzV0LqE6zGKNC6Z6krXn7tNf7kT/6cfrtlFQLPfetr/Oijd5gcn2GCpzMepzUTp8ENYY7F4EskAzpGE3iCF49oWmvZAZHmAuQQSNG4GckNotzQ0eBEUCQoloy7IXZoSBqPSl7cEPMuDToMjK2lTpQwVp4TSuGMog/QLRaotuNXPb7wAKlcUBkYMA4b2nRNaWEuhfHgHh68T5sOsYj2IwFdPq+MzUyb4rrbPoWNlO3w3lNXFavVCq2E5vbKlSuCjqdTsYYYy9bWVCwhxnJ0eBxpmF0GXyL0RPg552Nbida8VP9FhJPQdooi43OhMQCpTZKEZkmqEIJc58LYO7I+JptdomOGnxK05mvXAKtYE6KiolW0eKWFNSSXArl+TdnXJWBIie9KpefEhbzW9lJBKg8XQo7xLjeTpF8Mm80AeWRRq6xMJhrkbHlRhQBhAF8gW3t8SQgB5wNd3IzbbpULbqbk7vR7ct2nf6kop+s6iB6fFDaWzu/bln4VXf7ZmuVwvctFPLWK+ToMiluPkxDPWCE8j318CwHrQ82jZG2rJhVaV9SxL1zfMz86wbUdvQ4cXLzI9WefY2trm2kzYXdrh+l0hmo0NoauidFBEmSHsAexaCeLVMK/Tq3V2NEK1wuV8mw2Y2u2NeQGxntWdU3bu1i7R5T9qplIDuCiIyC1eQTEgKlqvPOoyPBmjUUbLflI0dvWO2Eb6n2gbhr2Dy5w5dp1PvnwNk4Zlp3HqY5F54DT1Imgq0w+EbShS2x7AZSyWReV5PGSuGRg0ExrJK3zEWFHXisQfPQaMZgZXGTB08pLMq0fJ9OGAJ0HtIAXrSSJnSDess611HVD7zXKTKhibk5lLTNrJIfK2GjkGEgXlBLQpWIiOFERM9qK1w5PbWA2scyaBgNsT7f4nd/5DtPZDv/X/+K/ZLlYsFousxFoMpmyXC6YLxZsTacCviK4T8ajQUmEQYHvuXjxEnfv3uXy5StZlvV9h1aWP/7TP+UH3/9rvvfnf87WtKZpKnb3L3Dh0iX29vaorOX9Dz7gkzuPIYDFiqGhXdG2snYBFos5fS9MhbK2Xa5JZbSspLbtWXU9KAGRq7bl4YNH1JNaatBUlmba0Ewqnr1xjevXrojOr2CgRw55fZS7pSoMXONvCyAVQEh8VHHd8HvyJI/uOfzF+BgAktoQKje0w+dLnfNFWzwlnXZWaJXsNyenJywWC5KRk6z4D9bsTYalZBUf7WuxJQohLdjb3WWxXBB8J4qhlz14lG+U36nwlqT7BkCrHH4+AifxeRqVw3ubpuHJ4SG7u7t03mfiEojDmsKD/dCngcgoGjFrCOf1pE3G3mTUNUZqhAWUGCyUynm34uFJLIrj/U/0LQkbS+AvkUEl75oKegNAkmiNFsfaxiiAMZAjXbLROfWBjEzeUXtfzi+J4vAqFFEnjlTvKBm+08Pk91SsdugT5/ohykIHvBMWvOxVUiH+zcgwnsNwlaKqNFo3VNZQV5bKGpbLJUtW+D4S9hAIKLxSslbjntXSMpnMeO21V3n7nfe4cuU6W5cvcOlLL/HoRz9l1moar+hCXCO5GG2hsxZ9HYIv1vvnHyl6QBVzdH3syjD0cUguxViff56CHAY89iST7zUyjgSZQ1opjo6O6Nr2V3oH+HcAIJXMYymsLrn81hVjePpgpo5PE3ldUGTBXQiMEZreALLSs8tJMgq7CmKVLa/XWqzfqgjFSZSRkmtgePzkCUofidDzsFy2KCMu45TgnCYTIDkXiPASxh2VJ6eP8bg+DHWDkmUnhJj0GQZQmSzTIfhM31yGZpzv82FTWD/KPi77pejIdKII4yTVw3D9wHJTLMBsCZS/EpuKUgPQKxoxAmsjJSAVeEuLsPhGlPwhJ4MQIkua5NVkQRtCrmcSfMhhNF0rtMxd10lydrsSOue2yx4W8bj0qCAApos5FM55+q6TULR2KWAp0UA7l4V7H59Z5pSFZKHJYRBDaJ8izv04H7UxsaaVCHZbaZSus1eyaZqYNGzwBqppE/Nt6hwmZCNBgC0IB0TpjZXUjYnMcx7X9Zw9OeIXP3+bd958CwJcuHSZb33nt7CTBm0qTKylkR0iI4t33j3xhCFMIM0/BYYIoLWQDVRVxXK5op5OMfUEZWt8VPzx4FdL+pMFi9WKxWIhYXUoTs6Wcf7JvX3vCJ3U9Elhdq7ztH1HCO1AU1/OSyVEJ0ZbqBpuvvQlnhyecHD5OiuvaJd99IanMDNPoCMpeEnmye8KHMW8c4MdPfSEotgwqgglQoBIDltFRYAQ0Hh832KtyRu/rNNoBY85f0m2mSjDhMGqhhCyUkUQ1ju0R2lRgI3S8Z+itpbKhjwmxgipxHTaMJ00GEQZkTDHSQ4bDgSCAasNW7MJezvbTOsaAnStJ+D50muv8uxzN7jzyWcs5mf4XkJ/mmaCMRXz+YJup0epKo7PYDU9b2iBvnfs7u7xzjvvRiUzytEIkm7fvs29+/cxSjGpNHt7O7z1zvtobZhOp4Di9PSEv/jeX4nimZRDH3KeXRqHROWcvLJJ3khNKSNzyHsBPVrhgqNrW6xRGGuEhbCu2Nvf48H9uxLmGufA8GoqG4tGu2KSeSHloo2m0HCaPy/b/22OTZ6TTWclp9BoT41bw3pDswKnPA8fP5LQuVwUegjQJ51X/Bw9c+0c+V36p6lrlFK0bYd34knXqooOyQFkJ+KkFP6d9o0kyAJhVP9t9FyIXgwhl9nd2ePRw8fU9QSllcj6MOR2eBdLFARD8FqKEitPwOFUjDrwIRN3roOkdJQ5ldba6HExiO9GPAB9EVWitSm85cM+6FKYegJIGSyGIaIjjD1qQPSqlfMy/Ra92IgnyPXi9XGxUCteiSekMHIIcYRCGzGopT1qyAl3gI/7YTK2q9RqtPbkvOGoB6aQOh8NfqpPOUspN0tqQSViGwnFG8LsTTIUWjMCSUZplss+630hyH2Fx8fhlEZrj+97nr3xDB9//DHHx0+Y1/DMb3yF+7/4gHB0Ru16lILeSP6n8YNOun5IDqgnMb8+7Ri86eejr8b3G3vOykOCEs87MMpz1/XwdWP66LkhEGLO27pR5vOOLzxAKoVP2aEpSbFU1ksQUw5euk95r3XUK18NYKfrJNG7ZHFJzygT1srJWCJ3nVz7a2BLFFGhh6RQsANECwys+haUJrhA1zuck/ojOQZ8BDoiiOgBJWEG5bulopE++NHEStYu2Zjl3Usrm4+bcgIQaZ4P/VkAmLV+3nTIJhfO1T0QhSCGkG24j3hwVLZ8hAimyD9B8NDgFUteMglZG5JWISa2K4XEzw45Nt5JG/q+J3QSiub6ntWqpes7FvM5J6en9MsVfdtFV3mXSQS8c7S5iFw/CjULwRMicUDwQ5hDQMBcF2PaUdEzEFnRZG9VWQHVeS5Cqk1kjFjltRo2OV3JvwRybMxTq+qapqkjJXSVQ9OslTA1nfJqogVfR9ailI8g3oIExnwaxhQ5Kq+QGRUlJKkPEghTIVaj6XQb18Pt2x/RdyuquqaeTgnWgrUEbXEorBkzUEloko0bWwpqjPW3KPJyoqVJNm1HcKBtw7LzzNs5hycLUTST4cVLPDhKo3XFqhcCFu8i5Ws0GJDlg4QygHgZS2NJVgZQEAzOOzrfS62ituPitRv83b9/FTNrODxZFtN4YDZKgCQumghqs4qXr0nro6osYkgeEqrTWBEtyZUxKKsy/bWPbHTWBEiKglYYXRLLRLrswqAEsuE3xqCChMrVtQDqpmmo6wpTIbTiVUVT1WxPt6iriklj8FbWvLVJcYkT2wd0zu8pwpoR0NCHNn6nWJ7NOTs+haDEAOE6prNtrly9xFvvvMP8bB5z2QKqEg/8armi6yS0TZMCswY5NSh7Q78aY2O9oi7LOR9lTprvq3bFbLrNa6+/xo9+8mMePnzA8Ym803yxoK5qvHcYTGbsSmF8SXmQ7i4MUdIjqKDARy80AmCCVllBrIyFVqGWGmU0J2cn/N4f/B6emDMW508Ky01HcsCIaNe5FhhKZc9rAk2bj0D5jSr+n79NS2CUL5SxabZO52vWQFMo7lj+LvcZcjjzPYIsycOTY/HkojAYghKwkvtizVgnf4Q89iqHGxVt9oHZdBrrlTlUkFLboW9HOkX5HgGVIwcSCE0SK8GITUQOuvioaSZ89NHH7O8fYCqL05Ao4XEx1NU5uWuw9L4HPC50eOVzfqFiIKwqAWdpgKnrOu8R2miR/yrKb98NslUpQutyjlNpWEzMtyULbfouFKkOIeorg9cOgjJZJrvesVothXRlPmd5dsZ8MWe1XLFqV/mcvusJbmwkH3QsldMwEkiqqorJZMJ02jCbTdje3mY6nTKbzaJRQ4wfSsm+J158jYtrp9cCYHT0cGuj0d5jvEY7AZXWh9h/OstxW+xhldGYpsFE450xK7QOLJce8IQgkUhdL/NFY3Cmp7aWN15/lT//7veYHuxQHxxw8ZWXOf7hTzFtj9GavoqGzn6c51wa8FPez2j6bwBTpaE/6Zub1s45T2yhu0moZLEu2AyIynSRddKYUQRYlFOz6ZS2+/chdvkoFfaUk+DDsMHAuCM3IdJ0n3Q8TYkvP8+EBmG8CMvE9tIrlEKZYOCPt0aPAERpEUaJUOmjNUYmlSgwfaYjJt5fCh/Kxjls5GnTyZ6MzuF9UrLlvn0vScs+umHTRp1ARMqTSm0S5TL2h6LgyC+9NAOlcd4wy35Om/6Gfs6hFfkZ0Rvoh3hUlIQb5HuFccx0ysNKIWHKST+mopp9CilbLelWcwE5MSwtCd/edVlw933HfL5gsZizWCxRvSP0LufVpPA11/eE3ufnluA8jQFqqJtkjcF5sdgYPRYsqQ5K23V0vsMjpByT6ZRm0jCZTmPi9iQqn5Jzk4S9tZVYkCPJgLVGmMu0JmiNr2JOR5xTpLWgkpKd5rTMR2M0ylgJAYnJ+n3f46OQrZQmKIP3kVQBkzWXBKRL76sPgdoaDFpqQcSxW/Zn7F68xHR3j7OTQ1RVUU+meKNRRrw3Ckm4LteNaFZDgmyaCy4kK2kCKD4DJJQissPHTV3mtoSoiFdIxi6NTfLODYaEsq9KJcP7oaq99z57rcR72KNVHcMYW8nlc4HgFUpZWPSZklvi/A2pxpCE5UarrjWZlVABVfQeO+eoo1VbaxUHYLAEhyAsbtpInHdtUv0SHT18lrquaCYKhYSeVJWEGuaaMSBFWZsaa1MIsWE6mTC1sZ6IlXtmi70KEERR63sh69Bag+sIrqOPIYHdKmRFOss5xyjRPUSXgScQlORhik1JizE6hQ7j6IPi0uWLLFdnrBZCy963jjABa2u65YLFYileGUXMcBxv7ut7hTWGumo4PZlT17UYmJTMj4uRRY7gefzkCXc+vkPbndF2p4X1U4r9KqUJ2tMDzvd5rg7P8+fakbx/ae4GBcZWmKqS3yvJS1FKcigsludffIkvf/2btL3MyySTffBR8Q5538zitxDPiQAkPrHwAMRlx3lZvn5kw08hF4f7qzzm69EH69tEOI8d4j1A8pOKfSZeu2hbKUKuiIbJREgSc2iC2nhP2Y/Xowzipd6hFUyamrZbReOMGK60V4NMlbMLORHlkyJ7BLOuEs4bFYfnlYBSxULRAnpCzMvS0SPb91K6oOtX+NAidZQcvXf0MZ9MANJ5BbhURtcV03Rd74KAUS97fgp1807GKwGh4ZqB+KkM+w5xDjp8Hq4Q9/O+71m1HYv5itPT01xeIdWgC30PBT12qVATJMCuJFQY2uFRXgyvidE0Xd91UmvIe58NPJPJhN3dXQ4Odrlw4YCt7W3qWopTB1Jag7CtJvmYcidFziqMcThjhAwoheBpjYpGkWSYtVqhqyrWI1IYq9AGlos2pksECAqvPMHEcG214tLFCzzzzFXu3LtH0Jrnv/ZVfvDOe0x6j43kG+tOoRGJWdanSs/yWOY9TS8u580mQ/im9V7O7/Xvy8/T3HuaDp/Pd1Abm8NKf9Xj3wmAlLxHpQWk7KKyo+E8fWn2iKydt36UtI5pkAba6/Ucl4F+PD2jvH9SZJJVNn2fPFKpEKuPAiT4QF3XoFQkZnAMsd9a+GczKJHDOU/Sj1S0XHV9ogHv6bpW6tQoCCpSkxfudxWVhVxDiRSPW1qqKRaVGtFnpvfUSkXygGQ9YNQn5flGDzSZzjm6aKENIWAItKtVzr9xfc/p2SlPHj/h5OiYxXLB3u4ely5dYtWKUF0ulrTdiuVywWKxyIUYV6uWvlvhu1Wmi075FclimtpY5l6VABYGqlMAbTW2jgLQmFG4kDEGXQ85M4ktTSslXpKmihYz2RxWbcvZ6Sl/85O/oT+T4qCvf+WrPPPss8x2tpjOZpiqQiUK9wLclGFPPviszMQm4z1YNXg+y1C0pISqNLWidctoK4QGSrYxMUgM4kUSPHVkpxFLWbHA4pwZLHg6xFCsICDGqcjcYy319hYXr13n5PSYejIhRWD40IMXa2VPYemM89JHSnDvBsp0pROZhycolXPVlFKjfCnvwYXB2JLGXsDAUGckh6BBXKuFUllsJkpJfL7MFwtazjK2QusaY6bRutsJ4NQadI1SlkrpCJAkvC6FcRij47itWeq0BCwYPeQglu2oDFR62PCn0wnGWMm5aixbEyGmMEYAjryXzOds/S3WqMg3QSSDMUTGOIRAHzphSewCoS2UI+8xsY9d9IC62JfCQJhC/ATMqmyMEeVu3VuVLNRoFckjyFZnH+/tnCOsVly/foUQPGenZyzOFnStgJGqqljOz1jMl1S2krWr/FDdPU/h8wad2WyLJ0+ecPHiRQG+9CwWS15//Q2+92ff4+zkBEXg52+/DcFhI5W55MsNRDmrto/7FqPcMDFEjFBKQVHsMDFvMSAhVJUCrS3b+xc4uHDA/sEB1565wXPPv8DzN29hm5kYdFLIbdxjklz2YfBgDI+MgFyR5Ug5BiIzYkL3r3IEskd3/ZIQAdoYjG24dXjKHp1ZKkuPgSjCZ4u5vJvWBQBW4olTQkRUvvPwh4/rjXiv4SujhSpfQ8wbS/uZKODpXcv3I6SQzFDcM8RryXtvPr+43jBuozGG1Wol5DAJxCkPWmO1Zmtri8VqznK1wIccD5HDvRPh0rr+kgwpaW8r9RMfpL6ec/1gjIIIeEIMaxsY8YBc58cVZELpp0tGSN/mItyryGq6jPmCvhddJvWXkCd5tLYopakzi2jDdDqhqmpm0watKKIgTPbcaKNQWt7f9T0+CLA5OztjPl9yenrK2dkZZ2dn9H3P4eEhjx8/5sMPZd+eTqfs7Oxw+fJlLl26xGw2wzZy37ZvxWDtxcPe24D1Cu0NNoCKxX1tDL9TRuYRSX+NMq6qK7Y01HUMSVdzlkuJQJF8c2m76BKavlvx2quv8NmDhyznKy5fOmD/1nPMf/o2M68wqDy/zs1xiNFHg/FaIiiG6IRS5pZgKcP/DQCoPJ4GktavXd9DSw9XqS+eA/WI0bxrW7Zms89tS3l84QFSEqoZkJixtyZtquVC3wSG1oX+Ortdelb6mZWgDeelIwnotLitsVlQrAOtdF8dlaE+KnshFhD1GoIVEKSl6Ej09CALnqTADQJLBGY0kkXg4nqXhXbKh5EOUJLQmTavCGo0UtdHm4HCNYO+KNxc32dB17YtvXOslm0OJ+v7nuVSQIokj3a4PlmC+kL4enwvZAHtStzly+Uq34PesVqu8MGLZ6XrWKykHo7v+nPWjhz/PfLODOMiOUQu5zsYa7F2IjkkWlPZmrppqKJXJjGbURlMLV6aSdOgjaapJf9G2xh2luKPo4Xf2krcylGZG1lkVIqzDpH5TTxSp2enfPzoEfP3foEylguXL3Nw+VIERgZlrAAkim1UQVCi2AYlVjkDo5AGrRWWoU6XsBrGy1Oh3HLOx409uGGehgBGmcEqGGQeSsHOQPa6xEmY5yWBvvcorWh7N1CYevG6tV1Hu1zxyuuv89yzz7J/cMDjx8fYqpY2RiXYEXJIaQlmlSzekUFCQiMUaE3r+iwTyuKFPiiCEm9N6gvJJTJolcIIBYD2vWMymaC1UGGTZUy0xiWvmzaRUCDdL8ohwCiF0fJCSgVJetaWEBQTNdRJqyKI1kbyVKZT8dik+VtXQvttjcZon69JoZFaa5oKKhOyR1FF+RFCQIce5bts/e5WK7oo3yT8cfAuZiu3F8MLyaruk8dHFNBO6RGN/GC9VOCiIhXEmj+wXoFxorr64p5p03YEUAHlEuV+eqYYYBIpDRE0pNCwvu3pe8+k2UIrxXx+yun8NHruXOxnw2LVUa96rImhqXpQ0kumUkXypij29vZ5/Ogxu3v7dH2Pspr5YsXBxYv84X/yn/Cnf/LHnJ4csVic4ds2W8UBlPHM53MIAdcJ6JlOJ6AVfZ9CRFIOUupIUMpEj50CH8OZMBhdE3TDV7/xLf7J/+afMtkWOeacp+scs91dFm0XZeJgvS/HNAvIQZREldqDSgXCy70yFCDgKYBGlX8PSfoKMsNjvizJ7/FFUfwURjeGUD81fBjPzSEP8Rka1/csV22W+0qpCMblurL9pTxJLU5gfQzU5I+6qWXva6M3MO3lqQZdAX7SdeIALGXpoDwmq37SU7JeESQcOR1iWGs4OjphZ3c7K7aV1Tz//E2uXbnMtasXOTo+Zr48Y9l2LJc9v7h9hwePnhBCyjUcxiSH6CF5MqWSWrap93HdMni8shwIg5E0zank8fEREAXEu9vHnNm+71m2EiLnEzFQqq+jbCTLibMnOKaTBmsMk7oWT4v0sITWuQ6F5vRkTtvNCRH8NI3kdQs4k5FNz2hqCSufNA0XLx7w3HPPsrW1hbUVEFgsFjx5cshnn33Gw4cPOD054e7dU+7du4vWmu3tbS5eucCzzz3Lzs6OyM5eDIjWeZzVWBONznqIoLBB2PEknG6Q+VKnLpEOWcBAMCglESzB+ewhV97RdQJWZ5Mpzz9zg/c++pjD+RmvfO03+PG7H+L6BU4SVDF5o1fZGB1CDDdHCCtU3m/8MG/jEkl203Jh58/SWKyBnHPgKq3cQf0Z1rMar/5smFaR8a7QR8YGBsk92qprmmnDr3p84QESWuI7IRYgLQTOOrhJeQVQKtHjwUznrnt81gBrPnd9EpTfye+JWSUOcLRemciYIoJ3cA3bqopeo5h3FP9DIcpYAC0xJLG8KJjgMMFF3UBiq4Ny9N7Te09lalzboZxDQ078S27u1WqV85CWq8iK5lys3RIyfeliscjntm1Lt1jiuo7lcoVzfQw5i6Co68UlHIWg610GRMr3sU/Sqgtx03YSG52UH8gWUwA6iXvWlcFUFm1tHv+60TnfpsyrsVVFPdvK1rCmaZhMJhKK1sRaBJE4oKoqUTZtKhI3hHGJdy2OdQQ65RwYJloaZznW432z2hFiLky04oqLXaOUB+eYVjN8sNy89RL3PriNMbC1NcNWFcpW6KoCpXOoGXGulGnHPiqXCiWexDxHVVI9ZZOL/axj+KYUy01rQ5JaQ+gJbiC8KDf1tLkSChrxJBRjaJhnYD30IQidbQgopwhOalBICEEkqOg81FucLB2271BqADZohY/5P4kUIXvxEECoVQwd1EIEUVUWj8LaWCw6J/lH2m1touKbcgPlnzEWo4qCgCFg0vyIoCuBo0yxHoFXrQMmcqDKqaLcVtay3cDWtMnkFQnoqBBoDALK64rK2qGtIaCMeCD6rqPr+5wgnuZaecg4Cb128IG+dbi2HSkvOgm3wEgeglDLlh6FUJyT7PCDgYo8t53yuQ5Lspqno5TRae14PIlNc9T25MlVisGsA6HcuNOnYZivSfEOLgibWO852Nlie7rNfDlnvjxl1S/o+wXWTlDa0jlYtg5jhUTCGhPX0xAu5L0YE6yC4Ht2t/f58PbHtL2n94Gw8iyWPV2AW196mWdffpFV14qyvFpJWnt0ny8Wc/71v/7X/PAHP8CEgDGBP/zDP+TDDz/k3ffeYzGf0/Ut4mFc34sCWleSBysmHjCWa889xz/5oz/CNjWtH0J9bWWFQr9bFvNibJgLISb4bwA3IUg9lczF4M7vn+vzbvhj8Lpkg2SIY6n8+qVPPZKhJilR6e/kQS4NluuH5G306GgUIgJpuW5kP2M4IXZBGOYXDAa2EESueihyHobQ26eF4JdtLAkEyuuyXGW8dgYAGbDKMJk2HB8esbU1IyhRbmtjOdid8dnHv2B19oDJpEGjuHvnDqaZcO3qRR4+eoiPJAvEd0nLV2mdiSxGNYCKdrsCvLkYU5eIStaBUQghe4Z0ECXWEVj1HauukxIRzmdWO62ErKCpalwneaV4GaO6MgR6FA6lHI01zCZTZrMtmqZhe3tLaPitZbY14fDoMW3bsrU1Y3trG5REDfQ9rFaOx4/k+9nWjJPjEw4fH/Lo4RPmi4UAq+wt2mZ//4CvfvV1tra+hdaaBw8ecOfOHT755BOOjg55cnLI7Tsfsb29zY0bN7h69Sqz2Yy+d1gVw42thCmjPS6A80ZCYrXHWvEwCYGERnkt4BBFUxnUTCJ5tILlYiUgNEZAqKgHeB145aUX+eTeXbq25+DSVWZ7F+nbu3jfYrRESuQ5niwEyTgeDREy/ZLHjmwYzcAoMIoqSstHjEdqZIzd5GDIj453CMX1pbFzdE3Wm4brk54jkSJGjHxaojJ+1eOLD5AYwE86yrjFUoiXOUHr3oZ0n/VjEGKDwrzp3HIilF4l7/xoM1FrE6A8cl2XELDa0HcdCqiM5BfpIC7E05NT+q7j9PSUJ4+POD4+YTKZMp1MefzoEYvFkuVyRec8KM18sWQ5X2Sgs4xV4KWdWlgMupiTFC08fQzPEuWqICjwQuaQCsCFon8S+5UoTY5EI5uSnKtKYvXRIizato1uXCRHxiiMbpjUdRyrISfr9OSUkyeHQGBrNuPlV7/EbHubZjphMpsxnUgy5WQyyfkbKnnBzBB2lCzv6XeVqD0ZKww+BvGvz49k/QgIWJANUxeb3zh7wWgziikfQogia5gBW2w+QmIg11TW8Mz1Z6gnMwJgmym2mhCMBmViO86zJ6YQjUEYFsQPYVBmS6UjVfEOeKm74H2OIc8J6EEAxEgxCtHqGRn9UlifWHhS36WaCirXNVLRIlQF2QSUshgTkBwbi60aghUQbM0AVHXMyUFVYrElAZxhfFVB913+9D4wicVhE2nFIBtMBkJJGJuY02N9i41FDqvKDmQXMTxWwK2MdfIyTmdTZlOY1CYnOad5aI3FeImRT6QWonEpCB7lE2GH1FnKShmQQq6UEgvoslDExscAxIlzdVDyChm0piSXR1BqUIopLMUBdKIyWFe2YfBghgRmhu/8CCANRgaZb8Ozy00WKCqhnG/rurKe5b8LuNaBd/TOcfHCBY7vHLM4m9OulqzalqqSgr99NO54RB4lCt/y/aS/FF4bet+zNZ1ydHIcr5PvnJdCry7uAZPJRBSKZhLnirRt5+Ai//SP/hlBW37y/e8SnOPh48f8p//Zf0bXtdy58xH3H9xnuTzLBq2+65gv5mitWS5X/OIXv+Dxk0Osqbh09Tr/7D/9T6mbOucYpXlfVdVIGV8fs/yZH+bD6DwgqFSSem3+rM299UiK4NW5cRlmlDs35z7vONfeYj/9vCPlbMEvP/fcodaz0eLH8X8JEDwNKD6tr8vvy6PMC9lk8IBo1IhAYD6fx9w9heQZeX76459w9Og+D+/fZTKtuXT1EmeLlv1LVzi4dA2jFe1yhVc23W30jE2MvKldZf5QkkElMNoEkLwXAETcGzrnWLYrCa8NsoMZG2Vp9BKoEL1zrsfUkdq8NuztHrC3u8P21hZbk20m1TR75PqupXc98/mSs9MjVitH3wcOHz7BuYcZIEmJCk/KW18tV0ynU5659gxVXYvxVWm6vmexmHN8fMwv3nufN7slVV1xcLDPhQsXee2NL/PNb/8mZ/M5d+58xDvvvsvR0SFvn5zwi/fe4+rVqzz37HPs726jncHEAukm5jj5aGhzOvWri6x3QoSh1yMJcoqHpl11g1fODZ646aThpVu3eOv9dzmcTHnx61/hrf/lPnUrBEoush2DGBHrumI6nbI8PqNftQM1vPKMi7mO52CaG2yY99lpUBiQ140E6+dvmue/zpHmrQ9iwPxVjy88QFq30It7s8/frSd1pUW9LgjSUd6rHFQdCxWW91n3OpWfl0qAjkpyImsoz0+HUsKM9/jxY3Z2dvBdz+LkjI8++oiPP/mYe3fv8fjxY9rVilXXUlc1AH3vsVXN3u4+06ZhEpW6jz/5lMPjY4lvD0hCZ9uTWL5SHhIgrDd+eNegIuV3CKDF0pSssloNHjttdAY7NiqydV1T1RV1bWmamiZ6a1zfi6UtBJzSGCuFGW1lUYpYPE0KU1aVJIPrmMvjnOPh/fv89V/8Od57di/u88bXvsJse5t62qBthVLi+UkbeuxkAiG7jYvOjrWpIMWzqzTuaWwChKBG9azyxhb7KI9hrp+A5PqWVFAg3gldeBlDQIUi5DMt7kIBTcKvqhu+8o3fIgSwk23OVj3aWhHwQUIayvdKeThaFfeLirJ4q3xiVBWrXxhIC0TA+Og1SJs4OQdO1oDJiqu0WQwTOtbFUNHTlujB0z00A1AN0VIpyfsF5bdKwMRIGISV8AqKtaaV5ASpkKiv1xawOGnzPFAM+XE6tsUUgCuNq9UGiyFEFqoE3OvasN1MubgzYRYtkXVTS76KMdlzRn7WMPYhzKMS6AihRzkFDtqVR7kh91DqCflhyqihnltqZ+rHpNCECEBVUU/kfEcMMiiF1FHcU+ZeAjo+3zMdjjXFLlvwBkteqUQP56nx58U9XP68BIUFu1+6x+jeYS2Hfl1lHa/P5KXx0Yjje8dqtWJvd09Cd7ue05NTtnf22JrtxpIKXUzYVhibiozbId8qP1MUiJQP4oOXAq9hqLoSVGJPJEcBYCqIhCSpj2xt+ad/+Ec8d+0q3/vzP+PPvvcX/OUPfpiLwYpy2efyCz54CadBCnVWtVDDv/zKq/zWb/8Oe/sXhBxCD+GzaZzbth2N7UiehWRQ8aOxEjEo4+TFPHxu/vxSZSbo8f0p5nNJPf9LjvU9/Gl/rxMKDM/9twBHcpNzVu0cOcBgnH0aQNr0s9QB1kFQ2UdPA0g+QFCiT0hhbh/zHSV0cDbZYmFqtpttjo+f8NFyzqUr13FtKyFpPhav9QHPOEVg0HcGo2Ifc13KNv66ACmEEKNI+igTwCphWEQl4yEyz/uUX6PZ393h6tULHOwfsDXbEs/5quPo8IiHnx6ymq84OT2lbVuWyyWr1YrVUnKY+k5C1XvX07XdYLyjjzJewmm1NtR1RV3VNNNJJGYQMqSd7W0ODi7w4s2b6EnN2WLOo0eP+fk77/LWz99hd2+Xixcvcv36M7zx+uscHR3x05/9jI/ufMQnH3/Cp598yuULF7h56xZ7BweSp2wtpq+obE+IofjOazonZE3GSi24yprReCQ20BBAsWS5XGZDdxojaw0v3brJ7bsfc9Se8cJrL/LW97+LbVtU6OmjkVYMehIhUVc1i/4Y7ZNnl+hFlFC7QMj5ZKXzwXuPEQSV58a6njUKE12by08DTJuOXw6aZJ+oY9TFr3p84QFSuQnAePGmv8tQqPL3TSCl/E5FRTp+m2PRy2vV2iRIwKNUDteFTykw07Wp3T/+8Y958OABOsDDBw/4+M5HvP/eeyhgNp2xt7vLtWvX2d7Zpq5rus7hXZDimYDxPaenJ1y4sI+tpcaHthWHh8cslITHVbUUm6wjeJlMp2irMTGcp04saZWlnkypG/HM1LVQ9U4mU7GK1xWmihTQObFcx3wli7D+SycslktOTk5YLhbCHte1mUGm71uc7wsGGqiqGqPj9c6xf+Ua9Wybs/kZQVfY6QxV16iqQdkKpWthMo+LP48pgVDkiQSfwn9A6JdsBlIkZVoN7lsXlQRtkhs6iGWkkAthZHhVEYCkzcwnrJFDPF2ZwOpTaKEfJa0651gtl7Rdx9VnXyAEeHS0QJsVqXS1NpEYQd5SvFVr3pvk2QkiVSG3VaFibo1KLnaVQtaGWg5pjuuUxMkAWExpYDA6hpsVHpgEfEIDQY8IOFKYW6fF0rTOmhRCQI+U5tKKHzD4DNAkBDNZVz3arbKXJ9GVV1WF1ToXUcxrVsXwt6Dwrazb7Z0dtran7GxvMZnWWC0ge1i3PfQ9rkeYpUIaeaIhIc6dUT2GqDBHwJKUQ19MniyPTBwnBuA1jN0AXAcARAxV2LyJhCLMKfVxBjfSCrJRgOF9/DpASsCoeI/h88E7GQikWK11JdqnVhbKd3qDbIAqZGbyOJWvdu4987tIm3TkQ07eOd+L5+Xa1Ws8fvSYvutYLZa0q5UYruJaEblt6XuX3yXVFMv9o8DhMCiWbYuxFSenp0y2Zpkq3MfEb2XKulGGzPeZwFNQmHrCf/i7f8Bvfed3+OzuZzx+/Jijo+NssVdKgNr29haTyQSlNbPplP39A+pJQ91M0EYKzboQ0DHaIHV5qWivA4uNvxdCrQS+6yB4fU8bz5FysM7PyWQIST6pX6Ygre/TTwMOm/b0rIT9ktouT33251wVGIOdp7X5aUCpVBJh/F6ZbGojCB2o7s/OzuR67/BevB4Xn3mGmzdusJrPOZsfY6cGlKELii7WQoTE+Dm8XQJFNhqmSnADjNpZgqEyUmf9s/L33J9K0VSVGBRijmjveskv9o6LBxd48YUXuXTxAt55To6PefzgiA+PP+Xk8IjTkzOOj445OT7i5PSI09OTDI66NtYVdC0weLvKfXjoT5X3eiFOMXnPSntHpvqeTam3trh8/SpXr17llZdeAgKPHj/m4zsf8vGHH7K7u8P168/wm9/6Nr/9W9/h3Xfe4c033+Thw0c8evyE3f09XnzpRXb39jBdT19ZnJGyLtbpaCTWmOCwzuOdyh6klCJgjNRSSyVilsvlqJ+7tmU6m/DKrVt8cOc2em+LC7ee48mTI6yX/S+tPzwoA8tTKZ4ctFgXhYJ7CLMXeTXWWdN82LR2ByNhitwYGOg+7/jlIGiso6dr0j6u/RDC/KseX3iAVIbLJfrq9U5MCLvrukx/u36PciMpgUsJvBLYeZrnqLQmZeEXrXnrdIXJo5SsMEkx/MY3vpGv3b9wwI0bNwghcHJ4hGs7PvvkU8K9u1y9do2+d3zyyWdsb23zwgsv0rYt9+99yv37D3jl1Vf5xm9+m2YyY7a1JaFfukYpHcOEbC5kpqzFG5WVl2StlYRKCatKikxSjKPaMAAPyOEjAMFbAkPdlLra4uLOJdp2xeL0hC4WRpUq8atYILGn79tc5K6NgCloha6n7OxfYtE6bDNDV1OCqXHKAjFOOXoxRpsTYlEWKumYQ5O2vRh2lJSr6GiI7Q/Z2k0oNsJkRWe8AQ5zRmiGfQxVzAnpIVXVVqPNIymKzkt+lfdDMqsQNmj6XuZPZaVAn44C01pDyLkyg6c0zaU077QxI0uoRPeZrDgkFjujjbxV8u5E8EAQxT8DJpnwuZ6RPKjwciiy0qm0RocKXFyfndRlMLlYo8cjeVdZCCslHr1Y+C2vmxBiHHZAEdnfUMzqKm8c+7tbHOxUbG1vUVmLtVUOqdQw5BTEF0leH7GoFgUCVfSuuBUqqGEusCbIS2109J0iZkPlz30RQxaUG5T6MMyhiA4KWFgcQfpr7GkZrkkhkfIqIb+31GkaW9ZDHCwffF7X6+/2NGUakuMsa+HZmh6y36TsnuFvN36j0TNFhm5WssuaOZ+3kWqt6VNYs4LOOXzfc3xywv7BHk8ePeLh/QdcuXaF5UqUKqPFG9+2wkQma4m8jkfWfCW5WQHFsl2htPysphOR/RSENirJH8RUFPIt4lKUD/oQsJMZz7/wEjdffHlkJEh1qbIXOPeNEu9+gM55kV4j4+350PHx9Yw+y2NVNNKHp/f5aC6sAZbxkbIdz18bOA+uNt5hI0j4nCeugbbUjhI0/ipW6889V6lz4G8TKNr0eymj18PzSuPsejtK2SKej+jlCZG2H2HOfP+jO1TWMKkrCI6w7JkvW1Z9EGhvJ/TdSu60loA1EFqNdZWxEWTY79ZlxCawVL5vVVUQpEg0wPzsjOOjIw4u7PGlN17j+vXr9G3L4ZMj3n7zLQ6fHPLk8RGPHj7k8MkTjg4POT09ZXE2Z7U6o3fLHF42hIIHUD3ayN7b926Q8QBYCCZ15WivNEr212zwTgVfrYXaUr81YTKZsLOzw/7+Pi+88AIv3HqBqp7w8OFD3n7rLT756CMuXbrEszdu8Nqrr/LeL97nxz/5CY8fH3J0/BMuXbrE87dusrOzhTMa03WSg2QN1mpsZbDaEyw5lzqEMGIVrOs6929b5JUGFei6FS9cf4aH9+7x8PiQZ15/hc/e/DlTE4TgoRjroDX1dMZ8tSSYWN8wSIQLosFFpssxkC69qOtrYNNekuZw+fso366YR+vnlfMrgcVyXsl30pgQQo5w+lWOLzxAKgXKekemI4SQE+8/T9gmYZitTiOLydiWtK6IloKh9CbBUHQyXQeM3PLlvZxzUohMiWLTzKZ88tmnWDSh77l77x7VpOHatWscHx0xPz3lH/5H/5DLV65yfHzE7Y/vcOvVV/kPfvf3ePmVL0kyP9D1EHQTXc4uGaQxMawqhGFDF4XdY7UCH5PWo+fAF+9CvAfnJrZYI5LHQSkI1kr1emuZNDNWq47lakHbrqj7tgBIC7zr6WNYTIhhJX3vuHz1BvNlz96FK6w6cDpIcUQfCL7DGD9QVhebvgvkUKLSkgSgPIPyUShhHgEs5XiV863YbUcWaJVyg1Kh1AQSsiVZ5oQxkZlHCfBwusoxuwmUCYDRUpU9SBKuMQqjBwUrRKrTdevM2AOUxiahv/RdfF7sL/FuxXmep7rK4CQ6HkjKRrmKgoueK7lEwuiUkdpb4RS81HUySoOX3K8KzZZGNgUb8+8yA5ymrm3esM//k/WZyDWqKrG7BVRIzIgO1zlS6VhRKgrFpgBIEn/n8AjQ9qneRAxJFQAiL1gqhOtg3BfeLOg2ngcRrK9fX86r/Fm686aj9GQnb8dwrzHwOK+ICmg7rzCPnjA4FDIYCwAFU52O7F1pHTGq3bP+3uffLxkQBgbBUHRD/P2pAEm+V3HiifdI5VDOVLz19PSU6WSK6x2fffopz794k3YlTJv1dJplr3M9AmzVmhIrz0ogN6BYrVbs7O5wNp8z2drKSX9axWcXvjEdBsZECrAEkUxFiyGHuBe4yHiFl2eJI2sgxUDFfMdoPQ0x80jk+sDSur4nbQJI2aiohoTpTec97fi870ZGp7XzckjvWujdr3P/jc9cM5DGP9D8etZlGMTgxraV+0ihC8CwX3xe+9Lv6f3WwwPXz0uHVgizbByzvutomkbmMCHmDiqWXQd9KyymWLyGzil6FKa2ONeiGOduDwZnNcoXXAfZ62F16ftNgC+DrrgPur7n8ePHLM7mvPjCLX7nN38L21gePnzAT3/8Nzx++JBHDx/x4MEDDh8/4smTx5ydnbJanNG2S1y/gkjq1Hsh91n3kspzVTZAj/bH0A3eXGTd5WsYaAOS4VHF6Bi3VKgTiUx48Bk0TcN7P3+TnZ1dLl19hldfe53nnnsOgLt373L37l0uXbrEjRvP8Y//8X/MT9/8Ge+88w6ffvopj5884datm1y9einuYRZbWUyvqZ3BGkfofS5km7xaqS6e1kbyG+PRdRKN0/kei2WK4tkLl/n57Xd55cWb1FcvEE7mmKDoujYbk1utsROD2p2B66Vgfe9QHmwQavm+yGFOoCaBlKcZCdYB0Kbjc3Vxzu96m5wS4xsiIZZt+9Rnrh9feIDU9332Cm3aDNZBjzYpDCm540IMhRGOexct/ipaEgQ4iKVdFBrZ+BILXcodyPStRHd+CCiVWJB8VEpTDRW5VwImOiXOKYRFJi7fdrXikw/v0K5WtD6wOD0DwIRApS2PHz7km9/8Jl/92lepJxParuXmKy9w9ZkbmLrh5HROpS1WWfFmoHBKU2mLtpUwSimxqpswWA89Aa18pB5GakXEQ5l66NtiHJL1d1Ch5f+5Bo9SKCuavVWGqplQrSqWyyXL1QITAZJxNat2hdIdKphoFe/wHVx65hYXrj3H1vYWT47nVE2FqZZRM00FTW22FqWwCpcEaFQI0xipwZSbvSJJeRFhHlnN4rikc0z6rgDCWSBEaugkoPMWqxJtdLyfSiQUJnvgyEBnENACkqIXUokHQRFQWhTikOi6y5o/GQAMoRha6YR+o64ZC9dGCxEq0isrj1TVSQDPx+LDIdf8yFS0MhEIIVCpDq0CVWUjKUHFZNIwnU6ZzhSTxtBUDTvbW1S2oqlrmqqmUl58lKPNOQpYxjHtst5czJ0i08FKSKLHuVboYym8uWvKaMpbSnx/JEOI8iQyCyJ7Y8LSCegnADOyrFMwvZ3bLBwEn63N5ddBGVF4KTaKEH2b5XlJIQ5D+9NKHQOq8yF23g3EHyPIUio8JANBbP9oz5H1kDbH0WamVEyyPr9xJUV905E8VnL3dN0AQMb3Gd7x/P1K5ZEoXwN9F0NEvdT0cZHdc9X1HBzss7W9xdGjx8yPT1ktVvRdR5hIzQ9jo7ErDMQkg5Es9lSS6cCq67B1w6MH9zm4eBEb9wQfxyvlISUzxJpGfe6Nco0SZA8Qgh8dPYApVExAlPeR2osEmEiTNfbrELJ6nkSgNCamv+XaAYeKkSS1X62NSzlO62EtTzvv/PvG1fU5SlR6B7mgfL9NJ8JglFJrX2XrzgAe5Y/h2vFtRut5mJ/pxJDXdfk+aVUNfZLm0NhAURo2SgU9GSHKuTKELBXtj3Nra2vGfL6QenGxWb0TbsMQAiooTCCSLw1GDaWCFCcv9vbkoQhBcs4UQ+SM1CFLgDuGzSV6/7yOk/4le13wPjNwGmto25Z7Dx/h+56XX3qZl198iW654oP3b3P3s095cP8eD+7f5eHDexwePebs9ITlck7ftXRti/c9BMnpTJ50V6yNuKEXkRyDp8M7X8ydYswUkIGg6Hqh9E7ENG3bi84k1PkSLu76Fcul5vj4CZ999hnv/PwtdnZ2ePGFl3jjy29w4eACTx4+5P79h1y8fIkXbr3ACy++yE9/+lNu3/mQd999jydPnnDz1vNS5L3vqCqLcxZrHa3qaJyQ/lh39ANtAAEAAElEQVRjqULAeo/RnspKLbVJU0PwLFQsbRMUnQ/0PvDMM8/w/p0PUNry1b/1t3jw/m3a01MhB+raWLsLvFFM96/QNDOUD7jFivmjx/QnR1il0H2Lj0b1JO/z1hPCaL0MBZgLhtS0ixZ7u1IKZfS4+HfcfzTDvphlD8MhjLtr6zma8dvFgsXxCb/q8YUHSKNwhGKjTpa/czGL3meqWWOGMCCQxZEqq/q82OMQqUFZkQ1y+F2RWMVkzJyLRVej8im1AkSp7GOblC42uyh0tNYYa+j7nutXrnLpwgWe3HvAJx99zM7ODsvTOc45tmZbLOZzfAj85nd+k1uvvIitJxLa4Xvmbc/JcoWuLMZUGCwqOKmqrjTK1vighW0qJbQXFlqjFFqHvB+sE13Amh6VxqEAqdkqZuImUoyDDoGqAq1r6kozm9YS7tK2rDxQTdBdh6okT4lVi1c1od5BBU9QnmAVfQj0XS8gU01QysQCjzFHhlis1ZrR5pND0pSKHoMErsriqQUxQGF9ku8GT0fa4LLH0QxhVanv8rV6YNaDFL4jQruKDAJlKE06EpOYfF5saFpllqigC+U07nseD1GhIwk0J274BAxCEnhE6xAB4VOXGGTlBThYpZgYxVZTsbNzwNbWFrPZjNlsymRSs9MomkrlfLTkwRIg2jN4FVShY0Q6CB9QymeDQn6/4UUz0K6iSBusl1KLyScmHx/ovKHr+xx6kcIvXO/RQceaUynckijskwU+zpGoEEmfD9629dyAoBVelQrPWBEqyVlGimJwxXnpf0MXjY5AnhfDs+MXTzmGgqOiwnhTtMuPy4E+zVNQytPPy/tYV3D///E2bARjrHNtFWBCJU91GDZvQlQEFfSKPniCllDiS5ev8OG7b3N6eMxqvsJ1nVjkdSA4kQ2BEEsqpDDQof8TVk35WdWkYbGMRppkEElJ8AXe9ISnFyMtzgtxLg/vmbz9WRvIoZQqDGQe2WDBYHxJ99scl1/I6GiAkSKVwxmJ5EKeMS5aW85FlQBWGo/y1dbGcQymk2f9lx8jQ8GGOVc+a93QEr/MMj1/R+6l8/sZRZ8zzLf1owRiY+Cjsswt18hgtC3bPAAipZJRYp3QIu1dQlIjk9Bjq4pV34mMlBNF5hRv5mK3hZjnqhDFUGj8h3257FOfa/WNSS5SXl/IQzHUpAqxP7QWsoGqbmJkQeDup3c5OjniG9/4Bjefv8njh4/4yY9+yCcff8yDe/c5evSEB/fvcnJ6yGJ5RNst8L7D9T0aKyHXcf9TCHmKYN4YtBsGIE9i0YxMm8MAMRp/Gee1kc+LSK5Pir93YorU2qG9po96gXYxb0v1LLoVy5NDnjy4x9/88K+5du06X/uNr3P95i2ePHrE48ePuHL1Kl/96pd5+Usv88EHH/DhnY957/3bPPvsM+zv7xDoafte0iC0oguOqu+oq5oJAe8NlaliGJxFa8V0YlFUtF3AKQXK0mpF0zRcu3yFxdmC3StX+cvv/RXh7Ax6yaG1RpiDm60psyvXufSlN9jbvUgdDGf37/PZOz/j9O4nqCePMa4FnOgcSomZVkmhZBX7KKt5IRDJcOMcZ7TtJz3RoAYvv0zCqIuKrmyLfZZCH1eQ88HjUEkOvNJ0bUe7WPGrHl94gFQqoN777GosPyt/amNGn3mfwEyykoypvNcF7XqoQgnMkrUuW2HW4nHXw+zWwUS2lMf8k/39A27evMnWzg6z2RZ92xOU4vjslAt9x4VLl6gnU4ypMonC8fERSlm06jFWgba4IOEYXkGwCpRGUi2Sp0VTmq03eePKd3/a3+X5yf1fevDyPQECVMZQGfP/I+9PY21J8sM+8BcRmeecu9+3V9Wr6qrq6qpeubRItriMRciSTI1NDzyyRcA2QMxYMAQIA0OWBBuyv0gag4b0wRYg2AI4Q1i2DEkYWOBINEhKFJcmJUpqskn2Ut1V3bW+V/X2d/ez5BIR8+EfkRmZJ8+591UX5UEpul/dezMjY4//vuBDkjbrHLOqZlGKdKMsK+qqohyXArB9dMoPc1MSFtM7R27Goo1RrUo/BhYwqg22kYZ9RiVkexxr/DZBGCmzLf90E4hhyfGwl5W98QtR4FUMdx18qxr/JPAqCzivlRQ3ZyPwmC1LHpGfT36Tny75xkUMLR0ESCXhVn1IHKe8a/4ZHJk25KOMje0JG5Mxu9tb7O3tsr+7w872iPHYk5msmVOEh8a3fhbSv0ekffH+tGekwwx0pNk9JrzHbHT2qUd0+GCnbT2MnCZG6LPWUpXiBFyWFbaWxJllXVPbkJPJ0eZviglKGxNRuSUR8DsvGdJtrKtpcjoN3ZeuZDi9LMOEVTrXTvXes6G/V9VxeLC6I4Fe1dY6af8QLFjvfzLczuqXw/MQgdTq9vrjas6Gb7WIURNz+fJlvl1WHB+fUBQFi8UCZ1t/UGlDExNl9uF4n5BUSgVT4FZbPjTPQCMMvlPJf9eVvoBKJbCnLyDstL+Gge3Mhe7VjHA6/tFq/IJfkYpnXHU+XKcR6uPRi5YnqT903zzD5zwyJP3naZ+r1mvtGFKK8AlLKvTttxpxkxYbZra2tjibTgXABrifEv39JvrCznWO80M+Rv21SIXTEbZnIY8RznN8fMLtW7d56aWX+NEf/VGOjo748m/9Fu+89SYPH9zj4PFDjg4OODs5oVgkUT+J/qDtXpqEdos4bpWMqE+XpfTHkDCrv/5x7Zq5O4f3deKj1cKZLESVNSZorkqwteWdd97h1u3b7F25wnd//vO89ImXuH/vDg8f3mf/0iWefuoG127c4P1gcpflho3NSTPeTAc6I/O42oP1uHyEGqvWZFdpskwz2RijjaJy4JQEhFHa8PwLL/CNr3+djz17kwrP6WyGK8vAIGk2tjZwbsTm5j5s38BuX2Zz/zJPf+KzPP3yJ3n/tVe5+8+/Svn4Efhj8HMJgOE1GRLgSrGMv3wcH8NCtKH1Tvdq3R4O7rcTS5dqUXD3vfdW9tUvH3kGKeZvgXYjvBefo+jAFn8HYZCipiB+E+3PXZBk9xmaWA9a36EUMCiGkdMQIxTHF02D0gORhh8+OjzkvVu3GY3G/NE/9sd47/Z7XP/+6/zWl75EVRQ8/eyzXLt+A2cdr3/rWzivJGKd0kw2Nrl8/QZZnoMLSdxwIQKTSJIas604tjVr3Jd+rSodYNljJPtMZCTcmwAPWUYGZKMxWxsbOO+xdU3dZOH2klgtyG+VDv4kSBQqQ0ykFrUWrfN9TGiZhuxWgYFLwwd3pX+tGVNK6IYVofEH6O+3oitpTU2fGwq1wWX4ELLMR4mcbiVykdmJ+UmWgUNkfkLrSgIYtJG/wly9T+qKdFHjmIxzdrY22dmcsLs1Zntrk62tbTYmG4xGOeNRLhoV78k0OF8GJi8kLFYpElc4l5wR365Jn4YeItDXSYSHnvUZpFgUkTkWzU8eErN6L2Fmq8pSliVFWTEvSsoqMOG1FYYp3BdlRGmPFoMnHdZQxtrO25vE1HBptAFwDxI73Tn1id/u+8ACxz7Czw7i8b11CGa+3iM5bOxqRmYt0/IB6n2QIstrO0RJKz1f1iCtGleXQQp3KIQyrqqKp566QVVVnJ6eMJvNKBZF46MQJeZpu+edQWNMY6qyEnmvha7Lba5614E10AnKkX570X3qCyAUdCwJ0qKDCWP4EgkLEXR3SuP0MA4cms+TjjMl5hv8sWY+fefvRurMMj6K8+lT2heBR0MCw6F9fNJ7MygYQjUSdkksLgF1RqMRxcHBEo5atU5LMGKFBqk/ligoSJ+n/yJBPM7GaCW+ym9++w3yLOf//Mf/OGVZ8tv/8ku8/fZb3L9/h8eP7nF6fMjZ2THFYoazIehOkovOWhdMw7vnv2HMWBY+9QUFq4QDq/ZniLlu19LhfSsEj98WRYFROoSXVmhVk2Ujsgzq2vLw/n2++Cu/zO/89pf4/B/4A7z0yss8fnifk+Mj9HiMUTDOc06Ojsm0YWtrI5jMi6bQ1Q5vHLa21NTUxqCUR0m0GPFHyzJJYF17ahvMtx3sXbrM5vY2Tmle/PQneVsriumcjSxjlGeMJiNmxYKT2ZzTWYEflYytY2tjg/0XPsb+9Uu8tPcy7/7O7/Hw/tc5O7mFLku8ldQd3piG/h2K6NgRYp5DP/ZLn/keEk5FJYdG/Jt97Tg5PLpwHx95Bsm7Nh4/0DA/TXhHJ1LkLMuC7wStODu2EYjnvrNf/Jk+6zNNSqlG9R/764+jzyhFqUP/QDUMk3MUZcmjhwcoZdjZ2edk+i3q+w/Q+Yinr11jsrmJyUYcn045PJlKNmrnMFnO5mSTZ64/zQhxxLPKUTmYV6KudiGwQZyJRvXMuJaJ0P7vq4B+B/D0/o7f6YSBirp5aT9KbwNBmbWZzz2K2kXTtSjBlI8V4pelk3H1JXhDYVOXgGdi5mC9awBw/zyECARLa9CM2ydroWic+73PxPkfmhDZkanyvgrSs5YY1pHxwYtZHC3QF2Ih5nHo+7JEP5sgacaTZUoylI9ydra22N7cYHd7k61xTq49I6NkuZWYiyo82peBQXJQe9oWw5qqRCLXA4Rx/pHoTAnfzpr7YSKvWZuB39N1WAa4rf+BCtJUZWQVMqMZ5RmTSc6iKJlMRizKikVRUhQV84UwTs55qsqK/4o24K0kRlXR/DKZp0vPu19BYLpOHTnvFyeaOjU7RLLvvBQmQ/ZCuZboi2dhFXEwtM7nSf1WESL93/v9rWpLzDtNc7Y739M9eUMETV/gBcHUSKnGjKgoCjY3N9Fac3p6xnQ6pazK0EebTDi2sy54QBSqmSRiUpCrLJUUFqUE5dA6pHPq933euvYZqf7arCLw+4RvM8cEXironLUlc7UenFw35nUMw3lMVkowrftmcK4DZ1vq+YB7uv7Kq/DgEMMa37camtYsbdU+Pcm6kOIi367D5ubmUh992qUPK1McqVJB75q59TVaaXt1XTMej8WcXSuODg948403+dxnPsuLL7zA66+9xptvvsmd927z6NEDDg8ecnJyQFXOwdV4LM5XMiIveE18f01z71ed3VawsRx5OH22clVX4JWhtUzr95lPpaCqSiR1hkShtbbGGEl27mrP4eNH/Oov/xJf/9pX+P4v/AAff+kTzGYzdvf2KYsS5z3zkzOMlwTTDocta7RS1Lqi0iVGGxbzBfk4J8skUIMxkIeARqgMEyLvoTT5aMIzz32Me3fvcvOFF/n5n/9FyvkCX1VsbUx46eVPsLW7zd72BnZ2hJtk2HKDstTs722wv3+ZSX6DPNOc/IsH+HzB7Oghel5hq5gyZRnn9+ng9P0Q497HH+fdiz7Mjz6GWim2t7ZX7ne/fOQZJB20An1VcXyW53nDPEVnbp0tm9FJpBDVQZDpu1WMg7TRSvNSU40+1xy/i34RKSEQGTkdpAZGZVRVze995fd45tmbfOEHfxBtNC9/6lNoPKN8hNYZZSUJ1YQu0ri6ZmuUc3z3Lr/9L/4l8+mMzc1NXvnMZ3j6xY9T4KmMxypABY+dDpE1zKnHd+mzVcg3EsyrvuuYAHTkq+L7YwJF1ITkDtWNbuvJxwoar6MQuUklxFWArkOMWttKwxk29TUquIB2may0rEJmWvmWSvLtOGTWiR1/ouVRCoyuiX4wPozDZCEvg5JoNqM8ZzQek2cZJssk63YTyrnN3dIyStEe3DPKNXmuGWUZ41FOpoRZMFqjsaiGmA6MYdC6acA7CTZgvcInsvwm4EFg6rz34Wfkl3xcxQ4Dl65dvLbriI7z1ryztwTzk/iNCmakwUzOKY/JNFqPcZMxk2jSWdYs5gum84LZomRe1vjKNtEVGw8PFYmtpkPSQ7IKF/vI7Db3ohsJb928VyL4geWIRpj07mN6r1dF4Vse8/K7JyE2+t+sak8I8OV2m74uQFDH3/tRRdO9KcuS3d1dvPeiPSoKFvMFs9mMje2tJgBGKuhK2x7qSykVkjf64L86jCNcb7M6bYX7k+KcVQxqQ8jCEmyK36c4qB+mvA+3O8K/HjESGUzCHWrPvMzTh1DyXulONMRh87DlskoY0n93Xolz7Psdr+svfSb/lts8L2/LqvEPneWhb89bo5QxEbPf2D5oT2MaOp/PiULGOJY+TOm3q5SCJNCQ975Dk/RLeib7zNTGxoYQ5N7zzttvcXJ8zA/94A9RlyW//sUvcuvdW9y7+z5Hh/c4PHzMfDalriSCnlEKURLFfH5x7YJPqEI0+cnY05KaDPZdG9KxP0kZgsUy32VtVSxG+5BfKprrWpyz6LpGVxKlVRtJ0/Hg3h3+0S/8PDdv3uTy5es458mynLqyTKdzrHVcu3GNy9evoFASwl2J4HxjMkEZwf/Oiw+zdTV1VZKPcvb3LmF0xnw+Z2NzwtbWJltbW5hM8+InXubf+MP/JqcHR5SzKY8ePeS1b7+BN4rLV+7yI3/oj0C1ibYLNrIdblzZ4dL2GPYM192zfC7/IX7v12aokxlGnYEvJArlikiUKYM6xHyvu/9pKO9V+5f699qQx9Fpxe7l/Qvv9UeeQbIhg3CfA1VKTCqstYzHY8qybBYzlfqmSCl+H0sEFv2QnX3gFhFxKs2IJnSxfvp83SVuc+PA3bv3+J7v+Tx7l/YFXGiF947cGEkkOi8xOmuIWe89owxM5fkn/+B/561Xv8HJwSHeOX7rV36Nl773D/BH/91/j+zSFWoFXjkcquNv8ySIqb8mcR4Ng9R71xbfINt0bUQCbxMgTAswvZfwzfJV0lSPiA7EfcN80hIcfekQtMyhbxtYyRQ1VXwyiqa91u5W6AepY4Kvk9aiejcm9YPK0EaLT4+1EoklBDcwRhL3ZsaQm7avLpMO1lXgJVpX551WZDqTENpGM8phNBKfrzyLzueWGN/MNbMQfzW8l3cx4iPgvMX7upm78yE/lpffIxPgfVeSGsM4LwE6RTCFC5pb1SUt1p3FofuebmFar8PIB5M3HQNrjEQS58eOapSztTFhOi85nRecTudM5wW1b5MLN3scTF7EyXw1c9OfcLtGYmff7uXF7t2TMCH931MCtr8+69q86LieFHZ0iI+4ph+wdOBIAoPSw2CtZTQaobViPp8xPTujKArKqmTsNrp3lm6ujT4yT4mxPMvEzGYjW7kGTfqBobH32l03p2Y8LPPHfTyWjnuI+RqSuKejbwMoRBwRxxXnI4O30CSgjO11/bbW8rjfURmaZ/ozhdVDO6Oa+7teSHGR0jJn609yh/HpLUzqw7ySsA9CKYUQkhJ0ZVlLFP+ltEbnLMc9HJjz0PzTfEFx3fM8Rymx4Pnd3/kdrl3a5ws/8APceuddbr37Lvfu3uXO+3c4OT7k7Owui/kUHMEyAYmEKdLAxnIihqyHaCnSzWvT0Af9SIUr5j+0/qvK+czUsH+2RDP2KHRgpIILBZbMhIh6WqGMQWlNVZW89eYb3H77NngxJzQ6w3vRnL1/6z1GuxN2treZjMdMJhM2RmMu7V9i7/IV9ncusbu7y8bmhCwkm1UKxqMRG+MJQvk4yrpEhSS4Shu2tnd5/9b7jLXhhRc+ztM3b/KVr32Vd969Tfal3+Lf/OP/tpwXJ23hFdWmY+O5bSaPL2O2LoF6jGYBzLFKAn2sOy/nlaE1T9OqrKqbwi6lFZUTenY0Hl+oX/jXgEHSJsM5Se4HsmjGaGpnyfIRXklgg9FkIrbiLubb6Drh6hDNTXmC/T7gWn8KpTXeBqjkelxwKkHvXUxx7guDDURAak/cAHgvwM46i1aaylaMN8Zcu3ENVAhnqUJST+/ITMYoGzeEHgTaXnnuf/PbHN6+jZpN2c4ly3p9OuX1f/5bPLxzn3/7P/wPufriCyycx2uN81qiHJNEHgn/Wye9WUvA9g79Ut2hT30iyYvfpwxrh0jpXSyVmrj1ch012hHfSETDJON/UCqJpuLFKCcdskqqK5xEYOkRxipoazKjyLIcY7Imd0GWGZSx6MAgRWZAgLpG1XQ1ecT5eVQTXQ58kNjEudeBCSEwmEaL+abRmo2RYpRnIQGdmJgJcS/FxYAEKpXc+dC3a30c4jmFlhnH423drLPDN4ErpLQhtpufQwhLXLDC2qdS2JDvo/k7kWQrhVfde5YiR63aZy2QTpha5yVqmRd/oiwz6AzyLGe0YZhs5EzmGZuTjNMzw+F0zrSocNYKk2hdGJ/ChXxS5wkYus99Z7NXAf2h96uk832E3a+zRDD2GMxV411FNJ73+0UZpnbPaExpVGRuVjEUqXykifZFIPptQjSLUEkClGisr8lHI7QxlOWCYjFlsVhQFCWbIdqW9p7ReEJZVZS2bLWPzR77RpggoX4t43yEq2r0BoNwrTHd7RDhfa3FMpGeChriHBshHKl0NmarF41OPPPL0txW0h5NyuWbmABaxiTwKs1BJlYP1taJ2bprxl95F8ItIwSi82gdI41VOG8xJlhnqLAiDawP36kgmUqibgpMG9r/sLeJQEr+dg1MTeF6A7tW3A+fwJ54dlpcsiwx66OouH1d2wiZ06rAHfF5ykC2QlK7VD8KnogSvPCd1qqlV9Qwsbnq7vfP6nL0v2FTRmlLBANaw+zslC//9m/zmU9/mks7l/jaV77O++/d5u77tyVk9+EB8+kp1k0Dbu36+qnQXmMy3EQFlfNiXRLVMTBNSoe8Vmp5bH2hwKoInEPz6pfluu39Td/ZMC+lBB8rpQOFIL6teImq610dcE6GVoqqLMGD1hlVVeC9QquMqi5Z1DPmZ6dMJhMmozHGGB7ev8/G9i4bO3vs7e1x+fJl9vZ22d3dZWdnm9zkFEUpOQG1YpxvyFoZzdms4NPf9d2czmZ865vf5OYLz4Gr+XT5Kb70u7/Ht9/6Fle+8hR7l/bw/jrvvP0+z924xmh7RG0yshvX2HnhOe6++W1ybyXZuTLikjywpg0jna6nc03495amWF7zeA9dqCNHP9yZFftjFNiqZJR1Gep15SPPIOX5KIQp7UkPkEOhvQ9J9uSnR9TT1qaqeEEyPhCi8WgLoPYtUYVq4ul7L35LCoUN5l1NfpiEOJBDkJi2JABbK90kMBXtiWvMLbx37Oxvk49F9ZqZGGpY5uW9b/xSGnpfgclGPLh7D+YFmffC8RiD9uCt5fDWLf4//+//Fz/2E/8BL333d7NworpXPuT5wTdScQ+BkOszRsv70AF4qZSqrdG2opr/NGsU210JzJO25f2AKUVAkN0b6RvCS9O9kD6pGxFVfKMbpOvbPQxvtfKMM4XWBmMk748JxIRRFqPbnBLpGGvlAyMRkCJxlR2N0CxZE5FAKUyM3wp4b6l9LYQgCkvIeK0kaeoozxiPRmSZZpzBKE+Ckihhs6yXVWhD2beEZoukh3znRPMUCa0WYYPzdcfMpouUWk1ThxgBsK3/VGefEb+yltAJjGTkXFUfebfn0ujk7NhlLU18Ls8k9DcGdK4YkZGPcgldvrXB9saIyeaEw7M50+mU+bzGekkVEIxqaRPyqiWpWSpVb/qOjN8FBQ6rng8xVk/GqK0nDuDiUsCh8awrQwITle537935fQrMamg/1eYhEkm5wjvN5tY2G1ubHB8fMJ+dUpaF+J15j7eOcWa4fvUKt957X5JoRzOzOAylGzNa0VQbJvmIalGgdoWxG0oMrrVqzn+7T+1epX9L/TbaZnoXI+OSth33PlonpEGIYr34t7WtKXgKd+tacstIPrGaqiqbfiPeQvXgQtD6NsIp6xCyVaO8IlMiqNQ6OJwbg/NQOyvpwYL/fcNAJrCYyPwN7LlON7mdZQd+pyWF493nkfTqClT6ws/lEs1Ce0/T8SRjae//suahO+blMTZ/L+GpoKlXiqKUdBg62fcUdi+NLfwdc5J1iNkukm5Kak2jFGxOJhhjOHj0iH/+m7/JH/yDX8BVlt/57S9z784dHj16wOPHd5meHrFYnOJcNFNOzEMjU4cHb5szlsLRKIzrrElYJ2ddp24K+/oMU3//+3fnYiWlhXrfBH8pD+HsJlGLldwVF4QR3tVYZ8lzj9EjUFAHxgkFjlrgSOlwdYVyDh/MHwtjODk7g4cP0FqSpI9GI7a2ttje3mZ/f59L+/vs7u1y6dJldnd32dzclEBFRkGe871f+H6eeu4Znr5ymVeef57/5Wd+hheee5rX336Ho4MHzKennBydsFAGXxn2t7Z5XM7ZvnGdnY89g97ZoDrzWByucjjbCl7S9Y3xAWSvulZYMdcU/b3un9dQpzkuCUxI76AiJOO2juNHjy+4n/8aMEgpwmmk6iG0a1mWS4Se1pqqqjqXqUFC+JBUUa6kTlW4sjtEIZgnAVQsA6A4LjHNcaggMaudbRgirbRcmkCsOmcDorHgJEKNc04YIgcNBOkDjPTiO8fZyTFbkwkLL3b3Whmcl3wtuVPYx4f8/N/+u/ybf2LOp3/wC5TeiyQgthF8kzQB/6WR2FZEOQpcSFK/V8/3K1+sXEQK3a93HuHY1l1nVuED1xcuoRJftFGeM84Vk5FcrShljUUr0+yQSD/a0NtWWOnhCfguMm6AhYeiji9kPA7fSH+VEu1pnksAhnEuSViNUYxMCnwiExvnHBkdR8yb0hJwrnmXEnVR6xHfgZyHeF/Su9ZlkCKCGiBUVAxy0gLCWAwpAaECLaYi9dtZvpYZjYzwMmMiTFRgsmjNGbX2qFq0yLKfwvhOJvJzvLnJ1taC45MRxyc5Z/MFs0VBbW2TL2lI45KWi57j88qqCF7LhNcH62/Il/PDKus0XPFMPmlb6f1OYXlsU85ka7K0sbnBZHOD4xPFdDqjWCwoy4KyLBvT5el02rGd72vFVGC8fMgTlI9GgSkyIX7LMqOcEt6pliKNXNoR8PXqRgFbVVVLjulp++2cu3BNBcatL7wbgpXp+sV+G4uCDhMg7Rrv0daSGcPmxoSdrW12d3ck2JB1lFVNWVUUZcWiLJnN59TRtOqcLf+w7s1FGPbvpK8h/P+kY1g7pshIhOfG6EaAJlFpk8AkAwx0nxFQSolJF63PXZ/Ahfb8x3ultWacZ2Ta8OjBQ774q7/Oj/zIj3B8cMqbb7zJ44d3efxYAjGcnhxQ1wVQi3teD3StWo9+FMJVdeP5TYnzIYapb7LYF/xdtKwWVMEQJ933y4luF3meA1CWBZkhhAkHgmYw/oxpKuLdjfSgc4XkddOaxUI+efhQ1iDLRijE934cTPN2dna4dOkSl65eYe/SLjs7W2xsTCiLguOTE65eucrdO3fZMBm+KCjmC4rK8f79A6ZzzdmexY0yTu8esbV9mctPP8e9e3ck4JeVCJ6dJMMB/tS1Jc/zJca0T3v3/UZTHNdnnobOcr+cnp6dt5VN+cgzSNCVAjQhpFULLOLBjJK9FMHE0uRGor1Ahjb5q2iPbCNDMANR6Pol3ezoyCbArU00KhNAfEaUtKmMwTu5EIKgWmDVn3faF96jncWVJfV8TuY9GyYjMzlV7bC5wViFrTzV6ZRf+d9+ltJWfM//6YcpnIQBj9yQRolk3YWEo0trHvtNH6bjTC9FfBf/7koBnqR8EIItJaKGos/0W4zEdGtiEpLBZRl5nqGVQzeJWR22CZAgzG6XzRImx0NMaZc8D4CaQPg3YkISMzqFbXzmPN7ZwNRApjV5phmNcjYmI0Z5LmGtjWn4B5Esh5ATKjI3Ho9oL0Wb1Y7fE5gpJ4wdUYLnwXoJtx7bgBC50ccz3jJVrZkIQSCQSPFSgEk7TuiaUSq6Es2WYKUhzsSxnOSdD+He5cM2+W9sp+ogfaWiT5LwXMIkhXy/iFZuQysyBZNcCMCDkzPU8RnT2QJbVR1iuk/w9glf4l6fE8VuSNrZrMQKYu6iBFifSE7LurxGH4SA7AuvPkxC8jx4qACDwgZC3BiDBvYvX+b9O+8xnU6ZzWbUlQTNyY3A39l0tsRsDhFVKjAMG5MJ9+/f55lnnwVFQxT09x9YIt7Se7RqX/rEXR38blOiIcVFqxiftvhGUh8JZBmbaTLb94Md6CQkdCTilFZkJmPDaPa2t7h65RLXrl7h8uVdFJ75fM7hScGDRwfgPAtb4GuL8QptMirVnrUl4j0JjNTf16H7cF4575shZ3LaGS+VJ9E89Bns8+qtfK7av2O+PK00k8mkwySkDMEQo7wqYEf3WTfXTzyfk8mEDHj04AG/8eu/wRe+/wd4cOc+777zLg8fPuT4+A6HRw+ZnZ3gXIlWDrwNglXD6hXtzncdY9Sfj+A42/k2hfH9urGsi6YWy3l7ltQknVu/v1T4EJkeYwxlWWBtzXi8ASE0lOAzwUNKmWDaKjkU8zwX/snVaK+w3jc40Fqoy4IsG1MVC+bTU5RSPHpguJVlTDY2MXnG5uaYvf0druzv8f7162xsboC13Lx6jXu3b3P77XdwfsK8MszdhEWt2NnbwSmHIWfvqWe4bTJGGCQJ/Aq47ulYVfXvWJ9xTGFaf0/S8zxIx7kQrsv5vux0bfnIM0jpZU+5ba+7F8R70QDUtWxo5HhjYtn4vqrbDY/JI5XWGJOJtDtIa1ww8SrLks3JBnVdd6JqNJJMBUprbF2DVuKgZwXBZVkmuYlCWx4f8nk6yqJgPJ60Y3HpRW2lJrGvBlCUJcVshq9KJtow0prM5JS+xmmFcYraWyqrqKZTfv3/+3No7/meH/khKqB0LmTeDnb3OmjAloD8shYmMkZDeCMSsVEzcx5qWUdI9YFO+mwIaQ0RCz4w0c0cws+WGTJkRqONprF5VgpweFdT2brTfuyiuzYpARQrtOsh78Kl11nDSMX1ieOsvBBj3ntwYm6Zq2BONzaMRyNGWUZuDEaJqM4jfmt94ioyXU55amvDgEI9F7U8PebeRY0SOJ8kEAQxHYhMES6862qiItAXZ+LQY2C8OuxkHzDiAyMUmQrVLGFqgpT+VEpMIJvEwDYlVKPNvjSlvOTZ8LYm0xqjFFp7tHY4F+oqGccoU2g9JstysnxEno85ODri9HRKVdWdMbTnYPnsNVLaHoE7dGb7xPUQsZ1K7NJn64i3CDsucldW9b1qvN63a3+e7X/atlaKxsj3nPH3YVG67vH+WmvBeUzIi1ZUFXiHMYq9y5dA0QRoqGoJdKKVwLyiLJb6aoO+0BKqGjKl2dzclCANRmN9VwMztJZDa7EKfqXnICUS1mkSV61ZxDGyXvJcQpWL1tQmJksxipQJeQNFgKDQIaKWMWLekxlDpmBkNHVtuXvvHo8ePUDjOTk95uisYjovqepaYFIcv1d43cLgzvr41qyqv25DmrgnKavu5RATKxVZgkvpdymDu66/VfcyvbdpO0PBOqwPTIDURKPD/giZF/P8Dc0zPUOpX2afiG+J1+4crbXCHBnD4YOH/PqvfpHPfe6z3HnvNu/dusXB40OOjw44Pr3LdHaCOKSK2WbEiJ6uMHId03pRBnRoPdOohvHvPqN0oWAYSf2hc5PUos/49dvtM2aRdjOZ2JnWdUGWjYiRheWbGNVWsGZdVzSmeyK7lnyR8QwpEQnVZRnolRilUJD63E7JMkO1mDGfnvHo3l2OHjzgj/+RP8Jzzz7He++/B1nGa69+jfceHPL085+h0puQ5dQ6Y3tzgnWKnRs3GO/vU50dNbg8woqu4IbO877LAdAxRx66Q6mgJjXzXMZhnkyLAOz0+HTlfvbLR55BsnXdmMw1gMRaQHc2DgQhxgWv6xpjTMPYNIjHi5md9zFCHmRoirLAmDyKxNFoqrrm8OiQ8fVRZ0zpIbHW4a2EC1YosjwPKlUfQiTK4Y19uhCkwWRZo4ptEUIkhGLbXZ8npRTeWWxZgLWMlCJwYBiPULdaYccZVI5NB8V0zm/87M9hUHzXD/4A3mhKW2OVQSmHasywUqDbzBTVwWurpd5RKhVBpIrauRUIY6gMMUOrEMK6caS/e+8Qx2aFMRkxD5PRQmjroD3zNoQdEEo/bbGDPyPhH0s6LtczT0zPiWukRz2GBi/JZr2klM20Ymw0k1HGxmREPhJCJc+EOVINwSyOoSmj5cNZc0GqHut512qJRNOjRIOUqLydc1jvhXl2bTLa5r0P5zmclyhciBqnuCSe6CshcwoOgmE92rDlUtcFxigyREmQicjARA1f+FZpCRPf+IDpkEBY66AZUg3TpbVpogwSckkpJTb2JlPNuYiSWm00Yy2h10eZZmwgNxmPDo46SHnonPXPZ5r/qUu0dM/NqrML3Uz3Q4h+nUR6HfE+VPrEaIrMUkavhb/dd6vm0LSpUi+/5TH1iadVJYWJ3gYPPS9tV85i64q9/T2c9xSLBcWikGingdHXhEA9qkuIxzmrFMl7j3W2SQNhre3o2tdp44bKKti3Dt7F0jdFybIW9Xck6boNrR+/i4SG1hlpUJ4sy5q5ZVrWtCqrRvBXFgVz68S53FmMlogrOoFDlfeSgBlPjJoW8lt2xteZnw/pGppl7hLw8dk6YcS60hFUDHzXWefkVK4SKFyEmU+l50PvY+mYayd7Gn2VA0WK0aYRLIAkVSdYnPTbizRQKsQgzi7B630GywdBV1VVTCYT8jzn5PiEX/vlX+Pll17m3vt3uH/3DkdHjzk5PuTo6DGzxYlEoiWyDXH9guHzE+zVkzC//bp9i6GU0E73v2+OOtTW+WMWBuYi443rH/uNTIPAzEpM5HTrr97eAYdzNXUtQcayLAclScxtM7c4hoj7fUgyr3GqxigHLsNasLZiPMo4PDrk3Vu3+MQrr/DWO2/z7M2nOJ4V3L3zLmqyy3jnEseLMeYsZ5RlXL9yiUtPb/H6b+5z9H73/Nd13ZwxE6yg4hqvYzTXwcnYXp85St+BMIfWSXCu7a2tc/chlo88g5QSaTEZrMkyateG2daiq2zst02wNY/aowgYnPdUtiZTWWjTYkwWTM9UozWyzlF7QcT7ly5RlpWc5YBo4iZGJkgZjQp28LWtQ0jkHtEUaAoXTN1E09Ui5rKo8D6G1VxGkioCSmsl67l17G1tUxQF3np8rciBAg9GkSlDXtSMnGI2XfBr/+B/RwGf/ZEfpHROclsoifYVQ0F7lsOTer9aKtfbKVQn8phrvk/RZR8G9QSLKBX78Ul9T8wF1WdQ8P1xQQQkWqUd+NCOmGhKqMto4x36isyQp0PMdQjAxiOnN3svQDRCvD5R4HyrNUq/EdZJbLizTHyMJmPDJM+Y5BkqSHRVOK/4yByBc7rRSHWEAMhxi8wK0DBBEuJbN0xPXdeN5qd2jtq1DFjULEUzO0dct8gsuSWtVJdZA1y7Xl3jRJDQiq32R34Ghse3iK4xmw3MkAm+RFmeCyMUmV6jMFnqZ6RbqZf2OExjYud81CYByqBNhg4+6ZmBrXFGvreFycfoLOfRo8etjXmWkeUiTHHxPCbz70uHl89Jl7DqLEnvzvcRzxCD1i99qfGqclHhRdpGn5FaVWfduM77vv+8P5+4ZnmWM9IZ6IyxhqIyzM6O2NndRWtNUZYUpTBIrjHzoGHWIrzv3FVniakFlAflBH9Uldjipz5Q64jwdesxJElPGdD+frcO9qnpqOpIbqPvQ1WVZHmMvNhKcOu6JiaYttZirWWxWDS4Vfs22E30jdBKS0JMLTfYeI/GEJLsCfw0Nd54VCCQfQPniCBX1oBoMiYCDD1wRM4Thl20rBMmnMfQ98tFieK0rVXfpHvY918REOJjg4AK8MXhrGuI0yEfwu3tbZRSzGaz7nvVRmJN75EIlNucYOPxmNFoxGKx4Fd+5Ve4evUaD+8/5O7dW5ydHnB6csDx0SMWi6ngRqXxQdDbiWa7Qph60XX8IKXvzzJ0787rO2WiVsOh1d8PnaeW4K+JPq9KBQG5DoxsEJoGggNPyPfjJepde98zIpMmNFLEsZGxCPSLs+CDdt9anNXUVc29+/f5zKc+jckyirLgs5/9JMe/83WyzFGUU/xixDjLmU4zjieean7KpaeucvqaoZp3c8a159dielYKq2BYyryu0iL18UKk+xotUoAlJgo9L1g+8gxSVVvGNnCwlTAt6EDSK41Xmspa8GC9mDoZFLUHZTLxK+oQ+wYXLI+UMngHVSmSQfE7SbRS8TslRKX2WqRlXiTOSmvwlQSN8ELciWRdxm10htGmIUa9cxiTYZ1IBQQPe+q65PTkGK00GxsbFFWBQocEhbC5tUXUFhRVRVkuyLxnZ5RjqpLaeawBvGOEwjhH5sV0YmEtYxTudMav/oOfwxrFp37wC5TK4bEiQfdKiAGi6C9I4QkO8eEOdwIQeN84jsrhlv5jpKooqVQqAfyAostepOxL033QqHjv2woh/HkrZPNJAymQVglgCaNohNgSTS5qESMCilnRhXaKkrXWzKxTlMyh6TU5W/LMN3+kxA+qa5rWkY5oyV00Ho2YTEaM8ow81yhDiI4DtVchMkxgjrxv2pOzlWh7ABdC0MaoVtYGbWcAwJHYj99Ya0UCHyJdeSfZwl0QRHiXMj+Ourbhnae2NGuWBngAj/et/9PSUjb70pX4GiXmcEbLGSYyPFkuTI8SBGSKEm20JNs1GqNVCIMuCEkYJIfRhtp4jKpCNMKQnK/RIFmMj/kewBiN8pIn4orJGGUKX814fHSKR4QhulboHMl70QgvAjLxPhCLNJJy70VqrkwrXnfO0mrV2qhT7fr0pJbeB41cOH3x19Bknwg8jzBIGZY+I5LWabsf2sNlP5zBer3nq9pK21xVNzIHuQnJv4Ha1tSuxnnF3u4VMpVDVVPOFpSLQghMFQL0ONEq99dIawmq08zJCZwwIbKcUq1GM44rHXNaukRXcsZVC2dQNKHzUylsV+uz7FPbEdJ50QDUdU1RCDPocSEUt24YHvlOdiLCKOfbM6Q6MFrOo3UiMYjJmJ2XXGlKiUmeV+E4qlYAGVMpGGVQKqxPkB016xqIf4GlKggeXQOTXLLfHebD9+RdS8W3fQ299dHkV+B6q8VqL1L6ne713dnfDs6JHUjbJsx5SZDXzFc1daNIzUeahsCYh4ZjoBDtwfgYudG3/QfYMp/PO2Zm6eBMyNGlUE3aEOfBOo/RGRujMa6q+Re/8Rv4omChZ7x3+12mZ4+ZTg85PT1kvjiVdfPtPBP+N0xxeZ3669+M6gMyTH1hQopb+oEozusrvU/nj9HhezkZ5bUitRaIAj/Be9F3KGiTRmG8TgJomBAZL5EiCB0rEI08zxBLKRvajRrCOLa4AzIuiwVXYpzBIIG/aus5Oj5DZZrdKzucnZ2yvb3Fj/87/w5v3H6MxuNqy7yomI89jw/nPDh9gNY5i6pEexvwmW9xWGDK6pib0bfMqQowxjR0lG/cSrwnuHS0goBG4O3khDof/eMVJssFPiqFN0602B6K2WxwP4fKR55B0rSaA6UQ4OIEMKug0vdeorlleU5RlrhCbMzzPAetg9+REJi5yQLR2F6siLjSMMY2aKyUUtSWIIVrNQzWWZyrUNoDLUEYf3ovCTm1NsIQ2eAAL5OR0NFZhveOYrFgMZ9itCYzcHoqNpY7O3t4D1tb2zhrUVqJhqquyZRC1TUm5MgBj/UO4zXGevIwJ0YZtqrY1IbpYsGv/IN/yPalPZ791CdxRjRZxkvUnMggxSsX7dJBmtJJuDuXgMcODUdEtq0ZTgpWPG3oxg4wgiYnbAS/3XYdqeN7B3Yl7bT29xFoJpq8OHbnUF5C0rYA1idAZ3l8q4j8blkGuPHvFJj3gXymMkZZzigfkWU52igwouHzzuOtx9ou0SVpXVrn2kZ75JwwOV58kCJT5Jyc6ehTZGsrwSeClsg6K0EaUkIlME61taKljNokJ9G2CIyK8yoJ+NDIxJolaeiL/vL5dM2TMKG+wiC5FEwmERoJZgfGaHKtyPOsZYJ11CCJX1kW/CqkvuSoMkFzlBlDpg2ZcWRBGhWFcEq1vgRxb0ZasbcxQj1zA4vn8PBM1hmPMh6TCaOTZVnIG6IbaW88e33NSZQg15F4DX03Efd70jat5W7q5CY1hBa0WqzeeVunlRk6p33fmj7DtIoZWCW17XwfEfvAN0PfriJa0nMecyJVzlI7K/ngrOXKletMRhvYci4Rm+YL6qpukTXdu9yVQouZ9Gg0Qnuoy4qNyaQRvOR53hEspExNWhqtDcj5y0yTMy0yNWlKib7ENRVcxDs3VFK41P8+JmluhTQDnEP4O2p/4l/tOy8WPZAQgra5rQ0DhJxJE5hXCZixmsntELZJkKVoYZHWS8+DjiaCagB/xLF70MYst0E8l1nDfK5j2qP5mE/WSXpofSu79yN+1RlQM8CG/fLiaN7ch/BYB85OQaOZUUoYnDwIdJQP5vphJDFUfV8r2cw7DEwF+gdCPsbKBSHsCK0Ur776dd55402eunGd27fe4eT0kGJxwsnZEfPZKT5Y1LTzDAxRf569Mawq63DpeRrEobkOtTvEAA19MyQYGu6//3fXBUHaknotzRosiwJOaML4e5pcSX14JN+7IKhXybN+X6n1C6CEuRKBt6KqarTSnE7nnE1PuX7tKg8e3Ofe/Qf821/4Qzw6/B1clrEIwr3ZoiTTI269+S7PZYbSOXLvRaQSyD2vfCPIcwjzAjGiL41Q2lnfmZcKQpaUwW6sd5ILJngwBGeyDp2PsHjqYImigMf3Hy3t1arykWeQnJIMukopCNJZk2VBgu0wWchVVIcDpbOQ9RjKsqKqqmCKAFVVB98GQ1XVDbKygflQAbBHZqwKGiuFEEERgENrahHzGjUSHy+Sd1tbJAJIgbVCQEUkUBYLdrcm8n04JIvFglGei2lIUWBMyN5uxIyoycFXOzk4iA+VDhILjVg+iNWSwnoYBUGVNYqZK5i4DKZzfvnv/m/8X/+T/xv7H3uu5e5pJVzRtzb+GxLHNTlI+s8TE5TzSkoUdBHwcF04n1G5CPCL6566DKX1+gRf33F4XRkiWPrMUXymlCLPMvJRxng8Is8l+azC42qPV5LxusvIAT5Ka7s+RJEwss6JNshKEjvnhLmxtbwTgiRofyIx7x21ryUHk3XN+xgJT6PBx3VQkqTZBz8hPKYncIiR8IzPGyapj2BsKtkOBJwiSKkp8YgETOYu119pqHFUlemY0ZlgilglDJLJaoyODJIiM2KWZbMs5B4zwtQoj62F4cizLJjyabQRqZ1Rms3JhOeffZb5/G3mi4rK1YyswpWOS5f2Oz4AVSDGU2dTICTj7Jo8psxyQ8QOnCmluz48aenx9Z17tY5Q6Z/p/vk8j7Dot9OMNWoKVhAe676HNsv6qn5biTGQsIYeIUD29nYZj8eczs4oikWjYXHOoUwwr3NuiUCWtkXYZq1lZHI5U5VoHouiFO3sAHzrw4x0HZ23UHXHH7Wycm668xqCE32YsmpdO4xHz/xoidAfYDzXlVXwMV2DjmSfZT+6of5Sptd7jzIrtAB+mThuxpQEphgaY/8sDu390vl2vmGqunWFMB4SHrSdLk2hM57Bb3rfK9o1dc4F6b1oQRt/pYTB7s9p6N5EOFXX4ndktOLB/Xv8+q//Os889RR33n+P05NTFosp0+kp89kZDTHrfCQSumU9L7Ry/kNlHcOzTuiTnrF1d+Simqvz7sI6pqp/X9NgEtGHUgSRtbh49MYNcm/qejiC3CBslhfNGLxz+CCkKYuCR/cf89yzL/Dq117DOMXZ0RH14pSXP/sSbz6ak5uMcnbKwemCRw/ucePaJl5nWIQpj/dZ8oWGsaoOMBGGSGvR+ASc78OdjdZG+Bafi6lgOq/gyRYFdRrKqkDlgpOdk3ZPDo/W7k1aPvIMkvWOqq4ZjUZUAcnlSECGLMuoqzpJCivIzHrfmFBUVd0ctszkQarrG38myXosqs6yqkSlreMBFD8W8bewDaCC1rY7tq1UCKPq2whEMfoVtEixowaXLnBO7MG1Uk2ejvF4wubmFgTCU+yGnSQVC1I266MpoDjGEkyj8KCVQ1lH5hVj7ai1pSxLts2E+eMDfvHv/j3+L//3n2Ry5QpOq+DE7IW4VKADbvWrAIpSkeptLmyKIIdKHwj03rZAf+C7ISTXDmUZqEbJRJTELREfng6DNBTxJv4eAVX/+VD/faKzL9WNBHPUeIzGY8ajnDwwx3FcEtvASQjj0J2NbbjIINnGdDMSgM6JJrF2NbV1jeDAWfneNsyREGiRiHfe46ixvl4iALXRGC9mbpA1iLslHiyeLrEfx6JDHoW++YVIl8RTCqVCNMG4oAh0JGimItDFC7DGUtcepSzWGrSWHDUSiMNgjUMbiyprjJHw7ZmRkOl17TG6xihhpPI8D8xT8OXwMdiDhJCOmsssy9kYaV54/lm+/dY71NY3+3FychoiTbUmEFqrjkClc/ZWnFulVee+DZvMrC/rpKtDJb2T67Q6F/W3WUucrOh7ncZoqI+2nlgCpHBIKcV4PGZ3b5fjg4cURcF8Pqe2Nd47FFkDumK/HQfvcEzrusbXIojSWkyfq6pCJX5tqcZtmdFq4cDQvCMznAZ26a9HH16uYqDSZ/020rmtG+fy2q6G7UN7lT6PQhej2iS462B3HJ8wcUFQMoBHvPODZ03+gFVcyQfHSd02LsLss3oYK9uRs0CjZW91Bt20CB5JnkrM5egFZzole5xlWeMrt6rvPM+ZzWbkuWE0yikXC371V36F7c1Njg4ec3Z6wnx+xqKYMp+GgAxRSKYMfmCpLsJMPEm5aHvnnd0P2v4HrQtdYSjEKJJt9Lcm2bPOcE4sm4aYa0/LUJlEG5r2szROH7U0rY9w7TxlVXL//gO+93u+G+/g7PhMQmi5kqev7/Lmoym2WnDnrbd4+7Wv4heP+ez172e8vcP8bCow0ben0nswWkyQU0YepcTSBRe0x5EB8hKjnMRsNepnE7JA4cWsGR9oM4XPDZeuXWF/b583v/VtrNOYAQHKqvKRZ5DK0mLMCO8VdS0MQV1JFLuqSqMpCZFY1XXLOBAzi4ujm3M++BpFoG+aKD5yaPNGs6S1boI+RBvQaGeZmkBIiRHqfLgENN9FCUIE0jHhoDwXqUxd11y+fJmd7W1qa3nuuecaM7t4qSQWfnDqU8EJ32is82jvsVXdRuezNbXzktHcKJT2ZNph6wpXO8Z6g5M7t/nFv/d3+Pf/kz+FH4/FXCc3eK2DlKg9tv0SieN27ZcR90VKn3mI6qp1UqAnA47LBEK3Xlez0wduad0nAcYp0ZCaxfUJDYkiZcKFD2enjpypqNnLIMXEdzVFYlalxNTTts+FCRJ/DDlbQQvlWlvoqOWUNn3DICktfj9Z8OnRie16plQTuUqrNvGycx5nK2Lo+hh9xzuHHClPbuSe5aMQtTH4KU0mo8ZUrqpq6rrCWkdVVsznwQQQFSIAmsCgiTAgkLOA+FcpVAgwUWOdR9WqCVdcW4/Rnjo3gTmSeebGUNVBk5RnGAPWS0Zzow1ZrjDaYQxoK1rH/Z0dnr5xjffu3EUpg/eKsqwxJp4hAoPUPa/9szL43NOYzUVGOn3f/75tQwJXXKScO4Ze6RPGF2FoBgmiXvPr4MQ6YnZ53K0GLSJqYzL29vZ4T2mqsqIoCuogKEMRcraowTWO2oGmB9/6NsznMyabGw08WKUpT6XGvj/xzhwDgbCC4Rhifvp1hxiU9F33+fL56TPwq8pF9ys9y9bZzlqsY96buUIH5fSZoNWk9qqVHmbuL0S0K5olW5q/HxhfeO5ZPc5VzKJPPvJe/iO6+XYftdJ4JWaiUZiKagMvxD0diuAW35VliVKKUZ6jvOPVr32Ne3fusLezzcHjR5SLOXW1YDE7w9oKhQPvJDjHapJgLfz4MBio/n0Y6r8Pmy4C3y5a+jTJKljc/+l79zsVXGjtG+ui/t2I30X6pQ+nUtqpmbcTSyjnxbQv5n4ry5Kj02NGGyNMnvPW2+8wPTvD1iWbkxHagK1Kbr/9Ogf3b7GR1xwcHmCVofYqSN+78MRah4k5NeP8A/LzPuYqUkEBEMYcF6Rd1eb8CuxGAr8ohcpyyDMYj/n0F36A3e0dbt+9z1n1OIznYuUjzyAVRcl4MqEoK1Gja0NRLIJ/RcsgCRAWItB6cTSPyK1WtjFv2RhvhEhxgbiqHWVVglKYzHB6etZEdZHw4qCU6QD5LmJUrXM2qaOgbhIK2mSs8n2wna9rVAiTHLUU3jlMCP8tbZlG44BXeA3eGLYv73Flb4+TRwcsFmfNt7V3whgpD8EeNbOwoQ0qh2ldUVtRqd597Wv8i1/8eX703/sPmNoKnxusF62aigd8TTmPkLlI/aZuhypZ/V1KqJ3XXyqdWWZyfAd49YmQVYTk4NhX/D5E0ERgFjNhR6LfWvGhEPNGATTOe4rwM9VAgTyrrW1M5uI5q+u68S2K9wGvcK5l4GOSVwFqEiRAmAYnSXIT4qk5v3WJq8VUSWsl+YKyjCv7+2Rac+nSPqPRmK2tTSaTSWOTrJJcDyaLSFY0leM85DZDhXwRkVBQwnjUNacnpzw6OOTg8IjDo2MWZSnR9EIbWhmcU4FZccHHJNxtL8Swqy1Ot9K8UZ6Lds06MuswylBVNuR+iblhHJn1kFu0g7HxGGXQ2vPU1cucHB1yelYiEZ1Em+vxjalf65c4fEYHme7eOe+cu3VMSJ9Gu8DZHSqr7lSfOEiRcr9uLEOIPcZsWjXWVWNZWfqfBk6pKksuX7qM9475Yk5dV5RV2SDq+Fnf5yreLRUEXgQBgEL8WaNmpA9/lobVY2hT0r0PgxTrzaKGvxsuq75NGenukWrncVGz6H7pazmbvjzEgDKx3ioGqR/QovtLOg8aM9Pl9Vj2B4llSMAQx7ByXf36NtM5rDvD66JUDvY58Lq9a4kvWfzEOUajcXMvUx+5Iaa5LMsmv9XJ0RH/7J/+BpPJiIcP72PLgqoqWcxnFIsZxiAaKx8As1fQE8SsEx5+GOVJmJwhGDvUzkX7vci8hoQUqVApvRcp7JTAKW3Kgq4PY6sJGoK3q/r10ESk1cHJzWuhEw7PDih8wfd+3+d5/bU3+eI//adMtjcpbRXCjldUizOMK9gMEQ2dyqicb/Zf5pYwaYTQ/z76iwf4qXQQQkmJllbt950FTGhAUDoLDH/GMy+8yIuf+RTq8iXUxhbf+8M/zK//8i9zcnpy4X38yDNI82IBp7qTM6iRqATisjWPcoxHY2EwvDjCjsZjtra2RMLiAS85kqqqkvwygYlBKfLxqMlinkYR6jhLJwffe1F556ORMDxBvZ3nYrs+Go8aMxutxaSHwOlrV7O5sQneUywKlPdMJhvk+Qi0YmNjE60No9FEcl540RZ4pdjc3eaH/sAf4ODWLebzGcWsoCoXYjKlwedazKi8qCtxoCuxX/a5ZuEKjK3J6oovf/FXefEz38vTn3yJhXc4r7HEpIo0mqRh/4eIeFbt3hqRE8sATKkYna0nAYqIw6d9Dkj0et3I+FUH0MR2U8OXvrR1HaDtP19FLPWZpDQ0bxZyYLXSmNi3Q1kIjmE4oFLRbyjN5RUCJdi60R7F+TnXBl8QxsgTo+lE3GqyPIxFN2aNCoV2JQawtWW+mAc/OsXOzg5Xruyzt7PF9s42GxsbGG2o6opiUVCXFeWioJxOOTs8kEhaIaBDVXuclfD3cQ102OvMW4wSTdpoNCLLMra2ttje3mK0qdna3mbv6Ws8/+wzOK+Yzeccnp5x5/CAxweHHB+dsljUxNCmDTKKxvnhL+9Dwj1bB42XaMGsttQhUEPuhDGKwVni714Hsz7nmegMpQ2ZUjx/8yavv3EL61ppn0jxwOkoCeudxx7CXCKw4gc95BqfmRX3SKkuO7aOGBgKEzxU+gg4vRurhQ7Lvh3p77o3/qU+5DeiX0X4C3p3NWmh+U0lfzrvuHLlCgBVVVFWFVVZtdLJhImO9VMH+qYL74kaHjGxqztzvCiTFPscmsMQobOuvWa+T0jwDbWXEmZ95iXd73U5vFKCsDNOJZHsLsJQ9t+1bOyQ+dGK52s0SOl8Y3+D63wOPZzOTR6km9obfXOlV5skdto8Zwxp/T4u3tjYYDabNeZb0c8l3qnYZAysY4wYD/+zf/ZPmc2mlFpRFQXeVtRVyWI+BWxL0IZIi3Hth+azhLN7ZYihlfpPcrbXMayqc898c4/jmEnepX2to19Wl6ExD8FFpVh6Hplda7v3p5m3av7TYZBSU7shpkxoA4Fs8Zt4Hs5mJxydHXA0PeZr33yVT1Q1H3vxBeaLQvp1ljwDrSwb4wxtNPnGBkXtIHEx6JxDrVHBvSWNTmc0bYRMBT76UrF872R+MQCbwTvFUzdv8spnPsOVm89gdrY4q0uM85wWBbOqon6CDfvIM0jf++nPsbG5SbyY0bSntdWXoA2SuKoNuGC0aew4Y6JJG5K5NqprGkFRUzoHL7ySDewyRyng6xMN8adXEjJYQ8NwyDgzsDnjbAOAzU2Ld5p8vIm2EoJ2MhFmD6XJ87GM2udUOqN0ln/+9a/w7NUrVDubFHWN29tmXlXkoxGjwPRt5jlnJycsTk+Zn52RaU1eayYWSldBpmAx5Td//mf591/5f2B9Tu6MHCrjcYnAyAfJQPwrLX2YJQRIW61LHHTrSrvymwo2tE18/biWCZ/kPXTYG7+Em5oxebrAKpViyv1NBxgkqZ7+9JYJGnz3s/DM0xLL/RKZ7izLyfMxWud4p0FprJKxeCdZt5skrkDtq6AN8o05nbUSca7yMb62jMHWksDPx2gGARBLQEMVIjiC1jlagYQNFe3QbDalXiwYmYz9vT2ef+5m0AaNKcuC2WzOfD7n6Pg+VVVSVRIAxdYWu5hTFkUTatjWdfD5gLKoKKu60VqlzGKujQSnyHLGkwnj0Yh8lMu515CPcjY2NtnY2GBnZ5ednR22d3f41Me2yV76ONPpjAcPH3F0fMrDRw9ZlDWWjEznoMX0To6FaJc1Bo1p8pzV2qMNGO+o8WQ+I/MOHaLSGWcxhDDcpsZlYLQjyzPGmxP293Z4fHgczq8CFcJE+3gslpFfCjeWpO4QTOxSRk8OmiKaBodbk55JlgS7q0t6NvtETa/N/ncx44ZKnvXr6TDeZlzhdycHr6UtPUmesuAArlTnPWJzmLC6qucDITDaNDBEomuWzrF7+bIEy60K6sWMaj7FVSXYcbBEUM1kMi3RRJ1LIgrG+QT/TGUU09MzJLmxxtNqn9IE2cnQmvbX8zIX84FZzk+34rukPwlG4btEWmeAPcHXEs+hWD4JsR2Bz2niZ+jPtY2i1i8+heGq/T2Qs8PfJwzKEsPZX/4BJmiJEQvEZPr0QqSX701pmGcf7HcVblARucX6QZCUEr+N4JYWn2ilhZqxdYObjFI8/fTT3L97H+sAo6i9xWkxd1bK8ejBI776e7+LtzWlrVHKUtULFsUp1hYo5UO+9CS4RyqFGJrjwHH0zfu+YEbeCqrqMufdhqLJq/ipxjQSbbhpaScyjqlG1CNEvHcxdHxDFaQj64wnPj/vTp73vt3n6LMeBWatfzvehwjLFq2j5YLBOdAqa2Fd1MTKxgeBajzj7ZpprSXAgRI4aJSRLIvOU8xqpidzbjx1jVlxSlHPqOqS92/fYXt0mVovsErjtaEoasqqwhrF1Fkxr09WS6KtijVXbR0SpEkz2djg5s2bzGcLTg6OJIpecFXJg9JiXiywQXMmmqu4FhIl+ROvfJqt7W2mi4qdeQXVGVVZ8P7RLV790pewswJfXVzb/ZFnkJQSf4Co5VGIs7kJ2hgV6qhImHohtAG8dXIlrMdriThH8NNQxogfOB242/hHRCAFSHthH513TfQwRcxtEQbbI46djmFcaVOCRZWlhUjWKGVQOmM2L0RFXjm0yuSiBNwbEVKtFGxtkO9vo69e4bkXn2c6XeA8XHvqKTY2N7l0aZ/p6Rlbm1vcu3cP7S3f/O0vc/DeHY7uPgAF5WKKzzT4mvfefI133/wWNz79XTIuBU5H5iRFob79r0+AxDCeXgFKExS9VKlFlB1tju8SSnRGtOwE3RlBwsz2bdGjT0Ja9AopR/p7Z49dzM2k8Eky21i3SxDr4H8WzEEDs9fVcAW/HucQMCfMRRruV3yQHE6HoBzOBwTrGuQZJzYa5ZJXQGsypXHGgXJUZcF0dkZZzNje3OC5Z65xee8yRmXMFzOmZ6c8fHiXxWJOWZaUi4JiXnB2dsbpyQnT6YyzszPOzs5YTE8o5vPGjDUGjAA65qUNgxoRns4YjXLyXDSteQivPJlMmIyFKdrd22Vvb4/9/X22NrfY2t5kvJGztb3J3v4+e7viE/TCc0/z4PEB9x4eMZvN8T4gVC++Vcr7sNYigHDK45QgTmdFeyfBLQzaajIXTO6chGX1ufgbZRk4VaOc4vKlfY5PTyUYizYNEeGJPgPLphbxbA9pkprzNHBzBHR1/eVajdnFS3p2VQM/o3CgfacT+Bfr9qXFDSPU/y551zzXuuNw3laTRWsD4wwzkatKzAejUGCCb6b3XL56hTzLqW1NWSwoizkuJEXuAB4fzFHCHdGxLWm0GUeWZdR1FQRnfQY3VA6lvcthjGtt5tebcXVqrmCuO/CqR8Qas2yas679Tp3evDol4Um6e7TcxrnTS7juiM9XVVvJcKoes8fwei0xTbTfrcYlw4MZGsfQ6g5qf5rlSYmHeCfbMwZdP5O4JfGu5iFUtNaStNUYw3g8pigWrf+tUjgbTV4FLn3xV3+Ncj4nyzTOVigsZTlnsZjRFcCs38Alxnuoru/KZRotbrOGq314lE/hnCYzrel3SranQgD5XjrWSuMD/Ac6mo4Wl8e/WwuTdeUiAo22TqvJWl6D4FPrLVVdgsoxWcyLF019fSPoTbVCcaFTGBTzEIqGUPqs6ypEUIbHDw955ZOvYIy4eRRFweHBEZvXrwmtmeeSU9M6zs6mZCHdSBTaAm3whdC+NuGsapgtZhweH7K/u085GWOtZTIZSQJ3k+GcxdS6SSei0SijgwZfaM17D+9j793BOcfm668FhtFRzM5w5ZzJzibGWXj/3C0A/jVgkGrnqVwqORMpv62dED5KEXOoNOo67zCIb5AOSeg0utFQeCVoEFSb3K4hZoEgcW6YAA/EnDQ+lRyGSxVxrW8vWVMnJJ0MsZqxIWywLatGFe69Zzwec3JygjGGciF5nJoIY4mNdm1y9p65yUsvPkcWkPWktDx8+Ijbb77GlStX+KHnn8EZh93cZGt0g52NDRau4sVPfIJ//Pd/FuNz/MKjvMVoKKqCr/72l/l3P/M9FN5hQwZAbfpSny5xddEypJI/r953akKSthMJynX24P2+V42zT9B263WRSdo3BG1ikATL3rr2bPnUjy36CXmsLTvR0BpmCon4Ij60AXiF/jJtIPjCSNAFHfIpOWbTI+bzM0Z5zsdu3mRnexvvHKcnJ9x+911mZzPKcsHJyTHHJ0c8fvSIo+NDzo6OWcxmzGazYKJaUtcWW9dYWzbrEAFaGx2vlcqnkgRBjroJfx9NCFQIkGC0Ic9Fo5Rn4q81Go/Y3d3j0qXL3Lhxg/3Ll9m/tM/2rjBR125c58aNZzg6PuXO3bvM5kUI+S+XWSWJITNjog6g0TzHcccx6SB9FAFN4o9lg7mkztna2uLs7CwkzIyh4xvgseZkJozJBfw/IlHRP1ND53Dd3VnnsD4ULSmtO5SEcajeqn71wLga7a4Sv7OU+TuvT49vYsk00vVAJO7t7TGeTJjO52JmV1ZUwYeoz/zF76MkPxXSxLFvbW3hHrRwJI5rVbjoVWZp/brOroaHQ98PWSp0++pq9fr1n4y4++Bl3fn8oP19kLkMlc73F1v+J+rvg4xLwOOydUoXfyWHs+0MpRQbGxI8ZDQa4Zzj5OSk4TtdCMiTZzm50bz/7m2+9do3MVrh6grvLM7VFMUCH/DO7wcu7g47CSbhfef+pkIl5ZdxcfQ3Txcjhi+Xspwwtnmv+sxRglNdy8R023+CQ5KUIbjQF4al9EDMnZaZfGV7kVlK2xwSAiilOvRlVZacTWdMNjYYjcegoCxKHj8+hJ0CrzT5aIzJM0bjEUW5YGtvl42dTbJo8h/Sy5jgE299BYHhlkTuBozjeHqEGnm2R5sYY9jQk2ZMu2YPHwRS0azeBMGpxUNI8u69ZzKZcO36NbY2N9nc3mRza4Pt7W2U0fydn/znF9qDjzyDVNQVpiobiYmiZYRiksjImLSXQjX1ffDR0CFutQpx/F1dE42lbBPGUnUAVdReeITbd9a240je9w8+BImvcminggbKS2QvRIpTl2WToylelLIsGY1GlGXJeDzuBH6I5gDjbMy1a0+TjTfJcs18UeDHGdnmBjrPeP/uHY7OTtFGU7qaEsfMW/Ir+2ztX0JvbeCcRRsxe5G8II53vvkNqpNT/HgTqw1N/lvtE63Ek5chxLgkiY67llzwLhDQDWAYQo4pwbgKeZ4nSRySXq8a/6p+/aCUqGsekWrGvBfTIo9NmOA2Wp1kl68GxxDvgVYKjEF5LzmxUCHBaiZhdq2lLgqOD49wznH9+lU++8lXKBYFjx4+4tGdx8zOppwcn3B8fMC9e+9xdHjAyckxZ9NTFgthiOpijvKeuqqW9sd622TXVnWcX5RqNYvVSL5aQl9RhKhK3su3zR551YRCl/xEOUorRtmEzEzI85zJ5gb7ly5x/cYNbjzzFM/efJb9y5e4cvUqn3jhebzyvPPObR4fHmNCgj6lxQyOILVCBe2FawURkehUSgQFckeFacoyg/cSeVCbjMlkEiJORm2w7I5PNIMpMbDq/KVnZuj3dWXwfJzTT//dk9zvFN6lks2hd3Axn500qW789rwxCfgdnvtksiHM62zGYrGgqkpsDITTMLFt/c7ces+9l7QQ07OzhgFLCbl+G+vWfGis6VzPg08XbXPVt6vW9EnaP6+tVXWH4P7QvC+y90NliHC8yD27SLno/q5jZGFYwRK+bOBi/D6uQxpWPgotY726rqgq0zBGUYtvrW1UNDE4jVYKase//Ge/SVUUjEZizuXwYimwWAR654MxBOvK0h1L7w5dAUcDM9Wyf1zrD26IGhhZN02aV0clSeUjPJe2W6uR/pnMzAiPMAKtNl1sf9L21pXz4G37ftlnKe6fVhl9udCqdlO/6k5AnF5gB1s7To5PcNazt7uP0RlFWfHgwQPMpROybIxSYU21QmWan/gPf4Ly7Cy4iIgmSbkoYPIoLTg0yzImG4KTUaqhcxuBm2otFURIKdZfefDFlv0xIQCZGNjqIMzMcrGAsa5uzvLh8dGF9gL+dWCQqhpdttGDYkQ3Zx1YsLYkzzO8J2Qd9kFzFDREKfKGRn1tY8hXpZrAACnw6muVVNA6KRXDFraHWi60bqSk1kn/XgNlAHJaNwlelVK4qtUgpdLruq4pq5LNzc1mLM3F8jDGQGUZ5yMuXdkHFCfHJ6iixuzNefPxIUf3H3Lj6ackD5LSWO/xkwm5ytjc2+N0NpMM3CF/TaZg/ugxB+/fZf/jL2G1wkBrthjKk0gFzyvpfgKdfVqqm9pzPEHpMzt9IJ2+G5IE979ZNd8W8C0DvVQ6H5GcD9KpxvlVOZyrO4Cy//0Q0dBklfeezGSYgFSyXHLyzM6mHDx+jNGaT7z0EjvbO9y/e5/Xv/YGR0eHnBwd8+jhIw4fP+bRw0ccnzxkNj8SH6OyxLoa70OQkWAnkTKSXWJA5hWZ/XaoQZvSfNN9roJGJ/4M00HcQeSMAlRVKT/zipEpObMOfZLx+OAht997h8k3Nrh69RpPXb/Bcx/7GE898wxXr13n6aee4rmbN7l1+30eHRwwmUzI8kwSfvpoy63xqpu8Nd7NCo3kgLBEn8ZIJJNVkjcsJK72gSBRSoV8ai2WGyKkh87Y0N/9MzwkSLiIdid+E7/XA+Mb6jPtd+gOdH37ls9H/DtKtPvt4kFooe5ZP4+IjUg3ra+1DsShY3d3l3sPH1AUBUVRUJZlc5bTaXSDtyxLYiORqkP6h/Tdk8CMZSENXBSwDQrhEsLvIt9epN75Y/7gMP8iY7hoO+vKOqHcEgPv19/NdW2uGs8QYxbnLkLYgbVU3W/7d0fonsBY6DYSrnOeoig65tdN/yoIf71YFRileHD3Lm+/8QZGgbcW78UKQJgjh1Fi+s05a7xq/OtYwKEijFD7TRQYR4Fj6leUnh951vfv1Akj0zI+nf0dgH3N/UeYAB1NspUE9JIpDZs+X3SOq0qcT9y7SA8qlTVb0Pned/FKWjqmmOGb2G5dW4qiYjabk2WSD7SuLEdHJ1xalGxtT0CLj6eQuo6Pf+LFJu9mPLcaoQsFbNdASPvhXQPPGsEtyforFegHiMJEay35aNT4iXkB6NKf0cHg1Qn9amu0c+RKkfUSia8rH3kGqaxrVFlBsOuvi1IW30twBrxHOzlEZch10Uggolo12paGf4SL5pWiCoks+wRGK6mQr6K5Hr5LSGVZhgsSGwNgJOlsUVaQWKyY6HEXmKc8YT5icljvBdgpWnOwCPyAQHTBvJyjc83+ZfE1yo1mI8upxxN8bTl8fMAzzz5LZWsyk1FaS5aP0F5z+eoVzu7fF8LQS5Qug4L5gge3bnH5pU9QJQyJ9x8MsZ0HFD6IhPC8vvoMRfw5JLkcGlNa/6LjS4mo1FpmiMgSxlqcvIT/Ft8X76vGJK3tH85DNvFtnuWCALXGKM3Z9JSDx4/JTMZ3feazlGXBw3v3+dq9r/D44SMeP3jI4cFjDg8ec3Ym2dKLxYK6LnCuxtoaEN8drUF5S3RnDqvUELsqPItaUsK82gVKR6q6j9cgnMgvxX48cu9KX+KU5EtCK5grlNFMJhNOjg+4e/sW3/zG13nq6Wd4/vkX+dgLL3D12nWeefY5nnr6Bm+9/Q5Hhwfs7e+TGR3yRjlMCFuemrNCyB3lBK5kzuCMmCvmo2DepTWj0Yi6XiRnYvnOpGZZH1a5yBkdqhPHFSV8q4j8VURxn4D+MO/y0DhW9d0cjN575xxYy6VL+0CIZFeWlFUpJiz5aOlqNfs1wNxEhjgLQg5YDls9RBD3x7WOOR6CsSsFRgmReBG4nMLA38+9umjpr9sy4du+6z/rv1vV3u9nWbe3q/ZQBLCqpUEGSsqcp+1WlfiR6MbPUUmgEdemUIjMf3csrb92ZjJypfnd3/4dyvmCLAtMlnPUZUFVFhKExZ9v7tufe5hp/P/gOg35h6k4j6SteNe8D0lxk9KkOwGUMqhIYEWGrsE1nib6bl/4hF7agEbo4drvlWpN+ZyL+O/Du0cpMxEZ4Ai7xNzOYky2dMd9+HidcCalI5p2vZjUzaYzNje3INCY9aJgviiZbMJ4siEBM5TkA3z06AHjyqN9sDby4J3kO5zNZqAVuVYYpamd+DWP8hFAk3C+jsGcnAvMLty8eZPJZMKv/dqvAbC5tYWta4ySHIzWSi7HqqqbNdnb2eKpa1c4PT3lG6+/fuF1/sgzSLVzqJAFPc9zvAaT57iqpizF90EFUxwbOWitsXXdCRkNCDMVGCdoTdcccgB8R11pAiNUEznesiw7Go8+4Z0SuaIVCupq7zHBST5GFirriio40BljmM6mKKUpyhLt4fDwsNGcROBntEZpS0FFQY3ZzKnPJOeRN555WaBHOY+OD3FGUVlZs2pekemMalFw7dp13lPfbCQt3nvxU/Fw591bfEZB7SyZVx273ijpTSVdF5W4rUMgqxu4yPtlSWd/DP09Sh1yV411bbc9SWQnupRXS8A3zj0y1RDN7IK/m/d4xJyu1b5EINf/u52zAnRAfJkxaMBWlvfffw+l4BMff4myKHn161/n3t07PLh/n8cPHzE9O+b0+DEnp8fU1YJyMQNfo5QX3xpywGFMmFfIA+OVamVovpWCipBHdRCIShiklFnqMn0+zH3gHAVEF9cHpRqGCe+DZsuDC3bLFuq6wOiMKp+zmI+Znp5y+9Ytrr3+Gi+/8goff3zAtaef4fmPfQzrLK9/61soo9nY2kKHHEkpAo4aZO+CjyIxClGIJugdPvMhoW5Xs6yUIBKnWs3hEzHe3kdJTufxKuLjIox/+k16JofaW9euohvM4cMtA3eY1Bl7uV66tvFvrTU6y7h+/QYKKIqFMEil+PP5FJAxNPcuPIh3vApa/z5zdN5UltYx/BmFdavGMUxsD8+9K2UeGM6HzDisYlA+SEnn0Y/WF3q7cDthcE/wVbdmf6vWTa0R+yjVoCOlImyMm5w2EH3mWhje4qFhpisySB3NJWKRQiDeXeIXnX4vIMxhjIRtPnx8wDe/8SqZyYhhvJ2zzOfzMKaoeVKDN3FticKFOO00GmcD8hOcAR1Ym96pbl6sFsdC6msUglk8ISxKE3Evf6t6d0zy/VmrQFmxamiYj96XK/D+ueNRrXa3daWo0TonyP9ji8SFG4ILfUFDCheiBmmxKJjPF2xtbTGblQHNaGazKbv7lyVwGeI3X9WW3/jir/Hgq6+zk08oFgW2rvDWi9l+XUuOzSyjKIul426dxRiJpOtsGyPAGM2N61f5whe+wOGbt3jvvfcavKu9RlvdBqMIzL3Wmo3NMe9sCLtz686dc9c1lo88g4Rz4kRoLZVQTEyLEo2Y2W1MJhSLkkuXLjEeSQ4hbTTHJ8dMp9OE6AzROLxDOdu1d9U6mDvFJI+SWLMsapTWaBX8QqKEI0TVq2uLw4oMPQCHqihCbqRcrrD3VGWN0xozmYhWyzm8NizqGmNrnPJMF3OckkhZm6OMxWzGaCz5lY6np5yenqK95/LeFqPMoGqHKj25HmG9p/KOCti9dJnReENC19YLJnrEaXGK3h5xZiu2b1xltL0FjzJqW2GtIke0SA/ev40vpmTjMU4ZrKJRO4t46HyJZv9ZLJHBisCtIbJ9RBKKVHjV+donfcT/REAlnSVVgyNjBDbRN8a375vxqXjEVkvN+gxWv3TN4bpO7gLsQHmPrevQcxuIwTdAxXcAXEQWznt8SNrbMCpewi1rAzrTEsXIKQ4ePeLg0QEvvfBxvHe8+pVXef/920FT9JCjw0fMpmfM56eUxZyyLFpkEO+GVoAEP/HQRvlNJbzxP6q7jtGHREztVpwTEsYKGsS+YuVJEULcP+ttULx3TWKtdThbgffMqwVGZ+TznNn8hIcP7/DG69/ic5/9PGevfIKrN67zPZ/9NPcePeD9u3fY3b1ErnNqZ6VdY3AovFIYBTrADTGjE4BdIzmVsjxvRiKrZpuFi/s7lBtoGHm2iDll45d4pQT5DbXSjRanOj+b8yUPu80uDWeIyOu232/jwyDBPdHOPf4VV8EvaY0UXpzNnW8EyEYrMBnXnn4Gj6cq5thyTlXOkTDdaVh0D86CUsHWvj137TRF62/rSkKKI/6kzRqqGJwjWYMOLdhlXjrQKtznJUYPFUKR+w74FRToAj5z6F7zsLyP7RiGCN/kux7T0ye6fj/KkKZVZhBhw/CJ6vCDIY+VaEDiaQl+gEszbuGW8u1969dp6P2OgKcV7nRcUlLYSDcCHY3QJEZuS3ZfpYch4K0gmFFK8h4qBE+L9UpoKwR80q49G+n4mn3DYhTkuQEsr732KmdnJ0yMJPfEiU9pVReCktHyT0KidpfGL5+rqM1qS6IhT6LPRWYmoPuoowk5e5QE0IrMSaAH+qZiy/DSkW6CUvEshXfN1nRH7XvWWe0J0ImZr4ywhdvRB1qiCrtgddDC8eH70YfzfSFxOr/0uXUW7Qq8b4OJJZXa7+LcEholauR0EGgGLhmPBDybzefB70dMKnEVujjFKQXZmExZ0DkLm+HnJacP7rGIwlxausqFMxgj6nrXCju1Nm2WEVqzeqU0tob3b035ubvvi69XVeG1FgGsA+VaBklrja2DhrQ64/BEmPqqLgfXe6h89Bkknck/NFXQ0GQ6w6PRuaKohVR6dHgM3gtToUWd6AFjcuoYHMEY8GKXi5KEnaLtqZkXJSBRtUQa7EDnlFUFhOSRmUQXsYDOJN9KZctEcqwoQnJN5cC5WvIvoamth7Imy1VIGGspq4rJZIy1NScnJziVMdnYpNYIV66F+y7LEhvyyDgnyTVtWUv4cuuYnk05PTujtDVOiVrdJgEetBLTK4tj5/I+k81NRuMJZwtRkyoMWWY4PjpgfnqCyi6hsiwEwoiXOezHKpyypjRAIL3TfaDiu8/6gC1lYpa0QokUJn3nnEuQYJ+BcwEJLn8b+0slmmnffY1Y/NckXqVljpLpdcaWIsxVgDICuYAXpQ+lwllUoEU6/s4bb3N1/zKfevll3nrjTd5++y0eP37A0dEBR4ePmZ4dUyxmVNWCslgQI7J11zisQyQgSN6nuHLlvrffrZacLZMr60tKdSbrDY2GN60afQudc1RUVHVJUSzEAXlecvDwgDfefI3Pffd387EXX+DGzWf41Muf4q233ibLR0y2tihr0SQrYwCF9oEgid14T13XwiiFcbXRJqMWSjRq8QxGhjeGOz9fspgQ6c1/SP5eRrSdrwcI2iVCoddWr5umztLzVWNfcc8uVJY69oHxSJvtcyDLfXakzlnG1evXMSajrkuqqqCqysTfqNuESsbdvvOdOpPxuCGsmxw1ocKSCVH6W4c/8p13/b46jtbBDy7UDP3QrE3bUQo7hq5oS5x+kLJuP5dMmHpwsf9unaayJTY73AcXQjbet4GZEkKx7bztq4G5gxEIpbLWLbGefN6tm3wUz0Mf7kecp5Y+GphaBPQqhaNd7UoUKgb9CUYpXI/xisVZK4GsECuU3/u938UYMeuOcysK0R75INjyXuFT5iNpdhW8aTV36fOWsI+Mi1KqiViWttn4ZUV8nN6QgfMyhK99lI6wzJisLkHX14EjbXvpfH0SNEjgfb0ES9KxDZV1wtau5kdMzGpbYQLtq7oXvgP70r5TbVQcnPeCF6uqYlEUjEaSVqNWNXiPreaYzOCVwjvLoijJjbiz4CzWtdZRrdav9RPzeKy3LQzDopXk6PIJbPSuRgGZMrhSfJs8iKtHOC/KS3oTpST8fBQAlJWnchUosYy6aPnIM0gnsxJTtup3pWDhZGONyYRx8IJYnHcwL1BGJYdXtWYRAegtFgsmE4m6UVUVRVlQLCqMycnzHAXM53O2t7ex1jJfLBjlOSYLOWwSfwLrrTBUXhJ1GiOM13Q+xQTzpziWytXU0wXeWsbac2V/D1vX5Mbw6U9+klkpTnQjDffvvMfWxoTC1uxub1GXkrwtApjFojUbkTDDHpMZNjY32d/fD9JURW2t4EclEputzQ2yUc5kMkEdg/dChO9sb3FQLJidnbJ35ao4xrk2IzcMAZJhINRHhOchzaHnfaZkqKzy6Yj9DYUtTgkRl/ze7y91eOxLVvvE2JOU1rctBBvp+bwsl6D1BLLMkJsshNlU3Htwj3t37vLySy8xPTnln/3TL/Lw/kMOHj/g4OgBR0eHLOZTymIOXkK5etcGFFm35kN/fxgmOv21TJ8NnbNV/Q6tWSptjIxM/GcrS1HMmRWn3Htwjxc+/gk++13fw3PPv8BLL36c9+7c4eToiN39S9SROA2aZ62Xz2hd12RKYVXMON9GKexL32MUqTjuD9sX6SLloszUk+7x78cZeZI+UgFD/Ke1xnjY39sjH+XYqqCqQhLjAA/7bQ0R7+nfWmvyPO/s5Ydd+jBzlUb+IoEZhopPtJpDfV64nYQA/f3Y7w9aLqLtWsWk9YsIo6IEX0pjWjrAhK7r94No4VLhnAhtl3GR1hJcJppnx3lFvOK8Z5TlKKW4f/cu9+7cZayN5IKsK2ortE808Rahjo66rKXx9xmPZU3IMDPTPyt9TdcHLatoiScpq+bWryOMlPwdGaV2DBfvMxW69Lvrj11gTTZIZbX08DI8X0U7WedYLBZsbExaGgeNDQGGWvNFT1mJUF4p8VWL8+4ycolAKpw5eUnzPP3ZTDzSXaqXeiUsilhBCqNkjOBgSfsr7I67YERB+NeAQSpqGAUmw9XtYoo0tm5/D+JGuZACVDwxtr0H6lYyoQyzssbY8B6DGcnhqII2KJtssKhFAjPe3KSqaqrKYowQmK4OGh0roX+V0ljnqa2oHFEjFkWFD2MUMz4JCKHw2HJBUZbk2R4aS55vso2Cq1fwdcWVS/t455hOp+zu7jAej/DOkmsh/KuqoigKshAq0dY1DqhsjVfiR+QV1FaYSRUA7SQfkY1GZHmGtw6vNY4QXc/VHD16xN5zL8TglhJ2MgnTGwGKRnU06tACvFWSch9FaQNSqaHyQd6lwC4FeksARQUjDN/a6fY1PP3f03opgFhFwHW+DdMeIu76viCd7zVNLp7cGPIso64qvvXat9BG8/Hnn+fNb3+Lu7dvc3TwmMcPH3Jw+JDj08cUizm2roLk2SGmOabDAH4QQqu/3kPPVjE76fr0319kLENr229jiJmZ2TPKas6kLijqgrPplHt37/HJT3+WT37qkzz3/HNc1vu8fesWV67faPtA7nvaZ0QG1llc1bX/jwxRHGsq0ZtMJiwWiw+NMOiHxe2v0br1O6/ti47vwz5DqwQyFy3tmjvG4zF7e3scPHxAWRYS7jskMY4+dkPCnK7kuN3XCHMjcTQUvvxJ97YPV9N+L26auR4etpO7+HfpONa9X9feBzvjXQSxClak42vWMNFY9Oukf/f3ddUcbEwFcM58OmPo4ZLzGLJVc1p1nztCoES7FeFS+q1EMwXtPF/73a+gQ5CniIfLcoG1Eqm07WA5efpFzoCMe/mZjGvZ9Lz5fkBbNHT/+uuwClcP9bEOx6xLv5DuaWayJSa0wQO2WjoDF+0/fZ7SA5GO8s5JEnKWlUZ9PJeuWXo3xKRaYWsb4FcYt6+bflxIjO49GCMhwLXS1LUl6+Hc2OdQXsl0HSPeS99pJQaVMbkxwVJDKdF0Gh+Ft0KBZpm8t96hgw+p7ROea8pHnkGaTmcUVVDfxbOgaFTQ6WUSwkRs0mNSQNnUuGHyMxL9HYK/+bv1p4jPQSIhRXOZGO1KQsZqieGehGksCwm1XFtLbduxN33gcV7UhVlm0E4cwLWRjMfajJhkGUorrly61ETIy0Y5RrUJtgDyPGi9wsWqQ0S8+WLRBK6QsOitFm28OaG2lswYKocwdmXF1uaYR/fu8LyzVFZyz3TNX3sXfeCunwdMFUoyJyeAIL5bx2gMtTXU9xAyaRBeGh5SqWZufWanf8n7ffSft+cISGyX+2PRvX5inSZqTwJMom2vcp7JKGeUS8LU6ekpX//q13j25k2quua3v/QlDh8/5PDRQw4fPeDk+IjZ/IxFOcV5K+FKW9JB7gDtGM4rFyFyziPchhjlPvHXJ1rO6/c8hqC/986L2WlRLnBeEnQ+vF9zdnLMydEjjg4+yfMvvsgrL32cN995l8vXruFRkpDaLNvDGyP5IiLhHE0vVo0RuuZT3ymjsuqurCoXWaN++6va7D//Tpi9/vfrxnnRb7VSwQxTs721zcP7d7HWUYXcc866JsJouqfn9RfvaF8DKOt3cYZy1d99on0IhgzBpFVjXlfvvLu/av/XEfxPMq7zYH1/X9YxMvI7REuJVQx3/Oa84CRKCAb6mqL4+9DK9eHDKhwyhE+GxgkQ8+KkbXXhptArSmlMD4/GuiYzzM6mvP2tb5OhJCKZEjO6xWIeglAJUyQR3johJgbXaB3s6e9bpKni6qU0VzN3htduqKw7t0PM0tD+X7S97nfLFiux7dbszi8xDavbXz6n/XvvfUxZMzyudcxWH06JskDM7DY3d1FKBRowo6prhBnJmlDy0T9Y7kLbdhtsarnPdB5DP7MsI1OaEcIEGW0aqzBtJIKd7tDiCpOJBq2uaxZlKVGei2LFmi6XjzyDND87Ix/X4rim5MIbbXDRmTxsVp7naCVhBW3wBTBaLrwn+JS4oK42ojYU3xwhdDJjWBRBugshT1Jw1DaG3Cgs4ldkKxukkCZEppOxqBCWcTTKAYU1mqLsHmKRPnoyJABDnucYB8pLGy5ovUzQ7iskkt50egreM8qzxnfKOZGSaq0Zj8fUdU2e58znc05PT7ly5Qp1XUtQiVrG67ViNJk0jtrGiO1pWRSQwaP794IjnhImghXA8Bx6IL0Y68pFiPQPo/SJj1XvPyhwjt82kpKBsPEpAB0ys1pCHAomoxGjTPb88aOHvPbN13jhY89z/+49br37DkePH3Pw+AFHB484PTmkWswlxGaQDjWBMGJQjDg9dXGC5jspfcTX18ClwH6IWF1XhhBMH1C3ReMcIdBCIWe8LrH1gte+UfL48WMePXrEJz/zaV5++RVuvfc+W9vbTVbviAjrkGw0SuVi4saqqtYSjt57CY36IZW+cOiDlCf5fhWR8WGdlw/93AEmy9gPob6tFelpVZZrYdcqIgsQs2TVFZx1e/zOSmqmsm69+wR3HPO5zKWoGla286+yPOkdP1cAsKLtoe+HYMVQi10DOxpUqFAMxaF5EoY09U1cNQatNXVdMx6PO7CzO0rxlxqybNBGhLnvvPcexweHkosxaL6rug6BetLJRd+kVoh2nnCiC79153nKDKVM0lK7Fzx6Q8zNEBxs5t/TsK/a7/Pu0NA40rZ0CNrVx2vfCUwT5shitSXL2ui3abmooKIdrwjztre3JJWHF8G6DcqEaMppjJGgCz76h0np0zAprIzwMAp7vWpzlsb3WZaRacM4aIliX9FkUSua/FMt8ynv8twwGhvqjQwzvfi6fuQZpOtXLzPZ2KQsikYbIra3Njn0kom3ripspsV50RhGeY42ptngKOG1QbNjgl25bEBGWY3Bt+9jmMGNjQ1G4zHeORaLIpi2BRGkU3jnRXUYslWPJ2OqqsbhqOqoQhRJT5ZlIdOwRJgx4RBgW22XUjQOpMLJSwAAEE56Mpk0yQ93d3fJ8jwAXMPWlhB1RVFgtKG0EpveVTXKQG0tu7u7GCOMZl076loYL1vVHDx6hK1qVDbBOkeWqSXEfS4iTkpHWpcS6L1yvhQ7UR/260Wo3vBzq+s2QHRFn0P1+wh1delqh9L6UcLUbzuuj3M2JIhrAcp4NGaUi7Pj7du3ufPe+zz79E2+8eo3uHf3DmfHR5wcH/L44X3m01OqYgZeHGyVVmhlOoEq/OplObdclJlaBcRTQBqBbLq269pcJ3FOS4oQh6VcQYPmPXVdihMoNbV1VJXl7GzKydkp80XBZ7/7u7l1+zZb23sYnQnsMC3At9aSmTYEewcB041klZ6fVfOT7+IH3Xfdb1pio4vwPyiBO7SHyVlZWXpnqvf9BxlDXziQdLNmGMk6J9U9ko39xo2n0Er2qSxL5vO5aJDyFSPpEVLp+ud53qR6iMRDbwrNKHxvXBcpUesl0/LN3IYk+r6R8EJqAhrfx3fynM7z2FdnXL0z1t3XJzlbfSCz4tv+wYlyt2Q+0MMf6cHsE9zed7paOsPJ2jRwN1ZYcdhVJA6baq1KSe54W28VbohtOLp3OQo503retfvtQt2yLMnzvO2/nZCsj/cSrCmdRzg7MfLdN7/xDbwVWia6ABTFPJyhxOwu4Od1jLNW3TxCS8FJBoSEcV5p1Tak9bKGZyXj6v1K4KJUwv97mnDeKZ5Jx9ifX7M3a/rwCW2hlA4BLzwxZUrUJA3h+n7fF5VHxIBKqoksqJqfq3BiimtSE0J57hiNxmQmo67ke+uiD5LgubqqSM8XTnJSRcsfWSdZJh38mY0xIW+iwTlLZSWJeqSJCXYs3jkq51BO/s7EwSVYWjl0MicdmaMsJ880mVbk4xHK/B9sYvf+++/zX/6X/yW/8Au/wHw+55VXXuFnfuZn+L7v+z5ANuAv/+W/zE//9E9zeHjIH/yDf5D/4X/4H/jsZz/btFEUBX/hL/wF/u7f/bvM53P+yB/5I/yP/+P/yLPPPvtEY9nbgMnYwWTUgtxwiCOzFLPeGzMO51uFSFNp4i1NPolYMQ+q68ggaZyr0CODUmCyMSBRYJwLNrmuYLQxpsoyqnHwtaktGxsbnQsoCLQi38zxzmJ0RhYCP9TWNvbC2Jqt3KN9BSjQBm/j5esiBWMMo9FI5qJgPB5TLhaUi5KqqhlNNqitY2wN2oxR6gxbe8b5mKoo2RiNKWzFeDKmPjtjZ3OLDM32aJPMlxRe7JBt5VgcH0ExQ43GoDK8N52LGAFOptuD3yJzubzOt+Sh4C0fAGuLBM5jNpaQRwOYAnJKgXgI8dvgzIgnGllYG4IyQuk0ul0Hh3v6mLWRpnjvJepfDxC1kkAfJD/LEfc0Kjj9J98G5sV7G46AOMgqFPk4YzzJMa7m29/6Fmcnc/a2L/PbX/pdTk+POD58wPT4PgcHj1nMZ9RVJfMNWCKuUcoQNoD/gwu2Bss65BP/7iOqvoPpeQjsvH5j3VXMlvdyBpwHH+GF1lDVaDfHek/tK+y3Kuq6pK5LPvdd38WdO/fZ272EMZIMD61BSwLBqqzIs4ztzS0JzDKdUhRFcta644pnxNoapbKlcbZEa/fb1qwmnVuKx5+EgO1vfrfdZgRLtEmf4bwoB7Ou73YMLVE0wIinZyA9JwmcCYOUUM9KzIgwhivXr1FZi/KKuqiwixpXWZi0Z3CZsVg+VwAaQzErBLkrApzw7fhjSP7+XiVkZH92fQIzrrNuW5YzEGp3mK+GqWjNmPp9t9J7OsSf8lGwFM6mbg9Ue4eejOmWdAVNz+GMprBaNfXW+lkn73QE6JE4TUM7h8oCM7tnVojv5MRFIUaMnAWNGKPByUTwH9ZFmSgGkHox7Hporzv3lhvt7GgYd4yE6cPAl+Ba5ztJgeqsoy5KMZ9TTghyErP02GLLtyERxRyZVmQaymLGO++8ic4UXouvifUV82IKOmgCGl3Z8PnvFt0ZZ8swggpWCpHpUZ28Rwrl217EsiGc1VVCtbAuzXqroNVrIhTGe9fTWOl2D3Vmwt7LdwTi3oVz0AS0CGejaae3hS1z1GrEtDZJSHR5lmU65EuKeQ27jEu31VXMXls/+jhlWR6+afWaFxFQtsJCuTvW1oxGuTDFODw2RF0N+UCdoixrmYt26HB2FUjIeiUnwGhFhjBIWVBE6JDMuKwrVKZ45plneHD/PraqRNMZxl2oCPc8lFUcqDQfYXIQjBhtMMYw0Zrt0Tho8VdItwbKh84gHR4e8iM/8iP84T/8h/mFX/gFrl+/zptvvsn+/n5T56/9tb/Gf/ff/Xf8rb/1t3jllVf4b/6b/4Y/9sf+GK+//jo7OzsA/Nk/+2f5uZ/7Of7e3/t7XLlyhT//5/88P/7jP86Xv/zlJ4oCtLORs7E1br4RyYP47ETHMm3GKMSO0VmPQlPVFXVV47xDq3HD4aZSaxsYoCzTaD0iMy3xJodxRG0l8petLVrVjCYGvTVqpFBZlgWJgcM5L3lplMJ7Sz6S7OuN1NyYRhOkvCHPJJdFRH8uSMFE+tGVbEwaszhPtZDEXJf29sB7RqOccrFgWi5YzGecnh2ztblBrRwq19iRYoFiNFZMD+YSKrr27OgctMUZSVyL1xSzGa6W0OYRAA1JYQQwR+TVRai+R7ho1SbXhfMA8HCJezbUhkhKEi1PShDAwNgRNiRhpFKQmKLzLm2mOvPqt71OCzZEMDf/8E2+Ju8kVH2e5+Dhm6++xtnpFE3Gb33pS5ydHnN6csDx4X1mJ4+YzWYt8d2H6u0gB1b0YvtwHiO7ikkZXPOBtjqSRt+et4tEensS5mnVGJ0HrKNGkk4777BviAmKd47v+74f4I033uby1asSsj8SyyE8vguBVKL5FSCRAs0qR/CWyP0g92DVfC4+//P6bYmAdeWDDf0ic+5rFFv4Ad259kmMhpAKBL9zjitXroZkjxbvPGVRNsKzQYaoB7tU07CMw7uWWFfhZeMPS8wPsjzv7nUcvqgpfGvOf0I4B9quEQQ1UDekLBgsvcmkhHTEMsNwrfvzIiXhv8K3fROsZEw9cDU43oYxSgjtDjxOBXEpHmr7H262y2R1YFXDfCZMZ6jXaKgHtNNJpx2GpdfdQPVuv6p9gdaasizZ3NyQR4lLQWfeaV9BMxYl9w/u3+fw4ICR0UIQByI5DQPd+Ul/7P017dZIA2MYbToCsLROX8jar9PXWqVMklaSoiXFK1HY1LdsaZibgYPrA33V19iryHglWr2+VUDU6GndP9Pir5P6ETd5DNedk3NKwxwpi3WWTGUJQTLMUPYFhL0GG5rXGMN4NKJYzIOvswhojRbmyzmhQ8YbG3gTlAZK4eu6scLSISy4VYpKe/TYYMYjnFbUpceXlnfv3BXf/FrOZGSQNT1z+zA+5wL8DCVGacR7MqU4y3I2Nzcw48mF1/FDZ5D+6l/9qzz33HP8T//T/9Q8e+GFF5rfvff89b/+1/mv/+v/mj/xJ/4EAP/z//w/c+PGDf7O3/k7/Ok//ac5Pj7mZ37mZ/jbf/tv80f/6B8F4H/9X/9XnnvuOf7JP/kn/NiP/diFx7O5lbO1NUoISo1HGBCtR2HDo4+AwmpRI2ZZhhtrqrIiy8XRy1qHNqIcl0MlDmpZMMvThPwHsa4WJzFrK8Z5JkBL6YaBkuB5Fm1iRLBu9CGFlsutgs2yd400Q+uINsV8zloXpKfrD7/Hs7Ozw/vv3mZrYwPrLUZ5Mhy2mDE/PcYWc/avXaGcTXFVSaUdVbUAW/PovTvog2NYFBjr0K6XxbqqmZ2esX35BjYFhEvEbov2L6INGiKY15Uu0zEcLCH92aqQv7OoUqvG0bRFwkCpLsM9pPKODEBMODhUxwdgoYDxaCSmoUrx6le+xtnhCYt5wTtvvcVsdsrZ6SHHJ485OXyErYolYD3UR38eFykftI0hBqmP/Prtrav/JGMfqtdK24PMqnderLV4Fdau9hQLz4lXvPnGt0XLjOKVT36G9+/e5cZTzwCeOiQWjcmnXQif2uTOMiYIcboEeHtW3Ae6E4Pz4oOvV7+sOz//KktH+AEDDMdyvaHinGNvb6/xzwQ6uZCGwmWL5LvbTjThzdLodUTJMYNEVypkWVVWwbT4+6CEGPDhLKuB7wb7WfMunkGXMHHnCTb6MHHo+VA/T1x8jydK0KNK3q+d4AXGMsQotwTyMAE6tEZLTNZ3WJRSTKdTtne2O8/W3f3oRD8aiRD3zTffFBgXmSsfzPIuuGjLazXsOxt9MjuMyhr4n74fYiRUoJvwXV+Wfp003HaKi+Pv0Xoo1veBwViFe/rft6aA7fgjjZdlGePxiEWxaNa9K8gP1iEfoJy3Pqu+SUtnTWiZLq3FDcQdTYPAx0kQsGBCrrRYS2T5CJ3laBeEQ0qjjYSPt87hFDgFJZ5PfvoVXvz0p6iM4tG9B3zrN77EYj7D1sEKy0meQJwnU4lvUjM2gruKJIH3IVm99aIR1TjObEVmC9Ti/0AN0j/8h/+QH/uxH+NP/sk/yRe/+EVu3rzJn/kzf4b/9D/9TwF4++23uXfvHv/Wv/VvNd+Mx2N+9Ed/lN/8zd/kT//pP82Xv/xlqqrq1HnmmWf43Oc+x2/+5m8OMkjRpyaWk5MTALRyKIIJko5EqsI5hVJiP6uiFsNbjI4HSknW81yhtBxWYzySCqm9pLkBpVzIoi7EiwRJ0I0QQmcGCGF9vaVNGhalGIIsW+lCkCxUrlH9a6UkGZePzFz0l3CB2ROU532Xi+5LXrSWkJOPHtzn67/zZa5cuczZ2Smzsyn2wRGcnXFtdxv14DEHDx/jrGWUGeZnU4qy4Ntf/Tr23gF2NhefJETVbIzBekdVVhw8fMzOcx9H6VYUll6+FBgOjfM8BDv0bBWDE95CsmerGKGhvuO7JUAvlTtt9sfSHx8Q8k60oZxXheLtIwlh8to6LcMr59F7j9GGcTbCoPnGV1/lwZ0HVLOSt956k2JxxtnZAdOzQ87OjqiKBVq1uZzOI0BWMSYrJekDc79Im6vK0Jr2CY5+yNVVbV+ISOl93yG0QmmQWLj/MeRoyRznHe++/RZYMZn8ru/+Hm7fucP1G08HM5UAJ4zpINLGX2/FmZI6q8fdYQ46vy9N64nKuvvRL2sZzTXtXUQY0ZfMnnvmziE2hwgd773kcfOeUTDLqCoJxVsUBWVZdqIxdcbQ606gsgi4YoLFKLlWKn4bfDlQLUx5QngY61307EeGv1+n33KXuOPChPEHKf09TaOUdseZmij24Aiq9Zkkrv+qohp6QLQrXRwx+EVvPEPncIhgjqXjI5bMuz2voa1B/NFd/U7fSnVNScP7siwZjcZrYVt/rpGhqGvL22+/TZaJ0z1KtJxRgzpUVsH0/j1Lf49jiJqUofkNBSDpr2FsLwpsYyCptK/4jdZtm0NrM9S2wF5zYViafhd9wmNfkRm6fPkKVV1yeHgoEdZUq/nL84y69o0LSHeMw3sZf6Z1I6yS1DXQjxCyDu5297nFt9FtoKorXF2hlW/86q3zFJWlsh5qB1byfTprKcqyOds1DpcZ/GTEjWeeZe/aNRbKM55sMXvzHl/73d8L50IETM5ahA+yEhAiBlLzYUqZwiqNzgx6nKPyjNFkjPWeycRw5ZJE37vx1FPwm796oT380Bmkt956i7/5N/8mf+7P/Tn+q//qv+JLX/oS/9l/9p8xHo/5yZ/8Se7duwfAjRs3Ot/duHGDd999F4B79+4xGo24dOnSUp34fb/8t//tf8tf/st/eem58k4YoBiu2osGxiiR4mU62mR6fMw/khJeQBb8X8TMovUDUtCYs2mlG5t2pYSr1s2FDJx3853YU/oQDjyiqsYZLRxWY3TzLibbUkp8H6KtufMWQwpUaJi0JUCNxyJ2mfW84F/82q9zfW+PjfGIN179JpwWYGW9FB7lJbRtVkNeeVymqOuSkfVoZym0x2YKFwJEOBzeWg4fPeYlFM73iXzCXCQgRLNHAwi6pW+WCaJ1DFNEQKukJn2E1lHlD4w1BXKd5G4eUiC1LnTl0ngj49zzo2kTrXX7jh+lDFKnH0BpzWg0QivFW99+gzdefx2c4t23bjGbnVAWp8xmR8ymx9iy7A5nDVF1HnO6ypRtFSEx9PeqfuLzixDlsW665v3zv6q9VQzqqr67+xIJGot3CqcsWPClZ3rmee+92+T5iO3tba5ev8HJyRHbu3so77G2lSambWutJYdKMv60z74ZQWccvd9TonKVqHzd+q4i9IbKKqFA+vtqIcb68ZzX9+qi4v/P7TfN7RUJgCwz7O/vU4b8UymDBL3z71uGKHbt20vLeDzm+Pi4gc0twSGWBfE78QVcTbD0hSh9QUGst8rBXOCXT5iktK9z9njlG9UMed056M9l3bMhBiQybJGZXIaFvsW7DT6OwpPEvK03JK00Tg2bcPdhSX+sQ4KidFjn3Z3O3QiWKAzMvT/sLmO43E9kkDY3Nzv1Vwkl4pkxwSxqenbG3bt3UUosZDwSydcFTdKTFoGT3b87MJrV4xqaW38NoGXu1sEt2a+WcUjxeoS//d9bxjaZy0D/aZ/tuRNNRj8PUpZlzOYz9vZ22dnZ4eHDhxwdHTXfRZpjKOrb0JWKY0kZqsiM1XUt8xwKn5iMex3sjWsW10bm4yVXopOgQ9EFpLKOs/mceVliFxKh1VqLrWvRHjmHVxqrwZUV3/jqN1hYT6ng9W98k8evvUVR1VhvAQVaCZOlFX5kUMozHkvUvKIouX79Gh976SWu3Hyam889x5Ub15hsbqCMxgGbGyPyYLZ+Np3C//OvrFyHtHzoDJJzju///u/np37qpwD4/Oc/z6uvvsrf/Jt/k5/8yZ9s6q0CQuvKujp/8S/+Rf7cn/tzzd8nJyc899xzwowohY+RMpxDKY2zLUcaL0Br+tBKSKIMok80xYOXOthDVPmp5Pdwqbxusvo2RLx3Mr5EItxFCtKGUgQmKEianQvOfVDXVeNvAtH8LiCDJcAAFsgUbGQ5jw5PePed2+i6ZnZwRF4ijKQSdanCkynIvCb3GWXl2DAaagmbbrXMQfwtLNpI8IX7d++ivTgcorpALv7u/cVlkem3F8lBMYTQhiRvF+07AoP0b6F+1n+7/A1ClOjWdG5oHun4lvIR9AikyCiP8px8lPPo7gN+44tf5PLePm+98SaL2ZyqnFEUp0zPjiiLhZiCesN6T+fV65GWIYlov+7ymNcTC6uQ35MS1U9Sr0/gDBGfq4p3Dudj3mNxVgWoK8Vsesa7777NeDzmB37oB8nHGxSLBeONCULD+caMowlx6j1K6ebd0LhXIbMPWs5b2ye9Mxdlui5S/19V6RI9ghNGoxE3b97krTfeYLFYsFgUjTYJVkS5ij+DEMVDIx2fzWYCEntzT8UMqke9O5bvQV+4ko4//p4KXDpCDbUadvX7Tqs5lUwureMDZ7jWIPD8MsTMNe13+ut21WeeBPvJM0m3IQKtznL59qdqGqVz55eFDHTq9Mf2nZ7jzrcXuG799Un3LhL+aWLipT5iV731FQZJ8+DBA2azGZOQ5BREmh+jrF1kpn2YCv2/2/Os0R3LirQMRXZLmZjYVtTIAw1tN3ymWi1SH8an+ej6DLtY+XQjqQ4JKPo/Ix5P6Ym6riX5dFVy9epVnnnmGYwxHBwcJJYlumGSVsHgoXWJa6iU6kQ8lEAhauW3q0ojVAlzESZMcF9dFdRVSRYsn0yWCTOF5qAqQjLhoDlTTgQRRmCiB2xZ8jtf+Spfff11KhcwaF0y2szRZszm1hbPvfAxXvj4x7l6/Rq7ly+htWZ3dxetNcdHR3zs+ecZb25hJpOGNFNKYZ2jLAvOTk9YLCrR4j8B2fOhM0hPP/00n/nMZzrPPv3pT/P3//7fB+Cpp54CREv09NNPN3UePHjQaJWeeuopylLUjqkW6cGDB/zwD//wYL/j8ZjxeLz0XGGwtZMADA68CxJFpXHOJpdWyz/v0CoDFSJ3IBoSMYNQGC2HzYe2RHofL4FtmBMC8SoO9IaRkUNTVRV5HhNZtapgiJeZ7u8qRHULfzcasNBee5lbiB99mZakbwgQVcDe3h5HozFqvMmzH7vGq0e/BwQg5ER75J0NznQwpQIlDFkW/I60l5zERhvQUIfEpIvpLMS/j867sWdAdVXfafGByeu+9MncWka0BXrdv6MvThfAtuZpnfUYIH7T8K3Nm/i3C7bXPh1PW6fPhEXfAyCEzVZYF5F1z445yOi0cLgNEM2zTPbftRK+VsLkcNZhRhnj0Yj52Yxf/IVfQKN46403mZ2d4WzJYnHKfH6Ks3WIYTPM1DwJERxLlFatKg2SSttvDznQ1aR1GGnSHX8y8quV4kYH+Pb7PtJbGr9SiXQ9yh5Wr40LvoE+nHlFHQQolmIxR6F5+603ycY5P/xv/CEODx/x1ORmMxYPounuEdmeVsgi0lffrGdDoAwQynRme7Gymhhd1sqd10Ynal5v89rPu8yyit+rOH46H4bptyZTqt2SlMCNlTsmagA+MZMc2EuV7DdKCZwFsizn2rVrfOu115hOp9i6oioLbF3DaNyG6g53WMbXrn8UcmmVkRmDtXUgeNp8WC7xLe0sVqe0cC7OV4I76M4XKVj0jRNza74Xv2/v4/BaxGVqppe2nY4qtKHSDVmxxkv90DtvKu6Rj4ADFI1GBe8Ds+hRmA7RJlc2zM9DjDCXNSF9Vfhu9dmKc/feNbq89FsfxtT4cKnkTKUtRnjXn2vcwzi6pM+obUxIV5b2ps8YLtdo5tL4MStJDL9cTw3ea6VUk+/o1rvvyppbG+6TxzuLtzGqGWtKlykZYo7iOvgQ3czjBxn//rjjmDuwIzWnCybKAveXGRdnhVkZjUdMJhO2t7fZ3NxkPB43UYmVUlRVRVEUWOs4PT3l+PiYxaKgtnXrSx7W24VQ16kgMGWe0sAL8VlZSmAfaxT379/n5s2bPPP0MzjrODo+CrheIiXHJK3ybboiq+9vuk6pL9Q6PN+nGZMXche1pA2xwaLJe0dVW6ytUDhqD9f2L/Hw8SFOa9jf4ukbNxiPxzzzzDNoJbm5yrLk0aPHlEWJNhmTyQbjySZXrlxhvDlh9+ouO5f2uHTpEpPNTUyeYX0bmU7GYjBaM76yy1ldMZufMnaVJJANw65rCZK2M9kUq43acnR2tHL+/fKhM0g/8iM/wuuvv9559q1vfYvnn38egBdffJGnnnqKX/qlX+Lzn/88IKGtv/jFL/JX/+pfBeD7vu/7yPOcX/qlX+InfuInALh79y5f//rX+Wt/7a890Xhqb8kRbZHWEkVIaUWmFd7XSAKtKO2X32tbLV3EVgojfj8Ao1EWfDi8ELVofBqwwAsCa8Fo9B9wDXMkVducFLGPhhlq4KjCGGHc5KLJIa5rhwwn1TJ0HftSYGKsIrOOvWtXmZiMnd09Nq9dQo8z6nkZDr5HkaF1JnNSCrRDeyS8o9GI7k0zIUi6tUa5CtAUJ8d4LCobBWYLtArIzBNyS3XT6HWBSQu48e13KImG0q5bnB9hD6PzqALXXYP0usdQreCbiCgRiEQzxzgmQLR1PiISLfbqvqsyJzkvLs6HZJyeQNBEraBuAHW0fTdRo6Q1dVWhEX+x2lqssmhFAzTB4ZwlzwwboxHGen7lF/8J9azi9PCAYnYG9Zy6PqMsz3CuCmrtoHVagn/LQLPPSCy972/AQGnWdQXi89AQo0lnw20NPu2OtYuMxR9PKxoCUUoS5CCJ9tWfb2rznhLWfeLCo0BJ8BeNnFHrLL72kGnmiyn+yPPu22+ztbXF937+8xw+fMD+9adFAOLaxNGNj2M8T1o3GmanWhqp0Swl/7pEVcpwBUZ05epdjJlap7XqP9dhLClR2K0bxqpo7mLDRK0YWgof253yyfzjo+5JkXHLM+fbfhKqGIVvNDVaeTQOtEQyvn7lGraqcbbC2jmuXqBsjbJ1m6cjwqTIxIU+oj8rKLQSZ2HlbVgfmaAh5obpm97FtUyXI2VCwLu6mY5WmlY67Nv/+dRvLa57wpD1hDtJZ51fdb/v+LcPu5DC5KTu0v4wXC+aNTbfqZToDTAyToG631DDMYjPl48D680nPYc+UaKHfG/OCc4NMKnZDyC4+SZjlM1uj2V3HTv3rQN7WE4TERlCApJtwJVvp+E9JsXzvXvQUAphjNa6EKlXUffSY3Tom7AqdV2jnEd70B7uv/c+I6UCTBIfautqbF02670sWAkuBNo0Zz8yQ/Gyy3vd+V3Rtfzoa+bWCW7wwec7rnDEJwp0FkzcnAUvyZqfuvoU169fZ2tzM5i6GVBBi9UwVdJ+DBJw/ZmrKBRV5Tg5PuXe3XscHB6062k02nsyoynLCu8jXgl3HwlOYAKsiLRNXZaYPMc7uHvnHlevXuXpp5+hKErmi3mH/rQ2WhSs1ibFkgqIO1qycK7SpLz9nIIpo9d8m8B+6yy2qhCf/QxnJhigqi2LfJvnXn6Z9957k5ufeJE/9Mf/EPuX93HOBWbTsrm5iVJCL8d+syAIVojWxzorzA0J3JatxnoCXVTjPJIz1DmMhnJ6hrOWsizJsiwEG9Hsbe6S5zmZh0tPwPV86AzSf/6f/+f88A//MD/1Uz/FT/zET/ClL32Jn/7pn+anf/qnAdmQP/tn/yw/9VM/xcsvv8zLL7/MT/3UT7G5ucl/9B/9R4BoN/7Un/pT/Pk//+e5cuUKly9f5i/8hb/Ad33XdzVR7S5aYiju2LfzkmSqDnbgUaInQKU130qJ31RF3cS997KJIg3sXuaUuMrznLqsIEgRYnAFGQ+dKClR0hDHGn/Gi19VVWIvGxmkGogHux3DkAYpUKMYk7G5s402Gb4ug1Yrp9aCWJQPZh2hvhAMhJj2oIzCAYYQKUYJ0W60wWM4PTrG1hVabdCuKN2xsAzw5H1LJLT1uxIRidonodFTzVE3W/SABCS+WeE3s1J6FTHIirkMSt9V75MEead1G3OFBFC5XhhhfDyrNnGglTrj0ZhMab76la/yzVdfJVOaxdkZWlmqumQ+n1KWRdextkP4PJn5VMq8XISsjkB2iLhOex1ixi5Gtp/fd/9ZNJHoI+NVUtV+6a+XUi3zFRnCeE/rukKFpNSHB49584032N7e4WPPfwxblZh8hLeCR51PGHQBSB1ecSjvTl/rtGqccUUH56TavVgnveUCdfrav6EyuH7yYmlgqQ66c716xO7yX50OE3YkqZ/A3a70Pomq5R2XLl8GJXtZ16X4INmgZfCeqJ1av3KSTkGk092R9Ge9tD5rWh3WHnbfdWCuDz/VGljVDmTlOIJYIHnR7nh3LbsM0hPNDd9hrAc/WgLzwuj2pfnpyGNJ8Xa3qUggh+fhLkYibZXfZf/Md+fql571Jf3t2IaZgyigWxqzCsewx1TUdcV4POr0tYSrwtzS+WulKYuSe3fvNvwaaLyvmkSmXQHlefhDToBSCh3TlCSHrg9rz2sv3Vcd6aMgpOvseWB2rLVcvnyZmzdvcuXKFUajEcZkGGPIsoyqEuFhXVUUtkYpoTEkytxEfHsDzl3MS/JM/OOrquLhw4fcvn2bxWLBOMsaX5/+2eqvffq7BNIYURQFp6enaK157rnnuHXrFotivmReJ7+uh8HpmYkCSmstRufNt8vwgcHn8fxLmwprHZW1aJ2hTMZkYxvvPcViASg2NycYA/l4jAXeuXULlOLq1atsbktExTowTAeHh9Qh/PdisZA8gN5z9epVrly5QlVVjZYvyzKU0jgvNPlisWA+nzOZTJr5Nv6hSlFWFZtbWwAcn5w0DNOiqtaer7R86AzSD/zAD/CzP/uz/MW/+Bf5K3/lr/Diiy/y1//6X+c//o//46bOf/Ff/BfM53P+zJ/5M02i2H/8j/9xkwMJ4L//7/97sizjJ37iJ5pEsX/rb/2tJ8qBBC0RER3yREugQxQp18R1Tw9slM5G282U6EkJvqj6jBmQYz1oGawYtShVc2ZZ1vQVfw4R2X3g3pcKxLnIGOP33QO/RJQqMYUbbW2QTUZUsxlPP/00b2QZCx1NBrVoeXxEUF6SfXmRkIs0L5gVEdbSO4xW6BCavFwUjLfWAAnoSkMJsBrVwOxBjYNfdnYEkX71fbnScl6oyy6jNTDegT0aCvN7XonSvXQ+/fGmGpfINEtwkBh5R3KyjMcS0vvk6Ih/9PO/iLeORVXgvaWyC+aLKYti0SCA/6PK0hkcmPO/yr7TMNlDDFRKXK1qJ937PnKPMEGkhA6lFbaumE2nHDx6xJvf/jaX9vc5mc556ROvoDNNUVYSmtSYlQTrkNBjHSO3jnnqjHnw6++w+GgCNoyEh+/NMjncCSOQ3h2f8OpPxN8vr9WQ1DoyEs5Ztra2yDNJDl7X9RPdpz6xUpblEhx5UuJw1XyGpOwp/utObnU7F+3vg5TzzsHvJ0x4Elgd121IILFqzVfhq6F368ayak28Wu8P2e+jKAqyLAvE8bKWAHpwQQmuB/HhPjubNqbckTiOjJxSGtSyJkP4Er0k6I3zcknwmaWxXETwkvRnQo5IVvglW2vZ3trmxRdf5PqN6+R5Tp7nlGXJ9GxKXQv9Jznoorm4RilPVZUUxSnz2ZyyEm3Ezs4uVy9f4cqVKwCcnp4CcPXqVR4+fMid27eDqZ0LGrRkjZVG665ANJaYQmA0GnF6espoNGJnZ4crVy7z6PEjqqoaDDd+kTOU0kvOuY5gYx0uSX+2Z17OR1WLpVA+3kCbEcpIMt2qmDMZGbKgnd7b3+flVz5JURUNzIy+tlVVMZ54dvf2OhEKxcTRNHR4HHtZllhryTIVkt7K/ud5jgjNJSHsxsZGY4qYBt/QWjfPUx+z88qHziAB/PiP/zg//uM/vvK9Uoq/9Jf+En/pL/2llXUmkwl/42/8Df7G3/gb39FY4iLHhYkXnkTikmqZZIC0BypBMn1Ek0YyUko1Uvr+4W2DP7ROhJF5UkqcaYXA1y3jk9gQx766Uc5ayWpVSabkKEVKmbEOQFdASIA42drEjEdMi4JHDx6CDSMM9yB+25XyizO6V+EfIkn0IViDciKZrKuKw8cHPHP1GnXiyNj3C+qJIDu/rQKWQxq2eBnaSxzHu1obsAq49BHiqvLBEbkAmX4fQ8R4x0HfegxK8gFUlkwrRiZDA7/8j36JYjqXTNU4qrqgqubM5medvC3fSWnOEl3Sah2Btm6NVmlB0r76bV6UuArCxBVIWN6vCy4BXbOEPuJI7+7QeCKsGY1G2EqYWbSmqgrmszPu37vL6699k89+93fz8P4drly9htHiUO6VQoUIj/2xDwlPurAmCDN6Z8mHBenksO8LEPzFkjBf9NwPSiHXtCO+g6oFC4FY8wOS2OT1IOO3ap0uWrwXX0AbvptMJkwmExaVmIjUVSXmSAME89AYYptlKdqnZr4JPll13vptLK/DasZmKIBES+AOt7lqn4bOYKc/eTn4bmgOQ/ty3tlaVXdorS8y9lWM6qo1GHLo79cbErDEZ0Mw/iLwbamdFdqDBmeHvT89PWVra2vpHKThrX34m/BNFnzi7t69KwSpTgUzMYVIyyitWu80QNHQ/FKB87ozv2qtUquEhiLyreAS4OMvfpybzz3Hzs4Oxhim0ymPHx1QVXXDMNa15fDwKESWFPpsPB4xGuWMxxO2r+3iPcznM46PTnj/9vvkec6NGzd4+umnuXTpEoeHh+R5ztM3rnPr3XfD2qVrrvDYBu+k916pYF4WfIyyLOPw8BBrLbt7u+xWuzx8+BDoWjKlOH3Vee+/t1bMDKPP/Dq4mNJrcubETNd7mC8K8skGSo9xLmOyuY0xmpOjA7bGOdiana0ttMko65r5YhECiYlWdhHS8TjrGi2eUqph6OMeRmFUnudMJpPg8yXmm+lZqaqqob/n83kzt7IsG7o6z3OyLCPLMiYDsQpWld8XBun/n8oQIPWIv0d6yKIWCNUCwqgujQclHmDoElhxg+Ilb9XQckFyk4XD1QUWEVDFduP3TWjI0EYK0OK3IqVpL1qWZdS1pR/eO503KKx3WAV6PMKMcvLRiLffeou6LEEryW4cfHGUEtvcBqlqGssMLybEYkLndQhxFJwAreP05IS6qiX5VFJSQjWOqTWrW96zdfuZFlmzZQbpIkR6v/11yHdoDOdJcjoMildLgD6VavQRcGSKVehXko/CZDQmz3LeevNNXv3K18i0wXlPbWu8r5nNT3C+/o6Yo0EAqlRHAnVRAqffznkR/FJkvw5xDq99a4qSvpff1xNNUUgxNLYUAa1CRrFeXHejhSNztkZ5x/TsDIXivdu3uHHjOspkXLt6hcwYvLeSYFoN59oYWochAmOICF1FVK0q5xErF2hgjbnR8hgbX7zI3cb3Ke+Xfh9yx5HOccXYBqNJsnzX0zqedp+1an3VqqqiSjLC99vow460z8ViwWg0WsojMzTu9N4OaTmH/l51x2KddbBs1dlKy9rv/XKQmqaOVFzbznntr3u+fMcvVvciJYUTEQevMrG7SFnF+J7H6Dbf+u67VedZKcVisWB7e1toAqM73zVnJpgjxVaiE/69e3exdY3JWym8CJLFvM651s9naY5r5pQKgYfG3WknOdd95ieFbWlI7CiY+tSnPsX1GzfIxqKVOTo6oixLTk9POTs7Yz4vQvCtIPgOEYWds2SZaaJObm5usr+/z9WrV7l8+SpbW5vcu3uXV199lTfeeIOPfexjvPzyy8IoPXrE888/z6VLl3n99W9RFGUIzOLQpju/Zg0CfIE27HhRFA2suHTpEtPplPl8viSUW4eD0vf9NRy61+v2QCnJu+lqoScePnzM5vYOSk8oa8XlK1cBxcnhYzLleO3Vr2LrisnGJrNFwbyoOJstKMuyETZJ/qKqY02llATGgFY7GGke731IYyKMU2SwR6MRWZY1dFKEr1UQYh0dHXF8fMz169ebuovFYnC9hspHnkFaRyAOAiXfJlpNFz5ewFRC08mLQ0vs9k2kus13CbPIIPXVgX1NVV/i3SSGdS0AFQDmO313kIeCGBwC49m9vM/sndvUVS1OjkHT5b3Dq6whPhxQIc6bEfg5L89qFCEwW4MElVIcPj5oxtsH3PJ7yyiti1xzHkLrEobd52nfF0GMfYJmFdBIx3We9Au6hIoLi9X/Pm0jEth9k0q8xztHnueMRiOctfzSP/pHaC9Mqa0tHsd0ekptS6q6PHdsv59lFeGyiqBf9S2cTyilgoX+fne/9Q0iGuormgCct2ZpH/25xL/LomCc5QGe2LCvFWVZcPj4MW9++zWee/553n37bV546RM4L8hUgrN853uWni0xz1k1me58PpTz4rsu5OvGCDQRoWJADRWYpCbEtY9AhmaMKjJhHupz4Ox5Z2yIaHDBYT8mJPReMsBbW4sPas88e6ik56Ku607I3XQe/Wd9IvxJCfv+mFL8IUFalu/mReHkUIkM5RN9c8E7ftH3q+oMCTaepKQ44SL46IOu4VBZ3pPVzF6Kr4wxnJ6ecvXq1Y6wpX/HVWCOfBIdVSnF0dFxl6nFdy1tLiwn6eH9ge8i0zQET/tzS4UhTdthvs45dnd3+dznPsf+/j6Vddy794DDw0MODw+ZTqcNAT4ebzAejdDaNPTW/4+9/2qyJDnzvLGfe4gj86SsytJV3dXdQEMDA4zaWfHu8n3N+AVIfgaSVy8/CnlDMxp5w4sljUbjxd7SuLuz2AEGOxAD3WhZulLnyaNCuDsvXIRH5Mms6hmukcSst1Vn5jkRHh4un/8j/o+vU+s6rP/VsuD57AXPn71kNBqytbVBmqYsl0vOzs64uLjg8PCQDz74gHt3bnPu8hh997vf5Xe/+z3nZ1MrQ16Kxo76JlK+2ASxmQNIGXkvY29vj9evX4c2dkH7m+Z06xyI+i6+dx1IasCRTTGT5xlgODk95cG7H3ByuiCtYDzZRGnFfHbBKCmZlSWjwZDdnR2yLCfJLMzohphIGsp4Pw98KcsyuBZmWRZiqGql0LoZbyFEqCOOzc6yDCEEN2/eZH9/P9TtXfHetvzRAySfNM4nZfWlNVHcwQcWQCCMo0iFulZ47nsrWLXZc+I6Y8ErHmylVUNVCiFZnaGZhD5QL26bH0ivOYg3X2vCte0tyoLBYBjAhl84NgNxo5H126lJnP/maEhva8Jmvs2LizlmubCGoERSu2SzYAkbjHAsPwg0htoJJRWeIUejpWXxK+uanZ1tEmGvEW4cWmZxx6Tm6cDbwg9cdRDERBpx/zeQq3s42TZffWh1D5n2s2MgF3yKRfyd6VxrtfXG/Wl/N74ZSCHQzhJnh8cx/cimD5q5GSWvxFmHgF6eIwT8/Kc/5fmzZ/RJ3SZRsypmFOXSbfJt7eAlCVlEmno/N/1X4ZLLjELx71cBjXV/Xy4NWF4nnHc/Ww+s/AFMcHtCCLI0ax34OPcQL6heRU/uhQCfMmDdO9g+odXu+Ds/ZlVdkwiJRIS1KLWhLFcUZcrBwQHbO7v8/Oc/496Dh8g0RxqolbJUpk1PXOq3a3s1OuhC+0wHrriuswqPNc+J12PrPtMsNgdm2sU06/CK8b/U78Y4Rkdv7aJZM1FDLmlPRXPoEuYRwY5s3B/2PsGlfjR+rXXb54QumUACWZ4xGA2Zzi4wylCVlWPCtHvwpXxirt3CA0/XbdIlFffJFLvCjn+2Z5+LWkTYa7rdLeL36s7Fhm7drlMT5q0QXFpXVwmmVymMWgJtp01rejvU3xWGu9fEz173+7r7um32pevqdZ1SJm7juvquuvdNdbqr3APCTfEf7bUi/NkQt0eEs2Lde8bt96UoCgaDgRufaH6ZqAnx2ShAJpal9eTkiCxNiOfWpVCE8D6XKm2/ebwfaYMWeu18u+qsEUI4i0NEttKZi7VSbG1t8Y1vfIPNzS3mszkvXr3i+OSE09MzpLBsdYONEUmSk6R9kiQjTSVVVfLs6RNqVbI5mXBz/5ZNYlpVKFVTlQWr1YLFYs7F9NTG0JRVYF2cz+f8/Oc/5/TkmK9+5SvkvR6vXh3w1Q8/5NNPP+Xw4AhiL5mwbzp5qqOgqFWNqASFi5Xa3tlmc3MzKNPt5Y13yJsUG6EfvSwSjWlzbyNzNOPhc0UJsjQly3sIIbl16zbvPn6fk5/+hs29HXq9PtVyRrGckSQl9/b3GPRzNiZDahyRmVLOmqacq58lA1PKM0LnrFYrLi4uKFycpneFU0q58xO359vPPNiVUro4Mnv2ZlkWlFGDwaDlnbN2Dl9T/ugBklY6nF9SCEc5LS1rlNIgGyCijWVrS2VKpSrHQ2BQtSbPk3C4xEQM3WR88aIPBA5aox0Q8EjXH+7KmQt9AFmv12u59cXPartMKDwxg1IVWtdOwBBUyukrnLBo3MZiXIxQqTW5ksidCVtfe5f9jQmzckV+0OfVy5cslwVlbf1V7dYqLNW0ASWgNIZaCmpjSIQhxZAlOVqkFFKi+j3uPryDFDZuJhFWWyBpwJKQSbRw24epiASj7nf+KPbvhFvcJrxvdKXw46I7tTRCta8r/tseIl5o8J+JUB/g3BtN5ObY1OGFRu1dDk0zftpZ6HwzWkIKXqCLm2k/r7Sh1jW9PCdNBcVyxl//+/8nmTQYDZoaxZJlcYahQGnvxhO5xNEu8eei6YzQCWFe086g/TZa2EuARxgCvb3PYYJVPFwWUNeDY7hMYBFfZzdCa1UtiiIoDLyWvxuLGGvq/TO7ZCvNd12hCbf+1gsEvlRakaWZy2VmBRyjKlarBefnKS9fvmZV1nz8h094/6tfs1Zad60XqC8LZLI1Fl1hoduG5vcIzOJmhmgY2LygK4VoYpKgRUlsovhI465d0wENQHHP11EdIgAagusoGNDO0hUBH+lZuxxw8LM5UO+7gGCfpDdmtgwAJeS1adoXHu4xtttHQnJvrREYlFaIJGG0MUG8PkRiKfhrVdp6pX9mXH/8GCvp2rkIAo3waR1olCDXl86+EO018ZhGOSF8b7S/w+5hWmu6rr7rSlf7/ybrSLxtva016qpYwOsA0VVzvWvpidfGdcJ3d61cF5/YsrxcJ+A74CDwdNaEsTFe2PMrr9Wu5rogRIe/W0Trl4BZ9/29uxkijiU2zbx0LZBg5ZNEQAJVvWJ+cW7FaaNA+L1L41OItBQjrXfhEkhqAUwH+rquzNeOLyCVa7cQmKTZ//yZOpps8LVvfpPJ5jYnp+c8efKUg6PXVHVNnvTZHm8gE4MRKb3hTUS2QdLPGfQzElFzcj7j5Ogl59Nz7rzzVcaTm9RliVErDl8/4/TVc4aDhEE+QisQJiUREq3gxt5NDIYvnj5jOpvzrW99izv37/H06VMePX4HI23eTykkaZJQ18rSfRs74MLHcEsC6FK6ZrVaYrSh3x8wHIyYzxZUpc3BhEzRurzUV+v6z5ckTbCxRH6eeBr2Zi+Jp7zWCpBIaRDpiM2tG9y6vc8//+f/nMOLFaO9mww29unJjOPnnyFFyWjUJ01T7t67Sa1nrAqF1k3cridb8JakLMvoyR7HJ2fO5TAhTXMWiwUgKYqC0WhEVS/J85xer4cQJpBreKI0Ywyr1aoViuItUHGi3aqqArnG25Q/eoAElzdBX7wg5DfF2PoCTZB80HgZExJkxdcG0LPmWVdtYp4RSSJC4iywLB7QBkRtcgbfboOUaRC2rQ/tZdNhe+OBWltApkvDeGPCi08/YzIYYfKMRVmhRAJJijYKVTuBTkqqJKPGMC9LCq2phaQGUilJBeRJQp73GW/v8M/+6p/x8viED/bvkJjLNM9rtXRXjN21h2ykUQoaucg1qRX03b4xPPFanV+njd1A6qvvswddS2a6YtPqUniuO9Ab4R+yJEEA/+Un/4Xj4yPyNKWuLUBeLufUdek2NitIX/WCXYtRt8RA4e00pFcJ5e6dJAjR5L9qAFISAYH1h2WzRq3lxmu8fFmnmPCPj+MBfYnB0TphSykV4g9jYTvMmY5wdZVw12gEVYt8xT+jWBUcHR2S9Qb87d/+iMcffIVESipVW+XNGyxFV5V43JpxNlfWFuEDX4FdNyKIPaHeVj9esa+u7ZM1z1zbluhebyW68kbRCGqi8+XbCt6xVC9l22JvhRdLbrGzs8NnfEJVVjYOqapo2BAvv1Gjb7isPFt3JjhUcW3frC8melj35ug7on2pA3iuOrPWlauAi3AP6O6NbwLy/pqu50W3ni4IehuFwJvWZrcNfk/oKnfi53Xru+677nXX/R2tskvtba5ta/i79cTnk4+L9soJH5j/JswqpAj0yV7ZYNCtcypuj29zt1+74621tsH48vJ13ff1zwh1uG4JOMxfJyyxTa/f4xvf+Cabm1scHh7z+edfcHx8AolhuDFi3JtQrJa8fvmEWht2b5Z843v/HNkbgVGoasVXvvldDl/vo+uKfLBBqRRJmpHlGTdu3eXo+BWzxRmJ7LMx2rRKY22V2tPplDt37rC1vcWTJ0/4u7/7O77zne9w584dXr58yTvvvENd1xwdHVHj5Lk4xlBIlFN0eGFeKWUpr7VlFByPx4zHY8qypCiKlrx63XztFm2aEJA45Ywfo7gYY+fU1tYW9x6+x/e+/33ee/9ddm/e5Pnf/5a9G3uYZIBcVbx49gWJMNy/d5fz4xO++93voVRNXWuSJAvty/M8yDP+52w2A6DX64XzemtrK7zLarViOBySJAnL5TJYjOLSTZfiPUC8q14c6+RZA9+m/JMASN2JZKLP43if+NC4RLPcmYT+ZwyMWsGUtDf+uO54MOuqcffpPufyhkT4TnY2msV8wXA4CiwzcQkLRgiyRKKVwtQVea/P2XTGr86nDIcjxOYGwzxHLJYM0wwpJHnepzcakg779Dc2SHo9TJ4h+z2y4YDxxoTBYEA/7dHP+owmE3SacnwxQyapO6PXB0OvK28+SNr9ENdr7A1r6uxovFpfXg+S1rWheyBeJ1D469YJRV1hKbYQdp+plaaXWwrM5WLBj3/0I6uNqmoEkrouWSxmVgtlDIlMbBLhIMBd387YQtQV6q4iLXhTaR2SwgvcHpQIIM7K3QCWqqqC5ce2zbjv0/C9MZCmCcbR9QvRsAH5rOZdq2s8Xn7trxtLrXUASM29EM+U9j5wNWC2gE7RBdcWhJUsZjNypZlezPjis8945/H7JEJSmxr0+vxRb1PWARQvnKwrEU6w7sjYNRPD6Eug9wph900C7HVtXSfUvk3x93X3525b3rQGukW6+TCZTEK7PIBet1d3n+1/2jGvL60vX/yufd2e8qZ9qH3d9cK0v/+q/viyY9A9r9YBsHXv1rXUruvHde256rr473XvF5/b6+Zdd6++SgHQBWzdEj65Ysyuepd173ZVP1w3RmVZ0uv1HPnJ5XndANvuJIHFcoGKc/GZy+dDvN7W9Xe33TaG1ipqYitSt0+uej+DO0Nwa8Upy9Is4Wtf+zo7OzscH5/w8cefcHp6xmAwJB/0yYZjBv0JRl5QmGcYqTm7OKWmdqyiC6piiakrBpM9hDEoJKouMcpgtMKoitsP3uH89ICNwZA8yUiyjKoqKIolR0cnCCF58Og+7777Lp9//jm/+MUv+N73vse9e/d48uQJH3zwAVVVMZvNLo83l+ejtfKCko3VZTweB6tITAL2ZVzG4tFetx90AfdgMEBKyXw+4+Wrl9x5cJdssaA36DOUUFaKs7NDjg+e8/DeDlubG+xtbnJzf59Xrw+YTpdMJlsMBgPGLgdSfAYKIYJLnJ9P3oMqSRL6/b6lBHdz2ecyOj095ezsjPF4HGT4OCbJGxx2dnZYLBYhX9J18e7ryh89QIo7zv8NkOZZ0LS08iDpJjDYC1LgEapG6Tpwr68DRf4ZfvJ6E5+/xlN6+7/TNCWJhLX43njT9htKvJC8Sx3AyekJJydn3LlzN7Tj0kYrJT766bNPP2V/7wYffutbjAYD8iTB/OmfUJUVWZYzGo1JkhQpU2SS2FxHCGpASYnIMnQiLS1xkpLLFKFBaYPWMNnawmCzcMdteFO57pDsvtN1n7XqXHdNZ1O+6iB8m/qvurZ7eNrDxm/xtqwDxc34usDwWiHA+gGnKT/5m59xenxCniYICaquKasliMbCaTqa4nUlPvTWvc86Ld91fRIrFrqW2fZzDVImpEmGEDL4IVvwZE36lhrbi+k2z4LWjhUOCc4FTet17WkUCOusfusO5K6A5PeNhjzFuge+qXTnkq/f0436Z2itqauSqiysVk8k/PKXP+edd9+1bmu60bque0b3PZq/rxB4uZqkQQhrJTE4ec4LusI/J66/Lfiv+7zdnsu/X3VvV+Ba187u329qy7o1sO6ZV7XfCAHGsDG2yRBViE2tLz37qn3EF1U3KScuKd2+PAZ+w/MMxlwGSb50g7uvWutdkBeXqwTbdWBoLShcAwS66/EqJUe37kvCJZfH5aq5Fp+5XRDQLevm1/q2wdsO6lXgcd3zrmtPfI1nsFNKOfKlK9pPM/f8d7OLGUVZkiaO3U3Y/S8+t64D6933CbKX0Ugus+mt6+uWoB4H1XsLoxAgDPcfPODOnbucnZ7zh48+5vT0nMFgaHOX9Sf0xvuMx7vcujdgvLPP0dELRqMtzi+WLNSCyXjEzvY+g16PLJGkUmJQgEbXBlXX1NWK8/MjxhtDitkMCWwOB9RVyWw6ZbGYc3pyhkHz/gfv8/jxYz7++GN+8Ytf8P3vf5/bt2/z5MkT3n//ff7+7/8eVdeW/EU0yrVuSAWut70ypqoqxuMxk8mE1WrFYrlw3XGZer6738VnjroCTF2lTCjLkvl8jhYnfPbpZww3xnzvT/+U0XBEWS8oF0t+/5ufISj58CuPGfVybt+8y9bWNpVeMJlkjmHZekx5oOPPNi97e5na//P5kPx+6ddor9fDGMPW1hZZlnF8fBzY7PI8ZzabBQXnjRs3yLKMnZ2dVrqf/waQohJrgWO3uNh9zpcgHEUuOSF2RGvquiLNktb18eSON4V1GipfZ0zpLZxAYowJh27MnBcfXM2mjtOSe1lGMByOmF3MrGk9aSeiDQeG1qS9DKOshunGjZvcuXOX5WqFRlPrCqWsAGCEQIsEZaCJecBFAdgYolRItLAxStppLGVqE7clxjKfBBeYKzb+q/5eV67bULtFAG3T0GVN2XXPXic8dDU1XaGie/CuA7pWFnoLjZlp2NaUVmRJQpak6Frxkx//mDRJEMZalmplg0gNlmGrqcvFX0SCgK+3K7C8SbPyNt/FdXSBkZ3TAA58KDDBCmqDgY0Boyzdql0W9gCxrk+mUV6EblofF2EVEY0rW7we43/r4pm85sp/36YhJfo9XpfrNehxWfdcYwxKVTbRnoBP/vAHTk9P2JhsWssFV4GG64Sm65QLLb1AGwRHt4to3KycdzXAXPf3mz6/qly3ttcJAa3vubTCv3TpCnkCAoHPwLl4YEzLgnTdXtQVFOvOXAzPw2vGr94L1rUzbmt8XfP926/ndUDzKhDlr1s3/64TdN907VXXrKvzbcB3t56rzuN1Zd0ZfF25dF2DSC616bp+u66/4uviErOw+Wvm8znD4XAt8PV/G2PcxGvv2ati5c4NK6cY/JnR3Nt93rV9QSRndeTztwHqxpgA8gwgEkmtFMPxiEfvvMN8tuSTTz7j5MRajjbGG4zHE/LRNv3NO0w2b1Fpxe6djGy0RbWqGA83ub0zYTzqk0qoiiWrxTmrsqQorbIxlT2bC2k0YLJxn7LaYzY95/TohOViRpblCJlwfnbO5mSD46NjhBR87Wtf45133uHjjz/m7//+7/nud7/LzZs3ef36Ne+//z6//c1vrGTk3lEZjSRp7Q0NqYoJ7HZ+TPv9PsvloklN0+m7dXOoWa+X9/HWObBmLMqypD49oyqs9Yok5YP3P0SvVnz6218xPX7Fhx884uH925SLJe+/95jt7W1ktoUQCQcHhxwfHzOZTAJ5QtyudW78XWCUJIl1OYzk416vx7179yjLJtfjZGI9mvI8DwBPCNEidPj/eqLY/18qcVZen5QqSRKKqrxE2+0nSkzFGgtONtFUYw2K7+1akq7bQHx9jdAlAkDybkIx8Irr7Gq7pGyTREgpw4a2jjdfOYaszckmz5495+GjdyDLUI7kAampa4WQCVJaVI9M0NIKDJkRGAVC02iD/OR2GmdL1Wsi4HS1Fveqv+PyJm1dGOsO8AhXvMEA9KZ631S6c2XdBhSehUCK9iZ1lbDhx1trzbA3JEtTfvOrX3N8dIw0Bo2dJ0W5sjmPVIUNohWtQ6/L3BLP1fjfuv646l2713etRN5M3mhz7dtbWlUsQDL+MG0rKZrPhLsn1q6JsGb8RufXTFyH7zd/WMcHTxfMdN8nVnjEhA7r+sHfe5UgFX/m12QQvrSiLiuSNMcA89kFv/n1L/kX//K/Q5UGrZXLHn79Nt0Odr720la7GnDU+PkDyLgO8cbl848uX1ar9//JctW+JDodORqNwnyuqoaC9jrg2C0m8o2/9rp/wB70ZUq3nesUP28DDq4DHG/bJ936YmVOvDddu6e+JdD6MoAnFtiuu6fbrn/s2F0FCLvtuuo+LwPM53Pu3r1rrxe0NCPr3sfukXafXCwWbs+ze7TWJlj5/7HlqnP/TWPiny6EjTsSUvDBV75CmuV88eQJr18f0O8P2NzcxGg4Pj7m1miT7b0JlYaL5ZKz8yOyRHP3wQNG/QFaF5y8fsnJ0SvmFyeoconA5npCSLSWpNmAPO+xMRlx8+YeW9vb7OztcXp4xMHLl+R5DykSZtMZG9tjjo+P+eyzz3jvvfe4d+8en332GZ988glf+cpXWCwWpGnKzZs3OTw4wOEVBO353nhhNAq1qqpYLi1RgSUnyIOc96a+a899eYkgozvn4vPOn+M9mZHIhNn5BR//9g9sj3d4+sVTnnz0e+7dvsF3vv11pNCMR0MeP36XJM0wsqYqK4bDIQcHB5ydnTEajVrP9HtPrJDwFiDfhi6o8R5Y3o1uNBoFa1NRFK38pUI0Mf7ei6P+bwCpXWIfR18uaSiiDc5TLsdo1QvcwR1ICMsK4hK2KmXdoBKXsNMY3OeaPM8a5o5A8SpxDwFhtbap425XTsO8zqGncTloDg1LmyiYTDaoqpKs17cLxxASKjp9BInTCu1s7/Cjv/kR9+7fp5dnUGhODw7Z3t0jSTKMsHmR0CaAHEtZLJEShDIIIxHCapgQoDz6NzaGwbK4+XiGtva6bcLp6DojNiYT/m/1rI1Fyn0XoyDheH+8pquh/+EqtGSwLD4mrqx7yHmQHB6Kc1kyTfXGhJ9WMxe/kRf0vVbavZExYKyvsc9DgYja7Z6dCEGeZQgEf/vjH9l5lkhUrWwgZFUG8GvwVMnWUVRVl60abTbE64kGrgJvDVCxc9le7/M3JUHJYIVKFQCSjW9pXODs/U191mrkSRQaUgavRfLXGyOQIfmh18HbQ923y2bclm6JyaChT2Tixi+m5fdKCBO1pVF0dC3CsTDnXZmuE45izZivTxtDrRW51ohEYpTi13//9/zlX/yl3dxNAwLbe1QMFJu//eSUwq+48FGrX3DfejcPEX8YKxaidv/XAjBdgLFO4GwO8MtzxtUSvYDAdNZ4E0ll514zTNEZEALN/bVuAmA7Ls0zCxaNYx5VyqWCaD/btrn99LjR/cHAVdtmPDPi6rnj+6Mr5Mc/u33WfvN2cY+Pro2uj+qQsvk91Clo/4zeLe7/uFti9RCdoE8T9nX/QVNP/E7d+XBVMYDpKlxwyhh3ogrj91m35ptTxbXI2G3ZCDCyWRetudg8L9QZnnO5/42fTuFEM2Eg/LnR9FJ7TYTntQ+8Zg0IHPNrs79rrRmPxw1Aim2sIvrTNHtDIiWJFJRF2RrfdSCx+TV+W//d5fEJoQ2ybT14E6CUUrpUII0UALC3e4ObN/Y5Pzvn2bNnJEnKaLxBVWuePnmKMXBwes745h2UGXJ2NmM4HnD31i6p0ZwcPOPV8ycs5lNAIU1FIrX93U0/I0HoimpVcXBxxtHrF4w2Jjx48JCbN2+yMRjw8vlzitWSxXzOaDygKFe8evWK7a1t9m/uM5/P+eSTT7hx4wY3btzg888/5/79+5ycnKAq+ywvZ4X5FdZho+T2pBsXFxeO/S2lrIpwLsb5hK4r/vo476adY9bJWghL9Z7IBCFlcF27vX+Xu3cfsLmzy3hzi08/+ZTf/urXPLx9h69/6332djeZTY/4zg/+FJkKalWDsWCzKApu3rzBalUwn89aStM8zymKAqUUw+GQPM+pXFx+kvjQEytDWBDUvKNPi7NarSyI6/UYDAZorZlOp+GzNE3p9/uhf6bT6Rv7yZd/EgDJbzJbW1ssl8u1LBZhI5aOktZJ9NoJ/0iBMNLtacIdcPanNgYhEptsVQhEoMhNyNIUgd14WkKncocbJlDqyjRxAM0+p6ptAldouwpazbg/IL37i0ZpePHqGUWl2Nu5wag3RiKpVIlRFWkvRasaISSDYZ/ZxTn/+//d/5Y7+7d4/uQpJ4dH/LN/8z/hL/7Nf8+8qkmM48VTGrTASKiN1WiL1G5ZMhJggwbaWbUEhgRD4Flfe1zTxUrNWUv3wPGHqxsrv3GHe6PrWmMbCwTRY42xmmLTtMzT/LZySLk6W/dibM4o1yYThEv7uZetWnd4GcPVbWILhwfL4RXse1V1xaA/IE0kR69f8/SLz0mkQBuFNopVWVA7xpu6tvMAoRHCCc2mrZVq+qQ9Fl2QdPVm264vntOJTNFGo5VBCfDky74Nvv89+AkCfadtzbO9kHb5O3uQRJowr2MU0e/g1pYdDGM0UljLKBjqukIIFYAYdIOOm41c666A0BZG/XR5mxIszlJijKaoSoZpCkZzdnTIk08/5t77H4R4xdglz7avOz5OsDMGoQ0iSTrKiNAFTvQUCGOFjsR9biJFRxDefNVryjqN+VUMZK1mvG0nXX4i7XkQgyQPanyzRes+Zfz89q6bHUDhrvNgvHmeRAuNTgS90YDesE9dlqBrUDU4JZRwCQw0gPZ7WEvCRAjQ2lpQDdIprnwfxtr5q8bXfmYBduzSLVp7W9wn6+GRfeMGsKtLa68NnpqeNS2UbSACIjYWsFnH2qnkGpprX1dnrXvrVQsoCJuKgwiAGg9820DJdPZpjUC3AJJLtuDOjaAo0ZHLvZs4UsowdbyyD2Ec5HP1aNOeXp1e9lu4bVLnHPLftwByF7S7dBiuq6184PfJBih5sG8VlPZv6XI1GtN4o1ih0sZPt5Rh0rZIu7ZIZciEIAWM80TQphsTG++NnXPZfxiNcdcCuM4i6MfyWkWMEM7lWGCni+D+/UfoWvD0yQuKVcF4sk1/uIlGQHIAqkaIlGJWcLFcsLW5y61bN9DlBU+e/Jajl0/BKc210lRatdolpSJNM5IE0iSh18+p65rF2Rm/PT3lzt27vPPoEQ8ePkRIyenZKUkqSBYzLs7O+OKzz5mMN7hz5w4n0zN+9/vf85d/8Zfs7OxyfHzM7Tt3efLFE6RntBN+TxZuzrmoULcXxOeABTlpYDwWwsaK1VUdXMni/ozPjiSRIUxECIHRFhzZmGDo9zIGgyFp3iPNcpQ2/OVf/jP+8l/8K45Pz3j57Dl/97f/hRdPnrA12eSbH37AzvaQxXzK5tYu481tjs9PEMIy1mVZxmQypiiKEFe0WCyYzxeAIMtyNjc3A/HScrly3lpZME403iRWOe/ZQ/154z1IyrIM+ZC2t7cBAvjyIDNJEqr/xmLXFD+5tra2gk/uxcVFmDCxG47WOvCq+3vXkTDEJWjjO+e+vzc2D7Zpg92Gbi4TSfh7k+iZuqWt9JsKQbMABKaTT375a37/m4/IRM7DB4+49+AuYKiqGqQNRBRK89577/F//usf8uuf/70T2iV//cMf8dXv/Rmi16fGII0BozFCkKYJSZoijQ+ml0gBiWiY+VqB/8Iuds/tv85y8abSkTPsZ75PrtDqde974zOi32OrUFyJx8zxXSIGTW301CrrDoN4A4sF4Phzv7DTNEEKwW9+/Su70SQC7RixiqJwm0Pl41fxuYUsiGhTv1/X52+yGjUHXJv9TQgbZGnzGwnnSqZbIKoLgroueVeVtxGou+QlLatvJPB6zZxdk86iLHx/mRYIWrc/vF25/rqw7ltxSMq6jWDdB375y1/x6MOvUVeNy21XsFivzRWBuvVym801AjOt601nsl8Hpq/qly9jcWqD0svAy34efrvi8zc+hQCF3rAGWtp8N196vR5ZlrIqVlRVHQ5eb6HoPqNbn3VTUpfoafF3NP+L6uq2nwgcxde0AaFoNePyuwpwFg0LcnRnD3UyaARHPLyJlRyN+6z9RkZCP+73+B2j+Rp/IUQQ8EFYdjIakBFV0OodP0W7+68BjNDdLThUovEESR7EgVfg6Uix0ljWROgfiBRnofmi0y4Tfl5ag/5a95FwiZF1lLvLW9AC7qPJIRaE6bg+V2HiBEfvauSFUaUUSSpZNw/A5zzzlP32My9k03mXbrlyGXX2Dm/RsmvFDmQD9teDpuvKeGOD3d1dzs+nvHx9QK8/Ih9t0p/ssLV7g73bj5hNzxiNN1jVhs3NTW7dvkm5uuDj3/2C8+OnCF2jKmuVsGt70ArH8HTaxphggej1evSkzc3z8sULlosF7777Lg8ePEBKwfHZCb3egHpQsVzMePnyJfce3rckDZ894dmzZ9y5c4fpdMr+/j6vXr2yynqnwEE0e9NlYiPbVx4E9Ho9VsWSNE3Z3t7mX//rf82//bf/NnhKtRVq7XPXM8HZeNs0knMNlVIsz85R2ipEbt26w72HD1ksF/z217/iZ3/3d9TFincf3+Mr77/P7vYGmhJj4PbtO5ydnbfk5izL2N7eZjwes7FhyRpGozFKvWI2WyClChYg734ezxcvBwEsFgtWqxVCGJcPSbiwlzS84/n5OcPhkKqqrEwirIudl5OSJKH28/styj8JgJTnefB9TNO05YPZHYzY9xGaAy7+F3/vwY3X3vgBjgW2+KePaWjurWncO2zxoEfKpAWM4gnv2etiYGVjrDL292/zh9M/8PzZE/72R/+Fnb0d/vv/6b9h68Y2MkvJ04xcSO4/fMD+/j7PvnhCVSlIU37wZ3/BcDRhVTkaSayLnTaGolJIZVAasjQjzxOr7RBXg8iuleFNY/VlSpcc46r63iSsrROA32bDjufGpTqjE32ddWSdoNy91s8nIW2271/84mdkaWKpRzFUVYkQRHEyhiTJ7Hj4zdZcZrmJ29F9n+ve1R92IFrtb+pvE5bEwOjLAKKugHpVu2MA0wVIfl10AYYVPkzrHtu29QQc8TOva9fbvlu8XtsEMDVpYl1xP/v0Uy4uZvSGw5ay5ss8900KiDZ0evO6u0oR8Tb3vXWbrtknvL7lTc/4MnW+TRFCIJFkWUaW5awQwW1EK/XGnms00k3Sw5b1A64FM64RkUzeWE2sW4xo3d9qTwS6Yi2+cft5UAi4zxCidY/9zaItD5D8ekuShNiCFMDTFe/fUr6sfcWOh0Wk2CC0oAFoHjzEz/DPv2pMrKO5Dn1AlLC7cyGN14PtZ6P9c7rxiH5vsN3X7EPt9ttbXF+675sk2THoAXTjWiSEsPGm2lrmMVZGqas6WJHquqKqK8AKxz4RppdD7LbXVRg17bc4uUmoXVV1/GZ4V+S33cNbtUfjL6UMqLsty1ytkFtX7ty5A8CzZ8/QBvLRJvl4i8HWDfqTPbb3h+xrxatXr0lqw917d1jOp3z8219ydvQc6qUDColNwjpswJE9c2WIV69r6+7lPY/6g0Ggnj47O+Ojjz7igw8+4PbtOyxWK5aLOf1en2q14tWr19y4tc/uzh4HL17z2Wef2XxJW1scHh5y584dvvjii1ay7W5fxLJJCzwJazmpqoqTkxM++uijACTite5/T9OUyWTCZDJBCMFsNnP04XU0XwVpmjEYjtiYTNiYbDEcb/D7jz7ixz/+MUeHr9maDPjqh9+mnyfcv3OLW7f2ef7iJQ8efI3JZOIAV5TjSUrAurkrZcgy60K3v3+bLDvl/Oyc2cWCVbFCCsnGxjj0r1e8yiShl+eMhpKNjQ3SVEbWJeHc8irquma5XHJxcYFSil6vx3A4DFTlxlhjSeFil96m/NEDpDRNKYqC58+fMx6PLUFDWYZFGgMlD2C6Gm8PnPzvvrQFr2YDiuuKk7wGE59Dt/6wiAFT/MxEtrXBMZpOkoYW0QtRWmvyvMfO9g693oB+b0BZVnzyyae8//l77NcFG1sTNkZjEAlZnvPt736Hg9ev2d7d5c/++b/ir/7Vv8AA/V7PnZVWw6VpFq7WhrKqEFIiU5uzZZ0g1N3yusDzKhByWXvs9ZiEQ/lNQlF3k1lX/5uEp641wf9ujHH9cVljaL9ra0zjurpuSF3BIP7djmeOFILnz59xdHxoD3lj4x/KssAfYFmW0iAyJ+tE7VvHtNh996v6YZ17Xgx8YguoFGlrDvtrvoyA331W97vuvAdah0OX2ce/e+N37dtE0N4a0wCWGHhB+/Or2hu/X3ctxH93rYX2HSxAyjNLYTpfLPjii8/56te/canut+2/q68Tl38ztHIkXXXvlwVpb2pjt96rAGgz5uvvv650lUtvuj+sy3gpCJvEcDwecXZ0iFLKHciBaeQSeuu+k5+XV7mTtolKIBa87f8aDX8Tp2PncvNO4bbwzK4HhHFt1QbrMheDDN3EQERv4qweLrYIe58yphXr1mC02FLku6/5zAuecYZ73zdhPXcE5xapjK9bNnPCAkUbvC8T2Zonrb5QmiRtBKuATx2Fv/1MO4sRljXT+DjKWPlj39gqoITrAgekjMGYdW5kNh1D7VhGPe2xf+/VakVRFNZiVFnPgOVyGaxA8/mcNEmQNIku89yC9jzPkYkgy2zyz+fPn3P79u0gi9i+avbHuG99PKjFybb9RVFE11mPAUtOFe1xa6ylzRi13evivTQRdg/ugi0/Jl3CEP+dFeENSZJy88YNiqLg5OQkxJ2MRiNG4w0Gow3SPOf0+IT5suS9d99F6JovPvkNZ0dPMfWS0aCH1obFYkVZFtR1wWAwCPOpKEoXv+pz7tl+LMsSpW1ONJ9Tx8cYffWrX+Xe/Xt8/umnXMznTKcXDEYDDg+PuP/oAXs3bvD82TNevXrFjRs3ODo6Ynd3l6dPn9qQ66tknjU/kyQhyzKUqplOp2it+elPfxrmUvds98Dg9PSUk5NTdz7a8Izt7U2yPEMIyPMevWxA1ushJcxm5yxXC36na3Z3NvnK+w+5efMG4/GI8aBHUS44PH7Nw4cPuXFjP8ypujbBKmTPupLp9MLJJLaPpRSsViVJYuWF0XDk1oXi4mIWzsjlcmVl9jwnTVN6/RytDWnajqXy+8pwOMQYw2Kx4OjoiNevXweAmOc5g8GA07OzS3PsqvJHD5A8zZ+UkqOjI2t2k3bRt7XflwVU/3OdMBuXLjBaxxjmBSPPpLH24HIlz/OQDKzbNn+vFwJjDbMQgvliQZL2GY02gAO3sCvKokZiXet0VVNJjTI1f/rP/oJ7jx5w6/Zttm/sAxlC9FCRv75BBXc2/37GGIyuUUo4LcTlhSmkuFLt+zaa5Mtf+A5v9338/uvKus2nO07xtesEwe488SCp+71xwswbPK1C/V0Nmv8Zk4okacrvfvcbqqq05AyqtpZHo1G66rT1ep32OuGs+3t8XQwwmne87PLlr/XjECsG4vquEoKval88VuvA0nVA++rnNADJqPZciMFfvFbXAcv42VfNvbeZY15AtHEDGXVV8dFHH/HhN74ZXA/eFhytf991FwGmrcR4033XAT//fRfwX9e+t2mnHxsb17i+Pdf1/3Xv8BZX23Y6ITLPrWBVOVakqqrs3HCXWo3+1UAujg9YNyfjDW5dM2MwZP9uz684Xs8KI233cf9MpXUAR15BFwPCRgN8ef8W0dYWB0ybLn9zfE9kUPHzHAj0vFYjbsGJiACX5x7xyaX9niudIE8EmBDOPc+I8CxvYfHvIkRCw5YgLCCUgsS59WEMxjTkSMYo6qpCUCNlwqooLHuhVmilgxuWf6+LiwtqVVvna6NZLJaAZ5rVbj+xOVu8p4l3l7LWFcFwNKKX9UhkEgRhsEmxhRAkwrJbYmwwfbMH2niyNLUuYwcHB1cqxeIzxyBsHJ1pLEXL5bJ9Hhk/HxtZw3q9xPMi/qP9+VV75HWKpe51CEvwM5lMGA6HPH3+nFrVbGyMGOUJ417KxiBn1M9ZFiWz6Rl7O9uMehnPPvsdJ6+fIPSSwTCnPxhxenLKcrUEoK7LwBAnE+kUEJZW2id29daIqq65uLhge3s7KLnPz8958uQJ7773mL3dG8zOpqyKkv5wyOHhETfv3GF7e5uXL17w9OlTbt++zcbGBtPplM3NTc5OTlt9s06xGMsXPglwnueMx2POzs4uyYvdMWnON2vF08aCjDRL2dqakKaCQd5n2B+S9XrkvT7D0Zid3RvcunWLQT/BqIqtrTFSJpyfW2B2+/Y9er0B52cXri/rsNf4Z/b7fYy2MfXaWFdyKROkSEP8r2XsswvepwRZLJYURcF4PMIYWC4LzqfngGIw6DMcDoPRozuHBoMBd+/eDX0Xe259mRPgjx4gQWMd8kJbIpJLWipoC4Pdxet/dhd5mJDGhI2hYcZqC1dxTEZTj3BBlI2/pacp1O7A8JMtBkVSpi1A5idJXdUkaIaDIVneQ4jE0RxWoA3DvM8w77FYLBBSoDB8+0+/7w4oMCZB14pMZC5dmgEjSJ2i1GqOnKZMW2vGkydfOD/cjglefLnJ+GVLd/O4/N16ALAWMF3hEhfX//aC+BpgaJqv3lRCED/Wh1crxe9+97uW+4YxGpkIdHGFYNJ5l3Wgb33b25/Fh1tjXTEti03znRNAOvWtFQhF1EjW9/dVAng8HnFbu6DlqmKv8ZrmJKi62+/YpkLvApp/SInbHluStHa5n4zTVgNPnjxlsVgEX/G4jv8apWsli0fmumd2R/DKXhfta2M2vzfVGapYI0RcNc5vquMqhYD/3YILt4yFdUnb3d3hI62pXV6SoiwaBZW3KOuu7bgp69JHhPZ6lMX6/az9VuvbDaLzHlf0k4jAmGjHcrbb1gZqEfa43LJr1puMrV+2Vjv3tXFJQBuiolZEl3d78gK8+zwQJ3ldlIuj8i7p/j200pRV5XLD2bN1tbJuRUppyqLgYjZzc9C4GIcixDTYGBTLQmtlB3uWe2avJLFpP4bDIb1ej8lkQppmjhxBRu78iQOsbUZG6WOQQqyyde9CtZU1XlEDBonCk3xIaUGht+RpRzyxt7fHy5cv18owzRSIgCPgmWMNsFwuA+gCnDumDvPpv0ZZp5gMshJN321ubgFwdHiEQDAc9FCrKb/5xXM2nj7n29//SzQSVa64eecO5XzKq2efQr1gPMpJM6v8LZUlORICyqqmrApkssEgH9LvDUmSLIAQ77KV5zn9wYDZbMbFxQUbGxvkeY7WmoODA7Z2dtjd3eXs+ISjgwMwguVixfnZOTf3dtjc3OTk5IT5fM7W1hbn51Nu3rzJydHxGla59lr2Qr4QgtVqRX9gYxm7ir3rQKYQzuVcGMpyhVKaqiz45je/zmQyYpjlTEZjRuMN+oMBQqYYIej3BxhdUlaG89NjjJFMNnd49PBd8l6f1bIK4MaSvsjIWk6whFomOcI1jdXWhM9jucKy9eWMRsNQd5r2SVKrJAjhLc5SFfdhLEPFTLAAuVM6vE35owdIUlpGOOV8S43TAMqw4TlsIzwQsQJo1y0ogBunHfLJFEPQpGm7z8TamzRNLRhRjlHLEEznNijVCyXCtcXGedS1E1qce5tyZn6ZpGjVBkyJ80cFiS4LRqMBw1GfJLMqv6qqMAp6WQ9Va4qysodKUnF+MePWzX0EgtWqgjyhVpqQms0YUD6jtvdbt/okrQy3bt1qCTotYfKasQnaKbr6Uzq/2dOwAT3e3aM5yHEa0+Yk7goZ62sN1zutWEsD4773Bn6tTdA0ItzB5K8XXgtpmZS87tnXG+oz7U3PUqJHWndvcTSGLE3JZMLZ8QkHr17Zt9YKjEY5piGfGLZdRNRrkSQR90YEoLoCWXyIN4eVjIIeHdWxhjSxdPB2nsrQn7Fm27g5JATWeksEbsG+U/RsYyyzkDYay46Fe4bXevuxcvPGs+QJ0X3N1rtGnyCEA30u+aeRYFmnBKpW1Mq63dgktdquedEG5W1hYf1cs5dctqr4A8/uFVZY0rqmVhUguDg54vT1K+7cv+fyXWE16VZfcf264orvTQPcPRmXnx3aaRVlR8h2UpEdQ9GayRih22vWDmzzfCdQN+2xdyvjnh993zxORHU0Y+qJA8KbdYBG2HMu9YV/Zzd3TGzxwa09t/eGQHKHmYXAIEEYtFLs7NzAYN1AlosVi8WSWilyY+M0HZq07+Tb5cg3EIL+aIgy1goSzoK4n0ObvYa+vVesFXZF+90FMggrHRHYnXX27NJR/S0LqbTrubm3Dd5sPdr1ZfNceannm33HaPtMfy7WqnbWIXtnWEtuovjAda3rQIihHZFJURSsVitqo1Fas1gsqCqbw6+uFavVgjSVlj1WSuqqIklT+v0eqcwwWtDLe+S9HkmSsDnZYjAcWgKiKE+iBzWJTEhTiTb+LAal2+72RkOckqA5h4ybgSIAOeH7JSh0PDscZKl145IYkjQJe0+a+f3csvtBkxi22ek9vb9VXEoH8v0cJBD0uf3TWz6dsk3VCkyK0ZrZYubmsMagMI6uOU1j1tBrSrQBXRLYY6C8RphfC5K8G7cx7O7tUpQls9mMLE1JheDw1QvOpgsOj06ZbG5z++4Dtjc2GA9yPn3yEbPZOXneYzzeYLEqmM3mof+8XJWmGYYEZMLW3g1u7t9mZ3cXjGE2n/PF559zdnZGJhM2NmwMT5omjEYjelnGrKh48fw5H37tQ/b2bzJbLFB1xWxxwcnhMTd299ja3uPo+JzXB8e88847JGnOaDwhSdM2+QaNzNmNQa1ry1S3XCzp9fsIYSm5lVSkSYJRKrAwX94v3LmqXQwhNXmasbe1xb17d5BG089ysjyj1x8yGA5YLFecnh6zKlYIKch7A+7cusOt2/coC2Up4RGBLdHLyXluwWXMGF2WysV+5SSJpKpq2ueptGvNydE2Z5yIlAyZnYOJYrVSrffTWoc4pNhAESuI/PXrvDquKn/0AMlrmzw7DgLH9AQmaLsl2u1p/jCI44e89UZKSeJMlN5f24MrrxWLEW3QZomIOhy/KDW1UiSBZcweENrYDS2TiQMgbRe9sqrD4qmcpSnLcytouwB6lGY86jMc9THC0T6DpTjOeiRS0KsVi8WCYlXx+sVrbm7fJJMZgyyhrGuU8Juo9vjD9VVbI+ndBPwkjbXCbfraNcUBpLhu+9MdLYZwiNjL/e/u4Omc4t7iZq+IARStjbkDFaKfbbeB+HM7d0yQ0URzvDR9IQRG2ESb2gm+nvXI1+vzVRhiF0bbwdKAcv2gtKKXZmQy4fOPPkaXFVmaWD/7aENo+sPV2z2PAtDpHkgmzN3u9W2XOv+zjqxEEp9EWAiba8i7a4X3jLWXCIS0oKTx8W8Aoc0B5RUQzv9faMt2JYwDKu5zo4MmN4ykf0eci40QGJOE79ubpCYk0w2zwYHdqI+sd6hAkCCFRJkq3B9bq9pzaF1pgFG8L/h9xbZPARJtaoyxmjBZFTz9+CMePbyPMVjAZqyrmY7W1WWLloMckYDhn28DzGP3Xve9kCDsXlcTi9ZOKAsgo/u2wu4v/qm6UWJ4Mo91PWOMwDhlk6USbr6TiCiPXLstAdnQYbD0Ymekfb30PK8J8wBQOOtIpNgwjRRp9z1t40mUEZhas7u3j0xSlNKsllbQqmpNpQz+WGjmvQgAEez+vbG5xfT8nNorWrqgyLTduV2mvMsHundtEzh9S7MWpGdjlB4sGWvVEo4FzeXsstpoP/445ZtdC1pbNzYhmripjrOaW8MOMCiFri1REW5e10o5V2BDVVfMZjNw1y6WS7t3Iahrw2w2R0rp3MlsDEye5+RpFtzTLNNYRpKmJElOmuekWcbujcZak8iENJOkqQ7r1wMTjLFAxjQeIrEAemmO4hVX9i8JGFXb/V3glCkakJCIoECxfejpRD0IvnyueIsMNPTdxkCeW1eyJAEhdKt9YQq70TZaW3nBrzlHi75cXFCVS1Rl3f+EBKNVAOpCNMoAIcCoClXV5OmQxWrJdHpm9yejMMa7cysnIzXArlsa63MzW/xnIWZ1bXbHTt93BXshEIkkFZLRaMRysaBYFQyHI5I0R6Z9DEvSJGE06LFazNm/c5/Vas7R8UtqpdjY2CTNhqjZClWVDHo9hgMntyBIs4z+YMSHX/86jz/4KsgksNj1t3a49/h9zs7O+O3Pfs5iekZZFqyWC/p5Ripz8iRnenbG+XTKZGeX3uExxXJOXhXMp1Oq2rCxuUuSPuPw+JxH76b0hxNWywXD4ZC5c+XrekJcPmvsGlquVqR5LyiA/NmJ0XYPjfqvpQgRCqMhlZI0yRn1+ozyPjlW3ixrxWJVwPmsiQsUgsFowqPH73Hnzl2MMZydnbFYLJlMNlguVkhpXTs9i2pVldYVFEs2liSNFdVacH0CWB2us3mPfA5FmzvREuIsybKM168PuHFjj8nmiO3t7XCGrlarcL76ueb7KZZTuyE1b1P++AFSJ9bHlkZoiBFsvPC9wB93pgUp9gJPyxtP4Bjt+8klpbTWG3cAejNgHJQaCzH+QDo/P2cxX7C3uxsWipSS1WoViB78s71vuw361AzyIXWt2NradP6bhtWqAGEn63A0ZFVUjEZJMFWenp9z5+ZtRxctocYeKpGQ2+1T13i8GPCPMb/HE1gk7U00Bp0xEPN9Ftfhy2UNP63vuuVN1wqPjMLnrF1s/jIpGm1b65q1AAYnnFsho3IuIUmSoJXmoz98ZLVDTjBWznxc11fFNHz5cei6Nfjf43icLhGDEKJFXR+3I14Pvnizd7yZaa3BGFwYQquvLO5pqKsvb3ARSKIRFIwRGN18niRW69oIK22AH/ddN6bP/27/jtsWa6XePgYmJmjwdft+icklMIYvPv+cf+HbqJ2gm4jWWnz7cnm9XL5EtBiVfNFX3mM687ntOnz1Y/xY+L/b4Mt/b0xQTVx+8jXvEX/XKFkuv393/Xatx6FVTqmxs7tDnvdQdUVZlUynU1bLFcPxRkQa0N4z43He2trh+fNXVLU9B6yQezmeI35srOm+FIdnBFp5d1GrZNHKgJBILZ2VTgagoJVPnmxnkNYO1DjAVJY1AmXdz8qKura5Seq6CqkxtLbCz3w+D+dZXSvqsiJLMrI8s0K8MeS9nH5/QJJaUD8YDMn6PXbHG2RZ7lzQhIuvse1MUyuSSCFCXFQQHP2YCIHprKOGSAGkUM0gegAhQKYCE1x4IEnBGHnpnLffe1uPRyXexcwrIELjwoPsb03yamPqMH999WG844e5PciCFgvMNc24xxqELhW59sqiluxwxKCfgrExconwrk9u37IbrTvfBcVqRVlWCODFi+ecn54G90cVKXJ8v/i5+Ta7UCz0hzF5i9K2nlohPc6jY4y2FM95jw+/8wPKqmY4mrC/f5vnL14xGQ84PHjJxXRKlqUMhwOUqpnP5gggkSlpZt3oZJbT6w/4+je+yYNH76AMVLUilZlLvm5YLQpGgxF//hd/wc/+y49RuuT05JjlcsnGOCdJU9RyyevXr/nqhzesO11l3TXLVUlZFIwnm/T6fc7OzqiqmsFgwMX0nMnGhPlstvYMWfeZMQZVq0BdbYzLgYXPCeT3Tn894Q8hDIm0+YSkFPTynPl8wdnZud3/k5SqqtFa0e8PuHPnPg8fPuT2vfukeR7O7t3d3SCTGQ3Hxye8fPnSWX2s8sSy7EoGgyFK1S2Z2ssWPo7Ln9v2pyWRSBLp3O7s/Lt1a5/J5gZ5noQcgdPp1Cr6iyKw9HnmWmNMiBUty9Iy4knJ0fHx201C/ikApAiINIvVaX5oDsnG+tGYpqGNvoUQKP+dsSpO5TQzaZZTV3UDGIyzYdTWjc77G3vSiMZ/0h8OjbBkjKVEnM1njDfGVpg0sCxWLkbBUFR2wDHCajqxW7TGsCpLMILt3V1u3r7F7z/+mKIswz7b6/VJkjS8X54nzGZzVlulda9wWmyDAbUGBMSaCQPKbdqelSguXeH9KsHmktZozfP8OMTj1tWStMf5suB6FTj6MlqFbl3r3tELN1cJZ20BMdY+E6yXWZZRq5qXL15GAoCkKFZtt5h/BDBt2nC5Dr8BrvNtjgFr/G7dvgxCjLFsbf67WPCTa+7xdfmkw3Eb1/dndK/xsRP2uuCqGr1jV+iMAU8MDH2dXnizWvF18UnNXLiqP+O64uf5vSAeU601h0dHzOdz8tHQufdYweYfOt5XrQkPRuL2de+7plZ3n62nAUn+nsv7R6MxX7+3tMHn1e8CDcBOxHr/ey9fXjlXrvzb4JOT2rUJo9GImzdv8PL5c+q65nw6ZTafMdneJk+b/TQe13g+ySTjwYNH/Pa3H/GVr3yFNE2Crt27/jXj4OdnA8CFSELbrHBs3YNAhCBtK5RYK9B8vgzXrpwQ7M+holg6QN4wtGZZ5uJt0sAQ1e/3HUXwZrDi+Pf0Lml+vH1uPC9/++sai6cTgLSxwfAA1DY5u3dPdwDC+E3R96lL5Cmks7D4xMauWilBGWUtnpH+xINDu0Q1QihrVcLW6fP/GGL37OZ+TOzhYP9pXfsv7TjpaDdvAVh/XTO/2sDLfa4jJYRxM0K5ZLXGRHUajI4oit05Y5pJjlKGF8+/YG/vBqvVhYthMoBLCCwEWikLMrVGa5hOL9AaiuWSv/vJTyiLFWmaUVWaulYtZe+6mMHW+znL6aXP3Xheb/2m9V1ImSKss79PPGotBu7vXp+Nm7fZ272BFJL5xZQ8T8kSwXx6RlEsGQ8HCKM5Pz9DVZW9L01JM5f/KMt59PBdHj18F4SL+RISjXbx6mCkCW6e3/nud/nxj/4z5+enFGXJUGvSLCWpEs7OrHVpc3OTo8PXpElKYayb3ub2DqPRiIODA2azGb1ez1qWJxNevnxxZb/6/midF45Qw8oJOZUpSLOM8XjsGBINtTur/B7iHQsEhkQK9vZ2+Oa3v8X27g7D4ZA06zMabjAej5lsTiyznIB+r898vkC5eD2lFMfHxxhjySt2d3eZTMbc3P8W8/mco6NDyrJkMBySpTm9Xo/T0zOMMSyXC5RSDAYDF2Zi10ie92y+RykcWZFEJglJKtgYbzB0Z6B9/zrsTzdu3MAYS20/m82YzWaMx2OAQKLT6/VcPJOND/xviWI7xR98DbWo1Qj54Me2O11bkx0LMDJJUFG8hHTAREpJrRWkNq6oLMqwwJVSpEJSl3aDUkoFhGtNgGC0Iu/lKGU3pCyzwtjO3h610UirAKM2msS4wyKxQEmr2m12Vgup3GdJkpJIwf0HD3j0zjts7myzsbmJVpYifHdnz1oFjCZLbXLci8WCzc0JqqpJk8RtpBYExgRKXctIzFjWZl5p7rkKhKwTxmLGvPiatnXhagG0K1x9WQC0TpC+Spi76h28UHZJ+HYCUQwjPaDy8W3QWDam02nQ3gIuqahqtWm90PvlS2zd8HMVCJuRdq5wUjTgKF4n3cPTGGdJNRr7lW7NGf9M9BXCsO83J+TF864LeOJ22zgn4Wh6Gxewxu0jpvptPzt2jfV94IGajRVIWwyDl5vcnWuNK2PXAuD7O1aYeC1wKlJmsxnHx8fcGY9su5Trv3/AWHfvaM+XdS6YX75W/57N3+vHte021KzxSxaSTj3XgfGur367XJ6XV9Udv5sQIoB3ZQypENy+fYfnT564gH8bgL1/+zZB+F+zV4Q5n6Zs7uygheB3f/iIGzf2LC2tNuDiCYuiDL78WmlWThni99iyKKNuF+CICbxrigXyVunmaW39WrFxNjZPiRAElxaI/fUJfduMV9vCFWT5yBLiXZqD63G0hpLuGst8bp7wBKSwQjypW6c28ZCT6xwhgRDB2mZvN9blTVpAmLj4xgBBjHXZDPcIg9FRElR7eFsCCK+woa1g00q59tj2ejdhIfy8SRxLn3WbRzTO1558Ke5Pr0zx7on2rNNBwWC0iwOM5qYOhCG2/TG5g9+jlLIAe7lc8vnnn3Lr1g0OD16hjbYss9rm7PLU4nVlY5DLsqIoKpIk5eD1Ib/4xc9dOxRGmKAQurT2Oqsl9BnGxe+1P/e/d4HWurXogVEz/zRGWEAEsFqt3FyWZFlOkvUQSYrAUNcV/X6OFIr5bIrQCqMVZ6cnzC8uMFqTJnZ+ZKm1KEwmG7z3/vuh0WmaWNcvITDSnT1CgBaIJCFLBI/eecSLl0+tdaiqyDObuNTHyI1GY9IkYb5aobWlaRdCMBgMQl4ln5vTWrdU8MaI96R4L2kpWxyQSxKbBsRguHPnDv+b//F/5PTkhIODA54/f87R0RGHh4eWYbGurdu6Uezs7vC//F//r/jmN7/Op599Spqm7O3sk6R5GKMsTandPrcoVyAIIGNra6s1TkVZoI0mTRPu3LlD4Rkfa8v2OBz20dowGPTwKQ08gLEgvqLXyx0BSkaatdkeGw8Lr5gwYS4YY4lTdnZ2wnVaN8mS4wTASimy9O1hzz8JgNSwxMSJtERLQPFFShGBl/ZB7BdqEGik9W2uVQ1GksjM3et9vm2siVb2IPFuSkmSUJYleZ5TFDUYYTVbAEZQFpbC2aa7ECFnAoBJrXlVa03e69lN1gnNNqGdQZoUbWqWVcHN/X3u37/Pe++/x3hjbM2vGvr9AUKIJmM0hun8gt6gR55mqLomlRJlDEbKa0hcLwMKuFoTvQ7kXCdsrvsZl+vuXQd01tVznbZ63XdX1dN83363GDwSxWb7w9gt+eZvY8izFJlInj59ilI1UrQp4+2Cv8ws1BVQ36bE98TAxc95P/eklCQyxWuyrwOhfv0YL4jQgMV4PK3A3/TJ5TY1h4J/5rp5sx5gNcKSEP454to5Go9Vc0Bp50KlwxqOD3BbRRssxtYD7wK1zoLTnSfBjRAbm/Xy5UvuvfMwhJ0YY1oxQW+jdPB9EX8Xg8B1970d4L68vv3nplFqR9/739avp+7v8WdXKQGsZvrLArvLbb60V/l56TTiUkpUVXH//n3+7id/G1xczqfnLBZL8v4wsoq06/ZrXJkaZTQ7e1tsbk+4uJhycnaCUjWJEWSeAc0RBuSjnN1sL8y1WCDx8ZZa4jTszZ5khWvw7G7GzdeY5QlnMbGv2Ky1IIA0b0GSxukrTDOXovFPRDTYxhC6QnilT2OlFDpSOlFd2sOMew+jbDyFFNYKpU1DRKBMQ31vlAig0iqhon3IeIWeU5Y4q057Tnmbjv2pHf230TZ/TCKkY2w17kw3FtAJ6+nhlapaW8tXs5bVpbmtTWMxj2MR4391VYXE857VtnJsfLoqQy4lYxoXIgPMFytOT0/pZRmf/OHj1hzURlFXdu8qyoLT01OKVeGShdp41tPTc8rK5mPDATMPqLxS6joLUpgxovu3WwedM2Ddur/q/BJCBOtl7ZRIUiZgNKmoyRODMBpVFwz7OVpVlMUSIQwCS11erFZgFKuFYbCxgUHR66Xs7m0zHPZcWpLEzS0csYi3aCToVFBXJWmWcefeXfqDAcvliqIsSFPrMlqq2sXmbJKmGQdHB0xGQxbzuc1159zUZrMZN27ccKAofat+9X0ihAgU7wAPHz3kxYvnlEXB9vY29+/dQQpL9CGEoCxKphdTm0h1PkcYw2g84t3HjxlujPn2d77DRx99xMeffcLt/Ttsbm3axNhpRg5kWcqqWKG0CvmEVqsVVVU5ubqmLFdhnEajkaNFHyAckIvPm3geddlw/boBg1IVSlXhHg9yvFteVVWcn5/T7/cD2Iyp8b1S1wMmb/H2ISlvU/7oAVIjpIjgMjAYDDg7m1KVVUiQ6H2f7UA2G2gc96K1RqRWv1OrGlNH2l8lSJLGupQmKUXpBkLYA6Msy+A7CQ5BK7sh13XttEFOu5emGGkDXJVS1kIkBaqq3IDbQ6x2mZCNMZZlDIk2julMGxKtePDOI/Zu3qDWGokO5A6LxSJQepZ1RWVqDg4Pub1/ywWKJla7L/8h2mXWboRf5t5/THkT+PqH1tkIwf8gRX67P4KQAIi29csLM59//nmwpAAhi7pPcPqP6aZ4bfi/vfDvNyU/v5v2r7eSuNdpvcOVvv1CBFksFtCuA57rNLGxO0cs+NvN0LfV52vxet2Gorx5f/+MdjvBA0WBZXNqhCqvlbL/XM0RGG7aCcZczkLfFfr9fY37ng3KevbsGT9wFh6vTY8UtF9inawHQzYAvy0SX1X8e7ZrjVitfBuN1/wTfvoxd2/ZriMCjusUKM3zr5of160DLwBf8e0Vz75UjD1wb93at64x7rBezBcslwvG9SaZbNzP1j/LIKShVvYc2JiMmGyOrVVZCWRwoWva5uuy+c8a0J25NBAIBdQuRtHPQWtNkCK1hAKJXyTWGiJk7Frq+yh60dYYWzcysMQPzVcmuIUJsABCN6QCLYWGjtGyCMBMYIK7mp8jQkTfG2+haiJ7vC5FGhXaIqRAGo3QlsFP60YAMsbQnMoGoxqA1NXW+9J1ddUhd4zGFMqSqThrj095YIFNbXNMORcoY2zajaIsgtVZ1YqqrsDgFKu2H+uqDvTjRqlAoqAcMPNtlb7njLWqFYUFSIdHR7x49Zp33nmHnZ0dFvNF0KB7EiqjJfOLOU+ePuX58+fOOm5BXyITEJIEm9BWC+FSRrUtGI3l/rr9oq0Iiz51OSjbSomuIvqS3CCaZxtjrXrGKSGlMFAuUMUFWZohVEXay9FaUZYFibRKhbJYYYxCq5rlokJhrEdOKtjd3caYmuFggDKGqlJoIZDaWoSK1ZKLsuT8/IxePrCMb9LSqZ+cnNoxj9o5n8+wrK8pGNy4qta5URRFsBh5OvjrFLXd/tJKI5x16+DggLqqmYw3KVYrenlCmihUbUizjCyT7O1uWtmzqKjKiuFoyHK5QKQJeb/P+1/9Cg8flbx88YLlakaWT6iUU6xkgp7IHQ29dYvb3NyMgI61HFkLdhNbbNe2vGQF8nH08WfeWtQYEXwiWEss5Pe1LEudjGz7Ym9vL/RdDIh8SoVYljLGsFwuOT8/v2butssfPUAqa0NSWeLlne0dJhsbqKpGDTSnxSkoMEKgtbP2GEtraRxjVF1b03RZlGgEiUob61IkqdS1AioSt4GUVY3AMgfVRiPQFFVF5n2kjQc/VgullCJNUrv9CQF1CVIjZBT/VFpgZQETlIXCqwutuVyTyAQjLNteVSkqpbhxc48sTyiKFWR9iqpiuaoC1WdVlXZDV4ZlveTw4JDNjQ1kZoNohXKuCkHRGGl+vGYufNUIol6bGd/SHJz2KiBQpvuDQHR81uOEhLIVDN2M83WAxZhooKK/vfDcFfoDfqEtAAshGvEhelZLnDCN48k6Yc+7omAaJrEgPDhhOgF6iSRB8/LFUwR2Pgph54zBbj5CxM9Y//LefcP3Wzxpu5YU3wdKaTwltBCCRGZOi25ZsBohHpr8GVZL7N3AhJT28BWRQO/mm+jGA2EfF8Y/ABYnnJk1Gn66wM0J/EYQKMXinvF/G+PY4tzm6WIAG2tTM79iK5Jll3QuNXZlu/ljtV2x1bkLPOO58CbhIhySRoMWHL9+Dc4n3ucBtePejoNyr9buoxYgagsgbReXWEANU9HNTdm09lLTRZjr7a9tnf5v3//RKm4q8g/EWtqEuBzDGN4TGlBsIlAnfGNp1Wmw01OuGYfoxqZut76J1rAQwgr4EjCC8da2pb+9uGB2fsZiPmW5mLv1mCFEElw7u30hhe8zwAXPewuYkH58RdhggiDp9guJAb//aat0S4SrXStbDyKseWEqu2/79WOarhLOVVxI0RoK2+JGILbcWF4ZYYUUf94Ir6Tx1lMHaOzvzZ5uSRMiNtaAtARC+tiraO+NhtUrN7wiqXmOU4iE9dIAGoQOe2mzHiUYjVZVUKJAk7jWKyG11iiXj8V7biilUUpTFCuKcgVYSn6tDaquMcqT5tShDVVVIZKEOlLG+D3FuvaLYNWLlS1aa3Stgrukj88SWCtamqRBaVWUmsVizscff8L5+ZS93T3yLOP48Ig0S5lMJkghkImgqiqqqqIoC6QQJN6qpu1e7/PSlHWFlO5MFn4OEPo+nBOXN4Po++hvonMm7LHd/bC9N4XVGT5zOeuMdaVsznrD9PSEX//y5/T7A37wZ39OkvXxVPZCSpLE9rEyGuXqUkZTKUVa1VxML+zaEnZMy9KSr1RVyfn5NLCvVVWNqiuGk01SIRB5j0F/aOVHx4zq217XijTN6PeHbG/toOrCxpMJq2QR0irYkzQhzTLL7CclxjFLhvenrUBrK9Q0qq4wScKqKKnqigcP7nPvwR2qckVdrWzcYV0zHo+RiX1WmmbkA23fp6qQqxVJmpKmlsji3r17zGYzBoNBmIN+XgopSdyc9W2x68gmdrUKHDt3V6sVRWFJGkajUSsHnHf7tX2WBvdCgCxLMEZycXFOsVqxubVlZWoHpjCQpj3AxkbZ+eYIIRIRrOlVWbo4utK5ka7CPjg9n/K25Y8eIFkTn+LurdsMewMykZAkgq3RmI3hiEopLhYLprMFtVZOfFWW1UWIwL5hjAGRUNSN36QPnLYbogVhOvFdan3K/YJQniPeCFRlfYABqlpTO4CUp5A64UUrS8mYpn4ygj/Q7WZsXeq8q54V9A2VqcGxfkkEdVGjTxWbkwlVXWIQLIqSfj5E6xql7VlmNKRpTlUWvHj2HHH3DqNBn14vx8sk4fCjs3HSbHax1scLRfb8arsb2fTd611SRBQz0AU+JkInbe2n3zyiE3b9jAj9GYDQGgHcf26ClaIBRwGSRMDO90lL/FqjlTYYTGSh9LDJNQ2jFakQJBhUseLs5ABtLMOQdvmPhLBaKZ+PhFZ/mfbTWqDP/+3Hq50nwP9ulZZ2bvucXPY/Sdz3Qni457O7e396S4srBMH62Bqq8M4OADvBQaaO5CNI1pbJ6tLhgGXtSZPUzS0vCDXxcMbX4x4lRPNnYKLCgHDaXo2jNm4H2wdLmnFCt5t/RntNs3A5zpokd14Q8vU079uaLpcAanCv82Omak6PjlhdzBhuTKy7KwY7Oy7PcTsmyaXPoRFM1lkFtQdeshHYQ/tMG2xegcNbbbATOcyUS9e05qgTmpr36YBbv/GAdXvzddAIyYAN6g/f2RtDUyIFi4grtDe2n2W8IIeb+zZ+zpImCHqjEaPxiNnpIYcHZ/R6GY/fe5eqXNLrWRpqI0RQrtj4FePmoEHiBDzXUuH3HqGw6RiERVLWv9rlWnPgx1UVZpS28zfqSvtMD3pVNEscQNIYpDEI09A++3tF9LvBgGMyswJS1//fWzOa8TBeuaA1OG2uVgpFjXCsbForB5AIi9Ja4yxzZ5gbxvaNchTA1jJkPS20Uu47HdZd/E9rRV0rFwNhQY4BqxBUtbNAWBedWlmihlVR2PvrOgAog2ObNdalz1vwvDUoTVNMrWgAvu251Amc2qHRPM8RQoT4DWPyYN2J3Y28hcGSZHiteIrWDWCq64okkaxWBYvFiu3dHc6mF0wvLtjd2yHLUgaDfrBODAZ9hqMR04sLlktQ05rRxpCNzTGHh0c2Jo0ERILSNtbOhLhnv+eZZo5Eq+eqU1a48TPu8A7KJtYDpK4i6ZJVz4DRgqpSLudUkzD94OAV8/NTpqen/PynP+VP/vTP7bhrQ5LavkuShNFozIW+sGPr0ilgBGmaU5d2PBOZMJ/NqKuS5WxOKgTj0YjxeETq4rQHvT66VmSO2lsg3LlBWBsmpC5I2NrapVjOqIyhVopa136jtmtLADLBkrRrd26aQJK4zrJpLWeCVAprZTX2ZP7DR7/n5atn3L61j9YZSeqUdki0EZydX9Dr9RiNx0y2h62YJ62sRbbfHzAYDIPCr4lNbGLMmrPVpwawFsrmWoGUKXW9JEkIFqIsy8LvgLXUaU+iZt1F0zQjTRI2NzY5qRSHrw/Z2tqi3+9zfHTMcDgiTTXT6ZTNzU1WK+vaNxhYd77jo0MWiwV1XZNlWaBqx69lrTk5Obli5l4uf/QAKQMeP3zIjb09To6OUZVF+lkiEVojZUa+tcXFxYyL81N6wwEGQVk5gSeS0NNMYoQErGVJOLc5aIQBT7vprT4ae/Yp45NB2hwRxcreJ5PEZarGfpZl4HK9SAmVqkCIoJ3WSllNPgJVlzbfRLVCJo5O3Bi0sAGNaZJQFSWlKKmqmnffeZez8wtWywWS1PnyAkJaocAIlssVv/jlL20QnpvwSZqwTgjvmsbXCbKY5rqYuQwZW5euAzTt4oU7v1l0iQViAfO6Or7MM32J/WC79XWeQAPExNpru+4FvnhfWSFsMrrVatUQGXSSAzd14ebcZY1T3PdXtcP/a+KP7IEUM9V1r3cZxpzmyGqIY4E1fo7dWJtcR7YtogWEfGLcjcmE8XjMxsaGy1SeNcBNaZarJbPZjMViwfR8Ztl1HNOiTARK10HgiNvQAPfIWhD1jZ+TkqvdrWxAuwhzILgj0iZ36PaxL5etS+3Dz9dpjItTwO4vx8cnjCabVuhyYDMkdBWdXr/m+QLRWi9hfKL7uoKLw9VfukhBOOTdw5t39RMnLsZr2DsAprnAgtToXZpv8IbM8CgBgayjoTW7VGW7kX5K+rngE+M6ZjXt5vju7g6vn37BcNBnOj1juZhRrRaofo8ssXulQCFdzi+0JwqxeeVihRHhX6MECyBTgM9ltKYb3bg1jEyx8gOj2++mCaBNG4OI9uKuddNb7PWaa/z3QrTJGzzxg8VVDvC72NgE44gCTEMy46xslQMkPmC7diDFEwl4IFOVVThXtVEuPqZqrZu4H3xdWjXxT1VVOgHUW0zc/uUAT1lVeIBjXX5sLK92YKjXs4kvh0PL7Nfv90mlJWKSDgAhCHTCBkGapeR5z0+20D4p06jfbVtiV6Esy8J5bhlnLb16kkiGwwH9fsVoZOWIra0tbt26zfb2NkBw3/LWqsXC5tp59eoVq9UqyhsTxwO1z/XLcZbtfUX7TNNrinGbxlXWj6tKFyjFf0spQ+yIj+NRSjEcjjg0BiMk440N0iylLFfIRNDr5QE0e3KEoijIsox+r89oNGY4GnJ4eMiDhw8RwO72jq17r6bf7zvrnY17EkK4+GwLvqfTaVCg2fbYOZimiVs/VsG9MsbF7nrgZN/B5g1KrfX3LUq8FpVWJNoDa9tftarJs5ytrS3voAI0cT7j8djOzcS3r0lDY98DoJED/E/7nQihHUkiO2MpkUHnYftjNBoxGAyCVXW1aph3KxcmYl0P7fq38fgF0+lrBoMBw/6Aoih5+fIV8/mCra0tlNIcHx+zWKxCfavVisViEZ7R62Usl8ugxFgul0wmE8qy5PDwkJOTk2DVfZvyRw+QdrYmCK04OzlGYM3ned5DVVZjpbVGZhnD0ZCTs1NWRYkWKUKkKC+Au81c19Z/3Gs8tbb86j6pnjYNo47f6ATW0tMwzljw42ONDBU+RkFoKwQIpyEvy8qaUY1lCfGTC6xbnmdG8ZMhBH2iGQ4HbIw3SJOEVCb84XcfcevmLYaDAa+nRyglyfLcCh3usEswnJ5PQUjOzs/JezYZnxGSJGkL8+HQ7Gxqcemaz+PPzJrrrwIta5/bqXfddfHzrmvjVXXEn8WWlque0TyrEfKueqfuYRD/TKQNCj48PGwJ3TocXG3BugFIl4UEn9g0jg3wfunN/U377aHYBFN2NXxNn3l0461G2rltXPWuzmXDfhC+6w8GbG1tce/ePW7cuMFoNHIUrBn9fo8ktQKjjftT1HVl867UNVWpWSyWnBwf8/zFC16/ekVRlgFExOXS/OsAeikby0U8zlfNFw/Ok8TSwGayARUt60wHmMYH/1oLowdfqQWRxhheH7zm0ePHdjyjmIQwNhEyCL92xs2yDzY0/O2Afa8tjt7XaQhblV4q1+iSjY+WCrWHEmMgK5jpxr3s8sg198n16yrc2rFoWK+uzlyI+1sY2i59dk4bR8MlnVuWEJpaV6TSuuFsbIzIepk9yMdjlosLiuUMMx4gTOaSfyubs8ZrSEV4Wcua5sfQa9alDu/QLCPj8hQlnTb69zAYUzV95Oo3/mckeDXz3V6nXRyMJyMw0XW+Dm898ZYgY3DuZlbosbmSHIGQj3sNbmkqZLbHmAB2/OfQKAWgobm28TvNO9RKhfbEwiGJHeOGlc97J1g3cxG5sNW1tcDnMmM0dEKiEAyGw6ZX3TkqpXQeGY0LnhQ2kahXzGXudzsn29Yfvy8IIVgsFjYPVCKpqtpRqFt3JClSfKL6mBDHrnFDIjNEZtuuasVqVVDVJTjvlqIoKcua+WzJcllw8+Y+r14dYLTh/Pw8BMgnyUvKqqRSitPTU6fQ9Vaw9l4VK/5a6+sa4LKuxNbdeB/yloI4R2Drvmhf67KUQsNY5sFOWZbs7u7y/T/7CwaDEQ8ePkQjuJidIgRMNsYBrHqw4xWQ/V6fNJEkQrh8RnP6/Zzh2LLPGT8Wbmx6zgrodRDn5+ccHR21xg839j7hcVBYa8sUbN2zJQLJcDBCYPMcSnHlBntpLLzSMngCOIIN7xJ6dHzErdv7SGSTU8z1db/ft/d1zvWmPv+vod33Y+i9JSxRkXcndGezkGFd93q9QByyXC4ja1EVwExZllYhURacn09d7iQL7MuyZDGf08t7VFXF0dERxhh2d3e4uLDJph8+fMhgMOA//If/4Ag00lBfmiZhf0lTm67g5OSE0WhEnufBsvS25Y8eINkzymCkzRZe1hpNhVaautYkWUpVa/L+EJHmzBdLZJ5gD58Ev2dUlaFeLu0ixh042OBKK/TZg0wbT1uokKK2blhu8uZ5TlkUjh3FInFL76rIshStFPNqQekmSu0mmgCkM7l7RpuqsubP0XDU0kThzJ7LRUGxKMnTFCkEF/kFv/7Vb3j3vccURcHxyZTxxhYyS1yQpiQTilcHhwxHY86nFwyHQ/r9vvPlvcxcBlZLclUiSe8zGguEPlhx3R2xwHoVeHoTqGriYy4LUuvquKredfXHzIb+u+va+qYSb1K+LqUUZHYzPjg4sIepc9H0rkJeKImFhk6rXZ3r31W6+CCft8RbP7wAI0QSwE58eLcPLa+yXw+C/UEU3i1xrhYu4e329jbvPX6PGzdu0B8MmGxsMBgOAj1qrWpUrVC6xMcDDtMmP4uUCVrDfD5ncfc2j99/zMXFBa9evuKTTz7h+OjYCn7RGBljSIQIMmbXMnYVqI3fq2tts/W362tcQNaXt5njITbOGA4PDsL1Qoh2XI2OlBQOz6y3YjWgrtsORARgBCHmoVFmdAWky/1lwnzwzzW0cgN0DvlmEGx8V9TK1j2dHmrq6Fbd6UurDPXB/pHioFN/lzDCCjru/bR7Xwx5KjBGgalJU8FoPCJJJKPRAHTNYnZGtTHA5ClJ1kMKg0KhhaI2nqG0WTLeTRRjY1nsmFrAgrJxNFKCqQ2QrrUOa61A1EHw9PF/fjy0VkFIs2eHCgJ3XddNnhSlnUXGfu/rUUpRlEUQflTtQJJzkxNS2HuqCnTtwKQVIuM4HwxBqDKx6460Ap6UMgSqx+tbJkmgMM6zhvK3rCqSnqUB9pTH0n1n6/aaersg6rqm18vtvuZdCD4aLwABAABJREFU4I0VoIqyQCsfKG6Zv7wLoO033QJhfqbafrXvNxqNAKtkLKvSESvY/Gurle3/5XJhA+uFsDkJtb3e5qcqqGtFUdhcVVaAtDFNPn6iLG2ciY11k6RphtGR5ceAxFoxtFYcH4tmnQqbv1FrD8K8K7A3YJpLZ9s6paZ9R33purBu3qLELnaxQqlb5yUForACtLXgDQOgrZXixs4e+/v7DEajACR1XbK5uUGeWyuS90h48uQJRVGAse6WdV0iS8HHH/2e7/3JnyBcChUDZKnNQ2jjVL18BapWfPrpp8xcXiDv/uhTwIzHY3zKFjv/FMMsD3NCyoQ877FaFSht0DTJUFuY0DT7VReY+lyeXt7MZMY777zDe4/fYzgcsFoULBaWqMMzvAkhSNImybuXN3z/p6l9Py9b1I7Myya2taAjy7yrnJ+bhYvPczKrIxsbDoecnJxQVRVJklAUBbPZjPl8HrnCWotQIhOmFxfMZhcs5gsQMBqMHKCaU5YVWZayv7/P+++/zxdffBFyHvlUBtaNcki/32MymWCMCQoaYwzHx8dUVUWWZZyenr7VXIV/CgBJZFzMloikIEkTaq2p5ivsdiLQhWK2WPDF06dUjvs+Mda6pJRlnLHaBIPNzdBovQIQcgGN2k1nrStLty2lNfmuVhhVUzqf6MTlQUqSJNS5mC+pq8qyEzkSBoEgEYlzS7Cba5bmJCKjl7kNuagpiiK4BWijMcLGQ9VaUyxWYAypTPjNr37NZHOCMZKXL17SG16QDwZk/Zw0lQySlFevDtjd2eb14RF53mM4HDEaWQBlE2U2rkXBShF39xXapcai4SwdkaB6VekK92/ahNdtrFeBruu0YF8W8Kyry9+yzoJ1lUbOA8oksQf+8fEx0BxeXrAondASBOqIp0kI0ejrvZEn/q4jPMcaqaDRNTowX8X9F9qIDwQ32BiIzoOgJYiH5yWSza1Nvv71r3Pr1i36/T47Ozv0ej2WyyXT6ZTDoyNHPatCYlbrLpoipAjf2Q09ZW9vl929HdI0ZbFYsLW9yYOH9zk+OOE3v/kNrw9euz5t3Ao8Vf91c/W6EoMggw3UXufad9W9fi7GlkD/3KqqnObPIKXNZO+1aDY2saE37hhNMP6d1rxbDHgu/QxuXbbIbr9E+KsZ5gbV+Aii9vpyIIl1QF2FSq1Pexwrc437Q4xtMM0a44qtxDXYmPV1iu60FcGG5F7PWy+ty2OtFUoV9Hs5t2/f5uLinDyzXgLz6SlHiUEaxcZoYgU/t0ZEcLETNq5HShs/E7myec00OAWerhxhkCfgaSwz2pEIWAtO6YTexmLswUldV1S1s+JgXd5s7jv7XK+sCu7g2uDjGu0as/Uqx5SKcNZttx/4PH8WpAhkYpVxSZpYgT2xucPSzLp7J1EyXT/HsqQtsFmvC0flnNlgbwFWyywEdVWz3ctRqnGvvri4IBcpg+HIenQEy5Htr/lqSZ716A+HJEnW7GlSkmqBEgptKqqyBCEwbp/RWjsBUFEsV0EIVEoxX8wtm6ib+5X7vCgKlAOdZVFhdBP7EMcYelDrJ6ofP2g0+jZwfhiESq0VBkcooLAWiRAj6s8cr9lvyJAsqI0siI4kRbgN5Dol4SWg4tqnTRM3uA5I+RK/0zpPhO59Vyl3fF3L5dJSUGdZAEjLoqCsa4ZO3krThKJYMplsMBqNmE6nzOdzdnd32dnZ4fXr19bd0vj4Qs3Tp0/Y2dm2OSM3t53FR9DL8vCOQthYtc8++4zf/va3VC7prJeLPDnDYDCgKAoWywWnR4cINMPBEBDBJXw02rAU4asCQe3OO7+24l5ar8yVLpa7rupwtm1ONtne2Q4MiMvlkouLC4CQKFW5PvTu+9PplMFgwP7+PovFEmNgNptRlmVwk5vNZi5hsObVq1dhTL3FyNefpqkFn+Dc5aacnZ1R1zWz2YylMzD4ZL+CJLj3ZVlGmuSkac3p6SlG4cBWQlkuqGvFalXyy1/+mtVqwWQywVN+B1dIIcgy6566sbERvp9OLdnGbDYjTW1+wbctf/QASRsbM1QsS7SoKCobj5Olfcq65vzigpcHBxRVTZb3rD5xVTtaVWXZPgJrnQVJsTkV7ORQRlPW1u+5SdgnUaW7v66sCTBL0XVF7QQhoxSj0ZDRaMTF+ZS6LO3n2mCQJCgqU6G0QteW4cZrsqRzW+rnNvmWMAJphKXoNDZmRStFVZSsjKEoVvy7f/fv2L99l15/wrw4o1/VDNSQLJXUwMHhAVJC5rT14/HIugZ0zLL+MI6F46s2wHgD9YJ4G1a17/HCVhdMIERLU2zln/YG0rUgtX5395tIMy24fAg0wGM9MHuT1mwdKIrdt1qfuxKsOM5tJJGSs7MzrHumChqdYGUiYgS8ygfKtJ/XNc/HANL3deasV/7eriuJFZrsT+MC2MN3jnHK/+03LSkleb/HV7/2Ie+++y6TzQnb29uoWnFyesLR4RGj0SgkLpZCsipWiNIe/rWCXk/Q7/eZbI7p9XoIAUpVHB4d8vkXX5D3ch48eMDd+/dYLVdsjCbs7+/z5MkTfvnLX4aDojvOLSue/aIzlv76Zvxa428IgMS73nRj1K4qnm3sUjviOWcMJycnGGNddpW27mjJOlAuBCasUxqLBY3mNgZo0Z2wJr7HBKndA6mmH7x2vakz9GDUYc07tBSjutPHcTtoGM+aNnSvc39HHyRrIJJvv5RRfbFCx3Sgle7sO0G7re2XApazKb1exp07d3jxwjJLalWxWs45qlZMT04YjzcYDW3m94vZjJPjY6bTC5bL0grYjupZa03l3aUKB2xMDUKxuTVmf3+PJJWIpHGNjFk3Va0gilFqKaAAy3bZrEHfJ+Eow8fL2JjHPE9I0yy4p2Vp2hDRAGkq6fWyAE4TKcN+pQ0kSRpyo3hAb4yhqosAypr4DDufU+d+vpjP0UYzSAakWUqSuChHCUVVkZAhhUQJz0aWUNf2/dK0B0aymBcsl0vKyoKkuqpZLBcsFwueP3+FMTbQvyjtOHhXIFXXrAprSfJpMwLhirZz14PJZt454givNfDnoo95AqSxrJ8EMG/nm1IKl102nOUWHMqO9VkEBj2tTYiB9HuM72OfvDuVlrXNuhxF+wvGOn0665ExzRpHiBCL1LWU+9+b9Xb587dVWsbXr1PUXauwpGGAPD095datW4zHY6bTKWVZsSwKlkXBxGjSNGU0GnJ+dsr9u/fY399nOp0ynU5dbh7rVlmsVmgpHPuZJFmm/OQnf8uqWPLe4w/Y2tpx54xwSsmS1WrFJ59+xk9/+lOOj48tgHIAwVsqxhtjRqMRp6fnHB4ccHF2xvZkg/F4DAiWiyVpmjIYDh0xiKauVkExIOJN9qr+MMYRNtnrU5FhjOLzLz7n9evXbG1OKIqCfr/Pcrnk9PSUuq6ZTCYsFguUc98fDAZsbm5ycnLiwNIFxliL6Hw+5+OPbS6tfr/P1tYOT58+xRjD6ekp9+/fD0DDGOvW6am6e70e0+mU4+NjLi4uEEIwn89DP3kF+3KxcvPBpjCw1qChnetCUBYVec8SkGmlmLuUCmlqXSZ9vVVVObfLmqqy7fVgCAh94c/nmzdvXtu/cfmjB0i/e/KC8WSC1pqycoxvxqCWc8qyZL5cUnoSBeNoQ3VjqrabZY0xDtHKFIE9nOzhqMhSg0wkeZbS7+VYEgXLCmfVXxkyMZYpLkmQIgl+uPYM12xORkwmEy7Oz5jP5lRFhRESkTpKTpcNu6pKhIRUC5cAUCCEpwm1h2FCCsKgpGXM09gM0waDWsHnX3xOlvUZjje4IfbJZA1JikhTZrMLyu0t6qrg1cslW5MRW5MN8iRBC0mWZ2hh3SyME4YvR3zYYsD680dCpjEGLUz43ZeWGd9p5m3XeB0dDtxcN9oR7XCjkg4/jKMINYhIAe41Npfb5CVM4X8KwoLWrgIjGu2530yFoWF48kKq+7N5GxPV5wUcZYXf1M6N8+mUhhJZoVzOkKDRjbT4Vxd7Texf7H82Vj1vjbCWK2FvCC4rELnaKTvvjbN8NqxCWEYd77csHeudgBv7N/ne97/Pzs4OOzvb5FnO7373O86nc7I8JwGOFyccHhxyMZ1yMZtS1aXtn9ogk9StO0kvzxkN++xsb7J3Z58bN2+wt3eDuq75/LMvWK1+z8MH97l77zbz2Yysn7B3c5df/v2v+PTTTxGJdGNtHG03AQNYzjIVNHTtQ7vN9AdRHI8WwS2o6dfLAD8GpV1rU0sw90KXS+a5WM6YLy7Y2NrC1BqDBHE5BhAI1MsyXNN6A9cG3TqEA0zoKB98slQRqNydtchOePe9I08wTV2teec+jJUOQaESPyv8XYdPvAXD9p19Nx/fEPdlLHz5w9UrQQR+zUVQ0elZYsuNNh4I2b0Smpi/2hEIVHXJ+dkZWZqQb2Tcvn2L169fsVisrBAnJcJMefLsCxaLFYeHRxwcHLNaFu68IIyvcbEIgHOvqe2+nkp2d3esm/TSku9kfavFljJxuWnsXtHv920/OYFDJtY1ViYJaZogpAnv64UXrTWJTINCJigzjAlKMaV1cK9BiAAQvCeDVope3iMNeV4UZ6en9Pt9+v2+9Z6IXN6ytE9R2LiDSvs5CGjH7FXVKJWwXJacn54gsKDo9PwsWF68+46NaYKqVIG6OrbQaGXjoPyc80oM7fZtonkTF62108rrAI79lJGO7MOThARlqbekY90wwVtfnWJJ2M9DvigX7yUcc2Z7b2hWhFdMxQni/XNNeK5dOcZYEgFtNDWCxFnk/AnqLZCeitr+ax4qgVRaVkx/NoQ2uXiV2HIU9j/TbnPrN7/23PvFCjP/nVcqmfj66P39+zZKQIWQgvPpCffv32VnZ5uzszNWyzn1as5qNuUEazEY5AmvXx9jbu+zv3+Tp0+fMJ1OOT09YTQaunAGwXR2jtJur5eS/mDAdDrlyedP+cpXP2R3dzfErbx+/ZqnT5/y6vUhi+WK1aogTTN6+RCMRNUCLfvs7d8jTTPOjg+pChuDkw0GDDY3qZVmMZsxGA5J+z2Oz86RImM2nVnSHdcH3jPB96pXRPk+afrfWkr3b93g7OwErS2IKIuSYlVQlZV1+awVi8Ui5G/b2d3lwYOHVFUVSIBOTk5YLpcslyveffddlFJMpza5rAc3vbzH3t4N3nn4kF6/x6DfpyhWnJ2d8/rlSzenJcfHRyFGTEqby6jX61kZuiox2p6V/b51M0wze472+zm9fp9aVeRJai3gZUmWpdSVZe+9dWufqi6RiSDLc1Jl66rq0uZmEiK4Yvp9wVuNhsNhcDl+2/JHD5B+//Q5w+EZibAasSzLLIrPM/JeD6UMGkmSJs6tLQmCf0Pz2pj/ZWIBUuI1P8ZaWzB2ARusn6cGaudfbUSGTEHXNueAxFIUN0KYQtUly8UFUsLe7i7nJ1Pm84VdKMKQ9jKElojMUn3q0gav2g2xiSGxOYlckiwEaZ5TqRplSpfMz5CnEq0rZtMTqmLO48eP2djaYTq9YDGfopX1gV4slzx/9pTdrU362W0SYRBZQsy4BNg4CNOxnAgrmKiQK8MqbI0/METjPy28xCLsYe9BROv/pqGZbBUT/yqI2fbittjmeqGyK8g5cNQNljQiaK5wbTCO0coIE5IM+w3fYLV0KbJNjtWctTZA238Wa9ndYScTqwWsa7vZ+Rfw94Q3fUNgZ/Nu9jcZNIVNMKaV751oGnJhpG4cdUuA8u+Py0yOscHLwo0ZWI2y9gcg1tXm8XuP+fo3vsHGZMLe3i6vXrzg4NWB05rXHLw45PDogLIoMVpYgobegNFoiJTQkxKtBYoEre3cPz+bc3p8xkeffExv0Of+/fs8uH+fRw8eopTm2bMnPHv6GR9++CHvvPOQ168PSJKE3b09fvbzn7Msli63gp9XVqErnOBvBWzVFhaExM+ty9pO24eNC4tHXfEcaGtpPdBuLFRRkHYAMLZRZbliOj1jtDnG4NSGkgAU2sXFD4V5QgPS0QhjCUDiu6QQJGHvuPxmAdb7NejWcbMPuGe4tdXoMxoB1YMW/15NXxGEVo1BmDpU0HLdES7eUTdUtxAxrQXriV1HXqC3oL5hSfNjoLQKnxts4sbVasVsdkFV1lR1RZomkSurVRjs7+/T7w9Ik4wss9rqw8MDzs/PrZuNWlFVJa9eHXB4eILRkrKoUcrGMfl8ZFYIrpAiIctS8r6kP8jZ29tjZ2eHyWQS3KaH43FwG1t3uMeeDIF5SlqXOq8Y8ox+VV3Z88snanQueamwwnvl4pY8oDLGun0maYJIUkypqFVJUdbMlzanzmpVsFqWXEyt0rERUGpWq4KysPFORhsWi0WYFzbO1sVARTFL3pJuMZRpxUj60lWutdxF8XHC8Ry3Spx1c9wYR1nu1kUD1l1xoNtfGwP7hlzEz/c4Aa92Z40HK8268fXF6791fAqILbTNvGmnZrBnvqMtrzVQhHne7af47waQSBJ3LnjvAv9MpAXIwSIZKQFDX1+joPPP8m6YgJ1Hvm1BXdKAgbi0LN2OOGU6PaeqSzYmY8f0V1IuZ7x8tuI//uEjtNZ88MEHPH78mKPDA27fusvt27dYLhecn59Zwg4BaWaVDUkq7Z7hmRWV5uWrVxwdn5Dn1uKwWq04Ozuz4Gs05mK+IklSBs5trq40dW0Yb22zubXDarlkubhgZ3uTi9mc3mhMNhgwPTyhLmt29/fRUrJYrcizjNn51FqvXdqMMCeiPvfnQ3MeC/fsmhcvXqB1iUzGfPT73zPoD5jPFszn8+CSWBSFte4mCeONMbdv3w79fHZ2jhCSra1tBoOC58+fB7bD+XzOxcUFRmvu3L7DyfFxsGB6JjnvztpYNIULE9FOzWfzEiVJQubcEbO8hxGCvJcGIofFck6aJQwHPabTC7IsIc+HVHVJXZdUVYHWQza3JiyXS8DGDHplTlGsyLM8xB71+/2wzwhhSVOEEP+N5jsuw+EWvf4AXddkeZ8sTRnsTBCJdV3SxtDLRyQ+B4uxPutW2eRjAixpA0aTCcjSJNDs9vOeHXRtCR9OT8+xDhmCXpaBkOSZoCgXpL3UBqtq66uepZLhMEepwlqiBrmd2GdnDPI+wmjOzs+RiUQYm1tGIsmSnKSPpX32gbCOkSURAqUds6zQqFpbkJJKWw8SNMEfvFxV/OH3HyOEYDqdoqqKjz/6PTf3dinLgjxLePViwrAv2N3dA1Ej0x4+YabXZDVaXy8dWaFIyMQJaMbx+0LiBM1I8exV2FhNfuM6ZoRxLII2ZiM8zn8fb646+jIuAV1YwHPpitgdPNaIxfgFcIgOY5w2MRzKjQDotT/dZ7SxYyP4dd2qUqcFXswXrJbLgHH8AeoT5XWaurb4jdULmKJlFXEaVTz7kwhWTfucZnNuW5saATd22xFCBGEGIUiylG984xu898H73Lh5EyMMv/vdb8mSjPl8wcvnLzk7PkHVmnQ0oL8xIcuGJGmfJMvo9TJevXzG65PXZHnGnfuPyQYb1Mqg65qqWGDqM6pyycd/+AN/+Ogj7t69y9e//nXeeeddynLBr371W27e3OcrH3yVfm9EnvcZbYz56//011YjhSO/8J0ZCeRdLXMsyHRdUeJ4vDgX0rpr19UdFy/kN0xeoFVNVa6QaPLEWuZSZ8km0lDbMfVsaE07/FTx75A4joSgscVag3ysTKdFFhjhlBvaRPO8tXACSPLWmwiZOYDTuHy1ro37StngdxvMb1lHcVrwsqqdm5AOgr2njg6sU15odLlwrFbV+tsLIRgMB+TO1cLH52hlAVJRVLx88ZrT0ylKVbz3/jtsbm4yGAwYj8dMJhOyLLdxNWlCpiVJCll+iyxPXKxDRa83YGdnjzwbcnJyznJ5Gqj7m7WjGI36jDdGbG9vsbU9ZnNzQpomlj46tYxnNomjjbcYj4cBsMR07caYwNbl3YFUqclz6yKksTGtNj8MaKXQusRA0CKvVjYeIs1T5vM588UCrRRlZQOxq7JCKUNZVqxW9rzyGlqlPbtiA/TjfcbHRfl1ELvgCd2QnVyyCHqLWzSPu0L65dlqaHbly2usC6z+MUVASKjqi1//8Trv7gFxX1zl2hbvvUDQhHfBSrw3d0Gkr9N/F7tWN983rtcxvbNV7Fqygnhd/WP6zRNxXFW6VuHWuzgF7Gq14uLigslkM4ovWiKEtbgiBJ9//oQPP/wap6dn7Gzv8ejRI46PjynLktlsRr/fp9fr0+/1KauKfi8jz/vked+BccN8vmC1Sri4uKCuK0saIg2L+RKUoT8a0e8P0NpQVBVplnH37h16ec7By2cYY+j1+yxWJTu7e0gpbWwNsHvjBksHPgYI5rO587y4rASI531c7F6sERLnHaT55je/ycXFBdPzKVVp2d12dna4uLhgNLJkXiunCDo8PGQ8HgcAsVgsKIqC8/PzAKh8zBBY19FPP/3UugcOBq252SaCsSxxeZ6zubkZYmo90NzY2HDxwssw3+L97Pj4mF6eU1cV8/mcXq8XKMD9vi+lDPWsVqtA+66dAsazUfqQhNFoxGg04uzsDFgfH33lnH3rK///tIzHG0iZkfRsFmAphMsnUltXN2kPEFVrsjTF951yNKiDXkZRrABDnsAHD+/z3nvvsTEa03cMGv1eH4Sk1Jof/vA/8/TZc2SakqQWIPUyCWbI9vYOG6MNikWB0YY7t29z+/YeeS9B65r5bM6PfvQTPv/0KZ999oTjkxMOT4545913LfuOEORJ6gTpFIyhcjSqsStU1stQuqKqoNYleT8n0YkNdK8M0tiEtEppjFJUtSJJJONhj36+Q1UWnB4fUpUFial5/ixnMIA0MWxu7dFPUnwuJit4OUGchskFmkiCRpMcOeN5QBTK5Q3AfyaEIUn8gWdYCwwcMHE4bS1Oil0ALn3jFVVt8xKxedsDDM+s1FTjBMdW60OFIadN+J9p3stbr2xyOJvjSgCr1YK6LEJ7bb6Ay2xDbyptH3CnxTTWAqW1ciZwn+yuHZvkN63WYe825dhX3m84/j2lFPzgBz/g4cOH7N28wenZGbPFjFVR8Icnn/P82QsSLRj3xwzyjDJLyEabpL0JMhvTH4zJsoRPvnjJdFkhVhU3RM7dB+9RVJrVqqBezXn96RHzCxuwKQQ8f/6aV6+OePToId/97jf51je/w8cff8J/+k8/5Hvf+x4PHz4gy1P+5b/8l/znH/6Q5WLputc4AGn1z20Bzxbt/Pn99V5ISxKJMAk+iWRXcOkKOu2D30/WtiAYtOcelmiDckHFxhjSVJBJPze9NdvPIx9j4/5288daEuqmDdo4fYJ1A/KUzn6+uQvDumoBGWel0Q7I+DbHQpp3d/KxNtAEq9s52FgN4nty4ee7A67GumFprVFOYPMlgNK6DkHLsdbaB7bPFzOXK8NQlINoLIyzSoEUGVoZPv74M2YXc5JEcPv2Le7cvsdkMrE5S2QWkkJa6uYSm0gcdnd3GI2GnJ2ds1wWqFqwXJQtrbzSlgq/1+8xGg24/+AOG+MRZVUyHo/o9XrOyyEPh36apOR5HyFqqko7q46kKi14Wa1W1JW1eHlAM5/NWBUlq2XpYmhrVqtVyA/SJgwgGocmriWOPdTGA11ByKIbTV8fUxbAibDeGMadEB2R3SrvEKhak0R7TnfNdWMZ/dztCs+xogbTpphuzZWwINYUpzCIBdJ/CCDwVrd1AKm7n8Z1X7WnD4dDvvWtb/Gzn/0saMBjoBHXHwOkLhBs9VHnxbsubb5+IROMENFaWm/Fe1P/xOPXjWntNKUFsv11VvnW5D188eIFW1vb3Lp1i+l0ynK5ZHNzk52dXYqi5N69e2xtblOViqdPn/L48WPef//9QEqwWq0YjQZsbEwoipKey4mUpjkYK8OUznXTu2XZ+C/LuDkej22qGGNYlQUKw639fba3NymKJUdHBwhtLSwyzdjdu0GxWHJ6ckqvP2T3xj6zxYKyXGKq2lm1YtKLdrf4+Le2S6YIngIGSGTC+fm5y/OUBzA4nU4pigIhbLzOYDhAGwskDg4OAqCZzWah35fLZQAevv/LVRHmb+ni5D0Jgp8vnrAiniO9Xi8AoDS1yhdPPqIRCM/u7EghlsslZVmFmCHfvs3NTcbjMTKRlFURQFwMhLI8w6gm/5en8xaiIV3Jsoxev3/tfI3LHz1A6mduwbuNYNDrWQ2asZmMe70eUggq18nlaoHRiv64j5CCRAoG+ztsbm4wGQ0QdUk5O8dkkkoVvPjiU8qy5N79+9y+d58P3rmPKpcsi4I87zMYDplsjMAoVosl/4//6/+FTz/+FK0Muzu7/A//w7/mr/7qz+j1M7Y3NsgTyS9+/lM+/+wph0evQQpm52d87RvfZDDcQCub8RkBaZaR5jY7cVWWNukeBqFrG7ScSHSaslLWxaGqKqSGft6nlyaYNKEsLVNPVdsYl8ViwXI+o1guyfOUYtDj5PiQp5lGGEOe9+j1+giZIH3qGGchUlpbtzNjwk/tDy1D8LtuABVOca9bm4LwcT0O8HgBzV3eKQ2U8okd/Yba1m432tv2id3oG4V7NpGveeyS0RxErt26yTEkpYzkhgjIGQLjjz/Am5Y3vxhjc5PIzJIPnBwdolXt6LbbWti16G9NiQ/m4OEsGvcaH8vkAYJnVWuDwnaPe41i/N7x84QQ/Mn3/oTHjx+zu7vL68MDLmYzFvM5f//LX3N2saI/2GAy3iQTiqeff8ZFVbL/4DHf/sF3GWzcJMn6SDQ/yHr88if/L5TWvPPhN9m5cRcjElStKJcXfPyrH3F2OmM6s37TIulTlhUff/IFh4cH/Omf/oD33nufV69e8sMf/pA///M/5/79+1RK8Vd/9Vf8x//wH6lcpm2ff0XIhHXF50KLXVBiYOXfP849YbX94lIcQXO97fOuC5Gdd7EF0IBRCF2hK8uW1UtGkUUxYjDD5sXxYBoaoUSbCu+Wp1yEr3J06mCc8GyBkqptMs6qrMLcDeOuGkui0rWLa0nCuovfRdUq9NE64dML6ElilVeLukZAq8+sBVTaZI1R/4f5lyYIQ4i/8LEviaOUX64WHB0dMZ1OefToER988IEDLp4yXyFIWS5KjFHOm0C5OqwLc+PKDGhFLSVCJM6qYnPj5Xmffq+mKmEwMPR6S6ScBsIfgWAy2WBvb5c0k5RFyWldo1XNalWSJuehn+u6tvu50lRKRPE2muXSut52wU6MXGzOEtd/tsPQyubTiQWfIJiZkM8WjECQhHkY6nWPaASzWElEhx7b7ZX4hKRJsGBaIO/uQbbWT1hbUT1XKR3Wldg6GZd1wnwMzKSw7vJd4HXVs4Lgjm5crTvAyN8fW5Vja0z379Y7uFKWJcvlMtAs+3nvhcL4Pg/O1oGtdUDMXqtbc8FbOqWLP9LuXh+/1pxBb1dCXR3LWRcoSinbZ6MxxGu8uUdycnLCdHrBZLLB5uYmZ2dnFL2K+/cesrW1xYMHD8iyHru7ezx58oQXL15w69Ytlsslv//977m4uGA+n9t438Qm8g3gSClqZeNybXMlaZqjlFXCjAbWwwGgrEqKqmJnd4/9u3dIEsGTz57YfWy5pChLdm7cJkkzDg8PKZYFDx6+Q3845uXzQ9JEcPjshX/jTs9FZCuuX2IXWztnHYETJoCoi4sLy66oGpc8f8/GxgZVbcHKYrEIVsPpdNpSUklpSRB8HJHve+8K5+N7/PeeSt27unkg4uesH19/zi2XS8va5yzc3iXOxxlqrSlczivA5e6ylqY0SzHY+vf29jg6OgpncuVykvo1ELt2ggVrvV4vxFS9TfmjB0gZNf0sJRGWIneQZYjMrkWlKjLsIb7luPU3bt5iezJic2vC5uaE3d1tl7FbcX56QiIEn37yCSdHB2RJSuYQ8+nhARfnZ4wnG3zl8SOOT07I8h7z+YJEGFKZ8X//d/83/vZvfgwItDIcHx7zxSefcPTqNX/6539CkiX84Ad/wkd/+Jha1WQ5LkhQ89nHH3Pn7gO2tnecr3QatPUSSZKlGHcIqqJAK7uBJgYyoKprymKFKitmWvHyRe023tJNUJfh3JFTSGFdCbcnY7YmG/z5n/0FP//5z9na2mU4HAE6CJPe1c44gGSMwSjRkC1E4EZ4a432kASn9WuKd+gJG2YANZcPPWMagT4WEsylOu3/1wOkWNNI+NvpxVvXhrPLOIlCuPiHIDbQkGO55zQuUDYotnvceouBUjWDfp88TShWS/teRthM754eWKmWgPGmEmtem0Sb9l+TMLZrZVrXz5GAYdZrfIUQPH7vPR4/fszW5hYvX71ivpjz+uCA3/7yt2hSxpM9BpNdhhtjjl8952S5AgOqhsnmDS5KuDg/oVxdoMoZD97/EIPg4GTK61Pr+50mCZNBzv1H77NY2MSHm7u3UUozn89YzGcs5hf8+3//13znO+d84xtfJ0lS/uZv/oY/+4s/49GjR0gh+Is//3N++MMfWnc7KUFdoxEV3srWiftxIKlxoWoONEt9moS4i1iA8YJDS1C9JEARLJBZIlnNLyirAmMEiWxyVRjjqMaVolKldYfSNvjdx974g6d2WeBtfokSow2D4cBq36Jx9u/jBT0fj+XniJ1DLkBdCGpRO2uBBZtNMkGbw83fm8gEI4yLtUtCUk//TBvX1hxqiSMcAEFZV2HO+jwxHuwJIE0zlPss9IvSrJYFv/vtR86FWvLNb3ybLMuYz+cUq5okyRBSkvcysixhuVwiBBRFxdnZOWVZMR5X4fC3fWopnYuyZOVoc5cueHsxX1oa79qyqPkxreqK4+MjLi6mbkszQZnklUQCG2QsE6uRFQhI0gCEodm/bAC9doH/8ZwVeHfI5hM73zwDpF/n8VK3+42zZotmrzNNJTQ0OHYe+NlgRHRl1BSBCDFQjbXC50dqFEdrgU9HZrwOSIS/O3tXGxABcr17jdXIN8+JrS5xPX49hNQLxrLLxu+w7p+/N/4Z/961dvmyXC756U9/GrT1UsqQMPWSRSHa679s6d5vXezs+HkXKb/e/NxYg8OuLV0FSQye7Lncfp+rilKKg4PXvP/eVxxL3QXL5Yo0nZNlOaenNl6o1+tz48YNXr58SZqmPHr0CICPPvqI5WKOUjVFUVKsKmbZksaDAqpaBYBi9/HcWpFTa1EtyhUKwc6NXR48fMRwPOLZ55/z8sUze5gJMEZw+849KmV4/uwZaZpx5+59FquS07NzNrKE4+NXQSrw+6fto3ZOx1ZsGDjFqw7XykQymUxCf6Zp0lK8eQCSZlkrDsy70XkyCm9p8eDUWyyNsxR7S5Hfdz1NtydS8QrC+Bzz1iYPdPx4x8BICMsC66+RUraUAmVZBqtRksngMh27bfs2ZVkWAJIHfH7+xgqLtyl/9ADpwb1dxqMxGIsw0yRlMh6TSOP8vQehIweDPlVZ0ssSHt65yXK14Nnnf2A6PSdLE4RMOD4+QyvLdw9eo244Oz9lYzwkkZqq1kzGQwpX18X5lIODI37/+z8gk4yqqKir2tKQKs2P/ua/8PVvfoO0l/CrX/+a7Z0tKlXS6+XW7U9oFos5z589o1hV3Lp9G4M9cKHR6B+fHDM9O6OeLyhXLrlcVaBUZTXF2mY8N45txMfNaOOSDOJ2PffPKEOepfwv/mf/c3b3dlHa8Nlnn7K1vcVmJkhl6tiZHDsQBh1l5/bAQBvtQJQFFBYkpQiSxkWjdS5GLmxhF27cw3yxFh83CgYQVqshkwQhzKWDaN0BFQMG92V0LrfhEZ1nm+i9jGncf9owSESHigDVaNfjz42xcSBpIsnShPPzMzCWccrIJkjXGG+du2bS+ycL0XmGeydtLQa+79I0xTNq+eEPJBDRSRjq0d764WPFbNnb2+Ob3/wme3t7HJ8cM5vNePnqJb/97e/oJQP6wy3627fIJzts7mxx6+5dsn6P5ekZDx++x+efP2NWCfJ+zuakx4272wx6PZI0pzYJq6KiLktm52dcnJ+QDzb46je+y8Zkwq39WxRlyfHREWl+gppLFosLfv6zX7BarfjTP/0+xmh+8rd/yw/+7M+5d+8eVVnyne98h5/99KfO0nH1oSy8uTMSLuPv7IEjiCnZbaB7Q90ba5VjS57f6FtClXP30UqR9hIW8wtOTyTL5ZyyKpnPJuFQ8v7ixWplWYtUozCw+TWsC6DAAh2vxfP501Rd0xvkdk+Q9kBMsgwBJGlGmubNnBONRllg17YNvs2aQPLY5dI0cWlWPnXfJUlYO8Jpj429Ca+jqKqGUEC7+E/vxmlMe02AJbMwbi+z1hdFUVQYk7B/8w55L+fhw4fMZyuUnjO7mAVL1apY8fLFCy5mU4Q0aC34+ONPePr0WQCufg1Y2lnnRhiBlsaVyL6XbbdzD1QKoRVa+ID4FDyTnbakIP59srTv+jsJ7HqNFUU2oEK1XZ4uz9n2HDUYYgOp77cAfiHEEgnh9mbTMLTF7nWWnc06gUohmmg0uzG2l5Lrk0bn9XaCsCeWiPfLqywk0V0NsOsCLiFatOVdsCWiZ8TXeOVGLJAFYcs4S5/WrXvXAb6rQNC6v+PPfUxFDPzjPaV7f2w1eNsSg5Xmn4TICtZWDkUawC/xjKs+v6SEu6ZIKXn9+jUPHzxie3ub3d09Dg8PWS5X9HpLzs7OybKc3d2E4XDIjRs3ePbsKUorHj58SJ7nfPrpJ5ydniKlpcq34QHaYneRNG6GTnD3bbLWE7vH3bhxg3uPHjIYjXn6/BlPvviM50+fMhoNGPQH7N+5R97r8eLVaxaLBfdvP2R7e48vDl9SK8Xx+TG6rhEyd2/WWM2UalvQY0sauPnlrbPA7du32drassxxQmK0afIDuXV0cnKC0prMZAHke1CxWq3CvOn1emG/80o9KUSI9/SAQwjBYDAIFiM/L70yLna3a1sBhYtbNMGK5fdIX0+eZoFm3a+5LMsYj8dsbk1I0iTkcvIeVZ4IwjjFte8rb723hDKrSGH95vJHD5D+xZ/9Cb085+zszG42VR3cK8qyJE0kg+GYlfO7vHt7H4TmN7/7lUPXPilWiUxsfgErJNj6jbQbeZZmPHr8mDzPmc8XHJ2cOL72IXs393j58jm93AavVaUFK1VtTY0ff/EHXh+/4t69O5wenXByfESWpGFyrpYLMBVGwcnxc7ResLV7k/5wiKqt//nnn3/BwcEBaZLQS1PQ1jVHYBlEtK6dQNNodr1dR7iF6QOjMQaTWMH48ydP+T/8H/9PfPjhe7z77rscHx3y4tlT8lQyGAztgSPdoQqWvEBZs6+XKaWzLnmrjhX+qqCZFhhMIFhwpuMIHAVrkDGB9DoIVKbRYgqjkcYgffSGiVzuvBtKCwDhhIFog3aAwDOw+Jwgl60ojonItVNGWeSlcBPDPcBbzYRDdFI0gkajETaAppelYDTnp2dWmDWEgH1Pr+1ZkZoDKgJ4l4oVwjw4EgK0roEkHPreXB+uQTuhyAlh0RiEp4hwRXBV/e73v8/t23coy4qz03MODg753W8/op8PmGxsMtjYId+5webtR2xu7SLrFe9/IDk7P6NGsn9ji2/fu8fuzha91KBVQVFVVHWNQSBFjzzLSORtVF1xfnHOi+cvefbsJZ8/e8H25i57Nx8y7E/4+NfPqCvFYNjnV7/+FUmW8O1vf5tVWfKTH/2Yf/mv/hV3795DK83x0RGffvoZlqHvcj964ckQxxnJQNuLSYAUjD/UYtc2E+Z+nMUcouSJxusPAWlzmgh8zI6iKBW//OWv2JgMUap26Qa6xBmW5a2uC+e2l4SD3Wr8JGma2bknJUWl+Pkvfsv29g7vPn7I5s4kxMHkeU6W5xitbU4upxX0h1sQ/GI3LhnFOXjLhSHsnwab4kBIidEivLdXniSpTY2gjXaJdzWmtukEKpR1D1sWTmBULBZzphcXrJYrli7AuChWwfVj6ViYyqJiuVyFQ/vF09f8zX/6cbCu2Bgkg9Y2xk8I615n3ec08/mitT8IIQLboV+X0sW2CnQwjiRSYnQdODWFEGhPFy26Vho375wQIlJPYuPmmTHBQmMZCF0cpNFB6d6dtXYnDTYRRJRgwO/3eD2Ln89CooRAITFIvMrHz0eEtHl+LCoiEQaExlAjyIEUg3LvRgB20s1uKa17ZlcAbvbXCLQhwt/NVmmac0aIwH5nHCCT0gpHynilhQzz06E9TCR4xv3mr4tlJ6sEcgl0lUEkPv5U00DCy/vF2wr61xV/b6zNL8vyEgCLr133Xbe+Nz2zNc8Tm8LD97EXqqV0ID0+w1r94FScxlukvGtYYx2OwWPjtuevv/w+9lv/vY0R//yzT/jqV7/GrVu3WCwsa5t157TXLJcznjz9gqoquXXrFi9fPqMsV9y5c5vhaMjLl695/vy5Y0SDBOei6wiokE44R6GUnZ+ShMFowt7tfXb290myhM8+/5zZdArOfS3tjcjHW9y885C6rnn1/ClJf8itR++wrCqmhyds5n0+evoKKVN0SPTu533kSu/mW/iJV5JYAhttBEIYRqOBDYkolgxHQwb9AaenZy0F3GI1R8qEXn87WI68BccrAWJrSwySJD55tL3OW3vKsrSxam7ctBAgE3q9Pt51F1zS8yiXWK0UibQJs/uDAWCtWUJasrE8SUmTlFrViESgezXVckUy3mB6em5DY4wgJcHUhvl8jpCCRblA1TakpImJt2tfa7t3lUX5xrXgyx89QHr2xWe8+/9m78+Cbcmu81zsm9nn6tfu99mnbwrVF6vQFFoCIgmKFEWqpURJlnwl3XtD98UOx/Wj7Sc/3Ag/6M3hB79YoRt2uBNFWRQlkUFKIgGQAApAAVWFqjr92Wef3a5+rexz+mHOmSvXPqeAosRrUrCyYtfZzVq5MmfOOeYY//jHP65fp9UIVJfrrCBazCvd90ajwc7ODpubm3iex5PDJ5ycHlcRukGcbN1Zua5YpayytttCMJpM6HQ6NNstWp02YRiS5znT+Vw5t7oLtm1bCKHkOfMiJU4j0iwGUXJycqSjYsVRFwKyPENKVUwss5zxSG3q3V6fZqPJwZNDFuMxLd9XvOFSF9ILG7fRwBIwn09BlrrYcPVQ/VuWzk+hObjCspnOF/zuv/s9vv6N32dzc5O/9/f+Hvv7+7RaDba2tnFdB8teRcaWm1atALRc9kAwRkAtbv2l3X5FyRC6ELwWIOmgpFwxmnXDrAyYBjBrmy3a8VhF6OvH+Y1hieJLyoKq8a65BkVtWUrHSimxdFNFEyTK2rntFVqHWB0XKZVjLmwcSygxCikZjYYY1FeyrKmSqNevHqubXz0NL7RBNb+rKyHVU/fL52fOYcaqrP5gjGCFDhjES5a8/MrLXLl6Bc/zefhwn9FoynvvvY/vNej1esSLBYWY89xzW7TXNxlPFgyPD8jnU/YuX+H6zes0A58kmnOyf5vjw8dMxiPiJK5UcoyCTrfTZWNrk7WtDV588RbXr13l0aND7t/fZzqP6LWbDIcj5vMxO7s7BEGT7333bRw34NatG0xGI77z1lt89rOfZTQc8uprr3FyespsOqtizvOotXr29f5Biv5ohkIIpXIkdRNds87KmqqVGe+VMa/mnQoyKC2ddVqiX5ZtcffePZqtAM/z8Dy36oxurtPzPHw/oNVu6P44VJQcU6waBk11ncJhOo2ZTGYMRzOiOGJn94v4fqhoJLYNUmBZDk6NTqFsoQoVVZbWpsjLJWqo10KaJBXlr9BUlSzPlr1sMqVoZJSTiqKoZLZznREzsrT1Pjd5Jklqm5uhd5zPyJpxO4+0n7dJq9kCBdSg1zW1wFWZGpP51gsL46hTyd1bqKBZGGRIzyMLibQElGYOGCl9iZR6fminc5mhMSBWyfJsdUdXVoH7M49apsbYwwr1FzYCQ4+mZstUtspxXQ3ylNhGDMTYOY3WloUSeLEsGylt1UdQCMDWWSplm23bwndC8lz3RXHsihKoGAeQ50UVTNWphMa2PpXpEU+DVki9fkzgWK3Nehanvk+tDBSwKiax/EyB69hcuXKJbrfLu+++S1GAtF0l0CGLyqbWFex+3PFxg6dnZZ1+VCZm9do/zueeZxnU1kptvFazR0sp9uXfDHBYP7ehcD77es4DRWUhn/pb7VTVN2ZPPTo6ZGdnl25vg729PR48eMB8PsfWrTI+vP0+R0eqxmcyGfP5z3+e4fCM2WzChb3L3Lx1i43NTc7OzhgMBkynU0X7KpVAV1ko4EAKge26tFptNvqbdNfW8Roh8zji7r3blKkq1XAsi163D07A1evP4XohD+7dpixKLly+wtrGJo8fPIIiZ3o6IpnPsa1yZT83e64BW83+a1rNqNeYImgD0EiazSYg8QNfN6NWpRJxHOO6Dq1Wm+3tbUajMUmiVCtlKSu6nSxV3allL+uTzLNR2Su7ygqZbJbZX5I0A6n6SVkaOBRS7T+q0XGBkBog08Gao0UvHFuJ0riOgwUkcUKe5QhbAXR5llEWJWmsWBKe67FYLHTdql01ezbtGgzgbTJnBpAxgZ2UsqJ8f5zjJz5AWizmPHnyBN/3aDSatNttfN+n2+1WHXbb7TZnZ2cMhwPVUVtvWoYmY5wz4/zX09HmKIqc4+Nj9vf3sW2V2jWISyFlxdcsyyVn3LYsStumlJI4TrVTkJOlOWmakaZJNSFNmltKVRScZpIwDPE9l3azwTwMSLN0pYhSFW2jO5PbqGB61Vidr4Ewmvbq/bLi7c/nKVl2zG//9u/SaPhIChzPptNuqaaEYolU6DhCo3q6/8SzgiYp9UYmzv19tdjUGGupEUQTvEDdkVj+H7WfV8bFvLf+30ryxXDhUdQZc+5SKgUtMzZVAb60NLJUQ8CEg43JyLiArqewLBA10QOsakMBXZ9ReyRK+lIynU60k6ycBUPdqs6zsoF8xGYrVl9XD4jO76FLBHd5OfWA8dnnV+fe2NjghRdeoN3u8PDeI7Ks4L333gdh0+72GE1nHD7aBydg58bLWGGXw8MjAhs+/eYb7GyuMZtN+P5b3+H+3dtEs6lCp2VZZekEUAhBPBoyfPKYBx8I7MBj+8Iez7/wEs8/d5Xd3W2+/857HA+esLa5zmQyYjiYcPnKJbKs4LtvfZd2q8GNGzf4zne+w927d7l06RJxHPPaa6/xB7//B0+NiRm382NQpw6Y8VeKX0bIQT+32hwuanNp6QTKlWdh1k9RLPn+zWaLIAi1epKH49hq7fs+cRyv1CcoRFAFFIrCqoJ8KSHPFyqAKxWne/fCBQZnQ0BwcjxACEerNqkslaoptIiTpQKa2lwjLbsKaaIy2NEiqjapNFFCEmVN+aoOnBjBkboYSIVWWpbOQJlxM9NMgLR0tmeVzlT/vp5RWx3r5RpYnfNLB3rlb1iYLHAt3lHXqDGC80GXlLWssvm8WgF/aemsdFVj9R+fYfh4hwGQzJf+TGmDdFHOpkRQ6MxUjmNLLEtlssMgoNUMCTyXJE2ZzyIFGJUSy/KQEsKwSavVxvVc1tb7tNtt1tf7rK2vacesyfVrt7j/4CG/8Ru/waNHj1gsFtVelheK7i2l0AHv6l5h1tESCVdofpEv1121H6P69lhW3TE352BlHMycWtYvsFKzBcvam06vyX//3/8vWN/Y5H/7v/nf8eDBvgK9pEVJiqEy1oVF/jSPP1bmSq/L8zWU1XqFp9aI1EBlhcNJ+SM/s77+DPBjzlX/+qhA6vxRV8X74IMP+OSn1uj1uqTpLo8fP2Y+j1D9nZR8d1EUtFodut0eYdjk5OSY999/n15vnY0NJQN+4cKFqm9QkihmT4lA2Cob4vkBfhDi2Upa+tGD20wmE6VKKWwmgyFJklNaNjeuX6fZUiDd8emAXneNm9dvMRoMGY+GtEKX2z+8C5ZqJ7MauJ+jTQqesmHotxiAxrZtNjc3mE6nNJohUkotcgCNMFQ07DjmNM3I0ozFIiLXynJZqhsr69EvypLA9xG6b6ipDzpPMZVS6gCowLXsqkVIWZYUssARFjIroNSsHv14y7JYaRFgWRZZnFR+Z6ZroKb5tPKZVUZIASxPjg6BpZx+XQil2WzSarXodXt4vldJjPd6PTqdDmEY0mg0cF2X33/rmx9rrv3EB0iKX6mahNWVwIwBCMOwKghTSipLeUkzAeqpYGMETaEamIVukSSGApJXBWuWpXi8zWZz+cC1FLbpWi5LyXg0RkqLdqtDHOVIiVYsmlYyjea68yzHjnMeS7h0+bKmhFD17amyLZpm59gOruOS1O7lWY6B2WhMMLg0kgJwyAvBN7/9Ft1uk+liihs43LxxnUYQKBlyfSgu/fJ7M3bqMww6vrpR1Sc8LNO76lqhbjzP/3zeeD+VmhfL+pu6o1Z/rznqn1tKleXTxBhKqVXfWNaRqMtXCn4SXXSvX2MJC0uqsTM1HCrUs6qCf9t2EECaZZQyx7YFi2ihayGonMXqumrP7aMCl/OI+mogv0TWV99j3idqWbinz7/iECKRQvDaa6/RbLUYjycsoogPbt9mtojob2zht3ocnY2RlosQNmkccbD/gP5ajzdee5nAhTs/fJsffO+7TCZjTe6RShilUKIhhqdsWzaWrednWZIvZtz/4IfsP7jPjVvP8+Krr/HJN17k/R/+EOIzPD8kDFQGtSgki/mY737nO2z87M9w48YN3n77bba3t9nd3UUIwb0L93i8//gj7/mjxnl56CxDzV7UM1JKMS2vBalFFSAZBNbQ6nw/wHM9Op0uQaC6kMdxpv+FNC1x3UQ12EVqRaOSPE9BaIUzLbOdabGGPC/IMy0ukCgQBgRxEvFv/+1RFdjVex0px5RlYKLXhcmEKOUyWYEg55FoIYTmwKuhULWOhXYq6w6ZGj8VwJnA6Dzyr85iNuwKwNFH/fPrh+G4Q53OtawtqT/jau3odbo0MzqTiK7zF6v2x3ymbduKZqxhFtuq1SZaint//hosLbZQlssMpSWW5/hR8+7HOabLa9P3g2IvWORAASIHkdNselzY2+WFF5/jypU9ms0G165eYXdnmzSJ2N/fxxKu+rIV6NUMO3S7G7Savar421DBYq1UdXJ6ynB4Srfb4td+7VcJw5DZfEaapIxGI45PTnn0aJ+DJwcMBgPiOCZLM/JCta/I82KFTmpZqs+fLK0KMNMziyobJ8y9gy4q0WOmM//akTONh+tZ3fMBb7PZ5B/+w7/PZ958A7D5b/6b/5r/4X/4PzAezbGEjW055DJ7av78uGzPn5XDOJd1wRgwa6nAUOzqrANYDe2f8ikqm/bRma5nZa3OX9f5eV4fY7OGFos5H374Q27deo6NjTWyLOPo6IjZbE4YBuxd2MP1PHZ3d5nPFoRhyM7OLtPpgpPTM05PT2k0FMuh3W7TarVAlFg25EVJmikaW5aXjMYTpsMzkmhBmieMBgPWemtMo5xoEZPkkstXb9Bf32CxWHD/wUP8sMmt51+izAsOHz+mGXo8uPc+eR4jKMCytL1YHR9V37hs6F0fj7pgg2UJ2u02lmWRphFFqQSdbOGqGkyhbM58uqjVBdU+rFRrSGXdHJ0V1VlxlPJbp91WmXtBRaszta+u61Km2kcSS8XWFNWixARChglg7sO8rmpsrZ9rnuc4roNlaN1IXN+n6Xk4tk2j2cBxHC5c2CMMA/Isx9UqeleuXGFzc5NGo4Gps3ddJdyDEDi2qi0bDIcfuR7OHz/xAZKwVA8ZofpwLZ2HsiTL0qqIWvk1FqrL9dNqVSZQMrru5zdj09CwvniXahmikla1nirMFoDFeDxlsYhIs5zbt+9wdHSifk7jajKZz8qyDJGp1P7pyRFh2CDPU6TM1UYrbSxh5J1l1cxu1bl5Wl7V/K5e5GmyPPrdlLJkMp3yw/c/UJz/rGRjfZ1Wq6XodqaGwrKqjd8UhtedGeP0mmDJIOqO7VTPqEK1pCaaiaUDJ8zzUle5cu6POupOW1kuFcDqBmclMEPrdOmUt2tZmlJiUGz1OpVpdKugFiGxLK0qKC1kUWBT42EjAFsjNooypGhJGVmWMp9PmUwm+lmqq6hQc56V0Vh1Nqu5f24TqnPJ1b+1jW0F9jbnXO3BUHceSqk46Fubm2xsbOB7HvcfP2Q0GvP48QGNdgc3bNLqrfNT2xc4e3JIEDZAwM5mj1dfe5Uii/mjr32Dhx+8B3mGKFTBsyxVq2WzXmxhIcuSJMt0Rg88z8f1bBxhUcQR737/uxwdPuFzX/wiL794i9CFB3cf0QzbCAl5mpPnKcPBiHfffY/XXnuVTqfDd7/7Xb7whS8wHA557bXXOHh88JEB0fk5ssyYloAxMGoAi0L1nxGca5BKXeGnqMbZBAhCZ49mswm+HwAFw2FRrQ/12vNAQKk3onPF8XpuLIOweiZhiZgvAYQKtlDnEYIyf7pmUf3fUrLItXljLSFlDRyYn5dxhhFsWN6Luq+6UIBBep71DM4H9uft9FPBWe1v57P+z3pv9TtpEFqhi35rzqGlGm2v2nhFVbYRuLa9HE9Td2QJpGUoeEtnwMyFMl/y9JdCHjqQEueAm9r3deTfjKcJAMCq2TbI8xTLsumvtbh4YY2yzOh0G3i+xZd++k16/TaeZxOEjrKvcsjJyUCr6Z2xd+EapbSYzabaCVkgGWFZLkgfpKLmOXZJGDqkiWRzo0+z1aLRaq04tVKiVcFchLAqNVVFVSs5PT1hNlOI/nw+YzAYEkUR4/GI73//Bxwdnmn6jton8qLAcvScKsGya0wFbcMVTcnSgKKi/yk7o+a7AfaEEDiOkhH+m7/2N/krf/VXKMsSz/f56ld/ju+89T3+2a//BnlWYGNRFst9E1iZE3/Wj7osvxJ0WVUho1Yz9BR75qMySM+I6is/Sc/vOjBR/V2sSsWf37dg2Wy2/pmHR09otZtc2N1ja2sTEJyeDpjPFpQNH8tyGI8m5Jnqa9RqtVSdYhRpSp7N4eEh+/v7ANh2icJ7LeIkp5Q2eSERlk1gW9gWPL5/jyiaQ15QlA5SuFy6fovdC3skcczDhw+RAq7evEWj0+Pg3l3yJGK8WHB2dohtSQS2ysbWh+6Z4MfTA2pslGVZXL9xgyiKCAKXJI216Is6l5HmdnTrAs/3oW63bMhAgftOWWVdiiJWAH5RsJjOyIqcpFYDl6Zp5RvY2JVgTBzHWLpGyXWcyt45+nsjw23sVqfTYWt7m3a7xdbWNkEQsLW9BfayvxEoup6rG3wb9oQQSvHTjIdRuTPkz8BXSQyVj5BkZUFZgOt7fNzjJz5AUjudKsIFcBylIKQWXYGkxDIqGmWunMZazcazNlzjGNWlcBVtaxU9qt6HUlaKoog8y5eLHrXgw0aDr3/9G3zta4rikyQ5ZUHF2a/ryds6CrYthzxLmU2neK6LY1lklTMLysmRFRJp1N2ME/es7MKzvlf3po6yFNqphyhKee+Hd3i8f4TvOro2wqsCQdM0zHEcHFcV3KE56aYY0NyP7/vVa9X7NNJnqzSv7Tha2EDREiu0y7IqikAdDa7fX/0wohAVxUfdoHpGllXVKdVmjpK31M/ecdwKdZQmcKk1sDNF8UJYWPYSkTPXq+7b1tdikBM1B0ajEWmcM51OODk5Jk0TTPPRvDA9Wayl0/Yx2AgG1TEoaR2tUc+z1HUEFrI8985zwVV9TIuiwHYcSiTPP/88nU6HyXRKmqTcv38fy3Zotru0u33avTUuXbnG1es3efDgPrbj8cbrr5JGC77+73+X44NHiCJVQiSA7wdKRUeWrK2tY7uudnAkUiNRo9GI8WgMi0L1NghCXEswPD7i3/2bf8Pnv/RFbj33HFkG+/cP6bY6dLtr5FlEnnl88MH7XLy4x9WrV/nWt77FZDJhfX2d+WzO3t4ejx8//shsxEcdS5BBVLU4lqWaUxfFs7Nx4tzGaHoiKec5xbYFo1FSO7/xSFQGBb1JGhpGLU6uPee681wPrlezC2YCyOr/JjuqRUdYZmE1pKG/VqZNdZSrn7zqxLNqZ+rjoCCdVbDj/Dw041EPEn/cczoP/tRBofPKglLKSnRBAFKuyrG7gW6OqG2Z2bw9z2Ozv0a71cbWrIFmq4WrbVvQatJfXyMIAvI85+joiEePHjEcjvjhO+9zcnSC57i6V4lyaKQQlGKJ9NfnpVmL9aBxZVykkmZQmaICx4Wr1y7x3/2jv88Ln7jMwcE+3V6TvEgYDI959Og+Dx/eJww8rl27hmMJkiSi3Wri2g6NwKcobRxLMp2NGY9m9Hs7FEmBEC4S6PX6BEEDSkm/18axXUrbwTKqr3rcTc1OlhvquWtSP1i2zfb2RrVAiiKnETZA3/P9e/f5wQ/e5cGDB1V/qyiOaLfa3Llzl8FgWGVqbdvWapJKlMb3/Ir9EQQBQRDQ6/UIGyGO7bC2vka73ebChQu8+OKL7O7usphPGM6mCCHI0oJf/pVf4ttvfYuHDx8hCxDlaq+f84DI/1THn8T5zRyq90wzjqhEqAxHzRf4KIU8s8eYtWNe//Q1Llkcq/ehWgCY85wH5J61DwmhgIe8yHjw4B6NsEm73WVnewfXCTg9O2E2G5NlGWmaMZ8vaDabTKczHjx4yJOjQyzL4ubNm9y6dauqZ5FFRCN0CBtt8gJOT8dYlktZWqRJxMMHD0mimF63S5Ln2EGDS1c/QXdti1mUcO/2bYo848bNW2xtX+Dg+JT5fIxtJdy/+yFC5CjraGii5cq41APCFWCmFpwKDWLZtk0jDAnDENsGiYcsJGUiybMCWapm1UoWG6aTGQqjWgp/xElCqllKlT0Ryv5XzB69D5v11G6rGvtWq0Wn3SWOYsaTMZZl0+12uXr1ChcvXtKiJpJWq0Wp2SBFWeA6LkEYVD6f6bfneR4IwXgy1gCexPcD3eoBBoMhjuuwiBY4jkOz1SRNM+I4IghDimhBv79GksTYjiotsRxb9YYqC90o9+P38vqJD5CKwqT3chVY2EtELQyDanMxEqvUuJTngyBYGgKTLqzQ4FJWxbp1pEWlSqVKGwpBnmcUuRJCsISF4/o0G02SJCZJIk25ssiL5SZSXzCWpXpZ+K4PQJLEDM5OVSdo4zShVFgsHSDF8aKib5iI/sc5f3XKgZSKaqbEGBRfXNUJWsymMTOtjCd4Oji0bFttevVNHC0NW0PiTWbEGApQDrHjuFWD2aXzYq04Y+Z3quDQ/FasfO+6qtGjCbSEQaueYXwrxEa/1hhqs3EIIXBcG9e1q9oPUzTvui62Y2kEU/cksG0838e2LK0ItizCV4iYzXQ6xfcC9h895s6du0hp+gaIKkh2nKCGDq8ez9q06qh9PUBavmf5XllL8y+zCKvzxATLxpA2Wk0uXb5MGDa4d+8e4+mEo+Njuv11wkaDdqfL1u4FHM/n4PiIRZbz05/9LGWe8q1v/AFH+w8hT5ktJnieSyNsYFk2URyTZhlSWHTX1/GDAEdzlG3bYWOngeOHzEYjZFEwn81pNVs4lk0yW/C13/v3fOHnf5bnPvE8k2HMbDyj22ozGXm4jsd8EfHhhx/y6U9/ms3NTb7//e/z5ptv4gc+V69d5fHBwR8vOKp9p1QZjZOhqa/lOXGXcyMNy8BFiSGIKnC3bQPmLJ8XOlNpHATKOgWjfs5nAwUGeVxCH8vslABkRX8T1bo2WcVlJssEX08HZk8dNdBG/V9Q73lS8e8EKltYC/zq1yxWodYlyIEWeDnnVNWDhTrt1wA0as06uJ5Hp93m+vXrBEGI53l02g167RZra31c162U8BqNkGa3TX+tj+s61T6heidZvP7KqwqhzZVjUZRL+hKOrcAeS5DpDVsIizRNefft93nvnfe4e/ce9+7dZTweE8cxURxTCuMciWoumOdr7GqViSqlfp0S6XEsoQI5R/DmZ9/g7/7dv8XGeodHj+6zv/+QjcUae3u7WFh87rNfZD6NKPKC06MJn//cmyAl+w8fslikJHNBo9Hi5OxU2SPhcf/2Q1qtDS7sXUAIycP7d/H8gDhKOT4+5fr1mzT7a3T767iuw2KhgJBGo6nskWXheu5KkGpZS9l3x3EoNTU9LwpOT47Z2trky1/+Aknyqaq4/rlPfILA9zk6OubRwyeA6gXTbDZZX1/H83yKIlMSzI1GRRc1PYUkUtdGlQqEs23Ozo6ZzcYEfsDgbMBsNmM6mVBS8rnPfZrB8JjxZIFjO9RpQ/Vs0scN4P80j4pJYSv2h8kiCFu1NjkPPJpeNc8KYFzHAbnMcp7fl+qCQeZQ51kGYPXPqv9b9y2W7zUiMRnvvvcuL7/0Gr4XKtECAc1mwNnZGZPJlCRJWSwi5dR3O5wNzzA2bjgc6j1SNYP91OuvkBeCw8MTDvePyPKYOM5J4hjX9uj3+sRZQnejz86V5/Bb60wXCY8fPgDg+o0bbO3scjocMhgM6PoWd96/TVkkCFGi6gBtwAKRsRQpWQZIlmXYJhh0ayXoFEIxk5IkYX44wbYhy1OyOAPdoLwOqqiSjgIpiwpo7/V6WOlS+MZxHC5fvkyr3cZ1HBrNJoHvY3uqV1yn0+HKlStcvHgR3/eRUuIHIX4YViAmwtDZlJBJludVHZGUkjiKq/YQZaFA5jRR1Nq0LGiEIY1msypViZMYp1CBVLPVJMtzwkYD27bJtGLdaDxGWBZho4GpIo9iVRdr7H1RFLBYkH8MtlE1Hh/7lf+ZHo5jFqSq9zAoaLVZC0sXOS+b8dX7xCj1OBMcLXXjFaKqNjgpSyVbKJbGxAg8GAem4vJLpf4jUCpQlhC0Wg3mM0k0j0iiGM8LFF2GVSOxNLYWtuMhLBurlCzimHkyxnE9fN/Dkig5ZFswm02J4lj7IwLb+hHB0Qpra+nMCKEdDKg2rup6JAhUBsI4KzquUKfRtPqyNNxvdf9pXW5cooqEddAkizodr05XWNLr6nbXOF9SGDpFzUkqy6eoR5bu4VI5/HpJLcUc9Hn1V3WftXoqZZwcJWdpCvO1Y2euwaChjuPgua76XnP1bZ1BkkidEVSB+Hg8YWNjU2VlJo+rMbFtUGIP9YdUpxs9XXBuWyrjZBvnvCgqZMiyHGzb0XNRUMil1Kj5qp+v+t5kKmybi5evEDbbJGlBmhQ82n+E7QmaDZ9W4LG13qPXbTKcTTk6PuOTr71OOwh5+9t/yP79D0DmzOMZzU6Pzc0tJuMRs/GY6XSMLAuyOGIRxTRbLSxhEfg+mRYAiBcLZFHQarXUBrGY0261EZYgWsz49h/8e778s7/AJ168xR/94TeJ85Injx+RZQs2trfZf3TEzRszLl28zre//W1ef12ytrbFaDIhbDZY6G7bZoOqZN/FM2TfzczXlahVLaAEISW2EOS6EaiShjaqRI62NTqYUXr46slaDnluaJDWcg3WgBoplWCIqGbwuUCnonOuKnQJjepVs6gEp7AoLMh1fY2UujuIQM0NeQ4RtqhsilLnRK8hnc21DLCkheaFhSVcyhJsIbEcsyDVlSppf1X3YJrB2o4CV8w8zbKSIi+rBoOKwqqeS2melQFexDK+ElokxXZsHNui1Wrx/Asv8NM//UWuXrtCEAR0Oh263a62GVJlscol5cRkh4uiYDKdcHh0xOHhEzoaSQ18n26vx3AyxnM9irIkjiLyvNA0bhuJ6l3neT5lWWhUe05Zlmxur3HrE79U8fUXiwVnZ2fcu3eP/cf7HB0dMZ1Omc3mTCYT0iQhy1WfKIPydjod/CAgiWPKPOPizhaf/dyb9HpNXM/ixRefYxFNiWYDvMChv9YHCSdHp6yvbfP4/iGff/MrIBR15eDJiDxNuXTxOb739ttM5gleAIOBoiVtb++yu9uC0iKXMBiO8b0G3V4fy5qxteMQNhu4Xohle0gpaHf6Wj1LzX3HUSyBxWJB4CkFrv37D4kWC4JAKc96nqfvOWV7Z5toOuPJkydMJlM8z2Mxn/N//x//r3S7XV595TXu377D3t4FuhsbBK7LYjrFbilq3+BESTtvbm5y69Ytjg8PK9pOkqR8+9vfYmNjg3t379HtdZnP58ymc3q9fsWMEAJ67R6//It/kX/+L/4V01mk5psFmczBUaCICZL/LB9q7Wifx0igm6AHFVy7rqsadDs2cZyT5amyHkL5BgCWKPE8jzff/Az37z/i0f6BXoN6F9XbeSmeFrmqbIpW+j0PyqkE97J2ZcnGMG0S1D6YpznvvvMDbty4QRTFJEmKH/js7Owym00rlbo4jnE9j83NrUoc4PT0tOrtVvTanA5mDIdjPvzgNqPxlDwvybOCtJCkRUHY6HDt2gU2tncphcvJYMCT/ScEYYPL12/SX1vjdHDKeHBCyy65+8E7JJHaU5ZBoAR0WUQtMKoHnbbGiqSUei8xbSD0e8k4eLKP6qNmKSpdXuKgQGTHcQj9gEbYoN/vkxU57W6HTqeD67p85StfYTKZ8PDhQzqdDmtra2xtbSGlks4OgkA9L9uuFEQty2I6XzDXrXE6nS7OdKpATSlpNBo4tk2SpuSZqpFtNpvkWaZZMUr8J9MZOyOWJnxBnmVVJs8ENe12+6kapjiOcRxHyX1bFtvb2yRJUpVmZPo8dcpo1UD2jyGm8hMfIBVFiesuJ2VdaabOcVxVR6rzvZco5Co/dHkOM6kNAmDQSasq0FUFoVKbI2Gpv5WFUulq6GIzy7IJAg/bcojjaKVGoJ6yz/OcrMgJPRfP9nD8gDTLKEpJnGY4QBxFSFmojs+FKv43ErQfFSA9IwlR3axxjmXt3o0DZNK9P+4wlC4zXmXlDFq68lnWDO+SQrIcg/Mpe4MooYPP5c8rFCmxDCvUOesFp7ISzaD2mup7/WYppeqFoYMgIRS3Nc+KSiFQiGW9iUFvnsrAiNp41j6vnkEYDIYrtMGyLBVNsSbRbQLR8wjdihMrltQcM38VNUg5nkJ3KFm5d549CarNTAMMErh85QpB2ODJwRPyvGR0NqTZCKEsuf3+D4mSnJ2LFxkOTuh1Wlzau8Dh/j3e/cH3KIucxWJBp9dnd/citm1xenrCaDyiyDME4Lg5i/mcMGxQypIoK0jimCxNFdorFY98d3eXNE2ZzqZ0u1082+Hs5Ii3v/sWn/zsT3Px0gUe3vmQKF6QRDPWNrdJ05x79x7wyU9+kjBs8uD+Iz7x/C1aZ20uXb7ED997zzz96v6fmaXTc88E02ZuGHVGWagMsrIjqr+UsLTUaFlgCSVH6vsujWZIv9dh7+IlDg+G3LlzT1MrtWR4zQbUr8cERiajYDLPlmUhtHhKFejXI4fq3gqkVSCFi0BJfAtKHFFiSYGU7hLd1/WENmrOq94zKmi2WGY1hFXguEJTMZqEfohr+4Rhg163RavVwnZsRaG1Ha3Q5+L5CkgKwoBWs0UYhvT7fXw/4Ox0zP37D7j/4D737t3jycEBw+GINEvJtES1cupEFWQ5jo3jKkTzypWrfObNz/DZN9/kwoULuJ5LFEdVhqcs84oCUpYljm0r6pWuN7IsCz/w6XQ7XLp0CSklURSRpimTyYQsy3hyeMh4PAGUkI9yLg2t1qo2f/OMfN9XlLsi42xwguu6DAYDgiDg8pWL3Lh5DZO9Bqr3GsfCSPKWZclisaicyCJNkXnE5Ut75EXKYjHjd377d/jpL/80hcyZjBesr29z9coV7t+9R5nbjAZzNjf2GE0mWJbFJ557GT8I+M633+LgyRm3noM4K7l87RbNZhtZQqvVptloIYVDf31Gq9ViPl/QaPUBaLc72H4D2/H0nlco0l+hwMUsVSpVruNQFAVnJ6cMTk8ZDUdMp1NS3cw5S1LKoiCNlRx8r9Oj1WgRBCpD8MB9yNGTI37n6Lf5wQ/epd/vs7e3x6NHj1SNpO9j2xYbG+tsb29zenxCEqlm6o8fKyDqC1/4Av1uj5OjY65eucJwOCT0A8bDMXmWEQQBk/GYdrtNEsdsbmzyqTde5/e/9nWVGbFcJIJClsgy18HDx0er/zSOlf209r1ijaheO4biX2XFylILdag1ZwlwHZfPvvlpXnzhebZ3djn9zd8imkdoBFUDkct9sC7KZOiP9WMVgGJlz1z1xRSAZLJQWZby4YcfcPnyZRzXZjabq4xwp0ur1WY+n2u1uvipzzcZtPFkwsHhsVISTpRTr4AOl6DdYXtri/X1TRzXY7pIOD07ZjKdsb62zoW9S/hhyOHhE6LpCEemPLj9PsliVqvR1OMulkDkCq3u/DPS929AVQW8CjY2lbx5EAS0Wi2uXbvG7u4uo+GQXrtDs9GsQBNPM10KJF6g1E/LsqTf7xM2G3R63aosAsBzPbzAr7XYcAkbTYQGT4QQuk1Dynw+r3opCSEYDYcEQUCkaXAgOT05qRg4/X4f33EoUEG1EX2QUlZBjAlcHU2TW/UDlY89m82wLCWOZmy4UXV1dM/ByWRSnSMMw5XWGB/n+IkPkIQQFepgVDxMcaxxPswGaH6uL1YTRJkHYB6UmdTGCbZqqIh5sCaaRXM3W60mZydn+J6DZStFJ2FZuK5DEHg0GiFFYWgS1gq3efWeoCwU7cpzPdbW15VKV5wQLRYUaYrnOjpbI0jSWGe7fnSAxIqtFCu/r//48SdYuXQgRZWPAU1BWt9Y5+bNm5ycHHP//gPNk1XOY4VOS+P8CYSo1XzJEhMrVPdlqCeGrqH/JmsBpuLEasdW31y9T9Eyw2gCv9VNw4xdPeCu/75OGzyPkhlKUN3A14Nv81qz8I0D5XkelqO4v3Wp6B9/PLuWSP/pP+owAWcYhLSaLfJcBTrDwZAsy+h22oxGI05PzxiMZly9cZPxZMobn/o0WTrlB2+/RRJHZElGELTY2b5Er9djMDhlOp1VNUeO7WDZLo7v4wUBoe8jEDSyBqPhiMFwSCnzSjRle3ubgydPWCwWtFpNHNvj7t27XLv5AteuXObw0T22dnY42H+oaDS2zcOHD3nuuedYX1/n/v37vPDS81rlaIf33n2vCkDNPFoGGT9qfMy4g5SCElvNU1XMhmWXOI6g2fK5sLvJpUt77F3YZX1jnbX1PoHvM5lM+b/8k99YmVeFljk1KLY5zlN46mpt54GVp+kuGnARJdIuELhY2NiixCpjWp5UVF6ptgnHdlTwUAjSLKPREwg7psilDgRUUOO6PmGry1/91b+p6BrNNq12G2UHLUI/wBKiApFOTk6YTqe4rkuWp7iuS6PRULx6DTJlWcbOhV1+6o1X1KaYppwcH/Pk8JD33nuP8XSiaKx6I1xfW8N2HMIwoNFQtSb9Xo+w0dDjp7JkjUajWqtGZdB13copNA6BCUZgycs3KKdBLJMkIS/KqoDYrOtKIRWqFhPmHKb+0hKyclB6vV71/tPTU4bDIYvFgo2NDVqtVsX/932/Op95vQHnFvMpSTRVqlzAeDyku/aQrHC5dPk6Fy8/RyMIsW2bTmuOkJJPf+pLpFnK48enPPeJ57CwaQQdXn/9M8ymCTduvMTW1rYCoqTAdTwNLEoWUcT65g627TCeRnzwwR3SNOXTn/o0nl2QpRFlWVS1c4vFgtlsSpyoQvl+r8fWxgZlnrO+ts721jYbGxsV4GT2042NDS0QsVQnvHjpEi+9/DLz2Yxvf/vbdLs9jo9P2Nzc4Pr1a9i2w7Vr1/jWt/6ITqfD9evXuXPnDsPhkGazybVr17Asi/F4TKfTAWA+n5PnOePxGMexOTh4rNeVzdnZGa7rcnBwQKPhcf3aHvcfPqKMSzzXJssFJSXSslj2dfrP/6jbGrWTK4DXc21uXLvKtatXCAOf7c0Nrl66yO3bd8h0Fu1ZI1BRT3m6DchT/gerPftWbdoqcFoUBffu3WNza4ter894rOqQTL3Z2tqaEmlIEt1kOiXLcopEX6tlMV4keJ6P44U0g5BOp0er1cLxQyzbZZYkjI8HTGdz/CDk6o0brPXWiKOIw4NHFFlMHk94+OA2ebqofI1njWm9jOIpv0yP9fkxEULwq7/6N3jxxRcQQugaJOXLFnnObDpjY2ODIAiI45jZbEYWZzRbTSaTSSV3bbKnxkZZlkUQBMxmMwDCMNTArPJ14jjm5OREi0IEFcXP+NRmf1Ly4Kan37KnUpZlTCYT4lgxpYIgoNFoVIkL9Xv1fvN9WZaMRiOCIEBKZSejKMJ13QogqoJcSzEEFotFVR9qlKorVek/xvETHyDZtk2SJDSbzRVn9XzBuolabY1kmd+bSLYe4ZtNr+6UFLLEtUU1QUxvkiRNKCVMZ1MVCIUermNTlrmWH7QIG6HiaRYZtm0K/VW9kI1dZQDM9bqui22p9GuWpRRZRrffV02+5jM90RVn3XVtbMciiuYfbYCgzjqsjuVrnoWc19AdxLMXNxIpcyzbAVkSBAGXLl/mueee4+atG2zv7qgFphfd/fv3+da3vs3J0akq2pMSRUdfjns9A2TbBk3Qz4qaiIGJxUAhyzogshTEjeFJK1oQFX2KysFdDXiqz9e84HrwUy+Uro/tM9F+jcw9ayzrzu0ym6kpeDqDdB5p+6jDZMdMHd2KoIhcFtI+6zosazkGz9zcJbQ7beIk5sMPP0SWypGzsfG9kHExRwhVA5BGEaFjc2FrjXt3P+Rg/z6UBWVRsr29S7e3jpQ5w8EA27ZZW99UYhRC4Loez734Ajdv3qTT6eDZDkmS8PjRI77+ta/xwfs/VIo5nken2yWKY4W+hwGO47JIM77/9vf48le+wqWLe2TRlN3dHcbjCdPplCiKmE6ntNttHjx4UKlzNRoNLYihMkA/9qitHQMImCBJCAvHdUCo2gbXlXzpi5/hF//CV2m1fRoNnzwvqoapeZ7ze9/+JvsPH1HvOl8Jk5zbJOvP7VnP81nrsp7xBiiljbRcLGlhixSXBS883+fX/sZXaLYkpVRCEb7vV4DA2dkZnX6HNM8ZDSeUhUW3s44sba5cuUlv7RX2Lr5CtIixXR9hq8xOKQvyMsWxHabzBScnx0gJa2trVSNg1bhaZ+/1+vRtG6XWl1OWgrxIWNvos7W7yfMvPIfjqfq/2WzGeDwm0K0HkiSuaNZSSkajAY1GA9/3VYNCz68aD4ZhqBDQ0YjT01OyWkBq1rXJDBu0MwiCWv1PSbPZJNCBR6vVotvtVo7LYrHg4OBAt56ISZKE6XRKr9dVKphakSmO4yrouXDhAru7u9X6NUGBsQ+qQSQVmGIOx/NotrcxzRR3Ll7jV/7KJRXMpSme42BblgIihApEy9yhyAvu3HnECy+8Rr/fR5Yltz94j0cPD1nMUzyvSRQnnJ6cEUUx7VZHOTiF4N/+y3+FEIJPf/rTBI0W3/jD3yVstsnzDKmR47OzM05OTrh165YOKFWdQTSb4yBotzssNEBkGrkvFgs2NzeVkE2a6qDS5e7duyrA63TI85z9/X1u3LiBlJJr167ieR5vvfUW7XYbKXN+7ud+locPH/BH3/xDkJLJdMLG+kYlYPR4f5/5fI7jOLTbbeaLBdFiQZ4XZFmuUfEY3/dJU9XAukwz9va26PU6vPfDD5nOYspCqvEsxVO2v348E6T8M3ScBwdXMtioPcR1bH7q1Ve5cf0aZVEwGg6Yzxe8+ak3OH7yhOlsTiEV3Re9J51nVdT3yfMA5HL/lSuvWf5NsBQ8Wh3Po8ND5vOI7e0tsiwjihakaYLnubh+QKPdobe2jmXbyLKkKFWdQGnZCMfF9wNtc+0qQBjNIsbTE9I0pdFscvXadTqdNlLC2ckRSbTAomB0esjp4T4UCRYFiKczZPVxPe/jVM+AVTtv9oArV6/ymc98ugKETFbZBDfNVotGs4nnuURxDELQaDZxXZdOt1sFFXmeVwGLybBEUVRljubzubZHPcpS2bx+v0+3260YLSYgMRlsY6NUBt1mPB5Xwg4mo66EalRAOh6Pmc1mFXAkhOqJ1myqOsXzwRosxcqklFX2ybZtTk9PK7th9nZDiTfU7I/rQ8H/HwRIha5TqBsnk7Izi2+lSVrNCJgHXRdtMANsBrkKpiQrD2LZp0NRuPr9Ln/77/waw8EQWZT80R99kx++8x5FWdJohFUPJSUPXJDl6VKenCXaYvjw/W5PKXNISZrGjAYDJtMZZZEjpAkiVCGECtiyqhHfswKkZ8RHK3/jmfQiXVQpV4OApZETdHsd9vb2eOWVV7h58ybr6+u6OFd9YJblBKHHxUu7bG2v8/IrL7KYxRwdHvPo4SMGwwHz+ZwiLxQPPUvJUhWcplmqZCPRRdGlMh5FudTlN3K30jrX9FSgVf1A9WV5VkZtqVZYGWqpGu/W7/P8xlcPaM3PJmB2bIuiXAZW9bE87/A+S5yjTperv/ZZGSwpVS1IXYGr/h7z/bMcbJUBecYmqWlMjUaDOIqZLZR61HQ2xfMDHMfjhZdeZpEmXLl6nbKErc0tyHMe3rtHkWVkSUS73aXf74GQPDk4YDwe0Ww2lYpdGHJh7yKf+9znWNteV9TOUvULa0nJxuYmn3jxRX7vd/4t3/yjb1KUJUmasraxzniiejF1Wh1cGw4fP2I8OGPv4h4PH9zDDXxaRlEyzxkMBly7pmhMR0fHbG6v4bquuqfJdDV1+tQY6fFEy6TLJd3NFN0qdcQC17NZ67b563/1l/nUp14hDBxKVD2VLAosCbbt4jser7/2U/zO73yHOFmVxTcI2vm58qygqR4MP+vn1cNBSBfXSmi5M776My/zF3/pFdqthLJMKKVSfxSWahpdliWdZoe0LDkZjBAiZn1tgygak2dwfHSP8cSi198lzyyyKCJoNmi2GwgBnu0hpMoSN1otHMeh0+vq+7QrW5emaUXpM33EHK0c54dBVcQ7GA0ZjUY4jlOjUykVuFarhRBKEVQ5eBaPHu2zt7dHFKUIa8HDhw9ZX1+vxtlxHBUA1pSaDFvAjJ+hz9WzeQCj8aTK/pqMkHFebNtmd3e3WqPGWZBSNWs0j7Gu4mXsT13+2+xXJmAzdjhJEp1dURnY2SyqrnU+V13o1c8+siiJohTXKbmwe5F//Vv/irX+GnES8+ILr/D9t99ld3eX8XjMd77zHVqtHmmScefOXRZzJSa0mEf80Te+ydVr12g0Qq5dvca9e/f4vd/9PZWZuXqNu7fvUBY5zWaD48ND0jSl3W7zR9/4hqZvKXbH9uYWRZpx+dIlijzn8ePHKgPYaDCfz9ne3mZvb4/hcMg777zDzs5uNVbvvPNOlQnMsoyXXnqRb37zmxpNbvJTP/UaUkrefvt7PDl8wmIxx7Is3Xcpqp756dkJWZaxtrbGaDzUtWyKutVutxiPx3p9eZRlQRj6WJZHUeQgBa+9+jIf3r7Hk6MThOUg0xJpWxUt8j/3wwQuUkqQJa5j8dzNG9y8cR0hwHUssiTBpiR0bV5/7WV+/2t/qAMPS9VEWk/bocqP4GnfpAIKa8O3asM0mPwsEMiymM0mzOdTNjc3CQKf2WxGUWQs4gTbC1dUDqvDE5R5RpIrHzFNiipT6vgBW9s7tJoKZMmzlMHpMUkU41qQR1MOHz8gnk+wRKEyiayyUer7+7IGdfVvRqikfhhb0Ov1+Lmf/VkdwKkMt/FJ5/M5/bU1AOIsYTybIBD01vsqA25ZVebF932mU6XOuL6+rpt/KyC77suq7O0SFDI+qLGJJpvT7XYJtVhDlmU6Cy9pt9uVnTLJCmVLqQIeQ30za/Hy5ctMp9MKOPR9v6IRm3losvsmUFosFnS7XcqyJI7jKsCqU0STJFlRhf5xx098gGTbNhsbG0gpGY/HKwGPQQbrFIjzTVLNxDWbnpmI51Va6hS++mLrtNt0+z0Oj45ot1v0u12EgCtXLhL9hZ/n/v19Ll+5xr/5N/+WoswpipKyUEWTpujbnM98dp7nuLbD3/qbv0aUxPzu7/47RpMJWZqqJqUVTcwITlgVRcEESH8Sh0q1q0DIZFdsy2Z9fZ2LFy/y0kvPcfnqHs2G6n+jKDo5UhZgCYpymZkrypIsTVXGrci5efMGzz13iyiKqmDTFDRPJhMGg0HFOVUoaUY0jZlqzunZ2UDz/VNms/mKcTefqZ51iaQeiCzVriSKGWU4sq7rEidx9d7zwZFZ4L7vV46K4ukm1T1kWY4pnoTaBvAMx7UuBmBQFzMH69Ks5x1kcz5R25B+FNXq/CEllYP/1P3pkVlbW6tQqKIoiKOYVquF32iwvrvNF195lTzP+fY3v8Vrr77KfDpl/8E+SodA0uu1lVTwkwNGZ8dKTcxVyN6ly9f4ys/8OWVIrYI8S/VYqSZ4ipoq+PO/+Iu0Ox3efvttpKVq0JqdNoOzMwK/geM6xLMZD+/f5eVXXiVoNsn0czSy8sPhkGvXrtFoNDg7O+PKtYs0m032Ll7kvXffXeHN14ONcysBkzEyM0c9A5AyB6vk4sVd/rv/9h9w6cIWlCmebRMlOUVeYuExG89RjfokvdYmly5e5vbdByu1dObrj9Nn5aMyxqt0mRzXStleE/yNv/IlPvupPWwxQerst+UEIHNkvlTWTKKI0gqZTwWu3SXPPGRpM5vOaDVgtjjkW9/89/TXLjKepOxdvsIFf4+CHGkLPMdTSkT6GURRTKPRqK4ty3OKUimNuToIyXMFjERRzHwxZ39/n729i3R7Pba2trAsu+rPsQS1JEmc4LgunudjCQdr06HbXdOUvoznn3++svsmQ//mZz5TKZwZFckgCFao08ZRME6B53lsbm0jZQ04Y7XmwthwM/7GflnaJuR5XjkF5n2e51UUFOMkGdofQKvVUlmYKKqANsMjLoqC+WSG6zkcjAZaedMjXqhGj3maMRwM+fDDD2i3Wnx45zZJmvDlL3+Fs7NTjo9PuHPnDjdv3uDevTscHDwmjhNeeukViryg3Qo4PT4gzTJG4zHNRgNZ5BwePGZjY4N+p60ArCInbDVZRAsEks2NdYXqxzH9/hrz6Ywfvvce8+mUbqfLzZs3+ea3vsV8sWA6nWp55ikPHjzgW9/6Nt2uCqi/9KUv8dJLL1UZwOl0QlHmvPHJ17l9+zYXL+1xeHjAcDjk+OQY27Yoipz5PKbZDIki5XCFYcjzz39CN8CMK4dwsVjgtXx8P6CUhfrZdwGFtDeCANd3VX1K2ODixYt8cPtD3v7+O5Q4pNmSon/ejvzndiwDdoswCHjxhU9w7epVdH6INImJ5nNcWzAdD7hy6SIPLu5z78GBItaXJXbF11gNhs6PSX2/Ur2CrGe+zvzumfunAIVFSo6Pj0AoR7zVbOGGHnGaYts2UZKqEgnbwvN8wiAgDBuAau3huT627eI4qtl5lmVEiwWz0YAiT/EcG1EmPH5wn3g2giLFF5ICSQGUwsFmCUAbIPOj9u/69yaDDkuQ/C//5b/ML/3SLzGeDLC1iEb9/mfzGaX2RTJtu2aLOVtbW4yGw2oPNPS0ZrNJGIYAVV8oY+NMdsb3gypjbehv5j6iKMJxHAWaxjHT6RTLMtelsuWGfWBamqhslV/5441Go7JnlmVxcHCwQpEzFHMT8DiOozJlzSZSyqqmyvhlxl83X0IoWm9DK1h+3OMnPkAyKDEs5V3N4jM8SuOs5nm+UswPyxRvXTXFRKBms1Lobsh6f53T09Pqb0YG8ezsTHHpNSKVpim2ZXHt+jVeevlV8lwVO25ubvLOD95hf/8xloXOIIkVKWnjKNsOnJwc8d/+o3/Ez331q/yTf/JP+d3f+z3yolTpXLm8j1Iuleeo3V+1kWojQr1E3yDTtWBBvxNlEEW1gF3XY2Njg5dffolbN2+xsbHB7u4uhUwYDE+0XG1UjZdyhD3iRBXJZmlGmqUUec7ZYEC6yNne3kUAI80Lz/O8QjayLMN1XXq9XlUvEMcxRafAvXoVgEwHNVEUKc5sHOE6ahwRgkQ7JrZtEzYDhRQ3mwRhyPr6Op1OG9fz2dza4q233uKf/tN/yqc//WnyPOcP//APq0Vo5ofnefR6XdbW1pVQgOchpeT4+Jj79+/j+z5nZ2cVrc88AxMEPQvxr3+5jk2r2UQgcB0XIxzxow6JzvjIVfljAGnJ6lXPfOe5wGiZLVGB7ubmJlOdUlepdbWmCgHNTgcv8JkO5kgBzXaDh/ceES8iiqwgDALKomA2GzMYDknjmEbY08W0HT7/hc/TbLa0ulKJsC3ViE4IpFCS+XmasogWfOazb3J6dspwOELKgm6vy+BsoMRZHLVJHj55wms/9Rpr6+s8fPCAru9XXbWHw2E1t87OzrAsG9tx6XQ6y/s+N86rAa1RfAKjf1B/uaSgyFOCwGUwOGMyOCFezIijOaPRmDTNmU5mnJ4OiOOEslBCK0fjGYYiKSxRPcOPeubnM0nnr7NO2pBC6d4JAbYFrp1z40qLv/03vsD1yw6WPEWUkjyzEY5NLtUmaebtbD6jLCRpqRoQjkcDSjkkDJqkWcTxyT67ey8xGp3w+S/8DJ3uLgUOpZBIUWJJiyIrybICzwtZW1Md3EfjCbPZFKCiY8znc+0gtypgSm3QCRsb29i2ku+3LRfbccjSHNsS+EFQ2WvaSsEUVODS62nhEi2PbjI9JjNTliVJHLOxto6wRFV7ZYKWip6iwQ4DEkjDMigK8qLA9zwWWv47z3NcT9G3U63EKNFOTJoxm04oy6KyZ1mWEQYhc53tcBynynqCCooMwup5HgcHB/i+TxRFrK2tIRDMxjMcx8LzXaTMiZM5BwePabZaSCnUdeQF0XzOyckTPG+PKJozX8R85ztv0el0GA6HtNsKiV3Mp3RbIeu9DuPBMWv9dS5cucjDh484Hpwymkw4evKYZrNJq9UmjRecTiYgoChLBoMzbfPUOCu6XMhitlDIfp4zn874zKc/zeHBE7a2t5lOp5yenvKbv/mbvPrqq7z33nuEYcjNmzdoNlscHx8hJezu7lAUSu1uvpgyHA7IspQ//MOvk6appm4KVeeb55WK1+npKY1Gg8lkonqnaOcwS7NK1CjL1PPq93sIoZpqdrsdzJ4Zxyme76lm7XnCrZvX2Njo8c23fsDBwTGWtSx2N2ItSpt/uTCfXqV/+kd9X6pnpjudDm9+5g06rSZRtKAsHALPw3Eder0uo7MBhS0ZTY7otNu4nkuZlVWfwfP40rOy4iu1IlL+yAFZrftVYJXJ66v9tVQbgZRkWcrZ4AzHj1jb2KHX71HkBUmakMQJaZogZxatdhvHcQFBWWQKEJKSPM2RElzbQmYx0WzCw+MjosUcT6ZYZYaQRvxLILEplfSNuZlKya26Nqj2jpU5YFkI/Toj8d/ptLn13E2GowFZFjMejytWjus6Cuy3LRLtI81ncx34eZyenuI6y9YEJkkwGo7Islxln/o9HYC4eJ5b1TAJYXF2Nqh8Z8dRn2WSDJZlVWvJtu2qNjjL0so+TiaTqu7P932SJNH0V5W8mM/nSnZc27vzvbnMnDDglAGo6vVLjUaD2WxGkiRVlitN06rnmck4fdzjJz5AMpveeTqTLKHIVTdjZQRKHNtDYFU1IkbCGyzy3MhQFxSFRIhlJkkIJZV8dnZWPSRT0JamaVWTZFmW+kxhkeUFtutRUHA2PKXdbfC5L3yKNz71KtPphMPDQwbDAdeuXa14lEDVWEvKjNOTU/4f/+x/5Jf+wq/wd/+rv8UffvPrLBYxuclKIFjKddtoZQhtjVX2RwpNDZJUjqjJDNm2jSWVDKjtOLiei2Pb2LaqFRCWYL3X5fLFXba3tul2lVN5dnJENJ+QlTmzSCHjs/kMqdGGIAxphiGWpYQqzDjZjk0zaNHyBWkc0e50uHblsqY6CLrdLo1mq+qGDVQFeJZl4Vk2caRU+5IkIdLfTyYTptMZi8WilgoOVHZxc4OgFdBut5WKludXvN80yUijjOHpCbtbm/zar/510jTj7gcfELYa2LrmYW19XRdOB7iOqygFqJqTsBHg+Q5hw8ed2qRFRpEvsz8GaalvRCZLZBw827bwbYtes4ErbBxscnKU7p9u6FczrFU2TGj6o7WsuYNlrVVZZsss2rm6qGdRuFSAZSEtmyjNyCVIKYgWCbKQWJaNb7sEwsJHUMYx7UYIQjIenkKRUZY5vt8my3LOzgZE87mW5p4ThiEvvfgc62stsDIoSxzLQkoLaQuysqRA0Tscx9aUSnjtp36K3/7t38Z1fUXDcjySZEEQKGn1yVQ1klxf7/Pw7h0oHLI0w7ZsFlFEVuS4gc/hyRFZKSiFTZTmFKXKKCKVEl19Z18GnAAK+FjWHQnKUgcnpcCzfB7ce8z/6f/4f4ayxBY2Ra6yI7Zt02g0aDZbdLubbG9v4boeQTdk/8lj/sN/+H3SLMbyA03Xk1gsM4v1wPc8HbL+s4VEiIJM+pTSx7bBExFNL+Jzb+zyy7/4Aq1mRhHNKWSmuqALicxzyiJHWiUFBUmWM5lHJElJmuSMhimLRU6cpLhuSdhogddElj1eevF1okVJEOY4noPAxrY8RFlie0tVN1M8q8CF3kpRvhA2/f4aUqr6QVkq6kyeZ9WctiwLS0CuqVymebPjWMoZEVCi5oztqE3TlgqwCkKVfRFAWcv6eLZLPE9wHZtcpDi2TVnkpGmirKmtlCCjGjpqWRbTyZS8KJjPlRz3xYsXyXMlJpJYVCjpbDarHMHBYFB9r+qs1HocSPX60WhAURTMZrPKUVBOgs1oMGJzc4Ner8/BwWMVaMQLwiCg2+3heS7z2YyyLOi3e7h7Nqdnqg5rd3OXLM/Zf/QIx/PJS8kbb3yKyXTK5uYG8/mcLFOUFN+3sS1BXkpG4yHRIubOnTvs7OySZTkPHj5E1aKWdLsd8jzR9gWms5kWzugxn88Zj8cVUIYsOD05QgiLyWRMs9nkm299k8997vO88OKLOK7LxtYm/+E//Af6G32++gs/R6vZYj6ZMpuOOTw85ODggFdeeYU8zzk8PGAeTUm1I2SJkmbDZ7GY0W63cRyLRthStDgknY6iT671+mRJziKL6K+tsZgrdD0PcoSw8Fyf0WhEt92jlCWu45DGGevrXRBlJYk8m02J5xPajYCf+dLnuH3vAW+//Q4LWZLlhipagoxRstbWueBomWH5s3DUbb/rurTbbV54/nkaQUAaL0jjmNkkJUtT8kL5FklWkmYFJUpFuNlqk2n2jqmrhKcBvmcFSbZtI+zlmBiGh2E4IAVSZvq8gqKoiTlIC0oLC0eDhWqndATILOfsySNGxweEoba/YUNlisKAWFPPbNsBHdimWUoRJ0SzqQ6oI30dBbYEKQQFDgij1GthC7AkCLHMZBRFfm7/qNBsDPtAjUGJhaXvTWI78MlPvcpzz11mMp1QFDmdTpvFYsaDBw/odrv0en2dKWliuRahH4KA2WTG9vY2hd6DhYAoihmPZriuj+8LbNsjy3LdM6xESgVmFIUECsIwrISChBBVkGOCku3t7SrbbvyZxSJmsViws7OD59n0++uEYViBEovFgrluqbG5uUme5wyHwyqwMQkJE9yoNexUGawoimi3lTCUuR6gasZtMlSTyYTA1wyA9L9Q7Kojz5/uPl4WqiDPIIcK2QEzOeuovkEUDdXCLNx60GVSfFLLUJsJUq8XqSveqQjc5ejomP5aj/5aj8l0jEQSNnx6/YtsbW9WkXedaymE0EWvsLWxxWIR889//dd59ZXX+eTrn+TrX/+GQhukCXRsSinJClWYixRVLYtxwj3PIwgCEKp/UrPRoNfpKjRAWLieh+Upp9Jxner6iyKn02yQxTFlkTMajaome3nuUsiShpZi3d29UKk7OY5DsxHQCEOlLNPv49W60QshVFo2CNT5rKUSiqKvlCvPxFBSPMtiba2vUBRtZFTjVkePf47ruJRSEi0WSMB2naoni0njmmJtRE6cJKytrxOEIbdu3WJza4s7d+/w01/5Mu1uh3/8j/8xk8mkuu5cqwumaUq329UNakVl7BVVYFn/BlQZSYOM1OecEEplr9nwaTeb+F6j6m9UUa7KZ9eg1AUlDGpSzyio5IgJjp4lsrE8lkZbNb+Mooju2hpxnDKfKpTbtlQjXiGhzHPm0ymeRnHm8xnUqIyj4YjxaKTWklSGLs9Srl+/RtU8C9OA2aIEAs8jzy3VPLMosIQgjWP2dnfxXY/5fE673cGxLbIkXqbWNfWoqesUPrx9m+PjY3b3LlAm6l6EZbFYRGRFieN4dLs97QQv77/KuZ1HOKuMW51qp5+dcHAci3arwWc/84YK7iyHRqjUyF566UVu3LypOPK+j+04zOdzEpnw8OFDvve97zIYqq7ijqXqVbI8x7LEiq2qFzXXqZnVsxMCWVio/lcgxIL1fslf+Lk3ePP1bSxOSHOFbivxExshFJ0xz3MKCVluMVtIhiPJwZMJ86lkMk5wvQDXC2i1e2xuXeVzn/sCl6++RJLZ2vGdYjkxtusRBA2EplyBAkg836uuvVJi0vbJ9xVgYVk2FkZYBYStEMQsz1XdqGPjaTTRZPSKfKn46NhLsRsjU5smCa5rV6/zPI/hSEnUFklGkRq1OkVbs+zlmnMcl2azSVnkzKaJLuTPeHJwgLAEQRAwHJyBLGk0GprKBYvFnOFwSLfbZbGICMOgossp6WElHS6lpN3uEMcRnueymM/I0gTHVo1VkzRhNo1Z6/ewLZhORuxsbxF12pWy1MHjR5RlSbfbJU1TxuMxURRxenpGs90mWqg+TaoOQcnmpmnO/fsPODo64ubN61X/kdOzU/IsodttV7YsSRLeeusttcdia+fKYTqdcOHCLghF8ZZS0miEZJmir21ubmjEeEYjFBW663kuo9GIw8ND/uAPfp+8lOR5waVLF/lrf+2v8sGH7/PkyYjhYEAaJSwWEbPZDN/3+f7338bzXKbTCc1WoPZIHaypgMxSn9doMptOq6BcCMF8ppzE+UwxSg4eH1T23ChoSVmSasfKdV2aTUXBevLkMb1+D8tSjm+v19O0cIfpbMYrz9/EpuDe/X3OzkYsogTbFhQFWl1VUkp+ZK3jn9Zh7t84w+vr6wRBwPHJCWcnT1RWRGg1XsOAQFHKSkRVs23ZSm4/z5fKkB/1ec8Ceup/P/8zQlG2q7YGQrce0cHGsi5UAY1UwFKBZan3LmYzZpNpFbxJS1BqZoBtW5oRoDI/Vmn2JjQYps6luRXIClQ3ALXElDso5V2TQfw4D0AL1RQFti344he+wF/6S79MkigQ/mwxpN0OdUb1pgKRLIHvBxRFqflAJYEfYFttVK2WJNd17r1eV7GXShgMTnVz+xYnJ6cVs6rRaOA4DtPptPJj4ziu2Dym3lNKyWQyqfzfNE0rRdC9vT1Nf51WNZtSSlqtVpUt7/V61W0bgQVDl+50OhRFUdUZmmDdiOIYv9z3/UpsAqjqP+M4pt1uV4I26X+pQVoextGUUjKbzapBBqreEivUo1I18zNOuan/MN2jzwdN5igKJQygCvcylY7NMp1NgELT9zqdDhsbGxwfHxMGAUWe8+jokDAM2dzYYLFYcKqpWGmieOKtdlupupWyQht7zTbjyYTRaMLZ2Yjf+H/+79nZ2aXX7DCP55hqEcex2djYpNVsIoGwGVST3jhYo9GIXrdDI/RIE4WWBp5PoxHi2g7NTptmr0u31yXwAwKdfbGERTNs4DnuSq8Qw8l3PBcpltkLg7JaKnWEbasaIlMDZgIjPdBVM7A4iijKgiAIcR2vWpT1ZyyEaorbbDaxHLsWTOYgFa3NchySXCmZCN2E0rKN4p+FbTukqdL1V0XfHs1Wm1yWXLt5g6OzUzZ3d/jrv/Y3iBaq/06322U2m60EPIaXawJPE4j6vs8iipeFrix53WZO1QvBTQ2C63r0+322ttZZxLnejBVF5/yGUg+QVEM5sTJGldNs/QiVuh9zCGHR7/exXZc4SvT6UgHe8fExd+/e5Qs//SXCZqO6rzhe3rcJCF3XXakX8TyPMFRc51Kv2SLPKzpnmisEP00zyrIgmk91IGOxvrbGwwcPSJO0wmBV5lFtkGma0mi1kEimsxlJlpLq4uk4ikFArpUT3ZpioKw1e6ycgHNI50ePkzBkVPr9Pr/yl3+ZS3s7bKyv0wgaWK4LUrCIFuR5znQRk+Vqw5jNpzQbDf7cl7/M//vX/wVlIZG2hYVFXioJ1fMUz3qWvD7HlCNhY1kOlm1hOwXdts1f+0uf48VbHUo5QgpXByUuua4VMOIn83nKaBSzWFgsFj4PHow5O02wHR/XbxNnFl13g4uXX+fWrRdpd28SNDYIkGR5get5FKXEsh2MNHCpr8vzPR3kq2yhnqwqWyQlud4kXdfFkoqqlaYpvuchhdBaL4Lh2RlhGK7U6liWpexwURJFx6pmpNlE6vmYJDF5mhDHCaenp2xubjCbzbFti8APCVyfKFI1hEkaq98HyvaYwmQjDb6kicyq7EgQBNy9ewZIkiRFyqJS0Hv8eF/TUFRhtJHK7XQ6ZFmqA96SPM9Is0iJCsmCvEhJUgUaeJ7D229/j+3t7aodgFF9MntWp9Ph6OhJJQjx6NEDJtMZF1zVn0TRFSNsW9DrdTk+PuXixYuEYcA777yLZUF/rV/tn9PpmDRNaTU7GgkOmc8jKIW2dar31WKxoNlqVLVBx8fH9Pt97XSqQvNGo0GRg+8HlcjGZDKpmj//81//daRUAglvfvYz3L79AUkSAaqhpOu4CCHxfVdnpob0+t2VRpPGaTNg2ng8rvb9xWJBlmVMp1NarQ5pklfSwqZeWe1HJXmR4+igXMqcKFL9dVz92iUFSNDpdImjiM21Hov5nFvXr7C7tcl8EfPh7bs8fPiIKLXJCgNO/dkLjmDp67TbbdrtNqDGLM9zKFQjZUMZN/tYWZbkpdRdDVZruZVN+vGfa3yup5Xsni4TMMBV/TVLm1yCqKs76PcKlY0WQmoQTWV7DE1cZfk1xyZf2n3bgGBCZUpL3QPKBDxSlFUWSH9gNTYqa1SuXP9HjfmK3UZdW6PR4Fd+5S9x/fotzs5OCAKfMGwihGri6/swGAwVvVYIoKx81tPT00oVLo4X+IFHlmU0wgwpYX19g0U0rVRAYVnv9Pjx44qxY4IWY6dGoxHj8biixZnaIqP0afoTmt5EvV6vAr9MraR5zqaXUhAEFSgTBEEVCFmWkuE3FD7XdavacCEEOzs7zGYz+v1+JaZSF2pwXJeF9smOj45+/CTUx098gOQ4qmbn9PSU2WymMiU16hksN9M67cksduPgGW642cyM82smQ5Zl+K6nu6erTXM+n9NqtSigolm0Wy2KPGd9bY12u83R0RN2tncUIhcnTCdTSp31cl2f6WRG6qYcHR5X+u+z6YyD+DGLWUSaZggsmmFIIwj55M++wSJdEEcRQRiw1l+j0+1gCYu8yCmFZHNri729PTzPqxSaHj64RzRXfFYLoVSF8pxm2MD2PXIbzfn0SFPVrM91XTzHxxYOlqZxqbSmFpawVL8UE+jUa7iKLAWUKkqr1apQiPF4TLOjNtg4jsESBM0lciBKsVKMZ3qBlGVJI1S9cuIkJs2UHKztOLpOQHFmEdBqt/RzVTU6huqjJDMbOpgJKaV638ngjLTImUcLHM+l3e3S7nRWeK5m3ph/fd/n8PCQzc1NPM/jxRdf5MMPP2Q8nWHrpsRm7pnDzBs1b50q69Nut9jcXGNja43FIsfzXcSMGkK1pCfU+dgqg7EsVjRG71lG+rzD/5SDXf1NZUjKoqRI0upZG1rq48ePieKI3/qt3+Jnfu5nCXQ2znbsleyrkfRMkgQpVPftXq8HUo1JkqWcnJxQ5jkNfY40y5QQiVD1C0WWsNbr4VgC33MZD4fEi0jRLs09SkWdAvA9D8u22djeJM2z6v5yXR+AlLpju6JrWZZFKRRtpJ5Bqm9i58fI/K4+jnle0GiEPP+J5wh8mzieMxqeYbu+Cka0wZdSUsiCoBEQBD4SwV//a7/K7/zOf2A8WSgao20otkv71Gq16PV6VZbAzOV6FhIhsV2whCT0bXqtBt/4g+9x912H9bUGnTWFsAWhr1FTpdwURZLZ1OP0JGIwmGvhggaet4btWzieoJQ280Ty9T/6Hm+9fYdWs8OlK7v80i/9efb29pBCaLqbmtuFvmc1jxRgketnlCQJaHQxzVQT0clkgu8HONoum+LcSmGpKEiThNFwyMOHD9nZ2a0cN9u2SdKkKjY+OjwgLwq63S7j0QjXsbUTLSnyDM9zSOKEs+kMSggCn7PBGa1Wg9FoUqkopWlKq9Wq0EoD9LiuQ6MZ6saSgrChenpc2NhRTVKl1NnljspazudEcVRlsQ4Pnyh1vizVAQAkaaKog6VSw1PCLzGddkfLlbvV/DH3aZy2yWTCwcGBrtlRvaVcz1PXmOWcDU5phA0ajZBWu8mdO3cpCgUSqMLpGEsI1tf75GlKWeacnZ6xmMdcuLDH5uYWcbzPeDLBcT3abSUtHIYBfuBRlkEVnJn+VmmasrW1pajPE1Xgvbe3x/7+Pmtra8RxXFHUsywlTSN+8P3v4fmqRQaAbam99OTkhDiJsG2LbrdDWRQURUmv1+P4+LiqBXUcR1Mhi5X6CyOoAxauk1fqtsaR6/V6PHnymDSLtRJaUFEqjdy4URxr6ILxJE5xHBebEtcShM0maRTRXO9zce/zHB6d8P7t+9x7uM9My2DrXst/LHbdjwO3fpwz/nHOb1lKbt1IOJvfi1JRuM0+aj5PCCiFrGiu569DCPsjr7vO2jnfb9LsG8+6p7oC3tPnVgGointqzeN1j0ZD2ROWokOXZYklSiwhlz6iBCFV7ZQUNlIqypvKHkn9vQmUnt4HzD0YVsFT91D78XyGzFBBr1+/zr/+rX/NgwcPGJyd0el0eOGFl8jzKe12R1+3w2KuMpSOq6j7YRDy6NG+lubuEYYK4B6PRtqOJQwGp8ByPzFMnizLqvIOsxYODw+rTI2phz87O8NxHK5cuVIBEdPplNFoVNWSCiE4ODig0+mwvr6uGCjdLlmWcfHiRc7Ozmg2mxX12GSXTOsCkxkKw5A4VrQ906TbiFctFosqsDKvM+Of53lFk+/UslU/7viJD5CAyuDt7u7qrEJRaaKfV/cyznKappXihQmYjNNRV/cwjme/16fTbOl6lwmdfp9uu00YNmi320ymE7qdruIvuy6ddoeDJwdMJ1M8xyFJUqbTqVIES2LSJGF//wn7jx/zeP8xruuytrbGjZs3WF9bZ3Ntk63NbYVGNxo4juIHu56rSo1qjrK5N6E55BIqZSSD7GxsrGFRcHJ8TEurfXW6Hcq8ULLZOkNk0M2qQ7wlSLTTOp1O1aREZczSNCXR49hqtSotfMdxcGyLJI44Pj7mwoULKhjQizNNUsJGQ4tRaAENjSoUeVE9N7P5maACSz0/LwhUb6ksI8tU1qHMs6ouIIoibMum2Woq4QZhk6YJrutVKE8UxSi6kcN4oIQENjc2WMzmaowtC7fRYH19nbt3767QJ82GbFRdwjDkH/2jf8Rv/uZvcnh8wnQ6W+HHmqNuOOvZJIW0W3iehcRTRC5LICpaF0+do8p0yrJy8OuHokM83ZPio47636RUafo8l4SNkPl0XgVqnudVRs6gOI5tEwbhSnC2tbWF4zgcHh4SNhUnWanuZPgEOpPjIgV42ilqhp2Vxry2KHFdB89zSBPVtV2W6ncGoTKBm+M4unYl59KVK7iux3g00kXzqs7CQtEHy7JkMVf9TyydvUI8u9fXszbsp7j1KFrX44MD4sUM33NpNds4uUXYaGLbFmmcVvzuLMnJ4pzxZMrR0QnNRovJeEaZpwrZFEsaibFt9QJWcw3GbqlxlzQaFq+8/DLrvT5CFvg2ZPGc2SIhKRxOzyzKMqeUmWoXYIEsbWTZw7Y36a85JGmmKa45WAWZzBEl5LpOME7nzBZT/IZNp7dGmhf88Ac/oNNqsb6mqLSO4xLrzU3x1JfN/gyi77pu1SuoKAp83a/IjHYURTSbzcqOTSbT6v7v3b1b0TxmsxnT+bSiYhgHwGScfc+tCvYfPFD0rl6vR+CHFFlhAGOEaNDrddna2tCBzJHqc5fEtR4iDlmecHys+n5Mpwr06Pf7nJ4eURSlptJF7OxsU5ZLWooBfDpdBQ7ZjlUBWKrWQRKGysFvt5vM53Nc1+HC3g6BHxDFChiIoxg/MN3olQLUIppxcLBPq/UcnW6L8WTKcHhGu91he3uLoii08xHQ6XQYj2esrfX13qjaIUgJW9vb2Bbs7OxwfHRKluWMx5MKzBodHdPvd8nznK2tDaJoges5VS8V0/zX932ePHlSieQYIYbT09Oq1uDDDz5EAEEQksuCxWxKEqkMXp7neEHA2eCUsBFUKncIqd8fV/UKJphWwWVeBUrnKfNFLun3+wyHw8ohNCDoCy+8yHwxxXVc8qIgDIOqjjTww8oPOD46qTKBQghchQAwnc2xXYeT03vYjkuaqwL6CxcuMB5PmMzmpFlGmilVS54263/ix8cNnlb21/rvMfYQqBSpy5Uo76Ns44/67LrtND7MMsB4en8DKhq5ee0qvXjVXi6p0BKEiUqFCnoEimYmlw3qV45SatluDUBosQ2zl6qA6tn0QDNWT1EEq++XrzPgpPIt1R/effc9bt++zde+9g2klHi+z80b36XX69LpdAkCpbToug7r6+ukqaLB5UVB4PuUheD+/X18z6PbE3heE9sSRFHCfB4RBL4GJPKVRqtCCObzOb7vs7+/T7vdXvFx1tfXq9ok01PJKOEZ0GY0GtFoNOh0OrqHWFplpIbDYQWsKwZJyGKxYDwe09X9mgyryIBTxme3bZu1tbVKACUIgiqQNzTAJEmq8XRcFyxBnCYfOf/OHz/xAVKWZpXaBqAllx2FEudZhVQYSo1RRIOlct2S6qQ2HJNBStOUZrOpAoCwwWw8Ya3f59LeHmmWcXJywtnpqeo27bj4+j2zyZTjwyOOjo7wfY9Hs1nVRHA2m6noPc0QlsNrr7zGL/z8L/Dqq6/S7/cJAkVB8jyfvFA0tbzIEJrzW5Y5SIkQiu+aF4VqUOm5Ko1cLPX3XdepFqxtO0gsdi9dVophOlMmHJtWI0Tq/iOWZVHqHktmHGVDGaRGs7kiOmAWkgnCDDpnKHaNMKg2yytXrlTPQVqiCiDmNaU0IQR5otSdTOamjgRKa5mhKMsS1/NwXJf5Yl41kCyKAoQgK3LGkwmWsCiyoto4YVkL0W62sYVFww8okpSN3hqLyZT19XVc16OQJZtbW7Xiy2WRt8kiGbnMKIr44he/yP/rn/06cZxUTuGPQtPMBp5lip7jupYqANU1TBKU0s0zYEdbi2nIQmKUtsx5QW0qP2oTrqN/z8qWNBtNzsYjwtDCdRxdzFlw4cIFNjc3+alPvkGz3eLw6EjRbBrhinNq2zabm5tKoCNLKzrLZDKl2Wrh+75qkClLSk3NrFMUpJRKxrUscBybwydPcB2bZjPEtpZdtYUscRy3yvbmmqKVl0ppTAjBZDxhMZvpjhUKCVTqY2qcykI5//UM0sc/ZCVs0mn36Ld7TKczOu1NHFtliZIoZjiY8ejRPvfu3ePevXs8eXLEaDRiOBoSJRG+71GUBZ5vk5dKBMJQVpMkYT6fV3PGrDcTdHiex8Zanyt7O3iOw2w+Jc9ypBRkqZJOl0QgFZVIILEd1UfI9DBpNtu4jk+epwhRYNmq75gtfEqNlFuOQ5zE+L7LL/3yX8T1QxbRnDt37tDvtGkEL3A2n6Ga57qcnJ4wOBvQbDWxdaYtzzMsy2Y6VcIqUkrdc8ghXkTMZora1Gq3ODs9Ub100hzH8YgWC0DV9PXX+tVc67QVGtnttomjmCD06XV7jHxX9aBCspgr0GJjfY0iL1jMZwhh42kw5OzsFNdTa2g+X+jgy3DqhVIwA4JAZVFUE0Spriua67meMB6PKrlbKSW7uztVxqSp7WcQKDs0m821KITEslTdUxjaOtgIcR0HR9uWNE2Yz5UYQrPZrJya0ViJOKRpWjUrv3XrBkUJi0XE48eP8TyXLLORUmUux+MZjx49oixVMKYk1FVDxzRRdT+XLl7Bth0OD48Yjcb0+n36a+tMJmOkLBUVnJJer1vZb1NMrWiEma7bXSpcFUVRKc5atkWRZiALhHBUY3TLYjIek2YpgabKO45dUY5N8TtIzRSBZrPJ8fExm5ubuv5jGZAb+zsej7GETZ4rJ9wg1J7nMdIgiqmVMA63qdmKomjFeVegmo0sJRRKVKSUEiyIkhhLO51JkZNkRWUL7VJiFaVSevyYaaT/1AzRjzt+LP1aLOsu1fc//jwf95LrQY7512TE62qTUoJtrdLuVoOkpRiCUU9Ur9PjrKIWVB2Rbs4I+vvz18MyOEJ/CZA6+6JJefr11D5bzQsTpK0Ed6JOyVtevwlKTV84EwSo31lkWcHtD+8o+6PvQSnYqWCj0NRw27GxLbvK3EgpuXz5IlevXmVre5N2u4WwBL4fkqYzBoNBlRU3iYLpdFqVTRj1YCMao0RkRopyb1SBdW256VNnQHHbtitbBwo8evToEdvb21UwY4JhU5cohKj6M/m+X/nHnU6HbrfLkyeKPmyEX0wmSUrFSmm328o2lCW5XNbTfdzjJz5AApQijUax4zgh1spqpj9No9Go6iLiOEFo9a/5fEEjbJClGfP5giROq9S6mbS+HzAeTTg7OsGSkEQx8SLivffeI0lSms0Go+EIWKo2WZaSdk3SBMdRFBDP89jc3OT5TzxPr9fjwoULNJptNtY3VVYlU1r9png5yRMQkCQ5pVSbg+d52I6FLAW2sBFlieO5WLa6HynBtpepat/3qFRlVCW0+l5KbCEIGk1VGK1Tk6ZJqOMsDU2dlmhQUBVMOhj1OTXpl9mQsiyUU68na6PRYP/xY/YuXMCybUqkVqxayqhX9QW5MhLm5yRJGA6Hqj8REs9XWaq1tTVsy6aQBd1Ol3a7zc7ODkVe4LiOdnohiROieVTxVk9OTnj06JFCRecLrFJxeOeTGb/727/D+vqaEvfwffxGyHg0Ar2oZVEiLAvLXqWn+b7PcDjkzc+8yYvPv8AfffOblXxmtXeci1fqdIOqt4tt41kejqMUrHIdyOoS0Oq9xkG2bVWDYX53/t+V7GJt5/pxtDFZqkJys0n5gY9lKwqn63l84vlPcOPGDQajYZUp6PV6VcbPGHvHceh0OhwcHmA7quj7/r17bG1tYGlqpAru1OCYDvV5USgMUI/76ekpaZawvb2N47oMB2Mc2wFUw2Qv8Gm1WpwNBqBFDlTwqWo87t67o8QeLl/BsVU2N1rMKctCiWr8mLE5f6xSPUzYJVTDwbxgMo55751vcPvDuzx8+JDTkxPGk7HaPLKMvFBN9NTmWxD4Ht1+lxu3rvGZN9/kn/6P/zdOT1XrgKIsybOMyXiixFmKHM91eP755/nyV77Me+++y5e+9NN87rNvMhkMeOfdt/mD3//3xNmCJEtx/UAJYZSlFn6gog0LIclkihCSWZzTCFqaMpjhWgIhHaRUNLC8UPQrR9js7uxgC8G77/wAgeTq5cu8/d3vYgGuYzMYDgnDBotowWQ8odVqEpsgT6tFGVtiGqyWRVkJtsRxxKNHD7l54waB5xEGAfNZRKvV1PQ5VZg/GA5xXYdCKmSzLEomkzGepuQGnkeSRDSbLTY3NxmPRiRpyvramlK7K1SdgeNYhI0QiVtRi5vNRhXIJHFcNY+eTsc0m40KwTS8e9e1aTbWkKUSCPJ9j0jX5RlRGAPuNMIGj/YfKfpzUYAoiWOVIY2TiE63o2pFHQfLIPnAwZMnOlOWVTai2+1oEEnVFwyHI84GA5qtDlEUEccRnU67yja6rmqSmySK+tZf6zI4O6WUJXmW0tA1goPhkFZTBZ65DmyCMARUvzrPcxEWxLEq7t9Y31CS+lnOaDgiiiImkwmytGi12vS6PbqdDnGccHJyrNTGXIssT9nYXNd0Spt2u4OwIMkyWq0Wk7FSqIyiaAWo6na6TKcTSikJg5D79+6TFzlpmpEk6VLcJ8/pdLtMJjNtTyVJEusAFl3LZCNLqv2vKIsahdUIi7jkuu5pOpsq2lnpqD5ntkVeFkxnE/KyoCwKkjyl0GyO3LQwkCCw/ljJo4+Twf6f5jDUcJM1McEMnP/4Z7EXPupYvlY+tS+ZwwCtyxOeyyhZolL6VD6IMqZLCpypcdWBLUL7QUZcoR4oUe2vZZUlM/TBUr9s2RLlfNZoNZv1EXuuePp9BqQFdD84ofdyQZGVCCGZTmfV3x3b1mApCGFRlqKidxdFymg048mTE4QQvPfDD/FcJR60sbHO9RvXaDYbXLx0gX6/W2XnG41GRd9VQIqnlS0V+6rdbi8bU+v6QVjuHwZkMOCP8WNarRaj0ahSFDbtdgyoncQxtj6fyQAZG+kHAZPJpPL/Op2Ospma9WTEVXq9nhZ+UUJsWEo8TGX2Jx85/84fP/EBUp5KQq3a1uuskcQ5FBbD4YDZTBXjr6+vV7rti8UCx/UrIYCJUChRkRca3WvgWiGFLEnTgvcefqD6qHgu/XaL0/wUx7FZTBXtYDaZIS2BFFbFl2w2mzTbHS70+vT6XdbW+uxs79DutPE9H1Cy2uPxhLTMyTNZadyrFGgTodFh112qglh6EthVZmLZxLXQEpyW1JkHUZfDlNoI6LoYKclL/ZtqQWvjJZYbhaHtqUWJLusukRQUusfIUiQAjBEtymXTRGyLTr/HD3/4Q+49uM/VK1e4uHdRGZOAyqFWnawzoiQGBEdHR0SR6hRv6H62ZWNjkywSRnKkUGTHxfFr2v+27kxv6b4mjsTt2ISh6ir9/POf4PLli5yennJyeMTZk2OKLOGN117l9OiQFz/xHHt7exTA6XiEZzm4llLCUnNE1bFgKTU3IVF1QFmOJQS/8As/zzvv/IA0Scgdhywv9Niquo/zQZJlWaRZhhAOsgDLtXB1gbXaxAWFzFcMsXmvuudlkWxd2EJRh6wVg22M9rM2sDqFwThIV25cJy0KkjTDa4QkRU4uc6I0IU5jPM8FJNF8TqfXxWsExFlCIQvGkxFbm1u0Wk3Vhdx2SKIFH7z3LtevXmRraxNKm9JRHCdLWGBJMpmBUMX/NqoHzre+/R0kFmsbm0zGU5I0o9XsICyHgoz1Xo8gDJmNxgTCpuW6DJEISjzPxvVccpkStJsIyyOJE5phgEALWwg9i89tdD/OEZFS1RRRSh48esT/8n/1v6bMC7IkI0sz8rIkK3Jdm1JW608IycWLO3zyk68zGo/5tV/7m1y/fp12u4XvB+zubJMmGf/8N/4FP/j+uxRFie8H+L5Hq+3y0ksv8Q/+4d9nb2+PXDeqLMuSXnePqzcukaQR3/r2t2A6U1nZXBWgK+qmi+e7mg4WY+MpBzv0cSwVdDquLpJNMqSlm6bqImfbdmg3WwxOjmk2mwqdtwTvvvMus8mUl15+Gc/xGOlGzmWWUaQZDoL1bh/XtSvHNssyus0ek+mENInwm00m0zG2ZdEIfY4On1SZxzRJ6fV7VRPhLMvIk4T5VBUqy1LiOQ6baxs8fPhQgVSeA5RkScx8qvqtxdGc05OsogMDWHhYsqTMMrI4Vqqdui41CAJVrJ5l9Pt9Dh8/Jk90zzbpIEoL1/LxnIAw8Ll54xpZnjOZTnF9RdnK0oxO2EFgaRAs48bVqzw+2FcIsA1h4OrCZEkazZVojdfCsXzyrGCt36fRCDk6OiAMeshS9RlrtzvM53Mtm55ycnLIYtFWiHGSVmh1Esf0e/1KHGI+n7Gzu4VlSTzfIS8ybNunRNBs91jMF9y995A4VrWerXaTOFZgSFn6pKlSXfVcn8BdEAmVHTbzTUpJmUqiaMZ8MsXXGR/bsgj9oEpIpFnK2dkQx7bxgwDHUSwPz3c4PDgkS1OkVHVatqWbcecZT8QTkKqXYKHpylleIrEqUMkEU+PxgoJSNfXUznfVg0VKykKAtClLqZ08pVZ3dnaG43mqDYZGx4Gq9gFD1ar8YFEV7WOyF4BqE0LVcuM/9fiTCpp+VGBjgNWyXM3S6Ff+iLP+KAU3FWgtP6b+/bJ2qc7WUEIsBUIKvafpLI72VSxbVPWI6Npzae5FCg0KWdXnoWuLTLbRBB0K1IVKXrx2q5VvdO7eV/ZjVLsYk4FUN2Koec8OpixLM0aMf1ZTC7SEBo1sG2HZyk/THyfLUrfdsFRrCKk+PdPlIJRq7iVZzmL/kEePla22rZz1jTabm5uEYchXvvIVtre3K1EVlcl3K/qyuRbD5jGUYJMlMiCqKa8YDAbs7e2xWCyUSp7n0dP+ja2FUzxdN27EbIwYgwnUKl/PZMp0wsAIr5gaVUOjFbZNCUoAqCxYzGaMdcLi4xw/8QHS2toaSqpzzPe+93alLua6Li+88ALXr1+v6iGUcVcLydDtjCKOotc1VLGwRjellDx8+JCTkxPyLMV1RJUmdB2XIFSKccPRmFa7o/udNCslDoWEFJUUtJSSNMs4ODhgMBjwU2+8vlKsD0t0up7Bqaf463UHykleShALC2Shk0U6LQsq4kcISrTCmFB0BtCOsTBBTlmhB6buwbbtFafeOI+GWmYCk3pGpJ4GN59x+fJlHj16BEJwcPCY05NTNjc3qwzKUlFQKUeZTsvb29tVb6i6WEKSJMxnqreO53nV+xVqGleIY1EUOM4yq5amKqt48eJFbt24idCS4o6t6ENV7xUJGxsb/PxXv8r9u/e4c/s2th7TPE2VSp4xZpZVpaA/++abXLt2lSh6T22+Mq1kyy1YSSOZZ1ylpIuCZsPBdmyyLKWUSkYZa3VDOm9oTbBUpztKloFT/bPOqzOeP0xQdXp2yq0Xn8eWMJ8uCMKQ6WRMmqQs5nPihepP0AhCDp884eatW/T6feZaYevsbECvq4QFjDJSkgSUsuRrf/AH/NzP/axCtgtrOSZSKvqnlBoUlLz//m329x/TbLaxLVs7gyrNn+m5d/HiJZVpOj5RUsCzEciCLE9ZW1vj4qUr3Llzl83NHfKiYDqbksZJNZZIqbKrH5GNOz9e9TVg3j6fRUTzGEqp6poQFBQVAmk7NpYAz3PZvbDDn//qz/AP/+t/QLRY4Lpq/uZFzmQ85I03XkMg+MRzt3j4aJ84UrThTqfN5nZPIZxlwcnREZZWilzM5zSbLZI04ZVXXmF9fZ1vfeubPNrfx9LZSyXTrh2fIsOxHdJUIei+51MWJY1GqBHKEj/wyPMCRf9UxctBEHL1yhWixVzJracJiyhiNBrywgsvMBicUeYZsiiIo4Uqxk1TBsMhWZbSbreqzVdRVFMcLROcpgmObVeF1eqRqF42hndu246uCQqQUim/CWHT0NRoIQSeq1oUIEuERUWfNvUnwvd1XaRa6waIMdeUJAm+71c0Etd1q8aJL7/8MmmW8ujhQw4Pn3D9+nVt422KwiaOS+UQOA6O5dJqt1Xn+dLCc1wirTJVljnXr19Vqqanx0tFSklVo3U0OeLqlRvMT2bIUgXIF3YvMJ6MAYHnBQwGQ6WKOJuxvr7O66+/oWhxA9WYeGtrk2SxUKIrWcb62hq7F3ZpNhusrfdwHJfT0zOKMifLCuIoIQxDnhwcUpSKZl2UEoGmtHQ6xFGsg9ScgydPGJwOK+nxKIro9/rM5io4d12PslDtFIyYT1kqiqtl2wpM0/uXotMppw+pqGtKpVRWKHZeFEtEXmo6uXZqkzQjSYtK/KMsy2U9cqlUZleETYwtLQVCOCv71nSuaDwyjtXeWatRPk/vquyyybKo2VSBh/XfqF/9yVPn/mPoeM/aB370eVSAUweP6lmTj/GJrGRuVj7/6Wbq5jXm2Zuxf5bA0Mol6o9S+yIIsaoutzIHdA+8SqnuxwSaH8XKEEKJ0iylyFcDovrPlSJiLSNVzzDXa5NL829RDzx1r6iyVBTimi/X7Te5dGmbVqvFlStXiCIlPuL7Aa5j0et2dA1TWvmpeZ6ztra2UkNsVFMdx6lKF4wqpPE3jM9j/Ma9vT2kVLV+vV4PdE1wEASVzRdCVEwTQxM2IlymTqkoiopeHukWHqZWydFtMoRY1nXGcVztb57nESf/pQapOoIgYD6fs7u7S6vVYnd3F9d1KzpOpJuH1qNQyzId2x1cV3EnPd/TzoNV0cmklDz33C1u3rxBUWQoNo7uBVOro8kzlSUwDjmwsphNMGGuY319HYDRcMjm5qbKSGjjYTuKVmP6HFlCpZQVymCKB6VW7pLqtUVZLU5LqrokE2kbNC8IQ7zArwrkOp1OpRsvpVTcaVjKNMYxpZT4OoVpFq5BEgxqXV/45qsKrMRS077b7dLpdNTYZDntVruSkWxqdSDzPoArV65UC9SgBWbhGMffBKtSyipIMuosRltfFdWm1aI2jSsNR95CICzloPmeTyGVEECudfmDbof/2d/9O/yrf/mbyhCkKbksSXWz2tlsRrfb5fLlS6pGIPD5yk//NA8fPCDPC5IkpfwICnfFR86Uo22cMd/3VfBlsnx6TpnxNEGpoR6cVwA6LwxRD7pNDYv52agLmkPq+x+PxxR5QaBpQJ1Om8HpqaKPaIe83WrR7/c5Pj7mEy88z87ONk8eK8GR2XTGcKgcp36/z2w2ZTgcMJ2OmUxGRNGCn/mZP8fuhV1dRF1WioNSz+l33vshb731HYIgJE0L4jhRtNhGQ61hDWzcunWLJI4ZDAY8fHif46N9tnd2kLKk3ekThC2kcNneuUiWZrp2T2X8TEWAtQToPtax3CAtTM+iMlM9ewzRw/Ys2u0WrueQpgl/9+/+HV597VX6/S6dVoPR4Iz5fF4VjBsFzaJQc3w4HOPYAt+D2WyM65Tc/uCI9fU1xmNF2TO9S6bTKWenJ3Q6HcUTDzzyLCWNlWCJZVHRYM26sm0PI4FvPrMojGJagaez3er3ud78ulgW5EXGyelxJRCxvrFGUWaMxkNsKZXSWSNAUrKI5jQaAb7fZbGYYVmwvb1VSe6ruppGtbaHw2HVtNKsccVZVxtps6noGFG00LU7NnmhMo/CEnS6LW7cuMHu7g6DwRn37t3j9PS0mue+7zOfzypbZ2yUaYJoPtPUpozH4wqkCUJPUco21+j22pSywPVsonhBXuTaVoHtKVGaNMvwg4AizkjzhLzIKFHBWzReUJYFm5tb3LlzR+8Rqt4PhLLZnottC8bjkZLF9RwODp6wWCzwgwZh2GA+n9NsNomiRLVJ8AJkXmBJiSMErlZ8Gp6eMJzMOT45UXVNecbFi3tIKZhMI5CSyWTKbB7hh03SNMNzPcpS08ezgjxSzkqRqawowibOcuZRgrAEjhdwMhhi6M2gFCPrTl6qhYBELWttaobU3qkyC5YO1E2tg7CUXHycqaalpi7J2MK8KAFbr+dzzeOVNURKtWbNb6U02eMacCRURlIBTSrrZPbxj2MXzjvPf9LHHz+w+ZM//lM/7+l7eBqcMnu2AYXN+54F/D0VqIlaePqMoMsc5vz1z/i4R/3zLPtppkb9PqrX1ee5LEGugsrL4G31XlfuTQd+pu6nDhz7vsNLLz/HL/zCn8e2bRaLBWEYMpvNiKOUVkP5XbOZaqxsao/MHmSkw1UyYZnRMtkeYxsNBc5kc3Z2duj3+0t/MwgopKTZbGphs2nV88gEWsPhsAp8jU9mfEvj58Cyj6QRmzF+oKI2u7phtCBLUw2czz72M/yJD5Bee+01Wq0WjuNU9SqgJk+qi7/MpF02ds20M+3g+66mpylXySRUCt1sy6T4JArVznVfC2O4VbNJwWw6q+pp6sGQKjy3K2e0LFVjP9tWaPhcFyXXgw+1edTT3XXUZXWB+55bvVdKWUlTO45Dr9erIv7pdEpeKqffIAfmvMZJNhPSsW0lmVxtWEulMFNQZ5wLc311etf5BV13xItC9U0xtWEmAzgYDBiPxywWR7rx7G6VXTINXoGVzzTPBqgcmyiKKnngVqtFs9lYyg/r15sF5vkeuUZGJtMpY90T4M6dO8ymU7rtDs8/9xybmxv8/J//qpLERFAgQdd6mTmg1K4iZFnymU9/kn/5L/8/quDQdZCpCq7PbwrGOJv5B2Bbikerze0z54A5VLHw8rzLrOVSNrX+/vPom5pPT2dHJFSKgI12B9tx6HS72LZFEsdkacrXv/Y14jjm1q1bWLbNaDjkyuUr3Lt7j+PDQzzf48mTJ+zu7lbFo0ruOWexWPDuu+8SxxHPPfcJLl++Qq/XrbK69+/f5+23v8/J6ZBLly4xn0dYwuL4+ATX9Wg221AqcODCpQv0ej32Hz5gvpirbK8WH3Bcj/WNTUqpuohv7+yyiBa4jsNsNl8a4Y/YQH+UE7BSuI1yyKQA2xHYlqqv6/ea/Fd//39OWRQsojmf/ORrXLq0x2g04uz0hOl0qjOdOdPpjMlE9WZZLOa6p0WkN70Az/WQMmVne4fA93DX18izXNEzkayv9ZlOppyenJDnql3BZDzG91zNelHginr+pkGixLZ9TWXIdXGr1LYvJ02Xgiag1EE7nTaj0RCEYDafEYYBzWYL3/dYW1MUrtl4RLfbQUpJu90milQNie/7dLvtygHIspS1NdUZXsnJq0Ct3+9re1RUdrjX6+q1nWo1Ssnm5oamUE1VDVJZ0mq1uH79GvP5jMeP97l06RK3bt3inXfe4e233656CcVxgmZ9URSFUlvUgYQRvjAytO12m5OTE65fv850NuHg4HGlgFbPgDfCFgKLIAzwG0r5qTR21bZI0xhhW1iOhRA2RVoyn02Zjmc8//wL3L59m8VC9RSZz5Wk7YWdXQaDM+I4Vg2GdZZsPJ5QyindrlLoezQ4IIkTWu0Wi/kcWeRKDns85saNmwzOBriuy2QRMxyOyfKMZrPFvfuPlGy8ZfP6668jZcm3v/0WrushhJKs9/2QPE+0mIzUGfFCqxQCiKqZpxCK/pSlKdrLo6yBW2Z9qcyPAifMM146liqQkaU0SQvdb1Cdq9Rz19CXhDD2Teh9XNHBzdvVdZh1XXesdVa9Kso3BkCJSJTSnH+prHXeZv7/Klh5lp3+OK87/9r638+f4zwz4Vmv+ZMPjJa/P3+d9S+jJgxLOW8T1DzruVQ0vGd85kfdUz2Y+XF7wPlr/ajrqN9b/fqrPVsLS9TB5eX34pnXJiwLUXtWil6r6m7PTof8q9/8HU5PxvyFv/CLpGmMs+URBCGB18C2nIpiF4ZhBVJbllUxesx1gKnRs6prNkCS2c+Nzbx//z5PnjxhZ2enysBHRj1WM37MOqoaeesgzARAvu9X6nr1en7jt5n7NEJhic4Uebq9R6vVIoqiFYD4xx0/8QGSGTgjyHDhwoWqEdXh4SFRFHH58mWOj4+ZzWZsbm4QNkIQkqLMK5TBdlR2SVYBleKjFkWmgyZBlmakSbpE8IHxcESz1a6ux0wCVciqZKWTJK6i7iiKKofREkI1SdWFyghBbDJejqgcF+P0mgyMQSEEgiJTqUsbVS5usj3mWkzA1l/rQ82gGKMjhHLmFL1DXZNdFVDnKpNVQ1hMUZxZ9OeNwfnJ+SxExdZZAiFEpexk7m0+j7hz5w6Hh4eVdO98Pq+0+EEpF5nAaj6fV3Q6pUK0pE8eHh7qDOGy75VZ2MPhUKHQccTh4RFXrlzm0qVLhGGoGqOhHLhkEXH7zofEiwWj0QBZSnJZEqdJpZ4CVNmqIsu4ce06X/jcZzk6PtYLGuIkpSiojDYsDWWqm5oalNStPUM9q1bGs3qvdgWqTJRG4Os9qc5nkOrGrn6+5fxVn5dnGSenJ2zs7NAIQ7I4VjUci4h4EXHv7j3SNOXs5JQ3P/tZ3v/hD/nsZz/HjRs3GJ6dIRCkccLx8TEbGxs6M+YRxwVxrJTQBoMB3/7Wt/nB2z+orvH07FQrXpXs7F6kLBWddX//MVlW0G53lNBCluC6Dm+88QZlWfL+++/TbDZptzukmYtEyby32h1OTge0Om26vQ5379+lKEtGo6G6d+0zfdTG/aMOtTFmgMCxHTxfcVybDZ+1fpf1jXXu3Hmfr37153Aci92dDR7cv02eF4R+gG1Bu9XUNUI2O9tbCCG4d+8+6+tr7O8/YjIZEy3m7O3tkaYRDx7cw7IUpSzVdFhTH2GkWM0GZJTbXMdFceuXnd6zLF25D0er2uW5sakq6Hc1XU2t1Qa2rXqE5HlW9d1xHJtWqwlIms0GWbxYBmmTsVY1U5kxhG4kKyWlLJjNJghLMJnMcGyboiwJwwDLVhldx1E0i5PTYwA8z6HRDEiSlCD0EcKi2Wyxs7Nd2f92p8PZ6SlPnjypVNO++MUvcuXKFb7+9a8zHo9ZX1+rACvLsmi323ieR7PZZDQakWUZQRDQarXodDrs7OyoZqe2g3BMuwCH/UcHXLsWIGWJ7ylbZjsuvkT1lKspo1m2hyxLokXEbD5lNlPS5aIoefz4gN3dC7z77ruMxxNmsxm7u9uEDZ/5Ysb62jr9fp/33vshruvhOAFRnDIaTbUyoMXW1hYHBweaoqcykiUW2Qd36HQ6nA2HTOYL8kJlY0/PhsgSWq02n//8FxiPR3zjD7/ObDYHKbBth0ajyfHxoNoL87yeudEMibKkKFZBhvNUtvP2C5byJuoPICs7V2J67zy15tB9eQxVTWd+pfmfrE63/DypX18H4euf/QzaWynlyp+fBTZ93OOjApQ/zvEfG5jUwcofFTz9aWal1Ef/aJCqHrw969/6XqfOxgrw9VH3Ut8P60FO/To+KlhcGTNJrf5MHXUW0fnnUN+Xn3W/5qgHT9X3paoFNeBwHRAtCsF8lvONr3+HvQtX+KnXXyOOCjxPZVlms9mKHLcBguqMnyiKaLVUL8n5fF7R5MqypN1uV7Q841MZ1ovnebqnnY/jOMzOzipaXFEUVQAEivlleqYBNBqNKoNlfLhOp1M1tjV1SkEQVOUy5tkFQYAAIq2k+ceZtz/xARKoDd3IfhonUAjBlStXNMf7tJLrjOKYKF5UEt4q+2ScgwJLNworiqLipidJgmvbqgeLbVNIiNKEk5MT7t69w4svv8KtW88xGA558OABnU6nokttbm6QZcs6DMuyODw8VMiw52HXImXDe1f8eYljCZCqiPDh48ckccz62hqJRuKMzPR0OkF1Ww5wHLcKfEwmRXVpL5nO51U/GmMQKklEKcnTTBW0p0aC0lJUA1t3mtYL8jzKUP9d3RH/KDTK0AfrC7z+LK9cuYLn+8ph0shRludEi0Ul4VoPBA36WC/s832ftbU1iiIny9IqaHIcRzXMDALGozG2sNjb2cXGYnQ2YIRavOsbazQaGxw9OeSb3/wjhFT9QdZ6fda3Nil10GyCRbNwizRFSOh0O7z/wQe8+977LKK4QjvqRx2lybKMOIoQwiJsND5yrpvxNRlMi/O8+Gejf/W/PZWyrx1lKRG2QuCODo+4ces5ut0uw7Mztre2uf3BB0RRxJqm1pWyZGtzk+PBGYPBgJs3b3J8eMjtD29XgMB0OqXdblOWOUHg43qOkjF2HWQhSBJ176WULGYRZQGWsAmCkGgRc3JywmIR0el0aTSaJLFCpp5/+SV2dnZ4tP+I8XjE1to6V6/dYDgaMRwOuXTlIp7vMxwPuHT5MkWp1OBmM9Ux3BZqU1PF1WoN1DnkP+oZmLG0HaWe1Ou3+Nu/9qt897vf5s99+UtsbW7g2A6Bph8sFjPGozN8X9HXTk6OsS1LKepFC0BwdnZKEIScnoyYTxeMxyMW0ZywEaj+Ze22RrQtooVay5PxmKPjI3rdHv7/l70/jbVty84CwW/O1e/+9Oee2754TTTvvegNOGwcJsIYqLRNka4yjUSZrmThP1jYYJAAYclhyyClyUIghJKSXaZJyllAJVVUJc4khXGEsXE4IhzvRcTrb3/vafbZ/erXnPVjzDHX3Puee98NiEqjEEt679xz9l5rzTXXbMY3xje+EUeoygJZusJqlZJekwSAhpSfBMxaR0amMN55mPka+L5xiAAaDTxfQHqA71M9oKtX34OkQxSy0KcaGMvl3FR318iyFTyP1DN9J7K7WMxtbqjSJNvueQSqeHPn+jknJyd2HueFidQ3NaQRZiiKHEVZoNfrmTpHEQaDEa5du4ZOp4NXXnkVn//8b5DS2XCIoqC1dz6f44UXXsCnP/1p/Pqv/zrSNEW3K21kuyxLqp/meXazL8sSZ2dn6PV6mEwmZs3zMJlQHaT65Bx1XeO3futVWxwWIIWly9euQnoetne2sbd/gCCIAA30Bz3UdYUHD+7i9u1bWMznGAz62N7awvb2Dr73e5+z9MkkiaGaAt/93d+F4XALe7v7+J/+p1/CzZu3MR5PMJsTVSXwA3zHd3yC5Hnr30Cns0KlFB48eICzyQModQ+XL1+G7/t44613UFQlqrrBdL6EgIckWeEX/x//T8wXU6imglI0Jihoc0b4Qj5a50UpZaI8ngU37jokjcAPn0J/NwYhTaDH0lq1y0nWFwhjP+ZE1z23bnDDrR3/6PG4z54SzzxthOcbdTzufu923yd9/r8VIHrccRFA4cMdV/y7yyYBsA5EtDZr3OOvt2mj8FrwpCiXe7iOx6Zp1gASX9u1R93z2khpq2i3/hwtFc+1t4Sg3DYhTEFlB9hQLUCBIPBw7dplbG2NICVQ1RnCqAMhPOzv79s2MnOJC8ByPTEhhAUjTP1mQMWRH6bCcY04TtfgdzIej60QDkeAWB6cHHK+fW52LvNnDLxcu57by8EBjkxxygC0XksRedrjmx4guQlqACwFjJNG2ZgOw5BySuIYSlegWg5j+L5n1TiSuAvfD+wgWS6XlgbTjRMMen30el34QYA8TXH3zh00VY3FbI6FqZmwu7uDMIzMi6eKw0WRW3471+7QWhNnsiHPbl03KMLChDArCFSIwhBRFCKOIrzn+lUAGk1VYDIek1fYDGhVVVhMJ0jiDgam+NYqz3Hr1h1cuXqNOPdZhjAKrWEUhjTgi6JEWZSo8gJ1XWExn+P05AQnJw/xgfe/H8++8AKUashzanmxjTXSAdp8qOCZiUZJUmy7aKHRWgMm6Zf5E9rQJKQktblOJ0GaZlCqMQp3DTjkzNK71Id036YxtZccwCKEQJplxuiFDQu7ogHSk4ijmIzzpoGqScZagOproZNguDXEH/qv/xBOj0/w4MED7OzvQkiBOKactUY1kNJDkefIlMJ8OsP0fIKsKPDBlz+It9++iVWamUVtfb9tF3NqX5bnqKuaEtCpt5z/Lo4iuYDYDX9rTTknNsKEVnFw3SsHZ7E2bBSlIITE6ckJ5tM5Dg+O0OkNICGRxAmyNMPWcIStrS1cvXYVl69fQdFU+MIXvoBPfvKT+OAHP4jZfIbjh8cIIqpfk2cZpBQ4unwZW1tDdDoJ5SZoD6vlkirO1wq+F2I2n5nxWeH27TtQSpsq4R2oRqFuFHYOD/HBj3wERVni1S+/gm6nizwrUOQl8qxEEMQ4PLyE5XKJsqrwvve/H6t0BSE0Th4egzcnfiFPLzDlGGuCosxJHOL3ftd3Yjjs4pOf/AS0LvHw4R1AkYfr/v078APfRHQqpFmGumxs4eI0zSz/mgz+AVHGtMLR0RHiOESvR4pxYRiZHCIPZZnj4GAfk8k5gsCDLyWU7+PS4SFu37lj6odIhKagH0QrrR8ElEuplLJRTSEFfOEbr2AIKQSk5wFaoWMKjXIep22v8QpSVHZK3kMhUDYNFXBWGtdv3EBzcookjhFEHknDVyWkojU7yzKk6QpCSNRVbTe4MIjgSVIyTJII83ltiwsCxjiQAtPJBHVVwQ981HWF4ZA8j1ma2SLXb7/9tokoh9jf38frr79O9X1GI+QGcAshcH4+QWnKMmRZZhOJgyAw3lRga2sX4/EJraWSjAQpJFarDH7go6wqXLl+HZ/+9Kcx2t4iSlpNToeiLOB5Eof7h3j+2RcAAHVeYH9/H+fntK5fuXwDVVXh+PghlCrxyiuvoqokqhJ4//tfxunpFEWh8PxwF57vYzqZ4LP//tfx+uuvo5MkWGYFVs4zKdXgwemYRBEaYldIQw3XWiArKqLqooEURnZYSBOVEeAaaGvgx64h5PCySpCCZ0nrxTfu9Y1ZRHPHWQ3bFU5oA5AcMLUW0dnwssMNErkhJMegvnAuO1ew6Gnzm4+nWOk14Mbehva42M42e557q6fBJRc9j9kWXBDKbRNr74EXOfqf+6TtWiYe25TH9h1fVrzL9/gWfNoFX3wSkOGrt3Xy1sUcNiMzBE4MCILj8BLcjvUcl3cDhm6UZ43G5ziFlR3LrpPYo7IrdlTSC2upc0QD5H23BWlsz7aCXJt2Lqs+9rpd9AcDYkbFCS5fuYT3vOc69vZ2EIQeut2YhHACCYHA1pvk52cKNOWZNqYgNq11XOjbFchiZzBANHwAlpLMdkhRFBiNRugPh/YaNrcabEMqC3S4v9h248/42q44BOddAS0Yq6oKnSSB73nk+PSfHvZ80wMk7lC30BajUh68w+HQ/k5eTB/bWzGGw200dY1ud0A5BJqNTt9SFg4PD+nleZ7ZVIh6NdzdwUe/5eP2XnmeIkliU5y2RtNQe7hdDIz4BXN4UOkSSdKzcoeqadDt9+DrCuOzE5ysVoBq0NQVxmen2N7axq/9+m9glab4Pd/5e7Czs4MwCjGMYyyXM0zTKaKkg6LS2O73UeUVorCHfj9BEPqo6hpSSBRlAykCohB6MbqDLvJ0hTAI0YlC3HnnTXzty19Ali7w8sc+jqYu4PsBhCZpTFbDqmpt87DoEFRTAsQZ36R4aU3yyzTpPft3oBW5yPMM8zkl9cVxDCkp/4EXfv5Jk5oKtDVaYrGgyAAXQiOObAyYgn08VtgzIoSAahpcvnoZYRhRDpoQRmKdJDsjUOjWi0Js7e9BmsKSnvBsFFAIiUU5x2w6Q6MU9i4dYTad4Ts/9V149auvI/vSl1EWDXSZo3bqRdnFVQJl1aBsFIqqgvA9iuKYXVBsuD7Zm9Q0CtprPUtASxkQQqA2FBhPetagAUBeX2McsVecuSoaVIPBg4QuGpzdP8XW6ADD7X3kWYVLh1dx8603UYUlhrsj+EmAymuwd7iLu+/cxpe+9AV87OMfwwc/8iH8+1//NTKadYimqlCVJR7ef4DlcoHR9hBRHEFpAUiBeDBAWTToyhBhdwt5XmA+n0MIicGgj063h6qukBcF4l4XH/72b0PQ7+E3f/WzqIsCO6MtjMdTovBVNZ59z3vQ6w3x2htvYG//CFu7h3j7zTfgQ+H+3bv0/MbfLBxp/IsO3svM8IYA0GiivXoAukmMQS/BfHKCbjdBFIYIo8TUpTnHajnD5cuXAa0RhhHNP4/UDX0/QLdLUqm8RnV7IQbD2Dp3eMMgcEK5N5y3p1SDF1/8AE5PT7G/s4vZbEYbiRCIgsBuIpImDskWOxsQ/wzCEDDrVFVV8D0PtRln7Akc9Psk0lEWKMqSag6FIeUgBSHKvES6zBBHEulqiZ2dPXzsY98CP4zwgZc+jDu3b+P+8S3kteGOBz4W0xmJLJQVRcHDAIBEVdWYzxaAFuj1u1CNQhxHpoaNB5I+jzCbTdGUDfJ0RbXHigJJHKMbx5Cej/Q4Q56SeMH47BxKKTy4/5DGlvRwejqBUgplRXk4FOUXaNQCUkhoCJK6jhNcuXoND47PcDI+Q9JJkC6WaFRjI5ocRb5y7QY+8OLLiOMuxicTarPwsJwvcHp6itVqib39fSzmC9y5cwdVpTGdTDEajXDr5i0sjYBEWVW49/AhTk9PSRnP8ww9bwkNoBItrcdGkSeLdtBarGAAStMAgvKf6kYbpwmJKFjajzaDnI1/odGwgIG1DblmDB1KNzbng6WuaZ1qjeF3D06sR3vsZOP/b1xgLTIFJ/pg19WNyz9tdOQiK184k3/tqw7EEFgLUT0eLLSLCffTOuDTG9+98NYWEbZrloO2xGOu98g13D+8W/882i7t3vPC77nHeoRxk9rnguVNOho5ZNf/3l7zUZraWmRJaprHa+N3YywZCXEAjmDWBT2gqZ1K8dwRxmYwinRoAZqrStmYsil2zV2L/gSo6wahKeeitLLlM4SJ+AdBiOFwiCRJcPnyZWxtDXDpaM8qz+3v71shK3b2VmWOTjJEXSoEQQLdKKP+3doJVVXZQsmsLMesqbIsbZ44O1qYEsc5Rjzner1WmbTX62F7e5uYUMYZx2wq92A7xRVbYCDITl4ANqjAII2jSm4Eke2fsiwhfR/C+y85SPZgABJF0VqY2Sa/m98ZRLnS1AEAEYs1hA604VGXK8rXEVIgECFGRhue5Q/TNLWJyBb8GH4mt5OTVH3ft+ohottFnlNibhAESAYDUsKqBaJOH+fTBZI4xnQyR9kAN+/cx7PPP4/ZbI7P/uqv4ujoCO9973tJslZrLJdL7EYJirJAAx+h5yHLM6iMjCMKQVZYLhc22dn3fciOD/g+wpCU/b7n+/4gxmen+Hef+yzi3gBHly9DqRWGwyGgyGOidAt+3CRb2qhooXHD3tazIki+umnUI/3s+yF63RBh2MHx8TEePKAcltWKqtWnaYooogVDKcpnaJRCrUj8gt8fT96mruF7wk4yS/NzeMdac62QAkVRmBByAKUak+sFDIZD9AcDC54rA8TIiy0RRCFG29vwfTI0lzsr3L//AH/8j/9x/LfnfxtVfRMKCo3JR3O9X0qRhHFRFMjyjIxo6QGocZFn0nrE9Hoiq5sb5/apO34vpg+sGwAasLVE3nzjdVx75j1I+gMoCAy2t5Gc9DFbLuFFPoKzMzy43cUz155Bub+PO3fv4tVXX8V73/c+QACf//xvYnIyReB3IJsadVNicj7HdDKD9CS8wDd+NSq6qLUHpQDP8xEnCaIohBcEWBU56qZBb9TH7/rWT2B/bxuvf/XLuHv7JmLPw3Ixw3w2QZrlCOMubjz3XtQAJosVvu0jH0WalSSEMB4jS1NSyNK19e6xcfV4kNT+nfuZqKs1dne2ceXyEbQuEfk+mrpGHNPYuHz5CLdu3YIQAoPBwHK+i4I2J65C7q4Ny+USZVkaimhjQUuv1yMjOcvWpPjjmEQcqqrCcDh8RKq/BeOwwgM0DgQ4OZ2VEgHYNbJ1WBS4fv06EiNK0NU9KCgslkuUZUX5llGM05MxDg8vIc8yLFcp+v0aR5ev4P7DY6Tn57hy5Qq2dgf4whd+E3maodQVpOejKCqTM1MjL0qEQQSWFo/jDuq6Ql2SqEoU+agrooFNJjNopaEVcD49BRVbVOgkHaxWS1S1Ql5UqOsKcZwAmvL9iAdP4IfnDtcSEmY9aWwxXaLP3D8+Q7/fx+7uPp599r3QWmMcjnHznZtYrVakFtVJEAYhfuvLX8Xdew8RBiEBoLqCL8m7maWZNSwpb6wCtBEBkCRSIUyejYZGZWhCjVmL7HwH0IiLDE7zEp15vub1dvJ2nHiL/d4TowDikX+s3XvzXjRvnuJyF/793QGNEK2D1D6/+W8tnGWv++7XfPT5HUDzxLXzqZpMX3M6ZXO92YwEvds1NoGG84W2SY+9jHj0gS+6p10rLm7D09ILH/e9x1HanDPxuHfwuLHn2iVPolxd1NYntWctisS2hGaxqNaWdJ2WntlXmA7n5pD7foQgoFy/OI6xt7eL7e1tbG1tIY5DDEdD3Lhxw6q/jUYjZFkKIcjJtVwubYoIAGJmmOg+5w6xbcZAhOlyAGyOupuPKYSwdDteA5m6xuIITLNjKjLnvlZVhd3dXaK+meflqBQLbjFVjvNnWcGuY1ILeH/dfId8X6bVsU3H74WL2r5bRNA9vukBkjVSHWNwU3GD81h4A+QQ3WaI1jUugUcFB2zexwaA4orEnEjG92RJaQ5L8mZrJaaNV9g3hbN4UIRxDCE7CDsD7OxfApTGlevPYDIeoywLVEWB3YMSl65cQ7/fQ6M0oCU8CXhRgrPJFF4QIYwDpFkGP9QAJIQXoMgzQABh2LEVjYX0sUwzipIFAbwwgi+Bw04Xv2+4hf/wG/8BUZzg0qVLYJY3hYW5snPbp7wAQLS1BYQgwQmWl4QCmrpBr9c1Sd4+VWqPY0CTwhRTEqtS4ex0giiO8OD+iTUkF/OU6EdJBxAatart+3IXxKIooJvK1rxKksS+Pw7/Mp2SFw3P82wi+Wq5RK/Xw/jsDJ7nYTgcIopjhHFMct8lKbkkvS7KooCAwGq5gtYKzz33LKT0kGX/Z/zNv/k30egGZV3ZcdACxwZlWSFNc6SrzAhXeND60YXdBTkM+rmQm6vuw+PYNSCeauEQBMiUoS2mqyXu3rmJ97zwXhxdvoQ7t+/i6MZ1vP6VV7FcrRDOAhzfuY/Ei9Dt9tDrdvHOW29DKYUXX3oJnU4Xv/VbX8Wdm3cgpEQURohUA23y4lTTQKsGwlPwBNVNkR7RqkRA9ZzSMocWAgdHl/CRj38Uuzs7eOf1r+GNV76MuzffQrZa4cb1Z5GmGdI8w4sf+RZ0Btv40qtfRn97D5cuX8OD+/cBCLz+2mvkTTMeyTWTULdKjo9TwnHnved5CATw3heexdZoACEaCEXSrdqosmVZhhs3btgNiCqMh7YeF485jj4IQbV4lqaeFL9bu9ma6DM7gLguxP7BPoqUCnlybTeek7x5t1652m5KvHbahPu6sV5CLvhH1cwlFoul3eQ6vS4yk1s3nc5RVw2m0ylee+0N7O1tIYo6mC+W+Kf//X+Pj37s43j+hffhta99FTeeu4Hv/u7fj//ll34JeUr5ZtDkNKlUASGALE/NXKD1iWu3NY2y7c+LHKppEEUx8rwwc4rEJ5TSKMoCda0QxQlUo3A2JuU2fn913ZigSmPXDHLa1GgaDa5srzUlRZPozznefPMu6lrBN7Xt0hUlHSutsFqVlC917/iRuQrZznlmKrAjx8SBiL3gUcFSAisaWrTjsFaNEyh4NKrs/nw3I3Vzz7vIWH0S8PnP5WADj4Wavl4DafN4GlDyn3q4zsLNddnNx33Smu1+712PxyRftXWZ3r29j/v71zMu3H3pSde94E4mekNAqT3tSdGeC6CuPbE9b7Mbn9Smtt30u+e1dD4egwwwGHQwOBiNRja6cnR0hPPzc3S7Xbz//e9HHFO+dF1TgeKyLBFFIYoyR57l8HwPRblCGHmYzs7QSTqAoQ5KKe05ZVkiCkMkcWyUQZVpJ1HglsulpcK59YaY3cRRpMViYSNHSikkSWLZOVznk21sztviQEWWZTg9PUWv36eisCan0wWWLm2QxxDvRzyfAdi9j/vezTFncS+OePG7E0JY6t/THN/0AIkV64A2WZ8VNgBYY4HRrqsbvzkZGKxsbgyMdqfT6ZqnUQhhFaMGg4EtWuouHO4g4t83Jy+HJznaJIREAw8KGtKP4EmBThihNxjR5FQEEphiVpaFrSkynY6xd7CHOOmiboAgiKE0IKUPwBieDpCUUkILjQZ0TU8KKogKohoORh6+9Vs/gU6nY+mB1D/G4274sm6lY3oGvbb48sRrmgahF2K6mBqe/YlN5o+iCMtFbmk9RFtJTMjaQ5pn9j3N5wvMZl8zeWURhN8amTx5yOPhQ4l2YvL44InI/TAYDNZAhoBGVeQUCFMag14f/X7fGld+6AMaKAui5vi+R95sTfckvX4CUL/rd/0O/IE/8PvxT3/xF40qWCvLzmOB8iAaZFkOKQMISAhIkJd3HSjx+FJarYXH+Xnc8cUAyU1IbY3lNrInqcgXtCa5agqoEAntza99FVeuXEZvaxf9rSGEJ3B49Soe3LmFYLaELyRez76GV7/yFSitce3GdQgpkOU5PvzhD+Nbfue34PK1q3jtq69hcjqG0gK+FyDwqT6PNpWDtNnIPUkFIYuqRK0ajLa28Ox7n8dzL7wAL/Dx6iuv4M5rX4OnFWaTc3zogx9EmtdY5RkOL1/Bs8+/H5PlAmfTOb7jO343yqbB+GyMdDrF+ckZpOTcGzNGhfGkq4uNQ+uNdX7SOAHCyMeVy5ewXMwwGvZI3bBUCMMYtaoxn89tHRcuR1CWBTodqmEzn88RBAFOTqjaebfbtRsfg/jpdIper2edPnmeI45jeJ5nVX6qskQ36SBNU6xWq7X3XZYVKKlXQwguxEpJ+FRHyEdV1VaZbLFYYjqdmdw/YHd3H0J40FogimJMJhMsVivESYzz8RQPHjzE1tY2ZrMFDg+PMJub+6sGX/3KV/CF3/wSPvWd34nv+NSn8Nlf/hVcunwZ73/fi/jVz30Oxw8eIktTyleSRK0oihIaAnVFjoOmUdCg5+Eab8p4FekRSUYWTgSEJOUbNM2E5r7WqEoGSEQ3qZU2c1ajqqk+llZcxYqNMlai4jIGRKdReWH3BlZca8y6XCui1JCDSANCoNbK1rNjkKSbxlC7lZ2Pjalpx2NSQxlnlCCvlCnYpbW6sLbaRcfTesk3//Y0xu83CjQ87XFRG9kBt9mex4Glp414PO68zejNo1Ggp+u3i753kWNmM+LUjqG2PY8Hs20EbL3NF9si7vXdaz1NZP2i40nP6H626XRev4i0c0Kptv4fNvrQFUbY3PM2n6ttf0vPpP8ACKrBRZ+ts2B834fv+8Zx1Ee/P7AO8iSh+mxJkuD5559Hz9QJ7HQ6VpHX932kKdXyS9MVpCRBpyzLUOU50mxh1HFLBIGPwbCHPM/R7faMPeOZtynt3s+0aiEEqrpGaBzu3CdcIqDf76/VgeToS+uobYvec7QmSRIow87hXCVWpuMo1cqIf/H5TdNgMZ+j0+utOfhWq5W1hZlpxQcLa7l9fH5+buoCtoBOKVIu5n2P/8YCXFJK5EX+xDHpHt/0AImVhzYnAv/OyJ4nDQBTCJELIJLxufnCgLbzOXTIIUu+LkeGWNZwc9Fyr8PHpteIjR53kiqt0ChACyfBUJP9RrWazGv1AN8XEH4IP2rQHW5h79IhcVrDCFVFVeYbpSCFD62lUR2irZfVqoQAPEO18YxXk4pv0UAdDvq0NzthYyGAqm6sC4aV2BiAaCgEgW+V9hhI5nmOCjUEPERRgjhKoDXgezUCP8LuLk3sMAwxnU4BaJL6zVfIC6oNEviB8cwQXTDLasjAW5v8bh2qwGvDyK0Xt1WPYU+uGwIXWkOGEeKI3vdm4iC9OyDyfQilUWYE7JiXzhGrsqjg+wH+6B/7I3j9zTfx2V/9VRs9ZEAvpcBqlaIoCpt7RQatGUMXMBzIYMIjbXLD0vzMm4cUAloaGg975sz1qXK3pMJ3DclYp4s53nz9a3jhpQ/jYO8Qi/kCu4eHKIoMk+NjSFCkLktJQvjO7dt46aWXMD49w//6b/4N3v/yy3jhhWdxeLiH4/snuHf3Hk6PT5EXBVTd5g62+QsVkk4HBzv7uHrtGq5fv45ul0QKfuPXfh2zyTn2RiPUZYHr128giBKc3LsFGSd4+SMfg++H+OpXX8O1Gzewf2kfD+/chgeFV7/4RUgIw8WmO0Ks6ditzVGen3y46wqtJw36vT6euXEFnU6EPFshCiJoTyBLCyzShaXPpWlqo8dRFCHLctR1Y/nW/HwkgR5ZpwFvxryOMb1Oa43JZGLnalmWyKIUWmu89tobGI0Glv7rjgkey7z21XWNPKd1NM9zA1AK60SYTmeI41PkeQ5oIAgD+m5RQEHDkz7m8yX29y+hrmscH59glaZ4+UMv4/T4BFlW4Llnn8fZ6SnyxQJ/4A98D+bLBSQEPvnJGLfeeQe/+H//RcwXM2RlBumRU8CTPg4ODtHv7+Cdd97BMs1MQWWaXywwQzV2yFGkGio2zO9Jm/HM/14z1kxRcD5cj/y6eAAdvG5IwM4ZrfUaNdGlcCkYhTczzCBa/O22g2rtODQuaLOkakuPEnSSAfFOO/Gogfr1GqxPG3n6RhxP8ur/x4IW17j7es552s/XhswFe7feOO9p2vG0kTn32Tav67bl3QFa+/m6o8yp5aYvlp7maz8pov6kaOVamy9onwuWLgKcDITs79K9l3bo0a0z2taudJzTrtNJCI0gYFtAQnoS3U7HqAD7GAwGGI2G6PV66PV6CEMqDg0Aw+HIfj4wlPu6bqwdStR8V4SAi2FHWC7n6PV66Pd7hl4mESck1JNlKeI4QpalJr+nQVkoW19zVs/Q65KDTUAizwsLUvI8tzmsMHZNmqZGxbOwQIbXuCzLrGy3rV1mDgYpYRhaO9llK7hjiB37HHio63pN0KEsClt+h98D12taLpfWRmKnMV+naRrb30Txzm1EjKNGTNNz2RK8Fzb1f1GxsweHAV3vgbugsGHBf9uUTmSAwl54BkRubR1WxWPKC9O/AFghgcctVnyvTfqe+2++L7dXSgmpDAWioarrqqkRhaamD6QTNTf8Vp9pYR5kQJ4PSLKsfd+HJz0CTJ4wtUzc3CsCSVISvYMqnBujqlbI88ICCDa0yrIETF/WdY3ZbGYpa2VZIunE2N2lQT6fz5EkCQ4PD5GlGVQNTCdTZGmOVqlOGeoP5XmtUmq750mEkYdOd4j9/R1TWd43oNSz3lXlbAJuPSCYSBAnGgKw71oIYUEw0C7WeZ5D1w1CjyteaxRGzrJuakrmrmqTMB6gRoEip0ryDRS01PA8H74fom4qW1Dxz/yZP4Pj01O89dZbawsWACzmC2Rphtl0jrLWhmL37uOfaZ9uwVwe5zy+HtnchDCiDQyQhK37YTcpurr1P7752ldxeOk6Ar+LK5ev4M6927h09SpUXdlE+xvXb+B8eo7RaAs72zsYjUa4c+cOfuPX/z22d3fw/PPvxY1nr+H6s9eRZjlm0zlWi5Wt1+P7PqIoRL/fw2A4RDIYkaLOcokvf+m3cPuddxD6AQ5GO9BNifPzKSB8vP7WO6hFgI985FvQGYzw6pdfQRwG+MhHPoTlYobp+RjHN29iOZuAYSd3rQbZp5ve+PV1BHY+cOSPNlwP733vc4jCAFIAvU4HUnhoaqDyGzR1Y9WNOI+Ia+2cno4tn3symWAwGFivX1FQ/Sj+G3vput0utCahmePjY2itrThAHMeQghwBH/3oh/G6kWNfLBaoa4WmpjFZlAUaQ6Nrk2G1pXXR8zF9AhC+RFNrnJ2e2/Fa1zWSboJVukKWFQAk7t9/gPlsgXSVYZFlyIoSN65dxXd9+vfixrVr+Pef+yz+r//df4dv/c5P4RPf/u3wfR95fg/37j7AC8+/Dzdv3USpani+j6IosZgvMF/keHg8wTs37xGlzgA7fgcs9FI2auO9mTcruJ6Na2CycbtOztHO+kH04PV1mqaLgIQyJzL4cYxdbBxr007DEWbbGGzStssgOeccB7ivXW3jD1/H8TQRjt/u43FUsyeBj/8UcPf4cx8FoE8CJP+xbXic7fC467r2zjro2TxPgiWh+bx2DVt/BrcNmyybJ0WQngSQ1r6LdZvHve7jonP0odt+NyJGJQlcJ6FSyqpOcrH4OI6xvb1tKWL7+7vodjskFjQaYXd3FwcHBzYKwjXR3OdIkgT37t1bU0dmoQMhBBYLYgrs7u6iKAobzfA8D1tbW/A8z5S6UBY0dbtdFEWBwWBgc2w6nY6JkEl4XgDPC42YjwfyxQhUVWFsD98wERLrFM6zDJ7DwOFnGg6H5OQyB4MSBjaughzbY7QfRxZouukqURTZotr8vjjaxO1ZmpIsACy4YrDERWJHo5FVzXPtsNlsZscW29rswGbhInaCx3FsI16cvvK0xzc9QNpUY2KDd9Ojzt9xDR8eAHlOtVZcNO16NDhq1DQNVil5abvGcAFgteA5kc2NaLmLF/90qVzuS+fPoMhgaZqaePZhgDgi2V1BFwUrkAkhaH+193PqAHgBecwNgPQDz4lGKUipIYVGXVWoiwwaVPNEgWhkiwXJLy/mC1vstmkUtFIIoxCpkevlKFon6aDX7yGKSJa42+kAQqCTJEb6XCLwA9SlsknlnPgXhCHVaQlIwlJrTUn8UqLe8HKwPDF5X41UNTwT/aBoABejrasS49NTlGVpi4g1cYI8zwDzXSFowlN7akjpwfckFikBQ6IoAXlOtXrqskLg+SbcTLVQpJDI8gxJr4O0SI3cPIFOouAFCDyBP/2D/yf8rf/Lf4vSeOvrmqJIs8UKk8kCUTyHH0QWwKwZ85teXkHvsW5Ishy8YZqIGXSrDMjAu50PLX+aNkzYfDKtFRpN0UTdNETyq2t84fOfx7d/agdRN8H27j5OHj7A5WvP4G7zFqbzOQb9Hi5dOsJgOMLtW7exf3CI69duYDY/x9nkHP/+c59FbzDEweERdg/2sXuwi6NLR5TEavncygKCh/fu4s7tO5iOx1jO5uh1u9ja2cZiucRkfIb5YoFlmkHJCB94+cPYPTjCrbv3cDod4/f83k8BqsHdWzdRpUu89dqr8CWsV5+jVQKOPWqOR7zyhvfOjClooh4GgY/3Pv+8fUMaAsvVCp4I4Hsm9zCMaA50OphMJiir0shap5aawBzyTocodwICw8EAgR+gzAtIIRCHEXzpIS9KTCcznJ6eYLFcWmNAmnzAoiTAtVqukGYZqFB1hTKv4QcBedcE9YOQZv2ByRmEkWsWvqFzSVRK4+z8HFoDdU25QGEQoFINtCBJaK0VojjEweEB7t67j+Uqw+T1N/Haa69j0OviyuEhmrpClq3w2u37+P/+0v+CXreHt958E2+8/gZgnCpFU6E2tDkBAj8M4hQM/c2CHFLLrFXTghsh7PvVWtP6IA2dzZBW+dCgQrXuO3ZtYQVl55OCMkpXrMJpT7Jqnu785Ou7YEgIYTKNHjG5CTiJ9e/aG+hNem37728EzBFiMzLgAsPNL2985YLfHwFx6zdzTmv7gz5yDV+DGbFuVFvXhr0vR93a6J3Z+pxrbq6bTtTBXvXxoGfjzgYbt+DYVHraAEmPRkW4leyQ4LXHLuVCbBj/HKVkUADrDBRmwHBwRQi55uFxn4SfTWv+rrD9QHksrQP3IrBzMfgRj/nctNMIi1iVPv6O1jYCJFlpzMxTj+04j/Yk6USzXOczR3T8wMeg30fSiW1eD0faO50Otre3EIYRhABGo621+o91XWK5XFB9yyCwQCUIAuzu7mK5XBLTxbCGhsMhTk9PEUURut2uVXBzDfder4coiiyNTQhh1/Q8z9ecsf1+3xEo6GC1zCCFDwFi0XBxbyE8QDcI4ggwIGW5XNp1K4ljNHWNIEkoF1+SDSCFsLlFbF/N53MbfYnj2Nqs/H7c3HkGS2VZ2hqGDMStOJFxzHKJHLIxSEBHQKBuGvjMejCU8Lqq4BnRqzAIcTY7Q1mWGA1HBCblei2opmlQN7VTqxNkYyWUV1qVdK88IwohR8u0evqV8ZseIDGNBGhBkltQCoDlNG4uBHVNOQKc/8LnMRXFzVGJE5KQ1QL2hXV65NGtysp6DVwqlhvJcq/JoUtuswug7O9NBQlQtMfcg0FfrcgT7UlKKuawZZZlENLkRTkRIo6QzRczNE1tvSMEEGNUeYHVfGWMqtQmjgPsqaSq6tBAkoTodjoYDAZYpUtk2cp6AnqGc8qTCYr4/kkUW+DnSwk/lohjGprUv+TNqusavG5y3ldpDHzuM45ecSiYPRFMS6nrBoCG7/loVAMojdj3sZhOkYQh0tUKp2VJtZoUhbbZMGU5+OVySeppvrTekzRNURYl/IBCuKslVW0ej8cWgNCCWmE8JkEHz/eQZzn8IEBZlBDQiJMEv+PDH0SZ5zg+PYcG5Upkhcbtu8fo9EZIEhIs8LQCJMB2+UWHBuVTQBCg1E1jNlRtk9qBFpSvU+5YSEPbjVIz3UeY+0pJSetSYjI9w2/91ufx4oc/iuFoF2WtMRuf4sZ7P4AHN9/G+ekJkkqhaoA8r5BmVNCzE0W49/Y9zJcLXL1+DcUyxxtffY3oY2FoACTNz6omD1BZlJAQ6CUdFOfnePMrX0WFBu//0EtotEK+SDFfFRBhFy9+5GM4OLyMB8fHePv2LXzwd3wUUb+DB7dvQqUZvvTrvwZV5rQZm2gQjT0zB+1Ahx27Lp2OjF3qF6EBoQAhGmwPB9jb3cbkfIo0pXo5YRSim0jM5xOEYYDRcISqrkm+NY5RNzWKujI5fQEmk3NkWY7RaIjz83NUZYVslaKpSbWNPaFZmiLNcmjt4fz8nOibVYWqOge0RhTHWKQrs2lrS/uA1pS/Aw+qVgCIZisgILQg+9v2iVF2M0NAmYhU2VBNLaL/axRVDqUbhFGIwnjrFDTG03Ok+QppnkGZCHg5XeJs9qYdceLBOfxXvgqAhFoaRQ4XosKpdqALDah67T3AgMA1I5Xfj/O3Nc+1ct/xJhJ2f7SAZs0gN2CNv4I1MibQaEY3j0MTzqntndbAhcZmprhj3Kv1a+uN6379h2jRh7lya+OuG+dc0Lv9lNuv1353m+SCj3Vw4/ybDd7Nlj0mmiClWJ+LNifTzEnh/iQA4lKm18aQ01wXiGq0+y8/iRAC0tnDwdexBrsT+XOgr3b6ja5J36U2KFpAtJmDTBnTDFhaSpgQ63Ll0lDu+f5tn1+cS0QfMnOFa1upFlQZ5yD18Tp9XgjPuUcL7oQQ8GRgnZPCGLzK5O4JLQCvLY5qi7UKQzjR1F7KKxbGqQn4vkQYBvANfV5KiZ2dHRwdHWJvfwsHB/umUHhiGT2+5yOMQnimRmNRlMaGE5jPF7h37y6uXr2KokhRVQRSmFrG9kS/30dRFOj3+1gsSHafBb2ANuLBqm4MLObzua2VxnbParWydiXnHTGoOD09Rb/fX1MZ5WiL7/tYLBY2GlWWJYJ+gKYmeppuyMaRIsBw0F1jRVVVRXbMagVmF3BkhYVLpJQ2P8q1g9lpymOH7Sx2qnJKCTOmpJS2rxhIhUFkx4aUEmVBCq1kI2ukpo4clLJOawgyLoQWUJUCFCAh15Tuer0elrkpd5C1gFMIgdALMV/NLT1PKYXQDxGH5KifTCZ42uObHiANh8QVLYoCy+XSVk1nsMN0qqIorOIdg5WyLJHnOfb399Htdm1Eww2vKqUwm80gTfiWeZacNEaDMoAnWw5kuzgoG2XiScFArKWIsJJR63GSUiIw4UqKpHioeYCWJWbzuSlaWNt7xHFs84BY2YMnSRAElA8U0+RZLBa2ncvlElVRQTcKUSdGfzQw5/h2EW1zWchrxaHs7e0hmqaVom5DpO0ir7UysrxEoQvDwOQMNGg3MirwCNBWVZUlgjCwiwA0sMqp5kiWUqLggwf34QcBeqY+Dif5zedzlEWBbq9nFPMo4tPpdHDv7l0sFgscHBzgjTfewOHhAaQncHxCAPPuvTsQQmA8HmO1WhoqIo2xyWSCLMuoL73ACDCUdkFiYAjQeOj3+zY3jXNKBv0eyqrBt/zOb8X7X3wJ/+Dn/2+4//AEKiePzPn5GG+88QaeeeYGedLRbmSPunPp4HHmUkp54YQWa39rwfujtSNaI0Je4FU2n6sat956Db1eD1eeeQ4H+3uQAGaTMa4++wLizgB379xGVk5JMj3PsOp0MD47xTvvvAMlaKP+zk99igztokCepqirGqcPKXfl6pWr2Or3IUYeVOBBlRXuffkhyrrCaDCAWuZYZhnmRYWt/Ut430sfQXe0jeOzMW7evIUPfuiDuHb1Mm6//TbS6TneePUVLOYzBKDcPhhvK70p0fatM/fcfrmoH1TTALrGpcNDnJ2cwJcKy+USw+EQWlNkSWtge7SN89NzTGcz5GWBoipRWGobqI/KEk1d4+2337EGiaobq8jFa1AQBJjNF1BKGPGBxnhqQUaKoOfjOai0NlLmyiT++5SjY+Rg3aik+6x0XWUNRmXmqFbaeg7ZO8yeQikEfvnf/ao1iKqGPd/r5RPMHeyayPfeHIvml0fewdNSwzYpT5uGOj//pkHuHq75/nSQ5IJvPdn5/tjfHzHoL/Ti/0ceYv3Z3OMiI3vTi7/5Of9027wGqlxD/oLPL7reRX9zgYtFdJrplC5YIYcPK4y14LWljLmsEjqYdt9+7iqA8drpOpfoO20EkYATfeZJnyKURnBDQBgRHGq/RmMjOi1KJ7AiINcjXGtdIi98D9Q/7b/dyBUV/abnl1I+8u4Z7Eop4Jl9m5/FXgN6fRxAmCLU9GwaGoEX2P2e+yQ0ZUWkQUa9XtdGYXZ3d7G1tYXRaISmqXH12hVo42jtdLtomhpbW9soihyr1dzachy5aZoGs9UMW1tbtsQKR3Lo3TRUrLTft5QrYoOUtsRKFEUWQFBeaGbPZ4ZRYfJomHbGQgXsrGUK2mAwWBMZYDDF0ZnRaGQFvFyQRvlJFMnhnKJOpwMBoDSO736/j+l0aul0nMrAUZ7BYIDZbGbV5ZIksUpu7GDjHHBX8OD+/fsYDocWDAJYEztgm4b7i69hbYyyQl4WSJIOhBBWUIEpdNITtt85T8jSE4VvKYfL5dKCUpfFxf3O96yqyubmMhjk/uZc28flXT/u+KYHSJwEvVgsMJ1OLcrkpC5XK93lOPJLZvnDNE1tdIe/ywvCwcEBtNYINFHWtNJYzheoTVIcAMvN5PNGo5G9Dod3m6bBbDZDHMd20PHi624yWhOlyTMhUY6SVFWFNEuNlC0VLBMwNBdFIc0kDrG3QwXEIFpFEPJiwebtuB4vKozY5lt4nm8Hpi88NHVN4Uzj9dHaQ5amBGDM4kmCBAWiOLbhWsozyOF7HiAEsixDlpHiljbep6KgopFaU5i9NDWhlsuFUQzksPcCSimMx2Ocnp4CgJHdHqEocghBBQ97vR6WiyXqujL0oxASpORy585t3L17D1/84hfw4Q9/GCenJ/B9iV6vh+PjY8wN8EySBHFMlEDOydjaGmE0GlLC5vYuAj+wIXYehxy+Z24yT1bfJwWx88mE8kBmc1y9ehn/x+//Q/gf/tk/x507d6FMxGxyfgYhNEW/PGlyWB5v0LiLyRqFTtDmvUkrZY+mcsLQroEqxKNGEn/ugeS5X3v1i7R4SoHtnR1Iz8dkPMb+letI+gPcvfUOJvMpyrJAnmfme9vI8gy9XhezybndKDpJjLtnVGBWa8oXe+GFF1CsKqRVhaIo0e8PEEfkaTudzCGDEC+89FFceeY5wA9x6+4DnJ2e4sMf/SiuXTnC/Tu3kM2nuPXOWzh+cB/QCo15boOFrDHEVFUYKsumQU/ziIoVNg3RF6hCusBgOMBqvkTgAR96+UNQSuHk5AR37tzBYrFAN+kjCCKUVQkFYL5cYDafoaobo8amqXCzbCuma5t70TojPM9DWWtABKhVhapW5v3RJmUV1kRLqXTzhbSmSIQyEV2mVDLdx3nbEMZAV4pKPbPogZSSvL12XBgPqwzIow2grEoy8kyyDV/novH0buDHXX9dg9W9zkXH04IoBiKPO97NmH/SsXnu07Rp8z7uNZ50/tffvsd/fxPMuMb440CP274ngaiL/r2ZZ/Skf69Fe5w1kSM5RBNdXxPXwZBcuy6PLwBwnUZtPou0RpsbXeExTY4SrF2DDU2eg2HQSvIzE4HYHo2NirX/8TMa1424aEwAHDXb7OO1QuCCI14APF7vOYLUznnbdwI20sPL32YUbD1i1cD3aV/zPFKNZUO83+tgd3cXcRThxo0buHR0hEG/j0Y12NneQqOYoRHD8yR8n+rypOnCPmNVV4iTAPPFuTWYWwcUOf8YZHE5AlaSYwOdqWRsTHNUh+0+NqrTNEUYhlZhl5k4dV2j2+2iLEvT3sg+J99DCGGdoIvFAkEQ2GKqQghrWwJAr9cDACwW9JxsH3ZNHUxWibM57mUJT0orBMG0OAYprCrMeaxurhCr2rkOKrYxWTQLAHZ2dixd0J0XPG+4PfwMPJcYoOZFQXahYRq4gmmNapAulmsS39xWrQHpt04PplGvVivbL/z+eO6wyBEr6Lk0wDiOLfuH85Ce9hD6qXeMpzvqusZf/+t/Hf/oH/0jPHz4EJcuXcKf+BN/An/lr/yVNe/rT/zET+Dv//2/j8lkgt/5O38n/s7f+Tt48cUX7XWKosCP/diP4Z/8k3+CLMvw6U9/Gn/37/5dXLly5anawZSoe3fuIo5j3Lt3z04mRuRsfDPSZGTJxohrPPJgYy+y673lAUMFHgv7Qvn6jOgB2ITpnZ0d6z1wBQJY8hdo0T3fg2lQZVmiMJ4KKaUVgbDKLMKAPN+zHh1+DmW8vwIEGKSkArIaGnVT2vydpmkgpERd1QjCAJWh6gkh4DmRLQkBVZkilkGAyWQCrbVF8pyfxXKSWZYhNFWRldaYTiYYjUaYzecWSPmeh8lkQgUZjRCGEAK7Ozt4+OABsiyF53tI4gSLxRxFWSIwoeH79x/g+vVrePnlD+LevbtYLJbkJa8rKK2ws70N1v2fzebI8gzPPfsCfvM3fxOf//znIQRw/dp1vOfZZ7FcLhCGAcqyMB6Q0irRkGJYijAM7AKwWJAks1Yk7831ijyPoi5VVSGMAggBjMdn2NvbRxD4CENSpZGCAKMGUFY1hPTw4OEx/vm/+Bd45+ZNlGWFsqL30mgBLYyHVLcRRgCPbFz89yiKbC6VEJIoVLqliPAmTptnO174WvQ9Dy69wjWUhG7I+yl8eEGMD3zoY9i7fBVR0kfVaJwcHyP0BEJPYHxyHw/v3UGWLhH6ARJDKeO+jQy1ToCigffu34Pnebhy+Qol1BYlVKGQVxWypsGqqqCkxP7lIzzznucwGB1gmeZ46+ZtaAAf+8iHsD3o4fTBHcwnJ7hz8ybe+NpXIVQDI2tivJ2t/LKQbOxQFIQBpdvXpEyo0DQ1mlpZ8fXBoIPD/R0c7o3w+3/vp/HKK6+iY+gSOzs7eOvtt3F6fI5v+7bfjcOjS+h0u1ikK/wPv/iLmM3mSIvcOD7a+1gDUxD9rKoq1E1NdFGzIdXNeoHjdp0i8KOdd9k+h3Dkq9E61XmlcJ3VG2BaOQBqzWCGB+bicTTJjhe5Hhl6Eph53Pb0OJBx0bXWn/XxxrZ7qJaYt3bu5nV+OwHSpmH6NOe9+yGeSNN7XJvXxifWlVldY+zd3unXEz3iv7tApxUP4PZIQLeRIrckAq95dG/bCvs5U7sB6eyh7XeoqGZMHn1B12dHFIOVuiawwPVuqqrC6ekZlFI2X4btjtlsZo1wKtJOjgra/x8FxUzNYzuAnmcdINl6es6Tra1dhlLHv1vHgyS7wfd9SE+iqRtr4F++fBlKNZhMx+j1iBa2v7+P4WAAISU8D9jd3bUMlWeeecbkcmdYLmZGECCzTmGKcMwhhFm7NEXjfM+nIus+0eHZGbxcLhHHsZHGbhCF8Zo6WpbRtUejkaW4u1QwV5SLRXHKssTOzg7u3LkDALbwtsvmYSc3jzOmbz18+BC7u7vWwGf7gt8J23Nso9mC0+Z6bqoHAwxWKHULevPzhWFogo2kksz35XM8z7MiDwDW8oms2qYJAkgprbovq7+5dPtN0FGWpe2D4XCI+XxuIzssvsCqeJR77VtGkVLKRseqqkJRZjbyx3OYCqGvEIWxZVwxeOVUF+5/7l9mU7h2exRF1hHIdD/+/snJCb7v+/8gZrMZBoPBheuKXSO+0QDpM5/5DH72Z38WP//zP48XX3wRv/Ebv4E/+Sf/JH7yJ38Sf+7P/TkAwM/8zM/gM5/5DH7u534OL7zwAn7yJ38Sv/zLv4zXXnsN/X4fAPBn/+yfxb/8l/8SP/dzP4ednR386I/+KM7Pz/H5z3/+qUJkLkBKkmQtesQDmwcfL748IFxhB3cy8QB3vZz88gVACWiC6rsUeY7CRE22trfR6/ftYHDD8jwhmPPKA4U3GL6XuxFAc/J4G9pnEEXEIFr0mtpMBhPpKPLCcoN93zceXYp4lRXp6gMw0Q2JLMtNvwgoM8gYwLGiSrpaWf5pv99HmqaoygpVVSLLCtTGkCN5xRp1UxsZawJBrWdDGu8IedeiMMTCFMOUUmIyOUen00G/10UcRYgM8OJwcFVVGA6H8DwP9+/fo2hUmiHpdDAcDqB1jTzLUTeUnHh2dmbAZYJeb4Asy3F8fAxpvDJJkiCKQgwGfaxWS8xmM5ydjS1vOI4p6sgRxdVqCd6YwiCEVrAc/V6vh7IgPmwYBVCqsQtL34yLsiwgpA8BgTTL0Ol07MR+88038cv/7rP40pdfwXKVQQsJouaajV83T0XzcbnG0ISr3OJrvBF4HrWDx9e6l7qVP94cl1S4VlMpFiGhhI9n3/cSdg+vQAQJ0jyHqksEnkC/24HQCicPH+JsfIbZbAYohcAPEPg+fM+DJyQgGkg4hTNNm5qqhi6AGoDodTA6PMSV9zyH7mAAQODkwSlOxhNcOryEF557Fh5qnD24i2xxjttvv4633njDzCMNwYAIAoC0AAlQJkJH/GjL8UdroFKbGoog1aQqFvoBdnYG+NDLH8C3f+J34f/z//p/4+TkBKPRCN/2bd+G27dv4+Mf/zjCMEEcJzg5O0MUR5C+j5//+Z/DZDKl+j6GukbKiGR0aUMhquoKnqTIK1HejOIgWgeO0srW8QGwNka0dgDAhtG6FiUT65SrNdDFIEI4X3ZPfMyoFJryirj/NiMTX+9x0Tmb13S/8zTAhLDdu3/vaQHIRcDg3eiaX+89vp7j8aAUawDpUQrk46/nAqTN6M/jIl7uXvhubXxSP7h7srDzVBBQN/OaRuymqIVDzVv/hNgQ0FCNe006p40m8WewUVuAo9BcU8y9H33G0SK2Mdhrz9/hdZdBEF2T80GF3fO578IohFK100aTGM+J7c56xVQvgEQPpEfRjMPDS8aAbbC1tYXd3V10uySqJITE9vYWOp2uoYSHSNNWORMAprMZ4ihClqfwPQ9BGBpwQGUKiryA7+Rtc8Si3+/j3r27tk4YO31938fDhw9RVRX29vahNdVKjMKQyq54Hu7ffwBoWAobOSopCsPqb9oACaaX8efcFxw1YXlp2vvJLmEhBXaAM/jhaAQb/ryvMuDgtAa2EW0NHqPsxiIJLuBy1WaZ6sc1h+bz+SMUTs+8Qxbi4fu6jnRuL9uJeZ5bG9tN6+BnlVJadpVbLJbpfQyA2P7jZ+Oi4Ryt4uepSqqdl2WZtXWsom5dWNDFTAgWRasrZcW92DHPeeccsHCDEFq3lEi+Fke4lFJWoKHT6WC5XOLTv/+7fnsA0vd8z/fg4OAA/+Af/AP7t+///u9Hp9PBL/zCL0BrjaOjI/zIj/wIfvzHfxwARXIODg7wMz/zM/ihH/ohzGYz7O3t4Rd+4Rfwh//wHwYA3L9/H1evXsW/+lf/Cr/v9/2+d20HA6T7d+9ZlY26rnH79m1Lmdvb20MURTapn/NF0jS1UR9GpBxBkg6tjV8268s3dQ3P86G1QhzFiOIIvW4XwvNItcNEg1xwxIuFJyUqZyC4Gwd/Zy1q5ZzbgiOQmlxdIgwC1HVlIxdCkAJdWZWIQooiLBYLQu+SABBHN87PJ2hUg9VySVGkskRdkGLbZDqF59E1Z7O58aDT4pskCZ599lmcnZ2ZGkUCaZqZQUjgzc2r4tpSu3t7NmeiriuUZWW4tDT48zy3k3W1XCDwfeRFQX1mDPyyLOEHpgZLlmM6nVBhzV4PvieRdCK7GFC/0QJXlBWSpGcXwAcPHuDSpSN4nkSSxGga8jpNJhMsFktIKUwdJ9oMkyTBtavXLJWQomrGU2qMWwZRAMymKKyXJ0kSszkKeIZOMJ/N0OuR90drjdl0iqpp8KXfegX/8//6y5itUjRaomqMj181jyhdtRv+uqHIHicAaCplFx9XGMSTnqVlbXrfAQkp/Qv+Dmh2NAgFKTQaDSgR4tLVZ3D12feibKgYZl01gKYFuNPtwPMEsjTFYjbHfDrFcr5AkZJqohSNNSSAtuhwp9NFd2cP2/sH6G3tIOn0UOY1pqcTHD88QTxM8Ozzz2NnewurxQwP7rwNUWT46pe/gPPThxzPQGsOmg7UTAGDyQUgZ4MUTB99NJLwKEDykSQBLh8d4Px8gjwrTGSWx79Ap9MlR0Jd052lQFGZ37WGbtoX6ubxeZ5Hif/GJewahhoawmvf29o70jDZC9z29bHytDY4OYMoqqRFG11yPesAG8zumY7RDawBt//U4yIA9I0ESP9btPFJxzcCID39NdYjSF9PGy/qY/ezi/p9E4A9Da3ucffnCA/9dCKZTg7RJhBaB1aPAjIWYOHrrtGUnWdxo1jrY2/9Pm79Hfbmu3YBgaPa0tM9y0AQgBCWoj0cDs01lSlKOsBw2LdiUDs7O/a6165dgzZ5vd1ux+bReL6POIlshGi0NUKSJFbEKc9zzBdzjEYjLJfLNdrSaNSH5wkrolIaYSPf87FYLJEkVJKAoxqc3w2lkaYZwrDNdR4OR5hOJ6jrCsPRELPZzDprpfTQNApJ3EFpCjkfHx8jCAJcuXIFSincvXsb/X4fg8HAvkvOpVGKCocOBgMrTsBAhKnubNcJIWzNIJcFxG1nKhmDUwZATCljtTv+LM9zC0gYRHGfMFBiAODmKS+XS8znc+zt7a2NKY6U9Pt9Etwy48h1rvPzc3FxlvpmYOCmkfC+vzm/+DlZcY/7wiqiGqDiRtcY7C4WlPrA4KYsWuDP4Ir7rCxzRHFk28+5UJ70kGWFVQTkZ8tNegX3u9ba9h23k6NmLAvOkS/Ou+92u5hOp/je//r7ngogfcNzkL79278df+/v/T28/vrreOGFF/ClL30Jv/Irv4K/9bf+FgDgnXfewcOHD/Hd3/3d9pwoivDJT34Sn/vc5/BDP/RD+PznP4+qqta+c3R0hJdeegmf+9znLgRInCzHx3w+BwDjAebwm8DhpUPkWYaqLFHVNaqqhFaK8lRAeQajrRGlcypFIWOHPqC1Rq/bgZRtJElKAd1QLaLxeIzPfe7X8Mwz78GlS4eIwwBCkWJZmWeQTONriPvfNBUAAe15lDApJcoiR9OQUpk7ODjMm2U5umaylWUBKjzWIIpiKN1gMaUCkVxUjPqF5HensxmkJB35KIqxXC6xt7uL88k58iJDWZB0Y1EWSGIy3gW0LdnRhlEDNFWN4c4OwijEKk0x6Pdx/PAYURThyuUrdhMoyhKxGeiNUuiYJMGqrgFojM9OkKUZTYg4QrpaIEuXGG2NMJ1MUVYViiIzwgIKWbZCmqbYGo1QNxWkEtBQOD15aL0fWmkURQatGgRhgG43RrdDfaaUQhgEUE2DChWapkIYxrh//wFNSNXg4clD+L6HKI6Q54VJrFdYrXIDnhIslwsICNy/fx++76HfHyCKIzSqQVXWKIsCjVIYn51RzYV+H51OAoCSNrvdrg3vp2kK35PI0hVGW0OslktEYYiqKFFVBRqt8LGPfgiHh4f4N//2V/DOzXtYpSVRwqBJahimros1BDii2C5+LrBnsAGs0/Eaw0dnI1cpbUEweSLdBdUBYix1DJPDpDWkVLh/+x1MZjO8+MEPoxP3UEcA4CEvS5xOFvCkQBSF2Dm8gqOrz0BoQzUtCjRG4c3zPPiBD894ssI4RhNEUBqYTue4e+8mVpMltrpDfPADH8TwcISmqXDrrTdwfO82pqcPcHbvNlSVwwN7Y02zwREkCQhln4tsEmkAEhtcDvvMHmwk0c9GK+RFgTfffgeABERrDEETGJqnnBjcQJgIL707A7LZwBPreWZNXUFTiA5ar1eDpy8YmW4Divi9ta2/+HBzzlyjddOwN0181OHu0Hjp+8o5rzWMydAjz/vTwaNHkP+jx4Zhq7EJAA2gM21vZb+fdM2Lfl/vRY7arf8Nj/aNGUetdLNwBhI/gmNUb8xZvrd7Co9HMuA3ruN8kdrDamLtcwvnM63bvz0ZIAnzOoRr+ZvuN2uNkFSGATS2aTwoa+SzUdNedx00tREd0ebO2ad3OtcBO1rDOh60NnMDPN48uEI2biFRVknjOcQKcfY9aEWCCvaltqUGWJSonYMkJtQ0tQEmLXByj5aqRcVIgyC0tO0rV65ie3sLgILnUxTl6OgIOzs7WC6X6Pf7tC9EEXq9HvIit0AImnaBbrdrc5waRTnNnThB6Ae20DOrrjZNhdWyhB/6SOIYVVmgrmj/73Q7qMrSfGdBRUrTDGmWUoTflzg7O4Xn+1AmmtLtduFJgdFwiCRJ0CiFssjBdRrJidwQVbwsMRiQuBFRqLrY2hpBCIF7d++j1+uh2+2aNbPC+fnEAIoYV69eBSAwn8/R6SS4ceMGmqaxggJnZ2cAyLHKOTrsIHejK1tbW5aSxqDFNaZZ4nsymdgoB+cU8fX5O/P53BroaZra+nNkr7W5Q1pTNI3zrznSx8CTHZgsLAbAyn5zzTs+b293F1q3+TcALN2tKArbfxz5YYc0t53BBwNFBj1EXaRcq52dHcznc3suK/HxNQFY6iKDULYp3MKwHPXUzoIpPUqTaJRhbNAUpVpPghSY84L+GEYR4jhCUZZ2uddao6orQJC8NzRsYVzebzmq1TQkysE5/097fMMB0o//+I9jNpvhfe97nzWQP/OZz+CP/tE/CgB4+PAhAODg4GDtvIODA9y6dct+JwxDbG1tPfIdPn/z+Omf/mn8xE/8xCN/r+sKjaKJMZ/PcXJyQiE8I/lIFKwh+r0eGY2eB8WRDq6jYCQwq6qEx7kkhjfpFlOsqxK9fgef+vR3Yjab4dbtd7C3t4/RaIiqIjDGOTmWFicplJ8XbWFQnjSrLIeEwGq1In5oFCGJYyzmc6wEkKYrsHIKQCHuwA+MKIGwYWPfcHhn0xnm86WNnLFKSmkiNKEXojPo4OjwyE4kIQRWqyXKsrDRF6bZdXsDrFYrhGGEOIzR1Aqz2ZyUYbICQmgEIYVg33nnTRu1qwcD2nSM96soqOZSUaRomhJa1xBC4nx8ivPzc/LAQEKr2hjsDXq9DsqqQBgGVs0EqoEnSCUsjhP4PoWUo8BHFLTylgxIet0eyrxE4Es0VYmt4RYmkwlOymNA0LMEKYXz07KAJwUCnyI/CwPA8yy31Mq93T34no+T8Sn6/QEmkyka1SBOEqQp1T7a29sFA3YGvrxo0iYdojaLK+UjaYy2tjGdnSEMBW5cO8L3f9/34JUvv4bPfvbXMJ3OUUmJ2hjYUpgaLfZY36CZ/xv4ARq09EyX0imlMKDB0GaMfUGHhhDrqopM7aRPmQomrSEl0SBfTPCbv/rvcO09z+LGe56HH4cIoxBxohCG5Hkan0/Jq+UHCMIAURgjSqhOEIQg50FdYZlVSM/HKPMSTVUhTjrY293D+9/3AfQ6PeRZipMHd5EtFzi+ewu33vwa8tUMUtemfziaY9qtSXxCSpOnw8Ya1mlDhG4cW1m7BRMBzzdABwpFTe/D8wQEGmgQaKcBvLFINWxItsZZwwBuo86NBtbOJwU6BlMmf4qNY/sc5t1bg/ICT78zTHj82PNtnRVtbGQ+vzXOqZ/aJG8CI+tAi/tcrRm5jz9ao9n98mNOctt/oWCDcOz7iyNIbjSAkMxmtJDH+KP3deDlY9pnMtycd+W2eQ3obrRLOuphm1Q2rRp7HY5wtO19nB4d7NzUPKbtNYWZEpyX2L5XAQ9BEFmKDNNrmHINwDItqqpCA2OQavYiE5iS7dKw9iyKDSUICEhIEbQdzA4acJ5NW9xAgyO8LMTwKMBjJ4GU7XvWWtuaehASSsNQcngMS7M+tiCKCnJSVDkMI1R1bq4p4XkCgQ4Qxa3Xu6kbdLpdbG9vo5MkkJ6H3d0d7O0Osbe3g6OjI3iebxkyLFMdxzEWi4U1RpkSnsQ+hsMhRV88gSxdkq2wogjP3t6eNaB5X6wNeCmr0qrxBlEAXVK0mxocTqwAAQAASURBVGn/q+XSGurKGJRlUaKuKvieh+lkgu1tEngq8xp7OwfWVsnyHFVZosxrFLqGakxkAVS/BlqYeomFpcKdn49Nkj9Fku7evYswDLG/v2+jVU1DdD+mbRGglAYcEcNjMNix++hqtbKOP2aWuFEVrbUVxWIDn6NcDI4YILCBzwCk1+uBmTIMjsqytHLSHJ1iga3VamXZL0II45Rux0an08H5+bkFFFwTiW1KphqmabqmGEf7t2+d5kzfYwDIezoDOs7h5rwc/j2O4zVAwe1nVV22k1jIzK2RxLLnbh1FZnporW39o04i1sAbt9mTHuarOaAFATkIVFWDPCvQ1Aph5CMIDT2uLNCoNh3GD8iuo/HgIc9TBAHNU24Tr1FpmrbRS7PGLJaLx62KjxzfcID0T//pP8U//If/EP/4H/9jvPjii/jiF7+IH/mRH8HR0RF+8Ad/0H5v07NyUYh783jSd/7yX/7L+PN//s/b3+fzOa5evWonsFJUgKvf7xujTRjp7Wbde940EL5nJZo59J3nOZaLJQZmkhRFYcOxSin4noQnBKaTKUajEVaLJT77K78C3/Px8W/5OLZGW5ZXGicxqrJEr9fHYrnAeHyGe3fvwvN89HpdBEGIhw8fQigypKfTKYbDoU3EU0qh36NJ3ul0LEKOogie8S4ppSyfloFmukrh+x5u3LgO3/dQ1w2SJLYLA3FJVyjLnOh4ZuPTmiQ43QWIvVA8AZmnyyid9PC7UIrA1N7eHn7lV37FemKUUnay8MLF3h2mCcRxjK2tLes9S5IEk8m5pZ+5i+1qtcJwOLSJrgSk1FpYuKoqG8rlxaLb7aJsapRVhdVqhdVqhf2DPaxWcwghMZlMMRwOkCQdSwlg3nJRuNTMEHfu3MVoNILnSSyXcwyGfbPIRYiiy/A8aQCyQFHkAGjR3NnZRpJ0TK6WZ6mP3W4Xd+7cMcn4DbK0MEIRAT784Rdx6dI+vvDFL+HV11/DbF6Qwa4puVZzfhL0miEmhLALuoRnx7ybvLlJOblorl70d2DTx+78XRFd7eabr+H+vbt45tnncXh0Bb7wIBqJwz1K6s2zDGmWIcsyTJcLNA3QKPKAK1CYP0pi7O6MEPWGFHUMfVRlgSxd4a1bd9DkOZrFFJOzE7zz1ptoqgK+oLpPwnDgiRYAAMa7boxhN0F17ZnZveX0I/Os29ohraFn6XdODhdH4B53rHuvH/+9i/p98525zpYnnX/RfVwD8klUsM1z3ee+6Htrxuq7rPX/KcdFVKmv/3scKvs6Dg0ATu0aB2DzeGmh1KMUROmc50bOpGyTnDcBEoMNl2LWvrcn5w9d/HgUufF9H7Gh/5RlCQ2NIIjg+4GNQvD4d8caO+zaXF4B6fmQpo0G4hjFQydqpNvaN1JKU4eubT+NLWX2njYPcv15eL3CI/3Oc567WKkGa7k97MlHBSGFzaGpqhrDXh9RFGLbCPwEQYid7W3MFwscHe3j8uWjtXyM3b1dVBUZdOOzM3JIxjGKPEfP0P2LbGXYH7RHHR4eANDWMGfDuyxLnJ+f22hHWZZ48OABer0emqaG1j7CMEAc71ilMwYTe3t7tgAo77MsV822g+/7VHxatApko9GIas05+TfL5RJXr15FFEU4Pz+3hj/loyzhez4QwEYIWfWXAfNyubSREc/zEMexfT7e6zlCwcDAzfNpc4f0mnBBr9dDmqY2f8jNucmyzOYGcdoE1zXiwtxMV2SFNQYrXM9Ha43d3V0LtLgMCstKu/k/vLdyhIqpZvz8XNOIo20sNsGCD5zHPZ/PbUkWfpfL5dLKonMf+7JVeev1evbaDILCMLRy3oPBANPpFEopm0fNYIyDBxwB4jEIwAIldoAwsOO6TDx+OTefKXAATO51bfuBaYVsj+/s7Fhbmu2Pfr8PDY1OJ7brCM9/nsdZltk8MhY9Y9DI+zbblpzOwdGroijQSX4bI0h/4S/8Bfylv/SX8Ef+yB8BALz88su4desWfvqnfxo/+IM/iMPDQwCwCnd8nJyc2KjS4eEhyrLEZDJZiyKdnJzgE5/4xIX3ZaN18yizDLVB8Fq3dTxUva7uwkVht7a3oAqFpq5RZDTJoUmi9v69O3gnL/Ge97wHDx48wO7uLubzOQGSukK6WCLNUmRpiulkgmeu38Crr74KVTeoqwpaNVjMZzg9ObYJ+KvVCp1OB7s7u5hMJrhz+w5WqxWuX78OKPJ27O/vU3VgsxHNZjOMhn0bKlwazw/r+XNC3Wg0wtnZmQUcL730EoqiwMOHD+2iw/SA4ZC4mCwvypQyKYX1INR1jePjY2RZhmeffdZya3lB4oUCAIbDAcbjM1R1YfnBH/jAB/Daa69BSomDgwML5LTW1lPCCYAMZBg8sacjimJr1LN0Z5ZlmEwmCKRnJyIv7lxjgOUyefKz5r4f+PAAzGfnUErD8wJkaWYWagJ8tDimNrTu++QtGg5HtqYAq7gAwPb2Nooiw3A4somdUkpMp1PTfoUoSiAEcH5+bnjWBFLyLIfWwHy+wGw2N3lgAmdnp+j1+tgxEu0UwQvw8Y+/jKs3LuPhwxN88UuvYLHKUFWaIjkQgGjWDFKXshmHiX0mXuD4O64xBjxqVG8az27o3P2dvmcoQUpDSg91usTXfusLePv1r2G0vQ0vSDAYbqPf79k+jD2KPmZ5hcATULqBFkAvDnB0dADpB1g1wGR8gny1RFNmCIRGtpzj4d3bmNy7jaauIJSGxxENKa3ZyeMe1mBqawS5Xnj7nGgNShfM81gE9CN9tNYv38DjSdfcfG//MQcbS08CRo8DzY/7m+uE4p+b93ya48Lo17u07UnH465BEZ/2Myndd7t5Dffcx1wPj4oyXATQLm67gBAeuO7a5rksP890NgL/8pF2XnRsjllSavQBTaqdfH++Pu8x7rtkQ8RdN9wokysuAK3h+YE1kjbXnbYx61RPN8LWOjfaZ+C56nkSvudGnQAZGM+zKWdR15R32ul0bG5rGAbY3tnCwcEB+oMBBv0+9vf3UVUVtre3oTXlfrh0raZp4AfCGrJRRNGGxWKJwJcAahwd7SNJYkMlaxBFEnXdYLlY2j2d83u4lg0bkp1OB4eHh7hy5QrSNLX0Od4XWWWNPfvn5+c4ODiwBqPneej3++j1epjP5yiKAru7uxgOhwBagZ4wDG1eC7MZ5vM5Tk9PceXKFWtDcFtZNZcjMJbSZ0Ax5+1MJhMb0RoMBmvveTKZoNPprO39DJ5YoIglmdn52+/3rQHP+4SbZ8RjkRXoOBLDtC+uhRkEgQVgDObG47FVGuTIXRAEFiTFcWyZTZwDw20uisICNQaUDBI4Ytfr9ayyHAMCpv/dv38fgVEA5hwaFlTyfd86dpn9IYRAnmWk7mdyraqqsmp1SikMh0MLXjjawuIMAGyUi+0hpuO5thbbSfwuNsVEeE66Yg+c98N2m+d52N7etnsls5DSNLXgBSD7fTweO/nGrQorO7N5neFoHgcx+F0BAmVRmbw2ytFbrVZ2LSqKwlLunvb4hgMkfnD3YG8TADzzzDM4PDzEL/3SL+EjH/kIAMqL+Lf/9t/iZ37mZwAAH/vYxxAEAX7pl34JP/ADPwAAePDgAV555RX8jb/xN76u9hRZjrkGApOwyJ6HpqqhlcJ0NsWgP6BQpfRQ5jlqVWE8HlvvAR9Hh4d4+51bOD09RVmWmE6nODk5wdWrV+ELykUJfB+L2RyXjo4Q+AG6SQe33nkHl69cwv7+ASooBL5Er9uh6FXTIPB8xGGEwPNx6fAQywUl03E+TdM0WCwWNuxaFDmUqi0w4gWyKAqrw8+LA8tNMkgCNPb3d6E1cHZ2agZ9Ca2V4eNSgbumqSElEAQhalOYEiDjnycub+jdbtcurpx0GIYRDg4O0KgaWZZiuVziYx//OOI4xnQ6te1yAQ0nj3IYn41QBmK0yFHkhYuesfekqiocP3iA5ckSly9ftgWCeXF1w8iujHqjFFSjABDn9dbN27h67TI8j+5V1xmJFgRc6DdAHJMntdNJEIYhojCxC0XgR6irBqPRNrIsNZ6ciBT4+gMURYnAD9FoBU962N7aRZ6VmM/PkKYrs7H5JE+qGhQ5AUzVSEynC6xWKaQUWCzmODw8QByH6HcS9J99BkeHR3h4fIY33nwHp2cT5GWJRkiopn4EzKimLc7GC4gbRb3ImGMPsAsG1qIjNm/n0WKLWisIaDS1ET2ARJ0rjB9maLSHE59kvA8PD3H58mWifQgBeKS0lJt8rmxxjrs3UwKaCJAtlxifHmN2foYyWyBfLUi6W1QQWkNqoDG5UcIWY2wNacqvUmuR5IvUxQhyttEZ12tOm0htv/8kcLRpkG724+bvT3NsgoL/1AjN5n0fF9ly2/j13O9J7bvoudvfHx8N47XRjdhtfse990X3d6OnsPENjki0Y8IFS5ugj6Mmm22n2wnn348+R/ssJO/cOvAIELhxJftdC/D5Op69l4B0ADNL0oMKCEuB9YQprnFD67/BMtwz4EKr7vh0+5mdQGxws+eXDNza7EutF5hqv7Fjhp9hvayAK1bkrjP0LHTfMArR77UKsYDGoN/D9evXAADPvudZ+AHt/aPREFVdoiiIyfHMMzfg+wEmk3PEUQQ/IJpSXZHXOwgDbG9vY7FYQiuFxXwKP6Ck98APQLLUCrs721gsFjg5fmgMwhGausZyuUJTV7hz+wTbO9sYDCh6EUcRyiK0463X69ln3dvbQ6/Xs5QqorCHtqbPbDajCJSj3sUqsfzfxJTOYKYA2z0Mptiu6Pf72N7etuBob28P5+fnlD/UUD2i27dvo9vtYmdnZ82OYPYFR5c4OiWEsDVnrl69ulbDxy2VwgCF9584jh8RTuAoUF3X2N/ft6CD82dchyeDKqYLMvWMgZzneTg4OLDGPEd0ut2ujYTxd3ms7e7uWpnruq6xvb1tbRXf97G1tWXH5mKxsCptDEh5b+D32O/3cXZ2hk6nYw13t/QGzyUGGu7aykCN5olC1O9DG9vGsofMXGHQx0CewRWPj6qqrO3I843zoABYWh1T09gZzZFNdtDyOGVw5AI5zsOrmwZVWdk9k/uT+43tMc/zLOOLIoKlfYfsLGc7hYEbR8x4LKlGWec1O19Co3jI84QFJZ72+IYDpO/93u/FZz7zGVy7dg0vvvgivvCFL+C/+W/+G/ypP/WnANDL/pEf+RH81E/9FJ5//nk8//zz+Kmf+il0Oh38sT/2xwAAw+EQf/pP/2n86I/+KHZ2drC9vY0f+7Efw8svv4zv+q7v+rrac+vmLXi+B2VQZ5wk6HV7qIx04mKxQLaVYX9/H+lqhZs330YQ0SD62mtfw5UrV7CzQ+Hr1YpC0+PxGFevXsVXvvIVzOdzPPPMM8hXqZWw3NnZwT//Z/8MV65cwUsvvoj9/V1keYrx+JQmy5IW326na+vx8AK5OCP559jUEWI+Mqt10MZDmxvnEPFCwGFrXsh4wnCUgBZSibqpIUDt5GiN1pQYKhqNpjEJexEtGkkSo6oa9Pt9vOc978FkMiFZZrS6+oPBwC5WpPJXoCwL+EErBHDn9m3s7+9b4MIJh+xJAmCL5AJEk2yaxikgpu0kZa+bVYDxfTz37HNrWv2s65+mqX1+XgTZa5VmGU7HE8xnK3gywGw2Q3/aw9bWAFFINLoiL2zxOiBDnkeQUuD0tLGTLs8Lu9lrrdHpJCirCp6UZsx1DTecaARUL8OzNItOp4M0zQBocIJvVZUASAmwqhrjIYoBENf21q17xA+XHiAkpOdjONrB+55/DsP+MRarFZZlgYVRr+HwNC8Qbc2NtvgxL6ibHmKgVb7h3BsGU7whbXrP2dujNaenU84DGWANhFKAlhBaQakaWgjcu/kWju/eMptpiDjpIIyIhiADHxpAaepE6LJBkWVoqgpCN4Bu4HsSummgfEALwdk01CDBYgfCtK02AggAU57cxfOiKAlvAK3H2jMUqMYahe53L1qMLwJDFx0XetYf07Z3+/vjjqcBYk/6/KIoyEXnbBrWLiBwc4bWI4+banTr7+ZikE7HppPuovOe+ExiPYLEf6dxzr8TiHDzdDa76nHt2KTYtXk+gJCeMz4EhPvc9lwjoHJBNEsIqtmlFJz2apPLBCihANu/rSgC328TiLpgyPOE0w/rfc5GiUvRoT7wUNccWVo3Oaj/OMeqWXs2oN1feK7ROQ08X+O5557Ff/U934MbN24QQAoCVFWNyGuT6MfjM8RxjP39AwgJCE/g+PihyQ9JTSSGSx9oBEYsaXdnG8vlkoQKTO5OXZXI0xQw7AvP8+BJibqsMJ1MEfg+yqJEkVIOUBSEkJ6H/d09UtkSFXStMFvNEMaxWfNTS2967rnnKH/X1Aucz+fWGclGJfctr9UseDEej5HnOQ4ODjCbzSxFjIGDlNJGoZhNoZTCbDZDnueoqgrz+dzSrbQmteF79+4Z2riH8Xhsk//Z5mCaO3vsmdblylLzPrFcLnF4eGiNYGZ5cDSJaYD8TKy+xn3B1DR2HvP84v3LzX/Ruq3FyMY+G9ur1QplWWJ/f9+CJb4vG/HcbxydAigaxFS1nZ0dTKdTa5dwqkOv1yORK1MP6/z83NIv3XpDHH1zy3lwVGo0Ghm7cEaCGZ0OoihaU2bjsitMc2P2Dc9JjgINBgNrYzE45H2c5yvT97gPeN/m9grR5hFxDhQ7rdn+4fvzWGOqZxSGNpdXa23pjd1uF57n2XIn7r2VaiyQZvU9dpjwfbjgLgBLuaxUtUaNd7/HUTsA9rynOb7hAOlv/+2/jb/6V/8qfviHfxgnJyc4OjrCD/3QD+Gv/bW/Zr/zF//iX0SWZfjhH/5hWyj2X//rf70WAvzZn/1Z+L6PH/iBH7CFYn/u537ukdyAdzvm0yniOCZwFEbQdQMoheVigdl0Sh6aIEDW66Gpa4RBgCjysTUa4Hy8g14ngS8Fbr79FrTwEEYJZrMZ5vM5ZrMZTk9PzUtPcPONMba2tvD6117D7/j4t+ArX/kK7t29h1W6QKcTASCwsTUiD0tdlRBCod/r0WRTCsfHx9jb20OSJDg8PMR8PrchyoODAywWC8MlbazKCNAWR2PQxN6MlalTxNGjRtWghHSBpqkhpEZiag6UZYlev2sXY4AGX1EW6Hb6Vu6aQ5us2HN+fm6rFTM3+cGDByjLHAeHexb88aLM0SAOM7PRyd9hyhovkKwKQ96teK1i9WKxQF3XWC2XUDUZ61tbWzYkzlKZy+WSnsXxgAEksnA+PoeAj/5oBK2B44cnkBKIogB1rUwUjTyCBEKX1ltFnoncLMy5meAaWVoiM6o40BMIw/kVQltJSu5foK0Hwt4uAMiLwhTwBKqKpJ7rmjwlyiT8N3WNQArESYyDS9u4dLCP0dYWqrrCw9Mz3Ds9xypNcXJyAiEEbt682XrZFdYWTKCtN+Qaumu1wUSr6MhHy/HnQqsXGNRCAvBAEgltMrrWiuh3GvAEebibsoKqBKpcIl0u0Jg2NZo836zUJ7UyggkakAJKA4VuIDxAGPUpotGxepjxwut1TjNEC/4eB2yEUayygM8xDuu63Shc2oA99zEg6SKA9LjIx/8/j3e7z0VtelIk5uu55rqxDXB08lGgJR7ps80IxpNA6UXtv+iz9h6uduf6QYCIo621cYyYmjgbAONJ73YTjLP4BY9J+/cLaHs2KuS00XVosMPCFV+hnwRI3u3ZL/qc6dd8Dx7nlM9jwJy5RhiFaGuptY6Fi/rk0TY+Cqbd36M4wie/81vw6U9/CnESY7GYGHlqBSjAT8jxOBh0oZoKRVlgNj3H7v4ubt+7g6ossb+/h/5ggAcPHlCU3w8ArdFJyFO+WiwxXywACKiGov2BH6DyiB0hhMR0OoMnPSxkikGX6NQIPJRFAykk8oJylKtSQTUCi3lqx2jckda5ycXV7969a3NxeB/liA8Dg+3tbcsYYYOe81eYXsXRhLqucXJyYg13pRTu379vJZin06ml+fPey0Ys5+MwEGPDlvO4p9MpJpOJtS1ms5k18l0wG5paSGwQn56eomkaK3xwcHBgPfzn5+dgZysDCldCm4EcO+QYWHA/8RrO0QZ+Po4ysJDBaDSyeUt8cE4WACwWC8RxbMWvuK+Z/j8YDGzeNbNgOKpCEuWBtcXctA8e/wyK+L5VVeHg4MD2Y1mWFkQx5Y6B6NrzV5WN9rHjl3OueJ6ywhzR+yM7j9xcID74XTKFksU+2CHIYMyNFgOwZXKEIKobO+SFEFitUjuWOF+bHdtuDUb+nfu7UbWJCMMqMfMawuPT3bNp/WxtER47PG+YAsrCE097fMPrIP3ncnAdpF/6F/8jGYxVBa204e0GGBt62XJFyV6NpkUNAMqqLXbFtLWyLMlLH0Y4Oxtbzfbbt2/jwx/+MJ5/9lncufkOJfovlrh58yaiKMJHP/pREBe6tpsI5ztxYdM8b6MjX/7yl/He974XdV2T+tlqhUuXLmG1StHpElho6hrSI48Ze0sA2HZ2OnFrCADwpESWZ1CNQhS1SZO+H5gCXzRwqWAsSXi7CXVBECIM2iJcQkgzAEs0SiOKI/T7A1QV0Rco5BqirkvUdbnGFeXQqO8HOD4+saIO/V6fwGoUrtU2Yq7sfD5HU9fw/ZaHyovo6ekpZtMZmrqxNLjDQ1LYuXfvPqIoRBhTKDuJY5pIZsKMx+c4P5thtcowGm3hi1/6ErRWJJYRBkjiBMrxyNQVFfAsS6JKNKqBNLUqtAbKokCtgCwrANGG7AUERe6M/eEaar7nwfcDAqyC1NpU00DpFkwFZlMuy9pM8gxlWaOuKoqcBCQeAUmLaVmVaJRCpQTqpqWtaK2ce3NujbCLOoMht31uXsFawUQzvlTDIgVG+taZh3bxElyPxAgVuMYiDG3JMZLpXGNyGuAE0SbOk1fKUN0EgSO4NCZzL62NXIWAvTcDJKYEQoCSt4WJcrFbnkMEgu7HUSKltQWuFB0jj7ybJ8GfbR7rxuH633mRp3s6wsZaO8px1JbHy5O599wQR9btvyW9sLYR4tGzbFvWHwCc28GniUeuJdabItyWtL9bIKABV676YoDkXBdOPxoqGiUTk4dU2LGkaYwLae/uKvIxXYu708pBU5YatJa2rZSTyTcEPI+UmLTWZl7THK+axgzv9XwawZNlrSvdl8g1cniT5/YA2uQTcXtt1AoCEiw17dnP4phq8GXpCnVN4igt4mr7TEqBumlMTp5nvqJb+Wt+r/adKPi+hygKbQ6r7wcYDAcoixIHB/s4ODhEHEfY2trCtWvXMJ3O8Morr+Ff/+v/2VkL3aEh4Kr0Ub+Z4qsQVCAZCkLQPLty5TK+7/v+K3zwQy9gla6sw2Iw6BMVrtE43D/E+fnYXreuKpRVhcFwQDLVYWApOUFI+Sm60YAmcYbFYoHK0IbqusZiscDBwQHCIMDZeGzycSuKEgiJbo+En+q6QRRHWC1XCMMAGkBkPPOVKVtQGGNyMOxBSIkHDx5YWpabT8RCACxQxAwNZoewwQ7AGoDS8wDH2eh5HmYmKrRZTJQZFJwoz2wVVmPTus0NcnOiOP+HAQm3gT38HD1ggMeMDyEon/fk5BTT6RSHh4fWMOY8Yq6HyYCt2+3i5OSE2uV76HS7RmLct8/COUhVXaMyIgyc/0T5csIa5d1OF0VZ2HHY6SQWdLCoAgBr83EaAEdRVmmKjqlb6IIdu14JYWsNsVObHdScp+ZGZDg3ajweY3d3F3merykXCiFI/ELD0u2jOLKgUNUNqSCbfq+rmlRzHcqZLc9hxklVlhBSWLDCNExuY11RLc/haGgBUhRFWC2X6PX6SDNKofGkZ2pqhtAaqBsa33Eco24axFEMz/dQla2SMoMazt/jqBH3CY8hrTXKiuohNapBr9slnYCqRlmVaw513gtpHGgUhskDwN7DpftGUYSyKvGp7/70b08dpP/cjk63B2iBplY4PT3F6ekZdra34ElgPqdIDITGKlshjiMEfgBPeKhLWoy6CSHQVbFCGCfwPB+DwcB6EyaTCQAScegO+4iSGHmRo6orbG9vodcjz0cc9yzSp4N43Z7nIwjIsJ9OJ6iqEt0uhVQpITJCVZXIshWCwANMTYk0TTHJc5uvUxSFNWLn8xnCKLADkCdBEPgoshxQGlFAk6Nnwr9akZc9NlGRbtKxoevVagVPguSwmxoQAlpVqMocGgJN7aGuSlCtC6rJVBYFOp0Iua7hxzGCMLAeRRgDM4kSCC0gIZGlGZq6gQiAXtJFmmWAAhYzipjdvn0bAHB0dAgBqv80m80RBOR1qWtWJRKoa4WHD0+sJ2s6nWOVpYiT2AhTeBifndECqgWq3MjRNgqqrrG1NcLO7i7Oz89xfk7KL3meI4pjeFIi6SS4dHgZ29tbiJMYR0eX0e10IMzmUCuNKO5aLnBZlpjP57h79y6+9MqXKUpiE1tru2C2lbm18W4ZoABAgcAJGwQWnBjvjqgbIC9pg+Q+BkdNXMNyowCs+XfdNFRS0aFFuOCoNWDaZEkbBZCwn1nD197PGL/KNXoBGIqR1jCAw/GeO8Ycm+r2ilrbXiHsIin6ZK9rnsrIY5Px11IKlFLQipXnhDXE3D5qawe5NLCG6jUwcDEe9EZRRIye5WJa2eZB/cmP2YKR9nTTHnv+OqDEY67LxvvGX9prrtG4pH3WCxpoTtaP3MuNRLTvv+3fNrJD13YjRO41hPPsLt57NAL0LhE1A2zLqjaRRZMDJNrxJJxtrgVBgBAmurjhsAAArUisgMd+Xev2uTQVBReisY2g7qRaOjZMudFm+QRXJHU15+MoZ8w2xknQqtwJIag2mPQgDUiSUkJIal9d1VSXTzcIfIokUR0kQ1kz70NKiTgK0VjKmMRoNES3R4yLwCdqUn/Qx2g4wmDYw87OFvr9nk3Al5Jq6iUJGZsp17OLIiRJjPG4i1/7td+AJz1Umhxftn8YEJs6guSRNkaS0kCj4Qmqb7SzN8LHPvohfOLbfhd6vS6qokJTNrbuzOx8bj3G09mU6vMohbzIbY4GU5+83LMGooCAqpVVZB2fn5lnJrXaIPQRRgHKqkCarRCEPnp9yrlNsxTD7aGlV4URlSeo6gKHhwfI8xyz2QxVQxGMUAQoqgIajY0SRWGIwWBgGCUVoDUqUzewqipsGUW5qakXxEdd11iB0hHqurZiT2EYUn1BM0ZDQ9efGZEGZmUwjY+L3ru5MAyCzs7OrHob1f1bWqEIjiBKKTGZTMjwNHYGR3GYoqW1xnA4NJGkno3AsZ+M7aBeL8RkMjWOzwpJ0kGvR8VK4zBAU9fwwhBSCNRVBSkEojC0NS9Zjny1XAJaY29n11LThRaYz+Z2jTo42AeEYUcIAsZakeBUbMYG21SNAZQ9kwogBRXZLYoC47MzuzfGSQLfRFAmkwn6/b4dZxwJY9o/v0MAtm9ZLIFtvyiKkIRUuFcrjTAIoRuqeThbzSxQKorU5nB50kddNTYviMCpXMv94lIWbr0lSjtI4HdN2ZSyRp4VBNqbHFoLLBZL6+BobI0wWnsCIQFN+Yu+R1L5y+n8kXHFoJOjk+6+wUCJwDLnOIWYTGYmT8+DVkAUrSscdrtdunfTUvP43bn3cNfapz2+6QHSe1/8AAaDARarFb74m79JnoWmgqwVtBDwbBJjAK7a7HshJhMqtsqJelVVYZXl2DETqNvpYrVc4tLhIYb9AXyfio01FSFmLoBGam8syalNfoyHJInB6kNFQVSs973vfQBgAQ8rpPHhvmTmtfLfOcJRliWyfIW+7EMpwJMe4rhjOMZL5Cl5fobDAai2UwPPC6BMrag8L6BUYwYWJ9zWNspFko3kQZrNZoAGOp0uVEWUOA8SSUCet9l4hm4nRl1XCEzkqsiJw5wXBZqyxCxLTXKdD8/3MD45wdkZKbtlWYaiLFAWJe7cuY3T01N0Ogl293Yx6A+sNwMaWKUrBL6Pynj2wjCE75kcpTBEEEQ43L+El156CUopnE8mqMoSk8kMX/jCl0jxJ47x8oc+hKPLl1FXFS5fu4HrN27g8tFlSE9iMBigY7xQnTjBfL6wUqHj8RjT6RRpmuHs/Bzn0wlOT08xnc1QVzVmsymyLMMqp4gfiUO0YXY2LN1NEGiBCoSEFi0tjIHNJl3FGqJmIXNzBdYMTNfjD6zlz3DonMEYL1yPo4653vyLDhNzAKDsb+vXWb/eux0CT47ObH7kgr1WkvtRIQb3IdzQvVIKtUNHcEUtxEWhgad8CJeO9W6B/E061uMv6kaw2vclBGzE48k0tBYAXSQTvQZsNtrD1DP6Vdr7cF++e/sBjuC0/XrxeW4kEwC0IiAkBSc3Sxtl2ZSE5uK/3F8cBbMRJQjAo3fD84eNQaWUAZje2vi3mzG5gQxQg/P8m8Wv2iiOdWGYOcmJ3dx/vsn74UhUoxRIe1PDlzDCOjR/PU8iDkIo1SD2KHqxvb2NbreL0WhkjZRr165hZ2cHB4cHaOrGCt14vkQYeYgjymetmxpZmhl6TYPBgKjbW1tbKIoCx8fHODo6sv0zm03R7XYwnU5wfq4wny/w8OF9eL5AGPnW88vPT3lHtcltMmq0cYxet4skiHHjxnW8973P4/qNK4jjALP5BNPZuaUBFUWB4XCIhw8fWrEgzjthytTOzg48z8PZ2ZlVbGPaDkfOmQbEogjswed9mNdmpj4ppTAYDKCUssCAqVaLxQJf+9rXsL+/v5bLwvsuO8xYnIAVvzjHhNkrnBfCUSR2TPGYYjloVgpz6x5yhMX3fcO8oDym6XRKRWZNLRu+D+dlsNw1G7HM+JBS2j5jR+9iscByucT29jYA2Fxhl/rGarEs3+37oZWCZioUt5mENEZr6nJMHQw8gbKk+cBqcG40hiNO/Mw0Fijnl1X9+P0wrbAo28KwpEo7hJTS5j5zMVmureNGflwqGucZKbR5t65KHr8vlxrIQgIcafM8D71ez+ZWc+5VkRZr75zBFVP8OTLD39da27+naWqFGbivIaiWF9MmmUYopYTvtUJmvAalaWrX7iRJ7LxgUM3UO7dUC9+P8vZXa6IbTKllZwbPJabdMVDi7/Jc5r7kNZgjj9yf7j7DoB5oi9XyUVUVmg0b60nHNz1AqgWgfYlOv4uP/I6P4/U33kC6XELWtaEw5dBKwZMBfI8WhDwrbGiXebfXr1+HFwTIqwqNahCEHrZGQ5yfn6PX68A3Ie0yL7Czs2MnziuvvIL3v/99CMPADgauaVTXFShRv7ReGTfkywORubes9sFUN87V4U1nsViY2gI5tra20Ol0KPfKFATrjDqYqHMIAaRphjhOUBQ50pRU5ipTC4j5m57noakb+EGAqiJgV9eV5St3u10sF0tILXE/isjLYpRt5vM5VFMjCH1EYYTBcABO7l+tVijrEtPZFKvliowSIexmUFdAWVbIsxxlVSIIQgx6Q5R5hf5ggPl0icl4Dg0gMYuUkAKlqhFFMZK4C8/3IIVEksQIoxjf+onfjd/9nb8Hs/E5xuMzvO99HYy2tvD2W2/j6OoNaA3s7e0ZT0dlqHtjfO21t/DlV76K8RkBIKUVCXukObIst7xZfrdKayjdQEGtGeGcvwJplKQ00c6EEFQUVJH3n34ISzni2IlWygIXN6KzaYBuGm18/82Dzc82QuLk5KA1gXlRB9qEaTdSsGak2v/hgvtq5ycbomTwKXWxRPZFx5OM6016G/++rlwj1gxQV72H2+few+Vpu32+ljeh10HS5ru48DnM/y3V6EnfveCzi/6mHa88fcdbj4w9EaS82z02wPAFoJCBB0fmlGpBmhRO3osNUF3UT07kZwOgudTCNtJIgEorzp9rI6Dtdx4FdO0927Hs5sgI4dlokTsHuOwDTL0x1zngCYrsQAqbq2fvKS/eajnC5ktpPbsu/QxCQKOGH5CRKgBEcYROp4t+r4vd3RGyLMPloyPESYL9/X1IIXBweGALPF+7dg2podsxvYqNn6Zp4CUBosiDRoU7d97Bzu4W3h6PkcQxlNY2yftg/7CNWDvG7d27d7G9TaIGHBkBCOyMRhKf/q7fg4cPTzGdThAEIZYm8Xxvfw9BIBBHEYQU2N7aRq/XI0p0EGHQ6wPQSNMV8iKltVFoAI01+JVSuHv3LgCiFp6dndkcm36/j9lstkbrGQ6HVsqZBXw4H4cN0F6vZ3NJ2Hhmo5/lrt3SDQxyuG+YdsWRGFdxy61ZyIY7G5ss9czvhg3dy5cvYzKZ2HWLa+gwSGiaxuZouAqCnLfSKGXlyvm6DIjdXJXJZGJBGds+XDiVhYXcXB6eN+Px2FIEeb6wGFBL02d57s6ayi5T6Dn5nw3g8/Nz25dBEKAqMvtsnBPEfcmy5Bw1YWVcpTQEpLWbANj6QIC20S1ez3nccvQIaBXT+J27OTYMrlh9V6tWpIRpj9xWpvXxWOBCs5wmwHlirkMzDELIQK7l3bdRIWEBvJu7xO+MxwcDb+7/MApsfSimKLpqh3le2CgMF8xl4MPiWdwnDK44QsbXYPEGBnE8Lpiy51Lt2JZwpbd5DLiMK1eBjgUg+HwecwAsDdS9N9+DAd1vq0jDf3aHRwaoFkDc7eCDH/4Q8jRDtlji7OQYDx/ch6orMqbjBALAakm6+IeHh9jd3bWDeDqbYTAaYj6fI9zeRlNXkNA4H5/h7PQEWZEjDiOqeaQ18izDgwcPsL09wnDYNxM3w2q1sPze+bytXu15Hk5OTqwePy/gly5dskW+XNWVqqqsF4wXOb5Wmj5Yk93M85z+W7X1fPI8x9nZGba2Rkg6BPKUao1GHqRhSBrzjWrAyepFUWI6mUMKCd1Q2Jm9FY1SOD05QRyF8KQ0FBzyYAtjRDRaIc0zcFVygHjwvu8hiXuQjUCUeOgNRoiiCFtbI7z08odRKYUwiuB7HvZ29xAZpb1OpwPp02bLi8FyucRiscAqy/GFL76Kz/3q5zGbk7BGnuXo9XuYTmcoqhKrVWoXXa01lFaoqhoa62pN2uSoaGXoAZKKG7qRGwg28xpLd4MQENIjAMX5FhbAoP2eQ71SujWVXC+Sa1iuRY2c46KEaPfYPMcFQcT59h/5G9Ny3Pu6IM36/C8EOBqkIsf/bsEbAyT3+Z4I7jaeidvB7eXvbIKu9m8Xg0t6T+1326gTFZN1F273mm6bNtv+bkDVbR+3/6IIz0XXv7hfNqMl64BmE9jSc2LtPHesue/b3bDad792t/baWsCTDpVuA1e5wPwCHGb/IT1pZPhN2yxNkNtBUUkCRhfXgHpcfzIQ4ufkd90+y3p/2HGhlEmHE9bJwO9PQxhjerNuDwE1bXJ8qP8A3ydjod9LoA1dpNfvY3d316qDxUmIS0eXyNMsSRUzCALs7e6gqjIoTUI/J0YwiESJKLl7NpvhbHyMwWAI6QnMFxNIj8Z1GAVI08I4/BJAhLh2/Qpmsyn29natJ7fbPYIQAkncxWKxsiAhDEPs7+9juVxiNBrZqIjneTg+PsbOzg6WyyWGwz5eeOF5+D7R0+/cuYMoisjwXk4xGg2sN3s2n2Nn9wrKosByNaUImwFFStWmKGpk81NZrS2OY0szY6BzdnaGnZ0dS0Hr9/tralu+72OxWFijmvfetlRFaIGLq/jJQMstlgrAqsgKIbC1tYXxeIzZbGZLUrB3fLlcWlpekiRWNc5N6ueoFxuPLKnNCnVsiHMtHtfYtjlJZkyPtrbgG2cqzwPOlWGjn20OtkO4gOnZ2ZnNKzo7O8NgMLDvlb/DkTueV9PpFIPBwKqPcc4UKam1dXfYqOVnYzltjmCwgZ6mKfrdZE1cialaHEEYjUZr+9NsNkOW5ShyKlLPhjIzbSA0mpLuxZERNqx5DLPhzXYUgxw2sNnwt3uCbJVzeU1xozoMNjm/jIEZ5ybx2OQIiPQkIj+y9+Rxyf3AEScA1gZkYMDUObYL+TmFBOI4svYBRzaJ7hnbNcsVUOA+Y/DDwMSNgnmehzRNrVogA94kSZDnuWXaMMBjmXabQ1a1RXFZAXAzh4j7maNWrqOT/2MJe3ZIaK3tOGVn9pOckZvHN71Iw70H9zEajdYAhCclPGMQ3Hr7Ldy7fRtVkSMKA6wWS7z1ztsoigJXr161k2c0GuFsfIbMDJTlaoXpZIJr167h5PQEu3v7SLodDPsDrJZLfOHzv4k333wTvufh+effAyG0UZJplY/quoFSGmlKk4gT9DhZkhcrRvs8eVerlY008aDlwbxYLGzBNSk9O0mkFEhXKQLD7x0MBk4SZmZseIE8z+xkbRXVxIZHRRrvE3uNKY9DSgnP95DE1GdFntkCcVEYYTQawg8CeFJie3cPSa9nB/BwMDDh9I7JwaGidFopxEls3908yzA+P0dZFJjPZkjTDEWR4/T0DMvFAvPFAqvV0kTeCnuehis5zfkrhlrGRh+wRrdpjFIcG80WmKA1cFpwQN8TQkALZXM7Hs3heTTrY91z3Rrma4dj5G1+ZsHbuwCLzXPcCNJa9MUsfq4qEW+urnoNn8d/kyb/46J7awgnQd52OUjhihClC/xco3TzOR8Hoi4yjteeV1P0Soq2/9b6UnBES61tIIBRSQPseNp8Oi6Nw/3hetovbJMxmF2qmDtW1qIPzvjZzOdxo2PUbx44j83exvbBxQCC2uD6ylqaG1O/tKa8QeG+l4vGGAMrZyxovSl3bb0AeJRuuf7c63OHr+Mm9NMz83NfDEof7U/njo/0iTBRTe7fzfchoYmBZ1wCSjngVihAakRhhE6HqFm+KUPgmcKT169ftzSv3Z0d9Ad99JIYeZYi6XTQ63Ux6JOS12QyQV4VazK1ZMAR/bkoyYPNteXG4zH6/b4FSkyLcp0dTPvinAj2FtP5ZwBA9LFGoTF06zCMUJU1lCJDng0mdopFUYTTUxI+2t3dxXg8tgbdytBktre30TQNptOpKaZdoCmodEGSJDg9PcXOzg4mkwkGgwHG4zEGg4FVZ+OIB9G/ImvQMg2Lc1F4/jHounz5snXyuAwNNmRHoxGWy6U1+tnDzTaEW2aCjTY2+vlgkMTqZr1ez6q7su3Bn3N7mQJ1enpq80EY6LgUo7qmGjxBEFgQen5+juFwaKN2bMQzqOUIj1IK/cEARVlaqhhF6ShqxmILvPawU5YLmrpOm52dHShFDAqmF65WKyslzZQ4KaUFSExF42hWXStbhoOjVWzXuOsYO4GllMRegbYFWhkIuEXk3YhUURQmKhICWqzR3di2CcIAeZ5aqpeU0rBvSguSOaLEFEOupZjnpE7IoJZB4mK1slFBrltVmZIUvJ/y+3cd2wwkeG7XdY3pdEoiXoYF4Ebl2NDnechgPjECElYMxbxPrbWNHFNOo7K2H9MN6R34CIPIvgtur0sJ5HHJ9EO3XzhixmOJ28EHR5k8z7O2K0efeMwwhZUpkdwfLpPDjUqyTcfgyr0PjxO2Y2xOWdPgD3zf/+6pRBq+6QHS7Tu3sbW1RUnJWlNUQCuEQQwWcp2dj3Hv1i08uHcPy8UCe4f7uHXrJi4dXsLxw4eAWUTH52OcjU9R1zVeffVVpGmKF198EZ0O0bXibg9REGI6mUArhX/5P/5LXLt6FYeX9tDtxnaD4yS8uq7R1GQg8mBZrVZtyNYgZSGEDb/zYkRVuUOsVqmRgmSjmpLpKIKVk5KIGYxVVcGDsGCLBAukXdi4fbzpaa3h+T6kIOnNra0tuykOh0P4vo9ev4+9g0N0ul0kSYIkiRH4PuqqBjRQ1TWWqxVqQ8cQgkKk81WGZZphMV9gOp1gfDYmTnVd2WTaPMssPQAA6rpBpSmK0xqBZCgR15rEBow5DsBwghXRXtzvsxKZFBLQam0jcA0ya9hb9hIreDnV4fEoXcjEKS6kj61POAZarr15wZTciDC493IjHWv3uWBq23Oc7110Lx5/LNTBhohLAXA95AyQXIN/rT3AmoIYP4tSCtAtnYnbyJEH9xpu9IOBrgus1ql0aw8ElhomWXH1mP7RdmzxZ7zYSykp+ndhZE5DYL12lAtoLopo0EXWi4rydZ8UJaLT5NpZ6wDJf6Qv6Z4KWrdc7fWjBUhtZKZ91k2wuhmp22w/fffiCNhmH6wDp0cBkvt9F6S7/UT/ftJ92vFGnzsqfGId7K/1j5mYfA6NfcBDgyj0KVodBrh06QiDfh8aGu99/3OQnsTu7q5Jmg8ghKFOqwa9Xhe+H+DOnTt2PYXWCDxSFmzqGqt0hTgicLNcpRifj3F0+QoWi4Wl+OR5hjiKIX0fVVkCQiDwTfV6n+rzLIzBv5jPkecFrl69QnK/cUx5n4FP9XtCAnB+EKAsSpvk3+32sLu3i7ffets6GdmwZ2EGzidgA4c9/nEcW6/x7t4OprMp8jzHtWvXbG0XrTWyxRJxFFvDBcawqqsKe/t7FhSRkUTqdmVRoKoJiLhRBQY/nD/C0SU29tjoTdMUe3t7GI/HWBmVWKClX/G+y15yPp+FC5g25+b5uDLEQEs7YrloBmc8Dpnm1Ov1MB6PUVUV9vb2UNc1jo+PMZvNsL29besNcpFSl7LExUBdByrncjAwU0pBAyjM5y5tikFDFEU20sX2BTtdXelr12aYzWZrdRf7/b59D2wEM40qTVObK8ZCShyZ4fQBBrg8hhj4eZ6HJI4RBj7KsrBtZsAFwBrSDH7430VewPdD2w5ODSCnr4bnk+3DUUdeH9zn5vEEtKUEgFYciaNMnuehrCrkJrrK+TcM4lxqHJ/PwMPNGePnK8sS3U4XVVkBGjbSwucxS4b3Ze5v12HJAIJ/KqVQVoWNWvNYtXt83aYFxHGM5XJpx9Rmng+PDx7PPO74+zwuGKiw3QfA1iZiQMv2HTsteH3nNvN85r/zmsAAm+ctPyfPSW4b9w/XXCrL8qkB0jc9xa6pa1RGMlB6Ep4EtKZiVL4J8W7vHWC4tYPrzz6P115/De+89TXUTYXXvvoqhFbG2i3w4MEDzGYL1HWD0A8gkg7KooCqGxRlQcpWhg8ceD5qVWE6nyCOA2g1gJACdVVjPl9h0O8D8FAVOZraDHLpY9gfoihLCy6ouniDDCV8L8Tduw9QlRV0I6AaGqhleWwmT2NoHuRF0GC1JUPXMoZ4FIXWi5EkCS5duoTDoyNcvX4NSmv0+31b0bvb7SKJEviSPFOz+Rzz2Rzj8Rl5etIMJ6cTrG7ew71796z3ZjqZYDyZYGm4yxyWbjhMKiSqprES0WTUtTQurclb3dQNtAE8WmtAtgIF1lOvFKpGGaufjGtlqtGDjV0jaU3eXmNoG+UaDSqO25qHxpASgFYNOMIhJRtiinINNEMmtOhGCHhCAkalh/OuXMOLLm0WSvZwWwlsgBO81zz0UmyEA+hZWQBaep7pS9NPQkM3BOKskcfABszie5S2tWmgutFJd3HkZ+JNQykFGIEqjiauNVZrSqQ3tCutzLyChhCKqDQWhLoRshZEbPYhwHOT+74NTa3BF34RBtS2ILXtC34PDUch2k6gM5WylMdHAYaw3zNPRJQ8fk0Qa33NF5dC2rHsGvH0XWVzUNpxTRv7ZnkeF+Zpvd5P7WN4UPDWzhEG/HvCA/QmdROgfA/6puetgyKO3qxHgjh6JIwch1ujgj73PQ8azC+HofsSbZeNk6qqYcULBPd3m9cjDa1VOfLVPH9Jbr91kNA1DPAxfStIdhFCAJ4vraeaPfHdbgdhGNkaLUHgY29vz471o0sH6HUSUq3yW3Df1DU6vRjCo9o5paFAV3UOzxdo6gZl7kEHNZ65fhWTyRSr5ZLASRIjiEJAa3ieDwiS4B4M+mgaBQmBwPNx6eCQIg5eQGp1Nc3F5XKJa9euIUkSvPXWW9ja2sLhwSUcHx8jjjvY3t7FapWhKCoMBiMTcYrg+wEC38hFNxpBEKJpFMqKinEzHaYoCqSrlaUy7e3uYjqdQkppyhT4mJyfGyGeHJ6UuHx0RDTwvMDWcITuETn+qrDCcr6kfFVIG+mPohjdboJet4/x+RhC0Gej0QhlWaEsKzvSGMBwkUs2rgCaq5wXxB791WqFk5MTa+wtl0tLH2JPe57nVuCH95YHDx5gsVjg6tWrNnmenZaTyQQjozLH3vyqqmxESut1VojrUWeDdjwe2yjOnTt3rCPGDwIsVytAMiCs4QcBZvMFlssVul0SaZrN57hkiq/mRYVEekizHFlO4PD09BT9fh9ZnmFrawtlWeLk5MQaq9xWXns4QtXr9bBarSxFbDgcGhGi1AJT3hN4f+BIxGg0QlWR3RHHMebzBbrdPuKYpPg5osYGL0f7yrxAk1QIgxCB5yNJYipnUZQo8hzDwQDT2QwCAp2ka2jPtC7WVYNO0sW0mKFROTpJB0EQQkpvjcolpTQOYPp7FMUIwxhZmkJIcjIoDeSmXAmD8263hyzP7FhpNKUMKKVQ1Q2K0kh5x8x24bVHIs+pJIeUrahImuZO6QBBc1x68P0QZTlHFMVYpSnyVWZFQra2tmw/V1WF4WgECALbzGCpqsru95wjyEwgAmOBjUBzREVrAklSKEuBBGCBGwMSAPZ3Bi9cNJbBEPcX0ApWuEISfC47HdhpLmVbT4qdLq4yMzvsmZLI49V9No6cMiB2wSjXzuRo49Me3/QRpLfefM1GZEgpzYeERFlUaOqKvG0+5dhEcQRA4/jhfbz2W1/Gr3/2sxh0E2ihkZU5lmmK1YJEE7h+BKNXP/AhPQ9lWSDPKBltPB7D8zzsbG9DNZXZbGkRp6iNgG4IWTd1Y0ANgToIQCkCSUCrUtQ0hv6j2fiQ8NizDxhFFMD3fPQHfYRhiG6ni16vh/2Dfewd7GEwHCKOqODqcDRCp9uB9HyczSaYTCZYLJY4n5wjyzLcu3cPJw9OkC4yTCYTSgYsShtWBRf3VI211OqGokdKALVuvfE8+JuG9Pt54LEh1ajWG+KG0l2AIcSjUQ822CTWoxvuBLGRD2hb74p/104bN73+m5EZ/s5FRxs18GyuxGYEROl15To+zzUC+b5r9C+5bvC6kQy37Zxf1n5nPdrjGsFuv/L1bHud/ttsq5uP5PbvZu4K3+eiKNtmvzyuf7Xm+kkbhr/JS7gw2gb+86PevosiRzzO2JHgRk422+Oec1GkbPNzjqjxd11xh4v6pT3Im07Amf4TIAlpLZR9ts3omXRAkCtqAADKierYdyUlhIat6+RGCKlN5KzgOjsUEaWr813sdwFTl4OAHPkzpKWbwoA3DVITdGk1LZWN8a62tDm+nyeF2ew6dpNrAXqFra0tkuk1lJr+YAApgP3dHfT7AwhB6+eVK5cBDQyGfQipKKditUInIXobe+2Hw5HZRwaYTCZrNU/CMLTr4f7+fpsXomqEUWhrwVBUPcHJyQk6cccYboFNmp9MJphOp7hy5TLu3r1nveFcl2U0GgGgfNHBYGCNBo5OCPNdTtDmuj1Jktgik+xR5ajHfD63RcbdHBx3zWXQwdGFLMsQ+L6lILPh4o5l1zCh0hYUxeDEcS6wyTQtzr1gGg3LVE+nU/t++Vy+B1MHGfhIKXF6eoqtrS34vo/5fI4gCKzw0AsvvGDp4tzW3d1dnJ2dWREHzhthkJUkCabTKZ5//nn7OQsVuB5ujjCxgAFLibMS23w+t0XLJ5MJ5vM5Ll26BCGEzZdioQzOwaAxtE6Rc6MDYRhbrzrT3tM0tcVVx+OxjZYxQJxOpzg42LOy40zh2t3dtYIPvV4PWZbZNm1vb9v9hO9/fHyMpmmwv79vxSl6vZ6lCHIO1WKxRNMo+z55njIQ6vf7FnzzPhLHMR7ef4AwCGwkjdXdGFi675Aly/m6HI1xc1e01jahn+W2mcLFESXu99VqZaN0WZFDelyv0bdRIgJUbRFeAFZkgpk/nJ/DESguUsv7Ju8zLITFz88CAvy+wzBEWRRWFZn7goFInudo0JbhcKNEUkh4BoTyZ6xwyG1xI/LunsVRLlaiA1olOI6Kcg4i94279zNVkccfKzPyfOVIGtvN/K4AWJEuty3MYuH7cqSII5/c55x75+4l/G+m/gEkXDKdTvEH/w//+/9CsRsOh3j91VftJkPGNyX9zuZzBIFnKA8SRZWjqSskSQ9CxNBVg//wuc/ia1/9CjxPoKhKnJ9P0ZQUAq3qGqvlClVdtWH9nDaiMAoBDezs0AaYZksUZd6iZylM0dYIAhLaLIie54MNC6UVPI8KqgZBgOFwiKTTQRiEGAz7kEGLrLu9Hnq9HjpJgu2tHSRJH9ACo60teL6HIs9RFiWyPMfZdILpZIqT01OcnZ1hNptRVezZFFOT2Ng0DeqmJg8lb5p1W9OkNt4hiuhINJp4oFK0hRXJmFKom/YagGMMGkAHcB6KsosAS6LzhruZFM+GFBugdkJcULHdNYrdieMCIIh1ALFJt3Pb7v7tomgLe6+55ox7L44eCLGeCM9HUzdgw/MRULYRtHBBivWqy7aoXdsHLT2Jf7pG+kVt1GqdgnZRRGKzHZvGEh/u4rn2PE8ASO7v2jH4OaLg3B2PA0j6MaDoIoDEz0HGOx4BgJuAbrONDG43P+e/u33SClK0z0Tfx9o1bL4QJEhIgOrZAICQGizn7ebKCCEgtBvpWb8mHDrZI9S2jb8z6F0bI2h7230GGwEzYIj6mOq1eZ600TPyuDZg3Ob5/FwacRQhiiNEEQkMBEGAra1t9Pt9aG3ECzoJrl2/jh1jvFV1jSSOqQi2arCzvY3FcmFqrdCmq5WCbtr1qjRG9XKxQBRH1uAGyLk0m80scHMpV2wsTqdTW52dC1K6xk3STbBKV9YrPxgMoLUmeeVOD570rOHCKmWu1DFH25m+xHQuzktlZTQ2eBRg6WSXLl3CZDKxKqlMOWIDjqMnOzs7Vr3N/bm/v78mtLBYLLC3t4fj42P0ej34xpBlw4WNGzZ0oiiyRheDO/4uJ3Fz/lOSJLY2DpeyCMPQAiemoLPiHFP73IgNGz9nZ2e20KYrTMTS0uxlZnDGgHA+n9t56QIB7mfuw36/b6NQfB1+Xn4eduxx+3k9YTGGpmms559rN+V5bnN0ptOpNbZjph9mmVU8i6II29s7mM3mVp1sNptZo5UNePb6c94PSYTTfDg7O8Px8TGef/55LBYkFMUKcJybxvkfbOiORqM1kQqOGHBEJssyO04YNPl+gLKkNnGelOvpZ2ObwQsDjrpo1dncfR+ABTzc/25EiEEJ0/9YlY3FMJRSNm+IgRSPKTbW2eEQBAG0IKYLr3MsWsHn8TjivDF2hvM4YeOdxwQAq/rLOT/srHApYbzu8rlaa3honcTc1q2tLQJXUqxJwFuRC89DFNC6xWDGlWznnCgGQq5jw50vm7/zGsXvwbUp+J0xdZbfl+vQcYUv3D3WjTQx8OS1hd8NjwdXFZLnGOd68T7FYwOABYTcnqqqMJvNnhogfdNT7OqiQpWV8AMfeUk8YelJFHkO30tQZCssygxBIFHXBeoiRbe7izhK8K3f8QnsX9rFW2+9BQ1gbz/Fw3sPsFqtcH5+DogGEAoQigql+hJK1Whq8lJduXKZ6vNE22iMccwDDAD29/axs7OD/Z1dSN9HbLxXjeENC0n1KDrdLvwggNIK08kEqzTFcjXHfDFHnuc4HU/xtdffIq5zo1CWGmenZ0TTqGtkhgNcNQ0yE/5trHgBGStNs24Qk6EjTKSKKDoU6RGotWqpYFpTFEloVEpBaGM4aaKn2etpbScIAYzWaJbMLlMA2XdEuWGjxF0EudBja69ySFdAbBjd65GIRyMndLYpuuqAns1oi3tN99+bURV6Fgk3L8YFWG5bNiNj9H2xFt1qn/DitvAiyt67dUOcwUProd+MGLlAci23pnXjP9oWB5RtAqhNQOJedzPCtNkfa6DIfVbRPgNMLlHbK4/WlrHXUG1CqXvdTeDnttM+Ox4FEE/KlTF/sT/bekCci9PmVElpyGc8SVwamfPYCp7N6aJ7t/1r1SCVgpRtW+x8EsxFF/Y8CMAzm/AmwBfC0OKUqeMjBODBgh3PJ2DDlEBWYROmBk8cx0g6CcIgtAbB9s4QcRxaqloYBhgMh/A9H91e16w/TPf1MBqNEMeRoZNI62AhQ5TUPwGTT5EX6Pe6RmY/hxANtrb7KKoUW1t93Lx1CwcHB7RxA5hNzhEEPqIoNu9GIop91HVpDUk25JIkobwdk+/DidoAFczmxGSWhY7j2BrjaZpisVhAafIgr1YrJEmCO3fu2E29k3RsHgtTVDod+hsbMbxpM+3L9br2+31rAGqtETr1R/i9sqf25ORkjS7FBsfdu3etQXt4eGhBUp5TeQiOTuzt7VkjnI1bAIZCVdnICQMLjrIwCGDlVH4uPn84HOLs7Aynp6c2j2R7exur1Qr379/HcDi0oKvbJfYDq2NxjRuOvLChH5qCofzZYkEFxtmTz+skR/Y4asIOIxY+4kgDgzYppY0ccWI91/hhEQo2Tt0EdVbVWywWa3WZONrHII4NOy4QGkURKtMmpjYCsDlOdr5KiV6vh8ViYQ1MHmMMUPldEZ2MIng940xlw5/3AVdpj0E9e+fZCGUwzGCMoxP7+/s0Fk2frFYpyrLNqeIxwAcbwUyJcnOi+v2+BYYM6Dmqwtdh4Sz3HfH+x4Yzvw8eEwBs/hH3P+9NDNaZFilkq1bKNojWJDnO74htElckoaoqG71z5eH5nbEjRAhhQTX3OUfH2JHAczuJYttnPK7yPIdn2sTOHQYpRJVr9zUeIwDWwBs7OhjAbNYU4nfEFFTeK3m+cNv5c+4Hvh5HffmZeJ3l89xcMY7m8X3d98T2H4uG8Ltw3yELZ/T7fQs0eY3kue+ycR7n7L3o+KaPIL3y+S+g1+1BComyosUpiiN0+j1AaHTiEE2VYT6boCozExqMqfaPQazsyVWNQp7mCMMAjVLI0tSEbGtkeQEpAsTdLnHjQHkNUkh0On1UtRlcdY3VKqUCqGWF+WyGPE1RNw2m5+f/P/b+5Fm2LEvvw769T+ftdb/N6yKyMiurCqURTBNpogYgUARIAaQk0x+nxkwGjsSBTBySEkhRlIgCChIpUBIMTQGoykJmRkbEe++2fr057dZgn98+yz2iUIlpWLpZxHvvXvfj5+y99lrf+lanh4cHff78WbvdTs+7vfaHg/q+S513ouB5Dc6r63uFIYwT1Kdwa0zHmxLYEth1Xl2wzkV8JdAYJmxMbY5CfI4EYt00AybzXvJSP8TDdO40DNLQy7tpsCbC3ve9hkCLXSJIJjrkI7inMI+DGSMk5ag0e/X9eVqY01Q78n0OknUerMPGRG0Mz/cV4v95jo5dv+n3F2DXpPjJKdVJXBY+Eiayiip9l2JjCeuU8dlLx21yBL6/293337Ndx++PtFw6RPZlv9euHf+2ztElOP/zFJZxd9OfAOd47+fO2dlnjYGzz/t9z3D2c28jMJdRIqVnOb/OmAL3fetyUUNlX9bpsuTB+Fsx0yc+X68s8+p75vKcO/KcMR+UomB5lmkY0+O6vpPcFGmMKRJZzNN3Tpn3iXl7//5DSr358MU7ZZnT7c2tpDiD5/2792NnyVaHw6s+fPiQQD1Gr6pyBcUuaczIAUwfDkcd9jGNRyOo8S52e/v86ZMWi2WKfMM413Wt2aJKgHM+n2sxX6hu6gQILeikwLgoChXjWsHmk6ZxOtXKsjIx0m3bpkY4tiAaow/bXVWVvv3229SeGFBX17XqtpbzLhXgO+f0+fNnbbdbXS2v9PXXXyfwT+oQ6Sp853K51FdffZXaE9/c3OjP/uzP0nBWoh2S9PTykpwMIlqAWF7b7VbffPNNAnakBwKCY7TuOrUffnl5SSkrb968SWvW1LW8c+n+uW+K7ImwkT7onEvRCWbweO9TcwGAGg4K4GsYhtSJFQeB+oSyLPX6+ipYe5h9WHm6vRGJI5UQcG3X3nazQ3YB2XT4kpTSufgsdoL7JS3tzyOKSFmEXAIMS9Mwbtutaz86COwrkcUos42uxo6v2HuiOyGE5FS9vLxovV6nFLg8Py+ox3F+fX3V/f29hmHQ9fW1Pn36pNVqlbJu6AiGA2Y7kVnmP4SQopuvr4fk3BIxYV3onmZlMZFuw1TfSmQXoAxRsN3GuV9ERC3hh5PE7yQZTBRBOTJA5zoiSeiHWFPUKbipFfpUt5Qn/WZrZZAH9tU6dtyHTXdjr9HfOCM2otK2rbxzmlez5NhnWZaix0MIcplP0WbWB8dKQ0gRW/bGpprj2HBftkECWAv5tg4OTg6RT84uDgt2HkeMtYCgsLVLkCZEuZAHbCOfs9gQYsieJe6R6Bt2lkgwe0Rk9+Hh4TcRJF4+L5VXsXAur2Yq5nNdX1/r0DQ6HPZaXy1UlQstZlt9/dUvddgdtN//Stu7O62vr9X0sWi4OR1VH2s9Pj1rv9/rdb+Pzs3ppM3VRt3gtNvXSbgexoLVw/EgDZkOhynFbvey0x//iz+OCro+qWunwVU29NinSIQTDQL6fpw+7pyk6GCoo54m5v5bHHYerQipTS8KlutLUlBsSBDC2IRAUyqNG+JXOo0O2RAdoNStarxMcJNj5jRG1MyBkzQCtqAQunT9iVXXeF1qrvq0HpLGgw7zPqZAjTeQ+e8CbpgyrsVhsQ7lpaNgjdyfB+D/PLBtozSX1+NerdPA71kzywSffZ/5XvaPl1V8vKaow7mT9G9iT9LvLpycX+dllRj7ZZ/Fgnn7/j/Pybt87vE36ach0P3v3EFKTNEFa3S5Pnb/rbNm32vruS7v69zhM3VSks4HnNrnmqJo53sV63bO1yQbFf9Yd6dBWeaUh9hUIdb/jUajLBTr3qTMxdS19XothRBn6tzeSs7p5u5Wfd/rd373d/T0+KTVeqW/9Jf+kjQELeZztU2rtmv1/v37ZMTLstDxGNOdSLf5Z//8n+t6e63ZfCbvY0QnzhZxautei+VSp2OtzeZKmXN6vL9XCEH16STvvdbLtXKfaRiB3eexe1VVVVqvVnEP+l6HMeqRZ5lms0r1KepXWuhGkimmcC2Xa3nn9auvvlbfxzk1t7dv1NS19ruXcR5HM0aHKNCv0kDRp6enlJIDCN5sNimSBIN/d3eXOowhDzh+MKrb620CZZ8/f9abN28SULi5uUnpRc655JRYMsg5pw8fPuh0Omm32ynP83Eg+SqB5f1+n1L9aIdNTREA9Pd+7/f0Z3/2Z/rZz36WipQh/Pb7vd68eZNANc9sZ+5Y8LLb7WJ30pGtJZJDa21AunNTOg1ACkAEwMERITKG4wTzvt1uE4tOdMh7nyJvsMnUOXRdlxxjIkFEWN69e5dk+fn5OdkA0gaZxxNCSO2tsyw7a/0MYGdPifoB5olmoX/QHTYNTFLaF8Aujt5ms0kA1nuvn/zkJ2n4KqM+cEJ3u31i2WlpzRgSnEKc+inS0app+gTsX15ezhzf2F0uyvLt7W2qUbMtmVkj1tXKI1EAauSI+BAxYf9oWc79A+idi6zsrKyS00K0k2gS9U7UqBDp5RyRquacS1FD0tLYu8Vikbqm8Tvun2jW8XhUlufqw3CW6mmBfwjhbDCvpNT0AhIF+4fzg15nPYk24bgzH4k6IZoJcK+cMWlsFZ/Fpl7IG/KIw7KYxbbhtg08KXLoGuSXaAvXx+GwaXREsHkG5B47ZlOFmUtmo56JjB5tJ2ef6NGl3cVho1si0SCcTus0UoPEd6BruE+wJ7Jy2Uf43/T6wUeQfvHzX+nm5kbeOXXdWIitoDYM6rtB6oO6U6PmeNQv/uzn+rv/2X+q+0/fan61Vrlc6VA3et3ttX9+1f5w1KFutXt9Vdd2Y95qpd/5nd/Rhy9/W8c2gq7jYQovRtZnr76tU6iXVIKH+3v1Q6vBFGQ658aIEOAwFo7n2cSIDEMvhU7eKRWVn0cibHqWAfkh5rFxqM4jJTGSws/PQpIhyJnaifiesaBaXkO4iLAkp6fXECYFYcFhP3h5PzEx9iBledAwEIq27bRHp1AuMQnTs0th6CRNz8VzWHDM7yagPiQMexntsA7Q5TGxDpFN2Ys7dp6OZe8zrvO5U5Uci4FQ+ffU7Ljwnfv5vijQ5f39eQ7S9zks5obP3v9viiZdXtveo3WQbNTl+xzL73VCv/OT774uWdv02QtH0/7e3svldWTu5/vS7FJu+AjykoMUJgPA7+J1SJnkmhM5EdcoSKmDnTPvcWPBeCW5oOVyLrmg1Wqp9WKjzGe6u7tT3/f66U9/qs1mIynoarVQ3TR6//59Ykc3Vxs9vzypG7oRFC4SGxjlLigfwTCsL10nq6rQy0scUu2zeFZXy5Ve9696ed7pxz/+idq2keR0OBxGQBCU54WqaqbN5mrspDZX2zYqy0pZlms+X+hf/It/oevrrZkAf0oDREMIqftUTNt5VVbGJjtVWeqrr77S1dWVHh4ftJgvtFxuUuE3Bt45pzzzmlWF6vqkEJQYVe+9vvnmm9QZKssyPT8/J2BL9InhjdRlkOrDzBwAUhqMuJyLVvGktAAqDq8HVeU05NQOO+37XldXVyktDzDPLCOY/i+//DIBwhCCsrE+ldQxgDMNEU6nUwIPFJLj8F1dXZ05AFGGlAAu+4kz048MeQghDUptmiYNCrW1N7DWRBJIKeRPOuABmrkX5spM7ZjPwWUIIdWBtG2rDx8+pD2HCFwulykC2ve97u/vU/RtPp+naJVl0amLOZ1OqRbHgiyijEQzcDSJoOGs2fVmSCZnCblumiY5P33fp1RG52LksR3vmeYBzMiJDniMwEhTXQ7RNfaK9acRRN93aprI/BPpo+aG+iBas/uxzgxSk+J6ZAkdgXPDfrGeMUJ4SnqSmhFbZ8az4Gx4H7v/FlnEA4vFIqaqDlODCktAIBuAcOuQSEoyDRDHKWbNJKXn4jt41XWtoiqVjU4fDoyNvNjUWwA7tma322mz2aTnAugjY0QCbU0c94QDg+3suk4+nBOpCbN5r6ZrU0TLOihEnhgiDKlCTR/6Q5q6wJGiah0enGRk4fr6OsmpvZdhGFIa6mKxSAQLBACOFtFH2vGj49lfziKfpSkO92z3+LxcwyXH3H4PpE1VVUnvsJZ/8O//u7+JIEnSP/j7/62KYq5j3Wi/O2j38qLX3V7HNtbmNE2tw+tej/f3en561mH/qkxBTd/L57mci3N0vGLbVbqyRTBVaH/o9M//+E/1+fGkL378Uznn1Q1OdX1SUZbqQ6e269XUtQ7Ho9yYYjBbLFQdj9o9P8ZUmiFIii1jvcYDP7aTznxsfpBYqjAodkW2oG9sDDAMKUrhXUw6c2OEhrbf3lNjNLbYHqQ4vDbW9/iQcGI0xJoiQ4m1zzQ6Qk4+TM5C/E6N96m0hiHE2q8o5EGZy5UXZVKOGFafZdJ4X0SlhiG28maGggW3ANAhNWjoYurh6GGSJkjRO+mCNJOQMSjBOmLOT8M/0/+na6bImxvZf+pJuG0X/z4M42+8H68/dQmj3oN7lfOxDbbc2A7bpfexDtwv3xPTKcf27sHcbfhuKiU//76XVT7JSZgWOX2fdTwuHcfLv9uo4fc6Yjof1GodpjOHh6ikdcQd9xXrtoZgnXo3+qFjW/aRGxjitsvLawh9MuIozSAn76ZarvMoUUwp9ZmPaa3OKc/jEGWfZWmvLz+b526s1clTe33aBZdlVNy3NzfK8iyBnZ/85CdaLOa6vb1TVZUj69VrMYKN+kjUJLLdT8/PUgh69+6dmuak4/Gojx8/ajvO2en6WqvVQk1bqypzHQ/RmIUiV9t22lxv9OnzJ53qk5qmVl7kOh6O2l5v1bzWqmazNKdk6GPV3nZzrTyPQOIwsqfX1zGqsnvdSSE+c920WizjVPd+iI0VvM+0e92prMq4dsi5k9q20enkU7va4dTLZ15t18VaqK5XE5o4SNVnutlEB+fbr7+Ks+jKyPzjBHR9l1Ly9vvYPAGDSd0BIMKCc0DQ1dWVXl5ekvHf7XZ6+/ZtAgWn00k3Nzd6enqSFEHO/rDXer3WfD7XerlOwGVWzZKzFcb9enp60vX1dXIwSOMhtYzC8/mY+cA5SYSLi7OTijzXcpyb45xT18ZZQmVRaP/6qmq51GI2i7YkxDSc0/EYUyuLQmEY1Jh6oTyL82cg3PaHg4oxCvbmzZvUJY7uUrDYpHg1TZPAR9M0+vrrr88AOalWd3d3en19TWlROBM4U7YQHIBzd3eXahhgnDkPnGXSo+o6tgmnKJ40MAq7cYzQOaR1Adyis5PLyatre7VNp/kstrmeVfG9tY/Pn2eFFvMstY1+GVuZz2eL5Az2fZ+uk/lcbdPp06d79WPa1NAHBe80ny/Sd2dZrq6LKeUuxNmNONN5lqutax2PJ/k8S45K38eBvLvdTu/fvx8dgVx13Wq3ex11fiQqnKu1WCwVhwDnCezGCFSmrqvHdF+vzWarsqzGPR+U56Vi5kPQaWwtXlXl+F1RholOAvqpXyL6e3d3l+xcCIP2x4NkQHNQkLxT07R6enmJXSzbXm0/lhKMjqb3Pp077z0WW8f6pGpWJdB/Op3UDbG2seta9SOmY88HBXnTOY4oRZZl6ZwTKZIiGU/qG8QHtXDUrJHuyXkhncw6mLOxRTgzkUIIclmmIcS60yEMaro22cZ+dM4smcd33T8+qq5PY/fbaL29z1RmXl5Onz590mazSWlqz8/PicglOmdt+Wq1Smmk1qHk9xBN6E/0ATWJROuw79QN8Rmi0ThLi8Ui1ZARoeSsE42nbhIyC2d3uVymZ1osFulaOLW2rvQvev3gI0j/zl/5n8vlcw0hk3e53BCFTS7TsY7zGobQjczOKToQLsSZFW2cR+TGTWu7Vt3QJkU9q6roPHmvarZUVkwtOFEIeZ6rqQ/q2qgUYBUBeplz8poMHsDWOa9BXWoLDdCU4iEo83ggEFYbjg1dHC4W7efYWWoYa4rGFrvDaPgGs/1p1I6LAJPW3f3QKzhY/svuVU6Zz82/p4hJlmem7e80+yF+PjpKgFoApfdeGqZ2lzCRyYHy5y24+c97pyE0GoYpb/XyP/s560z8eVESfmffY58z/j1e57KG5DKSEj8/fSdpk8xl8t7LKc6Esa/LNLDL5++HTsPQipoU+/2X0SXrjNh7+4vWwL5ixOH7Cx4vP/t9tVSXa0MEg+iJI9BJ5FNmzdwU3AohpMGz6UO86Xu+i99558a+eHFmjq2PC/LKslJ451mWJ4OQ+UgxEDWYz+Yqq1KzaqaizPXu3VtVVZXSqZqm0RdffKGiyLS+isDt6uoqMc+cV4wpYBsWH4bWAkcY5k+fPqXzcXt7G4cqj2lPNlce4Hl3d5eMN+w5zC6jCFarVUppIC3k7du3CSRSDN62bWopDLCktbI1VLvdLhXY73a7lBrDQEmKhAGjsPTWQEpTYbEUnQXLaA7DkMDJfr/Xu3fvohM3TB2fKMRfLpdn9UTsA84P7ZlJO2rbVp8/f9ZPf/rTNO/m4eEhtfXebrf69ttvE+Npzw7OFHti01U4v0Qpvv32W33xxReJYee9Dw8PSTYB9G/evEmMLzVd2+02RTZsWhVgA7AAc825Y3gpjR+IoL179y6BJUCejYLh7K1WqwSCYOdJ44G5vb+/1+3tbVpnHCjqnGazma6urlJbdZ7fe5/Y51R/NpulcwBLDCjlmVhfGHuAPo4ShegALPtMgFP2HkctdsGSvDtPNyIlilbTRGUAuDwLUQebVkdtkU2rhFVfX12pbpu0N4C52SwOYC+y/MxZZG/kYqddrgW4pAsg+gQnHHDKXsDS41yxTpJSZJb26qzlMAy6urrS6+trugbzkqx+sl3xbD0Ttoe1w16hF4hI8V50IeQHUdvCT2lrNiIiF7OFLKi39TBEcfi9cy6Be5yiYRjS2hHhoe6Khh6kb3FdnodIBpGsw+GQnETsiO3Qhg6xHfvQ59iyEEK6Lg6YfT9pgjgV3Dt6KAxBL09PyekpyzJFJInQ8bLZNlk2DfZFvyKXlnxg/dg3XmeY15wLsI2N2NqMIp6D9bbphqzPVLrhz84aDrrVD1IcevybGqTx9ZOf/o6e963qRqrrTn3bKDintu/kyzI6AS6P4GvoNF8u1NQnuSwuJu2u3dj4YJCTfBYjHUWpTLGrU9116k+7szQcBLMoy+joOKeh66Usj0yQ93EwWderKGJL3H7o0iHpukZ9PzEK0rnQAnAxANN3jjmdQ2QZhiE2c4iRpxjhiayYU+i7qdFDGu/o1A+9+h4QGo165rORqYhOXIzEjMA/SBF0TvmkeTkOYBy7X7kxajOkoZDfTYHq+15e5+l4Np3JvmzUI65HrMEaxjXkHnHkJob/slMcTl84f7bxd/yZAhpEmWwbAYZ4pggOtWTZeP9K13XG2fSewsw4rPMS4KNMbCqfrVXIfCbaXeNg2PW0DsJ5bYzO3p+c6TBo6hRnn9eshj+Pgk2/DGd5cSGM6YY4hs7+zjhyY70aa8x+xfs1dUSD/Swd4sZLOx+DSiktLkZQ5WhMEK+XZ5ly58YBgWUCeb/927+ttuu0ulprPovOw9XmKsneernUarnQj3/84xhxKPIpPSIEra9WCkPQfozOHPZjutkY+aM7mHMutfSVlHLHbXcoAAhgxgIDcvdtlINUCuoe1+t1SqlYr9fJ8MMKv7y86NOnT7q6utJ6vY6zP47H9B+FzA8PD8mRApCS8kAXKYCdcy51eaP9LfU8ND3geQCZrAFF3ETWYHoBrLvdTl988YVCCGmmzXq9lqRUS7HZbDQMQ3K8uq7T9fV1cgYeHx+/kx7EPdECmJRQQDwMK2vsnEstdUmloR6Fjm44MewPAIe6ivv7e/V9r/fv32s2m+mLL75IzhkAg/oEmkqEEBIQBXzhENFa9+HhIT3LcrlM9yYpzfnBgQXE4DzAnhdFoW+//VZt26aoi6QEmK+urhITC/igtunp6SnNI+KMrlarBEIA4Dg4gNxf/epXcs7p3bt3+vz5c3peZOXp6Sk9Mw0R0H3UfQBYkVGbNkjHM+qWiLwA4HHGcTQgNQHavGxHua7rEqgEMEpKNV7oadK/bCF5XdepeQfgWZrA6fPTk4J3KRqGTeS5cAg5z/yJ08/9sZ+QA3zfMAwJQLIG6/U6gV6cbOwtjhFg3taXee/T++/u7lI9GXtEmib3wn84y8gSoJ9r8nMcf9u4g72FMJKkYqzftK2sowUIasdRJdw3n8MpyfM8dT97fn5Oe0JE1+4BzjBkD9Goq6ur9J2Q1MgSMobets4R0REcemw8cod9wqmybbZtowwcSkg39o/vRraqqlI96jpk2t4PUVkbvbZEHs9EpA4yje/gvixeAMdxT33fJz2GA8fZo0aO67GOOGDgaZvWaHEEtWLIPc4TThfEhHWc/qLXD95B+p3f+139//7Jz1TlM2VVbCyQZU7lrFIIg5omhop95nV//1lD36saa4XKrhWd0uIraBj6NAh1UnAhFifPy7NIAxucF5V85jUMMCchGazFbKE8i5Od27bREHrleaaua9U2tZr6lFpLckhi4XKEpuTqoqwkUovCmddOSllwUp4Xms3m6rpW6txZh5PMk77klReZQhiUl/nZgeu62EXOey/n47+Lcsxt7frE7me+EPU0w+ioOR+LC70PY0RgmrxshR2liJLgZZWjZRviWg/qhz6l27EWpNJJYyRnzLWi7gPPxzk3doobW4/HLTdFfS5dE88iZj+681qv8VoiHdFN71eIjTJCCBr6uB5hkLqhlx+7+tm1YO34t2Wa4vf79P3nr6leLP0kOaM4RJdOpxv367Ku6bsOUxidHv6Mb3NpT92Y1un82JrbTc9jny++yyfnLTYycOO1J4c2Gtwpysi92/8mI5xruZprNptrtVpqu71Wnmf68OGDvvziy1hTN4KyeC2v3/7tn+h4OqoLncpiBJNlocxnI8Md5EXziU55XiiE2La77zs9Pn5OoH+/P451JYO6blBRlKm7F+ldpMJgfKwxxaGgEJU0oMVioZeXF61WqwQgYAaLokipRzgyX331VXI2AFi73S4V0WJ4MThEba6urtT3cb4MNSsYMNoUczafnp6+02CATmMAeElpECXGGNCEcwX4wbkDaHZdp7/8l/+yPn36lNo248Cg7xhwSdSKiBj1Qxhn5pRwprquS0ND5/O51uu1drtdeg66W8U25eUZ+dV1cSArc3x4LtaGfbAZBaSHAbABiUTViG4xYBUZ4Rn57jzP0wBaUkkATKTySEqgjWuhJ2FaWe++j+2VKXYGjEhKjiK2hEYI6/VaDw8PCSDR7pz3vb6+arlcJifZzkMCiD8+Purdu3eaz+f65ptvtNlsdH19rc+fP585HbDHnB/0IMCT6CDRLMsoIwM4xt7HJgM4j9wreol9hrjIskhcAaiJCtKy29a4cDZwGgBs7MUwxKHE7IMUo684g8MwqJrN1HRtcqhxzL799ltJ0nZ9leSJP5umUd00yusiERrow8PhkPYUZ2O/3yeHm722ZBFnNsuys6YeOMNckwwBrmH1Mk41z06hvXMupahaXc65pIPgdrs9c9IgKmw6GlG2vmnPnIyUkqWpYN/WVyWsMzoirAu6FJwFgUCECHngZ+wbUSD0MM7/YrFIkRW+k2e1qZA4OpxVnpcGC9LUxRG5tveHvkB+0Rd2mC7yWYwOGVkHrDn3b4kC2/2NdYxz6cJZ3R12iHXiHlkPIlq8qNFiPZEj5BaSDmeH9UbOaOFu9xD5res66V7WE1vBdxHh/XVeP3gH6b/3+7+rf/LHP1fXScoyuUwaQq/94Si5aGy6ttPQdypGQzor4wTgeTUVK0YH5KT5vJJzXqfTUX0/qCwLhSFoPpey4M82LSlhxfobFEcqsHVeTRd0amr1XavYbrpV29UR3LaNhr5P6RIY5q7rlLkYpeBAAEZCCOraIc08kaZoU3Ax3a3teg3HY4wU9UOsfRkjCBoBaZaNQp5n0gjIsywfIyJewxC70cn58dlGpVxOIU8cyqgEKejsFcZ5Jn03pcrgEA3DoDIv0vqxXtIErnkfTDBOat/HKIN32ZnDgCIGHAxuOPvZWfpidj4kVqnc5fvn/sR/6yySMgyxDowfUYifolfBjT7F+Pfxrdwf17h8XUbbkAkqa+yLlDuuZ1/2vqdrICdeeX4exTpzasI0B8deKzni5jsm5e/U9518dr5uUw1QpjDE7mthiBHQCASL6ID6WGdUVmUqMp7NZrq9udV2u1GeF3r//p2qstLv/O7vjOC20nw+U1GUyotcXduO83ROqopC2dgZzCmCsI+fPirPvRbrhU517Kp1fNknwDqrKj3exxb8Hz58UJ5n2u0OI7s70+Gw13y+UJ5n2u9fR0NXq6oWyaDjJGB4um6aG4FhfR47YwL0MdqPj4+JQSa1xTmXGFrAIWkfz8/Pur29TSCOdQ8hpHSYLIuNHgCSgElIiJubm+Q0AIItuPvVr36l7XabZt5wD58+fUpghLk91KwAlDHgrAtRpbquU7ME0qT6vtf19XVKmXp+fj6L/PAdtvsa0TPABvcPOLbGm+Y5XdelhgMYaOdcAsOQU/x8u93q9fU1OaufPn1Kzq/tUAWjCcggDZPuZ09PTyktiHUALACA0HfPz8+pix9nEx2GbXh4eEjOMo4e98S+26gkMg7QoynEarVKYIZ7BUzTWAPQQgSNKAOOA893d3f3naL4u7u7M6eVNKXZbJYcKyKCnBdJyRki5Ybn4XuJitIOu+u65IhYh5W0PVI0uS/sC4x9bAefp5oRuh7O5/P0J444ZAagFF3IM7L+gFNSMYk4Oe/VhyE5lRAOzjlVI7CFMCWrJDW62Mb0XGSesyadz7PB8eI5bftqgL91ggDN6CpsCtgInWAdCuSZOVUAfwYt2w58AFqcZ/QPeop7ZNYO33k6naQRRx2PR11fX180Vphq+NC1Nl2NtEqeg/2iFomuZ8hY0zTJwbV6gDPDmeXarClrZjv3YS9xnHBisaGAefQZ7+N6DLS2kW/wAw4+jkvChWMDh2wkrWkggbNGBAldwNpDSkBoYbtJX+bc8172D+cQssBiBBtVZT/R28iqlT30ADqKjpCQipwv5AqC8XJ/iKD+uq8fvIP0k9/6oLe3t/rm8z6mmQ296vqoPKsiKCsz1eNskSIrVDe1QpZrMVvIeaeujcXB3vsoWCEWuLZqNJ9HByqM6Vl916cC1Lqup7aCboqSNG2rYTQcWZ5LIRZ65+OQ2aBePstU10epbZQ5nwAOgtS2rQ6vL2d5m5IB8bA4RgFaMO19PkZZYuEmB0AaklHDyy6KQs3ofTs3CSzGwme5apMHPgyDirGtehg6zWbFBOzaQUMfozzSFK5FUacoSTsNjrMA30ZnEPwJcE+pVCGc19SQpjZFIGxLZSnPvzuP5mw99d3ud6zXeGdnMmdT2axSuIwwOTc9U/xZlCPpomnCX/By3qc7wImJjR401vecrx+NK+ytJ2fQ3GMIYRpcS72WlJpLSDrbI2TU7mlUmqVia/rJqbMGJMu8vvjig/IsVzWLdTw/+tGPtFqtVFVRya7Wa11vt3FAp3daLVe6Gtv0Ho+wunM1daP94aCXl2eFoVeRe/Vdq75r9XKK0ZgheHV1qzz3KWXCe6+m7VS0RXIiYJOHYVAYpO32Rm3b69tvPirPC11trhQ7MebK81J5Xuj5eae+DyrLQlU1H2tAIrD++uuvU3rWdrtNKVw2zxynAYcAo4GRYdjjL37xiwQw7+/vU3oRwA6m19YFAXqIChwOhxSVsQ4NMlsURRpg2nWdnp6eUt3IMAz64osvzoAHQIu0M1JsJJ21ty6KQtvt9iyaQdeiEELqpEcNDLoUoMWQU+4L48zzk7ZDehFgB4YTgM3+0iabVEVb7A/wX61WaXYQxtrOHyI6xLnYbrfJoH/8+FG3t7dpb15eXs6MuaQUmXh6ekqk12azSUADnWCjduh1SQkMIR/UocCc2rbUeZ7rmgYeo+5mXWBh6cB2Op30r//1v9bv//7vn6UKkT6HvSNCcXt7m0AwgAsHerVa6dtvv1VZllqtVqlpA0NiAUTWzqGPcAxwRgFhMMI8nzTNlWHd6NCGviIShHN7c3OT0hph2vn+tm1VFlWKDgGkWR/uZb/fJ5BKuhhkDvcE2AWs4uBYwiRI8nmW0jbtZ+/u3mj3/JzknDWfzeLcRiKznHGcaxxafsb1iA7wGUAvTiPODudmtVolJwn90HVdqiHjPHEtvh/HASeSPeHszWazRIoQkbgsU8ApIf2ONK+2aVL3O9aSaPn66kp9mGqX6Nxp18Q6EOwXe2zT5bgH6ojYF9aHfZAmB9u+bMogL/Q0epD9AUfZdDIcEewypAmyyvUvs2pwyFLEfYizIvm+tm1Td0UcfOSX9WcfLTnGc2K/LGlsa0QvyR5bb0bUzxJIvDiPdv04v+g6CCVsHMQHHTYhOMAlrP2/TQTpB9+k4V/8sz/Rf/0P/qn+qz/8R2q6QY/Pn5XnTlWxlhRGY9qrKMYwZNuoKmIqydAPqV5mv9+ra1sNXasgqcjzsYvYoLKIc0jatlGeF2PaXkwtKstCwTmVVYw85UWe2Ieu65X5Ut7ncn5QlkmHw05Ne9Tj44NC08gNUz6zJA197CqnYXIOSJNAyIoqgpW2aeV8PNx0QgvBqyhQ2r3CMCgv8jFKNDJnY92TwpjPfDxG5iE5GlOOqM8LdUPsruaNkm+bRkPfKM+kjgiQKK6PkZMQbDRjAuXZOCMFxwdnAkaFl2Vb+Cx1NDHz67w1NmyJc44GeSlyZa9pD3s6Hk5RHpIjNzW4iBEmPzkbwxR9stlp1sm9fO7498kRs87ZeNUz+bbRodEnTj+XZH733eN9GQlDebG+lw4iEbQ4Q+s8WhbC5Gij8Cj+vLm50fPzk66vb/TTn/6W3r1/q+12o4eHR/3oRz/SbDYbC+P3WiznaW9I/6jKUmVV6uO332q1XquuT6ng/Gq91nF/0KyqlI+GU1IaxLxaXcn76IA9PT5qCNTAFKpmVQLYGIqmabTZbvT88pLYravNlWbVTM8vL6ryUq+7KcJimeiqynWqT0n58/y73U43Nzd6fHyUcy797nA46Pn5WdfX18rzXC8vL2muDkAB1nKz2eiXv/xliniwR3SV22w2ms1mqaifFBmMB6kxpOrBSuMkrNdr/exnP0v3wjNIGltvT8X8GG9AC5EJ8vWRO5wam56H4SXqtdlszkCxnQWDM2jTUgAxPCOy9/LykiJuRD5o6YzxBQTyeRxPokkwqYAg3k+bZcuao/u4HnN7AF4M6LTpkbvd7owYwTHo+163t7eJSAOE0yoXprNtYwrRbDZLUTSifewlgIn6teVyqfv7+++ALP6NEwZYARgShWKvSR+kFo6hqPasE4HHCYckIT3MOu+WRbddvp6fn7Xdbsc5VbGpALUypPhQL2FrmHhuvp8ICOcHZ4kIRN/3Wq1WopjdNj8B9LOOpP6s11eqT9NcFklJ1qy+JgoiKTnHNjoDmLWAlyYaMPZ5nmt/OqZ7tCRgkecauv47qYvDEDNGmm6amWOHpbIPnKXVanV2BkjfhGXHWcYxyPNc3377bToHNk2VCAaOPecHx957n1q4kyIH629tn62HwwGg3tDWneEYIkd1XWuzWqf7xpE6HA5yPnakI1Jk7TzyC/mMPkGWi6JI0WvWIO2DSQ3Gcbd1Wuge9CbgHZDunNPt7e3ZeyzZYc+HtdGkdrLWOKJEfHgGntOmYeMIDiPm4/5xqjgzyCfXtyQ85xAHDFtE9Jqzgz3FhpDSx30R/UE+0Bm2to2XdfbIULBpgOgxzip/shZlWcVyFVM7dzgc9Df+1t/8tZo0/OAdpH/1L/9Uv/p6p//9f/R/1PPLUU3Xqh86tXWrvp8iH7GuKKiuj+raUwTZ1J+EoK7rYzjXa8qhz4vYxc7FFpR5HgfpwYAoRN49hEyb7Y1Wm43m67VUZCoWM/UhKBu8cpfpdDrq+flpHLg4qO86hfpVzw+fVR9PyryTD0F9G++71zBGtkjNGNT3sUNdWeSaVZXarjtrBx2FeUjOUt/H5g0+G0PQp1pOLj1HlmXqR4aWDC6iD1meJWZ9dGPks1iQ3w99bD86tOrGhgnOm+YClOSPjgyOU3w5hRDrQpyLDR1iy+DYBCHzIRXjp8jF+P+hj7U+fR+79OVlObYCHZS7SfkCcoo8Krp+iJGSaABiHVJU4FLft2eh9Hj4gvq+G1tyT6/kWPhMXrmCgoZ+SM6S914+fH/6HM/uTIMKugjGRhlDijjx+bMUtXHALwomhfFDkM+mIX84QlG+h3HmVmxokOX52AY+tosv8lzFmEK6Xq+1WC50e7OVz6TFfKFqVikMQT/57Z+ktsnL5VKzaqZqFqee03FtfbXWqT6Zrj8naazpyczcH85jGGLb9d3rq0II2l5vtXuJc33u7+/jwMjFQq+vr8m41vVJq9VaXdupPp0igzjKsSRVZexsRM45BkBSmrlwOp1UN41mVaXFcnnWUel0OEXyYEwBzceWuCEMen19TZPrmZFjI2k2neDjx4+xI9sIKLquU8lckdGQzUfmFeMDYH58fDwDGQApwBXNEySleS38Hofp+vo6GXrn3Nn8oM1mI5oKEMGwgIi1kCaQwbNxPQt8rczZhgaACmp4yOfHgXDOpS5hyAzPBfsoTfNUACG2ThNgjkxh7AHRgK7Pnz8nwMmfgBaY5/l8rtfX15QOFMLUPObl5UXL5TLdJ+lpAG7W2tYUkJ6F0SeyaDv12XMuRZD/8PCQIjasN6DARlVsobut+bKpVzjSgKfIJq/U1O0YqXqUc15VVY5y9aqiLFIUEMctfjbW5VVldG7rpsYwRAd0dGjKspL3YwODPNd6BOh9T5p1r+VyJeek5+eX5Lgfjwc1TatiJC8Xy+VIcMU6YuTySDF822o2m8uNJaZlGUEz6Wiz2UwFIHk8M+v11aize/XDoP3rq1brOIDYzr2xHSNZC2QM0IxTimNk602GYUi5B33fabFcKs8yHY5HhSHoar2KzQWGQX506Lfbjfq+1+F4UpZnCXTOxnk3zkm5z9QPvYo8yoZGsumbb75RH4aUdsqZtemVPB+RBqK9sPFtO9VF4QSd1UCNHRWJsOAYIpvIKUDfploiu6yXBbik+n7+/Dk5cLZpx2w20wBWGWcm5kUhJ+kwpjPnea67u7uUymrJQKJGRMJxwCAIuA/0GOtF8xCipdgPHFabYUGzFSLl3DfPzznE1lhHwRJDOASQFehLZI/vZX9Za6LvVVWp73pljvppnwgEotOW7LBRGSJIRHitjrcztHgeapqIYEOQYG+t7kpk++gkxejtVPbAOamqmer6JO+npl3YSEoKnPOjPsgVU/tNO/c+1qc3Ta2/+bd/PQfpB59i13a1qipT7gc19UFN12sIg+rT1NqQwxpC0PGwV9cczowOB8R7r67p1LVjq9Fm6vMvOTVNBKn16ZCMr3NeZTHT7iXWvmTzKrYD73q5PFOWxzlBLs+1vNpoebUZc+9fVfet5HPVXa8sBPkQFIboqHVhUB+CpE6nuh5rXiLQ7LpW++NRU0eykLzu1FVNpFU5hXqswxlGIHGqx4MX/ytns7ENQBxYy4GVpD4EhRBrgFiLeVHKOSlrTvJEKMLIQo8RuThGaapfGcaoDP/3Xsqz2I49vif+O37vpAySspPTEHoFhXESdnRKiiKPzRBCbGMenJT5TE5D7ACXO+VhbE7gIzCvxg5lsTDfjQ02grwbla/3CqFX2zWpwYMdaJv7ImKDILksdvDLYEWo3VKsE9LYUAMZjN8bD37upuHAIUTHjPocom/IWNzQKdXNudgUpBhbVfuxFiimIjoVRa67u1vd3FyrLCtVVam7N2/0utvpxz/+LV2NKTCRWeo1n8d5Atc3W7VtHWuKxrxq8r4j27oeU7kGffPNfgRlTk9PDyqryObEWpvHyTiNjkFZjFGPw34qXh8ioH16fB4V81G/9Vs/joZmCJLzqmbzlMYTjepOQ5hSZFDuxzFliGJtOqbBCkOqAN5Pp5NWy6WGYUhOT+XLpA/6vtfbt2/0+PiYIgHUQticc3QH0SBa30rScrXSn/3Zn6nrOv3u7/6uHh8fdXd3p9MIxPf7uIaPj4/68Y9/nPQUDh4MILVNy/F+SXeixga2FHniea6vrxPDenNzk9oQM5tnu91KmsYISDpzZK+urnR/f58iCxTrW2dFUkrdaZomDTYlbWe73Z51eWJeEd21Pn78eFavhQMgKT0TUToiAbZ21AIJ9u7x8TFFinBycN5Il8GpAvj0fa/tdnsWdSTVygII1qaqqtS1brvdJgeF/SEVyNZZEBmBwSZdDqBHWqYtvLa1QNbZQU6YS8TPt9ttYun5Oeu6f421dJE5J2Lp1bbRiY9z16ahllPtaNDpeFIYpkGonL/FqDtIRXPO6c2bt7q/v9d+f0jd5Z6enkawGNccR/75+TmlZ8XvLeTHdO9hGHR9fZPSp+az+fjcE2nR952en49j7eJ8cj6DNKtm41rYQZJObdOqKErtX/fJ6SdTg8gdOvsy6wAyA8ICucNh3u/38kV0BpjPY9uQO+fVj3vSd502V1eR9KlrDWFQmU2ty1OXt75XmRep8QeRv8eHh9jBb2wBzn2zBpBCRLZxfMFFpMiGENLwYc7UlJo/Nawigo1OssQJEYtLbGXXDrnifHEmOcOcA5qyaEQe+zEKgZxACLD+RGPQUc655LhwZi0hgeNr6/cgaKhn4ywReeYMcT0pRmhpAoIOYvSBc+5MXycMapqs4IxipyCs0H+QHTgLfI9trIAd996rnBfSEFJGknXEiMjh5BO9Yd1x1th/Sd+pP8JxlpSiTugkUkJtfaIdSjxlJp03pIp7mKeIkI1q0ZHSOnNRzhgeHM4+ZwnTX+f1g3eQvv7V15Jm+q3feq9/9ac/U1AEuD7L1IyMAQseDXr7nWGYHOT4u9g6O4Q4fV6S5ouFBjpW5UWcGzTO8un7Tk13VH9odOoPqtXq/Y9+ovl8Jvk8gmiMPhOzxwN5UK/6dFJwmQ4vLzGqFAZJ/jvpUNPLq1eMsuTlLM2s8dk0j6YoS+VZHECWZ1lK3gp9jEaMPcRGgQ1x1liIjQdsvZMUq3D6EJKylaYwb5EX8mFqKtC6OJ+p7Vo5Dcrz+F1Eq8IQUxrD2PTNZ5mKfHISnPfq2kxB48DOEOTcEAeAOikrYjRsCEHq+xglG8ZBuyMh4RSkwcm7TAp+/M54HRfG6FnbJUOZ+VLDmLc7Kys5pzHC5OVdrW6sl3JZSPU+mc/k3Hm7cD86XzSIyLJsnMEV5woNPjayyLM8RXWmeqjRWXWxQUJeFBr6XvNUO1JpuYwg6ebmVtfXW2U+tqleLaMRePf27RRuLwplmdf19UZ9z0DGqMAen55UFYVWywgYXl5iZ7CqLLV7fdXz88MZG20ZJ1v0jIGBPZdzakeQ632cz0InrL7rtBrrTh4fHyVNc79QkoAN2FoUJ+lWAM+2jQNGN5tNMq4wXUQCbB44ypX7lpRYfWourDHACMEYDsOQmFNANi2Wu65L9T1d1+nx8TGxafP5XIfRuby5uUmAcj6fqx2jKlIEHu/evVNd14nBhYEFvBB1gE17//59YjIBmDbNxHuvN2/enKUyAARIdeO7LwkigI+kBESYZUNKEywvLDcGkb3n+47Ho15fX7Xb7ZJxI3pDu2gcCMD4fD7XbrfTy8uLrq6u0vfBcgLgYFJfXl4S6LIsJ86BpBTpombn9vZWu90upQ4SMXp8fEz76ZxLTilROgy+rfnEObW593Rtw2lA1ngPMvfhwwcdj0c9PDzo5uYmrYUFZl999VXqiGcZ2MfHx+QsIuN8N99BdMZ7n+ZHSU4aU8/oDoczXRR5YqUBS6z30+Oj7u7enNW38D6KqrGxRC1Zc2SXFurYD2rCbBSQCJAFVc/Pz6nt+7fffpucdBqbAOiQZ863rVHCCUavAdxwggDVrCP4gHPFmbRRANL/cAz4zGKxkMsydX18DoC+TaNsRwcaPbJarXQ4HpXlWQLofDfdydCDkA38u+sisYF+uDyT2BocJKK99p5xDO3zD8OQ9DxRD4AwAB4HBCKB70ano4OpKwL0SrGOj0gX+4FTaJuyhBBSWi2RZjuegL3FsaX26Fe/+lVy4CBj0Hc03kDubPT6EgPZZhg4IpwPW5/D/qKPWWf0ArrGppBh/3AsbFMCWy/N3733qSaUtQkhJJko8lxN25zJKdfmZ5xpfo8zYwlp1ooINeSLjQYim+hn7tk6xkQfkTvmc3XddH3OO/qD66Nj+B06FB3CubQpw+CDX/f1g3eQlou5bm4/6N/5q/8j/b0//Afa7Xdqu0Ft0yXhYvFgCrIypsfhlU551RHokd5Q183EymdB1SwKX9e1ognCIMkNnZr6KN83qpYLdXWt6rqUsnJMSesUDCvYD4O6MKiYL3Tz5r1u3wQ9Pzzo87ffyDupyLIUfen7WASPgvbeqxu6sX30MLbVjlGM3Aqnjy25s9FR8s6NnjtRqF5Z5hM7Ffp+dD7GhR3rk9q+V0gh2GEEkbnC2FJ8GOtqgoKGvFBVzaS2iY0rxsPki1L92N7ZhTijifsILs6HCv04JXmxVl5QHD1TkRdjGmOIn81zOS/leaanp0cNQ6/meNDr5086jDUP6ZCH2FhjfJxx7eIDRmNZyuWFQs8wvli3Rbe/IqtUZFPuLqy5G9c6KqcIOvjOPBujX4qOW+a8vBu73fig1Wo5Ojo3Wi6XqZPYfD5TXuT6nZ/+dEwhHJRnucqqUFnmKRd8GPpRSceI0e71Ra+7nW7v7uRdnMEzjBGbp+f7saajVF44ve6f5dygx8dPauqFdruXUbn36rpSWeZSiB32n7VieCjhd1jJtCajbBdFoevr6wRe3r59q3rsRgSbTz0OraK9jwW5+/0+dTCzoBxD9PDwoBCC1quVXsa0ENK3GMYKYwf44l5w5IqiSIMOmVVjwT9Gkee8ubnRL37xC5VlmYpdbQoKz49zend3pyzL9PXXXysfARrFsYCn6KRPRup4PKaBqNTvnE4nffnllyldDOBPuhz/3m63Z0WxdMeLuqNPz0zhPPUHtm6CMxNCzIvP8zg7hHQ+G83leWezWWpeYB0K2E0MIR3uAHTcK0AYg/c8FqfzHKQLElFBf8PWAqyJFDGzA6MKwIIBBYDhUD89PaX1xzG+vb1NDRdI1+G+bToh8vJ2JCVYN+twkpJHHc3rmEpaFHHYZlmW+vz5s+7u7iQpgR7WmAYJtsbLe5/qum5ubhLwRPew35bFBUCSAliNERUIA56laRoFDSqKKXKAgxRCSA4+EU3OCP+29R7UauEc2RRAgA61HDixpG4RxQE0Amb3+31KRQU4W9lAtgBoREwsOCTNyXYGw/GCYMEJJlppa43sM7Mvkqb1G/UCGRXDEAcq4+ijl8osT/oOGYypWZ1OTZ0ceZ6Ttvx90yZ5IvWJtKqTiVguFoukS3C4U9rhiHkgTHCu0ZusO/dlibI8z7XdbrXf79M54lzZKIdNGeOaOKvoI9Ycx4n32JRiziiyyHmyKWAAfBu9pQaLayFfOKSAa84BUT90NBETmlQQPUm2zk0dLtGNFrTTNRMHjGtcko72uXkfESGb5ovzYjsjcn45/9aZIJvB1kDZuiAbtWIdqZ2yKaNWt1DHZskE9sY6VjwD2Js/eU987ohvbe0Uzp6tl+KebB0ZpCYyzJ6zRosxLf/Xff3gHSQnqamPulrP9T/8H/z39Z//F/8Pdb0b05ymWg0W3znF3F/vpwLIEfgNIajrB3VDo8OJRgzjprrY+hpB8NnUuUPOa+jiINPj4aSvv/paq6trbTZz+SJXcNME8rwcp0QvF9IwqK0b1ceD5DJleanT4aAyzxWGOIsJ5RwbE8R5TnlWxNqd0YmSzzR0fXRCskJhiI0eXJZpGLudDUGSj80LgvdS1muQU1ZWcn2voWujQzH0yTAfmwiksjxTcF5BTnk5l/dOeV7EjK8sdikjEpKNbbSdHzuSVKWqslI+Gt7j4agw5JrPFinvfwgh1o9Imi2r+GzjDB4O9NAHta1TnhVyPsQI1amVFJXj8fGT5rMRoCgTtURVGWuFIiicyAXvnZzGEG+RjfvTKjaBaNW1MW0tggGUIINye2U+pgsuFqupK9diobLINJ9Xevfuvb788guFIC0Wc/32b/+2dq8vYzQgT58p8kKH4yGBFeeirG22mzRw7enpQYf9LoGMoe9SkXM1r9R2jYah09PLi6SYIvDu3Tu5UwQPdVObdAgiTLEYPrbTnen1NbZrjYXNU5QA1gcFSSQJ5V8UMe1jN9ZlABYxWs/Pz3pze3tWkEqrZ9vq+o//+I91d3eX8r+LokhpObvdTm/fvk1AYb5Y6GHMWafj1ldffZXmb1RVrI/6+c9/noAUba6ZD7HZbNJ8HECupARMYL4eHh4SIKITGu1pMahTjVSdHIqrqyt1fa+mbVNKWlmWurq60ul00vb6Wpurq8S2Mkj0zZs3CVADIDDUgB/LfJPeRSc42FwML449s5VsVyOcYZs6BNiDUcX4WJaeCMVut0sAHJno+14PDw+pHglDyqwm6zTRYtqm88AWf/z48Yy9twDMdsuyoJBojk1JtAXUgMS6rlPUTlJinEMIev/+fYq04ZjSrQ3Qx0BVG1kgooXcwLADeJjfQbocDoFl9en0B0hBtiQlx9WCTuSPOhSah8Dopu6NY+RkPp+PHdvaFLG09XROLqVssmY8x3y2UNt2KTpjgTROBXUY7AckBylApN8RHcGpjgRRdIJoyMHnrMNDd0AbMeMFmMfOWvBq2XiiBTwzjjiyTsSa6CLXsfVuyCzpb+hBKYLcLM+1f92pms309u3bBPh3u13UJXmRcIWVq/X6Sv0wqKyivmEthmHQYNKaONN8rihioyhYd+6XrnQ2hdOmiBHtJoXU1uYhQ6SEIo/U8aA/IMpoiDGfz1MqF7qD82qL/Fljzh1Rg+fn5yTbfB4HF11DVMbKAc/E+ceZQv+gm9CLnFUaL9iMIqIlONeQX5BBEBOWLEIOWH/2hvPC2APGJViiAJtKgwYiaURveAZkE3mzQ3qliLdmVSU36iwcCH4PiUiDDGQPu4EjYp0osDP3wj7YKCF2xNaXWb1tu+dFHTa1iZeUmtJwBpEvZBCZ5U8cOVLCkfeUhuh//QjSD75Jw//nv/1vNF8s5bJKf/T//O/0v/7f/B297htl+TwtNiCgbVt5F9R3dUon4D1ZlqntOvUhOhHe+dT6OISgIi9TWlZZxjS+oR90PB40n8/GznClsqLS4Ly2N3f68OWXqlYruTwWGHoXK32aJg77y3yhrmk1dJ2a40FPjw867ffyUqxJ8mY+zRhxGYagMA5hjUoyFt7TTSAedmpzhtQ8IMti3Q6HJfNTa9iu72JK2RhRulpfxeL9EJsANPVpPAAUq46efNtqUOxu57xXPoLdYRjU1kwCPyofGYrj4SA5p9eXV1VFedb9ZLlcqus7nU6vOh6nzlLOxXbmMSJYjHNtvE6HV52OO3knDV2jbGwWQTe+fuhVlZWcdxqGblQGU251UZSKc7LGNrpFOaayrVQ3tfKs0G63l8+icp3P5iNDMddyOdft3Y22263evHmjN3dv5LzT/nWvIo9jXbuu02xOmg/FhGUCl1OaUCvJqRi//+Vlp6apR0MzE8WJy+Uysee2zXFWZimUDdsa0/syDUPcpzhnK1PT1GPNQ6nTYT8atVZ5Pk2iPp1qLRbLszSah4eHxJhmWZaYeYC1c07LcXYISo3v3Ww2ypzT119/nZxCDE1ZljqNIGM2m+n+/l4fPnxIhbF3d3fa7XbJ4YIdur291WEcVGmBowVP1LTAONFR7+XlJYG/tm1TRz0YevQFhfm0aiY1ZLVaJQMH8Lq+vj5L1WOtumFIBnsY/w7ork8nffvNN/riiy+SDrKsKOxpCOGs/gcAzjpLSg6RZXJJW8MAW4a77/vUgQ19QMSQ9AuGheJkAPKci3n+GCwcZBxo8v77vtfj42Pq+CZNjCkpWTCF1P0QdYQBZwYN6XwvIwFAmglGmbXAOEtKrbwxqKRA2ogBQ2N5RpwTzijOO+cAncRe4yQABgC10jTnxAJVfsbfAUGcFwAZ4I06OZjWw+GQ2sOz74AvagNZU8AK+yRFIDGfL+Rdls6UbVbhvVPbTek5D2N9SwSIpU7HU0pjRSbQZZwdgK2VG5w0GHCIDewVqUXW2SDCRBohL5s2Cmi3qZ/WoQd4kZLF93GP6CLq/SQlmWefuV6K/I4phfYsAzqt49CHoPlifhaZCiE2hKqKqcMgz9M0jXyWqQ+TM4bzH8aMgNB/t7FAtDNzDZrOtq2TI/KDQwWQ5NmY00R0iee1HeOso8MZttFvnDYi6ayFbf5iMZiNXlvnBzIB3U36FanH1vm3+8ce2nRB9C3PDrnGPREd57lxRm2KFzqNsw8JwO82m036Hr4b3WLTna0eYg+QfyK4rAkkJfrEnmHW3q6VbRhSlqWKLI+p/aNN4b04YVwXshBnFhuMPsAZxqahP3CYGCpMkAF5YP3RuayHlXcyiKxscsZsOiNyjk2XppR8SYm8wVFiv0/1SX/w7/313zRpkKT962vsNpb3+tEX73VzvdVu93Us3HeXNUadpKA8G2eiFIXqplGW5SqyTLfbG7lsWjLLBoQQB4KGITYJYMNiOpVT5nNpBEV9kIa218evv1axWqlcLhKbKsXam34Yc13dIOeDsqLS+mqrIi81dJ18GNQmb302CkkuOakN40HPvfoQVI0hXQWpnAXNZzP5zGtWzdIA2yzL1TRtbMSQF2edT7q+03w5T6zCy8uLjqMh6ZtaXrEAvm5q9V2fDrcbpLZuRFOCaJgic9k3TezJn5zQflKaapTn00HyzuteQZn3cmPnszzL5IvYNaksS2Xr2BXMO+n9uzdq64OqMtPmaoxCVAvJxWF7s9lMd3d3KqtKV1frGH0LMb1tGIaxc5xXkWdy2dTiGOciDs7MVeSl2pYuMKQoBjVtLVq9395s1fVH+eD1/PxJm6uV8syrbk6Si7U3p9NJ1Twycd55LecxzWV/OKQaMe+CmtNRToOKLIsNQoZhrCcr1LW9vMvknddiHh0Dp6DMx3qj/etR79691eF41NCHsc6tUtcNqqpFGqpZ17VeXw96eXoaJ9vf6he/+IXW67Vms7mKokoAgjST5+dn/ehHP0rg+DCyqzZ94zQaSpoHMC19s9moaxr95Cc/0cePH1P6FsDCOae7u7uzVIPNZpPYZxhhImZ0XuN8Eu3h8y8vL8qyWO9AET3PAxhFMWP8N5uN6rpObbFJDURnvHv3Lp11mC8YxCgbPjko1sA3JsUBQIIRapsmDYYkXcV7n5j21WqVgB/XhbEjIgSIIIWMdZiaWTQpCgXTCftJtAHnyRoxGENJCayTUgIoxKBnWRxye3V1NcrWawIBgGuMJY6GpLQ/j4+PyVlDpoiu2BRoW4uG/gGYAIjozMU64aCQDo3cMfuL54cNRYdJSoAD3YDx5b3Wmeb7IAwAOi8vL+N+1Irz+eoUKYzd+yr1fZf0swV5pLeu12vlea7X19cYlWy72MCgn1hbmF8iuKw3wGc+n8fPZV5d2+np6f5s1g5piMvVIgF2QCXnDKeJ4azo9dlsliKeVn82zTQIdL1ep8iZddCJauFASRMgsk7j6XTSer3W8/NzihTCOOd5nuqxcE7tOeE7ccBPp1NKa+S5AJ+cQ4AcNoHIq+2ChvwQnQNkI+NFnqWoOe9v2zam9o8jE2wNSIomyGm9Xqfztdvt4r30vdbLVSKEqqoy7eVDitxboA5gBcT2fZ86X6LDeD8YCbCKQ3lZ10Nkgue0KaqcC84mtScQC+wr8pXn+dkAXwvGiZR779NMLc6jJWesw2UdRKJ7dm9x8NDFRPb5bgvCqb1EDlkfnB+yDmwEB/Kj7/sUhUWuIaOxZRBOpFpCtFgSSZoik9wHzhMvGoYkfDk2LWBtOLecB3QZ8mFlHbzMs3BmLekwpc9N9fHIsCWs7P1b8i6ub6cQXCJzsF3oWl7WJiFTOLe2tsvKPNkuv+7rBx9B+nv/9f9ds/lC3hc67Fv9x/+H/0T/73/0j9UNsZ5mGIKC8/JZPjokTr6IraKzbDKg+dha07swdkwb1Hexa1rXdZpVc+XZCLC6QXleji2wner6pPlypr7rU8tlSZovl6o1qFgs9MUXX6goch1oGxqk5thpVs51f/9JTX1SWRYqilwvuxcNPtahLFfLMUI1ApeiUC6fijbrsYCzburYya2Pgrt7eVFZxe5lT49POuz3ymjG4JzyPNPhuNcwdBr6IA1jgVw/6FSf0hpo6FSOzkyWR4Ae62mcqtwr87FTEEZuNp9puVgoDL2qWan5fJ6YgfUqDqmsZl6bq5XmoxLcbDbKvNd8sVBZTB1xQgi6vb2VNLaGVhhnUjntX19FR7/Veq2X3atms1jgnXkvNzKI8fDEuU3e5CtPLNTYwWk8dFEhBbVtBKbr9Vq73S4pRoxA28Yapvl8PkZYcoUQD//xeBjvX2N0LToBh8NJ3keHMA7+K3Q4xDk0h/1eVSpojvfUj+ka1FNE0LnSbveitmm1XE1KuG4a3d7cqG6asS19vL+6bjSbTfMvIoicwusof8BqWZYpP9129prNZnrZ7fQ6srGAh3ZU7GHcI5hVSQlwAPqJYJCCVBSFZuU0u6oZ2SsYzdl8ro8fPyYZwVAvFgu9jG1YLcuHMufvAITHx8dU71VUVUpNmI2h/6IsY7fCMHXwIYJDPrMtSoaFxiHDCADkbBceC8IwsPv9fnTQ89SUAEYQsMAcJIAHho36CRw9jM9lG1kbGeJ9NtJjawQwQKw9TgD3zbPzd4gUjBmAwg6htUXyvAcHk1QcO08Eh63rusRKkxZDdI3hrOT5UztaVVVKhQS8Rzk/KfOZsnFAcdtEMNX1sc364XAc92WQc4wVCKqqUrvXXXL6rANmIzKw0VJ0npt6LMaezdKMvVk1U993Wq3W0XnMM7XN5NDOZpX6PqZV7V/3CdAVRa6u68/qF7puGqzqnE9AJLbVbtS2kxOz3x+0WMxV1400kmIw6IAi2GJ0YggxM8E5l9K7qVe1dV3WqVgsFmNqsDvrkgWgpPZJmua/2KJqdLSt9QDAIvOkH7He9kxxDixhCWB/fn5ORAPACaebM4YuQl5tnYiNEOK0WAfPFr4ji0RhhyHoeIzOCNkMXR/ta57HaD4gH5CHoxTGofTOOXV9H229c0k/oSNoZjCbx5Ei1FfxTLYWjfW2NR/oDdYPgIpDY9PySEe1ESxrp8kCwWGhBg0SQYr1k6wxOtJ7n+wN8gx+wiYDwJEPG81Hz3Iu0UWWcEG2Ikm6SoO3pSnSTDQSPUwEHeeAqB7XQ6dZBxn9xhpBquAk4RRiH3G8bfqhpNSUxBL76GDsq03jYx8i+SxlzidC8f7+PjUVWq3WKstKTVPrdKrPnK84kmOKlONkxsjdzNS9hpHM6cZMpeysTo/OqvH8TmMayrIYMfd0z/wdGWTvLSZB/yJz/HzSg+e6ADLy3/sPfjMHSZvNRv/kn/zjMeXFS6HUz/7kl/rf/u/+Iz3vO/WDxqhOr/liLp/lsevbMOhwHNkWxRoNpwi2qd9BMIuiUFPX6jXIFZm8y1SWlbIs1zBI9alRXmYqqyKyes6rms10Oh51c3Or9fWdytlCq+VKzsPExTxMnxUKcqOw9ZrNKp3qsX1oEYvomraJTo2Xuq5V1zZq9rH4tG1atV2buscMXafuuE+DwqyyCX0v9XHOREync8oyN+ZEew1dq+1moy+//DKxp1mW6eZmI6nXYhEdtevttTYjUOnbRnfXN2raJqUBbTdbtWNXnWpWqm3as9z6+Xymh4fPatpY6/GrX/1Kb968SUCQw8Ykd2oCUJTUBNgUjbaN3/H27dvUMcjmaJ9Op8Tcfvvtt7E+x7kzxs9OEUfRotybptHDw4PevXunvo8F1HwX75WmA0y6EmkspJaRjgLrSqqSZcvZM2peALTcD/NXAJpt26acZSI+KF0UOAqbgX6klAE6aHQAOHDO6dtvvz3LeV4ul2N+fJXC76TFAW7ZB64BeAC4zmZx4KlNd1iMNUfv37/Xz3/+81SDNF8s9Du/+7t6fn5O6TJPT096eXnRhw8f1I1RnuSYmwLky/Qk6h36YVA3fi8Oy/F4jLU0TaNgGHGcxTzP9enTJ7158yYxsfyc77LNCkhdAPyxDjc3N2rbNnUsI6+fgtxhGFLdEbrH7hdOD99PSkiMdmYpwoTMAyowVvwe9pKapaqqUlocbDcOKw4VKYUWRAAEKDS3KTc07wBEYcCowwAUAQjYD7o84TDCbPIsgEicbhws9oJaixRxPMR6OsBGXdfJgeW8AjZ55qhXgoKGVKMAO0p3MRtV4MzE94WxfXRx5igAZImYWKaa9FCelecljYuILO+1KUAPDw/JaSFyCfjkGW3uP2w/LDp6BWBB1MieX3QbUS8iCcgKtVXoJNKmsT82Ekn6VQhxADBEhk29kqbIDnrDzlhBlmjCIikNHOWs8yzWAZCmTpykFjHPCiKHiCI2k7MAIcI1OAMWWpGSOXX8mggBe93owMb7toNokUe+C3nHySBVz6bPkY6V5bl8PqUXssdEQLg2Mma/z6aAcV5tXQ7DVAHoEDA4O6RGUbvJsOHHx8ck29h+Pk8zFxvt5X6wX0Q9kB1LbKLzkSf7zFYfhxCSTrXfj1OO7sRJRadd6m/2nb1FPokqkm4GuWZT69A71uGUlOw6OpVoDVEdznsIsWU3OpUsDtY9yQCRSO9VjvMfpakza5T1tebzRcIONpoXx3OcDxJH5iSfmjrYdMqYAjtFgZDLiUiehidzPUgOu7forunsTDWD1pmWpqHIrDNRTb7/dDrpcDjob/0v/me/cZA2m43+5E/+5QiAMoUh19e/utff+Tv/sf75n36rbhyS6rI4KHa2qDR0vfLgVJ/irBdAcpZl6odBxzFMj3DDmPWuVzYrJI3zG2LXg3hIFzMtFrNRmY9tYuki5yq97mKBMoeZuofOSd3Qq20bnU5HHQ6vOhxeY9i2j40XjqeDhqFX37eSgvquU+6koZ/CjafTKTaNCL0K3ygvct3c3OjtmzdyLk51rspSeea0Xq30o9/6cuyAJ33xxXsd968a+ph6YBmXzXYT61fyCMAenx419FMB4aJaqmti97vjIQLN9dVVbDXZtIpTjqfUksgM9nIuDsHlIK3Xa33+/DkBH8sISTprdwoQK4pCDw8PCRwBVqwBsOkCIcR2yLbzEUqWQ2zbRMM27vd73d7eJsO6WCz0y1/+MhUeotAwJKQV2Vzj3W6XQPpms0kg8dOnT7q5udFisdBXX301Mr+RGaOJADUu+/0+pRphoFHWpEMQpbHsOuCTdDQLjrMsSzUesDG23gMFfnNzE2eVjKk0d3d3qfYB4Hxzc5McBtIwAN+k0pEWQ6Ska1s1YxoGYAinbTab6WrsmERBNcxyCEEvT08JDOHUMEeC50IGpKg4P33+LI3GCKMahzRudToetR6dT9bDMs2WzcNxx8khZQXlzrNauWPfqqrSy8tLcnQB8zDVwxBTwe7v79PZwEAgO3Vdp5lGV1dXKooiDTaUlJjSYRjSjBkLlGznvsti91SjaFJncO5tSgtgnnQ8WzuDLA3DkMDnzc2NPn36lEAVzj9gAplmHTF+gHj+s86YTbngM/wXgWVQ20wsLnqEdccJBYzgAA9Dr6KcUuZYD4w4ck9KGY5bfWrGbIT8rAYHMJ3neTqbrLvN47e6C/vDmvA90lSUjGzRqAQg+/HjR7Vtq5ubm/RcACiIIZs2CLBj/zlrpJGytwBLAJSkdFZgrG26C/eIPBDVAJBLSsXfOASsC/tF5IK9555t/Q6fBQjaonnIJ8grvhOdgHxZZ8juKbJpHUDk1uoFwOz0fe5M93Ivcc2mzlt8J9E1nDppSvG3Tjpn+CxtzXsFN9W+sN/IDhEMHFK+73Q6naVgoQ/QRaS/sW+kdwFSbUMO7DXOBffHntmUQmwPDjjfiS2jMQVOFGSiHamAPsU+QFiQQmj3D7kl8oIDQuQKmUKXICO2Fgp5Zg6ejQTR2Y8IP+tEJIoumzhfRMJ3u53W6/XZeWGdeH7rWINPeHGG0UUhBGUuZiZwRm262zDEeUGXEcuoD9t0ziEqIFyen1+0WEzdUa2cVVW0F7Z5y3QuzzvY2XPPMyPD/M7qPZ4RWbF60EaoORNWBv7D/9V/8JsaJIl2zbny3CvLneR6yfc61rWenl80X85ja+6+k7wUwhDTtJxXURaab9daLJbK80ynutaHzUZSHCwXa3nirJ6iLDV0AIeTQoiHqG5qSYMOh71Ox1ZDHw//breLHcqedwrdIOfi5Oeu7ZTncf7Qfr9T2zbq+lbeOXV9bCueead5VWi5mOuLm5VCyLTZ3On29lpNU2texlax19trXd9ca1ZVms3nyjKn3E+pC947zapZbI0tSWFQ20ZjXJSZTqejirxTnw/a3LxRMQ5QdWFQ19R6fniIndx8puPhqL7tddgftN1u1HadjqeDMue138Vn3mzX8l4qSq8Q8jENrdBstlbft/JesabHDWrGYbwYHBQ3w//W63ViGemWhQPFwEFJyQBtNps4c2cECURbMJQABsLhKNa+jzUORCOYv4KCBxSjtD9//pwUB0XTRVEk5/Lx8TFFCoh+McPBe6/7+/t0fzjNu90uzYU5nU56+/ZtisRsNpuUokJ4mXuyhp40EOp2cMJpqCDpbK1ZGwwjzg0AwRp/jAR1Rk9PT2nI48vLS1L4GA3rcAH4Qwh69+6dmqZJxa3DMKgbIyRd1511QGrbNtVw0N0Kp+Z4PGplOgHtdrv0HhQs+4syTdE3k4aR57nevXsXAeZyObbCn9K52rZNbN3V1VVqVnF7e5siW4Duvp86Z61WqzTvSZLevHmT8v1fXl4Se2hThNgXoiw2hQ0AhtNL6hcR1Y8fP6ZBrdQoEEWwoA7WDVAAA8m9bzabZARJx2StLOiBNbWtvNlr/iOawwsyg2gU+817LMiB8U2Ox8gYsmb8nOvR+QrHyfuxHbbzms9jlM0CWQyxNfSkdZ5OJ5VVkcAkZIakKY1lNO6w5QCNPD9P8ZTOaxtgV0nPtE4Rz0b6CNE91h39YaNoklIraNYNsoI6LkkpmkyaEDKAA4IjCFANISTAQ+Qa/YHjQjQH58iSF+gCSCIL9khd4pmx4YB+G423joAFWZwDG+mxES1b02BBF2DQe59qpvg8Tqp1LLgH9KPVowBP+xlkMK7BxHpbHRvvaUjpf/Z6fJ71u76+TjKCA8dZQOa8j0PEW5MxAUHQNFM3St6LM0n0A+eItaLOCifeOgJcxzqOyC2RQ0jC1WqVokwWcPOMkGcQbS8vL6lWDVyQZvsURUoT49zadEsigjhgRGRItWNPqFHL82kmHnKPY2AdeM4aEW2ceUsio1sB5hAwXBsnhmu+efMmnaftdpvkmnMaQqwlI0uBqDVn8vn5OdleSF5kuKoquXA+W86mQMZU+2leG7V58TnbtKbWAcEugT/Q3TjOcR4kM0Y74zi3yvMiES+QtVaP2Ai+zU6wpBjnDP3PtexZQ4/T/MXK61/0+sFHkP7RP/pH2mxWKspSXTvo5fmg/9N/8p/q//vPfqGuC1pvN1oslmq7Tm3fqagqZVUhn/lUH/P6+iqF2HVGmfS6e03Aqx+icxNOQS8fnzWE6Ay9vu5GIxcN3uPT4xTmJM3Fe7muVu7jIaStsnOxmcDb7Vab1VLVrNJ8PtNyuVCWeX344r1W25kG9VosYrpeXsYubN45zUfDmflsVFTM73HquiExQNvtVrE5Q6PT8agiz3U6HbVaLdX1rbqOmoVC9WnKDw0hTk0fhkE+y3RsYpG2QtDzy4uGvtdiuVTmg/p+GtSHlx+BTq8iL5UXufIsU9PGtr/1qdbL7jmlhWCEpXO2AEV+dXWV6jw48J8+fVJd1/ryyy+T4rHGGJYoy7IUnbKtNa2i+/TpU1K8RAOkqfhRmgxc18XBlDDypDnRNpk0Q9aB1BMiSADqyMo8JzCFQQDAYAAAFjZVkCndzCXCmFkjjNEjl9lGX66vr88MFwqdv/N5FI812C+7ne7GVDNbp8RMFhQcKUgoV8AyzGs11gEdDgfNqirOizIAIjUTqGtlJjUIINH3vcoR7NtnOBwOyZE9Ho+pZer19XWsDeg69SYyASDL8zzVIElKzs2lUcRgWbYbg8ye3d/fJwcUmUQFE53EsQWYc23rEEk6Mw42J5xrdl2n6+vrZCQx1pLSGg/DkNL7eNmUJiKWwzDo9vY2AYr7+/vkDJOyglNjnSYYYXL5Me7svWVBpSn1FQAHyLCOlk2zyLKpayKRLH7OM+PwcT91HRuolEXsvkYKFvqAFFNLsrAu8X7yWD80yuEwDGntAemQLERcuq7TYr7U6VQnht5Gu0n9tZFaIn/oBvaf++JlwTfRWNYWnQb7DLih7bJNyyNSy77bdDgikTYliXW1+sA6LjhaNlWH72NfONOAUmwTugu9hf5nPZFXZJ3ntLV1dPa0TTsA6zhAgEjOEvqTPedlATfrwj0ReecZ0c2WEbdMdlwbnYE6wHZ8xizJM/YIWQGUkl6LXLDf2EYi1LNZ7KD7OhI5VlbQSXGUQ4yeIG9ZliUHhDW29UmWIOS5cX66rktEJnoZ4oS/W8af9cVGEL1B3nD+2V+7nzaawr2he9kDdBBnjnNFuqhNdWMfOEOWcCDiLinNULLkQpZlZ/eGzkYG7DBc/uRFqjJny3YitamxvBc9eXd3l5wPdBX7y7qcRRq7Ts1pqqvj+yKxsTiTO/AGpL9zSnKPHonpoUHOTREeZDDinv4sBZPzHTGdTzaUZ7Q2wabj2WiW1QXsG7KEc2VTXyHrOHuHw15/8O//wW9S7Dabjf70T/9U2+u1yrJQGJzaNuhf/auf6+/90X+nl91B+2Otpu7V9lJRVPrqV7/SoZ66RO33e72+vo4GP0iuVdd2OtW1hr7XicPbSzNfKA4GHXR1FaMlcnFw5XrstFJVpX7845/o7du30QjmQZmPyvLNmzd69+5dBLX7vZZlJQ1BdX3UEOLg1jDON+pDr65vtVzMVTcnFWWhtm00q2YK/TRRezar1LadYupaprqdDk2WxSGx3Xi4J0CSSxrGWqGgqprrsK8TaGzbseCx61SOitWP842GftB8MQ6hy3PVdQTCQdJquVTTtppVlU71KeUmo8CIlpxOJ3348CGBLcADjsp8Pk8dy/g5zgZAEUapLMtk7C2rRl0W/0apWIcjyzKtViv943/8j3V7e5sAJ0P2SG8i5YzPeu/18PCQUrtQ6sMw6OHhIYWqUYQAi+12m4CLTRdkvzAc1JxgtHB4uB7OmGWk7dwcjCPpNkS5LHuLEsMhsUP0UECwWCgq572WY6TC5knDBrFPrK8FM6zhbDZL0cG2bXU1RrKoKUApO+dUN01qtoHswt45E0UjjQHnFlCLsgdwBSl14MNAArjbptHc1PHYlCzWLs/zNIwWwHVzc5PSkfg9hpHIIA6JZRetUYalZU4KjCF7w55jFPs+Ng95fHxMaXYWXPR9nxo84LxD+JDOhwy8efPmjJEHvDPYdBiGlELDebXGqSxL7Xa7lP7y9PR0Bo74j7Ntnxc5tyksFM7bmjyb9sfeME8EVhiZgoGO65Upz6a6NAwz32FZcKJHEaA7HU+HBCCpYbJAG5mE7cyzXEVRJbnjzAMIaBsPcx+7RsZaN2qTWG/Auk1XwtnhPegL/kTWqeGyzgf3yMuCQ0Cx/R3/2TRnPs/zsB/sIfLBNaRp+C33yf4hw8gEoB6Ay++BLvye/2wKrE0rRf8ToUWG+r5PHcsgOfgM5wASgMgrRA/1MqRzAfK4b/aKc0dKInwLayMp6R3svHVoALSAYVKyiXwQdeGsolPn87mGENT2U5MCyDsiatvtNu0dZ4o9xS5z5lh7PovMAd6t48V6scdXV1dp/XBUbZMIzrglSbBp7BGRtctUL/YAh87qFZ6NM806U6tsHVmiTZZcI9sgReSkpMcvoy2sF3aGe0S20NlkAUCu8RzIHKCf+jSIQ6Kb3A/kEl38GHvBQGWb/no6ndS3nYp8qrtFPuP6x+Yu6BL0bVzfOK/Rpj3z2a6bomA2HTBijKm5FfI6nd2JeLLRRktqW9myBIm1kxMunWq4LBnCPvGZx8fH3zRpwEH6l//yX6osY2ciJ6++k2bzlX72r3+hP/uzX+qXX32rz5+f9fnzsz59ftTrbqfQRWNZjKBzv9+rKEuVhVdVRYD+4f17rddrffr8WV98+KDb262Wi1Kz+UyHw06//ds/UQixU9vVaqX6VCsMU+cNgHMaeqo4qgigVhaFui5uft1ENrYsMr3sXqKxzWfKs0KvrzvleSbvFRWrJB+KWN+UxTQ257zyYgw751OkY7VaJcFtu+j0bTZXY5e6oCz3Oh4Oms1nGoZesWvS1FLxdDrp/du36vtWTi6xVfWpjjVPytW24UzJTQe6UN3UCVxK0ViQ+kUraBQuc3IA5ZaZw0DgdMAa2nQ6FItNkSD1A+WJMnIu1mV98803Z/nOgDHbupNUJNKQiBIBfvb7vYbRGpK2hoGBOcGB22w2qVYJtv3u7u4sxczO9kHxeR/3vRnXGCXCmqJgSFPAyeH7qFchmkTtDGCY50XBSZNTgeLP81xd32sgLB6C8pEBBHQTvbCOHfuG03p1dZX2sBiNbzmCNRhhANDezOrpuu6snWk5Ah2UJ/dOWh1O9/X1tY7HY2KYcgPqZ1Wlz/f38qM8hDEaR+E2KVywrjiLAF7vvd68eaOnp6fE/NIWvRmjrjgSRABhqDHirDPOGOBoNpvr+ekpnWuIg1/96le6u7tLhowz0vf9OMsrntGUelLG72na2OHqm2++kXNOy8VSeRGfh1RW7qMsKx0O+zFClqvr2hQVOh1PyvJM2+21uq5NLayraqYQhpSiA7scp6ZPw1jzPM5ny/IsgZ0I7OIYAyJacZoYdXZedT1NjKc9Ni/bdW9ysMfcdjd1rqTmgqJquzdZFmenhSGomsX0ZPY0viYjH0FkN8plL+fiHuxe9mfgmfOL8SYSBvlgU3HQPUR0LPOOjrROghQZ6/1+r/1+n1pXw4JfXV2lc8i5wlm2AAVdZOuUbDG6dZovI1w2GmezAGzUEECEbbBpUBLOFN8zNTtgzXBIJlZ6csC4V0lpfThDFkjZdaagG2BmIzvc62KxSFkLRCTRX9w7qanIAyQEfw5DTLPjvOd5bmp2pq557DF/Wt2JwzIBa6e2bWLjqa5TNdqGfhjUjucBMI9zTRYBs7JIjaSuBztmHQf23Hb44zWfzVOnw6qqFIYQz2kboy1t1yY9GIaQIrFVValrO3X9lGaHLnUu1msjP9WsSvcwkR2TnvSjAyhJuSFPbA1MlB8vZvxxniIOqBTGeVM2Ukozpfv72JUWJ5S9sqRl3w8KYUrbdM6nCAypcNSmcn3Ohm2ikfks2QVJcSalj50M2UvOZRiCur6bCMTRqbWkV5nHWZHoU/AI92jbc0/P0ivP/YgNGlXVNJ8y3nP8nHXk2Kth6DWfz9LaWGe270NyYiCFOR+Qwzajwjqc9oUeQo9Y0oYzwufyPNfT85P+6h/8ld84SJvNRn/3P/s/a7vdKM8L1fVJXdtpe32tEOLhWa3Wqk+NPo1NAPqu1+PDQwo7O+d0f3+vIQy6ub5WNjIQQxgSKFsul2MHn9N4YKKS8qOQkusKo8PhhU28uro6YyAxNk0zDX2Mc4uqcdYQGx476+VZrt3rLkVUmrpNTEY0DIPqesw7LUip6OV9FNrDfq/5fKEhhPHgTylZ5LguV8vo+Hin4+kkPx5428lMigKYZ7Fdet8PyrNcbjS4T0+xnXjT0qkkS1EBW/9gO6LQAtqmSnAAPn/+nJw8HCKYUkAhKWa3t7dnRbesP8qStUZpcUABChh1DCzOGukqAJ/D4aBhNKp0dLMpZOvVSvUoDzDMthkAufF8383NTVKeAKvT6aTNZpMY58eRVQNkJSa7bZX5acI2QIKIEkoFg8ggTkA46Xy2MxRpKTbNy6bdsUZDCKrKMnV8bMYoR9f3qsoytaW1ICyC0Jh6ejweVTeN+jHthXtkv2ARqcXquthKnPbcOFmkLWDMMD44hLPZTMvlMqXbzWYzVbOZnp+eJiAxOh+vo1PFMwIyD4eDXl9fvzMPqe9jR0OMOGmj7EOe52nIIdFqSWf1QtQ/sH9t22pWzVUUpXzm9fwU01EXy4WOh6Ne969aLpYJNGMAvfd6eXlW1/Uqq9JEw/KzegMbSWUujpy0mC/Ge81Hx6FSnscW2af6pMV8kaKyfd+nobu02u26Vrvdq5qm1mw212q9knfkknfK85F5z7zcOPR6StsYW+J7W6jbqyim+VVDGGIEcmTn2SPn3MiCtvI+U9sy08mlNbV1Nqyb807OZyqKPDr93msYQiSovI9dR9007NC2m80yCDmNOrpTPg7mRqfZNCAAkq2H4J7YF8CaTXuTzgvyrYPAc9zf3ydAYoeLcl3q+i5rUVg7QI91Koic8P1W1vgZ10JvcQa4vo16WhBKem4EZ9EBb5p6bOpTjiltCx2Ph6RDAak4SThqlp2nnsWSS0SpLqNn3JdNN7IRM+swQiDhOFxdXaU0UhxZnAvOb3Sgpk5qT0+PaS5OUZQKQWeRXe+9drsXE3kvk2OMvj+ejho0RceLotAwRkYXi4XkwpkNI6obMUirEOJ143Of5JzXbBYHptM8aRjnFoYQi/2r8dx1bZeiIc45lVUZx4AMQ2phfqpjS30c2rqu1Q8RwOZZrqBINqyWq2TjhmE4Sy9lP4qiUNM2KtJg+ihvTRtrtbMxdbFtGjkfa6RP9Ul5NqZd5zGlvx9lk86ayESMqm1UFIUeHh7TeVytVskOsvdWLiC/2FdwDPaq7zvV9RSpTs2Iuu7MztoW5X3D8NQxMl2VSY8MYUgD6vu+V9u1sf27d5rP5slxy/Ooo8M4rga9isPLmbVpfci5vdfowMRIE85Myr4Ik3xZwkaSlsuFmmaKBkfZjTqdelUILAgSG0myEWGr53B6rGNko1HYTe5tOks7/ZU/+J/+pkmDJA19r6EftDu8JO92Pxa1z+dzPdaROV7OR2avcFp8+XYErFH5/PjHH0agU6vvpSG0I+u2183N9bj4UlHEaeOSdByVZN/3urm5SSx1URSJmbEdSWDGYWKpf0I5pHSRMCnwGFaMrIE0TcYuylynWuqHTmVWaD5fyfk4bKw9NslZ2+/3urq60nK5SHUVZZmfARGU+ul4SiAax4tOUwhlVL69Xl/3KQJBS89YcBpiNCoMiTG/vr5OYXfnXBx2aNgUQBaKH8XUtq22221SVhhXIka0UyZtjLXHGaNLDOB0uVym4sbPnz+nQ/n4+Ji61HEgeTbSULgu1ytGx8Cm3JA2M4wGnCgNQB3Hg30n2gFoncLgsR33ZrNJRvhquz2rdaBxQ55lsb5rVBSAgd1ul+qeMOKXaSe2hbTNgQZwsAeshc3Ll6S+6xSKIrX+7dop8sh3zWaz5IDjEIQQUgpBVVVajkQFNVucGRwjUg5xLIdhSJ9hj1DwtBAn7YAIQNM0qdvXer3Wz//1v06fYU/60Rm7vr7W4+NjYl0BuKSPYDAxuOv1OqVVck/IFvKOE/Thwwc9Pj4m40BEj3sglarvopGpfCQMqNdaLBZar9bJ0PPnfr/XmzdvNJ8vkizWrjlLk7FsLU49+1TXtfoysozH4yn9rCiik+DkkjxjzEMIZ3V9pK6Rtmrbfef5NFB4upc46oDzY1PHMMDILc7EfDY/Y5Qt2ZRlear5AASQiodRRz7zPDpFzemori8S2MEZozrFAhf2p+tifdR8FtPJkuM5TPVqlrWFVUVvdV2XGn8AMEjxAZQQ1SB6y17TARGdygBNiA0LMkkDQmfYyJY0RV9sSp+kRAjxc2lqoGHTLbFbnA/eTxomOoQ/IZ44s9EGBHVdnUgq9vJ0qs+axFgZwDmw6XNEd4jOJwdiPOO2Ff3EbvcJrOEEIXN277AnYcwQ4B5ZZ9aaM87Zl4Kapk6kjE1VLssqMeusd4yKEomdmHfsUVM36jWlF0IYZnmufBzdcTgcUoc4Sbq/v9fV1SalfFXVZO+jHB5VFF2KlFv2v8wLVSZSwXdio1gfC5RJg+L8dqcuRobCCGI1Rf5shMimo9uOr/mSqOCUwo08RrvkVRQufYfdq6qsdGrqJH+cK57hdKoVwtSh1PtpALWt38RpwhGB/ACQc3100Ha7SKmLVl/YqCdkZ1VW6v2kX9iXlJqsadgwn8dWcu6IIqGLIiESZcSm26PrJSVnhfPOn4nEHM8URIatG+J5IHyITIEPwGvonuVymWSD++Zc8R6bfp0IMePYke5obas0tWwH46Bj/m1eP3gHiYNtWxujXLIsS20fMZZ2QvTPf/5zXV9fp4Nxc3OTlC1FnrZfPcqHgwJTYw28LcbFqFFA2PdT9ywUD8oBhs9OfJaiEKzX65QiQl0Dny3LMoE/Usr4XoTn48ePKTWJyBOHrus63d7eJmYD0J5lWWpuQNGgrYexqQuwlG3bntUu5Hmub7/9VsMwpO4tMPKAHwsSYecAfkSVMM6AdnLs+X4+TxSBdYOlsc0TMNDOuQTUcVpvb28T40F0DXDz+Piou7u72C2trkVY9ttvv9Vms9H79++jEzeyiX3f6+7uLnUGw4hiFNgfFA9gAjlNbbq7TsdxT6krkaKROOz3ysdrs7YUasNswqrMxhbdyBMtt6ndQSlynjCkGC5b9G2V5vF4TO19WX+ACY4w0TXAy93dnT5//qxhGPTx40f91m/9ligm/vz583fqpPgulG2WZfr06ZPyPE/vhfH++uuvdX19rZubG+12O338+DHJZ2QMH7Rer5POeHp6SqCWPdhsNunc4uBw1kmVpEPU27dvExngnEtOgc2V5ywDrDh/tgkILdrrutZ8tkwMPMCW7oiwadwrr8+fP581AgFko1MAckQnMPK8AL2LxSIZIxziw+GQIprIq3XokUmiaOhfALmVc8AGz8H7uCeuTVMEPmcjE6RInqXdjDoasMHfAaaAMuQ3OlRTwwELbsMQUooMa2Ofh5eNFl6SCxYkoXfYC54f8I7zbZ1enBLb2rcYCQmIAtI8OQOsHalg6E3Lutr0Nc4WRBDnnp8jRzw3KTE4xOheOweJFwAawhASgD0DTFuiAyAX7yM7I2boLMpnsdOkTHLWsPvIXd9Pc+hsSs/Dw0OK9mHvWEOAOAQAQ5Bt9Gm1WiUdAVi16YtEjNgvzkfTtMqyIulEGw2z4wwsaPY+djPtNTm3EBbRcfA6nY6JGERW2G/A/3K5TI0d2Bv+BPQSdfKa5jJxLm2qnc3q4Owh05e6CYfTzlvDHvE7vsfWNXIOsuw8jZE1Y03RJfwuyzIdTydlxRQdBFwTwQTMg5twXpHju7u7dA7Qg5CJdB/EkeIzFtRbQhO550z2fZ8GCPP8nDHbotxmwiC74CPsC84twYG+78+a0oAbwQXYaYhjq4vZVxwN3me7N9rIGM9q5R+dndLyu2lOHWuGneO7UtTSnENLZLB2khJJjh61OBYZsXbtL3r94FPs/uEf/n1tt9sknLvdLnVagUEHuGEcOQgpIlAUSRisM4VzgNEC2GdZluag2CJVaWLbAMYcfOk8P9iG5mHHUfQWhAK+cMJwjCSlNr04DeT9A1IeHx8T84NRJSqz2+3SwEpShe7u7vTzn/9cP/rRj9IzYdAAfUTC+H4cHQatAmKmdIEi/SlNjAGHmQO83W716dOntE43Nzd6enpKh+Cbb75R3/f64osvUgqZNLVoxTFCqVuWkT23ufWPjzHtoaqmGQUAO2QghKDr62s9PDyk9pqkiT08Pqbhs6SrSdJ8NLhFUSTwbeWD7yGqRg4/oPn+/j4V1lZVpaZtlY3yQDQG8BpC0MowuqSDErG8u7tLChH2FwUDIFqv18mpRwHa7kkhhARG+TzG1g5ozPM4uNKmFmJ4IAYwKChYzh3yhBKkG52ksxbw0lToChhCAduoJGAIRhnmnQHBkBEoWtYDQ3d9fZ26DAK01+u1np6e0gBgmgI8PT3pzZs3CXyj9AEfNJAAYFMgjo54fHw864y0XC7VdyF1SGS/siw2WSDNA6ePz9kaDJs6Ydk2zomt1bHpDxhZAL+NFlkG/tJBw8Dh1ANsbXdFIrwWsPEdkE+QGTCJNvID2EXekCPkmmfnu3l+HC27JyHEmtBu6FPUCd0Ra6R6NWMUA/lFd0nnbXQx4HSXww4hjxaY2NoiCzrRYYA5GxGyzCvPbtNeLekjTQAfpvxSFojmQlbwnkv2ms/xYm2RB+4fPUFWBOsM+LRrwnMjL7PZIpGOFsjGMxJ0dbVOJAJg2Ubd0EWXup4mOwBNfmbZa5xISFAioIBaupVa3ICsQ/7YZ+HcAS4hJ+17sd+S03y+OMsUgXi0nQcBzUVRqB96dcPUwhvCKd5X0Ha7UQhB9/f3yvOpjXXbdur7uP40puIeOd+WxEpEQN/LO39mK5Av9hjy0jpKyIwlNqwTxF6DedARrDWfZc/LspA0ZQKwh0R0hyFmTjDPLBG33mkwpB3XtnXP2BELwK0+Y9/ACDYSbyOY3D840UZ8wAfYOs5hURQKw6C2bpIO4vzxQu/wJ3aY+2vbNhHMPAt64FJncX9gMfaDs4PjZiO52HVSdqm7s2tmCQv2hu/kZxDbnBdIgClTYequybMgb1bfcE2+l7VHb7MfdV3/2il2P3gH6f/1D/4oLSIbhJBikJnbAqiktkCausFZZQdQYK4OQgS4YE4KhgC2Y7lc6vb2Vn/6p3+qDx8+JCV5PB5T3qntVMLm8jscISJUMM4oSRsVsykSKDkK4XC2drtYt2Tn1tgwJtciSsAwV5vDTb0B3ZZgWWGlAaSPj48JtMKaYags0MLwSEoHHOBjDTP7VxSxFTeHAFAI8McQcJi5NxwGlBdsIbN1Xl5eEpsGWIMt8d6nrnYcWK7djg5LNh5IQBed35wx4IBcWCbrKNoUMGpEPnz4kPaHORKLxUK78Xmsg0+kZ+im7kU2MkikBOUnTTUuRNNCiMNHaUxweXZgjvI8Tx3Q2G/LjLJ3KEsAJHuVZVkaTHoZebQsv6TEusNKETmq6zpFslgLIhqsJcYIcIZRwIm3gI10sP1+f+ZYIfO830ZqWXfrbOz3e202m7Q3RGg4QxhFa1xsuoBlC2FQD/vTmRFumial8aKv0C0W4BOVYi1xZtBbnBH+A5ySHkx9HnvPumD0cIos8SFNDgP7hcyw9jaaBiMP0CR6hr7FyLMmgC+ua/Uzsm4NKHvDPrFW2AZ0vvNe8tMe8Nm+7xX6QYNJs7pkJTH2AA3SGnmx7jDF9rzb6CxOJ2tCpIA1ts/NfvAslunluugo9C2OF9fBWQPMor/s2WUtbMQMQobrcg6JtLPX3CeOi03XwemmQUlcp2k0A/eKk9w0Uz2pBV3YCn5ndUlRFElPYTttdIPoZQghpT5jc7GhdCblvpEXvpdzyb5bAnK326UIxZQueEqyyJlrmlaz2TzZdmTGOvmr1SrpatpVd2GagwdxE1O2lqKpyGU3uqqaKc8nObDE0mXUDMLWe6+h7VKapsVA7CO6hzN4mSYKoWGjOqwJZ9iCYGy/Td+MhNEiNQ2wWC3uZam2nc6Ajdq0fZfqY3lmzi3/4eDZ1FwbFbe2ivUD33B/1iGy6W4W8zCew+IVdER7qhMpCxnAvdoukDg89pxz7+ApvpO9teQIZ4515L3IgE175P7Q+ZDRlkjkGjgq6CUcIpx+dAsYyJ4nGzXiXtl75JK9sNlWnBWrv2wQomka/U/+2v/4NzVIktKBIS+b0BsbsFgsEvC3oAPnhsOKoWSjL5k76+Gu1+vkFaMQpQjumB/SdV1ih0nxohnBZrP5TtoXdQ8AIsuGAOwZwEYdDwrfzioBEFtPG4AJeOi6LoEIBBNFDHjDyLBOi8XizMDC2mI4UDg2rMqMA9YRAGtZYtt5bmo6EZLxoMgeZoBBqzbVyTI7Nm2De9lsNunAsra///u/r7KqUgt0aZp9hEGFoaBIn33NiyJ2rtPkYCMfnz9+TBEWwDqGQlICD3Vdp/uyDjeAAWZtt9upN2wt94bc9OMe3d/fK4Sgu7u75BAxeJPUKqKhDJRFKeMgLxaLM5bdhssxqgwvBAixxrPZTJvNRl9//fV3IoNcd7fbqa7r5KwjI0RRaVmNESW9BuYL5Y7zZeWOM4wxBPyQooSMQEa0bZsifDwj6SkYPL6f1BRpSodDmfOczrn0PTbCQo2dlSnmUElK542aJ5wXoskYJSJPpOFYsGOJFGqjJKWzAKCwDCEOC04IRtbu7cTSnhssjDu6I6Xl+CmfnOeTpi5tFgAi6xjYpmnOpsqjuwAtrKd1lCw7bckKwKutCQLsAvKyLNNsMT/7fAJIxvGykQIAHkacdCGiMZfRAO6P9EnuA8Bio7XIITbJssrSlJpyCWCsgwWgtQCVyB3ZELZwXJoiXcgK6TvWObSOCLodPYC+Rr6IhqPfcdQsM841m+aoqpqdRTXt+eM8WjBmIy3YDe4X3YpzQLoScmxTC6kFJTLrfayXIKqLg8h+cuZXq5Wen59T5BXnmHPC+edeaCIzpfHfqm0nuy5Ns2eI4pGRgE0vy1LOOw2jU8KecsaojUaX2P1AL6GTLNFh5YuobqrvGX9n07cB7XzOPi8ZJLy4rh0hQDSONeUs4JjaIn7ksO+HFC3DuWZ/uS+cD/ajaRr5LFPbnc9ewsbhCCKb2D/0A+fcrpF1+KwTir2uqiqlV0OCIMvoHJvlwrOyVmAlsizYJ0sUWWcuhJD0JcQYUXtky5IdNjqDPQeTcQ0b3eZs8d32ZXUQesjWT3INbKi9H9bVkgzWmbS2DJ2NnQczXzrT7Dt7TUbMr/P6wUeQ/uEf/v0U/QCMPz09JeHabDZnhatd1+nz58+p1SueOeARZUqaHsw1h5uDYQEPTDhhfxTGYrFICtU5l8Lf1iGwuZi0Y73Md+fQXAL5S9a6KAotl8uUm348nbRcLOKAzO68EJDneXl50du3b7XbvSZHrO+nsHBsVzp1RIoAKJP3EzPB7JPNZnPGxmIgMUKkQ/A7mjt0XZcGwkpKwIbwPUYRIxiNYmwrHLvoxQP4+PiYnD6rDFlfFCsNAFgrlB+gzRbP4iQS9XMuzueZzedaLZfRcI7Rqqqq9DrWCQGubb0KssXf7T5YxUCzgrIs1Q+Dur6Xdy4O7TWtr51z0jCcKRquRx0dbbWZ32M72VgnkudEyXI2bBSBfH8ANrVSWRZTTiEM2EOiBzh8FlCQxkjrbtg1vhc2DacWJxSDj1KmfoPnYN0toLp8Vv5O8SfOmzSxZOgCIsMo76ZuYpt8dz4XBZBKkbU0KfhhGNLZpv6L+glqwLyfOvu87va6vr4+Mx6kM1rgb51ZABwdDVlj7+NsIggNZAQAgwEk6spZQ9atUbdpXPyMZ5Qm8GzBGddHxvgM0U6bfiVN9YSWwSXiB/iwzHc01k50ygthAkR2fawhd87JZV7eZ6qbOrUqds5p6Ac1da0yRXmmltRRB53PM+F31onEpgBEyCLguXDuWX90/aUjirwjB5bF5n2AGc61XUMbbecc8G/W1UbVuG90AedlAoSxFTf337adZBoHcFbZF2o9sJXsBWC474OyzItxF6xXCDR/6BJJcC4fsQNbCBqL6adoH3LIGqHDbPSdyCJRZAilSz3C9yHjrCH7aVN/bep8xA+rMcLXJnl/edmNJGJxth9EhskacD4OhEfWT6eTjqejytFZkZTqYOL9NAn45nmUgf3+oNjRsVDfn7P6zsUh8/3Qy0nyWab6VCvPM4VxHTJN6ZTgJ/YIEhGnab1ep1RtnAP0I3IA4ZLAsIK8izqaLpJcL8uyOP9u1DdB47nop1lDck55Fttty0lOI1mY5+r6TqdTraKa2s8jC9hazgqZLuhvbAMgHD2Es2Cjac/PzyqK4qwVOp+D/MEe83P0LPqorRvl2dRUxnuvru+T/snyXNWo6192O3kfm+aAUQ+Hg+aL2FIdXQIWBHshG5wN60jzGTATssxzW0KI88Uasq84jtTPW52I7UWH2SgR5DK29jISBNFgZReHGlvDs1iSeve601//m3/tNyl2m81Gf/T3/lB5nqfIjQUPbDyC771PwypRMLYIkQN6KVwYN4QMJwmlD+C2rBUGyNYeWKAEULEvmDTLjDFQEyCHEHD4KBz/9ttvdXNzI/lpirVNRanKUi+jo/by8qKrq6sklMMQ5PNCx+NB3mfpmvv9Xsv5QkWeq+1a03aT7mFxrgFzgnDybMoCzMHpdDpLr+MaGE3qITh4HFieJc9zvTy/JkWNsn58fJSclGVTqgWFjABfGBbS6V5fX9M+W2aDNBYLDuhs1jTN6Dz2qTj3yx/9SA/395KiIcUBKsvYOOMymoWyBiTa9uEwUawPawPQRFEAypEly/DwXqJ9u90uGSlJiQ20dS0ALyKb7DuNDLhHCvUtm+WcSwQC6VmAU+SYSAj3zfOjlmwKDiAeJ9EyezyXVbb2Wpbh5j4A9TaygaNoa2wu0ytxRhjyKjl5l6lpG/Xd1Dp4sVik6ECU0UxVNbHn1Gyx37vdTnJxlghEzjAM2mw26UyyLgBDnqtt27O0Rp4dI2R1Dc7NZW0OwABZQs9ko+NtDRS6iMgE+goZJkIvTYaQM8+eIvPoXpvKYvUr+4ehZb+sscS4AnKQg2iAs3QP/KzrSNk9b9XNfbRtdKhspASZsNEwztnEmGeKIxQm0GCjGJfrYokdngGZxn7wTPzd2hbW3DLmyIRNpWKd+D50r2WC+ZytSYU8svvIOiBzEZDEuXtE5Kldjc87pYdy37DhdR07jUJcYSPRBaRncqYmomp6H/bI6kQLWom6xlbVfbIdzIEjywQnGxuDXuEsw77bWj2ug8yzb0RXrNMKCRSdoClyyXoga5wDuz9N02gIg8L4nvl8nhrMcG6RC9tRMerBIOqMpKlJSD8Sa5nzZ9HPHqLCOMmcUXQN9hmiaiIjlCL+pPOv1+vvOMecZc5VWVVqxojObDZLQ+ibseERZwPyhgjffr9P98P6kUJtnV50P3Jma1QuiQRkDF3BGeN7yJTBNtp/c39gHJxqzhe4C73PfiDnrA3XGoZBfdfLZ9OAZDAAoN/aOeTAEn3Z6FRJcb6ml0spq5aks/fJ2nHW0RmWFOOc8ayLxSLVuludw382Ui9NJDkyhVPKXnL+bbQJktjaNWvrsa3IJ3bH1sbXda2/+bf/xm9S7CQlMHN7eytpyuVls2zY3XufDrM0FYDVdZ2iFTAdOCc2tYMZRxgUroG3bQcQooSpdbGd3phsjZLHaUNJ8XPS0XgODjBCTciVNLqiLJWNUS6iJ9Qf7UflDRiUlDoonepa7X4qnic15ObmRpn3cmM/+9lqlgRSkj59elSWx4NDkaR15mCiYVyur6/lvU/d6ihG5tmYKcNzMYCzqir1Xa+6nlqI0qGpLMu4xouY1vbVV1+dpRZgyCTp4eEhOWGswW63S6Hx5XKph4eHM8N7c3OTDi+dlLIsdsirx9xiSWfpNkQjaUXO819dXSWWjX3koANYberm27dvdTwe05BH3g8jjyOCg8p6EJnj323bpvu0ha6AZ5xJurrBiKGAQggpOohzyLVYZ0AKQJvvhWXj/mwuO8DcAl6MMsoVIwIo4CxedoMkN9xGLi3gZo+GYUiGh4YHXdedtXMlCoYxf3neabuNshvKkAq8AYVFUSS2nJ9zZnHIaDpBsav3PnXaCyGktEPAHXUQ6ARrLEjZYR9sap5NQ6RVLcaQ9ePZuCbXZf1xYmhiwppj5HE8LZgHCHK//B1ZtY6RNcDSlDtvnQGbYmZ1unX4+LPvp0Jh0oDis8ZInnXCMLJFUZ5dA6DDOcRBs1GrKFPTrJzvA5U2MmDX2b7Hgj1+zhrbtFHAGGDPgh2eB33B9SyDy9oCUpApy+ZyRrCTklKNqz1P2Lq+7/Xw8JBkOMrWeQoe94+c3NzcpOdDH9JB1DZkwQZ2Xa+imIZf2toW1pi1CSEk4iRGWON3o69wSHhOG41C1gCS7B26hu/iczR1opssQJ10MPRmvI/oUFrH8TKaxV6zv0VRaHBTfe2HDx+UZVmqm7WkhY0IWABpzyJA2ucTUch3837kCWcWmSeDg9+zflbOLKFr7S3XY32Px2PsKpdnmo+kjcazU5pUMEvi0ADLEqK8D2KQ5yHChU2HWLXpcBBfyDx1QawlpBE6yeIsu868F70H6Yj8c49gJO7T6lHsVtJpmnQlNhWbZ+0018W5tvpnOZ6RIi/kDVFD6iFrANlssRp7zM9t1oi1Z0Tb0CHoF1vjZ53CPJ9m/dnzRJkHOsiSRqwXa8NekilidSpn0Tph2Klf9/WDd5Dm87nevHmjh4eHM8EBRC+Xy5SzexkytYYTpbhYLFKEAQbLhtO5/nK51OPjYzqYfCcCYw0hXWcQNISDv69WqzNmYhqkF9mP5+fnZKyIPtkiTg5q17YqRi8c56ht25RqdRqdwbdv36a0muVyqbKqVJSzpGxgCLIsU5Hn0jANyMOIEXGoZlUq0GRoIeFWFCeRL/YEVgiw9fr6mupVUHK//OUvJSmlqDVNo/3rUdvtNtWtsE6L5UIh9PrZz36mzWaT2HvLgM7nc33zzTdnoALl8PnzZ93d3enp6enMUEpTvrCtBSAqY9OErNNA97GyLFPXM5xBmC8b2QCkSUppfVmW6ePHjwk0ooTevXuXGFXALVEdnH3SPVH22+02yRr/cU3Lqn78+PGMWcNQOudSMwMr67DEKEOYT+qu2F/WzSp/lD5F0eSZWzAKuLNglX8jVxNjm6eaIwwCKTu0nscY8uwAcUDI8XhM9YGsbV3XyvJzRw5jB2NJ3jtyZdMWKWSHxcaZRffQaAJjbgd0WjAC4OG+IXUwkPv9Puk1QLVlHK3zYlPA+LwFWfb3OIlWh7L+AAZpSmWyYAH9x14gI+g/5InnsmCE5+W+L6Mnkwz1cm5Kg8JY8kxZNoFFnj0WomcKQWkveQ72PLGzJqo2gZtpbohldrm+ZWpt9Ie0EMAXoARgTYE8QMACZ1LzbC2tBR2sDesIEcH6Qtjg5Nh6LUlne2vJCByTmA7epPtEduLzT90muSeeGQfCyoONfsPwWqBWFLkOh6MYeMna2jQvCEnItfgsE0DlWSCbIMCwwaw917ekmD0DRDGen58lKaUYQ6jYznpZliU7s1yukx7F2bUjNgDuOOnJiRqHq0rRUYVs416tDmPPeF7W3erZpm7kNUVJeL8948gq32v1U9/3qSW3jbxZecYGWb1rz9N2u43vc1O6p3WkOQvcn32uy/P83fM/7Z9Nu7JAHXsH5sL+WqIQWYYgs2TUpS0jVd1mB1giC+zm/ZR6b5/PkjycQewyz4l8WNnnrPNZqy95dV2nzE8ZE9h38Ks9n9ZZ5rxYR4m14T5sBMc64FZ38czIIEQ+eJKsBtYEmwOW43kZQ0IKIw67xdtkaFw6qDzTr/P6wTtIx5HNtaye9VwxMrDRlr0DUF6mQpDGZoEpB9d+5vPnz6n2IuYYTylk3Mt6vU5K2hoxGBjpnKHBs7+7u0uAnvQl0pSIKs3n81RwD9CsRwb19vY2fTfKcTmf6/3798mYvXv3TpJU9oOCm4Yz0gzh8+fP+uLDBzWnOgE56oSiI1clYEukiMN6fX2donus2dPT0xmw5RBjgPu+H41LNJ7r9ToNwfz06ZM2m9jNB6cJYHW1vtKpPqT5NdI5W0toeLvdJqcAw1PXte7u7s72mSgfjhkOH84Oe4bDulwudXNzkyITXRebGcCwkZJiWRZAEUoTQ8Nn+LeVKZx1wD7f9/r6mpqAkA6E3Ly+vqaUK0CWjQDgVCAzPL+NjEpK0S0YzM1mk86XZUitwsLQYWxsOiPPiTPCmlCfMwzDWQtTHD/WAWBk62IwTDgjEB2wVgATIqWcOZ6PBhGAGqKbznm1zVSsb8E9ZxlnEofaFrYSmfk+Q26bZPC9GB4L3KwjzXNa48Z92ZlrNg8ex5915sV9op8uI2A4etYgs3bfZ2AvU2AlJXlFpuzZZF/5tzX2nGNADt/NmkbDPFOWTVEU1oJaFucmYH4JSLzPkm1ArtApfBefmwiVKZXPpguz/9yndaosA8x7OTvoQeTBMtiQPOhVgARZDMgIupNr4NDaTqNEdLk2e875silSnHUGj8bnnGabcB45886FRBhZ8AbgQh4A2IAs66BwFqIjcVKsJ5ucGV7IJDbHAqO+71K7a2wipIU9o977s/oYzieOAvWIPOtl5MkCPPQQ8v7w8DCuRaVYv9ucOTaSUtdIzir3JDcNgCXlF4CI/iaVDx1hdTM6Ftkoy1LzaiZn7huZQ69AGFiSzqZPsQZkXnD22FPea89130/dG0nn7vuxjjb3KfImxawOiGgbCZj2dHIYWWd0qXReD2nPa57nyc5jpyFqIaGRC/YRGbZ4D53Hutj0WNad72d9OWPcDwQauBL9z+eQPXRTnufJjmMvL9PT7LU5u3meq5xVGrqpgQ66Gx1ARI/v5jm5ttX71q5YPcm6c26xg+g6W6aCXba1mHzW6mXI1uVymRpOWTxaVVVqjkb9LnJkhxxf2o+/6PWDr0H6L//uf57m/qB0Ufrr9TotZNu2qVUuwmhTtWB6Cf0jkJKSQcCgAGh4D4IGG0jUh7Ag77N56GwLrLJVLnmeJ+8Yo2lTERBKFP4vfvEL/fSnP40hccMEA6hh6P14DxxilFrTtgry2m63+pM/+RNtNpup85ZzausmMUlWsWaZV92c0n2lSNboeGB4OBCkIhAS5+Aw34colAVzOJTz+Vyn4wRGGY748PAQQYAPZ46qBamkzm2322S0F4tFYmNPp5Pev3+vl5eXVEQPwL65uUm56KQI4qjyXcgC4MU2l7DAEkAF6MQAYgRsaiXKmL0m3UGaUr+Q9f1+nxynzWaTngvlz/wc5mRZw2/ZfF44Qva+UOrcLwqJzwHuLSmB8uV5McYobQvyLMAE1KHMUXp0U8RAXDL2lt1CfjjnGAFkiz/ZFwuKeZ7pnDr13XD2rJx5wI0lQFhDew+smY04sMbsqa0psY6HZe/Qbay9ZUYB2rYJALoAo4WuYfilBT2AQD6LnAAgbNqbNZDsn2UdbRTQsnrcr3VwbSqn1bF2wCGAL6UimWhV308MPmcuRjxOyjL/nfMV5T2kCIW9JrJmo102BSnPM+X51Kad9bVMap7nqWEPa4wDfMnkEpmzzykppW3yXuuoUtQPILZMLbU0NrKJ/Nm9enx81Gw2SxEc9hfZsnIc9VA+Rt3C2VmOzx9rsziLOObYIGTFgkF0DkQIenSq98hTTQJ6k/ljdBS1Mh733+v6epvOE+3j+R6YeWTYgsNhGFKkWVIibrhf9KbV5zZqY9ctkjCLtK6w5tS/WEiGQ7ZareS8V1bkyXbYyIqNitjvZ3/s9XieEEJsABCmejfkEKcNzISMWznAgSU6wD3wndghm9LE90tKTahYd2UTaLeygMyg1/m7xXLsE7JsdaG1H/xpm1qhG61DBwFAhIW1thE/9IG9Z3Q+Oo21tNkW3KfFesgG63t+tiYcyfu4F65jiUWrl2xKmnNORZ6ryKZzzJ+sETrw8r7s2ly6DDwX98p7OUfYMj5rv5P15wzZPUNX2z2Xpmg00Uj0icUfl5Fp6/wPYdBf/YO/8psaJGnq0W/DoDYkDWvFvCKMMYbFKlrvfaqlQTEDNjB8lonjMwitVZYYD4rbbe0BihbwB3Nmc74B+ABmyxJaxgcwTiTgNAqqTfE5nU7q2laDATAcwPl8rrpplI0G7osvvkj5yt57aQiJkfTe6/PnzwkIF0WhvJjuF+EHLHHPOHqkGaCUpSm86r1PwzlhHzjUtGlnTVFqpPx57zWbl0kx2rAsbMmXX36ZgCFMKN3kyInHmMLioUQZsMdzsZ8YCfaBWjBau9JVj8NPh0Lk1Crr2WyW2k7bttHS1BocxwNAjzNqAZYF0LBWb968SQYFh8s66RbwHo9HXV1dnQETlKJtwmBrr+w92fQKDBw1XhgcFB/7j/KDTODeMIw4IXZmFmfAMuisqWWwbYoOCpX6LNbi6enpLLpjWcO4v5mGfmLWkW2Al03HYP35Powd77F57RYkYjSs88hZQE7tmvA+GxVnj6wM44TYSBfRMuoqpPOmIN/nCJEayHvtnxa8IzNWp+Jw2+6F6OXL6BhrhJMDM2mjK8jLpG+naCW6PerWVs5NYIgzFRnSXmVZpXVHzm3004JH59wYuZ4yFrgvnsdGNjlb/B0Hj7PJutjoGXaD9cIRsk54lmUpFRnnFt1MB0ML+qWJzbZONBEBWyMJAEMm2dsoS1PzDs7ppR63Og09JynNCey6LkW50R2SEilmGevYRCNPOqNpGj0+PiZ9jf6zYJEIDnKDzDG+Ah1BbSg2Cd1kgSlpQZw3Osdyf1ZWrINNxEIi/XNKacKe40xzdm2kIvipDs1GCWzExmYUkM7MC8fCRnM1TOmq1CaTKsgaWT1siQ50FLJn9Y/VCeh19lA6x2b8G3uNQ2JJRBxD6wTw3Dh3yDj7ZnU+th5yin2idhJQb+8NJwMChfeBASEabIqbdWpsRI/75r6sg4CDgX20JAINiWzWwSX5znpZW8EzctazLFORFxpMpoHVAzaKb9fO2iK7dqwDZ9A6ZLa2K4RYRw+BDKa2a231KzqGKCn3auUWGboky9kjrodesfcymIYlf9HrB+8gEYWY8pBJs/Da7V5VloWcJiVE6L4oyhEMTAaurhtlWWQXF4ulpMgyOjl551XMzttzxsM0pEhN0zQqi1Kr9WqMwLR6++atstGxcs5pVs1UlIWGfhz22XYaQpCTlOURiPX9oOPhqCzLdToeNYQQu9DtXlSVY8eylKYQD9Jhf1CW53p5jm2mszxT13Yqi1Jt10pBOh4OWiyWattpQN3+da+6aeR8p6Hvtdvt1Ladrsdoy9V6rdPhmACwVayPj4+6ulprCIOqaqZmNHgMwQP80MLYGtSYtlTr9XWv+Xym/f6gEIbxcE2zUsqyUua9juGk0/GgOPguT2zi/f29iiJGkPi+t2/fqh1TDWkjnmXZWaQo1ifFMPZ6vRplaZxbs1zJyY3pIEFN02q1Wuqbr79Jhr/rOm2326TgcG45tDDAvMqyTAad0LBViNSzYYBI/cBBjmvm0nMVRZHSSCzzjhJHwcZ1nea/DP2g192rZnO62GXyfpBzsRtSHBgrrZYrtV2nYZjan4agM0XmXFReVRWN3nK5kkLQ8XRUnjG410uaiuOpZZDOW4HaSJaNlnDGQ1BSrlVZaQiDsix2rpKkoR9UlFM0ou+H2HXRxWJ9771eXnbyzo9RvlqzqtI+HNQ0rfJ8ylm3jmbX9SqL7KzeDEaU75ImlswCfQCuBV4W9FnHBtKBSA6/g5TBOcNI2sYz6C8MmDSl3eCEAEwAmxg5yxzigFtSwzKaNmJnjSXrACjlniWlCAlyfTweU0t36toAZTwvoI99QGfYRjbTi4LeKZoWAd8w6p4pNcxG3TC6NiXaMpJxDf24vkT3OznnE6iczeajIxjOrsX6WwaYLIeqqrTb7dIz4awj9zbjwIJke01LSLVtBC7RAfRaLheKHc2mgmbkBeeRFtd8n12XrutShIbGMFEuQiIFrHMUdVKnLPPJHsZzWo16J9fd3RudTscUEez7uDf7/UGrVWxsRLOS6LgWCmFysgG+s9kspQ2SWgORQ0ZDlNdJ58xmcx2PJxVFrq6bBm5a3Rt1aIyERfkfdDyeFNuMd2NX0ELO4axOzT3QTXXdaBh6xbba8RoQWJZYIL3L6gSbjtT0nQrOw3h/RRExDE4CssE55nzZszg5A07OjUPCu079MMhn542giqI4m/0VQebYPEBOWT6y/d5pGIKKstRhjJCiHzibfR87skkuDmPWCObzXEWenRFkvP8yA4B7sxkHnAX0F1EGoqzobZzjy7OI3FoCmzRHzglkEntDRpHVv1ZXouOjDZz0MfqEzA1LwnN2rc1G5/CclhCykSSrczl/2KmpVrmOe5Z5KUx26VTXMRvIRMrsf54shTCo70ZiRZLz0/y8fjBdLrNp9AqDZG3UzEaFwJrYBfbV1nDZKKD9DPLB87OGVjci69iPupkiqn/R6wfvINEFBWGJ/2Xq2l5hkJyi4r5aj93l+qCymOl4OE1h7F4q8iIxU0Pfa/cSD0afT4zJw/2D8jyySWUxS7VBx+NRVSnd3rxJh7jvexX5GG4dgrp2GIFlr+OxPjOKCLk0TQ2ez5dq6lZVNR+NVK/V8iqxDZnPlWdS3w86HWMDg8Vioaqo0qEIfVBbT45jnpUqi0qnYx0dmqZRkFOeFSllbTGLnfeO+4Ny53V4jX37bZ95cqeDgrKsUO4k7zOVxchaN52cvOrTNOQzsgbdGWvgvZeTl1Om1XKd9pR5EPWpVb4sVdetyqJSVc5SxI1DI0nz+UKn+vCd1q2XxtCG3odh0GI+135/VFNHllRBKvJKRRFnKhFhqKpKXTtou71JjgEpiNIEqmGdbEpCvL95+j2KDZBi09dsyhvvtaF1QCsGls5plk22zFbfBd3eRAexqZuz1BwFr74LijNHphaaXTsB4aTYsil32zmvpqY1aK/5fKG+66XMqVNUZkVeJeNhmfHMezV1J+8yhYEIk5NzRaoJAPBEGcnUtWNjCPlR6Xs1JtKk4HU8jNGu4PX6GhuGxBkf7iyCEoFMq+VyrTC4qCeaRkVeJkOVZ2MUuo2M/2I+1ZlIU4oYbDBMp43GSROAIZoIQQPAsalgGD6UPvrMRqa49iVriExYNhTZuXSquF/2+pLtxIGdnKFBeV6cybIUHYbIkJ++915tPYeklB7Ketg6C4BmqlMYI46WJYWxtesMAGKOFj5TWeYJtJblefoeBApnuCyrZPytzsjzLF0vkjZ0oWvkfa6uG+R9TDkrS58cMSJoNoobwYgfn8GpaTplWaGuG9J6xtbhU5t2W5uKfbBRgri/QXle6HSqEzlYlqWen3fjfecj+MHBomlBnF2ErGA30T9tGzteAoRwbLNsqlGglsBGGmHqY2S3V9sexnVdqG1r1XWrrhvkXJ/s42q1Hgmjk0JwyrJc8/kiMcxEhz99+pR0OM5ECFONYd/HZg9N045y58X8n1g7VSjPC+12j6NDMGVgANSYV1RVM0lORVGeEQRR/rvxWrmyrDfAbDp/EZxPHdzatk3NeWznSRtJsOfQDUHd6JC3XZP2ta5rDZqiEjaSxZm2wN4C9mEYdGzq6VlGomJQUFkWKv1MQxhSOj5njLONTh6GQYWPXW2J5KA3cNKyshgdFtIxx654s2mYN9e2ZAf6NJ6zKUNAmmZREXkLYWrZbvXpMAwpmkodDU4N948dI43e6hnOnJ01CPlEmiT3Y51JIhq2gQajZMg0ITrGvRBRZi3400bs2Eue3UazeZ91QoiUBQUJeQiDBicVVanmVKcsIp4BW1FUpfowKHe5+mHUiZCEfS8NvYZxxlzw475lXn3bpQj0JXaZghUuOdPgHeyWxRqWCLKNRmwqvo0i8R02W+Lf9vWDr0H6b/7oH6YGAjaUOKumblHSNB8FQbMsJBtKiBTBZJNQZhgpy+xStI+iQrBRwBxcnIxhmAZsofgAWaQeWNBsczM5jJcgre/71DWO+0NhUcQvTWHpCexoZPJiTc12u00KgkPJVG+6ZKF8yC9G6dH9js8BkHlGpl3bnGaYTYwu6Snb7Tbl8ONc2JxgjDmHrGkaHU97kfplU4e4J+41Ro4WKSLS1G1q4gCrhBG2qT6z2UwPDw9jHcdcp/p4Fi0AzFgnkr0npQH2hiJrolt5nqd28DRvsAaQZ4Rdt4whRgzlzPsPh6PaZmqv/Pz8nJxgq7hsGgIyaiMjyLCNGqCY7HA3W7xqO/dwJjlDfA9GpWlPSc6Q+8TCuWhM+QzRh8qQIn0/1aOROmMnx3O+OPMAFZx0WwRvjQZOB+sA0MFoY4zsubcRFgtc+A6AM8qc82z3krXlvLOmNpp2meLGmeQ+rV6zf0cvsCf8HL3Da0ohiTOgrOPFvUkTm8f3ELHiXPB7zp+t87KRSNIoYWXRT+yDTavAQLK2XM/qWoym1Z1FUaSZTlFv5BqG719fapeQAZsGIrkUEQfos67R8ZjSqrh2lOvhjF21ut25kBoOkGJnibMp8tInPRafqUryxWdookLnSvaX33VdOw5ZnRhYdMrlPrDGcUbXRrFuyyWSin2hnoX0dEkp6k2dJufn5eUlyTx1PpdZGfbMQJrwzKwL+27r5WyWgmXJL51xy8Cjoy7Bs01351o2ZYrXpX222IF7tmnQOMDoHlsQP2VXTNGlJCPepfpiUutIzQYPWFLQngsblbC1Pugi/s7zWPCOs2KBqTMpe3wveKAdzpsNcG+WTGINk1NldKXNwJCU6jQtCWOjnZASds1YS54FGSTyaGcD2sgba0cqWrT1i7Ru6B0GuWO/+d66rlMEGPmFcLLn2T6vJaf4vW20gWxfyr+1bZwB5NeuIcRqVVXqmlbhghjhmn0YkkOEnNqMAn6OTCQb1/Vpn2zWjLULRJnAcJxBuxbeyDYv5JNnsSQl68S6YE/Zn7/xt/7d39Qg8bKKEMeDAw/zZL1VhNgCUDZDmphaDhRAHIDN32kLTapKnud6fn5OyhFgTWoawmzBHcYZAG1TZCxg431449wzCgFFae/79fU1GUjui3xsFLMk3dzcqKoqPT09nYXA6ViHcoAJpmNblmVprhSsomWhL/+EhWEN7Z7YuhWbH86BsozDJWjI81zr9ToBIArQYSps7YwF4V3b6Xis07rirGDo7CBQZKLrOtVNndaI99u6A+QBuczzaR4Uh/v29lbPz89JmeEo2hA+azIMQ8qBt/nnU5rNedtlAJ09F4Bgq4j5HkLdvGC5bNE+94lssgc2cguwYr1RzkVRpDoknETusR+m2o1LpTqEiT1iT2wdBwb26ekprQ/OGvduUxXYGxuJ4P0YXuug0BiF9DR7zjFaNi0SGcIJ5vrsCfLNXnVdl/LSLUuKgUIe7F5asMOaYETQSxZo8cwA32EY9Pj4mIZfSjojUNAL8Xm85vNp8CLt5eM9TqbFPjt1ItwD90UTHNaKNDXu0+plnsvui2UK+Qy6zjK6gEIAmM1ph5iKr+8WPSMv8WdTfYkFnUVxnvKDYY8ydt5gBNAUaxmW33u+48+mQcXW8WN4sE2LnO5Pen3dp/sAEC6Xy0Rm5fk4SFtTxC3W8U3PatdWmrrEIfPOuZGA9BqGNj0X9oy1g3hADohEDMOQ5s2EEBsnsT840+gbC/pYJ2sbqdO0RIJNu2E/kRPW0epdzquVE9aBs0W3UrvenGX0mT2TfJb3ACZZG4gUdIO1sXZv8nzq6kctKj/zLpMfI0PW/tsBz5eyam3TJQi/dI6sfeTMWdKIc1PXdRxEatK70JWsl20aASmFTmQkCPoZwsam1dkoE/oQEtBGWHifBeysge06yIt1A4eQSnrpTGOzIeWsjPb9+aDj/X6f9DUOFc6RjeYjo9ZOXhIzllgm84Da5nMdNM3a5OxbZ549Yc2TUzeSILaeKWUwdJNjj71g7y1hg35Ldmj8NzJOhg77ZAlz/m4JenuGsefYTrtG7Kl1Ntkv6gUtRv51Xz94B8kqHcvYeKezjUTIEQIKDC37ySGFkc2yTLvdLoF5GAsiHTYahSAzFNYOo7RhRDqJWRbdhoKl8zaseOUASoQaxc5zoVgsIy1N4WCb90x6BEzZ4XBI0ZqyLFP0huJ+DNLd3d3ZNblX730qJLftTBFYjL+NYDk3NZiQploySWf7QjErBpVmFJZpdM5psZzWhPdzsAEPpO5gIOfzhebz/jspbjb6QDMC6wBFR/k8RYl1sF24UIY8n3Oxda+de3IZMbAFurbLnTUOVklYhUVOdezC6OWrafCxFNORlsvl2QBblKh1vCyTxn3BmtlQN/vMiygJ68m94SxxDcCeNLHAAHjus8gL5flk/GCRkEWMMwBhv99LUkplgDHm7zaSwV5Yp4P1JD0lhJAaffAcvPg3+oZ9h+3EaNloGYQC64nTAPi1oMs6XDj43Bt6h++7dEw5kzatwzq3wzCMdXtF0k+AEAgOoi+LxVQzhx7KsizJlxvnAS0Wi8TQXk5ZZ19ZF+SDtaUQmiHR7DMAmxRXHEHWwYIzQA3OIetm9/nyHoYhJLBgGfx4LaUuooBZvpt6Iz7H+sZ1jPKKg47sRPJjAhkW/LNfgEt7/gDJgGnkn3pX7MJqtUrd3Yqi0GazSefv6uoqRaWIwHo/kQsAWNYR5xV55RlxWLkv7plUYWQQPQgw5GfoBus4W3kHtCGjnEmcWhsxQI+hRyEa6D6GfrHfYZ1Z9hvbwPeR/obTgJNzGZ2xEUyAM7YOObXOlT3H1unApqM7QwhJ7tAJOH11M2WasK7IEPdi9THXHYZpKDp6ypJhdg3Q05AFOLxgjmRzTxOxcWYDvVdnahdZc/AS8miJUTvbhvTXophSrtH3/GftqSU4rLMQQkjkLtkT3JPVn5xdG91HnyH31nFBN/Z9n+ooScUD0+FgQEpydu7v79P4EvaCNeG8rddrFWP6I3iJNbBRdGTSRtW5JnV54BnqnUOIzQv6oJTlgk6M69LpYJqQcJ5tDZglGqYzPNUosTdckzXj3oZhyp7CBvI8VudZos5mG5CBZZth2PWwjtmv+/rBp9j90d/7w7NQLc5SVU7TsJ+fn3Vzc3PGpFhnxHrtWRaHRgKSURgIAR65NOXNEgG4ZBY5WCg6hI4DxqA7rg2wtK0z7WDWPM/PGBgUGQcbY0ykwbJaMHD7/T6lQuBccFBRAESfSG9jMNrl+tk0Bdbr8gDxfThHKCPLimBwyGsehuFsrhIGD0OPk4uB9t6rrKbuaRhRyzJzP9LUxto5r74bzhQPDQkAcdYRoDA0y71CmFLquGcMIal6NhXARpRsu0vk5zL1AeVtr33pTCGf7L+kCdT4TH1/XsdhQ+U8p3VQbASK69p7hJWzTB+GjTVDkWLIbQjdhv+RI7khrSvrnIyDsjPHlD2VplA864vS5/m5J2v8LgEpAMCCCc4r98s5B3BZptlGnOzv+Cx7xH1Y55t9wJhZkG+BPCm83CfPYgEp32n/Yx2QDcsQQwZZ4M8zwZLHKFAslmc9kceoYw6SQgIIlqHnXF5GK21EFNnp+/47aZDIl2UwOVPoXEse8GI/7PpbZ501Bcg4N0VeLJs7DL2qaooasK/xbEyzWBjGDKAahigvXA8iK8p3lUDvOUMaZ+ZAUlhQyNpg33B4eTXNNPOD36FrbMSdtYlOfxULuY2u4axgi2gcYeXEOR/Tdk06n10zq5fJNiAF6RLMWv3AWUZv2n3kPHNfNprBOuD4sT6sq9WFVmdZosE6Gfz9Upb4vQV/ZCnYqAzny9oa63whM4wcgXHnfizJdknsSoqNFYapK6FNg7TsuSWQ0Bk0NSAqYckSiBiLFSwYBa9YJ9DLqR5Ze+em+VchBJ2aWhqJQKu3eB4b7cTedl0sL8DRuLq6SkPncdosycyZGobhO04HjizgfrfbnUU0AdCsE+cGXWGzIpBzax8glsFF2FHS+Nh3Uvlx4i0GZZ/+6T/9p8qyTO/fv09ngHOEXr0cDG1xK6NKDodD2hsyP9ADVl4UgnI/tddGTw7DoEEhOUgWD3AGub6Vtb7vVWS5WmqfxjW0Opl1s5+VJszH9VlD5AHS5dIO2OeyuAc975xT0zb663/zr/0mxU6STmPNAYqEPzkEePKwTxhVqxSkqT6HjbMHx4J+UgSsMyRNXjwbxcZhJKlxsUACICQpOVikLuBMXEbGmEpN6gaG2LJePP9sNku57Rhfew/2/QBUBBzgG0JIU7Ttc7NWrLcF+awL9SAAPZ6Vz3HwcAr5PhQagMIqe77fMkAoHHLVrcN8CdTPFIcmVo3PYsSpB4KlR5k651QWuV73r8nR4LsAyaQsWWBuUwJQGBbIcX/IEutvHSXuw75XmhSFZaebtolNLgzotGlspApgEHCgrSPF+9lTO0MMsoA0SIwHe8j+IBM4pTaiMQyDnJ9yifkugEHmzxsj2DxkC6DYc/sctijXOZeIBQtaLMuMMbRsoa3nsZE79tQ6FRh/6xBihKwhskqd99ko5KVTjcG03/F90UfOMAQRxIFl4Yj+AFItcIXVg+yJTOZJRTGlp3o/1RIVZl4LINY6fAAh1oGoB/V/tmbKAifrPHE/AGSMt5V1C2JYY85AURQpPcsC5Shj0+cB8+cRpvO6AVJRqyrWt9EgALA23U+W5vrY0QF9P6UKWTKJ/aPtNnsjTQDf+5ihQPRXok6iSOcCp8s2iUCv4ThE3d7pcNinZhlWF7Fv1pYxGmM+X55FBtgX7AcOg42eoDst0Lc2lRfrbm0jZ886p5yny6i6HTvBWbZdVLFFyD66CHmxEWZISOqjOD88qyUyOX+AYfsM/NySTRANEE1EatH5yK4ldZAT7zMVox3gDFALbM+9XV/O0Gw2O+uSaTMHbBc2S+DZaDQOHfeUOXf2TBbHXM0qNe003NnaVCsH6BT0UlVVKdpBquhlyq3V2YB3u3a2syhrsVgsEmHMvhKdQqfzO6LVrLs0jQgg7ZIoOaSOjbyB9cAPx+PxrBbJYg/vvX7v934vXQ/HACeH5yXrxZ5xzgdpjehL0vTZf2SC5ynyXKGfup2i5zijRGCx4Zbc4jOQX7PZTF3byo11iUSXrRxabMI62Sg40Wf0ymWU2dol1oO1s7qD9bf659d9/eAdJIUxpeQUmwQ0oVFmGFoLpOq6TjN+YCVtvQj5vdaIW6FnI19fX1NjiEugioFl+NvDw8PZz1Hc0nn7SRTw/f29yrLUer0+S+NI4Hx05AAWgD6Yrd1ul9IHUY7ci2W1bJcUnqvv+zQ8zeYEo9T4HhgLnt/mmKKoABV2DhDfiyFGmLuuOxvSB5vCi8/a6NVkOMZ0jpHpzrzX6YSi9CrLTGEIyrIRmGS56jpGn8pZqePhmAw54IIiSdabQ899vL7WGkLsdDYMg4Kkvo8zV9q2UxhiukGeFwrDoCHErlp932tsMCNmZEhOmc80hKC+6ySN9QAhdqlSCMrHwW/9EFvAe58ptsMt1Xc4706Hw3FUtkfZ1uo2FRQ2NBvXIQRpGIKyzKvrejVNKzlpfzgoFmXHPfDeKyRQ49R1/QiQczk3qCicYjvk2HqY9wGwpSmVA4Oa57mGENvZHk/HBCCzbEx3HSb2n/NiwQcyELuYTc4jAI2zAUOJo2ojvjZ6i/NjU19sEbUFh1mWnUUeWSPSY4hwWsbWkiKcD86APZvWWOBc2DRV1gTSxRr7y8geANCm82LQbCQP2bCpq/FeYJpjx0HaSGfZVDdk9ZTdG+7DMv6w0bxg0qUpXQ/jH9vsD2kfrBOLk8gzAQi892fNQ1hPO3SV58LBwYGJ122MQ9sn8qnv42ceHx+TY2iLhNFTpHvhyAJIy3KqEQWMQdyFMEU4wnjuP336NO5HrpubG3mfabd7VV2fRHt95ANHDFmxESQG1aZC7a4ba0hrNU075vVPkUUcj67rR/JtrqapVdcnMdICeYdsY8+tY8TeOufSvDrska0948zaCKrNqkAubDTHRq2sE2ZBNACas27TquwZRP5DmDIY+JlNWeMagE0iCDaqwGclxU6beaZ8KOQzryyL9zqbz9WP92KJP7CIdST4Xfx3q2AITsAsgNI69Mi0JXG7rkt2e7/fJ1KAbBQIIRsJ4MzYPffeK/PRpiKvNqoRNDl+2BoclLQ2zTSrEb10Op1SKp4F+ZzhS9LE2hKbFsi+s77IPfv2/PwsSSm1V4o1mJxJSEOyZzinEM6X6WE4c7YWjDRJ0uWsTbJ4jugQTrJN+bUpbpxLuzeWHORe0a8Wk1r5apsm4mXF9t1yTnJS13fy2dTkxN4r92efmTOJ7bMOEDaEe7HzkmwUcr1ep7lJnCvIA5uxAPGJXeb5L7+Ltfi3ff3gU+z+y//L/zU5EzgP3vsEmjAalpnGmOA0WeaahebfCABKgANKGgJMGssMk0AOLE4RytZGugBQHEq+i1A4QmINuTUaFJETEQDUWWWUZVNHNdYIZYjS4TmtEPJZWCCUlj0oKED+jhGxxo39sODPMrJ8D+ua5jJocjjX67XKstTDw0PaL/bWKhfLtqMQuR/LPrEH1vlB4VglwDqQXsj62pC+NLFhljWzRrvrupRSyTqy/wAdrnkZNQJo86wYGyKHNmUKYI2xZY0Bq3xPZM+/O1MgyzJ1Q69qbFGKwvr8+XM0ykWZZnMgb/bc8OJ7JoZ/iojY8DyssGWH7P5hoCzwt5EW7sNGp6QpLdWyXnZPrWwCAGwTAxheij9hsmyKp3WqWEfLBtuIhVXBXdedzb6xLB0ya8ENBv+SQbOGEgPKzyCHbISPdeP5MVxW7i2ry/1wHc46AJdrWTbPnjGK5S1wwFkLIZx1igLM2PMfwlREzctGE9hb/rQNYYie2EJ3q//sNSwRhN6R4hwt9BN6EWeDc2WZTxo7UKN0OcQ0y4qzek9SiQCT1kGxaTzcO3Wj9j1t2yZwZOWxaRptNpuzulDsngU9khIbbq91OBwSeGVdi6JIJBa1FVzHpuRALHImrW4AaNH2ummas/QgnsO2EAcIWVmHtMDR3u/3qqoq1cJBHOIMEA1iTbH/yFxsET45xpxZq2c4C6wTezabzZJOtk5eN/TKxv3iXhMb3nZnzRZsdJkzMQxTNgmf25+OZ5ktyAfrin7ECfy+rA7OA1jCNsew9o2159lttCFOhjy3A+i2rJzqpqz94ZrWeWJPh2HQ8/NzwkKfP3/WZrNJOAEihMwA1t5G/7gXslNsAxDkJsuyJMP8DvtlZZC/g+XQ5yGEs3Rw1pnnsw4u94Pes7iSZ7H2bb/fJ5zEPdgaOIsRLO7i35awZn047zwX38/+oFMt0c/nSfHjrIFVcT7BLTTsoH6PtbIEhTR14oO8t+fPro80dVHFsbK6357NS/lE9zw/P+tv/y//1m9S7HjhRXMwLMiQTF1GNk3ORtHBzFqhRqlbUGGLmFFaKKZL5gYWj/QGQqjWUUBAAbMoKkDaMAxJwDmAPCOGEjCB0NPAgCiOdD6/xXr2l6DIGgIOLhEUroUjyjUtuLIgzLLaVnjtPgDOLp1RSWcKv2kaPT09JWOMwmV9LeCl1TltnjncGD8Uiz1o7IGNhtnZCtbBA0hxLyho1tAqUrsu9qBbg0IInvu9dKqswUOJ0K3wMgVCOndM2AsLYCe2vFccIHgu58jIMMQOjZK+w5jxnewPxaoWHGA0JuU21aAAFmw4HSBqjQBrbc8VBtA6jDYNFaPL3gDSWXeuZR0b9oL3s76XKTV26OOlM8jnkXUMlP28NboQEzwT6X/ItAUuyLA9m6z/5ZniDNuURXvWuYYFtDaVifddpo3yJ3qF99D8o23bs9bS7KdN6bTsoGU8kQNr4GBWifwQ7YJkAmQD/JF3zoQFC9TBsLboD/SCPU+sWYxgDKnjYVEUKbUaoGFTgJ+fn/XhwwfV9UllWaSWti8vLyNLPUXJGRKLk4gMwnIjj3meJzABSLRppJwhC4A5C2QL4GgCTK2DYdvxeu/PiLYsy3R1dZUcJWym7WxnIzqcdXQr582CW+yfjayxjpxZ1sVmD1xdXZ2dc6vHkVk7W4t1AQxzTVKZkBVL8jGk2xIwllhETtkrbCxEw6UuKMtSfuglQzzu9/u0V1VeJH3BOg7DkMZsIP+vr69pvS0pYMGsNAFKa8OtbbVEHvVylhjFkbU6AHmSdKYv27aVhji43jo5VtY4x6wb+4d9tLa076eGB9TTWPnlGuwnqfi73S6RNeiAsiy12+1S3XNd17q5uUlnGscZG4MeQtf3fZ+iRZZstlFNW/OLPvLep+HWthEH9+6cSx0p7V6yJ+h6KWIC8KK1hZDhNlqD7kcPoXOJrCDLlmBHz3AW67pOeNU662BJXhab8grDIJdNJSIWO4MteUaL8fI8TwQZtW7cF/bJEoi2ex33aAlhZB0bNZtNQ6D/otcP3kFCKeOMkB/J4eVlvX3+bkN1tkkDQNlGVmwKySXrI005mrwHwOWcS46VZTMsg7larRJDhxLBIcvzafowylmKArvdbpNyQMClKeqA4rJdyiwriXKw0SYOD4CDa/A9HEYAwmUvekAu17XKHAFHYVpjifHn3i2Tx17wYu0lpXWCGSQ/3TpeKC2r+DhkKD8YEfaJbiowTvawWyb80iGy0Ry+7xJAoEBhUjnodu0lJUBtZR1AiVKwkSj+tHUgvIfzEP/skwG0TklZxmFxFujghBZFobpt5d05ILLrjQxZp6wsSx0O5wXROGPsNfeAzNkaMsAIBvMyGsBeShMJwPnhHi8V9OXfMXiw4ZZ5teCCfbdnxYIKa5Q4t+yBPe824mxrJGzqCOeYZ7Ygxd4vegGZtfrLgiDrWNoIra1LIKcd44TusGwm+036WwghRUZYM7pG4aD2fZ+IIt7Hd1LXxl5Z/cl8Mhw2IgGQNvYc2mgkMojjxv1ybVvbmGVZcgSwG6dTndprt20ssEZXAtBsGvJ2ux0dzXh+GYNAqna83+YsCkkEAX1ux0Bwvi4j25bMs5Fwm8bJWbS1BFaukE0+a88f54rfX0bqLBCx6Y7I2OFw0DAMMdXdRL6tLgOM2kZCOOmc/+12m/SObR/Nd1qHiJfVxegOu8fYeH7HGtqMCc4nxCSpqezFpV2x5A3PgRz1Ou8kCwAuikJ9MxEorAfDeblf9g2SwWdT10sb/bGg3ZJrrA3X5F6w3dwve27XEtm0zpsl3PJsSoFjbVmbYSRALtOhrGzaZ7DRPAvoAcfoIq5DSQR2ou/7s9olOstZwkNSOov8G/yCbKHPLJGEk4p8Wgecl7X36IioQ07prIEvcDxIj7RnDl2NPcMmoMdwJrHhNkJIfaKtvbW6wWZAcEZsjSpnCp2B3ICrIXCwr+xDTOx3Z3jBOkg2omZtI3Jh7SLrw5nCsbb3aJ0mu17WxhZFoa6fcP9f9PrBp9j9V//F/03r1TSgVNKZA1JVlR4fHxNzkPq+91PLbw4aShMBRDAYbodjZGtkrOMlnbecRVAsQ34JomyKh3XI2HQrNDa8CaBEiVjAB0tqhcyCG54Pg2O/8/vuwRpTPs/LhoR5futQWEbOrg9/x0EBTGFkLFNvmQnu3UZNLCjintt2qn+yioHPct88A9Ep61gOwxT6ls7naVxdXWkYhsQIS+ezi7h/G1mw68F3W/YfoMf68zOUnjUQ1nhYp4prABgxxIDMCIh72SGZPKtzTqf6pGxM0wOcJPDt/f+fvX8LtW1b73rRf6mXdu2XcZlrzpmly5jsnYi3E0UwxvOg7hgjmxgEIUIgiIgGBCUYUXxTkEjyoC+++BYQwTeFbDzZxvOgwjJKAm6PEgVPoqzEzKzMOcbovbd7vZTzUNqvlH+tY8Q11zmew2acNJizj956a7WWWsp3+X//7ytf0f5plx2Kg3bAG4DCGZ90eGYpg5w7Xg+qvWTI96egez6Xzl7zrN49EF1gvvmeyznjJWjBQc+DI0ALYNSzMm4vWA/GQnt9wDZzxDozF77fxnXMzbez9ugQjgFAi64CfhyMcF3mgqwBe0Rw1j5nXjbrJRYEoOgvZyS9ePEiB3uUGrPhmvkFoDkYAvAxdzzHOI56fHzUy5cvJxlOAAaf47lYG94nKKMUijXDaaMXMUbd39/r4eFBfT+o78vetsPhkA8jpvyNIM2dfzpfqGzwdvkYx6hhmLYl5gwVB5KeWc2g0xhjJwYgfvy5+Y53XnRwgQ0BEL+rNBm9QBacnPCskKRMSAKGyAg52GPNCAyxK6wZsnu5XPLeXphtnw/AoRM7BPjYDEjFYRhyBs4ZZ3QHO7rf73O2jiDMCQLkHRDLM5Ddcb/NMy8WC5370hnWsUVdVQqxHDyNf2VNXQd53kzGhHJIveMCdMvHyHUBucgyuuG4wYkkX28nLdzWxGFUZeAUAN8Pg5rF9JBxD3SciKH6hcwyf3eAjh1CR8A+vE95qGMy92eMl/njOuiIz4cHVB4Q4deQGyeMkTMnNhkL32eOkE9kwTHinMRy/8lcIF/YNSe4IV3Asj422mrznNhA2oHzqus6rwP3pPTWu9cic6yBxpgPnwWDuW310nX+5kHTXE6cpHYSElvlL7d3rM0wDHp4ePj1g2J5NXWT2UG6h+UIN07T5YA6ByLStHYeo4fzyYKgt7vtYERxiAjcfBMi93OgwcuN7DxwwTiwAdQP7pSmwQnK7iyUND21HtbA2WsXXD/nAoDNd3EeGFCADIrsissYPHXv5yAxfxgN368gTdtCMnfMv2c8WBf+TaAhaZKZwfAApsnsOXDwcROkMU8edHENUuqMFyX1OXcGi3kiyPIAz52egxQMqRt0Z76cJUbO/Ho4BWSK8qVUbjN9TpxEVMmG8n5+fiu3w5nNAxnK7XzvR1UFVVVpl+5BnWfAaKrg13RAi7yhx34YJVla5gxwdeD8AAEAAElEQVS5mwct6AZrN2c4YTUBvxh9goL5ejqRQKaE8TAPHuwvl8sMKD3rxH8eHLFuLmcxlvayzCdjI+Dwkk63b7yapsklKDCr2ALk6tmzZ3p4eMh/4z+6UhI8PT4+KsZ08LGXe2CTYS9dXn39vTSDrBBA+3K55IOouTZ2BFDG+rA2ACUOJwXQE5jC7FJy5raXNQ8hTEq1Wf/1ev0WW41MMoZhKOROjKkUMDXTWCtGA5nXvyHbTkzNZcJtCkEkDL93H0O+Mxiv395TyX/oe9d1ev36dZYDAKaDJ8bpQS3j9AwevsqzATDu+B63eYAh1g7w62DYyyqdqAAEMn88F+81TZPX3DOZvl+JucV/up7BgDspx3UfHx9zkOy2KsaY9X00/+Sl8lVVKeYGN3Uus5wfu1BVVS47kqSo0iocf8C+Vl8nJxM9e8KcOwBm3rA5yDFz4oEUtuh4PGrZLnKnOrdXq+VSo2L2IR5U8JxkGSmlizHm0jnwEsAaXwzugeQmsPRGM27H8eVOILp99xI/bIHPA5VIlLS5PGOfIAnY344vcn3zChv3MeiqEznokmfzmHP3a47L/H3mA/vCT9e3ENIhyP4+5MM8SEPWGQdjRM9y4D6MaozA9WwaGXnG4jiG8eAfmFeXX8c+vmfKA3ZeU8L417vY5ZfXUDqYq6pq0nrUU9yUIHmbRBYIYfNSLyLrOSjFYMFQcW8Uax40SFNjzt+kEp3DcvC715e64nvNqTTt9MP7CJeDODccUjEajI1/e9kSisR8zoNIZ02cucLAOQDiHp7h8O9wb8+quMISYDm75Rk9xoI84ND9Xqy57yOaM/EeDHtg5uvq4/XAwZ2QG+85y+TOxQ2dB82sgYMbXyPWw+fw2bNnE+DnRoh7n8/dpCsP/x6HUQurBwZkVVWl0DTarjc5OOLvjBeAA/CmxarLKc/cNE3eAMtc4mQ8G+O66cErjpRrSmUPADLpBpk1wbEwHsAw95oHmFwb0OJgFMfPHMFWe5DA/dyAIzcEOcgiZAssn7PmDmJoN+s6E2PM73vgwNjRCeYRUAJLCpnw+PiY9ZrveKviEEI+Xf7169eTvXCMB2YXuQX8MD5aLj88POR9oAQz6AcA3I8YYJ6x29vtNre29bIiuki5vXUbLqXOVYBc3/i+WCy02aQOmDhoxkd2EjDjdi7ZsyipzgwtAbIDK8C/B6wALmSQYBR/w/uuQ7ywLawfnQ29vNJ9icsCduzFixdZ3gHz7O8i6EC2+T66TyWHB42AxjnpwzN5xQYy6uw+6+X2E91El/AryAl2F2YceSSgRZ4BoZCAyGOMpYQTAst1xu1cVVW5JM6zmDxbCEGqUke3ue/t+15VLGXiXBd7wnwjz8zd4XjUEMfcdY61wh56YOV+zu8xDEOuLsEXECDw+xzAY0O9pL47n9XUpdSZZ5ekfihHMiCrnEVEpg6bRJklgSzj9iwYARQgGf3w4IyyV4J6b6/vZBQYgjUlS8f9PFOKbDJucAQ6QMMlz/Y4QeUAXyp7sdBj5BjZcPIcXMJ42rbNlSzce71e5857HlRQFXA+n/NerjmudVKC53RZw944+THPhmG3+D7X9/2vHsC5H+P62FTma05++zi5H2sx96VOoFQWpH6t13sfIFV1NTGUDqhROlg2qUyyZwN4IeBsGMTRuAHxrBBtw7kG1/bFw1jTR//58+c5WHDlQ1G87tQjbwwAApc74oylvM4ZB14YSO6FgHtpgLOgOA8H+YA+jIwDWGe+XdmdzZsL9rnrdT6dtGlaRY06x17jKC2bhcJ17rprHWmVqDgNSm2uGxtDXde6v7+XpHymA2AFp9X3fZ43B8AJhDbqOsoQOLk8qu/LOTMpuOiuGZBWqVNVUNtyjglGdNoFzANPN8rjOOYOccw/z+NG0wNlX3NP8c8BAvXXrEP6L+p43Oe1TwF+/5YDBCBtNhtduovadqHVYqmoa6nfOKoKRT6QYV44Sw9USwBXgjgyEOM4TvYHuXPEeUnKZIYTAcmwnie6m2QurU0pkasVY2q9DrM0n1eujZ75eVi+oZ/nhXn28iPWHYfqJUBkG2EZPXsIcEXPir4NappWqZFGCcq22xt1XSE+yPD4OXBVRYa7VwglIMLx8PyHwyHvyUglcL1S6/jldcxHK3lKY9zt9tdgZ8it8ql6SJkkZcdNxgUGn/svl6urTV7pxYtGl8tZwzBqvd5ouRyv36tykJaPKBhHKQT1w6Cb2zsN46BhjBrGKFXKfw9Vpa7v1S6WCte1SDbgch3L8pqtjNdyrFaXS6e6TnNe1831vVJ6jWzSpMbJMs8ypVJSMiNRXddfD9lO7fSdnfV9CdhgbxjhmU4HosgIfwPQUV5EqSSBpJN4+ALPcCF/PANlbWR+sCOUrhHs8h5j5nPsr0BmsYGANQdAzBXVHc4uAzDRZe6BL2PcXsYG+MOesReFQLiqqqwrVJXgmyBasWUEOv5c2G+CHn7yXA4Yh/46x+Ooy+mcyZAYoyoDf54Rc3+O/+XZqqrS4npkwulwVN3U6rqUBVy0Cx1Px7xeHpAxP9gqL2Gn/Ao58vG7DWR8kBGVgvqrPHqJLAQD2ULHOQR0BCtk8eYy6aWcZHPmxDBjw4aiU2TQ+Dz3JwPKczthRiCAnDHn3N8zaMgGwJ71c1vOe3MyHb1wHIa84zNYf3SM+/l79/f3mbRifX2PuSSNQyrlPB4OOh1PUpBWq7W6S6eo0swGEsIzR14i78Qw2ND91TiOWrStQhWuvioFyCEkcoDrME7WqPi5ck/Wg2DX7YfbPyf/PNHAGjh59Hle732A1F06XZqy2ZsJ9cyPVBwSe0ZYYGennMXHGHgZhlQWiJplDMw8OHBAzKbHjz76KAdBgCYW1ZkfN46+BwBhQHGlaXmgM4nu/Pg872FopFLHidNxBkEqiuB7GjxlPWernE1gbJ4ZUAjqq1GLcdSNBtUapWWrGIM0SJdBehwHnauoEIPq0EiqFKtrytmMjzvuEEqHHndkzAfAF+eYlG+8ApcErFPr66C6bq6B0nDNBLRWJlCpqoKGISoEHFGlEIoxcOaWeWJuWEecAM/CmPu+zydww+QiCxgPAlbfOEkpTwgh76s4nUr3vtPpnE/epqEJjD5g6HK5aOh7hSj11+BAMZ2+nWS8ymvuAbBUwB/OK92fks5RTVNPnCnz4nsgGFtmYVW68rh8p3WtMpBNMlcpXs+aooW5pFkb/2bSgcrZdfTAHTtBqQMzgBzkCSw1+91w0l5awT4YHKHX3aOfPEfKwNxd11CSgsZRWixSYILOE2xig1IQX+ty6SfPlZz0RU1Tyq08yE1ZhbQnbRyjzudTlokYpdev3+jTTz/Vl770Jd3fP7uylDfa7XbZGSXZ3GRHWNdFDiidBUzu94fre5QUtVd5rHW5dOLcrK5LTO39/bOkR1Wtpk3r1ywW2bGFENT1g0J9JZqusoNDvVwSEbZet9fMTXUNnNM8p/kfJoFOXde5+x3r7HX87mPcUccohVCLM8ZSZqKQBeg82UHkCODhhJIDL7KU2DnstpNq8/1Vvp8S+UV/sEdeiglgARQzD87MAkwgWtB7AkknEwgG/JmQOeaDa7NPb04IeSbCfSU644y3j8mBraRJIALD7+y5lxixrk44ejaEazIOL4Hyio31+gpIY1TVBtVVJcWo1TVIQA89U4WNA/BiH+u6Vrff63RImbmbmxs9PT2lZ+97HWKUqlItALj2cTthiH3CDnkm3ln+rutym3Svnhi7UvXhZGRd11IsZdnzQJZMNOsDTsGGYPvnmS5klXXCP7ht9mwHHe4gItE5ruVHhTBGJwp8LMgZc0jQDe7x4Abfvt/vc0MN9MDxB2MngEL2nPBzOUMOvKEIn8VGIXdD30tjVIjS5XRWBWk7DFosWnXX53XC0QNp35/tgZPjSvxy0zR2fqNVIwUpBpn/jxO7JSmXKHJtD9TmFRDz+UHXkG+3w13XqbsUMulrvd77AElSNiaAFN/IiiAz6R65A6pheaVSe4tBRSj5jlTa2jqgwrj5xlmMK4D1k08+yUAMh0vWwzvvcd0EbE8Th8H9PKDzaHxu2HHCHlkjrBg3xuQODYWDrZCKspK1wAgSxJH98kyVVAAdY1qee8XP3ugLYam7eqGqiarXG52fDvp/dmfdvLxTP5y1XK5Ux0rnYdBi2WjVNIpDqSPm3swlG4ad2cfgOTPJHKT1fHsDP+OGuXDwhDPgOx5ApveK8+QeLguUdQA0uK83/bhcLpnNdMPrYyFIctbXnfb5fM4H2N3e3urx8THPCcwRgczcMPMeJUWspwf/PB9jc3Dpe1XSmKt8Pz5PIOHGGLn0FvVuyB1shTA9w4l58gyUr2nTNNfa8sME6Lms8jzYAQiVm5ub/Cw4W5ywB+mwzOv1Ord4Ridvbm4yg+rlHx4kOUAdhiFnnVlv9nKR6fKum8vlShzQy7WYY6nV5XLOJSXYw/TszURPYWz3+31m/V+8eJHnmZIIQIrbGdapbUtHRSeJku0t+wMBZnTx9MzDq1evdHd3V+xgd5nsG2LMAGy38WQ2ukunuirdpWi/jc1A3jxjgZPG3k2DrXIuEkQFJUJkk/ieBwT4KGTIwQ567iXHrJ+X/M4JK3yEg378m8tzkYHyIrjmWXjPwZL7FoJdXx8ISI4DwMb5dRz013XZ0+PXwIa6vvq6oIcOkrzblmduuD8ygu4j87x4pvm9yLT42jtgc5KGuZ+3N/asG+uLb8TeYPOQM9cdromd4Swr9M0zaU62XPoiV4yXQJSxEigih1wL/YHIBNgyHnQl32sYtVpMz1dzH8JaeJDHWiAn2HiapziJizxDCPp95kG7Z43IkJHld4zmeI41Z86dAEAG8I34dR8HtsqxoW/J8BJlyBWem/nEprNHEplD1t2mum12W+ByCq5pmkaq0jW8u+8wDGqXC40W4DDnfk/uxX+OVZzU8LJEvuN6h1/wTKtjJuSEe/O7Nwhyu+TrznXAowuTxaZpVDe/XmKXXwAygKU7NyaZheccjKqqMoAjBcxCYTykYqBdMBz8IsQAHRwJxtY3prpispBu3J214wWodOeIgHmdrqQri1ycjLMtLlAOVtwZu2PE4WMknDFFsanzxahRisizA1h5Hj53OZ/VHC/6+Z/5f+hnfvr/0MsxaNkutH12r/sPP9L4bb9Vqxd3aqtai6ZVHKJi32m5WGq1aLW7bgpnTp114r25UjnD4/JSVUExlsDTN0jiCH2jrDPmvMfaYEiHoWzYRvaQG9bSs3YezMEUu1Ojnv/m5iaPnftivHw/EHOSsmBJHjk80dkgZ+ZwAO7oIAy2222WK4w+zgEH5qxWVVV5D0gpRyrGEeaQ+xMAMGeezXSH7oaR7/r8z9lP5JE9CazZYrGYOFUvdXL2lXkgCPGyI8ZWVWkvz4sXL7It8uADWUHvvSsgY2YcMcY8nylrNOZzsshUJfuQ1oj9NzQLiTGVynm77ZK5KY1ZnDFOzn3QcrmeBA9sZAcEA8Q8iwkL3TTpdPr7+3sNw6Bnz54phJhPrHcAkYBfeWYO3KQcDx3gvg6WXM55oU9OVD09PZnNC+qv5aQAEeYVIINt48WaMK+svYN3gCh67F3dkFHPFjlBBDCmFTLjQnYh9zwABVA6yLhcLnnzulc4sO6QbsiA+w/XdWTeZdLtdd6bOJZGQ07qFJkteyLRb/dRXiLohApjxzZgJ30/Gn7JCRgvw+J6nslAHlhnz6I4aGZsrmfsnaR7LTaQ61Iux1w4QHYybB44ICdUBiBXfmjy09NTDprv7+91d3eX9+D4WVngl8Uigd51Ww579fPJPIvhfoX5Qf88iOD72H8PDE+nUzooNkxbmGdAe21AEWPM+2YciKOL2EcOTvbAmblAxjxL5yAZW0aJ6TwoxV/NiU3kkjny7KLbZ/+8y6YT2FRv4FsOh0MOjLD/c7IeuwkmQTdo0409Z508gHGCkvI6J7frulaoSmWQ6xv3G8cxd3dDTx0XeJYL2zTHxv5vlyfkK0gKVWkm4TbFfSL34V4eBLvt5PPIgpN6lOE73vy8r/c+QMKheSvGOVByw4lyoVAIhlT268B+8D0HYSwgi4SBxVjt9/t8LdgoXhgpwIcbD4+mvRU5js7vx3Uw+igkBghFcsHxe+FAMerOfjBPDh59jqVpu2Z34iiYO32v1Q0h6Hg6ad8s9Nn2Rt03f6O+ejoprBb65t/x27T9n/9n9aHSue801FHny0VVDKpCpfPppP50VJgFqmTeMDSArvm8evaFwGIcS+bCZcMZpsVioW/+5m/WL/3SL+nVq1cTw+NyQ2Cc9irVuRMOcgSLg+EGRHtXQOaPwN2bB8ybdWBs/LsAKcAh1+L7GF/knLG70+B6lBZ5ZmSz2ej58+fabDZ69epVPu/Gs1+sjQdNPscYfA8ikD3kycswGCvOHEYsxrLZ20sVybgydgKkAq6nh/tSG+5z5HpGgBBjzMGHs65kI5B/3ofVKuWOp0k5lduVsk/mPAFczBH3lKTT6ZD1jRJJ9pqcTlOml3XtuosOh0M+XwZdaNtW+/1B53M3acnqAJY9RYAAZJ4294C+pmlyQDcMXd4LMyeZnHF3lt9bT/MeNlchKIbCbCJD8xJPB/fn81kaoxZXu+hBzuVyyfsfWJPL5ZKzhVI5bNdtN//BijOP8yyqpAnY4j0vPeIa830oLufYN78+36N0MYQwadmL7mJrAPJ8n7lA5gCxnoXlc2SmnfTy5+ffDnaYT+bA7RNr5gE6QAh9xz6iw+6LxrEcgM54sP2e4QH0uj2drwOAdrVa5ZbdbdtmGYZIcRKO+aWsFjl1ID6OqS09beGdpHl4eMg2B5/kJfQExszNnATieXgPX9suWlVGvGFjvDwZOcPG+bzO8RHzzwtdyPplMops4u/6ayMJ9iFChJxOp0yEOH5ym+J6gL9hPJ6tgEDxvSr+Pff32BGIXwJA/BI2zzGer4VnM5A9AhzXGWTSq3KwNayBy7M3QfE1duLSy8PxCXzO8anP4zikbrOemQE79MPwls44DnAyGzzL83lmleDOCXvHROkZouIYr/uTijxPgqhQ9hjOgyPPkPN9J7GdNHU5dB/yeV7vfYDkexYw9L5oDkZQJibR9xF4KtSZJgRyuVzq4eFhwlx5sIRi4Zi4F8LmJR3ch7GSrfEMkDOOrrQeACIcXjMN+0V5lHdzQnjd0HAfVxCMCcaYsfK8sL3zVLELqpdjkSlYrVaKY1RdrfR/+b3/V21/z6CuP+vYRGm11GcxqLlcFJugoQ7q+07D4azlaq12vdRwuWgcy5p6CQuBwJwN4XfWCTnAUfR92TfG55hv5vlyuegbvuHj7Cw9Cwdzw1wtFk12oF1Xzr2Zlwo4CPbsyJxFpWwUWXcAA9jBaPA3ZzZxMDh2ro8cZ9YplFIgZ2TnrN3r16/11a9+ddKgwcsRWAcvH2vbKavDswEQMOAe1CKjOEnfU7FarXQ4nLIeScplKJ6NOp/Pea9M0e+y78mzvASPkAesK89V13XO0Mx1GnCFY+R8G67N39HrcUyNOnDYAKSu63R3d6cY+wmgdwaN8kieEzlO9ioFdAAaAMpischlgjSVYdz39/fXJgVJlh4fH/O8E2yyFtgnD5hhv7uuM7a5NJlhjEW+p6VY2BeAI7aE8V0uF92uVhpiaWADOGDeWCtk3gN09wN8hnv2fT8pT6XtMHIEiGDukSHWhOvwnJ4t4DvohK8boHoeXLldRl6c4faA/nA45IADcsB9jjPRz549y+vqWQTWxfda8Az7/T7vrZsHG4A3ArS2bXV7e5tthoNe3zzOPXkePudZArdbzIfvG3RCk+fh2rxcJvBxHqTPMwZN0+RSQS9rHccxl+BDcECCbLfbbFuwv2RgHVNQbYE+4EOYZ9efw+GQ58XJHwJ+jgjAr0jlmBBVJTPoRKuX0jlOYZ74OwEvwB0f7yA265mCFMs+aw5SbttWTZX8zXa7zQ0F5iSXpIkOOLGKnmKLCWLQBdaaTA1nzTnpBbFFJQO+CDLVnxn5dbkjM0vGH3vQNE2u5OAYB8g1/CzBv1SqPBwPgFGwJ06uQmqzXmSNIQxZH+7ndo0uoGM1KFoQ7UFQGxaq+7KWzJUTIOi3lwJ7ZgYb6piAn57lHMdRqtK+O09WeNmw660Tp+4T8MFuLzzA9qAqB9FmC77W670/KPZ//99+UtvtNk8SAu1GyIGnOzJnv5h0Jh4WDmbZBQGnhRNyQZun7T1zg3Ji/FDIu7u7ye+MC6ZwHMdsLJwBcGPH95zxc4fAGD0F6QwpxtA3byNwniHyQAMWk5IAXi7AsLOSCrsYFgpdr7E7amyitGpUqVHbS2Mc1C9q9U2lZpCWQ6W6bnTsO419p9WqsDdeqjXffM+6OyuFYhemNyjGacDqMsHnvQyN+XYA4mx/CFKMZc+TM0fzwBOZYE39AEUyEBgWAm9/vnmJnQdXMUqp0UQpNcBAI/+UUmK4cBSejUWOmTPmyUsqD4dDLhkhqEN/0ph6rdep3AdA788O0PNnQQY9y8AzJ/krgZw7RubBZRgQFIIEtgKwEsBeLpf83H5AJbrhHZhcZxxMPz095b8NQ2rxTD28t8lFxvidYIpAcbEoDprPkxk9HHaTZ0Rn+35QfW1UwJ4o5Kdpag1Dn9cWp7lcLrVcrnQ8lg6QAG+yDB5YkKHEqSPXlPJA+JxORw1DkVVnUA+HoxaLZc60OfDCwR4Oh5yhyjJQT6sDHAQ78cV8DMOg5WKh7lw2crtuuzx7JogXgAnZY/xOjnFPv5YHbsiB2xEP5D0IQN89Y4g8My/4Feyw67JnAbi+72/ievOMjANVL9vjmk6OOZvr3/dAj7li7Z3p5x6MyQNDfr9cLpNjMryMzoEh33USDDCNHiOb/GT8HoC6ryTrif4gu65vBO3zkjuCVweDXkLHM2LH3YYzR/hHSDnG+PT0pGfPnuVs7jzAVJCqqyx4wEgFCcGOE6ueWZyTAk4IeBaDDoDd+aL6ei8ysdLVj1beSCdk2+qkHPcj0814AcWsB/OH7DgBjR32sk70xv3L6XSadFB0ksKzKOgtsoKN8OCFZ/IKEMbOT0hqJ2kJbBj7MAzZH7gOY3eYe8ZEa3THLvMMXF63MWq82hSydVn/JakqGUK3cU4cOfnPnHIdxu9YkLnCT3L9OqQSZyf6uCbvOfHumBX9xecwJ7wc8/j9hyGddfbrB8VeX+v1OrPQGACcvxtFlFWaHoQ5B/MYH9gcFz43lhgxaXoQl6RcOoEAS8qGGyeXFDzocul0PJ6upTKnK4jDcR6zAnsnKFpKS28fPuuOg7Hx/AQ6GF+u4d9HwD1AxKEyH84qwZjwvoMD1sEzc03bqg9RnQapbRSaSpehU31t9b1arqQ6aOgHdZdeldI8aRzVLlKL6su1SwnMUnFk0ulUDvejFbdUWj3ztxhLVyI3nG5AubZnxwogLRtvCRbS3A+iux0d8U6n8zXIKp0JMco4tWEYtVgs8xqnlsuLqzMubaurqhj2JD9T9rUY25Ju5jo4HAIb1niz2by1dwUGjjlOQejJSqpqnc8pS5kOmtyK0lQcK46lqkqgBcjBOMPwAoa93nsYRjUNYJIyyn4C8LyUDWdGByHmIrenrSodj4creEzPsl7z7L2aJnV8a9tysCTAAb3GcKc5aK6yGHQ+X3JAmsiDcl4JbDvlNrvdTq9evdKzZ89yYFIClqV2u0MuD/Q9FItFq6q6yc9NiR2BzXJZOqHhWJlzWNQ3bx50e3ur1N2t1es3bxRClTbvxqi7+3udL2dtNlsd9vtc4uXHHlAigj2FzWWsUVKzSO2H66ZWuMppVFTdttpc93TwfOM4KtSV4jiqH9Nm4mEcdemuJcphuqmfYM0BngcGBL2Z/azqVF6iqEpBw3gtTW6uzLGiqqZO59YotWFmzPNSO3QXm+bsqgcu6JcHJnMyhe/A5Lt+eHDpRBvyVNd11jEPUvBJGaTUZfO5Az23GVzLM3CeiedFUMD1DoeDbm9vJ89A+ZEHnciPZ7mQXV7+ec7HIlMCmPWypkJylfIkMj8EK/My+kIeTdtpYwMBsPg1yA30j3JWStQIRvyQUHTAA1nfq9s0jc6Xs87XYLSukixVdTq/pQ1B9TiqXS7UX23d7d2dqqZWqCqtt0mnF02b5TiEoLEfFGql/UFVUF3V0hhVN2X/0byaou/73BEPfJLXZIy6nM6pq2kIqppK+91Ofdcn4qErZy55oDsMJeOD/yTT4/s9PYBAh8BG6AyyTGaa9XFykiAIGUJPvCEINtnxIfIDSYYu+hYFng+5nAfL+DH8I1kqJ7h9DiA60XE/9J114bmQVWwLeDb742FQFSqN8Yplr+SKYlS4BqWu83V97S4XpX6MCnVQkFRXqSX9EKf7d95FprPWc5/I57E7pYKllON65o65xrY4tkIm/J7orpN7bg89QeHB5ud5vfcBUtf3WhijJCnX/eNEpVKzjCFncXBkCDQMkS8SzsSZX++k4wZcKh2LPNJ2B8i1079TO+nLpZsY1arCiCWgmNrTBsVYSmdQaBgrd+YIiwdtnllxhs1ZL88eECgQXPF9Ps88+334HClfnJorR11VCqo0jlJ/6NWGa4mSeh2O16CjqjSqSsCpCqpipXEYxfkrySkpO+MEcBstFoVZOhyOeS6Y5xilupb6fshlfx5cIC+uvMgOz4JCYig8mCIoksp5C7SgxlmmOatVVTBmdM1r8udTWRrn4JQAPxlwzklJ/yGvyHsyitO9c5y4nlj8spHUjd1ut5uU9pCl5Tpps/94DQ5P2fjd3t5ouVxnOem6Tjc3N3p4eNBisbgGUJtcenZ3dzdhbj3L5kxxjEXuErAEqJZ9BuyhQCZ9IzOBLc4/XT/N8zAMOh7TeUqAnr6nfCq1vE7n/5TyAQAFzjrpP7KfzimiRGUcoxaLZnImEMRL3/e5Q5tnrjH8z58/z2UZrltJF5Wd6na7zcHver3RalW65wEEsFFPT7srUBpUVbWeP79LTHnbqqprrTbr7Ng27VZjjNre3KTNtlfZ2+12We4hDhgj4LGua0UFLVepzj/vXwpJlm+va79crxSDru2JU3BSt42i0plGx7PZlroECQAdL1l24obnzhvzh0GjUi38xbJJp/NZ1VUeFII6K/eproDTy0nQPalkXgFEDpIgoPius/ZuRz3z40ERcut7eTzbwVgICAmSkMd5Ngdg4t9HVwi0ea52Bqw8CGH8EBmSchtlfB7laO43POvme1m8oQ/zQrkZ4zyfz9mOsKfHgdU8I47u932fmx14UB9jzPuNkBH8OPNBFoEMZiF5yjo6oOZanuljjtFhdFeSmraRQtBiudQYo86ncljq/s3rPKaqqtQNvaqmVrtcTI54CCFcZbpSu1goKDVHwNZrkFRHtU2jUFWqLRhHviCUCVRd5kIIClGKYzr/rm4abVbpAOA6lOyFVDbro3dNU87pw27jNwmQWX/PJDB2AnjPQLFdgBdyw3oh8wQgXv5NkOt77bgG8oFdkTTZk0VQ5IQY+A9dhyxCf7GNlE8zLl6u/9wTG48cQlDju8B2WTfGUf1YAtFhGKQxqu9KIEiFjycFCKiWV9sVx6uvraXe8DHySqaUsXFdD57QQeacOQkhSLHICetUkgOlizKy47jUcZeve/G70wofJ+ir+vMHSe99gHQ6HlPUHMJE4FB+TwlKb3fcYFKdgXSj66wbyuGpX0lvlYv4TxaUQMaZbRyQH/rlQYikfIieZ3667jxhTXleyve4rztiBB4WArbLgxie19kxjJ87V2dDPcOA88RJuQP066bsTppr2CGChhDKZk1/Fg8qmXfW1hkiPuepexSNg/E4M4T5fhd7Q8DI35kbGCZnWnmPNWPuGMc8fQxji1Hged0oEbhxL597T7/f3d2qrmu9efMmd2RM3XBahVBPysyQX1LvGCuehbm5vb3V3d2dXr16Jc7sSiCj0v39nR4fHyebx9Mzd/rww4/0+vXrLL84CrrGPX/+XG3b5u5DLos4gq7rcrbC95ow/5Le6vJFqQZrAFtNxhT9q6pqcmggQJuM736/nwBw9I5smTtgHE9dVzkDLBWHnMabZI69Lb6nA1kl28V3LpeL7u42b5EwxbGU9qc458S4b7LtwrHzvCEE7XY7NU2TAzPAfd02aq7zDjCD/AhVChQAzswNsuRsNGPquk63t7eKSvvVbm9vFWOcsMDYm8I0Ts8P8xp41p3vYWMgSZg7/sb8MyZkL8aYP++2jkwdIAdbGYcxj53vF6Ig6e/t7W22QR68sfeB+aAMySsR0GX8Ql3XORPhRAc2B5vqvgi92O12WV6dofb9dE6G8Blsp5MS2Kx50O5+i3lk7dq2zTaV75B9Q794duSMOWVzv4NJ5o3vEeB4EIWt2263OeMEuPXMA8/LT9bJ55V7N00zKX/3IBa7wx5fQOA86wG4xe44YG6aRnGM6sbiL/D/3JuggOf2qg8P/lMW/NqtcLlUtO6pTh5Ipbzc7S2yJpVyUmTl+rX8nMfjcRLIkt1gTlerVSZWYzVtuOBBDPsuWU/mjOf2syF5Di9pRW9Lp9Y6VzR4h0CqYNxWeOYB3XD/TvdL5nteZo59cOIB/OQkH+vkpaFOXpPhdllGzjwj6sFPIvOOBVdKuZOgYxueGbuPDDKPkBKOP5GJse80jGXPsjfzQP7RG9bdAyrG73arqaa2w/24Ey9zEpr3GCO/s/74Npdb9y1fz+u9D5CYOAfldV1n5gZBc4VFCaTCRjhTBGh1YWCBXaD5jjNZGEvJWz+Xzb6U7hQhqN7psEMI2u/3Rdiash+oqt7uVgSYmLOWjA9HBUDEYflZAxgEHARGxY08Si2VlsEA2jnzyE/Gx/UYgwcV6TmVM2cOetzJMfcwXawZjpXgYbfbTdZqfy0XYqPrfr+fMIMOlpGreaaI+87T5c4KZfZEpcyF+WYuXN48y8j8w/wwN16Tj9FNhmzMG2RxVNw/HYapSZc1Z/53u90ElJKRcIBPpufZs2fXPTinDGqQjwJ4EjtL29aqqnR7e6tf+ZVf0WLRaLvd5uf85JNP8pqxXnwnM5ghaL8/ZOeKk3GHyTyydrw8yHRAyZ4M12MMK7omKW+IZl8SmTM+T5lO6nJVznzyYDqtqyb65BltlzHGn8YqPTw8TLoI+jpVVWr57uD5+fPnappW/bXFLoAfeYV9ZD5ub2+zY5eU94Y1TTM5cHTsBy2ucgjoeHx8zPI+J3RwqIfjQev1Ws+ePcvz7/qGnjmj6EAYkCOVQBCgwnMAGp1NdlvB3wHW6E5q8HHIa+ABOH7idDpp0ZRDCOf+AUAHSzwv/aK0j0CejdWMj+9QdgRxIU2zvui/kynYOP7GNR2A4QP8oEzsNwQF93XykM/FGCeA0Z8bGfesA37Wn4113m63+bvOxrPmAE/3y27bHSj655bL5SQTjRxCrBAQ+1o4weV2xoNKsmp81gNzAjkH44wRGfC9WfzE3gBi2+saH49H3d/fTwIiJ3JZB57TbYkTFJfLRXWYZiEyZhhHRZVMju/d4L7cGzlL81kO3/XMlbP+DoizD551m+T7yANjcFnFz87PM0P2PIjG9hfyanpuoweIMcZcCkymyIMuJ7GRCfSX6z179izrHGPgefHJ+F4nUiGmfGzIvesC64ju4++wJeAODw7qqlaIZQ8ba+aBNMEbc4JNwA54wJE+2ytUJclAkOZkGGPjGb06q1R9lIxR3ZRGEi4TdFL1vVpO2iD/3MeDKV58zgk7z4Z/3td7HyAhRBgxFsP30EhlIp0pw5B4jSQgfn5tFh+BlUr3LoQRZXe2jX+7Yygb1cPE+XF9Tslm4Z0JSWMsrZt5tjkAdyPKNRin9Hb3EJwae1F8TGSRMCQYBy8JdAPgGS2p9Pf3Oed7i8VCT09PE0bC07c4I67njLOva9u22u/3E6DEZwG8yAgGzMfjQJzn4X1+J1hiLjz7wnpLpQSR+2Gk6rp+K9UPuO77flKCwPXO57MeHx9z9xyf7+R8k0GkrKoE72nfVd/3ur29zc00vPwAkOLsHgaJGnxJufXtarXMzsAzRICKw+E4YcwJUpqmHMDHvNzf3+f7+QGFDgqdcQeMkJHy/SY4HQ+gXH6ZU8CKt9Fv29S5zZsOMH4YzbT3Z5rFKDpZTRwHDHX63JCBBusQYznbinnjZ5pTiS5wrJGzbJdLATjIdwpsDgohBaw0i4BEOZ/Pev78eZZFAPtisVBn2fN5Frk7X3S52jeArneE8mCQ+wF0CKggUHw8njVhfbCjMZZ9OqwhOuL77Shza5omZ1B8rwhr4pkqD0T9+z6G4/GYzl+7zhPve4baCStfB88EOsuKzFKCCCPs16CMCLmAUGAvrBNMgIC7u7tMLDA387FWVepUKCWSCNvk92K+AJHDMLwVhOMDuLY3MjkcDjl7NWeGPTgEnALcPCNJ1o11x9Y5CPNsJcGGAz3u6wCTIM9JTb7nhAz3wd8g1+i1Z5bcv7OefP9dvgIiCBCnKnWL2W632edhzxxMQmzQDdN9fLExo4KmB8XzSnMV1XUl2+eEg/tJfH6et7pRvSpZFyf7nGTl82RN2uVC0e4/95k8gxOCc8yEncEWYFN9fd0fONnLZ3hhrzzjOb8vMsXco5dO3IxjyShzffy62zKuw7XmGSL8GZjFgyeu4/MzDyJ5sR7z8j1JWY94LnRA0ls4NXfIU9TQlwOuh6HsZ+SFHDDWKbn9NjHO8yArvNAF1xlsKtfzOfE5c7zleu74etGWPXBf6/XeB0jUgDuzB3OBg5tHoC6ILnx81gMNvofCIJAIoLOermh8xjMFzo6lzxbA4Uz+nEXid8BF33diL4gbTs+iOCOF8Pj1ADKu1DB+jBFHhpHyvVU8K4wdh7N5zbGXfMBM8zssgrMkaSyFJfV78/J9Vr4G+/0+Pz/GEiMIEPK1YS4cpHFNZMQNiFT2q0llw/LcYM7bfGIsKIGh46KDLUq8kMu2bXMmxjMZviYJnJSDNclseXlOVZU2o5xFAQvGnPj1+T4BF+w6AC4FXSX17gYa50fwwvw8e/ZMbdsoxjHvQQK08/IsAutIwwJYIfSP/TkAXebS92J4ySvrCZg7nU6T0iOeD73b7/eTds9J3lI2CHIDgJL0OO3pQe4Zb7p3Ca7nawgIZHwwn8MwZpnlsEoyeH3f6+Zmk0EB675er7Xb7dW2iwwiAeV8dl424kFJuywsvWduNpu1dk+7SYacfSapmcQuAzl0aLlcaohjzibe3Nzo/v4+AwEHBpA+zBf3gdxyIIf9YWyAI8pVvO2xl3RwbW/TTDDsjpyxpaMICovN9x1UH4/HSYMYvu+ssAfg6JQH/MwnthswjBxgzwEBfJfvd12nTz/9NMsFn2F+vHwHO0L2hPFiF0IoG9XRG+STbF8IIevc3d3dhETDzhPY+Vlk3mTBgdS8wQ7PQBb8zZs3EyJIUg4wz+dz1kPk1YmdOXhzsgn9dJuP7UM+0A0P0iDrIMx83Tyrg11xwtPtfN/3Oh5Pk8CKZwCHsL6ljLfOgBW8c7lccilxFabdQHn2ruvU9b1imB6J4dkz5pN/M8amqdXURa8gKfBRXZeOJCB4Yz7Ha2WfEwnYRtfpd2VIXL55XrcTTkx4kAQGcEKDoNSbBc2JAa6DnEP+zW0CJMJ2u52c7+TkiZMyrKWTaa7ryBzy72VlHsyznjxfqfQJCldfw/eQHeSHuXJdYK55ZsYzjqPaplU/TPEk8smzse7ut5hnnhkcE0JQ7AuhDjmCnHpgyD3c5vqcOe520tmJci/fG8bPfxbSex8g1U2TwTBG14EShpkyM4TRN1piFKTpRDuIdbaJa9Z1nU+55j2pbGh1dtEFopR8FFCAQCCIzibxKpvTSjDljoLnBADwHIzJHbVnaZqmyfu15qdwe6DDc3BtnBkMrqTsaFxxUSZXylwacDUCzIFUjK0Hi/7CCPA8OFxPTxNgeYkG6+e/A8Jd6dzgdF05y8jvPzfmfJ6AyoENssjvflCig7u6rrOBhn1HztzpEQB3XSqtgSHGKAJaYkzy8erVqyuI3k3KIcex1LHjHKRyThHyx5rWddDlkubCzw05nU7abm9yxoln4R6Pj4+qqmLIAIOsg6TMSBOYpaDn8s6sjxMKzso5+8tzcm3mxUkC7k02C0Dq+1HSNaIul2Iv/MRzmoN4JkACxI9aLNoM7Fg7Wo8yDzHGrENJpwhQNpMSyePxoPP5+BbLeTqdrkC0yXucUjB1o8fHx8zw+/MDHtbrtZrFtHQKWTifTnr58mXOpGG7IA88EGX/WtsmRyspky2AfUgU30w/juMki+ogkbEC0uu6zh0WKQvkebGTBIEALAd+PANAAVvm906ArlPblGY6+BayOU4QeHbdgRW2kDkjoMbmuV9BX5fLZS6vxN9kAGNVDlzbx41NnbPh7M/zzAHzit1zMsEJQuQOW4WPQca9ZAq7QUCOfHtQOC/3xfawFsMwZOLM5Yw19M50zDHBJDbDnymz45aNgZxB/r1Cwe8lKTcwYD3ABmTJ3Q8xB/h2XwfWiLFiwwCLBDrYZTLMzBs+nq6ijPH29jbNr4L6YcjNZjy4q6pro6NYzkz0gMYJK4KB9XqtOqSuks7m89MDH37PQXxdK+ptG+u+GczlQTfvO3gGGzg+c31w4oKxEdgTTHANZMr9MrLOGCB/8Cn4ESdbGIMTBMjv3H7h35ygZk0cn/FMnmVxG8E88QohKLzjvozNA2EPurDt3NOzcKEuWS73sayF4wrsJC/m3kv50jhL1scDP5chl0d0xtfUbZaTmZ58cHkJIeh8KuTr13q99wFSd+k0LEcNw/X03shm2sI8eYeNpISNQkgdV9L3Uqc4gAXK55klVzhnN3BU7ljcoACK+B4Lme5RKUaEcFRdN+r7qK67yPfiZENnAoFxxyl4FmceXKA8DjZgXJxNktKZC4B5B+YoEkLu9eo4HDIuzMHhcMgsKvNDAAcYBxD7fNGpLr2imob9Ven3tp22wk1rW9giNz5uFDD+zibBDuJEWSNnk9xpwsB6Ot9LEzDGbZu6fiFPnhLHMBCEUsI0jqm8EuMIwE1tmS968+aNPvjgg0l3mmHodXt7p/V6rcfHJx0Oe10uXdKFkM4gCnWtS9/p5u5W29tbdZeLgqbAzQ0Y4IIAkj0tY5RWm7Wqutbt/Z2enp70tN/rzZvXijHo/v4+O403b94Yw9aqbTlnhf1niwKo+/4q71HL5VrbbX0FcKvsTJhjZ+bQQWeJcZo8D2DFmT7WzR2zM+tk+ZwNXK04mT61YO/7kxaLNmdtaKndtm0+jDVl0jotFmRlSne8ZE9OWi5XqqpwPR9oodOpHH4LoHJZBeQlG9RpGE6qqnIOCIB9vV7r4eFB2+32rW5GHBmw2Wx0OB50upwz8GUfGnqLTfHzJLgHgQJZgpub1IJ8jKXsAbDy9PQ0OR8LcObgwDMGDmTGcZRiVHe+pO5aw6BF0+p4OCgOo5p2ofX2JgGFrtfF2P3D4SA1UYOkTqUTYAhBIUZ1l4vaplFbpz17x/1Bj4+PiqbjnKWCbCMrnoGSNAFQsLQ0OEGnWCdkF7/kWVeuSRXEcrmcZDaRX/wUMo+8zxscYJecYScQ4RVCyP7EzwHCbnIPJzBc57gHmfJoMuCZFe7ve2FYe2TFx4R/cwDFT4JjL5dkbubBKlk/91vYYeSQfxOooTcOwCDesOdeSeBzcTyfpHgt8VJUpZLZRW6YUwLOua0CuPOe71ljbc/ns1bLlZqqmhA32S+2bc4geSkx92MOkJfM8A+jur5T3dSqlLpMKgSNMWoYU1BG0OGBklTWibV1osMxxTiOEzlALr0yA13yIIxg13URO+2Bj5PWPJ/LFrLJOjOvfj3PWDgedBlAzj04wT6AG1hzD0CkaYkmzzvPXDOXZRyjmmq6r4e/MU70CftyPp+VWpJW0jiqbmrFoOsRB42iopq6lKWzVu43kD3HCU5k8TsYZ4yDhgj5MqaW4mPBk57hZx49OHI5RTd4LrdJzKWTV5/39fU1BZf0L/7Fv9Af+2N/TF/84hcVQtA//sf/ePL3GKP++l//6/riF7+o9XqtP/gH/6D+w3/4D5PPnM9n/YW/8Bf0wQcfaLvd6nu/93v1i7/4i5PPvH79Wj/wAz+g+/t73d/f6wd+4AcyK/31vGJMLZsTE9Dl/4YhlXns93s9Pj5OzutJf09tftlHwCZnHBuKIJXMDQzPdrvV7e3thL10J4Gjadt2khHwxU8CRV1uOkhzGHotFq2Wy9QK+e7uLt/DMz4AJ0/TPj095fKCrutyKRFlKGQuCO4o+XGWBSdDAEVDgzmQ5jkxOLe3tzno4V4EHOv1OndN8xIfjLKXjFE20HUXxTiqbekq1KvrLleAWEmKV5AjSWnjet+XEjPS5XNlv7m5ycYEY7VYLHKnMUpclsulbm5SRoSObuv1epKNgrV32XBmA2AE4MRAezDIeChzQdGl6Yn3x+NRm81GX/ziF/M8ATLqutHxeNJnn73SMAzabNL9FCpVdaVQVbq9u9ViuUznbCxabW+S/NLCmwDEgwIMNd3dACkKQUMc9bTb6c3Dg5arpb75f/qf9MEXPsjfAaDf399npi3pVqvUqjsZzBDSWQkpyGjUNJw/Uauum2zsXP5wMDi0XId/Bfh+3gbz6N170Gme1zOP6L4HsWQqOIg1BSOLqyyErNeHw2GiayW4GtV1qeX8cpla0+/3Bx2PJ71+/UaPj496etoptfEv98bZUz4qSS9evNRqtdY4xjyO5TLp583NrVarVS5x5PvOiuPYttttHt96vcklnhxGyXfHYcwyjMNn7vzgQ2xOJo2acvDwZ599lp04dsdZYdYOQO6AGBvWNq1Wi6UWbavlIp0P09S1Xj5/obqq1F0u2j09pXOblkttNxutVyvVVaVn9/cKkpaLhRTjtXVxlKLSOU0hHR/w6rNX+vRXf1VPj49ar1b64IMPsn3lIG/Oszqfz3rz5s2EVWbNPYPMfDBXBJvVFcw6qwv4cBvKXlRKGSG0kAcylvgVZNUzNsj8fr/P4/XgDD3xQAt7jV3woICDSodrxsJtmssC+ukBIWXDbBLHFnM9SA3PDEjKtpaxY2fwF+5TmRf0gIwL9hv54rk9QPf5lKZ7OU6nU9ZxWogfDgcdj0c9PDxov99nuTifz7lV/e6w16XrdDge1fW9WmPZGSM+wjNe3kTFs0boMfbq9vY22y0qOvhbVVVq2iZnbG9ubial3Owl9aoSCL5hHBSqKp/PlAIk6Xw563Q6TxohuF3tu3KwOE2deAYnROiOyjjAUI5B2DeMfNKpVCqZEw+8uQ/zUTBiabSEHAP4wSpc14MMB/7IsO+h495OogLSmX/sm+MGzyCS/cEXOVnNy4OT9Fxl3xdj9rF41tKrG9p2oTGOGhU1jOMVDyy0WpejClzmWC/sMzbaM0L+3zxTfu4uUghZdrqhV9f36Uw6e3b0GrlnvMwXgfN83ZhbSEMnqz7v6+vOIO33e33bt32b/vSf/tP6E3/iT7z19x/7sR/T3/7bf1s//uM/rm/91m/V3/ybf1Pf9V3fpf/0n/5TPqvgh37oh/QTP/ET+of/8B/q5cuX+uEf/mF9z/d8j372Z382C+73f//36xd/8Rf1kz/5k5KkP/fn/px+4Ad+QD/xEz/xdY3XmQXYkzTBpbzMN40nA1uMhu8xWSxaxTjmsz08nYdQICDUI/vnvCwJAUMAHNQBALg238eZANqcuXCwA7NJVy5AOQwzHaO8BhXB96gfR4oQInAYAQwm12ZcgB3u62NDyVNJ0HHyWQwXjtxTz3yGDBelDw7spBIgEtigWE2z0GJRDuRDAfm+G23q/N2w8uxkoVij3W6XHT7A08u1+Mm9SulVOeOBjnE4MEBi3/f5oEVnkJg/MgDO0tP5Zc68YCgyK3gdAywZ67rZbFSFoNWidElzucVY40TJknZdp/VmrWEs7TRvbm7yZm53BJSKAYoYg8sz8g6okcqZVshuCCGf6+NMIuuI7MyzEL5GHtRyX2coAbWuC96yGLvibCiAk+dCv8dxzK28GWPf97q/v1dVVbksh/HR+MBZaGwUNmQYhrxhnzXZ7/c56CZgdn1hX5KkPAfMUdkHkfY39eOgp91OL168yMw/pVJVFfIRCsgVY6BDGhvN0ZnD4aAhRikkZ/vBBx9IUt6b4vLI+qMnnp1GHsg+O/nDMyI7HhBSriQp72d7F2vL/dBtytCaJjV92G63+vDDD3PZkt/HgRvZFpd9HDpOG1nykmAHpZIm+/JijPm+AIbkn0omhcYpXNvHh83DLhMQEDDA/POazxH2iz1s2O05CPHAAv1B9o/H44TtnzdNcpKM58NG84xeVoTfYAxOOno5Hn6Ze2FLvTPZvKyHNWDeCh6YliCyhu5Dua5n3C6Xi6q2ycDfCUevKHFilTb8rAfjwV6xRp65IAjuu04hahJEsmbD6aTVZj2ZRwf9HqAiA/z0DLpkhw9XqZMaf2OckjRGqbH1YV0d/+ADuaZnKjzj4hgFPIS9Y4xzDFJV0wYi+ERwg5fmMQfuv5Bl5IZnRmaxcZ6Rdf8GNuOZua77amyDk0M+ZvyS64PP8eV8UR3KlhJsGXLFczJv+LquL+XAdPQF6/lzerXGnDR1ffX15PsQSegSY+c7Ppf+b2wJ2Nqxmeu1Y1qw/zxY/HpeIX693/Avh6B/9I/+kf74H//j+eZf/OIX9UM/9EP6q3/1r0pKSvnRRx/pR3/0R/WDP/iDenh40Be+8AX9/b//9/Un/+SflCT9t//23/SlL31J/+Sf/BN993d/t37u535Ov+23/Tb99E//tL79279dkvTTP/3T+o7v+A79x//4H/VbfstveWsssLO8Hh8f9aUvfUn/+//2T3MNu6f/2nYK7pzFjLEsjJdXJeNfSqFYII9sm6bJqWxaA2MkcewImF/DmRRXWi9JQ5iSsNUTYfNmDlWlCaj19eJ+KCGGycEjJXHuAHwDKA4QYfS5ciOEY4B1pLMQAu0O14MylAnA6JkBNyawPsfjMXdDQkkxDrD7bVuYI+6BwwBosjZu+FFOwBpjRo5w+J6N6vs+G0LAmgM+mE3OuGF9nc0hK1Qab/STmnjkDoMKyMCRSNJXvvKVScmdp7n7YVDdTvecISuLdqFgjhYgMd/XwOf5d7NodLk2aQDIA74vp4tOx5OeP38+2cjp5RbugAAKyB8OwxkqvoezwOGiI+iLgx7mbW64HTgxH4BpOvgxJmTGATnz6uNwBhw7M9dBrsfz8R1kiOD3dDrp448/1n6/11e+8hU9f/48Z754Tpzf8XjUzc3N5Iw0bBPzic3yunDWERkex1HtMnWy416Mab/fS+Oopi514u7kGTeZY+zBfr/X9vZWm+0m22nKelgLSjd5NqkQFMwrIC/buGFafsF3sJ+A/vP5nIM3Z96xwS53vLbbbZ4TJ4SQLXR8Xp7pZBKBJc8UY8yliowFx0/mBR8BEMJ+EtSi++gkBAyBOPKA/3OQXlVVzvw62eGgD1nxEiZkPsY46R6IjGOLnFhiTuZ6iQ1gvTwwZeweJCJP6BHrit/ET2OTmCsH+NyX9s5zsMnL55mM2vl8nth7QJ77A2REUt6f6sFTDparoKquc+bqzZs3OYAna0Q2AT/EGvpGd+bJyVQfU4xRVQiqQ5VlDd9dJZZYqkoJptsBJ/g8yHMCizHzzJfLRYu6NAjwsYQQFKtkI3g25A65dBwhaRLIOMk19xdgFCcmwR0eSHjQG2PpoujZFAIdCFleHojiA1hn133GxX0dLzrW8bn05+LZ0SHmnTVjfbiHBxtt214Phe0mfhKygesip4whxqiqqTWYvnMvb9KBTfAMnAevjJ919Ln1rK5jOHTHg5gwTveoud/kWeeHI7u8omusn/uE0+mk7/pf/7AeHh4mpeHvev0P3YP0C7/wC/rkk0/0R/7IH8nvLZdL/YE/8Af05S9/WT/4gz+on/3Zn1XXdZPPfPGLX9Tv+B2/Q1/+8pf13d/93fpX/+pf6f7+PgdHkvT7ft/v0/39vb785S+/M0D6W3/rb+lv/I2/8db7TDITjcJ2XZh0PKOeOxnDctgfgRGsQN9fJhGsswvOPlAGgcNgLCgfAQxnBcGoS8rtqLuuy6VYOG0cOE5iDjSTwI8ToAxrhcJvNpsssHPDgWDNGdXnz59LKuw/jC3fR1hRdMrDPPPhztZZDMBH16XON77pdc4WYCylwlASkPp8sO6pDDDodLro6ekpf465pIGHK3A2NNcXKXE2ZOKEvXmDB04ASEAeisocoxfMIUYedm+73eru7m4iN9zPgQyGCpnCSSCPH374YXaeGESM0XKx0BhU6tStLbNiVFs3mbX0QAi5ZQ6RYUBe0xZWH3YYEIfcIOeMh7H5hmjfTFxIjTaDUdaKTmjOOuLIvHzMwYMHFRhUd/pkJpBbb8qA3B2PxwycIUBwmj7PjMefCdsAUEe3nVFjnMjAdrvV4+OjQgj6hm/4hjy/2DayOjHGXPLGfPsck7Hivg4gPZMMezj0ZS8RDpO1juOoEIuN6ft0vtjt7W0GepTz0uwklR0dtN6sM2BmjBAC2D3Ghgwy59gQb29cWytjD2SwibD1ACZnyp14IWB04OEsNnKEY2bdnehxsEKAxljmAN6BOplkQDzzRxbOg3zsDlkcZIt70XIYQM1cYyMIXAFxzrgjj8xJycKnrCZ76BiHNA0oCHCx/dhAACtyCjjlPtg/fAWEnLPyriN0/ZwHKL7mHoAhL24b8AOuBw4sGTv34Pt+DeyJlxoy57e3t9lPTvxXFdRd15/SwmEYMqHx9PSU58Z1DznzoNV9JTiHe8WY9tHFatoeerfbpfltap1P0woOzwr6PcmGSppkD9EZfBPZIyeIkJW+H6QreHZS10Eu8u9z7hmEORFDwE6gDrgnyKmqavJM6CyfQ7Y9CPTGSMwxto/1hIDxcjJ027/Lc3kGmPlB3xxPegkg9+F5PThCNjx46PtedVXICmyXy5KvDeRgjFExSLWmGXdso3+PeeM97BQ2jTl3+0hjEb6DnoBj5/Zaw7QlOLrI8yMLfj3m2e0JY2UenLz5PK//oQHSJ598Ikn66KOPJu9/9NFH+q//9b/mzywWiwy4/TN8/5NPPtGHH3741vU//PDD/Jn566/9tb+mv/SX/lL+nQzSnFkrTEwRQI+Yk7CmCQTkS7CC0wXx77Ztm52dOwZK6dq2tGbu+z4ftIdgsaCLxUK3t7c5sPKa2ZL27dW21eSeBGdJ4YfJqfAILVkGaXruE1kvFNaDF/6DfYVtw9AidBg2gi+cL/cAaBLBI6gEODFGvXjxYpKFgmFnTM6aesnLYrHQbrebPJdUOr2kphuFbeOEey9fg2Fxw8R1fB8Rz+msl382hJBZajdozJEbYwIIrl9V6fBGDIzLJdeGJQVceAaD+yALq9VKu91uUmrFetV1reqaQQKAAWKGYZDqcojsu8Ax8+QB7Hq11qjCwuJE1+u1LqeLxiGBs5ubmyzLOA7m3rMP85ISz3qyMZ759o5vHiAXQqTLOrvZbPTs2bNJh0kCSc/ieLDNmhEMOVhGj/05qEf3rKXLFQwb+jXP1iE3zJ87SuwCwTDjRYawNzhkACt/c6CNo8FWoNMxpj0Jwzgq1OU9ApO+76Uxndru7POLFy+yXfLnIBhYLBZqlkmPP/300wyIHeTgUD0jilyzx8fZ/rqqFGIJ9sm0eM0+Y0emmXN+EhR4eZODrWFIe2pg9pnzeWvo5XKZx47NklKAiw6zfoBSZJvPMscuD5AMTdO8VZnA9R08OyPNdx1w4sOwpXO7yTiqqmSzY4z5DC1JWWekEpgA9iD5fP8Ieu1+mHlCFrGHfA8ygnFBBniWlvXxIIFAGzuLHkNG4psBs1yPOWItPCtNsEjDFbKCcxvizRvmtnwYBkWV0l/mD1IGWSVT6yDQy85Zdx8vfoQX2GAcoy79ZcKwgz+iyv44xkP1g1c08Lv7I88yOdgNV9LTs9MEBelHIUxZG2wldogxYc95Prdd+D/KTfm8Z/ZYO9ZzTrBmX1iVLsSebeDvPkf4TN/L7LbZSVPGy7WlaXMHB+3uo+eEJt/juSm7c1+cvxOCNMaM4dwnerDn45GUS59ZV+6Fvjl5wL/n18beorNl3UtQyE/fZjAfX13XimPpRsg1fq2sI9/xzzp+RQ5ijDocy0HgX+v1/5UudvMIzTMAv9Zr/pl3ff6/d53lcjkpP+K12W60XCwnyt33naqqOL4MCoWBL6wZC5K+L6UuaSW74AETAu7AmSyCs9kYZxQPgeQZvKyP7IMD6uR80hxxGr3v45GUgxAE009uxuAAjDygQ7AwVjgInIkbZq5b9m6V9PBnn302YQ6lohSr1Ur7/X7CvMA0w2wD2MnCUSO82WwmLcf5nhstN4B8b7VKDp4AjmeHtWMczBtBRVVVenh4eCsTw/WRq8yqX4Gll+Qhz8jI4XCYdBQC2JGd8xI/STlYBvQRFCHvnsFknpGpm5ubXI7kGa8xjhr7tzvgOIvmm3SdbeJ5mDeyA/3YS6GUNiFvp9NJYz9KsQAoZ9kBd+ybuLu7e6usB/1h/1yMpRRJ0iTYYO74XF2XElTm4OHhIcs3cwcjPzey6AcOmY3XNzc32m63WR6dZXvXfg9nprEpBIqAJ89kAR6QUwKMuq4zwAEE+YtOh+gPJA0yDMCTSo3/vOVyztb1nYZYSojRiaZpNHSd6qoE3ATjDw8PWq/XWq1W2m63evXq1eR+N3d3Ol/Oed2RAR8PGUXAE+sD6EJPMyhSOajXy+A8s8LzedYW/cG+FlA5ZtCGTEGYoYt93+eN4VVVTUgp1tqzGHOGGZuNrWGtXB593ggabm9vsx1Fxubky5xB5Xk9m4X99hfz7QAI+eW52cy/2+3ys3qAzjz6XHsAwpj4O/cAiHkpooPsdBxAlf0n13QgKpWuXE4eMC4PyJzA8ECE5+S+6Jrr6RyMOZPv2Qzu7yVnMUYNKiWHrDV/95Iw7ot/xQZ59sqBOnPspBKZXmx613X66KOPks+vK20XRffm5V3YJNbCK134u4PYJAelQzDvg2HGoNQERcVPeZWNg1pIMsbs2SX8gDStrHAyGB32AMTXGLnxgAQdcTxIwM0cMwb0HjlGFhgXsuh2Cdnw7D1z70ScB2o8y3xN/L7MXdM0GvpBQz89K8hlc07u5qAlSL35GSfL+LzLvgdvXBd5JeD3jNucrHLin3twjUXd5Iw15KNXrzjp63Lv8zQfp2cpP+/rf2iA9PHHH0tKGaBv+IZvyO9/9atfzVmljz/+WJfLRa9fv55kkb761a/q9//+358/8yu/8itvXf9Xf/VX38pOfa3X7mmnfjVlZxHWh4cHte2020bfl5IzZ6ySYJ9VVbVC8I1y/dWRXSTF7Li91IB6cOrMify94w4LOS1BatV1g8Yxqq7TuS+XS6flcqGmqa6GE4a5VtNUattSQ864YTwJ0DCyCKwzH3yO7zvwnwN3SRNhdwYNJXEj6CAcA+hMIYYyPeNS2+3mOh+9Vqu1YhxVVbWePXuum5vb6zMoM5b7/eHaCSyq78fr2tIhrdSkYtRhHNNcN5N2sJ6F8PG64nuWjbnAEWPQUUgPSgko2J8AOAAYePCAo+V7jA3wBKCHtWGOvTbfAyBfu7pKZxHEYdDYD6k+PErVtVzJz7fx9XbHDnN6Pp+1XC3zZ4ZhUNu0CjEoxKA4lj0YODgMNJkuDPxut8uMn5c2+r4T5sn3BUlTB4vBJL3vMo9jYTyScrANsHGmzPWUcQCY0WvuOS8ZZC2c+QI0ImfYBe6LrPo+BuQCp4P8OuMJ0CNLii0D8HmmDTIHGUMvuq7TbrdLzS+ujP5ysZBCVKWgqKCmqjRWlS7DdQzjqNVmrRiCFqultut0YO3j42PWAzIrHCbMng5sSghBVeo1q8VyqbpuVCuora9rfpWt1Ma7UQiV+ksCuV3fZeeKbPr+GjqdzQNvWH6em3XzDAL22Et4lstlPmeGrAdyRRMHsi/ch8yyz7mTCJ5Ndv3FDjVNk89awsZ66QjBtmd+AQxk/bw7nmd4eEaewecNkMV+Jrrt0VHPCRHPYqBryL7LIuNEx5EB9Ah55jv4IcpG3R85Q4xOeRaP52VM6CljmgcpDmIhmQDHznAzZn9+B8rcg/E4CKZTV13X6oayd3pQ6gLKNT0wQB4d1HI91yGeKZctVZVSJ95Go2I6iyglGRT7XpXJCfPKmmPj5zrj2dmJT6nTPpau69UqSkPyMf0wKFSlVJy58ABlHnSyP8vxE/NP1YNXUGDj3Ed4dgi/5Jk9J8md7PYDdx0Pvov0BE+hl773yGUFfOSBjhNcjo34zLt+uv56YM9zduxJGweFOEohaLspZ8mNkmIVdOl7hZC6PA9DKn308Tox6bLHmJE71sGJRM/YOcYk0HYy3jHKOKZ23+AtruGfxea6XWENfc4ZD3bk/53X/9AA6Zu+6Zv08ccf66d+6qf0u3/375aUhOKf//N/rh/90R+VJP2e3/N71Latfuqnfkrf933fJ0n65V/+Zf37f//v9WM/9mOSpO/4ju/Qw8OD/s2/+Tf6vb/390qS/vW//td6eHjIQdTnfVGyRmRLHS2CCBg/n8vGZKl0TnNWKrXtTe18E5g658VLYLKkZVFcjDmMG62xyaAAkCnfILBIJVStUrveVKqU2n1ur8ocrk61ugYJpcMcETbCjGBhgHDGjMfL7nB87lgxZJKyYvA37oeQu7NBSWAkHORzdo4bM7JAIdTXoOqixWKp5XKVsywAPIBLCCHvLVqvNxMDm1ojBx2PpxyQugMm0OBZAaY4AIwpLLGz3AA7B7vO2PC+G0pYNEAcRh8w46CYwHYcx3xf9ImxYhjcmR0Oh8kzYmgAGDgF5C7qmsHqz4XhsqypP4c7HVhNPidJVajySeJt2+rx4TEZf8scITsuc2TOvvrVr+YAdb/f5+CPOQFU875vAnXAwt+cbSZA5Z7IG/9mX4RUmCdnxt3Azvc9kJFhHRgna82ccV0CYxgyAkzfuzVfax+zB0ToKwek4sixcx5Qc28nTBaLhZ6eniZZZPa9EKA3dTmANY6jgqTz6ax+HNRfgTtlXIvlUlHpLBRn5uu61m/8jb8x2YxxkGYlWejJer1WZ5utM5C5yoHr1Bj7tJduRuywdjHGySHAZEs8WMOZOsnhABt5Yh5ZtxhjLuulwxy2g9JP7DiOm/ddNxkjsulAHPuAPXf/xHWdifYyKwd7/M2zunyX/XDIGuWcrA0y7cCS5hIEf/NnYpwASc+ueHbDQQ7rgvz5dRkPpZN8Hh3wjAOlgL4GzAM+2Rl1z7Y52YLMeJmyX48Xuujly8yVA1fkhBLSPGdGhHHfqFI9wfzM/Qo/PSCYvxLZWNq6xxg19CWT3fWXvD+Q6/FZPs96YdeRVQgtDxy8aqJpG43XOc8AWSVI9vXw8monsbGLEEReCiuV8i/0kYwEc4k943q+R8sDQpdfJ6ux6R5cMz78LZiS63k5q2MpgjfPQjJnVVUOhvWgzUk8ntcrlHifNXK/Ute1muscV1Wl/TXIRM7dtzdNo7opJX9kbbguMo7fdp300jtsh9tiD3x4Bp935MfxTAipqYj7XAJP1siDnnlPAJ6fqhy3Ab+Wrvxar687QNrtdvrP//k/599/4Rd+Qf/23/5bvXjxQr/pN/0m/dAP/ZB+5Ed+RN/yLd+ib/mWb9GP/MiPaLPZ6Pu///slpVPp/8yf+TP64R/+Yb18+VIvXrzQX/7Lf1m/83f+Tv3hP/yHJUm/9bf+Vv3RP/pH9Wf/7J/V3/t7f09SavP9Pd/zPe9s0PDfeznQR0kQEpgWXxivHXahRpiZeMq6UNK6brRcpuCBNsDOfnv3JO86A0CmyxtZp7SPYKGqqvN7XmZ2Ph+zQUZpnD3HacMkeyCDoM+ZVjcAGHoPpGBtKKljXhhbCCEzLzClzhzS2pV7UWfNewDDvu+02WxzgOfGzw0LinF/fz+5lzMgPOv5fM7nlbC+Hgg68+a16b4vwOXEQZ1UwAT3hSXzzzhAxllS752eu58YZQc+MNDuTDC8MK9zB+MBrztWngH59hbJlJPA1nkds7NWDqowpo+Pj1kO3KljNJFf5oH54YwuMmIYPoJyxsHemuyEzXFxPYw0a4SeIz/8zsvBgJcROeM1D74oIeL5Ca68VAoZWCwWk/PFeHb2QTw8PExApXfTgy3HKTE+nj3GqNevX2u1Wunu7i6DF56H+x0OB93d3U0cM7oLQAGQYTscYABQ0CP+VteNFMo5E8hc27Yar2UezMVms8lAkxfyxH0ul3TQa28y5A7YMw5OYDmLi67xN2cqeV4y1U4aOBgg+EeevIyI65Ht8+yR738CKDmIRe64L3pEGTZ+At2pqiq3i5+DYWQRG+YMNvLmNomfHhQAOGDMsXXzbBJrRgMBJxNcblgnABjXwJY6MOEaDrq8TA4/7AQFc8NcevZqThhxLQ8yPNOArccuQOixpq7zTjy4z52DbPywfxcf4mOFbackk6APG7G6Vk54STRz6+BvbiOdPKH03YmeebCQSMX1xPa4jCIL/j1Jb+1/ndtEZNLnD1n3gB9/wD29THACluvSgh6/+vj4mLGXYzRkh2fg+2BAl0MH6e/ydW7zsVWQBcgSthgf6PbJgz4Pap0wQDZZJ353++zrygsZnmcusXnoLXbIcZcHVu8KtD3AZA6Qe+aK77v94HfG4SSHYwcn7twfZyJQQdXsGj5uLz9G15EFcLuPG9vt9uTzvr7uAOlnfuZn9If+0B/Kv9MY4U/9qT+lH//xH9df+St/RcfjUX/+z/95vX79Wt/+7d+uf/pP/2k+A0mS/s7f+Ttqmkbf933fp+PxqO/8zu/Uj//4j0+YoX/wD/6B/uJf/Iu52933fu/36u/+3b/79Q5X7SIpC8YHgAmox8E504vDYhO3l7Ss1+sJYMGprdcr3d7e5O5LfA/AMAxD7v7jKVmpdEnDcJY++FExKrOP+/0+36/vB1HS50IoTc+Lwdk5uMHYwB7SKQ/F9HbSlDUQrPDMOLD5/DnwZY4IOp49e5aNPmeQ4DhwfGkcjbAHTdNk5henNC/tGIZBz58/12effTYpe+P6KGTbtrncyp2Pl8vhDFlz1oSAzA0xxl8q6W2yYxhnBygY13lQDrjychmMgaRJW0zGg7Nxx+9gxQ0LhoIx8gwYRwcmfigtskbw4lkznzPkSCqG25l5N4yu48zRZrPJQJ9reIkIJS7ok8s6z4FDoNsVThK9xRF7cO6y6Xt0mAt3KoCiqqryHh93iM5uOkhzhvFyuej+/n4yHmdevZU4AMj3TvFysoB2397U5fHxMQdgADHmjuYWOF1kFpmiBJXADpn0IIQzOVabdWbcN5tNLsskQBqv+uE67qQTwRh6vVgs0qGtM9uDTEAkeZaFw385/4s190ATQMi+BeYbGXDZ9BIxqZRglqCwZCCYFyfgfvVXf3WSmfKyScAHNhbbxJzwd54B+cLm0ZabZ3dwiJ4jo/yH3GHvnSkniPJ9Wp71QxZ9vh1QcT8AoWeoPHvi9sZBUYxlj6QHUQ5a0SO/3jyQ8qwHz8ja4PNZS74DiELPnXRy9h774HbPfRHAzO0ttoJAmGAHWWG+nHSQlJl7fy4Hpg7ImSfG7aQUfgvfwbVijFmG3Fajax6EMl8EUMgBOoB/JWOH3m82m8m+ZD9jkqAIv4XMeBkXJA/Pgyyx5qyB7+1zEsdlDluJbPHdue3GFnmQgQzwN/czrvf8Pg/AuQbzyn353UkFdNwDMdaEMmr3fW5L5xkS1o219ooi1zG3Z1yPF++zhvPAlfthX/066CLkHPPm5ZHYAMbp9oIxLpvSFp17uV10EtX1wgkFxskaonf7w16f9/X/0TlI/2d+PT4+6v7+Xj/1T/6Z7u/vJ2DIF8ODGAf1AJumafJZHQROLAjCkBZ61GIxPW1ZSovz+vXrDPJZYASmrsuJ1XOjH0KpK4edRlCapsosnLMSCMXxeMydRLy0iud2tpC9QFI5m4X5gF32LkoASWcaMZqS3tqfw5gBLc6qY8Bg1tLclLp45phAyDuZMc8ANLoteXkVZXUOCJ29xWjPGVZnWZEZxu/BsQeOw1DOhPA5xFA424es3dzc5Pti4JELB6du4Hguz3QBeHi5M3EGBobPA2MAoz874A3j5m123cH780jFaHpdNWN2p8BPWnTzvcPhoM8++0z39/fabDa51IsDeZPslzQ9oJ05cMbONxOz3q4Pc5aPtXWWnTWG+PCgm2fygIYg1MGNA2B030EoOsmaMjfoO0Grrz9678Enz+ggB5kFGGEj3IEwduRgzmii81wzg+G6UnP9DllI1iEOg+JYupfxjOM4qm4bLUyXADcxRi2aVkNfOsJht8mEVVU1aSzgASn3ooSYNXRihGd3thjdZezOantGlnHwPeQ9xqhXr15lO0wwMrfNzjZ7IwPkxuWNucH24BMA2wAnZ5IhWTjkkbUlAEBn+Tfj4ZmRLfZiYv+d7ICgcX3DniMbXgblGRYnZ+ZAh3Waj9PtGoEvOsO1PYD4tWypA17/m5MUfAbfiN5TOcELWXCA7/LmeuDr6TZ4GEpzIGf8u66T6pIB5m9ucz0olkq2B/vkwajbMQeRBUc02ccNw5DJD+Zxu93mChICHQ8aHLPUdT1pSe+dzBi/k7PoswfCbCVwmcB2cC23u9hafDjrgA3wc6uYd7f1LhP4NicWHaB7QIougI88C/f09JQJKs9muc7wLPMAjAokt8eeJeLzvHw+sOeM1/VkHozgf+bP5EHgnMjl+8is4w1ejjVc7tAvZJa/I9uUmcaYOqMumnaiR+5DkC/3h44/5xiEv7HeD48P+s7v/l/+f38O0v8ZX1Vtm7/q6b4KZ+5RLibzckntoMl0SAV0wqi4ga3rUvbAfVDeb/qmb9KbN28mdeYurCiBVAB6GkdptOBAKrE20xp/Z5FxCtvtNr/Hf7Avbdvq1atXWUAxVlKp7ZWm3VVQHp4RA+XgwdkYZ1HYaAk4f1epTZn/oHHUBGjAlACW27bNYAHgIJXyEEATYIqsxHa7nYAuBw+S3npGz1agsJ4hYNM0fyPg4PPOSmIw1uv1xFAiWx4oYLxwKi4bzCnG3Ev5MBqsDbLo2SoHldwHWXXgEkI5jRt98SyQO2YMKTLtQMGNoLO7dOwDCPDdDz74IANA5gIZ43M8E3PmRAKA21P5fI9584Yb8wDegyycpDtq1tF1petS5y/GjDymPXXTPWNv3rzJe+m4JrpBlyjYXN875w5ysVhk0M9cs96AFA9KyXzznGSrQijlfnWduuN5BsSZcV7OziuUkjMA3zAMGvoh7w9iXAQ9zaLV8To/nnFkPoOmgQ9zQIkl9pd1Z0xe8lPIltKCm2d1NhL7zTM62z53zMyR2w8pZfk4msEDECcpfD8TcuBVDDHG3ACBM9R8jAAISkjn+40AgwSqHjQyJuRhHEsWHrl14gM9dSDHnDFH6OKc8CA48s/P7Q/ve/ZkvkfUAxLPWAGEHfS6bSBAdKJzPgYn7dyvYdsAv074ISN+L4IdD/TdbvMsc//hoHoOJEMIulyD0LquJ/vT5o020E8Hrg74sRHoC7LiWwBcfhgz2Ib5Zb54Fn53P4ENZ3zINzqKnHn1A6Qma0GQ5eN1G8/zIgfcn/XyPcI+Tg8WkS3GPCfG53OKjjuum8sm43cilbUgg+yBrTcA8WAMW8nz83kPBOaZTw9+CLCkgoPmOMPlk/chv+eY1kl7nwteLrvoCfaCvzuR5LbPvzsvJU0XuR7fEKadMLkG4/WM/xx7zm1AloX+7cDu13q99wGSzPhh4NjMxv4WDBbOzA18VVW6u7tT13UThq6qqiz84zhqvb5VCMqOEDZBKh2KPEvizImzyjGmsoPdbqfLpexHwXggpH1fUpsO5BEYr9fmfozNFW673Wq9Xk+6FbEJ18s9qqq01sU4ki2BpWQ87mjSEsSJMM8DAHdK6W+ldTYBHSwnGZC+7yfRv4MPr1/3LIrvxaHeugSjJcOGXAC4na1jHlBQzjtyQ1TX5ZBhrsV9N5tNBicOSrguRtMduzMtno1w4+AMqaQMsgEeGDsHljgJxuxgCjDKWpE95T4eQGCYHUTzzOgA1yKA4TuMCwOIbA7DoE8//TSX9fkeOphGrk/WhYDaSwAckHkpUQhpoz6OvW3bSevY5XI56RCIbAzDdO+aM97ekZGyLmR2u91mB45OIq+Mn3Ix9mLxftGLcoAs+kfTF0CPgwnsAfrjpX2AFPTKbRZr53t8vJSKOUkyXGt/2Gewj9yEOAXByNf5fNYwY/W5R9u2qkJQH8v+EIJNLwH2IJ81OR6PWdeRc7JpzubOyyg51wj7wXiQU+YdGfJyQGelnTmu6zqXAnJdAmLPgqDf+Bv0f7vdTmQX0IStRQ+9YY1nfJhLSAgAKu9xlpSDNOQCYOaZBGeisRWAXQ9sfaxuZyVNZBxdh2RDT9A35htd5dmdwJkHqciXkzVuM5nncRxzh0a/F2P2IK1pGj1//nxC9KCv7h9ZDyfbXA69uZBXXyAXlPKTXXFbSvULcu9krc89pdDYCyeoIA88YODZuS5rzDoh+06MIR9go5ubm0zo1HWdtwAQNHrlBveeE5quy75GDpYBtzSKcRvg9tb3S82DC/yNE2v8zjwtjNBhbt2OojvMC+SwA3OCt3nZrwfUvMd8+jx71Qj6Na9A8OdxDMPY+d3JXr8OL+yQl4ZzbcbMPZEZ7K3bAydn3VbyWQ86uWYIQbq2nsfWZCJYqZNuVddSnGafHRcxZseS3Bs5Q/7859fzeu9L7P7Z/+2nZgcHps5m6RVEz/4E9sbr31LJXBJ8ouZUZwvgQAhJCVdVrWEoxgeHjiEAWDmghD1kbBiSuq6v3chW6rpS9uMAFIDjZVtc/3jcZ4PHs8+ZfxTZBRMwiuH3TeVupN2YSdPuQ4ARHBgAybNmCVzXSl36Kp3PqWNfXaPEhYEFHDEvzqo7wAJ8O2uFA/LncAeCsyBIcwCdlViaOOKqShun7+/vM0Al2HHWxR0Qvzurj1Mr81HYP0/nu1IzNi8P8uATptoZyXmWBTlgft3AsJ6sFYbT2XDGLxVGyQNIru3ziry74/PgGfnBeeFEaPoAKHz58mXOGgK8aHwC8PTMIPLHmgFumCdnuf05kCXGfDgcNI6p0cDDw4Nub28ne2e8vMOdEqfVs6Z+xhIvBx0AVmeanYHj34zPg+Q5E853yBa4nXD5JPDxbKODFGyY7/VgrhSSDe0uFy2WSw19r1Clc+bGmMzrYrFITq4qe2xCjLpcOjV1rVBRs57Ov9pfSykBag4mPAvAOhMsU1rLXAM0nRxDJvn3PAuC3Dhp47LhesF8YQP4jBMB2FjWAf1zG85/BLrOxDuwcV1hvABwJ+M8AzYnqHgG1xUHV4yfPWPz7Cv3xhZ4Btk34jvj6/PtNgyd51nRN5flecdZZBZ7xd+8JNJZbpdVZAC/4fbV7di71tj9G/92xh+5w4bS5h0CZ7vd5vvnoLttFKqKk1OvfvBKSChO/GuMcXIYKnbN/ZhnSpxkgzjCx/g+NN+n6ACXa3AdryKQlJ95Hjz5y2UAuWLOd7tdtoVkwfFbzA9y6VkbSCBseLKbg6owLeUvGYSgMY5v6YPrCL7Ys9FO9CBf2cdF6Xy+XO/dqbnulem6yzXgL2XvqXFNOrbEg/uqTo0I0oG5tfqhT0disBZV0DhMS1GnWEtXHFtpHAdESKG6VhMM1tigCqrCNZBuG/XdtYFMXapH+r6/fqbseZdSF+AQlN/r+k5tQzVL+l8a56gQqjz21Ka7zmvSNLViTJ2WR1uHuqoVgpT2nF+zViPltIOCiq/rh+EaUI1q61LezgtZQYd9X2CS3aLj+/1e3/W/fuevl9hJyo6n1Hsnzz03COkVlRojlD1Eh8M+OwVvn+wlHc5m3d/f58wSzg6l9oica0glwHDmLBnYMFlYv+8801BAbznJm4AC8OblHDhvxnY6nXLpGowjRsoBFMEf93Sg4sZ1nh3hOXGsbVvOCCkAX5ltY07ICjgbhUNk8znzwjpRjkNGwsc1B0vO5jszSSCB83aDzxx5LTpAyEslHWg5Q41R4j2yIc7sIX8eCDk7SWBLMMd7vsfIWSfWDfnymmBkBPl0xs9Bm7PCXB/d8Xn0rBSfcdDN/ABcPAiWEmtKEMr4+77PjUo++eQTxRj1jd/4jddM60U3Nze5HIXsCoAApg8ZYI2QEZw4c8OGfnTI5873fXjZm5+1BAvNuuLQCezZd8VzOQhFz5g7n0v2jDHHXjaDfjur6tkZ7uf2zgNy9BwyAfDlcsFaZOZZZQ1pza0YVYVKTdvo0pUDpOX2pm7UXtd9s9loHEYt2laHa8c2DzQZO3qH3fZx3d7e5s/GGDNzy/1YGzLlXlLoYNCZYPQfe+DE1xxAcm/2cTKnZNwBdre3txMdJlhALnx9nMTA/vL86CWBzDAMk8NMPfOLrnOmGTbZM6c8N2vFs7vOFqAxPesLmfT9fsicpLcyj+5Hse9OVHkASNBEAIlf8qwo6+gZMS9pI7jYbDaTOYX4GIZhssdoDq5YI168h71jTXwP1mazeWdp/GT/jqQ4lvLJGGMCs3XJyvs887t3YJzbU3w5vzuxxtoz72R5PKvCmB1YEgT6AeruI7BZ7uOdLHJCBtn1knoC8mwnri8v4/TgxYMgSQpKQQA2lHtmMiJMu615UOn+jvG5f/AGCKxhInYJ2st+RMhe7BVzfbl0OQhjrc6n0qkyhEpVKM2sQgjSUI6LYe743Qk2l8tMDMQZSTlE6TqtQ18yZ/7ZMVB1UjBE+lylcbRgO5Rqp7TmJdEAEed+jDETYMUYNF4DnRCC6rbOuuvkRAhBYyyNYXojXaowPUYAGzKXM5dR9yWO7T/P670PkIZxmHQBk8rhexh3JnzOFGEo+bsz7LBwpJURDmfyPb2PkEmlLtQVSiplSYzTmUNnPTAq3vZ5+t3p9505ciPBfbwrl4N02BNKhHAI+/1ex+NRz58/nzyjj2G322UB5nr8TKVnlwnI3263k0YA0rSzC0bYnQVKgkHGcQDmPHBj3gnGPOAhoOJ+3hDCAwhSwZRaMjbmaR6UOZgFCOEo3VF76Q9lWlJxcoAm/s4zAeTYB8N6OgDm2TEiDlZ4Bs8O+BrCbvNyw+TgAPlGDpB95J21QJbdGc3nqmlKm3wH5Kzl8+fPdXt7q3/37/6dHh4edH9/r/P5rPv7ezVNow8//DAHKO4oF4tFLikDaEjKwRPrBPD0sgoHYYC3pmnyWWboP0HTbrdTCCEHQmyadwDjgaUD9NTC/zxhunkGWqCzboAliALXMZjszWaT9YH5dDDBc2O70Gf2sxDY8XcH1+gQ9ocgZhgGnbtO7aKdOC2eBVny77odI2PH3AJasGPOxiNn7Ntx0OY64DbSS4Nx7H4/7Cq6jAzzjMimM/OQFE5mwE4ydsaNLO92u3xN/qN824EgcoXN4PvoE8/n4HlOsngwzbOgA6wLa+d76pzkcTn1gNIzWtgYMnoEW5QxegmnE0u8eD4Hpthc7CC2bL/f5/Ej89K0xTv3DCHkMkw+3zSl2yVzRcm0l6J68xTvpEjQyrN7yaP7DdZ1s9mUjehVKedu27KfFt/M2jA2rwzgjC7sh5drMy5Kjz2jh/wcDodsM12mIV18TtABLxH1jByAGZsGXsKvMB8eiHgJPP7WCRyel9JhbJYTrh7sIsvMD5/r+15jLHZWKh0y0W+eGRn3sfLTKyku51Kq6hkybJRjN2wROsJnvXSa9ecabn98zvCR2ATmwzEWc4o98Ewp10e+GJcH0cyR+945OeKEgWMFr1pwG5EDN3sxRreX7iPS2JUPFnZ7EcJUjubVNXOb5JidQM2DzK/1ev8DpH7QzbaU4UjKG+ulYqCkt1kXGB93El53ilJwanrf93nTIcLJdxAUFpAXQAUGCuVLjFzQYlH2Dbky+AZfroHBSZ97dztH7okguvIA8F2hAUsIG2DM2UwMMkYKFn0OCmj7mRzmJRtmQBFK4OPg2ZzZdMaRlysmLYdRXEA4xpt54xk9YJ07WeSB58cQYcSlwuA7e8a4vXTJ9wwhe/4ZMjPOyPqa8dMdFNdhjGRLAezIjAc6c2bPAxh3XMw1LCK/EwQ5IHLgyBjdsc5LIpkT7kfAz8ZimmlICWBSroa8/Pbf/tuzngCWHh4etN/v8yGRBGo8F4G4y/i7mEP0kLNhaDDiQSmNNujwxBzg8FPr/3LQLbqCY5h/nvna7/c5APd9EoAdB4/IKE6XkiTYSHSVefTMp2cqIA0c3DsjDnjjfowFUMj8QkR1XadRUa0KePQsGZk1Mi6+Rr6PwB2/yzKfRWYZk5Mh2Ch0DlvBc6M/XlLFM7jdZN1oR+32l/GQufQ5wV65XrpPgTDhc9hP7+75LlLNHT6fQz/5CeDj5bLoQAxSD/nhefy8GOadQNB9maQJa4wd9mfAJr+L8PDMlmedeAayyw7efF8UhAbXdvuFXCHPT09P+ZnwCw68fG8jgTfjdT9EJotxcE/WARvne92wb56ZqWOly3XNOITV9zTxzARlkGPDMOSyeewILyeC0UOXVdchrsG9kBmyyGQRvEEMcoje5IyHNDmQmTXwFvdOunlHTCcWnbRzvOZBkZOfCWsNCkrrSVOqQpwGtc0yg2lkEZIX4sCrXpgf5Jw1Q47W61ohlL10jhnme/UcsHMPfJxXJ7gczv2j22HWk59OYLA23NeDM/TK7aOPDXuEzmBf8IeOtXg272rI55mrvi+l7eAZJ1UYqxPakFbJ9naq6rdL8NMz97ks1XXlXTrj5FbX9RM78nlf732ARNmYR/iwBp7KRgg8tS9NuylJ5UBQHByC4EJJ8CCVA8+kwuJL0177sEUOXNNnpvsBpNJBbc7cInjJeKe0JgENTkaaCjhnGPDMlC7AGgNiPFuw3++zsNIxKYSgN2/eZPCBw+DfGDPmNDnnpch0OVODQSWb5IEdzBn3dAfMOAEhOI8Yp7XsBGiAPRweCubsujM1DiwcuGFg/Hn5O3KBPPFdnoXvcRgk3QUBPwAo3vOygHexxAALGE7AMLLm68MzSpoEbn4P5NA32c+75zmrxPy40/Bzupzx4W/uLHECPhYP1L3jlWfGFouF7u7uMjB7/fp1PnML4Md8eXDi6+q6yjydTqfcyMHLGclyuUMABOOMmQd3pMgjAZbPmTu9Z8+eZeCI/vh1mA+Cbge4nglBV1hHD4g8YFgul5M9KYwDmZyzkcgbgQ42DOfdNI2G6x5ODrFlLqV0xoVnVAF7rn9kRr0pAX/nGee2z5lMAmGAiDtMfncwDakACJsDKoCAA0Bk8nQ65UNUWRMnaJwA8rIdghSeA9afe2K3AEHYCXSDn8gQ8s48eUAybyk+Z6ddl5FRgmvGNGVjS5kZJYzMmwfwrg9eVujrBoBivdwWI7v4bbI+/lkYd3TY7Qc/PRh0YoXrs15uD7Cv7g8Yu8+tzwt7aPy5PNDMc3yNKbkn4y8gsRwgi71CN+lmx/ew+/grsonYR9cdlwsHxjQzwcfSLdEzJFyXeffsuxMXjIXnYe1ct8Ac2EUP9pgLx1TzPZKMq6mbXBpGRpbPObDHRvOeZzKRVeYFGzPPHg9DOrog7TcvjQrmNtPXybNeYDbPfqEXvpcUXfLGKS6fzJ1jQie80QPHtu7PkQPXVSdjvIoH+fdslX+H+zkZ4O95EOUyPLfd3GsYBo0xajR75PcLIWi5KuSUy938HvPs6TjGicx/ntd7HyABOnnFGHM3KdgGBI30MkBQ0kQYWVhn3PmuB1IuuA6qHXzDtAE8PaKXKIsodeHcw5l+B+UYhjT+0mgAY3pzc5OZaVpfu5PjmhgsHFBVVTkocoXm+oAwWvwCJkMoB+1SYoTRT4HYWqdTKVVzZSI4gl1wQwVI8LpTZwwceDpY8gAYI7/f7zMo4sUhd4BwgLCDOYyWVPaEwaTvdjtJyo7cy3B4/tvb20nJBkEsJU3IAxvAkRsHAe60MRKc+eBMisudB3eUZbD/zMvH+Duyydx7wwEyQwBY5MdLw1yu0CeCb9huQCBAlvK64/GYnaIDcWSg6zrd3t5m3ZBKq+Bf+qVf0he+8IXsBFlLgCDP40AYZzTXb9aS35Ep9mZ56QZAmgAI3a2qKpeosj673W6SdSPokkqb2hjj5Pw0uqTxdxwUQTZg+/Xr15M24gBTwIuXSLAOHmyzfk7oeDDNMzkYJ+NHCdLxfMrjfvXq1SQwDuO1Fv9qj8ZxzFk4Pz/IASi654CP35lHLyPlb+gKz+VdpBaLhfb7vTabTQZtrqvSdN8kOsgcMPfefGOeActArikds9BD5IHPzjMInjUE1GHvsbFO4rA+2E5Ktpgr5BibwL2QCZ7Z9RdA5MyvE0PDMORGKXNgxBo4CeIgMu9Bs2dgbrxVP/YGEmK/3+frk+HgurzmzD7XIrD36gWCPGQQufE9hB6IekbGgavrBf6R8bnO8ZN/40O9QmL+bw6RDSHkdvDICXpPCZ8TYh7IcD3W3rPYzAtZXXw+a+alkD5u7JbjBrcfvn+VdcFOUgXjgTByjL54lgrsgZ8JIagfpvtRUpZnXfZoqTTRcRznpCh67LLJejqeSd8tY3AinPVznQGLsA4eRGBjnPBGvtBxfIxvifCGJE4so3ce/Pp4/LmQacbgwSDzw3rgq90/OE51e+GyAc7zuSn4dFoS6OseQlAdal268+SaGZvr2uHOCEfH3azNPJuZxlv2p33e13sfIG2320mnKwc/c7YNBcEYwK7y3hyQOmCTSvpeSqlADypilMYxSpouKPXHybG3Wiza65kal4mTYNG5L0ru+zUkatLDdcypgwjfQVFTI4rCuiYhKuCIlwNzNywYm67r8n4BxsAze4DGfQCqMBiwbZSX3N/f5/IkZ4kx7CGEHIhwTQylOwDAkhsEZ6klTU6Z5qwagLLLB/Pg5UXO2I5jKenDgc+bR/g6Eji600AOmF+UmxIrN3w4MYy3AyKYOzKBzAX7asj4wTQ7+9r3vZ6eniaOCsCKYeP+PNOcWey6LjOPztbxPDxD13X5Osw9zh1nxXvOxLnO+h6jObstSa9evVLbtnr27FmWnXmA50E5suWOk/cczPEM3Je5vlwuk0Du4eEhl0h41yXGisNCt73sl2flegBnSl096GWvEBkHSn4vl8uk5A37hKwBNnhWL7HBHqGnPC9rPS+RkZTBKoHh+XxWqN4+GDeEoFBVigaK+TzX8rIqtykeTIzjqJubmzzfHoC7fYK8gOhiLZj/u7u7CevrWWsPFBxw+3ic+JHKGTfMn4MNX29neJl3Z2nd0c8rAPhvTnAxJl+nOWOOTWLN6FwKuPDncyaf7/MZzr1iPh3sOTHlwMuBMLb6cDjkezpJiF9wwAUY9wAYP4Nf9zXDXvl8sU74HOYP3aSUl/XCpvA5xg0hstvtCkNtQW2MUYfjUXVVZcIP0Ov6OA9CsFP8zQMp5FNS3o+IvfCAlGAJ/XWyijVlzBxUzrM5CegZG8/4XLoun3FGgMb3WGPmnECddcceck3WGjvDXHhmicZZAX96mRJmdT0t8cZeK0h1XQhnx25u/zxLhm9H5iiHy+SFSjYlzZl3k5tWc/BvD4qwDdzPx+O+14NZcAVyhz6xRo5b3Ua4r2FN/XsenHjGzbFcND3gXk5geXDltin9nmYsP2eQ2kUrRanrLhqHUe1Vnge7B3YNPUe3MyERNVkDXnyWNQPflOC5BN+f9/XeB0jOFjpb4o6UBaaGlRIl2GAmPn2u0jBEVVXZA7Jcrg00vH1QoG+uS4a+1jgOappWUqXFYqW6JlM1ar8/KIRKdNsjCALEMD6Aowt/GmfUMFDjHhQj5Xps/E3BWHJaUXXdqqpq1XWrEGrR+jwpaFSMNH6oJFU509F1pY2wVKnrhuu4Lte5LiwVig04vrlpMrABsGBk+Y40PUEbBXFHy5w4kMQgM/8O8qldZ0284x9MIi+MiyTd3d1NsnXuNGIsJTRN0+jx8THLHorK8zvTxfOeTifd3t5KKkbIQboDWeYQpw1o4Tq8x+vTTz/Vy5cv9fr1a93d3eVOXjgpP8D37u5O2+1WDw8PObOE8cVQA3QoUXLWkMCYueTwYeSeYEhSzjgyFinJCvPMXDGnHqAR3DFP6Cm//67f9bsUY9TP/dzP6XQ66e7uLhMdMMW+YZuW3ciOA0Ev35k7AN+b54AYuQTgMzYAGV3XaN7hzGXf97k+PoSQ25O7LLIeZOvc2c+ZPLcX2DHmDgDkG9LJantQhNNBBp1ocn2FAOm6Tst2oX7oVcWUMQpjVIyDQlVptdmq77pMnjh76IDCA2y3CU3TXBu9lL0yrJVnH2CpkVVng509xQ4R6PhzIyNOanltPjoOqGDMEELIsOsvawngxJZ4hsMzaL4G+CHkBtA3D+bcfiDPzg6jY968xwNwX2tJOXPPNTyTic673PCcztajX16axbpDsOCTeSaYeCdBWE+ux7+dEKP0nb8h376uLneenWdsPBc+C1sPcXQ8HtWPg5rreNs6Bf6hqdVUlfqY7NVysdDmNlVwjEEKTepIeblc8jlLTiLh5xxYE0h2l059P0zWorv0qpt6otvuM1gb9xnuI+Z+CXuFfJwvF1VXmejJaEoT++9AuQrXRjinixSDFIMu51KVMS8ZL+um1NFy0apuGsUxNUVAXgMtp1WpriuNoWQy0EF8YwqogsYhqut6KV5tXlMrXDFad+nVtI3aptX5fFEcU4ZoHFIZnUJQHJWe4yonqqLGOKqqEwleNwuNMZWFKaYzHBfLNpNTbdNqHKNCDG/p5DxYwb4jqx5EOSZwTMrfHQO5LeIFOeUErGOruq7V9b2iouI4aOyv2yzGKAUaJsT03P2gqk6yMMZRCvQZT03R6qpO7dWVAqyqDlK4Nsg5HtUPg+KYgqNxHJJsxWsCII7pb3WTOt4No6SgS3fKz+yNh/ycSebAsSDygf1L86DP/XrvAyQ38p5mxIFKpVEDThRQ41kliQAnKaV3G+MVQnHsXloxB7yF5Ss19hiPvi+b7jD+vo8IoMV1MGiercHBFNarycbRGWE3oLDVOEdnd7zspTjaKgcXsH0hpLNrMIKLRTnbCIBdWNzCDJBqdwDhQu41zcwJTtWZI+9QQ1ervi+16oBfMinMj3cDhFnks1y7bUv3Omd7PXtIVgVFdRBUVVU+ZA5DlWQmZMaSZ8fgsRZN0+jp6SkzS4yPrAYBEo6dNVmtVvrwww81jqO+8IUvZMa2bdssU/OMz+Pj48QAU4I4H9cwDHkPnmdRnIn0Q3Gl0vrTGRxYYT9klfnBgJOpYe18QzwOA0PIdy+Xy6RLE6CG7wAivMSBuW6a1IXr6enpLZBB4ASg9vV2GcPeuCN78eJFzpYwJt+MzHwzV4zHjynoutJyFxlgfQDudV3n7IqTCqydpLfOrZk7Ws8sYTNZG0gHDzKYP9+X2He9mroEiYzn8eEhr5UHdm5vY4y5RMXnx20SQNsDRGwGdiCz+8aketDhWRoPxCmzJTM3X3/3C86mupOmhJQyWyezfM4Y4zxThB55uSRr53uosEXut7AVXqIrKQeAPA+y7fqJLuE/eV7kkXlmbSAV0Sf2tBHwME7slGdonKRgPGT9nFxgzsZxzH+r6zqTMPhD/JrLAfLh5V/+bMwT3wFkuh90MIrNiTFKQ8h2TJJGfGgVsv0bhiHLEPN9c3MzuTYyztiZS9Ypb2IP5ZgOD2KPx6PaRTMpYUK3vWzNZdTtPnOIv2QsusohWxXOu911HEHddU2dcAghTJraeMCy3+9VN1MCAHs5jqP6bih7EQ/HSTMD1gudcJnEJvhz4BdPp1PO+uDD0QNJqkLKQMV4zvPK2mMLuG66Z58CBptjZDo9a6/zebrPUSKoqzPBgj13QgXbMA+knPhwmeZ3dIH/eJ/1dUzgPsDn7nK5qB+GfC4dNpDPDUOvxjJRZPx9fib37krWPZHuVyweU9atbhst28Vb+uV2Ad103cceOCHk5BO40clMJwL57ud9/f9FgOQC7uwJykd9Lx3ovEMXQpQUt3zfN/V5apeFQ2FhZzFSHoQgCNTqOpsACyaV7iMYIJRyzggTTHkWgvdJE7tjZg48Lc48oQiAxfmY2rbVdrvVbrfL50nw98KMlgPTpJINSkCuHCbm/zEG5ssZcuag7/tJeR7z2jTNpB7+fD5rv9/r5cuXk+cli+QOA4acuWLvFobOS2kcBHlQgkNwNmdeHywVwO9OhDI3jGdVVRMZ4/q+2ZjsAGtI8JAZIQPZADVYaMCLB83+N3c+GCfWFaNTVVU+L6jv+8n+LzrAMV+spRvncRxzUP/q1avJ+UqS8t41snpt2+ZAnLHudrtJcO8A4MWLF9putxm0f+UrX8nBogdU7owIOJAxZMP3t/h8ECAz35Qe4XT4GwbavytpAmgJmviOr6Okt3TEGXycOY6We2CTXGY980BGCxtJEM93uLekCQGADZtnpzzTNJdVSA3ujawxtwRzPKuXR2DLfH24tpeCenYCYOr7JD1LBMjFoWKfkG3sBzpbVVVuxsAczrMkyAdkETLNGDxo8CYGbv/dZswBgAf1HgBho7xFsGe6WH/PoCFL7q8IrLAdvO/7lPCNMZbD072hjJfm4Ytc3lwX3gVwV6vVpGyMwI2xstZOdkBysqbMnc+fE53onK8l+uJZHHyq70dy8NWERoPZscJSvx2QYt+xX8gq9wEHSMp6hf56i3AnG1jH1Wqlpi02wwMuB8bYIvybYyKfU+b1XYRe13WSkVledl7XtRTDxO7wfgo8C6jn2ZPuVNnHeUCMbjPfTmAzvyXDFLIOkIVnzKyBB0kE406YMj88r+Oxpml0Op+0WBTSk3V7V0BNGWRVVRqHUefztNLBM6aOEXzusFPIJXPjwZyPkzn08lpsjX+fOSmB3/W64/Ta2VaEMsdcZ17W7NUrjit5MYdZXkJZH/6TlKs7mAtk0ufGAyXG4/jYSSPWdG5LP8/rvQ+QfK+BNBV4V37fNM/f5mDRmU4UeV7y5eyGd5ZyZ4GgzLNQGAPfY+IBECU60tsHiXFfd6q+mZixozQYRAcaPk/+WZyUMxUwh84kOIhJ+0eirjI/YTjSMxdnjVMnm+FMJo4Z59c0zeSAP54fUMCaANDoZsVnCEYcnAFQeC4HpBhVDCHzSiaL9aPJwvz7rBPAgTWWUtkKZW/zciuA5NwZuJOs61qvXr3K90SWyY4QrLKWvgkXZ+MBaQghN4YAhMyzCw4mXDYkZYLB5xSZ6LpO2+12InNdlxotzPfCsJeFeeXZn56esqFsmtL9z4OD3W6nm5ub7HTIpA3DoLu7O/3Lf/kv9S3f8i36+OOPcztwZIH5njt+9K3rusxM+h4zd1KencAm4LAYtxMqrK07XLdDzAn2gXv4/PpmXkCcEwqMgzV21tKdjAccgDXGhQ10MEBARctzB/8u+w5oq6qaHKKLHDHnrjdus5AZJ1vc4ZGxQEewrdhySvIAzQ4sPVNJtodAzMkmroX++fuSso4NQ2oWQ9msB2HYFK7F+mCT3Iew3ozN15K1ZTxesso958GpByB8l0wZNkEqLbT5ngdGdAH1vYuQcp7N45rIPPIMKcL4IaqQTV9T7nG5XCb7mdyWz0tEmXu3HcwHGVtsomcY3f4wZwRH7gsAXxlDxFHBAk0AHOvE2qKbzDegHyDu+/pYA67ppFdTl/GxDovFIrdFRh7Yq+X7frmPN0fw58bG45u6rkslUldd8cY9owFWSrGdsOT66BMyGjWtXmH+pVFjnO79RO75ybxT+eABAD5pGEpHXtbKdZdn9DV3cM41kTPmLft0myO3o4yTNfe1HcdRiqVJCPqLHfKge05g8X3He35fnoXss5MiPLtXKnBtlzOeNYSQSuzMnvm8hDDNliM33gTJ7bbLo5MG2V9q2jyC9fLnBDejM25LyQjhQ+bzj+3hWtgrf/6v9XrvAyQvwXID5c4AwCpp8jcm3Y1djIWRcEAwV0iplGGw6LCYHjwhhAgxwkMKFsPgrCcL7OlCBB/hcVbHjQOpYAQcwcYAunPwwMDBsZeKYPgys6SidGmPVWnrSiYqXbt0USFIYv6kYhh9DwFKhPEnq4ORZI3c4GBA+BxG/C1lraeNGVgXzwhIxTlzcj2gHGfL3Hjp2jx7iMI70+rO2QEcjtVB1DxAAGCQYUI2YZNYd9YGw09gBqAhEAUYl2B2ep4CsuBzQpYKGcGZMi7fN4SD9lI71msOlHgWnA0btx8fH7XZbPImc57Ts65+/fP5rMPhoC984Qt5rmk9vV6vcxkbgSzg1c8ywk44WPVAyMuPeB7mw+eOZ5uUsqi05GXszD8lKawpZMk8oEeuAYwhhFyvzZ4H7ueBJuvoAMiBpKTcOYtgyZlSAmACM88oOBPKevqcOcvMnLgNQn/4vIMhgBefQ86xGS6782yBs+PYcf5NkO/klxMofI9rO3nmoN+/M45jXh/G7DLqwYzbBc+yuP1xJw9A8Gyc6yX2xYNwl09k12262xTu4d9lnmlAQFc1xgqYIUjxwJb78D7y4WQOQa8TXw7mfF6RB9aRe1ANgp/1jLzvSZgHph6Q+xlz7jeYM42DBiOy0D8nQyEF0Enkw5sAQeT52vl6DUPa2xHCtJU5sh76oNV6mbvPIUesH7qPz/RGCcwt8pBl1ID4HIPU1fQgUf59Pp/VNu2k2sDLUtmL4iA8y7aCmrZk1Hwt0N15BYfbMicC+C4y6WvvpIHr1DxD8y5Coh96tWOb7ydNy6HRRSdRlsulgkrQ5AGLE1Gu8z4G5JS/8T38AH+fk0bII/LA8zn288C+qmsNYyGAeO70/SpnDX1enWB3DOOkE9jBqy9CCHRxyL4dOQWTOunLM/ATe+H2kmvjL3we0U9sxed9heja9h69Hh8fdX9/r//7T/6zzHACzKTpAZzuQAHtl8sls/oYjuT0+typjPILqSg6gi4pl1ghvM4cu2F3wfdAByacMRIxe92vX5/r8BwImm+oR6k9M8ELYfQ9HtLb9fYoplTKFClJ8qxL113UdckwU25DLTVNKFBUZywxDM5CSiXwgrV0UE7whQGaszr+fDhwjBlZBkm5pIu1pDQNsITRA+ADdsgMOZBgDhkrL2QKII1cEJw4m+gZxXnWwo2PM0+svwNYnpVAtKxRyYY4iUBDBTJK3n2Jz3iZkrNfMcZ8pgYME/Pvjo2/8ze/hssa+wyYS2cst9ttXh90zgE2zo9W5m3b6uHhIcvc6XTSN37jN04YbRho9GzO3gEuMLjO/HqZAfu9nDTBuQHSvMTG7Qhygk5gJ1x3sT8+b4ASD8DnLChZMJcfZ4J9P4jLk4MTngUQ6oEWQYYH7W/evJl0KmT+0QtAgwcN2DXmi2CZ5/Qz0bCHPBMyz9w6y+iZWg9uvKzL7Sky7DrrmQefYz5f1+XsIc++sL5e8uK6yHUdYLPGDjzcxnmmx7Mb3MvJEmwY52wRcPta8z5BJiCNbIDLIfPJ7x6g+D4kt+1OQLq/ZU0dHHkg58DaSUJsLkEaxAz6xbU2m83kQHIPcr3MDR3i+h4YYNvy3pqQQD3PR4DhZVwe/POe2yfWE//JdZh3l7e6mu6lZOzr9UpVPS2hYk4hLgjwHJyz7nOiQZL64e3KmAy+LYviJGzf9woqASHf43WtqsrXnX4mSLHsw0WWvZzK7SRz7l0y0V2uOQfDORioSlbcy6+cMIGwnn621mK5mFzLMx/ougd2IaRmD8gdftjXfhimRxA4VnTM6Oc9Mo+MDTnxoMqJY3TB8YLb1tSMoZqsafbvSh0B0U3Gx/PyDNhung9/4SVvuZQ+Fl8xfx4PCgmGsMFt22aMxhog205yIGPoAbKw2+/0nd/9v+jh4UF3d3f6773e+wxS1/VarUpzgwROKzVNcUrubFJN6lmXS9m0lwQvtc3mPT+zBIfv4EhSPm+pGMnUyAEBRXic1fTMCcbaMzA4wvl3EBY/bBBDTXDIfXluFO7x8VGLxSIDcb8niuDCJk0bXjjLi4Ij+CiFO7xhGFVVydg4Q+oKhzIQUDlY8A3mKBxjYr6lYmi9exXPPQdM7N8hU4A8ULPsc+ABgZcqcE3+5sESc4JBlgqYdicFqHMWyGXUQYizyjgSZ57YSwfLxPtkSTwzwzOw5vO59c337qCdgcrlHhacORPH+nI/5Mf1gd+RJYAlARm15d7YA2CE4XbmDEaLAHqxWOiDDz7I8n1/f6/lcqnPPvtMz5490zAMuYTD18ADI8/M8QzIBUSLVDr10VAAXfeSM0gPB0zMhaTsCHg2nNlisZiUNDrY82CKz3tmDDvI+wA+so/85ywp8sVzIieUsvmevflY+NycocfZIuMAG/TIOxShI8y/gxxnlMnu1nUqP5qXWCPXXM/1iYDNbToZONbOm6Ign1wXO+j2GPnlBThyMMpaOTjipxMmni0GxHm7e/SD7Dpj9j1x6K8HYfg934PoBAh+Al3rul5tCxscVddlv5OD/hSQh8n8l6Cu2AMPfLjnnORyPXOyz9lrGHwfQ7vgoOhepys5VLLbqYkQstC2gMXh6p+aHCRUVaWqrlJntGgNa+paobru+xvG3E3Ou+uljEvqEtZdLqrqEgSnDFWQdLpes5EUM9HjALaqSrczMkHFdkSFqjD/c/KqudoE7E6S4dJ5dBgGVXUtDm8/XnXPyRdv2DNeQXNMi6rKAo+qKtkOD6gJFPqevTeL7KeSXF4mWXJ0YxxTS/+u73Uye9j1V5sYRw3jNJvC+qCb2Aj3oWADtwvMneuag+26rnKlgZMZ6Lb7WYjEdN8kO046LBatpOkxDFyraRuNw9WnK2rZJhJqjKPqWGeS1mUdX+AZZroYSyVQkFJXOuaCn3WTuhOybQJChODIiXLfY+RnIjoG5HO8PNhN81Se2QkuPzyba8wxqAdG2F4nMZumHLHBGhIQzhMD/73Xex8ghVAptbgeNQxRpxM1z4V98HKlZJSWoiNd111U141CkNq21PYDwEo70cIidN0lOyjqrTHCIeh67wKKfc9R6WbXZ4aboEdyBrpPRjG44LVqmtSy2xlEWOy+7/PBpwQ0fk6LM8QhhAxqMKLOtPI88zS0G4ikKJXO504Syl8YbgeNKJKDl8xIGfNIkIgBWK/XE8DBdclYDebgJE3Gzr4Er2emfG/OUPLvuSNHQZOsldIPZ4CcseR6jKtpmtw5jvXFCDHf3BPGD8PopUfuDN04e5bDszXOpAKePTDhvtzb9xx5Zg9nxWcw2OzJwvD53hXmljHxee+WSMCDw7y5ucnlI8iMg3HPDDN/NLxg7Ojkfr/Xxx9/rDdv3qiua71+/Vrr9To3fMDJzIE4usq/CTD4O/IKGEVGCJLQKd/wDfEhFfLBy66wL13XvSUnIYScQZszkABhsmYeRKMrrO30rIiSmUS3sQu8kDPmh+DI9zG4vLNn0B2Yyy3PAkvo8u7y73oJQPRyTQ9SPHAhEGBukBHPuKGLXvrsgSYvdMuZ/qqq9IUvfEGPj4/5b86s8jlfH67lpU6ud2RNPbh02yIpz7sTDYA69pp4FYQDFAgN1gNWFj3263DtNCY2PEcNQyFlhmHMwamTR8vlQglGl3N1kr5A7inbBp7Xg2Fk2UusCIS4D89S17V2+71ClbrbLZdLXbrHBKxPJy0vC8Vro6VRo2IY1A3Dtcoh6NIPE9lcRKmuG9V1pVBXqi0wjWNUvC5lHKLGIQG+7tJrrEuJVSm5kuIY1feD6igNGtWFXnVVyu/Hcbx+ptc4RC0Wy9Q2XOmQy7oqlQM0HyHj2/e9+m6QNGgYr2A/SovFUlJQ36d1PJ1pfxx0vDYDSnNcqe8LaVVV03K1tl1cpTZkfJHHPYzqh0FSVKhq9dcxhWHUqChVJYvaVLUUKg1jlK62cnUN/OJYSKiCl676cDyktttBuvTdNVhNktV15XDypimEbndJAbrrPLrmoNzJL4gI5NCDrCS35XxMxzlzotPLrEsQKHX9tQ13nfb7EKDHKDVtnQPwYbhmgapaIabMW9PWOp160fyqbkpWKIR0gGr6sErrbV4haoyDOvb81Y2aRbLfTY0NTnK2XLRqmzQHQW/vPwb3eRDL8zpG4PPYgnlg4tktfLonGdD7OTE3D/7xj6wXaze3m/jpr+f13gdILsR9z4bSwiBI09PhEyNWgJyDFy9dcmBPRmmzWYsDwyj9kkqnFV4heM1s2deEYDAmACT3kAorG2Opy0aIiuMZjSUqLY73+33+nRdgAEcOGLq5uckC7CDBBT89S8hBG2y4B0/L5TLvdUHgF4uFDoeD9vu9nj17psPhoN1ul9laDAvAGmDPNQDOKN6bN29ypzoArjt7npPnc8MIK+ZZD2dl2BzsneX4nisw12WDOA7bg2nGQV17Xde5/avLK2Nzo8MaovxSAcnMmWdqfB9ECGUvFWDdyz0k6f7+Xg8PD/l3Z5hdTjwo8rp6GGiCL/YPMD+M1YNdAI/v32Psno0oYKuUVOHMCI7ZB0aQ7PvmyJB0XTrYGPlwwPn69etMHmw2Gz1//jyTJ4zHs47Ik4NtqZyb5FmAeUmCB7KQFF5iA+CjNBNCwfdXcV/sEAEgf2fOkDHsDxkYZBcQj/Nwe+LZTAcr6JU3MvBrOnB150bmqqqq3Iac+1L+hA2hbTTz6CQHxBPPA8GE8+aefN7tNXLt2VaeH+fL+8iMywCg1LNP6DtzxL5WiK55ZlMqDQScQGOeARU8H6DOg1oHYF6qi012XUUmCOYJuhibEzr4F2l6AGn6fgnm/CdzDIFBpjzJz6B0WHlpyOF74cZRudSWa5Y9rGUvwTxrx/r0fZ8Z7/S+Utmb2b6c7bkCQJ4VnV0uC2Pdtu1kX1QIQefLRavVMs+TZxmHYVTbtBO7zJy63LNOAPFxHHNnMHwZn2cOPUgliC0BzPSMp6Zpss+D/AvV1cYOvY6z5h0eEHjTlDmR5rLOXAeb3+mapDbYOYMRpLZpp76jrrWoyl6YEIr9Y00ghjxT2g/Tsmsnejjk3vU2hKCmbuQVO9hcl28AtGfwIWmcUHFMQsaQZ2JNHIT7/k2fQyoTuG4h30aB3Slv9XuWzP+UoOdaLj9cl/nC5vtzoNNT4qxk2rAVzBO40QMSbBJZJJ616Fvx92ABxjj0vdbLtE3FCVNsH34J+869GI9nohzTOpnpBBb2nz3Xn/f13gdIbdtMQFOJ8oswuQAvFm1WWBYOg46BIOPAgakAIuqOKVVw5pIF9b8npSqHtrKofgCiKzPCm8DLSn3fvQU+peJo+a4DNMbB97qum+y58BIOB0WAcL7D+w7ECWg8OILBhyn3Mh6CTzfIzKGDFmcGAC2AgcslHbYHY8oaAcRwdvOSOpSfEjoHCM7sOggMIeS5WiwW2u12k8AZ5+kyQZkM2QNkAKPkoIn5ZZ0Iypzx97Xg+QDZBOrIilRqvD3I9vdx9G/evMnGybuiOTPvZXnOJPEe+7ecVeOe7riYawyY3wfGmrXwIMxZS+QTlnyz2Wi73U7YZEk5qOI/An82lwOEGPd2u9Xj46Oenp7yWSUYYGTZ59EDVJ7Hr4u8skbuuJyFc5CKHDG/nrHj+j6vPo6mafKhki4HnpVylg075t3E3Nm63vh9sI0euEN+kJEq7Hk5eNfLdLgnNg/74U7YnRxjIhj0IMIDG/TJgc9cDh1EsMbIF2vghAQ2ZE5o8Dmvc0e3AWPcz4kJ1htb5vs33e7yLGTGyR6wFpJyMFmyAaVRgq8BY/A1chDjWW8HSMhqWvMCyrClPDN23c9tSnNRq+87UdoeQsm4prUs5/z5Pefjc/KIIBSb4fudqqus8z76iQ54gOe6RIc+gpnc2GA1rTTwYLQ24gF9waaO4zg5J4//IC288sDBMPLjfho9c8KMcnDsg8t6CWpbdf20GYiDb35HPlh75LFpmkmDH2RB0gRfMHZ0DJ31YNgBMPdCv0MIGiwzgDxlIsOAM2uYfk+nx3r2mjnq+yGdLKviWx2oI++A/fn8THHVdX7jKA2lDM9L9v35/awv7udkBLrDdX09XP8dL2ArmFvG7jbKiTzWxEvryDhin7i/6ysyil3ifhDh2BbmgPtKynLpY3BblcmfUErkkCs+Ax5w3Ob2CQKBAB2/AXbgPrx8vhjf53299wFS07ZarxKonbKLpeWq1+aez2edTme9fPlSfd/nzawYcAfUOPd00GVKocJW45x8fwCOxBe9MjZCKpvMnb2OMeY9FHxGiuq6siHdHVVdTzupYGxg03EWlO9JxYBR9uP7bgAzLrAEVoz76ekpM7mwMH1fuoDB2nOIHGOAPSNYclbMBZvn5HsEZzhSlL5tW+12u5wtSWs9PYjPwSjGWJoePOeBCh28YCu8HHFeL03mghfGywEfxs+ZQzeIMcac6eDvm80my6BnrNg/xnUpOcSQPT09qe973dzc5PE4U8scUGrpm7YxPsjS5XLJpT+LxSLv9bi5uclpdu4BKQGDyjz7M1EmwvO7A2Ct0Q0PWqlRZj6RfQf3AIxghhg9ubm5yWNivL/hN/wGHQ6HLPuPj4+SNGmL7iyxB6AetLpjxPnzGW8R7oe9cl2ch3fV5LsepPleQQe/Tg4g954VcNljXglYpGkHTz7Hs3iWg/tuNpsMiNEf70bpzB3BE+uBLeKZHWQ5i4m9ZSxe9ggYdb1l7A5ysCNcl3HwXdbPiRBkCgDOs2DLHLx7qbBUyj3RGRw+dtQJMuQFvXaAjJyxJm7H+Am4I8Pq5y2RGXDg5aQGeiwp20/PFqDPU6BYyj792mSQOSfKwXbXddpub6/Ztz6Xudd1OUgccsMJJ3wQPseDWm8nzedDCOr60vHK95+5TfbMBPOFX+JZvaqEuadkmOBuGAY1daOu871AZV3K/pOQ9W++b8Tl0WXKM/zO3COvfm2u9ebNG63X60weYAOrENRaeTYBsmdB3E653AFUvSMj13VSgvlwW+bVKdK0lTlz4EShxjiRcWz++fqsbsvwzSkAKuAZOUi+ZaFxmJbwl8zVdI29BMznwcmhcRxTTV8oRIsHN04U8+xgB2Sbe+Nb3Z66Xvt75diUaYk+68T9nLx2e+FkCTrB9Z2UmpNjyCq4ALtGBtozMTwPNhU/ThUEMoKtBMN4aZwHQu73PJDlPtjOh4eHrB8ErJ5MwGdgC5OdL9VcX+v13gdIOFo3Psko9llhcaBeurLb7bKSLxaLfJiipFwihpKmBUq1sCwgAN07NXkWBCXpul7LZSkBAmShUJSf9H2fWdYk8JViLHW1BFBVVedytf1+n6/lCoLC4FjY5J5bhlq0fz6f9fz58wwe50wXAaS3U3Ulwxkxz9K0ixt/Q9kcyDrwAXxJb7PggBZJ12B1lR2f19nDiGBoGAvGxdkXZ274DPegpOb58+eTIMSDIX9GgkXGgGHGOeDsnGly+Q0h5AMZJWm32+n29jaX9Tw8PGT208shWReM67xMhUxRYnGXk3Hx8o2XfMfXyQ2pZ12ZN385E3W5XHR3dzcJKjGazhSii+iA69Q8cEYWITQc2OEIHDCj7/5cj4+P+uCDDyZBmG989Yywr7WvF5kmPoczAfj4fOJQPZvggBAZnYNwZBYQWsiROgcOAEAcNDIgKY8Lp+rBjMui3w8w5/oMU819WTfkj2s5e+zMIhkZ5gSnyLN4s5a6rnMZl2e2HIzxHuPwbCZ6jEP1wAhZIuAgMHPCxpl8QKqvFdd0uzQM5VweD3xYAw/oPespKZNkkDPuw3yOPRj3ueNZsf08GzafQ5S5BqU9ZOKlskG6lOiV/TLMI+NiPp3QcDlJQUOnGK+BYrvQ6dQrBE1sMPeGCPB9ocynM92+RkHTDnnYNq8S4bnwKbzPcwBkcxmPpjLAK1UKLKRYqjSQcWTUMyaSJngADMB4AHcuq14axTh9nw6fh3TxTCNB7/lyUbxiCdbZM3gewLv8YJ+8ZBQ8xdj5rI8RwnLuT7DTYB1s+jiO6i4XdZdydp+TdHVVabEsm+s9MByHVMLJfADOM9mhUhHh84nd9fXEJs/JTPQyyULKGnItt/8enKDvyBc4wAkjlykP7rCzJcOafLgfw+AkDTrGvLvPc4KA53VSD/vglSz+ea8ImmfN2H6An8Hv4Ks8yHe/m21YLPPO/PH3efUD8+IBK77ZM6j4Pbet6F3GCtWvB0j5dTqe1DZlQyfC1LYJkO12u0n2KDEUhQEn6g0hlX95JgdBSMI4VSRn+XEi3voTI5M6DKXrwRSgWDhIV2hOgx/H6cGzbLpHAQj+UBQA5by0iCj/dDrlPSg4t91ul50LWRkidp4BRXPQhNICvhkXrZ+lKUM9V3TGitI7czIHLB74uFNmPjC2Dthx8KydrxPzQtkK7zu4xMj98i//cj5sdLPZ5Fp6wAT3o87WlZ61dkDAXPBMOA9nwx0A87m7u7tJcP3w8JCDKM8OMK88xxzkkF1E7qVSSsA8znXF2SsCcOaHEktAQYylCQaMrLOjDmrQP+TGDTtr4KlygMEcJHhzEw9umF9kgGeHVPj000/18ccfZ5lg3jDilFA6uGQe562KXc5YY2fy3GbwAmB1XTfpVgdgZA54PnSt2Ldp2S5rzRoBWv2eHri4M8OBuxN0BtU7ahV7WICyO+wYYw5yPHsolSMDPLO62+0yUJZKZpBnc2ePzHrgzOdZCxp3OEBg7phHdB8bzHNIpaRuTtBQVuvsLffLYO6qy76nEl3w0mO+w9r7mvATncPPsLbMja8hjC/6iH1zNn8Yhsn+PL+2g8R5loe/A0wIuJDNx8dHXc5dajgQo4ahV9O2aQN9DOr6ki1lzpxcYgweMPuhmIBz1ulyOep4BXwAWHTXsxw8M3LX930+0gHghWwO/ZA7zzEuxno+nRTCtPzTZQO9xn45aESe3Ubw4lnnARdEqc8ZusGxIAQrGW8oaozF/zAOCAF0jrEybg8SnRR1QmyeBfHME/MNweoNVQDSzH+6RrkP1+Ceo6b7bsexNIdZr5bZdiD3SRY6BYWJHWYvLjLN/Zzc5OX+tmRPSrdgJ38kTWwdL+bu9vZ2Mm7P/LDergPDMOSjNjyrxLz4C/vmARDXRPbw6fNKACcRkUfHVVQl4Fd8jl3OCaQZb9/3mWSc462maRTHqLqaZkWxx1wXGcQeOUHF2rEOTv7wn/vdyZ7N86+X2OXX/rC/Zk2ClsuVUgvNs7pOmXl1ECCFHFF3XZeNzuvXr7NSe6QNWGJzIsINWy8pXzfGwtZ6xA5L4FkPZ3ARdAemkq6sCGNoJF379F+Nu0fRlMRJhblyxtgFyEsQENAYo87nU77m6XRUCOkwWAfKCKak7Gx534O4u7s7xVg6jeAECfYwBl4a4QabEgYP0hzMYPT8vCZn+TAMGAHvOsicOOCaB0ycDcT19vv9RFFZV34HnMSY0u5eZuOG00EzjojvkBXhmR2ceqABMEAOWHPmjednjG5YswEz1tOZRWQS+fNrOcPN/jwMmQe7PifoiINk7s0aI1uefRmGaTtuX0c3jsX5Ft0BgPvc0+Thgw8+UFVVevbsmT777LOsixhlQApzAihiXpkvL6mZ6y+fcSfNes/L3FhPB3w8G7aBdXXWj++jiwS6ACfWnYwBzsgDNQ8qWWcH7DhAdJQgwWWFtYOwwQHyPnPKPZyo4P7cE2Don/GsIfaYUkQAr/8N3cYeQBh5mYbbHOwIpMfhcLg+d9rfOo5Rfd9lX4IuYYs8Y+ElRm7TPDMmaRJApu5h8Up8POb3563a89kiVa26rq62caHUIGHaPpuXk08F3FWqKkoxUyl6sg1SjGkPUvIFpbzOyQK3kdi7EEJqyXztfnY6nXKDgnEc1bStGss0ra4k4Pl0up7LUg5ph2isqtQiO0par1ape16VNtCzlsiTj4O1xM7xc94xkfmKMSpUQaMFiqxpXdcah3Gik+/qvOh+Hvklg0uGwffGYJ+wUZTV4kfd5roNgsA4n88axlIBERS0WJUyPj7v5c5VVamuqlRBBngepgGL6yVtvdum0fpK6qKLdV1N9rgdDwc1V1/c1LUGeevmJHPoDHbSfVPTpFbXTlKk7JCujSBKRs4DVLrYNdf21eH6b2zpGK8+cBw1jm9nQus6Ne2iw3FVpz3qc1vtBAHrgUzxu2evITKcYCfQYPxcy0uPkSfk1/2uE140inJf4OvuQRLjwXY7JuEzHGIMzvNKD28g8q5MchXSAbNcK1zXoaorNVU55oL1Z+2cGHbc4JlAXo5hCPy9FA+5cdn6vK/3PkBatI2aBoWjtXLpvOROYrvd6nKhDKAwg77/iIXxnwmYLZQORi3sE4t1Op0VQnVVmLOqKioEzpgoXd94ETjMSzhglZIiLNS2xeClNHNU35cacpQQB8o9UDhP6eJIUFYChuTUK1VVKhO6vb29Bk+6OuXCxEnKTBFCy/W9dIqMgLM2BD7Ocnk2hXE7m+gMCV2/HFxiYOZnsGCAeO6bm5sJIKPU0DNZnGXDPDpolzQpo/K6eP4mKRsswD/BGHNPORTzw/klVVVNSos8lexA2x0f84Ax3e/3k+AaYOWpfubcA0kAtWch0RcnCGiRvd1u1bZtDsbJPMz3G/n+DrKNgIntdjupCXcw486aPXAAd19fZAdGXiosHTLk1+TlmaWXL1/qzZs3Ez3n3h48A6KZDw82CSI8IMBgO9PnwJLrzo27VDa5wmjyLE56+L8Zu5MfrgtequHBDHqYwdJYykT4m5MJrCGsLgCB8aBbzBFjY+z+vF5i5cSNj9s3rCPHDvQ9m0UWck56IKesHXPlpBJBt6/NarXW5XLW5cKmdcBOOsIBkscBKGvlrHEp06xF62Sul8qnB7MP3hp+UOooF1VV6ftJDuL1b6kUjkARwBajdD5fJraVIJk1nO9Zwi7w8izsnPhwW+1MbrsImRDy8uGmaXQ4XXW6rqUorTZX0iRUWm9Tk5RFaxntcVSoGynQYztqiNLpcgWsVa2mmpZh+dr52PEb+J2maTKRxTNhV5HVS19so2Jqee06BLkI+YNcQdwg51I544w1cAzgwNubSznB52XtXddp1KjjOVUxxN4CiqbWcCVI6iokubnqK/Ke1nJMADYEtU2tLo4KilJM3eaC2NNcMoSSFMe0z2mzXl39xShVQd2lv241SEETDbOWi1bjOC35qptaTV0O1Qa/jOOo5Sq1O5diHk8V6rTHyDKBvlZ936fA9hrcD/2g9SaRnP3QTQilKlSq6qAqBg1Dr37osw8KIWi5SrKrWPY3evWAZ1ywbfg/bJX7UvwfMumEkVdFuP33/ZaeafFsJnJyd3c3wTdgJQ+ukSeCEs+ikenb7XaTjLaPExsCxnVs6T5nvMpdFdN2sRCC+uv87Q0nMVb3cawjxJj7dgh8t9++NwsbxLXwn+4XP8/rvQ+Qbm5vJg0PmDCCCJxf7lizXGoc3z7xGAfrjhkjyKKx9wAngCBvNtscdAHqAPYomrPQrugAQRhDL7nzTk4xlk2QGGbAiIMLd3rcEyNJSZZ/Jilmp3Ec9MEHH2TBvLu7s2xO6XfvWSqezefZMwoObKqqlFyxVg7SHcS4MmJUYM6ckR/HMR/WixN0J7bdbidntDjz56yfG0JvL8xPAjNP8wIcvISiruucLuY1d8SbzWbSBVEqraMz8zWWAwQ9WMPhz7M2zKk7egwT4JxMCXMx7yaHHNLdibHAJm02m0l63AMGqTCG6A1gzJuG+HwzPrrTuFwCqF3XHAShe3yfABE74HuxCKw8Y8vfHh4e9JWvfEVVVen+/l5SqZMex7Tvz8fD3/kdJ+LAExvja0Gw7PvfXC48eOD+peSj2ApfZwIYZI8197VxGefaTqbgyMkg81lsHXLM9z1LhHyiO8yPB8Vc3+WMfZbYJsbvGS6eG/lFbtGH8/k8OeeL7Cslcw5ksLcAkKenJ223W9V1rfv7+zxG77JHWTYEEiSAVLKqTdPk/VXomNfHO+N7PpegsoDVYcKWIj9e5sucpbkqLXch8rBH+It32UBnX/np4N5tldssruVNRlgX9I9yV0i9qqpyZ0juzTi8tMuDN9aQf3N9votsOsHmQZGDOs+eeadYdI0ghveddOL63uADGWc87FXk+3Obgm9EhpkH1hvf7viCcQDsnGBgjaoqHfLp6+ABKvaReWS82GSe39cXOwWo99JA9AW5Rk5cr6RU8sfv3kmNcThxAhmCHjiu6i6dur5gN3SVShMaATBPh8MhP5uvue+jQt5ijOrHkplq21bN0OR7e/A/DINCH7JtxXchA75fx/0kz8u9vdyN+fB59Col9J+19iCAnx4E8R+2QCrd8nJWpyoNVrwiwPGok7GuD+4nXG4dX3vioW2aa4auyLUTNFwLO+64ZbFYTLpAOrHkmIHxe/DjgSyf8+ZHn/f13gdIi7Zs7nsXmGDS2B+zWJQMAZ1t2BdU13XOBlCmgtNaLNoc/KCYfi6Ed0IiOJsHNA6KUCxvNzoP9KTCxmO03fA468zfMcLOKqOE842VXCcBummJDYZzsSjMGGUkzDFCDrjkPTeMJQNWntfLlXCgzLkbfebTU90YBgKX+XNihPq+1263y+OC5cEw+z4cAC/172TY3rx5k9cZRSeD6Bk4NxpuwNzRtm2rzWajh4eHSYqdWl6el58esFFm5kECpY0Ep9zT97UhGzCnGCHvbCUVJv18Pme5J4VPxmAemOJIPWBw9tRZLHRLKkaOueGzyALjcAfiNfG8RxDgBpjvMo+w/M6W49SaptHd3Z2+7du+TeM46tWrV9lJbLfbPHZkeLVaTdpre4B7OBxyNpB5QVcZLyW2zhhih5wUwQn7PVy2PROFXDhBwX44zw65XXId8YAF+wnIwCa5w/Xgnr9j29ijhz0BFLuseAMIwEoIpUEJOs38sCfMSQiAi5fbYl+QA59XssPY3Zubm7wOLod0/koOflRVtZM59PI/7DcZAg/syVpB6jDfdV1NAgmfY67n4BFZQt6cZGE88xIeZIt5Zv24BzaC+XBQxO+MwckvZ3yxH66DvofAg/MYo/ohbXzHDzvo9ywwZISz3A7GnVSb7x2mIgBiiXWclw0xJmTFs7fum7F34AeCBychAZJ8H5vsNpA5R8c8wCNAZq6Yfw90PNBVeDu77DIT7He3G87cu3/xtWft2rbNZfOQW7ywhzy/l5A7ueK230sdL5dOitNzwXwuuD9Zasc5qfPwKcsWtsPvze/8G5xBAI/tx/f5PVxWfF+sB1ysN9/3bRL4QccuHgw7sCeAcLKWMuD5OJlnr4iAbJvjF8/68JOSTAIlZBAsN187z35hf92P85qQxHHqwx2jub1wMpGXZ4kKDi0kCfLMe3MM7MQl+uvz+nle732ANAyD3rx5kzepMnkAGzblAigPh72kEq2u1+sJG0fJB+ltmA8/sdm/K0mXS5cdHkqD8XbABqDhd69Rdme8Xq+1Xq+12+0mYASDAhODkvDMXNcBAODYW/W6s0mGMp0gHULQ3d3d9VDczVUx+G/MwRElbQgwLxwLJVfMpz8DY2WOnOHk5SyZNGVuMEKuEPOSJsrLGI8bcloxM36M1RwgsF5VVenh4SEbT67pzSg82MEh8JwOnAE1pPdhpnk+DB+GEAPJs2E4MGIwXDzDfM+QVBhfskE4Re+i4+vhjo/P4ehZD+QIuUUf5mvr+/HmGSyu4Qww88cc8zmfB2QA/UJWATdcl5+QA/yNYHUcx6yPh8NBL1++1Ol00qtXr3R3dyepgDpIEJ9/xuW2AuDnoHI+38wL3yM4pQSTMW82mwlIRv6YU+bdM0VumwB18znnOcgieVdLvhdCyAFyXZd9QFyfn05IoQ+eSWZsBF4+nwQB7tAdqGIvOB7AM0MhhNwAxVltgAr3c3bXv3c+n3P2B3IB3RvHUS9ffpBlYL/f5zI29saMYyltdtCNDYcVZd3S2pVyKR8Pesb30XVkHsDEXDvznVnvGXniDW34rNsEXxe3q54ZdPDMOB2AOKnHOnhWILPJmgYgTjDyPtlKD5wl9uAOGTzhk+Z+AKISO1D2v5RmHsgseuRA9V1+he+ir6yNB2Juj+aEiAN/rs38IE9OEPE76+xnEzEfo97ejJ99jUp5oZftu13G7vg8+jWcYHXi0n09ctB1XbZRTlB5FossL8+oWDr4OklDcIRtQ479jLt5pQHEie+xdPn2YI6x0ShlHtw46Pbgw+eIsYJZ3pX5cRuJTXI9I/B3wM8zYseQT/AkY3Y9ZAzI4nxOPUBhzKyxE2aMA53lJ3pX1/WkQyfP7XguhLLXl/l0e+w+CH3xLJCfbYjt42+uk25PmTvXSScY3J99rdd7HyABON1ZexYHAQsh2MGQpWMG4M0FhozQNPovbDjODGFJ9yqOikDG708GwReb1tqAdmfEQwi6v7/Pe2O4J06f3x2IMTaP8HkurnM+n98KCtmY6A4FwB+jxAnrGF8UyMufpNK1yR3pfGMzQaPPE8LtYJzMBfNEOdF2u51sVvUgi7XjXnPg6qVX7vBZV4JZP0h4uqG6zZ1nqqrS4+NjzmKRefMgknHgmPq+nAfC+mHk2JiN7PmeJ2cSXX6cxXUn7MbJy0HngSefI4j2ta/rehJMZsATS6cmQC5s3Lw8CJ10ZpV5doDhQTbfwcHBQAH4COBYV/TBdVOaGnScGfMEOPZgAR29ubmZsP/oGtd3xhGgM46jXrx4kUuz6rqcI0GGGJBRVVUu5yXLXFVVPrsJh4ccuaN3B4iDJKOCfDDP+/0+BxFeZuug3MEjgA79cWfK33kW1pdg3nXVCQb/3UkEz8Z6UMe9kFUACPOAriN/yArO2jPRfMezOIwVQM4asr7Is5Q2bh+PR10uFz0+PmY5iLFsnodAQ7edgKCBRGHoy9w7eHGWlOfmfXf0yLyvlxNLHuTMn8dBswNlZIb1cfvAvbE/AB/Atc8z68ezQ1SmfTOarKXrj8sG9s+DZcY7933IohMJniEva1U6sDoR4N3zGDcy5LLv5N27fB3fnZM+jgvcfnMd5NaBLKCPZ/V9stI1K9KXMrZ5ZjVIE1/n88hzIa9uR/BRlKmi3y576BIBCfbLZRaCi7XwLF0OWkMB407gxBg1xiHbTN8TSADsJZvIO99nbZxUQS88yPGzody38jkntfkJwenn33mJnNsjt9XDkDK1Nzc3E3l07MHco5v8HVvJ+vA35Mt9MXqPvoM30Svf4+mEyDwT68E9dhPSzvH0PPCO47SrKXJMwJOSEuXIHEg55MDPJ3N9ma8R9/Z9r8whtoG5YT0+z+u9D5A8azBnEhAgQDqOcRyV2VtAszMfLABAJS1eqcfkWhgDMizOijkrIJU6ZQ+COKvCg7thGDIb60AZQcfA4QwwNl7r7OwVAIK5CCHo6elpVgIzarVKGabD4ZDP4EmGppQloXAYsaZp8h4fXjwfTsNZIWfZyFZ4WYAD33kpDw4UpXanjoGUNHFuzkySdfOgAGfFesKEOZNzPp8nCg34BXD7Pivq5buuewu0+p4N1oTsxel00gcffJBbZIcQcgbODZKkLDfMicscMgRI5x7cGzCOQXYGHJlhDZEtxu815lJpbe4MDwCfMSHXfI9Ocsi566hf25khZMczgr4mzJcHMdK0wxuZWmTpdDrp7u5uMn4C8K7r9PM///P68MMPcydG34vkYJ17EuwRFBa9ihPDj06tVqvcYh9d8EDWM5z8jhOB/cTR8aw+97xHcD4HZh4EzW0pMu2gEOLCgTD3R8b4uzsv5gjghR2WSgmKBxXOwDpoRQ6dPfY1x775nhHsIuUrVVUOU6R0xtfJM8CffvqpQqgmmZhS5txlQsHtEfrPGBk/tggb6oDH/Q6+i+94dcB6vc5+AJu53+8zcHPw5YwwIJX5hgDyslMPCBi777PxgNoZbOyFZ1SQQ+SirmtVBn58PlxWfU+D65pvXPfsOnPmZZiAWve9njnimjzHnCxDD3l2Jxv4nJNHBAXzoNdtmmc8HTzyGQ+aWCsfi9vm8/msui16h+z0fa/1aqXlVT7mBBNrDxHr4yHgwSYyf/gTZKbruhxAoc/YLiemXPY8+MCvXs4lGEcPmVuFkp2D9MF++z445god3O12uSSNwMBLtLGZ/M3JMtaYdfdDnX0eXa8YE4ET8ub7q25vbzMe5Sd4EVlHPsjOM0/Ik9sIZJ559fI7t52M/12kITrkvsPxIjLlpBJ2FPvL/ZCXtm0Vxuk+T9ddfIWvJSQLZJs/H+uKfmP/GB+BM9fyIJ/PVVWl6tcPii2vqp4ynSxoyujo6mhSp7kU5KSOLY+Pj7q7u5soszNdDppQIpyYg7FkGKOkZqJQcwYQoXNgSLSP4mA4pLJ3xOvnUVAERipldwgTRhhj4kwPgomwXS6XXHKSxl3pxYuXGsdB4xj16aefqapS3T6GBgcHK4Di+sZvng+HiFF0JpfPOLB3hkUq6VgMvJ+X40EbjpD19xIN5sedHcwx15MSoGS9pbJnLcaYz6biWVxmkA0Ue7VaZVbZQbez8IAz3+eBPDrodDaSNQwhZUJ9/pydYT6QIQcJyI/X1XtphKeuXZYdFPD9ObvtgABDSeaI+fXPoSPewcbl3tlVDwaoRUdfkHPWyvVvHMv+CAdmlA0wByGURinjmLJB9/f3+XvL5VKvX7/WdrvV69evc2kefyeryjNiO3zOYLy9wYDPtZfbeGZ1TgbwPvfys4sAKcjk09PThKRx8uL58+eZQHBW2TM8rAMvZMTPwpqDPndkAAPWBFIKuUa3WU/0Qiot8LFxnlVwUOCAH3n2oN4DH16AKwfszFPJ6LaKsb3OPQfXjoqxdLfyA5rnZJXrVbF3ZPsrVRWVC6PW69tsUwBVAB50xufjfD7nYwjobnq5nNX3w9V2l/NlXMcBOF6ClTqPjTkDw3d8czc6QhDochtj6pgWY9D5fFGoKnVd6lIXFaQwLTviHsh436f9WSUgkEJIh6Rj19yGFZKzjBm22svGHTwBPKlMcF/JM7iNmAevHujMSSH3X7znlRBt2yhK105qqbU2HQslXZsvpGNCsj8dy7gL8TCqCo3i1bcje/hv7FlVVZODo/GXTm54IyLGyfjRfQeuZLe9kQm2krl0mXUMQgnrOI6KiqrqSpeOTou92natUAWt18nf7na7CdHBPXx/MgHR09OTpLKlwIM0J0L5LnIDWYPdwK663WCunHBFLqhEcvyzekeAiu2BLPGSWeabNfJsOXLP/dwGO1HlL7DFHAtIemtOnTDgfugkcgl2dOKO+6ITfd8rxJjPIWVOPIPjRL1nyyXlPf0eVPOdOfnp2Nx9o9sm93Wf9/XeB0i8mHSMYVURdUdJgy4XIuBmkl4E+DoriuOVCpPTNE0um/AsR1qs6Snqzn5iUACWzhBLpYTB9yM4yEXp+Q6HucLqOJCG1UHgvH7Uo3qUCAPszO04pjlrmlbL5Uq3t7cTo8F5QCgX2RTPGDhA9aCC53HlhQ1lHiaO1xykp4NdEVF8NtBLemt9eHF9MnObzUa73S4HQZ7p4fseXLA+UjI6zD1ZtO12m2WALI+P0xlmGBRnZedODZkgE8C1AWI8D9fzPUk0dyCLxXrzDN7Jag5wnf1jHVgTsmO8cEh+3gffJwhEn9jf5oYQEMg6OPuFjDgo5tmRI0kZNDVNk7M+ZBT8mswj8sP6epaPcpPlcqnHx0c9PDzo9evXevbsWQ4snVCBOCEY8YAcufeyAAdtrDMBmpMffv6PO/15diKEkm28vb2dBImetUSmmcv9fj8pNeJz3N9b6uP4HUg5keHOyjfkIv9kWpgT3sdRAxq8+x+fpXGKB2TYR+yeB2mso+ugZzTJOHiJktuHOWuZnjPocjnn62Oj3Tc4iGY83jWtsOF0qWyVWoaXTcqw506mlQqGkonCT9V1pb73ToilcUbTFPuADib5kvoe5pxmQOkMvBiLr3D/5cHpPMMRQlDXR+32T1qvV4qDFGNl2aOSgQNgA2b7vjD86Ofp1GkYesVIK/Ry/hL6T/k0Jc5TX1yaaBAsMH7KeTxjBhBEpllX9MT9owfSrDv/dtaddY4qJftjHDRey/DXm9Uk4K2tCkChUhPqyXNXdaWqbrOdXV0rB5Ddpp4eLYBfJxgEpDMHzJPPGWuCj3CC1cvApdJABf10oo89oeg5+pcChFanU9LJ0zn5wvPldA30yrERnt3zNXUQ7c23fL2l6R4k1p7PkEWp67S/5unpaRL8YuN8XbF/6AVjQFc8SJ9XJFECOie1HCO6nuFfPHMDKYWdRg/5vAf52AbGzzjnfpv3sXtzn8JY5z7YCb3NZiONYz7zjO/Ng3Jk0jNuHsi5bPF59JxxOpnpPoLP4zv5zOd9vfcB0nWuJgx53w/iwDucK/9tt9vctMHZbKmUfUllYzhKVdeV1uubCTOMwhyPJ20227c63qAkXhPqY5FKeYxH8xgsgh7AVNM0enh4yAeb8Qw0YSBj4cwQQk+Qg2FwR+hGBAOCw0KJUETPROFkSGE7iEKoUSbvnDTPRmHsAfsAJQy8b05nzkIIeT+Br6Gz+cw7hp715Kez855hcgXG+LkzZU7YTwQb7cwbhtFbwxNEXS4X7Xa73C3NA3ICDW8B61kZmCiALc+N3DIOz7Zxba43Z+A9iHGA4GDTwSzgiOsAQqQSnHvjBOYLGWEsrD+yQckgDCnzCrBiPO4onTVy5gqDjhzA/OEseCZnAkMI+uijj/TZZ59Jkm5vb7VarfRf/st/yftQXrx4IUl6/vx51g9khfFLiR3zoB1nSEC43+8zgYE98ZJPL53ytcJREohgp/gc3x+GVLtPeUPZVDs9K8nX9fHxcVKGw8vbF+Pg3Dk72+v703DUvg9RmjK+XlLB3x2cuGPmOzyHl+I8PT1ZY5l0MDBzSHabgGnOpmKLCN6HYdBut8t2ied1IgUnjl2B/OBZPAM3J724rzfOcQLJ9dhlgHlIcpWqFgDR6ESylSWQ8Kx90qVSxuuBfhpfpfN5yIQUcsE4+d3HK0lj5BDTRQbqCZDWGoYxl5ViV/AfDsS4fgKYnUKIed3S2NI5T+v1Rhxui032Z4As8qyAs/PMI2uKjXLmGR1xmwi+8ACL+zmjjq/u+3ROj3+HuePf6AVyxJjwWeiRP4tfx8t8+Q5A2JtnQKY+PDzkuSKwIcPi+3Ul5f2L7EMFB6Hf+IUQQj6XBz/JuJkjPxheKuV8yEnf93r16tXE96IX2HDk2QG8l2ZBFHmw4/eAaPE96dhEfKljBZ6ZteEaYBf+DY6bN9XwgMEzMy7vXN+xEXPMujuZDj51Uox7IFfMk9tkumq673XSnc/yN4hLfCXf5x5O1ipKw1j24CH7rkf8zpq63Wf90H/ujy7Ngy5JE38yt89f7+u9D5D6rnSZwagktq8w9wgkbAPChVNEuDEemdm5GlLKpk6nwyTLhCGG/cXxe2kRQYrXNDuIJCDBsM2zPTh23sdgMFbv7uMvBMfr/jFizlLMWTECrRhj3mA4P9uHPQUesHgg5enueUmVX9+DN2cB+Mn8+7OjoCg5c8X6syY8LwbAO+7gXBzIOEPlTHnTNDlT9+LFi3wgq5ekeGDoayMV9pr5hY3jADSXM4I3ZJNAiQAT44dsOBjjmWBXAQ4EZ344InNC6aA7E57b74+h9BInQGXbtlmevLSRvTLexc8NnWez1uu1bm9v83x7iaEDKZfBruv0/PnzfB93GgQYzp57QOmOZx5AoodeDvCbf/NvzvvDfv7nfz43ZGCMgBSAC8/GeJF13z/E+y4vHoxmdvj6bAAYZxql0ixAKnXxHrx67biTFpAqLhO3t7dZH5wRx5ETADhYdPZSKp2rcFrMpQctnNzOnMG+OlAZhiE3SWiaZhLwo0cObPk7sv/ixQsNw5Dn5Hg85n0PDpQBHJ4Vg7hgvnHg+BeehyAHdhp75HPi9hebw7ok3R4m13a7jl1EDvFFt7e3Vx8TJmN0oC1pMq/YAwefDsTTs6yy/XZyxrMo3A97Wde1okY1bTmsGR0+n3tJo16/fq0YU1k2Pi91Jyzz7gx4sk+DmoY9DVExSn0/qGlSG3Zn6bGZ85cHIe47PSDjd9c3J56cCef5sJ9OpmLLMvhTaQKC/3CcgtzNswLYJc8IIZMQhZ79nANixvb09JQJEg8e+DxHWABEAed85nA45L2bEDI3Nzf5Ow5Q3X87ieifYa4JvMFl7hfwIZ6lQUe9xN2zwZ6ZINiAhOI/vz/6z7oxRveB7D1HzxkT84tMeHDJGvI3D0jQb/dTzAU65OvtwSX6CG7g6ArXY8c7jsnw1/5vZJR5cAKT6zBuD1h4OW7ebDYautKp1n0qY/RgEayEzLnvdftUVSmrThDvfyOb5hjdyYQ5Tvhar/c+QIKdAoTgFGMsoMMzGc7IMpHeLQbBgTFBsKuqKBmK5MJd180ErDjDgHHG8PlPqQgiSkgQM2ciACQwuhgKj6ydEXbDw3NLhd1xocOwAZAI+rquy6CHezFHfIZrumHs+z6z7Q6037x5o7pOdfA3NzeTVLPvz9nv9xnowrgDDOfMo5cmSgUs4Wxvb2+z8SVAgxnz7nNca74ngzU6nU56fHzMWT2fN+TBwW1hdAv4mc/7nMl1B8xcE3S7s+N5uBbz7uvshp9sDMaS9z1L5rLqLDKZCwATWUuyWTgRZ4dw/ARS/A25Z22Qd2d2PYhDhgEJq9VKr1+/1jAMOVDn2Z1h9GyAZ1ucseLvyDVdJQmoPRPH83/rt35rngPGT3lYVaW9jRzIjB2AFfQSSHf6kCRt2046W6J/BKSu2y5nDqrQYZyvN3VBVjzY8KMH0B/2EDmbx70ccDggx5HRQWpOUiBDXubozzCO46TUFkBJ2SPP7R3zfFM7YNNLZpqm0ePjY54jJwzmG/75HVn2c2DmOsp7XnbjWRkACPaD50K3eSHzkDoAPmSDe3nQQwvxBGaLDeDvySdMz0Fjzwj38s3WtFFHRlzGYI+RPR+/y16oWtvHWqoSVitIpJAzYn6f83nIgSL+L9mepYah1zCM1/8gm1oNw6i2nWZ73M8ic/O/43NYHydA3P47aHMbis677+R5kT0nDxgHds5tPddEtj0L5uCPuWaNAMe+LwRw+vT0lMuDIQQAmU6CQsIR/BC0Ou6h8QG4ah5IIH+3t7d5ztx3cR0CevTNZcDb6mN/b25u8jMy9wQ9zCmYx//txKnLJteQlEvaWUfmCZ/pZKtUKhOo1kGH5seyxBj18PCQZQvd5d7oAtjFSWCfN/83GGiegeeaEMHzPdQ+JieauK5U/NE80GMdPeDlPQKaeSb8dDyqCoVc4JrYMcet2FR0B//u5LATFTwnMuvlf5CPzAtzlQO78dfPQcovByelzr3V4+PThEF2hpf/PLsBAHXj5qz7+XzReD2RGUMOa1/XrcaxRLEYJbq9eJCC0ZCKEnp3EUkZSLlhkKadb9xY7Xa7ycb9uRHf7/eTFHJVVfkUbByGlAww4F+adtdCiQFClBPt9/tJWQjGTVIOhtw4OPs6rY0vPwHgfBYlcEbDGSJS+D5uslWsNWuKs/eMDHLB3NBWtKqqXArHmDHwbCj1EgACmsfHx+z8CDi5no+TcXkGCOV31odrMTcEZ8g0AIs1otwH+cd5eDA7Z8VZY8blDBXOHxDhwJRxM1bmFkfk7KKX37jhpvRpu91mGXa5w9Dv9/tc6uZ7CKUCkAko0A8nC+aEg6RJ50sCaL9vjDE7+b7v9fz5c9V1aUNP4MRY7u/vs31wVppxcR9eIZTN+ARiyDky4+cHMT88L86BLlMESASUzh4jD76myBnXm7PxOCFnHJnHeQBOR050iwDBdZvuh74uPDv2wY9dgM1l/PMyHHTGnStAjAMv587XQa0Hh54ZYQ6cTeVZmUcYXQ8a+Rt7PVhPZ6g9UEv3ffvgTIAAuu7rTnOHGEvtP89NsBajcjCMDCYwVIg37B9/l4LquqyZl4th292W5nUcJIVSisazJFvWq2nqHPixtuln/ZZNK+VIlKQPSnuSouqqlkJUCCVz4ftDPMjAp3r2yP0BNtP9Ef7fMQI2k/u4XHjpttugvu/VtCW76c1A3P46CefjxLYyXifNeJ+/YZd5VsgHZIlyMDLg2Gts+e3tbZZXqZwTR/UI50uid571cHCNTIQQckkWOuJ2Hd0leOP5kTEPft61hu/at+O21u2i+xwnm/x7HggAxF1XnVxnDefZF9dRz16wPtgVz165/XEbzHXBAR68+BxDLiNPbgN5BmTY7QjNjJxQZl08iOb7c3vLnGCn2rpWXZU9l76Hzf0fz4IMQRp6YOtBI/MDrnff7frCfHkWz+Ljr/l67wMkjAUdiwoQLHtKWFAUEcPkNfR3d3e5FAmhhfVMSpH2IXl5k6SrAtcTRYDBgSkBLDp7hKI5Y+jlAFIBznwXo+HBlhtoZ4qkpIRPT085A3R3d5fny9O4XN/ZKwChl205o4HzZH6cvYCBdkADK+6bjFmDvu9zGSMAjODJmQ/PXAHimRc3/HwP4O4G7eHhIT+nt1l25sXBJsy+VJojeBkfa4xSo6ysK+NmPRwE+foSXLjjB5gy126Ij8fjpNQQY+xz5qwU60RQC0jgul664GQCMoL8eKZRKpvpPePjxpTrecDjDJuD5OPxmIN0N67IKM8CcTDPBHNfN/DMNWP0eXGHPWGgrrrpmZC5zgEgC1u+yutC5oy19vIK7vGutUPOXd48MGeMyCjXgBHme8wZ6+b7ERgnukMbX77D33gubKHLgs+7B22UOGJXAW9ka72cyxlP9M8BGGvKfLLuZLz4D5DlgIjPtm2b91Iwv1LaP1ZVVc42oc/IAjJN8AOgQgYgztAdyiedGXbAje9xEIUMzdlXzzhIZe+as9vYhxCUG4pw7lUJrvpM5PA83rmPF5nQYUgldtyLz7lu+T08uIghdcJzuUrzkzrJOjkwjmOWB6mUJvr6jOOocUhMcBylpi4ZRMk74E33/GDH3LehIy5TDrp97ahaYE3cpsyzeugA9g3SBJmUpufUeJmjE5LMP2Mnu8ccemaDoAiAybgYjz8b8gX5AnbgGtvtNgdNnsXDLzqgRZ7d5nJYPATpPDMz91d+mO9c/rA/Tqb4PiWCc98DxZq7//CsBXPNs72rYQ36zhzTbIm1dqLL992wh9tLAT2wme/fc1lEP50URZe84QXy4GSDX3+xWOSmI/Mg2vEYssWcI69U/8yJLtdf/EWyDctJBQhVOGM/KF4xEGtPIOZjYT18b7LjHewOMubZPTC0Z+C8BLzYm/GKNcqep6/1eu8DpPP5omF4MIYhOY6qanKJAMGTszNSmVhnWngR8ABYkiD7qeWVQugUoxSCNI6l85pU2iRiNOZpRIwWn4WJBlh52RkGywELqXYECOPOmAH21Kx75O0Mk6QJ8HKHMwcxGGEHsF4q5ELrYMOdH+V7zsa5YYsxZsXn+dhX4GDWHR9z7saW+TidTjmjcXd3lwGi1ykz/4wHo+/MIEDTAQaGy0sDcQzMN0bC2adxHHPDgDmbT6CAMfI9ST63ONp5KQ4/WVMHtIBYl3+CRBwH42S+Ad6ASG8G4Z/zAN6dCftIHMx6uR/jRTddfp1MYK2k6Tk885IL/w6lKU9PTwawpi3HcWaeAfN7oZ8eZPFs6KlnLh1UOuiWSsCDzDMmnDTPhC4ikwCNp6enCdu+2WwmjpAxsaZ9X7rhwQi77jhbB8ij8QvyK5VSHoIJ3huvz3c6n9TUdera1TTqh9JdTpJCVauqo4bz+VqSUWm73VyzcDDylEam0rE0j6nhTtfZPcdRKdNBMJv+K8RYselSEEcWJJ+QDvQehjdKDQUGDcMlX2ez2Wq9TmdUlWsXGUd+CX7cfrlsOtlRWGM/30TXrMiYx9Z1hchjXbz5hoP2EErXQ2f+/1/tnWuwZWlZ3//rti/n3jNtT9OiCBVTJIJIwGgiCalckEQk0aokIo5U5UtIiTImRaDKWKZSlYCmYi4SpUhZqUqZFH4ZKU0q6JjgBEoUa4ZRFA1UgqDGoZnuPufsfS57r8ubD2v/3vVfqxt6ZpxmsFlv1anuc/baa73v8z7X//O8z2riSxsz5Xn3vifKmdpuj+2LcJHh9ZrgZUPr9QZEDEFFnqlpNtm/NFOWT1RVQVXVKE2lqto0FUol2lSX67XSLFOSpCqKXCGUqqquFA2d1cqqJLXtnvOccsVVS6sQFJpmQ6tNMBYaZWlXigeN3eF1OfTzITEYTaSmqWMlRF7kmm/NdbI8UZ5vGoEAgjZBVV1pUhSqqlpJmmiStcFP3TQq8kKTSaGzTaOgPM+Upps1JDfbGA820b3wkTuNtwJhd3d3tVgsop5C5j0LCo8O9Q2AFrp7Pp/H6gd0GfdAH2HHuAd6eTqdxuoJdJQH9Q7S+RltbAh/41me5XXAGh5xx9gBGg/AXGaGoBudPSlNPT4+1v7+fvQJHBD0jAx600FD5IlyMf4Ob3kwCZ3dvmJnnG/ZTwIgfncaYX/QMw6WwUv84FcObZjrcc+AU2WAXyKpNy8HdbkHFSrT6VShaFSu11H3Ewgr6UBqnuVnXr1kzsFPp5UDg14C6zRhXr4P3OfJjLs+QCrL9vxPi5adRwecrInXMUpda2FHsqUONXOEZ4jMF8V0I7xr5XmqqupemucRNoKCAiHAcgeX68ickGnw8g4MoaP0q9UqMqikqLRQUO4wOnKHwLlCZc1SlwnIsqx3eN/TrNCCYA66EGC4onCHj3bTBHt+8N5T3qyZffOghPuC9HjpmCNf7B+KgMOE7PVsNovfp2yNEioM062QauZIvTYHYD0TNURD2EsQDxd06r+lrpEDioIMnQf2XqbHGr20zZFP9sV5AOXnqXVo7bQ4PT2NdHZnD0fLjRT3woCyZ+4AuIFFMaNwQZycP6GNZ03ZO0+tO2LI3nEvz4qAuEEPV/TIuBsZ7yLkNOQ5jqIiF/Cnzw16++8OUmD8CMgwSkND5+//2N/f76FxBDvoHi9B4D44MGQxMUTsIesJIWh/f1/z+VxXr16Nego95kG/JFVNrcbmv9rMKU2CghJNprM4z6Pj45YHg5SmiZq61ulp9z6dDiwhA93KHuV4OP5SW+rc8kK6uea0xyvoDkmaTjugpg3EWv44P69EpzfWiM7gNQbdnrXBRvv/VHmeaT6fdQ62IfZDHmVtreMWlKZZTx7rOmg246xY3qMxutnRYP5PW/uWj9v3INV1uy+AK1J3thaasHd1TWlzC+7Bv1UpNU2iJMlVV6XSRMrzTQOANFGebBzVjJJnaTqdaLVaK0sp583bzE9o31FYh66k1Ev7Wl6sI82KYi6pDRazrA3ykLl2fzLlIVXbojzr0QTd4rrIAY+6rlVMCp2vzqJ+TdNUSoII0La25xFISbPN/fI0BlV5kW2yC5uKhw0PrMu18rwt/ZvOplHn1HXbCRFwFB5zMM0BJ95VQ1ah3acuWEK2/TwbuhF7DA0cVOQe0NEd/SRpK0xw5D0zgE5Ad2LLKdFyUIB9aAGOs16XStYLj2FDfA3uswwDA+wl83DHuKqqXsMkP5tCaeDZ2VmUaWw1suoBhAfcnkVCVh0slRSrTBxgZQ0eiCwWi+hjuL/ZlZJ2JeueycG+Ehxyb/wSnsO8fS3ur6DH2W8y6549ctvl+olzTvhR8BX0CiGoqmudb/RMHRqtN68QSM12Qht8P0B9QB54h/l5tYDbVOjnQSh2j73L83x8UawPd5xJ/0uKWQqYmGukrrlCmqa9tKCkKHSgpSCvlCtUVdU7YMgG4/CS2SH4QWEiZDhVLlBlWUanDsZjDggmf/czM+5AXbhwQXme90qvXFBRLI6Eu4NNvW9d1z0ji2Jar9fxnUjQEGVEVypnduYIygmCRcDFnPwgqDfLKMsyvk9hvV5HAT0+Po70y/NcBwcHWiwW0aiQ8UBBE8Ts7Oz0glIUIW3CEUAUNgHharXS3t5ezxEmRQ2ahOKXuja9joBwbwxLCEHL5TJ+1wNmL7GAX1gH60LhuYPm2ZDhPuDMebMCUDB42LMedV1rZ2cn8h50Qra4F5+hxJiXl5Z5kA844UGsBy4YCkcAod8QLWKNzAlegz+3t7djQMtcPNvVOa79N4d7NnM6ncbyG3d2CcS51zALhFODYwBfOBrKMygnQJbhAdbqem6IEuMItmUFLf/7uUUHgTww4h1IXAP9jo+Pe0G5d1DEseoyT90ZOgx9p1u7OXlWpCgKJSEo2/A4c3a9dytEsZcBUHcubrhf/nd0FjLozibXwivsgWfWuDcyzlrTtHsBtAM07pQ4Es4+1XWru6eTzXt7ig1SXtdtRiZJlGgz/0RKlKhuGjV1rXUo25xPCMqLvM2slXXUDSfLUxUbeSzXa62TrpQrNFKaZGrqRryUtc0iKeoZaDwp2peWtvvRvt+vLNfKslQhtKiwNi/7rOtaWZ5ptV6pqivlSa4kCcrydIMoK77wtA1C+k1XPOPQLxPreGn40tFWz3Ul7A4soEPTNI3OqJ/FhC+64LR1gk9OTmI5k4N2lK16IOyONXzhmW/kkf2nRJPvuOwCbqBbd3Z2YhCLbvNmKR4sU92AswuNPEiA/5At1uVdHAFvKYNl3S5D3Asb7M8n+Ol4vGsD7VUEXkrFXnBfvov9Ya4OFLk98xJK7g1t3AZAy2GDEQ8qnffZfwJZ/EbowLXMfwgOsreuK9Ch3twBXnfAyoN5bCg/lEK6Xodn3K91HQxPemYMH8V9CtbsATx+TlVV0Tdj/VRjcU/PYMJTnsFkLQTrdBKlqmRnZ6fnrzrd/d2G8O6QT6CFV31MJhOdnnWv17jduOsDpBC6g7wESTAxBIOJUF4enaN8YB6MOpkPHGicZa6nk5wLDs8AkfeSPTfKKCqMKZkVz3g5QhNCVxrl0bIb9KEQYgRYF3Nwhea1rcwPBThEh2B+nAM3MHTccucYh+/o6KjnPJL5Ia1OtoAA6vz8PHYrQ8FTxsQz2E/S/JIiWuQoHAJ/q0AZ4+w1zdzfFYA7u9AfukALeMYzAjigXjsM3SXFLBFBg2eIuAYD5iWX8BuGlD1zZxsnHXqz574O50sccpQlc/CAEKfDSx8ceeLerN+DBn97PUYMhwY+Yg2eOfPMK0YSGXaHy42qpJ7ceTDF2QdHWvnxLBvBEc6bn/3AyKK8fU3Mn7+5vPM79AeEgN7n5+exUYyjxsgp6/TsgTuPnu11hHGYAcJwsk4cCTdK/roBD7z5Xut418qU9fiN65MkUaKuWxhrSZJkU65U9XgN2jk45GtDB3I9+0oAirPGHsesQVH0aOWoI/KFcwhvwePQk0ALvpe6pjDcx8Go9Xqtk5OTyDc4smVZq666Dm7wJXM6X3cdvuBJR4XbjEequmrMQUw29fZJ+z6Suo7ZrpbGbeYsovVZ3paR1V1QC43bDF97nqA9O9QGSEXRnsWazPqgQBskce4lUwiNkjSR1P6bJsmmxK47h+YvKXUQijm4PqbMiT2Frg7OuBPo8ulZhwgKJl2GAp4H1HI+x3agA7DF6CF4Hd04LM1Hj3A/l5mTkxNtb29H2y8pApPwHD9e+stzyQJhTxaLRWyygI1gr10X+NlAKiDYR+gPEORAF/dAPtGJ8ClznM1m8fUXHiixv5QSSq3do3IC24OfgjxxRhb94ef7XPd6EIROJ3uEHEuKFTH8HTqy76wV3ezgnPtTnn1xHqZ1fQghyj50dxCTwJgAzrMf+JzwdVVVsZEWWUjmgV5x8ItKAXQka/CGOdgRPh+CSQQ3VPxwPAGaetMybDdBNWCU1JXfZ0miNEljt1n8wyzLtLe3F+2U8z8NsbzM3vUUw+cOWIHOHIKLn2/c9QGSd6PBcYKYvKuETZS6YMOVMgJLVod092q16nVWgfFRUDwXpBUj7i9WdEccB5g0KelyapWLoogvkHTECiFGkeFUuMPg5U0EIQRHjmh4yQUKyR1LDL87XR7AoVT5ITAji4QTh1EkQ4exQxA9KEMp01KWdYMwD5EE/o6yRzny/hJQC5Qsw5F1aAOiQVbKDYfUvXh2mKnAIfSzOO7UcYjeS8ocBWHN8A/KsnPE1CtngHfZq6Fjyz46z6VpGsslOKALfZgLTj1744is85m/1NSDCx9OI4YbW5QdxgKZ8DIOaA4Psn5Hqhwl9fIMD5JwPr3c0p0HR/+Yp/99iGB6tsDblXJvroE/GA56+EHvqqoi72xvbyvP8157cL4DmOLZKHdkkHvo62vyefB37g+PwW8YfPaFZ7CXGC+MY5FOFNSVH/q6k815FF8vdKjzPL7de5iFdzl1hBc9Ca/4+hzQQSfx3GGg57pEUnRu3TnxvfTSJA/qh8Ab+4l8erlqWZatTp/t6Ox8Fe/ZlpPRRhg93PT04WSSb3gyES9Kbb+bKEkyuR8QgtR2U22UZbnSFDCwPSfbNO1PVVWq6rZ5ArYCuxmaNvuXZTgubRC2s7MlpanW5VqzWXvWyfcrTckCt2dwQmg2wdlaUlemhZ1DxuE9bx7hJT7IuXc19KwRus4DB3SLZ41iIKVuXz3z4/LpABX6hXIfeIB9psrBS2+9PBg5ovU9WXt4FP2O3sdR9rNLZMu8iQLzgJcAwqAlOmNtQbf7OwQ16BLXfTjxriMAfZIk0fHxcbTzfJ/mBlwDYE0LcUkRZPAADDAE/YP9YY3DqhTOEPtrR7BVrke8sYs7zARcbr9ZMzoMerE+5jiZTOKrH7wSoWmaCHa5TkBn4xvixMNzTlPmh+5g/9zGD4Fa+KuVvzTaE6lf1YHd92dgZ70Swkv3oHHTNLGVO5lUgk30vZc8kmhg3QpSEzoQ07N/DkTzuwdwDtAD8Dk4zTp9n6T+y+ifzLjrAySPNBEqGNjP4EidkOIII7CeSkzTttYf599bXHobbASNtOPx8XGvDAon3lO3HijxXJ5Ja1LuTQQvdR1zcAZhOOaFg+sONELuyKw7ru64SYpZDFAoShj8nqwry7ruJh69o2CKooglaJ4hkhQRAgRKUrwHSl3qd0NCqNwo8j13aodjiKhI/YwfAuvGl8Dagx2UH2vk+fCKO83uKKF4PDuEEaZNNPvoL9/1kgC/l6OSjr55VsRLmqTOgeWsGrR0dJrMAftIiYQHUo7UQlNHeFxR+Rkzng/t4EcCNww/yjKEfjMMnnErYILn+V6xB6zZgx3nIw8+uBfBvAcFQ2UMcOIOIs/G0WBe7pjwN0e80El+T0eS3fh7WYqj79zDjT9z9/mxXmQBWvnf0U/MHZpQOtxDprNMSdplFKBbCCGWViHjzCvLMoWmK28igHXHF7lyHrtVIE62X1KvDNJRXmQSHYyOdWcCnmJPeDZyhEMLALdadS/2xklxZHWoZ/luWVUKQVqvSzVNl2Wdz7d6fBuDzA2/zudbapsK+KsbkKtUkwlZp7YCrigmapp+xkFqS+MIlBJ15y8ATWazmYqc7l00B2ibLTRNo+l8pnSVqK4bzeczhdBsSmYmaluOS5wh2t7e2swnUdN0Og75hr+QJ/aHd1Yhn+6ETiYTbW9vxzMd6GQHS3BAh+dgXEe5jkQ/o0M9UK7rOr4D51aZ57Istb293WsdDg8hI0OnD/l3p1hSlC2AOOwlOsBBAXQqOo/7U64OoOvPd36GlugTpwfrhdcd+UeOoBP2DL/Ig1P4GNrgA3iDI3fUh9lEB24dYPQyaeaDDfcAi/1DlijxvpVPiE/hQNnQdmC30Qc0mwDY8jl7ZRHz9S62DtrCM8MsmYMxTgvW6cEza/BmTl5BdHBw0LPn6FfWQ6ZtOp1qsVjEfefsEACF87DPa7FYaDabxdfM5HneBVt1Z6OYE0C0+57IsfOEPw9edwByWD3hfurQXny+cdcHSDhkOA7uiLljdO3atRhgUP7m5wMwtihJHDUMrwvYtWvX4oFmBPXChQs9h4r7SuoJvyO5zIf63tPTU+3u7kaFjcJEEbjA+jknVyQ8DyWOwOEcch4I444SBiEgCOKAngcYlAC5g0LbcK/ZdacHA0O6NssyHR4eKkmSmzrMsJ+8jBXmpzxhZ2cnKtmmaSI65c4vguPpbeaE8CGkoDQ4RlwP4ueKdBhkeeDmQQ085whXXde9kkFHF1EaQ0de6pwrAhXm42cr3NixLgalFDgmOBf8uMJzA46iHYILHrA4muMKnUyGG8Otra0YCHE405Ee9gHZ9bOE/Mv1HojBG8zBjYQ7D/Awc8N4+fA96BzRfmcs/wx+QWfAI9ATmntwwkDJT6dT7ezsRKPK/eAj1ukOF5+xJrKPfIbsw5c4LP4+IBwJdwrYU5wzB3Rcx/CcYjpRYug7739ar9darzrjytxiwFfXvXIbXljJdSCS0JtyNuQJGvnrGOBD/9f3giDUwRDPvtZ13WtM47rI7QrOBMGXI6Dwo+sg9i5NMylQlouz1GZrWl3AC5nbLEwH7LQNGMqya5LS7nemqmoDpCQh6GiUZZPNc0HT28YWHT/VSpJG6eZ1FZ6RbJpGp2cncc6z2UxplqiqNo5V0gY/SRJU1xz+z1XXldbrjre6zoGUauY9hwq9gJ7DHkndSyzRb1xHYM58fWxvb2tvb6+XhWGvaD4QaaIu8M+yrhVxknRZHg/e+AEgwMbyjNPT09jx1PUSz2e96Hr2wbMUri9dBtgT7Lyk2MzJ5Ql+d1uO/DtowvzQp352jowMe3Z+fh6BBKo0UpN1ZG8+n8fKEc/yESTyHQIEeMQrHpwnoAdyDU2cXtj+YVBE1gJ6OsDqthx5dv0OL/qzuZbhASXnWhmedUaPuo+Jnoav2QP0hoM50M4zf55F5H4OtpE1Q8a8nbuDhSQC/FUx0ML9FujldPaqAioJ6rqOr44hyOJaSWpURT/LQW0HgYZAFjLOv26PuN5p7zR0nnqy464PkIieCZI8dekOaghBBwcHvfI6rkWA3UlzlNeR/Pl8HhUyDOjBAGicIwmOILChUv99LHVd9wINhBHBBQEg8IER6ro7sEeG4fT0NCpGrkP55HkeU/hDlAea+fsGcGC41lExrsNx8trsNE1jW1LPdKRpGtt+uiPrSAUDdGp/f7+3Ln+vihselEdVdW+vB33zlC7/L4qi16bUgyAcSbJhUie0KDCfJ4GuK3mUkTsIWZZFBcP92W8CdYIcnu0BiAcqBLPQcJi1cKXt33EDMHQKKSVABjxwI8jgmQQaDgzQyGQ6ncb28o4WuZPrRsede3dk3SB4OQay78YJHeDn7uAtLxHwDAnzAHX1vYN2KHeMggeuPMP3xjNhvhcexDjvHB4e9uYEHbg3BhY5GjoLOEJu5Hx/uJcjdk5r9sWdepwHQAMvd12tVipjEF9pa2dXWZIqCdKkmGhaTJRluaqq1Gw6UQicUwlS4JB7ez6mfYnoTgQqkkRar4OahkCdstG8x9vDANCdTxrrwAs4JDi6OMTwH3vPfR10w5Hib3XdZTPbXIyUJKm2tmaxW1aeF6JteYue07hBmky684ISwFmX6Q4KSpKgNJPyIlVZnm8+CyommdogJ1VRMOdKTVOqbholZf+ll+4AtTIoSaFHK+dPLwEKoQP1yrJU3dQqy0pNaBSatuPg/v6+Tk5OdF7XqkJX/59sslUrmhnVtdZWeoaOTC0jCV8iI9Npy+vTTTDdNG3DimLSlkRvbbfg2NnpmdIsjc59fVZpZ6erUjg7O227lFaV0jSJ6+Y58DoBM89C3sm4ODiArZa6QAP9g7OIXnebgg6gkqV7H1T/PBXfwSHmXugqgEwvvWavCErwCdhrnGJk2QFV9BqZbL7jLxl2sMsBMG99jR2FJoAbbnOlrvkGOg+fwZ1xB31YL4G762D4iTlPp1Mdb7pm+vVOZ87CMZ9b2XIP2LyiAH2D7KBPPGvsmVIqarCn6PLMeJ/AyO0MPw5WwoMeuLHf7h86mOblkpT7OtjDXjh9eB7zchvo/l3TNG1tb9P+JGkLqKjZ8PDmfh7sIU+szQN45uR0cDsHPbkP6x/a2DQZu9jFMZlOeiVMUlcz64THUXZGlLpD9M7k7nCyQZTboXx2d3d7tbdS53C6YoOZvN00jgeKlzIsykO8TAdBGqaXUeoEX6S9SXGCrLjDBPOR/fGSOVeCoK2OZPM7jowjYBgCFwJ3NjBeGEBHc4ui6HW5g/Y8lxIM1g7toI0jdu70bW9v95B7/vVUrzv+nslhTUVRxLeAo2ikrkMiAt40XYdD1owiha4EFey3ByrunHmgMwyw3LFzlMmzWFKnNN2JHCp6HEDWWxRF7yV+KGEMrxtjkB6+y17AY/v7+9re3u6Vk/p3MejQzrMyPidoDl1u5SA7Ukug4GcMCO4dbfNglHvxHNcLTgsO+GLo0BMeWA2Nigc6oHweqDqdHSjxzDV8jaMKLzvA4WfkPDPk+ozAEB7FcLlBRQcOacX+4lB5AJGmqdarleqqkkKI5VuhqZVnXWfQplaPBztEt9kAAV0bXGQG/djNuSs/Qee5Y8ge0unSy7dOT09jGTHXQk/kEt3DfTxQ9/1dr8tetrKua52cnKquOyACeWnf65Qqy1oePV+1jWSCGtX1Roc2LS1Ds8lQRiR6pSY09GDY7EmtoE1AlSVqQqm8SDRJi00JIEF6oroOStOguqk0nVFO3J05hH4AU3meqa671sZN0+mIpNo4omkX5J+eLJVI2t6a92TF7V5VtXxwvulgVVWV1jQEsAACMIiXp67LFjVfnix72R3kuSg23U6rtUIJAJCorEo1wbrKFbmqulJVlTEbQiUEttqdR8A7dAb6DX01BCq9Exx6BxtIdUUIQdeuXYuygA103QRYRzAzBGHgNbd3rgPdxtCZj+8QzHk21s+l8GzsjINryAA2gnJs7J/L4XQ6jeXpZD0AlIuiiN3YuN51DXYVPe+2QlI8X4y84YsNbS0ACee70CkeELnjXdd17HgKf+ErOoDi//J99Dx77wAqvg5BCDrG7R7ywv/xCVynpWkaQWqvCHGbwR44+IaN86AJ24Tf47xKcOn+IjRi7swRu17XdVtGl2ZtEW/TKAktbFQMns1wH90DZ+jP5w7wuH/mgJgDecy7qipV9fii2DhgUN5l44PNR3kMmZ3rYWBHW1EIXpNPEIPhdqeM7xM0ITzc0zt98DxS2wxSz5J6CtoFAyR5uVxGRByjTjYEhUf2DKEhm+POH4wFwzm6yEHL+XwehRSFz8sUYXJ+uD8tQR2dccdwKKSOknhtsSsTAhNoQ+CKgGEIaJDgtEWovc7aBdPp7kEdjro363CUDUWfZV2nPPYe/vSMAcEyCgeD6+l9FACKwYNdd+oc5fKsgfP5MPvoNeWS4tkq0DC+gwzwLzwMzT17xz5Hp8RKRbw8wwNPd8CRKfgaZxaHlYDBnTDfJ187z+F6529HBJ1mONMcnIavHQFGjqCDO884GjyToAXAwh0NNzquo+B9jLSjo+yBI4j8nQ5V7CXP8dJDd3j4Hs6Eo3geMBGgOFqHDhyWDLkBdP511HFodB3k4d7sHfy0Wq02OrHffMSvd4eB/7NW16844Dg9rBG+4ToCJQ+CHZga8h284rrz/Pw8ZruRgyEC6qWqZDt9v/K8s09d2VSi9boDJPx77N1s1h6OrpugPEuVF4WyQJOMVQxEk6SrbGBd2AW3o+6weDYeWQZ8dLlkHW57kCHKfLIsU2Ly2DSNrl27FvdjXXbNDJz3d3Z2op2kGoS9Z789wGYveacW9osGAlRgYFvdtsArntlaLBYxy+4gg+sIzicR6GCLsMfYbRx0D/QJQLAPzjfIJrbOGwQ50Alg5zZ1Op3G8787OzvRp4AXeAa/QxNozfM8w+AAI/KM3c6ytlJiMpno8PCwZ88JHMj0U9YHn7G3/jJmeJUsMPLL9fCqA0rMyzNwXiaJzeMZ8L0DOQ6aOXAET3INZbzsHcEo9tXfI4QfRec7AhOXK57BfNgfbCWfo7/d13M9hVyi6/CRHIT34euDF6CjN8SKQHbTPw8MH6LX/T4e8HpiwfU6voHT1ocHxQ4iwjueyXsy464PkKqykqb9bkpeX+uZDZjYS75QTu5kIeBsOAxD8INBwOD6WSZXFAjjcrmMio+3WNd13escQkYJVIr5rNdrXbhwIQokgZVH/H7Icm9vrxdYuGPkBowA4FZOpQsNAuUIAs4AaAJKwbMNPJP226zPBVdqBYCAhueh8N0RcVphYDE6Xmvt8+N3jBbfd0WKcHvgxv66Ywdt/D5SV46RpmmvRSX3xwmCx0AhuScBhN/byxY9u0SQ7U6pIyuu3LzkygMLD4D52zBY9MwQ17hcQRcPaD1TV1WVjo+PI/3hRUcoudYdeEo29/f3YzDHujwz4k47MujBtxtvd4DhJeTGg0131t3o4Bjh5GKEPKvpjq2keKYO2SCo8jng5EDnrsSsM0guuwT46DV3PF0X8Hc/P+iBKY4PxsXbwzoQ4wG7/421UyaCM+aopme4WDvzR7f5/cn0oItZAzqT9fnzfe1DeRxm7hzoiIbdAmr2yufrpR7sI3PwslgPMOE9B31wormOe8Bn3MvXRIDsDqs7JlzvzgM8U9d12z2q2bTGb7r34SjQdbO5iX9a/uuvA55xgGEITlAWQ1kUzmBXcVD1MnnYwCRNVW5spzu07OGtADP2bjabxXMg6AlsuuvvoTNGxsj5xB1q19ucmfTGCdDLARAPZtI0je/uA0CktM0zxgCt/B/neVj6JrU+BY40NPY9GQIV2B/sBWtz/sdGOnjDwFYhs8vlMsoE+9A03flfmpjgQDsgBY05g+z8FELQ3t5eXOv29nYEVqElVSXDJhDuR3iABx86uM1nBCU0skCnAfah6wmGAfe88yJ0Qpc5aM67Ek9OTnrAXAjt2d/lchnfaeQyRiYR3vOqCtbmsjqbzWLw6PLvFSnwFXzuoBq6hz3B/iDPDiyj/9Bj2Ar3MdAlrhscGBtmOtE3BPPMETne29uLdm8IRrk9gh7YBM+euT243bjrAyTPEGGAPNWJg0nkjoAgJC7EBC4oESJSjDob5wrVHYcsa7u70Qrz6Ogodskh84Pxo9yjaZqoRHkXAMzjaCjKByWPMoTBcXakzqB76tydA5zsIQKLs+AC4hkcgjovIXJHDqHhftyT+Q1TraxnsVj0shqedUERO6rtQuwOB91XHL1mfvwNYfMMjTuirMPLFrxkRuqQekcGMZzQmX1HsQzLF4ZKCIXOfTFeOA5eIsp8Hbljr1xRwufuUKEEMYB8BycDRUaQhvGr6zp2avRgGkfZla8HosPSOJ4JPzkKy/XDc01DVAhae0DJPg8bhqBQ/SwNez08eO3vAuG5HlzBP+gU1gjAQNMFHB2uYU89k+DlOuwvskdwfHBwEEssT05Oem3a77333vj34+PjuF8e8DJ3lynnGXdufK+gj+s29sNRReiD48TwoM/5nft7Joy5UGaLTkMmOj3VBUcYaF/LsCzRs+XMx884Dh1y9h3+BnXnWtcf/B1d7o648xxAjcse1+K8or8cBHBbw766vDFn5zsAhnZ9ifJ8sgkwqw0Ptq23FW5uPoEeQu6hgXdZHaLbOKQ4565HkUn2y/ec85xnp6c6Oz9XYsEh95jNZmpCF0Qiq2SBsIf8//T0NDrb6FB/bwu87cATzZA8sHJ+xblj7wAX+Mw7rnqzIHgS/SQp6gOCDC8Rwl46iDWdTnuVKDizDpp54DiZTGJJc5Ik8eyvnyvxbLADu+7DkPX04MrLMNH1VVX1rsVeus7gemRiKO/wATznWYO6rnvtwfGXho0s2BfX78jB0E/geq8yAYB2PoO/PSPEHHHICYqw+35GGaAKu4DtGFb6ODjvzSjQbf5c9pF9Ya6u1/kbtpHne3Dk59KinG2+D3BGwA5NmLP7d56MyLPOH3b/jsAee+/22GnuwTsZWn+m61MPvvm/22tovV7d3Mzlc427PkDKi34TAATBEXzQAEk9xerKihajvin8jkJGMFEEIDFlWcbDblJ3eHw2m8WGDY4So+hwzOjeA/rkh9hI5ZOd8IAGZYrD5qlzd374F8TEFRAG1lGJPM9jithRc0fEhw4G/7JOBJYgDfrN53MdHR31UKdbOXMIuddss484O74+RyeGJWru0PIsR8kZjqaw7/42d3+Z3RDl4P+OcLtDRWnJ0JFAIXoGhmd7uQ8OyVB5uNPO39kPqTXeKHp3LHgmysoDQObm57Xm87muX7+uEELPIfC0ts/N5wD9CAK8u48jTqyF9XI9vDnMCvGMLMviW7qbpom0JrOBckXunKbsuytg3x9H6TwYY53Mn+/gRLkzzP5g0KG9y6VnPnkG76Lw9fK8q1evxvXjFDjCKfXfcbRet++o2NnZiSix3xu551qXE9bnmVCcEBBTdJaDS26kvfTPM/aOjsPvrNV1TQj9jBEyMgQMXM69zMide8+w+p44cAEN/SwH13hW2sujPHBzPkFXOQhA0Owyx7Wsm/30QI+zMx4Ec+9ujYnqio5jK7XNCdKbeHuYFSyKudrOdF22i7l5JsvBAXgdZ955vssGdu8i9JeJBkkXNo2TeOF464hKq3U7Jxq9MEfkCL4rikIXL16MZ1ycDxw8SpK2qcTZ2ZmOj497QRnXIU/e0MB9CfQhepM1ceYXuajrWjs7O3H/dnZ2ev4B8xuWprKfXsrEuvlBXpgfug/bjrwOzxGjW3iud5JDdzRNo6Ojo9gtlrlCL3+1h9t61uMVKcgG2R72nMDDz7FgD7CVABVuI5xvvaoHnmQtkuLrVghksSUOenNPADUaUuCLeSYJfcIz8IWch5grPE7Ahiz589ErDo6y1+gHzmqxd54twc45X0pdEIhu4L6U5jHwD92OuS13cNZ1Mfaid75tMu3ZEtcP8DD74n6H389BOc+aOSA29MtcJ3nlRUvj8T1IcUwn03j2B8Xgjo5naTBqWZZFxxFDVdd1rOen9S7CInUoDIqC1LOkGADgICFg99xzj9br9h1J6/VaBwcH8V4uZMPgxB0LZzpQMe+K54b4xo0bEVVG2cNgOF4EbtyTTjoICEobZYdw+lks/vXyEAKtpmliQwoUDIqauRF4VFUVFRF7g6AwQAQRNHciXaB9DuwrAu7OG8LI8AyDB4COqHuWjr3xLMetjJDUlQn4GqCdO0FOZxQsa2R+8LaXMzF/D6rcGYQuPIf5cS8CCalz4jw76HMIIcTsIfsCf/mBX9YJ3Rzpd0eTeXv5EbLBfV1eoRt7SamCB5qSohxLrbEj0M6yTI8//rgWi4UuXboUnRzfH1fg3AtnxHkTXuNzlxucfC+V8f3BCXBnCTQamiBHZERBH7kW48kz3IBJ6iGAoISglhxE9yygB/Y4DaDArBn5cZQYYMgDSTfMOHDoK88kUCbMcFADertc4GT7/hAEDQEP/o8NoLQPXcszusCg6PG9B6KS4jrhe4IYZAMHD7nyjCY6jufhzCC7BJR+pg9HFJvlqC7z8yCW53TOaqp0c99WRnIlSSptOuQF1artILODI57dgFa8IwW+cHlzZx05BrBq59K+nwl+gs5ZlmlrE9R4th79jL1xlN351J14ZHm5XPY6hKE74DX4dHd3N37Xg3K3gR7kw8foxyzLdPHixfhdz+J5dtTLXPO8fVXF9vZ2D1Ah6+BOtjcySJIklusNdQlBPu+gQZ/BC1QEuA2r6zpmnJum0WKxiDoDPkVeqLjBprpuZsATdGbFPgEKswav3oHnJfUaKhBoooccIIUfsTc4+ezbfD6P60Rm3T643wKoTKCN/ONbDfUAfDPMqBAEuc/gQL3zD3vrQS/8zl6zX5Ii/Xi2B9A8E/1EVZGDilyLDcX2uo11e4oO8M/Qb9yPvXagoG76WXEP5pgbe0vW0nWr+3bYUvbd99Bp4fvCGplnXddK0v65pc837voA6fDwsJe+ROF4KZDUj5KlDq1mM2Aesj4wAQLpSpcNg/FPTk56qc+dnR1tb29HBCPLMt1zzz3RAFKvCjO6sx9CiO9W4Pn87jWjzuwEVzhvCKLUP2DPvXCWeTYBIwgI34UhadAATUIIvUYFrjS4BwaO63gmBtedZwwqiCWBlaMYrAVaDTNPlCJwX3fqvH4cI+ZBg/OHG1I+Z83USQ8NBfdiLTyL//O+DUc1ff2OjHpZBIJPIEM7aGgAiuRlGo6GOmIILw1RNw88UJKOpDNX5oXx9gDUnQwPnHB02FPq9pE9jCb7yDzhY4wjBoS5QyscGUesoINnpZCB7e3t+DyXI3gFR4QyXTcO0BheZj3QBmfl8ccf13q91u7ubq98xeeIbsJI4uR7MIpTB5jhoIrvjZdNuJy5k+2It9QCKW6A3Vh5adTQAPHvMIPA7z7YS5cn3zPnzVYH5RvZLA2txxlX3AdkzNu14wQM0Ub4kOc7EAR90pT39gRJOFTp5lD7lg4PjzSbTeN+EcA62sm+8iwPBDlfyf6SrYcnkCt4UOqcO/jj5GQZg7T1eqW67s61tY4XZaCUlEt5VquuGxVFrqbpmj00oVaSdCXHk0kRs4vofl6R4Cg3/OZZSUf80akewLZ82T5rsVgoTduXyp6cLJWmqQ6Pj1sHDduVZDo5PVGR58rrftdOdC2AGzqdANxl41aglQfqfjDfZZz98Gdi85x3mIc/h+BkCF5xH3iOl6bu7Oz0wAaXIXQ4TiJ20QFbsiQHBwdaLpe6ceNGXO+tQKY0bV+74bqWvcM3kBS7tvr5Zs5tI3vY9LOzMx0cHES5Qy45c723txfPH2Oz/Dw1egZ5d/vngIUH5g5kwofOd55FJ9giaPAgCdlFhgjsHOjxwAxdzmDfHYjHnnkFkYMFACjYDGwSNgz+ZW7MgTlL3Xk6txfs+TDD5rYCXeIBhwPAXs7M/EMI8Z1KBKXYZYJ/NZ2uZa2ekfc5ASQMAQi36Q74wKtF0XY69n3xZ/r6nuq46wMkgiHKn6qq0uOPPx5f5IqSlRRTyZ4JwMnJ81wHBwfa3t6ONaW80NS7y6VpquVyqSRJdHR0FJUDwnx+fq79/f2Y8id6RumhWIdnc3BsEA5qoCmJkbpULE4na/CDjc74OCdbW1sRbXXHh7WhQGD8YWoboYRWHrH7Idbd3d1eXStCUFVVL1Ml9V/YRqAJ2spaCJS4djKZxFatOPsII99xB4418X0PFlCO7B0KzTsjueFCiEnHO2KN4nXjNEQ/pS7wc9SR74IA+dkaV2AExyD2vl4/U+YZGs9OsZfOX2QIUNoeoPBceBYasLcoUak7w+HGHqSdzoNHR0eRHnzfeREkH8M5RA7JELvjxrxdCc9mM52envZKYj1IRpHCJ03T6Pr162qaJmaNqZ8/ODjQYrGIc3J+IvBwpyFJEt13331RfshsOyLKdzFo8DmBO46Kd3ByxA0aAIw4yLJer3sBp790Gv2DM+yZZw924Vd0pj/fSy7hd+7jmT7fC+5/KzmF57rzAkmUidZQF3H+Pl/mBD0988Tf4EPnE3hYkhaL417ABc87H1dVqbquVFXITqk0zSJaDS94yelqtdLOzs5NmVv2aLlcRh0O8OUyxB514B1nIHOt16uek7Zed+8W4h4t4NK+SLZtD56oCRuwRLXahuFtEwcp6Oys75yxP5J67+RzJ8eDRT+Ujk5F1snkS9Lu7m7UKezXZNrqX4VGaZqrCY3Ozk5VbN4z6Nc7EMQeOZDiWTv2B5n080CuG/k+uhH+4RoP6kHa0eV7e3s6PT2NmTV3NLHnALfQBqAiSRIdHx9HPnAAg0wG32O9nnlAR6/Xax0eHka9TTDRNE3sBIrNInNFgI7d5uwW2Rv20svJ0c0O8pRlqQsXLkR7Cc3yPI+v2EAHsw+r1ap3VMBBKZ53dHSke++9N87Pyzy9PJn7b21tRTDaz3khQwCaDqDDM94wBn+C9cLnyMYwEPNsKPf3OTigx5wI7gnomRPPdx+W583n81g+ToDvcupg+N7eXuRPBvdxP4vvcy10gH/gObKQQ/uFHJ6dnSlVosySDO7PEgANS/+wWdzPwSt0r6Re5Q9r6bLinZ73QFVq38X3ZMddHyCh6CRFx+bSpUvxd69t393djUESjA9zSO15Der+cUi9PMqZ0ZkMY4BAoZRQkO5ISh3aiGC4oyKpF7BQYuPr8QCJOaCoUE7DrAEK2x09qQu6uA6nDmFZr9exnAFauJJG8HAwQFs8OzdcuwuTK6Uh4iappyChAfvnAQ/Pc+XkB5oJ8DBCzEXqsj3D++L8zOdzHR8fx71wRArhxIDwXQaZGYQ/z/OIqkFHVzwEAKyXa6bTaezc5DT1DIsHMpKiY4kiZ7hDhcJyxAclTnCKjFGu5inuYZaP+yJzlNBgjHGi4QN4FINH/T/zRWEDFPAsEHSnXZqmunHjRgx2AUDIsDJX5Il5uOPlQXf34s9+ptDLfzBolMNJ6p0FxPlHTjzghgboD7Ki/jnGBbpzBsFLO9y4wzMYZK/3T9O2vAiUmPXgAFFmyT7DE575czSfgf7wICOENgvmAY+vhft1c0+UJB2SD5/glDtCit7yjnxuVBkeTMBrPDsE9fjY0c+hjnSQAAcPcAG6IQuUUQ9RYGSa68go4Hyv1+uYbSKwbPe/dWJYK/fxgN8zsi39ukYmOIKAK6enJ5pOZ1F+0HNkuZFH12fwsNMVXQWPkMFZLpfRsfHAO0mS3rmhuql7gSv74tUagHfsXV3XsRkBOnQoj1XVNTBA5pgzjq0HRq4HnD+YAyVo8B38enx8rPl83pMVvxcBAfT0MlPPTjCQRWyY34smDfA3JfSARw7YICvQQVLsCoodStNU+/v72trairIN0MQeELixj/hKyB6grGdTvXsne+tAkvMofpkHn3Vd6/Lly1FnY8ex3QCt8CzyfX5+ruVy2fNL2HMHr+Ajr0BA1h1ogj+wwdgz9gUb4eAxgRB2wJ14D+6GIBGva3Gb78/1M8PwWgihd6YI/nIwlvVhRzy4daDJwUhkmO8iO0MQ2H2TPM1UbII7eBddBn29mogs4/CVNtiFW8nlkN4OiDioF/e8efKtvu/6AAkHwc9BeDodJAXl6RGwO9gYY0kx00KUzGawqaBhjnJ7QMW1BCygGShLSsFgnqZpojOG0pO6+kwyQD5vf/9Jmqax5IR74ExKiuVxkiJShPKTum5RODeegXLUGMPhZXhS16Ico+0HjelOxXpQ3DhOoHJudD17hMBBCzfI0M9RF0fmHZGAHkOkzI2qP9uRehpWSP1MkhtHR8XIBHnQJ/UPc3Kex1PH0N6dn2Hg54dGPfsgKdIRJcreQnvuh4ywd9Skewcvnu/8EULolahxTxxfeNFRWEmRFiBkQ3RNUuzSxD34LogXBstlyxH/EIKOj4+1Wq20u7sb372BQvc22PywnyhvaI2yZ00u4+gJjBbOI0aFtXuA4lkOR2JxPqE5MuDggjuivnceUEMzqStz8Gsp1/OMC3LkDij0BHGHv7iv7wO8gJM/DGygAzQj2wW93OHm+rbMTXHfJfUO9vv5Dl8v98C58fUPwQHAhrquVJb9dsTDkpRhINcCJu1ZC5xLeBieGIIU0MztjJdiwZM4jB40htBvCICc7O/vR5TfEV9Kt1tgrQtOoAPBAevzzBl86GWht8quANoN6c/cPPDn/ujY6XTae38ecu7OrqSYdQXI4JrhO8qweegpB6Zcxr1Eze2wB9aOrqMP0FnQMc/zOLetra3Y2Kksy15jBXiI6hbW7bqMPfEMo9S97we5Wq1WOjo6igAVND8+Po6/ExDyd+SSebCvrH13dzeeMWI+2CzfQ8oNPQBz+SIIhHcAD8lsIQ+ceSRIcpAZH8xt3+7ubtxP9KwH+g7gsm/wCGAUcuD39X1Btpum6zBHcIUdwU/D72JvPbjDWce2AW7gnzmIAK8gT/D2ZDKJoJoHE0mSxPdQUrnipd8MByOd/922OaDmwRv3IlAlw+jAA3YNOXFdn6rfXATd5uATMsvekJ1y+Xdf3HkDO4wdYG0Elf59z9o/2XHXB0ggz2wIzjsbA2FhMIQF9Enq0rvucCD4oM8wi0e5Q2cZtJ5gCbSnLEvt7u7GkgrfUATVHTk/4IeBh6EckZa69CzKR+rQZxzwNE2jcBFcOCoN/QhaOI9E+Z4rNJSUMyQKib+78KdpGtH/qqpiVz93wBAab7BB4ITwuwLjPkOUFsfbUWRHB/kuf4d+KBPo7YLrjr476cOD9tDUnY5hpxie586GOyquIFCsHgBJ3aFYfjDM0MwRIndCoB8Oe5IkPZQOpeXKnHkwf5QPChfZYe0YK997N4ge4Hr3RfhgePaHe8IfyBbZWTIjrAdEl/0kY4qO8IDSHTkCeeTEW9CSlZbUk0XfQ+cfSkPYP9cXIXSHuD3A8oymZ/U82GQu0MnLHqA74EWet+Wojk7i3HgXrGHw5gErnzEvzwQgm6zByzbcIce5Bz2FHzwTgh5p79F3uLmeZzIPd6rYK/Sggya+L/Ar+rMoitghDWQTGYcmyA1OX/vcNvtE8LuzsxN5B8eJMzwcbqcJh+tobBBZEWiHHMIvUueQcS0OG2dD8jyPncb87BpVA47Anp6eRLqj62ncgZ5m72n6wzrPzs56bfS9rNIDEviJMl5oPplMYslt3TTKs1xBobe//sJ3By09eB3e08EqL7PyjnnuXHqXMRxe+I3n+Rkc+DiEEF+aToDq84FfvESO4AbbgZxCZ77jyDx2h3nw3dPT015pvp9tQ9/wr9to5zcHSQh8aFpB5sYzXgQ4yBuAMQEWPpADzg5iwvOeaaH02jN22HRsCvf0TBh8hc7EFhBMHx0dxQwTtPBskts1KmXIhnkJJQAIPuHR0VG0TegS9ge5ZO7sp2cIoT3zIUD3DOrJyUn0NbGP6CP0HHLioAX8Ap/7+gCDPUPlGTYHzdCh3qwJ+eNsFfvhFQRB6tnD1Wql5XLZaywk9btFEuwif/6Zzwv/B12M3YCf3Dfj+yEEyfb5duOuD5Bc8TjTuPN+cnKi/f39nqLhjcxbW1s6ODjoRddsAveCoTHCbvQxRihGHKbd3d14XgZUBkXsXbZgCowHDR+yLIudYVDmwxSy1ArH7u6uqqqKwYwHb9zDOyINnX+QEAQNgXCHyRUt/0ep4nhLXWaCYNWVhZc0enDDc4fOsXfSgwZ85nvN5wgUCoH98kCFNXlgKnVd+6ALCtUzbf45gYobHA+yUKY891Y85SiKGyUcea+b94yLB8sECdwb44QScqXIs+B1ZAY+9ADNUWLmNAx8PRj0tbH/nlXhO+5ko+iGSDXPYG18l7GzsxM/Wy6X2t/f7wVXGBiMDg4O+wGdcCYJOuAZnGwcAK7F6USOvEYb2WCee3t7Wq1WOj097QXw1OF74AftbhVMelkIWRj4AuPhGRKu9/cKIVs8B73AM6ALATOG0Ut9XNYcSJC6rDQ0cR5GLhyNpIzMS/fYB3iKucH3Hty7/Lte9v1FXzh9AbDacrJa16+fxuoD1sM8hw5Vl6XunNimabuAwZ+Uffl+E0zgZOJ48yyMvpeiss6Wph1tOMvqgWAI4RZlYF255FB34qBCcwfbOOuHbnFQyTupecmwOz3+d/bHA3AQanRbWnR2ZAhUoV9d7x4cHEQn1vmCIBC5Rxe4fHi50d7eXu88FdkA9hjZAExwXoYuDgZiq+Fvt7GATPtmFQAAUVVJREFUElnWlgkDDEFXB1WgNw63Z0ddptxv8GoXz2jAI8MfZA+6YKs8OzOdTqP+ILiHhnVdx3LMuq514cKFeN3Z2VkvW0RWyQGZoZPPntOJj8wTPtbR0VE8S4lv5uAotnwIRjoIgJxBR/SOZ+RYF7Tz4Bqedb+LfUBvLhaLmLXzzsee1WbvXUagKXLkIAO8hw1yveP208EhX79X3gwBLs/MMW8HEQlA4UnmAMDMdXVoVK47nefnaJkPegq9hswxL7fd2BDWQ/Ds+p3PuAd6tssKd/bwduOuD5BwDr1swRGEum7PPgzf++NdWdxAo1gxdDs7O5F5uDdKWmpr0o+OjmKGCoMvda2TPUsAs3RlFF3al9Q9DFKWZXzxpDsDzG0+n8f3JGFY+QznaChErNNLXHA+yDi50+LCBbM6AgCNUbju6EArShEILj3yRxE43ZgT9wTFcEQII+MlauwvQojwu3PvDtwQZfJ5cU9HfaAH/DVE/fyMhRspsow95CV0GTgPuuAZjJA7zkNnGjrhoKK8uBdrBAGX1FNCrAVFA8+ghH2+/l0Phvn/yclJNLSugKE1Bp/7EpB7Sp25My+e6WUoHtzhdDRN97JlrnGjC4KLI0HGlGs7dP00ghOUidC4g/NMKHnu7fPm+TgdXjKIk+gOPvMaZmBY3xBhhU/d8OAc+LlF5B9+hWYe9LMedyLdCUDXIN/QTupKqeB19Jo73HzmuqHLinRvhUc+Wrp2sk9A43Lm9yE74qCOOzw4I+50rlar2MUTR9n3Dl3jQFLTNPFcG7KeZTe/hBMbQVaHeXp2kL3JsiyeGaWzGQ6CX9+e5ShuorXrTHgHWk2nUx0eHsV5uIPVylHVO+eDI+pBtwfNHuyQcaqq9kWh2AFJvW5cbjNwGLG5Xl4Z0iTqSfgN3sa5ns/nsbV9WZbxfUkODtE+++zsLAY/7hMgQwQqHnzwLzLr2daqqmKJ2ZCn0QEEVPCB21rPLKLTkX32eyhfXuHgesSDLvgaRxz9yLsU3aa57XZas398hsxzf/iL55KZZw9ZCw0fOHcCDyPDZIvIJjIv1oTjDN/v7u5GvcjrT6qq3/Vva2srPpcAwEEqwFhozXPd3qPzWRs8DM2QBX4nE8z3oRslyt4ch5/9/f04P9e/HrDyHAfE4Cn2h3VJXbbSAUjfP6/i8HI9aMy+wo/IM/fh3h4cNU3XSdC7XSZJomrdZcYcEHawELqzdvid0QE7XQUX+tPBHK716iNspFeABY0ZpDggDBtKlkJSRARA8XCMQOL4nA3w1CbGnLMRKD+YX+pqWSXFDE5dd2UQfnDy0qVLsfyiaZp4mFXq3uLs6CpOyNBweaCEooZJHJni/x0jBrUtYjsHCsd5Op1IVkvq2Teeg+LFUKzX64i0EQgMywNx/EGsUIJ+3gNljGPtzQFIneN8eSkCAuQv4MNguvOBsoYmUuuw8qbyDhnu1u/onn/HU/GusDwLgvJxpBjnwo0/tMWgsL/O19CPPXZnBZ6R1KM5z3dk3ekNb2Msh5kX5uGpbEcs4UWcSP6lBMczI26oWZOjXB6sYlC9C5Nnjdy4SOrxIteBKnlpkwefRVHo+Pi4h1LTIne5XOrg4KCH3h8cHGh3d1c3btyI6DodKouiiCVsnEl0RFBSDLZ8b8hao5MADNAF0MTlF8fEMz3uaBDQsRfwNLxD9oG99hKmYbYIOnqwQxCNMXXAwYM53inipbI4iB4Qs479/f2I1Lf0k9I00XpdKcvadtshNMrzLvtJBgccAz6YTicbh5JDze05HFp0VxWZkqCtrdaROz9fqe34Vmu14mxMqrpuIjCWJFKSpBvAgg5pIeoo7EoH8qSScoXA2cGWnw8PD7W/vx/3aJj9w7Fxx8sBEUA5/m0dzCIeTi9Lzjg1kgBdKmXZVNPpRGdn5+JME/KB7MG3OILoloODg8gvTdP0Xp0BbwPquM6CF8iqDAEPbFy1LpWn7TmGoijUZI2Wy4USqZctRUbm83mkIXTk7C485C9qTpKk13wC3mavZrNZPEsG4IjuT5K2zMoz0IBx2BpklH2iYQLOLU6609iBBGwB9HYACZ2LrvG5AzI44ImdRe5cluE1LzH0UutbgW98XhSFtre3YyYcfcAcWf/W1paWy2U8SuDZRHde8UfgI/wHr17ArhOAuu3DjnvmyG2CdxR0P4HKHA/Y0aXYF3wP11mAZjzDn+3AhGeCCLTR5x4AOQiADYJPucaBS/YZUMUzOvgOnhxwe+OBC7wH/fzcmiRlaaaQNkqCFOr25c6pWr1arUslQSqyXDvzLeWb+zRl9/Jz+IJ/4X1ow/wcGET/YT9YK9d5Wa37iugUB6ABxCaTydikwUdedMgTyghicuAMAXTnFocJJcxGoNxBSlx5IVQIDRE1TAqSwHV+GPDo6Ch2YAO5w0mC2ckIuQNDZxhnDIQTlAUHkfUQKHDvVrGl2tnZ7hncEBolCVkXRScKY+YlOtCYNTF3lCFz8IO1GFaEABQXx410POvzLEGWZTG1juHBkNH4whWPI4QocC+zYz7cp3Ve2pKPxWIR1wa9EFAPVl25uwMKXzlKI3Uv33PeQmGzZvbDERwUmx9UdyOBUsLQO1qLkWC/CO7JpNFlxxWqGx6cBuQCXoCv4D13OnCQQHtdObNe5ocBYE9QrtABumAE4BsClCtXrsTvcD/2H9lg3dwHlA8DQ7Zrf39fUota7u3t9QJIUHZK66bTaTxIi7NLEOcvZgUthV7r9TpmgT17g3LHoYP+GG2XOXe0PDg5OjqKf8M5lbozlejBk5OTmw4Rw9/+TJwnB4LYR88+8Xx4AUfHDTUyJinSydHyJOla/Hrg1Oq1DizwTDYDGciyVGnaNbBo32fUtYbOsjSelyMbgG46PT2LZ9ncyUzTTHXdROQS/t/e3okAmDuzBAhtqWUWUVn0s4Mb7jhQYih1bdB3d3fjfNnXs7PTXqYawI/vkcl0AIT3tbUg0XSTXWvfQQRKTokRsse+8dz1eh1fho6OA1BE5rg+y7J47gpdhTwNu50RmGAXV5vzutWGFxMlSja8vbu7GwEvdwzhNfQr90KPOmruMtm9+yqNdMCZhTexnTiQ169fjzqF+0EP6OSyga5irpzZcv0IX7jMzmaz2FiG53nA4hlM6O5217PbrN8zZZ7B9rMu7I2XKDkQhR11QIt3HQGwuv07PDyM16Nb6PgHaIUMcfbNnV+vTvC21vAlpdPu+FO+6oEF1TzMi3XiG3gWyOXU6QvYzf8dpGVO7A+yiSx7wIyORPcMM0muE5m7A4B8hywV++aZde6Pj+mljsgR80Tu3a+d5LnWq1Y+66pSswHtqrLS7s6OEkkNoGzozvlAQ2wdTZIcoEQu4VXWDx3df8EuQdchQAw/u68wlA/fx9uNuz5AWq/WyrPupZI4wAgCGSEcpTRtWwE7yuIleY5cuAIaZnNw/thcqW0T7pvP5kpdKY47F0PmJnDC4eF7bD5KHMMsqYdm4IxSh833u2i+335SSjSZ8OKuOip0PyhLIOFpfhQNgQMlD56qZR8cyXEkkLnC9CgthE1qjSTrYy7QiZbRPBMaQmMcfK5HiNxRdbSDfWQuKNujo6N4T38Git1LXIZBqxtO9meYbYM+HgAzT+c95wf4ygNKlIk7tLPZLDYJobsRQZ9nqKAhPMs6KaPESXRkCqQOBMezFa6sMUDsVQjtmTnP4Dn/O0pKGYgkHR8fx4DGDRS047mOVEGf5XLZ44ELFy7oxo0b8R1Hly9fjkEM9AA5Zk9B0t0RQ1+wT9AX/sABfuKJJ6LxZ7+n02k8WM9ZpZ2dnXimiYAf58ODXujtug19B594gMU8eE8Gz/CMtdSVZBAIeEkvfOlZUA8oPXBnTcg7PE8W2fWto4A830EjN3yus+lk5VlynCPv5oQu86xadM5Xq1iiCRLtegAHhczZ7u5uPG9BYIK+ghdA1QEXPKPsgAXOBKAU51dxZKBDWZZR1+BYst7Vat1zrDxb4Giuz5N9lLrW4Tii3DuEEGUmhBABE2gLeAjoQFe9YVmm6xB0S57nunHjhvb29mJ5Ifvr5UGTSdfgCNo63/mZBdftOJgekHEWEfvK9QSVBJQAfp7NABBEp8MTlN56pod9dcccGaTxEXYFeUO/O93QOcxhvV7HzIwDTKzBAx704NCB536AGMwT2sPjnt1AnrAP8BoywXrYW2SY/ZO689bocwJsso8OQriz7eec0GvDAMZ5naCEzD9rQ7fwfQIHaOHBvgcx8BY2y8Fmz7a67nNeRje3YMxpzFwRaHu1j1ddoJvRdd7IwwFHDz7gB8A2Bz+dp6iuQNdx77qutaobyfjO/T4vm4Ze0NbtTJqmMQvrYC321H011ueJC+Qb/eaZUUBddJgfGXD/MMsyZWlXtXK7cdcHSDDndDq96XClC5VnDhAsjA+bgsDwXW8SQMYEIz5EeFBQZKykrg4T5vBzGFJ38B3GwYjicEv9HvQoLQyZOx8wM4yLUMF4bbCQbrIv9NBPNjXuqarq7Cakw5W2Ow5eSuWOh0f1nllB8XowgpIkiHFkBdQbNA/jiLC6U4Xy9+f4s9048znZQzIwCKsbFA824B2CbM+euLPljt1QqbBvjiazT9CdNDp86egKn8GbzNuDJJQJtHXDQbMO/3GHwQNtDBb3ZY6uCJ23siwbHJKsb3qWZ5L8gKbLCegq+3t8fKytra1ovJFvnCNvLuEOPHKBw+SOI7Kwt7cX51MURe+wPY6BB3U4tnwPeZW6VwngYDEPL8sFuc2yTIeHhzFb6CW8nhGVpIODg5jx8/uAvl68eDHukTve0Bq59PefEeTVdXsgmyztcrmMmVlk0ks/k6QrV8L5gXZJ0pXt+HtOPKtHqY6XreAcADI4T6HHhgATARZOusvG7/7u7+pTn/qU0jTVc5/7XB0cHCjLsniGiHeatXROeuc34Se3KU3TlnpSagWogWPvWVCfL4fVkyTpdeTi7NJyuYx6C15m33FMyFy3pYZJjz58V+oCBubhegAHDl3BjzshOBoegIQQ4otFnZdYN+ebiqJ92S1O8NbWVi/D5XNjjd74hB9/WXld1yomE602wRsOHZken6cHotAN3YwDjH6C56ATcoC+HFaZAAYhXw6YsK/u1OIIQifszmKxiOXp8DCIPnvjTSU8CMAhvHHjRnyxrLc2p3rFg/QkaTOzgCGeleFZ0M4BCJxnMh9OE3wqaCx1jjv6wZF/6E7Gg/1A5tETzMf3jGvcFqCHsEX4bGR4WCO8zbqd5gA3AFf+EmTfY5cV9JYH96zdAV/2w4Mjz8r6WSX+hYedVxwYd9/CwXq3o57NormGv6LCgXPX41Qp9fw1SZOiuEk/cI1ncB00RBehF5ijl4q7T+A6BRpzf4JA5JrrPdiFX7201+9Z17XKqjtff7tx1wdIk+kklisQGbPBGKsQQq+XPJ3UeMEYgszmwFg4HR5t+0F6qWtxWNd1L61fFEWsY18sFpHBEXoyMiChBGN53r6JmjIgnFI35I4Geb3/sMsWjjpObVs+UqssWwHNskzL5Ymm0845Rim44uP7HiCgPJmjpFhq6E4pc0TxgMCiRHFAhxkzhM0VI2g285LUy+JIig64B79839P3/N/P36CQhii2K3/P3riC8WARY8MamR984e+f8AOsUr/NMbQ8PT3tIW2enXLnkh/2DFo62sPvjq4ND5h6WR3nHeBrPyAKf+V5Hp3NjtfSnlL1ufEMBy2KoojGG3rj2CdJooODg2io3Zny0jQMEPvogZsj8GdnZ9rZ2YmHfbkWucKRx2iF0J1NdLTbedzXDirvMu86hXeoMN+LFy9Gx9FRavaD8051XcegaGdnJ2YAPKvk/Ai9vGyXdTRN22nTg206blKOhtF1UIg9RIb8++508LmXucKryCp6mPee4IijC4bZRze8Tif29fLly7p06VLcN7JD8/lc165d0yc+8Ql91Vd9VXxJZpomvU5lXlLMc9Cp3vnUwRkc/FaG+sBXnuexGqF9EW6/fAkZdnlhb7py7CryuwNlntFnn3g2ziDywZw9YEF+3PFyVB0bQHDnuhXeL8uuiRAOLw4RMs690Y1klCTFckTu7boefcDzmCcBAU4oNgc7h/wfHx/3ArvhOR6e4/RAlvEjhuAdfM1nBOsErfgC6Cjo73a0adrOh+hDbIrLDL6EA4noaPcffO6ur+EPsj/QH100zES5D4P9IhiDF7e2tnplx86LyLcDjD53z7oQFLouctljD7gff4PHkUd07BBkQ18BQgz5HD1DFg0aeOULw7NL2P+h7XS5cECVZzswtrOzE+0U98LPwl/x0nCehS5wHmW+XOeZH2TLm9g4+O0ywGfa6H+A3iGPuW5yQIa5c43bcHjA+XwIfDldobmDy+gK30vABL7PXmBbmrGLXX/gNMNgMBB15I4e4zB4OljqGArB9IO3lFTg4CCMIGigvyBrKAAcBs9wYLh4No4UjkeaphHBQdEMX1SKUXDkYSh4KElnrJOTM5XrUlVdSUFqQqNEieqm0u7uTs/x9cyBZz88WJPUU76ewUEYh2caECKuxwFyg3p+fh5rqD1j4MgXhscDAXfW/NA5DgLXwS8oM4QVheNBBcKepm0mkHQ5+y/137EAwsW8QT/9b863XrblSouDpDgUrgSGZ62YM3NA4cMrKOFhKYMHjXyP/QVc4F0TjkiyB1LXHp3vARIMAyV4ABpLXYbCn+33AsUG6V0ul6qqSnt7e6qqrvVwnucRKPAgxR0mnC34wZ09R6mg62Kx0HQ6je/K4bvO3zhDHlxhIKLh2XyHrCtZCObDHvI3nu+vCKBshJIj7uEG3x1A/i61zgfdlHxewyw090H+uR45ZK8JMJ2n3Gl255r36hAs4NDAc8PnerDMOoZBN8/00q2yLGOWR2pLGv37SZLoOc95jra2tnTx4sXNHnblHThblLx5VgK9wzyXy2WcozuSyJwUokOO3g9Bapo66hr0JfvkJUCsp5XpVEnSPwAtcc6za9fNs1y20fmOxg7v4890Zy06Gk2X5arrOmZz2X8CZ5wqP/+Ajse+QUMHozwL4sj/dDrV6Un3MlB0BFk17IGfRYX3kQ/kECeRcyrMb7lc9nRrXXevbnCeY77YwaZpIojA3E5OTiKAAc+R+UWX+/cl9UAB5g3fAJa5bJOZw75R3ucyzX4gIw7OsA4aGOEDSYodIOu662zGvF3PeeADH5Mx97JdD6rd/rjcuD71s2JuB+AHziqhJ93P6GUOLEDlnI3LOM9M0zRm790vcJCAwMwBxyFggGyxBvw96A/tXA9hO6Gv0wv96MGI+yQ8x+04QJbbeuSR70N7qTsbCk/HwC5JlSZdK3ZkF33ttHY/xkEN/GXW4PeC/znHy5ywDz4X9xvgB3jBQQH3T3vBbz6W2MXR1P2ONsN0pKc5syy76fwLjqe37XWmRekQsed53kuLUu9KuhSHA2FGWD0aR5BAHh2hlfp1mDiKMIPUnXVC6I+OjuLzaJPpSMPh4aFu3DhUCIkUCCgr5Xmb5drb3VNQh5jBlFJX4+mIAkKOEUFoHTFwxMydGw86PJByJG6Y+WCfhu1pEQrPbKEsXVihI89HIXt2zffZS9PgCZwjR58cFZO6F5tyD4TfM1eu/BjQFAUBP6HgfD/gIfYAJJN7Q2dfv7e4HwZiONse+LriyrL2zA68gFHAIee7nsIf1vkPjYSjSBgx5JNyNQALrjs9PY1d4yiRkxSzQdyT93FcuHAhPm+IXg3LdNgjl/m9vb2esoav3IB6QOM0gB9wDuGnum7L2jwQwIHBkYM3aM5CMMhLOv0ZoPbwtGdnCUjI7DkyCj08kwsdKA0bngHw5i2eDSRAkrrzPt4tDx5Adgh6h3wI/agGoCEA/ItskDnAUWSPkBmcky/7si/TZDKJZ9eqqtKlS5diQD+dziLK7IEQe+ngmXdIcsSejCp83863OxNI9ULrbPSNv5e24ojh7PO8NrDsyi7dsSnLdaS/1D+k7/zqyLY7bvyOrUzTNJ75gwfQYwAzLgs42u7MwIM0R8L2klEnE75YLFSWpba3tyMQCbAynU61LtdRDrk3++6Zl6G9ILjyTKaXRRGwUDbpetaBImyag4WUScEbDno6H3uWlOwoskwQ4TYfu80zkH+yq9DYHVtkzHU9wMXJyUn0SbgHn7M2dAEluQRgtM6Gth5Awsus2ffLgS70K0E/8+eeBLbwE3oDOh8eHkaZktQLnpE5B7o804becdvl4C46iXWzd8ic87LPG1kis0gJKdcSJFZVpYsXL8aGJewZcjmZTFRWlULTB5g9iPD9ImuGreh0Qhf0os89cHG97zoNHYMewzdtbdW5tre2Iz+hi+A3eIZ5O6iLnm5sXa57+ByfmcG93S/CNnvQ5YEjwLrrTOQozqEau9jFAZKDwk2SJB4AB9nEwFLShkBj5IftgD2KZ4MxwgiFlx6dn5/30qeuQAimHNXP8zxmiXi+o9g7Ozs95JLfOSjqjJFl7Uvq6rqtx0VpLBaLGGQcHBxsyk3a1q+SlKbZBtVs0c0sm0RHiCwF82ag+HAmcWJYc3vfzpgPDTMG3ZUPQsX6pe68AQIE+ocThdLw+zviRWtwD3DcmHvg4soF9EVSLJMYOhaeLcMwogAkMnUnMYh15NbPh3igxDOghQc4XmbkCDTrgi8dHYP/cALIYrlTC02GBtRT+/yf9TtaTSDjjoU7vfCOO63wiu9v5/CV8SwDjrs7Luv1Or5oEYciSRJduHChF1ikadrrYISjO3RmWAc0YSDflO3gQDDPNE1jiQo8xfwwkugXygTRLx6gDTNAyJ0bGHSAl0Cyn+wZ5UeOHhPUOL97tmIyaVuNI3fMCb3E/dBhzAcj7kGn1NX3A/jgNADYJElbIokD4+CA7+dQd7gTijPrmTK+44BKkiT6si/7shhkOI0cNGjX0bYVb9c/NcexiDpyOm11HZmLsqw0mZDxb7RaUSUwlZSoKHIdHy8iL2VZ3tMRaZrG4JPmNp5JZs3wbIdSB4XAC4zX8R0xdOHk/lyf513FAT/t2rogzx3XWwUFAA7oMXQQ8u/Biwde7B3yTqYXR/jg4CCi3lXVni0kaEiSRMWkUGP6gf1GZhyMI7PF75SvcfYHvXr9+vWINFdVFfWX2ze3H/C86zVkG/rAWwAVALCu16GJBybIoutAQE3miIyzD+wRz0eOKbXFIff5wf88n7khSx5oksHhfVKsHTuP3+HyPqxeIKjqeD+LWUWe7620XTbRd+ho9LLbCniGjBzgycnJSXyOA9+UxGL7vOyRAIm5u5O+Xq/jMQcCR/aMDBY6Hl3q2fidnZ3YGCTPc6UmE1LbDe58tdLcmiV5WRky7B02HQRwoM6zv27btre3dXx8HP0laHq+6Rrpfk+apsqms6gXhnbabRF7CaDLPdDRnq1jPrz2huASucDPwV8gAHUA04NHfB1kAv51EIh1Pdlx1wdI7jy6kZUUWxZDOP6GYsWphiGcwBgKR/sc2UXpoChIa56cnEQhgZndsUHJ8QNDcC8CHBwTFJ6X8pAaZp3MlUDFkXNXLK0BLHpGoc0GzONauS/KBCVF+Ymk6DB49xynE4yMk4lCZI/cMeZ6lCmOjNQJCLQmK4PCgn4eAOEUI8jQAgHl/RxSl8VxhN0Fj/MpzN8PPsN3/l0MNzznqWSv7fVDngRHQ34KIURkyulEcOhGk2AW/kVhw3ceiCIflIOCzngg4QYcHkPxeXofejp640AChhjHz1FNvicpyiDG0vfLS2igi4MW8D/7gKPncszesF/MSep3YGMN0BMkmsHc3UFDzi5cuBB1gwc+gDW+Z8g1tGV/cXCgN/LHWkMIsfMdPA4vwSfuoKGnkiS5KUjzYErqWtIPHWacABwAD/Dhe3SZyyBnUxzQgG+gAcikzx9ZoEzKAyGG8xm0BR0m+MQpunjxYswU8c4cfxb0crQYB8j3yA/vb29vRxR5a2tLi8Viw1OVzs+7tt1S232NF2V7+153rgECPJvmZ+nW635jGhxEglHmfnp6GjuyFUUbIC+Xy2iLkB3KJpnP0dFRDxhhjsgt+s7PfFDeBg+QwcBB9qB0d3c36rbT01Plea6DgwNJXYbUgZZWZ3UNJDzL6Z332BMct9lsFs8a7+7uRqcNGWKfvQWyN1WC9jiH8J+35uYa7LbLtGcL3MfwPQWgpbzKy8rQK/AxmTf0Kc9xoMfPfiHr+ADoagcXWbPTGtsKv/F/ZHFvby/SgH3m2XQwhDeGHXAdDDk8POzZJ/iH67nPyclJbLoFLWkQIrXNa7DTnnH1/ztQ5GALgDYZlltluuB7ZBw9kGX9smFoOqwMATRgvyix5/OwoU1V9883DbM2LkPofw+yCQw6menO+rI2fCsvCeZ+AG/SprHEhs7Qz0sNPfhC72GX4LOi6M6bA2qjiz0L7foWW+4+ofuSyP1wT9k35NR52HnuduOuD5AQ/hBCrCsm9YvxcdQT4hZFEevJvSTs6tWrUdD9gLwzEo7yZNK+G4I+/wiGBwO+uZyRIlPlQQKK9ezsrLcmST2HzpEXmAvFglBBF2p3XUG4g4PQu4PvSEYIoZeZcCWNUnCl7sbAkb577rlHk8lER0dH0UBIXStmd/79rAhr5Rrm6N/luZ52l/rt1D3AdUc+TdP48j9Hbzyj6N+jrASkrK7rXhMAqUMOJfUUjJdT+ecYIlcO0MBR/Vuhj+ylNxBhXShED3yhG/vq6LKj3DieZApxjpEjOrl5mSMoJryJYuQeOCmLxaIHYlRVW96Ks8EZL+hOcE4bbG8aMES7nSehFYaV66ATjhUOCMYJefZW6ARzzBsdAj2bpul1JuMaz/R4yZDX9rus8AzQSXj49PT0Jv0C0o2O4m+egWF+jhh7VpB5OXrrSBw6iXmii1x+0AXoUcAcMlE4/pIindl79KZnz7gnfA//ehkyIIkHbZ4dYC2Uqfj5CacJzpTP3XUftEDG4RtkiIw9jn9VdQEt8nJ8fBz3TerOALjsuhOxWCxicwnmzcDeSF2HMGjPPiDXyAN6ihIhrsMh85IXgmEyUk3TxCwMQSF05VwiAZuXwMFTPI8KDmQGOwXf+nvX6rrWdDZVsvkegwxelmWxsdKtwDCCOfiTeaOH4Hv+ZTi/oms9ACRw9g5l8J6DU8wR3kF/ZVkWzysTXHEtgZADV+4oouvhPed3zoTB87xLCzvDd/y8nJ8BhHfgBfgXenB2lucTJKCvPOvlZZ7MsSzLmOUZ0oAfHOqmad+fdfHixZjFwndhrdAF8Ap/hdd+SF1WGqDSZcMzVlIH2MA38Dz2F3tBoA0IxZ7C5x4MeRY1yzLVG1mG7oDH6/W6fb9Q0+86SkDoGXpfKzZ66Gu43kE/UXKHPKBr3Q9kHZWVeCIfABJDmXHQ220Vv/M5NIXuyDw/nu3hjCu8Bi9xz2GZN7rTweLWzj75sOeuD5Am004gt7e3exsO0yyXy/h/WuzO5/PeoWN3IheLhU5OTqKjwWZIXYDE5vJ/hAzD4iitZyVwIEC8QNQw2l6TyRpc+cIwfAdmZG7OkDAfSLDUlSq44XXmhnHpsgVNSVXDtCgF70KEouZ5jk45ks6acEJwahguCFF4zYGEvjgnTmvuy3Nd4Ny5Zr0YZ9bA/aGXH2BlH6Ah+xBT502/yxG8wz7xfxQha8bQoxAJ6OApDJJnHFCkODXuILPnzNGRRYwZCpc1cAYGUIEyPfbAAyccdnckKcniTBBroNTAS5zc0WSvF4tFRClZQ9M00aDnea6rV6/qvvvu6xlVnu0KG+PjwYHvn5dvQDMP9ra2tqJzyruJPEhH7uFH6Iqzyr/eRQgd5GUeXhoHT0IXspfInweVHhhkWRbPHTqIAp96gAu/eUYLHnC0HCTcDS7fAXhyGUL+HIHGmWKOOCfwk6SYWWCODu54ADsMzjygc+DGgSNo6e3nuS8OIHLiJbLs3xBFdyTaQSH2rnXUOx5z5wG9A594iQvAFnRpmiYi9I74Ig/oA9ZH1tID4LIsI/otKfIydKqqqhe4+TkP5uLgBvvCuiTFw9YEeQAs6IGiKKKT53y5t7en09PT2GUuTdv3EpLVJzDOJ11bZJ6LDT44OOjZLL6HQ4YOYx993z2jhNNG5hbb5JlGdxI5G8ke+7u4XHYdJMSPcMcUm8VewNOSYukk8uZBCDyHjWSvWYs7/WRp0IHwH2sBpOR+lKgxt6IoYudQaAidJfVkRlJ8JQNr8TI4XsiMHRiuDfCAufPD9S6LnnWYz+dxr1wHEKQ4yOyAFmv3hkL4XayRYNiBRIA+ADPmtb+/H+WVYBc5Zw74MS5ffv/9/f0YyHrGHdkegnxeweLrQ1a4xgNA1zNOj7Ista5XKvK8F+DBB26z+A70wba6znP95nIE7f137uVzYa9Zq4OJ6BH+NtznEIJkfHm7cdcHSOW6jEaC4ARjAZNBTMojQDa8TS6Cj9MlSfv7+z0DDZPCQDiEoGnelhSBwciz4TAp6WNXZDhV1IkOy6B4D8wQpUYZS/2XhtKpxrNEjhwQALnw4+RwgJb54xjRScyDMe+a4rXwzI/7OA1wUqA1a0BouBbnH0Pkjg5/cwfMswlS/23TKCBHzRF+lIkbS/bHA0p4h3tjtB1hc3QHQ+GBriszggKMGkEyShyjh6FylB0l5MgfBh/auQLy4HVYQslz3cDzLD8bgWHgGVzjDv+NGzfinJ944gndd999krqzNl7Ox945OsXZPWhzfn4ez5XAxyCW8JnX5kudIfe1ez25OyegpQ56gPB6uZ6j014yCZqIYoe3yEbixPv64Nv5fB4bUjhNp9NpLMvwLJeXFjIvN2bsITTww9V+ngjH1mUJdJTgmH3HUQfZ5BkEia4DCIBZqxt6N3xe8uLgh5dOUAnggAjAg9PW+Qqa+MtNvXQQviA4w4DDn/wLTVyO0JmerXb5JJh1PnHQCWcQ/eGlLL6HknqdqeBF7NVyuYz3uueee2JTC+bBOkDsHUXH8YTPvPzKy8OYN3bPG9TAk+yD61cCTs9eoF9wtOnOCL/gpFZVFTNWXnbr+tUDVM56OmDowbvbdObhQAM85I023H9w0JP9cgB2b28vZjrcWUVu8jyP5yn4P+CoI+esjzmSjWafvCubZ8IAV6C9A0bsCS/DTpIkyjYyBS9TEeOgqQOfAGVN0+izn/1sLCfm2AA+wXOe8xxdv349Am7YNGyE85QDG64v+Yw5eYYTGUb2blXtgh7wTq/wC2tkPTwb3nLnnGcxX+iOvWB//VwxfOiZ8hi8pf2KHPQMNKBygvJPdBr87DwDKO8+G3Losu8ZUA/MPRiE3qt1qTTpvzbBgWeu45kA5l7+6f7AcM/wQ9EL0N15jmdBA+g/9G+HwRif8/NUxl0fINHlh01DKLIsi06+l9A1TRO7g2D4CVL4Ho5qmqZaLBYxVQkSBHLQPj/X7u5uVDowk0fcGEQCHkerYWyP7qlzBW1xB0JSr+THAxGYm8OFOEiOFHo61J1IdxI8++ClZJ6xkPpnPxyhPj8/j6WJGEbowDXUGpMlQNlgMFH83qUGwUA5IexD1J41u5PiQaAfRL8VGg0duPcww4SB5McdZowqAwPpZXsoUi9T4LPPhZy4s8E+eOp7qCyg2bDUjh8Uu2fc+N4wc8Da3QA4zaEXSOC9996rk5MTnZ+f69KlS/E8itPM0Smei1NOmak7F/CTZwTc4LJfngmQFMtoHVFzWiVJEjMwGNOqqnR0dBQDMgIglzlqtTmAjlMEv7gTArCBM4acYnQ9+4N8gpyy59DLARD22EEEnDmXAc6cuH6SFLPXzA1QxQNnHHUMLnzijjx6l+e74edeyJiDGOyxG1ecAZw36MDwYMPRUeRgiHoS4JCNQJ+ii+EZ6OJIupfroqORG5x5z5aFoCgf6AzWUNfd2UmnFaV7XIsDx5zhQS+7QjcfHR3dVFrTyWWXPUMWnL8ddWX93giF0hwvmaMSwAEr9BhoP7YHfUfQ7uh7CCE2F4A3AAXKstTW9rZ0ftajPY6l60EHe7gPIIgHDsgjZVdeEogNmc/nMSMEjd2Z5+9eKg1IwEumpS6zQqBINg0Z94ARfsSGYNsAm9gP7rm3txcDnmGWc3iGi/0lW9c0TWyYQrdCSt+ROYIywDIyInt7ez1bKynqia2trfg+taZpdHBwEB1c6OSgjZc380NDIexaWZZRX6GjWQ/rBURkb+Avt8PDAJff/dUs7Ct8SVCHbmB+7Du6A0DWQbFhk4zoc4agUHUNYzy4dbskde+ygndcN8F//l0H7LGD8Bf08yzkEEBmX+bzuZq6K3tH5l3W0WnYAnjNQTvuj6/gz2DOyI4HSPh07G2apj0/lP1zYJN7uL3PskwagA+fb9z1AVK2YVKyHChylCqGw9EYCExak0yGMxJIV5K0h1jplHN4eBgREoQBRM8DBhT3MOXrRsWNl9Q50cPaSg9kfC2ejcFJOjo66iFpIEduLDDifj7DgwQcSJQ8ZQJS/yVrRVHo+Pi4VysqqVcXTZel9Xoda4IdhfV1ozhQGMwZpelpWhdE1iSptz6pOwjugZXUfwcLSoi/Sepl8dgvD3yYqx+u9qwHmSYU0b333huRU55FdsTLL0AH4Q13CFCOOE5Sl4Vx5efGgefwOe+YkhQRetaPM++HPynHwHi5w86zWSPPBeEik+B75YBAWZY6Pj6O6/VyVZwKN0iLxSLyFwE/jiQ8xDOQZQ9A3cC7YwUfeDkRraFdGWNo2X+cOvjMMyA4uk5/6Oy8SAbY+R2U0vcenvTy3mEQDa/jfKOPHJTBCQdNdkPGvbzcE4cbvnPE3403ARuGfShfGH4Pur28lTmyZzjPHoxSNsYZAHS7I89Dh4O9QM94iRXBn6PG6BBk0VFsX6Mj4shAWfbfF9c66k2PXmQ70e8eQOEcIN/obWwM9sODBs8q8pzlchE/d/5PkraDHLLgAdBQv2ODGH6ovaVDqhA6R4jvOVDo/2dPnLboTHgGJ16ha4Tiuoj9Yl/n87kU+qVSgCtul13HpWkaAQsyH0nSlb3DR+54oWNYO9dSfUG2Qure++POG/ILf2JXnb88y3f9+vWY4aTxhYOlOMgEwGXZdous67pXGn90dKTZbKbd3V2VZRk799HhzwETr1hwsJDnwrc8H/ABfoT+yJbbY/wyaILsoHM9E+a21jNLQ/txK33K766jkH+/n5/VdcDSAWFkZJiFYT51XUegHTvvVQzQJk3TWPKFTYy6umlUWGbK/UMHDeALB8WQTS9ZdLAU4Ac6Y29CCDHryjVlWWqSd/s/DELcDwE4Qg6kzi/FhrDH0M4z+9BxyD8O0HIdAarrDvaadUJX7tvyyhggxVHXtdJpGhUeSt+zEWQiUIAoI0e2uJ5sEptF6QJOOcYDZpO6EhiUAkrHmdIFm45Rbri4NwYBg0m9uZfKEFyQ6UL4UWgY3rOzs9gC3JEY7lFVVXxPCIjzzs5OVEgYBkk94eWQ+XK5jEYc2iFYXpayv7/fQyJRLFzDPR0ddrog1KA0zAfBQll6ds+DGfYChYwzC3LEZyh6dwRBnBzp5Zk4Jh7ssc90kyKgBZVBAXMtaNWwbAcnYtgFLc+7tvWOQEmdc+OIvJckcX9vG816Qrh1BzQPKLkXdGCvHbF35yLPcz3++OPa3d2NBpj9hAdpYU/whiGG7+k4BK9Jiug2tHbH3gOeEEJ0huB3DxIwiJ7Sh8az2UzXr1+P9Kyqqtd5D+fOA2w3/u6wksHBCRxe50gausUbPLA+HCUQTXQehoRMEHoH+eDFmOgH/o5eQV5x3JFTz7zwfAcR4BE3Vt6e2LMlyBa6A/mDj+AlB0k4i8G9MYwOaLnT6DrZnWYCGJwv+MOBIfYCZxr6OmAEr7H/brBBrquq7SDXOkGZpFRSkNRv0w5tKKF2niS7hb4DVOFZyIAHqKy93f9CITTa3t7Z6JW2/Xhd+/v/grKsVtMEVVV33qiuG5Vl53xmWfuOlPl8S21L9KAsy3sOELrdy5dxTF1Puv1EHzroh7yzP+6gk0lZna9Ul6WyJJHqJmZDrp89IaWJckPYvcScfec8FqVl3gAHHcm8oWld1/HdNg4U0EYZPirLUjs7O5Ev1+t1zK64fyFJn/nMZ2KQjh3g/mQaOdtCYA9ogP0h+zqZTPSZz3xGW1tbMVuPbmM/dnd3dfny5Zghga+rqnuxrx878GzHdDqNL6klCOUa503mhR7yoIfh4B+6Fv7wYN5tm4PFnk0GaHUb4OXv8Kb7PnmeazqZqqpq1VWjNM2UqH2Zc5qkSpJUWZ6qboLqJigvJqrrSkGJymrzjse6UVCiNM3UBGldVirUdVRel6WSTWAE/eEvB66TtOsAhy5Ed2MPpA648qwOgDhjOp32XiTuwA/PC3WjarVWpo1+yzcBcd1oXXdVEh54+kuw0eW3KinHX2It2AsPMN3Pxdbxd/YTEJjhgDi8jr8Onzjw4Lb0yYy7PkAq8iJmJjD2UufkeRDEpvP+CDYG40S5CE4sCpZrCYIcseeZWdbVezua4sg1TiCK0j9z5AkG8PKSzrA1Oj4+jkbAA0KYGcVHVi1J2rQ6z82yLJ55wPDAtJJuympwf0c63XFEQFgTShJmBXU4OjpS0zSxxeswC+b7JnXnR1iz1AWf7hA5WpUkScx4uVH2tC5zR3l4Ng8lTyaF/fGzQkVRxBdektXAWLhj6KlqHE+65nk7Yl83SoSsCPSWFJUifIKC9IyLO+DOCwzvkIUB8owOytidwahgQ1fnzf+HDSWQNb4L4CApOhnwKV3AQNWSJIn0xDEnK4ohd4Pih9/ZUw+4kVmMi5d/uZ4gcMFYIysENtCYFzJnWfvyXPQJa8a5KYru/UeU7aBfqM0HHfaSOy8v8KyGo7roARBknr27uxudPuSD/XWDBq8iw/v7+7E9NPeCltC5zUosY1mOI4HoPeYH8OHZAujkWVdHTaEN8sUes588h/1zMMN1sgdmQ1TadRl2wevnoT26ivt44OuOFp+5bN0cTLXvUmpt03mvisGz5Ogf5NxBBK824CwN+pjvp2m/q5fvMbw0m81jYBBClxkeItfIu4Mk0+ksPtNReQfjnGehRZqmN5Uhotu8xMwDJubdlOt4f/R+u/ZM042MLlfLXqYtLwplRecQA0ogW8wB++fVBX4uDH5AR+MXuJ11PwFdwXzJXCVJW3ECWJnnuZ73vOdF2eNf3lNYlqUWi0VsUQ4Q4O9Sc1SdMrzJZBLtOXwKOAT/ohc8s4Ae5r09ru+gk6Re0wvXCx7s++foAug+BITYS2wIsozulNQDUuAp9sazQtgr9w0cCL7Vv3XVAgMO4NRVrWQTjOVWItrSoF+2zfwJglt9UcfAkf1h8Fxki/uuLYPrPiXPQt5cvzho43pQUtT/8K0HLlVVqdkEu1xDWeF0E3QAkBGksXeswWngsoOsIV9eSopecUDbZdF1zVDfY1v5zIN6B8D5DvzkOvl2464PkGAkFD5RK5E07RWpO4VBQgi9lqkEER4ceKkICvP09DQKtUe7ZK/oxoPxRvHeuHGjl+J1h9SVhqPHGBMQA0d8cKBhQHfembsfunXEB8SY79yqNMcNrKfHuQ805N7e3ELqMil+lsMdXE9De9bDa6mhO/dDyHhOZ/C7Q9reoIDv5Hl3WJ2yExxIOq5RwoMCaJomInCOTnlJxLA0whFVRwtRRH7uAefMETuCPhBElBaHtB0R805rjpoxJ5xUBvvnZacePGF8oc0QiWEuGEAvK3BFCQ/xPIJh0FSUMMgk9ON6DCBZKtYLr+LAMheMN+tnTWQacBKgJ/dh/ZQbeqCDLON4QW8yfU47L0Vype2BjmdtPBMxRN0JsDCaGCmnEV0V2QP0DY6mB8nMd+iIM086EXLm0UsZnEeQL9BwnBcPTn1PcOwcmHA9gUwzD9Bz75roOsL3DjDFASt38nkWtMPxQob5cT7g/sg9a0BW0NmeiWffcD64n2eufI7Mk7lxb2SeMzDYBG9N7edH2WvaIoPgc++maWJGgN95FnrOZZn9hV8Ag7wygSAYenqQ3jYY6Zwj+G+9XsczpshWURTxRa4MOnQyH/Zd6hxLsmjI2TTvgl/2p6VxpiaE2LzBbR0OPfPm3vfcc4+SJImt/eHrz372sz07wZ5Pp9N4Dmsyad9r9MQTT/QyFAQ1165d03Q61f7+vra3t2NbdIASP1fGHpHxZo4ER/ASQQ00JbBKkiSCJNgV+MZlDn+FeXrTEGSY6zzIIlPn84bX+V4IofeeSQeX2UfkAp3L/fHFmD9rJKPowTl7yD3gY37nX/gXHwqdE5rQZo6SpKdjfJ+5n/srng3CjnX+StLTZ9iHIVjp4GHY3Be7gO/nskRQ6BUa8LLLL7YIQAX+8IC+KkslofMTHBRm3e5Doj+84QV+hftAng30wMeBVfwCp6HbS/S+y6br/i5YVdSf3APdh250v+V2464PkFbrfhcaFzB3ZrzDy3K5jKU7KCg6EGH0PV2Ms4Nji+H3w7SUBXGdp+c9m0KQxjkdsjKk6ynNwmiyLqmPbsGMoAG8rJDPPcDzbAABZF13hw9dIRNAMAcUDPRzx84RYJwFqUMXpC7T4/MG2XA0CIfPjZLU79SFQ06JFc+q67r3AkEPKthjnH5Kd1BEnOk4PT2N12KMWCOoNzT14NPPNPgbtVkDDos7SOwTvERpw8WLFyNft8htP0jAyXGFSIDkNdc4IPAo3xk6FO48ucPEc3y4guN35AynyIMk3zfkh+ukfjDHD3vn++9zg//hLdaCEXNUq2na8wzsEfSDN7zk1t/rFEJ7gHx/f19SFxjCmwT7rIkzD8gQBp19wHmg1a3zdNN0HZEI5pz/2TMP2nkmugy94FmSodPgIIPzK7rSeQcd5/rKMyXoAAeHyC67DsG58qwP8uPGzlFC5sp9bmVs4QsAMJBDN57cj/W6Y8WaXa48KwtPeTDswIuXgTAXL+1w20MGf4iKOljkehP+9uyNI7Z13VY10IiGTm/ulLJH0NUDR7ItrNOdXGiD/nIdgRygf/kudnMyKaJ+cLlFtzjoR+ACzRaLRS/zQJCC7pIU11qWpbbmc4XJtGfXmGtRFGqkCMq4E8ca07R9hQV6CR2LfYOOdV3r8PAwVhJwH0DUCxcuSGrtG0EWDj36+Cu+4ivicwnsAT6Yi+svnE9vAMDee6DPnmBXkWHm70ECtgD5cHR/2Doaveayh/xwxolsGGewnb5DoIogHXlgf9FVZKD8es9iuq/lABa+AuCT77U7x26zenrBKk68bHy9XiskXdMS1zXYjxjchK7xTKsPckkh+hd0pfOggQoKRp7nagwwQ095hpl9xKZ52Rq6BN0Arzrv4EOen58rS/rNK7i3+yEkGeAj1yFDkJE1OB9iJ92XYP3Q0vfU+dkDHff5COC5JyXZ7rt6ltoBmNuNuz5AKtdlL8qFcRAWFDuEZgO9pARFQmpbUk/ZgOghcNwHFI+DlF7ecH5+HlEcSZHpUQ7Xrl3rIZGguARKOO2OxqMMWBMH7mFiBAUEPaaP6+6APYwMsoSQIzA4xjAZAsPapO5Qngcd3MezTTwLIcFJdBTBgyVeKOcoCwLu7YXZXy834PmOsEFHrkORk2Fk1HUdz8J4TTrZAYJmHCf2ADRfUnxnBPs5RE7YH3+/FnRmP2mly1kXzpi5UxZCiE4re0SQjvODLHgJBAoWI8W6PTMJbeEzjBDBNOseInnwNYrbU+aOVLpjhnOHjDJc2VVVpfvuu0+LxaIXHCVJEoMpP0SPIwuvuCNM+cPJyUl8LQBoLXwrdecJm6aJTh2yj8PrGR5X8tAPPkd/EDSxB9AGxNUBFAyeZx08owNCxrOZJ+gfiLOX2uEQQQv4wIEXAkT2DEPGZzgw8CK6wuWd+Xg2BP5ABzv66WcbhnN1/nY0GJ5B/w3r1aGvG2IvhXIEG53gThY6C/r52j1YoFubI7tlWcazc5Rquhx4WSH87c4eoIg3HEGnoG8cnILf0RHsDY4vvOfZLbLa7qxCU2wbetdBGe4BqNQPstbKsrQHUk2nU128eDFmW3iOdHPgBz8SkOd5riwE5UUef+ccZ5qkmm8yI/5d5luZrKC3vUwWfQlPkdEiWM3zXMvlUpPJ5CbAYm9vL+6lpFhyy/o8CEdP4MShI7g3NtA7GDKHvb29CAI2TRP3yUtCHZBAtrEx2FjAPK6FBg7+esYZvYIcedbGz82RmfBqE/gQHUagy/DXFjgIh3x6MA6fAVJCXw942SsHX9BvXirMWlgHMt7UXVMbt9NVXasJHVAOv3IvZMx9ylae+xko/AbPXPk5aoKjyaZJCXLigDrD5wEg5zbbAznXs8hMtK9J975K9g89hI8ACAA/sSbsH/vkQaTTcBhcu5+DXwQ9eAaDvfY1IcueNWT/HRzx7Lrz3e3GXR8gsWGOnOPsgKp44OLOmH/HDxtCYGrGqTOVuq42GNwsy2IWB4XEc7z1KalmlJujWk888US8J0gA83Lkkuc7gyKIrtSGaW8/2MbA+JK94DqpCw5xevkd5eClGD4vRwwdAXADicOE8cUw0mmHEkgCzCFiKXXGG+Sc80l7e3vx3syR/1+/fj0KE8YHZwFh9lKWYRMAlI2jq+wxCO4TTzwRz7fBJ5SrUOPNuRMUEfyIo0ygDg+6w4OCd2UGHxFcwccoZwwwgSHOFs9HuaDM4CEv4STbCtqNkfQMA6CBZz8cSYI/3Nlnb3H6oTVBJKWxfm4LnoKuvtcgrDgSlNWiYLe2tiLP+kFWHBpkwY0I66A8Brpyf3gS2XZQAMeT+8NrHoSy/8gVa3O6eDYSh8nlx+nnPOLGijn5XJEVR7f5HOfbjRpzqOu2JIYgAb5gzQBGPIf5sV4PzKLD0vTL5HDiCDShIXqHe3hg5lkcPuOZ7mR4IOSGFR2ATJBFIHOIk8AzTk5OYokYawHU8kColZe65+TCj8gRepuACf1WVVXvReYAFR5sUMo2DC5DCPGsJHRfLBYRGCOQwQ4wB2yJB1rQiIwPTnvLp5XqurMbzMvnubW1FfU/mSjAxbIse6BGkiSaTLuXm0sdcKG0e80FAeV63Xa4vH7jhrIivylznCRJbGbiLycGhLxw4ULP9lEJsre3F0vvcDzhfYJS+Bwa7+zsRN2GzvemCJ4BybIs3t9LpqA3Ohvb4w1n4GHnY0AHwEZ4C5vjCD187uWn7uN4AIN8ksnyDFg/SOi/I9Kzow5Ye9bAwTt38Fk//I5OAux0ORwCRvCY8yPfb+W0Ul11gQr2jDVVdXesgX1xGeJ58LeDY/AWVUJ5nsfyVPcdNpPqBbjoIEqf8VudNp75gUbcG9n3kl/m44GJBz2eefEsHd/1a1z/O1DN3J3uDtJ7MOR6G7vAPsJrDo4BuLFHzmMOXEOTIeB6u5GEp3L1H6NxdHSkg4MDve/nfj4a8vnWXHW1SdfOOsRvvereoZCmqfKiezFrud6k79LOwamrOjqsaZrqfHWu9WqtYlLEDayrjaOabRR6MVFVV1qdr5TlbS/21QqUpe1YkqapsrRDz9blWk1da73Jgs1mU9V1o+XJUtNJ1yLZkfokkRIYqerKUTxT4M6ZM1/MEEy6oKOpuzIfZ74sb/89WZ7EQDMvWtSjNfat0ccQebtLz6RE5DFNpBAUgnqofFmulReFtuZtsJKmqZI0UWi8rEZar0tNpt1b1derrotblqVxTut1uSn5CErTROt1qdl8FoXm7PQsGurpbKqqbGvC1+Va21vb8RlVWUUEdntnW3VVR8MGGhQV7OZdXOdn591ByflMiZKI7pdVqaos1TQtMlquS+VFrtm0RTdn85mKvFATGuVZ+96flt7dObR4fmrDh03doS/FpIi8XFWVikmhYtO6k3viECRpq1CWi2U8BxTLfaYT5Vmusiq1Xq11etY2Gdjf249ZIJR63WzOOKzW8W+t4so1m7Vo4fn5mdIsi/Ixm850eHgY9y3NMmVppqqu4t5++lOf1mq9UpEXWq1Xuvfee1WVlaazqdIk1fb2lrRZP7y6Ol+1fF1tunoVG35OM9VNrfOzrhUvKB8Bmiv1sixVN7WKvLiJf0MTlOXdfNvnt7zpJQroCBR2Memc2aZpVK5LTWdTrVdr5UWu9Wqt89W55puD9Bgiz45keaaT5Ulb2jLpZLsqq1huGTNPG/0WmqA0S+N+KmzeMh5ClI+imKgJXXCSJl0nzNZJWsU98sxGCEHnq3NNiskGKGh1FwFD3dTtezWSLnsSjWlVqSxbHj07PYs8PSk4bNw+M4SgSTFR3dRKlPT0mw+yK94pED3P5+5YeACZpRuUOfQDtEkx0dnZ6SY7kkVZZC8kRXnDmcE4102t+Wx+UyMUjH5V1SomhULTqK6bGCBFNFYbRDsvdH5+pvPzVQxmi6JoMyvFRPOtuU5PTjcBVBL3VEmi0DRtR7e8A8+SJFFZdeXPRkBtBKPlnyzXar3S7k5XVpUkSaRRCEFF3p3NaZqWnuuyvW5vd1fT6SwGbjhs86155Nm8yHV22jU48nLHJE1VN7Wmm/38nd/5nfjepK2tLV28cI8kxWCOTFBQUB2CptOJ9vb2I0DSAj6l1uv2XGjd1O0aNzwDaOayK3n5kDbAS9Vz4txRxtY4wEommTl6yWbrmKdxb5lLlnUIellWKopcVVUryzY+w7orN5pOaQZ18/tn8iLX6nyls/OzKNOAC2W5jnybZXkMWFuaFqrNrhA4t90Zu+DIgx1kCj7L81xn52eaz+YxqHJZdfAVnoYn4QUc39PTE6VpF2i5XnWwxfdF6prUYDu5rg1S0mg7uAYbWTe1zjdlp9AZmazKtoFDlnbnjrGdq9WZsixvebCiY+0srpvAjExTBMbyVjdnaaaqKjf0mESwxO0tABpZYebA3sOzyJSXLqdp2nbfazp/QpLqpo66RFLbrGLjH+CDsW9+xKMFXyeq665MEUArzdL2PkbztrNniLqzvX+jpunWF0JQMSlioKYQVNdN97eyjC3Tm83fQwjKs1zr9SqWTi4WC33rt71Gh4eHsVT+c427NoN07do1SdKrv/Wbn+WZjGMc4xjHOMYxjnGMYxzj+GIYi8XiSzdAuueeFkX69Kc/fVsijOOpjePjY33FV3yFfu/3fk97e3vP9nTumjHS9c6Mka53Zox0vTNjpOudGSNd78wY6XpnxkjXOzPIKF+5cuW21961ARIpwv39/ZG57tDY29sbaXsHxkjXOzNGut6ZMdL1zoyRrndmjHS9M2Ok650ZI12f+fFkkybp7S8ZxzjGMY5xjGMc4xjHOMYxji+NMQZI4xjHOMYxjnGMYxzjGMc4xrEZd22ANJ1O9UM/9EOxfe44nrkx0vbOjJGud2aMdL0zY6TrnRkjXe/MGOl6Z8ZI1zszRro+++OubfM9jnGMYxzjGMc4xjGOcYxjHE913LUZpHGMYxzjGMc4xjGOcYxjHON4qmMMkMYxjnGMYxzjGMc4xjGOcYxjM8YAaRzjGMc4xjGOcYxjHOMYxzg2YwyQxjGOcYxjHOMYxzjGMY5xjGMzxgBpHOMYxzjGMY5xjGMc4xjHODbjrg2QfvzHf1zPf/7zNZvN9LKXvUwf+MAHnu0pfdGOt7/97fr6r/967e7u6tKlS/pbf+tv6X//7//duyaEoH/6T/+prly5ovl8rr/0l/6Sfuu3fqt3zWq10vd+7/fq4sWL2t7e1mtf+1r9/u///hdyKV/U4+1vf7uSJNEDDzwQ/zbS9emNP/iDP9B3fdd36d5779XW1pa+7uu+To888kj8fKTr0xtVVemf/JN/ouc///maz+d6wQteoH/2z/6ZmqaJ14y0vf34X//rf+lbv/VbdeXKFSVJove+9729z58pGt64cUP333+/9vf3tb+/r/vvv1+Hh4d3eHXP3vh8dC3LUm9961v14he/WNvb27py5Yq++7u/W//v//2/3j1Gut48bsevPv7+3//7SpJE/+bf/Jve30e63jyeDF1/+7d/W6997Wu1v7+v3d1dfeM3fqM+/elPx89Huj57464MkH76p39aDzzwgH7gB35AH/nIR/QX/sJf0F//63+9x3Tj6MbDDz+s7/me79Gv/Mqv6KGHHlJVVXrVq16lk5OTeM2P/MiP6Ed/9Ef1zne+U7/2a7+my5cv66/9tb+mxWIRr3nggQf0Mz/zM3rPe96jD37wg1oul3rNa16juq6fjWV9UY1f+7Vf07vf/W597dd+be/vI12f+rhx44a+6Zu+SUVR6L//9/+uj33sY/pX/+pf6eDgIF4z0vXpjR/+4R/Wu971Lr3zne/Ub//2b+tHfuRH9C//5b/Uj/3Yj8VrRtrefpycnOglL3mJ3vnOd97y82eKht/5nd+pxx57TO973/v0vve9T4899pjuv//+O76+Z2t8Prqenp7q0Ucf1Q/+4A/q0Ucf1YMPPqiPf/zjeu1rX9u7bqTrzeN2/Mp473vfq1/91V/VlStXbvpspOvN43Z0/T//5//oFa94hV74whfql37pl/Trv/7r+sEf/EHNZrN4zUjXZ3GEu3D82T/7Z8Mb3/jG3t9e+MIXhre97W3P0oz+eI2rV68GSeHhhx8OIYTQNE24fPlyeMc73hGvOT8/D/v7++Fd73pXCCGEw8PDUBRFeM973hOv+YM/+IOQpml43/ve94VdwBfZWCwW4au/+qvDQw89FF75yleGN7/5zSGEka5Pd7z1rW8Nr3jFKz7n5yNdn/74lm/5lvD3/t7f6/3t27/928N3fdd3hRBG2j6dISn8zM/8TPz9maLhxz72sSAp/Mqv/Eq85kMf+lCQFH7nd37nDq/q2R9Dut5qfPjDHw6Swqc+9akQwkjXJzM+F11///d/P3z5l395+M3f/M3wvOc9L/zrf/2v42cjXW8/bkXXv/t3/27UrbcaI12f3XHXZZDW67UeeeQRvepVr+r9/VWvepV++Zd/+Vma1R+vcXR0JEm65557JEmf/OQn9fjjj/doOp1O9cpXvjLS9JFHHlFZlr1rrly5ohe96EVf8nT/nu/5Hn3Lt3yL/upf/au9v490fXrjZ3/2Z/Xyl79cf/tv/21dunRJL33pS/Uf/sN/iJ+PdH364xWveIX+x//4H/r4xz8uSfr1X/91ffCDH9Tf+Bt/Q9JI22diPFM0/NCHPqT9/X19wzd8Q7zmG7/xG7W/vz/SeTOOjo6UJEnMLo90fXqjaRrdf//9estb3qKv+Zqvuenzka5PfTRNo//23/6b/uSf/JP65m/+Zl26dEnf8A3f0CvDG+n67I67LkB64oknVNe17rvvvt7f77vvPj3++OPP0qz++IwQgv7hP/yHesUrXqEXvehFkhTp9vlo+vjjj2symejChQuf85ovxfGe97xHjz76qN7+9rff9NlI16c3/u///b/6iZ/4CX31V3+1fv7nf15vfOMb9X3f9336T//pP0ka6fpHGW9961v1ute9Ti984QtVFIVe+tKX6oEHHtDrXvc6SSNtn4nxTNHw8ccf16VLl266/6VLl0Y6Szo/P9fb3vY2fed3fqf29vYkjXR9uuOHf/iHlee5vu/7vu+Wn490ferj6tWrWi6Xesc73qFXv/rV+oVf+AV927d9m779279dDz/8sKSRrs/2yJ/tCdypkSRJ7/cQwk1/G8fN401vepN+4zd+Qx/84Adv+uzp0PRLme6/93u/pze/+c36hV/4hV5N8XCMdH1qo2kavfzlL9e/+Bf/QpL00pe+VL/1W7+ln/iJn9B3f/d3x+tGuj718dM//dP6qZ/6Kf2X//Jf9DVf8zV67LHH9MADD+jKlSt6wxveEK8baftHH88EDW91/UjntmHDd3zHd6hpGv34j//4ba8f6fq5xyOPPKJ/+2//rR599NGnvP6Rrp970Pjmb/7Nv6nv//7vlyR93dd9nX75l39Z73rXu/TKV77yc353pOsXZtx1GaSLFy8qy7KbIuerV6/ehNiNoz++93u/Vz/7sz+r97///Xruc58b/3758mVJ+rw0vXz5stbrtW7cuPE5r/lSG4888oiuXr2ql73sZcrzXHme6+GHH9a/+3f/TnmeR7qMdH1q4znPeY7+9J/+072//ak/9adiE5aRX5/+eMtb3qK3ve1t+o7v+A69+MUv1v3336/v//7vjxnQkbZ/9PFM0fDy5cv6zGc+c9P9P/vZz35J07ksS/2dv/N39MlPflIPPfRQzB5JI12fzvjABz6gq1ev6iu/8iujHfvUpz6lf/SP/pG+6qu+StJI16czLl68qDzPb2vLRro+e+OuC5Amk4le9rKX6aGHHur9/aGHHtKf//N//lma1Rf3CCHoTW96kx588EH9z//5P/X85z+/9/nzn/98Xb58uUfT9Xqthx9+ONL0ZS97mYqi6F3zh3/4h/rN3/zNL1m6/5W/8lf00Y9+VI899lj8efnLX67Xv/71euyxx/SCF7xgpOvTGN/0Td90Uxv6j3/843re854naeTXP8o4PT1VmvbNQpZlEe0caftHH88UDf/cn/tzOjo60oc//OF4za/+6q/q6OjoS5bOBEef+MQn9Iu/+Iu69957e5+PdH3q4/7779dv/MZv9OzYlStX9Ja3vEU///M/L2mk69MZk8lEX//1X/95bdlI12d5fGF7Qnxhxnve855QFEX4yZ/8yfCxj30sPPDAA2F7ezv87u/+7rM9tS/K8Q/+wT8I+/v74Zd+6ZfCH/7hH8af09PTeM073vGOsL+/Hx588MHw0Y9+NLzuda8Lz3nOc8Lx8XG85o1vfGN47nOfG37xF38xPProo+Ev/+W/HF7ykpeEqqqejWV9UQ7vYhfCSNenMz784Q+HPM/DP//n/zx84hOfCP/5P//nsLW1FX7qp34qXjPS9emNN7zhDeHLv/zLw3/9r/81fPKTnwwPPvhguHjxYvjH//gfx2tG2t5+LBaL8JGPfCR85CMfCZLCj/7oj4aPfOQjsZvaM0XDV7/61eFrv/Zrw4c+9KHwoQ99KLz4xS8Or3nNa77g6/1Cjc9H17Isw2tf+9rw3Oc+Nzz22GM9W7ZareI9RrrePG7Hr8Mx7GIXwkjXW43b0fXBBx8MRVGEd7/73eETn/hE+LEf+7GQZVn4wAc+EO8x0vXZG3dlgBRCCP/+3//78LznPS9MJpPwZ/7Mn4ktq8dx85B0y5//+B//Y7ymaZrwQz/0Q+Hy5cthOp2Gv/gX/2L46Ec/2rvP2dlZeNOb3hTuueeeMJ/Pw2te85rw6U9/+gu8mi/uMQyQRro+vfFzP/dz4UUvelGYTqfhhS98YXj3u9/d+3yk69Mbx8fH4c1vfnP4yq/8yjCbzcILXvCC8AM/8AM9B3Ok7e3H+9///lvq1De84Q0hhGeOhteuXQuvf/3rw+7ubtjd3Q2vf/3rw40bN75Aq/zCj89H109+8pOf05a9//3vj/cY6XrzuB2/DsetAqSRrjePJ0PXn/zJnwx/4k/8iTCbzcJLXvKS8N73vrd3j5Guz95IQgjhzuaoxjGOcYxjHOMYxzjGMY5xjOOPx7jrziCNYxzjGMc4xjGOcYxjHOMYx9MdY4A0jnGMYxzjGMc4xjGOcYxjHJsxBkjjGMc4xjGOcYxjHOMYxzjGsRljgDSOcYxjHOMYxzjGMY5xjGMcmzEGSOMYxzjGMY5xjGMc4xjHOMaxGWOANI5xjGMc4xjHOMYxjnGMYxybMQZI4xjHOMYxjnGMYxzjGMc4xrEZY4A0jnGMYxzjGMc4xjGOcYxjHJsxBkjjGMc4xjGOcYxjHOMYxzjGsRljgDSOcYxjHOMYxzjGMY5xjGMcmzEGSOMYxzjGMY5xjGMc4xjHOMaxGf8fvAt79JbPX/MAAAAASUVORK5CYII=\n",
+ "text/plain": [
+ ""
+ ]
+ },
+ "metadata": {},
+ "output_type": "display_data"
+ }
+ ],
+ "source": [
+ "plt.figure(figsize=(10,10))\n",
+ "plt.imshow(image)\n",
+ "show_points(input_point, input_label, plt.gca())\n",
+ "plt.axis('on')\n",
+ "plt.show() "
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "c765e952",
+ "metadata": {},
+ "source": [
+ "Predict with `SamPredictor.predict`. The model returns masks, quality predictions for those masks, and low resolution mask logits that can be passed to the next iteration of prediction."
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 15,
+ "id": "5373fd68",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "masks, scores, logits = predictor.predict(\n",
+ " point_coords=input_point,\n",
+ " point_labels=input_label,\n",
+ " multimask_output=True,\n",
+ ")"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "c7f0e938",
+ "metadata": {},
+ "source": [
+ "With `multimask_output=True` (the default setting), SAM outputs 3 masks, where `scores` gives the model's own estimation of the quality of these masks. This setting is intended for ambiguous input prompts, and helps the model disambiguate different objects consistent with the prompt. When `False`, it will return a single mask. For ambiguous prompts such as a single point, it is recommended to use `multimask_output=True` even if only a single mask is desired; the best single mask can be chosen by picking the one with the highest score returned in `scores`. This will often result in a better mask."
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 11,
+ "id": "47821187",
+ "metadata": {},
+ "outputs": [
+ {
+ "data": {
+ "text/plain": [
+ "(3, 1200, 1800)"
+ ]
+ },
+ "execution_count": 11,
+ "metadata": {},
+ "output_type": "execute_result"
+ }
+ ],
+ "source": [
+ "masks.shape # (number_of_masks) x H x W"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 12,
+ "id": "e9c227a6",
+ "metadata": {
+ "scrolled": false
+ },
+ "outputs": [
+ {
+ "data": {
+ "image/png": "iVBORw0KGgoAAAANSUhEUgAAAxoAAAIzCAYAAACHlG8YAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjcuMSwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/bCgiHAAAACXBIWXMAAA9hAAAPYQGoP6dpAAEAAElEQVR4nOz9ebhtR1ngj3+qaq29z3Sn3Js5IWFImIIYCBBASQgQGbSVRxRFWtqRp6UfxYlWm6+iNLRoMzzi0+2AOLTMirat/hAixAmZIYQEEgIJmW+SO55hD2tVvb8/ali11l773HNDxGm/eU7uOXvXqlX1VtU7v28pEREWsIAFLGABC1jAAhawgAUs4AEE/c89gAUsYAELWMACFrCABSxgAf/2YKFoLGABC1jAAhawgAUsYAELeMBhoWgsYAELWMACFrCABSxgAQt4wGGhaCxgAQtYwAIWsIAFLGABC3jAYaFoLGABC1jAAhawgAUsYAELeMBhoWgsYAELWMACFrCABSxgAQt4wGGhaCxgAQtYwAIWsIAFLGABC3jAYaFoLGABC1jAAhawgAUsYAELeMBhoWgsYAELWMACFrCABSxgAQt4wGGhaCxgAQv4dweXX345Sile9apX/XMPZQELWMACFrCAf7OwUDQWsIAF7Bhe9apXoZRKP+985ztP+Mzznve81jO33HLLP/1A/xnhC1/4Am9961t52ctexpOf/GRWVlbS3L9WcP311/OjP/qjPPaxj2XPnj0MBgPOOussLr74Yr7ne76H3/iN3+DGG2/8mo3n3xKsr6/zqle9isc85jGsra2xZ88envCEJ/D617+e6XT6Vff/F3/xF3zrt34rZ5xxBoPBgDPOOIPnPe95/N//+39P+Kxzjre97W1ceeWVnHrqqQyHQ84++2y+8zu/k7/927896bFUVcXXfd3Xpf37n/7Tf7ofM1rAAhbw7xpkAQtYwAJ2CL/wC78gQPq58sort21/xx13iDGm9czNN9/8tRnsNnDZZZcJIL/wC7/wT9Z338/XAn7lV35FiqJovXfv3r2yvLzc+uyyyy77mozn3xLccsstcv755yccrqysyHA4TH9ffPHFcvjw4fvVd13X8pKXvCT1pZSSffv2tdby+7//+8U51/v8xsaGXHnllamtMUb27dsnWuvU38nu9+55f8lLXnK/5raABSzg3y8sPBoLWMACThoOHDjA6uoqV111Fbfddtvcdn/wB3+AtZbzzz//aze4f2YoioJHPvKRvPjFL+YNb3gDP/ETP/E1e/d73/teXvGKV1DXNU972tN4//vfz2g04siRI2xtbXH77bfzjne8gxe84AUMBoOv2bj+LYC1lm/5lm/hlltu4cwzz+QDH/gAm5ubbG1t8c53vpNdu3bx6U9/mu/5nu+5X/3/wi/8Ar//+78PwI/92I9xzz33cPjwYY4ePcqb3vQmyrLkrW99K//jf/yP3udf+tKX8v73vx+tNa997Ws5cuQIhw8f5tChQ/y3//bfEBF+8Rd/kbe//e07Gs/nPvc5Xvva1/KQhzyE008//X7NaQELWMACFh6NBSxgATuGaOE877zzkvX11a9+9dz2F154oQDyqle96t+NR6Ou69bfv/u7v/s182g85SlPEUAuuugiqapq27ZbW1v/5OP5twRvectb0jp++MMfnvn+7W9/e/r+qquuOqm+77vvPllaWhJAvu3bvq23TTx7KysrcvDgwdZ31157bXr3y1/+8t7n43k966yzZDKZbDueuq7lkksuEUDe//73y3nnnbfwaCxgAQu4X7DwaCxgAQu4X/B93/d9APze7/0eIjLz/d///d9z44038pCHPISnPe1p2/Z1ww038Ku/+qs885nP5KEPfSjLy8vs3r2biy++mFe+8pXcd999c5+t65rf+q3f4vLLL+fAgQOUZcn+/ft5+MMfzgtf+ELe+ta3nvTcfv/3f5+yLFFK8XM/93Mn9awx5qTf90DBZz7zGQCe+9znUhTFtm2Xl5fnfre5uckb3vAGLrvsMg4cOMBwOOScc87hsssu4/Wvfz0HDx7sfe7qq6/mO77jOzj77LMZDoccOHCAZzzjGfzu7/4u1treZ2Lez+WXXw7AH//xH3PllVdy2mmnobWeSdg/duwYr3nNa3jSk57Evn37GA6HnHvuuXz3d383H/nIR7ad81cD0dvw9Kc/nSc/+ckz33/Xd30XD37wgwHvyTsZuOqqqxiPxwD89E//dG+bn/qpn0JrzdbWFu9+97tb3/3FX/xF+n3e8694xSsAuPPOO3n/+9+/7Xhe//rX84lPfILv/d7v5VnPetaO57GABSxgATPwz63pLGABC/jXA7lHwzknD33oQwWQv/mbv5lp+/3f//0CyC/90i/Jhz70oW09GtFiSogl37t3ryil0mdnn322fOELX5h5rq5redazntWKI9+zZ08rbr6PzG3n0fjlX/5lAURrLW9+85vvF55y+Fp6NFZWVgSQF73oRfe7j09+8pNy7rnnpjFrrWXfvn2t9XjjG98489yP//iPz6xhnp9zxRVXyPHjx2eei3vqsssuk5/4iZ9o5ScYY1pr9JGPfEROP/30Vh7Crl27Wu997Wtf2zuvPN/gZL1qm5ubKdfhV37lV+a2+8//+T8LIGecccZJ9f+6170uje3IkSNz2z3oQQ8SQJ73vOf1vnfPnj1zn51Opynf42Uve9ncdjfccIMsLS3JgQMH5L777hMRWXg0FrCABdxvWHg0FrCABdwvyKvQdL0Gm5ubvPvd70ZrvaNKNZdeeilvfvObuemmmxiPxxw5coTxeMxVV13FE5/4RO644w5e9KIXzTz3jne8gw984AMsLS3xlre8hfX1dY4ePcpoNOLgwYO8973v5du//dt3NB8R4cd+7Mf4mZ/5GYbDIe985zv5L//lv+zo2X8p8MQnPhGAd7/73bz97W/HOXdSz99222180zd9E7fddhvnnnsu73znO1lfX+fw4cOMRiOuvfZaXvWqV3Hqqae2nvv1X/913vjGNwLwwz/8w9x5550cOXKEY8eO8cY3vpGiKPjgBz/ID/3QD8199yc/+Une8IY38IpXvIKDBw9y+PBhNjc3k+fslltu4dnPfjYHDx7kBS94AZ/85CcZj8ccP36cgwcP8v/9f/8fxhh+7ud+jj/90z89qXmfCD7/+c8nXF500UVz28Xv7r77bg4fPny/3jXP85N/d+211570s865NId5z4sIP/ADP8B4POZNb3oT+/fv3+mwF7CABSygH/65NZ0FLGAB/3og92iIiNx6662itZbV1VVZX19P7d761rcKIM961rNERE7o0dgO1tfXkxX77/7u71rfRUvuD//wD59Un12PxmQykRe+8IXJKvyhD33opPrbDr6WHo2rr766VaXojDPOkO/8zu+UX/mVX5EPfvCDsrGxse3zL37xiwWQ/fv3y6233rqjd25tbckpp5wigHz3d393b5tf+7VfS2P6+Mc/3vou9zT8xE/8xNz3vOAFLxBA/uN//I9z27zhDW8QQB772MfOfPfVeDT+7M/+LD17zTXXzG33p3/6p6ndtddeu+P+3/Wud6Xnrr766t42hw8fTl6loiha3+UekVtuuaX3+U9/+tOpzcMe9rDeNnGdvumbvqn1+cKjsYAFLOD+wsKjsYAFLOB+w7nnnsszn/nM5MGI8Lu/+7sAfP/3f/9X/Y61tTUuu+wywOd95LB3717AW5DvLxw/fpxnP/vZvOtd7+LMM8/kb/7mb1K+wL82uOyyy3jf+97Hwx/+cMDj5d3vfjeveMUruOKKK9i3bx/Pe97zeu9U2Nzc5F3vehcAP/MzP8O55567o3d+4AMfSNb7eRcg/siP/Ahnnnkm4L1QfaC15r/+1//a+93hw4d573vfm8Y2D773e78XgGuuuWYmj+RVr3oVIoKInHQVtPX19fT7ysrK3Hb5d/kzJ4JnPOMZLC0tAfCa17ymt81rX/valAtV1zWj0Sh999znPjf9/t//+3/vfT7v9/jx4zPf33LLLfzsz/4sKysr/MZv/MaOx76ABSxgAdvBQtFYwAIW8FVBDG2J4VM33XQTf/d3f8fevXv5tm/7th338+d//ue88IUv5CEPeQirq6utS/6iEnP77be3nnnuc5+LUoo/+7M/4znPeQ7veMc7uPPOO3f8zrvuuovLLruMD33oQ1x44YV8+MMf5rGPfeyOn/+XCM94xjO4/vrrufrqq/nZn/1ZrrjiCk455RTAX8D2l3/5l1x22WX8/M//fOu5T3ziE1RVBcC3fMu37Ph9n/jEJwCvdF544YW9bYwxXHHFFa32XXjYwx7Gaaed1vvdP/7jP6awnyuuuIIzzjij9+fRj350euYrX/nKjufwzw379+/n5S9/OeAVtxe/+MV8/vOfp6oqbrvtNl75ylfy+te/nrIs0zNaN+z7oosu4ru+67sAeMtb3sKP//iPc8stt1BVFTfddBMvfelL+aM/+qP0fP5shB/6oR9ic3OTX/qlX/p3VY56AQtYwD8tbF+WZAELWMACTgDPf/7z2bdvH//wD//AjTfemKrzvOhFL0pW2u3AOceLX/zilqW7KAr27duX7no4duwY4/GYzc3N1rPf8A3fwOte9zpe+cpX8r73vY/3ve99AJxzzjk885nP5Hu/93t5+tOfPvfdv/VbvwXA0tISV1111Y6t+P/SQWvNZZddljxB4G8sf8c73sHrX/96Njc3efWrX80Tn/hEvvmbvxloe4XOO++8Hb/rnnvuAeDss8/ett0555zTat+FeUoG0FIe51W86sLW1taO2u0Edu3ataN+8+/yZ3YCr371q7n99tv5wz/8Q972trfxtre9rfX9hRdeyPOe9zze+MY3sry8zHA4bH3/27/92xw6dIgPfOADvOlNb+JNb3pT6/snP/nJXHDBBfzBH/wB+/bta333lre8hauuuorHPe5xSeFZwAIWsIAHAhYejQUsYAFfFQyHQ777u78bgN/5nd9JpT2jp+NE8Du/8zu84x3vwBjDz//8z/PFL36RyWTC4cOHufvuu7n77rt5wQteANBbRvenf/qnufnmm3njG9/It33bt3Haaadx++2383u/93tcccUVfMd3fEey1Hfhm7/5m9mzZw/j8Zjv+77ve0CF039p8IhHPIJf/MVf5M/+7M9QSgFewHygIPZ5f9ttVxY4JjkvLy+n8KcT/TyQ4W9nnXVW+v2OO+6Y2y7/Ln9mJ1AUBf/n//wf/uqv/ooXvehFPOpRj+JBD3oQl156Ka997Wv59Kc/nRTtPs/R2toa73vf+3j3u9/N85//fC688ELOO+88LrvsMn7913+dv/3bv03KZP78sWPHUuncN73pTYxGIzY2Nlo/echW/OxkCw0sYAEL+PcJC0VjAQtYwFcNUal405vexO23385FF13EJZdcsqNn3/nOdwLwgz/4g/ziL/4iD3vYw2ZCO06Ug3HWWWfx8pe/nD/5kz/h4MGDfPazn+UHf/AHAfijP/oj/vf//t+9zz3+8Y/nqquuYt++ffz1X/81z3ve82a8Jv/W4IorruBhD3sY4O8viRBzKODkwo6iJ2K7G+KhCXvrVqzaCZxxxhkAjEYjbrrpppN+/quFRz7ykWlPfu5zn5vbLn53xhlnpHC1k4Urr7ySt73tbVx33XV85Stf4R//8R9T7kTMrXnqU5/a+6zWmu/4ju/gve99LzfccAO33HILV199NS972ctwzqV7RvLnY3Uw5xxPe9rT2LVr18zPrbfeCsDb3va29NlnP/vZ+zW/BSxgAf++YKFoLGABC/iq4ZJLLuExj3kM0+kUOLkk8CigXnzxxb3fb2xs8NGPfvSkxvOYxzyG3/7t304C1Qc+8IG5bS+55BL++q//mlNOOYWrr76a5zznOWxsbJzU+/61wdraGkAr/OaSSy5JoWr/7//9vx33FRXK22+/nRtvvLG3jbWWD33oQwA84QlPOOnxPuUpT0mekKiYfi1hZWUl7aUYntcFEeGv/uqvAK8sPNDwD//wD3zhC18A4CUveclJP/+e97yH48ePUxRFb6noBSxgAQv4p4CForGABSzgAYHXve51/ORP/iQ/+ZM/yYtf/OIdP7dnzx7AVwrqg1e/+tVzK/hMJpNt+463X5/otu6LL76YD37wgxw4cIC/+7u/49nPfvZJVQ36lwLvf//7e8PLcrjmmmsSrh/3uMelz1dWVlJC8S//8i+f0EMR4VnPela6b2Fe1anf/M3fTHkWMczuZOC0007jW7/1WwH41V/91bkKTYT7e4fFdhCF+w996EO9iu973vMevvzlLwNN9asHCtbX13nZy14GeCUm3peyU7jrrrtSRa8f+IEfaOXTnH/++ScMQ4s5Oy95yUvSZ1//9V//wExuAQtYwL9t+BqV0V3AAhbwbwC692jsFLa7R+OVr3xluhvgN3/zN2UymYiIyF133SUvf/nL070O9NTxf/azny3f933fJ3/5l3/ZulH50KFD8upXvzrdO/Cbv/mbrefm3Qx+7bXXymmnnSaAXHrppXLs2LGTmqeIyHg8lnvvvTf9vPnNb05zzz+/9957xVo783wc28niWERk//79cuGFF8ov/dIvycc+9rGESxGPzze84Q1y4MCBhO/PfOYzredvu+229P25554r73rXu2RrayvN65prrpGf+qmfkj/4gz9oPZfP8aUvfancfffdIuJv1P61X/s1KctSAHnhC184M+b8ZvDt4Etf+lLaB6eeeqr8zu/8jhw9ejR9f++998of//Efy/Of/3y58sor576nbw/uBKqqksc85jHppvqrrrpKRESstfLud79bdu/eLYA85znP6X3+RO//yEc+Iq95zWvkuuuuk+l0KiIe53/+538uF110kQBy+umnz73f5M///M/lTW96k9x0001S17WIiGxsbMjb3/72dKP4Ix7xiN7b2U8Ei3s0FrCABdxfWCgaC1jAAnYM/xSKxpEjR+QRj3hE+l5rLXv37k1Kwktf+lJ5yUte0ivoRKE8/uzevTsJfPHnBS94wYxAP0/REBG57rrr0gWBT3ziE1sKzE4gv6DvRD99AudXo2icccYZrf611rJv3z4ZDoetz3ft2iXvec97evv45Cc/KWeffXZqa4yRffv2pfUA5I1vfOPMcz/+4z+evldKyb59+1qXBz796U/vFXJ3qmiIiHzqU5+S888/f+Y9a2trrfk985nPnPue+6toiIjcfPPNrfevrKzI0tJS+vviiy+Ww4cP9z57ovf/yZ/8ycy6GWPSZw9/+MPlhhtumDu2N77xjaltURQza/akJz0pKYAnCwtFYwELWMD9hUXo1AIWsIB/Vti7dy8f/vCHefnLX87555+PMYaiKLj88st5xzvese3lYW9+85t53etex3Of+1wuuOACRITRaMRZZ53Ff/gP/4E//uM/5j3veU/vvQHz4FGPehRXX301Z555Jh/72Md45jOfyZEjRx6Iqe4IYuWiSy+99KSfvfHGG3nPe97Dj/zIj3DppZeyf/9+1tfXERFOP/10Lr/8cl7zmtfwxS9+MVXy6sLjHvc4Pv/5z/PLv/zLXHrppezatYvNzU3OOeccLr/8ct7whjf0xvi/4Q1v4IMf/CDf/u3fzumnn87Gxga7du3i6U9/Om9961v5wAc+cNIlX7tw8cUXc/311/Prv/7rPPOZz+TAgQOsr6/jnOOCCy7gRS96Ee985zvT5X4PNJx//vl89rOf5ed//ue56KKLUEpRliWPf/zj+Z//83/ykY98ZKZ07E7h8Y9/PK94xSu49NJLOfXUU9nY2GD//v1cccUV/K//9b/47Gc/O/eeEvAhbD/6oz/K4x73OPbu3cvGxgZnnHEGz3ve8/jDP/xDPvzhD3P66aff36kvYAELWMD9AiVygoDeBSxgAQtYwNcEbr/9ds4991yMMVx33XXphu8FLGABC1jAAv41wsKjsYAFLGAB/0Lggx/8IOCTbhdKxgIWsIAFLOBfOywUjQUsYAEL+BcCH/rQhxgOh/zCL/zCP/dQFrCABSxgAQv4qmEROrWABSxgAQtYwAIWsIAFLOABh4VHYwELWMACFrCABSxgAQtYwAMOC0VjAQtYwAIWsIAFLGABC1jAAw4LRWMBC1jAAhawgAUsYAELWMADDsVOG37j1z2eb/iWb2Lfg85GHJQYQGE1aKUwoU69cw5rLSJCYQpEQERwzuGcA0BrjVKKqqoAGA6HWGsB3zZ+H/9WSqU+4u9aa4wxAFRVlf6O73fOpX6UUlS2prYWay1lWQIwGo1QSjEYDJhOpwCUZYkxhrqu/fud73M6nVJVFUop6rpmbW2NwWBAVVXUdc2xY8dYXV2lKAqsq1HKYYxhOp2ytbWFUgpjDEZr6mmVcGSMQUQYDAZM6gmnDJe54kmXMtyzjLvnPo7/wzUsVRYpYVCWCQ91XaO1Tnjt4qgoCpxzCX8RlzElpyzLdLdAHIvWuvVvvhZaa99eKZy41LfWOuHbOYdGJdwuLy+39lB8Xz6OfGxxzfJ56PCTQ5xTKYrRQDEQxWlnn8k1f/lBBgJLu1Yoy8K3AZSCCTXTQth7zuk85ikXc9+RQ5iiRBVDzPIyblBilQKnMTUcvO4m7vvsjeyqFBZhYgStQIkgSqgHit0POZuLnnoJRzaPoZSgdIFDgSpQRYlDs2UGnPv1l7C8tAtrhVqESTXm0LHDDLViz9oe1Ooyylk2br6V+268nmVVg4JaO8Q4lDjEGtbdgNMefhHnPOTBOCV+vGiMFUqrufn6G6iP3stHf+cP2XVkk+MywjrHstXYwoTzJzPnEa2w4s/P0nDAcFAiAkoXGK1xdoopNNXuJZ72n76dm4/czYoolsVghwPMcABK42oHleOur9zO+vo6NQ6J5x0FCozWmIHiIRc+GKUUzgG6AOX3lghI7UCEsRZWdu/i5qs/xtZHv8CydYy0pVYw1AVMazCaLSM89gVXYtcGFEWBLgwOsM5SW0s1nWLHUzbvvJcvf/hT7K0NWEetBF0UKDTj8Zi6tlgrWGup65pqatPvzvnzvHfvXpaWhiitiNsy0pi4N7sQv3MiuOw85u1rFOO65rbbbmM4HDIYDNKZGxQlGiiNYteuNQwKxOKcxSioSsMpDz+fPQ89F71rlaIcYLRBFwUDU6Kcw1rH+L6jfPovP8jeMWgljI2AVgytYHHUB1Z58guexwjlb3gL5zvRdXGoac09H/0c93zuJkRBbRTGgbEOh99flYbdDzqTpzz/uRx0WzgUQzHojEZZaxmPRlz7/7ua5Xu3KK1gxTIt/HndVQ6YVpatSZX4RFEUDS5p06ecBlprW+POeQXaMDY1F176WMwpq5RrawwGK5higCoVqnaUZYlojZrWfOJ9H2J8531oC8YYqkKhdi0jWmGPbuKmYx75lMfxuG98MvdONthynkcYURhMOAEOV1u2Nrd431++n2NHNrn17oOM6orJeEpd1Zx1xgGWlwsuvfTxPOMZT2dzcwNrLcaYjM4LVe1wDm695Su8/6+uwlY1OBiYkt1T4dThKqeu7KIeTxgrh9u9zJOffQUXPflJqML4/SdQimJ8dJ2br/sCn//op7j9ttsYDoZMqymENRIRNKrFj+NY8r0bv490Pa5xTvPnQeyjj+/HMYgIzDlj/neV+Gh8pu9c5vwwjjd+l/NJJ651TrtnOj6b9+/bKRDd+qy1X3vmG/dtPo4ubvJ+8rnkPH+mDbrVR8578z5bchae13o65fyYM5z0PRuft5k8kI+z770RuuPO18WSrUenXb5WUfYQ8fgF1Yu3fE/E52O/UW7Mx9GH67heqX+tUBn96eIm57P5HpMevtHsTYNWbfnLv09wyqGcoK0GFK5wPOzRF3LBoy6gUprNyYjDR49w9N5D3HXTLVSHjrNvaZXN8YRj4y22XEXlLENt2DNYZrUcYmjObgtfHpW9e6Z7Xn7zpo/PrG0XdqxogBfonTjEgRMQFA6NUoLtEBgRYTKdUJiyhdDu5skXue+Q5YsWFzv+CyRi3IWcEFRVxbSuGE8mSQgvy5LBYMB4PEZEqCrP0ESEvXv3AqC1wQrUdZ2Ugsgkq6pK741KRFRGTKExhiC81BRFwWQyCQqOf39RFEm5ioK+iGemeLoaxqARarQ2LUJkjEnzy5WNiJeoFDUbtcFlzrC7xDJXMvJDltZEqbQB42dRIBIR6mnV2oTd/ncC2xGnlpISDomzjnoy8TidTBsiGNtbC8qhteLQ3Qc5duwYo9GIlRVDUYT11RpnNIhCIVRSYxXU4kB7AqycQyEIgrOOe++8i631DZxYjNGIc9ROQnvtW2pHoRXj0RaCYWoto8kmo61NvnzbbTzqURexd/cKRmmWVoZeiRGHBqx1CNa/VzRiLasry2j8XlGKRGCrqqKqvYIyKAc4WfcYUlHgihcEN9CsKwgWnKBrTWkKUCDOegXKGHBCtTXm1i/chDplhakO59JZTF2DNjjr+yiXlxjaGl1VuLC3lfKvFyfUleXo0aPs2b2X2gnK+edRCusEaocSqKhZXV1lNJmgjEasI8gV/twDFqFWjiPHj7M83Ieg0EJQiMFZcLUgKFRZ4rTBofx/yjMOrdrMrCvkdJV1fwDivycPOZOM6+d6BJ+0/wVQEgQZQOOFAq1B/LgPHTpEceZ+lleXsPUUrQ3KWZxxGKVxzmILhS01zimkqtP8a3GIUayPtji2vo4tS1TYN/nZndoaI3C8GjPVXunGCcqCcoLSeFVDKe47dB/Hjh1FVoqg9Akuw6ENRh+zNKQ2WxSiwCkQhyjPX2ygazkNSiC0lIl8jVKTDv3yiBYw8JWvfIX95hyWtGLgFLqoKazBoBClcEpQ1uGMwvqNhhLBOkE7hy5K0Aqn4Jav3MJDHvsojk02caVOioZWkS85xDlGo5E3aCk/N2ut30nOEQWka6+9lkc+8hEMh8MwNxCpG3osCueE48fXCbsabTRKK2rlqAuYFMDKgIdf9Eie8IynsXzqPkChLBilsdOKW798C9d+9JPcfMONyNYUnDAejRr+qjQiriVQdoXrnCfPU7C7fL2vTfy+u8474Rs5D+z2l++DliKRCcV527ZAO0sr8/FExWa7ueVyjSiSUGqtnVF0ujJNd/5dAW87Ba47oh3zX9WWu+gRMGfe1SPUR6NMV/nsyoB9SkAzlNm57wT61jr/rg8X+bp339W33xtQrT3QVfy6+EmGXKUaAa8zx3n7Pyq+WnnlxjnBmAKNQqzzBqeNEeNjG7hJhXGeFtfTirqqqSYTaldjxVErh9MD9ECD0DLMpD3Zg9fuuE60/3M4KUVjNBp5IVgrxELUIXMCEQmVtwIKlmYSUSCPz8TNGAedt8uZR1y4oihaxC5f4LiI3UMYNd4o8APpd6UUu3fvToguioK6rhMTHA69dlkUBcYYrLVMp9P0e1RAosWsruukjESPQldQ93us2bxxLGVZMq4mvn0Q4grjx6tQiPOW9NhfflhzgrmdVSSuTzwMuSUq19Zz7T1f0wjb/R4JafcAngx0LU85pHmH/0nAT115L1ERCYx4YdXgrXJFEJzqqmY6HgN+b9jJxM/fGCpbg9P+ueUlpspRa4UWQRxoF5QMLekgTkcjrBH/FmXw8rxFlMYhWJmwtX6cfftP5/CRdY5ubDKpRigU+/btpxZBIZQKNicjRCwWwdYOi7cq4QQTFCapJ6ggYChpCIIuDKYwiNYsLy9Tx3Mqjki2uyQhrqsVh8KhlLeDFRKtcBZxAqbweLYOtz6m2L3MlqpwS0toa1EKtJGE9z2nHWBSVdhphQho1Vh9xFovSFoYjSae+WpN0A4QFFLXEGjHxvHjOOcxYcS1rCyiocJRGYUyBheUGC2C1t6aXFUVzjnGVYUeDtDLQ6bTCYNI2LVC62g1tkCz7/Kf9M5whuftz+1AKe/57VqrRASbLc6scJ0p/uK8YO/to2ijqZ1lUJboovB7x9YUSRn3e18U6JUlDpx/DsduvJUVo4IU6xWNKbDrwKlMpt4Yg2qMB4kua82krjj9oedz+I6D6NGUwvmlU+D3owKrhOVda1RVTbVVgzE4U7ase9FLdOq5Z3HXvcdQdU2BeI+hqOSxmMfIlG6vSVc561MW87lY55jUFRqHtRWFVtTWMRCNAFaDVDVnXfBgrrv7HgbilXsRz+gFsDgqvGK9vrnB1E7BGUR7RUMpjRPvCUUEUxQMlpYYjeqwFwyqUEzGEwjKl4iwubmZeTNMCwfWeSTv3rObwhiq2gW+phirig3leNhDHsSlT30qZz/kPOpCIYOCsgZXW+689Tau+9RnuPPLt3D04H2oqokkiMKl0hqtFNZ/MVdA3M4gNO9s9CmDJwKl1AztavcxK7Tm/c8TdFPf3WfmvC3fW31z6ULL0wPJo9GlK913zMNbn3LS/TtMIM3hRGPM5xINc8SxSfvZvrVrtc/G0Wcc6M6t9e68bbBlug6eT7hXpGOInCNb5t/nSmdX4cjnne+htI+08oYVaSI7unPr4k5lSkbf/Lt0LH6vVTDChDmiwdY1dlpRb42wlePYnQcZb2xQbW2hK0uJxlYV9XSKUZqBLjDiKLX3LjvnjVB969WnaPSdlZ3yvx0rGkoFS7hW0YiG0QaryKymjVspKRHSCP759yJN2FBsnwvA8Z19zD721beRc+E4/u2cd4WaoBDEn6hg5OFGS0tLKKVCOFeNON2yMGitGQwGiHghJoY4DIfDNM6qnjIYGKqqSgpNbBcZytLSUsvrEEO3vJVLAY3Q7oVBwWTzjP92CWh8Jg9Fy7X7XLHIGX6ujUfFqRvGlPDtGldqN3ShtnVikl0imGvtfcpQ3lf62zdI88vfGU45IJSDASLOCwHiqOsgNAcm5d3hiuHykrfcLQ28wBj3pbNoUyDKWzTXTj0FtbZEvV5RVA7i3tUgWlFJzYFTz8Q6B8Z7VZT2App4iocgaIFDd9zO6vIqRaFZXVvhtNVTsbbm0OFDFGVBoUFNpqzfdy+uqqi0eKVGgQvueKM0hdYcvfceDpx5FqgCH73ofSzaGMxwQLXumYxzzlu+47mhTbhahBQfSqOMZmo0Y6MpvEsFhfdg1kZTK+fPxdTCUDOxlqHSqGAltgKmKJk6WN21i3prRFmWXoByMbAGbG1RymCtQ4nCEAmbQjRoHbxUtuaee+5hXE29MpY2TLCKA3UBe888jeW1VVw4S1oZvy0yhqmLAjeEcy98GAevuQE7rhHnhcCowPu9Hs5UZq3qCqnC9sp2n7CTcN7DUCQIsX19+f6CIB82rKhm30+spVxbYXXPLpbWVqi1otCGsigQXaCCYOz8InPh476O2ym494YvYWqvhE8V2KWC0887B1EkwTWnBUoplDjU0pDi9FN49FOfwBc+/AlkfezbivhwPqMYYznvvHOZVFN0OWjRsZaBxBj2n3MWxdRx56evR00yJUGBDbQyD6nsGlX69nP3O2hoX2UtasmwZ99eVnetoYrCe8u08p7IEHLiECrl2HvmaTzqCRdzwz98ikJ5BUgZjdNglcIZxWnnnMX61iZq6HeohLNrnQ2WRy/A68LwqEc/mn/88MdBgTYaaz2tG4/HLK+ssX//AbQ2TKcVxji09nS8ocVeANuzZw9f99jHcs2nPpNo9IHTTuU5z3kuj3/c4xkUhfcgaVAWxsfW+dynPsMnP/IxRkePoytLUTu0+PBnCTjMjUpRKe4Kufl45imD8wSQvrPR3e/d8wGzgk+3j64w2OWNfePqviO920lSZLvvyeWPrqLlPYQ91vlAo/ueP5Gxok+pyRXoXHmP7bTWWDfbR2uOPXiXKAcQ6ZE09KZnDDlN6+K+z8vVfXd3LVp7TLVDU+dBnK/HwWyI1TzBPd/XuWGnqzDNw3/kKy68M1cy+s5Lq09mz0F6h/R/F5/XwWjkraxCNZ5wzcc/hZtYNjY3fHpAbdFOGBQl4FhZMSwp7/0X5Q1D2g8C62xLIU7jpzlz85TbE+3dHE7Ko5E2sXXBgm+x0ma8uQIhAtV0ymAwSMwqP2DdOM4o+McJRS0x9hnb5xZvEUlhSEqpVjxvnq+xtLSUhOecEEXPhDGGpaWllvLR3ZzR+1DX9UyOBPi8B9+noqrqNG9a+CG9N45jMvGeDDGhgfKC8aDwCpHYysfKZ0QlVwzy/vPxdg9Nn4swP6hxLXIikT+TBH8dQ086FhUAadr2jSNXKuYR+i4Bz3M0ZpiCeOukV4I1rraIgFHemmtFQCumzuJMwbnnncvy6goUwVqoDRgN2qALA2KYWMvSnjUe+bjHcsPVH03KjrU1KE2tFeWuVc5+yHnosvCxk0Z7K7DSKF2AMWi85XPj0H1ct77BGQ++ACmHjCdjhkVJqQuWhksYEUZHDjM6fIglbai1D+dBaXSpfXhKDQOjufeO2zDDZR50wSNQOojoQfm31uck5BD3m0K34mzbeAeDwuoCt2uNXWeeyfqh+1iaKMq6RoliC8dZj7qQcvcautSsDA1SGgqn0UUBRRmIF2gLw917GG2sY6saJxYrwtTVWOs4+9yzGA6H/jyaAqUMojz+nPbeCEWNLTWVEi581CP54i33Uk+qJMQ5J5iyQA0LHvzICxkuL+Pi+Q6WJhQobXC6RomlKivWzj0bdWzMwetvosAzipjDIEF43465NBaw+US2K9ym88asgaRhrM2zswS8UROdeCuURO1jWHDqeWdjDuxlsLxEOSgxpvBeDG0o0BitmYilRhDleNCjH84dX7yJZbwXotKOR17y9RQH9lAMBgyHQ+8Rymg1+HNW45AVw+5zz+D8h1/Alz92Ddr5PVQjbNma8x/7SPadcwZqWFIOhyhtiKFYcb5RAXXLwlmPfCgbdxxk49a7/HvEhw9GJp4/l/B1AuGpu34ift9IWbD/zNPZe9qpLO3bC0tD0CXGlOhCU9qQWzgwWAQmNQ9++IUcvvlO7r39LnRZBNxrps5y5nnnsHrKHgZLS6jSoAdlUuoQvw+VEu89cnDe+edx7Ngmt911Nzaud6CFw+GQRz3qUd4opUz6LvIQHTwpWmvqac1Fj76IleEyn/rEp3jqU5/K5Vdcwa5du1DeP+nX9vgWX/nSl7nhmmv58udvwE6mDEQHA4xCGxUMI15Q9rQ24FM1Ckj3HHSFuHmKd9869P2+3TN9a9tue6LvZ89p1+g1Izx1nsmNbt1+0jnP3pWHo+Rt+/DUxV8fX87b54bbXE6Kz3bnPE/pyj9TKuzV7Lsu9H0W92T3u27Ow7z16ZMNoFFuunssH3N3zeIadMfbh9t8bF15JX9u3tr04WPePs9xBbP5Lq01ztq1wedWhU1GbS2FVsi0ptrYwk4sxgrKQYH2hF0EjKYIAd8msAyHC4ZQ/L89eyNH5Dw+1z0L28GOFQ0JXgFrLU6EaTXFmMKfR2lbtmNYlIj1yZmZ8uDn5pGcW7lEvIegLMvWAepzz0blIEdCLnjH76OSMhgMMEWRiEd8Zx5KZYxJeRRxLP7d/pn4ea4kAEwmE5aWllKbqqoYDIeI1BTFMLWP/xKUL2stg4FPXp1Op9S2xtUCw2V0IPhx/lpptDFYW6d55hp0xFfXQxRxN8lyU6C9kbuKX1cJjO1zPOcKYU4EcqUrx/N2DKVLROL7csLTJTJNW693p/U0hY/vV57JguBwTGuLHRpOPfcs9p1zBq703oeyHFKjfcKb8soTWlOUhqqq2XXgFJZ2ryFHNvw7jcZqYYLj0Y+9iGJ1mboICVw6JDKDD33TGodGO2HJKI5ubVLbKVPrmEynLO3bj1aa1ZUV7GjEfbfeSlHX3mulDH7rKawpERU8HK5mqdDccetXOONBD2YwWPP5QtMKXS57pcc5YnhjixAoUGjAtfAMniaVquCYMaw86Gye8r3fw8ff/36Ofu56zPoIVSv2nXcOD33qJRw5doQBMBSFcxqDwbt5fAhSCvHDeg+Lsxw49UyOHDrE3gP72draYs8ppzCtJgFvpqVoqBCCpZ1hqA1OaobLSyztWqVeHwXC6JXP2llW9uxjsGsVK6BD7gX4kDHnhKqqkdpSK8fEORBL5TNSUDbk3Cjx4VlOAJ15OZs9mu9b78Gdb3WaZ+mJ9KmPkfQp54le+hmlIgzOd4ZSiuV9ezj1vHM4rq1PUK5rjA3WVePDkERrRAlivMK9fvwwU2dZch5b5fISp513LlvGMq18TK82PbHH1iIIIywTW3N0soUYhdOhQIQCs7bMBV9/EdOlAqu8EuykKRLRNeBMlSCFogqeQuUc4nxieAyfyj0aSdDNlK8+gbFvTURg9cA+zr3woWxon7dXuhKNYOspYjVLZoC24o1o2mN/Kn6+Ufjxia8KZ+CRX/cYzN5lH4IXeIwUjdXRG7hdynNyKE4/4/SGxgbLIgqe8pSncPbZZ4W8xsaTBE2EQMRJaUrcwPGYix7DZd94GWefc44fk/OeezepuO+2O/nSZz7HFz93Pcc3jqOtpXTeZ6O1otbgtEIFCVNDoJtpU5LH7Xfz/f4pobv3+r7LBtrSC3oFp23e003K9p7pfkWnO562XEOrTfsMzwrFfYpLn/A6o2TT5pHdBOymXcOzu/PtvjPuRYn/eSKbQpTzsYhIa28i/TQvx0GfLNCdZz4nF8KUT6SAdr/rfrvd++YpMF2Ypxz7jvw/+R6ap9g1nbT/bK3HfH3ZKwkRL1qjcJTGUBA8xtahgwzi8Clv4PkiotBIUDQ0Dm/Imac07QS2W88u7Dx0Smsm47EXJJyjLAY+2dI5TIfIR0HdC7vtDdj1AkTB1VqbkqfrumY4HKbqUF3BN3cd5hWT8mTtGB4VBXDPnMKGVt7V7604sDQcMp5MMMZQFIUX3LTG1jUiLoQ9KZ/sWDvK0isHk4nP1xiPx0nIL4oClFAHgXc8HjMNXp2iKHDBcpoL60k4VB7PohVFUSJKMaqnFAiucmijWwejb+GLwvhwnoyIRQUj4ikncLmHJz8ksW2u6KU1UA3BjPj26zpfkOoqDd39kL8/70MrlRKK8/HEoFcNGOMVs8pZCkCsw2nv+lcojC6YYlnevYYrNOPpFmVRok2JdYKYAudAOVA4rPjwhEoppuIolcLZGlt4LwkC5eoqTnsvFyZaL5XPqtCCUr5KhHO+P2M0e9Z2MVUGU5RoJezbtxctQjUaMd3aROrKJ30VgxCfKt5DEcIlBKimY/SwDPk7HqeDpaFPRK8mlFpRuzqYmAVlfChYYiKBiM/QQAdOGSaDgvK0/XzDd347/zAaMfr8l9DWUhlgbZmNQwdZE40JVMyqMArBKwmByon4hFVdGIrhgLV9exFx7F89QB0qwKE0orwHQpDoz0VsjXI+zwURKiwb4xEDJU1ujnWI0lTOMrEVSgYUGAjFKgiygtE6rAe+6k7hqLQXHsvkGfBCqHUOk4VMxDC6aLFLNK6Duz5Fust0+trmoFHEV3cFEBNoD04Q58OKdMjSOLp+nIOH74NdKywrhcH/FMrnDJlQmKDQeH2wEPbu38/S2ir2vg0KrdkabXHw0EFkdUhZFhRRsNA6MDSCcqd9An7h160YDqjEEWL0cAomzjIWy+ZkijKGoRqgRXmXvdJeoFXBU41gFTixFCtLWBEGSqNxKI+RxnAVhHif8xAzVFqLkBT9uB+zrzxOFWxOtji2sc50CMtr3hCknPdi6MLTcOssiPEMWmswoJcHHu9OcLWjWF5CFQUUmsrWSC0Y57AiqMIgGqyL6y0URiMOlGiOHDlCVdXUdTvs5dRTDwDCaLSF6RRRERGKsvAhfUBZDDj99NPZv28/hSl9Qqj2PtSNQ0e46+Zb+dK113P7F27Cbo1BWW+8IpyJoKwRPvPHKirqzT7MhWjx/0uJqSp9EbwKvTt7Fk4k1PUJrIRzCrMCzv3VeXK+lycvw+xc+hSNrtLV0AhP70ne0UZh6yoH3fnmAvm8/iPkil+enO6fb/PYLm/v4sD/Edc5/UlO7PLwr5a819dXD677IJ9/E77qIDNu5m37+mopC75Bq30fdPNRoxzZVZjmyStKqaSI59/nRvK+dUvvoP+8eNo132vi+Y8Ec5ov7oD43FMdw30bFCTepQRU3OuBr7VcWH0D2YbPeVyr+c93YMeKhlGa6dbYl1ZUfke62qLLwlfcyTZBjiQVmEr8rFt6Nh949BpAf6JZvmBxo8TchxgqFX+PwnWyFAqUReGrfdS+5KUxhqIsQQnLwyVv5ZlWvkqRc776jtFU1YRCFRSFX966rlHaL1oM1YpKhnMOpUkhVs65NJYoPBhjUlncuq6bjRnsHpVS4AxmaZnpriXs0U2W0CkGPRdilFKhypUOOIVCh5wPFasOzbN40FJ6Ir4i/qMi0bW2ojruvkRgpPV87D8myudEMZ9H93Any5Jq4j3zzxuFR1E6UsL0RPmEZuOcrxSjoHS+kkwhsLm+zi63z3u4tEE5RWEGoEuUWUIVJYWIVzaMTybXy0PckS2MKKbKsWeqUcOC9eMb7FvaxxIGZ7S37ofKSZgSiuxo1ZZ6MmZ05DB6aZmtqmJTHKYcsrS8zLKqEVdRD6BQBRI9aUpRKqBQWO0TwQpd+qpv1QTlBkzqClvXrGjNdPMoy1ub1G5KLZYhpQ9D0ZLib73Fvr0XlAi1shROWLKa5cESam2Fi5/3bD50++8xnGxyfGMdW1Usa82qKqhLqAYajQ9Zy0tnKoRCFHazYqKm7HnUKXzltmu44KEP4fBd93DKgVOwZUExKL0yoTVK+R/jaqYF1KWhrL271y0ZVk/dw9bxDaS2mChuCayuLCPiKAYGp12YnxeYnDgKo3AYBiGeVg9KlvftpsIh4kVawYfOudpb00V8ecVavMLqtK8ANlAm26/0QldAaDNylUq8xrYRNArt/D6WAm/dj95MhEKF6nzeHp0YyMrSCgOtsU4oBO8qDyUSHV4RdIaQ46VAacxwQFEOsWYLi7C8NODA3l3cV296T48pfBUwQCkTrN3i8xesYyAK62B1126kKHBTX3bRlAWFVlhbUUtFWXqaWqiCUCqroUTK53wsKV/Zbfepp3LvF2+lqBRaNEZKps6H5toQBhSFCBvx28vlorcjroEX+LxRTBgoYWtjneHKPrQuvPJkfOlgjPF5DYHmGPw6SAF7z9jPfbfeidSKUgYUZki5ssqornHjCYPBEoXWlFqjTIFSGleCMsbzE/Fr7Kzl1NP2ea+nNDzLGM3Bg3cgspe11b2tIiQ6hk4VhsIZVtd2sf/00yiXhlGb8cLSeMLtX/wSn/3Hj3PvV25nujWmsjVO+fw+JX4+NsgHRcwpCMKSePQ1lmXrvLcjCHDe86FSWGrjWQrCcxC+nEgo69uzOhlPOZFg2hea0S+w9gvq8yD/fp6Hou+MQn+4SNPeZbkd0SjhaUVetrRvPrmQmwu9QCtSocs38/yCrvIV/+waLvK55hU7WwnRwaCGIhV5iIbafG0aj8182G6Nc4NraxydtnlUzDxlScLE+ww/8+aeKxxd6PM2teciLRznY5k39/QupTyt71Uq2vs5eXR9TTyvYIiAs2ysryNoRBlfKAIF4kIIVehXebVGaOeSmHjm+/DT+bslCyrFnCWdCztWNJy1/sc5H79bO4qiDEQrLnTDAFRg9kgW3xgWN2a8u85hihPKPRl9hz4viZuHNHmLfjFjMYjPxbK0ufAfvSmxBG1u6XciXrAJ1g6vJPnKU4i//2M0GgGEuObGOm9tk8cRhWwRL/DF8Uyn01auBwjTEFblBQXFvjNOY3r8ZpaMbvXfsnw4H7YQvTpx/kopxLWTOnPCFOeaH5KciHU9Gukn7omAx6SU0F7LvM+uBSc/YH3ENkLMC+kj/E78XkQco60trLOhKgu+jGUYr1Xemrl3/ylM64qVsqTQKZAIEwQgL8iE/RtKdg6Lkql1FFYY1mBEYUvD/nPPZrK1wYpSUDu08XdB+PkGpqwVSmlEOUo0hcDQlBQoqumE6XjMpJoyGR2j2txgIJZC62ApMYFJeWuwRVFbAQzTquae2+9ksG8fg7U1No4eYWl1FRlXVJsj6mnlvRbOBS+LhApV/fkHCiisUFSW1WKAEoMuh5zyoPM58LALWF+/nrW1XWgMqhZU4fGrnE/Q9lYY/xN71YCuHFuHD3PD332M4/fdxyduvp2zH3Qu5sApFCjKIL7GcCuF+PsHtHftmtpX29JKMzAFIxeZpye3lbUMBks+Yd41XoEUCiIhL0IErEPVDl05VOUoHKja50VZ68KPzc5I24KqcmYokvOCFvTt05wZd5lKOg8hZEhC984JGJWUphkBKLSzzidIVHXN1NYorbE4DCEmN+xJjd/PEpQZYjU+BNEl1vowM6MMrq5Rxhf7QCStrVP+3oxpCDUrBgPfP35/UzlWi1V2DZbY2BrhdIVTJc54QTrnXgqa8EYRyqUhlTimNngYbIl1jirkHSljMJlQnNOEecJEWpNsbZaLAaoWmFioQw3IoP0YCeGP4lMsYr8FwlD5+2qMFV97HsWgLBmUJeO6QhW+8IMShQ4Vpww+lMnWLlSNCcqedZiwV4twBlTtOGV1N2pa4wY1qmyMUyoI78vLy5x5+tmsrK7ixCvzYgU1qTl67yE+95lr+Pynr2F8+DiFlaAM4HlxTzh1sm528JgbxLr7Obdyn0iYP1GbuevVI6j5rdIvwOU8o8mh0r1tu+OLz8y0VTsbe5eHtfpRfuQS5L98rHmoVgw1bwmVc4Tq/F3b7f/8kZ300f09tWN7JWI76BtXn7egV7mLzDgbf2zXjcJIxmvl+UKuWM2jDX3vPdF4uxDpedc43vWO9Ckb3gvY9N2kEegWvZrBmf/Cl54HHyFDVCMk8ApavslIP1qyI1EB2dl8WwqRbzgXL32wc0UjuK/9QisKYzwTD6FTJmPE/q4Nz6h9DHawcoeJSNwotEs5xoMWlQVgJtFJRJKlp88S3t1A8SdPBI+bNQoWsWRtV1EZjUaYGPcextoII/4dXQXDOUdtK6C56GsSSqgqFfAW2o3H4zTnqqooC52UGAFfIrUoscMBtfVCV5xnHgJlCp8UnGursV1U7kSkuYQwO7Dx7/yZPiLdxTPMumuV8p9F5S96ayQbQ581JOKvm8uTQ/6e/Nm6rjFlyWA49EKW8xdgKW+8x6Gogam1oYyrLwtnSh/DbpXDqhp/ZZrC4i/os87C1AtuNV6g1pWjKkuqXcuo/buZbK0zdD72XYKE4vDKiwrxBKJ9mUgJlvFyaYhyBaY0GGtx04mPl3RTRBwYjVY+LEga7oQ2Gq0KNDUydQyHS2g0o/Utjh86ilrfohpPqDY2qEZjdDhXFi9Lxaim7tmIRMfn6vo7P1BwdDLh+MY6Zz3u6/nMF75IURgkhIFV+DsRNDrFdCfiiLd+1SJUdc3xu+9jj9UU61scmW5Sn3E6VV1RO+tzvHRG8FQQ7rVXkKOAW1tv2cYJwWnhlQetGU0mrFpLke2p5C0NP075nAznBGqbql6ho0VWUdU+P2G5KAJRltY9DlorT9M6Z6B7fvK92m2HSCrZmD/n2+PXX6Iw7cMGxYnfO9FgQ1P20eeWCFVlGVdTqkkFKHTpK09FC7NNezLgsq4pjC964IL8vzWeMJpMGGKwS15hLwrBqMYzLMqvfSUOZ2uvHIVSxPFupVKgGk/9paRKo1XlL/UroYjW+WCscGF+BBrp8GekQAclo2ZqK+raogtD6UXyhom2UNsvDuVrIYgPt6trmE4pawvWQjRyuWCgiffgSMz5c1CFfYOvOIXRuJAQPhpPvAfIGIpCYZSglceJaJJ3KOUNWevv51DWh1eG8U0mUxSK6aSipMTowvPaQcEZp5/B7t270cUAlPfQqknN1n1HuO4Tn+KLn/s8h++9j0IUurLe+xSqzolzwTjdpqvbGXhgNrykD68nUvJOFuadnZ0qLH3zmPddHoIdv/dC7vw5dcfUxUHOn1oyiBNQs4nFfcJulx/n3+VyUq6s9AqzPb93ITcC5v31zj3FXDxwkCtX8xSrLrTpZlugd6EE7E7eG+W8k9lb+Rgk+7xrHM0N1n1yWXedk1IflYBM/s0VJ69khL6VwhiNc8bLjMFwk0OuoJ/cWZUZPHbpxcnAzkOnWoJ9cHmZ4A4M3gkd4q1NjNe3FtC+fKAEscmFGFvdxD7HSeRxkhHx0+l0RvGIZWFjiVqlGi9IvsB9G6ibxxFvCo9CeN7n8soK4+kkjSWGSfn8D4WiSJsg/hvHVxQqjTEf16Ac+LKeqqlgE7+31ifyaaW8FawocYMB46LATMYsqWaTxg2slLeUadNO2I6g9WyN5Nxi1cdEukmpXY1dQROnq9RMabcYQha9HbmGH8cS8RLx1qf5pzF05pQILgpdGuoYwx32oCC+8oKQBEnxdB43rajEeIeBgVoJtdQUyoIoKqIw56irKWOpmWpBa2/JHGmHOeMUJsOCUV0zFAFToJSXii2ACt498V6FQS2MxzVFJZhx7S+5E8GUJXYFaltiCoOdVhhxOLGIMjjVWHAFEKOonaJWwsbWBvvW1hgInH3aaZi65rCzHL/vENXWmLKuvfCarZnvbJYJ1eKw2t/ovL5xjGo6oljbzdHphHMfeQHF2adSaV9xa2ot48InfxcKKvEJ9yiNDYzU1Q6nFE7D8fXjbJZDqukEtDCqpmzZCussYg1KXFA4gtKrFBN87L7FKyxja5kqobYO4/z7xAnaFGxsbrJ3WrE1GlMuLVGUvkSxi4oeXvkT7T2E48mUY1tbjJX4lRbFxsYG61tbiHMMlxW1k+S6bxifZ7PR26FNc9b6LKK5UJD2uTTx7V2GKoLPvxBBh/dZa31lMWX8PBRUzid9R4+rspbjR45RFxoZ1yAGcTWUGlcKIr6EsA33ykyqKTIaMywLtsR5j6cVNo9usrG5jtsFZTlGaU1Rlgy1QhmT7mQRJ7hphRtPUdPae0msw+oCW2hqW7MxGrE5GvtqJ9qHnBYQlNNGYbIi1OMp02ObjNY3Eo6sCFLXjKopG+MR4hyD4aBh7qmMdb9QktOZnA84EayGyjkmoxFuc4sSoRDHEKAMpQ2U8mcQTyvrumJUTam1YMVRDgtUqRApGDvL5mSC1RpnDMYphjqGrjm0MT4/BW/0mYzHHF1fp3Y1EzdFEGocY2fZmEyYOsWqmWCsV4zPO/dczjzjDIaDYbBCaqRyTDdH3HTN5/j8Jz/DsXsOUW2NGDgfBmnCRYGilI/LplEyuvsyftZnXW6UbN2raOT/dj/rE922sxznAmOXF0TZYb44eOIQli5vzMc6w1v8LzPfdfdb15iZ43V2ju0bprvjyscUocu3u3w4H/+sEW6+4pEb+LrjzyGdnUCPRLXXvEvf8r5PtNY5zOP9+Tu2U5zytYwG4BMpEPP2bxeX2wnV0ZiVyzDd9eoqGfl3fftGiEan2X2ZlGDlQzC11qnKpO/L8yafi9Hk17nsPX04ydcqT3PoXKPS7C+tWgazncDOq04B4mI1qSaG31YVyph0uRwEQVbEx8Hj2zjnk9makoUqXJbVCMg5YcsPda5Y5FaW/B6KfLGa8KUmiTgiMRd4Y9t4cHNX8XTqmYBSqnUzePzbH2VJoVH5s/FdcXwxPMr/XiHO9RILBWgt1FVFVVtWVpcY7N7D7jPPxN1+B2patbwIkQHEkP64SWJSex4a1ceUc1x3P+8jGEm7ZjZBKlc4cktBnGdeJUzr5i6SqPR1Q8Lyd+fQOsgxJEiCgqY1Tnzui9EGdChDChjrkM0xRw6tY4qS/aefjlkRGA4xRYnbnFKWYIoBtbVMJ1Pc1gQ7mniceG2HSise8ehHMbAKjo+og1AyMM5bRrXGTmoGq4a6qhjbio3phC1x2LUhG8bhfNg7GhhI4WO1JzVMa+pKYQYGKaxPYtYhGR6onc8dKmzN+sG7mRxfZzqtWRsusXtpyOieezhy593YyRQTldnoFwl4EtVe0yjcVUoQ5Th6912M7r6L5eWC3VpRKMWjLn0CN3zm00wOr1NvThhNK4bLA6wVZDDEoSicCVVrHDKtcRPHymCJelqxsblJVU3ZUpWPG98cUTuLtv7eDUpBaa9wWBRSgrKCqgRX1UzrKUb74gi1hHwDFcJGxhX1xpjh0gpIBVahB8qXG9Y+KVJbhx3XjI9vcuTuezh25Bi1wESEAn9x4Pr6JoNBKA6Axjkf+hitR576Bxol3ijQZSx9+zQ/e93d3K88A5lYFelMHEMdzooxxuegTAyHbrubCmHIgHJlGTMcUgxK1vbsYnXPLsolX4J4fX2d8eEjTI5tMNrYTPOhEu674yBHjh+l3jXCbVp04b1ug+Vl9uw/heWVZUpTMFofcfi+e5keXUcd2sDYkFeGoxIYKsPR+45w7PhhlnavYVcqjBlQlCVlWbK2toYZDChMwdFjxxkfPc7oviMcufMg1BZB4QKd3ByPOL65gUaxuroWLM2zmRk5ncmZPsxWuRqPpoysxR5XaFVQbU0oVpZQqzXDZcXy6ioq3IptrWWytcXW+jrHjx0LIa2GwoQ7YKxl6/BRNo4cwa1OYSKYYoxbrhkuLVEMSp8HphWurhlvbLJxfJ3p8RGmdhShP+uE6XjC8fUNFDXWaR76sLN5+AUXsra84u9/QiPWwaTi4K2387G/+Xvuve0Oto6u+1vZBcqIg6yggVaKUpmWVXMejW0pCrL9/u5Cm4/MCpL5O1rKd7ZWXUWn00la91llosmZyoX/rjGrO8cu5Aqp2Pll4+fNuyuk5kJb7L9PyO6DXiE0fNbd093P/TNNxczue3aiDHSVKOnR9PqE8e14N7SLZHTnm3s1bGd+fYJ8d/6yg/f3jX+n7WaVTJKMeKJ90n5uVlFrnunHY5RZRSQldcczURRl+Fvjswtpnu1RVNM8OmPM91z+bDoXSW71BjyldaIrJ4Kd36Mh0SrnXcnGaS/0lCUlCrGZC876fANjQrIbiiLEnCLehe5DSnJNtO0VyBOU87CbCPH7+NNFYlQ08gOTH4bc9RgVhRyZUYGY2iqFAuUuMRQpcbSbrOzf3VyEF0v2+gpFhU++7d7DIUIdfw+IGi6vUKwsM10aMlhdxdj11oZLAr6rk9U/93Q0RHiWIMR2OXFqlaxj9rDG9VdKpQTFLkGKfUdc5p/n30fcxDC4LqHsMoe8nzRGCTkWRrfCtLznKewP5XBKI7rmyO13c2zzOONjE75Uf4HTzjuHB13wMJxWjMYT1lZWWV5ZYWv9OKPRmOnGJtU9R9FbU7SEBDUHa7Zg44t3cPTaLzEuNPfZTQoL+089ld2nnEK5sgyb3nNx6PC9HLdTRhbWz7mHpZVdoWygoEWDGKZHjjG+4wh2tMmgGLC8spvBrl0MlgZegQx4r6dT6mqKmVpKKTkwWMVZhRzdYDq+h+M3fonjB+9JNzVLiH9Xgq/EZNplWRvGijdfjCvUkWN89n1Xcd4lX4/SBQc3vsRQadyhDe679ibuvecu1vauYTSs7d3N0mmnsLK2ht2YUBrDdHPE1r2H2Dq2yX233IkeV0yLMUrB/t27OMUM2bztHibTCfXaqk+iHQ4pB0PMcInl1RW09fkVk4NHueeeu5kWML7nCDiwRoWqSxpb1cjWhMN3HKQ8dNznWdU1y2srrO7Zzd79pzAcDjl28Ai3funLHDt2jGOHj1Ad32TJKhDFJHhji7LElCXT2l/kV4fcrSTcZPuQcK76oI8pNTRjNrRzHkSmKXjBR4eQNuus9+A5b7SpjlvqkJtxy5HrQBt/14NSGKNYXlliuLYKSjHa3GQ6GiN1jYzHLDkD1jFd3+S2z38J64SN+h7K8hYcXrHVwwHFsGS4sswp+05h8/g6h44dRaYVyzUMrG9XW4fRBeNDx7jhI5+mVhZdlFgXvInhzC8vLXHKKfsxxnDnnXcgVeUrOU0qVG2Z2kgLLWjF7n17KbRhOBw2OO7gt8vUu3itqioJItXBQ14QV4rRXYfRwxIpvNfdqIJdu3axd+9eRIT19XW2trYojGZ0/AhL1jP2rYOH0KtDwHLfxpfZ2DjOelGwa89enChMUVAYr+it7dlNVU05cugwh+69j2rqQzvPUEscE8GYksmSwUnF5t1HOP3sU3nyk57MWec+CKM0pdJogXpSsbW+wQ2f/Aw3XvM5Dt99L1LVKOfDLUUrapFkjY8Qs+Wc3t5qPG/vzrPs7lRIy5/t8mGY7z3vvqNPQN9OSM9/z/lQX7hw33z6zuiJzuy8sTb9z/cedGHeOLtjy79vFYrZpu8+nh0/z4X9rhfLdcaf+mEeNTyxwL+TfZS/Kw+zmgfb0Ybtnunbgyd4ihPxgXnjmj+O+c9EQ5TCy57OWqxz6bLo6HHySkf2vGqfg85AW+9KcpfqM+mENnhjs44h5juAk/JojEYTQmxIsJQqCHHgSnz8r1LRAtckfKfL9sKka1tja697xQMYBd+yLBrmqvx7p9ELYEO5XK0b/CQGHOrei/iYWonVlBobocoEaR28KYUpGFvrrVTOUQcvhApleX3oui8dOJ1OQ6JquN04JO7GAz6ZTkMsu2C0v13XL6wfU11bQFFonSwEEnDrby5XaF3irKBE+02nNVJozKAEo7DW+QOP12yFhoBG5Sr3bDjncDYeToJl1idzJqupCrHq4oi3m3aTtyEkzoebJON2jUpZTsyrqvL5PNpfLONyhQ8vLAkxRMGX9o2VwqxzPhTPhVvAopKSgqCCNh0W1a+VwVl/a66vzlNTTeswbotSmpqKg7fcgdKKoR1QWMP6zQe59rZ7wWhs7fGhVEjex4dKGesoLFhtcFphJxP+5v+8BxFhdWOCYBkPoRBYv+0enxBfFChjcApkUjFw/k6Nj33kS2BKb21HGCvFtNSUbopsrVOID9/CFOiBF4BQKpU1ntYV1bRCAUuDZcpi4MvSVjVuOmEy2vL5KdZ5a74KFiTAio/V7oZORdDWh3eoSc0NH/pbPv+PHwVTUE0tmAIzmXJU/Nm9pwBna8ygxK0NOfW00zh65IivYjOpmG5uIZVDK8OB1d2Itd4zsznmlk9fT4UN51VhnbeMKFNQlsHyvWuVejpleu9RRtWUqRbWplC6UE1MK5yzGFGM1zdZv/FmcMqneGifDK2MYWXXGqurq6zfe4SqqqjqilJgYA3G+pvjrVIMh0vem2KtP1/hriBjipSgDc3N5vHMnIgxxT0eHmgUjaxNOntYHDYk7sdQkEB/wt/xHJpYgEGUvzHeeM+xVpraOn+Dt9aYqUPGm2weWg+hRo7ShbNUlNS130tKNDpU+CrEUIx89ZxagKpCRjVufcqhe46DgqHyiquxwRJZGFTtE+wHuqDeqii0IFQ+ZyAkjCutka0RG8fuxDlhmcgP/L5XukCUwzpfH35t6PMRlPiqW8mxE3Di8dMWjrXyHpHID0yo9lO5GgHMVAK+QKYOGU+84lr44gvrhzc4fstdvjR2WNupqzFGGKgCZ4V6c4SbTlDOselqFEItcOzwFs4FpUqEu5XClAW2qn0uiPN0yyjFg9dOoVoVnDG4wrBr/x6edvllPPrix6BWhr5ylXXYqma0vsXNN36RL1x7HXfd+CXU1NfMN+Crpalwv0ZUCgi5LBKFEwVKeqtZJoFdyGhrTmP7w1b6LO2pXUf+6hNq097PvpsXUqQiH8jWWAfe2+03FxjzXMATKQ2tsammoEn00ufKWPe5PoEd2hES0L1pXSferWgLhl0vzzyc5CGbM/PcRvnuGgVPtC6Rb+e8Y57iOCMpM7tn5ilK3XHmkIed9QnxKtCJ3Jp/fxXFLp67c8zXsCXQz3m2Cx7nQBbyF3pJ/CYqFcS1jGdEaSSEdSqlmFY1g4GXy7zh28tNkvJphChsRlm0PVn/jgxzJOGKeH5SQy/nKeVDnJ3j+HjrhPiEk1A0rCh2rezy1XgGha9sIr5sng7lS8FXKnGByMd8zjrTeuL3IKHYR1wgiIXkLYIyuolRx1+G1GjbYIJAL+JjzD3jjWEiXuiNNfHrahqImE8k14WhqrxAW0vF8vISIsJ4PMFaf/u3rX2YVaF9mcG6qsD5OzVwLigHQd3Smul0koiftZbSFN6lDVRVDVZR6gFlUeCUxVlfP95XjRFfe905lDKhbeETV6sphdHogaFWUOMoS4Or6hAaIiGHpSE6uZdHISAWRLL7Q5xnJsrPwQTGG+5MQytSMmTXomW0CYJyYwGJ32utscom5S/GSyoTPDfRgxVwp01zo3vtrL9QRqkwr6Cw+gLQSZO2vtglIoSLaECcYWlpF4oSpSxeG44lUwOOKDCuQIu/REspKJwgUwvUlHGfOxcOhY9Jj8y2wiUFbGlj5BlCaDeYeuEC56u4uKpGKUuR8KO98FdNoPYheQgs4avZKCXYGrT2eSaucrjRKMVIuhBmOEQxDDxJxiOsbHnLRlDOtDgK8bHw08xbKECtFYJLdEYRLeWhVCqaWnyydTEVVD1FmIYkay+s+PwC0MFKjXOUkzFHD93qlU3w4ZXhfOhCwPm9J9ZLH+IcyjoGwdNWW18XC+XfNxVhevfhoOQrlkQYhnNUi3iFwl+bThU9hlaaeFLlBTBlHe7IBscPr2PQDMQFwRjPIAq/rkYsKF8O0IUzH93h2hkqqf2O0wakDgJPm5F1Y53j3RtKhRvKwxnRxtMHE9aF3EAgFjE+h8B5gkuBZaB1YBpNFbicgVkbLVi+7KtSIfnXOWrVsBWdGJAXbFxt083UIGD9obBKfAJz4oDiqyhZl5S4REsUOF/rFFPolGOiMOAaWTOJv8GLK5mnCJFwc61v6ESlfIbCNoKl7zDQLP+G+FSzP51DlA+7sNGC7wTl8CFKpQbRWKWSDUPrIJA7QPkNopQPa4x3RikErUooFKIdZSicIEq8t9T5kuKeR3shP45VWccQHS7SEpwSnFYYF0rqrg559BMfzxMv/wZW9uzGFNqfVWtxoykb9xzicx/7FDd+5lqmG1u+wGUQPuK6a4l5GFG4iXuCdGaJ9DJgK9EBlW0SiXeU+DkEf3JLqdgOmjYN7ck/n2fp3y5HL7WjGWbqz80rohunE0wEc+Ln42fdi4PjXtrOo9I3j26/7WdcWp+4VqlMdZBz4rN52HPksV0FJH9vN3KgO+a+z3NFo08hyxWZ7szzNYMoqza8PdK21t890IerRuZo51volpLWMS5knpx5u/REHoZun929m3tU0pjn9HFib0aey0Nn7tIo1Tl+CcqpgK/yYEATQomDtwmHaBAcNc3FxTEMsFEq8pFIurwPlC/OElt0K9Wl8RhqEUZG8eXjR2bm2gc7VjRq51haWkacUE18gra/wElTh1u0lfLx5K62ITlZJ6t1K1E8hOz4Erg6IVsFZirOdpKYVaj40mheynmyqUPytsQLwJzX+qzzQkERkoSHQ397t79IUGNCrJkKQnVVTxOhVSjKogw3cWufYxKUh7ryYUo6EOgYKz0I45iOx9i6ptT+HTEnw8/JC/QGr30TEncAEIdRGq29Z2UyncKWUGpDbR3T8RSxlkFZgvOlDhGop9MQGjB7J4W39tNU+co02nSgeywLOlg/44HoJgW2yGcW7tQNIesmwueWphZxyA553peIUNdTj+88bM13ltimrxLU5IfE9Wkf+MBQAxHzBoUuAaZFqHJLTjQMJCtD68AGITzHayQeThDlkgAbKxdFohitE4gvg5njKVoxvHCo083QOY5z4hcvRPNVrNq16iVbd9IuiOvnld7Yr4ggIZ9JpFEYBW88UKrxRCnCjfMuKymYWegitJhlbBOEn65lLuI9WmjjhY0J39ZCOLcz6xXmZ4xpcK1pPS+prQsVxly6EBFFqIwEzvr18jdBO0yoitXFZWv/MgvNudQtgSJn2EYbitCPvzgwJkbHan2h2pQ0BpQ07/B9I4B5Jp1j1eb7JFjcJWz4vL6/iOCk07lIME5IK/7f65p+32il28/l80/4osl5Sbhp6Lp4XTSc7cbaF4VlT75CXpmb2WK+rQuJkCH8LUzAK77h4sBICnyFmqgk+nfGTq1kZ1aaS8Ti72mvBcaf4y/tQeervUUhuVaCKzW1AsoBZz34PL7xymdy2jln4kw4U1YwlWL90GG+eP0X+NwnPs3W4aOoqfX3rKh2MnCD486eyGhbX7hJl+bGz3aaK9eFVpu4jtl7uvQof66b5xD/3U5A3cl4uvOY10/ON/Mwx9hHN4xpXn99OG19n94LMXpAMlxF6K5BV4DN+8/DYboKBJy4zOtOcdxV8rpz7vu7uwbb5VnM+yzfB317J3/Pdn1t93y3fdd4lD/Xyq3dRs090R6d9+7uGW3NK723WV/BRwRUzkd0RJKkwgPeRNP06TJZwDcORt1u5ncHcoOEJlRtFMI9bSeGHSsa5dDHixulGGh/w7UTsLhw46gK4SfeRWi0SYtSqEbgtFXtFRGlIOTPqnCZU7T0FsGCV+jCo1L5cBtDI5yaoHzYukoKgrUVrvZ3YuggNagQTpOsaNYnnVb11CfR4C3Qdlr7i64GJWVRUFU1Shmm0wlFUaI1IfTJ3yKrtEKbEhGoa0epNXYyYRASghX40AQRBoVh6mxIYLUoDaU24TbX5vK6pcEgXYayNRpxdP0Iq0ZB7ZiORgwgzENRVxWl8eFGSsF06kvoziSLK5UCdXPLjdaaqa1b+Sjp4LoYqtEfGkUPMYmbMVcgoHk+z0fJw7zimLtu5lw4E2dn3MmJCCWLviQhzmvm7XJ521mnusI3tC0s4SOiJbsLIsHl2WEKXlDx9Vi7wrRLXrE209BaJyE5J2RxHl18t96VCUFdgh7xEslV/s6ozEMTKpDjLYXSdQlfUG7iOuZjCdpha1xpzNJmkPMsQDnOoqKTM2UbPHNeaZllNPEMRBwnkTaOSRy1c9QhnypXRXwlPQWh1GlV1d7KraKg0BbkYLb8bA7+bDQ2+D5GXmh/sZ2gsOKtVTVCqWICXhSQ836DVYz2PlZaJc9rfH8u9CXhOlzoqYiCs0rhpuFJH/YWPFte2A/zkEC7IdGLPohj80aA2T2kMpyKeGWhObOhvUhSppyQDE/xBbEfF8IHBAEHdeE9fMo6SutwRgdlR9Ic/Ht1U35dJJVtjszb2ugtzzQVgtLZQ18UChVKkjutscYXkpgYYfep+7n0ymdw4aMf4b3R2uNfOWGyOeLOz3+JT3/4I9x710GUdWgheESam9HzM5/jsjmzjXLRp8h3BesunUzPaNV6pq+f+O5mx0iLVvQJ6/nvfXM5EXTpVvxnXh/bWZlnaCXSUty6dOpECkds0y34kn0byJWnyX3954a7nO53cdVVhrrfbzfGLmyn3MUDnhsec1kiPtv1uvTx4D4Fr4sjEVL4ejd3s4vTNn767yCZ92yO73zM84yjucEMxcxzs+OZVawindtuHbYDFQzk0WhTlgPGtQsGsUbTSGcZWhXDcj7R7PXGgNb/zub/BgdUbNVgd6Zn7FzRWF5b8wOzDrE+OVGcr6evwgS8hV8HixTpNuKogcWyt0W406JbKSS/zK4gVFUxhjpU5zBK4ZTvp9AFTqwPz1JCXdUYSGVuBY1RUBalZ0DiFYSlwTAkZy+1iPLAhDtCjMZZx7Ac+PktLTGtKupKsbQ88Lf1hhi78XjCtJpSh4v+jEBZeI+EMYZo+6+rGl36Eqbj8RitC2rn3dP+tnKvePkLsnwc/NZoxOboOGY4QI0n/pZH60K5Ur+TrNQ46+/tiBuorut0GaGILwFqdJNsnSfWG9FpbYpwR0pT3le3DhlkhzXK3plikR+uvopXUYDOY19zItLHyFTcR7SJbyIkzgXBAtY31n0uCt5a5GwMsWkTpFwoTu/IGLcTZsYTFQmfhEyrzwiSn4Osb4932+orZ/yu83caY4aK7YjsdvPLCZ1/b1tRacYYrbvSIqSeaehGCCSXJv3aWWYvxxQRXw412zctBYi2MNP3fMJPsjBGIdsLdrGFxgvLKtuT8blklSKUlrWNGVzE+XMtrtVnrvh5OUZhaz9vG9rGfRXPk3MunZ9YbjAfS/xdKX9reUxObu1nCfkqIc9Cm1B9yQnaCVr7an/iSJ6eeE9G3EfJWxAk927BhrgGUWmI/zkbwmvC7m55JlR4p3eVNXiRJmwsrp3L92y+p8mECyIjTAuBksjoSMxSBL+mKtIbFcbsB+g9yg1tih7mVMpRFMoYRlqYiGMoisIqHDZVXvNKi6Tx+jK0xitfUVAJAZ/O+hBdj8u4l+O4ZCaW34nzOUtKUWlhpBxm9ypPfMqTuOSpT8asLoX7d7wSUY+mHLnvEB/7hw9z9+e/hNsYMwj92ar2JaCND1no0srckJMrG13DTN6+76y192qcf1ymfmG4H2Yvg90J9LXN59InsHkts/Fsdr09OS3Mxx9pUjyDeXGZnN72vbvbZ59HJn4/ozQExTW0AAKPzehvfDavVplD31p2f49nbruwsS5eWuue8QJ/GLNw5g6eu/jqw0MXZvhrp41S/c/17bk0bghns4c/d/brtkoVzMwj5yst5WWb/ro47pMr+uaUGwmaNfX823sRwrPhnZtbW0xs5Y0ivuNGaVCqRZdnxqP8HWzp722UjWZegtWOiRNqdeL2cBKKxitf9fOsrK56Ymx0st4WZZEsitEjEQcdBVcVs7qVZxVCqDyVW6VoGJfXZP2NvaOtkfdmROVEKQbDIVtbW4h4a3hd15RlmSzBZVkky1YUbLU2dO+UmE4njEYTtFaMRmNcuETMBMFbEEajEc4JS8OhvxRONcKZ0pq6qsMFhU0VJaWNrw5jbbj9u0IFy691NVujMXfeeWciBF6R8jgcGp8MX9na3w3hhHpzzMAG6634PJcYh00mvMXNnqqsiCDatg5JXJtYAtfz/IYQJgET1WJIkB0I1Vgy4nM2hdr4u0/iQekjvMlqL20PTHxHl0F2PSJxnDrtccXy0jLloKTe2PR5CuJQbvag5/+mp1tKgPS3Uwo1S+PSd/H+jijsJ4YBoOZYtpRqzSl+n4hmduhzPPWNL8dtXsY53ZqqfYUrL2Xl7wtzp9kb8aJJ30djJYrMyyeD+WejJXw7wSMfb9pbzFrg+oSCpKQ4SZfLtRihCrqDiopnzz0tQUGwrvHouSBCCj6+1SfTtWO+lfiwqdpZRBxF8K7GxOru3KKSLx3FKsOEZxbZOud7wXsIVPIWO5S/TyQItwgUhU7hSkqpoGgFHMbQmhCmWtu6RRfaSn30KvpXx2IRLuDL09p4F01TCc+HuvnflSJVe1PaJ2DnEGcn4kOs2rQm3LOkolfFg+sohQ2OVKOkQLrpOimtAT9OHBZFIYIVxW1H7uOW++7mUWc8iKVijUpsiwmrjtfM6GaMgvhcPRfDWr3i3SgbUV/KPMhZiGdVaMbK4YYlD7/463ni5d/IvtMP+PMT8taY1hy77wjXfvxTXP/Za5mMxphxxZBQuMR5hdHzVu9tctm+y+n2PEEv32+5ISEXrPN2zW6VXqGt27ZPmO0TsubBPIEr4rTrkcnpQi7s7QS6feX95WPM57SdoB/HGfvN6U6+J3IFwPfRGZPqp4Xd9/bRybi2LeVujqCeP5fPOafh3c9EJOVdzuM9ueLRiljoeXdbgO6fn6j25337e8aQQ+MNnbenuuu83ZmB/v2SPxtpWhcndD6fx+O6uO7Oufe9NLTV48VhXZ2MlpHH6OgR6o4ryNpWhLwcbpQj5801gtXO372lhJKduTR2rGh8+Zabk6AfL9eqwwHpCwuJm6nv4HmC7m+ujf2lCwHxjNxojSkKVldW2NraShfsFWXJ8vIyzlqOHT/uQ6aCwG2CJX8rXL6Vo9fWdeZaCsRbGkUlF3rLskxW+aqqsNYyGAwYDgaUg0HyzsRNu7q6ymQ6xdY12hgGg4GvxILC1RXLgyFra2upNPCx9XWWBsNQBShzReITF5WDqa2pa9BVRVGUIZmWJkwkMouwMaL1A5g59FEY6JaRxTRzyC9L9OtW0IQVNOvmB9GOaU0KZSbQRM9SFHbzPvqE0u7hz8OIYuhRznicc5RFQV37SmdboxFVVROtjTpYJbvv6GMcOROYxyC9VXxOP1EIp4eg5P/vIYA5k8oJtgolOGP7XJHLn8/n0MsgIO3ljIzFYaexAemOmzbTsQmNEozaSil/aZxq+uriWKQJk5nZP9IebxfffXHFgq9OJAE36dIg5+s1FbStii0ir4I2ItFqnnm1vEE6KB+k533oFMmD4Zyfe22tF8RpM+VWOEEnZCUpy0pjpX2HTloRicm6OnlqrUjyAscQpbyaoNLgXD2zZ/M+JRtns8/i2ufjJ50dpbUvVjGTDUi4Q6f9rFJeKUPNrme+fhGi9d85B9Io8CJZWJd/WfZkTyiKao64BGufFecrxDmhQji4cZw7N49xrquZWovopijF7BlSWN1nxfbV/kQ0SuVeDYIi3owpt0aOsZx94UP5xmddwekPOc97MMIcjNK48ZibrrmOaz/yCQ7feTfKCkVQvmoVc81CvlnEj3/pTChSfHcffbv/oGivXOdb1RiC5gm129H5ruB8IpqWf54Lh/mrZ/Zdj1A9Dxqa0J73vD6huQB4O7y36HEMvetAfH7eBW/dfvrw0lJoevhM9119gnCfcdD/2x52Ts+7+ImySFJqO/jq0v45k02HW2X7vW8d8/HnHod8/l3oU4rz/vL3dJWvfIhdhWgedJWZedOfp3hAZuiUcM0AgnOKsiwYlCZ4tVWSc7XWIbJIGgNNkOE9rgRHo6hrNb9scEvRAF8EA1gZ7Jo75xx2rGj422F9fKutPTG0zrbq6Hrm2oSKxBu9vZDkB+vDehohuSzLRvkwptWXCKyvrzeaVrC8HTt2LGvTXPqWI6R5b3NQrK1T+2TR72wmZx2jehTG28T+eyLgsBsbLC0t+WRs/HgOHT6cwkzAKzwKn1RqjGa0NWL9+PFUdUZrQ2kMFs906+k0COZegCqKAqk1Rgl2Y4vCWp/PEUpZJoEBv9F90YpgEY0cSSRo+I1XJ1cK8hyNiK+cSXqFzxNFpTKBOfQvZAfceaZb2yYBX2sfgoY0Zf0ivvLL+5IgGt+Jx3ssvxtpfu49ic/ZQIzEObQvG+TnYIwfX8dTgFIhtGoOY3MOyeLPw04MQmcIDQmE0wuOpHWwQeBTAVkSEqgdeWJp7DEQey/JhtARSaEszcK2GQHBwgiZByEn5BJKO6PIvSjxM8/oWiyU6CytCUljiepoVCJuvjIFEhJWlQo3H0dchUWSDLfGYILo7PHTMACj4o2lLh9MmGcM3fF7uGEcGT5cTGDzY1FArbxCpAIBrENOlvgNiHMeD3Ff+P3jb4lOIWFhzjFcyIoNoVV+/TXea2GtQ5lm78RwQ2NMKiEab2VVkPJb/F6dFbTipnDivcVWfClsI2CcMNEKb0Pxe0aFSyiV81Z+owiXJ/n5umh4MSbg0LYFBfHJ/36/EoR9l3BqqzqNOS+q4Glq3Xg74j5WgZnpbGe5Zl7x2fSBhPAzUcH61igT0IQTRmUi9Wnr5veMcUcrXLAvpnC4yglojXXC1njC1nCJwoRb45NMmQkcApi2UBD3pMJ7P2L+imfRKuQahgIHhVcQHMLe0w/wrOdeyYWPewxWAYWnuaq2rB8+yvWf/Ax3f+U2jtx9L/XGCFP7wiAaFcrVRq+yCbNSviJgtoiRJnta0BaQuoJSzitz5aAbi97CSb5mmbEkrUGP8DUDbWI68+x2CkDXKDX33dL3htm+us/mkIcA+8pb/cnASrX7yr3H3b5zQ1zzWZPTFDd38p5lBrkcclzlykTko128+B/VeHrj8+G9kq1lV7FIqnXcCzGvLGMNfYJ+mn8+jqyveQrQvHnSM6e+tq05O4cxWahv9lyfAbFv/27Xbrs2fdDdc33t+hTU3GjV7J8o3EGMSIi8uTCGvatrTf+S0TffhPRB4AMRR7kpqT2KRiFuqLM0+yfKnMOdGTV2rGiYEIPslMIUgQD7+oiZSz60NUVLMDQh/yEiLlYGceIZgQqCr3XtpF7/vMnKsrYFZ38AAjGKd0ZIo9lGV35cABfxbAzKGAQfUy1BMJesbWRgLpRWdXhX1Hg0pRwOUylJ51wqYZneXfvQpenmFOd8Sdzl5WWKgG6t8xAGGAz8zY5KFxhlMBjQiqmtsNOKetMngqswvhQ+FH43WjEoCm9JCOEOWmn6iLhk4wZaGzptiuAZUopWkrgKgliq+OIaYVCpEMaBop76RPXo9QGFKI/f/LbUJqTHu/+8UuOFGBXujmhVacoUkzjG2lZYW7O1cYzhwDAxKlwe1ty1EpbXJ8cGZdDjISpV0foO4fggBE8M2d5QUdj1QmqK74ZG4VPRGhvyG0KYocO1hS/nyzvrkF0sQaHRQQiTfNyJbqj0/3g+ohcijsOJV/C0UUnwFOcFS29Mi8Jl5sFAURGUMzrx3wKKOt1GKv7BdB5sQ4887nSzz2xlg+KqW/kygqDE+VKfoXRt9AY5UYj45GcXFNik7IcxpsniwzK11j72XsIdEuLHlmhDMFrUTjWGkZATYTMLo1cyI74UViuc0yk3Q5wLN4d7PAqNEqGjR1b7PK+4k5RqYoeNNsm7FM9c3M8u+A+KpRK7uYEWh7U+KVwwuDrccq8IAqgCB5pwkaSNOyMshlL+7pSApwZnUZlziHKtcUa8CIZIDiIzSyusTEhUl8T7VKzGlXEtF/XdpKym7CYkusaI8kSgz4EeeLLSCDhR2W9ImacTEvhBVNxjXzZU3ZoqYckssWQNm5sjNga7KWv/OpHgMTAaxHuOCqXANZ5fCXWwYwUvFbwMIg5/e5QvNGKc99BPp5alfWs84fKncvE3Pom1U/YgKnj+nDDd2OTWz3+RT//9P7J+zyGobEJWEsyUwiivjIOvjJwLwS3BRKKZoDFEdPM0gJl/4+/RQJeiBYoecUAyqiMdYVDP9huXzHSUv7Qvkpibte8R0uPnOQ/rerTSD6o9rgxyL378Pv8776951u8DhQ6REX7PNuGFNil2XYG3+/6u5ykJjRm2nDRY6VurHLqKS1/b6EnOjV4QjBG5wJqNObb1H/p1IhzTeGfaPGGZOKPYr8rC2ZRK57PVXroKXBYmK82umWsU7FG+PK319KYbapXPs6/PXGnoe1f+jvi9VrRuMD8RNHJPcyb6FJrc4N7eP8HwqkkRO0oJy0tDBngDvg7r7TmBx711NtMzGiVEFKAbI0UbNCrIq6KibOGjB+JnXYVwO9i5R4OmXG1kqEZ74dYpFxIPJTBBnXIzxDVxikr5W7jHk3GIZ/bMOeVfZAQ1IjdPiGpZHTLXXHcTdDdZfD5qimlRNa1+nHPNfSBBcDA0Y1RK+bAt5xiPx2ncMSY/xsMDVNU0vXs0GlFVFcvLywyHQy+EZRWgmgPgEGVw4nM26rrC1lNKXGjfxOBDVkXK+duxc0bR50bN3ZZKK7TTKQktd/9GxhOfjbhMVaJ0kTTipMRlOB+Px+k29eFw2Cg1tA97XFMr/pK0OOao3MT1i/MtiubejSIoVkp5ZXFrc5NqOvWETXsvQlS6XDZGCBfOiKB1PIyKcOVVi4GkQxXZecaHorCGNFYflcl5Hi/WXwwnGk3jjUhWYK2oTbz5W9BGhUpKOoW9dC0zQFCWNFW4myLF2zuvTLh4j1AgBj7u3VfrIf74XUIyEETBUSRTFpr5xMml6mDO303QtQY1hF15xcwF5cM1765xOOUyZUqyuTYeJedIRomo/mWyZhqvTw72H0ZlWIu3BqeQMwTrSAJ07F/iuOJez76rBawD65S/30HCxYchgS6e//yM+YTvtkUyPztdYS+thDIYrVkaLIEy1A5UsK4PlUaJxlmPQK3x93ooRZXClYISkpcbTIpqg7eIiybJOuyTnGGIp0WqUz7Y0/f8L2mipaQdIhE+Ii169pXSPg8lekzzIiAq9CPBKKAkVCR0bZxWtfUKobOp+Ib39krwvCsmzrI0XOPcsx/MQDTjSnxp2ThpGvVHC5QaCqNxtQ3nWlNNK++pshat4vq5gGuFKEelNWageNhFF/GMb3k2p511OmpQoJzP66mmU47ce4gvfOazXPfxT6MnNcrNCrsNglSKr94J5LQ0xqj3hef1te8W58iFnLx9/LfFQ9jZ+NqdzRoz5gmT242/RRN7BMOIgzzSIZcB5r0r8STX/B3PVlI+dbt93v+8OTUCbuZxUO0+us/2fZfT2K7g3AjbEJXOvM+TCa1TkAqc9LXOre3NO786aM2783mfAteVb6Kxoau8xDbJONeRD08EJ1L+uu26c+lr50Mxm5DinYwlzsFojTYE5hUMW0EmScZEGu9nLHs/0x+NjJMYKvkcvIqJkO7Ey/dX7uU6Eey8vG05QOugTKhGuy3LgR+maicHx8/8gBvCUBQly8oLuMY0DDiPU88reMTN7G8NL1v956E+uUAcqxtNJpP0ey4Q9FlJonUnCsi54hPfEcda13VKmFVKJWF6Op0mpUMpT7ynU69wTCYTJpMJS0tLlGWZ+lhdXfU5HcE6XVc1o40talujpWKpMOkmVHF1KxysUaBqbxnPcB3nmHsQ6rpOCpNPOJUkjHbx2lXmGoIdE64aIpZufg+/l2XJ1tYWg8EgKV8quIdbHqms327+SE4MouKRh9jlpXEHZcne1d3cob+Cs5baCjk3sDZj6MrHYXshSbw3Q3IF1TbKAo213QHWtmNbbRDOdVBTUggbwXLnwIj3UkQGi8QkLY0VYSI2WWWRUMY5zMvfryct4gn+Qku0DrfTq3QmnXiJ3oeGBAk6CI3OCaIaBVEFXEjCc6NU+TvZmn2UfDyKeEOc9xgls1PELSSWowi5FKBj/D9RgQPCejfuf6+c5ATRiReo/doI5LfA0eCTgHcBdPSSIf4mIyQI315ZsE4lwds5sFn8arIy4QNjalHpQiQRhbL+s6g5RUEtp2/WZvsn4i+jjfMYkMKXBx+WS0jtGUCsMOes3xOJGVlLUYR9GL1fIdQmrqNf3pwu+rdIRFk+DtURGsUbllLjrF2uejiJ+G32fN5HXO84lvRVHQQ96zHtL/oLhgEl6e/WfmjzQGpPuLAIlbXgakzYHsqCdqGCnIKVwSqqskwrS6WaYiNe33KBeQu1aAqlQxlzsHbqv3MOo6LHVhBr0cZfzkmhOPshD+KZ3/IcHnzRwzEDv18L8fM7fPc9fPH6z3PDtdexcd9hBlaha4fo5oLFGUFGXJrsToTwyKe8waHubdO377pGvu3ekbxN0TOg1UyfOxKWOqJJ14iyXV9dATKduzlt4phzfpjztvzdjbU5ep7bQmOSE8TSVb/zdl3BP/adf5buJZKIEUkGv+68Z0Ov2r93lY34udaqVZSkWTedFL1eWiTSKG6d49+day5TbSdw7kix6Y7nBIpovl75Zyr7rK99t+rkTsbaVQTSWm4zrXnKY5xnft5yw+uJxpbTc19SP+7V3BAnwRMe1jIn7cn4E4ugdC7LzOltoO8uKtnNtvDPaR07PCHsWNHwSkYchaYoGmGxmYSfdCMYdQ+ytwZpXaBxKC0ZkWzXKu47ULl7N6+m09Xo48/KykpLk80XNj/ASWAdDFqhQvnYcuIUn4lCUhyLj9+OZfJU6iO6p2ObsvShUuPxGGstu3btQinFtK6oJlVQNCoK5VjWOlz45pI3qWupMbp9MV6zZrO1y2M7a8MN3jQ4yXMgoKkoE/vwHoVGociVglzhi3iaTqcopcJ8Id/xeb/O2VSyrZtk1meViGONCltRFAyHw4R/I5ra1tTORdEg4cmJC3H5ADYRp7B103xUM9BmnDSWgZb3zXpPRHMOmooPEwfRRSDiGYqRYEUU74VwIuECSf++qa0pXJODgWrCHJRSiC58yVVASbT6E0I9fG5LTOwVyAojhKRmF5U7726trcVpl5SGhlxFBclbdDMalfJwcobdIq0KdGG8WyBOI8xPoTBWJYU1hkilBxNBzcMlvCW/wXHHIizBhqMAGkub1gqRuqUMOOuVHuscUyVpTT3d8mPRynsK67qmsjVaBC3B2h6sSHFs8d+qqhKCusaA7lnMjQDO+RLVtfVhl1okVZSrxeLEYnQR4o+9oFLg97MRhVE6KZM65GXMsP4gtCchPsunaCddK5So1iV+LeWPJi8mzkMplQTPuG6JmUX6n5TVuL4BFwGn0WCS8APgVJqHQrX3p/b8xWigCAYhfFluV1c+BEqEgfb1xbQIAwGLDfqq789Vof/CIGKpXeNNHRQGbQyaIGgbbwxSRQEa1vbt5fIrn8HjnvJEitUhrlQoo5BpTT2p+eKnPsu1n/w0hw/eA5Vl4JSviOecv4jdzFqnc+vwTpSM/PvcE9ylpX2Q78Xtkm3z8TUP02sl7XtHi5fHdcy+m6eA54pAV1DrGtTid7nBK/ci9ikpfWP0+A+h3Z3oivh9HH/sqyuH5DjrKlLtqnMBI4Em5nPq4qHLF/OffHyxrXMyk5sJpDLOuaCe1jY3GhFkVMnOcDbf7vpwgj2a4yQ+2/WwtOfdzCfHSZ+Xap7C2yfnxT66Y+kK/X3znR1jO5yvT8ns/p637Rtft20+NsnwpRTNhbaundPhw2pjOdygIEgTjtbwV0FitUw/qrT+Ch9mrP1Fd55GE4zFIv7dPfOaBztWNBqqkiNeNYxZR2LnsgMad268BKpBklIGpX0/uedgHvHJP+sesK47tKtt533kG1YpxXTq8yjKsmxZ1/N2+QbNw3vyOylEJHlDlGof7qqqkqAY6+0752vvV1XF4cOH090JYp2vPKW80INSiIs33LYPXiIW4lLoQ+4ZyAldVAxy4plD32GNFbny+y/i/PqIeL52kSBEZWUwHKTxxXFEnCLimXxWOQtgaam562QymaSQrq4ipLTm6NEjWFtT1TV2an2sfwj90Fp7ISGU2Ix19LuKmVIKJ34MAsHr0wSrW5qwgvi8DUJr17oRmYdT4HKvmwvFAhRJMYr71ZhQqUyEWofCBXG9iYqkCsTBC2xxr9naBgZJuugovs/FcCzt85aSIqWmPplVKya28idVNee8YUY+mVipBid1sJwmkVNFF21jElGu2Vfx5nSlfFgTliyHJ6s2pKLi5GmL3yO+qIK1URnwQmazFnEcwVIdBGGt/T0GEorXS2iccrecF7hnToM46sqFu2ss2ll80rVQKjCalnLfKmecKUdR8GvlYuShm8Tz7KhdjdKwPCzYu7rC8fEILdqHbmof2qeDEK8CblXw2qhwq7hS+IyNHp7vC1uQGJQArSpRadUjnWw+bDPCpk08G0HFQ3TMWcsMD+HiSZM8Uy7sR9W6VNP311FWRdEcrFzgUGBcuoRKqSLl8XnlWlNYhXKOWkFtvF4ycD6nKCoNMY8teqCVjoqoTfcuec+coRaFLjVWgV4qeMTXPZrLn3kFe0/ZB4MCo31uhRtNufuWW/nURz7C3V+5A7s59uGTzheicBpcqZNyFfHbElg6a9dHp/J/mz4UVdVEA/QJ2X39aN0U6OgKtN31by1Pp6+2QH1y4SndMc37vE+47hqwohI/Twbo9hPHm9rM1aC8LOOrRTbyRDfiocWb8/Ci7LtgRwh8fjZ/IB9jd53nCaNtPkyL13fxGo0cedi4mpl5W/Poyl6pz5NY4+32xDxFK/+7i98+Wab7DLSjNPqejfjL5bZ8T/QpLN15z8NPd/zd39u8oD3/ruetiweA0WgrGc58YRzti4bQ0GyyscVzYV0oOaGUVyJEMj4gKTJCJHqrw//FzfLME8BJKBqNZTFq5Z74x4nHja5C207iTEtxCApKJ4YwJ7ZdRSO3mEObYOSxpvkC9B3y+Gy+mMeOHWP//v1z3Vl9Wng3LyS2iZ4LY5qFjUpMEiYDUYqJoU35WQ1aY5TBOR/H67FM2gTx3bnnJWZhdglnnsMSP5t3MPueT0JiZ51iCFT34HZxDl7JqqqKoizSBWJx3qmUn/KXGg4Gg+YdgVlE135c3xz36V+lMUaxvLxCvT7CpwtlwnhIDHYhqTjEwoD4kJGcYeR7i6ziizGFD9fIQXkLQKzEFMFmTFYpjcsS86OSKiKURYEr2muciIP24Vg6Iw7xd/933NeA8YnLIGhdEJPcu4zGe11MEsi0bso0r7hBUtpUPr+wPtEans5FiLOXOV5IlDc+JO9INg6fx9CUlc5/HD5B15ctzs87KLxXNX4WDRTRitNWvmNlMIWJVZq8doWki9eiQhj2bqgy5xW8kMsTwr8KrSjxFmktXvFyTqXzmyyo4QzUdU1VVSilZs55jo80P5/Fx7AsePA5Z7K+NfLVk5QwUDpUJmOGRjnr8wW01o2YoGh5API9HdfD0aYFyaYVvBkJ911yEcq5NvRRx2NA9FwJ0uojKRaqMYI1fKGp8+7nkglVXcUjbS2FNv0KFUCF+BAlBxUOa3x+jbFNGICKykXYj97r54tIRPyZogARnDZUuqTWwlkPPY8nPf0bOf1BZ2O1g0HhlaFaOPKVO7jpc9fzmU98nK2tTQZmgLbeeKS18XqT0VRKQW1TqOWMIKLaU9tOMMsNSta61t99AkpfH13hp49nprHF3zt/z6zRDoXPfJw7faYriOVlx+P3uaKznSCft099B1rXNw8VdN9uDsw8QXBGSXB52+xMyqxA2lWqevvrkYf8Z40M1hpXS2ZrGy2dc6kIQRfyPZW/y+Pr5NZ6hs/2zFc1BLtXED/Rvo795+/IZcRcnsyjBfr2YDeyJc078v6sXY6rfG7dcbX5YVsunadY5Z4k3yTwwVARtp5MQMQbAcXvAAWte3cASHQ2ykSze93Lmt4g4mjy75KJ7+TsBztXNJoN1p8wFqFvsfpi5kChlC8Da10sFWgCMxKUml2cvP8+bRDaCkm3XO7sGGA4HHL6aaelefnAiHAxkvOhLblSkc+njRda788tRFqbhLvY1Ogmr2E4iAnTYQ5K40T78pWTKRofE09on9+pEIVTrZtD0x2bClYYSaUxo76q2gcfPwQv7IakcG2C9THU+A66ZFSWYs7FvIv30mG2LtzNISk5yeEvw6qrmubmY+8lMMYnvzpXobVOpYhbuBZw+Opce3bv4Zwzz+RQ5dBWvMWIZs2ts74ak27KtiZBHUleD6GTjK4aAd7nXntpyUVc5sI4XpDK40C9gN8hznrJey6CJ8SPL/SnQxiM0LL4xhK7EqwJMdTKX0KnkxAnLlTjyUoz+z2lQDlMYRorfFAsEHwpWhVD/jqx/UHwinHEdV0nS3UMM8g9TREfyVig/J7WmcJXOwsMiDHRHl8hFyZjJkn5Skhuexgb2hLPlU6MWxu/1kYHZUOpTBgLeHGZAJwL5lrhNOk6I4VQBmVPo3B1FtsqXkjWoVjGdDJpDAGhjb8zKLOwxn0XEKy1QuPDI5fKkqXCMK2mWIQBGiXBmxAYcAy1cKVJ5xEaZdCXj81oaMYYJU42JnuHeUfnelRY0uWVyn/S5GQE3TPcZ+K/C/dKmEjHQ8hiOId+zgLpzIT5SBbmpWkWwI+goTeotK6CUEhTelelFfI9DbXxidtWMKKow5ppJdT+MIRoRv9sLJur8cqJ0t4zV2jPDyqt2Xvmfp7wDU/hvEdegBoUiFEoZZhsbXH07nu54VOf5fgdd3PkrnuQyYQl757GKF9B0CGh36A0a5UqzsUzhkQ2HjdjpCltYdMv56yQ5o1VZob2xvZdoTSHVOSh5507sQbnn+UywAxP6qxw31y6c0wKldaBPjZ8xnuGZi8dzIW+eQpMl2+nz3vGGL/pGk768NA3F7+0XqlNez8y3LCnlZqN2sgF6y5/3RZUOKvxXLh0yhDatDPfO03FkIzqdoThfL4N/8sYYI6DfEg9Y55V5Dr9Ze9Ja+7cXFx3X9H33Dx85v3mc/PhsqS1D8KDP8O08TJPyWgripH+xZ/4fP/eap5r+m2MhQWCZuosk7oOOoOkg6aUCtcLRIW7yVn1MlfkUY3yocDn/oW52ChHqMi2lK8l0lnr7WDn5W2zCks5Ucq11O6hywXzXCvMD7VzLlXzSBPVDqWa+zlyC3ZcyD7i1ifo5uOJ/+buQgmEqnkme0fmlck3UJ78HPvpCtrRwkmwWJXloAlZkRCbH2r9a+2tZ1H4E0BpgzECk2ny/LQuuiLf1G3GlLuNCQTN2lAGMhG4OEcgxHNGYTLioTBlwyRChR6tG89C/hPbRQtzruQlL07Ip6iryre1IZzMBA9HnYfkBS+DaiyPieEEoQnrE58rcejCINWUteEgxLlnMbYqCOCmUQTzfZD2GFA58RV+wlp5iysQksQjgyiKrvgb9jqCU43S6BTeWk0TehcXprmjBazyjFQXIGiwkpRHREK4FyhlQp8+5CxssbTWMchOqWY90zpoBcorNKQSxkGxSASzOS8iXth0zucYSUzsD8qiDqV7FaBNjwgR3y2gcGAD4RPvqVFK+bLHMWTFeQUrKvsq4T4KvBpUU2pWo5FAO3yFMfHqm3ihzgRGrpR4gU8JSI2OQjGRsEZRlaYMLw5jBUPmaY2xwd4U0QhgSqcQNWfboUOkM9cwQZXRn0RrJHotBEWNEUchNuCpUab8mQ2bBsHE8UfUx1/tLBMQkdY9rhJw26VvxH3nbMBQKFPeoocEBaAJn0L7tC8V9pg48eXBW2E0ngnGIgaJ2ca9mDNp4vlo2ibFmXC7fGLSiUWGkr/eG6RQmNClBKVawpwSypQOiogJqT4GKRQTpRiurfH4Sy/hgiddzGB1GVX4u1KMwOaRY3zxs9dyz623c/ftd2BHE2w1wQgUEtY/3kNA2L4IZRD6lG7uuEmVYSRhM0HO67qCeMMPNcbMeq37BMTunpgnLPcpDOnvyFh6nun221Ik5onwHWWj+7sLNCN+lufIxZyznJbHPvtkkz6ZoY2fWSE2hWGxTRWfrK+ufKJVETwvXWt8UMQUrfZxHt1x58VdunibOcdAk6uXz3mOAhrm1yhB4Zx39kiOjyS8z6KjF3K8zFMykkKU8+Yd7Gk/zzbe82dOpKTl8kzqE1IlJ8j4Q2d/5wph933deSdaRoPLvLjO7PgaQ1waUzjzTimOrm9gK4cKFRuTERNBCdROEq8DUCbkOYM3uqCiDTspHmTnyn8ewmMhhf2dhJ5xMsngiqIw6Mwi1QiYubCZL2Yg/No7cRoC0PQbNfz4TBx8nyDbFQ5j37nrq+vSjM/n38eF1Lq5ObGrUKT3SLuvHPqIV/f3vrGQ5Sh0K2J5y7NCxAarKa2LzaKykVs+fCncdn5DWwlpf5bGp2YPSVIYELQ26T2pWlXGyCLuq6pKQnRUMHKPTqyqJSJMJpOUy1JVFWVZzlTuaVnOmF2D+J0xhtpF5cznPgwGAyY25G5IRjSMVwe6jCBfU+dCuVqa/IG0Jn6BUr5D3LVJSIp3J2RrGHFchMoQWquoBQTrfnheKX8BXFSglE+kVgJV95bVLL9AqZjs3BAgbUhKGnhPRRi8t20FIXw2eTHHQ6PQdr0zcY3jmsWbrpVSWdJ5s1Y5bvvO8KxxIIj+8YySydDhMiZ6whfJ9mR3rwQDNUopCmOQYDBpxtDeVx4bCm36jRrduXXPlTb9oZw5LevmasQ2M+GNklkiM5xFyPPE0lh6QiTzs5XeF/ruG0cbvw1WuqFbDQ7aOI9Ci1YKFbyRjbAadltGb9P7O0aoHPL3dUP1thMi4ifhaKGEpHwgXnD01XgUFJqpUbilggu/7iIuedpT2XXKXqz2+08D4/UtPv+pz3D9pz4D05qt9fVYwsyfCQS09+CZcObzvdonQM0TULqC8Dze4gXW9hpHA1/O/7r7PG93ImifrVhSsy0wNXJAM/4ZmCOV5nPv4iDfJ216odK842fxmW4Yb87rutDCc6DXfe88EXTliK7w3B1jGl82pPyd89Ysl1P6lMvtaJUXLF2LFiilmLuzOnswlxX6lJvWOzP61ddvF+YpAX1tunPM71DbVpHpeW++x/J2XjecP6a+ue9kr/TR0G5/OW7nzSfmF5fDAUVZkJRDAktUiimxLLXn7d0z4ZzP/4uXp2qtfQid9UWIPP2ItMRf7mvxsvr81W3DjhWNojDhpXFBZjVAlWvBrX8jQe1hAir2k1l6hRSWkh+obZl7ZqmOEL/LLezd78X/kv6ORDm2z4n2vPfGzZ0rDDOHOwpOKtoASdWnWgxUBW209rq5Uv4CNuss3ZC17oZUqgnZSgxnm0OlaELMcqbknL/PI8dDFI5yAamL+64A1HpX9n0sAxwriFXBw9Gdi/+7LcSkOQTGqrVGiY+t3trcxI1Grdu/u8y9RUS6whWg8Dcto8JauHgxnoAojGpfAKVVm3h1196Hd5CUusRysvMTiZnS/k4RnODFlVmGpLWmdnaGiSZcJcuFzBIC1dz9kK9hLmzmZybiJuYY9OXtmHDHRYyvjx45RFqhW0qgiAnBHSGiNUdp4kG7Z6iLi5YA4CfRrEtgwPn+bSU+doSU7c5u11uJtPGV74f4bNewkbfJ++p7X1co3Y4xNuW0Z4WRHLr7vis0pPeFtYuQC8N956jbf3d8eR99wk9XmOrSkHnz9ze1t5lx7lnuxQF+H+qoaHgmlnJxaq2wpeb0h53PJU//Rs44/1xqDVOjQ2EAx6G77uGaj3ycu2/+CtWxDagtbjrxBR5QKG1w2isaZOc335d9a7OdcLIzQaa5e6O1np1z3bdHikwRnBG0RGaMW2keHeEYmrDRWUPGicY/y8/yz0yHbqRZR/rKLG/O++mG20Q+F9/RnnMonqHahrX0fXRtbwNxHI3Bclb+afZ+EwrT/lzNfJY/242qmHf+2/SGloIPbf6d99CEWfaf/Xzf9J1/aBSsefPoGyuqMVTk8+sL3ctxRWb0zsecr0WE7plLAncWeZPaZe/Z7hzNkzm60B1X/q44ju34XT4GrTV7T9nHEy/7BobLSwwGA4+7gEdtDMVwCR0ibOL9bqBwobpK/g4blQsRXF0zmU5CARvjDSZGY8oByhThCDzAioZzTX1ukbggTQ18P/F8ATKTERqlYizaHKtTKyFF42Q2dMq/a9Zykm+OvO+uZtsn/It4N3+Mn46EMlrpo6usm6fR3Rx5ud0ouEcvQOuwZu+P8xGRVI0q1uEXkRBD39wLkrOo/K6RvvGlw0lzG3LEXcRVvEAv37xRqI5rGnGcCzR5yEcXn10LeJeg5X3mbfpyS/xYmnyUVn+S4UHDeDJJf6twa3LuZu4jFLmA0ghaLoQ4KHwpZoFwQZeOV2QSciQC78gF9fiu9I7kzFTppmFPCGgODrEf75P0426S+aJHo1XVpPMeUp+u1W2LEIR9lef4ROWgdk31tvh5rpR0mX8SokPXLYYqpBC8WDq1FUqXCSn5nknv6CHY/t05+8kLL6QAohlGFnEZz3RXIYiFLfrzyPpw3LTPPTRpDwstD2mEvH3ed3cPdt/bl2fWtfTn7fO16LNUzxMMWv138N/ygnTe1Z1L9/sunZi3n/K2+d85nWu1sw6X4X5mHbL3tf9WIdwMRClcoamNolbC7tMO8KRnXsF5j3wYDEsYGJQIhdJMj23whc9+ji9+9jqO3H43QzRl7c/21DqU8pZFn1LuvYb+Ikk9M7du5b18T81TROK/O1mDnYZPdfnjvH3RFdDmvb/vHV36rkLpzfz77Xh7mlOPoB1x2TfW7rndCe6a9ioZgvoiJLwg0zv91pi778r3QLvvxjPd54XJobtHct6a05Oc1+fjySNQcjym+eeCOrOKwgwuaNOxfJ55H/nadnE0gzcRULFUeRt3ffsrp3V2ThJ/TsO6NKE7h74zENv00dMufro0L/+sT9npUyzyPvM17fKpoig47awzeM53PR8X8vKikqHCvGPRUt+f+CgJ5QvBmCBnuFClKsknSrzBxI8EkUzOFvwdSBJDsk4MJ5EM3k7owjVhGJ2G7b+VQpwNFzJFYaHPfRtd9LOMeN6h7TKV9jBmrRpdSEJ6qDqSC1d1Xc94O/JNFdv2WXm7B6orKHcZQXxfURSp3KjWOqQFKJTRSbjMPRapD+XzHeJGjhuyzyIYnwd8KEBGmNP8Qgxx1wWfW2n7hI/uPLsHJCee8V25INFlJM41t3V394FzDmV96I5tvd9hLRjaN5t317y7D5oxSvuwKk8qfW5dkzTvlRIJMfnNOZidt1dklfEXL2ZL5nd63DuIv+k4fRa08gCteH6lwi3IrqNw+rGrufOdJdJ+DfJ7J2ariPXhy+/HRilQNPtGRFIYVQqnk0yQTUEs7XH4WOXZfTCPCLcUyfC+vK+4T5tYbpeEE38OvCc1v3m+K/gAqXpU+k4ahhzHkdbbOtCzzKYrVOa/52enqwj0CUzzwkO7/c+DeUJMX7t5CkHf8/POWVd46tLR7c5k/l1LaOzQn+14RHeMopQvo2w04wLU7iUu/oYn83WPexzD3btwBt9/7RjUjttuuolP/eNHufeOu7CbY0pRoARtCqytGQ6H2cWkyhdWCHHw0aOYG566482FsNyg04fj7SA/vyKSwmlzYXw7Ibuvvy6/SuOmMUbFz/N+cs9Ga+1RM+27az1vPDmfjX3neZDbPdPFd3eeEbyxQFCq8Yx1Q3ljWeXus92z25qLNDHvM4JoR+6BxkiWC6i5gNzlqXn7JL/0CKqwjVVeSPy2T5Pqrk9+m3yXZiY5pCMPxDZ95yCNR5HOTj6nLr/rPtvdNS2aTVtR6NKeuefMM/uTOjd9kNP2vj5y+aqL5/z85fnBQLqjrdZCrSSYOWKkji92IlZad7ApbRiNxxinGYZoBZUpdhH3/kJnSXxVK4VTkgw1KFCzdpFe2Hl527wKlDQap9ades0djS0KiVragliOSADdCZWK9dO7BAnalpiIPGnLZa3DlW+w1hSiACvtcecelNrZziEX8vKh3VjrvtjrnCiYQARyQSgX3IkCnIK8qoo48XH72cHYTnjpHpwGT23NPSdWLU+Faidz53jJ++6GbsS5xjnFuyIiQQISA+xzU3atMHkOT3c+SiuwnjGUZZnCqWBWqcsJdhc/jQCqEYnWddIPvscsLKlNxDoF0tr7WikvmEZLS1jjzgOIOJQxGA1KfJljkTbzSvih7YEi6iXNC9K7WvPswWHzTTzPs3db9OE+vkAy66QJ3jAFqZQxkOWThHPl/PaKT7YYaA8e01mmOafd+GBjPB5yL0P8EWnfPt8W1jt3GLSE07Au2XuiopEPNF8fX+q4/3zOY2b5eexaK0+Gme0UuniFLLyJ7a1UOX63g3lCYx9t3E6Y7tKmtI+CUh37bJ3HLu2jWS6lvZJhRbAFPPRxj+HxV17OrtP2gw6lZ4HCCsfuuocbPvppbvnCjWxtbiGTilJgUBRgNFNXY0qDdo0XKFIJl+XMdQWcrtARx3sinJ4I+hTBFOLYUTYiHlOJ8TnQFdayb3rIWEYLMiNXiyfqNv/vrlXf3vRvI9HNnK5H3j8PH/ME/z4+BpH++bC3nG+ksShaPGmeADoTyiRCXnQmB0dm3KIf57HPbv9RoRSRFIrs6WFTRj/vI86tLwLEix0qGXvCDGfm18VJbmXvfpcrGV2e3O2zNedgw8rHGZ/t8+gopVrXJeTfd/G4Hb2Zfb4pYdt/Dprxd8fU16YPP/kZyfvJz0lfaG/k1dV0ClWNKULkRFQmA890RiUFvwrujcHS0MsmsdaP+BLcEIz+Iphs7xijfTi/cxhtEE0ogLIzPO5Y0RjosqktL+EyD+VVmrIIh90rzOHgRyWjYWTONVWXtDJobYLWBBITnpVGh+oloSnWNlZ8F4iVjkKf0kARBA0b3tdYk0R8FRjibbdExtNYX+MYuwTCE+NByBfxJRK90JKFjqimln7cNHn4UN5GRHBapxAO5xwrKysZfvwN2UprjC5Q1oGb+kvDFCmvoXsDrApad34Qcs3X+VgWYnlRCfO3tfW14qNgmg6wJCKVKxlKNTkgOZFqCQHKxwUmoQ5Cac9ZS3GE3NLcZcIRL30MwirQForab3gRRWkdKBdC3mKdBAl5D42VJFrxI47iTdeuJ+wlztcJ/vJEpQIR9PcpGG18dZ2oMARFMfUT9neKdfSmI0/CQ7KoWEI5hybvI4reHo9Z2dZk8SGMxSXvmyc0jUcmyYzSVMYKK5x4SJGdQ7+vVQopQiliireIhMpVUQGeFfRytbDOLHhxJeIQUsUtCfH2SmVezQbnEr4TPAHUhDMqPpcm7jmi8BS8f8bEkrsATY5JVBVNEKxjpTfnLM6CwrSswvk4UvWkjFGnQg2ZcpJKHhLWNJ4XZueWCxg5xO/iMyr7aUFnnN1x5//G33uFjPTiKPBKg/u4vpkJK+K8EQxmrYM5jUpz6oyn8XKHl6cNQlIkIh5U+NxZF8r9+nLIqMbrC/7cKPHVpnT8QGusCMYUjLHse/A5POFZT+fcR1yA1WF+xisN1bFN7vnK7Xz86r/n8J0H0U6w43FzwZ/R/h1ROcvC78TFct9FK8+wu7Z9oXI53vK/u33075cozAe8Zh6SVhXCDBrlvhHuUITC50GgThtP5S3979kwZsYYDB7xfLSUhkxQyufTJ1ynf1USLGaEzj5anf/ex3e6uG6H9Ya/M17p2/o56XDegwmwc+Y6hte4v1UmwGd7xnfR4DXnffnYuoJ9oj+ZIpnjJT7fVQKaOfbTC6v8mfRRwi2Bbu5+7RofEl3t0NHt1qTbzrmGV+fttjPE+N/bwnxXltiun+670njD/3Tcz/4trb0R55D/28VTPp6uApXz0HmKSuSRxPeGOzAmozHOKYwz1NMphTFMq4rBYOBlKqWog8w5CEnhSjfKhTGFlxmso7Y1RVEiQZ5KfEgXSG3ZOLrhDaKDkrVdu7YxSbVh58ngSuHQYDRO/A3DrcMvJI0oEjwRAe2TSxpGHISCqCpEZqTj5gg3G0KyhBY65g0IRRlKEIq/RA0MSGCe+bSDwCbaYCuHYFHGjzEKwBLDudLie8u7C+5YHUI+vPBIciv6C0ystzwzS8C6Gy4PqdKqUVByi75SimgoEfClZasKV1u0tZ5hBgtUl8CWZYENnoP4nrSp4ziCXBkFMecUIl541vna+IG3wk0SSqUdmpXmFD/LErynk0mDiw7hjEpFa38V7a2YvCQdt3h+GK0SSjSFKCaVBa1Z1gWVTKhcjaJtVYOGiDZ9NcwlryXdDz4COzFO5T1xEBUEP9VmuFncY3hv/C4S8aAGZUJ1KMFpXYuZRQUmtlFKpZtAcxzHsrepApSEeeo2g5uxnERBXUerMTjaBFurbE4SbN86hB1qneYS52NCsqDPO5KWYpLvYQ14F4dN+zRhPMzFKxSxClVQOETQStKdIpLPgfC+KHgplS8MUXFQNIqM0f4d0f6jVOOOj0J3FOxFBUWJuF0aQQMC7aJ594wwlK15ax0yiHQqZ0jx82aHNc/mpcdz4SnvOxf++0KaRGIJ3MD8Mssuyifl5mcwCQrpf/Ohy4Al7CGdPu4Kbs0Y4mQlMfqssIYihDYmbHgvtYTzWBRMcThtGK6t8oSnXcrDn3IJZtcytVIMlcGgmG5NuOOLN/Olz3yOu754M5ONLUTBNF7wiKCKgjqOIZ2NhhZaaylj+G0Iucs9vF2Bom8P5DS3u+Y5b+kKWdFIkrfthr/OeFYCXqMykfa7/zNdPiqd/U2b23YXOhl14u/ds7cTmFEQsr2X778+hTnHb5x//Lw1/6yP5ke3bQfRQqwinqMBKRYLUalNGov4cJR0dw4QU/wEkvFG0VRLitDlufMUpDw8Lf9uHm4iPcsLtbTwrfCW6hj6GY1BmfAen+uuQz7WltKRvbvPw9s7N5r3dt/XHXd3fbufdd/V3Rfd77vnDLKCLxlNb8SEpl08Y7PKD62/t1NIck9VvrbOZXJx4gteTjh6+Ajv/b23Ma0rVldXOf3001OO8e7du6md9YbwwKs3NzcZjUbUtUXTRNiUZUk1nXqltTBQ+HDvQmtWhssQZI/K1kyqKbt276aaTnn+Yx7BiWDHikat6sTsDUJZGF8qMhzAZC1UClUaEB8/L0qBCjesZkg2SqHEektzNJwEIcfZOlkdlfLPLRVFc2FUSP6MF48A6EGRxhIXJgqNIpa6nmJdDarIhEvQpkC5cAlXUEJq67yQZCvKIA9X1jIYDKnCjcVOwAWhv0sM4uaIseC5gN5VFLobzyc0hRArF+LQA3nKrRf5gahrm9yGOUPpxjPmwkUUWPNjkCs/RbjXI1om8jwNaG73jvHrANOqYjIepzHGqlo55AeqSwxzZhzBZUy8lyiFA69NKLcYmZo07XLCZ63F2ea9ZVkmb0Z3HbvQFdKakr9tt/iMICgyw+R9W2+56ZaeTFaEuC8IFpQgPCka2YCZPZTJW7QJW463Fg7//6z9Wa8ty5EmiH3mHrHWHs587sh5JpOZTCZnJnMgmVOhuqBqdBc0QAVBj1LrQQ21AAECpCcJ0O9oqboeBEgCVIBUgrqhRnVVZ3UNmcwkmZzuxDuee849457WWhHupgd38zC38Fh736zyi3P33mtF+GBubvaZubm5Ucg2FM6RK3HJtj59W3gltDEZplbxaX63ymoa3VS0AJfnbBy7Xku6/xpg6M+F5lKf5lf5TPNoU2k3gKIuV+WlVlmik/wtRRw+wpPy/VJcvvY+akPDghuhcatfH7bovuuSAGyEvt2jpeibtCICE5Xbb3X4YsfJKIoEhJ5wQRFxvcIXfvu38J0//gGOn7+DnU+7y2vy4IsB7771Dl77xS/xyl//Dc4/eIy13MOTd/D02q0vYyUAdZhpUHpB00CPzc7nVXhIA48WT6ZdDZqBT5HVGrxcFex/mPmu5+fqdexbA4UXF0K/7PstfbPUh9aznDGG7X9LV2uZqZ+x8wygGGqXjdn2ax9tLA7YN9YW4J0baTQBWSOXddSBvUdMtynPtEJhgbn+uEqx8qP1fgHkXO+07XvHljZNrl6qszxcG7L7Mujp9pc+1zpV/hZs5hh49vY9hHHEsxDx1l//LD0bI7q+hztcA0iZY7u+x2q1wvHRMQ5Wazy6937G3g5vvf8+njx+XAzhMTvewfkeKmYcrNcYxxF+1ePo8BC+6/Af/W//l5fS5uqHwSnFZiEGIEZ0XY+1T2Et0XlQ1wFg7IZt8vQTAzFiHCO6viuHVyfCBTiHdFlXhlLp8i2H85MTHHQdDg8PkW7MRTIUwohVv0IHB+8dtuOIYTciMuPw8BARDsMQsNvtsM23805CPWAMA0IIuHbtGoZhSAe/B4dVtwJ5j75P5Dg46EGUgj04bLHd7dB5YLs9x8VmB7dal8Vksz8BNcNpoW4tfvk3Lep8+ymmdHeyHU8ZPLeYsaXQLMizljIzg2meWQjADITpGHoxNjabDYYh0bPv+7TQ1aLSQKYAcgWGxJDR7WqwJKXayoYS+umF0t+u7zGGkHfGgBgYhPqwnBgH9W5QX7aiNT33KSwNfIrCI9fsv5gEmn71nNWAo8RqOlcfi4LaOg9ySL4VKjMBdauwrCDV7+/buYo0zU3lDWNJ4tBWcnrMlp+s8p6E6dyDJ2kUrdfKzpGuV+8a2jm0QKU1Nxbg2TG2lMaSMdJSxvve0++3+l3JmiyHhE66TTsX2qhonRm4ikK3dJkenj3afFe34yyPXxEwiuxySOEMLmngZHzkzwIIgwe2HeHOpz6Bb//ZD/Dxz34GoSPs8gWOPRPik1O89pOf46//1b/Fow8+AIaAPgASuBhyqGRH9dkl7TiwuemLk8tNHshWuFrl9DG7Ty1aWD0ypy8ga9++rzNdVXOM7Mk2crgFmJbmZNZH5eldBvOXl2pn3rxT11vcLotF09T+1M8QUXZXz/us5Zf+XfSY6DnRfVpm6Uvf5D1p8yo7GPuMUf3ckgyypW2kASW+f6FYA1rzsL7UWdoWbdTCQEuAnhrOJjtGKXpuYpSgvzYPt2ixj7eX5PX00NyAXOrzvnrs+Qutn6p3FG9op9Kw2+HsyVM8fPBAjSl3kCjpb5knTE63lJg+paZfr1fY7YbiOPZdyrgHTiMcYrpC4GK7AYiw2xAunj698lq+sqHx+MljXL92Hbdu3sS6X6F3aVvl4nyD7W5E3/fYbi9wfnEO54Czs1Nsd1tstwMODw5x/fr1BPby7bmMAO+B07NzbIcdDg+OAdfh+Pg6rh0d4XDV4+DgIN/fkVJypZCSgJNnJwAYm80mt7vBs2ePAOoQOHmVht0Op2enatcjIMSA9WqFs9MTrFYrnJ2d4fDwCOv1EY6PruHgICtr+LzlyWDv4FcrPHn0GI+fnqDv17i2Wpdt+xaTVGEhauEVkIspKwcw7Q5ETrsXjK7E4gEooFM2tmdeSaAwkIQg6UWiQb2875yvbijWgs+5FN++zSljRYgAKQPPbreDc67sBMgFfJHqOwesATGag2m6aBA7GYcqtj+X6iA5M5gA33c4PDoECoDxoBhATKWv0k+XQ3ycbx/+F0+BntMyD0roz9KONpRIjLEIo7aAm+bNKrNiMqi/UZ5Pi78Vf6v7tCjIDcjXY9M8Mgm8uTd2qmuq0wIqWQPa4NR01cBX12Hb0HQRsKQvutQ0b70jdVvgYvlUtptbStF+pv/pti2gXJoDqatlCOk+t9ZJRVvVL92uHdu+Ptm5189aulpDppqnhfFqOs12DhWm2EcrXZxzKQEcExwTOkcYY0yX7YUUQhk7h4PnbuG7P/g9fP7rXwWvHNh7dJTu0Ng9PcMHb9/Dr/7yx3jvtV9jc3qGjiPimLMOZceJMLjs8lrPLsCQDEUiOwpt1LzoXWY7Nxb0tfi0BTys3KAM8EV+S51Sv7RvQ7kELGlgvLSDrH9vybTSL/XZZe/adWALERXAY9dhfqKyDa4CLC2dZ3Kw8fxVdIF9dgmwttZRRb9Gm8Bc5ltdZcds25cwUSKqM1AaOaGdwpYPdRuad1uhmEtAe4mupT8ZCVl6tGSklISHaj6x87ovvMn23eoCaaPUxbVT0cpeXb/GgEtjsnSYhcKr97S+jRyxGTYYeJw5EhABxwxP0xlljhEcRgzMCNnRuT3flXf7rsfIIVGfEn6JLv1LIoYLrrE0WCpXNjQIHTabAb9++g6891j1K/jOg2M6MD2OZ2AE9L3HZrfB45NnePLkMe7evI3NxRk4jjg4OMB2u8XJyQkODlYgn86zdL7HZjOAHNB3I054g9Pzcwy7BxjHEcM4gnOICcaIYbNFOgAbMQw7eA+88MIL6FeMa0fH6cD02qPvgO12h6OjI4QQsdvukqETGQ4OYYjY0g4nZzs8ePgUQAKyafs77ZRcDOdgAKuux9HREbr+AHEcwMbDJYzR2iLTC9c7B1YeD9k9SLsjA9B7dF2HYdhBYn8TM6VZ0IKg7DTEAO/r26NFMQFt7xZRDj1wroB3GbsIMH0PyDAMJQxstVpVC0ErTyilKIWZEXK6YLsYl4DUBESoAtzVTxLlGbEbBwzjmJO7IRk1eWvR3r4uB0etktHt6z4K3VolfZ/+aaWjt45lTmYgFqjic61Xk6o2UmUERgiMqLpTK7L5zkwrLMYqEivA7BiFX2WXMPW1VigVUPF15hbdphX+1U+ekKdV7HZXS/7WoSwVvdS7S0pO12e/W/op79j01rZd/exSf1qxxZe1Le8RUTGu9WdL9JV6LO8v9bu1Pi1Q02MgA9z2AcypzxJvXI9jLy0JSPHvyRERI4M94QIB8bADDg7wm9/5Fr76u9/G8e0bKR7eJe+d3wx4du8B/uKf/znef/0txPMNxt0AMOA7SrfGcyzZSCSVfGX0V2OZ7isYhqEGzUTgbBjrXeOW3NF0tSlul8Copmf6bJ7VqLWuhXeZa6CgnQuyvnTWotluiOn/xA9cZcazzzbn9LLnjDxcMnasjGnxrx2vdrQBk5HR6lOrPWs867U98XWSay3gasG8rV/qEFm+qC8W5Ewto0Qn1enSJ/7IINLwp/RZy/iWLtcG7D5attaALfuMlLaOdgDml0vqenS0xZKM2VdaekO3o2nRmo+rFC23NZ5ryXGiZDBSnxPS5EPeyM86TA5NWeu6j3nvKc2dT87bkO8Nk5FGpDDUyOmOMuccKOdAYXe1MV3Z0Pg//h/+T/j0pz+No+vXcHh0iMPjY/TrFQ4PjrDqjhDCiK4jhLDD8bUD3Lx5Hd1qBe8dbly/ng6V9D2YI27dvIHVusdmtwXIYxwTgz47OccvfvEqhjhiN2xSCNRuhzCmwywnJ88wnG+xOTvHxfkZQAzngM99/jP4H/4P/vs4zDsg4zhmA8ThxvVj9P0KMTj0/iB5Lb3H2dkZhm3Aj//6rzB2PXy3KkYIwFiv19gNAwafD99ywAt37+CrX34O3jk4RDC5avEtgbWWcBNBPm1nJwsxZUNK2YyITFw/1V4tvUWp67XMbvumF6kYCVqJSL0CKjebDbz3JV+8jEOHVEk/loQdIwERa0joxWrrSoJrDj5K/5HSVEZmOO9B3mEYRqBL3kcGz3Z40u91KI8VXNbYyC9V46qFyVyBlGcAwePzkBUkzw1aYC9GAFQOIKfdkTyvKrd1+ZfpIaFMuj0BxBNN54BQG6kVvQjl/I9Vpgl81UqzBbybF1cqBVgbEKlOywfaYCpCUt2jodtrKUg737qeJdCn15Ktt2W8LbXfKtY40O/L9y0FY79rlRYQs3O+NK7LxrFPqVr5YsfapgMKsLHrcSZH5R3bJ0cYHcDrHh/9wufwzT/5E7z48Y9h4IDgXcpQFoHH9x/g/mtv4LWf/hzvvvYGupSJGMGlmGTHQEpl5sF5R8NnQ0jCi2a7AZySnUgab+ZJ5mi+XqKNpqkuFmBqusxpmI1uThKltcsudQK13uCYdoV1SKvusy7a+NH1aV2WfifYIbXGaHlJfm+VfcaTlRdL9NJrQcuO1livEgooxcqlJWNAP6PXv/7cFk1zMRBtqK8emx2PrTfEAKLaq16MGI5F+FrayRwvGXC6j9rRWXSgemZJ9lR1UvnfIm3seItOXehjocElKZ33lVq/o5xdvIyHtVPmwxock5yd0yLpYcJB53FGAEMSI00lUt615MlRI/uYPmMMzgOaZIODz587YowxZ/JkBsZYzopetVz9ZvCB8cZrb+KFl1/Ccy+9iOh2OHQdAu3Qh3x4mD08pcuKPvbCixi3N+D9lGbv+s3rWB+uAU6xxZv7H6D3HfqOcHBwjO12wDvvvQuAMGx32Gw2OD8/x8X5BS4uLrDZbADPODg+wM2XXsCNGzdw4/oxPvLi81gdHIK8x8Vmi4uLDdarFZx3uPPcc1it1njy7BRxu8P59hweAd26ww6MrXOA77DJZzYYQNf12DEQnMMYAhyl22GH7Yi+W4EygI3D/HyGTiUon1cL1AALAYLTuQgJDXGIIwDnSrYKQu1BKcqIk4dC0t/qRS/tS1uTYEv/izn2jjjHWOaL5U5zZoL1eo2Dg4PaexsTPYTJgdw/5yFpFpEBr88XojEYvutKWlHOwBnMxVtF+feYadF1XU4pjHQBVsztZRlLHBGGESMnA21FHivnMfosQJ1D51J4A2clTC5nqpG6KiU1FxiysNNirL1O5dk8OVPWqiwQcoo+yaAh2UkEEJT6ZU5C2gb1zoPJq8hjLjs1IBRPbqIBlbH43EYylbNhSpJJypkD5ZQMP5kDw8dFmOXnwSnjEzmvjIG0JcvZ4iACvAM4pr/FSJQMLCgHysM0H5luwlucU9w6RftiRmWCiDKzoMiCagskWgpY/229zjFMGY5AlHk204nzWs5zSlkxyg6VrPl9CtL2QQNLq1DmSmduINn2SP/kBJid4e8l4GqBkBStKO13FFHlJWcoAwRUsr3p7F3Jm9befndZlgSghEpRDpfywYEcYSBgWHkcf/R5/MGf/RAf+8JnQaseO0Q4BnwIuHj0FG++8hp+9dO/weN33sO42cIJIEzVInJKfZsyljmlkGsnR9dJSGwazDCEkl2q8x4hRsSQk3OokBodcpXop2VP5lOIrPGFjwiSGVB4YNLw1sC1qt+uZ+tM0npKwsJ0WTIOrH6ZP0tFlto67XtLn1ljWRwpdszCQ/oz7cjQOs8aIOnnlMoZ7Mrc6LZs3fL3DNwjOb4ExBEl3irpCNWzFngKRrLr2hrfrf7YeVqSOUQpfEZ2HoF5iJw8Z9tqyRqrK1t9Bup502F8LQNC6FjWhJHZug47PwlgU8EVgpemOmsatXY9bHvWgKr72dabNX/VNGvRp/V92/hNY9PfM3M2Hg+QNjKS/Kpeq8ad68G0dtL8yPkkBjOBHSEIrolpTXhKqXFjDMkhT+2EIa1y9Xs0ujWGccTbb72D3Rjw4sc+kg4Tbwf0Bz3Wh4fwMcKFCIxDOpA3pHsaIoCja9dxcHiEw6NrcM5hvT4AuRXOT08QxgGnJ08xDlvcf/A+Tk8usDnb4Pz8AkSEw8MD3LxxC5/61B2sb6xBKweGQ9f38MxwfY8hBNy+fQe77Q6nZ++BfIfDoyO88+49vPTyS3Bdj7jb4sWXX4BzhPfvf4DD69fg1wfYRQa8Q0CaNEfJGw7n4JEA8LjbllzEnmTeHYjkXg3hg4TKJI2u9n7p+FftzS1GACcvdogRYxDhyggxIkRG5+vFOYVpzRe+jhWW9qzQdW4ySooBkxVlCAHr9bo6LC7v9X46N5POnFBh3sj1wqo8ZSSpgxOzz+O1qYCiVC+mfOMsYD2nfxXg5FwCwIR078gYECllX/E5vCKr8BxmlruaQXjpa24DGQxUsdaU71lQ46qEbwadU0Wp3+V2bMnxz9LIZDRy5h0RICnTWuYjBSi41C1KiyFxkkXoEUDw5ZEEhrgYtwLYtaCbhaqZwllop3/I76sHSHWr7LrEFBNJkuwAMzBZC13xDHMxYuSm+0ro0vTuLDTP3Iyr27DtaS+iHevMuFE0EPCpFU4MKvtYToNNDUW4RFvtAdT91Iq7pcTLGM3YLGCTdNqTIp7WDpTM0HLAGhK2zn0gQ+pPHcL0k6bvEhu1QYYeY3A5tIcJHh4cI1Yun5NwDmPv4W9dw9d+79v48ne+Dne4hlul712M2D07xb3X38KrP/0Z3vzVa+DdgC5EuFx/xHSWwjsH76aQUX2mTeS7KObkUU4ycrfblfTKQm9y9SWs5dZwRWvCBH6otKL4AlluiWErvxu9rudGNjW03JX1IOtD9ys/UK2rFi8utWfnC8hhvkhOHssn+lktQ/VOrwV8GqzaOuR72UHRBoZt0/L5JNeTPHPUiWLIRkIbvC+B/fK3CMPs6AGJ42cZjO+Lhlgq+jmnaK3r1DQq/aaaTvK77IgtGQ4t42ep2DNrhc/38FVdJsegjE3vmLWM0laf5L2Klxrzp5/XY9f82zLCRaVbw+GydVPpGYOD9tGmZWgRpcPcHCW9NfKlubqeWpeIDHaOEJkmbEHJISmX7jJRSoZR3pM2HajLUTRX3Nf4UFmnut4hjhFPHj/CGEfcef45XLtxHYGOEdih71cJ+EdCYIeD42voeo/79+/jxo0bOD6+hvV6jfPzcxB53LnzHO7cuoWz02c4O7/A6cWA9969hwCHW7du4+VPfgK3bt2sLo0LGADHGAPDuw6Hqx6bi00RpNeuXcNHP/pRAMDR0RGGYcD7995HdB0OD1f5cDBhtVpl5skHnbOwk0xKctgvWYuJwHI4uuu6BJiN1LcMqhm9ANc8jr7vZwe5JsEphktWWt6Bh+nSwiIYkD1T1Lr5nMsOR6uPMg4iqrJzxRix2+1AROWQt31PYuJ3OedyyTrVKERT1qAQ41zhqnELYJNMUHosWimVzzJQSJcZpn4fOYfkA20v7MTL9UFNLbRj4zMgA191Adc8tr4WwkR5m1vVZ41LUUyWHkDyGkCFzlkFb5VA+h0Ay3melkKoFUkV6sTLwNt+tqRsNc+XuXFuRi9QLQa1oJZwQXsQTv+u+97ymFoa1WCsNgJmvHGJsLfF1tPinasoaBmT/L707FWVPTDRS4Pmwou8rCKW+mGBkJ2P1jOtvmtwowGx5fFdVoSrAPSR0Lk1djGA1msMBx4f/8qX8PU//j6Onr8F6ny6oG9k0PkW9999Dz/765/g3dd/jfPHz9AFBo8hZzacy2ctE/XYpJ86xJQ5JSIhSrsYteyuD8fKWOy9QfuAswXjFV0w7awu0Vf/rvusM+61ALztz1XLTB40ZMm++i1Pa3pWdTfas++3eLbVxvSZdnIRWJ0Ra/W3Fe5ZniGkA7eNOVySK3rttORZywC5iozSwHypzOchOYVgQHZrPWt+3yfzMniare/9Jc2BGKAzXdwYVxqvOK3qPpQ5qsZ6+bxYHav7IcBb9Leub9/61XVberX0rS4ca6egc/lc7fERur4vn1kn3NLckTpnrPshz7jOw3lX8KGl6Uyv7ylXNjRu3b6Fs7NzjDHg4uIc290msUOI6DYB66MjrFYjPDEGB5xebPCRF+4ijAOef+4FnDw7w6c/dQznPfouYLU6wAY79H6No8NDXN/ucLFj/MZvfBnr69dBbjIupi1uQudXiDGg75JhAxC22y04AuOQDo1rcHP79m1473G62QJINySeX5zj1p27WK3WSHIxMYOkal2tVkW5yBbRtOWdJ8E7cKhBm54IXbQAkXY0s0lb3nkg3/IcYwSUV136KOOSxea9R8xpey2YsAfTtZAMIVQ3lAu43263KfVvZlzNTFagtxaXfG/HKoaBKHJJL9xaBDI2mzrYgjlAtkfTTlTf9wAuph0Wnt6pzrBErgCHblu3UYHZBrguQoRQ3Q5cC6SJB+b0wTTXqJ/TPomWIrVznRR87v8CH+r25T0JmQg88ZTM+RKY0W3aMwalb4q22ji0Y7E0ScqlFmLy05MDqcP2ek5nnlq0Abvuo+VZqyC0grRgcglgy8WIup4l5aEVkRXkul/6XIAFHJqOtj3tyKjqJppuOTdja86l6kurry3Face5NL7WM+kDwDPBB0IXU2KBrWNcHHR47lMfxR/+8ffx0mc/gXDYY/CAj0C/Yzz69Tv44K138eO/+BHOT04xnF+gD+msBUeAuyQbdDirvlVZxtx1XUl+Yde7zIV4gSWZhtC8JVf0+GOMKbwQ1KSdXn+Wv3SdtjC3503a0Ouj8B7mAMzOS0u2L82f9yktZlCJTCzPWr1h+VN4vupDNU7N/83u7O2vfj+tZZRLetP5BQl+mp5v6T5NqzRfEVHV33L+tfqwtMOqS4tH9o1Rf1+9y2x26/Q7OSrZfKexhK6vpYMsn+6TL61SPs/hZloHWB6yc0AELBmKIs9Bbfmj69U7bBr7WANHdK0UG7Fii6Wb5cPLaGO/l35enF+Ar1+v9Mk++pYd7jIftZ5O7zeyXjXwxz6e1eXKhsbvfu+7OD09xZ//+Z9jPBswbLe4987bePLoEV782CdxcXaOfr0GEHHgE5McHx+DMzFWqxW6boVxHLHbDfB+hb5fg+II7zocrD2uX7uOo6NjBDj4vkvnBdSkjcMAUL4QBg4cgYAIH4GuW6HrugrIPv/88wCAzXaLAyZ0ncPzd1/Ao0cPAXK4e/duAomZAWWXQUB4IiwQxoCVd/Be4lg9iNJWu534yhhRE1QmpqFY5HuxyCUGTs5NhJhiw9PZjekg1zAMAFL/vKOy5S9KsMS9G2aw2aJijGXczIx+tSpbgnocwJS1QX6Xvmg66HGVZ1w6V6ANCAuihIbAPHZ05mWltGUYU7RZuThOe9OlPgvMJLTI9lsUrwbJRUkTIaCuxwpUu7W7BDJLe5gWu36XKJ/B2CMUdd9KW+LNWQJ1hGpLVeZd96nQoTEGSxMtkPV7RFPfhWf1XMMADQtE9ZxVIEk9Yw+423mwaZaX1pydS+HFFmCcgWEzF8DktFhSJvadJRCzZJzN2uPa86fH1lI48p018i8DEbZd23fhJQ1o7ZzqedgHYCkhBqwigYNDIEI8WoHu3MC3f/B7+Pw3vop135X7XfoR2D09xWuv/Bo//Zf/BvfffCcd7A7pnIZkjkrABSA3B/+alvKdTQkO1ODROYeQvX0WHNti2yM3hSK0lLYNKy1tMADUz1veW6Sp6UuLT3VpyTcr9yz9lj6Xf+IdtanMbb9a7+tkIvPv9wO0feMTfZJ2NBig9nO2v/b7KIdpUK9LKS36aLraLHb6nct2J2yxa9PyVusOK3I+h98tz6Ouw2Kbq/ar9bulq6adbXefnrUyp6xJpZOkft0PawzN1paR3zNMgRqjtNZhS3a25K12cGoeIXLVnOn6BQuK7rP1tuYgzWGt9yYHXkSOmqrC1/R8Wf7eV65saHzr29/C5uICN2/ewD/5J/8EngghjAjbLR7ffx83b9/BuNtit9vgWdyBEHCwTsaEDH63G/ICZIxjulPDgxGJAXJYrw9xcHiE4FwyIFw+KA2dQjVPBnkwEtjuOoeu63F8fA1d53F0dFQYIxEkwHceH//4x+AR8frrr+HsfAPqD1L4z+qgXCZXLex8iLbvHTyxyb4TAfIVw2nm9b4WOJWgxnyxJ695TIY8JkbxzmM7TpmepFQpZTPA1MpeM5RmDn1bOdHEWMMwYLvdwmWaw8Y25hJjLAeRtcWrDQNppxLwDDBN/dbMq2kk74uX0CrDlsInENbrVQMsTX0uQpeTcaLDD+qFOxfmRAS7XOsQiTS4JrhjTMbsQmmDOYkVXlZsM0HLze6nZyIjso63bIMV+z1QGwv6HStkdEaUdCajvpSq0Ex2KA2YtUpIGxnye1CeXus50iBGPtfJEVq7NBoEa34jmu8oNelq60PNK0vval5uzWfrM/l7ybhoPddaX/LckhKy86CdAEuKuGVIXIVmtZw2wIwIYe0Rrh3iU9/4bXzt+7+Hg1s34PLFql2IoLMN7r/+Fu699mv87C//GsP5BbAb82V5ybsZOKZD8Hkdelffbqxls96BtZ5m7bwpSnkP2NJ8ZWmiwfGHAWpLJfHrv3s9UrTBDbQNXs1/877UXlKRH3r3aAmoNI0Zt3So+28/xgrols9SvLs+T2vnR/dZwqylkhZAXWq7RVO7NqzTpUWv1hy06rPvWOAsuzpWriytae3o0fJaF5010YL7maGj390jN7XMWSq6Pcp9WDKgbGkZ+bp93Uf9XQ3U54bEvv7avs/mj5GyTWqeVfNydHiI+5kXWw6BFj8m6Vjr38IX0qzqu965lc+vKruubGicnp3g/PQML730Ij77mU/jlV+9goP1EcZhQNic48F7F9iFgBTWxHAU4Z3cAB0zAcSrEeD9CN/18M7DUTo7ul4f4GB9gLPdFn3XASCMu+n+BgdC5zow5UPTIWQvucM4jNhsNrh9+xaASbClMxket2/cSEQh4OLiAiFEPH32EOMwYAjAbhywWq2QYsQzU0bA+ewpQsolnASlS/94LlgAWYDT7oMIVLslpxeMGBrkHLxzCGMAeNqWZ4z5sCkVgc2cLFmHaRFpT6/0aw7AJwNFnhvHEev1unwnAgKYZ83SAtCCmCVPbAtYyrOVsFZlqd+yGDylbXrmRNfdbocQY4orjJOhUQnvnM6xnqu2ANfzWg57yyG/6hmAeRLe1QJUn2n6pH7V7dSemvRPCwG7hannWN4PBmxogVWy6ahyWSwv0XTGpqVUrEAWGkTmcihaA8lxHOHzRY/1Vq1eR21Pl23Xjt0qOmuItISijK/Vjs7QtE9h26KNWD0+K/jtfQm23hYQkWIN+da86DVm21gCOvLskvzQ79rQzEWFDFQGsK0f0OsrPRtBGHqPF7/4WXz9T3+AW5/8CMh36KmDHyOGsMP5k2d44y9+gl/8d38JbHboIyOO6eLQJHMybQjlHg3CJL+EPhowWS+qHTNg1rACFlaGWVlfy7F6/bfWYIvv0VjfS9/Z0pqnpaLluzbEWjSx604HlFhnkV0Dlk8s0Na/axrbPu0br25Pf1fxfjH6cuz9Qj8s7fQ5xxgimGr+tg6BVv+uCtisrrVja9HS1p3GNt/hAGTe6vmxsmRJHug+VFgoM7qVo02+0XR287Vgx2N1QWpqWpta707JWua6Y06j+i6yJR0guKaMdUHW6u+X5s62LZ8XPAXhzTlfeu9BjmbOk/JT8XPd/oQv9Hoq8kmds9RjaMnJy8qVDY1//I//C7z/3vu4uDhHGEfstjtcv3E9py/dYhgiQoy4dv0ann/hDrq+B3UOKQwoIEU+pFRyR0eH6DoPULoJ25FPqSQpAjTC9x7wHbbbbRIsPmUc8T5l1BEg0zmHcbsD0OPw8AjXrl3HarWqGOXg4ADP3b0DJmDYXYBWK9x57nk8fXqK+w+fIux2iOB8i/mugCBH6aCfYwAxCRDPHgSC8z4JpsiAyi6UZycdEHT1YdWi2EIomWKEiSVsyYkyJErj7Dw4BJBb5ywBmbkjpzAyTulFwemgNTAJdgmjskV7mIjSZXf6cr4iLBhTP5EOuSUPXi30hfGstT4DbY4QwxS6BJKD18nroQWyvSxQ00/qDiHAxZT1IBDQbQPWvsPo0jx05EuWKOd8qT9lYqo9s9rjGGIo+toaDY5QUsgh7yLlSzJBXqY/JRiQyCftFZ8pIAIYkzCxW5RJ7IuglhixtBNlhay04cs0pMY5jbY6t2F/FsMA6l2jPMpIpD0jYFreRjTmruu6Mrcy76IE9K212jiROUrhU4kwkZM3WYzsZBSU3sORg5yK53ziReoPmb+RFRMV73cx72ZKs1Kear5aXm8PSme4tEIT+afkvBbY1gvWml9bltacVhxSNODjPNclhTAAa2a7VFGam/yc5FWnVGH6qfsnPCS0y32JYESK8CAgZ4OLyGmmwejh4DnRfQBw0QHXPvICfv9P/gif/NIXEfp0q7cnBxoChrMLvP6jv8a9N36N9998G2GzRRhGhBjKDoOeoy4rYklXrPUDK37WfWagZJMitfssn5OinaZ5Cxy3DIgkL/QFl4kWmftSGlKg3PwurgcuDgjki7nSG1lMIKmDGlTYvlmwLxd5LfGbBYdL39txLwFoC+5aYG9m7GJ+lm16PtGjVa9ex6x4I8mnHI7J9Vokt7w3pHdXdd2SGl+cdxx5ms0EDgAzJi0rNXDTz7RCU1sGRz3H044SiKudLnJA4DryQdpxRAgNINvq1xIvWOCaIkPa5w8sb1Q3rGMy/qjUm/BjpLkDJfWpvWNd+BeV+G06ofTYWuunql9I3NCrlgelDcuLtn5r3FSRIunhqt9St4T1zxyHzCV0NAr2QnK+pMv3CjUSb+REP0QEL1RTkRCOUqr9qX1cqVzZ0BiHdAleyZZEwMnJCY6Pj+GdR+TkET88OETf9Tg7O8eTp8/gkWL60xmNLoPEESHuAAR48ujcCiESTk9Psd3tsI0MphEgwna3m0AictZMEEDJOEAcEQKhz/VvNhsAKBmXvPdYrdcYxi1CCNhsNrh16w6uXb+Dn/zNL7HqVzg736GcgciC1+WcwcNuBDgpsJ7WkEUsKqYwUUxbrpPinrI2iWCIMaf/jLFkatL5zDmEDJxFqSWvcNet0fURwIgwBDHds6KvY+2lT8zp0kG50Vt77ibLl0vqxSo7FZf/AUhCcwzp8LaOSdaAULcrxlMFmkCzBSnpZQscNAtcex21MVDaj4wBEfCEzek5ep/jtscAl+97EKtddqmYGRHzON+ifJQnxSq+TI4EAGI9/6O5PG6qI2WQsgInxljm14ZWlJ+qDwI00vkk+cv0DWKYYNq1Iaqe1s8ugQFKkr3wM9T7AiJFCcgNwK06ZA22dhZmwAKolLulV/nJE/2mzibDIiBkGy8BZBbDTWWHKwZOAcNUNJCmt1ZkrbDAfdvglNDeJLcoZU8SQ0kbT0uGhKaPVlAtXrF81/I+NxqYgI/tQ/5Odi+d5ksDzO24m2sgG96IDOLEj/laDIDSGQx2hIEjutvX8K0//F188Ttfx+roGIx0Fw6HiPHiAvfeegd/9a/+DU5+/Taw22GX9YN26GhvpHMpdBaxNmA1bZjTWSlJvS3PtWLmwcmpI2fVnPcYF4D4PgCu/9b0A5Du08H8cyA7t0q/ywOLfKT7oUGOBanycx+I1HxoQbAtIrdbbV0FqNo2od7TY9rXvqavPm9T5iGmEOf6Itk4Q6Qtfmm150XOcR6HfIdatum6Wm1Y48g+s8/wk3mJOVGNI1d2WAsvUx3mWnRYdqjGGGvQr95t8Y0tFZ3z+JfGpN/RYYvNEDEgu4zm709rvr37dllp8aQF9HP6Y7aDpb+347Pt6DXSes/KCtFjlrcjR4zjUHSDpV06meAgEVEMkb3S5hRxMvWhvWtRsMQVDQwpVzY03n7rLcSYsjjdvnMH3nvcu3cPRIQhBIAIwxDw6NFjeA88+uARbnztayUeVghU/rmM6SJA6ABH6V6O1Qp+DIg5zKPrupIdiVldeESEvke6WCQyHj55jFs3r+H2rRsAptApAPAsl4URnO/huoDz8y3u3Xsfb7/9NoYRcKsVDq8fw+WdhRjT7YesbpF2jtK5DefSFjzVYyrx0GrCNFNwNhB0vJtmNkmNhxgBUjcnS/3kkrHGKdQpjmMBsVqBSiYhC9ytBU2U06N5XytVw0RaCLYEkH1Gt7ekcMTIKoKR65Ar23e7uOR35x2GGHBwsE47YDGWcCrxgExiPu8MFGM/tVHmwniyZNEuxbkvFb0w069zRQugOm+gaajHq/tZ3t2vY1XJnr4Jm8z62RJyFtS2AGV5z4RJ6LbFE6LrtL/rz5bAgwXkLbrouuT3JTB0lTlsKVSr9HWf9TMieywfJ6w9r8PW3QKiLRBv/9bPLhl3rbI0v/sUZqv9Vt/k+XQom9IFk0lwgsghOmDrGHS0wue+9hV8/Qe/j+O7NxEdAZHQMRC3W5w/PcHP/uKv8OqP/wanDx9jxYy+8yVph9Dcnt0RgKmTWGh6aiNF85nNzNMyEqobthu8sESTffQtz3E9F0vF1vNh5zlmcAnMQ7xa/Wrx4WXFho62QFlL/ti+a56qz0nMAaGeL/3sBJ5q3V4PtD2HSwbTEt2uSqclD7Yeu9Snx6TnQkcDJH5W9zGhdphw4/MiM0jtHpu2WwC+JZO0sVCFRO4pV+etFEmwL8SxhXla7dm/l5xHrb4JTrLhzLb+y/hbYwvLO606dBtiEHJkHB4ezeonkqQyZudG61wzVr3D/u+zXP2MxukpDg4O8NXf+R1cv3Ed5xcXON2co+96nD47xXi+QRyTl/302RkePniIMAa4fr7IE2MnQ4O8A+Dhuh6vvP4Gnp2dIxAhjBGr1ao6jJbec4ghYDfsQN6h9x7OE9659z6+8bWvgrgOu/HeY7PZYLfdJe/TGOBdh9PTR/j5z3+Bx4+f4tnpGW4/9xyuZyOFOZ3ZcFkYdZ7gsmKJOdQoDaXtVdSLXjOhLDyt4ORz730OUUohBckYS1ao8zmdIpI3PnIsoVPOeYQw3f2hd0n04rECOJ1pSEpa3wpbmBT1opLxtBaGDstoxZ3L8zZeV4wWRht0Cb/ocydlAeQFI6FsTqVDnnxIk+cBSGFapV9KGFb9j6ESAkulEnRcZ/GZC4x26mPBEy3gLb9bwRnjdEmOVajMPHkcFBXkFyvClxS+FnAtAdiqwypaoml+NZ9fBraWPH9amet+WoAvv8u86nnSfNUSpHYeNL9phWJBp+6r7C7aNUBU74LquW2HAfBsfovyUMCgNTe6vlYf9827pqdVbLZPVwWdBABMiW8p3XTNziE6Qug9nv/0x/Ddv/vHuP2pj2L0hA2ADoQVCMPpOX79y1fwoz//1zj74BH4bIuDyGDH2Ib6cKLupzbe5V8IITuJpudsLLamh+V9K+/s55ZOdv1anmnNoXy+ZDAkUcZV31v91XOzD7TLeOTzfUaNfsburLWMA90PS1srKy8DhHYeLouHl+8sH0/tAckZZZKWpDdn7++jRWvtzOb+it6hFr9ZMK3Hp/uhP5dEL/vklOY/IkLnHcbYTjIhz852+Br9quQjT97yD1t03wsd4/Jas+vhMppZ+Wzn24L6mUymxClWHug6W3q11e+WY7iqyzgr5VnBexcXF3DOVQ7sqZ60UxdzOF+K2c4hkyYdu6bd0jwLrriK7JdyZUPDEeHmzZv42Ec/imu3buJXr74Cv+rRHxzgVr8GuWd4+ugpHAibiw3+xT/7F/jhD76P23dvl7SzzDzFaAMAp3zi5B1OT8/x47/5KUakeLO+c8VbJcRMXvwAIgdyDkyEITLIEX7x6qt48MEDvPTcXex2u3KwOcaUUSndtj1lwvnRj/4K4xhKzOtqvUoe5mGA8ynOOsa0hR3GgLUAyewNcJQOHAuxJTypAPEMNjQDSeiUlBjnB8VSyA8hQlLaphAhqiY6x4Tm+rq+L4JMGwO73W4GiuxCskxZmNgoHzFi7Hai9iASTfcyiLW9z0Iu/XAaHs9Bq9BPvDUJUBIgB78Y8D5ny2K5ZT1/gQR6a09a+mlTfFpwoOdIvtc0Kp9lRSKf1+Bn2iWR71rx+JpGGqguLWYt9DQt9feyca2VnG5Xe2SX6tKGZalXvqf0PyuwhfLOUVWP7Xdrh0hopunVKpZ2llaXgWDhXfuZ7oelsf58SZFZwFrxTCM8sMUHMm7528ZT17Rqj23fuHWxjohZn83ca7ppPm55GGVtRI4g5xGZQN5jBGH0hKM7t/CdP/gevvDNr4LlPgzn4AMQzzd4cO8BfvXjn+C1n/0Cw7Mz0C4AY7rIMqq7cHRf7VisDGnNGzOXQ90tXrZjbdV/Gd11H1r9qcbAbQ8tEVX6ozVvSzvMeg7tWiw0aPTF0k8bRpeBRytnrO7Q7bf4W9NN/95aW63vgfYOQXougrnWZ2WOU6VVn7UzSssGvRaI6rur9HOIXNZ/a3x6rVkv+T4ArOvThgVhvi4EvyDWgLmMzYxT6z0rt/S4W9ig9Ae5yTgPV9ZFeNR+Z9dsmU+avtdjb9FWntu3PjWNWjvorX6Ro8In9hkrl6Q+KyflPR3KZusruiDMsVcIAX3nsd3mC0RVNAuAfN4rOXe8dwgxIuTQTAaDUGMbfba3tT7LWC6RdbZc2dBI6Wl3+G/++X+DgRknF2c4OD6E7zv4rsNz3QEc9Th5/ASIAfffv4//7s//Jf7+f/T3y43QwowxptS1xATKZyF++rOf4YPHTzBmYToOO+y2W3RdOhQuE3DQrxEjY+CA1eEKwzgg9itwjPjLH/0If/bDH1TCrYA2JI9ajMDFxTl+8Ytf4vTkDBzzXRVjwLDbgfJZBRH4znfouhVcFhIu354ZQgTzHKTJgrE3TJfJVwxmt1wjM9hFON+n8xrqVnJyDshpGocwwsnhM+achnfO2MIoVsDHGLPB5zCOKUWwHKLXTCW/68W8T2DoMdndCw2abIy7xB23lI4V8AUc0tTmMA4AUowsKuUtP1Ps5jSOhUVCU4YlKwjk99Z3aW6WvQJOhZtp0CCCygpxTc+FjjYBoJAlGaWYFBulECqVkGM2rn1FK5Gqn4TKILXFfiK8Z4H0vtJSFBagLb3XMuRbwPAyJWTf0++2vmt52fV7LXDYmvsWoLoKzfT7dh1q4NQCzy2gulS3VcZLzzvnMcacDco74HCF3/zON/HV3/tdHN68hpANjIMI0DZg++QEb/7yVfzqJz/B+2++CQwBLt8rFB0wusZOmFH0S0DB8vzEy+2Dt3a8VwErLTCx790mkBZbXs05c3JgyeFaC3L1v7kDa/95iiUgK/VrYK09sLqOaRAoOkmHPNuxtvrx76Nctt4LIMfk3tLrJcRYxcMDE/1suNxV+pHaqh0ouuzjjRbIt2PU/S/fcQox0kZMek4N2tKEAJg1IM/Y8dpoDGBy3M12UixIbYxZ87P+m3m6YLDIyT1ssiSTiGhKrNCYu8uMIEvH8mxjbJZmesw2nFU/a2mg5QZR62SKPAfsdvXxgslooXR8gSglNPI+9TkGBMUf2sBtta3HI7TUDrDLypUNjVW/wuHhIS62W1DncfvOnRzbSYghZVm5ffs2MAacPH2MEBj/9J/+f/D7P/gD3L59G875cjg6xohxGBF2I0AOu8D45//iv00HwZnRh5g8V4C6OE97ZTJxh3QAZgwRHAJ++jc/w9e/8hXcvn0LYmxwIUgKuXLU4V/963+Dp0+fIUbOt4rHDFhHIAasVmv0zkPOalxsL7DqPI4PVrkvLh+6rT0bYz6x770HcgiFTFjJQcxcttvkHQn18jk0DEhbnyFExEgIuy2244C+mxg7hpDrSpms9EKwgkkEqHwuN6BLv2W3SGdTaSmv1mKzRS8ULYx0+1ohcxaIk76vQZVejHohTIuP0XUeDMYYAhwnQJJlba5PFjtle2BJ6bLYCxXw0ovP0jPGqM+PL4JOuyCJUtiXLFgLBPaDmvllUOWbmLIESSalwHFSpmp8uh9WSNp+MPPs3E+qrw3Ay2ei1WiihfCbPNuOBZ0MRE0Lzc9XMQxknlrfzfp6SV12jOnM/TLNrhJeI3Uthf9o2SK7eXodtMCHrsOGe8kzFmzbXat9dLAyptCjPCRrOdEIhJRyue8QHOETX/ocvv0nP8TdT3wEu95h4xieHLptRHxyioe/fhc//td/gXtvv42w24CGAT6ndQzEYE8IDqAxZ9y7QmkZnJpGdmx2DlrA2oJyzW963i6j5+LvPJcZzMlpYflK8xtRfYfRkvFQ2iGUQ/CtsVlwPt3BNNcNpdDcGN0XzteiwWXPXuX9fe/moVfPlnM+DTlT31u13L8lA6B6Tiu8hbJkYMh3++Rf+k7OJ6L85CSwK9Bq9XxxXoqMW+iDHZ8GqhXfGHrtm9OWMaPfKw6vmQerZXvU6ylyrTNaRkMF6hvruzW38kxr56wld6282Fe3/CuJdbBsY0lEjWBQ5xz6rk90iMgXhCqdkqM/GFPEkG4zifDL9e2/d0Pj5gsvY31wgPV6nYSdeFM4Xbg3cgB1DrdeeA6BGCdPn+C9D57g//7/+H/iH/yDfwBmxo0bN7Ln3GEYR2x3OwTq8P/753+Oe4+fprRlYcTFdkDn+wxuApiToU2UYggZQNellLjjbkB0KbPLgydn+K/+2X+Lv//3/i52uws4RwgRiEQgDuAw4NHpCf7yr3+MXWCsDw9wfnEOjiPCboO42wBdh+gcRgRwiGB4dM6jg0cYxiyUO0yHjRvWLER5x5x2LGQhli1ys5hKetu+S5cXckipGjNnOe9B4wCKE9NFJG9yiDEZUKC0JYrEW7I9GmO6YC+OoezcMDPCOKabHxnonE9GW98n4ypEeHVuowUo9MIRoDwdRKvjFjVA1Yc2p3qQve71lq3U0wI26V8ExxGu91itOjgHOBLP2ZSmrQbIDFCAHEidDjEQ0qV7KaOaHbMFErXiVBOvChFVdVnPtQBV6aMd31LRoMjOCbr6sD6HmM/6UM5W1fZU2NICXTOFh1rmayGdUtcmgw+MnCY6A1uiaidE09JVxl5KwMAs4IsrPmnNUUUL1e8lQb4IlhrvlvXkHDgohSf9xcROSwpVUl2ShLQxikKX8Du9g7RPwelx2tICzvY7eb+1tpZAdXax5PSIrpJnlDfiPfKa9Q7RE4a1w+FHXsL3fvCH+NSXPo+u79IuBjO6yBjPTvHorXt488c/x5u/eAXPnjyFnERiMEZwSg/s0vkKDom/7D1Fur+LhpwGE4C5v2N57JbWS8pX79zbxBk2FMUakqXvSGMtYFQA4AIf6/5pGarlyiLPXGIw27VT1moStmn95vNvZTmoOpeMHemj7Z8O3bB0ktLaydGgTbdlweNEc4Kjafd6FkaZQ07EGVhS2ANlt6YFjHV72jh1UARSRjiAkh1Pj01+b8qQhfFW80qMlPhE5CmDcs56ctMh7aoN5tJPycRNcOCQ6tL82jIIpOjnCJMRp5/dx8d6PvTcT/TFRLzcb0DSZrNK16zok/8vYD3pZprWm5qzlr6wa1fqZNV33dcl+an5YknOyLOz3f+YdLluT35f9T0O1gcYaJd2mRyBOMkN8rXzz2WZTSCMMfFIuqYiA8KYkuzoHlXripMz96qOHuBDGBqH16/DOw926WyEk9guMGIcEJEH4Ai3bt9GiBEX56f4t//2L/Ef/8f/IANuTndV5Mv7QCnH+lvvvAOQT2FQIaUmleKcz9erJ7A0yGGXQNjtdmlCQp44T3j73Xex3e2QfNwRIQJMHh0HOPJ4+uwUm80OzMB6tcZ6tcLZ+ZAZLmV2GoYRcB3AhJGnXZd19Cl3PxFADpHngrOABEIxLtL3sl2bJlVbqnKWou/qA8V6PY3DCLjawwbkhWtAidRtPQy67u1mi3SlfVbGZgFI/bMbvlEbGfqfLAh9+7emT2shpr/rzzRw0IBLtw0UjJbogYjVwRq7Z+clnZu+vEfeLUqVMi0E9DVA5pLymglJ00Zd6rFV7ShlI98Jva3wrg2UuSd7CXAWgR257KDo91qKbKndWT+MsGydZ5EwPb2rxQJWFY/U4X1T/dVdMDSfK2sIal5s0rzx99IzSyDmsrLPSCyAR4zM/C9kmWF37ZYA4j7jsNXfJcVu16OdU/t+UczyLy9C/X10QOgcRk/A8Rq/8/vfxZe/910cHB8BLgP/EEHjiIfv3cM7r7yGn//bv8L49Axxs03joKmtKRYw9auzoFC33TA6dKnTePOM1haUWiBaO0j2G2VWZrVAczSAj9kIhWxkLM23vTTR9uMqPKvHbp9vxd6n5yI4WhpMMtXSotW3pR20K60fA+gve9fSXssnGad8bmVceT7z4771Yddgy1FW3oH0gcutzy0g3pK5euwakE7PpfT16X3MQGNLNlDpEWaZCokcOjelytVlSXZomrTm2ur5Srcb/rV60/ZNJGoU5w3quSjnOtHgS7XGNX5pre+KhvnI71KfLU/oYufXGql6Psuco42HmHM0TsaclGmE/E6I8/vUZKa98xXfAe3QX9032/+rlKuf0chgoSzQPJtiPTqXbsp2LuWov337NrwHttsNYoy4fv06nEsHvLfbLTrvk6fA92lnQzwbSB58ZrnVe549KYRQpTWcgEXEOKbdgePjQwDA+WaLwIy0o0QgeIQxIgwBm7MLbM836c6MfIlUGFNcm+sSM0fPGCmWvO8hBowhonNzhaS3r/UZAvnpvZ+MIjVxtTWdUvG21INeyDoTExOVw4xS7HkKrTCm2DpG1/XlWYm31HdgtASf1KvTeNoFIL/rRdgSJEtAsWVY6L/TTk025hxjl0PgnCMgimesBdgoY5ZMS1aKEZzdFHMPhdSz5JHZV5YUyNJzFR81Ck2ytFlH9azUIUCN5x6YJcVh52rWD6JyqRmA2ijA3CCVzzR3X9ZWxQdop0rW7dkzPUt8V/qyAIZsv+WzqOSU/rzUnb0DLcDZGqv0uVN0aZ3Z+NuUpbHp7/Z9b3lDDIAc3AnHdfYaECE6ws4Du57wqd/+DXz3T/8IR8/dBboORIBnAnYBZw8f47033sLf/OhHePbgA2AzANsBDg4j5/A/orJr0pqr1vjEoNXFxkVrmbhEE1tawK9Ft+muqDB7Rq9v+d2OLSX5KCLoSmXf+vx3LTbN79R3Lp7SJSC2BB6BRCd76LQF0Mu7qMyv2fg0HW1/ddvSrxgZ4CkcsSVTlgwEK79agHLJUGiXenR27S3x3j5+1eEwlfxNLwNwzbEt97BO279UbL84e+Fbob77gKvFEfqdfx/FGkdkPtPfLfVZjE6NC+SZy2RJC1vY+m1/W/f6iD51Ll1Muh2me84E21gsVfEXoQITcoY2nZtt0+xvU65saHRdV+L39AQUQJt7FSKXA7XXjq+h9ynr0263K58Pw4Cjw0PEGDBgMj6cePQ5nYPQoTg+GyZCME2YTAWs+8k62253SHdMpIwIQ9whxhFhTJd68RjSzYch4PDaMTrfpXAjT/l3gDwhnZ1JKWV3wxYxhhzDSSUVrd3+jTGlDRPQLp9LelzCFFokAjX9TLF25BzGMFZhJM67fD/ExNgFTMVpoWjwonc+iNJ9EcJsiW4OzFNmL+Q6RFla5rf1Sz0tY8EKFT3eOeiuF45eDFawWqWVdjMY45gPSbp0aF6/VymT9GHC3CzeWSrdoJy22AodO75Z/+0CVt+3FrquU49d8/uyIlgGWrbOQntHxfBqjU334aqFwVW6Qe0UsHxQCW8AcG3wuEQ/IpoJRV1aXk2ZL7vLsgSMdFstOpQ1p8ISZ3PKy/NiPe31+CZwqTO3tfprjZiWQWTB29L6adUvz7aAIgNp5zcrKSaAHRA9ITqH2Hvc/vjL+NYffx8f/cJnEHuXdsEBYAjYnp7jnVfewC9/9GPce/PtdGfSdocu3+TOlGQdi8HPUx+lH1Z+WECwBDb1PFm+bBkzrV3VmTwxfGszxuk+Opcurt1ut7P+yDNJl8pZvWk+lsqS4W1poNvSPKOfW1oXWtZP9WH2jjWqdFu6v7MQ0gZftvpu51ToxYpHrrK2J7qhHPrWdzotzQszpzBUPz93Z9ea/ru1w1b3lWZja9FO+mF3PW0CE91Oc44/hIwv7+esWTos1M6R5bHy09BEl32OI1uWQsmKXDafW76ysrLgJ/W8fqa1C1PeYc7R1/MsgxYnaPq0aGRlRavoemc0UDZBwTQiOnnuGCl9U/Xp8ZY6GvxtaXHVcmVDQ1uzMuH6ELF3PscxTgu/6zscHfSVp5yZ863YCfj69SFWfZ9uNsyxnpHTLdvau7vZbGb3Y8giLtuHcSJkuhF7B9+tAcnQRGnHheMI7yIcRvQugMctXDhAHHbo8jMeAI8jHIXJ4935AlTTzkNbuYeQwrTEUJJ43RBCElL5xmU5IC6THeXcRyU4UcKaCFwMrjqmlwtKsULOKsWJsXKKSOaqDy2FpBefZTj9ud4Jke/0c8CkaPq+r8YoYSOt9+0iBpCzljF4iAgc0fWduBgybet7PqTtJGhtSFeEpBW2Rs+S4quK8RzUAkvu9Wgoz7zNuySELB0melTdNGNpG2OepkszW0ZgS4houuvPl0qlkGmKodftlb6ptrWXxta/BJCktOKD9/XP1rnUplWmFQ0wKU/7fhLuc4P7MoCvDyvaEEZLP7sedX2ttbe0tu1zrfFXijl/5yTWufOIiAi9w9gRju/ewVe++218+Ztfw+pojSigZIzgzYD333wbP/u3P8KDX7+Di6fPsO5WwG5En28LZyKQdwiZhvla1EIToWeLX62RIH9XOy7q2X3Feg11sTLFykh5V5/PkDaTA2w7q0v6U8bF8/XWAkh2LBYo2d9bYOsqxcqV9JNKFIINr9oHSOzzS/rCfm/n19ar9VirD7rt9HtIoS8LZNBr0VCj2YbWs3UY3HxHzY5VdLj+rvWOnUO9e7cUhmb1AREBVGcZ2iczp35Ozh5ZV/Y5izf0+C0madFgSd9ZGtjv1EPNMKFpfLV8tWO09F1qp6x5cLXeW3qlJXMtzVuyzNKEM0iyZ0QBFAcGcwQuNuk9YWya6rQ4kIjKuUmrq2R8mteWeOwq5cqGRigCCpDov8DJ008RSfGC4JxHDLJ9A8QYZlfLbzYbhJAu5GN110ICfA7jMJY4dAHVsvhEWOs7GhJABbY7vXswwvsOXd9hjIy0RQEcHq1wsPagSLh14xArugl2HY5vXAOtVkDn4X0HjCnFne9yFg8QDtYHiNl4cH66fK81gTHGajejfB5iea/ezRCvJjdv04wxwtGcUWOMZadDiv7eLkz56X3aQWGex+Hq0Ci7UOzv+wCZfk4LxSpOGtleMwqlNQa98EKIcCGkMwcEnJ6eFSGoF4l+p9QV60vviAS81EJfe7eI5obUUlkS4BqkENFMKNq+XlZaClc+nylBA7R0O/Z5G350VQEj9VoPsNBSl7n/qR6TLlN/5s8uKcl9isKO/Sp9AAzA29O+PGdTelq6a36iBZDRKpaWul3b95aCaK0L/Z2NF9YlQUwC5exPofeIR2v8xje/hq//4A9xeHxcjAXPAHYRFx88wq9/8Qpe/enP8cHb72G82KD3HULYocvgJSJ5CGMOm+oaYLQly5aA0hJAB+ahaXYe9RwIIGvRcIlPWgAJqOdiH9Cw/W/9va8Pdof9MrnSMlbs5/N30HR2tMazBKT2FQ189tW5Twbo5+xP5xzA8yyGUqxz6rK51jqrtX6bMrl8ttx/W4fsXrRCRC8rBWsYOizpdI25UvuojJRW/fLTgmVN3w+j41r1X1Zaa97qDw2gZUz6fWAKT18qjtLOq6ZHy7Gh67zqXOl+7tMx2hFfUvhfsh6KHEyfVDp6Cvmcv6vn78MaHVc3NHLmJIBSxqKcNpOcS+FAOU1BiAExBnBkDMMOxIS+7xFCSht7cXGhRkElXd4wDPBI6bgmQ8MV4yNGRoyjSiHrMI71reEBcYrpBaXQrGGA63p477DdbXH3zi38Z//Zf4qTJ08wnJ9g5R0Oj25gFyLuffAAN+/exapfYdWtEMcR4ADmfNmfczg5OUlGFjinUW0rLGE+mTxhwLQzgdkz6XvZOYrlsKU4XQiEEMbKgCkCIdeXmp6YTIffSJiXBn1CV/2sFTRLSr2lyDQYl8/tIlna/mwp5/IcM6Dad/nwFzmCJ48xjumMBuet7cgYI+ddCocYA8S0d84hyCHxvCjFMwEgXx6o+sETKBYhr8csFN+noFt8sVT2Kc7SdmSkXAoNIKiEgBYgMabLKfUct7wwuq0lz24Ze3KyzPqn/27Taxno2nq0wmNQ87k5cObMMlaxTc9LRiyiOZi5VBFwGvgS7YS2l4GAluxgpB1M1s+Y13U/dQYvp5UpTXUKJrTrVLcrL5KML/dFzzWloCnAEYJ3GFcOL33+0/jmn/4Az3/6E9g6QnAeHRHcELF7eop7r7+Jx+/ew69++jM8vHcfvB2w6noAEeg8AjO8IwTmdGMt1Z5kUdrWgLUARiu+EFJ4rPNzYL8EXivcrHin5aG1c9CaR6Gvlnc2Zt6u1dYca1ls+7y0E9mSpft2dKzNcKn8yfK4qqPRv6XxtJ5tyQO9fhhQa1brJEDAUqtYGk39mN/zZJ0AelxSolorrfFZvm2NRf9tjWgpLVDelBd76lguKnsi1+lirVEw0T/JVEmB36zVYAeZN1Lf2zHu6/NVeVsXRy5FxKg+tEo136peS9clPSWYgNQug8ZWrX4v6YJ9Y9L8IlFFek2LDLnYbHB8dDi9R0jOK85zSIoeWtDlMUA5V4t+VFjow4S4tcrVQ6diumQvjCFdGpT7SQKcY8QYAjabLXbbLS42FwjjDs/fvQmQS5cajozIDl23xtNn5wBHHBwf4c7NG0AYEcAYQr78hSSmP4XYUPFWB/iiQNKiHseQrDnvcXh8nJ+PQAwApx0WRgfvGDEwTp49xPXjA2zpABfn5/jMJz6Kg8NDnPybZ3jywf0EFHLmqzHG5HnmtIPT9z2Ojo7yHKVJ8d4X0CYCJsbJCy7MkfrMBdzPmJKRs60A65ExOmCzJvQccAgC5+dD3sUQQABllCVGECGRU/Rl5nCpUbWwUmNhHNMuAzPAMR3Gd1QZQtZ7orfwbLyzFGFKHf/aVNgMyG1y5FxKsZfpIULdUdqqZ07plL1ziJIEMxL6/gCx6zC6iFUMIPYgSoeaUn9RjBXHHgQ/tU3Zo6wNt2JgJPoRJhA0G2OMcwMFyhOrf6+EBVWKc1/IRl23PJP750QgilhvearrOZF50TtNFfBS/V0MrQNXQH2ptBSXTpbQMmLt+zJuySQm/D49zwhhLGGa6XOUnwJIWuCfuQbhS8K0fKcEuJTi0coe+dbaaAnqQufIkFjblEUFYEx1VWsiD0qepbxO5F6jaVDKS1e+mdpxcs5MjcWB4DhJ1uAAuNxyiOh9B2aHTe/QvXwX3/6zH+Bzv/2b8F2HERHOE9w4goaIk3sf4P3X3sS7r76Bd974NYZdCkuNK5eUnifAJf5hAvQNtaJUJTsf5TNoKaxUKVqZNycXsgqd85gjw0+jznqKC0OQ0N+ENjKn94gI1HVlbjjTmVzqLWU6LYXvtcBiC2xY2SDgpeI5U1oOBW2U2fVmd3HqDiuJwZCEfDmcbd5ukmnZ4cNzh8SScXQZSLHP2zWa1q8G2/P3LC2rYWrwiJruTTDZArLKGLZ9F1lZeNicp1iiTczMueSAagFRe1laq6+WBkWOEoCS5Woy3ohcmVN5fpJ5KHhGeM/yZmvHrjXjrfNRs74jZ9IiAuWU+7KKU2B7k1AAuJyh02MWfVvAdVbyGrRPPJayMbCkZ6eJr2KMiDzdawFOWISTGy87exjkfb7UeR4Z0Zqn1jq3hrCOdNGYwTmC79KVE+yQ0n8ruccsMk4UoZL1GUPDeYyCVYVG8l6RB0YHfYhydUNjCNiNKewHjHTTYL7XYXNxgWEYsNlsUp+dw2q1xur4CHdu38bFxQbn5xvcufMcVqs1QmCEEHF+doKDo2MQE548eoLjGzfBxOhXPUr+53wQWwCNd34SMBkMe5K0Xoxrx8dgAL5bYRe2sqYwDgHOpcwnBMLjx08ApPsqXvv1G/j4xz+Bu88/j7OLN9N4kbfAOo84crnrQrJlrPq0uyMLy8ZiA9MJfvlde7QKXasDOBnsAugoKWR2aaERJi+LrhPMefdHapwrtajAItTCAk+GkSwIOTAONynultdNGyH2O120oG1ZxVbY2O81yJ2BXUpersSPeclQCkkiTBdbEVSqW8Zs3orSZq7GnasrRocYLTokRvphlYelR9sIm0BR/Xldh+6rc+niSe8dasONF+tIP2W3rDlN1Xv63RZYKgoI85AT/fvizg3VfVwyMqxhU5c5iGDmyqiNcTrDZfuZ7O2aHnb7e2lsucGqbSkxMhh1aORlZQkQLYXg6Tlxtl+mUOsPArqsCJMCV/NBhJ1LSsZxAvOeHKj3iI4Qj47wG9/9Or76g+9hdfs64FOi8449eDvi/PFTvPvaG3jrl6/ivdfeBIYRu03KMug7DyfhKkWIoxhNmhYteSI7PbJeC23M/Oq1U+Yxt6mNf/l+CeCm92qapy8wWS5c96fMi+L9EioZGmkmF+ZvHyjXoEUbERo4f5izS0ttt4BP1Qf1nZXTut0YY0lwoD9rGUQtQ2Fap2TqTb+3wl6k1AfYVXvGXmgZRvo7XTcvPKMB9JJTzeq2NKo6o1MbJNdlnw4Vmmia1i9PoJFI1c1cdgPsDlhO5liNw/azlawHe/jY9r0aZ54fFseI6HoA4lCdz1dtIM3Hng0VwduqWH5s6W9pRzCg3vUimjFUsy81T09Y7FI5wFzu0JjNa24jxHQxtUQMIK+byJyMBqp5GKxjBJTMVGPW/aje/ZDlyobGmO+/QGRwCNjuBpyfn2G73cF1Huv1GteuHaPvV4gxIEaGd8D1G9cROeL6tRvl/gwigJzDxXaD87Nz3Lx+A48/eASHDv3qED7nJ9aDZGRw68UqTZ5cMXgIgCPGQd8jhojgOkQ4rPwKkSM22y2Oj4/hHMH5Dv1qDSAAO8KTp09xcvozxBhyGEKqX9oEUGXASv2pAzkqUGEEmA5RCZkBrGKYwHMKB6I4bVdaASuldSCrgOZcvPMIYayYehIUdeYrKQmsJV+gFcDyzwqimWI3xfarFSctf9u6NdAuxlOMCBwQshCSS5QYAtLyNjd06Ej+p8hm+yFKZCYYUHsR7FzYOdc0as21XtRa2GoaLG1X6svu5Oc0RzXNq/dQlyUgvRdgq88dXDmsq9+Td8TQnvcjCWVrYLQUawWaLgFfEq4k7+n5s2EMEtJoFZ2eq0Wwxzy7j8Qa4/b9pXWxD0hMIZU0m5+9/btSaRuCkQiDY3QxGRkApTsxeoePf/lL+Pqf/BC3P/pi2plwhA4O2I24+OAxHrz5Fl75xS/xwbvv4+zpM/jI4DEkz79aZ3/bfltDQH63itfuItl37Lt2vmU+l+hu56wFUBcBlCpXOYxr622tU1kjGrBYY8t+v1RqkFh/Xo2FqBKk+3ZjWwCrpVPGcZzdI1Te5Vru2TlqAf8l4yG9wxVgsu/btVueacgpWau2fd0vO95at9Rt67mqDGpV9MWGtr+tv0u/UieadTKLBT1fa6k+nvGSBcwfhpeXDDHBVlqPTPJjj3OF5w46mZt963CpP0BeAuZdjZmW+CTtPuzXAXYtXxZWbdvWfXTOo+/7hrxL0RxknHtgLkac1EvIBnhzH+rfrVzZ0Dhe9zg7P8e426FzHh6Mw1WHm9eO4PouZ9NgbM5PsveCETng8PAIYQw5pMEhhCFZpgTcvnMHzjs8//xzuHZ4gLDZIG524HWP3bjJFED2JMcMFLlcmidCSXYajg5XuHZ4ADCByePajdvwzuPs9BTO9+CcKYq8B6FDHCPIe3jOZ0S8T4e8tSBo3MWQmKFWmhWQVAwm3pxSuAY1lVKUQ/ViTDGyV5YKQwhDVkqbJ/BrD+KWZtV7hanJVXUJAJMD5rITImOzcatWmOti+2kFrA3HsbHQVvHrOgu9s5ERImO33VXgHWCEmO9hKYEjTqIR24JHtTcDKTSFWMw85GZrtAa7c8BT6i/NLm+r6vFLkTAyK5imeap32QCULG6MuYCzoKSMWT3TUiIinIQmug+6Lr2zB0xeqraiWwaAudKZ8t5HP7tWtPGWvvMzwLcPjOk+a0UmOyne++kMkBnT0jqxfy8pbOu5XlRylTJrjQEQr6Cmc5IJhFVIl3PBAWPncPDR5/F7/70/w8c+/xl0qxWGHGvTRUa8uMDjt9/He796DfdeewPvvv02HAhdTKEE5NIlp2KQXhUQFd5q8Kp+z3rS5+uvTfMWYLd/z8Bu43lydWikBTlalrTaaYKPBh5q8YNtr1Xs2vhwYGty3Oi6Eo/WO5otua3nahZSY2SsfKf1QEUbagM1yxMtg9+e7Zl+n+tw3Rf9ewF4qHcL7O3vluYtWsz6QbUOsfS0/dF9mgPLeh51u0RU3XBun89kbsrwtAuC6jMtS1uGh9THmOSalNYOYKmLHBiTEVWfdQ1wVQIhY0AqntTnX1s0apW5/Kx5zspgacPyf8yYoaWrbNkb1qj7hhpb6v46R3mnZYRHxrmc5PTUN2f4KYc+y3wbXrI8rHui279KubKhce+dFGfbdz0673OeXsZwgZxetId3Do4ZcbtLIU2+w82bN3D37l3EmMKlppPtDhfbHcLIePGF53DYE2LYgEPAGJOAC/nOCmHS3XaLkA+eEzlswpi30xjedxgvety9dQsgB3I9QH3e5SZ438G5rsQFRwaYnNjOcN6nzCdZiYptL9tQWvno2Ev5ZwGNTJJ4WasMM2qSKgVF06LUk9p1fWkDmJSr9nrbPk311wyhhaQ+HN7y7Ou/tVdhScAJbQDMaNFS7rZPMja9BWuVtW5zDCMCp52Ls/OzSqgQ5XMZAnCg08K1FYymuu13up9j/r0WLNbTE6PE2Lf7L/zVookFLkuCaAmAyHfT2JYFQksJWsPB9k0DAOEh643ZB/pm4Mp83gqtaIHOFp0s7+l3anBuBW89r60+FoFs+lIUH3g2J/vmzioiSxv73VK/2nW155wojd2uXZ/DqZzzGEFY372Br3zvW/jyH34H8foBRk/wkdCRw3CxwdOHT7B7fIKf/8Vf4cl77+Pi6TP4CLBkUyMqfKfnyTog9Pea9sxakbYzBFkguQ982c8WD4ab+bI8ZOm8NI8tGWjrFVosGQp67LaPesf0qrs4+nM7ztZ6ae3USr+1gVXJGlsH5vyt5YvWG/J91bcMIC29WwBtae5a/GbHvLSLtUQPO25d9Ny05k5+ElE6l4n23LXm8io7B1cBrrN5iyl0yqZmFixkdd5la21faa2pqg5DZ6C+VqFVn+2Tpv3SPNl3Z31TfSDan+zmMhq01rLul57XlryoiGLa22636PsOznmA2ZynKEFvtZOUucjndE/KNOCWrP13KVc2NP5X/+n/IhsaHdb9Cp3vcHx0iKOjY/Rdh9PTU6xWK6xWq3I/xPVbt/F0sy3KV0Kq0iAI2+0It3a4e+cm/vf/u/8Nnrt1A4QRIAfOh1O8T4Q7OTnBkydPsRtGrPo1xhCw3Www5FvFx3FEGEd85KUX0x0NlEKnCATnOvRrD86AEM4jdSEBSCbkC6KmBU/UBmc10SdrXoSUAHLmKWRKMmuV942wk7sxZgzsUjyg7LRQrD2yEzO2FWp6ZrogySqDGENlrFTMz3VMIFBfkmQXpn5XQEurWGUm9QJJ0OtUyHY8+vcYYzrDQpPh5p0ruzRcgqiR+CkKvcXHcnmZgVa11dgS9ha4MOde0HSmw/LP0vutvpQ6De3ngH7hcD4m4Gd5wQpqK1xa2/Qx7zLKGrCeHe3pb/Wj1Y7mtaWwATv2Fr/Ic3bHpx5v+tyuqX0AgjnxgK67MsDj5X3SdS0ppyXA2qKVruuyrfepTkDWh8gqAKDOY7vu8bmvfQXf/Ds/xPHztxEc0IPgAsFtR2w3Wzy7/wH+1T/75xienWMdgeFsg5EjRk7Z81wOPXXSlgIndp3Yz3QfyayzFhjQfNJeDwbYNeikDSD9jAUp1gAnoukAqAE5tn5b9PxXfLEAKK6i8Fvret/7V+VH3Q8g08GEammZaEGTXQ/2HFRrnU4No/LM2v4v8Yflh/pdqmSMPLOU0tTWs28uWrpL84s9U2Kdmfbdpc+X5Iym+1X6J/1IZ14n/VqF2mVdtoQH5O9m/aqf1qloebS8orZQbAhxSyaUuWzsnF513cjP6nmiqs7W2SsrNyacUddt6WPHfRlfLRXBnUnXAsiOzemCZ3EuMabzLUAEIecbSf9rrCPd3+mzhKE+TF+vbGh84qMv4GC9TsB+HNF3HThE7LbPMF4wxs0W1w9u4/TpA5yfn6Pve+y2Fzh87mV432HYbRAjYzcMiIHRr9cg5+G7DgAjhC0ePHgLRysH3/XYhWRlScaBrutw89oKMXY4PDjCwcFBBjceznmsViu4/gC7kO7ycJ0vFwoxCF3fFZDg8wV+lMNpkhSjsvshll2ir/XEyMJABhzTxCRG9HA+AqH23GjmkhhDLXyAFGcHTyC4dMAxMjwcdsMOnWGCfUqhBsG1RarDn2KsL7SyoVUA4LsOId9WTlCLgVNoFYGqsBGf64khVKmGZexLfR6GodqR0CFbulSC1THCGBFixGbYAcMupSRGyszlfQrhQ54v7zsADjGO0CC/6lMDbMcYwSGk9JvmnQn8197V1pxYBaNtoQ9T9MKfK1OqeHJ6CZOQkXcbdeoxtYoeoygnHcKoS2uXLb2IQn4LHDUvtvoFww8cI4IBUwJ6WgaJrqsFWqd6KrmrCVVkRxpb2iGLMRZapPYpy4ryIuxkT4rHhpUkIllQYw3faS1YsJ7alRlOjhSasglx+p/0xnUdhhjB3uGFT38SX/mzH+KjX/ocxrXDBRgH8FhvI4Ynz/DOO2/j16+/gYvTM2wePsXZ46fwgeG8wy4MpR8ck5xzzmcDvR2eV34Xnsp9SrIGs0mwsq8FlOU7AY2aH5aAjS0ahE5hGxM/a6W7D9hp3lva8ZvFZjPN5MI+pb5PH+jPZSwfplg6F3CZ1yIhpZEvgMv0R8av5bo43kRn2L7P1yUnj2sD6Ft5OwOlDTBegy8UWotebwHAOWHSe5QemO2Gz/rPcwNgAs6Ts4woOSsWDavyMwko7QxcMm738bqESyLv2E8idup7EdcCekyxxl2DTJVObcnembylSUlonKQdkU1grivhyTiS2pbW0YzO0j+1Q90yjm0/6j5NYxO9y8YpIm21eG6f4SHfuzxvt27dwt27d3B2cqr0ifRhcj4K7ogxgiNSlI/Qd4GPdZtipIjcu6qxcWVD49n77+K901M8ffoEr776K4zjDswR5xfnGIcRR0fHODo6wrNnzzAOI65duwZ/eAP/4T/8n2N92IG6dEbCd2sM4wYuMg7z4WzqOty8dQvj+SP02OFo7TAE4OL8HNePrmO32+H8/ATnp6fYbk+xWXcIgfHs5AyPHp8gRgI5j9XNl/GDP/l7aaNoTGcuyDmkIKGueL+d70pATYgRjj0Al+8GIQRO5xfGMKYFj4jIlP+lpSex3VMojgALBuAgN0IncBvAnO7AANdnH/RdFwGcD2Ayti5FKXZDAAMYHSplLRPvvUcc2zm/RaBqJpHfJ6FXCwE5ILvu0k3bcUgH9DgE9WxWjMyFqZPAC0BOKcnM4DEAPh9ci6EAQq34dZ9t2FVLMWoQGgGsImEXGAe3byRw9+59RCIAHuB0Wz1IBFkoyqXCvUppyYK87ACZDZOy4WxSrwBBC37L92ppt0LTpEgqWjVpzTknqoWmFmJdVlNBGYGseqBBvq5jKdTFbm/rA4o21KXqI1IiB6lb6tWKSOqYhZYI7yqDiYjUhaJtfpJdQ7vzAghPUOFlWc+VUlX0cDSBK87/5VDXzGPSX0bXOWWAJUeFNTpT9XknoBgfoYDQ5CyQMWlDJPVxWtuSyCLZxD0DAweMzoF98l51keCYAQ4JrPgOW0cYblzHN/7sh/iNb38LB4drjB3BrTzcGEDnI9772Wt4+2e/xIP338XDRw8RQ3ImgHMIZozosrOmIwd2eRebYzmjo9d+WT/AZAARISIWwLOswNtGl0664ZzD3bt38fTpU+x2u8IP+xT3PsCkvZfmRRAnuV30unAPoYRUFiBO85AnDWRSO1P1+hkLTOR3+5k2bnS72qjZR9dS9zScGXjP6ggELjfFT8/mCxjNuCwtpd6l+ZgZH0YutkKdluppGR8xDmnXLYO1xKMAkQfzWLVdtSMyK8qOdRp/ZAblrJjpTGm6v8m5VKekvGfFE0m3TkY2sTgAqDg0lISe1gtNhldr/Ba8apmKOJ3T6HIaf5YborPflQggp50jGbAijS05KQt8x2Vpzi1IB4DIofIsFMcNyVqr+bmMVckLO/bOeYghzNnJOJkM+w12oc/Sjpb+ab+b7wDFKXwJKVFRFmq5jrn+burYhX7Y54d8dhqSCjw9gLS7keSzGKegtOMc5ZAro9yLJxeljjECvk0rqUenEb6sXNnQuP/gXTAzDg57/NZv/yZOTk4wjiPW6wMcHR6l3QMQxpDuZHBEOB8J169fLzH3Gowx55vBY0oxC/I4OT3HnWurxCRgbIct/MZju93hYnOB9x+8jxi2OFyvsNnuAKQL2S42FxhHxic/ch0o23kBXedlRqYFnvPcyw3mgAgRgDjtfkguaQE0MrcanMcMYFugDoopbfgHZZSrgWdtyeZF7lOWY5dXPYOrbAuVVe8IHXUzUJaYYC5gC+BSWXqkyELTALClKORzHTKmBYJdmGMIyYBz9QEtCxikfqAOpWqVcRzRcwqXgpND0BL2Vpabmbu5N7S0613hF/3s5N2o3y9jMN7Sqk3Fe2IYFsOm9TxqoKC/K9+nD6p3pjIB5lkMdyVAJ17OUqk5Zk0f/bcofucn4ar5QRdL71mP1fvyt+1HK1RNgzhLL6lDQoKsomsBHcsPE1VQgRwNFOy8yoVe1vut15A1qIB8uLahaOZhRvXvduyinGWHBUToooD5tCbYEYIHYucR+g6f+MpX8J0/+2PceOF5sHfoAfgQwecDHr13H6//+G/w1s9ewfbZCcJugxinbF0xr8+u6wrgsnOgx68/K+CHltO/tko93vnlXNLe/fv3975ri5URS7JpCRwLY5d3s0Ft61h6X8sFqLHo+26E9/Ruzdxoba/h1hqx7VuDq0Wf8jxqXq7mBPXfej20+qnbtI6O3LnK2J9wxByU2f631ng9ppQUAtw2MnUd0tf5GtZyLK3nZLjE4sCsPDO5FPk1+0YNvaHHagNkXpZ2hC2/uFmq9rotLW90exMds0xRmEYXjjEZYFQ/Q0Q54qR6Orc57QDZM49pzhfopOddz4tQTLW1tAZbny+tB4tX7HdWf9s6WjRpOfVafbTfPXnyFEcHB/XY8/nlqUGpwNTXiO5wzs14oTXGq5arp7fFgBAjtpshpbR1HZ4+uwC5LYCnAFIq1a7rcHR0hIPDA9y4eQd932MYt5WQZOZ8Y3fyJAxDBJPHW++8j2eHHZyLgEO68AQfQLZ6uvUaFFcgAg6ODnF0dB3+2Rl24THidsBLL780E3hElJidMsNnz4X3HjEMKYMPUaW0ZXtXCGzBaWEI1/YilYkykyQCxTKKtFnFAnqHMCbrczcM6BfmhZmzhzUWr6FO8+nIlbAE6VMR0DRnHjECRLnpmFUZ92yrX31nGbKAB0IF+nTR9bcMGk1baT/dlSE3Ric6nJ+fQ0KEQDU99TzaudLb+kvx0aC637VCjiCVj1krI+25uGxhWg9di+cAgPfUI9nZgOXbbdODqHczUAM3XSxAmAyNen0ID7aA1b6xt9rU49W00H9rwE9EJWbcgioN1uxa1vXNgGUDRGhBbPkq0RGTlxT1Wj88PEw8ivkZlJlHzNDaygwNtJpGk3cYiNGxQx/ymQnnsfPA4AmDJzz/mU/gG3/2J3j5C58BdR0iOfhIwDBi++gp3v7Zr/DmL1/FydOnOD85ATFjt9sV8CzrVf7ZvkvIkTWw9PhbPLII5M38axpZ2ljD5iqlBR51fZeVFo/v6+di28UorOdZ822rXv15C9hI0Wvmw4RSLYGNJgBT7du00/o5uwaXxqjfbe26tkoL6M1kaenX5IFOz0y7bvbZJZ5loOCI9Oxy/1pr4rIx6M8Kllhoo2VQLRlRwgfi4NXvqD9Ka226L+g3qneeq/k3jy7pgYruFiSbeQWWdyW00WTbaOmCy8oSTVvvLu2mWvl+WdvNNosezro6hzDmuL5Lx2HrB5CiQy551urofeXKhsaPfvxTgNPB6t1uxJtvvoPNxRbjEPDiiy/i9p07iPkGbebkZf+9P/wjtLzKRKQAcPK6rVZHeOud+3j19AlAI3bjNi+mBGjEW81jTKE5IPiuBxPhg4eP0PUr/J3/8LnKs14s5xDRibPapTMQfd9j2G3TTdQRCDmdmhzKLlmWvLHQZZKpLTRbwgiovfT6+QpEZFK5fDNwAT1CM+czkLRtoApPkMuRkhFSh8ZoQEU5XMwKd83oc4E891zI8zp0xs6B9ELHO1tQ3fpdntEpUkUZR05xhkzA2dlZCsfJOs6pG4ZadTcVGaZzJ3rMaQ7mhwdlPMxceR21wGTZW2kYEDHKZZRtAKJprunB5pka1M7fLWFqea0RTd4r511JHx3jvE7bH80jzjkExR+Wv/aBelBb6C4BpZlSt+0AKSQol9YOgm3LjqtFe6hxNds1AFfWreU3Zi4Xmi6NT4fWtPpnwXmrrvIdAexSqGcKC3WI3mHbEdZ3buK73/89fPHbX0e8vsaWGJ0j8GbA7tk53v3Vq3jw2puIT85Ap+e4ePAI8ISRpl0UoaHkbpfPrFPCKnE9z6IHCLURv2+uZvODBm8BFb0uK3YOdb3W4XRVYK7Xv/zdNAhV3wvNGjrT1rEUL26LBtaWJ+3FozPQ3wCdtr0maAOqG6Zb42yNzYbO6jbEgbIkVyx9tWPT6lq9O5RowwlROAcUh1Gt7ywf23lITipxMuRwFU0amnSIFL0jJXXoNuc0MMaaoxmdpW8zuaTGYDMnyecOmJ13myiBYjTM5eUUOmX1oy5aFgLI4dZqd0XxsNaReixpd8hX/bPj1u/U+Gous7Us0nLW9rv1+1X0tn1nX2nJl7LOkUJ2QXNwn9ZyCrms1jJRSYLj3Hy3UmMaLR9Er+uU5HZurjomKVdPb3v/FOAcAhMifH+ILnY4357gvQePcP/Rs3xdfFKSR0eHeP7Fj2AYh3z4C3Dk8wJMMc0xpjS3zAT2HSJ6/NVPfokYd4ikY5Sn7XUeA1w+VR9ixBAC1ocH+PRnP4t+tS6X/lQT4YyAYKDv+yIQtBARD35RVGqRV0zmxAiYe2T2MR8w32qbvmM4SrsIA4eSUrXsIqgbMXV9nfdTqKNilhhj5VkCNBBIdWtFJMWGsLQW1JKw0m1pgY+FZ3XdAg5bu0Gzv0V5OCCMA567dQtnz87BzoE53wrdUD4t8FEEFk/AoAXmZM4tsMvwsinwNY11X1IfuAqBkHdatGn9bsF06o9r85qaAy18xtzjBwABAABJREFUKQOKtN0/V65WuGhhKM3YsAj97Ey4NUCh7lPVtwVBrtsodFZt1H2cz6fl01Y7SRDX/bROgiVlDtOWHZemhZ7rfbHr+8BEyyhJ8ckAO49t5xG8w9h5/Obvfhtf/4Pv4drd2wgegHNYA6DNgLP3PsA7v3gV777+Ot7/9Vs4YIfxYouRIyI7BDC82hVdMgj0560zAdJv7ekWUG/pqumn31/6TAPLFr/pz5baatFUfyb81eIb3e50+et8DlvrvNAKSX5Znm3xXDXnjb7r962zi3lKuy6Okstoog0c6/Ev7RKK3NsHSux3S/OVwpQJwHzd2vHbf9I/OzZLW2YUmZweiRUv6bIU4if1ME+/t9rS4K4lE1q0kHcr+jToaX+fyUnMjRf9rC1a38p1Xq0QOOmN1UdNuSpzhfZ6sOtrxkc04S6LH1o60tKqqacXyxRyZcO4l+ZI/956xpZ9c1DJkyTSF+tLmHbCrGBxDC0YRVTPUwvDlYuQTf9asn5fubKhsd2tUsdiBJBCm9gBIwPerXC22eHmzRvoug7DMODazbt4/sWXEcbp/ghmJewZSAcege1uBA4O8PLLn8DF5p/BeY/dmG4fd86hy4bDGEasycMTgTxhO+4wjBHRDXj+hZcQIxBpil8toSMSYkNIIS6UPHFpezQd+LZCvwi5nB5W/0sgpCaw9Z6S+a4CfEuCEgaQQ3kIFEjWAsr2Vyvs0qfIs2dQYmgnL48FaFYpS5H5bIF2LYRagF7q1IdDbVv2HaAOuxLayN9932N9cAA+PsKzEABIONV+z29TEdJUr34vxogY6n5WoUm+Ha9r94etgSYx7vqfbtfShHnyzOjPJsU6NVq9y+l/8p7vfN4qF6DeBrZWYVWCiBcMNkWzFqjfH118tdICEMVcXwA2rdIUwLlYb6g+81KNR/NRY74sENTfWWW0FJa4VM8+Qb+iDqMjXPTAS1/8DL79w+/jo5/5NOAdQt8jhgB3EbB98hTvv/prPH7rXbzz6ht49vQxur7DNowYXXa6+HTGp+U51zstVl60+lyFRCI7PTAZHi2Z1gQcpmi5Yml8lWKfW9o9uip/ERG88qzvc6Dodyifs7K0awFl7RW/rC/yjlwga9e4dRjAzOG+uvfRxI5b01ADwhbIkjnNR4+atLBrcaldrbPseFxx6smw6/W+bzyqxxBIW9GMgORQbc+7lf1L8mJfaeoJ873lHVssiLXrKNKSMZLetnLKuSQzomq3xgdcvaffXwo1AiTi43J5oMdKwGIokOXHauwGG161LNZ3hfdac7k0f8yc7j+hSReW71mebYcZEmo8VmEe++yH5EdbrmxovPb6O4gc0XUOq1WH1aqH9w7d6hCRHdYHh3jy9ATXr1+Hcx5HR9fQr9aIkcER8N5BMs2kTqewF995dD4R6zOf+SwOjq9jc3EG36/hIxBDxMnZRYoNJoezGHG0PsDRtSOEwAiB4SPw8Y9/EsMwgGnaFRBqJStPbtWYvGneO4xjcb8AyOBR5pFQLrGRg6eaAVOClLlnLXJ9mZFeNDHGknfdAl/kOEfJACB1eO8Bksw66QBXzCFizFxi02U3R9r03ifvGHQ4Wc7KEAXgTnM8juO0eyLGEeWhKlBJTOg6X8KuJkHR5p1iRHH24IdYUvolwFpf+LakcFJYnGyhAxyS8TiGgM3ZOYbdiADAI7letOGk5yeBUhUiZdrSfZhA7PzGZhGIvusgH09GDMqcMs+FVQJZVO2SWGVT0Y8nj1Fkbj6X/m63leifhXu+1RccS9rIvClj6pobgHq3kJB4VYch2H5p/iiebc7tS6M00cOaIC0BZxWTHaujNk1taYEVO367tluKQHuIOcZywLJV15IilzU7DAMODw/rOc8KIWZysZ4seYZSTC3lxAiRGUPncfzic/jOn/wAn/2d30R/eIAxRvjOY9jucP74Kc7uf4C3fvYrDE9O8ODNd7C7uIB3aRwjR3A3hSl0ObUWpw+0mIScU3Kq3945QFJec8omFYESYguX6kuHywXAiUe5UKmsdznoXvOEBa5QPzV9y2+zudHFzncL6C/x3byy+s8lRa2BVWq3vvhUry/LR/vAVksOtNoG8l1OIZR5Sus0EX7f3RKSWKQaM9e0Wj7bVu9E6fHMSUl75bRdl6L/RO6IXrOGqBSJtCVq8di8763PiDDJtaS8FQtMsk3mTztLdH37DA0rM4ppk/UoMHH9okGxpGtkoS2Mf4mPkq6bjF6XQ6KYUQxEKcJfyCHFjPbZRytrddtTMooav+h+6z4W3sph8JSHqten5Us7Tj1f+8pVwHhpX/2N/Bk1koKU9beACRItE37ynUcYRziSqKF04L7dL40DJyNZvgPV6/Sq42uVKxsah8eHJbMIkOMQAXRdnwBHCPC+x3a7xfHxEZ57/jms+hWGMUU9evLw5OAcIxCwHTIkZMLKOTgC7j73HK5dv4mz81NgHEFgDMMOYRyw3VwAAHrvcffuLYQ4YgwDAMaN6zfwsZc/ipVfIZIHB04KOTD6VQ8et/AupV4hpAuWHDmsVmtst9sUj5Zj0pjSeRAxLkZwiltEFoaRwSEZLRH1Qb0KcGAOdKvvjXBNNPX5fIUAsDT5RJQkoSOAHDrnsc0CyjuXgLtSCCLcx3FM/QwA59ST4vHmSIhU9+fw8DBdfBjGlNpOvgcqZmUkAUJEcD4ZjWkXRbb95yFeRGnrjyLDE5XUaAyAyeUwgwbAV2dIrPeuY0b0wBgjaEgLcfQOfkhpdkmlZ6sWiKN0eWOe71KU1LICq8TgKoGUdsXEmJgEYgovUXHBVIeJFL6gqc19IV3WuCHnSj5u/awY8EDtES/8xlyknMSCSzpFKz6sYGkpJjE+W0LIZsVpGgJixSKlduas7IUKNYBc2IGqO12fh5HnjNKsQDwlUC4JFaxys/xY5sBoON0/AkoChjQ61b8ydhQ6SB/I8J+84zgBmEAofU1hlREOKc00xSQ/YuexAaO7fowv/uH38Du//z2srx2BXJIBGIHN46cYHj/GO6++hqcfPMIH797D5ukJ4nZIIJcBDAyPiZ+JKKesjXBULRWAY3o2g4dkOCZA0TkCxwASOmZHS+QIiiwCCenekVHRluF9WkfaiJgAiFBRwKEG/pYfCYKA0xzN+XmfQarr0rzRAp1pLO2D8fsMAnufRJXQQ+02a92hAWtrvco7tm3LZ3JhrfNST9ZfSEjRynKRJexSbL6EaiS9SoXiVRsGQEudIvNsGJ2maZIlEy1aZd/uudYf8p2c5Uw8AXBOcw2XDNsQGs6ahbkr/SQClKE24cAk5/SZGJlzC+grOdLgR/2ZIw2cuXioBSS25JitYxb2pj6f725xJUtr2qSwMzH8q7YorW+iaUef8iW6k9e9nrMWT9vQv8ShrJiNqvrsnImYIJ5kbww5SZCv665wG++PutB9tDKlRXO9tSKrZVp17fq1XBP5onleMCwQAZocsij+gqUdrZBwGxGIRF9LPyaHWWt887qWy5UNDQ1i0wKZmDzJo0TYYUhnMp577jnpYvUvMduYFzdADvAuXwrHwPHxEbbbLYbhAtvttrR/7do1DMOAWzdvwHmP84uLdAeGc1iv17h+4zpWByuEOC0wp+PLYoTzSRDK96vVCkAd0iXEE6AS1U3fIuCnwzNTWkZ9CF28Q3pC9ITp56SkNlHAEWUCxRini+9c8hg679B3Xemb9GFJ8a1WKzBzdbCxFZ6x2+1yrK6Hc/O+aiCmFdgUWx2FI4qCqMdXZ6YqdCZUC6cG1vNDotaa997j/OQEPSclIYeZWsq3os9UMVpF99eRKwe3tRBM/U+JiKedoMkLLIpcfq/ie5VcaSmxJeVgjQz9PHPyEAN1ON9S3WLs6W1UC+gtSJjqmPqv62wBrdaYLADQY209d5nite1IPSF7XWfGAlCMxyUQoWPXW21aHrOKewnA6k/KmqAU0mm3sAOldKHS5yRzkxcrxJxm2zvEzmNcdfjkb38Z3/mjH+D6Sy+AvAc5gmPCcHaOzZMT3HvjTTx4+y08ffgQF6dn2F1ssNlu0DmfzwgYg1DTzAyFKntu+RyBnhNLw6UQlSWD0rYhn9Ue1Xl4zr6+yLqeAOi8aIBvgXGrT5eBj1b9zJwF0xwMyveW52byVD2rdZf0uTrb1eqI9JHrcei+kNIfdl21xqWfbYVJLZUyd406dZui22bnM40803OwxKetMS3NseYhbfxZp4Ut8mzrsLc+yN4aizilrkrzfbSueOZDvKfXmaVD3QCKcaL5jmhu8Oqf+87DyfupH7MRQRs7eq51OL30Q+SdHHzWc110I++fy6uUWf/RHnu4Ak+25ztiu1UJlFIjCwu81vvSVl3v1dbnVcuVDQ0AxQKvFC2AvutAjrDdjvC+y7saxyierWxgxCjAGPDZLcYci8HAMeLmzRs4OztF37tUByZFfOPGDaxXK5yfnyLEdCPwdrtF4IhutcrPpUvyuq7L/U1x6+Q8vK8Fjj1P0DImxFIsk0C1ApCFLxeCAWny9jFFoZ0ReummRmmGyi6KB02H4ZkRw5TSNYQA76ZwKVtvWBDqFoTqhZh2VabzB1axAtNN3jUt6nsD9DPae6N/OucQQy1U6/5OgmPmxQucvLgZpMnnEksOqhfRPgC8VIrg48nYmAGMBZqW8TTHhWnLu/Vd42/b95YQdo4QAjd5jwzvCk20p2pJ+bWUQmzUv0iDBSU/U0A5xEC3XQGjS9aUbk/TSK9HrVgdzbfEtcLX4EyPc0mRWR6V7/YZRAKknOpnUGd3onicOYVROaYsKzxGTwgOGHuPu5/4GL71p3+El7/4WVDfgcjBEyHsBjx98AjbJ8/w4M138Oarr8PFgO3ZGbYXF7g4PweIMHBE51y5cNPSL/d4Rs/W3Lc8+HbtXzafer4siG4915p7S/8lIKXlS6sNqc86XCwIna0Tsz73Adqpz8objrkh3hp7i6Z6PHuNuAZv2vpsaFOMMYVgNnhB96HVT60j9s2RyOsQQgp0Xeinlu1LvKFlm9B0mWdqR4Jut7WjosPeWu+0yj5ets44+70+G2jXSHoIAMcmVNyrZ5iL00/Xv9T/pfnWenYMAeTmGaX2rdl9fNTqh/lkJpeEh6Rvs3Vq6qkNornx/u+j2PFOtJnS09vx7ZsPZuD84jzLHAi4kDeXOjGTr1P9f3ujqlWubGh0XbcIPMZxBEhiIdNtmHJpHwAwB8S80zCOA8ZxgF8l42QcxpRJyhE63+Gll1/AjRvXwZx2CeTcwfHxMVarFc7OTrEbBowxYLPdJEOAGeuDNYCYzmx4VwwMZsnjnuKApb5a8LVTuDKzMpkzQ8Q4E5A1o7Q9EcULAZQDglLHJLySF3EYA6KbGEtSl2khPy2AWggOwzABlBjhGMWQs4rDGieVAnD1IrNbqXUfhEKEEGt66LhYu/jley5x2FTxmVViGhA6l7f8kUKJ5LbrNJaYdhWU4SM7MEnojMAVlEGtwNM27T7FrelbDma5OpuQprnmD6uodL01j0zv6N9boRQtACDPV0CQcppEc1xOA0bbHyALaONdA2rFa3cElgBcWUdUf2bH16J5a5yV8FRr1oIwnZ7X0napTt225eu58X25wCZK2wJL4TAdA44phUdFAthhABDJYdMBxy/cwTe+91381ne/DXe4wtg5jATQLmDz7BTbJyd47/U38fCtd3H68DE2p2c4Oz9Ndwhx3rnwcv7CyiRN6+mchF6T8nxrPjT97KHxfYCiBQjr9ViXFlBt/U6Kv/T3rf7Y93URuaaLNbLJGGy23iVeSmGlddYdLadbBkSLllZ2LMkSBpr9tGPUc6EdS0tz0jK+NM/osVsZZr+HCkXVnmkZzxJPaLrNQ2/mxiyA2Y3Hehyt+ds3F7Y/+jlrvMlYbJ16Pi1NLUAukQ2uRcN5HzQN2IzV7sqIbG45fbQ8sLJbSstIa8ldeV92GFtO0ZYM0c/Y1M1a9gitypwT5dDNeXpxe7fIEk3tmFv6ofR7AcRbunvv9zrYio7glDHSkUvneJGwkT39vrRGNd0muqIatcUBS9hiqVzZ0LBCZgoTSbHriJOhQZQup9rutgihZriUUlYOtqQbNNlTOnSdveghjJADcavVqhyOPDs7w8XmAjEG7IYdhjDCO4eu7xDKge2AEEcwd4VAXZfOFMiOimTdkIWpdzD0zoY+lFcOSi8Qt2J6SrF/rUUiv7eAZYwRY966d+TLxWyMFNvYqfdcHps33lgB6lPhshuiS0s52K1NeU4vUhHeenu3MJ2hh9A6xlhSr2leEHoLzaxiSPVOMZNVH/JKYGYEHhHIAW6a88Rec6Gjx2+FhSxuu4DKPKFWSFYZ6bq0IlwdrCs6T89F6AOutj39d8VLCwIj0by9m6FpOhtXjGA3fVZ505UynPWPUAw2mZdhGMp9Ktq4A2rgveSlFWNc2rQC+zJlXo1L3k1/zMaxr1iFflWhetk6W1KMIKrOl2hl6mOEZ4CYEEDYERDWK8SDFb74u1/BN3/4B7h+5zaYCAGAC0DY7nD64CFOHnyAX//iFbz/5tuIFztsLy4ABkgpVu99cYARULyaGpxN4597oPcZDhZw2OfsGgLaxoWmlV1rLXq2gFoLxC6B5FabrXFLfwWgVCA2MiLm9VuemrXfAHlEdRifBiStOuXdltOhogOV/+2loaal1AujD/S7dgewRVcLzPb1QX+ux2VLCyxqvbJU6vmdh/ItyY0WXy3xU4t3WuNcWh+X1U+UHXWYhwIt8VoFkBt1F34iAjdIoIF8613bP/v3kkzVMqUlV3QdEy0BoP38ZfoihtogrbJDzs581Y4sYO5UstioyHLvEcJk5FiDOYBndYgeDWFMyUaUnGFOriEJqe+4w7jbQc4F2bFXc0SYhU5NWIeaiWquogNb5cqGhk3LKf9izAekOWaPKItOzxeMpIvWfJeMkFW3Aigx7hhCChUihxgCOu8gqbiICKvVKu2MOIfNZoPNZoMYGWMI6Po+hU+FUDz2u2EL77scKsUAMchxyv8c5p6EKR53LiQEoMQ8kVHOYVwisHItFTCuw6rqUiuG7HHhCIrAOGTjJoR8nmU6BDyGAEcE33lQqL3kleefqPKsLZVK6KMt9GW+l4QrkVwQNvVDBFDLI19tp6rwKB2ilw5ZN/oTuQhGR4RVv0JPKesCxZDDy6j0Q0IehmFAwFxZtRTgbOfB0WzcS7TcbDbw3qPP52NsG7lGENXASQOIqyxqq6y1J7SlyPUaljkJUbJPTXXq7GWLQJmByKHqv1ZoFhjqNu0YSr08GXT7wEirX3Z9yxrep9SvWpaA7YetbwlQgblY90In5/JBb+cQOCASEFY9dusV7nzu0/j23/kTvPDZlwHHGL0HAgO7gIuHT/Hs/iM8fOtNvPXKqzh59ATDxQYcGQERvu9zdqjUd59PDIqxkQb14eixFAbTmsc6bK/t9NCftcJilgyED1Pm6/FqRdrVt823vmfmYrTZPi/yAdAMrdZ01LQUWa+BR+udFmhLL2CWNGMfbUWfEcek7Rt9aoHKpXWzpEdsWZID1ohYAv1XkdvTSygX4V3GG6251f0tfyMdtrfnK2xfrc5pgdt9fdEy+7K5vKzM2lswJKxRUPGEmeOrAH+p00ZR6LZaoJcIIOeh07m29J78LXIlOS2n58dxrFJAk2s7R6zebrWh5wTIuqmGnBVdgFqP6TocEWKjnXTsIEUSFf0q/YJO8rAsN+0cEqiSQUt0vGr5UDsaqTOiwCdvLABwjNgN23zwkvDw4UMQEXrvk6FBybO8Wq8QxwGBGYfrdMGeIyCSZINiEDFWqzW6rkMIAefn5zg/Py8T5n0HAtD3KxCNePzoMTYXGzA7HB36dKgRAGIAYgbnMWU78S5la2EAMYwQptSGUwF6Gcyen58XgM+YM5IQvoSj5J0Z8aTLYXEgpaaFpGjN51QEEAGJycMYAHYIMaTvvUe/6uGGHUIUJ5R4k7ikuu3zOZVsj6YEBJRCR4S3Of/bByRIqTrNlC0vW0toaENE0h9qQ1X+lmej5FtoCErpalGWolAjF+veO0J37QjX7j6HJ0+fId5/AMdTSFZmWjjvEeRMT86gJv2fhE6cPOBa4zcEg6aYeA+AdH7l9PQUR0dH6X4PoxjLokcNLvWYrWBrhbJUc2bmwioZq6irPuUwiBgSv7lMZxFuwvMtRarXgzDZOI7lULP16lhQYBWP9h4tKcp9Qm5GFywAtwbtLiuXCevLCiXfR8mulRtPxkSmM2Ve9M6nDHhIhiCtemwJuPbSC/j2D/8Qn/nabwNHa0QaQcyIw4hwtsHjt+7h3iu/xtP3H+DRvXsYt1uMF5viuSKabjD2ziNbdimDDdceeKJWiGRNAw0GmrzFaQ3KR6me1oykYncz9E/5XXvQZzTeY5Ck3+f1LRk5++opPwnlYr6gdGQWCFPykVJXrlfkP1DRjCiFn8qa19/JTqFd40DtXGr11c5jxe8N3m8Bi8ow4Gm3ecm40HNi6dqSV4k6VP6vTS+aKi4/JfX8kjFh6WrH0Zrf8rliiauO7TK5oDGGfb+iAc35wj5riw4LizGCVeiUnnvh0dxivQxpPraiF8EYG8bsfH0Zw4llt6DeXYMKl27JXruTXmMCUus4r7fCFnNjp4VRNJYRDKJ3D+R3733KUikRL8wFf1ljzs6b1EE0Tx7R+j3GWBLHaBpO/a2zbtZtA8NuB++peg9AuUdtqbT6n9KKcr6GIDmlWpjxKnoT+BCGxjAM6YUu3YdBDgAxhnEoXvdxSFs7q77Hq6+8gh/+wR/Cdw6egC53kscBB6u8G8FAR+nGSVp5EBgP7r2D60eH2I6xeKAl+5QcVBaQveo7rPo1ttsBP/vZL/Dtb30LPAbwOII6Dw4BlI2cyNlL23eIHBDjiO32FIQRwDyGXCZUmCXEFFISlaBvCQRRInpSyiIPoRhqyH2ikrYWYEcpJCo4RM71OsLokiGGkD1XnD0FQMqVnO8liJyskJhyzyKq3SGJNGQWz/Xk7dXKKs9SGYsW4nos9kbr8lNl/dK7E8zzeP9CnwzUm5Y2ZGdsSkmY1DqBqUef5+mEA774rd/B6vnn8JP/6/8Nh5QUUbnoL4/J9x3Y5H4v/WW1lyNgwcyjHqsUeUvvRKzXa/R9Xz2vBU5L+NlnW7/nD6o+WYVq+RMw6foaggpgdCrms/BYpj2b9sr7JvTLO5/owXNgoYtdO+WZvHYsaLDjaSl47Smf8W1N5OpnK6yiBS7suQHdhihC64XS9adbbVJ4EztKWYgDgxiIlFcoE3zMa7vvMXJA6Hrg6ABf/f1v4zf/4DtY3bwGdgSPANoFjGfnePbgEd5/4y08fud9PH7vPs6fnYCz4yJSzsAHQod0oByglNqYpi1ygEAxQu4SEGCehjEZ5HbOluZZaJDC+SaSy87tNCttQKU/08DDfq8/s/ypi+6byCb7vXY0afmm+UBK4oc8j2nfO8kpTbfIgIBhBiRsWNLDW91hDQNLj9YasGNvGXx2nEsAryVLbDs2jPoq61TTzr6jASQnouja8s61dmhkQw2AJ5dT0ocKGNv2NY11+NkSrVpzr+uxY2u1pfVdCjXbL9+X5ssCe91eU2dSnS67kkPM5fxGIiMX/QuiWZ1cdCLl+3Da4xfdZouDeofTWcC0ltOZQDsH+u9FPooAOV92ncA0Wy+tdduq267nVqg7iTpUMlN8hDYhirQ/D2FfNqqq8VFt+0lfBFcu0QQg7IYdjroDAFO0B2PCJ3NeURYaUMk9MKGjfFaj9JlKyO0+fm2VD5V1KsaA09NzDMMOjAjvk8WXwHxiNN/3GIcBP/3JT/Due+/i1p1bBXQ55/Dg3gPcuXMHIUZ4n8JKHj15Au8I7779Fn7+858DAA4ODnB2dobNZlMtyMjJk6095c45/ON//I9xfHSEz3/+C6B8wd1qvcZmuwMz42KzwWrVI3LEbrfFOO6w2WxhzTQRVmmBpVAULpZ3PkcxBoxjQNclxqlSlgIpxEndKG4Bn93m1qFckQFETvcKxJTTnpFCpfosKJh5ym0fGV1Xx9LrHQQ2CroKscrGhgVOjLS49il0qyDLmLKhocMdimfA0Lkl3IVGNqxpDp7T3IRhB/Ioh+gvLi4SzZMVVdFY6tUHzmcx6KLVtBftCkX3T3ZL0k/MxlEt3IayaI23ErSm7RpgXN3LYPtuD0sWwZwFUqte7V0uxobE/F/SZmt9EFHayVP9sUKtpSSWvrNjsXxnP2vxd6vY8J+lMer6R+ZysR4zQDGtM8fACEb0BILDLgKdTxnOonN48cufx3f/3p/h7gt3EdYdqHMgBsaLLbaPHuPRe+/j9V+9irdffQM0BMTtDjwGSBiaPSvDzDPerkFPHa+8pCAtIGkB3/QT0Fyr6SJVLM1vC0gJ/a080rK1dbaoVazxMdFgmd8q3srArYQhijPEOXhyVR/3reHKsOG5s6bVZ2lH5L3wrB27peNMvmTjfh99rAHHHGcgS3twW0BP98/OHZCB3J75ahktUrQMsn1dcoppfVjLADc7EH5Z0XTady7TjsP2R77TEQD75J3tuxgGtOf5FPJqL3OYGztlLhfGavvUkuVyDkCee/nll3H//n1sNhv0va/7gfm6lja0/I5GF7V+bxkw8r3GGRPmaTsnNN9OOnbiV1t0uHy1pveUuVxo4y2iukXdH+9ccfoxi8y9vLR4THDEVfp71XJlQ+Ps7CwLNmC9XqFfdWUBjzGmy2riJEQePXqEf/SP/hH+Z//JfwLfRYxhh9Wqx+07dxMAjIyL3QWYGYcHhzg9PcH/5f/8j7DdDvBdh2enpylkKQtTOashwk3alkX9wQcf4P/1//6n+F9/+Tex3SXjgpxP2aiYs3eZ4F2HcTjH+cXF4lgL8CLJXuWTcTGMiEoAaS+K9oQRau92S/jpn0HOYNC0ZewdYQzJuEvGzAivAIC2coFJaNo0bsIwc6A+LRRZEBo0MbhcCKTr1/XoA+FTvP/UN+0haNFXSsyHorUxJDshmIFzvSjy+zHi4PAAnfPgYURP2W9sFJ7tvwWYWohp8H5pyZJdL9oCDhggN+0A1UadhJW0BaEd794uqDo1jT+MUJC1q+OIOQZEULrDxc3jlrV3EJjWBDdMjZmgpvqcTP5wceerBZhsP1pgomVgTM21Adg+5aAVyWVFA4ZI6V9uDZ58NpIZPWcDxHmEzmPoPW6+8AK+9f3fx8e/+mW44zVizkS8PbsA7QIevncP7/70F3jv12/h2dOn6XLOYUyZ9ZzLF1PNz0G0jCpNxxkQNWOWe3O0Ip+to2rXrE1zKxtbwKwFypb6p8MxLzNWWnxkZYxVwpWTRp1vkuxLtg6GXH61fNGcHVcagyspy5f4VvdRA6fWWY3W33pcsgPZ6pOtb6IFFyNWy/vWPOrxSR16vV4mZ1uy345jiV8AzMLN9NhinJLDTHdhLXZlb/+sbDNPZQC4XxZZWoouvIo8L3Uyl3Af26/ckwrQa9othuiaZu2a0H/XfazX0TAM2Gw2OUokFlrrZ/T7TQMRfkaXq/Cc7quOVoEB9Et01c8szZ+sQS2LWrx5BdVR6pzGPf8OyOFylM5iJNxxtcoFLfxtDIcP+86VDY2joyOUjFFgMEJOa5sPL3OCrc5NMcC//NUr+Msf/RW+8Y1vYLVaYbVag8hhN+zAIKxWBzg/P8MwjvjlL36F09MzrFY9nj07wcXFpoqT0wtCT54I5xAC/uZv/gY/+9nP8aUv/QbGEDGMAV1gdJ3H4eExttsNdrstDg4O8sHyEcxJe2sFpic3hUtxzp5FSClTCZvNLh06p3TJVnVpn5sL0CnGEOVvLUxiCMiX/MI5mmUr0b9LO10+LMoK1tlxWHppho9h2iHR7bQsdVsfgHLIfRongWh+ME9AQDEeYMJVuBYwlWA1/SjjQQqH8j5dYhiGEZ3zKTwlsWjlpdB1W4ND5oBce/FYoaL7ysylk1JX5eGnucdJ94nVnMl7VmHb9mOMlXAsbWWKyW7arJ/mWc0b+4wbe2u7Li1gKv1bDIdrCOzSJ/OMBk92vFomWM+RHmNlQHMdOqH7oGlglYMF0q3+aJrafhJRuYGZcggVkOTkAMaB78EMbIjgbh7jt773bXz1D76H7voR2FPaDWFg8+wUp/cf4d7rb+L88VM8ePUNXDw7AcWSZya15+r7MFpjsnORfm8rRqGPpp+eQ+1UsPW3QtOmPqX4bQt8dL376rDzYuXUfK7aQEK/Z3mpZdTotc6NZwBkD/2cDklm1LKxhNd5D+3k1UlFNE11vy2/6XdEP+o1UBnlhl/teIUuNmTO9uUqAFjLYF1/eYZzIM9CXZo37Dk/GZc1WmwbVr/L7vNsNx1zJ5rU18IgVjfOaEKYyewlWmla2/Vg6WF/L7yFSY/aezf0OGxphcKlelFhDP1TinYQFT3PrDztjPv3709rp2G82LYt76UPa3m9hHW0XtN6oh6XhDnWa6alNy3tWjpEyxA9hpq2y/JXzmHYNoHiz6zqk/4zczq6wOkpyk6pMIZCf5kjqZeZZ6FwdvxWXFraXMbPUq5saDinALlK0MuR0XmfY1EFXAmTRfzVX/81vvTl38BqvcZuHAEGxjBiHAPCuEOMDO87/Pmf/0uMY4Rz6aD0MA7oug5931dMw8wl2xQzY5d3L9LnwPv3P8DnPx/hu3Tr9zAGbLZbeNflA92Evu+ypykdgGVKB1jfffddvPDCCxUhxSMVYzI2xjEg5NS1wzCWnZaK6WK9RZzenzKDaOavPJ7MJR4QNGVLWvUrOOfTYs/nNAj5QClnpkFbGFklWglCoMyVFRLay9VSZPJ5C7hY4KZpYA+O6n7qEIFJmEUQ5gt/WnDpbMrZs2eIw5A8gTHfDeDmXha9kLQAZ5GkZuFYJSV1VECWCIHn4xPjytZR5sRR1d6SkrLAQj9vF76e/tbzrbHZ9qo204MFkCw+Z5Vg+nJBaU300LwUY2xupQPzC59024tnf5TcsOF4LRC9RAv7nPTbKu7W+/V6o7zLkL4PHEGdR/AOFw5w3Qqf/K0v4as//EPc+vjL2HWEnXfoI8PvRjz94BF2T0/x2k9+jl//6lXEiy0oh4YmOiRHiJMkE5jzsp0vDSRb49TZx1q8J/RfHLMBovN5mg6Uaxkp7+h2dP+vouDafao/02PQP22WRb3mZ7JAyZkK5CCWENTZuAzY0Ge3kqNqTsvLihgsljZ219HSp8Too9ZT++bVuXmY5vIcz0tLrkJxrDUQbD9q4DkPMbkKCCpgyzgYLpObeqwALtWHAIp+ls90uNuiwaCKlZMtfVnWMlGVJrXStTQHz7rfTXmtfrMyeB+Npvqnv6s2qK59qZ4ZD3JNp5ZcsGtR1z3vOxazier+6rUl46qx4vx83gJRZvOsHWrzx4uJB2C+hrMNW7Kala0Kzrtzaj3YUGIs0JvrDxZpc9XyIbNOTX+L4RFyaE+rSQLhxo1bcK7DdjtkL0E64B3HiDBGOEcYY8DXvvZ1vPqrX5XJ0tuZ0v44jhjGsdxpIQrfe4++73H3uRfxhS9+CZvdgNXBIYYxYDuMSQCPAYcHa3jvMAxjIbpYkev1Gs8//zyccxjHEefn5+j6FYg8hmGLEJIBNO4CwISu6+Fcj67zMyWsJ8KCUv0dUDN/jDGFPLiUMzlmL2UytgpR4bsOlBdYyQoUFwSGAzhMwF8WpnOuAB4RfLVhMJ/RfYsovdt+T4oV4FK0Eds0hkwdpS9IBhHHiOfvPpdC94YxHRZvgG49/paCdOTKofGlfjeVHqb1audb+qdBbzE0I8rFiHpsrfHqfuinLL10CNqSwlw6/7KgKhBNP3X5MMKm1WerJHQ8b+tZW1q7HbMRGGWq67rMY/yhigKHdl6A5IgjAF4M2q7D6AmjB25+8mP41h99H5/44heAziMQwbOD3wSMT09w+sFD3Hvzbbz3+ps4ffgYfjMgXOzgSpaNucdL87oGjZcZf3YMLWNKPwPMz+pYI0yvj/r9eT+0nNF12LNwrf7vHxsgB92ltIwZ/fm++qbfacZbRFTF+c/7V4OGas5Me8t11HNgd+5KSvX8vU1Z7fKOuMTo2/bsWE2voGV2izdapUXnaQ7az7dkoAVMmteX5IWMvQDyhbDe5MhLuszywWX8IP2Z+ifPYAbyP0zZJwN1u+mPhL00jTQQjtze/f13Kfvqa51ZSfKIFx1ttiz1sdIdFaabr5XWGa7cMCIvJ6vRfavrq9P5L43DyhRtUNtnHBGYasdO0V/GztC8qeujUt+049rayVmKOLhq0Xx+WbmyoVF2MShptMLESAJVyCeC0juP42vX8bVvfgNDZLgQsD0/w2q1wm4YsTnfwJPHZrdF33X43Be/hOdefAlPHz3Car3GEaVzIdvtNt19oJUMJaDfdb4Iz9V6jf/g7/09dKsVduOIJ0+fYr1eY7VeA0Tw/QoRDmEICGGAcx4xhuSNCoRhN2C1Wk03a2ePg2RwYgBDGDGMA1K2BJT2W1tu088pNdkUrzsP2RCjAayAKSjlzgdAkUEhpPA0opJmLW2LzT3D8rscSLReG92u/lcBO8yFh65f/yyLqfxPW+GYWcW6PQDwRJgur8uclQWmRPyn5/OOAVwxtnbMGE9O4MKAD959O6XU4wjmeQaSSmDnBSrbh3Fh8WmAn3Z6Ulx2dveDmaYsGMCUTpgmY0LTq1VaRhir7/RnzCjgcXJfTMZOy7iw4LN6ToGfss064VfIVnWekCm2EzWv1/1kNfXLytr2z5NDyX3GAHMs93zoosFVC5Ta55bX5/xMSOHNQlSC7A9U4CQRB6x2YTwDHg6RCMExAnNOWQh0Eeg5ORJG7zB0BHfnBr79/e/hs9/6HfhrBxhA8ExYRWD75AQnDx7i/utv4tevvIL333kPFCI8KN0SLsAlCQVQVi5A5jvSQCdlOiKqAb48MxkMNXC2IGXSdKz+5jxX1kkhddVzrX+Xd1ohKqndaU6dEw9uVKB08sC0jDvpR1kb6lPKcl1u/yXkBQshnDLs9wFETrzOWXZDQhdAJV3lNF7Ro26iUgNMy9qyvLk8Rj2HkxNOy3RLY2krI+BEY8rg6QogZB/4nupuf98yJq8YWl7VPfH1fId83y6ofCb/arpI1EbmXQIIWV8UXs67Ci45TyFAn8RVFdWQCKC5B5wZOVJhrhe0vGqBeGvUVrSJSSY4ccRlsSDyLKnXIr3z+p9nxbK7yZGRnXgody7t40fOQoHRlruR4yxZzVKpxmvbwLTbIGGCOkTaGqK635Nc40KbDA1SeCujpFDWa0h0L1HdP7sr256z6TB+eY+n1Ngin4tko5xttsSaKSyi/gox68r8mdP8a/RjklWc9Eab4un/+fuoaP23KVcPnZL0i5iAYPrdIeSQqDwv8L6D7zr8j/7h/xif+/wXy+EfCEB0Hs53iBE4ODpO4Uce+If/k/8p/ov//D/Ho0cPCoC4uLgAEZUQJaHcJKTSQvjhD36I3/3d76HrD6pdDjDh4mKDYYw4OjyAz4eknPdw0SGMQ2ImFccYYoTrPEK+2TWCCgiNiGAEhDhgRfom6sSE5eCZE2HkFMaWiWrH97m8+L1zadvdpexIAw/oyaHvukTDgi0oXUwX6/zPetExz42gIoB5it+1IGxSdbnne5hspnAKcFd9gwPIzxSf9z4bVzkED6hoIzyW1X5axBnDekQMHBF8j4O+xzoGPL1/D94BHKmqq8rKogyzJeOi0EHoQpnxsxSqMq7IQiYUek/elXQWZsnjoxVhFaeuuEX3JWHbdCP89L4I6baHWP/UdC1ClgjskjCLJKpRJCjUz8kIUSKg4h0NGvSZFy2IW4aAXQfCn4QEfDrnEHi+32TnbZ/C0jTQa1bTpQIkoQ6TIhFw8nwOgGl5tYjU+RVwviPIAc5j8A7j4QE+882v4nf++PtYP3cTgQJcDOgYoM0Op4+f4eE79/DWq6/hwZvv4OTRk5S227l0XiPLOJ/nIgEB67VC4QsxiGXS5nNGmS40A0SatpMO1WueQCR1aGNBZ0ua+LA1P0Irfft1jCj1aeAofRD5n+Z8nzdS/a6aDpJcQ/SaI5CEMEVGUBOrjYKpbc5y2JURyhmD4nRAOks2yZipAy1AkvhsbpDJ9/rzpoFveVjRTrdRvccSsuWmsfKUVlwAqAZuMH3RNAHmZ7daY9Blem4uG6x+0u0tAXK7u9OiidWLNX1kzdTdSn8LOAdAEc6LASkyTjlF1VpKWD6nW88pn2O546CmU4uXbYhWq5T34rSrxvlyX5ZdDkIVzVCGx9noNvwiP536XsLtGHNjo+q7obf8nkIT2+OYdGetG6Znaxlv9Zml3Qzb8JShTp71xXGYsRWmkKQIatIk5nvO7PkyKVbX1f2SMUmdmYcytqP8YZFxNvKBxZzITh7KxgtN0kPfdaz1W6UjiwiwO4IEkAMxTYaiq41RTYvLyofY0agBS2F6Iywl1vTll1/GV37rt7DuexwfHRXFOAzp3o1wHOB9j5A9lsNug09+8hP4xje+gf/6v/6vwMQ4yJedaUYKxjPvvcdqtcLXvv51dF2P1WqVdjJWq3K+w3uPk5MzgNI17eR6gEfstmmXYRxDofk4juXyFsmsIQsDWQCNIWA08bB6Ap13GMNY+m2f0XS0QtCJomIHonRYu++7/D0AUKH5BJJq0KQP20EpCG2NhxBAkWd9mgDtJPzswtULzioTy9D1tun0ud51sUJ/H/OW9jitSE8OLgLbkzOcfPAI22enuM7TFqR+pwD1PaUlpIQeLaG61F95Ru/EtRQEm+fLT/XdHExP/Wh5KfeNyR7q5ITUsgGzP+OTntPEWyjG9UwxuVrAWoFrgYAW1NUOmYAvolpyNvrXAl62//ZwsW7bCvKynhte4CVhGwgYHKEHoQ+ENScDNBIwdA7bdYeXvvAZfP2Pf4i7n/gYgiMQA30EVuRx/vQEH7zzHu69/ibuvfk2Ht67j7gd4HM/uq4rcsd7DwfxwrXXKjA/AKh5wJ4r0rHjooynsCsxZudKdcmQbNHIfq4vfrPnAnSZxReb+ViigX526R4A+fsqoQBLsdgzHmw8o4sFyLW+WPYU6/f1WrJrRp83WZKt+4CRLVeLI2+vj6W5WQL6LcCo+1Ged/M13zIi9tVldVL9WSjzMdUNCNi1On6xqK9Ffst7dn0ugdMZ9rqExpYfpHG7g1LqydhFt1PkcXbwiZHCSCqYL3H+CO2kD9oY4JosM0ykaVTtJCwsC803lgdtsfikhdGWytI6sZ8LFm6tuctwzlVK/X4yOLwX/ZbDwYxzTNr/sKXoA8x59CrlQ92jYRWT/L5epXsyBOADKUvVg/sPcPc5h/V6Dec9+r5D5zusDg9wgW3aMYgRIYwYwwiMY7rrQik3UXzFm6L8PXqw52dnVXYFAEUxhxBwcHCIrkubic4BIRCGIbUbY8TFxQZAPqCpcyDHZGSFEApolzMiWrnqv+2i10xvvRLW0NBGhjCJ7zpEAWFhOmDIOZaUiIq3f9rWy3SgiUlslg7d/xnz0fJC1WPVGVOk7RYdUrtzb3ZLmNj+LYG6GHOmqTFi7Xo8eS+BMhcYzDFdcqjmIP9RS7dGsXNTDBSqaTaF7bjZ7oMcJrV8UbWTRW1LMIqhMesHi9HdppHwrR0P85RPXr+XeISmNi8Rzpo+AhIFyNT5/tvb1Utzqvu9BCJTV9t3a1haaKChw6s0yNbPtAT/PjZZErYSZOUjoYspBHPngU0HHH/kRfzOH30fn/rqlzEceGwohVL5IYJPzvDog4d498238PqvXsXj9x9gvNimUClH1eWPNsRIemENIg2e5HebgUaPXRuNkkWvasfwv50r6d8SvfYZAPqz6TkLRdoZ2ZaMDKHVVRXstLaWjY0WuNR8pnkrgss5DSsLbZ+E/slAmcBUC4i3QkLsYXZmnqV1tQaIHVdz/c32tienkb4UrgX0rwJGZN2LHN33nqVfCAEOKRRRh6K0gGrLgaL73nIatuSoBbOWXssDBWTbgNk+XztQlkCybd8W/blOLlC/i4IZdCnrpAHU65+pjpB3RpDlz761Zee07CbscRpZvtZj0H1aetfSw5al8KZmGC0SPef3pVFxzkmdS/y7xHtLuNHSoYVJ5B2X20xJjibDj2MEZ1nS0r0an1gZw2x0osgdMvLhEpkq5cqGxnq9xnq9xsHBAbz3WK/XqYKuQ++7kiZOCHJ0dJRT2ibDY7fdggD0vsM4jhiHAdthxG4cwEipuUApVOrk5ARH147LgfDigadkZOiwETEmDg4OsLm4gPN9lelnt9vl7UKfDlEjgkMsEzOMGwCEN954A89OnuHzX/gC+vVKyJiMoZBvBw+MIR8u1wJbG15J8deCTX7KOGR3pwnCeBLuSfAmQyxlzBLmA7SqCDFMN2Bbr58DJOpdxy0mRTTfnpR3pWghXW2do14sclbGxgVP9U/btVIsk7cUqv59JuiJMIQAYsLu/AKnT57C53bGwOBMJN0fKVYZtoRS1R64xCnOlXUSwNpLDtT3rLTAiR3rInidgbm6j7bPS8UKmOo7BeqWhLkVSLLbJ2OswzOSUSCA1RqgUn/LOLCKdpobqvoh9LXv6bm0itaOu2WEFGFt6rP8aWlLROiY4INL8dErj1MKiDeP8Jt/8B185XvfQ394iHHlwD0BY0C82ODiySle/csf4+1XX8PTh4+wvdgkPo7pjJXLa1v6WoFGFRqpgaWWTXqns8Vrlqc1beuwlXlMsp2r1o7REnBK/a4BoqanxEHbz/Xvdt6tEpx5+4F8oercc9wCKMyMEs5gaK95r0XXyxRyaz0wM2IYIaC7VSxoawHkFthe6oMGWdXYjaFX0xsFKFrDV/Ncaw5sKe3GuRNMt6vXeUU31HOi5YI8p2Pn9by1iqabpYmm9UzvN3ii1ClGJwhEES6HRccoLqWJfq3dVj1uu970mZyWLNN6Wl61Y0qAmkFcz6UuCVgrhxQD5Pfv2tlPrVzXY5fv9VjsO/ZZzW96t0ToKH1rhexKO+I81un3pzbTmOV97WBMj7SNshnt1Lt2rC1+nM1NQxfzNJmIMWC3G2qZ4upwenvxp5UR9Y6lokMeSozpYGAL215WrmxofO5zn6sUkWZwDvXCAJIB8tJLLyEGwmq1Aq0PMAwDOp/OWgze43yzhfMe4zhgtV4hbLf42Mc+ls50dA593+Pg4KAIjt1uV66d14pxvV7jxRdfxPG161gfHqWQgvxd13U4OjoCUQciBnM6AL7bhbJYYgz46Ec/irvb57Ber1MsOEsq2yn2OaUrnWIwI8fqUjs9gfKzNRE2Lly/Jx5RUDKo0s0QA4ZxxIqT15gldpwIUMJEt1eMraW+cO4/Wl6kicll8ekzDnYR2a3fq3g7nXPlDg4pdpFb2lnDJLp8/gEO675H5zsQgDGEZXc0TWDJ9q01V3X/2lWK4G3F+y8J4KU29pUW0NXttuq0c9tSoNGMvdXv1lwy1zxSKXKmkl5YnBC2Puudbin/qi9UqyULJCxdrMLR71kgY3f1yPBJax5b/SUAznXYeGB31OHFL30R3/rT7+P2R18Ckwdcj44ZdD5gc3aOd195FY/fuYf7r7+FJw8epjNNoHRewCHxa+cXQQ0n5quAmKWbXVf7QKddB/X8TAaHBp26PRt+ouvSgKieo+l7q3RbAE/+1jRpeShtbP80Q/WcLq3RYRjArNK3Y37Xim2zphuqMyFLa1HTL30+H3dZq43wMSsDLHjRdGjxxKL8yXbGEq+I8WX7b8u+kKyqH9Km7sKCTK7oo2jTllO1Q0TzqdTR0jXyvo4UWKLjZeGr8qz0LtWveb3Wjbrt6n3DP80dakO3Che4dHjdOu5yjXvmMclDMUGb2KVF+1RrcwxiIOrvWvLHjkeo2OpnC0/MRmJ4v9WeqlEgVNF1Ux1LezLzftu7Y5bkmg5dlfldWp92fOM4JOcxytItbLWkZ1tGjow7xnyW2TlEIDm8qK7vKvgG+BCGxvHxMUII6Pu0YyA7BensQlq8XZdCo0DprEMIAd6tKi/+OI44PDzEGAKGYcDq4AB932PYbdH3PT7ykY/i+PgYu2FXzlnUdxGgpCITodH3fT5QPnnVQz4AFTKgdU4W5ohxt8HTJ48wDFu4bKEdHh7i8OgIb779Fn7xy1/gG9/8JspB6sh5F2aEY0wGT2SwazOMFM0oGpCJ8GqFC1Fe1C7FeJWD7S6M6d4PyzBmcWmhy7FeSEWIEcOhW/Dy1OBAPtcAR7cnceMyfruIdNHv6xhieymjzKP2zmnmJiIMiGBKl/YBadkHTrdk0nQ2r1mWFJCdwwoMLFcGSSvbAlhLC5KIJu/QAr2W+rOk4FsAzc5Zqx85ycqVhIduI8aahq1i4+51G3uBzrynFQjTRWRESzFrBbFPaFfzL5K6AeKneUNxCsjnwXucuYhrn/wIfvfv/hE++sXPwK96EAMddQhDALYDnr7zHt742c/x/ttvIex22F1sUz/7PiWjICo7t4TlHa+0xtupPhep2OAJbXjasL/p2f3Gp/5M+qBDX1ve4XS+LFa7MdP70yJujVv/3gqNaX1mvwdQyWPrARQeJ7MGl2RFBQyuqISFb63h1hq3fW8fP9vx23V4Wf3Shp0zYJKFVia3wOa+v6vPeb9nV/dZ6wrkNSift9Iga7ms5+gyuajnw871VYD29AJKXyVaIX0tfNRuU7fd4rslsK37Y+uUv1u7fVflWedcOe9kdX4lgxr8Vvq8R+xr+aHfS/JuGSC3wLT9Tr7X7SzRNamCeg0VWez2ryXdXsuJYsfa0u1X4VP7PbkUw0J5ABrr2N0IbeAs1ck87W0y5kcFrlKubGjcuHkHEuuVFnKXJoCBYdzBgXC4PoB3Do8fPcoHqoHt7gLn5+eIMeLOnTuIYHSrHhebi3xSPuQdiASmfdfjE5/8NIaww+biAmdnZyBOh36ff+FFrA4O8NZbbyUm57Tdtxu2GMKAm6sOYRxAHHF2dobdbsDt27dwenoKkMPBwQG6rsPmYofTswv0fSLuGEP6FwKYCOvDIwyRwREYtzvstjtsdwFDSKQ+uxgQYz7lLzxDmSFpSlUmRRSYnBeR/OZWIHIEqEv2uidKaW2JAO/hVyvwdgsi5fEiSmc3KqFrPIfp4ZnwijEihiHtyGQOkv7bex9agskKAF1va+Gm6Zryt2uBJ+3orT27/W8FGBEBAaAUG5YMyRBAnLJEUE6BKXqoyHSuBfjMOHAZRIJzFqnclqwynkDmVLJ3g3mvQCnzXOajBqm6P/bQat3nGjRXAlSe0dXnuSXQJDTlM5IwJypnQqqR7RUmadw6dK584yjFTu/ZvZN3r2J0VMpJSz0gjdXVSlX/tPyjaeZymKMYWSmLW5It6YyUjIkRwGmtuUS7Dg40MggOA1E6BH73Fr7xwz/AF7/5O3DHa0QCPHv4ISJeXODi2TO88Ytf4uyDx3jvjV/j5MkT9F0H7x1WXZpX73zV5xgCJBtU6ruEQBAkzWbxDjqaeFyN33o+Q+aRsqZi2lkofE+JpkyY6OESxaCyxTAEUEx8Vw7oAlMYGqVMbeUgKaR/akq95HpBMt7zF0SpHyUET/iY53yF0lbMoZrpniaitEtkaWKBSStcE0gbGrJm0zPKuCYu2etC1EZfg38X/tbGTqJfex1cFrZgwVQLeM/pNf2S1UX6SfXzus+XAmvVBw107Of135NuqQ2JeRs1HWKZGxCjmMRcv2f1R6tP9ndmSUGLzG+p4pahaUvVf5FZRWglOZPkXzucZt/8tuig+14i9YlyNjEGB64cW7pOCat2qOVmeZb0+PNu1h6PvvSDmRE5lAxmEoUBlh2shZ2QBvAuv6sMqHLdArkky0PMd6AQl9uxk1GQ8JXQzDqkpMzDnLlMmZYP6QNM6wX1ehcHnMVCSzy39JkNtVoqkRmddypxEJVUxPt0uHYAFeyR5RsjAEj6TSmfUuc+jGPLlQ0N79cl8xI5h/VBepXBoLEDxog4Rmy3G3xw/yHWR4d4+PAxnpw+K9mjVhfnGJ4N+NjhAajz6L0va8+RRwwA+R43bt7BbrfB9Ws30fkPcPL0KVZdj5OnT/Gpu3fxmU99Gj//1S+wGwaMYQR5wmZzgRhGPHj/IWKMODo6wsnJCVZ9hydPHiNyxJ07z8F3PUKIODy+DuYB2+05QgzYhREhRtx5/jlQ12O7G+GcR8g7GUNgDCEpyc12yPmK65SSBahzAnUCnPXuC5BCSTTALgzpJw+mA7AbR7gYMYQRq65HYAJFQk8eIMbIAQFcYo6FcUp/siKHEarT74xh3KU0mTnNbBlHkVPtuGetEKw3TgMbGb98LqW1dW37bg0C+V1+eqQsCCEGOMdYOZdS8ImAytJ9ancSHE3DBUhAUt0bETlO+qEc+pC6JqWshWJLSc5BtgaM9vM2Hac6i9aaL/goRkaWgGpHy3kHnUmtvJfz0Ld2gJbGoQ0UHRpVKVbMBakeQ/poLnhbYTBpTaH8zKakdKqgIs1LWmG2xiIKL/1LwxcgDEqGvstZoThrFXYAiOFD7pPvsCVgOFjhi9/4Gr72p9/H0Qt3010uMWJNHuFkg5NHT3HvjTfw1muv4PTpCU6ePAGFiA4EHwBCSqkt43M07VT4PDeSHS91fTqzpeemyBkZPzCjbzJMSBi3OG309DNQ5IoAznIzAKf2NW2LwUg5PbjLCRLE8NFpPDNrBllbSQGUZSWGi4BPCI+HUIwUz21ARJRvRaapPvld3/bdNnwn0KVLZOFVKgaLxLsneueD0aBJhgvPmfh5XWy/7bm9VtHf6R2ZlnGts4fZg/3VPNcWUQZykziwoK8AJtM3CwgFuITGLnxLrjAYjtxsbmSMbeOEq1Aa5kl3iUEs8kDas2DShuRObSoQCUpoFhHMA2Ksd3CWZGQZGwk852JkM6Ki9fxshJ1PW/9sR4LKapqM+fwzMk9plkGzuovxbdaBld9aFleOK1VqfR0nucLJeVDaU1PVot0iQE5CrThX5AJC5yUHXxo1UaY2T7JJDPoWtmjNpRjfdmyVni9fTs+JQ6QV1lxqXsAMltb2Hf15+T7/XK3XAOeLtLMOEdnSkj/2bHUxNIiQUpab3QvmfD/LHNPtK1c2NCSeXocrOecQYgB5wuG1FcaLLR4++ADb3Q6nF+e4/+AB4BwuzjeZQB6biw1eeP4lMFK40jDsEHLdZ5tzxMhYHRwgxoAQRty4cQsX5+eIMWDkiA8ePsRv/85X8fxLL+D/+1/+l3C+A8jj9HyDt959DxdnWxwdHYHJITDw7OwMIQJnmy0OtjscsE87FyA8ePgQx8eHU3rbCGy3W/iux3a7QwwDxl26LHDYDRjHAILDZhMQxjBb6H3fI4SAzWZTzonEGMvBeVtEAIow9s4lxvBdMmR4svwp705MAISLN4DBOTxsUmbaS///5+0/nyVLsvtA8Hfc770R8VSKSl0iM0u3Ris00BDdAEiMzewHmu0MbWz+t5kPa7s7trYfdtdszMgBl8MGAYIggBaoalGiS6usSv1kxBXuZz8cP379eni8fAWS62VZ772Ie137Ob8jPRKRgkBQ2uQpIU6FhFTbp+5OWnKCBKxnVFCGUDK75e4K6UGKiQBywsgqrDmslitg59w4hlP2f9rXPEArLaXArVJdsa8AcmKRz8mkPmAC7s8SAJd+l67duNaIQgYjuScEgsXZBHe6RDOnostppWwqlXsX0rmIzwSgWApKzOdmuq5YG1NpPvK+5OZtrSMHjXn/iabMQ9vxBHQGMCyX8CkQIDDIERZssTTAcrvBxRdu4nf/2Y9x+blnYOsacAMqMvD9gNX+Yzy68wU+ffcD3PnkExwd7aNfteBw8Z6JzHpdGaA/83OaltxVLzJOEhhQ8uFO6YoWXZ+8vqn7FJDeV5H+VLqx5gaazukTGLw+U1rH0t9az2nMfAp6pi4Ea3soG48Wkk6u9WME0FOQn9aVj++0tpTGppacTe/lZdNYgPV0vJvoUfr7aftO94LP6ikB1xJgzOuPc+G90Kds/lMQtGkO0nZKY0nnIVWQbepfqDWrk+MZSOlUaQ60T5tcHifWtLXRrAsP630b68m/Y0zPdn5eS/sqCnKZEirOeXZZkPK6tKXT5iJfb1a+tAFM50U/2+Syk9af90dw2Pi7tl+KJc3niKKA+OQyPSPrZ3vjvs/o0mnrlM5Hem5UoeSjMsWMWIDK+Cyft4kwf0rb/5RyZkFjuVxiNpvFuAxmuedia2sLHh7t8QmOj4/x6NEjrJZLODAePHiIy9dvwHGPZjbDybKFMRYHR8dYtS0GBtzg0K1aGAIe3H8IQ4Sd3T0AgHMDHj9com7m6PsB1gKP9/exv7+P288/jwsXL+L+g4fwTHj8+ADGzDFbbOHew0doFlt46vIVPHr0CA6EwXkMjvHo8AhffHEXh4ePcf78DurgP+0Gj76ToOuuGzAMkonA9X1MZ6ugt+86rFYrdN085i3WRQOApmmwWq1ijEmqedKiGz0F0p49PIfL6ULAltyKLGZWaww8DxHyGCP3dRhjBQ1hSsSZOWbYSk3zWggGxsjmHoZhQsxzop4eAF1/3Qs5o8/dh8aDMxVYYj+IolVljcknxCMXiPQzYwyMFcEVvJkwbDr003kb52fizkBUJN6xvuzzvK2i8HEKk2P5YwPRoUK/NxGGhJBEAq9aGoogCgWG8aQ2lOmmc5TPQW79yoFhWm+6b3JQmv4sgUTwyPLSOT+NWEfxJFnYybpy0FIzUJEFGOLOaAxODGH7mWv49p/+ELe+9VWYpgLIgByD2kGyoD14jF/+9Gd4dOceTvYP0A89UIkbqDcAvNxqvEnKy90i0rnRv/N+T87KKXMmos06KNtUZE6FLpX6ksZb5aA7fT4HYkRlUDk+j2IdgZOfYf9PtdbpvipZWovzQHIBn2ZQizQnKobKAL4EtPLv076o1UECdk9fj7yfJWEAGF0j0vM3WYOsL6lgXgKH4xjW1RP5eSvR+Zw3TGhGQh82uU/p96W5LAmcKbBMlR7pecj51NhfGee4Fum/08smYDnd+zr2KQ3I+duT9oE+F3/PbA3aVklQSzGBWgjy+hC+1bkIlawJGU/qa3kPlcexqZ5NZyy/s6K0npvcDtO9v+6KNrVonLWo50CJt51GqybrUaBvOU3lsA7iHkdo21ZHFfdU6dzlc1Ka71PpKj2ZPqXlzILG8fExiAjHx8e4ePGiBHD3PeZbi6DtH/DgwQO0bYtV22L33B7atsOdz++hqmrYahVTiD18fIh+6MXU5QXQw3kcHx2BvceVq9fgvEO7WuHipcvoBycxHd7BeY8PP/oIt194AX/84x/jX//v/194D3zy6ee4e/8QpqphjcWDRweReBtjUDUV7j88wPHxEn0/oOuWOFoeYXv3Bblhuh/Qtj26QdoYBoeTkxMcP34MYxsMbDAMDj07wPVYrpZYrWbY2tqKc6RMrO97HB8fT4SMEoHRAzIBDuF9piCJD32sm9QlQe/0CJflpERUFz/GaWREdCSyAPGYgUKtL3nqXu2XbjrdsGk6XX0n1x5PD5mJknUptS/zaJXJQSIRTSw2OYBV0qpWNyLVQE+JySbzewqSUtNx2jf5ff3iNkDh6johyIlEus5EFPNwj3OUjBllDeHYRpk5MsRFChyETKPALIgVlEAEhlg5ghOSNRa5EKAl3cdxXKGyNNB6XL914JmXnAHL/uIJYc+BWk4sY5syYWtrl/Z9rU5g4ls72ZMMNCwWDWLZswOJu5bZ2cIrf/wDfPUPfhfNxV30cDAemDmC2z/G4wcP8Ntfv4E7H3yE/fsP0ZAF+h4V6a3WXoL1gjCgrms5GMjXV8/oEwP3CoAznS/F6fkcpQBaz5K6eYYZgiY92MT4UqVKGjiZn6dxPcUdJT3XWpxbz+Km72n82ZOYXQ7aco1mPm856CQSC3J+T0POuNNLK1NhJv17k+U07Wv0j86Ap5azCC/pOoznaupKWBr3pjrz/ueAPp2rTQA7fS59b2LBorLgl87xpnkrzdPoWbne7mlnpESv5DMRtIkUdK8rZPI2JvupABKF59Oa6FLiI/n3JYUDoMMuC4KbACWg1u8RJ2iSl7GfmABbcqOwkdOBtI8loBzXntYFVGA9k2Wpv6U5yvGDPhtju3g9TX/++2kAO9/PJUxRmt/S2dhUt47j1DWezEGwi4fkGam7ovcehqcCVmms+k7J8yDHrsnROnP5UhYNa2306To+PkZVVei7DnVd497hIQ4ODqSzzuH555/Ho0ePcNw/ArNkraqqCjvb2yBaoRs6VE2Fru1wdHiI1XKJbiV3bdx87hk8+9xzeO+991BVFc5fuAjvHe5+8TnqpsbDxw9xeHyMV179KvYPlnj9l7/G/sExdvYauJMeVVXh4PAA3jls7+xgZ2cHDYuUOQgSgyeL45MWDx8f4MLOAs4FYaPv4TxjcB6f3/kCn7z/Pp5/8SVUzUIsG65HU5ngSyoLeHJygsViAWaOF7ucnJzg/Pnzk4xZ+eLqdynz0/88QzRl4Z3BDWjCxiPnxPoBP7kZNd1MkfElm2TdjYQnBKXE0PJDlLsvlIQGLRMpHtOUgTnhSZlJiXBvtAo5Dw/GYBBd8DwzqgI4eRID8wXmNL5zGmEAjF0nejnjyvtQYh7xd/lgrU15D0BC4InG3PEgRNM5BzkmBdaAMjVOhiQCbro+ad2b+pgzifSnCaC8NA/psyUtU0ps83kq/Z7/TEF7zgDXCDyPerkJ+GCG8R5kLHxlsCQGthZ47qtfwbf/9EfYvnEJzjCYCY0D7KpHd7jEo8/u4NevvYbPP/4UbtWigYF3HWxlMDgP8uJuZgzFOI6qqoIP7Xo/0rHmYy8xovhM4TwmtU320LT+UWjO51b3OrDuwlAGZuXLI4E03SMArIP3sY5TwEaBro4dmD6rgk9+DtP526h1TDBbLojoGFJaWTozm5h3aW7SeS69V6KP+fsli+CmQqBJrOGmfo19k32SjzcHYZvGmvOqKZ8pu50+CciV+gkgZmks9Sd9Pt3Pa3vWB5UEGRBZMEY3301AOp+P0/s8taSXntPfc55cpGkbXKfOWsq8ONyDReHYFaxV/7nlNH6YWk5L+/E0XqDf67UEp53FUj0e64JC+l5J+aO8OFc6lASy0vf55dOlkmKbCTkPtMwk9U+eTX7Xou2lVr/NZTMN2lTOLGhcvnwZVWUxny/kwr75LKa5nVu5yO/GjetYLS9gZ2cHz926CdgaO2YGQIk4MIQDXTcNQAxbWezs7GCxmEvsgWfUzQzWVrh+7ToODw8wn81w8cJ5nDt3Dqv2GM73ePT4Ea61Lb7z3e9i7/xTmM+3YesZbFXB2go7u7sgAFUdbhqvDHrn0dhGJrkyAAY8fPwIfnWCyloMgwfBgL24EV29ehXbsxnmiy2QrbG1vQOwQ2UYVT2mdF0sFhHsAcB8Psezzz4LY8wkf3LK1FKiMX4nWmJDBk7ddiBZL5yT+z8YBFtVqA2hGzp4YvDgJ0xXQRYwzYyVbjK5jyMA7MR3Nc3hnAd7pwerdGCALP1buhlp6tC0bqLEmiCUHogckOZSuQkXm41CjZvUk7aZH+zYDtYl9fFZBrisSSasM4T8YKftR6KlAkFGLKH92ADk5D6DqYXBGCO1KcAHi5Y/I5CbBKf0MsVUOD5N0MjBmfbT+6kArM/mxCzOX0a00vnaZGEBMAGPvvB9vs6xLaIY3xPSCa2vPREGA3BFcLXFxdu38O0/+zGuvfQiUEkWmooZaAe45Qr379zB27/6DY4ePMDB5/dgHECeQOxhrYEzBEM2Znoi0Bhk7T18EEDS+ci17zmjSNe/ND+nlbSu6dqNwDkHNmLN2NyWgq8cbOZMOO4RInAW1L2+flPt6CSNMXNRUM3PTR73kfY9j0fLgVyocDJH070UMt5tACE5Q99U0jqZy4ApfTb/TP/WM1MCzsV+kPzTG8zzsrn/QVj25RiE0wLbN1p4wrnQvm56v1RKzzLzJI4k3fMlILUO+MI/AuQ276A1pnVanoP/J/V7DVSnvydjz/fqtH8o71fORY0ymM4LAWKpKALosB/VBTH2p2xtSdvJ5+asZZ02rfMaoBynlvNe+ezMTZ86nlQBVhb0ygJQmbaU29o0jvz7SBO9h8ZLTjg8TXlKCc8BstbDMIxKLyPxg6U+E+n/zl7OLGj86Z/8kTSi/p7JoOXKNADM8CFIWjKoGDhQ1BTr4AY3xH5qVh8fzORVVQEhi8CVS+dhDMENA4yRCPlh6OH8IIHZxgIw+P53vymbKGgciASc68Z0CjpJQLz3DBBjGHoQMSwCUOdgSTAGq7YFzu/A3rgiGn91nxh6ODdgZ3sL1oqLwWw2iwuhWgC9aDDfbOL65MO18eNBNerTAgqpOsWNxEqlwNCDvANzD08G1lQgZvhhgJUQVTB7EI/BT97rHSeI7ac58pEB4txHvsT4iyA/MLcS0U1LyY8fEBJGRjg2qcYkCF0KBPM+eC/7xoZ5qoxBU9VhmQ0I5axWCuxTbT7FlKDr2qxpGYFPNBmHfZXOTQ7gfHyW18BsTv0mxKsoIOjcqUuSMEAiGYPnqTm7BAJKwP60ILSUUCmIATC6r2gq4WAtIRPmkUb4roxb6pJh58SvpJ0vMbEi+Artj5OEKEAYlv0lwh1iNicwg0M6TMsEE/L4OzAGIhwbi52rl/H9P/0Rbn/zazCzBgN5GDDIO5jeY3nvIe68/yHeefNNfH7njmSI6gYYEKpKzqGt7ZjAAYj0yFY2CBcoltTCtAnElITn8ffRJSPsEtnrXvZP+s7YlgeRjTREYtCUhjCYp++VBOkSc03XN+2jCBq6luruOLo9pvs3dZf0zo9CtWoO9RzQ9L3Sfs8BQk7X9L3IlDMAPNa72WJael77vw6Ckn9Yt8jlmsayUFYGnqfRZfZcvN1ZzopQEk3XrgqVkZ5N681/5rRLf6b+9JMxBeGbOcQj6pnhkXbkAlhpLtL2jZ0qZHKregmAj++Ly68qcNKzlNOo6buyr9VVR93lRxhIkR6UboBP+XFO61Kem89D6W8tuYWrpOiLuABYn5vQc2OCElTXL8EWaT83na3JeQjfKxYaXxktbCkO2SSkTOgfp+2q4MpQ9VuJf5T4K3OSdSuhJzl9WxtTrKe8P0v8vISJUrp5Wh1Kg1Laq5a2OG8o0yatV/eGChmxjaS9TbRtU715ObOgceHCXjyoOaFMB59PTNoZye7EAOrkwNSxLvURYyYYY5OFrdD3ImCAgLpuUFUcL+orETr1NRYGN17kB4zSGzBLDuyY9qyuazi/ha5t5Q6PJDWY99KXujKgYAHoug7MHAPAU4aoQdbp3ERfaxKQPO7JUXOoeeyJAlHyAnBUq+JCbngLAxMyCTkfNquod6PPa048SkQmX8tNm7zEtHVMJTex2C7WN+aEeMrIoMJXJMs0Xgqn78S2QzCtJQPwky/oStvRxxT05mCtxJRTRDi1z5RBPQuCGv8GYsyEMqBSeyXmPJ33cX7GSiS2gZK+pWdC68gBh/7cdK7jvGWgSH83QSiWsaplZEyZms9NSpdS7es45vV53QSu0vGskTsKBFbBkAqtBHVDljF4Du/K3SXeGvQE2J1tfPuHv4tv/PD3MNuZw1nZKHMmdMdL7B8+wuNP7uD+ux/j47fewer4RFK06hwS4AiAJbmzAokQGBhX3/cgohAHIVaNEvEuMbd8HnJgRwEYxceTzxxPBZhUOyvPE5zziQWjzGjUQqXMLdemb2LIKXjWxdJ+es8wZh28p3OQChVeGaL2r/BOCZSW5jMH8zmA1LbTddFm15n/+Hmp/yUrz9gHURqkc5i7YKSfp/3Px5mPOQdMRBRp51phBHg21sNJfAJnfdrE+zcBqHX6Ko0mS4lRwBgBU7pG6XyUAFxJ+5yvZYnGjvOkzyRzwKeDLxXrGRTIswlZnlO+o8AwmWys77NNgD0fe95/5TNFPgYU91K6XkVaC4q4I439fNL7JZAc22dRMhOl67O+FsDUbbu0t+T59N+4RzTrVD6XkznLaFZs24xrchpgn8xrwutKQt5p65r3aVJvNgZjJB5T796pmxq1NTg+Pgwqm3ULUAlbpDiaOShWCkNV9HEaziqVMwsaShxzrVW6WHqwXbj1m1kyU+kgmUcwoyYfHaAuYt/3a/54JeDFzNHUo38TrecL1sUoBVlq/X3fRaYZA6CC7zTCpOv7VVVJuloChiAYdV23Vr+OLz0QzBzXLmeAOjaFwkQGJkiqhgi992CWfnkFdmEDsy8fnBLQnDAjlDd16bO8z3l7uVvYaYQ4J/jwPmrJSoRjU18sEYbBgUluaz842A9Ah4NQVijMUVNXKpvGHr6ctJ/PS7pv47txTafvbWJy6XOn9iXrb/wbI33YxOTX53jdBaAElrSOPDC8BI5Jx15gaOke1Hkbz+hm14bSXGwC5pO/w0Vt8OEsp7pFNiBrMBhCP7NYVoRnv/IyfvDjH+H8lctgA3hiVAxwN6A9OMLho8f47LOP8Yv/+HeoOgd30o6uYoEJbwLam9YipUk6x/n6F8FZ8m5Ol1PmmrpHpgkoSmuStpO6UqbPM48aP72ANAcApykq0p+lPZq7zeVjTelM/nf67GkWypw2p3M3rXvd2pc/m45/U1tpm6Vx5WcvHdsmkLN250fmYpf3gXmM34vP0LripNTvUkn7WKL9+XhzHlKag1IsTa6UybNjpeNL20gt7aVzkrZbGnu+N/M2Ty2TPTMdc9HlD+v7IKcP+u5pmm6OVqBpX0t1TbvLAJUVkemQiFSUAnJGmp/9vJRoQbpn49nPBC/9vbSvN9W/6fPS+zlf0zOiLuwlvpjjrekzoxCZ7+V8P561PAlzAcD+/j4sAdZWIwby4/sAJgrwdOyTNaPNlnYRQjZ8uaGcWdBIJ6R0eJV5pWlSVdhImWfqu5kzI3FNmloAdNE1/WnaRmqCLTHCdPOM8zc1X6epa1PGWVWVCBp+BABpgI5eEpNq8FRIARDHrtmSohVFxMG1OWUWMdw7j4EZbG28OE4vzvJe0t0aEGxinaGMMOQEKZ2bicm1cFDyucvrXQczUxeljSX7btIvbGaMyHxA07V2wX2KQ/WLxVZwTRuK0ngcRzKefJwbCdkpY8vfmYCUDeMrzTuQCNcb5muTyTv+LpUWmdVkDjYw0JL/5lkY7Fo7GeBMhe4SWNvUlu7ZEsjOiXcJcIDCjdQAKpZcZJpRNt72bAxWllBfuYA/+JM/xPPf+jrYEhyH+e4HtCcrrB7u48End/Dhu+/iw/ffAw0eQz+gMhaeEP2b8/Fpn1Kf5tyPPhfe0vdLtPe09VAwORU7p3Oa/p7T89S6pfOerxWRKIV0XdN9k76TM+h8nfJisjnM13qTZn9y5pJ9dhpN2gR4036q8OvcVNGW0718XjeV9Bzn7en34PG26ByclPZH3o/T2s3fJaI1DWWcM1I3x83tpetb6uOm/VoEN4VxTH+eLuykYwVGvrmJXpb2ZPp5Omeb9nOp3lGomPZRXdAmfSzQCt13+X7Ox7zxLDEwMdtifX0VSOcK0tjXhCZonRwUn5KGX7wuyFAUUtNzsYnXpW2V1i2OKRlOiRakv+drc9qabzofKa9J6yUaXQaLVr+sjohvMVVol85uSVAo1Zn+nmMFxcaRbhNha7HA47aN7meadSrlo3l7Od9nr67P0/kDM5jW339S+RI3g9s1M6T+rkU/V1+vVMBIQbp+rm5H6eLq+wAm1gp9Jp3YdPHyjaLvpQxdJ1MFCRV86rqKsQtpqtYcGDCLu0MdAsxBo8avaZrYrgoV+l3uk3qaZaiqDFznwBgDHvUZY2ywsoRDmc1BWr/+rXM/go8klSUMPJ0ej5H2LWcq6brm+yI34+thzRmLDbfDq29uToDFT9xO+p/2w1gTL6nR/aIpM3MhRb6cau/yQ57u8UlfmaduT1nR+UgZrDFmzXaSM92ciZRAVL7PtZ/5Z4IrTQgMW7+DIZ+7dMxpvTmx3gQU8u9SAOXC3D0pv3nKeGVMZQvmJmbzJPCl80IcLA0MMBF6eDgLOBiYrQYvf/tb+NYf/xDNhT10lkDWgAaH/uQEy4NDPPzsC3z4xtu499FnOHj0CNYYELNkq/MeVFlJg5ucwbRfcuYJ3q9f9JmPJZ3rEqAp+S2v00Jd2/W1K4Fk/T3VFOcZ4PJ1yRndOM51jau2k7sepZ+VrM76bgn0pWPIf3/SM6cBIW0v7WepXiLV7JWVcHmdygtOA9fyvVS5iS7o8ymdz+vJLRul+cjBbAlMnQZ08rGlZzDfjyX+Uqpz6saXtj3V9eQKtLxuIhLeeaoSa/33Es0rncG8Lv0na6uCGoCQ7OA0WFai7/l66ZoqRsnXMqfrniXNebr26RrnN8UTiUJGeVxOo4wxiDdJykvTdzMMsWntc3qvz6zdXB3kynxtSnspB8mbsGmJp+V1lrDQk/ZCTrfDp8g/SvuwaZ9vKvlZnnzmfYhFSpVEgLpE+kESAuV7IGKohF7H+TE02bOxbako4ponnQ0tX8qikZu40u/UMuATgKHAzyVAMGdKzrmJGUc7r/nbjTGo63pSTwnQbSKo+cKqhSFNTcc8tqsbXsfrB3ED67pu8q4xBr0bJoug7Wm/cmKeLkz6dwRoJOn4jDVyMRjJ/yJhMKE+JxqF3EUjrzfXGClBiG4Z7NcISqmk75xm8k3Ho/OXzme6J6eaAz9Zg7QudV/TvZVK75UZL9FqW4fVagkizbQ1zbkeiRAI1hCG7GZz3dclgjkS783MSutI1z3Wl7nBbHp/jVAW+qBzN+nXBLhM1+FJFif9LHfVyceUz1Opv+m7hihcInS6Fkl/pveyMK/3v9T3kvap1H+5mNKAHYe00EBngb4iXH7pBfzuj3+Ey888LcKCMZh5gm8HHD96gPt3PsfdTz7DR799D8eP9uHaLtzoDTgwnITuogk0wQTwmQsaKR3SPqe/n2We0vXWc5Xe37BpP8Z5KNBtPdtpn05LrZgDiFxJlFufU3qYgotSyWll2k6pLyX6Uxrrk+Y1H1/59/GdCTjhUXuZv5PzgJTJ53QunScNft5U1PUhV6qV+l5qo7RPtN5shtae3zTPm9zc0v6cNt9aRy5El95ZW4PCeDf146zPpO3n4y+do7RfmhUwr/KJ9H4DP9VSWu+SIAFgVFRinSen5zYVjIlOWbPsc0PrlssnlXS8+f1ha/s0G1uqwDgNd6Tuopt4YL7Wp9G50545bZysGQCy+tK5eqJ3Ak0FyNKzOldicSX0/YC+76H0wzsflRbpOc/pbGEUSAcQ5xkksUdfsnxp16mUycUuFZjMBKwnzKxEfFPA1zSNuAglGZtKYL3ETPR3BZ8lU1e6yVPrBRFFgUd/ei/pdrU+bUOtGgDWrCv5nK0TQ47S5abDY42RgE3dkGRGQSS4C1GcS2CTuiT3ndaia2jIngrk0jnL/y4JFvq7gpXJ5t6QJ9x7DxcuHkwJ4GTtXUEzgimRHIYefddHeig/C0wh/KzrusiAcuKifSIiwG86lNO+a13y+fQG2tKeLLWZ152ftxys6KQ4jEQsr6PUln6WM63Su3lfSntmomksCG1pHbnWdRTOxn6saVo2gB4CoquEutRpQHpMZUsEbwx6CywuX8QPfvRD3Pydr8PO5xhC5jJ0Du3jIxw9eIR7dz7Fu2+/jdXRMY4fH8D3kk2KCfDSIEw9Cu+VtTDGTtwqU+FCS+4j/yTGVwL+JSGiVE+pDZ37/Nwyj1bD9LzlZ10/U9pVAkwl8LOpjECnDAp0v+cCb/p72l5p75f2z5cBD3lfR1AMIEn5W+JHJUCca+TXFQLrAksKDNLsMPk8pPx4olh6wpjWQTXWLAKp9WnT2pbme5ObyGmCZwmcTedoM3hP69f2S0okGefmeKIS3dR6c/qlRfosqfJ1GU87Aae5UZXqVmVn+mx6BpgZMLS2b3L+mpY4z5mVa/x+3JGnjaUkBKTt5/sgH3N8nwpjKsxHOm+yxpt5BDAqt08r+VnDhvq+DP3Iz4Oe4fLZXx9bvs/0c2M0A6z8q6oRexuieH71nZwfpOuQfs7ARNcR14qgORu+VDmzoJE2pkQs1ayqK9IUGEhvRsFDbMJxYr1MhjUmaov9MAAJ48kXAsCa6bBEtHNtp4JufV8LkUiBUzBooSBVMi1S9EX04RCDCNZU0Awp1o4b2JpREBuGXiL/Y3viTqNAPAWNZIChZ7DXux4BYy2c5ZBC2IjrB4vhSsdtyUTXJB1fOv5Ue6DCDQAwETwDPviiq08fA8Etq0z88rpy4qdznRJqH/YDkWi7PSUyM1EMTF87BABcnPOwTwhgY+LcWg+5ZJEYjhg1AyATLqxLBdxAMNlEJqDrEsdOwfRN43oRSYaxNMB8GHT9AoGDuNJRSKcI5pAlBRJ+HMcW5oQ5Ki45zO+ExNAYVJzuVf2ODQViHJIpKcEwgIWJZ81aAe6aHUpLeoZywrzOIBIwENZE104JmtEsKiEITscIKEhU5gVA56UAbvJ+5GA4/U77ZMigCgkAWu/gTQBIRlLW2sHAW4NuUaNbVPj6D76Lr//u97B94Rx6eLDzsB4YHh9g+eAxju49wvtv/xYPHtzD4eGBKAacg63sBORp7IcJtA+BxqUMNbXwIpz7nJHHcVgz+suzF+GcCFXdBNrj4XlASLIm8wiKNIVBILIAsQh5GBlTySVO+6CKh6ihRBYcnu4HP6aI5pTW83hnAUGETN0nkRal2xvj+Y570vtJW+m+UFe8yBuScQDTvZSOS2lTum/099yKl78/9gPgcdJFW0kjr41MX7m9vDj+nnwee0wEwMhasVwMKQoosYCqMkr7mVuDcjCUnpGchuoajvRD/ueVxiMdK03oO2PajxJo0WfTfqXtb5rjtH9p/3Oal7af7+cS8MwF4LSuTeDwSQqg9LNcaZrWL88AgA80OLU2UvhOrWH64lj3JhqXzkU6/lTgmGAgKoP+TeshH5QVOrGPRHJ5ofYBIx1Kz0LJalJaq3zuJgLxhv6WcGGsl+VOmwCGNFImNCD8uOTamCrD8z5Kdq3pVERebcKc5Gct9muc08iPSHhzpPPJGDcpUkp/62f6z8OjCvetCU9GwIpJn7OzqWNPz/SkLc1+CsGKwU4TlcL5/jytnFnQUC2/avKBqXUiBZc6ACXSIyAbP/fhLgn2PgxiKj3mfr6Ufa7/SoxD+5Qye7W0ME8tFAqWUwFKN13TzOC9k8Ana2GCO5gGfVuTTl9g+CwB2zbZ/LkWqLSphSmTXDoHYThMDO8GmOCWwW4agA6iNaak8xSFngRApJcHcgCBZCwIwtyM+pP6dbej9FBo30vmz3Rt0sIQQaq2dQQLujYlBq9rGqYWRAZwYS3i5yTWDsnrGy6BJLCTC+M8MzxSbbCaNMW3nhIAEPN48xRARHGZJZNDSuCkj9LBEqOKCwsloOHdMETvZY3jAZ/sps1lIqBkf6t2Q9oa94Awt/X0lznxzgFEnOcERE4Jks6rgpk8/kDeIhqf199za8VY37SPTyoMRm8pBnlj8KisHUH4rIFrKlz5ygv4zp/+ES5evwLPHo4ZtSf0Jy32Hz3G/uf3cOe9D3Hv0zs4OTzEqltFJUlqxY1MtGRpCCNIQe6E8WAD4NGFYwGx3nu5fyPMqXNq5UX428FaM4LYhKkoLUIBrKRgUseVnrvU3S21Ska6Gs78mhYu9H0iWOVAJulDPFdIhITkd30OegZTZh4+zwGTlhKYQF5HvodOYZjMmATyav/HM+/X1/SJe1fBmZwfoTUyLr1TavJ0BgZKfc/PU/p87lPN4+xPnp3MY9iLpf2zVn+BhudnXL9LQXKxrwWAnP6eg6WcZ6TzIUrD9flLQVoJNKVCT743NnkBlIF9GL8nqJJJhQx93WvabVq36OXj0mdy7JKCxhRgp+NaB8Ib3Okm27jAj+WPsT7mKe9K5jOfd137XDm87g1AcU5K6316vzmxxCWfMdbmsASW879LJ1nxRDreNffBjKQQKCpg8nOVep/oPJXOQ9penN/YvsPW9nns7Ozg+OhAWwwsohwXmI55QsOyNQUFZY+Rizp5nUSdWr6U61QuoZb+zt2AUqLvvQRJ13Ut2jsnf4tPmQy+aZoJIU83YMr0lRFqGwreUw17HqicumilwoX3PsaEaD9UQ080bTetq0Rw8zmLoATjXROpsBT7o4QNCJpYAw/Vjjp4P90IE6Cutxuf4VCnP9Px6nPGyA3b7EcLUPpMPqaUqKfEOf9erUE5sygd8tzcHYXT5Ccg59go4xoYJycnGAaHWeivAr58ffI2p5lzsPacjI0j09I+xrEZcacpQRUiAjFN1mQ8zBgzixUY2qZy2ljW2qa0bYrE1lr7RF/88NsE1OXPbup3zsDT3/XxdC9NwUkCPs8yLwQMlaStNY4wgwU7hmkqdJYwu3ERv/fjH+HZV18EzWqwZ9TWwq06nDw8wMN79/HRe+/jzsef4tG9+zDqRpX0UX/PBY70Zw40SnudaLoH4nwmoEb3Vt/3Mc6t5GZWYkC6j51zxRiu9Hzq50rXIr3M6Efantaday3T+teUDAUwWPo87X9Om0p7NG8jZdL572feS4VCJFbqkgKl1I+03+ln+vmTSipul+o7TdhI91pKv/ROJn0mB51p/1JhJAVnp5Wc1qR9ScGw/q7KvildmIKslHeVxp+fzbwvT1qrvP/533n7+fyc5mOfu/rJe+VYqrScZa43vTfZA1i3TKfP/ufUnxcBu9O/UyBfWi99LucBcd55DKrPz+1p67r5nI/K5yfNfz62nIbEPmWKo9RVLd+PKW4hMwoH6TNENPG8Oa2kcyrnSqxNhwcHcF0HIFhjNsQKnUZLJm1EuYMj3iKUsc5p5cyCRqrJzw+ydjZ1C0gZa6q5SF2GwFNzbASVEJchHWAJ5KRZsLQf6jKUMgRloppuNg1SzwmbZooa3YA4jj3N2LSJcUTGHfzmcm2h9jHXPEWBygA8sIAka4P+ncOtxhLYk87tyOTXiYCOh2gUzFJLijEmCnhpXyJxZV5L17kJQKQWm3xeYr9I3Dxyt66cOennmzQ7Ja2d5rpWwTAKJbQOBksMQ4micw4llwgdZ++crAOCm0vIwkHGgGN0BIqajNI8p8Q5F9TycU8J3JRQnSYEAEgY+jjeHOzmGp4ICsyoFSrt9XSOUuaanpP8DIjQPPVzzvt9FmAz9oNgvYlB2iDGUBuYCzv4+h/+AC9999uoF3M4IlgweHA4eXyA/bv38fjjz/HJhx/h448/DlbW0EeeKibS9Lyb+lpyKUzBVZi5+N4wDCOjze5DSM8Whecnt7byaHFI+1HaE/l50z5uWnMkTDPtT8psc2102me9Gyn/7jQQddq+T9uJ4yvWsg6iS3s2b+PJZTqX0/6Ii2KpvhRIrfdh/Wzrs0RTxU5eZz6WtK3SZwyOvEM/y5Vy6dxH7wRjolW01Gbps9MEuvTzkitfPrbJd1k9JWFUf99oXcZ0f+Q0Ki0lepzXs2k+ngRkdc5HkE3RZTDPSjbuiSmdzd0BJ3wxrLmWfJyb6K5wM4ZYW6Z7t7SmsU5MWV7av1RBks5r7tGxRi8wrvlpa/Ckz9I2Shb0nLY8CYQ/iX5NBIoC/ayqSnh3YnFSfpy+s2m8OV2IezSYyPphmAorAojW+p9jyE3zpkLFNPnQtE9nKWcWNNRlKt9wuonHW71H9xlm0X4psNcNGBmcm2ravZfL75rZDDa5Dj0dfAl8qXY2JaIj8Fz3GUyzYKWbT/unFw6mwDUd79jf6WKXXInyDaRtafsT8ycYVm8JDhvRkIFz3WRjpRYdbVt9cHOwo+2lfU/dJlJmHPuOJAVuJsylB0rfLz2bjp9ZNBTOrx+knPDnB13rTYPxI6EIfv+WxBK22FoA4feu76IbyKaSEpxIEM3ocjJ5FgD7NN3nGNdhMPqnp2vPzGLNSATBCRMkxIve0rnIBTbtHwkCAXh6W3oOoNaBy/TclATCfC3iZ94DVL4f4jRAmH6/Tryn67tOrNbBVD6WdD/a4PZHMHC1Qd8YPPONV/GNH/0+dq5dArvAuJzHav8Iy/1DPPz8Lj55933cefdDtKsVPDMqawEKAZzhX34WUnqXWjfSjHj5HOjzaaBeDpRUWZCOTfeQzc5Fuo4Ty1q2djkY2Qjas3VKx5GCwRJITPe69ju1Duf9KoGGHADnZ6W0z/I9nlpcUsadr0VpnkpncwpipyBFFTi6bsaUYwvSv3PAlbc7BX4clBjrypzyeUFxX03GndGKnO+m/R3X16+NIR9PWlcJqOX7YNNe3ARkRyAlrq2pEjGlB6mCcaIdL8xRPv+lchrge1Ip0am0vbxOX+jTk+YjF0AmfJED9C/Q19xtbbL23keXo7w/m0oqbJT6kYP5dK1SfBTn4pRzktZZOt+baE74MvDO8jg20YwUZ+lzaZUw5TOV9iPHgeqSmM5H6TyW5q6EjwDh08wexmtKWwfPiYdKQhu15Bae0n4DwpTp/IVPlCae9Xx8qZvBU210SnjTm8DTTkoQqpkAYtXimbDoqaYwZdw5WE01aGsHNTPTpaAgzSxV0jjm6Xa1nr7vw3vToOrU9LupP2mfcmKg9ejfE3cl9mDDgA0xMTYgHRYBhPphCjpDO4anxC1nnKWDkPYrJdzjWmUaJZpqVNNSGp/2Mc7DEwxueVulvueElomBwUftgBvEXaSUVeK0AzGZn2RsKfGRTEIU/P6DVE+jtC/GgmB50gMa1k7S7T6ZaW0SACaEwHvAKhJ+8tjGd4F8/jcRFn0vnikzNTtvAoqn9WXa1ua9oP1M1/k0rQsQssxZC1cZ7D5zBT/8sz/G5VvPwsxrsUz0Hty2ON4/xMn+Ie589DE+/ehjPLr3AK4TulVXVTQNM4SmWkOTPVACt9pHPRspE02ZqtIiBaU6llG4p7X4l5xBpXMwtZJM5zhfj1R7ms5dLjyk/UnXO29rAgCTzzfRmykAmvY372sJUBfBS2HMJXqb97nUr5RnpALTZL6SfufCENFpQvNYpu2Xz5BYsAIdKYCufH50j6TKI3VL0v5ZY2OcS9q/tK6Un0dBkabnNJ8ffb60v9KSWwc2zVE6psl8bKCFpX2l/UuVd5vKJnpyllJ6Vvufg2hmBngaIzd5L2g0SkJQCViWwPba2ZIP1/pbwknx/cD/SnioVEf4MG1x8n3+rzRfOU3Vfz65tDJtO5+PfK5Kn4/zUZ6rTe+cpZTeK9GdTW1uaq+0N0trUSp1XaPzA4gDHXdcpCX5upTOERkjiXg4bW/sS24M2FTOLGi0bRtNMt77tcxCaSdTBpwzXGGmJu7P9BkF8kIUPYaB16wS+YSkmvuUIY5WlVHblsdo5CUFNtqu1t91XdRiOufAfmry0jZ0jKbAgEtuJcMwjJfWqREyzMVALKltrY3a+5TA6JyCp4Qod/MqHWYtsc/pM7H+dVN37j6VCwC5SVwBlnNy40C+5iWgkIOcXFMVDxsoZIkCQIBzA7yX9KaJ3VWI59pqh5IdXo91RicTEKxG0KqDxgiI1icKggeH/ug29T6MnFSAU5oXf5nsE4qBonFo47xifJ8TUH7K8NK/xt6XCF/2HYFi/InXOY3gI+zYyfxlLRElfeWoYaO19lNN09jHfD+NcyPPkAmZnsCg8zv4+u//Lp7/7teBRYPeGFTtANsN6B6f4PG9B3j84AE+fv9DPLx7T+hXuAzSE8ExjwHkSb+sZpSK8zkG11FYT2AK1IgonFkfx22txTD4CEq1GKN36JDMjxG3S+c1BTXpSoAIcI6TduNUxfmKoAUcGQ0DY1/CQqV0O7XG6POpsKdnLweB+a3gkc7qPk7obQoCcqaZ0yiZFzNmmgKiC9+4/UiyypKcLwbHuSCItVnXKTltkS6XgEHadvo30frZSMcOjLxg3L2Y/B57RhT7xTxVksX607NSABi5EitV6qRnRkuqtMsFqpICId5rRQDTSIt07vT8UqbMAyGuyZoghSdrQFPekvY3/S7nF/p7DjIjbz677HDmskmoKgE3pYHhg+J7yjfGv4VJ+MLz6bqfBopT/nqasKLPAsm6hg7lAmLO+/Wds5R8P6YKlHQvxrMIZTdT7Jfvh3x+8rkZxyk1RgCdzQFiq6ePbLK+hJjCXbFOjq/yd5IPp22EP09b201rMPZY6ov4kNSVeT3MId8PpX7GOXLBDT3SQKmzhKE3lTMLGiZEm7dtB+9dciPsOoGWMYWUslZSstrAeCtjYUM6xoFHYSB1fwLJBSSzWRPbkKKTs+4SoJNVMr1LYKRodhCBOkXmK8A6vEOSclBSdsqBC2we7BlDsCqAIWlrA+IjkmBUZYbpIqQHNgXrROLmMx46yVpljMApQ4BBjcpaWFPBc78mPMjmZnAQCsT1J8RCVFb8zo0k2GWW9JHEAkQMxkObHhRmBjSjjeegzQeYJR0uAFgy8OI0FMZMIA7jN1VEwt45wFgYmJgOc7qvwu3ZFAAtOGiSRctMRLCoMGhAPAR0gAHjGGwMYAkGHrWpJO1luNUy6IiDe9IGwhGRSyAcLMBVfVURQD9DLmhLVSOWTIz5GdyAwbkgZIb11JS5FUXCyUYPqzDlCG0JMJzsmaBEiIRV+8ss6WyjgBHS5bGC7wAkFHylhbTvPApCLGZQcoSKQuCxrGoAGoAnsa7JvktyszODvIJepZTjvA4h5a0hGkGnMXJLN1cgEAxNhS0mJ5nCWGdeFCqeAZgK3gEVEYwluNqgbQye/cqL+M4f/RC7F85jcINY/roebtXiwd37ePDpY9z55A4e3n+AoW0lS5kPNIMYFjaeX0SrlIdnB0sVYJC4GnDodwIKwTAUaBgznB4SI+fMWjmHtlY6I/9km0gfhJCPjEqEhGDtZRbxioHKJhYTAzg4eHC0tOmYBCmYuO7eEBiJ4iAkpxSNl8RkwQuNB4UMKGE+GAbejQBIAwJV2pFdKLeiez2bxsT0ikIfRuWS7GMft4wJ+1wVLiLUBnoQkiWAx93s2YckEGGHGAJ7VQSIm40IWyoMA2pTNVEekYs7EcbELCkiU9cRIqEFIrRIdj8j+aOnAAwsqcID7/KBnhkwLLHQlLDvYazMKUFOWWgjBmsnggYzg2LK4zANBbehFDCltLwExtN/Wk9aHzMn8YxG6BoRuLIABlTsUbGD9QZEcwzs4IzsRQMP6yURO4esZ2kWMxV4Ux496V+yP5EoH1L8kwuIm8C07N8RXKbgLwVWqUIsfWYTiM8BfBnwUsAogYAqz8iVAvo+K4jkcEbGcwXOwfD0/XQsEwUGnS5kpeB+4goJIR/KFrVKljz44z6KazUKxdqvdF7Tvmq7SktzLLTW/8K48jXOQXnuhpj2w9jgEGBG/hX533RyMdLpdewQ+0MKczKBrSAsqEA+FaYFo/gABixZuT8tGbeOR7FxqkxI54SC6zCzx+DETT0eoEzAz/fTpv0l3yWxXRiFUWOmyZCeVM4saCig8t6jbcdB63dTwhZMNQiE0TNa18qSVYAxiIS1JKExM4wdtSWz2Wx0uTLTlG65mTglHGnfBu4DSE0ClSgAcmCyoMBUuBBmaCL4ZK8+11UCQKZgPf23KbtPevi8l8wg3vvYZuwHBS1jRuSqqorzAox4jYjixTtavzLQOEd+tMCkKX1HNzUkdephY+idCuMBoxhn4LyXuz4CsVRpmkgsD9p26grHgalWlY2WI822M0kcgPWDbMMN6mwQzYNQIclPCSA2HIpIUjgETKb7UNuK8zrWo3Nsqwpb29sgK8H17XKFoe9lrVjJ1VirpaTuwIgEHGKyjswiXFC6b8JhB08J4OSOCo/EKjMdq0EKSpQYBsZiDTgQPRFywjgZmPMsSX0c+h9u2NZ0AtpzBbwGhEoteNo3AJaBgYDe+smZStfDBGEPRLE+UlHLAoMBBuNx4Zmr+KM//D1cuXEdDoz++BhwHn3bY3V0jM8/vYMvPv8Cd+7exWrVStrzCiArcwFDcOwCIALYmABeCcQGDY8XNVamljUyYSzx3hXplmMHw4SKJFucAieAgAGwtkbnBngzAqnUblWxQUUWJtzxwuSDMECyv8MZZvYwZKNAWbEL1k4/3UskwFlpmA1bV4Vox17G7FmsgkTg8LzSSWJR+JCxoh1zLvRB1skqUw8bWy7eDHvLBj6u+5mScRPgo0TqAQMQ+dAXhif5tvZe9mbcC1I8E7g3cf/r7paz4BGbikiV4g+5kyismWxkARsEeJigiKEgM49gqkawnBEieNSzSUFwAMm86e8WjCqo+N3AGDyDvIiFCPfgkFEeI0IKGRq1CmnRoWZnehPwTjODkaEAHsvgLC/K5z0AbwlXbj+HKy/cwi/f/DV2tua4srODw88f4ouPHwjdZgK5cE8RrIBsGrMMTkB+Zk3RMVCkbeO4StbzuMYJL5sIfbnVJBMKcgCczkc+l5vKWX3TKZxfkR/XE6mslUjXOeyv0Y1z/dHNwpPwvfXnS7+nlqL4OSF6gGiq5U1ANZ7K0PV0bjcJu6f1P23jtPXYtAaptS9/P/feGL/La8n6lgjAnO7pDJuUhHogsTBknj6lsRFNY9NSYSOfs7RdE8+3GTEj+4hvSvOe78EiPg0xpj48L948gDGbXcJK5Uultx1CRPsYKE0TSStdYP3neLxIBEFiRhU0ahkgB0YXDe8RU+GmQka+OTcBUf0ZJWdmsHOo63oCsHUMudl2BLN2soFyi0nuNqDvq8SXS+xpH9P5UlDunJf8/MaAqtH1QLOGxL9T819m4syJ7uRwIAnkC5pXvSVbP89Npumc5nsiHVPqIpbPWTrmcY6m7hgurI/Wkab31LVI2/Yc2gouC/0wiDXD8QSgn8YU0vbzko5fMaP2O+3/arUSrarOA6UM4hS3LSDeMq0AcWxbrIhp//P9nfY/fp6tR/wOos0FEzxHOBmFRlBwNWEOwC4QKDYg1OGZMB4O9jAPzDLJTIENLMPbADwJ0Q2AKwGOxAyYFBRKsZ5g/HhRmFqjTAi6G8jD7C7w7R98D7e/9hVYZriTY/TOYeg8ulWPxw8fY//hAT77+DOcHJ/A9UvMgoKvspXEXYV97oJW3JCBrZQRAIYsLOZgDpZABEuMMSBL6DlkGdM9xuKyZ8jCUnIemNH1PYxtUDcGgxH/Y3WFzHYcyKoiJQg9DAwW0UyvQAIQdy/rZF1zIMHkQKaTRXEMywwLIxY/MDrTi2AgHCpY8ziA30r2hkdQzFgRZkmsLOOZHu/VcN7Bk4zJWgO2qfsRTVxJ5d6AwIxZ5s6QKBuGwUUBUzbsaJEUJUwQiswoaLAiVBblkck31aTweMwSYEUkWngTDi4hxGWBYEm09br3VRKIgmSQDZgB4tE92IQzTGTg3QBr9EyrJWbdhUm2FI19w/Tcc2IBzMFPSuOVPunvnt3k+8mMZPswegJ4j6qpcOx6vPi738btH30fR4ePYdsV7r37ET68/1fYYqDuGMYBngycFUsZZVZ8LSnf0/FGoSMRhkogKOfr6lWRz1E+tpJwkc/fk+bkLILF+ntav/Z//Zzmbm55kWbLIL/UdnRxPeM7JXCpmCjfT/naRPf05PLYtJ5NgDoH+7mrYv78Jv78pLn4p3xXKvlY4r4+5fkSj87xSEkQKqGFzUJJqE+eCu0keDPwrieNrdTO+L20EGEQCd85DTeVypdwnRoJoQoZ6SUjUbJKfOqZGX3boWMxx25vbwcgMt6xnBKj0SXAwFAS85AxKZWm0slJXbByiZJ5BJ6plLnJGlHcANlG0wsA1cyczo38m7p3pfOodaR/GyNBN3UlJh/H4+2eCgbJmIlPYHwvMKaU+KbrkQauT4QIs+7Klc5dUcIt9D0PuE/3Sh5roe21bYumaWSOEk14eihVs2aMmWSy0X1hyYBNcLmwBlUjgNhz+I43S93p3ohCZpjH4vhJlJCg6UGX/eHgfSJIUbjVO5KNdc2efKpiSFi/pHrPom0uCUt5PRPBB1ONSpxPABSuY9e5AbNoz1mAAhHCbfE8ptAFg02P2LnwHgDAAi64SCg4G11PfHAdUm0vye3H1sB4YMHj82EGpP5g8vdgsJE9LyDWoqoIr7z8PF783rdAiwbL5TG47cHdgOXgcffBYzx++BgP7z3G6qRHu+pRmQqL+hyaykTaYgOQBxg9uXi2jLpQMuCNwYmpwFGTTRPGysECZ4wZ73JhRkcqkFB0WSRj0BsDRwS2Y6Y5RJlB3GyMQbCSGonNMpJeGMZElzvds/HGWhf65eSiUBVG+r7D0B4CbpCECb2DGxwwOFgmVP0JuO+DACf1Ou+Exhihs54EXIv1g2DIiiIEDKbxPiDHDGMqGD+A2aOGWGZEWBUrqMYkABhdlCAZw9g5wDFqa2AJ0Pvq2rqCt/kdK6kGdqSFqXLDwEYwTvosAGKgGUiEXEa0xBoEKwSPVgBrbdibogASeUncaiNtJbnpl8xobTGVDS6Pss9MoLPeG/h+EEv+eJDX6IIxJvgeb9IWTrXVJV6Vfyc0VM7zJnqoz6cKqsYaDIPH4b0H+MU//BQvfO93MD93DkePPc7dvoEf/Yt/hl/8u78BP1yBnLhueDYwFjCJW3ROw1Iwm66r8gDtsz6b8tD097X4rYxG6rpPsEWGG3IQuGlO0ucnsQQb3iWiJHPY+NmmdUvnRX9XF8KzllgnP0m9lfQxGVfahzS5BZDcsYNCcD8BQ8LjNgmLabslvjZZH3Ccv7Sfpb1UEmTztvN9kj+T17+pvbT/sr/Wn8vnYJPAlY8r3a+b+p73FxAlnoXu80I6aubJPiqdlxJWUiyjl1ATEcjSmZW4aTmzoJEKFuqOlAJLBbmRaBDh5PgY3arD/sE+tre30fc9dvf20LsBOzs78aZrLdEFita1HTmRSBlLejCGYYD3Hk3TjEFtCECCRlNUyqBS4pr7j2o/0lS4KQjWnPE6N3VdhzbXA5zSDZofNmttMKcL42X2IGtgwUA3ZuoaMhCZEuYU5OfCho5nmr0LgF8nekVQXDgoqStU+kxVVTFrVzrXqYCmfdb4Bp9op/L21oVNWYfey03JbuhhCFKPAh9MGVKJMawRl2R8+RiFSSMqinS/E4lmw4OjX3pAJQF8M0o0X/cIMAp8HN7T70qCXolI5u56G4sNrjg54WOgUhAYQZgBGYOBPVo7aAcEWClB8oBxokEzCRA2lkCDRYUZQCSxLUSwNgjRxEHzPGqFvPcSQA2LIbTFBHHJ8YxzF87j1a+9it2nzuFx3+Lw5JHce9P1OHzwCHcPj3Dc9jjYP4J3hPnWFupz51E1M/RNDV9VqJsaVV0D1gahBqhrQlVXaJoGTV3DWnGHtJUFVTbcYTO6a1prYOoK1aIJgoCJNIAoCAV29J+tqwrWBOWDsbBURS23uucQAd4wvAkBt8GaoXsoxkSE7ScucOHuFxanMlYhCIB3Dl3bYlgdYVit0B4eoT06wdHDx9i//xDL/QPYwyP41Qq+H+D6ARgcjKnDvmAwHIw1AIfEHxpwAYKtLIyxMg5jADKwAMBG4lpQwfdjenEyNgicIblFlVwkCoZjObeDJ4i5W4SSBgbslHYIeGf28J5BZoBnB4KmGQ+CjWfAWyhG00s2hWaIkgpKFzXLIRGIGJa7IBjK32KFsWI5hR0FbVMBPjimhT1gCFJfUPyQNairJpwXYPAnMNTDquDk13lfPLsZEJn40Ic9A5RBbg6+I93IrMdpyelGpOfeY24seADe+Q8/w71P7+FP/8V/i0sXLuNg/z6qaw4/+Oc/ws/+4q/RPVrCklioxri+dfCpqDvt+8irRsFQ+5W6RevPTWPUepXP6eel+6xyoSytQ0sOwvNnU8CdfZvMua7jNC2v/kz7lbuCMU8Dwjf1J+dtzDwqfzbw803CwDAMEdulz5Xc0vV9zxzOTBn05/OZA9wiiKbNQkhab76Gm/h7Pnf6XsmidJrQkfZXlSild9OyCXvkHh2k54emAsqmfT5ZGwmigzEWdV2jbVdgHzBVglnyuk47A0TBldqLoklxiu6r/PnTypkFDY2F0IOf+vXrwdD0t8MwoG1bEAj//ic/waeffYqbt2/j+9//Po6Oj7B7bg9d36Ox01tvdfK8dzBkJ5si3eTpgUqfSWMhlstlJEqq/U4zSaVFCYbea6H1pnVGLWQoaR8U2AOjtUfRZX5A9Jl0o0fwz6PkacjAg6IFwxgjLkEJ81FBymRjSttTwpH2JRLHJGBYv0ufTQ9nibjlz+g8pneqpAKgPmetjS5sxhi5BT15P3eR03VI/Xq1WGvR+QHOO/TDECKHCbx+3ov9nswXRKOfr5dzLgQzrzOiuP+CYCC3cVIULrSZEtESISUEkwYXI9IYgeCSUWIIeR3pv3TYa0zeVOBE28UqFBGh80HzymEsQQNqGDjn9CK8AHpVy2WBrpaZM9ZElxEiYAChszWosvAEwBB6K1a73hBcJfEteu6apkFd1zBVhappYOtKBKPK4tzFC3jq8iX07PGQHQDCtloUvcO2G3C9nqGeLWDrBnUzQ1M34r5YWaCRfhhrZB31ZlaCAGq1TIRAZpBouSvPcQEpgEwOGyXGHOga8ag558keTRgLGBTpOkc3JGYRvHi6tZMaaGQWAIbkzBkKa6PPhv29DYD5kgAtJlgGfDegbzs8uHsX+5/ewWcffIiD+w9BJyu4kxVc2wPdANO1sDTA+UEuw2Qfgktlb4KMxG3YkLLXBrA9q4DByVx7Hy58Y7EAWQtjLXqle4HJefh4H41PmL73HsYbmLAvI1hEiK8Bg4L2jp1o7BkCjokpMjbVEFrI2eoh+eVBBEfBqqZn1S9GGmQ1gQbL/Tlh3ZQWmYpgTVC4BWHFBMuqCXusqmeYz7ZgKwNvH6PvWzljbhBLkxtQorHyY4MP+wa6dlrhsdLIo0v0b+09AgbysD1hrzdY/vYzHLx3B7svXMd8ewdH7TGqi3t4+Q++g7/9i79C0zMatgEsjZaXCe0KfSnRs1QTn/KAlK/nGvYcvG0C4en3yj9LAkvp3Zze5mPK32EOgd2Yrmfaj9MA2hR8rn9X6l+6j84K/sb+jnWm1w3kc5N6JZTq4EJ9m8aX8/KJcKXuX4VxTEB5+D63fuXPpf3X53OB6ZTOrlmH4rwYmuyhTfswtzKm/czHkEGMNSxSEr4MkUbjxdg9Eyzo6byU2szP4QRLME8FfRKBOa3vTHOIL+k6VeokBxN7CuLrukbf9+j7Hu+9+y5u3rqFhw8ewBiDne2dOCgF6CUJlVl832ez2ZpWPEVx6W3kOkF1XUcNn0sWMCc0Op704jz9LD0IefxGOidpv7zn6DIFjMJKSiBT03wqCAEQAOdDViGjQoYuMpJ2Emk8AIExo5P4gGv8hbocleI1KAY10lofA3KK85wzOMY6gY5WKOckA5MKTUGYcmHPOM8g52BtFWK2DaLbgiEYmKgRM2RgyEpebVDMHiYZOiQ7ElkD1/XaMcmAEzKMBbWxaB941Az7mKItP9njWffBlURAjAdBMnqlz0UCG/zpJSA+PBB+jFYANd+PGnJ1IPLBTUoBPpKUuAh7nmMXRy07aIx/EOI8uiWqcACI9rYnAwRgxED0hvJMGGwlIJwoOoyACIO1OLIVTEh8UEXhoEa1NYfbatDMZpjP56iqCrPZDHVdo57PYGcNZvM57KwGVRVMbVE1Deq6QV3VMDZYAgBUdS2BpdBhGLClEEPBgLXowbAg1Gxgw63svSH0xCGTlayVx8hsiBiNl2A5CZBGzBJEJO4NwtOCOlX3NXl4q4kPOLo66d9MCVHWtWHph50Q72nqaCYf+CfBk1qKQvYxThh2mH8CxAKU7VH9YTlkjOKppskzo7fixuOZ4Bgw8xrVrMaV3Vu49OItPP8HP8BwvMTq0QEef34Pdz/6FPc++hi4/wBDu8JqtQQ7C/YDVHauqIa6eZpAW6yxcMbAVzUABlV1dBty3oGtgTfiimSCUGoCDfRWYpRUWUJkQg59Atd1EI5H+lVVlexBnonVwowXpwIc6OEKJnjBafwIB+C37RxcUHrERBrMABugb+AGN3FfYGaQ61ENy5hpTMG6CpgqYBsjQoZazmbNAvPZNqwloFmgbU/gfY/Vagl0S2AIUDRY4cP2k0xUzFMBU9eX9eQmJfRhM7xjCeqn9RvdS8Anjt0SVnCYUYVmYLAf8PO//lv84Mp/g1k9x/buLo73D7GsAN6p0e+3mDGBPMAwxXa0jTim5HvF4ynQyZVfuYCh/HCTEJDy/Pyd9Pu8zdLv+Xyl7aXPmCBgi0Cl36+DxFLJeTRnz+ftRvfFMC+j0hJroPUsAkA+hyUXtjWFn+7N8HvabNpiXnc+b/m6nSYIliwZpZ/5OykmSbFY6e6tUv3p3+wYoHKinxyET9Z0w3hL9aQlx55xLRQT06jw5/A5e00pg8neLwmkaR88h4yhKX4hBMP2+NyT5k3L2S/sc5LRpzI23ikhjXuQFfBTVyZcVQ4YYsxnNV568SXc+ewOXnr5JezMtzC3tQBG4S6h0wKcFIRVdWAuzsEPEu1oQ1AwO0m+GYUCAFUaa+E9/DBE6VonO2xxjAKAbpDU9STdEDqh482v6WLJwkwlxqoKLhHwcEFblRIqzVLlPcY6Q7vGELwTtwDHDPKMxhAMDzAzK8GntoJ3TnxhHaMii54ZgINnAdpkTNgg4v8svv7jRoowhhnsCMQmgPdx47KTtIyaIUmZP4Dgux8uO6TE1QkKjCXQ1QSm79ijapqQ+rGGh5OsMbCwzUzkIdfBcA9FmT74zeuKGVgQRpcLRnB1MIx26GAbcb8CGcyowtx5SccK0aa2BHhjUTtg7iTjke6hCNDDAbJB6PIxqDMxC5ON2nzv/HiRHSDa0UxYE7DA4rEEBqMKgR6y8Wz4DwZBox207Eb8/MlDtPompM60FNxKLGAMfFWBKyNg3BDYErwRUC97rUJdV6iqGqauMN/Zgpk1qOYz2KaGrStUM7EekDVoZg1msxmapkEVXI1MVYk2OtSZxoOIPz/FcxaZTRxi8DWPAF75n0ncPxDPsQhNCdEJ4Bbh/ITEoHBwYDv6yFpoEh9Ji2uhDE4adISYJjUh7cIUNY0iEH2Cx4aDEDLpGIcAZgWBrE/En6ldSZnvWO2YdnLKuwjp5LHSqvCdmTw7GUWMp0nbZDIi8PD4PMfnQ3O1QXN+G7NzWzh/8xpufu9r6I6Ocf+3H+HN13+N5Z0vJB0wscTbWEK12MXW1hzzeY351gLN9haaxRaortDMZ7DWYjYTYbKqZP9RJfsV4WyJkiW4HRGg/gJxCCoBG4rZz8bPAyN0Ed+EeVTmrftufEmmQdbNjC/E93Qd2CMG6TsnN+167wHnwW2Hoe/R9R2YJeawXbVo+wFd78HOw7c9XNuBBwfjGLXdxmL7ImpL4IOHWJ3sw3UnoKN9dCdHcKsleLVC1Q8w7QoUYmgcDxKn4iV/vawvB9AwasrTXec9gzW1mOegbQ2Wc0a82yQFPHGGCn9zAMnWWrAhDNbDG2D/3h189tqv8dSzF3HSPUZVNdibzfBHf/gHeOMfXsf+Z/cxpxpIFGwpKEyt/yl/VFeyHISlNDUVKuJe130CCJ83Qls0PXd6yE4TdEpCQA4M0+dysJ0+K8oFqLomCBm2GHOQ17sGPpM+p/NYdLtJz0oqoG4okd8X3s/nIwXmpbkzmK6ZlhDRVaxX69F/qeJVhX19fiLcA2t7Aljfx5N5xHTvp4JAKUY16fBUWspK3q+4hwkx+6MklQjzwWrRNfBpxQku0EuHtd50fOmYIrYExusNIHfemYBD867naz3qTQUE+YB9NflQinE40GUiyYyYXuD9pHJmQaOyFpWtMAR/WvWvT7X6Ml9yyK21cIPDn/yzP5ODFhipC35jzjuQYzAryB/vAxj6qctNOjGDuttk/1JpO2pCiFA3zUTil2eGESxlB0fHkkvMWqYbSpZI5lqFDKxtYm3LBOBv1FceiNpbANE3GCG9p2cnc1dZVIsG3cFhEJDEkmSNZMDxXi4dY2YJbDRBKCODhkUT5YIvvbgDSDjmYGU+nQt3UKi0a2SLDuSitUNdRQiI8Q9RqwuaXCjoQ5pLPVQuCGwWg2TDIYN5ZdFYj8E7wHkQ1dIGBQYJyeLDlgQoMgPsgkAh42i8xRwzeLbArEJz4SLaS+exanvMj1ZomHACj9nTV8E7C/RM8CuH1cEBlifHcV10vYiBOrF6yEETIcwT0FWSMnTcBwFkBy17ZGSjjlusM8HFgqwVgVldd+oK/awRS0IlWcYE/M9g53PYpkE9a2BnDZrFHM18hmo+g5k3MDNxMTJNJcLDrEHdNGi4Qk2SKcioG0foaw1xa/ABeDsgABnETD35OThN67HpbIQnVfSMhDrgW0TEiAk+Hh/K/+TsYwrMK2BzSoBmqZoIxrOyRoTXnlgvqZa5VBijUJPXGoX0+M30uU2YoDDTp30Zay12c9L9sOZhD8AY1Od38cx3v4HLr7yAx/cegj1ja2db9qytYJs5mtrAVizg11i44ALWGIron5nRdx32Dw7gwdjZ3UXTNNNYhNiHdc0eUN5jZ/lubT7OWKd+vwYaGLBkI6xPizfigmURgridhwUBvYMbCMbU8INDd7LE/uMHODl4hMePHuDo4BAHjx6jO1liuX+A/vBYYvH6AbQ8AroO3Pdy5wsziBmWDWCGCGDF3VQsurAmWvEpKJlyrXQ6FyUAWgKRyotUrm5A+M3f/wz16wZddwCGgTUVdmZ7aA9O0HgL58SFVTXFuXtJqlXVdktbPwWgwOiurVbViDkSN+KiIFIY4yZrROnzklAwAdMJUF0HXqnKbHwn9eQoabbT3zeNZ9PYEFqaUJdCO4rj8pL2K9Wcb+QNKrAnXhOxHcKEyOd7ILdGxZT2hTnIlb2nCVGnlU0CSRoK8GXqLu2RUYkxxtmoF4hiJ8ZmAS9XCKzNa94mqVJdz5tH1w5rN3fnZzz+xLjfNUTCkrpDj7uJTmN+p5QzCxpqZs5BeH4w9aA1TQNrK5xgGTMhNep7LS8CEOnJGInL0DpSdyjd6G3bxlSnLnPLSX1O036kz6SSYZ5RISUquvC5BiEdq74zbgSx0ycKiPh8qgGROgEN9kzbFEFILACeWC7jciKEDESwTRMvUrPWiDk+3p9gof7EYGUyAEDwlccAB68uQDwKMgCD2KOqAFuJyxMRAyYILGCopSlK3CKq6/IFIVI1ZiRCXLgPxNjRvcASAUYyHpExqA1CjnkWDT4qye9iKMRDBCCDQQJNgyuUQxXzzlszB0AY2MMZD3PxEnZ/52tY8oDDn72JrR5Y1hYXv/ZVdE/toa8qtIdLXNrewd7uLpbLpQT9KvryjKHv5b6AoP0kYzD0Pdp2hT0jvuDGhPgCkFgMarEiEAiDG7BarWCNwWw2R9PM0TRbmM1nmM1naOZz2LpCXddy63RVoWpqVI1YHUAEDlmHCCFuIgBBD0hArQ/uMhG5jzea61DE/SlYE0Q9BBPS/goYRrxLihUfFs6E/l467/L3VKu3XkbYO56NfxqxelL5p7GdtOTs+bQny2PgcEbTKiPTjP9L20u/fFLfzvzwP7kwAV1NMOe3cHFnjkcP93HgfIitIMzhsW0t5k0FY2SPORJ3R/hwRwQzTpYnePjwIS5cuID5fBGUK2N82khLRQMMnA6c1hn56VrSTeWsAspU80dgGjO6TZ6TWzfhMMjZrEjcdWsRKh0YxBb1uW1cvraFyjwndIYZfT+gX3U4fnyEo0f7ePjFfdy78wWWdz7B6sE99IdHoM7Btx182wPOozYEYJBLIckDVmOqEOjxFKjkYLUU/PqkedA19YNc1IeeYVaMLQ4Wc3h0OIRxQEMNekrvi1n3iU95Z2oZyGlL/nn691QYWnfL+s8pOaAufZ/jhf+ctk8ThvQyzrw/mwSk2Mesv+l7qTBUcu9Jx7wpJuMs49COMDaf3XxN43dmGitQmucn9asE2ktn4knj2lSIaAyQXiuj21zah1yAyN/NEwiV5j/v62RtkSR0yQXC5NloNcI6nYhrwoILJGbmdAXbk8rZXaeSAafBzM452CQjk2YbIiK5B6G2MDbEQVgjJniW25/hxc0KLNlHVOgAc9RQaJYi7/0k65VqSowZU5+mfoq5FiUlcnlAeT7Okkkt3+Tjz5QAqImRo+83eDQ7gpVoMJgdvAvClDXBUuHhXB8Di53rAarApoKBgXUE8oQaIeMXD/COYcjDkoNk+zfhJuUQmA3CAIKp5NZir6kqQWicWDOstbDeiktT8H2PAFKFEkYwTVugkvSRKkgwRDAUXz5ZCzJjjAWFbFpO59oauLoCbA22HObBxJuwOWxqBkBOAI7Ot2XG4Byc83hUW/QNAc6j8w6fnyyxePpp2IZAJx6re49gZnMM585jNZvB1w3qZgcr36LrTsCG4YceVVVj1jSoqhowC9igjZs1MywWCzThhvpmPsf2zo4EswdrnrVWbm7HqEUcHV7COFiAffgwmpP1oAPy/aBjJqB2HrUTLDEyHMRK9BZxIsruonBiKwsCHgfpl4gwUEiZHPqBlFElNeSEeDNDo+zNEhheZ8LM02dPA5TpMxsJ7ikEcBzf+vtrWp3sZ/rcBHx4SSerdERpkfdeNFU01dSNmr+glEiAFGMEf5S0NyaVmM5RrgFLv18HPOsm9+n360XOs+xQWxNggZ/85D/g4LjD3vmLuHzpAl5+4SauPnUes8bAGgp3rwQGJ5ONw6Mj7J07h8XWFjSDVknbnGvpnrQXngT8nlTyzD9nqR8UxkajIinubvao3KgVBBmw4XDmw50fDIkhgkHnJZkB1ww0hGo+w8XzC1y5dQ3Pu1fheo/h6ACP7n6OLz7+FHfe+xD3P/kMRw8eg7se1ckxzNABPMDCxzSy0oi0nd+BkM/RacBlIsCFv32g/5UxcIPD3FbSHtdiIQXgPMullF6yJQIOubY6V0rmfUvXRxWam6whab0c6i4lC0nHVxp7SXmYfn7aeUv7ftozsZNJOc3yMl2D8jOnthVo1CZ6VxKMSvOyRvc2nFXm0dUpFWREyXj2Mzz52zPSLBf5epQAfIrxSn3eNDYtRSGcE/fajM4oLsrnI7QiT2Sf57y0xHPSfZxevJnPV16PJMWYtpNi2dyFUS+BVYytz0cBZTJpMiKvlrkNwtqmcmZBYz6fwxiD1Wo1Aeo66FT40EMv/uHiJmWNpNmyegGXTo4f4ncyBIatLGxVr5nZBXy7yQSqlUP/3nSBj/ZR+z1xsQrj0dS4eit1qY5U4jTRKuVRVSGAGR4c0i6CJfhRXJwJfhhk05JabCTg2KIOGVQ8qiBsdcOYutExw9YzGFvDQIB810pwcmUqeHQho06ayg8AGM1QYebqEGiKwJAAEGHFnQRuhpS85MegcrJyw6vcSREu5nJyh0BrKQZJE5n4jg9ClrhSjTEdDGCAQQuxZmggqQg9BkQMIpaA48rC1nUIDq7gqgqoasxmsxhobEMGG8wsTGXRMMndDHu7sHtboEUDfOv7qFGhNhbN3i662oJhUDHgFg5U65pqSlGEPPthzQJAgJoUyWCgcLEhT7UOxgOUXfoob4rFyATwH6qLwJhp8vCEJhMBrpp8Hd9zqBEcNCLIO4UFxRrWHBSYIy1PLROnEY+Uscp+2sAICSDiyRxO6hlzF0zryEYyEuIwAiWwSvSDuObD7djMiZZGNTHBN9o5J2ZsJMksgInJXzU9kdBrwHBg3ko7qsySEwGQGa1LqTKGguAnbXNIcypCB0OC9etZg8pW4UwM8ZI7UUbYqLSI7SZtazC1/hPf2jLwLguN49/WObnXgwwu7O2hW3a4/8UjHB05LI9OsDebY7eqUO8uMKtrceExBBdMnYZIzm8t99oMw/S+hGkpa+xKfT0NKKfP5iWl39P9u8G/Pa8XANOYJjJ93gJoPEULIsLFhgCie4SCDtmHoS9uAOnlNZBLNGEIZmZQzXdw+akXcP0rL+EbyxYnjw/w2Ycf4+1f/waH73yI47v3MWh8h/eog8LEmfV1zX/PBYoSoJy8A3FhBUmAqAGJ5dsYDMaIy6z38AQ4HsCWxDPUj3WlZyttL8cQ4KlGdxNAS+sCkMR6rmuE0/VN3aeBqfU2nYMcsOZ7KC9PElpHemXWPi+NM5n8Yn152/kaMiQGgKnk0sOZG/m6wLPp743CfNjWUdmSgetckEz/zuuOfydrmguPmwTXTUJjqf61vZd9lo+1JOj4oNBLPWbGfqiHy2ZhUt/Jv9tUSsKGfi5u+UJvVqsVZtXoCq8K+nwMFPhasV7VGRFpVpmoFJ3w31Nod1q+VNYpYwxmsxmICG3bhkZ4Yl1Ig4YqW4PYx2Y4mAF1YPU8ZKip60na3K536AaP2Ww2Mv+EGGh72pecMKXWl5SglbQdKYHSv3VskWlnizESTD/ZdJHIAdGtCUn7znkYcoDrQeFyPqoIs8aAQmD14B1Ouha980C4idjAYHHhEg4f7IuLkmcM/QDvBpkjsxDtvHOQvPEJgBosDFkYGvP9A4LtlnCwsxm4quC9GzOTVAbGjvnyrTWYz+YCdqyBbyqYAPYbBf7GwNoKlZUgYzJGNP1WgohhLRyFeAEDGFuBAVTzBnVlUREBVgCSrSpxK7IG3oomXsHfRMMVQKNm7EH4mw3Qk0FFFnZw8AYgI6C/8QCbGt4FZE8UwJ5I66uK4uGTvSEuP4YZlR9URgOxi4fREWPVbIjpAcMkDCBaNAioPKFyY0inTfbYQIwhMVWkwoR1QF044EzAYHi0nmSl8pgIG/E08EhEYnsFArmmfeG0V5nyiiWeJWfi+lx6YWmJWOm5T8+++o7m9CA9f+NZcxHQIwvw1TVNmU+qRFAapn875wJYHhNOGB7dSZ1zMUGGGzxWq04uxwOjbTv0fS+KGjCGoYUbxJV0Z2cHV69ehXMOJ32LLvjX3rhxA+fOnZtYNciV3U/SPao0Ts6iga3GiwP135kKI7jVeZiqwtXrN/DGO59j6ZYYaMCn9+7h2rWnsFg00i5CZitSxmTw7rvv4tq1a7h27Vqkg/m+klLWvG7aE6cBvvQ5LXl7m3zSn1QnksQXaZ0OwKDzngBropDygEYRn2OQOksSDhfOnR4jwwCcJBuwldDjRYOd+SW8euMKXvzuN3F49xHe+Nlr+OTt3+Luu+9jODyC6XoQWZBvwTxaAfIg101xh6cVK/6ucJBsiOKbATjIfUXEktGtIsCxg4dehjmW9biccR4n8SN+jM3My6Y9QSoAJXxhkyB91jrzz84CAktlAsT+aVWsldP29uQ5jHQtB/76boprctrwJKF9IoCkdyhtcM3L6fVpoF6fT7XrJTyXC7JpXaUxl8a/abzj9xT5fOkZxrp1Kp+L3JqgnhDA1DtI68zryD1s9Ll0rg1JDCh5FzCK1JNeb7AmuMuoJu2lqaTHr4TIi8v6OBf/VQSNWV1hMZNL8FYri3lTy8VQfS9BweG5pmnQdh0W29sCiocei8UidpxZtHPee8y3FnDDgGGQIN/5bA5mxvFyicPjJSprsFgs4JzD4eFhuJ1QwgWausJ8PkNlq2SwYbOlU8iSBYmSRY8bVCcRYxyHMQZ930eQIfEQku9GwPh4n8Ns3oiwoIQ8MNShkxtyWcdLouXb3d5GZRizikdtZfi/3HhuAFgMfY+jrgdIsrN0bYeV6zCc30FtK8zncyzCHSTMDNM0QMgworEwACTweHcObwmLxULczGyFZiYpSameoW5mmM2aAMpsvKwMJlzSQqLt1ptyCQY+HvAMXAIiMOnY/JTISvhxUIBYIzcOh31BPApADGHezIyaHWaarpdZ8s9HnGsCo2cgZKSyEPcvZ4KlxRK8cXDWA+ykHV8j5MWS7oWsJWDGrB8D3MdBBYZGLpw5JZb6NWPmMkIZhk1MqLyNn+n4ROCw8JQkwyUCQjC69SypS9O5DefcGQabMRKAE5rQuIBXVIsa54rgQkxMbC9WwBg4/TNjwDz6m6qZXAfkvYI0+SD9TrP2MI8EKj1zWPs9zBGLpc87j77vsVqt0LYr9F0P9efn0E+dN7kDhCdEXGt3/ajBcyEjnQ/uTzrWvu8xDAP6YcDQ9xhCnI53Dm3XwXuPJihE3OAks10QMrz3WK1WcM6h7wa4zuP45ARHh0fo+g7L5VKUF34AYRRmmqbBSy+9hGeeeQbeEnbO74GZ8fmdL7BYLPD00zdw/fp1WCtCtxB3PxEKNQmDbh8KqQjl7gnAWoOqskEZYKNSAChr9wAR1BEuVXQM3HjuGbT8U/RDD9sDd/cf49HJMXZ3F4CBXJjtDVzYVOQJnRvw1m9/i8tXr4KYR0tpxpxUWTXVinL8fMJ3WQFU0KSPG29cbwUacd9ObApxr0YwEoWBsHtZd5fGFCmvCJ/pfiP5qyeghSSHs8YA4c4RQxTj0USY0OQYoSVnQGzA8AAxqBIXVBCjIQv0A0AUve0cHLghzJ69im9e+zNcffVFfPTar3DnN2/h4LPPgZMlqDUwwwA4Jxd4geEQ3CNAcMyT4FzJnqY9QnSVmoBZAGwoxA4KHYlCPRjGMywD8IzaSrY+8Q5bj5tEUn8J5BONAeQpCErdHkd+mV6w60NcXxmIjvtsWvL+rSlSsj31ZcsEVOtkbniupFUWMHi2dnNBUt2Q8+9ygJ8qZ4F1gSMtmywIyitL4FPdtDfN32aAP36nZ05pncfUapXWtUm4yPuWKp7zPVMSVFm6MAarByGETOxh2tp0PChbZdZcALN2NwlM+fwrHzJhzWezmbjPn+JKGAWUbB5L1jykfeAnC1ilcmZBY68WC4L3FbpGzPiDG9B2PYYgsXVth1lTY2EMmqbG9vY2To4OYQnY2pLLkJbLJSwxjtsV+spguVyBSG7Uns8lQ9TQd+BZhbqy2F408M5jbmRgj/b30cwXmM1nqA2BvZiFYiyAzIvctcAeDgJqiWoABIeg6TQW49yxcukI3LuuA8AwxCD4qL0kALMm3B5MknG0rkXY6PseXdfBsGh7qqZC5wd49mishDtvVQaNUObYrofDAMnCZalBAwn47cNYKtPg6a+/giuXLmLv3DlsbW0F7ZmOmZK9TpGoESimTI2CHlQoXHOkSQqv/abATjAsReY0Bgjo3Cd5ldf2+Eg4OBwMo/Ov2ZySBgPUgIMZ61KOGPoRf/gw3tBCxSIUqHxihzHTF4IWcTwjiT+iQWDNI4hF7OO4vyb0MURcK/ERl6nwKhGcHt7s/4YIVaKBiXehkKSzTTMlTTQioQOpKVMBvR8IsgQygXqHADPDhWxgYIS7V4LbAzMGQkzD533iBhZ8y4XYaFwOohCuFDhOh57BMFEpMVIBTm+zMMaC9GLOkNbGMWFwHocHh3j86BHak6UANwCSttTHTRnvR6Dgk+w1tgFiSRh6uMFhueohbuweJyfLSETbtkXfebRth7Zt0bYrDIMoE46Pj7Fctuj7AW4Y0HUdVm2Lvu8AyK30bdeh73rR9oT1cyzgTl25xv0ia0bJPiIi/MOv30Fd12iMxfUrl/GNb34NX/nKK2hMjXfeehu/ffNNPHfzNm48/Qy2dhYC8oLEKcyFwgV2gaKEjHrE4o7jHKMfGMa4kG5WXKqsSVJsIwVdXi5OhxGJgw3O72zD+g5wAPeMbrnC0dES/SVC7YFKGW4QcJmAm8/cxL/6V/8KP/y9Hwaz/siovE+gbZCSmYGTk2MR+FwvypXlIeDFmjQMQ8xW6JxHt3IYXFAiEYIr51SrzV5i0FS765yHg5WfiZuonm9mJ5ZamlqBDCimvQaF1JTeh1vh9ZZ0UYrpxZNNXWM+FyVO09RRWSUubRTdHDw7WAtw30tcG8SSSbaOAqExFDL8Sea+uibcevkWnn3uaTz8/nfw7tvv4v233sHxe5/AP9xHdXSMyq3geIXOOAzoUXei7FqxhyMRiipPIM9ojQB7lwifmilHQaS6CnIQzqsQX+TZBZdZpd8kkmfiuTDezj4CKflO1im63EBoFMwYY6ByUcwmHeqRZpS3Te9b2AR+UgtmXPcMeK8Lwdj4d64VL7UX62Raq/8shTAKG6mGfJOFIu59TEHxJgHsNKtCPu78/XzOy9aRqWVNzqGbAG0g9RLRfQdl0yLYIwB9Hj1NSvOdWz/WtPgZSE/nNX1uMv9BGhe+FzCUEf4DnyTZSei6CWdAFM0mBlSnmCJvPxd2S33K93AUGDjcDhA8fYahh0eIeU7eM8qrGSA/Xe/1OU2+96KsiJjqCXs/L2cWNCwBTWVRVTPwgoMGr8LO9jYciyZiuVoCAIZ+QFVZzOdzbM9nuHv3Lg4PDsAsQGBrsUDdNDhZtTg+OpTc/bVYSPb3D9C1Lc7t7mJwDk1VwdQEawh91+H87i7mW1uhV8G9h4TgE4lLl7jrKHETZuNhxHXJjfEZEaSQj7+PGTJk4quqDi5FsqGaEDRMhKBdl7tFQMAgDQbBqYJjDwNG33cC8qoa1swQQbX+8wR2Ak68YbR9j64bMNvZxQsvvoirVy/DVgRrDXYunJ+4EJXM4en2oVSzsQZ1n1zSrVTeWHTqn6Uvo4aHT3+Fsl9KPS72iaa/j+zy9IOhbgzxgBPlNGFj+8xj/UQGKgYwT+mKMltmhlO3EQ4WAwTg7zlc2qVBXALMRlci+adgSZ+RzwhDcBtSoC+BXz4yLQ4di/uABVM6l6bBHIMoDAczb9iDdR1u8vYWjamAEItBxoz1BmCQa2d0polkLvTOA/aMwXkcHB3jo48/wcMHD1FZi3kzAzEwaxr0bYt2tcKqXaHvBfwr4+rDHQdt22K5XKLrOhweHqJrO/QOOD46jpaFtmsDeHVwA2MYXASmNDlX4h4ZN15yjhw4MSWPu0szw+UMXYtBokXzHr3rcLJqURuLx/uHeOeDj/CX/+Fv8P3vfwff/d7v4NzeLn777vt45733cev2bTzz3NOYL+YxUxhoPNfA2BfRcolQQkGz5T1HdzLxgpymCI/7WdeJATBhb3cXdW0wsGjKh2HA/sEBVm2HWSVAXB418b1z5/bg3IBHjx5hb29vMg8jzWLAW9y/9xBvvPGmWEyChu3GjeuY1dtYtiv0XQdbzVBXcxjnAN+jrhjgIWo3RcgWhVDf92GPi7nFCDpA7wY4EPregZlEyA39GXoH5xnG6P05o+Up3mMTgHHX9SAS631jK1QOODw8kLNiDZYny+SiVIetra0g5Ems2e7uLmZbc+zsbWN3ZxvzRY1mJsoqYwmOSW5YJydCSQDVxgJEvQB5MmjmNa7ffAbXnn0aX//Ot/Dx2+/ivV/+Bvff+QD9/Qeg42OYdgXTG3TGxT3D3sEZFy1XKe1ay3JDGOm0KpgycCkXYOY78MklB4alMu0LQbWrqXtjCtBKrjslwJaOodT+acLIJktJSRCJvxuCuo2X4hjyOkbhCyP/26Dh1rbUDUf4gou0LO93CvZPK5v6t+a+ibJ1Srq+PuZN9ZaS74QvRwuWAJr4bOkCSi25kqtkuThNONWxhb8iPphioskbGJsf+Xw6DkQ6MgqC6Rg2jaUkEE8EP/WoYODk5ESEopDyeiLIpN3Nxrx2DgrCbJitLy00n1nQkHS1Nm6y+XyO5XIZmmWAPZoQmL01n8f3jo+PUYdgY9Eattjd3Y1mZkviUrSzswMiwmLWYGcxx9bWFpgZJycn2N7eRlNXAHtUdY2mmU02rjFy14G1NvZBN7cD0FQ1Bga6XszJ1mre7ZA1ZnAhZqKGMRTcKEQo6tpeAjQRbppmuViPIKZiYwzcIJm2XN+Le4f3mDdzzJoG3dABPUDsUNkGqrJXzT15gGBQo0YHj94DZCs8/9KLePbW87C1xdB3cJ3HhUzIAM6WrrC0ibV8Gan0v1RRzT+AUw+6FNV+hn2fALtpNPV/uX5RQtgnWjjluqFLIhzEPAxR26r9VgFgFC4QkgyMt9Z7JdbM8UZPzzy9ZHHyDxg4iVMIFfsAXEE21qmN6qqbIACBc3AqwpGCf41jAORsezeg63usVidwrscw9Kgqi72dXVzcO4/dvT3YcMmmxHsgaoBSzVUOKuR3H+f5s0/v4PVfvQEGYV438OSw/+gAH3/4ET678xkePXiMk5MlTo5PMAwDBjdE1yXP4f6WhIDLHOk9LmpV4qBtCj7nPDUdE4/BkhRu8aZIqEdiOzADlsY51feD9ns6Rt0/I4ZXYi3fAQ6Sda3rHE7uPsTdf/Pv8Lc//Tn+8A//AN/7zu/AEOONN9/Cu++9j+dfuIUbT9/AfGsR120sOdMf944Cs6qy8I7gg1uVAk3NDhVeA4LAVNc15rMZ9k+WMs8Qutx2LYZFHVIxj68CosV+/vnn8cYbb+AHP/jB5AbZdL77YcC/+8lf4+jwEMfHJ+g6cVvd2fktrl25DjDh6OgIB4eHwY1NrEwnxycYnMMQrFb90GPo5Y6druvFJdc5eO+immFwDr3vgcDcNX01he+6bogaP7WQGxKrMNXVJG7HWouqqtCQxcJKnOF8scCsacDMWGxtYWd7F4vFFgZfwfsVhmGIPBMhhXnT1NjZ2cL5C+dw6fJFPHXxAs6f28X21gJ1VcHBSeIAoympXYy7cWRgjdxvdf7SOWw/9W3c/Nar+PzDj/Hea7/Gp798E8OdB/D7h/C8AvoeVc+owfDk0RsnF6r6Os5RWnJNaylzTQmsjS5o66UESHMQpW3r8yXBIeV/+tnEgnBKe5O+bhB0cn5U0iKf5Z28rdPeL72bzqX2NU/Gk9dpjFwGl89N+u6mwO1NpQTOT3s20hwguHGOsQilts86J6KkpFHpk4wJKKeDzUF5qrlP40Dy/qf1l8aoQo+2Hy+x5hGzaB2T/YZRCbeZL47tpFYfpT/lIH6ZFrnfjtC3q7U9kI/hywgL43vC586yF7R86WDwdMPqBNfWwFiDugqByGHS9/f3QUZiBpgFuB8cHERJ3VoCs0PXreCGBlvb22hbmcSDg8cwRoKQvRvA3qGqJGha2hmvjWcgpCSVSV2tVtLpOBGMwXGi7VIG2oTgTjFpq5neO4c63F5bNRJwXoXg5b7vgn+wpFkd3BA2PtC1XXRJGYYWhhx2ZjNc2L6Itl2J5s+HC5eIQDAjqGSC8wTMGrz69Zcx29nDqh8wdD2GvsPWYhYzbKXly2yUf+rGWi9TTUkkhJO21t86jagp2Fk/oEAWWzgeZB5N9GcVttLflXmm76cByPpMfDfxh08Zr36W3jWjZ0CGo25bLHEBCIHN3o+uRhzcPHicTErA6Nh/0SAO3ku2tqAdUbcx6wkVUleCYC1hESDUAiIvjcK/Cr5jfJKAzq7r5fZyAijEeNS1xer4GO989Bm6YcBTly7h9vPP4+JTF1HVNWzINFfSiGgRpiMk13vg8ztf4O///qe4dPkajo+W2H98iDfeeAO//OUv8fDRozDX4tce5z+x0vgkS0nUtHpxL9TMZ2Dx75fYIIOg9gFYTMzOSX3hKncwXCIshflkzSkeXEdkB45jhGQh0z6mQrWmNR6fHfsFY8AgCbxlj2414OTz+/h//2//Gv/w05/hn//Zn+DlF19A27V47R9/hfff+xAvvvQinr5xDbPZTOozhDFAX1xtcnATwaElMIuQUVX6TthviQAvwcWMqrYYXI/Bi7Vs1bZYdZ0IywbJXe9SnHN4+eWX8X/8H/8OP/jBDyb7ID1TR0cnuH//IebzOT788FO8/dt3MPRywWjdWAxDj8ENazE1Xd9KXV7Bl9xfEc9jCs7AUJc9NgmAC3MvR4EAtsGqOILYCITT9TUSe6FxdgpeJAbORjcuaypUVYNz585LrEyIj5vPF5jPFrh06QrO7e1h/+AuPvn0czBLHND2Vo2rly/h8uVLePrpG7hw4Ry2d7ZhQ6wEVQY9D2AwqqqCr0R7basGW3s7eO4br+LKC7fw6He/i/d/9mu8/9qvcfTpR/AHhzBMsH0HN/TgyoCsCa6RI38oBaemfD/d2zlgj3NP68+k65/Wn36fuvuUrAqbhII0aUve57zNvC/pGDZZKk4TIlIgm7rvpfMn8zLtQxpnks9HBJLpvBbaznlX2mZaZw6Y07nKvSLSuS7NTQ5w83mI/Q39z0Gx9jfV5OeAOk8KoOAaULw3jiXvv85pmho271/qEVISyNI5z5XacS2yvZ8Kycpz8zVI28nncdMe1WfTbGFr+zR5f3AOe1s7WJ0cxz33JCGj5D6Wz5fuR4/N52lTObvrVGLN0E7UdR00RqKhV/Pg4AcMbYdZ3QDGoJnN0HUd9vf34+2wTSOB1E9dvCiB1bMZ2HtU4b4CPzicnJygNiZqoOq6hmOZVBkzoW0lCHOwFnXdwFqxMDg3BMnOBnbuBSgRB7OixeA6VFWNrWYRDgQDLMHMunkl5S3QhxvRJQPNAIBhQ5yFCS4j3jtUtoKtK8xmDeZ1gyaYryoIMBqGENBuq/C23HXRuwHnnrqESzeehrc1Ohf8vYcBhoDFYl4M1DmLNkLLaUA/fy4vk/fSiGZkyqt4mEbtr4JaQ3qRYAK3mKDZmUNLic9jcDVK6UgkvhAfbC+Hz4d0xCK4iYDCSEANq1ZXASrWNf8pYQkDU2HHGAMexvtCnB/TH6fMeV1DouAtaEdILGKWJMZB45tUE65gCUwYQgyFzqP3Hm4Y0DsHBmHoe/RDHwTcMMZOhFNjDOpa0vEOwxD3rf7d971Y7voezjmsVi2Oj46wChnX9vcfg1WecyNBrpsKTz11Ht/81jdx9dIVeGPwxb17+Ku/+ms8d/M53H7+eTz11FMw1ai1SplEspC62ujaDr/5zZt45pnn8Pmde3j4YB+vv/463nzzLbRdKxEdwcgilgEKwT3ZLduJMl7kOxu2qc007okJOYBIH9ygUlN53LppnfIQRnc8xLnXJsZvaNzvrDJAwnAne9pDkw0TGVRBCdK2Dh98+An+r/+3/xVf++pX8Kc//hFefulVPHxwH//489fw6Sef4ObN53D9+vVoORYALA5euj/H4ep+NyC9c8dB2tcsd0Txfk6G5GYn8vDexWBgic9rw7xTGOuUbly4cBHL5RJHR0fYiu6umaDPHrPFDJevXMXig4/x6Wd3MPSy2J46eO6Kbh5R2aDMnSi4jMi9REjmfUKhkoQI01UgpEFlKsQSEYgZVZbGOYIikn9EFAWM0EFZx6rG/vHDmPEsZgWjBpZqbO9sY7HYwrlze7hw8QLO7e3BDVs4Of4U73/wMezPX8Pu3g5u3nwWN65fx5XLF7F3bgdkDDzULVjcd6nrQHUFaiya7QWuvXwb1249i1d//9v48D/9DO/8/DUcfvY5hsND8GoFSyxZaiT/+hpgysF0SahIwaoCxCjYZYC1BKaYx9T4+XdnyZI1BXepNXJd2Mjb3cRHSyAsnY9SELHygBIwB1QgfvJ4coCraV7zYO1cwEnHIPxjes5OG2cJBGtJXZRyYWF8dz0j0lTgWP9c60itAKmwmPcn/c6DkceflDw7SlcuaPu5da60X0q/522UhC79vSQoAwgX4Y3jy4XSfB7zOtO+GBNUPGF/GWuwmM+xt7eHxw/ur/XlLHsiL6Vz7/m/kuuUxD7YiW+kADjROHs/wLAVv7DeoR9aLLa2ASO+p1tbW+j7PqakJYJkldrbAUCorAEI2NmWQGdnepwchwvsvEfTzIQBWiO+tGQAyzjRIMFeLAuVmcG7AfMmpMYN5vbWA0wksRvVmKGi7ztwj1i3tRbWWAxO3KyaykTJu21boKmAcDs1OwmwVC1YVVfwzmNwA4whca0Ch7nxI5MLTNID6AH4yuLKM7dw7sJF9A5YdQOY5II9xx5bW/MIGjW1b0lT9F+zjJsMAK8H1Y3PTP/WgFMihCDZaWpSDQJkHm+DBwujdyHYM93QEVCHtsRVideISN4vBfwpsU+1SZuEq8hcyIA1IUAQFjT2IbYb1n4YhphWTlIaW3jPMZZABNYBLgS5DoMEHIMo/O4AI+nqXMjsRhBrg/MeXdvj+Ei0FZ4ZfddhtVrh8PAQbS8ZklarFVarVbDYMZx3aNsWXdfFMbRtJ+BRBjjRimj2sqZu5LIxIlR1BWMJH9+/g5/95pfwzuP2zVv4/T/4A9y48TTee/d9fPLpZ/j617+BZ28+g62FZD9L76TReRVgKj8PDw9x48bTODw8xCcffYIP3vsYH7z3Ifp+gIecS0nJQLGfBGHePghvakVQoWwS6GuSBAWy2GNfgjUy/1z+pNFMn+JTAlKtv6WxjqmgMQ2wE3UHT/5mVoDlQJK6IrZtjd5T4NC2A37xi9fxzjvv4g9+//fwoz/6Izx/8za+uP8F/vEfX8fHH3+K54OQN1o4Qi7SUPRceOcArxdsekicjNxnw5BsU0qrQjgurl67ik++uAsQ4LzH4D2Wq5Vk52qqALLWNabXrl3Dxx9/jFdeeWXNesjMmC/maOY1dna38NzNZ1E3EvNDZOFhwdRM5nLcR8JgxYqDqEFX61Qq0E3W1STy5mSteY026KsEROtFXDioUEoh9oEDHwiugMwhBofhO3HhGrMpAYaXgPfYP5T7iogkC9lsNsPezh6uXLqMa9ev4amnLmI4OMKDf/wlXvvlr/HU3h6evnENTz/7DK5dv4qt3QWIgQEDPDGMd8BgwIZQzWpwRbh88zquXf/v8NIPvovf/PwXeP/1X+PxB58B+yewXQvPRzKaDYJFOh86V+kar/0bp6hYchCvl/Pm1oD02cgrNoCbkoBxmpY4H9N/6bIGfGlKF4rCf/J3FDYGHy/f3QT0S0U/zoWjEuBMhY0SAM0zE+XPaQxUyntV+73er/X4AsVXm1Ib51aJfG4nQk02n7kQltaX9qf0e+m9vO6SkFBal8mzZnqu8r2rv+cucqXzGOdlcFGpe3R8jLquIp/c1I+07tIeTN+Z9t/A8PoFrKeVMwsapfz1qVTomcFuEPcfQ9je3oGtKjgeNR51UwcrgxGLQ/BzVWbPLH6r1kjaUiLxzwUkJiTgE/R9h7qWHO7z+UxMacHdwbPD1mIRU+FW1qLrW1iq5OI7I25eBApuTgbwQ9DaiVBAxNjZXqBp6qhFBYBhmOPx48dBGKngBsl6s7Ut2jrvPJarJRpTY9ZU4t87DGN6RysLL1YShjcVmp09XHvuJupmgZNVj9WyBVUVYBlu6GGtwWJrIfVH8DS6ieVF98dIaNJvM8EgCD1r5IBHzZD8OcYbMIsGlHmdUMe9kWiDWceOUaug+ygGNgcrg7osqIuRZ69q4DCeXNvh4+V5iEJOYr4HjwHKYZyqCXFO+6EJA0JwcEgLGQUA5yWDw+Dg+iFaSxDG0nWd3GmicRfOBUvDgLqq4D1jGOQ5vZ/Fe8l+1AV3un7osVwucXh4GAWRZduiDb+LkCJWCNWl85BqigxmswZkDDrysHWNZjaLCRJsU2FrsYft4I9OFO4qMQZt16NuGnSux6ypRSucbJqu7eC9MA0yhFlT4cqVy1gs5jg+OMR7b76F//l//l/wxz/6EX7n29/Gx598gp/9/BdYdS1eevE2ZrMm2QOqhTZAdNcA+n7AhQsX8B//5j/hzp07ODjcFwALAkMyFnFgZiqnc9gPYSPKr56jW+Nkb2ZENN216WNTYEKwtgqWEJqcE8peFHAVhA0G0hOVAy+r5xI6Ft37A5DczUIk/SYiSd3JEodyeHiMf/tvf4LX/vE1/Nmf/Am+94Pvous7fPbZp7h//z6uX7+Omzdv4vLlS0EAIkBENFhD8MkcSkamQcZajTOj8gKFBTLGYHdnO9Tjw7ljLFcr9EMIogaPY0t4xKuvvopf//rXePnlV6JygFQoAEuMwu4WlqsVrj39NC5cuoyDg6OQXWYxFV6AicWP1IWTkvgjndwM2JUWfwIOoILGVCnBocNpulDv9WLCcJ5CgH3MrhTTOkuWNNWs6oWw3nsQd+jaE6z6ZaB7hOMTSUn+4MFDfPzJp2jeqLG3u4vLVy7h2rWreP72bfSDx5tvvYO333kXFy5ewPVnbuC5m8/hqctPwc8sDBzs4FARMPStHLOmQt802L59Db/77H+DV3/wPbz796/jvb9/DY8/uQN/xOC+hWEX19dR2Mdet/U0xaXOsa63ngEfTI8pmNpUNoHD/O+S9jcHxyVN+Fna13IaYEqB7vS9NO7KgOA3gy9OLJ+50CFEYw1QKjdU61BalJdqKvvoVpSsRaRErFZ+QoHbT4SR9Fb5fF6j8JPMR8SANLat/dMzXhbtEdvMNeb55/pdBN4QsCtKtJACnpOzn4xJ6XFpP+VWGhWO9MxTUDB5nsaWxGeJokJhkgglrsPaTIfPTRQeVQDMY9hKwkUpAZDyVqHvUm/XSUp1IhrnJ1Gopfxo07mJCjskLsoJPuN8np9QzixoADIZVXLjYNRQyTTABd9uIkLdVAL2jQBChmhxl26It4w31SIOKi6gJ5jKoq5n2N3dg3MO8/kcbdvC+Q6D81h1Hba3TQBMdZyoKgADMeGO90zMmjmIJBtPXcllc4AAfrKEPkhn1hhYAubzBluLRhYWY8C4hUV70qKqa5zbW8CGez/quo7jmM9ncEOPKmi3BpbALAcALhxma7FywPa5c3jm9osg02B53OLw8BhkCI0xgHOw8OHujSoZD0WQkGqR0iKLv67Bl19Vk8wY/CD50b347Ptx98APLq0wphIFSNzUA/CLwoI+amSekRwIL2g+xjjoAdZCoEhoVejwTgmnOpiNxG5wQ8hSJHceuMDEu3A5mnMDnOvA4S4GQFym2q4VC4NpADIh85AXy0JwbRj8EF2N1N1otVrJhWzw8R6Ftm2j8C1Bni2Oj4+jZaJt5W9hulVYMxEw66ZGXdVgOMm/X1Xx8FdVhflshmprG7vBojFfLFBZG12f6maGuhZXw7brojvG8aoTQT/sRTJi/dtfPIfHAQRV1spdEd0AtjP469+ErWoMx4+BO69Ds1nJDccW/vo3wCZoyAnA6jEu3r8LPHgP1/cqvPDKq3jw4AH+t3/9FzhcdvjhD38fH7z/EV5//Q1YW+P287ckDTV7MA9QFyEyFYjCnThNjbtfPMSHH36G/cND1FsV6nkNt2rlBnQGYBgVhbsHAuMEABOy5rA16Z1qowASlAsTgJn8oUxkZM5JFQEATASMOBGYMhY9i5g0FawWU/Y+1QgDFhYc7sFJlTmaIlEprAyH0PYDPvviPv6f/6//D/7up/+AP/uzP8PXvvZVPHr8EB9++BHu3buHW7du4tlbN7G7twXvB9Q2aAPZyvk3DBcEm8EPoGC9MWSilUiGKbaky0+dR2UIFRwMxM1q2Q7oesANBFuVwdDVq1fxl3/579GueszmTTiL4noqS+TwzI3reO313+LK9Zt45vbL+NVbvwIwgNmCoBZjAffsxckQPlihQzZAJGBI3b80riYFvY6nPtm6SAyAUxe/ZD2FWY9pKg2PApjel2GDi693DuwcSPNNmlCX86isF2sSMyzNsGgWkdZ49hj6Iab37bsWqxVwfPgY9+/fwbvvvInXX/s5rly9gtu3n8ft28/j8eESn/30V3j9H9/Gc889h1vPP4NnnrmOnZ0tDOTAfoCxgAWD2IHIoLYNLt24iov/7Z/hlR98B//49z/H+3//Cxx+cgdm/wB2tQRzB089PAEVWSC4zYWDBsN1OB1DFC5kSlTwWwdJwBjnqQoZBU2UrV0OfFJgm2KF8QyVtbL6/Wma/1IdKdBOy1QDrLgFIJLEAkwOapnP35HL1BDjwBgcY33AANPIfyfgF9PYhSntGOci19JbCN/VO5VSuuSydtSSkAsYa2NIns+tGunfkzq4PLdp30vCYVqXntf4fKot0bnQMZrpXEUargJeAqwnF02DgqiYKqjkf+k707UJzpZByEg/V7pPiS5MFRlE05goqWIM0s/nNh9/bCcRSBVSKd2u6xrd8iRRuox8j0O/1RJbmnsm0hBYwfEQzwKZ/3UB5UnlSwsaKgXqQlVVNdmoOiGpmUWXZmt7G9459MOAedOg7/t4SZxOpprhiOTikeVyidlshtlshtVqBaYBNRjHJycCOochpA6sUNsqao+slQv9+n7A7t5uzEyiAbeVtajncwF35OFZQE9lDZrKJhJ1WCIjG7sO2bcUHIrrVDLxgAgy3mFgETB671HP5qKNcw6r3uPilWt4+tbzcLA4ODzC/sMD8bEG4eOPPsKzzz4La2yw5ExNdHnQV0nY0CL3WrDgfM9grz6foiXXmAb5TOMd/CjZB5A0WiA4ZkSKQVK6gQkgayR40/kJEfTOhWB4RteL+453Pq5JPzg4N0jGmADylRkpM7bWRBck1Q70gTmrm9B4S7Nc7qYCyKpdhdiEASfLFsfHSwAENzis2hbtSuIcnO/RRUtConUI46+bGnXdxMD8uqowny/QNHMsFtsgouiPLtYJRjMXgboLF79tb2+j73ssVycgw3CeccIzAfjMWCljGRyGgUBDj8FYtJe/E9Z0jC/hOhBSU4Fv3IIG6qdxA0qFUo1vJMDHLcAtgAp06TtCJFXzoX6YPvHlrc7j8/oC+MZLuEPAuZPP8ZXZCl/96tfwk5/8BOfOncPLL7+MTz75BL95401cfOoiLl44J3vBq7XLgyCWpbo2uHjxIn76D6/h3t37MBVw45lrODxcYdk6ONYLz7wIGQoekTAqQEwFGUNLz0xaUsZHMS5i3TXBu3WXhbR+BZr6WexL4dm87bxeInGhMWa0Fov1DQH0hovJiGCsBXuP5arDO+9+gI8++r/gq199FX/+5/8cL774Ej7++CP85jdv4s7de/jq117F1asX5V4EEBhjvI/u7XSve+9DYLqOiQEyWGxtiTU4gkKxRK3aFry9gKSLnc6x9x6z2Qzb29t4/Pgxrly9PJkhCkt2+/nb+Df/9j+A7QIvvPgi7tz/Ar1v4Xsf914KSLXfJRdSIpJE74W1jmOikclrHTLuaqN7jgmxB7nrqiHV5IdEIt6DgnayqitYG7IYth0c5N4T0n1HBsZUoNCebRxq70Fesml1XYth6NGvWpysVtg/PMTn977AO++9i93tHTz7zHO49dxtXLt6HW+99SZ++87buH79Kl544Taeu/k0LlyQCyCHfoDpvPClyoMrj6pusHvlAv7wv/tTfOv738av/+6nePvvforjTz6DOT5B1baw3mEwLghMJggbAorhBfDpfEzO2gZBI8cHa8Ct8LyudX6GTuN5eUkFmbw9/e7LxINM+giI2MBRbxyE3vFbBL6nQ9BYFi0TZYf2tdB/YP2ug5zGTbBCAIcpDUqfVwtbCcjmVpxN4xeQv67hjufDiOIiatMLoL0kKJY+S8eQ9i3t66YMUUSSSEHnPY+nAY0pfyd8oFBX2p+1+Zc/kn5TEDISgSKrtbR2m4TjTUJwqt5iz+jaVpQhllTqWasrt/ZM2xtxnsTyqZAxYkWln2cpZxY0yEqQN7nRZOXYg9iLeTV0UiPuPXO8ZCc9OGryOlmKyXhnZ1tyz4dsPBVVcENy8KzkMR+GQYKsK4uG5hPJrw8Bre2qBQdNszFGghWZMZ9LjAMZA2LxBaxquUSJDIGticBs3kgaXQWWgBANXYxz587FcXrvo6uJMQYu9KWua/RegrnbIEwxCG0ni7+9ex7XbjwD54GTtsXx0QlmszlmswZ/+e//ErduPQfvPXZ2dieHaVMweK7pGJ8RUDcKFuKL7V1wTRrEcqCa8tQ9Djy6M0VXpxA34UMGr67r0HWS7lSDi3v28YIzFRb0TgcXbl9Wwq4ZwGAMVl2HdrVC1/fRb3e1WmEIz7Rdh5OTE3jn4Jmxv7+PQQUCHm92Hgm1WFYk+4uNmo66rlEFYUE0M4T5zi52LzRwg4OpJOCZSG6It8bIDeuh/4ZMyE/NcN6jrirM5nO4IVxa2fc4OlnioPVYVnswh3fQNYAjid/hvRvws5fBDQPbwSWNKtDivNCDBCQJrwquQBD8RGG+Jtqj8BwNDOZhfF9B1ejjMO4R0hYIkk0qYXCqbQGHSwPlLLP3IDtNrbdfXcMvsYuvDf8Jly5dwk9+8u9w7dpV7O7tYP/gMd548y384He/J+NKhJ/0huzKNLh79y66rsXOfAtPPXUJn995gPnhEierPs6FMgQgWMlMxhCyc6F0IC8lhpqfKz3jpTIBBLyuhc3byp/f1F7KcHRuNHOZXkzm9ebpkGTCe49V2+MfX/sVfvvue/ijP/oh/uRPfoyjo2N8cf8u/u7vforf+dbX8dxzT8MaAoiDmX1UDqlQAyBmU2KW9adwFs+fOy/WbDOOo++H6A6Yu3ekc//KK6/gvffew9VrV8IzqvMTLd+5c7t49tln8dnn9zHb2hNX0ZbF6tKPKR0nYMsQoBeWqqDA4v5khbNDLzRVwYjZS0YxUf3Bkg2uAeHuE5l8pBcZIvTUG4BBMLaeZP8jXS+2qCpx11WBI4Qdom4aNHUNdkIbVYHCnmFYU2A7kBMhhfyA2lhUzQwARwtH263kjqX9xzg6OsKDhw/x1ptv4tzeOdx87haeu/k8lu9/hLfefgc3nr6Gr37lFTx381lcvnwRhsX9sxsYQ+VAthMlYV1j+8ZT+L1/8ed4+fvfxG/+40/xzn/6Odo7D4DlCeCPAHbRwkxEwvMJoxUvAWcl0JKDsxxgpiUHqqVzop9tAt9pOc2PXM+Z8r203YmAmpzbNQGHR41youPGKGSEz0mo8CR7EnOM5TuLdrgE/E8DpPm78bMAfNN5S5UNTxLgUjAsWGG6lmvCEKbPbFL8lEq+B9J1KM2XYoC8v8oLcyFFlQWbFEL/1KK8tLSXJPHIqOTJBZZc4Mjr1fc29TFaypCIH6X5IprGnk3aG3GvYnq1rskcfrk5OrtFI1xgB0nKJNk2nIMnE00phsQnTDOTSGd9sGoQKisBzVvWikTkhZF5ZslVDoIHJLc7EFOAtgFs2vCssaETwXessXKvhrpk6Rl3gwODcXR0hB1rUNUVnA+WjbBQ88UcxhpUVSXBus7BgIHEfUc0zXJPgq0q+FCHZw6gukdVi4Wj73vM/AztcgUQ8MYbb2A+n2Nvdw9VVWHVdvj+D74CY2fovdxgTGTgeodP7n6Co6MjzGaSyrZpRpcsLSlBLBH1dAPqRW/OaWA14PyArhULwOpohcODwygorNoWYIYxFn3foe06uCAY9AH4O+dAEDeetl1htWolQH8YcHxygpPVCj6s29BL7MEwDBIPsFrh8OgILjDifuixWq7kQqygFZHxsfjHU3AtCVYvGasJ89PAWnGbm81EaBALWYW6qcGQjE7O+Xh54zCIhthWggCc43hRl+9CZqbOA0uxPnQOQQATlyfNOjXMzoH3nhXBK5pzATYzmGf/KByWSrIeuQ4wDYimmgwiGjkUM+CU2KhqSKV0eSYCbeHwUBLCUXMmwo8XLJm8m2hllODF/4W7M5iiJSPqZYKAEezRQcDRekI2J8j5W5pdfNRdwM2nB/z85z/DW2+9gW/9zu9g1W3hk08+xde+9lVsb82QXgIot3iPRHi1WqFtW5yzu3E9RZYg9M5B8+/G8RoKwDJMYUKq9FxsMvGfxhTzsknLVjqT+XP6+0Qo3AAmcjCjfdN3xL3GgZjgIDERQutEIBi8w8HhMf71X/xbvP3Oe/iX//J/wNVrT+PBg/v4+3/4BRaLbVy5fFFkM5rOxyRg3XPMQAQaBd/FYh7dZm1iBVmtVnDDAF9VwWw/BjcqE3366Wfwy9f/Ar/3+z8IAojOjwjR1hK+8pVX8Ju3/gLn7Ry7O+fQDT3c0K/Na9ToqSAcxOiqqhKXnDgauOCbrklEGIjc1yOxfMX6glCS0llDcm9KEMrF9UsqqojiJYxkTXAJrkJShx7wegGguAQbYzA3FjAGwyDz47yLiSGYvVgwu1XIbuhhACy2GzTzBYZhJfcqDQOOjo9xcnyCo+Mj3H9wH795421cu3Ydt2/fQtt2+OijT3DjxnW89NLzePn2s7h27TIsWQw9w7sevetRuQ7zaoHBWuw9ex2/93/+P+GV734bv/rrf8AHr70OuvsphtUKpqtg4VGxh/e9uFUkPu6p4k9ByCbgpgD/NPB4FtCXKt9OKyWtuP6eewekdad92yTsIFhW0xuY4ybTcaHsjpSOL5/H/Jn0uYl2PAOppZ/pOEBCxn1hzlNBqvQv75d+7rM+aFsxlimPbSjMd/5dPj+lMW+qK7dKipJ07FM5M+SGPqnfUVJyWl3aG6W1mAiGNL3EcNP8pGclrUMVUZO+BHpmKknk0i5PJJwhS9JxGj9cGz0J1hBslloYp8L+k8qZBY0333oTwzDg8uXLqKoKVVWh67rg1rQIvrIGbdticA7zmQRpMxhVXePxo0f44MMPsbuzg/Pnz2N7exuuH3BycoKHDx+K1uz8+TgZzazBYr4QjUNiamwW8wCexs2jWoH0kHoXo9hgjMEXd+9K35sa7BnHx8c4ODhA23VotubB3UlS4Ip5W6w2Xe/x4P4D3Lp1SzRbzqGu64m/qWcv4w6g/O69e6hsha7vceeLu7hw/jwePHqMy5cv4/kXXsZ8+xx69mgHB+eBBw8e4ZMPPsLf/qe/xb/8H/97PP3004Gpm42boCTp5p+J5Unu5/COcHKywsMHD/HgwUPs7x9gtVxheXKCk5MlDo8OsVwu8fjRI3HxYbkn5OT4GMvVUjaak5TDqnTv2lbAfVXFlK/OS4Caxq0ws2RTCUFrbCwWu3JTriFJCtDMZjAhBkFdpIyxaNsWfd/BWrkMrus6qcN7OM8xHmLVdjL3gbAREbphTO3pmaPLHnsPHyMcRXPb9w79znXYZ78nwIUIuHABtHdjOteKuwOhSGT/BADJc1EosDOol7365soY5OvUzWMUIgDxTZDKJvIHMmCdrjmp7SJUrrEJY0czmhmej/cgaP9EG8yJSR8JkVShh33onwf2Z09jaD/DfD7Du++9g698/WuomgZHx8c4ODjE1tYCHFx3RjFJzmbX9iEbFmLqa9EahwlPACGRlRlXpjfRHI5l1MSsu0zkTKrErEtMPn0/fTf3Ic+fSy2RX0YLFBkLEWAs/CDugAYGzC7e4UEULsRicd95+7fv4v/+v/4/8D/+T/8TtrbP4ejwEL/61Vv48Y//AMYyABf2XUHzBwG+BiHNNMQtRBQfDayxMcbNeYd2tUI/9Jh5i9LQiORmcQBYnpygCckB4qYkSbbw4ou3QUQ4OVlib+88vrj7xdgn5sk6ynyLS64KBHpRpuxnCgKoprz1ay4Nsq1Gpg8EZYcc3sigSYUt3bSMaGGkIIRrialrg2JkMIRB3USD8GIAMDsYD9jKRldfHZdzDtz1WJGB5yVADHaDCJm2Rm0M6moufQzuVW3XousdliuH49UKn975DOcvnMetW7dwsmrx4Ucf481rV/G1r30FN289gyvXLqGqxTrmBo8eAGY1fF2BKouLLz6HP372Or76e7+Dt/76b/Dur97Eyf3HcMcnsH0Ha0VhNQr/uVCwvq827Xsdtz6TurJtei8FbJvOXP5efs5LdeZ9Ln2/Bi4J4z6aVKCCDIPZAWZ068npQQrg8395/9Pf8xSvOYjWPq0Fb2Mzrds0D5uEDVUMpnVN+lmoo1RyoS8XcEp1lOjrZuDLESingoi4TE50L7Edk8X25XOV79k0oFvrKP+tNGc61rxeLXlM0nTuMdIiIV3R5f7gkVqcxvcnwukprIgzZea0j2JAOIu7oZYzCxoMj7d++yZAjJu3bmJ7exur1QpbW9swNGreq6ZG13VxQasAGkxdoe07XD+3h0/ufIbFbI5rV6/CscdiewtHR0fonQges9kMprKogkZ/uVpBfcmaoUczn0fztcZoMIDeDfHKddHGi/asdwNsU+OjTz9B33XogpvPpUuXcOGpi9ja3cHgHJq6Eo2f99jff4THjx7hwsXL2N7ZwfFqia7rJGaisiAnWsW+6wGSfhwcHODo6AhVVWFraxuffX4HO+f20LoBdV3j3IXzeP6ll9A5Fi91T7jz+V0YABcvXsJLL76EK1euous67OzsrJnwx02wWYpc19gYdCuHe/fu4/333sfh4TFW7QpffHEXb775Bj786EOsVisBd3UNa4wEH4e5t9bi4pWrsFaA/43FAtbWY6yF55j5ou3akC0IYgkZOyKH240uWMt+vNGXDw7h3YA+pHlVlzSvJm0SaVpdpeLFeGoFCS5aJeAXCRgrKAWYhIA8/fSzWA0Af/N/QL33dAANidY6PYnE8TRzai5Ifvr07CohCf8BCq1GBhUhN8VpEmDDDIKNQot4idD4QKhfnpMq4rtEQBJ3MIKjKV3h8D9K2lZBhVmyEwmo14r1kjvtd/g7BLi1W9dw+KjFYmuBR48e4OjwEPPtPdR1g4OjI1zFFUm0GhrWcRpj0HWr4MvrgzCZph1GFHo4GURkYDyaqNNS0hKVymnM6TRh4/+fRU3tVTMDscQysaa9DP6zotEKTA/A+x98jJ/85K/w53/+56jrOR7vH+PkpMXObg1jQkBisiMm4CZqqwAERirCXw1bS7YypU1d10VNPPN62knvJb3ztWvXcOfzz3H79i3x9Y9gR1Kjb+/s4aUXX8Bb73yMra1tzOYLtCcna/2LQZNRj+Tj5tY5YI1zAaYglijuM+9DkgmiKFDErFHeww8DBnbxHXUT0rMAAsjYEO8tQpkqw0TZb2HNLPpI+2GIsW+AnGdrgNAkjBGrizHA4D2q2RyLqpa/hx5dt8Iw9ICzYGIQhZz5iwbz2QJ916EfBhwe7eNkaXF0coQHDx7g3LlzePrpp3F4sMKHH3+OWzefxqtfeRHP334G165fBhOjow7GD7C9WIN726Gualx99Tau3HoWN996D6/91d/h8zfexvDwPviYYb0BDd0GwVwtjWWhPV3T0v7LQabsk7LAkb+vn+e/a31nAaUlkL+pD+slfcYAYFhbByvhuvCkdKoUBPzElmgaq6TnraSE1Of1HOQuO5vqP004iG0VvmbmMT73jGPK1yYXXnIB6iwlrl0w16dZnkYFotLDse/jv2kMTXGc4XO1oD8JgItL+ti/XEn+ZcYV209eZbDEiQYlCSXzmo4vxR752IWeltMNa/sTgfsJ5cyCxvmLl/Anf/rPce7cHpgR0hoSPBOapolmMmuBeVWPd16Eibh0+Qp+//xF9H2H+/cfwgOYby1A1mCHRBN8fHSM8xcv4HIAtqoVH5z4iK5WS5y0LWAreBDquoKtm7h5KPjtemYMnmGqCk0zw2J7B957XLj4VACoAoSNkUvNPIkTSN3MQWB4N+DSlWuYb+1ie7GNtuuw2N4JfuQ9jAn3iTgnbjxW7t3wIJCxePz4MVarh/ji7l08evQYi/kcN2/ewo0bz+KLL+7h4uVncHR0iOOTJa5euQJLFv/m5/87nn/+Nqoq3EheSVzBZHPHNc3NX35yMAQsyHtt5/DeBx/hvffeR9d2ePRILkP75S9/BU8eL73yMq5dvYqmadC1raRq9Q4OHGIwOrT9AO56tG2Lw+MTDIND17Uh3apsumFw4Q6JEKvQdZIqNmipNUDcDRKAPiF0IaPJuMkpCifxQEGVR7Kf0qAuBUOGSDRHNoT4hjmqKgogepzLrh9w/twFmPM38Nml5+WmXA7a44QxCbihCLp0/jXDCgXtBHFiPUjOffSUjM+a5PdETar/T9uOlYU5IW1b3jMU7A8+yEhKjLVNZfiQ4FPV1ip1icNRZsFifdze2Y6uhe1S/MKR2iE4CBvGiOGFRWvXtT0qW2HV9vj88y9w6/lzMMZIEgfmuB4By4b1lWxcW1sLsGf03YB2tYStAGYXxLSQfYmmTFPPsu6LtJRAx1nKk54tMbqSu0MKTvLPTtMgltoiKGEHwIS6auBIY+VC+kFl7ATx9yeD3/z6N/jqV7+Kq5evYOUGHByeYHvnAuTejA1tM+tsI6AjYYYA/NChmQu90+3Ydh1WXY+twYEMRfepCVODx63bN/Hb376NW7duTppzzgnaZo9vfuMr+MU//hp7zSVsL7bRLZeIorrOnWYbE0lTUqHr5ZkKtmw4A0RRuUHBvVP50ahRBNiErCpM0pfaYtZsww1O0kQ6H4QrgFhjcswo8yMIGxHIyam31qKq5iAmUXB1nfQHDMOMoeuCdXZM8y0xjNKxqpaYmNl8hi2/QN/3aI+XkjEuZAxj72BtAzuvMSOhy23bY9Wu0HYtjpcnePjoEXZ3zuPa1WtYtkt88MEHuH3zOXz1qy/jhZdewO6V8zDOo3IdfNuibixQGbjFHF1T4cY3X8YzL93Ce794A7/8D3+DO++8je7xPqoTA3Q9DLxY0+Bk7plHL0vdSWHLy/2r43nIlQEKulNLzyYBQvdXyktOc6UqWQ820Ycc6OZCTfgNo7YmvyEHMJZi8hmDNMHC9F6LHNCXaEdpLGl/WDVHgU6myHO0CqjSZry3YVMb+VyVLAvxJ2HMWJnWAQg/9gRXeLc0Hn0mBes5bT1NGE37mfZRP3fORcVM5KtZexOBB7z2WWme8n2VKr9GDh/qB6XXMAHgmO0v4WiIipMwFsccEYzReXfBuorRW8INLgowHGJYQ+fiM7HllK2HfnP828cvGeLpI3hDaLpcP4AzlTMLGpevPYuu68FGbvSuATQLcV856Vy86A7M8PBgsnILtrEKa2Aqg8bU+Ma3vo2Dg8d4fHQkmYC6Dr33eP6Vl7C3uwcYC2MbcAiUayALvdg7F9O69n0PUwU3itBHnTPvPbb35olrE4dDLwfMEqEKKW/HC79EaDLGAsai94xqtgPHBnWzBes9btyQIO2269DMGjk8QTNWVQ3s4HHh8g6a+RaWx3IJ2e1bL6BuZrh86Qp+/eu38OrXvoH9/X2QMdheLHBycoLlcolVv8Lla1fgvcPOzq5owsDQTDOSsE4j/8ebq3UTxJzvLDo2sQoAH31yBx98/AnaYcAndz7D66+/jg8//BB7T53Dq1//OpgZDx7v497du1gdL9Etl+j7Dp3rMAz9JPd7DBYPgHX8XTdp6GfSr1jWiKmsGBGBTD3RKIw+3MkzE0Y0An1Nn5cJ9ZM/KDSoh468B1mg9YzzDWCNhzM1RE7ResORD/WQWlFVgUNp5YWfsR+JkKA0JBVIwvdK+DiSjIQCJMJDpI/wQShC0rHxeW2a8wYTAhvXjMIpImBwPbq2hQmZ4MiS3CqZmhJ0PTlMDEvUwPHsKuZ9C++WOD48gWVGTQTf9SGzznhWvQNEVtS7BmqADdwg2t8L57dA5GCogWcDiUyYMp9NIL3EeDY982XezUFRSWBImfJZfcjT9/MxcQDTiGYpWUNb1agCUJPsZnJfjzWEyli4YUB70uL9d9/G9asXYI3B4f4Jrl+/BM+DBExn7cR/XjIwMYILkvdY1BV25w08E2pjJKaaPDo3oB08vJ57SjVmoW4wrl69jL/7u78NQlAQYqBMzQGuxcu3n8P57Rna5RLzeg54ArGkEAWPAD4qAGh0N0rpAwftJSNcpmgI8b5UmCjogghkg9AAhiGGowFmtgBshbmdodnaxdHBEVb9EjNTgQLNMxZgeLig9UuFDbBY0mtbS5+ZUTUE3w9Y9a1c/BroSA6MDDOUcnrPQO9BtkJd15jNG5xfbKNrlzHl9nK5DDRE6pjNtlDXfkzOEf6tlic4OHiIzz/fw7XL13B40OLdd+/ghec/xCtfu41XXn0J5/Z2gIowtB1qbyUwvTbo6wb1YoaXfvgt3Pz6i/jVP7yG1/7yb7D64FOYgyNUyxWIehAGeOvEVS0miBlBOSVMS9crD2xVoV3doacKNY7nKj03OVDfJExM98hmwBhB2hnohoIxz3KLt14g6RWkGeHVjm3kVdqHvK+b6Ep+npJey64jk9QR5ppCUn0O6Z811zIhgte8zTHT5npJhThdg6mw49fmOY6FaCJY6ef52qa0Mo3rSLOabsqGlQof+n5ptoSMsjJH4bmEybuTuiH0g4jGJA48javQ9lIh0vug/Jm0LX+Lx3EiPAf3LYk5RmTXqSs4mFVVGPk1e3FGBjOYTTxptqpEQRLmLKb3DjgiuogSADIxwYv3PhGAVChJ1oh0bghgE7H2WcrZs04ZC1upxENxA9WzGfq+x9HxMba3t8OmkJziptJ0gRDzjQcG32N/fx9f3P0cRBJo++KLL8ZA7n4Y0Nh6Q9CzaJUATDJ/AKM0lgKECQELAeT6mWpMfMiOUtd6H0eSOpTlZm5JOysXovSrlWgOjQV5N8mhTCFOZXfvHOZNjQsXLoLIYrlsYaoKg/PY3tmBret4QdswDHjttdfw/6Ptv4NtOfL7TvCTWea4a5/3eDAPHmgYdtM0KbIpkmK3yJGhODsSSW1IOzO7O6tVrJkISbMzK2m1sSH9sxPBUChiQmM0O7KUSEriSGSzLRvtgW4ADW8f8PCA5981x5bJzP0jM6uy6ta574KSkkS/e86pysrMyvz9ft+fXVldZTga1mNprb8x9UvfS3x9dW0rJFghHOazOZcvX2Y4HPLaa6/xxhtvcOPGDdbX13ngwQe4fuMmb7zxBjdv3LD530u70a1vtm48U4jaXUIKayKM41r4tOvuHAkCjUE10hYY8JpaAiRO8FtXaxNDKaOKaNqewk723uv3h5QSo2A+n3MqlehsAvGaC4R1a1zJ5k5L5AloCGhE/ZhwBo3vAq2GN06EGMLLj164CFmzwFiXjQ6hWiMQlcKhZuZ+gG7U1dytBSUQ9k3tZ14RaovbmM7nCHychqESCqthixqACTBSIoxGxUPSJEFrw3g8BmOZRJ4X7rxZAQLtXbQscYuiiH6/h5SS0mUy6qVpc2rBXA4CJNrM6A/bDgpU2kyqS8DZT6PX9awujWv7OVLa5AhaSVtYUttkFlZ7p7ny0UdMxmOGg3UmE1/XRSJ0uAn3TK5a59Cv3GZvi5zlxGqdjbbxaZZey8oPuj3Hfr9Pr9djd3eX9fX1YE6WLpRlycrKGvfccxcvvvI2K6MhSZygy8IJBaYSEqwQrqqMKT5rjHIZ6YCKYTbHYkGaP4ta28yJEguqS6UwMiKSNnC7UDb5x+rhTZK8z2x3F20MsdYILStgUFsybHp0gSCOJP20x/b2DuPxuIov85Z6VaqKb4TCc1mWyKjOkmeMi00zBpGmRJGo1rIsbU2qPM9ZLOYoZVdHCEGSJPY5SlmwkS/IiwVlmTObTLhx/RpHjhxlMt3hvQ/e4e233uHhhx/gnnvPs7GxQp4ZpFTIsgBlIDGIuEc86PHDP/VjPPjIg3zvmW/y2rPfZ/rRNaLxlCTLGeY5OoaFyBHSJlIxsnJaRRpJ5BRhYYagkLaH7m5dWux2tp5lFaX9+/+4bkld57QLBNSfHV3VLetbwBXsnjsYPTroOKkEQc8ITON7+8wwrm0vr/XPapcosMNtAoYuK4MQotpzofBda/P3PhOaYG8Z6GvvDX+fL7GwH9hoKE665tTxbttzcxPAK1LbY2zf1wa8vq/we8tnmyvi123POFr310By7z4y1fsWTgZ0dL7jnfhmXXI1RtVWmGrN2D+uKjyLB2kfA2hY4usH4YU2ZTRpr8dsMefDKx/R6/VYW10jCTImGWO4ffs2s+mMosiJk4SjR4+yO97h8KFT9HqDKvtUHNsMPWGEO9Qv2hONkLj4Q+C/D1GnX+h2juRQO+Lv7fV61XN8fZD5fEEUJ5XmN0l7qMWCRZZV2Yx8n0mSOJ9kC8BUqZEyZmv7Bt///vP80i/9EkmSMJ5OmU6ntpbCfM6HH37Ij/zIjxBFUZ3dZUll1baWxgdjWaBRX6eU4qOPPuLYsWM88/VvcunSJXZ3d9Fac9ddd3Hr1m2+/73nGY8nRFKSxinEdo5NzUYtslpNQM202wRZIKvKw37P1Hu1hhX2HqulNcbg/fyrOYb7joBoG6oiZuFv4f6o7hN7f/PgB2wl+SyzWbQiKSmMoz2mSnTp7nXCdHWvaACGCjjU/1iyb0zL4lATjervwMJQgwxnLqW+1YON+lk14DGN0bq1q+ZQMx+Ntn6qnglVWjDwTElU2S3cPLQJ1ix4l9VX9p34MZZKubOrWLggYZsGOavcpIQQNujEV5nXNsPYysoqSZJQKpsRbX1jtXUGmuDCr2FbMPeti7guu9a3LsbxcQSUsO2noexqXcyu6742gPH/Rs6dqcita4BxblTT6YzpbMZouMHM1R6ymrLa8th8MLXSIni+lJLDhw9zfXtCEidV7SOjSutyWZaYNGlo9trzP3PmDJcvX2Ztba16mDACXRoiIdAq58knHuV7L77CcLhCv5ei8gwjdO0n7Xa7rXmjiWREXuRNzbiw+8trCz2vEkJUDi4GqqBxVShMbNDSFmW1SSo0IkoonatWNOyzksTMd3fJ5guklsRIa+mUDrBjQU8ax8SxpCgLrly5wnA4pNezRS8Ll74b6j3qeZBvSit3VrEAw4GNOI4RcV2IVkrJaDRiMBi4mlNTsjyzRQEdfZAycoH8EVm2YJ7NyPIF88WU3ckOt26vc+z4cWazOe+9/wEXLtzDo489zF13nWM0TEEpSlWgck0RFfQHfbRWDI9v8uN/+he58KmnePYrf8DF772IurZNsjsnNgWxsDRdSihNiZYGLYw996rJw9pJG8IsO+H+Cc9+pSjUy6txt4XO/RQP+wmly0DGnmta1zdpkOg+bx1tP8F3LwgKOIcI76l6c+MQ1GkDm88K1/JOY2gL022w4PurZDJZr0v7PYRAMpTV/L3hOnYJ8e0+23spvKZLYdQ1jmWtbYFadl8bGPjv9gjkS+5rt/32XrMDqMWJvUA5lOnqM6H3ZAyrxtK6v4sPtsHnfu3AQEMT1lOopDJ3wCBNU06fPo1Sit3dXcRcVNmZ8jyn1+9z6NAhALa2t9jZ3mbz0GE2NjfdBHxGBOWE+u4iMqHWI0RVXRvW3+tNXhVzDACG3wBFUTS0Tv5wam0dNqR0Oe2FpNfvO5eFDKjNdEmSOMHZUOTW3zbt9Tl0+DBPPPkkR44cYzyZMpkuKr91H5R+6tQpkiSh3x84EOUPWvPAhJvX/62dcOhlQq1t2smyLJkuFly8eJHxeIwxhs3NTeI45p233yabzRn1B9XaaOORtrCWmkrggJqgeYIlasm62qBQmZyM81ptKQcq8mgIPtkdVk802ODV/1qNTNgaVc9bB3XpwRTCmfwMWZYjhSS+9gLi5Kers1+BCz83/4WorQFWIgvSxmHwLhseOOCJILJaVxP2ZeCuI33+1q9+gv/mH73IpZuLStCrVqyal6DK8lKBhnqVfMG0GqzUq2d78nupZnpeaxHuqepzfcSr91v3RYVhrHbGZqHwmhQP7P258xpv6VJkG6v8tvcYXVkn4yQmyxZkWc5g0K8y2aFcfiW3Zl1EeT+gedDWRUih6U/d7r9NaNsKkXYLLarh9QdhKEuZLDgmY7NDob2JX5PnGePxmMObqqo1Y+NfwrMYjMFymAaz9H8PBn3YnrhsSc7SEUVkWU5ZKoyJq372as80p0+f5sUXX+TRRx8NgjGtNUxKEEJz733nWR0NWGQLVoYjZrtjIqeUcJ1jtCaWPsW5IYms5VyAE7LtHkySxFk/6iBsW5Xe0TdTM13tqnPH2qCLEhHHKDRGSmSSYIQFxKtJQjaZkI0nrgiiJIliYimRwiBcynWJRKuySacDYOFBt9fs+3WrFBB+/yht8bzxdY5kBQQ979PaFkZM04SyLJnPF1UMnSdVIooZDEckhavJUSwoVUGWzRlPply7dp0TJ06wuzvm/fcvc+999/L4Yw9x16lj9PoRRAZkwUQp4l5Ez2hSMeDo2dP8/J/7j7n05Cd44Utf59prb2G2d5Azg9AKoRVS2+D5wpQVLQzH3ph7IDCG3/vrQv4PTcARrkn7LIU0Loz98Bry9rkK/24Djj1npvrO0qnO+j2m1jh1uf+EfS6L+fLjrfv2vzUFzOpLRBV0bOdRa63DZ7ZlJ//dsriEtuBusO8hTGtdX1wHU7fvawvq/vdQqG8L7V1jCsfcXsOwrzag7VrjvZ+792X47PYYQ5DUBTpqnt7sp6vfcG2WXd9UiFlXKQ/22mvcXn8pa1m5se/sQxvvIxxXG5jeqR0caDjOZIwtbiTd7hZSWvNzZH29BIb1jQ2bQcMJZkMzrE3a2nD48GGSNLUMN0kpihwjJEa4F9nBpMLMCp7otlGu/90Tbn+vLwwXCge+v1AT1hYAhIBSaabTOaurqy6O1/rDIWy9CR8bEQYnW183QZTErK1v8PwLP+CTn/wU4+mELCvJCzs+z/jvuusuVlZWSFwRwbAtE5hC03EomtriT4b5fM7hw4d45nd+j9lsVs1tc3OT2WzGzs4uadIjkpELRqQGDAh8lJDfdq1tXv8Z/GAPkWpe5i71rjb7iFFLf/G/7V2K5gEKx9E+XO11lK4IpDEQ68zp9OsIifBcV6CBSr7Gu6cJD4JwAV5eUPDzDqZW4bVgVv/bP3ovP/Xocf78Z+7h//0br+LX2r8JE/ThK3ULUb8X/2yLHYyraVMDNLFkXU3Yg/CApp5wtV4dt7cZmhBgCgsu4qTOBucra+d5TlEUDAbW3cNaQep4kzRNWF1dod/vs7OzzWw2cymPZSUkitpDsUH8DqKNulPrOmNdfbb3lP/uIEwjvHbZ80Im2NXPsjEZIdxRs0DDKIGONGVpNeG7u7s2i5vWzGYz+oM+Lq3Y3v49PekQLjY2Nrl8fauKlZBSglbkRY5SJUonS+entWZzc5OJi8urGLdztzTGYHTJyrDPvfee47nnXyd1VuWKobXWSAT7QUppA26lqbR0SqnKz9ldaTXqdkRUhWMcgEVryvkCUxpkmiJ6Ah3HEDlhVFp+t370CPGRw9y+eo18kRHnINBESQyRQJWWDvr9H2ppK7DhE2O04gWMMahSE8VunzuwYd3DanfWsD/Pv+I4QcqIKEooywFZZuM4sjyvLO1xIkmSlLKwIGOeZ2SlYZ4t2JnssrG+zsnxKbbHYy5d+oBHH3iAhx+6n1OnTyAijTIlCoXONTLSkMREvZR7P/Ew5+67m9e+/wNe/OrX2XrzInoyIc4zZAFoRWwMWga0MeC37dSgYQv5fJdQGZ6v9hlqC6vhet+pr/Cd7Ecjlgt9res67vfCa3ssy/h+KGjbOkQgJC5eyafTNbZWFKKSu2z/NTdoy0ztuXcpb5cBhPbcgy8avy27t4tetq8JwaEf4536Dgsx7qcs8v2Fz2gCqW7AGl7XptnhXvNZpbrm3LWHulrXvgzfS+iippWP1+2OBQrPxFI+amr3qfYcPW1dVhC3qx28YB/U7hyVQErlA5qkaVUl27tgaD8xP3A3wCjuMRwObQparSmVJnYim9V4Ns2AQnih0FTaz2Xm0tCFyi+iN1v7hfSWB695BWuR8QyrfimwtrbObDZje2fH1oeIYyfJCVfkr6w2dD0eG1Q+6A9YLDLW1tZI05TJZIbWduN5C4qvTWKMYdDvVy4QZomAGK5J/V6s+GuMTbHq5zWbL7j47rvkeV7FoPR6Pa5evYrWmlhECJszBB246/i5U+nBRS3lAYjAkkAt6OzxxRQ1YTPQqhnRuLAmSh2XLD+DXuzfD8B0C2i28rcNeBdyYLXA7XGIxh8VgAhXnuqAGnxOfYN1CTFu8OHwm3vW8NmnTgLw2adP8rd+4xV7jXEykDEhaqimHIKMxmDtTQQO6h3rReMeYfwYRfM6/+z2o2gy3mqMCEwyxChPfDWlKolj4XzIFwyH/dY6uNSOaeTiNPoYF8eRJr4Cc11F2YjWQJa0ZcCji1gftHUxwy4aFApEXRofT2PuBJAOAjLC36xroaWbUSRRUiKkplSK+WxGkeeIkWA8HrN5uL8UQGqtG9W/QyZz6NAhVPmWtWa4OQhXKLMoCozuI+JuQc1nEhqNRmxvb7O+vl5Zt4QRCJSNEyPiE48/yje+9TzDwSrDwYDdoiAKXSKEQOg6f38N/oWzvJfW4gHWdcOvkaOPtqiFLQ5rDbTeZRTQCq1ydGkQRmL6IKMYjCRKI6JeRJQkrA6HnDhxkt3r17ly8SJFkaF7CVLYTIq+VIlXfMVxHDB4my2mSq7RFnwxWMOMnVsURa42Uerm0cyyJBxQUsrXCrBgIk1t/ORsPme2mDsrkgI0cSKJZIxKS/I8ZzafsMgi8jxjdzzmxs2b3D52gls3d3n33Us8/siDPPjwfawfWUULQy4KC4CUJFEJSWLjNx7/Iz/MXQ/ex8vfeI6Xv/5tsivXULs7iDIDIav31hamQ+tGuG+skqU+M/u1OwF6/30orHcJ1O39u+xzew5VJsIuYbo1ztA9bJlioWt+NSCpnQC1NtYCZk3MwVj8OL18EMwjAHvh2t+JdrZBh28hLewCSvsBxTu19n37rdOy93kn2t/uP7w33JVtwNN+Ttd8Qxp6p3f8cVqDbrTA0GI+3wOk2mDBksLmPOr90Vyvtkua3zf/3oGGgUZqQO+zrrUh7fUrEAEgHQMoXXBeEscorcmz3MpN2rlT+MXHm681OvKp8WSF0qxwHrt84gVJYivUhqCjvQHDBbKfwdcFMEZUnz0x9+5A9ru6j1JrBoMB2mh2d3cQCIajEXFk09tGkSSOZcU0ZFWYRzMYDPna157h3nvvdVWrha24vchcbRDIsjm9Xkzai+n1UxuIbQyVGtv49W9u0JAwOIMoNvODzbseJwmvv/ASs0XmYkesRrIsNVtbOy5wELfCtbtT44V702z1VwfCdwJOGHzpm5WRTdVXA4gsOXCi4+9mzERARBp6f3uHcRpKKqa1FwJpByhsOt6CUXGdLaMQIq4BlaiFYf+dt1hU4q4Qdb91pT73vbvOUNkVRHWnvesT5zc4fXgIwJnDIx4/v84P3tt1YMZUIMU577XmsRcYVG/Lg6GGXN4W0hvIIXjTfjq2T+H+brwtN28/Nw8g1cknKS+9ixCCrMgpVIGIEpQ25FkJ2EKMBu1ev6iUAgbN6urQpfe0Y42kf3feRcjN01BZS9ttGTNaRuCXaZa6hJQ2c+lygejSjN1JYyeEdTP1yhT3bTAuE/y9tw8vaFoy4DLLiAhVFkjRYz63tYNkJJnNFmASQvbZYD7C7c9qA9VW5tXVFcqyqOt2GIOMJGVekJUlpdZIbZzsXu9DIaw7SRzHnD59mg8++IDNzcNVqkmDxpYfVERCc+G+ezi0vsp0kjPs95mOx46faPApFYWpshiJaomMy7wlKwWAX6dm3nzwC2YVIH6gLuscCqWcO4EuiQCTpghh06mngz6jtSEbwz7nTmzw0H1nefY73+H2zZvk2ZyV4Sr9pE8Ux/Rc/aiyEHXMmgAhbPyCUqrWExhIkwRjoJemRHFEEsX168C4AoV7BSkwrtCpd2vw5wBGwyFRnJAXmU07rmzSABHZ+/txQtLrMZ/Pmc6n5GXOIp9xe+smRzZPMN7d5urVK7xz8SKPPfEY5+45x8ragCzOEbmhKHLSJCdOU6IkYXR0gx/9j36O+z/xCM9+8Su8+/wPKLZ2MPMFUZEhi7x6X9oYV2VcVqouI4JXYqwkEAp7bYVgqLVeJkh2Aef2OWz3F34f3ldz3JC7iCo5gb+2KYQJME33mhAohm3Z56YAHTl3wzbY8ZZiB0CC+yzQNs5tdS+9C93Rutavi9bZe+1i7KFrfo2Cexpyyz5Ao02Hu9x32n972huOzbsQ3al5mu3/reRGP5HWGoTA5OM0D54NzffSBY7u2E+wNqGUY4B5lqGFQAfgF6wSAiczam3wSmT7nixArSQWIatipW61q/6NEAjvvnqAdvBgcGyqwErL4AavjUYSo3RJmVtmFkexze/tgoylEOhSUWQZZVFQLmzwXn/QR7nUl0Y5cVfZdH5Gg3Ip+6SIHBOIMMJuhLIs65iIYPGh3pyhVcM4GbAsFVFEhcZsXKpxBV0EVQAsFhDFNmE7K8MeaSwZj3eZ7G6xubFJEqfVC5RJVLlpgSFNew4UJaytrbFYzG318KLAKI0UmvcvXWJtbY2V1SG9fowRwcb1CY4r1ENjng3hwBhw6T+NgFzlICNeee0NjBEkiQ2wj6KU2XTM7s4UiNG+7xYixhibArZ12CsU3BiO34IixEWNNbd9SGjTr4rv1xcKJ+ALx1y1MZWPZ2MsHh4Zu+lrccwTN1kJOeE6CSFQRjjtuCHPrJuOcQxOdoCahiRQwR73vw5Y1HMPjZgElgL/jXcDEXz2aVt5/O89+/f4Lz75X/C5p09boNFY2xCcGLcuwnl9mGo0PvC8BjP1P80+oKqpgZ9WEyS5ruz6e5ARCMAVbfHCqBAuDaljnnGE0opZPkMmaxgiFnnpKolLQFUdaG2I44heL2E46rtaGvbpw9GA21sLtx8EaO1Wt0lU/bvq0mB1aaDC39uti3G0tVKhNrnr2q7xhP2HY6rju1KbDly0z7dXonSPWThAaCrgLcEIR+NyjBbkua1rIyXMphmYHrDAsJd5O/yHEAaEsdcIa6EaDAeURQnGII2wsRNSojAUWlMYiTQ2+xKAdPSiOndKcfr0GZ579nu2dI4WaOF9xzUGjVYZaysbXLj7HN/73iv0+yMSGVOoAmlwSiJTq6GcQI1TzkRSEicphSr3CCcyACDGGHzideue5/iFwNIGbTB5bguJFjmsDhGRIHFW534acWg9ZRBLkvUNfvazn+GVH7zEqy++xva2YX0UMxxGbKyvcvPmTVSZWxDgYu8iEdEfDdC6x87ODpGMieOIUydPsru9zdpoxdYfKksLvpVymmvLF/wcQrCrWjEhdt52D/XTmCQWJElElknyoqDUCiGdtUYqVqLUFQZckC2mlMWCIsvZHW9x8vhJdiZT3nnvIx5/9DEeeex+Tt21QZomEBnysqA0iqjM6Js+Ikk5evcJfu7P/zLvPvEYz3/pG1x/6xJ66xboKbHU6CIHbOYvZRSRAPx+qxJN2L1Wxw/W56jN75ed4fDstgPN25r4MFC/U/jztMSz5fprJ5A1teHLxtgeb1uA76Jl4ZylDOKWWv37faG1IZK1MhZqflTRz2BduvoK+wzXIhTqaQne1bXS1nEIC8aFgKbrWV1rHtLd/azBbZrcXvtwfCHAC9d/T30TcEkjArC2bG/QBGxLlVUdQLILuBxkX9djqaGvEaIq0aCwZycSHjhUVWwIUmu6/vzcLTmtsth5LYwfB17mCgS8O7QDA40rV65w5MiRxmJsb28zGo7QkS0UpLQiSa35NY4jpy2yke2TyQRjDJsbm67IkhWKvaapuWiOmOo6WCtyKf/iKEGp0tbfcBk8ul58VUOjCp7yFheD1gobuFVbNLRRCF1nYPDjsrxJVPeurq5y7do1bty8zuHDx2oBWdYbVSnNxvoG0+mUc+fOMXMVbuM4RivF9es3uPzRh4wnEx588EF6vR5JnCA7M03VAkfY9moO7MbRRlOWihs3t7hy5aoDVprRaIjWhvFkwnQ6RQqBItjzJnyaA13u+/A748ZSiZ1eMHVfhHOwB05W1zRm1XGIvM+1dMKsBwoenxgIUrfVYMQIPzZTaSAsCGmC0HYAkzGQZRmjnq2p4ucWHqoaKYWrXQ/IAKFHT71W/l7vP1kfaq89+NzTJ9lZ7PBXv/hX+dXHfpXPPnWSv/0vXq0YVgNE462JzWeHQ7Jyf3AN9VnyV7TEc3wAe2WdaDH0qiD6UkbpZyxcnRLng25cppy1CAXMZrb4mqdN3kqhnYY2jiJSX6CzVIydFjuSEiUdGNKik66FWqYud6U2I2/f19dkhZAAAQAASURBVNB2t37z9+/XT/tZ4fW+r67maZSU0tZWaD2roTHc53kIV6AyAIACm3WqKEqyxaKKaZvP55RFSdLbL+VnkyF7YSyJY+aLBVALJp5hZ3luaxJJX0tib+wBwGg0YjqduT6t5bcWeqhc5z75yaf45je/T+zcbLe3t+uEHG5NQjtbKCjYBCQ2dXm1N9xQvAuW1nXGFQ+ufPV5I+xZsIZpg84L8vGUshQIETPqJ2jVR0YWHCdCUCaSH/rUU9x913m+/fVnuXX9OotswMrKiJPHT1qeJAQikiQu9kQIuH3rNtliwYnjJ5jOptY11xgS5zrolWrhPLuEkXZAdFv4McZaDnuRTWZijGGRZUxnM1ShAOGSl/RI05gid4oxNSUvMqaTMTduXOPMyTNsbd3knffe4MmnH+PBBy9w9NhhW/VclCRJhCom9NMUooh+f8Ajn/wE9913Ly994zle/uZ3uPn+ZYrJBGMEkS6RqiDR0hUgdYKkpAKRHpwhlp2P5lzbn8N92j7LXevUpUSohF2W04D9zrvRrr4Ley0w7SDlsK/w+rDvkBW0rxfCensURdkAHf4dNyl8MztWNz2gMT7/XxUAHigUfD9erloGWrpAwLK1a9P2dkD4sjF3PXPZtW2gVl3n2PZBAKNv+1nWPk67Ux+NvUxzXYSwhbR9PJw2tQQCVDJUY2/JZuY+Tw8BVEP+3LtH79QODDR6vYSrV69w+PAh5nPlBP0MGa2QZQs8osrzjNlswrVr13j/0iXmi5ynn3ySQW/A+voa2iiMUhXQ8ONWpa2+aoPLS2tZcMKWKksibU1geWlQpUJjyIrcmbpdLnMpEcbYaolaIaPILZBDX8IQxT71mrKWBemL27miT6UVtvxL0IWicFWubR2AgkU25/r168xmU1ZWVonjmF5vUJkc07Tn4jdUFfuR5zlXrlzhow8/ZDaZMp5OGI5GnDhxgjRNkZEvJHVnQrZXmPFEUdt1jGJef+11iqJsCTMLbt286e7fx0QnQIgoZOOWsDnq1nRasdu3qWmx31elTozXoAREsgtogPPXDsRj0XxaSOysQEOdstLdZFfESrThuLRz31PaVEtWFIUtThdJKpe66mEOJlgJ3s0gHHe9tyq3nmrsftwOBhqvQLDzfOjsOuePrfAPf/APGedjfufN3+FXHv8VHjyzxuuXd6tBGPfs5pjcHx7Q1D95GNN4NxWyCcbhV9ktoUuhG4CXACwZh94ETRzj8YfxjMYFI/rYJe86CYK5A9t+pMZYwc4W4LQCzmhlBSltPYj5fM5oNASxXQmgDZQRTpMmIwkZdpemKGQa3nd+mVax656DNM8YlzFO32cYDBvWoGiOKWQR+zzTj1P481orWJRSLs1wbOuUJNaNdM85ZC9T9uNYWVmxNTu0QspefQaBbLGgLAp0L3HAp979fs72P8na2hrb21scPnwUpWoLn0G61LKK+y7cw9raCpPJnF7P0tOGa5lpZrPxTWuDKUuMtvwkDCTHGIwI0t2a+iSBdQ027lKtNSK2CU0oDdKUaDVlUpTEpmRzmDKfLljtpQhhbHyRKjhx6gif/cWf5ZUfvMaLz79EuZ2zMlplMBiAEQhlT7PS1gK9srLCaDRCCBs/E8dxlW3Nx7X4ZAq+eGq4j7pAsBcuvcLNX5ckCaWxlciFEBxZWyXe2maxyMgWCxsbaSxIlX1JkvSZuZS5RVFQqpzZbMLhQ4dZZHOuXrvBO29f4smnHueee86xujYkzxSxNCzyOSKNUcZQ9jTpRp+nP/sT3PfEo3z3S9/kte99j8mVq4j5jCgTxEYgjYsWNJ4m1RY1hzKquS+N6egQ1EMNtr/GB7K2NfFd57apJadR46T9/P2UEe3vlVLV+Q8Vo20AFPKwpvKpeb78v5XSVmuEqJPUgCSWtbUovG8Zreqie2FMqpSyYi+h+1E9Rq8Rb65DOyvUnVrI99sWg/a67AeYQqAUzm/5gz3nP5hgHa7TUsvGHXs5WGsCoqYroGh97gJ2xphGjIZRqo6vNsbJVW1YiqOlNPq9Uzsw0Lh48SKXLl1ysQYRcRwxGAzp9/sIImQkmEzG7Oxso41CqZLhcITBauviKGJ7e9uCBl91OI4qzWae51VV5iiKSZLUarC0qsyR/tnGGKQrFhWmVQszV9hqufZF53mOoQ4QN9oCjsV8QZZbv1VfMNBr1KyW06bfRPj6DZa5qVIxHu9y8eI7FmSkfQ4dOmJzv/f7PPnEUywW1uUjyzJu3LjBlStX2N7eZj6docqS4cqIRx99FCGlrdkhlxcdqt9vUxMQEkYrNEYsFlPywvDOO+8ColprMFWRQFsjJIGo1ko2BDUAIzHUrnLaodsokoiOoG5vCRBOoK0kWGqXpK5DaCdjfbq94OoBhK9FEZ5T4/oEMNppCUUN0LSvpO5dMlqamEpz6cDXYmHzzke6RFXgqhbiHYxyQIKmGin4EAr/xk6w0oB5gd5Oyl7/2adtEPhvvvab1b+/8viv8LmnT1qgUXVvEC4rj5C1s5TpenbIkKtFa4KR6v24xWyAuBYYtO9eNGbaZkW1hoRaQyws01zM51aj4miArx4rpa8qal2CtPPfj2NbDM4LxoPBoB63lBilG8BSyKaZvOtsLAMLy5h6u/nfvUWgi5AfREvWfkabwQu3j70FtykA6YalcL/0nWBBmY2jsDQxy3JHzywttICjj+z01W4KLXtBm7dE2Ba5qtXeKqSURvr6QsF863MIJ06c4KOPPuLIkWNOUPHuT6C0wYiclZVVHnzoAb71ze9VFm3rlmqbdlV0fb8VDdOeXovKd9mDDA/y670srCLDrVMdg+X2jjIYVxhQaOM+a3avFVwqc/oC1nsDSGDYS4l6PZIkwgjDk596nPP3nOe733yOq1euUqic0WCVQdpHl9ZiLmNrYfFaRz9WH3vo94X/7JOIhBWK77Tv/H1KuexgToiQUpKmKatrq/QHQ7RR7Gxtk+cLdFkiRYyMIgYrEl2W5NmCRbYgL3KyfMHueMKhjWNMp1MuXbrEQw8/wJNPPsbZs6cRvQghFCorKRAURhMnCWmcMDp1jM/88i9yz+MP8NyXv8rll19Dbe8gZgswygaL69ICVWEw0mVOMt3KqfZ82wJnuI9Di89+rkJdaVBr3mgQzhNimf9/l6a9Vhg0LRltGrKfcmPPNcbyk1AAb7iKBufXjrUd17WXZnbNI/zcFWNR87i9MS9dVscuIbhL+F8GCLr68WPrKjwYjqfLetS+ZhlPCMfSzla6Z006aHPzvTX3ZtdzlrWu/Spa7zHLsoY83HV2KndEQf2eKuBCJY8v2zMfpx0YaCwWM44dO8Lt27c5fPhwNSYpBdZ6Zv2LJ5MxvX7KcDhgNBoSxSnvvvu2WwwYj8e89cabFKrkwUcfZlhVE4dIRjYALrEZNixTzGvEaiCOE2xWDRuf4TN6gHNNCjVYIsxWZUGL3yCLxYJskREn9p7eomc1SZEVinyBpCSJGQz6Nm2iskzMSIMyCikNxiiULphMxoBkY32TXm/A7du3uHjxIpcvX+bmzZvM53MWiwVrq6ucOHGcJE05c+aMrfJaWTSaG9BviHbbu4mtkFIUmsUiZ2d3yo0bN60GzQGZPM/Z2dlBRrbwlkFQ6rregbd6eIFEGx80ZJsgoqqSLdrjsVfUxAan0XfXN66j6jH8q/YdxWq5EVThgY0blwmGVlsaCSfoG9WQdNrES8oIbWxhuTiO4PrLmONPO2Yvat/bYGwNa0FDmKdR7VMQ3l/P37tQCeBzT59imk/5/NufB+D33v49pvmUzz19iv/vv36zBgDVWAzOp8P+LaTDNcYBsmC6XetjHDjxXdBF0Jrgxc9Dmua8q0KEUGmuDQITpcyNVUIUSpG5syuJmM/nKKWJE4Fwe8sTrqIsWV9fZ211jdhpcBeLBaPRSpVYoWM6LjB273yWCeBd37WDB9uMfj+wsAyoiI4zvKz/kDEZU2cYyrIsUCLU67+MSYYY2FDvTc90PFiSUlj3J9OjcUAO0OJYsra6WsUC2AnZMZdl6WitxhjpNGW1Ri9ci1OnT/Ktb36nEvw83RNEVQpxUDz99BM887XvoJSi1+tVNNmnSK4ACk3FhVHa1l4J34+ps0BV64hTkHg+RqiYqC0mIpIoDVGSIEtrkR9fu8UbswVqmnHu/Cn6vT59GSFERG/QJ88LVg+t8NOf/Qzvvn2Rl154icl8F4MmjXpoo9GlrixCys3JC0ulU8iFgbleQPZuw2Hdgi7B0b/zStPsBGUv4ApgMByQaE0Sxwz6fba3tplNpzaW0MWuxElCHKdkiwVFvmC+WFCWhvlswfbOTXZ2jrC1tcXlDz7kqaee5JFHH+TIkTW7K5Ugm5eUhaaMS3QqSJOEux67wOm7z/Das8/z3Je/xrX3P4DxmCjLiGSC1KWtryIAadB1KZRqjl7J2AYPy7TkbSGwSyhs99/ljqbNXpoSvqPOz8EtFpCrRtaeZcJl19hqHtZ9XWWtCR57J+G165o9Csh95t0FGvYTurv6WkYb2zS2HWcT3u/BVjuoO/x9GZAIaUl1Rlru7F2Ap+vzMlC87Pr2vO+kTAqvhSYl9/Nur3XNT+p7jafLeNd1z8+pgGkt12D5vzFtYe6O7cBAY2VlhbzIWVtbpdfrNdC8EBFKlQhh6A9sKtnV1RXiOAEhiUTMaDhymnRJmiZIHdHr9zh0+LCN53CINI5ilwI3Jk0ThFjFUGcNEUiksK4uRV6QpEltDRA2IE4KGwPitTYGULoglSlKlSBiZCTp9VIi5xOrtK40c8N4yGA4qHKXexO2kLXJtT/oM+gdsQHjsbXqDAYD7rvvAru7O3zjG9/g5s2bTCYT8jxnbW2N8+fPM+j3EQb6wwGHDh0iTSxwkjJC6xqBHkS7UG80Kw5boTnhnXfepVTWRB7FVD7gRVEwHI6cdr5pggxNmRbTSYzLdKSD5ygHKvaeERn868dUb8j2tgy1oo3vDeAtC9VNy4hkoJ80ThAX9rl2vE0CWWuOBQZdaQillEhNZbIXbhyVidlPtkMj4e/wwvev/uR5Th+qNfFNEdC2fhpx/6k1/vkr/5x5OQdgXs753bd/lz/z8J/h//m/eYRFrjrv9e2jW3P+4dfes09YykRa97tXEgKhpfcZAncqH4djKgGlWnb3mzAGooQyHjFQU5t1Ks+rvbVYLFxslAVIsqGFUwwGfRIXoyGEtV72ByOkjADVYJrV40UN/Q6qFepiFF3CexMALAcrXQCiPY5lDLoNMnx6TO9S4ZUs7Yq+ddzZ/k04N6Q8zyorbRynLOZzEBt3vH/veAVRFFcZmfzYoyhi4ZQzWtsCoNJtklrJUK/BcDCyleOLgsi5jGJ8/I1GRoKizLhw4W42NzcZj8cMBoOGFhFsvng7z5a7S/A+G8wfXOpet5fdGhks/fd1MiJHB6Xr22hjk3mVRb1nCsW8MLz+gze4eesWjzx6P6fOHKE3SBBSkPZ7EJfkWc65C2c5ceoYb776Fu+8+S4rA+jFMaa0YLmKHdMaU1qf96IorDtWIHT4Z4fxMcvSbYZ/V/+5NTBaEzlFndKGUtkYEOu6GJMmPWbTmYvRUBiX+rvXH9okJ4sFeT5Hq4y8mDGbT9ne3mY6nXPz5jZvXnyXJ59+jAv33cvKcEAsQZeaUmoWxS5lz7kar/Z4/Kc/zV0PP8C3v/p13vrWd5lfuYrJMigM0u2HmsdVkwL/jg5wDur92zyHd0rr2smDA7q1n9b7oOPpUmaE/LhNf+o90KaI9e8HzbR0kLF10cG9gnrNc9t7NfTzD7/v+tyOFQn39X5CfHtM3m29HXu3X2HGZWNqb72Dtjbw+sO09rsP12SZtafN8rWq4ybbliC/g8J9WCt86wQ74e8Gy+vlx5zTgYFGFMf0hLDuRllmi/JVqElQlILUaA4dPsL29m3SXp/hcARCcv3addJen9W1NeI45p4L97EzHrO6tlEFpoEjvtqQ9l0aTF1vdunzojuGLKWsTMCe2XmAIqWEwAcTXIo8rYhk4sBChEyt65bWBhFZYTFJU+uf5szukayrzkZRDEKilaY/GCJQCBEhiUmjlI31I6yOVvnN3/ptLn3wPnmes7Kywn0XznH82FGKMkcrTZ6XnDlzptJeSpv6CtlQS7t9s4SBNA+JRZ3zRY6MEt5+5z3m8zkyTi1hlBFZVrDIMmQUU5ZOcHNaIpsNSLhT5QicCIlMk9iLUNKsPlcDs3p7U70scJ8b2gHTITi6P+Qextm9Jk1Sa+NuqoNIPSfhBWecQOfmLgSURWHXXji3JCOqOgK1maA10uCAV4cXWOlH/M0/+xhpfDDm949e+kd7Pv+Zh/8M/+nP3nvHe/NS86+++yHjRVEJ2h4YNBYzHLaffCAAdjcvsFknJenX0s87zMzmM/T4l6GNBf5ao/KcIi8gjZgtMvKyJEmTav9Ygc8GKqZJStpLSVIryGaLkv4wQgib9rRyenHzqAigG/EyJujfUTMJQDeD7mL44eeu5xwEuHQxzG5Npf2udAKtTXW9v3a2ejY14DRC2PSggRA9mU3JioKk32c8XWCNs8KXfgnmunxnCOD0yePcvL1FHK3Zs2VAuqKfRams1QCrPa8TMgcKAQSRjFhdX2d7d4fDhzctndd+fbDxe2XJxuYmF+4/x7PPfg8pB6S91AoP6MpVoP0ujGOCoctfte2dOU8QMmz7UKEFpT/uwlpHfVyQkNK6V2kDzmXLWkAKjBBcuniZ8c4OFx44z70XzrO2sWr3ciQQPRDkSHp84unHOXf+LM995zl2p2NGgxHCgM40ZVlUgj9Q1fipNKvCPxNEFBOnIEpbe8TGbrggeep1xCk/Gu6bju7Gvh6Utunby9LGVPX6PVs4N4mI56kDhDmqtHtRG0gGQ9JBjzK3XgHlfEpeFswWc7Z2t9ga3+b6zZt88P4VnnzsMc6cOkEUGYgNBYrSZJQ6J0pSekmf1ZNH+Nlf/lM88thDfPv3v8SHb7xNubWDXCwQ+ZxY+ZyKNu2tpeMaibBgRFraFKaM3U9zHgpq4Xlsn/dQ+10JfcY0shB1udCE/VWadREKns20+120YT8A1DiTwTy8cA32DNZFdx29FCEv318J4vsLx2U1SjhW4Mfq9pzjm14YrfoJLLHQjAXpCtAPm3+XjbPdSv7TXu9lyiI/j7ayIpxv+MygZ9o0sesZe/ZJx3xaAw7WqO5XRlEFpHHKkFDeoQIE9T0V3XdxzRIB2nqGaAPS2MLSXq5RKLePnXt8xYv9fMGg0cJUn0LFpMHSy6bj9f7twEBDClsZdW1tg/l8Dka476DUJXFirQSHxGHGk4kTelMGgyGjlVXS/gCZpMQy4tzd91AqTZLWlhEhvFtUvfG0sDESwgl7XannPMgIN5nfUOEBtC/KPSt4SVIItFt4IWNEFFlXEeEyTymDFDFG27SoQsRI6a+12q5YxEQy5e677uXypY949jvPIWN44sknOHbsKEJCls9RqkAI6xp2+MgRkiSxczJUMQPLzGn7aQIQxqYrVIbZZMZHH10nKwpiKzojS8U8y6xwIQQgXWFgn/63BhTW/7ROadk8lO2YkJaghWd0Au82YVMiO2bX2pftmfpD5UNATPV9+0o33lB+waNsjyScn7hLYxtW1RXCMiiNjeVBGxLmdfVyY6sGB9N26UNNvX8qRu6EFq3ZnWv+wq9/i//2f/cUx9YHvHP7Hf7y7/1lbkxv0G7TYsqrN15tfPcvX/+XPPL3HmGUjPZcf3R0lF//+V/n3kP3cn1nzv/1f3iB8bwAYSqaJTA1kXLAyX8VCnrtVuMPB66k9xev59ggmoGQ5oV9/whtbB0DoQ1GlURSIkVMoTPysmBI5GqcRI7W2bXr9a1/e7+fsL09ZjEvOTkYWaFSKAQxLj1EBXj8M8Pz0fV3lzauDQT8vw3tTUsA2LtuofDQ7CPUSO7X6mdQAeWGEHzQ5ueMi2Fx705r6+Y5nU8pVImQMdN5gVYCI6RTAPgumpbKPWM3hvXVFa5cvercaiK0sumMhXApU5Um8e/VeDpgaxT5pozh6LFjXLt+jY3NdTtqWe8lY4wr0FjyxFMP8Y1vPsNskZAkCZm0LiNadTN0IZoJHUJlFYCvyBDuHeNAkbRyec0vpLeyGETlDuZckIxGIDGqBC3Y3drlhe+9zO2bW9z/4AVOnDpGr2fjV4gMRWT5zOrGCj/7uZ/hzTfe4dWXX2eU9oiSyCo8EGR5YYO1qemWVazZsWghEcKBKRFRUiC1oSwVGFXxSkfq/P9UIMELB14xJ6M6DXipbMr4JE1sDEwkiHsReZ4wn88trXQem0YJ0t4IGaUsFnMW+QJlSubFhMl0h+lkymx3zofvX+GHnn6C++8/z/r6kKhSAZWgNIVSEBuSuM+ZRx/kT9x9Fy9/63s8/+Wvs/v+ZZjsIpgRaTs/IzTKtM4entbvBfZtF5rwvtCH/U6pqqv7gp3cFmxDC8keGoTBmMKm7Vc2jq1WtjgZvkPwb6drDWmN9bKg8RxwQN1EeN1QWB28msQd5hqumb2g/tPfXoOvGqB7hVdFhwKhuE2b225p4bNDoLXMghGOIVy3vQWU6+cvy7DVBjwN3uD+Du9tx8N0WRi6FFXC8+dgTHvmZQI5o6M1xB7XNJYuCIcotQGZphAvgAiBDTMwwq+7RmiQInbP1M3AcKBK6xmuIX74ouGKeqf2sSqDew18O+WsME2NYRzHrK6uYgzs7Owwn885fPhw5ZOota1MmqS9Rpn4dknz9osKmbfvy3/2vrvhC70TYhetDdRGvgCmrJl/l2+gdHnIV1ZWWVld4ctf+DLz+YKjJw5x9uwZZ7bSKGWzfmRZzvHjx+j3+86asX/F0/bm7RJeDDbIM00SXvzBq8xms8qdzP+7WGROa2YFAJshqLs/EJX/e5gVp712neP2cn71717kfqfWJgBdbdnzq4O65B4prUVKu8+qVGRZxrD4gN3jtbnQM2xPrYVn3k6rDjUhsLEP9olfe/UmP/c3/oD/9i8+yWceu5e//wv/Pb/627/CV977yoHm3gYfAD9990/z93/hv+fU2km++tI1/m//4/e5NfaWDP/sEHjWgrjxdE10E2x/XWXpkAFQESKIPQmNqvW8hWiutVIGEYuqBoC9zrh0twVCDKjkYNw70Jo0tVnbvEWyLEvStGefIoUNuXE4cs/4O85IF+Ns76v2d+2MPqGPdnhP+1rf2oCmTSvuBDzCc3VQAt6eo79XQ5VBRCnFbDolz3MQwgWDewDQPY7wX9+0MWxuHnIZxGpBLna0OMvzKouUF0AcayJ0ldRac+rUKZ577jkeeOABmiDY7gxjbCG4Bx+6n9FoyGK+YDRKnWBl96lE7lnv/eYTCptd1/pUztYS5P52RalK7d3bXHCyNjZ9rjHOemQLJL77zkVu3rrJgw89wF13neHQ4XUEEf2ejZMTwu7tBx5+kHNnz/O9b3+Hm1dukM8ztIHZfEpZ5KyujiidlSLCWemFc5lxZ9UIQUxEUWTY+hOhcmZ5i5wrsDHGZW2s6bzn7YPBgDi2Gcr85/l8zmw2s1XgjVUYyCim1x+SFxlZsbAuk4VivsjY3t7m+rWrXL1ymUcfeZAnnnyMs+fOMBj2MK44ryoLynhKERXEaZ/+cMQPf+anuP/Cw3z/q1/npW9/m+ntWzDbJSpyYqVJtUYjUNKg/Fo463ztAoxzea4FzK6zuExAbAjuQRyI3Z1NWSSkCW0rSLtvhI+tqMXFg575pmxTv+Sm27OpBNkuIbx9fdhv1zrVC1aD1HA+NYCv79EuIUNb4G7Ps4uuts9q+7plQnz4uRH71erzTkojLyM0QKvomG9rzF3PC9d/qby0ZBz7/b6nH0dnI2/BxpAJzSd+6IfIyoIb21vs7uyQZwvm0ym6yDBliVYGXVibhqZZr8y2qCIo4b4QQiJEDLok7iju2NUODDRms1lFeBraAVNrB+bzOdPptO48jlgsDMPhsEKBQgj6fRss54XX2qqxV/MgA2bpP4eHuA5groWJMPtACBB8v5XA6TZkEseVG5a/xvcjg03UIBxAWSgiaU1Up0+dYXt7l+9+91nKsuCB++9HRgJpvPUgxhhI0z5nzpyt4lza5sOwdRHGZdfN53OSZMhLL73EYrFAxi5FYhQxnU5t0Sl8Ok9Btsjweb3ba2Np2F4/ybCF39XEhlBKX0oY/rDtIIew/tdrI+vmBVtPE4WwgCrPc4Tsuz0avuNauK6ZQt2bCfsLit7d3F3w53/9W/ynP3Mvf+2XHuaLv/ZF/vY3/jZ//at/nVLXOfHv1GIZ8zd/6m/yVz/9Vym14f/1z17mf/jiuxXRD8fiJm7/EQHZD9bA4Yfg+5r5NfZ2pXWp4ABCUDFZL3BV4MTNWwDlySfQ1/4A47KzFUUBIq0ERykkSINxRbh8BeM0TUmShJXRCrdvbVEUBUWRu3E1i1PVU6uF0mUMqM2kQoLZRbS79nUXgNkzltZmu1O6yK6xtr8Lr+/6vk0fwr68wCHdnp7OZhZoAHluU6UmzsVPIhBRKOwvVySMRgN2d3dddqmm9tNmOimd7zzVHhNi77qurq6yWCxc0HMoVIRCW8nhw5vce995XnzhdUvXpLeO2PPWpoldgkzXO11mcRIOxGgXCF3VDBKSSEZVgLTBYJTzP48Epau8jhbsbO3y/Pdf4NbNW1y4cA9HjhxhOBoSW38nhFuruBfx6R//Cf7x//yPKBYlUgrSfkp/2GcymyEd8DaqRLpMR9WplNbLQKkSJIg4QpeaxvGG6vrw+EQuaYr3IAh5X7hG3uIuhE2qMhwOnbIsYzGdossSAURCMkhikjIhy+Zkuc0wVxQ21f329m12dna4/OEVnn7qSR5++CGOHN2AWGOUwagcHZfkuqBUJSYdsHr2ED/1n/wCd33ifr7x5a9y5ZVXEFu7iOmCuCzQQqCEjfuIde1i6AvH+4w54RYOz0xbGAx5f3vfL4uXaF/fRYfawrUUAi08DXU7rnWOlyknmmfSpZYOMivW+50qVLK998O57gFBwd/70cjw9/qBVOyinnvznv2E8bDfZefX/9aOQelSNHXJCm23ra7WBRqM2Atm2gBi2TPD67rWchld71JoddEz14stZur+TwnQaO579CEe/+FPkmyusphNKRYZ0/GYjz68zI3LH3D9ynV2tybcvnXb0XTLr7NsgTES8NYOEMYCGYxBGUOU9Ig6xr+sHRhovP3224xGI7TWzGYzzp07R7/fZzAcMFvMMMawWCxsp3HMjRs3sNWoY3q9HuPxmNFoRK/Xq/0I3YKFUf7hoobZkPxnIUSdeYSm5jEED6oVoxFuhsYm8osVZPAIr7FpFEXVv89sJYQkjlN0qVlfXWdtbZ3vfOM73Lx5i0NHNjl77jQ+nae3HmhlWF9fr7RFYRrLO23Arg3px6hcfvXtrS1u3LhptcGRzdwlhU2xO5/Pq4PvCx5aItflJ+nG0yBe3UFr+wn/dwIGy9oyoStcq/0EPiFqlwf/XyhglMbWF1GmdNaggmQ4tILrnhzjnoiaBvgC9sY8GGzKVbduf//33+E7b9zk7/7nP8R/9RP/FZ85/xn+3G/9Od7bfu+Oa3B+4zz/5Jf+CT9y5kd49+qYv/TffY+XL+1Uexbj/W49wKGJIvzS17iqKaoLr6H1c7V9alODTYQI3MlqjV6j88A8IYSAdJU4SdDGVFne4iSuMnwhcKlq6/vD9x3HEWVpFQdxHJOmKUWxsIKEAzMNANGeVzDWLkbaJdw3liXY1wfN8b7fc/YIskv2bUgDw1S6XeeubbIPxw2OiRoD0lbC1tquvQ3Wtum97TPqZyNEEAen0bqp3bN7QrC+vuFSh6vqdwsUE1RuY9DsuB0Adf3Vu5BqXayWfMHKyohwmTy4VLqkF6U88shDvPrym+AsI1JEGLk3Pqei77quRhy+w9BVI3y/dn5ULlFS1tnrbLC2wQQuKj51rpXnbN0mH9MWRRHaaObTjHffep/d2zvcc9+9nLv7HCurI0QkiXsJSgjyecZLr7zOZLpAaoGMIS9yjm4eYXZt5twUrMXES9AGbcGHcTE9wrrGaWNrS0kpXbyZ08S78yWccsBDNCGEBf2iBmzhGoZ7aTAYkOd5xbfjOKafpMynM7JsYZ+tFVGc0hM2YUBRFJTOcpZlC+bzGbPZjPHOhMsfXOGJJx/n3nvP0R/aDFPG2DTCcz1B6Yx+kjLs9zn/iQucuHCOH3zlm/zgq99k++IlzGQCqkRROvIuKtrs3dusp4XBmDrOoD23ZedrGX9ZJnR3CcbLrtU6AAP483VnHtol+Ie82p9FS0dqv/2wn2WCe1sm6qJ71oK4jN8Hcpt/FgFz8Vct4ef12ugGCOoS+hu0/w403hYtLFra+L19tO9rgAbH37voeFtZ0SUPde2lLmCyDACH17cV4XW/pgLWGoPCuoH+5r/8bf7g+9/lJ3/x5zlz9gy3bl1jfPs2oDh171184kc+xfrRY2ilmM1m7O6OKVTJxXff5fr125Qq4tqVK0zGE4pFxmQ8xigXr+ySc4TFRPdrBwYaq6urDIdDxuMxSZLYatZJQlmUTqdZb9jRyPqY9/t9FoucW7ducfXqVVZWVjh+/DiHDh1yhfPqRQ3dkpoMwF7jfUo9E/bfh0y5vYFCgaMNbqpmTEOL3QYaaCsweRRdlqWzFEg0kiiSnD17jiIv+foz30Qrw6OPPkac1IHyWtu+y7Lg2LHjldvZfn6h9fD2R8pek9jr9XjxhVeqisp2zWxKXwsyrCBRlooiL4I+m4zXOAFWyNpatN/YGt93jPOgiPegrX2Y7wTIms0Lp00NU1HkJMJprrTGCGfL8MK7k8idPF0/S8qmkFsJ4lRn4uVLu3zub32Vv/XnPsEvf/pHeeF//wI/+7/8LM9+9OzSUX7y1Cf5wq99kfX+Gr/x9Uv89X/6EtNFna7XgwDPDgRUfrFOH23nKryw5wX6xmAb48ZQz7v6rp43Dbrb2gfV63eFML3W19WkSR1ztWlV63fhe1HK1spJkoTBcAgYSqVIkrQqqGcFOBVoz0xrCnu1Wv7fZcB1v3YQQLJfazOKZfe1lSttS0hbwLgT+PF9SGEDC6WwrmmLuc1uppWtxJ1lGSujvnuIBZ1ecGn3F7Z+f1DFaNnftbMgx+RqTlG6+kXubLiVb8zH05kTJ05w7do1hsN7KhrthWRjDKYsKFXM4594lN/6zd9BlQqMV84sUWT4Pdux9u3rQ/5gwZlzfTHgFTClAS2US7XthFgBQrpMiUrbGD/ARBF5VliLCHb8N65uMR6/zK3bW9x7/z1sHNkgTiN6vYRnv/NdXv7eq4B0VXkLstImW4mThLSX2hTRRlCUJb1ej7X1NbQxzOczB0JsVhlrKJQkaUIc24xSeZZRuMQCVklQaVDsuggHAu8ghHuXaS9U2OQoghUZk/Z6TGcTijxDCIOMYlKZkCSGIl+QZ1OULjBjxXwxZzKesLOzzdUrV3n88Ud54slHOX5i0yaPyASz+Rwp5vT6MfN+j2F/RJym/PAf+xkuPPIoz/zO7/Ly178B0wkU2sZTVkfCqx0EuNScy4rr+XaQNKJhULTooDnt1haS28Km5ds2Rs2nnBZiuVBarbl7F3bc3srcVdvCP3uv0mXZeEMQ3mXxMIZGMpdmf23OWH/Vte7LwEHohdJ2Wd2vLVPm+CyiXcHjy8bhv6/5h59Md2u/11Au9b93AYuue2CvS+7H5VlSCGIpGA1HjFbX+PD9S3z9q1/l+Inj7OxsMRvvYrQilpIjx4+zceIk999/P88+9xzD4ZA0TXnoqU/w6aPHiXsjJrtjJrtjyizn2kdXuHn9OjKOUcZ6DWVZdqCxHRhonD9/niiK2Nzc5MaNG5SO8CVJgintAvZ6PVeYy1ZKjaKI4dDmQN/d3SXLMt577z12d3c5efIUac8yukroc9qzMDNAGGDVdoEKs0z478LUf/678MD7/nyflikucfExpvJz9mlQq42jLdleGa1w6NAhLr79Hu+9/x7D4YizZ85avzdjg16liNAo0rTP+vo6cRxXh2m/APBw/F2/+fWwfrQJb771FkqVlYCmtSFbZIzHY5fj3sVo4Is41YJF4zmOsOwJIms9/983iDhoC0HWx2teALdCMMI4N4acdWFgvo1JVqtnVPPzgmrwv+4iy7SNFfRxDNjqc2riPlto/sv/6QUWueLXPnM3Dx99eF+g8fDRh1nvr/E/f/ki/80/fikY+T7PNs7iUtU68dd6FBAO3Y/P1L+5a90vFciqYIoQtPmJH1NYYVnJAfM8t3VhsIU4054VdhbzhdU0qpCpY8F7ZK2FNqWnBeWLxZwktu4bxitOhHWTMK3BNJlD899l7U6//2Fbl2broK2tMIG9Zv79+q7AiveddUuUF4XV7hmNFJKismj6azydhLbMELY0jRkOhxZQ+uup3V9V6VNKeqGvCWD8udVac/ToUV55+VXuveeCnTeycqWz/L2kLAtOnzrJyZMnufjuZeK4b+sClXnVX5NZ10kb7tTa2uu2ksqOyRVrFdIWLXUWPOu2Iih1nUJT2hwSVnElBQibrWo2XfDWm29zc+smFx66wNETRzl8eIMTJ0/wfPkSCIkQEf1BypNPP8qFCxf4/d/7AiKSDIdD6/KmNWVZMp5OrJLOvjHiOKlSsUsZEUcWmPtAbxbeDcxaXpD1nAWiSt3r59+lRfbv1xbqtalD8yxHC5vJRkjBYhGR5a5ImLZKkLQHUWyYzyYssjlaa67fKJjs7HL7xhaT3QlpknDt2hqPPfYA7138iK995Ztk+RghS5IkIkl79HtDDp84yqmTJ7jwR36UeKXPs5//feROSa+w1FZG1tNAKyp6baDh+tyxAwiI3x5Q75tXdvjU78vYXluhEf4brqcPBK9bAMmX0I69GZqcdSTIZtUUUrtBURtMdinuuhR5onVvQ7nrp7Ckda3DsutCee0gLQRSfg38Oviiye0xdI2jPWcvn3Up1vZrXUrvNohtA79/F35hO7WB917JKA0sJlOGqyuspn0mN25RTCasr6+h84KTp0+ysb5OVuQkQvDum2+RT2dc+/BDhsMhl959l3gw5PDJ0yxmczZW1zh++ChFPieOYH19hdNnzzCeTNCBInq/dmCgkfb7aKVYWVsjSVNKVRInCfNsQRRHdXrZyFcxjZBRjCg1w9GI0coKeZ4zHo/Z2dnh4nvvcf783bayuGhq6tr5jqFmUAYonTnb18rABfhawmKD5owXmqREIKx/WdVEdVCljGzqPOdX7DUNtnq0QTmGZg+6JRBa20OsKDl54gRGGb777WeZTiY8/KmHGK70yIu520AKKWxV25MnT5EkSeV+5QsN/mFaeLAgZmdnxoeXrwJWM+DT9C6yGXkx59ixo5w/fw+vvvo6k90ZWaFwidBsP8Y4RuoXvJuw+L9rmTXQgv8HbuEhDj93ao4bTj5WKDBCONO1y5iARGDrFQz6CXJ+ExzQCIVy31v9v06oB2wK2FD77wT94G77QfPA6TWUVvybt/7NvvP8t2/9W5RWPHhm1bFCU/VbsSThRuD+9aby7nfhuaPvIwQhAYFtTDyQOP2aN3ijqTJxVbcJAaPDKDnC6B2yRYExpbPuSbKFxmgJKHzkrXEZMJTKWVnt0+/bQnLa1X8YjQbcur1jib6UaKOcMFwLE3Y4e03N/yGARPsZy7SFy5hrW4gJrw8FgGVm+TtpURv9YKz7lClBKXIXQxGnPRa5QgmJNiVR8GqFaO6J5kMMUhjStEdRQg+DFAohNJFIUEqTF6U9Y8b35Rl7cw2FEKyurrI73sUYUyXyqOYLGBOhShgNBzzwwP1cfPcDfNBz+10sa/vthXCtlLbWMqMdHTR1Zr1IWAuFLyBaUUkhkJEk0bFzu8K662jrOqaloTDGxr9ow+0bO/xg+grn774L7jvH6eOnuPfee3j1xdch7TFKe+zs7pIbxbkLdzMbT1hMZ6ysDJlmC86cPcvx0yeQUlDkBbu7u9y4fh0mIKREGkffjLQ1rKKCnoBssbDgx73Zat9i71NCV+9X2/w1BEesIcQKYV2XpZQuBksiImEL7eY95os5RaaIZYQ1fGlW12LmswnzxRQVF5Rlxjwbc3v7KotszI/82I8ynRe89877rG+u8XM/9x+RFzO0KdDGuvlu7U7Ynuxye2dMIWNW7rqb7PJl8q0tIqsVIxHSFtMVkJkSJY0rDloX/ZTCZRczNmi2LLXNjOfkBOuZYWu5GOPOkKe/ci91bYBS767nz6+3TgYKK4v56ngSEK5eSzdt6MqS5OOU7HMd70HYNPXGziOUqULPhC6hNnQ5N1hZwMZN2X0f7oPQ2lH1484HfqUcLwgF7aUApnU+27SyDYzCMYfXhf11uRgtUz7dSciXUjayzylls6DWNLbup/2OQtC0LBFFl5KjLWt1rV/YjOPovkqB0AY1y9jd3sGMeohSs9YbcvTIMbRRXL92jcVihpSCa9euow0USrHICqbTjOl8wSeeepIIe8a/+IUvs7a6ilEGXSriKObokcM2pqMs+cwv/sLS9fPtwJKukAKjbcxCVlhf343NTaIkdq47fbTWezZ0FMdIY10fvJCdpinXrl3nypUrnD9/vvkcUZvN2ofMHgRh60AIqzGymiarcRXCmqC9/3Hlc4zTQBn/QmvTuxC2fLsHGTWjlSA0cZJUB9mmEBTY9GGCtJdw+PARxtsTvv/ccwxHfR585AIiNkQ6dlo/TeasIUeOHKmroB8wWj9s4cb1mzfPCyKZ8u47bzKdzBFCVqZtpWwF2RMnjvLQww9x6tQpMIZvfeu5iikiRU1Mw02/5OBDkL3BrUudBU00Dt4fpu13X1uwMMZUmbt8fFDVT/iXAETk4g8ioAyusGsIxmZ0gVouD3oSrV5rQCEa11UCunDWBrciR9b6/NB9h/jq+1/h5uxmMDrBhcMXePPWm9V3N2Y3+Nr7X+Mn7/spjqyl3NjNms82xu79SnTwzlKmcV2ASjrm0tVMfV1ASMN3UmuxhAMgdYe1eCtARIC02WjyGf3eBmVhGaNNzdlkYNqUjFZ6bGysYTPzFMwXU9JeaoW9KKLUCmVMa057mcVBNUT7AYSDtNDCGj63DUD+MONpr3n7upBxtgNZPQ0z0iBcsTRVFhTZAq1KhBywyEpb7drLYY4m7qeZxFgX0sOHjzJfFAzXDUYqMBoprDa9LEqU0rYehKitZm2g4ePd4ihmOp1WxekajFhEFIWmKBSPP/44v/u7v4/WJVEUEyeWdbWLclWqhTvQkT3Ci7GnyJMAnyXL0kIqwVwL56su/PGSrm6HqdIKC+NcqowAqRHGCj+ygMU4493XL7Jz+zYX7r/b+tOjiRKBkDAarZCXBbku+MSTj0OhePa550j7CUdPHWN7Z4uLF9+l1+sxGo04e/4sSik++OAD8myBMBKjpUs7HBOh6IseZaTJs6LhSmKMQVQ5wgN6ZtGIFYpFHesYrqm3cERxhFKJBYpRhIxj8rigyAtUGSNED6MKBsMVkjhhsZhTFDl9k5DvzvjByy+wO5vzQz/8aa58+D7Hjq5z/NQRjDD0+wlxLEAYikxz/dYur75xkdfev8q2ipDDFVSWsbY2pJjOMLOcKM+RBlJf20e5uQhZ0RvlMq4JfAkOga0fRbUWbvtSudmKvSCjLSBXQM7/1t6VxtNGJ3+4/n1GwGVguL1v671bu0jZVs8xPMjLUrqG+7/KOoaxbuHGVIDIC+8imHNI+zQB+G713fbY2K+GRXuMbWtFG4jtR78PooRoZ91q91NZkcJ6br5/7eIZQwthBx+6Ez+5kyIpBIv++r1Axd5jPfQNkbG5AGQk2ZrP6PdTeouMhVKUxiDiiEW+cM8U5IVCIUj7Q27e3uHG9i4vvPRqVUx1PJ2T9AYcP37SPicv2d6ZYoxhd3d33/n5dmCg4TeN3yhJkqC1rtynKmDhTOgeKEgXqO0XsN/vu00KN27c5PLlyxw5csQyHacpaTPrppuT91GsF973H6aW28+tpv27dKkSuypH6iKvCEMURWCsiVppzfm7ziMRvPSDFxmPd7nn3rs5evQISE0sI8qyPqxra2usrIyIIlkR6YOseRcSDzd0li2IoiGvvPIKRWnzoHuXJx+/cvbcWeI44tatW0RunVVpa4RY4hcSq70Hb38hqSXc/gdoXYKW/z50aQuvDUVqT/i9KVTK2kdZgK2cHOSUr5REdRdBT3ubqH4x1ScRsh0DP//USaQU/OZrv1ndd3R4lH/wJ/8Bn7vwOf7Nm/+Gv/Cv/gI3Zrbmxm++9pt85u7P8MeePMk//IP36gF5ggZV9XLP4mo7i3t2JT90vJ+GwN6abPub8Nlddg8HWMHY4FmXBEGVyla3dmPO8pyyLImTphDu/xuNViwNcEGqUkoOHTrEW29dskqAO8Qn+HNx0CDurvtDV82wdTGu/bTlH7d1AZRl14Xj6BKaQ+EZYTWsRVGwWCwqRZB3c6myQzlsaWl29/P9fI8fP8q7l66h1CqxqemorWZeVEJX+97237av49y4cYMzZ87smYsAiqJEacWF++/lyJFD3Lq5Qxyndo98zNZeu1Cp1dYiNtYz+M7a47oFwvAkVQJgcKl/VpYZrl65ymS6y+6OBVlJknD06FEeeeRhTCzo93pcfP897jp7jp/+Yz/LN7/1Ld6/dImHH36QxWLOZDIB4PLly/R6Pe65527mszGXPrjseHXkjIwxRBIprOXV5LkdknN5MjiwYQTCFfzySiQvwywT2rxM4F2qvE98OSxRhbZWjPmEMjdE2AD7NE2Zz2aoIicSkvl8xq3bt3jmmT/AlIq33ii55+7PMxgMOHLkMEkSu2QGc67euMXrb7/PRx9eQc+m9LM5caH5uV/6U6Sx5Dtf/gMml68Q784ZzAriXJHHBUpolHEF/xBoLxzq7mxbUkjqWFAA7+7kksO0grdrgGx3iNfBGVODGCuON0G3EDYgv46229v2Uz7sS3uCPd0lwIb9VOfBFQ5u0zX/2SfYaVtbvb09HOeyZx6UVrbpYJtftJ+1bG5h/MpBXVDb1y4DeyKYdfuMhLLofs/yLZStu2hSO1ti+CwpRFVUFFzVImmTMpjSyq/Wu8UWdPb1hMtSIaQgTntWGRJbpW0kRWMsa2urTKdToihiZbRCNltgCkVeFFXNszu1jwU0fBR/iPbCv31a2ao2hmiasbxmMkkSF6uQMJlM+PDDDzlx4kR1774bR5UIsTd/entz7A2qkbVwZOqMVkJYl5rQHN/IfBDFWNcO5Q6YvbCX9jh25BiL6YJvf/M7YOChhx9ikS+IEkHirCPWqlJaAAKNIPBlQsUyrUNzPnUl0J2d23z00UfVvPqDAaUqmU6nTnCza7RYLBiPxy7blXcPwEuTDdP6fq3a9MY0dPq+r72Ie/kcwt/20+Lux+z2VDBtXlH9FgWg1wrrVsKylXUNye23mJ+5K0AZHrR48d2rMd33ezCWqP5tjF8IPvvUKQB++7XfBuBn7vkZ/pc/+Q85sXqcj27P+eP3/3Fe/D/8gD//L3+NL777RX779d/m737u7/LZp09ZoCFEILSIjmf78YqAwZkaZBj/dyBV7hl3PWevxW0uhZ+3qPGJAzKWHzs/dq1JkoSiLFzyhAiMoSwKtNKQyuoxfh9rrUmSmH5/UL2n6XSKlAk4k7Xhzpq/tsDeZrQfR2u4DLD4670w0ngDHaD4oMw1pD0Hvcczfmjm8Xc91rYuY4t6evqqbfVOwLuNOgvZHUCOlBGrq6tsb7/B0VOH8Bl/bIxNQlnWWnNRoZhuzZ0xhmPHj/HO2+9y7ty5hiXbXm/nUuQL1tbXOHvuNNeu3USWKTrQzIdrXP2vYc+7aYOJtua0PddqLzREiuqCCqh7WmItIqL6uXTut10p2JVRbG+N0RpOnDzN+bvOgim5ePFdFsUCI2G0usosmzO5OuXHf+rHefnll3nt1Ve5//77uXTpEpPJhLIsXVbBGefOneCxxx7hjdfeJl/YAHZflFVIaWtgGV1l4mkU6DLW5Uvp0sXz2ffQHw0qReKdAlU9b1exgh4M+ymLRZ/dnR3m8ymR7AGa0UiyGI/RThGR5wvkIiGbZ0x2J/zrf/27bG4e4uiR4yRJymKRMRlvszubcHNnTJbnxGhWk4hRnPK9V17j//R/+T9y16MP863f/zLvf/dF1Ie3EJMZRKX1WHAaaCMESkiM0aQNC0B49iXSJUjwMUNWL2gVKSLa68JrdwLV+anP7/LzVPF/031NFz/s+q5LGelTsobfhRk8l73DUGHrY1PCsYbnogIc2nRO8yCKmPB5XTSi/TmUmdpjWtb/srUL6Wb4ewji2mvrnxlmdOt6Xgg42vSl3Vf47DB7KrCnlhM0Len2Pi+XuP61dfTM84w4TSCSjGcz3n73IsZo1tZXGY36NmRAgVGK8XTGZDYnWxSkaQ9BfZ4LoRBCcuPGddbX10l7PdZPn6YsSyZBOYv92sErg4dpDkWtOQz/DhcyDLpuX+M36crKCoPBgJs3b3Lz5k3OnTu3RFhsahuXbciuA9ceb5IkjXHayTXvD1PjSmljMqrYDRcEfvz4cWIR8+a7b3Lx4nucOHmSY8ePsigWREagiSrLTRInbGxsuvHvHVv4uas1CEiAcH3E/zvvvMNsNnMbzK5TWRbkec7GxkaVDnExX7C9vV0FhfpUrJaZWqKrO95l+zA03kvniP/d2zJieKfx1ONyB7f9vQhjFBxQ0VYgSMudWqgQ4dyCOBQnXNSCBnuFkErssNdujhJ+9IHDfOPSN7g5u8nf/pm/zV/59F8hKxR/45+8xP/05Xf4i3/0Pv7an3mIL/zaF/g73/g7/Ndf/q/55gff5Ecf+BE2Rgnb06IBhu08qgHhJX8TCED1OEUNVIQfcS2MNt+iaP4lamBhsYapqgOHWp3wfwvRo+eIYZ7nzBdzems2W44Npm0Sfk/Q+/0+vTSl3++jdc5ikXH06IYF5wq0amqI2oy0DSqq991xfsLfw3996wIZyzLUHPQMtzVcXfe1mdt+e9w3T6/CBBpCUCsSXF+z2YwiLwBYZAun8W4WshLBHmsLJv6aw4cPM5/PKz2mDza22uqpcxsyxL74Y8da+Lmtr6+zvb3doGvVdVimWZQZWhc89tjDvPD9lxFCEAUpzhvr5gSfLmDZ5gXQ/U7DZgUh49xt3AK5o+XPlPFnzK2It3wbIyiquiKyUZDWGHuuBJKd7V0+jD+il0rybEpWLBiujLjnJz5NlKbMsznvvH+R+x96kK0bt3j++ed55JFHmE6nXL9+HaUUaS/l+vXrnDlzjkcfeZQXn3+FPCvIFhmRgLQ/oCgKEtGn1BqFQbgsW0oVYGxsytraGmfP3Eccx7zwwouUZVHxzK419XPz+89nDtNoZCTp94f00h7TyYTxzg5FkRFJGI5GTHZ23b6ckvQGFGVBVmRc/vAyt29v8f77HxLHKcZAUSzIVUGmFUbYvZVnBj0a8v7b73Hz6i2OnT3DL/zqf8JbDz3Es7/3Za6/9Q7lrkKUgsgAhUJiiADjYlr8EWkrJ6SLNbVZ1TyNrF0+OxUW0sai1eAarHtTE7+LiodYC4n0Kq+WPLNsP/p1D2lFex+HSXHCvd7O6NkW0pfJUOG/YV8VTRP1fmgL0G360fXbsnmGALd9f0hH2uUMwv7bAKkNIsJrQzrUxWuaz+lWTuzHY9rySyjTLuMPbYAVPs/95a6vFdjWil0y3NigkJJMKWL32/VbW2yodVcvyPJo5dztRysjtIEkiSsFg5UNhSv6XNLr9+mlfXrA0WPHO99fu32saOSwaF5RFNVkw0j/kEF1vTz/fRTZrEdRFNHv99nd3bWE0E8uWFQfKGgnXWvdQrBT17doHiAboB4RiTpHvR+Pty4Y2dTWhBu27d9oN0fE2TNnKQvFs999jrIouffee9navk1/rYcUMVoLsrn1rT927LgDX5H1yT2AcNJ1CMLfjDFV8cSXX36J2WwGoiYAqrTvajgcMOj38RVlZ9OZnYMPmvdEACprRtfzDiLw/PtobaLQRZzaxGzpOE39ffhf5ZcbaD2LsiCKeghMZS3w7KXSCxsso9lP81tp+O3dxsDPPXmSOJI8f/V5vv4Xv86nTn+Kd66O+T//d8/x8qUdEJL/8Yvv8t03b/Lr//nT/JVP/xV+6q6f4rkrz/FjZ3+MP/bESf7ZNz6oRuIVYP6dVf96S0OoRfYDr9awBhjGISqxB3y4K1zHHkQIIao4HpuGtPqRCp0ZjTrxCZIPnyHLZsxn8yqORpVWEBEyrurW+H1WliX9/oC05641dTaq6p36iXYte4vIdwlF/vs7MbeP+9uy37sEgWX3tRn8sjEua3uvd/TSKTu01mSLBXlhk1uURRm4BO2vcazGaB/E+vo6ZVkERi17f5LEjEtFlmeMBr0GyFjGJHtpD4CiKBp1hexFjgabkqJc8PgnHqE/6DGbFCRRvMTNTVSxVstA3X5z7RyvoHLVUgFdss4wzWry3m9bCkkiI5CisiCEKdIRgiRN8Zm2bt68xZnTx0iShJMnj9Ib9m2QdS8ijQeYSHDl6odsrm7yyU9+kq985SscO3aM++67j8Viwe54l7KQ3LxxiwcfOM2NG7e5fcMqlYaDPhtH1llbWwMpULpHUZau8rhBxIr19XUefPBBVlZWQMBkPOHQsU12bo8b2tUQ1Hq+XLo6TlUWSESQ4lqDNkRRwmi0RpbNKYoZ2qXHLMqS2WxCOhiiUZQmY5rtkKuF45cxGFDaoIxGS7u+Jo6IopjSlMzmM958/U02jx9FphEP/ejTnLlwnu9+9Rle+uo3mF2/hZrMSEyBVMq6kbW2ffN9h3TSa+61+zvCmHIJf7IJY+z+NYggA6C9zPZhTHBeDVRk27VlSrbwtzvRh49zXfVf6ze/Z73cBDQApf/saUh4f9fZC+W1Lj7veXs4pj00IRhbuP5dWUaXzdWPLxxXOx1teH0XIFu2lm1FePv3rmeE13aBumXPb6xfuDbGxtnkZUksoD8cVd9JGWEWC+aL0imb7V43SGRkZe9+YmvfIWtrqI2pE2xvb3P40FF3DgxHjh7dd018O3gweCCkx7EN4MvzvAIGvnUx1C7B0OYpr+M9BoNBtXh+c1WDjOPqN+u+XWvZQkDTxUz85o0i6TT9tRbM+5YS1d83kKR9gMuMU2spjh8/TiQjbl69xcsvvcKhQ4cYDAdcu3EdtjQrq0MOjTbo9wYURcnx48cRTjaNomYcyn6xGsvAhnAAoSgKtra2+eijK04oi0iTxFV3zIiimMFgyGAwIMsWztQ1sUHq3v2mekDzmV1gg9bl1Xp/PJlo3xauS5fZ0Y/NX3swAOQJvb/fMgSBjdnQ2qZr7A9zTD6DZODvaojfwmui9gjlpgIYFqAYpNdTCcPnnrJBVH/pU38JgH/2zPv8jX/6MrNFWWlHjTG8dGmbX/hbf8Df/LOP8R//+A/zw2d+GICff/oUv/GND+pnewuDRRfuX+dzbQLO1UYi4bCN1c6FgmIQyl9Nq/a+qh5YjVe4edvHedc7UcdoOPNylmX00xKJrAq6he/Qn4c0TVhdXWU0GnHj1o6teox3v1Q0yemdW8jYwvaHAc3N83dwd6j/0K2t9Wr8JiVRwICzLHN1j6BUJVYYkphGcoTuZ9h9ZWPuVlZsvvVQyFdKETkBvyy84GmTbLT7DhmnMZr19XVu3rzJsWPHOtbVuquUZc6JE8c4deoEb77+AUQ17W+AjWCv/mFjdfwYq3+da4jWtliejK2A7Iu5+loUVoEjHH+yz46jiEhKlNZ7XDyVMpYGGUufFos5Kyt9jh45ws5kl6IskUYTJRF92SeOIiaTMb0k5XOf+yxf+MIX+dKXvsTJkyc5duwY62ublIXmX/zz3+Lah7esBRDJTOcQ7bCyssLGxga3b99mOBxw7NhxVtZGxH1NkqZsbKwTRZLhYMjOZIuNI+vcurFNonUVg2FdnXLnHmczwNVuxaYCGhhbRAwDytXaiuOUOI7IM0khIE9TSqVQqiTPF8SJRMgSbTJKrSx/coU9y9IGKCPtnhLKpr6N4xEMYq5uXScvMqQS0EsYHd7gp//UL3DvhYf48m/9r9x66x3E7i5xvsDoHKM11r5R7xvvBmwaQMNZBoRPLFO7GXqFqbV4eHWUt2jUlg9RBaLXBFhK6YC0Vc6ETLRNH8M9c1C60xaQl9E8/968VVIE8ltbUdIFFCqvFdndfwgkQkVzqMhtC9FtYOK/89eEY/DfhxaW8NkHaVZ5vDfYukuw3691KdfD8XTRo9DjpyzLKk65fe+y99clg0VRVFuDi5JY2p0tXCbYtNdHINC6RMSCtNejLAqbkQ2I49oaJoTAuDpyPr7YaEOhrAum4WCxcgcGGmVZopSq/PbiOGY2m7GysoKQET7bkQ1MiaqXb3Psa0eU6pgOY3zhWlEVAlwsFvR6PXeAayTrhXFjVXNWI1DpWU1F1LwA6dG5T0tmjKkYbpjqDWxRlyRJmClXiRX/4r1GWHjvW/dyFCePnQYleP7732d75zZPPfUUyhQV8pvuzinGBVGccmjjMEkyJE76IAQyqg9dOK87akyx62iwfuGlKjAI3nzrXcazOcbl7YuihCLLGO9OkJH1ee/3B8xmC2aTBUZ7AlEiibwUaZ9g9gr2Xeh+33HuQxCXaWq6tLr1PtnbTxtY7iHG2AwMPqjbOAHZV702GLSo3SGEtP6Mm5ubCLVAx4NqWYJR4jVSASqr168aSyCkIFjtx/z4wxb1785z/tr/7wf8r89+VHfZUK0JZpnmv/wHL/C1V27w//nzj7M2SPmJh4+wOogYzy1AtHxc19Vfu9bc+B79WrUX0T1b1CHkjRv930JU8zTCgVNtXO0ZP1eDMaKy1oEgihNEFFFkOf0kJRb2zCuj7V61cqs9C0phlEICSSJIU0kkYvJ5wWiQgsmJXdYwaQ+2q1FTj7iLuHs60kX0w+/abgchI/T0zsem+d/vdBaW/d4F3kNmHt67TDO2jHl5muv/tgKQRJgIoySq0BilEMbGvJSlwqShbF6j0rYwUGsuNb04oh9DbASxjvFRDHESI6Stbm2cW5A/K1VKzxYjlyLi+PHjXLt2jRMnTlTKLA9CjAFkjFKGQV9y34V7eeuNKygDIqrrqwi3N/fqZfe+92XvLbyz2l/aYFyWeiOMTa+sTFUNG2/dNKXjdQKhLD9ElSA1aZJw9z33c+mDD9jZ2UWVtnqzNmVlvTPGsL2jKcs+z7+0w/l7znPj2g0OqcOsrKyQJin0EkoRkRc5O+Mtfv5zP8sXfv/LvPna29y6uo1B8f77H2AUmBK0EcgopjSQLayV4oEH7qcoM558+gnuOn+WtJcwX4zRWnHi5EnHOw2nzpzg3bfe48p715wQpyjLgrLMKUtlz6xLNW2cmximdsEVAhsbIQSFLsjmc0bDIadOnWI8njDeiVFKM50tEMZQLGb0e2sYg83NH9BqS9Ajm93QgVejFSQx/UHKytoQIbBZt6TNttjr90jThAufuJ+NzT/L8898h1e/9SzZR9dIZlOisiDXJbkw5CjiJEGUmkhhMwolXrFiN4as9oykDu622ScRIJxw58hhVam5ZhECIeLqXFsZxFp+ZLAfQ3rkvqiUQXY4Xu7xv7ttinFKrnqf+/7atDFU5rX5umm4dvsH1a66bb5bCft+dVruS1U2q5Yb5jJhvP25i06H14TgI+w3pKFdHir+b62bZQbCuI0QILX78evj16QNVEIQBE13/L3WoOaz/fzadL5LmVStgXtXQljZp9TanstFToygwBAlEXGaIJREFaWl3ZHNUCdEbGUBlzlOyogksRkf53qBlHa/FEVGnETISFLMi9ql9A7tY8VohJMdDAZMp1O7gFgNjv3NvyiX756wAJ/97M9viNzSNOX27dsMBgM2NjYqd4vwBdsKwhDHEVqLRkCbDF6CEFaolEJWSDvsywdx+owZ1Qt0zDn0PdZOYyyMwGjD5vohVoZrbN2+zXPPPku/3+PU6RNM51OSOAZho/1VWRIhOXP2PFGUEkWx3QRaI+LlWbG6iIL9Aaf50GhjtV8GyauvvWXTDRtDJCRRHKNmM6bTObPZnEcefYRr124wny+4fv2W9TdWCksoIzx1MtSm7/CgLG13ABzdtxzsnlCQuyOSX9I0zbXUStHv2wKRWb6o0lP6lmUZStssDAINQlZElgq116DAujB5wCEcwQ+IsJXhOXVoQBpHfO+d2/zlv/99Prg5w2u/jLO0hBEdnjP9zrMf8fzFLX79P3uap+89xInNIbvzOpVc49lAIzq8+kdUz6pb87oaZtbP9tc53SR4sOK7kI27bO0AnMBBTfyVc6kwSpNnGWnas5/9re4/qxXUxHHEaNhnZWXglHx2lZIkosghEgJcUTTRen++dTLBFsBdBni7Wpj8og2E/11bV8absLUZ7jLGHF7fuEdYTWwkY4SRqEKRLzJLq41AlSXGRDRNm92aRfCKG02axhzZXINSYRRWiSM8WKpdhSxtcYJYa919/8YYjh07xttvv70n6FFIg1ESo6EsLM16/LFH+f3f+5at4xTZjSCE00XLAMR0rNu+TbQ/OsHEuIxFLp4B5eK+pLBABzBS0OsljFYGnDp1it3xjA8vX0NKweb6CBlFCGndWEGwOx5T5AWRS0+qhA067qV9zt11D9duXued9z5Ea82hzU3uvvtubm9tsVjMefzxhxkMByg0W7u7/NRP/zTfjr/L6y+/ZXlCaatgWGFcI6ViNFrBaEVZFBw5cohSLfjoygecO3/SxSIIbt/e5tjxEyCse9BgGHHf/ffz8vNvcuXKVSJpLQpRkoJUKF2itastZQxloTDKFyyVJFHMvffew5UrlxlPtsiLOYvbY3YnW0gZWetXJBGRzXJTFgVlXiA1oIwDyspuIW2w6MmRp0ggoog4ilhfX+XE0aMIbLKTKI7su8K+syJSrJ85yqf/5M/z0FOf4Jl/9W+5+uprqJ0x8XyBKnMSp/g0AoidHEBZkVYDKGN3RCRkJQuIyO5Ng6fH1srrgVZ4hmCv/70QAlXxmL3CtjFOGdboy8s4oWIg2O/spU/LaF6Xhr1xXWPMzeva3gb70ao2HV5GB0KBPfw+fEYXHfF9ehodrrN3j/cJDtrP6hp/+Dmk/XvoK3vnEf7b5hf++y5AEY67K6YmnGf4t3CbzThgD/ZvLbD7uCgRxirMSq3RZWGteaq07vXKyr9ZllEUBWma2uxSKyusrW+4MImyGtfu7i5nTt8Fwrp+Zi773Z3ax4rRCBdEa12lqvWfwwVoC6zhooW/e/eljY0Ner0eeZ4znU4RQlT9t12ewk3ShbDb4+g6aFV8hjFVNXP/W3gdaOsrKiSl1pw+fRpjDO9evMgHly9z9z13EycJMo/QxpnGsZskSRLOnDlj10BKZOQ1E2bP+O7crAlWAqVSaA3Xr13n8uXLNuAvSuj3exhjg3viOGYxn7O1tc2x48f45je/DcbWAlHKa+aD3peslf8tfP/7jrL17g/S2mt/IMGg477gF/v/wTo3sqG1zNRgKycLAZFaoHobAcho9+2BhHDaTsv9WquJP/BvXJnwE/+PL3L5xoxSG4QJgraqHgNmIWqHrQ9uzfnlv/MNTh8ecOnGrLI8eFHKmOXPrv8K/m4AieZ83ELW9zsBohqhaAU1+suE7xuM47peyPS+vMopHQxecK+zuWCsFsW/h/6gT7/Xr95NkiakScJC2Jo0QjrLFKJTe12tQgdjPQhQCPd4m8kcZF92nZW9NIWln5eNKWSQXYw6fH5FHwncixxdmEwnTrsWV/WG/FkxaIyR+ygRrHue1ILjx4+xM53TH42qMUgp6aU9m+JUKRfoWruSLGuDwcAKVa0sXn6/GWNTMRZlyT33nmdjY5UbN28DLsuTlA1N7H7re6fMSe1mBV6N8jUFpLQuBElMr9+nUAoloD/qc9d9d3H2/DnyUpNurvPR+5dYFCWnjhzj6rUb3L69hdX8S6IowRhQxjvbaCbTjPff/xCFYeze0+7OjBs3tm2a6EiyyDN+4jM/TiQM/VRQlIaHHn2UH7zwGroASUypCmQEaS/m7OlTHNo8xNWrVymLjBPHjtHrRXzhi5/n1KkTHD9xnEyXnLnrPCU2zTvGKkHG4ylZVjKd2KrevV6P1dUVVlZW6Y36qAiMtoUgYyHsOZ3N2L69zXQ8Ie5F/Ik//Yusrazy1ptvUBQ5K2tDxuMddrZ3mOyM+fzvfR6EJMsLekVeyRLC73FPV3QV9YYkwhirmNjYXGfzyBFXRFhRakWpNZGyADHtReRRiexFmM0Rf/w/+xVe+Pq3+P6X/wB9+RbRfAF5htEKZaCIQRlFpJXbtdbBVkgJwoIyqUJXPdGwCC6jEV08v5KNHFDuVqx5q8jefdpFV5YJ8+E49uOzS8+Dsbyu7dYjhFdnNZ/RRWu7ZML22A40ln2aV0j71rbatF3AvIu2v7ctu3TJRR9nXO09sazvg8wLltQhaXgk1NdrrSizjMViQbq6Qp5n3L6+RZ7nFIuMbJGRuiyPeZ67OAwLCQ4ftpZUH48dGhmm0wlRlNPrWavhQdqBgYZHsLWwZs1B2hhiIRqCfxvBdaFSf7//zcd6JEnCbDZjOp1WDNNPsixt6j0PEpIkaZmfmm4Q7SxV7ReulE2v1zU+P0frDmafMRwOWF9fZ7GY8+1vfxshBA88+ADj6YTaDcYWSpFCcPTIUXq9tEoxK6UkknX8Sdt0tl/zbmc21a4V5J599jmm05lF69iA+MVizny+cOAJnvnaMwgpGQwGJInN4CGdG0qtKrFjr8yGrXVqjsOtVafQuj9IaAt/HxdQhPfe6dpKG9XSFNTWg0Bj4Q4aCKIrzyPu+1xlsm9M0xNVo6saFnh7dSvfrNcuIAyXbszxlXmtT7y7pjKHu0sD6GEwoEEJeP/GtB5vCJJE69nVEPwfNRrYCzLC8YZ/16DC/1LNybsxCOHL6zowItxUnTZv4xxm6/sgcO4ltt5Lr+eLshHcC1rp6hyORiNGKyNAsLa2xqA/cFXup3501NbTgwXpha0LgCz7DE0f2nYf++3Drv3dpok+UUV3UPNeoSGcaxtchM+sPstagMFpseazuXVNSWJn9vbuKfZkuI4afVfPcu/OGOj3h7x3+QqHjhyphHxjbIHWxXzuaDtV3zaWqHv8URTR6/WYTCasrq76J2OMworhNuNflmWsr69x5swxrt+4DqQ22N0VRvWFtbrW5g/TvGuFckJnFMdESYIRBhlFyCgCpWzFeqE5dOwwpdSYFM4/cBf9QcLldy6yKEuiNKUoFWi3b7UNcAaDkdYSNJvOWSwyV77a8hCtNONyipCSOIZrV29w49pNjhyzxV+V0fz+5z/PfDYl0alVlsQxhpKz505z/PAmcRQzHKRMJhkrg4Q4OkSR5Vx8620efOBByiji6tWrnDt71laEFoIPL13in/7j3+D6hzdtNWSsm/HO9haDwYD1I4c4fv4MRw4dA2FQecZkd5vecJWTZ4+TL3LGu2O+8vWvsbYy4pd/6Ze469x5EBm7k9uMdybMpnNeeuUlrly+AhKUKh2N8e/d7Ssd0ElAu8zM/X6Po0ePsjJaIUoSQKC0tv7mLvMZOiFJBSKRlGi28hk/9os/z5n7L/Ddf/slLr74MuXNLeI8JwJKZa19ERqhrfuZQGLQ4GuReNnCA38Al1AmDFVo04e2kFl5EFDHEDbOh/DB5938OJRZ2vu+DSZCeuTH3+5vWf9+jl0019gL8DygPa72XMPv91gwg3kso5/tcYaAzX/vwUP4n+83zMznvwuVkF3u2m1lejh3w95g8a4+lq2BX4f2nMLv261SJIXPXSKLFWVpZZs8YzKdcPPWLVRRYEpLn7OiJE1TkiSprBnG2AyF29vbDIfD6hl+fG++9SZlYdg8tEmapp1jbLePFQzu3Y7CB0vRXNSuxW5npQrRrF98j6S8K1OlDe3YAGG2C1/8zmadMhhTVgCkaw5+I/oX77+PY+s/6QvA+esUml7aIyLm5PGTGANXrlzljTffYOPwJkmvx6LMsdmInIArJcJo7r7n7iqbjhUomoewy+fwTs0YwWKRM5vOeeONtzDaMv0adUPhKrcLKZAmIk6SCmTYegQCjKgCv6ymQqBNd2GYsC2Lm6jmARVR6lr/PcJQ6zu/Ll1BYgddp/bomn0YV8wmQinLzCJJDTSigCD7CTlB3GarstnSTGAvED7mwDEMYyoWaa0eIkiNCYGnigB09X3YZ329vzgYk/tNVveEgChYnwpvmNYX7jpjXFYi0/itmrcxiMp9yj7TGBPAtHo8FvM4wXZ4CKXtuue5c6PRtiBideakREaRZeCBMJ+mKb1eDykFu7u7TKdTVlZWuH1rgVJ15jtDbRnq2o9t5tP+/kD7qCXoHwQcLwM/Xc9bxuy7BJT9+mnf22Bixrqq+Ri2RbagKEv6su9cp6y7C0JU+yfso/E8UYO8k6dO8uIrr1bg3TO+NEmYjMeosqw3pVi+dgZLc44dO8atW7dYXV2lAqPB3jYIm+lKGh77xEO88OIrNa0Swo17r9a0vX53cldr/1ZdIyVxmlqfZremVoNuCxwarWxAcylJ+n2kgTOnT7DeH7CztYN0aUyFsadE65LInx7twJgPnHcuSULa/5DWJVmYCCkjLr99kSMba8RpwreeeYYbly/RIwadQySI4wgRS+azXSap4P5776VYzBjv3CKWEbGUjHp9elHKzavX2Tx1nGtXr3D00CGS0QrZfMG/+Cf/lMsX3yMyCV6/kBcZCCgXUxaLMbu7t5ifPcMDDz3AYH3Eoc1Vbm3dZGd3h8Obhzh0dMO+O6X5wle/QiQl58+d5PHHHmA4GBDLmEcffYRLF9+3vDfPLEXUvm4FVSIWSzbqOLAoEoxW+mxsrNEfDllZWcMIG6Po3wtFSVyCVCCUZnNtlddefY31lQ3OPfQAh+86zQ++/h1+8KVnGL/3IXp3Rqw1RucILZDC8sWyUFZB6PeQz3DpLHzKxzbSAuYd57KbloR0OZAR3P96L4i2IB5evwwg7Pd7V1s29prTNGUYISwo1qJ5ZkKFrZel2uMIAUB7Tvspc8Iz7ltoaWnLEW06G8o4oSKpy1oTPnMPDTOmem37rXVbvmn3HT7/Tu+xkXTBgw1wLnjBWIQF6HluXaJirdlYX6dQpZVxjZU04iSl1+8TxzGDwaB6Tz4wvW3xSZKELCuYLybIHRqeRvu1j2XR8MK/1jbi3JpzI9K0XwGFMMi5rQ30Gy+0FviFCZFmmIHKL2gIcNop0LTWLBYLhLAAoiiKanODNc23xxIGYnvXrK4YhTRKLdIjZn1jA60V3/ve95hOpjz+xONMZ1PKsiBKYusnJyUykgzSHpuudkbdREhP9iVKe1C1kE4DKSlLzeXLHzIZT5CRrVI+Gg0pioLJZGJ9VR0A00oxGAycZsT6wuKFUmMqVO6JWa2h2DsmP+bWL3s+HwQzhf11/d2+br8+On+zF9xhDFQMwoPaGN3Q7vr/9QwQU1YpQ+vfq85wSkoneDs/S2M1gnGcVDELBuOyzXgLh/YIzX0OiHsIGISrI+v6hFrI6lof4YRDDw8qKOECHar3aaXR1vrJPc8OKGsFi3z2Kt9NWVpNfRInGGNTLUfSr6FnLq0X4X5bGa2wurpGFEVkeUae56RJssflrft9du+pO13v237Mbdk9H6e1mYtvISHvGs8yINX+3DU2W9PB0Ov16PWsayVO2K1cDLysTr1m4SNrRond2xKOHjlUx+CYWrkUu5oLPnmIza5Tiyl7xk0NNF577TXuueeeOvC+wtl23xVFjtIFDz10P2kak2d2n+ngvbUVWKHmb9laLmue1xkDURwhIhvzF4kIZQyltgHhQkMsIjZGQ7Zu32ZnvMtwtEI/tfFZRTZlPt4mNqVDVtAT2sYBGGu5Mc6t0pIfG0RvHNAwQqCFoJQSmUdcfeddLo36FEXGS9/+Nnpe2IB/AVKm/OKf+NOMZxO+9tWvMLl9g62rV0BETCdjdrZus7W9zXw2o8xzXnz+eX7y+B/FlDmTrVusJjHPfPmLvPPqKy7oPXLvye0BDKWQ5JOIfOcWxfYtPnr3LZ781Ce576EHWN/cIC8zrl2/QilLNtcPIYygyAveeuMtvvzF34c848TxEzz04AMM0x4CjTTeIuAE6wqcaoc0vcDt6KMwbGyss76+xnA0IooTxpMpo9VVjLAxFEWpmUuNKkoSFImWnD19htdefZ0nnnqKdNTnR37uJ7nv/vv5/le+wevPvsjs1q4NFM92MVohtEbGGlWWCKOJI1lZCYUQKFwsaCTRSmHrbCw/x23QK4So3cRoKUhafXS5zfh+wuv2yA7BmQjdisLf2lrrcDz+2T6ZSphgo5IZgjFC7bLkz+R+4Kv9Xfhc/7eXG/14Q5eoZck8/PVefgxjH7pARNutyl/bBhHVZ+fG274unEf4jK55dvW9HxjpAmO1vBCsq/u2KCyw6BtI0pRTp05Zd1PtEpzIuMp0NRjYWjtKKdI0rdbR8w0/ho2Ndfp9mzCnLJv7aVk7MNCoKspqXaW48+ltoyipXijsjewPF6a9oG0kF26m8PswDWy4ycO6GHFsM1l4sOE3pw8E8gHmfgHD57QPIFjmIjEUecHa5ro1Hd/a4dlnn2U4HHL8+HG2d7YqwQ80ErvBz5w/izGGOE6qoPMo2pv+t0v71sUMvZlWacvA33jjTTwDtm5kKXleMB6PKUuFlBG9tEcqLQrNs5KyDAQap6XCeJjRfPYfTqCqdB6N93SnFhKEZebCpU9sHdRl2ojl91u3hbIs0UqxonfZ1gVCptU8vObCa0+rgy3qNfQtkNcs8KAW78uyrO0JLlq8toI0hfyqx2pO9bOt4jMQqsPrqcckRE0I94h3IsAOHgCHfTngVF+/1w/Uj68OEw/WQTathCKpFQVdW8v/1u/3WFkZkaY9jDa2JsNoRBIntrBY46bWehkPffa+l87mmWQD/4d7OBxos69lPYv2h1DTFKyUH14FdkPG6m5rnsX2E+txhvSs2veCKofBcDRifTRCSpybpW115htcXiVb1V0LC4DrZ7snOrBnjGE0WkEb49xd6vNn+UFUKW6WtbbAtba2xnw+rz7vObPuY55nnDp9gqNHj/DR5evEUYwWBR4RCyGqWI82DbC8JvyOeo+IcE39ufD3OF4Q2TNgUzzaxBGRFERAIgRb128ghebU5ibXrl5jUmpKDfPZjHw+JRGayWTsXrxGm8JmrzIarUs3Z3vCpZCVyy7CgbgoJici293m+ckWN29eZzaeEIuYotCYnuQzP/2zPPX0o/RGQ+4+f5rf/se/wdUrV0DY4M0b16/x4UcfsX37Nld6PXrDPrevX+PU0SOMt27TF4Lnv/sdyvncZnnCpRn3bqcO9CitKY1mdvsWvbVVnhmPuX7jBj/yEz/B4cNH2DyyzrWrV9na2eL0qTP0S8Mjjz3KzctXePX7L3L54kd8/7vfY2U4gLIkShLroRDHCGOIhEuTbYxTlHj7rbXaR5Hk0KFDljYkKUJInn/hRZ588inSfg+ETS8+1SW50iQC+kT0+n1Kbbh+9Ronj21AHHP07jN85tSf5uSjD/PM732FD9++SEHOyePHOH38CG+89ANMkREZhTSCSEVI4y3Rri6KtC5WEi/oOnyktdMfdbt6CoHVLgsqyyIBHVAYIhlZAGasFbcpYJvges/Xl7sPSuEVU12aqZpXQX32PcDwY/C/NUAKHe48gQJsP2VJ3WdtPTfBWaz5ejMWuL6/YyodwMG7SO2ZX0vx3aUE6pLL2rJbuy2TO9r3tMfRvn8ZAGk8t6UYElh5WOTW5XQN675cGkNZFOjcev6USrO1tUWv1+Oee+5prIF/n96y4Xl5HNWKbyn/A1g0/EvzmqpezxZbsu7adRVwpULwUG/OtltOePjaWqdwMUPXKWOo4jmKosTHLsSxzaDkgYUXWr3px2vYPGIDWF1dtS/DQCSjivMbbX2NExmjtM0Bvrl+CK0EL7/8Krdu3uSRRx5CUUBUidV2rlphhOTc2bsB64ojIxDSBXNLm2XDyqwhQWgGaO/RygoQUjKflkwnBe9e/BCNRKmC0coKUsZoXZDnCkyE0ZI47iGi2AmxlmAL4c1tToPhiYsxCINN4iuwWqH2GFyTQjQT1VDvc9OYxd62DMjsJ5R8HNDjx6wdgd/bh52rFBHSWcDQBgqNLmz65pDYiUoK9YK2CSR0Ecy3/kv4e4UI+qIllFMBmIY8X3VQC0A+qgRqIFCFjHsmVZ0fN0oRjJ8On9eWdqS5wqbq389KVCAkFORxmY0cYzBeXjOYUhFLgTTGupRENgVlaaxPu3UXEdU6KqA0hjiNGa0OiGKBMQpdGtZW1lxufjtP78RgjLYMH1NV+PXM0tKqgMa0sFDlAS7cufPCfIM5xNVsTbUajkZQa81Cn2AhjHspNYjwuyfy62zc9/78GT+iYCe5veOFlvq1mZoe4FxqXKdSGoTwsQ0glGQwGHLu7GnGOzvW9QXD2soIacCUBqNcLICx9yujiUyEwGXiqYChcXvazm80GjFMe6iiQCiF1AppIpIoJpYxeVagtEK5/LOhANPYh9qmivWKpCzLSJLErY/Tpktb9M3oCFUK1lZHPPTgA3x46Tpop6CQC2wq3wQhwWUncBVvcefM1ayoHm0a58AIW9fGK3WgQGB5XT9NMMJaHnRh3f20MUgMKi9RYsD4+lWuXbvCg/dfYHbzOkVeoMFmmCpyRDmmyG67bFDO0ugEVhmcXY0rA+gyK2FAGAmmBBFTFhnXP9xCqZI0sZaMUsL5R+7j6Z/8UZRQ5MWCRx57mLv/2v+df/kvfotnv/UdolRw6fJFrnx0haKYsbNzk5Fa4Uuf/yJlXtBPEpJI8tEHl0EXTqhVRHFksyuZoG6CEGhsGtrpeExRKt556VXy8Zw/8rM/zeETR7j71L1khzM+eP8Sx4+dIO1FbK6uIZRClwWFKphPxxijrLuXlJTaurLGQrianjaFbKWec8sURSnrG4fp9UcIIen1Brzyg9foJys88ujDJGlsrU3Su0lLshJIDWfvupvXXn+VI4efxuiMCEPSi3nyxx7j3ofO89L3X+SbX/4GH7z/ATHHefCP/jGEUaSpQC0WZOOZi90pmU4nDAYDRitDrrx9kfzmtqWVBoQ2COcWZ1ziEL/7rILUadg1RDjB2NE1T6cS6U5ekHre04DIU3cjUC4WLnICSSlUzZEs4iGWEUZGVhmrrDxh3H4zDuD42lLCK1+ldQ8TxsZJ+ShHpHSlKi19ioSP7fTAsCJkhFxQO5CowYFIaxG3wFpUayWEBbL2GFgFsj2n1gWdijY6q5ejhZ72hcJ5KHd2pTtvK8iXBanvtYLYGmtCWnmqAnE02Uj7/pAXt60xywBZl+IkbNLH/jrlmZAW9MYyglkOmU128Opbb7KztUNkYHN1g14SM55OWFtfJz++sGmehc1IWKiSDEj7fSeH2PcZIdGldjWCDgYhPlbWqaIoiOO4AhhVrISy/qaeWQiB0xxJfHYZr2Xq0ppbzf/eobTNWDXy80KzqPLcG7ezw82TODO+MdZ1IARLi8Vi78t1ggzCCtNWk2MYDIakSY/FLOM73/oOcRRxzz13szvedRtFuGdZJr++us7a6gZKeS2Vy2lsAhcEr+sOBAkPzPz4w82kndtUUSg+/Oga4/GMsrQHOklTjBHs7o4RCJIkxaax1WhlwYUTFxsuZJ2bmkCI7QAZwv8XSj/V+Pd0t7SFfR7U8nHQfrUTxNjnYApHAL3gJ4Aiz0nipHEf1OvhBfxKKKX+Bw++PEBrFbLxsMQ4kGJpQksj0UhR6xFICGNErekJZTVAaO0EYDdiJ8TW7zEESG68InxxdswVMzQVyawYRjUPIV1EpgOknqUJW6hQaZvNKJZWQ1UWOWVa1vI8Xkh2NMIxFG0MaeoKwvVT5vMZs9mMQ5tHAE0USxtX44JDjdENi03wRqt3ZIxx2kYvTDoa4emEiCvQXRXQql6aB6vebctU70gr4bJ0RKRp4hQY9pxbATkUret37FMBW2Bvgm3Uhnq1ssZogRBR3Udrvp7ZSqymHSKkgEgYnnjsYaSUTMc7aKU4tHGItZU1dna2beyZjLFV0XS1rSydCumR/dfg6hEZWwV8bW2FxXSG3lwjkjaGSQpBGqeW9gQgpdrHba0g9l1KKdnc3GRra4ujR4+6Oflz4lJ8GkmelyitefihB/jql76J0YZY2lg6Kw1HCOODiqnnZYyNk3DgQhunpdfeLUShcEBD15b7siwQkaTUs4rXaKUd0LOPkALK3FDMZ+zevs1LLzzP6ZOnkLETDiXs7G6zmE1JYmwcQWHrIBntXYHqvSccABFaYdCu8J3dg6U0oA1l6TLBIDGRRPZjHnr8McqiJJvNMYni2RdfYuv2bQ4fPcxoZYjRhg8/uMStW7fQZcFTTzzOseMnePn1t9i6eQvV63Ps6GErPFlkRqlUFUti/LqZmo5J4YrWlYqd29vE8jJf+Def5+FPPMpwMGA6mXLt6lX+4MMvs7u7y62PPqIsclRZWP6IcudYI0TsSJ6NF6xojnT0ptpGlsdtbGxWPKcsS+azjO9+51nOnD7N0aOHSKS0+gxlAaeRYLStQJ/2ely89AGnTp0kEQVGlxgdMVxJ+fRP/RhPPvEEH16+ypuvv8PO9g79UZ/Ll9+jLHIG/R6j0Ro/9qkf4tSpU2T5gvHuDrevXWfr6nXKrEAXBbpQmLygLAryvHB1SJRz07UuLbPZnKjU9KQV5P01XnEbG43Qdj8YpSmVreaOadZWMCqy4FUb9/5qhRlauz1r65pJ4+CCF7A9BTcG4epsCSOIXVV241I8K1w1MePoqWcfQmOkG6cLmhdCumQpTmnhaZww1iXQmEqZ6WlL6Wm5tMColj+cAseBGlsI1LkXBjyyq4UyZPh3W/G2nzzSVo5X9EQ490YhKvZAQyXVdMlqj6tpmWrJVB3Pbrt+Na3CotoTyNrlOUkSiiJnsrtLtDbCGGvpkKUhWyyQokeSxJRlwSLPGPUStFGMd3e58eE164afxMRJQm/Qd2fTMBwOOXL4sJWXDtA+VjC499sK61CE5qkwQ5T9HAVasb2LGAYDhQvfNiuF7k52bZsvPtxAHmDc6aVJKW3aL1fhVivV+K1Cmgg2NjaRQnL50nu8++47nDx5gl4/JVUxhSpIkoRhvwcGJpMp5++6h7K0oMwDKG9JOKh2vmuzl6VNFfrOO+9QltaNpNdLSZKU8XjCYpG5dbc1O4SwJm7/t38vXf3vWStqWVYGghlgtdEHaO25Nk3GzXe87Lf9Wvvg+8/S+U4eFL54YpVnOelohBRWw96YC5b4VqtSaYAq8aAGAYEGJ4BtjtAGopsI7mtofvY+2/sdOzRMrdWun+BFzwD9VM8GUVdvNdX/OFBEBYzqvhyh9PfXm8GOUsqKGRhtrP3frU8UnFchqE3Wxid78EvYtGgqpUh7CaOVIf1en+2tbcqyYH1jjTgWLJyCwVurKv2bxRJ71s9nhnElOcIFrfeN8EzQdPArx9Q90BA1IEui2P6tFUIrpLfoWj1SpTkPltoJv9p103peeCFtcB8FlYlNta72XVl3TZ+OWDrgkaQxP/KpJ3jowQf47nefs4JdWfLgAw+6miYRG5trBDrKPc8OXSDcYmGM8EmROHLkCJc/usJx5eIYZFRZuqfTqXNZTatkCV3NK3aUUhw9epRr165x/PjxwIrdtHR6q/R9F+5mZaXPeHdBvx9RlMZGRJoC9AKjyypLoQWA7h3qAh8TEZ4hhKg0tF6YRikio4llQi+2Qqrdq7UrCcIWuBLCunUlsUQirLtUkZMGCi7/n3df8wCjrcixdMWumVFOQPbgP2KPkFkqxcraCh+99z6JEWxubvL1r32NWzdu8pnPfIbpeMJ8OmM4GHD79m2yxYLVlRV+7Vd/jTfefIt/+/kvMRoNOXXqJJtra1W9Ks8T2xXNvZIG5x4poxhbsNcw3p2S9Hf44u9+nmyxoMwtn1JFYelEldzFWyzq9xpH3eJI7f2ALSgWSeIkBilYuJS4cazJsgVXrlzlnXfeZW1tRK+fVnTaKzv9v2fOnOHVl17gyNGjGGOIkwitDb1+ijGG0eqIBx6+wP0P3k9RFBRFwXwxo8gzcvfMzc11ZCSggN5qj9XTRzgXP27pnLEitqikTgvSlFJoFca65sSlIVI2iUue5+RFQZEXlEWOKBQqz8kWCzuOsiTLMvIsoyjsv4vpjHyxQGhDmeVk8wypBbq0tVOM9hY4m/IUo6rq7WiD9LzTWAc1rTRCW/c14bIlaiAP3MBCraIWtqQljl94jw2MrRNicIlU3BXW4CstuPcWaSERkeWFGqA0VcigT2uOt9SKaE/wd5fiNJR3QpegZbJhyI+WyUdePmx74oSAod3vnVqXMr1TMdoBlsCuqzaGCGllblFbl6QQpIMeypSYImPQi5lPrMvrvMwpKegPBwzXV5hmM2QaMV8smI0nJDImHqxYt1opyecZQkj6K0Oifsqt8Q6bm5t3nB98zMrgPtagEs6dFjWMnwgXD+r0bF2WDN/aLygEDZUbjKlRrO/TVyr3fbSF6RBNVoGJwfOrDDYB4AlfuIwkWklWV9Yx2vDcd5/FaM0DD93PeDp2kfkRa2sjBv0Bea7IM8WZU+fI86JK/SWlLd/ezjLVXodaW05jrfx1WZaRLRa8//77lIW1lhw6dJi8KJnNZmTZAiF8zRF3cII1DQXztnC/pwVyUFWh1zNls/wALQOV+x1eP5725zuCoQ5Aaoe39769oMcLObWLSlmWVlhabKEHxwLhqBa9hVW/Vk/xa1yJY36h/NhFbW3z2rjG/wocgKHqxQS/N6M8sNW5CQRnEcZOODegSrCl8Tn4slqEejTu2cE7roFSfa+EysRvK3Qrd7s1f/t9LqUg6fXo9SLKUiGEaryj9jvxGmQhDWtrIw4dOsSlS5eYzxdsbm6wsjJkcnsLhM+kJPAWCFeovNEq0CkEqtLZ2UkIIaqq8X4vy8D3uWIexG4JHGHHWVIRSBMjXYVyXQqEjpEE/TjhXbp3bIyx2bWodV6RsMXFMK7AmmnXkfCZbQqiyLmlaldhFreWQhPHViBPewmHD21y73338tSTT9FPY777ne+ys3WD8e4Wjz/+BD/01BNc/vAyTzz5OGkvRnjwFGxBb+ERRuxZT2OEK9ynuPvus7z/wSVUaRAiqgBcmqbs7u7W6cvpZp7tdvToUd54441qP8iom8aUZcHR44c5fvIIuzvvkcR9JnlGvphTZhqtZmDq2D3hzoi18ihb2E82tYoGiIS1REl3VoXWKGMr9Alls7AYbSiVS6UrQEhDtigwcWwtFlHMgw/cz8rKkBde/AGZS9scBuKWZWnPsXO5qNbbn21dF6A1Fpti3TRwRQkDviAESZxw7OhRpDJ89N4lnvnSV5js7nLk0GHee+NtFou5TW9clkx2d1ksFvT7ff7e3/27vP3ORUoNptTsbG2zfeNGVZlbCrHHhdY3KSUyjomjFGQERDiYy/atLeZzm54e4wrJapz1yCsefDyRcCBFI+KAbAa8O4qiCgwKKYniiOHKCKW1TYNfKsrScPbsWS5duszrr7/GAw/eR5I6ayV1n3VVZkF/sMJ7713i7NkzyLK0ml1lBeVUJtadWgAR9JKU3sgCF7t3fAFiTUofgyE2BuWzUylHfwjUP8Y0eIr3zJBCOhfCWklb8cvSuQ2aeiZ+P2ldWlftUqPzAkqFygqyRYbWUOYFeZbb/xY25X2+WDCf7jLZHVPmhQMmc7L5AlWWqLLAlCWmVPb8lwr8flc+AYkFwBjrIhaRII1CYwF95GItDNZVVgtL66zXpQHteIiQlJ5/CKsUVdp7JNT1d4S07lWm4m9RQ0ZsKynbn32yHyHqQPa2laJL2K/eVGv/t60foWKmeq70rlxmzzUhqAn7aFs32vyozT/DJhCVHIsQVkTRBlUWLKZjUqEYxpL1tEceR2RZaSuAR5ITx45y7PhxIiGtxTe31cTT4YCkl1Yudj74/YGHH2Lz6GGe+cY3uHjp/c7xtNuBgUaojfEafx8gEv7eRnphlqkwNZdfeL9wYbGm2gWryaC8+5AxqvKN9i30dQvHED7bB31bDUjMysqKy2qTIpSqLCFVil0Da+trCBlz6+pNXn7xB6yujjh8eIOb27eJpGR9ZcTm2orNqa5zjh89wcpwjcV8Uj3Hb6pq/sGaNje1E+zcdyFy1dpqbD744LI1fWtbQCmKYorZgvF4jM+QUq8xePectqDfxfQbgnvzF6tN8u/D6887wEA7IKyhBTsAug/HsQyYLmvVYe7oY+mzqEFHURT00hS5dREGx3xP1OK4Bxn2055X578zBJW7A6nf4AQ7/4W7ROBcapw9wUv7AkB6eluBIhPe3ujOfekYONX6uds9oxNV59UM/bN90tzGs4N5ehuHt4R4Buizxayur5PPdinLgiOHN9EmZzabsrG5ThRHrK2t2diJ4LV4S2ipSrQqWVkdct+Fe3j55Ve4dWsLIeGppz7B733py0ij8XlwbLEzaSuGO6vDnj3pBKYKfEkbsumFIFDYGjLC+SV7hiMR9BwQcH1XK+CWyFjhVBf2nkQmKJUjpdXY2nkpd44hiu0ay2rjeHdSG8vls394ZU6v1yNJEkajlNU1a+Xp9ftsrK///1n7r2fbkvy+E/tk5jLbHHv9rVvmlusy3Q20AxogCcISEVRQHJAYgUYjhSImQhHS/yE96FFPipjQ04hSxMQEKVFDjUQOSQANoBsNtEV3eXvLXn/cNstkph5+mbly7bNvdRWDq+LWOWfvZXKl+eXv+zPfH7P5nKIoQi2Bi1K87OCQolQcPTzik08/5Yc/fZvXXnuNo4cP+OVf/gp/+I//C5597kleePEm1bTmbHEG+OApkznhPXgVrWZjmSq9rhNQunrtMqIj+VBrQc6pqirtFdY5YWxSY8rqkcEjKNqz2Yy+l5ASYcsahzlEWd73PdOZ57kXbvLGa2/jraVdLemaJTiFUVbyOiKsy7wi4s0IYV1EOSHrwuWEDEqBd3gv80PIRWwK2zDRk2+t/O4s3ln293a4euUStz/9lNViQT2bp7zA6NmT+hdJo06KtPeSG+gLl1iv5f1l34pVrzUeFQ1sheHxm0/x5DM30crw6s9foTYFajqnWa64/fHHTCYT+rajMIYmtPnk5ITv/+VfgjLU8z1WyyUFcPuTj1FOSEy8lzCMuLfmhbtMUco/XaB0IX2nCjyKrulSvLp0rHjdPAqvJfSmLEsJS1OyRqIsGohTBlrNOAe1EcW/qErKqqLtOnprabsO7xV1PaEsSz788ENOTk7Y2ZmiTDmac4OR0XPt+g1+/vOfcfHSFZQShVbrEA6mjHymAuNYsBZLzRQfxkb0YRXkpfYKTUZag5difypa8aNhStoQfcjWAFoHoCvgNcn6qcnk77D/Rm+cViGZ3PlQVd3iUfRKiXklUic7j7c2hAuKp8P1FuW9AI62w3lHu17Rrtb0bcv6bMny7Iyzk1O65ZrFyYLT42Ns29Ou13jrcH2Pax10ErLlrIAdHfLwPB2KXkhyehtkpoTCKe0plJOoCy9t1z4UaFY+yKFeQIbP5Dskg04OHkRGjIkgotzYZgzP94ltCvym/hF1uM1c43h9rsNK2sh2ALSpM+d6cf79o37fBEk+Ari41wVDWkwXXB0d45qG2il2yordi1fo9yxN19H4nqq1rO8+oC4ryqKgWDU0qyXUNfsHu3S2Z900tOuOy1ev8OLTT9M5+M2//Rv8u//478/127bjcwONKABy74JY1NTIW5AfsY+2eRryz+PvOQtUTmcW/16tVtT1BKXM6NpNirYc3OTt3wQ5RVHQdR1N01BXVaLFjYVLUIqDCxdxDn78wx9zdnLCL33tKyzXK5SG3dmOxIJWGmc93nqeunmTxemKelKMclbic42JyeCfT3nON9emaXjllYE/XujI2uRy7fs+KE1SwdTaPJxjOzDYevhMtsFg0/YBCG305Ta0/1nP+UUg51HXfp62R8Vh0KnPWyfizwjGVLCUNU0T5qEatHO26PRBL/OMZMlGn2XPj+cK0kg385nHYAAPm/2g0kfxeQk4jJ43JIen542u80PoFMP1iiAUI4d/7v5Ij8+8LEnhi1a2wUq/O99hNp3Qvv7vuHrpgGvXrnL79kd0nXj3rly5Eqime+GpH4VYKWxvWTdLrl69xGOP3eCxx27wzruv88GtW/zWb/9d3n7nXd548y1Z715jFcS4bks3ansuV8zmWsuQmlIubGQyYYow9kqBs61AMB2VPulgBfjChfh0kUWTySSElnqKUjGdzaiqiqoUprv5zozd+YyqKEPxzJKdnR12dnbCWi6Zz2YYXeKByWTKZDIJ7H5L6rqk62xglNPUdUXX9bSteC8XizNee+V1Hj68z61bt7h16xYP7p9SVRV/5+/8HX7/93+PF196jmvXDuhtx8OTU6ztgnyN8y3MHeexWAERTmaJ1gIySPlejgsXDtnb3ZWQjraHucjZqi7RxtA0TZA/w5jk+wAEyujs+/l8zmq1Yj6fh/l6frOW0KOel1/+Ev+//+Hf06yXTCcV7eoYI8EfuCw3YwN3EkPAPCFpV2lRqJUZagt5J0WtlFhevYfeBs+HGVhYvJewgliTpCwKLl28wGuv/Jyua6GRvI6Y4B73T/ChCF/BZDJhOp2m0OTFYpXWYtM0yZO/Xq9YL86EVCAYlK5dvsRTTz0FSvPpJ5/wyccfC7V0sKw7azk5Pgl5HhIWE0Gys46qrvDW0rcda73m5PiEaT2BYJ12G8pV3KdNSASNyrdRJR4jSb1awgcDeksx4w5JVq6qkr5vadsmMRqBRB2UhYCM+XzOcrkc5HcApGVdcXjhAl964QUuXLyIMqLgrZYnWNtT1zUnJ6c8fPCAy5cvUgWgMcyFTLk0BVU95c7d+xwc7It3NphcjC4gyAZTaBQGrUuUMnhskgdS4FDML9orjM9EpyCLADR8yuGLeVVpTmqSgFEMLE8K8Fpnhq6wl0QjSSSVCfPBaJPmVYuDCJzQ4h0sVDhPUQahJrqceGLBS55FWJ9GaXwI88KJh9NZS9+0dOuWdt2wOD5mebZktVhz9OAhp0cnLE5O6dZruqaladY0bYPrJQRMWY/v5X69a/HIOsM66C3a+RTOJf3ag3Z43+O9DnvfeN/ID2PO63kw6JS5rrppnB5kxFj5zw3Xm9flx6DjmeCtHH+3CYA2QcSmDp1/tmkkzg0wgjl1UhWUUqGmjGE2mVAUodj1/Yd0XoV5Ivk2BsfiZMXCewpTUAZSJK/AV4Y7d+9jCiO5QVpx5/4DvnfWsH/lOr/6W3+Hr7z4Ep/n+ELJ4JvUYslbYIaYudylJYM7oMptiCz+vWm5ioOdD65Y8A3GFKNQoEe5k/LByWlz82dVVcVqsUzUisYYicdcrajqCcYUtMuWH/7gBxSm4ObNm5y2J1R1ycHBPjvzOZ6OTlmqsuLqlWsslw2VL1IbvCdZSlVQ3HJv0KjNwbqWv4NSMlHatuOtt94Ri7CR8JS2bUN1cCkq5FxA+0iCqFjgPge4+IwjKdpBOY6VgDfbv3URbWrEW64bThyeOAalERBsXOHH94/2nq1vEOdaWI1ijRoEt1YqVFN3FM1DCZ+IseVKFqXPn5OBgjiu3nlsbwcHRGxLYrrJwEBsTQIz4WwfVYyxwh9fUzwJg2UrBPSM3i1ulgkYEpW0c0OR9fG2z9PjE1gWS68fIayyLDg4OODChQt88u7rqFvf5bFv/wrGaLquo3cd165e5cknnxjapGJuV+wtuf9iseTi4SUuXjzkW9/6Fvfvf8Kffuc7PP30s/zv/3f/W/7N//D/4Wd/83PaxrI4W9O0PR6N00oSvbN3csFybbKtGiRsoihKCqPRWpSb+XzOZDJBB+Vvd3eXuq6pqpKqLrlw4YDJpJYqqlXBzv6U2WyWQjdnM1EUvVM4Jxt3UZY4LwaStm1QOPCKpmlD0mefFOejh0fc+eQOVVXRNA1nZ6cSauI9Dx+c0HU9fW8l6XW1YrlcorWm6zynp2c4Jwmm1vYYo5nvzPnmN77NN775dV566XmuXb/AtetX8L7jbHFM23ZicfVelCo/rDMP4olwA9PfAEvjjPCUVcn1x65z794JbdsmmRwT5CPFrYzxeVa5BKTD4Zzj8uXL3Lt3TwAYfrhKDfNYKei7NTdvPsne3g5Hd+8yn805O74ridQBNPuwYWYzGu91ehWV3TtaAcFTVbUUYgvhLNoYVCoI69GmkNoWxHwkuc1qsZRCeGXN4myBMUUqfCWCJgAcH8JDUqic4oUXXuTpp2/yH/7jf0QXhv2DQ8qyZLFYpP3qo48+xBQG4wegMZ1OuXPnDj2Ojz/6hCYU52qd1J/RIXytrIQCVl5VkqnjGFgnMfAPHtzHeUvvoTRa6v6oILNCvpN2okiVVU1hJgLSMChtQJkAwpQUKQ0KcQzrEGAuYnWxOKMqCuljLSGBPrDETSZTrl27xu3bt1FKU1UVs/mM3b1dLl+7yrXr13nsscfY3dsVub1Y8eDBA2GhdJ71es3du3d55tmb1Gq21cgYZfETTz7J66+/zje++XVcJKBD4W3QSbQTljEUWrkAyoOip30IxQoyTAUcPnwS9hqVwEAc72xGovuB7ZGwb0dAor0iTuI4dmm9+FgHJ+5pgcxDKZwO+pEP0RzRiBQMkS4k4HulQoKbtLEI+0k0vsnvGlVqob2mpJhVVB6mKC5wA2fAaR+SycF3PX3bYntLt3Y0qx7btnSrhuXZgrPjExanZ5yePmCxOKVftywfHtMt13LtusM3La63dF0D9IDFWsmvctYnql2tdWL0IhqMMoNGlD/OO5SRsHtFBB4yP8VwNdYbVLDmJc/RlhD8GIYXDcpFLOSYxvh8WNWmsXfT6L4JKDYBSf7dcB3DHInXWfGqVyqMvS5Csc4CpQrxQntPH4wBCiQvxwcd2XtU06O0w/sWr4KcMIaPX3mN5VmD/7VfZVL+Z64M3vf9iMUpd/sYJbGr1rlED6q8Bje2SMUjTyaPnZWDhvzvvLPFJc8ofGuENmNRu4DYoq1VFqAsLK3FhWvxEu+sFGUl4GI+2wmFCCWB7WD/gNrD37z+Orc++pCbTz2JrgyF1Vw62Of6hQNMqVi3Pdprdvf26awLRhyp4gpKYm5NJLc8D7LGR1g0wVrskXCoru84Pl7y8OGKoqqYzjWmgtYrmqYDbyjLEtvLwrLW4+x5K87nOkJfEq4d+GiSGjdqexqj9IYqDXuw3xDfJntI1geOgdknCE0tGs9ghY+q+7BRKK8ZkphjDKsPYUiGGPoj8nsAo8IuEyq/960kDHtPbzuMgd3+PmZvzuWLlzGF0EtqRaJ+c87y7nvvS9yn1pSlxLr3vbiBI2LwTqzhXimhOQybmMOnojlRb896Vf6fv7snnadBFOr4DPzAbyVShgRbwh6lctAWz0ldLZuMVgGcBIYmbYS7XQdFyhQFpRGFQqEoykIUytIwqWtWqxUfvfrXdH/93+LPjrlwcMDbb7/JarHm+Rde4Ktffo6LF+dBQ9JEWmqjIxWxKKPrlaXbtTz7/A0Wy2MeHn+LP/+z7/Iv/sX/g3/8X/5D/lf/6z9EtX/AyYMj3njjTV57921O1iscJWU5YT6fU1Ulk3qSQlz2dydMpxOKsqAqK6qqZD7fwRhDXWqqciBtsMH17p2n7SzrZp3GES95UqvVmrbrWJ4Ic91qtUxEDMpp1kvLydkpbSceg7ZrOVssWC9WGC99uo4x021DURS0bU/btGkzg5inYChD+KX3DmMKyrKQ5HALe/Mply8fUtU1u7u7zOczLl++LP8u7XN44YDrN66xu7vDcrlmsViwbjpsCv1xEHK6QHIDrBZa1d5pVA+mNGgXowZD/pfWGK957LHH+PST+8KCZAPbE5ayLlmt1vQ+0JNux7JhbQ6eisuXL/Paa68Jp7u3GyfLTZz32FZz5cJlnnziOg9u30bpGnSNUpayUDRdk4oVjm7hssUWAEZkoLLBY9E2YX9SjrLQFIWmLMQ43/eWrj0TC7BSeFWgfAkYbKeYTvZYLiyL056uAWuksB8YrNehAJ7BIExHynpc73j+uRc4OT1jueqpyorFyemwZoHVakXfdBhVhWZrJnWF8wXHD894/vnnaZaOxUmDUsEzF2s7qUB1rmNojqIOe2nTSV5UZztWzZqyrCjQgTFukOhaF1gkF6csSqpiQq1mmFjE0EhxQa1UYD5z8ndZ4LSid5IAv2qX4HtU44CGHkOnLa2xdJ0S5qfpjMdvPBbyEA26qKhqQ1VP8Q66dYe3UJsapRQP10fcu/eAZtXTrBpWiyVnizMsLuzx21l9vLfMplOcsyzPFkymEzEKKQVYEZM2KuEerwKdvg772gZ2ViEsLMrZ5MGIYnxsQ0wrwHqLIuowmYFIBQAS25sZ+JRSw77siYJ+MMDqtBOjlMvuAiqSXMT9e/gCm+3t0eg52Bnibj6Ap2EtEdbMsFGpyqCrkvn+VPS1jesjEPXW0YYE99VyxcnxMWf3jjh9cMzy9Izl0SlnR8e0qzW2aelXC7qmwXU9vrNo63C9DdxWK9FHnJXwRC9G117BylihY/c6sXFqIolGT9RgFBrtoxdO4dTQ79tC9LfVntgc523eDzjPLqqyAVH5pPFD/obbci4qM6p4od2O+oTWFQ4nazQk4QMYDSqGCqvYJpvG0ftA/KS15NWgJffI91i7wBWOYlbzeY4vlKOhtaZt24Tc4qZotNuQ53ECD0puXok7H6AYjpV7RDYtEPnf0UOSK7nJtatNSKr0Ie4zuzZ0vA8bdmQd8UBZFBK2sV5hjFiRDg8vsLuzi3KeP/vOdzBG88yzz7Bu1sznMw7396jrEDNqDG0HFy5cZrFcYkwZLLYSGmCMYixtPmPXDWZ6z/i9y6rkzt27rNcd86pmd3eHh0cPKMppSnSSe6hkeVOh6NM2V+LWx48EcVTbYTzzB0EXEbtPbSYJki92qOwfIuxDH7hQkyXFZGZ3F0tETNx1RBf20NQMlGRvkuBvzh6DMDHgPVVVsFaKxx+/EShVJQ67LKrwvo6T0xPWqxUoxXQ2wdqexaKhWfcETCH0fkoFKr9g2fMpy4FgNEHFeCiUWGQhJNy6tFFJroCKOOycdUsXJlguZAQKozGmECHhJb65MAMpgTEmgQmUCptkACexmGCoYI5DLOYxxt453NGHrE5vc9q1dMsjmrf/HH96l65tefnll7l//z6ffvope3u7/LN/+k/ZO9ijMIq264dZooItAi2KaABxx0cnXL50kRs3rmHMtymLmu9+93v8t//X/xtv/+R1/tk/+kO+9uLXeenpl/n9vmWNw6s1TbtKcqXrYlKkp2k0q3UblDXL2fEJtz++z2q1Yt0sU1X4mJC+Wq3k2l5c7U3T0AWLfW/F8mrtOEQz5X4ZI0qrs6AUpijQIRxEoSmVSXlbk0mdvCSmgNlsQlUJ3WA9mTCbzsQqFSy6ZVlSFCXT6YTZbEZVV+hCM9+dh/CbCUVhKIoy3EfjnGK5WvPRJ3dZLldSzdp7sVR7SBTBXkIuTAAZk7pEVRVGqyCSwprXJLmitOGxx67zgx/8lKZZZ7UBPPWkTp7WsbJ1PhQh35UPDg5YLBZR0IyAwnCd/G2M4uWXv8RPf/RDkcs7u/TtEm09E69Rwbsb6ZNBKH+jrMKF35R4MzozVgQdFu86cAa8kbowRSGhlclQYilqsd7Wdc2NJw5pu4covaSoGspSQ6pJ0gPCgmV8gXKlgDBr+O53/pKT0zMqNUH3Bh0ohpUSw5pb9Uz1QQiDEZKCnekOxlYUSmOXJcXScG1yWUJzESVV62DRLusUFmaMoa5rJpMJ3ikKP0VZRX+hxXhFoTR1WVIVBgxoZShMiQ6hUnU9oagr9KQKzIqaqiopqkK8hIiMLKoSVRQ0tuPhyTHrtmHpGkyp6M6WnN5/wLpZc9atuH30gI9uv0fv1hxcmjHbrdk52KVpwDlNR8/xasHKdqz7jk55KA37e1IZfL4z5yc//C6r5QJrO84Wp1Jg0TkwWwpAMtRUeOrJJ7l16xYvvvjilvPUsGnE/S6rzzM604+TjdNc3WKRzo/B7jPkvUUNP5J/yInhvCins/uma8I+mhgKs2eEtxmB/s13yLGTD8aseN743LGukD9LdB+XKeA6rRmIe5cAj5TLY0DPJ8znE/avXxZwrAuUQ8KtWkezXLM4OWVx+pC7n3zK6cMjTh48ZPHwmLOjE9bLJb5tcH1P17SSHN/1eGtR3jG3YX9ACB0wSsC3t1hFAlYopIaHCfl87rOL0m3zOkS5mocbPsqrsRkKRbpfPvfO9/wo3AtGMhbCPGEga3LOS+2bdJ+hCGPyCoXD+kE/9hupEd5bDg73KepyC3DefnxuoDGdTgES41T+QlF120y4kRChofz7ZqhU7q3YZJjKQ6eUGtgiIk0sjEEJDMAm/p3T8qlUJE+lxJ3ownYOylJyNJTSXLx4iaqsqesJH334MW+++SZ7e7tcuLgPWC5ePGB3dxcdaTtVAUoq8K4bS5HF48ZFJkpm8HYwRsefdcRzqqoK7uGO2WwGwGKxYL5ThrhtmWh1VWL7JvS5T5aGvG9/0ZGAQ9aXA7ADQb2SOAuZ0PUMEm24G8PS8Buf5/Mn7ws1+l7WXlDEs0Un8tYjmZP5fSExMI3uGX/16GilCAo/HvqQe1AVBc16za1bt0CFcCjnUMoIM4ezIaRCozS0TUNZVUGA+7EgJ2IIHeZ0sAxonYS+MQZltLB1KIUxRSpgpZDvi6KUNwjJilqD9kO17U0Xbc5yE3/33Rnqw5/iXE9vQ+JeWm8iGL214lvyHnX8IcXqHt7alO/jvZNx75uQ/Ofo2hYU1HXNl7/8MpcuXeKnP/0xBwf7/NEf/RFPPPE41jnWbUNCV+EZuZAW0FfQd5aHD0948cUXUBT8yq8UXL1ylR9//6e8/rN3+T+//99w88YTrJuGo+Up676l7xd0XYOzDufsQGsKdBR0NiTumsGqq1BQjKV4WZZhzXkKFEZrptMJk3pOnOtFUTCZTsUoqAVcTCaTEEqlMNpST8W7ooqgeBSirIlHJSpoRbhuSlkpTKFCnaKKST0J7ZQQFh1itYsAEJ21Mjc99NalMKVV29AuToW3vwPbezrbB4+dhPVZ54iZEz7OmaDVGqMpC8NsWmOnDufEi6crYdnKc5I8nsODfWazCU3b0LZtuI2SWktBSY7hDHGMh/U73kUlpEeet1qtmEzrkZKWZBBgfYcqHF/92kv8q39pUM6xs7PP8QOLbhxOD4pXkYkWnYXXpZsR8geMHkkoay1atShjqIx4yJySmPYk85TGlBW6UvRtR7Mo6XZq6uISk4kBIwVsi6JktVzR1+LxnNVTKlPjQuL1rJozPzykqmoKYykKpGZJ9u4SbithS3Vdsbuzy3xnRyyVSqG+8RJFUTCfzpjWM8qipAwJ24WWMOBoZJhMBJSWVQGlozACzApjMEpTmYKiksR0uUYobL2Tuk3OE/IHAkOWFpZGHS2jygfFxtP0DQ+OTuhtj1aeidGo3mPXHc7Bsm344Pan/B//T/8H7h3d4/133ufjDz+lKGvqeofpbAddG9Ayl3trOVsueXj0kF/91V9lZ7bD7du3uXPnU1kfheLixUOpMp6N1aNCRC9fvsxbb701YrH8Tz0281BzJfJRR1wzcRnmW2gyirGhN4W+HRbk+dCbjaeEZ51XiM+fNTxv+D33vg85bUDKYYvvq/Wm7uCIUfd5+3KSjmEeadxqJSE9WuSN7R1GF9TTmunBVXaLqzzxrS+jrAPr6FcNZ8cnPLhzn6M7D7n36R2O7j/k+N591mdLFienuNWK6bLG2V6KxvousGRJlqHXoShl0DucUlKF0DPyXEWj9i8y3AqQGuu7n0f/yo2pnz2ejz5GOctEHSSyUsmeFQFeJGJ4VFs29QqQPqrK8gu17QtVBo8PjJt1XhF3s4E5GNhU7nNwAUOHDsr5dtqyOFhxUeXgZOjI8QSILB/RmpwnmOfvpZSmLGu8g6ZtuXTxCkppvvvd77FeL/nqV1/C2pbDC/sCMkL8Yu8leKUoJvQOCMJ3TMk7HLlF/rwSf956N/SzZ7Va4Zyjqkru3PmUruvCySIEikJCwJyX0CCp9CuejWhpadv23Dhte/5gyYjCL2cAiUmcUaCEBGoGECUKzNhlK+fLzxRbmJ67qYgM1o/cihmrPXvvUxkgFMmTBYQoqbFHTJ6pEZo8OU/rkIYRrT/e4vqe65cucufhW9wJbDCRaE8jSV5oRaUdtVqBcpRlhXnwKRfPPuTyztO0kysyPzMmIbx4JURZkIqivlux8+BvoO+xrU1xytYKK0hvBdDY3oYY/AAYnKPvGorTT8LG7kbx/jH2FCQUaAAcfbKW5ODfey+Wn2xt5uso9zjGMZL1CYWp2Ns/YG9vh93dHY6Ojnjw4D43b97k937vd/n2t79NXU9YLBd0XS+U0Vn74v3iuGsleYGr1Ro44fkvPc+FC4fMZjOefPwp7nxyhw/efZ+7t++wWq85XpxK0SRbYfScohSPQWRtKgqN1+uUoD2dTJIFv5pMmO3OKRK4kLo0dT2hLAyFEuWzrmsKI8CgLEu00cxmU6bTSVI6i0LCtcqiQAIzQRsNRtiMXLRwhVoTYjzzYS0NYA9EZlknY9o3Lb1t6K3H9gEwdH3i5O+th0AnKXUjrHjDnE+Vlb0Kz4DEse4yRcHHRR3WpDHQ9j1t19FOagEmrmaqtCikSodwAit5Gtev8MGHH7MOXP+RNUirQeYPq2gY81yexMNay97eHqenp0xnkyQfRvMPiU/v+pbnn3+Gf/a//CMKpbly6TJvvvYmr/7sZ5wcHQ9sMyomykL0YppoKQ4sUkVRSo2GQEVujMEUBX3Xi8JaFpRVKcp/BJt1TVlNmM1309gf7B8wqSp+6ctfoagrqaqLoiprAfJOZGVdG6pSnltWpeRThDYapSi1wWgTqohrMWr1PdarVO266zrJ2SgMOOi1w/YOqd0rye2aIniVdLpG6D4tRG+Wtfhe+nndCiBX3lJooT/tuy4pwM16LQC38dh1NObJ3IwaWd/bMEc9nevp+p7FUjyHPb3kb/ReYvG9wSrNyWLBE9MX4eQDFt2SxdEJK8449veZTEp2L1yimki+Ra9WNEXB8sERywcnzHZ3ef3VV1mvl+zMZ+zvH/C1r31NcjoptwKNqMdE2Xj9+nU++OADbt68eQ4U5IaQuHdt+z7eN36WK2mfDTY2PHzZEdXOQTaHPCrvB4puhn1y7NnI2xcgi/dYt11J9kR9YYuCq4Z2bH6mrHjpE/hQUc+JMmVoS4xMQAWreWifQgm5RyyGqbzUXgGWyxXWQ1FW1G1NURmKUK+mVIay0kyuHPLU9Ss8o8QtaduWxdEpD+/d5+4nn3Lvk9vcf+cDjh88YHlyjFouMLbHrtcUOHoP2vtQyR3QYiAQ3WJQ3HO9Lv69bS7E2kGbxrR8PsRjFO3DZ4Pizeek+5vc4+BH33mlAutZiOaxAUgxnq/xZ/77piFQ3k3IKZxzg/f5FxxfqGBf/uBo2WuaVtgiynIEEsJFSbGJn2+iutgZserqqIP8uHhe3pZN5SeiNyCBn1HnIRvs5qKX77LE7KC0zuc7rFYNP/zRjymrghuPX0Mbz2xWUxSSXmq9CHDnFJPpLl0nyTLKqLTOx5MzgqPznoLN98tBhkxE2bRjESqJtZYY8cODA87OFigUq1WH1qIsCL99UOD0QEccldKcji3vx9ybMAyj3zgn3jeCv4G6V4X8DhUs/LlTLheIQ5/7AXVH46dSwtUdPA4m5P44Jwqz0qFyKRHwhDwPNSxykMRUyC3VBHpCRVUUsO+wfYdRUNUVTzz+BM899xw7772HmbxKXVXYrsU6h0ZylNbrJc4uOJwb2mbN+riRWkJK0R//NYuPl3RtS9dLgaW+76VIkxMvQhcEaN933A+dIuPR07VdAqryz6ZQuJjcL3PKJ3aQmOwmcafZGMV5H0kbIptWGIeYHOqdD2w9Q05GmptKhQ0thuKpsEZEKSuKSQg9dCwWS65du8pXvvIyX/2lr/Lll7/ClSuXOTo5EQYi78Sbw1jAjSwnYWZ5L0nObdtxeHjA1y9e4OjkiIs3DnjqxcfEety29NaG8RYWHKWkroA2sWKrpyqgMJGgQoU8h0rmRGEoypIqKZGawpiQPDskHcbNEe8TsUMEBC4o0yu7ZNmC7QModFKHoQ8VfW3waKYExZib4gEM+IIYcpD/610M/CSMdx6lKzHFnnyNBoDohQnJe48PYy+FLP2wXrPNMNwdoz1tKnZnh/kGzCa1zB18smA/88xN3nn3vUTj6rxP1vNIiarLIj1rkCuh/Xo8H65du8b9+/e5ev0q+PNMheAladk5dudznn3uWR7eP+Lw8Cq/9/ee5x/9l/8L2nbNcrmUtV8IC5ZSDPHWXmhBRaBIrYdCmRTPPySyS0hujF2P8jz2S9N19C5WkCDkKHjm0x3W7ToUJFMsF8uwdqFtWvAa5bQYF6zFKFmfXduxXkDfKZr1mvV6nWRn27asuw6tDdZZmiYUqzOGvuspWqFYddaLFVhJ8mffWWHUCsBP6WH/LFRBaYVFKybWxveI30XncCwrUZYF5bTATCVstK4qJtMaU4Q4fCX5GiqsQVtYWtPSdT0L33HSLun6jsJYlCqw3jPbv8KVb97gaHHEK++/xivv/A1nzT26vqFfLzi+6zHFJMiLod7ELfUOrhJvb6Vhb3/Of/1f/2949tln6Bx4O1a6N9dQVPJu3rzJ9773PZ599tmRfBK5mekfShEDjDYVxlz52/RsbN4zPwZvRhYyM3yb1unm3+MwJ3/umuzbYc8l5Etla3FQSMNQJ6PediU6vy8QCv2N9YOhL9zoupyYxqY6QWqQBUp0vhIodKAUrizL1Rrd9yhThOJzOtRIUnRKcvG0bnAmeuA05aUJ1688wY2XngQU68Zx8uABd299yIevv8nd9z/g6JPbnDy4D51Cd1J4tQCpwq4sTpPA13i8zgOI/P01KtN5zgO3bcZd74f9ZrMkxGeNh0fkWZ6qsG3MNgsvn9fpht83wXl612CM6nuh++7toz0i+fGFWadyLwSI0HF2cClprRPowG+x6GdAZBuaivfZPHcMLtS560DQf7YiU0eJVcsPiYCbzw5hOeKt08xmO1RVzZ//2V9w7949vvSlZ6jqkkuXD5jPJxgT6Xc7vC9oWs9sd4JDYuOHhTNY46KAlHf4bLS62f6iKHBeEiUBjo6OmU1nfPDhLfb2L/L4E4/z85/9XKqJ9n0aK+c9BAuqxHfL5h+ZbfIJfH7ReKJbNgdx0jAR3ioonUqD0oHhArFGxPvmiq+LwNEM/UEQfNGaa8xAL1mUsmnFTVAsj4aqEvax0gh9qFwjnp7pbIpSwsZlTMF8NqPtWrTSTKZCF3q6WOACuYHyjma9wjsBXx+8f4v3330P8Hjbg3cpd8N1jq7vsF4UROssffASSDy/sP6IIjKO3x88f7mnYABtudCPHpjYx3lfxfkq1VFjRQlPaQpUMa5tE61vQ9xwUA43EtrwHm1DEbjs+yhY0ENyuIlWfa0pioqqnnB4uM+lSxe48fg1nnjiBlevXeapJ5/k6tVrLBYrzk7PhJUIH7xwohzn6zD+1GpswVssTlmtlhK+NJvw9FOPCykEnr7votEM53tRhJRUDR6sbxpcgWJI+nWBzSl6j6SQmKfrLda2CQi0zgowDAp3WieIVT+uC7HkhRXihPxBik85oXPwMldc+NwFq50kmQfFDE2gS0rAMfZL53oBx1vDIyKo3qYIBJBAeNesvanSeOr/IAecJPEW/ZC3Et9NKRXYawqpehzYgq5cvYwpdPBotFS2DmCupG0FpKfrM/me2p8dzjmuXr3KrVu3kgK2ueeIzCjoeinw9dTTT/PDH/y/+O6f/ZDVWcf+7j67OzvSd61Y8F0Ain3oEx3AhTDkdIHWMbDSKGnHcrVKBoLeqmSoksrOwWLfgaUKM1oFsSnzyvoOhw3jpun76OHVeCYoX4si5i1F8K7GBO6xGjl47VVZSi5NoNCMe5YCJhYMoqAZidFEK8Wk1hS6whgx5hWFCYYCjSk1TCxFKbVbyqKkqiuquqZQBXUxYTKpJJRTwWRSMplNqA8q9B7MdqZUVUldl8GQkdTPseJtg5HEOvp1j3M2GUN8IGAo9ASnDT9943X+xf/zX/L6269y784HtKsTut7Tui4ZooqiwFRiMNg9OOTa1cu8/KVn+Af/4H/Giy+9yLrtoXepMGM+f0aGjfCzqiqm0ymnp6fs7++fA8S5TM2JRfLjPIje/t35CyXxluCdH5/pRx8MRljEIqrGn2+5RD7KvRjJ2Dfond4HsoNguBN9azARquz/6VcflWo/UiSjEWZTmZZ1NXpt0SUsAWCEYocenA7kE0axt7fH7t4eXdvR9aEwYCh2GGgHsCqEAyUxKnPRxHozxuBLxd6Ni1x+/Apf/fY3aM+W3Pv4U/78j/+YN3/8E7qjY8qmw7U92NA2Btm+DWDkSnn+nc1eNKeGzvsovz5+FiPh4r226dz5XIiDl+8X+fdaj8Ndo0E3dPMWLkBG77OpY8e+OD2V8Fy90aZHHZ8baMT4xdxzMVi25eHRChQVGx3czLl1PlrSN7mM84mZD0L8fOzaGa4ZWSY8SbGSAmLnFZn4u3gyYodHB6VsbLs7e/St5Tvf+Q4AL774AtNpzeHhPnVd4yxCpQcy8b1JsbbOCrtVDFXIvTiDd+acKBn/nbU19nVhCm48doP9/T0ePnzIjSeucHR0zNnpMYf7hzz77NO88sqraKPELU5kPJL79FYASNu1QehndLtqKHhDCOdQcbEynuC50I6KQxrrsC7zsS0i9XGI4ZX49DJ5dyaTKXVdBOo6oWucz+chQddRlQXGaJbLJV3fY7TQj66bBtd5ClMKj/pqGVh81lg7AK47QZnMvQPWifdA9nVL33d424eiWDXOOdpmTQQbSdkK42pddFurZOUWK6AAJOddijeNQGo44t8qCEGdhXUMfQoSo610tMwTYiujkquCdd7g3QDgIlOUKBL5+CnKSjamGFMdqaKN0pS6FAtoAKQRsGgjlXi11kynU3Z25uzt7THf2WFv/4CDw0P29vfY3Z0wmZbs7s3Z2ZnjPTw8OubBg4c0bZPCdmRz06gY+BosMXER6LSJx2Q0T9+3NMcN+uGRhLwYaacJCpZCBbrRwRiSgAGBHDHIkgjYfLRWO5WeI4BhAMVWDe7xXDkWkGRSyFGUcyrMBaKi6VwKmXIRXNpAExiU6MjSpJVNBgofvB0ueCOcHvoCn/dRBFlJtRu103vSdTHvxqV7xHCtdPagfDipsWD7LtBUdilkD9vj/ZSpqlHaoZUA/MeuX+PsdDHU7rHCQNisliMgtHXDDcMfLXrT2YSua0MeSmZQiopOkFnOCdPbxYuX+O3f/h2++2d/xd1Pj7h/64STT1rWzZpm3STZZ53Dh6Wmvfwrwmg656DQgR2QZBxKhi0lidCyJmUNl4WmKC2qDLUllOT04KE0hqLSlJV4x0zwKMQ8G6dBaYMxwrxWl4a6LCkLQ1kakZVlSVGWlIUo1EVZiFtBD/Tx0eNdlAV6rjCVpipNSAj3FEZRmgKthKAk7SeFGSU1F5XkGRodalSFOY0BbWKYq+RoaROKwSF1G3xQWWScQtFYIvFF2JO9pgAMNc6GeH8l1znbBiXL0zvHyTsPeeIrTzJ/4iKnx0csT4/pbRNktuTxVJXkOu3Od7m0f8gLzz7Db//mr6OV7HXiyQvMV2kfy2sj6Gzuy/HSSy/y2uuv8Wvf/rXRdyMlXg36jny3DTRv3HiL4j/+2meMUuM9Nl430l/CDd1nWJM3gc1AEENgYzqvE0WPhidXpIc32sznGNrLUIAyfGatG+RZfJ8IbDKdNW+llC5TaO+x2lEqLd4LH8gnCi1pE04NIZle2hXzPZQL8kJrvFa4pg0EDpap8TSrJb0pJa9qp+bg+af41uz3+Nrf/lVe/8GPeeOvf8zi9h1UK5E6WB+iAmSu+qH5aYxyxTx+hovMX8N5EdkNBqtB7m2Odx6aFfXVR4ZpRYPgxtgn43wEMD6ymMm5ufcKn+VzbNwfRBeJ+2ks8tism3Nr6FHHFwqdygv2RYrZrutQphDKzkKszA6fYtnjIs2tqFGIx79HHb1FkY1Kw6DUquS+ds5RlqUoXNaikbj0WLhFus3RdyFuWgWFLFhUnXf03mKU8MkbCvZmu7z/9i0+eOsWV67tc/nSIQf7u5SmxltQOIyBHoPrhWHFekepJT7V9oau9JRaCb9/sDxoHfmGhIkksoBknUyMdRwDEyiKkkuXLvK1r/0Sf/wf/5x24Xn68Wf5+NYt6qLg6aef4Xd/97d49dXX+PiT26zWDRBLQTjavqGzrUwo5SmqEu0lVyBZSsM011qjCkaAcdjUNEVQUqOHJC6Iqp5QlJM0jkpJIq2EewmNYpxDtu9p2pbCKFzfQQgFWp4uWJ6cUdcTTk5OsN0aa9uQhD0kMOdeAtvbYDF2ySqbrI8p9GhwRdqg+MVl5IJ7t9B6oOcjLsKoGHlQHmUUZRmU8GAVFDq8gbImVYMPFkejRaHXSjwD+MDwEykhM4tFrtwMQixQzJrAeOMUhRZlpCiKpOwWgSmmKstQA6JKCq0xislcrJV7+7vM53PKopKchMmEyWxKWVXMpsJmNJlIfHxdV5R1kdpZlUWyxosiqyQx1Dms62lWHafHt1k1Lauuk5yB2Bdpmnvh1vORTSvfpMYGgLSZEABF7/CdRTVdmncAFk0IqU0WJe9cMHQQwkV8Ao0pjBJ9bpyjJc96m9ZEnEPpumzM8rjjOLb5HIyHB5QRoOSD0E5gQClR26JhRAVAhuQjCAAJgEcPBgGfWUATeArv42zaMkY/FR6cSgqYgJGwGSkvFkM8vY2eniVN6+k6D9bhvMJ6xcTXTLRHGc9TN5/ke3/xV0ynu5iiYoIkLfenp0J7q3ygMrYZUAqKaQhMyo1j01lF06yZz3aI1bjzV9FYNIp2vWY2qXn+pae5fO2Q1197k9U9z8HuRY4eHvPee+/Tdi1xCxcgHShrS0NVCfGCrG0XlPsihAUW1FVFUZW4kKgfvavR6FaUBWVVhBweMwD0JDOjlzGGzOb7QL6xh31Rb2S1+dzwxqMPBTaGpQT662H9DN4wss+TIhE0jjgPSXuBD+sh/OYCs58Lsi9ojXKbYGjChCrFQ9NcZk3vWYsMT2uQwAQpSvCD4wVvvPUByk2YTyuKYsJ8fx/vewhGzMKUTOsJZVGxM5tSu46bTz1Bbx1d12Kd5KkVSf+KCpkd3tv7wOxHUrKuXD7kZ3+zxPZrynoalDSd2jmMQZiLwWgin2cAP7klRJ7INWM5MEYeYw9LPjZ9on0fXyP3eISFe+Pv3NpOkGv5OcN3Cm82PZ3DdWOANfzu0hyQQww/wUjKWGGNpLwKFa2ZYT4SPL0K7RSF79HeoApF77ukz1nvcNbgrcb2IqcVGhvndJCnUoNTnhFl7Vr75N20rgMlOU66UBR7c178zd/gS7/+d/iz//Hf8u4Pvo85uketHC54mvsAFGR9E4X0yJAcxy4q5vKuo54RT2rovzwhXoV+jeMVZcimR25zjJORNz0hG6MoP9T56xRD3RRPTBCPwFcWfbrMOQkH8x7jYKecSej6ljZtO74Q0MiTR3PXSo62cuapTWS12VG5dSu/b54ckz8jWmYjnWsEH865ZMGOEyF6QyIVL2QWsSBs0+9erNzGKOazOZN6wp/+yZ/gbM+LL74AeHZ394JiVuJxnC3OUBi6ds3+wQzPwHLl/IDmz/fjgFytdSPQtWn3yPu7qjTz3ZpvfuuX+fnPX+XOnds88/SzONfy/jvvgLU899zz/OEf/EPu3L3He++/z8nZgvW6C6xUUqRJkXmCnAuCcojVjpaCopaiPrGvo7XUOQfByxRzRkSxsyy7FtQRSVnzQhcacxKsl7bEELK27cL9/GBFDQnRZVmyXq/FYuLGyD7TPAfFVEVhl6H88LMM+R1xAOrM45LPY2MM2ovHYIg1jptS9M4M1VeLmD8ThFq8Rw4YjDKUIXfAFCacU0hOQGHwgfnCmIIqWOom02mgNhXLfRms99PZlL3dHWbTmnpSU5Ulk8mU6UwqTVdlSVkaptMJZVUE20WwwGqD8ySLnCjp0fJuaQKbVt/3dF3PupcQorP1EowaFA2GEMAIJmO/RjIGWbviZRDrm0rAXma5A2fTPUdsdR6iVTTNS4Ky5AcDQ7Tq2RCC4UOFcBc3xQhiEIBB/C5T/j3D/Nm0tDsf6sek9RoZ6obE7XiNxSb5lrvJz6//bBMYPgp/C4NUfu4wZQcjQK40eO8DPTDjczPFYXOHiVAj6UJsyGE8+A7U0Pe9syxWy0QZfND27FvLvnegHBMqrl6+zHIphdOscxxe1BhTBq+DrGl09Eaf3wdg2GQlfOoy9+/fZz7bTd7PXLnRyqCVeCnPzs7Y3d1l/2CPX//b36Zwkpsg5Am/Rtx+xVIboqeVhBIqI3HhMkcGQByVchB9wkYgSdyXRqO40efj7+T1QniDClEZqb/lX5SrWJFj+TPGYzo+8o+8etT3fqQnqtF7bCqn47bnY7VpvX+UjrF533xfIcsbsp4gkyTCXxUFr7/xHk3jQRXUlaGsSyxSL8MQAJ4pKIzkZSjvMMpyeHjIet0Qd3atB30htVgNoXhD+3xcDoDiqaee5L333+VLL3w5GYwyRlDZ1/IUKdgY92wGPAI85N89qu9G7cvHI5te5xmktgOBOH+cCyGbWzwT2Qtm9RjS3SJkOtcM+WP8/nGeaxVXXZBdUe74UEAvXBfb6kIdEotEEnjrcAWjfDvnYujiWCfI+yxX0qPnXCkVcjNB90o8iUbTdx0XLlzk/v17fP/7P+LwwhV+7fd/n8euXOEv/8d/w/roAbW3UsxOhT5QAq500IG2gYHN8c1nRzIAZOdvHpvjt+2eqd8+w9PxqPvn1yuVy5xHtM0POZ7OOdr1mvpzFuuDLwA0omchJm3HiZujLxhCfTYb6pxL1HGbiVK562kbuMgt/N4PCcgpgS07P0eWMcxLAMCYOWCwHMcYV3Elz2Yz7t2/x49//CPmsxnPPvccs9mMsqzoe2EBunDhgNPTM2F8QWJ7i7Ii5kXEdm1HoPzCSTacK+8theE8V64ecu/uQ/7+3/97/Pf//b/i/fdu8c2v/yrvvfMab7/1Og/u3ObWe+8ync2o6ilts6ZrhebT9j2LYKnNcwe896NQjagsl7X03cnJCev1Oimkznq89UN8e6Z8WduBl6JdMR8jxnw7gmvWDQxSSSEnWFczpa9t1xSFxlnJ21DFwMUdF0a4SxbmMHzvM4anOMYxt8AEIJGPkykMhSnwdpw4H+dQ3HRijktZFsIYU5aYQmFqUmjRbCZF46qqpioripAYO5vNmM/n1LW4/VXwQkyn0+CVi3koYlF1MTHT6BDqINZtVI/CZUn9Q02b3vUcN8fY5RBW6D2BociQKhNbCS2IANlm20hUpJNiHGvCeJc2n9hvKoT85KBNFPoAc4JX027Q6MXNTELRss8zEBTbEAGH4JNhw1QEi6TSUqdERaVNNueh6rga2q4iKFXB+3k+ljZMTsCzCUbj79FbG/srX6+fdXzWxjLayEdK0hjEjc/Z/rzhMY9QaPJmjO4jY0dSOOU7h2PddyyPLQ8XK/aOjrl8aZ8rl/bZ350zm06Zz2c8fPAgzOuKyWwua7mLsfWBfMC70fPia+V9c/nyZd555xZP33x25NHO3z0C3b63LJdLqko2PusbumBt9MYnbTwq9EqpwDHv8V0+z6qhXs8GYPNxjHL5nf6Xy/UE34bffexOUVJimEyuqfsIgmN/bP39vKLh8rxDNf4uWi1RKmj05/uZzft6NmZMrrzG8+XvR+YabtwjeuM8PvS7C6qrkgKg2oPSWKt5671bOEJMvdKgDIWZUBQVGil6qxBl3zmH8p6rj10NRVNlpo5DC7fnU+T9kK/tZ599ln//H/4DL738S6kP80iOHPR/0eNRQGBbuwaZAnGSnR//PEzyPLjbvF+at5pz5+XGTuUZfabUkAuy2c7N3zdl4uaFPqwBkWmDxw0AS1pnDo/tLK3OyxwQQN52xqdNsLFp9PEB8GsH1im0VSkMe7qzw1NPP8V7739C3zqe++VvsOw8P/h3/1+K4zv43mJSm0OYbtbHsY35PPlMWZ+1Mz8vv08OEDdznfNnbOuHzfHZdvyi77e1G2QFrpartK4/z/GFPBp5qEx8sPcSLrRJdZsDgHj9Z1n9coCQ/54PnuRr6JHw2AQr+aDEtuQVs+MxirlWwurkgcl0wl/86Z9zfPyQb33rW5RFyc7OLt/97l8ymdS8/PKLiGHXsFouqeo5fe8oK0PvpJK3MeNJEa1kufDYNhEVwyTM+6jrOlCO3d0Zly7t41+4yR/8wf+cf/2v/9/86Ec/5pu//CK//zu/wU9/+nN+9srPOV2s8F68DNYJf74LYUdxw1NKpRoK+eQuy5LZbIauCpp1w3K1TJ4arSU8qFBlGuMYDiRgrZLS9YqQSyDP0EqlImHjRGQp7KMIeQNb5oMJbDFK6cHCBCmMoa5rIpNQVZWUZZX6eWdnHgCiWNGqSsKJtIfSFNSTmkk9CbUQCorSMJtV7OzOmc/mmBg6UUqYxKSW2gj1pEaHWOaqqqgmFV770E41mrNRwRos7HJIcq7kezhraV2H67JwMCnrPrY6MyhLg6BVI6UkWrhjfH+05Up8pU5hDMka4iW8LLLERC+BXCdsYtb6TFkSMKBCiI7WhGS+sXdMIeQLKmwqY+OISnuLtKdPipoLlt88pjitmTxOSO4aQI5QCXslVU+t21DMPHgn1jTl4ybuM+UvKNfhJaOXA3VeEKsIVPT2TSXfEDY3kfhZuk+23s8pHiNF4bwSka4Zd0m6d7TeBiS2YQnN7z1ckwwwarD+YsVlLgqWAl2wbhua9ZLjh/c5erDP9asXeez6dXZ2dvng1kdU9YR6OkNp2V7apsM78a6NMhNHSvlwGGPY39/n+PiYaPg47xGX94rhZet1Q9t2kuhchPFQmyBwUI4jkB2BCd8O4xaekECBU2nuJ/wQZbX3SX7FdRiVwCEMUP6vUKOxy8ME8/unuUn2Dr9AwfUqjvNYAVQKiV3fOD/WkhnNPbURupU9U6tYbzjKjuyy/KpoBAgvIvWcIrAQGSMELQIklNYoXfDWrQ+4/+CMsppJNFdkFlQe7wo8EuLmM9lme8vNmzcxRvL8JF8qrO8t3XVuz91Yh1VVsb9/wO3bt7ly5crW8/Kfo/7f+Gww9HwxYLJ5XX55NNzk/36Rp2Ss62wHCCPjXZRlmVFGPoqEJGw8M78sGoYyAwLDvHaZO8g7L2G3cR1l5Q9wIWStj8QI5xOTt8nX+K65MTuFJmsxdETGOa01jg5lxdB447HHcKrg3Xc+4MdvvcPNr3yDmw+Pef/P/x1quaByUn1cKk0ZnGIUBrVNjuegMW9/XtgxPzbHdBMkPmof2NSd8udvJqNvu39+/uaayNsex7Nru8Da9/nm9ucGGn1g6ck315yHOm/Qts571ELdRIERUHgvHon88+jR2PaMCDC2Lbptm3luERPaP890MsVow3e/+xfM5jNe/vLLKKX59JPbvPHGm3zjG19jMpnStT3eKc7OVjx58TFWyw6x+vYUpYTW5MmESqmNDV6N2pzak73P5mCv1x1FWXDz6aew9n2++ksvMJ1V/Pt//x/4m5/9jI8/uMWXv/pVnnz6GVbrlgcPH3J6dsa6aVitVrRNS9M0KTwmUq5679PfsX191+PaDm0M88l8BArKsgJHVnF3GAvlCWw2KrmuJU9AAENVCVe8MEqV1JUwoaC8VEOuJ6Ocg+lsSj0pca4HpYInoKYIycCTyYSdnR20FhA8n89D7kFJVUlRtbKU59d1lQDPpKqY1CGPQhm0KVLMsVNrIMTXZwJ/qN8RaWoj9eiKZrnE2sBPHix3cU6DKMBRuR0EsQhoB+lesZKoHvgHh7kcFWcPngLnVPIO5cImFmJDFcma6V1MSu5xUg55JPi9l6whlZgryJQwhwuWxPxQnlCvYbQK09pUCC95zqA0rEslRf+USp6xSKDQeyesXhHVZM81iUR0WEbpb43Qa4YaA+NEyZCsHUDZcC2ZFdinx4lKNMT7npNZjMMaNwX45maQmhsteRuKQkyy21T4hr4e2Mo2N5ZtbvgBhGbnjhRK6QetlNB/xs3YuxDbL8YBjRK6bsQDYJ1HqR4f2L0Unnt373P84AHHD0+w1tK2LcvlkvlqhSmEIWm1XAWvW4htjv2dwMK4/5xz1LUUyGvbdkRNnWRNVFoZ1o5zkselegN6g0rdxzUkV4vsi2ME4ED1nIdtob8kmz7NS5/kuc+UczVeJmkOnx9TRmP2KMtiDlI4d96g2MUffnhGaFNci5uAVLakAMY2rc6j8wbg7IYPOddPo/04grzQLjVQZmNqbA+f3rnHJ5/e5nSxCim2mntHJ+hyCjrmhOXGJ6GUV0Fwag3OWabTmv39g61K26ad4LPAQozYsNbywpe+xE9/9irXrl0bEc5sW2eb99mm6G/KhM1jc12Pzw05Ziqu65yt0LHN2LHt+cM/8YoPoUVjoFHEqAB5NAOwiFgx8+pmCCOX+6M39X6Qbdn7eaJ3Ory7c/RZHl2PRBJ6bzMD8XmF+LNkb270Dr/InHISJeG8lQLKIc9yWtfcuHKJ5dmST26f8OZHn/LsN3+N1cM7fPLqz9FnJ0x0CN2NYGtDxxzrquO9I/9+c75u/r4NoGw791HXbj4z/p2fvw0Y/aIjjXGo9VVXny986nMDjdigPPlXwpKGGOsxteaj75MPRrxfXsU7LoBYbG98zRDPvTkgm+Bl00OSb7xDexy2k4TWg4NDTk5OuH//Hk88cYNrVy+jCsOf/MmfcuniJZ555jmuXr0GeE5OFyglnCXGhHh4pUYAIw2k9xnjzoZimCFvkd9jd+hwGBZnDbOZ4bnnn+a99z7gOfUUj934Z/zw+z/gb37yE777l3/NYrVCa0nELKsabTRt7/HaoMuavm0CPavkFzjrKAtDVU6GJ5lCkpaVwsSEZy3VfhVi8YwsRDGUbjKZsLO7gwquzvlsznQm33ddR6E182lNXdXiHZhOmNQTKapUaKq6ksrKoaaBhCeVKG0Sy0gct7IqMDoq7ALQCqPRugwKjVjbZY4GoeaENUeqRXvaPoZ9tUOcv/d4Zel6STSOYRRRGd80wCZFxoHCZPMwPtcLAA3JtcP3cQ6IQSBSrTon1cZNDCfYVFLCddb1WDe0J7Y/BaEFb1IU+hFoeCUet/xdkgU1hFGBAIhk+fditcnnpNRicOB1okmN/eGInh0JkJC13SdlWu6h6W2Y/8l7IT+td4G3XDpaZRZwP1KJhrAs6eseWtFsYgLuEPakUD560jLDh95cYyTwBcLQsRmDG04Z5gTnFYX8GP8tQDXKz03vcO6KJ/t9E2hEmedCPHXMHdm0+MVrclmklISMKRcSXa14s7x1Q8FTZ2lDTQzlJX9K2mdZrpchfLDE9T3Nes0HH3zI+++/R10X/PLXvk7Xd7RdR931lHVF20kF6Pie2YtlU1yN2q8UHB4ecnx8nGi9t2+KITRSyf0SyLfj8Rl3q1jVvY3zYSAM2K7052AujCOx6Wqw3jNU3I3vN1YZxyA5v/+jAUfeR+eP0V6mGHkgfGrdeB2pDAikrtnyaJEf6hHN2vxwA6x4EtiJley1Nnzw0R1+/to73Lt/X9qnDR6NMgXaFJgUQqoCbsr7xQ//lEcpy43HH6eqCqEiJ8qzbHRGe/14vW7rR+89BwcHrNdrFouF7HmfARS23TP//VH60NjLMFb8Nvf9uFd4PxiW4vk5mB5CjPJ1pMafK5HnMVpgTEQCRg2yN4KE+N0gkx8NqOKsiV/rFM0BcUzi774gezeHtSbtBW0vjHJ9rxLjnY0RM6EcQf5u28KHYj9YayGMofIhfDPOTcQgVijo1mv2pgI26nqX9z855s7Ziq/+1t/n5OiM9tY7+GaBUS6x+P0iZX1Tz837apsHYtv1j9pTHnVdfn7O8Lrtfo8CyducBcMf4tE4Pjqm+px5Gp8baIyqF2aNMMUQ973ZmbHBmwAgHjF/YihKt51zePNecYFFMDIAifOCJS3K8P9hw80UPqSy72w2586nn/DtX/s21y5fZf9wn3fefZeXX36J5557lr7reP31N7j96ad8evsOv/zNX6NpO7QRXv/IUx4tp95FvmcR2FGwbwqlod255B8fovQ5Tk/PmM2mPPnkDS5c2Ofunfv89u/+Ft/4xjf48KOP+ejjj3jw4Iij45NQzEwKPUX3vrAuOLQyVMawu7PDZDINYyfKz3y+Qz2Z4L2wxMQQpclkwmQyEQajumY+n1MUUjF5Np8zmVRgLFUt+QnR9VoGNiRsLxSQWa5ObmXJhWYEsh4j/7LNo2nWJDYpxgI3/svrHogWMcy9qJwBoWpu3HwV1mtSOL/Ag3C5HimHcr5Om9rY+j2EBuFJ+QkjweQlMMn6AUA479CexCEesEX43g4C2dtEJ5iAa/C4aGXiC8ZVM4RRqaFd43Xq4wvLXzZYsHwUaNtYShwKLR4SxkqUjfHYDM+1WTXwGKHv/cBIM6xFztWhGUDRsI6BtLbSaKW5I22OxZ9wHgnt2tjQcfgM0G0+UxOTR6MyOfTXJjCQDTA83w+b9aY8jN3sAWWHcIVzikk0PCBVrAl9FDNnYv5OmInByiT1HdquE6+kCxXl+56u6ySZu2lYnJ2xOjnDhTVirZUCoCEXC2+FFrbrgpcysMyVhrZd4fHUkykSV+9YNw1d1zKdFhy8f8ATTz5F27YC6LsOjWK1bpjOJpQ6KsNjFXzzsNZx/boU7rt27Vq2bwzzety1OsjcnhhekxZPGJ+BBUzCuBLICBTHpBAfkszA+0D7GeZP/Di8g0fWSQwVdeGZ20LvRqFG2WMEoGyE2+bff5btbmTNjP2Sr+ctAEaFMLgg30YAKMc1Sb/fDoCcc8O1OZAJ+7fk+mqcA+s1P/jRT3jr3U/oXAm6kjkeCn+aogClMVrofj1DDaaxePIidl2PxnPzyesBEI/zflIr/TaFPk6N4b3Eaq7Tun7yySf56KMPefrpZ1J/yncMgDw9xo/mYjQqRY9jnIc++5nnu+WGA2lfPlFItse0BuLcCHugbLMCIkT5Dv0fmc+0ycAGod5Q9AgMIEThQk2T2CaSVyz25QA2xnrWAG6GpTM+BjAU+y7mVMr76kTc472nKH2IHBD6+q7vsX0vYeB28Hw47ySBPBCEaDUUL41tAYnIEHYsm0LZtVZSyFRDazsq41nbFVcuHqLLlmULn9w+5qio+NZv/x7f/Zf/d1y/pkDWcmfdaKxzgJd/lvdPPrabucpZhw59lu8LcaklwDaWofGURFsdpso20PtZ4OZR3w+6tCTTO9czqf8zA418MSg1JNK2XYfaKP4UX+hRwCO/Xx6zH6/J8zMiIstByhC/vT1ZJk9SHiaAl4TRQAFo89AKD9NqyqQqqcuKf/AP/gu6tuP27U95/Mkb/M5v/Tbvvvsur/z8Fd59510KU3Dl0nX2Di9wtlgxrXVwRxZoNMoVGDSlKYPipyV8hqDkM7RtW/yczzY8Wdfhu3DucrnGGMN0OuPpZ3ZxvVSJffHLz7Jer2nblrbpWK5W9G1LH6rzxvwLE6plK6WF2rSWAnge4Uuu6hpj4kaEsCuFkCalzUhgxp/WScK5CFGfqDa9F87lrmlCvPMAFGPfi0V2DDDiAvNB4OXKcjwcEXjGlpLuEfsxWsGzPQGbb6b5RiAzY/gmvd94I9nOFDZs6GNA4RDii0E5jmFCjsgaJBJRiopJHzmnh8TnrA3RIk4UJGoQ1g5oQsklGFtNAIzXg8KshnHwHrQfEqzHLCIem3sV8nfDIaSsWTwv4FUEPkPIRE73p9UQAhU34wSUfAR3PlMG4sYkACLmpiTZouI7BQtW2pA9qu9RzgdFcIjNB1Ba0+mwWYQhUorEvV8gc723A01hnNvRir1pMIBI0yjn23CuFFjz+FDALcq+LoQstqsVfdPQ9z1N00hNmK5jtVyibY8LdV7atqXve6kY7T2E0M+u70IdmZa2EaY320ooUNs2UsnV5ow/Nr3DOHlWlI9Yh6UspJZD33mMnnGwf0GUl8JQVGWgyvRcONynbZdY19L2Db3r6ZyQh6z7nqXr2FOWUmu0Ew3GYRgvTkbtuHTpIm+++RaeF2UsM8XB+fMhCCIHiuDNCN6jMC+sj5bQgQoyKiMUErMtilUEkNJGHycFit45yV/BB+3PB2/BoDwpFVjnotdkpENsKgZDvHtuSJEjjskQ4rWtj0bfRcUwaaLpSYzBRgZmw4nbnrHtswEAqZCcHWVQdg8vnxktz+6d5q9+9FPefP8OStfoMtRF0Lm1fVgboFOF5LiQDNGLFDxYHg7mEy7tzPG+T97TNFzZuyZJ5sef400mZ/ILPTduPMb3v/99bt58Gpc8Xx4JqQwyOYPMsaRSkMYZBfXY4r3NCp7ff/NwbggrzZVXMWbGOSB5odpojImWfhN0NDMKQZPvhucoFeeXSnTsuYK82dZsdozBVT746d5xXgwgcNARwxgQ805kDsTQ14KhT5wX3aLvhdgmeTuip9zLHu+sEzrgsB8MGFNC7rQK2oD14t33Uo/KOYvX0CmDVgW2g53dHeriHrMSThdrioM9bv6tX+Gd/+l/olpr6GwqsBnXcL7fbqYD5B7nTRCS95fyNjU8dpFCJVCfdRuGSNOvUKpI3a+yMUv15PKR2wI88nZt+z1vY297euv49PbHTK9f2zI3zh9fCGjkoGCc9M2og/Pz881gFDPLWGHLN+x8cm8bjLiAc9CyqbjnIUybeST5NVJ/A/b393DO8corr3B8dIyzsLsz53d+9zdkM9aGb37rV+g7R9f1XLtxA60NXdexu1uEKomD5ycmB8aaCJEBR5CgS5vmeCGr9NmAZiNMDe+sNVp5oSBdN8FLIRU1hfVoJykx3hNqiwxJisZoPDHcRCZgn1U+ttayalbyvKSEx4UTYsnJ6xTITWKNC0Lxv9T2TUVdxVcbQmmCNhBAhwsb/iDAR/OCXAXO2WA250sMU4lWlqEBLtv9Ny3TZO9MNkZRqfDZz1xZyFdyKqAW39XmVrWorIIlUKgytF0sZl4Uy96OqirH9nk/WExzisBgo8/oCTeBWbbtJlCgUlif9KNLm00aL3JKUpe2V48agGD6PvZNEHhZO3wEB96lznHhmTkAyPs8rhsPdH2frNKRYjcJ7Phucb4EQKcQ8JLGzMdxlTkaqVPH8co+KAwuwrKQRzKEjEYQm8u2+Ll1lrZpabs25T+tV2u61ZJuvWK5WtK1HavVisVigXOWxdkZXduktdj34o0A6H2f+jS+sxShi/HbwgqTj7VWGu1VWrdd2+CcAI3Dw0MOL11kMp0ymUzY3d0lsp1NJhNm07mER9U1sxAeCZIHNalnUiU6TAmhlz3lvffeomlaiiALtIkc+bJyFsslzh8EkCZzKplS0hqXK+J7TKezVAR2c/4H1ulz+47sTXEvGdYFPlhvw9pcr1ehsGlYdyE+vypLChOK1xmD6y1t30MknlAqFI4bQiKVEpKSQd6FubMRirWpsOWKyPnP3eicbcejjHjjk8JK/QLWzM868ks39/ThGSptXx7P+x98wAcffowpKsqyBrazuW0quHmb01xB8rrwnseuX8VoJeyPSQPznKN9TW3P9Q8F58Bq/M5R1xVFUXB2dkZdTchZKwWMBl9u1F+iTElMSrE5g0EuXp/2HD/06aOARiz6metHCTCo6AnTAWgoiiISqJhzci1rbjaeQ/usRcIkk7FrRAcYbpC923CT0V4ejXvEvZHB6GTt4BXRekguH36Sbq6UvKtRBYWRyvXOOWonRYm7rgvy1WJtT99retcnw6WzcV5KeIB1Y+U59o/WCoyK1c2EOpueJ594nI8++CGzvT2O1mfceOlrHL33Mcc/f4Wq8GAtGSTYCibOzeNNMOIcKJ3mn2I7AIg1oWIf6xDykPtBB7NBPjxq+NvH+Ssy1zvPIHvPz71HyQmjlORotB02lpX4BccXztHY7DjpAHMuhCkHI/HakReB7R26GWuXXx9rZkRvykjR2Ghfn3VA7g3ZtECKN0Q2WK0VV65cYbVc0bWWL73wAovFEqMNZVlR1TXXbtzAWsfO3j7rvk+MKPGeMbF1EzANfw+hFefBhgi/+F5R2YrfyQLqktKBH0I2hjWqkjXIgyj/PvMUyCnSRyFuPsY/eu8GBS0qXeGCGOIGSAHC2OagsMZ8iBGdYHjB+Iz4mWJMDReBRlQSctrEqGaOTo9ALGzuY6AxFFAaNpYxEvDZ8syt0vm8yBswmn8+JlOnhjMWkkEI+Myqkd0uFQrMFe9Bhwp/B3Sk9fBV9n4JA4RfEk0xHpsLfbW5xjZ2iLxbvB2dl1uDxjSWQwig8IHk82oQslEZ2LTECZBxxHx3l8256LFL8yZtxBL2YsN8A4a8E0+a/3HzzV+v64Qdo+96VqsVfddBkAe27+nXaykGaS1d19N1LV0IO7JdE9z1PW3byWbWSWhSzOOJ7ZS1Hzc9K9Y261KCqbU9WIfxbnSNMSLHilAIERD2NKNxSlHVFc5MKCYlRksF6LquU62Zsp5S1XViBIyy0RiD8rBarTg+esh7b7/N8cMHeOu4fuM6v/Qr32a+tyt5VkYKL5mkmMSCkcI0lzZHD6UuxaqvpXBlXVVMZ1PeevMNVquGiZL6FZG6MhI1LBZLbG9RZUW+bhhtleP56b1nZ2fOyckJBwcH5Mej5WtYP8lCocK80pydnPLg7j0WZ2es12tWq2Vgq2pYr9bYrkuFNWfzOQcHB1LMTxtaBwcH+zz++A0ms0mYkwoJ0bPJajwoGyqA0WzlbFH2twGJXPn9RaDgPwVAfC6A8gtvAo7xfYb7eqnMjKbtHa+/9Q5lPUHrEheIRDYTkbf9HLUx3hcJndJKcfXaVbq+ZQhLjvNhvMc/6r3xdtTXw6s5fN9z48YN3nvvPZ5/7oUwzgHIBJkWjTpicCGwGQ2Ku09J2340P3MwHF/Lb+xj8XBuIB7f9FArVFKUy7JAGwlpiWt4k9p3s3/iZwncRTrwABbSzzQCPtujhlHZHK34fTLCyZuM3kEMwJG58DzoJHvnzet0KFhbhvxd62yq19X2it46eix9Riris/7OAbKMhehd2iuMt2jfUWmpk/XyS8/zN6++x+6Vy5zYnhf+1u/yV5/cwT/8FOPcSJfIj3ztbo4boftU2EfHuslgcNsEKI96xi9av/m3SaPwoR+IfXC+zh2wdX3gPNoo7t2+wxPXrn7ms+PxhYFGfLlc8YzKv1LjUKd80eThTbkibUPxt7yi6rmBYTzhcqU5b1sOHiLoifcfKUEjxcdT1zVHx8fU1YSnnnqKSxcvY7QgaG+lzPp8voN1nmuP3WCxXLFar7HWUdd1UvQk3EioVvM25wBKB+XRoxLrU94uH2k2kfoIEJl7PH2wlubXOCuKS5zu3pMWatzwoqci9U+w9I6oUHPaUwUpxCYCBe8xLiaUSV6DCPcstMeJkM5gchy84fdw5Em2PgCNkfCN7xPsI3E6RIpjcbeOGZQ8JLfwWGiHuRuQvNtQqkfPy/6M9I8uCCoX8iTy66Kg0IE6T5TYKKDj87L7x35zslHFvpZx8MNJBLdo5pEDlSr+RsUvKuEQwoLydZedK1a08ZqJiqBcPIypzM64PqB3kbo25JuE+0blP86fGHMrcbMSYhDX6rDeQDG4h1NfbxgLvPfJmh2V9Xa5pm/bFEI0kim9ZXl2xnrdYK1luVqyXq04OTmhWTe0TUPbtGlOxeeIlX/wkPgMIEIfLIZhjiqSBSoaUXOFyRhDWZWUoc4KhcEYYVIzRag0XZfUkQTBGCaTmrKsKOtS/oUCjWUhFNJlVYICE4BEHINYLVsFhp4oY1zIj3FW1MD1asXi9ASvPD/90bF4VPHsX75MUU0oq1LGRjQDkUt+kF2EzdwE9ild1Rgl5AtFIWEZu7t7eDTOKvrOyb9AtmC0RmlN07Q0TYurK4pQkdmTe7SHeZnP0WvXrnP//n0ODg7GYMKP5Wo+b1wIC3OhEKhG8eEHH/Gjv/4hn3x4i9dfe43j42NWq1WyiipZgGmeJqVGa7xSlJM5X3rhS3zzV77Jt3/tV9k/PEAFr9YwHiaEfoiCqI3JFLVHH48CCNs+Hytj43O2ffZ57rvtHp+j0Zl4Hys84m1yeG348JM7rJoeqwvwEoa76b3YVKg26eljG7XWBLI6duZzdnbm4C3WukSTmrcnXjeI7ExpSvJzS18pmVf7+we8/vobPPvMc1ibVacnhrmCDXte8pZuzE/5PBgWGL6DgXRCcoTGoCTKWB1M0SNvZZZ7EfNbTRFZunJgMPTdGJS7c58nY6zKAE/aW0MfZsBj8OrL57lRa/RdvC70Rb6uDGD0EMqV5kWwQj2qTovWKuSNFeHehrossM7RdC1t19E2Hb219J2l7wNLJGM9FEj6oVcGE8IUCxR921IUBZcvH3Dh9pzT1Yrpzj7+wPD4177Ge3/yb6Xwr92u8H/mGvTRU6MCcx5xQkh4f3aPfG/ZNNSP9dhNg+sY6KTPYtu8FxauoLNvyo7Na/NnaqXxfcfR/Qfs3Lv/6PfMji+UDL4pkFIDvQxYWZYURTHqkE3BGI9NFJvf95FIUD4lX3g5kMiZq3KB1fd9qsGwORmi9e87f/odfuPv/AZf/+WvUZU1H334Cbdvf0pdaN564y0cit5Ba3t657BIKEcZCvVFS29cBHA+Xi8CK0kO3maRi+9HOjeyF1mP1FxIeSouKY/K52JliEmNiDVWRE6VkQnCJvZhDFuJwi6Macq1SMIoJlMPDsM0QRGQpBiHEMR3SQI0HLIxx8/FojB4OTJhnFs2Qr/qoLwP9pRhkQ00tDnOCdbG2N/Kp7IJm8cw90A5FfK9VUqmzzFUGi7vafs+KOexT0K/qPPKU/oXro9K3vDucYzkY+cjOM/mRwScasg7iKEged+PhIx34h7WkjAnBf6koKLKmLfiutFaByA7jGmsMh+BQIz1B2itpetanPP0bUPXrmmataxN54Tm1NmQryEV4r3zmMJgTBGs+5JTcHa24Pj4mLOzM7FUtS3dYkm3bpOHIHmvggtawl/EkxVDE1Jfu5z5S0Jl0ApfSB0YKcBYYEyRfq/qkiKEzBRFQT2ZhOrrNeV0lmiWi6KgLAqp0VIU6MKMKFmTJ8xolDGSpxXkTppQOq6iwVAAwcuAkjwfJdZg4wcSDb/hQVQE2YBkG+l6glOap559njfeeIt2uaS3ip3dQ6zPqu6OJIj8P8oPU5TEApw9nujql3wajTYFRVHR9x7TQ9v0gd0tynlDu25ZrRrsfCbh62q8/DaVofjZ4eEhr7zyCs8+++x47YwA4XC+UE8GYBti/U+Pz/i3/+bf8dorr/Lh+++wWJyl8LS4hvTIGKJGa0026GOO7t/jk48+oG1XfO2bX+fCxUN5D2XD/JXt1PYWpQx9340Viez4Il6EbQrMtuu35UR+0edtXv+Z120oJXEvj8qMU54PP7mNNxW5l2yb52LTcn3uewiKqozV9evC/iiEB5qMa4J8b91mkJR7PxpwSb6IEy+B1pycnjKf7dB1Mp4xR9RBIAoYFPOcFCSG7m7OUWl3DO0EEjFBDkxkjhslcj8Citg/xhjxcAYDRK6c5kVxN403oXuSLIx9FOnqfTp3ACRRrox6a8t63aaURgNiOi/sd0qBUVAaI6GYahzurrRQ+W4zPOuwNuMSVUrCnYzRFKWh7kq6sqPrLM26o9UdbdfT9RL+Go2ug46osEqHvWkIDcb3eOV5+eVn+bO/+CGTuuLB8pRrL77A7Tdeo/3gFprm3Dzb1h+jfsrOj20YAPE4OiJf71EHz8Hh8JwBuG96J0aMhAyAIw7IowwU2/Vv2aoKr/C9ZWe+c+77bcfnBhqxIbly3rYtIDkCmy+0GeKUKzD5Sz3qZT5LoOZtic+Jn+Xn930/hBFsCK/Ypjh4v/mbf5eT41PatmVnPufu3buURcmVyxeZzWcs1g29h365xHUtTvmkMIjyJZbPoiiS0rg56DGGm4wbeqhXAGOlefBCeI882w+hUoNMVRtAA7FKhPwJm+VC5Mq3cz4xBg2xgkP4UmRiGUASRFHjYzXoEBseEbLYwTc21gRecggkh42ehUAvGUHC+PJMIVexDWHD8nogO4lgIinkg7ItwDTeO5Tc8X6oTDrquzAnxXydcsNjv8SezllDPIGe2UdVMQo/6Z9NdqJcUGwKjU2A0IcEe6WG8LQctCVL1OjepHNkfclGZHzMCRlvQF3bYrs2MXcoJAfAWsk1aFbrlITctm1KVvbW0jXr5HWINRTatmW9WuJsRx9DjBgU4AxOpnFKc5AhRDKvCJ3eJWyqQ3ytrO9yUqfCilJlfTAsiOVdFIR1s+bDDz7k9PQU5x1XL1/jm9/6JhcOD9nb28ME0GCKgp3dPXZ2dlgul5yeniZFVpuCPlKihveIxgWHx5tMyPuQVxV+hoEMm+mYVEAwgyi8eTE1rcxAxas1GlmD2hhctmnE81GhRoaG0lRUrWXPGx5/4mnee/stTFHLPArx3QHdDLLYR5kscsT2Mpc639HZnkJrCq2oi4JedexMZ1w4vMiH73+Mcz55L2wvDFCFMRhdsDhb0B/soUP/uCQTtieeag27u7sS8tb3o3O8g9wDmmQVnr7vJNSt7Tl9eMZffe+vee/t9/j0o09ZrFb0QX6qQnLbiEqdHgwJeb6PAqpC5PvDB3d5+63Xeerpx9nbn3Hp8iU623N8fBry5lpmsxl1NU0A9/Mc+hGAJK6beGwqBZsKxX/K8VnK4qPOkweeBzUqGGMUiqOzE45OzkCFsMAYNsggezb37HzPyZ4MDEZFh+XwwoEQHLgWawtSGGp2X9jeJ8O9twMNIR6QtX716lU++fhjHn/8ycGAhQpAPsizbA/EDYAhvUdU3BMgkR5IymYONDKdQQFOSaREHhIZf8+NtdaGGjiRpECZUT8Mv6toyxoDDR081BGAMIR3xbYMaIaxZTx96QZZIhcOlPKhHX3fJzlTaoUvLNYWSeGOIYixnuMIfCRdMXqlBoAFWV5sVYa6XY6qrOi6nlXTsm775AmP8kQMEwplTUAwDm0FBHmvcUWLLjRff+Em3//xT/jKt77FrTff4qVf+7v88M6/wtj2/Lr4BYdiMGpopSL/y9Z5mhvM4/zfJFDKj032Ve99ph8OlP1iSHZ4PU49SG3M94PN9nuHQbE732Fv5z8z0Oi7PiQFQpyskW0jD1HKG5le9DOEV75YhpfdRGPjDTmGCMSFaq0dVY3OnzdUtZYNNSq70RNjTMGNx26gPNx6931effUVjC756U9+ynPPPcfFCwdY59nb30cXJbt9zxtvvsl0vkOzatK7OucwoVp1HNRNSw8Edqa8CFDmMYhAI71fFoPuQrjGYB2IahobxXYHa0Q8K1c8pU9CuFOY7zFhNApSoQsMQjUAkGGMQlKxBh1zCXym7GTJYvl4xj6Jv3tIG9UgwAmW53TqEAecT/rwbiqE8eRjvpmQlWL242LygOEck0c8v/cy3+J1Eduk2hHhDfyGZBgpQbmAUCQq2tg+CGFRHvG9M14H8RmKIeY71v/wIbfAOUfXdyFh3A73DhuIy/IEemtZr5b4pqFrGpYrCf1ru5aubSWsqBWWI+cdOI/tLK6XmiLWdXR95oVzsf1eEuJGoYw+ACPpr0iZrALLjFIqrBPxBBRlSVWWaKMpCgEJVV1ThMrtVVUxnU4pyxIKHXj2CynAGPIHilK8CDqsPQkvHJiuPB6vNV3Xc//BA8q9XX7413+F8prJzpybzz7LweFBoIFUUuixKNGmoihLdO9weiUGDWdDUqEongmUhnfXSoMxQT6qJB+9jzBcgckUyyg/MuODGD9kHnpcCmXySPikUuLqtz6jC/fjddL3Fq8N4uQqwJR85evf5OpjT3D92jVW6xZTmMTkAjH0R+P9sKlHud61HbowUhNXiaV1UhgOdueYQvHMM0/x3jvvsFq3rJYN67VYEa2zlKXCFJqzxZnQgU+qME8yetRcEQvrzoYQRKUUq9VKQlmjcmQDoPZw9PCI09NTbN9hCg1G+m5S1uzs1Dzx5HWuXrrI++++xw9/8gPu379HlzHxFUVBVVZUwZMl3qya6XRKVVVUheH6lYtcuXaVq9ev87d+429TTWvu3r/Pwf4hzmmqcodm3XDv7nu8+84tvvKVr0RxvuWIm/jwiexTKjt/kJ15CImzIR8pheDmd2Usqzfi0ofDZ/8ff5eUynimH86NSl562sb947UCvA0ff3Kb3lp8jIbwwS3nB+IWvA81DdS4r/xgtIkfuBAJsDOvmNQ1bdugnIRDRhINkZHbdYl0t7jfZthusCiHZ1nJv9zZ2eOVW69y5ep1QEILbbhlMvDEfvJCDxv3i9SuuO9kz5G6Tj7tdYOBiDQ3tNaBijYqj7DJIBXlG8E7PEiigZEpPTdtsuNQrahjOYS1yQ1KQ7iXD7rTow+VvZuES4YdTGlM8KArpShCTqsYsjwtHm0HJtMEKqxPfTCAkPCPYOzWsRBrpmBreWYkwykKR2UriqqkaHqaphCm1IZAletEnnsLRpQb6x0dHq8VunGUwOULu1y7uMdbr/2MSxevUZa7XHjqaU7fOEVboVK3oW6O9uocCI/sT9JPNs1362yg5A2gTftz/ZzLxLSuo5FGxfkT5Ef4IOlbCtC5JzE8J/z0PtAMZwbRTfyS+z9AQtucc0wnNZcvXPiMWTEcX8CjIS5w5yw6rFDFQFEXvQM5Yh0sqoPyvAlCcq/C5usNAjmztI8AybCZ5wpj/uw4OcXSELrNeUIWF9N6yqQowcOXX36Jo6MjLl455Gtf/woApjYsmhV3Hz6QWFAHqrfY9RqTxc/HhRI9GtY7tHdjBOlcABohrtdGzqFoRdApxt7amKMhh/P9kGQuFw2TM0248QYif4z72qffRVmP4VFiCY3Kusf4uGnoUE8geDkUOKQ/LYPgI71JbEGYvC5uMIPSQAB5QxsdkcM8Kj2jI8npgT0oF95JoKoBBOhAb6m1GXjPQ3t71w+LnkHAewWt9wloKC/30cFaYxnCcnwMOcrm2rjNfujbLK8meqn6vse2Ha4VsNC0TUho6+naFtf3uFYIDdbr4DXoLW3XYvsWa4UG1fvAgGIdqShhBAi9zRjFLKrrcK6n8xZLsIJJXBbOaHwARYUq0A4KL2/eVZnrXivKqkjhRMZoqqpmMqlD2FEp+QdViS+EBjUWXzRachgKY4LLXEgY0vdGEm/XbZfJBB/YhzqapgvzQ8CFD5YpAFOZxI+eA/lo5fKmpMewsAU3ntK8+fM3sOsloJnMdkAV1NMpdVWn8IjlqqM7XUq+gypBS8Kl63uUEo/hIN8CSNAFoEcKoyIm3YU1oxR93Ii8eDqcV2gjnPHOKrQuQhFHqditlfDKKxWNEyHPyguFbVRUnbOhTxTOFhLu2bV01tEVE/Yef4qmMDw4WeC9TwYa75z8rjVKS0iXMYN1TBuDcxrjC7SBQlsK7Xns+iW+9Y1fwijPi8/f5L/77/41R2cty2VH0zla27NTaUzjWXUNZ+0aMymJ1m2jMmIJGO0R3slc3Nvf58HDh1y+fHkwLjkPTvHe2+/z0x/9lK98+WVuPvk4+3tzqpnBlCYRddy99zG//0/+IbbrObp/zNH9h3S95GZEb7gUZoviSGRjXdfSJtvjfce66Tg9XfLTH/2M08WaO/fucefOQ5Se0ttOcriUo7Mde/uXePzxx/C+TzJv2A9JMf6ZuBBlAIVnkBcyt/ITRUlki6U+etXPyc/4gPEHSbkde1PGyn2kwc4Bs7Qr0gTHtgXQqBSBeJN7Dx6ijcL6XsIUdSgo6qJVV64fwOagOOVNiY+RZ/ZcOjzEBTY3DTjXJYNZbkkHhVCYesjkfHyUU5zbS0LPYNCsW0tRzVk2lrNlgykKHNCH0NFk4AshzspbtLICRhw4r7AwAnyDDjOEVUUFUpqukvJclprSMCpAGjvIOUdPln/noqEweBBSoTwxOvkwB5yTPS2Cm+FwWDwtdoCSgdrNeS8U4WEjzq3m0auh0xTzeGPACcuTMToYJYXSXBuNLgu8N0nH6UN0QB8qlqsQ1S3AVTy9JiS6g6dQFmMcPjMuawLjZ6QiV4M32xgvOSxVRVEXmPUaXSjW6zVd56CTfVAh4NMpMaz7QmMUaN2z1iXPvfgif/qnf0G/09J4zxPf/CV+/MEbTE4WGO/ojMNqzcRqsEP4Wjb44llHB++2wzvx0MW1Fj28aS5ACm0TjZuR3CDIDR0MN3hFhDTRSOpDh/qo8ajoVfQhL82g/cCwmOtEEaukOaEU1ih6D91qhWpbPs/xuYHGZvxnUrAZh4NsHnER5MnQ8RjcfoM3ZNshFrp+1Ib8eXnsWtxcNt2xMRwgb4dzjqosaZoGrYTe8cqVK4LWplNB56ZgPp8KMjcFx0cngX7UJhAjwkOEiLUutJVgXYr1A2SRC12dKAQuFXwBEG77KHzy5G3v5Trrx9b6/Gfsp/P9OGbkyMFfunYD+Am6DRu+VsECEyfokMQGpPoHeV/nindMsFUqPicsiI2254pGfljvUwxsLpTjPj0I7QE6yOJQSSmL9J/JEqCyhcgAYkC2yPCS4D3WebqwqbVdkwqfxSTS+Ht0ycZ/sTia7ToIHogYDhTP79uWvgmu3GRdsdjepmJqWoV8BgYFqMdK6F6oeJrGPryFgN6hZka0/pSTEq1LqtAXtu9ZHp9i245eew4vXuT6408wn+8wrSfszXeZTmeoWlOEkCQB75KIN7izxcIaLSQRR1q1UaNBK2wvFKKz2Yz5bD7kToV7llVF29tQ+0GU5rKeSI7UqsMjtR0EDIApK5x1qMDIVJgCbaTidazt0lthB+mdp6prDg4vcOXadT56/z2sMqw7h1Udq84CZ7ETQZcpyd1rQxfZsTwoVSSdTpJUc4KEMeXfQIW7QQyQ1gp4F7wYDHDdBtYqrZwk7blx0p730DlACwjQSpJl8eK96WxLVdX0TqPMhDLkLpRFwawwkmNiimAsGJK7lRLwokLCKUGhMboQLxKOysBsUjCrawywM53z67/+baazXf4v/82/YL1a0azXyZgymUxZr1csVyvm06mAmACSoxFmULZgUIR7Ll68xKeffsrly1eSLOv7Dq0K/uQ73+GH3/8B3/uLv2A+rajrkr2DC1y4dIn9/X3KouCdd9/lo1sPwENBIYC9bWhbWbsAq9WSvhdmMVnbNtU0MVpWUtv2NF0PSsBY07bcu3ufalJJDYOyoJ7W1JOSx29c4/q1K6I7KxhoQX1aH/luqTJD0fjbDJB48H5QROK6T7LSbbI6jv5ifAxAQ20JgRra4dKl1rqsLY6cRjYphkr2m9OzU1arFdFYSFKgB+vqNgNNtNKO9rXQEoUkR+/v7bFar/CuEwXLyR48ysdI75RZ7+N9PaBVCiseKfnheRqVwjbruubh0RF7e3t0ziWCBAjDGsM+3dCnnsAAGLCf9+f1pG1G02gcNUZqzHiUAH+lUl6ieBwi69l4/xN9S8KBIoiKpDPR26O83gI0JHqgxbKxMQrw8qTIi2S8jX0gI5N21N7l80uiCpzyWRSEJdbLiAbk+DD5PRYNHPrE2n7w+muPs8Jalbwcyoe/GRmYU3ilUpSlRuuasjBUZUFZGNbrNWsaXB+IQfB4FE4pWathz2ppmUxmvPjiC7z+xltcuXKd+eULXPrSs9z/8c+YtZraKTof1kgqCpjprFlfe++y9f7ZR/Rmq2yObo5dHl48DrUkG+vzz1OQwjvHnk3SvUZGBi9zSCvF8fEx3X9uoLGZ0xDDpaIrZ1PBzBu+2SnxBeKE2FxwSQBmC2+E7raAlfjsvLNH4TRerIT59VqLNVZlIRaRKk1isQ0PHj5E6WMRHg7W6xZlxBUYEynjoAASk44IAWHIUGmQXYhXdH6oOxEtDd6H5DI/gLNoKZVq0D4pkcnydq7PB+G6eeR9nPdL1pHxRBFqUTr64fqBlSKbyMkyJX9F9gOlBsCUNWIEekabaSy0Eydz9o0oy0PMOt4HViPJO0gCy/vEh++dT+ERXSt0pF3XSRJoK5WMu7ZLFn/xAPQoL0CgCzHm1jr6rpMQo3YtoCPSn1qbhGQfnpnn3PhoMUju7SFkSxHmfpiP2phUuV1rTVFqlK6Sl6yu65CcaHAGymkd8hGqFP5RhETkIktsFuUxVIY1JjBFOWzXs3h4zNuvvc4br7wKHi5cusw3v/2rFJMabUpM4GJPBvqRBTbtQjj84P6N80+BIQBRLUnNZVmyXjdU0ymmmqCKChcUaBy4Zk1/umLVNKxWKwmXQnG6WIf5J/d2vcV3UhMihk/ZztH2Hd63Az1zPi+VECoYXUBZ89SzX+Lh0SmHl6/TOEW77oN3NoYPOTwdUVGKMk9+V2DJ5p0d7Lq+x2dFH1FZiAii0KdwRFRQtL3UWO9bisKkDVTWabDK6qz6tHMSNkDwNBUVBNkctTJTFKAdSosiaZQO/xRVUVAWPo2JMZK8Pp3WTCc1BtnUJXxtksJBPR5voNCG+WzC/u4O06oCD13r8Di+9OILPP7EDW599Amr5QLXS0hHXU8wpmS5XNHt9ihVhvEZrHjnDRbQ95a9vX3eeOPNoKwFORrAxnvvvcftO3cwSjEpNfv7u7z6xjtobZhOp4Di7OyUv/zeX4sCF5Us51MeUhyHSGEavYRR3khNEiNzyDkBD1phvaVrWwqjMIUR1rCqZP9gn7t3PpXwxTAHhldTyegy2hWjzPMxV2c0hYbT3HnZ/p9ybLPkbzsrOilGe2rYGjYbmhQh5bj34L6ERKXinDEYNL7T2Go7eubGOfK79E9dVSilaNsOZ8Wzq1UZHGQDWI0ELTGsN+4bUZB5/Kh+0Oi5EKzqQmKxt7vP/XsPqKoJSiuR9X6IfXc2UHN7g3daikMqh8diVfCCO5+I9jbBRjzynLOiKIIHwCC+BLFI91mUg9Ym894O+6CN4ccRaCTQ5YcIAz/28ADBy5PPy/hb8KoingnbixfChoJ5OCWW+cxYIAnqCm3EMBX3qCFn1gIu7IfRaK1iq9HakfIqgx4YQ6VcMJypPuZ0xNwVqSUSCTQkxGoInzbR4FaYEdgwSrNe90nv817uK3whFqs0Wjtc3/P4jcf48MMPOTl5yLKCx375K9x5+1388YLK9igFvZH8OOMGnXTzkBw5R2RqfNQxeHfPRwON7zf25OSHBJuddwTk527q4ZtG6dFzvceHnKBN48ajji/k0ciTTvOGxWSoXOnNwUDeCflLxO82UZh8NYCGrusSyNnsnDwxJh/UHEnq6LLdAC2i0AktGpmi6iFYBKDpW1Aabz1db7FW+OtTjOxIeQ/KeA8ocR/n7xaLdznvRgMUrS+ywcm751YfFza3qIjH+TL0ZwYENvp52yGbhT/Hmy0bawgN2nIf8SiohMR9ACWknyC4YvDSRK+NhCINyXFAqiYt8YVDDoKz0oa+7/GdhBjZvqdpWrpeqiWfnp3Rrxv6tgsu0C4lKztraVMxn34UQuS9w4cEZe8G97VHQFEXYn5RwVIdWIxkj1JJkdNpLkKsbWGMWIm1GjYLXcq/CBaKkMdTVhV1XQUq1DKFHBWFhB/pmHcQLMo6sIzEeG2xXkdQ4+IwxohAeYXEgCahJr2XAIcSsWJMpzvYHt577wP6rqGsKqrpFF8UUBR4XWBRFGbMGCMhJ0XYIGKwWqjfQpa3ECwfsvlZvAVd1Kw7x7JdcnS6EoUtUh07iZdFabQuaXohenA2UB0G4E2SD+KiBvF65UaHtKmiwBuss3Sul1oXbcfFazf4zb93FTOrOTpdZ9N4YCKJin1YNAEcJlUpXRPXR1kWiGFzSNyMY0WwbJbGoAqVaF9dYI8qjIe44WqF0TmBRaCJzQwzIBtnbQzKSwhUVQkwreuaqioxJUKnW5bUZcXOdE5VlkxqgytkzRdFVADCxHYenfIfsnBVRPnufRu+U6wXSxYnZ+CVAHnbMZ3tcOXqJV594w2Wi2XI9fGoUjzCzbqh6yRkSRMDbgY5NShNQ78aU4R6F12Scy7InDjfm7ZhNt3hxZde5Mc//Qn37t3l5FTeablaUZUVzlkMJjHsxPCsuAlLd2cGHekRlFfgglcUAQJeq6RolaaAVqHWGmU0p4tTfuf3fgdHyKkJ8yeGW8YjOgREtOtUSwalkicwgo/thyf/RmX/T9/GJTDKp0gYL1lL0zUb4MNnd8x/l/sMOW7pHl6W5NHpiXgWURgMXonSn/piw+glf/g09iqFkWRtdp7ZdBrq3ViUl5Knvm9HOkX+Hh6VPNkRzEWJFdXxbQnjOvuorid88MGHHBwcYsoCqyFSIWNDCKO1cldf0LsecFjf4ZRL+VeKgRgnB265IaOqqrRHaKNF/qsgv103yFal8K1NOSC5gS4yVeaskfE7n4Ww+6CvDF4k8MokmWx7S9OshdxhuWS9WLBcLWnWDU3bpHP6rsfbsbF50LFUCq+PYKMsSyaTCdNpzWw2YWdnh+l0ymw2C8YBMSIoJfueeJU1NqydXgsQ0MHjqo1GO4dxGm0FnBXOh/7TSY4X2R5WGo2pa0wwghnToLVnvXaAw3uJjOl6mS8agzU9VVHw8ksv8Bff/R7Tw12qw0MuPv8cJz/6GabtMVrTl8Fg2J+v6B5/j3kRo+m/BZTkBvOob25bO+c8g5nuFiu+p3XBdmCRpwFsklOMIpKCnJpNp4EQ6hcfXzh0Kgr6GLPt/CCoNxu0DSFtdsqjlOH885Q47ceTOU+gzb0UMUQFBv7hwuiRIp5bKFGyOPtgHZDBEUWgTzScsR+kAJVsQMOGGIV3sqx3Fueisir37XtJjnTBvRY3vKiMxzyS2CZR0kJ/KDKO5dxrMFB5po0n7+e4eW7p5+QyT88I3ik3xOuhxI2c7uXHMaUxTyWG+igr/RiLm/UxVKhZ0zVLAQsh3CgKsd52SQD2fcdyuWK1WrJarVG9xfc25R3EsCTb9/jepefmIDeOAWqou1EYIxWLtRJ2mdgHQXFWIIXYXIdDkv8n0yn1pGYSqiNXof5BzEmIQrMoSrFohmRmqZwcEtK0xpUh5j3MKeJaUFFZjXNa5qMxGmUKce2HpOC+73FBWJVK45XBuZC8jUkaQASkuTfQeU9VGAxauMTD2K37BXsXLzHd22dxeoQqS6rJFGc0yog3QSGJnfm6EQ1lSMSLc8H6aLWLir5LQAOlCKzIYXOUuS2hB+KlkLGLYxO9RQMgz/sq36ydG6r0OueSF0W8WT1aVSE8rZVcJ+vxTqFUAas+UdFKHLQh1qiI1aS1llyTyCKmgDJ4M621VMHKqrUKAzBYJr0X1iVtJA62MpH/XgePU0FVldQThUJCCspSQshSzQGQ4nh1RVHE0FDDdDJhWgQ++kLumSzIyoMXhafvhRRAaw22w9uOPoR6dY1PCmmSc5ZRQq0PJmyHxyvJUxPbjBbjaAwJxdJ7xaXLF1k3C5qV0BH3rcVPoCgquvWK1WotXgJFyAAbb5Kbe0VhDFVZc3a6lOrA3mGVzI+LgfUJ73jw8CG3PrxF2y1ou7PMGidFF5XSeO3oAev6NFeH57lz7YjeqDh3vQJTlJiylN9LidtXSmLMCwqefOZZvvy1b9D2Mi+jTHbeBQXWp30zid9MPEeigfDEzCIdlh3nZfnmkQwomVwc7q/SmG96wze3CX9eBw/3AMnfyPaZcO2qbaUYrCIY+CLxQcgx2KjcHQ/Zjze93uFSZ9EKJnVF2zXByCEGIO3UIFPl7ExOBPmkSB6qpKv488a54Xk5MFOhYKeABx/yVnTwEPa9UHZ3fYPzLVKHw9I7Sx/ybQRobGf3yXMecgUvXtdbL6DOyZ4fQ5iclfGKgGK4ZiCYycN5fZiDFpeGy4f9vO97mrZjtWw4OztLtOKxhpHve8hoYXPFFC+BU3ni9tAOh3JiwIwMhPH6rpNaFc65ZCiZTCbs7e1xeLjHhQuHzHd2qCopEuqJ4erCjhjlY8wtEzmrMMZijRHSkRhapTUqGBeigbPQCl2WoZ6FwhQKbWC9Eop2az14hVMOb0IYrmq4dPECjz12lVu3b+O15slf+io/fOMtJr2jCEn+m06KEVlS0qdyT+dY5j1KL87nzTaD8rb1ns/vze/zz+Pce5QOn863UJkihAz+YlkEX7BgX9zY44QakPH4vHyxbCKjZKHfOG/zyOnM4ssOdK+bOQA+tSs+I79/VAiilTB+Hz0ksSCeCwvRO09VVaBUSAC3DLGxWngXk3Ivh7VS7ThWCPUouj7S30rF4b4PcdwqUPJmblUVNt1Ug4MYr5hbTskmpxrRxsX31EqFJOWIZhn1SX6+0QM9nLWWLlgMvfcYPG3TpPwE2/ecLc54+OAhp8cnrNYr9vf2uXTpEk0rwmm9WtN2Dev1itVqlQpiNU1L3zW4rkk0qTH+PFrwYhvz3JQcCMJA8QegC01RBUFizCgMxBiDroacgshupJUSq31dBguOCNmmbVmcnfE3P/0b+oUUaXvpK1/lsccfZ7Y7ZzqbYcoSFamLM5CQh7M475JSEJqMc1CowROXhxhFZU7FqRWsLUYXkjitZDsQYD8sVUkk04FNQiw32QILc2awKGkfQmy8gAGrAtNGUVDtzLl47TqnZydUkwnRs+58D06sZz2Z5S3MSxeocJ0dqIKVjqQBDq9UyuVRSo3ySZwD6wdvXRx7UaoHnvoUWgRhrWbKWSaUlZL4ZZkvBWg5yxQlWlcYMw3Wxk6Am9agK5QqKJUOQEPCpqJ73hgdxm3DcqTFEW30kKOVt6M0UOph45xOJxhTSE5KXTCfSAK8MQIU5L1kPidrZLZGRb6JZj8YFWSMvff0vhNWs87j20zJcA4T+tgGj5wNfSmMYTF0S0ChSkYNUZI2vSfRYopWIUmdZAV14d7WWnzTcP36Fbx3LM4WrBYrulaU+rIsWS8XrJZryqKUtavcUK02TeHzhpHZbM7Dhw+5ePGiAEh6Vqs1L730Mt/78++xOD1F4Xnt9dfBW4pA4Sv5RAMhR9P2Yd9ilDsjgH6k7WfUnBYT8ro8EhpTKtC6YOfgAocXDjk4POTaYzd44smnefKpmxT1TAwjMZQy7DFRLjs/WNSHRwZgq0hyZDM30gfmpc91eJKHcfMSH4DOGNRsubV/xB6dWOVyC7YolIvVUt5N6wxIKvEMKSE8yd95+MOF9Ua41/CV0UIRrSHk1cT9TBTZ+K75++FjqJ3P7unDtaS9N52fXW8Yt9EYQ9M0QkIRwZByoDWF1sznc1bNknWzwvnkn09hvJHYZVN/iQaJuLfl+onzUp/J2n4w6kAADj6EKw0MVkCqE2Ez0pL400ZjnmtTMdQmsBCuQz6V60WXif0lJC0OrQuU0lSJ9a9mOp1QlhWzaY1WZF55kzwJ2iiUlve3fY/zAhAWiwXL5ZqzszMWiwWLxYK+7zk6OuLBgwe8/77s29PplN3dXS5fvsylS5eYzWYUtdy37Vsx/Drx+PaFp3AK7QyFBxWKLBYhrEoZmUdE/TXIuLIqmWuoqhBqrJas1xIRIfm40nbRJTR91/DiC8/zyd17rJcNly8dcnDzCZY/e52ZUxhUml/n5jiEaJjBCCwe/cFbnsvcHHQkGL0FSOTHo8DG5rWbe2juccn1xXPgGDE+d6EUxOc5Pj+9re2TkpQUezP2HsTNKV8w20DFpvDcZKPKOyEXZNvOSy8fBF1cJIUp0oLbBCzxvjooFX1Qmnwo5OY0+ELAhBbS+uB5QBYOUREaFr4InmC0CQDA9jYJv5gvIB2gJHEsbgIBHGikLoQ2A3VhAk9BSNi+TwKjbVt6a2nWbQoT6vue9VqUfUGcHbaPlok+E2IO10tSctuIG3S9btI96C3NusF5J5b+rmPVSD0F1/Xn0HeKjx15C4ZxkRwLm+LBTVFQFBOJsdeasqio6poyeAkiExGlwVTiNZjUNdpo6kryE3QRwolifGawOBdFKe7CoBSNLAQqxqH6wNQkHpKzxRkf3r/P8q23UabgwuXLHF6+FACGQZlCgAbZdqTAK1EQvRIrkYGRq1prRcFQ50VYyMLlsWBhPufDBuntME+9B6PMYKXyMg+lcJoneQHCJEzzEk/fO5RWtL0dqPuceIHarqNdNzz/0ks88fjjHBwe8uDBCUVZSRuDMmnxKVQwB4VKFu8I2IvLW4HWtLZPMiEvIuW8wquhirLIBINSBq1ieJgAub63TCYTtBYKWJKMCdah6AXSJiQux/sFOQQYpTBaXkgpL8mVusB7xUQNdXbKAEa1kTj+6VQ8CHH+VqXQ3RZGY7RL18SQN601dQml8cnDpYL88N6jfY9yXbLGdk1DF+SbhLUN3q5kdXViwCBaeV30QIgi1yk9ok8erGkKbFBIvFiXB5YaMFZUQJfdM25+Fg/Ko2ykmo7PFENGJL8gKN8x5Kdve/reMannaKVYLs84W54FT5IN/WxYNR1V01OYEHKoB2U3ZxZUROu+Yn//gAf3H7C3f0DX96hCs1w1HF68yB/+k3/Cd/70Tzg7PWa1WuDaNllpAZRxLJdL8B7bCXiYTiegFX3fhZ6LORqxI0EpEzxIClwIU8FgdIXXNV/9+jf5g3/8j5jsiByz1tF1ltneHqu2CzJxsCbnY5oE5CBKgmrqQMVCrfle6TNl+hHAQOV/D8nAChIjW7osyu/xRUH8ZMYrhhAuNXwYzk0u+PAMje171k2b5L5SKoBauS5vfy5PYosj6B0DHvmjqivZ+9rgnYp7eaxhlIGIeJ04pHJZOihhqSq03yhy5iXMNB5ioKo5Pj5ld28nKYhloXnyyae4duUy165e5PjkhOV6wbrtWK973n7vFnfvP8T7mIs1jEkKvULyCHJlL29T78K6ZfDAJDngB2NjnFPRA+ECsPCIt7EPOYV937NuJfTJRQKSWJ9BFYGUI8web5lOagpjmFSVWP6lhyVkynYoNGenS9puiQ8goq4l71VAjoxsfEZdSbjwpK65ePGQJ554nPl8TlGUgGe1WvHw4RGffPIJ9+7d5ez0lE8/PeP27U/RWrOzs8PFKxd4/InH2d3dFdnZiyGusA5baAoTjLd68OgXXtisJExqkPlS5yiSmxSAAW9QSiIqvHXJY6ucpesE9M0mU5587AZvffAhR8sFz//SL/OTN9/H9iusJPBh0kavklHX+xBGjCTGq7TfuGHehiUS7Y/5wk6fxbHYAAvnQEpcuYP6M6xnNV79ycCrAkNVpo+MgbrkZsyrism05vMcn9+jIS1IsaPWu9HC3QQJMe46dkIuaDfdPpseiA0Alc7d7Mz8O/k9MiGEjgrWFBMYDkSADS6/oiyDFyPkZYT/UIhS40FLbEAo8wbGW4y3YY+V2FOvpMJy7xylqbBth7IWDSnBKLovm6ZJeRrrJrAYhWrh3vtE27dardK5bdvSrdbYrmO9brC2D6FEAVx0vbj6gjCxvU3AQrk+9EmcvT5sflZiR6MSAcmCB0AncaG6NJiyQBeFjL8xVLVO+Qh53kFRllSzebLO1HXNZDKREKM6cFmHBOWyLFNVZVFGh/Ac8faEsQ6AIZ8Dw0SL4yzHZjxk2r59yBUIVkVxnWqUcmAt03KG8wVP3XyW2+++hzEwn88oyhJVlOiyBKVTCBFhruTpjS4oaQqpXD7MURVVONksQj/rEJYnRQvj2pDkOe97vB0S6/PNMW5S+Iw+NwqXEPLjGFjKnPdC4+g9yiq8FQ5zcQ2HRPjOQTXndG0p+g6lBoCAVriQHxGTr5NXCQFWWoWQMC0J52VZ4FAURSjamZKJA92sNkGBjLlT8s+YAqOywkzeY+L8COAlgoxELRwATKU9JnD/yamiJJZFwU4N82mdkuQjYFDeUxsE3FYlZVEMbfUeZcQi3ncdXd+nRNQ41/JDxkloZb3z9K3Ftu1ICdBRuHlG8hCEUjG3cPvsnGgXjlZoHzZvEO+UI7tfJjtzGR3XjsMR2e9GbY+eRaUYzCPg8w0wfuqH+RoVWG+9sP/0jsPdOTvTHZbrJcv1GU2/ou9XFMUEpQs6C+vWYgpJVi+MCetpCANxTkB5ocC7nr2dA95/70Pa3tE7j28cq3VP5+Hml57j8eeeoelaUTqbRtJnw161Wi354z/+Y370wx9ivMcYzx/+4R/y/vvv8+Zbb7FaLun6FvF4be5FHq1LyRMUUwmYgmtPPMEf/NEfUdQVrRtCOIuyEOrobp3Ni7GBy/uQSLwFJHgvfPwp59ue3z83593wx+AFSIY9H8ZSuc1LH3lEg0dURuLf0aOZG/42D4lr79HBuEIApHLdyA7FcELoAj/MLxgMVd6LXHVIeKscQ0jlo0Kr8zbmicr5dUmuMl47AxDzFMowmdacHB0zn8/wSpTEyhQc7s345MO3aRZ3mUxqNIpPb93C1BOuXb3Ivfv3cCGZm/AucfkqrVPC/KiGRNZum4EgG2KlIiHCJsDw3idPhfaiDFo8Td/RdJ1Qo1uXWKi0kqTouqywneTd4WSMqtLg6VFYlLLUhWE2mTKbzanrmp2dudBPFwWz+YSj4we0bct8PpNq0Uq82H0PTWN5cF++n81nnJ6ccvTgiPv3HrJcrQSgJO/FDgcHh3z1qy8xn38TrTV3797l1q1bfPTRRxwfH/Hw9Ij3bn3Azs4ON27c4OrVq8xmM/reUqgQRlpI+CnaYT1YZyTUUTuKQjwekqiuUU4LyEJRlwY1k8gSrWC9agTMBY+8CnqA057nn32Gj25/Stf2HF66ymz/In37Kc61GC2e+zTHI9KORuYA6GX6RQ8SycCYAIZnFOUSl48YYdTIqLnNUJ8eHe7gs+tzo+HomqQ3DddHPUciF6TMBdrjfFyPn318IdapGHOcMwnlcV25MMxzJjat3+OXGj8jKVyZdfKc6ybr0NzL4awbCWW10ZH5keoCeE+hDX3XoYDSSP6F9uIaOjs9o+86zs7OePjgmJOTUyaTKdPJlAf377NarVmvGzrrQGmWqzXr5SoBhnWoaivt1JIt3YWcjWBx6EPYjSgpWSK0k6TxWIjHZ/0T2WpE+bBE+sSYTFmWEsuMlkXXtm1wzyE5BEZhdM2kqsJYDTkrZ6dnnD48Ajzz2YznXvgSs50d6umEyWzGdCJJW5PJJMW3q+iVMUM4SbQEx99VpLRjvPG6EOS8OT8iGveI0i0bj842kXF0t9FmFHM7hIYElh8DRSbEJVlarikLw2PXH6OazPBAUU8pygneaFAmtOM821l0vQ9CJUsw94NSmG/eqcoxDnSY99lQVK/8AAEAAElEQVSGKMJDFPGRguGDFS4wcMVwLbE4xL6LnNwq1cVQwUJRehGmShUY45EchIKirPGFgMnCDIBPh5wFVCkWRCJQGMZXZTS3+U/nPJNQpC8mxw+ywSRAEYWaCTkPhWspQrGpsiyGpPoQ9iggUcY6er2msymzKUwqk5Ip4zwsTIFxEkMck+dFc1HgHcpFYgCp05GUGyCG0iglFrl1ptCMjwHQEubqoCxlMmhD2cwPr9SgXJJZLj3omDK9qbTC4FHzERQM37kR0BjAusy34dn5ZgVkTPrn27qp9Cb5bz22teAsvbVcvHCBk1snrBZL2mZN07aUpRRe7IORxCHyKFJX5u8n/aVw2tC7nvl0yvHpSbhOvrNOCu7ZsAdMJhPZmOtJmCvStt3Di/yjP/qneF3w0+9/F28t9x484J//V/8VXddy69YH3Ll7h/V6kQxDfdexXC3RWrNeN7z99ts8eHhEYUouXb3OP/3n/5yqrlIORpz3ZVmOlNrNMUufuWE+jM4DvPIpW2RzD3uUkQ3AO3VuXIYZZc/Nuc86zrU3208/64g5LfCLzz13qM1snfBx+F9UrB8FuB7V1/n3+ZHHzW8zHEAwDgSFerlchtwmheRhOH72k59yfP8O9+58ymRacenqJRarloNLVzi8dA2jFe26waki3m30jHyc4tpKFdCz/Ioog3KAsQ1oOCdAgrA3dNaybhsJm/Syg5kiyNJgtVY+eItsj6kCpW9l2N87ZH9vl535nPlkh0k5TR6ivmvpbc9yuWZxdkzTWPrec3TvIdbeS0BDqNld0h+bdcN0OuWxa49RVpUYMZWm63tWqyUnJye8/dY7vNKtKauSw8MDLly4yIsvf5lvfOtXWCyX3Lr1AW+8+SbHx0e8fnrK22+9xdWrV3ni8Sc42NtBW4MJhWpNyAFxwWBldexXG1iqJOFeb3q2U+i+pm26wUtkB8/QdFLz7M2bvPrOmxxNpjzzta/w6n+8Q9UKUYsN7KQgxriqKplOp6xPFvRNO1AiK8e4qN54Dsa5wZZ5n4zvmSF2E2xvnr9tnn+RI85bFwDi5zk+N9DYDF2K/6J7OuZIbFrQ4gLYlo+Rd0beOToUjMrvs+kFyT/PN1MdlM2cJWsbUOm6jgcPHrC7u4vrelanCz744AM+/OhDbn96mwcPHtA2DU3XUpUVAH3vKMqK/b0DpnXNJChHH370MUcnJxL/65HEsbYnsvLEPA1AWCrc8K5eBapb70GL5SNaCXVQ9kDCqSJoKIJCWFUVZVVSVVIpuQ7eA9v3YvnxHqs0ppACWUVZoBShiI0UCCtLSTrVIdfBWsu9O3f4wV/+Bc459i4e8PIvfYXZzg7VtEYXJUqJJyJujKGT8fjkDsw6O9Q2gRjvq+K4x7Hx4L0a1UNJG0ToozSGiX8bySnMqVtArOU683p5j/JZKF9cJJkiF4VIWdV85eu/ivdQTHZYND26KERQenFV5+8V8xS0yu4XFE7xnrjIJChWKD8kR8tCdcGKHTdDUo6QrAGTFEBpc6xyHzw+wfMTaXHjPTQD4PPBciZJwhnVrYoKvhH3diFuc7K1ppXkTCgfKV83FrA4DdM8UAz5Qzq0xWTAJY5roQ0FBh9YYyIArirDTj3l4u6EWbCMVXUl8fzGJE8O6VnD2Hu/DMqUxfseZRVYaBuHskNultSjcMOUUUM9oNjO2I9RMfAByKmMj/58RwwyKIZKkd1T5l4EDC7dMx6WDQUpWZQGy1KujA7nqfHn2T1s+jwHVxkbV7zH6N5+I1d3U/Ubr8/oNXDBGOJ6S9M07O/tS0hm13N2esbO7j7z2V6gEu9CYqhUDPfeBxazkI+SnikbcYyXd95JoT0/sPZ7FdnOSF5pTAmB+CD2UVEV/KM//COeuHaV7/3Fn/Pn3/tL/uqHP0pF+URJ6xPtuPNOwiSQgmllJZTIzz3/Ar/6a7/O/sEFSULXQ1hkHOe2bUdjO5JnPhom3GisRAzKODkxV56bP79QKfB6fH+y+ZxTLv+CY3MPf9Tfm4nLw3P/E0CG3OSclTV5ssNneQ7fZpu3/cx1gE0wkffRo4CG8+CV6BNSINWFfDAJCZtN5qxMxU69w8nJQz5YL7l05Tq2bSXUyIUigs7jGId+D/rOYJyLBY/zNn5RoOG9D1ENfZAJUChhRENFIxwyz/uYf6A52Nvl6tULHB4cMp/NxZPbdBwfHXPv4yOaZcPp2Rlt27Jer2mahmYtOR59JyHIve3p2m4wgtEHGS9hklobqqqkKivq6SQkgAvpyu7ODoeHF3jmqafQk4rFasn9+w947Y03efW1N9jb3+PixYtcv/4YL7/0EsfHx/zs5z/ng1sf8NGHH/HxRx9z+cIFnrp5k/3DQ8njLApMX1IWPT6EWFun6ayQwphCagmVhRmNR2Tv8x4Ua9brdTIYxzEqCsOzN5/ivU8/5Lhd8PSLz/Dq979L0bYo39MHY6cYxsRjX5UVq/4E7aKnkeDVkhAqj0/5NrkR3zmHESSS5samnjUK/9uYy48CHtuOXww+ZJ+oQh7s5zm+ENCIwiVfxPnL5b/nL5VbqvP75d+poJCGb1Osbn6t2ujMqMDnStbmIs4FT7w2tvsnP/kJd+/eRXu4d/cuH976gHfeegsFzKYz9vf2uHbtOju7O1RVRddZnJVKxQowrufs7JQLFw4oKuGI10XJ0dEJKyVhT2UlRb+qAAIm0ym60JgQplFFVqOyoJpMqeppqJYsFJWTyVSstFWJKQP1aUpg1SGfo0BYo6UTVus1p6enrFcrYXvq2sT40Pct1vUZYwSUZYXR4XprObhyjWq2w2K5wOuSYjpDVRWqrFFFidKVMPiGRZTGFI/P4ui9i2EdIHQpRQIkRKVUDW45GzZbbaJ70QtSz9aXHxkCVVDk46bgos6eQvdsnijnYsiYGyXHWWtp1mvaruPq40/jPdw/XqFNQyzFqU1IwJa3FO/Jhjchehq8SCdIbVWokHugoutUxVCkgQs8znEdk8UYFH+TA3WjQxhR5hGIAMLX4PUo0T+GL3VaLB+bLCfee/RI+cytyh5DBO6WvHK7xqFtk7wOkaa3LEsKrVMxq7RmVQhr8grXyrrd2d1lvjNld2fOZFpRaAGrw7rtoe+xPcIE4+PIEwB5mDsjPu+geAbFPypZLps8SR6ZME4MAGYYuwEADkCC4ILeLox9Fr4S+ziBBGkFCVwzvI/bBBoRYGTvMXw+eMs8nhiDs6mMutjKTImNb5AMOZnMjB6Q/NXOvWd6F2mTDjyg0VvkevEEXLt6jQf3H9B3Hc1qTds0YgAKa0XkdkHf2/QusSZN6h8FFotBsW5bTFFyenbGZD5LFLkuJJgqk9cdMSR+vghCvMJUE/7ub/8ev/rtX+eTTz/hwYMHHB+fJAuyUgJ4dnbmTCYTlNbMplMODg6pJjVVPUEbKfhnvUcH73fs8lxh3VTQt/6eCbUcQG6Cyc09bTxH8sE6PyejQSH6SH6RorG5Tz9KAd+2pydl5hfUBnjksz/jKs8YNDyqzY8CHLmyBeP3SqQ2W8Hc/5+3/36WJMkTO7GPu0dk5lP1XunuqtZi5M7szmJnsOIOsAPu7AAccXbkncEMv1Acf+V/RN4vpBlxRjsaCOJssSRvNcRidlaM7ulpWdVd8umXKoS784eve4RHZGS+V70N+Ez1y8zwcO1fLdoQz7PZTN53FudECn/z3j1ev3+fYj5nNj8n2zKgDJVXVCGXFsQIfe3sInORBQFPyiQAnXGmTEVqOdL/Lf3crKdSjPNcGPPgQ1fbWvwvneXm9Ru89eZb3Lp5A2cdF+fnHD8/49PzR1ycnjG9mHF+ds7F+RkX0zOm04uGyajKkJfKlkCrfUnxcLueqsH1EqDBNDgr4o4mxO32FqOdHW6/fJe7d+/y7ttvA56j42M+e/Apn336Kdeu7fHyy/f47t/6DX7ze3+bX77/Pj/72c84PDzi6PiEawf7vPX2W1zb38dUNXWeYY2kM8isDsJWjfGWzDqcVY1GI5p+GyO5eGJqhOVy2VnnqizZ2p7w7htv8PGDT9D7O9x441VOTs7InOC/eP9woAwsp5LEUjK36xB6tjWfFnjVpVnjeRi6u62wLVoStBGjNpXLmYkujR7fiXhcu9Y09SrlyowGdM2gYtjW/mAix1dVVRP2sd9GCpBTBiBlYCLTsE6TkUo3GiASpEv9MF1RwxGlApHA+s53vtO8e3DjOvfv38d7z8XpGbasePz5I/zTJ9x96SXq2vL554/Z3dnlzTffoixLnj19xLNnz3n3q1/lO9/9DcaTbbZ3dsSkR49QSgfzj6xJKKOyDGdUQwRE6aE4bom5TCQIIoEZ0G9LwEMn47J3GZ427v4o3+Hm3i3KsmAxvaAKCeok620RElXV1HXZJBsqA+PhtUKPttg7uMWitGTjbXS+hTcjrMrkyLhWqt4B8oiEU0KoBh+DiD6COUkkUoLgO4zfN9JXfIJQolSXLiJpz4yE13TBBK1xfPUxS6jqAOFIcFkn/ifOtU5z4hiuqWs5P3kmiZJ0ADxZZvCNL0GruYtnKZ47bUxHMidWW6ZBwDGggtFGZhW1DYEIxwsB3TAecuCbfBjSUSJ1VzTEm9Ia7XOw4X5WEtfbNEmzHA7xS2mAmVKiYQoJeJp7432wU/UoQrQmFNujvAHAB9d2uL6Xs7O7Q55lZFnemMppaG2uw0SiFkIkfEmiJhWk/bZAedWeBXoAMaXqOs8UwVuk+b2TvV7Zljj27RkKVHbCXiXFy3p1Jf/tO9HUTabim3lLno+upNeHzXLeNfe6P7d1RClERU5DzTbSXd/I8dPlab/b7ow6fQoMHSZW05CFmxCS1po6mqsqqKzF1TXnFxccXN/n5OiIw2fPufPSHZbFMmTZFu1wWUrkILlLNPe4I11W4rviUSzLAqXlb741EdhPEjhDRfiDiFx800S4ivJD7T3ZZJvX3nyb1996p8Nsx7wmjVayWRsl2mYPlXUCvTrCxFWT4O77dH5r9ioZpPPr17xzFnqEf7dEb7DVdz2rTMpgC4PE9oYee8xPHEfKfF1FirqxrlIrTNQQczH0OYXRfbOrVMjZH0cKW0QS32bDzowJgRTgo4cPyDPDZJSDt/hlzXxZUtReWORsQl0V0lLPQaUNnNOlVbrChBbf9WHEENORzjfPc/CSrBNgPptxfnbG9Rv7fOUbX+Pll1+mLktOT874xc9+zunJKSfHZxwdHnJ6csLZ6SnT6ZTFbE5RzKjtsjEbak18PagabQT31rVtYTwAGXgTl7KDK40S/NoIjmPivSyDUcbo5xMmkwl7e3scHBzw5ptv8uYbb5KPJhweHvKLn/+czx8+5NatW7xy/z5f++pX+eDDj/jhj37E8fEpZ+c/4tatW7z2xuvs7e1gjcZUlfhoZIYs02S5IdMOn9H4mnrvO1HARqNRs75l4nfnlaeqCt58+R6HT59yeH7Kva+/y+OfvceW8eJInuy115rR1jbzYok3IT+WF4sLhIILkem6DGmq1evfgSFcEs9w+rnjj5Sco3699HxFpis9V/JMBuO9byxuLisvxGikA+4PKJ18dPDdBLQiUGmkIB0Ovivb6BN06QVLtRvQJv+K7wEddWvaVsz+7ZUQCOPtLT5//IgMja9rnjx9Sj4Z89JLL3F+dsZ8OuUf/pf/kNt37nJ+fsYnnz3gja9+lf/kP/t7vPPuV8RpGKhq8HocVIk2CkgxwVzG+xYxCuHryLQCF5xjgyTbJXMhtMHKARHuOErAlQKfZZKNN8uYjLcpioplsaAsC0Z1mTAaC5ytqYO5gw/mAnVtuX33PvNlzf6NOxQVWO0lSZXzeFdhjGtDtSbI03oaE5FUsgGgHC0ST4gZhxD+6X7FOXrfth8Jbu99UF9GEzvXEJBKtyGCvZczYUyIpKGEgLc6b2waI3MjjICWLLNenP2MURjdEio+hPjrSwu6Gom4N5GLis9Cf2G9RNsSznlz1Nss0kEQTkTa6S3yNmhS5BUxj1JGcrf4KTjJC2KUBie+MTmaHY0A1yz4JzURmzSjUdYgvtV/cj+jE3+ex2hMHuVjJDOLrSwxhZ8g54RASBgNsauyOIRhdTFeeTA1FEJeJpgSVn2m1iXaFagG60Fgevvvp+eq+S22PFRSzWqUvrdtdQn4VYJOmJ9VwrPTQyvgbpgaD5BEltIh2k68R3RyP/TnvTq/yIi3Eb98sgzh81pGQ56rcPBEm6EaE72YRG86nbI12cLWlsePHvHaW69TFhIZb7S11cBea2uEQVQ9YlD6isyiR1EUBXvX9pjN50x2dhqnKK1C34muRvs2whkJ0wEhaIMWgQgBF9gQoQYnfYlipXW+RwV/sCDN88EzQ+B6G1Wxj5OGGI1GOKdax8yheuvKpmcd4U2vXmOq2TOpepH2B/vsCRrDFzRXl3Y2r/Xa7A6s22cKg1Of0XXji5/j/PpmX/16sWiFRIIMe1ZXFePxWM4wPvhWKZZVBXUpUQfJcBoqq6hRmFGGtSWKrm9rK7hVpP5UfWa1by4Vnw8xTg3zEvCgrWuOj49ZzOa89eYb/NZ3v0c2zjg8fM5Pfvhjjg8POTo84vnz55weH3FycsxsNqVYzCjLJbYuIASPqZ0EEelr7aRf1QhyO/jRV612Ebl3zTu07slRgKeCtYZdKtSFaMqfP4bxeMwH7/2Mvb1r3Lp7j69+7eu8+uqrADx58oQnT55w69Yt7t9/lX/8j/9rfvKzn/L+++/z6NEjjk9OeOON17l791bAYRlZnmFqzcgaMmPxtetkL2+SJmr5N5lMminFBNKVq8nI2ELxyo3bvPfJL3n3rdcZ3b2Bv5hjvKKqykYoW2pNNjGoa9tga0kcXFuUg8xLSOU68fGMtHYk9tcx231GYqhspMVZxXpDwv1ug4jpXFGs7TMtV2Y0IrGeMgh9oNpnHrSJ5iVtvG4biIksywJxKZLpmJzOB8mvEAaCQGLUqGhb3YQtJKhpvUepGLXEBeIuxuCXtiKBr6ODjkKiPoRrUBYFn3/6gLIoKJ1nMZ0BYLwn1xnHh4f8+q//Ot/69rcYTSaUVcnr777J3Xv3MaMxF9M5uc7IVCbSdRRWaXKdobNcIsAokfIa30qzHB6tXAi5icQaj5ttRu3aJnsRpZEtKSr/bXI4KIXKhELOlCEfT8iLnOVyybJYYAKjYeyIoixQukJ5E6S0Fa6CW/fe4MZLr7Kzu8PJ+Zx8nGPyZaDwYmK5rJFeRHW5jYAoEFZxj1QrWmyk9JEIEKAYohCFfYl1THyWMJTNxQohUSOga1CViuFSQ3sqOrubRiNEwzC0gE6YjZjNWSTaCo/SQlj6GKY2zRnRENKtil0rHbnIQLOFBIJBYoEKYUWVQ7IyREbJhSSQvokZ34RglIOA955cVWjlyfMsOD/nTCZjtra22NpWTMaGcT5mb3eHPMsZj0aM8xG5cqIz6yC5AKjo2vzKfbPBt4QmDKKYmjmsLSVsIol2sUfURb+OGJ+LKFBQjug0T4i2FnnSyDBHRqAj6SWJzLQCdC1410g/08deGSEcSQCuD7q2tF4kLH07/nhTu4zJqumUs22AgQ7pnxIOREY7jL8Du+U+RCTTQQpKBWfOVQQQCd6hEjUo0np8ryXku+20c1xtLyXCCPDVU1fB9M9JTggbovEVVc316wfs7O5wdnTM/HxKsSioqwo/kZjxJgtCI98GQGiFTWGlIkwHiqoiG405ev6M6zdvkgWc4MJ+RT+NyM73KNOVGTUx7hEcIIFEdNBIRRMgYUacC6F4iIwH8bCGdW1NEVedlVOhXPwu77b8nAgb4vhVb1/SfeqbK6yrtzrfcLs2ECNxDvJCOr+hitAKd1TvUSMlaZkw+dK+222mc5/b8xkr+uZep/OJt6pdk3iGuox+KiBICd3IzKdnpTVFScYfztbOzjbz+ULyDYVh1VZikXnvUV5hPCHISyscUMpLktgEt0eJuffik6NoLTkkj01kXIM5VAxr3dzjSH8JrvPONRHzTGYoy5Knh0e4uuadt9/hnbfeploWfPzRJzx5/Ijnz57y/NkTDg+fcnp2zGx6wXI5p65KqrLEuRq8+LxFza5N7kZA6IllQSt5d9YlZyfZMwU0DJXQej6Vlgc31qwWmklCRosZsK0LlkvN+fkJjx8/5v33fs7e3h5vvfk23/jmN7hx/QYnh4c8e3bIzdu3ePONN3nzrbf4yU9+wicPPuWXv/yAk5MTXn/jNUm2W1fkeYa1GVlmKVXF2Epwkcxk5N6TOYfRjjyTXDyT8Qi8Y6FCSgevqJyndp579+7x0YOPUTrjW7/92zz/6BPK6VSCkFRlyP0Czii2Du4wHm+jnMcuCuZHx9QXZ2RKoesyZJmPxz5qnmlgc7wvbSLMJKJhxKIJbldKoYzuJmEN+EfT4sUG9tAWiZDZu89BHF4uFszPL7hKeeGoU42aOUF4URK1YtPlXBNi0ZjWvAPkkMUMd665NGGqqkX6gmjaz4oYBUjmbm1IfheIOIk1LcRZHcakdII0wuXVWrL91nXNy3fucuvGDU6ePufzh5+xt7fHcjrHWsvO9g6L+RznPd/929/ljXffIhtNRGXvauZlzcWyQOcZxuQYMpS3kiVWaVQ2wnkt0WGi42wiMTRKobVv4GrfoR569EhY3yjZT+tqE4Bxsg/ae/IctB4xyjXbWyMxYyhLCgfkE3RVoXLx46AocWqEH+2hvMMrh88UtffUVS3MmpqglAmJtoIPASFpXmY6QLwxNVIqSLAjk5ImsUsckBNpiDxrJe8RUTQaMNOay8S1a97VbSSseH5VAH558FROTSSac54gmFQybbRqorp4nRB5AX84HMTM7REwWFGvRgLbR8BBkFbgkTjCYqOpnBDgmVJMjGJnnLO3d52dnR22t7fZ3t5iMhmxN1aMc9X460SNijB0kg26WZQGVwe3c+dRyjWMeTO/dqINw5oH8NBK0ySXh4uRN5yncoaqrhuVelSr29qhvQ45S6IZHQFoRolwOCOBsJA1b7U/fdtprxVOpYRDl6BIg0B0CC5vk3rxP+0SdYqnORdt3+HBmtImfhNSwJlkXK6blm2d5DqFp5vs4vuE4t9E+j3I1NCPjZMQ5SpqTn2LBPGBoFJQK2rv8FpMRG/dvsOnv/wF09NzinmBrSqREGuPtwIbPD6EEm8zhDfamgAWo/9KPhmzWAZhRxQsRGfbhG9z+PVJ4ZJ6Ppzldp5R+9xg1cZETvk2aEDD+NMKMWJ7w3bLCYwOggxJFtbWiM700kc3eWB6FlVkVOJ+pFPr7WOXKY2a3stLh+EeOHNpX32BRXjYwPTmGc0qreIzkjWnPW/9kjI0XQZCNTA3vSOt8DMdc8tYKBWZ+77jfMRdSugNDzhHlucUdSUwUioKzElmZsOy+eAHqBAiS8JXt3g5XVPX5HrqOtNHvyffbEWgncI/FZK8GS15PkTT7Xny6AlnF2d85zvf4fXXXuf48Igf/fVf8flnn/H86TPOjk54/uwJF9NTFsszymqBcxW2rtFkYkob8J9CgjQI7xiMMX3LEBOj3oXIeO0G0dl/2efezjeXSN6PBLSzItLT2qKdpg50gbbBr0XVLKqC5cUpJ8+f8uO/+gteeullvv2rv8bLr7/BydERx8dH3Ll7l29965u885V3+Pjjj/n0wWd88NEnvPLKPQ4O9vDUlHUt5u1aUXlLXleM8hETPM4ZcpMH86YMrRVbkwxFTll5rFKgMkqtGI/HvHT7DovZgmt37vLnf/YD/GwGtfgYZkYifY53tti+8zK3vvIN9q/dZOQNs2fPePz+T5k++Rx1coyxJWCF5lBKxJ1KElaqsEYNmec9IXhlOON00H6kEw2q1TrLIQy0qNDKWYJnSehxBY2/bNgq8RFWmqqsKOdLrlJeyBk8JeScc40KKf0t/auN6fwWmRX5blFpXoI+4KALKPsalCg9aqQCPXvFvvlUnyhvJLfBPv/g4Dqvv/46O3t7bG/vUJc1XinOZ1Nu1BU3bt1iNNnCmLxx1j4/P0OpDK1qTKZAZ1gvananwGcKlEZM0aPkX5OKUYe0Q+nc131P60e1bl/b5H1L+ObGkBuDD8lyrHPMq5plKdx2WVbUVUU5LgXw+ej8G+amJBycd47cjEU7oFpVbXRgNqp16k/DnaIS8jeONb6bAN6UaZV/unH4XnFw6mWZbezmFXgVw7wG35PGfwO8ygLuaCWXzdkIvFrL2kYk4pNP8tcl77iI6aSDcOMlzKAPCXyUd80/gyPThnyUsbU7YWsy5truDvv71zi4tsfe7ojx2JPFjOCqJQ6Nb+3QpX+PSJ/i/WnPSIeo7khXe8xsj2jv7FMPefsY5trDyGliRK2YXb62tUReqyWBWVnX1Dbk9HC0+T9iorjG9E9uSQSgzkvGVxvrapqcIEP3pSupTC/LMIGSzrVTvffb0Pd1dRwerO5IRNe1tUn6PAQLNtvnD7ez/uHwPESws769/rias+FbrVbUDNy4cYNflhVnZ+cURdFkH+7YHStNTFjWh+N9gkwpFUw8W+3t0DwDrh18ppL/bip9QY9KYE9f0NZpfwMj2JkL3asZ4XT80mqggt+FimdcdV7cpKHo49GrlhepP3TfPMPnPBL2/d/TPtet18YxpJTVC5aIn1bvimpwkxbbVHZ2dpjOZgJgA9xPied+E32h4SYH3SEfjP5apELeCNuzkAcD5zk7O+fhg4e8/fbb/N2/+3c5PT3lL/78z/nkow95/uwJx0fPOT0+Znp+TrFMovQR/eXavTQJ7RZx3DpZS58uS+mPIaFQf/3j2jVzdw7v68SHpYUzWYgCaUzQpJRga8snn3zCg4cP2b95k29/5zu8/c7bPH3yiOfPn3Jw/Tovv3SX23fv8nkwpcpyw9b2pBlvpgOdkXlc7cF6XD5CjVVriqk0WaaZbI3RRlE5cEoCTyhteP2NN/jZT37Ca6/cp8JzMZ/jyjIwGpqtnS2cG7G9fQC7d7G7N9g+uMHL73yTl9/9Kp+/91Me/7sfUR4dgj8DvxBHe6/JkEA6ilX85eP4GBZGDa13uleb9nBwv51YXlTLgs8fPFzbV1peyEejrutOuMpmk0Ks4rIsm89AyNhsOhOI9rkuSFb7jEG6GGlo3JbDGgbyQwxFHF80+UgXNp3H6ckJnz14yGg05j//L/4LPnv4GXd+4w5//v3vUxUFL7/yCrfv3MVZxy/efx/nlUSYUprJ1jY37twly3NwIZkOLkRMEclGY44Tx7ZhjfvSmHWlA3R6DFmfGYsEcONInmVkQDYas7O1hfMeW9fUTVZRLwlugjxR6WBvj0SNMcSENlGK3jr5xsRiaahaFRihNGxmVxrVmqekBGNYERp76f5+K+hI/lLT0IbSa3ACPoQY8lFCpFsJUWQaYnz71UsWmYjQuhJH6TZST5ir90ldkXZpHJNxzt7ONnvbE67tjNnd2WZnZ5etyRajUc54lIuE33syDc6XgVkKiSNVigwVziVnxLdr0qdFhwjdTRLKod/6jEYsishkiiYiDwnyvJfwilVlKcuSoqxYFCVlFZjZ2grjEe6LMqKMRYshiw5rKGNNMgCbxIRsZbQBAA4SDd059YnI7vPASsY+wt8OAPe9dQjmm94jORDseoZgI/H/Bep9kSLLazvIvZXmrmo01o2ry2iEOxRCeFZVxUsv3aWqKi4uzpnP5xTLorHhjhLctN3LzqAxpjFBWIsEN0LX1TbXPevAGug4/6fvXnWf+oy8go5mOy06mKaFNxH386BLUhqnh3Hg0HxedJwpUdzgjw3z6TuZNlJQVvFRnE+fYr0KPBoSvA3t44vem0EBC6qR+EqCVwncMRqNKI6PV3DUunVagRFrNBr9sUSGO/09/RcJy3E2Rivx5fzwlx+QZzn/8B/8A8qy5Af//vt8/PFHPH36iKPDJ1ycnTCdnlEs5zgbgnskuYysdcHkt3v+GwaHVSFOn+Fex2Sv258hJrVdS4f3rTA5vlsUBUZp8iwDFFrVZNmILIO6tjx/+pQ//oPf5y9/8H2+8+u/zttfeZej5085PztFj8cYBeM85/z0jEwbdna2gim0aK5c7fDGSeZzampjUMqjJCqF+OtkmSQSrT21DWa5Dvav32B7dxenNG9+/at8rBXFbMFWljHKM0aTEfNiyfl8wcW8wI9Kxtaxs7XFwRuvcXDnOm/vv8unf/nXPH/6E6bnD9BlibcSst4b09C/QxHYOsLAS+jHfukzsUNCnqgs0Ij/p68d58cnV2r/yoyGCTkWsixrnK+aNO6uDW2W1pEzvHr4hFvuOhWlk4mf+8yHUqpR6cb++uPoMxyRC+5vTMN4OEdRlhw+P0Ypw97eAeez96mfPkPnI16+fZvJ9jYmG3F2MePkfCbZNZ3DZDnbk23u3XmZEeLwY5WjcrCoRA3pggN1nIlG9cxzVom5/ud1wLNzgXvf43s6YUSizlXaj9LEQJhlbSZXj6J20SQpStTkZYX4rehkXH2J0lC4wBUglKivrXcNIOufh+DpvLIGzbh9shaKxonY+0ycjKEJDRuZE++rIM1piUodGQi8mDvRAk9BujEOeN/WP/ohBMknnixTknF1lLO3s8Pu9hbXdrfZGefk2jMySpZbiRmgwqN9GRgNB7WnbTGsqUokRD2AEucfibeUgOysuR8mlpq1GficrsMq4Grts1WQ7ikjq5AZzSjPmExylkXJZDJiWVYsi5KiqFgshQFxzlNVkiFdaQPeSoI6Fc3qknm69Lz7NYSa69SR83514qNTs0Ns+s5DIdZlL5Rriad4FtYh2aF1vkwKtQ6h9z/3+1vXlpjttZmIO+/TPXlDhEFfcATBhESpxjykKAq2t7fRWnNxMWU2m1FWZeijTeoY29nkpByFU23481ao3C8pLEoJs6F1SOfU7/uyde0zJP21WUco9wnIZo4JvFTQOWsrZkg9OLlpzJsI78uYlZTw2PTO4FwHzrbU8wH3dP051+HBIcYvPm81Bq250bp9epF1IcVFvl2H7e3tlT76tEsfVqY4UqUC0w1z62tY0vbqumY8HouZslacnhzz4Qcf8ivf+CZvvvEGv3jvPT788EMeffaQw8NnnBw/5/z8mKpcgKvx2JDNWYX8UtE30jT3ft3ZbQUEq5FC09/WruoavDK0lmn9PhOnFFRViYSMl6iR1kpmc51luNpzcnTIH/7+/4+f/PiH/Mb3vstbb7/DfD7n2v4BZVHivGdxPsV4SfTpcNiyRitFrSsqXWK0YblYko9zskwcwo2BPAROQWWYECkLpclHE+69+hpPHj/m/htv8ru/+3uUiyW+qtjZmvD2u++wc22X/d0t7PwUN8mw5RZlqTnY3+Lg4AaT/C55pjn/s2f4fMn89Dl6UWGrmCpgFef36eD0+RAD3Mcfl92LPsyPPlhaKXZ3d9fud1peyHQqSqn7KsD4W57nDRMSnUZ1tmoeJZ79qoNo0mfrCHBpo5UupSr4PhcX34t24ylCjQyRDlysURlVVfPXP/xr7r1yn+/95m+ijebdr30NjWeUj9A6o6wksY3QFxpX1+yMcs4eP+YHf/bvWczmbG9v85VvfIOX33yLAk9lPFYBKng0dIiVYc4xPkt/W4fEIuG57r2Oarcj7xPfCBMoiyYUbahudFtPXlbQeGWESCsqIVIClBpieNpWGg6rqa9RwdWsy6ykZR1S0Mq31IZvxyGzTuycE62DUmB0TfQT8GEcJgtxvZVEnxjlOaPxmDzLMFkmWUSbEKZt7P+W4Yj2sp5RrslzzSjLGI9yMiVEt9EajUU1RGlgsIIWSAPeiVOz9Yo0E3njWB2YI+99+Bv5Dh9XscMIpWsXr+0m5H3Zmnf2lmBWEN9RwTwwmD855TGZRusxbjJmEk31yprlYslsUTBflizKGl/ZJhpaYwGvItHSdEh6SNbhNB+ZxuZedCNXbZr3WkQ5sBzRuI7efUzv9bqoWatjXn32Iki7/8669oSQXW236esKhGn83I8CmO5NWZZcu3YN771oM4qC5WLJfD5na3encbRPBUZp20N9KaVCEi0f/PuGcYTrbVanrXB/UpyzjtFrCEJYgU3x/RQH9cPz9uF2R4jWQ+qRUSPcofbMyzx9CKHsle5ELxs2+1kt64QK/WeXlTjHvl/mpv7S3+TfapuXxf1fN/6hszz07mVrlBL4Ys4Z2wftaUz+FosFUVgXx9KHKf12lVKQBDTx3ndokn5Jz2SfKdna2hLC1ns++fgjzs/O+K3f/C3qsuRP/viPefDpA548/pzTkyecnByxmM+oK4l4ZZRClBYxH1Rcu+AzpxDNcjL2tKSmYH2T9XTsL1KGYLHMd1V7EovRPuQniWaYkoFc1zW6kqiK2kh4+mdPHvH/+Ve/y/3797lx4w7OebIsp64ss9kCax23797mxp2bKJSELlYigN6aTFBG8L/z4uNpXU1dleSjnIP96xidsVgs2NqesLOzzc7ODibTvPnOu/yn/9nf4+L4lHI+4/DwOe/98gO8Udy4+Zjf+Tt/H6pttF2yle1x9+Ye13fHsG+4417hV/Lf4q//aI46n2PUFHwhUePWRI5LGb0hJnbT/U9D2K7bv9T/0YY8YE4r9m9ev9I+v1DUKecc4/F4hSNSSlTl1lrG4zFlWTaDSqWQKXDvTzheun6ouj6QiAgt5a7j2GL99PdNl6HNrQCPHz/hV3/1O+xfP5BrpxXeO/KgySkWJUZnDVHovWeUgak8/8u/+J/56Kc/4/z4BO8cf/4Hf8Tbv/br/Of/+L8hu36TWoFXDofq+CO8CIDvr0mcR8No9J61xTdIK10bkQjbBJjRAh7vJWypvJU01SNGA5HcMHG0iLsvrYCWyfJtA2uZi6aKT0bRtNfaJQoeljom+IJoLSpVY1I/kQxttPg8WCuRE4ITtTGSQDEzhty0fXWZXbAuZFvv+EMolFZkOpPQsUYzyiXLdW4MeRadXC0xHpFrZiH+PHgvz2KENsCFDNdx7s6H/CpePkdi2vuuZC+GL10BGIpg4hQ0iaqLojedxaH7nm5hWq/DEAdTJh0d+EciGfJjRzXK2dmaMFuUXCwKLmYLZouC2rdJHps9DqYM4sy6nknoT7hdI7FDbvfyavfuRYj5/ueUEOyvz6Y2rzquF4UdHSQe1/QLlg4cSWBQehistYxGI7RWLBZzZtMpRVFQViVjt9W9s3RjtfeRYkrU5Fkm5hNb2do1aMJuD4291+6mOTXjYZXP7OOxdNxDTMxgWPjOmBsIHnBEHFecjwzeQpMILLbX9WvZyCv+jcrQPNO/Kawe2hnV3N/NzP5VSsvkbD7JHQaitzCpj+daAjkIdxRCkElwh1WtRfyX0hqdsxz3cGDOQ/NP803Edc/zHKUkhOxf/eVfcvv6Ad/77nd58MmnPPj0U548fsyjzx9xfnbCdPqY5WIGjqApRyLXiVSt0eTHUM0QLRe6eREa+qAfWWzN/IfWf125nCkZ9l+V6KMehQ4MSTCNx5KZEAFLK5QxKK2pqpKPPvyAhx8/BC9mYkZneC+anM8ffMbo2oS93V0m4zGTyYSt0ZjrB9fZv3GTg73rXLt2ja3tCVlI+qcUjEcjtsYThPJxlHWJCskIlTbs7F7j8wefM9aGN954i5fv3+eHP/4Rn3z6kOz7f87f+wf/SM6Lk7bwimrbsfXqLpOjG5id66CO0CyBBVZJQIFN5+WyMrTmaTqBdXVT2KW0onJCz46SsL+bygtoNIQgc06SLMXOjdHUzpLlI7wSB+rRZCK2tC7Ga+86++kQfUl5gn0z4Fp7c6U13obb7XpcWSrR7R1wcSKKAw6S1UCkdAC/D6ZgzqKVprIV460xt+/eBhXCuKmQXM07MpMxysYNwQSBRlaepz//JScPH6LmM3ZzyRpbX8z4xb/7c54/eso/+qf/lFtvvsHSebzWOK8luidJpIDwv03ShI2EYO/wrNQdetUnkqX4fsr4dZB974Cq1HSplyujkdb7RkIXJhn/g1JJ9AMvxhbpkFVSXeEkYkKPwFRBe5AZRZblGJM1sa+zzKCMRQdGIxLVAhw1qqarWSLOz6OaaFDggwQhzr0OxDyBUTNazPKM1myNFKM8C4mAxHRIiGQpLjo+q1SS5EPfrrUBj+cUWqYWj7d1s84O38mILqnZfHM3onZnBaiELNguzDVdb52MNd6ZhuFS3XuWIhmt2t9aYJcwh85LlCEv/hZZZtAZ5FnOaMsw2cqZLDK2JxkXU8PJbMGsqHDWCrNlXRifwoV8JJcx6t3ffWez1wHPoefrpMV9xNevs0J49Ri1deNdR3xd9vmqjEe7ZzQmEioyCesI81TO0ETnIRDPachzEc5IIASN9TX5aIQ2hrJcUixnIaNwyXaIjqO9ZzSeUFYVpS1bbVizx75hyiXEpWWcj3BVjd5iEK41JpkdYrYvRV8ldlOGPc6xEWaRSgtj9l3RMMQzvypdbCW/0VRY3omJOGVMAq/SHDaihbe2TsyRXTP+yrsQZhQhtJxH6xgZqMJ5izHBWkCFFWlgfXhPBQlPEiVPYNrQ/oe9TQQ78t01MDWF6w3sWnM/fAJ74tlpccmq5KmPouL2dXX1Mqd1AQLi7ykj1gob7Ur9KMAhSsLCe1qrll5Rw0TburvfP6ur0bqGTdSkLWGwtYb59IK/+MEP+MbXv871vev8+Ic/4fPPHvL484cSqvbkmMXsAutmAbd2faFUaK8xBW2i+Ml5sS6JwhaYD6VDXhS1OrY+c70uYt7QvPpltW57f9NnNsxLKcHHSulAIYjvH16iYHpXB5yToZWiKkvwoHVGVRV4r9Aqo6pLlvWcxfSCyWTCZDTGGMPzp0/Z2r3G1t4++/v73Lhxg/39a1y7do29vV1yk1MUpeSU0opxviVrZTTTecHXv/VtLuZz3v/5z7n/xqvgar5efo3v/9Vf88uP3ufmD19i//o+3t/hk48/59W7txntjqhNRnb3NntvvMrjD39J7q0knVVGXDYH1rRhSNP1dK4Je9zSFKtrHu+hC3Xk6Ic7s2Z/jAJblYyzLmO6rlyZ0dDaNKZTKbIXQkgWV3sfkh3JX4+oHa1NVawCrH0g6OIRUWFyDXGCauIxey9+HQqFJWZ+ts3h7iBcEpOFBPBppZtEciLNd40a3XvH3sEu+VhUapmJITZlXt77xm6/oZsVmGzEs8dPYFGQeS+cgzFoD95aTh484P/xf/k/81/+k/+Ot7/9bZZOVLLKhzwR+EZK6yEQRH0GY3UvOoAjlZq0NdpWVPOfZo1iu2uBYtK2PB9QkQdE0z3ZviFgNN2D7ZO6EeDHJ7pBXr7dw/BUK884U+H8Sd4IE5CyURaj25jk6Rhr5QNBHpALcZUdjRAnWRORiChMjFsIeG+pfS0EFQpLyOCpJHndKM8Yj0ZkmWacwShPgh8oYVesl1VoQzi3BFuL7IZ8i0QTEgmWFvGB83XHfKIL3FvNRwepA9jWv6Szz4jfTUswBIYscoCqjwTbc2l0cnbsqtYg/i6/SchbDOhcMSIjH+USsndni92tEZPtCSfTBbPZjMWixnoJkR2MJWkTI6oVKU4q5W36jgzUFRn3db8PMSgvxvBsRrJwdanU0Hg2lSHBg0r3u/fs8j4FZjU0lGrzWIjkVuGdZntnl62dbc7OjlnMLyjLQvxyvMdbxzgz3Ll1kweffS7JTKP5UByG0o15pGhODZN8RLUsUNeEQRpK0Kq1as5/u0/tXqXfpX4bHS+9i5EBSNuOex+15Wmwk1gvfre2NfFN4W5dS24CyUdTU1Vl02/EW6geXAhayEbIYx1C/mmUV2RKBH5aB8dWY3AeamclvUzw820YsQQWE5mogT3X6Sa3s+zA77SkcLz7eyRhuoKJvhBxtURzv96v6XiSsbT3f1US3h3z6hib7yt4KmiOlaIoJQy8TvY9hd0rYwvfY06bDlHYRdJNSa07lILtyQRjDMeHh/y7f/tv+dt/+3u4yvKXP/gLnjx6xOHhM46OHjO7OGW5vMC5aH6amP1F5ggP3jZnLIWjUajVWZOwTs66Tt0U9vUZj/7+9+/O1UpKC/XeCf4kHsLZTaKMKrkrLjD13tVYZ8lzj9EjUFAHBgQFjlrgSOlwdYVyDh/M2gpjOJ9O4fkztJZktaPRiJ2dHXZ3dzk4OOD6wQHX9q9x/foNrl27xvb2tgREMQrynF/73m/w0qv3ePnmDb7y+uv8X/+H/4E3Xn2ZX3z8CafHz1jMLjg/PWepDL4yHOzsclQu2L17h73X7qH3tqimHovDVQ5nWwFGur4+0Zi6nlVQzFVCf6/75zXUaY5LAhPSO6gISVGt4/T54ZV284WcwVPA3Uh5Q0jDsixXCCatNVVVdQ5lA8zxIbmVHG2dquZklkShjCe58Kxe5DguMblwqCDBqZ1tGAuttBy+QPQ5ZwPAtuAkooRzThgLF5ez4e86fTWfnWN6fsbOZMLSi12yVgbnJd5/7hT26ITf/b/9M/7e/2bB13/ze5TeC2ca2wi+G5qAR9LISWuikgRqPqnfq+f7la9WriIV7de7jABr625Sl/vAPYXDrMRXZ5TnjHPFZCTHNEr9YtHKNDsk3HgbctYKSzo8gZiWPZmDSNSgqOMDGY/DN9JIpUSbl+fi6D3OJRmeMYqRSS9xZAbjnCPD4Ihx91tCyDXPUuIoSuHjM5DzEO9Lete6jEYE9AMIX8VgCi1AicWQImIVaBoVqcjO8rVMXWQoVwl8YUYCs0Jrpqa1R9Wi1ZT9FAZyMpG/4+1tdnaWnJ2PODvPmS6WzJcFtbVNvo0hDUBarnqOLyvrIu6sEjBfrL8hX7cvq2zSuMQz+aJtpfc7heWxTTmTrSnK1vYWk+0tzs4Vs9mcYrmkLAvKsmxMUmezWce2uK+lUYGB8SHPRD4aBebChDgRqwxnSsCmUvN+xMT4vF83CqqqqlpxgE3bb+fchWsqMEB9IdgQrEzXL/bbaLg7xLS0a7xHW0tmDNtbE/Z2drl2bU+CmlhHWdWUVUVRVizLkvliQR1NZi7Z8i/r3lyF8f2b9DWE/190DBvHFAny8LtYckTtgOvkZhpiRPsEtVJKTHVofZL6hCK05z/eK6014zwj04bDZ8/54z/8E37nd36Hs+MLPvzgQ46eP+boSBy+L86PqesCqMV9qQe61q1HP2rYurrx/KZE7hDj0TdF6wvQrlrWC3xgiCPt+y1Ec/o8zwEoy4LMEMLjAkFTFf/G8Ozx7kZ60LlC8gJpzXIprzx/LmuQZSMU4ps8DiZXe3t7XL9+neu3brJ//Rp7eztsbU0oi4Kz83Nu3bzF40eP2TIZvigoFkuKyvH502NmC8103+JGGRePT9nZvcGNl1/lyZNHEljISsS9TrLHAH/q2pLn+QqD16e9+351KY7rMyFDZ7lfzr/shH2xpB03oVNVe+na7MG2mVh/sE1uDdqDaGLWZQjaDNvwtGYgalS/pIsWHWYESLQJ32QCiE29kjaVMXgnB0sAfXvp+/NO+8J7tLO4sqReLMi8Z8tkZCanqh02NxirsJWnupjxB//TP6e0Fb/6n/w2hZPwt5Gr0CiR9LqQ+G1lzWO/6Y/pONPDFZ/F712u9EXKFyF8UmJkKFpEv8VIlLamAyEpT5aR5xlaOXSTIM9hG0dsYRq77IowCx5iaqHk9wDwCAR0I7YiMY9S2ManyOOdDcwBZFqTZ5rRKGdrMmKU5xLO1ZiGDhdJZ3BtV5FJ8HhEmybalXb8nsCUuJABO0qUPFgfsnInyXKccyHbfQzH22aShXgVxTSrZZ7SdWjHCV3zOEVXwtYSfjREjjiwkjzzIcyxvNgmYYztVB3kqVT02RDeRZiNkHcR0RJtaUWmYJILIXV8PkWdTZnNl9iq6hClfcKxT0AS9/qSqFND0rdmJdYQRVclZPrEZlo25cX4IoRYXwj0ZRJkl8FDBRgUNhC0xhg0cHDjBp8/+ozZbMZ8PqeuJDhHbgT+zmfzFaZtiDhRgfDemkx4+vQp9155BRQNcu3vP7BCBKX3aN2+9Imkuq6bMfXhWkp8DY0/tNhIjiOhKWMzTabevlO1TkKhRmJIaUVmMraMZn93h1s3r3P71k1u3LiGwrNYLDg5L3h2eAzOs7QFvrYYr9Amo1LtWVshgpMALP19HboPl5XL3hlyWqWd8Up5EUl4n1G9rN7a31X7PeZb0kozmUw6xHZKWA8xnOsCA3R/6+aKiOdzMpmQAYfPnvGnf/KnfO83vsuzR0/59JNPef78OWdnjzg5fc58eo5zJVo58DYIKA3rV7Q7300MRn8+guNs590UxvfrxrIp+lEsl+1ZUpN0bv3+UiY+Mg/GGMqywNqa8XgLQggawWeCh5QywWRRcnDleS58iKvRXmG9b3CgtVCXBVk2piqWLGYXKKU4fGZ4kGVMtrYxecb29pj9gz1uHuzz+Z07bG1vgbXcv3WbJw8f8vDjT3B+wqIyLNyEZa3Y29/DKYchZ/+lezw0GSMMkox3DVz3dKx8+nesz4ClMK2/J+l5HqTjXAgL5HxfBrm2vFBm8HjBItfXSG5096B5LxLpupaFiRxYTPAXn1d1u3AxiZfSGmMykb4G6YELpjtlWbI92WqyD6ecf1Q5K62xdQ0hG3hlBVFkWSa5LUJbHh/yqjnKomA8nrRjcemBb7n42Fdz4cqSYj7HVyUTbRhpTWZySl/jtMI4Re0tlVVUsxl/8v/6l2jv+dXf+S0qoHQuZBINdsk6aGRWgOWqViAyGEPwNxKDUVNwGYjeRJD0L2/62xDwH0K6PjCjzRzC35apMGRGS7b1gFSFeHV4V1PZutN+7KK7NikhESu06yHPwuXRWcOQxPWJ46y8EDXee3BiRperYCY1NoxHI0ZZRm4MRonoyCN+PX0iJTIvTnlqa8OAQj0XtQ49JtlFDQc4nyRyAlEJR+YCF551NSMReMaM1CqOJZyyZLG6ZwAfGIpInKtmCVPTkvSvUmLa1iRotCnBF22apSnlJU67tzWZ1hil0NqjtcO5UFfJOEaZQusxWZaT5SPyfMzx6SkXFzOqqu6MoT0Hq2evkRr2CMWhM9snUoeI1lSClP62iQiKsOMqd2Vd3+vG63279pfZRqdta6VojDcvGX8fFqXrHu+vtRacx4S8OkVVgXcYo9i/cR0UjSN4VUtABa0E5hVlsdJXG1yCluDTkCnN9va2OIMbjfVdjcDQWg6txTr4lZ6DFNlu0mytW7OIY2S95HcJ0StaPJuYosSoLybknRJGXKFDBBxjxGwjM4ZMwcho6try+MkTDg+fofGcX5xxOq2YLUqquhaYFMfvFV63MLizPr41l+mv25Bm6EXKuns5xAxKRVbgUvpeyihu6m/dvUzvbdrOUFAAm2SCB4dGh/0Rkqk1I1+dZ3qGUr+1PjHcEoHdOVprhckwhpNnz/mTP/xjfuVXvsmjzx7y2YMHHB+dcHZ6zNnFY2bzc8RhT8zxIkb0dIV6m5i/qzJyQ+uZRiGL3/sMx5Wc7pP6Q+cmqUWfgeq322dwIu1mMrEfrOuCLBsRI4HKOzEKpWDNuq5oTLJEBiz5xuIZUiJaqcsy0Csxqpgg9YWdkWWGajlnMZty+OQxp8+e8Q/+/t/n1Vde5bPPP4Ms472f/pjPnp3w8uvfoNLbkOXUOmN3e4J1ir27dxkfHFBNTxtcHmFFVwBC5/e+KTnQMTMdukOpwCM131vFYZ5MiyDp/PR87X6m5YUYjchcpP+Eu9WdBQBBLHHgMdFfZBAaAO7FfMp7sHWNUpChKcoCY/IookWjqeqak9MTxndGnXGli22tw1sJk6lQZHkeVGU+hAaTQxD7dMEZ3GRZo2JrAWskKGLbXZ8QpRTeWWxZgLWMlCJwMhiPUIlaYccZVI5tB8VswZ/+83+JQfGt3/wu3mhKW2OVQSmHasxrUuDVzBTVwQ/rpbBRShJBjYraojWAd6gMMRXrAOumcaSfvXeIA6XCmIyYx8NoIVh10OZ4G9ybhWJOW+zgoUhAx5KOy/XMztJz4hppRo8xwEvSPy+p/TKtGBvNZJSxNRmRjwTh55kwGaohPMUBLWVYfDhrLkh5Y72YDZvAYHqvRKORqDKdc1gvmbe9a5MCNs99OM/hvEQmPWpA4pJ4oi25zCk4UIX1aMP1Sl0XGIzIWCTO7JERiBqn8K7SEh658ZHROskWD8aohnnR2jRRwQi5SJQSG2STqeZcRMmhNpqxlpDDo0wzNpCbjMPj0w5yGzpn/fOZ5g/pIv/uuVl3dqGbuXcIYa4jwvpI/CrEWp+oS5FCyjC18Lf7bN0cmjZV6gW1OqY+EbKupDDR2+DB5KXtyllsXbF/sI/znmK5pFgWEp0wMMyaEBBEdQnaOGeVIkvvsc424c+ttR3d7ybt0FBZB/s2wbtY+iYGWdai0Y5kV7chpeN7EWFrnZEG/8iyrJlbpmVNq7JqBGhlUbCwTpxYncVoieygEzhUeS+JMPHEKEchz1hnfJ35+RCmvFnmLiEcf9vE1G8qHYZ/4L3OOiench1jfhWmOJXmDj2PpWOGm+xp9OUMlB1Gm4ZBB0luS7CA6LcXaaBUGECcXYLX+4yKDwKjqqqYTCbkec752Tl/9Pt/xLtvv8uTzx/x9PEjTk+POD874fT0iPnyXCJHEsnvuH7BoPUF9upFmMh+3b4FS0qwpvvfNzMcauvyMQsjcJXxxvUfEpJDJaZPuvXnbe+Aw7maupZgRlmWg5JksraZWxxDxP0+JPvVOFVjlAOXYS1YWzEeZZycnvDpgwe885Wv8NEnH/PK/Zc4mxc8fvQpanKN8d51zpZjzDRnlGXcuXmd6y/v8It/e8Dp593zX9d1c8ZMsMqJa7yJYdsEJ2N7fSYjfQbCZFknQYD2vuw8GmmnzrkmKZ/JMmrXhpfVooNq7Ftjor+ozYgXzHlPZWsylYXDYDEmCyZFqtFiWOeovSC0g+vXKctKzkQA2HFckZlQRqOCnXBt6xAKtEd82HbRvSJoXtq5lUWF9zGc3CqyURHgWCtZXK1jf2eXoijw1uNrRQ4UeDCKTBnyombkFPPZkj/6F/8zCvjm7/wmpXMSG11JdJ4YAtWzGpbP+/VSom4Rf4L2Xde8n6Kd/l3uCbpQKvbjk/qemEukT+jj++OCeCG1SjvwoR0xvZMQb9EGNvQVmQpPhyjqEFKNx0Jv9l6AUYQcfeQqGYwHGCEcLti4Zpn4YEzGhkmeMckzVJAwqnBe8ZHJAOd0oyHpMNOEDPG0KufITEhoW90wD3VdN5qI2jlq1zIyUdMRzacccd0i0+FWtCRdpgdw7Xp1jc5AQqG12gj5GxgH3yKMxhwyMBUm+FpkeS4MRWQejcJkqR+GbqUw2uMwjemU81G7ASiDNhk6+L5mBnbGGfn+DiYfo7Ocw8Oj1gY3y8hyEUq4eB6T+fellavnpEugdJakd+f7AHyI0emXvhRzXbmqECBto8+QrKuzaVyXvd//vT+fuGZ5ljPSGeiMsYaiMsynp+xdu4bWmqIsKUphNFyjvqdheiK879xVZ4khtZUH5XwnO3jqI7KJmN20HkOS3ZSR6+9368ibmgSqjiQx2oZXVUmWx0hprUSxrmtiok9rLdZalstlQxRp3wbViLbjWmlJTKblBhvv0RhCkiaBn6bGG48KhKZv4BwR5MoaEE2BRBCgB47IZUKlq5ZNTPlljHG/XJW4TNta9066h337fgEhPjYIqABfHM66hsgb8rHa3d1FKcV8Pu8+V23kxPQeiWC2zSkzHo8ZjUYsl0v+4A/+gFu3bvP86XMeP37A9OKYi/Njzk4PWS5nghuVxgeBaSf65Bqh5FXX8YuUvr3/0L27rO+UGVkPh9a/P3SeWsK5JvoEKhUEzTowhEH4GAgOPCFfhJcoVe19z4jMjtBIEcdGAj3QL86CD9pma3FWU1c1T54+5Rtf+zomyyjKgm9+86uc/eVPyDJHUc7wyxHjLGc2yzibeKrFBddfusXFe4Zq0c051J5fi+lpzdfBsJQJXKfV6OOFSPc1Wo0AS0wUHl6hXJnRqGuxGc+CxqKuhPhHB9JYabzSVNaCB+vFhMWgqD0ok4nfRYdoNrhgUaKUwTuoSpFUiV1+oiWJ7ykhzrTXIr3xIgGVFPKVOKd7IZJE0gtVbTE6w2jTEHXeOYzJsE64VMFnnrouuTg/QyvN1tYWRVWg0CFRFGzv7BCl10VVUZZLMu/ZG+WYqqR2HmsA7xihMM6ReVGJL61ljMJdzPnDf/EvsUbxtd/8HqVyeKxIdL0SpEoURQWpMMHxNtyFjqOz942DmhwS6T9GlomSM6USAAooumR6ygY03QcJv/e+rRDC/rZCH580kAI7lVzQMIpGqCrRn6JWKwLymOVVaJAo6WnNhzpFyRyaXpOzJb/55ktKRKC6Jkcdbl1L7ovxaMRkMmKUZ+S5RhlCNAuovQqRHAKT4X3TnpytRPsAuBB6MUahsTZo3wIgi0RzfMdaKxLhEJnGO8l+6gJD713KRLhwN+V+1pZmzVJHcvB43/qHrCxlsy9dCaRRYuZkQtQ5IuOQ5cI8KAHkpijRRkvSQ6MxWoXwvwLYhdFwGG2ojceoKkQPC0mSGo2GxfgYLxyM0SgvccZvmoxRpvDVnKPTCzwiVNC1QudI3PRGCBCAsveB6KKR3HovUlxlWnGvc5ZWy9NGiWnXpydF8z5oiMLpix9Dk31i6jIEmxL+fYI+rdN2P7SHq34Kg/V6v69rK21zXd1IZOcmJGEFaltTuxrnFfvXbpKpHKqacr6kXBZCqKkQCMSJlrO/RlpL8I5mTk7ghAmRoJRqNWxxXOmY09IlXpIzrlo4g6IJGZ1KBbtaiFWfw46wy4tEuq5rikKYKo8LIWh1wzjIe7ITEUY5354h1YHRch6tE847JsV0XnLtKCWmVl6F46haQV4MIW6UQamwPkEG06xrIKIFlqogwHMNTHLJfneIeN+TG60U3/Y19NRHU06B661Wpb1I6Xu613dnfzs4J3YgbZsw5xWBWDNf1dSNoikfaRoCgxsajgEJtAfjY6Q13/YfYMtiseiYD6WDMyHHi0I14fKdB+s8Rmdsjca4qubP/vRP8UXBUs/57OGnzKZHzGYnXFycsFheyLr5dp4JHxmmuLpO/fVvRvUFGY8+U57ilr7D+2V9pffp8jE6fC+nlzxWpNrrKDgTvBd9K4J2YxTG68RR34RIVgk3LnSsQDTyPEMsd2xoN2qs4tjiDsi4LBZciXEGgwQYqq3n9GyKyjTXbu4xnV6wu7vD/+q/+q/44OERGo+rLYuiYjH2HJ0seHbxDK1zllWJ9jbgM9/isMDc1DG3l2+ZPBVgjGnoKN+4C3hPMNVvGepGcOzkhDof/YcVJssFPiqFN060qh6K2XxwP/vlBfJoSNbkOGClkEvqBMCpoKr1XqIvZXlOUZa4Qmxw8zwHrYNfhhBquckC8dUe0IgA0vCdNmhQlFLUliAVaiXe1lmcq1DaAy1hFf96L4nRtDbCWNjgaCuTkZCpWYb3jmK5ZLmYYbQmM3BxIV71e3v7eA87O7s4a1FaicakrsmUQtU1JuRYAI/1DuM1xnryMCdGGbaq2NaG2XLJH/yL/ze71/d55WtfxRnRrBgvUS4ioxGPbrTbDWeiycoNEdC2iJRm5hFpteYV6fX0tCHLOpcamtx8EYx123WkDrYdGJC009onR+CTaJbi2J1DeQnF2AIqn1ze1fGtI5a7ZRVwxe8pUOwDy0xljLKcUT4iy3K0UWBE4+Sdx1uPtV3iRdICtE58jTbDOWEWvPhoRObCOTnT0efC1lac3IPWwjorzuApwg8MSG2taM2idsNJdBwCwe+8ShzLGxlNsyQNnu4vn0/XPAmP5ysMEovbZBJRjaBONkaTa0WeZy0zqaNGQ/xusmB3LvUlx4kJmozMGDJtyIwjC9KRKBRSqrW1jnsz0or9rRHq3l0snpOTqawzHmU8JhOGIcuyEHdeN9LHePb6kvwo0awjERj6biJN96Q/Wsvd1MlNaggWaLUqvfO2SUswdE77vgd9xmMdUb1Oith5PyLIgXeG3l2H/NNzHnNqVM5SOyv5hKzl5s07TEZb2HIhEVYWS+qqbpEe3bvclYqK+etoNEJ7qMuKrcmkEWDked5h0FPmIC2NFgHk/GWmybkTmYM0lHpfApgKAOKdGyopXOq/H5NltsKOAQo8fI/aiPitfebFUgMSgso2t7VhJJAzaQITKI7565nFDoGYBHOJGv+0XnoedDT9UgP4I47dgzZmtQ3iucwaJm4T8xvNgnyyTtJD63vWvR/xrc6AmgE2bIz3TZL5pi7B2TVskUr21CgtAUC0aLaVbkVdMURzX0vWzDsMTAX6B0I+r8oFYeYIrRQ//elP+OSDD3np7h0ePviE84sTiuU559NTFvMLfLDwaOcZGIv+PHtjWFc24dLLNFpDcx1qd4iRGHpnSMAy3H//e9e0XNqSei3NGixdAk5owld7mlwbfXgk77sg8FbJb/2+UmsMQAmTIoJjRVXVaKW5mC2Yzi64c/sWz5495cnTZ/yj7/0dDk/+EpdlLIOQbL4syfSIBx9+yquZoXSO3HsRTQRyzyvfCMQcwgRAjMBJI9x11nfmpYKwImVUG2uS5IIJHgxBYKxD5yMsnjpYRijg8Mmzlb0aKlc3nQrAsblIQVposixIVB0mC7ku6rAxOgtZHKEsK6qqCipmqKo62H4bqqpugL4NRLwybd4OqW+bBXLOdrKBN3aBPiWehbu1Tgg58dgvsFYIkQhMy2LJtZ2JvB8We7lcMspzUfkXBcaEbLRGzEOaXEi1kw1AfEx04KA1otEWaxSF9TAKghNrFHNXMHEZzBb8/j/7n/hf//f/ew5ee7XlNmklLtGHL/4bEg81Mez7vyemBZeVFLl2EdlwXbic4L8KEInrnrpUpPX6hFPfQXFTGUL8fSYj/qaUIs8y8lHGeDwizyUJoMLjao9XksGzyxABPkoPuz4WkcCwzol2wkoyIeeESbC1PBPEHrQRkSj2jtrXksPDuuZ5jFyl0eDjOihJlumDHwUe02PcY+Qq4/OG2egDaptKWsNdVwSpKSUekcjI3OX6Kw01jqoyHfMoE0zMqoTRMFmN0ZHRUGRGzG1sloXcNUaYA+WxtRDueZY1mcW1ESmSUZrtyYTXX3mFxeJjFsuKytWMrMKVjuvXDzo20lUgalOnNiAkReuasqVMZ0MMDpwppbs+Dmnp8cede7UJ4ffPdP98Xoag++00Y42S6zUIfNP70GaNXddvK8EEEhbLI4h8f/8a4/GYi/mUolg2En/nHMoEsynnVghNaVuEVtZaRiaXM1WJJqwoStEWDsC3PsxI19F5C1V3/FFLKOemO68hONGHKevWtUPA98xKVgjmAQZuU1kHH9M16EiaWfUzGuovZR699yizRirtV4nMZkyJA/zQGPtncWjvV8638w1z0q0rBOYQE952ujKFzngG3+m9r2jX1DkXpMmilWv8ORJGtT+noXsT4VRdi1+G0YpnT5/wJ3/yJ9x76SUeff4ZF+cXLJczZrMLFvMpDVHofCQSumUzT7F2/kNlE+OwSXiSnrFNd+SqmpTL7sIm5qR/X1On9ehjJgK9Wkz3e+MGuTd1PRzxaRA2y4NmDN45fBB2lEXB4dMjXn3lDX764/cwTjE9PaVeXvDuN9/mw8MFucko5xccXyw5fPaEu7e38TrDIsxtvM+Sby6MVXWAiTAWWosGIuB8H+5stH7Bt/hcTMDSeQVPnyjw0lBWBSoXnOyctHt2fLJxb2K5MqNRlhUmE4fu0WhEFZBFjjh+Z1lGXdVJcj5BCtb7RjVeVXWzaZnJg5TRN/4eMXOwB8qqElWljhspdv5ij26bCw+t7WtsW6kQPtC3EUNitJq4+f3oCFH865zYy2qlmjjv4/GE7e0dCASc2FU6Se4SpD7WRxMvccAjmLzgQSuHso7MK8baUWtLWZbsmgmLo2N+75/9j/zX/4f/LZObN3FaBWdJMVMzCnTAUX7dxVQqUo/NwU8RzVDpX6be0xZ4Drw3hCzaoawCp8gpR8nQChL3dBiNoQgV8XO88P3fh/rvE299KWMkPKMEfjQeMx7l5IHJjOMSH2onoTtDdza24SKjYRuTvEhIOSeardrV1NY1DLiz8r5tmAwhdCIx7LzHUWN9vUJIaaMxXsyXIGsQYIuELZ4u0RzHokMc7r5aXaQd4kmCUiH6V1xQBMoQNCUReOEF6GGpa49SFmsNWkuOA3H4N1jj0MaiyhpjJGxxZiRUcF17jK4xShiSPM8DExJs3X10KidkhxdNWpblbI00b7z+Cr/86BNq65v9OD+/CJFhWtW21qojmOicvTXnVmnVuW/DphCbyyZp31BJ7+QmLcNV/RE2Ivk1fW/SYAz10dYTzXQKh5RSjMdjru1f4+z4OUVRsFgsqG2NZJbOGtAV++04koZjWtc1vhaBjtZi0lpVFSrx+0k1QKsMSwsHhuYdmcp+ZukOod6Dl+sYkfS3fhvp3DaNc3Vt18P2ob1Kf4/CC6PaZISbYHccnzBDQeAwgEe884NnTb7AOur+i+OkbhtXYZpZP4y17chZoNH6tjLsbjhwjySxI+YC84IznZI9zrKs8SVa13ee58znc/LcMBrllMslf/gHf8Du9janx0dML85ZLKYsixmLWXD8jsImZfADS3UVovxFylXbu+zsftH2v2hd6AoVIUZ9a6M1NUk3dYZzYmkzxKR6WsbEJNq5tJ+VcfqoNWh9KGvnKauSp0+f8Wu/+m28g+nZVEL1uJKX71zjw8MZtlry6KOP+Pi9H+GXR3zzzm8w3t1jMZ0JTPTtqfQejBbT0pQhRimxvMAFbWZkJLzE5iUxR4z6woQsUHgxVyUk4Ubhc8P12zc52D/gw/d/iXWanC85M7jzYMsYU1xR10JY15VEnaqqNPqJEFtVXbcEODFTqjjUOOeDL0YEnqaJuiGbnzeaDq1141webeSiHVqq2m6WyNNIca2leS9ytBHYxcRP8rtICeq65saNG+zt7lJby6uvvtqYT8XDKbGUg/OQCs6+RmOdR3uPreo2mpatqZ2XDK1GobQn0w5bV7jaMdZbnD96yO/9j/93/tv//v+IH4/FDCM3eK2D1KLd/n6JRGa79qsI8CqlT4RH9ckmqcSLAZlVRNut19U09IFEWvdFgFqKfFNzpz7ClqgvIpWPDKWtI4cn6tMySNXwXc2FmMsoMeGz7e/CTIi9upytoBVxra1o1LpJm75hNJQWv4gs+DzoxLY3U6qJNKNVmwDTOY+zFTFkc4yW4Z1DjpQnN3LP8lGIshb8OCaTUWMCVVU1dV1hraMqKxaLYNqFChG7TGB0hKkOZCEg/icKFRzZa6zzqFo1YTpr6zHaU+cmMBkyz9wYqjpoNvIMY8B6ydBqtCHLFUY7jAFtRQt2sLfHy3dv89mjxyhl8F5RljXGxDNEYDS657V/VgZ/9zTmUJEhTZ/332/bEAf5q5RLx9ArfQLzKozBIGHRa34TnNhEFK6Ou9XoRIRnTMb+/j6fKU1VVhRFQR0ETihCzH81uMZRWt304Fvb78VizmR7q4EH6zS3qRTT9yfemWNAtGsI9yEmol93iNBPn3V/Xz0/fUZ4XbnqfqVn2TrbWYtNTHAzV+ignD4zsZ5kXbfSw0zylYhfRbNkK/P3A+MLv3vWj3Md0+WTl7yX/4iuuN1HrTReiflfFEqiWgfvuKdDEZfis7IsUUoxynOUd/z0xz/myaNH7O/tcnx0SLlcUFdLlvMp1lYoHHgnQQDWkwQb4ceXwYj078NQ/33YdBX4dtXSp0nWweL+X9+736kAQGvfWLv070Z8L9IvfTiV0k7NvJ1Y5jgvJlsxd1BZlpxenDHaGmHynI8+/oTZdIqtS7YnI7QBW5U8/PgXHD99wFZec3xyjFWG2qsgxe7CE2sdJuZki/MPyM/7mOtCBUF6GHNckHZVm/MrsJsm27jKcsgzGI/5+ve+y7XdPR4+fsq0OsK7K9xdXiRhn9IslwvG4xFFWYl6VBuKYhnsz1tGQ4CZEFPWi0NrRBK1so3ZwtZ4K0R2CkRK7SirEpTCZIaLi2kThUEyjINSpgMsuwhGtU6gpA5JuknsZJOxyvvBtriuUSE8aJSae+cwIeyttGUaCThe4TV4Y9i9sc/N/X3OD49ZLqfNu7V3wmAoD8FeL7OwpQ0qh1ldUVtRlT1+78f82e/9Ln/3v/nvmNkKnxusFy2Pigdl0/ZcQhBcpX5Tt4Pd17+XEjyX9ZdKC1aZBd8BAn1kvo4gGxz7ms9DhEEECjGzZySerRUbczFbkwvrvKcIf1ONCMhvtbWNKVQ8Z3VdN74X8T7gFc61jHBMtifAQZyRhfh2kqwwIUKa81uXuFpMULRWkm8iy7h5cECmNdevHzAajdnZ2WYymTQ2myqJFW6yiKxEczbOQ24cVIg3HhGuCBbKuubi/ILD4xOOT045OT1jWZYS/Sq0oZXBORWIfhds8MPd9kJUutridCtdGuW5aHusI7MOowxVZUPugJhbwJFZD7lFOxgbj1EGrT0v3brB+ekJF9MSicAi2kWPb0y4Wr+t4TM6yLz2znnn3G0i5vu0zhXO7lBZd6f6SDZFbv26sQwhyBhjZd1Y141lbem/GjiOqiy5cf0G3jsWywV1XVFWZYPw4mt9n5R4t1QQHBEYaYX4+0VJfR/+rAyrxximJHAfBik2m7sMvzdc1r2bMqTdI9XO46rmrv3S17o1fXmIgStivXWMRt9xvvshnQeN+eDqeqzay8cyxKjHMaxdV7+5zXQOm87wpqhyg30OPG7vWuJrE19xjtFo3NzL1IdoiPksy7LJj3J+esq/+dd/ymQy4vnzp9iyoKpKlos5xXKOMYgGxQfA7BX0BBqbhHBfRnkRZmEIxg61c9V+rzKvIWY/Fc6k9yKFnRKgoQ3V3fXxajUTQ/B2Xb8emgiSOjgBeS10wsn0mMIX/Nrf+g6/eO9D/vhf/2smu9uUtgrhdiuq5RTjCrZDBDKnMirnm/2XuSXMDiHktY/+tAF+Kh2EOVKi5U/7fmcBExoQlM4C45xx7403efMbX0PduI7a2uHXfvu3+ZPf/33m89mV9vDKjMZ0NqMsS4pwOdIFFiRmmonI747xaCyEuheHu9F4zM7OjnD8HvCSY6OqKslPEFOoK0U+HjVZWdOoHx2nzOQAeS+qzHw0EsYhqC3zXGx7R+NRYz6htZhqEDhP7Wq2t7bBe4plgfKeyWSLPB+BVmxtbaO1YTSaSMx0L9JrrxTb13b5rV//dY4fPGCxmFPMC6pyKaYwGnyuxTzGixoKB7oS+06fa5auwNiarK74iz/+Q978xq/x8lffZukdzmssMbkVjWZj2D48AvB1O7hBBMIqIFAqRlPqSSQiAPZpnwMSpl43Mn7VubCx3dSgoS/92wSw+r+vIzr6zEYakjILOVRa6UDs26EsBMcZHFCp6FeR5oIJDtm2brQZcX7OtU7ewmB4YvSLiKNMloex6MZcTaHQrsQAtrYslovgZ6TY29vj5s0D9vd22N3bZWtrC6MNVV1RLAvqsqJcFpSzGdOTY4l8ExzHq9rjrIR9jmugw15n3mKUaHZGoxFZlrGzs8Pu7g6jbc3O7i77L9/m9Vfu4bxivlhwcjHl0ckxR8cnnJ1esFzWxJB+DVCPxsvhm/ch8ZGtgwZGtDJWW+rgEJ47YTBiEIj42etgruU8E52htCFTitfv3+cXHzzAulb6JFIlcDpKZnrnsYd4VgiV+EIPScXfzJp7pFSXrdmEVIfCYw6VPiJL78Z65n3V9j39rHvjX+lDPhHtzsM36N3VpIXmk0q+Ou+4efMmAFVVUVYVVVm10rKEGY31U0fdpgvviRoHMZ2qO3O8KrMR+xyawxDBsKm9Zr4vSDgNtZcSOH0mIN3vTTlgUsKqM04lkaeuwpj1n7Xs4JBZyZrfN2g00vnG/gbX+RK6Mp2b/JBuam/0zZVeb2rWafOSMaT1+7h4a2uL+XzemOV0co8lTcYAHsaIUei/+Tf/mvl8RqkVVVHgbUVdlSwXM8C2hGGIjBbXfmg+Kzi7V4YYQ6n/Imd7E+OnOvfMN/c4jpnkWdrXJvplfRka8xBcVIqV3yPTaG33/jTzVs1/OoxGakI1xNwIbSCQLb4Tz8N0fs7p9JjT2Rk//vlPeaeqee3NN1gsC+nXWfIMtLJsjTO00eRbWxS1g8R0vHMOtUYFt4U0mpTRtBHtFPjoa8LqvZP5xUBPBu8UL92/z1e+8Q1u3r+H2dthWpcY57koCuZVhXVX27ArMxrf/to3G+lrPODRZKO1ZRbncEkg0jp2G20aO7eY8MuGpHqNSpJGcDG8geGRLESXyUgBSB/5xr9eSahMDQ3hLuPMwOaMsy0Atrct3mny8TbaSujFyUSYJpQmz8cyap9T6YzSWf7dT37IK7duUu1tU9Q1bn+XRVWRj0aMAvO0nedMz89ZXlywmE7JtCavNRMLpasgU7Cc8W9/95/z337l/4T1ObkzskHG4xIBhg+cavyWlv7dF0TeVusi2W5daVc+qWBj2MRnjmuZ8BveQ4dN8CswvhmTp3vpU6ma3IN0gEGy5+lPb5UwwHdfC795WqKzXyLzmmU5eT5G6xzvNCiNVTIW7ySLaJNMD6h9FbQTvjGTslYiRFU+xpWVMdhaEin56DUdAJoEIFMh4hponaMVSLg80VbM5zPq5ZKRyTjY3+f1V+8H7cSYsiyYzxcsFgtOz55SVSVVJYEWbG2xywVlUTQhNm1dB5t4KIuKsqqbe5wyXbk24gSf5YwnE8ajEfkol3OvIR/lbG1ts7W1xd7eNfb29ti9tsfXXtsle/stZrM5z54fcnp2wfPD5yzLGktGpnPQYlIlx0K0nRqDxjR5cmrt0QaMd9R4Mp+ReYcOUaSMsxhC+FlT4zIw2pHlGePtCQf7exydnIXzq0CF8Kg+HotVJJLCjRUpMATTqZRhkoOmiCaf4dakZ5IVQeP6kp7NPnHQa7P/XozYrpLf+vV0GG8zrvDZycFraTRPkucmOJoq1XmO2JIlLKPq2YgLjDYNDJFoeKVzXLtxQ4JEVgX1ck61mOGqEuw4aMZVM5lMS/Q/55IIYHE+wX9NGcXsYookmdR4Wm1Imqg0GVrT/mae4Go+Aqv5jda8l/QnTu++S+x0BtgTIK3Q7orVkxDbEficJuCE/lzbqEf94lMYrtrPgSwcfj8h9FcYt/7yDzATKwxNIMrSX69EwvjelIZ538F+1+EGFZFbrB8EMikR2QhAafGJVlqoGVs3uMkoxcsvv8zTx0+xDjCK2lucFjNWpRyHzw750V//Fd7WlLZGKUtVL1kWF1hboJQPeWuTIAIpNz80x4Hj6JvnfQGHPBVU1WVyuw1FU0bx44vh09swq9JOZMBSDZ1HiGHvYsjkhipIR9YZT/z9sjt52fN2n6NPbxQ8tf6/eB8iolq0jpp0g3OgVdbCuqgZlI0Pgsl4xts101qLI7USOGiUkSxdzlPMa2bnC+6+dJt5cUFRz6nqks8fPmJ3dINaL7FK47WhKGrKqsIaxcxZMZtOVkuiI4p1UW0dEgxGM9na4v79+yzmS86PTyXqVXBByIPwf1EssUGTI5qUuBYS1fSdr3ydnd1dZsuKvUUF1ZSqLPj89AE//f73sfMCb6+mfb16eFto4j5HrYNCnFpN0A4IrtLBYUWAnwo75K2To2U9XkuEKIIduzJG/E3pwK/GfjxedkDaC+sh2b5dc7AlNG48EF1A4nQMX0ibmiWqoixE8kApg9IZ80Uhqs/KoVUmBy7gsAjYa6VgZ4v8YBd96yavvvk6s9kS5+H2Sy+xtb3N9esHzC6m7Gzv8OTJE7S3/PwHf8HxZ484ffwMFJTLGT7T4Gs++/A9Pv3wfe5+/VsyLgVORyI/RUW+/a9PLtswvlsDkhJUt1KpRTgd7YLvEhx0RrTqbNkZQcIU9m11o812WvQarjv93NljF3N7KHySVDDW7RKWOvjnBDO/wDR1NS7B78E5BFwIkZ6GuRQfDYfTwfnf+YCoXIOE4sRGo1ziUmtNpjTOOFCOqiyYzaeUxZzd7S1evXebG/s3MCpjsZwzm17w/PljlssFZVlSLguKRcF0OuXi/JzZbM50OmU6nbKcnVMsFo15YnRMBzpmgw2jFxGHzhiNcvJcNH95CCs6mUyYjIW5uLZ/jf39fQ4ODtjZ3mFnd5vxVs7O7jb7BwfsXxOfiTdefZlnR8c8eX7KfL7A+4CYvPieKO/DWgsj75THqZDx3Io2SZzoDdpqMhdMqZyEI/S5+GNkGThVo5zixvUDzi4uJOiDNg0y9kSb6lUVejzbQ5qN5jwN3BwBXV1/olaDc/WSnl3VwM/IZLfPdAL/Yt2+9LJhKPrvJc+a37XuOLa21WTR2gAcw8zYuhLzCSgUmOC75j03bt0kz3JqW1MWS8pigQvJKTuAxwczg3BHdGxLGm3GkWUZdV0FAVSfUQyVQ2nvchjjRpvizeY5nZprmNQOvOoRg8asmlxsar9TpzevTklo++4erbZx6fQS7jXi83XV1jJuqsc0MbxeK8wH7XvrccnwYIbGMbS6g9qIZnlS4iHeyfaMQdcOP25JvKt5CJGqtSTPM8YwHo8pimXrn6gUzkZTRoFLf/yHf0S5WJBlGmcrFJayXLBczukKMjZv4AoDO1TXd+UbjVaxWcP1Pg7Kp3BOk5nWpDclf1NmWt6XjrXS+AD/gY7kvcXl8Xtr8bCpXEUw0NZpNSuraxB8Dr2lqktQOSaLeZWiCadvBKapliIudAqDYh4r0VhJn3VdhYincPT8hK989SsYI+b7RVFwcnzK9p3bQmvmueRks47pdEYWwuxH4SfQOnmH9rUJZ1XDfDnn5OyEg2sHlJMx1lomk5Ek0jUZzllMrZsw+hqNMjpolIXWfPL8KfbJI5xzbP/ivcB4OYr5FFcumOxtX2n94QUYjcqt2oV5H5zEaycEhFLEGPyNGsY7DOI7oUMyII1uJOZeaSKIaZIMNUShLGc8f0pFJsM3TEjsK25ug7N8e1ibOiH5V4hRig3hMm1ZNSpO7z3j8Zjz83OMMZRLyQPSRARKbFhrk7N/7z5vv/kqWUB6k9Ly/PkhDz98j5s3b/Jbr9/DGYfd3mZndJe9rS2WruLNd97h//v//OcYn+OXHuUtRkNRFfzoB3/BP/7Gr1J4hw2ZmLTpSyG6RMpVy5Cq9bJ6L9L+ppJKgzbZy/b7XjfOPmHYrdcFymnfELRbOs0u79qz5VM/n+hH4bG27EQvapgSJEKD+OoFIBD6y7SB4Csgzt065ONwzGenLBZTRnnOa/fvs7e7i3eOi/NzHn76KfPpnLJccn5+xtn5KUeHh5yenTA9PWM5nzOfz4PpYUldW2xdY23ZrEMEDG00q1ZKnHLkgmR0E/Y5qoZVcMQ22pDnouHIM/FnGY1HXLu2z/XrN7h79y4HN25wcP2A3WvCjNy+e4e7d+9xenbBo8ePmS+KEOpaLrNKEnRlxkSZdKMJjeOOY9JBGmZ08P/w0d8qmMHpnJ2dHabTaUhcFkMmN8Bjw8lMCPwr2MdH5Nw/U0PncNPd2eQYOxTdJK07lAxrqN66fvXAuBptoxK/nJSJuqxPj29iVjTS3kBs7e/vM55MmC0WYj5VVlQxu3KPiYrvR8lyKuyIY9/Z2cE9a+FIHNe6MKnrzI36dZ1dDw+H3h/SnHf76mqZ+vVfjEj64mXT+fyi/X2RuQyVzvtXW/4X6u+LjEvA46q1RBd/JYez7QylFFtbEqRgNBrhnOP8/Lzh31wI/JFnObnRfP7pQ95/7+cYrXB1hXcW52qKYinZpfFXhidftKR3xHnfub+pcEb5VVwc/XHTxYhhe6WsJu5rnqs+k5HgVNcyA932X+CQJGUILvSFSik9EHPvZCZf215kOtI2h5hppVSHvqzKkulszmRri9F4DArKouTo6AT2CrzS5KMxJs8YjUcU5ZKd/Wts7W2TRVPukFbBBJ9h6ysIjKsk1DVgHGezU9TIszvaxhjDlp40Y7pm9vFBsBPNpU0QQFo8hGS73nsmkwm379xmZ3ub7d1ttne22N3dZW9v90rrf2VGY1mWYQFbDl7RMhQxWVck8NvDpZr6Ptiw6xCvVYU40K6uiUYwtgnfpjoXPkrTPcJ9OmvbcSTP+wcIggRSObRTQSPiJRIPIlWoy7LJ8REPXFmWjEYjyrJkPB53HMyjmnecjbl9+2Wy8TZZrlksC/w4I9veQucZnz9+xOn0Am00paspccy9Jb95wM7BdfTOFs5ZtBFzBokr7/jk5z+jOr/Aj7ex2tDkIdQ+kZK/eBlCMCuS0bhryUXpXibdXLAhJJMSXuuQ0GWSrSFp6rrxr+vXD0otumrvVFPjvZiMeGzCTLbRpSRbbjU4hngPtFJgDMp7yamCConuMgkvaS11UXB2copzjjt3bvHNr36FYllw+PyQw0dHzKczzs/OOTs75smTzzg9Oeb8/Izp7ILlUhiLuligvKeuqpX9sd422UJVHecXpSzNYjWSmJZgVhQhCor38m6zR141IYAlv0WO0opRNiEzE/I8Z7K9xcH169y5e5e7917ilfuvcHDjOjdv3eKdN17HK88nnzzk6OSsze6sxbyJIEVBBWm6axn6SLwpATzhjgrzkWUG7yVSmDYZk8kkRIiL2knZHZ9oqlKkuu78pWdm6POmMng+Lumn/+xF7ncK71JJ29AzuJpPQ5rcML572ZgE/A7PfTLZEiZwPme5XFJVJTYG3GiYwbZ+Z269372XcOiz6bRhZFKCqN/GpjUfGms618vg01XbXPfuujV9kfYva2td3SG4PzTvq+z9UBkiwK5yz65Srrq/mxhCWOUTkjcbuBjfj+uQhlOOwr9Yr64rqso0DEbUKltrG5VBDIKhlYLa8e//zb+lKgpGIzHTcXjRXC+Xgd75YoT1prJyx9K7Q1dQ0MBMteo/1PrLGqJGQNZNk+ZlUEly3wjPpe3WiqF/JjMzwiMEdavdFVuUtL1N5TJ42z5f9emI+6dVRl++sq7d1O+0E3ij50Bua8f52TnOevavHWB0RlFWPHv2DHP9nCwbo1RYU61Qmeaf/NN/QjmdBtN/0WwoFwU1HqUFh2ZZxmRLcDJKNXRuI7hSreZchH1ijZQHX1XZHxMCHYnhpA5CwSwXiwzr6uYs17ZeWYehcmVGoyirRvKUEgBaa4mGYMHakjzP8J6QRdEHTUbQWKRIEBq1pI2hDlWbETwFAn0thwpaEKViuK72cMjF0I3Uzjrp32ugDMBC6ybRnlIKV7UajVSaWtc1ZVWyvb3djKU5oB7GGKgs43zE9ZsHgOL87BxV1Jj9BR8enXD69Dl3X35J8mgojfUeP5mQq4zt/X0u5nPJKBryH2QKFodHHH/+mIO33sZqhYHWHI14Xq4upbqspPsJdPZppW6qp3+B0mca+sAufTYkmey/s26+LQBZBR6ptDgiCx+kJY2TnXI4V3cATv/9IeTbZMn1nsxkmACcs1xyOsynM46PjjBa887bb7O3u8fTx0/5xY8/4PT0hPPTMw6fH3JydMTh80POzp8zX5yKD0ZZYl2N9yGYQdB/pwxZF6nKvCLT3A41SPebd7q/q6BhiH/DdBBzeTmjAFUlQocqrxiZkql16POMo+PnPPzsEyY/2+LWrdu8dOcur772Gi/du8et23d4+aWXePX+fR48/JzD42MmkwlZnkniNR9tXTVedZPoxbtZoZEY4pbo8xWJTbJK8s6EBKI+IHalVMjH02KLIYJ06IwNfe+f4SGG/CrahvhOfF8PjG+oz7TfoTvQ9X1aPR/xe5Sw9tvFg9AU3bN+GTEYkVdaX2sdiCzHtWvXePL8GUVRUBQFZVk2ZzmdRjdIxKpkMBJ7OoQ9T5+9CMxYFXbAVQHboDArIaCu8u5V6l0+5i8O868yhqu2s6lsEm6tMMJ+893c1Oa68QwxOHHuIswcWEvVfbd/d4TuCQS6biNXOucpiqJjVtv0r4IQ1YuW2yjFs8eP+fiDDzAKvLV4L1ppYTIcRolJL5es8brxb2KlhoowFO07UfAaBXep30V6fuS3vv+bThiCloHo7O8A7GvuP0JMNxnYlQQOkikNm7RedY7rSpxP3LtIDyqVNVvQed938UpaOiZ24Z3Ybl1biqJiPl+QZZJPrq4sp6fnXF+W7OxOQIsPnJC6jrfeebPJ2xbPrUboQgHbNRDC3XvXwLNGAEqy/koF+gGiUM5aSz4aNX40XgC69Gd0MGR0Qr/aGu0cuVKoXkLXdeXqjEZthRlwkShR1EUpk/DiBI73aCebUYZY6Q1HHNVl0fYu/CMcWK8UVUgo1kfULecsb0UzLHyXIMmyDBckCAbASPK/oqxI84qY6NkTmJA8IeJjkj7vBWgoWjOfCESAQLzAolygc83BDfHFyI1mK8upxxN8bTk5OubeK69Q2ZrMZJTWkuUjtNfcuHWT6dOnQmB5iapjULBY8uzBA268/Q5VQth7/8UQxGWX64tIrC7rq0+Yx79DkrShMaX1rzq+lBhJrSCGiBVhUMUJRvhY8Q3wvmpMjdr+4TKgHZ/mWS6IRGuM0kxnFxwfHZGZjG9945uUZcHzJ0/58ZMfcvT8kKNnzzk5PuLk+IjpVLK/FssldV3gXI21NSC+DVqD8pboNhlWqSEaVfgtau0I82oXKB2p6v68AXBHviP245F7V/oSpyTfBlrBQqGMZjKZcH52zOOHD/j5z37CSy/f4/XX3+S1N97g1u073HvlVV56+S4fffwJpyfH7B8ckBkd8o44TAjXm5opQsg94gSuZM7gjJih5aNgtqM1o9GIul4mZ2L1zqTmNl9WucoZHaoTxxUlTuuI5XXEZZ8Q/TLv8tA41vXdHIzec+ccWMv16wdAiDxVlpRVKaYJ+WjlajX7NcAkRMYyC8ICWA3XOkRY9se1ickcgrFrBS8JsXUVuJzCwP+Qe3XV0l+3VQKyfdb/rf9sXXv/IcumvV23hyLIVC0NMlBSJjdtt6rEzl43fmBKAhq4NnR4ZKK7Y2n9WTOTkSvNX/3gLykXS7IsMCvOUZcFVVlIsAd/uRlnf+5hpvH/g+s05D+j4jyStuJd8z4kJ0xKE+YfUMqgIoEVGaMG13iaaJl9IQ56ZQMa4YFr31eqNdFyLuK/L+8epUR5ZCQj7BIzKosx2cod9+HlTUKOlI5o2vViKjWfzUMiaKEx62XBYlky2YbxZEsc85Xkkzo8fMa48mgfrF88eCf5subzOWhFrhVGaWonfp+jfATQJP6tY9AY5wLTCPfv32cymfBHf/RHAGzv7GDrGqMkh5e1kgusqupmTfb3dnjp9k0uLi74+ONP+N9951cvXeMrMxq1t+BjojGJEe01mDzHVTVlKbbhKphY2MjRaY2t606o1Li7OjAg0JokOWQhfUcNZQJDURM5sLIsOxL4PgGbEouipQhqSO8xwRlXmAhPWVdUwVHHGMNsPkMpTVGWaA8nJyeNJD8CEaM1SlsKKgpqzHZOPZWcGd54FmWBHuUcnp3gjKKysmbVoiLTGdWy4PbtO3ymft5w/t57seP38OjTB3xDQe0smVcdu8coeUwlL1eVAG0CxOsbuMrzVclbfwz9PUod/9aNdWO3PclYJxqMVytALM49MqcQzaeCP5D3SFZt1xCjLbDof2/nrAAdEEhmDBqwleXzzz9DKXjnrbcpi5Kf/uQnPHn8iGdPn3L0/JDZ9IyLsyPOL86oqyXlcg6+RikvvgfkgMOYMK+QR8Ar1cp0fCuVE6GD6gBilTAaKdPRZZ58mPvAOQoII64PSjWMB94HTYsHF+w6LdR1gdEZVb5guRgzu7jg4YMH3P7Fe7z7la/w1tExt1++x+uvvYZ1ll+8/z7KaLZ2dtAhx0aKyKJGM2Zhhxg1JET/8g6f+ZDYsKvpVEoAslOtJuuFGFjvo0Sk8/M6JH4VBjp9Jz2TQ+1talfRdRr/csvAHSZ1+lytl65t/K61RmcZd+7cRQFFsRRGoxR/J58CMobm3oUH8Y5XQQvdZzIum8rKOoavUei1bhzDROvw3LtSz4HhfMkE+DpC/4uUdB796Fqhtyu3Ewb3Am91a/a3atPUGvGJUg06UirCxrjJaQPRp6iF4S0eGmZeIqPR0aQhFhIEItglfqPp+wLCHMZIuNKTo2N+/rOfkpmMGL7WOctisQhjipoQNXgTN5bIpMdpp9HzGpCf4AzowNr0TnXzqrQ4FlJfjOA0/4KwKE2Iuvqu6t0xyRdlrQJlRcveEPG9N9fg/UvHo1ptY2siX6N1TpCjxxaJCzcEF/oMewoXokZjuSxYLJbs7Owwn5cBzWjm8xnXDm5IgCTEr7iqLX/6x3/Esx/9gr18QrEssHWFt17MsetacrRlGUVZrBx366wkIlZKIg4SBTaau3du8b3vfY+TDx/w2WefNXhXe422unV6D0yy1pqt7TGfbAnr8OzZs0vXFV4kM7itJWqAszhrqYTyYFaUaMR8amsyoViWXL9+nfFIclBoozk7P2M2myXEW/Ce9w7lbNceUOtgxhKTbUmCs7KoUVqjVbCbjxy3lsNe1xaHFZluuGRVUYTcGrlcBe+pyhqnNWYyES2Lc3htWNY1xtY45ZktF7iQaXh7lLGczxmNJT/H2eyCi4sLtPfc2N9hlBlU7VClJ9cjrPdU3lEB167fYDTekpCN9ZKJHnFRXKB3R0xtxe7dW4x2d+Awo7YV1ipyRKvx7POH+GJGNh7jlMEqGnWiiCsul7D1f4slMioRSDTEqo/AVpEKUzpv+6SP+J944aWzpGpwmIqXNvoO+PZ5M74w3E3OuH1GpV+6Zk5dZ1oBGqC8x9Z16Ll1+PbN5fQdQNFkoPceH5InNgS/lzCj2oDOtEQdcYrjw0OOD495+4238N7x0x/+lM8/fxg0F885PTlkPpuyWFxQFgvKsmiBarwbWgESZMFDG90ylTjG/6juOkYbezGhWnNOSBgUaBDkmpUnBaxx/6y3QaHaNXW01uFsBd6zqJYYnZEvcuaLc54/f8QHv3ifX/nmd5h+5R1u3b3Dr37z6zw5fMbnjx9x7dp1cp1TOyvtGoND4ZXCKNABboh5lAC+GsnJkeV5MxJZNdssXNzfodwSw0ioRXApO7zCcyRIZKiVbnQn1fnbnC/5sdvsynCGiKVu+/02vgxS1hPtgOO3uAp+RYuh8OLU6nwj0DRagcm4/fI9PJ6qWGDLBVW5QMLTpuGAPTjJsCy2yO25a6cpWmhbVxJKF/G3a9ZQxSAAyRp0aKouE9CBVuE+rzBMqBCC13fAr6BAF/CZQ/eah9V9bMcwREAm7/WYhz7x8h+iDGn+ZAYRNgyfqA5fFfKgiEQ+npbgJ7Uy4xZuKd/et36dhm7uCEpaIUnHZD+FjXQjRpFYY0h7ye6r9DAEvBUEHEpJ3iyF4GmxpghthcAy2rVnIx1fs29YjII8N4Dlvfd+ynR6zsRIkjWc+NxVdSEoGS3/JIRhd2n86rmK2pW2JBrbJFpUZAoCuo86g5DzQUmgnkjkB3qgbwK0Ci8d6SYoFc9SeNZsTXfUvmd1054AnZhvyghbuB19RCUKqAta8BaOD9+PPpzvC1vT+aW/W2fRrsD7NmhRUql9L84toVGihkgHwWDgNvFA7TzzxSL4RYipHK5CFxc4pSAbkykLOmdpM/yi5OLZE5ZRKEpLV7lwBmMETO9aoaHWpo2uT2surZTG1vD5gxn/8vHn4gtTVXitRZDpQLmW0dBaY+ugsaumnJy3wZGuUq7MaOSj7WBvK6ihChqDTGd4NDpXFLWQHIcnZ+C9EOda1EQeMCanjk7YRjITW+9ASeI00T7ULIoS0CEdfAB4OqesKiAk8cokGoAFdCbx+itbJpJMRRGSnCkHzgmjZNHU1kNZk+UqJO6zlFXFZDLG2prz83OcyphsbVNrhEvUwg2WZYkNeQickyRntqwlbK91zKYzLqZTSlvjlKhLbeJIrpWY1FgcezcOmGxvMxpPmC5F/aUwZJnh7PSYxcU5KruOyrLgcB8vRTzo4e8LUBTNZUrvRv9y+u5vfQCRHq4VLUUiFUifOecSZNJnhFxAJqvvxv5SCVvad19DE/81CfBomYxkep2xpYhnHcCJwCLgF+lDqXAWFWiR1n7ywcfcOrjB1959l48++JCPP/6Io6NnnJ4ec3pyxGx6RrGcU1VLymJJjKDUXeOwDhERkzxPcc7afW/fWy/JWUX7m0tKvSXrDY3GMa0afa+cc1RUVHVJUSzF0XFRcvz8mA8+fI9f+fa3ee3NN7h7/x5fe/drfPTRx2T5iMnODmUtmk1lDKDQPiD22I33IUO0aXJGtNHholZENDzxDEbGMYb5vVzSlRC7zX9Ivq8irM7bA4ThCsLttdXrpqmz8vu6sa+5Z1cqKx37QMCnzfYp+dU+O1LQLOPWnTsYk1HXJVUlWY9bf4xuEyoZd/vMd+pMxuOGQG1yHIQKK6Yh6acOn+E7z/p9dRw6g59QqBn6oVmbtqMUdgxd0ZbI+yJl036umKb04GL/2SbNWUu0dah4roRsvG8DwCQEV9t521cDcwcjhkllrVuiN3m9Wzd5KZ6HPtyPOE+tvDQwtQjoVQpHu9L+KJwL8nyMUrgeAxOLs1YC5iBWEX/913+FMWKuG+dWFKLN8EFA5L3Cp0R80uw6eNNqktLfWwI5MgBKqSbCUNpm47cS8XF6QwbOyxC+9lHKwCqBv74E3VMHjrTtpfP1SXASgff1CixJxzZUNgktu5oIMR2qbYXRGdEKIo45mXB3Ngkt0+DG8N06R1VVLIuC0UjCydeqBu+x1QKTGbxSeGdZFiW5ETcFnMW61lqn1UK1fjQej/W2hWFYtJIcLz6Bjd7VKCBTBle6Jou58lFsqFBewvorJWGXIyNdVp7Kic/2sHhttVyZ0Tg+m4FSAbHHCwdLJwtkTCYEuA9pzr2DRYEyKjkEqlV3B+CxXC6ZTMRLvqoqirKgWFYYI5nCFbBYLNjd3cVay2K5ZJTnmCzkQEjsra23wph4SZgWMz/PFjNMMGuJY6lcTT1b4q1lrD03D/axdU1uDF//6leZl+KsM9Lw9NFn7GxNKGzNtd0d6lKS6MSLuly25gASXtNjMsPW9jYHBwdBuqeorfi5RAn5zvYW2ShnMpmgzsB7IWb3dnc4LpbMpxfs37wlDjiuzTAqZ7t/IYc3vI9QLkM+Q7/3ifuhss7mPfY3FK4zRegu+dzvL3Ws6kv6+kTNi5TW9ycENej5BKyWoIUDssyQmyyEl1M8efaEJ48e8+7bbzM7v+Df/Os/5vnT5xwfPeP49BmnpycsFzPKYgFeQhh61wYu2LTmQ9+/DNOL/lqmvw2ds3X9Dq1ZKv2KDEH8ZytLUSyYFxc8efaEN956h29+61d59fU3ePvNt/js0SPOT0+5dnCdOhJ5QROq9eoZreuaTCmsihl026hifWlwjPoSx/1l+2pcpVyVKXnRPf4PcUZepI+UUY//tNYYDwf7++SjHFsVVFVIJhngYb+tISI4/a61Js/zzl5+2aUPM9dpiK/iAD5UfKJlG+rzyu0khNx/iP3+ouUq2pd1zE6/iFAnSpSlNCaDA8zcpn6/iFYoFXKJ8HMVF2ktQSyi2W2cV8QrzntGWY5SiqePH/Pk0WPG2kgusbqitkL7RNNdEY7oqFtZGX+fgF+VzA8zBf2z0te8fNGyjpZ4kbJubv06wpDI98hwtGO4ep+p8KLfXX/sAmuyQSqrpYdX4fk62sk6x3K5ZGtr0tI4aGwIZNKapXnKSoTbSokvT5x3lyFKBDvhzMlDmt/Tv83EI92leikHwqKIdZswHMYIDpb0i8I6XPXEXN1HgywsQvCXqNtBiXSwbj8H8ZccbLmcnhgb2QN1ywkpw7ysMTY8x2BGsshV0E5kky2WtUgExtvbVFVNVVmMEULN1UHDYCXkpVIa6zy1FVUSasSyqPBhjGKeVYWF8thySVGW5Nk+Gkueb7OLgls38XXFzesHeOeYzWZcu7bHeDzCO0uuhYCuqoqiKMhCiDBb1zigsjVeiZ+FV0gosCCFy7KMST4iG43I8gxvHV5rHCEalqs5PTxk/9U3YlA3CbeWhKeMF1OjVtIRxzrrJLc+inYGpCRD5Ys8S4FGCjxWLqYKynXf2jH2NQ79z2m99KKtI4Q674ZpDxFJfVv5zvuaJpdDbgx5llFXFe+/9z7aaN56/XU+/OX7PH74kNPjI46eP+f45DlnF0cUywW2roIk1CEmF6bDSH0RgqW/3kO/rWMa0vXpP7/KWIbWtt/GEFMwt1PKasGkLijqgulsxpPHT/jq17/JV7/2VV59/VVu6AM+fvCAm3futn0g9z3tMwJV6yyu6tpHR8YijjWVME0mE5bL5ZeGYPvhIPtrtGn9Lmv7quP7ss/QOsHGVUu75o7xeMz+/j7Hz59RloWEuQ3JJKMP0pBQpCvJbPc1wtxIZAyF7X3Rve3D1bTfq5vcbYaH7eSu/l46jk3PN7X3xc54F0GsgxXp+Jo1TCTo/Trp9/6+rpuDjSGwL5lPZww9XHIZY7NuTuvuc0eYkmhbIlxK35Xog6Cd58d/9UN0CCYT8XBZLrFWIgu2Hawmsb3KGZBxr/4m41o1KW7eH9BeDN2//jqsw9VDfWzCMZvCjqd7mplshZlr8ICtVs7AVftPf0/pgUhHeeckGSyrSow+nkvXLL0bYiqrsLUN8CuM29dNPy4kqPUejJHQt1pp6loyg6frEfscykuWrmPEe+kzrcRQLiaZJFgOKCWaN+OjEFQo0CyT59Y7dPCxu2q5MqNxenouCx/UNKkuP6oW00MpgxCb3ZicSRYnTlz+RuK5Qzg331t78/g7SOSSaAYRo9NIqETJ9uyT8GRlISFGa2upg8opal1UIHCdFzVQlhm0E0dTbUI2cDNikmUorbh5/XoT0Sob5RjVJjoByPOghQkHtA4RrBbLZeMgL+GAW63OeHtCbS2ZMVQOYZDKip3tMYdPHvG6s1RWchd0zQN7F2bgzlwGlBSyn+mFis82EexDbQ31PQSUG8SRHlKlmrn1mYb+Zen30f+9PUdAYtvZH4vu9RPrNFE2kksZbR+V80xGOaNcEtfNLi74yY9+zCv371PVNT/4/vc5OXrOyeFzTg6fcX52ynwxZVnOcN6GjNgNCpY7QDuGy8pViIXLCKAhhrNPRPWR/2X9XkZY9/feeTEnLMolzkuitOdPa6bnZ5yfHnJ6/FVef/NNvvL2W3z4yafcuH0bj5LEoGbVXtgYiTceCdCoUl83RuiaxfxNCf51d2Vducoa9dtf12b/978J09R/f9M4r/quViqY12l2d3Z5/vQx1jqqkLvIWddEBEz39LL+4h3ta6Rk/a7OmK373id+h2DIEExaN+ZN9S67++v2fxPh/CLjugzW9/dlE0MgnyFq7tcxrvGdy4IgKCEY6Gsu4uehlevDh3U4ZAifDI0TIOZVSNvqwk2hV5TSmB4ejXVNZphPZ3z8/i/JUBJBSIl51HK5CMFuhLmQiEwdV/bBNdoEe/r7FmmquHopzdXMneG1Gyqbzu0Q0zG0/1dtr/veqgVFbLs1p1r1H1jf/uo57d9772OqhuFxbWJa+nBKhO5iPrW9fQ2lVKABM6q6Roj6rAmhHP0n5S60bbdBbVb7TOcx9DfLMjKlGSHMhNGmsVLSRiJO6Q4trjCZaHTqumZZlhKF9csOb7uYTZvP1ondl8kka7CLTqth0nmeo5WE07LBVtpouTg+LJB3QQ0ZUrCL74IQDJkxLIsgbYSQZyM4hBpDbhQW8buwlQ1SMRMiSYUs5SEc2WiUAwprNEXZPQwiDfNkiKN3nucYB8pLGy5oYUzQ2iok8tVsdgHeM8qzxrfEOZHaaa0Zj8fUdU2e5ywWCy4uLrh58yZ1XYvzei3j9Voxmkwah1BjxDavLArI4PDpk+Dwo4QYZw1QuQSvpgdsU7kKsftllD4SX/f8iwK5+G7DuQ+ES04B0ZD5zAoAVjAZjRhlsudHh8957+fv8cZrr/P08RMefPoJp0dHHB894/T4kIvzE6rlQkLLBWlF43Afne/j9NTVCYO/SekjkL5GKAWaQ0TfpjIEqPsAry0a5wgO3YWc8brE1kve+1nJ0dERh4eHfPUbX+fdd7/Cg88+Z2d3t8lSGhFKHZK+RSlRTKBVVdVGAsx7LyEBv6TSF7J8kfIi769D1l/WefnSzx1gsoyDEOLWWpHmVWW5EXatI1YAMTdVXQFUt8e/WUnNDzatd59wjWO+lEkT0ffadv5jlhe945cy0mvaHnp/CFYMtdg1nKJBhQrFULyLF2HsUt+tdWPQWjJFj8fjDuzsjlL8SYY07dqIUPSTzz7j7PhEcnkFTWxV1yEgSDq56LvRCqMuY/K78Ft3fk+ZipTZWGn3ikdviEkYgoPN/Hsa33X7fdkdGhpH2pYOwYH6eO1vAtOEybBYbcmyNlplWq7K8LfjFaHY7u6OhLD3IqC2QSgfTfSMMeLc7ZMk1qzSMCmsjPAwCk29anPexedZlpFpwzhoLWJf0RRNK5r8JS0TJ8/y3DAaG+qtjKqsrrSGV2Y0Xn/lnuSVCIRwlM6LbaJNDo9kFqyrCptpcZIyhlGeo41pFipKHG3QNJhgdysTySirMfj2eQyvtRXStnvnWC6LYLIURGJOhaziWhI6KcV4MqaqahyOqo6qIZE8ZFkWMidKRAgTFhPbal+UonFUE85SHI1BOLvJZNIkobp27RpZngfAZdjZEeKoKAqMNpRWYhu7qkYZqK3l2rVrGCMMW1076loYGFvVHB8eYqsalU2wzpFlagUBXorQktKRHqWEbq9cLlVN1Fn9ehE6NnzR+roNMFrT51D9PmJaX7rairR+lHj0247r45wNiXraizkejRnl4lT18OFDHn32Oa+8fJ+f/fRnPHn8iOnZKednJxw9f8pidkFVzMGLI5/SCq1MxyHer1+WS8tVmZJ1wDAFSBFYpWu7qc1NEtC0pIhlWOoSNDreU9elOJtRU1tHVVmm0xnn0wsWy4JvfvvbPHj4kJ3dfYzOBHaYFnBaa8lMG3q4g8joRp5Jz8+6+cl78YXus+47LdLuIs4vSigO7WFyVtaW3pnqvf9FxtBnspNuNgwjWeekukeyy969+xJayT6VZclisRCNRr5mJD2CJF3/PM+bEOcRCfem0IzC98Z1lRK1MDIt38xtSMLsG4kjpKZ98Xl8Jr/T+T321RlX74x19/VFzlYfyKx5t39wovwqmQ/08Ed6MPuEq/edrlbOcLI2DdyNFdYcdhWJrKZaq+KQO97WW4cbYhuO7l2OwsK0nnftfrtQtyxLybgMvT7ks/NegsKk8whnJ0aq+vnPfoa3QstE0+6iWIQzlJhTBfy8iQGNGZubcfdO95CwLc4rrdqGcl3VOKxlAL1fC1yUSvhoTxPGNsUz6Rj782v2ZkMfPqEtlNLBsd4TUwVEzcYQru/3fVW+PgZuUU0kMNX8XYcTU1yTmobJ747RaExmMupK3rcu+mgInqurivR84WK29GQtwzLp4O9pjAl5twzOWSoryWwjTUywq/DOUTmHcvI9E8eFYPnj0MmcdGQyspw802RakY9HbE8mV1q7KzMa10aWSiPE02TUgq5wGCLTEbP4GjMO56R1IG8ToGjyScQueVBJRkZD41yFHhmUApONZZFDxm65+QWjrTFVllGNgy9Cbdna2uocZEFEFfl2jncWozOy4GBeW9vYU2JrdnKP9pUcHm3wNh7iLnA1xjAajWQuCsbjMeVySbksqaqa0WSL2jrG1qDNGKWm2NozzsdURcnWaExhK8aTMfV0yt72Dhma3dE2mS8pvNhp2sqxPDuFYo4ajUFleG86Bzpe3Ey3B6hFinIJnG/JLIH/PgCoFpheRrSvAOHmggcgnwLDENqywT0R3jaymTb0WoR2aTSqDi709DFUw9177yVKV+9Ct5IpHyQRqxGyNCo4FyfvBibAexuOgDjiKRT5OGM8yTGu5pfvv8/0fMH+7g1+8P2/4uLilLOTZ8zOnnJ8fMRyMaeuKplvgLZxjVLGqgGgX1zQMlg2AfH4vQ/w+45slyGCy/qNddcxLd7LGXAefIQXWkNVo90C6z21r7DvV9R1SV2X/Mq3vsWjR0/Zv3YdYyQpEVqDlkROVVmRZxm72zsSAGI2oyiK5Kx1xxXPiLU1SmUr42yJv+67rblEOrcUH74IIdjf/G67zQhWcHyfcbsqJ7Cp73YMLXExwNCmZyA9JwmcCYOUEKdKzEMwhpt3blNZi/KKuqiwyxpXWZi0Z3CVQF89VwAaQzEvBEkqApzw7fhjKOr+XiXkWH92fUItrrNuW5YzEGp3mJiGOG/NU/p9t9JkOkSU8lFAE86mbg9Ue4dejHmVMN1Nz+GMprBaNfUGtjlZhPajjgA9EnlpSNNQWWBm98wKEZucuCgMiJFuoBEHNDiZCP7DuigT2WmpF8MNh/a6c2+5us6OhnHHyHU+DHwFrnXek1R0zjrqohSzKOWEsCUxN44ttvwPEgHIkWlFpqEs5nzyyYfoTOG12OJbX7EoZqCDZLrR3Qyf/27RnXG2jBeooDWPzIPq5M1QklG66SlygquEfWd+6XqroGVqIorFe9fToOh2D3Vmwt7LewQi2YVz0DjOh7PRtNPbwpbJaDU0WpskFLD8lmU65NuIebG6DEC31XVMU1s/+oBkWR7eafVsVxH0tUI3uTvW1oxGuTCXODw2REkM+eScoixrmYt26HB2FUioZiUnwGhFhjAaWRDo65BUsqwrVKa4d+8ez54+xVaVaN7CuAsV4Z6HqJ3wgpsjjRQtlYw2GGOYaM3uaNwEcbpKuTKjMR7BZJSjtGoc8IQTFp+G6MCizRiF2Hk561Foqrqirmqcd2g1bjiuVIpqAyORZRqtR2SmJYJkU0fUViL12NqiVc1oYtA7o0YqkmVZ4GAdznnJa6AU3lvykWSTbaS4xjSaCeUNeSax0CMacUEqI9x4l9OeNOZOnmopCVKu7++D94xGOeVyyaxcslzMuZiesbO9Ra0cKtfYkWKJYjRWzI4XEiK19uzpHLTFGUkgiNcU8zmulpC+8SIPSQUEwEUk0EVMvkcAaNUmOYTLANlwiXs21IZw7onWIUWsMDB2hJxPGJIUtKRosUvjqM68+m1v0soMEZ7NP3yT78M7CdGc5zl4+PlP32N6MUOT8eff/z7TizMuzo85O3nK/PyQ+XzeErF96NgOcmBFr7YPlzGE64j9wTUfaKsj+fLtebtKZKYXYULWjVGStTtqJPmn8w77gZgWeOf4W3/ru3zwwcfcuHVLQlVHojOEhXYhYEM0qwEkspdZ53DaEotf5B6sm8/V539Zvy0y3VS+2NCvMue+hquFH9Cdax9VNwRJIJydc9y8eSsk3bJ45ymLshFCDTIWPdilmoYJOZ1aoleFh42/IDG+/Oq8u9dx+KKm8K05/wkBGmikRqDSQN0Qqnuw9CaTEqQRywzDte7fq5SEjwnv9k1rkjH1wNXgeBsGIyFYO/A4FWileKjtf7jZLrPSgVUNE5cwb6FeozEd0JYmnXYI/153A9W7/ar2AVpryrJke3tLfkpMxTvzTvsKmpooSX729Cknx8eMjBbCMhCbafjTzl/6Y++vabdG6oBvtOkIktI6fWFlv05fi5IyGzHJcopXotCmb2nRMAkDB9cH+qqvQVaRgUm0TH0tddQwad0/0+LPkPpZNnmwNp2TS0rDZCiLdZZMZQlBMsyY9QVtvQYbmtcYw3g0olgugi+oCDqNFibGOaFDxltbeBOE70rh67qxCtIhHK5Vikp79NhgxiOcVtSlx5eWTx89Ft/lWs5kZDQ1PTPqMD7nAvwMJUZVw3sypZhmOdvbW+zu7l1pDa/MaEwmXUJd/mk8QshrPQoLF22oFVaLeijLMtxYU5UVWS4OJdY6tBGlp2yOOMJkwdxKE+Jnx7panFGsrRjnmVx+pRtGRIJdWbSJEXy60UIUkjVYq2DT6V3DXWsd0Y+YRVnrgjRv8yHyePb29vj804fsbG1hvcUoT4bDFnMWF2fYYsHB7ZuU8xmuKqm0o6qWYGsOP3uEPj6DZYGxDu16WTmrmvnFlN0bd7EpQFkhGlv0eRXtxBDhual0ifdhp+z0b6sa/JtFgVk3jqYtEkZEdRnXIVVmJKRj4qehOj5cOgWMRyMx+VOKn/7wx0xPzlkuCj756CPm8wumFyecnR9xfnKIrYoVoDfUR38eVylftI0hRqOPRPrtbar/ImMfqtdKf4MMpXderLV4Fdau9hRLz7lXfPjBL0XrieIrX/0Gnz9+zN2X7gGeOiR4i0lAXQgb2OReMSYIQ7qEbHtW3Be6E4Pz4ouvV79sOj//MUtHiAADhPtqvaHinGN/f7/xXwM6uTSGwsSKJLbbTjTNzNJoU0RJJoPESyqsWFfWwbT4eVBiCfhwltXAe4P9bHgWz6BLmKHLBAR9mDj0+1A/L1x8j7dI0KNKnm+c4BXGMsRwtoTmMCE3tEYrzMrfsCilmM1m7O7tdn7bdPejs+5oJMLQDz/8UGBcZFJ8MLe64qKtrtWwb2H0WesQ/Bvgf/p8iCBXgW7Cd239+3XSMLMpLo6fozVLrO8Dob4O9/Tfb0282vFHGi/LMsbjEcti2ax7VyAerBW+QLlsfda9k5bOmtAyL1qLeb87nQXBiZNgQ8E0WGnR3mf5CJ3laBeELEqjjYRNts7hFDgFJZ6vfv0rvPn1r1EZxeGTZ7z/p99nuZhj62AV5CTPFM6TqcR3oxkbwQ1BkvH6kDTYetHQaRxTW5HZgkldXGk9rp6wz4DSTmQKkTj3In12TqGU2BeqKFX3FqPjxijJ4porlJZNN8YjqTTaw54bUMqFrLBCBIgztm6YYp0ZIISz9JY2eUvkqgXptNxu4HQr16h0tVKSFMVHpigyTy4wTYI6vO9ydX1JgNYSau3w2VN+8pd/wc2bN5hOL5hPZ9hnpzCdcvvaLurZEcfPj3DWMsoMi+mMoiz45Y9+gn1yjJ0vxGcDUSEaY7DeUZUVx8+P2Hv1LZRuRTPpIU6BytA4L0NUQ7+tYxTCU0j2bB1DMdR3fLYCMKVyp83+WPrjA0Lc8jaE6boQlH1gK8xSW6dlHOU8ei8Z58fZCIPmZz/6Kc8ePaOal3z00YcUyynT6TGz6QnT6SlVsUSrNhfIZYh8HYG/VrI7MPertLmuDK1pH3H3Qw2ua/tKyL73fodgCaVBBuH+x1B7JQucd3z68UdgxRTuW9/+VR4+esSduy8H84MAJ4zpIKTGn2nNmZI668fdIbI7n1em9UJl0/3ol40M24b2rsLU9yWFl565S4i2IYLBey95gLxnFNTtVSUhKIuioCzLTvSUzhh63QlUFkFRTHQVJalKxXeDrTuqhSkvCA9jvaue/cg49+v0W+4SSVyZwPwipb+naVTB7jhT07MeHEG1PmXE9V9XVEMPiLS/iyMG3+iNZ+gcDhGesXR8aJJ5t+c1tDWIP7qr3+lbqa6JYHheliWj0XgjbOvPNRLmdW35+OOPyTJx7kWJ1i1q9IbKOpjev2fp5ziGKNkfmt9QoIP+Gsb2ouAzBqxJ+4rvaN22ObQ2Q20L7DVXhqXpe0p3HcsjU3Hjxk2quuTk5KTxJ46aqDzPqGvfmPZ3xzi8l/FvWjfCKknZAP1IBJvgbnefW3wbzcGrusLVFVr5xu/YOk9RWSrroXZgJV+cs5aiLJuzXeNwmcFPRty99wr7t2+zVJ7xZIf5h0/48V/9dTgXIqhx1iL8hBXH8xiwyYcpZQqrNDoz6HGOyjNGkzHWeyYTw83rEi3rjTfeuNL+XZnRMIoQR1hDDNPqRSNglEiVMh1t1jw+xq9PCRggC/4Boj5v/SQUNGZKWunG5lcp4fJ0c7ADJ9i8J/ZmPoTBjSC/cXoJm55mio5JT5QS2/Boi+u8xZBeThpmZwXg4bGI3Vq9KPizP/oT7uzvszUe8cFPfw4XBVhhzBQe5SWkY1ZDXnlcpqjrkpH1aGcptMdmChcc0R0Oby0nh0e8jcL5PrFMmIs4nscyhOhaOmGVsNjEeERAvo6L7yOGjop2YKwpsOgk2fGQXvZNIdtWxhsZ0J6fQZvwptt3fCllNDr9AEprRqMRWik++uUHfPCLX4BTfPrRA+bzc8rigvn8lPnsDFuW3eFsIE4uY/LWmSitQ8hD39f1E3+/CnEb66Zr3j//69pbx+it67u7L5EwsHincMqCBV96ZlPPZ589JM9H7O7ucuvOXc7PT9m9to/yHmtb6VbattZaYvAn40/77KuHO+PofU6Js3Wi203ru45gGirrmOv083phwObxXNb3+qLi/y/tN80NExFplhkODg4oQ/6SlNGA3vn3LWMRu/btpWU8HnN2dtbA5hZxi6Y7vie+UusRf18Y0We4Y711jqwCv3zCbKR9XbLHa5+oZsibzkF/Lpt+GyLkI+MTmbJVWNhmXafBx1EIkZgt9YaklcapYdPcPizpj3VI4JIO67K707kbwTKCgbn3h91lsFb7iYzG9vZ2p/465j6eGRPMXWbTKY8fP0YpsdjwSORNFzQbL1oETna/d2A068c1NLf+GkDLJG2CW7JfLQGe4vUIf/ufWwYxmctA/2mf7bkTyXo/j0aWZcwXc/b3r7G3t8fz5885PT1t3os0x1CUpqErFceSMiaRqanrWuY5FO4sGfcm2BvXLK6NzMdLri0nwU2iaX9lHdPFgkVZYpcSUdFai61r0WY4h1caq8GVFT/70c9YWk+p4Bc/+zlH731EUdVYbwEFWgmzohV+ZFDKMx5LlKuiKLlz5zavvf02N++/zP1XX+Xm3dtMtrdQRuOA7a0RuVmP04fKlRmNZlOVwkfPdhfTk7ccUjxIrUq75dgjT9wnPuIGpo68TV8J4+DDBuF1k6WwIYa9E6YjkVB2gau0oRSBmQiST+eCExHUddXY40M0qwpAdeWCgQUyBVtZzuHJOZ9+8hBd18yPT8lLhCFTogZTeDIFmdfkPqOsHFtGQ11jnZVD4l2wR7doI07eTx8/RntxbEJ1gUX87P3VZWPpu1eJYT6EGIYkQVftO16q9LtQEZvfXX0HQe66NYkamkc6vpV41j1CIzKcozwnH+UcPn7Gn/7xH3Nj/4CPPviQ5XxBVc4pigtm01PKYikmft6w2aNy/XqkZUhC16+7OubNSHcdEnlR4vRF6vUJhSEibl3xzuF8zD8pTnEAdaWYz6Z8+unHjMdjvvtbv0k+3qJYLhlvTRBayDfq+Sa0n/copZtnQ+NehxS+aLlsbV/0zlyVeblK/f9YpUs8CE4YjUbcv3+fjz74gOVyyXJZNNoNWBOVJv4NwggPjbR2Pp8LSOzNPWXXVY8Kdqzeg76QIh1//JwKLjrCAbUedvX7Tqs5lUwureMDh7XR0OvyMsQUNe13+ut21WdCBPvJbxJmXgRDneXy7V/VNErnzq8y63Tq9Mf2Nz3HnXevcN3665PuXSSg0wSRK33ErnrrK4yG5tmzZ8zncyYh2RyIdDlGRbrKTPswFfrf2/Os0R1Nf1qGIjGlzEBsK2qIgYa2Gz5TrVajD+PTfEZ9xlesTrqRD4cY/f7fiMdTeqKua0kCWpXcunWLe/fuYYzh+Pg4sXTQDbOxDgYPrUtcQ6VUJ0KZBCRQa99dVxrhRJiLMDOC++qqoK5KsmCJY7JMmBI0x1URkjoGTY5ywtAbgYkesGXJX/7wR/zoF7+gcgGD1iWj7Rxtxmzv7PDqG6/xxltvcevOba7duI7WmmvXrqG15uz0lNdef53x9g5mMmlIM6UU1jnKsmB6cc5yWXVyyF1WrsxoSOx/SZGujRFvfhckXErjQop0GvAkztVaZaCCpz0isSfkujZaNs2HtnzcPETr0DiCByJQHHUNIyOLX1UVeR4TirQqvriZ8U40n1WIwhS+NxqZ0F57KVrIGX09VqRBCDBSwP7+PqejMWq8zSuv3eanp38NhMvsRJvhnQ1OOzCjAiWMTRb8MrS3ko1RG9BQhwRxy9k8xE+OToKxZ0B1VZrd/Qp1Ow99MreWoWuBR/d79FXoAqrW7KizHgNEZBq2sHkSv7tgm+rT8bR1+sxMtM0GQrhYhXUR6fXsPIPMSAun2ACjPMtk/10rcWolHg5nHWaUMR6NWEzn/N6/+ldoFB998CHz6RRnS5bLCxaLC5ytQ8yJYebgRYjJWKL0ZF1pgH3afnvIga5mp8OQku74i5ExrVQxOtq27/eRx8r4lUqkvZGHX782LvhO+XDmFXUQRFiK5QKF5uOPPiQb5/z2f/p3ODk55KXJ/WYsHiQPTo9Y9bTCCpEG+mY9G0Q/QHDSme3VynqiblVLdFkbnShXvc1rX+8ynSq+r+L46bwYpt+awqh2S1JCMVbumB4B+MT8bWAvVbLfKCVwFsiynNu3b/P+e+8xm82wdUVVFti6htG4DVEb7rCMr13/KCzSKiMzBmvrQDi0+VRc4nvXWaxOaeFcnK84kevOGylY9I2zZGuWFd9v7+PwWsRlaqaXtp2OKrSh0g1Zs8Yr/dA7byrukY+AAxSNhB/vA9PlUZgO8SNXNszPQ4wIlRmd9tZgpPa39mzFufsmo3cX7/gwpsbHRSVnKm0xwrv+XOMextElfUbtV0ICsrI3fQZrtUYzl8bPU0mC3tV6avBeK6WafBkPPv1U1tzacJ883lm8jVGI2FC6xP0QkxHXwYdoRB4/yED3xx3H3IEdqZlUMD0VuL/KADgrRP9oPGIymbC7u8v29jbj8biJIqqUoqoqiqLAWsfFxQVnZ2cslwW1rVtf27DeLoR4TQVqKROSOnjH38pSAohYo3j69Cn379/n3sv3cNZxenYacL1ENo3J8uTddEXW3990nVJfkU14vk8zJg/kLmoJl2+DhY33jqq2WFuhcNQebh9c5/nRCU5rONjh5bt3GY/H3Lt3L2QLrynLksPDI8qiRJuMyWSL8WSbmzdvMt6ecO3WNfau73P9+nUm29uYPMP6NpKUjMVgtGZ88xrTumK+uGDsKknkF4Zd1xKMaW+yLVYEtWV+cbV8VFdmNFCSvRBoMlt751FakWmF9zWSyCRKn+VzbauVA91KBcQvAmA0yoKNuxfiEI1PHaO9IIIWHEX7atcwGVK1jWke+2iYigYeKYwRBkgOrByGunbIcFKpd9eBKL2Uxioy69i/fYuJydi7ts/27evocUa9KMMB8igytM5kTkqBdmiPhDUzGtEFaSYEyavWKFcBmuL8DI9FZaPAtIBWASl4Qm6Sbjqj7qVsASC+fQ8l0QvadYvzI+xhdFJT4HpZltP1cFFG6JsIBvEyRvO1OCZAtEc+AmTJjp4S/enmeS8SbQFyyTg9gTCIWirdALxoG2yihkNr6qpCI/40tbVYZdGKBviAwzlLnhm2RiOM9fzB7/0v1POKi5NjivkU6gV1PaUspzhXBXVl0IKswJFV4NMnyFee9zdgoDTrugaBeGiIuqSz4bYGf+2OtYvUxF9JKxpCS0riTJ1E5+nPN7UJTgnUPpL2KFASZEIjZ9Q6i689ZJrFcoY/9Xz68cfs7Ozwa9/5DifPn3Fw52URJLg2gWfjAxbPk9aNxtOpltZoNB3Jvy5xkjIugaFbu3pXY0o2aVH6v+swlpS46tYNY1U0d7FhRtYMLYWP7U75ZP7xp+5JkXHLb863/STUJQrfaA608mgcaIngeefmbWxV42yFtQtcvUTZGmXrNs57hEmRGQp9RH8/UGglTonK27A+MkFDzC3QN6mKa5kuR0rMg3d1Mx2tNK200rf/86lfT1z3hLHpCUmSzjofdb/v+N2HXUhhclJ3ZX8YrhfN1Zr3VEo8BhgZp0Ddb6ihvMUnxseB9eaTnkOfKHVDviDnBOcGmNTsBxDcIJMxyma3x7K7jp371oE9rIZHj4wVAck24Mq30/Aek+L53j1oKIUwRmtdiKypqHth4Tv0TViVuq75/xP3H02SJHuCJ/ZTNeI0PGhmZGYlKf74636veU8PwSx2BbjhtB8CwGnxUYAL7jgsIBAIDiMQjKysYMj2TpPp7kf6sXpFMytpcA9nRlQVByWmZu4eGdU9DWhJVri7makp+eufE6EN0oA08Prr5+RCOJxkY0yVrlF1GdZ7XUHhXMNlEmDfCxX+sNvrsvVZ0PZE6FqKblKAYFxMrF9hT08EyNS5LmkFxhbNvHd0j7t37zIaDp0LUwLCWVWCcGL798HIdx8cIRBUlWZ6dc2rl684vzhv1jORSGNIE0lZVhjj6Yo7+9gg6MThCs/b1GVJkmUYDS9fvOLo6Ij79x9QFCXL1bLFfyrlLdzbrRu+xYrWltXGwVVcHLFbkyoWmMKzEe5XWqGqChvTnKKTPglQ1YpVNubRRx/x9def8c6H7/Ev/lf/gr2DPbTWTmhTDIdDhLD8sn9v6hSqAmuFUFpZIYEIb9utRhkcX1SjDbbmnNYkEsr5DK0UZVmSpqlLaiDZHU7IsozUQH//v3DWqcbEE0mzxhb7qJ2frNcw2cOpW8/G5rh402xKL7sYVjvVPhQxk5JlGXVZgZNqfRC3HQ+trAZe8vVj9X/9AaqqKvIn9IKGLf8eS7oxsMR9Oa6OJEkZ7oyRSYqpS2dlyailRdDCOHO9u98SXlxOZGxldCDBZXYQlvlNZIIh4fryClVXSDGgWVHaY2EdcdjrDbFt7m9L6DbLlk0JHFsy2tUvN0jk/sqWuIKt2hSPibfMZaM2WHQeiYhgfG8wQ0cHXnfSZ2I8rKooUM/e08t7pELys5/+jF/94hekQrKazZBCUdUly+WcsizaAXwtBuKbucXEQsBt2FOPrDYxqfFbNwk1t2N/3/7u7m/e9N0latu0fN3WXS8hGiHGC1b+nNZ1hXDFQS/Oz/js008Zj3d4/OQxqipJshyjLD3SJhJ0LUJqyVyb6jZ0rSDbxulXdOOcRLMXN2kTucU9XWvUprZx/eyFtYHFNtHW8eowjevfWi+M2Pro/gjvtrXJURYco9k/OABh97KuSxujoZzW2xi8teTmlbNpxK22tD2S7qzX1ueGXjdbs9rXWjjXuL/iBlzVDGTrOJx4HV1odry9lm1B4xvNDdMSUDc+tIbmrcDY1S7HI/ctptvtrjyj6X53Z9EzO9vi0row356rWfutq3luxraZyfaKrrUxCweGHea8rit6vbz1rjVa5eYWz18KSVmUvHr5Msg9IDGmCgXl2oq+t9EPCwFCCKRPzx8BXRfXvq2/eF9D5Wmn7GrtuRMalFIcHBzwzjvvcHh4SJ7nJElKkiSkaUpVWSVcXVUUqkYIy2PYrFB9G/voaO5qWZKlOfv7+1RVxcnJCc+ePWO1WtFL0xAL0YWt7trHn23Afk5RFFxfXyOl5NGjRzx9+pRVsVxzm7Ifb8bBMcx4RZ9SikRm4dl1/MDG3z382z4FSmkqpZAyRSQp/cEYYwzFagUIhsM+SQJZr4cCvnz6FITg6OiI4dhmQKud4HF+cUHt0t6uVitbR8oYjo6OODw8pKqqYHWylccl2liefLVasVwu6ff7Yb4hfk4IyqpiOBoBcDWdBsEj5udvat8oRsP/84E/VmstXdYXHfICxxvvtYXety1mHmLGyZu0fEVHfx80gorPMhKbr7yP2CampouIYiDoSql+LnaM/vk24Kwxd8K6OOWjAWk/p1osuH//Pp+mKSvpXcFslXJhPKI3tuiKsRpbq11y7iK4tTSaRAqkS8lbrgp6oxsOG7S1czichwi4b6MG3KwHVYHVxnRjXeL2thRvbYFlw3g37NGm9JZva17bFM+nO97YAuCFT5uEwGfKsDn9ez2bynZ6ecm//X/9vzFKs6oKjFFUasVyNWdVrAIi/f9XW4PBDXP+/+W74/SwmwSRmEnZ1k+8910i6XGC1VpphBSoumIxn3N+espnv/0t+3t7TOdLPvjwY2QqKcrKpuRLkq2M3yblwU0C0U1CSGvMG5/+RzbjXXs2E7PN52adrWyFK8dnx0Qy7zeSk9fXapMW1TPkWitGoxFZaou01nX9jc5Tl+iXZbmGR74pk7VtPpu0vjH9a09uez+3fd8/pL0NDv4pccI3wdUx79AV7Let+TZ6tenaTWPZtiZG3Bwv1n1HURSkaeqYzHWtNXTwgrC0HmA6nTKbzYOLrmcyvUAkhASxrlm3/L1cU5j6ecXVodfGchsFRvS+xJUuYEvcplKK8WjMe++9x93ju2RZRpZllGXJfDanri3/Z2sYeTdgiRCGqiopimuWiyVlZbXjOzsTjg4OOTw8BOD6+hqAo6MjTk5OePHsmXOh0s6iE62xkEjZViz65lNn53nO9fU1eZ6zs7PD4eEBp2enVFW1Mc3ubWAo5pe01i0FwU20JP7bwLyFj6q2nitZb4BMckRiixpWxZJ+npA6a+nu3h4fffwtiqoIONPHIlZVRa9vmOzutjKKWde1JPDhfuxlWaKUIk2FKz5o9z/LMqzy2RbmGwwGwcUsDvKXUobf4xicm9o3tmh4pqD5bLMmxFrlFiIWNBsTIesuwo4zjwjRVBPvAkETZN4EK3khRAgbtGcZZdkIEJGPpX9XOytRo+mrKlv50Ws1YqGmhRgF4ApR9UdDkl7OvCg4fXMCyo3QwZN/tq11tkGvRrh/WM2WcUHhQltNWV1VXJyd8+DoDnUUMNWNm+ioxFqftiGdTRYfD1TNYfDj3a6d3nZIu4RlW/uHE0R7WLvv2MTUtgKBlSFB2HzSlSKVgjxJkcD/+G//B4r50lbeRFPVBVW1ZLGctfL+/2NagCXaLMpNjM5Na7RNKx+/q9vnbZkUp9zaQszs9ZuC2KFtbu4i4PjsbhqPxzV5nqMqKxQiJVVVsFzMeP3qJb/59a/43g9/yMnrFxwe3SGRNnDVCIFwGdm6Y9+khGjjGqcU6MCScQvSqsnbFcTN7Yph3hbuN2rFbujHxlaJBi04psds0AxGlzcKUNvW6bbNGBsrpdxz/X6ffr/PqrKm/7qqrJvJBsZz0xh8n2VprSFhvhE92QZv3T7W12G7gLApUL1hFDf3uW2fNsFg63324sZrm+awaV/eBlvb7t201rcZ+zaBb9sabAoc7t63SVHhf9uE42+D39b62aLNDjTb7f319TWj0WgNDuK0rsZ9xz2Tupihly9fWsZOxgoOnzq/ETi2rXecCGXT/GLF7U0wv22tYit54IhMowAEeP+993nn0SN2dnZIkoT5fM7Z6TlVVQfBq64VFxeXLhOc5c96vZw8z+j1+ozvTDAGlssFV5dTnj97TpZlHB8fc//+ffb397m4uCDLMu4f3+XpV1+5tYvXXGBQge7E514I5zbkYjDSNOXi4gKlFJPdCZNqwsnJCdD2rIlp+jZ4715XyrqP+Zjim/BizK9ZmLPul8bAclWQ9QcI2UPrlP5wTJJIppfnjHoZqJqd0QiZpJR1zXK1cgmLrJVwVdg6FlrpYFUSQgTB2O+hV+pkWRYKTiOsW14MK1VVBf57uVyGuZVlGfjqLMtI05Q0Tf/LVwb3A+guuMH6w8eb5a0SiAaheDOYX3APCH4hfJ/+Pf6wNOZFC2hZkuIrT/smRJPH2ffrnw8p0VwfMWLwz1qtQQOwaZpS14puWtt43iBQRqMEyF5Okmdkec4Xn39OXZYgha3W6GIVhLC+i4E4SZpq2NbF0rpGGelSkrhgI6W5nk6pq9oWL4lazPD5MTXuUs3abGs3CyDrgsZtmN1u/zcRsU1jeJtmocXoG7GGMGMpu0vIvHAp3HttETjo5z2yNOPzzz7jFz/9OalM0MbYSvSmZrGcok39jxIyNiIiIVoakdsyCt1+3pZxKyaaNxGgzWvfuBjE1+3nm5kPL+xvGluMyLchdX+fX/dEWslGqxphNPPZDIHg62dPOT6+i0hS7hwdkiYJxihb6FNsztW+aR02EepNzNw25mRbexvRv0UHN7iRrI8xxCp5KdFfj2Wo+HlXe4h4jlvGtjH7G+tnPb7H0OyzFE0sT1VVVFGF224fXdwRv3O1WpHn+Vodgk3jjs/tJqvbpu/bzpi/5yZctg224nbj82Y9GUa4x954Yz9v6/+m39fP+O3uvU2L8YSnwdtcp27TtgmQbxMYw7OmfW0bPAshWK1WjMdjyxMksvVcgBnnZuJ78cG+r169RNU1SdZoha1C1rpNad3EQazN8YY5xcrUTeNu9RPBdVeIiHFbnArWK3i+/e1vc/f4mLRnrQSXl5eUZcn19TWz2YzlsnBJfpwC2WUA1VqRpknIEjccDtnb2+Po6IiDgyNGoyGvXr7kF7/4BZ9++imPHz/mo48+sgLH6SlPnjxhf/+A3/zmE4qidAkgbKHn7jp4Fx+fUMJ73BRFEXDF/v4+8/mc5XK5pty6iQbF17truOlc37QHQti6bbq2/MTJyRnD8Q5C9ilrwcHhESCYXpyRCs2vf/EzVF3RHwxZrAqWRcVssaIsy6C0sfUvqpZ3jxA2AB8aa5XneYwxLn2/FUC8oOqzSHk+yePXyimDLi8vubq64u7du+He2+KAb5B1qhvIvb6IGx4KJq94Ar6fWGPQqqtAwzR2XV+6Y4r/ekGja+bpWk66GthQoE83iMgiAtN6dwsJC/BB6CSGycEeiy+fUVe1DaZylhdjNEakgYhroMIGiXkkoo39rUbgEikFYiKE4OLsPIy3iwDt50bguCnTxNuAos1gtX+P330b4OoyBtsOXzyut2ljoE3wtVus7vNxH55R7brKYQxGa7IsI89ztFL8D//23yKNFe5UrTBo5vNralVS1eVbx/ZP2bYxANsY423PwtsZjlhA7+53+1kTEPqmd3nT7tvWLH5Hdy7+e1kU9NLM4RPl9rWiLAsuzs747Le/5tGTJ3z1xRe8+8GHaGOJkk0C8Y/fsxi2rNvFtsm05/NfBF5MO1T1pjECIYOLD9wXTtgIqV2NRzKEMQovzBio34Jn3wZjm4ivdoHBvjCUMbairVK1jdHruN1uajFc1HW9Rug24acYljeN9TatO6aYfthkEOtn87Z4clPzgtk3euaWZ/y217fds0lB8E1aTBNuQ4/+oWu4qa3vyXahKaZXSZJwfX3N0dFRS2nRPePCCRkmymYohODy8qotHGLanh+31jd06P6G57zwsQmfducWKxVC326+Wmsmkwnf//732dvbo1KaV6/ecHFxwcXFBfP5PDCyvd6AXp4jZRL4Ld+n1nU4/6tlwfPZC55//ZLRaMje3g5pmrJcLrm8vOT6+pqTkxM+/vhjHj64z5Wrg/GjH/2IX//6N1xdTi0PuRatGq1NpMSwhfoyJ2hk5L2Mo6MjXr9+HcbYFX7fBtMtOhCtXfzsJmGjETJsaYU8zwDD+cUFj9//mPOLBWkF48kuSivms2tGScmsLBkNhhweHJBlOUlmWfZu6ICkSZXs4cC3siyDy1iWZSHGpFYKrZv9FkKEPuLY1SzLEEJw9+5djo+PQ99xXZK3tdsLGto0FbR1G3hbC+4IiF1cq7a3qQGhrm3VbZsOV+PTEsab4VvMwMSLprRqUvRBKBpkaDbTBwTFY/PCh5dkYyRmTXN2vEVZMBgMA9PuAdBWVGw0hB4tmcT5t42G9PYm7Ob7vLieY5YLa5hIJLUr+geupLtwWTkQaAy1I+4VPqOFRkubdausaw4O9kmEvUfgUjzG5k6X+cinwW0zEbANocYB+/H6N6JLF8nbMW9H/l1k3X53LBAFn0sRXzOde6322Liv9rPxw0AKgXaWIbs9LjOHbNaggc2oiBjOWgH08hwh4Cd/+7c8//pr+qTusNWsihlFuXTIsq2tWuM0RaQ59rDpL4Vb1jOAxJ+3Meybvq+3RujcxOR2f9ssoHhCRnBnQQiyNGsRTpzZ3zN829LyemLa6/W2zsGuCa1xx9f8nlV1TSIkEhHOotSGslxRlClv3rxh/+CQn/zk73j4+AkyzZEGaqVsCr9mJdbW7cZVjQhGGJ/psP1u6aziYMN74vPYes40h80JBe1mmnO4Zf/X1t0Yl4HNW19ozkw0kDVtnmiIFwGOCHZN477Y5wRr62j8WeuOzzEvMoEEsjxjMBoynV1jlKEqK5e5zuLgtXo0btzCC3Bu2aQr7uqLWnWZBv9uny0qGhEB13SXW8Tz6sJik2bYnlMT4FYI1s7VNgZvm+KlxRh2xrRhtUP/Xaaye0/87k2fNz3XHbNvXReem5Qb8Rg39bft2bf16e5yLwgPxV/aZ0V42hCPRwRasWme8fh9K4qCwWDg9ieCLxMNIaaNAmRisyqen5+SpQkxbK25mIf5rHXannmMj7RBC70R3rbRGiGE04BHSR06sFgrxd7eHt///vfZ3d1jPpvz4tUrzs7Pubi4RAqbXWqwMyJJcpK0T5JkpKmkqkq+fvaUWpXsTibcPb5ni8lVFUrVVGXBarVgsZhzPb2wMQZlFbKkzedzfvKTn3Bxfsa3v/Ut8l6PV6/e8O3vfIfPP/+ckzenEHttBLzp+KmOoF+rGlEJChdLsn+wz+7ublBK29sbb4W3KQjCOnpeJNrT5tmG52j2w9caEWRpSpb3EEJy79593v/gI87/9pfsHh3Q6/WpljOK5YwkKXl4fMSgn7MzGVLjEiYp5aw7yrlw2aRDSvkMrjmr1Yrr62sKF8fWdzRYKRWqg1ucb3/zQqOU0sXZWNqbZVlQ6gwGg5a3yKZ6LNva7dPbOgLmGXYphEu1Km2WF6VBNgy9Nja7UipTKlW5eGeDqjV5ngQkHQd8d4sixYcnBIprjXYMtZe8PJFUzgzkA1V6vV7LXSt+V9sUrvAB4EpVaF07Qi2olJOfHdNl3AE1Loai1JpcSeTBhL3vvs/xzoRZuSJ/0+fVy5cslwVlbf35LIqyaYKVASWgNIZaCmpjSIQhxZAlOVqkFFKi+j3eefIAKWxcQSKs9CpphA4hk+gAtImSiBiM7jVP0vyccIfEhPlGdwq/L7rTS8Oc+r7i7xYZe+LrfxOhP8C5rZnIfa3pwzNf2ruSmWb/tLMY+WG0iD2eMYqHaX+vtKHWNb08J00FxXLGf/x3/yOZNBgNmhrFkmVxiaFAae+eEbk60W7x76JZjLAIAa5pVwS9jVZwTXAQhpDW2efAxwrw64zeZiET1gPl4/ssQrFWvqIoguDttc5+Dj5WK9Yc+3d2kzo017rMB+78bSasvlVakaWZq4VjGQWjKlarBVdXKS9fvmZV1nz628/46NvftVZDd69nTNcZG9naiy7R7Y6h+RwJhTjIEE3GJM8wSiGamA1opeI0UfyYcfduWICG0Xfv11EfIggGBJdAMKCd5SUSIKTPsuMYcA/NIeW0Czz0xRLjTHSB0Q91EZrxhZd7WdXhkVBkVWsEBqUVIkkY7UwQr0+Q2NTTtSptv9K/M+4/fo3lGC0sgkAjfDpzGmXCza2DFyJcE+9plAvdr0b7GhaHaa3punBual1t9Nu09THauq11ZFus1E2CxTZY71oe4rNxExPbPSs3xW+1LAE3McqOARf4NK6EvTGeafInrzWu5r7AjIbvrQTDawJOd/7ejQgRx1qaBi7dCCRY/iQRkEBVr5hfX1m21CgQHndpfOr8loKhNRfWhI2WoOaEp66L6o37C0jlxi0EJmnwn6epo8kO3/3BD5js7nN+ccXTp894c/qaqq7Jkz774x1kYjAipTe8i8h2SPo5g35GImrOr2acn77kanrFg/e+zXhyl7osMWrFyeuvuXj1nOEgYZCP0AqESUlc4ec7R3cxGL569jXT2Zwf/vCHPHj0kGfPnvHuB+9hJLx69coKO0lCXSub5tbYDRc+xlUShBela1arJUYb+v0Bw8GI+WxBVdoaHsgUrcu1tdq0fr4laYKNtfBw4tMPN7gkBnmtFSCR0iDSEbt7d7h3/5h//s//OSfXK0ZHdxnsHNOTGWfPv0CKktGoT5qmvPPwLrWesSoUWjdxjT6o21s2siyjJ3ucnV86V7KENM1ZLBaApCgKRqMRVb0kz3N6vR5CmBDE7xMyGWNYrVatEANvEYkLHno++50nG5eo1W4vaEQLv03699rH2HwXuyJBlGHGmFCoJL43CA8b3rUNGfgMJhIRCpgAIVAlFizaQeB+3AYp08C0Wh/DdRex9gGGWlvBRpeG8c6EF59/wWQwwuQZi7JCiQSSFG0UqnaMkZRUSUaNYV6WFFpTC0kNpFKSCsiThDzvM94/4J/92T/j5dk5Hx8/IDHr6U03ao227N2NxCrScAQNUeRy0goubT8Y3nijDqozxm7A5vbnLMFo8R5bDn83dd0mwtgw0ZAlCQL4z3/9nzk7OyVPU+raCprL5Zy6Lh2CsAzptgl2LRjdFjPct9PYbWNu3ZwkCNHUT2kEjSRiqDcTneaMWkuC18D4tknA96+P46V8i4WMTUyLUirEZ8VMa4CZDpOyjUlqNFSqleTBv6NYFZyenpD1BvzVX/0FH3z8LRIpqVRtlSBvsVxsa/G+NftstvYW8dm+A3tuRGAfQr+tddyCVzeuyYZ3bhxL9Ky3Wmx9UDQMj+hcvC0DG3PHUrYtyJYJsEH0BwcHfMFnVGVl4zSqiiZ72fqMGrl9XQm1iSY47vzGtdncTPSy7sPRNSK81BEcttGsTW2bACDcC7q48W0Csb+n6wnQ7acrTNxGsH7b2eyOweOErpIkfl+3v5uude+76Xt0ytbG29zb1jh3+4npk48b9UK+DwB+m+wnpAhpQ73QbtAtOhWPx4+5u67d/dZa26BfuX5fd77+HaEPtyxBnvH3CZtAo9fv8f3v/4Dd3T1OTs748suvODs7h8Qw3Bkx7k0oVktev3xKrQ2Hd0u+/+N/juyNwChUteJbP/gRJ6+P0XVFPtihVIokzcjyjDv33uH07BWzxSWJ7LMz2rXKV22Z1ul0yoMHD9jb3+Pp06f8zd/8Db/7u7/LgwcPePnyJe+99x51XXN6ekqN4+fiGCwhUU5h4JlipZRN9aptBrDxeMx4PKYsS4qiaPGrN8Frt2nTuPbHpRb8HsXNGAtTe3t7PHzyIT/+/d/nw4/e5/DuXZ7/7Fcc3TnCJAPkquLF11+RCMOjh+9wdXbOj370Y5SqqWtNkmRhfHmeB37G/53NZgD0er1Ar/f29sJcVqsVw+GQJElYLpfBghG3bpkA75HgXbDiWBCf5ett7Rult4X1bBF+abuBSTHyXUsv2tnMuG//vRW0RRuBxn3Hi1JXjRtH9z3rB7uZl+wc2MV8wXA4Clkh4hYATwiyRKKVwtQVea/P5XTG319NGQ5HiN0dhnmOWCwZphlSSPK8T280JB326e/skPR6mDxD9ntkwwHjnQmDwYB+2qOf9RlNJug05ex6hkxSR+s2B11uam9HyO11iPs19oENfXY0MK2LNwsbm8bQJSw3EWZ/3ybmost0xBar7ju10vRym/ptuVjwl3/xF1Y7UtUIJHVdsljMrFbEGBKZ2GKOgRG6eZyxxaLLHG0Ljn5baxEb4RlXz9wLIK4y2jD+VVUFS4Qdm3HX03DdGEjTBOPSVAvRZO/wVVq7VsB4v/zZ37SXWusgaDTPQgwpbTywXfC0gpGiK6RaYaZkMZuRK830esZXX3zBex98RCIktalBb64/cpu2idH3RH5Ti/ht62aKPTOxOLomPG5hGt/GCN401k3M4W2af66Ln7tjedsZ6Dbp4GEymYRxeUF0E67uvtv/tXter50v3zzWvgmnvA0Pte+7mSn1z29bj2+6B116tUmQ2TS3ruVw0zpuGs+2++Lvm+bX5Qm67+7i6m2CdFfw6bbwy5Y92zaXTXPbtg437VFZlvR6PZdkYR2uGwGxCySwWC5QcS0ns04f4vO2ab2747YxhlbhEVs1umuybX4GR0NwZ8UpndIs4bvf/R4HBwecnZ3z6aefcXFxyWAwJB/0yYZjBv0JRl5TmK8xUnN5fUFN7bIALqiKJaauGEyObPVoJKouMcq4SugV9x+/x9XFG3YGQ/IkI8kyqqqgKJacnp4jhOTxu494//33+fLLL/npT3/Kj3/8Yx4+fMjTp0/5+OOPqaqK2Wy2vt+sw6O1OoKSjRVgPB4HLX2cbOibJHyJd3sTPugKroPBACkl8/mMl69e8uDxO2SLBb1Bn6GEslJcXp5w9uY5Tx4esLe7w9HuLnePj3n1+g3T6ZLJZI/BYMDY1dCIaaAQIrg6eXjyHj1JktDv920qXAfLvhbGxcUFl5eXjMfjwMPHMRtecX9wcMBisQj1Nm6KB+62WwsafiKxVjZkacqzIPm36mjoJgDRMyS+L2M0Stchd+8m4cK/wwOBN934e3wqW/89TVOSiOmJn42Rnz+YMUB6VymA84tzzs8vefDgnTCONYQlJT465IvPP+f46A7f+eEPGQ0G5EmC+cPfoyorsixnNBqTJLY6uEwSWysDQQ22CniWoRNbNVwkKblMERqUNmgNk709DLaqaDyGt7WbiE13Tjf91upz0z0d5LaNoNym/233domQRdoeVdq2Sbhs9tcFoNYKAdZPMk356//0d1ycnZOnCUKCqmvKagmisbiZjuZyU4uJx6b5bNI63bQmsYDetRS232uQMiFNMoSQwU/TCiHWVGtTwnp21+bp1tplcUKCcy3SetN4GkF8kxVqE2HrMhoecTVJGnxF9ptbF5Z8/z7Nnn+H1pq6KqnKwmqZRMLPf/4T3nv/feuOpBst4KZ3dOfRfN/COLI9GFwIq7U3OL7IM4zCvyfuv81Ab/q9PZ71z9ue7TIum8bZ/f62sWw6A5veuW38Rggwhp2xLUqlQuxevfbubXjEN19l2J+T1pi/uSz5lvcZjFkXNnzrBpFuO+tdYSlu2xjETULFRuFqA0PdPY/blAXdvteYNNb3ZRusxTS3y0x32yb42jw2uO2mbhPCNr3vpvHE9/iMU0opl+Rly/hpYM9fm13PKMqSNHHZmITFfzHdukno7c4n8F5GI2nvZSywxK3F8MbJfLzFSwgQhkePH/PgwTtcXlzx208+5eLiisFgaGvf9Cf0xseMx4fcezhgfHDM6ekLRqM9rq6XLNSCyXjEwf4xg16PLJGkUmKw1bd1bVB1TV2tuLo6ZbwzpJjNkMDucEBdlcymUxaLORfnlxg0H338ER988AGffvopP/3pT/n93/997t+/z9OnT/noo4/42c9+hqprm2RCNEqqrqs8brW9UqOqKsbjMZPJhNVqxWK5cMuxnnK5i+9imqO2CCXbhPKyLJnP52hxzheff8FwZ8yP//APGQ1HlPWCcrHkN7/8OwQl3/nWB4x6OffvvsPe3j6VXjCZZC4jqvXg8QKDp22e9/Y8tf/n62l4fOnPaK/XwxjD3t4eWZZxdnYWsk/lec5sNguKwjt37pBlGQcHByG+6G04Om7fKOtUTKhjd6fYLSq+XwiBjlwtgm+91tR1RZolrftjIIkP1yaNie8zTmUrHGE3xgTiFWe6iglAgxxxWlvPEwiGwxGz65k1mSbtgoAB8WpN2sswymo87ty5y4MH77BcrdBoal2hlCWkRgi0SFAGGp9wnJe0jbFIhUQLG8OhnQZNpraATmJspoLg2rAFgW77vm0/tyGmbhNA21Sxrrm56d2biHBXc9Alzl0CtklgtDzFLTQ4psmOpLQiSxKyJEXXir/+y78kTRJbwV1pamWD1Qw2I07Tl/NPjwiq77dL+N8m6d/mWtxHV8CwMA3gmHgFJljlbNChMWCUTTNoj4VFxNalxTRKgLBMm/3GrUDfuCjF5zH+tynew2tS/PV2+j2iz/G53KzRjdum9xpjUKqyBY8EfPbb33Jxcc7OZNdq0tnGfN/EfNwkpLfk67YwGT0uon2z/NJ2QW3T97f9vq3ddLY3EdPWddZO+DduXWZJQEgUMnCme4xpWTRuwkVdhqvuwGJ4H15Tux0XbBpnPNb4vub67c/zJoFtmzDi79sEfzcxjG+7d9s9m/q8jRDb7WcbPd7UNtHgm9rafQ1nvzamm9btpvWK74tbnDXJ3zOfzxkOhxsFSP/dGOMAr42zV8XK0Q1XsBhPM5pnu++7cS2I+KwOn3sbgdcYE4QlA4hEUivFcDzi3ffeYz5b8tlnX3B+bi0ZO+MdxuMJ+Wif/u4DJrv3qLTi8EFGNtqjWlWMh7vcP5gwHvVJJVTFktXiilVZUpRWaZfKnq2lMRow2XlEWR0xm15xcXrOcjEjy3KETLi6vGJ3ssPZ6RlCCr773e/y3nvv8emnn/Kzn/2MH/3oR9y9e5fXr1/z0Ucf8atf/tJyRm6OymgkTTFoTyO8EOKzUfk97ff7LJeLpiRDZ+02wVBzXtfxeIsObNiLsiypLy6pCmtNIUn5+KPvoFcrPv/V3zM9e8V3Pn6XJ4/uUy6WfPThB+zv7yOzPYRIePPmhLOzMyaTSQjSjse1yT27K2AkSRKqhvuz2ev1ePjwYVMNHJhMrIdNnudBUBJCtALH/4tXBreBI8IRdBWKgyRJQlGVa+lq/YLHKQhjBsQW/GisE/GzXcvGTQfR99cwLyIIGt79IxZg4j672hcp28HoUsqAGDblXVYuo83uZJevv37Ok3ffgyxDuWBypKauFUImSGmlTGSClpbwZkZgFAhNo53wQOI0oDZFpYkEkO1axW3f4/Y27ZFvSYeBD3e8xSDxtn7f1rqwsukgh3chkKJ92LcRbb/fWmuGvSFZmvLLv/8FZ6dnSGPQWDgpypWtmaEqbLCeaBGPbraQGFbjf5vWY9tcu/d3rRbe/NloF+3sbTpBrKBhPFFqC/vNb8I9E2t7RDgzHsn6MxP34dfNE70YgXeFgu58YsVBHDi+aR38s9sYkvg3fyYDE6MVdVmRpDkGmM+u+eUvfs6/+Jf/C1Rpq1Lbaqg3o7x2UOWNt7bG1QgZjR80gIz7EG89Pv/o9k20TP+l2za8JDoLORqNAjxXVZN68SYBrNtM5Dt8433/ABz0TVp3nJsUKLdhsm9i3G+7Jt3+YqVIjJtuxKm3FFi+ieAQMz43PdMd1z9277YJVt1xbXvO8wDz+Zx33nnH3i9oaRg2zcfiSIsnF4uFw3kWR2ttgtX5H9u20f237Yl/uxA2LkNIwcff+hZplvPV06e8fv2Gfn/A7u4uRsPZ2Rn3RrvsH02oNFwvl1xenZIlmnceP2bUH6B1wfnrl5yfvmJ+fY4qlwhsrRCERGtJmg3I8x47kxF37x6xt7/PwdERFyenvHn5kjzvIUXCbDpjZ3/M2dkZX3zxBR9++CEPHz7kiy++4LPPPuNb3/oWi8WCNE25e/cuJ2/e4Ph+BG14b7wCGsVUVVUslzYg2gZB54HPe9vatWFfrgXid2EupneejvdkRiITZlfXfPqr37I/PuDZV894+slveHj/Dr/7O99DCs14NOSDD94nSTOMrKnKiuFwyJs3b7i8vGQ0GrXe6XFPLNh7i4Qfg+dhfPMeQd49ajQaBetHURSt+ndCNDHQ3qtgMBjcuF6+feMYjdgHrHsN1rVCPtVoLD15xjW4eQhho/hd4TylrHtL4gqnGYP7XZPnWRNpH1IbStxLQFgtYupy/yqn8dzkqNGYkhvka9OFCSaTHaqqJOv1LQAaQmErJx+TOC3Fwf4Bf/Gf/oKHjx7RyzMoNBdvTtg/PCJJMoywdTXQJggLNlWnREoQyiCMRAir8UCA8tKosT7eNuuS9/dua1PbJoWO7i3KnmLC/63er7GQuGuxNCFcng6veWnSdbBN6jDYrBsm7qxLLLywGV6Kc0UxTffGhL9WUxTPyDPMXkvqZmQM+Cr1HmGIaNzu3YkQ5FmGQPBXf/kXFs4SiaqVDbiqyiBEGnyKUOsAqKp1LXs7e9nNAc3bhKCG4bewbO/39T+SIKxb5kwFQcP6/zeuTfb5pj9rxfDB2k3wt9dq+PuNEchQhMrrhC1x9OOyFUSlO2IyaIwTmbj9i9NRe2HeRGNpFAZdC2XMFHkXlZuYjFhT4/vTxlBrRa41IpEYpfjFz37Gn/7Jn1okaRphqo2jYoGr+e6BUwp/4sJPrXXBXfXmexH/GAvo0bj/qQSBLqO+iXFrCOE6zLheogkITOeMN5EmFvaabYpoQAho9fc6AMAuXJpnVugyLlOgUi4Fevvddsztt8eD7g8Grtt2hiIjtsOOX48usxz/7a5Ze+bt5l4f3RvdH/UhZfM59Clo/43mFq9/vCyxmoVOUJwJeN3/0PQTz6kLD9uaAUxXcYFTajiKKozHs+7MN1TFjchYtGwEGNmcixYsNu8LfYb3rK+/8eAUKJoJG+HpRrNK7TMR3tcmeM0ZELhMjQ1+11ozHo8bQSO2+Ynoq2lwQyIliRSURdna303CVvMxnq2/tr4/wWVdtrXZbxPMpJQuBX7DBQAcHd7h7p1jri6v+Prrr0mSlNF4h6rWPHv6DGPgzcUV47sPUGbI5eWM4XjAO/cOSY3m/M3XvHr+lMV8CiikqUiktp8d+BkJQldUq4o315ecvn7BaGfC48dPuHv3LjuDAS+fP6dYLVnM54zGA4pyxatXr9jf2+f47jHz+ZzPPvuMO3fucOfOHb788ksePXrE+fk5qrLv8nxWgK9wDhtlsQ/uv76+dtmaUsqqCHTxtmlb/f1x3TYLY9Z5Vgib4jiRCULK4JJ0//gd3nnnMbsHh4x39/j8s8/51d//gif3H/C9H37E0eEus+kpv/sHf4hMBbWqwVihrSgK7t69w2pVMJ/PWsrHPM8pigKlFMPhkDzPXeV2RZL4kALLQ1hhopmjLwexWq2sMNTrMRgM0FoznU7Db2ma0u/315SLb2vfSNCIkcPe3h7L5XJj1HlAaNKlYnScsXZMNFIgjHS4QThCYf9qYxAisUXvhECE1JAJWZoisAe4xbwpRyQwIZWkTF0VaGcmrGpbSA/Wy88b4+fm3Ro0SsOLV19TVIqjgzuMemMkkkqVGFWR9lJboVhIBsM+s+sr/s//p/8jD47v8fzpM85PTvln/9X/kj/5r/5r5lVNYlweK6VBC4yE2lgNq0jt0ZcRIxg0otJXszYkGI8FWadOrrVljoZm0UXcnki5vfIIMDwb3dfa25iwRq81xmouTTMyn96yVYPE9dl6FmNrjrgxmcCk2d89j9J6wtNq17eJNe5e6AxTsPOq6opBf0CaSE5fv+bZV1+SSIE2Cm0Uq7Kgdhkq6trCAUIjhGM+TVtL0qxJey+6wsb2w9juL4bpRKZoo9HKoAT4pKN+DH79vRARGOPO2Jp3e2Zn/ZpFyJFmxuu8RPQZ3Nmym2GMrbotpS08VNcVQqgg0EA3uLFBiFp3CW2bqfPgcpsWLKBSYoymqEqGaQpGc3l6wtPPP+XhRx+HeK7Y1cqOr7s/jkEyBqENItlQWdzzzFj2RxhLvBP3u4kUBoEJ8l1vaJs0uNsyBrWGcdtFWn8jbTiIhQ0vHPhhi9Zzynj49i55Hcbc3eeF2uZ9Ei00OhH0RgN6wz51WYKuQdXglDnCJe7WANrjsBanhhCgtbXoGVwV9CCYxNribftrf7OCauyqK1q4LV6TzWKGnXEj+Kq1s9cWQpqVNS1p1UDE0NtYqeYca6faatK7+r46Z91bU1oMt7Ap6IkEOeMFyLbAYTp4WiPQLUHDJRl3dCMoHHTkSu0AR0oZQMcrzRDGiU6uH23a4NVZZY/C7ZA6dMhfdwKGF/Lawq9LA++W2vIHHk82AocXmq2iz36XrtaXMY13hGXObHxpS6kk7Yi0G4tUhkwIUsA4y7g23ZjBGDd26LL/MdrjrkVqk4XK7+WNCg0hnCupwIKL4NGjd9G14NnTFxSrgvFkn/5wF42A5A2oGiFSilnB9XLB3u4h9+7dQZfXPH36K05fPgOnfNZKU2nVGpeUijTNSBJIk4Re31acXlxe8quLCx688w7vvfsuj588QUjJxeUFSSpIFjOuLy/56osvmYx3ePDgAefTS379m9/wp3/ypxwcHHJ2dsb9B+/w9KunSJ+BSnicLBzMuag5hwtiOmCFhTRkKBXCxtLUVR1chOL1jGlHksjg/i+EwGgrZNiYSej3MgaDIWneI81ylDb86Z/+M/70X/wrzi4uefn1c/7mr/4zL54+ZW+yyw++8zEH+0MW8ym7e4eMd/c5uzpHCJthKssyJpMxRVGEuIvFYsF8vgAEWZazu7sbErwslyvnPZQFJX/j3WCV3D7bn6c33qPBVx4XQrC/vw8QhBgvrP2TFOzzHdZ1zd7eXvBZvL6+Dgsfu1dorUNeXr9Zm4K94xa0wx366Z+NzT7tdJkOMZq2S1T8bBK9U7e0Z/5wEiRdIGQm+Oznv+A3v/yETOQ8efwuDx+/AxiqqgZpA56E0nz44Yf8X/7jn/OLn/zMMb+S//jnf8G3f/xHiF6fGoM0BozGCEGaJiRpijQ+aFciBSSiyaTVCjAW9tD43NCbNOlvax16bX/za7JFy9R97q3viD7HVoq4Ey97xk+JWPhoSyGttgmpxoggZiTj3/0BSdMEKQS//MXf2wObCLTLYFMUhTtklY+Tw9emsMx42x/xpjV/mxWjIRTtbE1C2GAuWx9DOBch3RJGusJE19VqW7sNY9pNktCyQkaMo9cU2TPpLJzCr5dpCROb8MPt2s33hXPfitNQ1h0Ai6t+/vO/593vfJe6alwpuwR6s3ZRNAVK18ZsbmA8ad1vOsB+k1C6bV2+iQWkLdytCzD29/Bpy+9vfQtBpHjLGWhplx289Ho9sixlVayoqjoQMK8x776j2591P1FraRnxTzT/i/rqjp9IyIjvaQtWojWM9bkKcBp2KyzoDg51vFzE1nsxIVYWyBbBFsiIecZ9jucYwWt8QYjAKIOw2YRomPWog9bqeBDt4l8DGKG7KDh0ovGJWLwwBF4RpiMFRWPpEWF9IFJAheGLzrhM+Lt2Bv297ifhClTqqPaLt+gE+YmmBk1gSuP+XIeJY8A8I+WZOqUUSSrZBAfga+b4VNX2N8+s0plLt209Rh3c4S0s9qzYjWyE5s3Cx01tvLPD4eEhV1dTXr5+Q68/Ih/t0p8csHd4h6P77zKbXjIa77CqDbu7u9y7f5dydc2nv/4pV2fPELpGVVZLbs/2INANn7XIxwR4jXiv16MnbW2Hly9esFwseP/993n8+DFSCs4uz+n1BtSDiuVixsuXL3n45JENBv/iKV9//TUPHjxgOp1yfHzMq1evrNLbKUIQDW5aT6Bi18oz071ej1WxJE1T9vf3+df/+l/z3//3/33w3Gkrptp012dusvEKacTnGiqlWF5eobRVLNy794CHT56wWC741S/+nr/7m7+hLla8/8FDvvXRRxzu76ApMQbu33/A5eVVi2/Osoz9/X3G4zE7OzYofDQao9QrZrMFUqpgkfBuxTG8eD4IYLFYsFqtEMKEsAgbzpCGOV5dXTEcDqmqKlQHr+s68EkxD/629o0sGlpr8jwPvmFpmrZ81LqTin3DfB8x09JFHl5I8NoEv1Ax4xP/9T7fzbM1jdneNi88SJm0BIwYcHy2qVhAsTEoGcfH9/ntxW95/vVT/uov/jMHRwf81//r/4q9O/vILCVPM3IhefTkMcfHx3z91VOqSkGa8gd/9CcMRxNWlUufhnWd0sZQVAqpDEpDlmbkeWKlb7FdGOtqvW9q31Tb2Q3C39bf2wBrEyN5G8QXw8ZanxFl3KSt38Rwdu8NB0Pa6qU//enfkaWJTbmHoapKhCCKIzAkSWb3wyMts56VIh5Hdz43zdUTDRCt8Tf9txMjxALGNxEsuozetnHHgkBX0PDnosuoWyJuWs/YsW0O9I/fedO4bju3+Ly2E03UpIl1sfzi88+5vp7RGw5bSo9v8t63CfJtEeTt526bQH+b5249phvwhNdbvO0d36TP2zQhBBJJlmVkWc4KEdwBtFJvXblGQ9oUn2pp4+FGocANIuJtGy2+dXcQredb44mEl1irbBw+D4K1+w0hWs/YT1Zq8YKGP29JkhBbNIIQsmX+LSXGxil2LP6RgoAwgkbQ8Ux4/A7//m17Yh2IdVgDosKpnRtprPB2nY327+nGa3ncYJevwUPt8dtH3Fq6602x0lh4AHTjMiKEsPF42lqKMZZHqas6WDXquqKqK8AymdfX10CjgLFor6t4acZv5c2msGlV1fHM8C6mt8Xhrd6j/ZdSBum1zctsV2xtag8ePADg66+/RhvIR7vk4z0Ge3foT47YPx5yrBWvXr0mqQ3vPHzAcj7l01/9nMvT51AvHcOd2GJ4w0bIsDRXhnjeurZuPN4Tpj8YhJSrl5eXfPLJJ3z88cfcv/+AxWrFcjGn3+tTrVa8evWaO/eOOTw44s2L13zxxRe23sbeHicnJzx48ICvvvqqVfS0uxYxb9ISQoTV5FdVxfn5OZ988klgyOOz7j+nacpkMmEymSCEYDabubS5dQSvgjTNGAxH7Ewm7Ez2GI53+M0nn/CXf/mXnJ68Zm8y4Nvf+R36ecKjB/e4d++Y5y9e8vjxd5lMJk5wiWqESAlY92WlDFlmXaOOj++TZRdcXV4xu16wKlZIIdnZGYf19QpMmST08pzRULKzs0OaysjaIZy7VUVd1yyXS66vr1FK0ev1GA6HIUWvMSbs523arQUNz/QXRcHz588Zj8c2ELwsA7DHAocXBLoaWC+AxJsNdBiY5iDHfcXF9rzpxktbHunGgkf8zkS2tZOxdJckTTowz4xYoarHwf4Bvd6Afm9AWVZ89tnnfPTlhxzXBTt7E3ZGYxAJWZ7zOz/6Xd68fs3+4SF/9M//FX/2r/4FBuj3eo7mWI2LpjkAWhvKqkJIiUxtzv9NDEUXdXQFuG3M/Lo20+vVCMTtbcxF97Bu6v9tTEhXu+0/G2PceqxrsOy1tgYv7qvrXtIlsPFnLyRLIXj+/GtOz04ssTTWP7wsCzwhyLKURrJxPEM0vk2Z0bpz37YOm9yuYgEitshJkbZg2N/zTRjl7ru617pwD7SQbDcTh59745fqx0TQJhrTrjoeC/jx79vGG8+vexbi713rlZ2DFTTyzKbumy8WfPXVl3z7e99f6/u267f9PrH+ydCqsbHt2W8q7LxtjN1+twlyzZ5vfv6m1lXSvO35cC7joyBsYpHxeMTl6QlKKUfYQkaDNSmoOycPl9vcBNsJESBmYO3/Go1zE8dgYbmZU3gsvLNrkTdurNpgXaFiZl03PuLRTJwW3sVeYJ9TxrRigRpZJ7Zc+OVrfvMMXFyx169NOM8dBrSVvML3LRuYsAKXDRKWiWzBSWstlCZJGwYlyHkudbX9TTsLBjbLnfFxZrESxc7YKnKEWwInkBiDMZvcg2wa8tplBfTpPv28V6sVRVFYC0ZlLdXL5TJYJebzOWmSIGkKjuW5FX7zPEcmgiyzRdieP3/O/fv3Ay9i16rBj/Ha+ng5K2/a8RdFEd1nLdg2CU6E4zZY75o9artNxbg0ERYHd4UWvyeb3Fo8n2QwJEnK3Tt3KIqC8/Pz4Jc/Go0YjXcYjHZI85yLs3Pmy5IP338foWu++uyXXJ4+w9RLRoMeWhsWixVlWVDXBYPBIMBTUZQuvs/XbLLrWJYlStuaOr4mg4/B+Pa3v83DRw/58vPPuZ7PmU6vGYwGnJyc8ujdxxzducPzr7/m1atX3Llzh9PTUw4PD3n27JkNSd3G82z4myQJWZahVM10OkVrzd/+7d8GWOrSds9gX1xccH5+4eijdbvf398lyzOEgDzv0csGZL0eUsJsdsVyteDXuubwYJdvffSEu3fvMB6PGA96FOWCk7PXPHnyhDt3jgNM1bUJVgpL60qm02vHk9g1llKwWpUkieUXRsOROxeK6+tZoJHL5cry7HlOmqb0+jlaG9K0HWvi8cpwOMQYw2Kx4PT0lNevXwdBK89zBoMBVVXx3hqUrbdbCxpVVTUWByk5PT215hRpD09bG7vO6AUg38AUxq0rYGzK8OPH4CPfNxIA1/I8D0VZumPzz3pmKtZ4CiGYLxYkaZ/RaAd44w5IRVnUSKzLlK5qKqlRpuYP/9mf8PDdx9y7f5/9O8dAhhA9VOTPbFDBTcnPzxiD0TVKCScVrwO4kGKrGvI2ms31C37B22sfz39T23SIu/sU37uJoerCiRc2uteNYwre4kET+u9qdPzfOHlBkqb8+te/pKpKGwSuamsJMxqlq85Yb9axbmJyup/j+2JGvZnjuiuPv9fvQ7ea/SY437Rf3fHFe7VJ6LhJYN3+nkbQMKoNC7EQFZ/VTQJa/O5tsHcbGPOMlvWrzqirik8++YTvfP8HwaR8WyFj83w33QSYtjLgbc/dJED5613B+abx3Wacfm9s3Nfm8dy0/jfN4RZ323E6ZizPLYNSuSwmnr54ucBqmLcLRLH/9CaYjBHcpmHGQoX93oavOJ7JEvW2W7B/p9I6CBle0RULVo1Gch1/iwi1xYGZppu3NH4mUvB7OAdCWkqrobVMvogEF5/jwBf59DhXOoaYSPBAOLcrI8K7vMbfz0WIhCYqW1jBSgoS566FMRjTJGExRlFXFYIaKRNWRWGzjWmFVjq41/h5XV9fU6vaOtUazWKxBHxmSO3wic3575Wg3g3GavsFw9GIXtYjkUlgKMEWJxVCkAibjQ5jg3YbHGjjbdLUugK9efNmq3IppjkGYeOMTGO5sFXBI3pkPDw2vIb1wojhIv7S/n0bjrxJQdO9D2ETiUwmE4bDIc+eP6dWNTs7I0Z5wriXsjPIGfVzlkXJbHrJ0cE+o17G11/8mvPXTxF6yWCY0x+MuDi/YLlaAlDXZcjoJBPpBHmbTtUX2PPa8aquub6+Zn9/PyiLr66uePr0Ke9/+AFHh3eYXU5ZFSX94ZCTk1PuPnjA/v4+L1+84NmzZ9y/f5+dnR2m0ym7u7tcnl+01maTgi7mL3wxxjzPGY/HXF5ervGL3T1p6Ju1KmljmfU0S9nbm5CmgkHeZ9gfkvV65L0+w9GYg8M73Lt3j0E/waiKvb0xUiZcXVkB5/79h/R6A64ur91a1gHX+Hf2+32MtjHH2lgXYSkTpEhDfKTNsGUPvE+Fv1gsKYqC8XiEMbBcFlxNrwDFYNBnOBwG40EXhgaDAe+8805Yu9iTyGerelv7xjEafsM885OIZE1r4gcap/3adEC7hyVsrDHhgMXvjZmU2Ge96UfgKxnHDEeSJG5TGq1ALFxImbYEG7/YdVWToBkOhmR5DyESl96rAm0Y5n2GeY/FYoGQAoXhd/7w9x2iB2MSdK3IRObK1hgwgtQp7qwmw2lutNWuP336lfNT7JhWG5z/T9K6h3D92mZGeqPgscXVKe7/9gztBgHLNJfe1kKwMNbHUSvFr3/965ZZ3hiNTAS62ELgO3PZJDxtHnv7t5hINNp+07IgNNccIe/0t5GxEtEg2bze2xjZeD/isXaZ/23N3uM1n0lQvbbn2E4B3BUM/iEtHnts2dDa1Q4xTnsKPH36jMViEXxp4z7+KVrXahPvzE3v7O7g1lUX7Xvj7Ftv6zN0sYEYb9vnt/WxTbD2ny2T7o6xsK5Gh4cHfKI1tctrX5RFo+jxFk7dtWU2bVPa9DBeL62wGZ+1Z7V53CA689iyTiISakQ71q09trbAE/Hw6yO74bzJ2Bpje7Wwr40rxtYkRGlFvHh3Fs8Iu99Dghav03FxJt7V2M9DK01ZVa62kKWtq5V1F1FKUxYF17OZg0HjfMCL4PNtffRt1kjLO1ha7jPxJIlNdz8cDun1ekwmE9I0c0HYMnLTTpzgFwviPqteHMtp3XZQbaWHV3iAQaLwyQSktMKVtyxpF+B+dHTEy5cvN/IwDQhEAhjgMz0aYLlcBuEFcG52OsDTP0XbpOALvBLN2u3u7gFwenKKQDAc9FCrKb/86XN2nj3nd37/T9FIVLni7oMHlPMpr77+HOoF41FOmlklaqlsMhUhoKxqyqpAJjsM8iH93pAkyQIz711x8jynPxgwm824vr5mZ2eHPM/RWvPmzRv2Dg44PDzk8uyc0zdvwAiWixVXl1fcPTpgd3eX8/Nz5vM5e3t7XF1NuXv3LuenZxuyQLXPsmeWhRCsViv6Axvr1VWQ3SSsCeFciYWhLFcopanKgh/84HtMJiOGWc5kNGY03qE/GCBkihGCfn+A0SVlZbi6OMMYyWT3gHefvE/e67NaVkFIsMklZGS9JVjmbOYnwj2NFdGE32O+wmbXyhmNhqHvNO2TpFbYjo0IUsrWGsY8VJy5EZpsVW9rt3edShOMtgWXlPO9M04jJQPicDKC8Ay9ZeS67h5BSHDaCl/UKgRnmbZbRKxNSNPUMvXKZcAxBJOoDX7zxF24sVg/+Lp2xN+5LSlnvpVJilZtwSNx/nog0WXBaDRgOOqTZFYFVVUVRkEv66FqTVFWFjknFVfXM+7dPUYgWK0qyBNqpQklcowB5SuEer9eq9/QynDv3r0Ww9Biym7Yn6AtoavPo/PJUpVGePBm/IYg4jR4DUXrEuvNvYb7nZampRFw173hVmsTNF8Ih+D9/cJrxWzmE68L9f2G/kwbedhUwJEW2FvAjLGVwGXC5dk5b169srPWCoxGucwgvkBfu4lo1SKKHK9GJIh0GZuYGDZIX0bBVS7Fp4Y0sWmQLZzKsJ6xptU4GBICa00kEhLBzil6tzE2E4g2Gl/5277Da2H9Xjm48VmthOhOszXX6BeEcMKTK8JmJNgsMQJVK2pl3SlssUBtz7xoC7dtorsZ1uwt61p+TzgsrrBMh9Y1taoAwfX5KRevX/Hg0UNXLwWr2bVy/83nii3XTSMA++Q5Hjq003LJDrPquAu7h6IFyRih22fWbmzzfseYNuOxTyvj3h9db14noj6aPfUBymFmHYY94Jy1tfBzdrBjYgsE7uw53BsCVp3sKQQGCcKgleLg4A4Ga95fLlYsFktqpciNjWNzUpmdkx+XC/JHCPqjIcpYrXygBfE6hzF7jXEbV2xkGkV77gIZiH6HlXS0ztIuHfXfsthJe56bZ9tCkO1Hu7Vs3ivXVr7BO0bbd3q6WKvaWSvsk+EsOUDxAbJa1yHwXruECUVRsFqtqI2l6YvFgqqyNaDqWrFaLUhTabM9SkldVSRpSr/fI5UZRgt6eY+81yNJEnYnewyGQ5voJKqz5YWDRCakqbRVraV30Wq7URsNcSruhg4ZB4EiCETCr0tQjPhsTpCl1j1HYkjSJOCeNPP43GbjgqZAX4PpfVprqwCUTlj2MEhIqOXwp7fEOaWVqhWYFKM1s8XMwbDGoDAuTWmaxln+bmgRAlpjfGOBcwNTvFHY8O65xnB4dEhRlsxmM7I0JRWCk1cvuJwuODm9YLK7z/13HrO/s8N4kPP500+Yza7I8x7j8Q6LVcFsNg/r5/mqNM0wJCAT9o7ucPf4PgeHh2AMs/mcr778ksvLSzKZsLNjYxzSNGE0GtHLMmZFxYvnz/nOd7/D0fFdZosFqq6YLa45PznjzuERe/tHnJ5d8frNGe+99x5JmjMaT0jStB3kT8NzdmP0fJXw5WJJr99HCJuKVklFmiQYpULW1HV84eiqdjFW1ORpxtHeHg8fPkAaTT/LyfKMXn/IYDhgsVxxcXHGqlghpCDvDXhw7wH37j+kLJRNhYwI2c08n5znVkiLM7yWpXKxMTlJIqmqmjY9lfasOT7a1hwSkbCeWRhMFKuVas1Pax3iNGJFf6xo2abk2dZub9HwTJ5jcDwxTJwfpwnaV4l2uMEj1Ti+wlsTpJQkzvTk/Vm9kOK1NLGEFbQrIkqZiwduTa0UScgKZBGtNhYxZDJxjHzb9aqs6gCElbN8ZHluGVYXqIvSjEd9hqM+Rrh0p2BTe2Y9Eino1YrFYkGxqnj94jV39++SyYxBllDWNUp4ZKQ9Hx82NdaUePOv3+xYS9lO27ihOUEj7tv+dSjaEJCxvd1/dgi8Qw29BcjeEQsitBBch+WO/rbNwfHvFnZM4HVEg6abtRACI2zBM+0YSJ+lxPfr850bYtc0u8DSgHLroLSil2ZkMuHLTz5FlxVZmlg/5OhgNevh+u3i9SAwdA+YCbDbvb/tKuX/1pHVQuKLOQpha1V4N5wwz1ibhkBIy9w3PtCNYGVriHhB3vlHC22z0wjjGH73u9FBsxh20s8R5zohBMZVpvdjaZCNJhQ1DNDghMZojazXn0CQIIVEmSo8H1tP2jC0qTUCRowXPF6x41OARJsaY6xmRlYFzz79hHefPMIYrOBjrAuRjs7VuoXFse4Rofbvt4Gssdumuy4kCIvramIW1TE3gVnvzlZY/OLfqhtlgE8asGlljBEYp7SxKTSbaxIR1SFqjyVICHQyznn2zX/vwLRPBY6DGTtnp62PFASm4cYs3tPW314Zgak1h0fHyCRFKc1qaRmWqtZUyuDJQgP3IghaYPH3zu4e06sraq+w6AoXpu2m6yotrbvfeZclgdNbNGdB+uxp0gsdxlpZhMta5Gq+WO2o33+cEsueBa2te5IQTVxJxwnJnWHHeCuFrm1CFBxc10o5F09DVVfMZjNw9y6WS4u7ENS1YTabI6V0bkI2RiDPc/I0C25HNjNQRpKmJElOmuekWcbhncZ6kMiENJOkqQ7n1zP4GGMFAtN4LMSM3BqM4hVA9psEjKotfhc4pYQGJCQiKCLsGvr0f16YXKcr3kIATdpaYyDPrYtQkoAQujW+AMJut43Wll/wZ86lA14urqnKJaqybl1CgtEqCLxCNEK1EGBUhapq8nTIYrVkOr20+MkojPFuusrxSI2A1G2NNbSBFv9biOnbWB2ss/ZdBlkIRCJJhWQ0GrFcLChWBcPhiCTNkWkfw5I0SRgNeqwWc44fPGK1mnN69pJaKXZ2dkmzIWq2QlUlg16P4cDxLQjSLKM/GPGd732PDz7+NsimEnV/74CHH3zE5eUlv/q7n7CYXlKWBavlgn6ekcqcPMmZXl5yNZ0yOTikd3JGsZyTVwXz6ZSqNuzsHpKkX3NydsW776f0hxNWywXD4ZC5c9HqWubXaY09Q8vVijTvBUWKp50YbXFotH4thYJQGA2plKRJzqjXZ5T3ybH8ZlkrFqsCrmZN3JQQDEYT3v3gQx48eAdjDJeXlywWSyaTHZaLFVJalz2f9bCqSuvih01qlCSNVc9aFH0hPh3us3UzfA0uW3vLJt5YkmUZr1+/4c6dIya7I/b39wMNXa1Wgb56WPPrFPOpceKY27RbCxrBLWGN+DTEN5Zy4gPkGeeYObPMvr3Bp6OMASGWPv0mSSmtNcEREm/eiYPfYmbAI/arqysW8wVHh4dh/FJKVqtVCCj37/a+vza4TDPIh9S1Ym9v1/m3GVarAoTd9OFoyKqoGI2SYIK6uLriwd37Lk2qhBqLnCNmMV6HZim95madaf0mLQYEkbQBIRbeYoHGr1nch2/rGmda17rtbfcKL2GE39vwE/px/5Oi0f607tkoCOCYXEusK2fqT5IErTSf/PYTq61wDKZyZsG63ubz/c33oWuu9p/jeIVuwLcQopUuLh5HfB588+bM+LBrrcEYnJt2a62s/NCkbO3GVLVUZzQE1xiB0c3vSWK1gA3RbwvK8dp1Y578Z/s9HlusJbl9jEAcCO779uvSyoZhDF99+SX/wo9RO4YxEa2zePu2fl7WbxGtDCi+6a3PmA48t11Ct7/G74X/3hZi/HVjgoi//uYb5hFfa5QV6/Pvnt+uNTOMyikHDg4PyPMeqq4oq5LpdMpquWI43omCk9s4M97nvb0Dnj9/RVVbOmCZxXV/9/i1seZ1LU7JCLTyboBWWaGVASGRWjqrkQwMt1a+iKWFIK2dcOAEj7KsESjrVlRW1LXNbV/XVUgJr7VlIubzeaBndW0r3GdJRpZnlhk2hryX0+8PSFIrHA8GQ7J+j8PxDlmWO9ci4eIP7DjT1JJ3KUSIGwkMmN8TITCdc9QEbIMUqtlEz4gLkKnABNcMSFIwRq7ReXvd2x48d+9dh7wgHwYXXmQ/NUVEjakD/Pruw37HL3M4yDL/VsDVNPseS+LdFLzaK11avMMpg34KxsYQJcK7tDi8ZRGto++CYrWiLCsE8OLFc64uLoJbm4oUIn5dPGzeBgvFzHPYk1u0tjXPMrtxHQZjtE1tmvf4zu/+AWVVMxxNOD6+z/MXr5iMB5y8ecn1dEqWpQyHA5Sqmc/mCCCRKWlm3aNkltPrD/je93/A43ffQxmoakUqXaFlDKtFwWgw4o//5E/4u//8lyhdcnF+xnK5ZGeck6Qparnk9evXfPs7d6ybVGXd8MpVSVkUjCe79Pp9Li8vqaqawWDA9fSKyc6E+Wy2kYZs+s0Yg6pVSNlqjKuhgq8p4XGnv5/wRQhDIm09CikFvTxnPl9weXll8X+SUlU1Wiv6/QEPHjziyZMn3H/4iDTPA+0+PDwMPJmtxH7Oy5cvnRXCKiFsVkzJYDBEqbrFU3vewse5eLpt/9pg9SSRzp3Kwt+9e8dMdnfI8yTUmJpOp1ZhXhQhq5bPNGmMCbF0ZVnaDFZSslwuefLBh2+FwW8UoxEHgTRA7zQRNMSm0cY3Jsd4o0N2DH/NWJWbcpqCNMupq7phvI3TqdfWPcr7Y5ZlGRbcBzn6NHcNM2VTgc3mM8Y7Yzt+A8ti5Xy4DUVlFw4jrObNbhEaw6oswQj2Dw+5e/8ev/n0U4qyDPiq1+uTJGmYX54nzGZzVnulNZs7rarBgNrATMeSsgHlkN+mYihdJngbg7CmxdjwPr8P8b51pfb2Pq8zgNuEjBsZsC0tZiK67/dMwjYmp81oxdpQgjUtyzJqVfPyxcuIkEqKYtV2d/hHCHjNGNb78Ihkk+9nLPjFc+uuZWAGjM2u5K/FDJTc8Izvyxd/jMe4eT2jZ433Lbf3BRfEaI5d5i0WHGIBy/fpmSCrpd0Uv9HAwrb1jPuK3+dxQbynWmtOTk+Zz+fko6Fz27AMwj90v7edCc/Ux+PrPndDr+45208jbPhn1vHHxorT0bvaQtz2uUAjqCZis3+y59O2wsrW7wZfJM6eTRiNRty9e4eXz59T1zVX0ymz+YzJ/j552uDTeF9jeJJJxuPH7/KrX33Ct771LdI0Cbpf79LV7IOHz0aQFSIJY7NMpnX7ABGCQS1xt1aJ+XwZ7l05ZtLToaJYOsG2yaiYZZmLR0hDRpd+v+9SY+4Gq4Kfp3c18vvtayt5Ptbf11jgHCOhjQ26BaC2RXK927FjxI1Hin5NXUE1IZ3G3xeYdN1KCcooa4GL9BBeyLJHVCOEslYObJ++foQhdrttnsfEFnf7T+vaX7T7pCNs3hIE/X0NfLUFGPe7joR54yBCuaKBxkR9GoyOAlkdnTENkKOU4cXzrzg6usNqde1iPAzgCjMKgVbKCmtaozVMp9doDcVyyd/89V9TFivSNKOqNHWtWkrTm7TBxo+9u4wepxjeYo2ldS2UChDWidsXgLMabPe912fn7n2ODu8ghWR+PSXPU7JEMJ9eUhRLxsMBwmiuri5RVWWfS1PSzNXPyHLeffI+7z55H4SLiRESjXbxvGCkCe57v/ujH/GXf/E/c3V1QVGWDLUmzVKSKuHy0lo7dnd3OT15TZqkFMa6X+3uHzAajXjz5g2z2Yxer2ctnZMJL1++2Lqufj1a9MIF7ls+IacyBWmWMR6PXUYzQ+1olcch3tAtMCRScHR0wA9+54fsHx4wHA5Jsz6j4Q7j8ZjJ7sRmghLQ7/WZzxcoF8+klOLs7AxjbJD84eEhk8mYu8c/ZD6fc3p6QlmWDIZDsjSn1+txcXGJMYblcoFSisFg4MIH7BnJ856tFyaFS4oikUlCkgp2xjsMHQ20868Dfrpz5w7G2JTOs9mM2WzGeDwGmmRQvjp4lmWhJspt2q0FDd88AWlS6lkNhQ+yartJtTWrMSMgkwQV+ZNLx+BLKam1gtTGXZRFGQ6KUopUSOrSHnSlVJC4rGkHjFbkvRyl7MHOMsvUHBwdURuNtAoZaqNJjEO6iRU4tKod0rBaMeV+S5KURAoePX7Mu++9x+7BPju7u2hlU+MeHhxZLbXRZKktUni9WLC7O0FVNWmSOIRkhak44UlXUx9nGGpnSmie2cbMb2Jq4gxX8T1tbfd2Rq7LpHxTQWITQ7qNKdo2B8/crDGxjrGIxTEvmPj4H2g07dPpNGgTAVfcTbXGtJl5/OYt1rZ7WAXCodbOxUmKRsiIz0mXCBnjLHtGYy/pFsz4d6K3MJV+3RyzFMNdV3CIx23jQIRLT9m49jTm/DjFZfvdscujXwMv8Fhf6rSVEWx9yF1Ya1zUuhppv96x4sErRlKRMpvNODs748F4ZMel3Pr9A/a6+0QbXja51n3zXv08m++b97XtDtKc8TWNfaefm4Tari9zu63D5ba+47kJIYIQrIwhFYL79x/w/OlTF1hsAz2P798nMNEbcEWA+TRl9+AALQS//u0n3LlzZNMxagMu3qooyuDrrJVm5ZQKHseWRRktuwAXAO1dDqxAbJVXPp2jPys2DsHmuReC4KoAsT8zYW2b/WpbXAJPHGnmvatqcCmNzlDSPWOZr+0Q3oAUlhkmdefUFq5w/JELfBYiWH/s48a6MkkrWCUu/iuw8gZXX9k9IwxGR8XoLPG2geZe8UFbUaWVcuOx4/Xun0J4uElcVi3rDo1onGp9kpd4Pb1SwrudWVqng6ButIuTimBTh8QEdvxxELnHUUpZQXW5XPLll59z794dTt68Qhtts0JqW/PFp9StKxujWZYVRVGRJClvXp/w05/+xI1DYYQJipW1s9c5LWHNMC6+qf27/9wVWDadRS9gNPCnMaIJ4l2tVg6WJVmWk2Q9RJIiMNR1Rb+fI4ViPpsitMJoxeXFOfPra4zWpImFjyy1Gu7JZIcPP/ooDDpNE+vSIwRGOtojBGiBSBKyRPDue+/y4uUza62oKvLMFpDzMUSj0Zg0SZivVmht0xMLIRgMBqEuh6/tZq0tKngHxDgpxiUtpYUTiJLEpr83GB48eMD/4b/777g4P+fNmzc8f/6c09NTTk5ObEa0unaFmRUHhwf8b//3/zt+8IPv8fkXn5OmKUcHxyRpHvYoS1Nqh+cW5QoEgVnf29tr7VNRFmijSdOEBw8eUPgMbbXNzjYc9tHaMBj08Km8vSBgheGKXi93iRYy0qydna2x+HsB3wRYMMYmaDg4OAj3ad0UrYwLMSqlgrLkbe3WgkY7S1NTodtuYLs0u29SikgIaBM0D/CBMZDW97NWNRhJIjP3rPeJtb74WlmE7N1PkiShLEvyPKcoajDCaloAjKAsbOpSmy5dhJzbACa1ZjOtNXmvZ5GVYz5tYSGDNCna1CyrgrvHxzx69IgPP/qQ8c7YmtU09PsDhBBNBUwM0/k1vUGPPM1QdU0qJcoYjJQ3JC9cZ8xhu2Z0k7BwE9O26W/cbnp2k8CwqZ+btKebrm3rp7nenlsshBHFgHqi5o5O890Y8ixFJpJnz56hVI0U7VTJ9uCsZwLpMnq3afEzsQDgYd7DnpSSRKZ4zepNwlyomuwJOo3QFe+nZZybNVkfU4Nc/Ts3wc1mQaVhOoTw7xE3wmi8Vw2i1841RoczHBNC20Vb6Iq12d61ZZNFoQsnwT0MG7vy8uVLHr73JLjlG2NaMRO3Ed79WsTXNrmUbvu8va2fb/+7aZSs0XX/afN56n6Of9smTFtN6TcVkNbHvIarPFw6Da2UElVVPHr0iL/5678KrgtX0ysWiyV5fxhp6dt9+zOuTI0ymoOjPXb3J1xfTzm/PEepmsQIMp+xyAUm56Ocw+wowFpM2H08mpY4jW+DkyyTCj4bk3HwGmdlwWnw7RSbsxYIeTMLkjRO224aWIr2PxHRZhtDWArhlSeN1UzoSHlDtYbDjJuHUdbf3Fav1qGCNRhrvfBKHCWCcGaVOREeMl4x5pQOzsrQhilvY7B/tUt7a7StP5AI6TIsGkfTjRWMhPU88MpJ7aopN2dZrcG2No0FN47Viv/VVRUKAPsslJXLnqWrMtTiMKZxDTHAfLHi4uKCXpbx2W8/bcGgNoq6srirKAsuLi4oVoUr2mbj/S4urigrW88HJ+B4wcQrd27j3949puEcdGjApnO/jX4JIQKDWDtljJQJGE0qavLEIIxG1QXDfo5WFWWxRAiDwKbsLVYrMIrVwjDY2cGg6PVSDo/2GQ57Lh1/4mALl8DAa9gTdCqoq5I0y3jw8B36gwHL5YqiLEhT6wpYqtrFLuySphlvTt8wGQ1ZzOe2VpJzP5rNZty5c8cJF+mt4waCsJE0irYn7z7hxYvnlEXB/v4+jx4+QAqbUEAIQVmUTK+ntqDdfI4whtF4xPsffMBwZ8zv/O7v8sknn/DpF59x//gBu3u7tkBpmpEDWZayKlYorUI9itVqRVVVjq+uKctV2KfRaOTSAQ8QTiCK6U0MR93slf7cgEGpCqWq8IwXFry7VVVVXF1d0e/3g9AWp4T2ylEveHgL7H/xGA2fJjZoVpwpeDAYcHk5pSqrUKjK+4baBWkQURwXoLVGpFbfUKsaU0faSCVIksbakSYpRem0J8Ii3rIsg28ZOIlOWcTmK5J75jFJU4y0gXRKKWuxkAJVVW7hLDGoXWVHY4zNCoREG5eZSBsSrXj83rsc3b1DrTUSHYLIF4tFSGVX1hWVqXlzcsL943suIC2x2mb5D9F2shGhfJNn/zHtbULMP7TPhpn8BymW2+sRiC0g2tYYzxR8+eWXQbMPhKqwvtDcP2aZGkZ4XePkD7eH72b8m7X2bjqtOWz1fRYi8DQxo3OTALdJMxib6WMG2iIVP1af79/rGZvUvM38/Tva4wQvcAls9pWGOfFaEvvP9RwJlc04wZj1qrpd5tk/17hl2aCVr7/+mj9wFgev3Y0Uht/gnGwWKmygb5u13Nb8PNu9Rllo/BiN10QT/vo9d7Ns9xEJYJsUEc37t8HHTefAM5Jbrm5591ozlnDdu3dsXR4c0VvMFyyXC8b1Lpls3Io2v8sgpKFWlg7sTEZMdsfWyqkEMrhGNWPzfdn6OY3wmrn05wgF1C6Gy8Og1W5LkdrA5cQfEqudFzJ2GfRrFE20tcfWPQhsgHlzyQR3HwGWEddN8HJLMaBjqVMEAUdgghuShxEhouvGW0yayAevk5BGhbEIKZBGI7TNuKW91cK9v6HKBqMaQaOrPfat68KoQ+0BjSmUTdrgrA8+1bcVEGpbo8S5thhj080XZRGsoKpWtoq3wSko7TrWVR3S7hqlQrC2cgKOH6v0K2eslacorKBxcnrKi1evee+99zg4OGAxXwSNrk92Y7Rkfj3n6bNnPH/+3FlrrfCUSFvpPcEWFtRCuJIjbY16Y0m+CV+0FUrRr66GWVu47yp01/gG0bzbGGtlMk6ZJ4WBcoEqrsnSDKEq0l6O1oqyLEikFc7LYoUxCq1qlosKhbEeIqng8HAfY2qGgwHKGKpKoYVAamuhKFZLrsuSq6tLevnAZmiSNo3w+fmF3fNonPP5DJulMQWD21fVohtFUQTe1DO/Nyk8u+ullUY4a8ubN2+oq5rJeJditaKXJ6SJQtWGNMvIMsnR4a7lPYuKqqwYjoYslwtEmpD3+3z07W/x5N2Sly9esFzNyPIJlXIKikzQE7lLv2zdnXZ3dyOBwVoyrEW1ib20Z1uuWSV8nHH8m7deNMp4X5DPJjDxeC3LUscj27U4OjoKaxcLFj6VeMxLGWNYukQUDx4/uQF+bbu9oGEEqrYaDoHhYP+Ayc4OqqpRA81FcQEKjBBo7awPxqZzXsNFqwABAABJREFUMy7DS11bk2NZlGgEiUoba0dE8etaARWJO4hlVSOwmT5qoxFoiqoi8z6kxgsRViuilCJNUotGhIC6BKkRMooPKa2AYgUPKAuFV19ZM6gmkQlG2OxYVaWolOLO3SOyPKEoVpD1KaqK5aoKKe6qqrSIURmW9ZKTNyfs7uwgMxusJ5QzQQfFV6SJ8JqicKlh6Lx2LX6kIUD2LiCkCvYIVXR8euPCULIVdNns9U2MvzHRRkXfPRPaZZ6DHECbkRRCNGQ4eleLLJvGoWAT0+RdDDBN5p9AhB1TmgC9RJKgefniGQILj0JYmDHYQyxE/I7Nk/dmeb9uMdB2Nft+DZTS+FSoQggSmTmtrs1a0zDD0ORft1pL794jpLRETESMsYM30Y2XwL4u7H9g/B2TYzZonOkKQI5xNoKQAiheGf/dGJfdySEhFyPVWD8a+IqtGjYbnHOVsCfbwY/VvsRW0K4AF8PC24h0IDZGgxacvX4NzmfY12Oz+96OE3FTa69RS7BoE/K260LM6AVQdLApm9GuDV0EWG9ftn367379o1PcdORfiLX8CLEe4xXmCY1waSLhSPjB0urTYMFTbtiH6MGmb3e+ic6wEMIyyhIwgvHevk37eH3N7OqSxXzKcjF35zFDiCS47HXXQgq/ZoAL0vUWGSH9/oqAYAJD5vCFxIDHf9oqrxLhete2Srl3vzQGhKks3vbnxzRLJZwLsJCitRV2xA1jaXPZeKHeEntPb4RXdnhrnhMM7OcGp9vg7Ch7YpBYBEL62JQI90bb6pUEXiHTvMcpFsJ5aQQDhA64tDmPEoxGq6aILzQFBL0yT2uNcvn8m+rdGqU0RbGiKFeATUWttUHVNUb55Bx1GENVVYgkoY6UGh6nWJdtEaxMsdJCa42uVXCD8/ErAmvVSV0lZWuZ0CwWcz799DOurqYcHR6RZxlnJ6ekWcpkMkEKgUxsheuqqijKAikEibfyaIvrfV2Dsq6Q0tFk4WGAsPaBTqwjg+h69J2IzgQc28WHbdwUTmf4zdU8MtZFrqH1hunFOb/4+U/o9wf8wR/9MUnWx6dwFtJWSk+SBGU0yvWljKZSirSquZ5e27Ml7J6WpU3yUFUlV1fTkC2pqmpUXTGc7JIKgch7DPpDyz+6TIZ+7HWtSNOMfn/I/t4Bqi5svI2wygohraI6SRPSLLOZuKTEuExwYf60FVFtxZRG1RUmSVgVJVVd8fjxIx4+fkBVrqirlY3LqmvG4zEyse9K04x8oO18qgq5WpGkqauqPeDhw4fMZjMGg0GAQQ+XQkoSB7N+LPYc2QJ7VhFiYddWurfB4KPRqFVDyLtz2jVLg9sYQJYlGCO5vr6iWK3Y3duzPLUTSjCQpj3Axo5YeHOB54kI1t2qLF2cUencA1cBDy4WC27Tbl9HQ9rJ1VXFO/fuM+wNyERCkgj2RmN2hiMqpbheLJjOFtRaOTZQ2SwMQoRoeWMMiISibvzKfICmRSy2eoJO/PCsz60HLOVzDBuBqqyPJEBVa2onaOQppI4J0MqmIktTv6kW9HDvq2vrKuVdsCzDbKhMDS5Lj0RQFzX6QrE7mVDVJQbBoijp50O0rlHa0gSjIU1zqrLgxdfPEe88YDTo0+vleNoeiAgdBESDNGIthGcuLB1ou5HYcqSbXQ1E5FPdFSBMxOW3tXH+EEaUamMTYT2DQLGBkfW/m6A1b4SMwNpHApJfkxYbs0FLajCYyGLmxQ83NIxWpEKQYFDFisvzN2hjM4JoVz9DCKsl8fnsaa2Xab+tJTz5736/2nmm/WerRLOw7Wu62P8k8doL4cUmX63W+xvbdJBCEKxhra0Kc3aCpCPAMnXJBAKHajPPrCFZbJaNNEkdbHmGookXMr4f9yohmq8hcwwGhNM+alxKz3ZQb7DsuIrCHv6M9ppP4WrkNMWGPEPh+2nm2wKXNUEvuE35PVM1F6enrK5nDHcm1o0Rg4WOdRi3e5Ks/Q4Ngd9kpdJegJEN4xvGZ9pC2xZ5tjUGC8gBUtbuacGoYz6a+XSERI94wLoz+T5omE3AVbr21+yDYSiRokLEHdoH2+8yniHCwb6NL7LB2YLeaMRoPGJ2ccLJm0t6vYwPPnyfqlzS69n0q0aIoKSw/v3GwaBB4hglN1LhcY9Q2DTkwkok1m/W1epxQoTrKkCUtvAbLaV9pxceVQQlTtDQGKQxCNOkO/XPiuizwYDLPGQZja5/tNeuN/thvJCuNTjtolYKRY3AVwtWTtAgHEprHbKZ9gJsGLs2yqW+tJYKa/nXSrlrOpy7+J/WirpWzkfcCgsGrGJN1U4jbl0vamUDwldFYZ+v6yCIGFx2SGNdtbxFyVsn0jTF1IpGULYrlzrGTTupLs9zhBDBv92YPFgbYjcSr/G2wfheS5uidSN41HVFkkhWq4LFYsX+4QGX02um19ccHh2QZSmDQT9oyweDPsPRiOn1NcslqGnNaGfIzu6Yk5NTG7NDAiJBaRuLZEJcqMd5poGR6PRso7LC7Z9xxDsobdgsaHQVMmtWJgNGC6pKuZolTeHaN29eMb+6YHpxwU/+9m/5vT/8Y1e93ZCkdu2SJGE0GnOtr+3eujTiGEGa5tSl3c9EJsxnM+qqZDmbkwrBeDRiPB6RujjWQa9vCxq7lLYC4egG4WyYkLI7YW/vkGI5ozKGWilqXXtEbc+WAGSCTU6sHd00IanZJkubteQIUims1c9YyvzbT37Dy1dfc//eMVpnJKlTfiHRRnB5dU2v12M0HjPZH7ZiQrSyFsJ+f8BgMAyKsyZ2q4nBaWirT4ltLWbNvQIpU+p6SZIQLBZZloXPgLUcaZ991boBpmlGmiTs7uxyXilOXp+wt7dHv9/n7PSM4XBEmupQVX21si5bg4F10zo7PWGxWFDXNVmWhRTF+LOsdXjmbe326W2rkizNePfJE+4cHXF+eoaqrOSZJRKhNVJm5Ht7XF/PuL66oDccYBCUlWMcIk43zSRGSMBaOoRsypl7FO3TzXkrhMbSEGV8US6bY7xY2edkkrjKm9jfsgxcrQApoVIVCBG0pVopq1lGoOrS5iuvVsjEpdE1Bi1s4FSaJFRFSSlKqqrm/ffe5/LqmtVygSR1vo6AkJa4GsFyueKnP/+5DfZxgJOkCZuY2RhZbEIQxkka/r440xAytnbcJBi0m2eS/KHrBjDHjNpNfXyTd/oW+wl2++u8gUagERvv7ZqNffO+hELYokCr1aoJmO4UaWz6wsHcugYkXvtt4/D/mvgMi9jjzFLd+119XqfJsBrLmPGL32MRVFMrw45FtAQKX6BwZzJhPB6zs7PjKq9mjQCkNMvVktlsxmKxYHo1s9kwXGY0mQiUrgPhjsfQCMCR9jpaGw+Tku1uNDZwVgQYCG5mtIPIu2vs27q1o01EfJ/GOD9uLH45OztnNNm1zIsT2kJhPdFZ9RveLxCt8xL2J3quywA4+fQbNykIxNK9vJmrB5y4Ga/x7QgCzQ1W2Ivm0lzBG9bCqwSEpABNGqK1LtuD9CDpYcEXKHSZkLSD8cPDA14/+4rhoM90eslyMaNaLVD9HllicaVAIV3NGLRPSGDrEsWKF8K/RpkUhDUBvhbGhmV0+9YUxIqVCBjdnpsmCD/aGESEi9va5caCrDfc468L0Q4S9wHmVj5xgrOLHUwwLiDZNMksnNWncoy9DwytHbPvA5a9QFCVVaCr2igXP1C1zk28Dr4vrZr4kKoqHSPnNfgOfznBoawqvKDgK39rU6OdUNHr2QJkw2E/ZK9JpU34Ip0ggSCk0TQI0iwlz3se2ML4pEyjdbdjiV1AsiwL9NxmiLRphZNEMhwO6PcrRiPLR+zt7XHv3n329/cBgluOt54sFrZWw6tXr1itVlHdgTheok3X1+PQ2nhF+4qfG5pxSGObNn5b6woc8XcpZUjj7+MclFIMhyNOjMEIyXhnhzRLKcsVMhH0enkQPn0QdlEUZFlGv9dnNBozHA05OTnh8ZMnCOBw/8D2fVTT7/edNcnGhQghXPyqFWKn02lQRNnxWBhM08SdH6soXhnjYhu9AGLnYOtOpNYaeYsWn0WlFYn2Aqpdr1rV5FnO3t6ed5gAmjiI8XhsYTPx42vKL9h5ADR8gP9rr4ngsp8ksrOXEhl0B3Y9RqMRg8EgWPlWqyZTZuXc/61LmT3/Nl65YDp9zWAwYNgfUBQlL1++Yj5fsLe3h1Kas7MzFotV6G+1WgULxWq1otfLWC6XQRmwXC6ZTCaUZcnJyQnn5+ekacr/5r/9b9+63rcWNN5//Nj6oWnF5fkZAmsWzfMeqrIaFK01MssYjoacX16wKkq0SBEiRXlG1iFFXVv/Wq+B09rm5/XFjbRpMmB4hCGwlocmQ4QVInwshqHC+3ALbYmpcBrbsqyseczYqH6/SRZ4TMhk4Bc1BJehGQ4H7Ix3SJOEVCb89tefcO/uPYaDAa+npyglyfLcEm9HNBIMF1dTEJLLqyvyni2KZITEFlCOtbKNxiL+LW5ds2j8m9lw/zbmf+N7O/1uui9+301j3NZH/Fus+d/2juZdDbO0bU5dpBr/TaQNPjw5OWkxrzoQgDaD2gga68TWF5iLfae9327zfDN+S1yaoK2uxqlZMy8leCuGdub4bXN1pnj7Q7jWHwzY29vj4cOH3Llzh9Fo5FIPZvT7PZLUMl42LkpR15XN21/XVKVmsVhyfnbG8xcveP3qFUVZBmY8bmvw1xGMpWw06fE+b4MXL+QmiU1/mMmGOW9ZCzoCXkxAN1q8vBCTWmHMGMPrN69594MP7H5GPtthbyIOO3zs7JvNFtakn24HBnvtZTRfp7FqdbrWbtBtGh9NEnoPLZYlLIOjG7eh9Z1rnpObz1V4tKNht946HViI11sY2q5aFqaNS5sjnbuNEJpaV6SuevvOzoisl1mCOB6zXFxTLGeY8QBhMleEVdmaB15jJ8JkbZYjv4de0yt1mENzjIyrc5F0xujnYTCmatbI9W/834iBaeDd3qddnIAPejbRfb4Pr833lgljcG5ElnmwtTZcohIfFxjcjVSo1IsxQWjwv0MjXEOT3tXGNzRzqJUK44mZLBK7x00WLW8tt+7DInJNqmtrEc5lxmjomC0hGAyHzao6OiqldB4CjWuVFLagm1dwZe6zhcm2NcLjBSGsi0a/P8BXQbapg62biRQpvmBwnHjDnnFDIjNEZseuasVqVVDVJThvi6IoKcua+WzJcllw9+4xr169wWjD1dVVCMRNkpeUVUmlFBcXF04x6q0ybVwVK9Ba5+sGAWBTi62NMR7ymuu4xlTruQivdbMKQpNhyAsNZVlyeHjI7//RnzAYjHj85AkawfXsAiFgsjMOQp8XGrwir9/rkyaSRAhXD2NOv58zHNtsUcbvhdubnrNKeVn+6uqK09PT1v7h9t4XngyKX20ze1q3W4lAMhyMENg6WVJsRbBre+GVf8Ey7QL5vavf6dkp9+4fI5FNTRq31v1+3z7XoetNf/5fk27a76G33tuEKN5NzNFmIcO57vV6IUHBcrmMrBdVEArKsrSCfVlwdTV1tTesgFyWJYv5nF7eo6oqTk9PMcZweHjA9bUt+vnkyRMGgwH//t//exeon4b+0jQJ+CVNbZru8/NzRqNRqFQ+GAxuXG/fbh+jUSqMskWMjLTVT8tao6nQSlPXmiRLqWpN3h8i0pz5YonMEywST/Bnr6oM9XJpD4PbfIMN4rLMkyUI2vh0XQopaute44Agz3PKonDZDKxkaNMaKrIsRSvFvFpQugWv3YYJQDpTqs9AUVXWrDUajlqaEZw5a7koKBYleZoiheA6v+YXf/9L3v/wA4qi4Ox8ynhnD5klLhhMkgnFqzcnDEdjrqbXDIdDW/V7LWNJ07RWWwt6eZ+6mLHyQVGbnogZv21CyNuEkyZ+YJ0h2dTHtn439R9nIvPXbhrr21p82H1fSinILFJ78+aNJUrO9c67gHjiHhPfzqhdn5vnKl38hM9777XxnhEQIglCQ0wE28jfq5A3C5MeoYe5Jc6E7goP7u/v8+EHH3Lnzh36gwGTnR0Gw0FIC1irGlUrlC7x8VLDtMnvL2WC1jCfz1m8c58PPvqA6+trXr18xWeffcbZ6VmoVB0LB4kQgVfrWmq2CYfxvLrWH9t/u7/GtL+53QbGQ+yQMZy8eRPuF0K04w50JOw7uWCzVaURjrrjQESCgCD4hDdKgS6jsb5eJsCDf6+hlRO7QyybTbDxL9EoW890Vqjpo9t1Zy2tcs4HFUcCeKf/bmC6ZRjc/LSbL4Y8FRijwNSkqWA0HpEkktFoALpmMbuk2hlg8pQk6yGFQaHQQlEbn1GwOTLe/Q9jff3tnlrGH2XjDKQEUxsg3Wit1FqBqAMD5+Oj/H5orQKzY2mHCoxrXddNnn2lnYXAXvf9KKUoyiIwEap2woZzfxJS2GeqCnTthDLLjMVxEBgCc2JilwxpGSUpZQiIjc+3TJKQujPPmlSXZVWR9Gz6S5/qU7prtm+vObYHoq5rer3c4jXv2mwsI1KUBVr5gFSbqce7dtl10y1hxkOqXVc7v9FoBFhlXVmVLoDb1u9Zrez6L5cLG8ArhK1ppe39tr5JQV0risLWOrGMmI358P7lZWn98G0skCRNM4yOLBEGJFarrrXi7Ew051TY+l9ae2HGu3h6g5pZo22blIN2jnrtvnBubtFi16lYMdPtc00RJywjai1KwyAY1kpx5+CI4+NjBqNREMh0XbK7u0OeW6uGt5A/ffqUoijAWDe6ui6RpeDTT37Dj3/v9xCudIABstTWsbJxfJ6/AlUrPv/8c2auroR3a/OlD8bjMb5UgYU/xTDLA0xImZDnPVarAqUNmqYoXUu2Mg2+6gp4vhac5zczmfHee+/x4QcfMhwOWC0KFgubEMBnZBJCkKRNsV3Pb/j1T1M7P89b+GRKtsCgZd6zzLtAedgsXPyS41ldUqPhcMj5+TlVVZEktsr6bDZjPp9HLo7WQpHIhOn1NbPZNYv5AgSMBiMnmMwpy4osSzk+Puajjz7iq6++CjUzfApv6x43pN/vMZlMMMYERYcxhrOzM6qqIssyzs/PbwWrtxY0hEgQIuN6tkQkBUmaUGtNNV9hj6VAF4rZYsFXz55RudzJibHWDqVshggr3Rpsbu9GCxMEChc4pR1YaF3ZNLNSWlPeaoVRNaXzGU1cHY0kSUKfi/mSuqpsNhEX7C0QJCJx5maLpLI0JxEZvcwhtqKmKIpg7tVGY4SNF6m1pliswBhSmfDLv/8Fk90JxkhevnhJb3hNPhiQ9XPSVDJIUl69esPhwT6vT07J8x7D4YjRyAoitmBZ4zIStOatNd+s7Wg07E7zHjF821qXSX4bMtuEoLYJLzdpZb6p4LCpL//IJovKNg2RF8ySxBLOs7MzoCECnkCXjvgHxjTKqyKEaPTH3ugQX+swobGGJGgYjQ6ZauL1C2PEB5warI9450W0q7SH9yWS3b1dvve973Hv3j36/T4HBwf0ej2WyyXT6ZST01OXclGFAnnWDTBFSBGuWcSYcnR0yOHRAWmaslgs2Nvf5fGTR5y9OeeXv/wlr9+8dmvamIt9iuqbYPWmFgsTBhsQuslla9uzHhZjy5R/b1VVThNlkNJW5vVaHRu71aT17CjxMX5OG+YWCw5rf4O7jm1r1cEjOabZ5kY68BEW7fPlhA02CbwqdGp9fuNYghvcCGIZAdOcMbagEjdgYzb3KbpgK4JNw03PW9OsK1utFUoV9Hs59+/f5/r6ijyzVuv59ILTxCCNYmc0sQyUOyMiuE4JG/cgpY0viFyUvKbU1n6u0LpyiUl8oo/GUqBdsLK1KJSOeWwsmJ7Jr+uKqnZWBawrk62dZN/rlT7BzVcbfNyXPWO2X+UyGyKctdXhA18nyjL7tqqwFM7V1uCYf0GaWTfeJCpq6GEsS9qMj6+YXiuFzGxQqQCr9RSCuqrZ7+Uo1bjNXl9fk4uUwXBkPQyCJcOu13y1JM969IdDkiRrcJqUpFqghEKbiqosQQiMwzNaa8dIKYrlKjBTSinmi7nN/udgv3K/F0WBcsJbWVQY3fiGxzFYXjj0gOr3DxoNsw3QHQbmTGuFwQUuK8/f+Bg6T3O8prlJumKFw8ii5ZIxCIdAblK2rTH8bnzaNHFVmwQS3+I5bbKMd5/bpiTxfS2XS5t6NcuCoLEsCsq6Zuj4rTRNKIolk8kOo9GI6XTKfD7n8PCQg4MDXr9+bd3ojI+/0jx79pSDg31bc2x331kgBL0sD3MUwsbyfPHFF/zqV7+icsX/PF/kg8AHgwFFUbBYLrg4PUGgGQ6GgAiuvqPRjk2NuyoQ1I7e+bMVr9Jmpah0sa51VQfatjvZZf9gP2QsWy6XXF9fA4SCdcqtoXfLnk6nDAYDjo+PWSyWGAOz2YyyLIP702w2c4UbNa9evQp76i0Yvv80Ta0QB84Nasrl5SV1XTObzVg6Rb0vuihIgttWlmWkSU6a1lxcXGAUTmhJKMsFda1YrUp+/vNfsFotmEwm+FS3wcVNCLLMuh3u7OyE69OpDeqfzWY2BXEZFb28od1a0JjNS5I0QZFQLEu0qCgqG6+QpX3Kuubq+pqXb95QVDVZ3rP6rVXt0gkqG50fskxZYSM2k/lFVkZT1tYvtCmcJFGle76urGknS9F1Re0YCqMUo9GQ0WjE9dWUuizt79pgkCQoKlOhtELXNiOF16xI547Sz20RFGEE0gibms5Yn36tFFVRsjKGoljxb/7Nv+H4/jv0+hPmxSX9qmaghmSppAbenLxBSsic9ng8HlmTb8fc5olazGRuQyQxIvIMbVs8aT/jmZYuU44QLc2l5SPaB7Fr0Wh9ds+bSFMqWEemDQO/WcB5mxZnk3ARu+W0fnctWBWcO0AiJZeXl1i3OxU0DMHqQZTBa5tvi2m/r2t2jQUxv9aZs6b4Z7suApb5sH+NC5QN11yGGP/dH34pJXm/x7e/+x3ef/99JrsT9vf3UbXi/OKc05NTRqNRKCAphWRVrBClJaK1gl5P0O/3meyO6fV6CAFKVZycnvDlV1+R93IeP37MO48eslqu2BlNOD4+5unTp/z85z8PCLe7zy2rkr3Q2Ut/f7N/rf03BMbeu1R0Y3i2NZ8daG0cMcwZw/n5OcZYV0ylrZtRskm4FQITzimNBp1GkxgLOtGTsCH+wQTu1wskzTp4bW/TZ1jBaMGaObQUdbqzxvE4aDIUNWPo3ue+Rz8kG0QNP34po/5ixYjpiCi6g3eCtlXbiwKWsym9XsaDBw948cJmgtOqYrWcc1qtmJ6fMx7vMBraSrbXsxnnZ2dMp9csl6VlVF2KU601lXeDKZyAYGoQit29McfHRySpRCSNy1ucJU/VCqIYjpYiB7DZ6Zoz6NckkDJ8PIGNCcvzhDTNgttRlqZNwgsgTSW9XhaEvETKgK+0gSRJQ259LxgbY6jqIgg3jf+6hefUuRUv5nO00QySga2ynLgoMAlFVZGQIYVECZ89KKGu7fzStAdGspgXLJdLysoKG3VVs1guWC4WPH/+CmNsQHFR2n3wLh6qrlkV1rLh08WHxA7awq4Xyhq4cwHqXvr2dNHHhADS2Cx9BKHYwptSClflL9ByK2TJjjVUhIxXWpsQI+ZxjF9jX0Q1lTbLknUlifALxjrzOWuGMc0ZR4gQq9G13PrPzXlb//22yr/4/k0KrxsVfzQZ2y4uLrh37x7j8ZjpdEpZViyLgmVRMDGaNE0ZjYZcXV7w6J2HHB8fM51OmU6nrraDdZcrViu0FC5bkSRZpvz1X/8Vq2LJhx98zN7egaMzwin3SlarFZ99/gV/+7d/y9nZmRVEHKPtNefjnTGj0YiLiytO3rzh+vKS/cmOq1YtWC6WpGnKYDh0CQg0dbUKAraIkey29TDGJYax96ciwxjFl199yevXr9nbnVAUBf1+n+VyycXFBXVdM5lMWCwWKOeWPRgM2N3d5fz83Akd1xhjLXTz+ZxPP7W1WPr9Pnt7Bzx79gxjDBcXFzx69IjZbBbGc3V1FVLU9no9ptMpZ2dnXF9fI4RgPp+HdfKK6uVi5eDBpu621omhhXUhKIuKvGcTHWmlmLtU4mlqXeF8v1VVOXe6mqqy4/VCBRDWwtPn4+PjG9fXt1sLGj/74kt6eY/M+VyWlcvQZAxqOacsS+bLJaUP1jYuXZ5uTJAW6dQY4yQsmSKwSN4SGUWWGmQiybOUfi/HBmvbLE5WHZMhE2MzOyUJUiTBT9HSQs3uZMRkMuH66pL5bE5VVBghEalLReeqe1ZViZCQauEKMQl8pWNv3k1IQRiUtBmuNLZipsGgVvDlV1+SZX2G4x3uiGMyWUOSItKU2eyacn+Puip49XLJ3mTE3mSHPEnQQpLlGVpY87lxTOW6R7w7EGD9nSNmzRiDFiZ89q1lnnWaYrs0XmeEExJu2vEo3WajIg1/jEuNZxCRQtZrENbH5Dk14f8KwsHQrgMjGm2uR0rC0GRk8cye+9rMxkT9eUZBWSYytbBxNZ3SpAJVKJdzPmgYI63y9mbvif0v/d/GyuS149aSIuwDwRUBIhcqZeHeOEtckwUEmwHD+3VKl6VKwJ3ju/z493+fg4MDDg72ybOcX//611xN52R5TgKcLc45eXPC9XTK9WxKVZd2fWqDTFJ37iS9PGc07HOwv8vRg2Pu3L3D0dEd6rrmyy++YrX6DU8eP+Kdh/eZz2Zk/YSju4f8/Gd/z+eff45IpNtr49LVEnhpm2NIBY1Rm/i1M3NBFOegRXD3aNZ1XVCOhbuu9aPF4HrmxRVVWyxnzBfX7OztYWqNQYJYj5ECQspRGe5pzcCNQbeIWWC3O0K8L1onQgpjZ72wAO+uuyBt0/TVgjv3Yyy8B8VE/K7wvQ6/eI26XTs7N+//Ha9lzMR4IuWVCQJ/5iKRy+krYkuCNl6gsLgSmpio2gUqV3XJ1eUlWZqQ72Tcv3+P169fsVisLDMkJcJMefr1VywWK05OTnnz5ozVsnD0grC/xvlqA85torZ4PZUcHh5Y99elTfKR9a1WVcrE1TawuKLf79t1coRbJtblUSaJrQ4uTZivZwK01iQyDYqNoBQwJiiXlNbBbQIhAqPtLetaKXp5jzTUCVBcXlzQ7/fp9/vWmh+5MmVpn6KwftmV9jAIaJeJp6pRKmG5LLm6OEdghYuLq8tgCfBuGTbmA6pShZStscVAKxsn4mHOKwO0w9tEcBM3rbXTEusgZHqQkS6pgE9GEJSO3rKLda8Dbw10Chphfw/1Rlw8jHCZ7tq4oTkRXsETF+r17zXhvfbkGGODlbXR1AgSZyHyFNRbxHwKVvuveakEUmmz2HnaEMbk/PljS0bAf6Y95tYnf/bc/GLFk7/mlTMmvj+av59vo0xTCCm4mp7z6NE7HBzsc3l5yWo5p17NWc2mnGM12IM84fXrM8z9Y46P7/Ls2VOm0ykXF+eMRkPnpi6Yzq5Q2uF6KekPBkynU55++Yxvffs7HB4eBr/+169f8+zZM169PmGxXLFaFaRpRi8fgpGoWqBln6Pjh6RpxuXZCVVhYxSywYDB7i610ixmMwbDIWm/x9nlFVJkzKazUA1e4HFXg6+8QsevSbP+1nJ3fO8Ol5fn2ArkC8qipFgVVGVlXflqxWKxCPV/Dg4Pefz4CVVVhWQj5+fnLJdLlssV77//PkopplNb5M8LCb28x9HRHd578oRev8eg36coVlxeXvH65UsH05Kzs9MQQyOlrYXR6/UsD12VGG1pZb9v3cfSzNLRfj+n1+9Tq4o8Sa1FtizJspS6stk27907pqpLZCLI8pxU2b6qurS1PYQILnYeL6Rpymw2YzgcUlXVmtJxW7u1oPHs7MoONE1JhNXQZFlmpco8I+/1UMqgkSRp4tyVksBAN+kNG7OuTKygkXhNhLHaf4w9CAbrB6eB2vmfGpEhU9C1zVktsak5G2ZGoeqS5eIaKeHo8JCr8ynz+cICnDCkvQyhJSKzKe50aYPkLGJpfOxtTQtXrARBmudUqkaZ0hVVMuSpROuK2fScqpjzwQcfsLN3wHR6zWI+RSvrI7pYLnn+9TMO93bpZ/dJhEFkCXGGFItBPCMeMT3CEngVcq1bBaLxiFc0/qXCU35hiaZnxlv/N016tVaLlagI4uxY8VjscD1z1mWInJDRDcoyImhScGMwLgONESYUe/SI02C1RimyncymoVk2ENT/Fmt9HdGQidVK1bVFGn4C/pkw07cEkDVzs59k0Fw1QV+WT3YsXsilnrp91C1GxM8fV2kVY4MkhdszsBpO7QkJ1oXigw8/4Hvf/z47kwlHR4e8evGCN6/eOC1uzZsXJ5ycvqEsSowWNhC8N2A0GiIl9KREa4EiQWsL+1eXcy7OLvnks0/pDfo8evSIx48e8e7jJyil+frrp3z97Au+853v8N57T3j9+g1JknB4dMTf/eQnLIuly83t4coqGIVjoC2jqtpEV0g8bK1r3+waNq4JXnqJYaCtNfQCa2MxiYJBgyBgB1WWK6bTS0a7YwxOjSUJDHe7ufiKACc0wi4aYWyigfgpKQRJwB3rMwvisT+D7hw3eMC9w52tRi/QMHqe+ffzataKwPxpDMLUoYOWS4Zw8WC6SfEIUWakoM2358gzxlY4brIa+T1QWoXfDbaA1mq1Yja7piprqroiTZPIRdEK3sfHx/T7A9IkI8us9vTk5A1XV1fWfUKtqKqSV6/ecHJyjtGSsqhRysZ5+Ho2lpmskCIhy1LyvqQ/yDk6OuLg4IDJZBLcYYfjcXAH2qRBji3rIVOMtK5SXsHiM3BVdWXply+Y5VytUmGZ4MrFdXjBxBjrzpekCSJJMaWiViVFWTNf2poMq1XBallyPbXKu4bQ16xWBWVh40GMNiwWiwAXNg7RxYhEMR3esmtlEdOKIfOtq6RquQHi4yhjGLfKkE0wboxL1evORSP0uuaEV39vLCA3SQw8vMeFELWjNZ7pb86N7y8+/y3yKSC2GDZw005Jbmm+S9dba6AIcN5dp/h7w9hLEkcXvLXbvxNpBc1gIYuUaWGtb1B0+Xd59zogVKu2YzCtv12tWcvy6hI0TKdXVHXJzmTsMnOVlMsZL79e8R9++wlaaz7++GM++OADTk/ecP/eO9y/f4/lcsHV1aVNDCAgzazQnqTS4gyfCU1pXr56xenZOXluNeCr1YrLy0srxIzGXM9XJEnKwLlD1ZWmrg3jvX129w5YLZcsF9cc7O9yPZvTG43JBgOmJ+fUZc3h8TFaSharFXmWMbuaWmuqSxcfYCJac08fGnos3LtrXrx4gdYlMhnzyW9+w6A/YD5bMJ/Pg6tZURTW2pgkjHfG3L9/P6zz5eUVQkj29vYZDAqeP38espPN53Our68xWvPg/gPOz86CRc1nfvJuio2FTTj3f+3UZbauRZIkZM7NLMt7GCHIe2kIGF8s56RZwnDQYzq9JssS8nxIVZfUdUlVFWg9ZHdvwnK5BGxMlVeKFMWKPMtDbEa/3w94RgibnEEI4VzS395uX0cjGZCNRtansa7J8j5ZmjI4mCAS65KijaGXj0h8Dn9jfXqt8sP7TNvgcIwmE5ClSUgv2c97dvG0DSy/uLjCGtoFvSwDIckzQVEuSHupDYrT1pc3SyXDYY5ShbWMDHILIJeXDPI+wmgur65suXljaxNIJFmSk/Sx6U59wJ3LoJAIgdIuo6LQqFpbZj+Vth8kaIK/bLmq+O1vPkUIwXQ6RVUVn37yG+4eHVKWBXmW8OrFhGFfcHh4BKJGpj184TKvWWm0kJ7LsMyFkIljdIzLawmJY9giRahXqWI1y41LkBHGZf2yPu3hdf56jKR0dDFugUu3gsPaHbG7bKyhieUAwElGGOO0W4G4NYyU10Z039GWwRoGqusukzqt5GK+YLVcBlnBEyJfsKgz1I3NIyjPqImWlt5p+PDZWkSwstn3NEiubf1oGMXYHUMIEZgChCDJUr7//e/z4ccfcefuXYww/PrXvyJLMubzBS+fv+Ty7BxVa9LRgP7OhCwbkqR9kiyj18t49fJrXp+/JsszHjz6gGywQ60Muq6pigWmvqQql3z629/y208+4Z133uF73/se7733PmW54O///lfcvXvMtz7+Nv3eiDzvM9oZ8x//p/9oNSS4IHu/mBFj29V6xgxB18UgjleKa2lsundT33HzzHKTeQe0qqnKFRJNnlhLUeosq0QaU7unPntRMw4PKn4OiYvFDhpErHXCxxJ0RmQFDJySQJsIzlsHJwgb3poQSThOUGhceVr3xmulbJCtDRq2WQJxWtnSVV62LkZNhh7liFrbB976TFstn/VHFkIwGA7InQndxy9oZQWNoqh4+eI1FxdTlKr48KP32N3dZTAYMB6PmUwmZFlu4w7ShExLkhSy/B5Znjhf8Ipeb8DBwRF5NuT8/Irl8iKkrG7OjmI06jPeGbG/v8fe/pjd3Qlpmti0qanNUGSLaVl/9PF4GBj/OE2xMSZk1/FuHqrU5Ll1/dDYmD9bXwC0UmhdYiBoNVcr6y+e5inz+Zz5YoFWirKyAZ9VWaGUoSwrVitLr7zG0FfD9nsaM7pegRK7tMauVUI3SRXWLFTeAhTBcZfZXYdWQ4OV189YV0D5xzQBobCdb/78x+e8iwPitdjmstS1nnrNbJfpj3FzVxjzffprsctsc71xqY3TmloFqQ2Kjs/VP2bdfMD/tta1Urbm4hSZq9WK6+trJpPdKP5iiRDWAogQfPnlU77zne9ycXHJwf4R7777LmdnZ5RlyWw2o9/v0+v16ff6lFVFv5eR533yvO+EWsN8vmC1Sri+vqauK5ucQBoW8yUoQ380ot8foLWhqCrSLOOddx7Qy3PevPwaYwy9fp/FquTg0Favvri4wACHd+6wdEz8AMF8NneeAOvCdAz3cbO42BZ0rl0R3x/84AdcX18zvZpSlTYb08HBAdfX14xGNmnQyilUTk5OGI/HgRFfLBYURcHV1VUQTHxMBViXwM8//9y6fQ0GLdhsJ5yw9SvyPGd3dzfEHHqBbWdnx8VTLgO8xfjs7OyMXp5TVxXz+ZxerxdS33q8L6UM/axWq5DuWDtFhs8e513NR6MRo9GIy8vLAN+3gtdb3QVMJnsIsAEzPVvVUArh8tHX1oVJWkSsak2WpvhzoFz6v0EvsxW1MeQJfPzkER9++CE7ozF9F/He7/VBSEqt+fM//5959vVzZJqSpFbQ6GUSzJD9/QN2RjsUiwKjDQ/u3+f+/SPyXoLWNfPZnL/4i7/my8+f8cUXTzk7P+fk/JT33n/fZssQgjxJHUOagjFULn1g7OKS9TKUrqgqqHVJ3s9JdGIDaiuDNLYwoFIaoxRVrUgSyXjYo58fUJUFF2cnVGVBYmqef50zGECaGHb3jugnKb6Wh4gQhGfcfPNsS6PZjJysvGARHR1a3xouXwhDknjCYdjIYDsG38k7G+WN2LS7dsUrTtrmDmKzpWfUfSaUphvHgLVGHzoMNRHC/0wzL29NsUV6bI0UAaxWC+qyCOO1+abXs4O8rbV9ZJ1WzViLiNbKmTZ90aF27IY//C2i6ZBb7EvsiYefp5SCP/iDP+DJkycc3b3DxeUls8WMVVHw26df8vzrFyRaMO6PGeQZZZaQjXZJexNkNqY/GJNlCZ999ZLpskKsKu6InHcef0hRaVargno15/Xnp8yvbWCYEPD8+WtevTrl3Xef8KMf/YAf/uB3+fTTz/if/qc/58c//jFPnjwmy1P+5b/8l/zPf/7nLBdLt7zGCWJWH9pmlGzTzt/Z3++ZnSSRCJPgi3l1GYAuw9AmoB5Y2wxV0OZ69l4blAteNMaQpoJMetj01lUPR01FauOPivtgdN2MQRsnl1v3Dp/K1MObuzGcq5ZA4KwG2gkEfswxs+PdWHwsAjRBsRYGGy12/EwuPLw7AdBY9xqtNUrI1rEOwp2rnB4T5rh423wxc7nWDUU5iPbCOCsJSJGhleHTT79gdj0nSQT379/jwf2HTCYTm/NeZqE4l01ZWmILusLh4QGj0ZDLyyuWywJVC5aLsqUlVtqmgO71e4xGAx49fsDOeERZlYzHI3q9nrO654F4pklKnvcRoqaqtLMySKrSCgGr1Yq6shYYLxjMZzNWRclqWboYw5rVahXyy7cDk4n2ofH7j2OztPECoyBUM4zA18fcBCZfWO8A4yhEh/W1SjAEqtYkEc7pnrlurJeH3S4TGis8MO3Uqi1YCQdiQ3OCd8zY/UMY67hqclfQ6OLTuO9tOH04HPLDH/6Qv/u7vwsa2Zhhj/uPBY2uQNVao87Eu65Kvn8hE4wQ0VnabFV62/rE+9eN+esMpSWs+vusEqupm/XixQv29va5d+8e0+mU5XLJ7u4uBweHFEXJw4cP2dvdpyoVz54944MPPuCjjz4Kwc+r1YrRaMDOzoSiKOm5mhppmoOxPEzpXPK8u42Nj7EZ8sbjsS2RYAyrskBhuHd8zP7+LkWx5PT0DUJbjb9MMw6P7lAsllycX9DrDzm8c8xssaAsl5iqdlaWOLi+vSw+PqjtaieC5doAiUy4urpydULyIFRNp1OKokAIG88wGA7QxjLkb968CYLBbDYL675cLgMD79e/XBUBfksXR+yDrT28+MD4GEZ6vV4QJNLUKjF8kgONQPhsrC74fLlcUpZViKnw49vd3XUVziVlVQRhKBYosjzDqKZ+jE0zbNfKJ3fwWbhu024taPQSVyRPpsECMej1rEbH2MqMvV4PKQSVG2y5WmC0oj/uI6QgkYLB8QG7uztMRgNEXVLOrjCZpFIFL776nLIsefjoEfcfPuLj9x6hyiXLoiDP+wyGQyY7IzCK1WLJ//P/9n/l808/RyvD4cEh/81/86/5sz/7I3r9jP2dHfJE8tOf/C1ffvGMk9PXIAWzq0u++/0fMBjuoJWtYInAlpTPbbXFqixt8SMMQtc2ODKR6DRlpazpuqoqpIZ+3qeXJpg0oSxtZo2qtjEAi8WC5XxGsVyS5ynFoMf52QnPMo0whjzv0ev1ETJB+tIDzmKhtLbuRMaEv9ojf0PwS20EE5wiWbcOl/BxD05w8IyOx0Xt1ogkvsCWR0xtbWujTWxTvkb/Jdy7iXxxY1N7g9DduHVTo0JKGdHfSCAyhAwdnhA2I28+GGNz28vMBjmfn56gVe3SzLa1ghulqA0tJnDBA1Q0bhM+1sMz2j4LUlu4aq+413DF847fJ4Tg9378e3zwwQccHh7y+uQN17MZi/mcn/38F1xer+gPdpiMd8mE4tmXX3BdlRw//oDf+YMfMdi5S5L1kWj+IOvx87/+/6C05r3v/ICDO+9gRIKqFeXymk///i+4vJgxnVm/UpH0KcuKTz/7ipOTN/zhH/4BH374Ea9eveTP//zP+eM//mMePXpEpRR/9md/xn/49/+BylUO9fn7hdys7fC1dGLXglhA8fOPc5db7bNY87Nu7rdr3nUNsXAXW6QMGIXQFbqy2W16ySiycEUZh7B1FbxQCg1xtxXmLQwoF0moXBphcFWXnZVX1bYoWlVWAXbDvqvGsqV07fz+k3Du4rmoWoU12sTEeUY3SawSaFHXVjkUrZm1yElbNCta/wB/aYIwBP90HxuQuFTKy9WC09NTptMp7777Lh9//LETAHyqaIUgZbkoMUY567ZyfVjX1MZFFdCKWkqESJyW39ZWyvM+/V5NVcJgYOj1lkg5DYlFBILJZIejo0PSTFIWJRd1jVY1q1VJmlyFda7r2uJzpamUiOIRNMuldansCg2xBNBUJ3a/CuvOsFoVLQYiMDgm1BUEIxAkAQ5Dv+4VDYMTK1vopIV1uBJfGC4JFjUrELtnkK3zE85W1M824X1Ti61lcdvEFMcCjhTWDborwGx7V2CA0Y0LbUfA8M/HVs7YOtD93pqDa2VZslwuQ3pRD/eeuYqf80LOJqFlk0Bj79UtWPCWN+niM7R71sf3NDTodi301bHkdAUuKWWbNhpDfMabZyTn5+dMp9dMJjvs7u5yeXlJ0at49PAJe3t7PH78mCzrcXh4xNOnT3nx4gX37t1juVzym9/8huvra+bzuY2HTGxBxSBkKEWtbNyiHa4kTXOUssqM0cBa3AHKqqSoKg4Ojzh+5wFJInj6xVOLx5ZLirLk4M59kjTj5OSEYlnw+Ml79IdjXj4/IU0EJ1+/8DPurFyU1MGtS+w6aWHWJYrBBGHk+vraZkNTjauVf2ZnZ4eqtkz/YrEIVqzpdNpS9khpg619nIVfe+/i5OMf/HWfQti7MHmG3sOs319P55bLpc2y5Syu3tXJx2FprSlczRRoimJXVUWapRhs/0dHR5yengaaXLmadv4MxC57YIWeXq8XMmO9rd1a0MiTygoYGSTCpoYcZBkiszCtVEWGJYZ7Ljfzzt177E9G7O5N2N2dcHi47yqQKq4uzkmE4PPPPuP89A1ZkpI5Ce7i5A3XV5eMJzt864N3OTs/J8t7zOcLEmFIZcb/49/83/mr//SXgEArw9nJGV999hmnr17zh3/8eyRZwh/8we/xyW8/pVY1WY4LRtJ88emnPHjnMXv7B86XNA3aY4kkyVKMIyaqKNDKIqLEQAZUdU1ZrFBlxUwrXr6oHQIr3Ua7iq0uCF4K6yK2PxmzN9nhj//oT/jJT37C3t4hw+EI0IEp8y5UxgkaxhiMEk1QdyQkCG890J61x2mhmuYdNQLiCcLBOvEwpmGMY2Jr1vq0/98saMSaL8J3p6dt3RtogHGUWTj/8EB+aZLZuPc0ri02+K5LtrwGW6maQb9PniYUq6WdlxG2cq1Pi6lUi1C/rcWawKbgmf3XFO7rWj02rXNEqM1mDaQQgg8+/JAPPviAvd09Xr56xXwx5/WbN/zq579CkzKeHDGYHDLcGXP26jnnyxUYUDVMdu9wXcL11Tnl6hpVznj80XcwCN6cT3l9YX1j0yRhMsh59O5HLBa2ANXu4X2U0sznMxbzGYv5Nf/u3/1Hfvd3r/j+979HkqT8p//0n/ijP/kj3n33XaQQ/Mkf/zF//ud/bt2opAR1g4ZOeKtPJy7CCRuNa0xDGGzKvyT4pceMgCfALYZvjREhWMSyRLKaX1NWBcYIEtnkOjfGhGrKlSqtm4u2Qbah4rJD4LWramvzk5cYbRgMB1YbFO2zn49nmHy8iocRC0MuEFYIalE77bUV2pqiTrYGkH82kQlGGBeLlITiav6dNu6nIQ6JC2wGwf+Xuj8LtiW7znOxb2afq1+732efvilUX0ChKYAAAYgkKEoUqZaNrkyFJd17g/fFDsf1o+0nP9wIP+jN4YcbdlghhR3XjSjKoiiJDFIiiR4FoIBqUHX6s8/u9179yj6nH+acuXLtc6rqQOINUVmx6+xmrZWZM+ccc4x//OMfaZ5Vc9b0GTBBkwAcx6XQv6vGpSiJo4T33n1fU2MtXnn5NVzXZTabkcQ5tu0iLAvPd3FdmyiKEAKSJGM4HJGmGa1WVm2iakyVlGmSpsRaLjLSRaLzWaTka3OlemSeaZZnnJ6eMJmMtUmTFShjwBaBKma0bIUQCgTYThVQwsJ+qULdUhcY1+eswNDcFr9R880otpl1Xl/qyt7o7KpY2Dq5+BAWchtqHpjZIEXtlbVLEYiqRmSBnpv+GgsA5qkBxDnf66Mc8urnc7ZrObAArKdTdxRCvDhPPQtQ/xyzHirJcanUIOv38LQv8976v/Xvz2dfzBFFEW+++WaFHluWVTWuewLhrtn6n/Y4/35FnVLPz1BfzHozc+Mp8cxHHueBhnoQovbl5fv5sKMoCo6ODrl18xNaVWpCFMU4zgzX9RgMVD2F7wesr6+zv7+P4zhcvXoVgPfff59oPqMocpIkJYkzpm7EIqMPWb7oNq/suO7k7agMX5LGFAhW1le5fOUqjVaT3fv32d/bVZuZACkF2xcukhWSx7u7OI7LhZ1LzOOUwXBE27U5PT2ovAJjP9UYLfcEW6qdAQ1gltVrLdui0+lU4+k49hKAZRx5x3WX6mQMPcoUvRvk3wR5JoMmdebSZC6M3TXytEawwQBt9X3MZD9MwGCedz3AEEKpNprXWJa1FFynaVplMWzXqqiwdTquuSbXdatAwwROZv4+LQj/sOOZA40rF1b1Zqag9yxNcWyHTquFbUnNhw2rCwrDgCxN8V2bKxc2iOI5u/c/YDwe4To2wrI5PR1SFkovWT9vylIyHA1otxrYVkmWl3RaDRL9WZPRmKOjE37ykw+wbJcsycizXMnvFSXf/MZ3eemVl3F8mx+//Tb9lR5ZkeL7nqJziZL5fMbj3V2SOGNrexuJ2rjMQxVCcHp2yng4JJ/NSWPd5CdLKIpMIZel6uAqtTqAqSsopW72hLYe+ksWEs91+M1f/w1W11YpSsm9e3fp9Xt0XYFjOVpNRat5IClr3UaNg13KUgcjyjFXwYaDwF6k3pf2lxo1qZoYC9qPOVQGQj8FCQgVZVu2jRDyCYP+NENfd7z1H2v723KYwblzy9p9SbmgdSyHE6JmnAUUC7S3/nspFU/esS1cx2Y0GoJUCjHSWhQDSmmyRR8x8c2ZhTh3Dn1PpUKwzdg5joNRwDGPvyo2r+0o1eeUBo03tTTqWFtb45VXXmFtbY3Ts1Om0yn7B/u8++57+HZI0OgR9LfwOit0V3ps7ezgBj7RYMiVKze5f3+XaSbwAo9ux2d9p0/o+9iORy5t4iQjT1OmoyGT0Rle2Ob5lz9Fu9Nha3OLJE05PTnB8c4oZhbz+YQffP+HxHHM5z73GaQs+c63v81n3/g8Fy9eJEtTPvnJT/L9N9/UyPuHb27CpN9qTlr9b8pwC+pSxKqgdiFZWUc565klYzCXnBNN4yiLAse3mc8mDM4somhGmqXMpp3KuBs+bRLHSmWkWATeSp9dUbsEKmAwqJLpv1PkOX7oKZtgqY3Fdl0EYDsujuMt5pxYIJwCtbZVkZ+7KFitU+nkom5H+Xn6b7ZdrR2h0Uyp3oSJ9bNsUbhc6vo4Q8+TcnlNgCqal9qWqWxAQZJkSGmzuXEBz/e4cuUKs2lMUc6YTqZV5iROYvb39phMxwhLUpaC27fv8OjRbhUAmjWg5BY1Pazm/C8oIuq+1HVr2ldRIMqCUpjCWweM8lSpxAfM/bhOoMfbrtSwFqi+tXDOi2Uqy5NzdnmOSiT1hJ0ZtyqIhKrWQghtm+VCUalOm1JqSorcZwmxqNZRhnF5KekxWWBHz+ZQmgL2ur38MMS+9q5FgHQ+cBFiSa73fNAiaueov8aABHXHpgpkpc48leXSe58WOH1YMPG0n+u/N5zzegBdtynn319HsZ/1qDv9iy8LalmZZZClhqT9FOf4sN8/AWZ9xGFZFoeHh1y5fJV+v8/q6hrHx8dEUYzvRwyHI1zXY3XVptFosL6+zu7uI4qy4MqVK3iex927dxgOBliWkohWtO9SxcDCXtDHtANsrkmh+crGra+vc/HqFcJmi0ePd3n44B6PHz2i2QwJg5DNCxfxfJ+9g0Pm8zmXtq/Q76/x4HifvCg4HZ1S5jnC8vSdLbI4RbGc0a1ndkDPL5MtBLa3t+n1ekrpSVjIUi76S+h1dHZ2RlGWuNKtgmXjnMdxXM0b3/cre1d1uxeiqoczjrsQgjAMqwyGmZcG1KrTqJazUkLXdckqq2JspPkcz3EreWGz5lzXpdVq0e11sB276gViGD6m4FxqANiMlckmK+GKuAqGPu545kDja1/+vIpO05ThcKgWbZZXafM0TXFsi7DRIta8tJ3tTRAl77z3Yx3tmeYkKZat9KnVZqunhqUMouu4XL1xA8/zmM3mnJydab3fBmsba+zvP8b3VJFMliqnP8tVCun2gw84PD3g4sULDE7OODs9wbWd6iHH0Rxkhizg7PQxZTmnt7pB0GhQ5Iqfe//+A46OjnBsG99xoFSUC4Gq+C/LXDsGC6TR5BmEnuCmABMpkbZyMO8/fMT/+H/9v/HCCze5fv06pyfH7O0+wnMswrChDLelNydQRdKFSucZ38zS2Q6TZVBOVFYhpQKJrAq5dUqwFmRU2QkpK7HXyjGRC1RNyBJLSizDbpc1KpWhFywFEuhNtWbotGNtFBOMpvyTqL5WDtHXadW64lpCTwx9ApPFEToyssRiw14glBIo8V0HZMloMFROoaQqDDayskbFZGHoa4HSE4dyZkyQIQSUZQ7Y1eZp0rDVayi1c6GdmdozqM4iqldUFMRPfeYzbG9fIE0zhoMRR0fHvPfu+wReSKfdJWyv4K2s092+Sre3ipXH3HrOYjgakmOxud7jtYsXWV3p4TuSskhIsowsz5EILOHjuS62tU2RZ4wmI/Ye77O7u8/93T363VXWNq7QCDrcfnuXPCsIGwE/fvvH2K7Na6+9RpymfOeb3+IrX/0qOzsXKYuS05MT7t69h1LUenIcjRMiqddhWJVcJdIGHJBmc6hTlmQ19+tdWaHWxEoaPAuwlCa+wNQ0FCRpwY9+9GPanQZFkWuZ7fMF+kqVKc8TTceyqw1SIVCqm7AlBFgWSVbwgx++S7+/wvUbV+iudKo6Ac/zcD0PWaquyEY4wmwSlQNVp+dYNR64QdIllf2UKGlvYVnIUlT3bUAI21GS4KUsdQPEEpkrGe2MQtF+okQ7XgXz+YzxZEIcxUS6kDFJ4iqlH2nVlDTJiKK42vz2Hh3yjT/9VoX2qxoNSVnqDt1C0aYULapkNpsv2QchRKVOZtalpWv/BGUF1tuWhSzzSgNPCEFpZFLF+ayBnnd6MxeOEcvQ80zKKmOgFMN0nZgsKxD4/KxVlrTC6BE1YW1j7zF4hZnPwqIQggILiYWBTsx8RFiqT4SKLrCFBFEiyRF4gIOk0PdGFSBZenZbuhP4eUdyYV9rwQ+i+nlhKuVinxGiUquSOrCxLOVkFNIE/1Y1P3XUhKw5cPVxM6+r++cKTNGNDAuJsE19XskitHrSXjyrw/xRh3lvHV1WHcOXA5n6a5/2t/Of93HnXJrntm5qXC7qI4yjKZG1BMT5cdBQoTQZEkP5WWQr60HYgo5lXv/k/ai/mr+rGtr79+7w/PMvsrW1xXyuVJYUTU+9JoqmPHz0gCxL2draYn9/lzSNuXBhm0azwf7+IY8fP9YKRmCjqZda6AZLO7kUFIWanxY2YbPD2vYmK5ub2K7Nvfv3mY7HoGlJjt/Ea/XYuHCFPM85ePwIO2iwdfUaUZYxPj6j6wW8/+gAy3Ioq4a7Zt7XKNJ6vlX/YsAGJZRRSoEQkmYzVFT3JKLRbBAGIYPBcAnImsczLMvGD/pVJsNkFEwwXUf/68GGhWniqV5nsg9pmqpaHv3cSiHAsvH9AEPJBN18ttaLJi8KbEs1Lg3CEFDZFWEpUSPPdnBsh7zIEbag9HOyKMZutRkPRqrkQQocbGQumc1mCEswT+cUuSoVWNQMq7Vflsp2lcWz0f+eOdB4eO8uUkrV4KURqK6dWUE0n1W6wY1Gg62tLdbX1/E8j/2DfY5PjqqI0SAgtu4UWVeYUdZN2z8hGI7HdDodmu0WrU6bMAzJ85zJbKacRN3V07YthFCydHmREqcRaRaDKDk+PtRRmuLwCoHqTi5V0aLMckZDtTl2e32ajSZ7+wfMRyNavq94laUu2BU2bqOBJWA2m4AsdVHT8qH0/xdORKE5isKymczm/NG//2O+8c0/ZX19nb//9/8+u7u7tFoNNjY2cV0Hy15GahbGv1ZoVi40tM1iUotEf2n3WaXahS44rQUa2rkvl4xP3cApQ6ABtdqmhd7AlxHj+nHewC5QZUlZUDVANNegKAsLyUQpJZZubmWCLVn7bHspXS+Wx0VK5eAKG8cSquhdSobDAQaFlCxqTiTq9cvH8iZST68KbZjM7+rKJfWU7OL5mc8wY1VWfzDGpIqyDQIjS15+5WWuXL2C5/k8fLjLcDjh3Xd/gu816PV6xPM5hZjx3HMbtFfXGY3nDI72yGcTdi5f4frN6zQDnySacbx7m6ODx4xHQ+IkrlQtjOJFt9NlbWOdlY01XnzxFtevXeXRowPu399lMovotZsMBkNmsxFb21sEQZMf/uAtHDfg1q0bjIdDvv/mm3z+859nOBjw6muvcXxywnQyrWK38yiqevb1/hOK1maGQgilSiJ1M0OzzsqaCo0Z76Uxr+adctYpLZ0FWaAxlm1x9949mq0Az/PwPLfq9Gqu0/M8fD+g1W7o/gpUVAtTFBcGTXWdwmEyiRmPpwyGU6I4Ymv7S/h+qOgBtg1SYFkOTi1NrmyhCrlU1tCmyMsFiqXXQpokFZWr0BSELM8WvRAypUBilE5MR+U4jsl1hsbIMdb7JOSZJEkWXV1N2v58htCM23nk97xNWkavFeCBXtfUAkBlakwmVi8sjMNLJfNsoYJPYRAWPY8sJNISUJo5YCSkJaZrudDO2yJjYMCgksWn1R1GWQXATz1qmQNjDysUWtgIDO2Vmi1T2RPHdTVYUmIb0QFj5zR6WBZKSMKybKS0VR8qIQBbZ02UbbZtC98JyXOtq+/YFdVLZcAhz4sqKKlTxIxtfSLzIJ4Ef5B6/ZgArFqb9axCfZ9aGihguWh9cU6B69hcuXKJbrfLO++8Q1GAtF0lBCCLyqbWFac+7njWIORpWZCPygwsX/uznPd81ru2VmrjtZzNWEgQL/5mALj6Zxtq3tOv5zzgUhbyib/VPqr6xuyph4cHbG1t0+2tsbOzw4MHD5jNZthaIv6D2z/h8FDVQIzHI37mZ36GweCU6XTMhZ3L3Lx1i7X1dU5PTzk7O2MymSg6T6mEgMpCBeBSCGzXpdVqs9Zfp7uyitcImcURd+/dpkwVBd+xLHrdPjgBV68/h+uFPLh3m7IouXD5Citr6zx+8AiKnMnJkGQ2w7bKpf3c7LkGtDT7r2mxoF5jikQN0CF1gbPED3zdFFRR4OM4xnUdWq02m5ubDIcjkkSpzMlSVjQqWaq6PMte1G+YZ6OyKXaVpTDZFbO/JGkGUvUjsTQAJ6Taf1TDyQIhNdCkgx5HF9c7thK/cB0HC0jihDzLEbYCuvIsoyxK0lhl7T3XYz6f67o+u2q6aWTKDXBsMjkG2DABkpSLWpOPO569M/h0ihCwv7+P73s0Gk3a7Ta+79PtdquOge12m9PTUwaDM9UhVBt/Q38wTo5xoutpRnMURc7R0RG7u7vYtkrZGQSgkLLis5XlglNrWxalbVNKSRynenPNydKcNNWdxPWDNelLKVXxYZpJwjDE91zazQazMCDN0qViLVUciu60aqOCu+VFf54jbjSRzaQ3vObZLCXLjviDP/gjGg0fSYHj2XTaLdUcSiwiZ+2Pa5RJ65c/LfiQUm8I4tzfl4vajNGTGtEyQQDUN+TF/1H7YrVIzXvr/y0lAwxXGEWJMJ9dSqV4Y8amKvSVprt5DZERDjYmQ+ACmm9uWSBqxdXUOjej+eu1R6Kk1ySTyVg7m2rTNZSc6nOWDPGHbFpi+XX1wOL8XrRAFBeXUw+8nv756rPX1tZ44YUXaLc7PLz3iCwrePfdn4CwaXd7DCdTDh7tghOwdeNlrLDLwcEhgQ2ffeN1ttZXmE7H/OjN73P/7m2i6UShpbKsskYCKIQgHg4Y7D/mwfsCO/DYvLDD8y+8xPPPXWV7e5Mfvf0uR2f7rKyvMh4PGZyNuXzlEllW8IM3f0C71eDGjRt8//vf5+7du1y6dIk4jnnttdf4sz/9syfGxIzb+TGop4TN+CuFHlMwrp9bbQ4Xtbm0cKbk0rMw66coFnzoZrNFEIRa7cTDcWy19n2fOI6X+NsKoVKOuaImqmBZSsjzuQqESsV53b5wgbPTASA4PjpDCEerrKisiaq5Ul3ajWKR2qQiLTcIaaIyqtE8qox9mqiC9bKmVFMHIIywQV10oELPLKvqMG/maeW4S0tnH5ZpKvXv6xme5bFerIHlOb9wRJf+hoXJStbiBnWNOtY+H7xIWctymvPVCoVLS2dJqxqU/3jE+9kOA8SYL31OaYN0UU6bRFDoTEmOY6tO6r7rEAYBrWZI4LkkacpsGingpZRYloeUEIZNWq02rueystqn3W6zutpnZXVFOzhNrl+7xf0HD/nd3/1dHj16pLoT670sLxSNV3XtVj0O6nuBWUcLZFahy0W+WHfVfozq+2BZdQfXfAZL42Dm1ILfzVJNCyxqEzq9Jv/9f/+/YnVtnf/9/+7/wIMHu5qObVGSYihqdQGD/5zHT5VJ0evyfI1ZtV7hiTUiNeBX4VlSfuQ56+vPACjms+pfHxaQnD/qKlbvv/8+n/7MCr1elzTd5vHjx8xmEao/iJKtLYqCVqtDt9sjDJscHx/xk5/8hF5vlbU1JX974cKFqu9EkiimSYlA2Aqd9/wAPwjxbCWp+ujBbcbjsVKREzbjswFJklNaNjeuX6fZUmDX0ckZve4KN6/fYng2YDQc0Apdbr93FyzVRmE5AD5HhxM8YcPQbzFAh23brK+vMZlMaDRDpJS6mBoaYajotXHMSZqRpRnzeUSulaCyVDe41KNflCWB7yN03zlTP3GeOiil1IFEgWstGlCXZUkhCxxhIbMCSs0y0Y+3LIslaWzLssjipPI7M10jMsknlc+sMhQKqNg/PAAWMtJ1wYVms0mr1aLX7eH5XiWt2+v16HQ6hGFIo9Gg0+k80zx75kBDUUQEcayatdSVe8xCCsOwKjxRygcLWTUzkPUUnzEmpiAGzIKxSBKT2s+rwhjLUjzHZrO5GDgtAWu6sMpSMhqOkNKi3eoQR6oTuVIYmVTyZOa68yzHjnMeS7h0+bJO9VP1fajQf02fcmwH13FJavfytA3WGGwTVC2MjQAc8kLwne+9SbfbZDKf4AYON29cpxEESn5XH4prvPjejJ06h0Frlw1+feLAIm2nrhXqRuj8z+eN4BMpV7GoT6g7PPX3LuZMzfmRKuukCQ+UUqs0seDZq8tXilsSXdyrX2MJC0uqsTMcdxUyWVVhsW07CCDNMkqZY9uCeTTXXHEqp6u6rtpz+7AA4DzCuxwQL5De5feY94laVujJz19yrJBIIXjttddotlqMRmPmUcT7t28znUf01zbwWz0OT0dIy0UImzSO2Nt9QH+lx+uvvUzgwp333uLHP/wB4/FIkzZUd+ayUOIEhsdpWzaWrednWZLPp9x//z12H9znxq3nefHV1/j06y/yk/feg/gUzw8JA5XRKwrJfDbiB9//Pms//3PcuHGDt956i83NTba3txFCcO/CPR7vPv7Qe/6wcV4cGvWu2Yt6hsR0+l0Ee0UVaBhE0NClfD/Acz06nS5BoLqqxnGm/4U0LXHdRDU6RGoFkpI8T0FoRSItL5vpovA8L8gzXcScKDADBHES8e/+3WEVINV7ZSgHj4WDj+myrJB5pTQkKzDhPDIqhNAcYTUUqhas0M5Z3bFR46cbzusxOY9Eq08xG18FhOijfv76YTjAUKfpLLj39WdcrR29ThdmRme20PXEYtn+mHPatq07SCu4wrZqtVuW4iafvwZLF3WX5SJjZonFZ3zUvPs4B29xbfp+UNl0ixwoQOQgcppNjws727zw4nNcubJDs9ng2tUrbG9tkiYRu7u7WMJVX7YCj5phh253jVazVxWZGopPrJVljk9OGAxO6HZb/OZv/hphGDKdTUkTRWc+Oj7h0aNd9vb3ODs7I45jsjQjL5Rse54XSzRBy1J9omRpVcCTnllU2SFh7h006V6Pmc5Ea4fINICsZxnPB47NZpN/9I/+AZ9743XA5r/5b/5r/of/4f/EaDjDEja25ZDL7In583HZh78oh3HS6sIUYNZSgaFO1bPgsBwiP+FTVDbtwzMvT8uinL+u8/O8PsZmDc3nMz744D1u3XqOtbUVsizj8PCQ6XRGGAbsXNjB9Ty2t7eZTeeEYcjW1jaTyZzjk1NOTk5oNFTWvd1u02q1QJRYtmq4nGaKnpTlJcPRmMnglCSak+YJw7MzVnorTKKcaB6T5JLLV2/QX11jPp9z/8FD/LDJredfoswLDh4/phl6PLj3E/I8RlCAZVUd5+v3quq/Fo1V6+NRLwy3LEG73cayLNI0oiiVcIwtXFWjJpTNmU3mtbqJ2sl0s2WVBXJ0lk5naVFKTZ12W2WSBRVdytQGuq5LmWofSSwUFlOUspMJKExm2tyHeV3VYFQ/1zzPcVwHy9B1kbi+T9PzcGybRrOB4zhcuLBDGAbkWY6rVa+uXLnC+vo6jUYDU4fsukogBCFwbFV7k6Qpz3I8c6ChGrypHgS6yfdiEy5LsiytijWVf2ChunY+qS5jAg6jC3x+UzONpeqLwDjPICpJQeuJAlABWIxGE+bziDTLuX37DoeHx+rnNK4eijlXlmWITKVsT44PCcMGeZ4iZa42LGljCSNrKqumQstOwpOyguZ39WIyk3XQ76aUJePJhPd+8r7iRGcla6urtFotRaMyHHPLqjZQU4BadwqM82iCDoPwOrZTPaMKZZGaQCQWjpAwz0tPx/pnf9hRd37KcqHYU1+4SwEOWldHpzJdy9JUAYOqqtepzJdbBYcIiWVpFTBpIYsCmxpPFQHYGkFQk17RTTKyLGU2mzAej/WzVFdRobg8DWFfdtrMcd6Y17m26t/aBrEEw5rPXNbwrm/CpVQc3Y31ddbW1vA9j/uPHzIcjnj8eI9Gu4MbNmn1Vvnk5gVO9w8IwgYI2Frv8eprr1JkMd/++jd5+P67kGeIQhVWqk7jZbVebKG6WSdZpjNM4Hk+rmfjCIsijnjnRz/g8GCfL3zpS7z84i1CFx7cfUQzbCMk5GlOnqcMzoa88867vPbaq3Q6HX7wgx/wxS9+kcFgwGuvvcbe470PDSzOz5FFBq9EdQ1fcI2LQvUvEJxrVEddkaOoxtk42kJnM6bTMb4fAAWDQVGtD/Xa8wF1qQ36uSJcPTcWwUwd2V4guItAvAr/1ecIQZk/WdOl/m8pOdDavDHdjpGmPsv8vPDXTWH44l7UfdULkg1i8rRncD5APm+nnwhyan87n4V+2nur30mDGApdXFhzsizV8HTZxisKqo3Ate3FeJq6DEsgLUOtWmyqZi6U+YLHvBAM0AGJOAeA1L6vI9FmPI0jDfVOz5DnKZZl019pcfHCCmWZ0ek28HyLn/3yG/T6bTzPJggdZV/lgOPjM61+dcrOhWuU0mI6nejNfI5kiGW5IH2QinLl2CVh6JAmkvW1Ps1Wq+pubpxDKdEqPi5CWJX6oaIglZycHDOdKoR5NptydjYgiiJGoyE/+tGPOTw41bQMtU/kRYHl6DlVgmXXMufahlu6A7YC5hStS9kZNd8NQCaEwHGUfOZv/OZv8Df/1q9SliWe7/O1r/0C33/zh/zz3/ld8qzAxqIsFvsmsDQn/qIfdTlqJRyxrBpErabiCTbHh2U0nhIdV36Snt/1AL/6u1iWSD6/b8Gi6V/9nAeH+7TaTS5s77CxsQ4ITk7OmE3nlA0fy3IYDcfkmeqL0Wq1VB1XFGmqlc3BwQG7u7sA2HaJwk0t4iSnlDZ5IRGWTWBb2BY8vn+PKJpBXlCUDlK4XLp+i+0LOyRxzMOHD5ECrt68RaPTY+/eXfIkYjSfc3p6gG1JBLbKDtaH7qkgwpMDamyUZVlcv3GDKIoIApckjbW4hPosQxNytGS35/tQt1s2ZKBAcqessgBFESsgvCiYT6ZkRU5SqxFK07TyDWzsSpgijmMsXcPhOk5l7xz9vZGfNXar0+mwsblJu91iY2OTIAjY2NwAe9EfAxQNy9WNVk02XwhRSdUKISpVKkPqC3yVDFC4viQrC8oCXP/PmTpVFT4Lk90Ax1GKH2ryFkhKLFP1XubK+apx2p+2cRkHoy4Bqeg4y2hG9T6UEkoUReRZvlg8qIUTNhp84xvf5OtfV9SNJMkpCypOc12P2NZRmW055FnKdDLBc10cyyKrnEJQzoKskDGjxmScoaeh3U/7Xt2bHs9SaOcYoijl3ffu8Hj3EN91NHfcqwIq07zFcRwcVxX2oDm7pujI3I/v+9Vr1fs08mSr9J3tOLqAWtHNKvTFsqrUbx2drN9f/TDF5xV1Q92gekaWVdVxmEOCknXTz95x3AoFkyYAqDUSMsW3Qqgu7PXAbRFY2fpaTCSv5sBwOCSNcyaTMcfHR6RpgmkClxdG099aOD/PkGU2KINB7erogXqepeZZW8jy3DvPBSn1MS2KAttxKJE8//zzdDodxpMJaZJy//59LNuh2e7S7vZp91a4dOUaV6/f5MGD+9iOx+ufepU0mvON//BHHO09QhSpEjwAfD9QqheyZGVlFdt1taMgkRoZGQ6HjIYjmBdKGzsIcS3B4OiQf/9v/y0/87Nf4tZzz5FlsHv/gG6rQ7e7Qp5F5JnH++//hIsXd7h69Srf/e53GY/HrK6uMpvO2NnZ4fHjxx+Kjn/YsQjWRVWrYFmqSWhRPD07JM5tMKanhnJCU2xbMBwmtc83O7tC9NGbjUmv1+LN2nOuO6H1IHUZ7TYTQFb/N9k6LW7AIiuooQH9tTRtqqNcPvOyM8yynamPg4JGlkGD8/PQjEc92Pq453QeRKmDK+eVwKSUVXG3AKRcliF2A92kStsyswl6nsd6f4V2q42ts9jNVgtX27ag1aS/ukIQBOR5zuHhIY8ePWIwGPLe2z/h+PAYz3G11r1yDKQQlGKBPNfnpVmL9eBraVykKgFXmYsCx4Wr1y7x3/32P+CFT1xmb2+Xbq9JXiScDY549Og+Dx/eJww8rl27hmMJkiSi3Wri2g6NwKcobRxLMpmOGA2n9HtbFEmBEC4S6PX6BEEDSkm/18axXUrbwTIqjXrcTU1DlhtKsWtSEVi2zebmWrVAiiKnETZA3/P9e/f58Y/f4cGDB1V/lCiOaLfa3Llzl7OzQZU5tG1bq78p8Qvf8ys2QhAEBEFAr9cjbIQ4tsPK6grtdpsLFy7w4osvsr29zXw2ZjCdIIQgSwt+5Vd/me+9+V0ePnyELECUy70izgML/3Mdfx6fb+ZQveeOcegkQiHuNV/gwxStzB5j1o55/ZPXuGAVLN+Hkr42n3Me2HraPiSECuDzIuPBg3s0wibtdpetzS1cJ+Dk9JjpdESWZaRpxmw2p9lsMplMefDgIfuHB1iWxc2bN7l161bF95dFRCN0CBtt8gJOTkZYlktZWqRJxMMHD0mimF63S5Ln2EGDS1c/QXdlg2mUcO/2bYo848bNW2xsXmDv6ITZbIRtJdy/+wFCKKYNlTpluTQu9cBqCeCoBXlCg0G2bdMIQ8IwxLZB4iELSZlI8qxAlqppqJKDhcl4isJ6FgIDcZKQatZMZU+Esv8V00Tvw2Y9tduqBrnVatFpd4mjmNF4hGXZdLtdrl69wsWLl6rmxq1Wi1KzE4qywHVcgjCofD7Tr8nzPBCC0XikgTCJ7wda4hzOzgY4rsM8muM4Ds1WkzTNiOOIIAwpojn9/gpJEmM7qmTAcmzVW6QsCBvhM6+bZw40YJG6KQrVkt22FwhPGAaVkTbSgtS4ZueDCVgsKJMGqtDJUlZFgfXIX6XApEoHCUGeZxS5Kri2hIXj+jQbTZIkJkkiTaWxyIuFMa5PPMtSWui+6wOQJDFnpyeqs6VxPlCqCZYONOJ4XqXlTYT5cU5UPZUspaIQqaJvxadV9UgW00nMVAd0gieDLMu21eZR3wzRkog1ZNgg9WbBgXIsHcetGv0tnABryakxv1OFTea3Yul711UNt0zAIgx68hQjViEI+rXG4BkDLITAcW1c16648aY413VdbMfSiJrWtLZtPN/Htiyt4LMo9lUIjc1kMsH3AnYfPebOnbtIaXSnRRVsOk5QQyuXj6cZ/zqKXA80Fu9ZvFfW0rcLVHt5npig0xikRqvJpcuXCcMG9+7dYzQZc3h0RLe/Stho0O502di+gOP57B0dMs9yvvz5z1PmKd/95p9xuPsQ8pTpfIznuTTCBpZlE8UxaZYhhUV3dRU/CHA0h9O2Hda2Gjh+yHQ4RBYFs+mMVrOFY9kk0zlf/+P/wBd/8ed57hPPMx7ETEdTuq0246GH63jM5hEffPABn/3sZ1lfX+dHP/oRb7zxBn7gc/XaVR7v7f10QUbtO6WiZjZrTWksz4lInBtpWAQAquhaVAGwbRtQZPG80Jkzs9FS1lPr9c98esBtkLAFhLDIlghAVrQmUa1rk+VaZFZMEPNkgPPEUQM/1P8Fdc38ilclVL8jWQug6tcslqG/BViAFpI455zUne46ndMAHWrNOrieR6fd5vr16wRBiOd5dNoNeu0WKyt9XNetlKsajZBmt01/pY/rOtU+oXpvWHzqlVcVYpirDbooF7QUHFuBJpYg0xufEBZpmvLOWz/h3bff5e7de9y7d5fRaKS6eccxpTBOhqjmgnm+xq5WmZFS6tcpMRDHEiogcgRvfP51fuu3/i5rqx0ePbrP7u5D1uYr7OxsY2Hxhc9/idkkosgLTg7H/MwX3gAp2X34kPk8JZkJGo0Wx6cnyh4Jj/u3H9JqrXFh5wJCSB7ev4vnB8RRytHRCdev36TZX6HbX8V1Hd2hHRqNprJHloXruUvBnmUt5I4dx6HUlOO8KDg5PmJjY52vfOWLJMlnqiLe5z7xCQLf5/DwiEcP9wHVS6DZbLK6uqo6OReZkh5tNCoaoOlJIZG6dkR1b7dsm9PTI6bTEYEfcHZ6xnQ6ZTIeU1LyhS98lrPBEaPxHMd2qNNB6tmNZw2E/3MeVWbfVmwEg2oLW0n6nwfwTK+DpwUCruOAXGTdzu9LdWESc6jPWQQy9XPV/637Fov3GjGKjHfefYeXX3oN3wtVcbSAZjPg9PSU8XhCkqTM55FyjrsdTgenGBs3GAz0Hqma8n3mU6+QF4KDg2MOdg/J8pg4zkniGNf26Pf6xFlCd63P1pXn8FurTOYJjx8+AOD6jRtsbG1zMhhwdnZG17e485PblEWCECWqTsoGLBAZCzGERaBhWYb9gEGJloI3IRRTJkkSZgdjbBuyPCWLM9CNYuvghKLqF0hZVIB1r9fDqlGJHMfh8uXLtNptXMeh0WwS+D62p3oNdTodrly5wsWLF/F9HyklfhDih2EFBiIMTUkJJmR5XtVZSCmJo7iSRS8LBdamiaJMpmVBIwxpNJtVCUKcxDiFCkiarSZZnhM2Gti2TaYVpoajEcKyCBsNTJVtFKu6wUWD4gLm80os5eOOZw40jHpLlqldyzbytLVdTAhLF1MumiLV+wwotScTZCx0hxXCpzYKKUsl1yUWi9IUkhtHoOI6S6XWIVCqLZYQtFoNZlNJNItIohjPCxQN4txiWxgtC9vxVHfuUjKPY2bJCMf18H0PS6JkQG3BdDohimO9r6tO5x/qRC2xcRZOgRB6o4ZqA6iuR4JAIeJm09f+ufoYTTsuS8ONVfef1mV2JUtdtmVRp1nV09AL2lTdfhknRgqTJq85G2X5BKXE0j0AKsdZT81F0bj+XP1V3Wet3kQtckfJuJkCYO0gmWsw6JzjOHiuq77XXGZbZzQkUmeoVEA7Go1ZW1tXWYLx42pMbBtUUXn9IdVpJE8WttqWyoDYxsktigqpsCwH23b0XBQUciGxZ77qn1d9b5Bz2+bi5SuEzTZJWpAmBY92H2F7gmbDpxV4bKz26HWbDKYTDo9O+fRrn6IdhLz1vW+xe/99kDmzeEqz02N9fYPxaMh0NGIyGSHLgiyOmEcxzVYLS1gEvk+mC43j+RxZFLRaLWVo5zParTbCEkTzKd/7s//AV37+l/jEi7f49re+Q5yX7D9+RJbNWdvcZPfRITdvTLl08Trf+973+NSnJCsrGwzHY8Jmg/lsVs1/NY/Lat6fR8UN7UzoireqVkqCkBJbCHLdkE1JohoVEUfbGh0UKB1o9WQthzw39DZrsQZrgIeUSphAVDP4XMBQ0fSWFXWERpmqWVSCU1gUFuS6/kBKrS4vUHNDnkMoLSqbotT00GtIZxctA9BogWVhYQmXsgRbSCzHLEh1pUrSWvHCTVM+21EghZmnWVZS5GXV6ElRE9VzKc2zMgCGWMQpQosx2I6NY1u0Wi2ef+EFvvzlL3H12hWCIKDT6dDtdrXNkCqrUi6oBCZbWRQF48mYg8NDDg726WhkL/B9ur0eg/EIz/UoypI4isjzQu9DNhLV+8jzfMqy0CjrjLIsWd9c4dYnfrniM8/nc05PT7l37x67j3c5PDxkMpkwnc4Yj8ekSUKWqz4jBnXsdDr4QUASx5R5xsWtDT7/hTfo9Zq4nsWLLz7HPJoQTc/wAof+Sh8kHB+esLqyyeP7B/zMG18FoSgJe/tD8jTl0sXn+OFbbzGeJXgBnJ0pusnm5jbb2y0oLXIJZ4MRvteg2+tjWVM2thzCZgPXC7FsDykF7U5fq92oue84Kms9n88JPKWYs3v/IZF2CJJEdTJX95yyubVJNJmyv7/PeDzB8zzmsxn/0z/7f9Dtdnn1lde4f/sOOzsX6K6tEbgu88kEu6UoW2fHStJ0fX2dW7ducXRwUNExkiTle9/7Lmtra9y7e49ur8tsNmM6mdHr9atMvRDQa/f4lb/y1/gX//JfM5lGar5ZkMkcHAUumGDzL/Kh1o72eYz0rwkeUEGq67qqUapjE8c5WZ4q6yGUbwBgiRLP83jjjc9x//4jHu3u6TWod1G9nZfiSTGdyqZoZc7z4JZKuC64/Qt2gJEHV/tgnua88/aPuXHjBlEUkyQpfuCztbXNdDqpVKXiOMb1PNbXN6oi5JOTk6o3UNFrc3I2ZTAY8cH7txmOJuR5SZ4VpIUkLQrCRodr1y6wtrlNKVyOz87Y390nCBtcvn6T/soKJ2cnjM6Oadkld99/myRSe8oimJKAprvXAox68GZrzEVKqfcSI3+u30vG3v4uqg+PpShSeYmDAmMdxyH0Axphg36/T1bktLsdOp0Oruvy1a9+lfF4zMOHD+l0OqysrLCxsYGUSjI2CAL1vGy7UvyzLIvJbM5Mt4TodLo4k4kCB6Wk0Wjg2DZJmpJnqoaw2WySZ5lmaSiRkUxnkIwok/AFeZZVmSUTHLTb7SdqPEw/DN/3sSyLzc1NkiSpKPeZ/pw6FdCoND6raMMzBxpCqEi3/nDrJ6lzwJbVTOp82AUqtsyfW3yGmRwmIjVomVUVAqrCM6mXtbDU38pCqeo0dFGLZdkEgYdtOcRxtMShrqdi8zwnK3JCz8WzPRw/IM0yilISpxkOEEcRUhaqg2WhioyN9OKHBRpPAcWrmzVOpqzdu3EkTBrv4w5D1THjVVZOlaUrLGXNgC2oAYsxOJ+KNQgHOohb/LxEfREL91x9Zr2wTVbF+dReU32v3yylVFrqOpgQQnH/8qyoFL2EWPDxDZrwREZA1Mazdr46on12Nliig5VlqehnNWlaE9CdR4yWnEGxoFyY+asoH8qBE1rhfuneefokqDYFHahL4PKVKwRhg/29ffK8ZHg6oNkIoSy5/ZP3iJKcrYsXGZwd0+u0uLRzgYPde7zz4x9SFjnz+ZxOr8/29kVs2+Lk5JjhaEiRZwjAcXPmsxlh2KCUJVFWkMQxWZoq9FEqnu329jZpmjKZTuh2u3i2w+nxIW/94E0+/fkvc/HSBR7e+YAonpNEU1bWN0nTnHv3HvDpT3+aMGzy4P4jPvH8LVqnbS5dvsR7775rnn51/0/NGum5Z4JSMzeMmposVEZT2RHVn0RYCj2kLLCEkuHzfZdGM6Tf67Bz8RIHewPu3LmnKXNaKrdmA+rXYwIMg3CbTKhlWQgt0lAFzHUPvLq3AmkVSOEiUNK2ghJHlFhSIKW7QJt1vZWNmvOqd4EKPi0WKLuwChxX6BR7k9APcW2fMGzQ67ZotVrYjq2okbajFbVcPF8BMkEY0Gq2CMOQfr+P7wecnoy4f/8B9x/c5969e+zv7TEYDEmzlExLsyrnaNH13nFsHFchbFeuXOVzb3yOz7/xBhcuXMD1XKI4qjIOZZlXqf2yLHFsW1FqdD2GZVn4gU+n2+HSpUtIKYmiiDRNGY/HZFnG/sEBo9EYUIIhykkzdEmr2kTNM/J9X1GpiozTs2Nc1+Xs7IwgCLh85SI3bl7DZFOB6r1mgzZSlGVZVh3o8zynSFNkHnH50g55kTKfT/nDP/hDvvyVL1PInPFozurqJlevXOH+3XuUuc3wbMb62g7D8RjLsvjEcy/jBwHf/96b7O2fcus5iLOSy9du0Wy2kSW0Wm2ajRZSOPRXp7RaLWazOY1WH4B2u4PtN7AdT+95hSJzFQqky1KlKuPq7sGnxyecnZwwHAyZTCakuqlmlqSURUEaKxnkXqdHq9EiCBRi/cB9yOH+IX94+Af8+Mfv0O/32dnZ4dGjR6qGzPexbYu1tVU2Nzc5OTomiVRT28ePFaDzxS9+kX63x/HhEVevXGEwGBD6AaPBiDzLCIKA8WhEu90miWPW19b5zOuf4k+//g2F1FsuEkEhS2SZayf82TT7/3MdS/tp7XvFYlC9Ggx1u8rSlKUWBFBrzhLgOi6ff+OzvPjC82xubXPye79PNIvQSKQG9Bb7YF38xdDa6scykMPSnrnsiykgxmRFsizlgw/e5/LlyziuzXQ6UxnKTpdWq81sNtPqUvET5zcZndF4zN7BkVL+TJRzrAADl6DdYXNjg9XVdRzXYzJPODk9YjyZsrqyyoWdS/hhyMHBPtFkiCNTHtz+Ccl8Wqth0+MuFoDeEl3q/DPS92/ASQVgCtbWlaxvEAS0Wi2uXbvG9vY2w8GAXrtDs9GswAdPMy8KJF6g1ArLsqTf7xM2G3R63YruDuC5Hl7g16TlXcJGE6FBCCGElidPmc1mVS8OIQTDwYAgCIg0vQkkJ8fHFSOk3+/jOw4FKjg1xeVSyioYMAGgo+lPy36g8rGn0ymWpUSYjA03KoyO7lk1Ho+rzwjDcEkS/uOOZw40zI2bKNhU3ZsiPLOJm43E/Fyf9CYYMTdibthMDuNMWrUo3QyQia7Q3LZWq8np8Sm+52DZSoFFWBau6xAEHo1GSFGY9Le1xP1cmngCykLRaTzXY2V1VanqxAnRfE6Rpniuo7MHgiSNdfblowMNlmyOWPp9/cdnfVBKCYTqnAa9RFNLVtdWuXnzJsfHR9y//0DzCJUTVqGl0jhRAiFqNTGyxPjc1X0ZSoFJw+u/yVqgtugsXOW0lvpcLDJeJoBaNr5m7OqBa/33dTrYedTGUD3qhrIexJrXmgVkHBHP87AcxY2sS6R+/PH0Wgv9p/+owwRuYRDSarbIcxUwDM4GZFlGt9NmOBxycnLK2XDK1Rs3GY0nvP6Zz5KlE3781pskcUSWZARBi63NS/R6Pc7OTphMplVNhmM7WLaL4/t4QUDo+wgEjazBcDDkbDCglHklzrC5ucne/j7z+ZxWq4lje9y9e5drN1/g2pXLHDy6x8bWFnu7DxU9wrZ5+PAhzz33HKurq9y/f58XXnpeq5Js8e4771aBnJlHC2f9o8bHjDtIKSix1TxVxT5YdonjCJotnwvb61y6tMPOhW1W11ZZWe0T+D7j8YT/+z/53aV5VWh5P4OqmuM8NaOurnQeoHiSxqCBC1Ei7QKBi4WNLUqsMqblSUXRlMrkOrajnPBCkGYZjZ5A2DFFLrVDrYID1/UJW13+1q/9hkrDN9u02m2UHbQI/QBLiAqMOT4+ZjKZ4LouWZ7iui6NRkPxjjVYk2UZWxe2+eTrr6jNJU05Pjpi/+CAd999l9FkrOiJekNZXVnBdhzCMKDRUFz8fq9H2Gjo8VNZm0ajUa1Vowrmum7lXJmN1Tj1sOAtG9TNIGhJkpAXZVWoaNZ1pWgIlbS6+QxTn2YJWW30vV6vev/JyQmDwYD5fM7a2hqtVqviR/u+X32eeb0BueazCUk0USo6wGg0oLvykKxwuXT5OhcvP0cjCLFtm05rhpCSz37mZ0mzlMePT3juE89hYdMIOnzqU59jOkm4ceMlNjY2FaAjBa7jaYBOMo8iVte3sG2H0STi/ffvkKYpn/3MZ/HsgiyNKMuiqi2az+dMpxPiRBXk9ns9NtbWKPOc1ZVVNjc2WVtbq4Abs5+ura3pQvSFmtjFS5d46eWXmU2nfO9736Pb7XF0dMz6+hrXr1/Dth2uXbvGd7/7bTqdDtevX+fOnTsMBgOazSbXrl3DsixGo1ElfTmbzcjznNFohOPY7O091uvK5vT0FNd12dvbo9HwuH5th/sPH1HGJZ5rk+WCkhJpWSz6gvyXf9RtjdrJFVDquTY3rl3l2tUrhIHP5voaVy9d5PbtO2Q6q/O0EagohTwpf/+E/8Fyz6dlm7YMQBZFwb1791jf2KDX6zMaqToNU4+zsrKiisGTRDf7TMmynCLR12pZjOYJnufjeCHNIKTT6dFqtXD8EMt2mSYJo6MzJtMZfhBy9cYNVnorxFHEwd4jiiwmj8c8fHCbPJ1XvsbTxrROj3/CL9NjfX5MhBD82q/9Oi+++AJCCF2joXzZIs+ZTqasra0RBAFxHDOdTsnijGaryXg8ptFoLBVXGxtlWRZBEDCdTgEIw1ADnMrXieNYd2GPCIKgom4Zn9rsT0oW1/SEWvTkyLKM8XhMHCvmThAENBqNKgGgfq/eb74vy5LhcEgQBEip7GQURbiuWwEtVbBoqYz1fD6v6ueMsmylAvuMx09Vo2HbNkmS0Gw2l5y+84WxJoqyNbJifm8iq3rEaTaP+uZeyBLXFtVAG237JE0oJUymExVQhB6uY1OWuZbdsggboeKxFRm2bQqKVT2FjV0h0uZ6XdfFtlRaLctSiiyj2++rZiuzqZ4witPruja2YxFFsw9fyFBnk1XH4jVPQ3JraAPi6YsEiZQ5lq26XQdBwKXLl3nuuee4eesGm9tbaqLqyXv//n2++93vcXx4ooqDpETRdRfjXs9I2LaJbvWzolYsbWIaUEinDixMZ2TDI1V0DypaDJWjuBw4VOfXvMl6EFEvyKyP7VPRZ40UPW0s607iIrumqVU6o3Ee+fmww2RrTJ3RknCBXBTsPe06LGsxBk/dJCW0O23iJOaDDz5AlsohsrHxvZBRMUMIxZFOo4jQsbmwscK9ux+wt3sfyoKyKNnc3KbbW0XKnMHZGbZts7K6rorehcB1PZ578QVu3rxJp9PBsx2SJOHxo0d84+tf5/2fvKcULjyPTrdLFMcKDQ4DHMdlnmb86K0f8pWvfpVLF3fIognb21uMRmMmkwlRFDGZTGi32zx48KBS02k0GrrwXmUkPvaorR0TWJtgQwgLx3VAKO6360p+9kuf46/81a/Ravs0Gj55XlSN6/I854+/9x12Hz6i3kW3EkA4t9nUn9vTnufT1mU9AwtQShtpuVjSwhYpLnNeeL7Pb/76V2m2JKVUBem+71eB9enpKZ1+hzTPGQ7GlIVFt7OKLG2uXLlJb+UVdi6+QjSPsV1fdVW2hWpSWqY4tsNkNuf4+AgpYWVlpWrIqBqI6myyXp++baPUtXLKUpAXCStrfTa213n+hedwPFUfNZ1OGY1GBFpyO0liHGdRXDocntFoNPB9XzWK8vyqAVQYqkJBFSifkNUCO7OuTabSoG9BENTqI0qazSaBduBbrRbdbrdyAObzOXt7e4r6F8ckScJkMqHX6yrVOq2gEsdxFTxcuHCB7e3tav0a59rYB9WoiwqUMIfjeTTbm5imVlsXr/Grf/OSCorSFM9xsC1LBfRCBXRl7lDkBXfuPOKFF16j3+8jy5Lb77/Lo4cHzGcpntckihNOjk+Joph2q6MchULw7/7Vv0YIwWc/+1mCRotvfuuPCJtt8jxDaiTz9PSU4+Njbt26pQMzxcOOpjMcBO12h7kGWkxD3fl8zvr6uhLMSFMdnLncvXtXBUqdDnmes7u7y40bN5BScu3aVTzP480336TdbiNlzi/8ws/z8OEDvv2db4GUjCdj1lbXKqGUx7u7zGYzHMeh3W4zm8+J5nPyvCDLco3Sxvi+T5qqRqJlmrGzs0Gv1+Hd9z5gMo0pC6nGsxRP2P768VSw7y/QcR5kW8qoovYQ17H55KuvcuP6NcqiYDg4Yzab88ZnXudof5/JdEYhFY0TvSedz/LX98nzQN5i/5VLr1n8TbAQVlkez8ODA2aziM3NDbIsI4rmpGmC57m4fkCj3aG3sopl647ypeJ/l5aNcFx8P9A2164c7eE0YjQ5Jk1TGs0mV69dp9NpIyWcHh+SRHMsCoYnB5wc7EKRYFGAeDJjUx/X8z5O9QxYtvNmD7hy9Sqf+9xnK2DFZDlNkNBstWg0m3ieSxTHIASNZhPXdel0u5Vznud55fgbxD+KoiqTMZvNtD3qUZbK5vX7fbrdbsWwMI69yagaG6Uyujaj0agqIDcZXiWIoQK70WjEdDqtABghVE+dZlPVcZ0PemAhiiSlXOpsfnJyUtkNs7cbqrOh3DYajWea/z8FdUptDK1Wa2mRm1SMmcRLzWpqi8kMWL043GQpjMNXBSWSpRta6Lwrak6/3+W/+nu/yeBsgCxKvv3t7/De2+9SlCWNRlj14FCymAVZni5keVlE/4Yv3O/2VCW9lKRpzPDsjPFkSlnkCGmccUUUV4FPVjVEelqg8ZQ4Y+lvPJU2oou35LIzvTAWgm6vw87ODq+88go3b95kdXVVFwGqE2ZZThB6XLy0zcbmKi+/8iLzaczhwRGPHj7ibHDGbDajyAvF081SslQFeWmWKrk0dPFlqRZhUS50ndUztpDWueZzAq3CBUrX/2kZnoW6WGXwpGqAWL/P8xtIPTA0P5vA07EtinIRoNTH8rzj+DQRgDoNqv7ap2VUpFRc+bpiTv095vunOaoKkX/KZqPpKY1GgziKmc6V2stkOsHzAxzH44WXXmaeJly5ep2yhI31DchzHt67R5FlZElEu92l3++BkOzv7TEaDWk2m0p1Kgy5sHORL3zhC6xsrirKXqn6zbSkZG19nU+8+CJ//If/ju98+zsUZUmSpqysrTIaq14enVYH14aDx48YnZ2yc3GHhw/u4QY+LaMAl+ecnZ1x7ZqipxweHrG+uYLruuqexpPlVN4TY6THEy0PLBc0JlPcp9TMClzPZqXb5u/8rV/hM595hTBwKFH1JrIosCTYtovveHzqtU/yh3/4feJkWQ7aIDrn58rTgo96UPm0n5cPByFdXCuh5U752s+9zF/75VdotxLKMqGUSq1NWKp5Z1mWdJod0rLk+GyIEDGrK2tE0Yg8g6PDe4zGFr3+NnlmkUURQbNBs91ACPBsDyFV1rLRauE4Dp1eV9+nXdm6NE0rqpbpQ+NopSc/DKpiwbPhgOFwiOM4NZqMUm1qtVoIoRT8lKNk8ejRLjs7O0RRirDmPHz4kNXV1WqcHcdRgVRNWcVkr834GVrU+S6zw9G4ykaaDIVxAmzbZnt7u1qjZtOVUjXNMo+xrrpj7E9d9tbsV2Z/M3Y4SRKN9quM4HQaVdc6m6muuupnH1mURFGK65Rc2L7Iv/n9f81Kf4U4iXnxhVf40VvvsL29zWg04vvf/z6tVo80ybhz5y7zmRItmc8ivv3N73D12jUajZBrV69x7949/viP/lhlCq5e4+7tO5RFTrPZ4OjggDRNabfbfPub39S0HMU22FzfoEgzLl+6RJHnPH78WGWkGg1msxmbm5vs7OwwGAx4++232drarsbq7bffrjJTWZbx0ksv8p3vfEejm00++cnXkFLy1ls/ZP9gn/l8hmVZum9HVD3zk9NjsixjZWWF4Wiga30UJafdbjEajfT68ijLgjD0sSyPoshBCl579WU+uH2P/cNjhOUg0xJpWxXd7b/0wwQAUkqQJa5j8dzNG9y8cR0hwHUssiTBpiR0bT712sv86de/pR14S9WMWU/aocqP4EnfpALcasO3bMM0KPs0MMWymE7HzGYT1tfXCQKf6XRKUWTM4wTbC5dUyarDE5R5RpIrHzFNiipz5/gBG5tbtJoKrMizlLOTI5IoxrUgjyYcPH5APBtjiUJltlhmR9T390WN3vLfjCBC/TC2oNfr8Qs///M6EFIZV+OTzmYz+isrAMRZwmg6RiDorfZVRtayqkyA7/tMJkpNbXV1VTdhVYBw3ZdV2cQFuGJ8UGMTTXah2+0S6qJw060bJO12u7JTBvRXtpQqcDCUJrMWL1++zGQyqQA43/creqiZhybbbAKO+XxOt9ulLEviOK4ClTr1z9zjsxw/RcM+9WBWVlaQUjIajZYCB4NU1VPb55vVmQlgNg/zQM+rKtSpWfVJ22m36fZ7HBwe0m636He7CAFXrlwk+qu/yP37u1y+co1/+2//HUWZUxQlZaGKs0xxqfk8c+48z3Fth7/7G79JlMT80R/9e4bjMVmaqmZxFf3HFLZbVerZBBp/HodKoaqAwqD9tmWzurrKxYsXeeml57h8dYdmQ/VPUNSLHCkLsARFucgUFWVJlqYqA1Tk3Lx5g+eeu0UURVXQZgonx+MxZ2dnFSdPoXYZ0SRmojl5p6dnmg+dMp3OloykOad61iWSukO/UKeRKMaL4RC6rkucxNV7zwcZZqH4vl9t+IrHmFT3kGU5pkjLzNEPyxzUi44NCmDmYF2S8LyjaT5P1Az7R1Fozh9SUjnKT9yfHpmVlZUKFSmKgjiKabVa+I0Gq9ubfOmVV8nznO9957u89uqrzCYTdh/souqdJb1eW0lk7u8xPD1S6j+uQpouXb7GV3/uLymDZBXkWarHSjUjUpRDwV/+K3+FdqfDW2+9hbRUjU6z0+bs9JTAb+C4DvF0ysP7d3n5lVcJmk0y/RyNnPJgMODatWs0Gg1OT0+5cu0izWaTnYsXefedd5Z4xXWn/dxKwGQwzMxRzwCkzMEquXhxm//uv/2HXLqwAWWKZ9tESU6Rl1h4TEczVMMkSa+1zqWLl7l998FSrZH5+ml0+j8sg7lMg8hxrZTNFcGv/82f5fOf2cEWY6TOxlpOADJH5gslvCSKKK2Q2UTg2l3yzEOWNtPJlFYDpvMDvvud/0B/5SKjccrO5Stc8HcoyJG2wHM8pRyin0EUxRXSJKVUGd5SKQO52pnPcwUwRFHMbD5jd3eXnZ2LdHs9NjY2sCy70ndfgEOSJE5wXBfP87GEg7Xu0O2uaKpWxvPPP1/ZfZMxfuNzn6sUiYzqWxAES5RYs+GazdXzPNY3NpGyBkCxzEk3NtyMv7FflrYJqvt6UgU1JmAx1AKzpxk6F0Cr1VJZgSiqACvDDy2Kgtl4ius57A3PtFKeRzxXDbfyNGNwNuCDD96n3WrxwZ3bJGnCV77yVU5PTzg6OubOnTvcvHmDe/fusLf3mDhOeOmlVyjygnYr4ORojzTLGI5GNBsNZJFzsPeYtbU1+p22AoKKnLDVZB7NEUjW11YVyhzH9PsrzCZT3nv3XWaTCd1Ol5s3b/Kd736X2XzOZDLRsqQTHjx4wHe/+z26XRWY/uzP/iwvvfRSlZGaTMYUZc7rn/4Ut2/f5uKlHQ4O9hgMBhwdH2HbFkWRM5vFNJshUaQclzAMef75T+hGZHHlWM3nc7yWj+8HlLJQP/suoJDfRhDg+q7i74cNLl68yPu3P+CtH71NiUOaLajX5+3If2nHIvC1CIOAF1/4BNeuXkXnK0iTmGg2w7UFk9EZVy5d5MHFXe492FOE6bLErvgDy0HF+TGp71eq14T11NeZ3z11/xSgMD3J0dEhCOXQtpot3NAjTlNs2yZKUkV9ty08zycMAsKwAShJe8/1sW0Xx1FNZ7MsI5rPmQ7PKPIUz7ERZcLjB/eJp0MoUnwhKZAUQCkcbBZArgEEP2z/rn9vMrqwAJv/xt/4G/zyL/8yo/EZti7Wr9//dDal1L5Ipm3XdD5jY2OD4WBQ7YGGdtRsNgnDEKDqK2JsnMkW+H5QZVANrcncRxRFOI6jwMc4ZjKZYFnmulT21mTDjZS/yp74lT/eaDQqe2ZZFnt7e0vUJ0MdNoGD4zgqc9NsIqWsak6MX2b8dfMlhKJrNrRa1bMczxxomPqKs7MzYCFraCax4ZkZpy/P86WiYVik7uoqByZCMkZfoY0hq/1VTk5Oqr8Z+a/T01PFNdYISZqm2JbFtevXeOnlV8lzVVS1vr7O2z9+m93dx1gWOqMhliRUjcNpO3B8fMh/+9u/zS987Wv8k3/yT/mjP/5j8qJUaTq5uI9SLpSiliax2ZD0YqReCmyQ0prTrd+JMiyiWgiu67G2tsbLL7/ErZu3WFtbY3t7m0ImnA2OtUxjVI2Xcig94kQV42VpRpqlFHnO6dkZ6Txnc3MbAQw1bzbP8yrSzrIM13Xp9XoVnzqOY4pOgXv1KgCZDg6iKFKcwjjCddQ4IgSJ3uBt2yZsBgq5bDYJwpDV1VU6nTau57O+scGbb77JP/2n/5TPfvaz5HnOt771rWoym/nheR69XpeVlVVVkOx5SCk5Ojri/v37+L7P6elpRdcyz8AEE09DoOtfrmPTajYRCFzHxRSof9Qh0RkIuSz7CSAtWb3qqe88F2As0HsVMK6vrzPRqVKVMlVrqhDQ7HTwAp/J2QwpoNlu8PDeI+J5RJEVhEFAWRRMpyPOBgPSOKYR9nTRXoef+eLP0Gy2tBpKibAt1RBICKRQUtF5mjKP5nzu829wcnrCYDBEyoJur8vZ6RlFUeI6arM52N/ntU++xsrqKg8fPKDr+1WX0MFgUM2t09NTLMvGdlw6nc7ivs+N83JgaBRawNRZ118uKSjylCBwOTs7ZXx2TDyfEkczhsMRaZozGU85OTkjjhPKQgk6HI6mGOqbsET1DD/smZ/PbJy/znoyXgqlUyUE2Ba4ds6NKy3+q1//ItcvO1jyBFFK8sxGODa5VJuNmbfT2ZSykKSlagQ1Gp5RygFh0CTNIo6Od9neeYnh8Jif+eLP0eluU+BQCokUJZa0KLKSLCvwvJCVFdWRdjgaM51OAKo0+2w2045mqwJ41EaXsLa2iW0r2WrbcrEdhyzNsS2BHwSVvaatFAdBBQC9nhZI0LLAJvNgMgVlWZLEMWsrqwhLVLUpxvmvaAcaNDDBtjRZ76IgLwp8z2OuZW/zPMf1FC031cppEu0MpBnTyZiyLCp7lmUZYRAy0+i74zhVFg5UcGEQP8/z2Nvbw/d9oihiZWUFgWA6muI4Fp7vImVOnMzY23tMs9VCSqGuIy+IZjOOj/fxvB2iaMZsHvP9779Jp9NhMBjQbitkcD6b0G2FrPY6jM6OWOmvcuHKRR4+fMTR2QnD8ZjD/cc0m01arTZpPOdkPAYBRVlydnaqbZ4aZ0WDCplP5wppznNmkymf++xnOdjbZ2Nzk8lkwsnJCb/3e7/Hq6++yrvvvksYhty8eYNms8XR0SFSwvb2FkWh1Klm8wmDwRlZlvKtb32DNE01JU+oOsg8r1R3TGfo8XistPe1k5WlWSWekmXqefX7PYRQzc263Q5mz4zjFM/3VNPcPOHWzWusrfX4zps/Zm/vCMtaFNUaUQilSb1YmE+u0v/8R31fqmdKO50Ob3zudTqtJlE0pywcAs/DcR16vS7D0zMKWzIcH9Jpt3E9lzIrqz5V53Gap2Vpl7j0Un7kgCzXRSrQx+SZ1f5aqo1ASrIs5fTsFMePWFnbotfvUeQFSZqQxAlpmiCnFq12G8dxAUFZZApYkZI8zZESXNtCZjHRdMzDo0Oi+QxPplhlhpBGZEggsSmVxIa5mUp5qbo2qPaOpTlgWQhpOtcru9TptLn13E0GwzOyLGY0GlUsEdd1FGhuWyTaR5pNZzqA8jg5OcF1FpLcBmwfDoZkWa6yIf2eduRdPM+tajyEsDg9Pat8Z8dR5zJgvWVZ1VqybbuqnVRNsZV9HI/HVV2U7/skSaJpjSoJMJvNlNyutnfne7uYOWFAHgP01Os7Go0G0+l00bVc7xemZ45RuHqW46eQt13w0s/TVGQJRa66M6rXlDi2h8CqOPRGuhYs8tzIrxYUhUSIRWZDCCURenp6Wt2sKZxJ07Sq2bAsS51TWGR5ge16FBScDk5odxt84Yuf4fXPvMpkMubg4ICzwRnXrl2teGZA1eBEyoyT4xP+X//8n/HLf/VX+a3/5d/lW9/5BvN5TG5QcgQLmVobXYGurZrKRkihKR+SyqEzmQrbtrGkkr+zHQfXc3FsG9tWXGphCVZ7XS5f3GZzY5NuVzlnp8eHRLMxWZkzjRRSO51NkTr6DcKQZhhiWaog3oyT7dg0gxYtX5DGEe1Oh2tXLusUtqDb7dJotqrunkBV6GNZFp5lE0dKZStJEiL9/Xg8ZjKZMp/Paym+ANu2WVtfI2gFtNttpXrj+RUvMk0y0ihjcHLM9sY6v/lrf4c0zbj7/vuErQa25oSvrK7qAs0A13FVqhjFyQ8bAZ7vEDZ83IlNWmQU+SIbYSL/ukE3WQvjKNm2hW9b9JoNXGHjYJOTo/ukY1qo1ec36D4hEpVpqkXxQiirVpbZIqtzrm7kadQcFahYSMsmSjNyCVIKonmCLFRnY992CYSFj6CMY9qNEIRkNDiBIqMsc3y/TZblnJ6eEc1mWpJ2RhiGvPTic6yutMDKoCxxLAspLaQtyMqSApW2dxxbU+XgtU9+kj/4gz/AdX1Fr3E8kmROEChJ4fFENfRaXe3z8O4dKByyNMO2bOZRRFbkuIHPwfEhWSkohU2U5hSlynBhOrSL5TFW4wGgAIRFXYagLLWTXwo8y+fBvcf8X/7P/yOUJbawKXKF1tu2TaPRoNls0e2us7m5get6BN2Q3f3H/Mmf/ClpFmP5gaZhSSwWma56AHme5lb/2UIiREEmfUrpY9vgiYimF/GF17f5lb/yAq1mRhHNKGSmuroKicxzyiJHWiUFBUmWM55FJElJmuQMBynzeU6cpLhuSdhogddElj1eevFTRPOSIMxxPAeBjW15iLLE9hYqTKZITwXpvaXiXyFs+v0VpFT1VbJUlIg8z6o5bVkWloBcU3RME03HsdSmLqBEzRnbUZuPLRXwE4QqGyCAspaF8GyXeJbgOja5SHFsm7LISdNEWVNbKbdFNbTOsiwm4wl5UTCbKRnaixcvkudKtCCxqFC76XRaOVRnZ2fV96oORa3HM6lePxyeURQF0+m02nDVZmszPBuyvr5Gr9dnb++xctjjOWEQ0O328DyX2XRKWRb02z3cHZuTU1Wnsr2+TZbn7D56hOP55KXk9dc/w3gyYX19jdlsRpYlZFmG79vYliAvJcPRgGgec+fOHba2tsmynAcPHwJqH+12O+R5ou0LTKZTXaDfYzabMRqNKsAJWXByfIgQFuPxiGazyXfe/A5f+MLP8MKLL+K4Lmsb6/zJn/wJ/bU+X/ulX6DVbDEbT5hORhwcHLC3t8crr7xCnuccHOwxiyakmlJhiZJmw2c+n9Jut3Eci0bYUnQnJJ2OosWt9PpkSc48i+ivrDCfKbQ3D3KEsPBcn+FwSLfdo5QlruOQxhmrq10QZSUFOp1OiGdj2o2An/vZL3D73gPeeutt5rIkyw0FsAQZo+RcrXNBxgLx/4tw1G2/67q0221eeP55GkFAGs9J45jpOCVLU/JC+RZJVpJmBSWq30+z1SbTbBJTdwZPAmVPCzZs20bYizExjAOTcUcKpMz05wqKolY0Li0oLSwcDbqpndIRILOc0/1HDI/2CENtf8OGylyEAbGmFNm2AzpATLOUIk6IphMdmEb6OgpsCVIIChwQRlnTwhZgSRBigawXRX5u/6hQYUw2XI1BiYWl701iO/Dpz7zKc89dZjwZUxQ5nU6b+XzKgwcP6Ha79Hp9jdw3sVyL0A9BwHQ8ZXNzk0LvwUJAFMWMhlNc18f3BbbtkWW57jlTIqUCBYpCAgVhGFaCJEKIKlgwzv3m5maV/TX+zHweM5/P2drawvNs+v1VwjCsgvv5fM5MS8mvr6+T5zmDwaAKEAywb4IEtYadKqMSRRHtthKgMdcDVE1RTcZkPB4T+DojnS4aYH/U8VNnNM5/lYUq/DFIlkIaqB5yHWU2CJdJoZsFUKcwmNSN1PKrZqDrfPq6QpWKCF0OD4/or/Tor/QYT0ZIJGHDp9e/yMbmehUJ1rloQghdXAcbaxvM5zH/4nd+h1df+RSf/tSn+cY3vqmiX2kCBptSSrJCFQAiRcX1N86s53kqyhOq/0az0aDX6aroVFi4noflKefMcZ3q+osip9NskMUxZZEzHA6rZkd57lLIkoaWINzevlCpsTiOQ7MR0AhDpQTR7+PVuusKIVS6LQiWOoGrsVbGq/5MDNXAsyxWVvoqqteLVTXQc/T457iOSykl0XyOBGzXqTT9TXrOFIUicuIkYWV1lSAMuXXrFusbG9y5e4cvf/UrtLsd/vE//seMx+PqunOtBpamKd1uVzcKFJXRVCngRX0QUGXITKRen3NCKFWsZsOn3Wzie42qP0ZFpSmfztGvF66brF0d4VZgvQkynlbMvzgWxk81IYuiiO7KCnGcMpso1NW2VENEIaHMc2a6a31ZlsxmU6hR1IaDIaPhUK0lqQxGnqVcv36NqvkKphGmRQkEnkeeW6qJWVFgCUEax+xsb+O7HrPZjHa7g2NbZEm8SJlqSklT87g/uH2bo6MjtncuUCbqXoRlMZ9HZEWJ43h0uz3tTC7uv8oBnUfcqgxQnUKln51wcByLdqvB5z/3ugqSLIdGqNSDXnrpRW7cvKk4xL6P7TjMZjMSmfDw4UN++MMfcDZQXVIdS/H5szzHssSSraoXT9Ypd9WzEwJZWKj+KSDEnNV+yV/9hdd541ObWByT5gptVSILNkIomlqe5xQSstxiOpcMhpK9/TGziWQ8SnC9ANcLaLV7rG9c5Qtf+CKXr75EktnagZxgOTG26xEEDYSm0oACGjzfq669Uk7R9sn3VeBvWTYWRsABhK0QrSzPVV2dY+NpdMtkmIp8odDm2AtRDSPPmCYJrmtXr/M8j8FQSTMWSUaRGnUpRUey7MWacxyXZrNJWeRMJ4kuGM7Y39tDWKrr9ODsFGRJo9HQFB2Yz2cMBgO63S7zeUQYBhUNSkluKslcKSXtdoc4jvA8l/lsSpYmOLZqcJekCdNJzEq/h23BZDxka3ODqNOulGD2Hj+iLEu63S5pmjIajYiiiJOTU5rtNtFc9flQPG0lF5mmOffvP+Dw8JCbN69X+vUnpyfkWUK3265sWZIkvPnmm+R5QYmtnRSHyWTMhQvbIBR1V0pJoxGSZYqWtL6+phHMKY1w0aHb81yGwyEHBwf82Z/9KXkpyfOCS5cu8rf/9t/i/Q9+wv7+kMHZGWmUMJ9HTKdTfN/nRz96C89zmUzGNFuB2iN10KMCG0udr9FkOplUwa0QgtlUOVuzqWI47D3eq+y5UbyRsiTVDorrujSbilqzv/+YXr+HZSkHstfrabqvw2Q65ZXnb2JTcO/+LqenQ+ZRgm0LigKthigpJR9ZC/af6zD3b5zK1dVVgiDg6PiY0+N9hdILrZ5pMvIoqlCJqGpaLVvJTJtWAx+2z3wYYFL/+/mfEYqKW8l5Cy25r532Rd2cAuyoAJoCy1LvnU+nTMeTKgiSlqDUmWrbtnSGWjdZLs3ehAaV1GfpXD+yAqcN0CsxNHallGkyWs/yALQgRlFg24IvffGL/PW//iskiQKzT+cD2u1QZ/huKjDGEvh+QFGUmp9SEvgBttVG1bJIcl0H3Ot1FZumhLOzE91kuMXx8UnF9Gk0GjiOw2QyqfzYOI4rdomph5NSMh6PK/83TdNKwW9nZ0fTGidVTZuUqlu4yd72er3qtk0ht6HBdjodiqKo6rBM0GvEN4xf7vt+VdQOVPVxcRzTbrcr4YzzdXUfdvxUxeD1jXc6nVYXC1Ta5EuUklI1VTLOreHHm26Y54MPcxSFKkBWBUKZSrNlmUa3odC0rE6nw9raGkdHR4RBQJHnPDo8IAxD1tfWmM/nnGiKTZooHm2r3VYqTKWs0K9es81oPGY4HHN6OuR3/9//R7a2tuk1O8ziGYZN7zg2a2vrtJpNJBA2g2ryGEdlOBzS63ZohB5potC7wPNpNEJc26HZadPsden2ugR+QKCzAZawaIYNPMdd0po3nGXHc5FigaYb1M9SqQxsW9VYmBoZE2Doga6assRRRFEWBEGI63jV5DaHMYbTqeLyWo5dC8pykIquZDkOSa6UB4RuBmbZRqHLwrYd0lTpQqviUo9mq00uS67dvMHh6Qnr21v8nd/8daK56t/Q7XaZTqdLgYPhLZoAzgR0vu8zj+JFQR0L3quZU/WCU5OJc12Pfr/PxsYq8zjXm5qiXpw3zPVAQzX2EUtjVDmf1keoSn3surLo9/vYrkscJdpwq0Dp6OiIu3fv8sUv/yxhs1HdVxwv7tsEVq7rLvHpPc8jDBUXtNQbQpHnFU0vzRWinKYZZVkQzSY6ILBYXVnh4YMHpElaYYIqE6Y2mjRNabRaSCST6ZQkS0l1kWYcxSAg10pnbk3hS9aablWb6Tnk7cPHSRiSIf1+n1/9G7/CpZ0t1lZXaQQNLNcFKZhHc/I8ZzKPyXJleKezCc1Gg7/0la/w//2df0lZSKRtYWGRl0o68Dx1r561rc8xtSHbWJaju0QXdNs2f/uvf4EXb3Uo5RApXO3cu+SaS21EFmazlOEwZj63mM99HjwYcXqSYDs+rt8mziy67hoXL3+KW7depN29SdBYI0CS5QWu51GUEst2MJKYpb4uz/d0sKyyV3qyquyFlOR6s3FdF0sqCk6apviehxRCa0oIBqenhGG4VMtgWZayw0VJFB0pTn2zidTzMUli8jQhjhNOTk5YX19jOp1h2xaBHxK4PlGkaqySNFa/D5TtMQWQRhJ3kf6fVmh9EATcvXsKSJIkRcqiUrx6/HhX0wtUcaKRiOx0OmRZqgPHkjzPSLNIiZfIgrxISVIVfHuew1tv/ZDNzc1KBtuotJg9q9PpcHi4XxWeP3r0gPFkygVX6dsrGlqEbQt6vS5HRydcvHiRMAx4++13sCzor/Sr/XMyGZGmKa1mRyOTIbNZBKXQtk71TpnP5zRbjap24ujoiH6/r503VdDaaDQocvD9oCrmH4/HVRPOf/E7v4OUqhD7jc9/jtu33ydJIkA19nIdFyEkvu/qTMmAXr+71PDLOD8GlBqNRtW+P5/PybKMyWRCq9UhTfJKUtPUc6r9qCQvchwd3EqZE0WqP4OrX7ugdgg6nS5xFLG+0mM+m3Hr+hW2N9aZzWM+uH2Xhw8fEaU2WWFAnr94QQYsfJ12u0273QbUmOV5DoVqaGmowGYfK8uSvJRazXu51lXZpI8/r/G5nlSeepL+bQCg+msWNrkEUa8i1+8VKjsqhNRglMo+GPqvyjprzke+sPu2AZOEytyVuoeICRykKKushD5hNTYqi1EuXf+HjfmS3UZdW6PR4Fd/9a9z/fotTk+PCQKfMGwihGqm6PtwdjZQtEkhgLLyWU9OTioVpzie4wceWZbRCDOkhNXVNebRpFLtg0U9yOPHjysGiXH+jZ0aDoeMRqOK7mRqL4wyn+lvZXpb9Hq9CkQytWTmOZteHEEQVOBGEARVQGFZSn7aULNc161qZ4UQbG1tMZ1O6ff7lWhDvSDccV3m2ic7Ozj4+EnITxloGKrRyckJ0+lU87MWlCJYbEp1OotZNMZRMtxZsykYJ9IMapZl+K6nu8GqzWc2m9FqtSigSp+3Wy2KPGd1ZYV2u83h4T5bm1sKIYoTJuMJpVY7cF2fyXhK6qYcHhxV+sHTyZS9+DHzaUSaZggsmmFIIwj59M+/zjydE0cRQRiw0l+h0+1gCYu8yCmFZH1jg52dHTzPqxRVHj64RzRTfD8LoVRA8pxm2MD2PXIbzYnzSFPVNMl1XTzHxxYOlqbnqHSVLmC3lN6+CRjqNS5FlgJKxaDValVR8Wg0otlRG1Ucx2AJguYikhWlWCr6MVryZVnSCFWvhTiJSTMlg2g7juZRK04hAlrtln6uqobBUDiUVFxDBwUhpVTvOz47JS1yZtEcx3Npd7u0O50lHqCZN+Zf3/c5ODhgfX0dz/N48cUX+eCDDxhNpti6OaSZe+Yw8waoOIigNtr19RXWNlaYz3M830VMqSEmi7Rzna+qEPVFUZQxHk8zducd5ycc1epvCrEvi5IiSatnbeiGjx8/Joojfv/3f5+f+4WfJ9DZIduxl7KBRsouSRKkUN1Ee70eSDUmSZZyfHxMmec09GekWaYED4TidxdZwkqvh2MJfM9lNBgQzyNFpzP3KBUlBsD3PCzbZm1znTTPqvvLNX8aKXUHWkXDsSyLUig6QD2jUd8Mzo+R+V19HPO8oNEIef4TzxH4NnE8Yzg4xXZ95dRrwymlpJAFQSMgCHwkgr/zt3+NP/zDP2E0nit6mm2okwv71Gq16PV6FWpt5nI9K4aQ2C5YQhL6Nr1Wg2/+2Q+5+47D6kqDzopCfILQ1yieUlqJIsl04nFyHHF2NtMF0g08bwXbt3A8QSltZonkG9/+IW++dYdWs8OlK9v88i//ZXZ2dpBCaBqTmtuFvmc1j1Tgn+tnlCQJaLQrzVQzt/F4jO8HONoumyLAShGlKEiThOFgwMOHD9na2q4cINu2SdKkKmo8PNgjLwq63S6j4RDXsbUzKinyDM9zSOKE08kUSggCn9OzU1qtBsPhuFI9SdOUVqtVoWcGMHFdh0Yz1A2+BGFDacJfWNtSzeqk1NnOjsqizWZEcVRlVQ4O9pWaVpZqRxqSNFGUsHLRNTxJYjrtjpbpdav5Y+7TOD/j8Zi9vT1d06B6k7iep64xyzk9O6ERNmg0QlrtJnfu3KUoVLCtCjRjLCFYXe2TpyllmXN6csp8FnPhwg7r6xvE8S6j8RjH9Wi3laRmGAb4gUdZBlWQY/qjpGnKxsaGorSOVSHpzs4Ou7u7rKysEMdxRT3OspQ0jfjxj36I5ytpeADbUnvp8fExcRJh2xbdboeyKCiKkl6vx9HRUVUrZ7oI53pvNcCGEe4AC9fJKzVK4xD1ej329x+TZrFWLgoqqpyR2TUKQQ1dmJrEKY7jYlPiWoKw2SSNIpqrfS7u/AwHh8f85PZ97j3cZarlX3XPy5+KNfVxINHHObXP8vmWpWSGjXSp+b0oFTXX7KPmfEJAKWRFXzx/HULYH3rddRbJ+X5lZt942j3VFaue/GwVyKn4od51vKwyAFKCsBTNtSxLLFFiCbnwESUIqWpLpLCRUlGZVDZD6u9NwPHkPmDuwWS5n7iH2o/nMzaG4nf9+nX+ze//Gx48eMDZ6SmdTocXXniJPJ/Qbnf0dTvMZypj5riKkh0GIY8e7WpJ2h5hqIDi0XCo7VjC2dkJqql0WWULPE8FI4a2b9bCwcFBlTkw9cKnp6c4jsOVK1eqgH4ymTAcDqtaOyEEe3t7dDodVldXFSOi2yXLMi5evMjp6SnNZrOilJpsh5HsNpmKMAyJY0XHMs1SjUjOfD6vAhTzOjP+eZ5X9Oduv//U+Xf++KkCDaAyHNvb2xrlLipN3fNqPMbpTNOURqOxQMbKhcxpvRrfOHD9Xp9Os6XrAcZ0+n267TZh2KDdbjOejOl2uorf6bp02h329veYjCd4jkOSpEwmE6Xgk8SkScLu7j67jx/zePcxruuysrLCjZs3WF1ZZX1lnY31TYWONho4juJPup6rSjFqDqe5N6E5thIqJRODNKytrWBRcHx0REur83S6Hcq8UHKxOmNh0Laq460lSLTzN5lM1MNFZXDSNCXR46g6/3oVx86xLZI44ujoiAsXLiinWk/yNEkJGw1d9K4L9XWUW+RF9dzMJlJ1e7fU8/OCQPUmyTKyTKHgZZ5VvOkoirAtm2arqQrEhU2aJriuV6EOURSjaCQOozNVsLy+tsZ8OlNjbFm4jQarq6vcvXt3iRZnNjajwhCGIb/927/N7/3e73FwdMxkMl3iD56fr2bOmuyGQn4tPM9C4imCjiUQFV3nyTlfZd5kWTnK9UOluZ/UNP+wo/43KVX6Nc8lYSNkNplVAY/neZWxMKiCY9uEQbgU5GxsbOA4DgcHB4RNxdlUKhkZPoHOLLhIAZ52LpphZ6lBoi1KXNfB8xzSRHWhlaX6nUFMTADkOI7m9udcunIF1/UYDYe6OFfx0C2oukLPZ0o/39LZFMTTe8U8beN7gnuMous83tsjnk/xPZdWs42TW4SNJrZtkcZpxX/NkpwszhmNJxweHtNstBiPppR5qpA2saAHGNtWL5Qz12Dslhp3SaNh8crLL7Pa6yNkgW9DFs+YzhOSwuHkVHXHLmWmZLItkKWNLHvY9jr9FYckzTR1MQerIJM5ooRc11HF6YzpfILfsOn0Vkjzgvd+/GM6rRarK4oi6Tgusd4kFI930XTJIMyu61a9JoqiwNf9LsxoR1FEs9ms7Nh4PKnu/97du1X6fjqdMplNqhS72UhNBtT33Kow+MEDRdvp9XoEfkiRFQbARIgGvV6XjY01HRAcqj5JSVzToHfI8oSjI6UbP5ko8KDf73NyckhRlJoiFbG1tUlZLugGBjjpdBXIYjtWBQQpLrgkDJWj3G43mc1muK7DhZ0tAj8gilWAHUcxfmC66yrFlnk0ZW9vl1brOTrdFqPxhMHglHa7w+bmBkVR6E08oNPpMBpNWVnp671RyYBLCRubm9gWbG1tcXR4QpbljEbjChQaHh7R73fJ85yNjTWiaI7rOZUWv2nC6Ps++/v7lRiHKfg+OTmpuNgfvP8BAgiCkFwWzKcTkkhllPI8xwsCTs9OCBtBpUqFkPr9ccXnNkGpCtLyKuA4T4Uuckm/32cwGFSOlQETX3jhRWbzCa7jkhcFYRhUdXaBH1Z+wNHhcZWZEkLgqkiayXSG7Tocn9zDdlzSXBXqXrhwgdFozHg6I80y0kyp0PGkWf9zP541CFnaX+u/x9hDoFJiLZeipQ+zjR917rrtND7MwlF/cn8DKnqwee0ybXTZXi4orhKEie6ECh4Eij4kF42Cl45SarlaHcjron6zl6rA5Om0LzNWT1C/qu8XrzMgn/It1R/eeeddbt++zde//k2klHi+z80bP6DX69LpdAkCpYzmug6rq6ukqaI35UVB4PuUheD+/V18z6PbE3heE9sSRFHCbBYR6G7hWZYvNbwTQjCbzfB9n93dXdrt9pKPs7q6WtVumJ4cRrnKgB/D4ZBGo6G6lPt+BdJMJhMGg0EFUCtGQ8h8Pmc0GtHV/T4My8WAPMZnN4qyRmghCIIqIDb0LtM1XEqJ47pgCWJdx/FxxzMHGuYCpJQVL0tJjToKtcyzKnI2VAmjYAQLpakFhUUZbpPRSNOUZrOpHOmwwXQ0ZqXf59LODmmWcXx8zOnJieqe6bj4+j3T8YSjg0MODw/xfY9H02nVzGk6napoMs0QlsNrr7zGL/3iL/Hqq6/S7/cJAkUt8TyfvFD0o7zIEJoTWZY5SIkQig+YF4VqFOa5Kj1YLPSbXdepJr5tO0gsti9dVgo/OnMjHJtWI0Rq/XrLsih1jw4zjrKhxrjRbC4VN5sJaYIZgxYZ6lQjDKpN58qVK9VzkJaoHPFZTdlICEGeKDUWk0moI1PSWiDmZVnieh6O6zKbz6pGXkVRgBBkRc5oPMYSFkVWVBsQLLji7WYbW1g0/IAiSVnrrTAfT1hdXcV1PQpZsr6xUSvyWhSTmqyGkYmLoogvfelL/H/++e8Qx0nlXH0UumM2wixTtAvXtVShma7xkKCUKZ4Cg9m6aF8WEqOMYz4XlHH+qM2sjkY9Db1vNpqcjoaEoYXrOLporODChQusr6/zyU+/TrPd4uDwUNEnGuGSk2fbNuvr60oIIEsrmsJ4PKHZauH7vmpUJktKTbmrp56llEq+sCxwHJuD/X1cx6bZDLGtRZdQIUscx62yj7mm3uSlUgYSQjAejZlPp1rxXCFTSi1IjVNZKCe6ntF49kNWAgqddo9+u8dkMqXTXsexVdYiiWIGZ1MePdrl3r173Lt3j/39Q4bDIYPhgCiJ8H2PoizwfJu8VMXmhoqYJAmz2ayaM2a9Gefd8zzWVvpc2dnCcxymswl5liOlIEuVZLAkAqkoIgKJ7ag+FEYDv9ls4zo+eZ4iRIFlq741tvApNXJrOQ5xEuP7Lr/8K38N1w+ZRzPu3LlDv9OmEbzA6WyKamLocnxyzNnpGc1WE1tnfvI8w7JsJhMl4GBst+s6xPOI6VRRVlrtFqcnx6oXQ5rjOB6R7tydZRn9lX411zpthY51u23iKCYIfXrdHkPfVT1MkMxnKvhfW12hyAvmsylC2HgaVDg9PcH11BqazeY6iDGcY6EUh4AgUKi+akYl1XVFMz3XE0ajYSXzKKVke3urQvCb2n4GgbJD0+lMF59LLEvVhYShrZ32ENdxcLRtSdOE2UwVXTebzco5GI5UsXiaplXT2Fu3blCUMJ9HPH78GM9zyTIbKVUmbTSa8ujRI8pSBTVKOlg11koTVRdx6eIVbNvh4OCQ4XBEr9+nv7LKeDxCylJRfCnp9bqV/TZFm4oelum6xoUiTVEUlUKkZVsUaQayQAhHNai1LMajEWmWEmgKtOPYFZXUFNmCrJRlms0mR0dHrK+vY7p0G9tr7O9oNMISNnmunFmDmHqex1CDEYZLbhxXU9MSRdGSE6zAKRtZSiiUeEEpJVgQJTGWdt6SIifJisoW2qXEKkqlzPaMaY3/1IzFxx0fS6sVi7o09f3Hf86zXnI9WDD/mgxtXR1OSrCtZTrVcrCxKLo2amfqdXqclfePqrPQzb1Af3/+elgEGegvAVJnAzTZSr+e2rnVvDDBzlKQJOpUq8X1m+DO9BUyvqz6nUWWFdz+4I6yP/oelOKUctoLTfm1HRvbsqtMgpSSy5cvcvXqVTY212m3WwhL4PshaTrl7OysytIawH0ymVR0eKP2acQplFjFUFGpjYqnrr01fY4MuGzbdmXrQIEwjx49YnNzswoKTFBp6raEEFXvC9/3K/+40+nQ7XbZ31e0UCMwYTIbUiqWRLvdVrahLMnlot7oWY6fItDIcWxbKUhoVDWOE2KthGT6GzQajYo3HscJQqv1zGZzGmGDLM2YzeYkcVqlTM3D9/2A0XDM6eExloQkionnEe+++y5JktJsNhgOhtUEqVDLNCNJExxHpfY9z2N9fZ3nP/E8vV6PCxcu0Gi2WVtdVyh/prSeTZFkkicgIElySqmMrOd52I6FLAW2sBFlieO5WLa6HynBdF1WA+5RqUCoikuzqrCFIGg0VQGmTjmZZm2Os1iwdbqZQeVUUOZg1KLU5Fmg82VZKOdYP/RGo8Hu48fsXLiAZduUSK0ws5APrvjXuVps5uckSRgMBqq/BRLPV1mTlZUVbMumkAXdTpd2u83W1hZFXuC4jnYeIYkTollU8fqOj4959OiRQulmc6xScRxn4yl/9Ad/yOrqihIR8H38RshoOAS9OGRRIiwLy16mHfm+z2Aw4I3PvcGLz7/At7/znUo2rrLB5/z+ehq56g1g23iWh+MoxZlcB4S61Kx6r3E0bVtx1M3vzv+7lO2q7QAfRweSpSpYNcbeD3wsW1HzXM/jE89/ghs3bnA2HFTIda/XqzJQxmg6jkOn02HvYA/bUcWl9+/dY2NjDUtT3lSQpAbHdNzNi0JhUnrcT05OSLOEzc1NHNdlcDbCsR1ANa70Ap9Wq8Xp2RnoYmoVxCkO/N17d1RR+eUrOLbKLkbzGWVZqOL9jxmb88dyCt+EL0I1fsoLxqOYd9/+Jrc/uMvDhw85OT5mNB4pI5xl5IVqZqQ2sYLA9+j2u9y4dY3PvfEG//Sf/T85OVGS2UVZkmcZ49FYiUAUOZ7r8Pzzz/OVr36Fd995h5/92S/zhc+/wfjsjLffeYs/+9P/QJzNSbIU1w9UwX1Z6gJzKjqoEJJMpgghmcY5jaClqWAZriUQ0kFKRe/JC0WrcYTN9tYWthC88/aPEUiuXr7MWz/4ARbgOjZngwFh2GAezRmPxrRaTWITLGl1F2NLTKO7sigrYYg4jnj06CE3b9wg8DzCIGA2jWi1mpoWpQqAzwYDXNehkAppK4uS8XiEp6mWgeeRJBHNZov19XVGwyFJmrK6sqLUqQrFw3Yci7ARInErymiz2agCgiSOqyaek8mIZrNRIWqGl+y6Ns3GStWB2Pc9Il23ZMQnDEjSCBs82n2kaK1FAaIkjlXGLk4iOt2OqqVzHCyDLAN7+/s6c5NVNqLb7WgwRvGvB4Mhp2dnNFsdoigijiM6nXaV/XJd1awwSRSlqb/S5ez0hFKW5FlKQ9dQnQ0GtJoqgMt1gBCEIaD6HXmei7AgjlUR8drqmpKSznKGgyFRFDEej5GlRavVptft0e10iOOE4+MjpQ7kWmR5ytr6qqbJ2bTbHYQFSZbRarUYj5SiXBRFS4BPt9NlMhlTSkkYhNy/d193Ic9IknQhIpLndLpdxuOptqdSd5NXIJqq9bCRJdX+V5RFjZpoBAxccl0XMplOFJ2odFSfHNsiLwsm0zF5WVAWBUmeUmh2QW6kuyUIrJ8qmfEsGdX/eQ5D+TUovgkK4Pzpn5ZN/7Bj8Vr5xL5kjnqzZf3SZefdEpUyn/JBlDFdUJtMDaAOEBHaDzJF3PWAg2p/LausjaGFlfpli1YA57MYy9mVD9lzxZPvM2AnoPsJCb2XC4qsRAjJZDKt/u7YtgYdQQjVld7QdosiZTicsr9/jBCCd9/7AM9VIiVra6tcv3GNZrPBxUsX6Pe7Vba40WhUtEwFSHhaiU6xgdrt9qJBqK6vgsX+YYJ1A6IYP6bVajEcDisFUNNmwoDDSRxj688zGQljI/0gYDweV/5fp9NRNlOzcIyIQ6/X0wITSvAJS4kUKWDo2dbHs1OnpE2eSlxHqSz1OiskcQ6FxWBwxnSqin5XV1cr3d/5fI7j+lXB8Vgo1KLIC402NXCtkEKWpGnBuw/fVzr8nku/3eIkP8FxbOYTlU6ejqdISyCFVfHJms0mzXaHC70+vX6XlZU+W5tbtDttfM8HlJzsaDQmLXPyTFYaySq11URotNJ1F1X8lh5Mu0LKF830Ci09Z0mNhIu6DJzpZ6zrBqQkL/VvqoWhjYBYGFxDx1KTG10+WiIpKLRG/aIYmeoBF+WieRW2Raff47333uPeg/tcvXKFizsX1aIMqBxT1ZkzI0piQHB4eEgUqc63hsZlWzY2Nsk8YSiHCtV0XBy/ph1t6067ltbFdyRuxyYMVZfM55//BJcvX+Tk5ITjg0NO948osoTXX3uVk8MDXvzEc+zs7FAAJ6MhnuXgWkq5Rs0RxfPHUupLQqLqJLIcSwh+6Zd+kbff/jFpkpA7Dlle6LFVvPjzwYZlWaRZhhAOsgDLtXB1IafaDAWFzJcMmnmvuudFMd5Soxqhzlk3fMb4PW0jqKemjaNx5cZ10qIgSTO8RkhS5OQyJ0oT4jTG81xAEs1mdHpdvEZAnCUUsmA0HrKxvkGr1VRdVW2HJJrz/rvvcP3qRTY21qG0KR3FXbGEBZYkkxkIVWRso3oofPd730disbK2zng0IUkzWs0OwnIoyFjt9QjCkOlwRCBsWq7LAImgxPNsXM8llylBu4mwPJI4oRkGCHQBvdCz+NyG8XEbupSq5oJS8uDRI/7X/5v/LWVekCUZWZqRlyVZkWvuflmtPyEkFy9u8elPf4rhaMRv/uZvcP36ddrtFr4fsL21SZpk/Ivf/Zf8+EfvUBSl6qjue7TaLi+99BL/8B/9A3Z2dsh1w7CyLOl1d7h64xJJGvHd730XJlOVJcxVoaui5Ll4vqtpPjE2nnJUQx/HUsGb4+pivCRDWrp5nS6mtG2HdrPF2fERzWZTocWW4J2332E6nvDSyy/jOR5D3VCzzDKKNMNBsNrt47p25SBmWUa32WM8GZMmEX6zyXgywrYsGqHP4cF+lQlLk5Rev1c1c8yyjDxJmE1UQaQsJZ7jsL6yxsOHDxXY4zlASZbEzCaqX08czTg5ziqaJ4CFhyVLyiwji2Olsqfr9oIgUEWxWUa/3+fg8WPyRPf8kQ6itHAtH88JCAOfmzeukeU548kE11dUnCzN6IQdBJYGkzJuXL3K471dhUjaEAauLoCUpNFMiWN4LRzLJ88KVvp9Go2Qw8M9wqCHLFWfmna7w2w203LBKcfHB8znbYVgJmmFniZxTL/Xr4rQZ7MpW9sbWJbE8x3yIsO2fUoEzXaP+WzO3XsPiWNVC9dqN4njSHdg90lTpZLouT6BOycSKltp5puUkjKVRNGU2XiCrzMQtmUR+kEFkKdZyunpAMe28YMAx1GsA893ONg7IEtTpFR1LLalm6LmGftiH6TqRVVoGmqWl0isCpwxQcloNKegVM3VtBNbafhLSVkIkDZlKbWzpNSlTk9PcTxPyb9rtBaouOEYCk7lT4qqOBiDpgNKHp9Kav4/9fjzCj4+KkAwAGVZLmcN9Cs/4lM/SnFJBSyL09S/X9R21NkDSvChQEih9zSdVdC+imWLql4LXZsrzb1IocEVqzofuvbCZL+M867AUahkdWu3WvlG5+59aT9GtUkwGTF1I4Zy9fSgxLI0g8H4ZzV1L0to8MW2EZat/DR9OlmWWm7eUpLoUp090zR/SjX3kixnvnvAo8fKVttWzupam/X1dcIw5Ktf/Sqbm5uVeIPKLLsVLdVci2GXGKqnyVoYMNLQ5s/OztjZ2WE+nytVK8+jp/0bWws0eLqu1ohmmKJvE/BUvp7J3Gjg3Qg8mBo+Q48Utk0JSmikLJhPp6pGbHPzI+ahOp450Oh1VTX8dDplOBzxwx++VakBua7LCy+8wPXr1yu+uDKSakIaGpVRsFC0qYYqSqx1hX748CHHx8fkWYrriCr94zouQagUngbDEa12R+vlN6vKeRWZF5UEqpSSNMvY29vj7OyMT77+qaWiYDMB69FwPbqvFl65UNoyCwaE4lwXOnmh022gIlCEoEQrAgmVpgbtYAoTLJRVNGt44bZtLznHxgkzlCHj4NcR+np605zj8uXLPHr0CIRgb+8xJ8cnrK+vV4j+QgFMKb2YzpGbm5tVwX+9KDtJEmZT1ZvB87zq/QrFiysErCgKHGeR5UlTleW6ePEit27cRGgpXcdWtJBKu1/C2toav/i1r3H/7j3u3L6Nrcc0T1OlamWMgmVVqcXPv/EG165dJYreVZuYTCu5XguW0hrmGVepxqKg2XCwHZssSymlkg/FWjbs5w2WCTrqNDbJcrdwUXvGH404qbE6OT3h1ovPY0uYTeYEYchkPCJNUuazGfFc6Vs3gpCD/X1u3rpFr99nphVxTk/P6HVVAbNRMkmSgFKWfP3P/oxf+IWfV0hrYS3GREpF65NSg1SSn/zkNru7j2k229iWrZ0qlb7N9Ny7ePGSynwcHSsJzOkQZEGWp6ysrHDx0hXu3LnL+voWeVEwmU5I46QaS6RU2b4PyQ6dH6/6GjBvn00jolkMpVR1HwgKigoRsx3VHdrzXLYvbPGXv/Zz/KP/+h8Szee4rpq/eZEzHg14/fXXEAg+8dwtHj7aJY4UHbTTabO+2VOIW1lwfHiIpZXd5rMZzWaLJE145ZVXWF1d5bvf/Q6PdnexdDZNyRNrB6LIcGyHNFWIru/5lEVJoxFqxKzEDzxUB+UC11VFkkEQcvXKFaL5TMkMpwnzKGI4HPDCCy9wdnZKmWfIoiCO5qroL005GwzIspR2u1VtYop6mOJoecw0TXBsuyrgVI9E9UIwvFzbdnTNRICUSqlJCJuGprwKIfBcJc2NLBEWFS3W8POF7+u6MbXWDaBhrilJEnzfr+gBptN8lmW8/PLLpFnKo4cPOTjY5/r169rG2xSFTRyXamN1HBzLpdVuq066pYXnuERaFaYsc65fv6pUCE+OFgpykqqG5XB8yNUrN5gdT5GlCjQvbF9gNB4BAs8LODsbKBWz6ZTV1VU+9anXFd3pTDWI3NhYJ5nPlbhDlrG6ssL2hW2azQYrqz0cx+Xk5JSizMmygjhKCMOQ/b0DilLRZ4tSItBUhU6HOIp1sJezt7/P2cmgktyNooh+r890poJc1/UoCyUjbkRDylJRFy3bVqCU3r8UTUo5T0hFSVKqgrJCVfOiWCDEUtOEtXOYpBlJWlQiA2VZLuo1S6UKuSSgYGxpKRDCWdq3JjNFz5BxrPbOWg3nedpOZZcN6q9mUwXC1X+jfvXnT4n6j6FZPW0f+OjPUYFCHYSpo/jPcEaWMglL53+yqa15jXn2ZuyfJmSydIn6VGpfBCGW1aCW5oDuoVQpS31MwPZhLAEhlPjFQoJ3ObCo/1wpmNUyJPWMZ712szT/FvUATvcaKUtFDa35ct1+k0uXNmm1Wly5coUoUiIHvh/gOha9bkfXeKSVn5rnOSsrK0s1lkbl0HGcipJuVNyMv2F8HuM37uzsIKWqher1eqBrJoMgqGy+EKJiPhj6pxH7MXUcRVFUtOFIS9ebWg5Hy8MLsah7i+O42t+qDMczHM8caMznc9XBeDJhe3ubVqvF9vY2rutWNItIN3GrR0WWZTrQOriu4pZ5vqc3YauiCUkpee65W9y8eYOiyFAsC91LoFZnkGcKtTaOLbC0KIxTbq5jdXUVgOFgwPr6ukLI9SK0HUWXMH0yLKFShSrqNUVKUivtSPXaoqwmuSVV3YaJ/Ay6FIQhXuBXhTidTqfSHZZSKm4pLOTJ4phSSnz94MwCMJGtQVHrC8h8VQGKWGgid7tdOp2OGpssp91qV/Jpps28eR/AlStXqoluolczAY0DbYI+KWUVbBg1BaPNrIr30mpxmAZihkNsIRCWcnR8z6eQquA417rOQbfD/+K3/h7/+l/9nlpQaUouS1LdNHA6ndLtdrl8+ZLiUAc+X/3yl3n44AF5XpAkKeWHUFwrvmamHFbj1Pi+r4IYk3XSc8qMpwnuTEr5vGLH+QL0evBqOP7mZ6MGZg6p7380GlHkBYGmd3Q6bc5OThQtQDu27VaLfr/P0dERn3jheba2Ntl/rIQNppMpg4FyQPr9PtOp6uY7mYwYj4dE0Zyf+7m/xPaFbV2sWVYKYVLP6bfffY833/w+QRCSpgVxnCi6Y6Oh1rAGCG7dukUSx5ydnfHw4X2ODnfZ3NpCypJ2p08QtpDCZXPrIlma6domlYEyjGlrARg907HYaCxMz4syUz0fTALf9iza7Rau55CmCb/1W3+PV197lX6/S6fVYHh2ymw2qwpTjeJdUag5PhiMcGyB78F0OsJ1Sm6/f8jq6gqjkaJiGe37yWTC6ckxnU5H8WgDjzxLSWMljGBZVPRGs65s28NIP5tzFoVROCrwdPZV/T7Xm0gXy4K8yDg+OaoK0VfXVijKjOFogC2lUiZqBEhK5tGMRiPA97vM51MsCzY3NyqpaVV30KjW9mAwqJqHmTWuOL1qQ2o2VZo9iua6tsEmL1QmTFiCTrfFjRs32N7e4uzslHv37nFyclLNc9/3mc2mla0zNso0ozLnNNz90WhUgR1B6Cmq0PoK3V6bUha4nk0Uz8mLXNsqsD0lfpFmGX4QUMQZaZ6QFxklKgiKRnPKsmB9fYM7d+5guv9alg0IZbM9F9sWjEZDJQfpOezt7TOfz/GDBmHYYDab0Ww2iaJEyYN7ATIvsKTEEQJXK7QMTo4ZjGccHR+ruo884+LFHaQUjCcRSMl4PGE6i/DDJmma4bkeZalpwVlBHqlNv8hUlg5hE2c5syhRXda9gOOzAYa2Ckrhre4spVpwRNSyqKamQu2dCum2dMBruODCUjLJcaaax5m6DWML86IEbL2eF8pGsHD1pVRr1vxWSpPNrAEwQmXIFGCjsiBmH38Wu3DeCf3zPn76AOHP//hPPd+T9/AkyGP2bAOumvc9DUB7IuARtTDvKcGLOczn18/xrEf9fJb9JHOgfh/V6+rzXJYgl8HZRRC0fK9L96YDKFMXUQdgfd/hpZef45d+6S9j2zbz+ZwwDJlOp8RRSquh/K7pdKqbEC/EDkxdMqBB+UWGxWQfjG001CaTXdja2qLf7y/8zSCgkJJms6kFlCZVzwwTsAwGgyqAPN+J3Pg5sOhDZkQtjB9oOoerxp2CLFXtIqoWCh9zPHOg8eUvf5kgCKqI1/D5QT2EVBeZmIe/aLCXaafUwfddTTtSLocB+Avd9MSkbiQKZc21LroxgKrpl2A6mVb1BvWgQhW42pVTV5aqwZJtK3R2posf6068MsL1NGYdBVheKL7nVu+VUlaSrI7j0Ov1qgh0MpmQl8p5NpGs+VzjbJoH69i2kgqtDP9C2ccU7tRbyJ+n7ZxfGHWHtiiU7r6pnVlZWaEsVXHhaDRiPj/UDQC3q2yHabQHLJ3TPBugchCiKKpkMVutFs1mYyG7qV9vJqrne+Q6Uh9PJoy0pvSdO3eYTiZ02x2ef+451tfX+MW//DUlBYdQ3at1LYyZA0qdJkKWJZ/77Kf5V//q/6cKm1wHmaog9bxxNUbOzD8A21I8Q222njoHzKGKEhefu8iiLeQC6+8/jwap+fQkWi+hUvBqtDvYjkOn28W2LZI4JktTvvH1rxPHMbdu3cKybYaDAVcuX+He3XscHRzg+R77+/tsb29XRWpK5jRnPp/zzjvvEMcRzz33CS5fvkKv162yjPf//8z96bNtyXUnhv0y93zmc+c3v6pXVSgQY2FgYyAJECCpptRqRTvCEbIc7SGi/df0F8v+Kjvc/iSZsiVbptWTWiF2gyBBAiCAKtRc9epNdzzzsOdMf1i5cuc5995Xr9hwt3dE1X33nrP3zp07h99a67d+6+FD/PKXv8L5xQR37tzBapVCComzs3MEQYh2uwsoMrJv3rmJwWCAJ48+wWq9ouijSXL2gxC7e/tQmqqiHh7dwDpdI/B9LJerZjG7ZiN63ma6kSAKU9VaAJ4v4EnKPxoO2vjf/G//11B1jXW6wte//hXcuXML0+kUo4tzLBYLE3mrsFgsMZ+Ttv96vTKa6KnZPGKEQQitCxwdHiGOQgS7O6jKimh30NjdGWIxX+Di/BxVRTLd89kMURgYNgM5Kej9c6EqDc+LTIi6Mkl02qx9FYqiEU4ASM2v1+tiOp0AQmC5WiJJYrTbHURRiJ0douYsZ1P0+z1ordHtdpGmxLGPogj9ftdupGVZYGeHKt2SjDIZPMPh0KxHtV2HB4O+mduFUY/T2N/fM9QYquSrlEKn08HLL7+E1WqJp0+f4M6dO3j11Vfx1ltv4Ze//KWtRZFlOQybB3VdkzqaAeScYM/yi91uF+fn53j55ZexWM7x7NlTq1jkRmRbSQcCEnESI2qRUoviddWTKIoMwpOQvoQQHupCYbVcYDFb4vXXP48PPvgA6zVp0q9WJOV48+gGxuMRsiyjQo8majObzaH0Av0+KWo9Hj9DnuXodDtYr1bQdUUysLMZHjx4BePRGEEQYL7OMJnMUFYl2u0OPn74mOSSpYc33ngDWiv89Kc/QxCEEIKkmqMoQVXlRrRCmwhtbVTFAEDYompCEK2lLAoYtATlOIl4flEkgox8fscNQCODQCvNTnRTr4qupczYZVqKELy+CbOPE82XT6d28Lx2AaqJ8trkX14AKFldab5+o4SzvWb+uwL9V63TL/K97e+6n29fYztSftV3fvMGRvP37Xa6/7H6J9DI2LJxcNV7sfSqK+553TO5RsGn7QHbbb2uHe6zue23e7ZJYHedtM2/xZVtE1JCOO+KaJOUlzi6mOC////8D7g4n+E//A//GEWRwT8IEccJ4rAFT/qWOpUkiXX2Siktw4TbAXAOk7RtZocM7+e8Zj58+BDHx8c4OjqyEeGU1R4NA4XnkS2oaowZNiSiKLJqWG6+M+M2fk4WJOIq4aGRte90OpbO9SLHCxsaLJnJANvzPNy8edMWBDk5OUGaprh79y7Ozs6wXC6xv7+HpJUAQqNWlbV6PZ+iHdoaJsTXq+vSGB8CZVGiyIvGowxgNpmi3enaNnFnUsIcyanmeWatwDRNLfCSQlCxOpMQCSGQcQTGFxYAMHjkiABbxQICdUkhKQ+UlsrRB24LGz7DnSHgTEyevEIQKKKwPbXJs4maFUVWHIvfrba+ba1z29zjKgvfM15rIYRVYuFnW61SfPjhhzg5ObGSlavVymo5A6Q0wgbKarWyNCmu2M6A9eTkxESsmropPEEmkwl5RbMUJyenuHfvLu7cuYMkSahADQgI5esUH3z4PrL1GtPpGFppVFohK3KrdgDARk/qssSDl17Gd7/9LZyenZmJAWR5gbqGXfyAZsEpTHE59toFzjs0o2qjP+25Zku1kRHjEXZrmmxHNNxFw71eM37pflVZ4vziHHtHR2glCcosI477OkW2TvHxRx+jKAqMzi/wd771Lbz7zjv41re+jQcPHmAyGkFAoMhynJ2dYW9vz0RqQmRZTVXhowDj8Rg//euf4s1fvmnbeDG6MAo1Ckc3bkMpoik+efIUZVmbyuA+8jJHEPj42te+BqUU3n33XbTbbXS7PRRlAA2SN+50ezi/GKPT66I/6OGjhx+hVgrT6YSe3WCP6zbA5x20wZQABHzPRxgRd7HdirAz7GN3bxcffvgu/vAP/wC+L3HjaA+fPPwAVVUjiWJ4Euh22iaHwsPR4QGEEPj444fY3d3BkyePMZ/PkK5XuHXrFooixSeffAwpiSpUGJoj88dZgpAXclZaCvwAXCGeK9eWZbHxHL5RoaoqrmBPxnNgaEg0V1vwPNKYr6rS1m3wfQ+dThuARrvdQpmtG2NnPjMqRBSpgTAF/bSG0jWWyzmEFJjPl1TdWykkSQzpUYTR9yl8fn5xBgAIQx+tdow8LxAnEYSQaLc7ODo6tOt/t9fD6OICx8fHVuXod37nd3Dv3j38+Mc/xmw2w+7ujnX8SCnR7VLF7Xa7jel0irIsEccxOp0Oer0ejo6OqOic50P4LJPt48njZ3jppRhaK0QhrWWeHyDSoJpEjpKR9EJopZCuUyxXCyyXJNkraoWnT5/hxo2b+PWvf43ZbI7lcokbNw6RtCKs1kvs7uxiOBzi7bffQRCE8P0YaVZgOl0YJS+Jg4MDPHv2zFCvKEKmIFG+9yF6vR5GkwnmqzWqmqKDF6MJtAI6nS6+853vYjab4i/+8sdYLleAFvA8H61WG2dnY7sXVpUbSTARe6VQ15vG+jZFaXv9AhoZBfoA0HadU+DaDZfmHExdB6YgmUik5v9pe7nmftp833UKu/e+gs6ktN74+CqnzYse1wH9z3L8bQG+6/R7nhHy7zNKQrd+vrPHNYKu+unudXQ1bDiQrnsWdz90jQW3HdcZXRt9puHk59Dhslq234O7L1/1vHy4Roj9t6JcOXayuo7FuhZYLSv8xY9/jls37+Grb3wFWVojDMnrv1wuN2Ro2aHiMlDSNEWnQ7XIVquVpT8ppdDtdi3dijEVszDCMDQ1kSL4vo/laGTpTnVdW0MCAOI4tjV3AMLyHFFhDNfr9WyBQc7j4IrmbIQoRQpWAkBqlO9e9HhhQ4MrD3NhEX4x3On37t0zHNgLK1OXZhnSbG2lazudjrPJ1pCmYEtd15a7m+c5As8jDX/PQ62BtMhxfn6Ojz76EL/1xS/h1Vdfw3gywSeffIJer2dpMPv7eyjLhqcupcTJyQl5KsMQnmO5MS+Y+MUavhSApmSlR0+fIs8y7O7sIDeeIZZXXSzmoOqRMXw/sAYEe/ap6qzCYrXaMM6UUo0UmNaoipISZwuWXpMUQvZM5UwzsLet3qsmxFU8Sv7JtDB3ovDheR7u3buHMIoIeBhPRllVSNdrK13oGlTsDXMTiKIows7ODuq6QlkW1vjwfZ8Kl8UxZtMZPCFx6+gGPEhMR2NMQZNgd28HrdYeTo9P8Fd/9RMITfryO4Mhdg/2oYzxyUYXT4C6KCA00Ov38O577+HXb7+LdZpZ69s9XK9BWZbI0hRCSCSt1rVjnvuXI2oS27zhq71R7meXQrHOoZSG8MgjdHpyigevvoZ+v4/JaITDg0N88N57SNMUO4YypbTCwf4+zsYjjMdjvPLKKzg7OcEH739gDevFYoFutwulKsRxhCD0Sb4z8KFrgTynZ1daY71MoWpACg9xnCBdZzg/P8d6naLX66PVaiPPyFPy+he/gKOjIzx+8hiz2RQHO7u4/9IDTKZTTCYT3Ll3G2EUYTIb487du6gVqTctl1QB1RO0OVASJ80Bl2P7vHfAfen5pHYyGHbwn/2n/3P8zd/8FL//vd/Fwf4efM9HbMLK6/USs+kIUUS0pPPzM3hSkgJWugYgMBpdII4TXJxPsVqsMZtNsU5XSFox1b/pdo2HVSJd01yez2Y4PTvFoD9AFEcoixzpeoXVak36KhIAalJqETBrHYE1YbzFMPM18H3jWAA0ani+gPQA36d6EnfuvIykRdSg0CcN9eVybqrVaqTpCp5Hane+E2lcLOY2d05pkiv2PDJOeJPk+gtnZ2d2Hme5iRzXFaRJAM/zDHmRo9PpmDoZEXq9Ae7evYtWq4U333wLP/3pX5MyUb+PPKe1dz6f47XXXsMPf/hD/OQnP6HK1m1pI61FUVD9Hc+zm2ZRFLi4uECn08FkMjFrnofJhOpoVGdjVFWFX/7yLVukDyBFlFt370B6HnZ2d7B/cIggiAANdHsdVFWJ4+MnePToEyzmc/R6XewMh9jZ2cV//B+/YmlxSRJD1Tn+6I/+AP3+EPt7B/hn/+xf4OHDRxiNJpjNiYIQ+AF+7/e+Q7KU1V+j1VqhVArHx8e4mBxDqae4desWfN/H+x9+jLwsUFY1pvMlBDwkyQp/8n//f2K+mELVJRSVdaef+oJwurxcJ0ApZaIOnjUS3HVIGiERPoX+boAVTaBr6Yra5ZrqKwRhrznRdXNtAle4NXwvH9d99oJ2wYtGHH5Tx3X3+7T7Pu/zf1eGxXXHVUCfD3dc8e8uuwHAJqDX2qxx119vG6PwWvC8qIt7uA68uq43DA2+totH3fOayF2jQLX5HA3FysVbQlDujxCmsKVjIFAtKYEg8HD37i0MhwNICZRVijBqQQgPBwcHto3MpOFCfFyPRghhQT1Tetkw4UgEU5y4xhDT8PmdjEYjK7jBGJ1lccmx5dvnZictf8YGjIvrub3sZOdICVPBobWl/r8oBe6FDQ1+Ke5PpvZwchqD0jAMiXMfx1C6BGmBj+D7ng23JHEbvh/Yzl4ul5be0I4T9DpddDpt+EGAbL3Gk8ePUZcVFrM5FkZze29vF2EYmQ6kCop5nln+L2u/a62JU1aTp7GqauRhbkJTJQRKRGGIKAoRRxFevncHgEZd5piMRuSlNANDlSUW0wmSuIWeKYKyyjJ88slj3L5zlzjJaYowCi3ACEMaOHleoMgLlFmOqiqxmM9xfnaGs7MT/NbnP48Hr70GpWry5FneYG3BLkCLOBWeMdERSQpLV01YrTVgkgs5Lq5N+FtKUodqtRKs1ymUqo0iVQ0OJbLkJPUh3beuTe0OB/gLIbBOUwMeYcN9bnKy9CTiKCaQW9dQFcm3CgBlUQKtBP1hH//gf/YPcH56huPjY+we7EFIgTimnJ5a1ZDSQ55lSJXCfDrDdDxBmuf48pe+jI8+eojVOjWLw+a+1SyK1L40y1CVFSW6Um85/10d1XANSzesqTVx8m3EA41C2KaXCM6iZ1gGSkEIifOzM8yncxwd3kSr04OERBInSNcphv0BhsMh7ty9g1v3biOvS/z85z/H9773PXz5y1/GbD7D6ckpgojqH2RpCikFbt66heGwj1YrIe629rBaLqmCbqXgeyFm85kZnyUePXoMpbSpetqCqhWqWmH36AhffuMN5EWBt371JtqtNrI0R54VyNICQRDj6OgGlsslirLE65//PFbrFYTQODs5BS/y/EJeXBDGAT2Cop5JHOIP/+D76Pfb+N73vgOtC5ycPAYUeVyePXsMP/BNhKHEOk1RFbUtILlep5afSsC5R1QgrXDz5k3EcYhOhxSewjAyORYeiiLD4eEBJpMxgsCjytq+jxtHR3j0+LHRn5cITWEliEZSOggo10wpZaNsQgr4wjdeqhBSCEjPA7RCyxR84zw3217jpaIo4ZS8WUKgqGsqpKk07t2/j/rsHEkcI4g8kkQuC0hFazZVJl5BCImqrOxmFQYRPEnKY0kSYT6vbJEnwGyyUmA6maAqS/iBj6oq0e+TJyxdp7bY6EcffWQinCEODg7w3nvvUX2IwQCZMVyFEBiPJyiMHHmapjZhMQgC490DhsM9jEZntJZK2mylkFitUviBj6IscfvePfzwhz/EYGdIVKOKjPe8yOF5EkcHR3j1wWsAgCrLcXBwgPGY1vXbt+6jLEucnp5AqQJvvvkWylKiLIDPf/5LOD+fIs8VXu3vwfN9TCcT/OgvfoL33nsPrSTBMs2xcp5JqRrH5yNKvq4p2i8N5VdrgTQviYKJGlIYuU0hTZRAgGvobBgRdg0hx5FVbhM8SxqvsnH3bs0imjvOatiscEIbQ8MxSjYiDFteX7hBCzek4QDTK+eycwVrhWx/83rqjN4wgNhqb46r8arZ89xbvQi+v+p5zLbgGnPcNrHxHniRo/+5T9qsZeLaplzbd3xZ8Snf41vwaVd88XkGAV+9qbO0mTS+HSkgkG+MCTiOI8Ht2MwB+DQDy406uJjGda4qO5ZdZ6tH5QbsqKQX1lCiiN7F+25j7DCebYR/tnEuq7R12m10ez1i6sQJbt2+gZdfvof9/V0EoYd2OybBjUBCILD1yvj5mdpKeXi1KUxKax0XXHWFeNipChC9GoClmjIOyfMcg8EA3X7fXsPmnoIxpLIGA/cXYzf+jK/tJqFzXgrQGDVlWaKVJPA9KrTNRaA/7XhhQ4NfstaNdj83zl0Y+/2+/Z28aj52hjH6/R3UVYV2u0cca91UGedQ9NHREXWC55nFmSg1/b1dfO2b37D3yrI1kiQ2RQIr1HW50S42MLijOOyjdIEk6ViZL1XXaHc78HWJ0cUZzlYrQNWoqxKji3PsDHfwlz/5a6zWa/z+938fu7u7CKMQ/TjGcjnDdD1FlLSQlxo73S7KrEQUdtDtJghCH2VVQQqJvKghRUDUMC9Gu9dGtl4hDEK0ohCPP/4A7/zq50jXC3zp699AXeXw/QBCkyQcq9eUlbZ5Kmb6kSY5iFO7Td3RmmRHafJ49u88cKgvU8znlDwUxzGkJH44L6D8kyYHFcqptcRiQZ5qLkhDHMIYMIWTeBCzpS6EgKpr3LpzC2EYUY6OEEZamKTqIlBIzotCDA/2IU2BL094NiolhMSimGM2naFWCvs3bmI2neH7P/gDvPX2e0h/8SsUeQ1dZKiceiN2kZJAUdYoaoW8LCF8j6IKZjcRW6449m7UtYL2Gk8H0ISChaAq8VJKSgZ2oxtKW5DBXlrmIGiQhrcHCZ3XuHh2juHgEP2dA2RpiRtHd/Dwww9QhgX6ewP4SYDSq7F/tIcnHz/CL37xc3z9G1/Hl9/4Cv7iJ39J4FOHqMsSZVHg5NkxlssFBjt9RHEEpQUgBeJeD0Veoy1DhO0hsiw3VZUler0uWu0OyqpElueIO2189Xe+i6Dbwc9+/CNUeY7dwRCj0ZSoWWWFBy+/jE6nj3fffx/7Bzcx3DvCRx+8Dx8Kz548oec3/k/hSEJfdfCeYIY3BIBaE53RA9BOYvQ6CeaTM7TbCaIwRBglpq7BGKvlDLdu3QK0RhhGNP88UiPz/QDtNkkE8hrV7oTo9WPrJOGFl0A+5SZwXpNSNb7whd/C+fk5Dnb3MJvNaEEWApGJ+AIGGApBcp3OQs4/gzAEzDpVliV8z0Nlxhl7pnrdLokBFDnyoqCaFWFIORpBiCIrsF6miCOJ9WqJ3d19fP3r34QfRvitL34Vjx89wrPTT5BVhlsb+FhMZ5TMXZQUlQ0DABJlWWE+WwBaoNNtQ9UKcRyZGggeSPI3wmw2RV3UyNYrql2T50jiGO04hvR8rE9TZGtKkh5djKGUwvGzExpb0sP5+QRKKRQl5SlQ1FmgVgtIIaEhSOI1TnD7zl0cn17gbHSBpJVgvViiVrWNsHFU8/bd+/itL3wJcdzG6GxCbRYelvMFzs/PsVotsX9wgMV8gcePH6MsNaaTKQaDAT55+AmWJlG9KEs8PTnB+fk5KVl5nqFdLaEBlKKha9io5mTRDFqLuQ3Qr2tAUH5IVWvjfKBkbUvn0GaQM4gWGjUnSluMxTUH6FC6tpx4lnildaoBlZ/uLN+MPtjJxv/fusBGpASON9yuq1uXf1Fv/VVoWTiTf+OrDlQX2AiZXA+6m8WE+2nTcNJb373y1tayatYsx2oR11zv0jXcP3xa/1xul3bveeX33GMz4rVN2XKNzm2aETk2N//eXPMy/Wgj0iE1zeON8bs1lox0LgBHmOeKHtDUTqV47giDGYyCFBpDx1WRq025ALvmbkQjAlRVjdCUMVBaWdl4YSLQQRCi3+8jSRLcunULw2EPN27uW6Wog4MDK5jDTtOyyNBK+qgKhSBIoGtlVG8bnFCWpS1YyUpQzOIpisLm0bLDgqlOnIPBc67TaZQEO50OdnZ2iJljnFrM7nEPxiluUjcbVOwsBWCd82zscJTDjWgx/imKAtJg9xc5XtjQyLLMgvcoimwn8st2BxwnnbiSrAEAETdVdt1OcCeEe10hBQIRYmC0hVn2a71e24RHa0QY/hp3GCfD+b5vs/1Fu40sowTAIAiQ9HqkXFMJRK0uxtMFkjjGdDJHUQMPHz/Dg1dfxWw2x49+/GPcvHkTn/vc50iqUWssl0vsRQnyIkcNH6HnIc1SqJRABlGpSiyXC5tU6fs+ZMsHfB9hSEpcf+/v/ycYXZzjX//5jxB3erh56xaUWqHf7wOKLHilGyPCTeajBZ8mrBvOtJa+INnWulaX+tn3Q3TaIcKwhdPTUxwfE8d/taLqu+v1GlFEE08p4nvXSqFSlGTvDmIhBOqqgu8JO1gtfcvhZWrNWvM58jw3ocEAStUmFwbo9fvo9nrWCC2NQUNeVYkgCjHY2YHvE2Bb7q7w7Nkx/uE//If4z8f/R5TVQygo1CZfx/XGKEXSnXmeI81SAqPSA1DhKk+Z9dA4hrYbcgSw0afu+L06LLy5kWrAatF/8P57uPvSy0i6PSgI9HZ2kJx1MVsu4UU+gosLHD9q46W7L6E4OMDjJ0/w1ltv4XOvvw4I4Kc//RkmZ1MEfguyrlDVBSbjOaaTGaQn4QW+8fNQ8SutPShFlezjJEEUhfCCAKs8Q1XX6Ay6+Na3v4OD/R289/av8OTRQ8Seh+VihvlsgnWaIYzbuP/K51ABmCxW+O4bX8M6LSjhejRCul6Too2urLeJQcr1xkbzd+5noiRStenbt25C6wKR76OuKsQxjY1bt27ik08+gRACvV7PcmLznBZ5rqrqrg1LowVO1L/agv9OpwOuQu9KUMcxJYtTdez+JYnqxqiFTXCmcSDASbCsbAbArpGN4Z/j3r17SEzyc1t3oKCwWC5RFCXlo0Uxzs9GODq6gSxNsVyt0e1WuHnrNp6dnGI9HuP27dsY7vXw85//DNk6RaFLSM9Hnpcmp6BClhcIgwgsqRvHLVRViaog8YYo8lGVRO+ZTGZU9VwB4+k5qOiVQitpYbVaoqwUsrxEVZWI4wTQlA9FPGEyInjucC0KYdaT2hY1JFrEs9MLdLtd7O0d4MGDz0FrjVE4wsOPH2K1WpG6SytBGIT45a/expOnJwiDkAyJqoQvyduWrlML0CivpgS0STaWlAwvTB6ChkZp6B+1WYvsfAdQi6uAm3mJzjzf8MI6eQ2O/99+77leaXHpHxv33r4XzZsXuNyVf/90w0CIxjtqn9/8txFesdf99Gtefn7HMHju2vlCTaavOZ2yvd5sRyY+7RrbgN35QtOkay8jLj/wVfe0a8XVbXhR2th137uOquScievewXVjz8UlrvrYdc/wvHZuf2Y/ZyyhWZSmwZKu888z+wrTnNwcW9+PEASUCxXHMfb397Czs4PhcIg4DtEf9HH//n2r1jQYDJCmawhBzqLlcmmp/wCIKWCizZxbwdiMAT3ToADYHF43X00IYWlUvAYyBZ+TsJk+xRRTzg0syxJ7e3tEaTLPy1ESFvZhChTnF7LiVMtQxnl/3X6HfF+mSzGm4/fCxQU/LULFxwsbGnEc24iCC6q2M+SZ588bCYdetkNvLkjjl+Aelhe/ZYhwhUVOWOF7spQqh5t407LSqsZL6ZsCJty5YRxDyBbCVg+7BzcApXH73kuYjEYoihxlnmPvsMCN23fR7XZQKw1oCU8CXpTgYjKFF0QI4wDrNIUfagASwguQZykggDBs2QqNQvpYrlOK2gQBvDCCL4GjVhv/QX+Iv/rrv0IUJ7hx4waYBUvhPq5U2fQpTySIRptaCEpsZ1k1KKCuanQ6bZNM6lPl2TgGNCnCMNWsLBQuzieI4gjHz84sIFvM10QrSVqA0KhUZd+Xu7DkeQ5dl7ZmSpIk9v1xWI9pcjz5PM+zCaur5ZKqTl9cwPM89Pt9RHGMMI5J5rYg5YWk00aR5xAQWC1X0FrhlVceQEoPafq/wz/+x/8Yta5RVKUdB40BVqMoSqzXGdar1CTIe9D68gLpGgtsPHNBHVeNg8exuxG/0AQUZNgoQ0dbr5Z48vghXn7tc7h56wYeP3qCm/fv4b1fv4XlaoVwFuD08TMkXoR2u4NOu42PP/wISil84YtfRKvVxi9/+TYeP3wMISWiMEKkamiTN6TqGlrVEJ6CJ0h3X3pElxEB1QNZFxm0EDi8eQNvfONr2NvdxcfvvYP33/wVnjz8EOlqhfv3HmC9TrHOUnzhjW+i1dvBL976Fbo7+7hx6y6Onz0DIPDeu++Sd8d4yDaglW6U167zirjz3vM8BAL43GsPMBz0IEQNoUiyUBsVpTRNcf/+fbuQU8XU0NZz4THH3nAhqJbD0tQj4XdrNy0TDWVHCuuKHxweIF9TQTWuDcRzkjfBxktU2cWdNz+b2FvV1mvFhZeoOqvEYrG0m0Wr00Zqco+m0zmqssZ0OsW7776P/f0hoqiF+WKJ/+q//C/xta9/A6++9jrefedt3H/lPv7oj/4u/od/8S+QrSkfB5qcD6XKIQSQZmszF2h94to/da1s+7M8g6prRFGMLMvNnKIkd6U08iJHVSlEcQJVK1yMSGmJ319V1cbJX9s1g5wfFepagyv1ak3JlyQuMsYHHzxBVSn4pjbSekXJjUorrFYF5ZM8Pb00VyGbOc+Rc3aImLgERdM9KhxHoF9Di2YcVqp2HNeXo5zuz08De9t73lWg73kGxP+/HAyUWBHxswCNq44XAff/tofrdNtel11++fPW7BfloQPAdckpTV2PT2/vdX//LOPC3Zeed90r7mSiCWRwNKc9L/pwhcloT2zO2+7G57WpaTf97nkNTYvHIAN1Bu8MsgeDgfX237x5E+PxGO12G5///OcRx5RPWlVUKLIoCkRRiLzIkKUZPN9DXqwQRh6mswu0khZgKGFSSntOURSIwhBJHBslP2XaSdSm5XJpKU5uvQpm23BUY7FY2EiGUgpJkli2CNeJY4zNeS3M3EnTFOfn5+h0u1Scz+S8uQaaSwfjMcT7Ec9nAHbv4753c3BZRIgjMPzuPsuY/EzUKZcyxZYbZ8QDsJsuW1+u7vD2oGLQv73AsvU1nU43PF9CCKvw0uv1bPE492Hdl8G/b3cEh504+iGERA0PChrSj+BJgVYYodMb0CBXBLaZOlQUudWkn05H2D/cR5y0UdVAEMRQGpDSB0ylZdcgk1JCC40adE1PCipMB6KQ9QYevv3t76DValnaF/WP8QAbPqFbuZGeQW8sYjyA67pG6IWYLqaGh3xmk4ajKMJykVm6BtEREhOK9LDOmkrh8/kCs9k7Ju8mgvAbsMaDkCxwH0o0A5zHBw9o7oder7cB1gU0yjyjwIzS6HW66Ha7FqT4oQ9ooMiJcuH7HnlXNd2T9J7JEPnWt34bf/zHfxf/1Z/8iRUw2E7gJp54jTTNIGUAAQkBCfI6bhocPL6UVhthT34ed3yxoeEmvjWgs5mYkorEQGuSaSUHP5GLPnjnbdy+fQud4R66wz6EJ3B05w6OH3+CYLaELyTeS9/BW7/+NZTWuHv/HoQUSLMMX/3qV/HNv/NN3Lp7B+++/S4m5yMoLeB7AQKf6jtoU3lCmw3Rk1SYKy8LVKrGYDjEg8+9ildeew1e4OOtN9/E43ffgacVZpMxvvLlL2OdVVhlKY5u3caDVz+PyXKBi+kcv/d7v4uirjG6GGE9nWJ8dgEpOTfBjFFhPLvqapBlvYPOTxonQBj5uH3rBpaLGQb9DqmRFQphGKNSFebzua0DQMITVFOj1aIaCPP5HEEQ4OyMqre22227gbAxPJ1O0el0rPMkyzLrZGFVjrIo0E5aWK/XWK1WG++7KEpQ8qCGEFwQj5J9qQ6Fj7KsrJLQYkEFUCk3CtjbO4AQHrQWiKIYk8kEi9UKcRJjPJri+PgEw+EOZrMFjo5uYjY391c13v71r/Hzn/0CP/j+9/F7P/gBfvRn/wY3bt3C51//An7853+O0+MTpOs15XNICpnneQENgaokA7yuTcVn3dQIUsbLRY9I8olwPPIkpVyjric097VGWbChQTSCSmkzZ6natFJkVDSUDKJK0B7A8t1Ek1BZbvcGVkiqzbpcKaJKkKNFA0Kg0srWQ2JjQ9e1oewqOx9rUxOJx6SGMk4dQd4dU/BFa3VlbZ6rjhf12m7/7UU27N8U+H7R46o2siNruz3XGR0v6oG/7rztaMLlqMSL9dtV37vKwbEdAWnGUNOe643CJiKz2earsYh7ffdaLxLpvep43jO6n207bzcvIu2cUKqpH4WtPnQTsLf3vO3natrf0O7oPwCCarjQZ5usDC6wTA6YLrqmUDMVfKb6PkmS4NVXX0XH1JniQs4cZV6vqRbUer2ClCQck6YpyizDOl0YNcsCQeCj16dK3O12x+AZLqAs7d7PdFkhBMqqQmgc19wnLI3d7XY36ohxNMAF6FJS8WGOHiRJAmXYIpzLwUpSHDVZGZEhPr+uayzmc7Q6nQ1H2Wq1sliYmT98sICP28fj8djUlWoMI6VIaZT3Pf4bC/1wQOHlVx48d1wCn8HQWC6XtoO2BxT/zpYmDz4ApiAVF6IiELf94O5DcEiIQ1F8XY5UsJzX9uR3r8PHtheDwYM72JVWqBWghZPIpAkHUa0P00Ue4PsCwg/hRzXa/SH2bxwR5y+MUJZUNbdWClL40FoalRDawlhdRgjAMxQKz3jZqAgKvfB+r0t7nBMOFAIoq9q6BFg5iYG8hkIQ+FYZiw2yLMtQooKAhyhKEEcJtAZ8r0LgR9jbowkShiGm0ykATRKX2QpZTtrygR8YTwHRwNK0ggy8jUnk1jEJvCY82HgVG7UH9iy6oU2hNWQYIY7ofW8nKNG7AyLfh1AaRUoGEvN2OYJS5CV8P8D/4j/7T/HeBx/gRz/+sY1msWEspcBqtUae5zY3hYChGUNXRK4JeOBSm9xwIz/z9iGFgJaGnsGeInN9qkQqqQBRTfKt68UcH7z3Dl774ldxuH+ExXyBvaMj5HmKyekpJChylK5JOvPxo0f44he/iNH5Bf7Hf/Wv8PkvfQmvvfYAR0f7OH12hqdPnuL89BxZnlMVaZ4zlt9dImm1cLh7gDt37+LevXtotykZ+q//8ieYTcbYHwxQFTnu3buPIEpw9vQTyDjBl974Onw/xNtvv4u79+/j4MYBTh4/ggeFt/7mbyAhDFeV7gixoTu1MUd5fvKxvc4oVaPb6eKl+7fRakXI0hWiIIL2BNJ1jsV6YWlR6/XaRjOjKEKaZqiq2vJR+flI+jeyxjdvaryOMW1Ka43JZGLnalEUSCOqZvzuu+9jMOhZWqc7Jngs89pXVRWyjBKysywzQD+3xvh0OkMcn1MRJA0EYUDfzXMoaHjSx3y+xMHBDVRVhdPTM6zWa3zpK1/C+ekZ0jTHKw9excX5ObLFAn/8x38P8+UCEgLf+16MTz7+GH/yf/sTzBczpEUK6ZFx7Ukfh4dH6HZ38fHHH2O5Tk1hS5pfLGRBNRrI4aLqpkq0NkaHcv69AXpMcVY+XA/xZpIyHbxuSMDOGa31BuXMpeYoGEUmM8wgGjvWbQfVanDoOdBmSdWW9iLoJGMMO+3EZaD3WYHfi0ZCfhPH87zMf1vw74Kkz3LOi36+MWSu2Lv11nkv0o4XjRS5z7Z9Xbctn27oNJ9vOpycWkD6aslVvvbzIrzXPe+lNl/RPtfouMpwY4PC/i7de2mH9to4dW3tM904eV3njRAaQcBYQEJ6Eu1Wy6h2+uj1ehgM+uh0Ouh0OgjD0BZZ7vcH9vOeoVJXVW0V64hy7SY7c1HSCMvlHJ1OB91ux9CGJOKEBEHSdI04jpCma5P/UKPIla3PNqtm6LTJUSUgkWW5BftZltkcPxhcs16vjepebg0CXuPSNLVytbb2jTkY7IdhaHGyGz13xxA7yNmBz5W9rZM/z23ZCX4PXO9juVxajMTOV75OXde2v4m6m9kIDUcxmH7lRu95L3yRwprAZzA0eMPkMIxr6fO/eYPmv21LhjHQZ68wGxZubQZWsWIqA9N6uCOYFnXVpOd7bdOy3H/zfbm9UkpIZULbNVWRVXWFKDQ1ISCdaKjh//lM9/EgA7LEIQmh+r4PT3pkeHjCaOG7uSlkbFDFdG0qthpwUilkWW6BOAOWoigA05dVVWE2m1kqUlEUSFox9vZosMzncyRJgqOjI6TrFKoCppMp0nWGRllKGUoH5cGs1tR2z5MIIw+tdh8HB7umUq5vjDvPevuUs5i69SRgIhOc0ATAvmshmmrnQLPoZVkGXdUIPa7gqZEbGbeqrihptKxMYmqACjnyjCrj1lDQUsPzfPh+iKoubWGrf/SP/hFOz8/x4Ycfbkx8AFjMF0jXKWbTOYpKG+rUi80BWzgSsMaeu6Fc2iSEMMnhbGgIqxtvF3u6uvWHffDu2zi6cQ+B38btW7fx+Okj3LhzB6oqbULv/Xv3MZ6OMRgMsbuzi8FggMePH+Ovf/IX2Nnbxauvfg73H9zFvQf3sE4zzKZzrBYrW++Bcq1CdLsd9Pp9JL0BKWAsl/jVL36JRx9/jNAPcDjYha4LjMdTQPh478OPUYkAb7zxTbR6A7z1qzcRhwHeeOMrWC5mmI5HOH34EMvZBGy+cddqEM7b9g5vriOw84EjUbRxefjc515BFAaQAui0WpDCQ10BpV+jrmqrRsJ5Flyr4fx8ZPmuk8kEvV7PeqHynOqP8N/Ya9Rut6E1CVqcnp5Ca22TkOM4hhRkUH/ta1/Fe0aGeLFYoKoU6orGZF7kqA09qkm605auQ8/HYXFA+BJ1pXFxPrbjtaoqJO0Eq/UKaZoDkHj27Bjz2QLrVYpFmiLNC9y/ewd/8MM/xP27d/EXf/4j/J//i/8C3/7+D/Cd3/kd+L6PLHuKp0+O8dqrr+PhJw9RqAqe7yPPCyzmC8wXGU5OJ/j44VOiSpn1nt8BC0oUtdp6b+bNCq6H4AI1BombpAvtrB9E+9xcp2m6CEgocyIbEQ5oxNaxMe00HCGlrcEmbbuMReSc4xjAG1fb+sNnOF7E4/7v+7iOQvQ8EP9vYyRdf+5lQ+55wP5v24brsMN113XxzqbxsH2eBEuh8nnNGrb5DG4btlkfz4toPM/Q2PguNjGPe93rokX0odt+N0JDUtyus00pZVXiuGhvHMfY2dmx1J+Dgz202y0SJRkMsLe3h8PDQ+uV55o67nMkSYKnT59uqJlyQrUQAosFRa739vaQ57n1rnueh+FwCM/zjMS7ssZHu91Gnufo9Xo2B6HVapmIjYTnBfC80IiGeCCfhkBZ5gZ7+CYynljnapam8BxGCD9Tv9/fqJjtlobgvZfXf8ZjnPvMBpubhhBFkS1uyu+Lox/cnqUpRQDAGilsdHCxvsFgYFWuXBw2m83s2GKszY5gFkhhZ3IcxzYC4+K8TzuEfsGV8PEnj+xF+UEYOF7KGcBlTyUPhCzLrGHhfs4GAg+6uq6RGR5o2wAAIQTiOLa5BvxS+OBFgL3XwGayi9tO/gwQqBVV6FV1jSgMEARUcEUIQEmiMdjNk2YwtVuYv2nyjEk0YUS2+ik6Ygw0IVGVOeo8hQZp5isQPWixINnRxXxhiw7WtYJWCmEUYm1kKjmq00pa6HQ7UEqh02mTrrwQKPLcSP5SAnhVKJLUNYUVgyBAEIak8x+QdJvWmpKFpUS1ZXWzLKfShvpAw9B44wWoEjh9vyoLjM7PUBQFut2ueV8JsiwFBHmyhaCJQ+2pIKUH35OojFQyUU/MQqZNvRHPN2FE8jBLIZFmKZJOC+t8bWSWyXgjalUABYHHj5/if/9/+M/x5MkzZEVBXHGtkcQeXnv1NRzduAk/iPBnf/avMZsvDChWzbvD9iIsLAeT3jlJbnpGIc3labpRN0vL0kwpE2DlGE1al1Rnoq4hfQkFoDe8gd/5wR8haieYr5Y4OzmGrCs8+fhDpIs5et0O4laCnpG+PTg8QhSFmM3HuJiMsVyv0en1cXh0E3uHB2h3ughlSMlylu+qLLAeT2Z4/OgxpqMRlrM5Ou02jg4PsVguMRldYL5YYLlOoYSP17/0Vdy6/wAnJ2d49PEn+P0//AHiJMCHH7yDcjHHX/3Z/wRVFNCqJm8zjISm0DDEHKBuDDM2qmnuCAgJqLoB4gJA4Hv4X/0v/wG+/MXXEAQePCmQrlN4IgC0xPHZMZJWDAjK45pMJqhVjSROcHZ2YUPOfSMDyLK2lCToIXCktjncnOUFFosFzs/PsFgu7aYqTb5UXpDhslqusE5TUMHQEkVWwQ8C1FVNY8kZJ4KNKG3WJfO79CQ0gCgMoTVQVZQrEQYB/MCHFkCWZtAaeOmll5CuMzx5+gzTxQplVUFohV6njdtHR6irEmm6ws7hTRzduIFOu4MPP/gA77/3PmCcE3ldojJ0KAEyItgYUjC0pi0PqYnNmj+IZh3UVEUaspEh3VBewwZTbouvTsUEwXuAUY2BEKS65+xB0smh2DBOsGnJCEHROq2BzW1QQMCzz3Vp69PbtMmm/dr9wwseblSOTt/2VLsG1tZHYusrV/x+yRi64mBXxrY47MbZovnRtNe8cXvf5kuNdPfldm+um44X3F71euPBDUptPzaM4eo6JAhjXPbSc1iaDXuNzXFEdRNcEM3vynnnunkGOM8rhIS+prfp2aS9jhDSrmFA0+btPL7r6OVbPbD1uRnD6jK1ix/ARkiMEw9mnnoGo0mP2iqd6IrrxOUIgx/46HW7SFqxzXvgyG+r1cLOzhBhGEEIYDAYbtQPq6oCy+WC6qMFgQX8QRBgb28Py+WSmBeGxdLv97FarSAEJUkzEOcIMUuwRlFk6UlCkApSq9WyDIYsyyy45sJ2Lj7laDYXWRXCRGd8HzC4crlcQunaRNMJa8WGsu8Zb78UYkPpifOHpZQ2744NA6BRdnIdtOwwzvPcFunjCDhjXpadZfDveSTUEccx0VYVRUHSLCPqmHG0CUEqohcXFwjCAIP+wK6xbgStNtewRp8GYayE8u64/xkvcPQmjmP84A9/eOV8cI8XjmhwyISLofELcwt7ALCcr+0JVVXEoeb8AD7PHUB8TpyQdKIWsHrArQ55GMuitFasS7FxIyvuNTkkxW12rXz7e11CAhR9MPdgo6RSpR1YdV3ZcFSaphDS5I04EQuO2MwXM9R1ZV8cWawxyizHar4y4GRtE1TNuwUEVYmFBpIkRLvVQq/Xw2q9RJqu7OTpGE6enTymCnESUZgOSsOXEn4sEcf0mql/acGrqgq8/nBeTGG42NxnHE3hScqWMdMNqqoGoOF7PmpVA0oj9n0splMkYYj1aoXzoqBaH4pClq0WceVZBnm5XJLakS+t4bher1HkBfzAR13VWC2pCuVoNLKeAVqYSoxGlDju+R6yNIMfBCjyAgIacZLgt7/6ZRRZhtPzMTSIS57mGo+enKLVGSBJKDHa0wqQMELBVx8axDeHMMCwrs2GpW3yLNAYt5tUKn1pw9FM4xDmvlJScqyUmEwv8Mtf/hRf+OrX0B/soag0ZqNz3P/cb+H44UcYn58hKRXKGsiyEuuUCqu1oghPP3qK+XKBO/fuIl9meP/td4kWFIbGEDPV6CsSSijyAhICnaSFfDzGB79+GyVqfP4rX0StFbLFGvNVDhG28YU3vo7Do1s4Pj3FR48+wZd/+2uIui0cP3oItU7xi5/8JVSR0aZmohM09swctAO9cUy4gIxAI/WL0IBQgBA1dvo97O/tYDKeYr2megthFKKdSMznE4RmES2rimQL4xhVXSGvSpPzFGAyGSNNMwwGfYzHY5RFiXS1Rl2RyhJ75tL1Gus0g9YexuMx0fLKEmU5BrRGFMdYrFfG+6NtOB9aGzPKg6oUAKJPCggILQjH2j4xSkxmCCgTISlqqslC9GiNvMygdI0wCpEbL5mCxmg6xjpbYZ2lUCYiW0yXuJh9YEecOB7Df/NtACQIUStyXBDFSTUDXWhAVRvvAcaYooDCFqh3/rYB1pX7jrfDVu6PxjDYALbG6OGvYINkB9SaQd/1dBV7anOnDZCusZ2R6nh61ea19dZ1P/shTASlaVeDFTdBLhdWbT7l9uuN390muSB+00hw/s3Acbtl13i3pRSbc9HmrJk5KdyfHKFrqLCXjKut+/E7dRkPtCYKSGcPB1/HAl8nEuWAf+30G12Twb4GoGgB0WYOMhVIa1CCb0P1EWJTplcaKjXfv+nzq3Mt6ENmUnBtFGUNDhgnG/XxJi1aCM+5R2MkCSHgycBQ/mhfEGgcpEILwGuK1NmiecIQIDS1l5ycwjgHAd+XCMMAvqFFSymxu7uLmzePsH8wxOHhgSnYmljnr+/5CKMQnqnxleeFwXAC8/kCT58+wZ07d5Dna5RlZgEye8M5esFgerEguWnm+QONB55VmLhA3Xw+t7V2GPewMVJVlc3L4AjS+fk5ut3uhioge/9938disbCgvSgKBN0AdUW0I10TxpEiQL/X3mDplGVJOGa1Ake72dPPAglSSps/4uJgZs/w2GGcxSpPnCrADB4ppe0rplKFQWTHhpQSRU6KioSRNdamDhGUgmcwF3nLAaEFVKkABUjIDWWqTqeDZWZkvtPGcBNCIPRCzFdzS7tSSiH0Q8RhvKGo9WnHCxsaVJFWWLrTcrm0VWDZaGCaTJ7nVo6UQX9RFMiyDAcHB9ZSZa4YH0opzGYzSBOWYx4aJ6fQyw3gyYYj1kwyZfliPLjYoGlC/6w80nhApJQITBiKPIseKn7RRYHZfG5Lw/M94ji2eRKcic+DLQgoIhLFNAgXi4Vt53K5RJmX0LVC1IrRHfTMOb5djBquv2g8+0phZ6fvRA9cxZ5msdRaGTlKokaFYWA41TWaDYEKbYGGLMqiQBAGdjJBA6uMNOvTNSUkHR8/gx8E6Jj6CpxMNJ/PUeQ52p2OUbiiCESr1cLTJ0+wWCxweHiI999/H0dHh5CewOkZGWpPnj6GEAKj0Qir1dJQzECVsScTpGlKfekFJtG7sBObDSyAxkO327W5O8y573U7KMoa3/w738bnv/BF/J/+yf8Vz07OoDKKwo3HI7z//vt46aX75NlFsyFcdi/SwePMpQryAgQtNv7WGMGXtcebzVhe4eU0n6sKn3z4LjqdDm6/9AoOD/YhAcwmI9x58BriVg9PHj9CWkxJKjhLsWq1MLo4x8cffwwlaMP7/g9+QIA1z5Gt16jKCucnxO2/c/sOht0uxMCDCjyoosTTX52gqEoMej2oZYZlmmKelxge3MDrX3wD7cEOTi9GePjwE3z5K1/G3Tu38Oijj7CejvH+W29iMZ8hAHmmIUgRjd6UaPrWmXtuv1zVD6quAV3hxtERLs7O4EuF5XKJfr8PrUEVzzWwM9jB+HyM6WyGrMiRlwVyS1kC9VFRoK4qfPTRx403saqtgg6vQUEQYDZfQClhkpxr4zkEbfbG885zUGltJHyVSTD2KYfByCBq53ncZ6XrKgu8lJmjWmkbLWbvvAC1RQqBP/vXP7bAoqwJILnOnuao7ZrI994ei+aXS+/gRSk/21SWbcDLz78NbN3DhcEvBu2v+NbzncHX/n456vBva1xsXv86mderwOq2V3n7c/7ptnnDOHEB8RWfX3W9q/7mGgCNi59pci7oJ8cJKwI1RmDjoXe97XQw46H53I0E89rpOmnoO01ESzuhKk/60CDlPmH6m8Q2qP0atROpYGONQL+g2GrTFxtdIq98D9Q/zb/dSAoVX6Xnl1JeevdsNEop4EmnMrZr7EJvjgMIUwyUnk1DI/C4ELGyfRIaOX1pLIxOp40oitBut7G3t4fhcEjV7OsKd+7ehjYOy1a7jbquMBzuIM8zrFZzi+WY2lPXNWarGYbDoS0t4HkeOp2OeTc1FY3rdi1liNgJhS0tEEWRBeKUN5fa87XWFqhzjq5SyiZEs9OTqUW9Xm8jmZmNEiGEVZ1ib75r7FD+BkUW3MLSAkBhHMjdbhfT6dTSpJiizlGHXq+H2Wxm1aCSJLHF9NhRxTmybmL1s2fP0O/3rVEFYCOpmjEN9xdfw2KMokRW5EiSFoQQNnGbqVHSa6JjblCAjEzfUsmWy6U17lxWEfc737MsS5u7yEYV9zfnIl6Xl3rV8cLUqdWCMs/X6zWm0ymm06m1etiD62rtcijJpUbwgOK/uepJPLGYG81cfQ1SealM8g0Ay13j8waDgb0O8+TSNLWcarba+Rx3sdZao64qGwpjr31ZllinayPhSIVjBKiSq+/78D0PfuCj0+4YqlSTwU9eFdi8BtcDQwWqmvCv5/lNSExI1MagEcYLIT0P6XpNhoBZhCjxOUcUxzYMRzzsDL5H1AA2gEqWlTUWMkCLoyclClNTZLlcGIUvDmcuoJTCaDTC+fk5ANoE+v0B8jyDEFR4qtPpYLmgCsxEKwkhDQ3j8eNHePLkKeq6wle/+lVTGEui0+ng9PQUc2PAJUmCOCaql1LKUq54cO/u7CHwA8sdBGCNoqoqLHeTBz0bI5RL4SMvKgjPx1tvv4P/+v/x3+Dx4yeNUSokdnZ3sVyukGaZiTgw7WJzo26MOb3hteCwroS3YfTyZJZSQtXbBgZfT0KITVvfGpCCAKgXtfDFr34TR3fvo9MbYjqdYTIaIQ4CLGYTPPnkYyznU7TjEEkcQUBjOp0izVLcvnMHr776ql1wAY0njx/hpz/7GbTWuH/vPl577TXkRYl1WSLPC0wvRiiL0nh+VpBBiLuvfxG3X3oF8EM8fnqMi/NzfOXLX8Dd2zfx7NkjzEYjPPzwfTz+4H2gyuEZz6LSAlyUEMbwUaoCNAkhXCl9LahoVF2RCpeuFTxP4bvf+W3c2h8g8IAvfelLUErh7OwMjx8/xmKxQDvpIggiFGUBBWC+XGA2n6GsaqOepKmApmwqwGrLTW+Mev6vqpSJYnB+jzaeJo9Psd4oN59Ca/KMKxNhpDWKn9FdaumeDKwUYJOrpZTkfeRvCh+AgOd4QouyANM4rgOV14H77d/d9dcFftvX2T6u8+xeup+4Pkrofv9vA/KvmqefdmwD8he9/2dtnzZRgE/9nnN/F7hedf/nGUXPO287D+O6721/zmui+YYF6DSfLwuvXNWXPL4AgAuWbkY0sLFeuu+Sz1U1nGs0XnCeg64UNUfGiX1Q2yhN8x+3j/v7cp80RtXlPt6OcFAEhn5jlb0mqqKd8xp1Jfq96ePtfaa5fg3fJ6VFzyOVRwa03U4Le3t7iKMI9+/fx42bN9HrdlGrGrs7Q9SKGQMxPE/C96muw3q9sM9YVqXNaaMEZ6pCTY4cbVSY2pbyNJvNrLOP+306nVqcRfsyRRl4fWdwul6vLd2GmRIsuNFut1EUhWlvZHFgI+IirTNxsVhYGpabJM3qSMyC4d8ZH7oiQ8ysqaoKZVHAk9LWWVosFhtsHFYBTdPUji8ea0w3ZYGjICABD24TO6i5/TwP3dwMYfCaW2jPjYRwfaWyKG3NKDb2giCA0grr9dL2D+MTMio8BH6jIsW0rqIobL/wHOVnY5oW41k3ohMbzMk51WVZ4gf/wadTpz6TocFW3dOnT601xBYig1i2fHiQ8QPwAsLGhkv7cb2J/HKp0FZuXyRfny1MADYxc3d311qzboIKS10CjbXJ92DjqCgK5MZyllJaTp1VUhDGWPI962Hg51DGGylAwFtKKuSnoVHVhc1vqOsaQkpUZYUgDFAaCpYQBB4s+IGAKk0xsSDAZDKB1tpalqzCxRzENE0RmiqPSmtMJxMMBgPM5nNrkPieZ/jqyg4OIQT2dndxcnyMNF3D8z0kcYLFYo68KBCYwf/s2THu3buLL33py3j69AkWiyV5basSSivs7uxYcD+bzZFmKV558Bp+9rOf4ac//SmEAO7dvYeXHzzAcrlAGAYoitxY5IVVjqBJvEYYBhCGQrJYkBSpViRry/UuqIo4GRdhFEAIYDS6wP7+AYLARxiSioQUZHhpAEVZQUgPxyen+G/+2/8WHz98iKIoUZT0XmotoIXx2Okm4sUTnn93N9IoimyuiRCSqDG6Cf3zZkibUDNe+Fr0PQ9u2NwFe0LX5I0TPrwgxm995evYv3UHUdJFWWucnZ4i9ARCT2B09gwnTx8jXS8R+gESQxXivo0MZUqAolNPnz2F53m4fes2Je7lBVSukJUl0rrGqiyhpMTBrZt46eVX0BscYrnO8OHDR9AAvv7GV7DT6+D8+DHmkzM8fvgQ77/zNoSqYeQTjPetkR0VkkEDeeWlaDzwLoDQUFRfoVJWdLjXa+HoYBdH+wP83T/8Id588y20TBh8d3cXH370Ec5Px/jud38XRzdvoNVuY7Fe4b/+kz/BbDbHOs+MA6G5jwUMgmhFZVmiqiuiAZr8sKreLDTZrFNkRGhsAlX6KRzZVjROXl4pXOfplsNDYRNEWuAHD8yx4uiGHS9yM1LxPKPguqX+OrB+1bW2IyLXedTdQzWEq41zt6/z78PQ4HOeB/CvO+/TD/Fc+tV1bd4Yn9hUUnRBzqe9088SzeC/uwZDkzvA7ZGAbiIXrhQ4r3l0b9sK+zlTdimTke/RfIeKm8XkYRZ0ffbIMuivKgLdXC+hLEucn1+A8hQ7VkQGAGazmVO7gNSGtGaMcdm4Y8oV4wB6nk1D0dZjcp5sY+0yVCn+3RrwknCD7/uQnkRdEW2m1Wrh1q1bUKrGZDpCp0N0n4ODA/R7PQgp4XnA3t6eZUy89NJLJjk4xXIxM4nHqaWhk8d9DiHM2qUJrPqeT8VufaI5s1N1uVwijmMjCVsjCuMNNSMG14PBwFKXXYqPK/7D4htFUWB3dxePHz8GAFsA1WWXsLOYxxnTck5OTrC3t2fFOxhf8DthPMcYzRb+NNdzKfwMjllR0C2sys8XhqEJfmkLolmgiEsMcDI5AEvncscDO84ZwLNRwv24aTBkFrwz6NeaEsjn87mNNHCSNxsrlJvqW4aLUspGa8qyRF6kNhLFc9j3fSyXK0RhbI0aNgLZ0OL+5/7l6L6L26MosoYK07j4+6vV6jdraCznCzto3GgGDxB+ibyIccfyi2fg5S7q27xO7kQBoDKAOM0y5FmG3Hjxhzs76HS7tlPdcCsPLOYEcofzQu16jOxCbjyHfA3bBrPYCdDiUVdmUBnPe57lljvp+77xMFLxsOy1j1MAAQAASURBVKIkXWbuLyomlpl+EVDmZbEhxAoI69XK8vO63S5ZlkWJsiyQpjkqA4h8nyoiV3Vlkp/ImGhUC6Tx6pO3JwpDLExRMiklJpMxWq0Wup024ihCZAwYDvNx1WPP8/Ds2VOkaYp0nSJptdDv96B1hSzNUNWUBHVxcWGMtASdTg9pmuH09BRSSlvzJIpC9HpdrFZLzGYzXFyMLK8yjjejYKvVErzAh0EIrWA5zJ1OB0VOfMEwooriPEG7ZlwURQ4hfQgIrNMUrVbLTpAPPvgAf/avf4Rf/OpNLFcptJAg6qLZQHX9QvQNN6oBTfaJWwSHF1TPo3bw+Nr0Sjayn9vjkryFmqT8hYQSPh68/kXsHd2GCBKsswyqKhB4At12C0IrnJ2c4GJ0gdlsBiiFwA8QmOibJyQgakg4BcxMm+qygs5NbfROC4OjI9x++RW0ez0AAmfH5zgbTXDj6AZee+UBPFS4OH6CdDHGo4/ew4fvv2/mkYZgwwICgLSGBqCMKhTxRy0HGg3QozbVNqIhtEboB9jd7eErX/ot/M53voX//v/9pzg7O8NgMMB3v/tdPHr0CN/4xjcQhgniOMHZxQWiOIL0ffyTf/J/wWQypfoQhpJESmYEXrShhpRVCU9SJJCoTEYhDI0jRGll60AA2BgjWjtAegv8bdCZxCaVZsN4YTAunC+7J14zKoWmvAvuv21v/Wc9rjrnugiA+9nz7kU20qd/70WB/FUA+9NoeJ/1Hp/luN64w4ahcZnadv31XENjOxqxDZL5cPfCT2vj8/rB3ZOFnacmkd7Maxqx28nzDuVq8xOS+YaGqt1r0jlNdIM/M0qOYKMWaGrSuPejzzh6wRjDldyka3FxVTd5nPPlhN3zue/CKIRSldNGwhCe9CxmcL3s/D3pkVR5GIY4OrphgGCN4XCIvb09tNsdRFEIISR2doZotdqG6htivW6U7gBgOpshjiKk2Rq+5yEwVaEBkufOsxy+k9cqhLAJ0k+fPrF1Zth56vs+Tk5OUJYl9vcPoDXV2orCkLzxnodnz44BDUtNIocf4T5Wa9IGkDNtiD/nvuAoAcuq0t5PuIQTttmRzEYE54IygOZ9lYE7RyEYIzLQZSUmTsZ2DRdXHZIpXFyzYj6fX6LmeeYdsuAH39d1SHN7GSdmWYZutwtgk67PzyqltFKxbtE+pm2xIcH4j5+Nk8jzPLdREIq8UO2lNE0t1rEKmFVujReOyrNaVVUqKyLEDm43GsO43GW8MNWNr8URF06dYNqZ1hp/53e+de1aYvv4sxgaLlCvqgqPHj2yuRr7+/s2OYRzI4IgoMReE4VgC4kjGtKhK3GnsT5xbagvWivEUYwojtBptyE8D5UBje7iwO1SioBM6XSouwDzdzaiKM65jZEBUn+qCoRBgKoizzV5sEkxqigLRCF5tReLBVmTkgwJ9raPx6R+s1ouKapRFFZhaTKdwvPomrPZ3Hh0aRFLkgQPHjzAxcWFqXEhsF6n6BnwB2zmnXDobm9/33LKq6pEUZSGa0iDKMsyO+hXywUC30eW59RnBigXRQHfhACzNMN0OqHwaacD35NIWpGdVNRvpsJxUSJJOnYhOT4+xo0bN+F5EkkSo67JCzKZTLBYLCGlMHVAaFNJkgR379y14WiK8hjPnQGJbniRNhdhvQ5JkphNRsAzYeL5bIZOp20n0Gw6RVnX+MUv38S//B//DLPVGrWWKE0hYKFqksbc2Id5imwCLvaAAEBdKjuJXQECT3qWbrPtDQYkpPSv+Dug2WAXClJo1BpQIsSNOy/hzoPPoaipKFlV1oCmhazVbsHzBNL1GovZHPPpFMv5AvmaVM6kqO2GDDTFH1utNtq7+9g5OERnuIuk1UGRVZieT3B6coa4n+DBq69id2eI1WKG48cfQeQp3v7VzzE+P2H/OhpYZTpQS3ASOHGlyWiXQpriaZc925cNDR9JEuDWzUOMxxNkaW4ihTz+BVqtNhnkVUV3lgJ5aX7XGrpuXqib5+R5HiUYGxelC7A0NIRD7dp4RxqG3c1t3xwrL4plyalCUQ4tmmiH6+kFGHi6ZzrgFdgwgP5tj6sMid+kofHvoo3PO34ThsaLX2MzovFZ2nhVH7ufXdXv24bMdXSpF4nccMSBfjqRNSfHYtug2DRQLhs2LPTA13VZDu6zuFGVzbG3eR/LOvCamk0uLiAjo7K0Y89GxAUghKXe9vt9c01lisP10O93rejM7u6uve7du3ehTd5ju92yeQae7yNOIhuxGAwHSJLEisVkWYb5Yo7BYIDlcrmhNjQYdOF5woo1FEZAxfd8LBZLJAlJcbOXnfNfoTTW6xRh2OSC9vsDTKcTVFWJ/qBvqE5ck8FDXSskcQuFKah5enqKIAhw+/ZtKKXw5MkjdLtd9Ho9+y4510ApKuDW6/VsEjQDeqYwM64TQtiaEy4rhdvOtCY28tiQYAoXU7X4syzLLLBnY4T7hA0OqyLl5HEul0vM53Ps7+9vjCn23He7XaI6mXHkOqn5+bnIK0vctlotUqRimrN53qYIdDNm+TlZIculWnFfcS6y6yyKogiLBVHa2Ugo8saAZiOF+6woMkRxZNvPuSKe9JCmOdrttjWC+N1wdIqfk/uO28lRHJbD5UgM0/I51/r3/+gHz11PgM9iaCwW1EhnQcjyHFmaoiwKlCaUpgwAYuMgMck2nHfAPGO7wGiqY+CGMHVNtSxGoxH+/M//HC+99DJu3DiiBcEoDJVFCWmAQF0TN7quSwCNh4JeIlW79ZxB5hZxS9MMbTNoiyIHFYCpEUUxlK6xmFKhLi7uQlYfyU5OZzNISTrEURRjuVxif28P48kYWZ6iMPKYeZEjiQkEC2gr+d6ExwKs1yl2dncRRiFW6zVxLU0CFEvJ1XWNvCgQmwFTK4WWSUYqqwoALQrpOqWBFUeYz4hGNRgOMJ1MUZgICyUwm1yU9RrDwQB5QXSvWilMJxNrjWulEYQBwiBEEAY4ONizi5dr3adpBj+MEIYxPv74IaIows5wgIuLc/i+hyiOkGU5gsDHfL4wCwTzCReIothUdPbQ7fYQxRG00iiLCkWeo1YKo4sL+L6PTreLVisBQMlhLs+TuKBk9LY7bayWS0RhiCIvMJtPUWuFKErw9Nkp/tX/9G/w8cOnWK0LQ/WpTfTE1AWwGypvts0Gz94iUqvY3PSbDVRQ2NpEyJTSDa9eC1xWHKG7aFDejxSKvNZaAzJADYmkv4MvfPmraLU7qDQAeMiKAmlewJMCURSi3WojCgIIbSiEeU75PxxKD3x4xrMSxjHqIILSwHQ6x2Q0xWqyxLDdx/3799E/GqCuSzx98glOnz7C9PwYF08fQZUZkXm46JoANDiiId3eAhfPIEOjQdSMqRtDw3iRaiP7KyV8D6AIjwREAyqgYWgJMGOxhjARR3p3xlhloCQkKEG76W9t6BFab1d0Nw/ENAsTAeE1UD4n7nUd+NsGyBtAyjE04ORv0Hca7y6c8SeESXzVm4o51x+XLOhPbb97T/c6pnvh9uW119s+3TnPeRMNkHSveEVTBITNYRHcbxuebgecOlQz997uKTweCQhvXcf5IrWH1X+EvZ5wPjNT3j7d9YaGMK9DuAja6VPy7vueR/FAVZvxoDYAOjs33Otf9f6aautuVM3t8CZ6wAa81sIaBjTePLiCGa6ORaNqJOx3N8e6QlOvSJs2Sfs8m3OQREvqujIAvzFA3KOh4BBTIAhCS8e9ffsOdnaGABQ8n9bpmzdvYnd3F8vlEt1ul/aFKEKn00GWZ9agoHVJod1u2xyQWtWUBBwnCP3AFtxklcS6rqGg4Yc+kjhGHJNXfrFYoNVuoSwKrNPU4qJ0nWKdrhH4Pg6P9nFxcQ7P96GMd5+Boe+FSJLE7n0MQqX0UFc11usMAAHmyWSCnZ0dKKUwHA4ghMCbb76JTqeDdrttHYDL5doA8xhRFIKcmCu0WokRkKlt4vLFxYVlOfA+22A1aek0w+HQYgEG/wxMAVjDZDKZWK87O6SZcRIEAeI4tnK0LOvKn62M2hPR7CIL2PM8t3K1jO0AotZzzQz+W7fbtc42t77W/u4utNb2XXKki6MQrtQsj2u+Jt+b+4SjG5yvzDUxdnd37bNJKa1yFhsM/F3uayGaCt9EfwsvOcu1JgZNVZUmP8fUZZISWZ6j1+2SgqJShJe1RhhFkEJYmjw74dMss8EBaODg4ABZltli3Z1Ox9LKBoOBpbz9RiMaF+en1nJVSmE+n+Ps7IxCM0bqLDE69d1Oh77reaSb72zg/DKqsoTHXHur99sUtarKwg6G2WyGk5MT7O8fYDDooywrlKamBNBYxUIKq2vc8Esp7FmkGSToxaVpijCKkJhBLQWwXq+MQUHW2nQ2Q+AHJvlZ2MHmG47jbDrDfL60kRyeCO12eyNDnzWluS2r1RJFkdtoANOntNbWW8BJVrPZzCZHC6ERhBRae/bsmY0ikecB1huT5zlWq5WNHHGUQimF8XhsQ240cUimjpLWteUnlmWJ1XxhJ2gcJ/B9zyaGHRwc2IWDgX273cZ4PEaYRFA1sFikmEwmIAEtMtSCILR8P/bmsKIXT1xeEF9//XX4vo+zs3N0uz0cPzu2Os98v9u3b4HD3zyu3FCgS5lzN4bp7ILCfkpiNlvjzV+9ix/96C8xnc5RCo1KVdbIUFYOk+kDm5t5EARoJS3KKXAWXr6vm5+04TE34HVbB96CBUhoSDQCnw548nwI6ePuyw9w/+VX4cctVAooKoUwJE+IVeHwAwRhgCiM4HmRAbQCQkoUVYmiLKlGS1agLkvESQs7uzvY29tHp9VBlq4xn54jXS5w+uQTfPLBO8hWM0hdQQoqM6iUkfkVBISEaN7FtpdSCMf4cI4mMsm6841HliVZLdWSI5LXeGa3Af11KPyqv7qg7aqIy1X32j73quu5/fC86/F3XI739rW5r7apUs87Nq/D53z6uZ+WGH7d82zcT8Aamld99/pDXvmStr3dVwHQq6KE9FkjTOKOSQBglTC+5iYd6/q+cuc1/8793ID0hrpDxqqHIIgs9YFpE0ylBWAj/1xziCLuFYm5CY7Q1dZW2XwWpiwKUJ2UwHkGbZ+J8hAaUe/G0OBnv2woWWNbYqOfm34XUBqOkeBSo9112jMqbUAYRiirzF7T86g2URQ3Xti6qtFqt7Gzs4NWkkB6Hvb2drG/18f+/i5u3rwJz6P98c6dO1aeNY5jLBYLC+qY6ssU4cViYeVa67rGakURh/39fbuO8r7I8qtsDHBSL3Pzmc7NHnP++2AwIEorCACfnZ1hZ2fHOquIUkVYJc0ylJa/DytmszT0Z9/3bS0DpjhlBiS6+76LQ3g/7PV61oFIhpm0yqF1XePw8NBei8ci7/PbXn6gaZurLsr3T9PU5H5Ulup+fn5uJVW5X9z7cY4CRyQ4arVarbBarRAaqpdbJoHn6ng8tn3ANTUYU7IRw1EXNoLKskTgU920beoVX5ejLE1OprA4ht9/r9ezlcM5WsCGUGhobzyOORmd6V97e3tYLBYbObRsjLCokRACraRj+5nFf3iuTiYTK/PL68JqtTIUc3+D9uTmtnC0iPcajg4ppREGDVbjI0kSS0Nn7PoHf/yH166Ndu14UUNjdHG2kYhiPXWa4BBJzta2M9njLnzPDno3j2K5WKLX6diHcEu7+55EXRaYTmcYDAb45JNP8E//2T+F7/n4xje/geFgaHl3cRKjLAp0Ol0slguMRhd4+uQJPM9Hp9NGEIQ4OTmBMKXqp9OpLRfP8mndTssOTpYNi6LIGglKKRvuHA6HAIAPP/wQs9kcb7zxBnzfQ1XVRrnJtyFOCr1SATmetFqT9BwDZqZ28b+5Hex94MHR7bahdGUX/H/zb/4NDg8PcffuXSil7KBzQ39SShv+5UnG3pwwDG2uBgDLE+SCLKiVTahjo0gISv7f3d21oTS+hzWa6gp5XmI8mmEymeDgcB+r1RxlWWCxWKLf7yFJWjbUW5aFuX9hvBikXiWEMFYzy3xKsyhHVkWDDE2BPM8ACMxmM+zu7iBJWiaXxbOUtiAI8PjxY5P0WyAMQpOQHkDAx+npOX7+N7/AW++9a6RNCUTTNtkkQDbO+Ibe1W63IeHZPnCTxNz/3I3aeskdOoD7Uzv5G5dnrUleFxJh0sZLD17F0c3b0MKD50dotcnQz9IU6zS19MS6BmpTjV6BFsEoidHudhF1+uRFC32URY50vcJkPEKdZagXU0wuzvDxhx+gLnP4QqOuTK0ZIdAkQVKxQ6ZLuQU9N0Gd8+BonAG0KbD2/GZ1cP7eNqi77ngRI8Htb/f3bXDvOi1e9J5XfXYZvF597kbEd6udLrC7Dmg/r22f1dDYbueLGjZbV9kYyi+05WiAJUbNnTfGUAOk+bONVjq/c7yB/iBls4dtGxru2KP+d/vtxfIrNg+KWPq+j9jQOhhwBEEE3w8cAK7s+sHAgp/TzXWEoLwtIczaxNE7bqeUNlLI4InqGDXtd/dwkhW//D7c97zd70IYY0Tw9Wps5D6Y+czRI8oxCFCWpFQYRSF2jJBIEITY3dnBfLHAzZsHuHXr5gZffW9/D2VJDr7RxQU59uIYeZahY5xweboybARlVJXWVgGTnVhFUaAoCozHYwyHQ/s9llllXjzvaf1+30p7UoRgSE5J2agNRVGE6XRqwb3v+1QE1MzdsiwtkOY9XQii8wwGA0RRhPF4DM5ljKIIyyWJ7jBA5vbzGhoEgcUibGSwihMD9TiOrcecDRnOg2AAv1gsNvIJ2CnKIHs7J2E2m9ncCfayc35Cq9XC+fn5Rr+xRGoYhlitVtZhyu+CwT/vD2yIsMEhRFO3ix2SLP6zXq+tIAAzGZiixPkQ3Dfz+dzOp06nYytasxwwG8i+mV9VRWOU7ws0NCWW7u31ephOp3bvZ+cm0+vG47Gll7Fzmg1efnZ3X3QNFjZU+e/sJKXcVKpFx1iOnRRuVMTFH3EcQ0Oj1YptkWyXYsjjkfNsmJ1RlqWptxXaBHYe92wAAbAO3+9877ufvhK+qKHx7PEjoj1JVmSQVgdeVZtqDFycb7gzhIJCXVWAaCooF2WBR48eIc8KvPzyyzg+Psbe3p5VJ1BVifViiXVKA+rs7Aynp6d466238P3vf98Ue6tsJ7CFxdV/67rGZDKhqr2rFe7duwcobSc7l28HSJ1i0O9awM0TnQcVeykA4OLiwg5QDiOdnJxYziAvOCyvxguVWxzFXQAfPnyINE3x4MGDphiKmdhuqDCOI4xGFyir3PInT05O8O677+Lg4ACHh4c2aYi+H9uFc7FY2EWBFwnXipVSWGMiCALM53PibUriK/L3Wq0WgiDAzs4Oer3ehrfAGjSBj6KqcXJ8hqKosVyu0GpFWCynkFIgimK7qLnAiRdL1qRm1YV2u43BoI88T9HvD+zkklJiOp1iMNgx9/cgBPDs2TMcHR1ZT0VZkDoWyfLNTZ6MwMXFOTqdLnZ3yaPEUZksy3F6McbJyRn+5hdvYrFKUZbaRBcEIGqbP+JOGykl4jCx9+XJbyeZGfvbNBpoVjDSlwwRwAPEJiglcNkU1RLSg4ZErYEwTjDY2YEXJOj1d9DtdiyPlbxZCmlG1EKlNbQAur0ebt66CekHWNUU1ctWS9RFikBorJdznDx5hMnTR6Q05uQCbHqEGWCwqla9Ac4vgRY0wQg2GhhQUQ7FNjf7RT3gVx+f5fzt+34WYH3Vfa4aK+53XcfMde246j7bXv1PO/cqQ8O95XXnfJbnv/a+4vJ8aD7fvoZ77tX33jQOrqbVbI+75mAVo6uMOFoPXc8mXUdeaud17Wraro2yGkkT80eNE4K8+Xyea4jynNgeG+TdbZKYed3YNujdfmn6YlNGmz+ndWfzGfjenifhe24UBCYqYxSUpEBVUQ5gq9WyXvEwDLCzO8Th4SG6vR563S4ODg5QliV2dmjNZilR1znjB+Rco6RicsRRLl9TKyJJYkwmE1RVjV6vi6qqsVwsbX4eY4HFYmG92p5HFayZDsQAib8bBIFVRWJ1x/F4bOk7vO+sVit0Oh3M53PkeY69vT2TP9kIgbAjj/f+druN+XyO8/Nz3L59GxcXF1itVtg3uZTSwVO83zIglFJaUD2dTrG/v7+RUM3vMTWCJ0VRWBGZTqdjDRyiiKe2ja4Uq0u9Y+wxHo+tUUOO0Q4WhjrPuIQTgoMgQL/fx9nZmX3e0WhkDQGWeu10Ouh2u3ZsnZycWKlbdrQypmLDjw0fBtscQWIcs7u7S9LmjuTvs2fP0G63bTSFoxGJqeidpqmtTM5rRGkoRJyLkiSJVZdiA4H3M46+bHv5GeSzo5oVqzjaxAYRG3FsfPDhRoU4osFGCtOwVA1r7HNERwix0VcsFsTvQErKqeX1zJUl3o5EseIq7xFFXtrn4D53VWbZuPr2733n09fGFzU0PnrnHaOuRKEm16NdlxW0UpjOpuh1ewQ8iwJRHKJSJUajEbTW2Nvbs9dTSuOjjz+xobxWq4WzszPcuXMHvhB49uSJvc+NmzdxcXGByXiM8/Mz3Lp9AwcHhyjLwoQPSd1hvUotT7MoCni+h+WCknb4HszZawByhiSJEZrBwwsND0aOOHDokUNpFKIyMpcaJg+BFvMois1Aqi2/VBtuPFXTponNL44XXKWoiA7Tt9jLS4OoQq0qpOkaWmt87vXX8dabb2I6nVr5O7a62djgBYSjMrwZsbWe55ldeNzEpslkgtPjYywXS9y6dQv9ft9Gm/i73BecyA9QjZGirHB2NkaaFnjn7Xdw5+4tSE+be3nwpIc4jsz4CRDH5NkjfmiIsqysN6jVaiGKAnR7HaTp2ngWIruoVpVC4IeAoKRrTh6bz+dYm8rNnkeTrlY18owMteVyBaUVgoCUTBaLOY6ODuF5HsbjGSAkVqscJ6cXeP+Dj3F+MUFWFKgFSa9eZTAEfrjB3+QN253Ul6IWGpSLAGyADHoXHoTcBA7NtSnWUisGZhKQnpHq9eD5NAeOjo5w69YtYygLFEUN6XnI8hy1VhCeRBTHiKIYGgHS5RKj81PMxhco0gWy1YIka0VpqkkDtRbmpqSlL5xIj1IVNNRGZJO9LpuAUFtePI/L5hmVMTawcd51IN79ntu/2yD5b2NsXAdirzte5B5Xtemz3m8bgF4Fsvnn1f3nRjWac9x28JpxXWTFbcdV7d2kzjkEQNFEB7bfkfve6KdbDdrtH2C7/dc/C63PjSNM2h7gOIf97kYVbEM74ntp6RgeLMUMKuQoBTYTSprztL6cTM9rwXakjD9z/3M57EyhIrCwKVwCsNeb/q3Uppw2SYN7G/3bOC6o3WEUottpFB0BjV63g3v37gIAHrz8AH7gm32qj7IqkOfELHjppfvw/QCTyRhxFMEPyOtflRQhD0JyUi0WS2gTgfcD8qIHfoCqprVjYKhMs9kUnueh1++jrioslyu7N+3s7jSqPGGE+Xxpab/MQsjzHPv7+7aSNAMldhS6NSF4X+N9Z3d3F+v12ibkDgaDDS88e3iVUphMKIez2+1iZ2eHFBrTFEmSYDwe2+Tv09NTS63megfMfODkZ8/zcH5+bnMQ+N3WdW2NJpa63y4R4FJ12Fhzay3M53Msl0tUVYWDgwPrWF2ZatL8TJYebkA3g2XOJ+D8g263a//NY4xp41zQjZKUqd+Ojo6sY5jPYScmO255v3RVlVqtFhUGNkYUJ6RzLgdjOs75YAOPndb8ngDY53QNBb6/NmOAjRI3gZ3nq+tYdalX/Px8H8ZGPCY5OZ0dzpxEz31eFAU6Jt2AI2VsIDUOSpJ3LovS7pn8PFprIxIEi19dI6SqG7ElABv/dtvDRlVd11C1gucFFi9ypIOVppi943kevvW73752LebjhQ2Nf/mnf4ogCJHlGZTh2MVJQtWijWTYYrHAcDjEwcEB5XCcnyKI6GW88+47uH37NnZ3d9Hv97FapVinVAnyzp07+PWvf435fI5vf/vbyFZrzCcUUhwMBvjTP/1T3L59G1/8whdQlDnSbG1UoARWS1rE2q02pPStepPneVgY2dM4SXB6erqRYMQLTFVVSOII7XZro8Ijv4Sm+JtnJzJ7AXxfoqorsC44GzBaa8RJbBK7TGJQFEIK5k/W6Ha7GA6HmEwmmM1mdmLu7e1ZK7aqKmN0aBRFDj9ouMccIuXkJZ68PBAA2CgBAMzncxtR4Qqc6/XKhgf5nkEQQAqBOIwsZ5gXsu1Nj9vM7VinKc5HE8xnK3gywLvvvovbd25hOOxBCI08L2yIMIpiO/k5qsIelyzL7aaptUarlVASu5RmzLUNd1Za74qUng2ft1otrNfUb2zoEUWLa7TUZtGmInaLxQKr9QpVWcKXFEmQno/+YBdpmuP45BSL1QrLIsfCqE0I0RRFhAYEpI0K8QLGC5NLHXI9WIAwFaQbzwaPM60lIDaNE8uXNDQlrZuk3MbzSnQmAlZNEckgCBEnLYQReWdk4EMDKAyXVhc18jRFXZYQugY0URh1XUP7VOFBWSoJGxvM/xbEIde86TReV9coa45NSenGg0qGX55ndpwBjZF1ndd628jgc57n2d++zm/q+NtEX667/1Xe6au+4wLr7ZwKPn/bINjm3m8bJ26fP69/ntd2225xvWHjfqUZy9KO7Re51yZVqjnf2gh2LAhclZnOxoPS23KtxgEgJLhbORpC87TJhdjsp8YreP1za7hzxHUk8MFA0pVrbeb81e/FdYpdN2f4e3S9Gn6g8MorD/Af/b2/h/v375OhERDVKfLIeZZlGUajC8RxjIODQ8oT8QROT0+wWq2wt7dvHHONbDy0RlGWCA3dp9UmYY52u23zyHiP4rkfxzGOT04QmL2nqT5NyaycLM2sgDwvEMZUf+Pi4sKCrnv37tlK1WmaYj6f2yg5g7PJZAKgAZtuwm+WZTg8PMTTp08RxzG63a4FtSygwp5zVnJkI4QBODMdtKYaE0+fPsVwOITneRiNRsjz3BoYHDnJ89yqYDHtaDQaWRWoOI5tnunR0ZEFkxzp4OgG55GwNCwDYjaEuHYG9wWADaaBCy61bmp5MaWNQfZsNkNRFDg4OLCGBGMm3gNbrZY1ErjPWdp+Op3i8PAQ0+nU4ic2gpjq5AJy9txzBIHfB4ANGXsG0FwlnGng5LyMNpSUhHl27ThjObrDSlmseMVRIn7HPMcYEyyXy42iwdy33C53T+T+ZTYLGzEcwWAjhZVcAz9EUZR2/eCoEo+h+XxuxxxTI6lOGuEIVstiRwIXUGTHLcBKnhJlUSIIIjsW2CHOKQCc6yGEwO/98HuX1qHtw//Ub5hjfDGyIaROp4M4jKCrGlAKy8UCs+mUPAZBgLTTQV1VCIMAUeRjOOhhPNpFp5XAlwIPP/oQWngIowSz2Qzz+Ryz2Qzn5+fGK5Hg4fsjDIdDvPfOu/jtb3wTv/71r/H0yVOs1gu0WhEAgSSJMRz0CWiXBYRQ6HY6NGiVwunpKfb395EkCY6OjjCfz60qw+HhIRaLheHakRW9u7trJyNbpMwvZM4jh6YAjVpVoMRXAlpCaiSG51kUBTrdzYlcVRXyIke71bUyr7xossLGeDxGHMemEA8tYMfHxyiKDIdH+9aIYm+AGw7jxYgnS5ZllorEsmxc9XE8HiNJYht2rOsai8WCcjSWS6iKrOnhcIg4jk0y/r6dTBwmZO8HAGRphvFoDAEf3cEAWgOnJ2eQEoiigCIQQWg0tleGs7i0Rgx5Iqi/0pS9RhrpukBqVCygJxAmiUoIbRdT7l+ewOzV4A01y3NbCbosSeK0qmoD9Anh1FWFQArESYzDGzu4cXiAwXCIsipxcn6Bp+djrNZrnJ2dQQiBhw8fNl5f1UxSd7HepkS5fGuuJeGCAb6elFzw7gqQKSQAD00WCYiXrRVFCjTgCfK41kUJVQqUmcR6uUBt2lRr8sRy0rvUygAzDUhK5sx1DeEBQvoGNyhAsNqP8fvqJiohzB/5ma81EIzCDIMhF2RVlbIGp+uNsudeAa62gTIf13ni/395vEg0Yvu7nwboX/Sam6AV2AbAzb3FpT5zDYPG2H0+dep5htCmAeRq7W0eDExpblRm8zI1FbaA+vPe7aXICJxoj3D+fgUdy0YpsBmp5P6kPt2sx0Q/udL185/9qs8t/VGIjXFO+Q7GiDfXCKMQTS2ehmp4VZ9cbuPmO97+PYojfO/738QPf/gDxEmMxWJiZFkVoAA/IS91r9eGqkvkRY7ZdIy9gz08evoYZVHg4GAf3V4Px8fHFHX2A0BrtBKT87dYYr5YgB0rnvQQ+AFKr0IYRhBCYjqdwZMeFnKNXptosgg8FHkNKSSynHjqZaGgaoHFfN049VrSeli5yO2TJ09srgLvo2maWgNBKWUjEFyAjvdSKaUFa8z1r6oKZ2dnltqjlMKzZ8+s93g6nVr6Nu+9DAY5qsDAmyMv3W4X3W4X0+kUk8nEYovZbGbzB9gBA8AmFbvRj7qurbORKdRaa0t/6vV6luHhSseyQeRSaJgmzviHnKnktebnY4oNA+LBYEBec8cY5kgEACwWC5v8DMD2NQPpXq9nPeWcT8JGBUecGIsxJZ3mCY1/Ni74vmVZ4vDw0PZjURSWNsaJ0pxEv/H8ZWkTndmByjkpPE85f2o6ndq2CNGoU7l7Fb9LZpawqICbp+zmpzAmYKNCCGHpYHyf1WptxxInmbOB7Nbw4t+5v2vVKGCxShevITw+3T2b1s8Gi/DY4XnD1D63ePanHS9saBzsHyAKQwSm0EiZU2hKaEDXNfZ2dhBHAaBrPH32iGQXAazXC6yjNXaHu8izHLrW8ETDP+dQHVNynj59ilcfPEBv2Md8tUBRFvjLn/wloihCu9NGu9OC1pVdjLOswHw+NwXmtFGM8FBVGpPJGAcH+xiPR4iTBEWeoSqJj5dlKSlXRSGkRx4cXqQAWEuy3U6gtSl8F4fwpESapVC1QhSRp5iSswIUeWGAnobQwHw2RxgGyA1PtK5rhEEIAUXe95pqc9QVFeWrlTaSwAlW6yXKiqzmg8N9VFWBqiqsYUJqIdpUfw4wmUwNhUyh2+mS0ReFAEqKRGU5hJDwfZLS7XV78H1pF5nA99Fpt3F+fo75bI66ookznRKtqNPp4oMPPkIUhQhjKszTHwwoJ8cMvDTL4Asfq1WKLFyhyDPk2RpaUUX0JE6gjHcnyzJMRlSxvChyxFGEWtXg6t9aA0Weo1JAmuaAmfzsqa/qyjpKXcDje5R8X9c0RoSsoeoaSjdGSRDSRC4qoCgqrNcpiqJCVZbkyQ98PDkd4ae/fBN5nqMoC9RKoVQCVb1Z3ZvHOQxw4CgYT/ptQ8NNbtYciZBNfhNRqZjU0UxiBo5SClNjQ254DpvDfMdQRoAGmGhQ0mZdk8GglYFyWkAIE1kRArbshFlwKPXCJJha7zHTBjki4wA//smPwK5qG41pjBCltTUAqaaKcsBdA5Q/LRLBkasNcG3vuQn29EZbBa5fKjfpRsL9q27+Ld17uR3gnEXnbAF320HCXlNcupbYbIpwW9L8bgG1BhmD9vSrDA1s9IkFn2gEHzgSS7QgNgYpaia2zuMxZucjYI0F+s1UlDZtDQLfjk0IwPMkPKMGVfG8hUBZ12Z4O+3mqMdzox2sPNdUgrbJ3FLaa9rhYSSOJVhi1bOfxTHLka5QCS5AyZZL886kFKhqKvYppWe+oq3sqx0j9p0o+L6HKAodj2GAXr+HIi9weHiAw8MjxHGE4XCIu3fvYjqd4c0338U//+f/0lkLm6FByd+NkdhETUiO15MSGqQKp6Fw+/ZN/P2//x/hy195Dav1CmWeIwoCdFoJUZw0CZeMxyNI6UF6AoHvoShzLJcLxGGIbqeNsixwcXaGVhIj6HWpbo2mJPAiL6A1sLe7h6qqsFgsqW5Pq400zVCVlZXIr4VEu9NFnmeoqhpRHGG1XCEMiXYCrdFutVBWVHQzN6Cs02pBSInj42P0ez1SNDKMhjiOsTR5ipw/oQ3gZ4rVeDSyQMzSgj2SArVOO8/DzHiMuXgZ5/ZxRH93dxe9Xs8aL6zMyJEI/oxzRlyAyJ53nqe8BnKOAxsL7FEeDAZYrdaYzeY4OjqyALOqaqTpEnme4/DwEKPR2CplTSaUwBz4HlrtNrTx6AdBgMLsnZUBqKWhKiVJgslkAt/k1yYxebaTKIE0qqGtpIVWK7HgnZO3eYqkxnMupURkVKJW6zVahqLE9+wbSVchhFOjS2F/f99SpsqydPJ46DvM1GCFNq5r5iqNhWFo6w3VqsYyWyKKI4r6ez4gfZQlOwoloJV1htZ1DSk85HkBLiiZ5wXKooCQYkNZig2nsiyxXq2RZwX6g75dzuM4wWq5RL83wDo1YkDSMzXZQnjSR1VXSNepiazliKMYnu8Buimyx+OGc0KYScFRBsYe7JwoiwqZytFpk0BSVZKRr7VuGCSGqSAlSR/nWWMkc+TIlf7lvKwXOV7Y0Dg8vIHSDPS6Ujg/P8f5+QV2d4bwJDCfU2QAQmOVrkg9yA/gCQ9VQS+wnZBFtMpXCOMEnudbWbA8z21YrSgLtPtdREmMLM9QViV2dobodNom3NqxD2yWWAhBVZiDgAHyBGVZoN1uWTWHOI5AVbZXCAIP0AqeRwlXkyyzcnOsokThqBnCKLChMAaSQeAjTzNAaUQBDbKOUcvQiry+sfHSt5OWHQir1QqeBAJfEhddCGhVoiwyaAjUlYeqLECFhaimR5HnaLUiZLqCH8cIwsB6uGCAWhIlEFpAQiJdp1TJPAA6SRvrNAUUsJhRBOfRo0cAgJs3jyBA9UNmszmCgLwAVcUqIgJVpXBycmY9K9PpHKt0jTiJTbKRh9HFBSXPa4Eya+ogqKrCcDjA7t4exuMxxmNa6LIsQxTH8KRE0kpw4+gWdnaGiJMYN2/eQttsHGmaolIaUUxJVBwins/nePLkCX7x5q/Ia28MHTYu2NomTzsrdxhwD0DBM4Db0Av478YIEFUNZAVtNNzHYC++C9C2CvGZf1d1TaWtnPwEBvuup1/regNUA2R/82cWQNr7GZCsXPAIAJyQDQPcHW+uA4oY8toram17RRv6FzTFShpspwFDKSEQ1fDLlVLQipWiGISKjT5qak+49J4atTFqBAAYj26tKEJDz7KJJJ/n7deMZx1Q35wu7ALaPM/VgHvz0IC49Jfmmg49RxhvlGvAXLr+FQaP6xlv3n/Tv42RBStC4I4VvoZwnr15zy5l6IonuOq5jXFZlCzvbHIkRDOehLNlNMYEIISJdm0Z/gCgFSVF89ivKt08l6birEI0+RHUnVSLwYbNttosn+NIo67mfAXljNma4iSCZV3pmkqTl10aY0NKCWGqUFdlRXWddI3Ap8gG1dEwid2yqWwdRyFqYzR4nsRg0Ee7Q7WBAj9AkiTo9roY9Afo9TvY3R2i2+1gMplgf5+i1azuQ6pIqeX0J0mM0aiNv/zLv4YnPZSagIbtHzYsTR0q8pAaKVmlgVrDE0Rz3N0f4Otf+wq+891vodNpo8xL1AV5utfrNWbjufVgTmdTqu+gFDJDaeTchTzP4WVNPQQBAVUpm98wGl+YZyb+fRD6CKMARZljna4QhD46XaIfrdM1+jt9q/wYRiTLXVY5jo5IcnU2m6GsyaMeigB5mUOjtlGLKAytPDw5jTRKU3eqLEsMjQLUdDLZ8MBXVYUVgH6/b1UXGUSVVQWYMRoaGvbMJIMzS4DpWazuxyCY6TVJkuDi4sJ6gKlu1NImpHNEi3NQuPAxU+c4ksBRjn6/b5ygHRsRYn8T46BOJ8RkMjUGSokkaaHToaJxcRhQQeQwpHIAZQkpBKIwxHw+pz4pS/ieh9VyCWiN/d09SzkWWmA+m9s16vDwABAmWi/IwNSKhG1iMzYYU9WGytUxFG8pqNhhnucYGeqb1hpxksA3Hv3JZIJut2vHGQPeNE03alUAsH3LydeM/aIoQhJSAUWtNMIghK41FBRmq5mN5uT52iaoe9JHVdY2b4LUsKR9L5STSZiBBQVYBjmOE/htUy6gqJClRHNK6wxaCywWS+soqLWCJ31obUQBhAS0gFKA7wVQSmM5nV8aV2y8cbTM3TeYpkXJ74XJVQoxmcxM7ooHrSif2MVL7Xab7l03EsP87tx7NGvtbzii8epvvW49j4vVCn/zs59hMpkgq0vISkELAc88sO8HYFUN3wttwtTe3p61jFZphl0zENst4m7eODpCv9uD71PRl7qkPIWJWRgePHiAbrcDKtDHZd49JEkMVgvJc6LYvP766wBgDQdWNOLD7SyW0+O/s8e9KAqk2Qpd2YVSMInMxM+bz5fI1hRi7Pd7oKrhNTwvgFKVAdQ5XHlWpkhlGYWuKKmJuI+z2QzQQKvVhiqJ6uRBIgkoJ2Q2mqHdilFVJQKji5xnxPHM8hx1UWCWrqFq8lJ4vofR2RkuLsaQkvozL3IUeYHHjx/h/PwcrVaCvf099Lo9a11DA6v1CoHvo6xKywP0PZPDEYYIgghHBzfwxS9+EUopjCcTlEWByWSGn//8F6RyFcf40le+gpu3bqEqS9y6ex/37t/HrZu3ID2S82u12siLHK04wXy+wGQygZQSo9EI0+kU63WKi/EY4+kE5+fnmM5mqMoKs9kUaZpilaXGQ6GgnPApAzR3M+FJoQ2A0qKh+7CBsE1DsJPILAgul/qSZ9qZcG5+gU2UN0aNm/jvHttUh+vc7GQUkbm0HfXgpmxc51MOgasXi01Dpjlco6mRA71asrUBoU1IVimFygkzuxJ9Qlx+nhd9CJdm82mL3zbN5vqLuhElt8oyrAf++fSixpC4Sh51w0DYag9TiujX66M7z3/PZIE1/Xr1ecLJBQJgIl0+pODoGwFUwdGJjfbK5jksrY7ft/m7ZyIGjtiBTTYHNkQP+BnpMxNvEnLjM/dduM8jTWRCcOdqp/aK6T/f4xwC+kqtFHwyreGbwm9cT8PzJOIghFI1Yi+0qnukhjewm/3du3exu7uLw6ND1BXlL5ZlCc+XCCMPsVHbY08l0SZINUlKieFwiDzPcXp6ips3b9r+mc2maLdbmE4nGI8V5vMFTk6ewfMFwsi33nZ+fipqWcHzaNxEUYQojtFpt5EEMe7fv4fPfe5V3Lt/G3EcYDafYDobW3oH5wecnJzY/AP23jMVZnd3F57nWQVGBoDb4ilMO2ZvMl+f6Sicf+jWIWCREq55IKXEYrHAO++8YxOYmaLC+y47njjPgRN9mYPPTAnmzXNUgx08PKZYBtXzPOzs7NgcSevx5xoP5m9ZlmE6nVp1J85BYM82ABu9YDDI+Q0swMLeaCFIYnS5XGJnZwcAbC6lS2nyPG+rThblTPL744g9KxoNBgObv8ny+UmSIPAEioLmAyeo877ECcic4+H7vhkLlBPJ+R78fmxNjyKzCe6e56Hf70NKaXNDi6LAcDi09SLcSIRLMRqPSXJfoVFi4qgC59C4HntuLzswuZ86nY6VAebclXydb7xzNlKYus00Mf6+1tr+fb1e29wU7msIbdgzlS2XANNu32sEk3gNWq/Xdu1mFSy+litGwGPY5pAIYfKaV5dyOhhPuzVd3HwjHgtER083cpN5Dba5uaY/3X3GpUfxescHR1Vf5HhhQ6NQlbGWJVrdNt747W/gvfffx3q5hKwqQ02hCoSeDOCbjPUszXF2dgZO0u12u7h37x68IEBWlqhVjSD0MBz0MR6P0em04BulgyLLsbu7awfgm2++ic9//nWEYWA7lWtiVFUJSggurJfADeXxC2VuIicLMUeNcxl48V4sFiZUmWE4HKLValFuShxTAs2ghYkaQwhgvU4RxwnyPMN6vcZyuSRjarWy/DbPo0qefhCgLMlAqkwtApZuWy6WkFrimUla75jidfP5HKquEIQ+ojBCr98DDC1gtVqhqApMZ1Osliva3EWjt12VQFGUyNIMRVkgCEL0On0UWYlur4f5dInJaA4NIGF5MylQqApRFCOJ2/B8D1JIUueKYnz7O7+L3/3+72M2GmM0usDrr7cwGA7x0Ycf4ead+9Aa2N/fN5Y39fX5+QjvvPshfvXm2xhdkCGhtMJisUC6pqrizCvkd6u0htI1FNQGmGV+P6RRftEC2lTYrrWirGXBPwxfWze+fK2aOjBuhGEbyG2DH77/9sEwrvHYbyrC8FR0JW55Qrue6w2wZ/+HK+6rnZ9NbQ8hiEK0bTBddzxvkXDPc40ulwoGiA0gZ5PVnXa693B5rG6fb/DK9aaxsf0urnwO83/LLnred6/47Kq/acdLTN/xNiM1zwX7n3aPLaPyCuOKATxHipRqjB0pnLwAGzC5qp+cSMSWoSOc0EcT+SLDRCvOL2oics13LhtGzT2bsezmEFCVaNioqJsMSUNYbEbvNOAJijRACpvLZO8pr962OOLjS2k9jXZMmKiWRgU/ILAnQAXhWq02up029vZI8e/WzZuIkwQHBweQQuDwiJKfoYG7d+9ivV6hqmqbaMsgoq5reEmAKPKgUeLx44+xuzfER6MRkjiG0tomkx4eHDURVAckPnnyBDs7OzZpk2XWoyjCYCDxwz/4fZycnGM6nRBt18i47h/sIwgE4iiCkAI7wx1bsyIMIvQ6XQCaJKzzNa2NQgOoLXBWSuHJkycAiDJ2cXFhcxC63S5ms5nl5tc1VY8OgsDWKuJIxnQ6tUCu0+lYrj2DUAbPrBLoSpazscB9w1KuHBlgsM4UIo6wMAC2ibOGCs3vhgHjrVu3TCFZWre4BgODbVeV0hU/YV5/rZSV6eXrsmHpcvknk4k1bhj7sOQqC5i4uQ48b0ajkZXa5fni0qcYnFN/tCxo5EgJ/2RqjVIkV8t9GQQByjy1z8Y5E9yXLMfLXvxGCl9DQFrcBDT1JYCmSC6v5zxuOZoBwIrq8Dt3cxDYSOHkf61YpbOydDZuKwNcHgucgM70Ms6jcR2DYRBCBo3aEs8pxoZsCLu5HfzOeHywAcv9H0aBVRhjSjsbyuxo5qgAS9uyAcEiPdwnbKRwxIavocx4Y2OIxwXnfPDc4X7i5+CDx4DLAOKxwREPFjjiOcd9xPQ+9958DzaMXjSi8cKqU+s0bfi6aDa0bJ0iXSxxcXaKk+NnUFUJKSTarQQCwHgywc9+9jMcHR3hS1/6kh0My9UKvUEfk8kEw50dUq2az9Hr94kHmWeIwwhVWeKf/9N/hsV8jt3dXXzhC59Hv9+1CUY8ANfrNebzpbXCPM/D2dmZ1XPmhfDGjRsYj8fWklsul5bb5+or86Bgi475gJyknWUZstXaTpQsy3BxcYHhcICkRcaSUg344pcdhlShtVY1OCk2zylsJYWErimcyNZzrRTOz84QR6FTx4Q8qsJsxrVWWGcpuMoqDTAPvu8hiTvI89IuUFEUEZ1pdw+lUgijCL7nYX9v31YnbbVakD5tWjyplsslqTOlGT54/2OkaYbZnBL4szRDp9vBdDpDXhZYrdZ28SIeviLZWmyqq2gQzUcrE/aVEtL12AoBCAVtKtfawlQMZrSGMkYE4yY2UOgGDdBtOPwwHOzLIcDrJs42iNv+jt6aE9sgNDCLMB+uwoT7H3+fPa4Mzi61B6Kh6zjPSDSUzYrH25+7x1Uecu6Dq9Witg8F6dBqNpVu9AaQ5fGvtSkYyNQrHgt8nm7G8HbbrzL4GgAqG/PLaf9VEYfta15/XH2eC+A3/84RoKbvXA+am3DnLvyN0bV572YsGE+9jRxsNGPDwL36cUyUxJNWTpnbttnHytynKSC33T/X9af7H29uzbhqvn8p6VApCG0MfjSGP4khUD/5QTN/GkOXPuf1QmvA92nT7XYSaEMD6HS72Nvbo5yyfh9xEuLGzRvk+ZSkYhcEAfb3dlGWKZQmQZEzI0wSxzE6HUoiZXXAXo/2KKrHQ4nBQRBYWc9+v4+yrJDnKWazqQW5TE0QQiCJ21gsVhZsM8BYLpe4efPmhpf+9PQUu7u7WC6XWK1zHB5SraBer4fHjx9T/mK7jdVyisGgZ72rs/kct2/fRpHnkCYqBWhkWYowDKxXsyhqhGFknW68tzJlgkVEdnd3LdjiqD+3u9vtYjKZ2P2R997hcGiVkHgPYnDMIGZnZwdZltnEYQAYDocWBAZBgNFo1OxNspEbpXpKAwve5vO5NTQYvLleZXcdYZoaJ8VWVWXlcN0EaiGErccxGA6xNPWtXHDpgmcGyAw6+R6PHz/GwcEB1us1Li4u0Ov17HtloR2OJFFCPknw9no9W9+LDR6idsUbylUArGHG32fg7NZw6LaTDREXpuCwR9vdA7if0jRDnhXY39+3gJOdpBT51bafWRHMjTYwvYjXFe5X3oP5mrxPQDZKl7ymMBbjhHVWL+MoGhudLq2KAbEQApEfWaOev8eMF5K9p6J/7IDmdjGWcQ3eMAwhJK05HE3hOV6WJaIwRlE0haq5f3necL8wwOffuc+4IDVHwDg5Pcsyy/zgaB0bCmyE8PNxWzjyxHOP11L+t+c10tfufzbqbJ6bI418XZ5bv9GCfbPFfCO51Up3SgnPbKyffPQhnj56hDLPEIUBVoslPvz4Iythyy9oMBjgYnSB1HhRlqsVppMJ7t69i7PzM+ztHyBpt9Dv9rBaLvHzn/4MH3zwAXzPw6uvvgwhtFngG6WSqqKaFes1hbw4EYg3ATY+2PrkF8o60taLrpQduIvFwuobS1OngQa9wHq1RmD4j71ezxo7WZYaLCyQZakNuzUKSGLLwpfGG8JeTOK5Synh+R6SmPosz1L0TLJUFEYYDPrwgwCelNjZ20didKjjOEa/1zNh0hYoR4Eqm2ulECexfXfzNMVoPEaR55jPZlivU+R5hvPzCywXC8wXC6xWSxMJyu15Gs6CZPn9hjLEoMXACwusjLITxKaHnHNNuM+EYE69OVcoy32/nONwmRW/6UltqktvHBsGiNr6aAv44mqwv33OdYYGe2ZcFREGma6BwedZw8Pw4683NPhetstBijRspDRg2AV32895nTFyFcjceF5Nm4sUTf9t9KXgCEsj3+vSpTSwIf/nPh1XHHYXu21DY+MQDMQ3Fb+2n819Xr62e383WkP9xlWkdXMb2wdXA3Fqg+txb+hLTOnRmvKqhPterhpjDNydsaA1NsZMM9P43+7pm8+9OXf4Oq6BTc/Mz321cXe5P507XuoTIRojf9uwAcg89NiAAiUuWiNRKEBqRGGEVosoN34QIPB9eEFgo+NM39nb3UW310UniZGlayStFjqdNnpdUt6ZTCbIytx6bwGYTZYAQF6QR3U6JeNgNBqh2+1ag4PpLm5UkgE0gxv2XtL5FwCokrCqFWpDow3DCGVRQammLgNTHlgY5fyc6jLt7e1hNBpZMLEy9IednR3UdY3pdIqdnR16JlMTKkkSnJ+fY3d3F5PJBL1ez0qkMuhlDzzReiILDJlew1x9nn9svNy6dctGJl3GAANCrhvB4JkxAwu2MCWI10H+3aW5Mj2D1Yg6nY5VY2TswZ9ze5nawnUoXIPBpY5UVYWdnR1bW8LzPIzHY/T7fRtFYqciA0eOOCil0O31kBeFpQBR1IiiOKzWxGsPOzfb7fbGuNFaY3d3F0pRRJ9pY6vVyhbDZaqTlNIaGkwxYmOjqpSVn+foCeMadx1jZyoB1gIS2tZ8YgcR03UYWGutrbFDBlMIaLFBY2JsE4QBsmxtKTxsFDBY5noPACxw5sKEXPXaNUTa7TYWplYGS/5z7oMrsesmRLODmAE5z202Rvv9PjwTlXajRAyYeR4yYOdaGlZ0QWxW3ybAXUNDWezHNDJ6Bz7CILLvgtvrGl88LplW5vYLO9C3DTM+OOrheZ7Frmz085hhaiJT3bg/XGaBGyVjTOfWVeP78DhhHMNYOI5j/O4Pfg+fdrywoTGdUTjU86gwGLQmL7VWCIMYLGA4G4/w9JNPcPz0KZaLBfaPDvDJJw9x4+gGTk9OALMYjcYjXIzOUVUV3nrrLazXa3zhC19Aq0U0nLjdQRSEmE4m0Erhv/t//Xe4e+cOjm7so92O7UbByT5VVaGuCGhxp3MlT95g+WVxWLWpcF0jikKsVmtbiI86Wlj1jSzN4PnNSy3LEh6ENVq4CiMvENw+3jy01vB8H1KQ5NxwOLSbC1cs7XS72D88QqvdRpIkSJIYge+jKitAA2VVYblaoTJhdiEo9DVfpViuUyzmC0ynE4wuRsQ5rUqbtJelqQ37AkBV1Sg1RRUaMKWtF6SuKKnZwFq76dSK6Azu91k5SBq1BndBdYGNBciWlcIynI0WPZ/HiyTAEERfSQvaii1Y4N2M6iuG95bH270XGyZXefm3D3uO872r7sXjjwUBeEN3Q7uux5YNDRc4b7QHcAyN5lmUUoBuaCrcRvaEu9dwPdBsMLoGyiZFauOBwBKbJKerrukfbccWf8aLppSSolGOUeieJ7BZ+Xrbw7bZvezW3yzuxtf9tKgFJ/a65/BPaWV9t8eIgtYNl3XzaAwNqzjlPOu20ecaDddFCrYlWa/rg+0o1HUGwbaxu+3ptV165X2a8Uafa+f7l+Vh7TV0E4nka2gNeKgRhT5FT8MAN27cRK/bhYbG5z7/CqQnsbe3Zzy4AYQwlFhVo9Npw/cDPH782K6n0BqBRwpMdVVhtV4hjshIWK7WGI1HuHnrNhaLhaVuZFmKOIohfR9lUQBCIPADs2Z78KTEwgDnxXyOLMtx585tkrmMY8qLC3xMJ1MEIRlCfkAqhJxM3G53sLe/h48+/AiDwQBCCAuQ2bPOfGsGCsytj+PYejH39ncxnU2RZRnu3r1rK2BrrZEuloij2IICGIBSlSX2D/atcUFgg9SoijxHWRGgd73cbtEwpqN0u10Lmhg8rtdr7O/vYzQaYbVa4caNGwAaWg3vu+y15fM5QZrpUG4ehCu/CTR0Eo60sJHD45AjAJ1OB6PRCGVZYn9/H1VV4fT0FLPZDDs7O5QHCdgIiktF4WiU64hkrjsbOEpRPaHcfO7SYRh8R1GE2WyGVqtl8QU7L13JVxczzGYzI/VORkO327XvgcEk02PW67VTa4PWPM/z7PtgoD2fz+0YYgPK8zwkcYww8FEUuW0zGy4ALCBlI4L/nWc5fD+07eBoBjlPNTxf2qLIm2to89w8noBGQhtoIvyud70oS2Qm2sf5CWwMuZQnPp8BvJtTw89XFAXarTbKogT05egJszZ4X3YVm3g/ZiDOP5VSKMrcRlF5rNo9vmro3nEcY7lc2jG1nQfhRjyApqYZf5/HBQN+xn0AbA0MNgwZ3zXqpNKuB/y8fD02YNjAZGaPa7TynOS2cf/MTY26IAheyNB44RwNrWoDDipS6PAkPAloLaFUTfJnAHb2D9Ef7uLeg1fx7nvv4uMP30FVl3j37bcgtDKoMcfx8TFmswWqqkboBxBJC0WeQ1U18iInJRrDlww8H5UqMZ1PEMcBtOpBSIGqrDCfr9DrdgF4KPMMdWUGi/TR7/aRF4UF6VQttUaKAr4X4smTY5RFCV0LqJpeeFGcmkFI19Egq1aD1VFM7QEDaKMotFZ1kiS4ceMGjm7exJ17d6G0RrfbtRVK2+02kiiBL8lTMpvPMZ/NMRpdkOdhneLsfILVw6d4+vSp9SZMJxOMJhMsDbeTk81qpqMIibKmmhAMspmjTBOGvKd1VUMbw0FrTZKs2PIcK4WyVgY9E0hVLJXKoFELQ1MiioMQAsIoTRDdoUQDswwgETSG2OMuJQMaRVxszaYHGitBCHiCCtcZjHOJ0kGXNgsOe1xhCNWEyM0AdoCwFFvuaXpWA7dNYSinKrLQ0Cw7y/dmAwFokk+xGQnZBnputMxdZPiZePFVSnHhbRvd2misNtK00qhNKTOvoCGEIoqENebciE0Dxrf7EOC5yX3fhEo2zAB+EcY4bIy9pi/4PdTsFW86gc506G2Xgbqw3zNPRJQ6fk0QG33NF5dC2rHsgmH6rrIc/WZc0wa5Xd7BNZe03uyn5jE8KHgb5whjRHvCA/Rmng9dR9tvet6mccHRhM3IBEczhEn7dzXO6XPf86DB/FsYGifRMXmTJ8nGhnpFz9LkPUhDV1SObCvPX5KZbhwNdA1jQJi+JSlIon15vrSeU/YMt9sthGFkNf6DwMf+/r4d6zdvHKLTSkhlxm+M5Lqq0OrEEB7VXigMtbWsMni+QF3VKDIPOqjw0r07mEymWC2XBPKTGEEUAlrD83xAkPRsr9dFXStICASejxuHR+QB9wJSl6poLi6XS9y9exdJkuDDDz/EcDjE0eENnJ6eIo5b2NnZw2qVIs9L9HoDEwGJ4PsBAt/IpNYaQRCirhWKssByubSUhjzPsV6tMBgMoLXG/t4eptMpURwMWJqMx0bwI4MnJW7dvEn03izHsD9A+yY50MqwxHK+pHw+SBt5jqIY7XaCTruL0XgEIegzqnJdoihKO9LYEOBiYwxSAJqrnDfBHubVaoWzszMLmpbLpaXMsOc3yzIrJMJ7y/HxMRaLBe7cuWOTdNn5N5lMMDCqUG7hO46QaL3JUnA9vAwMR6ORjSo8fvzYOjT8IMBytQIkG1YV/CDAbL7AcrlCu01iMLP5HDdMEbwsL5FID+s0Q5qRkXV+fo5ut4s0Sy216+zszII+biuvPRwx6XQ6tsie1qQaRWIna2vg8Z7A+wN7xgeDAcqyKSQ4ny/QbncRx4kt3ubWb+LoU5HlqJMSYRAi8HwkSUwy7nmBPMvQ7/Uwnc0gINBK2rTGSloXq7JGK2ljms9QqwytpIUgCCGlZw003svIkUp/j6IYYRgjXa8hJBnrSgNZXliDjNSgOkiz1I6VWhMVXCmFsqqRF0bCNmb2Ba89EllGUvRU2JUMrvU6cySzBc1x6cH3QxTFHFEUY7VeI1ulVoyACydygnV/MAAEGa3MqCjL0u73nEPFzBQyagIbEWUPv9ZkbEhBdHGOvjEoZ2APwP7ORgBTENmo4P4CmsR4N2HdlZt1E8ClbOqRsPPCVVJlxzdTzXi8us/GkTw2LF2jjmuvvai0LfAZIhpnp8cGxGr7YJ7vQ0KiyEvUVUneH59yEKI4AqBxevIM7/7yV/jJj36EXjuBFhppkWG5XmO1oORs1h9na8oPfEiPKj1nKSW9jEYjeJ6H3Z0dqLo0mxY9KEURBHRNll5d1cY4AOqqAgSgFBkbQKMqUnNVZs2buITHnmbAKBgAvuej2+siDEO0W210Oh0cHB5g/3AfvX4fcUSF7/qDAVrtFqTn42I2wWQywWKxxHgyRpqmePr0Kc6Oz7BepLYieJEXNlwGLrKmaot4qpqiGUoAlW68wzyI6romSUN+oWCqUmOduyFSF6jz+9wYEAb4SGx6292BZj3xaOpI8O9ab/LuXS/0dqSAv3PV0XixKRF922tOBt+m0hSf54Ipvu8GrUduAkfXs+62nfNvmu9sRh9cMOn2K1/Pttfpv+22uvkabv/y93jh4PtcFfXZ7pfr+ldrD4ysNwC0SQq9MvoD/vNl79NVkQweZ2yQu5787fa451wVudn+nCM8/F03ifyqfmkO8u6SAUr/CZB0qhZNDZDtaI50jAk3eRoAlBNlsO9KSqor5Dyz20fC1GHgOg0UoaOr813sd0FRK0rINlQnIS2NEMYI0iD1L5cu0VCU2G7Ulg7F9/OkMJtGy25mjaFbYjgckjyloUp0ez1IARzs7aLb7UEIWj9v374FaKDX70JIRZzz1QqthGhL7EXu9weGPtPDZDKxnk8GG7weHhwc2FyBSlUIo9BWX6Yob4KzszO04pYBQIFNzp1MJphOp7h9+xaePHlqvbOs6z8YDABQPl2v17ObL3vLhdfUKuBEyMViYStKA7AePvbCz+dzW+x1sVjYBFp3zWXwzt7uNE0R+L6lljIAcMeyu8FzBW0hhE1QZb1+pt9EUWTbVVWVlWedTqf2/fK5fA+mhLEBIaXE+fk5hsMhfN/HfD63uSfL5RKvvfaapQFzW/f29nBxcWGTxZkbz8ZKkiSYTqd49dVX7eecEO16XDniwYnSLKHLyknz+dwWj51MJpjP57hx4waEEFaOlhPyuc4CjaFN6pPrrQ7D2Hp5mc68Xq9tkbvRaGSjN2xoUSXrfSu3y9Scvb09m1je6XRsXsp6vcbOzo7dT/j+p6enqOsaBwcHNgm+0+lY6hfnUy4WS9S12qhZwEDQzS1grzaDzJNnxwiDwEZ2WI2JDTT3HbJU73aeAGMMBr2cOMwys0zN4QgH9/tqtbJRozTPIL2mmjhHLcgwaYohArDJ7MxE4fwFjohwsUDeN3mf4Vwafn7Oy+D3HYYhijy3KqbcFwzosyxDjUZ+3o1aSCHhGWOOP+P8Im6LGyF29yyOurByFNAoN3GUjnO0uG/cvZ8paDz+WEmN5ytHdhg387sCYMWA3LZorTfykTlywZE47nPOOXL3Ev43U7oAWDrbD//uH+DTjhc2NJ598hBUTM2zN/VMcuFsPkcQeCaULZGXGeqqRJJ0IEQMXdb4qz//Ed55+9fwPIG8LDAeT1EXFNoqqwqr5QplVTbh2owW9DAKAQ3s7tJGsk6XyIusseakMMXzIghIW4zH86h6t9bkkfc8nzxOQYB+v4+k1UIYhOj1u5BBY+m1Ox10Oh20kgQ7w10kSRfQAoPhEJ7vIc8yFDlVqr6YTjCdTHF2fo6LiwvMZjOq8jmbYmoSqOq6RlVX5DHjzadqNPEr462gCINErYknJ0VT4IpAiUJVN9cAHFAlm0RYorUoO5lYCpg3LgZnLi2FPZ1CODUdrqhA64JLdwC6hgTEJhDfplG5bXf/dpX3n72pXLPAvRd7s4XYTLjlo65qMIC7ZNxsOdFdsG+9vMZb4xoObJgxl5ENPbd/ttuo1Sa16CoP+XY7tkEHH+4itPE8zzE03N+1A5zZw+3cHdcZGvoa4+IqQ4Ofg0AwLhlS24bRdhvZSNz+nP/u9glT6ZrT3QiNSxUyRiAkqL4C1UMAACE1WMbWzSUQQkBoN/KweU04NKFLlKWtv7PxuDFG0PS2+ww2ImOMCupjqvfjedJGc8gDWIPtH8/n59KIowhRHCGKKJE5CAIMhztUrEybJOlWgrv37mHXgKCyqpDEMRUjVTV2d3awWC6MVj9tXlop6LpZrwoDTpeLBaI4ssAVICfNbDazBpBLpWHQNZ1ObbVZLgzmgoSknWC1Xlkvca/Xg9aaZEVbHXjSswCAE65diU+O/jIthWk6nLfHiZ0MHBRgaUI3btywyc2sRsPylFyFuq5r7O7uWrUl9+fBwYH1aHO+3/7+Pk5PT6mgnAGEDAAYJDBg4GRVBtIUiSjs+sDecKbgcG0FlnAPw9AaIEwtZoUopmy5EQQGERcXF9jb27NAUIhGWpMiZOUGL5wNq/l8buelC6i5n7kPu92ujYrwdfh5+XnYQcbt5/WEa2zUdW090Vz7g5Nx2Rhg0BozrSxNrUJRFEXY2dnFbDa3akKz2cyCPwbC7IXmvAiSxqX5cHFxgdPTU7z66qs2iZ0Vmzh3h/nxDBgHg8FGMjx7sDlCkKapHSdsfPh+gKKgNnEeiet5ZtDKRgAD9ypv1JTcfR+ANRy4/90IBYN7pnVxQvtyuSTZWaVsXgUbJDymGPSy4R4EAbQg5gWvcyw2wOfxOOK8GnYq8zhhEMxjAoBV6eScCDb6XaoPr7t8rtYaHhpnK7d1OBySkSLFhvQx52v4nocooHWLjQJXqphzRtigcB0E7nzZ/p3XKH4PLqbgd8aUSH5frmOEnUJuDhLjA5f2B8CuLfxueDy4Km48x9h44H2KxwYAa1hxe/hav1FD4/ijT+wi4Ac+UY60hvQk5ss52u0EYSBRFCmCQKKqckjpo93eQxwlUKrGh++/hw8//BAaQLpa4+TpMVarFcZj8viXZvLlKVWx1ual7u3t4e7du3j3vffI429AJr8ogCqX7+7u4mB3D9L3ERtvSm14lUKSnnmr3YYfBFBaYTqZYLVeY7maY76YI8syrFYrG4JVtUJRaFycX1D4vaqQGo7k/5e1P/u1JdvS+7BvzohY/dr9afPWbaqKhOUHSxREFkmxNW353/CLX/3n2BZgUy+2BBCkHwzQgCzbkkCKVJEskkVC7Fys22bm6Xa3+minH2b8ZoxYeS7zELgLyDzn7L1WrIg5R/ONbzSzblsd+7Rem5qko9Nv2zGwBDD0VS8jZhZmIaL9vkyH6FqGqe2aobyoF7AE1H2WAEh8Q/wjyyMYoQwM0DzUI2ZiZCb3E+/byZnvOmf6YQpQZgBV27UpKPp1YHgEfD8TaJyDctaM342YcTc8rM0o8Aw222KX5ryzw36OKN/eU9yjcb8AjAqGa7Tf5wHHWSbHPqsFoLZBa3TPJkCTxgHH54KWXxfIyMVhBPa6w6p892yC9L5uPCGKz57vlWVxnetLoM7u/XP3/N37HRj+4TwJehVszwlTkoDtpjzIbHEXXOp5ifIz7GM8GHM8jjX9SRYhhFR+hNxlvTM7l1/n+nKnc/3V8H1d16ZSL6Ymuf4Mh9lspvlirkkxSTp2c3up2WySSpAmk0IXl5fKs1zL1bK3P5RxZrq6utJsNu3LBHzSyQjoZjqdjpL6evNTqdVq2Y+XjiD94jI6+eVioZ/9/Od69epV3FNJz48PKopc0+ms35uoY03TqiimqZzBNq9ut1tJGo1dpCzG+zjWlAADUHs4HNT1ZZXee+33e719+1a//OUvlWWZri6utJgvUp0/e0DtP3PlYfgkJYBE6el6vU7ApKoqZf2korKMY9XpnSiKQh8+fEhlMA8PDwmsl2WpFy9eaLfb6fXr1zocDgkccSAbDP3z83MCcXmWqTDlQ4xCZ6pSPPl5n0AFjbMw3VxztVrp06dPozr7m5sb7fd7/epXv9Ll5WUaMUoWh+k1tj+hbdsE7G9ubvoJitc6HA4pKwGzDDtNdoRpTdhDe2gd06ikocl7MpnooS8Ns+dK2ClA1LUzknW/38s5l84CIGtix2/C1rP+0+lUdX9PBDuAr9ev32iz2SZwW/UN3pYcIADjMxH4Zzr1ZT9dF8//AOxKsVyKhnvYZ2wELLjtN7DlY4BV9iSe/XVQVcWeE+ecnp6ekn8imKPRGFkPIaitYhDDHknDeHFK2wgm6GelxI0ghl4HgkTGvPJv21xMEzlnfqD/LvOq+mASgqEoipQxlDQiQe3P+A4L5nk+5Aa/RCP55xqdQwiaFIXm5nA663uzPFenIdgPwZQsuVi+zd5st9sRMCfryzqR9QDw22oKSASyrLzHTo1qmiYFOXb4Ac9OcGmHC9heGrJLBBZDH82AlxnAgP7zLGDDw+Gg9XqdAjaCTYIafs6e/S//N39N3/f68ozGH/881dl551XVMcU8nU21WK8kF7SYTdTWR22eH1VXxz7lM4tnR/QRFMxi13Y6HU6aTAq1Xafj4dCn4hodT6W8KzRbLmPNk2Ldt3dei8VaddOzyU2j/f4QD6Kram2en3U6HNS0rZ4eHvTw8KBPnz5pu93qebvX/nBQ2zZpUkZUQq/OeTVtG0/09u5s8W1JiRtQr/NqwtAIySuBrwADrtS7oNCf3Az4csMZApn3kpfaLgr4GHx3UtfKO42EJglzcOIkXBp1E/DzkalGsImaoyJPemVo1bbjch+nobb+nIW24NGy8BGEjRtNP9fwew4+7ffa4GNY8+F9tnRLTqmO/LzBirQFazRm9mMDuzVcfPYcFA+A+vPTqT5/z3YdP8/8W4D+OeD9nYDLfMYGGecg99cFGSbMSX8CQOO9nweb5rPdMJrWPu/nnmH0cz/uRfjc388zYxG4fj6Icmc9JvZlswo2CO9/K86EiM/XKsu82pZzHcaBdMraBqWsTJ5lPejNYjmjGzJf0fhmsY7ZOWW98+66Tq9fv0klFW/evlKWOd3e3EqKZzi8fvW6nwRX63DY6c2bN7q4uEjPEUs3cgXFqUacsUB50eFw1GEfyzPUO0Pv4nSmTx8/arFYpkysdVKzRSxNoZF2MV+orKKjBNTFMa11amQsikJFv1bpBOc+MD+dSmXZJDGkdV2ngRu28RJnDPs6nU71/v37NPYVcFSWpcq6lPMuNfo65/Tp0yddXV3pYnmhb7/9NjlvOy4TIEA98ddff53Gct7c3OhnP/tZOiQPMCNJT/1oVEkpw0JmmNfV1ZXevXuXmFLKvkIIadIRB5PRNEkpwosXL9KaVWUp3wMVAAmAkbGWT09PqSzMOZfYcs5w8N6nJmYyC7D9lgRhciKBHvXbAEJYZJhmgDPTmcgMUSJGwGPX3k6fQnYBZ0zkkZTKdPgsfoL7pdzI2iL7H6AWoJiIOo3HdQKC9n0mg30l0xVlttJFP6ERfw/YDSGkgG6z2Wi9XqfSpjwfN+4SgO52O93f36vrOl1fX+vjxzj+mJI9ggHApp0cZJlogG485ToGgZbBZ12YdmRlMQHobuj/I3AD4JLVubqK58aQoWPNCbKwBTZDwO8Ph0OSASZNkdnAPsSei0bBSbvdLvluAlXsm+0lQB7s+FSrH5JGZUzsNfabAMEy/HUdTz6fT2dp7HGWZSmb2YUQA6I++8n6EKCoCymDyN7YEmJ6k7gv24gN1kK+yeiUZZmCBQgZdJeSK/w8gTNrQbBgezsIDsm6IA/4Rj5nsSFBldUl7pFsEH6WzCR7RKaxLMsvymh8cTP4vB81y4Pn05mKfk72oap0OOy1vlhoOlloMbvSt1//SoftQfv9N7q6u9P6+lpVG5sTq9NR5bHU49Oz9vu9dvt9DBJOJ11eXKrpnLb7Mm0S7MfheJC6TIfDUDq13Wz1r//Nv46Grjypqat0zzal1AaAmhONyG3bn6bqnKQI1NXQbxBroy2ewdBFhQtpPKWNrFO5jmLjcwh9s7OGEgnX9QkM9YFNFwOJNF2mv0xIJxP3wVnXjAQ3ClGmpg0KoUnXl2FS43XpSWnTekjqFQYmuC9t6W8gVml8F3jjdK1hsIHZ5xjsz2Uu7OvXgVabpTi/HvdqwTe/Z80GEH0W1JjvZf94WQPCa2DBP3+a9+de6XdnwcKXvKwxYL/ss1hQbN//64Kl8+fuf5N+GgLTusaBRuprCeMRwefrY/ffBj32vbbf5fy+xoGT6SORND5ozj7XkNUZ75XrM3VhdM1oQPu+JHXKMqc8xObt2B/VG99JodgXFA+0zvJM6/VaCiGeyXB7Kzmnm7tbtW2r3/6d39bT45NW65X+xJ/4E1IXtJjPVVe16qbW69evkzOcTAodj7GMhTKKf/mv/pWur641m8/kfcwwxNn0TnXZarFc6nQsdXl5ocw5Pd7fK4Sg8nSS917r5Vq5z9T1AOlTP21mOp1qvVrFPWhbHXoWNc8yzWZTladoXxkdGcmayPQtl2t55/XN19+qbePBbLe3L1SVpfbbTc+IV322gkbggcF+enpKbDRg8vLyMk16YqrQ3d1dmgiEPBBAwbxeXV8lcPPp0ye9ePEiOdybm5tUNuKcS+DekirOOb158yad05DneX8w7CqBTk5H7roujYGl5wIg97u/+7v62c9+pp/+9KepGRLibL/f68WLFwmc8syccYDdBARst9s4TbDPUuR5nspuJCWw69xQJgEgAVgAFAD01GsTgEynUx2PR11dXaWSLw6b9d6nTBAMNXXgTdOkAJPR7957rVYrvXr1Ksny8/Nz8gGUg3GeA4w8/7YjTwEn7Gld1wmUAmDxbdg8WHKbPWdfAI0ETJeXlwkIeu/1ox/9KB2Cx4h7grntdp8YZEa5Mn6f4MpmpCLzXquq2gSQN5vNKICM06CiLN/e3qYeHjuKlDViXa08wkqTfSLDQPaG/WNUL/dvz4tQCJpNpgn8w25TPkY/CDX88/k8TfQi2ALsksWi3MiercKUI37H/cOMH49HZXmuNnSjEj4LoEMIowMSJaXmesgI/B9BBHad9azrOpXFFUWRztcgK0CmgHtFx6R+RHIWhwchb8gjwH8xi+Ny7fhjsjfYGuQX9p/rA9xtdsWez4Kts6eG2xLQ9XqdAhN+byseuB/eDz6zfpfAh+lmZL4I3mzwRY8G34Gt4T7BnsjKOSn5615fnNHYb09quzYxZk3TN3wqqA6d2qaT2qDmVKk6HvXLn/1C//X/82/r/uN7zS/WmixXOpSVdtu99s877Q9HHcpa291OTd30dX1T/fZv/7befPVjHesIXo6HIfUXWYi92rpMzXn7/V7ffPONHu7v1Xa1OtP45ZzrMxSArNigmmdDhN51rRQaeafUvDpmxm3ZjQHLIUhhKCkZM/d9CVQYWAWz4HKmtjy+p2/clFcXzhj/FDy06sKgaBZktZ2X9wMzYAUyy+OksGhA7BjZPriSS5Ht8Ox9qZaG5+I5LMjkdwPg7RIWPGffbSBxLnI2sDgvu3JnY4HsfcZ1HgcnCaB3nL79mZ4GF75zP5/LSpzf368LND4H/M0Nj97/78punF/b3qMNNGwW4HMB2meDue/85LuvcxYxffYsYLO/t/dyfh2Z+znvY4BtwoiNAo0wGFKbMh9Oh+eaQ5Af1ygWxhEYDu9xfWPqVHJBy+VcckGr1VLrxaUyn+nu7k5t2+onP/mJLi8vJQVdrBYqq0qvX79ObN3lxaWeN09quqYHV4vETkW5C8p7UAkLSanOdFpos3mKBjuLurparrTb77R53uqHP/yR6rqS5FIJjhSU54Wm05kuLy/6yUdz1XWlyWSqLMs1ny/0b/7Nv9H19ZU50faUyndCCKlUJjZr7pRN4jCP6WSir7/+WhcXF3p4fNBivtByeZkaTHGUzjnlmddsWqgsTwpBieHz3uvdu3dpkkuWZXp+fk4AkWwIJylTt04tPGcuADQAMPPlPJWRUg+Mcz7sDppOpqn3gj+p4aekZT6fJ1DMWRgwz1999VUCViEEZX3/Hs3nAFAar0+nU3LCNKwSOF1cXIyAdJQhJaDIfhIUtD1jG0JIh9xVVZUObLO9CbCoMNuU5vAnE6sAn9wL5SS2fMKCtBBCqpOv61pv3rxJew6htlwuU0aubVvd39+nbFAs7dmnLAPgkb4BTkE/BytkvWDXCdjI6BD02PWm3AtdQq6rqkpBRNu2evHiRTpYcT6fq+7vmSZlzliIgWzMCEhD38LnTusOIaSG87ZtVFWRiSbzRE8C/ROMJPZ9Hw7kIE28yBI2giDBlv8QUBwOp2Qnqam3fTg8S6o28XFaZ5FFPLBYLLTdbpMcone2hMqy7BbYS0oybcvbyDYAWHkuvoNXWZYqphNlffBEIGAzAewzz0FGB+Lg8vIyPReAGRkjM2V7hrgnAgF8Z9M08mFMSCbM5r2qpk4ZFgv0yYQcDocROUHPE/ZDGqY2TSYTbTabUeBAsIksXF9fJzm199J1XRqUsFgsElFBIE3AQjaMMdTYePYXXeSzDN/gnu0ej8rwe4IEObRZODIr2B3vvZbLpX7vL/xZfd/riwON/+6/+XvaHU+q607HstJ+e9B2s9Fuu9exjr0LVVXqsNvr8f5ez0/POux3yhRUta18nsu5eA6DVxw3yBQlgETbdiqKXHcv3+rtD38i53wfRZ9UTCbKs0x1dVB1it33zqSO7+/vtX1+lHdO6oI4CDouuk/1vmzsEHE28q6T03A+QKzb9v2ptT2r7Di5VoLdbusqlVpFUBtBUDxE0KdyKXoChoaskP7vnEvTR2SaVLuuS98pSV1oFVsxfLrHKCxBzuXKi0kyMjgon2VKJy33WZKuiyNsmcFtAev477W6roklZcE8R4iAG2AXQg/2+/ZWDDNr7Z0fnVUQBDger41oj00/44rDGqXv0xD0ca0hoCCq7NdGrh8D22db+u7Zruv6IG74nlgm1481Dmafesb/PNA4f50HBvZln18hPqEF8N/HDiCzNqCw7z///Pn70u/IktmANgrgyAAN9+/6eM4N/+z60jNJRZYrjYIOpodGTt4PvS7jrEUsFfSZj+WKzinPY/+Iz7K01+efzXPX9zLkaaw0YzInk2gAb29ulOVZAg0/+tGPtFjMdXt7p+k0gqGgVoveaZdHWPzIvj49P0sh6NWrV6qqk47Hoz58+KCr/pyGZW+wq7pMgBjwXNeNLi8u9PHTx2j0XexnOx6Ourq+6p17nubcN3WjxXKpIs+12+91eXmV+hlWy1gqtN1tpSAVxUTFZKiZpsxiOpmq7Zn49Xqtsp9QZA9UYkyjd06LfuLPbDaV650SAKPtGbH37+PzZn5o6C3LUk3bqCpPCWACmmOJxy45Y0AdwTGOarVaabPZJCe63W51fX2td+/epevRXyBFRnN/2Gu9XqeDv9KYyf7U3d1ul/oKnp6eRhN/CJKenp4kKdWk27p7S0rJAHAYQOfcKDh6fHzUiv6PHgymoNh7ZT0Qyfp1Y+JOarAMQfvDQUWflXnx4kU6SwNmlmwPoIZARorAD2YSgEW5x93dnXa7XcqS8CKAOW84BSxT440NgfFHlzkLguvyPFIEbgAvwLGkBGjor4AEy7JcbTNkfJgyOZvOkiwCqruuU9O2Oh4OqptGq15HCaoAQmRMTqc44ajty2EW87mCHxj6ofm/VdPUWszmaYJXLBfLFUKn4/Ekn2cJ8LdtPBgxyzK9fv1aVVXG52hbVVUsR7u4uFSWxRHC8bTooKLIE2iMGZGsl3PpcDhqNpuKE9lD6DSbzRXCcNYVPURZlo96cGym43SKUznJRt7d3SU/F3oi1NrSSFzk/RkoRy2XkAX9uO9uKK1er9dpj3uPrf1+l8p4CMhjAD9TVZVJhgC9eR4niNrAgKwGto7MhTSciQKQl5Qa/pnGBftvZZCgBYA860fjEtDWdR3HgYcQB2mELq1ZJGu7RIxwj+hOVUYMGkvg4hp6n2k+n8nL6f3794lYoMcBQpSyT4Kpuq61Wq1G07qkgbSFlCEYZD3p7UGWyUwRLBIwhhCPVNhsNmn9yexsNpuRHbAZKM5hwa+AAciGcTbMYrFI9kaK+Po3emDf/+5/+7/Xz375jVrl6kIm73K5Lm6aXKZjGed9d6HpmYaT2qaRdyHOPK/jeRY4t7qp1XR1ioxm0+gwvfeazpbKimH0HM4gz3NV5UFNHZWLzQIwZc7Jy402KLKfXp2aNA51APwx2pzkPi0awkKEHJp4yEv0Q/0kmI7TquNoya53IJ1ZynRUg4tAjZG1bdcqOFjn82kzTpnPzb8HBj/LMzPucpgdHj8fQTXCCjDz3segqzdKMGMpEPHj0bP8571TFyp13VDXd/6f/ZwF5b+Oted39j32OePf43XOa+zPAXz8/PCdlMNxrof3Xk7xTAH7Oi/vOX/+tmvUdbWo2T8Pwmym4DuBhBs3FP+6NbCvyICbbJe5/vlnP9drcr42MOqw+QS+KRMns2ZuSLaEENIBgOlDvOkz38XvvHP9HKt45sKo6UxeWTYRUW6W5YmRyXwsG8RQzmdzTaYTzaYzFZNcr1691HQ6TWUyVVXp7du3KopM64sIKjjlGOaGGnFGZ55Op2T8YQypN6YsgBOU0Y/b29t4uKUBVNQS73Y77fd73d3dJcCC4YdpZAT3arVKQBWH9fLly8TK0XRa13UapQk7yUhRHA6lNstlHKu93W5TyQMHe9GMCPCANYbdsgdm2VGSlmHrui41su73e7169UqbzSaVA+AgYdVtvwX7QBDBWFKAZF3X+vTpk37yk5+k8xIeHh7SONurqyu9f/8+MXBWdwhK2BNbhoD+wpq/f/9eb9++TYEK7314eEiySdbjxYsXiYGk5+Xq6ioBE1sug9OmwRzAhN5xiBxThMjovHr1Ss/PzymQtVkNWw7Dycg8BzJrG2Tv7+91e3ub1nmxWCSAttlsNJvNdHFxkcYJ8/ze+8SGpv6c2SzpAWAdcMczsb4wyABmMjY0vFLGZp/Jgjz0UmJqjeTduIyEUhdGrBLIWLBpA0BbLgX4tuVysLzriwuVdZX2BnA0m8WDcItsqP+3WQy5OBmTawHSmNqFPQFwA/LYC4IsghTWSVLKFDJWmLXsui6dAM41OG/D2ic7xcr2e+B7bFBLAIJ9sdkMbCEkAqRJ4YdyJMvQy8XqFfZZGkqxbVaB3zsXxzKTyQJ3sHZkHBJh0o/MpSyH6/I8MOtkVg6HQ8pU4EfsRCVsiJ2whT3HlxGsELwQyNh7ptwMNh+AnmWZQhe0eXpSCCHZfDJkZIx42eqPLBsOWMS+IpdZlqVAh/Vj33iNMK/RC7CNzSDaCheeg/W2wQ3rM5Tk+5Gu2UEelqjvuu43O3Xqv/1//wP9V3/j/66PjzuVlVSWjdq6kndOdXJWbWRMnVSejppOJ6r6Q/RgxJq66UFNSL0LeZZp1qc0vXNqO6lthmYehCI2GjUqy6PUC3LXxcPevPea5IU6DuzLvNquScLWNJXatkmTFOzmZ26I+DGkfGfOeW9djHq7ru0ZXTIOfemHXBw/2wHaxtmTtu3Pu+iC5F1iC2ONfA/iANAmG4Nw5pP+IKx+Wo3rswhkDj4HzKV4YoBlqglczgGrJBOESHKd2rYR43Fh9AmIBiZew/3rvJwofPZ3NtBwfYaI9/Lc9nm47yH9P3ynM0EbZTPex0PTzoEy90VAhXMYAqhObVcPG2A+cx44nKvNONCQlBil775vuIhiduMzgQzZo+GD6oOI/oMmQOWz8e+McR1nPaKs2TMjzp7DnC2Ssmyp3Clm9ORogI49PXmWKXeuP6hpksDSj3/848hAXqw1n0UQfnF5kRzQernUarnQD3/4w5iOLvIh7R2C1hcrhS5of4jg5rDvy4j6TNT19XUCN4yytGl39I1JM6SYvffJweLUbHMkjoK66aIotF6vU90qE0a2220atbrZbNK5DIAO1t5OyIHdgmGn3Ic+A+rhaUDe7/epFIlyKJ6RKU08L1N+JOnx8THJAoeBUVLDtJ+3b98K1hFwDHCy9dI8NyUwgGqAOGUfdlILJVqAIU4n3m63uru7S2VaZGUoDYA5WywW6SwFggHsPECBuvPHx0e1bavXr1+nCS0EOdZRk+Gg+ZssD8wd41Fvb291cXGhDx8+pDIRSnQBXQRTyCssIH9PDaY9uGW6FhkcGkA5H4I9kKTr62uFENJhbtfX10lH2QfWDhADSLCNmq9evUqTqNhXQDJAi8Zr7CF2AOBH8CEpBaFXV1fJZpJlsZOxbMkG9hqZAciEIM1niwRc2CMb8EpKPTD4KthfsjyTyWQUfAHIuN8si+NTg3ep/4a9SpkCDXoKMwxgy6dxfW3wazPKBAdkAy2oteCRhlr0GD+B/MVMbdwTAkP2G1DIWvIMAOL5fK77+/sRy0y9PdgJ8oHxx9yfPV0b2yNJs2Iyus8EzBVU1sPYU/s8kGB5nqdpRc/PzykwoBSQZyNTRLBopzhxmrrVObJfBKIEB8gEpUp2EpZl5CUl/8SesraUB3IfNnAjW83+83NKMMvTSdWpTPtMoI4fsQAduwCBzfvJGDNeGfJg6AX+bi8jf7Ztm+6b4MXqHus9EMg+BUDIJD8/x1r4AGwCpD/3Zu3IbzSj8c3XT/q//ld/S//gD/6FWs3UtLGBOcucJrOpQuhUVTEF6DOv+/tP6tpWHILbNLWYbKRedLuuTQfSIZRSUF22muTDBrMAzjlluVfb1vGzfTMzoGExWyjP4kmVdV2pC63yPFPT1KqrUlV5SpvBf7FBMgKr7XabQAoCkmdDjewIDIYI9qLjmqtp6nTNuFmdMu/jOR8dQLBLxgXD3DRm/KyP/y4mfe1f0ya2OfOFKA/quuHk8tgUG3qGerjPBOTDkK3AQfIcGETuh+g3rnWntjsb3ZqkZjh9OHQh9UmMaHJJw+nPactTqdSAb20tfwyezsfPhhD6rNK49l8hNuSHENT1gRz43LvxOLx4fTdSJOm7B9J0Xa1wNuo1BOT1u6VTIWW7zsul+mC6O+/7CKO/OnN9/rTrQzBlryc3zpzYDJ5CLBWMvx/KyeJ1hvedG63z/3BmRZFruZprNptrtVrq6upaeZ7pzZs3+urtV7HnqAc3yOOPf/wjHU9HNaHRpOhr9CeFMp/1jGuQ19DkTslAdFhNCgDm87natulBaaem6WIJUQ9KAVA4LthTgAZOHIdDAxssOcwhB44x1eXi4kJt2yaw55zT119/PQLFIcT6dkA6e09aG8DMtWhk5vtWq9Wo7hcWHMYZ4DubzfTw8JB0W5JWq1V632QSD2Vj7vzxeEw162QV0P+mafT27Vt9/PgxjSslI4Ej5+ccrAZ4pb8ClpT1pim2aZp0eNt8Ptd6vY5ALww9FpQzEYigewQigCuCBoAmY2axUwBDm826u7tLTH3bxgPeYCEBmABR/m6ZWH5+Li8AFfaIbNRAYA1NoQQnMPqwzoB9WFNbY85Eo4eHhwQyYLux5YwVBVwgt4C9siz1+PioV69epb1krO2nT58kKa0DbCb6w3MDSOkpYF1gLgE0TBkaiL+hhIV7xd7Z04nRSQggAqc8z1PQbXsA+DeZJfbSNtpaEpJ7JAB3LpYdV82QGYG9p2Tnan2RfB4yHEJQWVXKJ0UiBtD5w+GQ9pS9QMcJfgFoBHIWfHItskNc02bnbA8D+mUDDrKp4CXbowb7TskfcsngCWTFBmQ2c1rXtTK5RDIAqpumUVDQqQ9U2FeuYXGRnQTFvTOxiTU7Ho+jKViAZMArwRvrAUFgJx+BZezatW2bsg74RzJdlHIhlxb2ArjRe54Fm84UPAKdpP95LheGsd2sOfdyHvDgb8lKEehDpkCIYcPwVwSM2CQCAAItbCyyY/vqrA2zpWX8jL2wGRCuU5ZlGrPM8yGzBI7OOf3Zv/jn9H2vL586Ncv0H/zP/oT+4A//tZpGUpbJZbF3YH84Si6mlJq6Udc2KvpIfjaJNZrMMEY5yvKk+XwqjpVv206TSaHQBc3nUhaGRlFJgzFTPLvDZgpCCMqcV9UEnapSbVMrjlmtVTdlZMDrSl1vpK2Da5pGmYtsPRtIzWkIQU3dpZn50lDXHlwsY6qbVl1/bH3bdlI/t94539e9e2VZf8BhniUGO8tyxQMQvbouTo+S8/2z9Uo2GVJZBGZxc2kcaxX6efhtMzBCGPau6zTJi7R+rBdCgzLZlCbBXttKoYuA3QJ/mx3x3qtz3ehno7K0bHxYn1I7wLjR+TzD4Uwmous6JZwtDlUjm+Kj4wqS1P+9fyv3xzXOXzYI4bnJ1kjnjctjxsy+7H3boCXKiVeej7Mqo+AnDOco2Gt9J7thjIf3Tm3byGfjdRt6JDKFLk5LCl1Q3vcr5Hkh7xXL75zXZDpJzYyz2Uy3N7e6urpUnhd6/fqVppOpfvt3frsHfFPN5zMVRaynbuq6P4/hpGlRKMvjJB+naMw+fPygPPdarBc6lXEKznETa/Bns5lm06ke7+Po6Tdv3ijPM223h74MaabDYa/5fKE8z7Tf73qHUWo6XSQgRy0+QJjshQ2SnvtJdvRfABYfHx8TqKVkATBtG1jJcjw/P+v29jaBH5tBtKDv7u5O3se+MYA5wfzNzU0C34BJG6B88803urq60nK5HN3Dx48fY2npbJaYWE5qhqHEEbIuMKJlWaambMpf2rbV9fV1AjvPz88JhK5Wq/QddloS009w2tw/tcbWCZIBaJomNTYDipyLZU6svf351dVV6i+YTCb6+PFjH2i2o4kyAE3KAyivA7BRSw+DCZCBCJjNZsnePT8/p6lb6CY2DN/w8PCgu7u71Ato74l9t2UoyDhlHDSfr1ar1NjKvQJKyVjh4MnokBEBgPN8d3d332m+vbu7S8EmAANQSIBHiR36Ig2ZDUopeB6+d71ep0wKYHzTjwFmrXhmggZ7roQNcuM+xv4GgDZTyjirYz6fJ2aXpnIbDALM0HMCJGSLv5dlKee92tAl4gKSwTmnaR/ocd4GGYjUUH8Vyy6ReXRN0qhMBXDIc2JjAIsEmFyHDAm26jz4xSZYII08czAgAJoDL+3ELIAhIB77g53iHjmrge88nU5Sj6OOx6Our6/PGriHHidsrS1DIiDhOdgvAD6gGRmrqkq3t7cpYMcOoDPoLNdmTVkzO2nLEqfovA0YCA4six99YrweB4uuVqtR1QdYlXHM2FGwoz1jA/IFIoWMBraAtSe4hyzDd1OWit7zXvaPIMtmLXg+sJ0NgrDbyKqVPewANorAAfIb/UKubKBk94cM25e8vjijsXl41C++ftB//n/5m3r3aa+qC+q6UmV5VJ5Ne0Gc6nDYK8viGLiyKrXoF9Z5p6ZulOVxMeqqklPQZFJot9trMil64yspBLV1mxrdyrIcxmm5gdmr6lpdb4CzPJdCbCjN8zgKNig2UJflUaorZc6PIkuM1mG3ScLABg2pq5CMBko6AMoxkCYyj6/hQDcbUVY9o2Br7jFYPstVnjUpJuHuGs2mxQggdW3MOqjvSwHsj7IQYQCqFigjpJ9juOPzxDKbEMY9B0TQ9hpW0e3r/L02O8XneA2N1r++L8D+PWU3WO3PloOF0e9/3WsURLiz7+uff1y6ZJ79vMSJz7nxPYYQhgME6WdRDKp4j90j9sLuaTQ+E8WRzENwZA1xlnm9fftGeZZrOot9Dj/4wQ/6Jt1orFbrta6vrvT09CTnnVbLlS768ZTH46ln5Oeqykr7w0GbzXMahQnIw4idlxAwAjAoaLleJtYPFns6nWo+nUtB+vjxo7abjfK80MVlBDJDoDGeaBOB60p1HQ0dAJxSGXuCMw7w/fv3mk6nuru7S+DHljVcXFxotVrpl7/8ZQoS7u/v+/uYJ2AKuKcfg3IbnAnnGkyn09QPATgnEKB0pSiK5PSpq7fglnUEsPzqV79KpRHYvevra+12u8RgUhpCXS3ss62BpkcgNX4bsPz09JTeQ93+1dVVciSAdZhMbDHvpUmwqqo0HlaKmRdkWFJqEF+tVnp8fEzXpLSChnCcIiDcOsanpyfd3t4m8Io9h123/SQfP35M5BGlI7BzlNEhD9h1aVxmgcO3vRkWWFqSxZYtoCfsA2Du5z//uf7kn/yTKTsCwKEZ3ALJ1WqVwCSyBlhYrVZ6//59AuNMPaKZ3mYqyQxgg3legrpUc97bEnpOJKXvJHAA7GKjKP+SIqjk++3J0vjZoig0KaZqmiEjga6RdbJBEiw770GvWQOyXHYaFZmzqqpiZjvPUiOtZZTfvnmrbd/gir9k3Zq21fryYtRkiy0AiPEzC/5YU/wJ2UoAPwEPWcfzLDI9Acgg64des08E+5AIfB/T27AL4A57SCCfB/DbSUV1VaVpVWQOyTatLy7UhqG3w45Mtpk9SyDw7ATM6AsBNaSBnbBGAI6MoWf2ZcszeQGGbXkQ+2OzagQDBJngGtYDPSXAtVUevD/L4hS5aTGJtKTx0ZZoIet7XrbE92DPLaZgHfgMNoWMlCVNWG/+zvtsDxn3gu5YnIYdIFMJTsRv4Ntt6Sp6a4Okv/BX/6K+7/XlgcandzqUmf72f/37+m//7j9W1XR6fP6kPHeaFmtJoVeyVkURlbGqK02LXtHaYerTfr9XU9fqmlpBUpHn/dSfTpMizrGv60p5XvTlWLFkZDIpFJzTZBozIXmRJ+FqmlaZn8j7XM53yjLpcNiqqo96fHxQqCq5bjhmXZK6to2QrxvqMGmwxFEU037KRlXL+T411lPzIXgVBcavVeg65UXeZy16JqfvC1GIG346HmMknI2PkO+6Tj4v1HRxGpLvDU+QVFeVurZSnkkNGQnRxBuZ/PBr+iSyfsY+bH00auNGaPsZHAqMfAjdMCnJXB+Fda6fxqWhls9e02Yskqg5RXlIAdHQSB8zHn7oQTCTrSygHwdF4+eOfx+CCxvk9FcdybYNNEKwlVm2v+G7fRn2Z/ZZMRLnmZsQQsroxDNYxtkbAjwYv6ZpUpPZzc2Nnp+fdH19o5/85Lf06vVLXV1d6uHhUT/4wQ80m836Upm9Fst52hsaDKeTiSbTiT68f6/Veq2yPCXwdLFe67g/aDadKu8BsKR0IOZqdSHvI/h9enxU189Fz/NC09k0nVaLg6qqSpdXl3rebBLbcnF5odl0pufNRtN8ot12YPwtMzqd5jqVp1QnzvNvt1vd3NykHgR+x8Se6+tr5XmuzWaTzmXAEeNELi8v9atf/Sox8OwRU6AuLy9TqVKWZan0ASPMeQukr2FJAdvr9Vo//elP073wDJJSORLgCYcCswZTDuhG7ggOGKWK7tmSJk7TxjHZswQAQbbEwQJiAiOyM2SAYOIZZQqAIPvB5wngyG7A7OH4eP95ICENJQu2l4JyLxpw1+v1qGRgu92OSBIAdtu2ur29HQVBZArYM0mp7ALwBfsI8wfzT/BcFHEu//39fZIlG8ABHrg2+8leDH1vrp/2NUslehxOZ3WdjDDBLGCcYIHeCdYN8ENZFqUz8XT4WWpepk+CoIkSNQAFa47NRCdtpgNgBKBu2zhJDIBshywAKFlHwN56faHyNMz1l5RkzdprWHlJw9Qgky0ggGEv6BmyjcN5nmt/OqZ7tP0WRZ6ra2IPDhmfVHaZ56qa4cwFe2id7WMi4LM6QH8ErC/TsZxzySa8f/9+FPTgM2DUn56eks0h24K9YnQx4A8W2vo+WyINaD8cDikIs8QgvUU81+Vqne4b4Ho4HOS8V6chc2H9PPJLthd7giwXRZFII9Yg7UPP7IPLaL7HxmF7sJsEJwRhzjnd3t6O3mNJA6sf1kdT3spaE9ClKX0a+jkljYLyBPB7zMf9E0SgM8innXxlCWl8oyV6IZzQHfwpPoSSS+4Lggv5wGYQUNpgzAZNZMzRCWvH0FX+ZC0mk2lsQ6iHs32cc/pzf+nPfwcXnb++ONB4/+3P5PxK//rffKP/83/xN/S8OapqarVdo7qs1bYDEx/7LoLK8qimPkWwSn1+CJHRCPFQOJqwijyeEO6dU1X1tYmmnlehHwkaMl1e3Wh1ean5ei0VmYrFTG0Iyjqv3GU6nY56fn7qD77q1DaNQrnT88MnlceTMu/kQ1Bbx/tu1fWZFlLundo29llMilyz6VR104zGoEah6FLQ0baxSdxnfWrxVMrJpefIsjh2r67rVJkDG57lfTqvUxrs6jMvplTlWa66q9X0ze3ODyDb9SdNuD4gIADpt1chxLp552LjuALBRFDmQ2r6TUx6//+ujb0QbRunauWTieq2ldQpd4MRAywUeTQYbReZ+2hI47kl0RBKbVuPUqRRiIPaNg4IGHUyANB9Jq9cQUFd26Wgw3svH/5dmQoX1wYF7qd+DY364+h+VHrUH7SIoqb0bAjy2XDYEgFFlO8ujTr2zsWDikhNd12cctKXBq7Xay2WC93eXMln0mK+0HQ2VeiCfvTjH8XzGi4vtVwuNZvONJ3FU1yZkLS+WOtUnsyUjpPU9zxk5twI9DF0QUFB291OIQRdXV9pu9mmZsL5fK7lYqHdbpecVFmetFqt1dSNytMpMlq9HEvStJ9EAquNIZWU6nFPp5PKqtJsOtWiZ8spAzgdTjEI70v78n4UZAiddrtdOokXls6yRjZN/OHDh1iz3Dvmpmk06Z1L0TuEec9EYsQBno+PjyNnDSABpNCULWnU6GtLXGjgJQiw509cXl4qz/M0D541siUE7BPOmmfjehZAWpmzjdM456qq0r9x5rZJ2p7IzHNFBzKex48zt31stjmYQA8wgTN3Lp7cDXDjT8vsM+GGcbhkIgBLjGDkPik7OmdCyZxJSmU3OE8yXXayltVzKYLlh4eHxMjaTDfvt+ADoJH8Ve/YAbwEpICQuq61XK5UlXXfR/Mo57ym00kvVzsVk6EPhAAofraJQfwkBollVeIYYiDXBwaTyVTeR4CW5bnWPdBtW8pnWy2XKzknPT9vUgB8PB5UVbWKngRcLJc9URT7LJHLYw9Am7rWbDaX61vwJpMIPikzms1mKgCbvc6s1xe9zW7Vdp32u51W63gQpD03wU54s/XkAEJAFe+xJSqJpOstftvGcdF5lulwPCp0QRfrmAUNXSffB8ZXV5dq21aH40lZPoxenfXnJTgn5T5T27Uq8igb6kmbd+/eqQ1dyliis7Zszo7+pKTpeDym81Lquh71dFAaR4DMBDQmK9lMBu/Dr1kiJa5BO1ovCxQp4fz06VMKhCBDUoANVunP3MqLQk7SoS9TzfNcd3d3qUTRkmpkncjMEsjYagPrO1kvMqpk7/AfBH42489QBzK33DfPbzOh2HX8uCVYANYE/dhLZI/vZX9Za3oaptOp2qZV1n+G6/N3ZBQ5xw7xzNgMggNsvD2Dhecho0g2GqIBf2ttVyKt+2AjZhOHcnb0ZDqdqSxP8n44wwofSal4PF6i7Mv86YGZKfZbt2KE85//y98faHxxj0YbpNCUmk4z5b5TVR5UNa260Kk8DSO9bArqeNirqQ4j442gee/VVI2auh+x18+jjpvjVFUR7JWnQ3JiznlNipm2m9gbkM2ncQxu08rlmbI8ntXh8lzLi0stLy772uSdyraWfK6yaZWFIB+CQhcDniZ0akOQ1OhUln1PQARsTVNrfzxqmCAUUhQYeyyyAdw7p1D2fQpd75BPZS/A8b/JbNa3O8eDAxH8uMZBIcQeCdZiXkzknJRVJ3kY837WNhmiTJJzQ31/12cJ+L/3cbKXHNmK+O/4vd9N18VpVm2cqJXncW2cVBR5bLoOcUhRcFLmMzl1ccxxHk9bds6nCVvTfqJQbACOAVTXBXnXGzHvFUKruqlSB7Q9WDD3RfSxQXJZnLiVEaXT26LYRyENzdEYEykqUO6GQxrjSelD/wLZIGQsbuhQwuRcnKhW9CNafZal7/PeqShy3d3d6ubmWvGE5InuXrzQbrvVD3/4W7pYrZJx6rpW83ksNbm+uVJdl2rbaHCom7XTUWJ9b6d37/Y9uHF6enrQZBrZhdiL8DgY+R5gT4qehT/sU31/289If3p87g3cUb/1Wz+MBrsLkvOazuapTyA6p626EBJTiJE89mUFNIUx4QiWkgwBIPh0OmnVl/gQPEz9JNmDtm318uULPT4+JmaaWnHWhu/y3qfsBCMfJWm5WulnP/uZmqbR7/zO7+jx8VF3d3c69YCW8oHHx0f98Ic/THaKQAlGit4PSpKoJ6YHAfYOeeJ5rq+vE+N3c3OTmlOvr68TWy8N47MljQLCi4uLNEUGh3N5eTkC/ZJGJRkcMEc5xtXVVVor+jII3Lqu04cPH0b9LABpSd+ZXAUzDbtFOcQ5aHh8fEyZC4IFgiBKnwhOABCUZ9ksGCU01hGzNtPpVPf39+lztkyCz8L8ArRsGQEH7MEk5nmuy8vLoWykz8bYXgkbNCAnZVmm8lUmSsEa83PWdb+LvUaRySWD5lXXMRiO5/YMpQ34yK4LOh1PCt1wIB36t+htR9d1KUP04sVL3d/fa78/pGlQT09PPeiKa05AbKfbxO8t5J1PjPD19U06u2M+m/fPPQT/bdvo+ZkTpudDEBek2XTWr8VwoJfkVFe1imKi/W6fgmcqB8gkYbPPs+CQAgT+yB2B536/ly8iqJ7OpimYHTKWXm2/J20Tz7lp6h4Ih06TbBjZi1x2batJXqSSRTJRjw8P8ST1fvQt9z2UWbvU6wR4JHtJhor75xBIdGoouR4G45BRxSZZAgIG/Rxb2bVDrtAvdBIdRg+YiKYeeex7Vhw5IbBm/ckOYKOccykAQGdtYE8AafubIDro90GXyISiQ7a8qK7rNGwAG8TIb+fcyF4nDNpnMm2GFT8F8YP9gzQAdPM93B96jh+azAupC6lCxgY0tlyRCXtcm0wC9pNs2Xl/BgGopJQFseVpdoACARe2eqiUGbDkQCrlKUNhsyyUktqgKMoZ5XZh9LkY7H9ZCPHFgca333yjriu03zX6rd96rT/6458qKAJFn2Wq+giWG4+Osf7OoWQoRPxdHBkbQjxNV5Lmi4U6JszkRTx3oj8Lom0bVc1R7aHSqT2oVK3XP/iR5vOZ5OMEgOQ8Gc3XC/ZBrcrTScFlOmw2McsROkn+O2Uuw8urVWT988ksnXngs+E8Aw4S7Ppn4Aqhjex4P/On3/gQp4iG2OBMgMG1OsVg45wBIGPgw9APUrt4vkfd1HLqlOfxu8iehC6WqoV+SJPPMhX5ALad92rqTEH9wWkhTiXq+tKhrIjZmS4EqW1j1qaLk7TUB8hOQeqcvMuk4Pvv7KcbhT6bUzfJ4WR+oniInjSbTOWc+oyHl3elmrrP2GQh9UNkPpNz4zG5vg9iaETPsqw/wyWeS9H52DCfZ3nKMgz9In3Q52Ijdl4U6tpW88WiB11TLZcRbNzc3Or6+kqZj+NZV/0p0K9evhzSqEWhLPO6vr5U23ZpUlJRFHp8etK0KLRaRse72cTzEKaTiba7nZ6fH0bsqGVAbHMlhho2V86p7sGi93G+P5Nr2iYebJXnuR4fHyUN58ZgbHDasIcYIMpoAHB1HQ96u7y8TE4K5gVmmrQu983vYb9hmakHtkYVYw6D1XVdYvIAq5eXl8kwL/o9apom1fjP5/N46FgfpN3c3CRgNp/PVfcsvxQd+KtXr9LkGe7VggBYcNideEBXlewWh6UBzLz3evHixShFjUOlhInvPidaABDSMBWIsxBsbTz7RWkBgNcy+sfjUbvdLk3OI0Co6zqNSQWIA2rn87m22602m00aQ8ueUEJgM5BMcoogc2DdANmSUuaF3rrb21ttt9tUEkYG4/HxMe2ncy4Fd2SNcJy2J44gDxY2hDj56N27dwl8I2u8B5l78+aNjsejHh4edHNzk9bCApyvv/46TcixjODj42MKupBxvpvvIFvgvU/nj0hO6kuK6G8iKC2KYbQpoIP1fnp81N3dixS02PfRvImPJYvGmiO76/U6rRvyvVqtRlkpMhIWnDw/P6eD2uIp9DHYZYACwAh5Rr+xJYBQW+4DACKYAJyyjuAD9AqdtKw0ZV0AbD6zWCzkskxNP60OwGzL4+o+EMWOrFYrHY5HZXmWgO5oUpipRSdo599NEwkC7MO5TuJrCDTIPtp7JsCyz991XbLzsPAASoAwQJ6A3PYZ5Ma3274LbB/jlLmeDZrt8IcQQiqXJPNJGZslCuwEujzP9c0336RACFIDe0eDP3Jns6nnGMg23QPo0Q8CJGRgNpsle8w6YxewNbY0CP8HQEe2sBl8L3/33qe+P9YmhJBkoshzVXU1klOuzc/QaX5PUGCJXdaKjCkkhs1OIZvYZ9snhFyRDUPu6C9qmuH66Dv2g+tjY/gdNhQbYntw0EPk+kteXxxoXK4vVdVB19dr/ZW//Of1d/7u39N2v1XddKqrJm0SN0Hkmk1i2RNR0lB3GgETaeuyrAaWOAuazuImNk3dR1IxReq6RlV5lG8rTZcLNWWp6fVEyiZ9qVGjYFiqtuvUhE7FfKGbF691+yLo+eFBn96/k3dSkWUpG9C2sdkWQ+e9V9M1kXXvwXnmI6ue2032cRRt1gcc3rk+kiQr0irLfGJLQtv2IL5f3L5/o25bhZRao8E2V5BTcFLX9x0EBXV5oel0JtVVbJDvhdIXE7WuP+sgqI84430EF88XCW00+MvFWnkRjeh8PlORF315WoifzXM5L+V5pqenR3Vdq+p40O7TRx36mvCkLCEezNg/Tr92IRmPopjI5YVCy6FIsa+F6VxFNlWRDbWNsLiuX+uo5NF585151mdjFAOgzHl510+n8EGr1bIPGG60XC7T5J/5fKa8yPXbP/lJXxrWKc9yTaaFJpM81cp2Xdsbu5jB2O422m23ur27k3fxDIeuzyA8Pd/3Ne8T5YXTbv8s5zo9Pn5UVS603W56I9mqaSbKMpdSp7DRrBWHuJFWhSVLa5INs8Svr68TCHj58qXKfnoI7DL9ChxK5n088XW/36eJQxbcYtAZqbperbTp0/2U5XAoHgwSIIZ7ISCi0bjrunTWgQXROBee8+bmRr/85S9lR2ja0gKenyDv7u5OWZbp22+/Vd4DHabVAEJisDsY++PxmA6mo7/hdDrpq6++SmVAAGjKoPj31dVVcmTcoy1Z4Jknk0mq16bEgwwEOhNCrBvO8zh7njItm13keWez2ehUa0AibBsOhaZ1gBH3CqDEcTAuluegDAyGH/sNewhAJXPBQYQ4J4AKjBxAhsD06ekprT8B5u3trT58+KDb29tUhsF92zIx5OVlH9yzbjZwo9SKPoNdXyJYFMVozOvd3Z0kJfDAGtOIbXtgvPep7+Xm5iYBOGwP+21ZRTsNKWazZkmf5vN5epbYqNypKAYmm0AjhJACZTJs6Aj/tvXw9LIQZNjSLgADte4Eg5TkkFUAfAEK9/t9KjEEgFrZQLYAOjD4FmRRvmIn+RDAQFQQTJI9s70Y9pnZF2k4vwG7QIa/67p0vg1g6HA4aJLlyd4hg7HkptGpKlNAzHMyjrqt6iRPlLRQLnMyGbTFYpFsCYFrKifrMQ/EA0EqdpN1574s4ZTnua6urrTf75MeoVeWdbelQFyToA97xJoTgPAeWyqKjiKL6JMt7QEo22wiPSpcC/kisAOkogdkobDRMPg0lMPmJ1/nhol02EYLfmm+BvByjXPyzj437yNDYcs3CQLsJDP0F/23oJzsuu0RsX0TNovCOtJbYksBrW2hz8cG5eyNDVB4BrA3f/Ke+NwR39reEoIm20/CPdk+G8hBZJg9Z40gd77k9cU9Gv/yn/2h5DMF5TqVrf7G3/x/6P/13/z3qlsn52IJDgBxSH1JLtSjqM0C0yadLzFE9ZLkXRz5ynsxcF3XSS6OrPVZoelirfnySn/iP/if6/LyVr7IFZxM/f/gVNR1qstK5fGg436n3fOzToeDJnmu0MWzPDBy9GhkmVenPjNgol2CCp9lKf0NW+4cFUAuAe62bVPfRde2sQm+XyscHKnRrMiSgHLSdZ4XsZIni1OF+K6sHx/rfAQ6k+lE08lUee/AjoejQpdrPlukuuguhFhfL2m2nPaHJsaMQfreNqiunfKskPNBTp3uP32U1CrUpT79/I/UwPJKQ92oi0VhEVzFtLXU97T0mZPMR0cZT6uO/Q1xbbJkMNnrKA/xrJYgpcbOPM+1XCw0KTLN51O9evVaX331ViFIi8VcP/7xj7XdbXp2Ok+fKfJCh+MhOX3noqxdXl2mST1PTw/JKNP8SjPldD7Vhw/v9fLlS202G0kx9fvq1StttztlmU8AEwZjt91qMZupqsp+jORMu922r03dqKoiiwyY4eAhdIYyEvSgKAptd7vUK2JT2GVZ6sXtbWIVGZP6/PwcJwr1YPPnP/+57u7u+trxp3QGwdPTk7bbrV6+fJkYlcVioYf+nAkcy9dff62XL18m3Z3P5/rFL36h6+vrBDoAvxwWBVtNQ6/tlyiKIoEE9AHnTeYBxzT0kJRJXoqiUNO2qurh9GpJ6fCnrm11eXGR2D9KXGDm2XtbcgQja5nYtm3TGRaAd5yU7dHA6QK8LPtMdoDyNAw8QB1biFOGpeM/wCXrQM03WSGADnW8XJ/RqpQNIE+r1SodUIdjo1cHQAAI435tdiHLshS4sd+ww/Z+AS3cw3kASYBnAyX2GR3AMWPfbQ8F3319fa3n52cdDgddXFyIZlaCeQKU3W6XGmPZG1tCQUYE2w4YWC6XevfunVZ9OSS2D9IAuQkhaFJMVVV10kMCgggyMtXNcJI9+i7FA+3quknZAgtIAWL4Nb4XssAGeQSJeZ6nKWVkOihLXC6X6XOwpQxH4LnRCWlgngE6ACBALr9jXSWle5KU2GzAi6TUvwApcc5GE1xwDe6hbeO0ye1uq2kPGPnMdruN954XKTAHLNd1relsprbrNJkOII8AoG0ahXY8rpZndd6p6skOaxvYE5h1bDhrYGXI9i7ZkjEYdLJ/YCLsP9mY4/GYesb4XgAggZltJmaNLUgnILRBBT8n6MUPE/Qi1zwT+k+JItcH9BOUkIkjgEen8V0ErdgA7t0CW7I5yJI9TBJSDn1h6AZrje1gXwgeITjo+WBPbYBig2AwAT+fTaepdAo/QBkVARhTwGzGA6IAO2j1hz23DerWHnJ/ds2xV8gJjfQDLh32RFKaYId82wDFyjp7yAt/aO26915/5j/90/q+1xcHGv/0H/xDXVyuY3CQTfX3f/+f6P/wf/zr2u0rZfl8FETg8LwLapsypYl5T5ZlqptGbejBuPPmILegImd0mdNkEsuzurbT8XjQfD7rJzlNlBVTdc7r6uZOb776StPVSi6PjUyAXsbJZb5QU9XqmkbV8aCnxwed9nt5KfZseHO+QZ8B6Lqg0B+GRz1a2zRpIlJ0AvQudKlJOctiXwNCmfksRX9N28RSoT7DcbG+iE3CITYbV+WpT08j0H1kWdfqFMG88/2pzD0rV/eNwafTUXkfMR8PB8k57TY7TYvJaFrBcrlU0zY6nXY6HodJMM45tR0ZqqI/F8HrdNjpdNzKO6lrKmV9UzrTs9qu1XQy7Q8nbHqlGmpPi2KieM5KPz6ymPQlSiuVVak8K7Td7uWzqBDz2byPmOdaLue6vbvR1dWVXrx4oRd3L+S80363V5HH4/2aptFsTvkGTUuTVNYwlH/UkpyK/vs3m62qquwN9kw0QXFSKOCKoDCbZEmxAdixbCtT1ymBLu8zVVXZ14RPdDrs+6kstfI8S8DqdCq1WCxH5RGcSI3SA0AB9c45LfvZ8zgovvfy8lKZc/r2229TcAWgnEwmOvXOejab6f7+Xm/evEkNeHd3d9put2mM66JvDr+9vdWhPzAMBt4GgzgSgD9A8+rqSpvNJhnGuq7TBCwcDvaCBmDmdpPyX61Wo0ONsizT9fX1qASLtWq6Ljm+rhvGTnrvVZ5Oev/und6+fZtskGXpYPNCCKP+CFLRrLOk5FAsoUI5EsDBMq5t26aJSdgDQC9p9dg8u05BFiwjjhjDXxRFml6FY4UZfnx8TBOapDHYA7xTmua9T1kwGFnOMKBMi0AaYEDJDGthHdByuUxACNDN/UiRTeXwPp4RphAdJeuDHmCT2OvzALEoilHTLTJGIMjP+DtgwgJXG1TSRwTzx2GNAGMYWsC6XVPYzXPgPZ8v5F2WdMo2xXvvVDdD2cVDX/8fs3UTnY6nBGCQCWwZukOwaeWGYAdGFqIEf0VAyf4RzPJdyDl7z4uA1Zb0WeDD9C5Kbfg+7hFbRIAoKck8+8z1UiayGQ7WRZcBbwCzpmnUhqD5Yj7KlIQQB89Mi2EiGM9TVZV8lqntex0pv0RvizxXaL/bwBz9zFydBt22ARiZCLKYADKejXM+yHbwvHbCkw0Y0GGbjSWLAXBnLWxgYDGYzaYSXNh+A2w3ZTWW2EHX7f6xh9g+gi3bZ0RWiHuCtOC5Cdht6Q42Dd2HnOB3l5eX6Xv4bmyLLWO1digFlb38k1FkTc5HAVsdZu3tWtnBBJPJREWWx5Lt3qfwXghCrsvkQIJCfDD2wDk3OpcE+0HgARlHCS/ywPpjc1kPK+9UtFjZRMdsmRpyjk+XhlJrSYmEIYBhv/M8/6JA44tLp/IssiLyTi5v9YO3r3VzfaXt9tvYIOzOezAaSUF55lXV0XGWVaUsy1VkmW6vbuRMIwmfjYoUD2YLXWxG5sFjmYxT5nOpBxdtkLq61Ydvv1WxWmmyXCR2T4q9CW3X1wK6Ts4HZcVU64srFflEXdPIh051r4DT6axf7FxyUh16hcm92hA07VN1CtJkFjSfzeQzr9l0lg4SzLJcVVXHhu+8GE0qaNpG8+U8RZWbzUbH3iC3VSmv2GhbVqXapk1K4jqpLivR/BwNfGRQ26qSuqE5retP9K7rWk6V8nwQSO+87hXiqeX9pKI8y+SLOOVkMpkoW8cpPt5Jr1+9UF0eNJ1kurzoDz6bLiQXDz2azWaRHZ9OdXGxVuizP6tVZIfipCevIs/ksmG0JyA9zpLPVeQT1TVTGyg9C6rqUow4vr25UtMe5YPX8/NHXV6slGdeZXWSXOxNOJ1Oms5jtO+d13Ie2dD94ZB6aLwLqk5HOXUqsiwOIui6vt+mUFO38i6Td16LeQTYTkGZj/0Y+91Rr1691OF4VNeGvg9oqqbpNJ0u0uFmZVlqtzto8/Sky8tLXV/f6pe//KXW67Vms7mKYpocMczJ8/OzfvCDHySQeejZLZuWP/UOhyblw+GQzpJoqko/+tGP9OHDh1SWg4N2zunu7m6UQr68vExsKEwxGRwmJaGfnLPA5zebjagHp1mX5wHUYeBwopx3wThYSr6wGa9evUq6nmVZYgHPU+AYaxxlZVLXOHaMeV1V6YAuyhBgighoAFBcFxbMZjFgighCQggpEIVVoqEfAEDZG+vC+zDaMIoY76qqUqkA4ArHmGXxsMGLi4tetnbJmQJScToAdklpfx4fH1PQg0xRRmNLW22vDvYHBw+wYJIO6wTQp8wVuePsGJ4fxhQbJik5bmwDToz32qCU7yPwBjDAwJ9OpbquTZN76O2ZTKZq2ybZZwuWKFvkdPjdbhdLcOomNkr3wxq4Jz7D55FBmNambuL0wbrR09N9yi7BQtZ1reVqMWINOXsEIiPLsnRIHnZ9NpuljJO1n1U1HMi2Xq9TQ7sNdMkSEohIA7CwwdfpdNJ6vdZzf8YEBAP7RL8KQZ7VE76TQPZ0OqVyNZ4LEIceAojwCWTo7NQi5IdsEWAVGS/yLGVxeX9d17Fkux8Vbmvk0ZlOTuv1OukXp753bav1cpWIlel0asYqR/BHn4wtM+EZCRbIOmDDeD8YCdBHYHbe90AJEs9pSw/RC3ST2nwCdPYV+crzfHSQogW1ZFjIcNrxspbksIGLDbTINtm9JVDCFjPUgu+2YJbeNOSQ9SGIoGTSZhQgEdq2Tf1PyDWkLr4M4oYSOgiL88ybzVYQ2Nl1YjBBwpd9czRrg96iD9gy5MPKOniZZ0FnbfA+lEUN/cPIsCV+7P1bEiyub6MQXCJF8F3YWl7WJyFTBIm298XKPMTHl7y+OKPxD//B/9iXKHTyvtBhX+u//L/9Lf3BP/7narrYb9B1QcF5+Szvgb2TL1wqQ8IR5f1IOe9CP+GoU9vEKUdN02g2nSvPeqDSdMrzST/61aksT5ovZ/Ek7Gxo4JkvlyrVqVgs9PbtWxVFrgPj8oJUHRvNJnPd339UVZ40mRQqilyb7Uadj+VRy9Wyz5j0AKAolMun5rCybxQrqzJOXmqjAGw3G02mcdrQ0+OTDvu9Mpq++zT54bhX1zXq2iB1fSNO2+lUntIaqGs06YOCLI9AN/YbOE1zr8zHyR44i9l8puViodC1ms7iSc9EqutVPCxsOvO6vFhp3huTy8tLZd5rvlhoUgwTLEIIur29TYoWFPozTZz2u52YwLVar7XZ7jSbxUbSzHu5ntGKQhjP/fCmnnNgRfqJK73wRsUOqusI8Dg5GQODMa3r2OMxn897xj9XCFGJjsdDf//qsz2uP8n3JN+fgp0XRT+SMaZUD/u9pqlxMt5T2zRxfnpfbx7B20rb7UZ1VWu5GoxZWVW6vblRWVX9OOZ4f2VZaTYb5qdHMHZITg4jCuibTCapftdO4pnNZtpst9r17CBOuO4NZOj3CKZPUnLcgGcYddLURVFoNhnOPql6NgWGbTaf68OHD0lGcHiLxUKbfvygZZ0wivwdR/v4+Jj6YYrpNJVRzfreiWIyibWFYZi4QUZht9tJGtgTQBnZAMAUTgdGNIQwcvQWkO73+z7QzVPzMwwVTpdSERw4DoL6cgImjPj5+ESbqeB9NvNga6gx5LZUy5bG8Oz83aa5o+No07Nj9G0zLu8hUGMik51HT+DTNE1iSW0pCIErDhmwSeDx8PCQgATO6Hg8KfOZsv6gyLqKoKRp43jhw+HY70sn5xinHTSdTrTdbVPwZAMZmyGAHZViEFqVfdPnbJbOaJpNZ2rbRqvVOgZheaa6GgLD2Wyqto3lMvvdPgGjosjVNO2ovrtp6mQbnfOmpMCpLCvV9RAM7PcHLRZzlWUl9eQSjC7gAvYSmxhCzJQ751LZLv18tu/FgnPKIMlUkOkEmNEbIg3nB9jmTWy0rYUHCCLzs9kslaDw/NwDemCJP4Dv8/NzCthPp1MKbgCXyCDBPwGDZciRN8C/DZRsgy2ySFaw64KOxwjqya43bfSveR6zy4BlwBIBR1DsLXTOqWnb6OudS/YJG0HT9GweR+nTf8Iz2V4d1tvWxGM3WD+AHoGBLbei/MZmVKyfpioB4E9JHsG4FPvLWGNspPc++RvkGfyETwbIIh82u4ydRS+xRZa4QLYi2bjS/f19snlkPsmOYYfJ6AKyyTJxPWyaDTRtyZk0MOwEGwRX+EcCWO4Te8rwA0uQY4Pxr3yXDRAiiStlzidi7v7+PpUJr1ZrTSZTVVWp02k4QI9g1fshc2tLdSeTmekLDD0p0vSVM9moj4lJiFF/h/Hk8fDr8T3zd2SQvbeYBPuLzPHzwQ6ObQHy8p/+ld/gORq/+tUvTLTkpTDRT//tr/R/+s//Cz3vG7Wd+ixDq/liLp/lcUpT1+lw7KN/uQjSFUFr6NrUfEzUWZWlWnVyRSbvMk0mU2VZrq6TylOlfJJpMi0iy+S8prOZTsejbm5utb6+02S20Gq5irWUfQal61r5rFCQ6zet1Ww21ansx+YVsV6uqqsYHHipaWo1daVqH5vc6qpW3dRp2kPXNGqO+3Rgi1Xa0LZSG+eUxzIppyyLhr7Ivbqm1tXlpb766qvE5sU6/UtJrRaLGPBcX13rsnf4bV3p7vpGVV2l8o6ryyvV/RSM6WyiuqpT7XFsYJrp4eGTqjo2u33zzTd68eJFAlQILSfTvn79Oik6pQfnzaV1Hb/j5cuXacIHhgsGFybx/fv3evXqVUofY3wx0BhZDBtG6OHhQa9evVLbxkZNvsvWTqIIlKFQnkDJENE2LCAlKJa9Zc+KotDFxUUChtwP8/sBbPQtcO+UU+BgMKCS0sFKlArhvGmoxsk65/T+/fvEImOQY/3wNKVVKXcCJLIPXAMnDACczeLBczaNvej7MF6/fq1f/OIXqS9jvljot3/nd1LtPr0bm81Gb968UdNnHVKAaxodz8tOqL1tu05N/70A/+PxqO12q7qqFAxDS9CV57k+fvyoFy9eJGaQn/NdtimalDQginW4ublRXddpwhCNsDT+dV2X+jKwPXa/CB74flL9nORMxgOZxzlj9Pk9bJqtu6bcCfaVwI/AhFIx64xxqNTy21IKelIAIzgC+l4AFzhW9oM6eAIvmDaeBVtP8Eqgwl4w8jFlwA5HVVWTnHZZlikQRF8BbTxztCtBQV1qioStYxqQZbnRmfi+0I9NLUaAG0AIg2+ZU8r+eFael/IcMoS815Z2PDw8JPBPJs320EgDWLPsM6wudgUHTRbD6i+2jSwMzDayUpZlYu7RdYJxmF8+T1lNCCH1fUH6YN8BPqy9lRUYWvSMrA819eg6z2KBtDRMzqNkhN4lCBEyXPhMW//NcwCSBmY3vii1Gyb0DIG1vW4MBON92wMBkUe+C3kHrFOCZcuiUq19nsvnQ9kYewwjz7WRMft9trQHfUVmQgjpUDuALkQGQQMlLzSvc+jj4+Njkm18P5+nN8NmH7kf/BcsPLJjCUJsPvJkn9na4xBCsqn2+wlusZ0Ee9i0c/vNvrO3yCdZLsqIIKlsyRR2xwZukpJfx6aSPSDLgL6HEHsssKlUFbDutt+ibVtl3mvSnx8mDZMUo6yvNZ8vEnaw2aU4ln58oCsyJ/nUv2HL5GJp45CVQC4HQnY4xJLrQRbYvcV2DbozTNyyQak0HE7JOpNl4/vBdH/pr/0GTwZ/eLhX29Lglyl0ub795l5//a//l/pXf/xeTX9YncvigX2zxVRd0yoPTuUpnhXAjWVZprbrdOzTrwgJDE7rWmWzQlI//7sbGlpmi5kWi1lvFPvxiEx9clPttkfN5/OkFNSFN05qulZ1Xel0Oupw2Olw2MV0XJupa1odTwd1Xau2rSUFtU2j3EldO6SRTqeTfJbJhVaFr5QXuW5ubvTyxQs5F0+pnE4myjOn9WqlH/zWV/3EKunt29c67nfq2phStgzA5dVlrO/PI5B5fHpU1yv1ZDLRYrpUU8VpVcdDBGzri4s4Yq2qFU9tHEoGIlPVyrl4GCECuV6v9enTpwQgLEMhaTTmD0BTFIUeHh4SyMDpW0Nq08AhxDGgdlIJxgplsONRYb/2+71ub2+Tg1osFvrVr36VJglhGDDIlIvYWsztdpvA7uXlZQJbHz9+1M3NjRaLhb7++uueiYxMzeXlpT59+iR6APb7fSohwdFh9EhzkzWwbC8gjjIjCzKzLEs18LADth4eQxhPAH/WpC+RuLu7S7XhANCbm5sEvEmvA2IpkaLcAea+qWtVfXodUEHwM5vNdNFPOKHBC6YzhKDN01MCFQQHzCHnuZABDNDHT5+k3qjjnOJhWVc6HY9a90Ec62GZT8suEQATLFCKgJHkWa3csW/T6VSbzSYFjIBimNOuiyU+9/f3STcwtMhOWZbpTAyaizlgSlJi7rquS2cUWMBhJ20lJrt/pR4uUxJBkGxLFQDFlFnZ3gJkqeu6BOJubm708ePHBE4IonHKyDTriBMBDPOfDWpsKp3P8F8EaEF1NbCK2BHWnWAOp04g2XWtislQCsV64AyRe0qFCIDKU9Vnx/NRjwKgNM/zpJusu61ztrYL/8Oa8D2SEuhGtqbTaQIis9lMHz58UF3Xurm5Sc8FEIFgseVgACT2H12jPJC9BaABRCQlXYFBtWUM3CPyAMsOsJU0anhlPbAp2Fz0mM+xvrbMC6DIqF4bXHBN1pegwQZbNqiwe4ps2kAKubV2AVA4fJ8b2V7uJa7Z0FDMd5LtITiShtJtG+yiw6NyJO8V3NAbwH4jOzDqBHZ8H4MUbBkk8tg0TSprYt8o2wHscW3O1iDzwXrZIMaWiuF7CGT5TnwZDfAEI5BydpQ49hT/QOBPaZjdP+SWTABAnkwKMoUtQUZsrwjyzMACm5lgEhcZZ9aJzAhT8QhiyMxut1ut1+uRvrBOPL8NUMEnvNBhbFEIQZmLmXJ01JYxdV08b+I8gxbtYZ30nIAf4uL5eaPFYphmaOVsOo3+wg6JGPRyPHHK6j3PjAzzO2v3eEZkxdpBmzFFJ5CBLMv0V/+zv6Lve31xj0bTRJDeda3y3CvLneRaybc6lqWenjeaL+dxJG3bSF6KJ2vHA4GKSaH51VqLxVJ5nulUlnpzeSkpHvATex2y/gTliboGB3xSCFEYy6qU1Olw2Ot0rNW1UYm2222cKPS8VWjiqc+H41FN3SjP4/kV+/1WdV2paWt559S0cZxu5p3m00LLxVxvb1YKIdPl5Z1ub69VVaXmkzgi8frqWtc315pNp5rN58oyp9wPKWnvnWbTWRwJK0mh69erUzGJp5UXeaM273R580JFf5CdC52aqtTzw0OcvOQzHQ9HtXWrw/6gq6tL1U2j4+mgzHntt/GZL6/W8l4qJl4h5H15UaHZbK14Ardiz4PrVPWHImK4MYAcwrRerxPrtd1uk+OeTqfp4CcEFQD/8PCQnC3sPw4Hx0uaEwPVtrEGHHac+f0YSsAlxu/Tp09JAWnOLIoiBWmPj4+JuSYbwwxw773u7+/T/RF8brfbdK7A6XTSy5cvU2bg8vIylR6QNuSerMMkvU9fA8EsjduSRmvN2uBgCBJQVOtEMbb0YTw9PaXDtjabTTKcGF8buACcQwh69eqVqqpKTXRd16npGfumaUYTS+q6TjXu+/0+gR6CpFXPsqNrvAdDxf5ilFI2yKTX8zzXq1evIlBbLvsR0EOZTl3XiT26uLhITfG3t7cp0wJ4bds2MZSr1SqdFyJJL168SPXQm80msVm29IN9gfW3pUkAGYJHSnrI8H348CFN8qGGG1bbgiNYIJwrjBj3fnl5mZwJZXaslQUPsHh2hC17zX9kF3hBCtipSrCXkkZgAQYyAfiewWLN+DnXe35+Tg6ONdnv9/LOaz6PWR8LCHFo1mFSrnc6nTSZFgmUQQrgHG25FOwtDjvPx6V70rj2G7aPsjsbXPBslAWQbWLd7YQsWyrE9C3WjaCfPhdJKbtJ+QcyAJAnoALwhRAScCCTiv0gACC7QJBhSQBsAWSLBU2UpPDM0vhQMpsdtoDaghX0wGYebIbF1nxb8AKo8t6nnhI+T7BnATr3gH20dhQAZz+DDMY1GFhYa2PjPXWprMtej8+zftfX10lGCITQBWTO+3iYa20y+ATaVTWc18N7Ccpg4wkyWCv6UOzJ0ABqrmMDMOSWTBZk22q1SlkPC1x5RkgoCKvNZpN6ecAF6WyIokjlP+itLaMjQ0UgQ4aAEir2hB6ePB/OVELuAdg2EEbXyLASFFsyFttKkAORwbUJBrjmixcvkj5dXV0luUZPQ4i9NmTNyaKik8/Pz8n3QpYiw9PpVC6MzyZCt6NMxEocAgJ6l+JzDhMELZDHL4E/sN0EoPE8Mc6oa0wAWivPi0RgQHpaO2IzyjZbbskl9Az7z7WsrmHHGTJh5fXf9frijMYf/dG/ldT14Haipu60eT7ob/6tv60//Je/VNMEra8utVgsVTeN6rZRMZ0qmxbymU/9A7vdTgpxSoQyabfdJQDTdjFICKegzYdndSEGFbvdtncW0XE8Pj0O6SvKF7yXa0rlPgrzYjE0hU8nE728utLlaqnpbKr5fKblcqEs83rz9rVWVzN1arVYxDKsfBKnJnnnNO8dUOazXuE5/8GpabrESFxdXSk2gVc6HY8q8lyn01Gr1VJNW6tpqOkuVJ6G+rkQ4imwXdfJZ5mOVWwGVQh63mzUta0Wy6UyH9S2w4FJRJ0RMLQq8onyIleeZarqOO6yPJXabJ9Tuh9nhiBbpiOEeFopdfAozsePH1WWpb766qukwNapwVpkWZayJQsDTK3B+PjxYzJgsNPS0GSFYULgN5tNYogpX+F8BcrHWAdKCshoAEwjS/CcQAmGFSCAIcVB2xIwTh3lXAucgnVmOA9qPW024Pr6euQAMIz8nc+jwNbxbbZb3fUlRLaPgzG4GApKSzBSgE6YwGnfJ3E4HDSbTuN5I8YRp6blslRmSj5wyG3batKDZvsMh8MhBYTH41FPT08p0FutVnGqnGHKATZ5nqceDUkpSDh3Lhh+y77i2Niz+/v7FMghk5gzsmUEiABcrm0DC0kjI2trZrlm0zS6vr5Ozganh9MCbFK2lQysKVUhg9Z1nW5vb5Njvr+/T0ElpQgEBzb4gKGk1hknyd5bVk4aShoBQjhrG7DY9HmWDVPOyKzwc56ZwIn7YSzmpIjTkuy4yvV6nUoHLVnBusT7yWN/RS+HXdeltQfsQlaQAWiaRov5UqdTmRhjm32lpNNmDslEYRvYf+6LlwWxZAdZW2wabCgg4dgfymfLrcgcsu+2zInMmC01YV2tPbABAAGLLcHg+9gXdBpwh2/CdmG3sP+sJ/KKrPOctveISXx2OACgl0ACMIYuYT/Zc14WuLIu3BOZYJ4R22wZWsusxrXRCBwBWuMzZkme8UfICuCOsknkgv3GN5Ixnc3ixMtdT4hYWcEmxRHmkc1H3rIsS0CeNbb9G5Zo47kJIpqmSYQgdhkCgr9bBpr1xUeQTUDeCKLZX7uflt3n3rC97AE2yI6ifXp6SmWAtoSJfUCHbOBOBlhSGgdug/Qsy0b3hs1GBuyhhPzJixJUdMtODrQlj7wXO3l3d5dAPLaK/WVdRpmvplF1GvqO+L5IECxGcgfegDx3TknusSOx7C+O/Ue/kMGIe4YTwPFp4AjJJx/KM1qfYMusbHbF2gL2DVkiSLEljZBeNnv6e3/hz+j7Xv8epVPxwLYslyaTQqFzquugP/qjX+jv/P1/os32oP2xVFW2qlupKKb6+ptvdCiHqS77/V673a53nEFytZq60aks1bWtTihBK818oXhAW6eLi8jey8UDxNb9ZITpdKIf/vBHevnyZXQmeVDmo9F58eKFXr16FcHhfq/lhJnHR3UhnvMQQie5oDa0atpay8VcZXVSMSlU15Vm05lCO5wQOptNVdeNYklSprIehC/L4mF9Ta8kg2PPJXV9L0XQdDrXYV8m8FX3J2e3TaNJb6B8fz5G13aaL/rDgPJcZRkBZZC0Wi5V1bVm06lO5SnVbmIIYO9Pp5PevHmTQAtOGMDPqcKXl5fp54B2ABcMx2QyzNa3LA99K/wb5bTAPcsyrVYr/fN//s91e3ubgBvnJVC2QikRn/Xe6+HhIZXsYBy7rtPDw0NKQWJQcNBXV1cJANgyMPYLA0xNPsafwIHrEdRYhtSeu4CToYyCrItlEzEGAHt7mBGKDKuCwjvvteyZc1tHCjvBPrG+FhSwhrPZLGWr6rrWRZ9ZoeYa4+acU1lVqakf2YVNciarQ3razjHHQGGc67pWkNLELBwNwLWuKs1Nn4MttWHt8jxPhwICXG5ublKZCb/HwZCpAthbtss6N1jDNGd/OsyNh3W2zqVt45CCx8fHVD5lnXTbtqmRnCAY4oQyLWTgxYsXI4YYEMwBc13XpdII9NUa+ckknkFCWcPT09MIZPAfum2fFzm3pQk06NqeJVvOxd4wjx6WEpmCEY3rlSnPhr4dHBzfYVlZshkR6DodT4cExOjxsIAVmYR9y7NcRTFNcofO41gZlwyTHKe8xV4gejdYb0CvLUMhaOA92Av+RNbpcbEgnntMDtaALMCl/R3/2fJVPs/zsB/sIfLBNaThvCjuk/1DhpEJwDFAkd8DA/g9/9nSRlsuiP0nY4gMtW2bJgxBFvAZ9IBgmkwghAn9BJTpAJa4b/YKvaPUDN6CtZGU7A5+3gYGAENAJaW2MPFkAdBVbOp8PlcXgup2aIaGBCPDc3V1lfYOnWJP8cvoHGvPZ5E5QLANYFgv9pgzh/gdtsxmxfAbkA34NPaITM95CQ97QGBk7QrPhk6zzvRy2oCQ7Iclqch+pwyRlOz4OfvPeuFnuEdkC5tNVhqSiudA5gDP9O9AwJFt434gaZi6xbh3Dra0ZY2n00lt3ajIh75E5DOufxwigS3B3sb1jed92XJWPts0Q1bGlnlFjDEM0UFeB90dCByb/bLksJUtSzRYPzng0qHHxZIK7BOfqarqN9sM/v7dB8kFleVBTdvIyattpNl8pZ/+/Jf62c9+pV99/V6fPj3r06dnffz0qN12q9BEp1P04G2/36uYTDQpvKbTCHTfvH6t9Xqtj58+6e2bN7q9vdJyMdFsPtPhsNWPf/wjhRAnK12sVipPpUI3dMoDQNPhc4pHXQB4JkWhpomLWFaRHZwUmTbbTXRa+Ux5Vmi32yrPM3mvaKAk+VD0B/TF8iTnvPKiTyfmA/POYVDOOdVNDJ4uLy/6qVJBWe51PBw0m8/Uda3ilJNhlNjpdNLrly/VtrWcXGJPylMZe0KUq67DyFgMilGorMoE0qRodCnpYQQqhotzFgC3linC0ALeYbFsmRQKalPfpPQxQii1c7Fv5d27d6N6UECNHVlHiQnlJWQtABH7/V5d71UoR8JQE8kTCF1eXqZeDtjfu7u7UemQPRsCA+J93PeqX2OUkTVFUUk/EyzwfdTzk92gtwBQyfNiKKQBnGNA8zyPJ72T7gxBeVGkvaCGVxpKfTDcGAVGBrKHRe/EJj3ogaEESOzNWQ9N04zG+E16wIAR4t4plyJ4vb6+TodJhRCUG3A8m0716f5evpeH0A0nihNYLBaLxAISdAEcvfd68eKFnp6eEhPJOOCqzwICyMlIwZjiDFlnghpAxmw21/PTU9JrAvBvvvlGd3d3ySGgI23b9mfBRB1NJQWT+D1VHSfSvHv3Ts45LRdL5UV8HkoUuY/JZKrDYd9nbHI1TZ2yFKfjSVme6erqWk1Tp9Gt8cTpLpVewHbGU2CHA+fyPJ7vk+VZAg0RIMXx3WRY4mk09CF5leVwAi5jYXnZKVlDoNrX/rph0hw16TRv2r3Jsnj2TuiCprNYdsqe9m4p7VcEY00vl62ci3uw3exHIBT9xQmSmSGItyUW2B4yDJYJxkZasC1FBpVTmhnZCit7cXGR9BC9Iui0jh5bZPs4bNOrDT7PMy42O2Sz0jaLBbDAN9jyFomghO8ZmqpZM4D9wJKOD8cjSGV90CELSOw60zgKwLGZBu6VgwzJWNoGeu6dkkPkgWCeP7sulk+h73mem56GYcoVe8yf1nYC/AeA6lTXVRxw0zSa9r6h7TrV7XAIn53+RVabs1YoeaPvAT9mATh7bidy8ZrP5mky2XQ6VehC1NM6sv91Uyc7GLqQMoPT6VRN3ahph/IpbKlzsZ8V+ZnOpukeBtJgsJO+D6QkKTckhO0RiPLjxRlR6FPEAVOF/rwSm7ljaMv9fZwiSTDHXlnyr207hTCU4znnU0aAEid697g+umGb9TOfJb8gKZ5p5uPkMfYSvQxdUNM2AxHXB4eWPJrk8awx7Cl4hHu0Y2mHZ4mtBxEbVJpOh/PN4j3Hz9mAiL3qulbz+SytjQ0K23Y4rA9yFf2AZLUZfhu42Rd2CDtiyQ90hM+Bm/7j3/tT37nOd677pYHGP/1Hf6D94aDYLV+oLE9q6kZX19cKIQrharVWear0sW82bptWjw8PKZ3onNP9/b260Onm+lpZHxF3oUvgZrlc9hM3Tr3gRWX3/WZTCwjDgBLAbl1cXIwYMYx2VQ2Hb8VzL6b9WRUsXJyElWfxpFEY/qqsU2QdDWynsuzr8gpS5a28j5t/2O81ny/UhdAr0FBqQw3gcrWMAYR3Op5O8r3i2MlDbGSexTHBbdspz3K53nE9PcUxulXNZIEssdS2PtxOMGD0qU2BI0ifPn1KwRKBBcwd4IrSodvb21FzH+uP0WGtUX4EHYeLc8RREfRQhgCAOBwO6nrnxAQmWxq0Xq1U9vIA42mbjqkd5vtubm6SEQKgnE7x5GoY0Mee5QGsJGa1rpX1jpE1sRkOlBPHwoFogFnKtOwkF8oNbPmOLadijTjNnQltVc+6N20bT3l3cRyjBTMRzMWSwuPxqLKq1PblDNwj+wWrRa9K08QRuoylJVghHY1TwIgTWM1mMy2Xy1RGNZvNNJ3N9Pz0NDjkHsTv+uCEZwSsHQ4H7Xa775yn0bZxAhnOkHJA9iHP83TYFNlTSaN+CurD2b+6rjWbzlUUE/nM6/kplhkulgsdD0ft9jstF8sEPnEk3nttNs9qmlaT6cRkZ/JRPbbN7HGugpy0mC/6e817AD5VnsfRsKfypMV8kbKEbdumww8ZMdk0tbbbnaqq1Gw212q9knfU2jbK854Jzrxcf/jokI7vR0F72xDYqiiG80+6EE+on/VsMXvknOtZuVreZ6przgRxaU1tHwLr5ryT85mKIo/Bs/fquhCJHu/jlEA3HDplxyxmWdYTW+ptdKO8PyAVm2bLOwAatl6ce2JfAD22nEkaN/5aoM1z3N/fJ8duD3njuvQ9ndfqs3aABwvOYfL5fitr/IxrYbfQAa5vs3AWzFF2GUFODGSrquyHh0z6UqWFjsdDsqGAPYINAh7LFlPvb0kasibn2Rzuy5aR2AyODbwgYgDgFxcXqTyQgBCQjv7GQGSYfPT09JjOVSiKiULQKNPovdd2uzGZ4EkKMLH3x9NRnYZsbVEU6vpM3WKxkFwY+TCyjBGD1AohXjc+90nOec1m8eBahrR0/blXIcSm4mmvd03dJHbeOafJdBLH33ddGt17KuMoaQLDsizVdhEI5lmuoBi0r5ar5OO6rhuVDbIfRVGoqisV6YDgKG9VHXtZs74kra4qOR97SE/lSXnWl9PmsVS77WWTSXjIRMzyXKooCj08PCZ9XK1WyQ+y91YuIJHYV3AM/qptG5XlkDlNQ0+aZuRn7WjetuIQuz5TOp0kO9KFLh0U3Lat6qaOY4+903w2TwFQnkcbHfpjGrCrBI7orC3XQs7tvcZAIGY+CApSNUAY5MsSH5K0XC5UVUN2MsputOn080EEQTTYzIbNUFo7R/BgAwybHcFvcm+2euVP/Zn/SN/3+uJA45/943+i5+fnJNg2/YTBPDfWXHq/36f6Zu99qpmXlFggml5hVgClNKRibGAM+DtNrNTMUg5DOQuTEWBJKE+g4RWnRArUudgceHV1laJTznbAuXDoC44ZYENZBXXnBEK8j++0Yz0JYJgMw+ZibGEGnXNplB0BBcCfEoA3b94kY+9cPIwIhgYHC4MMgEN5cRzUcwJG+Q4AvD0Qij1kqgMgjylRIQR9+vQpCffj42OaKgV4PBwOuri4SH0dAOw0Dq8H2Ha6B/0aXduq7Pes6hudyTJgVC37zueH9GZUsMvLyyRfnOiOYlLb2rWtcpPRQFlxNLBR5wp7Op3SuFZGJsL4ErSwB9ybbSrHgdszUgAm6CHlKASQOOwQQkoNsycEkThwvgMDvNvtUoDWdV0618PWzbdtm0bnMtkJ4JRlWZrOc3t7q1/96lfJuALQJpOJPn78qOvr63SCNPIMc2IdD+OQQwipXA5HBdvJPiO78/l8NDYXmwQDiMy0zTDKj2klkkZTVyzjt9/vU8N50wwNeQTj57XXBMdMCcLJYsOQUXsGAcDMglpbEkMwX1VVuhZnCtgUPkACR3X+PNZh2DKY87Q8ssw6cm1b60tQjTziC2azmYKLwIUSIpxy0zTyimcDYQ8sGdE0zSiFj7xLSllMgj/Lstt+j4Opp+casOzcD4GNrQNHrq+vr1XXta6vr3V/f59sJADAZh/wI5bIkJTIMeTFZi0AftgVsm22jI5r4RN4vy0Bw+7gZ9AXfIDkhzWH4EsZ8SELCAjlOQCzrA+yQraY3yPLdgTzwLaOT0Wn9NHuObLIPVmCAFBssw+UnLKWNgsDqRnvfzoqm8F2cu82G4atPx6PajWMgiVwiZ+JI+sPh0Oa6HQ8Hvtej0vleewRIpPHWHVwDbjE2ohJXmhqmHNsBnKFPtrSKvQcG277qXgmejzsJCyus9lsko/H58TPDaW5yGPEH74P3MJ3ALDzXqcq+it6pvBzrJEt60oBW3/fBKxUKbBOEHjsMesAiYD+2+EbrAk6z+cmxURtH0ATKGNr0B1wFj4AG4Pc2NJSiFSIT7smVI/YUi9pmIRme8qQK3TZkhLYP2tbsF1lWaYgDbxhG7PZJxssWF8/ZKwnowDJZhJZO1u5AsbBRmVZ9psNNP7JP/xHo3QoQIUNx4DA8thm37qOjZvX19epPvrq6iqBf1hsm/5FQDEuTdOkFBmLCJhFGW29Pptr06g2fScpldlwn1VVab1epyZj6r4fHh5SKRJZAlueQTMzQQYlJwQVbDa9EBhky+RQqkIwwnOjjAgZALWu49QoG1jgXJm2YGf/k861E5JI51L+ZWsQMbLUIDsX62YvLy9Tj4FNwwFgKHfiMxhF2HKmQt3e3ibgALMISHh8fNTd3V0cY9fGs1Yk6f3797q8vNTr169juVkvg23bjg4wgulmDwDZrBHPRv05YLaqax37f1N3L0Vje9jvlffXxhkif5TWsJeAfoyYDaoBbW3bJiCBgyOwRl4tQLQ9GHwn4AU27Zxh7LrYkP7p06dUwvRbv/VbKS3+6dOn1EfCfiEPNnBgihHv3e/3Oh6PiUC4ubnRdrvVhw8fkvHl3tBdyARG81J6BmEBWIZkoIeCDMz9/b1evnypzWaTGvWpnQV8Y7yp9//w4UOa7mSHDSCrZVlqPlsm8ImzIECxAJsXjoBAluAY5wQoohYbQCgNhpzgyJa2AAYOh0O6ZwtabRM6WRNbM4ttQIeRR+7T1hgT1EJAIIO2LAV7hdxgl+1zU4KI07byPUrb53kqN2Gdkh3uYoaONbLZCEAo68m/bZ0y4Aw7Y0EMdf4EuvQXWZDBukDoUEc9m81S4AXgxs6iLwBsZI4AFsd+XmKCHLF2NoN5zv7zPpw8a0f/HH7Xyh8Ehg0gkde6bhPYA8gBnhaLWZI15MrabrKWZBIJQi2wlTQCd7ZU4+HhIekMz8wa4gO4Lrpt9xagas+CIPtFNtRmPgBVZVmlswzQCXQIMol9x5YkjKDhmQDrcT+8TqdjwjuSKafsz/wiS05/kg1qkRn6z7quk5eU+eEeeR8vG1Sjl+yv9WXcL7JgS3Z3u90IRPM7ehyKouj3Z5AD/BkllXk+DA9A9rIs0/F0UlbkIztMsIJvx86jjxYfWLnke61floaBG/hjroevQ2+wHeAzsiNd16mthoMDCf6RZfwlzwRxAumAXFAxY8kLbIDtA0QvwbY2s4DuUIaFr0d/kVHIPXAI94ZMotup3PoM+1oiheCWe8Y+YXfAStwLuoUdRAYtzkRO/6M//R/q+15fHGj84R/84+8wOETu3BAlLQBVG1UhzES5NOXZZkMMH4wrhow5+rYZDoFDqa1RZ1Mo17ApVwIOgCn3iZAg4GwQ38V4yrqu00xmUlWAE4IdywYfDgdtt9t0cBglIHd3d/rFL36hH/zgB+mZUGKcH5kZvh/ABMOLcg1p4CL9iTCdK/LpFA/U+/jxY1qnm5sbPT09Jef97t07tW2rt2/fptIgBNfW+WFMLOtlg0AUgdOiLWuMo0QGQggpqGOsHOU/D4+P6RBAypAkad7XVBZFnHwB8GLP+B4yNtQ4E/zd39+nBr7pdKqqrpX18kDghbMLIWhlGEbK/LquS+dd2KCD7AMMRNM06eRzDAnsDoYxhJBAHZ+fTqcpKLSsIKcz83mMOFkUDDPOHb2zAYSkND1K0mj0MYYG48Z+YtDQa0AFDCdMMAc1UkYC0GM9AEPX19cpw4lxX6/Xenp6Sgcxkrl8enrSixcvEtggKMGgAiRxNjSiYiMeHx9Hk0yWy6XaZsiQsV9ZFpu5Sd8TPPE5y57blDhO3IIsm/m0aW3rKG2QZMkWjL8NdHAMsGawUnYaGn1AODfbn0FGDFIAp2EzEYAa5A05Qq4t82adD47R7kkIsWeu6QZGHNuR53ksSTmVKZOKk+R9XBMHCkljs5LIowXeNrtoswDYMJwsGYpzho9nt8EA4Az7yvsgns5lgewiIIb3nLOpfI6XZfh5Hpv9ICvHOtOIa9eE50ZeZrNFAqg8u3Ou15Ggi4v1iO1HTyUlUgwbY209wzxsBsyO68anZlmWysS6rhtNV2O6oMUNyLoFSJYI4bMEprb3ijWLAZvTfL5IesW6Ul6DPQMcF0WhtmvVdMPoWiYTxfsKurq6VAhB9/f3qdJBiuPk2zauPxlK7hH9RmbASd57hbaVd37kK5Av9phgGF9uZYZ9R1YB8Ow1mAcbwVrzWfZ8MimkvuwKG8V+xu+IoBrCFTmVd+oM+cW1bV/oiHjIht4Au6dgtufn52Tf0TebucQX8aw8A/gAX4ceFkURD1Yuq2SD0D9e2B3+xA9zf1TQICf4VPsZaz+xSTyDxUmQycghwQkySWDAeyxpAaZhb/hOfnZeHUEwDVYkYOC6Vt6sveGafK/NGmPTwJS/0YzGP/offz8x9xgQjAubmWXD3H/AGbXX3LgdjcV1ptNpOpeBzcBJM2cfg7rdbhODfXt7qz/+4z/WmzdvkrGBaV2tVqPJAiwSvyOgyPM8OQrLPrAZCIVtZMSp2qBlu419HfbcA5yLvVae5wnc8m+Upm1jPTbTUUhd0SwLsHt8fEzgj+wGBt8CFgy4pKQoAAjr4Ni/oogjaBEmwBUAGoOKUnBvAG+MANE6ZW2bzSaNBwT0wF5479MUKgSfa9c98M96wQa8pLS5cYSARRg/G3BhxChXKctSb968SfvDHPLFYqFt/zw2UCbz0DXDtBGbqXp4eNB6vR4xEgB2smMhxEPgaIA+1x1YzDzP08Qi9ps9Zh+t0QGIsVdZlqUD4pIjkBIwwYBLSqV6MDRk58qyTCWLrAVnCLCWGHVAjs1g2HMJABUEIzZAQeZ5P4E9ukZwDWgno8bewGSjQziXz2UM+AzfGULMSB32p5Ezq6o4Qphnh/niezDsMIusJUGBzUbZ/2yZBew3zCqMn2W1CS4sgSANwNuy6zw/eoeMwBAD2PI8T8EYWVrrxAExXNfaZ2TdOiL2hn1irfAN2HznveSHPeCzbdsqtJ26th1d24JunCYOm/Kj5MD6daf8wOo7II0gC/uC46UPz8q/NJRo8SwET/a62Cjs7Xk5j2VLsRn4SHSXtbD9JBAbXBc9ZPqaZfMZNGGbWAFRsMnYBeeGkeTcK8FmVQ39dha84Cv4nbUlRVEkO4XvJJBlrbHXlLTic/GhlBBz38gL34tesu+WyNtutykDBViDsLRVAlVVazYbMgvIjA2WKTukjNd7ryYM5yhBgLRtq9VqKYYXnE+Pmk5nyvNBDixBA6gl0ID49N6rq5s0XcliIPYR24MOQtiwhxADrKsFsOiwBZM22wVAjcTLIjUnW6wW93Kiuh50wJYX122T+gd5Zps1JYAA79igi3uyvor1A99wfzawYO2RGWvvKCe1k9natlV9KhO5SVBtM8TWJ2FHWHfuHTzFd7K3lmRA51hH3osMoGc2UMTmQ+paQo5rAPixSwQWBM/YFjCQ1Sf2xt4re49cshf4YVuuZu2XJfMnk4n+w//kf6Hve31xoPHf/3/+v7q4uEjlRKT/cFSwsCggzh1nCuthU0ssmPc+legAmik9wLg0TZNAraTUoL3b7VLpxnQaD6Z5eHhICwEwsYCPVCkZBivolHZxEA6GAsPJrHuUAfbQNlizqRioLMtGZ0vYA+YQIhwAmZzztB5/77ou3Z8VMsChZfXZE4TSToqisZf98t6n/W3bNtUAMuoNht0yDbZfAWPAwTgA3rZtdXNzo8l0mkb/SsPZGTgmABQ1uTxDXhRx0pSGQJVn/PThQ2L8cXbspzVwHJBGPSjZFZhF9qAsS7W9cp9nC5xzauo4TvjDhw8KIeju7i4Foighcgvjs1wuEytu6x/tqePoBTrDHnCIlE1p0mezWCz07bffjtjHq6urVLrGwXoEvXkem1lxnoxq5fsJgCmFsVksW8/N363cXVxcpLW1pScE9W3bpjJFnpFUP4CdmfvT6XQU0HICO44KIwlrisw3TaOvv/469W7wPhsMsPb0ec3ncx32p1F2kxIRjL3tlTgnJAhApaE22bJzODWcLo7SGmpJCTCdM9KsD07hnM0CBNppNQS7NrNnA5Vz0MK6EJxgn/lua8+4fxv086z20DnLDqPDs8V89PmUge4DDXstZMQCJftZy+iyp9wf8mLfw77Znhj7bLbkC7njPmDy0GeIE4Ah+4xtKooiZefPGWr2D1nhz/PMiw067VpY8sOyqHyGvcZ+Y8ei/ag17Xth8F2S+tLEU5IfAA/yAJlh7ek5QLHywGcIFFg3Dr6klHc+n6csI+vHPkJIrFYrPT8/jyaIsTYEm+wb62gJMsCx9VV8DnA5n89TSSj9bM47lT0OwebwKopc3rsUWKPDkYWea7VapzIl1tJmYKwfT8FCG4d28G/W0AJ+roW9Zz1sYIi/QiatnlvZohyV/QL7xP/GJ6azv95napr2O8MLqqqSzzJVTZ2CczIKjNwns4cPs43oyLYNklkj9ILA2GaCIUUobUK/bBM2OCD1FZRVkjPu6zywRpYgaKwtY43sMBQCVeQAYglMAwYGH6ETNrNrwTt6ZUknngWiALuI7cJO4F9ZQ3stfm6DBbCfXQN+DolIYALuYo/Qw67r9Jf+2l/U973+vQKNu7s73d/f6+rqKjn4p6enpACXl5ejGuWmafTp06fUGIVxo0QK50r5lQXLCKItL4G1IujAYAK8MEzOuZTWZFHt/GoAIKU0CJM01AKeA+JzFrUoCi2XyzR683g6ablYxIPKmnHtMs+z2Wz08uVLbbe7xPi37ZDui2P6hgkm0TFm8n6IlJmdf3l5OWIHYTIo+yDNze9oIsfoU1ZCqpO0LMbaOhjGacapV9Fx04sCQMeosL4YD3ozWCscH0yjbbYi2CIL5Vw832E2n2u1XMaSiT57Mp1Otev7KFD6y8tLVVU8oRXZ4u92HyxYpLZ3Mpmo7To1bSvvXDw80Yx8dc5J3TCa1/txbxLAHXCMc7RlCrbsiKwZ05CsE8WAE0zWdZ2AfJbFUsK6rkd1+7DZXdeNem9wppTMAIJsqQqOAxCCUQHQYzSZ3c5zsO6Ap889K39nVjpMqKQREKPhmfKirutUlVUcD+3Gc/VhrqJcxnIGDGXXdUm36beiDpsgxvuhXna3jcGYLW+gTI1nRAYwwpTu0AvAGnsfz7aAVEBGAJo4MQgTdA1ZtyWJtjyHn1nAA+Nk2Wauj4zxGbJv50GMdWLsFRkonLhlYiM4d2KyVQjDGRN2fXDQqbky8/I+U1mVaUSnc05d26kqS01S1mEYxRpt0HgePr87B7m832a1eS4APeuPrT9n8qyT5t7PARegAL22a3hOMtlAhnXlOWxQgy1AXwaWPI6g5f7rupE0ZHvRVfaFfgALNvF78VlifwFj3lmvEBjC0KTyo7F8xIlJIajvvRsHy+gI63seEAHIyWqS8T23I3wfMm4DlvOSTlsSHfHDqs84DYH3ZrPtAW4x2g8ylWSxnY8H8yLrp9NJx9NRk75UUFLqE4j3UyWAl+dRBvb7g+IEtkJtO2aZnYuH/bZdKyfJZ5nKU6k8zxT6dcg0gGLwE3sEGQdgXq/XqQQX4Ih9RA4gLhLTryDvoo1m6psF4M57TXp7E9TrRTucVSHnlGdxzKyc5OTUdp2KPFfTNjqdShXTYewysoCvRVcgkbHf+AbALHbIEqzYfAYRWVKFz5H1wR/zc+xsCvDLSrkJnr33ato22Z8szzXtbf1mu5X3Tq4ftU21xHwRRwljS8CCYC9kA91ABiz5AWZClnluSHdrK1hDS24TjGOzrH22NswSUwQL+NrzzIQlM5Fdghp8Dc9iyd4Qgv70n/9P9H2vLw40/v7f+bsp/clJttYJs4A2EoT5QVFh9iwjd75JOAk2i2AD4wlwJeiwhtzWZlvAgcO3Lxhrvhfgbxt7WEyEmAbV9+/f6+bmRvLDqZy2xGA6mWjTBzybzUYXFxdpc7suyOeFjseDvM/SNff7vZbzhYo8V93UZtyc69cgzsXmnAmCJZuKJkI/nU6jsimugfOhXhwBRvB5ljzPtXneJYOH0Xt8fJSclGVDCp2pGgBIIn7KpGhYhxln/ylPsE52t9ul6WScCk0T4Fc/+IEe7u8lRYdEIDGZTPT8/JzYQWQHowfYsmNzYQZYH9YGwIbC2WZSJo8AKHjvYrFIsoGxl4aGNVv3D4Ahw8K+MxmGe6Qh+JxdIRCn7AaQhxzDzHPfPD8qblkjO+WL2l2MH89ljZa9Fs8ISMCQ2vXF0HNPOJLzsjlAPRPnJCfvMlV1pbYZRmYuFovEVkcZzTSdDtOFyLix39vtVnJxFj2ESNd1ury8TDrJugCweK66rkflajy7ZXGwNQQJ570LOFhkCTuT9QGsNfTYIhrFsVfIMMylNDgUdJ49ReYtk2pT9pbFslkF9ss6HZwUYAE5iI7su6cHNw2lmOMRtQM7HgMT5MRmY7Dt6CQ2LQLWTHF0+OB8sdXcn10XS5BY5hKbgY7bMjrrW1hzfm5l3ZbIsE58H7aXNbZlRrZnDxLG7iPrgMxFxx7PbWqaJpF3Q2Z7KPvjvmFnyzJOBoQAwkdiC8gao1MD4TO8D39kbaIFfzC2cUTr0ITLOUKw/ASr+BjsCrpMeYftZeI6yDz7RobUBn+QKTGYmIyCSJhm9oisNPtTVZW60Cn075nP52mQBXqLXOBnBjsYRB+GNAw1aHuCKnM+gUPv47kbIQR5E2yio9ga/DOEzxDUa9QwTKBxHmTaLH5d15pMpynDMJvN0mHAVVnGs8H80NsF8MS+cj+sH6WxNnjE9iNntob/PCBHxrAVtv+Lf2NzkIVzkgaMQ3CKfoG7sPvsB3Juswe8t21a+Ww4qBIMAHi2fg45sIRZ1gcnUjyfzWtovLdkl71P1s5mVNk7G6TbZ10sFqkX2Noc/rNZEWkgm5Epgjv2Ev232Q/IVuvXrK+32VXWM8uyUe9wnuf683/5z+n7Xl8caPxPf/jPtNvt9PT0pNvb2/QQ3BDCZAMDHhhHC2MDe07NNSCfCBrGAfZDGmri9vt9AtkYTQw9vQAYIK6FYoQwpL1tqj+EkOo0EXii78+l9Mqy1Gq9Tr0DsPm2P6UxdZ0YsIuLCx2OJ9VNO2o6lfpmb+/lglK/BxsrSR8/vu8P77pKoNeWS8CM4iDYAyZyUAZFORdKSO02B6FNp1O1TauyHA6vsiN6N5uN5otYrnR/f5+UyZbMUCdIMINQVlWV1pk6cWTDlmRhPCygsk4fx4oCHg6HEWNeFEUqA+NZCRZtGQ3y1ratXr58qePxmErgKB+ywVxVVWnsMdej54K9prSJ57VsHk6ubdt0+BwMIuV3BPAAd5yPdQCwkQBWfo8eEqzbWl9kDXDE7+i5sgE7zpXrwrIB3CilGwDhkNIH4FBbTsBOY3XTNLq9vU0Bx8PDQ3Jas9lMm+etrq6uk15SBgSAKIoisbc4IhwTgQ0jnO2whq7rUqYPww9Isj0P3D9BMaUY7APZTYAdz4Hjt6lsroXtsgYdB+y9H9U7Y1dxljYwsFkKC7ABnthYroksSWPgRoABQOJe0RULwi1LFu9jeDZkI8pKzCydZzWirMVD/awuAlgBEOgPP4v3HM/94HnPwRnvYx1YO1vPzb2wXpQ3scbYPFsTf17aMDDY+QjE0rfEC6BlM3Q2S2kBFYTFyP6ntYgTjLDV6FVchyGIQfZtEMl9o6uQbZQZkzEceh9iWQzyht2y5Sd8V9M0aSJUvM/4HHbkpmVdsfvIH6SI7W/jXgFa9G0wPOZ0OqVyK7J1ttcwrq9XluUj8HmeXcFusr9FUahzg9zQvE1fIfbekp5W9/g7tqPpKxkmeTFi620Aj5zyHOiZ7Wvi3ll/y1pbAI2+Ehixvk9PT5JzyvJM8z4QIOCwTLlde0CwJSfOSQn00voC5MASttwfPgidAs+BlfAZdsiG3SMyUxZ72EAGW8YaImNW5qwNggSyusx9W7KBtcAncx0bHGLvJ3khb2QXe4JvBZdZrIYM8HPWkmewmXVre3le2wNlg6s8H86KAncjwzbDIWnkO/FHkL+2coF7hUiDHD5f37/yv/7L+r7XFwcav/8//L1UKvDw8JBYAowRRs1OPLERmo3quEkCD2ruAD4EK2zCcrlME2Ng0DHMsOiU5lxdXaWSF4z+ebDBIttUHiD8+fk5gSg2FSWh2RrnPe/LqihpgpW6uLjQqT947OXLlymouri4UN00KiazkdPCsBR5LvVpOQID51xfN95qOpumw+g4PIrgC8EE2FmjChgiGGHyFD979+6dJCUWvaoq7XfHtJY0+4YQ4mE1oU2jQ2kGJeAC7P70pz8dNe7isE6nk+7u7lLplo2UuWcUi3Vzzo3KP+h5oLyIiV9MKarrOp4+HYYmJoARyoVTt6ldSsgwuLAKGCPGE5NlAGjZskDGNjdNk8p2WB8yQJYlSGVZGpgmW0aG8WUKlv2Mcy6dE5Dq4fPhgEpYT8uIMEWFf2OQcEg4HIwP+gqYwDgSTGBY8zzX1dVV6nEgCGJ9bQrZriXGbGDJW+XZMAgB82TrnDHE3Is1xHyPXQtrlK29gu2294ZtgGXFcdla7c/1Y7CWfBf7hjNDf1h3y1oi+wRrfBcye+7oAFEYfRtoSIPjsQ45gatuPGHK1vPaYNMG9vw7nsw9lLdYti/WrQ9lSXxnBMmZQvj1pU+WQQXAEbw4p9Eenj+TzV7abAT7jyzgT1hT27cxBDYDK2sziVbf7NoAiCyw6LqhdBEZtQEjz4mts+tMcD2ZTFWWVQpIbPai65pRsGT1BwBr/St20wZPPC/rejgcFU9bdqN7hmiCQLSTiJyTmqYekXb017Vtm4Iwm7UCNLLGNrMkaXRGlaQ0Dc8Cz3M9fvfunZbLdZIjmubBAJYcwV6ynnU3AFNslpUbe94H68EeWnCYsMwxHnBqZdPuK7IKgLW/QxcICFkPADz3xXphd4esYZ3kKc9zdW6w72AwSgttJpS1AERaW23JJsueW12RNJp4d05e2HWixNr6YFsyxPV4ZmwaANjugQ0gsJVUUtjnY724D+tTsJUWs9r3WeLGBtyJqJJT5ocMvrWz+FGwgfVB4ODzAND6Y2uT0W8+B1nGM+NL0DXwJMcloG98tyWTov4f0nogJxD/rDODjvBH9v1/9T/7K/q+17/XyeAYANLiAFoiKcsC2JpXnC7CzANQ4mGjuvM0J9Hvu3fv9Pr168TOUKOGctimZ+4H1ooSL4RaGkeHd3d3evfuXRIuehCKokjpQRT4+fk5sS5lXevp6Ulv375NjofUYOaGdCiBVFTQTsGkV8uy1MePH/Xp0ye9ffNG1alMRhogFBmyqeqmHjlJa0AA2ARBltVGGS1wL4o4YYrSlvV6raqq9OLFC338+FGTIs4EByyxXuv1WqfykIAvYBOgTzM9taUcRMhe3t3dSRoa15qmSad4oyC2nwQFXK/XiZGTNJpeBsOP7MXGvFm6Z57RluWhnBgw5AaZxmkTnNhmKMueW5Y9NRO6YQoE5TCAluPxqLKM54hgmHjvuTEgI0JAhwMfGjyrkZMGZHENVBuQQGbNnoUDeGB0HwYQwJLYmz4bhOFF1wDFrLO1AThOHJBN51pATsYjfs6rroamYAtUzq8bQhgxseiKDfww+ICP8xIjq0fYptRb4IYyJDIr3AcBG5k1nDwyYkuleGZ008q6BQO25tr2aFiwyt7aWm7rpFkTZMoGKqzPOVPGy9bNSxo512h3Zsqy8frxzLFfQyP5hbFs207eDzW/yBWBOt9lwXz87qFEy5a+2oDMliPhiC0jCSBiHdhj7AXAAbDM9XgG9BYZYUoSYIP7sEwvz2a/D59pAxCeEx8KOI5nPwz7iV+M6x71GvvIPljGFLm2DDD7Cmjmu47Hk7JsyPDxfqvryDcyFO+pSWNeCWgo/2Rt0AXIQDuSFxkio5PnebKnyLnVDwu0kHcGyNzc3Cr2Nw7jlQm2T6dT2kOIGu+95Jx8PgRVdpCIJaIo8UIXbIWG1ds8z5U5LyAY98r+YY/sMA1kmfdbQGvt+OeCbIsDqBJgGlXbtgrOyfcHC4I9drtdKpE7twt2H5F3m7H53D0BQsnaQy7RT4Gfot8UObaT8KyPssEMwZSVZ1vaZO2XDZDxP/hxdAQ7xvNY7MCzc232AHxiCQvWPs9zzWczdc0w5tc+C89wvr/8DhvD34fs71DVYdfCYgQIMIuh+Z21d/zMltCDj8Ck9/f3g/yahAH2w54vZIMvS+b9ub/0Z/V9ry8ONP7g9//BiDm0AQNAsKqqBHgZEWmjeRgNAAnAzKbAcaIAUYw072HD8jxP0eDz83NK9/A+W6drHTQOBUeIk8E5k00A0GKYSXH+8pe/1E9+8pNY1uWH9DrGOx301N8DDgDDVdW1gryurq70b//tv9Xl5WWaAuGdU11WIyCFsGaZV1md0n3B8JAVsmVrCAOBgDX8BAiz2Uz39/cjUAS4nc/nOh2rZCiYykGpk/Mh1bVzwijGbLlc6uHhQVdXVwm0ElljlF6/fp0ObIP9Y3oYtbrX19cjReK7kAUmgtgmdsv6olwElzbzYMEEhpnrkq7nBetgFZvAiUlWgMiu69L5C0w1sxkdC9J5AWztfaHANi1vjY91mtaA83kMjnVqNruILFsj2rZtYvSkyFLRpwHAtgyyZVlsqp37Rkb5rM0aQVhYED7oqVPbdKNnRecBLrbWlDW098CaWZbIBmVki1gn69Asm2SDIcuSWWdjm42xBQBWbM3pdEqHEyKTlMzxWeTk3JHY8gj+wyacs2DngIT7xQ7ZbBgBiQ2kyLoA7M+zIFFOBhCIzsVBGydlmf+OfkV5D6J0yl4TWbPOHmY+6k6mPB/GE7O+Q+ATmT1YcNaYTPE5oCIwsc8pKREFvJf7gBhgz8ngA5boNbAZcOTP7tXj46Nms5kuLi6Sb+KZLdgbfF3eZ4HCSJfj88feFQsoALTW/vNvZIA95EwaWP64R3mq2cZucn4N5ZxWxuP+e11fXyV9YmyyzZgRXFnQyvvtdDebCccWY5ew55Ydt+sWSaVFWlc7+dLqNrZku93G8i/vlRV58h2W6Wf9+F7+ZH/s9XieEEJsNA5DSQ9yCFFlgz96L5ADQDFTvbgHS9BSdXH+/dIwIY91Vzb0AlhZsEG3JSIslmOfkGVrC63/4M/zE6oJBrG3BNKQYUPJm0sZO5sd5Z6x+dg01pLvtUGSxXrIhs1Ifw5HWmLD+hn0ztoJm33ls0Weq8gGPeZP1sgSFvb77Nqcw2+bhbN+Fz3Cl/FZ+52sPzpk9+w8gGbtqCCC8MeeWPxxnim1QfRisdB//Ht/St/3yr/3Hf0Lgwswg2EDrLAZlIdQY4kw2YdkQTj4BQNnR/7BOp0zNWy+NToYYZpoLaONwQJEweRQeoVjpxTCzva2zDaOipR6WZY69RvOs1M61tR1GtmI0MLolFWlrHcUb9++TWyP917qBobMe69Pnz6NymXyYrhfmxYkMIHlJstBWs06aZq/OSSNaBjl4HwP1hTjAAvuvddsPkkGhiCA75Okr776KgEsmCWmPxXFMAoYg8ta0+9gwRT7ibFlH+o6nl/CmF6mYKFETBRDTq3Rm81m6YA/AgV7OjxyiEGDwSaYsw1rNkCbTCbpVHachQV2VlZg2Bn7iIPHuNhmb3o+cJ62rMcaUu99GieL4caAsP8YEYJy7g0HA5i3ddDogGV0WVPLqPIejKIUa5953qKI46FtOYBlseL+ZuragelFtgEwNs3O+vN9OA3eY1P+FmxZltQCy6IokpzaNeF97AnPjIO0WQ2bAQK0XFxcpLpzaTx84HMBBaV2vNf+aUEwMmNtKoGrnTaGXeYez5lwggXbF3WeERrsrRuVMNC/0jS1nBtABToVswax58CyhXb9baksP4tZvCGLxH3xPKwzDo97tYESusm62GwOfoP1wr/ZYDbLslRiSpCIbaaM2IJnaWBXbTBqx2/bEivkxwagUZaGIQGWmbR6bG2a7T1jNHbTNCnriu2QlMgl1jTe51BmSMD0+PiY7DX2z4KuPI+HhiI3yNzFxUWSnxDCaFw5OsEeW3vO+4uiSJMeuT8rKzZQHXrUKOsbSppsaSOZfmQNmxC8SzKDLcQmAdjQsaIoUpkqLwC67W9QN5S8UNfO9EDWyNphSxhgo857HiDr+G7sOnsoDedv8B7sJnKIbWFNCbAsmOa5CZKQcfbN2nx8PSQP+0RWCXBs781mZ212AQxIwI69gWG3JBWlx9w392WBNkAd/2iDccq8wDfYIvTKrpf1FTwjup5lmYq8UHeWzbB2wuIqq6+WqLfBhPXbNrDBbrA3m80mEbFgarvW1r5iY8jaca9WbpGhc9KZPeJ62BV7L1/6+uKMxj//J/9Um81Gl5eXI+MeNyLvnWshJ6f9Yd+nZmaq60rz+SIt2uHAWRixprfrQq/MQXleqO5ZoSwfUpOD8HaaTIpUljMpJlqtVz3Qq+PUhzzvnZ7TbDpTMSnUtZ2Cgpq6UReCnKQsj4Cmbhrttlut1mudjkd1IcSpUduNppO+3KnjcJS42LPpTFme68PHj1GY8kxNHRvl6qaWgnQ87LVYLFVVQyrYO6+yquR8lkqM6rrRD37wlXb7vS7Wa50OQ/MvQCQaqJMuLtbqQhfXuyw1m89UFMxzxtFGtskCON5/KkvN5zPt9weFQHmC02RSDKMAvddmu9XpGMeHMtZtsVjo/v5eRZFrOpuk+yJta9mrZT+KFvYsKl7MuqzXjAr0Oh4PWi3jDOq6qdV1UalXq6XefftOk8lEV9dxlPLV1ZWen59HhxLa8gUcE8AYRSB1bANWyxiTHbGpTBS2ruuR4QTwotg4NQzV8RhZzhhcSE1/wNFsPktr3TRxjyScm1fXtqp7YG4zJBgE5+J6oSOJHQxBx9NRTk55kSs2RWZqmiFIKsuhtCgasoERxChahy8psanocxc6SU5dX9NcV7WKSWEceycfb1KMmt1stiryXHmR63QqNZtO1fUsug2OnBsYwKqqNSkmis3DA7OFw7UGkd/hOAGKFsDYwAPDybXIQFoDDNhCtrqk90OvB0AX4y0NLJRln9AFnhdbZrNCNuMACLDZIN7Ld+N8uS5riPzhkCzwZpSxJR2wxRAAgDIAuaRUQmHtiERt7xDMxb1oewDuUqbGAoU4Tnhw1KyN7XFADqqK0285m6fuiaN5r8PD5Dyew8ow9wSYgvCKdnAo38L5M7yCa9rsCte2gLxtaTT3Wi4XOhyOojcF2bDT7whMAJcQLAAuMgaUd8bfhTTynGdDPuq6Sva9beP6TCbTXnZyZVmu0+mYMlS8Z7vdabVappKjaFsKTSaFum5oZMdOQrjAbAKakcssG4a9RCLopOVy1T9XrqZpVdfVqDyPvQ4hZmaiDnR9oBEnk8UpfkUfnE7EJLOBpWZyZZzMFe3cNJEhrLUlR8gmoF+JYGwbFb0+ZFkcN9t1nbzzklMqjTzPPCVGuxgan733ynwmB4hrmC7WKnRhlE2WG/ckdW0bRz73dlxBct4lbHTodRR7hiy0bassj34l6laQglRWlXyejYCiDdIA4dJQwjPOmo0P5MROMoTDEkA2GBt8zNCjhV5RfcB1IQp5HmSPvgx8Ljph/S33zndALA6TPYfD51hnyFnWwGYU2Reb2eB9FpjbwKNtW4Wuk+txrMJg16q6TlPGuAfrl3yWqW0aOe8E5HCSnI+ld957VXUt19twuTjJlOesqioRIDwThJHFMNhIsNpAZAxVRuefsdk9u4asq/Ux+J3f6Hjb/+kP/1lSPDY5/pepqdu0kUSuGCGElQdAoGFK4vzu4YwDPv/4+KA8L9LUGEZ6EmTAfOO8bSrKRrNEhzYdZxXJTjAi1Y6AEP1GQYn9FbAaMAx2o+1pjnUdJy1QqgRbSPpaisq/2Wy+A6LsqLV0anJVarlY9g55MDQYK8qnfl0Uy33C3PNinjgBgk33WZa1KOKEoIuLC53KQwo4YTRt6RHRMvfX9Qq53w8Te6Ro5FarVTrpvCiK0e/qutZqvVQcc9mNZooDBqbTaRq7zPrxnfxX13UKJmz9OYbYKh/rB+Bnn0i9IrdcI6WRm8G5WYaULAOyiRyiyNYg8x47EQIZc04pYEevkG+AtmVqpWEELwAyKP6bPh0yKfFZsxhAFIXR7fH5GOfOINUEd62c3IjRZ49ubm4Su4MOADhtVtSmwvk9QNSmz89rW1kzyiYIIL0fZpVj6C2rho7aYMSynQl8mIyJzdhwHQy5DU4siOA6Vl8BtzaYifP3ixT8cg+A6xigDg6PPbWAm4yXNJSR2BIyZAWggK5Y1g49tuUj1hZRmmJZRVsSZR018uKc12QynFyPLET7MVFRDIl19CLufZ4YYGzrUOoxyKgNnJ3zqfzI2n+JJvlBppEtmy3FFlj967oIyo/H4ygoYX1sxod1aRqIjfE4YWTMOnQbBMf9HZoyCRZt5ov1syUNZMLwBbbfBBll/bgGo7mx8bPZTB8/fkw23Q4Y4LNt26YyZfac7wQMF0WRysV4NtaWfY9YIZd6u2EBGbYZTGCDcsuOW/AImJrP56n+HNadYJ8gysoo/8YuTyYTlVWlTuPA27K9yBvrbrOoMNL2WQjy5/O5Mp+pC93oQEfWFx/Dnngfp1B2Zyw1a965IeOITtr1sbYIPbH7KSkRDbYKBDmz4NsG9RB3XJf9Yq8s/qC0GxttM9V5no/OqmJsKmSdJQQsZpOUqiUsAYj9I1sz6OJAGlhcyn7xHz+3ASv+yvoLyCFLCp0THtWpVGdIJ2sfimk8s4v7516sTNp1x0519YBfICOtzeR7bGYau2J9mQ2w0BurA9gHZAe7bvUG+5Jl2W820Pj//ct/lTbdsqGn00mz6WIEljASCJ9lxawxRjksCCFAsEYAh0p3PIsGg4QgIVyAdZSbUgYEHlDNvXKf5w1vNgUIs9G2bZryxP2h+JPJJE2MsKUTvGjYKopCV1dXCTyj2LPZLE3eQNhJW9tG+rIsU/OuBZo842q1SqVisPswbYBHDP7V1VWqcaZkxNZMAqIwElVV6Xjaq21jSY8tCeGeuNe6rs0J2FJV1mmSEyVoCKst4ZjNZnp4eOiZtLlO5XFU7mGdAobcRtyWHeSQGpon8zxPY5ABfFzXgiBKQNhby2zYaSQxID2qrobpFM/Pz6NgEgPA73GQ59NjrPJjZDE4dgIJAJp9t7XR0jB1yAb/klTVpyRnyH1imd0wgpjrWkYPneS5KImgJAe55L3oDE4MQ43zOc8I2XWwgSH3hJycs1PsA86I77CG29aw271kbdF31pQ14TOSRk6FQNNmybBX/N0GNvbn2B1eQ2lAPEPEBjDcmzSe0sQes0bWyaF/NhhmT1gbAOx5UGODb+TRBipcz9paAKS1nUVRpCEI0W7k6rrPry+9HciATe9HpnYoxbPrKkVW2zLNQ0A4zgBZ2+5cSGefnI86DiGYTEA7GudYFNMkX3yGYQ1MmmN/+V2cyjSUjDnnkk053wfWOJ7xcqnY1xLXH1uO7pxOp1R2LCllkehjQ38gsUIIqQ+C+2CfrM4QrPLMrAv7bvuJsMM2uLasuQXb9n38Bz4gW24BO/vGnvI6988WO3DPtrwVgIbtgdW1AYRlmpOMeJf6LymZouTWBjxW5y0w4/5tL4QlHdAlgj5bAkmwxnM4U4rF94IH6m7c1HxOHmA/h0zSuJ8Ooiz5h76PzZIZ2Bz2k/W0GUT0C9/CxCI7fIY9Q39ZO0gosmasG3aHAS34b76XYJr3F0UxmuBkAyuel3/zbJByloDk2a38W9+GDiC/dg0paZ5Op2qqWqEbmrOtzWtDJ+eHQRpgMmSKnyMTycc1A4lEhuncL5D1AMPZAMEGG8g2L+TTEkb4BdbJkkA24P6SZvAv7tHgZQ0KAB7FgUklQsPJ82/LlLEwbBaCCaC1WZGu6/T09JScKJv//PycjAwAlek3CIUFSTg5gCj3wP3ZCNJGh9wzioXBsfe92+2So+G+qFfFwEnSzc1NGoeLMQH8sok4E96PMnJYDywXz/25P2G3ziN4m3pEgWDPUjTeP/PnnG+e5ymDQD8JB84hD6yjBbNN3eh4LNO6AvpxGPZANmSiaRqVVZnWyLJyyBzygFzm+XCeCEpye3ur5+fnZBQIuNh/lFkaTpYmcEMhAbc2MGH9+G6eGzBpDRrfA9vPCwbINgdzn8gme2DZesv24wAwQPRpEGylMcrdUNt+bpy60KX9OmesbTD99PSU1oegh3vnvjFIZNksa8d+WVAhKQ1ggFWzeo7xZ/8xhDgedMWygsg3ewWzZtcQJ8+/AbLWOFugYIMA7JIFLDwzADJmZh/TGF9JIyICuxCfx2s+Hw7A4uC0eI+DmbbPTh0998B9MWyDtaI2nPu0dpnnsvtimX0+g61D1yx4BsjYml8Invj6bgYEeYk/G9g7C96KYpqAA/aI5+y68SADwEes9V5+Vr/jz4YDI20AxSGO2DGeOd6ftNvt030ArCgRxZY9Pj6mvZXU9zkNz2rXVlLaf2TeOddPHPTqujo9F/6MtSOARw5gxruuS6PYQ4gDWtgfglLsjQVPrJP1jfSx2YAcvbbBgs0GI5/8G321csI6oFuMJLfrjS5jz6xO8lneAyhjbSAksA3Wx9q9IdvFd2Jfm6aRd5l8lo3wSAjDyG4LynhZ33QOZs+DDOsfbRbEYg5siVdsOrZ+xK6XbU6H3MEmknG2ZzXxXdwT68L6IRuU/JE54n0W+LIGXN++WDdwCCWC50EpPhtyy8po244PnGTSKPbGTorjXqyMWj95TnBYgpZMOL2fYxs0rnLh2dEB9oQ1T8FRTybYfo80ercZAmT8BXtviQ9b2uRcbAvAF0eC8zDKzFjimb9botvqMP7cVoJYP3getLFf9FPxXhus/LteXxxoWBbVpqOjYmq0IAgLi0mZkWXjEHYYwizL0pkFGAqUDvCNQCIQ8/k8TR+aTCap0RlDx+QfuyA2xcfioxi2DpFNwQlwTzwHZV48M2uDk+XzpL1hbhgpSikY2QSaiDHsjIHlmtyr9z41rGIcraDgRG1GxbmhkV0aynOk8Qg2ymJwTDS9W+bLOafFclgT3o+C4IRXq9WIRZjPF5rP21GWxKb1ycRwH1aB67pLhtEGfHZqDkaF53POpUPgbG20ZVf4Hgw2BssaWatsVvFPp1NKf2eZl++dEizD8XhM/S1cG2NkAxjL7HBfsDg2hck+84K1Zz2HEj+Xsn+AWZ6ZIBUgzH0WeaE8H5wIrAayiJPD0e73e0lKKWoYTP5umXX2woJ31jPrnXkIIQ0U4DmSgcrzkYFk32HfbPoX+ScwZz0B34DI81Qw/yZQ5t6wO3zfeYCHTlI2gu2y6e/Y1zQcWogzhyggG7BYzNLeY4eyLEvy5frzJBaLRWIMz0+NZV9tOh4gSrZzsVjo+fl5xF4BVCkjJKBiHSzIARwQZLFudp/P76HrQnK65+VbzilN/QMU8t30Y9hyn2hL5mqa4TBJKzuRRBictQXR7BcgzeofYBNQivxTrolfWK1WaRpTURTprKA8z3VxcZGyJGQEvf/uiHHWkSAQeeUZCfy4L+6ZMaLIIHYQgMXPsA02ALXybmuwsW8hhBQcWgYbO4YdJWBnWhD2xX6HDQptGQqEAeuKTbLBwnm2wGbUAKD4OuTUBilWjy14x6djO0MISe6wCQRPZTVUPrCuyBD3Yu0x1+26oW8LO2VJJbsG2GmCbtuDQX9OCEH1aSAIRj7QezXV+GBFvhM7DtHJmoIX0EVAOlkH7D3/WX9qiQILukMIiSQlm889WfuJ7tpsM/YMubcBALaxbdvUZ0aJFZgOoA65h+7c39+nQ43ZC9YEfVuv1yqKIpV9Izs2YOXZLX60WM8ePgjwx591bac2KFVdYBPjujQ6mGEH6DO2F1tsA/j42WEcPnvDNVkz7q3rhmoefCDPY22eJbxs9tselGg/Y323/c7ve/17NYOjsNw40fF0Mk9G5vn5WTc3N6PI3oJ6G0VmWTyJE7CJ4rGYRIgoIg9sN8Q6VAQCJUHBMJYWnADQ7Mg4e0BenucjRgCDgILg1GC+LcsCI8QhfTCIKB/GBmaKRqYQQpolfr5+Nv3Mep0LIt9HkIFS2ygdw81Eia7rktO0bB4Ok2ARR+e912Q6TDvCGVnWk/uRhvGtznm1TTdSYDujnrXn8zSgZblXCEOpFPeMQ6EEy6Z4bYbDjnlDfs5T2hhBe+3zoAT5ZP+loc8j85nadlznblOgPKcF+jYjYnsQuEdYIss84SBYMwwSDtGmRm1aFzmS69K6ss7JyCobBXjsqTSeCw5QtoQA92SdyDmww5Fap4y+cr/oOcDFMp82A2J/x2fZI+7DBrHsg21k5JoWEFOayX3yLBbY8Z32P9YB2bCMJaSKBdA8E6xtzErEJlnWE3mMNuYgKSRHaxlj9PI8e2YzdMhO2w6HLBKcI1+WUUOnsLk2COfFftj1t0EvawogcG7IBFh2setaTacDi82+Rt0YmsX3+1iuOZxIH+WF60EIRfmeJvA4ZuycZrNpCvYtuGJtAHgEjryqamhq5nfYGpsBZm1i8DxVVZUjW4Ou4IuYymblxLl4iJ4t07JrZu0y2W977pAFCNY+oMvYTbuP6DP3Zdl11oEAivVhXa0ttDbLBuwWrPP3c1ni9xZEkTW3WQL0y/oaG8QgM4zahwHmfixZdU6QSpLPvJpumCJmy9ssm2uJGGwG/Xmw5JZ0gNCwWMGCOvCKDaa8nMqeRXbOJSwSQtCpKqWeULN2i+ex2Tf8bdPEsnEA+8XFRTr8l+DHkrXoVNd13wHvBISA5O12O8qwAURZJ/QGW2Gz9Mi59Q8QtOAie/6GxY2UaBMMWwzKPv2Lf/EvlGWZXr9+nXQAPcKunh/QaXErI/oZRgPZxH5Yf1fXtRSCcj+MlcVOdl2nTiEFGhYPoINc38pa27Yqslx1b9dYQ2uTWTf7WWnAfFyfNUQezs85wQ/Y57K4BzuPvHxJj8YXZzSsw0Eh+RNhIrKEDcE5WeWShv4FFsAKoAXPpH5tUMFm2gdmAXA29ABYhwygkIZDc0hJA8rPMzVXV1cJDAJYOffjHPhyoieLD7jiHuz7AXoICgAyhJhitGCX+7N1hBYssy7UywOYeFY+hwATXPF9GAYcszWafL9lJFBcanlt7ec54B0poAaWh8/iDOmXgDXGKDnnNCly7fa7BNj5LsAmpSgW4NpUL4pnARH3hyyx/jbg4D7se9EDq8ySVNWVylM9Am+2PIkUMIaVQNQGJLyfPbVn0BB0U96GEWYP7bAFjITdM9bK+aHW0qawY7A01GTiqK3R51rsuX0O7gu5J0C3zt+ynjgVy17ZfgebSWJPLTjHidrACmNuDbo1jrzPZsXOg1Mcj/2Oz2XD0GGIFgJwywqRjQDsWQAIywRpEpm1k5i2xR7Qa1GYef+AQRs4AShYB1h4+qNsT4kFIDYI4X4AmjhBK+sWDLDG6EBRFKnsxgLOKGPD5wHF44zHuK6aEsPpNPb/7Ha7BBroaYvXy9JkOzsyu23HjcQ2uJSUpt2wN9IAlL2PGXOykRJ15MO0N4IXAAI6CNOP3W3bRofDXovFIt0bMsq+WV/GhKz5fDliqtkX/AfA27L52E4LmK1P5cW6W9+I7tkgD306z/LacevoMnYMG0qWiWsREGE7WAfIPPpH0B+e1RKC6B+g0j4DP7ekDQE7hI2dPGh135IjyIn3mYreD6AD9Epavbfriw7NZrO0RgSOXdelDDhZXEuE2ewogRH3lDk3eiaLYy5mU1X1cMim9alWDrAp2KXpdDqaxoje8jznNhsQbNcOLJj8RxbLpCBe2VeyJdh0fkf2lHWXhtHYlNORtYUcsZkgsB74gUENZGgt9vDe63d/93fT9QDYBAs8L1UYVsfRD8rVsJd2siX+1RJeRZ4rtMOEO+wcOkpGEB9uSSI+A4k0m83U1LVc37dFttPKocUmrJPNypINxa6cZz2tX2I9WDtrO1h/a3++5PXFgcbpVMqjHKfYjFyFSplhDC0gKcsynREBS2br6al/tM7QCg8LwmnQ58EK7yGwWK1Wenh4GP3cTmEBJFlDdn9/r8lkovV6PUrPJ5DbB0Q4aMATTMt2u01lYRgZ7sWyLIBIG1G2bZsOsbE1kxgHvocImue3NXgoPM7ZniPB9+LQEIqmaUaHJRHd8+KzNpsyGOA+Td8zr5n3Op0wOF6TSabQxXHHbdsqz3KVZX9S/Gyi4+GYHCJOmmYs1hvl4T52u1Jd6EcTd52CpLaNM/vrulHoYho5zwuFrlMXgkLoMypBCkFixrrk+qkfQW3TSOrrpUOcKqMQlPcH8LRdnATkfSZGLbYNQbDT4XDsjdZRNKxy74A+2LmsX4cQpDjC16tpWlVVLTlpfzgoNn8qKXdI4MCpaZikkcu5TkURxzw6F0du8j6AahyDO2S/ErAMrZyk4+mYgFiW9WWM3cBGoy/WiSMDi8ViFIQBdNANGDMCPpuBtNlEgghb0mCbNS3IyrJslAljjSh7IONmGURLLqAf6IDVTWt0Aem2/JA1gbywTvM80wSQsmWaOAabWUI2bElivBeYz1zeOy2XC7Vtpywb+iqsnbJ7w31YBhp2lBfMrjSUYeFEOTWefbDBIMEWz4Rj9d6PhhSwnvbwO56LQIFAIF63MoGhPUU+fubx8TEFWLYZETtFGQ8BIcBuMhl66AA1w0S9gXEPvd5//Pix349cNzc38j7TdrtTWZ7EyGjkg4AGWbEZDQ4MTA2hTdP32JWqqrqvex4yXQD4pml7EmuuqoqjYtt2IHEkJdKKPbcBBnvrnEvnHeGPbG8OOmszejbLj1zY7ILNothgxoJRgCi6bstlrA4i/yEMGXV+ZkuRuAagDUbbstx8VpKqulaWZ8q7Qj7zYtz+bD5X29+LJdDAIhaQ87v471rBEIWAQoCZDYyRaUuGNk2T/PZ+v0/BNdURECuWmUZn7J57H0fmhm6QV8uyBw0BFL7mfFoY8mHLgTjt+TxTgw6fkw/Wl9hyL/ad9UXu2bfn52dJSiWbUuxRQych36jmQE8hbs/LfgiKbK8M5W+UQVmfZPEc2QqCTVvKaUuX0Eu7N5Zk416xrxaTWvmqqyqOKVYcWyvnJCc1bSOfDcMU7L1yf/aZ0Ul8nw0k8CHcC8GfxVfexzOxOHcDvSIItxl0CET8Ms9//l2sxb/P64tLp/7wH/3TxGqQ7gF8Aj4wvpYpxSgTfFgmlRvm3ywkyoSgk16G2eGWiWypESS4wGjZzAtABOHmu0hxstjWIVrjS7MqDDXgyCp1lg0TkFgjjArKy3PazeSzsBIovxU41p2/Y4ytk2A/LIiyDCHfw7raWe1813q91mQy0cPDQ9ov9tYqqWV/MSzcj2VD2AMbRKC4VplYB8rGWF+bqpUGdsayONb5NU2TSuVYR/YfwMA1z7MYAFaeFaNNJsuWwgBQcVqsMaCP74ls7rgemu9sulbT2SydRTKbzfTp06fo3IqJ4AqQN6s3vPiegXEeGHqbdoWltGyF3T8MvQXQlvnnPmy2RBrKDS0LY/fUyiaO1DZLwzjSZAazYkv3bHDCOlp20jLo1pw1TZNsh9Ur3oueWOBgwRDrax0OjoifQbLYjBPrxvPjAKzcW5aR++E66DpAkWtZdsnqGE251gET9IQQRpNdAAVW/0MYmjV5WXabveVPO3gCNt821Fr7Z69hCRXsjhTPYcE+YRcB7eiVZeJoIKeH4/wwuSwrRv1wlIgAyizQt+UZ3Dt9dfY9dV0nkGHlsaoqXV5ejvrm8HsWPEhK7Ky91uFwSCCQdS2KIpFB1J5zHVtqAUGHTlrbAGBh3GtVVaOyD57Djs4FUFhZJ/gnYGUcKr1CEHCAarITrCn+H5m7uLhIMmgJB2tn0AXWiT3jvCSwR7L5XassH8YZj9jZuhk1ddtsJzrRdUN1A5/bn46jSgvkg3XFPhJMfa7KAH0AS9gmfOvfWHue3bLfXu47fgDblk2GvhLrf7imDULY067r9Pz8nLDQp0+fdHl5mXAChAKZatbeZqO4F6ol7KAB5CbLsiTD/A7/ZWWQv4PlsOchhFGZL+vM89lAkfvB7llcybNY/7bf7xNO4h5sj5DFCBZ38W9L/LI+6DvPxfezP9hUS5jzeUq30DWwKkEcuIXBAPQ3sVY20JeGyVmQ4Fb/7PpIw9RDAhRr+61unssntqdpGv3l/9Vf0ve9vjjQ+Gd/8IfpAYlqAQN2UxFAFgdnQYM0WY10A24opeDz3g91gTgSFNwKAwuA4ME84Kyt8ZI0yqrYlHFujJQF4TgkfkegQCrUsmk8Cy/bH2EFh82WBmdgy1QwQoBPfs73WCBkWWUcuU1zWuNiI+FzYbdgwDo1DBcMLwYUY5llWRpvyr7jRHh2rm9T2OfBFs/H3nNfGA/LFttAg+vbhit+zzX4tx0gcG7c2R+bprcG0g4ZYO9YJ4w5jgbZGgKveNidVVSePy8KyY8nQbD/uc8iG+KGdDpNcdYx2yAi3mNkh9FRe/AawEHSyJiy1hhEy4LZwMsy9TyfpGRMbaMr62vBNGwZusD0NstcWXKAdeZlDSHfgaEHfNkgyzmXjDifoawLUgLgb0HVuV6s/A4vAAEAAElEQVRY4G4zE5ZMSD1FJnBFdq0+IMO8z5YDWlBvg2BYP2yGHalq2Vr0gSCF7IJtLLZ7Y5u4YQtt9oVngBG02Q2bBYLcoVzEe59ALbJJxtoypJFRr9W2XZpQBquJE7VAejKZaLPZ6M2bNyrLkyaTCMgpn4oTbmIW0/uY6QaYTKfTUR+YDUrJrLPu7DU25jyzTcCDHiDz1gZhH2xQboN+azMp00JebeBrfQrfY20f16Wnhr/jB7hfnok9JLjYbDZJ7zkfg7WHVWacOzIK0488AyphPS2ZZckGgl5sALKHv+d9tm+Le7d+zPZEQtjIAHCe0TmnaT7sI3ikaZo0Xh6m2653nud62m6STeHe0UXWVRr6ZSwzjk9hHe37rS20QQx7YIOvtm2lLh4gzL4CCpumkS/y4X39y9oY1od1l4ZzuZAR7hfbRnC12+0S7tput8lm4hMnk4m2223qCy3Lss8GDs+PnJNxsKRE27Ype8G98m/Khu2+4M8mk0ma8Gkb/tFF51yaIMc9oE/IJv72eDymKW28sGfci90rZAs/iO39HAbrui5ld9CdsixHukkAZ4E8MmXlI8siFsizTHk2+Agb1FosYzGelRt6gbgv8Bf3B6Fqsyo2SEQv0UP24/f+wp/R972+uHTq4eEhGQhAPfVjbDQvG33yd5uCsc3gADoLPq1ynrMQbDyG3UaNzrkUoNjo2jJqq9UqMUYYgslkkpgdy5bYMZlXV1dp0S2Yt0wStX0YDcuSoWQ2+4EgWLCMEbEKisE/n2WM4+K658EDjg8Fs+UFlgWzxo294MXaS0rrBPjAOFllQfmtAUFBI7AYInSbjsWAWJbCOkjuzSquzS7wfThQlAXFh9lDYezaS0rGjJetlcU42cwIf9o6eWtohj/bZOQsuJ9MJmpDNwIMBHNFUaisa3k3nqhl1xsZskH7ZDLR4TBuvATss9fcAzJne2zIYME4n7PT7KU0TM2xIN8CMfT5/O+AdthZC+Csk2Lfra5gfNETronesgdW320GFPAOmOZ96LHtnbK6xP1iF5BZa79sttIGaDZjaOu2AZYYbWyHZdfYb8qaQgiJqWfNmPJCoAdYWK/X6X18Jw6cvbL2k/NtCHxgpukFsXpos2PIIAEQ92uBttUjGHz8xulUprGydR0bObGVOD1bXnp1ddUTO1F/Gf9NCW6832qUFYPRxp7b8efo13mm1Qb9NjMLeEIHLKMM6LPkmw3Irf6hV+cExznraLOL1k8eDgd1XTz81WZirS0D1NmBJZBi6P/V1VWyO3ZsKt9Jf4kFs9YWYzvsHuPjLQiyLDQ+3DLBlBxaMGv9CqAYPbBZjlbjyY8Ef0VRqK0GIoL1WK1W6Zo2KKLE2WfDlDqbjUDvLdHDvdr95V7w3dwve27XEtm0oNYGYHk2lDaxtqxN12cTzstcrGzaZ7DZJUswkD2xABL8gyxhi2xvB5OgbO+gpKSL/Bv8gmxhz2wA6pxLvVjcP9/Ly/p7bARAGl0DXxBEQj5bnbOBGHrPs7I/6DzrjZ+if8v2JlrbYDPy6Ijt4UOnsBnIDaAf8hL/yj7Egm03wguWsLIZHusbkQvrF1kfdIoyMnuP7Ce/t4Er17Jlft/3+uKMxv/w3/3dkaDaxeUBptNpOhHUptjZZJyOddhsJAvMIUMEGLaHwAYwCKN1eHyHND6kxhp8lNYGNpYtYfG5Ft8JMLXpLxwpi25rHnlOy2LxfdYAn9+DdUqW4WetuQ+e3wJz/o4C21Qrhgdja8sILIPJZ6xRsyVbFlxYZpd6b6tgfNZmrGCXzgO0rhtSmtJ4HvvFxYW6rksMpTQ++8KyzHZ9rLJJ4wwPgIn152cYD2torRG2wQnXAHjh0ABrEVjGk4WtTHL9U3lS1pdf4eQTiPVe++0uGWYLfgFBlmEYZCiODAU0nzswG5zaUhBbv4/u2bXEgeNIm6YZTftCFyyTwrX4Gfd7zqSfBxk4f0CdzRJYe8F+cC9kTQGtrJHNSkga9SOcZ9F48XsLHDCw5xkdQIR16lyXtaDskhp6nJ5dM1sOaVPnBHLoL2ds3NzcpKCJElIaO1lfgI4FFQAn1s5mpjabjW5vb5OjA0hbsM1zsTf8nOCGEhf2DOeHXoQQdHl5qefnZzVNq6YZen8Oh0M6FJKyJoId60Tj+RRDI6mVj64LatvxOE5m8FtAhjwiZ+g4MmgDbAgU+9x8xk5Ks04aGwKw/FzJKXqBLNgg35aySErEHqCCrLsFTewZARZ2hT1DdquqSpmjsixTRo71AGRZgoRAGZsBOde2bcoIIU8WdGNH9/u98jxPJKPNbGF/6B1gDZjKaPXe+rzJZKKyGSY5WmyR+XiyNqDYsrDIDOvO8yZSww2svMUFNmtobSzrQj+CZa0tbrCEjN1vG/xbWxPaTt6NqxratlXTtson48NebcBgCQ1KJMl08nsLdLFD6AjYh59T9mcxmfVn3C/rx3XQEbseNjCxgQV+DbmxxCtyZglCm11Ax2wWAFmwGPGcDLL+k7VAvmxWnTWBvADL2ntjnCzPiQ1kDC6vLMvSPvCdlFTaaZPIHHugLqRDAMFg1rbakmR+Z4OPczmxZK8l87BV9mXtHXuDvv9GD+zDOcLkMe0nRVwG5FLiYdlwBIH3WRCOEU8Lqu9Ox8AY4VjYuPNmJ77POmxe1lidBwAoGY1m9gA1aQzybbrMZjcsQCKKtWyqFQBbzgBQ5bMYYQwRgACFsArAPbB2XdelRlYicRvM2HpuaTwOjbVj/S0Dz77wdwC7pFGmAAUGlJJpsg7Y3jfBDutkgxeucTgc0n1YJ27X3DIqrBPBig2UrPOwzh6DZA2jZWIsa4mc2ethXJGpqqoSo5Jl4+fE2AYN2Tl+np7/rJwIJ2QDAsrAbG28907eD2OCbXBkMzI0b9trWmCIvKHH9lAwsoasGXJ3Dv7RDfbunHGDZQNEYjwB1+f7aQNymHvuh3WwQTPlMrYO1e65DTLYNytnIQxjFVlP7g3gbmtbrX3jled5Ki2A6cMWIFdXV1d6fn5Ov+M/SvYIQjabjUKIB1BiL4tiOHMDNs3Kq91/21BMlgLAWlVVOhCUa2NHADfsD3sD4KD8AGBMgAfTSDmGtb3suXMuHTrIvRIEn7OnyCT30LYDSRJC7EeITftzhWDAWv87ZNsSPOcyYW0KwRiMs50WhHwnUJt9t+eM/9D3uq71+PiY5ACgZkEI92mDQ+7TZpTwVZadhgHG91ibB6hg7wCRFlQi49aX2+CE9eO5+BlVDkVRjDJrtp+DtcV/Wj37/9P2r72SJFt6JrbM3SNi33dmVZ0LQLQO2RgSkCioCZGcIUGJggD9akGgpGlK0xQ0I4gSwE/ToHDQ4GF3VWbu+47wi+mDxWP2uGd1Vx6AE0DWrh07wt1s2bq8613LzGFkTW5x3cfHx5ps2lflnKu9L4pPJOvEjjy1diBaZLbHjXddV9tJIiJytCNyiQfs+/M6mZQzm4/MDSSRGz4HPUYmTkjwRW9vb3HY7evJUvZXF4dDLJFrDDE4Z55UvTjJKedcW6LASwBUYjG4B7KYBM0tlfbjxHITcfbv2J/JZMuBzhhalazP+CeSbfb/Eotsb+74cIzBVk2IYEuuLiFzxzXjMr+PPPAv/LS9pVTa3/0+Sfw22UHXGQdjxM5qAjwvMYgIdXWHCjFjMY5hPMQH5Gr9NfbxnhInvry2xOu3vP6o4239VECDoq5rfWAG9zhRmKktyGPR3MJDprcFdxg+jAn3RkG34Dti7RT5G3MhWHkxCdy+DgE1oiU1BrW8zyIZDNkAUSKDOf7f7SgoJPLcJmPO4s2k4CgMJLiHGXd/h3ub5bfik6iYbXGFibGgDwRG34s1d+/zlhl2UukEx+vq8RqA25nbCW5ZDztpOwwnn6yBQYLXiPWwDD98+LACUDZm7n08jqtTNPj/ZV5ir35JwErXdZGGIa4vr2qSwd8ZL0ABAMvRgtZT5jwMQ+1PR5Y4a1cHbJtOAglIXDOi7ZdAJ+3YWBMcNOMBVHKvbaLGtQn+BnUEUGQEm2Kwzf3sCNEb94abjYR1MotrMMAxi7aZnHN93wCcsWMTyJHgDmtHUk5/vO3IR3SmlOrTcj9//lwDADLJuT2UFL0FRDA+jhp9eHioT9klKcA+ALI+Whs547evr6/rHgC3i3Dqi/2tfXhEOWkGsOgNtvv9Pq6uyol1BDrGR7UMUGA/V/xZjoi+MoYkmgYogGgnfgAXdJCkjnjD+7YhXvgW1o+TyNw251hiXcCPfffdd1XfAcXsfwG8o9t8H9t/fHyM+/v7VfIF+NqSJ8zJHQToqNlm1sv+E9vElogr6Al+F6YWfSQxRJ8Bc5Bp6GPOrTUPIsg2Yz/XdV1tdXJVjbmllCK6cgLTNvZO0xRdbu2/XBd/grzRZ2T3+vYWc17qKVGsFf7QCYrjnO8xz3PtdiAWALT5fQuE8aFulR6Pxxj61sLK3CMiprkdRY6u8iwLKkf4JNrn/IgCk7foDj6ANRs3SQ7tjCTHPlbapA4YgjWlasT9XLlDNxk3OAIb4GAXVx9M9BgoR7QTpbBj9BjdMAkNLmE8u92udlZw78vLy3pSlsE5Verj8VhPGt3iWif3zNO6hr8xibCtzuC3+D7XR+4mX02CoE8Q3zyQdJvQcz2Te4zFGHY7Fid6v/T65tapf/dv/2IVPP3/OGEPjgVflmWVLFjQKCclYQcBKwPPsYhoAId7mQUgqHAO88ePHyvo3rKyW0D1c4HH/5zV4qTdmhKx3uCFY3WwM0Nrp2+w7KQIpWNRccqAAIAW9zO4ZY7jvETMU1wNu5hjiVOeYlkiDsM+0rLEuCwxc6xqoYZijnzeeLRuobm/v4+IqGeCw0hYB+pmZgHJAsaGs+Pt43g8rZxd23uS43RqLVHlQX0Rux1yaEGiOZbWyoB+oJvoF+trQ2ENtq0MrDcsH+NEZwGGrB0BoOhGO/Us5+X8tylOp8b02iEfLi7iNJ5it9tH5Bw5WumyS12E7uc2IBJR5lIA29V5Tq1NbttaZUdkhtRA0SCrMRoNpDRbL5vcsZWIdhBEGUdaMcIAg62u4uAIyswJMALBgc1xDQcmM4NUBty+yRx99jnr/vjYNjqWYFr06vr6JsbxVJ0x1/Xxhvs9FYKIlDgpbln5P5IS9Ke0NrU9HQYl19fX5yCX4unpufpGbAq2+3h8j5zjXMloFQASLp5KfX1dHuLGw9xOp+PZnnY1EJIcT9MUj4+PJWAuSzmXMecyx6UcFX04HKIf+nJ0YzQWbhjOe3V2bbMxdoNtvb291TXp+3IcdZHRviaL+OlpmuqR48QTQEJLJOdYFoDW/ryh+7IeI23Ag8+0D/BzHgz0nMSZmKKChn2YfIFIA/QR8/guMjDRwbrzeXxSRNQk0WQK33XwN9D3P5NEvh+Jq9l4M5pmeB1z0Gfv82DNiJvIytUHbNTtpK5eEOe2MZa4aeKOdWM8Bl5zbn3nfddOe8o5RycQxWf8AEDmjb+b53Nb0u4s53kpOj9OtWL09v62IiQZk1vBiNXEKdpqTJiiE6ylW7hqgnoaYzonazwfq8psaM9XYm3BAxwmQ6XTlWDHBzCPiTwDWYgKdBl/biDrigw+Ct8MOGfNXSHdHl7gOMJ6eJ8FcRiwbCwAbiNuYNfImfl6YzoxySQ16wdeNLECYKdz4eLiIsZzMjEMQ7y/vUekiIuL88mm0Tb5s0YRsYqHW2LOmNQxN+cc+90u+q6rVaxlVheBSETW0oQ76+qkh4TMiQb+kte22kGcZZ36vo9/9i//afzS65srGmZxMXADXvecAdLoqWciBgZmlVG4rWNjIvR0UjlwZsrCoExsrvrNb34Ty1JKXLByBAwzEQb/7pFmsQCuLCJCN7PlILJNwlBwFg0w5jG7LE2QQq5e1C174uyWsZmpjpRi6pbYL0vcxBx9LBGHXeScIuaI0xzxuMxx7HKknKJPQ0R0kc9gdTgrGcpJT25KqT6h1wEBeQCo7Qj6viQN01QAKqcx9f0Qy5JjmuYzUNqp/NudgV+OlAgMXaTUel7NJCInZMM64kyZC2Oepqk+URRmEV0gQSGZ8wYtWjRSSjWAvr+307be34/1SaIcnAB4IFidTqeYpylSjpgA2bk8TRQwxpozB14OBsynteotMQwt+SGgm0FCvn7oEnbrCk8L6AUY8vcCquMctFqivT6+eqi/O5GznaO/gCUYIHSf6gesMawp+4EATC6Zs0+AZMp9ydgn88g5x+3t3XkNIyJSLEvEfn8R09RaPZdlqe1Jp9MpTqcxuq6P02lazasE0ZJMG+QSZArLXfbsLEuO4/G96kTOEZ8/f4kff/wx/uRP/iTu7z+cWbObespK082rCmz6vukBLZGAs5eX1/N7tIrszvrYx+k0Bs9dGceSHNzffyh21PUx7Mr6Dft9DRIppRinOVJ/Bv9n3SEwQRJcXu7OwbSLruurnIv8G0GDLpAIsc7uc3aMYc3Kv4iU+uAZNYUpbxU2bJ5EAD0igDupdUIBCDVhxhiIJ9v9J95vhv5iP9ukn+8AwH1yjZlCgDrgDLsHuAGk0AP7CMgH7uO4zT6mLbFiZtyxEpsxA+sxmWmOaOQLCQnJCPdw6wjrauLO7DzXZBxubXEHweXlZYynM5m5S9F3haS5OANl7NCVE3ycgSMAdnx5iffXUim6ubmJp6enMvdpitecI7pWvQakety8B5ZA7yAO+JzB+jiO9XhgV/OXsXUhsOboZOTWbmusADkL0cPaEiPRY3TJlRcnIMTzrW82YcSJVCQ2Tuq5zzYZYZz+jCtayJCN5uAe9J/P5Jzj5eWlbtzHDow/GDsJDrpnEG89Qw98cIGJVGJNzudncS05Uo44nZ8zN89z5HmO/X4X43m+Ju6ckHr/as5fHyLC/ev6cM9Qd0yKyClWrfr2WxFRW8+2xDn66Yr8Vj7YGvptP2xi4pde35xo4EwwSoK9N8yhEAwehQNQeMMf1zTrxeKawRnHdpqJGXJAo4EYZfecc/zhD3+ogIbABQu/zVQbQHxfOV7u58TI2eHWQRLMLHwWfcucOTCguF3XVceI0ufcjmVD0WG4t4x8RANGjOlwnCL/9CV+lQ5x1++jG3L0l1dxfHqN/3E8xs33dzHNxzgcLqLPXRznOfaHIS6GIfLc+iy5N7KkCkXyB/D1ejsYl/X8eqOwKzgYnh0Tc3JS1SpkLQhxD+sCVSUCNvf14QKn06m2HNmBeSwkG13X1U2TDn4ch/f29laP2kQmtCWQEGwdHO/RKmIm8+cM3vaBzOjlL2Nux7ryeQC5nRp6ib7hkBmXQUtK62eAbKsLyAaZDsNw7r19XQEm6yrzwQ9ATNzc3NS5ELQIZk526fW9vLysR5tikzc3N5WNc1nfyYaB3jzPtQrKerPXBTbOp+QdDhfBgxK5FjKO2MXpdKzsJP6wzH1Y2SltRC8vL7X0/t1331U5U+om2NvPsE67XTsBzWRL8b1t/xQAh1P3AKIppfj06VPc3d01PzieVvsqzJCR/OHjqVSMpzH6rp0G8/z8XJMfty+ZQSfY4e/WSUt7rgYJP60ftHXwPQPriPbEboAlcQU7B0QRNA3i8BmMlbk6uOKP+WcQvw28JKnMhfcMOhxbiLFeH4i8L1++1OsYGOL7XP2GQfY18KG2V68Ldmiw4dNxkLXBEjqC7aPzvJjT9l7L0loqXUlCr0x2IHvvMQLwIgPWl9iIv8HnoWe2Ha6Jn+FZKNgbgJ97kSycpqZXjJeEjrG6qgMgQxfwRyaIGA+2Uu81L3GxXz+fxzGEtXCyxFqgJ/h4DmkwGYo+byv/9in8P/rN+ozjuKo6YyfGc6w5MncijQ64UsZPxoGvMjZ0q71bTyEpmDfyxKezhwydQ9ftU+2b7Qusp+CaYRgiunINn8Y5z3PsDvtYlCggc9+Te/HPWMXkgNvN+I7tjriA3PnpKpH9Lr/7IBL7Ja871wGP7qWLyPhbXt/cOvX/+L/9u6+SCIzXg3VZEAH7OQRrlrs9GwIDwlFZsHbCdi44iWVZVgZL5mpghaG7J9Bgx4yLf/dCu2Lj4ImCbMt/jBFFj1hvUk8p1cDpvllky0kEnH2NErr052zcipRzOaFgeHuO//Hf/Nv46S/+3/H9kuKw28f1h/u4//VvYvmz/3lc/MP/WTzHFBcXV5HnHK+nYxzubuNqv4vn8+ZTAhfri1I6uUDxkTlyxZGVMbds2uU51teKix6wfqyNE42ItjGUsbGmOArGhSM0k2W9I1DBYuFIGQ9r7D7ZFmCH2O2as2SO1lsDcwIJAYPE+/r6ujpenKcBM+NxcuzjEQGeDiRm8NyGQWAiYcVBosPIvKzBOlFCF2xrOPB1FWNeBaftJm9sAjnAbKFjHnvXlb0O/hvXwYbQN4Mu3mft0Yd2Xniq7QGU1VvAbJVDqlKtReC6/m6bK61MRT7lyfHvqwTncLiM5+fnuueBfmCuAaApetWvQPYwlKft3t/fxzzPcXt7Gynl+gAuSJy+78/60nw1urssS9zf31cbQCcI/LvdLqbcwBg2yP3NxHoD8DLPMY/tGQZuq2H8Buf2iQAxfJtBMCDDvgJZmnF0FRiwjr1wDYAGftQb+wm8ADPABIwkier2CFjsh7YwJ2WsB4mP2z9MNBkUmjl2guPYxvXt792GYf2xnfE9gwf8CsDN8ZHPuCIM2HO8x6eZSOOezN26hH6Udreyt+zp6Sl2u131gegJbVDTNNWeeAMkQBYVaWIVx/Lyfm1FUpXs6emp2iZtwd6jYKKnsvC5VDRcIUeHkZ9ZYvy/5WYwvgWyTrCWZYkuUux37QRGJwI5ladNQ1SxZvgrk1VO7oy/iEsppXoqGON3BQkSl7VwYkSShYztD8FOyMjPcAD/oKf4H4NaVxhIdrDp19fXVbwwQT1N7dQnZEdiS2LF9R0XnbiDfSKitk0ZZB/2+0i5PaiZOY/jGMN+F8eznhIb0SuvL/GDGI/egD+se1yfNa5j6ftY5jlSrE+UMg6xf/HG+a0eon/IybbuxMa2/l//q38ev/T6o1qnUAAfQYZQapCa1puynVUiYK6HMrsEuZ0wQQkjA0js9/t4eXmp10KJvCCuANgI7aR9BC8BY+sYCA7OnAlqOFp68w0CYcAJVs4iLSeCHguHjFlsGzxZNorq4EkZmLm9vb/Hy7CPn65vYvzT38Vfv79HutjHn/4v/xdx/V/9VzGlLo7TGHOf43g6RZdTdKmL4/t7TO9vkTbMs3vZYdJZD8vV1QAA0LI052LdMOOx3+/jT//0T+Ov/uqv4tOnT6us3XqDsZbTlfp6cgV6BGjGARIsfYpXdeRn4OxNyttDAXA6/i4goxh+uxbfx4mh54zdzpfr0TJipv7q6io+fvwYV1dX8enTp/q8BFdjWBsDLsuYgMb8kaNb8FxeZ6wkQjA0ObdNpQ6wVAAZOz3jTgS3yR+A1UwWcvGTqnkGhFlAkir0n/dJXlob2/uqTcZ+BR+FD8N3GFABPt7fX6u90fpGL/77+5p5ZF3HsTyBmecTYAu73S5eXl7jeBxXRxEyfwgZWFXbBsc7E7CGoWxiLwB9rCcCmqzZMsBmnX3kKu/hcyOlyGndL4yf5oVNoXPH4zFiOfcQb5IFwKSJodPpVKtXEaE9Ws13myAi+cJmLLOIWPXCG2jgo7mG23oI8CYTnCyYHKAlLaW0OqrSCbqrInwfWaBzJJWuCvI5KqUGpp4//29GEnkiA/sn1sx7uQBO2Dv+ERt2LFqWZUUoODlxxcFEIWuyXQeA4cXFxerBfujwfr+vz4MgeUW+tEuipwa0y1KOY+Y4ZE64Oh6P8fDwUH0OMcmt0bSwIhv0b1vN4j1i7W6/i04EFj7GbafoGT7Oct3iIxMVtoVqX9JRdJN4N503rL+8vFT8wNPp2bdl/GSfYjsg3jjZ5P5U07xv1d9zvMePAJxzzquT8/B5xnheCxPW6J4JQxOYJjG4r9fA+uzDFrzGjZxr7d5OyPic8anluMzldEgn/GCHaZ6/shnjABMZ4Fnm50of5OvfRo6XOeTIS47UtQRvmzBhq/gNfIRxDfJh3FufYp/ktfiW1zdXNP6v/6f/y8rRmSlDYVgYgADv41hwuLAZOBIUm+8fDofK0jkjt0OIaCyCg4xBvb/HWKkeuHzs9i3GAnhhfhiXwRtsDJmug4CZbO6BcVjRMCLmxVhRTnpqXQI08GXMVhjamqZpjjntYjjOcT3PMU7HeBtyxMUhUk4xnE6R930c+4g85Zhfj3G4uIzdzVXMp1PkpQUM1tsVCfZpOMi4yoEeNJZ+Xdmx7gC0fve738Uw9PEf/+P/rwI1AwTrwH7fAjsBl6Bs5oc12AZqOwHWz0mSk10Ct/sSWY8SHBqId6IJm0vLj6uBzIlAYkYI2Y3juGJ0cUjch0Qdmex265MgSAaRo21j67jcj4tdlqcWr8EKgQFGH8bYDFkpYc8r/QV0Xl1dxcvLS03CzUw6SQJgEDyRB+COigBJT2UdlUDu9+UBXYBr7GNZlri7u4vTaVp918E456+f18Hf5rkdmUpgKnraRXlqdXlyLmtUAOtFnE5jlcPj42NERN3Pw4ZRxou/wjZIpBxcU4qYprHKjNaBct/GJm8TC0CXiYKnp6e4vbuLOS/1/hwr66TWLYXocOSIi/1+pZeMB18N8PYeGVgzV7rxi977gJ3avngRwrgu7YqunLlSZdafv0W0Fj7YSRJj9NAEj0GXEyBaJ9EL5E1rxfrggTYW9h7ZxyJH9oWQENze3q7IMMc4y8RsJv9vAMULGeMjXVExWPF8uK/X26y6gSg/AWxfvnyJm5ubKlsDPuwT2bOmVDN9gAHP2HBVA4C0rUp5ffG3/AObYAuwy964XK+TIvpd20TrmMdnIQTwjbz4O8QMhx/gI9EZrtf3fXSRInLbh/rw8NA6BLrWPtQIvdZaZHIBf+64iFywLbfBm4hBRvgoAL6Tcjaz+zkdrAXft15v9Rd5YqfTVA6xwHbAZLZBkmjkiT6+vLysCB702CSlYzxJNTpqkD0MQyUgkFc9Tr7rynNOuq9b2COlOE1fVwGNK62PJoCcsDlRQAeRLaTksiwRS47YYAnWyYmd7cDYFP9mX7HF3B6PcfG3PBn8j3pgHy8EimKglEzCjtTK7CQF52LmjeBiB8kiwBAzOVc7AFIGeCgLioZC393drX5nXDBXy7LUoGCB8g+B4zBQYDtWxmjH7wSJRfQmUSdbGA3zg+nmNBm/zFjAFkZEY7vSPtI4xTK+xTLkiIshuhhiN0UseY5p38c0dDHMEYe5i74f4m0aY5nGuLhobIJb1rabfK28BsFr5jFFzlHX14GM72MgzAV5e7+B2eeUyslUBswwGbAqyB2dYE39ICuMn2CHo/P83DplvWAjb9nQ3krIODr0H9CLAyCoujqIHiMz5IRuppTi9fW1tgKQ7LntaZ6nuLy8qCeQuGLB9bZzQQcdmJhz0b9WeTDgNAngSgNrA1EH8IOtPJ1Odd5+UBi2QbuY7QcbJTg8PT3Vv83zXJ8ODZjzBn7GB3iA8SssdzlRhaM553muydnr6/NqjtjsNJVT1FJKNYFsyXUf8zzVtSWxPBwOcThcxNtbO7GNNieAgwE6QITgiF5DrpBYvL+/xTw3XUUvSyL4Fvv9oVZ+DIypMLy+vtaKSdWBfl2tdoKBHJArtnnY72M8rtt+DJ7QP1cmeAE80D1XMSx7/DbXcsUSPbAfod/eeos/wa+6HxwdJw4AfmwzES0w2y96/wfX21YIDPgAZbwcP8zs4vP4vpMaJ2DovduGiQUACGyH30+n0+p4eOTttTaYxD8yPgiGLWBylciJnGMlVTjsB921vZGowtaThADm0QfbD39HTlsmGxkRH2GQGePT01N8+PChVhdNcKV0blUa2tPkWSM6GkgaDMRc6XJybRvZsuok+OPxFP35XlQGI85xtPOBHan6VuZv0EnllfFCTLIeW5ILuzepwf9zPXwT8eX9/b22HRvcW0+xAa5Fwu8kwPJ2RwJj5ydkr4ndnNt+Eb5LPLAN43eQPWPiSGBjl21FqK7bkmM5+xSqR9X+IyK6VrGyjzOphcyRhe2c8RsLIiviJNfvU4ppbAcCcB1X9fEtXMutddxz2yIfESvM4/vjT/+LP7AP43GJiiBq54LSMyg7RoNijPj19fWrRdxmTjhNBx4EAsvL/XGABItiKClOpzHe3t7PLRDvZzCEwN6qIfjklmFoLNvPKT0O2AqEsboNpzGh68qNW30A9U62nO2TwfO+gyzrwHenaYpht4sp5RhjjtgNkYYuTvMY/fmI24vDRUSfYp7mGE9TdFHkFMsSu/0+OJoVmTLnsjYR7+/tIUscQVsUc31uec6NKbMDsiPi2i4TN2DXNvgBuovs5+A0Kk6wen8/npOVdpKYmdAisyX2+0Nd42maK3t2OsFU9dF1zUEW/Wmnc6xZ1VZG5Do4bhIE1vjq6qq2BQFULy4u4urqqsq4JHPvapXp43gsLHx54Nd1rWQQoBpb1BIWwAJOjqoaoJIxlsCwxDAAymiPm1ZAyS1KBAVO/EAWtPGVJOL1DMLKXC4vmfsUw1BOaNrt2gO+CMDYNQ6wyGA462KK4/FUE7uShLfz7mF/aaN4fn6OT58+xYcPHyrAb8D/EM/Pr7XtC3awJJC76LqbOm9ap0gQDoe2n4sAhcxh9b58eYjb29sopzHt4vOXL5FSV/q8c467+/s4no5xdXUdry8vlTmD0SW5ILGMiNqXzFhzRAz7fex3++iHPtJZT3Pk6He7uDr3vDO/ZVki9V3kZYlpKZsW52WJ03huPU3rzcMkPQZKBtgkj5WN6/rSNhA5ukgxL+eW0+Hc7hI5uqEvzz2IcvwoY962UGG7+LQt20dwxL4M8LekBN8per22DydpJqzQJ9hG39MxqQb7vu0/MWCyz+Ba2KQJK2JERDu5kevxxHTPgbYSJ2/oj3vB0V1e/jzPV3EVwLFoTRa1thMqEYD+bXt0I2HyytfjAwGCxDVIAuyPNkWq2YB6P6wNG3BCiP9B7sfTMY7npK7vii51fR9d38cupeiXJXaHfUxnX3d7dxfd0Efquri8Lja9H3ZVj1NKsUxzpD6iixSpS9F3fcSSox/axnNXZ/G9nGAFPqlrsuQ4vR/LKYQpRTd08fL8HNM4lQR+bM/scMI4z+34VOInlQf0x2vC90zQYjPoMvtgWB+TfCQT6BB24oMH8MnGh+gPZBO2iJy4trtbtkkncYz4uCxL9ZfGm8gAwhAb98N3WRfmha7iW8CzNR7Pc3SpiyWfseyZpIicI52TO9t8359Pg8oR05Ij9SlSRPRdF/M0x5ybH2PMW1Katd7GRD6P38FPL0trs3RFBlnjW4yt0AnfE9s1SWZ/aKLfydMvvf7oPRpmfiKilvMJRnyWQeEEmDDAC4GwSHxv27YCK+sNbg4eZNTO/BxIuHb5/3KM6uk0rpxT1+EMCuAqxzKmyHm9eYpA7eoH88IgUAgz/WZ8zMKYzQZwk6TwfT6PnH0fPscDuAgOVrK+6yJFF8sSMb1OsUvnc7xjite3M3jvuliiKwCkS9HlLpZ5iePxVI0056hBrQDFIfb7xnS8vr5VWSDnnCP6PmKa5nh9fa0ADJmgLzYCdIe5oHMYnJMSkouI1obA0asEnSKzProOBodTrob6+dJulKIcndsS5eII9+f1K//QV/S9OJf13iKeIEt7EY7PTsMbm8dxrA/j4jp9X46qLUnWe3Uit7c3cThcVj0ZxzFubm7i4eEh9vt9ffIwLUV3d3crJtFVHzOXOTe9KwANB9L6sOkxRyeRL8mwWc5y/SLneZ7j7e093t+PFTxMEydclaNeU2qnkjkwE/SK/aP7Ka6vb7SZOcd+P9ReZfY40NrFiUqupOJAP378eNbf15VtFVtsZ55fX1/XJPLy8iouLtppVwRUfNTT0/MZcMzRdX18/HhXmNvdLrq+j4uryxogrnbXseQc1zc3kaLp3vPzc9V7EnDGCAjr+z5ypDhclD7our8jFV2+Pa/94fIicorzsZwF5Pe7IXJEzMsSb0f5lr6Bbbc/2UYNJl1tnuY5lii9widVN96Px+jO+hApxThp0/EZuHEv5oxvoBIIsDDYgMjhu2aR7UddiXBygd56r4PZd8ZCYkWygT5uqwsEeH8fWyFhZV67DUAxmGf8EAIRUY8PJeZxgqPjhqtA7vUn5nIv2pxcPTkej9WPsOfBAGVbocX2p2mKp6enmtzbt7AfAx0hjiMPWG0qao0saetoYMq1XHlCxtgwthsRMeyGiJRifzjEknMc39tD616+fK5j6rouxnmKbuhjd9ivjjZPKZ11uovdfh8pIpapVdBijog+x24YInVd9Epq0S+IWRI+61xKKVKOyMsSeVmiH4a4uijPwulTY9Mj2qEH2N0wtOc84beJmySarL+ZbcYOlnNFxIdXtHje1gudB8i7rZdk0XuRuIYPtCHGec8KyYWJJfAftg7pgv3iG9kPwrh42f65Jz4ePYToJXaB7aptLEtMS0vo5nmOWHJMY0uo6DgxuU5icjj7rrycY20fMQkfo68+YMj+10kINojMkUlKKSI3PWGdGsneNnCjO8alxl1e9xZ31x0nJrqdIP1dr29ONFAKAL0XDiPy3yPWpSF+uvyGArkSYMU368o1t20A/olgSAjMtOLICRZbMB8R9WFGrkSM43HF4jFf2rK4rwMaiuP9BZSmUQ7ma7YGJ+IgZXbOjDdBCGfvQOLrlmpDkTVsBeA7pdYG57k4OUPurK0ZCz7nkiwKS7+5n7zMOm3ZBBIv/o5sYDzM/LnfmnHxohxvRgAGEeNivjZuEiDuZdm7rHp3dxt938eXL19qf205vWIXKfWr9iH0l5IqRs9ckM3t7W3c3d3Fp0+fgme+lGDdxf39XTw+Pn51os00jfHrX/8mPn/+XPUXh8spTx8/fozdblfPbrcu4lDHcfzqgUjb5M8b9XBebNo2e0oFD/vruvXDmwCsVCA54YT3sTuqNw5kOPC+72pFMqIFtjLeonM3Nzc1yaDnHV2l+sJ3TqdT3N1dfUVmNAfdjv0jyBUG+Kr6LgIk800p1b5xEhxAcr8bYti1pyXzt/f390hdAdwAUGSDLpkdZUzjOMbt7W3kyPH58+fy/zmvWEn8TWO+1vsL0AMDbL6Hj4FsQHb8DfkzJnQv5/aEcvs6KkeABXxlnpc6dr7fEu5iv7e3t9UHOQmiNxx5+InTxB1smbjQ9/1XD+xz8MSnOhZhF8/Pz1VfzZh6v5FJBT6D73Ryj8/aJr+OW8iRtdvtdtWn8h2qQdgXc0fPkCmbiA3KkBvfI1FwMoKvu76+rhUQ8ICZcObLT9bJcuXew9D6551kIWeSKeZKfDMLD0jE7xh4DsMQeckxLuv9OfwNn+Z5uwvBSXSpyp6Pxj8cal++97yVV2sbtr9F1yJamyC6cv5anefb29sqIYRtR6Y87LXrCilYbUgEzTAMdZ8X64nMmLefLcY83KqI3bJBH+Iuoj2XAfljV95ThS5jG47vnDCGvLftw/gHJ/DgJ5NlrJNb/kwCU3G1LqNnrtA5iSik2FvDlXGuXKXWmkVbG+tI7CKpJJHE/9hf7/f7WKYx5qXtcfKhAeg/dmOCH8zD+O23hm7tOxzHTWBsyVzeY4z8zvoT26y3ji3/k1Q0GIDBbd/3lUlgwaz4KBOT3jIXgD8LFUFZMfiOmRWcTkTrI8NBpNTaVZowu58NfCmVo93qog1tv0TXfX26CEF5y6IxPhw+QAvH77OqMSwcLcZpZ4lxREQFjADDLRPGT8bH9RiDwXmZZ9RKjsGDgwWyh3lhzQhQgPDn5+fVWr2c20AOh0M9FcNMlUEnBrCtXHDfbRnULEXN5qO1LyBvZGF9c9UL+cNEIBv3LOO8ikNY4uHhoV5nfdJPYWt9KpKZ6Ofn5xW4gyE3UKby8OHDh/MehfcKDtCPBhwKW/j6+lrZstvb2/jP//k/x35fNnAzzz/84Q91zVgvvlMZtZTi5eW1BimctQMPcmTteDlZMzCjZ912jIPC1iKibrxk3waVHD5P+0U5laY9M8RJaVnXWNmTK6zWMcZfxlqe+O1Tv7xOXVeOOjYI/fjxY5QnYc+1PcvtBLBhyIMnXDMW9s4Mw7B68NsyzfUYS4L34+Nj1fctMUJgen17jcvLy/jw4UOVv+0NOzPDZUAJWMDHm+lnHoAvs5v2FfwdgIrtXFxc1NiALnhNSN72Q3sY1DY+AIxgLbctPbRskRCzUZPx8R3aSSAAItZVSOzfpAQ+jr9xTQMZYoAfWIb/JtH35lx0ls/lnFfAy/NGx82CE2c9N9b5+vq6ftfsMGsOgHNctm834PLnDofDqjKKHkJQkFh6LUwU2c84OaPKw2cNXkiIDGoZIzrgvSv8xN8ABnfnNX57e4v7+/tVYmFClHVgnvYlTvRPp1P0ac2KV8ywLJGjVRbc2859uTd6VuTZHoLoSopZaAPLGoM3p8PxffSBMVhXibPb5+Gge05G8f2NBFo/98uJVs65tnhSuXDyYjIYncB+ud6HDx+qzTEG5ktMJvaakNxupkc/TQ7j1/gcsmXeyIjvRZz3nXZ9pNz2+LBmTkhJgpAJPgE/YOBePjtF6hpZT7JjUomxMUd3C7UuhFbB6Id2IJJ1ggN1vJfF5Af6z32clPDicya+XJ39ltc3bwb/P/8f/83K8dnJmqXwgMzcYJAuMQOG+fs20DlbQiFsbCwyiohSY9QwBMUZplUQYSEMjjxOXn3fxX6/BunM0QpqgLJlLMxmmI2jV99jYmHNlPr6rnI4MHEdZ+g/972npydlyM0AAN04dGTpa/Dv+vq6bpSDyWCtt4yRZWmAgmPEMWBMKLCNhfE5USGgcD0nnzgWxsgccQLcB7nwPZwCrDj6Sqlymk4VCLpMW5xqAVG3t7f1lAyXlV1mdRsGDplNaIDPi4tDROSqyznnWnrf7fbx+vq2esBU13XnjZV99P36gXT39/d1XdAdt9cVh7Q+tYt5c31XiAhI2Kj118wWYNNMyU8//VRbFrx+sEhlb0SqAMd+IaJbOWAHyGWZYxxbhQ+gz2bT06mc5kRwLTKN4CnzXA89LfbRjo7GFvApKa032rG2PJPDc8Y2xmmqGwSxRdbEmz55lgBzd2B1uT0i4uLqMg56sj1JD+QIbCHMP4k8vsrsLewc16JVyQCPli4ApisCrpyg1ySQfN/ggf73oV/va0AH7UddSWeNHWhN0FxeXtbWMieeJNjEBMAuiTl7BamEce2IOJ9QVuaCv2OsjoNUd01cMTe3W6FXxDADDAgWfIYPTHh9fa0VBdaBCilg0JUO4o8rZOiCGVIDa4Do8/NzXFxcrKpZriTbHxi0m6DCntANAySSCANjdNtjcRxqpGEjNA1iHS9SShFdOZVieyqe479jCv/PT9ahJsGRIs/zah7oc44cJ+m/fSPXtD7gh3d96fdnfE40jAlYR9Zgd9gH4M3JuRNaYiH39PXxe/hK7MNxi3VDr0yasm4m0IwL0RHui00zLj7v6tHWP20xFLbs992lwP34h81xb+M87mviwslYSimGfoh5bCdioV/ohAkYZMnL5LeTkNfzfkvm7PWyj+eajJV1RkboWEREH+tTxFg76yfvkcxZb7jPdi2xA59w5WSk67r4J//8z+KXXt+caPx3/+3/vRoGwZEJcJLLNiNi0CykDRijcUk7Yl1atOAQDkEGJ7StaCBMt3EAUrYOy4uLUtsJFgZurMBt64AYkzd8e/6WAX3jzBEGELaH8WPsdk44bNhSnoAa0bJs2mvMlpD8kdU6ay9jaacuMC7WZhzHynp4DUgE3Ga0ZYCccFoWOB8nnSg4wBh5RrQKmQM762mWOGLdvkVrA7rgdXcfJTr8+vpawZD35LAmxcGkeHl5XrH+BOCy7kPVBxhUgzKAMwCBz+FkYHtJ1i4vL2IcW0nVziylLl5f23GXjLk89XmInJe6R4N5oCvM+3g8xsvLS2WgUmrHT6I3PgIVO0afSIDcysh6sNYuV7N2gKb9vhz5e3NzU+9REotSnUC/kHdxkKXlj/e8GXCeGzPrdgs226O7yIF9KOVggDIWnn+BHC4u9ivGDZv49Olz7HZt8yDglqBCYmcGKOcc78dj7A7rJy2ji4fdLp6fniv7hHPn53bPBsTAnJcYp9KfzlO/t3aJHM0CIkN8zJbxc/uOfSW64yNkt6CCVh7bvgOjgW9eytGMBqImgrDLLbjk/1lj/Ni2H57rcS2TMtg7rYAtwWzyQDddaTKgtf3xHqwwa8U1YV7dDmhfxHUAMMNQ2u9oxTMYHscxrq+vV20m6CFra5/NWsDyuir25cuXVYyOaFVs2zZrii5g3wZBfJ91cyUCEsKs95acIz7gK7k+duAqw5YwhCgqhEW599upxUIIEu6DXrBWjnXoOGtOi2iXusiqrjP3cRxjnKbIKeo6b5NI1pj/J1Zf7Pcx9O25TABa9MJrzVxTSrGkpj8kJq6eueKP3Fgn2y4x1iSREx10knXaJgPEMsgzJ818Bp3EPxCz7RNMxEJmOh5X8D98fWyrq5hbQtLMvduFbLNOfJD5siyxG4bIc3uAoxNTJy/GGKyJ/ZXHOOcc0/lkQhOozAn/ZP3H1+A3sN+6DlPbCE4lCT3zOhP/GBt64TjgJOTnYslWj/7pv/hfxy+9vrl1ymVYDJmb4UQJ+rQPsaje0AU7GtHYou1CEQy4NgLjqZ3OAM2QcQ2Eg1CLU1k/IwEl9EI452qbYJqC05dK/x2tLF4YxoQTYvG45jAMdT8LYNgJEXJkHlybVh16hCOiOmwbgLNZDMJKa9YrolspkRMvXjiAbeBy2ZGA6tI76+ffKbU7SXTGT1XBQdjjwxi2DAHj4G8GfX5gFc4Q+eDoCCTomYMHQXkcS/DjCbI4PFjgnIt+fPr0qbKBbnODtWcOJEYudyPLklCmOJ2KLL58+RIRZUPo+/t7XF/f1AoIc+Eej4+P0XUNLJKcsg4RUcE+JxEVENZAjh9i6YBixwjoiIg6T65dQeSGbYyICsKdkKEn5Ro5eLI2zBmsD4cQoNesbdGjJfb7XWWyWbu7u7t6bZw+NlRsqnyfY4JbW9NrHI9vK1vu+9LqUxL5oTLf01Q2rj8+PlbG2fMHUFxeXsawX7fEoAvH9/f4/vvva+80voskwQkd+3t2u11Mc/Gh19fXq4ouZIQ37S7LUsdGADZQI0mnrYokjXYv5oufBLjDqBtAbQMuvsz3LsBojN0wrIIXp3xh4078Xe21n8dn4N+Qk9lcYsTl5WUcDofaNke84ZqMkxiwHbdZ4ohW3Wb/kkkM5IrfM7Ns5teMPoA4pXbSoFth8Bu0KqHfxEXs022c+B7WAjDtmOjKlE+SQsYkcfgMzwlfzNi5hk8lcwXD94qImhg6EcAH02KKrzdxsiUpWSPG6soI9rvf76tfppKK3IjxnALIGG9vb4t8I8U0z/VQC67L91PfbAk5OflBJoC2y8vL6FNJuNEXdMBxhpjPZ+Z5jtT3keNrH+vYDObCHuyT0WGTSMZntgcSB5OxVANc2WZ9sEMDc+Sbc65kCjGFOMIaegzu+kB/t/6L+IY+GRcanzEnV/PsI5wI8Z30M/dlbIwdMs6dC7ZHZHc8HiP1LblxjN2SMN4HxgvZu0WrjLMlSnzfc2g4eP1MHK+pfRafNQY3ZuOz+Kdfen1zonE8jpESwjk/jTCzaa+14HhHfFHmIVIqJySU75WTnQjQKLHLVVZcnIYDgB20DRNwYQajBb4ucmYxl+j7IaYpxziewnsVqsOQYHGSOFcYULMVBtWMh6BNz6F7VSPKmd2AYgNcFNLsEsqA4962Gb2+vtaKBvIhEQLUAiwtL06WOqtxDAPVjfL7brc+ArKsbWv9sRHbuHCiyBAjZS7ePwPYQu7oEsyJqxUuc+LUdrtySg/6xLq47E0yR2vKsizx9PRUnQxAsRxHeoovX77EDz/8sDpNYp6nuL29i8vLy3h8fIrX15c4ncZiC6k8wyL1fZymMW7ubuP69jbG0ylSrAGQHQFBmkSMnv8ll7aYru/j9v4unp6e4unlJb58+Rw5p7i/v6/O98uXL1Vfh2EXux3n9LM/Z9+A6TSd9T3H4XAZ19f9GQhdVKf8cywMNmjWkuBjttXO0sDJAc7s8fX1dQ1Q2M/FBU/aLUcPT9N77Pe7WkXgKNndblcfileY5TH2e/YbtNOsij95j8PhIrounZ8vsY/399NXIMq6ClgqPmiMeX6PrmvnyAN8Ly8v4+HhIa6vr786fYSjsq+uruL17TXeT8fqoNmng93iU0iOsH2zz1QraQNbcnsKNUH/6elp9XwVQI6DrNsNDAiWZSkPfjqeymk48xz7YRdvr6+R5yWG3T4ur0sVah6nOIltfn19jRhyzBExRju5K6UUKecYT6fYDUPs+rKn6e3lNR4fHyPLxjmLH91GV1wRiYgVEKHixUEK2BTrhO4Sl7ZVCD5Pwvzy8lLbJ9Fft4IShN3mxBril7aVBsAxdkM88XMk8Jvcw0SAbY57ULnN0gHsk+vh5wFkbhfZjon4ZiDCT5JMt8Ehm23SR2ua4xZ+eNu+SsKD3RjIuIPBiaNB+LKUU9MinzfWR44u+hq30RtkCjDa+ioAMO95T487BS4OFzF03YoAqXFxt4ucCgh8fHxckZD4SWKU8ckyLzFOY/RDH12UU+EipVhyjnkpyQ3g3QlHxLoViWuCPYwplmVZ6QF6iTydyDmZIWm0LeKnnUCY/GV+1i10k3VGrr4escbko4GvKw4G+fgHd0h4XK4uUDlgvq6kbhOsMo4lBhEx/hvjxJ7wL8fjMcoRgl3EskQ/9JFTnI/2HiJHjkGVftbKccPtx54T9+V3MM6S55gzJMZSjtJdGp50xwRydJJhPcU2mJd9ErI0CfQtrz/iyeD/bZ2ogXxx8gVk5ZyrkwE4juO634wJFQfdziTnMzhWggHOdrupiUXHaW3L1AjHjonv06PKdS4vr2uCY8BR2I3TyrnjuBnH3d2dqh9d/RzGg/MmAeOpriRQDiZWYNpaGLuvxfy8WdeMOFk3oMxOIKI4wufn53qaCK0sKBprRRAzg1fGWVpYWEfaEABQgFX+boBgY+WFHrlk7CoH43cwdKXCoIHkw+dAwzTCdm8TUdjmz58/V6afa8/zXNeI8Vkmp9MppnmO1LcKGXPuuq6cn52682bm4ypRJngSgCJaG85pPNXzth8eHuLLly/x61//uhyzOuxjPh8JimOgvQaWkXswV+9dcVsMLKPthM9gjzDM7ic1MHL/OPLx5nCYLH+e/zeDiR1tk3cn8cgcR8hJcdgvOsepK6yhGXm39gBISAZ+/PHH+OGHHyqwYL52ysgdW6Zv3y1PZoWYc46I49haI1sL11yf7Op5Qxa8vb3VfQRuEd3tdtENQ8xL0YU//OEP8fHjx5X+IV82SeMT8XN+dsc0leddXJ1bAvExDkL2c65qcV1a9tw6Zv8REfHly5cqV54h89NPP9WKp+cIA2wGFALHSQL7QUxiMF/AhW0XOTsBtx0Clrg3iSA+mXvh+wA1EVHXFHvh2q4yoyMGV4zLz0G4urqqJ//4gAYzlOzZwJ9wD9YF9p57EAMA4k7iDFzRka09RqxPxeG76CvVd4g13jeZh02xPpBNlfVNXz8MmM+SHDPPcWkP3eO6+HnrOX6D6iDVC15cd3tCEXG167rIS45eVQLmtCxL9LshOlUJ8Fn+LH7EoNgxkO+QhHaRoj/bj4FmRMScl5iX9uBcfLWTB/vEbYsT4B/ZesyQmGa1Sdzx14wJ/4r8iBd8j8+baGPNLUMnHx6X/Qe/cw3jIdbJiQq6bN11EuJEg3VkrhGxOnWK9ULWtRVqbq3GjKUfhjiOX5MZ1m/P05gEHWZcXgt0AHKPeXjM2HGtqOT1Pg/0j+ubNHD7nfEn98X2bff/4n/738Qvvb65osFiMWAWuChSAwMcL4jj77phdU5xc3S7yHmp4MQKbVBPQLOgCbhMnioDTt3GzeJa6REijL/ZDebEIsC00Qds4EFgdcDguyy42SUCPvNiHt7IzbWtXAQPB03mhqJQGuezBDbaHlxS5DPul0XZWZ+IqInXfr9fbUAchn3s94eV47PjIah43wMyQC4ppWpwrNHz83N1iAR6t+Hwk3u1lpq2KZcTngh2BvI88MqMBvKDkTZrzEkNWyYAJ13ByXkMOG7W9erqKrqU4mLfTjWy3uLoAM0A0nEc4/LqMualHSN3c3NTT0Cyg6IF6HQ61UTKzhu9sdPAWbjcm1Kqz4Uws8U6ojtOBHGOrJFb57ivgx5ByLbgozrxKzhPdIZN/awFPoIjbBnjNE1xf38fXdfVdgvGx4k8ZkUNTtElAD1r8vLyUoEm5IfthX0b+EhXDgCwb29v8fj4GNMyx9Pzc3z33Xc1iW+gPNVEw0GM6gV92siEYD7nHJFKEvDDDz9ERNR+busj64+d8NNtKIApztJHp7fJDetLG0pEVGKEtTOLyP2wbdqLhqFsLr++vo5f//rXNZn1fTi+FB+MXqL7BG4SKnTJrZ6Ml7GQvKDT3BdSo8Snxuy/vb1VWZgw45rM2UAP8gYmmtdWRvgviAj8NvNxZcHxCx1nfGafnWhFrI8KZ34G/sRrXsQNH4QA8HGblfesGER6X9O2XYM1QG5OfABIJvYcQ7muK0Cn0ym63VCTFOyUpMwVWq7LnhfWg/Hgr0wo4ftJDqdxjJSj+hviS9/3Mb+/x8XV5UqOzHvbpYEO8NNJRoQeAtmVk4/4m5ODJUcMWh/W1fiHGMg1zZw72TFGAQ/h7wxmt4m7DyogJoIbnPghA8cvJ7HEaCcY+DhXCB3fwGbMmes6VuMb+BtYyWtMLEQOlvHpeIo+ta0C+DL0yqSHyahxam2e7PUB63me6IgTaN8DffB6OkHfHnDkKpZl6f/Hl4Ctjc1s18a020QM3/mtr2+uaPz5v/m3K+YCRSlCWIMks5g5twm6baZcq7W4MFGz2MMw1BIlp3jgbAiQLJSvAduN00f5tycatUXrV4tGICxzjBU4rILT4qHMGLhBGK1OdqSAQwcSFtWysjHjYKep9Guz6Q/FcOBycoNSArxYN1cJWAOCFuwnyu5N2dM0x27XjhjkHjheABtrYweKkpt1QJ8iWpLK+GGccChmycws0oaCPHAeZoZoJeEz7hlG73BMBGscckTE73//+1UrFZ/vui6meY5+t96Tg67sd/tIClgE5G3ft9mknHMM+yFO583gAGJA7On9FO9v75W9RtfMRtqRE3DRPzOc6BXfw+kSuLAR7MXgAbltHaABCPIAlFJpYEzojIGt2dEti06g3LYhuqWQ+fEddIgk8v39PX7729/Gy8tL/P73v4+PHz/WnnjmSRBhw7qfsYNvQp74LPfNso7o8LKUJxCPU9vjxZheXl4iliWGvrHUDpaMm0ox/uDl5SWub2/j6rpU4NyuwVrQksfcItYn6+GnndDHvC6r8x38J+D5eDzWJMj97Phg6x0vTtQywwkAQvYG54zBpAwJGnPKOdfKLWMhgNJSSowAUOA/SQ6xfbO1vE8CT6sSdmJ/SiXHpIHBE7ri1hR0Pudcr+s2CnyRCRpksrVLM6LYLevL2J1soU/YkSuKJFn4RwNLA2Xu643vBm28LGeqClSKsFMzv/gWdCQiapXaSUhNOrsUXV/2N+73+1oxY1wk3gbLrKE31CInk5IeU87lSfZ9Wh/SUlthz2MxKcqamChzsmQiiDEz59PpFPt+qOuxxV+5Kz6CuaF36KVxRESsEgKTRdt4AUYxwQfuMCB38phzrmPHPzI3MME2mXUMBGNsbZ9xcV/jRWMdy9LzYu7YEHJnzVgf7mHQvtvtzg/nG1dxkqSd66KnjCHnHN3Qxyx7516uJuETsEnWCPkwftbRskVXScCMKbDZKsNlvYfHcZO5bh9SaX3F1lg/x4S+7+Nf/ut/Eb/0+uZE4y/+/N99xXy04J8q8wTY5qjFZWknlXgTdXHCp8rCOLBa6Z1N43gRJKDGTBkVA4Kn2TkzHhhaCT5NQed5rgxlea0VARYFWeAscdpbR+yx8n2AM9kwm6AwYMAEwcCsEgqwZdJQUDZRjuMYd3d31aAAYBjvdoxOUux4nTSxTu/vpwocWTNK5s7UvUcFg0dpWSfGjcN3NQjZwSLjYNzexgswZwB8Op1qlcJrYSbfzJkBsbN+M6gYs0uXfd/Hkr4+kec8kNj1Q2XRDMwdwJA9gXp/sY8ltyfIAyiOx2OMxzGWuW0MRq6sM2VcbNRgzcAEUMdaARwjWgXPrBTzNYvia6K/thXW2E/edvIDK319fV1BIXqw3fCGXiFzWE7YXDPvDpKMj3FsGU7YSuyfKoMBMCSHZUwFxaQHtkJCy/vjOMaScwz7dmypE4m8LJFyVKA5TeX5NOwZwk7M8n/58iVS38V3338ffd/Hjz/+WNeJxBoQgszQdZJzAxz8SR+NoDDYA6ijxwYaJmKYF+vgVhT0yYyuN/VvY4CDPokD+o4fJYACLA3wsfvt2PGlXMv2tZ0LfyeJYX3wTegpYMj+zokWPgXfc319XfcYGcSQSHFNJ+5O6nl2BfMB1ODf7SeRFXtpmBfg8G8D+vxET1hzro1cPU8nJL4e1zDAwi4NcFhvt6Bhi3zX94muHB3N+PkedgIrbsBPPENfuDe2iz9g3aoOnE714WjoL8cAd0Mfx01HgatU1gHbFQDeFRyqSruuX7H4vs60zPXoXj/4keQRnebztifWgTVA5/ChrogawBIb8GF83qSmSSHu5Xhg2TFmCE3bPbbN3G3TW9DLNdElVywsA/sW6wP66r9FRPRdH120vcfIxNgJm+DvOefIqTzu1RVgbNh40ve3n+JvyMkta8Znxkn2VybuY163N27JZsbk6xmvbm0HW4wo+6L+7J/9r+KXXt/cOsUEAdVesGFoC+kMrgSHMuCbm5sVCOQhNV4os70EDRwvmTGMHQ8rm6apPvDI/fwAldvb2wqM2MSGoy5GOcVu163u6WCY87x6yq2VxWCOBSEAspAGp/yDDQRUGjyZ2bu6uqrXw3lg4CRQdgiU6XLO8d13362qIj6SlOAIs+RWBvZveF4YUHEe6z5vntjrtiQM3QbOdTAikp4tC+PPAu78/AMz604WSFi9X+bm5mYF4FlTrg1rR7A1o25wSnL4/Py8aqExYO/OFQ3aWwA78zxH9O1hfk4QDVwsk5RSXF5cxhItkaK14vLyMk7vp1jmElA5HpYxs85tvVqwi2iMiatwbMBF3j6hyc4IZ0VwWZay3+nDhw+rE+G8H8NBh2uxZlQn0UsDF8/jdDrVQLxleJ24OCG3w0VvkJ8DDn4B8sAJbNd11d8QaAB+/M3VHSdJ24To5uamPA22b+/BRk7TFLGUp9A6ofvuu++qX/I8pqkdtzkcih3/+OOPFfyxPvhH2mDMlu12u0pmOGHvuy5SjjpnmH9AAHYDycM9GTe2z7ranznAvb6+ro7sRB9cdT4cDnXs+KyIUhXBhlk/wB26zWeRsfWBZGIYhq8q5VwfXYY8Yz35roEbMQxfuvWbjKPrWnU15/KAOF7YDLEWW8257NcjWTBRwZi5NnJCF/GHfG9ZlkogYI/IG303eYV/IInHz2LHPGvFrLXHj4y8/497Q5JwsANAd+tDvEl868vneY4cDayZtcZvQ9zZHyJvx6fteIkjvNoRuDlO02lFYoA/crRNzYyHBM8Vdn53PNoCuVqx7bpVMmsQXH60Sgdr04jcqa6zGXfmZ99F/KON0Mm3fSL2hr5YhjUWdt0q2dn+3TIiZnpv0RZIOwH0tSPWm8i5PhjSpE2tOp1f6CqYjb3FzKd+J6WIRXt0FBOdNHk8EVFbWllX7oW9ESvQC8/TPjaldnx3W/eWXPHT7ePb8UFkbTuH/rYqGN/xZ41f0QNizLe8vjnR8DGANpJpGqPr1mcBI2wSDVhLJla+H8EDyXg58TDbCWihIuLMFieHArOwh8NhxXLCbgAoAFPFiZdAwNN1vc8hop0XzgL7SZQYLgDDiRELhNHjaL2BKaI5OvZBOHhHRPz00081UDooEEReXl5WDPs4jqvWBYAvVSF6KK+urlZH7fI9G78dCd+7uCiBkkSIuVMNYhzIDXDedV08PDzUIGJWx4kmAByA5lariK+Zcp8AAkCiPc2tWxHtyb+AJ5ILbw7GUSFndOrm5qZWyljznHMseYll+vrECjNhbLp1lYR7ppSq3NgQOy1TRGotK+jb+/t7LNMSkRsQMesLSKKvnKoWMjMzxP4imGJkZNCO7Phc37fWQmTw8PBQ9RvZ5ZxXduIgij6OY9no/PDwEDc3N7WqYcaE5MNgz04av4FtIFtkzXgIwugpQL3v+woUABN+cTIZ9gPZgQ4DlCJaD/T2qFEA9ziNMefWGurq2DyO0XctcSWpfXh4iMvLy7i4uIjr6+v49OnT6n43d3dxPB3ruqMDHg8VLkAI6wN4wU4ruIj29Fi3N2GTZtfNkmE/+Fc/n4C4gU5BPGGLMPTIxOQOa40NoUu2a3w2voa1sj5abtsnt3PtnyMxtmwt8+U9XutKeKueGkigv8z75uamkjs/x9gjR8vaQJ4x8XfuAaBxi5nBajkGu6vxk2sa0EW0U3SchDMuJzYmAgzomSf3xdZsp1tQw++M2wQNfsd+b47WSsZa83e3+nBf4is+iHUk+XFCgE0RO6g84tPHcYzf/OY3Jeb3XVzvm+1t23bwSawFe+usLwaDRQ/WD9VF15dlKU8GX9YVXHd9GBxCNjFm5AwGAtvgEx3T+Z1YiU15jdEbA3tsxHiQxBUZMwbsHj1GFxgXumi/hG64JQzZm9BywsNctmvi+yK7YRhinuaY1S3BZx1PjVEr+E8Rk+KMSSc+b913EsR10VcSZ3TZBBvXMoHOPWqlqB9qBRUSjxjPWoK3rfeW03acW9/3S69vTjS2PY4oEov+8PAQu92wUu5par18ZlCKghyj6/oox84CPHgq9SkiWvkOQEjZl/dgvAj8zsQIoK21pLRILUuOvi/PDTidxjgc9jEMlFxhPPsYhi52u1aCZ9wwcCQ6OCsW3pk4n+P7BtBbAIyCIVMzOiibnYnBLI7EzBUOp8zxENfXV2d5THFxcRk5L9F1fXz48DFubm7Pc4jKoL28vMbhcHEGFst5bctxo6y5gzsMWJH1sDoG0ay4x2sDctUHWRDQXJ41KwOgQbYYD2AQPXDiytq41Q8QAjCGRUDG7l12IuG167tylnWe51imufTP5nJixTRNq+cjeL0dIGHyjsdjHC7aA8/meY7dsIuUU6ScIi+tR51AgaOj8oKj5CQq1gX9dV8+cvK+iYh1oMLxcO68dR4HzXgioiatAAQzN7ZTxgHwxK6557YVzG1KBlYGv/gF7ouuus8bvcB5u7UwYn1kIlU7fBnAyZUfSBF0DLsYxzGen5/LJvszw3zY7yNSji5S5EgxdF0sXRen+TyGZYmLq8vIKcX+4hDXl+XkocfHx2oHMP081JGed3xKSinKmWcp9odD9P0QfaTY9ec1P+tWOb52iJS6mE4FLI7TugWItgbkwbNEtgksrLPblLDPiBKc8MfIifXiOQWw8OgVm8W7ru1Vw79xBK2vRaxyddP2ix+ipQYSypUobBI/Yb8Bk0+ygo654sAcmYPlBlhhvwdHGtMGZWLBrDq2hu5bFxknNo4OYEfoM98hDrnVmO+ZscSmXFVivowJO2VMW7BvMAhZA8g048qYPX8DTu7BeAwmJ1W6x7k91XqOFHNuXRgG2OijwSHXsw0xp9qO0nWR0nnNI5dnWaTzoXHTVE+d4rtm7vHxW5txtXAVU/rS5z+OU+wiR8wlxkzzHOn8rCSSREA967ZN3ti/YvyE/KnCu6KPj3OMcLWCuORKk8lmk8Z+irjx4M+Rh+Ap7NJ7M6wr4CMnDCaKjI34zM/9tP06QWaeI3t2ljlSXiJSiuur9iyiJSJyl+I0TZFSxDSdn2W2Ga8JPuue2z0ZN8kv8nAFyRiThNWktjHKspRjbsFbXMOfxefar7CGljnjwY/8sa9v3qPx3//F/7ACh4AOnLRPviCbt6NASQF4Zr7MIhR29SXSz7C5CBQHDavy8vKyYus4DhKAXkq8l9GdGcPj8Vh794tRpBoEzCBxT7Ln7SZzgg4MpNsTcFB+0BYn2BBA+CzXsRIhQyoLKBstU8zNY7NT40nBKTXlgS2B9QcoEbhTSvH09LQC6swFR0vgZ98ETtrAw07DTJiBCC8CE/chQeT7LjlvAw9gyAYBKHAiZKcI28u97fQsv64rx7W6VxeDJXHEuaJ3rKnPxneSzfzsAHGsjB+we3l5WZ+MarYdoMm9DEhw5uM4xl//9V+vEj0eUsbJXgBHkisCiwNvxPooO2TvuWAHfo++ccbIZ/AJ/G7mZXuSE+sAiEZv+D7XwCkDaqkI2t9EtL1LzNNjNiPF/igz6siBuTs58+9UR8wgU1kj0SW58rNhpmmKaZljOq8T7Tn1WOW+j7w0nY+I+ryVcWl7qPCfrNfl4SJGbepErtgG6+3xcg/01gQKeu1kD51DzgZyJPj46m27gAGuWyrxJZYtfpwkhJYd1pG1cNsU+giA4hQ5fJwfNoUfogpK+4pbgkhQDI54uXWXdXabnnu1+czFxUV9KNcWUCFf1pMXvo0x+31/15UYXxe7JE772pbXNE31GHjkvAVD9mtmj2G/sVd0wu2nvt7WHzMfJzv2IfZ1rIN9og8boNrh66Ir23mbONy+iC2WI/KDWOM5LFzPcYL7QeQxboNIxyJX8Z0gboGmiSHGj87ZdpAVhJfjbkRLUPFz+FnmjI/Etl0h9rojly3hikydpIIX7NvdDsg/dIBKumOV14O1ZV58zt0j6Il9IONgrNiyq3T2n65Iet+Xk3D0ggoSPgA9ZC2Na9xS5XZ2YyrHgC3Rgwwcq1JKMaT1ccQmYezvwdvWNeZPDLYPAC/9s3/5T7+yl+3rmysaLqUAanFWZKA4CrcsAC6tHBgIE6BaQvbW90McDiXL4/hLs7E+7cSnRBDYOZWJKkjps95H1/X1PbcPHY9v1bGRdZvNJfjBbLIIgHHkYObPhoRDdkICiwAwQi6MjWDadV1l7sxkkdhxL/pQeY/AP01jXF1d1+wZBXGQoLUk5xz39/erezkjZ67H4zHu7u5WjIZP6jIT5EDtvmnrCUruYOGACWvjzxhoAjABbxitgRUG5r0p3suAAyNZtpHzfbdc4NyYA/rtwwdoE8B43efpgGBwglN6fHyseuDgaMdtJhf5PD09VUDGEarIAwfBmBzMHAC4npNknI/1h995YS9cE2fswGj2En3yw7FIUtwCgw4ADpEXcwd0Pjw8NKZpacdio58AAQcL5p5zjs+fP8fFxUXc3d3VSinz4X6vr69xd3e3SlTs5GGnAL+MgUBNooodtWR3iEjtqczo3G63i+VcvkcWV1dXFbBVRz605zGQzKQc5ThOkRdb/+AWBOum+6D5m5kz5kvlFFCOj0e3lqU9rwBQDdDkelSfXM3w/hASL/4x5ohYJc3YLgHchxZ0XVePSfZ10AX0CNvFF6Nv9klmwLEPAnfOubZyIjt/ljXjBDMn5dYb1gkgwzVMevDiGugVNsBniMMmapANsnQ1ZZtUG7Dhe8184+sNytwuYpvHf/I+Mdd+Bv3d+gtiiMdKUgQxAKCqydy5ku9WVye86PDWR2LbrJX3nTnOuWqHvmJf1lF0YZu0bfcHbn0iOmn5oetuDSQecE/WzvPBD+D/iauPj48VexmjoTvMge+DAa2HrBv4ZBvr7PPxVSTd6BK+mBho/8Rn3NlhomuLC/g+39sSfn6hw9tKGj4Pu8UPGXdxX+6x9S34Pq8Leo+s+L79hwmAbVJl7GAy1vG4VqIiRbe5xjYxdxKFHYPb3FKJ7tgOvvX1zYkGC8FNYVoJjBgKTAZKieNns6hbFWBZzQyWAHMRt7c39aQavkfgned5dVqHBYyjxAG1c5Rz5Fyc9c3NTby8vNT7TdMctGp5MVkwrk/QMEjAaMn4eDqtKwUEdcrVgH7mbKbW8jOAREaA9w8fPlTnyRn2OGACSBnHENjVMAy1jxjnvi3Zz/McHz9+jJ9++mnVzsT1UWyYShIuDM1tUAQV1pw1IbGxQ8OJYlgEWCpAZuuQBfKwIwWkuA3CzKMrR4wHp+0Auq2kmD11CZk54GQc4KkWsH4k1eM4rh4KaJmhRxHNAeJQGYuDJC9kdHV1VQEz13Dpn9YF7Mm6zjxwrJzWQrDBbgloTnKtm97DgCzsnAEXXdetns6OjqIjBB8nD7TPnE6nuL+/X43HTKCP0AVIeG9JdYBKujnm1odHPD4+1kQGQIPs2ERP8EJn0SmfmkO7jatn4zjWM90vri4rO0kloz7peppjOduHbXxbhSLhZo4p4ivfg05AyLgSwkmBMP+suRM2gBV93cgbHbBubplhJzwO/E5ETWT9zd/8TY0Pfd+v2uEI4vhYfBMyMePtoIjP4zha5m6QhZ2jo/xD7/D3rjyQjHgfC3ptv255G5hwP4CVK8rYuUEgPo/YlHPbQ+ZkxOAPO/L1tgkJNosvQvbEP1fh+Y4rKwaO2K8ZW1ebDMDRGxN19hUklCQN6ArycvIeEbUf3fMywDOwRU6M2+QOcYvYwbVyzlWH7KuxNSdzyItEBD3ABoivHBKA3V9dXa32bfoZZSQXxC10xu05kCXMB11izVkD730yGWKdw1e6MuNWK/6OLzJYRwf4m+OM7Z7ft4ks1zDbjn92QszYTPQyDmQDVrVNIxPsj/mxbqw1MZb1sw05GXJc5n3WcJsAujppnXBiAcmF3Nz2hg9gnPYXjPEwtOOAuZf9oslI24UTc1dqTPbY9v+u1zcnGigtQBPFsiHhTAEJVjKSDs56JwFhE6od3Ol0qidymL1aliX+5m/+poJlBGWFw2hwkK3E3q/ACsEzIuLqav3UZsAp8zwej3XnPwqLgpnlmed2TjJJjtkk2E4cEMDAgIx78zsyRbFcojbr6k1RMD3F6e8ioikLBkuLhtcPg3EbmcuFtEjM81xPQvG9CEJOAswAbU/PYD4wkfM8r/YCATisUxic2SfWw85028phJtaOgnGxfuicAyYOyRUY5oe+ERx8chRz3wII2Cfmb5bg5xKqreMgyZnnuYKveZ7j5uYm+r6PP/mTP6lj+vLlS9zf31db2O128fz8XAOhy6/btgHWyEm2Ewd0jUAGSDBg8bxYQwgE5Iyt2Qmjg2bSsA3kDHAxmHPAZ27oD+SGGR0cMGvsJ2j7qOyI1m4CwOCedswAHca4ZdjcxoA/2O/3kfouhrOdUxVDFimtH3iHXueco+9S7A8Xdd5mhodhF/PU9pagswTW5+fnWrVi/JYPfsXJZ9+3PUH4YLf0IUPs0K0X+EavO0ArolUh2aiM3dL2xntOeqhout0Vveu6rh4ugK66+gJoBZxRGdgy5fgSHyVrcIq+GVQgG+83wcZMVLj9hjGSlOKrnCQhZ7dasb6Pj49Vp80oG8Dxss7ar/I33tuyxfhJ+3WDIPtbYg1j914N5mRdM7PPC/lxWAbrz5hc6eZzyDPnHNF30Q9tz6PbYUwCIUe3ZrFO1n/GOs9z3N3dVTCMPeM/Aa5OzNj8TfLsSqET46urq+j7fvWATgP3u7u7qhskvciYa6E/Bs6utvJ54i5jt47hG7dPSvfYHVudrKAXXl++jx9Al7quq2TpluB4enqqccsVXF6O67YRYyTWxmSU9R6/zDW8f5H1Ref4uQX1zNWYAd3kM06wDO4dI9FRdMY2jozxf45h1mWTbyki0vJ1+6X9Bnhrq/dci+TY92I+3/r65kQDwO4Fcm8ajtqgjwGfTuUYVJSJCWHYVoLiqLpVIHIp/x/8g38QX758WVVXvOgECi9UGUdaZcR8t7AI6yc0m9XEcV5fX9f3+AcbsNvt4tOnT9XBAaQi2pFmVirkZkeNocPKbUGus3o2dAFyf66Fosk/xbK0kjPACYBLC4afiwFQwPHhDEjwUL7r6+sVeAEUO/BuGSJnxr42DK6DkJ0LemfAz5jMqqBbBiQ2LBsM1yKBxpGY1WQcBECDJF/DCarBhR33dlOXE3Xvs8D40WkHGnQMIIG86S0noPLdH374oTI5yAId43NOrFhbAqvBoece0aqH3rtF0HUPuFtUtgmpEytsBfDu5DMi6lO73drx5cuXCui5JrZBYAfkUmmhmoZd7ff7Wp1D1qy3g73tAPCJr9juHej7sl/DjLyDCS+zxZFaKxHAap7nmKc5Dvv1Qw1zPp+kt9/F21k+roAhzxTrZ+QgA1rn8L+sO2NyKwcABFCOPGhXQS/x38zR7K+Brn27/UdEiTMcSW4QawbWp3qhB66q59z28b28vKxOlMMHUNExWcLc+76ve2Asuy2AAnBTaUJvzfhhp9ivwSwywhZZb34CiPz5rf/hfbP51nODMPyLmVDHF+KCQZWPajdTbNtlfI5r24TKxBk64nullGqbSde1tjfWmLls4wfg2ddhvCmlOJ2Tub7vKzEXEV9t6Mc+kRVyYc74CIMurolPtf4wZpOEgHPmiF/ETyIXfLiJLO99Rc9cjb+6uqrjQy74c/tb3mO+6AH3Z718cp3Hib2hMx7zlmDeytSkpvGjdZPxQwr4YBBINdZ4m7w6OcJXMn+ThYxhW4nj+/gx1hQctMUZ1k/eh7DeYlqTaJYFL+sudoK/4O/b5ITr+rvbFsFykfOx5ZtkxAmMk2Tsy75h6wPQhf/iFQ0mjRPBUbBpxg9gQ4HcJhXRsvFxHGtSgqGjRIVVu42U2oYjstuIdqIIwcEKz/ct7Jubm3h+fo7TqfXrY4Qs9jS1kpUBMYJ3Pyv3Y2xW3Ovr67i8vFydLsITa81ydV07UhInA5NK6wzjscNmDawUWyBt517+1o6MJTGCdaMHdJqmuLu7q+vsIO7snzUFZCBzWPyW1DX2Ar0AuKKo6AOy2u129XkZNui+bw975Frc9+rqqgZ5B3euazYIfeX3bZuFjcyMXURUsEoAx2kYoOFsGbNBCaCOtaKax30MxHFwBqPMGRvgWiQCfIdx4UjQzXme48cff6ztWt5jROWN61NxIjF1adfAxi0iMEcEyN1utzoy8XA4fMWUMy7v7SFAW7+Qjzd6X19f10DoCh9rxPp7rwrvN7toDxzE/g6HQ90Mji8gKOMPsB+zRgR77Mo+i7XzHghXuJBJ0eE+Xl5fKmhGb1Jeg0n063g8xpxbC5J94W63iy6lmHLrnydpc2unk2XW5O3trdo6ej7Pcz3ZjjXeVmP9BGYHNfTU1TnsBX8NEANUwWT2fV9bvLiuD7HwnjZ0YZqmav/X19cr3QV84GuxQ67pKhlgwe1hAD3e41kkBjvoBQCH9jjuz/zxFYBGJ4geq/1sRKx0HFuHrMJOsDezqfgq+0HW3ske+mXSwz7TlRBOVPO9GLOTnWEY4uPHjyvCBHt1fGQ9TFpZD32IiQ9XQC9o0Ybtty+9v79fgSWTnpY9La74CxM9JOEG3syd67LGrBO6b4IJ/QAb3dzcVGKk7/va2k3yBd5AF9DTlBoxaFv2Ghl0AhI58MI+wP7W+0m2IJ14Y4KK35HTXsQIsrUfxXaQCySrAS5J0Lad04kp7yFPyxmdRved5G2TfyfJrCX4kmsgK1+HF37ILb9cmzFzT3QGf2t/YJLTvpLPOnnjmimVpwMiUxO0KcrJl13fR+R1NdS4iDEbS3Jv9Az980/jlL/r9c2nTv35v/nz2O2aIy8376LruFEKznwuoGk5/y1FzrCHZHGlHE7gZjE5Darr+pjnZsQERgwKgGJgBpvF2DDIvu/PpwddxDi2krcFBFBwOw7Xf3t7qY6DHsstE41BeIEBdThQb161s7NTYGFRBoI6gQCg4SpOAal9DAM9/u8xDLvoe4yhMYKADORiltdABRBrFgVH7nnYEeN0SXYMRKsxRKwCWteVkun9/X0FeiQNZgHsyPndLDPBocmjsVGMHWdhB2C2g7GTxMGcmiHbsv7oAfK1obKerBUOyOws449oDIcTMa5tuaLvDiBOQtEfggDOmM3lgKvvv/++VrEAMBywAIBzpQr9Y80ACcjJrKvngS4x5tfX11iWsqH54eEhbm9vV3sLCExb587Td1lTP6ODl4P3tkWD39FB/p/xOdncMrN8B/bafsL6SQLh6peDPT7MLRjIKlLxoePpFPvDIeZpitSV5xQtubjX/X5fgkXXWkxTznE6jTH0faSOFozy/JQXnTBmG3Ri6oBM0sm+KPt65uJWO/TNCaftwISJ709Qs70hG1cfnFDjY1kH7M8+nH8kjGaGDRBsK4wXIGtSyxWZLdHDHGwrBimMnz0122og98YXuKLpDb9mIC1v+zBsnrlib9ZlTgyzDyWZNtjwhmKzrtZVdIC4Yf9qP/Zza+z4xv+bgXZLGIkMVUUOUeH+NXndDZG6jifYnePgObGPvIqvOefVQ+nwa45jZu5NVkHAEGO8T8f7uAwUuQbXcVU7Iuqct0mIX9YB9AqZ0/4I2UOctnzQS1cRIFPw4cVvztGlbmUnjdFOseTlK3uwjRCLXR01YYJ+1RiXI47H0/neYwwDpyiezolzO0imHJBRjut3ktz1ZcNzeXBhH9M8laPgWYsuxTK3JMoEYtG/OOPYLpZlRoUidefq9qwN1F2KLp0T0t0Q03g+qKJv3QzTNJ0/0/YER+RIqYuUor43TmPsBroryn/KOJdI51OiUpfOx9P2dU2GoY+co2BqrUPf9ZFSRNmTe66iLLTIzZGixbppns+JyRK7vp38xQtdwYa9b6ro7vpBl//yX/838Uuvb65o7PdtA2/rhy0RcGtY5ZWjbMBuO+tfX1+qcwW0MDEckdmV+/v7WukgaGAczhC5RlOeNZNTHFX6SkDcd8t8N/DYnkwKMAcEuUxPEGRs7+/vtSUJBgxjNxAhieKeDvh2Ulu2nnkSoHa7dsZ8A8rt6c/IBJba7AiBhU2uyIV1os0Chtzj2oIOs8tmygDkBEE7TmSEg2JOABzPtSWx82q9GBvO1Y6dNSoG0hIKs2Xu4Qdwwth6zw/6xrqhXwAh7k/Q4H7M1eDHLCXXx3YsR1dJ+IzBK/IBADiZjCgsHskc45+mqR6I8Ic//CFyzvG73/3uXPkrTxunzQB7J7DCPKEDrBE6QjBENmwcxoYsO5/I5HYmP6sDVnTbP0+CzL4U5mUwh50hO8uSPTXI2O0Q2LdZPlcLuJ/9nRNb7JykHBBjvWAtKhMabQ05kjZyji51MeyGOI3tQZ5hf9MPsTuv+9XVVSzzEvvdLl7PJyw5YWPs2B1+2+O6vb2tn805VyaR+7E2VG7dKmZQZWYS+8cfmEDaAjHuzcZ1ZEoFGIB0e3u7smFAN3rh9TEZgP9l/tglCcE8z6uHyrkSia1zRCg+2ZU85u09WE4+zGbaHmm5xe/wQuciWu+4kyTiKP7dhI8TKffnY3fbKjfr6AqNW5UA6ewhQKYQCPM816QgIr4CKawRL97D37EmEIro38+1PLPGJZmIyEtri8s5F1DYtyqx5czvPjFt60+J5fxugoq1R+5UHczyM2YDNJIpP8jWMQKf5Rhv0sXEBrrrVmkS2+onzi+35zkJcDIREZGigGl8KPesSX1an47k5MzxjvE5PnijNWtYCFKS37YfBtIUf4WsT6e2H461Or63k+VS6qJLbR9DSilibk8lR3b8bqLKelkT7Lwh++YccRbrPLVKjj+7JLogGoYon+tiWZS0ptZ9U9a8EfYQWo5jjJlEJecUyzlhSClFv2uPbnCSn1KKJbcDKCaRF11qyStrbpKedbSOOpbYl/3S6494jsb/syysemcjYrWpG8bfyoYTJgC4jB2xfpLsy8tL7a3GcbNx24GExYpoIKsqQ27nvxtsjmNzFM7CI6ImBYAhO5xpGs+Z7vrITsACSZdPlzIQcUKAs+IZH/v9Pl5eXuLt7S0+fvxYjdbKHRH1OSFOovhZwGU7AWyapvqEZZw3cjbo2LLGMLK8zxwAdWZGzO4wL65DYuKxuu0hom0mwzH+HKtGgELmDpToAQHHRuCWDh/valDlxAF5e04Aie1mvi1wcdCnouIAj86wrk4qfKKNgyz/vFHbjJwBlO3MgNebkLHXbdADPE7TFP/+3//76Lou7u/v43g8xv39fQzDEL/+9a8r0LeeEDyQG3MnCYmIVVteROv1ZT4EKYCPv+u5+eGDfd+vnm+xdV0OjqylW3YcnA18bNuw+QbJ4zjGw8NDBT0OWA6y2Au/s25+MJoBrtfENsnfIA2mZYndfrdy/rXKNDTWnDYhn0SDH/CcsSdY7q2+sa/BiYnli38g6aCiyFwBWl3XVWDKum7XieuTaGITJA8maNAxZGuChufD4MciYnXKFrpikgFf4PXHPjhe12xwxProbftpqsOsLfqw9ZEAHt+fe9vfNNA11KPaXfmZ57meUmSdN2CiSsOYeM/XQVe28dQv9M5EiI/UxR/x/3zfpyQR530gCG2N7ggwHmBtTSCxrvjnnHOkoawNyTYkiX0Mr5rYn23U+MJkIrGGii1zxFcjk9fX1+oz0fFtMo/emQixnJCx47UJJSflJMbGB07kHKPRfeTFxmh87RYrFXKjPdPLBOc0TbHktv7oMTpDAsM+Or7zcyAVvHY6rg+6AfRCNCC7bdUeEscJBGDcnQNOmp2csDbIzrjAvty2v123rZ38bSAcn8bYjYEsFz5rfGdc5aTNsQedZq14z50S8zzVBzwa/3Wpi0W+HULC84TM2LaWk/D0ff9ftqIBMOKmCJkNvBHt+DcPnMmhGHa27stDkDwFdpqmurnJCoCTREmcuaPgMCIocQk8Kfb7tq/CwN0bCbegrHzu548x454InPeZixMSDJE9GwTlLbuGYwMgwupug+vpdKrM0vv7aQW+WJPtOOxQXGWw04pogXlZlnrUJoACR4qiI7efA+3IiPGjD8zfSaKTNNYB4OVkDdBhxUf3/BmfpuH9MawZPw3CuA5jBCDi2NEZB64t08SYuZ+dB47UbX7sPzCwQI4GtABy1t5tFciE+3HcJxsY2bQfUSoPtCGhL//4H//jaic5l6P8Hh4e4uXl5fzQx3QuXTd2k6BiHccW7BSxQ54twEEG6AlAqu/bM2aQAQQFoM/EBTLCh/jzyOvl5aXuBXMfOUmqASw6CjgEhDu4myxwJc4JKMmBgbQZWsAd92Ms+FbkS7AfxzGWyLGL3VcBMaKdhASo9hq5z5p/2JuvQUCNiDom5BvRTr7D5vAVzBv7casMc7DfZN04htX+l/EAEi0T/JXt0jGF5IrP4T/9fCYDA3SP34kH2BDxjXlXhjNipYvIsuu61WEpjD+l9fMGkDsMrWNZRKzAFX7YczCQdEUMvYMgcRWEOVDtxMegw3wGYsAA0jIyMOVESGyev21jjo8dZryOQ1RWGAf3dM+49ZhrkNQiqz53cTqvGQ859Z4P5gzBk1I7khty1ERHxPoYdOzQumob4hrcC50BEMNq+yAK9NCkAfPB9xjw+mhnbAmiDR1y9wG2Vn3I0ioRxAz8NqTBNM2Roqwnh980IJ5iNxxq0oMush+PpNZdGMgHPXdC1Pd9XF72kVLba2TMsN3LROw0OUCMc7XceriNj/bDrKeTUcbF2nBf7MF2Zf/osTkBsM8iHhprMTd0wofvICtIGObtRMp6RCyE/EZ/pmmMrv+6tbrMearthraVn7MZ4l7xW+1EM/uvv+v1zYkGzCKlFdgbWJht9oUhul/U2WNEY4cIFAjUi7tlBQyYWDAWweyqAWD5zLpfmgW1sdXMXWzAblfKVVtmcqsosEvMmZI0FQHAAMYJc8iic8JJSim+fPmyYlAAPAQWHBFzv7g4xLnJe8Xs45h4HoITJD/V3cGCeVbW4XRaMSDu9SXRcRJqh+sSLGvvxNLg1Ibq+fJ39AJ94rvMhe/xUC5OAwNEAETMDG2TV+sTARrGDVCJrnl9mGNErBIg3wM9dAVne9oVawcw2zpfM03MgxcPeMLwcaYeixNen1DDd/b78gyMu7u7CnA+f/5cn9kCgEJeBvleV9sqcnp/f68bxt2mNgxDXT/kAJgkqCEHByT0kUTFMnPw+PDhQwVg2I+vgzxIXg0U0Sl028SGEwsD78PhsOrZZxzo5JYdQ99IGPBhBMFhGGI+73HjYYLIMqKcke4KH6DJ9kdLhzc/83fmuPV9fC8iakJJQHfg4XeDUpJzwMwWmBBQDaTQyff39/owO9bERIeJFLdjAPaZBwcbcE/8FmACP4Ft8BMdQt+Rk4H99ihds5IQCLyHjpKkMiYnOXwGQGkbdyJse3C7mNcNIGJG3XNgbZGd9zSllCoDjA3bf/DTSZUJCq7Petkf4F8dDxi7ZWu5+JlCbkvzfHLOkc+5Gfdk/A1stQf54a+wTU6f4nuurGC39pW2HeuFASaHJhBjqYyZsTfbblsn3kW0fUpO9lg72xaYA7/opAlZGFNt95AxrqEfassPR6DzOQNkfDTv+dALdBW54GMMVJFfXsq+Clc6tz7T68Q4jNlcncQuvNcOW/IBDdZPZGdMaOIYOzC2dTxHD2yrJjXQQa5jwtY+1vHASbXfczJiHd76bu41z3MsOccif+T7pZTicNFIHuvd9h4mNoss8krnf+n1Rx1va7aWyXD6C9kvC0YrEoCKRak9lKmx615QJmpHwncNTg1iYX4AcM4wIyght3YV7mHm2eAWAyvjbyVAnNLNzU1lSjny1cGCa2L4OPKu62pyYcPg+oAZjrYElKXUHnjIue44z5LQXMb7+7EakJWSJINs1wZPsHVfnjNYAziDDieSOEva3qwfPGwIMAugNCjC+CPanhmY3efn56Kk54DojXjM//b2dnVqDckgJw6hD2w0RW8cTB38MDbK/s7srXdOkii3sz+H3/mskwtk743NVCr8oCTWj2tYr7AnkljYV8AUgJB+9re3txpcDGjRgXEc4/b2ttpGRDsi86/+6q/iV7/6VQ0mrCWAivkYUOLUt/bNWvI7OsXeFX5nXxTvoUfch9ZD1uf5+XlVBSJ5iWgtWznn1fN3ONWIv+PoSVYBrZ8/f14dn+uWHoIWesQ6OGll/UyMOCllTga1VKA4Pejt+F7H/enTp1WCmZZzr/LZHy3LUqtCrPUWyGF7Bk78jhwZD/6L39FPxsfvtIFeXV1V8GNbjVjvK8MGkQGy9yb/bUWmAqKhnXCDHaIPfHbLaLuKBTjC3+NjTYawPvhOWnGQFXqMT+Be6IRbGAygHCO21d95nuuBDFuAwRqYTDAYq3t0NAdk4yOq8Tck8zwPaZqmyrhzXV5bpplrkSC7mk6yhA6iN95j5YTOFQIDQNsF8ZHx2eb4yf8TQ12x3/4/D/NLKdVjkNET7P7q6mpViWet0Qmux9q7qopcqDL6uTMQNds5IC9XLrg+/sP7+1gX/CRdGU4o0WPsxVUTsAdxJqUU07zu1y9Vh8u2hyXWD07GH5hcxI6tm6yn8Uz57rrlybEPO0HXwCKsg8E4PsbEMfqFjRNjWHd8hGVpLOLrb8fjeaHTjMFJFfJhPYjVjg/GqfYX1g1wnmXT8GnDe05umEOf+jiNx9U1KzaP84lUIu6Mu1mbbXWtjLft3/mW1zcnGh8/fqzKwwAMIrbsjz+LghCwHaytXAAfFr78rZR4DM5zjliWHDyIzkrSysO72O935zPZTytni/C4L8YCMHMG2vfs8Sg7/vkOCl82vK/7W5elgYytAm0NFKMdx7H2UzMG5uxEh/sA+MioYX9oG7i/v69tJ2YtcZAppQrouSYOx44U0GHDMmsaEaunZrpH00HRyabbRswgLktr1SIQbjepex1JwOx80QPki5HQOmMHQjDACRpYwCRRmUIWbBylAgXzaTZwmqb65PqI5uhJOLg2vztJ53f6l3FcZkexA8bHdZA9QRKnz3tmhmyz3gO1ZVsjIj59+hS73S4+fPhQdWebKDm5RbccgHjPoIg5cF9kfTqdVgnRw8NDLX37lBTGiuPHtt3OyVz9DJmIqC2MTh55dgIMOK2cp9Np1cqEf0LXCNrM1a0T+CPslPmy1tvWh4j1k7uRRerWR3fXgNt1kQUu+TzXcruMfYpB+bIscXNzU+XtRNb+CRIAwoi1QP53d3crFtJVVANuA1ePxwRKRHtGAvJz0PZ6m3FE7mYNHTC3FWn+bYkixuR12jK4+CTWjL0oBGnPz8wy3+czPDcFeRo0meAxgDGgxFe/vr7We5psIy4YuABqnUgSZ4jrXjP8leXFOhFzkB+2SYsm64VP4XOMG2KBromccyxKDnPO8fr2Fn3XVeIM8Gh73IJ5/BR/c0KCfkbEai+fWX78I75iS/ps99Pc3NzUuSI/2zrXdgXiNI71GTkkOnyPNUbmJLysO/6Qa7LW+Blk4UoHB/Qk4ulpTTz1/bp1F38dKaLvG3Fr7Gb/56oNsR2do82pkgDR2P0iM5/+tO4u4P+dXOAbuJ/H49jrpBBcgd5hT6yRcat9hGMNa+rvGeS7AmQsl2UH3MtEkJMU+6bye5FYnWeK2O13ETliHE+xzEvszvo86x74Newc266JfY7VGvDis6wZ+KYloS2Z+ZbXNycaViz3AaIIOFMERY8frSewk0ygfK6Lec7Rda1H/nC4VPD9+oFN3sRTHGYfyzLHMOwioov9/iL6nsrJEi8vr5FSF5yORTIBGGB8ADArURlnjnmmBzhFzrRhcWJDSWqK88/R97vouj76fhcp9cGRv0XRc+RckqdyfEFXmfdxbMdnRnQxjjwdmw30jTXBQACZNzdDBQgEfpwV34lowJH52ZlFtIf8GJDh2JC/wTK9vayJT+iC2bL+EJTv7u5W1SM735xba8QwDF897dYJkpkX5vv+/h63t7cR0YzZYNeAEBkS/Aj+XIf3eP3444/x/fffx+fPn+Pu7q6evIOz94MU7+7u4vr6Oh4eHmqlAyeGwwMw0HpiFosEE1nyEEj0nqQiImoFjLFEFF1BzsgKmTrRIUlCTtgpv/+Tf/JPIucc/+E//Id4f3+Pu7u7ShjAXPLcBdbGumNA5baMrSP13iUDS/QSoMzYADacksRBE2bSpmmq/cMppXosr3WR9aB65KC5ZZbsL/BjyA4gASDFp3gsTqrRQRM2tleIhHEc47DbxzRP0eVSwUhLjpznSF0XF1fXMY1jJSHMZjkwO1G1TxiGsqfBewlYK7PhsKboqtlJs3n4IRIGzxsdMTnk3mVsnODMmCFW0GHbL2sJcMOXmHF3RcdrQBxCb4hx26TI/gN9NluJjflobieyXuuIqJVkruHKGjZvvWGeADnHYbfcsO4QFcRk5gQzbDKB9eR6/L+JJVqa+Rv67XW13rlazNiYFzELXw8B8/b2FtMyx3Ae764vCXQa+hi6LqZc/NVhv4+r29JRsKSINJQT5E6nU31Oh8kY4pwBKgnZeBpjmubVWoynKfqhX9m2YwZr45jhGLGNS/gr9ON4OkV31omJClvEyv8bcHbpfODG+ykip4ic4nRsXQLbVuC2blFOoNvvoh+GyEvZfI2+Jo5ajS76voslNWYdGyQ2lsQkxTLnGMcpIp993tBHOmO08TTFsBtiN+zieDxFXkrFYplLe1SkFHmJMo+znkSXY8lLdH0hk/thH0su7T6RyzPA9oddJXl2wy6WJUfK6Sub3IJ+/Du66mTEmMCYlL8bA9kX8YLkMZFpbNX3fYzTFDly5GWOZTq3zy85IsV5Y3Yu857m6PqiC0teIhLn60bMyxx915djhaMkKl2fIlKZ6/vbW0zzHHkpScayzEW38plIz0v5Wz+UE6rmJSJSnMb3OmcIP/CD5cj/u9U1olX1i2y+bY/GN5869f/9f/1/VsHfjgc2ks2e7uV15sngIuIMDIpyU67kRRBzBukqxM8pmUEkRohz4wXbQo82gQLnzLUROo7aTKKVbavAzopJihwA5rk9DAtAw3dx0GTcKZVnH6DI+317NgZK3djUKY5n5wNzgYODrfd3mI+ZCYIk7DQv2qIAGYwVEAmzj+K6dcdg1pk07JXL2pU5ifYgP/6GXDEKQK71kfV1MupKiJmJp6enem30dp7neuKQdQH5u9UC3Zqm0hLHg8rQU+uny6z+nXkiewAfAME9pegi1RTmZIca0Zjwjx8/rpgl6wzBNuey3+bu7m71nhln1vV0OsVPP/1U58pTyCMaG+INvKwR+tj3ZQOpARd6yjUYryuebjdC5tgNlQYn1N6rwzgcWIZhqK11+AtX7ZwYeE+KQW/E+iGZEQ2gkQCha1uZus/cwNEJznbcfI5qj1tNtgwtP61nJAGAWWRstht9c4ncAQY/gIzcwkAgZqy0eDihJUmhUlSD8cZPYROAawc7iAt0apuU21cADpHNtpXDNgPDamBtJplru60IWTuxtW9DR5AxL8aDvQPCSZJ3u10l5xgHe37sF4i3+AQTZKwJv1OFsv7xPvEQe4XMQAeIp5YXeuq2Hs+t7/sV2cD3nRz6Wnwm5xzjPEWIUPL18d32wU50nFyaNSbp8jrVzdapVd+4Dz5vtx/qOMz4ujJoQGYygXtDntXK2jlmsH/w+fk5hmGI/W59+mJEaxscTy3xBE9VsmRYVxjwl9M0xTS2E7Pwz15LYxX01YmzfRSVI2I9+MT7YfGDtFC6AuDqCGtW7jlFpDZ+4j73c/x123tJjvoaI8ANjmOMyxjPWNEJsu10y/jzProHSWHfjB+3H5zmuT7XyNcvn48Y+vXpgj4syZg5olWWLc8Vpui6OOz+9lhlG8JWXGHibyZYuIdJN+sP+tn3ffzv/g//On7p9c0VDYIbi8FC8h7gkv5HTozyiToscAkC7fvePGSlZOLcG/AFyDFIZ5EIdM5uYWUi2mkBMAAIfctQYlBmxXnfisF3kME2SHFPxu3efz8Y6vr6Op6fn+t55Py9MXXtwTWsRwQtSe2hLv7nQMl3kL/BstuukOswDKt+4ePxGC8vL/H999+v5ktVw+VwnJoTO+TuPlveQw8IvGZUzC5s+ycjWpKLAdJWgyEB0q1jXN+bGmGrWUOqAwZFOD4ADwkUjsAByX+zE8dBsK4GazxvYpqm1f4YTmxy4vxzQRiH++nTp9VRuhFRQSpVpt1uV5NKxvr8/Lw6ttIB/bvvvqsJ1bIs8fvf/z6WZYlf/epXXwEGfgLc0TF0w/3/lgdtk8iblhIqDvwN4OfvRrSNdwAv9N7J6rYMz7qYUQaQEUC4Bz7JOuuAQ4WFYEEyzHe4d0Tb0+YkeFstceVjq6sEeu6NriFbAiVzddkbX+b14dpu8TNbDknifWSuWhAYCUD4J3Qb/4HNdl1XN30jQ8scefLe4+Nj1WnG4ADszdL2//YZJgEiWjUTcMH18VEw76wFvtFJBbJHlxyvTGb4fe/jMDDgIbY+uMItVya3kI9twUARHSQRAQiTYDBW1tqAnfZB1hTZWX74IdbS7Wq2F66LHUGWEKsNYoY0xCw/xn2c2Dl+831XdrgPOCAiql1hv7SWskbIn3W8uLiIYdd8BokLa+gkm3Y8bM2EqtcWP4B+c71xHCNyayN3O3Hf9xE5rfwO7xe2vYFj5l5sp6sxDl2wbSNvE8HIF/1JKVUboCrMmFkDEmPm7WQE3Xf11HhsGIZ4P77Hft8O+2DdkK+JK5LvrutimZc4HteVd1fwjBEsO/yUSRavDzrNOE2Ym/Dw3h3sw0lJve6yvnb1FWl9lC6JID5pm2gYV/JChlVfkhOZljib2LY9WjbIkXu4Qua/o3v2y9jGL72+OdFwX6kZA7NACNybc80QGXTxj8EzOQvU2bazSDtdBL6timBU7sF3IgGrFPH1A124r4OTNy0ydrOK24DtRfBncfZcy8w/vdV8H6df+utznHWnfo+AF9GCHsGRErn30xDgCCLDMKwetMT8Ca6sCUCH02f4DKDeIIdA74w4ojEFrqggVxhh1o/N3Nvvs04EYNY4orQj0M60baMBkG2dqoNN3/fx6dOnVRbPNWCGvJHNm/1w2k7sUkqrp53bVghSDsrWDRyEWQcDOBh969w4lg3d270C9PojV+b+9PS0Yk9o5zDIfn5+jpubmxVLSw/x3d1d/Pmf/3n8w3/4D+O3v/1tPQYXXUDe2wCKvY3jWCtIrjzZ2Zu1xCeY2WPduA9r68BlP2TGme8yZ+TrTYOAISfmjIM1NktmZ23gDuhhXPhAB1USE476NYi27hsYdl23epgheoTMbTf2WeiMSQuDSBh0bMTn9gP0sU/GB0Bz5YzqAwmNSRuuhf35/YioNjbP5VAK2iGdzJh9dIKGT3IMYb0Zm9eStWU8bkXkntskz0Ce73LwBT4hoh0dy/ecYHBqn/d2QW6RNOMfWUu350EuMH4IH3TTa8o9TqfTar+Hffm29Q/Z23cgDyqS+ERkbqLBXQkkGY4FgJiKIfISSQmbWWS+x1jRA/YhGsB73xNrwDVNHg19Gx/rsN/v63Gg6AMVEO+L5D7ehO154+OJTeM4ltaXs624gsETnllPZO8WaTAQAPTy8jJytOf4oI/FfpZY8npvHHrPT+TOKW8G0sQkKjJuL7btMkevuUEu10TPkFuN6WldYbGd8cKXuoUwcqt0YL/4ISevWyKI7xvv+b7MhRYikwvMHb1HNz3W7b6OHG3+3KP9//rUPfTGh63Yb1sfnXzXeBnr7gnWy/N09d57FsEvrLdx9Jaw5lr4q//iiYZBPjfD0O1UAX4Rsfobg7fTyLllyA6sW8Xm/jhgBApTse3fRRlYBFolMDCzcAgK4/ZcWQSzDDYySnwoCgqCI7GTNcA2yHTZGwdSmY5oylv2oLTjDKmMlGu3Uw9INpBfRHMw7rFGGXGifkozn98aLobI53CGXyl9v94AzrqYoY5oQY4n8QJuCVrIxpuit9UsDMfMn4OcgRABymBkC7QJ1FQ80E3YDdadtcGBkuAADEjoAJgtKVyfx40uWCZUTdARghLj8r6K7cPuuAbXMeBgLjhtyIPHx8e4urqqm1mZp6uAvv7xeIzX19f41a9+VWXNkauXl5e1PYmEEBDoZ2HgJ+xTnFC4rYT5IA/LjrmZyUL3uK/bamgRZE0hHbaJMXoN8Eop1dY9esK5nxM21tFAwoAsIupJNyQdZu5IJElwzHCbmWM9LTOznsjEPgj74fMGFQAYPoee4zOsu1v22mwtfpz/J1k2iWQigu9xbZNQBs/+zrIsdX0Ys3XUSYH9gll/+x8HSwKtq0O2S/yLk1nrJ7prn26fwj38XeTMRmdOQWKsgALAvhNEt+v4IXcmRUgeTSAZFFmu6APryD3oTiDOukK87tleJ3hObP2Mom2L7jAMEcscswgh7M+kIsk1Nol++LARCDGvnddrnkvve0rrI3xre/CU4uLyUE+LQo9YP2yfmOnWSWSLPlQdFaDdYpC+a21F6G5NDofdqvrNus3zXHv1DWarbkeKYdcqPF4LbHfbUWBf5oSa76KTXnsn37apbcXg5xL7aZ5it7TWvYj1qWbYosmIw+EQKVryYeBvQsc27zGgp/yN7xEH+PuWfEEf0QfmZ+znBLnr+5iXRqQw7/L9rlaxLFcT1cYwJm/ADu4GSCmxW7zGdvQUTGrylDnwE39hf8m1iReWI/aJr/iW1zfv0fgf/t1/Xxe07/sKcBgUSuZABPg9nU6VZcYAS/CY6slClNVtMCgMQnM50EymHaQVyAkDzCxjJINjAQCfrq5Y0CyYN+5iHGbKq2BTq+5sqzT+Hgoe0drPaDVxFWAcTzGO7Ym3OO5iAGWzOwpvBg0DMysW0RIYWDSDW5IYDHnLMnh+BEKcAqx3RNRWHdaSliNAB84DoAxooFLhgIwMvT+A8RuQoheAfLNbrnBtWXQbsZkQ1t9AkLmS0LU1auy8k3E2blPh8GkpfMbtJ2Zjcs71THYYD+TvAMHf+ZuvYV1zHzYJAQHy+vq6rg82Z6BKEOEI391uFw8PD1Xn3t/f43e/+92KYYURxc62bBJBGsdlJtLlY/Z+mXwgSAB23DphP4KeYBP4Cdsu/sdyI7g7kd2yclRlrD9mJgF/1m38opNP7I1jLn0fJ0sXFxfx5cuX1cliyB+7IPgafOPXkBdJJ/P0M3Xwh8wJnUe2Zr1cOXSS4HYd+1N02DZrJtwy5vN9355d4WoA6+tWBtsi1zVQZY0dwO3jXHkw2869TDrgw3hOC4mr15r3SdYAO7DT1kPkye8G+t6nYd9uIs/xljU1yHBCZIBqsg2fS7IDwYF9ca2rq6vVg2GdLLp9CRvi+gbY+Db0MKcCjpkfQN3tOU6iec/+ifUkfnId5G5967v2Ocvv8vIiun7dGoNMIQBIlAxyWfdtwh4RMc1fd2pUECtW32TmNE2RoiVWfI/XuVumXnf9mRSR2yEC6LLbZOwnkTn+wVU+rrkFlRVUd61K67YaEw8Qv+vP9rE/rJ92bSbepLaxSF5aBYQ47LWf5/XR28aKxox+XhhyZGzoiZMTE7DYgvGCfWvZ9L1++neN71FO8MI2GR/zZQ74buZHvHArU22Rzi1WbOfj5IqkAh+82+0qRmMN0G2TBegYdmBd+K//1T+PX3p9c0WjnNSQouta61EBeV0MQ3PudtqlZ+8Yp/MRaixi15XjYnnPZ94TOA0yIqI+r6M5m4iUGjBkEcyymcnH6bkiQEDZfgeh+6FPODySLO7LvFHcx8fH2O/3FdD6niiUFw1DcHIEGMFQUCCUy4FjnpfoumK0ZuysuCgViYmDLsZmxWVMyDuiOSyfNsO8t8DDTz/GSPgcjt3OEYfrEjTX5G9OOpAJji2igVI7e8CRWQnrqIO5WU4cspkQ9hrBevA+rL0rBcyBNd/K1g9ndKAzI+JN9PwzM8T6cj/0x/bA7+gSAI3Eht5bQEzOuQIMHKCZHBgWEtH9fh8//PBD1e/7+/s4HA7x008/xYcPH2Ke51qa9xo4wXCliDmgFxAWEe1kLTZ3YutuJYI8MPBAFhFRHSpzIyjs9/tVq5pBk5MSPu9KDX6Q9wFOVMP4Z9YO/WKe6AktStsN1x4Ln9syxgQtdByAgB35RBFsBPkbLJjhpNrY96WtxMcYo3dOrmxPJD726VSEWDuSNGzUQAw/aH+M/vICZBjUsVYGGfw08eDqJWDIxzxjH1R7GbP3DGG/TmaIe96jZSKBOIGtjeMUux3sZI6+b/tBDJ5LYptW8m/JUfMHTiC455Yssp2ZNDObCqPsMez2PLBzivczydKqreWwEnRhtwN0zef4NFSw3XVddH1XTjLK7ZCM1PeRuvO+qHmppz/5IJZSASin+oynU3R9SyZLxSRFxPv5mkNEtCfIGwh2XTsYgMpE8x05UteY6C0JNJx9An6n6HA7KXCe5+j6PniI7tvZ9kxi0CK3LEssZ/CZy6JGJwDfdevDcKzfeYmYJvYm7GucKnp5WlVtsY1lKUdZj9MU7/KH43T2iXmJeVmz+6wPtomPcAwFG9gvIDvbmkFr33e18m1SANt2nIWQK/ctuuPkfb/fRcT6+HGuNeyGWOZzTI8ch10hc5a8RJ/7SnZa14kFrnhy6mhEA9wR5RQpZMHPfiinidEOD7FAkmHC2Xsw/EwtY0A+x8tJY5FTm7OJIj/ElGtsMagTDHyvycBhaEfLs4YkVh7f3/X65kQj51QVvzj2HO/v9ISun3RMG0ox7kOkRIn1FH0/REoRu13rfQbItGP0WlY7jqfq6OlHxZmlFOd7N3DpPRk+fQrGleSBxSrOZyrOJXkBdzEM5ahaM1qwqtM0fXXKjc/5N2OZUqrgAGdk5o/5bMuLNrSyoF0cj2NEYESNcTX4QiENAipDIiaMZAtDury8XAVurksFZVagiIjV2Onbdr+nnyIeEauxOdnBkaPoEeuSvhkJM2hcj3ENw1BP6mJ9MWbkzT1hoHAwbilxULGTM+vu6oGZPUCoAT735d7ek+FKE06fz+D42LOCA3FvP7JlTHzeD2sjcSDw3Nzc1LYAdMag1pVK5MfGesaOTb68vMRvf/vb+jT7z58/x+XlZd1YjrPeAlpslf8HqPN39BVQh46QbGBT2weBAUQJem6nwb+M4/iVnqSUakVny4gBKKniOBnFVljb9Vnj65Of+OmqDXqGfEgy3OdtfWdPlQOB9Za5wFpZ363/tkuAltvwDPadAACokQ064goQtuiWVidsvLAtM89d18WvfvWreHx8rH8z08fnvD5cyy0stjuqeE7S7FsiYnVqnMF2qby3o33xoQ70EAOsBywhduzrcO0yJjZW5pjnRm7M81KTPJMwh8M+Chxtz2Uo9gJJFtU3MF8nleiyW2dIKLgPc+n7Pp5fXiJ15TSqw+EQp/GxANT39zic9pHPB7ossUROc4zzfK66pzhN80o39zmi74fo+y5S30WvBC8v7eneec6xzAU4jacplr61zrRWmoi85JimOfocMccSY5qi71pb9bIs589Mscw59vtDOS43ysPG+q5VsjnkgArkNJVTmyLmmJczaM4R+/0hIlJMU1nH9yPHfqZ4Ox86UmTcxTQ18qfr1m1Iu93+rLWp4os67rmcWBSRI3V9TOcxpXmJJXJE16p6Q9dHpC7mJUecfeXFGZ/lpZE5DS+d7eHttRw3myJO03hO+opmjWN7SOwwNGJ0PJVE1zaPrRncmkQioUcPnawUvW3PVzPO2RKGbp9tyVTEOJ2Pn+3LfggS3Zwjhl1fE9l5Plcluj5SLpWgYdfH+/sUHLLTD61KkVJ5kF35cLQjZ3mlHEueY2RPVD/EsC/+e+jxwUXPDvtd7IYigxRf788E9zkZZL7GCHweX7DtoHG1hZhush673xJc2ySa+Mh6sXZbv0mc3o7jb3t9c6LhiSOQkpW3jDZi/bTbwtA0QGQQ4JYUA2QqHFdXl8GDW2jpiWgnI7Rxuaew7ftAwIwJIMY9WJTivFrfKovRHPgi1mKqZdmXl5f6Oy+CKgERUHFzc1MVwcHWCoSMSX5gZ52EHA6HuhcAxdnvy5HCLy8v8eHDh3h9fY3n5+fKHmKgAFQAMtcAgKLAX758qSdLARQdNJkn87ODgaUxC2+WgE2IPgmK79kQuC4bUQl8TkoZB32/fd+ehM2LQGdnxfpwTfTE1SDmxhzcJ55S22sC6HUZPyLi/v4+Hh4e6u9mPK0nTi7cdwwjShJDfzXyYaxOGgEO3t/E2M2ON9DSWmUICiSZ7JMh2fS+Ihj7cSwPmEQ/DNw+f/5ck/Crq6v4+PFjJSEYj6tg6JNBa0R77oZZ6W2p2Qkhyb5bJwBOtNyRmHv/CffFD5FI8Xdkho7hf6gIoLuAYZyw/Ymraw762JU3TPuaBoAOElRSuq6rD9vjvrS14EN4ui9yNFkAgcN8IGoIgtyTz9tfo9eu/jF/ghjvozPWAR8ZzZiwd2TEvj8Io22lLaJtVDYRhZwJzswPcOTk0EDGLZj4ZNsqOkFSTPLC2EyMEF8i1g+CK99vSZF/ImOIACq3RX/mKA+NbRv/vVdoWaK2UHLNtsev9Vpvq0iszzRNlYEt70dpZ5LvQzYAKeaKzR4OjUHd7XarfSMppTieTnFxcahyctVrnpfYDbuVX0am1nvWCUC7LEs9yYdYxueRoZM9ksGWCKyfETIMQ415kGjp3MkxzVO8bQ4JMLD24QxbQsq6jqyT5Ltek3L8a2XUU8Ru2K1jR9/Hvmt7BVJq/o81gWBx5W6a1+20Jkx42LDtNqUUQz+EO0jwudZvgKgrypAdJiaMSahgMSfWxGDW+9ssQyrlXLeRWEucp1jbFn3PVoleE91cy/rDdZEXPt/zwKbXBFSr/OArkBO40cAen0RVg7k2e2vxHizAGOdpisvDRT1WOGJ9UBNxCf/OvRiPKyPGtCYFTQTh/334xS+9vjnRQDCw9uuexLYoVoT9flcVHwHgGDE0GHAeXAewoC+TErSZNATjvxflbA/PQzh+NoONAiUoIOAipmn8CsRFtIDFdw10GAffG8dx1ZPu0rzBBWCW7/C+AS2JgZMMGGWYW7dnkMTZsSFDB39nqgR/gurpVJ7BAIPHGgFoCBrbVimMiNYoB1ozjQZTKaUqq/1+H8/Pz6sElCBknaD9ATYbHcC4DT6QL+tEcmMG2mvB/ACrJLzoSkTrgXWy6vcJmF++fKlG7lOMzBS73crMBu+xv8UsD/d0AEDWOALfBwaVtXAyYxYN/YS1vbq6iuvr6xW7GRE1OeEfCTSbWAEUjPv6+joeHx/j6ekpbm5uViwqumw5OtFjPr4u+soaOQCYFTLYQ4+QrytIXN9y9TiGYagP97IeuEpi1gc/5tN/HLRsN74PvtEJMCQCFZLG5rYHILr9gnvi8/AfDmYOFoyJpMpg3AkC9mQAsdVDB2PWGP1iDZzY40O2xACfcx8wtg2o4X5O8FlvfJn3t9nvMhcqtbDZrEVE1KSssdNtQ7bXgDF4jQwGXIU10EBXy5o3cIMvZc74dXxu83N9TNMYtCyn1CqAZS0vapuc77kdn0kYkjl8hveDdGdd533sExtwomRb4kQtkoK6gfpiXfl2Utcrgcde8KnLstR9VCaySP5dCTeoRH8cp7EzE0+0+eIfrOstOdzFOK0PHTCI5Xf0g7VHH4dhWB0kgi5ExApfMHZsDJt1Umkgyb2w75RSzGKq0adKCAiAsobl9/IUP1dTkdE0zeUJf9FiqwEv+g5o3spnjavO8s1LxNzaq9yK7fn76fLcz0k9tsN1vR62f+MFfAWyZez2USbEWBO3TFEBwz9xf9srOopf4n4QyvgWZMB9I6LqpcdgX1VJlNRan9ArPgMeMG6zfyIRJ9ElboAduA8vy8vx7Zde35xomK3bLnrXtaMG3bt4PB7j/f0Y33//fUzTVDfN4QgNTAmSb29vcXFRSmOwpzh594ThkC28TtlxRNvMajY151x7zPlMRI5xbBtf7fD7fn3yAUYLu4vTpS0LRej7vrZzeF8CoMALT4LCuJ+eniqzCCswTe3UHlhknkTNGGBzSDrM0lhBmCffI8khIGE8u115qBDsPXrAdbegDqeGQtrZoz+cuEP27DazbT8pTDovnICBE07ETJYdS865Mu/8/erqquqgKyjsr+G6tJLhEJ6enmKapri5uanjMXOIDEjGvTkUI0aXTqdTbenY7/e1F/7m5qaWT7kHlQUYPeTsOVH+Z/52pKw1tuHkjx5O5Inu24kQqJMcGnZyc3NTx8R4/97f+3vx+vpadZ+nu/s4YLOWTuSc/DnAEET5jI/GJYFFXxoBklen4PFdJzveS2UQ6SQbvTdLbd1DrgD/iPWJe3yOuZh1575XV1cVWGI/Pj3OTBJJCOuBL2LOBitm1fC3jMXtbIA62y1jN1jAj3BdxsF3WT8TCugUQJa54MsMgt0CGtHa+LAZAid+1EQT+oJdG2iiZ6yJ/Rg/AUlU/Py8DphqAxiTA9hxRFT/afYae14DrtbO52tT0eQ5Iwat4zjG9fXtuRo01fblvm8PdIUkMHFDDCLmODn0Map8PqXygDls1ftz7JPNlCMv4hJzdZcDsqcVlCRpnucY+iHG0Xsl2rq0/vz2QL9tX7310TrlirOZZPTV1+ZaX758icvLy5qE4wO7lGKntlsSTbPy9lPWOwCfT1Djuk7ukYd9mbslItZH+CIDE26x5JWO4/OP57nalxGbSyLRQCh6UGLLPpZ53ZrdKinrNXZrj+VgULosS+nVSo2wcJJgwpW5gx3Qbe5NbLU/tV37vfa4gHXrNevE/UwC21+YdMAmuL7JnS3JhK6CC/BrVET5nbUyeUYcpyqPjuArwTBueXJC4bjnhJD74DsfHh6qfZD4mZQnZuALsedveX1zouH2IxtxcS5TVXwCkVsSnp+fq7Hs9/v6UKuIqK0/KHuZaOkVRBAAXZ+sYlYeZRvHKQ6H1toBWEExaSuYpqmyfkVxusi59R2SiHRdX9uQXl5e6rWsaCgeDprNtPWoPGWfx+MxPn78WEHYlnkhEfMxglZWnDpyRikBA/wNpTUgNIAAxER8zcoS/CPinPRd1ADiPmQydAyWsWCkZgPMJPAZ7kGrxMePH1dg3kmF50jSxRhwcDhZgoaZD17MjwdjRUQ8Pz/H7e1tbdd4eHiobJzb3FgXnNS2/YDKRWEVD6tx8fIGL77jdbJDchUQufllZuR0OsXd3d0qOcP5mLnCFrEB29Q2AUUXIQYMkHCoBp7Yu+f1+PgYP/zwwyqZ8QY7Vyi91l4vKh98zk+NJUhu2Saz2wZW6OgWzKKzgLlGMvQVgAOkCHToQETUcRGcnBRYF30/QJHtGeaU+9qRk6zg+EkqzHRRIUAmBBfm4kMh+r6v7TmutBjU8B7jcHUNOyYwOcFAlwDuJDgmPswsA/a8VlzTfmme23MdnECwBk6MXYWLiEo2QXI4hlnGTmotO+aK72du+HweZsk1aNmgMhzRNmK21qu2nwA5Mi7kaWLAelLA9xg5nxOu3T7e36dIaX0UPfcmofa+OeRp5tVrlGJ9ohW+zV0LzIuYwvvMA0BY2zNirQO8SuV6H5Eb1kDH0VEz+BGxwgNgAMYDSLKuuuWFcXofA5+HvHDli+TxeDpFPmMJ1tkVJSfC1h/8k1sBIQAYO5/1GCH+tvEEPw3WwacvyxLj6RTjqT37yWRX33WxP+xXiUBNnufSmoc8ALmVNIhWobc88bteT3zylhTELosulCoW17L/N8jH3tEvcICJF+uUkyT8bKv4lRju48dNdmBjyN0xz4k28zU5hn9wZ4U/7w6VbRWHtnLiDHGHWOVk2XG3+rDc5I78+Pu2Go9cnPgRm13RI+5tKxfYtAmHX3p9c6JBS4QXkEXZ7QqweX5+XlUzSsbcGFmysJRKW48rCwi0LOpaIc0644x95B3GWk4EKdcjc0VBCTQ2DJ5uuyzrBwCyuRdFIolC4QBm25YRss739/fao0+QeH5+rk6aKgEZJHNAYQ0+UH5ALOPiyFOUC0XYGgxjxXicyW8DvxMIBzfkgdMy8CVQsnZeJ+RCOwLvG6ThLP7Tf/pP9aFvV1dXtdeYoMz96EO08bDWDqzIgjnhhM3OGkjyubu7u1WS+vDwUJMRs9XIlXlswQLVLvQeG3KyvrUVsykkssiH1jmCa85tsz0Modk6gwPsD72xg2QNYFyZ388FWx+i4CQB+aIDzJ3k/Mcff4zf/va3VSeQG86Q1jiDNOS4PaLTesYam1myz+AFUBnHcXW6FMALGTA/bK35t3U7JmvNGgH+fE8nAA4KBEIHEzN6PgGn+cMGOB34cs41WXA1K6Idle1K3/PzcwWcEa1SxdwcNNFZJ6B8nrXggAAHWmSHHLF9fDDziGitUluig3ZJs4ncr4Kisy17zxm24JZSvsPae034ic0RZ1hbZOM1hIHEHvFvZpfneV7tX/K1Dba2VQf+ToAncUE3Hx8f43Qcy8bmnGOepxh2u7JRN6cYp1a9Q2YmaRiDE08/nAyQyzqdTm/xdgZOAEFs16w7c0bvwAr4DuwqpRTzNNeTohgXYz2+v0dK67Y+6wZ2jf8y+EKf7SN4Mddt4gLhaJlhGxyHD+iveCNyLLnFH8ZBYo3NMVbG7WTL5KKJpS0r70oI8oao9MENAFLkX67R7sM1uOcS632Jy9IOobi8OFTfgd4XXRgjRVr5YfYqotPczyQhL8fbxua30z1NokTEytfxQna3t7ercbsSwXrbBuZ5rkfMu8qBXPzCvzmR4JroHjF9W5k2GYc+GldRJSeuWMbWcxJSxjtNUyXrtnhrGIbIS46+W1fp8MdcFx3EH5noYe1YB5Mo/HPcdbugidy/6/VHnDq1xMvL+5nFT3E4XEQ5Ou4Y4xiVCXQwjUg1wxvHsRrv58+fq3E48wN0sAkKJYE9RkHKMyMae+gMkqzVLLwZRRTGAC8izlk6Yxgi4nzO89lJOquj1SmiMSlmML0QLi2z0DnnOB7f6zXf398ipfJQPgNOFjgiatDifSdDd3d3kXM7GYBgQtKEUTkDteOjNO1kx6AA5+HnfZh1wsAwJp8ShkwMXLaJB8+W4HovLy8rhWdd+Z0gn3Mpp7p9wg7I4BOHzndg6ZmzQZ4BOwHWm56sl8yfMdpBVUcgFs5MFzqJ/vlaZlzZv4RDcNJomWAjBpvcmzVGt1wNmOf1MbReRzuZFsSa7QBkLXs2k//www/RdV18+PAhfvrpp2qLODeCPTIBXCBX5OVWia398hkHO9Z7277Eeho4MTd8A+tqForvY4skjAAQ1h0GG6fuhMfJGets4EsgwUYB29YV1g7ig0DC+8iUezjh5/7cE4Dlz7iKhT+mxQzg6L9h2/gDiBeX3+1z8COQB6+vr+d5R5QjXnNM01hjCbaELzKD7tYR+zRXaiJilYiV037ymUB4rO9vjyiuZ9N3ffR9d/aN+ygbsdfHxvIyidNAUhddR4tdaTEuvqHEU5595LYpJ932kfi7lFI5irRrTzFmI/SyLDHsdjGo8nFxJtOO7+/nc/3bw3Ih7LquHA2bI+Ly4qKcdtWVjbqsJfrkcbCW+Dl+bk84Q14550hdikUJF2va930s87KyyZ87Kc1xHv2logjj7b0D+Cd8FO2SxFH7XPsgiIDj8Rjz0iryKVLsL1p7Fp93G2vXddF3XekMAoTOa+Bvu+Q4290wxOWZHMUW+75b7QF6e32N4RyLh76POXxkadE5bAY/6dg0DOWIVyf7pVoR5w3nrULkRI9Tp4bzsa3p/P/40iWfY+CyxLJ8XZnr+3I4ECeSdn3Zw7v11U60WQ90it9dTYUQMFENYGf8XMstpegT+uu4a+KIA2kcC7zuTjYYD77bmITP8DBJcJ47D3xQwc9VNrtUHvTHtdJ5Hbq+i6Frx7uz/qydCVbjBlemeBnDkEC7xQq9sW59y+uPSjT2+yGGAcXlSNF2Uoqd7fX1dZxOlHcbU+X9GUzQPwvA2Ud5QF1jQ5j0+/sxUurOineMrsuREmeUt1OaLDjKfQZesBxFofax2zXHUcqHOaap9diizAQi7oHiutKDQ0bpAd4lOHbRdaX94/b29pyExDm4NWYoIipzweJzfbfEwFCbRSCBMOtidp9xm91yxs4pPQZpGOr2DH8MmXnf3NysgA0tZK6s8CwE5GjwGxGr9hj3DfO3iPbUckA0SQ2yp80F+XD+fdd1q5YRlwgNWB1AkANO6eXlZZWkAlBcwkXmTsgApq6KYS9OtDka9vr6Ona7XU1qYcK3+zHc/071i6B8fX296pk1KHDQY48QANjri+7AEEc01ggd8jV5udLx/fffx5cvX1Z2zr2dhAJGkYeTNsC4gTWOz8yTARrX3TrJiLaZDlaGuZg88P8zdpMItgWX4J0UYIcVdCyt/M/fnJSzhrCMBFrGg20hI8bG2D1ft86YAPG4vTEWPTZgdnWFqtiWPEBPWTtkZXKG5NVrc3FxGafTMU4nNscCGsrR5ZAlBnKslVnM1n7XB0eGcr3SFjvLP/hI5DnKCVA5uq58v+hBPv+ttDiRcAF8co44Hk8r30qyyRpu93TgF3i5KrglEOyrzSzu9qkSK2YTh2GI1/ezTfd9RI64uDqTD6mLy+tyGMN+pwrrskTqh/pU4cg55hzxfjoDv66PoVu313jtPHbiBnFnGIZKCDEn/Cq6epqab4xcjnq1DUHSQaKgVxAg6HlEe0YOa2AMYADrQ2xMlLldeRzHWGKJt2OpqudJwHzoYz4TDX2Xit6c7RV9L2u5FCCYUuyGPsa8RIockcvpUCnY89kqVhEReSn7QK4uL87xYonoUoyn6dxCXpKP3e78pOz9LpZl3crTD30MfXu4KfhlWZY4XJRjfiNyHU+X+rIHQ5Upr9U0TSVBPCfJ8zTH5VUhC6d5XBEzXeqi61N0OcU8l6d/E4NSSnG4KLobue3/cjXbFQB8G/EPX+VYSvxDJ028uEpv/+/9aGb+XV1DT+7u7lb4BqzkJBV9Aty7qkPl6fn5eVVh9TjxIWBcY0vHnOWsd10u22lSSjGd5fcinMRYHeNYRwgmx3aIcPtv713BB3Et4qfj4i+9vjnR+Pjx4wpUYMzNobcgUk+YOBxiWb5+giOBygEOZ8Lk6c3GmaIQV1fXNXkBHAGQUVizojYYABUMllupfPJKzm2zFXMmqDtIO3hwT5wNrTb+TFHwMZZljh9++KEu8N3dnaoL7bxkV02Ym+VshtsAoetaKw1rZbBrMGClxjhhcswQL8tSH5pIMHEwuL6+Xp3xbybKLJQdio/V5CcJjst3BGCXxvu+r2VAXtuAdnV1tTq1LKIdmVqZmKU9yMlJD4FzW0VApg6YGDggF+YeWWxPf0IPOY2FscBuXF1drcqeBt4RjcHCbgA1PpzA8mZ8nCZhvQSY2tYMJrA9vk+iBUj2XhUSFFcQ+dvDw0P8/ve/j67r4v7+PiJaH+myLPVJz05WzEDhjA3g8DFeC5JO7w+yXhiEc/9Wym++wutMIoDuseZeG+s41zYpQUCkosln8XXoMd931QL9xHaQj5NLrm89Yx8avonxu+LCvNFf9BZ7OB6Pq+fEUA2kFcqAAH9LIH96eorr6+vo+z7u7+/rGH0qFu22EDEk0xGtyjcMQ91/go25f9gM5PHYkrMG+uYVe4f+uH0TmRVZtaMmIcTwR8SLn/OBZgP5aZBsX2WfxbV8mAHrgv35tEfmzklu3JtxuGXHSRBryP9zfb6LbpqocnJhcORqjk92xNZIBnjf5A3X90EC6DjjYS8X39/6FGIjOowcWG9iu/EF4wAgOVFnjbquPGzN6+BED/+IHBkvPpn5e33xU4Bjt3xhL+g1emK7iiitXPzuk48YhwkISAXswLhqPI0xTg27Yat0PrDhGDm9vr7WuXnNvc8Efcs5x7S0Sslut4thHuq9nUTP8xxpStW3ErvQAe9ncJxkvtzbbUzIw3J01wz2z1obTPPTyQT/8AUR7XSrWmXo2kEOrlAbj5rUtD04Tlhvja9N4O+G4VwxanptooNr4ceNW/b7/erUNhM0xgyM30mEE0I+5z2+3/L6o56jgZNDkbZBmZuzf2C/b4w1J1Gwb6Lv+8pO036A89/vdzWJQMF9rrhPLiHJ2SYGBhcoqI/Z80lUBtssOs4c5TcLyt9xZmY5UebtBi6uU4DRunUCB7TfN6aG9gBkjLIA0njPDqZVZNp83YZCIELmdp7I0yVMDIwEYDtPjHmapnh+fq7jgnXAwXmfAsCR/mAqPl++fKnrjMFQ0XJFyMZnR+CAtdvt4urqKh4eHlalU3odmS8/nfjQPmSwTcsaSR739L4fdAMmD2P2STQRjdk9Ho9V7ynN/twToc3wGHibzTOrgm1FNGeBbPgsusA47IjdM8x7gGk7Mr6LHGGd0UfWC99wd3cXf/ZnfxbLssSnT5+qs72+vq5jR4cvLi5Wx8o6UXx9fa3VKeSCrTJeWifNYOGHTC4QzHwP67YrI+iFE332C7laYb9kGzHwx38SrPFJDlxOkvk7vo09TPgTwKV1xRvNCfoptYMQsGnkw54ZJ/MAALdR4l/QA8uVaiV+9+bmpq6D9ZCTekqgXKLrdisZuq0L/w1j7QSZKgrkCPLm6dpu+/Qpbug+P9El9M1kBePZtmagW8iZ9eMe+AjkYXDB74zBJJIZSPyHbdA91k5yc84xzXN9GrH1xcwpRAZ6YhBuGRBPt3srqVBD0LCO23YQxoSuuJro2Iy/Az8Awk3mAcj4Pj7ZPhCZY2NOlEg0kRXyd8LghDHS19VO60zS7/YbZpIdX7z2rN1ut6vt0JBEvPCHzN+twSYp7PvdwnY6jRF5/VwZy4L7UzU1ziknhb5X3cJ3+N78zv+DM0iE8f3EPt/DuuJ9g05cWG++7/Z34qCxi5NKA2SAuElP2ju340TOJtMhrbb4xVUIftJqR8KBDoLltmvnagz+13Gc14pszesYboxmf2FSjperFg2HNrIBfea9LQY2AYj9OjH8pdc3Jxq0a3z58qVuhmMQAAQ2/wHMXl9fIqJlT5eXlyt2iFI+ZUsycT+B0t+NiDidxho4UD6coIEPwIDf3cPpoHZ5eVmfZOygjmHCDKBszJnrOpACMn1EpZ12cTjliZgppbi7uzs/nPDqrGD8W2qSQasSisALB00rDfL0HBgrMjLjxsusTcSaScCYrVjbVhXahhiPHSJHkDJ+jH4baFmvruvi4eGhOiGu6U3vThpwrMzTABRwQNkWppT54UBwKDga5oYB4gxgXJjDdk9FRGMgqU4QXHzqhdfDAYTPETBZD/QIvcUetmvr/UrbigrXMCOJ/JAxn7Mc0AHsC10FJHBdfpJk8zeSvmVZqj2+vr7G999/H+/v7/Hp06e4u7uLiDVDAkDmd8ZlXwGAMjjbyhu58D2SPFrrGPPV1dUKbKJ/yBS5u3Jh3wQ42sqceVDV8Cl0fC+lVBPNvm/7JLg+P03sYA+ubDI2EhjLEzDtwGjAh7/gWGxXKlJK9aAFs6wEfO5nttHfOx6PtRpBko7tLcsS33//Q9WBl5eX2p7E3oFlaS2rBq/4cFg61q2sXWuD8XiwM76PraPzAA9kbSa2srAbEsIHZ/BZ+wSvi/2qK1UGoYyTezAm1oV1MEtd2c1YA3kTdbxP9cwJaAR7FOcKQohJ2zgA4YcfaPsD2qEB6Cx2ZMD3c3GF72KvrI0TGvujLbFgAM21kQ/6ZKKF31lnP9sCeSzx9abfGmuitY25Hdt+Gb9jOfoaJipNADrWowfjOFYfZaLHVRWqjswxcjtx02QHSQa+DT3GRyFvV74hILwHzfrtpIixcSDDNkkweDWIt4wYK5jl5yoR9pH4JNsZCbSBM3PEj6Gf4EnGbDtkDOjiVqYG+oyZNTbxxDiwWX5id33fr07UY97Gcym1vZDI0/7YMQh7cVXCz8bC9/E326T9KbKzTW4T9W95/VEVjdPpVEvhzs4wHBYqpaQHdLUd7oAgC54KxTobbewsQQGhl3s1h09C4PvDaFtoHCkL+DVDm1KK+/v7uneAexI8+d2AhrE542ReXOd4PH6VXLEByo4Z4JxzBE+MxYmhiG5rYcFd2s65lW9xFiRflhNKYlALk46caBO5vr5ebYpzssLaca8tAHRLjQMn60pS6Ac6rjdu7upJEV3XxePjY62qUAlyMsY4cPDT1M6TZ/1wFmwARfe8J8TMlvXHrKKDmY3cbX7bBI7PkYx67fu+XyVlFTjkdrIKYBF2aNv2gU2a6UPODtROVvkOgQJGBOBEIsS6Yg+2zYi1YyQoICdApkE3Nnpzc7Nio7E1rm8GDMCwLEt89913teWm79s55FQsCdZd19U2TaqeXdfVZ38QONAjB0wHEgINDD/6gZxfXl4qGHf7pMGtQRjACPtxUOLvzIX1JSm2rTpR9+9Oxl0ddHLEvdBVAjlywNbRP3SFoOfKKN9xVYGxAmxZQ9YXfY4oG0Tf3t7idDrF4+Nj1YOc2yZdiChs24k8G9UbY9xkbxBg1o55874TQHTe62WCxsnCdj4Gnwac6AzrY//AvfE/AAhAquXM+jF3CL+yryBWa2n7sW7g/5x0Mt5t7EMXnZC7YtvWqp2Y6ITap10xbnTIum8S7OdiHd/dkifGBfbfXAe9NSAEPDFX7yOMOLP0U2tP2lb6UqyfUG05Mi/01X6EGEX7IfZt3cOWAPb4L+ssRBFr4apRTf5SA7UmQnLOseS5+kzvmSKRdCse+s73WRuTE9iFkwU/W8Sxlc+ZHOYnRKGfn+TWJ/sj++p5LpXDm5ublT4aeyB7bJO/4ytZH/6GfjkWY/fYO3gTu/IeOBML28qgk2T8JuSX8fQ2gc3L+hRC9JjEoZD77VERkFvogZ9vY3vZrhH39r5AZIhvQDasxy+9/qgH9nFxHJyBGAsB2CXALEtUNhHw6UyciRDwixBavxrXwqhg/M3SOEtF4AQdAi1nnTtJmue5soMGnCgMjoK5Y7TuBTWbQiBGFimleHp62rQ2LHFxUSoer6+v9RkOxWBbuwmKizMYhqHugeDF/HC+ZinM+sCeu9xrALlt0SAQYRwOjjgadIL3zZRRBTK4xumznjAzZhaOx+PKMACRAFfvQ6GfeBzHr8Cfe9pZE9j09/f3+OGHH+rRsCmlWhGyYUdE1RtkYp1DhwC73IN7A2pxbGZk0RnWEN1i/O7BjWhH+ppxACgzJvSa73HyE3puG/W1zVSgO65QeU2Ql5OBiPWJTFQO0aX39/e4u7tbjZ9EdhzH+Mu//Mv49a9/XU9O814Ng17uSdJEctXsKq8cKDZ1cXFRj5bGFpwQuuLG7zhj2DgCBnO17HmPJHcLcJxM+GVwbnAFAWBAyf3RMf7uIICMADD44YjWWmBwbkbQ4A89NJvpNce/uacev0hbQte1h1rREuF1ckXyxx9/jJS6VWWgta+ONTG3P8L+GSPjxxfhQw0cHHeIXXzH1erLy8saB/CZLy8vFQAZxJihBOwhb4gUtxMaWDN270NwYmpGFX9hhh89RC/6vo9OIMLysK6659u25g2yrvYiM7fXAQ4de13J4JrMY0s6YYfM3Uk7nzMJA7jeJo/2aa7AGYTxGScfrJXHYt98PB6j3zW7Q3emaYrLi4s4nPVjS9Sw9hCaHg+JAz4R+RFP0JlxHGsigj3ju0zwWPcM4omrp2NLarFDZBupVYsgT/Df3ieErLDB5+fn2moEwHbrLT6Tv5l0Yo1Zdz9c03K0XTEmEhD0zftPbm9vKx7lJ3gRXUc/qBYjJ/TJPgKdR65uq7LvZPw/R75hQ44dxovolMkZ/Cj+l/uhL7vdLtKy3gdn2yVWeC0hKyCtPD/WFfvG/xnfO647WeZz+LJveX1zomEmAaeAYEqFIc4Ou5wMVZKFcsLC4+Nj3N3drYzCzIvBB8pIMDCoKZPKETGsFHPLSLF4BlhknyggBogQbTRWdASPUqEwLithlGYeWGAW7XQ61VaCMu4uvvvu+1iWOZYlx48//hRdV/qaMVgCBVkqBuANpsyPwIJzMbPIZwyQnfFHtDIbjtLPW3DyQ0Bh/V16Rz4OGjCZXC+iADPWO6Lt6ck512ebMBfrDLqBgVxcXFSW0+DVrDAgx33w6KPBm9kx1jClVJ8CblYMnUQe6JCDLfrjvmOXvF2StC47uPL9LdvqwIrDoZKBfP05bMQnTljvzfYZVNOri72g56yV7W9ZWv+4AQ7lYGSQUjuQYVlKdeL+/r5+73A4xOfPn+P6+jo+f/5cW674O1U+5ojvsMxgYL2R2bJ2G4Urfdukmve5l599QbBHJ3myu+VIEvPx48eaiJvldMWBdeCFjvhZKlvw5IBAgGVNIHfQa2yb9cQuItrRz/g4s9wOrgbO6LOTYycQvAApBr7IqVUYd5Hz7ix7HiC4RM7tNBo/KHNL+tiumr+j+txF11FJX+Ly8rb6FMAJwAGbsTyOx2M9fpvTCE+nY0zTfPbd7fkEtnGAgltryklBS60I8B1vIsVGSKastzmXE45yTnE8niJ1XYxjOVUqR4pI63YS7oGOT1PZv9KAdURK5WG1+DX7sEYWtjHDnrod2CAEAEel3LGSOdhHbJNAJwxbcsXxi/dcmd/thsgR55OPypGynDAWEedN3uV4/BpPlzbulsAv0aUh8jm2o3vEb/xZ13WrB3gSL00S+MATxsn4sX0DQKqtPjABX4ksrbPGILQmLssSOXJ0fRenkZPRptjtLiN1KS4vS7x9fn5eEQbcw/s3SSyenp4iorWKO9kxoch30RtID/wGftV+A1mZuEQv6Iwx/rn4mUQP3wPp4FZI5M0auXqL3nM/+2ATPn6BLbZYICK+kqkTb+6HTaKXYEcTYNwXm5imKVLOsRvaxnFjWO6FDrp6GxF1z7OTU76zJRGNzR0b7Zsc677l9c2Jhl8MHqfSdWSBOSLmOJ3IyIZV2QgAaZaOAIbAmSzlcLPuZdLrp8KajcMwAWhmLBGSg7DHE9GeKMt3eKgeLIMBKSwDC+f+OmeZKCOOzEzishSZDcMuDoeLuL29XRkfz5NASWH3zWAb6BmcMx8bAewcclgFMAUal/ms0BgQG3Uj4qv14cX1qRRdXV3F8/NzTSZceeD7BumsT0QxXmRPVef6+rrqAFUHj9OMJxm9WcJtcEAnYKa5NoCG+XA979lgEzlVFdabOfjkmS1QNBvFOrAmVGt44dh9XjzfJ5nCntj/Y4cCmGIdzMagIwaXzB09iogKPoZhqFUIGG5fEzmiP6yvq060ERwOh3h8fIyHh4f4/PlzfPjwoSZoJiYgIAD1TmzRe5d7DX5YZxIdkwh+foSD55YtT6lVv25vb1fJlqto6DSyfHl5WbWQ8Dnu76OkCaAGJCYE7PS98Q/9h/lHJrxPwCP4+rQuPssBDU5s8I/4PSc7rKNt0BU2GHC3ntg/bFm0Ms8Up9OxXh8f7dhgMMp4fMpRY2c5VW4X5ajcthkSNtekVKuot8oIcarvu5gmn1zWNugPQ/MP2GDRr4hpgsnl0JHyDKWcW6xw/HKSt2XcU0oxTjmeX57i8vIi8hyRc6dqRqsIAVQBhdPUGGfs8/19jHmeImeOAG7P78D+aYuldXUdi9tmfUA346dNwxUcABU6zbpiJ46PTkhZd/7fLDDrnKO1Yi95juXcXn15dbFKHHtVpSN1MaR+Ne+u76Lrd9XPXpwr2eju0K+P1Cauk1QBdpEBcrLMWBNihIlKt/dGrJ9yzt4J7s2eOewc+ytAexfv78Um348lFh5P7+eEqR2X7mqT19Rg1If8eL0j1ns0WHs+A6vf92X/wdPT0yqJNHHNuuL/sAvGgK042d12yNDatyWHjBFtZ8QXVxIgd/DT2CGfd7KMb2D8jHMbt3kfv7eNKYx1G4NNjF1dXUUsS31mDt/bJrfopCtAToisW3weO2ecJgUdI/g8sZPPfMvrj0o0HMCbEObgwUMEKf5dX1/XzeFmVyNaOw+Tcw9y33dxeXmzYipRvLe397i6uv7qhAqUzT1zHgtC8ZG6DnIkD4CSYRji4eGhPmCGObDZGwbdTAXKQ7KAgTmg2BgxRBw/yohCuzKCs6Y0aTCCcqCUPulkWx3BaQKaARw4Sm+CRWYppdpv7TU0u4zccZisJz/NFrviYUPAiTgoIRP2W8COmgnCwfhIZJKR0+kUz8/P9XQjJ7YAdh996CoBzAgAkXmjt4zD1R+uzfW2jLCTAQdagzaDQkAG1yGYR7Qk1xu0kRc6wlhYf3SDVjAYO+QKQGE8DjhmMcyk4BjRA5gonC5zMjOVUorf/OY38dNPP0VExO3tbVxcXMR//I//sfbpf/fddxFRjtbGPtAVxh9R2BonvwQVEquXl5dKBOBP3MrnlhivFQEHQI+f4nN8f57n+hR0s2gApC0jm3Opqrm9gpeP7SRQOMiZffT+HQKe92lFrBlIl8r5u4O8AxzfYR5usXh6etIBFkt94jjrQnULWzEQwReRBM/zHM/Pz9UvMV8TEgRD/AokAnNxRWhLHnFfH9BhIsZ2bB1ADkWvShUdMIpNFF/ZALmryMWWWnumE+Yyvi6Ox7kSO+gF4+R3jzciYsk8TG59AuQw9DHPS20XxK8QPwxouH4BamOklOu6lbGV54RcXl4FDxnEJ3sOkC7Ysxl6y5E1xUeZCcVG7BPBF05UuJ8ZXmL1NJXnPPg7yI7/xy7QI8ZEzMKOPBdfx+2bfAdA6U36kJIPDw9VViQIMP7ezxgRdX8X+/TAQdg3cSGlVJ/rQJxk3MjID+iNaG1a6Mk0TfHp06dV7MUu8OHos4GwW24gXJw0+B4QFt6zi08klhorMGfWhmuAXfh/cNx2876BtysF1neub2yEjFl3k9LgU5NL3AO9Qk72yZyC59hr8prP8jcIQGIl3+ceJj0jR8xL6yxC921H/M6a2u+zftg/98eWtslLRKziydY//zGvb040zNYguIg4s0+NSWZhyX79NGseoIZgHDhxSLTDvL+/rqoeODTYSAKoW0YYo3s+DcYA9jiIbfWBAMn7GB5j9WkcfrEA7ovGGThr3rI0JCw557qRaftsCHquDfydkLiMuW2V8fWdBDkr5Sfy99xRdIwFWbH+rAnzxZB8QgZO2oDAjImZ22EYauXou+++qw/Gc6uBEyyvTURjU5Ev7BAPorGekQShmyQcJGo4EXTDoIY5wfYRgEly/JAqZEJLmJ0y8/b9cThuXQGc7Xa7qk9uWWMvgU/dssNwdeXy8jJub2+rvN06ZkBiHRzHMT5+/FjvY+cLULd/cGJmB75NxLBDl3n//t//+3X/zF/+5V/Wjd+MkWAPAGBujBdd9/4K3re+OKmrbOV5bgABM18RbVNyROsbdhLo3lon/5AT1onb29tqD2ZoCYgAaYMus2kR7aQZnD+yNPjnSbTIDDbQAX+e57oZexiGVeKMHRkg8nd0/7vvvot5nqtM3t7eal+4ASeB21UaCADkTSAkvjAfkgXYUvyRZWL/i89hXYptz6tr26/jF9FDYtHt7e05xqTVGA1YI2IlV/yBQZwBbZnLRfXfJjnM6nM//GXf95FjiWHXHpqJDR+PU0Qs8fnz58i5tNsS88ppYuunNePri3+aYxjo+c6Rc8Q0zTEM5fhhs8b4zO3LYN6x04kNv9veTOCYmWV++E+TkviyCqKiHTZA/IBIMGDcstT4JVco0EkIN1fjtsCSsT09PVWiwSCcz3N0O4AOkMtnXl9f6942iI2bm5v6HQM9x2+Tcf4MsiaBBZc5LhBDXDXARt267OqkmXJAO2QO/3x/7J91Y4yOgezNxc4ZE/JFJ5yksYb8zcAe+3acQhbYkNfbSRr2CG7gyHbbsfGOMRnx2v+PjiIHE4Fch3Eb+PMybr66uop5bCdLOqYyRiddYCV0zrHX/qnrSpWXZNh/o7pjjO6k3Pb9S69vTjQIiCwyWVcB/i14m1k3Q8hgfboDC0AGj4J0XVNWFNJK0vfDKug748XJ4UD80wuKMpMMbDNjAjsMIwbnTM8MpQ2YebMgGKCzWxwzABHHAXjgXsiIz3BNO5hpmir7a8D65cuX6PvSJ8wTu5m39y+8vLxUwAgDDMDaMmFuOYtooIOgdXt7W50YiQ5MjU+L4lrbnnXW6P39PR4fH2uVyXJDHwwSG8PYQMRW7ltm0YEMWZO8OmgwH66F3L3OdqBUB3A6vO+qjXXVrCZMOsCDKhrVFZyx2QoCKAkJf0PvWRv03UyjkyF0mGB7cXERnz9/jnmea8LL3M14mZ02+28Ghb+j15wCR2LqyhDz/0f/6B9VGTB+2n66ruz94sGY+AFYKre2OXhCNux2u9VJdNgfiZ1t23pmcIINE8R8eAS6YtDuI7exH/ZYmF3iXg7cBrYEBE582Sb76JDb1zyHZVlWLZQAM9rZmLdPuML3s5bTNK1aIYZhiMfHxyojJ97bjcX8ji77OQJbG+U9t1O4SkAgx38wL2ybFzoPOQJwQje4l5MHjs4toLD5AP5eYsL6OTr01HMvb+rk+GB0xDoGm4nuefzWvdTttM+vVckvLiBjUq3Q+D7H41wTLuJf8T2HmOcp5nk5/4O02cU8L7HbrasPjrPo3PbvxBzWx0SC/b/Bj30oNu/YyXzRPSfhjAM/Z1/PNdFtV2UMopA1awTIdN88IO/p6am2fZJYA9ZMJkJmkUSQ/Bn3sMGaauEWkKN/t7e3VWaOXVyHxBh7sw74OGn8783NTZ0jsid5QKZgHv+/CUjrJteIiNqqzDoiJ2KmScuIVimnewQb2j6OIOccDw8PVbewXe6NLYBdTKZabv5/MNC2Isw1IVS3e0w9JhM2XDeixaNtwsQ6OnHkPRKDbWX2/e0tutSSdK6JHzNuxadiO8R3k6xO+JknOuu2Lkg85IKsXFX5ltc3JxouORloDMMuHh+fVoymGUf+mW0HyNlJmAU+Hk+xnJ8wiUOERe77XSxLy6owbk5nMNjH+KzMPg0gIiogsYGx6O5r4/PPz8+rDcJbZ/jy8rIqDXZdV5/qieONKI4MEB2xPg0HYwBQ0Cby8vKyKvfjJCKiJhU2MrOB697h9hMgy2dRJmfYZiwozXrcVE9Ya9aUoOkKAXqBbDhOr+u62uLEmHGUbFxzaZfE4PHxsQYREjeu53EyLlckMCKzEFwL2ZDkOMG2w/ITizFQJ0RuQWF9WWPGZcaEIEowNsBj3IwV2eLQzXa5rcIOkJYWnvKOs+KzOMyXl5fawuQ9VhENaALMsQ8n3dvEPSJWJ9WRiPq+OecaLKdpio8fP0bft+OXSUAYy/39ffUPZkkZF/fhlVLb9EtCg56jM37+BPJhvjhZToUh0SAxM5uJPnhN0TOut2WHceZmwJDjNpHlBD1sC6Bt2+a0Mq8Lc8c/+Lhx2EXGv22vwGYcpAA0PHhsG8QMDh0/zNQjA7N7zBU5wjA6+eJv9MKznmZMnfCU+379ADMCKrbudWcTec7rpz4DporeRk0q0cECKhqBhf/j7xEp+r6tmduA8O32pXUd54hIrcWIuRRfNsUw9DWBYm3Lz/4rn9baTGg1nqPs2cjRd31EypFSY9LdP2+wTkxlbWBCmTc+0/GI+G+MgM/kPtYLt+TaB03TFMOuVdt86ID9r8ksjxPfynhNPvE+f8MvM1eSeHSJNh8qsvhrfPnt7W3V14j2nCG6GXg+GXZnFt4gFZ1IKdVWG2zEfh3bJQli/uiYk4ifW8Of29dgX2u/6Jhj0sbfM6AG0NpWTVKzhttqgG3UIJf1wa+4mmL/Yx/MdcEBTgIsY0ha9Mk+kDmgw/YjHJpiYpZ1cTLK97f+Fpngp3Z9H33X9qR5j4/jH3NBhyDfnCA6+UI+4HrHbtsL8nJV6VsTjZSR6i+8/uLP/7vKyHHCSANUba8DARewgIGjaMuyxM3NTTVAFh8FKQszRt+3UhCKVAJFA8FWMBSW9zF8gg8OlmzRZV6U1gwSC2Rgi9GYubAyf/nypVYkeAgVjsMB1gvIC3kA2nEGriyYTcJwkDfAAAP3qVduvZmmtvkUILPtKQTAutLDuAE26AFK/3NlwpeXl6qUPu/drNTl5WU8Pj5W2ZDEMW+ClEGrkyU+R4Lg8RlM4Pj5nnUPFog549B4uR3PwB0Z4jQIhNyD5JBxbpkBJzBeV66DfaEnZlqwKVfOGDsBwn/H+WwTEm8MgzxwTyrnkxOgzIhErFtbLGuziRFrBgfSAftxcuz2GieWzBGQYvDNmFhLl/yxLWRusMi4Ilp11ft/CELsM0NW19fXdUzIwoHR5WrkwNicyPMTO0cfsTdvMN8GcWSx3btB9dBtOmbgXLliHmbo0Sufa8+6GVTiU/k7eu3qQETUAy6ofjiRMWtmcsD3ZM1YY9risDH05+Liou6HQ/7ofQ3Uu12k1K32FdiP25cDOmD7Uop6cAFVk5aktAR8C9R2u2YfzGWeS+sUvsXtMdyT45nRheorUjm5yjZV5DNHaXtaVqAIfWCPieMwsl7mVo2wb4i0xMVFS4z5HrLks6wNa4gu2T6IF6wd97Itcj3uZ4C6lS0s/X6/PydELaa6nZU1Rc6MnWoDcneM416sGSdHkeR4kzP+dsuG08aFbpJ8WNdZQ/tUg3TuZ3KMz51Op9ptwVyxcT9U0Sw8cYy4gHyc1EOAbG0InXDPPtfg/pCiEA9eZ9bXPh0sRVyxv7av9r18HSdjEFH4EJJAfBPyc0LnlnTmZ6KKddrv9/VwA8bh2M09IKu3uJJ19XzAXibo+QwHy3AvKmbLNEde2l4O7g3Z6TY31p8Y7uTDMsQmbPfoMj7e7YLYGXF3nuf43/zv/1X80uuP2Aye4v39uDoC9nQqDrjrhjp5DNpsAQM0eDEbz+TIpopC+CmsXaQ0Rs4RKUUsSxMIiolQCDZ2cAQsPgszCgPndiKAsQO/Qd/7+3ttNWLMtGLQ02unZ+AV0Ur4BoZWXidpEa21IqI9GRZFAOygzGZyIqK2ZZkdcpkt51wNiPnhpLmmM3iz77zv1qv39/ea1Nzd3VWGz32cyJ/xUKUxUwXgtCPAAbjlC+Bu5UcvAH0ktmYNHLgIAGaYmSuyBXhsWyz4yZoiL+ZA9YB5AVS3QR15c6oYQMibzv05xuN2w4ioffboLAme+3DNDll/XZVgrSLWz3HYltL9HVoOnp6evgJtyIUE3RUZ3wv7NCgzYCEJ4HMGZwZPEa1/Gp23E/WcsEV0Euf/9PS0Yn+vrq6+SnwgBbAHmHUYStuOk0kCDQdMOJEwIYFf6roulvP83o/vMfR9OWVnGGKa22lQERGp66Prc8zH47nU3sX19dW5KgRDTMtbaQkqciwHe4yj7rksUZh3WP7yrxFMzadHpOCo7hITyoNV5/lLlI3Lc8zzqV7n6uo6Li/LM07atZuOo79OLFlL66YDeGMxfT5+nFn6pY5tHNvmR9bFm/wNflNqp5SZiV7qw7P6GIYGMgDA5XS28kBCbPh0otJ2lvXpnLznHLuhj2U5kyhdH/2wj2nKMU1LdF3ENJ0PL+kiOJ51PJ2i6/tIqYvdboicx5im1mKEzyq2GhFRjjkdBtrQjkVWOUdelrOszpWHvETftRYrgyQTCK4EuqMgpfK8hmWZK8AddkNcXl3Gy/NLDMP5wIGzPeclxzRPsd/tYprmSF2Kfb8vY16W2A272O938XY+kGQY+ui68xzS1zHGgArfix4Ra7F3/Ac2fXt7G09PT9VPYfOuyqGjW38DGMd3X15e1mo8voxr4I+IY1wDv3w4HGo1Hx+FTTgBA6xC3BFDeI97uepoggIdMcBElsRV/KBtxkC767p6Eh8th4+Pj/VByKtkObf2IvtNJ2/YkwG8dYvr4BcgAZAvccZ6y3qSSPC7ZUT8wc+YdHIialy5jWH2467IQgqDSyJiNS5k4ISKJOJwOETeLTGeTtX3k1BGavumuZf3BLoVCgxT40VaE7YQ3NiEZeLkCRlwnV96fXOiQZDKmU3T7xXIwuKbscP4KJESSJmce9gj1i0eJUM8nI3gFMPQxTS1hxfR6mNwiSGSqBgo8jk2mpv5dhWDU05Q0OPxWBc6IqrxY+hb1tRld4NOMzooEN/1JmGXz5AFSRFyAajb4AycyIZJmszcu5RpJXNZ2u1vKZWH3LklCMfIGDA0gBMnaEQU58/3YappjcHBw5xuDXie59rPykY77svYMW4zJLALNhj6YyPahnEMjqqNE2Szc8zRLUtmLFgX6wBOxFUrZG1ZvL6+rtgkDB7AYmdv1pO18Fh8kokdHI4Lds36iWzQU+TisSNngBlrx7V4yBQyYm7MGX3Hxu2sfeqHZch9zCBhF+inx2a2hd+d7JtR4u/IxQHD58ff39+v2CGSBnyPS8tcByBA+xUOnTVkPjnnuL+/j8vLy/jrv/7r6qfwY06eIyKmZY5F4z+ex9SlHDlS7A/tyfYPj49FB3NE16VY5jleX9vzGBrpQOtLsT3arADQEaWFtehCd/7M60pX8B0REYdDIzxKrCj68f4+BSczMUd8BtW+tmYFtJf/72IY+ri8vGhAVazvVkddIVuWHF3Xr+xxnnNcXLCXZljJGN/MemGr2GEDreU5GvNc1gWSIqLtPXTFqcRA2MpCkqG/0xixLClSGmKexuhSxDCcmcMuxZDOgK+nAhZxOOzjeDxF39GmOUReSjLV9V3MubUKumWr6GKrCu52lxFRkq6+L8kSNlfWp48hd1GO5u1XMsG32BeZOJjnOXb7Xbwf31YMeKQcJDpX15eVkOj68/WGriYnw64/s93nCvxZB07jKYahtHQdLg7V58xzObkMkhEdMyll4oZnHcByl3VqSQe27f0++EbisavYfmaN21kMmFMqD+8FEM/zXPcvuopN7J2mqbbeOLlmHQpR8LbqJmC+6BgxxHMwZtkCbOIl4zDApDPCnQkkIFQI3t7eqk0Tq7FVA3Enrq5quErh+EGrqolKd2Cgk09PTxVjGG+2FsHWisw/5uYqNNcGl3Afxu25GK/gx1lvOiSwDe7Hmtg/sQ8EHIVeIa+cc0zzHO9nPzPnJU7no7M7xU5kA/aDHIcsQXcYn6vXjqmuoJtYM86yLv3S6486dcqLQ1mXBTE44jMRbRN313UV7DibJbifTqfKBJZEprB93siEoACOVBpIInA8KCvgxIo5jmMFRywgY0DBed97CgxEPn78GMNQnvXhkj/KiIGamTVQpfQ6z/MqWGHgp9OpthwgQ4yaU2SsNIwR1s0bVN0C4g1n3pQ/jmM9j/t0OlVFf3x8rPIbhiE+fPhQn3QeEZWBx9GRDNBqw7rgUDgeF0XG8ZFYHY/H+hRpJzzoF+CAUjbjd0bOtXHQOef6lGw7cXQEp4C+MA/mheMw0DE7v10HQJE3RcPKoMNm4ed5jpubm6p7yAnb4lr8DWfAuNwy5GSZJN/JoBMAHK4ZKeS3ZS+YI2NC19BPWnD8UDVXXxoAXD8J1dW1w+GwqpbyHRJarrWtSnhDIYFyy85xD8rE2DI6wFx5OWGBtQRQLUs7stf7ukymOMHgGRp8Bvk9Pj6uklufeAZAaZWQ9dPdeRVf2sZkln6320XKOfqzjjNm+72fY7hWjHS0fUPb9fL7+Cxs0KCNz6IrrIErPVwbG2euXdcexGmiw8HdzCzrNM/Fdx/25+c+7M7M7TyXCkFKkeI8/hSRIsW8LLHMc5zyWGoQOcewG0qlZ5yrb3h5fo3d2R7H0ylOqT3fIy8RXepjmZfg4XilqhHVzyDj/a48PK6sR3k+1Dieou+7yLmwlHF+6No8z9EPfRxPx5jmKYY0REo5+qE7M5xRHzxXwPz6cAcz4PiSsnZNl7YPfyt+rq8xygk6PrTrugrqvFcNvWhJXgGTLy8vtW3J5Bcbpp1QGqCiF67EYo+sP/t3+I5tF5IA30rrtuOoD2Vw0km1HdCIjAy20T9si3n51DVI0NPpVKuj3szMWhFD3A4DAYhPQfcZg6va+G7ktq30m5hhrCZcHM9IroxD3MrMNZHl9iADJ2fWfdafhBDciBz4LOPfkmysrX0FPtSbyNF1Ez9Oiomh/Lu+vq5VH/vqLa61DzYuNlEBbjXO8RpjR8QAsBnzpzuIa7qihk65osZcSHo5+Y8uh5ubmxVetdz9bCx0d6snyMJdCNbfX3p9c6Jh8AIIxGBQBPcU4wScLWLELALBESYeIAro5PP0IloBuQcMsVuxHNwweIISTL8rMGYMcm4tL87eHBi3yowzZV6MwY7BvX+MD0eyZStQIu8RwVFzQo5BJsDp4eFhBcKoRFAudf841+d0IRwl7Sncg/WkfBsRlb0wK4Th/FzCSZDb9nzyPmtu0Ij8kYuf/G2WAB2JaCDKyV9ErPaaOCH1ZwgEbqVD3whIrJlBK2AXebPmnof1EmCL02EMTqwI3i5pmwnh2szf4NtP4yUYAAzQI+bgSo4rgQQbbNjAxcEpIlZ256SE3nAzf/xz1YckAxCEDjB+9Ao5rKueLTGyvfM78ieZR97v7+/1QAqzmNgp8zSbbRDm6qMZr21FggDEPAnIdu4+ZtsJLN8rAHaOPvqVvvH5lFKkaKf7MJeU0rkNZVrpGrIzyeK54QP5POtKIgfoYY0ri73brWRlFgz7AmShW+g48iRhQe8j2uETXMekzul0ipeXl6o3AMJxnGOetAdhWbdZvJ/aiTzopFnKwsB3MU+LgBZ7MVI5z36ea/WlyLhUcip73A+lPWhuySEyLhWn0m9d9laURGO3Kw9521+sk+uSbExnefaR8xKpSxFRfnYpnVuncpWxHxZnMocx2B/TvsKaIleTHAZTtk+z4JVcS40xR+chh6znxA58ALEYP4Su4xu3Ldf4Ea5nm3l5eYnr6+sa+yPa3gp0jn9u6eS+VCWIJ09PT3UzNzGCtbYvYH/bbrerFXnWEflDqJgw4hrYJz4RPWWMFxcX9dh3JxysLy1iESXuUckn9oBTsCdOmMR/eP+Tfa+TCXw61QzsOCJqhwbvI0fWnbnim01yGU+5GmAd5sjmnHO1feRuMpAEk0TIbDyYE72epqke2ENVjHHgV0wiUbnGRzIHH8xBHOHvW1KGJIEOFNrOkakPRyJ2k5xC6kS0tuo+pehSV0+HBB/2fR93d3c1Tln/OXjH7dP2U7w8dpJ+fOaWpPvbXt+caOBUAGoAEAbFWfcIg0VhUxDODcWnykAZ83g8rjYlo0AYOooP80cw9AOuDGgBkpS/KIPSy7nb7eqDvMygYAw4BIKzA6/bVgDzJBnOsF1Kx7AN0AigBi9OhHBO/CPBoaoBGCK4UDEiaKDQTm5wbhylyLxhPLeZLe/jNHEynH9PFo2z4mWmF9mQYVMlsQOOaA8A3DLnACvvVTA4ury8rEnSz2XlzBn9wek0QBOrMjW6y1ptASLraJ3ruq6WwTkBDfkwFsAxa2OG0Hrmh8sZpG/t0T9ZOxw5TgOni024PI/M0UHmb+bErJ1LpU42AHFuo3MQNhvFOP3+llEze+1j+rg2n0E/eJk8IDgA/tEdnijvY3H5DqSEqyMGBNg98vWcPA7e5/roGPpG4GRduAdrSRAgyOy6feRobWWedzr363u+yGEehtLrGusjwLeMnBlH/CS64vmZGMEncd9twmRfEhEVJDrIey3dcuLkeEtgsZ7Yp9sQx3EsPv3iJt7ej/WapU2I4zPxw8vKH+73w1knU/DAuvLdFCn14Xiac0Q5/XCJvh+i6yDVyj7CZSn/pmmKaZ4jnfesQOLM81ySx36IvgcAlGTm5uYqouviNJ7i4qLsBfF6dR1VybJHIeflnOScIqK13xDnsHF0z5tg3bqBnfsUMuwTf+lYbBLNVYyakERbV1cibJ8mevAvtHGgA6wzVXe3VLrtEztiAzRVZHQU/47fB3B6bwfVGz+3iXGgSxBKyBKfcVLyarxDcoAvse8DDNtHQJ6klOLx8bHGeb7/+vpav886n06nenRuRNv47kQGUgH/Q/xhjtsuCfZY+rh9YpX9CPHcMY75EFdYG+aMD0NezI8x7vf7euS5K+PLslTSyD4Bnw02BAyjc5Yp48N3sH6O8VvCE/0q9tfVeBKx7jIg7vsexFlX5t2ShYyXZalHGFPZI2nD37uVDcKeeUeOWHIjA12NMqHL706ETHRDlJnkZZ5ep4j1Q4F/6fXNiQYLg7KhnCiC9yhY2QGUKL5LRF1XeqEB0T7azce/orCUkx4fH1ftLYBhl+SccHBf7snpKVybjBLhAQQMmBgXQNFAFGP5/7d3Z0t2JEmamPVssW/IRGVVj3TLzCOQQgqFc8Onp5BCcvgEfdN9NVnVmQBiR5zFnRcen/nvnmAlUqQuj4tAAESc426mpsuvv6qZJ1OYADABEOVKVkRpOu9pXqvVqm1iy2ySoW42m9ZalBWLqvFt2hSzqto9OMeqmhg/5czg4nsJDufXPMOnM75L8TOISVAzaeBEzNHz6UqCzwQcDDirFYKZ41GtY74EMUu9ea9kyZINSpY+W1WqRiBoLw9ZJluKybaOSt+ZkCRzSKbJOKTB5x4czyc7+igByheT0dPcdO8Z30rwPS/XyhqYcyYNqUcJ4t1LUpzgeu7UEBAJtDxbwDauDPB+lgwMn5T3TGYzg2i2GyQb7B4ZRI09x2e+bIGs8uf8k7GTiZbQCVO6WtViOTLc5Nb3fWuZYePGtVqtqu/GthWJYAJIdpU69q2EVvW5ajzm3HqaA5vkg/nYDMp0ypp4NjsCDBFZb2/jC1YF+2T65n7Wd3f7ffV91Xa7q64bq37n5xcTvW3J2ru+np9f1LB5OY8sZ1fLOjlRBRk6mzabk+q6KQNeNbQ8STgWNfanIx/Ozs5qsz55l41NyMOm7q7r6vT8rJZvizocujo/P6u+795bIU5qOGq3yh6Ly8uL9/EsqutGH8e+6Rd7sj7eecI+E8ydnJzU5eVl63nnk5N0AOTm+wTSR6WP5J/50Ew4D4dDe4fCtyqhu92uLi8vJ0fm0iE2MgdP7D/BZVU120JoiZd8QCbXfCqf5/7akBGj+fzUZ7LkT1Ie5kvXk4lmR+QknsFFmeTRY7KBAfIglQS88+pWEqBJ1GX7q/GI4ZmoWD+2pHX3W5gQpkjCaR47xG3+wKZ2BFGOOTtdjDePJ0/yk87MqzZJaqQszDOTUHPIQ2Oyo+Xu7m4Sz/lX81H5OT09rcfHx7bu9lZI9FOHc1yPj491dnbWTuZcr8cXHNdhjFHGhNBN7MmOUyfyeXQ9ibx5NT9xatrW37v+0B6NZAYFJQqbAOPXX39tQF1bU/ZPC1qcDcAjgKWi/vrrr23jJIX/8OHDBJi4L+VNpiozOA7m9fW1Xl5e2huSseFZQkzFz30gaZCexxlSXCDLfglBkjOTsUomVIoSqGvtyEDvTO/saUzwwFErw61Wq/ry5UstFovfnAhRNYAxL8WjRMrOV1dXzVl1XdfYkgSRFDDLlsZEiSk71gDA8HkMVDqkebKSCVAmB3QuGZfD4TBpBSN7+uBP6mvVCFIAfuPJ3vMMGublUiIX4AVpf9JxZCDksOZJegL/ZBfSMWLWM6hcXFy0hMImsGQerAPbzb1W/vb5TGjohjGks80gTIeNTRDIK9dgBHTTk2zyd/SFz6Aj5EnmCfJdnOXp6WldXV1NjoTk1+haMp7mn3NSDfM7tk8vBf58n4SAnMHVmgI5SYykj/GczelJLYIN9v6Q7XZb27cxSBlbS5zebYHcvDjM5zBk5K1NiT2RkbbFeXDxd66FZC5JhawGHg6HyQEY6YsyrgjKkphk5Ohj+iBrt1yuqnrtlkDHUD0YfIEXYw5VgZEgGTZ673bjYQzDeq9qvx8SjcUCeO9qtXKMNXZ32EA/6tOhFouulu/HtGeFrOu6enkdj70+Ozur5WpRw7Hu3l9RtVj0dTjYZLyuw2Ff2+2oW+NJX1rw1hNgwi/wc+JR1fgyMf7N5yS4xpvX5eVl3dzcTKoC1som5yaTGhPo1WrVmO/FYqw6ZBLkj0RbjPWMl5eXdkJh+iXPN1++3joka57+Mm3AmojzVdUOjUl7ou8Zy9l/kg/Gx5/m3iIVAmv29evXlpDrGliGrbO98/Pz1smQVSfJlu8A2nQkK/CpE+TBrskk5SX2z5MLLDp5JlGZsZw9p3+ni/lsn3VlYmbfn4uvNzb4KAkzVbsksviNJEXILitRWdVyvyStVHHYGD/RSKH3xAmhbv1SFolbyCvlnFVule3D4VA3NzctqWdrrR299g1nJTmcZMqcEGLj/s545PMp+5Rh6tT3XN/9Ho3/9n/+vy1TswAABUXiGF5fX+vu7q5taMqAxEjy88k6JrOcpSMKQclSEBn4GFpVNWZ8DloJljL727zyZULJ9MhAMzt8eXlpi8YxJWCRIFG0w+HQ+mfJUmVCpSEz2cViYAcfHh4mSpC9q+Qq2354eKjdblcfPnxom4ISvGfmTLmN6/b2tv18vV63jXNz9iEDwf39fTMKTiwdbjIDnMOcKZCEAIJZ2s3KlCsrEcY/ZwBWq1UzVBvC04l7ZlW1taKbgJyxA58ZYNJhZLsR4O1nrnSgmI48xSzZgky26Yrvu6cDE05PT1sfpoSUTNORp6O3Dtk2ZV38O4NrBtKsumiL83t6r/Q7Z52tizUkM/c0T84wx8jmkrEzjgScbI2u8z3WPKsIvm+Oqedp/1kFyOCZegAYZ297PoM+JNs8T7Lojevt7a1W73PZH/Z1fXXdKrD489Vq/Q6Gh9ONhj7+vqq3mXbYP3ByMrxHYmSUd430yGTTBnNjnCdS5r9arRqBQResqbcnW+vUXTo2/zt1dfRB9vOMMeT8/KwRJuv1phzXO7C5h9pszqrvqw778cSyoVow7vlZLocjg6vvq6/3U5r243tiur6v5WI82U4Q3u1278etjlU++pls8PvK13ozJqWpn7nu2rXIf7la1m63r67var1aVdWibm9v6/n5uZ6entpaDHFgaPPKCqAkLROH5Wr6pnTk1WC3w+9O35PSrhs2xtdiIJG0dLy+vNZytRxB8ntsMTeE2W6/r+Vy0eKU+ScwpUt0nR/OJDsTDv4sCcM8WSd1KddFZ8X4PpFxr0b6Cp8F0HOtsksgyVU+ASbgg7JakC29fEpWyzPBM8eMm2KR2E+W8ziaY0iAyd8mQZVxX1dHVvzZOKIzO1Pcz5gfnHL3rhPWmB5lXMx1TnLUmsJ56WeSdUdGZxWcT/AZNpQEU1aHrQkZp13OSbI5UGf/vk83xNuMI6vVqp3ARb6JK8XmrMJlDKyqCf44HA7VHQ51ejJ2SuwP+1qv3vU15JCEalZcMhGmV0nS8X3mkkRb2pg/1uN//F/+h/q96w9tBk8AY1LAm4ExIhljsotZhkyWNgUANCv5fP36ta6vrye9iQRhkZPJWC6Xk2NWgTVOS3uNsn+2X6QSZNmQwUhiKJzSFVCcQJPhcujZCjUyUiNwyoTM/wGCZGRSIb+lBAxekE920eYw7HwqurEwRIqaPbnpeBM8ZYJRNQLJLOEBY8Y+d5abzaa91TSBVr4HhOMBsDO4cCLApIAlWU3ZJgtFZoBSAik6lKzHPEHKxCV/l85QMDRfGwVTl6tG4J3OWAD03XQA+/3wduzLy8vfJGMJgFJ2WSXIMZE5uaQ+JzComrYPJZCQJCeY5rzokTn7e+5P+r5vGwklYPwE/+Ln9IYukSPWyVyMO39PLllJTTCcFQ+ySqbM2hp3+jMJFh2VLPvZHJCkrKxvOvwEU9u3tzrs91V934JL3x3eAek7oD/URAdHhrF7T+bH4x/ZDP84jnlsK+DzEmBZQyfTZVvOy8tLaw/1WfJkl3yP+2QFJNd3u91NqmeHw6Gen1/qcBhbOtjL8F6QZa1Wg45+fRsOrOirq8Ph3Yd2gyz77r1i1siPt+r6zl7v9zU5VF/vycBqUV2/q/VmUSdLpBB2eFGHQ1/LZV+Hbl+nZ9pExz1Z5IfgGcD9SF503egjFvv3k9eWY5Ly8vxUi6q6vDif2ErGvf1+0AMJwH6/r62Nx5PkZNPa9Pb7fW13Azn49Pw0qTaw583mHejvt9XvbAZf1G6/q66PU6A269of9rXf7xo7rzIvVvMF9kcmeca/8VcJ6BAoCDZ+RwxU7e/7vn799ddmC5mAJUmHEZYcZ6UkCZe0Y3qaMcZJWr4DI2V1MPv2PVucyWSeDYgR2mzFv7TD09PT1naM3D0/P6+bm5vabDbt9CSfT18jrvLzGSuqqu2/ZG+w2DzWbjabdpoRObHxBOhs+XA4tBMK6ResyPfS90zOEdGZdOUeCVgHmOdjMu6xF/9OgjWBvqpvdihkzLAGxicO0J/Ul6xMpK4ijxMvkpGxG2MjNw6HoT1quRqaM7uuFv1Av2xmz3YlRs8ElPz9PomSxGdJsEq+EhfMidS/d313opEL5F0IeREiI5wrjc9ThLGndTzDOnuWJQMCYIIb35d8UEL3zJ35nqdk6VJSrJq+YTUV7PT0tE5OTurp6akxtIKjDJ/jwL4mMynJyIw7E5os79rQdX5+3pSd4/RSqywxZxKjciTgen4afiq7pCBlOmcQAHyykQBSVA7VRuyULePIPtRU8JR7JkcAbx4KkKficJir1XiylbWno/5dNb7whuEKXFm2ZUgMLJPGBEdklhU3Op+MXQbH7LmtmlbYkmlgA/6mw2SeVQ3r3IJ7tABk2T0TuASybIpeA4WAH+CdYCbXKefuOT6f+p0MVcoMKLVBk14nS8uOyCFBKMfmmcC/xD8Ddjrv9FF0X7BLht4aJNvj506UsZaeky1lCRx8T1BOVikTD0Df+Oiy76XtZiBJ/U0WbB68kixxb2tHn97e3t594vSQg/x8Bt5k/JbL5cS/ArLAgznSG5+TcGQymQTPXO/oSvrOr1+/tqoyO/B5sssWRJWmXK/1eoxPY9VuUdvtmNjn96zd2dmwCfPQ9bVeLWu92dSqtxn/rSV0i8VYaTevrKqmvzIG9p8EExIv7dI8MvawIe0bq9WqFmGPXdfVr7/+2tZjuxs3TafuX11dtTjpUBdrb70zUbWW3skiftmofDiMR5zngScJNIHG1WrVqmK5wTtjNb28vLxsCUPuK/P/PPI7E2ZAPjsc5rYp1uVBJEkYIr4ypp6enrb9kVdXVw1TJLsvETQOMa1qPKGNHdD1OfOdlYjLy8s6OTmpL1++TOI5AK7yrF2LnlnbfCkmXdXGlhXm1NV5lVK8ocfZ9SDmeQa9T0IkyackYOikz+gesXaSOvE130MBRzmpCsBPu/IM47E+YqXf89+J9dJPsUu+DkZKMjuvnB9dIMc8eKcRwt10vyQ95NfzPpk4JkGffh02SNnmlcllknF0x7p+z/Xdica3Np0y5GRJKR5lyE20jDzBCkMhOIKXRHCsAlfu9UiDo9RPT0/NgXgr5+FwmOz0V+HAkhjPdrutDx8+NMWWoGQGmpu5bm5uJgA9AUYGAkD6W+AslY9iZkYrqMpuGVey357p2FnzSwOgSBIDz+M4M6CnrAQqzjtbaHJ8/s/5+346JEaSCZD1TYBENvN2KYF0uVxOjmZzf2CCjmHF3DNfyJb7N3JTnzWUrCa4y0w/nQSgOQfomUj62TzpykqFz6RdkUsmhlk52u/39fDw0ORPF5Mx89kEwg5DuL29bUmReSVTn+CXDWYSm0EwgSRdYjeZtCXoTecNYACLnHlW2RIgVlVroWEbkpMcA7BAznxROva03dyAmfM3vzxBpKom+6sywQMgOOk8FjEJjUx882fmrvwP1CTLlhUXczd+vi3vr/LAF5sDn2l++fyc+9we55WkJAxagIy4Ya1yvGJArqMx8G/0Ya7TSZ4Aoz7nHvTMvXJOEs0EfhngfT6DMJ05HA7DaS/d+5HQ3fg+heqdktf9Rn8G/ZvOg85koj5P8rW1aHcBqsYK+H5SWRIDF8tl7d5jZwJDa/gt4snanZ2dtT55fkJMT/89BzXZUkJPEpim37anLDdok1cSCZkULJfL9u4nRJx++KxgIiz9GwjNlibXer1ugJSMc03mCb/4I16YW+q/GJkkiEusYrNPT0/NJqxD1437Ix2WAIgmsUPG9mimPvV9Xzc3N22ul5eXjaAkS10O883miSMyUaKHSRL7HXBvwzyfhjTj6yWVSLI8KY2c+LIkn71r6/n5eUJw9f2wN/Lp6am9EyNtTGWL7mWV39zSVs/OzloSlvafTD69oudJTvE91kT8Yc9J0PJ//JhYkRiDL0nfkATTvPLG30iKjZEd39zctLg3J3UyHpGHmJDVnH94omEg2TbECVSN2VRmkhQt++0ZgwSAMcqQBEcCSMeUAXi1Gk5jcgTc/f19O9VCJUIQUcbvuq45I32aFiHZudy/kCdhURSggSFkZUMw4KiB1TkjKOimomVFQXKUrSEJiCif+7mn8c1LaObz+Pg4YdmzCsChJcuaxpCB22kJyaYan59R2qwYJKAzjyxHZytE1cgcJ1MlAJGzdWeg87L03Jg5RvcVBATgbP0z3mSSrFU6HHqewIQzEUh8R7DmECQ7gsjhcGgnq2VSCnCmE8uEbt7y5Jn0KVlBn08A73N5kXUmZtZ5fjABx0SmwDonnwxXniXvuZmk0B8+xRwl6jZ3Aww+Y02T2c42DOvL9iSZd3d3rXXu+fl5cjzxjz/+2H5ur5Rn0jNjT5tKnUmQkGtFPunbrEeyXOQDgLgyeUp9d/+szBiL9kk+jU2MfmpMMgS6nMu83Syrt8ZjfelF+hvrTr+xwD6b/sPP+fIEtKlzCI+0PZ8FAuf7oTLAsvfsi06gnHonUR/mt6j1+uQ9UXt/k/t+OHK2+t9ucueH2D0Z5KmIc7YVsANy04+ySeuVa26/2+vLS71+/VqLSLLc4+zsrLo+9+cMtqoqIR7698vLSwOtfGie+0+3k8Bx6EomKKmvQJK1k6T7XZ6QmIeS0En+qaqaPwDWs/VDvEwy6PT0dNIZARQm+ZQJ2MnJSWtVXSyGvUj8C7lmdTIJ0sQwqnCZpGR7HV+/3+8nnxUv02f4PJuY2zs9oHPJYh8Oh8mxuPDSfMO8dUn/zg7mOMHns+sBkZt6Rr+zQmGMgK3kQtzPPZwIH3FB7Jh3niTJnZve+bZ8rnW0Lsaaft3PxEbPzyQj98w0O3v/PgJK4ksmxpz4Lkn99WrEw4nvJMjifcbjlHkmwSqG+cz0p5nE+nfG6yQ/vuf6Q61TADzGlUIloyw7raqJg0qjd7ReTs7/OTYKzqAwA7vdrm2qIWRJx9nZWeuPplwcBoDjtA1sSG4wUqLFlmdiwCkBPlkSTRDhbxl8GrJAlVnyer1upb9kcZOhnQdqf5snxZfskN/5+Xnd399PWJBvgSLGkj2t1hFoyPlltjxvPUpg6FnJ2royu7fu+XbafKnQPOv272RcE5jkG9AzIHMsWRHw7GzjENjnRpjg18+tR9UQBHOTH/3wTEafiZSx5X6W8/Pz+vTpU/V9PwmsdJjef2sM5AdM52kcyYCYi/n6PN2cVyk8Y7VatQMGuq5rssa0c1LsLmVq3dOR5foka5RJjXkav+8AIwkqrY/ASPZpl1mJ8wxnmed8Pe9vf/tbm7/gmoxb1fQdGdvttr2BGGuZ92b3Ppt2Yn5ZmRPMMXh8VpI0GeyypSsryMnWZoWa3o2+YVrBYCPzxDvtPNtHEiRnxS/XJAkAMsxed5/JKmm2vWQClHrCV2UyLflMm/NZ87aemTDZW5DJpHuPc1zUYe+EoLcaNkEvf6Pb8yrVZnNew0lSY/XF2LKykkk2XQeKU+fH6tT4Lqt8qVtfVR/eD2jx4tcB0FW9bYcxXV9fN30gt+Vy2fRus9nUx48f2x6A1IMkYRaLYfP66+trPTw8TJIbn2NPErZk/IF198vN4fnGZMnN1dVVW7+rq6sJPjC+ecuh9cwWFfP2h70YH98ntrPX+T5LvsVz8+QnvqPrurq/v2+nOxoreeWR9hnrzSc7JNiG6oM1B+Czz188ECsl/BkjUm+zy4ROmktVtdcMSAjFkiSP3RMx5SQ8WCwrG/yJZ8BCqUPGSsclPmwpn8+vJMlorfkHe1msXbL34lzqZdWYTPEN7qvlygUfZhzLWJ4kZ/pi8SJ94unJ6SSWpH+gw9YlcUfeL8mtrOIksTTHZemTshNAHP2e67sTDSBWTxwDS8CQVQPBYbVaNQDG4R8Oh9bv7MhJSkdIGImzs7NWUqyqBqQBDYr6ww8/1HY7vGNju93W3d1du1cq6xzkZ4DOxcPS5LnMGdA+f/7cWE5O00IBMBIg93TyBUXj/DgNSp57VfydZX8JS9d1beM7Q+XwjA2A3+/3zaCtDYXLNRZc0mGSHcPIMVhXhpIgiFK7kvHORCoZ3qwaWZtk3b/lzBlwVioyMCeYSDlzVOZofHQ721SMP5OTBFXk4jnG514AedUIhrJalWPo+75Vs6wL/cqNheZJbsk8J2Az7mwrYRvum/ZKbtZSCToTtqpqdlw1BA0J62q1qp9//rkeHx/rp59+amAh1ycdoXsJ6qmbdM3v026A5WyByPURTBN0YEfJhB2p0GHDfFYQ8owMBFU1YaSwVlg0G16zKpUJsuCLlTRn9pOsJYIlE7IMcIAQf5XMtvZPV5ID5J12Aazm+kgm5sSBf4sBWrb4Ws8YAfZmoveZ0FVVmye9lwywDUCJXWWFjY/zPKCA7UrMcs8TQCdmJctofJkMes4I+pa1XIwnji2X61osljW856Kvvg7lrd5py7kO7Gi5XLYz9ulF2luCXnaM+BnGMrzfgz6R82q1qov35CCrx/yzeJOsb+ppgmG2/PT0NDnRh+/IN5Ivl8v2Nu20V3/YcibL9Jh/XK1W9fHjx/bdrCpltS7bF9fr8c3gSUxgwROs5obpxWLR2rDmvkSy7B0G/BldUKHOGHY4HFoFtOu6enx8bD6DnrIXHSBiavpmF51wkqL4lKf7SZ4kD3S+qiYbtyVs/FASjfRRvAGWrZu3ZwOZ817+xC3IWQkr+4et5n6A3swZfslEYoYkvFN/rG0mj/TdWluvqmry8+xMRD2Tf9LlkuScz4qhYm/G2IynfED+jn9zP2udCfehm1ZpMykyNmuripa+NbGdWGrdcw1TFrku5micOc/fu7470bBZMFlkhpstHhTDIlWN7KlJGZwqBGFS7HReJk6BvHZeELy6uqrLy8uWUa9Wq/rhhx9aINHPZ1ETNPd9387m9nz/z566VBpJChBEoQmeArpXZn0cpxOHUtktrI3gZNL3/WRDdBqfewgUPueZAleCUIEJgyZByazaXMhqXglRYnbfBEfZXysYJPhO/ciA5PfmrI907nDdy1w8y7+d154sW84/mbosdzMgCcGXL1/aXOmHgDgHsxxBMrB0LFmgBPCcTTK7xmpcgmAmchmsMwEBGKypvma2J/hYR+Okx4IMR2zsZAUQJINCDlklYQOXl5fteWlHdEVAR16kkyVjumw+ZCPo//zzz7Xdbuv6+nrSlpBj5JsEG2A5kzrgCCmQ5ESuzfwISTqbYDUZ2KqBkMhAlk4/W17mjtzfc0bb//OylmlPuWapm4MPWr/b5i7YY6C22jqwsTz2WTCds1/00POTUCGf5dJ7H/qqAkyW75tnL+rLl/s6Oztt6yURTPbNunpWJlT2n1lf1WM6wa7oYNUIkujH8/NTS3a227c6HMZ9PwOA0d6nVbhqvTrU4dDVZrOurhs3lXf9oRaLsZX05GTTql18vzexJ+tK37JKlgw0n5qJ4KCXw7MeHx9ruRxe7vf8PByH++XhYQA6YtdiVc8vz7VZr2t9mJ6yx9cirvh0iWzaxrfIn0x4cwNw2rj1yGeKeak7xpHPAfLnJJD70DlH/V5dXU2S9rQhPhzYEheT+MTa393d1dPTU33+/LnN91tkzXK5rMfHx4mvtXawQVW1UxZz/6d9rWxPTPfKAHbHLu1Jvbm5afszxazcb8rPsPeMf5n4Z4KbhCA9TL3Lqq6kBfjOZIPtsiEJUhImmeDw5S7rnoS2eJYdLZl0IyLEDDFJDKO/xmYMxlw1fet3VjxgWTLK+9GFOXBPIjXbVI2/7/v2Tg7Jnbgsia5u9LXmmhXiHJOEfJ7IZ0xP4oSubjbDyaS5LvnMnN8fuf7QHo3sTyWEn3/+ub1Qj7OqqsnbmCk1sLBer+vu7q4uLy9bz50Xy+VpUMvlsp6enmqxWNT9/X0zMkbx9evXur29baVc2RznwUHN9y4ACJRMj6hWB8aT4M0ccgNVKpAgf3Fx0di/BBDmxhAp0LxkSbnJKjPI3Cx3fX096fujTPv9flI5sXbGImHD/pmLhMNnT05O2hGFQDOl9p0EQubk+wm6ORlrxzHkSSYZABiDMmsyqBxYOvk5G1c1JlDJgvkuPc69B+kIJJkY5Jxv7rnJikFWS6xl6hfGmvNLoO+5dJYMrC1nVDX2uGfQxPw6Kez+/r7Jw/dTFzHLAtCcyVKxTABk3OnMzs7O6uXlZdLqmMkmh0RPuq6rT58+Vdd1rYqpv/ju7q4eHx/bmFKfAPgMvovFov785z83+9ntdq2XOR08ciSrUBJgAT9PXEkGiAwQDElWbLfbSeKWL//kf4DKrIRm0khf+cx8frbS0Xf3ycpTroX7f8tO6dzYT71oNjEEvE0bf47XmMgzKyF+Rg9TT+hwVdXj48MkcaHzqcf7/a4Oh33t92xnV8vlqrGndCFbCd/e3urq6uo3lURr5J0Tm82mEUhpQ9ZoJMHsEVvXdvs2ATvb7dsk2RnZ8+GFfsOxuIvq+nfSoQ41HJQ7bBav6uv1dQpyrE9VtSTW2ICFTLpy8yufytZVlquqrq+vm0+xXieng/+tvqvlcl1d39Xr60tt3l/Al59PQsUaJSGRVSTrwyZzv0T6Rt/nG+mPz2RyjPnly29uburl5aVVehKwiecqkWQj4V8shreg04MkAjDrvme+yYTz0dvttr58+dL8NlDedV07uU/MUkmR6Irb9raoJljLbBPmm5Ms2e3Gd2KxZX7c0fJ8sHV4e3ubtIAnueN59/f39eOPP7bxZftetp26/8XFRSN1cx8MG0IMJhFNZ/JgCnjCfOk525gnNFmdc/8cQxJjxiRJlhgbk+cnhvW88/Pz1hYsUU47TVL55uam6afLfRJn+b7PkgP9oXOqYvP4xQ5fX19rWYtaBVmfeFYiMW/pErPcL0kgvreqJp0o5jJWaUc/nwmf733P9d2JhkVxYwDhp59+av/P3t/r6+uWbFAgQq4a+tn1RQN22faSi5qLxalSTMbN0SQgqxrZLwqWAT8FhdGQ+JhPJhrGwOAZ+ZzF5vgSMFWNyYvPAUeUbrvdtjI1WaSzo8ACtew/q0XzuadSpnHPGaCqmjgaMrB+mTh4Xhp5bpyUKHHmxlI1fdN33heIOD8/by8cBEbdl5JzxL7rUilgROv1evLWcmPLxCtBlc+cnp62k1ZSpsn4Z0JQNb5wkEN0JTBh+MlAcIaSPEFZG5LvCYDpDNyXzWmNENSAUXpARwUO/dHGy/FJuD0Lo5uyWy6X9fnz55Y0IhJU/IyVPRlHAphMXvPlRj4P1FhzPkibU1VN9koB0ewkE1cy4D9U6fL3nDS569HOkn0GSTojsGU/9HI5tI1gLc0HkNA+Z53pRFaikl128R8J1vt+qMpk4pBzcb9x7ItaLEZmmZ4At8nY8Vt5glYGJ1eCcrrm2X1fEz1ONm7uIzPZBpQk6eTGFrTHzllJNu1zGG7xa7vdtuqHBG1Y/wEMmKv7ZOKcFcJBfuOBCQAVkuLl5blOT8+a/fBzqq7sMf0ZHU658lV0REXh6empAYRMYBeLxWRfxaE7TBJA65LdA0gwa3c4HNqmZz50bo/7/bhRms0ZM4CYCUb6gdQPY9BaRO/o68PDQ3vzeFay3QuwJs9sH/SZtFm2KIblvWwGp99ao5EwSXywFXKoqnaKnzi0XC7r9va2Li4umm0jbKyBBMg6wkpsD7mZ1b08bc/aJiGTOgqXZRJ3OBzqL3/5S/PZ4rjYjbCks+z769ev9fT0NMEl1jxJIHqUFXG2noQN/RCDxTPrIkYkCSuhEAcSDGeSNCdbvKYgY34+N/dU0rW+7yd7LuhXkprmJ45kkpiETZJ6bNh32c6cTE1ssl6uavOeJNFdvox8s7tF1Wv+Kgdx4Vt2OZd3EgtJjuWaf8/13YlGZtHZJ55lUpk9J5QZWQJVQa2qGvMvazMpwsHOJOuaiYnPAv6ya05Hi49F6LqugRrOo2rsX1ORyHHn+fnL5bK1ErgH2VRVa3uqqsZccCJV4+kuQEJWRJLF5ICzvapqPJpX8MsNjU6TMR8OEADBEmXwymoGxSWLDGzklyxAMsWZIZPHnLnJ4JTPTubYxviqaWUjg0yyNCoTmTxVTTeN2e+QJUGyTxAxT6Byc1qy4VXV5MgZWVuydz82Yu307OaJO56f+tH3/aT1yD0BSLqYrGBVNVlgbOZsT1W1U1Xcw3cxMBx/2lYy0H3f18PDQ729vdX19XU7u51jzONf/bGenCBZc5rmlDbOT3D+QBjnbO4J9JN1T2YQiCNzNpBJegK6XLtMTMmMT8wAulqNPepZAWBHCeTIEwNMv9w314EuAMvzBIEcyEz1hbwSuPr80L5Ubd2rarKBOPvfc77uASTk/OdJtqT9cNjXbjc9hnPeajBPiAbiYehFB9LoMJ2YJ/tklnEmW2zoJOCVyVffTzces5Pb29vGOicDqSV3IKhGkE8OQLb5ZSWHHma737fYfuTXXP7Glgm0+/Oxp6enk/cvsfMEjVXVqoAIAZ+Zv+NGzOOnkuBJG8/Wo4zDmaAm28sf8FnkuF6v29guLi7aATK73W6ygZsOaeE27/Rl1iQrXlXj+yLY1dvbW93f3zeih8wfHh7a/yVWfs4ujcO6mvv19XXbg2E8YlauoTayTGTSviRTdAcJp9LCHuwJk2wkWQuDZezz1vdMMDNhTiLUutERpA47yPvmurDtrhtPhJKkiCNwGtxlbTNJAnrFNiQBfJbJOF1hT3T75OSkkVMJyheLRXuPmU6KbOl1JamX+p+xLYmpTILcS8Kn4pUJvLjGTtLXL2t6iAHfliQOm7U2qiVp/4nFUzfEYXHA3CRn+f2sIn/P9YcqGgkSkuU0QQO0UJQOG1I1lu0ycDMgbCihZ9Y1B53YY0kH9mG329X19XUrladgKHwCotxIJFBamGRIq8ayGyOmvBw8kExJgfRkSckP+LdfQ1tWOgbGngvLsP08jWi5XDY2er/ft1O4EshQvtzILwFhROkI3GfOGgKwyWomW+W7fk5+jJK80wASMCfYnW/oJdMM3vOTHTwvg3YG/DQ0DioTiapx850/AhyZJWORwZz8AN/FYjFhjRh/OkXjMH5GzHGxHXPn9HPtM7BkopinpdGD+d4I96QfbEu1EFNvPhhG66mCt1wuJxubU1bGkHaSRy+qklbVxBZzDVN/lPytX/qLvh83i2aikhW2rDJl0mYs5JTlbHJHAqzXQ5thsmVAQp5aM0+CMvHzO+NKZpptmkOW4xPYAsnYPPqQzDw/MtxjClx93jONI8GJteIHk3zIdaGv/Odms2knGmHaMqZktRZ4Gp47VEMkkVdXV013ABB7HGyitdk/fbQYhKUnO3ZIX6pGYOOzgI/e+fV63U4Gyr09qtjJCL68PDe58/UOCOCnrb3DRczz9fW1gdFMwpL4Sb+jPZPMT05OWivloetqvVpXX/1kffPFu0n+ZRI4v2eSPtk+kydcJUjLU4EAR/rmeblHgR73fd9eXivRy/HQl2x9kiSIHeyUnH0nmWJxxzh89+XlZdJynXt/+Bt/Z4xOfUuyQQJhc7xKQlZgJArsDfEqUYGBkrhNMpDOJ/OvpTYrSGK6mOKeWZmhV3ymWCApvb+/bxUPssjqRsY1nRuqM9kah0iACe/v71ts4kusD7s0duuZzDrZG49ENyt6z8/PDWuKj/wRP8dOMvmnL/Q854dUzYpJVnySfOJD81AY9mfvifXIinZfNYmHb29v9fT0NDnApGp6upukkf3l73Jc8A9fLG7Qp8Rmvp9y+b3ruxMNC2HB8yEJgp+fn+v29nZisN4weXFxUXd3d5Nsz2Tci2IIZhk8OXUOBvC4vr5u+wmwBBxanopDuJywjeWr1aqd5MApzkuDVYOSXV9f136/b0lBJkHukZvm5yBaZk5hKVYCj3RYKXOAw+eMTdKXRpetapkkeO4cZObJV2Tgd7nWfk8xGZb1SsBvTpngVY2nbJELx5SVn/w9wJ+OO5MVTslzv6VTmdWncweIs684KwCZdALb7s3JM+Z0Lp5F19kMPcxEJ1lLY5onkJlU5dysf7L8vpNglcOYM6eeYW6+67q6umq/e3p6qtvb20mSwlFz3oCC9SAnoAx4pzPAqkDqs8AbO8oeVrZhnDc3N/X29tbeVpxlfGAx5eDveVKW5X5VAXrBCSdj7/P5Xgq25Tn8gmeQi8RTgMkWjrS1TMirxiopmaQOs4tkx7QHZUuWdaBTxkbvM0lO+0+/nOvLX6R8EUFDm9ChPn16adVw8zHOOTAZq6YjGOy64dQe+qmdJ9cbKAfWAFjPEjyzxdA8B5mOsrHXLxOqvu+/0d4ztsHNfSegR+ZJWtkLxbckOZMnH2UraIKH/Ln1yUQWY8q3LTdjHJkTPvxr+t27u7sGBlMvJFPsni9I+8g2kpubm8l+E+y0NWYbkvLUZXJJUk2spt8ZYyX3q9XQ/olgIdckJ8gbcM1qXdpU4obsvkiGnY7Mu/Y9PgAAQIdJREFU/7A9chGrslpwenra/IckmQwPh0NrszscDvXhw4f2udfX10n1QpUjiY05WLbmTs5SCYGx7u/v214z2CxJRrF8TuplMs3OyJHfyQqReZFdJql0NnGXdeA3Hx8fWxUpTyrNKqu1TxshU3aUyTrdE4PS72T8TJIl55+dIHOiKCtFxp1knESOThoDotbnDn1Xu+3o83KfofHwU/wamzOujN1iiPlIQtO/+5178LNZKPie67sTjWRVshydGe3hMPSGz98bkacoZKDjoASMq6urtgjuzdlVDT279/f3rWJiPFXjkaHJWhP6WB4fy3lKsgS92+3aC8AyqBrb+fl5e8+GAOV3QMZcGc0zWxcEcRWQDP6ppBY9M1Iy5rgSMJCVErMkLTNRBpVyMyb3lFUnQ8FZZ+uR9aXMjChBcgKhOeuR43LPZCHIg37NWajsQU9nr+o1YQKiIpTJC53hzBOAzkEpOQF6nIB7mSNGtqomxmwuDJbOcGY53vxuJpX+/fz83AJWOjKyFjjdV2KbpVJjNy7PzPaCTJIE764bX3rpMxm8MIoCsgqez45s70tL8pX/HRBgvwdn6d45bs8XvLMVDNhKoGxc84qA+c0ZP3qaDlyQzX1d7J++klkmz+aTYCyDKV/DvsmuamyRoev8WgJXv0vfMLL041tu2ccg19H2JQZpZ3kfbH2SIwkcBPUEb29vb+3UPYAz146vSUKm67q274etr1a/fRmaGKHKYJxZrbI2q9Wq7alzEpFAm58fet03v5F1+ky6Q1anp6f15ct9G0cClcGO9pN9EABdJq+ZfGbSoAKy3w8vbBMHqmpyek7GDMBLzM22uX65aH6SvtFtIPX8/Lwd6bzb7dr7NpJkcWzs6+trSyIS5LEhgD9BvL/ZbFb/9vt9ax2a6zQfIDGhBxlrs9LFp7N96z23r6y4px/J5IVeA7T8o3dxZUzL2J2ytn5+x+bdn355rkqxNTQXG8v15dNhNqx6obplXOYEgNL76+vr5hcd+7/fT0/puri4aM8FpJPsQWqStedmvOfzzY0Okxlb8H+VSd8nN62neQiHP7e3t2186X8z8fOcJJbolPUxr6qxepZEXq5fdhVkGxYZW1f6yJ7dx70zyei68eSvPJ1usVjUfjtWapJYTdKN3M2dvrtGgmRMFPjPJEV8NrthxMjsSMqOlr93/aH3aFgogsGaV1XLULFKAAZmyO9NJEtWgqLecU6EElWNvX4Eqy8PY5kbtH766adWVu+6rm2asxCcDMZBMJ8HgEw4ODzCTqbEv8cF7Ws4GnEEIgDo6elJVfTaZTXIczgwDne73TbmB6Cet30B0BgU65X98JwagJqbkJVEgZgsMVPEfBGSwJNBnNMjk6oB+Hnz6shUjvNPtim/kyXWNPxk5RlxMpeCdAZRsuWYrW8zgvV4ZKA1zqBPZ6pqInPPT6Y35U23BZ15JcA4skSZDBpdBMb8rbUimfoMeOaUrEsmfQJTnpqSVYx00lU10UWfw3Jky0omcZvNph4eHiasqaMhn56e6u7ubsIm393d1fX1dX3+/LmxvU6U22w2rTXJnq1kqKqqJS25NqqofJLEmy8gk7RfAT4rDxmwJUbWgk7THWy4tc7WlHn1ghwzaZCMCkqZuGdS5Ez6bIEEtDKxNI/b29vGHA/yq1ouF7Xd7mu1Go6Z7fuu1uuxGqeigA+gB6enJ+/AzObJYZ+Co2n3e8x9XxcXAyD6+vWthhOaDvX2Zu/Asg6HrhFMi0XVYrF8T/ydaDS+9VxcGcmSZVWtq+/trRr0+cuXL3V7e9vWKBM8tsEOrUcSC8gtfw9AbdM2we529oB0VYW82NdqdVqnpyf1+vq17PlgH2yP3grSfMvd3V3Tl67rJkfG023kSPosuoDlnxMHYtx+u6v1cujz3mw21a26enp6rEXVpHrHRs7Pz5sMydHeRjqUL8xcLBaTTe5021qdnZ21vTaIO75/sRjaZ7IiitQSa9iodbIxG0gEdlPGmZCLBeSdRAyfy9fk2CXrSRyKs+wubZmuZetYttB+i8Ty+81mU5eXl60yyx8Yo/lfXFzU09NTaxHP6laCQHiEHsEPWU0X1yVyGfvE8axkZEzIE8ASJ+gUycSXLxVfYI/0Wcgnz8hnZ4KflQkJK3+eiUQm02IQPfWZJACtM3IiKwywQ5LsGW8yAaB75Jf7eqqqVstV9cuuFn1Vfxhesrmswa/ut7ta9FWb1bquzi9q/X6fbje+hJZe+Jvuk43xJcHG/4kf5upz2S6ZWJFPSSIXsTTfP/z3rkWflvJ3rv/n//hvzWiVfbwDg2MDOk2MIIDiOaO6WCyaUjJMi0U5KR9D8SwGmGxyVl2cmIRJSiNfLBZtMxUGM8eVpTQGZOOOn6WzyLaOkfUamfnMlLtuOKnE3gkKw2iTWaVAejs5lZHtGxUq58F5AeYcO0UHnqtG8HR7e9sybwrGkT89PTVGfZ6QZd9mlhXTWVLU09PhZVTkyVFzdpn0ZZ91AjlyZvjWLB16soJ+7+eMKwFGgsdknOmA7ycLl4kJh2Z8DNCpGFkFFMgxM3lSUK5fskR0PXXU+tJHcjd342JL2c6ELXI/zImxAfr/6T/9p+bY5uxbPtc60RHOFau93W7baSzWjg2lLgPbniWRvb29bafoJJOuJajrunYQxN3d3aSCkAHd2fb8CB8GLFmLrIr42xGZGazzb/adJ+24tzWzvthI9pmJ9zwIWCe64I8jiMktE8Bk1gEPaySAJjlBTzKhTJsRiBKg5V4Gcgbcdrvd5Bjal5fXttfH/STY/FySPxjWIXk4aWMGtIf21V17Drszvufn8VCS1Mc522z/k3V9fX2ZVE6z+rBcjkRS+pWTk7HlUEUAG4m1TTIkCY5k3IF2c0lg5TtJEElAyAU5k+06CbySaQaCqqq6vq/dYdgUzO5VU9J3Z8U0W9aSxU1GfXx3ysiAZ2Whakhw8rS5POI3WwnJw3ySpMlxiB9kZX3ZqDU7OztrB1hkjDc/95vHQnqBBPNziWEywn6X1VXjyop7+ofLy8sWIzOePT09teNUxayvX7828pYtWqc8Otwa2BtkffhrsQTQthb8Qb7zgg2nrVtrNiB2577AlAlsaG8tG89kyLqKC2Qvjnk2IJ/xmu9Nu+Fb5wS29jPynPv3xKlJ2iSeU+3NSjAflslQJqgn63Vt38YTyIzNsxO7wNAZ17V/8oVJ9OVYxZHEQOmDMsZIGN0/iW86dziML+bMBOd//q//U/3e9d0VDVkeEGBhs+cSCAA4lsvhCMzMZbLVKjPpBNBzMJuAwSJ7G3YGyxSo+1SNfXRZFpKApCNMx0CwHHlVTbJriqBP1ffH7HJ67FrVok5OvEDl0JKL3JDH6LJ8y2AB8HzLusBsHZJZSGbKWCk7Yxd0q6ru7+8nGaq/D4fxqFTPJEMyBpR9nuFnQMrs2zoaC+B3f3/f7pnPUBXL1gVOCyBJR2N95tUf8snAMQdqyQTNk4mq8YSVLA2vVqsWNHe7XTuNRI9rVkzIkM6ap/Y4ACCdfSahc/bc93PTpbXq+2FPUVaUUv+TtVPer6p6eHio29vb9rlMuvO5meiSz9PT00QHPnz4UJ8/f27vyPjLX/7SWhQz4bJugpe2j2RvtOZVjS/Roh8C5S+//NLASSZaNvDay3F1ddWSVq0eHKrSdco7fRt/R08ER3ZXVRNgYF2BwKqx1K4yKzDNS9XWYA7+sVvmxN7pvOQ2/W2yUp6fCQbflz60qhr4zKot8J6nr/BlWeUBTN/e3lrrHWY0/QCQoZJzfX3d+tG1zvFXdEFyIUnPCqe14E+BYEDP59mAcfI1EijzfXsbfXICtWTl2U+SRGxExV1Fwr0BSXamPZdskwyTdFvLrNamD+Fb1ut1ff78uW5ubhoQTgBCV09OxoNUyDb1Lnu607cDmbkXxF4t8TXJm+Vy2V7ECvwmu54JUxIRWiqz8mBdjZm9S5L4K2vCV6S+kXlWf7fbbSP1MlEyh9xEnAA6yUf3S3IpYwwdz+SGPYkPScjkfKwtG7Z+VeN+VP5coqoaRlfJgZ7mPhB+zdiML3VdBT6JnSQFfR8AJ4sE/+IQH5DgnixhTeubvi91mW8eSI2XRp5JWLP7JLsA+OYk75Io5xsSxNMHxEBWN1KnJFt8XYL1t0NXFXqXuC/bYZME8jnyXC6XrSpobLCiFrjsHuGzjYN982+ZCCU5yv7JN/Fhxovfu7470XC6h8A938SVyknQqaCcuMlRPN/NzciyS8EQyMpsTZDOwMcpEfa8dCYYqLJQpHRCGXiypSKDOKWgAJTTAg6ge/nOsjqDefHeA7ys/f61KYfnpvPLAJwtMhnAk5EGrMwvwYT7WAPPy/KoSkkCIUqf4IQTzefkszPI+b02GowUpU/HnKCd7khWrb3vZEWNnObGad0EOWNJ5ljiTC/9PH9HN407kw1GSbbpgB0KkH8y8GbCyvG7rzGmQ0ndyirSXF/8STYkN4KlnWD7rO/Dw0NdXFy0IMi+gYzcxJ5AmF0AHgnA2MLNzU0bz2azmWzqFWAzOQIQfY+9Vo1HaAMqxpFsFXZztVrVly9fWvUqWzOzxF5VdXd31ypQeZ/VanhR2sePH9saJYAla3aZ78+RLB0Ow8ZPGy2fnp5aBYZNZsUA25bMLtktFosJg8x/ZZVJC0a2IwiykvXUKX5sTtRIVIDdtI1/+7d/q3//93+v5XJZ//zP/1x3d3e1Wq3aHgvvxBnkvJjsb6NPnuX5Ly8vrYUGOQAgZxUzxztnJdm+vR1PT08T9jX9hACPCR9ayBYT+fhu1W/fFJx+IFn3ZMEzmAvYCeT7vm8veEtdMm8V0s1meOkgMHlxcdFaledjM8c8YMGffGns4XCozclJvb0nQYCRym2OMxM6cuObAUn+KbsQ6Ka1JI8EPUgV9pXEg3VNcAhQkZO48/j42CoxdPj6+rqtyW63m2xeTzANWH3+/LlVL/NIXy/ezGR3sVhMqg1iIdtHWCQxw6fCH0k0kG2+J6FqBMBZxTEGcs/KbAJsfsJ4cs18JmMBPyQWwWyHw6G159F1MS3Zdn5Dl4NqXVaNrHHaCr+VSbK5J3GaFZeqanPKeJNzF1/ZaVYaPCOxRZLeGUd9TxKXJ8IlCWcs/Ny3Xp7cV9XJZvMb/+Az7pG+KCs5/IIxZgtwYoL0KWTs/pKp7CRI0tUY4P0kSNwzE8ffu767der/+t//7wYwKFcCDacn9H3fSsiZ/XvBDIOgGH4veGfGnRt2CSgz3XRmwOzj42P7PwVRIcgzoTnjy8vL1t4B3GVAtCBYFGNIACsoYciGBV00UGiBBsB00s5A9icrMoyRorl/MuFV1b5rH4oxMrZ0Mn6eb0+n9Bx5JoV+BtAn2JmXFAVvoIJ8KLWEoWosnSeDSAe+BZKzYjXPwsmN0zZH65hBjrHmRjlywrzQk2Q/qsajR4GadHR0bj7eBNsSVaXu3MiWlwCUe5Q4E7os6fSMrDTQWw50zv5k8j9PQKuGSoQKiPskKKkaS8XWiz1w3BKgTPKen5/r6uqqvXXVmJIdzdKwP1W/Le2mzRmPAEAf5k6/aqjQZJU1W0/oarJhgn8mF3S566ab4ZPpsnkWGJEcZeXUXJNZ17ue7YQcPl+JrZZoJ7A0JzLIily+/4FO+F22fc1bmNix+WfbRu5/Mw7VisfHx/r111/r559/rv/yX/5Le1lZ30+rY/MjN41p9J8jyKBzgPJgQyP5AEDQieGFhFMyhE2kvXimAHs47Ce+LpOgxUJ71Wtbp6qq09OTCRkzb1nxuWxzTHBOd8mdPZKze2MZrX8ewSlhTwY7ZUYH7VdKELJYLGrfjy+MzeoSMJiEGl0RF5bLZXuhnkquK6sE/Gzq+MnJSdv3kkx3ssTmbm4SDTJOkuHx8bERJElOAtHkmyf+IKbMebvdThIMccFa5NwyucjODmt2dXU1qYwgQc0NEbBcLtt7WfJYbUkbP8BW0mflupiLRISt+0wmgwlm5+CSz8ijdh0Awd/RN/vnrDVAz/9lCzu7pptJOiaRJz6lvaRPyjb7TBz4zaxm59pab+QiWWXFTQwgp8QQq9WqJV5kQL50hk+hq+Zr/fq+r0XfV9+NJ0/BBLmmSXBmnM0xG0u2rcEmWQmxNolTM+nwvfT3SVSSWyZ9dKzruvqv/9v/Wr93fXdFg3PD0AFtWC8GkmymkxmyzFdVjYUilNzgp1QOGFFKoBobiekRpIDlZNwThJiDbNvCAhUEPn9hHGNKhZ4rMAeVxvb8/Fq77a72h31VX9X1XS1qUYduX9fXV79RrEygKH4mPRQgW41SIcwvGW5Jlc8DgeQDHGZSyIiTieEoPI+BpyG4KOM0gI9H2DJGgVPWbJ7kcnZ21oze+jP+THSyrQoblz9zYdVyH0ACai1wCRoAtSy7GrMxCGB0JYOXMWZ5vxneejwSEbh1VnkyZNagajwW2PcwG+aRcvRctpib2Dw774VVxTw+PT3Vfr+vm5ub2u/HIzfX63UDnJ6bVQUMSLZlJGhK1oRcHx8f6/T0tL1rwXdTvyW/dI9uZ5DxHQkZVtx4rKGfeX4eja0dQCuJe/AJHKxn+XnVEDCdfpLjmldF3Yf9+zw7tNaqB6lTCT4TpObb3LFeqXPz52bSaR6ZrApWqknGb1+Ecf7yyy+T7y8Wi/qnf/qnuri4qI8fP76v4Vi2B/QynmTyytf1/dBSZIzGK24M9tU3UMPv931V1x2ar+EvE+Sk/EY/tKzFYrrRsqreSZnxmFrPStvm85MdnN8nn5mgxzj5dmBfddH6A47ACQCXb8zOZNP4MrHHyicTfXp6Wi/PIwHHR6jyiAcqcH4vAeA3YQJEFlLi/Py8np6eJr71cBiPLE+dM15xUFJPBxEXWs3onEokX57fr6r2Ujpy5uO05rnYtkqR+KZtK23aerARMs552LMKA1VVA+yHw3gSkXGnn2NLyeKr4GY7ZianGX/SbtKfmke+OI/PRQj7Hdvkh5PJpudiJ31n454pIR0PofjtizslOEmizRNvtmUO8F4mivBYksF+Ro8y2RTDUp/Fd8/JOH5xcdGOaSdr9uj7mVDxWXS6JUiLZS1nRFf66zmRSJZJDsDL5pD3ov9eTGhMWanP6q7x0we6kERJ4tOMhZl8/73ruxMNjFYq/bzMlOUrGddcuQjAQHPxGe9+P24KzHKXfkBZs8DNKCh9totQSExYtmNVTfvUAC5CrRr3gjCe+/v79jzHwxn7fr+vL1++1OfPX6rvF1XvL5s6HPa1Xm/q6uqqbq5vqq+x3JUtZxZewBGQEtRRfk4ojXMOEhK8Z0Li+7k2uYYZdAQlysXRpdNJpSfHOduU1Z5c52w5ohNAhrEBibkuyRADagmszMN4XGTK0OgTR5HrQYeS+cnSMjnn/PNo53lCk4ciJOjIUueHDx+aLnCuWamyRr4z74OeO1v/TiaKfWpDkvj73MvLSzvlSetT1UAQXF1dtXs6z/3Dhw/tefTSZ+btF9Yobf7m5mbi9OhVBqJMDFIG9AHISmb35eVlAqgBgWSfuq5r1VZJFdY6n6H9gE4DKblPQnuQe1tHSUQmy5LkxWLxmx5prSH8AxuXaFSN+yHydCs6wHYkj3M9JD+b6W0qpb9sIw8qyMoNmxHk//SnP9XJyUnb27Pf7+unn35qifHp6VljPTOhsJZJQuWJJvwJ/cn2uGG8456prJa9vU2DaLYsAjRAs+cNCdrYTpcAYbfbNvnPY2HqazKtCYD8X6zEnALi7NKfrLwkYE1QQAcdUiL2qow5LODx8bF2u11dXl42Qg9BcXp6Wtvdttmhe1t3upfEFZ8sScm2mGx3Afy1w6WfTcJFTEvSDStNN5I8TD0GiPyxt8IY4AfxRtz2DPafTH0m4fx6Hjhj/q+vr/X8/NwwiXv4vbnxBaoeEhlHxpJtJmJ02ZxzvZIw4l8lz8bvnhJE+sRvkPOXL1+aTVXVJAllc0kYZSvevAKWiQGwah3Fb7Ihz3mc4qf4S0kkWfLVnvXx48fW0m/N2OXJyUnt9vvquylRm2A810s7lFgx+oQxeeTPMwFIv58+jY/hx2DTIVZ9rcuLy6ZPfBF9ozPGneQoP93FvNL3ZCeP31eNBwYlLhKbM3nJBAxBnT6THfkMn/h71x863hb7x3EtFou20RTTJlBpVWIYguX8GMzMKglKMKNc2VLy9evXBnY4ZoYoKUmWeb1et6qF5yerenV1NWHS/N+GtBTwajW8LOhwGPoVGd/j42MD63d3d+9tBMORh4ORrN5ZtoFtW61OGqDAmhu3iwMByoABc2Z8WaLPACcwphFTTvOngKmI2ChghPHl/ZOBcSRuJgoZFDMBSCPFBlRVa9GZB+is3ggwDImBaVcBqDjn7J/PhMMzyCITBYlGVl/mTLC9CORP/9iFqkqCQzKZByI6Qx7J0CR7KiHIAJ3gke4k+KMrub4jcNq1Xm8AOAHAdrttL7wSmBeLRX348GEC0JfLsb2C7RrbfM0SMLvYt/K0QGycy+WytR7QKeMTbPiXzWbTWjZ9VyCeVyTYXTpqPiBb26ynNdOyl2ym5CD1Pdnzk5PhiF12Z0z8kvvxYcYjGGbyxg9jpx1LqvqiInR3dzc5ocWV6zn3HQnmgMKs3PhOEhOLxaL+9Kc/NbCeMsrke5jHcJzuMP/TAGDeFL2q09PB12HSd7t9nZyoQHf19qZqfVpVi9ps1vXw8Nh0abVaT3zEcrlsSZxDNLKyme0CmdgPJwN6keS2tTw6Ecj9fX69Hivg/gxzG5OlBIDfAtcSd36MD2L/mQRkAmPt2LvKI0B5d3fXWNj9fth7BXwvFovanGyqC/9gvdlMkloqLf7/+PhY6/W67Y3gVz99+tSYz/1+3/xXxreMH3Q+/RrbJh+6JeFHZKZfJ5ME+GwxfSBy0BjZuHWwRp7Pjq+urianIub46L/nGxtbyoRNRcH7SMxdnIc70t7n1XTJyaj740mbnp9HyKZt8nd8NL+csYLOqBAhIZ6fn9tzkkC2L0fsk8CIxeST3+HLta9LwKxZ7plAcHqLOJlqT6Nfy7CJqqrucKivb291HoeyZPsZG5bw5xjnhFdWIzO2XV5etvZcsYWPTsKxxfrTs+YX5nE6Y5G1RIy6Bx+d1SPj8boHSRq7gHPgBYlcEoGZhME6bIL+JpmS2P33rj+UaMyFLFhVVTsn2wD8jIMCTgk2mTYON9mnZBoZL4NTrnp+fm7KRikSIHAW/hCse0kUBHiOI1s0lPzM01gB/mRy00CHQLKZONeBnT5vc3VfRsnYtRVwPkBFKgE5UQhgLXu7AW1/fJ5Tyj7OZCYos/IuOSYzTg7WM9kJiu5896qxqpCMbyqwjdnGnxssOdn8rgBI57JEaO2tsWRVkjHXp77vG1OScpJkZfDJfQiebw5ZysxqhTY/bEEC8gyEdIwDybIteSabkAm5gAZAJcvme1XVbFDQyfXK1ghyyeSf/lsHgCnt2NpYL2Oqmp6YZA7kiRl1GXsCHXb24cOH5hsygUB65Jqxa7K1voACebM/c+37vp1URcfpEj1JoMNPLRaL3yQ7mZRUjcdjzoGnYCqQZqJM7/mytEGneCUxQG/IAFOW42cL2l8yoXClnpEttlISB1x8/PixVS4cW5rPIq9kLwGJXKPcJHx5edlYzYuLi3p8fHzXqX19/Vrt+1XDaUleWApo82kZXLPd0P9HEmF6AAagJakz9peXl3aC0mYzJJpPT08tFrEd7XDGc39/PyEYjJHd8nd5BLW2JTqAUQc0M7m7vr5uvu3lZXgb+93dXVWNFbskLAafNW5Uz6pbnpRlTQCgs7OzOj8/b0evAz9syDrn0Z95eAvZA1n0z8bktB9xO2062evEGLmmiE5tM9kuxK/QY5Ug/tRzkjAB3BO/wAB8dZJ05pyyFlvpm3+zxZubmyYD6+zZThyjG/MTKxP0ffnyZRKf6I/Pu8/z83M73IcsHURQNRySIU5nBTD/nYRLkhaIYYz/tyov9J6N8wOr1bQdlEznnQqSb+ulddrv+3fZ7A/T/R/zKkLaEP+fySqAPdrMuPfH3GCrbPV0PwRW1fsG9nc5k1+2kGUSw++JS/Rss9k04gQ5zBdnVTT9rViemDCxJLufr6l1Y6epw//wRGPeZ6fvMjdnJRC1EAKBftts9fnb3/7WDGa73bZyby4IwHlyMpynbuMZBUtQnUKyh0TlJME2B/X6+tocQwLuNF5ByiIxUMpZNTgXvY1paAkUGE8C5cys+76fMOXp7BhXOsd0qsk8/fDDD3VyclL39/fN0VaNG5QSRGcvvbn6jDHmdz03y6lV02OEM1FMQLxcLttLmJJNyApXfk+7AObmcDg0UMqArHlVTQw122Ty9xx6GhkZJMv8LTbMWgq4Wf7lWDKBJDfrmmxnsq4AnMoVkMmOnLyU7Wu5oVNSoeLHyWw2w+lOSQbs90PboqBtDwy5S3Id/5onhmVyQM4ZYDnTLL2SE4AikHPy7DmPAJYUGTcfQp5d101OEvKZrDxkK0j2PqeteAa2jA6/vLz8xr9gXvkoP8uKgPElg5lVKuNKNjGZIT4pWaK0V2ufSTJSRGUEgK6qJmdrz29mNcc96T39zfZSZEMmP8lWm4v2g+wvT5kAJTn29H1kwcZz03Df962CDEDv92NiyF4eHh7aulWNPdJpuxmMHx8fJ2+7z6Ap3lRNDzDJdWDX7IGf0vrhc4BNtjJIKlVIuq5rVQHJFbnatyXxydYmOuV5OgrYjDhFb4E+enp6dlqL9++5VJRWq1U9PT21JGlOKkmK6Kdx80P03t+u1Fe+NhMpCWieKET3kuQxRrrDf61Wq7afU5LisxKKJIAScPH1dC/13Z4ZOn99fT3ZWO47uZ8o90jRHbpAf8nD3kLPB7b5q6zCZPueMe52u1Z1mMvAH8C067q6ubmpjx8/tqoK7GKu5IIEglccd181VkkRfmkbWUGpGokPekPnxV/xQsKKzLGm9DyTiqzqrVarOrzbMrkjYbfbbS0ijieYRohXjTjBXMXoOdZIv8M/aaViD3xt4kDz2EfrHvuQ2M9tJsnjjFX+7/dkSu5s3h/2xaeJ4Rl/3HPevst3Juma/vD3ru9ONLLVp+uGEk0KjvCfnp7avx0teX5+PtncmGDs8fGxvYyLwlASiQYh+Tdl5aCTNUyWXCDGwGB4BL/sWTOHdGIE7zsW1dhyYS0iZpISWRxXKgkFeHh4aGVtiVA6EsaVL8Hi8Dwv2ZJkds1JMAcOXKlQzQgCiJGvIJ+ydl/PTcVNkGq+gpw5uD955Ua5LM1xPBgEsvW8ZBisk39zKOYsYHIsEiM6xbEnA84hAQcJNK25MSbTJShwXOZgj4DkXPuVNcgEBPBNQKbVxp4Jc1BCztaVBGzW2guhgEfyFBjX63X97W9/qz//+c+T4OTZ6fg48QTZuX5ZliezTJqchNN1XXu3RSa77J4+kisn528yxSwDMvQ5W57oJLmoprG/TM4SYK9Wq7YvK8kIepqJIn3LCgsdSPYWM5uBy3cQOGlD7C8ZUaDEGAV5+lRVjek2xiRJMhGcJzmZGCUBkgQMWeaxy+4LSLGTbH20fnNWN5nRJFes3QB4Rx3LIMzv0JNsXUAQkUvXjS8wTAaSPfAH5qeKlonkbrdrbGxVNV0mp/1+P0mAsg/eWJIksC7mVVVtU6dkCVHBD2w2mwaWUi9vbm7q5eWlHh4ems58/vy5VZklmOuT8ThQzxWD7+7uJjHL9wAbPsw65rpnhQP4UUkUm7LylWDL3jFrnO9ySdtNsi1f6slWxCxrQaerqrXEsbcE83ROjLTW5pLgWdWAD6R/5oLscz+tR8a22Wzq7u5u4t/IuaomNlNV7Shyc8n2Ji/VEwfmc5OEG7s/Pp+2mCz4+fl5W6v0AcB+krVJDJl7HlwCd5mjpDIJOYQZ4sm4vK1eO31WVYwBjkn7yvt7eayfJ1jOZIbeZEdFzo+t+EwmUulnUh673a62h7farNeTRIkeZMzyHfIRW9PnpX9LOyL7/L975VistbkmKceP+Nl8nenc91x/aDN4gmYgn9O1WAal7C3TZnSMv2p8Q25V1e3t7STQWWwLAVhhdyhOtn0IlgRnsZUF0yEAJ/ro5u0tjsmbs6acWtX05W1OlsiqRWayEok0ImDBRj3jBzCc/JNJTZ5ykL3Cxuc+KQPBnqzNgfL5LBDNoSdg8LMEMsluM1LggSEni8uIGGUGHeuTOkZ33FvwS8Yn2QYONxPGdArAteAg2eQMBQ8OP1lfxpxMlMBJdmnImQTOW+M8NwOlZ2XvOAfrGT6TwPnz589tzL/88kv9+c9/rqpxL0K2aVm7ZEvsbSKbr1+/tr57eoxBo2fZu1w1BsSce/bbZpDH3iV5gHHMNqxkS7MVDrvFQdIt1TFgOOdHbx2xm2/HZXPK7Vl1yZYx48qgYA3JIDdx5n4LADFtCVsnybTuAC+mzTMkW+kDJJLmmgEzA0i2MiSJkCVxlekkFiTwKdvUKzLJl8xlSxi9kOQIhPTT32SSdsRnZvU07VNSmHqS5A1QxX9ki0KuYVVNTpKhi+LV09NTu9cPP/xQNs8bh3lgkJPVBeDoWbbVZNuPcYt7eRAGnbQO6V8lbsmm8y8Aq9PU6Auwt9/vWwUl2ynTv2aiZy9cEm+ZBGdMN45M2OlQbuhP/JDkofVKIvPm5qYx7wn62M16vW795v6NZEwm1/yMUXXUOuUpSlmZQVKQfRIv1sRLSReLRbNtNkWXdWgk+ZgEIsKp67r6j//4j9Ymqh0cJvinf/qn+vTpUyOuxDQxInUqCYL0l35nTFlxY8Ns71vdF/xAnsxIX8zRfDybbiXI9SzjJXfxwvrmvkt6mJXblgQtpx0i/AwZ5GsYfC9JndQZ5HZiNnaYtp8VuUxwM6ki77ftrpaL8X0+CeDnGISdw99JbCU+yTWDQ/kFck+d86w8rjeT9vQDmdT4/beqJH/v+u5EA7Oak6dcq9WqgeVsjeq6ru3mF0CBfd8D+JbLZTsH22ez3F41OJDr6+tmvBYlM0CBReKQ7CkFyWxTH6DsPwNxVU1aORLQUxKbmACNZK6yzJVgLINtsuHZIpQMOsVLZXTfr1+/tpYzAYYcfEYvJtaa0Qo8HGieKkHBGDmjmbPI5pzBPpOp3PD6LXaUHNx7XvEQaPxJ4Ck4uQSabMfikLL87Hf/f5l8Bm3rkCXNudGR2byFyh8OMitAvjdnss09HWnKnLwwUz/++GM9Pz/X169f66effpq8dTvniC3xXOBW+2AGafqUDHUGLuuVzHRVtfbIZHhSVovFolUEBKX9fngjvMRGIpE2p5fVRlfggr5kMEcQADXsVPDKagT7xORZc/JKIsEaZzIOFKUN6MlP/8R/ZuKEnMgEFOAVuOhJAmJ+1/MzgLoXG0sywBpnkBJUgSBycCVoT7aOHcxZOIkCdpw/5YvpDLkks5ttmHw0uwGKs3rT99Xsg88wh8Nh3FuWslKV91lAyJjpYLbT8M339/e/aZkY7XKs5rCF1O9kAc0/D1zQcpGtUCrTSfzwY9hnsYe/k/wmG9z3fdvETDck17vdri4uL6u+vk5kD6ClH0zSxH2QCQnA2aN2mmz1EkPOz89bhYKMExT7ebbASra97LNqZPolXKo7bDwTL/oohohtSBvr4Z43NzctcZhX3eZ7XKyv6lHXde1gBqeLaWlmc5IbpBOG3vs0Uib8xMXFRV1fXze7vru7m7wEOfW1akxQMxY4uERc2+12zV/x0eZjvsg4a0O/Mg7PE0X/z1cSWFd6KTniG4zPuvMdiM0kl+ab8Rvm7Pvq99MXLfOTGZeqxneh0J30TfQvv5vEtzhIv8gvq2JzIta6nJ+fV3cY25nZfNo6nyYW0LUkv9wfVshnGDPbyUQDprO2y+VygkOtXxKE7pHxPmPp713fnWgkq4515xA5Jw442QEDVa7CrOeCYF4Wi2GznJMtvnz50jJ2SoVhSuDNAc5LeemcMwhUjWB03nuWCUHOJasDwMb9/f2E2cFkpNMVDLN/PcE2IMZZKv9SFnPabDb18PAw6aWrqknfqFNRtttt65lMVjDnzQAZnjFTniy/pUKbE0U3P4bAQWV7RhoBY/azqppUlaxXJhDGmps4k4VX+WDQP/74Y2PyPAtbn2V1bBXdyMDKyQAgVWNVIJ1IOlnP8XvvKKmqxhibP1Ccm8yU2QWBBL6ebY6ei3HBbOdaZWK92+3q4eGhzTfbEAXndOyPj49NvyTOABkd8gy2nIlcBsoEKPQg20QciZpOTcCy/sARPUtGHmBM+ZNz6qKKZOo71izXnk5m2+Y8GaXrQCx/lOQGMJsETbbGZKJZNbYS0btkoDMISnwEyLl9CaCZvGbbojFaMyA0kzrtQHqk+fZkQueB21rwM9k6I4lKFpMPYYvJquYck6FlA7vd9H1DA+DtJvJSfePfMxERZNk3vy3GiB8JvrPK5TlPT4/t96n/i8Vw4hNbyERi7t/FIFdunh3ksKy+n754UJVF0pj/tiYpWz6TzgDD1Y8HLqQvsl7W9fz8vKqftsAgKTIup49bLpct8cfELxZjOzM9SgDDx5i7z+oGwJ5Xje+NSBDEfumnuJr6lVWnT58+tYqbDfZJOgKaEsndbjjd7XA4TFqe7+/v6+zsrL2J3ElbTuRK4iEr6Em6eS699XxJPH0kf7aV8RguIxO2w+dmZSZjbVY65vHjW/7U/9NHsf+8X+5lTOIviVU2Mq8KGM/hcGiEtTifVXWyWS6XVUF+sYndbld919UmKiWJDzP5phdJLrHNbEVL0hGBQs7iTd/3rQroM7vdrk7W4/rPwXziEAQMO6gacakYYo3JLivN5DjXnyQ6fU6il77DWpsnubpvJkS/d/2hU6eSDXh6emrOM9lxzDhHwqiTafF51Q2TVpIGbjlhi1Y1tjYwLsabi5sG4oSXDADuzbEKPPpxswUCSFd5YUQcgwD2+vrajr5NZsA99vt9O2ceA3p1ddUWi4PNRQQCOHLBkOwoaLYb3N7eTpgxBuoz7plsZcqFcWANjIeCcjpZbcqkwFpwbEAhJsPvOMwEVBiQZB49U4DPpMk6O/1FYogl4Mh8Fnsyb8cQjOenFq3X43HNyYhUjSAhGeJsNXH/+ZvAyetbJxZlYuZe5GCtk0HOIL1er+vnn3+u6+vrFsisJx10dLMkSECj904IoWtV1dhWsk6AnIlD3/cNVND3BNsCS5Zqyfjs7Kw+ffrU5Lnf7ycnZQFJmahmEE3gp6IATM0/l8wO35Ibyc0P4MCw8XkcssoEv8M+vKCMf/BzfoW9AsDsNCsBnp/JOB1Jp5/HciZ7z7b4DvZHj+hSkg161d1bgEliKMFX+uQEnxIBIIZ+JMFiLYBS8k3iha5Z/wx8mNT9fjjxaQATq6paVlVfVdPjiclGa2zqpGoLf4ec8Cw2kImeuQ/rv6m+7+ry8urdrwzH7h4O+f6ovlarQ3VdX/v9uB/jcOhqtxtB3Go1nLF/fn5Rw1HAfa1W6wmQ4NuzLRXASz+Z8ZM/TPKMvVufBLqY/bevb3XY7Wq1WFQdusbOf3r9pWq5qHUwvtk6bN3tV9EylAdt8JHGTaaHw6G9GyETbseH0qPdbldXV1dNL7fbbWP7E19UVf31r39tya444P4qX3r/JciSb/FHNfDk5KT++te/1sXFRase823W4/r6uv7yl780xp5e7/fjCxaznTzZ99PT0/ayQMmcz6RuGhc/lMmDK0k0vpZ+ZFKcsS1J16xuIiwzBmRbM91M7LNer+v05LT2+0Md9l0tl6ta1PBSzeViWYvFslbrZR26vg5dX+vNSR0O++prUbv9+zvCDl31tajlclVdX7Xd7WvzboOr1aq2u10t3hMM8qdfSQAvluOJTXwh351gOSsXZI1Ydp2enk5e6JoEiuf1h672b9ta1bt/W78nloeutoexap8JXL6MlC//VqswvGQu4kUmaolzxTo/t57IVFcSy3QdXqcnmcBnLP2967sTjcyeV6vx2LWqESxlMkF4zh83QU5eGwAwyFH5rGQiGWTPXK3GftjM7pNJBaY4nPxdMiEEmW0DY4Do6uHhoTnTTKwoBQeiyrNYDOVSz12tVq0nnAO3+FX1G5bd/ZN5SwBG0cyJs7HosuD7+/vquq4dbTivyuS6UTw/c0RkMjDmmuzJYrFoFZgMblmuM3ZGmNUlzhKzb31yL8Vms2kvHsOyc7oJsLIECcA55SqP4cx5M0YsPXlXVXMu9ISjyQpAAtnUBVeeaMORZ4WBU0tQ1RxVP/bB+vd84zpb812Je1W1YE1PndqD5VksFk2eAK4qnYCYjjk32VrTTFzZLCedbT3pJyQAgh5bkSCQsRdjrlbDSwz5E3MGEjab8f0Z2jH4F73L2MpspcqycbLsyTLyAxhNz76+vm7giX1Y3wwMdJUN397etmNR3YssyXlgyZ9au0UyU/ye8SEQkr0mp6wCJotHNuzLGltPz7F+SQqkT84EZ86Spi8TF7K/mOz5KvfJBDIBi9+lbf02KRnexTHEpq+TqnpWbfkfdp7JeFa/7TXgj31/uZyewpNrTJfOzs4bwO77sVI5Z1LZe5INp6dn7ZnJEieplTpLFsvl8jftZXxbtg5l4mHc3W7b7s/vD3Nf1em7jT69PU0qP+vNplabEVhK7tmWMYh/We3OfTP0gY+GCzLOJk7gK4xXJWWxGDogkH7r9br+83/+z832/O09V7vdrh4fH9vRvBLqfBdPsrzaq05OTlo8p6dIFvrLLyTTzQ9770P6O3Kqqsnm+vQLmTTn7/kCcp8TK9ZSDGHLfGdVTQgJOmVtskohXiU2SEL1W38f9kOCnUTIYX+oxXtSs47Wv0EG03Zc45dMDv7i0BIw6+PyXLblvtuoKCam9Cz2lv4lyY/0g1XV/D+9zQRgv99X9540+ox2sdN38I5okuxYO3NIGaTtsDX2lS2C/EoSw2mL6Wvm/l5s9btMjpNI9h36lD75713fnWhQYEzKZrNpWZTMzrFi+vIIuu/7yVGBwHiC7GwB4Hi82Re4YxiqKU7PEAQ5sM+fP09Kdwns0viSzeSUZbDJQACiFjJBsLHn5r5kIDCYvvOtlosMVFn2dB8ydO/cRF81MvvZ655AMcuLycJnrym5ux9l9ZwxcI6bQXMjtO+s1+OmWO0EgJgTkrRmMKSuG9/8nGxJlrrnJe9k+JK9YtDZFw7kJIMkecJoMX6bQZOhyZORksUxJmDPZf2ynTCTEEGMbObMgLEIJFkuTodDhzxPUond48wwZeTn8wKJqon50lVA0FgEQfM3J8y3YEue7mP+2sgyYWDLAAx5qzyl7LLFJJ1fJgxZRUhmfM4CS1QEH84+ZeQUNGvA3wBsmWwa7xzQGqeTw+wJyxJ16gj7ws4CAZnk5ZoASJngp59g08aBzc1TztJH5NohJZL4SbDsWWQHwLBhf1IP3J/dmwNb4bOzMmzdBHH3y0pKjtE4jc292bw9AmJCHsma++usteNAMcru3XVdY6j937P4ubRl60tfkCpZKZdMkmcmu8NBBiPIoH/b7bbtwWNbm82mvVDP5UQ947HuVSNAU9VhZ6frMYm0PoOMV9X1fdsknrEOMDZu9/7hhx9qsVi0I63p9X/8x39M4oQ1Pz09bftUTk6G92L88ssvE8ZccvDrr7/W6elp3d7e1uXlZTsOGOGQ+26skQqsMUoy6JLkgEwlKIvFopEN4gq9SZuDV4wzDydgwz6XyUq+Nd646brv9X0/eU9ZkrTWkV3wue4Pixm/OapwZZJrDd2DHvu/v+kvDMXn9F0/VDIWi4mPyXV2v8QrWZ0Qx0a8spj4M/FhTvolCde/31dcgP3SliRX2TFAl9N+xSLEBP3IxHi/29WiH3FCkqvmnRiS/8iN9XBFYqCsTmUCkQQlXJAyzHjJ76dtpu8fk75q/tM9+D6+MXHL37v+UEVjvlk4FTVBQZ7I8PT01FoyGLoTQwTPLAMCDQCiAJqb9rR7+FyWXZPdl+zYx6BKoAyr5UbwMS/Kbq4WVXbqpVF+n4lSstMSscNh3OSUjg0QNwaGSn4JkJKRFHSrxmyXQWY5zj0ZSpbYE+gaL0X1XMkEUAK05oucEpxbY+BZSwa90fP+8vLSPsupmyMWlkwzicue73xDqDkI/Ak0rBNdUrL++PHjxOjmYBtYSMci0cieVIGcjvrOPDAnCEng4Tl5paPwf3YGXGSykevGfnyOQ8gEONcu1z/HRv/plrkIBsmydN3Q722NyI9uZCtlvhek74eNqre3t83HJNMjaTYnPeFsSGC0DoKwIx5Tp7tuPMFEUpT6b80y+fVMvoxfSNZ+HnwzWU995StTd/i49FfJ3PMBSbKodqYPAVKyCsF+Mmgka2Ws7vOtoEUvEEmYrAxC7me+CVDMOe0qq4R0KpPKJDCyvG8sWbLP2KOiPGfpknRJv0m/s5qQDOLhMFTZHXjhZKYEd9aIXDMBw/6bZ4JFsuG/0kewA/7Xd8XNk5NN8w9pt3xLkmcSADJ7fHycMOHAPt9VVW2uu92uLs7Pqz85ncQ1Y91shjeKIzcSDJnjcjkc3c4v8bHiGzkeDof68uVLq2y7DzLyw4cPVTXEN8kKYMwf/8u//Et7rgQZgWAs6b+AuNxobO0zYbYm4iobNv4E22IB+0i2eX5kKr+Wtsd+7AFRnbFHNeU7J3wku+zB+vJVKiL5+ayqJdZKIghWQOLkWifIzJg18QvRAZHtwNvttvrFeDhC+hrxoyUJ/XjAxeAP1lXVN3zhFKkE3yr6rvV6XV0QT/xUVjyto5iW7Uh8Cd9AV1N3YMivX7/WajHdJO/eiUOQ9fQofcicrDOH1ENxMrGE+ZNlrmnqcyYMifkkwu6p1Taxa1ZNzf33ru9ONCiOQM6hJqjhIA2YILJVgEEqWZpUso/YEaADuwAsJDOgcoBVqKqmPIzs119/nTBjWEUJB/Cb7DCjMicbeykDhcPotrLgYdzISyEwHYyF4gGYDJ7imRu5z8G7+2T1w7MoG7CVWW0mHV7sk1k/Q8ljNa1vlpE9PxkfcvQ5DlHFy3U4HNpegezZxVZLPgEQa4Bdrqp25rj1nGfy1iffz0LO1tMRkvYC2IOT4Kbv+wb+rJFkF4hgC1na5qg4e/POShnZ0jPOXFJq3nNmiV5zgFkKTeYsAQ6QxEZd6TT2+339+c9/rsfHx0mSsVgsWlKSm3UBQrqSgFJZ+/n5ub17AHtIb6vG/VZd1zVwxPYBx6w4pLMkP3rOf0g+rAHZYACTiBA4kgXPCgPGxrONExuFAc0WKsCCLOhBEhgSLWsmIPgdIEAX+Yq0d+NJdp5+8MHJxmXv93ysqd/JTtIZ/m/ez0u+GdCyxSUZVT4hwQqfRX459wTdTldKpnG327W9RVrw0g6yXYx+J2hCLuTBBnwKf5MkD33nI6wNAEn3stqiypqgj0zFNn43yQ33QM5Mk5VtrVbLCdlzenpaHz9+bOy/51T9NoGijxLb9Xpdq76v9Wbd/m+f23KxrPN3pj6/a7z7sBV+O9sf+Us6pcIi6Vuv1/X09FQnJye/Sfxvbm7aWlZVa6U0v0xm+QlgiI9wbzEwTxwzhpubm0amdV3X1ilb/TKxZ9tijBiLFPNZMkgSNSug/Ao7yipC7ivClGf3Az3kwySMrjyuO8ks9plJLT1D9pFvJo7WKkkM/i1bQM3FPNh4dxgPz8g4vT8cqutHwpm+uhcbS0w52PO0IgI3ZCUl95lKMk7eD0NgJ0lMu3IciK2M2ZkQpZ9lMy2+Lsb3nVk/fghGkEzTJ3MS/6xTJmMpw3mSmjgHLiIPz3BZ65wTW84qlvVPkiGrvWL5711/aDN4Ah8OwINk+ZkAJKjJ7+SmJpPUU6sPr2o8hULgWq1WrarAsD0nj/xTQuQkkmX55Zdf2j1lpsaVTJrn50JT6HQO83JmbqBxCWLYdJ+rGpMs4NH/GVmW2HNcyWBlRpqBBvAQxAQYJ2NobZOozRm0qjEIYnLt37i5uWn3Nkb//vTpU1NKTlzQZRTZojDfbMxok+2zxhjFX375pe3/oSfaEPTA6stn0PQR4JTw0sEEDhxlOgV6JEmhx5ycQCbBAlo8n5FyCnQoW/NU/7Cvgk0y3pLvZOOT2aAfCZqtLfBM1pIxLY+5r4VOkWuuNcZPQNYuyVFdXFw0nc0Nc4ABW0hnbB7aHsjV/ekk287kGoBzf7qWyZz1Z1fmlnLJ6hjgkfaT8ksdSadvTDlWtpJsq98DsRkcjOFwGFodgG16Yc6IF88xPvPNBKcF/m7a/gQMSdjIkN9xj0xwsqrgd56ZwToTigxQfACbwGqrZAm2nvH8/Nxaf8wFOZQJxWAvhwlYpI/siN+WePBv+/1+8kJZCX+Cdi1K8ySt7/u2l4zcHx8fG8EkIRAHjEEsyYSFjFQggN9BT/d1OIxxw7hynBcXF83/q4wg6Xa73YQcWCwWdXI6vmS2aiQAajke7y4x226HE+k+ff5cq836N5XMxWLRDk3Il0Qi8z58+DCJfToTbm5uWksVAEf3JXf0nIyvrq6ab+Pzc/N1MvKr1ardP1thyJvPFnvyYAs6nHoseUfa0S0xJxljep5thYlxMhFgnyorWZGZgu3pO8ayWpfEb7LYSYIlUDZ/+s4nIQ3TDufECx1LffT9wU73ddiPgF88M6f9YWxXty5pQ55Hv5Nkolu6VtbrdWs7TOzwPqhJosgHaWmFW1M2WYkgI/dm+9nKaTwJ8DN5mFcCMnlJcjK/k3gs/WfKPcnuTCrSb4sL1pGuJcmEuLJGqWNJAJPJnLj8e9d3JxqYFafDcNQWgDLLwAmPwxO0DHLOjJt81XiKCUEQhr/dN5UJI8FBJMvOiez3+3bUnIz36elpcjSoRaYoBD3vVdeqkQwbReHoEhwCNAwugYX7clJag+aKzPgFLEDMvZIJI3dJhACbTJrPZMsVxmReoqPgQCCQdnJy0vZb6FH84Ycfqmo891/LwW63a/tuLi8vJydLdd3Qn6gPVoCQYDBI8nYaFCMRvHNTV54cJEmpqlaK5sSAuEwarLHn0vXX19fJZuAEVYw1GWmyI7NMCgUSnwHyyctn6b6EhMMEjLFXKgnmf3FxUZ8/f27zATro1HK5rP/+3/97Y+Le3t7q48ePE3ZLIs72lJtzD5AqYVbPjI3tpZ5yegLZZrNpz6Fz7JfTy1YHOikZch+JgTHR+UxGEBTG4/vW3TzNkU8yJ3afbDTbZ4OSplwnc0jygh/kJ6yRhBOzTgeS5FB51HdN7skY0zugRbJrHFU18UMCEVkDU3n1fd/aOdgaX5QggF37fwKIqt+yvUkGZQBTXVQxyCQuW0uyrfdbujP37XScPH02mcNM5rMCnGO0fpJA9+Ojs1WNPzP/ZLCzXSZBLTvJKmPqrpfXOumMbefRnl3XtYMS+PpG7CyX1XWHWr9XvP71X/+1rq+vW3vhn374scV48x1aX8/r0I8nHT4/P7cWWuuNcGNPHz58aPYhKaJzDw8Pk/iVJyNmJYNepY1JBvIY6fy9tUnwnckM/y5GsR1kIbCdn03Cle7zK+zQemalgI9IbCCeiY/sla7x/ZmI0h+/F4cTi2UinCA4AXD+nP9JMGmsSVrkvY3F75K05YcXNWKcCQnRjQdyeN7c9jJ5YqNfv762uJlJS/rpJIA80xrNyb55xwC588PmRDa5xvxfducsl8vh1KluJKfokXV1JW5I3EaPzSNJRnPKdc1kYZ6gZWXE/Nj0vBKT8SWJvEx26EsSZr93LfrvTUmO1/E6XsfreB2v43W8jtfxOl7H6zuv79vJcbyO1/E6XsfreB2v43W8jtfxOl5/4DomGsfreB2v43W8jtfxOl7H63gdr3/4dUw0jtfxOl7H63gdr+N1vI7X8Tpe//DrmGgcr+N1vI7X8Tpex+t4Ha/jdbz+4dcx0Thex+t4Ha/jdbyO1/E6XsfreP3Dr2OicbyO1/E6XsfreB2v43W8jtfx+odfx0TjeB2v43W8jtfxOl7H63gdr+P1D7+OicbxOl7H63gdr+N1vI7X8Tpex+sffh0TjeN1vI7X8Tpex+t4Ha/jdbyO1z/8+v8A5RjUPqGPmQIAAAAASUVORK5CYII=\n",
+ "text/plain": [
+ ""
+ ]
+ },
+ "metadata": {},
+ "output_type": "display_data"
+ },
+ {
+ "data": {
+ "image/png": "iVBORw0KGgoAAAANSUhEUgAAAxoAAAIzCAYAAACHlG8YAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjcuMSwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/bCgiHAAAACXBIWXMAAA9hAAAPYQGoP6dpAAEAAElEQVR4nOz9d7xtyVXYiX9X1d7n3Pvui52jWrFboYVQRCjQrVZASOAxssgYIewBM58ZjzEDY/zRgADbH8t8LPljnPCQ7J89EnhgGI8BGYRamCSUU7darayOr7tfvOmcs3fV+v1RYdfeZ5/7XkNj0ln9uf3uPWfvCquqVl6rRFWVNaxhDWtYwxrWsIY1rGENa3gMwfxpD2ANa1jDGtawhjWsYQ1rWMNfPFgrGmtYwxrWsIY1rGENa1jDGh5zWCsaa1jDGtawhjWsYQ1rWMMaHnNYKxprWMMa1rCGNaxhDWtYwxoec1grGmtYwxrWsIY1rGENa1jDGh5zWCsaa1jDGtawhjWsYQ1rWMMaHnNYKxprWMMa1rCGNaxhDWtYwxoec1grGmtYwxrWsIY1rGENa1jDGh5zWCsaa1jDGtawhjWsYQ1rWMMaHnNYKxprWMMa/tLBrbfeiojw5je/+U97KGtYwxrWsIY1/IWFtaKxhjWs4aLhzW9+MyKSf97xjndc8J3Xvva1vXe+8IUv/MkP9E8JVJU/+IM/4E1vehO33norV155JXVdc+zYMZ773OfyQz/0Q9x3331/4uO48847+dt/+2/zrGc9i2PHjjGZTLjmmmt49rOfzbd927fxb/7Nv+Huu+/+Ex/HXyTY29vj13/91/kH/+Af8LrXvY4bbrgh7+nHUmE9efIk3//9389NN93E5uYml1xyCS996Uv56Z/+aVT1gu9/9rOf5Xu+53t4whOewMbGBldccQVf/dVfzS/90i8d+N7HPvYx/uE//Id89Vd/Nddeey2TyYQjR45w880387f/9t9e75c1rGENfzTQNaxhDWu4SPiRH/kRBfLPq171qgOfv++++9Ra23vn85///H+fwR4At9xyiwL6Iz/yI49pu//gH/yD3lxFRI8fP64ikj87evSo/r//7//7mPZbwj/5J/9Eq6rqjeP48eO6ubnZ++yWW275ExvDX0S4/fbbe/grfx6rffSBD3xAL7300tzu4cOHe2v5qle9Smez2cr3f/VXf1UPHTrU22vGmPz3G9/4RvXeL733H/7Df1ia07Fjx3pndzKZ6L/5N//mMZnnGtawhr88sPZorGENa3jUcNlll7G1tcW73vUu7rnnnpXP/ft//+9xzvH4xz/+v9/g/hShaRqOHj3K3/pbf4t3v/vd7O7ucubMGXZ3d/mlX/olHve4x3H+/Hm+4Ru+gU9+8pOPef+//Mu/zA/+4A/Sti1f9VVfxW/8xm+wv7/PmTNn2Nvb49577+Xtb387r3/965lMJo95/3/R4cSJE7z85S/nB37gB3j729/OVVdd9Zi1fe7cOb72a7+WU6dO8dSnPpX3v//9bG9vs7u7y7/4F/+Cuq75jd/4Db7v+75v9P3Pf/7zfOM3fiN7e3u8+MUv5lOf+hTnzp3j3Llz/PAP/zAAP/dzP8dP/MRPLL3bNA3T6ZRv//Zv51d/9Vc5d+4cZ8+eZW9vj3e9613cfPPNLBYLvvd7v5d3vetdj9mc17CGNfwlgD9tTWcNa1jDnx9IHo0bbrhB3/CGNyigP/7jP77y+RtvvFEBffOb3/yXwqPx4Q9/WE+fPr3y+8997nPZs/A3/sbfeEz7VlV90YtepIDefPPN2jTNgc/u7e095v3/RYa2bZc+u+GGGx6zffSmN71JAd3c3NTPfe5zS9//o3/0jxRQa61+6lOfWvr+27/92xXQq666Ss+cObP0/Xd/93dnL8dwj95111163333rRzbmTNn9KqrrlJAX/7ylz/6ya1hDWv4Swtrj8Ya1rCGPxK88Y1vBODnf/7nR2PHf/d3f5e7776bJz7xiXzVV33VgW196lOf4id+4id4xStewZOe9CQ2Nzc5evQoz372s3nTm97EI488svLdtm35t//233Lrrbdy2WWXUdc1l156KTfddBPf9E3fxM/+7M8+6rn9u3/376jrGhHh7//9v3/R7335l385J06cWPn9E57wBF72spcB8P73v/9Rj+tC8JGPfASA17zmNVRVdeCzm5ubK7/b3d3lrW99K7fccguXXXYZ0+mU6667jltuuYV/+k//KSdPnhx97z3veQ/f8A3fwLXXXst0OuWyyy7j5S9/OT/3cz+Hc270nZT3c+uttwLwS7/0S7zqVa/iiiuuwBizlP9w7tw5/uE//Id8xVd8BSdOnGA6nXL99dfzLd/yLbz3ve89cM5/HLDW/om1DcH7B/DN3/zNPOEJT1j6/n/5X/4XDh8+jHOO//gf/2Pvu+QxA/je7/1ejh8/vvT+D/3QDwFw/vx5fuVXfqX33U033cQ111yzcmzHjx/nda97HfAns2/XsIY1/AWGP21NZw1rWMOfHyg9Gt57fdKTnqSA/vZv//bSs9/1Xd+lgP7Yj/1YL759zKORLMOsyGu49tpr9a677lp6r21bfeUrX7kUWz6dTnufDeEgj8Y//sf/WAE1xuhP/uRP/pHwdBC87nWvU0Cf8YxnPOZtp/j8b/3Wb/0jt/HBD35Qr7/++ow7Y4yeOHGitx5ve9vblt77vu/7vqU1LGP8b7vtNj1//vzSe2lP3XLLLfp3/+7fze+fOHFCrbW9NXrve9+rV155ZW7TWqtHjhzp9fuP/tE/Gp1XmV/0WHnVHiuPxl133ZXH9ou/+Isrn/uar/kaBfSFL3xh7/N3vvOd+f33ve99K99/2tOepoB+8zd/86MeY1qbra2tR/3uGtawhr+8sPZorGENa/gjgYjwnd/5nQBLXoPd3V1+8Rd/EWNMfuYgeOELX8hP/uRP8pnPfIbZbMaZM2eYzWa8613v4gUveAH33Xcf3/qt37r03tvf/nZ+8zd/k42NDX76p3+a7e1tzp49y/7+PidPnuSXf/mX+Wt/7a9d1HxUlf/1f/1f+Xt/7+8xnU55xzvewf/8P//PF/XuxULTNPze7/0eAM985jMf07YBXvCCFwDwi7/4i/xf/9f/hff+Ub1/zz338NVf/dXcc889XH/99bzjHe9ge3ub06dPs7+/z8c//nHe/OY3c/nll/fe+xf/4l/wtre9DYDv/u7v5v777+fMmTOcO3eOt73tbVRVxbvf/W7+x//xf1zZ9wc/+EHe+ta38oM/+IOcPHmS06dPs7u7mz1nX/jCF3j1q1/NyZMnef3rX88HP/hBZrMZ58+f5+TJk/wf/8f/gbWWv//3//6Sxf7POnziE5/Iv998880rn0vf3XnnnSvff8YznnHB9++4445HPcb3vOc9wJ/Mvl3DGtbwFxj+tDWdNaxhDX9+oPRoqKp+6UtfUmOMbm1t6fb2dn7uZ3/2ZxXQV77ylaqqF/RoHATb29vZiv07v/M7ve++93u/VwH97u/+7kfV5tCjMZ/P9Zu+6ZuyR+T2229/VO1dLCRvCaC/9Vu/9Zi3/573vKdXpeiqq67Sb/zGb9R/8k/+ib773e/WnZ2dA99Pcf6XXnqpfulLX7qoPvf29vSSSy5RQL/lW75l9Jl//s//eR7T+9///t53pafh7/7dv7uyn9e//vUK6F//63995TNvfetbFdBnPetZS9/9WfZolPg5d+7cyuf+2T/7Z/m58rwlb8OJEycO7Ofv/J2/k9f30cA73vGO3O/P/MzPPKp317CGNfzlhrVHYw1rWMMfGa6//npe8YpXZA9Ggp/7uZ8D4Lu+67v+2H0cPnyYW265BQh5HyWkWPQHH3zwj9z++fPnefWrX80v/MIvcPXVV/Pbv/3bOV/gsYTf/d3fzdV/vuVbvoXbbrvtMe/jlltu4Z3vfCc33XQTEPDyi7/4i/zgD/4gt912GydOnOC1r30t/+2//beld3d3d/mFX/gFAP7e3/t7XH/99RfV52/+5m9y+vRpgJX3SfxP/9P/xNVXXw0EL9QYGGP43//3/330u9OnT/PLv/zLeWyr4Du+4zsA+OhHP7qUR/LmN78ZVUVV/8xVQdve3s6/Hzp0aOVz5XflO+n3g94tvy/fvRDcfffd/K2/9bcAeMlLXnJRHso1rGENa0iwVjTWsIY1/LEghbak8KnPfOYz/M7v/A7Hjx/nr/7Vv3rR7fyX//Jf+KZv+iae+MQnsrW11bvkLykx9957b++d17zmNYgI//k//2e+5mu+hre//e3cf//9F93nAw88wC233MLtt9/OjTfeyO///u/zrGc966Lfv1i46667eN3rXsdiseAZz3gGP/VTP/WY95Hg5S9/OXfeeSfvec97+KEf+iFuu+02LrnkEiCEbv3ar/0at9xyS1Z6EnzgAx+gaRoAvu7rvu6i+/vABz4ABKXzxhtvHH3GWpsVq/T8EJ785CdzxRVXjH73B3/wBzkM7LbbbuOqq64a/SnDhr74xS9e9BzWMA4PPvggr33tazl79izXXHMNb3/72zFmLTasYQ1ruHg4uCzJGtawhjVcAL7+67+eEydO8Hu/93vcfffd/Lt/9+8A+NZv/VY2NjYu+L73nm//9m/vWbqrquLEiRP5rodz584xm83Y3d3tvfuSl7yEt7zlLbzpTW/ine98J+985zsBuO6663jFK17Bd3zHd+QqT2Pwb//tvwVgY2ODd73rXRdtxX80cPfdd3Pbbbfx8MMPc9NNN/Gud72LI0eOPOb9lGCM4ZZbbsmeIAjKztvf/nb+6T/9p+zu7vLjP/7jvOAFL+Brv/Zrgb5X6IYbbrjovh566CEArr322gOfu+6663rPD2GVkgH0lMdVFa+GsLe3d1HP/VmAcj/s7e1x9OjR0efKOZXvpN8vNOf0/cXsv4ceeoiXv/zlfOYzn+HKK6/kt37rt/IarmENa1jDxcLaNLGGNazhjwXT6ZRv+ZZvAeBnfuZncpnO5Om4EPzMz/wMb3/727HW8sM//MN8+tOfZj6fc/r0aR588EEefPBBXv/61wOMltH9gR/4AT7/+c/ztre9jb/6V/8qV1xxBffeey8///M/z2233cY3fMM3ZEv9EL72a7+WY8eOMZvNeOMb3/iYC6d33303L3vZy3jggQe48cYbuf322x/TS94eDTz1qU/lR3/0R/nP//k/IyIA/PRP//Rj1n5q84/63EHlY1Np3M3NzRz+dKGfP4nwtz8pKEvL3nfffSufS98dPXqUw4cPL72fLma80PsHlbKFoGTcdttt3HnnnVxxxRW8+93v5qlPfeqFJ7KGNaxhDQNYKxprWMMa/tiQlIp/9s/+Gffeey8333wzz3ve8y7q3Xe84x0A/M2/+Tf50R/9UZ785CcvhWdcKAfjmmuu4e/8nb/D//P//D+cPHmSj33sY/zNv/k3Afi//+//m3/9r//16HvPfe5zede73sWJEyf4rd/6LV772tcueU3+qJCUjPvvv5+nPOUp3H777TlP4U8TbrvtNp785CcD4f6SBOXYHk3YUfJEHHRDPHRhb8OKVRcDSTnb39/nM5/5zKN+/886lJWmygpSQ0jfPf3pT1/5/kEVpdL7B1Wmeuihh3jZy17GHXfckZWMYX9rWMMa1nCxsFY01rCGNfyx4XnPex7PfOYzWSwWwKNLAk8C6rOf/ezR73d2dvjDP/zDRzWeZz7zmfyf/+f/yYtf/GIgJCyvguc973n81m/9Fpdccgnvec97+Jqv+Rp2dnYeVX9DuPvuu7n11luzkvGe97znglbk/56QrOHT6TR/9rznPS+Hqv1//9//d9FtJYXy3nvv5e677x59xjnH7bffDsDzn//8Rz3eF73oRdkTkhTTv0hw00038bjHPQ4gh/8NYXd3l9/5nd8B4FWvelXvu5e85CX5AsZV73/xi1/kk5/85Oj7CU6ePMnLXvaynifjIKVkDWtYwxouBGtFYw1rWMNjAm95y1v4/u//fr7/+7+fb//2b7/o944dOwaESkFj8OM//uMrq+TM5/MD207C14VudX72s5/Nu9/9bi677DJ+53d+h1e/+tWPqjJPCUnJSOFS/z2VjN/4jd8YDS8r4aMf/WjG9XOe85z8+aFDh/jmb/5mAP7xP/7HF/RQJHjlK1/JpZdeCqyuOvVTP/VTOc8ihdk9Grjiiiv4H/6H/wGAn/iJn1ip0CRIVbD+PEGqmPWOd7yDL3zhC0vf/8t/+S/Z2dnBWsu3fdu39b7b2trK98X863/9rzl37tzS+295y1uAkJ8xVqShDJe68soruf3229dKxhrWsIY/Pvxp1NRdwxrW8OcThvdoXCwcdI/Gm970JgW0qir9qZ/6KZ3P56qq+sADD/Tq/gP6hje8offuq1/9an3jG9+ov/Zrv6ZnzpzJn586dUp//Md/PN9m/VM/9VO991bdDP7xj39cr7jiinz78kF3GozBpz/9ab3mmmsU0Jtuuknvv//+R/V+ObZHi2NV1UsvvVRvvPFG/bEf+zF93/vel3GpGvD51re+VS+77LKM74985CO99++55578/fXXX6+/8Au/oHt7e6qqOpvN9KMf/aj+b//b/6b//t//+957P/mTP5nX93u+53v0wQcfVFXV3d1d/ef//J9rXdcK6Dd90zctjbm8Gfwg+OxnP5v3weWXX64/8zM/o2fPns3fP/zww/pLv/RL+vVf//X6qle9amU/Y3vwYuH06dP68MMP5590g/oP/MAP9D4v77i42P7Pnj2rV111lQL69Kc/XT/wgQ+oarjj5V/9q3+lk8lEAf3e7/3e0bF97nOf062tLQX0pS99qd59992qqrqzs6M/+qM/ms/CW97ylqV3H3roIX3GM56R71658847/0j4WcMa1rCGIawVjTWsYQ0XDX8SisaZM2f0qU99av7eGKPHjx/PgtH3fM/36Bve8IZRRSMJ5enn6NGjevTo0d5nr3/969U5N/re2EVrd9xxR74g8AUveEFPgbkQvPGNb+yN5corrzzwZwz+OIpGElRLXJ44cUKn02nv8yNHjuh/+k//abSND37wg3rttdfmZ621euLEibwegL7tbW9beu/7vu/78vcioidOnOhdHviyl71Mz58/v/TexSoaqqof+tCH9PGPf/xSP4cPH+7N7xWveMXKfv44ika6oO9CP8N9erH9f+ADH8jKVFqnpKQB+qpXvUpns9nK8f3qr/6qHjp0KD9/7Ngxtdbmv7/zO79TvfdL7/3oj/5ofmZra+uC+/ZiL3NcwxrWsIZ1eds1rGENf6pw/Phxfv/3f58f+7Ef41d+5Ve47777qKqKW2+9le/+7u/mm7/5m1deEvaTP/mT/Pqv/zq//du/zac//WkefPBBZrMZ11xzDc973vN4wxvewOte97pHNZ6nP/3pvOc97+G2227jfe97H694xSv4zd/8TU6cOHHBd9NdDxAuAjx//vyj6hu6ykAvfOELH/W7d999N//1v/5Xbr/9dj70oQ/x2c9+ljNnzmCM4corr+RpT3sar3zlK/kbf+NvcOWVV4628ZznPIdPfvKT/Kt/9a/4lV/5Fe666y52d3e57rrreNKTnsRf+St/hW/91m9deu+tb30rX/d1X8e//Jf/kt/7vd/j1KlTHDlyhC//8i/nr//1v853fMd3XDCE7ULw7Gc/mzvvvJOf/dmf5Vd+5Vf46Ec/ypkzZ5hMJjzlKU/h+c9/Pn/lr/wVXvOa1/yx+vnTguc+97nccccdvOUtb+G//Jf/wj333MPW1hY333wzb3jDG/iu7/quA++xeM1rXsPHPvYx3vKWt/Cbv/mb3H///Rw/fpznPOc5fM/3fE8OrxpCuW93d3cvWBAhVQFbwxrWsIYLgaheIKB3DWtYwxrW8N8F7r33Xq6//nqstdxxxx35hu81rGENa1jDGv48wjoZfA1rWMMa/ozAu9/9bgDe8IY3rJWMNaxhDWtYw597WCsaa1jDGtbwZwRuv/12ptMpP/IjP/KnPZQ1rGENa1jDGv7YsA6dWsMa1rCGNaxhDWtYwxrW8JjD2qOxhjWsYQ1rWMMa1rCGNazhMYe1orGGNaxhDWtYwxrWsIY1rOExh7WisYY1rGENa1jDGtawhjWs4TGHi75H46Vf9lxe8nVfzYnHXYt6qLGA4AwYEWys7e29xzmHqlLZClVQVbz3uVa3MQYRoWkaAKbTaa7Lrar5+/S3iOQ20u/GmFyTvWma/Hfq33uf2xERGtfSOodzjrquAdjf30dEmEwmLBYLAOq6xlpL27ahfx/aXCwWNE2DiNC2LYcPH2YymdA0DW3bcu7cOba2tqiqCudbRDzWWhaLBXt7e4gI1lqsMbSLJuPIWouqMplMmLdzLplucttXvJDpsU38Q49w/vc+ykbj0BomdZ3x0LYtxpiM1yGOqqrCe5/xl3CZUnLqus712NNYjDG9f8u1MMaE50Xw6nPbxpiMb+89Bsm43dzc7O2h1F85jnJsac3KeZj4U0KaU63C/kSYqHDFtVfz0V97NxOFjSOHqOsqPAOIwJyWRaUcv+5KnvmiZ/PImVPYqkaqKXZzEz+pcSLgDbaFk3d8hkc+djdHGsGhzK1iBEQVFaWdCEefeC03v/h5nNk9h4gipsIjIBVS1XgMe3bC9V/+PDY3juCc0qoyb2acOneaqRGOHT6GbG0i3rHz+S/xyN13siktCLTGo9Yj6lFn2fYTrrjpZq574hPwomG8GKxTamf4/J2foj37MH/4M/+BI2d2Oa/7OO/ZdAZX2Xj+dOk8YgSn4fxsTCdMJzWqIKbCGoN3C2xlaI5u8FXf+df4/JkHOaTCplrcdIKdTkAMvvXQeB744r1sb2/T4tF03hEQsMZgJ8ITb3wCIoL3gKlAwt5SBW09qDIzyqGjR/j8e97H3h/exabz7BtHKzA1FSxasIY9qzzr9a/CHZ5QVRWmsnjAeUfrHM1igZst2L3/YT73+x/ieGvBeVpRTFUhGGazGW3rcE5xztG2Lc3C5d+9D+f5+PHjbGxMESOkbZloTNqbQ0jfeVV8cR7L51uEWdtyzz33MJ1OmUwm+cxNqhoD1FY4cuQwFgF1eO+wAk1tueSmx3PsSddjjmxR1ROssZiqYmJrxHuc88weOcuHf+3dHJ+BEWVmFYwwdYrD0162xVe+/rXsI+Hmtni+M11XjyxaHvrDT/DQJz6DCrRWsB6s83jC/moMHH3c1bzo61/DSb+HR5iqxRQ0yjnHbH+fj//6e9h8eI/aKU4diyqc1yP1hEXj2Js3mU9UVdXhkj59Kmmgc6437pJXYCwz23LjC5+FvWSL+vBhJpND2GqC1IK0nrquUWOQRcsH3nk7s/sfwTiw1tJUghzZRI3gzu7iFzOe9qLn8JyXfiUPz3fY84FHWBUsNp4Aj28de7t7vPPXfoNzZ3b50oMn2W8b5rMFbdNyzVWXsblZ8cIXPpeXv/xl7O7u4JzDWlvQeaVpPd7Dl77wRX7jv74L17TgYWJrji6Uy6dbXH7oCO1szkw8/ugmX/nq27j5K78CqWzYfwq1CrOz23z+jrv45B9+iHvvuYfpZMqiWUBcI1XFID1+nMZS7t30faLraY1Lmr8KUhtjfD+NQVVhxRkLv0vmo+mdsXNZ8sM03vRdySe9+t45HZ7p9G7ZfnhOQE3vs95+HZlv2rflOIa4Kdsp51Ly/KVnML02St5bttmTswi8NtApH8Zc4GTs3fS+K+SBcpxj/SYYjrtcF0exHoPnyrVKsodqwC/IKN7KPZHeT+0mubEcxxiu03rl9o0gBf0Z4qbks+Ue0xG+0e1Ni5G+/BX6U7x4xCvGGUDwlefJz7iRpzz9KTRi2J3vc/rsGc4+fIoHPvMFmlPnObGxxe5szrnZHnu+ofGOqbEcm2yyVU+xdGe3h6+AytE9MzwvP/WZ9y+t7RAe1YV9TdOEDefBKyiCxyCiuAGBUVXmizmVrXsIHW6ecpHHDlm5aGmx079AJsZDKAlB0zQs2obZfJ6F8LqumUwmzGYzVJWmCQxNVTl+/DgAxlicQtu2WSlITLJpmtxvUiKSMmIrg7VE4aWlqirm83lUcEL/VVVl5SoJ+qqBmRLoahyDQWkxxvYIkbU2z69UNhJeklLUbdQOlyXDHhLLUskoD1leE5G8AdNnSSBSVdpF09uEw/YvBg4iTj0lJR4S7zztfB5wOl90RDA97xyIxxjh1IMnOXfuHPv7+xw6ZKmquL7G4K0BFQSl0RYn0KoHEwiweI+gKIp3nofvf4C97R28Oqw1qPe0XuPzJjxpPJURZvt7KJaFc+zPd9nf2+Vz99zD059+M8ePHsKKYePQNCgx6jGAcx7FhX7VoM6xdWgTQ9grImQC2zQNTRsUlEk9wet2wJAkgStd/NtBt66gOPCKaQ21rUBAvQsKlLXglWZvxpfu+gxyySEWJp5L77BtC8biXWij3txg6lpM0+Dj3hYJ3atX2sZx9uxZjh09TusV8eF9RHBeofWIQkPL1tYW+/M5Yg3qPFGuCOcecCiteM6cP8/m9ASKYJSoEIN34FtFEaSu8cbikfCfBMZhpM/MhkLOUFkPByD9++ihZJJp/fyI4JP3vwKiUZABDEEoMAY0jPvUqVNUV1/K5tYGrl1gjEW8w1uPFYP3DlcJrjZ4L2jT5vm36lErbO/vcW57G1fXSNw35dlduBarcL6ZsTBB6cYr4kC8IoagaojwyKlHOHfuLHqoikqf4gscumj0sRtTWrtHpQJeQD0qgb+4SNdKGpRB6SkT5RrlRwb0KyBawcIXv/hFLrXXsWGEiRdM1VI5i0VQEbwo4jzeCi5sNEQV5xXjPaaqwQhe4Atf/AJPfNbTOTffxdcmKxpGEl/yqPfs7+8Hg5aEuTnnwk7yniQgffzjH+dpT3sq0+k0zg1U244eq+C9cv78NnFXY6xBjNCKp61gXgGHJtx089N4/su/is3LTwCCOLBicIuGL33uC3z8Dz/I5z91N7q3AK/M9vc7/ioGVd8TKIfCdcmTVynYQ74+9kz6frjOF8M3Sh44bK/cBz1FohCKy2f7Au0yrSzHkxSbg+ZWyjUqZKHUObek6AxlmuH8hwLeQQrccEQXzX+lL3cxImAu9TUi1CejzFD5HMqAY0pAN5TluV8MjK11+d0YLsp1H/Y1tt87kN4eGCp+Q/xkQ65IJ+AN5rhq/yfF10hQbrxXrK0wCOp8MDjt7DM7t4OfN1gfaHG7aGiblmY+p/UtTj2teLyZYCYGlJ5hJu/JEbwOx3Wh/V/Co1I09vf3gxBsBHWQdMiSQCRCFayAiqObRBLI0ztpM6ZBl8+VzCMtXFVVPWJXLnBaxOEhTBpvEviB/LuIcPTo0Yzoqqpo2zYzwek0aJdVVWGtxTnHYrHIvycFJFnM2rbNykjyKAwF9bDHus2bxlLXNbNmHp6PQlxlw3gFQX2wpKf2ysNaEsyDrCJpfdJhKC1RpbZeau/lmiY46PdESIcH8NHA0PJUQp53/J9G/LRN8BJVicBoEFYtwSpXRcGpbVoWsxkQ9oabz8P8raVxLXgT3tvcYCGe1ghGFfVgfFQyjOaDuNjfx1kNvYglyPMOFYNHcTpnb/s8Jy69ktNntjm7s8u82UcQTpy4lFYVQakFduf7qDocims9jmBVwis2KkzazpEoYIh2BMFUFltZ1Bg2Nzdp0zlVTyLbQ5KQ1tWpR/CIBDtYpckK51CvYKuAZ+fx2zOqo5vsSYPf2MA4hwgYqxnvx664jHnT4BYNqmCks/qoc0GQdLC/Pw/M1xiidoAiaNtCpB0758/jfcCEVd+zsqiBBk9jBbEWH5UYo4oxwZrcNA3ee2ZNg5lOMJtTFos5k0TYjWBMsho7oNt35U/uM57hVfvzIBAJnt+htUpVccXiLAvXheKvPgj2wT6KsYbWOyZ1jamqsHdcS5WV8bD3VcAc2uCyx1/Hubu/xCErUYoNisYCOHLZ5cwXwRiDdMaDTJeNYd42XPmkx3P6vpOY/QWVD0snEPajgBNl88hhmqal2WvBWryte9a95CW6/PpreODhc0jbUqHBY6iSPRarGJmY/poMlbMxZbGci/Oeedtg8DjXUBmhdZ6JGhRwBrRpueYpT+COBx9iokG5Vw2MXgGHpyEo1tu7OyzcArxFTVA0RAxegycUVWxVMdnYYH+/jXvBIpUwn80hKl+qyu7ubuHNsD0cOB+QfPTYUSpraVof+Zowk4Yd8Tz5iY/jhS9+Mdc+8QbaStBJRd2Cbx33f+ke7vjQR7j/c1/g7MlHkKaLJEjCpRiDEcGFL1YKiAcZhFadjTFl8EIgIku0q9/GstBatr9K0M1tD99Z0Vu5t8bmMoSepweyR2NIV4Z9rMLbmHIy/DtOIM/hQmMs55IMc6Sxaf/dsbXrPV+MY8w4MJxbr+/y2WjL9AM8X3Cv6MAQuUK2LL8vlc6hwlHOu9xDeR8ZCYYV7SI7hnMb4k4KJWNs/kM6lr43Eo0wcY4YcG2LWzS0e/u4xnPu/pPMdnZo9vYwjaPG4JqGdrHAimFiKqx6ahO8y94HI9TYeo0pGmNn5WL530UrGiLREm4kGdGwxuKEwmrauZWyEqGd4F9+r9qFDaXnSwE49TnG7FNbYxu5FI7T394HV6iNCkH6SQpGGW60sbGBiMRwrhb1pmdhMMYwmUxQDUJMCnGYTqd5nE27YDKxNE2TFZr0XGIoGxsbPa9DCt0KVi4BOqE9CIOKLeaZ/h0S0PROGYpWavelYlEy/FIbT4rTMIwp49t3rtRh6ELr2swkh0Sw1NrHlKGyrfx3eCDPr+wznnJAqScTVH0QAtTTtlFojkwquMOF6eZGsNxtTILAmPaldxhboRIsmocvvwQ5vEG73VA1HtLeNaBGaLTlssuvxnkPNnhVxAQBTQPFQ1GMwqn77mVrc4uqMmwdPsQVW5fjXMup06eo6orKgMwXbD/yML5paIwGpUbAR3e8FUNlDGcffojLrr4GpCJELwYfi7EWO53QbAcm470Plu90bugTrh4hJYTSiDUsrGFmDVVwqSAED2ZrDa34cC4WDqaGuXNMxSDRSuwUbFWz8LB15Ajt3j51XQcByqfAGnCtQ8TinEdUsCTCJqgBY6KXyrU89NBDzJpFUMbyholWcaCt4PjVV7B5eAsfz5IRG7ZFwTBNVeGncP2NT+bkRz+Fm7WoD0JgUuDDXo9nqrBWDYVU5WBle0zYyTgfYSgahdixtkJ7UZCPG1al2/dz56gPH2Lr2BE2Dh+iNUJlLHVVoaZComDswyJz43O+jHupePhTn8W2QQlfCLiNiitvuA4VsuBa0gIRQdQjG1OqKy/hGS9+Pnf9/gfQ7Vl4VjWE81lhhuOGG65n3iww9aRHx3oGEmu59LprqBae+z98JzIvlAQBF2llGVI5NKqM7efhd9DRvsY5ZMNy7MRxto4cRqoqeMuMBE9kDDnxKI14jl99BU9//rP51O99iEqCAiTW4A04EbwVrrjuGrb3dpFp2KEaz67zLloegwBvKsvTn/EM/uD33w8CxhqcC7RuNpuxeegwl156GcZYFosGaz3GBDre0eIggB07dowve9az+OiHPpJp9GVXXM7XfM1reO5znsukqoIHyYA4mJ3b5hMf+ggffO/72D97HtM4qtZjNIQ/a8RhaVRKSvFQyC3Hs0oZXCWAjJ2N4X4fng9YFnyGbQyFwSFvHBvXsI/ct9esyA77KeWPoaIVPIQj1vlIo8fev5CxYkypKRXoUnlPzxljcH65jd4cR/CuSQ4g0SPt6M3IGEqaNsT9mJdr2PdwLXp7TPqhqasgzTfgYDnEapXgXu7r0rAzVJhW4T/xFR/7LJWMsfPSa5Plc5D70PHv0vsmGo2ClVVpZnM++v4P4eeOnd2dkB7QOoxXJlUNeA4dsmxI8P6rBMOQCYPAeddTiPP46c7cKuX2Qnu3hEfl0cib2PlowXc47TPeUoFQhWaxYDKZZGZVHrBhHGcS/NOEkpaY2kzPlxZvVc1hSCLSi+ct8zU2Njay8FwSouSZsNaysbHRUz6GmzN5H9q2XcqRgJD3ENoUmqbN86aHH3K/aRzzefBkqI0PSBCMJ1VQiNQ1IVa+ICqlYlC2X453eGjGXITlQU1rURKJ8p0s+JsUejKwqABo9+zYOEqlYhWhHxLwMkdjiSlosE4GJdjgW4cqWAnWXKcKRlh4h7cV199wPZtbh6CK1kJjwRowFlNZUMvcOTaOHeZpz3kWn3rPH2Zlx7kWxNAaoT6yxbVPvAFTVyF20ppgBRaDmAqsxRAsnzunHuGO7R2uesJT0HrKbD5jWtXUpmJjuoFVZf/MafZPn2LDWFoTwnkQg6lNCE9pYWIND993D3a6yeOe8lTERBE9Kv/OhZyEEtJ+E0wvzraPd7AIzlT4I4c5cvXVbJ96hI25ULctosIenmuefiP10cOY2nBoatHaUnmDqSqo6ki8wDiYHj3G/s42rmnx6nCqLHyLc55rr7+G6XQazqOtELGoBPx5E7wRQourDY0oNz79aXz6Cw/TzpssxHmv2LpCphVPeNqNTDc38el8R0sTAmIs3rSIOpq64fD11yLnZpy88zNUBEaRchg0Cu8HMZfOAraayA6F23zeWDaQdIy1e3eZgHdqotdghdKkfUwrLr/hWuxlx5lsblBPaqytghfDWCoM1hjm6mhRVDyPe8ZN3Pfpz7BJ8EI0xvO053051WXHqCYTptNp8AgVtBrCOWvx6CHL0euv4vE3PYXPve+jGB/2UIuy51oe/6ynceK6q5BpTT2dIsaSQrHSfJMC6jeVa572JHbuO8nOlx4I/WgIH0xMvHwv4+sCwtNw/VTDvtG64tKrr+T4FZezceI4bEzB1FhbYypD7WJu4cTiUJi3POGmGzn9+ft5+N4HMHUVcW9YeMfVN1zH1iXHmGxsILXFTOqs1KFhH4po8B55uOHxN3Du3C73PPAgLq13pIXT6ZSnP/3pwSglNn+XeIiJnhRjDO2i5eZn3Myh6SYf+sCHePGLX8ytt93GkSNHkOCfDGt7fo8vfvZzfOqjH+dzn/wUbr5goiYaYARjJRpGgqAcaG3Ep3QKyPAcDIW4VYr32DqM/X7QO2Nr23/2Qt8vn9Oh0WtJeBq8Uxrdhu3kc170VYajlM+O4WmIvzG+XD5fGm5LOSm9O5zzKqWr/Ewk7tXiuyGMfZb25PC7Yc7DqvUZkw2gU26Ge6wc83DN0hoMxzuG23JsQ3mlfG/V2ozhY9U+L3EFy/kuvTUunutDyK2Km4zWOSoj6KKl2dnDzR3WKeKhwgTCrgrWUMWAbxtZhsdHQyjh35G9USJyFZ8bnoWD4KIVDY1eAeccXpVFs8DaKpxH7Vu2U1iUqgvJmYXyEOYWkFxauVSDh6Cu694BGnPPJuWgREIpeKfvk5IymUywVZWJR+qzDKWy1uY8ijSW0Hd4J31eKgkA8/mcjY2N/EzTNEymU1Rbqmqan0//EpUv5xyTSUheXSwWtK7FtwrTTUwk+Gn+RgzGWpxr8zxLDTrha+ghSribF7kp0N/IQ8VvqASm50s8lwphSQRKpavE80EMZUhEUn8l4RkSme7ZoHfn9bRViO+XwGRB8XgWrcNNLZdffw0nrrsKXwfvQ11PaTEh4U2C8oQxVLWlaVqOXHYJG0cPo2d2Qp/W4Iwyx/OMZ91MtbVJW8UELhMTmSGEvhmDx2C8smGFs3u7tG7BwnnmiwUbJy7FiGHr0CHc/j6PfOlLVG0bvFZiCVtPcLZGJXo4fMtGZbjvS1/kqsc9gcnkcMgXWjSYejMoPd6Twht7hEBAMIDv4RkCTaql4py1HHrctbzoO76N9//Gb3D2E3dit/eRVjhxw3U86cXP48y5M0yAqQreGyyW4OYJIUg5xA8XPCzecdnlV3Pm1CmOX3Ype3t7HLvkEhbNPOLN9hQNiSFYxlumxuK1Zbq5wcaRLdrt/UgYg/LZesehYyeYHNnCKZiYewEhZMx7pWlatHW04pl7D+poQkYK4mLOjWgIz/IKmMLL2e3Rct8GD+5qq9MqS0+iT2OMZEw5z/QyzCgXYfChMUSEzRPHuPyG6zhvXEhQblusi9ZVG8KQ1BhUFLVB4d4+f5qFd2z4gK16c4MrbriePetYNCGm19iR2GPnUJR9HHPXcna+h1rBm1ggQsAe3uQpX34zi40KJ0EJ9toViRgacBaiaCU00VMo3qM+JIan8KnSo5EF3UL5GhMYx9ZEFbYuO8H1Nz6JHRPy9mpfY1Bcu0CdYcNOME6DEc0E7C80zDcJPyHxVfAWnvZlz8Qe3wwheJHHaNVZHYOB2+c8J49w5VVXdjQ2WhYReNGLXsS1114T8xo7TxJ0EQIJJ7Wt8RPPM29+Jre89Bauve66MCYfPPd+3vDIPffz2Y98gk9/4k7O75zHOEftg8/GGKE14I0gUcI0EOlm3pSUcfvDfL8/SRjuvbHvioH29IJRwemAfoZJ2cEzPa7oDMfTl2voPdM/w8tC8ZjiMia8LinZ9HnkMAG7e67j2cP5DvtMe1HTf4HI5hDlciyq2tub6DjNK3EwJgsM51nOyccw5QspoMPvht8e1N8qBWYIq5Tj0FD4p9xDqxS7rpH+n731WK0vByUh4cUYBE9tLRXRY+w8JsognpDyBoEvooJBo6Jh8ARDziql6WLgoPUcwsWHThnDfDYLgoT31NUkJFt6jx0Q+SSoB2G3vwGHXoAkuDrncvJ027ZMp9NcHWoo+Jauw7JiUpmsncKjkgAemFPc0BJc/cGKAxvTKbP5HGstVVUFwc0YXNui6mPYk4Rkx9ZT10E5mM9DvsZsNstCflVVIEobBd7ZbMYienWqqsJHy2kprGfhUAKe1QhVVaMi7LcLKhTfeIw1vYMxtvBVZUM4T0HEkoKR8FQSuNLDUx6S9Gyp6OU1kI5gJnyHdV0tSA2VhuF+KPsv2zAiOaG4HE8KejWAtUExa7yjAtR5vAmuf0GwpmKBY/PoYXxlmC32qKsaY2ucV9RWeA/iQfA4DeEJjQgL9dQieNfiquAlQaHe2sKb4OXCJuulhKwKo4iEKhHeh/asNRw7fISFWGxVY0Q5ceI4RpVmf5/F3i7aNiHpq5rE+FQNHooYLqFAs5hhpnXM3wk4nWxMQyJ6M6c2QuvbaGJWxIZQsMxEIhFfooEevFjmk4r6ikt5yTf+NX5vf5/9T34W4xyNBQ5vsnPqJIfVYCMVcxJHoQQlIVI51ZCwaipLNZ1w+MRxVD2Xbl1GGyvAIQaV4IFQNPlzUdciPuS5oEqDY2e2z0S0y81xHhVD4x1z1yA6ocJCLFZBlBWsMXE9CFV3Kk9jgvBYZ89AEEKd99giZCKF0SWLXaZxA9yNKdJDpjP2bAkGIXU9FEBspD14RX0IKzIxS+Ps9nlOnn4EjhxiUwRL+Kkk5AzZWJigMgR9sFKOX3opG4e3cI/sUBnD3v4eJ0+dRLem1HVFlQQLYyJDIyp3JiTgV2HdqumERj0xRg8vMPeOmTp25wvEWqYywagEl72YINBK9FSjOAGvjurQBk6ViRgMHgkY6QxXUYgPOQ8pQ6W3CFnRT/ux+CrgVGB3vse5nW0WU9g8HAxB4oMXw1SBhjvvQG1g0MaABbM5CXj3im891eYGUlVQGRrXoq1ivcepIpVFDTif1luprEE9iBrOnDlD07S0bT/s5fLLLwOU/f097KCIiqpS1VUI6QPqasKVV17JpScupbJ1SAg1wYe6c+oMD3z+S3z243dy712fwe3NQFwwXhHPRFTWiJ+FY5UU9W4flkK0hv/lxFTJX0SvwujOXoYLCXVjAivxnMKygPNH1XlKvlcmL8PyXMYUjaHS1dGIQO/J3tFOYRsqB8P5lgL5qvYTlIpfmZwe3u/z2CFvH+Ig/JHWOf9JSezK8K+evDfW1giux6Ccfxe+6qEwbpbPjrXVUxbCA73nx2CYj5rkyKHCtEpeEZGsiJffl0bysXXLfTB+XgLtWu01CfxHozktFHdAQ+6pSeG+HQoy7xIFSXs98rWeC2tsIAfwuYBrWf3+AC5a0bBiWOzNQmlFCTvStw5TV6HiTrEJSiRJZCrps2Hp2XLgyWsA44lm5YKljZJyH1KoVPo9CdfZUqhQV1Wo9tGGkpfWWqq6BlE2pxvByrNoQpUi70P1HWtomjmVVFRVWN62bRETFi2FaiUlw3uPGHKIlfc+jyUJD9baXBa3bdtuY0a7RyMC3mI3Nlkc2cCd3WUDk2PQSyFGRGKVKxNxCpWJOR+Sqg6tsnjQU3oSvhL+kyIxtLYiA3dfJjDaez+1nxLlS6JYzmN4uLNlSbp4z/LzTuERak9OmJ5LSGi23odKMQK1D5VkKoXd7W2O+BPBw2Us4oXKTsDUiN1AqppKNSgbNiSTm80p/sweVoWFeI4tDDKt2D6/w4mNE2xg8dYE636snIStoSqOVuto5zP2z5zGbGyy1zTsqsfWUzY2N9mUFvUN7QQqqdDkSROhFqASnAmJYJWpQ9W3Zo74CfO2wbUth4xhsXuWzb1dWr+gVceUOoShGM3xt8Fi398LokorjsorG86wOdlADh/i2a99Nbff+/NM57uc39nGNQ2bxrAlFW0NzcRgCCFrZelMQalUcLsNc1lw7OmX8MV7PspTnvRETj/wEJdcdgmurqgmdVAmjEEk/FjfsqigrS11G9y9fsOydfkx9s7voK3DJnFLYevQJqqeamLxxsf5BYHJq6eygscyifG0ZlKzeeIoDR7VINIqIXTOt8GarhrKK7YaFFZvQgWwidhivzIKQwGhz8gll3hNzyYwCMaHfawVwbqfvJkolcTqfMEenRnIoY1DTIzBeaVSgqs8lkj0BEXQW2KOl4AY7HRCVU9xdg+Hsrkx4bLjR3ik3Q2eHluFKmCAiI3Wbg35C84zUcF52DpyFK0q/CKUXbR1RWUE5xpabajrQFMrqYilsjpKJCHnY0NCZbejl1/Ow5/+ElUjGDVYrVn4EJrrYhhQEiJcwu8ol0vejrQGQeALRjFlIsrezjbTQycwpgrKkw2lg7E25DVEmmMJ66AVHL/qUh750v1oK9Q6obJT6kNb7LctfjZnMtmgMobaGMRWiBh8DWJt4Cca1tg7x+VXnAheT+14lrWGkyfvQ/U4h7eO94qQmBQ6VVkqb9k6fIRLr7yCemOatJkgLM3m3Pvpz/KxP3g/D3/xXhZ7MxrX4iXk94mG+bgoH1QppyAKSxrQ11mWnQ/ejijABc+H5LDUzrMUhecofHnVWNZ3ZHUKnnIhwXQsNGNcYB0X1FdB+f0qD8XYGYXxcJHueV/kdiSjRKAVZdnSsfmUQm4p9AK9SIUh3yzzC4bKV/pzaLgo51pW7OwlREeDGkIu8pAMteXadB6b1XDQGpcG1944Bs+WUTGrlCWNEx8z/Kyae6lwDGHM29Sfi/ZwXI5l1dxzXyKB1o8qFf39nD26oSZeUDBUwTt2trdRDCo2FIpAQH0MoYrtSlBrlH4uiU1nfgw/g797sqAIK5Z0JVy0ouGdCz/eh/jd1lNVdSRaaaE7BiCR2aNFfGNc3JTx7geHKU2o9GSMHfqyJG4Z0hQs+tWSxSC9l8rSlsJ/8qakErSlpd+rBsEmWjuCkhQqT6Hh/o/9/X2AGNfcWeed6/I4kpCtGgS+NJ7FYtHL9QBlEcOqgqAgnLjqChbnP8+GNb32e5YPH8IWklcnzV9EUN9P6iwJU5preUhKIjb0aOSftCciHrNSQn8tyzaHFpzygI0R2wQpL2SM8HsNexH17O/t4byLVVkIZSzjeJ0Ea+bxSy9h0TYcqmsqkwOJsFEACoJM3L+xZOe0qlk4T+WUaQtWBVdbLr3+WuZ7OxwSgdZjbLgLIsw3MmUjiBhUPDWGSmFqayqEZjFnMZsxbxbM98/R7O4wUUdlTLSU2MikgjXYIbROAcuiaXno3vuZnDjB5PBhds6eYWNrC501NLv7tIsmeC28j14WjRWqxvMPBKicUjWOrWqCqMXUUy553OO57MlPYXv7Tg4fPoLBIq0iVcCv+JCgHaww4Se1agDTePZOn+ZTv/M+zj/yCB/4/L1c+7jrsZddQoVQR/E1hVsJGu4fMMG1a9tQbcuIYWIr9n1inoHcNs4xmWyEhHnfeQVyKIjGvAhVcB5pPabxSOOpPEgb8qKc8/HHFWekb0GVkhmqlrygB2P7tGTGQ6aSz0MMGdLYvPcKVrLStCQAxeecDwkSTduycC1iDA6PJcbkxj1pCPtZozJDqsaHoqbGuRBmZsXi2xaxodgHqnltvYR7MxYx1KyaTEL7hP1N49mqtjgy2WBnbx9vGrzUeBsE6ZJ7CXThjarUG1Ma9Sxc9DC4Guc9Tcw7EmuxhVBc0oRVwkRek2JtNqsJ0irMHbSxBmTUfqzG8EcNKRap3QplKuG+Gus01J5HmNQ1k7pm1jZIFQo/iAomVpyyhFAm1/pYNSYqe85j416t4hmQ1nPJ1lFk0eInLVJ3ximJwvvm5iZXX3kth7a28BqUeXWKzFvOPnyKT3zko3zywx9ldvo8ldOoDBB48Ug4dbZuDvBYGsSG+7m0cl9ImL/QMyvXa0RQC1tlXIAreUaXQ2VGnx2OL72z9Kxc3NiHPKzXjoSRa5T/yrGWoVop1LwnVK4Qqsu+Dtr/5SsX08bw9/wcBysRB8HYuMa8BaPKXWLGxfjTc8MojGy8lsAXSsVqFW0Y6/dC4x1CoudD4/jQOzKmbAQvYNd2l0ZgevRqCWfhi1B6HkKEDEmN0Mgr6PkmE/3oyY4kBeTi5ttTiMKDK/EyBhevaET3dVhoobI2MPEYOmULRhzu2giMOsRgRyt3nIimjUK/lGM6aElZAJYSnVQ1W3rGLOHDDZR+ykTwtFmTYJFK1g4Vlf39fWyKe49j7YSR0MdQwfDe07oG6C76mscSqiIRb/G52WyW59w0DXVlshKjEEqkVjVuOqF1QehK8yxDoGwVkoJLbTU9l5Q7Ve0uISwObPq7fGeMSA/xDMvuWpHwWVL+krdGizGMWUMS/oa5PCWU/ZTvtm2LrWsm02kQsny4AEuC8R6P0AIL52IZ11AWztYhht2Jx0lLuDJNcIQL+px3sAiCW0sQqE3jaeqa5sgmculR5nvbTH2IfdcooXiC8iIxnkBNKBOp0TJeb0wRX2Fri3UOv5iHeEm/QNWDNRgJYUHacSeMNRipMLTowjOdbmAw7G/vcf7UWWR7j2Y2p9nZodmfYeK5cgRZKkU1Dc9GIjohVzfc+YHA2fmc8zvbXPOcL+cjd32aqrJoDANrCHciGEyO6c7EkWD9alVp2pbzDz7CMWeotvc4s9ilvepKmrah9S7keJmC4EkU7k1QkJOA27pg2cYr0WkRlAdj2J/P2XKOqthT2Vsaf7yEnAzvFVqXq15hkkVWaNqQn7BZVZEoa+8eB2Mk0LTBGRien3KvDp9DNZdsLN8LzxPWX5MwHcIG1WvYO8lgQ1f2MeSWKE3jmDULmnkDCKYOlaeShdnlPRlx2bZUNhQ98FH+35vN2Z/PmWJxG0FhryrFSucZVglr36jHuzYoR7EUcbpbqVZoZotwKakYjDThUr8aqmSdj8YKH+dHpJGecEYqTFQyWhauoW0dprLUQSTvmGgPtePiULkWioZwu7aFxYK6deAcJCOXjwaadA+Oppw/D03cN4SKU1iDjwnh+7N58ABZS1UJVhQjASdqyN6hnDfkXLifQ1wIr4zjm88XCMJi3lBTY00VeO2k4qorr+Lo0aOYagISPLQyb9l75Ax3fOBDfPoTn+T0w49QqWAaF7xPseqceh+N0326epCBB5bDS8bweiEl79HCqrNzsQrL2DxWfVeGYKfvg5C7ek7DMQ1xUPKnngziFWQ5sXhM2B3y4/K7Uk4qlZVRYXbk9yGURsCyvdG555iLxw5K5WqVYjWEPt3sC/Q+loC9mH6TnPdo9lY5Bi0+HxpHS4P1mFw2XOes1CcloJB/S8UpKBmxbRGsNXhvg8wYDTcllAr6ozuruoTHIb14NHDxoVM9wT66vGx0B0bvhInx1jbF6zsHmFA+UKPY5GOMrelin9MkyjjJhPjFYrGkeKSysKlErUjnBSkXeGwDDfM40k3hSQgv29w8dIjZYp7HksKkQv6HIFR5E6R/0/iqSvIYy3FN6kko6yldBZv0vXMhkc+IBCtYVeMnE2ZVhZ3P2JBuk6YNLBIsZcb2E7YTGLNcI7m0WI0xkWFS6lBjF+jidEWWSrulELLk7Sg1/DSWhJeEtzHNP49hMKdMcBFMbWlTDHfcg4qGygtKFiQ10Hn8oqFRGxwGFlpRWm2pxIEKDUmY87TNgpm2LIxiTLBk7huPveoS5tOK/bZlqgq2QiRIxQ5AondPg1dh0iqzWUvVKHbWhkvuVLF1jTsErauxlcUtGqx6vDpULF46C64CaoXWC60oO3s7nDh8mInCtVdcgW1bTnvH+UdO0ezNqNs2CK/FmoXGlplQqx5nwo3O2zvnaBb7VIePcnYx5/qnPYXq2stpTKi4tXCOWRWSvyuBRkPCPWJwkZH61uNF8AbOb59nt57SLOZglP1mwZ5rcN6hziLqo8IRlV4R5oTYfUdQWGbOsRCldR7rQ3/qFWMrdnZ3Ob5o2NufUW9sUNWhRLFPih5B+VMTPISz+YJze3vMRMNKq7Czs8P23h7qPdNNofWaXfcd4wtsNnk7jO3O2phFtBQK8j7XLr59yFBVCfkXqpjYn3MuVBYTG+Yh0PiQ9J08ruIc58+co60MOmtBLepbqA2+VlRDCWEX75WZNwt0f8a0rthTHzyeTtk9u8vO7jb+CNT1DDGGqq6ZGkGszXeyqFf8osHPFsiiDV4S53GmwlWG1rXs7O+zuz8L1U5MCDmtICqnncLkVGlnCxbndtnf3sk4cqpo27LfLNiZ7aPeM5lOOuaey1iPCyUlnSn5gFfFGWi8Z76/j9/do0ap1DMFqGNpA5FwBgm0sm0b9psFrVGceupphdSCasXMO3bnc5wxeGuxXpiaFLrmMdaG/BSC0Wc+m3F2e5vWt8z9AkVp8cy8Y2c+Z+GFLTvHuqAY33D99Vx91VVMJ9NohTRo41ns7vOZj36CT37wI5x76BTN3j4TH8IgbbwoUEVCXDadkjHcl+mzMetyp2SbUUWj/Hf42ZjodpDluBQYh7wgyQ6rxcELh7AMeWM51iXeEn5Z+m6434bGzBKvy3Ps3zA9HFc5pgRDvj3kw+X4l41wqxWP0sA3HH8J+exEeqTSX/MhfSvbvtBal7CK95d9HKQ4lWuZDMAXUiBW7d8hLg8SqpMxq5Rhhus1VDLK78b2jZKMTsv7MivBEkIwjTG5ymRoK/CmkIvR5df5op8xnJRrVaY5DK5R6faXkZ7B7GLg4qtOAepTNakuht81DWJtvlwOoiCrGuLgCc94H5LZupKFEi/L6gTkkrCVh7pULEorS3kPRblYXfhSl0SckFgKvOnZdHBLV/FiEZiAiPRuBk9/h6OsOTSqfDf1lcaXwqPC7w3q/SixEMAYpW0amtZxaGuDydFjHL36avy99yGLpudFSAwghfSnTZKS2svQqDGmXOJ6+PkYwcjaNcsJUqXCUVoK0jzLKmHGdHeRJKVvGBJW9l1C7yCnkCCNCpoxeA25L9ZYMLEMKWCdR3dnnDm1ja1qLr3ySuwhhekUW9X43QV1Dbaa0DrHYr7A781x+/OAk6Dt0Bjhqc94OhMncH6fNgolE+uDZdQY3LxlsmVpm4aZa9hZzNlTjzs8Zcd6fAh7xwATrUKs9ryFRUvbCHZi0cqFJGYTk+GB1ofcocq1bJ98kPn5bRaLlsPTDY5uTNl/6CHO3P8gbr7AJmU2+UUinlT6a5qEu0YUFc/ZBx9g/8EH2NysOGqESoSnv/D5fOojH2Z+ept2d87+omG6OcE5RSdTPELlbaxa49FFi597Dk02aBcNO7u7NM2CPWlC3PjuPq13GBfu3aBWxASFwyFoDeIUaRTftCzaBdaE4gitxnwDiWEjs4Z2Z8Z04xBoA04wEwnlhk1IijTO42Yts/O7nHnwIc6dOUerMFelIlwcuL29y2QSiwNg8D6EPibrUaD+kUZpMAoMGcvYPi3P3nA3jyvPQCFWJTqTxtDGs2KtDTkoc8upex6kQZkyoT60iZ1OqSY1h48dYevYEeqNUIJ4e3ub2ekzzM/tsL+zm+dDozxy30nOnD9Le2Qfv+swVfC6TTY3OXbpJWwe2qS2Ffvb+5x+5GEWZ7eRUztYF/PK8DQKU7GcfeQM586fZuPoYdyhBmsnVHVNXdccPnwYO5lQ2Yqz584zO3ue/UfOcOb+k9A6FMFHOrk72+f87g4GYWvrcLQ0L2dmlHSmZPqwXOVqtr9g3zncecFIRbM3pzq0gWy1TDeFza0tJN6K7ZxjvrfH3vY258+diyGtlsrGO2CcY+/0WXbOnMFvLWCu2GqG32yZbmxQTeqQB2YE37bMdnbZOb/N4vw+tvVUsT3nlcVszvntHYQW5w1PevK13PSUGzm8eSjc/4RBnYd5w8kv3cv7fvt3efie+9g7ux1uZVeoEw6KggZGhFpsz6q5isb2FAU9eH8Poc9HlgXJso+e8l2s1VDRGTSS131Zmehypkrhf2jMGs5xCKVCqm512fhV8x4KqaXQltofE7LHYFQIjZ8N9/Tw8/BOVzFz2M/FKANDJUpHNL0xYfwg3g39IhnD+ZZeDTeY35ggP5y/XkT/Y+O/2OeWlUyyjHihfdJ/b1lR694Zx2OSWVU1J3WnM1FVdfzbELIL6d4dUVTzPAZjLPdc+W4+F1luDQY8MSbTlQvBxd+jockqF1zJ1psg9NQ1NYK6wgXnQr6BtTHZDaGKMadocKGHkJJSE+17BcoE5TLsJkH6Pv0MkZgUjfLAlIehdD0mRaFEZlIgFq7JoUClSwwhJ44Ok5VD391FeKlkb6hQVIXk2+E9HKq06feIqOnmIapDmyw2pky2trBuu7fhsoDv22z1Lz0dHRFeJgjpuZI49UrWsXxY0/qLSE5QHBKk1HbCZfl5+X3CTQqDGxLKIXMo28lj1JhjYU0vTCt4nuL+EI8Xg5qWM/c+yLnd88zOzflsexdX3HAdj3vKk/FG2J/NOXxoi81Dh9jbPs/+/ozFzi7NQ2cxewuMxgQ1D4ddxc6n7+Psxz/LrDI84napHFx6+eUcveQS6kObsBs8F6dOP8x5t2DfwfZ1D7Fx6EgsG6gYNaCWxZlzzO47g9vfZVJN2Dx0lMmRI0w2JkGBjHhvFwvaZoFdOGqtuWyyhXeCnt1hMXuI83d/lvMnH8o3NWuMfxclVGKy/bKsHWMlmC9mDXLmHB9757u44XlfjpiKkzufZSoGf2qHRz7+GR5+6AEOHz+MNXD4+FE2rriEQ4cP43bm1Nay2N1n7+FT7J3b5ZEv3I+ZNSyqGSJw6dEjXGKn7N7zEPPFnPbwVkiinU6pJ1PsdIPNrUMYF/Ir5ifP8tBDD7KoYPbQGfDgrMSqSwbXtOjenNP3naQ+dT7kWbUtm4cPsXXsKMcvvYTpdMq5k2f40mc/x7lz5zh3+gzN+V02nIAK8+iNreoaW9cs2nCRXxtzt7JwU+xD4rkagzGm1NGM5dDOVZCYphIEHxND2px3wYPng9GmOe9oY27GF87cAcaGux5EsFbYPLTB9PAWiLC/u8tif4a2LTqbseEtOM9ie5d7PvlZnFd22oeo6y/gCYqtmU6opjXTQ5tccuISds9vc+rcWXTRsNnCxIXnWuexpmJ26hyfeu+HacVhqhrnozcxnvnNjQ0uueRSrLXcf/99aNOESk7zBmkdC5dooQMjHD1xnMpYptNph+MBfodMfYjXpmmyINKcPBUEcRH2HziNmdZoFbzuViqOHDnC8ePHUVW2t7fZ29ujsob982fYcIGx7508hdmaAo5Hdj7Hzs55tquKI8eO41WwVUVlg6J3+NhRmmbBmVOnOfXwIzSLENp5lWxwThVra+YbFq8Nuw+e4cprL+crv+Irueb6x2HFUIvBKLTzhr3tHT71wY9w90c/wekHH0abFvEh3FKN0Kpma3yClC3nzcFW41V7d5Vl92KFtPLdIR+G1d7zYR9jAvpBQnr5e8mHxsKFx+YzdkYvdGZXjbVrf7X3YAirxjkcW/l9r1DMAW2P8ez0eSnsD71YfjD+3A6rqOGFBf6L2UdlX2WY1So4iDYc9M7YHrzAW1yID6wa1+pxrH4nGaKEIHt653De58uik8cpKB3F+9I/B4OB9vrKcpeMmXTiMwRjs0kh5hcBj8qjsb8/J8aGREupQIwDFw3xvyLJAtclfOfL9uKkW9fi2qB7pQOYBN+6rjrmKqHfRfICuFgu15gOP5kBx7r3qiGmVlM1pc5GKIUgbaI3pbIVM+eClcp72uiFkFiWN4Suh9KBi8UiJqrG241j4m464PPFIsayK9aE23XDwoYxta0DhMqYbCHQiNtwc7lgTI13iqgJm84YtDLYSQ1WcM6HA0/QbJWOgCblqvRseO/xLh1OomU2JHNmq6nEWHX1pNtNh8nbEBPn402Sabsmpawk5k3ThHweEy6W8aXCRxCWlBSiEEr7pkphzvsQiufjLWBJSclBUFGbjosa1sriXbg1N1TnaWkWbRy3Q8TQ0nDyC/chRpi6CZWzbH/+JB+/52GwBtcGfIjE5H1CqJR1nsqBMxZvBDef89v/v/+EqrK1M0dxzKZQKWzf81BIiK8qxFq8gM4bJj7cqfG+934WbB2s7SgzERa1ofYLdG+bSkP4FrbCTIIAhEgua7xoG5pFgwAbk03qahLK0jYtfjFnvr8X8lOcD9Z8iRYkwGmI1R6GTiUwLoR3yLzlU7f/Nz75B38ItqJZOLAVdr7grIaz+1AF3rXYSY0/POXyK67g7JkzoYrNvGGxu4c2HiOWy7aOos4Fz8zujC98+E4aXDyvgvPBMiK2oq6j5fvIFu1iweLhs+w3CxZGObyA2sdqYkbw3mFVmG3vsn3358FLSPEwIRlarOXQkcNsbW2x/fAZmqahaRtqhYmzWBdujnciTKcbwZviXDhf8a4ga6ucoA3dzebpzFyIMaU9Hl/oFI3imXz2cHhcTNxPoSCR/sS/0zm0qQCDSrgx3gbPsRFD63y4wdsY7MKjs112T23HUCNP7eNZqmraNuwlUYOJFb4qtVT7oXpOq0DToPstfnvBqYfOg8BUguJqXbREVhZpQ4L9xFS0ew2VUZQm5AzEhHExBt3bZ+fc/XivbJL4Qdj3YipUPM6H+vCHpyEfQTRU3cqOnYiTgJ++cGwkeEQSP7Cx2k/jWxSwC434Al14dDYPimsVii9sn97h/BceCKWx49oufIu1ykQqvFPa3X38Yo54z65vEZRW4dzpPbyPSpUqD4pg6wrXtCEXxAe6ZUV4wuFLaLYUby2+shy59BhfdestPOPZz0QOTUPlKudxTcv+9h6fv/vT3PXxO3jg7s8ii1Az30Kolibxfo2kFBBzWTQJJwKio9Uss8CuFLS1pLHjYStjlvb83ED+GhNq894vvlsVUiSJDxRrbCLvHbZbCoxlLuCFlIbe2KQraJK89KUyNnxvTGCHfoQEDG9aN5l3C33BcOjlWYWTMmRzaZ4HKN9Do+CF1iXx7ZJ3rFIclyRllvfMKkVpOM4SyrCzMSFeIp0orfl/VEVxiOfhHMs17An0K94dQsA5UIT8xVYyv0lKBWkt0xkRg8awThFh0bRMJkEuC4bvIDdpzqdRkrCZZNH+ZEMfBebIwhXp/OQHg5wnEkKcvef8bO+C+IRHoWg4FY4cOhKq8UyqUNlEQ9k8E8uXQqhU4iORT/mcbaH1pO9BY7GPtECQCsk7FLGmi1EnXIbUadtgo0CvGmLMA+NNYSJB6E018dtmEYlYSCQ3laVpgkDbasPm5gaqymw2x7lw+7drQ5hVZUKZwbZpwIc7NfA+KgdR3TKGxWKeiZ9zjtpWwaUNNE0LTqjNhLqq8OLwLtSPD1VjNNRe9x4RG5+tQuJqs6CyBjOxtAItnrq2+KaNoSEac1g6olN6eQQFdaBa3B/iAzORMAcbGW+8Mw0j5GTIoUXLGhsF5c4Ckr43xuDEZeUvxUuKjZ6b5MGKuDO2u9G99S5cKCMS5xUV1lAAOmvSLhS7RJV4EQ2ot2xsHEGoEXEEbTiVTI04osL6CqPhEi0RqLyiCwe01Gmfex8PRYhJT8y2wWcFbGNnPzCE+NxkEYQLfKji4psWEUeV8WOC8NfMoQ0heShsEKrZiCiuBWNCnolvPH5/P8dI+hhmOEWYRp6ks32c7gXLRlTOjHoqDbHwi8JbqEBrBMVnOiMkS3kslYqh1ZBsXS0UaRcoi5hkHYSVkF8AJlqp8Z56PuPsqS8FZRNCeGU8H6ZS8GHvqQvSh3qPOM8ketpaF+piIaG/hSqLB09HJV/YUGUaz1GrGhSKcG06TfIYOu3iSSUIYOI8/swO509vYzFM1EfBmMAgqrCuVh1IKAfo45lP7nDjLY22YccZC9pGgafPyIaxzunuDZF4Q3k8I8YG+mDjulAaCNShNuQQ+EBwqXBMjIlMo6sCVzIw55IFK5R9FYnJv97TSsdWTGZAQbDxrcs3U4OCC4fCiYYE5swBNVRRcj4rcZmWCPhQ6xRbmZxjIljwnayZxd/oxdXCU4RqvLk2POhVcj5D5TrBMjQYaVboIb3V7U/vUQlhFy5Z8L0inhCiVBtQgxPJNgxjokDuAQkbRCSENaY7owTFSA2VoMZTx8IJKhq8pT6UFA88Ogj5aaziPFNMvEhL8aJ4I1gfS+puTXnGC57LC259CYeOHcVWJpxV5/D7C3YeOsUn3vch7v7Ix1ns7IUCl1H4SOtuNOVhJOEm7QnymSXRy4itTAek2CSa7igJc4j+5J5ScRB0z3S0p/x8laX/oBy9/BzdMHN7flUR3TSdaCJYET+fPhteHJz20kEelbF5DNvtv+Pz+qS1ymWqo5yT3i3DnhOPHSogZb/DyIHhmMc+LxWNMYWsVGSGMy/XDJKs2vH2RNt6f4/AGK46maOfb2F6StrAuFB4clbt0gt5GIZtDvdu6VHJY17RxoW9GWUuD4O5a6dUl/glKqcKocqDBUMMJY7eJjxqQPG0dBcXpzDATqkoR6L58j6QUJwlPTGsVJfHY2lV2bfC586fWZrrGFy0otF6z8bGJuqVZh4StMMFToY23qItEuLJfeticrLJVuteongM2QklcE1GtkRmqt4NkpglVnzpNC/xgWyamLyt6QIwH7Q+54NQUMUk4ek03N4dLhI02BhrJlGobtpFJrSCUFd1vInbhByTqDy0TQhTMpFAp1jpSRzHYjbDtS21CX2knIwwpyDQW4L2TUzcAUA9VgzGBM/KfLGAPaU2ltZ5FrMF6hyTugYfSh2i0C4WMTRg+U6KYO2nq/JVaLT5QI9YFky0fqYDMUwK7JHPItxpGEI2TIQvLU094lAc8rItVaVtFwHfZdhaaCyzzVAlqMsPSevTP/CRoUYiFgwKQwJMj1CVlpxkGMhWht6BjUJ4iddEPLyi4rMAmyoXJaKYrBNoKINZ4ilZMYJwaPLN0CWOS+KXLkQLVaz6teq1WHfyLkjrF5Te1K6qojGfSbVTGJVgPBDpPFFCvHHeFyUFCwtdgh6zTM9E4WdomUt4TxbadGFjxrdzEM/t0nrF+VlrO1wbeu9rftbHCmM+X4iIECsjgXdhvcJN0B4bq2INcdnbvyxDdy5NT6AoGbY1liq2Ey4OTInRqVpfrDalnQElzzt+3wlggUmXWHXlPokWd40bvqzvr6p4HTSuGo0T2ov/D7pm2DdGTP+9cv4ZX3Q5Lxk3HV3XoIvGs91Z+5KwHMhXzCvzS1ssPOtjImQMf4sTCIpvvDgwkYJQoSYpiaHP1KjT4sxqd4lY+j3vtcj4S/zlPehDtbckJLei+NrQClBPuOYJN/DSV72CK667Gm/jmXKKbYTtU6f59J138YkPfJi902eRhQv3rEg/GbjD8WBPFLRtLNxkSHPTZxebKzeE3jNpHYt+hvSofG+Y55D+PUhAvZjxDOexqp2Sb5ZhjqmNYRjTqvbGcNr7PvcLKXpAC1wlGK7BUIAt2y/DYYYKBFy4zOvF4nio5A3nPPb3cA0OyrNY9Vm5D8b2TtnPQW0d9P7w+aHxqHyvl1t7gJp7oT26qu/hGe3NK/fbra8SIgIaHyI6EkmS+EIw0XRt+kIWCA9Ho+4w83sApUHCEKs2KvGetgvDRSsa9TTEi1sRJibccO0VHD7eOCox/CS4CK2xeVEq6QRO17RBERGBmD8r8TKnZOmtogWvMlVApYRwG0snnNqofLi2yQqCcw2+DXdimCg1SAynyVY0F5JOm3YRkmgIFmi3aMNFV5OauqpomhYRy2Ixp6pqjCGGPoVbZMUIxtaoQtt6amNw8zmTmBAsEEITVJlUloV3MYHVIQZqY+Ntrt3ldRuTSb4MZW9/n7PbZ9iyAq1nsb/PBOI8hLZpqG0INxKBxSKU0F1KFhfJgbql5cYYw8K1vXyUfHB9CtUYD41ihJikzVgqENC9X+ajlGFeacxDN3MpnKl3S+7kTISyRV+zEBc08365vIOsU0PhG/oWlvgRyZI9BNXo8hwwhSCohHqsQ2HaZ69Yn2kYY7KQXBKyNI8hvnt9FULQkKAnvCRyVfaZlHnoQgVKvOVQuiHhi8pNWsdyLFE77I0rj1n7DHKVBajEWVJ0SqbsomcuKC3LjCadgYTjLNKmMamn9Z425lOVqkiopCcQS502TRus3JIEhb4gB8vlZ0sIZ6OzwY8x8sqEi+0UwWmwVrUotaQEvCQgl+1Gqxj9fSxGsuc19V8KfVm4jhd6CklwlhxuGt8MYW/RsxWE/TgPjbQbMr0YgzS2YARY3kNS4FQ1KAvdmY3Pq2ZlyivZ8JQ6SO34GD6gKHhoq+DhE+epncdbE5UdzXMI/Zqu/LpqLtucmLdzyVteaCpEpXOEvgiCxJLk3hicDYUk5lY5evmlvPBVL+fGZzw1eKNNwL94Zb67z/2f/Cwf/v338vADJxHnMUr0iHQ3o5dnvsRld2Y75WJMkR8K1kM6md8x0ntnrJ3Ud7djtEcrxoT18vexuVwIhnQr/bOqjYOszEu0Eu0pbkM6dSGFIz0zLPhSfBvJVaDJY+2XhruS7g9xNVSGht8fNMYhHKTcpQNeGh5LWSK9O/S6jPHgMQVviCNVcvj6MHdziNM+fsbvIFn1bonvcsyrjKOlwQxh6b3l8SwrVonOHbQOB4FEA3ky2tT1hFnro0Gs0zTyWYZexbCST3R7vTOgjffZ/d/igYa9FtzF6RkXr2hsHj4cBuY86kJyovpQT1/iBIKF30SLFPk24qSBpbK3VbzTYlgppLzMriJWVbGWNlbnsCJ4Ce1UpsKrC+FZorRNi4Vc5lYxWIG6qgMD0qAgbEymMTl7o0eUJzbeEWIN3nmm9STMb2ODRdPQNsLG5iTc1htj7GazOYtmQRsv+rMKdRU8EtZaku2/bVpMHUqYzmYzjKlofXBPh9vKg+IVLsgKcfB7+/vs7p/HTifIbB5ueXQ+lisNO8lpi3fh3o60gdq2zZcRqoYSoNZ0ydZlYr1Vk9eminekdOV9Te+QQXFYk+xdKBbl4RqreJUE6DL2tSQiY4xM0j6iT3wzIfE+ChawvbMdclEI1iLvUohNnyCVQnHuo2DcXlkaT1IkQhIyvTYTaHkOirYD3l2vrZLx+8HfeYwFKg4isgfNryR0od++otKNMVl3tUdIA9MwnRBIKU2GtXMsX46pqqEcarFvegoQfWFm7P2Mn2xhTEJ2EOzSE4YgLEuxJ9N72SpFLC3rOjO4qg/nWn2vzVLxC3KM4NowbxefTfsqnSfvfT4/qdxgOZb0u0i4tTwlJ/f2s8Z8lZhnYWysvuQV4xVjQrU/9WRPT7onI+2j7C2IkvuwYENag6Q0pP+8i+E1cXf3PBMS+wyusg4v2oWNpbXz5Z4t9zSFcEFihHkhEE2MjswsVQlrKoneSBxzGGDwKHe0KXmYcylHFcRa9o0yV89UhcoJHpcrrwWlRfN4QxlaG5SvJKjEgE/vQohuwGXay2lcuhTL79WHnCURGqPsi8ce3eIFL/oKnvfir8RubcT7d4IS0e4vOPPIKd73e7/Pg5/8LH5nxiS255o2lIC2IWRhSCtLQ06pbAwNM+XzY2etv1fT/NMyjQvD47B8GezFwNiz5VzGBLagZXaezaG3p6SF5fgTTUpnsCwuU9Lbsb6HbY55ZNL3S0pDVFzjE0DksQX9Te+W1SpLGFvL4e/pzB0UNjbES2/dC14QDmMRzjzA8xBfY3gYwhJ/HTwjMv7e2J7L44Z4Nkf482C/HqhUwdI8Sr7SU14OaG+I4zG5YmxOpZGgW9PAv4MXIb4b+9zd22PummAUCQ13SoNIjy4vjUfCHWz57wOUjW5eijOeuVdaufDz8CgUjTe9+Yc5tLUViLE12Xpb1VW2KCaPRBp0ElwlZXVLYBVKrDxVWqXoGFfQZMONvft7+8GbkZQTESbTKXt7e6gGa3jbttR1nS3BdV1ly1YSbI2xDO+UWCzm7O/PMUbY35/h4yViNgreirK/v4/3ysZ0Gi6Fk044E2NomzZeUNhVURJjQ3UY5+Lt3w0SLb/Ot+ztz7j//vszIQiKVMDh1IZk+Ma14W4Ir7S7MyYuWm815LmkOGwK4S1t9lxlRRU1rndI0tqkEriB53eEMAuYSI8hQXEgpLNkpPdcDrUJd5+kgzJGeLPVXvsemNTHkEEOPSJpnCbvcWFzY5N6UtPu7IY8BfWIXz7o5b/57Z4SoOPPiSDLNC5/l+7vSMJ+ZhgAssKyJdKbU/o+E83i0Jd4GhtfiduyjHO+NdWECldByir7i3On2xvposnQRmclSswrJIOFd5Ml/CDBoxxv3lssW+DGhIKspHjNl8v1GKFE3UGS4jlyT0tUEJzvPHo+ipBKiG8NyXT9mG/REDbVeoeqp4re1ZRYPZxbUvJ1oFgVmAjMoljnci8ED4Fkb7FHwn0iUbhFoapMDlcSkahoRRym0JoYptq6tkcX+kp98iqGrlOxCB/xFWhtuoumq4QXQt3C7yLkam9iQgJ2CWl2qiHEqk9r4j1LkrwqAfxAKexwJJ2SAvmm66y0Rvx49TiEShWnwj1nHuELjzzI0696HBvVYRp1PSYsA6+ZNd0YFQ25ej6FtQbFu1M2kr5UeJCLEM+mMszE46c1Nz37y3nBrS/lxJWXhfMT89ZYtJx75Awff/+HuPNjH2e+P8POGqbEwiU+KIyBtwZvky/2XUm3Vwl65X4rDQmlYF0+1+1WHRXahs+OCbNjQtYqWCVwJZwOPTIlXSiFvYuBYVtle+UYyzkdJOincaZ2S7pT7olSAQhtDMYk47Rw2O8YnUxr21PuVgjq5XvlnEsaPvxMVXPe5SreUyoevYiFkb77AvT4/FT6n4/t7yVDDp03dNWeGq7zQWcGxvdL+W6iaUOcMPh8FY8b4no459F+6WhrwIvH+TYbLROPMckjNBxXlLWdKmU53CRHrpprAmd8uHtLlJqLc2lctKLxuS98Pgv66XKtNh6QsbCQtJnGDl4g6OHm2tRevhCQwMitMdiqYuvQIfb29vIFe1Vds7m5iXeOc+fPh5CpKHDbaMnfi5dvleh1bVu4liLx1k5RKYXeuq6zVb5pGpxzTCYTppMJ9WSSvTNp025tbTFfLHBti7GWyWQSKrEg+LZhczLl8OHDuTTwue1tNibTWAWocEUSEhfFw8K1tC2YpqGq6phMSxcmkphF3BjJ+gEsHfokDAzLyGK7OZSXJYZ1q+jCCrp1C4Pox7RmhbIQaJJnKQm7ZRtjQunw8JdhRCn0qGQ83nvqqqJtQ6Wzvf19mqYlWRtNtEoO+xhjHCUTWMUgg1V8RTtJCGeEoJT/HyGAJZMqCbbEEpzp+VKRK98v5zDKICDv5YKMpWHnsQH5jps+03EZjRqN2iISLo2Trq0hjlW7MJml/aP98Q7xPRZXrITqRBpxky8N8qFeU0Xfqtgj8hK1EU1W88KrFQzSUfkgvx9Cp8geDO/D3FvngiBOnyn3wgkGIStZWRaD0/4dOnlFNCXrmuypdarZC5xClMpqgmLA+3Zpz5ZtajHObp+ltS/HTz47YkwoVrGUDUi8Q6f/rkhQypDl9SzXL0Gy/nvvQTsFXrUI6wqdFW+OhKJId8Q1Wvuc+lAhzisNysmd89y/e47rfcvCOdR0RSmWz5DgzJgVO1T7UzWIlF4NoiLejam0Rs5wXHvjk3jpK2/jyifeEDwYcQ5WDH424zMfvYOPv/cDnL7/QcQpVVS+Wkm5ZjHfLOEndLoUipT6HqNvf3QQ+is3+FY6Q9AqofYgOj8UnC9E08rPS+Gw7Hpp340I1augown9ea9qE7oLgA/Ce48ep9C7AaT3V13wNmxnDC89hWaEzwz7GhOEx4yD4d/+sEt6PsRPkkWyUjvA15D2r5hsPtxS7PexdSzHX3ocyvkPYUwpLtsr+xkqX+UQhwrRKhgqM6umv0rxgMLQqfGaARTvhbqumNQ2erUly7nGmBhZpJ2BJsrwAVeKp1PUjawuG9xTNCAUwQAOTY6snHMJF61ohNthQ3yrawMxdN716ugG5tqFiqQbvYOQFAYbwno6Ibmu6075sLbXlipsb293mla0vJ07d654prv0rURI1293UJxr8/PZoj/YTN559tv9ON4u9j8QAY/b2WFjYyMkYxPGc+r06RxmAkHhEUJSqbWG/b19ts+fz1VnjLHU1uIITLddLKJgHgSoqqrQ1mBFcTt7VM6FfI5YyjILDISNHopWRIto4kiqUcPvvDqlUlDmaCR8lUwyKHyBKIoUAnNsXykOuA9Mt3VdAr4xIQQN7cr6JXyVl/dlQTT1ScB7Kr+baH7pPUnvuUiM1HtMKBsU5mBtGN/AU4BIDK1awdi8R4v487gTo9AZQ0Mi4QyCI3kdXBT4JCJLYwK1p0wsTS1GYh8k2Rg6ojmUpVvYPiMgWhih8CCUhFxjaWeE0ouSPguMrsdCSc7Slpg0lqmOQTJxC5Up0JiwKhJvPk64ioukBW6txUbROeCnYwBW0o2lvhxMnGcK3Ql7uGMcBT58SmALYxGglaAQSSSAbczJ0rAB8T7gIe2LsH/CLdE5JCzOOYULOXUxtCqsvyF4LZzziO32Tgo3tNbmEqLpVlaBnN8S9uqyoJU2hdfgLXYaSmFbBeuVuRGCDSXsGYmXUIoPVn4rxMuTwnx9MrxYG3Ho+oKChuT/sF+Jwr7POHVNm8dcFlUINLXtvB1pH0tkZqbYWb6bV3o3f6Ax/EwlWt86ZQK6cMKkTOQ2Xdv9XjDuZIWL9sUcDtd4BWNwXtmbzdmbblDZeGt8likLgUMB2xcK0p4Ugvcj5a8EFi0x1zAWOKiCguBRjl95Ga98zau48TnPxAlQBZorrWP79Fnu/OBHePCL93DmwYdpd/axbSgMYpBYrjZ5lW2clYSKgMUiJpocaEFfQBoKSiWvLJWDYSx6DyflmhXGkrwGI8LXEvSJ6dK7BykAQ6PUyr51rIfltobvllCGAIfKW+PJwCL9tkrv8bDt0hDXfdblNKXNnb1nhUGuhBJXpTKR+OgQL+FHOk9vej/2q8VaDhWLrFqnvZDyygrWMCbo5/mX4yjaWqUArZonI3Mae7Y3Z++xtgj1Ld4bMyCO7d+DnjvomTEY7rmx58YU1NJo1e2fJNxBikhIvLmyluNbh7v2taBv4RHyB5EPJByVpqT+KDqFuKPO2u2fJHNOL86ocdGKho0xyF4EW0UCHOojFi75+KyteoKhjfkPCXGpMojXwAgkCr7O95N6w/u2KMvaF5zDAYjEKN0ZoZ1mm1z5aQF8wrO1iLUoIaZao2CuxbOJgflYWtUTXFGz/QX1dJpLSXrvcwnL3HcbQpcWuwu8DyVxNzc3qSK6jSlDGGAyCTc7iqmwYrFYMMLCNbhFQ7sbEsElji+HD8XfrREmVRUsCTHcwYhhjIhrMW6gt6HzpoieIRF6SeISBbFc8cV3wqBIDONAaBchUT15fUBQCfgtb0vtQnqC+y8oNUGIkXh3RK9KU6GYpDG2rsG5lr2dc0wnlrmVeHlYd9dKXN6QHBuVwYCHpFQl6zvE44MSPTEUe0OSsBuE1BzfDZ3CJ8kaG/MbYpihx/eFLx/KO5uYXaxRoTFRCNNy3JluSP5/Oh/JC5HG4TUoeMZKFjzVB8EyGNOScFl4MBAaonLGIP5bQWjzbaQaXsznwXX0KODOdPvMNS4qrqaXL6Mooj6U+oyla5M3yKugGpKffVRgs7Ifx5gnSwjLNMaE2HuNd0hoGFumDdFo0XrpDCMxJ8IVFsagZCZ8Cc4I3pucm6Hex5vDAx6VTokwySNrQp5X2kkiXeywNTZ7l9KZS/vZR/9BtVHjdncw6nEuJIUrFt/GW+6FKIAKeDDEiyRd2hlxMUTC3SkRTx3OkjLnUfG9cSa8KJZEDhIzyyssNiaqa+Z9kqpxFVzLJ303K6s5uwlNrjGSPBHpc6QHgax0Ak5S9jtSFuiERn6QFPfUlotVtxaibNgNNpxld3efnclR6jZ0pxo9BtaABs9RJQK+8/xqrIOdKnhJ9DKoesLtUaHQiPXBQ79YODZOHOb5t76YZ7/0Kzh8yTFUoufPK4udXb70yU/z4d/9A7YfOgWNy8jKgpkIVoIyDqEycikE9wQTTWaCzhAxzNMAlv5NvycDXY4WqEbEAS2ojg6EQbPcbloyO1D+8r7IYm7x/IiQnj4vedjQo5V/kP64Cii9+On78u+yve7dsA8EEyMjwp7twgtdVuyGAu+w/6HnKQuNBba8dlgZW6sShorL2LPJk1wavSAaI0qBtRhzejZ8GNaJeEzTnWmrhGXSjFK7UoSzieTz2XtehwpcESar3a5ZaRQcUb4CrQ30ZhhqVc5zrM1SaRjrq+wjfW+E3g3mF4JO7unOxJhCUxrc+/snGl4NOWJHRNncmDIhGPBNXO/ACQLunXeFntEpISqA6YwUfTBIlFdVkmwRogfSZ0OF8CC4eI8GXbnaxFCtCcKtFx8TDzUyQZNzM9R3cYoi4Rbu2XwW45kDc875FwVBTcgtE6J6VofCNTfcBMNNlt5PmmJeVEOvHe99dx9IFBws3RhFJIRtec9sNsvjTjH5KR4eoGkWue/9/X2apmFzc5PpdBqEsKICVHcAPCoWryFno20bXLugxsfnuxh8KKpI+XA7dskoxtyopdtSjGC8yUlopfs3MZ70bsJlrhJlqqwRZyWuwPlsNsu3qU+n006poX/Y05o6DZekpTEn5SatX5pvVXX3blRRsRIJyuLe7i7NYhEImwlehKR0+WKMEC+cUcWYdBiFeOVVj4HkQ5XYecGHkrCGdlYfKeS8gBcXLoZTg6HzRmQrsBFam27+VoyVWEnJ5LCXoWUGiMqSoYl3U+R4ex+UCZ/uEYrEIMS9h2o9pJ+wS8gGgiQ4qhbKQjefNLlcHcyHuwmG1qCOsEtQzHxUPnzXd4vHiy+UKS3m2nmUvCcbJZL6V8iaebwhOTh8mJRho8EanEPOUJwnC9CpfU3jSnu9+K5VcB6cl3C/g8aLD2MCXTr/5RkLCd99i2R5dobCXl4JsVhj2JhsgFhaDxKt61MxiBq8Cwg0hnCvhwhNDleKSkhZbjArqh3eEi66JOu4T0qGoYEWyaB8cKDv5V/aRUtpP0QifkRe9OIrMSEPJXlMyyIgEtvRaBQQjRUJfR+nTeuCQuhdLr4RvL0aPe/C3Ds2poe5/tonMFHDrNFQWjZNmk79MQq1gcoafOviuTY0iyZ4qpzDSFo/H3EtqHgaY7AT4ck338zLv+7VXHHNlcikQnzI62kWC848fIq7PvIx7nj/hzHzFvHLwm6HIMnx1RcDJS1NMepj4Xljzw+Lc5RCTvl8+rfHQ7i48fUbWzZmrBImDxp/jyaOCIYJB2WkQykDrOor8yTf/Z3OVlY+Tf/5sv1Vc+oE3MLjIP02hu+OfVfS2KHg3AnbkJTOss1HE1onkAucjD1dWtu7Pv940Jv34PMxBW4o3yRjw1B5Sc9k49xAPrwQXEj5Gz43nMvYcyEUswspvpixpDlYYzCWyLyiYSvKJNmYSOf9TGXvl9qjk3EyQ6WcQ1AxUfKdeOX+Kr1cF4KLL29bTzAmKhPSabd1PQnDlH5ycPosDLgjDFVVsylBwLW2Y8BlnHpZwSNt5nBreN1rvwz1KQXiVN1oPp/n30uBYMxKkqw7SUAuFZ/URxpr27Y5YVZEsjC9WCyy0iESiPdiERSO+XzOfD5nY2ODuq5zG1tbWyGnI1qn26Zlf2eP1rUYbdiobL4JVX3bCwfrFKg2WMYLXKc5lh6Etm2zwhQSTjULo0O8DpW5jmCnhKuOiOWb3+PvdV2zt7fHZDLJypdE93DPI1W0O8wfKYlBUjzKELuyNO6krjm+dZT7zBfxztE6peQGzhUMXUIcdhCSNHgztFRQXacs0FnbPeBcP7bVReHcRDUlh7ARLXcerAYvRWKwaErSMjhV5uqyVRaNZZzjvML9etojnhAutMSYeDu95DPpNUj0ITQkStBRaPReUekURIm40IznTqkKd7J1+yj7eIR0Q1zwGGWzU8ItZJYjxFwKMCn+n6TAAXG9O/d/UE5Kgug1CNRhbRTKW+Do8EnEuwImecnQcJMRGoXvoCw4L1nw9h5cEb+arUyEwJhWJV+IpCqIC58lzSkJaiV9c67YPwl/BW1cxYCEUB58Wm+gbWAAqcKcd2FPZGbkHFUV92HyfsVQm7SOYXlLuhh60YSychwyEBo1GJbyw8VzperhNeG32/NlG2m901jyV20U9FzAdLjoLxoGRPPfvf3Q54G0gXDhUBrnwLfYuD3EgfGxgpzAockW0jgWjaORrthI0Ld8ZN5Kq4ZKTCxjDs4twnfeYyV5bBV1DmPD5ZxUwrVPfByv+Lqv4Qk334SdhP1aaZjf6Qcf4tN3fpJPffwOdh45zcQJpvWo6S5YXBJk1OfJXowQnvhUMDi0o8+M7buhke+gPrK3KXkGjCy1eVHC0kA0GRpRDmprKEDmc7fimTTmkh+WvK3su7M2J89zX2jMcoI6hup3+dxQ8E9tl5/le4k0YUSzwW847+XQq/7vQ2UjfW6M9IqSdOtmsqI3SotUO8VtcPyHcy1lqoMEzotSbIbjuYAiWq5X+ZkUn409P6w6eTFjHSoCeS0PmNYq5THNszxvpeH1QmMr6XkoqZ/2ammI0+gJj2tZkvZs/ElFUAaXZZb0NtJ3n5TsbluE94xJDV4QLlrRCEpGGoWhqjphsZtEmHQnGA0PcrAGGVNh8IjRgkj2axWPHajSvVtW0xlq9Onn0KFDPU22XNjyAGeBdTLphQqVYyuJU3onCUlpLCF+O5XJk9xGck+nZ+o6hErNZjOccxw5cgQRYdE2NPMmKhoNlXg2jYkXvvnsTRpaaqzpX4zXrdly7fL0nHPxBm86nJQ5ENBVlEltBI9Cp1CUSkGp8CU8LRYLRCTOF8odX7brvcsl24ZJZmNWiTTWpLBVVcV0Os34t2poXUvrfRINMp68+hiXD+AycYpbN89HuoF246SzDPS8by54Irpz0FV8mHtILgLVwFCsRiuiBi+EV40XSIb+Fq6l8l0OBtKFOYgIaqpQchUQTVZ/YqhHyG1Jib0KRWGEmNTsk3IX3K2tc3jjs9LQkaukIAWLbkGjch5OybB7pFXAVDa4BdI04vwEwTrJCmsKkcovZoJahksES36H44FFWKMNRwA6S5sxgmrbUwa8C0qP856FaF7TQLfCWIwET2HbtjSuxahiNFrboxUpjS392zRNRtDQGDA8i6URwPtQorp1IezSqOaKcq06vDqsqWL8cRBUKsJ+tipYMVmZNDEvY4n1R6E9C/FFPkU/6VoQld4lfj3ljy4vJs1DRLLgmdYtM7NE/7OymtY34iLiNBlMMn4AvOR5CNLfnybwF2uAKhqECGW5fduEEChVJibUFzOqTBQcLuqroT3fxPYri6qj9Z03dVJZjLUYoqBtgzFIqgoMHD5xnFtf9XKe86IXUG1N8bUgVtBFSztv+fSHPsbHP/hhTp98CBrHxEuoiOd9uIjdLlunS+vwxSgZ5felJ3hIS8eg3IsHJduW4+teZtRKOtZHj5endSy+W6WAl4rAUFAbGtTSd6XBq/QijikpY2MM+I+h3YPoivR9Gn9qayiHlDgbKlL9qnMRI5EmlnMa4mHIF8ufcnzpWe91KTcTyGWcS0E9r21pNCLKqFqc4WK+w/XhAnu0xEl6d+hh6c+7m0+JkzEv1SqFd0zOS20MxzIU+sfmuzzGfjjfmJI5/L18dmx8w2fLsWmBLxG6C219P6cjhNWmcrhRQdAuHK3jr4qmaplhVHn9hRBmbMJFd4FGE43FqqHvkXmtgotWNDqqUiJeOsZsErHzxQFNOzddAtUhScQiJrRTeg5WEZ/ys+EBG7pDh9p22Ua5YUWExSLkUdR13bOul8+VG7QM7ynvpFDV7A0R6R/upmmyoJjq7Xsfau83TcPp06fz3QnqfKg8JUHoQQT16Ybb/sHLxEJ9Dn0oPQMloUuKQUk8Sxg7rKkiV3n/RZrfGBEv1y4RhKSsTKaTPL40joRTVAOTLypnAWxsdHedzOfzHNI1VITEGM6ePYNzLU3b4hYuxPrH0A9jTBASYonNVEd/qJiJCF7DGBSi16cLVnd0YQXpfReF1qF1IzEPL+BLr5uPxQKErBil/WptrFSmSmti4YK03iRFUiJxCAJb2muudZFBki86Sv35FI5lQt5SVqRkEZJZjTB3TTip0p3zjhmFZGKRDidttJxmkVOSi7YziYjv9lW6OV0khDXhKHJ4impDkhSnQFvCHglFFZxLykAQMru1SOOIluooCBsT7jHQWLxe48M5d8sHgXvpNKinbXy8u8ZhvCMkXSu1gDX0lPteOeNCOUqCXy8XowzdJJ1nT+tbxMDmtOL41iHOz/YxakLopgmhfSYK8RJxK9FrI/FWcRFCxsYIzw+FLcgMSoFelai86olOdh/2GWH3TDobUcVDTcpZKwwP8eJJmz1TPu5H6V2qGdobKKsqdAerFDgErM+XUIlUOY8vKNeGygniPa1Aa4NeMvEhpygpDSmPLXmgxSRF1OV7l4JnztKqYGqDEzAbFU/9smdw6ytu4/glJ2BSYU3IrfD7Cx78wpf40Hvfy4NfvA+3Owvhkz4UovAGfG2ycpXw2xNYBms3RqfKf7s2hKbpogHGhOyxdozpCnQMBdrh+veWZ9BWX6B+dOEpwzGt+nxMuB4asJISv0oGGLaTxpufWalBBVkmVIvs5IlhxEOPN5fhRcV30Y4Q+fxy/kA5xuE6rxJG+3yYHq8f4jUZOcqwcVmaeV/zGMpeuc1HscYH7YlVilb59xC/Y7LM8B3oR2mMvZvwV8pt5Z4YU1iG816Fn+H4h7/3eUF//kPP2xAPAPv7e9lwFgrjmFA0hI5mU4wtnQvnY8kJkaBEqBZ8QHNkhGryVsf/q1/mmReAR6FodJbFpJUH4p8mnja6xGcHiTM9xSEqKIMYwpLYDhWN0mIOfYJRxpqWCzB2yNO75WKeO3eOSy+9dKU7a0wLH+aFpGeS58LabmGTEpOFyUiUUmJoV37WgDFYsXgf4ngDlsmbIPVdel5SFuaQcJY5LOmzVQdz7P0sJA7WKYVADQ/uEOcQlKymaajqKl8gluadS/lJuNRwMpl0fURmkVz7aX1L3Od/xWCtsLl5iHZ7n5AuVAjjMTHYx6TiGAsDGkJGSoZR7i2Kii/WViFcowQJFoBUiSmBK5isiMEXiflJSVVV6qrCV/01zsTBhHAsUxCH9Hv4O+1rwIbEZVCMqUhJ7kNGE7wuNgtkxnRlmg/5SVbapJxfXJ9kDc/nIsbZ6wovJBKMD9k7Uowj5DF0ZaXLH09I0A1li8vzDkLwqqbPkoEiWXH6yneqDCbYVKUpaFdovngtKYRx78Yqc0HBi7k8MfyrMkJNsEgbDYqX95LPb7agxjPQti1N0yAiS+e8xEeeX8jiY1pXPOG6q9ne2w/Vk0SZiImVyViiUd6FfAFjTCcmCD0PQLmn03p4+rQg27SiNyPjfkguYjnXjj6adAxInitFe21kxUI6I1jHF7o672EuhVA1VDzy1hKMHVeoABo0hCh5aPA4G/JrrOvCACQpF3E/Bq9fKCKR8GerClTxxtKYmtYo1zzpBr7iZS/lysddizMeJlVQhlrlzBfv4zOfuJOPfOD97O3tMrETjAvGI2Ns0JusoRGB1uVQyyVBRPpTO0gwKw1Kzvne32MCylgbQ+FnjGfmsaXfB38vrdFFCp/lOC/2naEgVpYdT9+Xis5Bgnz5fG470rqxeUjUfYc5MKsEwSUlwZfPFmdSlwXSoVI12t6IPBQ+62Sw3rh6MlvfaOm9z0UIhlDuqbKvgK9Ht9ZLfHZkvtIR7FFB/EL7OrVf9lHKiKU8WUYLjO3BYWRLnnfi/cVzJa7KuQ3H1eeHfbl0lWJVepLCI5EPxoqw7XwOqsEIqGEHCPTu3QEg09kkEy3v9SBrBoOIp8u/yya+R2c/uHhFo9tg4wljCcYWayxmDgSRUAbW+VQq0EZmpIgsL07Z/pg2CH2FZFgud3kMMJ1OufKKK/K8QmBEvBjJh9CWUqko59PHC73+SwuRMTbjLj1qTZfXMJ2khOk4BzF4NaF85XyBIcTEE58v71RIwqkx3aEZjk2iFUZzacykr0r/4BOGEITdmBRubLQ+xhrfUZdMylLKuVh18V4+zM7Huzk0Jyd5wmVYbdPS3XwcvATWhuRX7xuMMbkUcQ/XCp5QnevY0WNcd/XVnGo8xmmwGNGtufMuVGMyXdnWLKij2euhDJLRpRPgQ+51kJZ8wmUpjBMEqTIONAj4A+JsNoLnInpCwvhieyaGwSg9i28qsavRmpBCrcIldCYLcepjNZ6iNHPYUwLisZXtrPBRsUAJpWglhfwNYvuj4JXiiNu2zZbqFGZQepoSPrKxQMKeNoXC13oHTEgx0QFfMRemYCZZ+cpI7nsYO9qSzpXJjNvYsNbWRGVDpBDGIl58IQCXgrkRvCFfZyQodVT2DIJvi9hWDUKyicUyFvN5ZwiIz4Q7gwoLa9p3EcHGCIYQHrlR12xUlkWzwKFMMIhGb0JkwCnUwtc2n0folMFQPragoQVj1DTZlOwd552c60lhyZdXSviky8mIume8zyR8F++VsImOx5DFeA7DnBXymYnz0SLMy9AtQBhBR2+QvK6KUmlXelfyCoWWpsaGxG2nWBXauGZGlDYchhjNGN5NZXMNQTkREzxzlQn8oDGG41dfyvNf8iJueNpTkEmFWkHEMt/b4+yDD/OpD32M8/c9yJkHHkLnczaCexoroYKgR2O7UWk2kivOpTOGJjaeNmOiKX1hMyznspAWjFV2ifam54dCaQm5yMNInxdjDS4/K2WAJZ40WOGxuQznmBUqYyJ97PhM8AwtXzpYCn2rFJgh386fj4wxfTM0nIzhYWwuYWmDUpv3fmK4cU+LLEdtlIL1kL8eCBLPajoXPp8ylD7tLPdOVzGkoLoDYbicb8f/CgZY4qAc0siYlxW5QXtFP3nNvV+J62EXY++twmfZbjm3EC5LXvsoPIQzTB8vq5SMvqKY6F/6Se+P763uva7dzlhYoRgW3jFv26gzaD5oIhKvF0gKd5ezGmSuxKM65UMg5P7FubgkR0hiWxJqiQzW+iC4+PK2RYWlkiiVWurw0JWCeakVlofae5+reeSJGo9Idz9HacFOCzlG3MYE3XI86d/SXaiRUHXvFH0UXplyA5XJz6mdoaCdLJxEi1VdT7qQFY2x+bHWvzHBepaEPwXEWKxVmC+y56d30RXlpu4zptJtTCRozsUykJnApTkCMZ4zCZMJD5WtOyYRK/QY03kWyp/0XLIwl0pe9uLEfIq2acKzLoaT2ejhaMuQvOhlkM7ymBlOFJpwIfG5UY+pLNosODydxDj3IsZWogBuO0Ww3Ad5jwGN11DhJ65VsLgCMUk8MYiqGoq/ca+jeOmURi8EazVd6F1amO6OFnASGKmpQDHgNCuPqMZwLxCxsc0Qcha3WF7rFGQn0q1nXgcjIEGhIZcwjopFJpjdeVENwqb3IcdIU2J/VBZNLN0rgLEjIkTqW0Hw4CLh0+CpEZFQ9jiFrPigYCVlXzLuk8BrQLpSswaDRtoRKoxpUN80CHU2MnIRDQKfKGiLSUIxibAmUZWuDC8e6xRL4WlNscHBFNEJYGJyiJp3/dAh8pnrmKAU9CfTGk1eC0Voseqp1EU8dcpUOLNx06DYNP6E+vSrW2YCqtq7x1Ujbof0jbTvvIsYimXKe/SQqAB04VOYkPYlcY+p11AevBdGE5hgKmKQmW3aiyWTJp2P7tmsOBNvl89MOrPIWPI3eIMEwcYmNSrVGueUUSYmKiI2pvpYtBLmIkwPH+a5L3weT/mKZzPZ2kSqcFeKVdg9c45Pf+zjPPSle3nw3vtw+3NcM8cqVBrXP91DQNy+KHUU+sR0d9zkyjCasZmh5HVDQbzjhwZrl73WYwLicE+sEpbHFIb8d2IsI+8M2+0pEqtE+IGyMfzdR5qRPitz5FLOWUnLU5tjssmYzNDHz7IQm8OwOKCKT9HWUD4xUkXPy9AaHxUxofd8msdw3GVxlyHels4x0OXqlXNeoYDG+XVKUDzngz1S4iML78voGIUSL6uUjKwQlbz5IvZ0mGcf7+U7F1LSSnkmtwm5khMU/GGwv0uFcNjfcN6ZltHhsiyuszy+zhCXxxTPvBfh7PYOrvFIrNiYjZgootB6zbwOQGzMc4ZgdEGSDTsrHhTnKnwew2Mhh/09Cj3j0SSDC1VlMYVFqhMwS2GzXMxI+E1w4nQEoGs3afjpnTT4MUF2KBymtkvX19Clmd4vv08LaUx3c+JQocj9aL+tEsaI1/D3sbFQ5CgMK2IFy7Og6qLVlN7FZknZKC0foRRuP7+hr4T0P8vjk+VDkhUGFGNs7idXqyoYWcJ90zRZiE4KRunRSVW1VJX5fJ5zWZqmoa7rpco9PcsZy2uQvrPW0vqknIXch8lkwtzF3A0tiIYN6sCQEZRr6n0sV0uXP5DXJCxQzndIuzYLSenuhGINE46rWBnCGElaQLTux/dFwgVwSYGSkEgtCs3wltUiv0AkJTt3BMhYspIGwVMRBx9sW1EIX05eLPHQKbRD70xa47Rm6aZrESmSzru1KnE7doaXjQNR9E9nlEKGjpcxMRK+SLEnh3slGqgRESpr0Wgw6cbQ31cBG4Kx40aN4dyG58rY8VDOkpYNczXSM0vhjVpYIgucJSjzxPJYRkIky7OV+4ttj42jj98OK8PQrQ4HfZwnocWIINEb2QmrcbcV9Db3PzBClVD2NwzVO0iISJ/Eo4UoWflAg+AYqvEIVIaFFfxGxY1fdjPP+6oXc+SS4zgT9p8BZtt7fPJDH+HOD30EFi1729uphFk4EyiY4MGz8cyXe3VMgFoloAwF4VW8JQis/TVOBr6S/w33efnchaB/tlJJzb7A1MkB3fiXYIVUWs59iINyn/TpheR5p8/SO8Mw3pLXDaGH50ivx/q8EAzliKHwPBxjHl8xpLLPVWtWyiljyuVBtCoIlr5HC0SElTtrsAdLWWFMuen1WdCvsXaHsEoJGHtmOMfyDrUDFZmRfss9Vj4XdMPVYxqb+8XslTEaOmyvxO2q+aT84no6oaorsnJIZIkiLEhlqQNvH54J70P+X7o81RgTQuhcKEIU6EeiJeFyX0eQ1Vevbh8uWtGoKhs7TQuyrAFKqQX3/k0EdYQJSGqnsPQqOSylPFAHMvfCUp0gfVda2Iffa/gl/52Icnq+JNqr+k2bu1QYlg53Epwk2QDJ1ad6DFSiNtoG3VwkXMDmvGMYsjbckCJdyFZmOAccKqELMSuZkvfhPo8SD0k4KgWkIe6HAlCvr+L7VAY4VRBroodjOJfwd1+IyXOIjNUYg2iIrd7b3cXv7/du/x4y9x4RGQpXgBBuWkbiWvh0MZ6CClb6F0AZ6ROv4dqH8A6yUpdZTnF+EjETE+4UwStBXFlmSMYYWu+WmGjGVbZc6DIhkO7uh3INS2GzPDMJNynHYCxvx8Y7LlJ8ffLIodoL3RKFKiUED4SI3hy1iwcdnqEhLnoCQJhEty6RAZf7t5f4OBBSDjq7Q28l2sdXuR/Su0PDRvlM2dZYf0Oh9CDG2JXTXhZGShju+6HQkPuLa5egFIbHztGw/eH4yjbGhJ+hMDWkIavmH25q7zPj0rM8igPCPjRJ0QhMLOfitEZwteHKJz+e573spVz1+OtpDSysiYUBPKceeIiPvvf9PPj5L9Kc24HW4RfzUOABQYzFm6BoUJzfcl+Orc1BwsnFCTLd3Ru99Ryc67E9UhWK4JKgpbpk3MrzGAjH0IWNLhsyLjT+ZX5WfmYHdCPPOtFXlnlz2c4w3CbxudRHf86xeIb0DWv5++TaPgDSODqD5bL80+39LhSm/7ksfVa+O4yqWHX++/SGnoIPff5dttCFWY6f/XLfjJ1/6BSsVfMYGyvSGSrK+Y2F7pW4ojB6l2Mu1yLB8MxlgbuIvMnPFf0cdI5WyRxDGI6r7CuN4yB+V47BGMPxS07wgltewnRzg8lkEnAX8WispZpuYGKETbrfDQQfq6uUfbikXKji25b5Yh4L2NhgMLEGW08QW8Uj8BgrGt539blV04J0NfDDxMsFKExGGERSLNoKq1MvIcXgdTl0KvS1bDkpN0fZ9lCzHRP+VYObP8VPJ0KZrPTJVTbM0xhujrLcbhLckxegd1iL/tN8VDVXo0p1+FU1xtB394KULKq8a2RsfPlw0t2GnHCXcJUu0Cs3bxKq05omHJcCTRnyMcTn0AI+JGhlm+UzY7klYSxdPkqvPS3wYGA2n+e/Jd6aXLqZxwhFKaB0gpaPIQ5CKMWsEC/oMumKTGKOROQdpaCe+sp9ZGem5JuGAyGgOzikdoJPMoy7S+ZLHo1eVZNBP+Q2fa/ZHiGI+6rM8UnKQeu76m3p81IpGTL/LETHpnsMVckheKl0ai+UrhBSyj2T+xgh2KHvkv2UhRdyANESI0u4TGd6qBCkwhbjeWRjOO6eLz00eQ8rPQ9pgvL5su3hHhz2O5ZnNrT0l8+XazFmqV4lGPTaH+C/5wUZ9DWcy/D7IZ1YtZ/KZ8u/SzrXe855fIH7pXUo+uv/LTHcDFQEXxlaK7SiHL3iMr7iFbdxw9OeDNMaJhZRpRLD4twOd33sE3z6Y3dw5t4HmWKo23C2F84jEiyLIaU8eA3DRZJmaW7DynvlnlqliKR/L2YNLjZ8asgfV+2LoYC2qv+xPob0XWLpzfL7g3h7ntOIoJ1wOTbW4bm9GNx1z0s2BI1FSARBZnT6vTEP+yr3QL/tzjM95oUpYbhHSt5a0pOS15fjKSNQSjzm+ZeCOsuKwhIu6NOxcp5lG+XaDnG0hDdVkFSqvI+7sf1V0jq3Iom/pGFDmjCcw9gZSM+M0dMhfoY0r/xsTNkZUyzKNss1HfKpqqq44pqr+Jpv/np8zMtLSobEeaeipaE9DVESEgrB2Chn+FilKssnosFgEkaCaiFnK+EOJE0hWReGR5EM3k/owndhGIMH+3+LoN7FC5mSsDDmvk0u+mVGvOrQDplKfxjLVo0hZCE9Vh0phau2bZe8HeWmSs+OWXmHB2ooKA8ZQeqvqqpcbtQYE9MCBLEmC5elxyK3ISHfIW3ktCHHLILpfSCEAhSEOc8vxhAPXfCllXZM+BjOc3hASuKZ+ioFiSEj8b67rXu4D7z3iAuhO67Xv8c5sPRvNh+u+XAfdGPU/mGVQCpDbl2XNB+UEo0x+d05WJ53UGTFhosXiyULOz3tHTTcdJw/i1p5hF48v0i8BdkPFM4wdlk532UiHdagvHdiuYrYGL7CfuyUAqHbN6qaw6hyOJ0WgmwOYumPI8QqL++DVUS4p0jG/sq20j7tYrl9Fk7COQie1PLm+aHgA+TqUfk77RhyGkdeb+fBLDOboVBZ/l6enaEiMCYwrQoPHba/ClYJMWPPrVIIxt5fdc6GwtOQjh50JsvvekLjgP4cxCOGY1SRUEbZGmYVyNENnv2Sr+TLnvMcpkeP4C2h/dYzaT33fOYzfOgP/pCH73sAtzujVgFRjK1wrmU6nRYXk0oorBDj4JNHsTQ8DcdbCmGlQWcMxwdBeX5VNYfTlsL4QUL2WHtDfpXHTWeMSp+X7ZSejd7aI0vPD9d61XhKPpvaLvMgD3pniO/hPBMEY4Ei0nnGhqG8qazy8N3h2e3NRbuY9yVBdCD3QGckKwXUUkAe8tTy+Sy/jAiqcIBVXsn8dkyTGq5PeZv8kGZmOWQgD6Rnxs5BHo+Qz045pyG/G7473DU9mk1fURjSnpXnLDD7R3VuxqCk7WNtlPLVEM/l+Svzg4F8R1trlFY0mjlSpE4odqJOe3ewibHsz2ZYb5jGaAUpFLuE+3Chs2a+akTwotlQg4As20VG4eLL25ZVoLTTOI0Z1GseaGxJSDTaF8RKRAKYQahUqp8+JEjQt8Qk5GlfLusdrnKD9aaQBFjtj7v0oLTeDQ65UpYPHcZaj8Vel0TBRiJQCkKl4E4S4ATKqirqNcTtFwfjIOFleHA6PPU195JY9TwV0k/mLvFStj0M3UhzTXNKd0UkggRkBjjmphxaYcocnuF8xAi4wBjqus7hVLCs1JUEe4ifTgA1qCbrOvmH0GIRltQnYoMCaf19LRIE02RpiWs8eAFVj1iLNSAayhyr9plXxg99DxRJL+k6yH315jmCw+6bdJ6X77YYw33qQAvrpI3eMIFcyhgo8kniufJhe6U3ewx0BI/5LNOd02F8sLUBD6WXIf2o9m+f7wvrgzsMesJpXJein6RolAMt1yeUOh4/n6uYWXkeh9bKR8PMLhaGeIUivImDrVQlfg+CVULjGG08SJge0qa8j6JSndrsncch7aNbLjFByXCquAqe9Jxn8txX3cqRKy4FE0vPApVTzj3wEJ/6ww/zhbvuZm93D5031AqTqgJrWPgWW1uM77xAiUr4ImduKOAMhY403gvh9EIwpgjmEMeBspHwmEuMr4ChsFZ8M0LGClpQGLl6PNH0+f9wrcb2ZuiNTDdLup54/yp8rBL8x/gYJPoXwt5KvpHHIvR40ioBdCmUSZWy6EwJnsK4xTjOU5vD9pNCqao5FDnQw66MftlGmttYBEgQOyQbe+IMl+Y3xElpZR9+VyoZQ548bLM352jDKseZ3h3z6IhI77qE8vshHg+iN8vvdyVsx89BN/7hmMaeGcNPeUbKdspzMhbam3h1s1hA02KrGDmRlMnIM72VrOA30b0x2ZgG2STV+tFQghui0V8VW+wda00I5/ceayxqiAVQLg6PF61oTEzd1ZbXeJmHBJWmruJhDwpzPPhJyegYmfdd1SUjFmNs1JpAU8KzGEysXhIfxbnOiu8jsTJJ6BMDVFHQcLG/zpqkGqrAkG67JTGezvqaxjgkEIEYT2K+SCiRGISWInREulr6adOU4UPlM6qKNyaHcHjvOXToUIGfcEO2GIM1FeI8+EW4NEzIeQ3DG2Alat3lQSg1Xx9iWUjlRTXO37Uu1IpPgmk+wJqJVKlkiHQ5ICWR6gkBEuICs1AHsbTnsqU4QWlpHjLhhJcxBuEEjIOqDRteVaidB/Ex5C3VSdCY99BZSZIVP+Eo3XTtR8Je0ny9Ei5PFIlEMNynYI0N1XWSwhAVxdxO3N851jGYjgIJj8mi6ojlHLq8jyR6BzwWZVuzxYc4Fp+9b4HQdB6ZLDNqVxkrrnDmIVVxDsO+lhxShAgpxVtVY+WqpAAvC3qlWtgWFry0EmkIueKWxnh7kcKr2eFc43dKIICGeEY15NKkPUcSnqL3z9pUchegyzFJqqKNgnWq9Oa9wzsQbM8qXI4jV08qGHUu1FAoJ7nkIXFN03lheW6lgFFC+i69I8VPDwbjHI67/Df9Pipk5I6TwKsd7tP6FiashPNOMFi2DpY0Ks9pMJ7Oyx07zxuErEgkPEj83Dsfy/2GcshI5/WFcG5EQ7Upkz4wBqeKtRUzHCeecB3Pf+XLuP6pT8GZOD8blIbm3C4PffFe3v+e3+X0/ScxXnGzWXfBnzWhj6ScFeF36lO576qXZzhc27FQuRJv5d/DNsb3SxLmI14LD0mvCmEBnXLfCXcIsfB5FKjzxpPyyfB7MYylMUaDRzofPaWhEJTK+YwJ1/lfyYLFktA5RqvL38f4zhDX/bDe+HfBK8OzYU4mnvdoAhycuYHhNe1vKQT4Ys+EJjq8lryvHNtQsM/0p1AkS7yk94dKQDfHcXrhJJzJECXcE+hW7teh8SHT1QEdPWhNhs953/Hq8rmDDDHh974wP5QlDmpn2Fceb/yfSfs59NLbG2kO5b9DPJXjGSpQJQ9dpagkHknqN96BMd+f4b1gvaVdLKisZdE0TCaTIFOJ0EaZcxKTwsV0yoW1VZAZnKd1LVVVo1GeynzIVGjr2Dm7Ewyik5rDR44cYJLqw8Ung4vgMWANXsMNw73Dr2SNKBE8VQUTkks6RhyFgqQqJGZk0uaINxtCtoRWJuUNKFUdSxBquEQNLGhknuW0o8CmxuIaj+IQG8aYBGBN4Vx58YPl3Ud3rIkhH0F4JLsVwwUmLlieWSZgww1XhlQZ6RSU0qIvIiRDiUIoLds0+NZhnAsMM1qghgS2ritc9BykfvKmTuOIcmUSxLwXVIPwbMq1CQPvhZtklGo/NCvPKX1WJHgv5vMOFwPCmZSK3v6q+lsxe0kGbvHyMDpRagyVCvPGgTFsmopG5zS+Rehb1aAjol1bHXMpa0mPQ4jAzoxTgicOkoIQptoNt4h7jP2m7xIRj2pQIVTHEpzO95hZUmDSMyKSbwItcZzK3uYKUBrnafoMbslykgR1k6zG4OkTbCPFnDTavk0MOzQmzyXNx8ZkwZB3pD3FpNzDBgguDpf3acZ4nEtQKFIVqqhwqGJE850iWs6B2F8SvETKhSEpDkKnyFgT+kj2H5HOHZ+E7iTYq0RFibRdOkEDIu2i63tJGCrWvLcOBSQ6VTKk9Hm3w7p3y9LjpfBUtl0K/2MhTaqpBG5kfoVlFwlJueUZzIJC/t9qGDJgjXvI5I+Hgls3hjRZzYy+KKwhxNDGjI3gpdZ4HquKBR5vLNPDWzz/q17ITS96HvbIJq0IU7FYhMXenPs+/Xk++5FP8MCnP898Zw8VWKQLHlGkqmjTGPLZ6Gihc446hd/GkLvSwzsUKMb2QElzh2te8pahkJWMJOWzw/DXJc9KxGtSJvJ+D3/my0d1sL/pc9vhQmejTvp9ePYuBpYUhGLvlftvTGEu8Zvmnz7vzb9oo/sxfdtBshBLwnMyIKViIZKfyWPREI6S784BUoqfQjbeCF21pARDnrtKQSrD08rvVuEm0bOyUEsP30KwVKfQz2QMKoT39N5wHcqx9pSOou8xD+/o3Oj6HfY3HPdwfYefDfsa7ovh98NzBkXBl4Kmd2JC91w6Y8vKD72/D1JISk9VubbeF3Jx5gtBTjh7+gy//PP/kUXbsLW1xZVXXplzjI8ePUrrXTCER169u7vL/v4+beswdBE2dV3TLBZBaa0sVCHcuzKGQ9NNiLJH41rmzYIjR4/SLBZ8/TOfyoXgohWNVtrM7C1KXdlQKjIewGwtFEFqCxri51UEJN6wWiDZiiDqgqU5GU6ikONdm62OIuG9jarqLoyKyZ/p4hEAM6nyWNLCJKFR1dG2C5xvQapCuARjK8THS7iiEtI6H4Qk11BHebhxjslkShNvLPYKPgr9Q2KQNkeKBS8F9KGiMNx4IaEphlj5GIceyVNpvSgPRNu67DYsGcownrEULpLAWh6DUvmp4r0eyTJR5mlAd7t3il8HWDQN89ksjzFV1SqhPFBDYlgy4wS+YOKjRCkeeGNjucXE1LR7riR8zjm86/qt6zp7M4brOIShkNaV/O27xZcEQdUlJh+eDZabYenJbEVI+4JoQYnCk9DJBiztoULeok/YSrz1cDhgyMNQOCMmxyUP2ytvC+8RbTrFdMj4yv0+ZFbd7DooCXh6bhjHXp6lcvylgFF+nnCe2iv3a/qs3KOjTHtEUCzhYvfSGKzCU/o7QTL4pD2Zvl8Vl19aH0tFYyjcJByPjevRQjn2EoIA6ylv9xhj9KO4EkFF8u23ZfhipUEp8gKuFvbF46cTbvyym/mKl9/K1uWXsLDBuzwVi+433H/PfXzu/8/an/XasiRngthn7hFr7eHM5445j8xkkslkjkwmh8zkVKguqBrdBQ1QQdCj1HpQQy1AgADpSQL0O1qqrgcBkgAVIJWgbqhRXdWsroFMMjOZ053Hc8+5Z9zTWivC3fTgbh7mFh5r78sqvzh3771WhA/m5mafmZub/+KXeOWv/wbnHz7GWu7hyTt4eu3Wl7ESgDrMNCi9oGmgx2bn8yo8pIFHiyfTrgbNwKfIag1ergr2P8p81/Nz9Tr2rYHCiwuhX/b9lr5Z6kPrWc4Yw/a/pau1zNTP2HkGUAy1y8Zs+7WPNhYH7BtrC/DOjTSagKyRyzrqwN4jptuUZ1qhsMBcf1ylWPnRer8Acq532va9Y0ubJlcv1Vkerg3ZfRn0dPtLn2udKn8LNnMMPHvnHsI44lmIePuvf5aejRFd38MdrgGkzLFd32O1WuH46BgHqzUe3fsgY2+Htz/4AE8ePy6G8Jgd7+B8DxUzDtZrjOMIv+pxdHgI33X4j/63/8tLaXP1w+CUYrMQAxAjuq7H2qewlug8qOsAMHbDNnn6iYEYMY4RXd+Vw6sT4QKcQ7qsK0OpdPmWw/nJCQ66DoeHh0g35iIZCmHEql+hg4P3DttxxLAbEZlxeHiICIdhCNjtdtjm23knoR4whgEhBFy7dg3DMKSD34PDqluBvEffJ3IcHPQgSsEeHLbY7nboPLDdnuNis4NbrctistmfgJrhtFC3Fr/8mxZ1vv0UU7o72Y6nDJ5bzNhSaBbkWUuZmcE0zywEYAbCdAy9GBubzQbDkOjZ931a6GpRaSBTALkCQ2LI6HY1WJJSbWVDCf30Qulv1/cYQ8g7Y0AMDEJ9WE6Mg3o3qC9b0Zqe+xSWBj5F4ZFr9l9MAk2/es5qwFFiNZ2rj0VBbZ0HOSTfCpWZgLpVWFaQ6vf37VxFmuam8oaxJHFoKzk9ZstPVnlPwnTuwZM0itZrZedI16t3De0cWqDSmhsL8OwYW0pjyRhpKeN97+n3W/2uZE2WQ0In3aadC21UtM4MXEWhW7pMD88ebb6r23GWx68IGEV2OaRwBpc0cDI+8mcBhMED245w5zOfwnf+7Af45Oc/h9ARdvkCx54J8ckpXvvJz/HX/+rf4tGHHwJDQB8ACVwMOVSyo/rsknYc2Nz0xcnlJg9kK1ytcvqY3acWLawemdMXkLVv39eZrqo5RvZkGzncAkxLczLro/L0LoP5y0u1M2/eqestbpfFomlqf+pniCi7q+d91vJL/y56TPSc6D4ts/Slb/KetHmVHYx9xqh+bkkG2dI20oAS379QrAGteVhf6ixtizZqYaAlQE8NZ5MdoxQ9NzFK0F+bh1u02MfbS/J6emhuQC71eV899vyF1k/VO4o3tFNp2O1w9uQpHj54oMaUO0iU9LfMEyanW0pMn1LTr9cr7HZDcRz7LmXcA6cRDjFdIXCx3QBE2G0IF0+fXnktX9nQePzkMa5fu45bN29i3a/Qu7StcnG+wXY3ou97bLcXOL84h3PA2dkptrstttsBhweHuH79egJ7+fZcRoD3wOnZObbDDocHx4DrcHx8HdeOjnC46nFwcJDv70gpuVJIScDJsxMAjM1mk9vd4NmzRwB1CJy8SsNuh9OzU7XrERBiwHq1wtnpCVarFc7OznB4eIT1+gjHR9dwcJCVNXze8mSwd/CrFZ48eozHT0/Q92tcW63Ltn2LSaqwELXwCsjFlJUDmHYHIqfdC0ZXYvEAFNApG9szryRQGEhCkPQi0aBe3nfOVzcUa8HnXIpv3+aUsSJEgJSBZ7fbwTlXdgLkAr5I9Z0D1oAYzcE0XTSInYxDFdufS3WQnBlMgO87HB4dAgXAeFAMIKbSV+mnyyE+zrcP/4unQM9pmQcl9GdpRxtKJMZYhFFbwE3zZpVZMRnU3yjPp8Xfir/VfVoU5Abk67FpHpkE3twbO9U11WkBlawBbXBqumrgq+uwbWi6CFjSF11qmrfekbotcLF8KtvNLaVoP9P/dNsWUC7NgdTVMoR0n1vrpKKt6pdu145tX5/s3OtnLV2tIVPN08J4NZ1mO4cKU+yjlS7OuZQAjgmOCZ0jjDGmy/ZCCqGMncPBc7fw3R/8Hr74ja+BVw7sPTpKd2jsnp7hw3fu4Vd/+WO8/9qb2JyeoeOIOOasQ9lxIgwuu7zWswswJEORyI5CGzUvepfZzo0FfS0+bQEPKzcoA3yR31Kn1C/t21AuAUsaGC/tIOvfWzKt9Et9dtm7dh3YQkQF8Nh1mJ+obIOrAEtL55kcbDx/FV1gn10CrK11VNGv0SYwl/lWV9kx2/YlTJSI6gyURk5op7DlQ92G5t1WKOYS0F6ia+lPRkKWHi0ZKSXhoZpP7LzuC2+yfbe6QNoodXHtVLSyV9evMeDSmCwdZqHw6j2tbyNHbIYNBh5njgREwDHD03RGmWMEhxEDM0J2dG7Pd+XdvusxckjUp4Rfokv/kojhgmssDZbKlQ0NQofNZsCbT9+F9x6rfgXfeXBMB6bH8QyMgL732Ow2eHzyDE+ePMbdm7exuTgDxxEHBwfYbrc4OTnBwcEK5NN5ls732GwGkAP6bsQJb3B6fo5h9wDjOGIYR3AOMcEYMWy2SAdgI4ZhB++BF154Af2Kce3oOB2YXnv0HbDd7nB0dIQQInbbXTJ0IsPBIQwRW9rh5GyHBw+fAkhANm1/p52Si+EcDGDV9Tg6OkLXHyCOA9h4uIQxWltkeuF658DK4yG7B2l3ZAB6j67rMAw7SOxvYqY0C1oQlJ2GGOB9fXu0KCag7d0iyqEHzhXwLmMXAabvARmGoYSBrVaraiFo5QmlFKUwM0JOF2wX4xKQmoAIVYC7+kmiPCN244BhHHNyNySjJm8t2tvX5eCoVTK6fd1HoVurpO/TP6109NaxzMkMxAJVfK71alLVRqqMwAiBEVV3akU235lphcVYRWIFmB2j8KvsEqa+1gqlAiq+ztyi27TCv/rJE/K0it3uasnfOpSlopd6d0nJ6frsd0s/5R2b3tq2q59d6k8rtviytuU9IirGtf5sib5Sj+X9pX631qcFanoMZIDbPoA59Vnijetx7KUlASn+PTkiYmSwJ1wgIB52wMEBfuN3vo2v/e53cHz7RoqHd8l75zcDnt17gL/453+OD15/G/F8g3E3AAz4jtKt8RxLNhJJJV8Z/dVYpvsKhmGoQTMROBvGete4JXc0XW2K2yUwqumZPptnNWqta+Fd5hooaOeCrC+dtWi2G2L6P/EDV5nx7LPNOb3sOSMPl4wdK2Na/GvHqx1twGRktPrUas8az3ptT3yd5FoLuFowb+uXOkSWL+qLBTlTyyjRSXW69Ik/Mog0/Cl91jK+pcu1AbuPlq01YMs+I6Wtox2A+eWSuh4dbbEkY/aVlt7Q7WhatObjKkXLbY3nWnKcKBmM1OeENPmQN/KzDpNDU9a67mPee0pz55PzNuR7w2SkESkMNXK6o8w5B8o5UNhdbUxXNjT+j/+H/xM++9nP4uj6NRweHeLw+Bj9eoXDgyOsuiOEMKLrCCHscHztADdvXke3WsF7hxvXr6dDJX0P5ohbN29gte6x2W0B8hjHxKDPTs7xi1+8iiGO2A2bFAK12yGM6TDLyckzDOdbbM7OcXF+BhDDOeALX/wc/of/g/8+DvMOyDiO2QBxuHH9GH2/QgwOvT9IXkvvcXZ2hmEb8OO//iuMXQ/frYoRAjDW6zV2w4DB58O3HPDC3Tv42leeg3cODhFMrlp8S2CtJdxEkE/b2clCTNmQUjYjIhPXT7VXS29R6nots9u+6UUqRoJWIlKvgMrNZgPvfckXL+PQIVXSjyVhx0hAxBoSerHaupLgmoOP0n+kNJWRGc57kHcYhhHokveRwbMdnvR7HcpjBZc1NvJL1bhqYTJXIOUZQPD4PGQFyXODFtiLEQCVA8hpdyTPq8ptXf5lekgok25PAPFE0zkg1EZqRS9COf9jlWkCX7XSbAHv5sWVSgHWBkSq0/KBNpiKkFT3aOj2WgrSzreuZwn06bVk620Zb0vtt4o1DvT78n1LwdjvWqUFxOycL43rsnHsU6pWvtixtumAAmzsepzJUXnH9skRRgfwusfHf+0L+Naf/Ale/OQnMHBA8C5lKIvA4/sPcP+1N/DaT3+O9157A13KRIzgUkyyYyClMvPgvKPhsyEk4UWz3QBOyU4kjTfzJHM0Xy/RRtNUFwswNV3mNMxGNyeJ0tpllzqBWm9wTLvCOqRV91kXbfzo+rQuS78T7JBaY7S8JL+3yj7jycqLJXrptaBlR2usVwkFlGLl0pIxoJ/R619/boumuRiINtRXj82Ox9YbYgBR7VUvRgzHInwt7WSOlww43Uft6Cw6UD2zJHuqOqn8b5E2drxFpy70sdDgkpTO+0qt31HOLl7Gw9op81ENjknOzmmR9DDhoPM4I4AhiZGmEinvWvLkqJF9TJ8xBucBTbLBwefPHTHGmDN5MgNjLGdFr1qufjP4wHjjtbfwwssv4bmXXkR0Oxy6DoF26EM+PMwentJlRZ944UWM2xvwfkqzd/3mdawP1wCn2OLN/Q/R+w59Rzg4OMZ2O+Dd998DQBi2O2w2G5yfn+Pi/AIXFxfYbDaAZxwcH+DmSy/gxo0buHH9GB978XmsDg5B3uNis8XFxQbr1QrOO9x57jmsVms8eXaKuN3hfHsOj4Bu3WEHxtY5wHfY5DMbDKDreuwYCM5hDAGO0u2ww3ZE361AGcDGYX4+Q6cSlM+rBWqAhQDB6VyEhIY4xBGAcyVbBaH2oBRlxMlDIelv9aKX9qWtSbCl/8Uce0ecYyzzxXKnOTPBer3GwcFB7b2NiR7C5EDun/OQNIvIgNfnC9EYDN91Ja0oZ+AM5uKtovx7zLToui6nFEa6ACvm9rKMJY4Iw4iRk4G2Io+V8xh9FqDOoXMpvIGzEiaXM9VIXZWSmgsMWdhpMdZep/Jsnpwpa1UWCDlFn2TQkOwkAghK/TInIW2DeufB5FXkMZedGhCKJzfRgMpYfG4jmcrZMCXJJOXMgXJKhp/MgeHjIszy8+CU8YmcV8ZA2pLlbHEQAd4BHNPfYiRKBhaUA+Vhmo9MN+EtzilunaJ9MaMyQUSZWVBkQbUFEi0FrP+2XucYpgxHIMo8m+nEeS3nOaWsGGWHStb8PgVp+6CBpVUoc6UzN5Bse6R/cgLMzvD3EnC1QEiKVpT2O4qo8pIzlAECKtnedPau5E1rb7+7LEsCUEKlKIdL+eBAjjAQMKw8jj/+PP7gz36IT/za50GrHjtEOAZ8CLh49BRvvfIafvXTv8Hjd9/HuNnCCSBM1SJySn2bMpY5pZBrJ0fXSUhsGswwhJJdqvMeIUbEkJNzqJAaHXKV6KdlT+ZTiKzxhY8IkhlQeGDS8NbAtarfrmfrTNJ6SsLCdFkyDqx+mT9LRZbaOu17S59ZY1kcKXbMwkP6M+3I0DrPGiDp55TKGezK3Oi2bN3y9wzcIzm+BMQRJd4q6QjVsxZ4Ckay69oa363+2HlakjlEKXxGdh6BeYicPGfbaskaqytbfQbqedNhfC0DQuhY1oSR2boOOz8JYFPBFYKXpjprGrV2PWx71oCq+9nWmzV/1TRr0af1fdv4TWPT3zNzNh4PkDYykvyqXqvGnevBtHbS/Mj5JAYzgR0hCK6JaU14SqlxYwzJIU/thCGtcvV7NLo1hnHEO2+/i90Y8OInPpYOE28H9Ac91oeH8DHChQiMQzqQN6R7GiKAo2vXcXB4hMOja3DOYb0+ALkVzk9PEMYBpydPMQ5b3H/wAU5PLrA52+D8/AJEhMPDA9y8cQuf+cwdrG+sQSsHhkPX9/DMcH2PIQTcvn0Hu+0Op2fvg3yHw6MjvPvePbz08ktwXY+42+LFl1+Ac4QP7n+Iw+vX4NcH2EUGvENAmjRHyRsO5+CRAPC425ZcxJ5k3h2I5F4N4YOEyiSNrvZ+6fhX7c0tRgAnL3aIEWMQ4coIMSJERufrxTmFac0Xvo4Vlvas0HVuMkqKAZMVZQgB6/W6Oiwu7/V+OjeTzpxQYd7I9cKqPGUkqYMTs8/jtamAolQvpnzjLGA9p38V4ORcAsCEdO/IGBApZV/xObwiq/AcZpa7mkF46WtuAxkMVLHWlO9ZUOOqhG8GnVNFqd/ldmzJ8c/SyGQ0cuYdESAp01rmIwUouNQtSoshcZJF6BFA8OWRBIa4GLcC2LWgm4WqmcJZaKd/yO+rB0h1q+y6xBQTSZLsADMwWQtd8QxzMWLkpvtK6NL07iw0z9yMq9uw7Wkvoh3rzLhRNBDwqRVODCr7WE6DTQ1FuERb7QHU/dSKu6XEyxjN2Cxgk3TakyKe1g6UzNBywBoSts59IEPqTx3C9JOm7xIbtUGGHmNwObSHCR4eHCNWLp+TcA5j7+FvXcPXf+87+MrvfAPucA23St+7GLF7dop7r7+NV3/6M7z1q9fAuwFdiHC5/ojpLIV3Dt5NIaP6TJvId1HMyaOcZORutyvplYXe5OpLWMut4YrWhAn8UGlF8QWy3BLDVn43el3PjWxqaLkr60HWh+5XfqBaVy1eXGrPzheQw3yRnDyWT/SzWobqnV4L+DRYtXXI97KDog0M26bl80muJ3nmqBPFkI2ENnhfAvvlbxGG2dEDEsfPMhjfFw2xVPRzTtFa16lpVPpNNZ3kd9kRWzIcWsbPUrFn1gqf7+GrukyOQRmb3jFrGaWtPsl7FS815k8/r8eu+bdlhItKt4bDZeum0jMGB+2jTcvQIkqHuTlKemvkS3N1PbUuERnsHCEyTdiCkkNSLt1lopQMo7wnbTpQl6Norriv8ZGyTnW9Qxwjnjx+hDGOuPP8c7h24zoCHSOwQ9+vEvCPhMAOB8fX0PUe9+/fx40bN3B8fA3r9Rrn5+cg8rhz5zncuXULZ6fPcHZ+gdOLAe+/dw8BDrdu3cbLn/4Ubt26WV0aFzAAjjEGhncdDlc9NhebIkivXbuGj3/84wCAo6MjDMOAD+59gOg6HB6u8uFgwmq1ysyTDzpnYSeZlOSwX7IWE4HlcHTXdQkwG6lvGVQzegGueRx9388Ock2CUwyXrLS8Aw/TpYVFMCB7pqh18zmXHY5WH2UcRFRl54oxYrfbgYjKIW/7nsTE73LO5ZJ1qlGIpqxBIca5wlXjFsAmmaD0WLRSKp9loJAuM0z9PnIOyQfaXtiJl+uDmlpox8ZnQAa+6gKueWx9LYSJ8ja3qs8al6KYLD2A5DWACp2zCt4qgfQ7AJbzPC2FUCuSKtSJl4G3/WxJ2WqeL3Pj3IxeoFoMakEt4YL2IJz+Xfe95TG1NKrBWG0EzHjjEmFvi62nxTtXUdAyJvl96dmrKntgopcGzYUXeVlFLPXDAiE7H61nWn3X4EYDYsvju6wIVwHoI6Fza+xiAK3XGA48PvnVL+Mbf/x9HD1/C9T5dEHfyKDzLe6/9z5+9tc/wXuvv4nzx8/QBQaPIWc2nMtnLRP12KSfOsSUOSUiIUq7GLXsrg/HyljsvUH7gLMF4xVdMO2sLtFX/677rDPutQC87c9Vy0weNGTJvvotT2t6VnU32rPvt3i21cb0mXZyEVidEWv1txXuWZ4hpAO3jTlckit67bTkWcsAuYqM0sB8qcznITmFYEB2az1rft8n8zJ4mq3v/SXNgRigM13cGFcarzit6j6UOarGevm8WB2r+yHAW/S3rm/f+tV1W3q19K0uHGunoHP5XO3xEbq+L59ZJ9zS3JE6Z6z7Ic+4zsN5V/ChpelMr+8pVzY0bt2+hbOzc4wx4OLiHNvdJrFDiOg2AeujI6xWIzwxBgecXmzwsRfuIowDnn/uBZw8O8NnP3MM5z36LmC1OsAGO/R+jaPDQ1zf7nCxY/z6r38F6+vXQW4yLqYtbkLnV4gxoO+SYQMQttstOALjkA6Na3Bz+/ZteO9xutkCSDcknl+c49adu1it1khyMTGDpGpdrVZFucgW0bTlnSfBO3CoQZueCF20AJF2NLNJW955IN/yHGMElFdd+ijjksXmvUfMaXstmLAH07WQDCFUN5QLuN9utyn1b2ZczUxWoLcWl3xvxyqGgShySS/cWgQyNps62II5QLZH005U3/cALqYdFp7eqc6wRK4Ah25bt1GB2Qa4LkKEUN0OXAukiQfm9ME016if0z6JliK1c50UfO7/Ah/q9uU9CZkIPPGUzPkSmNFt2jMGpW+Ktto4tGOxNEnKpRZi8tOTA6nD9npOZ55atAG77qPlWasgtIK0YHIJYMvFiLqeJeWhFZEV5Lpf+lyABRyajrY97cio6iaabjk3Y2vOpepLq68txWnHuTS+1jPpA8AzwQdCF1Niga1jXBx0eO4zH8cf/vH38dLnP4Vw2GPwgI9Av2M8evNdfPj2e/jxX/wI5yenGM4v0Id01oIjwF2SDTqcVd+qLGPuuq4kv7DrXeZCvMCSTENo3pIrevwxxhReCGrSTq8/y1+6TluY2/Mmbej1UXgPcwBm56Ul25fmz/uUFjOoRCaWZ63esPwpPF/1oRqn5v9md/b2V7+f1jLKJb3p/IIEP03Pt3SfplWar4io6m85/1p9WNph1aXFI/vGqL+v3mU2u3X6nRyVbL7TWELX19JBlk/3yZdWKZ/ncDOtAywP2TkgApYMRZHnoLb80fXqHTaNfayBI7pWio1YscXSzfLhZbSx30s/L84vwNevV/pkH33LDneZj1pPp/cbWa8a+GMfz+pyZUPjd7/3XZyenuLP//zPMZ4NGLZb3Hv3HTx59AgvfuLTuDg7R79eA4g48IlJjo+PwZkYq9UKXbfCOI7Y7QZ4v0Lfr0FxhHcdDtYe169dx9HRMQIcfN+l8wJq0sZhAChfCAMHjkBAhI9A163QdV0FZJ9//nkAwGa7xQETus7h+bsv4NGjhwA53L17N4HEzICyyyAgPBEWCGPAyjt4L3GsHkRpq91OfGWMqAkqE9NQLPK9WOQSAyfnJkJMseHp7MZ0kGsYBgCpf95R2fIXJVji3g0z2GxRMcYybmZGv1qVLUE9DmDK2iC/S180HfS4yjMunSvQBoQFUUJDYB47OvOyUtoyjCnarFwcp73pUp8FZhJaZPstileD5KKkiRBQ12MFqt3aXQKZpT1Mi12/S5TPYOwRirpvpS3x5iyBOkK1pSrzrvtU6NAYg6WJFsj6PaKp78Kzeq5hgIYFonrOKpCknrEH3O082DTLS2vOzqXwYgswzsCwmQtgclosKRP7zhKIWTLOZu1x7fnTY2spHPnOGvmXgQjbru278JIGtHZO9TzsA7CUEANWkcDBIRAhHq1Ad27gOz/4PXzxm1/Duu/K/S79COyenuK1V97ET//lv8H9t95NB7tDOqchmaMScAHIzcG/pqV8Z1OCAzV4dM4hZG+fBce22PbITaEILaVtw0pLGwwA9fOW9xZpavrS4lNdWvLNyj1Lv6XP5Z94R20qc9uv1vs6mcj8+/0Abd/4RJ+kHQ0GqP2c7a/9PsphGtTrUkqLPpquNoudfuey3Qlb7Nq0vNW6w4qcz+F3y/Oo67DY5qr9av1u6appZ9vdp2etzClrUukkqV/3wxpDs7Vl5PcMU6DGKK112JKdLXmrHZyaR4hcNWe6fsGCovtsva05SHNY673JgReRo6aq8DU9X5a/95UrGxrf/s63sbm4wM2bN/BP/sk/gSdCCCPCdovH9z/Azdt3MO622O02eBZ3IAQcrJMxIYPf7Ya8ABnjmO7U8GBEYoAc1utDHBweITiXDAiXD0pDp1DNk0EejAS2u86h63ocH19D13kcHR0VxkgECfCdxyc/+Ql4RLz++ms4O9+A+oMU/rM6KJfJVQs7H6LtewdPbLLvRIB8xXCaeb2vBU4lqDFf7MlrHpMhj4lRvPPYjlOmJylVStkMMLWy1wylmUPfVk40MdYwDNhut3CZ5rCxjbnEGMtBZG3xasNA2qkEPANMU78182oayfviJbTKsKXwCYT1etUAS1Ofi9DlZJzo8IN64c6FORHBLtc6RCINrgnuGJMxu1DaYE5ihZcV20zQcrP76ZnIiKzjLdtgxX4P1MaCfscKGZ0RJZ3JqC+lKjSTHUoDZq0S0kaG/B6Up9d6jjSIkc91coTWLo0GwZrfiOY7Sk262vpQ88rSu5qXW/PZ+kz+XjIuWs+11pc8t6SE7DxoJ8CSIm4ZElehWS2nDTAjQlh7hGuH+Mw3fwtf//7v4eDWDbh8sWoXIuhsg/uvv417r72Jn/3lX2M4vwB2Y74sL3k3A8d0CD6vQ+/q2421bNY7sNbTrJ03RSnvAVuaryxNNDj+KEBtqSR+/XevR4o2uIG2wav5b96X2ksq8kPvHi0BlaYx45YOdf/tx1gB3fJZinfX52nt/Og+S5i1VNICqEttt2hq14Z1urTo1ZqDVn32HQucZVfHypWlNa0dPVpe66KzJlpwPzN09Lt75KaWOUtFt0e5D0sGlC0tI1+3r/uov6uB+tyQ2Ndf2/fZ/DFStknNs2pejg4PcT/zYssh0OLHJB1r/Vv4QppVfdc7t/L5VWXXlQ2N07MTnJ+e4aWXXsTnP/dZvPKrV3CwPsI4DAibczx4/wK7EJDCmhiOIryTG6BjJoB4NQK8H+G7Ht55OEpnR9frAxysD3C226LvOgCEcTfd3+BA6FwHpnxoOoTsJXcYhxGbzQa3b98CMAm2dCbD4/aNG4koBFxcXCCEiKfPHmIcBgwB2I0DVqsVUox4ZsoIOJ89RUi5hJOgdOkfzwULIAtw2n0QgWq35PSCEUODnIN3DmEMAE/b8owxHzalIrCZkyXrMC0i7emVfs0B+GSgyHPjOGK9XpfvREAA86xZWgBaELPkiW0BS3m2EtaqLPVbFoOntE3PnOi62+0QYkxxhXEyNCrhndM51nPVFuB6XsthbznkVz0DME/Cu1qA6jNNn9Svup3aU5P+aSFgtzD1HMv7wYANLbBKNh1VLovlJZrO2LSUihXIQoPIXA5FayA5jiN8vuix3qrV66jt6bLt2rFbRWcNkZZQlPG12tEZmvYpbFu0EavHZwW/vS/B1tsCIlKsId+aF73GbBtLQEeeXZIf+l0bmrmokIHKALb1A3p9pWcjCEPv8eKXPo9v/OkPcOvTHwP5Dj118GPEEHY4f/IMb/zFT/CL/+4vgc0OfWTEMV0cmmROpg2h3KNBmOSX0EcDJutFtWMGzBpWwMLKMCvrazlWr//WGmzxPRrre+k7W1rztFS0fNeGWIsmdt3pgBLrLLJrwPKJBdr6d01j26d949Xt6e8q3i9GX469X+iHpZ0+5xhDBFPN39Yh0OrfVQGb1bV2bC1a2rrT2OY7HIDMWz0/VpYsyQPdhwoLZUa3crTJN5rObr4W7HisLkhNTWtT690pWctcd8xpVN9FtqQDBNeUsS7IWv390tzZtuXzgqcgvDnnS+89yNHMeVJ+Kn6u25/whV5PRT6pc5Z6DC05eVm5sqHxj//xf4EP3v8AFxfnCOOI3XaH6zeu5/SlWwxDRIgR165fw/Mv3EHX96DOIYUBBaTIh5RK7ujoEF3nAUo3YTvyKZUkRYBG+N4DvsN2u02CxaeMI96njDoCZDrnMG53AHocHh7h2rXrWK1WFaMcHBzgubt3wAQMuwvQaoU7zz2Pp09Pcf/hU4TdDhGcbzHfFRDkKB30cwwgJgHi2YNAcN4nwRQZUNmF8uykA4KuPqxaFFsIJVOMMLGELTlRhkRpnJ0HhwBy65wlIDN35BRGxim9KDgdtAYmwS5hVLZoDxNRuuxOX85XhAVj6ifSIbfkwauFvjCetdZnoM0RYphCl0By8Dp5PbRAtpcFavpJ3SEEuJiyHgQCum3A2ncYXZqHjnzJEuWcL/WnTEy1Z1Z7HEMMRV9bo8ERSgo55F2kfEkmyMv0pwQDEvmkveIzBUQAYxImdosyiX0R1BIjlnairJCVNnyZhtQ4p9FW5zbsz2IYQL1rlEcZibRnBEzL24jG3HVdV+ZW5l2UgL61VhsnMkcpfCoRJnLyJouRnYyC0ns4cpBT8ZxPvEj9IfM3smKi4v0u5t1MaVbKU81Xy+vtQekMl1ZoIv+UnNcC23rBWvNry9Ka04pDigZ8nOe6pBAGYM1slypKc5Ofk7zqlCpMP3X/hIeEdrkvEYxIER4E5GxwETnNNBg9HDwnug8ALjrg2sdewO//yR/h01/+EkKfbvX25EBDwHB2gdd/9Ne498ab+OCtdxA2W4RhRIih7DDoOeqyIpZ0xVo/sOJn3WcGSjYpUrvP8jkp2mmat8Bxy4BI8kJfcJlokbkvpSEFys3v4nrg4oBAvpgrvZHFBJI6qEGF7ZsF+3KR1xK/WXC49L0d9xKAtuCuBfZmxi7mZ9mm5xM9WvXqdcyKN5J8yuGYXK9Fcst7Q3p3VdctqfHFeceRp9lM4AAwY9KyUgM3/UwrNLVlcNRzPO0ogbja6SIHBK4jH6QdR4TQALKtfi3xggWuKTKkff7A8kZ1wzom449KvQk/Rpo7UFKf2jvWhX9Rid+mE0qPrbV+qvqFxA29anlQ2rC8aOu3xk0VKZIervotdUtY/8xxyFxCR6NgLyTnS7p8r1Aj8UZO9ENE8EI1FQnhKKXan9rHlcqVDY1xSJfglWxJBJycnOD4+BjeeUROHvHDg0P0XY+zs3M8efoMHimmP53R6DJIHBHiDkCAJ4/OrRAi4fT0FNvdDtvIYBoBImx3uwkkImfNBAGUjAPEESEQ+lz/ZrMBgJJxyXuP1XqNYdwihIDNZoNbt+7g2vU7+Mnf/BKrfoWz8x3KGYgseF3OGTzsRoCTAutpDVnEomIKE8W05Top7ilrkwiGGHP6zxhLpiadz5xDyMBZlFryCnfdGl0fAYwIQxDTPSv6OtZe+sScLh2UG721526yfLmkXqyyU3H5H4AkNMeQDm/rmGQNCHW7YjxVoAk0W5CSXrbAQbPAtddRGwOl/cgYEAFP2Jyeo/c5bnsMcPm+B7HaZZeKmRExj/Mtykd5Uqziy+RIACDW8z+ay+OmOlIGKStwYoxlfm1oRfmp+iBAI51Pkr9M3yCGCaZdG6Lqaf3sEhigJNkLP0O9LyBSlIDcANyqQ9Zga2dhBiyASrlbepWfPNFv6mwyLAJCtvESQGYx3FR2uGLgFDBMRQNpemtF1goL3LcNTgntTXKLUvYkMZS08bRkSGj6aAXV4hXLdy3vc6OBCfjYPuTvZPfSab40wNyOu7kGsuGNyCBO/JivxQAoncFgRxg4ort9Dd/+w9/Fl37nG1gdHYOR7sLhEDFeXODe2+/ir/7Vv8HJm+8Aux12WT9oh472RjqXQmcRawNW04Y5nZWS1NvyXCtmHpycOnJWzXmPcQGI7wPg+m9NPwDpPh3MPweyc6v0uzywyEe6HxrkWJAqP/eBSM2HFgTbInK71dZVgKptE+o9PaZ97Wv66vM2ZR5iCnGuL5KNM0Ta4pdWe17kHOdxyHeoZZuuq9WGNY7sM/sMP5mXmBPVOHJlh7XwMtVhrkWHZYdqjLEG/erdFt/YUtE5j39pTPodHbbYDBEDssto/v605tu7b5eVFk9aQD+nP2Y7WPp7Oz7bjl4jrfesrBA9Znk7csQ4DkU3WNqlkwkOEhHFENkrbU4RJ1Mf2rsWBUtc0cCQcmVD452330aMKYvT7Tt34L3HvXv3QEQYQgCIMAwBjx49hvfAow8f4cbXv17iYYVA5Z/LmC4ChA5wlO7lWK3gx4CYwzy6rivZkZjVhUdE6Huki0Ui4+GTx7h18xpu37oBYAqdAgDPclkYwfkergs4P9/i3r0P8M4772AYAbda4fD6MVzeWYgx3X7I6hZp5yid23AubcFTPaYSD60mTDMFZwNBx7tpZpPUeIgRIHVzstRPLhlrnEKd4jgWEKsVqGQSssDdWtBEOT2a97VSNUykhWBLANlndHtLCkeMrCIYuQ65sn23i0t+d95hiAEHB+u0AxZjCacSD8gk5vPOQDH2UxtlLownSxbtUpz7UtELM/06V7QAqvMGmoZ6vLqf5d39OlaV7OmbsMmsny0hZ0FtC1CW90yYhG5bPCG6Tvu7/mwJPFhA3qKLrkt+XwJDV5nDlkK1Sl/3WT8jssfyccLa8zps3S0g2gLx9m/97JJx1ypL87tPYbbab/VNnk+HsildMJkEJ4gcogO2jkFHK3zh61/FN37w+zi+exPRERAJHQNxu8X50xP87C/+Cq/++G9w+vAxVszoO1+SdgjN7dkdAZg6iYWmpzZSNJ/ZzDwtI6G6YbvBC0s02Uff8hzXc7FUbD0fdZ5jBpfAPMSr1a8WH15WbOhoC5S15I/tu+ap+pzEHBDq+dLPTuCp1u31QNtzuGQwLdHtqnRa8mDrsUt9ekx6LnQ0QOJndR8TaocJNz4vMoPU7rFpuwXgWzJJGwtVSOSecnXeSpEE+0IcW5in1Z79e8l51Oqb4CQbzmzrv4y/NbawvNOqQ7chBiFHxuHh0ax+IkkqY3ZutM41Y9U77P8+y9XPaJye4uDgAF/77d/G9RvXcX5xgdPNOfqux+mzU4znG8QxedlPn53h4YOHCGOA6+eLPDF2MjTIOwAeruvxyutv4NnZOQIRwhixWq2qw2jpPYcYAnbDDuQdeu/hPOHdex/gm1//GojrsBvvPTabDXbbXfI+jQHedTg9fYSf//wXePz4KZ6dnuH2c8/hejZSmNOZDZeFUecJLiuWmEON0lDaXkW96DUTysLTCk4+997nEKUUUpCMsWSFOp/TKSJ54yPHEjrlnEcI090fepdELx4rgNOZhqSk9a2whUlRLyoZT2th6LCMVty5PG/jdcVoYbRBl/CLPndSFkBeMBLK5lQ65MmHNHkegBSmVfqlhGHV/xgqIbBUKkHHdRafucBopz4WPNEC3vK7FZwxTpfkWIXKzJPHQVFBfrEifEnhawHXEoCtOqyiJZrmV/P5ZWBryfOnlbnupwX48rvMq54nzVctQWrnQfObVigWdOq+yu6iXQNE9S6ontt2GADP5rcoDwUMWnOj62v1cd+8a3paxWb7dFXQSQDAlPiW0k3X7ByiI4Te4/nPfgLf/bt/jNuf+ThGT9gA6EBYgTCcnuPNX76CH/35v8bZh4/AZ1scRAY7xjbUhxN1P7XxLv9CCNlJND1nY7E1PSzvW3lnP7d0suvX8kxrDuXzJYMhiTKu+t7qr56bfaBdxiOf7zNq9DN2Z61lHOh+WNpaWXkZILTzcFk8vHxn+XhqD0jOKJO0JL05e38fLVprZzb3V/QOtfjNgmk9Pt0P/bkketknpzT/ERE67zDGdpIJeXa2w9foVyUfefKWf9Si+17oGJfXml0Pl9HMymc73xbUz2QyJU6x8kDX2dKrrX63HMNVXcZZKc8K3ru4uIBzrnJgT/WknbqYw/lSzHYOmTTp2DXtluZZcMVVZL+UKxsajgg3b97EJz7+cVy7dRO/evUV+FWP/uAAt/o1yD3D00dP4UDYXGzwL/7Zv8APf/B93L57u6SdZeYpRhsAOOUTJ+9wenqOH//NTzEixZv1nSveKiFm8uIHEDmQc2AiDJFBjvCLV1/Fgw8f4KXn7mK325WDzTGmjErptu0pE86PfvRXGMdQYl5X61XyMA8DnE9x1jGmLewwBqwFSGZvgKN04FiILeFJBYhnsKEZSEKnpMQ4PyiWQn4IEZLSNoUIUTXROSY019f1fRFk2hjY7XYzUGQXkmXKwsRG+YgRY7cTtQeRaLqXQaztfRZy6YfT8HgOWoV+4q1JgJIAOfjFgPc5WxbLLev5CyTQW3vS0k+b4tOCAz1H8r2mUfksKxL5vAY/0y6JfNeKx9c00kB1aTFroadpqb+XjWut5HS72iO7VJc2LEu98j2l/1mBLZR3jqp6bL9bO0RCM02vVrG0s7S6DAQL79rPdD8sjfXnS4rMAtaKZxrhgS0+kHHL3zaeuqZVe2z7xq2LdUTM+mzmXtNN83HLwyhrI3IEOY/IBPIeIwijJxzduYXf+YPv4de+9TWw3IfhHHwA4vkGD+49wK9+/BO89rNfYHh2BtoFYEwXWUZ1F47uqx2LlSGteWPmcqi7xct2rK36L6O77kOrP9UYuO2hJaJKf7TmbWmHWc+hXYuFBo2+WPppw+gy8GjljNUduv0Wf2u66d9ba6v1PdDeIUjPRTDX+qzMcaq06rN2RmnZoNcCUX13lX4Okcv6b41PrzXrJd8HgHV92rAgzNeF4BfEGjCXsZlxar1n5ZYedwsblP4gNxnn4cq6CI/a7+yaLfNJ0/d67C3aynP71qemUWsHvdUvclT4xD5j5ZLUZ+WkvKdD2Wx9RReEOfYKIaDvPLbbfIGoimYBkM97JeeO9w4hRoQcmslgEGpso8/2ttZnGcslss6WKxsaKT3tDv/NP/9vMDDj5OIMB8eH8H0H33V4rjuAox4nj58AMeD+B/fx3/35v8Tf/4/+frkRWpgxxpS6lphA+SzET3/2M3z4+AnGLEzHYYfddouuS4fCZQIO+jViZAwcsDpcYRgHxH4FjhF/+aMf4c9++INKuBXQhuRRixG4uDjHL37xS5yenIFjvqtiDBh2O1A+qyAC3/kOXbeCy0LC5dszQ4hgnoM0WTD2huky+YrB7JZrZAa7COf7dF5D3UpOzgE5TeMQRjg5fMac0/DOGVsYxQr4GGM2+BzGMaUIlkP0mqnkd72Y9wkMPSa7e6FBk41xl7jjltKxAr6AQ5raHMYBQIqRRaW85WeK3ZzGsbBIaMqwZAWB/N76Ls3NslfAqXAzDRpEUFkhrum50NEmABSyJKMUk2KjFEKlEnLMxrWvaCVS9ZNQGaS22E+E9yyQ3ldaisICtKX3WoZ8CxhepoTse/rd1nctL7t+rwUOW3PfAlRXoZl+365DDZxa4LkFVJfqtsp46XnnPMaYs0F5Bxyu8Bu/8y187fd+F4c3ryFkA+MgArQN2D45wVu/fBW/+slP8MFbbwFDgMv3CkUHjK6xE2YU/RJQsDw/8XL74K0d71XASgtM7Hu3CaTFlldzzpwcWHK41oJc/W/uwNp/nmIJyEr9GlhrD6yuYxoEik7SIc92rK1+/Psol633Asgxubf0egkxVvHwwEQ/Gy53lX6ktmoHii77eKMF8u0Ydf/Ld5xCjLQRk55Tg7Y0IQBmDcgzdrw2GgOYHHeznRQLUhtj1vys/2aeLhgscnIPmyzJJCKaEis05u4yI8jSsTzbGJulmR6zDWfVz1oaaLlB1DqZIs8Bu119vGAyWigdXyBKCY28T32OAUHxhzZwW23r8QgttQPssnJlQ2PVr3B4eIiL7RbUedy+cyfHdhJiSFlWbt++DYwBJ08fIwTGP/2n/x/8/g/+ALdv34ZzvhyOjjFiHEaE3QiQwy4w/vm/+G/TQXBm9CEmzxWgLs7TXplM3CEdgBlDBIeAn/7Nz/CNr34Vt2/fghgbXAiSQq4cdfhX//rf4OnTZ4iR863iMQPWEYgBq9UavfOQsxoX2wusOo/jg1Xui8uHbmvPxphP7HvvgRxCIRNWchAzl+02eUdCvXwODQPS1mcIETESwm6L7Tig7ybGjiHkulImK70QrGASASqfyw3o0m/ZLdLZVFrKq7XYbNELRQsj3b5WyJwF4qTva1ClF6NeCNPiY3SdB4MxhgDHCZBkWZvrk8VO2R5YUros9kIFvPTis/SMMerz44ug0y5IohT2JQvWAoH9oGZ+GVT5JqYsQZJJKXCclKkan+6HFZK2H8w8O/eT6msD8PKZaDWaaCH8Js+2Y0EnA1HTQvPzVQwDmafWd7O+XlKXHWM6c79Ms6uE10hdS+E/WrbIbp5eBy3woeuw4V7yjAXbdtdqHx2sjCn0KA/JWk40AiGlXO47BEf41Je/gO/8yQ9x91Mfw6532DiGJ4duGxGfnOLhm+/hx//6L3DvnXcQdhvQMMDntI6BGOwJwQE05ox7Vygtg1PTyI7NzkELWFtQrvlNz9tl9Fz8necygzk5LSxfaX4jqu8wWjIeSjuEcgi+NTYLzqc7mOa6oRSaG6P7wvlaNLjs2au8v+/dPPTq2XLOpyFn6nurlvu3ZABUz2mFt1CWDAz5bp/8S9/J+USUn5wEdgVarZ4vzkuRcQt9sOPTQLXiG0OvfXPaMmb0e8XhNfNgtWyPej1FrnVGy2ioQH1jfbfmVp5p7Zy15K6VF/vqln8lsQ6WbSyJqBEM6pxD3/WJDhH5glClU3L0B2OKGNJtJhF+ub79925o3HzhZawPDrBer5OwE28Kpwv3Rg6gzuHWC88hEOPk6RO8/+ET/N//H/9P/IN/8A/AzLhx40b2nDsM44jtbodAHf5///zPce/x05S2LIy42A7ofJ/BTQBzMrSJUgwhA+i6lBJ33A2ILmV2efDkDP/VP/tv8ff/3t/FbncB5wghApEIxAEcBjw6PcFf/vWPsQuM9eEBzi/OwXFE2G0Qdxug6xCdw4gADhEMj855dPAIw5iFcofpsHHDmoUo75jTjoUsxLJFbhZTSW/bd+nyQg4pVWPmLOc9aBxAcWK6iORNDjEmAwqUtkSReEu2R2NMF+zFMZSdG2ZGGMd08yMDnfPJaOv7ZFyFCK/ObbQAhV44ApSng2h13KIGqPrQ5lQPste93rKVelrAJv2L4DjC9R6rVQfnAEfiOZvStNUAmQEKkAOp0yEGQrp0L2VUs2O2QKJWnGriVSGiqi7ruRagKn2041sqGhTZOUFXH9bnEPNZH8rZqtqeCltaoGum8FDLfC2kU+raZPCBkdNEZ2BLVO2EaFq6ythLCRiYBXxxxSetOapoofq9JMgXwVLj3bKenAMHpfCkv5jYaUmhSqpLkpA2RlHoEn6nd5D2KTg9TltawNl+J++31tYSqM4ulpwe0VXyjPJGvEdes94hesKwdjj82Ev43g/+EJ/58hfR9V3axWBGFxnj2SkevX0Pb/3453jrF6/g2ZOnkJNIDMYITumBXTpfwSHxl72nSPd30ZDTYAIw93csj93Sekn56p17mzjDhqJYQ7L0HWmsBYwKAFzgY90/LUO1XFnkmUsMZrt2ylpNwjat33z+rSwHVeeSsSN9tP3ToRuWTlJaOzkatOm2LHicaE5wNO1ez8Ioc8iJOANLCnug7Na0gLFuTxunDopAyggHULLj6bHJ700ZsjDeal6JkRKfiDxlUM5ZT246pF21wVz6KZm4CQ4cUl2aX1sGgRT9HGEy4vSz+/hYz4ee+4m+mIiX+w1I2mxW6ZoVffL/Bawn3UzTelNz1tIXdu1Knaz6rvu6JD81XyzJGXl2tvsfky7X7cnvq77HwfoAA+3SLpMjECe5Qb52/rksswmEMSYeSddUZEAYU5Id3aNqXXFy5l7V0QN8BEPj8Pp1eOfBLp2NcBLbBUaMAyLyABzh1u3bCDHi4vwU//bf/iX+4//4H2TAzemuinx5HyjlWH/73XcB8ikMKqTUpFKc8/l69QSWBjnsEgi73S5NSMgT5wnvvPcetrsdko87IkSAyaPjAEceT5+dYrPZgRlYr9ZYr1Y4Ox8yw6XMTsMwAq4DmDDytOuyjj7l7icCyCHyXHAWkEAoxkX6XrZr06RqS1XOUvRdfaBYr6dxGAFXe9iAvHANKJG6rYdB173dbJGutM/K2CwAqX92wzdqI0P/kwWhb//W9GktxPR3/ZkGDhpw6baBgtESPRCxOlhj9+y8pHPTl/fIu0WpUqaFgL4GyFxSXjMhadqoSz22qh2lbOQ7obcV3rWBMvdkLwHOIrAjlx0U/V5LkS21O+uHEZat8ywSpqd3tVjAquKROrxvqr+6C4bmc2UNQc2LTZo3/l56ZgnEXFb2GYkF8IiRmf+FLDPsrt0SQNxnHLb6u6TY7Xq0c2rfL4pZ/uVFqL+PDgidw+gJOF7jt3//u/jK976Lg+MjwGXgHyJoHPHw/Xt495XX8PN/+1cYn54hbrZpHDS1NcUCpn51FhTqthtGhy51Gm+e0dqCUgtEawfJfqPMyqwWaI4G8DEboZCNjKX5tpcm2n5chWf12O3zrdj79FwER0uDSaZaWrT6trSDdqX1YwD9Ze9a2mv5JOOUz62MK89nfty3PuwabDnKyjuQPnC59bkFxFsyV49dA9LpuZS+Pr2PGWhsyQYqPcIsUyGRQ+emVLm6LMkOTZPWXFs9X+l2w79Wb9q+iUSN4rxBPRflXCcafKnWuMYvrfVd0TAf+V3qs+UJXez8WiNVz2eZc7TxEHOOxsmYkzKNkN8JcX6fmsy0d77iO6Ad+qv7Zvt/lXL1MxoZLJQFmmdTrEfn0k3ZzqUc9bdv34b3wHa7QYwR169fh3PpgPd2u0XnffIU+D7tbIhnA8mDzyy3es+zJ4UQqrSGE7CIGMe0O3B8fAgAON9sEZiRdpQIBI8wRoQhYHN2ge35Jt2ZkS+RCmOKa3NdYuboGSPFkvc9xIAxRHRurpD09rU+QyA/vfeTUaQmrramUyrelnrQC1lnYmKicphRij1PoRXGFFvH6Lq+PCvxlvoOjJbgk3p1Gk+7AOR3vQhbgmQJKLYMC/132qnJxpxj7HIInHMERPGMtQAbZcySaclKMYKzm2LuoZB6ljwy+8qSAll6ruKjRqFJljbrqJ6VOgSo8dwDs6Q47FzN+kFULjUDUBsFmBuk8pnm7svaqvgA7VTJuj17pmeJ70pfFsCQ7bd8FpWc0p+XurN3oAU4W2OVPneKLq0zG3+bsjQ2/d2+7y1viAGQgzvhuM5eAyJER9h5YNcTPvNbv47v/ukf4ei5u0DXgQjwTMAu4OzhY7z/xtv4mx/9CM8efAhsBmA7wMFh5Bz+R1R2TVpz1RqfGLS62LhoLROXaGJLC/i16DbdFRVmz+j1Lb/bsaUkH0UEXansW5//rsWm+Z36zsVTugTElsAjkOhkD522AHp5F5X5NRufpqPtr25b+hUjAzyFI7ZkypKBYOVXC1AuGQrtUo/Orr0l3tvHrzocppK/6WUArjm25R7WafuXiu0XZy98K9R3H3C1OEK/8++jWOOIzGf6u6U+i9GpcYE8c5ksaWELW7/tb+teH9GnzqWLSbfDdM+ZYBuLpSr+IlRgQs7QpnOzbZr9bcqVDY2u60r8np6AAmhzr0LkcqD22vE19D5lfdrtduXzYRhwdHiIGAMGTMaHE48+p3MQOhTHZ8NECKYJk6mAdT9ZZ9vtDumOiZQRYYg7xDgijOlSLx5DuvkwBBxeO0bnuxRu5Cn/DpAnpLMzKaXsbtgixpBjOKmkorXbvzGmtGEC2uVzSY9LmEKLRKCmnynWjpzDGMYqjMR5l++HmBi7gKk4LRQNXvTOB1G6L0KYLdHNgXnK7IVchyhLy/y2fqmnZSxYoaLHOwfd9cLRi8EKVqu00m4GYxzzIUmXDs3r9yplkj5MmJvFO0ulG5TTFluhY8c3679dwOr71kLXdeqxa35fVgTLQMvWWWjvqBherbHpPly1MLhKN6idApYPKuENAK4NHpfoR0QzoahLy6sp82V3WZaAkW6rRYey5lRY4mxOeXlerKe9Ht8ELnXmtlZ/rRHTMogseFtaP6365dkWUGQg7fxmJcUEsAOiJ0TnEHuP2598Gd/+4+/j47/2OcTepV1wABgCtqfnePeVN/DLH/0Y9956J92ZtN2hyze5MyVZx2Lw89RH6YeVHxYQLIFNPU+WL1vGTGtXdSZPDN/ajHG6j86li2u32+2sP/JM0qVyVm+aj6WyZHhbGui2NM/o55bWhZb1U32YvWONKt2W7u8shLTBl62+2zkVerHikaus7YluKIe+9Z1OS/PCzCkM1c/P3dm1pv9u7bDVfaXZ2Fq0k37YXU+bwES305zjjyDjy/s5a5YOC7VzZHms/DQ00WWf48iWpVCyIpfN55avrKws+Ek9r59p7cKUd5hz9PU8y6DFCZo+LRpZWdEqut4ZDZRNUDCNiE6eO0ZK31R9eryljgZ/W1pctVzZ0NDWrEy4PkTsnc9xjNPC7/oORwd95Sln5nwrdgK+fn2IVd+nmw1zrGfkdMu29u5uNpvZ/RiyiMv2YZwImW7E3sF3a0AyNFHaceE4wrsIhxG9C+BxCxcOEIcduvyMB8DjCEdh8nh3vgDVtPPQVu4hpDAtMZQkXjeEkIRUvnFZDojLZEc591EJTpSwJgIXg6uO6eWCUqyQs0pxYqycIpK56kNLIenFZxlOf653QuQ7/RwwKZq+76sxSthI6327iAHkrGUMHiICR3R9Jy6GTNv6ng9pOwlaG9IVIWmFrdGzpPiqYjwHtcCSez0ayjNv8y4JIUuHiR5VN81Y2saYp+nSzJYR2BIimu7686VSKWSaYuh1e6Vvqm3tpbH1LwEkKa344H39s3UutWmVaUUDTMrTvp+E+9zgvgzg68OKNoTR0s+uR11fa+0trW37XGv8lWLO3zmJde48IiJC7zB2hOO7d/DV734HX/nW17E6WiMKKBkjeDPgg7fewc/+7Y/w4M13cfH0GdbdCtiN6PNt4UwE8g4h0zBfi1poIvRs8as1EuTvasdFPbuvWK+hLlamWBkp7+rzGdJmcoBtZ3VJf8q4eL7eWgDJjsUCJft7C2xdpVi5kn5SiUKw4VX7AIl9fklf2O/t/Np6tR5r9UG3nX4PKfRlgQx6LRpqNNvQerYOg5vvqNmxig7X37XesXOod++WwtCsPiAigOosQ/tk5tTPydkj68o+Z/GGHr/FJC0aLOk7SwP7nXqoGSY0ja+Wr3aMlr5L7ZQ1D67We0uvtGSupXlLllmacAZJ9owogOLAYI7AxSa9J4xNU50WBxJROTdpdZWMT/PaEo9dpVzZ0AhFQAES/Rc4efopIileEJzziEG2b4AYw+xq+c1mgxDShXys7lpIgM9hHMYShy6gWhafCGt9R0MCqMB2p3cPRnjfoes7jJGRtiiAw6MVDtYeFAm3bhxiRTfBrsPxjWug1QroPLzvgDGluPNdzuIBwsH6ADEbD85Pl++1JjDGWO1mlM9DLO/Vuxni1eTmbZoxRjiaM2qMsex0SNHf24UpP71POyjM8zhcHRplF4r9fR8g089poVjFSSPba0ahtMagF14IES6EdOaAgNPTsyIE9SLR75S6Yn3pHZGAl1roa+8W0dyQWipLAlyDFCKaCUXb18tKS+HK5zMlaICWbsc+b8OPripgpF7rARZa6jL3P9Vj0mXqz/zZJSW5T1HYsV+lD4ABeHval+dsSk9Ld81PtAAyWsXSUrdr+95SEK11ob+z8cK6JIhJoJz9KfQe8WiNX//W1/GNH/whDo+Pi7HgGcAu4uLDR3jzF6/g1Z/+HB++8z7Giw163yGEHboMXiKShzDmsKmuAUZbsmwJKC0BdGAemmbnUc+BALIWDZf4pAWQgHou9gEN2//W3/v6YHfYL5MrLWPFfj5/B01nR2s8S0BqX9HAZ1+d+2SAfs7+dM4BPM9iKMU6py6ba62zWuu3KZPLZ8v9t3XI7kUrRPSyUrCGocOSTteYK7WPykhp1S8/LVjW9P0oOq5V/2Wlteat/tAAWsak3wem8PSl4ijtvGp6tBwbus6rzpXu5z4dox3xJYX/JeuhyMH0SaWjp5DP+bt6/j6q0XF1QyNnTgIoZSzKaTPJuRQOlNMUhBgQYwBHxjDsQEzo+x4hpLSxFxcXahRU0uUNwwCPlI5rMjRcMT5iZMQ4qhSyDuNY3xoeEKeYXlAKzRoGuK6H9w7b3RZ379zCf/af/ac4efIEw/kJVt7h8OgGdiHi3ocPcPPuXaz6FVbdCnEcAQ5gzpf9OYeTk5NkZIFzGtW2whLmk8kTBkw7E5g9k76XnaNYDluK04VACGGsDJgiEHJ9qemJyXT4jYR5adAndNXPWkGzpNRbikyDcfncLpKl7c+Wci7PMQOqfZcPf5EjePIY45jOaHDe2o6MMXLepXCIMUBMe+ccghwSz4tSPBMA8uWBqh88gWIR8nrMQvF9CrrFF0tln+IsbUdGyqXQAIJKCGgBEmO6nFLPccsLo9ta8uyWsScny6x/+u82vZaBrq1HKzwGNZ+bA2fOLGMV2/S8ZMQimoOZSxUBp4Ev0U5oexkIaMkORtrBZP2MeV33U2fwclqZ0lSnYEK7TnW78iLJ+HJf9FxTCpoCHCF4h3Hl8NIXP4tv/ekP8PxnP4WtIwTn0RHBDRG7p6e49/pbePzePfzqpz/Dw3v3wdsBq64HEIHOIzDDO0JgTjfWUu1JFqVtDVgLYLTiCyGFxzo/B/ZL4LXCzYp3Wh5aOweteRT6anlnY+btWm3NsZbFts9LO5EtWbpvR8faDJfKnyyPqzoa/VsaT+vZljzQ64cBtWa1TgIELLWKpdHUj/k9T9YJoMclJaq10hqf5dvWWPTf1oiW0gLlTXmxp47lorIncp0u1hoFE/2TTJUU+M1aDXaQeSP1vR3jvj5flbd1ceRSRIzqQ6tU863qtXRd0lOCCUjtMmhs1er3ki7YNybNLxJVpNe0yJCLzQbHR4fTe4TkvOI8h6TooQVdHgOUc7XoR4WFPkqIW6tcPXQqpkv2whjSpUG5nyTAOUaMIWCz2WK33eJic4Ew7vD83ZsAuXSp4ciI7NB1azx9dg5wxMHxEe7cvAGEEQGMIeTLX0hi+lOIDRVvdYAvCiQt6nEMyZrzHofHx/n5CMQAcNphYXTwjhED4+TZQ1w/PsCWDnBxfo7PferjODg8xMm/eYYnH95PQCFnvhpjTJ5nTjs4fd/j6Ogoz1GaFO99AW0iYGKcvODCHKnPXMD9jCkZOdsKsB4ZowM2a0LPAYcgcH4+5F0MAQRQRlliBBESOUVfZg6XGlULKzUWxjHtMjADHNNhfEeVIWS9J3oLz8Y7SxGm1PGvTYXNgNwmR86lFHuZHiLUHaWteuaUTtk7hyhJMCOh7w8Quw6ji1jFAGIPonSoKfUXxVhx7EHwU9uUPcracCsGRqIfYQJBszHGODdQoDyx+vdKWFClOPeFbNR1yzO5f04Eooj1lqe6nhOZF73TVAEv1d/F0DpwBdSXSktx6WQJLSPWvi/jlkxiwu/T84wQxhKmmT5H+SmApAX+mWsQviRMy3dKgEspHq3skW+tjZagLnSODIm1TVlUAMZUV7Um8qDkWcrrRO41mgalvHTlm6kdJ+fM1FgcCI6TZA0OgMsth4jed2B22PQO3ct38Z0/+wG+8Fu/Ad91GBHhPMGNI2iIOLn3IT547S289+obePeNNzHsUlhqXLmk9DwBLvEPE6BvqBWlKtn5KJ9BS2GlStHKvDm5kFXonMccGX4addZTXBiChP4mtJE5vUdEoK4rc8OZzuRSbynTaSl8rwUWW2DDygYBLxXPmdJyKGijzK43u4tTd1hJDIYk5MvhbPN2k0zLDh+eOySWjKPLQIp93q7RtH412J6/Z2lZDVODR9R0b4LJFpBVxrDtu8jKwsPmPMUSbWJmziUHVAuI2svSWn21NChylACULFeT8UbkypzK85PMQ8EzwnuWN1s7dq0Zb52PmvUdOZMWESin3JdVnALbm4QCwOUMnR6z6NsCrrOS16B94rGUjYElPTtNfBVjROTpXgtwwiKc3HjZ2cMg7/OlzvPIiNY8tda5NYR1pIvGDM4RfJeunGCHlP5byT1mkXGiCJWszxgazmMUrCo0kveKPDA66COUqxsaQ8BuTGE/YKSbBvO9DpuLCwzDgM1mk/rsHFarNVbHR7hz+zYuLjY4P9/gzp3nsFqtEQIjhIjzsxMcHB2DmPDk0RMc37gJJka/6lHyP+eD2AJovPOTgMlg2JOk9WJcOz4GA/DdCruwlTWFcQhwLmU+IRAeP34CIN1X8dqbb+CTn/wU7j7/PM4u3krjRd4C6zziyOWuC8mWserT7o4sLBuLDUwn+OV37dEqdK0O4GSwC6CjpJDZpYVGmLwsuk4w590fqXGu1KICi1ALCzwZRrIg5MA43KS4W143bYTY73TRgrZlFVthY7/XIHcGdil5uRI/5iVDKSSJMF1sRVCpbhmzeStKm7kad66uGB1itOiQGOmHVR6WHm0jbAJF9ed1HbqvzqWLJ713qA03Xqwj/ZTdsuY0Ve/pd1tgqSggzENO9O+LOzdU93HJyLCGTV3mIIKZK6M2xukMl+1nsrdretjt76Wx5QartqXEyGDUoZGXlSVAtBSCp+fE2X6ZQq0/COiyIkwKXM0HEXYuKRnHCcx7cqDeIzpCPDrCr3/3G/jaD76H1e3rgE+Jzjv24O2I88dP8d5rb+DtX76K9197CxhG7DYpy6DvPJyEqxQhjmI0aVq05Ins9Mh6LbQx86vXTpnH3KY2/uX7JYCb3qtpnr7AZLlw3Z8yL4r3S6hkaKSZXJi/faBcgxZtRGjg/FHOLi213QI+VR/Ud1ZO63ZjjCXBgf6sZRC1DIVpnZKpN/3eCnuRUh9gV+0Ze6FlGOnvdN288IwG0EtONavb0qjqjE5tkFyXfTpUaKJpWr88gUYiVTdz2Q2wO2A5mWM1DtvPVrIe7OFj2/dqnHl+WBwjousBiEN1Pl+1gTQfezZUBG+rYvmxpb+lHcGAeteLaMZQzb7UPD1hsUvlAHO5Q2M2r7mNENPF1BIxgLxuInMyGqjmYbCOEVAyU41Z96N69yOWKxsaY77/ApHBIWC7G3B+fobtdgfXeazXa1y7doy+XyHGgBgZ3gHXb1xH5Ijr126U+zOIAHIOF9sNzs/OcfP6DTz+8BEcOvSrQ/icn1gPkpHBrRerNHlyxeAhAI4YB32PGCKC6xDhsPIrRI7YbLc4Pj6GcwTnO/SrNYAA7AhPnj7FyenPEGPIYQipfmkTQJUBK/WnDuSoQIURYDpEJWQGsIphAs8pHIjitF1pBayU1oGsAppz8c4jhLFi6klQ1JmvpCSwlnyBVgDLPyuIZordFNuvVpy0/G3r1kC7GE8xInBAyEJILlFiCEjL29zQoSP5nyKb7YcokZlgQO1FsHNh51zTqDXXelFrYatpsLRdqS+7k5/THNU0r95DXZaA9F6ArT53cOWwrn5P3hFDe96PJJStgdFSrBVougR8SbiSvKfnz4YxSEijVXR6rhbBHvPsPhJrjNv3l9bFPiAxhVTSbH729u9KpW0IRiIMjtHFZGQAlO7E6B0++ZUv4xt/8kPc/viLaWfCETo4YDfi4sPHePDW23jlF7/Eh+99gLOnz+Ajg8eQPP9qnf1t+20NAfndKl67i2Tfse/a+Zb5XKK7nbMWQF0EUKpc5TCurbe1TmWNaMBijS37/VKpQWL9eTUWokqQ7tuNbQGslk4Zx3F2j1B5l2u5Z+eoBfyXjIf0DleAyb5v1255piGnZK3a9nW/7Hhr3VK3reeqMqhV0Rcb2v62/i79Sp1o1sksFvR8raX6eMZLFjB/FF5eMsQEW2k9MsmPPc4VnjvoZG72rcOl/gB5CZh3NWZa4pO0+7BfB9i1fFlYtW1b99E5j77vG/IuRXOQce6BuRhxUi8hG+DNfah/t3JlQ+N43ePs/BzjbofOeXgwDlcdbl47guu7nE2DsTk/yd4LRuSAw8MjhDHkkAaHEIZkmRJw+84dOO/w/PPP4drhAcJmg7jZgdc9duMmUwDZkxwzUORyaZ4IJdlpODpc4drhAcAEJo9rN27DO4+z01M434NzpijyHoQOcYwg7+E5nxHxPh3y1oKgcRdDYoZaaVZAUjGYeHNK4RrUVEpRDtWLMcXIXlkqDCEMWSltnsCvPYhbmlXvFaYmV9UlAEwOmMtOiIzNxq1aYa6L7acVsDYcx8ZCW8Wv6yz0zkZGiIzddleBd4ARYr6HpQSOOIlGbAse1d4MpNAUYjHzkJut0RrszgFPqb80u7ytqscvRcLIrGCa5qneZQNQsrgx5gLOgpIyZvVMS4mIcBKa6D7ouvTOHjB5qdqKbhkA5kpnynsf/exa0cZb+s7PAN8+MKb7rBWZ7KR476czQGZMS+vE/r2ksK3nelHJVcqsNQZAvIKazkkmEFYhXc4FB4ydw8HHn8fv/ff+DJ/44ufQrVYYcqxNFxnx4gKP3/kA7//qNdx77Q289847cCB0MYUSkEuXnIpBelVAVHirwav6PetJn6+/Ns1bgN3+PQO7jefJ1aGRFuRoWdJqpwk+GnioxQ+2vVaxa+Ojga3JcaPrSjxa72i25Laeq1lIjZGx8p3WAxVtqA3ULE+0DH57tmf6fa7DdV/07wXgod4tsLe/W5q3aDHrB9U6xNLT9kf3aQ4s63nU7RJRdcO5fT6TuSnD0y4Iqs+0LG0ZHlIfY5JrUlo7gKUucmBMRlR91jXAVQmEjAGpeFKff23RqFXm8rPmOSuDpQ3L/zFjhpausmVvWKPuG2psqfvrHOWdlhEeGedyktNT35zhpxz6LPNteMnysO6Jbv8q5cqGxr13U5xt3/XovM95ehnDBXJ60R7eOThmxO0uhTT5Djdv3sDdu3cRYwqXmk62O1xsdwgj48UXnsNhT4hhAw4BY0wCLuQ7K4RJd9stQj54TuSwCWPeTmN432G86HH31i2AHMj1APV5l5vgfQfnuhIXHBlgcmI7w3mfMp9kJSq2vWxDaeWjYy/lnwU0MkniZa0yzKhJqhQUTYtST2rX9aUNYFKu2utt+zTVXzOEFpL6cHjLs6//1l6FJQEntAEwo0VLuds+ydj0FqxV1rrNMYwInHYuzs7PKqFClM9lCMCBTgvXVjCa6rbf6X6O+fdasFhPT4wSY9/uv/BXiyYWuCwJoiUAIt9NY1sWCC0laA0H2zcNAISHrDdmH+ibgSvzeSu0ogU6W3SyvKffqcG5Fbz1vLb6WASy6UtRfODZnOybO6uILG3sd0v9atfVnnOiNHa7dn0Op3LOYwRhffcGvvq9b+Mrf/g7iNcPMHqCj4SOHIaLDZ4+fILd4xP8/C/+Ck/e/wAXT5/BR4AlmxpR4Ts9T9YBob/XtGfWirSdIcgCyX3gy362eDDczJflIUvnpXlsyUBbr9BiyVDQY7d91DumV93F0Z/bcbbWS2unVvqtDaxK1tg6MOdvLV+03pDvq75lAGnp3QJoS3PX4jc75qVdrCV62HHrouemNXfyk4jSuUy05641l1fZObgKcJ3NW0yhUzY1s2Ahq/MuW2v7SmtNVXUYOgP1tQqt+myfNO2X5sm+O+ub6gPR/mQ3l9GgtZZ1v/S8tuRFRRTT3na7Rd93cM4DzOY8RQl6q52kzEU+p3tSpgG3ZO2/S7myofG/+k//F9nQ6LDuV+h8h+OjQxwdHaPvOpyenmK1WmG1WpX7Ia7fuo2nm21RvhJSlQZB2G5HuLXD3Ts38b//3/1v8NytGyCMADlwPpzifSLcyckJnjx5it0wYtWvMYaA7WaDId8qPo4jwjjiYy+9mO5ooBQ6RSA416Ffe3AGhHAeqQsJQDIhXxA1LXiiNjiriT5Z8yKkBJAzTyFTklmrvG+EndyNMWNgl+IBZaeFYu2RnZixrVDTM9MFSVYZxBgqY6Vifq5jAoH6kiS7MPW7AlpaxSozqRdIgl6nQrbj0b/HGNMZFpoMN+9c2aXhEkSNxE9R6C0+lsvLDLSqrcaWsLfAhTn3gqYzHZZ/lt5v9aXUaWg/B/QLh/MxAT/LC1ZQW+HS2qaPeZdR1oD17GhPf6sfrXY0ry2FDdixt/hFnrM7PvV40+d2Te0DEMyJB3TdlQEeL++TrmtJOS0B1hatdF2Xbb1PdQKyPkRWAQB1Htt1jy98/av41t/5IY6fv43ggB4EFwhuO2K72eLZ/Q/xr/7ZP8fw7BzrCAxnG4wcMXLKnudy6KmTthQ4sevEfqb7SGadtcCA5pP2ejDArkEnbQDpZyxIsQY4EU0HQA3IsfXboue/4osFQHEVhd9a1/vevyo/6n4AmQ4mVEvLRAua7Hqw56Ba63RqGJVn1vZ/iT8sP9TvUiVj5JmllKa2nn1z0dJdml/smRLrzLTvLn2+JGc03a/SP+lHOvM66dcq1C7rsiU8IH8361f9tE5Fy6PlFbWFYkOIWzKhzGVj5/Sq60Z+Vs8TVXW2zl5ZuTHhjLpuSx877sv4aqkI7ky6FkB2bE4XPItziTGdbwEiCDnfSPpfYx3p/k6fJQz1Ufp6ZUPjUx9/AQfrdQL244i+68AhYrd9hvGCMW62uH5wG6dPH+D8/Bx932O3vcDhcy/D+w7DboMYGbthQAyMfr0GOQ/fdQAYIWzx4MHbOFo5+K7HLiQrSzIOdF2Hm9dWiLHD4cERDg4OMrjxcM5jtVrB9QfYhXSXh+t8uVCIQej6roAEny/woxxOk6QYld0PsewSfa0nRhYGMuCYJiYxoofzEQi150Yzl8QYauEDpDg7eALBpQOOkeHhsBt26AwT7FMKNQiuLVId/hRjfaGVDa0CAN91CPm2coJaDJxCqwhUhY34XE8MoUo1LGNf6vMwDNWOhA7Z0qUSrI4RxogQIzbDDhh2KSUxUmYu71MIH/J8ed8BcIhxhAb5VZ8aYDvGCA4hpd8070zgv/autubEKhhtC32Uohf+XJlSxZPTS5iEjLzbqFOPqVX0GEU56RBGXVq7bOlFFPJb4Kh5sdUvGH7gGBEMmBLQ0zJIdF0t0DrVU8ldTagiO9LY0g5ZjLHQIrVPWVaUF2Ene1I8NqwkEcmCGmv4TmvBgvXUrsxwcqTQlE2I0/+kN67rMMQI9g4vfPbT+Oqf/RAf//IXMK4dLsA4gMd6GzE8eYZ3330Hb77+Bi5Oz7B5+BRnj5/CB4bzDrswlH5wTHLOOZ8N9HZ4XvldeCr3KckazCbByr4WUJbvBDRqflgCNrZoEDqFbUz8rJXuPmCneW9px28Wm800kwv7lPo+faA/l7F8lGLpXMBlXouElEa+AC7THxm/luvieBOdYfs+X5ecPK4NoG/l7QyUNsB4Db5QaC16vQUA54RJ71F6YLYbPus/zw2ACThPzjKi5KxYNKzKzySgtDNwybjdx+sSLom8Yz+J2KnvRVwL6DHFGncNMlU6tSV7Z/KWJiWhcZJ2RDaBua6EJ+NIaltaRzM6S//UDnXLOLb9qPs0jU30LhuniLTV4rl9hod87/K83bp1C3fv3sHZyanSJ9KHyfkouCPGCI5IUT5C3wU+1m2KkSJy76rGxpUNjWcfvIf3T0/x9OkTvPrqrzCOOzBHnF+cYxxGHB0d4+joCM+ePcM4jLh27Rr84Q38h//wf471YQfq0hkJ360xjBu4yDjMh7Op63Dz1i2M54/QY4ejtcMQgIvzc1w/uo7dbofz8xOcn55iuz3FZt0hBMazkzM8enyCGAnkPFY3X8YP/uTvpY2iMZ25IOeQgoS64v12visBNSFGOPYAXL4bhBA4nV8Yw5gWPCIiU/6Xlp7Edk+hOAIsGICD3AidwG0Ac7oDA1yffdB3XQRwPoDJ2LoUpdgNAQxgdKiUtUy89x5xbOf8FoGqmUR+n4ReLQTkgOy6SzdtxyEd0OMQ1LNZMTIXpk4CLwA5pSQzg8cA+HxwLYYCCLXi1322YVctxahBaASwioRdYBzcvpHA3Xv3EYkAeIDTbfUgEWShKJcK9yqlJQvysgNkNkzKhrNJvQIELfgt36ul3QpNkyKpaNWkNeecqBaaWoh1WU0FZQSy6oEG+bqOpVAXu72tDyjaUJeqj0iJHKRuqVcrIqljFloivKsMJiJSF4q2+Ul2De3OCyA8QYWXZT1XSlXRw9EErjj/l0NdM49Jfxld55QBlhwV1uhM1eedgGJ8hAJCk7NAxqQNkdTHaW1LIotkE/cMDBwwOgf2yXvVRYJjBjgksOI7bB1huHEd3/yzH+LXv/NtHByuMXYEt/JwYwCdj3j/Z6/hnZ/9Eg8+eA8PHz1EDMmZAM4hmDGiy86ajhzY5V1sjuWMjl77Zf0AkwFEhIhYAM+yAm8bXTrphnMOd+/exdOnT7Hb7Qo/7FPc+wCT9l6aF0Gc5HbR68I9hBJSWYA4zUOeNJBJ7UzV62csMJHf7WfauNHtaqNmH11L3dNwZuA9qyMQuNwUPz2bL2A047K0lHqX5mNmfBi52Ap1WqqnZXzEOKRdtwzWEo8CRB7MY9V21Y7IrCg71mn8kRmUs2KmM6Xp/ibnUp2S8p4VTyTdOhnZxOIAoOLQUBJ6Wi80GV6t8VvwqmUq4nROo8tp/FluiM5+VyKAnHaOZMCKNLbkpCzwHZelObcgHQAih8qzUBw3JGut5ucyViUv7Ng75yGGMGcn42Qy7DfYhT5LO1r6p/1uvgMUp/AlpERFWajlOub6u6ljF/phnx/y2WlIKvD0ANLuRpLPYpyC0o5zlEOujHIvnlyUOsYI+DatpB6dRviycmVD4/6D98DMODjs8Zu/9Rs4OTnBOI5Yrw9wdHiUdg9AGEO6k8ER4XwkXL9+vcTcazDGnG8GjynFLMjj5PQcd66tEpOAsR228BuP7XaHi80FPnjwAWLY4nC9wma7A5AuZLvYXGAcGZ/+2HWgbOcFdJ2XGZkWeM5zLzeYAyJEAOK0+yG5pAXQyNxqcB4zgG2BOiimtOEflFGuBp61JZsXuU9Zjl1e9Qyusi1UVr0jdNTNQFligrmALYBLZemRIgtNA8CWopDPdciYFgh2YY4hJAPO1Qe0LGCQ+oE6lKpVxnFEzylcCk4OQUvYW1luZu7m3tDSrneFX/Szk3ejfr+MwXhLqzYV74lhWAyb1vOogYL+rnyfPqjemcoEmGcx3JUAnXg5S6XmmDV99N+i+J2fhKvmB10svWc9Vu/L37YfrVA1DeIsvaQOCQmyiq4FdCw/TFRBBXI0ULDzKhd6We+3XkPWoALy4dqGopmHGdW/27GLcpYdFhChiwLm05pgRwgeiJ1H6Dt86qtfxe/82R/jxgvPg71DD8CHCD4f8Oj9+3j9x3+Dt3/2CrbPThB2G8Q4ZeuKeX12XVcAl50DPX79WQE/tJz+tVXq8c4v55L27t+/v/ddW6yMWJJNS+BYGLu8mw1qW8fS+1ouQI1F33cjvKd3a+ZGa3sNt9aIbd8aXC36lOdR83I1J6j/1uuh1U/dpnV05M5Vxv6EI+agzPa/tcbrMaWkEOC2kanrkL7O17CWY2k9J8MlFgdm5ZnJpciv2Tdq6A09Vhsg87K0I2z5xc1StddtaXmj25vomGWKwjS6cIzJAKP6GSLKESfV07nNaQfInnlMc75AJz3vel6EYqqtpTXY+nxpPVi8Yr+z+tvW0aJJy6nX6qP97smTpzg6OKjHns8vTw1KBaa+RnSHc27GC60xXrVcPb0tBoQYsd0MKaWt6/D02QXIbQE8BZBSqXZdh6OjIxwcHuDGzTvo+x7DuK2EJDPnG7uTJ2EYIpg83n73Azw77OBcBBzShSf4ELLV063XoLgCEXBwdIijo+vwz86wC48RtwNeevmlmcAjosTslBk+ey6894hhSBl8iCqlLdu7QmALTgtDuLYXqUyUmSQRKJZRpM0qFtA7hDFZn7thQL8wL8ycPayxeA11mk9HroQlSJ+KgKY584gRIMpNx6zKuGdb/eo7y5AFPBAq0KeLrr9l0GjaSvvprgy5MTrR4fz8HBIiBKrpqefRzpXe1l+KjwbV/a4VcgSpfMxaGWnPxWUL03roWjwHALynHsnOBizfbpseRL2bgRq46WIBwmRo1OtDeLAFrPaNvdWmHq+mhf5bA34iKjHjFlRpsGbXsq5vBiwbIEILYstXiY6YvKSo1/rh4WHiUczPoMw8YobWVmZooNU0mrzDQIyOHfqQz0w4j50HBk8YPOH5z30K3/yzP8HLv/Y5UNchkoOPBAwjto+e4p2f/Qpv/fJVnDx9ivOTExAzdrtdAc+yXuWf7buEHFkDS4+/xSOLQN7Mv6aRpY01bK5SWuBR13dZafH4vn4utl2MwnqeNd+26tWft4CNFL1mPkoo1RLYaAIw1b5NO62fs2twaYz63daua6u0gN5MlpZ+TR7o9My062afXeJZBgqOSM8u96+1Ji4bg/6sYImFNloG1ZIRJXwgDl79jvqjtNam+4J+o3rnuZp/8+iSHqjobkGymVdgeVdCG022jZYuuKws0bT17tJuqpXvl7XdbLPo4ayrcwhjjuu7dBy2fgApOuSSZ62O3leubGj86Mc/BTgdrN7tRrz11rvYXGwxDgEvvvgibt+5g5hv0GZOXvbf+8M/QsurTEQKACev22p1hLffvY9XT58ANGI3bvNiSoBGvNU8xhSaA4LvejARPnz4CF2/wt/5D5+rPOvFcg4RnTirXToD0fc9ht023UQdgZDTqcmh7JJlyRsLXSaZ2kKzJYyA2kuvn69ARCaVyzcDF9AjNHM+A0nbBqrwBLkcKRkhdWiMBlSUw8WscNeMPhfIc8+FPK9DZ+wcSC90vLMF1a3f5RmdIlWUceQUZ8gEnJ2dpXCcrOOcumGoVXdTkWE6d6LHnOZgfnhQxsPMlddRC0yWvZWGARGjXEbZBiCa5poebJ6pQe383RKmltca0eS9ct6V9NExzuu0/dE84pxDUPxh+WsfqAe1he4SUJopddsOkEKCcmntINi27LhatIcaV7NdA3Bl3Vp+Y+ZyoenS+HRoTat/Fpy36irfEcAuhXqmsFCH6B22HWF95ya++/3fw5e+8w3E62tsidE5Am8G7J6d471fvYoHr72F+OQMdHqOiwePAE8YadpFERpK7nb5zDolrBLX8yx6gFAb8fvmajY/aPAWUNHrsmLnUNdrHU5XBeZ6/cvfTYNQ9b3QrKEzbR1L8eK2aGBtedJePDoD/Q3QadtrgjagumG6Nc7W2GzorG5DHChLcsXSVzs2ra7Vu0OJNpwQhXNAcRjV+s7ysZ2H5KQSJ0MOV9GkoUmHSNE7UlKHbnNOA2OsOZrRWfo2k0tqDDZzknzugNl5t4kSKEbDXF5OoVNWP+qiZSGAHG6tdlcUD2sdqceSdod81T87bv1Oja/mMlvLIi1nbb9bv19Fb9t39pWWfCnrHClkFzQH92ktp5DLai0TlSQ4zs13KzWm0fJB9LpOSW7n5qpjknL19Lb3TwHOITAhwveH6GKH8+0J3n/wCPcfPcvXxScleXR0iOdf/BiGcciHvwBHPi/AFNMcY0pzy0xg3yGix1/95JeIcYdIOkZ52l7nMcDlU/UhRgwhYH14gM9+/vPoV+ty6U81Ec4ICAb6vi8CQQsR8eAXRaUWecVkToyAuUdmH/MB86226TuGo7SLMHAoKVXLLoK6EVPX13k/hToqZokxVp4lQAOBVLdWRFJsCEtrQS0JK92WFvhYeFbXLeCwtRs0+1uUhwPCOOC5W7dw9uwc7ByY863QDeXTAh9FYPEEDFpgTubcArsML5sCX9NY9yX1gasQCHmnRZvW7xZMp/64Nq+pOdDClzKgSNv9c+VqhYsWhtKMDYvQz86EWwMU6j5VfVsQ5LqNQmfVRt3H+XxaPm21kwRx3U/rJFhS5jBt2XFpWui53he7vg9MtIySFJ8MsPPYdh7BO4ydx2/87nfwjT/4Hq7dvY3gATiHNQDaDDh7/0O8+4tX8d7rr+ODN9/GATuMaHHcPgABAABJREFUF1uMHBHZIYDh1a7okkGgP2+dCZB+a0+3gHpLV00//f7SZxpYtvhNf7bUVoum+jPhrxbf6Hany1/nc9ha54VWSPLL8myL56o5b/Rdv2+dXcxT2nVxlFxGE23gWI9/aZdQ5N4+UGK/W5qvFKZMAObr1o7f/pP+2bFZ2jKjyOT0SKx4SZelED+ph3n6vdWWBnctmdCihbxb0adBT/v7TE5ibrzoZ23R+lau82qFwElvrD5qylWZK7TXg11fMz6iCXdZ/NDSkZZWTT29WKaQKxvGvTRH+vfWM7bsm4NKniSRvlhfwrQTZgWLY2jBKKJ6nloYrlyEbPrXkvX7ypUNje1ulToWI4AU2sQOGBnwboWzzQ43b95A13UYhgHXbt7F8y++jDBO90cwK2HPQDrwCGx3I3BwgJdf/hQuNv8MznvsxnT7uHMOXTYcxjBiTR6eCOQJ23GHYYyIbsDzL7yEGIFIU/xqCR2REBtCCnGh5IlL26PpwLcV+kXI5fSw+l8CITWBrfeUzHcV4FsSlDCAHMpDoECyFlC2v1phlz5Fnj2DEkM7eXksQLNKWYrMZwu0ayHUAvRSpz4catuy7wB12JXQRv7u+x7rgwPw8RGehQBAwqn2e36bipCmevV7MUbEUPezCk3y7Xhduz9sDTSJcdf/dLuWJsyTZ0Z/NinWqdHqXU7/k/d85/NWuQD1NrC1CqsSRLxgsCmatUD9/ujiq5UWgCjm+gKwaZWmAM7FekP1mZdqPJqPGvNlgaD+ziqjpbDEpXr2CfoVdRgd4aIHXvrS5/CdH34fH//cZwHvEPoeMQS4i4Dtk6f44NU38fjt9/Duq2/g2dPH6PoO2zBidNnp4tMZn5bnXO+0WHnR6nMVEons9MBkeLRkWhNwmKLliqXxVYp9bmn36Kr8RUTwyrO+z4Gi36F8zsrSrgWUtVf8sr7IO3KBrF3j1mEAM4f76t5HEztuTUMNCFsgS+Y0Hz1q0sKuxaV2tc6y43HFqSfDrtf7vvGoHkMgbUUzApJDtT3vVvYvyYt9paknzPeWd2yxINauo0hLxkh628op55LMiKrdGh9w9Z5+fynUCJCIj8vlgR4rAYuhQJYfq7EbbHjVsljfFd5rzeXS/DFzuv+EJl1Yvmd5th1mSKjxWIV57LMfkR9tubKh8drr7yJyRNc5rFYdVqse3jt0q0NEdlgfHOLJ0xNcv34dznkcHV1Dv1ojRgZHwHsHyTSTOp3CXnzn0flErM997vM4OL6OzcUZfL+Gj0AMESdnFyk2mBzOYsTR+gBH144QAiMEho/AJz/5aQzDAKZpV0Colaw8uVVj8qZ57zCOxf0CIINHmUdCucRGDp5qBkwJUuaetcj1ZUZ60cQYS951C3yR4xwlA4DU4b0HSDLrpANcMYeIMXOJTZfdHGnTe5+8Y9DhZDkrQxSAO83xOI7T7okYR5SHqkAlMaHrfAm7mgRFm3eKEcXZgx9iSemXAGt94duSwklhcbKFDnBIxuMYAjZn5xh2IwIAj+R60YaTnp8ESlWIlGlL92ECsfMbm0Ug+q6DfDwZMShzyjwXVglkUbVLYpVNRT+ePEaRuflc+rvdVqJ/Fu75Vl9wLGkj86aMqWtuAOrdQkLiVR2GYPul+aN4tjm3L43SRA9rgrQEnFVMdqyO2jS1pQVW7Pjt2m4pAu0h5hjLActWXUuKXNbsMAw4PDys5zwrhJjJxXqy5BlKMbWUEyNEZgydx/GLz+F3/uQH+Pxv/wb6wwOMMcJ3HsN2h/PHT3F2/0O8/bNfYXhyggdvvYvdxQW8S+MYOYK7KUyhy6m1OH2gxSTknJJT/fbOAZLymlM2qQiUEFu4VF86XC4ATjzKhUplvctB95onLHCF+qnpW36bzY0udr5bQH+J7+aV1X8uKWoNrFK79cWnen1ZPtoHtlpyoNU2kO9yCqHMU1qnifD77paQxCLVmLmm1fLZtnonSo9nTkraK6ftuhT9J3JH9Jo1RKVIpC1Ri8fmfW99RoRJriXlrVhgkm0yf9pZouvbZ2hYmVFMm6xHgYnrFw2KJV0jC21h/Et8lHTdZPS6HBLFjGIgShH+Qg4pZrTPPlpZq9ueklHU+EX3W/ex8FYOg6c8VL0+LV/acer52leuAsZL++pv5M+okRSkrL8FTJBomfCT7zzCOMKRRA2lA/ftfmkcOBnJ8h2oXqdXHV+rXNnQODw+LJlFgByHCKDr+gQ4QoD3PbbbLY6Pj/Dc889h1a8wjCnq0ZOHJwfnGIGA7ZAhIRNWzsERcPe553Dt+k2cnZ8C4wgCYxh2COOA7eYCANB7j7t3byHEEWMYADBuXL+BT7z8caz8CpE8OHBSyIHRr3rwuIV3KfUKIV2w5MhhtVpju92meLQck8aUzoOIcTGCU9wisjCMDA7JaImoD+pVgANzoFt9b4RroqnP5ysEgKXJJ6IkCR0B5NA5j20WUN65BNyVQhDhPo5j6mcAOKeeFI83R0Kkuj+Hh4fp4sMwptR28j1QMSsjCRAigvPJaEy7KLLtPw/xIkpbfxQZnqikRmMATC6HGTQAvjpDYr13HTOiB8YYQUNaiKN38ENKs0sqPVu1QBylyxvzfJeipJYVWCUGVwmktCsmxsQkEFN4iYoLpjpMpPAFTW3uC+myxg05V/Jx62fFgAdqj3jhN+Yi5SQWXNIpWvFhBUtLMYnx2RJCNitO0xAQKxYptTNnZS9UqAHkwg5U3en6PIw8Z5RmBeIpgXJJqGCVm+XHMgdGw+n+EVASMKTRqf6VsaPQQfpAhv/kHccJwARC6WsKq4xwSGmmKSb5ETuPDRjd9WN86Q+/h9/+/e9hfe0I5JIMwAhsHj/F8Pgx3n31NTz98BE+fO8eNk9PELdDArkMYGB4TPxMRDllbYSjaqkAHNOzGTwkwzEBis4ROAaQ0DE7WiJHUGQRSEj3joyKtgzv0zrSRsQEQISKAg418Lf8SBAEnOZozs/7DFJdl+aNFuhMY2kfjN9nENj7JKqEHmq3WesODVhb61XesW1bPpMLa52XerL+QkKKVpaLLGGXYvMlVCPpVSoUr9owAFrqFJlnw+g0TZMsmWjRKvt2z7X+kO/kLGfiCYBzmmu4ZNiG0HDWLMxd6ScRoAy1CQcmOafPxMicW0BfyZEGP+rPHGngzMVDLSCxJcdsHbOwN/X5fHeLK1la0yaFnYnhX7VFaX0TTTv6lC/Rnbzu9Zy1eNqG/iUOZcVsVNVn50zEBPEke2PISYJ8XXeF23h/1IXuo5UpLZrrrRVZLdOqa9ev5ZrIF83zgmGBCNDkkEXxFyztaIWE24hAJPpa+jE5zFrjm9e1XK5saGgQmxbIxORJHiXCDkM6k/Hcc89JF6t/idnGvLgBcoB3+VI4Bo6Pj7DdbjEMF9hut6X9a9euYRgG3Lp5A857nF9cpDswnMN6vcb1G9exOlghxGmBOR1fFiOcT4JQvl+tVgDqkC4hngCVqG76FgE/HZ6Z0jLqQ+jiHdIToidMPycltYkCjigTKMY4XXznksfQeYe+60rfpA9Lim+1WoGZq4ONrfCM3W6XY3U9nJv3VQMxrcCm2OooHFEURD2+OjNVoTOhWjg1sJ4fErXWvPce5ycn6DkpCTnM1FK+FX2mitEqur+OXDm4rYVg6n9KRDztBE1eYFHk8nsV36vkSkuJLSkHa2To55mThxiow/mW6hZjT2+jWkBvQcJUx9R/XWcLaLXGZAGAHmvrucsUr21H6gnZ6zozFoBiPC6BCB273mrT8phV3EsAVn9S1gSlkE67hR0opQuVPieZm7xYIeY0294hdh7jqsOnf+sr+J0/+gGuv/QCyHuQIzgmDGfn2Dw5wb033sKDd97G04cPcXF6ht3FBpvtBp3z+YyAMQg1zcxQqLLnls8R6DmxNFwKUVkyKG0b8lntUZ2H5+zri6zrCYDOiwb4Fhi3+nQZ+GjVz8xZMM3BoHxveW4mT9WzWndJn6uzXa2OSB+5HofuCyn9YddVa1z62VaY1FIpc9eoU7cpum12PtPIMz0HS3zaGtPSHGse0safdVrYIs+2Dnvrg+ytsYhT6qo030frimc+wnt6nVk61A2gGCea74jmBq/+ue88nLyf+jEbEbSxo+dah9NLP0TeycFnPddFN/L+ubxKmfUf7bGHK/Bke74jtluVQCk1srDAa70vbdX1Xm19XrVc2dAAUCzwStEC6LsO5Ajb7Qjvu7yrcYzi2coGRowCjAGf3WLMsRgMHCNu3ryBs7NT9L1LdWBSxDdu3MB6tcL5+SlCTDcCb7dbBI7oVqv8XLokr+u63N8Ut07Ow/ta4NjzBC1jQizFMglUKwBZ+HIhGJAmbx9TFNoZoZduapRmqOyieNB0GJ4ZMUwpXUMI8G4Kl7L1hgWhbkGoXohpV2U6f2AVKzDd5F3Tor43QD+jvTf6p3MOMdRCte7vJDhmXrzAyYubQZp8LrHkoHoR7QPAS6UIPp6MjRnAWKBpGU9zXJi2vFvfNf62fW8JYecIIXCT98jwrtBEe6qWlF9LKcRG/Ys0WFDyMwWUQwx02xUwumRN6fY0jfR61IrV0XxLXCt8Dc70OJcUmeVR+W6fQSRAyql+BnV2J4rHmVMYlWPKssJj9ITggLH3uPupT+Dbf/pHePlLnwf1HYgcPBHCbsDTB4+wffIMD956F2+9+jpcDNienWF7cYGL83OACANHdM6VCzct/XKPZ/RszX3Lg2/X/mXzqefLgujWc625t/RfAlJavrTakPqsw8WC0Nk6MetzH6Cd+qy84Zgb4q2xt2iqx7PXiGvwpq3PhjbFGFMIZoMXdB9a/dQ6Yt8cibwOIaRA14V+atm+xBtatglNl3mmdiTodls7KjrsrfVOq+zjZeuMs9/rs4F2jaSHAHBsQsW9eoa5OP10/Uv9X5pvrWfHEEBunlFq35rdx0etfphPZnJJeEj6Nlunpp7aIJob7/8+ih3vRJspPb0d3775YAbOL86zzIGAC3lzqRMz+TrV/7c3qlrlyoZG13WLwGMcR4AkFjLdhimX9gEAc0DMOw3jOGAcB/hVMk7GYUyZpByh8x1eevkF3LhxHcxpl0DOHRwfH2O1WuHs7BS7YcAYAzbbTTIEmLE+WAOI6cyGd8XAYJY87ikOWOqrBV87hSszK5M5M0SMMwFZM0rbE1G8EEA5ICh1TMIreRGHMSC6ibEkdZkW8tMCqIXgMAwTQIkRjlEMOas4rHFSKQBXLzK7lVr3QShECLGmh46LtYtfvucSh00Vn1klpgGhc3nLHymUSG67TmOJaVdBGT6yA5OEzghcQRnUCjxt0+5T3Jq+5WCWq7MJaZpr/rCKStdb88j0jv69FUrRAgDyfAUEKadJNMflNGC0/QGygDbeNaBWvHZHYAnAlXVE9Wd2fC2at8ZZCU+1Zi0I0+l5LW2X6tRtW76eG9+XC2yitC2wFA7TMeCYUnhUJIAdBgCRHDYdcPzCHXzze9/Fb373O3CHK4ydw0gA7QI2z06xfXKC919/Cw/ffg+nDx9jc3qGs/PTdIcQ550LL+cvrEzStJ7OSeg1Kc+35kPTzx4a3wcoWoCwXo91aQHV1u+k+Et/3+qPfV8XkWu6WCObjMFm613ipRRWWmfd0XK6ZUC0aGllx5IsYaDZTztGPRfasbQ0Jy3jS/OMHruVYfZ7qFBU7ZmW8SzxhKbbPPRmbswCmN14rMfRmr99c2H7o5+zxpuMxdap59PS1ALkEtngWjSc90HTgM1Y7a6MyOaW00fLAyu7pbSMtJbclfdlh7HlFG3JEP2MTd2sZY/Qqsw5UQ7dnKcXt3eLLNHUjrmlH0q/F0C8pbv3fq+DregIThkjHbl0jhcJG9nT70trVNNtoiuqUVscsIQtlsqVDQ0rZKYwkRS7jjgZGkTpcqrtbosQaoZLKWXlYEu6QZM9pUPX2Ysewgg5ELdarcrhyLOzM1xsLhBjwG7YYQgjvHPo+g6hHNgOCHEEc1cI1HXpTIHsqEjWDVmYegdD72zoQ3nloPQCcSumpxT711ok8nsLWMYYMeate0e+XMzGSLGNnXrP5bF5440VoD4VLrshurSUg93alOf0IhXhrbd3C9MZegitY4wl9ZrmBaG30MwqhlTvFDNZ9SGvBGZG4BGBHOCmOU/sNRc6evxWWMjitguozBNqhWSVka5LK8LVwbqi8/RchD7gatvTf1e8tCAwEs3buxmaprNxxQh202eVN10pw1n/CMVgk3kZhqHcp6KNO6AG3kteWjHGpU0rsC9T5tW45N30x2wc+4pV6FcVqpetsyXFCKLqfIlWpj5GeAaICQGEHQFhvUI8WOFLv/tVfOuHf4Drd26DiRAAuACE7Q6nDx7i5MGHePMXr+CDt95BvNhhe3EBMEBKsXrviwOMgOLV1OBsGv/cA73PcLCAwz5n1xDQNi40rexaa9GzBdRaIHYJJLfabI1b+isApQKxkRExr9/y1Kz9BsgjqsP4NCBp1SnvtpwOFR2o/G8vDTUtpV4YfaDftTuALbpaYLavD/pzPS5bWmBR65WlUs/vPJRvSW60+GqJn1q80xrn0vq4rH6i7KjDPBRoidcqgNyou/ATEbhBAg3kW+/a/tm/l2SqliktuaLrmGgJAO3nL9MXMdQGaZUdcnbmq3ZkAXOnksVGRZZ7jxAmI8cazAE8q0P0aAhjSjai5Axzcg1JSH3HHcbdDnIuyI69miPCLHRqwjrUTFRzFR3YKlc2NGxaTvkXYz4gzTF7RFl0er5gJF205rtkhKy6FUCJcccQUqgQOcQQ0HkHScVFRFitVmlnxDlsNhtsNhvEyBhDQNf3KXwqhOKx3w1beN/lUCkGiEGOU/7nMPckTPG4cyEhACXmiYxyDuMSgZVrqYBxHVZVl1oxZI8LR1AExiEbNyHk8yzTIeAxBDgi+M6DQu0lrzz/RJVnbalUQh9toS/zvSRcieSCsKkfIoBaHvlqO1WFR+kQvXTIutGfyEUwOiKs+hV6SlkXKIYcXkalHxLyMAwDAubKqqUAZzsPjmbjXqLlZrOB9x59Ph9j28g1gqgGThpAXGVRW2WtPaEtRa7XsMxJiJJ9aqpTZy9bBMoMRA5V/7VCs8BQt2nHUOrlyaDbB0Za/bLrW9bwPqV+1bIEbD9qfUuACszFuhc6OZcPejuHwAGRgLDqsVuvcOcLn8V3/s6f4IXPvww4xug9EBjYBVw8fIpn9x/h4dtv4e1XXsXJoycYLjbgyAiI8H2fs0Olvvt8YlCMjTSoj0aPpTCY1jzWYXttp4f+rBUWs2QgfJQyX49XK9Kuvm2+9T0zF6PN9nmRD4BmaLWmo6alyHoNPFrvtEBbegGzpBn7aCv6jDgmbd/oUwtULq2bJT1iy5IcsEbEEui/ityeXkK5CO8y3mjNre5v+RvpsL09X2H7anVOC9zu64uW2ZfN5WVl1t6CIWGNgoonzBxfBfhLnTaKQrfVAr1EADkPnc61pffkb5EryWk5PT+OY5UCmlzbOWL1dqsNPSdA1k015KzoAtR6TNfhiBAb7aRjBymSqOhX6Rd0kodluWnnkECVDFqi41XLR9rRSJ0RBT55YwGAY8Ru2OaDl4SHDx+CiNB7nwwNSp7l1XqFOA4IzDhcpwv2HAGRJBsUg4ixWq3RdR1CCDg/P8f5+XmZMO87EIC+X4FoxONHj7G52IDZ4ejQp0ONABADEDM4jynbiXcpWwsDiGGEMKU2nArQy2D2/Py8AHzGnJGE8CUcJe/MiCddDosDKTUtJEVrPqcigAhITB7GALBDiCF97z36VQ837BCiOKHEm8Ql1W2fz6lkezQlIKAUOiK8zfnfPiBBStVppmx52VpCQxsikv5QG6rytzwbJd9CQ1BKV4uyFIUauVj33hG6a0e4dvc5PHn6DPH+AzieQrIy08J5jyBnenIGNen/JHTi5AHXGr8hGDTFxHsApPMrp6enODo6Svd7GMVYFj1qcKnHbAVbK5SlmjMzF1bJWEVd9SmHQcSQ+M1lOotwE55vKVK9HoTJxnEsh5qtV8eCAqt4tPdoSVHuE3IzumABuDVod1m5TFhfVij5Pkp2rdx4MiYynSnzonc+ZcBDMgRp1WNLwLWXXsB3fviH+NzXfws4WiPSCGJGHEaEsw0ev30P9155E08/eIBH9+5h3G4xXmyK54pousHYO49s2aUMNlx74IlaIZI1DTQYaPIWpzUoH6V6WjOSit3N0D/ld+1Bn9F4j0GSfp/Xt2Tk7Kun/CSUi/mC0pFZIEzJR0pduV6R/0BFM6IUfiprXn8nO4V2jQO1c6nVVzuPFb83eL8FLCrDgKfd5iXjQs+JpWtLXiXqUPm/Nr1oqrj8lNTzS8aEpasdR2t+y+eKJa46tsvkgsYY9v2KBjTnC/usLTosLMYIVqFTeu6FR3OL9TKk+diKXgRjbBiz8/VlDCeW3YJ6dw0qXLole+1Oeo0JSK3jvN4KW8yNnRZG0VhGMIjePZDfvfcpS6VEvDAX/GWNOTtvUgfRPHlE6/cYY0kco2k49bfOulm3DQy7Hbyn6j0A5R61pdLqf0oryvkaguSUamHGq+hN4CMYGsMwpBe6dB8GOQDEGMaheN3HIW3trPoer77yCn74B38I3zl4ArrcSR4HHKzybgQDHaUbJ2nlQWA8uPcurh8dYjvG4oGW7FNyUFlA9qrvsOrX2G4H/Oxnv8B3vv1t8BjA4wjqPDgEUDZyImcvbd8hckCMI7bbUxBGAPMYcplQYZYQU0hJVIK+JRBEiehJKYs8hGKoIfeJStpagB2lkKjgEDnX6wijS4YYQvZccfYUAClXcr6XIHKyQmLKPYuodock0pBZPNeTt1crqzxLZSxaiOux2Buty0+V9UvvTjDP4/0LfTJQb1rakJ2xKSVhUusEph59nqcTDvjSt38bq+efw0/+r/83HFJSROWivzwm33dgk/u99JfVXo6ABTOPeqxS5C29E7Fer9H3ffW8Fjgt4Wefbf2eP6j6ZBWq5U/ApOtrCCqA0amYz8JjmfZs2ivvm9Av73yiB8+BhS527ZRn8tqxoMGOp6Xgtad8xrc1kaufrbCKFriw5wZ0G6IIrRdK159utUnhTewoZSEODGIgUl6hTPAxr+2+x8gBoeuBowN87fe/g9/4g9/B6uY1sCN4BNAuYDw7x7MHj/DBG2/j8bsf4PH793H+7AScHReRcgY+EDqkA+UApdTGNG2RAwSKEXKXgADzNIzJILdztjTPQoMUzjeRXHZup1lpAyr9mQYe9nv9meVPXXTfRDbZ77WjScs3zQdSEj/keUz73klOabpFBgQMMyBhw5Ie3uoOaxhYerTWgB17y+Cz41wCeC1ZYtuxYdRXWaeadvYdDSA5EUXXlneutUMjG2oAPLmckj5UwNi2r2msw8+WaNWae12PHVurLa3vUqjZfvm+NF8W2Ov2mjqT6nTZlRxiLuc3Ehm56F8QzerkohMp34fTHr/oNlsc1DuczgKmtZzOBNo50H8v8lEEyPmy6wSm2XpprdtW3XY9t0LdSdShkpniI7QJUaT9eQj7slFVjY9q20/6IrhyiSYAYTfscNQdAJiiPRgTPpnzirLQgErugQkd5bMapc9UQm738WurfKSsUzEGnJ6eYxh2YER4nyy+BOYTo/m+xzgM+OlPfoL33n8Pt+7cKqDLOYcH9x7gzp07CDHC+xRW8ujJE3hHeO+dt/Hzn/8cAHBwcICzszNsNptqQUZOnmztKXfO4R//43+M46MjfPGLvwbKF9yt1mtstjswMy42G6xWPSJH7HZbjOMOm80W1kwTYZUWWApF4WJ553MUY8A4BnRdYpwqZSmQQpzUjeIW8Nltbh3KFRlA5HSvQEw57RkpVKrPgoKZp9z2kdF1dSy93kFgo6CrEKtsbFjgxEiLa59CtwqyjCkbGjrcoXgGDJ1bwl1oZMOa5uA5zU0YdiCPcoj+4uIi0TxZURWNpV594HwWgy5aTXvRrlB0/2S3JP3EbBzVwm0oi9Z4K0Fr2q4BxtW9DLbv9rBkEcxZILXq1d7lYmxIzP8lbbbWBxGlnTzVHyvUWkpi6Ts7Fst39rMWf7eKDf9ZGqOuf2QuF+sxAxTTOnMMjGBETyA47CLQ+ZThLDqHF7/yRXz37/0Z7r5wF2HdgToHYmC82GL76DEevf8BXv/Vq3jn1TdAQ0Dc7sBjgISh2bMyzDzj7Rr01PHKSwrSApIW8E0/Ac21mi5SxdL8toCU0N/KIy1bW2eLWsUaHxMNlvmt4q0M3EoYojhDnIMnV/Vx3xquDBueO2tafZZ2RN4Lz9qxWzrO5Es27vfRxxpwzHEGsrQHtwX0dP/s3AEZyO2Zr5bRIkXLINvXJaeY1oe1DHCzA+GXFU2nfecy7Thsf+Q7HQGwT97ZvothQHueTyGv9jKHubFT5nJhrLZPLVku5wDkuZdffhn379/HZrNB3/u6H5iva2lDy+9odFHr95YBI99rnDFhnrZzQvPtpGMnfrVFh8tXa3pPmcuFNt4iqlvU/fHOFacfs8jcy0uLxwRHXKW/Vy1XNjTOzs6yYAPW6xX6VVcW8BhjuqwmTkLk0aNH+Ef/6B/hf/af/CfwXcQYdlitety+czcBwMi42F2AmXF4cIjT0xP8X/7P/wjb7QDfdXh2eppClrIwlbMaItykbVnUH374If5f/+9/iv/1V34D210yLsj5lI2KOXuXCd51GIdznF9cLI61AC+S7FU+GRfDiKgEkPaiaE8YofZut4Sf/hnkDAZNW8beEcaQjLtkzIzwCgBoKxeYhKZN4yYMMwfq00KRBaFBE4PLhUC6fl2PPhA+xftPfdMeghZ9pcR8KFobQ7ITghk414sivx8jDg4P0DkPHkb0lP3GRuHZ/luAqYWYBu+XlizZ9aIt4IABctMOUG3USVhJWxDa8e7tgqpT0/ijCAVZuzqOmGNABKU7XNw8bll7B4FpTXDD1JgJaqrPyeQPF3e+WoDJ9qMFJloGxtRcG4DtUw5akVxWNGCIlP7l1uDJZyOZ0XM2QJxH6DyG3uPmCy/g29//fXzya1+BO14j5kzE27ML0C7g4fv38N5Pf4H333wbz54+TZdzDmPKrOdcvphqfg6iZVRpOs6AqBmz3JujFflsHVW7Zm2aW9nYAmYtULbUPx2OeZmx0uIjK2OsEq6cNOp8k2RfsnUw5PKr5Yvm7LjSGFxJWb7Et7qPGji1zmq0/tbjkh3IVp9sfRMtuBixWt635lGPT+rQ6/UyOduS/XYcS/wCYBZupscW45QcZroLa7Ere/tnZZt5KgPA/bLI0lJ04VXkeamTuYT72H7lnlSAXtNuMUTXNGvXhP677mO9joZhwGazyVEisdBaP6PfbxqI8DO6XIXndF91tAoMoF+iq35maf5kDWpZ1OLNK6iOUuc07vl3QA6Xo3QWI+GOq1UuaOFvYzh81HeubGgcHR2hZIwCgxFyWtt8eJkTbHVuigH+5a9ewV/+6K/wzW9+E6vVCqvVGkQOu2EHBmG1OsD5+RmGccQvf/ErnJ6eYbXq8ezZCS4uNlWcnF4QevJEOIcQ8Dd/8zf42c9+ji9/+dcxhohhDOgCo+s8Dg+Psd1usNttcXBwkA+Wj2BO2lsrMD25KVyKc/YsQkqZSthsdunQOaVLtqpL+9xcgE4xhih/a2ESQ0C+5BfO0Sxbif5d2unyYVFWsM6Ow9JLM3wM0w6Jbqdlqdv6AJRD7tM4CUTzg3kCAorxABOuwrWAqQSr6UcZD1I4lPfpEsMwjOicT+EpiUUrL4Wu2xocMgfk2ovHChXdV2YunZS6Kg8/zT1Ouk+s5kzeswrbth9jrIRjaStTTHbTZv00z2re2Gfc2FvbdWkBU+nfYjhcQ2CXPplnNHiy49UywXqO9BgrA5rr0AndB00DqxwskG71R9PU9pOIyg3MlEOogCQnBzAOfA9mYEMEd/MYv/m97+Brf/A9dNePwJ7SbggDm2enOL3/CPdefwvnj5/iwatv4OLZCSiWPDOpPVffh9Eak52L9HtbMQp9NP30HGqngq2/FZo29SnFb1vgo+vdV4edFyun5nPVBhL6PctLLaNGr3VuPAMge+jndEgyo5aNJbzOe2gnr04qommq+235Tb8j+lGvgcooN/xqxyt0sSFzti9XAcBaBuv6yzOcA3kW6tK8Yc/5ybis0WLbsPpddp9nu+mYO9GkvhYGsbpxRhPCTGYv0UrT2q4HSw/7e+EtTHrU3ruhx2FLKxQu1YsKY+ifUrSDqOh5ZuVpZ9y/f39aOw3jxbZteS99WMvrJayj9ZrWE/W4JMyxXjMtvWlp19IhWoboMdS0XZa/cg7DtgkUf2ZVn/SfmdPRBU5PUXZKhTEU+sscSb3MPAuFs+O34tLS5jJ+lnJlQ8M5BchVgl6OjM77HIsq4EqYLOKv/vqv8eWv/DpW6zV24wgwMIYR4xgQxh1iZHjf4c///F9iHCOcSwelh3FA13Xo+75iGmYu2aaYGbu8e5E+Bz64/yG++MUI36Vbv4cxYLPdwrsuH+gm9H2XPU3pACxTOsD63nvv4YUXXqgIKR6pGJOxMY4BIaeuHYax7LRUTBfrLeL0/pQZRDN/5fFkLvGAoClb0qpfwTmfFns+p0HIB0o5Mw3awsgq0UoQAmWurJDQXq6WIpPPW8DFAjdNA3twVPdThwhMwiyCMF/404JLZ1POnj1DHIbkCYz5bgA397LohaQFOIskNQvHKimpowKyRAg8H58YV7aOMieOqvaWlJQFFvp5u/D19Leeb43Ntle1mR4sgGTxOasE05cLSmuih+alGGNzKx2YX/ik2148+6Pkhg3Ha4HoJVrY56TfVnG33q/XG+VdhvR94AjqPIJ3uHCA61b49G9+GV/74R/i1idfxq4j7LxDHxl+N+Lph4+we3qK137yc7z5q1cRL7agHBqa6JAcIU6STGDOy3a+NJBsjVNnH2vxntB/ccwGiM7naTpQrmWkvKPb0f2/ioJr96n+TI9B/7RZFvWan8kCJWcqkINYQlBn4zJgQ5/dSo6qOS0vK2KwWNrYXUdLnxKjj1pP7ZtX5+ZhmstzPC8tuQrFsdZAsP2ogec8xOQqIKiALeNguExu6rECuFQfAij6WT7T4W6LBoMqVk629GVZy0RVmtRK19IcPOt+N+W1+s3K4H00muqf/q7aoLr2pXpmPMg1nVpywa5FXfe871jMJqr7q9eWjKvGivPzeQtEmc2zdqjNHy8mHoD5Gs42bMlqVrYqOO/OqfVgQ4mxQG+uP1ikzVXLR8w6Nf0thkfIoT2tJgmEGzduwbkO2+2QvQTpgHccI8IY4RxhjAFf//o38OqvflUmS29nSvvjOGIYx3KnhSh87z36vsfd517Er33py9jsBqwODjGMAdthTAJ4DDg8WMN7h2EYC9HFilyv13j++efhnMM4jjg/P0fXr0DkMQxbhJAMoHEXACZ0XQ/nenSdnylhPREWlOrvgJr5Y4wp5MGlnMkxeymTsVWICt91oLzASlaguCAwHMBhAv6yMJ1zBfCI4KsNg/mM7ltE6d32e1KsAJeijdimMWTqKH1BMog4Rjx/97kUujeM6bB4A3Tr8bcUpCNXDo0v9bup9DCtVzvf0j8NeouhGVEuRtRja41X90M/ZemlQ9CWFObS+ZcFVYFo+qnLRxE2rT5bJaHjeVvP2tLa7ZiNwChTXddlHuOPVBQ4tPMCJEccAfBi0HYdRk8YPXDz05/At//o+/jUl34N6DwCETw7+E3A+PQEpx8+xL233sH7r7+F04eP4TcDwsUOrmTZmHu8NK9r0HiZ8WfH0DKm9DPA/KyONcL0+qjfn/dDyxldhz0L1+r//rEBctBdSsuY0Z/vq2/6nWa8RURVnP+8fzVoqObMtLdcRz0HdueupFTP39uU1S7viEuMvm3PjtX0Clpmt3ijVVp0nuag/XxLBlrApHl9SV7I2AsgXwjrTY68pMssH1zGD9KfqX/yDGYg/6OUfTJQt5v+SNhL00gD4cjt3d9/l7KvvtaZlSSPeNHRZstSHyvdUWG6+VppneHKDSPycrIa3be6vjqd/9I4rEzRBrV9xhGBqXbsFP1l7AzNm7o+KvVNO66tnZyliIOrFs3nl5UrGxplF4OSRitMjCRQhXwiKL3zOL52HV//1jcxRIYLAdvzM6xWK+yGEZvzDTx5bHZb9F2HL3zpy3juxZfw9NEjrNZrHFE6F7LdbtPdB1rJUAL6XeeL8Fyt1/gP/t7fQ7daYTeOePL0KdbrNVbrNUAE368Q4RCGgBAGOOcRY0jeqEAYdgNWq9V0s3b2OEgGJwYwhBHDOCBlS0Bpv7XlNv2cUpNN8brzkA0xGsAKmIJS7nwAFBkUQgpPIypp1tK22NwzLL/LgUTrtdHt6n8VsMNceOj69c+ymMr/tBWOmVWs2wMAT4Tp8rrMWVlgSsR/ej7vGMAVY2vHjPHkBC4M+PC9d1JKPY5gnmcgqQR2XqCyfRgXFp8G+GmnJ8VlZ3c/mGnKggFM6YRpMiY0vVqlZYSx+k5/xowCHif3xWTstIwLCz6r5xT4KdusE36FbFXnCZliO1Hzet1PVlO/rKxt/zw5lNxnDDDHcs+HLhpctUCpfW55fc7PhBTeLEQlyP5ABU4SccBqF8Yz4OEQiRAcIzDnlIVAF4GekyNh9A5DR3B3buA73/8ePv/t34a/doABBM+EVQS2T05w8uAh7r/+Ft585RV88O77oBDhQemWcAEuSSiAsnIBMt+RBjop0xFRDfDlmclgqIGzBSmTpmP1N+e5sk4Kqauea/27vNMKUUntTnPqnHhwowKlkwemZdxJP8raUJ9Sluty+y8hL1gI4ZRhvw8gcuJ1zrIbEroAKukqp/GKHnUTlRpgWtaW5c3lMeo5nJxwWqZbGktbGQEnGlMGT1cAIfvA91R3+/uWMXnF0PKq7omv5zvk+3ZB5TP5V9NFojYy7xJAyPqi8HLeVXDJeQoB+iSuqqiGRADNPeDMyJEKc72g5VULxFujtqJNTDLBiSMuiwWRZ0m9Fumd1/88K5bdTY6M7MRDuXNpHz9yFgqMttyNHGfJapZKNV7bBqbdBgkT1CHS1hDV/Z7kGhfaZGiQwlsZJYWyXkOie4nq/tld2facTYfxy3s8pcYW+VwkG+VssyXWTGER9VeIWVfmz5zmX6Mfk6zipDfaFE//z99HReu/Tbl66JSkX8QEBNPvDiGHROV5gfcdfNfhf/QP/8f4whe/VA7/QACi83C+Q4zAwdFxCj/ywD/8n/xP8V/85/85Hj16UADExcUFiKiEKAnlJiGVFsIPf/BD/O7vfg9df1DtcoAJFxcbDGPE0eEBfD4k5byHiw5hHBIzqTjGECNc5xHyza4RVEBoRAQjIMQBK9I3UScmLAfPnAgjpzC2TFQ7vs/lxe+dS9vuLmVHGnhATw591yUaFmxB6WK6WOd/1ouOeW4EFQHMU/yuBWGTqss938NkM4VTgLvqGxxAfqb4vPfZuMoheEBFG+GxrPbTIs4Y1iNi4Ijgexz0PdYx4On9e/AO4EhVXVVWFmWYLRkXhQ5CF8qMn6VQlXFFFjKh0HvyrqSzMEseH60Iqzh1xS26Lwnbphvhp/dFSLc9xPqnpmsRskRgl4RZJFGNIkGhfk5GiBIBFe9o0KDPvGhB3DIE7DoQ/iQk4NM5h8Dz/SY7b/sUlqaBXrOaLhUgCXWYFImAk+dzAEzLq0Wkzq+A8x1BDnAeg3cYDw/wuW99Db/9x9/H+rmbCBTgYkDHAG12OH38DA/fvYe3X30ND956FyePnqS03c6l8xpZxvk8FwkIWK8VCl+IQSyTNp8zynShGSDStJ10qF7zBCKpQxsLOlvSxIet+RFa6duvY0SpTwNH6YPI/zTn+7yR6nfVdJDkGqLXHIEkhCkygppYbRRMbXOWw66MUM4YFKcD0lmyScZMHWgBksRnc4NMvtefNw18y8OKdrqN6j2WkC03jZWntOICQDVwg+mLpgkwP7vVGoMu03Nz2WD1k25vCZDb3Z0WTaxerOkja6buVvpbwDkAinBeDEiRccopqtZSwvI53XpO+RzLHQc1nVq8bEO0WqW8F6ddNc6X+7LschCqaIYyPM5Gt+EX+enU9xJux5gbG1XfDb3l9xSa2B7HpDtr3TA9W8t4q88s7WbYhqcMdfKsL47DjK0whSRFUJMmMd9zZs+XSbG6ru6XjEnqzDyUsR3lD4uMs5EPLOZEdvJQNl5okh76rmOt3yodWUSA3REkgByIaTIUXW2MalpcVj7CjkYNWArTG2EpsaYvv/wyvvqbv4l13+P46KgoxmFI926E4wDve4TssRx2G3z605/CN7/5TfzX//V/BSbGQb7sTDNSMJ557z1WqxW+/o1voOt6rFartJOxWpXzHd57nJycAZSuaSfXAzxit027DOMYCs3HcSyXt0hmDVkYyAJoDAGjiYfVE+i8wxjG0m/7jKajFYJOFBU7EKXD2n3f5e8BgArNJ5BUgyZ92A5KQWhrPIQAijzr0wRoJ+FnF65ecFaZWIaut02nz/WuixX6+5i3tMdpRXpycBHYnpzh5MNH2D47xXWetiD1OwWo7yktISX0aAnVpf7KM3onrqUg2Dxffqrv5mB66kfLS7lvTPZQJyeklg2Y/Rmf9Jwm3kIxrmeKydUC1gpcCwS0oK52yAR8EdWSs9G/FvCy/beHi3XbVpCX9dzwAi8J20DA4Ag9CH0grDkZoJGAoXPYrju89Gufwzf++Ie4+6lPIDgCMdBHYEUe509P8OG77+Pe62/h3lvv4OG9+4jbAT73o+u6Ine893AQL1x7rQLzA4CaB+y5Ih07Lsp4CrsSY3auVJcMyRaN7Of64jd7LkCXWXyxmY8lGuhnl+4BkL+vEgqwFIs948HGM7pYgFzri2VPsX5fryW7ZvR5kyXZug8Y2XK1OPL2+liamyWg3wKMuh/leTdf8y0jYl9dVifVn4UyH1PdgIBdq+MXi/pa5Le8Z9fnEjidYa9LaGz5QRq3OyilnoxddDtFHmcHnxgpjKSC+RLnj9BO+qCNAa7JMsNEmkbVTsLCstB8Y3nQFotPWhhtqSytE/u5YOHWmrsM51yl1O8ng8N70W85HMw4x6T9j1qKPsCcR69SPtI9GlYxye/rVbonQwA+kLJUPbj/AHefc1iv13Deo+87dL7D6vAAF9imHYMYEcKIMYzAOKa7LpRyE8VXvCnK36MHe352VmVXAFAUcwgBBweH6Lq0megcEAJhGFK7MUZcXGwA5AOaOgdyTEZWCKGAdjkjopWr/tsues301ithDQ1tZAiT+K5DFBAWpgOGnGNJiah4+6dtvUwHmpjEZunQ/Z8xHy0vVD1WnTFF2m7RIbU792a3hInt3xKoizFnmhoj1q7Hk/cTKHOBwRzTJYdqDvIftXRrFDs3xUChmmZT2I6b7T7IYVLLF1U7WdS2BKMYGrN+sBjdbRoJ39rxME/55PV7iUdoavMS4azpIyBRgEyd77+9Xb00p7rfSyAydbV9t4alhQYaOrxKg2z9TEvw72OTJWErQVY+ErqYQjB3Hth0wPHHXsRv/9H38ZmvfQXDgceGUiiVHyL45AyPPnyI9956G6//6lU8/uABxottCpVyVF3+aEOMpBfWINLgSX63GWj02LXRKFn0qnYM/9u5kv4t0WufAaA/m56zUKSdkW3JyBBaXVXBTmtr2dhogUvNZ5q3Iric07Cy0PZJ6J8MlAlMtYB4KyTEHmZn5llaV2uA2HE1199sb3tyGulL4VpA/ypgRNa9yNF971n6hRDgkEIRdShKC6i2HCi67y2nYUuOWjBr6bU8UEC2DZjt87UDZQkk2/Zt0Z/r5AL1uyiYQZeyThpAvf6Z6gh5ZwRZ/uxbW3ZOy27CHqeR5Ws9Bt2npXctPWxZCm9qhtEi0XN+XxoV55zUucS/S7y3hBstHVqYRN5xuc2U5Ggy/DhGcJYlLd2r8YmVMcxGJ4rcISMfLpGpUq5saKzXa6zXaxwcHMB7j/V6nSroOvS+K2nihCBHR0c5pW0yPHbbLQhA7zuM44hxGLAdRuzGAYyUmguUQqVOTk5wdO24HAgvHnhKRoYOGxFj4uDgAJuLCzjfV5l+drtd3i706RA1IjjEMjHDuAFAeOONN/Ds5Bm++Gu/hn69EjImYyjk28EDY8iHy7XA1oZXUvy1YJOfMg7Z3WmCMJ6EexK8yRBLGbOE+QCtKkIM0w3Y1uvnAIl613GLSRHNtyflXSlaSFdb56gXi5yVsXHBU/3Tdq0Uy+Qthap/nwl6IgwhgJiwO7/A6ZOn8LmdMTA4E0n3R4pVhi2hVLUHLnGKc2WdBLD2kgP1PSstcGLHugheZ2Cu7qPt81KxAqb6ToG6JWFuBZLs9skY6/CMZBQIYLUGqNTfMg6sop3mhqp+CH3te3ouraK1424ZIUVYm/osf1raEhE6JvjgUnz0yuOUAuLNI/zGH/wOvvq976E/PMS4cuCegDEgXmxw8eQUr/7lj/HOq6/h6cNH2F5sEh/HdMbK5bUtfa1AowqN1MBSyya909niNcvTmrZ12Mo8JtnOVWvHaAk4pX7XAFHTU+Kg7ef6dzvvVgnOvP1AvlB17jluARRmRglnMLTXvNei62UKubUemBkxjBDQ3SoWtLUAcgtsL/VBg6xq7MbQq+mNAhSt4at5rjUHtpR249wJptvV67yiG+o50XJBntOx83reWkXTzdJE03qm9xs8UeoUoxMEogiXw6JjFJfSRL/Wbqset11v+kxOS5ZpPS2v2jElQM0grudSlwSslUOKAfL7d+3sp1au67HL93os9h37rOY3vVsidJS+tUJ2pR1xHuv0+1ObaczyvnYwpkfaRtmMdupdO9YWP87mpqGLeZpMxBiw2w21THF1OL29+NPKiHrHUtEhDyXGdDCwhW0vK1c2NL7whS9UikgzOId6YQDJAHnppZcQA2G1WoHWBxiGAZ1PZy0G73G+2cJ5j3EcsFqvELZbfOITn0hnOjqHvu9xcHBQBMdutyvXzmvFuF6v8eKLL+L42nWsD49SSEH+rus6HB0dgagDEYM5HQDf7UJZLDEGfPzjH8fd7XNYr9cpFpwlle0U+5zSlU4xmJFjdamdnkD52ZoIGxeu3xOPKCgZVOlmiAHDOGLFyWvMEjtOBChhotsrxtZSXzj3Hy0v0sTksvj0GQe7iOzW71W8nc65cgeHFLvILe2sYRJdPv8Ah3Xfo/MdCMAYwrI7miawZPvWmqu6f+0qRfC24v2XBPBSG/tKC+jqdlt12rltKdBoxt7qd2sumWseqRQ5U0kvLE4IW5/1TreUf9UXqtWSBRKWLlbh6PcskLG7emT4pDWPrf4SAOc6bDywO+rw4pe/hG//6fdx++MvgckDrkfHDDofsDk7x3uvvIrH797D/dffxpMHD9OZJlA6L+CQ+LXzi6CGE/NVQMzSza6rfaDTroN6fiaDQ4NO3Z4NP9F1aUBUz9H0vVW6LYAnf2uatDyUNrZ/mqF6TpfW6DAMYFbp2zG/a8W2WdMN1ZmQpbWo6Zc+n4+7rNVG+JiVARa8aDq0eGJR/mQ7Y4lXxPiy/bdlX0hW1Q9pU3dhQSZX9FG0acup2iGi+VTqaOkaeV9HCizR8bLwVXlWepfq17xe60bddvW+4Z/mDrWhW4ULXDq8bh13ucY985jkoZigTezSon2qtTkGMRD1dy35Y8cjVGz1s4UnZiMxvN9qT9UoEKrouqmOpT2Zeb/t3TFLck2Hrsr8Lq1PO75xHJLzGGXpFrZa0rMtI0fGHWM+y+wcIpAcXlTXdxV8A3wEQ+P4+BghBPR92jGQnYJ0diEt3q5LoVGgdNYhhADvVpUXfxxHHB4eYgwBwzBgdXCAvu8x7Lbo+x4f+9jHcXx8jN2wK+cs6rsIUFKRidDo+z4fKJ+86iEfgAoZ0DonC3PEuNvg6ZNHGIYtXLbQDg8PcXh0hLfeeRu/+OUv8M1vfQvlIHXkvAszwjEmgycy2LUZRopmFA3IRHi1woUoL2qXYrzKwXYXxnTvh2UYs7i00OVYL6QixIjh0C14eWpwIJ9rgKPbk7hxGb9dRLro93UMsb2UUeZRe+c0cxMRBkQwpUv7gLTsA6dbMmk6m9csSwrIzmEFBpYrg6SVbQGspQVJRJN3aIFeS/1ZUvAtgGbnrNWPnGTlSsJDtxFjTcNWsXH3uo29QGfe0wqE6SIyoqWYtYLYJ7Sr+RdJ3QDx07yhOAXk8+A9zlzEtU9/DL/7d/8IH//S5+BXPYiBjjqEIQDbAU/ffR9v/Ozn+OCdtxF2O+wutqmffZ+SURCVnVvC8o5XWuPtVJ+LVGzwhDY8bdjf9Ox+41N/Jn3Qoa8t73A6Xxar3Zjp/WkRt8atf2+FxrQ+s98DqOSx9QAKj5NZg0uyogIGV1TCwrfWcGuN2763j5/t+O06vKx+acPOGTDJQiuTW2Bz39/V57zfs6v7rHUF8hqUz1tpkLVc1nN0mVzU82Hn+ipAe3oBpa8SrZC+Fj5qt6nbbvHdEtjW/bF1yt+t3b6r8qxzrpx3sjq/kkENfit93iP2tfzQ7yV5twyQW2Dafiff63aW6JpUQb2Giix2+9eSbq/lRLFjben2q/Cp/Z5cimGhPACNdexuhDZwlupknvY2GfOjAlcpVzY0bty8A4n1Sgu5SxPAwDDu4EA4XB/AO4fHjx7lA9XAdneB8/NzxBhx584dRDC6VY+LzUU+KR/yDkQC077r8alPfxZD2GFzcYGzszMQp0O/z7/wIlYHB3j77bcTk3Pa7tsNWwxhwM1VhzAOII44OzvDbjfg9u1bOD09Bcjh4OAAXddhc7HD6dkF+j4Rd4wh/QsBTIT14RGGyOAIjNsddtsdtruAISRSn10MiDGf8heeocyQNKUqkyIKTM6LSH5zKxA5AtQle90TpbS2RID38KsVeLsFkfJ4EaWzG5XQNZ7D9PBMeMUYEcOQdmQyB0n/7b0PLcFkBYCut7Vw03RN+du1wJN29Nae3f63AoyIgABQig1LhmQIIE5ZIiinwBQ9VGQ61wJ8Zhy4DCLBOYtUbktWGU8gcyrZu8G8V6CUeS7zUYNU3R97aLXucw2aKwEqz+jq89wSaBKa8hlJmBOVMyHVyPYKkzRuHTpXvnGUYqf37N7Ju1cxOirlpKUekMbqaqWqf1r+0TRzOcxRjKyUxS3JlnRGSsbECOC01lyiXQcHGhkEh4EoHQK/ewvf/OEf4Evf+m244zUiAZ49/BARLy5w8ewZ3vjFL3H24WO8/8abOHnyBH3XwXuHVZfm1Ttf9TmGAMkGlfouIRAESbNZvIOOJh5X47eez5B5pKypmHYWCt9ToikTJnq4RDGobDEMARQT35UDusAUhkYpU1s5SArpn5pSL7lekIz3/AVR6kcJwRM+5jlfobQVc6hmuqeJKO0SWZpYYNIK1wTShoas2fSMMq6JS/a6ELXR1+Dfhb+1sZPo114Hl4UtWDDVAt5zek2/ZHWRflL9vO7zpcBa9UEDHft5/fekW2pDYt5GTYdY5gbEKCYx1+9Z/dHqk/2dWVLQIvNbqrhlaNpS9V9kVhFaSc4k+dcOp9k3vy066L6XSH2inE2MwYErx5auU8KqHWq5WZ4lPf68m7XHoy/9YGZEDiWDmURhgGUHa2EnpAG8y+8qA6pct0AuyfIQ8x0oxOV27GQUJHwlNLMOKSnzMGcuU6blQ/oA03pBvd7FAWex0BLPLX1mQ62WSmRG551KHEQlFfE+Ha4dQAV7ZPnGCACSflPKp9S5D+PYcmVDw/t1ybxEzmF9kF5lMGjsgDEijhHb7QYf3n+I9dEhHj58jCenz0r2qNXFOYZnAz5xeADqPHrvy9pz5BEDQL7HjZt3sNttcP3aTXT+Q5w8fYpV1+Pk6VN85u5dfO4zn8XPf/UL7IYBYxhBnrDZXCCGEQ8+eIgYI46OjnBycoJV3+HJk8eIHHHnznPwXY8QIg6Pr4N5wHZ7jhADdmFEiBF3nn8O1PXY7kY45xHyTsYQGENISnKzHXK+4jqlZAHqnECdAGe9+wKkUBINsAtD+smD6QDsxhEuRgxhxKrrEZhAkdCTB4gxckAAl5hjYZzSn6zIYYTq9DtjGHcpTWZOM1vGUeRUO+5ZKwTrjdPARsYvn0tpbV3bvluDQH6Xnx4pC0KIAc4xVs6lFHwioLJ0n9qdBEfTcAESkFT3RkSOk34ohz6krkkpa6HYUpJzkK0Bo/28TcepzqK15gs+ipGRJaDa0XLeQWdSK+/lPPStHaClcWgDRYdGVYoVc0Gqx5A+mgveVhhMWlMoP7MpKZ0qqEjzklaYrbGIwkv/0vAFCIOSoe9yVijOWoUdAGL4kPvkO2wJGA5W+NI3v46v/+n3cfTC3XSXS4xYk0c42eDk0VPce+MNvP3aKzh9eoKTJ09AIaIDwQeAkFJqy/gcTTsVPs+NZMdLXZ/ObOm5KXJGxg/M6JsMExLGLU4bPf0MFLkigLPcDMCpfU3bYjBSTg/ucoIEMXx0Gs/MmkHWVlIAZVmJ4SLgE8LjIRQjxXMbEBHlW5Fpqk9+17d9tw3fCXTpEll4lYrBIvHuid75YDRokuHCcyZ+Xhfbb3tur1X0d3pHpmVc6+xh9mB/Nc+1RZSB3CQOLOgrgMn0zQJCAS6hsQvfkisMhiM3mxsZY9s44SqUhnnSXWIQizyQ9iyYtCG5U5sKRIISmkUE84AY6x2cJRlZxkYCz7kY2YyoaD0/G2Hn09Y/25GgspomYz7/jMxTmmXQrO5ifJt1YOW3lsWV40qVWl/HSa5wch6U9tRUtWi3CJCTUCvOFbmA0HnJwZdGTZSpzZNsEoO+hS1acynGtx1bpefLl9Nz4hBphTWXmhcwg6W1fUd/Xr7PP1frNcD5Iu2sQ0S2tOSPPVtdDA0ipJTlZveCOd/PMsd0+8qVDQ2Jp9fhSs45hBhAnnB4bYXxYouHDz7EdrfD6cU57j94ADiHi/NNJpDH5mKDF55/CYwUrjQMO4Rc99nmHDEyVgcHiDEghBE3btzCxfk5YgwYOeLDhw/xW7/9NTz/0gv4//6X/yWc7wDyOD3f4O333sfF2RZHR0dgcggMPDs7Q4jA2WaLg+0OB+zTzgUIDx4+xPHx4ZTeNgLb7Ra+67Hd7hDDgHGXLgscdgPGMYDgsNkEhDHMFnrf9wghYLPZlHMiMcZycN4WEYAijL1ziTF8lwwZnix/yrsTEwDh4g1gcA4Pm5SZ9tIXIdIwCFpMrgWxNhK0t0/CnaRYgQTMMyqIQmhtu9lwBb2QSiIAKxhZjLWAzcUGuHZzGsMe/td9tQe0dGkd3GrVVfoKwAoLS5OqPqAC91c5AKe/03M3zTWKkcFQ94QgYXF2OZxOeebEdNlX2lul6d4FTYvyTAaKrUOJljb1vGI2phY9bF/s9rbUYUGj7T9RrTyknUjAzgGO0yV8AgQIDAqEQ/a4cP9/3v702ZIkuxPDfsc9Iu59S65VudSaWWtXL0Cj0Wg00ACmsXCGRuoDzSTRaPykf4z6IJNEk+mDJDOacTjUcHqImeEMgMZSvVVVd+1bVmXl9vZ7I8L96MPx43HCr9+XWRhSXpb13rs3wnc/53dWB872Olx95RZ+/z/5U1x78Xn4tgXCiIYc4jBidfAID+98ic/e+xB3Pv0Ux8cHGFZrcLp4z2VmvakM0J/lObWldNXLjJMEBtR8uC1d0aLrU9Y3d58C7H0V9qfSjQ03UDunj2Hw+kxtHWt/az3nMfM56Jm7EGzsoWI8Wkg6udGPCUDPQb6tqxzfeW0pjbWWnG3vlWXbWIDNdLzb6JH9/bx9p3shFvXUgGsNMJb157mIUehTMf8WBG2bA9tObSx2HqyCbFv/Uq1FnZzPgKVTtTnQPm1zeZxZ0zZGsyk8bPZtqqf8jjE/2+V5re2rLMgVSqg858VlQcrrbEvnzUW53qx8aQuYLot+ts1lx9Zf9kdw2PS7tl+LJS3niLKA+PgyPyObZ3vrvi/o0nnrZOfDnhtVKMWsTHETFqA6PivnbSbMn9P2P6Y8saBxdnaGxWKR4zKY5Z6L3d1dRESsT05xcnKChw8fYnV2hgDG/fsPcO2ZZxF4QLdY4PRsDec8Do9PsFqvMTIQxoB+tYYj4P69B3BE2L9wEQAQwohHD87QdksMwwjvgUcHBzg4OMBLL7+MK1ev4t79B4hMePToEM4tsdjZxVcPHqLb2cVT167j4cOHCCCMIWIMjIdHx/jyy7s4OnqEy5f30Sb/6TBGDL0EXff9iHGUTARhGHI6WwW9Q99jtVqh75c5b7EuGgB0XYfVapVjTKzmSYtudAukI0dETpfTpYAtuRVZzKzeOUQeM+RxTu7rcM4LGsKciDNzzrBlTfNaCA7OyeYex3FGzEuibg+Arr/uhZLRl+5D08GZCyy5H0TZqrLB5A3xKAUi/cw5B+dFcAVvJwzbDv183qb5mbkzEFWJd66v+Lxsqyp8nMPkWP7YQnSo0u9thMEQkkzgVUtDGUShwjAe14YyXTtH5RyU1q8SGNp67b4pQan9WQOJ4Inl2Tk/j1hn8cQs7GxdOWmpGWjIAwxxZ3QOp46w9/xNfO/Pf4Tb3/0WXNcA5ECBQetRsqDdf4Sf//Rv8fDOVzg9OMQwDkAjbqDRAYhyq/E2Ka90i7Bzo3+X/Z6dlXPmTESbTVC2rcicCl2q9cXGW5Wg2z5fAjGiOqicnke1jsTJn2D/z7XWdl/VLK3VeSC5gE8zqGWakxVDdQBfA1rl97YvanWQgN3z16PsZ00YACbXCHv+ZmtQ9MUK5jVwOI1hUz1RnrcanS95w4xmGPqwzX1Kv6/NZU3gtMDSKj3seSj51NRfGee0Fvbf+WUbsJzvfR37nAaU/O1x+0Cfy78XtgZtqyaoWUygFoKyPqRvdS5SJRtCxuP6Wt9D9XFsq2fbGSvvrKit5za3Q7v3N13R5haNJy3qOVDjbefRqtl6VOhbSVM5rYO4xxHW67WOKu+p2rkr56Q23+fSVXo8fbLliQWNk5MTEBFOTk5w9epVCeAeBix3d5K2f8T9+/exXq+xWq9x4dJFrNc97nzxFZqmhW9WOYXYg0dHGMZBTF1RAD1CxMnxMThGXL9xEyEGrFcrXH36GoYxSExHDAgx4qOPP8ZLr7yCf/Knf4p//j/8fxEj8OlnX+DuvSO4poV3HvcfHmbi7ZxD0zW49+AQJydnGIYRfX+G47Nj7F14RW6YHkas1wP6UdoYx4DT01OcPHoE5zuM7DCOAQMHIAw4W51htVpgd3c3z5EysWEYcHJyMhMyagRGD8gMOKT3mZIkPg65blKXBL3TI12WY4moLn6O0yiI6ERkAeIpA4VaX8rUvdov3XS6YW06XX2n1B7PD5nLknUttS/zZJUpQSIRzSw2JYBV0qpWNyLVQM+JyTbzuwVJ1nRs+ya/b17cBihc3SQEJZGw60xEOQ/3NEdmzKhrCKc26syRIS5S4CRkOgVmSawgAxEYYuVITkjeeZRCgBa7j/O4UmU20Hpav03gWZaSAcv+4hlhL4FaSSxzmzJhG2tn+75RJzDzrZ3tSQY6FosGsezZkcRdy+3v4hv/5If41h/9PrqrFzAgwEVgEQjh4ASP7t/Hb375Fu58+DEO7j1ARx4YBjSkt1pHCdZLwoC6rpVgoFxfPaOPDdyrAE47X4rTyzmyAFrPkrp5phmCJj3YxvisUsUGTpbnaVpPcUex51pLCJtZ3PQ9jT97HLMrQVup0SznrQSdRGJBLu9pKBm3vbTSCjP2722WU9vX7B9dAE8tTyK82HWYztXclbA27m11lv0vAb2dq20A2z5n35tZsKgu+Nk53jZvtXmaPCs32z3vjNTolXwmgjaRgu5NhUzZxmw/VUCi8HzaEF1qfKT8vqZwAHTYdUFwG6AE1Po94QRN8jL1EzNgS2ESNko6YPtYA8p57WlTQAU2M1nW+luboxI/6LM5tos30/SXv58HsMv9XMMUtfmtnY1tdes4zl3j2Rwku3hKnmHdFWOMcDwXsGpj1XdqngcldjVH64nL17JoeO+zT9fJyQmapsHQ92jbFl8dHeHw8FA6GwJefvllPHz4ECfDQzBL1qqmabC/tweiFfqxR9M16Nc9jo+OsDo7Q7+SuzZuvfg8XnjxRbz//vtomgaXr1xFjAF3v/wCbdfiwaMHODo5wTfe+BYODs/ws5//EgeHJ9i/2CGcDmiaBodHh4ghYG9/H/v7++hYpMxRkBgieZycrvHg0SGu7O8ghCRsDANCZIwh4os7X+LTDz7Ay6++hqbbEctGGNA1LvmSygKenp5iZ2cHzJwvdjk9PcXly5dnGbPKxdXvLPPT/yJDNGXpnTGM6NLGoxDE+oE4uxnVbqbM+Mwm2XQj4RlBqTG08hCV7gs1oUHLTIrHPGVgSXgsM6kR7q1WoRARwRgdsgteZEZTASePY2Cxwpymd84jDIDzm0SvZFxlH2rMI/8uH2y0Ke8BMASeaModD0I2nXOSYyywBpSpsRmSCLh2fWzd2/pYMgn70yVQXpsH+2xNy2SJbTlPtd/Lnxa0lwxwg8DzpJebgQ9muBhBziM2DmfEwO4OXvzWN/G9P/8x9p59GsExmAldAPxqQH90hoef38Ev33wTX3zyGcJqjQ4OMfTwjcMYIiiKu5lzlOM4mqZJPrSb/bBjLcdeY0T5mcp5NLXN9tC8/kloLudW9zqw6cJQB2b1yyMBm+4RADbB+1THOWCjQlenDsyfVcGnPId2/rZqHQ1mKwURHYOllbUzs4151+bGznPtvRp9LN+vWQS3FQLNYg239Wvqm+yTcrwlCNs21pJXzflM3e30cUCu1k8AOUtjrT/2ebufN/ZsTCoJciDyYExuvtuAdDkf5/d5bkmvPae/lzy5StO2uE49aanz4nQPFqVjV7FW/ceW8/ihtZzW9uN5vEC/12sJzjuLtXoiNgUF+15N+aO8uFQ61ASy2vfl5dO1YrHNjJwnWuZM/bNnze9atD1r9dtettOgbeWJBY1r166haTyWyx25sG+5yGlul14u8nv22WewOruC/f19vHj7FuBb7LsFACXiwJgOdNt1ADF847G/v4+dnaXEHkRG2y3gfYNnbj6Do6NDLBcLXL1yGZcuXcJqfYIQBzx89BA312v87ve/j4uXn8JyuQffLuCbBt432L9wAQSgadNN443DECI638kkNw7AiAePHiKuTtF4j3GMIDhwFDeiGzduYG+xwHJnF+Rb7O7tAxzQOEbTTildd3Z2MtgDgOVyiRdeeAHOuVn+ZMvULNGYvhMtsSOHoG47kKwXIcj9HwyCbxq0jtCPPSIxeIwzpqsgC5hnxrKbTO7jSADb+K7aHM5lsLc9WLUDAxTp3+xmpLlD06aJEhuCkD0QJSAtpXKXLjabhJowq8e2WR7s3A42JfXpWQa4rkkmbDKE8mDb9jPRUoGgIJbQfmwBcnKfwdzC4JyT2hTgg0XLXxDIbYKTvUzRCsfnCRolONN+xjgXgPXZkpjl+SuIlp2vbRYWADPwGCvfl+uc2yLK8T0pndDm2hNhdAA3hNB6XH3pNr73F3+Km6+9CjSShaZhBtYjwtkK9+7cwa9/8Ssc37+Pwy++ggsARQJxhPcOwREc+ZzpiUBTkHWMiEkAsfNRat9LRmHXvzY/5xVb13ztJuBcAhuxZmxvS8FXCTZLJpz3CBG4COreXL+5dnSWxpi5KqiW56aM+7B9L+PRSiCXKpzN0XwvpYx3W0BIydC3FVsncx0w2WfLz/RvPTM14FztB8k/vcG8LNv7n4TlWI9BOC+wfauFJ50L7eu292ul9iwzz+JI7J6vAalNwJf+ESC3eSetMW3S8hL8P67fG6Da/m7GXu7Vef9Q369cihp1MF0WAsRSUQXQaT+qC2LuT93aYtsp5+ZJyyZt2uQ1QD1OreS98tkTN33ueKwCrC7o1QWgOm2pt7VtHOX3mSbGCI2XnHF4mvOUGp4DZK3HcZyUXk7iB2t9JtL/PXl5YkHjz//sT6QR9fc0g5Yr0wAwI6Ygacmg4hBAWVOsgxvDmPupWX1iMpM3TQOkLALXn74M5whhHOGcRMiP44AQRwnMdh6Aww++/9uyiZLGgUjAuW7MoKCTBMTHyAAxxnEAEcMjAXVOlgTnsFqvgcv78M9eF42/uk+MA0IYsb+3C+/FxWCxWOSFUC2AXjRYbjZxfYrp2vjpoDr1aQGlVJ3iRuKlUmAcQDGAeUAkB+8aEDPiOMJLiCqYI4in4KcY9Y4T5PZtjnwUgLj0ka8x/irIT8ytRnRtqfnxA0LCyAnHJtWYJKFLgWDZhxhl3/g0T41z6Jo2LbMDoZ7VSoG91eZTTgm6qc2alwn4ZJNx2ld2bkoAF/OzvAFmS+o3I15VAUHnTl2ShAESyRgiz83ZNRBQA/bnBaFZQqUgBsDkvqKphJO1hFyaR5rguzJuqUuGXRK/mna+xsSq4Cu1P00SsgDhWPaXCHfI2ZzADE7pMD0TXMrjH8AYiXDiPPZvXMMP/vzHeOm3vw236DBShAODYoAbIs6+eoA7H3yEd99+G1/cuSMZovoRDoSmkXPoWz8lcAAyPfKNT8IFqsVamLaBmJrwPP0+uWSkXSJ7Pcr+se9MbUUQ+UxDJAZNaQiDef5eTZCuMVe7vraPImjoWqq74+T2aPevdZeMIU5CtWoO9RzQ/L3afi8BQknX9L3MlAsAPNW73WJae177vwmCzD9sWuRKTWNdKKsDz/PoMkeu3u4sZ0UoiaZrV4XKRM/m9ZY/S9qlP60//WxMSfhmTvGIemZ4oh2lAFabC9u+83OFTGlVrwHw6X1x+VUFjj1LJY2avyv7Wl111F1+goGU6UHtBnjLj0taZ3luOQ+1v7WUFq6aoi/jAmBzblLPnUtKUF0/gy1sP7edrdl5SN8rFppemSxsFodsE1Jm9I9tuyq4MlT9VuMfNf7KbLJuGXpS0reNMeV66vuzxs9rmMjSzfPqUBpkaa9a2vK8oU6btF7dGypk5DZMe9to27Z6y/LEgsaVKxfzQS0JpR18OTG2M5LdiQG05sC0uS71EWMmOOfNwjYYBhEwQEDbdmgazhf11Qid+hoLg5su8gMm6Q1YmAM7pT1r2xYh7qJfr+UOD5MaLEbpS9s4ULIA9H0PZs4B4JYhapC1nZvsa00Ckqc9OWkONY89USJKUQCOalVCyg3v4eBSJqEQ02YV9W72eS2JR43IlGu5bZPXmLaOqeYmltvF5sacEU8ZGVT4ymSZpkvh9J3cdgqm9eQAfvwFXbYdfUxBbwnWakzZIsK5faYO6lkQ1PQ3kGMmlAHV2qsx5/m8T/MzVSKxDWT6Zs+E1lECDv257VzneStAkf7uklAsY1XLyJQytZwbS5es9nUa8+a8bgNXdjwb5I4SgVUwpEIrQd2QZQyR07tyd0n0DgMBfn8P3/vR7+O3fvQHWOwvEbxslCUT+pMzHBw9xKNP7+Dee5/gk3fexerkVFK06hwSEAiAJ7mzAkYITIxrGAYQUYqDEKtGjXjXmFs5DyWwowSM8uPms8BzAcZqZ+V5QgjRWDDqjEYtVMrcSm36NoZswbMulvYzRoZzm+DdzoEVKqIyRO1f5Z0aKK3NZwnmSwCpbdt10WY3mf/0ea3/NSvP1AdRGtg5LF0w7Oe2/+U4yzGXgImIMu3cKIwEz6Z62MQncNGnbbx/G4DapK/SqFlKTALGBJjsGtn5qAG4mva5XMsajZ3mSZ8xc8Dngy8V6xmUyLNLWZ4t31FgaCYbm/tsG2Avx172X/lMlY8B1b1k16tKa0EZd9jYz8e9XwPJuX0WJTORXZ/NtQDmbtu1vSXP23/THtGsU+VczuasoFm5bTetyXmAfTavhtfVhLzz1rXs06zeYgzOSTym3r3Tdi1a73BycpRUNpsWoBq2sDiaOSlWKkNV9HEezqqVJxY0lDiWWiu7WHqwQ7r1m1kyU+kgmScwoyYfHaAu4jAMG/54NeDFzNnUo38TbeYL1sWoBVlq/cPQZ6aZA6CS7zTSpOv7TdNIuloCxiQY9X2/Ub+Ozx4IZs5rVzJAHZtCYSIHlyRVR4QhRjBLv6ICu7SBOdYPTg1ozpgR6pu69lnZ57K90i3sPEJcEnzEmLVkNcKxrS+eCOMYwCS3tR8eHiSgw0koqxTmrKmrlW1jT1/O2i/nxe7b/G5e0/l725icfe7cvhT9zX9jog/bmPzmHG+6ANTAktZRBobXwDHp2CsMze5BnbfpjG53bajNxTZgPvs7XdSGmM6y1S2yA3mH0RGGhcdZQ3jhm6/jh3/6Y1y+fg3sgEiMhgHuR6wPj3H08BE+//wT/P3/8ldo+oBwup5cxRIT3ga0t62FpUk6x+X6V8GZebeky5a5WvdIm4Citia2HetKaZ9nnjR+egFpCQDOU1TYn7U9WrrNlWO1dKb82z57noWypM127uZ1b1r7ymft+Le1Zdusjas8e3Zs20DOxp0fhYtd2QfmKX4vP0ObipNav2vF9rFG+8vxljykNge1WJpSKVNmx7Ljs21YS3vtnNh2a2Mv92bZ5rlltmfmY666/GFzH5T0Qd89T9PN2Qo072utrnl3GaC6ItIOiUhFKaBkpOXZL0uNFtg9m89+IXjp77V9va3+bZ/X3i/5mp4RdWGv8cUSb82fmYTIci+X+/FJy+MwFwAcHBzAE+B9M2GgOL0PYKYAt2OfrRltt7SLELLlyy3liQUNOyG1w6vMy6ZJVWHDMk/ru1kyI3FNmlsAdNE1/altw5pga4zQbp5p/ubma5u61jLOpmlE0IgTALABOnpJjNXgqZACII9dsyVlK4qIgxtzyixieAwRIzPY+3xxnF6cFaOku3UgeGOdoYIwlATJzs3M5Fo5KOXclfVugpm5i9LWUnw36xe2M0YUPqB2rUNyn+JU/c7ObnJNG6vSeB6HGU85zq2E7Jyxle/MQMqW8dXmHTDC9Zb52mbyzr9LpVVmNZuDLQy05r/5JAx2o50CcFqhuwbWtrWle7YGskviXQMcoHQjNYCGJReZZpTNtz07h5UntNev4I/+7I/x8ne/A/aEwGm+hxHr0xVWDw5w/9M7+Oi99/DRB++DxohxGNE4j0jI/s3l+LRP1qe59KMvhTf7fo32nrceCibnYud8Tu3vJT231i2d93KtiEQppOtq9419p2TQ5TqVxRVzWK71Ns3+7MyZfXYeTdoGeG0/VfgNYa5oK+leOa/bij3HZXv6PXi6LboEJ7X9UfbjvHbLd4loQ0OZ54zUzXF7e3Z9a33ctl+r4KYyjvnP84UdO1Zg4pvb6GVtT9rP7Zxt28+1eiehYt5HdUGb9bFCK3Tflfu5HPPWs8TAzGyLzfVVIF0qSHNfDU3QOjkpPiUNv3hdkKMspNpzsY3X2bZq65bHZIZTowX293JtzlvzbefD8hpbL9HkMli1+hV1ZHyLuUK7dnZrgkKtTvt7iRUUG2e6TYTdnR08Wq+z+5lmnbJ8tGyv5Psc1fV5Pn9gBtPm+48rX+NmcL9hhtTftejn6utlBQwL0vVzdTuyi6vvA5hZK/QZO7F28cqNou9Zhq6TqYKECj5t2+TYBZuqtQQGzOLu0KYAc9Ck8eu6LrerQoV+V/qknmcZahqH0AcwpoBHfcY5n6ws6VAWc2Dr17917ifwYVJZwiHS+fEYtm8lU7HrWu6L0oyvh7VkLD7dDq++uSUBFj9xP+u/7YfzLl9So/tFU2aWQop8OdfelYfc7vFZX5nnbk9F0fmwDNY5t2E7KZluyURqIKrc59rP8jPBlS4Fhm3ewVDOnR2zrbck1tuAQvmdBVAhzd3j8ptbxitjqlswtzGbx4EvnRfiZGlggIkwICJ4IMDB7XZ4/XvfxXf/yY/QXbmI3hPIO9AYMJye4uzwCA8+/xIfvfVrfPXx5zh8+BDeORCzZKuLEdR4SYNrzqDtl5x5QoybF32WY7FzXQM0Nb/lTVqoa7u5djWQrL9bTXGZAa5cl5LRTePc1LhqO6Xrkf2sZnXWd2ugz46h/P1xz5wHhLQ9289avUSq2asr4co6lRecB67le6lyG13Q5y2dL+spLRu1+SjBbA1MnQd0yrHZM1juxxp/qdU5d+Ozbc91PaUCraybiIR3nqvE2vy9RvNqZ7CsS//J2qqgBiAlOzgPltXoe7leuqaKUcq1LOl6ZElzbtfernF5UzyRKGSUx5U0yjmHfJOkvDR/t8AQ29a+pPf6zMbN1UmuLNemtpdKkLwNm9Z4WllnDQs9bi+UdDt9ivIj24dt+3xbKc/y7LMYUyySVRIB6hIZR0kIVO6BjKEMvc7z42i2Z3PbUlHGNY87G1q+lkWjNHHZ79QyEA3AUOAXDBAsmVIIYWbG0c5r/nbnHNq2ndVTA3TbCGq5sGphsKnpmKd2dcPreOMobmB938/edc5hCONsEbQ97VdJzO3C2L8zQCNJx+e8k4vBSP6XCYNL9QXRKJQuGmW9pcZICUJ2y+C4QVBqxb5znsnXjkfnz86n3ZNzzUGcrYGtS93XdG9Z6b1x0yVa63XAanUGIs20Nc+5nokQCN4RxuJmc93XNYI5Ee/tzErrsOue6yvcYLa9v0EoK33QuZv1awZc5uvwOIuTfla66pRjKuep1l/7riNKlwidr0XSn/ZeFubN/tf6XtM+1fovF1M6cOCUFhroPTA0hGuvvYLf/9Mf49rzz4mw4BwWkRDXI04e3se9O1/g7qef4+PfvI+ThwcI6z7d6A0EMIKE7qJLNMEl8FkKGpYOaZ/t708yT3a99VzZ+xu27cc8DxW6rWfb9um81IolgCiVRKX12dJDCy5qpaSVtp1aX2r0pzbWx81rOb7679M7M3DCk/ayfKfkAZbJl3TOzpMGP28r6vpQKtVqfa+1UdsnWm8xQxvPb5vnbW5utj/nzbfWUQrRtXc21qAy3m39eNJnbPvl+GvnyPZLswKWVT6W3m/hp1pq610TJABMikps8mR7bq1gTHTOmhWfO9q0XD6u2PGW94dt7NNibFaBcR7usO6i23hgudbn0bnznjlvnKwZAIr67Fw91juB5gJk7VmdK7G4EoZhxDAMUPoRQ8xKC3vOSzpbGQXsAPI8gyT26GuWr+06ZZlc7lKFyczAumFmNeJrAV/XdeIiZDI21cB6jZno7wo+a6Yuu8mt9YKIssCjP2OUdLtan7ahVg0AG9aVcs42iSFn6XLb4fHOScCmbkhykyCS3IUozyWwTV1S+k5r0TV05M8FcnbOyr9rgoX+rmBltrm35AmPMSKkiwctAZytfahoRjAnkuM4YOiHTA/lZ4UppJ9t21YZUElctE9EBMRth3Led61LPp/fQFvbk7U2y7rL81aCFZ2UgImIlXXU2tLPSqZVe7fsS23PzDSNFaHN1lFqXSfhbOrHhqZlC+ghILtKqEudBqTnVLZEiM5h8MDOtav44Y9/hFu/8x345RJjylyGPmD96BjH9x/iqzuf4b1f/xqr4xOcPDpEHCSbFBMQpUG4dhLeG+/hnJ+5VVrhQkvpI/84xlcD/jUholZPrQ2d+/LcMk9WQ3veyrOunyntqgGmGvjZViagUwcFut9Lgdf+btur7f3a/vk64KHs6wSKAZiUvzV+VAPEpUZ+UyGwKbBYYGCzw5TzYPnxTLH0mDFtgmpsWASs9Wnb2tbme5ubyHmCZw2czedoO3i39Wv7NSWSjHN7PFGNbmq9Jf3SIn2WVPm6jOedgPPcqGp1q7LTPmvPADMDjjb2TclfbcnzXFi5pu+nHXneWGpCgG2/3AflmPP7VBlTZT7svMkab+cRwKTcPq+UZw1b6vs69KM8D3qG62d/c2zlPtPPndMMsPKvaSbs7Yjy+dV3Sn5g18F+zsBM15HXiqA5G75WeWJBwzamRMxqVtUVaQ4MpDeT4CE24TyxUSbDO5e1xXEcAcN4yoUAsGE6rBHtUtupoFvf10IkUuAcDHooSJVMi5R9EWM6xCCCdw00Q4r30wb2bhLExnGQyP/cnrjTKBC3oJEcMA4MjnrXI+C8R/CcUgg7cf1gMVzpuD257Jqk47Pjt9oDFW4AgIkQGYjJF119+hhIbll14lfWVRI/nWtLqGPaD0Si7Y5kZGaiHJi+cQgAhDznaZ8QwM7lufURcskiMQIxWgZALl1YZwXcRDDZZSag65LHTsn0TdN6EUmGMRtgPo66fonAQVzpKKVTBHPKkgIJP85jS3PCnBWXnOZ3RmJoCiq2e1W/Y0eJGKdkSkowHODh8lnzXoC7ZofSYs9QSZg3GYQBA2lNdO2UoDnNopKC4HSMgIJEZV4AdF4q4KbsRwmG7XfaJ0cOTUoAsI4B0SWA5CRlrR8donfod1r0Ow2+88Pv4zu//3vYu3IJAyI4RPgIjI8OcXb/EY6/eogPfv0b3L//FY6ODkUxEAJ842cgT2M/XKJ9SDTOMlRr4UU69yUjz+PwbvKX5yjCORGatku0JyLyiJRkTeYRlGkKg0DkAWIR8jAxpppLnPZBFQ9ZQ4kiONzuhziliGZL63m6s4AgQqbuk0yL7PbGdL7znoxx1pbdF+qKl3mDGQcw30t2XEqb7L7R30srXvn+1A+Ap0kXbSVNvDYzfeX28uL0u/k895gIgJO1YrkYUhRQYgFVZZT2s7QGlWDInpGShuoaTvRD/heVxsOOlWb0nTHvRw206LO2X7b9bXNs+2f7X9I82365n2vAsxSAbV3bwOHjFED2s1JpauuXZwAgJhpsrY2UvlNrmL441b2Nxtm5sOO3AscMA1Ed9G9bD/mgrtDJfSSSywu1D5jokD0LNatJba3KuZsJxFv6W8OFuV6WO20SGNJImdSA8OOaa6NVhpd9lOxa86nIvNqlOSnPWu7XNKeZH5Hw5kznzRi3KVJqf+tn+i8iokn3rQlPRsKKps/F2dSx2zM9a0uzn0KwYrLTZKVwuT/PK08saKiWXzX5wNw6YcGlDkCJ9ATIps9jukuCY0yDmEuPpZ8vFZ/rvxrj0D5ZZq+WFua5hULBshWgdNN13QIxBgl88h4uuYNp0Ld3dvoSw2cJ2PZm85daoNqmFqZMcukchOEwMWIY4ZJbBod5ADqINpiSzlMWegyAsJcHcgKB5DwIwtyc+pPGTbcjeyi07zXzp10bWxgiSLW+zWBB16bG4HVN09SCyAEhrUX+nMTaIXl90yWQBA5yYVxkRoTVBqtJU3zryQCAnMeb5wAii8ssmRwsgZM+SgdrjCovLJSApnfTEGOUNc4HfLabtpeZgFL8rdoNaWvaA8LcNtNflsS7BBB5ng2InBMknVcFM2X8gbxFND2vv5fWiqm+eR8fVxiMwVMO8sYY0Xg/gfBFh9A1uP7NV/C7f/4nuPrMdUSOCMxoI2E4XePg4SMcfPEV7rz/Eb767A5Oj46w6ldZSWKtuJmJ1iwNaQQW5M4YD7YAHl04FhAbY5T7N9KchqBWXqS/A7x3E4g1TEVpESpgxYJJHZc9d9bdzVolM11NZ35DC5f6PhOsSiBj+pDPFYyQYH7X56Bn0DLz9HkJmLTUwATKOso9dA7DZMYskFf7P535uLmmj927Cs7k/AitkXHpnVKzpwswUOt7eZ7s86VPNU+zP3t2No9pL9b2z0b9FRpennH9zoLkal8rANn+XoKlkmfY+RCl4eb8WZBWA01W6Cn3xjYvgDqwT+OPBFUyqZChr0dNu02bFr1yXPpMiV0saLQA245rEwhvcaebbeMKP5Y/pvqY57zLzGc577r2pXJ40xuA8pzU1vv8frOxxJnPGBtzWAPL5d+1k6x4wo53w32wICkEygqY8lxZ7xOdp9p5sO3l+c3tB+zuXcb+/j5Ojg+1xcQi6nGBdswzGlasKSgpe5xc1MmbJOrc8rVcp0oJtfZ36QZkiX6MEiTdtq1o74L8LT5lMviu62aE3G5Ay/SVEWobCt6thr0MVLYuWla4iDHmmBDth2roiebt2rpqBLecswxKMN01YYWl3B8lbEDSxDpEqHY0IMb5RpgBdb3d+AkOtf1px6vPOSc3bHOcLED2mXJMlqhb4lx+r9agklnUDnlp7s7CqfkJyDl2yrhGxunpKcYxYJH6q4CvXJ+yzXnmHGw8J2PjzLS0j3lsTtxpalCFiEBMszWZDjOmzGIVhratnDeWjbbJtk2Z2HrvH+uLn36bgbry2W39Lhm4/V0ft3tpDk4M+HySeSFgbCRtrQuEBTw4MFzXoPeExbNX8Qd/+mO88MaroEULjozWe4RVj9MHh3jw1T18/P4HuPPJZ3j41T04daMyfdTfS4HD/iyBRm2vE833QJ5PA2p0bw3DkOPcam5mNQak+ziEUI3hsudTP1e6lullQT9se1p3qbW09W8oGSpgsPa57X9Jm2p7tGzDMuny9yfeS5VCJFbqmgKl1g/bb/uZfv64YsXtWn3nCRt2r1n6pXcy6TMl6LT9s8KIBWfnlZLW2L5YMKy/q7JvThfmIMvyrtr4y7NZ9uVxa1X2v/y7bL+cn/N87EtXP3mvHktly5PM9bb3ZnsAm5Zp++x/TP1lEbA7/9sC+dp66XMlD8jzzlNQfXluz1vX7ed8Uj4/bv7LsZU0JPepUBxZV7VyP1rcQm4SDuwzRDTzvDmv2DmVcyXWpqPDQ4S+B5CsMVtihc6jJbM2stzBGW8R6ljnvPLEgobV5JcHWTtr3QIsY7WaC+syBJ6bYzOohLgM6QBrIMdmwdJ+qMuQZQjKRDXdrA1SLwmbZoqa3IA4j91mbNrGODLjTn5zpbZQ+1hqnrJA5QAeWUCS90n/zulWYwnssXM7MflNIqDjIZoEM2tJcc5lAc/2JRNX5o10ndsAhLXYlPOS+0Xi5lG6dZXMST/fptmpae0017UKhlkooU0wWGMYShRDCKi5ROg4hxBkHZDcXFIWDnIOnKMjUNVk1ObZEudSUCvHPSdwc0J1nhAAwDD0abwl2C01PBkUuEkrVNvrdo4sc7XnpDwDIjTP/ZzLfj8JsJn6QfDR5SBtEGNsHdyVfXznj3+I177/PbQ7SwQieDB4DDh9dIiDu/fw6JMv8OlHH+OTTz5JVtbUR54rJmx63m19rbkUWnCVZi6/N47jxGiL+xDs2aL0/OzWVp4sDrYftT1Rnjft47Y1h2Gatj+W2ZbaaNtnvRup/O48EHXevrft5PFVa9kE0bU9W7bx+DKfy3l/xEWxVp8FUpt92Dzb+izRXLFT1lmOxbZV+4zBmXfoZ6VSzs599k5wLltFa23WPjtPoLOf11z5yrHNvivqqQmj+vtW6zLm+6OkUbbU6HFZz7b5eByQ1TmfQDZll8EyK9m0J+Z0tnQHnPHFtOZaynFuo7vCzRhibZnv3dqa5joxZ3m2f1ZBYue19OjYoBeY1vy8NXjcZ7aNmgW9pC2PA+GPo18zgaJCP5umEd5tLE7Kj+0728Zb0oW8R5OJbBjHubAigGij/yWG3DZvKlTMkw/N+/Qk5YkFDXWZKjecbuLpVu/JfYZZtF8K7HUDZgYX5pr2GOXyu26xgDfXodvB18CXamctEZ2A56bPoM2CZTef9k8vHLTA1Y536u98sWuuROUG0ra0/Zn5EwyvtwSnjejIIYR+trGsRUfbVh/cEuxoe7bv1m3CMuPcd5gUuIUwZw+Uvl971o6fWTQUIW4epJLwlwdd67XB+JlQJL9/T2IJ29ndAdLv/dBnN5BtxRKcTBDd5HIyexYAR5vuc4rrcJj80+3aM7NYM4wgOGOChHzRm52LUmDT/pEgEIDnt6WXAGoTuMzPTU0gLNcifxYjQPX7Ic4DhPb7TeI9X99NYrUJpsqx2P3ok9sfwSG0DkPn8PxvvYHf+vEfYv/m0+CQGFeIWB0c4+zgCA++uItP3/sAd977COvVCpEZjfcApQDO9K88C5beWeuGzYhXzoE+bwP1SqCkygI7Nt1DvjgXdh1nlrVi7UowshW0F+tkx2HBYA0k2r2u/bbW4bJfNdBQAuDyrNT2WbnHrcXFMu5yLWrzVDubcxA7BymqwNF1c64eW2D/LgFX2e4c+HFSYmwqc+rnBdV9NRt3QStKvmv7O61v3BhDOR5bVw2olftg217cBmQnICWurVaJaOmBVTDOtOOVOSrnv1bOA3yPKzU6Zdsr64yVPj1uPkoBZMYXOUH/Cn0t3dZmax9jdjkq+7OtWGGj1o8SzNu1svgoz8U558TWWTvf22hO+jLxzvo4ttEMi7P0OVslXP1M2X6UOFBdEu181M5jbe5q+AgQPs0c4aKmtA2IbDxUDG3UUlp4avsNSFOm85c+UZr4pOfja90MbrXRlvDam8BtJyUI1c0AsWrxXFp0qym0jLsEq1aDtnFQCzOdBQU2s1RN41im29V6hmFI782Dqq3pd1t/bJ9KYqD16N8zdyWOYMeATzExPiEdFgGEhnEOOlM7jufErWSctYNg+2UJ97RWhUaJ5hpVW2rj0z7meXiMwa1sq9b3ktAyMTDGrB0Io7iL1LJKnHcgZvNjxmaJj2QSouT3n6R6mqR9MRYky5Me0LR2km738UxrmwAwIwQxAl6R8OPHNr0LlPO/jbDoe/lMubnZeRtQPK8v87a27wXtp13n87QuQMoy5z1C43Dh+ev40V/8E1y7/QLcshXLxBDB6zVODo5wenCEOx9/gs8+/gQPv7qP0Avdapsmm4YZQlO9o9keqIFb7aOeDctELVNVWqSgVMcyCfe0Ef9SMig7B3MryXyOy/Ww2lM7d6XwYPtj17tsawYAzefb6M0cAM37W/a1Bqir4KUy5hq9Lftc65flGVZgms2X6XcpDBGdJzRPZd5+/QyJBSvRkQroKudH94hVHqlbkvbPO5/jXGz/bF2Wn2dBkebntJwffb62v2wprQPb5siOaTYfW2hhbV9p/6zyblvZRk+epNSe1f6XIJqZAZ7HyM3eSxqNmhBUA5Y1sL1xtuTDjf7WcFJ+P/G/Gh6q1ZE+tC3Ovi//1earpKn6L5pLK23b5XyUc1X7fJqP+lxte+dJSu29Gt3Z1ua29mp7s7YWtdK2Lfo4gjjR8cBVWlKuS+0ckXOSiIdte1NfSmPAtvLEgsZ6vc4mmRjjRmYh20nLgEuGK8zU5f1pn1EgL0QxYhx5wypRTojV3FuGOFlVJm1bGaNRFgtstF2tv+/7rMUMIYDj3OSlbegYXYUB19xKxnGcLq1TI2Sai5FYUtt6n7X3lsDonILnhKh086odZi25z/aZXP+mqbt0nyoFgNIkrgArBLlxoFzzGlAoQU6pqcqHDZSyRAEgIIQRMUp6U2N3FeK5sdqpFIc3YpPRyQQkqxG06qQxArL1iZLgwak/uk1jTCMnFeCU5uVfZvuEcqBoHto0r5jeZwPKzxme/WvqfY3wFd8RKMefRJ3TDD7Sjp3NX9ESkekrZw0bbbRvNU1TH8v9NM2NPEMuZXoCgy7v4zt/+Pt4+fvfAXY6DM6hWY/w/Yj+0SkefXUfj+7fxycffIQHd78S+pUug4xECMxTALnpl9eMUnk+p+A6SusJzIEaEaUzG/O4vfcYx5hBqRbn9A4dkvlx4nYZoqagJl0JEAEhsGk3T1WerwxawJnRMDD1JS2UpdvWGqPPW2FPz14JAstbwTOd1X1s6K0FASXTLGmUzIubMk0B2YVv2n4kWWVJzheD81wQxNqs62ROW6bLNWBg27Z/E22eDTt2YOIF0+7F7PfcM6LcL+a5kizXb89KBWCUSiyr1LFnRotV2pUCVU2BkO+1IoBpokU6d3p+qVDmgZDXZEOQwuM1oJa32P7a70p+ob+XIDPz5ieXHZ64bBOqasBNaWD6oPqe8o3pb2ESsfK8XffzQLHlr+cJK/osYNY1dagUEEver+88SSn3o1Wg2L2YzyKU3cyxX7kfyvkp52Yap9SYAXQxB8itnj+y2foScgp3xTolvirfMR/O20h/nre229Zg6rHUl/EhqSvzZphDuR9q/cxzFJIbeqaBUmcNQ28rTyxouBRtvl73iDGYG2E3CbSMKaWU9ZKS1SfG2zgPn9IxjjwJA9b9CSQXkCwWXW5Dik7OpkuATlbN9C6BkaLZQQbqlJmvAOv0DknKQUnZKQcusXlwZIzJqgCGpK1NiI9IglGVGdpFsAfWgnUicfOZDp1krXJO4JQjwKFF4z28axB52BAeZHMzOAkF4vqTYiEaL37nThLsMkv6SGIBIg7TobUHhZkBzWgTOWnzAWZJhwsAnhyiOA2lMROI0/hdk5FwDAFwHg4up8Oc76t0ezYlQAtOmmTRMhMRPBqMGhAPAR1gwAUGOwd4gkNE6xpJe5lutUw64uSetIVwZOSSCAcLcFVfVSTQz5AL2qxqxJPLMT9jGDGGkITMtJ6aMrehTDjZ6WEVppyhLQGOzZ5JSoRMWLW/zJLONgsYKV0eK/hOQELBly2kfedJEGIxg1IgNJQCj2VVE9AAIol1Tfadyc3ODIoKepVSTvM6ppS3jmgCnc7JLd3cgEBwNBe2mIJkCmOdeVGoRAbgGsQANERwnhBah3Xn8MI3X8Xv/smPcOHKZYxhFMtfPyCs1rh/9x7uf/YIdz69gwf37mNcryVLWUw0gxgePp9fZKtUROQATw3gYFwNOPXbgEIwHCUaxoygh8TJOfNezqFvlc7IP9km0gch5BOjEiEhWXuZRbxioPHGYuKAgIAIzpY2HZMgBZfXPToCwygOUnJK0XhJTBai0HhQyoCS5oPhEMMEgDQgUKUd2YVyK3rUs+lcTq8o9GFSLsk+jnnLuLTPVeEiQm2iBylZAnjazZFjSgKRdogjcFRFgLjZiLClwjCgNlWX5RG5uBNpTMySItK6jhAJLRChRbL7OckfPQdgYEkVnnhXTPTMgeGJhaakfQ/nZU4JcspSGzlY2wgazAzKKY/TNFTchixgsrS8BsbtP63H1sfMJp7RCV0jAjcewIiGIxoO8NGBaImRA4KTvegQ4aMkYueU9cxmMVOB1/LoWf/M/oRRPlj8UwqI28C07N8JXFrwZ4GVVYjZZ7aB+BLA1wEvJYySCKjyjFIpoO+zgkhOZ2Q6V+ASDM/ft2OZKTDofCHLgvuZKySEfChb1CpZ8uBP+yiv1SQUa7/svNq+artKS0sstNH/yrjKNS5BeemGaPvhfHIIcBP/yvxvPrmY6PQmdsj9IYU5hcBWERZUIJ8L04JRYgIDnrzcn2bGreNRbGyVCXZOKLkOM0eMQdzU8wEqBPxyP23bX/Kdie3CJIw6N0+G9LjyxIKGAqoYI9bradD63ZywJVMNEmGMjHVYy5I1gHPIhLUmoTEznJ+0JYvFYnK5cvOUbqWZ2BIO27eRhwRSTaASJUAOzBYUmAsXwgxdBp8c1ee6MQBkDtbtv23Zfezhi1Eyg8QYc5u5H5S0jAWRa5omzwsw4TUiyhfvaP3KQPMcxckCY1P6Tm5qMHXqYWPonQrTAaMcZxBilLs+ErFUaZpILA/atnWF48RUm8Zny5Fm25klDsDmQfbpBnV2yOZBqJAU5wQQWw5FJimcAibtPtS28rxO9egc+6bB7t4eyEtw/fpshXEYZK1YydVUqydTd2JEAg4xW0dmES7I7pt02MFzAji7oyLCWGXmY3WwoESJYWIs3oET0RMhJ42TgSUvTOrj1P90w7amE9CeK+B1IDRqwdO+AfAMjAQMPs7OlF0Pl4Q9EOX6SEUtD4wOGF3Eledv4E/++A9w/dlnEMAYTk6AEDGsB6yOT/DFZ3fw5Rdf4s7du1it1pL2vAHIy1zAEQKHBIgAdi6BVwKxQ8fTRY2Na2WNXBpLvndFuhU4wDGhIckWp8AJIGAEvG/RhxHRTUDK2q0admjIw6U7XphiEgZI9nc6w8wRjnwWKBsOydoZ53uJBDgrDfNp66oQHTjKmCOLVZAInJ5XOkksCh9yXrRjIaQ+yDp5ZeppY8vFm2lv+cTHdT+TGTcBMUukEXAAUUx9YUSSb9sYZW/mvSAlMoEHl/e/7m45CxG5qYxUKf+QO4nSmslGFrBBQIRLihhKMvMEplokyxkhg0c9m5QEB5DMm/7uwWiSij+MjDEyKIpYiHQPDjnlMSKkkKNJq2CLDrU409uAt80MRo4SeKyDs7Ion48Aoidcf+lFXH/lNn7+9i+xv7vE9f19HH3xAF9+cl/oNhMopHuK4AVk05RlcAbyC2uKjoEybZvGVbOe5zU2vGwm9JVWk0IoKAGwnY9yLreVJ/VNp3R+RX7cTKSyUTJd57S/JjfOzUe3C0/C9zafr/1uLUX5c0L2ANFUy9uAaj6Vqet2brcJu+f137Zx3npsWwNr7SvfL703pu/KWoq+GQGY7Z4usElNqAeMhaHw9KmNjWgem2aFjXLObLsun283YUaOGd/U5r3cg1V8mmJMY3pevHkA57a7hNXK10pvO6aI9ilQmmaSll1g/Rd4ukgESWJGkzRqBSAHJheNGJFT4Voho9yc24Co/sySMzM4BLRtOwPYOobSbDuBWT/bQKXFpHQb0PdV4isldttHO18KykOIkp/fOVAzuR5o1pD8tzX/FSbOkujODgdMIF/SvOot2fp5aTK1c1ruCTsm6yJWzpkd8zRHc3eMkNZH67DpPXUtbNuRU1vJZWEYR7FmBJ4B9POYgm2/LHb8ihm137b/q9VKtKo6D2QZxDluW0C+ZVoB4tS2WBFt/8v9bfufPy/WI38H0eaCCZEznMxCIyi5mjAnYJcIFDsQ2vRMGg8ne1gEFoVkpsAGnhF9Ap6E7AbAjQBHYgacBYVSfCS4OF0UptYol4LuRopwF3bwvR/+Hl769jfhmRFOTzCEgLGP6FcDHj14hIMHh/j8k89xenKKMJxhkRR8jW8k7irt85C04o4cfKOMAHDk4bEEc7IEIllinAN5wsApy5juMRaXPUcensx5YEY/DHC+Q9s5jE78j9UVsthxIK+KlCT0MDB6ZDO9AglA3L18kHUtgQRTALleFiUwPDM8nFj8wOjdIIKBcKhkzeMEfhvZGxFJMeNFmCWxskxnerpXI8SASDIm7x3YW/cjmrmSyr0BiRmzzJ0jUTaMY8gCpmzYySIpSpgkFLlJ0GBFqCzKI1duqlnh6ZgZYEUkWniXDi4hxWWB4Em09br3VRLIgmSSDZgB4sk92KUzTOQQwwjv9EyrJWbThUm2FE19w/zcs7EAluDH0nilT/p75DD7fjYjxT7MngAxoukanIQBr/7+9/DSj3+A46NH8OsVvnrvY3x07y+xy0DbM1wAIjkEL5YyKqz4Wizf0/FmocMIQzUQVPJ19aoo56gcW024KOfvcXPyJILF5ntav/Z/85yWbm5lkWbrIL/WdnZxfcJ3auBSMVG5n8q1ye7p5vJYW882QF2C/dJVsXx+G39+3Fz8Y76rlXIseV+f83yNR5d4pCYI1dDCdqEk1SdPpXYM3ky863Fjq7UzfS8tZBhEwnfOw0218jVcpyZCqEKGvWQkS1bGp56ZMax79Czm2L29vQREpjuWLTGaXAIcHJmYh4JJqTRlJ8e6YJUSJfMEPK2Uuc0aUd0AxUbTCwDVzGznRv7N3bvsPGod9m/nJOimbcTkE3i63VPBIDk38wnM7yXGZImvXQ8buD4TItymK5edu6qEW+l7GXBv90oZa6HtrddrdF0nc2Q04fZQqmbNOTfLZKP7wpMDu+Ry4R2aTgBx5PQdb5e67d7IQmaax+r4SZSQoPlBl/0REKMRpCjd6p3JxqZmTz5VMSStn6k+smiba8JSWc9M8MFco5LnEwCl69h1bsAs2nMWoECEdFs8Tyl0wWA3IHcuvQcA8EBILhIKzibXk5hch1TbS3L7sXdwEdjh6fk0A1J/MvlHMNjJnhcQ69E0hG+8/jJe/b3vgnY6nJ2dgNcDuB9xNkbcvf8Ijx48woOvHmF1OmC9GtC4BjvtJXSNy7TFJyAPMAYK+Ww5daFkIDqHU9eAsyabZoyVkwXOOTfd5cKMnlQgoeyySM5hcA6BCOynTHPIMoO42TiHZCV1EpvlJL0wnMsud7pn8421IfUryEWhKowMQ49xfQSEURImDAFhDMAY4JnQDKfgYUgCnNQbYhAa44TORhJwLdYPgiMvihAwmKb7gAIznGvg4gjmiBZimRFhVaygGpMAYHJRgmQM4xCAwGi9gydA76tbtw2iL+9YsRrYiRZa5YaDz2Cc9FkAxEA3kgi5jGyJdUhWCJ6sAN77tDdFASTykrjVZtpKctMvucna4hqfXB5ln7lEZ2N0iMMolvzpIG/QBedc8j3epi2ca6trvKr8TmionOdt9FCftwqqzjuMY8TRV/fx93/zU7zye7+D5aVLOH4UcemlZ/Hj/+I/wd//q38HfrACBXHdiOzgPOCMW3RJwyyYteuqPED7rM9aHmp/34jfKmikrvsMWxS4oQSB2+bEPj+LJdjyLhGZzGHTZ9vWzc6L/q4uhE9acp38OPWW6aMZl+2DTW4BmDt2UAnuJ2A0PG6bsGjbrfG12fqA8/zZftb2Uk2QLdsu90n5TFn/tvZs/2V/bT5XzsE2gascl92v2/pe9hcQJZ6H7vNKOmrm2T6qnZcaVlIso5dQExHI0xMrcW15YkHDChbqjmSBpYLcTDSIcHpygn7V4+DwAHt7exiGARcuXsQQRuzv7+ebrrVkFyja1HaURMIyFnswxnFEjBFd101BbUhAgiZTlGVQlriW/qPaD5sK14JgzRmvc9O2bWpzM8DJbtDysHnvkzldGC9zBHkHDwb6KVPXWIBIS5gtyC+FDR3PPHsXgLhJ9KqguHJQrCuUfaZpmpy1y861FdC0zxrfEI12qmxvU9iUdRii3JQcxgGOIPUo8MGcIdUYwwZxMeMrxyhMGllRpPudSDQbEZz90hMqSeCbUaP5ukeASeDj9J5+VxP0akSydNfbWnxyxSkJHwONgsAMwhzIOYwcsfajdkCAlRKkCLggGjRngLDzBBo9GiwAIoltIYL3SYgmTprnSSsUY5QAaniMqS0miEtOZFy6chlvfPsNXHjqEh4NaxydPpR7b/oBR/cf4u7RMU7WAw4PjhEDYbm7i/bSZTTdAkPXIjYN2q5F07aA90moAdqW0LQNuq5D17bwXtwhfeNBjU932Ezumt47uLZBs9MlQcBlGkCUhAI/+c+2TQPvkvLBeXhqspZb3XOIgOgY0aWA22TN0D2UYyLS9hMXuHT3C4tTGasQBCCGgH69xrg6xrhaYX10jPXxKY4fPMLBvQc4OziEPzpGXK0QhxFhGIExwLk27QsGI8B5B3BK/KEBFyD4xsM5L+NwDiAHDwDsJK4FDeIwpRcn55PAmZJbNOYiUTACy7kdI0HM3SKUdHDgoLRDwDtzRIwMciMiBxA0zXgSbCID0UMxml6yKTRDlFRQuqhZDolAxPDcJ8FQ/hYrjBfLKfwkaLsGiMkxLe0BR5D6kuKHvEPbdOm8AGM8haMBXgWnuMn78tktgMjMhz7tGaAOckvwnelGYT22paQbmZ7HiKXz4BF499/+Lb767Cv8+X/xn+HpK9dweHAPzc2AH/7TH+Nv/8W/Qf/wDJ7EQjXF9W2CT0Xdtu8Tr5oEQ+2XdYvWn9vGqPUqn9PPa/dZlUKZrUNLCcLLZy3gLr41c67rOE/Lqz9tv0pXMOZ5QPi2/pS8jZkn5c8Wfr5NGBjHMWM7+1zNLV3fj8zpzNRBfzmfJcCtgmjaLoTYess13Mbfy7nT92oWpfOEDttfVaLU3rVlG/YoPTpIzw/NBZRt+3y2NhJEB+c82rbFer0Cx4SpDGYp6zrvDBAlV+ooiibFKbqvyufPK08saGgshB5869evB0PT347jiPV6DQLhf/7JT/DZ55/h1ksv4Qc/+AGOT45x4dJF9MOAzs9vvdXJizHAkZ9tCrvJ7YGyz9hYiLOzs0yUVPttM0nZogRD77XQem2dWQuZiu2DAntgsvYouiwPiD5jN3oG/zxJno4cIihbMJxz4hJkmI8KUq4Yk21PCYftSyaOJmBYv7PP2sNZI27lMzqP9k4VKwDqc9777MLmnJNb0M37pYucroP169XivUcfR4QYMIxjihwm8OZ5r/Z7Nl8QjX65XiGEFMy8yYjy/kuCgdzGSVm40GZqREuElBRMmlyMSGMEkktGjSGUddh/dtgbTN41YKPtYhWKiNDHpHnlNJakAXUMXAp6EV4Cvarl8kDfysw577LLCBEwgtD7FtR4RALgCIMXq93gCKGR+BY9d13XoW1buKZB03XwbSOCUeNx6eoVPHXtaQwc8YADAMKeWhRjwF4Y8Uy7QLvYgW87tN0CXduJ+2LjgU764byTddSbWQkCqNUykQKZQaLlbiLnBaQEMjltlBxzoGvEk+acZ3vUMBYwKNN1zm5IzCJ48XxrmxpoYhYARnPmHKW10WfT/t4DwPy0AC0meAZiP2JY97h/9y4OPruDzz/8CIf3HoBOVwinK4T1APQjXL+GpxEhjnIZJscUXCp7E+QkbsOnlL0+ge1FA4xB5jrGdOEbiwXIezjvMSjdS0wuIub7aKJh+jFGuOjg0r7MYBEpvgYMSto7DqKxZwg4JqbM2FRD6CFna4DklwcRAiWrmp7VuDPRIK8JNFjuz0nrprTINQTvksItCSsuWVZd2mNNu8BysQvfOET/CMOwljMWRrE0hRE1Gis/tviwb6Fr5xWeKs08ukb/Nt4jYKQIPxAuDg5nv/kch+/fwYVXnsFybx/H6xM0Vy/i9T/6Xfz7f/GX6AZGxz6BpcnyMqNdqS81emY18ZYHWL5eathL8LYNhNvvlX/WBJbauyW9LcdUvsOcArsxX0/bj/MA2hx8bn5X65/dR08K/qb+TnXa6wbKubFeCbU6uFLftvGVvHwmXKn7V2UcM1Cevi+tX+Vztv/6fCkwndPZDetQnhdHsz20bR+WVkbbz3IMBcTYwCI14csRaTRejt1zyYJu56XWZnkOZ1iCeS7okwjMtr4nmkN8TdepWic5mdgtiG/bFsMwYBgGvP/ee7h1+zYe3L8P5xz29/bzoBSg1yRUZvF9XywWG1pxi+LsbeQ6QW3bZg1fMAtYEhodj704Tz+zB6GM37BzYvsVI2eXKWASViyBtKZ5KwgBEAAXU1Yhp0KGLjJMO0YaT0BgyugkPuAaf6EuR7V4DcpBjbTRx4Sc8jyXDI6xSaCzFSoEycCkQlMSpkLaMyEyKAR436SYbYfstuAIDi5rxBw5OPKSVxuUs4dJhg7JjkTeIfSDdkwy4KQMY0ltLNoHnjTDMadoK0/2dNZjciUREBNBkIxe9rlMYJM/vQTEpwfSj8kKoOb7SUOuDkQxuUkpwIdJiYu05zl3cdKyg6b4ByHOk1uiCgeAaG8HckACRgxkb6jIhNE3AsKJssMIiDB6j2PfwKXEB00WDlo0u0uE3Q7dYoHlcommabBYLNC2LdrlAn7RYbFcwi9aUNPAtR5N16FtO7RNC+eTJQBA07YSWAodhgN7SjEUDHiPAQwPQssOPt3KPjjCQJwyWclaRUzMhojRRQmWkwBp5CxBROLeIDwtqVN1X1NE9Jr4gLOrk/7NZIiyrg1LP/yMeM9TRzPFxD8JkdRSlLKPsWHYaf4JEAtQsUf1h+eUMYrnmqbIjMGLG09kQmDALVs0ixbXL9zG06/exst/9EOMJ2dYPTzEoy++wt2PP8NXH38C3LuPcb3CanUGDh4cR6js3FALdfN0ibZ45xGcQ2xaAAxq2uw2FGIAe4foxBXJJaHUJRoYvcQoqbKEyKUc+gRu2yQcT/SraRrZg7wQq4WbLk4FONHDFVzygtP4EU7Aby8EhKT0yIk0mAF2wNAhjGHmvsDMoDCgGc9ypjEF6ypgqoDtnAgZajlbdDtYLvbgPQHdDtbrU8Q4YLU6A/ozYExQNFnh0/aTTFTMcwFT15f15JqS+rAd3rEE9dPmje414JPH7gkrBCyoQTcyOI74u3/z7/HD6/8pFu0Sexcu4OTgCGcNwPsthoM1FkygCDBctR1tI4/JfK943AKdUvlVChjKD7cJAZbnl+/Y78s2a7+X82Xbs8+4JGCLQKXfb4LEWil5NBfPl+1m98U0L5PSEhug9UkEgHIOay5sGwo/3Zvpd9usbbGsu5y3ct3OEwRrlozaz/Idi0ksFqvdvVWr3/7NgQGqJ/opQfhsTbeMt1aPLSX2zGuhmJgmhT+nzzlqShnM9n5NILV9iJwyhlr8QkiG7em5x82blie/sC9IRp/G+XynhDQeQV7AT9u4dFU54IixXLR47dXXcOfzO3jt9dewv9zF0rcCGIW7pE4LcFIQ1rSJuYSAOEq0o09BwRwk+WYWCgA0NtYiRsRxzNK1Tnba4pgEAN0g1vXEbgid0OnmV7tYsjBzibFpkksEIkLSVllCpVmqYsRUZ2rXOUIM4hYQmEGR0TmC4xFu4SX41DeIIYgvbGA05DEwAwiILECbnEsbRPyfxdd/2kgZxjCDA4HYJfA+bVwOkpZRMyQp8weQfPfTZYdkXJ2gwFgCXV1i+oEjmq5LqR9bRATJGgMP3y1EHgo9HA9QlBmT37yumIMHYXK5YCRXB8dYjz18J+5XIIcFNViGKOlYIdrUNQHRebQBWAbJeKR7KAP0dIB8ErpiDuo0ZmHyWZsfQ5wusgNEO1oIawIWWDyWwGA0KdBDNp5P/8EhabSTlt2Jnz9FiFbfpdSZnpJbiQecQ2wacOMEjDsCe0J0AuplrzVo2wZN08K1DZb7u3CLDs1yAd+18G2DZiHWA/IO3aLDYrFA13VokquRaxrRRqc6bTyI+PNTPmeZ2eQhJl/zDOCV/znj/oF8jkVoMkQngVuk85MSgyIggP3kI+uhSXwkLa6HMjhpMBBymlRD2oUpahpFIPsETw0nIWTWMU4BzAoCWZ/IP61dSZnvVO2UdnLOuwh28lhpVfrOzZ6djSLH09g2mZwIPDw9z/n51Fzr0F3ew+LSLi7fuolbv/dt9McnuPebj/H2z36JsztfSjpgYom38YRm5wJ2d5dYLlssd3fQ7e2i29kFtQ265QLeeywWIkw2jew/amS/Ip0tUbIktyMC1F8gD0ElYEc5+9n0eWKEIeObNI/KvHXfTS/JNMi6uemF/J6uA0fkIP0Q5KbdGCMQInjdYxwG9EMPZok5XK/WWA8j+iGCQ0RcDwjrHjwGuMBo/R529q6i9QQ+fIDV6QFCfwo6PkB/eoywOgOvVmiGEW69AqUYmsCjxKlEyV8v68sJNEyacrvrYmSwphaLnLStyXLOyHebWMCTZ6jyNyeQ7L0HO8LoI6IDDr66g8/f/CWeeuEqTvtHaJoOFxcL/Mkf/xHe+puf4eDze1hSCxgFmwWF1vpv+aO6kpUgzNJUK1Tkva77BBA+74S2aHpue8jOE3RqQkAJDO1zJdi2z4pyAaquSUKGr8YclPVugE/TZzuPVbcbe1asgLqlZH5feb+cDwvMa3PnMF8zLSmiq1qv1qP/rOJVhX19fibcAxt7Atjcx7N5xHzvW0GgFqNqOjyXlopS9ivvYULO/ihJJdJ8sFp0HaKt2OACvXRY67Xjs2PK2BKYrjeA3HnnEg4tu16u9aQ3FRAUE/bV5EMW43Ciy0SSGdFe4P248sSCRuM9Gt9gTP606l9vtfoyX3LIvfcIY8Cf/Sd/IQctMdKQ/MZCDKDAYFaQP90HMA5zlxs7MaO62xT/rLSdNSFEaLtuJvHLM+MEloqDo2MpJWYt8w0lSyRzrUIGNjaxtuUS8HfqKw9k7S2A7BuMlN4zcpC5azyanQ794VESkMSS5J1kwIlRLh1jZglsdEkoI4eORRMVki+9uANIOOboZT5DSHdQqLTrZIuOFLK1Q11FCMjxD1mrC5pdKBhTmks9VCEJbB6jZMMhh2Xj0fmIMQYgRBC10gYlBgnJ4sOeBCgyAxySQCHj6KLHEgtE9sCiQXflKtZPX8ZqPWB5vELHhFNELJ67Ad7fwcCEuApYHR7i7PQkr4uuFzHQGquHHDQRwiIBfSMpQ6d9kEB20rJnRjbpuMU6k1wsyHsRmNV1p20wLDqxJDSSZUzA/wJ+uYTvOrSLDn7RodtZolsu0CwXcMsObiEuRq5rRHhYdGi7Dh03aEkyBTl140h9bSFuDTEB7wAkIIOcqac8B+dpPbadjfSkip6ZUCd8i4wYMcPH00Pln1x8TIl5JWxOBmjWqslgvCgbRHjjic1itcy1wpiEmrLWLKTnb+bPbcMElZk+78tca7Wbs+6nNU97AM6hvXwBz3//t3DtG6/g0VcPwJGxu78ne9Y38N0SXevgGxbw6zxCcgHrHGX0z8wY+h4Hh4eIYOxfuICu6+axCLkPm5o9oL7HnuS7jfl4wjr1+w3QwIAnn2G9LdGJC5ZHCuIOER4EDAFhJDjXIo4B/ekZDh7dx+nhQzx6eB/Hh0c4fPgI/ekZzg4OMRydSCzeMILOjoG+Bw+D3PnCDGKGZwe4MQNYcTcViy68y1Z8SkqmUitt56IGQGsgUnmRytUdCL/6679F+zOHvj8Ew8G7BvuLi1gfnqKLHiGIC6tqikv3EqtV1XZrW98CUGBy11arasYcxo24KohUxrjNGlH7vCYUzMC0AaqbwMuqzKZ3rCdHTbNtf982nm1jQ2ppRl0q7SiOK4vtl9Wcb+UNKrAbr4ncDmFG5Ms9UFqjckr7yhyUyt7zhKjzyjaBxIYCfJ26a3tkUmJMcTbqBaLYibFdwCsVAhvzWrZJqlTX8xbRr8eNm7vLM55/YtrvGiLhSd2hp91E5zG/c8oTCxpqZi5BeHkw9aB1XQfvG5ziLGdC6tT3Wl4EINKTcxKXoXVYdyjd6Ov1Oqc6DYVbjvU5tf2wz1jJsMyoYImKLnypQbBj1XemjSB2eqOAyM9bDYjUCWiwp21TBCGxAERiuYwriBAyEsF3Xb5IzXsn5vh8f4KH+hODlckAACE2ESMCoroA8STIAAziiKYBfCMuT0QMuCSwgKGWpixxi6iuy5eESNWYkQhx6T4Q5yf3Ak8EOMl4RM6hdUg55lk0+Ggkv4ujFA+RgAxGCTRNrlABTc47790SAGHkiOAi3NWnceF3vo0zHnH0t29jdwDOWo+r3/4W+qcuYmgarI/O8PTePi5euICzszMJ+lX0FRnjMMh9AUn7Sc5hHAas1ytcdOIL7lyKLwCJxaAVKwKBMIYRq9UK3jksFkt03RJdt4vFcoHFcoFuuYRvG7RtK7dONw2arkXTidUBROCUdYiQ4iYSEIyABNTG5C6Tkft0o7kORdyfkjVB1ENwKe2vgGHku6RY8WHlTOjvtfMuf8+1eptlgr3T2fjHEavHlX8c27GlZM/nPVkfA6czaqvMTDP/z7Znv3xc35744X90YQL6luAu7+Lq/hIPHxzgMMQUW0FYImLPeyy7Bs7JHgsk7o6I6Y4IZpyeneLBgwe4cuUKlsudpFyZ4tMmWioaYOB84LTJyM/Xkm4rTyqgzDV/BKYpo9vsObl1EwGjnM2GxF23FaEygEHs0V7aw7Wbu2jci0JnmDEMI4ZVj5NHxzh+eIAHX97DV3e+xNmdT7G6/xWGo2NQHxDXPeJ6AEJE6wjAKJdCUgS8xlQh0eM5UCnBai349XHzoGsaR7moDwPDrRi7nCzmiOhxBBeAjjoMZO+L2fSJt7zTWgZK2lJ+bv+eC0Obbln/MaUE1LXvS7zwH9P2ecKQXsZZ9mebgJT7WPTXvmeFoZp7jx3ztpiMJxmHdoSx/eyWa5q/c/NYgdo8P65fNdBeOxOPG9e2QkRTgPRGmdzmbB9KAaJ8t0wgVJv/sq+ztYVJ6FIKhObZbDXCJp3Ia8KCCyRm5nwF2+PKk7tOmQHbYOYQArzJyKTZhohI7kFoPZxPcRDeiQme5fZnRHGzAkv2ERU6wJw1FJqlKMY4y3qlmhLnptSn1k+x1KJYIlcGlJfjrJnUyk0+/bQEQE2MnH2/wZPZEaxEg8EcEEMSprxLloqIEIYcWBzCAFADdg0cHHwgUCS0SBm/eEQMDEcRngIk279LNymnwGwQRhBcI7cWR01VCUIXxJrhvYePXlyaku97BpAqlDCSadoDjaSPVEGCIYKh+PLJWpCbYiwoZdMKOtfeIbQN4Fuw5zQPLt+EzWlTMwAKAnB0vj0zxhAQQsTD1mPoCAgRfQz44vQMO889B98R6DRi9dVDuMUS46XLWC0WiG2HttvHKq7R96dgx4jjgKZpseg6NE0LuB34pI1bdAvs7OygSzfUd8sl9vb3JZg9WfO893JzOyYt4uTwksbBAuzTh9mcrAcdkO9HHTMBbYhog2CJieEgV6K3iBNRcRdFEFtZEvA4Sb9EhJFSyuTUD1hGZWooCfF2hkbFmzUwvMmEmefPngco7TNbCe45BHAa3+b7G1qd4qd9bgY+oqSTVTqitCjGKJoqmmvqJs1fUkoYIMWYwB+Z9qakEvM5KjVg9vtNwLNpcp9/v1nkPMsO9S0BHvjJT/4tDk96XLx8FdeevoLXX7mFG09dxqJz8I7S3SuJwclk4+j4GBcvXcLO7i40g1ZN21xq6R63Fx4H/B5Xysw/T1I/KI2NJkVS3t0c0YRJKwhyYMfpzKc7PxgSQwSHPkoyA24Z6AjNcoGrl3dw/fZNvBzeQBgixuNDPLz7Bb785DPcef8j3Pv0cxzffwTuBzSnJ3BjD/AIj5jTyEoj0nZ5B0I5R+cBl5kAl/6Oif43ziGMAUvfSHvcioUUQIgsl1JGyZYIBJTa6lIpWfbNro8qNLdZQ2y9nOquJQux46uNvaY8tJ+fd95s3897JnfSlPMsL/M1qD9zbluJRm2jdzXBqDYvG3Rvy1llnlydrCAjSsYnP8OzvyPDZrko16MG4C3Gq/V529i0VIVwNu61BZ1RXFTOR2pFnig+L3lpjefYfWwv3iznq6xHkmLM27FYtnRh1EtgFWPr81lAmU2ajCiqZW6LsLatPLGgsVwu4ZzDarWaAXUdtBU+9NCLf7i4SXknaba8XsClkxPH/J0MgeEbD9+0G2Z2Ad9hNoFq5dC/t13go33Ufs9crNJ4NDWu3kpdq8NKnC5bpSKaJgUwI4JT2kWwBD+KizMhjqNsWlKLjQQce7Qpg0pEk4StfpxSNwZm+HYB51s4CJDv1xKc3LgGEX3KqGNT+QEAoxsbLEKbAk2RGBIAIqy4l8DNlJKX4hRUTl5ueJU7KdLFXEHuEFh7ykHSRC6/E5OQJa5UU0wHAxjhsIZYMzSQVIQeByIGEUvAcePh2zYFBzcITQM0LRaLRQ409imDDRYervHomORuhosX4C/ugnY64Ls/QIsGrfPoLl5A33owHBoGwk4AtbqmmlIUKc9+WrMEEKAmRXIYKV1syHOtg4sAFZc+yptiMXIJ/KfqMjBmmj08o8lEQGhmX+f3AlokB40M8s5hQbmGDQcF5kzLrWXiPOJhGavspy2MkAAins3hrJ4pd8G8jmIkEyFOI1ACq0Q/iWsx3Y7NbLQ0qolJvtEhBDFjwySzAGYmf9X0ZEKvAcOJeSvtaApLTgZAbrIuWWUMJcFP2uaU5lSEDoYE67eLDo1v0pkY8yV3oozwWWmR2zVtazC1/hPf2jrwrguN098+BLnXgxyuXLyI/qzHvS8f4vg44Oz4FBcXS1xoGrQXdrBoW3HhcYSQTJ2OSM5vK/fajOP8voR5qWvsan09DyjbZ8ti6fd8/27xby/rBcA0pYm0z3sAXaRsQUS62BBAdo9Q0CH7MPUljCC9vAZyiSYcwS0cmuU+rj31Cp755mv4rbM1Th8d4vOPPsGvf/krHL37EU7u3sOo8R0xok0Kk+A217X8vRQoaoBy9g7EhRUkAaIOJJZv5zA6Jy6zMSISEHgEexLP0DjVZc+Wba/EEOC5RncbQLN1ATCxnpsaYbu+1n0amFtv7RyUgLXcQ2V5nNA60Su38XltnGbyq/WVbZdryJAYAKaaSw8XbuSbAs+2v7cK82lbZ2VLAa5LQdL+Xdad/zZrWgqP2wTXbUJjrf6NvVd8Vo61JujEpNCzHjNTP9TDZbswqe+U320rNWFDPxe3fKE3q9UKi2ZyhVcFfTkGSnytWq/qjIg0q0xWis747zm025avlXXKOYfFYgEiwnq9To3wzLpgg4Ya34I45mY4mQF1YO0yZahp21na3H4I6MeIxWIxMX9DDLQ97UtJmKz1xRK0mrbDEij9W8eWmXaxGBPBjLNNl4kckN2aYNoPIcJRAMIASpfzUUNYdA6UAqvHGHDarzGECKSbiB0cdq48jaP7B+KiFBnjMCKGUebI7Yh2PgRI3ngDoEYPRx6Opnz/gGC7MwT4xQLcNIgxTJlJGgfnp3z53jssF0sBO94hdg1cAvudAn/n4H2DxkuQMTknmn4vQcTwHoFSvIADnG/AAJplh7bxaIgALwDJN424FXmH6EUTr+BvpuFKoFEz9iD9zQ4YyKEhDz8GRAeQE9DfRYBdixgSsidKYE+k9VVD+fDJ3hCXH8eMJo4qo4E45MMYiLHqtsT0gOEMA8gWDQKaSGjCFNLpzR4biTEaU4UVJnwA2soBZwJGx5P1pChNxEzYyKeBJyKS26sQyA3tC9teFcorlniWkonrc/bC0hqx0nNvz776jpb0wJ6/6ayFDOhRBPjqmlrmY5UISsP07xBCAstTwgnHkztpCCEnyAhjxGrVy+V4YKzXPYZhEEUNGOO4RhjFlXR/fx83btxACAGnwxp98q999tlncenSpZlVg0Ld/cTuUaVxchYdfDNdHKj/nqgwkltdhGsa3HjmWbz17hc4C2cYacRnX32Fmzefws5OJ+0iZbYiZUwO7733Hm7evImbN29mOljuKyl1zeu2PXEe4LPPaSnb2+aT/rg6YRJf2DoDgFHn3QBropTygCYRn3OQOksSjpDOnR4jxwCCJBvwjdDjnQ77y6fxxrPX8er3fxtHdx/irb99E5/++je4+94HGI+O4foBRB4U12CerABlkOu2uMPzihd/VwRINkTxzQAC5L4iYsno1hAQOCBCL8OcymZczjSPs/iROMVmlmXbniAVgAxf2CZIP2md5WdPAgJrZQbE/nFVbJTz9vbsOUx0rQT++q7FNSVteJzQPhNA7B1KW1zzSnp9HqjX5612vYbnSkHW1lUbc23828Y7fU+Zz9eeYWxap8q5KK0J6gkBzL2DtM6yjtLDRp+zc+1IYkAphoRRpB57vcGG4C6jmrVnU0lPXwmRF5f1aS7+NxE0Fm2DnYVcgrdaeSy7Vi6GGgYJCk7PdV2Hdd9jZ29PQPE4YGdnJ3ecWbRzMUYsd3cQxhHjKEG+y8USzIyTszMcnZyh8Q47OzsIIeDo6CjdTijhAl3bYLlcoPGNGWzabHYKWbIgkVn0vEF1EjHFcTjnMAxDBhkSDyH5bgSMT/c5LJadCAtKyBNDHXu5IZd1vCRavgt7e2gcY9HwpK1M/5cbzx0Aj3EYcNwPAEl2ln7dYxV6jJf30foGy+USO+kOEmaG6zogZRjRWBgAEnh8YYnoCTs7O+Jm5ht0C0lJSu0CbbfAYtElUObzZWVw6ZIWEm233pRLcIj5gBfgEhCBSccW50RWwo+TAsQ7uXE47QviSQBiCPNmZrQcsNB0vcySfz7jXJcYPQMpI5WHuH8FlywtnhBdQPAR4CDtxBYpL5Z0L2UtATMWwxTgPg0qMTQK6cwpsdSvGYtQEMo0bGJCE33+TMcnAodHJJMMlwhIweg+sqQutXObznlwDHZTJAAbmtCFhFdUi5rnihBSTExuL1fAGNn+WTBgnvxN1UyuA4pRQZp8YL/TrD3ME4GyZw4bv6c5YrH0xRAxDANWqxXW6xWGfoD683Pqp86b3AHCMyKutYdh0uCFlJEuJvcnHeswDBjHEcM4YhwGjClOJ4aAdd8jxoguKUTCGCSzXRIyYoxYrVYIIWDoR4Q+4uT0FMdHx+iHHmdnZ6K8iCMIkzDTdR1ee+01PP/884iesH/5IpgZX9z5Ejs7O3juuWfxzDPPwHsRuoW4x5lQqEkYdPtQSkUod08A3js0jU/KAJ+VAkBduweIoI50qWJg4NkXn8eaf4phHOAH4O7BIzw8PcGFCzuAg1yYHR1C2lQUCX0Y8c5vfoNrN26AmCdLacGcVFk114py/nzGd1kBVNKkTxtvWm8FGnnfzmwKea9mMJKFgbR7WXeXxhQpr0if6X4j+WsgYA1JDuedA9KdI44ox6OJMKHJMVJLwYHYgREBYlAjLqggRkceGEaAKHvbBQRwR1i8cAO/ffMvcOONV/Hxm7/AnV+9g8PPvwBOz0BrBzeOQAhygRcYAck9AoTAPAvOlexp2iNkV6kZmAXAjlLsoNCRLNSD4SLDM4DIaL1k6xPvsM24SZj6ayCfaAogtyDIuj1O/NJesBtTXF8diE77bF7K/m0oUoo99XXLDFTrZG55rqZVFjD4ZO2WgqS6IZfflQDfKmeBTYHDlm0WBOWVNfCpbtrb5m87wJ++0zOntC5ibrWydW0TLsq+WcVzuWdqgipLF6Zg9SSEkMs9tK3Nx4O6VWbDBbBod5vAVM6/8iGX1nyxWIj7/DmuhFlAKeaxZs2D7QM/XsCqlScWNC62YkGIsUHfiRl/DCPW/YAxSWz9useia7HjHLquxd7eHk6Pj+AJ2N2Vy5DOzs7giXGyXmFoHM7OViCSG7WXS8kQNQ49eNGgbTz2djrEELF0MrCHBwfoljtYLBdoHYGjmIVyLIDMi9y1wBEBAmqJWgCEgKTpdB7T3LFy6Qzc+74HwHDEIMSsvSQAiy7dHkyScbRtRdgYhgF938OxaHuarkEfR0SO6LyEO+82Dp1Q5txuRMAIycLlqUMHCfgd0lga1+G573wD15++iouXLmF3dzdpz3TMZPY6ZaJGoJwyNQt6UKFww5HGFN74TYGdYFjKzGkKENC5N3mVN/b4RDg4HQyn86/ZnEyDCWogwE11KUdM/cg/YhpvaqFhEQpUPvHjlOkLSYs4nRHjj+iQWPMEYpH7OO2vGX1MEddKfMRlKr1KhKCHt/i/I0JjNDD5LhSSdLY2U9JMI5I6YE2ZCujjSJAlkAnUOwSYGSFlAwMj3b2S3B6YMRJyGr4YjRtY8i0XYqNxOchCuFLgPB16BtNEWWKkApzeZuGcB+nFnCmtTWDCGCKODo/w6OFDrE/PBLgBkLSlMW/KfD8CJZ/kqLENEEvCOCCMAWerAeLGHnF6epaJ6Hq9xtBHrNc91us11usVxlGUCScnJzg7W2MYRoRxRN/3WK3XGIYegNxKv+57DP0g2p60foEF3Kkr17RfZM3I7CMiwt/88l20bYvOeTxz/Rp+67e/jW9+8xvoXIt33/k1fvP223jx1kt49rnnsbu/IyAvSZzCXChdYJcoSsqoRyzuOCEwhpHhXEjpZsWlyjuTYhsWdEW5OB1OJA52uLy/Bx97IAA8MPqzFY6PzzA8TWgj0CjDTQIuE3Dr+Vv47//7/x4/+oMfJbP+xKhiNNA2ScnMwOnpiQh8YRDlytkREMWaNI5jzlYYQkS/ChhDUiIRkivnXKvNUWLQVLsbQkSAl5/GTVTPN3MQSy3NrUAOlNNeg1JqyhjTrfB6S7ooxfTiya5tsVyKEqfr2qysEpc2ym4OkQO8B3gYJK4NYskk32aB0DlKGf4kc1/bEm6/fhsvvPgcHvzgd/Her9/DB++8i5P3P0V8cIDm+ARNWCHwCr0LGDGg7UXZteKIQCIUNZFAkbF2AuyDET41U46CSHUV5CScNym+KHJILrNKv0kkT+O5MN3OPgEp+U7WKbvcQGgU3BRjoHJRziad6pFmlLfN71vYBn6sBTOvewG8N4VgbP271IrX2st1Mm3U/ySFMAkbVkO+zUKR9z7moHibAHaeVaEcd/l+Oed168jcsibnMMyANmC9RHTfQdm0CPZIQJ8nT5PafJfWjw0tfgHS7bza52bzn6Rx4XsJQznhP4gmyY6h6y6dAVE0uxxQbTFF2X4p7Nb6VO7hLDBwuh0gefqM44CIFPNs3nPKqxmgOF/vzTk130dRVmRM9Zi9X5YnFjQ8AV3j0TQL8A4nDV6D/b09BBZNxNnqDAAwDiOaxmO5XGJvucDdu3dxdHgIZgECuzs7aLsOp6s1To6PJHd/KxaSg4ND9Os1Ll24gDEEdE0D1xK8Iwx9j8sXLmC5u5t6ldx7SAg+kbh0ibuOEjdhNhFOXJfCFJ+RQQrF/PuUIUMmvmna5FIkG6pLQcNESNp1uVsEBIzSYBKcGgSOcGAMQy8gr2nh3QIZVOu/SOAg4CQ6xnoY0PcjFvsX8Mqrr+LGjWvwDcF7h/0rl2cuRDVzuN0+ZDUbG1D38cVupfrGonP/rH2ZNTx8/itU/FLrcbVPNP99YpfnHwx1Y8gHnKikCVvbZ57qJ3JQMYB5TleU2TIzgrqNcLIYIAH/yOnSLg3iEmA2uRLJPwVL+ox8RhiT25ACfQn8iplpcepY3gcsmDIEmwZzCqJwnMy8aQ+2bbrJO3p0rgFSLAY5N9WbgEGpndGZJpK50DsPODLGEHF4fIKPP/kUD+4/QOM9lt0CxMCi6zCs11ivVlitVxgGAf/KuIZ0x8F6vcbZ2Rn6vsfR0RH6dY8hACfHJ9mysO7XCbwGhJExjiEDU5qdK3GPzBvPnKMANqbkaXdpZriSoWtxMFq0GDGEHqerNVrn8ejgCO9++DH+9b/9d/jBD34X3/+938Glixfwm/c+wLvvf4DbL72E5198DsudZc4UBprONTD1RbRcIpRQ0mzFyNmdTLwg5ynC837WdWIATLh44QLa1mFk0ZSP44iDw0Os1j0WjQBxedTl9y5duogQRjx8+BAXL16czcNEsxiIHve+eoC33npbLCZJw/bss89g0e7hbL3C0PfwzQJts4QLAYgD2oYBHrN2U4RsUQgNw5D2uJhbnKADDGFEAGEYAphJhNzUn3EICJHhnN6fM1me8j02CRj3/QAisd53vkETgKOjQzkr3uHs9MxclBqwu7ubhDyJNbtw4QIWu0vsX9zDhf09LHdadAtRVjlPCExywzoFEUoSqHYeIBoEyJNDt2zxzK3ncfOF5/Cd3/0uPvn1e3j/57/CvXc/xHDvPujkBG69ghscehfynuEYEFzIlitLuzay3BAmOq0KpgJcygWY5Q58fCmBYa3M+0JQ7ap1b7QArea6UwNsdgy19s8TRrZZSmqCSP7dEdRtvBbHUNYxCV+Y+N8WDbe2pW44whdCpmVlvy3YP69s69+G+ybq1inp+uaYt9VbS76TvpwsWAJo8rO1Cyi1lEqumuXiPOFUx5b+yvhgjolmb2BqfuLzdhzIdGQSBO0Yto2lJhDPBD/1qGDg9PRUhKKU8nomyNjuFmPeOAcVYTbN1tcWmp9Y0JB0tT5vsuVyibOzs9QsAxzRpcDs3eUyv3dycoI2BRuL1nCNCxcuZDOzJ3Ep2t/fBxFhZ9Fhf2eJ3d1dMDNOT0+xt7eHrm0AjmjaFl23mG1c5+SuA+997oNu7gCga1qMDPSDmJO917zbKWvMGFLMRAvnKLlRiFDUrwcJ0ES6aZrlYj2CmIqdcwijZNoKwyDuHTFi2S2x6Dr0Yw8MAHFA4zuoyl419xQBgkOLFj0ihgiQb/Dya6/ihdsvw7ce49Aj9BFXCiEDeLJ0hbVNrOXrSKX/axXV/AM496BLUe1n2vcG2M2jqf/X6xcZwj7TwinXTV0S4SDnYcjaVu23CgCTcIGUZGC6tT4qsWbON3pG5vkli7N/wMgmTiFVHBNwBflcpzaqq+6SAAQuwakIRwr+NY4BkLMdw4h+GLBanSKEAeM4oGk8Lu5fwNWLl3Hh4kX4dMmmxHsga4Cs5qoEFfJ7zPP8+Wd38LNfvAUGYdl2iBRw8PAQn3z0MT6/8zke3n+E09MznJ6cYhxHjGHMrkuR0/0thoDLHOk9LmpV4qRtSj7nPDcdE0/BkpRu8aZMqCdiOzIDnqY51feT9ns+Rt0/E4ZXYi3fAQGSda3vA07vPsDd//Ff4d//9O/wx3/8R/i93/0dOGK89fY7eO/9D/DyK7fx7HPPYrm7k9dtKiXTn/aOArOm8YiBEJNblQJNzQ6VXgOSwNS2LZaLBQ5Oz2SeIXR53a8x7rQpFfP0KiBa7JdffhlvvfUWfvjDH85ukLXzPYwj/tVP/g2Oj45wcnKKvhe31f393+Dm9WcAJhwfH+Pw6Ci5sYmV6fTkFGMIGJPVahgHjIPcsdP3g7jkhoAYQ1YzjCFgiAOQmLumr6b0Xd+PWeOnFnJHYhWmtpnF7Xjv0TQNOvLY8RJnuNzZwaLrwMzY2d3F/t4F7OzsYowNYlxhHMfMM5FSmHddi/39XVy+cglPX7uKp65eweVLF7C3u4O2aRAQJHGA05TUIcfdBHLwTu63uvz0Jew99T3c+u4b+OKjT/D+m7/EZz9/G+Od+4gHR4i8AoYBzcBowYgUMbggF6rGNs+RLaWmtZa5pgbWJhe0zVIDpCWI0rb1+ZrgYPmffjazIJzT3qyvWwSdkh/VtMhP8k7Z1nnv1961c6l9LZPxlHU6J5fBlXNj390WuL2t1MD5ec9mmgMkN84pFqHW9pPOiSgpaVL6mDEB9XSwJSi3mnsbB1L239ZfG6MKPdp+vsSaJ8yidcz2GyYl3Ha+OLVjrT5Kf+pB/DItcr8dYVivNvZAOYavIyxM7wmfe5K9oOVrB4PbDasT3HoH5x3aJgUip0k/ODgAOYkZYBbgfnh4mCV17wnMAX2/Qhg77O7tYb2WSTw8fATnJAg5hhEcA5pGgqalnenaeAZSSlKZ1NVqJZ3OE8EYAxttlzLQLgV3iklbzfQxBLTp9tqmk4DzJgUvD0Of/IMlzeoYxrTxgX7dZ5eUcVzDUcD+YoEre1exXq9E8xfThUtEILgJVDIhRAIWHd74zutY7F/Eahgx9gPGocfuziJn2LLl62yUf+zG2ixzTUkmhLO2Nt86j6gp2Nk8oEARWzgdZJ5M9E8qbNnflXna920Asj6T3zX+8Jbx6mf2rhk9AzIcddtiiQtACmyOcXI14uTmwdNkkgGjU/9FgzjGKNnaknZE3cZ8JDSwrgTJWsIiQKgFRF6ahH8VfKf4JAGdfT/I7eUEUIrxaFuP1ckJ3v34c/TjiKeefhovvfwyrj51FU3bwqdMczWNiBZhOkJyYwS+uPMl/vqvf4qnr93EyfEZDh4d4a233sLPf/5zPHj4MM21+LXn+TdWmmiylGRNaxT3Qs18Bhb/fokNckhqH4DFxByC1JeucgcjGGEpzSdrTvHkOiI7cBojJAuZ9tEK1ZrWeHp26hecA4Mk8JYj+tWI0y/u4f/93/1z/M1P/xb/9C/+DK+/+grW/Rpv/sMv8MH7H+HV117Fc8/exGKxkPocYQrQF1ebEtxkcOgJzCJkNI2+k/abEeAluJjRtB5jGDBGsZat1mus+l6EZQdz17uUEAJef/11/E//07/CD3/4w9k+sGfq+PgU9+49wHK5xEcffYZf/+ZdjINcMNp2HuM4YAzjRkxNP6ylrqjgS+6vyOfRgjMw1GWPnQFwae7lKBDAPlkVJxCbgbBdXyexFxpnp+BFYuB8duPyrkHTdLh06bLEyqT4uOVyB8vFDp5++jouXbyIg8O7+PSzL8AscUB7uy1uXHsa1649jeeeexZXrlzC3v4efIqVoMZh4BEMRtM0iI1or33TYffiPl78rTdw/ZXbePj738cHf/tLfPDmL3H82ceIh0dwTPBDjzAO4MaBvEuukRN/qAWnWr5v93YJ2PPc0+Yzdv1t/fZ76+5TsypsEwps0payz2WbZV/sGLZZKs4TIiyQte57dv5kXuZ9sHEm5XxkIGnntdJ2ybtsm7bOEjDbuSq9Iuxc1+amBLjlPOT+pv6XoFj7azX5JaAukwIouAYU701jKfuvc2pTw5b9sx4hNYHMznmp1M5rUex9KyQrzy3XwLZTzuO2ParP2mxhG/vUvD+GgIu7+1idnuQ99zgho+Y+Vs6X7seI7edpW3ly1yljzdBOtG2bNEaioVfz4BhHjOsei7YDnEO3WKDvexwcHOTbYbtOAqmfunpVAqsXC3CMaNJ9BXEMOD09Retc1kC1bYvAMqkyZsJ6LUGYo/do2w7ei4UhhDFJdj6x8yhAiTiZFT3G0KNpWux2O+lAMMASzKybV1LeAkO6EV0y0IwAGD7FWbjkMhJjQOMb+LbBYtFh2XbokvmqgQCjcUwB7b5Jb8tdF0MYcempp/H0s88h+hZ9SP7e4whHwM7Oshqo8yTaCC3nAf3yubLM3rMRzSiUV/kwTdpfBbWO9CJBA7eYoNmZU0vG5zG5Glk6kokvxAc7yuGLKR2xCG4ioDAMqGHV6ipAxabm3xKWNDAVdpxz4HG6LyTEKf2xZc6bGhIFb0k7QmIR8yQxDhrfpJpwBUtgwphiKHQeY4wI44ghBDAI4zBgGIck4KYx9iKcOufQtpKOdxzHvG/172EYxHI3DAghYLVa4+T4GKuUce3g4BFY5bkwEeS2a/DUU5fx29/9bdx4+jqic/jyq6/wl3/5b/DirRfx0ssv46mnnoJrJq2VZRJmIXW10a97/OpXb+P551/EF3e+woP7B/jZz36Gt99+B+t+LREdycgilgFKwT3FLdtGGS/ynU/b1Bcad2NCTiAyJjcoayrPW9fWKQ9hcsdDnnttYvqGpv3OKgMYhjvb0xGabJjIoUlKkPU64MOPPsX/9f/23+Lb3/om/vxPf4zXX3sDD+7fwz/83Zv47NNPcevWi3jmmWey5VgAsDh46f6chqv73YH0zp0AaV+z3BHl+zkZkpudKCLGkIOBJT5vnead0ljndOPKlas4OzvD8fExdrO7ayHoc8RiZ4Fr129g58NP8NnndzAOstiRekTuq24eWdmgzJ0ouYzIvUQw8z6jUCYhwnwVCDaoTIVYIgIxoynSOGdQRPKPiLKAkToo69i0ODh5kDOe5axg1MFTi739Pezs7OLSpYu4cvUKLl28iDDu4vTkM3zw4Sfwf/cmLlzcx61bL+DZZ57B9WtXcfHSPsg5RKhbsLjvUt+D2gbUeXR7O7j5+ku4efsFvPGH38NH/+Fv8e7fvYmjz7/AeHQEXq3giSVLjeRf3wBMJZiuCRUWrCpAzIJdAVhrYIp5So1ffvckWbLm4M5aIzeFjbLdbXy0BsLsfNSCiJUH1IA5oALx48dTAlxN81oGa5cCjh2D8I/5OTtvnDUQrMW6KJXCwvTuZkakucCx+bnWYa0AVlgs+2O/i2CU8Sc1z47alQvafmmdq+2X2u9lGzWhS3+vCcoA0kV40/hKobScx7JO2xfnkoon7S/nHXaWS1y8eBGP7t/b6MuT7Imy1M595P+NXKck9sHPfCMFwInGOcYRjr34hQ0Bw7jGzu4e4MT3dHd3F8Mw5JS0RJCsUhf3ARAa7wAC9vck0Dm4Aacn6QK7GNF1C2GA3okvLTnAM041SHAQy0LjFohhxLJLqXGTuX0dASaS2I1mylAxDD14QK7bew/vPMYgblZd47LkvV6vga4B0u3UHCTAUrVgTdsghogxjHCOxLUKnOYmTkwuMckIYAAQG4/rz9/GpStXMQRg1Y9gkgv2Akfs7i4zaNTUvjVN0f+WZdpkAHgzqG56Zv63BpwSIQXJzlOTahAg83QbPFgYfUjBnnZDZ0Cd2hJXJd4gImW/FPBbYm+1SduEq8xcyIE1IUASFjT2Ibeb1n4cx5xWTlIae8TIOZZABNYRIQW5jqMEHIMo/R4AJ+nqQsrsRhBrQ4gR/XrAybFoKyIzhr7HarXC0dER1oNkSFqtVlitVslixwgxYL1eo+/7PIb1uhfwKAOcaUU0e1nXdnLZGBGatoHzhE/u3cHf/urniCHipVu38Yd/9Ed49tnn8P57H+DTzz7Hd77zW3jh1vPY3ZHsZ/ZOGp1XAaby8+joCM8++xyOjo7w6cef4sP3P8GH73+EYRgRIedSUjJQ7idBmHdMwptaEVQomwX6OpOgQBZ76kuyRpafy580mektPiXAav09TXXMBY15gJ2oO3j2N7MCrACS1BW5be/0noKA9XrE3//9z/Duu+/hj/7wD/DjP/kTvHzrJXx570v8wz/8DJ988hleTkLeZOFIuUhT0XMRQwCiXrAZIXEycp8NQ7JNKa1K4bi4cfMGPv3yLkBAiBFjjDhbrSQ7V9ckkLWpMb158yY++eQTfOMb39iwHjIzljtLdMsW+xd28eKtF9B2EvND5BHhwdTN5nLaR8JgxYqDrEFX65QV6Gbr6oy8OVtr3qAN+ioB2XqRFw4qlFKKfeDEB5IrIHOKwWHEXly4pmxKgOMzIEYcHMl9RUSShWyxWODi/kVcf/oabj5zE089dRXj4THu/8PP8ebPf4mnLl7Ec8/exHMvPI+bz9zA7oUdEAMjRkRiuBiA0YEdoVm04IZw7dYzuPnMf47Xfvh9/Orv/h4f/OyXePTh58DBKXy/RuRjGc0WwcLOh86VXeONf9MUVUsJ4vVy3tIaYJ/NvGILuKkJGOdpicsx/a9dNoAvzelCVfg3f2dhY4z58t1tQL9W9ONSOKoBTits1ABomZmofE5joCzvVe33Zr824wsUX21LbVxaJcq5nQk1xXyWQpitz/an9nvtvbLumpBQW5fZs25+rsq9q7+XLnK185jnZQxZqXt8coK2bTKf3NYPW3dtD9p35v13cLx5Aet55YkFjVr+eisVRmZwGMX9xxH29vbhmwaBJ41H27XJyuDE4pD8XJXZM4vfqneStpRI/HMBiQlJ+ATD0KNtJYf7crkQU1pyd4gcsLuzk1PhNt6jH9bw1MjFd07cvAiU3JwcEMektROhgIixv7eDrmuzFhUAxnGJR48eJWGkQRgl683unmjrYog4W52hcy0WXSP+veM4pXf0svBiJWFE16Dbv4ibL95C2+3gdDVgdbYGNQ3gGWEc4L3Dzu6O1J/B0+QmVhbdHxOhsd8WgkESejbIAU+aIflzijdgFg0o8yahznvDaINZx45Jq6D7KAc2JyuDuiyoi1HkqGrgNJ5S2xHz5XnIQo4x34OnAOU0TtWEhKD90IQBKTg4pYXMAkCIksFhDAjDmK0lSGPp+17uNNG4ixCSpWFE2zSIkTGO8pzezxKjZD/qkzvdMA44OzvD0dFRFkTO1mus0+8ipIgVQnXpPFpNkcNi0YGcQ08Rvm3RLRZTQgQClnv72L1wAXtpHTRhAnNKST1KNqXTEVi1V6ftkrZcZGDkAVfdMS5dvogrly/h9OgY77/9Dv6b/+b/jH/y4x/jd773PXzy6af427/7e6z6NV579SUsFp3ZA6qFdkB21wCGYcSVK1fwv/y7/4A7d+7g8OhAACwIDMlYxImZqZzOaT+kjSi/Rs5ujbO9WRBRu2vtY3NgInNE+pA5J1S8KOAqCRsM2BNVAi+v5xI6Ft37I2DuZiFC0oqTpO5kiUM5OjrBv/yXP8Gb//Am/uLP/gy/98Pvox96fP75Z7h37x6eeeYZ3Lp1C9euPZ0EIFlEgriXRjOHkpFplLE208yovEBpgZxzuLC/l+qJ6dwxzlYrDGMKogZPYzM84o033sAvf/lLvP76N7JygFQoAEuMwoVdnK1WuPncc7jy9DUcHh6n7DI7c+EFmFn8SF04ycQf6eQWwK62+DNwABU05koJTh226UJj1IsJJb6DUoB9zq6U0zpLljTVrOqFsDFGEPfo16dYDWeJ7hFOTiUl+f37D/DJp5+he6vFxQsXcO3607h58wZefuklDGPE2++8i1+/+x6uXL2CZ55/Fi/eehFPXXsKceHhEODHgIaAcVjLMesaDF2HvZdu4vdf+E/xxg9/D+/99c/w/l+/iUef3kE8ZvCwhuOQ1zdQ2sdRt/U8xaXOsa63noGYTI8WTG0r28Bh+XdN+1uC45om/Ena13IeYLJAd/6ejbtyIMTt4IuN5bMUOoRobABK5YZqHbJFeammss9uRWYtMiVitfITKtx+JozYW+XLec3Cj5mPjAFpalv7p2e8Ltojt1lqzMvP9bsMvCFgV5RoKQU8m7NvxqT0uLafSiuNCkd65ikpmCLPY0vys0RZoTBLhJLXYWOm0+cuC48qAJYxbDXhopYASHmr0Hept+8lpToRTfNjFGqWH207N1lhB+OibPAZl/P8mPLEggYgk9GYGwezhkqmASH5dhMR2q4RsO8EEDJEi3sWxnzLeNfs5EHlBYwE13i07QIXLlxECAHL5RLr9Roh9hhDxKrvsbcnG9E3bZ6oJgEDMeFO90wsuiWIJBtP28hlc4AAfvKEIUln3jl4ApbLDrs7nSwspoBxD4/16RpN2+LSxR34dO9H27Z5HMvlAmEc0CTt1sgSmBUAIKTD7D1WAdi7dAnPv/QqyHU4O1nj6OgE5Aidc0AI8Ijp7o3GjIcySLBaJFtk8Tc1+PKrapIZYxwlP3oUn/047R7EMdgKcypRgMRNPQG/LCzoo07mGeZAREHzOcZBD7AWAmVCq0JHDEo41cFsInZjGFOWIrnzICQm3qfL0UIYEUIPTncxAOIyte7XYmFwHUAuZR6KYllIrg1jHLOrkbobrVYruZANMd+jsF6vs/AtQZ5rnJycZMvEei1/C9Nt0pqJgNl2bYr5CZJ/v2ny4W+aBsvFAs3OLvb3PdZ9D+p2hIgkAa1pOzRNB3AUawc5nF18GcG1aFlmNBAQSPbv6qlv45D0giAnQbImHsQ3cncLp2xXkisNoERkdV8QGJ+HERf3d8Ef/R2uNHt49qVXcfHgAf67f/4vcHTW40c/+kN8+MHH+NnP3oL3LV56+bakoeYI5hHqIkSuAVG6E6drcffLB/joo89xcHSEdrdBu2wRVmu5AZ0BOEZD6e6BxDgBwKWsOeydvVNtEkCScmEGMM0fykQm5myqSABgJmDIw7mNvO/1LGLWVLJazNn7XCMMeHhwugfHKnM0RaJSWBkOYT2M+PzLe/h//r/+P/irn/4N/uIv/gLf/va38PDRA3z00cf46quvcPv2Lbxw+xYuXNxFjCNan7SB7OX8O0ZIgs0YR1Cy3jhy2UokwxRb0rWnLqNxhAYBDuJmdbYe0Q9AGAm+qYOhGzdu4F//6/8Z69WAxbJLZ1FcT2WJAp5/9hm8+bPf4Pozt/D8S6/jF+/8AsAIZg+CWowF3HMUJ0PEZIVO2QBhwJC6f2lcjQW9gec+2bpIDICti59ZT2HWU5pKx5MApvdl+OTiG0MAhwDSfJMu1RUiGh/FmsQMTwvsdDuZ1kSOGIcxp/cd+jVWK+Dk6BHu3buD9959Gz978+9w/cZ1vPTSy3jppZfx6OgMn//0F/jZP/waL774Im6//Dyef/4Z7O/vYqQAjiOcBzwYxAFEDq3v8PSzN3D1P/sLfOOHv4t/+Ou/wwd//fc4+vQO3MEh/OoMzD0iDYgENOSB5DaXDhoct+l0jFm4kClRwW8TJAFTnKcqZBQ0UbF2JfCxwNZihekM1bWy+v15mv9aHRZo2zLXACtuAYgksQBTgFrmy3fkMjXkODAG51gfMMA08d8Z+MU8dmFOO6a5KLX0HsJ39U4lS5dC0Y5aEkoBY2MM5vnSqmH/ntXB9bm1fa8Jh7YuPa/5east0bnQMbr5XGUargKeAdazi6ZBSVS0Cir5n31nvjbJ2TIJGfZzpftkdGGqyCCax0RJFVOQfjm35fhzO0YgVUildLttW/Rnp0bpMvE9Tv1WS2xt7plIQ2AFx0M8C2T+NwWUx5WvLWioFKgL1TTNbKPqhFgziy7N7t4eYggYxhHLrsMwDPmSOJ1MNcMRycUjZ2dnWCwWWCwWWK1WYBrRgnFyeiqgcxxT6sAGrW+y9sh7udBvGEZcuHghZybRgNvGe7TLpYA7iogsoKfxDl3jjUSdlsjJxm5T9i0Fh+I6ZSYeEEEmBowsAsYQI9rFUrRxIWA1RFy9fhPP3X4ZAR6HR8c4eHAoPtYgfPLxx3jhhRfgnU+WnLmJrgz6qgkbWuReCxacHxkc1edTtOQa0yCfabxDnCT7BJImCwTnjEg5SEo3MAHknQRvhjgjgjGEFAzP6Adx34kh5jUZxoAQRskYk0C+MiNlxt677IKk2oEhMWd1E5puaZbL3VQAWa1XKTZhxOnZGicnZwAIYQxYrddYryTOIcQBfbYkGK1DGn/btWjbLqev9M5hudxB2y3Rdgt0iyV2d3axGiOW0SMy0Cat0zDInS+L/Us4vvwtDOMIUAL3qf4RwCqvHSO0++D9ZyaGC70bZFMbqBpjmLUCOeBknTU78qAF0ROS1t2uXkGkN4YbIsvMuPfoFNh7A/cQ8eWFPTzPf4M33mD85Cc/waVLl/D666/j008/xa/eehtXn7qKq1cuyV6Iau2KIIhlqW0drl69ip/+zZv46u49uAZ49vmbODpa4WwdEFgvPIsiZCh4hGFUgJgKCoZmz4wtlvFRjovYdE2IYdNlwdavQHO2Bhvnr+6OUNZLJC40zk3WYrG+IYHedDEZEZz34Bhxturx7nsf4uOP/y/41rfewD/7Z/8Ur776Gj755GP86ldv487dr/Ctb7+BGzeuyr0IIDCmeB/d23avxxhTYLqOSfbQzu6uWIMzKJT9vFqvwXs7kHSx8zmOMWKxWGBvbw+PHj3C9RvXZjNEacleevkl/I//8t+C/Q5eefVV3Ln3JYa4RhwikOnVPM++TU6yoZWMm/Otwp4FHBbYyribre45LsUelK6rjlSTnxKJxAhK2smmbeB9ymK47hEg956Q7jtycK4BpfZ8F9DGCIqSTavv1xjHAcNqjdPVCgdHR/jiqy/x7vvv4cLePl54/kXcfvEl3LzxDN5552385t1f45lnbuCVV17Ci7eew5UrcgHkOIxwfRS+1ERwE9G0HS5cv4I//s//HN/9wffwy7/6KX79Vz/Fyaefw52colmv4WPA6EISmFwSNgQUIwrg0/mYnbUtgkaJDzaAW+V5XevyDJ3H88piBZmyPf3u68SDzPoIUcAwZ71xopfTt0h8T4egsSxaZsoO7Wul/8DmXQcljZthhQQOa7yCiLKFrQZkSyvOtvELyN/UcOfz4URxkbXpFdBeExRrn9kx2L7Zvm7LEEUkiRR03st4GtCU8nfGByp12f5szL/8YfpNScgwAkVRa23ttgnH24Rgq97iyOjXa1GGeFKpZ6Ou0tozb2/CeRLLp0LGhBWVfj5JeWJBg7wEeVOYTFaBI4ijmFdTJzXiPjLnS3bswVGT1+mZmIz39/ck93zKxtNQgzCag+clj/k4jhJk3Xh0tJxJfkMKaF2v1uCkaXbOSbAiM5ZLiXEg50AsvoBNK5cokSOwd9msuewkja6CNUCIhi7GpUuX8jhjTDmr04SH1Je2bTFECeZeJ2GKQVj3svh7Fy7j5rPPI0TgdL3GyfEpFoslFosO//p//te4fftFxBixv39hdpi2BYOXmo7pGQF1k2AhvtgxJNekUSwHGiRs3ePAkztTdnVKcRMxZfDq+x59L+lONbh44JgvOFNhQe90COn2ZSXsmgEMzmHV91ivVuiHIfvtrlYr0bQzY933OD09RQwBkRkHBwcYVSDg6WbniVCLZUWyv/is6WjbFk0SFkQzQ1juX8CFK52kOfaULsdyGMYRnhyc9zj2lxFUkk+CR7+4gvH6t3HmG5zyRGzvxYCRFoiNuPABxsSKiUBxgykLFBjskTX1SKuHyODDoyxgUJqvmfZIFhxZo6jvcwLok4/DtEdIWyBINinD4FTbAk6XBspZ5hhB3qbWIxweneCjvd/F832Pp5++h5/85F/h5s0buHBxHweHj/DW2+/gh7//ezIuNlooc0N24zrcvXsXfb/G/nIXTz31NL64cx/LozOcroY8F8oQZFo4Z+zKc1WcC6UDZakx1PJcAbULjKa6LXippUgs66+BnfJ5y3B0bjRzmV5MFvXm6ZRkIsaI1XrAP7z5C/zmvffxJ3/yI/zZn/0pjo9P8OW9u/irv/opfue738GLLz4H7wggTmb2STmkQg2AnE2Jk5BJ6SxevnRZrNluGscwjNkdsHTvsHP/jW98A++//z5u3LyenlGdn2j5Ll26gBdeeAGff3EPi92L4iq6ZrG6DFNKxxnYcgTohaUqKLC4P3nh7NALTVUwYo6SUUxUf/AkwoOm7FWQYC8yROppdACD4Hw7y/5Hul7s0TTirqsCRwo7RNt16NoWHIQ2qgKFI8OxpsAOoCBCCsURrfNougUAzhaOdb+SO5YOHuH4+Bj3HzzAO2+/jUsXL+HWi7fx4q2XcfbBx3jn1+/i2edu4lvf/AZevPUCrl27Csfi/tmPjLEJIN+LkrBtsffsU/iD/+Kf4fUf/DZ+9b/8FO/+h7/D+s594OwUiMcAh2xhJiLh+YTJimfAWQ20lOCsBJi2lEC1dk70s23g25bz/Mj1nCnfs+3OBFRzbjcEHJ40yph03JiEjPQ5CRWeZU9izrF8T6IdrgH/8wBp+W7+LAFfO29W2fA4AW6u2OLML7RsCEOYP7NN8VMr5R6w61CbL8UAZX9VwVAKKaos2KYQ+scW5aW1vSSJRyYlTymwlAJHWa++t62P2VIGI37U5otoHns2a2/CvYrp1bomc/j15ujJLRrpAjtIUibJthECIrlsSnEkPmGamUQ6G5NVg9B4CWje9V4koiiMLDJLrnIQIiC+40BOAbpOYNOnZ51PnUi+Y52XezXUJUvPeBgDGIzj42Pse4embRBismykhVruLOG8Q9M0EqwbgjiOGPedECWLQ4gBvmkQUx2ROYHqAU0rFo5hGLCIC6zPVgABb731FpbLJS5euIimabBa9/jBD78J5xcYotxgTOQQhoBP736K4+NjLBaSyrbrJpcsLZYg1oi63YB60VsIGlgNhDiiX4sFYHW8wtHhURYUVus1wAznPIahx7rvEZJgMCTgH0IAwWMcR6zXK6xWawnQH0ecnJ7idLVCTOs2DhJ7MI4jvHNYr1Y4Oj5GSIx4GAeszlZyIVbSiijoVlcxImSrl/wtGcq8b0UbSITFQoSGo7MVyLVo2gaAw5jWUN8NQW4LX7QyP+sAhCFi3TPWu7cQWyD6BeIz352ES05pSWlyxcuGAWbEfjLnik8zg8kDPAAY0qVulM3lWoho4lAJQE/CITBJ6fJMBtrC4aEkhLPmTLT9UbCkeddoZZTg5f+luzOYsiUj62WSgJHs0UnA0XpSNifI+Ttb9bh35Xfx/Mkn+NUvfo533nkL3/2d38Gq38Wnn36Gb3/7W9jbXcBeAii3eE9EeLVaYb1e45K/kNdTZAnCEAI0/24er6MELNMUYip6LraZ+M9jimXZpmWrncnyOf19JhRuARMlmNG+6TviXhNATAiQmAihdbKvxhhweHSCf/4v/iV+/e77+C//y/8jbtx8Dvfv38Nf/83fY2dnD9evXRXZjObzMQtYj5wzEIEmwXdnZ5ndZtWNL0ZJOhDGEbFpktl+Cm5UJvrcc8/j5z/7F/iDP/xhEkB0fuTMeE/45je/gV+98y9w2S9xYf8S+nFAGIeNec0aPRWEkxjdNI1xycmjQUi+6ZpEhIHMfSOM5SvXl4QSS2cdyb0pSSgX1y+pqCHKlzCSd8kluElJHQYg6gWA4hLsnMPSecA5jKPMT4ghJ4ZgjqBxwNivUnbDCAdgZ69Dt9zBOK7kXqVxxPHJCU5PTnF8cox79+/hV2/9GjdvPoOXXrqN9brHxx9/imeffQavvfYyXn/pBdy8eQ2ePMaBEcOAIQxoQo9ls4PRe1x84Rn8wf/+f4dvfP97+MW/+Rt8+ObPQHc/w7hawfUNPCIajohxELcK4+NuFX8KQrYBNwX454HHJwF9Vvl2XqlpxfX30jvA1m37tk3YQbKs2huY8ybTcaHujmTHV85j+Yx9zgpYJUit/bTjAAkZj5U5t4JU7V/ZL/08Fn3QtnIsUxnbUJnv8rtyfmpj3lZXaZUUJenUp3pmyC19Ur8jU0paXdsbtbWYCYY0v8Rw2/zYs2LrUEXUrC+JnrlGErmsz04lnKFI0nEeP9wYPQnWEGxmLYxzYf9x5YkFjbffeRvjOOLatWtomgZN06Dv++TWtJN8ZR3W6zXGELBcSJA2g9G0LR49fIgPP/oIF/b3cfnyZezt7SEMI05PT/HgwQPRml2+nCejW3TYWe6IxsGYGrudZQJP0+ZRrYA9pDHkKDY45/Dl3bvS964FR8bJyQkODw+x7nt0u8vk7iQpcMW8LVabfoi4f+8+bt++LZqtENC27czfNHKUcSdQfverr9D4Bv0w4M6Xd3Hl8mXcf/gI165dw8uvvI7l3iUMHLEeA0IE7t9/iE8//Bj//j/8e/yX/9X/Ac8991xi6m7rJqhJuuVnYnmS+zliIJyervDg/gPcv/8ABweHWJ2tcHZ6itPTMxwdH+Hs7AyPHj5E34sb0RgCTk9OcLY6k40WJOWwKt379Vrc35omp3wNUQLUNG6FWXK9d/lvYJFuymUGjmKDtu3gvMuaQLmQyuPw4qsIfhfROUSeAqZOOQGCbC1It2c/fwto9wBSIWvSdCtTYQB8/CXgPGj3KTBbTbOTLEenIe3dlFOVGcwS1A9SFxH1nEc+4ErIEY32PQsZmAkb+U68aNdMhQikSmQDz+QPFMDarjmp7SJVrrEJU0cLmpmez/cgaP/UOjIPfMtMV/dbTP2LwGnscMYdlssF3nv/XXzzO99G03U4PjnB4eERdnd3wMl1ZxKT5Gz26yFlw0JOfS1a4yToGEBI5GXGlenNNIdTmTQxmy4TJZOqMesak7fv23dLH/LyOWuJ/DpaoMxYiADnEUdxB3RwYA75Dg+idCEWi/vOr3/zHv7v/+3/A//Vf/1fY3fvEo6PjvCLX7yDP/3TP4LzDCCkfVfR/EGAr0NKMw1xCxHFRwfvfI5xCzFgvVphGAcsokdtaERyszgAnJ2eokvJAfKmJEm28OqrL4GIcHp6hosXL+PLu19OfWKeraPMt7jkqkCgF2XKfqYkgGrK27jh0iDbamL6QFJ2gAHmzKBJhS3dtIwk3uhr88u/nHNZMTI6wqhuokl4cQCYA1yU2Ch19dVxhRDA/YAVOUQ+A4jBYRQh07donUPbLKWPyb1q3a/RDwFnq4CT1Qqf3fkcl69cxu3bt3G6WuOjjz/B2zdv4Nvf/iZu3X4e128+jaYV61gYIwYAWLSIbQNqPK6++iL+yQvP4Ft/8Dt459/8O7z3i7dxeu8Rwskp/NDDe1FYTcJ/KRRs7qtt+17Hrc9YV7Zt71nAtu3Mle+V57xWZ9nn2vcb4JIw7aNZBSrIMJgD4Ca3npIeWABf/iv7b38vU7yWIFr7tBG8je20bts8bBM2VDFo65r1s1JHrZRCXyng1Oqo0dftwJczULaCiLhMznQvuR1XxPaVc1XuWRvQrXXU/1aaMx9rWa+WMiZpPveYaJGQruxyf/hQLU7T+zPh9BxWxIUyc95HMSA8ibuhlicWNBgR7/zmbYAYt27fwt7eHlarFXZ39+Bo0rw3XYu+7/OCNgk0uLbBeujxzKWL+PTO59hZLHHzxg0EjtjZ28Xx8TGGIILHYrGAazyapNE/W62gvmTdOKBbLrP5WmM0GMAQxnzlumjjRXs2hBG+a/HxZ59i6Hv0yc3n6aefxpWnrmL3wj7GENC1jWj8YsTBwUM8evgQV65ew97+Pk5WZ+j7XmImGg8KolUc+gEg6cfh4SGOj4/RNA12d/fw+Rd3sH/pItZhRNu2uHTlMl5+7TX0gcVLPRLufHEXDsDVq0/jtVdfw/XrN9D3Pfb39zdM+NMm2C5FbmpsHPpVwFdf3cMH73+Ao6MTrNYrfPnlXbz99lv46OOPsFqtBNy1rcQc7Ozkuffe4+r1G/DeY71e41rbAPAm1gLo2hanweEYEoeiApmW/uJtrPafzRpohqQdjnCIyyvSV808xXqTdiI8CQ8xJ19W1lgSS/RSxqo1g1dHANQHGtKmbODJotBcAgDsJQvbOOh9AxMuV8FDPk/uRelGabbmAvMz2rOrhCT9l7qQ/y+gn/SXqX1KbcOrnJG8RGh6INUvz03zQ4Tk6mRSGWZwNKcrOidk2lZBhVmyEwmo14r1kjvtd/o7Bbit+x6HO89jufMuHj68j+OjIyz3LqJtOxweH+MGrksCq9SwjtM5h75fJV9eyZgB2LTDyEIPm0FkBsaTidqWmpaoVs5jTucJG///LGpqb7oFiCWWiTXtZfKfpSTQuhQT98GHn+AnP/lL/LN/9s/Qtks8OjjB6eka+xdaOKd7e87c8lxkbRWAxEhF+Gvh20ZiNRJt6vs+a+KZN133YpT0zjdv3sSdL77ASy/dTudXgYOkRt/bv4jXXn0F77z7CXZ397BY7mB9errRvxw0mfVIE43QOWCNcwHmIJYo7zNROujnIlDkrFExIo4jRg75HXUT0rMAAsj5FO8tQpkqw0TZ7+HdIvtIx3HMsW+AnGfvgNSkKFe8g3PAGCOaxRI7TSt/jwP6foVxHIDgk2tnypm/02G52MHQ9xjGEUfHBzg98zg+Pcb9+/dx6dIlPPfcczg6XOGjT77A7VvP4Y1vvoqXX3oeN5+5BiZGTz1cHOGHBm3XYvA92qbFjTdewvXbL+DWO+/jzb/8K3zx1q8xPrgHPmH46EBjv0UwV0tjXWi3a1rbfyXIlH1SFzjK9/Xz8net70lAaQ3kb+vDZrHPCL/wvk1Wwk3hyWrZv46GWN+1sUpZmVbUUYJ0Z8D2ee3VQLAtUxzg5nfMPMXnPuGYyrUphZdSgHqSktcumettlqc8dsPrbXtKA20MTXWc6XO1oD8OgItL+tS/Ukn+dcaV2zevMljuLUpKEjLzasdnsUc5dqGn9XTD2n5pHTmvPLGgcfnq0/izP/+nuHTpIpiR0hoSIhO6rstmMu+BZdNOd16kiXj62nX84eWrGIYe9+49QASw3N0BeYd9IjABJ8cnuHz1Cq4lYKtacc2Ss1qd4XS9BnyDCELbNvBtlzcPJb/dyIwxMlzToOsW2NnbR4wRV64+JRMJyEV4Ti41iyROIG23BIERw4inr9/EcvcC9nb2sO577OztJz/yAc6l+0RCEDcnL/duRBDIeTx69Air1QN8efcuHj58hJ3lErdu3cazz76AL7/8ClevPY/j4yOcnJ7hxvXr8OTxP/7d/4CXX34JTZNuJG8krmC2ufOaluavODsYAhbkvXUf8P6HH+P99z9Av+7x8KFchvbzn/8CkSJefvUVXLh0ReJKhh7jEHDKLU52buasS/dB4JEx8oixew7hwnMiKMR8WlLOe3Gji0mQUN/MyAxeC1DkGCD+314I0PoQyIAxHQQikMkYwwlFE6urxHR4BNyLEKAZIEiJkkyVfE6qtZC9FkNA1y6wXC5xcHgoN+Vy0h4bxiTghjLo0vnXeAhK2gliYz0w5z57SuZnnfndqEn1/7ZtK2Wp0IDJnOko2R+iykBm3KleTvMjN7qwShS6bLqBslDWtHKJmLoWrs/ELxzWDsFJ2HBust7EiPXTv432/b/EOI744osvcfvlS3DOSRIH1rbTckM1bZKNa3d3BxwZQz9ivTqDbwDmkMS0lH2J5kxTz7J0fTtz/ToE/HHP1hhdzd3BgpPys/M0iLW2CErYATChbToE0li5lH5QGTtB/P3J4Ve//BW+9a1v4ca161iFEYdHp9jbvwK5N2NL28w620joSJghgDj26JZC73Q7rvseq37A7hhAjrL71IypIeL2S7fwm9/8Grdv35o1F0IQtM0Rv/1b38Tf/8MvcbF7Gns7e+jPzpBFdZ07zTYmkqakQtfLMxVseT37BE7JPyi5dyo/mjSKALuUVYVJ+tJ6LLo9hDFImsgQk3AFEGtMjptkfiRhIwM5OfXeezTNEsQkCq6+l/6A4Zgx9n26dHRK8y0xjNKxppWYmMVygd24g2EYsD45w9iP4JQxjGOA9x38ssWCglg41gNW6xXW/RonZ6d48PAhLuxfxs0bN3G2PsOHH36Il269iG9963W88toruHD9MlyIaEKPuF6j7TzQOISdJfquwbO//Tqef+023v/7t/Dzf/vvcOfdX6N/dIDm1AH9AIco1jQEmXvWqyd19dJ6Qei11aiXygAF3dbSs02A0P1lQfN5rlQ168E2+lAC3ZrVJKk70l4qb8gBnKecfMbBJliY32tRAvoa7aiNxfaHVXMEtbjPaYw+I3xrurdhWxvlXNUsC/knYcpYaesAxJITCaHybm08pbbeflb2pyaM2n7aPurnIYSsmMl8tWhvJvCANz6rzVO5r6zya+Lwqf6EQabCOduf4WjIipM0lsCc5QKn8x6SdRWTt0QYQxZgOE5ZIy3Gyi1btp76zfnvmL9kiKeP4A2h6aL4xROVJxY0rt18AX0/gJ3c6N0C6HYkRuG0D/miOzAjIoLJyy3YziusgWscOtfit777PRwePsKj42PJBNT3GGLEy994DRcvXASch/MdOLnEdJCF3rl4Kad1HYYBrkluFKmPOmcxRuxdXBrXJk6HXg6YJ0KTUt5OF36J0OScB5zHEBnNYh+BHdpuFz5GPPusBGmv+x7dopPDkzRjTdPBjxFXru2jW+7i7EQuIXvp9itouwWuPX0dv/zlO3jj27+Fg4MDkHPY29nB6ekpzs7OsBpWuHbzOmIM2N+/IJowMDTTjCSs08j/6eZq3QQ55zuLjk0C1YGPP72DDz/5FOtxxKd3PsfPfvYzfPjhh1he2sPVN/4QB5dfxxfLZ3F2lnytNdc7GNFLhhIBhgxuGRwY/OhIUXEGx7MVMAd4RnzTwQHPCTeRywdTAYzgds516uPWtxTM8CoAzEDzXMInTJ9xuhWcnJe1byUgUgK9Uz7+LPggm1RJraiqwJlkjvrPPGwjJEzDmQQSFaLSeDiTDEMBjPCQ6SNiEopgOjY9r01z2aAhsKztkc4RMIYB/XoNlzLBkSe5VdIIGdqGxII4gANADswOznWIocfJ0Sk8M1oixH5ImXWmsxoDIArgCLlroAXYIYyi/b1yeRdEAY46RHaQyIQ589kG0muMZ9szX+fdEhTVBAbLlJ/Uh9y+X46JE5hGNkvJGvqmRZOAmty9Iq593hEa5xHGEevTNT5479d45sYVeOdwdHCKZ555GpFHCZgu2sn/omRgYiQXpBix0za4sOwQmdA6JzHVFNGHEesxIsLP9vRMEQLGjRvX8Fd/9e+TEJSEGChTC0BY4/WXXsTlvQXWZ2dYtksgEoglhSh4AvBZAUCTu5EFqpy0l4x0maIj5PtS4bKgCyKQT0IDGI4YgUa4xQ7gGyz9At3uBRwfHmM1nGHhGlCi984DjIiQtH5W2ACLJb31rfSZGU1HiMOI1bCWi18THSmBkWOG0tUYGRgiyDdo2xaLZYfLO3vo12c55fbZ2VmiIVLHYrGLto1Tco70b3V2isPDB/jii4u4ee0mjg7XeO+9O3jl5Y/wjW+/hG+88RouXdwHGsK47tFGL4HprcPQdmh3FnjtR9/Fre+8il/8zZt481//O6w+/Azu8BjN2QpEAwgjog/iqpYTxEygnAzT0vUqA1tVaFd36LlCbXKBteemBOrbhIn5HtkOGDNIewK6oWAsstzirRdIRgVpTnh1YA+b6tXGgOjPbXSlPE+m17LryJk60lxTSqrPKf2z5lomZPBatjll2twsVojTNZgLO3FjnvNYiGaClX5erq2llTauw2Y13ZYNywof+n5ttpCwTCYCzPmOnBoNFoWafJeTOPA8rkLbs0JkjEn5M2tb/haPYyM8J/ctsLp4pn4m5b1iA81XpfyaozgjgxnMLp803zSiIElzltN7JxyRXUQFCOUELzFGIwCpUGLWiHRuCGCXsfaTlCfPOuU8fKMSz6RlbhcLDMOA45MT7O3tpU0hOcVdo+kCIRroCIxxwMHBAb68+wWIJMXqq6++mgO5h3FE59stQc+iVQIwy/wBTNKYBQgzApYCyPUz1ZjElB2lbfU+DuTgJma5mVvSzsqFKMNqJZpD50ExzHIoU4pTuXDxEpZdiytXroLI4+xsDdc0GEPE3v4+fNvmC9rGccSbb76J/QsXsLu3O/WlmH/madE3ia/eri0gQbQWwNnpGT799FPs7u7irbfewjvvvIO7d+/CX34Gyz/8P+EedvHo0QFWD7+QOoNubD2MgKIH1U6o5lQGjBx4nGV3FSYMj+H0lfkxk/gZgIucEgKk50zbGURHTpL8FPMAZWYZxE8NWXLBeq5ENwtmYIjB7GWkQNg0xxmbp5aUgFoZhubjMR+bcdP0WcL4VobI0zzTZeRei3WnAqojCJQVDhMz1w6aVRNiYxZLhUOdrkyoWcZ9cnYG+v/R9p/BliTZfSf4cw9x1ZOpdWVprdHQINAgAAJNYChAzJIEwDVyh7O7s1zaijEjOTuzJJdra+SXHTMYjWZjHMHZoQQJgCSGBBpohdbdVd1V1aVlVmVlVep86sqIcPf94CI84sV9mYUZRltXvntvhKtwP+f8j8THaRiCUBiGLWoAJnDF9GzenizLmE4Me3sWjCZJQlGU7rxZAQLtXbQscUuShH6/h5SSymUy6uV5c2rRXO4ESLSZ0R/2ulOg0mZSXQLOQRq9rr66NK7tfqS0yRG0krawpLbJLKz2TnP5448Z7+0xHKwzHvu6LhKh4024b3JhnWO/cpu9LXGWE6t1NtrGp1l6LYMfdHuO/X6fXq/H7u4u6+vr0ZwsvamqipWVNe655y5eevUdVkZDsjRDV6UTCkwQEqwQrkLGFJ81RrmMdEBgmM2xePpk/9TaZk6UWFBdKYWRCYm0gdulssk/Vg9vkhV9pru7aGNItUZoGYBBbcmw6dEFgjSR9PMe29s77O3tOZdAgqVeVSrwjVh4rqoKmdRZ8owx9lljEHlOkoiwllVla1IVRcF8PkMpuzpC2HOYZZlNcFKWlMWcopxTVQXT8Zjr165y5MhRxpMd3v/wXd55+10eeeRB7rn3PBsbKxQLg5QKWZWgDGQGkfZIBz1+4Cd+mIcefYjvfOXrvP7cd5l8fJVkb0K2KBgWBTqFuSgQ0iZSMTLYqpFGkjhFWJwhKBZ0Y3e3Li12O1vPsorS/v1/UrekrnPaBQLqz46u6pb1LeIKds/dGT2603ESBEHPCEzje9tnHNcmGmOK+2qXKLDDbQKGLiuDECLsuVj4rrX5+/uEJthbBvrae8M/50ssHAQ2GoqTrjl1vNv23NwELN3pGGP7uTbg9W3F31s+21wRv277xtF6vgaS+/eRCe9bOBnQ0fmOd+Iv65KrrfLYjam2yBwcVxWfxTu5PgHQsMTXD8ILispo8l6P6XzGR5c/ptfrsba6RhZlTDLGcOvWLaaTKWVZkGYZR48eZXdvh8OHTtHrDUL2qTTNEaJmWG2TlScaMXHxh8B/H6NOv9DtHMmxdsQ/2+v1Qj++PshsNidJs6D5zfIeaj5nvliEysu+zSzLnE+yBWCq0kiZsrV9ne9+9wV+8Rd/kSzL2JtMmEwmlC4r00cffcQP/uAPkiRJnd1lSWXVtpYmpEbFm0/tpZTi448/5tixY3zlq1/n4sWL7OzsMBYDVn/oLzMj5caNmyHGJBES0sgFzUNnByiDpE70HR7lEu5vnEcnKVpELsJnjAnaSRNQfCzBewHbAxbfl3AInvrARTjDg/TQt5e7ozF5m4GQVnPu90xRVG4eIdGlG58bml8D16eJ226BKA2WmPg5ifrdNQRRD5Q8SLar5YhzBLMc2Kj7qgGPaYzWr4OfQ818NNqup2dCYf3dOwJEyG7h5qH9u3OwJZLXjAdhph6jkj3m+SG0vs7cBQnbNMiL4CYlhLBBJ77KvLYZxlZWVsmyjErZjGjrG6utM9AEF34N24K5v7qI67J7/dXFOD6JgBJfB2kou64uZtf1XBvA+H8T585UFtY1wDg3qslkymQ6ZTTcYOpqD1lNWdJEx6FjaqVF1L+UksOHD3Nte0yWZqH2kVEVhU+EkWcNzV57/mfOnOHSpUusra2FzoQR6MqQCIFWBU8/9RjfeelVhsMV+r0cVSwwQtd+0m6325o3mkQmFGXR1IwLu7+8ttDzKiFEcHAxEILGVakwqUFLW5RVCmkt50lG5Vy1kmGflSxltrvLYjZHakmKtJZO6QA7FvTkaUqaSsqq5PLlywyHQ3q9HmCzEsZCk/83FuKUVu6sYgGGAxtpmiLSOvudlJLRaMRgMHA1pyYsioWNj3P0QcrEBfInLBZzZospi2LObD5hd7zDzVvrHDt+nOl0xvsffMj999/DY48/wl13nWM0zEEpKlWiCk2ZlPQHfbRWDI9v8qN/+he4//uf4bkv/gEXvvMS6uo22e6M1JSkwvIlKaEyFVoatK0AGgQbv3/bSRviLDvx/onPflAU6uXVuNtC50GKh4OE0mUgY989rfubNEh0n7eO6yDBdz8IijiHiJ8JrblxCOq0gc2+4rW83RjawnQbLPj2gkwm63Vpv4emErmW1dpK4mXJNtpttvdSfE+XwqhrHMuutgVq2XNtYOC/2yeQL3mufR2095oNQC1O7AfKsbWqPhN6X8awMJbW8118sA0+D7ruGGho4noKXtKrtbx5nnP69GmUUuzu7iJmImRnKoqCXr/PoUOHANja3mJne5vNQ4fZ2Nx0E/AZEZQT6pvE2P8daz1iVNW1Yf2z3uQVmGMEMPwGKMuyoXXyh1Nr67Dh820jJL1+37ksLIDaTJdlNrgYYygLq/nPe30OHT7MU08/zZEjx9gbTxhP5sFv3Qelnzp1iizL6PcHDkT5g9Y8MPHm9X9rJxx6mVBrm3ayqiom8zkXLlywWrWyInvyzyLyIbs3bqDK0lqG3Cb3bkk1jqgFWpyw6yRSIuk53OeeCKDMSi3CY4va6kEMSFyAtZuD8fd4cOEF4cbzrukgPPtvPYyIls3C9MYhE+4dKa2tQCIlQtRALYALN+/whaitAXYAUdo4DCYAo9qlzB5aGeZl4rYM3HWkz9/5lSf5r/7JS1y8MQ+CXljNMHZByPISzdtP0hdMq8FKvAheQPNMSYR+urSGdg83AWR8+a2BIcTNGBcgi6wr//pz5zXe0qXINlb5jXX308E6mWYpi8WcxaJgMOiHTHYol1/JrVkXUV7GRD7J1a2tbPpTt9tvE9q2QqR9xRbV+P47YShLmSw4JmOzQ6G9iV9TFAv29vY4vKlCrRkb/1ID48YYLIdpMEv/92DQh+2xy5bkLB1JwmJRUFUKY9LQzn7tmeb06dO89NJLPPbYY1EwpkQYuzeE0Nx733lWRwPmizkrwxHT3T2rBPF72YGHVPoU54YssZZzgUtC4eh/lmXO+lEHYduq9MJZomumq1117lQbdFkh0hSFxkiJzDKMsIB4NctYjMcs9sauCKIkS1JSKZHCIFzKdYlEq6pJpyNg4UG31+z7dQsKCL9/lLZ43vg6RzIAQc/7tLaFEfM8o6oqZrM5RbFwdYrs0okkZTAckZWuJkc5p1Ili8WMvfGEq1evceLECXZ39/jgg0vce9+9PPH4w9x16hi9fgKJAVkyVoq0l9AzmlwMOHr2ND/75/9jLj79JC9+/qtcff1tzPYOcmoQWiG0QmpLG0pTBVoYj70x90hgjL/398X8H5qAI16T9lmKaVwc++E15O1zFf/dBhz7zkz4ztKpzvo9nk/SFJy7+l0W8+XHW7ftf2sKmOFLRAg6tvOotdZxn23ZyX+3LC6hLbgb7HuI01rXN9fB1O3n2oK6/z0W6ttCe9eY4jG31zBuqw1ou9Z4/+fufRn33R5jDJK6QEcsj8TtdLUbr82y++P5g3WV8mCvvcbt9ZdSNGTh+J3Seh/xuNrA9HbXnQMNx5mMscWNvAuLkNKanxPr6yUwrG9s2AwaTjAbmmFt0taGw4cPk+W5ZbhZTlkWNpBYuBfZwaTizAqe6LZRrv/dE27/rC8MFwsHvr1YE9YWAISASmkmkxmrq6sujtf6wyFsvQkfGxFXnLS+boIkS1lb3+CFF7/Hpz71/exNxiwWFYWrEO0Z/1133cXKygqZKyIYX8sEpmbWiFo0tcWfDLPZjMOHD/GV3/5dptMpQggmx54i3zwbiu1JmVjtuSAQfytcQ+0uU4MdE8ZSC/seNNRxBfYHDx5rdXtNaE3rs0fP/vu2mFw7VNWXf9r+6/97e2Et/OIOi8H6wPt5elNv3EQADXGfQoZ5+76NAxkimncQykM7dbsC+N/+0Xv5iceO8xc+fQ//719/Df8ua+BUtyFMRPSiVTABEBpX04Z9a7l/HaIWhAc09YTDvut4vM3QhABT2lotfv9WLsuOEDYzUVmWDAbW3cNaQep4kzzPWF1dsYH5O9tMp1PyXg/pfEcxxsfQuy7FPgHlf8nVdca62mwTbP/dnTCN+N5l/cVMsKudZWOylj67pmmaYpRAJ5qqsprw3d1dlKNL0+mU/qDvsih0tO/pSYdwsbGxyaVrW8EaKaUErSjKAqUqlM6Wzk9rzebmJmMXlxcYt7C+48YYjK5YGfa5995zPP/CG+TOqhwYWmuNRLQfpJQ24FaaoKVTSgU/Z3en1ajbERGsrA7AojXVbI6pDDLPET2BTlNI3L6Wlt+tHz1CeuQwt65cpZgvSAsQaJIshUSgKoMvcuf3aqzcApt+Xbl4uLawpSpNkrp97sCGdQ/z9zat8Z5/pWmGlAlJklFVAxYLG8exKIpgaU8zSZblVKUFGbNiwaIyzBZzdsa7bKyvc3LvFNt7e1y8+CGPPfggjzz8AKdOn0AkGmUqFApdaGSiIUtJejn3PvkI5+67m9e/+z1e+tJX2XrrAno8Ji0WyBLQitQYtIxoY8Rv26lB4yvm811CZXy+2meoLazG6327tuJ3chCNWC70te7reN4Lr+2xLOP7saBt6xCBkLh4JZ9O15CkVhmoG3ONXJNbMlN77l3K22UAoT336IvGb8ue7aKX7XticOjHeLu240KMBymLfHtxH00g1Q1Y4/vaNDveaz6rVNecu/ZQ19W1L+P3EruoaeXjdbtjgeIzsZSPmtp9qj1HT1uXFcTtuu68YB9WKAmCifvb+4BmeR6qZHsXDO0n5gfuBpikPYbDoU1BqzWV0qROZLMaz6YZUAgRalR47ecyc2nsQuUX0Zut/UJ6y4PXvIK1yHiGVb8UWFtbZzqdsr2zY+tDpKmT5IQr8leFDV2PxwaVD/oD5vMFa2tr5HnOeDxFa7vxvAXF1yYxxjDo94MLhFkiIMZrUr8XK/4aY1Os+nlNZ3MuvPceRVFYn93hOkmSMJ1NMcYGPgvqYnk02nT9GGq3If+7A53edFA/a7MQBA8dTK15FxDnc25ACfe8F/XDPb6tSPRuPt/8rQY7bixL1tAKKdaFxGgbxIcvuBfmWM+vbl80sZO73zN/n1PfuHlbHNYU9Zt71vBzz5wE4OeePcnf+fVXG/P2dTticEIEIuqRuL/tQ0QO6u2ZN/oGJ6wJ0QIk7ffdfLRBWMN9AozGpEN3j6ZSFWkqnA/5nOGw31oHl9oxT1ycRh/j4jjyzFdgrqsoG7F/H3Rdy4BHF7G+06uLGXbRoFgg6tL4eBpzO4B0JyAj/s1gAlhMEomSEiE1lVLMplPKokCMBHt7e2we7i8FkNqdhy5GeujQIVT1trVmuDmIJAkBx0b3EWm3oOYzCY1GI7a3t1lfXw/WLWEEAuUy1SU8+cRjfO0bLzAcrDIcDNgtS6sM8AKcEAhd5++vwb9wlvfKWjzAum74NXL00Ra1sMVhrRXOCmxSAlqhVYGuDMJITB9kkoKRJHlC0ktIsozV4ZATJ06ye+0aly9coCwX6F6GFDaToi9V4hVftm6QZ9w2W4znG/sEXwzWMGPnliSJq02Uu3k0sywJB5SU8rUCLJjIcxs/OZ3NmM5nzoqkAE2aSRKZonKrdJrOxswXCUWxYHdvj+s3bnDr2Alu3tjlvfcu8sSjD/HQI/exfmQVLQyFKC0AUpJMZWSZjd944o/8AHc9dB+vfO15XvnqN1lcvora3UFUCxAyvLe2MB1bN+J9Y5Us9Zk56LodoPffx8J6l0Dd3r/LPrfnEDIRdgnTrXHG7mHLFAtd86sBSe0EqLWxFjBrYo7G4sfp5YNoHhHYi9f+drSzDTr8FdPCLqB0EFC83dV+7qB1WvY+b0f72+3Hz8a7sg142v10zTemobd7x5/katCNFhiaz2b7gFQbLFhS2JxHvT+a69V2SfP75n91oGGgkRrQC59aG/JeP4AIAOkYQOWC87I0RWlNsSis3KSdO4VffLz5WqMTnxpPBpRmhfPU5RMvyTJboTYGHe0NGC+Q/Qy+LoAt0mY/e2JOSKFZF54yxlBpzWAwQBvN7u4OAsFwNCJNbHrbJJGkqQxMQ4bCPJrBYMiXv/wV7r33XlvYLhG24vZ84WqDwGIxo9dLyXspvX6ODOlcIZIq9wGPmDA4gyg284PNu55mGW+8+DLT+cIG6M4XpCceRRvDYl4EP20Ttx32XL3ZvGhn37fr0wnb4XbhUL8fdnjcETgs/dN4Omgi6wgt+dcEAb3+qe6tuQ41XAn3BYQUHQATcE/Uty/05/26rXsWESH2wrD/zlssQn9CREvmxugEIRPN29sVotUE4MnzG5w+bAXzM4dHPHF+ne+9v+vAjInAl/M1apCT/cDAhIHvw0jtD82/42fDdGyb/t03dp/fF25uvuigNoby5DPw3jdZlAWlKhFJhtKGYlEB0loB0e71iqAUMGhWV4cuvacdayL9/vEuQm6ehmAtbV/LmNEyAr9Ms9QlpLSZS5cLRJdm7HYaOyGsm6lXprhvo3GZ6O/9bXhB0x5ml1lGJKiqRIoes5mtHSQTyXQ6B5MRs88G83Fntt5AtZV5dXWFqirruh3G2EKbRcmiqqi0RmrjZPd6Hwph3UnSNOX06dN8+OGHbG4eDqkmDRpbflCRCM39993DofVVJuOCYb/PZG/P8RNtaZDbfJ6WiLBExmXesuONhb5m3nzwC2bApoFxR92OR6GUcyfQFQlg8hwhbDr1fNBntDZkY9jn3IkNHr7vLM9961vcunGDYjFjZbhKP+uTpCk9Vz+qKoVLV457PzZ+QSlV6wmMrUlkDPTynCRNyJK0fh0YV6BwvyAFhiSRkStE7Y46Gg5J0oyiXFAUBUrZpAEisc/304ys12M2mzGZTSiqgnkx5dbWDY5snmBvd5srVy7z7oULPP7U45y75xwrawMWaYEoDGVZkGcFaZ6TZBmjoxv80H/0Mzzw5KM897kv8t4L36Pc2sHM5iTlAlkW4X1pY1yVcenoo7Hpx/0rMVYSiIW9tkIw1lovEyS7gHP7HLbbi7+Pn6s5rqfm9i8Z0Q4PYqJRg2m618RAMb6WfW4K0IlzN2yDHW8p9vWo6ucs0DbObXU/vYvd0brWr4vW2WftYuyja36NomcacssBQKNNh7vcd9p/e9obj827EN3u8jTb/xvkRj+R1hrEwOSTXB48G5rvpQsc3badaG3qfWjbni0WaCHQEfgFq4TAyYxaO8Wsl2mEBahBYhEyFCuNpTGDkwm8++odXHceDI5NFRi0DMb79WskKUpXVIVlZmmS2vzeUpKnuTXrVYpysaAqS6q5Dd7rD/ool/rSKAcwlE3nZzQol7JPisQxgQQj7EaoqqqOiYgWH+rNGVs1jJMBq0qRJHUVV6vMdpp3IQgBsFhAlNqE7awMe+SpZG9vl/HuFpsbm2RpHl6gzJLgpgWGPO85UJSxtrbGfD6z1cPLEqM0Umg+uHiRtbU1VlaH9PopRkQb1yc4DqiHxjwbwoEx4NJ/GgGFKkAmvPr6m9iqvhlFNoDeGqpULgA8qc2qCKstrlGFhXhRnzU7c1s6Ho8gaMZjrOJRs5M23NeGhh9M6Lvpax6Yrz8+ToCPoUYMdoKs4ZoO9wiPimpToI4GqXRFmuUgcOL8fkLakARC/+6/flwB48RGTCJLgf/Gu4EIfu7ZUwD8g+f+Af/Zp/4zPvPsaQs0GqsegxPjYlWEA3u1u5oPPK/BTP1Psw0INTXw02qCpGj50R5kRO9LxC/AAyLjXdGs377SimkxRWZrGBLmReUqiUtAhQa0NqRpQq+XMRz1XS0N2/twNODW1twJtQK0dqvbJKr+XXVpsLo0UPHv7auLcbS1UrE2uevervHE7cdjquO7cpsOXLTPt1eidI9ZOEBowaBbXyMcjSswWlAU2rlKwnSyANMD5hj2M+/6DBoQxt4jrNvOYDigKiswBmmEjZ2QEoWh1JrSSKSx2ZcApDv/fj5KKU6fPsPzz30HrcBogRbed1xj0Gi1YG1lg/vvPsd3vvMq/f6ITKaUqkQanJLI1GooJ1D7Q59ISZrllKraJ5zICIAYY/CJ1617nuMXAkuPtMEUBVpVlGUBq0NEIsic1bmfJxxazxmkkmx9g5/+uU/z6vde5rWXXmd727A+ShkOEzbWV7lx4waqKiwIcLF3iUjojwZo3WNnZ4dEpqRpwqmTJ9nd3mZttBLqGAkpXd0iYxMpUM8hBruqFRNi5233UD9PyVJBliUsFpKiLKm0QkhnrZGKlSR3hQHnLOYTqnJOuSjY3dvi5PGT7IwnvPv+xzzx2OM8+vgDnLprgzzPIDEUVUllFEm1oG/6iCzn6N0n+Jm/8Eu899TjvPD5r3Ht7YvorZugJ6RSo8sCsJm/lFEkAvD7LSSasHtNm5qm+nPU5vfLznB8dtuB5m1NfByo3yn8eVri2XL9tRPImtrwZWNsj7ctwHfRsnjOdpxNxUP8vAebiayVsVDzo0A/o3XpaituM16LWKinJXiHe6V0HgNx+t39Pv8H9RM/FwOzLjrdpsnttY/HFwO8eP331TcBlzQiAmvL9gZNwLZUWdUBJLuAy53s63osNfQ1QoQSDQp7dhLhgUOoYkOUWtO15+duyWnIYue1MH4cWHnDW9Hv5LpjoHH58mWOHDnSWIzt7W1GwxE6sYWClFZkuTW/pmnitEU2sn08HmOMYXNj0xVZskKx1zQ1F80RU10HayUu5V+aZChV2fobLoNH14sPNTRC8JS3uNjK0jZwq7ZoaKMQus7A4MdleZMIz66urnL16lWu37jG4cPHwkL7DDk2aFyzsb7BZDLh3LlzTF2F2zRN0Upx7dp1Ln38EXvjMQ899BC9Xo8szZCdmaZqgSO+9msO7MbRRlNVius3trh8+QplWbFdpUwf+pOArT9SVpUTKOq4hkB+9pkrqGVQD3zi3xzIMF4IdmDDb9ZAfKND4A9v3YQXdIVrz95ru/LuPcR7PfQbjooQ4ajJMIVwpAJAgijGwVh/RpGZMOC4SI1b6Pg1tH5zfe+T7Wtw42YQ9V+vz2eePcnOfIe//rm/zq88/iv83DMn+bv/6rWwZg0QjbcmNvuOh2Tl/uge2gsXx3a4VsOa+z3UZOjC08WljNLPWNRCHxa8F0VBupaggOnUFl/ze8lbKbTT0KZJQu4LdFaKPafFTqRESQeGtOika7GWqctdqc3I2881tN2t3/zzB7XT7iu+37fVdXkaJaW0tRVafTU0hgf0hxChKCXuX4HNOlWWFYv5PMS0zWYzqrIi6x2U8rPJkL0wlqUps/kcqAUTz7AXRWHr0khfS2J/7AHAaDRiMpm6Nl2q6SD0EFznPvWpZ/j6179L6txst7e364Qcbk1iO1ssKNgEJDZ1edgbbijeBUvrOuOKB1e++rxxdMcapg26KCn2JlSVQIiUUT9Dqz4yseA4E4Iqk3zf9z/D3Xed58yi9/QAAQAASURBVJtffY6b164xXwxYWRlx8vhJy5OEQCSSzMWeCAG3bt5iMZ9z4vgJJtOJdc01hsy5DnqlWjzPLmGkHRDdFn6MsZbDXmKTmRhjmC8WTKZTVKkA4ZKX9MjzlLJwijE1oSgXTMZ7XL9+lTMnz7C1dYN333+Tp599nIceup+jxw7bqueiIssSVDmmn+eQJPT7Ax791JPcd9+9vPy153nl69/ixgeXKMdjjBEkukKqkkxLV4DUCZKSQE88OEMsOx/NubY/x/u0fZa71qlLiRCEXZbTgIPOu9Guvgv7LTDtIOW4rfj+uO2YFbTvF8J6e5Rl1QAd/h03KXwzO9YyDX08Pv//EAAeKRR8O16uWgZaukDAsrVr0/Z2QPiyMXf1uezeNlAL93nR5A4Ao78Osqx9kut2bTT2Ms11EcIW0vbxcNrUEgi4NZUt0Cebmfs8PQRQDflz/x693XXHQKPXy7hy5TKHDx9iNlNO0F8gkxUWizleiCuKBdPpmKtXr/LBxYvM5gXPPv00g96A9fU1tFEYpQLQ8ONWla2+aoPLK2tZcMKWqioSbU1gRWVQlUJjWJSFM3W7XObSVoXWythsF0niFsihL2FIUp96TVnLgs+S4wtJVVbY8i9Bl4qyKFDaapSqqmS+mHHt2jWm0wkrK6ukaUqvNwgmxzzvufgNFWI/iqLg8uXLfPzRR0zHE/YmY4ajESdOnCDPc2TiC0ndnpDtF2Y8UdR2HZOUN15/g7KsmJaanYf/JFk2RFeKxXxmCYMDDAJTC/+i9nc2QgbmbAmUJ24GV/Ku3rjCBKbvCYwxtnJ1kJL8QQ39GIct3P0twllnmWJf9Urbh3DeRLWUHzJCYrWp9rDY76RjXNp4out8FJ3GxZpYlQNUhIYMXoPvDeTxKOu9Fdx6IKxOA+YYr0CwB/7hs+ucP7bCP/7eP2av2OO33/ptfvmJX+ahM2u8cWm3nq/ruzkmP8vmokUwJry3Gg01x+G1FB43GieMNeCrG69dw/3vyeMPY+q1NBBil7zrJAhmDmz7kRpjBTtbgNMKOKOVFaS09SBmsxmj0RDEdhBAGygjniZNRhIz7C5NUcw0vO/8Mq1i1zN3cnnGuNQK4dqMg2HjGhTNMcUs4oA+/TiFfa/eDO4D92ya4dTWKcmsG+k+rRn7mbIfx8rKiq3ZoRVS9oLwDLCYz6nKEt3LHPCJzjsxGJSsra2xvb3F4cNHUaq28BmkSy2ruO/+e1hbW2E8ntHrWXracC0zzWw2/tLaYKoKoy0/iQPJLd2L0t2a+iSBdQ027latNSK1CU2oDNJUaDVhXFakpmJzmDObzFnt5QhhbHyRKjlx6gg/9ws/zavfe52XXniZartgZbTKYDAAIxDKnmalrQV6ZWWF0WiEEDZ+Jk3TkG3Nx7X4ZApVtd9K0wWCvXDpFW7+vizLqIytRC6E4MjaKunWNvP5gsV8bmMjjQWpsi/Jsj5TlzK3LEsqVTCdjjl86DDzxYwrV6/z7jsXefqZJ7jnnnOsrg0pFopUGubFDJGnKGOoepp8o8+zP/dj3PfUY3z781/n9e98h/HlK4jZlGQhSI1AGu3ScHuaVFvUHMoIc18a09EhqLc14V65sCwIu31um1pyGjVO2v0fpIxof6+UCuc/Voy2AZDvpy3ANih9RO+C0lZrhKiT1IAklZH3QvTcMlrVRffimFQpZWAvsftRPcZaNojXoZ0V6nZXDHLaFoP2uhwEmGKgFM9vecee89+ZYB2v01LLxm1bubOrCYiaroCi9bkL2BljGjEaRqk6vtoYlwq8DUtxtJRGu7e77hhoXLhwgYsXL7pYg4Q0TRgMhvT7fQQJMhGMx3vs7GyjjUKpiuFwhMFq69IkYXt724IGX3U4TYJmsyiKUJU5SVKyLLcaLK3w5kjftzEG6YpFxWnV4swVtlqufdFFUWCoA8SNtoBjPpuzKKzfqi8Y6DVqVstp028iCJlWtNGoSrG3t8uFC+9akJH3OXToiM393u/z9FPPMJ9bl4/FYsH169e5fPky29vbzCZTVFUxXBnx2GOPIaS0NTvk8qJD9fttagJiwmiFxoT5fEJRGt599z1AMDn0CCIdIIBK2YxXUvpgTt+yJ+S6jp3wxX2MBxTGAbqkQfAjchh9Mq4Wh2MODiHjhVkB+HSorpW4KF3Tlav2Oa1/97vcjbshcLqChQ4UeUG6bgc3Jiu8K1UDTlAesoR2/dyF08Y3aWZz9rGoj3eP8fDEAQb/yM89a4PAf+P13wj//vITv8xnnj1pgUZo3iBcVh4ha2cp09V3zJDDy22ujxCR0Gpa7gjRBMOaB4tFe8Zx39Rrm4/QriDXfDazGhVHA3z1WCl9VVH7frTz309TWwzOC8aDwaAet5QYZV1cgvG3ZSbvOhvLwMIypt6+YqvHMkJ+J1qydh9tBi/c/vQW3KYApBvWzoPSd4IFZTaOwu7vxaJw9MzSQgs4+hZ8txiQPaZNkNb87C0R9kpc1WpvFVJKI319oWi+tRAGJ06c4OOPP+bIkWNOUPHuT6C0wYiClZVVHnr4Qb7x9e8Ei7Z1S7WXdvV3Yg20McbFnvksPK5GjwMZHuTXe9nSpGBZ98DaATChDMYVBhTauM+a3aslF6uCvoD13gAyGPZykl6PLEswwvD09z/B+XvO8+2vP8+Vy1coVcFosMog76MrazGXqbWweK2jH6uPPfT7wn/2SUTiCsW323f+OaVcdjAnREgpyfOc1bVV+oMh2ih2trYpijm6qpAiRSYJgxWJriqKxZz5Yk5RFiyKObt7Yw5tHGMymXDx4kUefuRBnn76cc6ePY3oJQihUIuKEkFpNGmWkacZo1PH+PQv/QL3PPEgz3/hS1x65XXU9g5iOgejbLC4rixQFQYjXeYk0yGwdQjBbYEz3sexxecgV6GuNKjh/xiE84RY5v/fpWmvFQZNS0abhhyk3Nh3j7H8JBbAG66i0fm1Y23Hde2nmV3ziD93xVjUPG5/zEuX1bFLCO4S/pcBgq52/Ni6Cg/G4+myHrXvWcYT4rG0s5XuW5MO2tx8b8292dXPsqtrv4rWe1wsFg15uOvsBHdEQf2eAnAhyOPL9swnue4YaMznU44dO8KtW7c4fPhwGJOUAms9s/7F4/EevX7OcDhgNBqSpDnvvfeOWwzY29vj7TffolQVDz32CMNQTRwSmdgAuMxm2LBMsagRq4E0zbBZNWx8hs/oAc41KdZgiThblQUtfoPM53MW8wVpZp/pzXtWk5RYocgXSMqylMGgb9MmKsvEjDQoo5DSYIxC6ZLxeA+QbKxv0usNuHXrJhcuXODSpUvcuHGD2WzGfD5nbXWVEyeOk+U5Z86csVVeg0WjuQH9hmhf+zexFVLKUjOfF+zsTrh+/Qaq0uj+ISu8aWuZEVLQy2z2H6sktsWwjLExMHVl3RoUuG0WMik1RU9Leh3NC4K986COBF4I2ngDvu5DaF3ISOi1N5r4YHrNglefRO847lsI6dEB/o8gbPhxeeJgjK0G7NY7zM2I2veW+hA2rAWmObe42qfto/47Fmw86f3Ms6eYFBM++85nAfjdd36XSTHhM8+e4v/7b9+q1yKMJX4ZBhvnggVMxjQtQl2EyriVCO+zi6A1wYufhzTNeYdChBA013YPKHRvHZEPUWrOwp1dScJsNkMpTZoJhLGBNJ5wlVXF+vo6a6trpE6DO5/PGY1WQmKFjum4wNj981kmgHd91w4ebDP6g8DCMqAiOs7wsvZjxmRMnWFosVgE4SFGuMuYZIyB43PnmU6txRXW/cn0iN/3nVxpKllbXQ2xAHZCdsxVVTlaqzFGOjpSa/TitTh1+iTf+Pq3guDn6Z4gCSnEQfHss0/xlS9/C6UUvV4v0GSfIjkAFJruJUZpW3slfj+mzgIV1hFL//B8jFizXVtMRCJRGpIsQ1bWIr939SZvTueoyYJz50/R7/XpywQhEnqDPkVRsnpohZ/8uU/z3jsXePnFlxnPdjFo8qRnLauVDhYh5ebkhaXKKeTiwFwvIHu34bhuQZfg6N950DQ7QdkLuAIYDAdkWpOlKYN+n+2tbaaTiY0ldLEraZaRpjmL+ZyymDObz6kqw2w6Z3vnBjs7R9ja2uLShx/xzDNP8+hjD3HkyJrdlUqwmFVUpaZKK3QuyLOMux6/n9N3n+H1517g+S98masffAh7eySLBYnMkLqy9VUEIA26LoUS5uiVjG3wsExL3hYCu4TCdvtd7mja7Kcp8Tvq/Bw9YgG5amTtWSZcdo3NjyX27orvC9aaqNvbCa9d98RC+e0EzC7QcJDQ3dXWMtrYprHtOJv4eQ+22kHd8e/LgERMS8IZabmzdwGers/LQPGy+9vzvp0yKb4XmpTcz7u91jU/qZ/1MpbBhOQa/r8emNZyDZb/G1Mfxju87hhorKysUJQFa2ur9Hq9BpoXIkGpCiEM/YFNJbu6ukKaZiAkiUgZDUeu2rYkzzOkTuj1exw6fNjGczhEmiapS4GbkucZQqxiqLOGCCRSJMhEUhYlWZ7V1gBhA+KksDEgXmtjAKVLcpmjVAUiRSaSXi8ncT6xSuugmRumQwbDQchd7k3YQtYm1/6gz6B3xAaMp9aqMxgMuO+++9nd3eFrX/saN27cYDweUxQFa2trnD9/nkG/jzDQHw44dOgQeWaBk5QJWtcI9E60C/VGs+LwfD4nTTPeffc9KqWZFiXq0H1Wu6cUWivSJA3itw8GFdi6IMZtNOOEfBEJN0GwdgK8ldNNYOL2VicUm/q+aMQNYhuEsVjj4W5DiPB3bNloE+taS1QLuyJ89Nond2+s2RcC727XcDEw9VREu2+ifxsgw7h52/H9yo+f5/ShWhPfFAHt1c8THji1xr989V8yq2YAzKoZv/PO7/BnHvkz/D//N48yL1Tns/76+OaMf/zl920PS5lI63m3NjEQWvqc3wOmXtfARHxb1L/VQMvWl9GVA7ZubefzuYuNsgBJilgLpxgM+mQuRkMIa73sD0ZImeAtTfEJsGOood+daoW6GEWX8N4EAMvBSheAaI9jGYNugwyfHtO7VHglS7uibx13dvAlnBtSUSyClTZNc+azGYiN2z6/f7yCJElDRiY/9iRJmDvljNYDyyjdJgmnJFqD4WBkK8eXJYlzGcV4N0eNTARlteD+++9mc3OTvb09BoNBQ4sINr7KzrPl7hK9zwbzB5e619MEr+BwxTtdnYzE8SLp2jba2GReVVnvmVIxKw1vfO9Nbty8yaOPPcCpM0foDTKEFOT9HqQVxaLg3P1nOXHqGG+99jbvvvUeKwPopSmmsmDZC0Zojamsz3tZltYdKxI6fN9xfMyydJvx3+H/bg2M1iROUae0oVI2BsS6LqbkWY/pZOpiNBRG2yK6vf7QJjmZzymKGVotKMop09mE7e1tJpMZN25s89aF93j62ce5/757WRkOSCXoSlNJzbzcpeo5V+PVHk/85I9w1yMP8s0vfZW3v/FtZpevYBYLKA3S7Yeax4VJgX9Hd3AO6v3bPIe3S+vayYMjunWQ1vtOx9OlzIgFxTb9qfdAmyLWv99ppqU7GVsXHdwvqNuxdO3V2M8//r7rcztWJN7XBwnx7TF5t/V27N1BhRmXjam99e70agOvP8zVfvfxmiyz9rRZvla6VphECjBPDwzNfRhkPuqY1/h3g+X18hPO6Y6BRpKm9ISw7kaLhS3KF1CToKwEudEcOnyE7e1b5L0+w+EIhOTa1WvkvT6ra2ukaco999/Hzt4eq2sbITANHPHVhrzv0mDqerNLnxfdMWQpZTABe2bnAYqUEiIfTHAp8rQikZkDCwkyt65bWhtEYoXFLM+tf5ozuyeyrjqbJCkIiVaa/mCIQCFEgiQlT3I21o+wOlrlN37zt7j44QcURcHKygr33X+O48eOUlYFWmmKouLMmTNBeyldHQfZDlRgOYJuHhIr5M3mBTLJeOfd95nNZhRpH6Q181bK1isREXH1xavsG6xjCvxmavQgCHe40TSE7aD1N+ElNYKkQTTlJW2csNvy4PRLEJoW7jvTEG5joT8UDjYm4Bnh18s0l7Sem+3fRBori+pFqCNQmwm65x0TEQGs9BP+9p97nDy9M+b3T17+J/s+/5lH/gz/yU/fe9tni0rzb779EXvzMgjapmvN42EbExb3YDLh19ZlkfIiip93nJnNZ+gJVKtm4KoobIazPGE6X1BUFVmeuWa8wGdjZvIsJ+/lZLkVZBfziv4wQQib9jQ4vUSgJta2LGOC/h01NN5LtEtdDD/+3NXPnQCXLobZram031VOoLWprg/Wzoa+qQGnEcKmB42E6PF0wqIsyfp99iZzrHFWhCzQ9VyX7wwBnD55nBu3tkiTNXv2DEiZoLSmrJS1GmC153VCZhG1K0hkwur6Otu7Oxw+vGnpvPbrg43fqyo2Nje5/4FzPPfcd5ByQN7LrfCADq4C7XdhHBOMXf7CtsfTg5hh206FFlSB9thYEh8XJKR1xVTagHPZshaQEiMEFy9cYm9nh/sfPM+9959nbWPV7uVEIHogKJD0ePLZJzh3/izPf+t5did7jAYjm/Z7oamqMgj+AGVZ2FTCXrMqfJ8gkpQ0B1HZ2iM2dsMFyVOvo1fONNw3HX1MfT0obdO3V5WNqer1e7ZwbpaQznIHCAtUZfeiNpANhuSDHlVhvQKq2YSiKpnOZ2ztbrG1d4trN27w4QeXefrxxzlz6gRJYiA1lCgqs6DSBUmW08v6rJ48wk//0p/i0ccf5pu/93k+evMdqq0d5HyOKGakyudUtGlvrSVLIxEWjEhLm+KUsQdpzmNBLT6P7fMea7+D0GdMIwtRlwtN3F5QZIlY8Gym3e+iDQcBoMaZjObhhWtwPNK5Fhu3A6wn8/66LcvarRMvCP8lNSvwY3V7zvFNL4yGdmJlJc1YkK4A/fjy77JxtlvJf9rrvUxZ5OfRVlbE8437jFqmTRO7+ti3Tzrm0xpwtEZ1uzJJApDG1IrScF8ABPUzge67uGaJAI1VCBmQxhaW9nKNQrl9LB2g8LzYzxcMGi1q5WGsmDRYetmUEA++7hhoSGEro66tbTCbzcAI9x1UuiLNrJXgkDjM3njshN6cwWDIaGWVvD9AZjmpTDh39z1USpPltWVECO8WVW88LWyMhHDCXlfqOQ8y4k0WNNTRAbQvyvUVvSQpBNotvJApIklcILHLPKUMUqQYLVBGIESKlP5eq+1KRUoic+6+614uXfyY5771PDKFp55+imPHjiIkLIoZSpUIYV3DDh85QpZldk7GCrxdObX9HA/SBCCMTVeoDNPxlI8/vsaiLJn1TwaiVTkf7ebBcYw37OsYcgisNokaNLjNidEuv3Idg4B/T4bwbA1E3GefHD2w/daciITHOmoZL5Qi3Ni88CWELcgVvVMTtR60EX7sxJEN9gfl/P4TWQe/W3cKUQ/f4Cw8pt4/gZE7oUVrdmeav/hr3+C//t89w7H1Ae/eepe/+rt/leuT6/ve6aSc8Nr11xrf/es3/jWP/oNHGWWjffcfHR3l137217j30L1c25nxf/3vXmRvVlJbojwYEwHoeVczEa15lyBZ4w+35rK2KPn2GkQzEtL8+/JdaBeEa7TBqIpESqRIKfWCoioZkoC2Gd/sdrJr1+tb//Z+P2N7e4/5rOLkYGSFSqEQpA7OhgmFPuPz0fV3lzauDQT8vw3tTUsA2L9usfDQbKNd4GjZVfcBWqvW+A58tHn5OeNiWNy709q6eU5mE0pVIWTKZFailQgJH2KwEfe5b+zGsL66wuUrV5xbTYJWBpkmCOFSpipN5t+rcefe1SjylzKGo8eOcfXaVTY21+2oZb2XjDGuQGPFU888zNe+/hWm84wsy1hI6zKiVTdDt2tX9xYrqwBEsOIS9o5xoEhacljzC+mtLAYR3MGcC5LRCCRGVaAFu1u7vPidV7h1Y4sHHrqfE6eO0evZ+BUSQ5lYPrO6scJPf+aneOvNd3ntlTcY5T2SLKEqS0CwKEobrO1Qu4+JkW4sWkiEcGBKJFSUSG2oKgVGBV7pyJ3/TwAJXjjwijmZyKCUqZRNGZ/lmY2BSQRpL6EoMmazmY2RcR6bRgny3giZ5MznM+bFHGUqZuWY8WSHyXjCdHfGRx9c5vuefYoHHjjP+vqQBG9ZqUBpSqUgNWRpnzOPPcSfuPsuXvnGd3jhC19l94NLMN5FMCXRdn5GaJRpnT2S8O7rPdAUbLsyFcU+7LdLVR2ei3ZyW7CNLST7aBAGY0qbtl8ZbJxTLeAJ0S34t9O1xrTGelnQ6AccUDcJXjcUVwcPk7jNXOM1szfUf/rHa/BVA3Sv8Ap0KBKK27S57ZYW9x0DrWUWjHgM8brtL6Bc978sw1Yb8DR4g/s7frYdD9NlYehSVAnPn6Mx7ZuXieSMjsthvcalsXRBOESpDcg8h3QOJAhsmIERft01QoMUqetTNwPDgUZGnuh742S82BX1dtcnqgzuNfDtlLM+h35oNE1ZXV3FGNjZ2WE2m3H48OHgk6i1rUya5b1Gmfh2SfP2i4qZt2/Lf/a+u/ELvR1iF60N1Ea+AKaqmX+Xb6B0echXVlZZWV3hC7//BWazOUdPHOLs2TPObKVRymb9WCwKjh8/Rr/fd9aMgyuetjdvl/BisEGeeZbx0vdeYzq1FcjLww9Zsi4ESmmXQ1lE+1yEGha2Ly/De+nc+YEa520thNUmG8AFmwZhFId0Y5V6AAf+z1rb0fh736Tdf0RoNRL07W/CdV5jgaYQ6kFGaNv35yQrn8bWYF3KpE+r2JiSb6TZdz2uum+PUr782g1+5m/9Af/1X3qaTz9+L//w5/9bfuW3fpkvvv/F9iw7rzb4APjJu3+Sf/jz/y2n1k7ypZev8n/777/LzT1vyfB9x8CzFsR9PD6im2DHyw3OJ9UDFf++3V31W67nLYLWw31nDOXmfeitKyEtp8G4dLclQgwIcjB2HyityXObtc1bJKuqIs97thcpMIoIyLbG33FGuhhnm7G0v2tn9Il9tONn2vfGc29rC9var4MIc6ydvFMC3p6jf1ZDyCCilGI6mVAUBQjhgsE9AOgeR/yvv7QxbG4echnEakEudbR4URQhi5QXQBxrIg4g11pz6tQpnn/+eR588EGaINjuDGNsIbiHHn6A0WjIfDZnNMqdYGX3qUTuW++D5hMLm133+iR5Pl5MCEJRqkp79zYXnKyNTZ9rjLMe2QKJ7717gRs3b/DQww9y111nOHR4HUFCv5dSFAVC2L394CMPce7seb7zzW9x4/J1itkCbWA6m1CVBaurIypnpUhwVnrhXGbcWTVCkJJQlgusYoflNDW6kpBlz7isjbVbieftg8GANLUZyvzn2WzGdDq1VeCNVRjIJKXXH1KUCxbl3BbqLBWz+YLt7W2uXb3ClcuXeOzRh3jq6cc5e+4Mg2EP44rzqqqkSieUSUma9+kPR/zAp3+CB+5/hO9+6au8/M1vMrl1E6a7JGVBqjS51mgEShqUXwsXw1FnM8K5PNcCZtdZXCYgNgT3KA7E7s6mLBLThLYVpN02wsdW1OLinZ75pmxTv+Q4g5PxyCWaYxd4aQvd/v5lLmG1Zaxev8aaRTtOu4QMbYG7Pc8uuto+q+37lgnx8edG7FerzdspjWIldehTdMy3Neau/uL1b49x2XUniql97Tg6m3gLNoaF0Dz5fd/Hoiq5vr3F7s4OxWLObDJBlwtMVaGVQZfeid4EF6v6SgJBifeFEBIhUtAVaUdxx67rjoHGdDoNhKehHTC1dmA2mzGZTOrG04T53DAcDgMKFELQ79tgOa9RqK0a+zUPMmKW/nN8iH1GjViYiLMPxADBt+u/8xsyS9PghuXv8e3IaBM1CAdQlYpEWhPV6VNn2N7e5dvffo6qKnnwgQeQiUAaiVX+pxgDed7nzJmzIc6lbT6Mry7CuOy+2WxGlg15+eWXmc/nTMQQ1s4ghPV3V45pSSdA6mDhIFZR1JrpfWDE3RgEBuMEzXjsnuj49yfw5Cl2ZYi7DDMMhLjW8MR3NAx1oglcLCKPWtO14B2L4F6wjUrWWBNjpUhS73sbv2Oxr5V4XKFvL9Hbw8CN3Tl/4de+wX/yU/fyN37xET73q5/j737t7/I3v/Q3qXSdE/92VypT/vZP/G3++o/8dSpt+H/9i1f47z73XiD67TUKDEZEZD/aLo11NdGPbaYoPDoJcAC/xMIB1TBvD/Dc3tHGYIZH0FqhKmW1oCIPgqMUEqTBuCJcvoJxnudkWcbKaIVbN7dsvZeycONqFqeqp1YLpcsYUJtJxQSzi2jH56vNXJZp19rPwe3TRXaNtf1dfH/X9236ELflBQ7p9vRkOrVAAygKmyo1cy5+EoFIGqdkKWMcjQbs7u667FJN7afNdFI533nCHhNi/7qurq4yn89d0HMsVMRCW8Xhw5vce995XnrxDebzuaPRXsrq9mHvem/tdVpmcRIOxGgXCG2c+yBCksgkBEgbDEY5i28iqFzldbRgZ2uXF777Ijdv3OT+++/hyJEjDEdDUuvvhHBrlfYSfuRHf4x/+j/+E8p5hZSCvJ/TH/YZT6dIB7yNqpAu01E4ldJ6GShVgQSRJuhK76Ov/v74+CQuaYr3IIh5X7xG3uIuhE2qMhwOnbJswXwyQbt6TImQDLKUrMpYLGYsCpthrixtqvvt7Vvs7Oxw6aPLPPvM0zzyyMMcOboBqcYog1EFOq0odEmlKkw+YPXsIX7iz/48dz35AF/7wpe4/OqriK1dxGROWpVoIVDCxn2kunYx9IXjfcaceAvHZ6YtDLZrEMTXsniJ9v1ddKgtXEsh0MLTULfjWud4mXKieSZdamlh9o3NGFzq9/17P57rPhAU/X0QjYx/rzsksIt67s1nDhLG43aXnV//WzsG5U6UsbDfbavr6gINRuwHM20AsazP+L6utVxG17sUWl30zLVii5m6/ykBGs19jz3MEz/wKbLNVebTCeV8wWRvj48/usT1Sx9y7fI1drfG3Lp5y9F0y68XiznGSMBbO0AYC2QwBmUMSdYj6Rj/suuOgcY777zDaDRCa810OuXcuXP0+30GwwHT+RRjDPP53Daaply/fh0hJEmS0uv12NvbYzQa0ev1aj9Ct2BxlH+8qN7aEYMNIUSdecRN1GseY/CgWjEa8WZobCK/WFEGj/gem0ZRhPZ9ZishJGmaoyvN+uo6a2vrfOtr3+LGjZscOrLJ2XOn8ek8beFBa+5fX18P2qI4jeXtNmDXhvRjVC6/+vbWFtev36AoChaHH0ImNjBRFwpVVUEWN9pq8Y0r6uWQQchuZNcE63bgngmcKj7g/ltjgtBJUFdHLM8QtP6RaBXrL6OsSY45+I7rD7TxTug7Ho3Guv64gxc0MaIWT8AGq/qcRcpoUqcNiItJiKhvK0i3XG6ieYswLnsYjTH8w997l2+9eYO//59+H//Fj/0XfPr8p/nzv/nneX/7fW53nd84zz/7xX/GD575Qd67ssdf+W++wysXd8KexXi/2+Vr7pelLXz4xYyBh3B7QHtC576s3clqjV6j8cg8IYS1gEiZUBoTsrylWYo2ytIHgUtVWz8fn9E0TagqqzhI05Q8zynLuRUkHJhpAIj2vKKxdjHSLuG+sSwR47jTHO8H9bNPkF1CmGMaGKfSbdOGWGHTFpwaTNQY6+YobGzafD53wdrW7dH2UfeNEFEcnMZ+1XRBFQjW1zdc6nAVfrdAMUMVNgbNjruO+tpXBNOti9WSz1lZGcVkBQ8ula7oJTmPPvowr73yFjjLiBQJRtaKh7aAEVcjjt9h7KoRv187P4JLlJSSxAv12sYQmchFxSeRsPKcrdtknMCXJAnaaGaTBe+9/QG7t3a45757OXf3OVZWR4hEkvYylBAUswUvv/oG48kcqQUyhaIsOLp5hOnVqe3fWIuJl6AN2oIP42J6hHWN08bWlpLS1v4wOE28O1++mKqngUIIC/pFDdjiNYz30mAwoCiKwLfTNKWf5cwmUxaLue1bK5I0pydswoCyLKmc5WyxmDObTZlOp+ztjLn04WWeevoJ7r33HP2hzTBljE0jPNNjlF7Qz3KG/T7nn7yfE/ef43tf/Drf+9LX2b5wETMeg6pQVA5JiUCbvXub9bQwGFPHGbTntux8LQPZy4TuLsF42b1aR2AAf772C6jttrsEf/tbTeu8/CNl7bcft7NMcG/LRF10z1oQl1ldIrnN90XEXPxdHZ/j9uLg/i4Bvg3abkfjbdHCsqWN399G+7kGaHD8vYuOt5UV7fm0x9ied9eYl4HWNhhu7i8TgLXGoLBuoL/xr3+LP/jut/nxX/hZzpw9w82bV9m7dQtQnLr3Lp78we9n/egxtFJMp1N2d/coVcWF997j2rVbVCrh6uXLjPfGlPMF4709jHLxyi45R1xM9KDrjoHG6uoqw+GQvb09siyz1ayzjKqsnE6z3rCjkfUx7/f7zOcFN2/e5MqVK6ysrHD8+HEOHTrkCufVixq7JTUZgL3H+5R6Juy/j5lyewPFAkcb3ITLmIYWuw000FZg8ii6qmwdCplINJIkkZw9e46yqPjqV76OVobHHnucNKsD5bW2bVdVybFjx4Pb2UF+ofXwDkbKXpPY6/V46cVX2dvbo9IatfmA8+ttWoO01mgVWDTNOIhajBRCBK2I85sKwmcbbNigIsL3QfgFbOmu2k+1LRqK6L/NhajtCewzc7gYCjceDz4AG7OBBxWi1Tet9uzzPm2xlNK6l/m+A+IyoZ94pMLPO3wRu4PZPl+5uMtn/s6X+Dt//kl+6Ud+iBf/9y/y0//TT/Pcx8/tn7O7PnXqU/z+r36O9f4av/7Vi/zNf/4yk7kKnft5e3Yg3Jr78QUIJ+J4m7bPf/RBCLcVojVvzTuAL/9bdIVCiY7R+5ShviZN7pirTasangojUMrWysmyjMFwCNi0w1mWh4J6VoBT9d4LIM8Pt8lw4n/bRPxOrjsBJAddbUax7Lm2cqVtCWkLGLcDP74NKWxgoRTWNW0+s9nNtLKVuBeLBSujvuvEgk4vuLTbi69+f+DG4MelnQU5pVAzysrVL3Jno32+/RyMMZw4cYKrV68yHN4TaLQXko0xmKqkUilPPPkYv/kbv42qFBivnOmg5XZAds92rH37/pg/SBd7prV2QrnT5BvQQlkhy81ICBDSZUpU2sb4ASZJKBalVe5gx3/9yhZ7e69w89YW9z5wDxtHNkjzhF4v47lvfZtXvvMaIF2SjpJFZZOtpFlG3sttimgjKKuKXq/H2voa2hhms6kDITarjDUUSrI8I01tRqlisaB0iQUaNNDzT+FA4G2EcO8y7YUKmxxFsCJT8l6PyXRMWSwQwiCTlFxmZJmhLOYUiwlKl5g9xWw+Y7w3ZmdnmyuXr/DEE4/x1NOPcfzEJmiNWgimsxlSzOj1U2b9HsP+iDTP+YE/9lPc/+hjfOW3f4dXvvo1mIyh1DaeMhwJz1sEuNScy4rr+etO0ojGQdGig+a0r7aQ3BY2Ld+2MWo+5bQQ7Lsv7sPThbrAn7cyd9W28H3vV7osG28MwrssHsbQSPXabK/NGeuvutZ9GTiIvVDaLqsHXcuUOT6LaFfw+LJx+O9r/uEn032132ssl/rfu4BF1zOw3yX3k/IsKQSpFIyGI0ara3z0wUW++qUvcfzEcXZ2tpju7WK0IpWSI8ePs3HiJA888ADPPf88w+GQPM95+Jkn+ZGjx0l7I8a7e4x396gWBVc/vsyNa9eQaYoy1mtosVjc0djuGGicP3+eJEnY3Nzk+vXrVI7wZVmGqewC9no9V5jLVkpNkoTh0OZA393dZbFY8P7777O7u8vJk6fIe5bR+RfgtWdxZoA4wKrtAhVnmfDfxan//HfxgQ/CtmvTMsVuxoQxwc+5LOMMICJo+1dGKxw6dIgL77zP+x+8z3A44uyZswi8z1ti61OgyPM+6+vrpGkaDtNBAeDx+Lt+8+th/Wgz3nr7baqqZHz0GcTKUQuSlKIoSycEqujMiJo+GM+CPDhwf0eECl0L8fVA6uetUGufDn79onavcr+E5+opu3v2HWYRfgGChkaArUzuxxX1bVzfRK0JD3oijBOgjntWa5s+VQpJRQ1Iw3uJ+m4QVN+3ceNzDNjQnPd0rvnP/4cXmReKX/303Txy9JEDgcYjRx9hvb/G//iFC/xX//Tl0Ks5qG/jY1m8MBSBtPhdxWsezBUda+5AVlg2IVpt0Fpz+3OlFLq3ac8UthBn3rPCznw2t5pGVb9rY7DgPbHWQpvS04Ly+XxGllr3DeMVJ8K6SZjWYJrMofnvsut2v/9hry7N1p1ebYUJ7DfzH9R2ACved9YtUVGWVrtnNFJIyqrCC83eHOcFii7c7688TxkOh9Yi6u+ndn9VlU8pWSsUYgDjabTWmqNHj/LqK69x7z3323kjgyudPZ8VVVVy+tRJTp48yYX3LpGmfdI0paiK0F6TWft4qtuvf1t73VZS2TG5Yq1C2npDjpZYtxVBpesUmtLqP6ziSgpwhUOnkzlvv/UON7ZucP/D93P0xFEOH97gxMkTvFC9jI13S+gPcp5+9jHuv/9+fu93fx+RSIbDoXV505qqqtibjK2Szr4x0jQLqdilTEiTNCiXZCJh7t3ArOUFWc9ZIELqXj//Li2yf7+2UK9NHVosCrSwmWyEFMznCYvCFQnTVgmS9yBJDbPpmPlihtaaa9dLxju73Lq+xXh3TJ5lXL26xuOPP8j7Fz7my1/8OotiDyErsiwhy3v0e0MOnzjKqZMnuP+P/BDpSp/nPvt7yJ2KXmmprUxSp0Qj0GsDDdfnjh1ARPz2gXp/eWWHlTf26Vn2Pd/1b7yePhC8viJIvoR27M/Q5KwjUTarppDaDYraYLLdX9fnsFLRsw3lrp/CkqtrHZbdF8trd3LFQMqvgV8HXzS5PYaucbTn7OWzLsXaQVeX0rsNYtvA738Jv7CN2sB7S8qtG9V8PGG4usJq3md8/SbleMz6+hq6KDl5+iQb6+ssyoJMCN57622KyZSrH33EcDjk4nvvkQ6GHD55mvl0xsbqGscPH6UsZqQJrK+vcPrsGfbGY3SUUOGg646BRt7vo5ViZW2NLM+pVEWaZcwWc5I0qdPLJr6KaYJMUkSlGY5GjFZWKIqCvb09dnZ2uPD++5w/f7etLC6amrp2vmOoGZQBKmfO9rUykNJp6jxTsAKQwQIFgbD+ZeES4aBKmdjUec6v2GsajMuspBxDswfdEgit7SFWVJw8cQKjDN/+5nNMxmMe+f6HGa70KMqZ20AKKWxV25MnT5FlWXC/8oUG/zBXfLAgZWdnykeXrjAvFerUs84NwlpjlKoYDPqsra6xtbVNWZTORcatRdDWuUPhhUoi4BW5FOGFUQ8yImETDCb41NcEP8L97uB6QBALxC3NQvjNC9E4gdrdbiVgbBrWCGyIerjGt+O0PxawaPebfcaC2qbGJhbKPXCp/xtBI9e350Cm7jE8bT9oHjy9htKKf/f2v1v6XgH+/dv/HqUVD51ZdXMyod2wlsKNwP1bA7Euonhna94EUtFb8wymwRtNCNAPjzmp1ayfQ+mUxbzEmMpZ9ySLucZoW4HdR94alwFDqYKV1T79vi0kp139h9FowM1bO/YdSYk2LrYoEibscPabmv9DAIl2H8u0hcuYa1uIie+PBYBlZvnbaVEb7WBclrgKlKJwMRRp3mNeKJSQaFORRK82APPOTgxSGPK8R1lBD4MUCiE0ichQSlOUlRWAjG/LM/bmGgohWF1dZXdvF2NMSOQR5gsYk6AqGA0HPPjgA1x470N80HP7XSy7DtoL8Vopba1lRhtXwFSHsSfCWiik2+067HmBTCSZTp0lD6tk0dZ1TEtDaYyNf9GGW9d3+N7kVc7ffRfcd47Tx09x77338NpLb0DeY5T32NndpTCKc/ffzXRvzHwyZWVlyGQx58zZsxw/fQIpBWVRsru7y/Vr12AMQkqkEW7tpa1hlZT0BCzmcwt+3JsN+xb7nBI+i59B2/w1REesIcQKYV2XpZQuBksiEmEL7RY9ZvMZ5UKRygRr+NKsrqXMpmNm8wkqLamqBbPFHre2rzBf7PGDP/xDTGYl77/7Aeuba/zMz/xHFOUUbUq0sYUgt3bHbI93ubWzRylTVu66m8WlSxRbWyTGgDZkQtpiugIWpkJJ44qD1kU/pXDZxYwNmq0qmyVPOjnBembYWi7GuDPk6a/cT10boNS76/nz662TkcLKYr46ngSEq9fSTRu6siT5OCXbrwg82GgBxs4jlql8HGu7HX/FLucGa5W2cVN238f7ILZ2hHZEHfdoeaz9Lha0lwKY1vls08o2MIrHHN8Xt9flYrRM+XQ7IV9K2cg+p5STFVr8pw1g2nE9yxJRdCk52sC0a/3iyziOrp1MJLRBTRfsbu9gRj1EpVnrDTl65BjaKK5dvcp8PkVKwdWr19AGSqWYL0omkwWT2Zwnn3maBHvGP/f7X2BtdRWjDLqytdiOHjlsYzqqik//ws8vXT9/3bGkK6TAaBuzsCitr+/G5iZJljrXnT5a630bOklTpLGuD17IzvOcq1evcfnyZc6fP9/sR9Rms/YhswdBULlMUARNE67aszVBe//j4HOM00AZ/0Jr07sQ0vmV2/trRitBaNIsCwfZphAU2PRhgryXcfjwEfa2x3z3+ecZjvo89Oj9iNSQ6NRp/TQLZw05cuRIXQX9DqP14yveuH7zFkVJInPee/ctJuMZlcgxIrVASNs1HA77bG5sMhwNAbh65bplJKF8tSemBNkzFuqN8FK9X8uuQCoRCRe1gN8EGfa+pije/D3y7MYfodgS0hDijXHuIYl1qyAi2C2R2+4hNzlhGb+noD5TTsAZDa2V2PdfwmrFvbQEdCHqOBHgyFqf77vvEF/64IvcmN5ozPf+w/fz1s23wnfXp9f58gdf5sfv+wmOrOVc3100+zbG7v0gOniQ1VrtGpV0zKXrMvV98XsUzb6tFks4AFI32CC9IgGkzUZTTOn3NqhKyxhtas4mA9OmYrTSY2NjDZuZp2Q2n5D3civsJQmVVihjWnPazyzuVEN0EEC4kyu2sMb9tgHIH2Y87TVv3xczznYgq6dhRhqEK5amqpJyMUerCiEHzBeVrXbt5TBHEw/STGKsC+nhw0eZzUuG6wYjFRiNFFabXpUVSmlbD0LUVrM20PDxbmmSMplMQnG6BiMWCWWpKUvFE088we/8zu+hdUWSpKSZZV3tolx+Age9x07hxdhT5GmAz5JlTA2aLDN3vurCHy/p6naYkFZYGOdSZQRIjTBW+JElzPcWvPfGBXZu3eL+B+627q1okkwgJIxGKxRVSaFLnnz6CSgVzz3/PHk/4+ipY2zvbHHhwnv0ej1GoxFnz59FKcWHH35IsZgjjMRo6dIOpyQo+qJHlWiKRdlwJTHGOB4Q0xHh0YgVikUd6xivqbdwJGmCUpkFikmCTFOKtKQsSlSVIkQPo0oGwxWyNGM+n1GWBX2TUexO+d4rL7I7nfF9P/AjXP7oA44dXef4qSMYYej3M9JUgDCUC821m7u89uYFXv/gCtsqQQ5XUIsFa2tDyskUMy1IigJpIPe1fZSbi8+SiE3/6qsDySA0usKRbi08exBOoEfsBxltATkAOf9be1c6+QUHvI1r32cEXAaG2/u23ru1i5S96jnGB3lZStd4/4esYxjrFm5MAEReeBfRnGPap4nAd6vttsfGQTUs2mNsWyvaQOwg+n0nSoh21q12O8GKFNdz8+1rF88YWwg7+NDt+MntFEkxWPT37wcq9hnroW9IjPV6l4lkazal38/pzRfMlaIyBpEmzIt5kImKUqEQ5P0hN27tcH17lxdffi0UU92bzMh6A44fP2n7KSq2dyYYY9jd3T1wfv66Y6DhN43fKFmWobUO7lMBWDgTugcK0gVq+wXs9/tuk8L16ze4dOkSR44csUzHaUrazLrp5uR9FOuF9+3HqeWWZRXwLyf+XbpUiV2VI3VZBMKQJAkYa6JWWnP+rvNIBC9/7yX29na55967OXr0CEhNKhOqqj6sa2trrKyMSBIZiPSdrHkXEo839GIxJ0mGvPrqq8wXC+YnP1ULiY74jVZWkYlgsZhbgikFUnkh0ulsNIQ0qT5oO0iC9T92L3cIexa5RLp+S3ZjEdiryboINp7oekGh1pUTk+zancodLm01cF6r712niMbg+9Zu2FbjY3/2gbFeC2WBVSQYdQnRrase9f5544SPn33mJFIKfuP13wjPHR0e5R/9yX/EZ+7/DP/urX/HX/w3f5HrU1tz4zde/w0+ffen+WNPn+Qf/8H79YA8QXNrboTXZ+xf+3oZOohd4x22Jtv+Ju67BVbsOIxDaSYqgGizeRVFEaqAL4qCqqpIs6YQ7v8/Gq1YGuCCVKWUHDp0iLffvmiVALeJT2ha+T755enCstS1/p52f3cCIm53dQGUZffF4+gSmmPhGWE1rGVZMp/PgyLIu7nIyPgohDtPSXf/fr7Hjx/lvYtXUWqV1NR01FYzLwPdaT/b/tu2dZzr169z5syZfXMRQFlWKK24/4F7OXLkEDdv7JCm+RJlx8FXe+1ipVZbi9hYz+g7a4/rFgjjkxQEwOhW39diYbhy+QrjyS67OxZkZVnG0aNHefTRRzCpoN/rceGD97nr7Dl+8o/9NF//xjf44OJFHnnkIebzGePxGIBLly7R6/W45567mU33uPjhJcerE0vrRAqJRAqX2rwo7JCcy5PBgQ0jEK7glxBNJcIyoc3LBN6lyvvEV8MKVWprxZiNqQpDgg2wz/Oc2XSKKgsSIZnNpty8dZOvfOUPMJXi7Tcr7rn7swwGA44cOUyWpS6ZwYwr12/yxjsf8PFHl9HTCf3FjLTU/Mwv/inyVPKtL/wB40uXSXdnDKYlaaEo0hIlNMq4gn8ItBcOdXe2LSm8stK7H3l3J5ccphW8XQNku0Pc8lkS60CMFceboFsIG5BfR9vtvw5SPhxIe6I93SXAxu2E8+AKB7fpmv/sE+y0ra3e3h6Pc1mfd0or23SwzS/afS2bWxy/cqcuqO17l4G92N27fUZiWfSgvvwVy9ZdNKmdLTHuSwoRioqCq1okbVIGU1n5VRvDfGELOvt6wlWlEFKQ5j2rDEltuYVEisZY1tZWmUwmJEnCymiFxXSOKa1Lvr6z1/nJgIaP4o/RXvy3TysbamOIphnLayazLHOxChnj8ZiPPvqIEydOhGcP3DiqQoj9+dPbm2N/UI1saMLjoi7Gqi7Cb43MB0mKde1Q7oDZG3t5j2NHjjGfzPnm178FBh5+5GHmxZwkE2TOOmKtKpUFINAIAl8mVCzTOjTnU1cC3dm5xccff0ylFNXmfS5w1rkjhPW37gFVWdrvlMILwcLN34sHsZgcqUsajNRL74IanzTvMZGwKqgL+DkCJTxcEPurToanmwKwCW3VRzy2GngRuCkKO8FfWG2l0bXrhV/HoLV0WXrqOTdBT9D2OUbTLl8R99l4Z0Lwc8+cAuC3Xv8tAH7qnp/if/qT/5gTq8f5+NaMP/7AH+el/8P3+Av/+lf53Huf47fe+C3+/mf+Pj/37CkLNISIFl909F2vUM3gTAQWTVj/IFXuG3c9Z78vmkvh5y3qFx2DR+/HbqzveFmVLnlCAsZQlaUNvM9l6MbvY601WZbS7w9CFrnJZIKUGWBN1obba/7aAnub0X4SreEywOLv98JI4w202j+IEbavmPbc6TOe8UMzj79rsT5Nxhb19PTVJkCwv9XZXtr7omt8Caurq2xvv8nRU4fwGX9sjE1GVdVacxFQTJM5xkz02PFjvPvOe5w7d65hybb327mUxZy19TXOnjvN1as3kFWOjjTzDS2o/69h37tpg4m25rQ917AXGiJFuCEAdQv87VoHjaeByrnfdqVgV0axvbWH1nDi5GnO33UWTMWFC+8xL+cYCaPVVaaLGeMrE370J36UV155hddfe40HHniAixcvMh6PqaqKxWLBbDbl3LkTPP74o7z5+jsUcxvALkQS3kWe52ijQyaeRoEuY12+lLauSv499EeDoEi8XaCq5+0qVdCDYT9nPu+zu7PDbDYhkT1AMxpJ5nt7aKeIKIo5cp6xmC0Y7475t//2d9jcPMTRI8fJspz5fMF4b5vd6ZgbO3ssioIUzWqWMEpzvvPq6/yf/i//R+567BG+8Xtf4INvv4T66CZiPIWksh4LTgNthEC5Okp5wwIQn32JdAkSfMyQ1QtaRYpImoJ0+Nd+aOz3DiLdWD8L6pYD+3hsy77rUkb6lKzxd3EGz2XvMFbY+tiUeKzxuQiAw2vwOsZ/O0VM3F8XjWh/jmWm9piWtb9s7WK6Gf8eg7j22vo+44xuXf3FgKNNX9ptxX3H2VOBfbWcoGlJt895ucS1r62jZ1EsSPMMEsnedMo7713AGM3a+iqjUd+GDCgwSrE3mTKezljMS/K8h6A+z6VQCCG5fv0a6+vr5L0e66dPU1UV46icxUHXnVcGj9McilpzGP8dL2QcdN2+x2/SlZUVBoMBN27c4MaNG5w7d65T8I6faWcjOFCjB/vGm2VZY5x2cs3n49S4UtqYjBC74YLAjx8/TipS3nrvLS5ceJ8TJ09y7PhR5uWcxAg0SbDcZGnGxsamG//+scWfu64GAYkQro/4f/fdd5lOp0x0hpG5ZYxGo5UKRQHBBmouFgu3EQlCiBdIhW/f1CChKc96waUxOBD73aH2Py1qYVfEByOaW9R+gA6BhnVoSAzRGVvetxB13za1qg5jN1iNrzbWVzcIFWLJvEU8l7qndt/1E4LNUcYPPXiYr138GjemN/i7P/V3+Ws/8tdYlIq/9c9e5n/4wrv8pT96H3/jzzzM7//q7/P3vvb3+C+/8F/y9Q+/zg89+INsjDK2J2UDDAsh6jUK/3oQ5z8ftOa1MNrkEqL5l6iBRQCe0uOLpqNbLFQmjhgWRcFsPqO3ZrPlGEwAcm3C3u/36eU5/X4frQvm8wVHj25YcK5Aq6aGqM1Iu7R3XffEV5vQ+6sLZCzLUHOnZ7it4ep6rs3clrUXX55exQk07JZv0uTpdEpZlADMF3On8W4WshLRHmsLJv6ew4cPM5vNAsD3wcZWWz1xbkOG1Bd/7FgLP7f19XW2t7cbdC3ch2WaZbVA65LHH3+EF7/7CkIIkijFeWPdnODTBSzbvAC632l8WUHIOHcbt0DuaPkz5RUnuBXxlm9jBGWoKyIbBWmNsedKINnZ3uWj9GN6uaRYTFiUc4YrI+75sR8hyXNmixnvfnCBBx5+iK3rN3nhhRd49NFHmUwmXLt2DaUUeS/n2rVrnDlzjscefYyXXniVYlGymC9IBOT9AWVZkom+zUqIQbgsW0qV4Gjg2toaZ8/cR5qmvPjiS1RVGXhm15r6ufn95zOHaTQykfT7Q3p5j8l4zN7ODmW5IJEwHI0Y7+y6fTkh6w0oq5JFueDSR5e4dWuLDz74iDTNMQbKck6hShZaYYTdW8XCoEdDPnjnfW5cucmxs2f4+V/5s7z98MM897tf4Nrb71LtKkQlSAxQKiSGBDAupsUEVtBUTkgXa2qzqnkaWbt8diospI1Fq+kgWPemJn4XgYdYC4lLrL5Pnlm2H/26x7SivY/jpDjxXm9n9GwL6ctkqPjfuK1A00S9H9oCdJt+dP22bJ4xwG0/H9ORdjmDuP02QGqDiPjemA518ZpmP93KiYN4TBtAxTLtMv7QBlhxf+4vd3+twLZW7IrhxgallCyUInW/Xbu5xYZad/WCLI9WLpHNaGWENpBlaVAwCFfMeD5f2CRQ/T69vE8POHrseOf7a1+fKBo5TpNalmWYbBzpHzOorpfnv08SiVLW1arf77O7u2sJoZ9ctKg+UNBOWjS0BjH6jje579cGqCckos5R78fjrQtGNrU18YZt+zfazZFw9sxZqlLx3Lefpyor7r33Xra2b9Ff6yFFitaCxcz61h87dtyBrwSfcvZ2wknXIYh/M8aE4omvvPIy4/GYxdo9kKQYTAA0aZaSJvV8qkrVoqWo/bJFbIEQghAMSUNkj0doP4v6l4bIailnsAX4z8EiIESwoNiUVoAL5HcUuiZg/lnXkzbNILtwi6k/eHBhIuuC0XayIhISBC4jizakSYLAhHbq5kQYlvApYJcxg9a8jYGfefokaSJ54coLfPUvfZXvP/39vHtlj//zf/M8r1zcASH57z/3Ht9+6wa/9p8+y1/7kb/GT9z1Ezx/+Xl++OwP88eeOsm/+NqHYSQhtIZ4jDUgiAX+MHD8PqsBhnGISuwDH+4O17AHEUKIEHRu05CGHwnozAc6HrqbauttZtNZALuqsoKIkGmoW+PfTVVV9PsD8p6719TZqML58BPtWvYWke8Sivz3t2Nun/S3Zb93CQLLnmsz+IO0gF3X/vsdvXTKDq01i/mcorTJLaqyCsLN0kWlZnL4u4ytBVRVZaSmsM9nWcpepVgUC0aDXgNkLGOSvbwHQFmWjbpC9iZHg01FWc154slH6Q96TMclWZIucXOzyqG4zzsFbEtpsqjj0lQkEFhnmGY1ee+3LYUkkwlIESwIcYp0hCDLc3ymrRs3bnLm9DGyLOPkyaP0hn0bZN1LyNMBJhFcvvIRm6ubfOpTn+KLX/wix44d47777mM+n7O7t0tVSm5cv8lDD57m+vVb3Lq+TVmWDAd9No6ss7a2BlKgdI+yqlzlcYNIFevr6zz00EOsrKyAgPHemEPHNtm5tdfQrsag1vPlytVxClkgEXVhQ61BG5IkYzRaY7GYUZZTq9hJEsqqYjodkw+GaBSVWTBZ7FCoueOXKRgbb6iMRku7viZNSJKUylRMZ1PeeuMtNo8fReYJD//Qs5y5/zzf/tJXePlLX2N67SZqPCUzJVIp60bW2vbN9x3TSa+51+7vBGOqfYKh/dcmjDHG8xmnAhOexto2jInOqyGqIUXYr53j4s7pwye5L/y/9Zvfs15uAhqA0n/2NCR+vuvsxfJaW/gPZyoCUMaY/TQhGlu8/l1ZRpfN1Y8vHlc7HW18fxcgW7aWbUV4+/euPuJ7u0Ddsv4b6xevjbFxNkVVkQroD0fhOykTzHzObF65tNh2rxukrbsmBP3M1r5D1tZQG1Mn2N7e5vCho+4cGI4cPXrgmvjrzoPBIyE9TW0AX1EUARj4q4uhtjeFbU8iRB3vMRgMwuL5zRUGmabhN+u+XWvZYkDTxUz85k0Su1ixFsz7lpLU3zeQpO0g+J3b3601I5EJN67c5JWXX+XQoUMMhgOuXr8GW5qV1SGHRhv0ewPKsuL48eN4uThJmnEoB8VqLAMbwmlUyrJka2ubjz++zM5CUz78R0ikRCvlsiNI0iQlSXxguq3OHNCFl0P9f4T3K47FV2otvyH0X3/rD4wVwsOj4VXEQmKk2on/dH3XczYhLSEx2PB9e+HICfVOpHd9C0S774A+/MLWApYPENdaQZo6NzrdmHdoRURttUGXB0PCklzp9VTC8JlnbBDVX/n+vwLAv/jKB/ytf/4K03kV1soYw8sXt/n5v/MH/O0/9zj/8Y/+AD9w5gcA+NlnT/HrX/uw7ttbGBy6CvP2aZo952ojkXjYxmrnYkExckgL06rfk6j3hRuvcPO23flIEduK6a0E8/JisaCfV0hkKOgWE1p/HvI8Y3V1ldFoxPWbO7bqMd79UtEkp7e/YsYWX3cidLavtmbukwKB/1BXW+vV+E1KkogBLxYLV/cIKlVhhSGJwa7zQX3YfWVj7lZWbL71WMhXSpE4Ab8qveBpk2y0225qFTXr6+vcuHGDY8eOdayrdVepqoITJ45x6tQJ3nrjQ0hq2t8AG9Fe/cPG6vgxhn+da4jWtlieTK2A7Iu5+loUQvhEB14whTRJSKRE6WaiFLtmBoENFhcC5vMZKyt9jh45ws54l7KqkEaTZAl92SdNEsbjPXpZzmc+83P8/u9/js9//vOcPHmSY8eOsb62SVVq/tW//E2ufnTTWgCRTHUByQ4rKytsbGxw69YthsMBx44dZ2VtRNrXZHnOxsY6SSIZDobsjLfYOLLOzevbZFqHGAzr6lQ49zibAa52KzYBaGBsETEMKFdrK01z0jShWEhKAUWeUymbFbEo5qSZRMgKbRZUWlmW4Ap7VpUNUEbaPSWUTX2bpiMYpFzZukZRLpBKQC9jdHiDn/xTP8+99z/MF37zf+bm2+8idndJizlGFxitsfaNet/4CLQ4+Yn1eLdV2O1urN0MvcJUewUWgrr4VG35ECEQvSbAUkrHeIVTztT7vk0f4z1zp3SnS5Pfdfn35q2SIpLf2oqSLqAQvFbaqe9b4/DntJ1YoG2Zac+1K5A9HoP/PrawxH3fyWWVx/uDrbsE+4OuLuV6PJ4uehR7/FRVFeKU288ue3/h+2hoSZLU1uCyIpV2ZwuXCTbv9REItK4QqSDv9ajK0mZkA9K0toYJITCujpyPLzbaUCrrgmm4s1i5OwYaVVWhlAp+e2maMp1OWVlZQcgEIVxVSiFCMSMppQvO1Y4o1TEdxvjCtSIUApzP5/R6PXeAayTrhXFjDGiby9oLR94VQwrpDrQM6NynJTPGBIYbp3oDW9QlyzKmylVixb94gqDrvG/dy1GcPHYalOCF736X7Z1bPPPMMyhTBuQ32Z1R7pUkac6hjcNk2ZA064MQyKQ+dPG8bqsxxa6jwfqFV6rEIHjr7ffYnUyZrd8NMsVW1LWbQGArs6dpynyuKAsrUNg6BBaINIEAYLQTPiD6D15nUWtARSCtxOOXwrUTCfbuHpx1Icjrfm7Co2odtRsBDAGxuSIAACFCP1aol3FXQTY2fk5GI+Lv3TiEC/6zaQ4FlapBUHTU8RqpWhCP0FIgjpGQgmC1n/Kjj1jUvzsr+Bv/v+/xPz/3cbTmEYpCMF1o/vN/9CJffvU6/5+/8ARrg5wfe+QIq4OEvZmy4rywczL7+o6ojQdmfs3b2ysCl00f9JiYuvn5cyBcbIg2rvZME7DJCOhImSCShHJR0M9yW3ndgDLa1mOxcqs9C0phlEICWSbIc0kiUopZyWiQgylIhY07kvZguxo19Yi7iLunI11EP/6u7XYQM0JP73xsmv/9dmd22e/xO2oztHY82zLN2DLm5Wmu/9sKQBJhEoySqFJjlEIYG/NSVQqTx7J5dMZawkCtudT00oR+CqkRpDrFRzGkWYqQtrq1cW5B/qyElJ4tRi5FwvHjx7l69SonTpwIyiwPQowBZIpShkFfct/99/L2m5dRBkRS11cRbm/u18vuf+/L3lv8ZNhf2mBclnojbC0io0yohu0ICJgqJKIQyvJDVAVSk2cZd9/zABc//JCdnV1UZas3a1MF650xhu0dTVX1eeHlHc7fc57rV69zSB1mZWWFPMuhl1GJhKIs2Nnb4mc/89P8/u99gbdef4ebV7YxKD744EOMAlOBNgKZpFQGFnNrpXjwwQcoqwVPP/sUd50/S97LmM330Fpx4uRJxzsNp86c4L233+fy+1edEKeoqpKqKqgqZc+sSzVtnJsYxrtZOJ2LsQqjUpcsZjNGwyGnTp1ib2/M3k6KUprJdI4whnI+pd9bwxhsbn5/BrwSRyfWEO7Aq9EKspT+IGdlbYgQ2KxbUqBURa/fI88z7n/yATY2/xwvfOVbvPaN51h8fJVsOiGpSgpdUQhDgSLNMkSlSRQ2o1DmFSt2Y8iwZyR1cLfNPokA4YQ7zx59peaaRQiESMO5tjKItfzIaD/G9Mh9EZRBJuLHMUACl/VJ1N+3lSJdn+PEPUG4b7h2+45qV902CArCvl+dlvtSyGbVcsNcJoy3P3fR6fieGHzE7cY0tMtDxf+tdbPMQBy30bay7HfNqnlPV0rdmIbHLlf7rUHNvv382nS+S5kU1sC9KyFs9qlKa3su5wUpghJDkiWkeYZQElVWlnYnNkOdEKmVBVzmOCkTssxmfJzpOVLa/VKWC9IsQSaSclbWLqW3uT5RjEY82cFgwGQysQuIF+IEITuD03Z4jaR91n725zdGbnmec+vWLQaDARsbG8HdIn7BtoIwpGmC1qIR0CajlyCENWFLIQPSjtvyQZw+Y0Z4gY45x77H2mmMhREYbdhcP8TKcI2tW7d4/rnn6Pd7nDp9gslsQpamIGy0v6oqEiRnzp4nSXKSxKac1Voj0uVZsbqIgv0Bp/nQaGO1XwbJa6+/ze50SvnAD7pUfTZvflVWVpAwm0xnc1RVMZsv8BYD32QQIonCr33/gBHSMXAfPEokoLrLZ4Dx1boxtduN8IJMDRLCXGPQEK2BwAkmThNkRxYF81OHrQdq6LSC9XyiWQrrbuUJSqUq6rdsL+0EHJuq0vZdAy3/rmpQYF2Y4vWw9wYCaJeIU4cG5GnCd969xV/9h9/lwxvTsA4GEeYX1sWN/7ef+5gXLmzxa3/5WZ699xAnNofszupUco2+AdoR+W6M7TWH5n3+Fw8Ya0Ri7TIeMgWACFEeYPerA/bG1MwIQDmXCqM0xWJBnvfsZ/+o+7/VCmrSNGE07LOyMnBKPrtKWZZQFpAI4YvCByLfvjqZYEtb1qU9W3bFyS9iJvmHsYq0r66MN/HVZrjLGHN8f+MZYTWxiUwRRqJKRTFfWFptBKqqMCbBWxPdU/v6D/1Kq6TI85Qjm2tQKYzCKnGEB0u1q5CVfJwg1lp3374xhmPHjvHOO+/sC3oU0mCUxGioSgVonnj8MX7vd79h6zgldiMI4RQTMgIxHet24CXaH51gYlzGIhfPgHIVGaSwQAcwUtDrZYxWBpw6dYrdvSkfXbqKlILN9REySRAShsMBINjd26MsShKXnlQJG3Tcy/ucu+sert64xrvvf4TWmkObm9x9993c2tpiPp/xxBOPMBgOUGi2dnf5iZ/8Sb6Zfps3Xnnb8oTKVsGwwrhGSsVotIJxiUCOHDlEpeZ8fPlDzp0/6WIRBLdubXPs+AkQVkkwGCbc98ADvPLCW1y+fMVayo0hyXKQCqUrtHa1pYyhKhVG+YKlkixJuffee7h8+RJ74y2Kcsb81h674y2kTKz1K5GIxGa5qcqSqiiRGlDGAWVlt5A24IrNCgEkApEkpEnC+voqJ44eRWCYz21NL200GvvOykSxfuYoP/Inf5aHn3mSr/ybf8+V115H7eyRzuaoqiBzik8jgNTJAVSBtBpAOd6WCBlkAZHYvWnw9Njacz3Qis+QBRr7aZMKPGa/sG2Miw1qtOVlnFgxEO139tOnZTTvoOx6/gzUY27e1w5yPohWtenwMjoQC+zx93EfXXTEt+lpdLzO3j3eJzho99U1/vhzTPv30Vf2zyP+t80v/PddgCIed1dMTTzP+G/hNpuVN+x+MA5sYAy6rBDGKswqrdFVaa15qrIlAZSVfxeLBWVZkue5zS61ssLa+oYLk6jCuHZ3dzlz+i4Q1vVz4bLf3e76RDEa8YJorUOqWv85XoA2sosXLf7duy9tbGzQ6/UoioLJZIIQIrTfdnmKN0kXwm6Po+ughfgMY0I1c/9bfB9o6ysqJJXWnD59GmMM7124wIeXLnH3PXeTZhmySGzlbezRl1KSZRlnzpyxayAlMvGaCbNvfLe/rAlW4qova7h29RqXLl1iuqggG5JIq1WxhQytILEoFgwGA67evGnlcWMcOBNOOxy5RZkWEBCirvId/+IBo//TaxKFF209wjDhvuhB/3ICKPVHVhBplkUMQZqicq2BNzUFjNcw0vz4v7yfrS2m6gV9E24LgFVKV+TMP9l+Nx5ICKftrOfdHIA98G9eHvNj/4/Pcen6lEob27cP2ormE0YczfvDmzN+6e99jdOHB1y8Pg3z9nOv12l/3/Vf0d8NINGcT72G7nknQIQRCm/BaHbjBX5hHDg0tTbY+/Iqp3QweMG9zuaCsVoUfyb6gz79Xt92YQxZnpFnGXNha9II6fzg/ftbcnUx1jsBCm1LQsxk7kRg7VIS7KcpLP28bEwxg+xi1HH/gT4SuRcZG/Q3noyddi0N9YY8XTBojJEdeyT0ZOMPtOD48WPsTGb0R6MwBiklvbxnU5wq5QJda1eSZddgMMBreZtz8QKVjS0rq4p77j3PxsYq12/cAlyWJykbmtiD1vd2mZPalxV4NcrXFJDSuhBkKb1+n1IplID+qM9d993F2fPnKCpNvrnOxx9cZF5WnDpyjCtXr3Pr1hZW8y9JkgxjQBnvbKMZTxZ88MFHKAx77j3t7ky5fn3bpolOJPNiwY99+kdJhKGfC8rK8PBjj/G9F19HlyBJqVSJTCDvpZw9fYpDm4e4cuUKVbngxLFj9HoJv/+5z3Lq1AmOnzjOQlecues8FTbNO8YqQfb2JiwWFZOxrerd6/VYXV1hZWWV3qiPSsBoWwgyFcKe0+mU7VvbTPbGpL2EP/Gnf4G1lVXefutNyrJgZW3I3t4OO9s7jHf2+OzvfhaEZFGU9MoiyBKhAKynK7p2kZUkGGMVExub62weOeKKCCsqrai0JlEWIOa9hCKpkL0Esznij//lX+bFr36D737hD9CXbpLM5lAsMFqhDJQpKKNItHK7VqARLiOhBWVSRXvI019xMKjt4vlBNnJAuVtj7a0i+/dpF11ZJszH42jfu6zN1oNW9dRy6xGB5zf76KK1XTJhe2x3NJYDrthiAOyz2rRdwHxWJ/9sWybrkiE/ybjae2JZ23cyL1hSh6QhY9X3a62oFgvm8zn56gpFseDWtS2KoqCcL1jMF+Quy2NRFC4Ow0KCw4etJdXHY8dGhslkTJIU9HrWangn1x0DDY9gQ+paCPUHUiEagn8bwXWhUv+8/83HemRZZjMoTSaBYfpJVpVNvedBQpZlLfNT0w2inaWq/cKVsun1usbn52jdwWwfw+GA9fV15vMZ3/zmNxFC8OBDD7I3GePU/4AtlCKF4OiRo/R6uasN4Cwoso4/aZvODrq825lNtWu1hc899zyTyZTpynkX2CMdUq1cOlC48vFlECLy/bPmbS8gxxu08b5ampIwjkh89T76NaUFI7x7kX8jnj2Y6BOu70gPY4RbvsaI/ORbGQCdmGmMu6UGLE1gYNv1QXnag4eG0Gg/Ky8Y+X3s5tYQrj1RNTrUsPDzbuebDfU8hOHi9Rm+Mm9wS/OrUn+I4JTrX4MS8MH1SWi74eQkWn3HyC+Qf4sG9oOMeLzx3zWo2P82/PsWvryuAyPCTdVp83C1ZgTOvcTWe+n1fFE2omdBKx3O4Wg0YrQyAgRra2sM+gOyPEebSf3mTdNP+I401n6mHQBk2Wdo+tC22zjo7HYBkzZN9IkquoOa9wsNbU1h13ga98hagMFpsWbTmXVNyVJn9vZ7vbYT0mo79OXenTHQ7w95/9JlDh05EoR8Y2yB1vls5mg7oW0bS9Q9/iRJ6PV6jMdjVldXfc8Yo7Bn22b8WywWrK+vcebMMa5dvwbkNtjdFUb1hbW61uYPc3nXCuWEziRNSbIMI1yh0CQBpWzFeqE5dOwwldSYHM4/eBf9Qcaldy8wryqSPKesFGi3b7UNcAaDkdYSNJ3MmM8Xrny15SFaafaqCUJK0tQWW71+9QZHjtnir8pofu+zn2U2nZDpHCHsOA0VZ8+d5vjhTdIkZTjIGY8XrAwy0uQQ5aLgwtvv8NCDD1ElCVeuXOHc2bO2IrQQfHTxIv/8n/461z66YeP9sG7GO9tbDAYD1o8c4vj5Mxw5dAyEQRULxrvb9IarnDx7nGJesLe7xxe/+mXWVkb80i/+InedOw9iwe74Fns7Y6aTGS+/+jKXL10GCUpVjsb49+72lY7oJKCdcb3f73H06FFWRiskWQYIlNbW39xlPkNnZLlAZJIKzVYx5Yd/4Wc588D9fPvff54LL71CdWOLtChIgEpZa1+CRmjrfmb5pQZfi8TLFh74A7iEMnGoQps+tIXMEJ+AoD5i0fkQPvh8P+2J228rXOPfuhQffvzt9pa17+fYRXMtS615QHtc7bnG3++zYEbzWEY/2+OMAZv/3oOH+P++3Tgzn/8uLskQW6791Vamx3P37uTxmnS1sWwN/Dq05xR/376CIinut4MXGWMoq4qiKKBYMJ6MuXHzJqosMZWlz4uyIs9zsiwL1gxjbIbC7e1thsNh6MOP762336IqDZuHNsnzvHOM7esTBYN7t6O4Y++LGE8OmovdzkoVo1m/+B5JeVemoA3t2ABxtgtf/M5mnTIYUwUA0jUHvxH9i/ffp6n1nyxdFW9/n0LTy3skpJw8fhJj4PLlK7z51ptsHN4k6/WYVwXCuRIZq0ZEGM3d99wdsulYgaJ5CLt8Dm93GSOYzwumkxlvvvk2RkM6GFDJJOw171JmiZV0ViFPsLwEKYJw6113fHVP4YRVY9pjarvhiCDkeqxhx+j/FtGX9k8ZCTZ+wIGQR83iBHkTuonv7+ibupswCS9/m8YvVk6WAutiLcHU+zMEVPsnIsHdu6Yp5R2vHODyMQeOYRgTWKS1eogoNSZEnioCIpe0uM36/ggQteYnwzPxckarEfCGaX1BWBgRzlX9W5i3MYjIZc0DtOit1qBJ+N1h95U+9ijVO1+iKJwbjVa24qyuNcMySex7j4T5PM/p9XpIKdjd3WUymbCyssKtm3OUqjPfWQK/PDVpm/m0v7+T89YW9O/EqrEM/HT1t4zZdwkoB7XTfrbBxIw91T6Gbb6YU1YVfdl3rlPavTMR9k/cRqM/UYO8k6dO8tKrrzlXuJrx5VnGeG8PVVX1phTL185g6dWxY8e4efMmq6urNRiN9rZB2ExX0vD4kw/z4kuv1to9Idy4azC27P3fzl2t/Vu4R0rSPLc+zW5NrQbdFjg0WtmA5kqS9ftIA2dOn2C9P2Bnawfp0ph6a6rWFYk/PdrRQx8471yShLT/R1qXZGESpEy49M4FjmyskeYZ3/jKV7h+6SI9UtAFJII0TRCpZDbdZZwLHrj3Xsr5lL2dm6QyIZWSUa9PL8m5ceUam6eOc/XKZY4eOkQ2WmExm/Ov/tk/59KF90lMhtcvFOUCBFTzCfP5Hru7N5mdPcODDz/IYH3Eoc1Vbm7dYGd3h8Obhzh0dMO+O6X5/S99kURKzp87yROPP8hwMCCVKY899igXL3xgeW+xsBRR+7oVhEQslmzUcWBJIhit9NnYWKM/HLKysoYRgiTJwnuhrEgrkAqE0myurfL6a6+zvrLBuYcf5PBdp/neV7/F9z7/Ffbe/wi9OyXVGqMLhBZIYWzMXqmsgtDvIZ/hEmvhU652kKAFzDvOZTctielyJCO4/3oviLYgHt+/DCAc9HvXtWzsNadpyjDCMlO0aJ6ZWGHrZan2ONppXZcBifYVn3F/xZaWWMb0smPcZmwViBVJXdaauM99NMyYSOZZvtYxT+hqO+7/du+xkXQhKEVxLnjRWIQF6EVhXaJSrdlYX6dUlZVxjZU00iyn1++TpimDwSC8Jx+Y3rb4ZFnGYlEym4+ROzQ8jQ66PpFFwwv/2gUbW3NuQp73A1CIg5zb2kC/8WJrgV+YGGnGGaj8gsYAp50CTWvNfD5HCCtMl2UZNjdY03x7LHEgtnfNitv1GyRPcov0SFnf2EBrxXe+8x0m4wlPPPUEk+mEqipJstTK7lIiE8kg77HpamfUl4jpyYFEaR+qdkHeIKkqzaVLHzHeG1tGvXKKNE1sdpaypPL52oXVTCeJjR2RQlhriBfAobYMEMTeWhCO5FzhmHkYV5BsJbUu1Bq2vYxP/XiEuE3jc70G9sAE24TXjsTPx4Kz69vrFezzkRnX+GfiNa7vq8V6ty/de0/igPLQvwgMEFOFlKH7x2dwSsowXKv5shrBNM1CzILBuGwz3sKhw5jrt2GiudTz1gCuTQ/munhHTeQ0Hh4EKOECHer3CbE6zsqcsmPNazTpYZHPXuWbqaqK/mCD1Be7rGxGIruGdeXwaKB2BbRmZbTC6uoaSZKwKBYURUGeZY5W3F7It0M72D2gfb+/DmJuy575JFeXxhH2F4xqj2cZkGp/7hqbrelg6PV69Ho925YTdoOLgZfVqdcs7rJmlNi9LeHokUN1DE6kXEpdzQWfPEQ6N8TggNkeNzXQeP3117nnnnvqwPtwmO2+K8sCpUsefvgB8jylWKhQnNS33VZgxZq/ZWu57PK8zhhI0gSR2Ji/RCQoY6i0DQgXGlKRsDEasnXrFjt7uwxHK/RzG59VLibM9rZJTeWQFfSEtnEAxlpujHOrtNm2reXZOKBhhEALQSUlski48u57XBz1KcsFL3/zm+hZaQP+BUiZ8wt/4k+zNx3z5S99kfGt62xduQwiYTLeY2frFlvb28ymU6qi4KUXXuDHj/9RTFUw3rrJapbylS98jndfe9UFvSfuPbk9gKESkmKcUOzcpNy+ycfvvc3T3/8p7nv4QdY3NyiqBVevXaaSFZvrhxBGUBYlb7/5Nl/43O9BseDE8RM8/NCDDPMeAo003iLgBOsATrVDml7gdvRRGDY21llfX2M4GpGkGXvjCaPVVYywMRRlpZlJjSorMhSZlpw9fYbXX3uDp555hnzU5wd/5se574EH+O4Xv8Ybz73E9OauDRRf7GK0QmiNTDWqqhBG21TxERhXuFjQxGZ7tHU2lp/jNugVQtRuYrQUJK02utxmfDvxfV0aeX8mYrei+Le21joej+/bKy/jBBvGRLTf1Mpbf48/kweBr/Z3cb/+by83+vHGLlHLknn4+738GMc+dIGItluVv7cNIsJn58bbvi+eR9xH1zy72j4IjHSBsVpeiNbVfVuWFlj0DWR5zqlTp6y7qXYJTmQavF0GA1trR7n6a34dPd/wY9jYWKffHyCEdWm9k+uOgUaoKKt1SHHn09smSRZeKOyP7I8Xpr2gbSQXb6b4+zgNbLzJ47oYaWozWXiw4TenDwTyAeZ+AeN+2gcQLHORGMqiZG1z3ZqOb+7w3HPPMRwOOX78ONs7W0HwA43EbvAz589ijK2Q7IPOk2R/+t8u7VsXM/SCsNKWgb/55luAQGmD2ThPIhOU1hRFGSp1JjIhEfX8ghuz8K5PNKiZcVJte+M2b3CSp9gfQRG0Ov4weMQfhFTfbi3cBl974Sp3G1PfEyt6gvag7jsMKxpfnYmp0VPUdzSkMBsRNGciSVp31jd77amJOjD1wtVPRGOuq5E4S5y/z6cTDprYppAfz8kDMd+3VXy21ry9Hu65IIS110HEr0WERallOxHNa/+a151FLjfxexU0rIQiqxUFXbK6/63f77GyMiLPexhtbE2G0YgszWxhscZDrfUy/m3ufy+dl2eSIl6fGGXHA222taxl0f4Qn69opfzwhGjSxfixJvBp91iPM6ZnItr/HrUPRyPWRyOktHvQP1lnvsHlVdIYrdHCAuC6b9ejA3vGGEajFbQxzt2lZoSWHyRBcbPsagtca2trzGaz8HkfDXQfi2LBqdMnOHr0CB9fukaapGhREk6yECHWo82ULa+Jv6PeIy1iKNxn+4zjBYk9AzbFo7KgQwoSIBOCrWvXkUJzanOTq1euMq40lYbZdEoxm5AJzXi85168RpvSZq8yGq0rN2d7wqWQwWUXR8PTJKUgYbG7zQvjLW7cuMZ0b0wqUspSY3qST//kT/PMs4/RGw25+/xpfuuf/jpXLlv32SzPuX7tKh99/DHbt25xudejN+xz69pVTh09wt7WLfpC8MK3v0U1m9ksT7jKxM5yJRzoUVpTGc301k16a6t8ZW+Pa9ev84M/9mMcPnyEzSPrXL1yha2dLU6fOkO/Mjz6+GPcuHSZ1777EpcufMx3v/0dVoYDqCqSLLMeCmmKMIZEuHpJxjhFibffeuWZ5NChQ5Y2ZDlCSF548SWefvoZ8n4PhFWATXRFoTSZgD4JvX6fShuuXbnKyWMbkKYcvfsMnz71pzn52CN85Xe/yEfvXKCk4OTxY5w+foQ3X/4eplyQGIU0gkQlSOMt0a4uirQuVhIv6Dp8pF1x3KD0afJ3IbDaZeEoV0R3BaAwJDIJ6d5DVs0gYJvofhFAfZdACj571hKLrh9DGJtTAHlBvCX8N0AKHe48kQLsIGVJ3WYz4Us8fs8DY5pSP98xlQ7g4F2k9s2vpfjuUgJ1yWVt2a19LVNqtJ9pj6P9/DIA0ui3pRgSOP5bWJfTNaz7cmUMVVmiC+v5UynN1tYWvV6Pe+65p7EG/n16y4bn5WlSK76l/A9g0fAvzWuqej1bbMkKiHUVcKVi8FBvzhgpxi+pzWjbixq7ThlDiOcoywofu5CmCX4jVlUVzGbe9OM1bB6xAayurtqXYaxQ7jm/0dbXOJMpStsc4Jvrh9BK8Morr3Hzxg0effRhFCUkXrhwc9UKIyTnzt4NCJJEIBMQ0gVzS5tlw8qsMUFoxjbs08oKEFIym1RMxiXvXfgIjWSPAWlvaAlrqGIKuHSj/oDWud2dAGWs1ijU0DC1VaIhNzYIRy3INQWyGhOYkC7VEEwjMdELAKIWbr0g74fejP2w7jvGCcS+N1HfGUZh4uw5pgmYhBeUHSG2Y5IIrewG1sa+90RE03c2EhH3ZcI+8d81V8ALiiYc+LBapiVqunk35PnQQC0Amda8AzgCX/swOj9ulCIaPx0+ry3tSJNUmtB+AJMBhDStRjazUf1e/TiNhlQKpDHWpSSxKSgrY33arbuICOuogMoY0jxltDogSQXGKHRlWFtZc7n57Ty9E4Mx2jJ811+9hl4LF9GYFhYKHuA+psgL8w3mkIbZmrAajkZQa81in2Ah3L4PMoPfhbYisZdnvWWhLiETpYKlZhZeaKlfm6npgTvXXiiW0mBr2bikFEoyGAw5d/Y0ezs71vUFw9rKCGnAVAajXCyAsc8ro0lMYs+c8XSIsAZ+fqPRiGHeQ5UlQimkVkiTkCUpqUwpFiVKK5TLPxsLMI19qG2qWK9IWiwWZFnm1seBfqnd+UxQlWBtdcTDDz3IRxevgXZVqeUcm8o3s0nwbHYCV/EWd85czYrQtWmcAyMqR4c8vSsRWF7XzzOMsJYHXVp3P20MEoMqKpQYsHftClevXuahB+5neuMaZVGiwWaYKgtEtUe5uOWyQTlLoxNYZXR2bfJxwGVWsqTUZhNEpFTlgmsfbaFURZ5ZS0Yl4fyj9/Hsj/8QSiiKcs6jjz/C3X/j/86//le/yXPf+BZJLrh46QKXP75MWU7Z2bnBSK3w+c9+jqoo6WcZWSL5+MNLoEvHMxRJmtjsSiaqmyAEGpuGdrK3R1kp3n35NYq9GX/kp3+SwyeOcPepe1kcXvDhBxc5fuwEeS9hc3UNoRS6KilVyWyyhzHKuntJSaUNiYRUCFfT06aQDeo5t0xJkrO+cZhef4QQkl5vwKvfe51+tsKjjz1CltvaUT7VvtaSRQXkhrN33c3rb7zGkcPPYvSCBEPWS3n6hx/n3ofP8/J3X+LrX/gaH37wISnHeeiP/jGEUeS5QM3nLPamLnanYjIZMxgMGK0MufzOBYob25ZWGhDaIJxbnHGJQ/zuswpSp2HXkOAEY0fXPJ3KpDt5pnYz8jQg8dTdCJSLhUucQFKJqDCvRTykMsHIxCpjlZUnjNtvRngZwJ4X4ZWv0rqHCWPjpLRXl0hJqDYlIBE+oYoHhoGQEXNB7UCi9ZwwTn4zDliLsFZCWCBrj0Hq6oIJwLqgE2ijCHKN368xnfQ02p/xrnTnbQX5siD1/VYQW2NNSCvvBBBHk420n495cdsaswyQdSlO4kv62F8n9whpQW8qE5gWsLDJDl57+y12tnZIDGyubtDLUvYmY9bW1ymOz22aZ2ETCZWqYgHk/b6TQ+z7TJDoSrsaQXcGIT5R1qmyLEnTNACMECuhrL+pZxZC4DRHEp9dxmuZGqanSJCOcxnHixlvkhr52c3s0ZYHIERI3geL+3Z6vV4DLM3n8/0v1wkyCIv8rSbHMBgMybMe8+mCb33jW6RJwj333M3u3m4IsLZ9WSa/vrrO2uoGSnktlctpbCIXBK/rjgSJWpu/X6unndtUWSo++vgqe3tTFouS+ekfJ09zMFAUVuMrZGo3nDEuyxL44kBeSLHCmXGEoL6CIOQlWP9Co7HZ+/bHwNSCfQQ29vlAEYSAGmzUAnpDeo4ebAq+TbG4pqgeQDWfrdfW3axrAc7fKwCjtAWOUcGtzr69UFpP2q5jBMza6+NhiXHztksaS5Bu3nSveQ0uWv3idpKLkPTvQHggiT83MUBy4603HgHQeWZoAskMDCPMQ0gXkWnXLzihCVuo0J/ZVFoNVVUWVHlVy/N4IdnRCJ+lyhjy3BWE6+fMZlOm0ymHNo8AmiSVKGVBipURdcNiI4iYmpuzMcZpG70w6WOX3DkTKd4HOhTQCi/NRy15ty0T3pFWwmXpSMjzzCkw7Dm3AvK+Xeoe9+5wzlUmvM421KuVNUYLhEjqNlrz9cxWYjXtkCAFJMLw1OOPIKVksreDVopDG4dYW1ljZ2fbxp7JFFsVTYdtZelUTI/svwZXj8jYKuBrayvMJ1P05hqJtBZJKQR5mqOUd7Wod6+ddpNB2rW39G5zc5OtrS2OHj3q5uTPiUvxaSRFUaG05pGHH+RLn/86RhtSaWPprDScIIwPKqaelzE2TsKBC22cll57txCFwgENXVvuq6pEJJJKTwOv0Uo7oGe7kAKqwlDOpuzeusXLL77A6ZOnkKkTDiXs7G4zn07IUmwcQWnrIBntXYHqvSccABFaYdCu8J3dg5U0oA1V5TLBIDGJRPZTHn7icaqyYjGdYTLFcy+9zNatWxw+epjRyhCjDR99eJGbN2+iq5JnnnqCY8dP8Mobb7N14yaq1+fY0cNWeHK0tFIqxJIYv26mpmNSuKJ1lWLn1japvMTv/7vP8siTjzEcDJiMJ1y9coU/+OgL7O7ucvPjj6nKAlWVlj+i3DnWCJE6kucSd3iaIx29ieh8luVsbGwGga6qKmbTBd/+1nOcOX2ao0cPkUlp9RnKAk4jwWhbgT7v9bhw8UNOnTpJJkqMrjA6YbiS8yM/8cM8/dRTfHTpCm+98S472zv0R30uXXqfqiwY9HuMRmv88Pd/H6dOnWJRzNnb3eHW1WtsXblGtSjRZYkuFaYoqcqSoihdHRLlYk+tS8t0OiOpND1pBXl/j1fcpkYjtN0PRmkqZau5Y5q1FYxKLHjVxr2/tKYoWrs9a+uaSePgghewPQU3BqEd/zKC1FVlNy7Fs8JVEzOOnnr2ITRGunG6oHkhpFP8OaWFp3HCWJdAx6eDMhpD5Wm5tMColg+dAseBGlsI1LkXtuSS9hXLkPHfbcXbsr/t0axpV/y3FM69UYjAHmiopJouWe1xNS1TTSDT1Xfb9atpFRZhTyBrl+csyyjLgvHuLsnaCGOspUNWhsV8jhQ9siylqkrmxYJRL0Mbxd7uLtc/umpTRmcpaZbRG/Td2TQMh0OOHD5Mlv6vnHVKCBH8tuI6FLF5Ks4QZT8nkVZs/yLGwUDxwrfNSrG7k13b5ouPN5AHGLd7aVJKm/bLVbjVSjV+C0gTwcbGJlJILl18n/fee5eTJ0/Q6+fkKqVUJVmWMez3wMB4POH8XfdQVRaUeQAlRLMi5u2urs1eVTZV6Lvvvms3htLIjdNWE1SWrUJHdp32uyA4pmEbDejb6+a9tr/28vPCZa2V8IDJnq/aDcsLnPXZd9pW4zX5kUVFBDGW2sff9x35nMZrgDed+74JBM9rBv1a1bjCC9d+UDWBDGoXY8eutCJzzLNtEBRY4htGFDRANRQyjRXzHYhobUVDQBEieq6h+dnft/c79mtUa7XrHrzoGaGf0DeIunqrCf9xoIiw5vF7d6ttn/dfulgLS8wcAdfG2v/d+gT3FAeogsna+GQP/uemRVMpRd7LGK0M6ff6bG9tU1Ul6xtrpKlg7hQM2rkjBP2bxRL71s9nhnElOeIFrWmB8EzQdPArx9Q90BA1IMuS1P6tFUIrpLfoWj1S0JxHS+2EX+2aafUX30jz/AuSqDKxt9L4d2XdNX06YumAR5an/OD3P8XDDz3It7/9vBXsqoqHHnzI1TRJ2NhcI9JR7us7doFwi4UxwidF4siRI1z6+DLHlYtjkEmwdE8mE+eymodkCV2XV+wopTh69ChXr17l+PHjkRW76U7grdL33X83Kyt99nbn9PsJZWVsRKQpQc8xugpZCi0AdO9Ql/iYiPgMIUTQ0HphGqVIjCaVGb3UCql2r9auJAhb4EoI69aVpRKJsO5SZUEeKbj8/737mqfBzXeNoyt2zYxyArL7LBL2CZmVUqysrfDx+x+QGcHm5iZf/fKXuXn9Bp/+9KeZ7I2ZTaYMBwNu3brFYj5ndWWFX/2VX+XNt97m33/284xGQ06dOsnm2lqoV+V5YruiufC0SrpshoktFKu1YW93Qtbf4XO/81kW8zmVU36p0rn0huQu3mJRv9c06RZHau8HbEGxRJJmKUjB3KXETVPNYjHn8uUrvPvue6ytjej180CnvbLT/3vmzBlee/lFjhw9ijGGNEvQ2tDr5xhjGK2OePCR+3ngoQcoy5KyLJnNp5TFgsL1ubm5jkwElNBb7bF6+gjn0icsnTNWxBZB6rQgTSmFVnGsa0FaGRIFZelc0suSsiipygJRKlRRsJjP7TiqisViQbFYUJb23/lkSjGfI7ShWhQsZgukFujK1k4x2lvgbMpTjArV29EG6eUuYx3UtNIIbd3XhK45dxG5gRHtWS0MNUU2wWMDY+uEGFwiFXeHNfhKC+69RVpIRGJ5oQaoTAgZ9GnN8ZZakewL/u5ybfJyKDTdopbJhjE/Wub25OXDtidODBja7d7u6lKmd82lCyyBXVdtDAku6Y+orUtSCPJBD2UqTLlg0EuZja3L66wqqCjpDwcM11eYLKbIPGE2nzPdG5PJlHSwYt1qpaSYLRBC0l8ZkvRzbu7tsLm5edv5wSesDO5jDYJw7rSocfxEvHhQp2frsmT4q/2CYtDgN0v9Ius2faVy34Zf/Lafmb+3jRxDBpsI8MQvXCYSrSSrK+sYbXj+289htObBhx9gb7LnIvMT1tZGDPoDikJRLBRnTp2jKMqQ+ktKW769nWWqvQ61tpzGWvn7FosFi/mcDz74gKqsmGWb9FY2G65hFnHWLgJBk+u1p9Hm9DKEZ7RW1gqn2woyAShALC0EolGrmSzTxPuBegHVhPbq+1yb7jYThMSmgN7UVZjwKI2+fdeybicSlOrxenur/7kGSl549Gk6ZZJYC0F4vBa9hVW/EmBVDJjiefq+RW1tcwtN478CB2C65i1oRnlga5sQCc4iXgUH5IJgS+NzYwHdWKPdYPvz+yEIvpH4LqyDjzfx2wrdKrxPKVyNASkRoqLnMkhVlUKIWjkRmov2v9cgC2lYWxtx6NAhLl68yGw2Z3Nzg5WVIeNbWyB8JiWBt0C4QuWNy59nKQQq6OzsJLwrlQm4TUSVfCPmQeqWwBF2nCUVgTQp0lUo15VA6BRJ1I7bWdK9Y2OMza6F3zmGRNjiYhhXYM2060j4zDYlSeLcUrWrMItbS6FJUyuQ572Mw4c2ufe+e3nm6Wfo5ynf/ta32dm6zt7uFk888RTf98xTXProEk89/QR5L0V48BRtQW/hEUbsW09jhMvMprj77rN88OFFVGUQIgkALs9zdnd36/TlMQ064Dp69Chvvvlm2A8y6WbSVVVy9Phhjp88wu7O+2Rpn3GxoJjPqBYaraZg6tg9EegSJELZwn6yBlLG0bdEWEuUdGdVaI0ytkKfUDYLi9GGSrlUugKENCzmJSZNrcUiSXnowQdYWRny4kvfY+HSNseBuFVV2XPsXC7CevuzrQkFaI3Fppa+aVxRwogvCEGWZhw7ehSpDB+/f5GvfP6LjHd3OXLoMO+/+Q7z+cymN64qxru7zOdz+v0+/+Dv/33eefcClQZTaXa2ttm+fj0orKQQQevcxbNlmpImOcgESHAwl+2bW8xmE8dzbIKNROOsR17x4OOJhAMpGpFGZDPi3UmSBB4lpCRJE4YrI5TWNg1+pagqw9mzZ7l48RJvvPE6Dz50H1nurJXUbdZVmQX9wQrvv3+Rs2fPIKvKanaVFZRzmVl3agEk0MtyeiMLXOze8QWINTl9DIbUGJTPTqUc/bEzdCTSNHiK98yQQjoXwlpJG+SlyrkNmnomfj9pXVlX7UqjixIqhVqULOYLtIaqKCkWhf3/fG4BynzObLLLeHePqigdMJmxcEV9VVViqgpTKXv+KwV+vyufgMQCYIx1EUvIkEahsYA+cbEWBusqq4Wlddbr0oB2PERIKs8/hI37UdrV+RJ1ohchhVNGev6WNGTEBp9vA3d3j/e+iYPU/Vr6NW8L++FNtfZ/2/qxzzMG3Jhlg8bEbcVy3TLrRpsftflnfAlEkGMRwooo2qCqkvlkj1wohqlkPe9RpAmLRWUrgCeSE8eOcuz4cRIhrcW3sNXE8+GArJcHFzsf/P7gIw+zefQwX/na17hw8YPO8bSvOwYasTbGa/x9gEj8exvpxVmm4tRcfuH9wsXFmmoXrCaD8u5DxqjgG+2v2NctHkPctw+KthqQlJWVFZfVJkcoFSwhIcWugbX1NYRMuXnlBq+89D1WV0ccPrzBje1bJFKyvjJic23F5lTXBcePnmBluMZ8Ng79+E0V5h+taXNTO8HOfRcjV62txubDDy9x8+ZN5osF6t6fJRMSpRVFWbpCZrYZn2cIcO4t7QPiRNoIfHiZ1Lp3OEHem0mphVwvCVvFxn6wZJzw7DX19W/xLFt9R9/XfdcgpBZX7DMeHjTaDnRcBOIVa168/B9cmJodW20PIgoY9SOqxf7gIIpg36vz3xmaAfF+gAYn2MWrQajqGa95jbukp7fRvFuLGT7XgC8GOyJ6r/Wai84190lzG31H8/Q2Dm8J8QzQZ4tZXV+nWCzQRcHGxgZpaphOJ2xsrpOkCWtrazZ2Ilp+bwmtVIVWFSurQ+67/x5eeeVVbt7cQkh45pkn+d3PfwFpND5c3xY7k7ZiuLM6tBmNF5gC+JI2ZNMLQaAI8UxSRr7AEkHPAQHXdlgBt0TGCqe6tM9kMkOpAimtxtbOS7lzDElq11iGjePdSW0sl8/+4ZU5vV6PLMsYjXJW16yVp9fvs7G+znA0Ik1TV0vgsC1etrFJmgm2t7a5fOUK3/3eu7zxxhtsb93iyScf4xf/9J/g3vvO8eBD58kHPcaTMeBcKN2GMwaM8FqzJk21qy4DUDp+4ihWRjKu1oK9J8/zwCuU1jZjk5ANASpm6l7QHg6HVJV1KbHZsppuDp6WV1XFYGi478HzvPXGuxilKGZTysUUtCARysZ1eFgXWUWsNUMHWinCgbU1E/xltbYaY+z+sMlFVHDbSLwlXyn7t1YYrVhfW+H4sSNcvXKF2WRCbzgKcYHesmfrXwSJOgjSxtjYQJPqkPXazt/yLV/1WvL/Z+3Pnm1L7vtO7JOZa9jDGe881HCrCoUaUAAxEQAlShQlihHqkNtSs00Nbjsc0RGOsP8P+8GPfnJEh5/asiM6OiRbbrltqSWRBEmAoDASqEINqOHWeOcz7r3XkJl++GXmyrXOuYUqhRZZuPvsvYZcOfzy9/0N359HRQNbYXji1tM89ewttDK89otXqU2Bmi9pVmvufPQRs9mMvu0ojKEJbT46OuIHf/EXoAz1cof1akUB3Pn4I5QTEhPvJQwj7q154S5TlPKfLlC6kL5TBR5F13QpXl061gVac4XXEnpTlqWEpSlNrLXjgyyIlPVTIhltRPEvqpKyqmgDw2LbdXivqOsZZVnywQcfcHR0xNbWHGXK0ZwbjIyea9dv8otf/JyLl66glCi0WodwMGXkOxUYx4K1WGqm+DA2og+rIC+1V2gy0hq8FPtT0YofxjOsk+hDtgbQOgBdAa9J1s9NJn9Vum/0xmkVksmdD1XVLR5Fr4Su3kfqZOfx1oZwQfF0uN6ivBfA0XY472g3a9r1hr5t2ZysWJ2ccHJ0TLfacHp0yvHhIbbtaTcbvHW4vse1DjoJ2XJWwI4OeXieDkUvJDm9DTJTQuGU9hTKSR6Vl7ZrHwo0Kx/kUC8gw2fyHZJBJwcPIiPGRBBRbpxnDM/3ifMU+KlhPOpw01zjeH2uw/oRfecYAE115lwvzn9/3OcpSPIRwMW9TkUdTP5bHxzimobaKbbKiu2LV+h3LE3X0fieqrVs7j2kLivKoqBYNzTrFdQ1u3vbdLZn0zS0m47LV6/w4jPP0Dn4nb/+N/g3//7fnum3847PDDSiAMi9C5FCNfcW5EfSXzNledph00GMz8rpzOLf6/Waup6hlBldO6Voy8FN3v4pyCmKgq7raJqGuqoSLW4sXIJS7F24iHPwkx/9hJOjI77y1VdYbdYoDduLLYkFrTTOerz1PH3rFqfHa+pZMcpZic8Vi+9nD6HKN9emaXj1VeGPPy730bs3cGGDGzZxsX4pYlIjJPU7n+wTEBCRsGx48ac8GCWzcCbFNd47D9jxA8jwmZKb7oJs4Cr/xhNsv9LeqDSreMdBHc6aM1GAY9OGZ8fOP/fZKsahR+FPsLyH+Zkrp9Nn+GkfjM+Lnz3xXhm4SgBkeK8xeJiMSQRNDM+b9unw3pO2ja7zQ+hU1n2KIBQjh/85fTzyWyWFL1rZBiv99nKLxXzGZrNm6/Rdbt68wf37n9B14t27cuVKoJruhac+80IqpbC9ZdOsuHr1Ejdu3OTGjZu8/c7rvH/7Nn/rd/8mv3r7Hd548y1Z715jFcS4bks3ansuV8x0rWVITSkXNjKZM4UUS0EpcLYVCKaj0icdrABfuBCfLrJoNpuF0FJPUSrmiwVVVVGVwnS33FqwvVxQFSXz+ZyyLNna2mJrawulFPN5yXKxwOgSD8xmc2azWWD3W1HXJV1n6ftIxFHRdT1t2wNSrfWXr77Oo0cPuH37Nrdv3+bhg2OqquK3f/u3+f3f/z1efOkLXLu2R287Hh0dY20X5Gucb2HuOI/FCohwMku0FpARMq0Bx4UL++xsb0tIR9vDUuRsVZdoY2iaJoSTDWOS7wPAQF4Rfl8ul6zXa5bLZZivZzdrCT3qefnlL/L/+x/+Lc1mxXxW0a4PMRL8gctyMya4kxgC5vFhPWlRqJVJceveOylqpcTy6j30Nng+zMDC4r2EFcSaJGVRcOniBX756i/ouhYayeuICe4DHbAPRfgKZrMZ8/k8hSafnq7TWmyaJnnyN5s1m9MTIRXw8m7XLl/i6aefBqX55OOP+fijjzDGUAbLurOWo8OjkOchYTERJDvrqOoKby1927HRG44Oj5jXMwjWaTdRruI+bUIiaFS+jSrxGEnq1RI+GNBbihl3SLJyVZX0fUvbNkO9JyTqoCwEZCyXS1ar1bBPBkBa1hX7Fy7wxRde4MLFiygjCt56dYS1PXVdc3R0zKOHD7l8+SJVABrDXMiUS1NQ1XPu3nvA3t6ueGeDycXoAoJsMIVGYdC6RCmDxyZ5IAUOxfyivcL4THQKsghAw6ccPsV4/xc2Y5X2qtgnCvBaZ4ausJfEjSuSyoT5YLRJ86rFQQROaPEOFiqcpyhVpL/3AVyJgUk5F9jlBBD4EOaFk33dWUvftHSblnbTcHp4yOpkxfp0w8HDRxwfHHF6dEy32dA1LU2zoWkbXC8hYMp6fC/3612LR9YZ1kFv0c6ncC7p1x60w/se7yN1/njfyA9jzup5MOiUua46NU4PMmKs/OeG6+l1+THoeCZ4K8e/TQHQFERMdej8u6kXJTfACObUSVVQSoWaMobFbEZRhGLXDx7ReRXmieTbGBynR2tOvacwBWUgRfIKfGW4e+8BpjCSG6QVdx885PsnDbtXrvOtv/XbvPLiS3yW43Mlg0+pxZK3wAwxc7lLSwZ3QJXnIbL499RyFQc7H9y6roO1oxjldzzOnZQPTk6bmz+rqirWp6tErWiMkXjM9ZqqnmFMQbtq+dEPf0hhCm7dusVxe0RVl+zt7bK1XOLp6JSlKiuuXrnGatVQ+SK1wXuSpVQFxS33Bo3anCvJDJOq73vatuOtt94WbuQLr4h1xVq6vpe4Snm5JLCUi7GTmet2GMGxohysLijOaZcfNNPRxyGA6bzPg4Id7hGBS4iLHxT4IQwqKtGprWp4YFLeYz+NtP0pHIhvSdKg0rMViUUpohsV5ogngGiIdEqgZFGO8tozUBDH1TuP7W2CTknUJKabSZ+jBmKueLbP3++c7vdZKErqOZ/uEV6YIYRMDcLHj8FJasVjQO8IqKhMOIZNIB5lWbC3t8eFCxf46KMPsW3DNR5Q1zO6rqN3HdeuXuWpp54c2qRiblfsLbn/6emKi/uXuHhxn29+85s8ePAxf/Ld7/LMM8/xv//f/W/5V//D/4ef/9UvaBvL6cmGpu3xaJxWgfFseKfI/W6yrRokbKIoSgqj0VqUm+VyyWw2Qwflb3t7m7quqaqSqi65cGGP2ayWKqpVwdbunMVikUI3FwtRFL1TOCcbd1GWOC8GkrZtUDjwiqZpQ9JnnxTng0cH3P34LlVV0TQNJyfHEmriPY8eHtF1PX1vJel1vWa1WqG1pus8x8cnOCcJptb2GKNZbi35xte/zde/8TVeeul5rl2/wLXrV/C+4+T0UGiwkfsbXRDjGAPeEk+EG5j+BlgaZ4SnrEqu37jO/ftHtG2bZHJMkI8UtzLGZ6luE5AOh3OOy5cvc//+fQFgZGU81TCPlYK+23Dr1lPs7GxxcO8ey8WSk8N7kkgdQLMPG2Y2o/Fep1dR2b2jFRA8VVVLIbYQzqKNQaWCsB5tCqltgQ9hgnKb9elKCuGVNacnpxhTpMJXIqsCwPEhPCSFyileeOFFnnnmFv/u3/97dGHY3dunLEtOT0/TfvXhhx9gCoPxA9CYz+fcvXuXHsdHH35ME4pztU7qz+gQvlZWQgEbDSllWaUxsE5i4B8+fIDzlt5DabTU/VFBZoV8J+1EkSqrmsLMBKRhUNqAMgGEKSlSGhTiGNYhwFzE6unpCVVRSB9rCQn0gSVuNptz7do17ty5g1KaqqpYLBds72xz+dpVrl2/zo0bN9je2UYrRXO65uHDh8JC6TybzYZ79+7x7HO3qNXiXCNjlMVPPvUUr7/+Ol//xtdwkYAOhbdBJ9FOWMZQaOUCKA+KnvYhFCvIMBVw+PBN2k8jGIjjnc1IdE/IrYpz1CVAohM1JGns0nrxsQ6OCs8JZB5K4XTQj3yI5kibt0LrQkI+o9EtGlcQnj2f3i/eT6NKLbTXlBSLisrDHMUFbuIMOO1DMjn4rqdvW2xv6TaOZt1j25Zu3bA6OeXk8IjT4xOOjx9yenpMv2lZPTqkW23k2k2Hb1pcb+m6BugBi7WSX+WsT1S7WuvE6EU0GGUGjSh/nHcoI2H3igg8ZH6K4WqiNwRFJHmOzgnBj2F40aBcxEKOaYzPhlVNPe5To/sUUJyNehl+G65jmCPxOite9UqFsddFKNZZoFQhXmjv6YMxIOqLxgcd2XtU06O0w/sWr4KcMIaPXv0lq5MG/51vMSv/E1cG7/t+xOKUu32MkthV65yECoHQ8bmxRSoeeTJ57KwcNOR/550tLnlG4VsjtBmL2gXEFm2tsgBlYWktLlyLJP9qpSgrARfLxVYoRCgJbHu7e9Qe/ur117n94QfcevopdGUorObS3i7XL+xhSsWm7dFes72zS2ddMOJIFVdQEnNrIrnlWZA1PsKiCdZijyRadn3H4eGKR4/WWDRcf0WEmlMhbEGHystyrfN+qJshmnv+COkXf05MfpKOEIskpXCo/CeCQA7WmhhSk6siSbhCCt9SYeEO0CI1kOhKUfiRUu/1uP1juHRWAZLvdbLciTVMpWdHxK60RtlonZfYf62gKAzbO1tcvngRUwi9pFYk6jfnLO+8+57EfWpNWUqse9+LGzj2pXdiDfdKCc1heG+HT0Vzot5Oeovwv55R8nY8T4Mo1PEZ+CF1XsV+Cr0b9iiVexLjOQm8ySajAy1xZGjSRrjbdVCkTFFQGlEoFIqiLEShLA2zuma12fDh+7dp1ivat/+ML339Au+++zbr0w3Pv/ACX/7SF7h4cRk0JE2kpTZaJYAHjs3a0m1bnnv+JqerQx4dfpM/+9Pv8c/+2f+D/+K//M/5X/2v/wDV/gOOHh7wxhtv8st3fsXRZo2jpCxnLJdLqqpkVs9SiMvu9oz5fEZRFlRlRVWVLJdbGGOoS01VDqQNNrjevfO0nWXTbNI44iVPar3e0HYdqyNhrluvV2w2wXrvNJuV5ejkmLYTj0HbtZycnrI5XWO89Okmxky3DUVR0LY9bdOmzQxinoKhDOGX3juMKSjLQpLDLews51y+vE9V12xvb7NcLrh8+bL8d2mX/Qt7XL95je3tLVarDaenp2yaDptCfxz0fZp3WimsFlrV3mlUD6Y0aBejBuVcpTXGa27cuMEnHz8QFiQb2J6wlHXJer2h94Ge9HwsG2TK4Km4fPkyv/zlL4XT3dvJyXIT5z221Vy5cJmnnrzOwzt3ULoGXaOUpSwUTdekYoWjW7hssQWAERmobPBYtE3Yn5SjLDRFoSkLMc73vaVrT8QCrBReFShfAgbbKeazHVanltPjnq4Ba6SwHxis16EAnsEgTEfKelzveP4LL3B0fMJq3VOVFadHx8OaBdbrNX3TYVQVmq2Z1RXOFxw+OuH555+nWTlOjxqUCp65WNtJaYqiFjCAyJU67KVNJ3lRne1YNxvKsqJAB8a4KFtFObVILk5ZlFTFjFotMLGIoZHiglqpwHzm5O+ywGlF7yQBft2uwPeoxgENPYZOW1pj6TolzE/zBU/cvEHf9Xhv0EVFVRuqeo530G06vIXa1CileLQ54P79hzTrnmbdsD5dcXJ6gsWFPf58Vh/vLYv5HOcsq5NTZvOZGIWUAqyISRuVcI9XgU5fi9xUE+ysQlhYlLPJgxHFuB/vXXEiWm9RRB0mMxCpAEBie12uXEbygnBTEfSDAVbLuMk0d9ldQEWSi2jwHX7Axv1HDZEBg50heGNiG7LrIqCKFLVoUJVBVyXL3bnoa5PrIxD11tGGBPf1as3R4SEn9w84fnjI6viE1cExJweHtOsNtmnp16d0TYPrenxn0dbhehu4rdaiMzor4YlePEK9grWxQsfutRhmlZbKJ96j6YM5Soku5aMXTuHU0O/nheifV3tiOs7neT/gLLvooIvFz3F8h/wNd865qMyo4oV2O+oTWlc4nKzRkIQPYDSoGCqsYptsGkfvA/GT1pJXg5bcI99j7SmucBSLms9yfK4cDa01bdsm5BY3RaPdRJ7HCTwgurwSdz5AMRwr94hMLRD539FDkntFkmtXm5BU6UPcZ3Zt6HgfNuzIOuKBsigkbGOzxhixIu3vX2B7axvlPH/63e9ijObZ555l02xYLhfs7+5Q1yFm1BjaDi5cuMzpaoUxZbDYSmiAMYqxtPmUXdf72HOj9y6rkrv37rHZdBSziqos2fQ9WhtRFhikmHcMScPDSIwnf7RwjwBP3q4A0oYZEO3kwcIdfonWhIRAAlhISGN6xxxkRFCgBqt5UrT9kLBL+nG4Q45hBcEQTfaDZ2Y4X0/eX8Soy57pE1VqrGL9xBM3A6WqxGGXRRXGw3F0fMRmvQalmC9mWNtzetrQbHpcAlexL/xQX8SnLIf0SirR+SqxyEJIuHVpo5JcAZW6eWrd0oUJlgsR5YXRGFOIkPAS31yYgZTAGJPABEqFTTKAkxDgKaBVJpS1LsW2E9hSmk3HUdfR2Z62aeiP7tD+5X/Ll56+ysGB5pNPPmFnZ5t/8o//MTt7OxRG0XZBUQ0v4hSAFkU0gLjDgyMuX7rIzZvXMObblEXN9773ff7b/+v/jV/99HX+yT/8A7764td46ZmX+f2+ZYPDqw1Nu05ypetiUqSnaTTrTRuUNcvJ4RF3PnrAer1m06wC3aRNCenr9Vqu7cXV3jQNXbDY91Ysr9aOQzRT7pcxorQ6IWYwRYEO4SAKTalMytuazerkJTEFLBYzqkroBuvZjMV8IVapYNEty5KiKJnPZywWC6q6Qhea5fYyhN/MKApDUZThPhrnFKv1hg8/vsdqtZZq1t6LpdpDogj2EnJhAsiY1SWqqjBaBZEUFCgtSq5WGqUNN25c54c//BlNs8lqA3jqWc3p6Uoqx46UrbOhCPnC3Nvb4/T0NFvz2SacrpO/jVG8/PIX+dmPfyRyeWubvl2hrWfmNcqREvbjYVSUr4ALn5QYUjozVgQdFu86cAa8kbowRRFyuKL10VLUYr2t65qbT+7Tdo9QekVRNZSlhlSTpAeEBcv4AuVKAWHW8L3v/gVHxydUaobuDTpQDCslhjW37pnrvRAGIyQFW/MtjK0olMauSoqV4drscpJfGgl501qjyzqFhRljqOua2WyGd4rCz1FW0V9oMV5RKE1dllSFAQNaGQpTokOoVF3PKOoKPasCs6KmqkqKqhAvISIji6pEFQWN7Xh0dMimbVi5BlMqupMVxw8esmk2nHRr7hw85MM779K7DXuXFiy2a7b2tmkacE7T0XO4PmVtOzZ9R6c8lIbdHakMvtxa8tMffY/16hRrO05Oj6XAonNgzikAyVBT4emnnuL27du8+OKL55wXhbRMVFFix2Ew6Uw/TjZOc/Uci3R+DHafIe8t7ucpL5L01SCns/uma8KmmxgKs2eEtxmB/uk75NjJp/2Wc943/zx+VqSHHxRwndYMxL1LgEfK5TGglzOWyxm71y8LONYFyiHhVq2jWW04PTrm9PgR9z7+hONHBxw9fMTpo0NODo7YrFb4tsH1PV3TSnJ81+OtRXnH0ob9ASF0wCgB395iFQlYoZAaHibk87lPL0p3ntchytU83PBxXo1pKBTpfvncO9vzo3AvGMlYiLrdQNbknJfaN+k+QxHG5BUKh/WDfuwnqRHeW/b2dynq8hzgfP7xmYHGfD4HSIxT+QtFFXKacCMhQkP592moVO6tmDJM5aFTSg1sEZEmFsagBAZgE//OaflUKpKnUuJOdGE7B2UpORpKaS5evERV1tT1jA8/+Ig333yTnZ1tLlzcBSwXL+6xvb2NjrSdqgAlFXg3jaXI4nHjIhMlM3g7GKPjTzviOVVVBfdwx/b+LodA33UUVWAACvxxJjI5WJfN0TFciOh1sEgMm5qcAwTGG59JKMUYbvio4AfF36fZnt1MJkr6O1pKkkBV0ROSoRLviXSdqUXJu5L1WSaBh0f4oQ3xXuEdVRQmakD7oTvCqbLIjTas1itu374NKoRDOYdSRpg5nA0hFRqloW0ayqoKAtyPBXnskhAqpHWwDGidhL4xBmW0sHUohTFFKmClkN+LopR2hmTFZD1M8z0yMcn7RgpFrwjWWlECI7WmC5SfsThZrGCb/g19EftWWEdaSXr1sQ6Bxx18RH/nNdyd16jdKb/xwhe5dOkSP/vZT9jb2+UP//APefLJJ7DOsWmbDDAyWv9xbmhV0HeWR4+OePHFF1AU/OZvFly9cpWf/OBnvP7zd/g/v/ffcOvmk2yahoPVMZu+pe9P6boGZx3O2YHWFOgo6GxI3DWDVVehoBhL8bIsw5rzFCiM1sznM2b1EoLVsSgKZvO5zB0t4GI2m4VQKoXRlnou3hVVBMWjEGVNPCpRQSvCdXPKSmEKFeoUVczqWWinhLDoEKtdBIDorJW56aG3LoUprduG9vRYePs7sL2nsz3OS00Ej4RFxcyJ0VgrkddlYVjMa+zc4Zx48XQlLFujmph49vd2WSxmNG1D27bhNkpqLQUl2U/W/yAWxruohPTI89brNbN5PZIjybgEWN+hCseXv/oS/+KfC0vc1tYuhw8tunE4PSheRSYytMqNJ6S56Ajx3dlP1lq0alHGUBnxkDklMe1J8VIaU1boStG3Hc1pSbdVUxeXmM0MGClgWxQl69WavhaP56KeU5kaFxKvF9WS5f4+VVVTGEtRIDVLsneXcFsJW6rriu2tbZZbW2KpVAr19ZcoioLlfMG8XlAWJWVI2C60hAFHI8NsJqC0rAooHYURYFYYg1GayhQUlSSmyzVCYesdlFUl9Sm09JcO+6s2OhTv9clQ4fA0fcPDgyN626OVZ2Y0qvfYTYdzsGob3r/zCf/H/9P/gfsH93nv7ff46INPKMqaut5ivthC1wa0zOXeWk5WKx4dPOJb3/oWW4st7ty5w927n8j6KBQXL+5LlfFsrB4XInr58mXeeuutEYvlf+wxzUPNlcjHHXHNxGWYY53cnjbSm2JYdEYuMlVgJ08JzzqrEJ89a3je8Dn3vg85bUDKYYvvq/VYD1PKEaPu8/blJB3DPNK49VpCerTIG9s7jC6o5zXzvatsF1d58ptfkmgE6+jXDSeHRzy8+4CDu4+4/8ldDh484vD+AzYnK06PjnHrNfNVjbO9FI31XWDJkixDr0NRygCanFJShdAz8lxFo/Y4DO/sIUBqrO/mOvDjDtHLMl3p15x/3jHKWSbqICqwUsmeFQFeJGJ4XFumoV8gfVSV5edq2+eqDB4fGDfrvCLutIE5GJgq9zm4gKFDB+X8fNqyOFhxUeXgZOjI8QSILB9Rac4TzPP3UkpTljXeQdO2XLp4BaU03/ve99lsVnz5yy9hbcv+hV0BGSF+sfcSvFIUM3oHBOE7puQdjtyFOQ2fmr5v7g1yzrNer3HOUValfE5Ktw9Kq8JGDvgkoXywWIvSmsBXVDQyC/lguPGDNXGEFwJIwU0oWRlJqKnHIlpefH5ueKg00+Gzd5mClQHPBOreEIuaejbgErm9Cv8fFGRF2vySuzd715jhIO8tfVfPKtq24e69u8EyGAQhkuSFVlRlEYrVeIqqxDvY3tpme3uXWNJDGy2VfZVwrngXmVOU0Bm6PtGbxnyC+FnAuVgG27ajaVYh1tQLVaWLRZhCD+ZAwfb41QPwPoEJGb9B0A0evfB3UMrt/bfw998abSQuUDD6o49R3WkABDLPC12yt7vDzqUttrevcnBwwMOHD7h16xa/93t/h29/+9vU9YzT1Sld14/C+/K5HteAVpIXuF5vgCOe/+LzXLiwz2Kx4Kknnubux3d5/533uHfnLuvNhsPTYymaZCuMXlKU4jGIrE1FofF6kxK057NZ6udqNmOxvaRI4ALquhL2msJQKFE+67qmMAIMyrJEG81iMWc+nyWlsygkXKssCiQwU8YfI2xGLlq4Qq0JMZ6FkL0ktwbviHUCHvqmpbcNvfXYPgCGrk+c/L31YX4R6kZY8YY5nyore8UwPxQhrNKPl25Y80qBMdD2PW3X0c5qmWuuZq60KKRKh3ACK3ka16/w/gcfsQlc/5E1SKtB5g+raBjzQa4MssNay87ODsfHx8wXs/D7WI4qJD6961uef/5Z/sn/8g8plObKpcu8+cs3ee3nP+fo4HBgm1ExUVYEiVJCEKBkcoe8nFJqNAQqcmMMpijou14U1rKgrEpR/iPYrGvKasZiuZ3Gfm93j1lV8ZUvvUJRV1JVF0VV1gLqnSTo1rWhKuW5ZVVKPkVoo1GKUhuMNqGKuBajVt9jvUrVrruuk5yNwoCDXjts75DavZLcrimCV0mna4Tu00KUDdbie+nnTSuAXHlLoYX+tO+6pAA3m40A3MZjN3E/kbkZNbK+t2GOejrX0/U9pyvxHPb0kr/Re4nF9warNEenpzw5fxGO3ue0W3F6cMSaEw79A2azku0Ll6hmkm/RqzVNUbB6eMDq4RGL7W1ef+01NpsVW8sFu7t7fPWrX5WcTspzgUbUY+J+eP36dd5//31u3bp11lMxAslnrddnwfN4//71YGPi4cuOZNZLelPY1/zY469UrhieBfBJIfAe685Xkj0St3+ugquGdky/U9aH/danR6fYh8l7R7YoVLCah/YplJB7xGKYykvtFWC1WmM9FGVF3dYUlaEI9WpKZSgrzezKPk9fv8KzStyStm05PTjm0f0H3Pv4E+5/fIcHb7/P4cOHrI4OUatTjO2xmw0Fjt6D9j5Ucge0GAhQY8U91+vi3+fNhVg7aGpMy+dDPEbRPnw6KJ4+J93f5B4HP/pNwttJxm5vA5BiPF/jv/nnqSFQ3k3IKZxzg/f51xyfq2Bf/uBo2WuaVtgiynIEEsJFkJ2fo8G8U7z3qerqqIP8uHhe3pY83CpdEz5H8DPqPEjW22lnKrLEbCWxyMvlFut1w49+/BPKquDmE9fQxrNY1BSFpJdaLwLcOcVsvk3XSbKMMiqt8/HkjODInxng6fvlIEMmomzafd9Lefiuw6oCX/nAmCU80UK1GfQG7wJjig8l6ZUoPqFc+MirIY1Ngk2U7gkIyt4pyRGCLT2Cg/i/EazgJ9creTZj0BXI44OBxuV3ksSkQAEp69pmsbAqvUs6P/3vkOhlClGQcguR0RpfVfgQl2+MZmu5ZGdnV0JRZjMKYyQMxnvwQnnYdR3WiRB0XpiAYpVhj2y0kdbUxe+9h4P38O1K7ocwwiRrr/ehJoNNVmZ/fAd/56/E0uJDzk4kV/CemITjIqAIOR/YHtYHw7yPpA0h6U/mmIBrpQR0hPR3SR7TmWBRKmxoYQ7NFmGNiFJWFLMQeug4PV1x7dpVXnnlZb78lS/zpZdf4cqVyxwcHQkDkXfpOdMNefBKkja04+MT2rZjf3+Pr128wMHRARdv7vH0izfEety29NYGoS4sOEpJXQFtYsVWT1VAYSJBhQp5DpWAhsJQlCVVUiIFHJaBQWrkNZKGJWKHCAjiOK7tilULtrdYK2DQeiseByvFqZyP8imCw6jwG/AFMeQg/6930Qcox7C5qbCK9OCZyNaN830Clz6MvUvgckj0HhtnHEZ72lTsLniwwtxezGqZO/hkwX722Vu8/c67icbVeZ+s55ESVZdFelY8ogKk9Hg+XLt2jQcPHnD1+lWRC+ncQdlz3tI7x/ZyyXNfeI5HDw7Y37/K7/3d5/mH/+X/grbdsFqtAMJ8kEKRKd7aCy0oTuoUGKUplEnx/EMiu4Tkxtj1KM9jvzRdR+9iBQlCjoJnOd9i025CQTLF6nQVDAfQNi14jXJCTe6txShZn13bsTmFvlM0mw2bzSbJq7Zt2XQdWotMappQrM4Y+q6naIVi1VkvVmAlyZ99Z4VRKwA/pYf9s1AFpRUWrZhYG98j/hbLF8SyEmVZUM4LzFzCRuuqYjavMUWIw1eSr6HCGrSFpTUtXddz6juO2hVd31EYi1IF1nsWu1e48o2bHJwe8Op7v+TVt/+Kk+Y+Xd/Qb045vOcxxSzIi6HexG31Nq4Sb2+lYWd3yX/9X/9veO65Z+kceDtWuqdrKCp5t27d4vvf/z7PPffcSD6J3My96LLjxXPGVv/xHMm/m94zPwZvRhYyM/ya1un073GYkz9zTfbroJAS8qWytTgopGGo1biPpu+X3xcIhf7GOt3QF250ndbDeTbVCVKDLFCyZ5dAoQOlcGVZrTfovkeZIhSf06FGkqJTkoundYMz0QOnKS/NuH7lSW6+9BSg2DSOo4cPuXf7Az54/U3uvfc+Bx/f4ejhA+gUupPCqwVieOuVxWkS+BqP11kAkb+/TsbWsT437cupLhz3m2lJiE8bDw+BM+csgByDvGH/P+/Z+ecpOE/vGoxRfS903719vEckPz4361TuhQAROs4OLiWtdQId+HMs+hkQOQ9NxftMzx2DC3XmOhD0n63I1FFi1fJDIuD02aHwl3jrNIvFFlVV82d/+ufcv3+fL37xWaq65NLlPZbLGcZE+t0O7wua1rPYnuGQ2Phh4QzWuCgg5R0+Ha1O218UBc5LoiTA4dERxc2Ck9MNZT1jubXFo4cPJZkxywCPryWxujrwV8uG5kI4hZxJAA1quBYC5Wn0DKRlM4CMiM2CkBqJyLS4BuU/eiMi3ohgJP1NSJ4mv1ec8IgSWIqCK/GdImBitWqtdeDsFxq+aGl2MV7eFHhr6XqplqpDsqhYtWS+nhwdcnLwEBjAS6T785ly6NcH+Lu/GAquffwzfLvGuj4pkXEep8/dZrD8QMo3yjeGwXor3+dzJ/YFXom1MltHOhQIMhHobu0RrW9D3HBQDicJbXiPtqEIXPZ7AnJ6SA430aqvNUVRUdUz9vd3uXTpAjefuMaTT97k6rXLPP3UU1y9eo3T0zUnxyfCSoSAtKgcxzbk/2o1tuCdnh6zXq8kfGkx45mnnxBSCDx936V56HwvipCSqsEq3VODK1AMSb/RMyRWfxvG1dP1FmvbBARaZxOrWx7+qRDQGo0bYskL68MJ+YONXifkWdZZXPjeBaudJJkHxQyh7JV54VNegfdiFXZqsHZNlYq4o53d9AJICN40m7U3VRpP/R+8Hk6SeIt+yFuJ76aUCuw1hVQ9DmxBV65exhQ6eDRaKlsHMFfStq0QJMTrM/me2p8dzjmuXr3K7du3kwI23XNAQuy6Xgp8Pf3MM/zoh/8vvvenP2J90rG7vcv21pb0XSsWfBeAYh/6RAdwIQw5XaB1DKw0StqxWq8lBNE5equSoUrCEoPFvgNLFWa0jIUKMsX6DocN46bp+5iUq/HMUL4WRcxbCh1i50MC91iNHLz2qiwllyZQaMY9SwEzCwZR0EQuynqa1ZpCVyL/vLCC6eBZM6WGmaUopXZLWZRUdUVV1xSqoC5mzGaVhHIqmM1KZosZ9V6F3oHF1pyqKqnrMhgyBok/UrytrClvHf2mx7nByBINPYWe4bThZ2+8zj/7f/5zXv/Va9y/+z7t+oiu97SuS/aroigwlRgMtvf2uXb1Mi9/8Vn+/t//z3jxpRfZtD30LhVmzOfPyLAR/q2qivl8zvHxMbu7u2cA8TD3PIlaanKcBdHn/3b2Qkm8jZa78Zl+9MVghEUsomr8/TmXyFe5F0OR7qHS9YHsQCRE0LcGj7fK/jd99FGp9iNFMhphpsq0rKvRa4uGbAkAw0Q1AKcD+YRR7OzssL2zQ9d2dH0oDBi8/YF2AKtCOFASozIXTaw3Ywy+VOzcvMjlJ67w5W9/nfZkxf2PPuHP/uiPePMnP6U7OKRsOlzbgw1tY5Dt5wGMXCnPf7PZi+bU0Hkf5dfH76KaFe91ns6dz4U4ePl+kf+u9TjcVeXP5jwuQEbvM9WxY18cH0t4rp606XHHZwYaMX4x91xEJSlO62gFioqN1gNXMwzJV+dxGecTMx+E+P3YtTNcM7JMeJJiJQXEzioy8bNYe2OHRzu+bGzbWzv0reW73/0uAC+++ALzec3+/i51XeMsQqUHMvG9SbG2zgq7VQxVyL04g3fmjCgZ/521NfZ1YQpu3rjJ7u4Ojw4PqE8/oGm26NqWuqrZ2dnm0cFBULqGxeGDYPRemOXjAo1jp8LK9kHhJH0foxVFQAzhUOFzBBkJKOiciTaM7ZBLkBa+NqO4WUlK1gRTPaYoJMclVk3VBq0QCl/vAxNfCMlwspE6j4QVWIuzYsWNlkT8KhPOPizKMObe49oVrjnGH36E+/hnFKv70K7o2kb6Jc0xD8na7En5IgEwKWKIVmA3Uyq5GLUiyywZ4iOLsgB0FtYxeP5APC5KR8s8IbYyKrkqWOeNeCS0DhbmaLk3Y88EirKS9saY6kgVbZSm1KVYQMtSNvFAv6yNgDetNfP5nK2tJTs7Oyy3ttjZ3WNvf5+d3R22t2fM5iXbO0u2tpZ4D48ODnn48BFN28hcUhFbalQMfA1jESeXTpv4ENrV9y3NYYN+dCAhL0baaYKCJfNRWFiiYE7AgECOGGRJBGw+WqudSs+R+REUI++xanCPj6i9EUpPAeiDnFMRPEdF07kUMhVBvbOBJjAo0ZGlSSub1kUEtC6sU6eHvsDnfcSw3kM/5O304V3EF0YCHXKPoe7OqL89KBdyfPou0FR2Yb05sD3ez5mrGqUdWjmqquTG9WucHJ9ibehXKwyEzXo1AkLnbrhh+KNFb76Y0XVtyEPJDEpRsihQSmRu3zsuXrzE7/7u3+Z7f/qX3PvkgAe3jzj6uGXTbGg2Db2VZE7rHD4sNe3lvyKMpnMOCh3YAUkAPxm2lCRCy5qUNV0WmqK0qDIaciSnBw+lMRSVpqzEO2aCRyHm2TgNShuMEea1ujTUZUlZGMpSZGJVlhRlSVmIQl2UhbgV9EAfHz3eRVmglwpTaarShIRwT2EUpSnQSghK0n5SmFFSc1EVg3yOskspSdI1cZ+QvC5tQjE4pG6DDyqLjJN4wj2R+CLsyV5TAIYaZ0O8v5LrnG2DkuXpnePo7Uc8+cpTLJ+8yPHhAavjQ3rbYG2PQvJ4qkpynbaX21za3eeF557ld3/nt9AKehs9eW7w5MNgHPCBiXKy8b700ov88vVf8p1vf2f020iJV4O+I7+dB5onNz5H8R//PBgIlRoDo3jdSH8JN3SfYk2eAptIzawUgY3prE4UPRqeXJEe3miazzG0l6EAZfjOWjfIs/g+EdhkOmveSokqVmjvsdpJMeJQP0MrjSq0pE04NYRkemlXzPdQLsgLrfFa4Zo2EDhY5sbTrFf0ppS8qq2aveef5puL3+Orf/1bvP7Dn/DGf/gJp3fuolqJ1MHKHI4U3bl+E8coV8zjd7jI/DWcF5HdYLAa5N50vPPQrKivPjZMKxoEJ2OfjPMRwPjIYibn5t4r/BBCrib3B9FF4n4aizw2m+bMGnrc8blCp/KCfZFitus6lCkkyr4wlKaSUJoQyx4X6dj6qrOJPA4jyj9HQR+Vhtj5Orh+4/dlWYrCZS0aoag0iWlChF/fhbhpFRSyoPo57+i9xSjhkzcU7Cy2ee9Xt3n/rdtcubbL5Uv77O1uU5oab0HhMAZ6DK4XhhXrHaWWsBnbG7rSU2ol/P7B8qB15BsSJpLIApJ1crJ4j4EJFEXJpUsX+epXv8If/fs/Y//29znY/hKnpTDDbG/vcPPmDR49OggxjT0EC6QnJuZJlVtU5mmKwCJa1cPGLgleEdXKppOS/mCwxGYWFW1CASdPqugt4FISdJWKwj4oX2EReO8CexX0XS9x0dpIcqkLFgwbw0z8kMAs2VvZ317uE4S1O76DO72fAEacV93d17EP3pUF1RzhuzVKKUpj6KJAIC7CqBh5ULJxqzIo4cEqKHR4A2VNqgYfLI5Gi0KvlUpeFBXcu0qPPQi5cjMIsUAxawLjjVMUWpSRoiiSslsEppiqLEMNiCoptMYoZkuxVu7sbrNcLimLSnISZjNmizllVbGYC5vRbCbx8XVdUdZFamdVikLiXQy7EaAnTEs9zbrj+PAO66Zl3XWhCKKaCF0v3Hqe5BHK5UxuAEibSZilvnf4zqKaLgliAIsmhNQmi5J3Lhg6COEiPlnoUxgl+sw4RyBpvU0WvZgvk67LxiyPO45jGxm6xgoCKCNAaUi6j5u8ErUtGgjCWlFIeJ4AkAB4QqKzD+ssKSMpZFTex9m0ZYz+VXhwKilgAkbCZqS8rDc8vY2enhVN6+k6D9bhvMJ6xczXzLRHGc/Tt57i+3/+l8zn25iiYoYkLffHx0J7q3ygMrYZUAqKaQhMyo1j80VF02xYLraI1bjzV9FYNIp2s2Exq3n+pWe4fG2f13/5Juv7nr3tixw8OuTdd9+j7dpkJhEgHShrS0NVCfECyqOMC8p9EcICC+qqoqhKXEjUjyFG0ehWlAVlVYQcHjMA9AQEgvdBxZDZfB/IN/awL+pRQGnQTcZK37mHAhvDUgL99bB+Bm8Y2fdJkQgaR5yHqJi55sN6CJ+ck3s7lbzKg7EquKIxoUrx0DSXWdN7NlI9Oq1BAhOkKMEPD0954633UW7Gcl5RFDOWu7t430MwYhamZF7PKIuKrcWc2nXcevpJeitseNGrXCT9Kypkdnhv7wOzH0nJunJ5n5//1QrbbyjredifdFb4No5B3DtJRs9R9fnklhB5IteM5cAYeYw9LPnY9EH1Z3KN3COfKWfBxVSvkr9FruXnDL8pvJl6OofrxgBr+OzSHJAjGiKdcyMLuvzm0jnRM+RDH8WcQ+0Uhe/R3qAKRe+7pM9Z73DW4K3G9oPBz8Y5HeSp1OCUZ0RZu9E+eTet60BJjpMuFMXOkhd/52/wxd/6bf70f/zXvPPDH2AO7lMrhwue5j4ABVnfRCF9Jm9DBYNDiswZ94x4UkP/5QnxKvRrHK8oQ6YeuekYx5y/4QnZGEX5oc5epxjqpvhkAI3AVxZ9usw50SW9xzjYKhcUuhgL7U85PhfQyLPtc9dKjrZy5qkpspp2VG7dyu+bJ8fkz4iW2b7vB7QWBrTv+3jT1LbohRkGPGrFJAUiInsbaGiXiyWzesaf/PEf42zPiy++AHi2t3eCYlbicZycnqAwdO2G3b0FniHR2vkBzZ/txwG5WutGoGtq98j7u6o0y+2ab3zzN/jFL17j/v0HvDx/nV8cWI79LfCenZ1dnrn1NJvNRuLb+04oOsNGE13sSUnP+iQh6yBUVSHC2Ds3UOUOmlGmbAYB5R29awliVhJfEdDnIkggsk+I1SvVnIiCPAk9ERLC6KUg9oPtw7xOmifu6GPc/bflHQ4/gEfvD/1sWzTCIpVGQinKzFqpZjW+rtK80148BkOscdyUJHZfZ9VXi5g/E4RavEcOGIwylCF3IIZ1GVNITkBh8IH5wpiCKljqZvN5oDYVy30ZrPfzxZyd7S0W85p6VlOVJbPZnPlCKk1XZUlZGubzGWVVBPgYLLDaSEqHipufKJFiebc0gU2r73u6rmfTSwjRyWYFRg2KBkMIYAKhoV8jGYOsXRVqp4g2rDOfjseBs+meI7Y6P8yPpEwHgKn8YGCIVj0bQjB8qBDu4qYYQQwCMCIgjXMsPioCm6ml3flQLC6tV5/AcVw/8RqLTfItd5OfXf/ZJjB8Ff4WBqn83GHKRsVvrDR47wM9MONzM8VhusNEqJF0odgH2SaD70ANfd87y+l6lSiD99qeXWvZ9Q6UY0bF1cuXWa2kcJp1jv2LGmPK4HWQ8DR09Eaf3Qdg2GQlfOoyDx48YLnYTrltuXKjlUErMWCcnJywvb3N7t4Ov/XXv03hJDfBWoe13yFuv2KpDdHTSkIJlRHvrcyRARBHpRxEn7ARSEKSUVPFa+jz8W9RZjkvIXM2f+fwn3MOrAUrSlv+jPGYjo/8K68e97sf6Ylq9B5T5XTc9nysptb7x+kY0/vGvVj2lyFvyPqQZhYLuBYFr7/xLk3jQRXUlaGsSyxSL8MQAJ4pKIzkZSjvMMqyv7/PZhO80Azy+Mw68tPaBT4uB0Dx9NNP8e577/DFF76UDEYZI6iApjxFCibjns2Ax4CH/LfH9d2offl4ZNPrLIPU+UAgzh/nQsjmOZ6J7AWzegzpbhEynWmG/DF+/zjPtYqrLsiuKHd8KKCnou4gv7tQh8Qie723DlcwyrdzLoYujq39eZ/lSnr0nCsl9TCUAt0r8SQaTd91XLhwkQcP7vODH/yY/QtX+M7v/z43rlzhL/7Hf8Xm4CG1t1LMToU+UAKutFIpOmcKBqbjm8+OZADIzp8e0/E7756p3z7F0/G4++fXy3ln597oWj/keDrnaDcb6s9YrA8+B9CInoWYtB0nbo6+gBGgGG3cziXquGmiVO56Og9cxO9kQEkejZTAlp2fI8sY5iUAYMwcMFiOY4yruJIXiwX3H9znJz/5McvFgue+8AUWiwVlWUmSr3dcuLDH8fGJML4gsb1FWRGZg2K7zkeg/NpJNpwr7y2F4TxXru5z/94j/t7f+7v89//9v+DOx3f4zhe3+Nmm4pFzNOsVp8fHwkRiClxQ8glAqicqEvH+LgisQZkTliaNDlWB26YR63AEHeEdUv2MoMApH8NDJCY58kh5Z/GbA7lGK6i28Zuj8P7SjmTDVgp3/y38g18JltES765QsqE8ejch9HhtgacwRRhPBfMhYdCYRVKEY+5QzFXREViEcTKFoTAFPuQbRcAQ51DcdLSWSrVlWQhjTFliCoWpSaFFi4UUjauqmqqsKEJi7GKxYLlcUtfi9lfBCzGfz4NXTidrqdYSGqII7FWF0O85b0H1KFyiDrV2qGnTu57D5hC7GsIKvScwFBlSZeJAbxsBss22kQGIBsU41oQJ8yWtGaVQIeRnyCWJjEYB5gSvpp3Q6MXNzDmHzeN2MxAU2xABh+CTYcMUL1xoX6RfJLq586rjami7IH0ZSzg3lnaYnH70XrmMid7a2F/5ev2049M2ltFGPlKSxiBufM75zxse8xiFJm/G6D4ydiSFU35zODZ9x+rQ8uh0zc7BIZcv7XLl0i6720sW8znL5YJHDx+GeV0xWyxRStF2MbY+kA94N3pefK28by5fvszbb9/mmVvPjTza+btHoNv3ltVqRVXJxmd9Qxesjd74pI1HhV4pFTjmPb7L51mVvFNTwObjGOXyO/1PLtcTfBs+R5EbwErKo5sqnmEO+CBkz34+q2i4PO9QjX+LVksx1pxVXIb+z9HKdMbkyms8X/5+bK7h5B7RG+fxod8DFTdKCoBqD0pjreatd2/jCDH1SoMyFGZGUVRopOitMPiFsfSeqzeuhqKpMlPHoYXn51Pk/ZCv7eeee45/++/+HS+9/JXUh3kkRw76P+/xOCBwXrsGmQJxkp0d/zxM8iy4m94vzVvNmfNyY6fyjL6TiIbz2zn9PJWJ0wt9WAMi0waPGwCWtM4cHttZWp2XOSCAvPMZn6ZgY2r08QHwawfWKbQVL+WmaZhvbfH0M0/z7nsf07eOL/zG11l1nh/+m/8vxeFdfG8xqc0hTDfr45wBNZ9P5x3TdubnnWFS9f6M7Muvy438oz5mus7PHr/u9/PaDbIC16t1Wtef5fhcHg1RgPSok7yXcKEp1W0OAOL1n2b1ywFC/jkfPMnX0CPhMQUr+aDEtpRlie3dSCiPYq6VsDp5YDaf8ed/8mccHj7im9/8JmVRsrW1zfe+9xfMZjUvv/yiWOWVYb1aUdVL+t5RVobeSSVvY8aTIlrJcuFx3kRUDJMw76Ou60A5trcXXLq0i3/hFv/gH/zP+Jf/8v/N66/9kq++0MBFzZsn29z9+H26xXV5n6BIxlCQGEoSG5HbJyKi1UpJBWyj6R68S7c6SpNJKY3bHMHtH0IU6OF2WqVADBRQht9c31I2RzJ+SkG9hWlXRJenD4z+OlqV9RCKMij88uziwoXUZzGMoa5rIpNQVZWUZZX6eWtrGQCiWNGqSsKJtIfSFNSzmlk9C7UQCorSsFhUbG0vWS6WmBg6UUqYxKyW2gj1rA5Jo1JMrZpVeO1DO9VozkYFi6ioh0OScyWZ1VlL6zpcNzBVRaarJK6VSqpLvLdzMQ9lUEqihTvG90dbrsRX6hTGkKwhXopbRpYYfKiOjUJs+lpo/pKyJGBAhRAdrQnJfC6sy/DOCPmCUsP8Su8eAUKcm75PipoLlt88pjitmTxOiABAtYAZbRReSdVTG+d7fIgH78SapvxAUjAof0G5Di8ZvRyos4JYRaCiz99Upkx40zV+nuXrXIAyUhTOKhHpmnGXpHtH621AYhNLaH7v4ZpkgFEM11uX1qZHgS7YtA3NZsXhowccPNzl+tWL3Lh+na2tbd6//SFVPaOeL1Batpe26fBOvGujzMSRUj4cxhh2d3c5PDwUI0DYW6YKsswrkTubTUPbdpLoXITxUFMQOCjHEciOwIRvh3ELT0igwKk09wdDTZDVQW5GJVTm8lmPscx8NRq7PEwwv3+am2Tv8GsUXK/iOI8VQKWQ2PXJ+bGWzGjuqUnoVvZMrWK94Sg7ssvyq6IRIBqinA8TTYUCoiHyIQAJpTVKF7x1+30ePDyhrBYSzaVVCM/weFfgkRA3n8k221tu3bqFMQXWdiFfKqzvc7rrzJ47WYdVVbG7u8edO3e4cuXKuefl/476f/LdYOj5fMBkel1+eTTcTI2yj2tDfj95j/MBQm68ix9SMdf0WyQkYfLM/LJoGMoMCAzz2mXuIO9CvmRcR1n5A1wIWesjMcLZxOTz5GtOwBLPTaHJWgwdkXFOa42jQ1kxNN68cQOnCt55+31+8tbb3Hrl69x6dMh7f/ZvUKtTKifVx61U3cEpRmFQ58nxHDTm7c8LO+bHdEzP89ZMz53uQVOQOU1GP+/++fnTNZG3PY5n13aBte+zze3PDDT6vk/W3djQnIc6b9B5nfe4hTpFgRFQeC8eifz76NE47xkRYJy36M7bzHOLmCQXe+azOUYbvve9P2exXPDyl15GKc0nH9/hjTfe5Otf/yqz2Zyu7fFOcXKy5qmLN1ivOsTq21OUElqTJxMqpSYbvBq1ObUne5/pYG82HUVZcOuZp7H2Pb78lReYLyr+7b/9d/zqrTe5cPcT/uYrr+CWcOfwQw6PjlmtVjRtx8HiaXpKeivJ+tx9DdaPcNan/h747iUW0XlP6TuKrJ+8d5RlYFhROlWrju+nPIHNRpQ/haKa16jFVYwxVJVwxXvvKMqSuhImFJSXasj1bJRzMF/MqWclzkm+iXgCaoqQDDybzdja2kJrAcHL5TLkHpRUlRRVK8sKpTR1XYXEcc+sqpjVIY9CmZRbopXCqQ0Q4uszge9cnIdDDQvnHL1b06xWWBv4yYPlLs5pUIliOCpHcRP0PvDLhHvFSqJ64B8c5nJUnD14CpxTRDrbXNjEQmyoIlkzJV/A4XyPw40UmghINKAScwWZEuZwwZKYH8qTPE7ZKhwMCAgvec6gNKxLhQ3xuJH5KRIo9CGR30dUkz3XJBLRYRmlvzVCrxlqDIwTJUOydgBlw7VkVmCfHicq0RDve0ZmMQ5rnArw6WaQmhsteRNFISbZTRW+oa9DiuY5G0sOqPJ2RAKDdO5IoZR+0EoJ/WfcjL0Lsf2SO6VRgVZaPADWeZTq8YHdS+G5f+8Bhw8fcvjoCGstbduyWq1YrteYQhiS1qt18LqF2ObY3wksjPvPOUddS4G8tm2zIorZZh2VVoa141wvifa9AT2hUvdxDcnV4tGLYwTgQPWchW2hvySbPs1Ln+S5z5RzNV4maQ6fHVNGY3YW0Kbnju4wVZKz7xSpLfFHBWktTgGpiOwAxqZW59F5A3B2w5ec6afRfhxBXmhXlsuHqbE9fHL3Ph9/cofj03VIsdXcPzhCl3PQMScsN0YKpbwKglNrcM4yn9fs7u6dq7RN7QSfBhZixIa1lhe++EV+9vPXuHbt2ohw5rx1Nr3PeYr+VCZMj+m6Hp8bcsxUXNc5W6HjPGPHec8f/hOv+BBaNAYaRajgPUytCCwiVsy8uhnCyOX+6E29H2Rb9n6e6J0O7+4cfZZH1yORhN7bzEB8ViH+NNmbG73DB5lTTuojOW9xPka0aOZ1zc0rl1idrPj4zhFvfvgJz33jO6wf3eXj136BPjlipodCuKL3jHXMsa463jvy36fzdfr5PIBy3rmPu3b6zPh3fv55wOjXHWmMraXvOurqs4VPfWagERuUZ8NLWNIQYx3DTX7dffLBiPfLq3jHBRCL7Y2vGeK5pwMyBS9TD0m+8Q7tcdhOElr39vY5OjriwYP7PPnkTa5dvYwqDH/8x3/CpYuXePbZL3D16jXAc3R8ilLCWWJMiIfP2j6aaN5njDsTxTBD3iK/x+7Q4TCcnjQsFoYvPP8M7777Pl9QT3Pj5j/hRz/4IX/105/yF3/5I07Xa7SWRMyyqimNZvfgdaQqtKVtxfIn7mnhXPdGo4qhX40pUmE5ExOetVT7FZAh82A+n6dQutlsxtb2Fiq4OpeLJfOF/N51HYXWLOc1dVWLd2A+Y1bPpKhSoanqSiorh5oGEp5UorRJLCNx3MqqwOiosAtAK4xG6zIoNGJtHxiiZFPyYb56PG0f6wO0Q5y/93gV6G+9T56VqIxPDbBJkXGgMNk8HJipJP7YjRTCqKR4LwaBSLXqnFQbNzGcYKqkhOus67FuaE9sv6iGoV5IJvQj0PBKPG75uyQLqnfD64VY2XieUWMrvdRicOB1okmN/SE1VaS5jghk+6RMyz00vQ3zP3kv5F/rQ05R2uTGYCu3q0TrnvR1D61oNjEBdwh7UigfQyczw4eerjES+ALxsk1jcMMpw5zgrKKQH+O/BahG+Tn1DueueLLPU6ARZZ4L8dQxd2Rq8YvX5LJIqUDm4EKiqxVvlrduKHjqLG2oiaG8R7nYPstqswrhgyWu72k2G95//wPee+9d6rrgN776Nbq+o+066q6nrCvaTipAx/fMXiyb4mrUfqVgf3+fw8PDROt9/qYYQiOV3C+BfDsen3G3ilXdx/I4fiAMOF/pz8FcGEdi09VgvWdglIvvN1YZxyA5v//jAUfeR2eP0V6mGHkgfGrdeB2pDAikrjnn0SI/1GOaNf1yAlY8CezESvZaG97/8C6/+OXb3H/wQNqnDR6NMgXaFJgUQhqMV6N+8cN/yqOU5eYTT1BVBT4wi/lkoDmrpE3X63n96L1nb2+PzWbD6emp7HmfAhTOu2f++XH60NjLMFb8pvt+3Cu8HwxL8fwcTA8hRvk6UuPvlcjzGC0wJiIBowbZG0FC/G2QyY8HVHHWxJ91iuaAOCbxsy/I3s1hrUl7QdsLo1zfq8R4Z2PETODtz9/tvPCh2A8x19N7j/IhfDPOTcQgVijoNht25gI26nqb9z4+5O7Jmi//rb/H0cEJ7e238c0pRrnE4vfrlPWpnpv31XkeiPOuf9ye8rjr8vNzhtfz7vc4kHyes2D4QzwahweHVJ8xT+MzA41R9cKsEaYY4r6nnRkbPAUA8Yj5E0NRuiyG9pwFmqPBeF60xJ/HNTxa/OF/hw03U/iQeguLxZK7n3zMt7/zba5dvsru/i5vv/MOL7/8El/4wnP0Xcfrr7/BnU8+4ZM7d/mNb3yHpu3QRnj9I095tJymIm5eBHYU7FOhNLQ7l/zjQ5Q+x/HxCYvFnKeeusmFC7vcu/uA3/07f4uvf/3rfPDhR3z40Yc8fHjAweFRKGYmhZ6ie19YFxxaGSpj2N7aYjabh7ET5We53KKezfBeWGJiiNJsNmM2mwmDUV2zXC4pCqmYvFgumc0qMJaqlvyE6HotAxsSthcKyCxXJ7ey5EIzAlmPkf+yzaNpNpJ/4gZrSW5hjsA13c8LwkuWKTXEV0rV3Lj5KqzXpHB+gQfhcj1SDuV8nTa1sfV7CA3Ck/ITRoLJS2CS9QOAcN6hPYlDPGCL8LsdBLK3iU4wAdfgcdHKxBeMq2YIo1JDu8br1McXlr9CDn6s/u7PZSlxKLR4SBgrUTbGYzM8V4BRGNswkt4PjDTDWuRMHZoBFA3rGEhrK41WmjvS5lj8CeeR0K7Jho7DZ4Bu+kxNTB6NyuTQX1NgENmsIOQsRYV0sp5jN3tA2SFc4YxiEg0PSBVrQh/FzJmYvxNmYrAySX2HtuukMrOTwpGxwGfXdTRNw+nJCeujE1xYI9ZaTk9P2Ww2sil7K7SwXRe8lCpQqBrado3HU8/mSFy9Y9M0dF3LfF6w994eTz71tDDG4Wm7Do1ivWmYL2aUOirDYxV8eljruH5dCvddu3Yt2zeGeT3uWh1kbk8Mr0mLJ4zPwAImYVwJZASKY1KID0lm4H2g/QzzJ34d3sEj60QHcO/CM88LvRuFGmWPEYAyCbfNf/80293Imhn7JV/P5wAYFcLggnwbAaAc1yT9/nwAJKxCA6gabh+szbKYcQ6s1/zwxz/lrXc+pnMl6ErmeCj8aYoClMZoofv1uOHVRuLJi9h1PRrPraeuB0A8zvtJrfTnKfRxagzvJVZzndb1U089xYcffsAzzzyb+lN+YwDk6TF+NBejUSl6HOM89Nm/eb5bbjiQ9uUThWR7TGsgzo2wB8o2KyBClO/Q/5H5TJsMbBDqDUWPwABCFC7UNIltInnFYl8OYGOsZw3gZlg642MAQ7HvdAD28r46Efd47ylKHyIHSmysZdT39Nbi7OD5cN5JAnkgCNFqKF4a2wISkSHsWDaFsmutpJCphtZ2VMazsWuuXNxHly2rFj6+c8hBUfHN3/09vvfP/++4fkOBrOXOutFY5wAv/y7vn3xsp7nKWYcOfZbvC3GpJcA2lqHxlERbHabKeaD308DN434fdGlJpneuZ1b/JwYa+WJQakikbbsONSn+FF/occAjv19OexuvyfMzIiLLQcoQv31+ssxQzTYHLV4SRgMFoM1DKzzMqzmzqqQuK/7+3/+f07Udd+58whNP3eRv/63f5Z133uHVX7zKO2+/Q2EKrly6zs7+BU5O18xrHdyRBRqNcgUGTWnKoPhpCZ8hKPkMbTsvfs5nG56s6/BbOHe12mCMYT5f8Myz27heqsS++KXn2Gw2tG1L23Ss1mv6tqUP1XnLsmSxWGCC90IpLdSmdS2eI4QvuaprjIkbEcKuFEKalDYjgRn/tc5h+z4IUZ+oNr0XzuWuaUK88wAUY9+LRXYMMOIC80Hg5cpyPBwReMaWku4R+zFawbM9AZtvpvlGIDNj+CW933gjOZ8pbNjQx4DCIcQXg3Icw4QckTVIJKIUFZM+ck4Pic9ZG1INlChI1CCsHdCEkkswtpoAGK8HhVkN4+A9aD8kWI9ZRDw29yrk74ZDSFmzeF7Aqwh8hpCJnO5P8nkyOUAGlHwEdz5TBuLGJAAi5qYk2aLiOwULVtqQParvUc4HRXCIzQdQWtPpsFmEIVKKxL1fIHO9txFMDXM7WrGnBgMgFeRToS2KwEamPT6QJUTZ14WE/na9pm8a+r6naRqapqHtOtarFdr2ONun0KS+76VitPcQQj+7XkCErP1WqnS3EgrUto1UcrU5449N7zBOnhXlI9ZhKQup5dB3HqMX7O1eEOWlMBRVGagyPRf2d2nbFda1tH1D73o6J+Qhm75n5Tp2lKXUGu1Eg3EYxouTUTsuXbrIm2++hedFGctMcXD+bAiCyIEieDOC9yjMC+ujJXSggozKCIXEbItiFQGktNHHSYGid07yV/BB+/PBWzAoT0oF1rnoNRnpEFPFYIh3zw0pcsQxGUK8zuuj0W9RMUyaaHoSY7CRgdlw4nnPOO+7AQCpkJwdZVB2Dy/fGS3P7p3mL3/8M9587y5K1+gy1EXQubV9WBugU4XkuJAM0YsUPFge9pYzLm0t8b5P3tM0XNm7Jknmx9/jTSZn8gs9N2/e4Ac/+AG3bj2DS54vj4RUBpmcQea8YK3CZxTUY4v3eVbw/P7Tw7khrDRXXsWYGeeA5IVqozEmWvpN0NHMKARNfhueo1ScXyrRsecK8rSt2ewYg6t88NO947wYQOCgI4YxIOadyByIoa8FQ584L7pF3/dYm3k7oqfcyx7vrBM64LAfDBhTQu60CtqA9eLd91KPyjmL19Apg1YFtoOt7S3q4j6LEo5PNxR7O9z6a7/J2//T/0S10dDZVGAzruF8v52mA+Qe5ykIyftLeZsaHrtIoRKoz7oNE2SVyKAidb/KxizVk8tH7hzgkbfrvM95G3vb01vHJ3c+Yn792jlz4+zxuYBGDgrGSd+MOjg/P98MRjGzjBW2fMPOJ/d5gxEXcA5apop7HsI0zSPJr5H6G7C7u4NzjldffZXDg0Oche2tJX/77/wN2Yy14Rvf/E36ztF1Pddu3kRrQ9d1bG8XoUri4PmJyYGxJkJkwBEk6NKmOV7IKn03oNkIU8M7a41WXihIN03wUgh9q7AebSUlxntCbZEhSdEYjSeGm8gE7LPKx9Za1s1anpeU8LhwQiw5eZ0CuYlYHyyo4H2IbZ8q6iq+2hBKE7SBADpc2PAHAT6aF+QqsErWi7PzJYapRCvL0ACX7f5TyzTZO5ONUVQqfPZvrizkKzkVUIvvanOrWlRWwRIoVBnaLhYzL4plb0dVlWP7vB8spjlFYLDRZ/SEU2CWbbsJFKgU1if96NJmk8aLnJI0UhVLTyQgmH6PfRMEXtYOH8GBd6lzXHhmDgDyPo/rxjMUbfTpmgGk+/hucb4EQKcQ8JLGzMdxlTkaqVPH8co+KAwuwrKQRzKEjEYQm8u2+L11lrZpaTsBBX3fs1lv6NYrus2a1XpF13as12tOT09xznJ6ckLXNmkt9r14IwB636c+je8sRehi/LYQL+RjrZVGe5XWbdc2OCdAY39/n/1LF5nN58xmM7a3t4lsZ7PZjMV8KeFRdc0ihEeC5EHN6oVUiQ5TQuhlj3n33bdompYiyAJtIke+rJzT1Qrn9wJIkzmVTClpjcsV8T3m80UqAjud/4F1+sy+I3tT3EuGdSG5ZDqwHsFmsxZvZlx3IT6/KksKE4rXGYPrLW3fQySeUCoUjhtCIpUSkpJB3oW5MwnFmipsuSJy9ns3Oue843FGvPFJYaV+Dmvmpx35pdM9fXiGStuXx/Pe++/z/gcfYYqKsqyB89ncpgpu3uY0V5C8LrznxvWrGK2E/TFpYJ4ztK+p7bn+oeAMWI2/Oeq6oigKTk5OqKsZOWulgNHgy436S5QpiUkpNmcwyMXr057jhz59HNCIRT9z/SgBBhU9YToADUVRRAIVc0auZc3NxnNon7VImGQydo3oAMMNsncbbjLay6Nxj7g3MhidrB28IloPyeXDv6SbKyXvalRBYaRyvXOO2in63tJ1XZCvFmt7+l7Tuz4ZLp2N81LCA6wbK8+xf7RWYFSsbibU2fQ89eQTfPj+j1js7HCwOeHmS1/l4N2POPzFq1SFB2vJIMG5YOLMPJ6CEedA6TT/FOcDgDGRT8g7UYrcDzqYDfLhUcPfPs5fkbneeQbZe3buPU5OGKUkR6PtsLGsxK85PneOxrTjpAPMmRCmHIzEa0deBM7v0GmsXX59rJkRvSkjRWPSvj7rgNwbMrVAijdENlitFVeuXGG9WtO1li++8AKnpyuMNpRlRVXXXLt5E2sdWzu7bPo+MaLEe8bE1ilgGv4eQivOgg0RfvG9orIVf5MF1CWlAz+EbAxrVCVrkAdR/n3mKZBTpI9C3HyMf/TeDQpaVLrCBTHEDZAChLHNQWGN+RAjOsHwgvEZ8TvFmBouAo2oJOS0iVHNHJ0egVjY3MdAYyiglFdAz5GAz5ZnbpXO50XegNH8i5TAQ8MZC8kgBHxm1chuF+uLkCvegw4V/g7oSOvhp+z9EgYIH+La83hsLvTVdI1Ndoi8W7wdnZdbg8Y0lkMIoPCB5PNqELJRGZha4gTIOGK+u8vmXPTYpXmTNmIJe7FhvgFD3oknzf+4+eav13XCjtF3Pev1mr7rIMgD2/f0m02qKt91PV3X0oWwI9s1wV3f07adbGadhCbFPJ7YTln7cdOzYm2zLiWYWtuDdRjvRtcYI3KsCIUQAWFPMxqnFFVd4cyMYlZitFSArusa74Qso6znVHWdGAGjbDRGCmeu12sODx7x7q9+xeGjh3jruH7zOl/5zW+z3NmWPCsjhZdMUkxiwUiI7GpKifJY6lKs+lpRloa6qpgv5rz15hus1w0zJfUrInVlJGo4PV1he4sqK/J1w2irHM9P7z1bW0uOjo7Y29sjPx4vX8P6SRYKFeaV5uTomIf37nN6csJms2G9XgW2qobNeoPtulRYc7Fcsre3J8X8tKF1sLe3yxNP3GS2mIU5qZAQPZusxoOyoQIYzVbOOcr+eUAiV35/HSj4jwEQnwmg/NqbgGN8n+G+Xiozo2l7x+tvvU1Zz9C6xLkAgieJyOf9O2pjvC8SOqWV4uq1q3R9yxCWHOfDeI9/3Hvj7aivh1dz+L7n5s2bvPvuuzz/hRfCOAcgE2RaNOqIwYXAZjQo7j4lbfvR/MzBcHwtP9nH4uHcQDw+9VArVFKUy7JAGwlpiWt4Su077Z/4XQJ3kQ48gIX0bxoBn+1Rw6hMRyv+noxw8iajdxADcGQuPAs6yd55ep0OBWvLkL9rnXh6u66j7RW9dfRY+oxUxGf9nQNkGQvRu7RXGG/RvqPSUifr5Zee569ee5ftK5c5sj0v/LW/w19+fBf/6BOMiyT+Z4987U7HjdB9KuyjY91kMLhNAcrjnvHr1m/+a9IofOgHYh+crXMHnLs+cB5tFPfv3OXJa1c/9dnx+NxAI75crnhG5V+pcahTvmjy8KZckRbK2qHQ2TShKR5T70UOSM4DDxH0xPuPlKCR4uOp65qDw0PqasbTTz/NpYuXMVoQtLdSZn253MI6z7UbNzldrVlvNljrqOs6KXoSbiRUq3mbcwClg/Loicwn040yLjKpjwCRucfTB2tpfk2skxGnu/ekhRo3vOipSP0TLL0jKtSc9lRBCrGJQMF7jIsJZZLXIMI9C+1xIqQzmBwHb/gcjjzJ1gegMRK+8X2CfSROh0hxLO7WMYOSh+QWHgvtMHcDkncTpXr0vOzPSP/ogqByIU8ivy4KCh2o80SJjQI6Pi+7f+w3JxtV7GsZBz+cRHCLZh45UKnib1T8ohIOISwoX3fZuWJFG6+ZqAjKxcOYyuyM6wN6F6lrQ75JuG9U/uP8iTG3EjcrIQZxrQ7rDRSDezj19cRY4L1P1uyorLerDX3bphCikUzpLauTEzabBmstq/WKzXrN0dERzaahbRrapk1zKj5HrPyDh8RnABH6YDEMc1SRLFDRiJorTMYYyqqkDHVWKAzGCJOaKUKl6bqkjiQIxjCb1ZRlRVmX8l8o0FgWJQBlVYICE4BEHINYLVsFhp4oY1zIj5EimbBZrzk9PsIrz89+fCgeVTy7ly9TVDPKqpSxEc1A5JIfZBdhMzeBfUpXNUYJ+UJRSFjG9vYOHo2zir5z8l8gWzBao7SmaVqapsXVFUWoyOzJPdrDvMzn6LVr13nw4AF7e3tjMOHHcjWfNy6EhTkriewaxQfvf8iP/8OP+PiD27z+y19yeHjIer1OVlElCzDN06TUaI1XinK25IsvfJFv/OY3+PZ3vsXu/h4qeLWG8TAh9EMURG1Mpqg9/ngcQDjv+7EyNj7nvO8+y33Pu8dnaHQm3scKj3ibHF4bPvj4Luumx+oCvIThTr0XU4VqSk8f26i1JpDVsbVcsrW1BG+x1iWa1Lw98bpBZGdKU5Kf5/SVknm1u7vH66+/wXPPfgFrs+r0xDBXsGHPS97SyfyU74NhgeE3GEgnJEdoDEqijNXBFD3yVma5FzG/VRj3oocbpoB9DMrdme+TMVZlgCftraEPM+AxePXl+9yoNfotXhf6Il9XBjB6COVK8yJYoR5Xp0VrFfLGinBvQ10WWOdoupa262ibjt5a+s7S94ElkrEeCiT90CuDCWGKBYq+bSmKgsuX97hwZ8nxes18axe/Z3jiq1/l3T/+19RaB2r3s/P4U9egj54aFZjziBNCwvuze+R7y9RQP9ZjpwbXMdBJ38W2eS8sXEFnn8qO6bX5M7XS+L7j4MFDtu4/ePx7ZsfnSgafCqTUQC8DVpYlRVGMOmQqGOMxRbH5fR+LBOVb8oWXA4mcuSoXWH3fp4Jr08kQrX/f/ZPv8jd++2/wtd/4KlVZ8+EHH3PnzifUheatN97CoegdtLandw6LhHKUoVBftPTGRQBn4/UisJLk4PMscvH9SOdG9iLrkZoLKU/FJeVR+VysDDGpEbHGisipMjJB2MQ+jGErUdiFMU25FkkYxWTqwWGYJigCkhTjEIL4LkmAhkM25vi9WBQGL0cmjHPLRuhXHZT3wZ4yLLKBhjbHOcHaGPtb+VQ2YXoMcw+UUyHfW6Vk+hxDpeHynrbvg3Ie+yT0izqrPKX/wvVRyRvePY6RfO18BOfZ/IiAUw15BzEUJO/7kZDxTtzDWhLmpMCfE37xjHkrrhutdQCyw5j2vSWyPfV9n2L9AVpr6boW5zx929C1G5pmI2vTOaE5dTbka1iiBy0WmBTrvuQUnJyccnh4yMnJiViq2pbudEW3aZOHIHmvggtawl/EkxVDE1Jfu5z5S0Jl0ApfKLQxoQBjgTFF+lzVJUUImSmKgno2C9XXa8r5ItEsF0VBWRRSo6Uo0IUZUbImT5jRKGMkTyvInTShdFxFg6EAgpcBJXk+SqzBxg8kGn7iQVQE2YBkG+l6hlOap597njfeeIt2taK3iq3tfazPqu6OJIj8b5Qfpihl/mstGUDB1S/5NBptCoqiou89poe26QO7W5TzhnbTsl432OVCwtfVePlNlaH43f7+Pq+++irPPffceO2MAOFwvlBPBmAbYv2PD0/41//q3/DLV1/jg/fe5vT0JIWnxTWkR8YQNVprskEfcvDgPh9/+D5tu+ar3/gaFy7uy3soG+avbKe2tyhl6PturEhkx+fxIpynwJx3/Xk5kZ/3edPrP/W6iVIS9/KozDjl+eDjO3hTkXvJzvNcTC3XZ36HoKjKWF2/LuyPQnigybgmyPfW8wyScu/HAy7JF3HiJdCao+Njlostuk7GM+aIOghEAYNinpOCxNDd6RyVdsfQTiARE+TAROa4USL3I6CI/WOMEQ9nMEDkymlMEJ+OzdQAlfdRpKv36dwBkES5Muqtc9breUppNCCm88J+pxQYBaUxEoqpxuHuSguV73mGZx3WZlyiSkm4kzGaojTUXUlXdnSdpdl0tLqj7Xq6XsJfo9F10BEVVumwNw2hwfgerzwvv/wcf/rnP2JWVzxcHXPtxRe488Yvad+/jaY5M8/O649RP2XnxzYMgHgcHZGv96iD5+BweM4A3KfeiREjIQPgiAPyOAPF+fq3bFWFV/jesrXcOvP7ecdnBhqxIbly3rYtIDkC0xeahjjlCkz+Uo97mU8TqHlb4nPid/n5fd8PYQQT4RXbFAfvd37nb3J0eEzbtmwtl9y7d4+yKLly+SKL5YLTTUPvoV+tcF2LUz4pDKJ8ieWzKIqkNE4HPcZwk3FDD/UKYKw0D14I75Fn+yFUapCpagI0EKtEyJ+wWS5Ernw75xNj0BArOIQvRSaWASRBFDU+VoMOseERIYsdfLKxJvCSQyA5bPQsBHrJCBLGl2cKuYptCBuW1wPZSQQTSSEflG0BpvHeoeSO90Nl0lHfhTkp5uuUGx77JfZ0zhriCfTMPqqKUfiFooUjgDWAzigY8nk7BQh9SLBXaghPy0FbskSN7k06R9aXbETGx5yQ8QbUtS22axNzh0JyAKyVXINmvUlJyG3bpmRlby1ds0leh1hDoW1bNusVznb0McSIQQHO4GQapzQHGUIk84rQ6V3CpjrE18r6Lmd1KqwoVdYHw4JY3kVB2DQbPnj/A46Pj3HecfXyNb7xzW9wYX+fnZ0dTAANpijY2t5ha2uL1WrF8fFxUmS1KegjJWp4j2hccHi8yYS8D3lV4d8wkGEzHZMKCGYQhTcvpqaVGah4tUYja1Abg8s2jXg+KtTI0FCaiqq17HjDE08+w7u/egtT1DKPQnx3QDeDLI61cRA5YnuZS53v6GxPoTWFVtRFQa86tuYLLuxf5IP3PsI5n7wXthcGqMIYjC44PTml39tBh/5xSSacn3iqNWxvb0vIW9+PzvEOcg9oklV4+r6TULe25/jRCX/5/f/Au796l08+/ITT9Zo+yE9VSG4bUanTgyEhz/dRQFWIfH/08B6/eut1nn7mCXZ2F1y6fInO9hweHoe8uZbFYkFdzRPA/SyHfgwgiesmHlOlYKpQ/Mccn6YsPu48eeBZUKOCMUahODg54uDoBFQIC4xhgwyyZ7pn53tO9mRgMCo6LPsX9oTgwLVYW5DCULP7wvl9Mtz7fKAhxAOy1q9evcrHH33EE088NRiwUAHIB3mW7YG4ATCk94iKewIk0gNJ2cyBRqYzKMApiZTIQyLj59xYa22ogRNJCpQZ9cPwWUVb1hho6OChjgCEIbwrtmVAM4wt4+lHN8gSuXCglA/t6Ps+yZlSK3xhsbZICncMQYz1HEfgI+mK0Ss1ACzI8mKrMtTtclRlRdf1rJuWTdsnT3iUJ2KYUChrAoJxaCsgyHuNK1p0ofnaC7f4wU9+yivf/Ca333yLl77zN/nR3X+Bse3ZdfFrDsVg1NBKRf6Xc+dpbjCP839KoJQfU/ZV732mHw6U/WJIdng9Tj1Ibcz3g2n7vcOg2F5usbP1nxho9F0fkgIhTtbItpGHKOWNTC/6KcIrXyzDy07R2HhDjiECcaFaa5PHIj4/HtHLEePmo7IbPTHGFNy8cRPl4fY77/Haa69idMnPfvozvvCFL3Dxwh7WeXZ2d9FFyXbf88abbzJfbtGsm/SuzjlMqFYdB3Vq6YHAzpQXAco8BhFopPfLYtBdCNcYrANRTWNSbHewRsSzcsVT+iSEO4X5HhNGoyAVusAgVAMAGcYoJBVr0DGXwGfKTpYslo9n7JP42UPaqAYBTrA8p1OHOOB80od3UyGMJx/zaUJWitmPi8kDhjNMHvH83st8i9dFbJNqR4Q38BPJMFKCcgGhSFS0sX0QwqI84ntnvA7iMxRDzHes/+FDboFzjq7vQsK4He4dNhCX5Qn01rJZr/BNQ9c0rNYS+td2LV3bSlhRKyxHzjtwHttZXC81Razr6PrMC+di+70kxI1CGX0ARtJfkTJZBZYZpVRYJ+IJKMqSqizRRlMUAhKquqYIldurqmI+n1OWJRQ68OwXUoAx5A8UpXgRdFh7El44MF15PF5ruq7nwcOHlDvb/Og//CXKa2ZbS2499xx7+3uBBlJJoceiRJuKoizRvcPptRg0nA1JhaJ4JlAa3l0rDcYE+aiSfPQ+wnAFJlMso/zIjA9i/JB56HEplMkj4ZNKiavf+owu3I/XSd9bvDaIk6sAU/LK177B1RtPcv3aNdabFlOYxOQCMfRH4/2wqUe53rUdujBSE1eJpXVWGPa2l5hC8eyzT/Pu22+z3rSsVw2bjVgRrbOUpcIUmpPTE6EDn1VhnmT0qLkiFtadDSGISinW67WEskblyAZA7eHg0QHHx8fYvsMUGoz03ays2dqqefKp61y9dJH33nmXH/30hzx4cJ8uY+IrioKqrKiCJ0u8WTXz+ZyqqqgKw/UrF7ly7SpXr1/nr/2Nv041r7n34AF7u/s4p6nKLZpNw/177/LO27d55ZVXojg/54ib+PCN7FMqO3+QnXkIibMhHymF4OZ3ZSyrJ3Hpw+Gz/x3/lpTKeKYfzo1KXnra5P7xWgHeho8+vkNvLT5GQ/jglvMDcQveh5oGatxXfjDaxC9ciATYWlbM6pq2bVBOwiEjiYbIyPN1iXS3uN9m2G6wKIdnWcm/3Nra4dXbr3Hl6nVAQgttuGUy8MR+8kIPG/eL1K6472TPkbpOPu11g4GINDe01oGKNiqPMGWQivKN4B0eJNHAyJSemzbZcahW1LEcwtrkBqUh3MsH3enxh8reTcIlww6mNCZ40JVSFCGnVQxZnhaPtgOTaQIV1qc+GEBI+I9g7NaxEGumYGt5ZiTDKQpHZSuKqqRoepqmEKbUhkCV60SeewtGlBvrHR0erxW6cZTA5QvbXLu4w1u//DmXLl6jLLe58PQzHL9xjLZCpW5D3Rzt1RkQHtmfpJ9smu/W2UDJG0Cb9mf6OZeJaV1HI42K8yfIj/BF0rcUoHNPYnhO+Nf7QDOcGUSn+CX3f4CEtjnnmM9qLl+48CmzYjg+h0dDXODOWXRYoYqBoi56B3LEOlhUB+V5CkJyr8L09QaBnFnaR4Bk2MxzhTF/dpycYmkI3eY8IYuLeT1nVpTg4Usvv8TBwQEXr+zz1a+9AoCpDafNmnuPHkosqAPVW+xmg8ni5+NCiR4N6x3auzGCdC4AjRDXayPnULQi6BRjb23M0ZDD+X5IMpeLhsmZJtx4A5E/xn3t02dR1mN4lFhCo7LuMT5uGjrUEwheDgUO6U/LIPhIbxJbECavixvMoDQQQN7QRkfkMI9Kz+hIcnpgD8qFdxKoagABOtBbam0G3vPQ3t71w6JnEPBeQet9AhrKy310sNZYhrAcH0OOsrk2brMf+jbLq4leqr7vsW2HawUsNG0TEtp6urbF9T2uFUKDzSZ4DXpL27XYvsVaoUH1PjCgWEcqShgBQm8zRjGL6jqc6+m8xRKsYBKXhTMaH0BRoQq0g8LLm3dV5rrXirIqUjiRMZqqqpnN6hB2VEr+QVXiC6FBjcUXjZYchsKY4DIXEob0u5HE203bZTLBB/ahjqbpwvwQcOGDZQrAVCbxo+dAPlq5vCnpMZzagptPa978xRvYzQrQzBZboArq+Zy6qlN4xGrd0R2vJN9BlaAl4dL1PUqJx3CQbwEk6ALQI4VREZPuwppRij5uRF48Hc4rtBHOeGcVWhehiKNU7NZKeOWVisaJkGflhcI2KqrO2dAnCmcLCffsWjrr6IoZO088TVMYHh6d4r1PBhrvnHzWGqUlpMuYwTqmjcE5jfEF2kChLYX23Lh+iW9+/SsY5Xnx+Vv8d//dv+TgpGW16mg6R2t7tiqNaTzrruGk3WBmJdG6bVRGLAGjPcI7mYs7u7s8fPSIy5cvD8Yl58Ep3v3Ve/zsxz/jlS+9zK2nnmB3Z0m1MJjSJKKOe/c/4vf/0X+O7XoOHhxy8OARXS+5GdEbLoXZojgS2VjXtbTJ9njfsWk6jo9X/OzHP+f4dMPd+/e5e/cRSs/pbSc5XMrR2Y6d3Us88cQNvO+TzBv2Q1KMfyYuRBlA4Rnkhcyt/ERREjnHUh+96mfkZ3zA+Iuk3I69KWPlPtJg54BZ2hVpgmPbAmhUikC8yf2Hj9BGYX0vYYo6FBR10aor1w9gc1Cc8qbEx8gzey7t7+MCm5sGnOuSwSy3pINCKEw9ZHI+PsopzuwloWcwaDatpaiWrBrLyarBFAUO6EPoaDLwhRBn5S1aWQEjDpxXWBgBvkGHGcKqogIpTVdJeS5LTWkYFSCNHeScoyfLv3PRUBg8CKlQnhidfJgDzsmeFsHNcDgsnhY7QMlA7ea8F4rwsBHnVvPo1dBpinm8MeCE5ckYHYySQmmujUaXBd6bpOP0ITqgDxXLVYjqFuAqnl4TEt3BUyiLMQ6fGZc1gfEzUpGrwZttjJcclqqiqAvMZoMuFJvNhq5z0Mk+qBDw6ZQY1n2hMQq07tnoki+8+CJ/8id/Tr/V0njPk9/4Cj95/w1mR6cY7+iMw2rNzGqwQ/haNvjiWUcH77bDO/HQxbUWPbxpLkAKbRONm5HcIMgNHQw3eEWENNFI6kOH+qjxqOhV9CEvzaD9wLCY60QRq6Q5oRTWKHoP3XqNals+y/GZgcY0/jMp2IzDQaZHXAR5MnQ8Brff4A057xALXT9qQ/68PHYtbi5Td2wMB8jb4ZyjKkuapkEroXe8cuWKoLX5XNC5KVgu54LMTcHhwVGgH7UJxIjwECFirQttJViXYv0AWeRCVycKgUsFXwCE2z4Knzx523u5zvqxtT7/N/bT2X4cM3Lk4C9dOwF+gm7Dhq9VsMDECToksQGp/kHe17niHRNslYrPCQti0vZc0cgP632Kgc2FctynB6E9QAdZHCopZZH+M1kCVLYQGUAMyBYZXhK8xzpPFza1tmtS4bOYRBo/R5ds/C8WR7NdB8EDEcOB4vl929I3wZWbrCsW29tUTE2rkM/AoAD1WAndCxVP09iHtxDQO9TMiNafclaidUkV+sL2PavDY2zb0WvP/sWLXH/iSZbLLeb1jJ3lNvP5AlVrihCSJOBdEvEGd7ZYWKOFJOJIqyY1GrTC9kIhulgsWC6WQ+5UuGdZVbShgn0fgFJZzyRHat3hkdoOAgbAlBXOOlRgZCpMgTZS8TrWdumtsIP0zlPVNXv7F7hy7TofvvcuVhk2ncOqjnVngZPYiaDLlOTutaGL7FgelCqSTidJqjlBwpjyb6DCnRADpLUC3gUvBgNct4G1SisnSXtunLTnPXQO0AICtJJkWbx4bzrbUlU1vdMoM6MMuQtlUbAojOSYmCIYC4bkbqUEvKiQcEpQaIwuxIuEozKwmBUs6hoDbM2X/NZvfZv5Ypv/y3/zz9is1zSbTTKmzGZzNps1q/Wa5XwuICaA5GiEGZQtGBThnosXL/HJJ59w+fKVJMv6vkOrgj/+7nf50Q9+yPf//M9ZzivqumRn7wIXLl1id3eXsih4+513+PD2Q/BQUAhgbxvaVtYuwHq9ou+FWUzWtk01TYyWldS2PU3XgxIw1rQt9+89oJpVUsOgLKjnNfWs5Imb17h+7YrozgoGWlCf1ke+W6rMUDT+NQMkHrwfFJG47pOsdFNWx9FfjI8BaKhzQqCGdrh0qbUua4sjp5FNiqGS/eb45Jj1ek00FpIU6MG6ep6BJlppR/taaIlCkqN3d3ZYb9Z414mC5WQPHuVjpHfKrPfxvh7QKoUVj5T88DyNSmGbdV3z6OCAnZ0dOucSQQKEYY1hn27oU09gAAzYz/uzetJ5RtNoHDVGasx4lAB/pVJeongcIuvZeP8TfUvCgSKIiqQz0dujvD4HaEj0QItlsjEK8PKkyItkvI19ICOTdtTe5fNLogqc8lkUhCXWy4gG5Pgw+RyLBg59Ym0/eP21x1lhrUpeDuXD34wMzCm8UinKUqN1TVkYqrKgLAybzYYNDa4PxCB4PAqnlKzVsGe1tMxmC1588QVef+Mtrly5zvLyBS598Tke/OTnLFpN7RSdD2skFQXMdNasr7132Xr/9CN6s1U2R6djl4cXj0Mtycb67PMUpPDOsWeTdK+RkcHLHNJKcXh4SPefGmhMcxpiuFR05UwVzLzh006JLxAnxHTBJQGYLbwRujsHrMRn5509CqfxYiXMr9darLEqC7GIVGkSi214+OgRSh+K8HCw2bQoI67AmEgZBwWQmHRECAhDhkqD7EK8ovND3YloafA+JJf5AZxFS6lUg/ZJiUyWtzN9PgjX6ZH3cd4vWUfGE0WoRenoh+sHVopsIifLlPwV2Q+UGgBT1ogR6BltprHQTpzM2S+iLA8x63gfWI0k7yAJLO8TH753PoVHdK3QkXZdJ0mgrVQy7touWfzFA9CjvACBLsSYW+vou05CjNqNgI5If2ptEpJ9eGaec+OjxSC5t4eQLUWY+2E+amNS5XatNUWpUbpKXrK6rkNyosEZKOd1yEeoUvhHERKRiyyxWZTHUBnWmMAU5bBdz+mjQ371y9d549XXwMOFS5f5xre/RTGr0abEBC72ZKAfWWDTLoTDD+7fOP8UGAIQ1ZLUXJYlm01DNZ9jqhmqqHBBgcaBazb0x2vWTcN6vZZwKRTHp5sw/+Terrf4TmpCxPAp2znavsP7dqBnzuelEkIFowsoa55+7os8Ojhm//J1GqdoN33wzsbwIYenIypKUebJZwWWbN7Zwa7re3xW9BGVhYggCn0KR0QFRdtLjfW+pShM2kBlnQarrM6qTzsnYQMET1NRQZDNUSszRQHaobQokkbp8J+iKgrKwqcxMUaS1+fzmvmsxiCbuoSvzVI4qMfjDRTasFzM2N3eYl5V4KFrHR7HF198gSeevMntDz9mvTrF9RLSUdczjClZrdZ02z1KlWF8BiveWYMF9L1lZ2eXN954MyhrQY4GsPHuu+9y5+5djFLMSs3u7javvfE2Whvm8zmgODk55i++/x9EgYtKlvMpDymOQ6QwjV7CKG+kJomROeScgAetsN7StS2FUZjCCGtYVbK7t8u9u59I+GKYA8OrqWR0Ge2KUeb5mKszmkLDae6sbP+POc6z5J93VnRSjPbUsDVMG5oUIeW4//CBhESl4pwxGDS+09hqO3rm5Bz5LP1TVxVKKdq2w1nx7GpVBgfZAFYjQUsM6437RhRkHj+qHzR6LgSrupBY7Gzv8uD+Q6pqhtJKZL0fYt+dDdTc3uCdluKQyuGxWBW84M4nor0p2IhHnnNWFEXwABjElyAW6T6LctDaZN7bYR+0Mfw4Ao0EuvwQYeDHHh4geHnyeRk/Ba8q4pmwvXghbCiYh1Nimc+MBZKgrtBGDFNxjxpyZi3gwn4YjdYqthqtHSmvMuiBMVTKBcOZ6mNOR8xdkVoikUBDQqyG8GkTDW6FGYENozSbTZ/0Pu/lvsIXYrFKo7XD9T1P3LzBBx98wNHRI1YV3PiNV7j7q3fwh6dUtkcp6I3kxxk36KTTQ3LkHJGp8XHH4N09Gw00vt/Yk5MfEmx21hGQnzvVw6dG6dFzvceHnKCpceNxx+fyaORJp3nDYjJUrvTmYCDvhPwl4m9TFCY/DaCh67oEcqadkyfG5IOaI0kdXbYT0CIKndCikSmqHoJFAJq+BaXx1tP1FmuFvz7FyI6U96CM94AS93H+brF4l/NuNEDR+iIbnLx7bvVxYXOLinicL0N/ZkBg0s/nHbJZ+DO82bKxhtCgc+4jHgWVkLgPoIT0LwiuGLw00WsjoUhDchyQqklLfOGQg+CstKHve3wnIUa272malq6XasnHJyf0m4a+7YILtEvJys5a2lTMpx+FEHnv8CFB2bvBfe0RUNSFmF9UsFQHFiPZo1RS5HSaixBrWxgjVmKths1Cl/JfBAtFyOMpq4q6rgIVaplCjopCwo90zDsIFmUdWEZivLZYryOocXEYY0SgvEJiQJNQk95LgEOJWDHm8y1sD++++z5911BWFdV8ji8KKAq8LrAoCjNmjJGQkyJsEDFYLdRvIctbCJYP2fws3oIuajadY9WuODhei8IWqY6dxMuiNFqXNL0QPTgbqA4D8CbJB3FRg3i9cqND2lRR4A3WWTrXS62LtuPitZv8zt+9ilnUHBxvsmk8MJFExT4smgAOk6qUronroywLxLA5JG7GsSJYNktjUIVKtK8usEcVxkPccLXC6JzAItDEZoYZkI2zNgblJQSqqgSY1nVNVZWYEqHTLUvqsmJrvqQqS2a1wRWy5osiKgBhYjuPTvkPWbgqonz3vg2/KTanK06PTsArAfK2Y77Y4srVS7z2xhusTlch18ejSvEIN5uGrpOQJU0MuBnk1KA0Df1qTBHqXXRJzrkgc+J8b9qGxXyLF196kZ/87Kfcv3+Po2N5p9V6TVVWOGcxmMSwE8Oz4iYs3Z0ZdKRHUF6BC15RBAh4rZKiVZoCWoXaaJTRHJ8e87d/72/jCDk1Yf7EcMt4RIeAiHadasmgVPIERvBx/uHJf1HZ/6Zf4xIY5VMkjJespemaCfjw2R3zz3KfIcct3cPLkjw4PhLPIgqDwStR+lNfTIxe8odPY69SGEnWZudZzOeh3o1FeSl56vt2pFPk7+FRyZMdwVyUWFEdPy9hXGdf1fWM99//gL29fUxZYDVEKmRsCGG0Vu7qC3rXAw7rO5xyKf9KMRDj5MAtN2RUVZX2CG20yH8V5LfrBtmqFL61KQckN9BFpsqcNTL+5rMQdh/0lcGLBF6ZJJNtb2majZA7rFZsTk9ZrVc0m4ambdI5fdfj7djYPOhYKoXXR7BRliWz2Yz5vGaxmLG1tcV8PmexWATjgBgRlJJ9T7zKGhvWTq8FCOjgcdVGo53DOI22As4K50P/6STHi2wPK43G1DUmGMGMadDas9k4wOG9RMZ0vcwXjcGanqooePmlF/jz732f+f421f4+F5//Akc//jmm7TFa05fBYNifregeP8e8iNH0PweU5AbzqG+et3bOeAYz3S1WfE/rgvOBRZ4GMCWnGEUkBTm1mM8DIdSvPz536FQU9DFm2/lBUE8bdB5CmnbK45Th/PuUOO3HkzlPoM29FDFEBQb+4cLokSKeWyhRsjj7YB2QwRFFoE80nLEfpACVbEDDhhiFd7KsdxbnorIq9+17SY50wb0WN7yojMc8ktgmUdJCfygyjuXcazBQeaaNJ+/nuHme08/JZZ6eEbxTbojXQ4kbOd3Lj2NKY55KDPVRVvoxFjfrY6hQs6FrVgIWQrhRFGK97ZIA7PuO1WrNer1ivd6geovvbco7iGFJtu/xvUvPzUFuHAPUUHejMEYqFmsl7DKxD4LirEAKsbkOhyT/z+Zz6lnNLFRHrkL9g5iTEIVmUZRi0QzJzFI5OSSkaY0rQ8x7mFPEtaCishrntMxHYzTKFOLaD0nBfd/jgrAqlcYrg3MheRuTNIAISHNvoPOeqjAYtHCJh7Hb9KfsXLzEfGeX0+MDVFlSzeY4o1FGvAkKSezM141oKEMiXpwL1kerXVT0XQIaKEVgRQ6bo8xtCT0QL4WMXRyb6C0aAHneV/lm7dxQpdc5l7wo4s3q0aoK4Wmt5DpZj3cKpQpY94mKVuKgDbFGRawmrbXkmkQWMQWUwZtpraUKVlatVRiAwTLpvbAuaSNxsJWJ/Pc6eJwKqqqknikUElJQlhJClmoOgBTHqyuKIoaGGuazGfMi8NEXcs9kQVYevCg8fS+kAFprsB3edvQh1KtrfFJIk5yzjBJqfTBhOzxeSZ6a2Ga0GEdjSCiW3isuXb7IpjmlWQsdcd9a/AyKoqLbrFmvN+IlUIQMsPEmOd0rCmOoypqT45VUB/YOq2R+XAysT3jHw0ePuP3BbdrulLY7yaxxUnRRKY3Xjh6wrk9zdXieO9OO6I2Kc9crMEWJKUv5XErcvlISY15Q8NSzz/Glr36dtpd5GWWy8y4osD7tm0n8ZuI5Eg2EJ2YW6bDsOCvLp0cyoGRycbi/SmM+9YZPtwl/VgcP9wDJ38j2mXDtum2lGKwiGPgi8UHIMZhU7o6H7MdTr3e41Fm0glld0XZNMHKIAUg7NchUOTuTE0E+KZKHKukq/qxxbnheDsxUKNgp4MGHvBUdPIR9L5TdXd/gfIvU4bD0ztKHfBsBGuez++Q5D7mCF6/rrRdQ52TPjyFMzsp4RUAxXDMQzOThvD7MQYtLw+XDft73PU3bsV41nJycJFrxWMPI9z1ktLC5YoqXwKk8cXtoh0M5MWBGBsJ4fddJrQrnXDKUzGYzdnZ22N/f4cKFfZZbW1SVFAn1xHB1YUeM8jHmlomcVRhjscYI6UgMrdIaFYwL0cBZaIUuy1DPQmEKhTawWQtFu7UevMIphzchDFc1XLp4gRs3rnL7zh281jz1lS/zozfeYtY7ipDkP3VSjMiSkj6VezrHMu9xenE+b84zKJ+33vP5Pf09/z7Ovcfp8Ol8C5UpQsjgr5dF8DkL9sWNPU6oARmPz8sXyxQZJQv95LzpkdOZxZcd6F6nOQA+tSs+I79/VAiilTD+Hj0ksSCeCwvRO09VVaBUSAC3DLGxWngXk3Ivh7VS7ThWCPUouj7S30rF4b4PcdwqUPJmblUVNt1Ug4MYr5hbTskmpxrRxsX31EqFJOWIZhn1SX6+0QM9nLWWLlgMvfcYPG3TpPwE2/ecnJ7w6OEjjg+PWG/W7O7scunSJZpWhNNmvaHtGjabNev1OhXEapqWvmtwXZNoUmP8ebTgxTbmuSk5EISB4g9AF5qiCoLEmFEYiDEGXQ05BZHdSCslVvu6DBYcEbJN23J6csJf/eyv6E+lSNtLr3yZG088wWJ7yXyxwJQlKlIXZyAhD2dx3iWlIDQZ56BQgycuDzGKypyKUytYW4wuJHFayXYgwH5YqpJIpgObhFhusgUW5sxgUdI+hNh4AQNWBaaNoqDaWnLx2nWOT46oZjOiZ935HpxYz3oyy1uYly5Q4To7UAUrHUkDHF6plMujlBrlkzgH1g/eujj2olQPPPUptAjCWs2Us0woKyXxyzJfCtBylilKtK4wZh6sjZ0AN61BVyhVUCodgIaETUX3vDE6jNvEcqTFEW30kKOVt6M0UOph45zPZxhTSE5KXbCcSQK8MQIU5L1kPidrZLZGRb6JZj8YFWSMvff0vhNWs87j20zJcA4T+tgGj5wNfSmMYTF0S0ChSkYNUZKm3pNoMUWrkKROsoK6cG9rLb5puH79Ct47Tk9OWZ+u6VpR6suyZLM6Zb3aUBalrF3lhmq1aQqfNYwsFksePXrExYsXBUDSs15veOmll/n+n32f0+NjFJ5fvv46eEsRKHwln2gg5GjaPuxbjHJnBNCPtP2MmtNiQl6XR0JjSgVaF2ztXWD/wj57+/tcu3GTJ596hqeevkVRL8QwEkMpwx4T5bLzg0V9eGQAtookR6a5kT4wL32mw5M8jNNLfAA6Y1Bzzq39Y/boxCqXW7BFoTxdr+TdtM6ApBLPkBLCk/ydhz9cWG+Eew0/GS0U0RpCXk3cz0SRje+avx8+htr57J4+XEvae9P52fWGcRuNMTRNIyQUEQwpB1pTaM1yuWTdrNg0a5xP/vkUxhuJXab6SzRIxL0t10+cl/pM1vaDUQcCcPAhXGlgsAJSnQibkZbEf2005rk2FUNtAgvhJuRTuV50mdhfQtLi0LpAKU2VWP9q5vMZZVmxmNdoReaVN8mToI1CaXl/2/c4LwDh9PSU1WrDyckJp6ennJ6e0vc9BwcHPHz4kPfek317Pp+zvb3N5cuXuXTpEovFgqKW+7Z9K4ZfJx7fvvAUTqGdofCgQpHFIoRVKSPziKi/BhlXViVLDVUVQo3Vis1GIiIkH1faLrqEpu8aXnzheT6+d5/NquHypX32bj3J6uevs3AKg0rz68wchxANMxiBxaM/eMtzmZuDjgSjzwES+fE4sDG9drqH5h6XXF88A44R43MXSkF8luOz09vaPilJSbE3Y+9B3JzyBXMeqJgKzykbVd4JuSA777z08kHQxUVSmCItuClgiffVQanog9LkQyE3p8EXAia0kNYHzwOycIiK0LDwRfAEo00AALa3SfjFfAHpACWJY3ETCOBAI3UhtBmoCxN4CkLC9n0SGG3b0ltLs2lTmFDf92w2ouwL4uywfbRM9JkQc7hekpLbRtygm02T7kFvaTYNzjux9Hcd60bqKbiuP4O+U3zsyFswjIvkWNgUD26KgqKYSYy91pRFRVXXlMFLEJmIKA2mEq/BrK7RRlNXkp+gixBOFOMzg8W5KEpxFwalaGQhUDEO1QemJvGQnJye8MGDB6ze+hXKFFy4fJn9y5cCwDAoUwjQINuOFHglCqJXYiUyMHJVa60oGOq8CAtZuDwWLMznfNggvR3mqfdglBmsVF7moRRO8yQvQJiEaV7i6XuH0oq2twN1nxMvUNt1tJuG5196iSefeIK9/X0ePjyiKCtpY1AmLT6FCuagUMniHQF7cXkr0JrW9kkm5EWknFd4NVRRFplgUMqgVQwPEyDX95bZbIbWQgFLkjHBOhS9QNqExOV4vyCHAKMURssLKeUluVIXeK+YqaHOThnAqDYSxz+fiwchzt+qFLrbwmiMdumaGPKmtaYuoTQ+ebhUkB/ee7TvUa5L1tiuaeiCfJOwtsHblayuTgwYRCuvix4IUeQ6pUf0yYM1TYENCokX6/LAUgPGigrosnvGzc/iQXmUjVTT8ZliyIjkFwTlO4b89G1P3ztm9RKtFKvVCSerk+BJsqGfDeumo2p6ChNCDvWg7ObMgopo3Vfs7u7x8MFDdnb36PoeVWhW64b9ixf5g3/0j/jun/wxJ8eHrNenuLZNVloAZRyr1Qq8x3YCHubzGWhF33eh52KORuxIUMoED5ICF8JUMBhd4XXNl7/2Df7Bf/EPmW2JHLPW0XWWxc4O67YLMnGwJudjmgTkIEqCaupAxUKt+V7pM2X6McBA5X8PycAKEiNbuizK7/FFQfxkxiuGEC41fBnOTS748AyN7Xs2TZvkvlIqgFq5Lm9/Lk9iiyPoHQMe+aOqK9n72uCdint5rGGUgYh4nTikclk6KGGpKrSfFDnzEmYaDzFQ1RweHrO9s5UUxLLQPPXU01y7cplrVy9yeHTEanPKpu3YbHp+9e5t7j14hPcxF2sYkxR6heQR5Mpe3qbehXXL4IFJcsAPxsY4p6IHwgVg4RFvYx9yCvu+Z9NK6JOLBCSxPoMqAilHmD3eMp/VFMYwqyqx/EsPS8iU7VBoTo5XtN0KH0BEXUveq4AcGdn4jLqScOFZXXPx4j5PPvkEy+WSoigBz3q95tGjAz7++GPu37/HyfExn3xywp07n6C1Zmtri4tXLvDEk0+wvb0tsrMXQ1xhHbbQFCYYb/Xg0S+8sFlJmNQg86XOUSQ3KQAD3qCURFR465LHVjlL1wnoW8zmPHXjJm+9/wEHq1Oe/8pv8NM338P2a6wk8GHSRq+SUdf7EEaMJMartN+4Yd6GJRLtj/nCTt/FsZiAhTMgJa7cQf0Z1rMar/5k4FWBoSrTR8ZAXXIzllXFbF7zWY7P7tGQFqTYUevdaOFOQUKMu46dkAvaqdtn6oGYAKh07rQz89/kc2RCCB0VrCkmMByIABtcfkVZBi9GyMsI/4dClBoPWmIDQpk3MN5ivA17rMSeeiUVlnvnKE2FbTuUtWhICUbRfdk0TcrT2DSBxShUC/feJ9q+9Xqdzm3blm69wXYdm02DtX0IJQrgouvF1ReEie1tAhbK9aFP4uz1YfOzEjsalQhIFjwAOokL1aXBlAW6KGT8jaGqdcpHyPMOirKkWiyTdaaua2azmYQY1YHLOiQol2WZqiqLMjqE54i3J4x1AAz5HBgmWhxnOabxkGn79iFXIFgVxXWqUcqBtczLBc4XPH3rOe688y7GwHK5oChLVFGiyxKUTiFEhLmSpze6oKQppHL5MEdVVOFkswj9rENYnhQtjGtDkue87/F2SKzPN8e4SeEz+twoXELIj2NgKXPeC42j9yir8FY4zMU1HBLhOwfVkuONpeg7lBoAAlrhQn5ETL5OXiUEWGkVQsK0JJyXZYFDURShaGdKJg50s9oEBTLmTsl/xhQYlRVm8h4T50cALxFkJGrhAGAq7TGB+09OFSWxLAq2aljO65QkHwGD8p7aIOC2KimLYmir9ygjFvG+6+j6PiWixrmWHzJOQivrnadvLbZtR0qAjsLNM5KHIJSKuYXbZ+dEu3C0QvuweYN4pxzZ/TLZmcvouHYcjsh+N2p79CwqxWAeAZ9vgPFbP8zXqMB664X9p3fsby/Zmm+x2qxYbU5o+jV9v6YoZihd0FnYtBZTSLJ6YUxYT0MYiHMCygsF3vXsbO3x3rsf0PaO3nl841hvejoPt774BZ74wrM0XStKZ9NI+mzYq9brFX/0R3/Ej3/0I4z3GOP5gz/4A9577z3efOst1qsVXd8iHq/pXuTRupQ8QTGVgCm49uST/IM//EOKuqJ1QwhnURZCHd1tsnkxNnB5HxKJzwEJ3gsff8r5tmf3z+m8G/4YvADJsOfDWCo3vfSxRzR4RGUk/h09mrnhb3pIXHuPDsYVAiCV60Z2KIYTQhf4YX7BYKjyXuSqQ8Jb5RhCKh8XWp23MU9Uzq9LcpXx2hmAmKdQhtm85ujgkOVygVeiJFamYH9nwccf/Irm9B6zWY1G8cnt25h6xrWrF7n/4D4uJHMT3iUuX6V1Spgf1ZDI2m0zEGRDrFQkRJgCDO998lRoL8qgxdP0HU3XCTW6dYmFSitJiq7LCttJ3h1OxqgqDZ4ehUUpS10YFrM5i8WSuq7Z2loK/XRRsFjOODh8SNu2LJcLqRatxIvd99A0locP5PfFcsHx0TEHDw94cP8Rq/VaAEryXmyxt7fPl7/8EsvlN9Bac+/ePW7fvs2HH37I4eEBj44PePf2+2xtbXHz5k2uXr3KYrGg7y2FCmGkhYSfoh3Wg3VGQh21oyjE4yGJ6hrltIAsFHVpUAuJLNEKNutGwFzwyKugBzjtef65Z/nwzid0bc/+passdi/St5/gXIvR4rlPczwi7WhkDoBepl/0IJEMjAlgeEZRLnH5iBFGjYya5xnq06PDHXx2fW40HF2T9Kbh+qjnSOSClLlAe5yP6/HTj8/FOhVjjnMmoTyuKxeGec7E1Po9fqnxM5LClVknz7husg7NvRzOupFQVpOOzI9UF8B+Fz5KAAEAAElEQVR7Cm3ouw4FlEbyL7QX19DJ8Ql913FycsKjh4ccHR0zm82Zz+Y8fPCA9XrDZtPQWQdKs1pv2KzWCTBsQlVbaaeWbOku5GwEi0Mfwm5ESckSoZ0kjcdCPD7rn8hWI8qHJdInxmTKspRYZrQsurZtg3sOySEwCqNrZlUVxmrIWTk5PuH40QHgWS4WfOGFL7LY2qKez5gtFsxnkrQ1m81SfLuKXhkzhJNES3D8rCKlHeON14Ug5+n8iGjcI0q3bDw620TG0d1Gm1HM7RAaElh+DBSZEJdkabmmLAw3rt+gmi3wQFHPKcoZ3mhQJrTjLNtZdL0PQiVLMPeDUphv3qnKMQ50mPfZhijCQxTxkYLhgxUuMHDFcC2xOMS+i5zcKtXFUMFCUXoRpkoVGOORHISCoqzxhYDJwgyAT4ecBVQpFkQiUBjGV2U0t/m/znlmoUhfTI4fZINJgCIKNRNyHgrXUoRiU2VZDEn1IexRQKKMdfR6zRdzFnOYVSYlU8Z5WJgC4ySGOCbPi+aiwDuUi8QAUqcjKTdADKVRSixym0yhGR8DoCXM1UFZymTQRNnMD6/UoFySWS496JgyPVVaYfCo+QgKht/cCGgMYF3m2/DsfLMCMib9s22dKr1J/luPbS04S28tFy9c4Oj2EevTFW2zoWlbylIKL/bBSOIQeRSpK/P3k/5SOG3oXc9yPufw+ChcJ79ZJwX3bNgDZrOZbMz1LMwVadv2/kX+4R/+Y7wu+NkPvoe3lvsPH/JP/6v/iq5ruX37fe7eu8tmc5oMQ33XsVqv0Fqz2TT86le/4uGjAwpTcunqdf7xP/2nVHWVcjDivC/LcqTUTscsfeeG+TA6D/DKp2yR6R72OCMbgHfqzLgMM8qemXOfdpxpb7afftoRc1rg15975lDTbJ3wdfifqFg/DnA9rq/z3/Mjj5s/z3AAwTgQFOrVahVymxSSh+H4+U9/xuGDu9y/+wmzecWlq5c4XbfsXbrC/qVrGK1oNw1OFfFuo2fk4xTXVqqAnuVXRBmUA4zzgIZzAiQIe0NnLZu2kbBJLzuYKYIsDVZr5YO3yPaYKlD6VobdnX12d7bZWi5ZzraYlfPkIeq7lt72rFYbTk8OaRpL33sO7j/C2vsJaAg1u0v6Y7NpmM/n3Lh2g7KqxIipNF3fs16vODo64ldvvc2r3YayKtnf3+PChYu8+PKX+Po3f5PT1Yrbt9/njTff5PDwgNePj/nVW29x9epVnnziSfZ2ttDWYEKhWhNyQFwwWFkd+9UGlipJuNdTz3YK3de0TTd4iezgGZrPap67dYvX3n6Tg9mcZ7/6Cq/9+7tUrRC12MBOCmKMq6qS+XzO5uiUvmkHSmTlGBfVG8/BODc4Z94n43tmiJ2C7en5583zz3PEeesCQPwsx2cGGtPQpfhfdE/HHImpBS0ugPPyMfLOyDtHh4JR+X2mXpD8+3wz1UHZzFmyzgMqXdfx8OFDtre3cV3P+viU999/nw8+/IA7n9zh4cOHtE1D07VUZQVA3zuKsmJ3Z495XTMLytEHH37EwdGRxP96JHGs7YmsPDFPAxCWCje8q1eB6tZ70GL5iFZCHZQ9kHCqCBqKoBBWVUVZlVSVVEqug/fA9r1YfrzHKo0ppEBWURYoRShiIwXCylKSTnXIdbDWcv/uXX74F3+Oc46di3u8/JVXWGxtUc1rdFGilHgi4sYYOhmPT+7ArLNDbROI8b4qjnscGw/eq1E9lLRBhD5KY5j4t5Gcwpy6BcRarjOvl/con4XyxUWSKXJRiJRVzStf+xbeQzHb4rTp0UUhgtKLqzp/r5inoFV2v6BwivfERSZBsUL5ITlaFqoLVuy4GZJyhGQNmKQASptjlfvg8Qmen0iLG++hGQCfD5YzSRLOqG5VVPCNuLcLcZuTrTWtJGdC+Uj5OlnA4jRM80Ax5A/p0BaTAZc4roU2FBh8YI2JALiqDFv1nIvbMxbBMlbVlcTzG5M8OaRnDWPv/SooUxbve5RVYKFtHMoOuVlSj8INU0YN9YBiO2M/RsXAByCnMj76sx0xyKAYKkV2T5l7ETC4dM94WCYKUrIoDZalXBkdzlPj77N72PR9Dq4yNq54j9G9/SRXd6r6jddn9Bq4YAxxvaVpGnZ3diUks+s5OT5ha3uX5WInUIl3ITFUKoZ77wOLWchHSc+UjTjGyzvvpNCeH1j7vYpsZySvNKaEQHwQ+6ioCv7hH/whT167yvf//M/4s+//BX/5ox+nonyipPWJdtx5J2ESSMG0shJK5C88/wLf+s5vsbt3QZLQ9RAWGce5bdvR2I7kmY+GCTcaKxGDMk5OzJVn5s+vVQq8Ht+fbD7nlMu/5pju4Y/7e5q4PDz3PwJkyE3OWFmTJzt8l+fwTdt83r+5DjAFE3kfPQ5oOA9eiT4hBVJdyAeTkLDFbMnaVGzVWxwdPeL9zYpLV65j21ZCjVwoIug8jnHo96DvDMa5WPA4b+PnBRre+xDV0AeZAIUSRjRUNMIh87yP+QeavZ1trl69wP7ePsvFUjy5TcfhwSH3PzqgWTUcn5zQti2bzYamaWg2kuPRdxKC3Nueru0GIxh9kPESJqm1oapKqrKins9CAriQrmxvbbG/f4Fnn34aPas4Xa948OAhv3zjTV775Rvs7O5w8eJFrl+/wcsvvcTh4SE//8UveP/2+3z4wYd89OFHXL5wgadv3WJ3f1/yOIsC05eURY8PIdbWaTorpDCmkFpCZWFG4xHZ+7wHxYbNZpMMxnGMisLw3K2nefeTDzhsT3nmxWd57Qffo2hblO/pg7FTDGPisa/KinV/hHbR00jwakkIlcenfJvciO+cwwgSSXNjqmeNwv8mc/lxwOO849eDD9knqpAH+1mOzwU0onDJF3H+cvnn/KVyS3V+v/w3FRTS8GuK1c2vVZPOjAp8rmRNF3EueOK1sd0//elPuXfvHtrD/Xv3+OD2+7z91lsoYDFfsLuzw7Vr19na3qKqKrrO4qxUKlaAcT0nJ8dcuLBHUQlHvC5KDg6OWCsJeyorKfpVBRAwm8/RhcaEMI0qshqVBdVsTlXPQ7VkoaiczeZipa1KTBmoT1MCqw75HAXCGi2dsN5sOD4+ZrNeC9tT1ybGh75vsa7PGCOgLCuMDtdby96Va1SLLU5Xp3hdUswXqKpClTWqKFG6EgbfsIjSmOLxWRy9dzGsA4QupUiAhKiUqsEtZ8Nmq010L3pB6tn68iNDoAqKfNwUXNTZU+iezRPlXAwZc6PkOGstzWZD23VcfeIZvIcHh2u0aYilOLUJCdjyluI9mXgToqfBi3SC1FaFCrkHKrpOVQxFGrjA4xzXMVmMQfE3OVA3OoQRZR6BCCB8DV6PEv1j+FKnxfIxZTnx3qNHymduVfYYInC35JXbNQ5tm+R1iDS9ZVlSaJ2KWaU1q0JYk1e4Vtbt1vY2y60521tLZvOKQgtYHdZtD32P7REmGB9HngDIw9wZ8XkHxTMo/lHJctnkSfLIhHFiADDD2A0AcAASBBf0+cLYZ+ErsY8TSJBWkMA1w/u4KdCIACN7j+H7wVvm8cQYnKky6mIrMyU2vkEy5GQyM3pA8lc7857pXaRNOvCARm+R68UTcO3qNR4+eEjfdTTrDW3TiAEorBWR2wV9b9O7xJo0qX8UWCwGxaZtMUXJ8ckJs+UiUeS6kGCqTF53xJD4+SII8QpTzfibv/t7fOvbv8XHn3zMw4cPOTw8ShZkpQTwbG0tmc1mKK1ZzOfs7e1TzWqqeoY2UvDPeo8O3u/Y5bnCOlXQz/2cCbUcQE7B5HRPG8+RfLDOzsloUIg+kl+naEz36ccp4Oft6UmZ+TW1AR777E+5yjMGDY9r8+MAR65swfi9EqnNuWBuoHg+PT2V653FObHCX7xxg6dv3qRZrThdHVHMDShD5xVdqKUFkaFveLsILopg4MlBAjBqZw4q8siR6Xf559SfSlGXpQDzkEPX217yL53l4v4Fnn3mWS5dvICzjuOjIx7eO+S9o484Pjjk5PiUo8Mjjo8OOT455OTkOIGMrg11qWwLDN6XfB8e+lOlvV4IGkzas+LekShuF3Oq5ZLL169y9epVnn/uOcDz4OFDPrj9Hh+89x47O9tcv36D3/zGN/nOt77Nm2+8wauvvsr9+w948PARO3u7PPvcs+zs7mK6nr4ssEbKGRRWB2OrxnhLYR3Oqv8/b//9LEmSJ3ZiH3ePyMyn6r3S3VWtxcid2Z3FzmDFHWAH3NkBOOLsyDuDGX6hOP7K/4i8X0gz4ox2NBDE2WJJ3mqIxeysGN3T07Kqu+TTL1UId+cPX/cIj8jIfK96G/CZ6peZ4eHav1o0Go1o+m2M5OKJqRGWy2VnnauyZGt7wrtvvMHHDz5B7+9w441XOTk5I3OC/+L9w4EysJxKEkvJ3K5D6NnWfFrgVZdmjedh6O62wrZoSdBGjNpULmcmujR6fCfice1a09SrlCszGtA1g4phW/uDiRxfVVVN2Md+GylAThmAlIGJTMM6TUYq3WiASJAu9cN0RQ1HlApEAus73/lO8+7Bjevcv38f7z0Xp2fYsuLx54/wT59w96WXqGvL558/ZndnlzfffIuyLHn29BHPnj3n3a9+le989zcYT7bZ3tkRkx49QikdzD+yJqGMyjKcUQ0REKWH4rgl5jKRIIgEZkC/LQEPnYzL3mV42rj7o3yHm3u3KMuCxfSCKiSok6y3RUhUVVPXZZNsqAyMh9cKPdpi7+AWi9KSjbfR+RbejLAqkyPjWql6B8gjEk4JoRp8DCL6COYkkUgJgu8wft9IX/EJQolSXbqIpD0zEl7TBRO0xvHVxyyhqgOEI8FlnfifONc6zYljuKau5fzkmSRK0gHwZJnBN74EreYunqV47rQxHcmcWG2ZBgHHgApGG5lV1DYEIhwvBHTDeMiBb/JhSEeJ1F3REG9Ka7TPwYb7WUlcb9MkzXI4xC+lAWZKiYYpJOBp7o33wU7VowjRmlBsj/IGAB9c2+H6Xs7O7g55lpFleWMqp6G1uQ4TiVoIkfAliZpUkPbbAuVVexboAcSUqus8UwRvkeb3TvZ6ZVvi2LdnKFDZCXuVFC/r1ZX8t+9EUzeZim/mLXk+upJeHzbLedfc6/7c1hGlEBU5DTXbSHd9I8dPl6f9brsz6vQpMHSYWE1DFm5CSFpr6miuqqCyFlfXnF9ccHB9n5OjIw6fPefOS3dYFsuQZVu0w2UpkYPkLtHc4450WYnvikexLAuUlr/51kRgP0ngDBXhDyJy8U0T4SrKD7X3ZJNtXnvzbV5/650Osx3zmjRayWZtlGibPVTWCfTqCBNXTYK779P5rdmrZJDOr1/zzlnoEf7dEr3BVt/1rDIpgy0MEtsbeuwxP3EcKfN1FSnqxrpKrTBRQ8zF0OcURvfNrlIhZ38cKWwRSXybDTszJgRSgI8ePiDPDJNRDt7ilzXzZUlRe2GRswl1VUhLPQeVNnBOl1bpChNafNeHEUNMRzrfPM/BS7JOgPlsxvnZGddv7POVb3yNl19+mbosOT054xc/+zmnJ6ecHJ9xdHjI6ckJZ6enTKdTFrM5RTGjtsvGbKg18fWgarQR3FvXtoXxAGTgTVzKDq40SvBrIziOifeyDEYZo59PmEwm7O3tcXBwwJtvvsmbb7xJPppweHjIL37+cz5/+JBbt27xyv37fO2rX+WDDz/ihz/6EcfHp5yd/4hbt27x2huvs7e3gzUaU1Xio5EZskyT5YZMO3xG42vqve9EARuNRs36lonfnVeeqip48+V7HD59yuH5Kfe+/i6Pf/YeW8aLI3my115rRlvbzIsl3oT8WF4sLhAKLkSm6zKkqVavfweGcEk8w+nnjj9Sco769dLzFZmu9FzJMxmM976xuLmsvBCjkQ64P6B08tHBdxPQikClkYJ0OPiubKNP0KUXLNVuQJv8K74HdNStaVsx+7dXQiCMt7f4/PEjMjS+rnny9Cn5ZMxLL73E+dkZ8+mUf/hf/kNu37nL+fkZn3z2gDe++lX+k//s7/HOu18Rp2GgqsHrcVAl2iggxQRzGe9bxCiEryPTClxwjg2SbJfMhdAGKwdEuOMoAVcKfJZJNt4sYzLepigqlsWCsiwY1WXCaCxwtqYO5g4+mAvUteX23fvMlzX7N+5QVGC1lyRVzuNdhTGuDdWaIE/raUxEUskGgHK0SDwhZhxC+Kf7Fefofdt+JLi990F9GU3sXENAKt2GCPZezoQxIZKGEgLe6ryxaYzMjTACWrLMenH2M0ZhdEuo+BDiry8t6Gok4t5ELio+C/2F9RJtSzjnzVFvs0gHQTgRaae3yNugSZFXxDxKGcnd4qfgJC+IURqc+MbkaHY0Alyz4J/URGzSjEZZg/hW/8n9jE78eR6jMXmUj5HMLLayxBR+gpwTAiFhNMSuyuIQhtXFeOXB1FAIeZlgSlj1mVqXaFegGqwHgentv5+eq+a32PJQSTWrUfrettUl4FcJOmF+VgnPTg+tgLthajxAEllKh2g78R7Ryf3Qn/fq/CIj3kb88skyhM9rGQ15rsLBE22Gakz0YhK96XTK1mQLW1seP3rEa2+9TllIZLzR1lYDe62tEQZR9YhB6Ssyix5FURTsXdtjNp8z2dlpnKK0Cn0nuhrt2whnJEwHhKANWgQiBFxgQ4QanPQlipXW+R4V/MGCNM8HzwyB621UxT5OGmI0GuGcah0zh+qtK5uedYQ3vXqNqWbPpOpF2h/ssydoDF/QXF3a2bzWa7M7sG6fKQxOfUbXjS9+jvPrm33168WiFRIJMuxZXVWMx2M5w/jgW6VYVhXUpUQdJMNpqKyiRmFGGdaWKLq+ra3gVpH6U/WZ1b65VHw+xDg1zEvAg7auOT4+ZjGb89abb/Bb3/0e2Tjj8PA5P/nhjzk+POTo8Ijnz59zenzEyckxs9mUYjGjLJfYuoAQPKZ2EkSkr7WTflUjyO3gR1+12kXk3jXv0LonRwGeCtYadqlQF6Ipf/4YxuMxH7z3M/b2rnHr7j2++rWv8+qrrwLw5MkTnjx5wq1bt7h//1X+8T/+r/nJz37K+++/z6NHjzg+OeGNN17n7t1bAYdlZHmGqTUja8iMxdeuk728SZqo5d9kMmmmFBNIV64mI2MLxSs3bvPeJ7/k3bdeZ3T3Bv5ijvGKqioboWypNdnEoK5tg60lcXBtUQ4yLyGV68THM9Lakdhfx2z3GYmhspEWZxXrDQn3uw0ipnNFsbbPtFyZ0YjEesog9IFqn3nQJpqXtPG6bSAmsiwLxKVIpmNyOh8kv0IYCAKJUaOibXUTtpCgpvUepWLUEheIuxiDX9qKBL6ODjoKifoQrkFZFHz+6QPKoqB0nsV0BoDxnlxnHB8e8uu//ut869vfYjSZUFYlr7/7Jnfv3ceMxlxM5+Q6I1OZSNdRWKXJdYbOcokAo0TKa3wrzXJ4tHIh5CYSazxuthm1a5vsRZRGtqSo/LfJ4aAUKhMKOVOGfDwhL3KWyyXLYoEJjIaxI4qyQOkK5U2Q0la4Cm7de4MbL73Kzu4OJ+dz8nGOyZeBwouJ5bJGehHV5TYCokBYxT1SrWixkdJHIkCAYohCFPYl1jHxWcJQNhcrhESNgK5BVSqGSw3tqejsbhqNEA3D0AI6YTZiNmeRaCs8Sgth6WOY2jRnRENItyp2rXTkIgPNFhIIBokFKoQVVQ7JyhAZJReSQPomZnwTglEOAt57clWhlSfPs+D8nDOZjNna2mJrWzEZG8b5mL3dHfIsZzwaMc5H5MqJzqyD5AKgomvzK/fNBt8SmjCIYmrmsLaUsIkk2sUeURf9OmJ8LqJAQTmi0zwh2lrkSSPDHBmBjqSXJDLTCtC14F0j/Uwfe2WEcCQBuD7o2tJ6kbD07fjjTe0yJqumU862AQY6pH9KOBAZ7TD+DuyW+xCRTAcpKBWcOVcRQCR4h0rUoEjr8b2WkO+2085xtb2UCCPAV09dBdM/JzkhbIjGV1Q1168fsLO7w9nRMfPzKcWioK4q/ERixpssCI18GwChFTaFlYowHSiqimw05uj5M67fvEkWcIIL+xX9NCI736NMV2bUxLhHcIAEEtFBIxVNgIQZcS6E4iEyHsTDGta1NUVcdVZOhXLxu7zb8nMibIjjV719Sfepb66wrt7qfMPt2kCMxDnIC+n8hipCK9xRvUeNlKRlwuRL+263mc59bs9nrOibe53OJ96qdk3iGeoy+qmAICV0IzOfnpXWFCUZfzhbOzvbzOcLyTcUhlVbiUXmvUd5hfGEIC+tcEApL0liE9weJebei0+OorXkkDw2kXEN5lAxrHVzjyP9JbjOO9dEzDOZoSxLnh4e4eqad95+h3feeptqWfDxR5/w5PEjnj97yvNnTzg8fMrp2TGz6QXL5Zy6KqnKEudq8OLzFjW7NrkbAaEnlgWt5N1Zl5ydZM8U0DBUQuv5VFoe3FizWmgmCRktZsC2LlguNefnJzx+/Jj33/s5e3t7vPXm23zjm9/gxvUbnBwe8uzZITdv3+LNN97kzbfe4ic/+QmfPPiUX/7yA05OTnj9jdck2W5dkecZ1mZkmaVUFWMrwUUyk5F7T+YcRjvyTHLxTMYj8I6FCikdvKJyntp57t27x0cPPkbpjG/99m/z/KNPKKdTCUJSlSH3Czij2Dq4w3i8jXIeuyiYHx1TX5yRKYWuy5BlPh77qHmmgc3xvrSJMJOIhhGLJrhdKYUyupuENeAfTYsXG9hDWyRCZu8+B3F4uVgwP7/gKuWFo041auYE4UVJ1IpNl3NNiEVjWvMOkEMWM9y55tKEqaoW6QuiaT8rYhQgmbu1IfldIOIk1rQQZ3UYk9IJ0giXV2vJ9lvXNS/fucutGzc4efqczx9+xt7eHsvpHGstO9s7LOZznPd8929/lzfefYtsNBGVvauZlzUXywKdZxiTY8hQ3kqWWKVR2QjntUSHiY6zicTQKIXWvoGrfYd66NEjYX2jZD+tq00Axsk+aO/Jc9B6xCjXbG+NxIyhLCkckE/QVYXKxY+DosSpEX60h/IOrxw+U9TeU1e1MGtqglImJNoKPgSEpHmZ6QDxxtRIqSDBjkxKmsQucUBOpCHyrJW8R0TRaMBMay4T1655V7eRsOL5VQH45cFTOTWRaM55gmBSybTRqonq4nVC5AX84XAQM7dHwGBFvRoJbB8BB0FagUfiCIuNpnJCgGdKMTGKnXHO3t51dnZ22N7eZnt7i8lkxN5YMc5V468TNSrC0Ek26GZRGlwd3M6dRynXMObN/NqJNgxrHsBDK02TXB4uRt5wnsoZqrpuVOpRrW5rh/Y65CyJZnQEoBklwuGMBMJC1rzV/vRtp71WOJUSDl2CIg0C0SG4vE3qxf+0S9QpnuZctH2HB2tKm/hNSAFnknG5blq2dZLrFJ5usovvE4p/E+n3IFNDPzZOQpSrqDn1LRLEB4JKQa2ovcNrMRG9dfsOn/7yF0xPzynmBbaqREKsPd4KbPD4EEq8zRDeaGsCWIz+K/lkzGIZhB1RsBCdbRO+zeHXJ4VL6vlwltt5Ru1zg1UbEznl26ABDeNPK8SI7Q3bLScwOggyJFlYWyM600sf3eSB6VlUkVGJ+5FOrbePXaY0anovLx2Ge+DMpX31BRbhYQPTm2c0q7SKz0jWnPa89UvK0HQZCNXA3PSOtMLPdMwtY6FUZO77jvMRdymhNzzgHFmeU9SVwEipKDAnmZkNy+aDH6BCiCwJX93i5XRNXZPrqetMH/2efLMVgXYK/1RI8ma05PkQTbfnyaMnnF2c8Z3vfIfXX3ud48MjfvTXf8Xnn33G86fPODs64fmzJ1xMT1kszyirBc5V2LpGk4kpbcB/CgnSILxjMMb0LUNMjHoXIuO1G0Rn/2WfezvfXCJ5PxLQzopIT2uLdpo60AXaBr8WVbOoCpYXp5w8f8qP/+oveOmll/n2r/4aL7/+BidHRxwfH3Hn7l2+9a1v8s5X3uHjjz/m0wef8cFHn/DKK/c4ONjDU1PWtZi3a0XlLXldMcpHTPA4Z8hNHsybMrRWbE0yFDll5bFKgcootWI8HvPS7TssZguu3bnLn//ZD/CzGdTiY5gZifQ53tli+87L3PrKN9i/dpORN8yePePx+z9l+uRz1MkxxpaAFZpDKRF3KklYqcIaNWSe94TgleGM00H7kU40qFbrLIcw0KJCK2cJniWhxxU0/rJhq8RHWGmqsqKcL7lKeSFn8JSQc841KqT0t/SvNqbzW2RW5LtFpXkJ+oCDLqDsa1Ci9KiRCvTsFfvmU32ivJHcBvv8g4PrvP766+zs7bG9vUNd1nilOJ9NuVFX3Lh1i9FkC2Pyxln7/PwMpTK0qjGZAp1hvajZnQKfKVAaMUWPkn9NKkYd0g6lc1/3Pa0f1bp9bZP3LeGbG0NuDD4ky7HOMa9qlqVw22VZUVcV5bgUwOej82+Ym5JwcN45cjMW7YBqVbXRgdmo1qk/DXeKSsjfONb4bgJ4U6ZV/unG4XvFwamXZbaxm1fgVQzzGnxPGv8N8CoLuKOVXDZnI/BqLWsbkYhPPslfl7zjIqaTDsKNlzCDPiTwUd41/wyOTBvyUcbW7oStyZhruzvs71/j4Noee7sjxmNPFjOCq5Y4NL61Q5f+PSJ9ivenPSMdorojXe0xsz2ivbNPPeTtY5hrDyOniRG1Ynb52tYSea2WBGZlXVPbkNPD0eb/iIniGtM/uSURgDovGV9trKtpcoIM3ZeupDK9LMMESjrXTvXeb0Pf19VxeLC6IxFd19Ym6fMQLNhsnz/czvqHw/MQwc769vrjas6Gb7VaUTNw48YNfllWnJ2dUxRFk324Y3esNDFhWR+O9wkypVQw8Wy1t0PzDLh28JlK/rup9AU9KoE9fUFbp/0NjGBnLnSvZoTT8UurgQp+FyqecdV5cZOGoo9Hr1pepP7QffMMn/NI2Pd/T/tct14bx5BSVi9YIn5avSuqwU1abFPZ2dlhOpsJgA1wPyWe+030hYabHHSHfDD6a5EKeSNsz0IeDJzn7Oychw8e8vbbb/N3/+7f5fT0lL/48z/nk48+5PmzJxwfPef0+Jjp+TnFMonSR/SXa/fSJLRbxHHrZC19uiylP4aEQv31j2vXzN05vK8TH5YWzmQhCqQxQZNSgq0tn3zyCQ8ePmT/5k2+/Z3v8PY7b/P0ySOeP3/KwfXrvPzSXW7fvcvnwZQqyw1b25NmvJkOdEbmcbUH63H5CDVWrSmm0mSZZrI1RhtF5cApCTyhtOH1N97gZz/5Ca+9cp8Kz8V8jivLwGhotna2cG7E9vYB7N7F7t5g++AGL7/zTV5+96t8/t5PefzvfkR5dAj+DPxCHO29JkMC6ShW8ZeP42NYGDW03ulebdrDwf12YnlRLQs+f/BwbV9peSEfjbquO+Eqm00KsYrLsmw+AyFjs+lMINrnuiBZ7TMG6WKkoXFbDmsYyA8xFHF80eQjXdh0HqcnJ3z24CGj0Zj//L/4L/js4Wfc+Y07/Pn3v09VFLz8yivcvnMXZx2/eP99nFcSYUppJlvb3LhzlyzPwYVkOrgQMUUkG405ThzbhjXuS2PWlQ7Q6TFkfWYsEsCNI3mWkQHZaMzO1hbOe2xdUzdZRb0kuAnyRKWDvT0SNcYQE9pEKXrr5BsTi6WhalVghNKwmV1pVGuekhKMYUVo7KX7+62gI/lLTUMbSq/BCfgQYshHCZFuJUSRaYjx7VcvWWQiQutKHKXbSD1hrt4ndUXapXFMxjl7O9vsbU+4tjNmd2ebnZ1dtiZbjEY541EuEn7vyTQ4XwZmKSSOVCkyVDiXnBHfrkmfFh0idDdJKId+6zMasSgikymaiDwkyPNewitWlaUsS4qyYlGUlFVgZmsrjEe4L8qIMhYthiw6rKGMNckAbBITspXRBgA4SDR059QnIrvPAysZ+wh/OwDc99YhmG96j+RAsOsZgo3E/xeo90WKLK/tIPdWmruq0Vg3ri6jEe5QCOFZVRUvvXSXqqq4uDhnPp9TLIvGhjtKcNN2LzuDxpjGBGEtEtwIXVfbXPesA2ug4/yfvnvVfeoz8go6mu206GCaFt5E3M+DLklpnB7GgUPzedFxpkRxgz82zKfvZNpIQVnFR3E+fYr1KvBoSPA2tI8vem8GBSyoRuIrCV4lcMdoNKI4Pl7BUevWaQVGrNFo9McSGe709/RfJCzH2RitxJfzw19+QJ7l/MN/8A8oy5If/Pvv8/HHH/H06SOODp9wcXbCdHpGsZzjbAjukeQystYFk9/u+W8YHFaFOH2Gex2TvW5/hpjUdi0d3rfC5PhuURQYpcmzDFBoVZNlI7IM6try/OlT/vgPfp+//MH3+c6v/zpvf+Vdjp4/5fzsFD0eYxSM85zz0zMybdjZ2Qqm0KK5crXDGyeZz6mpjUEpj5KoFOKvk2WSSLT21DaY5TrYv36D7d1dnNK8+fWv8rFWFLMFW1nGKM8YTUbMiyXn8wUX8wI/Khlbx87WFgdvvMbBneu8vf8un/7lX/P86U+Ynj9AlyXeSsh6b0xD/w5FYOsIAy+hH/ulz8QOCXmiskAj/p++dpwfn1yp/SszGibkWMiyrHG+atK4uza0WVpHzvDq4RNuuetUlE4mfu4zH0qpRqUb++uPo89wRC64vzEN4+EcRVly+PwYpQx7ewecz96nfvoMnY94+fZtJtvbmGzE2cWMk/OZZNd0DpPlbE+2uXfnZUaIw49VjsrBohI1pAsO1HEmGtUzz1kl5vqf1wHPzgXufY/v6YQRiTpXaT9KEwNhlrWZXD2K2kWTpChRk5cV4reik3H1JUpD4QJXgFCivrbeNYCsfx6Cp/PKGjTj9slaKBonYu8zcTKGJjRsZE68r4I0pyUqdWQg8GLuRAs8BenGOOB9W//ohxAkn3iyTEnG1VHO3s4Ou9tbXNvdZmeck2vPyChZbiVmgAqP9mVgNBzUnrbFsKYqkRD1AEqcfyTeUgKys+Z+mFhq1mbgc7oOq4Crtc9WQbqnjKxCZjSjPGMyyVkWJZPJiGVZsSxKiqJisRQGxDlPVUmGdKUNeCsJ6lQ0q0vm6dLz7tcQaq5TR8771YmPTs0Osek7D4VYl71QriWe4llYh2SH1vkyKdQ6hN7/3O9vXVtittdmIu68T/fkDREGfcERBBMSpRrzkKIo2N7eRmvNxcWU2WxGWZWhjzapY2xnk5NyFE614c9boXK/pLAoJcyG1iGdU7/vy9a1z5D012YdodwnIJs5JvBSQeesrZgh9eDkpjFvIrwvY1ZSwmPTO4NzHTjbUs8H3NP151yHB4cYv/i81Ri05kbr9ulF1oUUF/l2Hba3t1f66NMufViZ4kiVCkw3zK2vYUnbq+ua8XgsZspacXpyzIcffMivfOObvPnGG/zivff48MMPefTZQw4Pn3Fy/Jzz82OqcgGuxmNDNmcV8ktF30jT3Pt1Z7cVEKxGCk1/W7uqa/DK0Fqm9ftMnFJQVSUSMl6iRlormc11luFqz8nRIX/4+/8/fvLjH/Ib3/sub739DvP5nGv7B5RFifOexfkU4yXRp8NhyxqtFLWuqHSJ0YblYkk+zskycQg3BvIQOAWVYUKkLJQmH0249+prPHn8mPtvvMnv/u7vUS6W+KpiZ2vC2+++w861XfZ3t7DzU9wkw5ZblKXmYH+Lg4MbTPK75Jnm/M+e4fMl89Pn6EWFrWKqgFWc36eD0+dDDHAff1x2L/owP/pgaaXY3d1du99peSHTqSil7qsA4295njdMSHQa1dmqeZR49qsOokmfrSPApY1WupSq4PtcXHwv2o2nCDUyRDpwsUZlVFXNX//wr7n3yn2+95u/iTaad7/2NTSeUT5C64yyksQ2Ql9oXF2zM8o5e/yYH/zZv2cxm7O9vc1XvvENXn7zLQo8lfFYBajg0dAhVoY5x/gs/W0dEouE57r3OqrdjrxPfCNMoCyaULShutFtPXlZQeOVESKtqIRICVBqiOFpW2k4rKa+RgVXsy6zkpZ1SEEr31Ibvh2HzDqxc060DkqB0TXRT8CHcZgsxPVWEn1ilOeMxmPyLMNkmWQRbUKYtrH/W4Yj2st6RrkmzzWjLGM8ysmUEN1GazQW1RClgcEKWiANeCdOzdYr0kzkjWN1YI689+Fv5Dt8XMUOI5SuXby2m5D3ZWve2VuCWUF8RwXzwGD+5JTHZBqtx7jJmEk01Strlosls0XBfFmyKGt8ZZtoaI0FvIpES9Mh6SFZh9N8ZBqbe9GNXLVp3msR5cByROM6evcxvdfromatjnn12Ysg7f4769oTQna13aavKxCm8XM/CmC6N2VZcu3aNbz3os0oCpaLJfP5nK3dncbRPhUYpW0P9aWUCkm0fPDvG8YRrrdZnbbC/UlxzjpGryEIYQU2xfdTHNQPz9uH2x0hWg+pR0aNcIfaMy/z9CGEsle6E71s2OxntawTKvSfXVbiHPt+mZv6S3+Tf6ttXhb3f934h87y0LuXrVFK4Is5Z2wftKcx+VssFkRhXRxLH6b021VKQRLQxHvfoUn6JT2TfaZka2tLCFvv+eTjjzg/O+O3fvO3qMuSP/njP+bBpw948vhzTk+ecHJyxGI+o64k4pVRClFaxHxQce2Cz5xCNMvJ2NOSmoL1TdbTsb9IGYLFMt9V7UksRvuQnySaYUoGcl3X6EqiKmoj4emfPXnE/+df/S7379/nxo07OOfJspy6ssxmC6x13L57mxt3bqJQErpYiQB6azJBGcH/zouPp3U1dVWSj3IO9q9jdMZisWBre8LOzjY7OzuYTPPmO+/yn/5nf4+L41PK+YzDw+e898sP8EZx4+Zjfufv/H2ottF2yVa2x92be1zfHcO+4Y57hV/Jf4u//qM56nyOUVPwhUSNWxM5LmX0hpjYTfc/DWG7bv9S/0cb8oA5rdi/ef1K+/xCUaecc4zH4xWOSClRlVtrGY/HlGXZDCqVQqbAvT/heOn6oer6QCIitJS7jmOL9dPfN12GNrcCPH78hF/91e+wf/1Arp1WeO/IgyanWJQYnTVEofeeUQam8vwv/+J/5qOf/ozz4xO8c/z5H/wRb//ar/Of/+P/huz6TWoFXjkcquOP8CIAvr8mcR4No9F71hbfIK10bUQibBNgRgt4vJewpfJW0lSPGA1EcsPE0SLuvrQCWibLtw2sZS6aKj4ZRdNea5coeFjqmOALorWoVI1J/UQytNHi82CtRE4ITtTGSALFzBhy0/bVZXbBupBtveMPoVBakelMQscazSiXLNe5MeRZdHK1xHhErpmF+PPgvTyLEdoAFzJcx7k7H/KrePkciWnvu5K9GL50BWAogolT0CSqLoredBaH7nu6hWm9DkMcTJl0dOAfiWTIjx3VKGdna8JsUXKxKLiYLZgtCmrfJnls9jiYMogz63omoT/hdo3EDrndy6vduxch5vufU0Kwvz6b2rzquF4UdnSQeFzTL1g6cCSBQelhsNYyGo3QWrFYzJlNpxRFQVmVjN1W987SjdXeR4opUZNnmZhPbGVr16AJuz009l67m+bUjIdVPrOPx9JxDzExg2HhO2NuIHjAEXFccT4yeAtNIrDYXtevZSOv+DcqQ/NM/6awemhnVHN/NzP7Vyktk7P5JHcYiN7CpD6eawnkINxRCEEmwR1WtRbxX0prdM5y3MOBOQ/NP803Edc9z3OUkhCyf/WXf8nt6wd877vf5cEnn/Lg00958vgxjz5/xPnZCdPpY5aLGTiCphyJXCdStUaTH0M1Q7Rc6OZFaOiDfmSxNfMfWv915XKmZNh/VaKPehQ6MCTBNB5LZkIELK1QxqC0pqpKPvrwAx5+/BC8mIkZneG9aHI+f/AZo2sT9nZ3mYzHTCYTtkZjrh9cZ//GTQ72rnPt2jW2tidkIemfUjAejdgaTxDKx1HWJSokI1TasLN7jc8ffM5YG9544y1evn+fH/74R3zy6UOy7/85f+8f/CM5L07awiuqbcfWq7tMjm5gdq6DOkKzBBZYJQEFNp2Xy8rQmqfpBNbVTWGX0orKCT07SsL+biovoNEQgsw5SbIUOzdGUztLlo/wShyoR5OJ2NK6GK+96+ynQ/Ql5Qn2zYBr7c2V1ngbbrfrcWWpRLd3wMWJKA44SFYDkdIB/D6YgjmLVprKVoy3xty+extUCOOmQnI178hMxigbNwQTBBpZeZ7+/JecPHyIms/YzSVrbH0x4xf/7s95/ugp/+if/lNuvfkGS+fxWuO8luieJJECwv82SRM2EoK9w7NSd+hVn0iW4vsp49dB9r0DqlLTpV6ujEZa7xsJXZhk/A9KJdEPvBhbpENWSXWFk4gJPQJTBe1BZhRZlmNM1sS+zjKDMhYdGI1IVAtw1KiarmaJOD+PaqJBgQ8ShDj3OhDzBEbNaDHLM1qzNVKM8iwkAhLTISGSpbjo+KxSSZIPfbvWBjyeU2iZWjze1s06O3wnI7qkZvPN3YjanRWgErJguzDXdL11MtZ4ZxqGS3XvWYpktGp/a4Fdwhw6L1GGvPhbZJlBZ5BnOaMtw2QrZ7LI2J5kXEwNJ7MFs6LCWSvMlnVhfAoX8pFcxqh3f/edzV4HPIeer5MW9xFfv84K4dVj1NaNdx3xddnnqzIe7Z7RmEioyCSsI8xTOUMTnYdAPKchz0U4I4EQNNbX5KMR2hjKckmxnIWMwiXbITqO9p7ReEJZVZS2bLVhzR77himXEJeWcT7CVTV6i0G41phkdojZvhR9ldhNGfY4x0aYRSotjNl3RcMQz/yqdLGV/EZTYXknJuKUMQm8SnPYiBbe2joxR3bN+CvvQphRhNByHq1jZKAK5y3GBGsBFVakgfXhPRUkPEmUPIFpQ/sf9jYR7Mh318DUFK43sGvN/fAJ7Ilnp8Ulq5KnPoqK29fV1cuc1gUIiL+njFgrbLQr9aMAhygJC+9prVp6RQ0Tbevufv+srkbrGjZRk7aEwdYa5tML/uIHP+AbX/861/eu8+Mf/oTPP3vI488fSqjak2MWswusmwXc2vWFUqG9xhS0ieIn58W6JApbYD6UDnlR1OrY+sz1uoh5Q/Pql9W67f1Nn9kwL6UEHyulA4Ugvn94iYLpXR1wToZWiqoswYPWGVVV4L1Cq4yqLlnWcxbTCyaTCZPRGGMMz58+ZWv3Glt7++zv73Pjxg32969x7do19vZ2yU1OUZSSU0orxvmWrJXRTOcFX//Wt7mYz3n/5z/n/huvgqv5evk1vv9Xf80vP3qfmz98if3r+3h/h08+/pxX795mtDuiNhnZ3dvsvfEqjz/8Jbm3knRWGXHZHFjThiFN19O5JuxxS1Osrnm8hy7UkaMf7sya/TEKbFUyzrqM6bpyZUZDa9OYTqXIXgghWVztfUh2JH89ona0NlWxCrD2gaCLR0SFyTXECaqJx+y9+HUoFJaY+dk2h7uDcElMFhLAp5VuEsmJNN81anTvHXsHu+RjUallJobYlHl57xu7/YZuVmCyEc8eP4FFQea9cA7GoD14azl58ID/x//l/8x/+U/+O97+9rdZOlHJKh/yROAbKa2HQBD1GYzVvegAjlRq0tZoW1HNf5o1iu2uBYpJ2/J8QEUeEE33ZPuGgNF0D7ZP6kaAH5/oBnn5dg/DU60840yF8yd5I0xAykZZjG5jkqdjrJUPBHlALsRVdjRCnGRNRCKiMDFuIeC9pfa1EFQoLCGDp5LkdaM8YzwakWWacQajPAl+oIRdsV5WoQ3h3BJsLbIb8i0STUgkWFrEB87XHfOJLnBvNR8dpA5gW/+Szj4jfjctwRAYssgBqj4SbM+l0cnZsatag/i7/CYhbzGgc8WIjHyUS8jenS12t0ZMtiecTBfMZjMWixrrJUR2MJakTYyoVqQ4qZS36TsyUFdk3Nf9PsSgvBjDsxnJwtWlUkPj2VSGBA8q3e/es8v7FJjV0FCqzWMhkluFd5rtnV22drY5OztmMb+gLAvxy/Eebx3jzHDn1k0efPa5JDON5kNxGEo35pGiOTVM8hHVskBdEwZpKEGr1qo5/+0+tXuVfpf6bXS89C5GBiBtO+591JanwU5ivfjd2tbEN4W7dS25CSQfTU1VlU2/EW+henAhaCEbIY91CPmnUV6RKRH4aR0cW43BeaidlfQywc+3YcQSWExkogb2XKeb3M6yA7/TksLx7u+RhOkKJvpCxNUSzf16v6bjScbS3v9VSXh3zKtjbL6v4KmgOVaKopQw8DrZ9xR2r4wtfI85bTpEYRdJNyW17lAKticTjDEcHx7y7/7tv+Vv/+3v4SrLX/7gL3jy6BGHh884OnrM7OKU5fIC56L5aWL2F5kjPHjbnLEUjkahVmdNwjo56zp1U9jXZzz6+9+/O1crKS3Ueyf4k3gIZzeJMqrkrrjA1HtXY50lzz1Gj0BBHRgQFDhqgSOlw9UVyjl8MGsrjOF8OoXnz9BaktWORiN2dnbY3d3l4OCA6wcHXNu/xvXrN7h27Rrb29sSEMUoyHN+7Xu/wUuv3uPlmzf4yuuv83/9H/4H3nj1ZX7x8SecHj9jMbvg/PScpTL4ynCws8tRuWD37h32XruH3tuimnosDlc5nG0FGOn6+kRj6npWQTFXCf297p/XUKc5LglMSO+gIiRFtY7T54dX2s0XcgZPAXcj5Q0hDcuyXCGYtNZUVdU5lA0wx4fkVnK0daqak1kShTKe5MKzepHjuMTkwqGCBKd2tmEstNJy+ALR55wNANuCk4gSzjlhLFxczoa/6/TVfHaO6fkZO5MJSy92yVoZnJd4/7lT2KMTfvf/9s/4e/+bBV//ze9Rei+caWwj+G5oAh5JIyetiUoSqPmkfq+e71e+WrmKVLRf7zICrK27SV3uA/cUDrMSX51RnjPOFZORHNMo9YtFK9PskHDjbchZKyzp8ARiWvZkDiJRg6KOD2Q8Dt9II5USbV6ei6P3OJdkeMYoRia9xJEZjHOODIMjxt1vCSHXPEuJoyiFj89AzkO8L+ld6zIaEdAPIHwVgym0ACUWQ4qIVaBpVKQiO8vXMnWRoVwl8IUZCcwKrZma1h5Vi1ZT9lMYyMlE/o63t9nZWXJ2PuLsPGe6WDJfFtTWNvk2hjQAabnqOb6srIu4s0rAfLH+hnzdvqyySeMSz+SLtpXe7xSWxzblTLamKFvbW0y2tzg7V8xmc4rlkrIsKMuyMUmdzWYd2+K+lkYFBsaHPBP5aBSYCxPiRKwynCkBm0rN+xET4/N+3SioqqpqxQE2bb+dcxeuqcAA9YVgQ7AyXb/Yb6Ph7hDT0q7xHm0tmTFsb03Y29nl2rU9CWpiHWVVU1YVRVmxLEvmiwV1NJm5ZMu/rHtzFcb3b9LXEP5/0TFsHFMkyMPvYskRtQOuk5tpiBHtE9RKKTHVofVJ6hOK0J7/eK+01ozzjEwbDp8954//8E/4nd/5Hc6OL/jwgw85ev6YoyNx+L44P6auC6AW96Ue6Fq3Hv2oYevqxvObErlDjEffFK0vQLtqWS/wgSGOtO+3EM3p8zwHoCwLMkMIjwsETVX8G8Ozx7sb6UHnCskLpDXLpbzy/LmsQZaNUIhv8jiYXO3t7XH9+nWu37rJ/vVr7O3tsLU1oSwKzs7PuXXzFo8fPWbLZPiioFgsKSrH50+PmS00032LG2VcPD5lZ/cGN15+lSdPHklgISsR9zrJHgP8qWtLnucrDF6f9u771aU4rs+EDJ3lfjn/shP2xZJ23IROVe2la7MH22Zi/cE2uTVoD6KJWZchaDNsw9OagahR/ZIuWnSYESDRJnyTCSA29UraVMbgnRwsAfTtpe/PO+0L79HO4sqSerEg854tk5GZnKp22NxgrMJWnupixh/8T/+c0lb86n/y2xROwt9GrkKjRNLrQuK3lTWP/aY/puNMD1d8Fr93udIXKV+E8EmJkaFoEf0WI1Hamg6EpDxZRp5naOXQTYI8h20csYVp7LIrwix4iKmFkt8DwCMQ0I3YisQ8SmEbnyKPdzYwB5BpTZ5pRqOcrcmIUZ5LOFdjGjpcJJ3BtV1FJsHjEW2aaFfa8XsCU+JCBuwoUfJgfcjKnSTLcc6FbPcxHG+bSRbiVRTTrJZ5StehHSd0zeMUXQlbS/jREDniwEryzIcwx/Jim4QxtlN1kKdS0WdDeBdhNkLeRURLtKUVmYJJLoTU8fkUdTZlNl9iq6pDlPYJxz4BSdzrS6JODUnfmpVYQxRdlZDpE5tp2ZQX44sQYn0h0JdJkF0GDxVgUNhA0Bpj0MDBjRt8/ugzZrMZ8/mcupLgHLkR+DufzVeYtiHiRAXCe2sy4enTp9x75RVQNMi1v//AChGU3qN1+9Inkuq6bsbUh2sp8TU0/tBiIzmOhKaMzTSZevtO1ToJhRqJIaUVmcnYMpr93R1u3bzO7Vs3uXHjGgrPYrHg5Lzg2eExOM/SFvjaYrxCm4xKtWdthQhOArD093XoPlxWLntnyGmVdsYr5UUk4X1G9bJ6a39X7feYb0krzWQy6RDbKWE9xHCuCwzQ/a2bKyKez8lkQgYcPnvGn/7Jn/K93/guzx495dNPPuX58+ecnT3i5PQ58+k5zpVo5cDbIKA0rF/R7nw3MRj9+QiOs513UxjfrxvLpuhHsVy2Z0lN0rn1+0uZ+Mg8GGMoywJra8bjLQghaASfCR5SygSTRcnBlee58CGuRnuF9b7BgdZCXRZk2ZiqWLKYXaCU4vCZ4UGWMdnaxuQZ29tj9g/2uHmwz+d37rC1vQXWcv/WbZ48fMjDjz/B+QmLyrBwE5a1Ym9/D6cchpz9l+7x0GSMMEgy3jVw3dOx8unfsT4DlsK0/p6k53mQjnMhLJDzfRnk2vJCmcHjBYtcXyO50d2D5r1IpOtaFiZyYDHBX3xe1e3CxSReSmuMyUT6GqQHLpjulGXJ9mSryT6ccv5R5ay0xtY1hGzglRVEkWWZ5LYIbXl8yKvmKIuC8XjSjsWlB77l4mNfzYUrS4r5HF+VTLRhpDWZySl9jdMK4xS1t1RWUc1m/Mn/61+ivedXf+e3qIDSuZBJNNgl66CRWQGWq1qByGAMwd9IDEZNwWUgehNB0r+86W9DwH8I6frAjDZzCH9bpsKQGS3Z1gNSFeLV4V1NZetO+7GL7tqkhESs0K6HPAuXR2cNQxLXJ46z8kLUeO/BiRldroKZ1NgwHo0YZRm5MRgloiOP+PX0iZTIvDjlqa0NAwr1XNQ69JhkFzUc4HySyAlEJRyZC1x41tWMROAZM1KrOJZwypLF6p4BfGAoInGumiVMTUvSv0qJaVuToNGmBF+0aZamlJc47d7WZFpjlEJrj9YO50JdJeMYZQqtx2RZTpaPyPMxx6enXFzMqKq6M4b2HKyevUZq2CMUh85sn0gdIlpTCVL62yYiKMKOq9yVdX2vG6/37dpfZhudtq2VojHevGT8fViUrnu8v9ZacB4T8uoUVQXeYYxi/8Z1UDSO4FUtARW0EphXlMVKX21wCVqCT0OmNNvb2+IMbjTWdzUCQ2s5tBbr4Fd6DlJku0mztW7NIo6R9ZLfJUSvaPFsYooSo76YkHdKGHGFDhFwjBGzjcwYMgUjo6lry+MnTzg8fIbGc35xxum0YrYoqepaYFIcv1d43cLgzvr41lymv25DmqEXKevu5RAzKBVZgUvpeymjuKm/dfcyvbdpO0NBAWySCR4cGh32R0im1ox8dZ7pGUr91vrEcEsEdudorRUmwxhOnj3nT/7wj/mVX/kmjz57yGcPHnB8dMLZ6TFnF4+Zzc8Rhz0xx4sY0dMV6m1i/q7KyA2tZxqFLH7vMxxXcrpP6g+dm6QWfQaq326fwYm0m8nEfrCuC7JsRIwEKu/EKJSCNeu6ojHJEhmw5BuLZ0iJaKUuy0CvxKhigtQXdkaWGarlnMVsyuGTx5w+e8Y/+Pt/n1dfeZXPPv8Msoz3fvpjPnt2wsuvf4NKb0OWU+uM3e0J1in27t5lfHBANT1tcHmEFV0BCJ3f+6bkQMfMdOgOpQKP1HxvFYd5Mi2CpPPT87X7mZYXYjQic5H+E+5WdxYABLHEgcdEf5FBaAC4F/Mp78HWNUpBhqYoC4zJo4gWjaaqa05OTxjfGXXGlS62tQ5vJUymQpHleVCV+RAaTA5B7NMFZ3CTZY2KrQWskaCIbXd9QpRSeGexZQHWMlKKwMlgPEIlaoUdZ1A5th0UswV/+s//JQbFt37zu3ijKW2NVQalHKoxr0mBVzNTVAc/rJfCRilJBDUqaovWAN6hMsRUrAOsm8aRfvbeIQ6UCmMyYh4Po4Vg1UGb421wbxaKOW2xg4ciAR1LOi7XMztLz4lrpBk9xgAvSf+8pPbLtGJsNJNRxtZkRD4ShJ9nwmSohvAUB7SUYfHhrLkg5Y31YjZsAoPpvRKNRqLKdM5hvWTe9q5NCtg89+E8h/MSmfSoAYlL4om25DKn4EAV1qMN1yt1XWAwImOROLNHRiBqnMK7Skt45MZHRuskWzwYoxrmRWvTRAUj5CJRSmyQTaaacxElh9poxlpCDo8yzdhAbjIOj087yG3onPXPZ5o/pIv8u+dm3dmFbubeIYS5jgjrI/GrEGt9oi5FCinD1MLf7rN1c2jaVKkX1OqY+kTIupLCRG+DB5OXtitnsXXF/sE+znuK5ZJiWUh0wsAwa0JAENUlaOOcVYosvcc624Q/t9Z2dL+btENDZR3s2wTvYumbGGRZi0Y7kl3dhpSO70WErXVGGvwjy7JmbpmWNa3KqhGglUXBwjpxYnUWoyWyg07gUOW9JMLEE6MchTxjnfF15udDmPJmmbuEcPxtE1O/qXQY/oH3OuucnMp1jPlVmOJUmjv0PJaOGW6yp9GXM1B2GG0aBh0kuS3BAqLfXqSBUmEAcXYJXu8zKj4IjKqqYjKZkOc552fn/NHv/xHvvv0uTz5/xNPHjzg9PeL87ITT0yPmy3OJHEkkv+P6BYPWF9irF2Ei+3X7FiwpwZruf9/McKity8csjMBVxhvXf0hIDpWYPunWn7e9Aw7naupaghllWQ5KksnaZm5xDBH3+5DsV+NUjVEOXIa1YG3FeJRxcnrCpw8e8M5XvsJHn3zMK/df4mxe8PjRp6jJNcZ71zlbjjHTnFGWcefmda6/vMMv/u0Bp593z39d180ZM8EqJ67xJoZtE5yM7fWZjPQZCJNlnQQB2vuy82iknTrnmqR8JsuoXRteVosOqrFvjYn+ojYjXjDnPZWtyVQWDoPFmCyYFKlGi2Gdo/aC0A6uX6csKzkTAWDHcUVmQhmNCnbCta1DKNAe8WHbRfeKoHlp51YWFd7HcHKryEZFgGOtZHG1jv2dXYqiwFuPrxU5UODBKDJlyIuakVPMZ0v+6F/8zyjgm7/zm5TOSWx0JdF5YghUz2pYPu/XS4m6RfwJ2ndd836Kdvp3uSfoQqnYj0/qe2IukT6hj++PC+KF1CrtwId2xPROQrxFG9jQV2QqPB2iqENINR4Lvdl7AUYRcvSRq2QwHmCEcLhg45pl4oMxGRsmecYkz1BBwqjCecVHJgOc042GpMNMEzLE06qcIzMhoW11wzzUdd1oImrnqF3LyERNRzSfcsR1i0yHW9GSdJkewLXr1TU6AwmF1moj5G9gHHyLMBpzyMBUmOBrkeW5MBSReTQKk6V+GLqVwmiPwzSmU85H7QagDNpk6OD7mhnYGWfk+zuYfIzOcg4Pj1ob3Cwjy0Uo4eJ5TObfl1aunpMugdJZkt6d7wPwIUanX/pSzHXlqkKAtI0+Q7KuzqZxXfZ+//f+fOKa5VnOSGegM8Yaisown56yd+0aWmuKsqQohdFwjfqehumJ8L5zV50lhtRWHpTznezgqY/IJmJ203oMSXZTRq6/360jb2oSqDqSxGgbXlUlWR4jpbUSxbquiYk+rbVYa1kulw1RpH0bVCPajmulJTGZlhtsvEdjCEmaBH6aGm88KhCavoFzRJAra0A0BRJBgB44IpcJla5aNjHllzHG/XJV4jJta9076R727fsFhPjYIKACfHE46xoib8jHand3F6UU8/m8+1y1kRPTeySC2TanzHg8ZjQasVwu+YM/+ANu3brN86fPefz4AdOLYy7Ojzk7PWS5nAluVBofBKad6JNrhJJXXccvUvr2/kP37rK+U2ZkPRxa//7QeWoJ55roE6hUEDTrwBAG4WMgOPCEfBFeolS19z0jMjtCI0UcGwn0QL84Cz5om63FWU1d1Tx5+pRvfO3rmCyjKAu++c2vcvaXPyHLHEU5wy9HjLOc2SzjbOKpFhdcf+kWF+8ZqkU351B7fi2mpzVfB8NSJnCdVqOPFyLd12g1AiwxUXh4hXJlRqOuxWY8CxqLuhLiHx1IY6XxSlNZCx6sFxMWg6L2oEwmfhcdotnggkWJUgbvoCpFUiV2+YmWJL6nhDjTXov0xosEVFLIV+Kc7oVIEkkvVLXF6AyjTUPUeecwJsM64VIFn3nquuTi/AytNFtbWxRVgUKHRFGwvbNDlF4XVUVZLsm8Z2+UY6qS2nmsAbxjhMI4R+ZFJb60ljEKdzHnD//Fv8Qaxdd+83uUyuGxItH1SpAqURQVpMIEx9twFzqOzt43DmpySKT/GFkmSs6USgAooOiS6Skb0HQfJPze+7ZCCPvbCn180kAK7FRyQcMoGqGqRH+KWq0IyGOWV6FBoqSnNR/qFCVzaHpNzpb85psvKRGB6pocdbh1LbkvxqMRk8mIUZ6R5xplCNEsoPYqRHIITIb3TXtythLtA+BC6MUYhcbaoH0LgCwSzfEda61IhENkGu8k+6kLDL13KRPhwt2U+1lbmjVLHcnB433rH7KylM2+dCWQRomZkwlR54iMQ5YL86AEkJuiRBstSQ+NxmgVwv8KYBdGw2G0oTYeo6oQPSwkSWo0GhbjY7xwMEajvMQZv2kyRpnCV3OOTi/wiFBB1wqdI3HTGyFAAMreB6KLRnLrvUhxlWnFvc5ZWi1PGyWmXZ+eFM37oCEKpy9+DE32ianLEGxK+PcJ+rRO2/3QHq76KQzW6/2+rq20zXV1I5Gdm5CEFahtTe1qnFfsX7tJpnKoasr5knJZCKGmQiAQJ1rO/hppLcE7mjk5gRMmRIJSqtWwxXGlY05Ll3hJzrhq4QyKJmR0KhXsaiFWfQ47wi4vEum6rikKYao8LoSg1Q3jIO/JTkQY5Xx7hlQHRst5tE4475gU03nJtaOUmFp5FY6jagV5MYS4UQalwvoEGUyzroGIFliqggDPNTDJJfvdIeJ9T260Unzb19BTH005Ba63WpX2IqXv6V7fnf3t4JzYgbRtwpxXBGLNfFVTN4qmfKRpCAxuaDgGJNAejI+R1nzbf4Ati8WiYz6UDs6EHC8K1YTLdx6s8xidsTUa46qaP/vTP8UXBUs957OHnzKbHjGbnXBxccJieSHr5tt5JnxkmOLqOvXXvxnVF2Q8+kx5ilv6Du+X9ZXep8vH6PC9nF7yWJFqr6PgTPBe9K0I2o1RGK8TR30TIlkl3LjQsQLRyPMMsdyxod2osYpjizsg47JYcCXGGQwSYKi2ntOzKSrTXLu5x3R6we7uDv+r/+q/4oOHR2g8rrYsiorF2HN0suDZxTO0zllWJdrbgM98i8MCc1PH3F6+ZfJUgDGmoaN84y7gPcFUv2WoG8GxkxPqfPQfVpgsF/ioFN440ap6KGbzwf3slxfIoyFZk+OAlUIuqRMAp4Kq1nuJvpTlOUVZ4gqxwc3zHLQOfhlCqOUmC8RXe0AjAkjDd9qgQVFKUVuCVKiVeFtnca5CaQ+0hFX8670kRtPaCGNhg6OtTEZCpmYZ3juK5ZLlYobRmszAxYV41e/t7eM97Ozs4qxFaSUak7omUwpV15iQYwE81juM1xjrycOcGGXYqmJbG2bLJX/wL/7f7F7f55WvfRVnRLNivES5iIxGPLrRbjeciSYrN0RA2yJSmplHpNWaV6TX09OGLOtcamhy80Uw1m3XkTrYdmBA0k5rnxyBT6JZimN3DuUlFGMLqHxyeVfHt45Y7pZVwBW/p0CxDywzlTHKckb5iCzL0UaBEY2Tdx5vPdZ2iRdJC9A68TXaDOeEWfDioxGZC+fkTEefC1tbcXIPWgvrrDiDpwg/MCC1taI1i9oNJ9FxCAS/8ypxLG9kNM2SNHi6v3w+XfMkPJ6vMEgsbpNJRDWCOtkYTa4VeZ61zKSOGg3xu8mC3bnUlxwnJmgyMmPItCEzjixIR6JQSKnW1jruzUgr9rdGqHt3sXhOTqayzniU8ZhMGIYsy0Lced1IH+PZ60vyo0SzjkRg6LuJNN2T/mgtd1MnN6khWKDVqvTO2yYtwdA57fse9BmPdUT1Oili5/2IIAfeGXp3HfJPz3nMqVE5S+2s5BOylps37zAZbWHLhURYWSypq7pFenTvclcqKuavo9EI7aEuK7Ymk0aAked5h0FPmYO0NFoEkPOXmSbnTmQO0lDqfQlgKgCId26opHCp/35MltkKOwYo8PA9aiPit/aZF0sNSAgq29zWhpFAzqQJTKA45q9nFjsEYhLMJWr803rpedDR9EsN4I84dg/amNU2iOcya5i4TcxvNAvyyTpJD63vWfd+xLc6A2oG2LAx3jdJ5pu6BGfXsEUq2VOjtAQA0aLZVroVdcUQzX0tWTPvMDAV6B8I+bwqF4SZI7RS/PSnP+GTDz7kpbt3ePjgE84vTiiW55xPT1nML/DBwqOdZ2As+vPsjWFd2YRLL9NoDc11qN0hRmLonSEBy3D//e9d03JpS+q1NGuwdAk4oQlf7WlybfThkbzvgsBbJb/1+0qtMQAlTIoIjhVVVaOV5mK2YDq74M7tWzx79pQnT5/xj773dzg8+UtclrEMQrL5siTTIx58+CmvZobSOXLvRTQRyD2vfCMQcwgTADECJ41w11nfmZcKwoqUUW2sSZILJngwBIGxDp2PsHjqYBmhgMMnz1b2aqhc3XQqAMfmIgVpocmyIFF1mCzkuqjDxugsZHGEsqyoqiqomKGq6mD7baiqugH6NhDxyrR5O6S+bRbIOdvJBt7YBfqUeBbu1joh5MRjv8BaIUQiMC2LJdd2JvJ+WOzlcskoz0XlXxQYE7LRGjEPaXIh1U42APEx0YGD1ohGW6xRFNbDKAhOrFHMXcHEZTBb8Pv/7H/if/3f/+85eO3VltuklbhEH774b0g81MSw7/+emBZcVlLk2kVkw3XhcoL/KkAkrnvqUpHW6xNOfQfFTWUI8feZjPibUoo8y8hHGePxiDyXJIAKj6s9XkkGzy5DBPgoPez6WEQCwzon2gkryYScEybB1vJMEHvQRkSi2DtqX0sOD+ua5zFylUaDj+ugJFmmD34UeEyPcY+Rq4zPG2ajD6htKmkNd10RpKaUeEQiI3OX66801DiqynTMo0wwMasSRsNkNUZHRkORGTG3sVkWctcYYQ6Ux9ZCuOdZ1mQW10akSEZpticTXn/lFRaLj1ksKypXM7IKVzquXz/o2EhXgahNndqAkBSta8qWMp0NMThwppTu+jikpccfd+7VJoTfP9P983kZgu6304w1Sq7XIPBN70ObNXZdv60EE0hYLI8g8v39a4zHYy7mU4pi2Uj8nXMoE8ymnFshNKVtEVpZaxmZXM5UJZqwoihFWzgA3/owI11H5y1U3fFHLaGcm+68huBEH6asW9cOAd8zK1khmAcYuE1lHXxM16AjaWbVz2iov5R59N6jzBqptF8lMpsxJQ7wQ2Psn8WhvV853843zEm3rhCYQ0x42+nKFDrjGXyn976iXVPnXJAmi1au8edIGNX+nIbuTYRTdS1+GUYrnj19wp/8yZ9w76WXePT5Z1ycX7BczpjNLljMpzREofORSOiWzTzF2vkPlU2MwybhSXrGNt2Rq2pSLrsLm5iT/n1Nndajj5kI9Gox3e+NG+Te1PVwxKdB2CwPmjF45/BB2FEWBYdPj3j1lTf46Y/fwzjF9PSUennBu998mw8PF+Qmo5xfcHyx5PDZE+7e3sbrDIswt/E+S765MFbVASbCWGgtGoiA8324s9H6Bd/iczEBS+cVPH2iwEtDWRWoXHCyc9Lu2fHJxr2J5cqMRllWmEwcukejEVVAFjni+J1lGXVVJ8n5BClY7xvVeFXVzaZlJg9SRt/4e8TMwR4oq0pUlTpupNj5iz26bS48tLavsW2lQvhA30YMidFq4ub3oyNE8a9zYi+rlWrivI/HE7a3dyAQcGJX6SS5S5D6WB9NvMQBj2DyggetHMo6Mq8Ya0etLWVZsmsmLI6O+b1/9j/yX/8f/rdMbt7EaRWcJcVMzSjQAUf5dRdTqUg9Ngc/RTRDpX+Zek9b4Dnw3hCyaIeyCpwipxwlQytI3NNhNIYiVMTP8cL3fx/qv0+89aWMkfCMEvjReMx4lJMHJjOOS3yonYTuDN3Z2IaLjIZtTPIiIeWcaLZqV1Nb1zDgzsr7tmEyhNCJxLDzHkeN9fUKIaWNxngxX4KsQYAtErZ4ukRzHIsOcbj7anWRdognCUqF6F9xQREoQ9CUROCFF6CHpa49SlmsNWgtOQ7E4d9gjUMbiyprjJGwxZmRUMF17TG6xihhSPI8D0xIsHX30amckB1eNGlZlrM10rzx+iv88qNPqK1v9uP8/CJEhmlV21qrjmCic/bWnFulVee+DZtCbC6bpH1DJb2Tm7QMV/VH2Ijk1/S9SYMx1EdbTzTTKRxSSjEej7m2f42z4+cURcFisaC2NZJZOmtAV+y340gajmld1/haBDpai0lrVVWoxO8n1QCtMiwtHBiad2Qq+5mlO4R6D16uY0TS3/ptpHPbNM7VtV0P24f2Kv09Ci+MapMRboLdcXzCDAWBwwAe8c4PnjX5Auuo+y+Ok7ptXIVpZv0w1rYjZ4FG69vKsLvhwD2SxI6YC8wLznRK9jjLssaXaF3feZ4zn8/Jc8NolFMul/zhH/wBu9vbnB4fMb04Z7GYsixmLGbB8TsKm5TBDyzVVYjyFylXbe+ys/tF2/+idaErVIQY9a2N1tQk3dQZzomlzRCT6mkZE5No59J+Vsbpo9ag9aGsnaesSp4+fcav/eq38Q6mZ1MJ1eNKXr5zjQ8PZ9hqyaOPPuLj936EXx7xzTu/wXh3j8V0JjDRt6fSezBaTEtThhilxPICF7SZkZHwEpuXxBwx6gsTskDhxVyVkIQbhc8N12/f5GD/gA/f/yXWaXK+5MzgzoMtY0xxRV0LYV1XEnWqqtLoJ0JsVXXdEuDETKniUOOcD74YEXiaJuqGbH7eaDq01o1zebSRi3ZoqWq7WSJPI8W1lua9yNFGYBcTP8nvIiWo65obN26wt7tLbS2vvvpqYz4VD6fEUg7OQyo4+xqNdR7tPbaq22hatqZ2XjK0GoXSnkw7bF3hasdYb3H+6CG/9z/+3/lv//v/I348FjOM3OC1DlKLdvv7JRKZ7dqvIsCrlD4RHtUnm6QSLwZkVhFtt15X09AHEmndFwFqKfJNzZ36CFuivohUPjKUto4cnqhPyyBVw3c1F2Iuo8SEz7a/CzMh9upytoJWxLW2olHrJm36htFQWvwisuDzoBPb3kypJtKMVm0CTOc8zlbEkM0xWoZ3DjlSntzIPctHIcpa8OOYTEaNCVRV1dR1hbWOqqxYLIJpFypE7DKB0RGmOpCFgPifKFRwZK+xzqNq1YTprK3HaE+dm8BkyDxzY6jqoNnIM4wB6yVDq9GGLFcY7TAGtBUt2MHeHi/fvc1njx6jlMF7RVnWGBPPEIHR6J7X/lkZ/N3TmENFhjR93n+/bUMc5K9SLh1Dr/QJzKswBoOERa/5TXBiE1G4Ou5WoxMRnjEZ+/v7fKY0VVlRFAV1EDihCDH/1eAaR2l104Nvbb8XizmT7a0GHqzT3KZSTN+feGeOAdGuIdyHmIh+3SFCP33W/X31/PQZ4XXlqvuVnmXrbGctNjHBzVyhg3L6zMR6knXdSg8zyVcifhXNkq3M3w+ML/zuWT/OdUyXT17yXv4juuJ2H7XSeCXmf1EoiWodvOOeDkVcis/KskQpxSjPUd7x0x//mCePHrG/t8vx0SHlckFdLVnOp1hboXDgnQQBWE8SbIQfXwYj0r8PQ/33YdNV4NtVS58mWQeL+399736nAgCtfWPt0r8b8b1Iv/ThVEo7NfN2YpnjvJhsxdxBZVlyenHGaGuEyXM++vgTZtMpti7ZnozQBmxV8vDjX3D89AFbec3xyTFWGWqvghS7C0+sdZiYky3OPyA/72OuCxUE6WHMcUHaVW3Or8BummzjKsshz2A85uvf+y7Xdvd4+Pgp0+oI765wd3mRhH1Ks1wuGI9HFGUl6lFtKIplsD9vGQ0BZkJMWS8OrRFJ1Mo2Zgtb460Q2SkQKbWjrEpQCpMZLi6mTRQGyTAOSpkOsOwiGNU6gZI6JOkmsZNNxirvB9viukaF8KBRau6dw4Swt9KWaSTgeIXX4I1h98Y+N/f3OT88ZrmcNu/W3gmDoTwEe73MwpY2qBxmdUVtRVX2+L0f82e/97v83f/mv2NmK3xusF60PCoelE3bcwlBcJX6Td0Odl//XkrwXNZfKi1YZRZ8Bwj0kfk6gmxw7Gs+DxEGESjEzJ6ReLZWbMzFbE0urPOeIvxNNSIgv9XWNqZQ8ZzVdd34XsT7gFc41zLCMdmeAAdxRhbi20mywoQIac5vXeJqMUHRWkm+iSzj5sEBmdZcv37AaDRmZ2ebyWTS2GyqJFa4ySKyEs3ZOA+5cVAh3nhEuCJYKOuai/MLDo9POD455eT0jGVZSvSr0IZWBudUIPpdsMEPd9sLUelqi9OtdGmU56LtsY7MOowyVJUNuQNibgFHZj3kFu1gbDxGGbT2vHTrBuenJ1xMSyQCi2gXPb4x4Wr9tobP6CDz2jvnnXO3iZjv0zpXOLtDZd2d6iPZFLn168YyhCBjjJV1Y103lrWl/2rgOKqy5Mb1G3jvWCwX1HVFWZUNwouv9X1S4t1SQXBEYKQV4u8XJfV9+LMyrB5jmJLAfRik2GzuMvzecFn3bsqQdo9UO4+rmrv2S1/r1vTlIQauiPXWMRp9x/nuh3QeNOaDq+uxai8fyxCjHsewdl395jbTOWw6w5uiyg32OfC4vWuJr018xTlGo3FzL1MfoiHmsyzLJj/K+ekp/+Zf/ymTyYjnz59iy4KqKlku5hTLOcYgGhQfALNX0BNobBLCfRnlRZiFIRg71M5V+73KvIaY/VQ4k96LFHZKgIY2VHfXx6vVTAzB23X9emgiSOrgBOS10Akn02MKX/Brf+s7/OK9D/njf/2vmexuU9oqhNutqJZTjCvYDhHInMqonG/2X+aWMDuEkNc++tMG+Kl0EOZIiZY/7fudBUxoQFA6C4xzxr033uTNb3wNdeM6amuHX/vt3+ZPfv/3mc9nV9rDKzMa09mMsiwpwuVIF1iQmGkmIr87xqOxEOpeHO5G4zE7OzvC8XvAS46NqqokP0FMoa4U+XjUZGVNo350nDKTA+S9qDLz0UgYh6C2zHOx7R2NR435hNZiqkHgPLWr2d7aBu8plgXKeyaTLfJ8BFqxtbWN1obRaCIx071Ir71SbF/b5bd+/dc5fvCAxWJOMS+oyqWYwmjwuRbzGC9qKBzoSuw7fa5ZugJja7K64i/++A958xu/xstffZuldzivscTkVjSajWH78AjA1+3gBhEIq4BAqRhNqSeRiADYp30OSJh63cj4VefCxnZTg4a+9G8TwOr/vo7o6DMbaUjKLORQaaUDsW+HshAcZ3BApaJfRZoLJjhk27rRZsT5Odc6eQuD4YnRLyKOMlkexqIbczWFQrsSA9jaslgugp+RYm9vj5s3D9jf22F3b5etrS2MNlR1RbEsqMuKcllQzmZMT44l8k1wHK9qj7MS9jmugQ57nXmLUaLZGY1GZFnGzs4Ou7s7jLY1O7u77L98m9dfuYfzivliwcnFlEcnxxwdn3B2esFyWRND+jVAPRovh2/eh8RHtg4aGNHKWG2pg0N47oTBiEEg4mevg7mW80x0htKGTClev3+fX3zwAOta6ZNIlcDpKJnpncce4lkhVOILPSQVfzNr7pFSXbZmE1IdCo85VPqILL0b65n3Vdv39LPujX+lD/lEtDsP36B3V5MWmk8q+eq84+bNmwBUVUVZVVRl1UrLEmY01k8ddZsuvCdqHMR0qu7M8arMRuxzaA5DBMOm9pr5viDhNNReSuD0mYB0vzflgEkJq844lUSeugpj1n/WsoNDZiVrft+g0UjnG/sbXOdL6Mp0bvJDuqm90TdXer2pWafNS8aQ1u/j4q2tLebzeWOW08k9ljQZA3gYI0ah/+bf/Gvm8xmlVlRFgbcVdVWyXMwA2xKGITJaXPuh+azg7F4ZYgyl/ouc7U2Mn+rcM9/c4zhmkmdpX5vol/VlaMxDcFEpVn6PTKO13fvTzFs1/+kwGqkJ1RBzI7SBQLb4TjwP0/k5p9NjTmdn/PjnP+Wdqua1N99gsSykX2fJM9DKsjXO0EaTb21R1A4S0/HOOdQaFdwW0mhSRtNGtFPgo68Jq/dO5hcDPRm8U7x0/z5f+cY3uHn/HmZvh2ldYpznoiiYVxXWXW3DrsxofPtr32ykr/GAR5ON1pZZnMMlgUjr2G20aezcYsIvG5LqNSpJGsHF8AaGR7IQXSYjBSB95Bv/eiWhMjU0hLuMMwObM862ANjetninycfbaCuhFycTYZpQmjwfy6h9TqUzSmf5dz/5Ia/cukm1t01R17j9XRZVRT4aMQrM03aeMz0/Z3lxwWI6JdOavNZMLJSugkzBcsa//d1/zn/7lf8T1ufkzsgGGY9LBBg+cKrxW1r6d18QeVuti2S7daVd+aSCjWETnzmuZcJveA8dNsGvwPhmTJ7upU+lanIP0gEGyZ6nP71VwgDffS385mmJzn6JzGuW5eT5GK1zvNOgNFbJWLyTLKJNMj2g9lXQTvjGTMpaiRBV+RhXVsZga0mk5KPXdABoEoBMhYhroHWOViDh8kRbMZ/PqJdLRibjYH+f11+9H7QTY8qyYD5fsFgsOD17SlWVVJUEWrC1xS4XlEXRhNi0dR1s4qEsKsqqbu5xynTl2ogTfJYznkwYj0bko1zOvYZ8lLO1tc3W1hZ7e9fY29tj99oeX3ttl+ztt5jN5jx7fsjp2QXPD5+zLGssGZnOQYtJlRwL0XZqDBrT5MmptUcbMN5R48l8RuYdOkSRMs5iCOFnTY3LwGhHlmeMtycc7O9xdHIWzq8CFcKj+ngsVpFICjdWpMAQTKdShkkOmiKafIZbk55JVgSN60t6NvvEQa/N/nsxYrtKfuvX02G8zbjCZycHr6XRPEmem+BoqlTnOWJLlrCMqmcjLjDaNDBEouGVznHtxg0JElkV1Ms51WKGq0qw46AZV81kMi3R/5xLIoDF+QT/NWUUs4spkmRS42m1IWmi0mRoTfubeYKr+Qis5jda817Snzi9+y6x0xlgT4C0QrsrVk9CbEfgc5qAE/pzbaMe9YtPYbhqPweycPj9hNBfYdz6yz/ATKwwNIEoS3+9Egnje1Ma5n0H+12HG1REbrF+EMikRGQjAKXFJ1ppoWZs3eAmoxQvv/wyTx8/xTrAKGpvcVrMWJVyHD475Ed//Vd4W1PaGqUsVb1kWVxgbYFSPuStTYIIpNz80BwHjqNvnvcFHPJUUFWXye02FE0ZxY8vhk9vw6xKO5EBSzV0HiGGvYshkxuqIB1ZZzzx98vu5GXP232OPr1R8NT6/+J9iIhq0Tpq0g3OgVZZC+uiZlA2Pggm4xlv10xrLY7USuCgUUaydDlPMa+ZnS+4+9Jt5sUFRT2nqks+f/iI3dENar3EKo3XhqKoKasKaxQzZ8VsOlktiY4o1kW1dUgwGM1ka4v79++zmC85Pz6VqFfBBSEPwv9FscQGTY5oUuJaSFTTd77ydXZ2d5ktK/YWFVRTqrLg89MH/PT738fOC7y9mvb16uFtoYn7HLUOCnFqNUE7ILhKB4cVAX4q7JC3To6W9XgtEaIIduzKGPE3pQO/GvvxeNkBaS+sh2T7ds3BltC48UB0AYnTMXwhbWqWqIqyEMkDpQxKZ8wXhag+K4dWmRy4gMMiYK+Vgp0t8oNd9K2bvPrm68xmS5yH2y+9xNb2NtevHzC7mLKzvcOTJ0/Q3vLzH/wFx5894vTxM1BQLmf4TIOv+ezD9/j0w/e5+/VvybgUOB2J/BQV+fa/Prlsw/huDUhKUN1KpRbhdLQLvktw0BnRqrNlZwQJU9i31Y0222nRa7ju9HNnj13M7aHwSVLBWLdLWOrgnxPM/ALT1NW4BL8H5xBwIUR6GuZSfDQcTgfnf+cDonINEooTG41yiUutNZnSOONAOaqyYDafUhZzdre3ePXebW7s38CojMVyzmx6wfPnj1kuF5RlSbksKBYF0+mUi/NzZrM50+mU6XTKcnZOsVg05onRMR3omA02jF5EHDpjNMrJc9H85SGs6GQyYTIW5uLa/jX29/c5ODhgZ3uHnd1txls5O7vb7B8csH9NfCbeePVlnh0d8+T5KfP5Au8DYvLie6K8D2stjLxTHqdCxnMr2iRxojdoq8lcMKVyEo7Q5+KPkWXgVI1yihvXDzi7uJCgD9o0yNgTbapXVejxbA9pNprzNHBzBHR1/YlaDc7VS3p2VQM/I5PdPtMJ/It1+9LLhqHov5c8a37XuuPY2laTRWsDcAwzY+tKzCegUGCC75r33Lh1kzzLqW1NWSwpiwUuJKfsAB4fzAzCHdGxLWm0GUeWZdR1FQRQfUYxVA6lvcthjBttijeb53RqrmFSO/CqRwwas2pysan9Tp3evDoloe27e7TaxqXTS7jXiM/XVVvLuKke08Tweq0wH7Tvrcclw4MZGsfQ6g5qI5rlSYmHeCfbMwZdO/y4JfGu5iFEqtaSPM8Yw3g8piiWrX+iUjgbTRkFLv3xH/4R5WJBlmmcrVBYynLBcjmnK8jYvIErDOxQXd+VbzRaxWYN1/s4KJ/COU1mWpPelPxNmWl5XzrWSuMD/Ac6kvcWl8fvrcXDpnIVwUBbp9WsrK5B8Dn0lqouQeWYLOZViiacvhGYplqKuNApDIp5rERjJX3WdRUinsLR8xO+8tWvYIyY7xdFwcnxKdt3bgutmeeSk806ptMZWQizH4WfQOvkHdrXJpxVDfPlnJOzEw6uHVBOxlhrmUxGkkjXZDhnMbVuwuhrNMrooFEWWvPJ86fYJ49wzrH9i/cC4+Uo5lNcuWCyt32l9YcXYDQqt2oX5n1wEq+dEBBKEWPwN2oY7zCI74QOyYA0upGYe6WJIKZJMtQQhbKc8fwpFZkM3zAhsa+4uQ3O8u1hbeqE5F8hRik2hMu0ZdWoOL33jMdjzs/PMcZQLiUPSBMRKLFhrU3O/r37vP3mq2QB6U1Ky/Pnhzz88D1u3rzJb71+D2ccdnubndFd9ra2WLqKN995h//v//OfY3yOX3qUtxgNRVXwox/8Bf/4G79K4R02ZGLSpi+F6BIpVy1DqtbL6r1I+5tKKg3aZC/b73vdOPuEYbdeFyinfUPQbuk0u7xrz5ZP/XyiH4XH2rITvahhSpAIDeKrF4BA6C/TBoKvgDh365CPwzGfnbJYTBnlOa/dv8/e7i7eOS7Oz3n46afMp3PKcsn5+Rln56ccHR5yenbC9PSM5XzOfD4PpocldW2xdY21ZbMOETC00axaKXHKkQuS0U3Y56gaVsER22hDnouGI8/En2U0HnHt2j7Xr9/g7t27HNy4wcH1A3avCTNy++4d7t69x+nZBY8eP2a+KEKoa7nMKknQlRkTZdKNJjSOO45JB2mY0cH/w0d/q2AGp3N2dnaYTqchcVkMmdwAjw0nMyHwr2AfH5Fz/0wNncNNd2eTY+xQdJO07lAyrKF66/rVA+NqtI1K/HJSJuqyPj2+iVnRSHsDsbW/v894MmG2WIj5VFlRxezKPSYqvh8ly6mwI459Z2cH96yFI3Fc68KkrjM36td1dj08HHp/SHPe7aurZerXfzEi6YuXTefzi/b3ReYyVDrvX235X6i/LzIuAY+r1hJd/JUczrYzlFJsbUmQgtFohHOO8/Pzhn9zIfBHnuXkRvP5pw95/72fY7TC1RXeWZyrKYqlZJfGXxmefNGS3hHnfef+psIZ5VdxcfTHTRcjhu2Vspq4r3mu+kxGglNdywx023+BQ5KUIbjQFyql9EDMvZOZfG17kelI2xxippVSHfqyKkumszmTrS1G4zEoKIuSo6MT2CvwSpOPxpg8YzQeUZRLdvavsbW3TRZNuUNaBRN8hq2vIDCuklDXgHGczU5RI8/uaBtjDFt60ozpmtnHB8FONJc2QQBp8RCS7XrvmUwm3L5zm53tbbZ3t9ne2WJ3d5e9vd0rrf+VGY1lWYYFbDl4RctQxGRdkcBvD5dq6vtgw65DvFYV4kC7uiYawdgmfJvqXPgoTfcI9+msbceRPO8fIAgSSOXQTgWNiJdIPIhUoS7LJsdHPHBlWTIajSjLkvF43HEwj2recTbm9u2XycbbZLlmsSzw44xsewudZ3z++BGn0wu00ZSupsQx95b85gE7B9fRO1s4Z9FGzBkkrrzjk5//jOr8Aj/exmpDk4dQ+0RK/uJlCMGsSEbjriUXpXuZdHPBhpBMSnitQ0KXSbaGpKnrxr+uXz8oteiqvVNNjfdiMuKxCTPZRpeSbLnV4BjiPdBKgTEo7yWnCiokusskvKS11EXB2ckpzjnu3LnFN7/6FYplweHzQw4fHTGfzjg/O+fs7JgnTz7j9OSY8/MzprMLlkthLOpigfKeuqpW9sd622QLVXWcX5SyNIvVSGJagllRhCgo3su7zR551YQAlvwWOUorRtmEzEzI85zJ9hYH169z5+5d7t57iVfuv8LBjevcvHWLd954Ha88n3zykKOTsza7sxbzJoIUBRWk6a5l6CPxpgTwhDsqzEeWGbyXSGHaZEwmkxAhLmonZXd8oqlKkeq685eemaHPm8rg+bikn/6zF7nfKbxLJW1Dz+BqPg1pcsP47mVjEvA7PPfJZEuYwPmc5XJJVZXYGHCjYQbb+p259X73XsKhz6bThpFJCaJ+G5vWfGis6Vwvg09XbXPdu+vW9EXav6ytdXWH4P7QvK+y90NliAC7yj27Srnq/m5iCGGVT0jebOBifD+uQxpOOQr/Yr26rqgq0zAYUatsrW1UBjEIhlYKase//zf/lqooGI3ETMfhRXO9XAZ654sR1pvKyh1L7w5dQUEDM9Wq/1DrL2uIGgFZN02al0ElyX0jPJe2WyuG/pnMzAiPENStdldsUdL2NpXL4G37fNWnI+6fVhl9+cq6dlO/007gjZ4Dua0d52fnOOvZv3aA0RlFWfHs2TPM9XOybIxSYU21QmWaf/JP/wnldBpM/0WzoVwU1HiUFhyaZRmTLcHJKNXQuY3gSrWacxH2iTVSHnxVZX9MCHQkhpM6CAWzXCwyrKubs1zbemUdhsqVGY2irBrJU0oAaK0lGoIFa0vyPMN7QhZFHzQZQWORIkFo1JI2hjpUbUbwFAj0tRwqaEGUiuG62sMhF0M3UjvrpH+vgTIAC62bRHtKKVzVajRSaWpd15RVyfb2djOW5oB6GGOgsozzEddvHgCK87NzVFFj9hd8eHTC6dPn3H35JcmjoTTWe/xkQq4ytvf3uZjPJaNoyH+QKVgcHnH8+WMO3nobqxUGWnM04nm5upTqspLuJ9DZp5W6qZ7+BUqfaegDu/TZkGSy/866+bYAZBV4pNLiiCx8kJY0TnbK4VzdATj994eQb5Ml13syk2ECcM5yyekwn844PjrCaM07b7/N3u4eTx8/5Rc//oDT0xPOT884fH7IydERh88POTt/znxxKj4YZYl1Nd6HYAZB/50yZF2kKvOKTHM71CDdb97p/q6ChiH+DdNBzOXljAJUlQgdqrxiZEqm1qHPM46On/Pws0+Y/GyLW7du89Kdu7z62mu8dO8et27f4eWXXuLV+/d58PBzDo+PmUwmZHkmidd8tHXVeNVNohfvZoVGYohbos9XJDbJKsk7ExKI+oDYlVIhH0+LLYYI0qEzNvS9f4aHGPKraBviO/F9PTC+oT7TfofuQNf3afV8xO9RwtpvFw9CU3TP+mXEYEReaX2tdSCyHNeuXePJ82cURUFRFJRl2ZzldBrdIBGrksFI7OkQ9jx99iIwY1XYAVcFbIPCrISAusq7V6l3+Zi/OMy/yhiu2s6mskm4tcII+813c1Ob68YzxODEuYswc2AtVffd/t0RuicQ6LqNXOmcpyiKjllt078KQlQvWm6jFM8eP+bjDz7AKPDW4r1opYXJcBglJr1cssbrxr+JlRoqwlC070TBaxTcpX4X6fmR3/r+bzphCFoGorO/A7Cvuf8IMd1kYFcSOEimNGzSetU5ritxPnHvIj2oVNZsQed938UraemY2IV3Yrt1bSmKivl8QZZJPrm6spyennN9WbKzOwEtPnBC6jreeufNJm9bPLcaoQsFbNdACHfvXQPPGgEoyforFegHiEI5ay35aNT40XgB6NKf0cGQ0Qn9amu0c+RKoXoJXdeVqzMatRVmwEWiRFEXpUzCixM43qOdbEYZYqU3HHFUl0Xbu/CPcGC9UlQhoVgfUbecs7wVzbDwXYIkyzJckCAYACPJ/4qyIs0rYqJnT2BC8oSIj0n6vBegoWjNfCIQAQLxAotygc41BzfEFyM3mq0spx5P8LXl5OiYe6+8QmVrMpNRWkuWj9Bec+PWTaZPnwqB5SWqjkHBYsmzBw+48fY7VAlh7/0XQxCXXa4vIrG6rK8+YR7/DknShsaU1r/q+FJiJLWCGCJWhEEVJxjhY8U3wPuqMTVq+4fLgHZ8mme5IBKtMUoznV1wfHREZjK+9Y1vUpYFz5885cdPfsjR80OOnj3n5PiIk+MjplPJ/losl9R1gXM11taA+DZoDcpbottkWKWGaFTht6i1I8yrXaB0pKr78wbAHfmO2I9H7l3pS5ySfBtoBQuFMprJZML52TGPHz7g5z/7CS+9fI/XX3+T1954g1u373DvlVd56eW7fPTxJ5yeHLN/cEBmdMg74jAhXG9qpggh94gTuJI5gzNihpaPgtmO1oxGI+p6mZyJ1TuTmtt8WeUqZ3SoThxXlDitI5bXEZd9QvTLvMtD41jXd3Mwes+dc2At168fACHyVFlSVqWYJuSjlavV7NcAkxAZyywIC2A1XOsQYdkf1yYmcwjGrhW8JMTWVeByCgP/Q+7VVUt/3VYJyPZZ/7f+s3Xt/Ycsm/Z23R6KIFO1NMhASZnctN2qEjt73fiBKQlo4NrQ4ZGJ7o6l9WfNTEauNH/1g7+kXCzJssCsOEddFlRlIcEe/OVmnP25h5nG/w+u05D/jIrzSNqKd837kJwwKU2Yf0Apg4oEVmSMGlzjaaJl9oU46JUNaIQHrn1fqdZEy7mI/768e5QS5ZGRjLBLzKgsxmQrd9yHlzcJOVI6omnXi6nUfDYPiaCFxqyXBYtlyWQbxpMtccxXkk/q8PAZ48qjfbB+8eCd5Muaz+egFblWGKWpnfh9jvIRQJP4t45BY5wLTCPcv3+fyWTCH/3RHwGwvbODrWuMkhxe1kousKqqmzXZ39vhpds3ubi44OOPP+F/951fvXSNr8xo1N6Cj4nGJEa012DyHFfVlKXYhqtgYmEjR6c1tq47oVLj7urAgEBrkuSQhfQdNZQJDEVN5MDKsuxI4PsEbEosipYiqCG9xwRnXGEiPGVdUQVHHWMMs/kMpTRFWaI9nJycNJL8CESM1ihtKagoqDHbOfVUcmZ441mUBXqUc3h2gjOKysqaVYuKTGdUy4Lbt+/wmfp5w/l778WO38OjTx/wDQW1s2Redeweo+QxlbxcVQK0CRCvb+Aqz1clb/0x9PcodfxbN9aN3fYkY51oMF6tALE498icQjSfCv5A3iNZtV1DjLbAov+9nbMCdEAgmTFowFaWzz//DKXgnbfepixKfvqTn/Dk8SOePX3K0fNDZtMzLs6OOL84o66WlMs5+BqlvPgekAMOY8K8Qh4Br1Qr0/GtVE6EDqoDiFXCaKRMR5d58mHuA+coIIy4PijVMB54HzQtHlyw67RQ1wVGZ1T5guVizOzigocPHnD7F+/x7le+wltHx9x++R6vv/Ya1ll+8f77KKPZ2tlBhxwbKSKLGs2YhR1i1JAQ/cs7fOZDYsOuplMpAchOtZqsF2JgvY8Skc7P65D4VRjo9J30TA61t6ldRddp/MstA3eY1OlztV66tvG71hqdZdy5cxcFFMVSGI1S/J18CsgYmnsXHsQ7XgUtdJ/JuGwqK+sYvkah17pxDBOtw3PvSj0HhvMlE+DrCP0vUtJ59KNrhd6u3E4Y3Au81a3Z36pNU2vEJ0o16EipCBvjJqcNRJ+iFoa3eGiYeYmMRkeThlhIEIhgl/iNpu8LCHMYI+FKT46O+fnPfkpmMmL4Wucsi8UijClqQtTgTdxYIpMep51Gz2tAfoIzoANr0zvVzavS4lhIfTGC0/wLwqI0Ierqu6p3xyRflLUKlBUte0PE995cg/cvHY9qtY2tiXyN1jlBjh5bJC7cEFzoM+wpXIgajeWyYLFYsrOzw3xeBjSjmc9nXDu4IQGSEL/iqrb86R//Ec9+9Av28gnFssDWFd56Mceua8nRlmUUZbFy3K2zkohYKYk4SBTYaO7eucX3vvc9Tj58wGeffdbgXe012urW6T0wyVprtrbHfLIlrMOzZ88uXVd4kczgtpaoAc7irKUSyoNZUaIR86mtyYRiWXL9+nXGI8lBoY3m7PyM2WyWEG/Be947lLNde0CtgxlLTLYlCc7KokZpjVbBbj5y3FoOe11bHFZkuuGSVUURcmvkchW8pyprnNaYyUS0LM7htWFZ1xhb45RntlzgQqbh7VHGcj5nNJb8HGezCy4uLtDec2N/h1FmULVDlZ5cj7DeU3lHBVy7foPReEtCNtZLJnrERXGB3h0xtRW7d28x2t2Bw4zaVliryBGtxrPPH+KLGdl4jFMGq2jUiSKuuFzC1v8tlsioRCDREKs+AltFKkzpvO2TPuJ/4oWXzpKqwWEqXtroO+Db5834wnA3OeP2GZV+6Zo5dZ1pBWiA8h5b16Hn1uHbN5fTdwBFk4Hee3xIntgQ/F7CjGoDOtMSdcQpjg8POT485u033sJ7x09/+FM+//xh0Fw85/TkkPlsymJxQVksKMuiBarxbmgFSJAFD210y1TiGP+juusYbezFhGrNOSFhUKBBkGtWnhSwxv2z3gaFatfU0VqHsxV4z6JaYnRGvsiZL855/vwRH/zifX7lm99h+pV3uHX3Dr/6za/z5PAZnz9+xLVr18l1Tu2stGsMDoVXCqNAB7gh5lEC+GokJ0eW581IZNVss3Bxf4dySwwjoRbBpezwCs+RIJGhVrrRnVTnb3O+5MdusyvDGSKWuu332/gySFlPtAOO3+Iq+BUthsKLU6vzjUDTaAUm4/bL9/B4qmKBLRdU5QIJT5uGA/bgJMOy2CK3566dpmihbV1JKF3E365ZQxWDACRr0KGpukxAB1qF+7zCMKFCCF7fAb+CAl3AZw7dax5W97EdwxABmbzXYx76xMt/iDKk+ZMZRNgwfKI6fFXIgyIS+Xhagp/UyoxbuKV8e9/6dRq6uSMoaYUkHZP9FDbSjRhFYo0h7SW7r9LDEPBWEHAoJXmzFIKnxZoitBUCy2jXno10fM2+YTEK8twAlvfe+ynT6TkTI0nWcOJzV9WFoGS0/JMQht2l8avnKmpX2pJobJNoUZEpCOg+6gxCzgclgXoikR/ogb4J0Cq8dKSboFQ8S+FZszXdUfue1U17AnRivikjbOF29BGVKKAuaMFbOD58P/pwvi9sTeeX/m6dRbsC79ugRUml9r04t4RGiRoiHQSDgdvEA7XzzBeL4BchpnK4Cl1c4JSCbEymLOicpc3wi5KLZ09YRqEoLV3lwhmMETC9a4WGWps2uj6tubRSGlvD5w9m/MvHn4svTFXhtRZBpgPlWkZDa42tg8aumnJy3gZHukq5MqORj7aDva2ghipoDDKd4dHoXFHUQnIcnpyB90Kca1ETecCYnDo6YRvJTGy9AyWJ00T7ULMoSkCHdPAB4OmcsqqAkMQrk2gAFtCZxOuvbJlIMhVFSHKmHDgnjJJFU1sPZU2Wq5C4z1JWFZPJGGtrzs/PcSpjsrVNrREuUQs3WJYlNuQhcE6SnNmylrC91jGbzriYTiltjVOiLrWJI7lWYlJjcezdOGCyvc1oPGG6FPWXwpBlhrPTYxYX56jsOirLgsN9vBTxoIe/L0BRNJcpvRv9y+m7v/UBRHq4VrQUiVQgfeacS5BJnxFyAZmsvhv7SyVsad99DU381yTAo2Uykul1xpYinnUAJwKLgF+kD6XCWVSgRVr7yQcfc+vgBl97910++uBDPv74I46OnnF6eszpyRGz6RnFck5VLSmLJTGCUneNwzpEREzyPMU5a/e9fW+9JGcV7W8uKfWWrDc0Gse0avS9cs5RUVHVJUWxFEfHRcnx82M++PA9fuXb3+a1N9/g7v17fO3dr/HRRx+T5SMmOzuUtWg2lTGAQvuA2GM33ocM0abJGdFGh4taEdHwxDMYGccY5vdySVdC7Db/Ifm+irA6bw8QhisIt9dWr5umzsrv68a+5p5dqax07AMBnzbbp+RX++xIQbOMW3fuYExGXZdUlWQ9bv0xuk2oZNztM9+pMxmPGwK1yXEQKqyYhqSfOnyG7zzr99Vx6Ax+QqFm6IdmbdqOUtgxdEVbIu+LlE37uWKa0oOL/WebNGct0dah4rkSsvG+DQCTEFxt521fDcwdjBgmlbVuid7k9W7d5KV4HvpwP+I8tfLSwNQioFcpHO1K+6NwLsjzMUrhegxMLM5aCZiDWEX89V//FcaIuW6cW1GINsMHAZH3Cp8S8Umz6+BNq0lKf28J5MgAKKWaCENpm43fSsTH6Q0ZOC9D+NpHKQOrBP76EnRPHTjStpfO1yfBSQTe1yuwJB3bUNkktOxqIsR0qLYVRmdEK4g45mTC3dkktEyDG8N36xxVVbEsCkYjCSdfqxq8x1YLTGbwSuGdZVmU5EbcFHAW61prnVYL1frReDzW2xaGYdFKcrz4BDZ6V6OATBlc6Zos5spHsaFCeQnrr5SEXY6MdFl5Kic+28PitdVyZUbj+GwGSgXEHi8cLJ0skDGZEOA+pDn3DhYFyqjkEKhW3R2Ax3K5ZDIRL/mqqijKgmJZYYxkClfAYrFgd3cXay2L5ZJRnmOykAMhsbe23gpj4iVhWsz8PFvMMMGsJY6lcjX1bIm3lrH23DzYx9Y1uTF8/atfZV6Ks85Iw9NHn7GzNaGwNdd2d6hLSaITL+py2ZoDSHhNj8kMW9vbHBwcBOmeorbi5xIl5DvbW2SjnMlkgjoD74WY3dvd4bhYMp9esH/zljjguDbDqJzt/oUc3vA+QrkM+Qz93ifuh8o6m/fY31C4zhShu+Rzv7/Usaov6esTNS9SWt+fENSg5xOwWoIWDsgyQ26yEF5O8eTZE548esy7b7/N7PyCf/Ov/5jnT59zfPSM49NnnJ6esFzMKIsFeAlh6F0buGDTmg99/zJML/prmf42dM7W9Tu0Zqn0KzIE8Z+tLEWxYF5c8OTZE9546x2++a1f5dXX3+DtN9/is0ePOD895drBdepI5AVNqNarZ7SuazKlsCpm0G2jivWlwTHqSxz3l+2rcZVyVabkRff4P8QZeZE+UkY9/tNaYzwc7O+Tj3JsVVBVIZlkgIf9toaI4PS71po8zzt7+WWXPsxcpyG+igP4UPGJlm2ozyu3kxBy/yH2+4uWq2hf1jE7/SJCnShRltKYDA4wc5v6/SJaoVTIJcLPVVyktQSxiGa3cV4RrzjvGWU5SimePn7Mk0ePGWsjucTqitoK7RNNd0U4oqNuZWX8fQJ+VTI/zBT0z0pf8/JFyzpa4kXKurn16whDIt8jw9GO4ep9psKLfnf9sQusyQaprJYeXoXn62gn6xzL5ZKtrUlL46CxIZBJa5bmKSsRbislvjxx3l2GKBHshDMnD2l+T/82E490l+qlHAiLItZtwnAYIzhY0i8K63DVE3N1Hw2ysAjBX6JuByXSwbr9HMRfcrDlcnpibGQP1C0npAzzssbY8ByDGckiV0E7kU22WNYiERhvb1NVNVVlMUYINVcHDYOVkJdKaazz1FZUSagRy6LChzGKeVYVFspjyyVFWZJn+2gseb7NLgpu3cTXFTevH+CdYzabce3aHuPxCO8suRYCuqoqiqIgCyHCbF3jgMrWeCV+Fl4hocCCFC7LMib5iGw0IsszvHV4rXGEaFiu5vTwkP1X34hB3STcWhKeMl5MjVpJRxzrrJPc+ijaGZCSDJUv8iwFGinwWLmYKijXfWvH2Nc49D+n9dKLto4Q6rwbpj1EJPVt5Tvva5pcDrkx5FlGXVW8/977aKN56/XX+fCX7/P44UNOj484ev6c45PnnF0cUSwX2LoKklCHmFyYDiP1RQiW/noP/baOaUjXp//8KmMZWtt+G0NMwdxOKasFk7qgqAumsxlPHj/hq1//Jl/92ld59fVXuaEP+PjBA27eudv2gdz3tM8IVK2zuKprHx0ZizjWVMI0mUxYLpdfGoLth4Psr9Gm9bus7auO78s+Q+sEG1ct7Zo7xuMx+/v7HD9/RlkWEuY2JJOMPkhDQpGuJLPd1whzI5ExFLb3Rfe2D1fTfq9ucrcZHraTu/p76Tg2Pd/U3hc7410EsQ5WpONr1jCRoPfrpN/7+7puDjaGwL5kPp0x9HDJZYzNujmtu88dYUqibYlwKX1Xog+Cdp4f/9UP0SGYTMTDZbnEWoks2HawmsT2KmdAxr36m4xr1aS4eX9AezF0//rrsA5XD/WxCcdsCjue7mlmshVmrsEDtlo5A1ftP/09pQciHeWdk2SwrCox+nguXbP0boiprMLWNsCvMG5fN/24kKDWezBGQt9qpalryQyerkfscygvWbqOEe+lz7QSQ7mYZJJgOaCUaN6Mj0JQoUCzTJ5b79DBx+6q5cqMxunpuSx8UNOkuvyoWkwPpQxCbHZjciZZnDhx+RuJ5w7h3Hxv7c3j7yCRS6IZRIxOI6ESJduzT8KTlYWEGK2tpQ4qp6h1UYHAdV7UQFlm0E4cTbUJ2cDNiEmWobTi5vXrTUSrbJRjVJvoBCDPgxYmHNA6RLBaLJeNg7yEA261OuPtCbW1ZMZQOYRBKit2tsccPnnE685SWcld0DUP7F2YgTtzGVBSyH6mFyo+20SwD7U11PcQUG4QR3pIlWrm1mca+pel30f/9/YcAYltZ38sutdPrNNE2UguZbR9VM4zGeWMcklcN7u44Cc/+jGv3L9PVdf84Pvf5+ToOSeHzzk5fMb52SnzxZRlOcN5GzJiNyhY7gDtGC4rVyEWLiOAhhjOPhHVR/6X9XsZYd3fe+fFnLAolzgvidKeP62Znp9xfnrI6fFXef3NN/nK22/x4SefcuP2bTxKEoOaVXthYyTeeCRAo0p93RihaxbzNyX4192VdeUqa9Rvf12b/d//JkxT//1N47zqu1qpYF6n2d3Z5fnTx1jrqELuImddExEw3dPL+ot3tK+RkvW7OmO27nuf+B2CIUMwad2YN9W77O6v2/9NhPOLjOsyWN/fl00MgXyGqLlfx7jGdy4LgqCEYKCvuYifh1auDx/W4ZAhfDI0ToCYVyFtqws3hV5RSmN6eDTWNZlhPp3x8fu/JENJBCEl5lHL5SIEuxHmQiIydVzZB9doE+zp71ukqeLqpTRXM3eG126obDq3Q0zH0P5ftb3ue6sWFLHt1pxq1X9gffur57R/772PqRqGx7WJaenDKRG6i/nU9vY1lFKBBsyo6hoh6rMmhHL0n5S70LbdBrVZ7TOdx9DfLMvIlGaEMBNGm8ZKSRuJOKU7tLjCZKLRqeuaZVlKFNYvO7ztYjZtPlsndl8mk6zBLjqthknneY5WEk7LBltpo+Xi+LBA3gU1ZEjBLr4LQjBkxrAsgrQRQp6N4BBqDLlRWMTvwlY2SMVMiCQVspSHcGSjUQ4orNEUZfcwiDTMkyGO3nmeYxwoL224oIUxQWurkMhXs9kFeM8ozxrfEudEaqe1ZjweU9c1eZ6zWCy4uLjg5s2b1HUtzuu1jNdrxWgyaRxCjRHbvLIoIIPDp0+Cw48SYpw1QOUSvJoesE3lKsTul1H6SHzd8y8K5OK7Dec+EC45BURD5jMrAFjBZDRilMmeHx0+572fv8cbr73O08dPePDpJ5weHXF89IzT40Muzk+olgsJLRekFY3DfXS+j9NTVycM/ialj0D6GqEUaA4RfZvKEKDuA7y2aJwjOHQXcsbrElsvee9nJUdHRxweHvLVb3ydd9/9Cg8++5yd3d0mS2lEKHVI+halRDGBVlVVGwkw772EBPySSl/I8kXKi7y/Dll/WeflSz93gMkyDkKIW2tFmleV5UbYtY5YAcTcVHUFUN0e/2YlNT/YtN59wjWO+VImTUTfa9v5j1le9I5fykivaXvo/SFYMdRi13CKBhUqFEPxLl6EsUt9t9aNQWvJFD0ejzuwsztK8ScZ0rRrI0LRTz77jLPjE8nlFTSxVV2HgCDp5KLvRiuMuozJ78Jv3fk9ZSpSZmOl3SsevSEmYQgONvPvaXzX7fdld2hoHGlbOgQH6uO1vwlMEybDYrUly9polWm5KsPfjleEYru7OxLC3ouA2gahfDTRM8aIc7dPklizSsOksDLCwyg09arNeRefZ1lGpg3joLWIfUVTNK1o8pe0TJw8y3PDaGyotzKqsrrSGl6Z0Xj9lXuSVyIQwlE6L7aJNjk8klmwripspsVJyhhGeY42plmoKHG0QdNggt2tTCSjrMbg2+cxvNZWSNvunWO5LILJUhCJORWyimtJ6KQU48mYqqpxOKo6qoZE8pBlWcicKBEhTFhMbKt9UYrGUU04S3E0BuHsJpNJk4Tq2rVrZHkeAJdhZ0eIo6IoMNpQWolt7KoaZaC2lmvXrmGMMGx17ahrYWBsVXN8eIitalQ2wTpHlqkVBHgpQktKR3qUErq9crlUNVFn9etF6NjwRevrNsBoTZ9D9fuIaX3paivS+lHi0W87ro9zNiTqaS/meDRmlItT1cOHD3n02ee88vJ9fvbTn/Hk8SOmZ6ecn51w9Pwpi9kFVTEHL458Siu0Mh2HeL9+WS4tV2VK1gHDFCBFYJWu7aY2N0lA05IilmGpS9DoeE9dl+JsRk1tHVVlmU5nnE8vWCwLvvntb/Pg4UN2dvcxOhPYYVrAaa0lM23o4Q4ioxt5Jj0/6+Yn78UXus+677RIu4s4vyihOLSHyVlZW3pnqvf+FxlDn8lOutkwjGSdk+oeyS579+5LaCX7VJYli8VCNBr5mpH0CJJ0/fM8b0KcRyTcm0IzCt8b11VK1MLItHwztyEJs28kjpCa9sXn8Zn8Tuf32FdnXL0z1t3XFzlbfSCz5t3+wYnyq2Q+0MMf6cHsE67ed7paOcPJ2jRwN1ZYc9hVJLKaaq2KQ+54W28dbohtOLp3OQoL03retfvtQt2yLCXjMvT6kM/OewkKk84jnJ0YqernP/sZ3gotE027i2IRzlBiThXw8yYGNGZsbsbdO91DwrY4r7RqG8p1VeOwlgH0fi1wUSrhoz1NGNsUz6Rj7M+v2ZsNffiEtlBKB8d6T0wVEDUbQ7i+3/dV+foYuEU1kcBU83cdTkxxTWoaJr87RqMxmcmoK3nfuuijIXiurirS84WL2dKTtQzLpIO/pzEm5N0yOGeprCSzjTQxwa7CO0flHMrJ90wcF4Llj0Mnc9KRychy8kyTaUU+HrE9mVxp7a7MaFwbWSqNEE+TUQu6wmGITEfM4mvMOJyT1oG8TYCiyScRu+RBJRkZDY1zFXpkUApMNpZFDhm75eYXjLbGVFlGNQ6+CLVla2urc5AFEVXk2zneWYzOyIKDeW1tY0+JrdnJPdpXcni0wdt4iLvA1RjDaDSSuSgYj8eUyyXlsqSqakaTLWrrGFuDNmOUmmJrzzgfUxUlW6Mxha0YT8bU0yl72ztkaHZH22S+pPBip2krx/LsFIo5ajQGleG96RzoeHEz3R6gFinKJXC+JbME/vsAoFpgehnRvgKEmwsegHwKDENoywb3RHjbyGba0GsR2qXRqDq40NPHUA13772XKF29C91KpnyQRKxGyNKo4FycvBuYAO9tOALiiKdQ5OOM8STHuJpfvv8+0/MF+7s3+MH3/4qLi1POTp4xO3vK8fERy8WcuqpkvgHaxjVKGasGgH5xQctg2QTE4/c+wO87sl2GCC7rN9Zdx7R4L2fAefARXmgNVY12C6z31L7Cvl9R1yV1XfIr3/oWjx49Zf/adYyRpERoDVoSOVVlRZ5l7G7vSACI2YyiKJKz1h1XPCPW1iiVrYyzJf6677bmEuncUnz4IoRgf/O77TYjWMHxfcbtqpzApr7bMbTExQBDm56B9JwkcCYMUkKcKjEPwRhu3rlNZS3KK+qiwi5rXGVh0p7BVQJ99VwBaAzFvBAkqQhwwrfjj6Go+3uVkGP92fUJtbjOum1ZzkCo3WFiGuK8NU/p991Kk+kQUcpHAU04m7o9UO0dejHmVcJ0Nz2HM5rCatXUG9jmZBHajzoC9EjkpSFNQ2WBmd0zK0RscuKiMCBGuoFGHNDgZCL4D+uiTGSnpV4MNxza68695eo6OxrGHSPX+TDwFbjWeU9S0TnrqItSzKKUE8KWxNw4ttjyP0gEIEemFZmGspjzyScfojOF12KLb33FopiBDpLpRnczfP67RXfG2TJeoILWPDIPqpM3Q0lG6aanyAmuEvad+aXrrYKWqYkoFu9dT4Oi2z3UmQl7L+8RiGQXzkHjOB/ORtNObwtbJqPV0GhtklDA8luW6ZBvI+bF6jIA3VbXMU1t/egDkmV5eKfVs11F0NcK3eTuWFszGuXCXOLw2BAlMeSTc4qyrGUu2qHD2VUgoZqVnACjFRnCaGRBoK9DUsmyrlCZ4t69ezx7+hRbVaJ5C+MuVIR7HqJ2wgtujjRStFQy2mCMYaI1u6NxE8TpKuXKjMZ4BJNRjtKqccATTlh8GqIDizZjFGLn5axHoanqirqqcd6h1bjhuFIpqg2MRJZptB6RmZYIkk0dUVuJ1GNri1Y1o4lB74waqUiWZYGDdTjnJa+BUnhvyUeSTbaR4hrTaCaUN+SZxEKPaMQFqYxw411Oe9KYO3mqpSRIub6/D94zGuWUyyWzcslyMediesbO9ha1cqhcY0eKJYrRWDE7XkiI1Nqzp3PQFmckgSBeU8znuFpC+saLPCQVEAAXkUAXMfkeAaBVm+QQLgNkwyXu2VAbwrknWocUscLA2BFyPmFIUtCSosUujaM68+q3vUkrM0R4Nv/wTb4P7yREc57n4OHnP32P6cUMTcaff//7TC/OuDg/5uzkKfPzQ+bzeUvE9qFjO8iBFb3aPlzGEK4j9gfXfKCtjuTLt+ftKpGZXoQJWTdGSdbuqJHkn8477AdiWuCd42/9re/ywQcfc+PWLQlVHYnOEBbahYAN0awGkMheZp3DaUssfpF7sG4+V5//Zf22yHRT+WJDv8qc+xquFn5Ad659VN0QJIFwds5x8+atkHTL4p2nLMpGCDXIWPRgl2oaJuR0aoleFR42/oLE+PKr8+5ex+GLmsK35vwnBGigkRqBSgN1Q6juwdKbTEqQRiwzDNe6f69SEj4mvNs3rUnG1ANXg+NtGIyEYO3A41SgleKhtv/hZrvMSgdWNUxcwryFeo3GdEBbmnTaIfx73Q1U7/ar2gdorSnLku3tLfkpMRXvzDvtK2hqoiT52dOnnBwfMzJaCMtAbKbhTzt/6Y+9v6bdGqkDvtGmI0hK6/SFlf06fS1KymzEJMspXolCm76lRcMkDBxcH+irvgZZRQYm0TL1tdRRw6R1/0yLP0PqZ9nkwdp0Ti4pDZOhLNZZMpUlBMkwY9YXtPUabGheYwzj0YhiuQi+oCLoNFqYGOeEDhlvbeFNEL4rha/rxipIh3C4Vikq7dFjgxmPcFpRlx5fWj599Fh8l2s5k5HR1PTMqMP4nAvwM5QYVQ3vyZRimuVsb2+xu7t3pTW8MqMxmXQJdfmn8Qghr/UoLFy0oVZYLeqhLMtwY01VVmS5OJRY69BGlJ6yOeIIkwVzK02Inx3ranFGsbZinGdy+ZVuGBEJdmXRJkbw6UYLUUjWYK2CTad3DXetdUQ/YhZlrQvSvM2HyOPZ29vj808fsrO1hfUWozwZDlvMWVycYYsFB7dvUs5nuKqk0o6qWoKtOfzsEfr4DJYFxjq062XlrGrmF1N2b9zFpgBlhWhs0edVtBNDhOem0iXeh52y07+tavBvFgVm3TiatkgYEdVlXIdUmZGQjomfhur4cOkUMB6NxORPKX76wx8zPTlnuSj45KOPmM8vmF6ccHZ+xPnJIbYqVoDeUB/9eVylfNE2hhiNPhLpt7ep/ouMfaheK/0NMpTeebHW4lVYu9pTLD3nXvHhB78UrSeKr3z1G3z++DF3X7oHeOqQ4C0mAXUhbGCTe8WYIAzpErLtWXFf6E4Mzosvvl79sun8/McsHSECDBDuq/WGinOO/f39xn8N6OTSGAoTK5LYbjvRNDNLo00RJZkMEi+psGJdWQfT4udBiSXgw1lWA+8N9rPhWTyDLmGGLhMQ9GHi0O9D/bxw8T3eIkGPKnm+cYJXGMsQw9kSmsOE3NAarTArf8OilGI2m7G7t9v5bdPdj866o5EIQz/88EOBcZFJ8cHc6oqLtrpWw76F0WetQ/BvgP/p8yGCXAW6Cd+19e/XScPMprg4fo7WLLG+D4T6OtzTf7818WrHH2m8LMsYj0csi2Wz7l2BeLBW+ALlsvVZ905aOmtCy7xoLeb97nQWBCdOgg0F02ClRXuf5SN0lqNdELIojTYSNtk6h1PgFJR4vvr1r/Dm179GZRSHT57x/p9+n+Vijq2DVZCTPFM4T6YS341mbAQ3BEnG60PSYOtFQ6dxTG1FZgsmdXGl9bh6wj4DSjuRKUTi3Iv02TmFUmJfqKJU3VuMjhujJItrrlBaNt0Yj6TSaA97bkApF7LCChEgzti6YYp1ZoAQztJb2uQtkasWpNNyu4HTrVyj0tVKSVIUH5miyDy5wDQJ6vC+y9X1JQFaS6i1w2dP+clf/gU3b95gOr1gPp1hn53CdMrta7uoZ0ccPz/CWcsoMyymM4qy4Jc/+gn2yTF2vhCfDUSFaIzBekdVVhw/P2Lv1bdQuhXNpIc4BSpD47wMUQ39to5RCE8h2bN1DMVQ3/HZCsCUyp02+2Ppjw8IccvbEKbrQlD2ga0wS22dlnGU8+i9ZJwfZyMMmp/96Kc8e/SMal7y0UcfUiynTKfHzKYnTKenVMUSrdpcIJch8nUE/lrJ7sDcr9LmujK0pn3E3Q81uK7tKyH73vsdgiWUBhmE+x9D7ZUscN7x6ccfgRVTuG99+1d5+OgRd+6+HMwPApwwpoOQGn+mNWdK6qwfd4fI7nxemdYLlU33o182Mmwb2rsKU9+XFF565i4h2oYIBu+95AHynlFQt1eVhKAsioKyLDvRUzpj6HUnUFkERTHRVZSkKhXfDbbuqBamvCA8jPWuevYj49yv02+5SyRxZQLzi5T+nqZRBbvjTE3PenAE1fqUEdd/XVENPSDS/i6OGHyjN56hczhEeMbS8aFJ5t2e19DWIP7orn6nb6W6JoLheVmWjEbjjbCtP9dImNe15eOPPybLxLkXJVq3qNEbKutgev+epZ/jGKJkf2h+Q4EO+msY24uCzxiwJu0rvqN12+bQ2gy1LbDXXBmWpu8p3XUsj0zFjRs3qeqSk5OTxp84aqLyPKOufWPa3x3j8F7Gv2ndCKskZQP0IxFsgrvdfW7xbTQHr+oKV1do5Ru/Y+s8RWWprIfagZV8cc5airJsznaNw2UGPxlx994r7N++zVJ5xpMd5h8+4cd/9dfhXIigxlmL8BNWHM9jwCYfppQprNLozKDHOSrPGE3GWO+ZTAw3r0u0rDfeeONK+3dlRsMoQhxhDTFMqxeNgFEiVcp0tFnz+Bi/PiVggCz4B4j6vPWTUNCYKWmlG5tfpYTL083BDpxg857Ym/kQBjeC/MbpJWx6mik6Jj1RSmzDoy2u8xZDejlpmJ0VgIfHInZr9aLgz/7oT7izv8/WeMQHP/05XBRghTFTeJSXkI5ZDXnlcZmirktG1qOdpdAemylccER3OLy1nBwe8TYK5/vEMmEu4ngeyxCia+mEVcJiE+MRAfk6Lr6PGDoq2oGxpsCik2THQ3rZN4VsWxlvZEB7fgZtwptu3/GllNHo9AMorRmNRmil+OiXH/DBL34BTvHpRw+Yz88piwvm81PmszNsWXaHs4E4uYzJW2eitA4hD31f10/8/SrEbaybrnn//K9rbx2jt67v7r5EwsDincIpCxZ86ZlNPZ999pA8H7G7u8utO3c5Pz9l99o+ynusbaVbadtaa4nBn4w/7bOvHu6Mo/c5Jc7WiW43re86gmmorGOu08/rhQGbx3NZ3+uLiv+/tN80N0xEpFlmODg4oAz5S1JGA3rn37eMRezat5eW8XjM2dlZA5tbxC2a7vie+EqtR/x9YUSf4Y711jmyCvzyCbOR9nXJHq99opohbzoH/bls+m2IkI+MT2TKVmFhm3WdBh9HIURittQbklYap4ZNc/uwpD/WIYFLOqzL7k7nbgTLCAbm3h92l8Fa7ScyGtvb253665j7eGZMMHeZTac8fvwYpcRiwyORN13QbLxoETjZ/d6B0awf19Dc+msALZO0CW7JfrUEeIrXI/ztf24ZxGQuA/2nfbbnTiTr/TwaWZYxX8zZ37/G3t4ez58/5/T0tHkv0hxDUZqGrlQcS8qYRKamrmuZ51C4s2Tcm2BvXLO4NjIfL7m2nAQ3iab9lXVMFwsWZYldSkRFay22rkWb4RxeaawGV1b87Ec/Y2k9pYJf/OznHL33EUVVY70FFGglzIpW+JFBKc94LFGuiqLkzp3bvPb229y8/zL3X32Vm3dvM9neQhmNA7a3RuRmPU4fKldmNJpNVQofPdtdTE/eckjxILUq7ZZjjzxxn/iIG5g68jZ9JYyDDxuE102WwoYY9k6YjkRC2QWu0oZSBGYiSD6dC05EUNdVY48P0awqANWVCwYWyBRsZTmHJ+d8+slDdF0zPz4lLxGGTIkaTOHJFGRek/uMsnJsGQ11jXVWDol3wR7doo04eT99/BjtxbEJ1QUW8bP3V5eNpe9eJYb5EGIYkgRdte94qdLvQkVsfnf1HQS569Ykamge6fhW4ln3CI3IcI7ynHyUc/j4GX/6x3/Mjf0DPvrgQ5bzBVU5pygumE1PKYulmPh5w2aPyvXrkZYhCV2/7uqYNyPddUjkRYnTF6nXJxSGiLh1xTuH8zH/pDjFAdSVYj6b8umnHzMej/nub/0m+XiLYrlkvDVBaCHfqOeb0H7eo5Rung2Nex1S+KLlsrV90TtzVeblKvX/Y5Uu8SA4YTQacf/+fT764AOWyyXLZdFoN2BNVJr4NwgjPDTS2vl8LiCxN/eUXVc9Ktixeg/6Qop0/PFzKrjoCAfUetjV7zut5lQyubSODxzWRkOvy8sQU9S03+mv21WfCRHsJ79JmHkRDHWWy7d/VdMonTu/yqzTqdMf29/0HHfevcJ1669PuneRgE4TRK70Ebvqra8wGppnz54xn8+ZhGRzINLlGBXpKjPtw1Tof2/Ps0Z3NP1pGYrElDIDsa2oIQYa2m74TLVajT6MT/MZ9RlfsTrpRj4cYvT7fyMeT+mJuq4lCWhVcuvWLe7du4cxhuPj48TSQTfMxjoYPLQucQ2VUp0IZRKQQK19d11phBNhLsLMCO6rq4K6KsmCJY7JMmFK0BxXRUjqGDQ5yglDbwQmesCWJX/5wx/xo1/8gsoFDFqXjLZztBmzvbPDq2+8xhtvvcWtO7e5duM6WmuuXbuG1pqz01Nee/11xts7mMmkIc2UUljnKMuC6cU5y2XVySF3WbkyoyGx/yVFujZGvPldkHApjQsp0mnAkzhXa5WBCp72iMSekOvaaNk0H9rycfMQrUPjCB6IQHHUNYyMLH5VVeR5TCjSqvjiZsY70XxWIQpT+N5oZEJ77aVoIWf09ViRBiHASAH7+/ucjsao8TavvHabn57+NRAusxNthnc2OO3AjAqUMDZZ8MvQ3ko2Rm1AQx0SxC1n8xA/OToJxp4B1VVpdvcr1O089MncWoauBR7d79FXoQuoWrOjznoMEJFp2MLmSfzugm2qT8fT1ukzM9E2GwjhYhXWRaTXs/MMMiMtnGIDjPIsk/13rcSplXg4nHWYUcZ4NGIxnfN7/+pfoVF89MGHzKdTnC1ZLi9YLC5wtg4xJ4aZgxchJmOJ0pN1pQH2afvtIQe6mp0OQ0q64y9GxrRSxeho277fRx4r41cqkfZGHn792rjgO+XDmVfUQRBhKZYLFJqPP/qQbJzz2//p3+Hk5JCXJvebsXiQPDg9YtXTCitEGuib9WwQ/QDBSWe2VyvribpVLdFlbXSiXPU2r329y3Sq+L6K46fzYph+awqj2i1JCcVYuWN6BOAT87eBvVTJfqOUwFkgy3Ju377N+++9x2w2w9YVVVlg6xpG4zZEbbjDMr52/aOwSKuMzBisrQPh0OZTcYnvXWexOqWFc3G+4kSuO2+kYNE3zpKtWVZ8v72Pw2sRl6mZXtp2OqrQhko3ZM0ar/RD77ypuEc+Ag5QNBJ+vA9Ml0dhOsSPXNkwPw8xIlRmdNpbg5Ha39qzFefum4zeXbzjw5gaHxeVnKm0xQjv+nONexhHl/QZtV8JCcjK3vQZrNUazVwaP08lCXpX66nBe62UavJlPPj0U1lza8N98nhn8TZGIWJD6RL3Q0xGXAcfohF5/CAD3R93HHMHdqRmUsH0VOD+KgPgrBD9o/GIyWTC7u4u29vbjMfjJoqoUoqqqiiKAmsdFxcXnJ2dsVwW1LZufW3DersQ4jUVqKVMSOrgHX8rSwkgYo3i6dOn3L9/n3sv38NZx+nZacD1Etk0JsuTd9MVWX9/03VKfUU24fk+zZg8kLuoJVy+DRY23juq2mJthcJRe7h9cJ3nRyc4reFgh5fv3mU8HnPv3r2QLbymLEsOD48oixJtMiaTLcaTbW7evMl4e8K1W9fYu77P9evXmWxvY/IM69tIUjIWg9Ga8c1rTOuK+eKCsaskkV8Ydl1LMKa9ybZYEdSW+cXV8lFdmdFASfZCoMls7Z1HaUWmFd7XSCKTKH2Wz7WtVg50KxUQvwiA0SgLNu5eiEM0PnWM9oIIWnAU7atdw2RI1TameeyjYSoaeKQwRhggObByGOraIcNJpd5dB6L0UhqryKxj//YtJiZj79o+27evo8cZ9aIMB8ijyNA6kzkpBdqhPRLWzGhEF6SZECSvWqNcBWiK8zM8FpWNAtMCWgWk4Am5SbrpjLqXsgWA+PY9lEQvaNctzo+wh9FJTYHrZVlO18NFGaFvIhjEyxjN1+KYANEe+QiQJTt6SvSnm+e9SLQFyCXj9ATCIGqpdAPwom2wiRoOramrCo3409TWYpVFKxrgAw7nLHlm2BqNMNbzB7/3v1DPKy5OjinmU6gX1PWUspziXBXUlUELsgJHVoFPnyBfed7fgIHSrOsaBOKhIeqSzobbGvy1O9YuUhN/Ja1oCC0piTN1Ep2nP9/UJjglUPtI2qNASZAJjZxR6yy+9pBpFssZ/tTz6ccfs7Ozw6995zucPH/GwZ2XRZDg2gSejQ9YPE9aNxpPp1pao9F0JP+6xEnKuASGbu3qXY0p2aRF6f+uw1hS4qpbN4xV0dzFhhlZM7QUPrY75ZP5x5+6J0XGLb853/aTUJcofKM50MqjcaAlguedm7exVY2zFdYucPUSZWuUrds47xEmRWYo9BH9/UChlTglKm/D+sgEDTG3QN+kKq5luhwpMQ/e1c10tNK00krf/s+nfj1x3RPGpickSTrrfNT9vuN3H3YhhclJ3ZX9YbheNFdr3lMp8RhgZJwCdb+hhvIWnxgfB9abT3oOfaLUDfmCnBOcG2BSsx9AcINMxiib3R7L7jp27lsH9rAaHj0yVgQk24Ar307De0yK53v3oKEUwhitdSGypqLuhYXv0DdhVeq6RjmP9qA9PP3sc0ZKBZgkPqbW1di6bNZ7VUARTMO1ac5+ZCriZZfnuvNZ0bVE6GuKNglA8MEnNq5wxCcKdBZMl5wFL0kzX7r1Enfu3GFnezuYMBlQQavSMCfSfnRGvnPvFgpFVTnOzy548vgJxyfH7XoajfaezGjKssL7iFfC3UecoE2AFZG2qcsSk+d4B48fPeHWrVu8/PI9iqJksVx06E9ro4Z7vXYjllTQ2tHahHOVJkfs56RKGabm3QT2W2exVYX4NGc4M8EAVW1Z5ru8+u67fPbZh9x/503+zj/4OxzcOMA5F5g2y/b2NkoJvRz7zYJAVSFaCOusMAkkcFu2Guv//8T9R7MkSZ7gif1UjTh9/mjEi4gMkrx4dVc17+mZWcxiVwQ3nPZDADgtPgpwwR2HBQQCwWEEgpEVCHZ2tneaTFcX6WJZSSMy6OP+nBlRVRyUmJq5+4uX3dOApkQ+dzczNSV//XOC44tqtMHWnNOaREI5n6GVoixL0jR1SQ0ku8MJWZaRGujv/2fOOtWYeCJp1thiH7Xzk/UaJns4devZ2BwXb5pN6WUXw2qn2ociZlKyLKMuK3BSrQ/ituOhldXAS75+rP6vP0BVVUX+hF7QsOXfY0k3Bpa4L8fVkSQpw50xMkkxdemsLBm1tAhaGGeud/dbwovLiYytjA4kuMwOwjK/iUwwJFxfXqHqCikGNCtKeyysIw57vSG2zf1tCd1m2bIpgWNLRrv65QaJ3F/ZElewVZviMfGWuWzUBovOIxERjO8NZujowOtO+kyMh1UVBerZe3p5j1RIfv6zn/PrX/6SVEhWsxlSKKq6ZLmcU5ZFO4CvxUB8M7eYWAi4DXvqkdUmJjV+6yah5nbs79vf3f3Nm767RG2blq/buuslRCPEeMHKn9O6rhCuOOjF+Rmfffop4/EOj588RlUlSZZjlKVH2kSCrkVILZlrU92GrhVk2zj9im6ck2j24iZtIre4p2uN2tQ2rp+9sDaw2CbaOl4dpnH9W+uFEVsf3R/h3bY2OcqCYzT7Bwcg7F7WdWljNJTTehuDt5bcvHI2jbjVlrZH0p312vrc0Otma1b7WgvnGvdX3ICrmoFsHYcTr6MLzY6317ItaHyjuWFaAurGh9bQvBUYu9rleOS+xXS73ZVnNN3v7ix6ZmdbXFoX5ttzNWu/dTXPzdg2M9le0bU2ZuHAsMOc13VFr5e33rVGq9zc4vlLISmLklcvXwa5ByTGVKGgXFvR9zb6YSFACIH06fkjoOvi2rf1F+9rqDztlF2tPXdCg1KKg4MD3nnnHQ4PD8nznCRJSZKENE2pKquEq6uKQtUIYXkMmxWqb2MfHc1dLUuyNGd/f5+qqjg5OeHZs2esVit6aRpiIbqw1V37+LMN2M8pioLr62uklDx69IinT5+yKpZrblP24804OIYZr+hTSpHILDy7jh/Y+LuHf9unQClNpRRSpogkpT8YY4yhWK0AwXDYJ0kg6/VQwJdPn4IQHB0dMRzbDGi1EzzOLy6oXdrb1Wpl60gZw9HREYeHh1RVFaxOtvK4RBvLk69WK5bLJf1+P8w3xM8JQVlVDEcjAK6m0yB4xPz8Te0bxWj4fz7wx2qtpcv6okNe4HjjvbbQ+7bFzEPMOHmTlq/o6O+DRlDxWUZi85X3EdvE1HQRUQwEXSnVz8WO0T/fBpw15k5YF6d8NCDt51SLBffv3+fTNGUlvSuYrVIujEf0xhZdMVZja7VLzl0Et5ZGk0iBdCl5y1VBb3TDYYO2dg6H8xAB923UgJv1oCqw2phurEvc3pbirS2wbBjvhj3alN7ybc1rm+L5dMcbWwC88GmTEPhMGTanf69nU9lOLy/5d//P/xdGaVZVgTGKSq1YruasilVApP//amswuGHO/798d5wedpMgEjMp2/qJ975LJD1OsForjZACVVcs5nPOT0/57He/Y39vj+l8yQcffoxMJUVZ2ZR8SbKV8dukPLhJILpJCGmNeePT/8RmvGvPZmK2+dyss5WtcOX47JhI5v1GcvL6Wm3SonqGXGvFaDQiS22R1rquv9F56hL9sizX8Mg3ZbK2zWeT1jemf+3Jbe/ntu/7x7S3wcE/J074Jrg65h26gv22Nd9GrzZdu2ks29bEiJvjxbrvKIqCNE0dk7mutYYOXhCW1gNMp1Nms3lw0fVMpheIhJAg1jXrlr+XawpTP6+4OvTaWG6jwIjel7jSBWyJ21RKMR6Nee+997h7fJcsy8iyjLIsmc/m1LXl/2wNI+8GLBHCUFUlRXHNcrGkrKx2fGdnwtHBIYeHhwBcX18DcHR0xMnJCS+ePXMuVNpZdKI1FhIp24pF33zq7DzPub6+Js9zdnZ2ODw84PTslKqqNqbZvQ0MxfyS1rqlILiJlsR/G5i38FHV1nMl6w2QSY5IbFHDqljSzxNSZy3d3dvjo4+/RVEVAWf6WMSqquj1DZPd3VZGMeu6lgQ+3I+9LEuUUqSpcMUH7f5nWYZVPtvCfIPBILiYxUH+UsrwexyDc1P7xhYNzxQ0n23WhFir3ELEgmZjImTdRdhx5hEhmmriXSBogsybYCUvhAhhg/YsoywbASLysfTvamclajR9VWUrP3qtRizUtBCjAFwhqv5oSNLLmRcFp29OQLkROnjyz7a1zjbo1Qj3D6vZMi4oXGirKauriouzcx4c3aGOAqa6cRMdlVjr0zaks8ni44GqOQx+vNu109sOaZewbGv/eIJoD2v3HZuY2lYgsDIkCJtPulKkUpAnKRL4f/+7/55ivrSVN9FUdUFVLVksZ628//+UFmCJNotyE6Nz0xpt08rH7+r2eVsmxSm3thAze/2mIHZom5u7CDg+u5vG43FNnueoygqFSElVFSwXM16/eslvf/NrvvfDH3Ly+gWHR3dIpA1cNUIgXEa27tg3KSHauMYpBTqwZNyCtGrydgVxc7timLeF+41asRv6sbFVokELjukxGzSD0eWNAtS2dbptM8bGSin3XL/fp9/vs6qs6b+uKutmsoHx3DQG32dZWmtImG9ET7bBW7eP9XXYLiBsClRvGMXNfW7bp00w2Hqfvbjx2qY5bNqXt8HWtns3rfVtxr5N4Nu2BpsCh7v3bVJU+N824fjb4Le1frZoswPNdnt/fX3NaDRag4M4ratx33HPpC5m6OXLl5axk7GCw6fObwSObesdJ0LZNL9YcXsTzG9bq9hKHjgi0ygAAd5/733eefSInZ0dkiRhPp9zdnpOVdVB8KprxcXFpcsEZ/mzXi8nzzN6vT7jOxOMgeVywdXllOfPnpNlGcfHx9y/f5/9/X0uLi7Isoz7x3d5+tVXbu3iNRcYVKA78bkXwrkNuRiMNE25uLhAKcVkd8KkmnBycgK0PWtimr4N3rvXlbLuYz6m+Ca8GPNrFuas+6UxsFwVZP0BQvbQOqU/HJMkkunlOaNeBqpmZzRCJillXbNcrVzCImslXBW2joVWOliVhBBBMPZ76JU6WZaFgtMI65YXw0pVVYH/Xi6XYW5lWQa+Ossy0jQlTdP//JXB/QC6C26w/vDxZnmrBKJBKN4M5hfcA4JfCN+nf48/LI150QJalqT4ytO+CdHkcfb9+udDSjTXR4wY/LNWa9AAbJqm1LWim9Y2njcIlNEoAbKXk+QZWZ7zxeefU5clSGGrNbpYBSGs72IgTpKmGrZ1sbSuUUa6lCQu2EhprqdT6qq2xUuiFjN8fkyNu1SzNtvazQLIuqBxG2a32/9NRGzTGN6mWWgx+kasIcxYyu4SMi9cCvdeWwQO+nmPLM34/LPP+OXPfkEqE7QxthK9qVksp2hT/5OEjI2ISIiWRuS2jEK3n7dl3IqJ5k0EaPPaNy4G8XX7+Wbmwwv7m8YWI/JtSN3f59c9kVay0apGGM18NkMg+PrZU46P7yKSlDtHh6RJgjHKFvoUm3O1b1qHTYR6EzO3jTnZ1t5G9G/RwQ1uJOtjDLFKXkr012MZKn7e1R4inuOWsW3M/sb6WY/vMTT7LEUTy1NVFVVU4bbbRxd3xO9crVbkeb5Wh2DTuONzu8nqtun7tjPm77kJl22Drbjd+LxZT4YR7rE33tjP2/q/6ff1M367e2/TYjzhafA216nbtG0C5NsExvCsaV/bBs9CCFarFePx2PIEiWw9F2DGuZn4Xnyw76tXL1F1TZI1WmGrkLVuU1o3cRBrc7xhTrEyddO4W/1EcN0VImLcFqeC9Qqeb3/729w9PibtWSvB5eUlZVlyfX3NbDZjuSxckh+nQHYZQLVWpGkSssQNh0P29vY4Ojri4OCI0WjIq5cv+eUvf8mnn37K48eP+eijj6zAcXrKkydP2N8/4Le//YSiKF0CCFvoubsO3sXHJ5TwHjdFUQRcsb+/z3w+Z7lcrim3bqJB8fXuGm461zftgRC2bpuuLT9xcnLGcLyDkH3KWnBweAQIphdnpELzm1/+HFVX9AdDFquCZVExW6woyzIobWz9i6rl3SOEDcCHxlrleR5jjEvfbwUQL6j6LFKeT/L4tXLKoMvLS66urrh7926497Y44BtkneoGcq8v4oaHgskrnoDvJ9YYtOoq0DCNXdeX7pjiv17Q6Jp5upaTrgY2FOjTDSKyiMC03t1CwgJ8EDqJYXKwx+LLZ9RVbYOpnOXFGI0RaSDiGqiwQWIeiWhjf6sRuERKgZgIIbg4Ow/j7SJA+7kROG7KNPE2oGgzWO3f43ffBri6jMG2wxeP623aGGgTfO0Wq/t83IdnVLuuchiD0Zosy8jzHK0U//2/+3dIY4U7VSsMmvn8mlqVVHX51rH9c7ZtDMA2xnjbs/B2hiMW0Lv73X7WBIS+6V3etPu2NYvf0Z2L/14WBb00c/hEuX2tKMuCi7MzPvvdb3j05AlfffEF737wIdpYomSTQPzT9yyGLet2sW0y7fn8Z4EX0w5VvWmMQMjg4gP3hRM2QmpX45EMYYzCCzMG6rfg2bfB2Cbiq11gsC8MZYytaKtUbWP0Om63m1oMF3VdrxG6TfgphuVNY71N644pph82GcT62bwtntzUvGD2jZ655Rm/7fVt92xSEHyTFtOE29Cjf+wabmrre7JdaIrpVZIkXF9fc3R01FJadM+4cEKGibIZCiG4vLxqC4eYtufHrfUNHbq/4TkvfGzCp925xUqF0Lebr9aayWTC97//ffb29qiU5tWrN1xcXHBxccF8Pg+MbK83oJfnSJkEfsv3qXUdzv9qWfB89oLnX79kNBqyt7dDmqYsl0suLy+5vr7m5OSEjz/+mIcP7nPl6mD86Ec/4je/+S1Xl1PLQ65Fq0ZrEykxbKG+zAkaGXkv4+joiNevX4cxdoXft8F0iw5Eaxc/u0nYaIQMW1ohzzPAcH5xweP3P+b8YkFawXiyi9KK+eyaUVIyK0tGgyGHBwdkWU6SWZa9GzogaVIlezjwrSzL4DKWZVmIMamVQutmv4UQoY84djXLMoQQ3L17l+Pj49B3XJfkbe32goY2TQVt3Qbe1oI7AmIX16rtbWpAqGtbddumw9X4tITxZvgWMzDxoimtmhR9EIoGGZrN9AFB8di88OEl2RiJWdOcHW9RFgwGw8C0ewC0FRUbDaFHSyZx/m2jIb29Cbv5Pi+u55jlwhomEkntiv6BK+kuXFYOBBpD7Yh7hc9oodHSZt0q65qDg30SYe8RuBSPsbnTZT7yaXDbTARsQ6hxwH68/o3o0kXydszbkX8XWbffHQtEwedSxNdM516rPTbuq/1s/DCQQqCdZchuj8vMIZs1aGAzKiKGs1YAvTxHCPjpT37C86+/pk/qDlvNqphRlEuHLNvaqjVOU0SaYw+b/lK4ZT0DSPx5G8O+6ft6a4TOTUxu97fNAoonZAR3FoQgS7MW4cSZ/T3Dty0tryemvV5v6xzsmtAad3zN71lV1yRCIhHhLEptKMsVRZny5s0b9g8O+elP/56Hj58g0xxpoFbKpvBrVmJt3W5c1YhghPGZDtvvls4qDja8Jz6PredMc9icUNBupjmHW/Z/bd2NcRnYvPWF5sxEA1nT5omGeBHgiGDXNO6LfU6wto7Gn7Xu+BzzIhNIIMszBqMh09k1RhmqsnKZ6ywOXqtH48YtvADnlk264q6+qFWXafDv9tmiohERcE13uUU8ry4sNmmG7Tk1AW6FYO1cbWPwtileWoxhZ0wbVjv032Uqu/fE7970edNz3TH71nXhuUm5EY9xU3/bnn1bn+4u94LwUPylfVaEpw3xeESgFZvmGY/ft6IoGAwGbn8i+DLREGLaKEAmNqvi+fkpWZoQw9aai3mYz1qn7ZnH+EgbtNAb4W0brRFCOA14lNShA4u1Uuzt7fH973+f3d095rM5L1694uz8nIuLS6Sw2aUGOyOSJCdJ+yRJRppKqqrk62dPqVXJ7mTC3eN7tphcVaFUTVUWrFYLFos519MLG2NQViFL2nw+56c//SkX52d8+1vfIu/1ePXqDd/+znf4/PPPOXlzCrHXRsCbjp/qCPq1qhGVoHCxJPsH++zu7galtL298VZ4m4IgrKPnRaI9bZ5teI5mP3ytEUGWpmR5DyEk9+7d5/0PPuL8J79i9+iAXq9PtZxRLGckScnD4yMG/ZydyZAalzBJKWfdUc6FyyYdUspncM1ZrVZcX19TuDi2vqPBSqlQHdzifPubFxqllC7OxtLeLMuCUmcwGLS8RTbVY9nWbp/e1hEwz7BLIVyqVWmzvCgNsmHotbHZlVKZUqnKxTsbVK3J8yQg6Tjgu1sUKT48IVBca7RjqL3k5YmkcmYgH6jS6/Va7lrxu9qmcIUPAFeqQuvaEWpBpZz87Jgu4w6ocTEUpdbkSiIPJux9932OdybMyhX5mz6vXr5kuSwoa+vPZ1GUTROsDCgBpTHUUlAbQyIMKYYsydEipZAS1e/xzpMHSGHjChJhpVdJI3QImUQHoE2URMRgdK95kubnhDskJsw3ulP4fdGdXhrm1PcVf7fI2BNf/5sI/QHObc1E7mtNH5750t6VzDT7p53FyA+jRezxjFE8TPt7pQ21runlOWkqKJYz/sP/8P8mkwajQVOjWLIsLjEUKO3dMyJXJ9ot/l00ixEWIcA17Yqgt9EKrgkOwhDSOvsc+FgBfp3R2yxkwnqgfHyfRSjWylcURRC8vdbZz8HHasWaY//OblKH5lqX+cCdv82E1bdKK7I0c7VwLKNgVMVqteDqKuXly9esyppPf/cZH337u9Zq6O71jOk6YyNbe9Elut0xNJ8joRAHGaLJmOQZRilEE7MBrVScJoofM+7eDQvQMPru/TrqQwTBgOASCAa0s7xEAoT0WXYcA+6hOaScdoGHvlhinIkuMPqhLkIzvvByL6s6PBKKrGqNwKC0QiQJo50J4vUJEpt6ulal7Vf6d8b9x6+xHKOFRRBohE9nTqNMuLl18EKEa+I9jXKh+9VoX8PiMK01XRfOTa2rjX6btj5GW7e1jmyLlbpJsNgG613LQ3w2bmJiu2flpvitliXgJkbZMeACn8aVsDfGM03+5LXG1dwXmNHwvZVgeE3A6c7fuxEh4lhL08ClG4EEy58kAhKo6hXz6yvLlhoFwuMujU+d31IwtObCmrDREtSc8NR1Ub1xfwGp3LiFwCQN/vM0dTTZ4bs/+AGT3X3OL654+vQZb05fU9U1edJnf7yDTAxGpPSGdxHZDkk/Z9DPSETN+dWM89OXXE2vePDetxlP7lKXJUatOHn9NRevnjMcJAzyEVqBMCmJK/x85+guBsNXz75mOpvzwx/+kAePHvLs2TPe/eA9jIRXr15ZYSdJqGtl09wau+HCx7hKgvCidM1qtcRoQ78/YDgYMZ8tqEpbwwOZonW5tlab1s+3JE2wsRYeTnz64QaXxCCvtQIkUhpEOmJ37w737h/zL//lv+TkesXo6C6DnWN6MuPs+RdIUTIa9UnTlHce3qXWM1aFQusmrtEHdXvLRpZl9GSPs/NL50qWkKY5i8UCkBRFwWg0oqqX5HlOr9dDCBOC+H1CJmMMq9WqFWLgLSJxwUPPZ7/zZOMStdrtBY1o4bdJ/177GJvvYlckiDLMGBMKlcT3BuFhw7u2IQOfwUQiQgETIASqxIJFOwjcj9sgZRqYVutjuO4i1j7AUGsr2OjSMN6Z8OLzL5gMRpg8Y1FWKJFAkqKNQtWOMZKSKsmoMczLkkJraiGpgVRKUgF5kpDnfcb7B/yLv/gXvDw75+PjByRmPb3pRq3Rlr27kVhFGo6gIYpcTlrBpe0Hwxtv1EF1xtgN2Nz+nCUYLd5jy+Hvpq7bRBgbJhqyJEEA/+lv/xNnZ6fkaUpdW0FzuZxT16VDEJYh3TbBrgWj22KG+3Yau23MrZuTBCGa+imNoJFEDPVmotOcUWtJ8BoY3zYJ+P71cbyUb7GQsYlpUUqF+KyYaQ0w02FStjFJjYZKtZI8+HcUq4LT0xOy3oC/+Zu/4oOPv0UiJZWqrRLkLZaLbS3et2afzdbeIj7bd2DPjQjsQ+i3tY5b8OrGNdnwzo1jiZ71VoutD4qG4RGdi7dlYGPuWMq2BdkyATaI/uDggC/4jKqsbJxGVdFkL1ufUSO3ryuhNtEEx53fuDabm4le1n04ukaElzqCwzaataltEwCEe0EXN75NIPb3dD0Buv10hYnbCNZvO5vdMXic0FWSxO/r9nfTte59N32PTtnaeJt72xrnbj8xffJxo17I9wHAb5P9hBQhbagX2g26Rafi8fgxd9e1u99aaxv0K9fv687XvyP04ZYlyDP+PmETaPT6Pb7//R+wu7vHyckZX375FWdn55AYhjsjxr0JxWrJ65dPqbXh8G7J93/8L5G9ERiFqlZ86wc/4uT1MbquyAc7lEqRpBlZnnHn3jucnr1itrgkkX12RrtW+aot0zqdTnnw4AF7+3s8ffqUv/u7v+P3f//3efDgAS9fvuS9996jrmtOT0+pcfxcHIMlJMopDDxTrJSyqV61zQA2Ho8Zj8eUZUlRFC1+9SZ47TZtGtf+uNSC36O4GWNham9vj4dPPuTHf/iHfPjR+xzevcvzn/+aoztHmGSAXFW8+PorEmF49PAdrs7O+dGPfoxSNXWtSZIsjC/P88DP+L+z2QyAXq8X6PXe3l6Yy2q1YjgckiQJy+UyWDDi1i0T4D0SvAtWHAvis3y9rX2j9Lawni3CL203MClGvmvpRTubGfftv7eCtmgj0LjveFHqqnHj6L5n/WA385KdA7uYLxgORyErRNwC4AlBlki0Upi6Iu/1uZzO+IerKcPhCLG7wzDPEYslwzRDCkme9+mNhqTDPv2dHZJeD5NnyH6PbDhgvDNhMBjQT3v0sz6jyQSdppxdz5BJ6mjd5qDLTe3tCLm9DnG/xj6woc+OBqZ18WZhY9MYuoTlJsLs79vEXHSZjthi1X2nVppeblO/LRcL/vqv/spqR6oagaSuSxaLmdWKGEMiE1vMMTBCN48ztlh0maNtwdFvay1iIzzj6pl7AcRVRhvGv6qqYImwYzPuehquGwNpmmBcmmohmuwdvkpr1woY75c/+5v2UmsdBI3mWYghpY0HtgueVjBSdIVUK8yULGYzcqWZXs/46osveO+Dj0iEpDY16M31R27TNjH6nshvahG/bd1MsWcmFkfXhMctTOPbGMGbxrqJObxN88918XN3LG87A90mHTxMJpMwLi+IbsLV3Xf7v3bP67Xz5ZvH2jfhlLfhofZ9NzOl/vlt6/FN96BLrzYJMpvm1rUcblrHTePZdl/8fdP8ujxB991dXL1NkO4KPt0WftmyZ9vmsmlu29bhpj0qy5Jer+eSLKzDdSMgdoEEFssFKq7lZNbpQ3zeNq13d9w2xtAqPGKrRndNts3P4GgI7qw4pVOaJXz3u9/j4OCAs7NzPv30My4uLhkMhuSDPtlwzKA/wchrCvM1Rmoury+oqV0WwAVVscTUFYPJka0ejUTVJUYZVwm94v7j97i6eMPOYEieZCRZRlUVFMWS09NzhJA8fvcR77//Pl9++SU/+9nP+PGPf8zDhw95+vQpH3/8MVVVMZvN1vebdXi0VkdQsrECjMfjoKWPkw19k4Qv8W5vwgddwXUwGCClZD6f8fLVSx48fodssaA36DOUUFaKy8sTzt4858nDA/Z2dzja3eXu8TGvXr9hOl0ymewxGAwYuxoaMQ0UQgRXJw9P3qMnSRL6/b5Nhetg2dfCuLi44PLykvF4HHj4OGbDK+4PDg5YLBah3sZN8cDddmtBw08k1sqGLE15FiT/Vh0N3QQgeobE92WMRuk65O7dJFz4d3gg8KYbf49PZeu/p2lKEjE98bMx8vMHMwZI7yoFcH5xzvn5JQ8evBPGsYawpMRHh3zx+eccH93hOz/8IaPBgDxJMH/8B1RlRZbljEZjksRWB5dJYmtlIKjBVgHPMnRiq4aLJCWXKUKD0gatYbK3h8FWFY3H8LZ2E7Hpzumm31p9brqng9y2EZTb9L/t3i4Rskjbo0rbNgmXzf66ANRaIcD6SaYpf/sf/56Ls3PyNEFIUHVNWS1BNBY309Fcbmox8dg0n01ap5vWJBbQu5bC9nsNUiakSYYQMvhpWiHEmmptSljP7to83Vq7LE5IcK5FWm8aTyOIb7JCbSJsXUbDI64mSYOvyH5z68KS79+n2fPv0FpTVyVVWVgtk0j4xS9+ynvvv2/dkXSjBdz0ju48mu9bGEe2B4MLYbX2BscXeYZR+PfE/bcZ6E2/t8ez/nnbs13GZdM4u9/fNpZNZ2DTO7eN3wgBxrAztkWpVIjdq9fevQ2P+OarDPtz0hrzN5cl3/I+gzHrwoZv3SDSbWe9KyzFbRuDuEmo2ChcbWCou+dxm7Kg2/cak8b6vmyDtZjmdpnpbtsEX5vHBrfd1G1C2Kb33TSe+B6fcUop5ZK8bBk/Dez5a7PrGUVZkiYuG5Ow+C+mWzcJvd35BN7LaCTtvYwFlri1GN44mY+3eAkBwvDo8WMePHiHy4srfvfJp1xcXDEYDG3tm/6E3viY8fiQew8HjA+OOT19wWi0x9X1koVaMBmPONg/ZtDrkSWSVEoMtvq2rg2qrqmrFVdXp4x3hhSzGRLYHQ6oq5LZdMpiMefi/BKD5qOPP+KDDz7g008/5Wc/+xl/+Id/yP3793n69CkfffQRP//5z1F1bZNMiEZJ1XWVx622V2pUVcV4PGYymbBarVgsF2451lMud/FdTHPUFqFkm1BeliXz+Rwtzvni8y8Y7oz58R//MaPhiLJeUC6W/PZXf4+g5Dvf+oBRL+f+3XfY29un0gsmk8xlRLUePF5g8LTN896ep/b/fD0Njy/9Ge31ehhj2NvbI8syzs7OQvapPM+ZzWZBUXjnzh2yLOPg4CDEF70NR8ftG2Wdigl17O4Uu0XF9wsh0JGrRfCt15q6rkizpHV/DCTx4dqkMfF9xqlshSPsxphAvOJMVzEBaJAjTmvreQLBcDhidj2zJtOkXRAwIF6tSXsZRlmNx507d3nw4B2WqxUaTa0rlLKE1AiBFgnKQOMTjvOStjEWqZBoYWM4tNOgydQW0EmMzVQQXBu2INBt37ft5zbE1G0CaJsq1jU3N717ExHuag66xLlLwDYJjJanuIUGxzTZkZRWZElClqToWvG3f/3XpEliK7grTa1ssJrBZsRp+nL+6RFB9f12Cf/bJP3bXIv76AoYFqYBHBOvwASrnA06NAaMsmkG7bGwiNi6tJhGCRCWabPfuBXoGxel+DzG/zbFe3hNir/eTr9H9Dk+l5s1unHb9F5jDEpVtuCRgM9+9zsuLs7ZmexaTTrbmO+bmI+bhPSWfN0WJqPHRbRvll/aLqht+v6237e1m872JmLaus7aCf/GrcssCQiJQgbOdI8xLYvGTbioy3DVHVgM78Nrarfjgk3jjMca39dcv/153iSwbRNG/H2b4O8mhvFt9267Z1OftxFiu/1so8eb2iYafFNbu6/h7NfGdNO63bRe8X1xi7Mm+Xvm8znD4XCjAOm/G2Mc4LVx9qpYObrhChbjaUbzbPd9N64FEZ/V4XNvI/AaY4KwZACRSGqlGI5HvPvee8xnSz777AvOz60lY2e8w3g8IR/t0999wGT3HpVWHD7IyEZ7VKuK8XCX+wcTxqM+qYSqWLJaXLEqS4rSKu1S2bO1NEYDJjuPKKsjZtMrLk7PWS5mZFmOkAlXl1fsTnY4Oz1DSMF3v/td3nvvPT799FN+/vOf86Mf/Yi7d+/y+vVrPvroI379q19ZzsjNURmNpCkG7WmEF0J8Niq/p/1+n+Vy0ZRk6KzdJhhqzus6Hm/RgQ17UZYl9cUlVWGtKSQpH3/0HfRqxee//gemZ6/4zsfv8uTRfcrFko8+/ID9/X1ktocQCW/enHB2dsZkMglB2vG4NrlndwWMJElC1XB/Nnu9Hg8fPmyqgQOTifWwyfM8CEpCiFbg+H/2yuA2cEQ4gq5CcZAkSSiqci1drV/wOAVhzIDYgh+NdSJ+tmvZuOkg+v4a5kUEQcO7f8QCTNxnV/siZTsYXUoZEMOmvMvKZbTZnezy9dfPefLue5BlKBdMjtTUtULIBCmtlIlM0NIS3swIjAKhabQTHkicBtSmqDSRALJdq7jte9zepj3yLekw8OGOtxgk3tbv21oXVjYd5PAuBFK0D/s2ou33W2vNsDckS1N+9Q+/5Oz0DGkMGgsnRbmyNTNUhQ3WEy3i0c0WEsNq/G/Temyba/f+rtXCmz8b7aKdvU0niBU0jCdKbWG/+U24Z2JtjwhnxiNZf2biPvy6eaIXI/CuUNCdT6w4iAPHN62Df3YbQxL/5s9kYGK0oi4rkjTHAPPZNb/65S/4V//6f4EqbVVqWw31ZpTXDqq88dbWuBoho/GDBpBxH+Ktx+ef3L6Jluk/d9uGl0RnIUejUYDnqmpSL94kgHWbiXyHb7zvH4GDvknrjnOTAuU2TPZNjPtt16TbX6wUiXHTjTj1lgLLNxEcYsbnpme64/qn7t02wao7rm3PeR5gPp/zzjvv2PsFLQ3DpvlYHGnx5GKxcDjP4mitTbA6/1PbNrr/tj3xbxfCxmUIKfj4W98izXK+evqU16/f0O8P2N3dxWg4Ozvj3miX/aMJlYbr5ZLLq1OyRPPO48eM+gO0Ljh//ZLz01fMr89R5RKBrRWCkGgtSbMBed5jZzLi7t0j9vb3OTg64uLklDcvX5LnPaRImE1n7OyPOTs744svvuDDDz/k4cOHfPHFF3z22Wd861vfYrFYkKYpd+/e5eTNGxzfj6AN741XQKOYqqqK5dIGRNsg6DzweW9buzbsy7VA/C7MxfTO0/GezEhkwuzqmk9//Tv2xwc8++oZTz/5LQ/v3+H3f+97SKEZj4Z88MH7JGmGkTVVWTEcDnnz5g2Xl5eMRqPWOz3uiQV7b5HwY/A8jG/eI8i7R41Go2D9KIqiVf9OiCYG2nsVDAaDG9fLt28coxH7gHWvwbpWyKcajaUnz7gGNw8hbBS/K5ynlHVvSVzhNGNwv2vyPGsi7UNqQ4l7CQirRUxd7l/lNJ6bHDUaU3KDfG26MMFkskNVlWS9vgVAQyhs5eRjEqelONg/4K/+41/x8NEjenkGhebizQn7h0ckSYYRtq4G2gRhwabqlEgJQhmEkQhhNR4IUF4aNdbH22Zd8v7ebW1q26TQ0b1F2VNM+L/V+zUWEnctliaEy9PhNS9Nug62SR0Gm3XDxJ11iYUXNsNLca4opunemPDXaoriGXmG2WtJ3YyMAV+l3iMMEY3bvTsRgjzLEAj+5q//ysJZIlG1sgFXVRmESINPEWodAFW1rmVvZy+7OaB5mxDUMPwWlu39vv5HEoR1y5ypIGhY///Gtck+3/RnrRg+WLsJ/vZaDX+/MQIZilB5nbAljn5ctoKodEdMBo1xIhO3f3E6ai/Mm2gsjcKga6GMmSLvonITkxFranx/2hhqrci1RiQSoxS//PnP+fM/+3OLJE0jTLVxVCxwNd89cErhT1z4qbUuuKvefC/iH2MBPRr3P5cg0GXUNzFuDSFchxnXSzQBgemc8SbSxMJes00RDQgBrf5eBwDYhUvzzApdxmUKVMqlQG+/2465/fZ40P3BwHXbzlBkxHbY8evRZZbjv901a8+83dzro3uj+6M+pGw+hz4F7b/R3OL1j5clVrPQCYozAa/7H5p+4jl14WFbM4DpKi5wSg1HUYXxeNad+YaquBEZi5aNACObc9GCxeZ9oc/wnvX1Nx6cAkUzYSM83WhWqX0mwvvaBK85AwKXqbHB71prxuNxI2jENj8RfTUNbkikJJGCsihb+7tJ2Go+xrP119b3J7isy7Y2+22CmZTSpcBvuACAo8M73L1zzNXlFV9//TVJkjIa71DVmmdPn2EMvLm4Ynz3AcoMubycMRwPeOfeIanRnL/5mlfPn7KYTwGFNBWJ1PazAz8jQeiKalXx5vqS09cvGO1MePz4CXfv3mVnMODl8+cUqyWL+ZzReEBRrnj16hX7e/sc3z1mPp/z2WefcefOHe7cucOXX37Jo0ePOD8/R1X2XZ7PCvAVzmGjLPbB/dfX1y5bU0pZFYEu3jZtq78/rttmYcw6zwphUxwnMkFIGVyS7h+/wzvvPGb34JDx7h6ff/Y5v/6HX/Lk/gO+98OPODrcZTY95ff/6I+RqaBWNRgrtBVFwd27d1itCubzWUv5mOc5RVGglGI4HJLnuavcrkgSH1JgeQgrTDRz9OUgVquVFYZ6PQaDAVprptNp+C1NU/r9/ppy8W3tGwkaMXLY29tjuVxujDoPCE26VIyOM9aOiUYKhJEONwhHKOxfbQxCJLbonRCIkBoyIUtTBPYAt5g35YgEJqSSlKmrAu3MhFVtC+nBevl5Y/zcvFuDRml48eprikpxdHCHUW+MRFKpEqMq0l5qKxQLyWDYZ3Z9xf/p//h/4MHxPZ4/fcb5ySn/4r/8X/Jn/+V/xbyqSYzLY6U0aIGRUBurYRWpPfoyYgSDRlT6ataGBOOxIOvUybW2zNHQLLqI2xMpt1ceAYZno/taexsT1ui1xljNpWlG5tNbtmqQuD5bz2JszRE3JhOYNPu751FaT3ha7fo2scbdC51hCnZeVV0x6A9IE8np69c8++pLEinQRqGNYlUW1C5DRV1bOEBohHDMp2lrSZo1ae9FV9jYfhjb/cUwncgUbTRaGZQAn3TUj8GvvxciAmPcGVvzbs/srF+zCDnSzHidl4g+gztbdjOMsVW3pbSFh+q6QggVBBroBjc2CFHrLqFtM3UeXG7TggVUSozRFFXJME3BaC5PT3j6+ac8/OjjEM8Vu1rZ8XX3xzFIxiC0QSQbKot7nhnL/ghjiXfifjeRwiAwQb7rDW2TBndbxqDWMG67SOtvpA0HsbDhhQM/bNF6ThkP394lr8OYu/u8UNu8T6KFRieC3mhAb9inLkvQNaganDJHuMTdGkB7HNbi1BACtLYWPYOrgh4Ek1hbvG1/7W9WUI1ddUULt8VrslnMsDNuBF+1dvbaQkizsqYlrRqIGHobK9WcY+1UW016V99X56x7a0qL4RY2BT2RIGe8ANkWOEwHT2sEuiVouCTjjm4EhYOOXKkd4EgpA+h4pRnCONHJ9aNNG7w6q+xRuB1Shw75607A8EJeW/h1aeDdUlv+wOPJRuDwQrNV9Nnv0tX6MqbxjrDMmY0vbSmVpB2RdmORypAJQQoYZxnXphszGOPGDl32P0Z73LVIbbJQ+b28UaEhhHMlFVhwETx69C66Fjx7+oJiVTCe7NMf7qIRkLwBVSNESjEruF4u2Ns95N69O+jymqdPf83py2fglM9aaSqtWuOSUpGmGUkCaZLQ69uK04vLS359ccGDd97hvXff5fGTJwgpubi8IEkFyWLG9eUlX33xJZPxDg8ePOB8eslvfvtb/vzP/pyDg0POzs64/+Adnn71FOkzUAmPk4WDORc153BBTAessJCGDKVC2FiauqqDi1C8njHtSBIZ3P+FEBhthQwbMwn9XsZgMCTNe6RZjtKGP//zf8Gf/6v/grOLS15+/Zy/+5v/xIunT9mb7PKD73zMwf6QxXzK7t4h4919zq7OEcJmmMqyjMlkTFEUIe5isVgwny8AQZbl7O7uhgQvy+XKeQ9lQcnfeDdYJbfP9ufpjfdo8JXHhRDs7+8DBCHGC2v/LAX7fId1XbO3txd8Fq+vr8PCx+4VWuuQl9dv1qZg77gF7XCHfvpnY7NPO12mQ4ym7RIVP5tE79Qt7Zk/nARJFwiZCT77xS/57a8+IRM5Tx6/y8PH7wCGqqpB2oAnoTQffvgh/+f/8Jf88qc/d8yv5D/85V/x7R//CaLXp8YgjQGjMUKQpglJmiKND9qVSAGJaDJptQKMhT00Pjf0Jk3621qHXtvf/Jps0TJ1n3vrO6LPsZUi7sTLnvFTIhY+2lJIq21CqjEiiBnJ+Hd/QNI0QQrBr375D/bAJgLtMtgUReEOWeXj5PC1KSwz3vZHvGnN32bFaAhFO1uTEDaYy9bHEM5FSLeEka4w0XW12tZuw5h2kyS0rJAR4+g1RfZMOgun8OtlWsLEJvxwu3bzfeHct+I0lHUHwOKqX/ziH3j3O9+lrhpXyi6B3qxdFE2B0rUxmxsYT1r3mw6w3ySUbluXb2IBaQt36wKM/T182vL7W99CECnecgZa2mUHL71ejyxLWRUrqqoOBMxrzLvv6PZn3U/UWlpG/BPN/6K+uuMnEjLie9qClWgNY32uApyG3QoLuoNDHS8XsfVeTIiVBbJFsAUyYp5xn+M5RvAaXxAiMMogbDYhGmY96qC1Oh5Eu/jXAEboLgoOnWh8IhYvDIFXhOlIQdFYekRYH4gUUGH4ojMuE/6unUF/r/tJuAKVOqr94i06QX6iqUETmNK4P9dh4hgwz0h5pk4pRZJKNsEB+Jo5PlW1/c0zq3Tm0m1bj1EHd3gLiz0rdiMboXmz8HFTG+/scHh4yNXVlJev39Drj8hHu/QnB+wd3uHo/rvMppeMxjusasPu7i737t+lXF3z6W9+xtXZM4SuUZXVktuzPQh0w2ct8jEBXiPe6/XoSVvb4eWLFywXC95//30eP36MlIKzy3N6vQH1oGK5mPHy5UsePnlkg8G/eMrXX3/NgwcPmE6nHB8f8+rVK6v0dooQRIOb1hOo2LXyzHSv12NVLEnTlP39ff7Nv/k3/Hf/3X8XPHfaiqk23fWZm2y8QhrxuYZKKZaXVyhtFQv37j3g4ZMnLJYLfv3Lf+Dv/+7vqIsV73/wkG999BGH+ztoSoyB+/cfcHl51eKbsyxjf3+f8XjMzo4NCh+Nxij1itlsgZQqWCS8W3EML54PAlgsFqxWK4QwISzChjOkYY5XV1cMh0OqqgrVweu6DnxSzIO/rX0ji4bWmjzPg29YmqYtH7XupGLfMN9HzLR0kYcXErw2wS9UzPjEf73Pd/NsTWO2t80LD1ImLQEjBhyfbSoWUGwMSsbx8X1+d/E7nn/9lL/5q//EwdEB/9X/6r9k784+MkvJ04xcSB49eczx8TFff/WUqlKQpvzRn/wZw9GEVeXSp2Fdp7QxFJVCKoPSkKUZeZ5Y6VtsF8a6Wu+b2jfVdnaD8Lf19zbA2sRI3gbxxbCx1mdEGTdp6zcxnN17w8GQtnrpz37292RpYlPuYaiqEiGI4ggMSZLZ/fBIy6xnpYjH0Z3PTXP1RANEa/xN/+3ECLGA8U0Eiy6jt23csSDQFTT8uegy6paIm9YzdmybA/3jd940rtvOLT6v7UQTNWliXSy/+Pxzrq9n9IbDltLjm7z3bYJ8WwR5+7nbJtDf5rlbj+kGPOH1Fm97xzfp8zZNCIFEkmUZWZazQgR3AK3UW1eu0ZA2xada2ni4UShwg4h420aLb90dROv51ngi4SXWKhuHz4Ng7X5DiNYz9pOVWryg4c9bkiTEFo0ghGyZf0uJsXGKHYt/pCAgjKARdDwTHr/Dv3/bnlgHYh3WgKhwaudGGiu8XWej/Xu68VoeN9jla/BQe/z2EbeW7npTrDQWHgDduIwIIWw8nraWYozlUeqqDlaNuq6o6gqwTOb19TXQKGAs2usqXprxW3mzKWxaVXU8M7yL6W1xeKv3aP+llEF6bfMy2xVbm9qDBw8A+Prrr9EG8tEu+XiPwd4d+pMj9o+HHGvFq1evSWrDOw8fsJxP+fTXv+Dy9DnUS8dwJ7YY3rARMizNlSGet66tG4/3hOkPBiHl6uXlJZ988gkff/wx9+8/YLFasVzM6ff6VKsVr1695s69Yw4Pjnjz4jVffPGFrbext8fJyQkPHjzgq6++ahU97a5FzJu0hBBhNflVVXF+fs4nn3wSGPL4rPvPaZoymUyYTCYIIZjNZi5tbh3BqyBNMwbDETuTCTuTPYbjHX77ySf89V//Nacnr9mbDPj2d36Pfp7w6ME97t075vmLlzx+/F0mk4kTXKIaIVIC1n1ZKUOWWdeo4+P7ZNkFV5dXzK4XrIoVUkh2dsZhfb0CUyYJvTxnNJTs7OyQpjKydgjnblVR1zXL5ZLr62uUUvR6PYbDYUjRa4wJ+3mbdmtBwzP9RVHw/PlzxuOxDQQvywDsscDhBYGuBtYLIPFmAx0GpjnIcV9xsT1vuvHSlke6seARvzORbe1kLN0lSZMOzDMjVqjqcbB/QK83oN8bUJYVn332OR99+SHHdcHO3oSd0RhEQpbn/N6Pfp83r1+zf3jIn/zL/4K/+C/+FQbo93qO5liNi6Y5AFobyqpCSIlMbc7/TQxFF3V0BbhtzPy6NtPr1QjE7W3MRfewbur/bUxIV7vtPxtj3Hqsa7DstbYGL+6r617SJbDxZy8kSyF4/vxrTs9OLLE01j+8LAs8IciylEaycTxDNL5NmdG6c9+2DpvcrmIBIrbISZG2YNjf800Y5e67ute6cA+0kGw3E4efe+OX6sdE0CYa0646Hgv48e/bxhvPr3sW4u9d65WdgxU08sym7psvFnz11Zd8+3vfX+v7tuu3/T6x/snQqrGx7dlvKuy8bYzdfrcJcs2eb37+ptZV0rzt+XAu46MgbGKR8XjE5ekJSilH2EJGgzUpqDsnD5fb3ATbCREgZmDt/xqNcxPHYGG5mVN4LLyza5E3bqzaYF2hYmZdNz7i0UycFt7FXmCfU8a0YoEaWSe2XPjla37zDFxcsdevTTjPHQa0lbzC9y0bmLAClw0SlolswUlrLZQmSRsGJch5LnW1/U07CwY2y53xcWaxEsXO2CpyhFsCJ5AYgzGb3INsGvLaZQX06T79vFerFUVRWAtGZS3Vy+UyWCXm8zlpkiBpCo7luRV+8zxHJoIss0XYnj9/zv379wMvYteqwY/x2vp4OStv2vEXRRHdZy3YNglOhOM2WO+aPWq7TcW4NBEWB3eFFr8nm9xaPJ9kMCRJyt07dyiKgvPz8+CXPxqNGI13GIx2SPOci7Nz5suSD99/H6FrvvrsV1yePsPUS0aDHlobFosVZVlQ1wWDwSDAU1GULr7P12yy61iWJUrbmjq+JoOPwfj2t7/Nw0cP+fLzz7mez5lOrxmMBpycnPLo3ccc3bnD86+/5tWrV9y5c4fT01MODw959uyZDUndxvNs+JskCVmWoVTNdDpFa81PfvKTAEtd2u4Z7IuLC87PLxx9tG73+/u7ZHmGEJDnPXrZgKzXQ0qYza5Yrhb8RtccHuzyrY+ecPfuHcbjEeNBj6JccHL2midPnnDnznGAqbo2wUphaV3JdHrteBK7xlIKVquSJLH8wmg4cudCcX09CzRyuVxZnj3PSdOUXj9Ha0OatmNNPF4ZDocYY1gsFpyenvL69esgaOV5zmAwoKoq3luDsvV2a0GjqqrG4iAlp6en1pwi7eFpa2PXGb0A5BuYwrh1BYxNGX78GHzk+0YC4Fqe56EoS3ds/lnPTMUaTyEE88WCJO0zGu0Ab9wBqSiLGol1mdJVTSU1ytT88b/4Mx6++5h79++zf+cYyBCih4r8mQ0quCn5+RljMLpGKeGk4nUAF1JsVUPeRrO5fsEveHvt4/lvapsOcXef4ns3MVRdOPHCRve6cUzBWzxoQv9djY7/GycvSNKU3/zmV1RVaYPAVW0tYUajdNUZ68061k1MTvdzfF/MqDdzXHfl8ff6fehWs98E55v2qzu+eK82CR03Cazb39MIGka1YSEWouKzuklAi9+9DfZuA2Oe0bJ+1Rl1VfHJJ5/wne//IJiUbytkbJ7vppsA01YGvO25mwQof70rON80vtuM0++NjfvaPJ6b1v+mOdzibjtOx4zluWVQKpfFxNMXLxdYDfN2gSj2n94EkzGC2zTMWKiw39vwFcczWaLedgv271RaByHDK7piwarRSK7jbxGhtjgw03TzlsbPRAp+D+dASEtpNbSWyReR4OJzHPginx7nSscQEwkeCOd2ZUR4l9f4+7kIkdBEZQsrWElB4ty1MAZjmiQsxijqqkJQI2XCqihstjGt0EoH9xo/r+vra2pVW6dao1ksloDPDKkdPrE5/70S1LvBWG2/YDga0ct6JDIJDCXY4qRCCBJhs9FhbNBugwNtvE2aWlegN2/ebFUuxTTHIGyckWksF7YqeESPjIfHhtewXhgxXMRf2r9vw5E3KWi69yFsIpHJZMJwOOTZ8+fUqmZnZ8QoTxj3UnYGOaN+zrIomU0vOTrYZ9TL+PqL33D++ilCLxkMc/qDERfnFyxXSwDqugwZnWQinSBv06n6AnteO17VNdfX1+zv7wdl8dXVFU+fPuX9Dz/g6PAOs8spq6KkPxxycnLK3QcP2N/f5+WLFzx79oz79++zs7PDdDpld3eXy/OL1tpsUtDF/IUvxpjnOePxmMvLyzV+sbsnDX2zViVtLLOeZil7exPSVDDI+wz7Q7Jej7zXZzgac3B4h3v37jHoJxhVsbc3RsqEqysr4Ny//5Beb8DV5bVbyzrgGv/Ofr+P0TbmWBvrIixlghRpiI+0Gbbsgfep8BeLJUVRMB6PMAaWy4Kr6RWgGAz6DIfDYDzowtBgMOCdd94Jaxd7EvlsVW9r3zhGw2+YZ34SkaxpTfxA47Rfmw5o97CEjTUmHLD4vTGTEvusN/0IfCXjmOFIksRtSqMViIULKdOWYOMXu65qEjTDwZAs7yFE4tJ7VaANw7zPMO+xWCwQUqAw/N4f/6FD9GBMgq4Vmchc2RoDRpA6xZ3VZDjNjbba9adPv3J+ih3TaoPz/1la9xCuX9vMSG8UPLa4OsX9356h3SBgmebS21oIFsb6OGql+M1vftMyyxujkYlAF1sIfGcum4SnzWNv/xYTiUbbb1oWhOaaI+Sd/jYyViIaJJvXexsjG+9HPNYu87+t2Xu85jMJqtf2HNspgLuCwT+mxWOPLRtau9ohxmlPgadPn7FYLIIvbdzHP0frWm3inbnpnd0d3Lrqon1vnH3rbX2GLjYQ4237/LY+tgnW/rNl0t0xFtbV6PDwgE+0pnZ57YuyaBQ93sKpu7bMpm1Kmx7G66UVNuOz9qw2jxtEZx5b1klEQo1ox7q1x9YWeCIefn1kN5w3GVtjbK8W9rVxxdiahCitiBfvzuIZYfd7SNDidTouzsS7Gvt5aKUpq8rVFrK0dbWy7iJKacqi4Ho2czBonA94EXy+rY++zRppeQdLy30mniSx6e6HwyG9Xo/JZEKaZi4IW0Zu2okT/GJB3GfVi2M5rdsOqq308AoPMEgUPpmAlFa48pYl7QLcj46OePny5UYepgGBSAADfKZHAyyXyyC8AM7NTgd4+udomxR8gVeiWbvd3T0ATk9OEQiGgx5qNeVXP3vOzrPn/N4f/jkaiSpX3H3wgHI+5dXXn0O9YDzKSTOrRC2VTaYiBJRVTVkVyGSHQT6k3xuSJFlg5r0rTp7n9AcDZrMZ19fX7OzskOc5WmvevHnD3sEBh4eHXJ6dc/rmDRjBcrHi6vKKu0cH7O7ucn5+znw+Z29vj6urKXfv3uX89GxDFqj2WfbMshCC1WpFf2BjvboKspuENSGcK7EwlOUKpTRVWfCDH3yPyWTEMMuZjMaMxjv0BwOETDFC0O8PMLqkrAxXF2cYI5nsHvDuk/fJe31WyyoICTa5hIystwTLnM38RLinsSKa8HvMV9jsWjmj0TD0naZ9ktQK27ERQUrZWsOYh4ozN0KTrept7fauU2mC0bbgknK+d8ZppGRAHE5GEJ6ht4xc190jCAlOW+GLWoXgLNN2i4i1CWmaWqZeuQw4hmAStcFvnrgLNxbrB1/Xjvg7tyXlzLcySdGqLXgkzl8PJLosGI0GDEd9ksyqoKqqwijoZT1UrSnKyiLnpOLqesa9u8cIBKtVBXlCrTShRI4xoHyFUO/Xa/UbWhnu3bvXYhhaTNkN+xO0JXT1eXQ+WarSCA/ejN8QRJwGr6FoXWK9uddwv9PStDQC7ro33GptguYL4RC8v194rZjNfOJ1ob7f0J9pIw+bCjjSAnsLmDG2ErhMuDw7582rV3bWWoHRKJcZxBfoazcRrVpEkePViASRLmMTE8MG6csouMql+NSQJjYNsoVTGdYz1rQaB0NCYK2JREIi2DlF7zbGZgLRRuMrf9t3eC2s3ysHNz6rlRDdabbmGv2CEE54ckXYjASbJUagakWtrDuFLRao7ZkXbeG2TXQ3w5q9ZV3L7wmHxRWW6dC6plYVILg+P+Xi9SsePHro6qVgNbtW7r/5XLHlumkEYJ88x0OHdlou2WFWHXdh91C0IBkjdPvM2o1t3u8Y02Y89mll3Puj683rRNRHs6c+QDnMrMOwB5yzthZ+zg52TGyBwJ09h3tDwKqTPYXAIEEYtFIcHNzBYM37y8WKxWJJrRS5sXFsTiqzc/LjckH+CEF/NEQZq5UPtCBe5zBmrzFu44qNTKNoz10gA9HvsJKO1lnapaP+WxY7ac9z82xbCLL9aLeWzXvl2so3eMdo+05PF2tVO2uFfTKcJQcoPkBW6zoE3muXMKEoClarFbWxNH2xWFBVtgZUXStWqwVpKm22Rympq4okTen3e6Qyw2hBL++R93okScLuZI/BcGgTnUR1trxwkMiENJW2qrX0LlptN2qjIU7F3dAh4yBQBIFI+HUJihGfzQmy1LrnSAxJmgTck2Yen9tsXNAU6GswvU9rbRWA0gnLHgYJCbUc/vSWOKe0UrUCk2K0ZraYORjWGBTGpSlN0zjL3w0tQkBrjG8scG5gijcKG9491xgOjw4pypLZbEaWpqRCcPLqBZfTBSenF0x297n/zmP2d3YYD3I+f/oJs9kVed5jPN5hsSqYzeZh/TxflaYZhgRkwt7RHe4e3+fg8BCMYTaf89WXX3J5eUkmE3Z2bIxDmiaMRiN6WcasqHjx/Dnf+e53ODq+y2yxQNUVs8U15ydn3Dk8Ym//iNOzK16/OeO9994jSXNG4wlJmraD/Gl4zm6Mnq8Svlws6fX7CGFT0SqpSJMEo1TImrqOLxxd1S7Gipo8zTja2+PhwwdIo+lnOVme0esPGQwHLJYrLi7OWBUrhBTkvQEP7j3g3v2HlIWyqZARIbuZ55Pz3AppcYbXslQuNiYnSSRVVdOmp9KeNcdH25pDIhLWMwuDiWK1Uq35aa1DnEas6I8VLduUPNva7S0anslzDI4nhonz4zRB+yrRDjd4pBrHV3hrgpSSxJmevD+rF1K8liaWsIJ2RUQpc/HAramVIglZgSyi1cYihkwmjpFvu16VVR2AsHKWjyzPLcPqAnVRmvGoz3DUxwiX7hRsas+sRyIFvVqxWCwoVhWvX7zm7v5dMpkxyBLKukYJj4y05+PDpsaaEm/+9ZsdaynbaRs3NCdoxH3bvw5FGwIytrf7zw6Bd6ihtwDZO2JBhBaC67Dc0d+2OTj+3cKOCbyOaNB0sxZCYIQteKYdA+mzlPh+fb5zQ+yaZhdYGlBuHZRW9NKMTCZ8+cmn6LIiSxPrhxwdrGY9XL9dvB4Ehu4BMwF2u/e3XaX83zqyWkh8MUchbK0K74YT5hlr0xAIaZn7xge6EaxsDREvyDv/aKFtdhphHMPvfjc6aBbDTvo54lwnhMC4yvR+LA2y0YSihgEanNAYrZH1+hMIEqSQKFOF52PrSRuGNrVGwIjxgscrdnwKkGhTY4zVzMiq4Nmnn/Duk0cYgxV8jHUh0tG5WrewONY9ItT+/TaQNXbbdNeFBGFxXU3MojrmJjDr3dkKi1/8W3WjDPBJAzatjDEC45Q2NoVmc00iojpE7bEECYFOxjnPvvnvHZj2qcBxMGPn7LT1kYLANNyYxXva+tsrIzC15vDoGJmkKKVZLS3DUtWaShk8WWjgXgRBCyz+3tndY3p1Re0VFl3hwrTddF2lpXX3O++yJHB6i+YsSJ89TXqhw1gri3BZi1zNF6sd9fuPU2LZs6C1dU8Sookr6TghuTPsGG+l0LVNiIKD61op5+JpqOqK2WwG7t7FcmlxF4K6Nsxmc6SUzk3IxgjkeU6eZsHtyGYGykjSlCTJSfOcNMs4vNNYDxKZkGaSNNXh/HoGH2OsQGAaj4WYkVuDUbwCyH6TgFG1xe8Cp5TQgIREBEWEXUOf/s8Lk+t0xVsIoElbawzkuXURShIQQrfGF0DY7bbR2vIL/sy5dMDLxTVVuURV1q1LSDBaBYFXiEaoFgKMqlBVTZ4OWayWTKeXFj8ZhTHeTVc5HqkRkLqtsYY20OJ/CzF9G6uDdda+yyALgUgkqZCMRiOWiwXFqmA4HJGkOTLtY1iSJgmjQY/VYs7xg0esVnNOz15SK8XOzi5pNkTNVqiqZNDrMRw4vgVBmmX0ByO+873v8cHH3wbZVKLu7x3w8IOPuLy85Nd//1MW00vKsmC1XNDPM1KZkyc508tLrqZTJgeH9E7OKJZz8qpgPp1S1Yad3UOS9GtOzq549/2U/nDCarlgOBwydy5aXcv8Oq2xZ2i5WpHmvaBI8bQToy0OjdavpVAQCqMhlZI0yRn1+ozyPjmW3yxrxWJVwNWsiZsSgsFowrsffMiDB+9gjOHy8pLFYslkssNysUJK67Lnsx5WVWld/LBJjZKksepZi6IvxKfDfbZuhq/BZWtv2cQbS7Is4/XrN9y5c8Rkd8T+/n6goavVKtBXD2t+nWI+NU4cc5t2a0EjuCWsEZ+G+MZSTnyAPOMcM2eW2bc3+HSUMSDE0qffJCmltSY4QuLNO3HwW8wMeMR+dXXFYr7g6PAwjF9KyWq1CgHl/t3e99cGl2kG+ZC6Vuzt7Tr/NsNqVYCwmz4cDVkVFaNREkxQF1dXPLh736VJlVBjkXPELMbr0Cyl19ysM63fpMWAIJI2IMTCWyzQ+DWL+/BtXeNM61q3ve1e4SWM8HsbfkI/7n9SNNqf1j0bBQEck2uJdeVM/UmSoJXmk999YrUVjsFUzixY19t8vr/5PnTN1f5zHK/QDfgWQrTSxcXjiM+Db96cGR92rTUYg3PTbq2VlR+alK3dmKqW6oyG4BojMLr5PUmsFrAh+m1BOV67bsyT/2y/x2OLtSS3jxGIA8F9335dWtkwjOGrL7/kX/kxascwJqJ1Fm/f1s/L+i2ilQHFN731GdOB57ZL6PbX+L3w39tCjL9uTBDx1998wzzia42yYn3+3fPbtWaGUTnlwMHhAXneQ9UVZVUynU5ZLVcMxztRcHIbZ8b7vLd3wPPnr6hqSwcss7ju7x6/Nta8rsUpGYFW3g3QKiu0MiAkUktnNZKB4dbKF7G0EKS1Ew6c4FGWNQJl3YrKirq2ue3rugop4bW2TMR8Pg/0rK5thfssycjyzDLDxpD3cvr9AUlqhePBYEjW73E43iHLcudaJFz8gR1nmlryLoUIcSOBAfN7IgSmc46agG2QQjWb6BlxATIVmOCaAUkKxsg1Om+ve9uD5+6965AX5MPgwovsp6aIqDF1gF/ffdjv+GUOB1nm3wq4mmbfY0m8m4JXe6VLi3c4ZdBPwdgYokR4lxaHtyyidfRdUKxWlGWFAF68eM7VxUVwa1ORQsSvi4fN22ChmHkOe3KL1rbmWWY3rsNgjLapTfMe3/n9P6KsaoajCcfH93n+4hWT8YCTNy+5nk7JspThcIBSNfPZHAEkMiXNrHuUzHJ6/QHf+/4PePzueygDVa1IpSu0jGG1KBgNRvzpn/0Zf/+f/hqlSy7Oz1gul+yMc5I0RS2XvH79mm9/5451k6qsG165KimLgvFkl16/z+XlJVVVMxgMuJ5eMdmZMJ/NNtKQTb8ZY1C1CilbjXE1VPA1JTzu9PcTvghhSKStRyGloJfnzOcLLi+vLP5PUqqqRmtFvz/gwYNHPHnyhPsPH5HmeaDdh4eHgSezldjPefnypbNCWCWEzYopGQyGKFW3eGrPW/g4F0+37V8brJ4k0rlTWfi7d++Yye4OeZ6EGlPT6dQqzIsiZNXymSaNMSGWrixLm8FKSpbLJU8++PCtMPiNYjTiIJAG6J0mgobYNNr4xuQYb3TIjuGvGatyU05TkGY5dVU3jLdxOvXaukd5f8yyLMOC+yBHn+auYaZsKrDZfMZ4Z2zHb2BZrJwPt6Go7MJhhNW82S1CY1iVJRjB/uEhd+/f47effkpRlgFf9Xp9kiQN88vzhNlszmqvtGZzp1U1GFAbmOlYUjagHPLbVAylywRvYxDWtBgb3uf3Id63rtTe3ud1BnCbkHEjA7alxUxE9/2eSdjG5LQZrVgbSrCmZVlGrWpevngZEVJJUaza7g7/BAGvGcN6Hx6RbPL9jAW/eG7dtQzMgLHZlfy1mIGSG57xffnij/EYN69n9KzxvuX2vuCCGM2xy7zFgkMsYPk+PRNktbSb4jcaWNi2nnFf8fs8Loj3VGvNyekp8/mcfDR0bhuWQfjH7ve2M+GZ+nh83edu6NU9Z/tphA3/zDr+2FhxOnpXW4jbPhdoBNVEbPZP9nzaVljZ+t3gi8TZswmj0Yi7d+/w8vlz6rrmajplNp8x2d8nTxt8Gu9rDE8yyXj8+F1+/etP+Na3vkWaJkH36126mn3w8NkIskIkYWyWybRuHyBCMKgl7tYqMZ8vw70rx0x6OlQUSyfYNhkVsyxz8QhpyOjS7/ddaszdYFXw8/SuRn6/fW0lz8f6+xoLnGMktLFBtwDUtkiudzt2jLjxSNGvqSuoJqTT+PsCk65bKUEZZS1wkR7CC1n2iGqEUNbKge3T148wxG63zfOY2OJu/2ld+4t2n3SEzVuCoL+vga+2AON+15EwbxxEKFc00JioT4PRUSCrozOmAXKUMrx4/hVHR3dYra5djIcBXGFGIdBKWWFNa7SG6fQaraFYLvm7v/1bymJFmmZUlaauVUtpepM22Pixd5fR4xTDW6yxtK6FUgHCOnH7AnBWg+2+9/rs3L3P0eEdpJDMr6fkeUqWCObTS4piyXg4QBjN1dUlqqrsc2lKmrn6GVnOu0/e590n74NwMTFCotEunheMNMF97/d/9CP++q/+Z66uLijKkqHWpFlKUiVcXlprx+7uLqcnr0mTlMJY96vd/QNGoxFv3rxhNpvR6/WspXMy4eXLF1vX1a9Hi164wH3LJ+RUpiDNMsbjsctoZqgdrfI4xBu6BYZECo6ODvjB7/2Q/cMDhsMhadZnNNxhPB4z2Z3YTFAC+r0+8/kC5eKZlFKcnZ1hjA2SPzw8ZDIZc/f4h8znc05PTyjLksFwSJbm9Ho9Li4uMcawXC5QSjEYDFz4gD0jed6z9cKkcElRJDJJSFLBzniHoaOBdv51wE937tzBGJvSeTabMZvNGI/HQJMMylcHz7Is1ES5Tbu1oOGbJyBNSj2rofBBVm03qbZmNWYEZJKgIn9y6Rh8KSW1VpDauIuyKMNBUUqRCkld2oOulAoSlzXtgNGKvJejlD3YWWaZmoOjI2qjkVYhQ200iXFIN7ECh1a1QxpWK6bcb0mSkkjBo8ePefe999g92GdndxetbGrcw4Mjq6U2miy1RQqvFwt2dyeoqiZNEoeQrDAVJzzpaurjDEPtTAnNM9uY+U1MTZzhKr6nre3ezsh1mZRvKkhsYki3MUXb5uCZmzUm1jEWsTjmBRMf/wONpn06nQZtIuCKu6nWmDYzj9+8xdp2D6tAONTauThJ0QgZ8TnpEiFjnGXPaOwl3YIZ/070FqbSr5tjlmK46woO8bhtHIhw6Skb157GnB+nuGy/O3Z59GvgBR7rS522MoKtD7kLa42LWlcj7dc7Vjx4xUgqUmazGWdnZzwYj+y4lFu/f8Red59ow8sm17pv3qufZ/N987623UGaM76mse/0c5NQ2/Vlbrd1uNzWdzw3IUQQgpUxpEJw//4Dnj996gKLbaDn8f37BCZ6A64IMJ+m7B4coIXgN7/7hDt3jmw6Rm3AxVsVRRl8nbXSrJxSwePYsiijZRfgAqC9y4EViK3yyqdz9GfFxiHYPPdCEFwVIPZnJqxts19ti0vgiSPNvHdVDS6l0RlKumcs87UdwhuQwjLDpO6c2sIVjj9ygc9CBOuPfdxYVyZpBavExX8FVt7g6iu7Z4TB6KgYnSXeNtDcKz5oK6q0Um48drze/VMIDzeJy6pl3aERjVOtT/ISr6dXSni3M0vrdBDUjXZxUhFs6pCYwI4/DiL3OEopK6gul0u+/PJz7t27w8mbV2ijbVZIbWu++JS6dWVjNMuyoigqkiTlzesTfvazn7pxKIwwQbGydvY6pyWsGcbFN7V/95+7Asums+gFjAb+NEY0Qbyr1crBsiTLcpKsh0hSBIa6ruj3c6RQzGdThFYYrbi8OGd+fY3RmjSx8JGlVsM9mezw4UcfhUGnaWJdeoTASEd7hAAtEElClgjefe9dXrx8Zq0VVUWe2QJyPoZoNBqTJgnz1QqtbXpiIQSDwSDU5fC13ay1RQXvgBgnxbikpbRwAlGS2PT3BsODBw/43/+3/y0X5+e8efOG58+fc3p6ysnJic2IVteuMLPi4PCA/83/7n/LD37wPT7/4nPSNOXo4JgkzcMeZWlK7fDcolyBIDDre3t7rX0qygJtNGma8ODBAwqfoa222dmGwz5aGwaDHj6VtxcErDBc0evlLtFCRpq1s7M1Fn8v4JsAC8bYBA0HBwfhPq2bopVxIUalVFCWvK3dWtBoZ2lqKnTbDWyXZvdNShEJAW2C5gE+MAbS+n7WqgYjSWTmnvU+sdYXXyuLkL37SZIklGVJnucURQ1GWE0LgBGUhU1datOli5BzG8Ck1mymtSbv9SyycsynLSxkkCZFm5plVXD3+JhHjx7x4UcfMt4ZW7Oahn5/gBCiqYCJYTq/pjfokacZqq5JpUQZg5HyhuSF64w5bNeMbhIWbmLaNv2N203PbhIYNvVzk/Z007Vt/TTX23OLhTCiGFBP1NzRab4bQ56lyETy7NkzlKqRop0q2R6c9UwgXUbvNi1+JhYAPMx72JNSksgUr1m9SZgLVZM9QacRuuL9tIxzsybrY2qQq3/nJrjZLKg0TIcQ/j3iRhiN96pB9Nq5xuhwhmNCaLtoC12xNtu7tmyyKHThJLiHYWNXXr58ycP3ngS3fGNMK2biNsK7X4v42iaX0m2ft7f18+1/N42SNbruP20+T93P8W/bhGmrKf2mAtL6mNdwlYdLp6GVUqKqikePHvF3f/s3wXXhanrFYrEk7w8jLX27b3/GlalRRnNwtMfu/oTr6ynnl+coVZMYQeYzFrnA5HyUc5gdBViLCbuPR9MSp/FtcJJlUsFnYzIOXuOsLDgNvp1ic9YCIW9mQZLGadtNA0vR/ici2mxjCEshvPKksZoJHSlvqNZwmHHzMMr6m9vq1TpUsAZjrRdeiaNEEM6sMifCQ8YrxpzSwVkZ2jDlbQz2r3Zpb4229QcSIV2GReNourGCkbCeB145qV015eYsqzXY1qax4MaxWvG/uqpCAWCfhbJy2bN0VYZaHMY0riEGmC9WXFxc0MsyPvvdpy0Y1EZRVxZ3FWXBxcUFxapwRdtsvN/FxRVlZev54AQcL5h45c5t/Nu7xzScgw4N2HTut9EvIURgEGunjJEyAaNJRU2eGITRqLpg2M/RqqIslghhENiUvcVqBUaxWhgGOzsYFL1eyuHRPsNhz6XjTxxs4RIYeA17gk4FdVWSZhkPHr5DfzBguVxRlAVpal0BS1W72IVd0jTjzekbJqMhi/nc1kpy7kez2Yw7d+444SK9ddxAEDaSRtH25N0nvHjxnLIo2N/f59HDB0hhEwoIISiLkun11Ba0m88RxjAaj3j/gw8Y7oz5vd//fT755BM+/eIz7h8/YHdv1xYoTTNyIMtSVsUKpVWoR7FaraiqyvHVNWW5Cvs0Go1cOuABwglEMb2J4aibvdKfGzAoVaFUFZ7xwoJ3t6qqiqurK/r9fhDa4pTQXjnqBQ9vgf3PHqPh08QGzYozBQ8GAy4vp1RlFQpVed9QuyANIorjArTWiNTqG2pVY+pIG6kESdJYO9IkpSid9kRYxFuWZfAtAyfRKYvYfEVyzzwmaYqRNpBOKWUtFlKgqsotnCUGtavsaIyxWYGQaOMyE2lDohWP33uXo7t3qLVGokMQ+WKxCKnsyrqiMjVvTk64f3zPBaQlVtss/zHaTjYilG/y7D+lvU2I+cf22TCT/yjFcns9ArEFRNsa45mCL7/8Mmj2gVAV1hea+6csU8MIr2uc/OH28N2Mf7PW3k2nNYetvs9CBJ4mZnRuEuA2aQZjM33MQFuk4sfq8/17PWOTmreZv39He5zgBS6Bzb7SMCdeS2L/uZ4jobIZJxizXlW3yzz75xq3LBu08vXXX/NHzuLgtbuRwvAbnJPNQoUN9G2zltuan2e71ygLjR+j8Zpowl+/526W7T4iAWyTIqJ5/zb4uOkceEZyy9Ut715rxhKue/eOrcuDI3qL+YLlcsG43iWTjVvR5ncZhDTUytKBncmIye7YWjmVQAbXqGZsvi9bP6cRXjOX/hyhgNrFcHkYtNptKVIbuJz4Q2K180LGLoN+jaKJtvbYugeBDTBvLpng7iPAMuK6CV5uKQZ0LHWKIOAITHBD8jAiRHTdeItJE/ngdRLSqDAWIQXSaIS2Gbe0t1q49zdU2WBUI2h0tce+dV0Ydag9oDGFskkbnPXBp/q2AkJta5Q41xZjbLr5oiyCFVTVylbxNjgFpV3HuqpD2l2jVAjWVk7A8WOVfuWMtfIUhRU0Tk5PefHqNe+99x4HBwcs5oug0fXJboyWzK/nPH32jOfPnztrrRWeEmkrvSfYwoJaCFdypK1RbyzJN+GLtkIp+tXVMGsL912F7hrfIJp3G2OtTMYp86QwUC5QxTVZmiFURdrL0VpRlgWJtMJ5WawwRqFVzXJRqT+rdQABAABJREFUoTDWQyQVHB7uY0zNcDBAGUNVKbQQSG0tFMVqyXVZcnV1SS8f2AxN0qYRPj+/sHsejXM+n2GzNKZgcPuqWnSjKIrAm3rm9yaFZ3e9tNIIZ2158+YNdVUzGe9SrFb08oQ0UajakGYZWSY5Oty1vGdRUZUVw9GQ5XKBSBPyfp+Pvv0tnrxb8vLFC5arGVk+oVJOQZEJeiJ36Zetu9Pu7m4kMFhLhrWoNrGX9mzLNauEjzOOf/PWi0YZ7wvy2QQmHq9lWep4ZLsWR0dHYe1iwcKnEo95KWMMS5eI4sHjJzfAr223FzSMQNVWwyEwHOwfMNnZQVU1aqC5KC5AgRECrZ31wdh0bsZleKlra3IsixKNIFFpY+2IKH5dK6AicQexrGoENtNHbTQCTVFVZN6H1HghwmpFlFKkSWrRiBBQlyA1QkbxIaUVUKzgAWWh8OorawbVJDLBCJsdq6oUlVLcuXtElicUxQqyPkVVsVxVIcVdVZUWMSrDsl5y8uaE3Z0dZGaD9YRyJuig+Io0EV5TFC41DJ3XrsWPNATI3gWEVMEeoYqOT29cGEq2gi6bvb6J8Tcm2qjou2dCu8xzkANoM5JCiIYMR+9qkWXTOBRsYpq8iwGmyfwTiLBjShOgl0gSNC9fPENg4VEICzMGe4iFiN+xefLeLO/XLQbarmbfr4FSGp8KVQhBIjOn1bVZaxpmGJr861Zr6d17hJSWiImIMXbwJrrxEtjXhf0PjL9jcswGjTNdAcgxzkYQUgDFK+O/G+OyOzkk5GKkGutHA1+xVcNmg3OuEvZkO/ix2pfYCtoV4GJYeBuRDsTGaNCCs9evwfkM+3psdt/bcSJuau01agkWbULedl2IGb0Aig42ZTPataGLAOvty7ZP/92vf3SKm478C7GWHyHWY7zCPKERLk0kHAk/WFp9Gix4yg37ED3Y9O3ON9EZFkJYRlkCRjDe27dpH6+vmV1dsphPWS7m7jxmCJEEl73uWkjh1wxwQbreIiOk318REExgyBy+kBjw+E9b5VUiXO/aVin37pfGgDCVxdv+/JhmqYRzARZStLbCjrhhLG0uGy/UW2Lv6Y3wyg5vzXOCgf3c4HQbnB1lTwwSi0BIH5sS4d5oW72SwCtkmvc4xUI4L41ggNABlzbnUYLRaNUU8YWmgKBX5mmtUS6ff1O9W6OUpihWFOUKsKmotTaousYon5yjDmOoqgqRJNSRUsPjFOuyLYKVKVZaaK3RtQpucD5+RWCtOqmrpGwtE5rFYs6nn37G1dWUo8Mj8izj7OSUNEuZTCZIIZCJrXBdVRVFWSCFIPFWHm1xva9rUNYVUjqaLDwMENY+0Il1ZBBdj74T0ZmAY7v4sI2bwukMv7maR8a6yDW03jC9OOeXv/gp/f6AP/qTPyXJ+vgUzkLaSulJkqCMRrm+lNFUSpFWNdfTa3u2hN3TsrRJHqqq5OpqGrIlVVWNqiuGk11SIRB5j0F/aPlHl8nQj72uFWma0e8P2d87QNWFjbcRVlkhpFVUJ2lCmmU2E5eUGJcJLsyftiKqrZjSqLrCJAmroqSqKx4/fsTDxw+oyhV1tbJxWXXNeDxGJvZdaZqRD7SdT1UhVyuSNHVVtQc8fPiQ2WzGYDAIMOjhUkhJ4mDWj8WeI1tgzypCLOzaSvc2GHw0GrVqCHl3TrtmaXAbA8iyBGMk19dXFKsVu3t7lqd2QgkG0rQH2NgRC28u8DwRwbpblaWLMyqde+Aq4MHFYsFt2u3raEg7ubqqeOfefYa9AZlISBLB3mjMznBEpRTXiwXT2YJaK8cGKpuFQYgQLW+MAZFQ1I1fmQ/QtIjFVk/QiR+e9bn1gKV8jmEjUJX1kQSoak3tBI08hdQxAVrZVGRp6jfVgh7ufXVtXaW8C5ZlmA2VqcFl6ZEI6qJGXyh2JxOqusQgWBQl/XyI1jVKW5pgNKRpTlUWvPj6OeKdB4wGfXq9HE/bAxGhg4BokEashfDMhaUDbTcSW450s6uBiHyquwKEibj8tjbOH8KIUm1sIqxnECg2MLL+dxO05o2QEVj7SEDya9JiYzZoSQ0GE1nMvPjhhobRilQIEgyqWHF5/gZtbEYQ7epnCGG1JD6fPa31Mu23tYQn/93vVzvPtP9slWgWtn1NF/ufJF57IbzY5KvVen9jmw5SCII1rLVVYc5OkHQEWKYumUDgUG3mmTUki82ykSapgy3PUDTxQsb3414lRPM1ZI7BgHDaR41L6dkO6g2WHVdR2MOf0V7zKVyNnKbYkGcofD/NfFvgsiboBbcpv2eq5uL0lNX1jOHOxLoxYrDQsQ7jdk+Std+hIfCbrFTaCzCyYXzD+ExbaNsiz7bGYAE5QMraPS0YdcxHM5+OkOgRD1h3Jt8HDbMJuErX/pp9MAwlUlSIuEP7YPtdxjNEONi38UU2OFvQG40YjUfMLk44eXNJr5fxwYfvU5VLej2bftUIEZQU1r/fOBg0SByj5EYqPO4RCpuGXFiJxPrNulo9TohwXQWI0hZ+o6W07/TCo4qgxAkaGoM0BmGadKf+WRF9NhhwmYcso9H1j/ba9WY/jBfStQanXdRKoagR+GrBygkahENprUM2016ADWPXRrnUl9ZSYS3/Wil3TYdzF//TWlHXyvmIW2HBgFWsqdppxK3rRa1sQPiqKOzzdR0EEYPLDmmsq5a3KHnrRJqmmFrRCMp25VLHuGkn1eV5jhAi+LcbkwdrQ+xG4jXeNhjfa2lTtG4Ej7quSBLJalWwWKzYPzzgcnrN9Pqaw6MDsixlMOgHbflg0Gc4GjG9vma5BDWtGe0M2dkdc3JyamN2SEAkKG1jkUyIC/U4zzQwEp2ebVRWuP0zjngHpQ2bBY2uQmbNymTAaEFVKVezpClc++bNK+ZXF0wvLvjpT37CH/zxn7rq7YYktWuXJAmj0ZhrfW331qURxwjSNKcu7X4mMmE+m1FXJcvZnFQIxqMR4/GI1MWxDnp9W9DYpbQVCEc3CGfDhJTdCXt7hxTLGZUx1EpR69ojanu2BCATbHJi7eimCUnNNlnarCVHkEphrX7GUubfffJbXr76mvv3jtE6I0md8guJNoLLq2t6vR6j8ZjJ/rAVE6KVtRD2+wMGg2FQnDWxW00MTkNbfUpsazFr7hVImVLXS5KEYLHIsix8BqzlSPvsq9YNME0z0iRhd2eX80px8vqEvb09+v0+Z6dnDIcj0lSHquqrlXXZGgysm9bZ6QmLxYK6rsmyLKQoxp9lrcMzb2u3T29blWRpxrtPnnDn6Ijz0zNUZSXPLJEIrZEyI9/b4/p6xvXVBb3hAIOgrBzjEHG6aSYxQgLW0iFkU87co2ifbs5bITSWhijji3LZHOPFyj4nk8RV3sT+lmXgagVICZWqQIigLdVKWc0yAlWXNl95tUImLo2uMWhhA6fSJKEqSkpRUlU177/3PpdX16yWCySp83UEhLTE1QiWyxU/+8UvbLCPA5wkTdjEzMbIYhOCME7S8PfFmYaQsbXjJsGg3TyT5A9dN4A5ZtRu6uObvNO32E+w21/nDTQCjdh4b9ds7Jv3JRTCFgVarVZNwHSnSGPTFw7m1jUg8dpvG4f/18RnWMQeZ5bq3u/q8zpNhtVYxoxf/B6LoJpaGXYsoiVQ+AKFO5MJ4/GYnZ0dV3k1awQgpVmulsxmMxaLBdOrmc2G4TKjyUSgdB0IdzyGRgCOtNfR2niYlGx3o7GBsyLAQHAzox1E3l1j39atHW0i4vs0xvlxY/HL2dk5o8muZV6c0BYK64nOqt/wfoFonZewP9FzXQbAyaffuElBIJbu5c1cPeDEzXiNb0cQaG6wwl40l+YK3rAWXiUgJAVo0hCtddkepAdJDwu+QKHLhKQdjB8eHvD62VcMB32m00uWixnVaoHq98gSiysFCulqxqB9QgJblyhWvBD+NcqkIKwJ8LUwNiyj27emIFasRMDo9tw0QfjRxiAiXNzWLjcWZL3hHn9diHaQuA8wt/KJE5xd7GCCcQHJpklm4aw+lWPsfWBo7Zh9H7DsBYKqrAJd1Ua5+IGqdW7idfB9adXEh1RV6Rg5r8F3+MsJDmVV4QUFX/lbmxrthIpezxYgGw77IXtNKm3CF+kECQQhjaZBkGYped7zwBbGJ2UarbsdS+wCkmVZoOc2Q6RNK5wkkuFwQL9fMRpZPmJvb4979+6zv78PENxyvPVksbC1Gl69esVqtYrqDsTxEm26vh6H1sYr2lf83NCMQxrbtPHbWlfgiL9LKUMafx/noJRiOBxxYgxGSMY7O6RZSlmukImg18uD8OmDsIuiIMsy+r0+o9GY4WjIyckJj588QQCH+we276Oafr/vrEk2LkQI4eJXrRA7nU6DIsqOx8Jgmibu/FhF8coYF9voBRA7B1t3IrXWyFu0+CwqrUi0F1DtetWqJs9y9vb2vMME0MRBjMdjC5uJH19TfsHOA6DhA/xfe00El/0kkZ29lMigO7DrMRqNGAwGwcq3WjWZMivn/m9dyuz5t/HKBdPpawaDAcP+gKIoefnyFfP5gr29PZTSnJ2dsVisQn+r1SpYKFarFb1exnK5DMqA5XLJZDKhLEtOTk44Pz8nTVP+1//Nf/PW9b61oPH+48fWD00rLs/PEFizaJ73UJXVoGitkVnGcDTk/PKCVVGiRYoQKcozsg4p6tr613oNnNY2P68vbqRNkwHDIwyBtTw0GSKsEOFjMQwV3odbaEtMhdPYlmVlzWPGRvX7TbLAY0ImA7+oIbgMzXA4YGe8Q5okpDLhd7/5hHt37zEcDHg9PUUpSZbnlng7opFguLiagpBcXl2R92xRJCMktoByrJVtNBbxb3HrmkXj38yG+7cx/xvf2+l3033x+24a47Y+4t9izf+2dzTvapilbXPqItX4byJt8OHJyUmLedWBALQZ1EbQWCe2vsBc7Dvt/Xab55vxW+LSBG11NU7NmnkpwVsxtDPHb5urM8XbH8K1/mDA3t4eDx8+5M6dO4xGI5d6MKPf75GklvGycVGKuq5s3v66pio1i8WS87Mznr94wetXryjKMjDjcVuDv45gLGWjSY/3eRu8eCE3SWz6w0w2zHnLWtAR8GICutHi5YWY1Apjxhhev3nNux98YPcz8tkOexNx2OFjZ99strAm/XQ7MNhrL6P5Oo1Vq9O1doNu0/hoktB7aLEsYRkc3bgNre9c85zcfK7Cox0Nu/XW6cBCvN7C0HbVsjBtXNoc6dxthNDUuiJ11dt3dkZkvcwSxPGY5eKaYjnDjAcIk7kirMrWPPAaOxEma7Mc+T30ml6pwxyaY2RcnYukM0Y/D4MxVbNGrn/j/0YMTAPv9j7t4gR80LOJ7vN9eG2+t0wYg3MjssyDrbXhEpX4uMDgbqRCpV6MCUKD/x0a4Rqa9K42vqGZQ61UGE/MZJHYPW6yaHlruXUfFpFrUl1bi3AuM0ZDx2wJwWA4bFbV0VEppfMQaFyrpLAF3byCK3OfLUy2rREeLwhhXTT6/QG+CrJNHWzdTKRI8QWD48Qb9owbEpkhMjt2VStWq4KqLsF5WxRFSVnWzGdLlsuCu3ePefXqDUYbrq6uQiBukrykrEoqpbi4uHCKUW+VaeOqWIHWOl83CACbWmxtjPGQ11zHNaZaz0V4rZtVEJoMQ15oKMuSw8ND/vBP/ozBYMTjJ0/QCK5nFwgBk51xEPq80OAVef1enzSRJEK4ehhz+v2c4dhmizJ+L9ze9JxVysvyV1dXnJ6etvYPt/e+8GRQ/Gqb2dO63UoEkuFghMDWyZJiK4Jd2wuv/AuWaRfI7139Ts9OuXf/GIlsatK4te73+/a5Dl1v+vP/mnTTfg+99d4mRPFuYo42CxnOda/XCwkKlstlZL2oglBQlqUV7MuCq6upq71hBeSyLFnM5/TyHlVVcXp6ijGGw8MDrq9t0c8nT54wGAz49//+37tA/TT0l6ZJwC9patN0n5+fMxqNQqXywWBw43r7dvsYjVJhlC1iZKStflrWGk2FVpq61iRZSlVr8v4QkebMF0tknmCReII/e1VlqJdLexjc5htsEJdlnixB0Man61JIUVv3GgcEeZ5TFoXLZmAlQ5vWUJFlKVop5tWC0i147TZMANKZUn0GiqqyZq3RcNTSjODMWctFQbEoydMUKQTX+TW//Idf8f6HH1AUBWfnU8Y7e8gsccFgkkwoXr05YTgaczW9Zjgc2qrfaxlLmqa12lrQy/vUxYyVD4ra9ETM+G0TQt4mnDTxA+sMyaY+tvW7qf84E5m/dtNY39biw+77UkpBZpHamzdvLFFyrnfeBcQT95j4dkbt+tw8V+niJ3zee6+N94yAEEkQGmIi2Eb+XoW8WZj0CD3MLXEmdFd4cH9/nw8/+JA7d+7QHwyY7OwwGA5CWsBa1ahaoXSJj5capk1+fykTtIb5fM7inft88NEHXF9f8+rlKz777DPOTs9CpepYOEiECLxa11KzTTiM59W1/tj+2/01pv3N7TYwHmKHjOHkzZtwvxCiHXegI2HfyQWbrSqNcNQdByISBATBJ7xRCnQZjfX1MgEe/HsNrZzYHWLZbIKNf4lG2Xqms0JNH92uO2tplXM+qDgSwDv9dwPTLcPg5qfdfDHkqcAYBaYmTQWj8YgkkYxGA9A1i9kl1c4Ak6ckWQ8pDAqFFora+IyCzZHx7n8Y6+tv99Qy/igbZyAlmNoA6UZrpdYKRB0YOB8f5fdDaxWYHUs7VGBc67pu8uwr7SwE9rrvRylFURaBiVC1Ezac+5OQwj5TVaBrJ5RZZiyOg8AQmBMTu2RIyyhJKUNAbHy+ZZKE1J151qS6LKuKpGfTX/pUn9Jds317zbE9EHVd0+vlFq9512ZjGZGiLNDKB6TaTD3etcuum24JMx5S7bra+Y1GI8Aq68qqdAHctn7PamXXf7lc2ABeIWxNK23vt/VNCupaURS21ollxGzMh/cvL0vrh29jgSRpmmF0ZIkwILFada0VZ2eiOafC1v/S2gsz3sXTG9TMGm3bpBy0c9Rr94Vzc4sWu07Fiplun2uKOGEZUWtRGgbBsFaKOwdHHB8fMxiNgkCm65Ld3R3y3Fo1vIX86dOnFEUBxrrR1XWJLAWffvJbfvwHf4BwpQMMkKW2jpWN4/P8Faha8fnnnzNzdSW8W5svfTAej/GlCiz8KYZZHmBCyoQ877FaFSht0DRF6VqylWnwVVfA87XgPL+ZyYz33nuPDz/4kOFwwGpRsFjYhAA+I5MQgiRtiu16fsOvf5ra+XnewidTsgUGLfOeZd4FysNm4eKXHM/qkhoNh0POz8+pqooksVXWZ7MZ8/k8cnG0FopEJkyvr5nNrlnMFyBgNBg5wWROWVZkWcrx8TEfffQRX331VaiZ4VN4W/e4If1+j8lkgjEmKDqMMZydnVFVFVmWcX5+fitYvbWgIUSCEBnXsyUiKUjShFprqvkKeywFulDMFgu+evaMyuVOToy1dihlM0RY6dZgc3s3WpggULjAKe3AQuvKppmV0pryViuMqimdz2ji6mgkSRL6XMyX1FVls4m4YG+BIBGJMzdbJJWlOYnI6GUOsRU1RVEEc682GiNsvEitNcViBcaQyoRf/cMvmexOMEby8sVLesNr8sGArJ+TppJBkvLq1RsOD/Z5fXJKnvcYDkeMRlYQsQXLGpeRoDVvrflmbUejYXea94jh29a6TPLbkNkmBLVNeLlJK/NNBYdNfflHNllUtmmIvGCWJJZwnp2dAQ0R8AS6dMQ/MKZRXhUhRKM/9kaH+FqHCY01JEHDaHTIVBOvXxgjPuDUYH3EOy+iXaU9vC+R7O7t8r3vfY979+7R7/c5ODig1+uxXC6ZTqecnJ66lIsqFMizboApQopwzSLGlKOjQw6PDkjTlMViwd7+Lo+fPOLszTm/+tWveP3mtVvTxlzsU1TfBKs3tViYMNiA0E0uW9ue9bAYW6b8e6uqcpoog5S2Mq/X6tjYrSatZ0eJj/Fz2jC3WHBY+xvcdWxbqw4eyTHNNjfSgY+waJ8vJ2ywSeBVoVPr8xvHEtzgRhDLCJjmjLEFlbgBG7O5T9EFWxFsGm563ppmXdlqrVCqoN/LuX//PtfXV+SZtVrPpxecJgZpFDujiWWg3BkRwXVK2LgHKW18QeSi5DWltvZzhdaVS0ziE300lgLtgpWtRaF0zGNjwfRMfl1XVLWzKmBdmWztJPter/QJbr7a4OO+7Bmz/SqX2RDhrK0OH/g6UZbZt1WFpXCutgbH/AvSzLrxJlFRQw9jWdJmfHzF9FopZGaDSgVYracQ1FXNfi9HqcZt9vr6mlykDIYj62EQLBl2vearJXnWoz8ckiRZg9OkJNUCJRTaVFRlCUJgHJ7RWjtGSlEsV4GZUkoxX8xt9j8H+5X7vSgKlBPeyqLC6MY3PI7B8sKhB1S/f9BomG2A7jAwZ1orDC5wWXn+xsfQeZrjNc1N0hUrHEYWLZeMQTgEcpOybY3hd+PTpomr2iSQ+BbPaZNlvPvcNiWJ72u5XNrUq1kWBI1lUVDWNUPHb6VpQlEsmUx2GI1GTKdT5vM5h4eHHBwc8Pr1a+tGZ3z8lebZs6ccHOzbmmO7+84CIehleZijEDaW54svvuDXv/41lSv+5/kiHwQ+GAwoioLFcsHF6QkCzXAwBERw9R2Ndmxq3FWBoHb0zp+teJU2K0Wli3WtqzrQtt3JLvsH+yFj2XK55Pr6GiAUrFNuDb1b9nQ6ZTAYcHx8zGKxxBiYzWaUZRncn2azmSvcqHn16lXYU2/B8P2naWqFOHBuUFMuLy+p65rZbMbSKep90UVBEty2siwjTXLStObi4gKjcEJLQlkuqGvFalXyi1/8ktVqwWQywae6DS5uQpBl1u1wZ2cnXJ9ObVD/bDazKYjLqOjlDe3WgsZsXpKkCYqEYlmiRUVR2XiFLO1T1jVX19e8fPOGoqrJ8p7Vb61ql05Q2ej8kGXKChuxmcwvsjKasrZ+oU3hJIkq3fN1ZU07WYquK2rHUBilGI2GjEYjrq+m1GVpf9cGgyRBUZkKpRW6thkpvGZFOneUfm6LoAgjkEbY1HTG+vRrpaiKkpUxFMWKf/tv/y3H99+h158wLy7pVzUDNSRLJTXw5uQNUkLmtMfj8ciafDvmNk/UYiZzGyKJEZFnaNviSfsZz7R0mXKEaGkuLR/RPohdi0brs3veRJpSwToybRj4zQLO27Q4m4SL2C2n9btrwarg3AESKbm8vMS63amgYQhWD6IMXtt8W0z7fV2zayyI+bXOnDXFP9t1EbDMh/1rXKBsuOYyxPjv/vBLKcn7Pb793e/w/vvvM9mdsL+/j6oV5xfnnJ6cMhqNQgFJKSSrYoUoLRGtFfR6gn6/z2R3TK/XQwhQquLk9IQvv/qKvJfz+PFj3nn0kNVyxc5owvHxMU+fPuUXv/hFQLjdfW5ZleyFzl76+5v9a+2/ITD23qWiG8OzrfnsQGvjiGHOGM7PzzHGumIqbd2Mkk3CrRCYcE5pNOg0msRY0ImehA3xDyZwv14gadbBa3ubPsMKRgvWzKGlqNOdNY7HQZOhqBlD9z73Pfoh2SBq+PFLGfUXK0ZMR0TRHbwTtK3aXhSwnE3p9TIePHjAixc2E5xWFavlnNNqxfT8nPF4h9HQVrK9ns04PztjOr1muSwto+pSnGqtqbwbTOEEBFODUOzujTk+PiJJJSJpXN7iLHmqVhDFcLQUOYDNTtecQb8mgZTh4wlsTFieJ6RpFtyOsjRtEl4AaSrp9bIg5CVSBnylDSRJGnLre8HYGENVF0G4afzXLTynzq14MZ+jjWaQDGyV5cRFgUkoqoqEDCkkSvjsQQl1beeXpj0wksW8YLlcUlZW2KirmsVywXKx4PnzVxhjA4qL0u6Dd/FQdc2qsJYNny4+JHbQFna9UNbAnQtQ99K3p4s+JgSQxmbpIwjFFt6UUrgqf4GWWyFLdqyhImS80tqEGDGPY/wa+yKqqbRZlqwrSYRfMNaZz1kzjGnOOEKEWI2u5dZ/bs7b+u+3Vf7F929SeN2o+KPJ2HZxccG9e/cYj8dMp1PKsmJZFCyLgonRpGnKaDTk6vKCR+885Pj4mOl0ynQ6dbUdrLtcsVqhpXDZiiTJMuVv//ZvWBVLPvzgY/b2DhydEU65V7Jarfjs8y/4yU9+wtnZmRVEHKPtNefjnTGj0YiLiytO3rzh+vKS/cmOq1YtWC6WpGnKYDh0CQg0dbUKAraIkey29TDGJYax96ciwxjFl199yevXr9nbnVAUBf1+n+VyycXFBXVdM5lMWCwWKOeWPRgM2N3d5fz83Akd1xhjLXTz+ZxPP7W1WPr9Pnt7Bzx79gxjDBcXFzx69IjZbBbGc3V1FVLU9no9ptMpZ2dnXF9fI4RgPp+HdfKK6uVi5eDBpu621omhhXUhKIuKvGcTHWmlmLtU4mlqXeF8v1VVOXe6mqqy4/VCBRDWwtPn4+PjG9fXt1sLGj//4kt6eY/M+VyWlcvQZAxqOacsS+bLJaUP1jYuXZ5uTJAW6dQY4yQsmSKwSN4SGUWWGmQiybOUfi/HBmvbLE5WHZMhE2MzOyUJUiTBT9HSQs3uZMRkMuH66pL5bE5VVBghEalLReeqe1ZViZCQauEKMQl8pWNv3k1IQRiUtBmuNLZipsGgVvDlV1+SZX2G4x3uiGMyWUOSItKU2eyacn+Puip49XLJ3mTE3mSHPEnQQpLlGVpY87lxTOW6R7w7EGD9nSNmzRiDFiZ89q1lnnWaYrs0XmeEExJu2vEo3WajIg1/jEuNZxCRQtZrENbH5Dk14f8KwsHQrgMjGm2uR0rC0GRk8cye+9rMxkT9eUZBWSYytbBxNZ3SpAJVKJdzPmgYI63y9mbvif0v/d/GyuS149aSIuwDwRUBIhcqZeHeOEtckwUEmwHD+3VKl6VKwJ3ju/z4D/+Qg4MDDg72ybOc3/zmN1xN52R5TgKcLc45eXPC9XTK9WxKVZd2fWqDTFJ37iS9PGc07HOwv8vRg2Pu3L3D0dEd6rrmyy++YrX6LU8eP+Kdh/eZz2Zk/YSju4f84uf/wOeff45IpNtr49LVEnhpm2NIBY1Rm/i1M3NBFOegRXD3aNZ1XVCOhbuu9aPF4HrmxRVVWyxnzBfX7OztYWqNQYJYj5ECQspRGe5pzcCNQbeIWWC3O0K8L1onQgpjZ72wAO+uuyBt0/TVgjv3Yyy8B8VE/K7wvQ6/eI26XTs7N+//Ha9lzMR4IuWVCQJ/5iKRy+krYkuCNl6gsLgSmpio2gUqV3XJ1eUlWZqQ72Tcv3+P169fsVisLDMkJcJMefr1VywWK05OTnnz5ozVsnD0grC/xvlqA85torZ4PZUcHh5Y99elTfKR9a1WVcrE1TawuKLf79t1coRbJtblUSaJrQ4uTZivZwK01iQyDYqNoBQwJiiXlNbBbQIhAqPtLetaKXp5jzTUCVBcXlzQ7/fp9/vWmh+5MmVpn6KwftmV9jAIaJeJp6pRKmG5LLm6OEdghYuLq8tgCfBuGTbmA6pShZStscVAKxsn4mHOKwO0w9tEcBM3rbXTEusgZHqQkS6pgE9GEJSO3rKLda8Dbw10Chphfw/1Rlw8jHCZ7tq4oTkRXsETF+r17zXhvfbkGGODlbXR1AgSZyHyFNRbxHwKVvuveakEUmmz2HnaEMbk/PljS0bAf6Y95tYnf/bc/GLFk7/mlTMmvj+av59vo0xTCCm4mp7z6NE7HBzsc3l5yWo5p17NWc2mnGM12IM84fXrM8z9Y46P7/Ls2VOm0ykXF+eMRkPnpi6Yzq5Q2uF6KekPBkynU55++Yxvffs7HB4eBr/+169f8+zZM169PmGxXLFaFaRpRi8fgpGoWqBln6Pjh6RpxuXZCVVhYxSywYDB7i610ixmMwbDIWm/x9nlFVJkzKazUA1e4HFXg6+8QsevSbP+1nJ3fO8Ol5fn2ArkC8qipFgVVGVlXflqxWKxCPV/Dg4Pefz4CVVVhWQj5+fnLJdLlssV77//PkopplNb5M8LCb28x9HRHd578oRev8eg36coVlxeXvH65UsH05Kzs9MQQyOlrYXR6/UsD12VGG1pZb9v3cfSzNLRfj+n1+9Tq4o8Sa1FtizJspS6stk27907pqpLZCLI8pxU2b6qurS1PYQILnYeL6Rpymw2YzgcUlXVmtJxW7u1oPHs7MoONE1JhNXQZFlmpco8I+/1UMqgkSRp4tyVksBAN+kNG7OuTKygkXhNhLHaf4w9CAbrB6eB2vmfGpEhU9C1zVktsak5G2ZGoeqS5eIaKeHo8JCr8ynz+cICnDCkvQyhJSKzKe50aYPkLGJpfOxtTQtXrARBmudUqkaZ0hVVMuSpROuK2fScqpjzwQcfsLN3wHR6zWI+RSvrI7pYLnn+9TMO93bpZ/dJhEFkCXGGFItBPCMeMT3CEngVcq1bBaLxiFc0/qXCU35hiaZnxlv/N016tVaLlagI4uxY8VjscD1z1mWInJDRDcoyImhScGMwLgONESYUe/SI02C1RimyncymoVk2ENT/Fmt9HdGQidVK1bVFGn4C/pkw07cEkDVzs59k0Fw1QV+WT3YsXsilnrp91C1GxM8fV2kVY4MkhdszsBpO7QkJ1oXigw8/4Hvf/z47kwlHR4e8evGCN6/eOC1uzZsXJ5ycvqEsSowWNhC8N2A0GiIl9KREa4EiQWsL+1eXcy7OLvnks0/pDfo8evSIx48e8e7jJyil+frrp3z97Au+853v8N57T3j9+g1JknB4dMTf//SnLIuly83t4coqGIVjoC2jqtpEV0g8bK1r3+waNq4JXnqJYaCtNfQCa2MxiYJBgyBgB1WWK6bTS0a7YwxOjSUJDHe7ufiKACc0wi4aYWyigfgpKQRJwB3rMwvisT+D7hw3eMC9w52tRi/QMHqe+ffzataKwPxpDMLUoYOWS4Zw8WC6SfEIUWakoM2358gzxlY4brIa+T1QWoXfDbaA1mq1Yja7piprqroiTZPIRdEK3sfHx/T7A9IkI8us9vTk5A1XV1fWfUKtqKqSV6/ecHJyjtGSsqhRysZ5+Ho2lpmskCIhy1LyvqQ/yDk6OuLg4IDJZBLcYYfjcXAH2qRBji3rIVOMtK5SXsHiM3BVdWXply+Y5VytUmGZ4MrFdXjBxBjrzpekCSJJMaWiViVFWTNf2poMq1XBallyPbXKu4bQ16xWBWVh40GMNiwWiwAXNg7RxYhEMR3esmtlEdOKIfOtq6RquQHi4yhjGLfKkE0wboxL1evORSP0uuaEV39vLCA3SQw8vMeFELWjNZ7pb86N7y8+/y3yKSC2GDZw005Jbmm+S9dba6AIcN5dp/h7w9hLEkcXvLXbvxNpBc1gIYuUaWGtb1B0+Xd59zogVKu2YzCtv12tWcvy6hI0TKdXVHXJzmTsMnOVlMsZL79e8T/+7hO01nz88cd88MEHnJ684f69d7h//x7L5YKrq0ubGEBAmlmhPUmlxRk+E5rSvHz1itOzc/LcasBXqxWXl5dWiBmNuZ6vSJKUgXOHqitNXRvGe/vs7h2wWi5ZLq452N/lejanNxqTDQZMT86py5rD42O0lCxWK/IsY3Y1tdZUly4+wES05p4+NPRYuHfXvHjxAq1LZDLmk9/+lkF/wHy2YD6fB1ezoiistTFJGO+MuX//fljny8srhJDs7e0zGBQ8f/48ZCebz+dcX19jtObB/Qecn50Fi5rP/OTdFBsLm3Du/9qpy2xdiyRJyJybWZb3MEKQ99IQML5YzkmzhOGgx3R6TZYl5PmQqi6p65KqKtB6yO7ehOVyCdiYKq8UKYoVeZaH2Ix+vx/wjBA2OYMQwrmkv73dvo5GMiAbjaxPY12T5X2yNGVwMEEk1iVFG0MvH5H4HP7G+vRa5Yf3mbbB4RhNJiBLk5Besp/37OJpG1h+cXGFNbQLelkGQpJngqJckPZSGxSnrS9vlkqGwxylCmsZGeQWQC4vGeR9hNFcXl3ZcvPG1iaQSLIkJ+lj0536gDuXQSERAqVdRkWhUbW2zH4qbT9I0AR/2XJV8bvffooQgul0iqoqPv3kt9w9OqQsC/Is4dWLCcO+4PDwCESNTHv4wmVes9JoIT2XYZkLIRPH6BiX1xISx7BFilCvUsVqlhuXICOMy/plfdrD6/z1GEnp6GLcApduBYe1O2J32VhDE8sBgJOMMMZptwJxaxgpr43ovqMtgzUMVNddJnVaycV8wWq5DLKCJ0S+YFFnqBubR1CeURMtLb3T8OGztYhgZbPvaZBc2/rRMIqxO4YQIjAFCEGSpXz/+9/nw48/4s7duxhh+M1vfk2WZMznC14+f8nl2Tmq1qSjAf2dCVk2JEn7JFlGr5fx6uXXvD5/TZZnPHj0Adlgh1oZdF1TFQtMfUlVLvn0d7/jd598wjvvvMP3vvc93nvvfcpywT/8w6+5e/eYb338bfq9EXneZ7Qz5j/8T//BakhwQfZ+MSPGtqv1jBmCrotBHK8U19LYdO+mvuPmmeUm8w5oVVOVKySaPLGWotRZVok0pnZPffaiZhweVPwcEheLHTSIWOuEjyXojMgKGDglgTYRnLcOThA2vDUhknCcoNC48rTujddK2SBbGzRsswTitLKlq7xsXYyaDD3KEbW2D7z1mbZaPuuPLIRgMByQOxO6j1/QygoaRVHx8sVrLi6mKFXx4Ufvsbu7y2AwYDweM5lMyLLcxh2kCZmWJClk+T2yPHG+4BW93oCDgyPybMj5+RXL5UVIWd2cHcVo1Ge8M2J/f4+9/TG7uxPSNLFpU1ObocgW07L+6OPxMDD+cZpiY0zIruPdPFSpyXPr+qGxMX+2vgBopdC6xEDQaq5W1l88zVPm8znzxQKtFGVlAz6rskIpQ1lWrFaWXnmNoa+G7fc0ZnS9AiV2aY1dq4RukiqsWai8BSiC4y6zuw6thgYrr5+xroDyT2kCQmE73/z5j895FwfEa7HNZalrPfWa2S7TH+PmrjDm+/TXYpfZ5nrjUhunNbUKUhsUHZ+rf8q6+YD/ba1rpWzNxSkyV6sV19fXTCa7UfzFEiGsBRAh+PLLp3znO9/l4uKSg/0j3n33Xc7OzijLktlsRr/fp9fr0+/1KauKfi8jz/vked8JtYb5fMFqlXB9fU1dVzY5gTQs5ktQhv5oRL8/QGtDUVWkWcY77zygl+e8efk1xhh6/T6LVcnBoa1efXFxgQEO79xh6Zj4AYL5bO48AdaF6Rju42ZxsS3oXLsivj/4wQ+4vr5mejWlKm02poODA66vrxmNbNKglVOonJycMB6PAyO+WCwoioKrq6sgmPiYCrAugZ9//rl1+xoMWrDZTjhh61fkec7u7m6IOfQC287OjounXAZ4i/HZ2dkZvTynrirm8zm9Xi+kvvV4X0oZ+lmtViHdsXaKDJ89zruaj0YjRqMRl5eXAb5vBa+3uguYTPYQYANmeraqoRTC5aOvrQuTtIhY1ZosTfHnQLn0f4NeZitqY8gT+PjJIz788EN2RmP6LuK93+uDkJRa85d/+T/z7OvnyDQlSa2g0cskmCH7+wfsjHYoFgVGGx7cv8/9+0fkvQSta+azOX/1V3/Ll58/44svnnJ2fs7J+Snvvf++zZYhBHmSOoY0BWOoXPrA2MUl62UoXVFVUOuSvJ+T6MQG1FYGaWxhQKU0RimqWpEkkvGwRz8/oCoLLs5OqMqCxNQ8/zpnMIA0MezuHdFPUnwtDxEhCM+4+ebZlkazGTlZecEiOjq0vjVcvhCGJPGEw7CRwXYMvpN3NsobsWl37YpXnLTNHcRmS8+o+0woTTeOAWuNPnQYaiKE/5lmXt6aYov02BopAlitFtRlEcZr802vZwd5W2v7yDqtmrEWEa2VM236okPt2A1/+FtE0yG32JfYEw8/TykFf/RHf8STJ084unuHi8tLZosZq6Lgd0+/5PnXL0i0YNwfM8gzyiwhG+2S9ibIbEx/MCbLEj776iXTZYVYVdwROe88/pCi0qxWBfVqzuvPT5lf28AwIeD589e8enXKu+8+4Uc/+gE//MHv8+mnn/E//U9/yY9//GOePHlMlqf863/9r/mf//IvWS6WbnmNE8SsPrTNKNmmnb+zv98zO0kiESbBF/PqMgBdhqFNQD2wthmqoM317L02KBe8aIwhTQWZ9LDprasejpqK1MYfFffB6LoZgzZOLrfuHT6VqYc3d2M4Vy2BwFkNtBMI/JhjZse7sfhYBGiCYi0MNlrs+JlceHh3AqCx7jVaa5SQrWMdhDtXOT0mzHHxtvli5nKtG4pyEO2FcVYSkCJDK8Onn37B7HpOkgju37/Hg/sPmUwmNue9zEJxLpuytMQWdIXDwwNGoyGXl1cslwWqFiwXZUtLrLRNAd3r9xiNBjx6/ICd8YiyKhmPR/R6PWd1zwPxTJOUPO8jRE1VaWdlkFSlFQJWqxV1ZS0wXjCYz2asipLVsnQxhjWr1Srkl28HJhPtQ+P3H8dmaeMFRkGoZhiBr4+5CUy+sN4BxlGIDutrlWAIVK1JIpzTPXPdWC8Pu10mNFZ4YNqpVVuwEg7EhuYE75ix+8cw1nHV5K6g0cWncd/bcPpwOOSHP/whf//3fx80sjHDHvcfCxpdgaq1Rp2Jd12VfP9CJhghorO02ar0tvWJ968b89cZSktY9fdZJVZTN+vFixfs7e1z7949ptMpy+WS3d1dDg4OKYqShw8fsre7T1Uqnj17xgcffMBHH30Ugp9XqxWj0YCdnQlFUdJzNTXSNAdjeZjSueR5dxsbH2Mz5I3HY1siwRhWZYHCcO/4mP39XYpiyenpG4S2Gn+ZZhwe3aFYLLk4v6DXH3J455jZYkFZLjFV7awscXB9e1l8fFDb1U4Ey7UBEplwdXXl6oTkQaiaTqcURYEQNp5hMBygjWXI37x5EwSD2WwW1n25XAYG3q9/uSoC/JYujtgHW3t48YHxMYz0er0gSKSpVWL4JAcagfDZWF3w+XK5pCyrEFPhx7e7u+sqnEvKqgjCUCxQZHmGUU39GJtm2K6VT+7gs3Ddpt1a0OglrkieTIMFYtDrWY2OsZUZe70eUggqN9hytcBoRX/cR0hBIgWD4wN2d3eYjAaIuqScXWEySaUKXnz1OWVZ8vDRI+4/fMTH7z1ClUuWRUGe9xkMh0x2RmAUq8WS/8f/9f/C559+jlaGw4ND/uv/+t/wF3/xJ/T6Gfs7O+SJ5Gc//QlffvGMk9PXIAWzq0u++/0fMBjuoJWtYInAlpTPbbXFqixt8SMMQtc2ODKR6DRlpazpuqoqpIZ+3qeXJpg0oSxtZo2qtjEAi8WC5XxGsVyS5ynFoMf52QnPMo0whjzv0ev1ETJB+tIDzmKhtLbuRMaEv9ojf0PwS20EE5wiWbcOl/BxD05w8IyOx0Xt1ogkvsCWR0xtbWujTWxTvkb/Jdy7iXxxY1N7g9DduHVTo0JKGdHfSCAyhAwdnhA2I28+GGNz28vMBjmfn56gVe3SzLa1ghulqA0tJnDBA1Q0bhM+1sMz2j4LUlu4aq+413DF847fJ4TgD378B3zwwQccHh7y+uQN17MZi/mcn//il1xer+gPdpiMd8mE4tmXX3BdlRw//oDf+6MfMdi5S5L1kWj+KOvxi7/9/6C05r3v/ICDO+9gRIKqFeXymk//4a+4vJgxnVm/UpH0KcuKTz/7ipOTN/zxH/8RH374Ea9eveQv//Iv+dM//VMePXpEpRR/8Rd/wf/47/9HKlc51OfvF3KztsPX0oldC2IBxc8/zl1utc9izc+6ud+uedc1xMJdbJEyYBRCV+jKZrfpJaPIwhVlHMLWVfBCKTTE3VaYtzCgXCShcmmEwVVddlZeVduiaFVZBdgN+64ay5bStfP7T8K5i+eiahXWaBMT5xndJLFKoEVdW+VQtGbWIidt0axo/QP8pQnCEPzTfWxA4lIpL1cLTk9PmU6nvPvuu3z88cdOAPCpohWClOWixBjlrNvK9WFdUxsXVUAraikRInFafltbKc/79Hs1VQmDgaHXWyLlNCQWEQgmkx2Ojg5JM0lZlFzUNVrVrFYlaXIV1rmua4vPlaZSIopH0CyX1qWyKzTEEkBTndj9Kqw7w2pVtBiIwOCYUFcQjECQBDgM/bpXNAxOrGyhkxbW4Up8YbgkWNSsQOyeQbbOTzhbUT/bhPdNLbaWxW0TUxwLOFJYN+iuALPtXYEBRjcutB0Bwz8fWzlj60D3e2sOrpVlyXK5DOlFPdx75ip+zgs5m4SWTQKNvVe3YMFb3qSLz9DuWR/f09Cg27XQV8eS0xW4pJRt2mgM8RlvnpGcn58znV4zmeywu7vL5eUlRa/i0cMn7O3t8fjxY7Ksx+HhEU+fPuXFixfcu3eP5XLJb3/7W66vr5nP5zYeMrEFFYOQoRS1snGLdriSNM1RyiozRgNrcQcoq5Kiqjg4POL4nQckieDpF08tHlsuKcqSgzv3SdKMk5MTimXB4yfv0R+Oefn8hDQRnHz9ws+4s3JRUge3LrHrpIVZlygGE4SR6+trmw1NNa5W/pmdnR2q2jL9i8UiWLGm02lL2SOlDbb2cRZ+7b2Lk49/8Nd9CmHvwuQZeg+zfn89nVsulzbLlrO4elcnH4eltaZwNVOgKYpdVRVplmKw/R8dHXF6ehpocuVq2vkzELvsgRV6er1eyIz1tnZrQSNPKitgZJAImxpykGWIzMK0UhUZlhjuudzMO3fvsT8Zsbs3YXd3wuHhvqtAqri6OCcRgs8/+4zz0zdkSUrmJLiLkzdcX10ynuzwrQ/e5ez8nCzvMZ8vSIQhlRn/93/7f+Nv/uNfAwKtDGcnZ3z12WecvnrNH//pH5BkCX/0R3/AJ7/7lFrVZDkuGEnzxaef8uCdx+ztHzhf0jRojyWSJEsxjpiookAri4gSAxlQ1TVlsUKVFTOtePmidgisdBvtKra6IHgprIvY/mTM3mSHP/2TP+OnP/0pe3uHDIcjQAemzLtQGSdoGGMwSjRB3ZGQILz1QHvWHqeFapp31AiIJwgH68TDmIYxjomtWevT/n+zoBFrvgjfnZ62dW+gAcZRZuH8wwP5pUlm497TuLbY4Lsu2fIabKVqBv0+eZpQrJZ2XkbYyrU+LaZSLUL9thZrApuCZ/ZfU7iva/XYtM4RoTabNZBCCD748EM++OAD9nb3ePnqFfPFnNdv3vDrX/waTcp4csRgcshwZ8zZq+ecL1dgQNUw2b3DdQnXV+eUq2tUOePxR9/BIHhzPuX1hfWNTZOEySDn0bsfsVjYAlS7h/dRSjOfz1jMZyzm1/wP/8N/4Pd//4rvf/97JEnKf/yP/5E/+bM/4d1330UKwZ/96Z/yl3/5l9aNSkpQN2johLf6dOIinLDRuMY0hMGm/EuCX3rMCHgC3GL41hgRgkUsSySr+TVlVWCMIJFNrnNjTKimXKnSurloG2QbKi47BF67qrY2P3mJ0YbBcGC1QdE++/l4hsnHq3gYsTDkAmGFoBa1015boa0p6mRrAPlnE5lghHGxSEkorubfaeN+GuKQuMBmEJR1FWDW1xnwQpMA0jRDud/CuijNalnwm19/4lxjJT/4/u+RZRnz+ZxiVZMkGUJK8l5GliUsl0uEgKKouLy8oiwrxuMqEFG7pjaVaVGWrFy6yKULEl3MlzZ9bW2zHvk9reqKs7NTrq+nDqWZoJTxyhaBDWaUidUQCgQkaRAoocFfNlBXuwDjGGYF3s2t+cXCm8/Y5s95fNQtvnHWVdHgOtN0QpNuw8KBhwYjojujoQhEiBFptOe+vkajgNkoQHR4r5sY8vC9g7vaggUgN7vuWA1x857YChD3489DSDlubDbIeA6b/vln47/x5671xbflcslPfvKToD2WUobCdWsa7gjXf9PWfd66Ttn9864v/rx52Nggz9zYuoqGWAixdLk9n21NKcWbN6/56MNvuaxS1yyXK9J0TpblXFz8f6n7syBbsus8E/y2z37mE3PcuPOQyDmBxJAAAQIQSVCUKFIjB5Wa6pJUVcZ66ba26sfufuqHMusHvbX1Q1m3tUxlXdaTKKpFURJppEQSMxJAAjkg8843bswRZz4+++6HvbcfP3FvZl5ILBPlaZE3hnOOu2/fe+21/vWvf6l6Ct8PWF9fZ39/H8dxuHr1KgDvv/8+0XxGUeQkSUoSZ0zdiEVGH7J80W1e2XHdydtRGb4kjSkQrKyvcvnKVRqtJrv377O/t6s2MwFSCrYvXCQrJI93d3Eclws7l5jHKYPhiLZrc3p6UHkFxn6qMVruCbZUOwMawCyr11q2RafTqcbTcewlAMs48o7rLtXJGHqUKXo3yL8J8kwGTerMpclcGLtr5GmNYIMB2ur7mMl+mIDBPO96gCGEUm00r7Esaym4TtO0ymLYrlVRYet0XHNNrutWgYYJnMz8fVoQ/mHHMwcaVy6s6s1MQe9ZmuLYDp1WC9uSmg8bVhcUhgFZmuK7NlcubBDFc3bvf8B4PMJ1bIRlc3o6pCyUXrJ+3pSlZDga0G41sK2SLC/ptBok+rMmozFHRyf85CcfYNkuWZKRZ7mS3ytKvvmN7/LSKy/j+DY/fvtt+is9siLF9z1F5xIl8/mMx7u7JHHG1vY2ErVxmYcqhOD07JTxcEg+m5PGuslPllAUmUIuS9XBVWp1AFNXUErd7AltPfSXLCSe6/Cbv/4brK6tUpSSe/fu0uv36LoCx3K0mopW80BS1rqNGge7lKUORpRjroINB4G9SL0v7S81alI1MRa0H3OoDIR+ChIQKsq2bBsh5BMG/WmGvu546z/W9rflMINz55a1+5JyQetYDidEzTgLKBZob/33UiqevGNbuI7NaDQEqRRipLUoBpTSZIs+YuKbMwtx7hz6nkqFYJuxcxwHo4BjHn9VbF7bUarPKQ0ab2pp1LG2tsYrr7zC2toap2enTKdT9g/2effd9/DtkKDRI+hv4XVW6K702NrZwQ18osGQK1ducv/+LtNM4AUe3Y7P+k6f0PexHY9c2sRJRp6mTEdDJqMzvLDN8y9/inanw9bmFkmacnpyguOdUcws5vMJP/j+D4njmM997jNIWfKdb3+bz77xeS5evEiWpnzyk5/k+2++qZH3D9/chEm/1Zy0+t+U4RbUpYhVQe1CsrKOctYzS8ZgLjknmsZRFgWObzOfTRicWUTRjDRLmU07lXE3fNokjpXKSLEIvJU+u6J2CVTAYFAl03+nyHP80FM2wVIbi+26CMB2XBzHW8w5sUA4BWptqyI/d1GwWqfSyUXdjvLz9N9su1o7QqOZUr0JE+tn2aJwudT1cYaeJ+XymgBVNC+1LVPZgIIkyZDSZnPjAp7vceXKFWbTmKKcMZ1Mq8xJnMTs7+0xmY4RlqQsBbdv3+HRo90qADRrQMktanpYzflfUETUfanr1rSvokCUBaUwhbcOGOWpUokPmPtxnUCPt12pYS1QfWvhnBfLVJYn5+zyHJVI6gk7M25VEAlVrYUQ2jbLhaJSnTal1JQUuc8SYlGtowzj8lLSY7LAjp7NoTQF7HV7+WGIfe1diwDpfOAixJJc7/mgRdTOUX+NAQnqjk0VyEqdeSrLpfc+LXD6sGDiaT/Xf2845/UAum5Tzr+/jmI/61F3+hdfFtSyMssgSw1J+ynO8WG/fwLM+ojDsiwODw+5cvkq/X6f1dU1jo+PiaIY348YDke4rsfqqk2j0WB9fZ3d3UcUZcGVK1fwPI+7d+8wHAywLCURrWjfpYqBhb2gj2kH2FyTQvOVjVtfX+fi1SuEzRaPHu/y8ME9Hj96RLMZEgYhmxcu4vk+eweHzOdzLm1fod9f48HxPnlRcDo6pcxzhOXpO1tkcYpiOaNbz+yAnl8mWwhsb2/T6/WU0pOwkKVc9JfQ6+js7IyiLHGlWwXLxjmP47iaN77vV/au6nYvRFUPZxx3IQRhGFYZDDMvDahVp1EtZ6WEruuSVVbF2EjzOZ7jVvLCZs25rkur1aLb62A7dtULxDB8TMG51ACwGSuTTVbCFXEVDH3c8cyBxte+/HkVnaYpw+FQLdosr9LmaZri2BZho0WseWk725sgSt5578c62jPNSVIsW+lTq81WTw1LGUTXcbl64wae5zGbzTk5O9N6vw3WNtbY33+M76kimSxVTn+WqxTS7QcfcHh6wMWLFxicnHF2eoJrO9VDjqM5yAxZwNnpY8pyTm91g6DRoMgVP/f+/QccHR3h2Da+40CpKBcCVfFflrl2DBZIo8kzCD3BTQEmUiJt5WDef/iI/+H/+n/jhRducv36dU5PjtnbfYTnWIRhQxluS29OoIqkC5XOM76ZpbMdJsugnKisQkoFElkVcuuUYC3IqLITUlZir5VjIheompAllpRYht0ua1QqQy9YCiTQm2rN0GnH2igmGE35J1F9rRyir9OqdcW1hJ4Y+gQmiyN0ZGSJxYa9QCglUOK7DsiS0WConEJJVRhsZGWNisnC0NcCpScO5cyYIEMIKMscsKvN06Rhq9dQaudCOzO1Z1CdRVSvqCiIn/rMZ9jevkCaZgwHI46Ojnnv3fcJvJBOu0vYXsFbWae7fZVubxUrj7n1nMVwNCTHYnO9x2sXL7K60sN3JGWRkGQZWZ4jEVjCx3NdbGubIs8YTUbsPd5nd3ef+7t79LurrG1coRF0uP32LnlWEDYCfvz2j7Fdm9dee404TfnON7/FV776VXZ2LlIWJacnJ9y9ew+lqPXkOBonRFKvw7AquUqkDTggzeZQpyzJau7Xu7JCrYmVNHgWYClNfIGpaShI0oIf/ejHtDsNiiLXMtvnC/SVKlOeJ5qOZVcbpEKgVDdhSwiwLJKs4Ac/fJd+f4XrN67QXelUdQKe5+F6HrJUXZGNcITZJCoHqk7PsWo8cIOkSyr7KVHS3sKykKWo7tuAELajJMFLWeoGiCUyVzLaGYWi/USJdrwK5vMZ48mEOIqJdCFjksRVSj/SqilpkhFFcbX57T065Bt/+q0K7Vc1GpKy1B26haJNKVpUyWw2X7IPQohKncysS0vX/gnKCqy3LQtZ5pUGnhCC0sikivNZAz3v9GYuHCOWoeeZlFXGQCmG6ToxWVYg8PlZqyxphdEjasLaxt5j8Aozn4VFIQQFFhILA52Y+YiwVJ8IFV1gCwmiRJIj8AAHSaHvjSpAsvTstnQn8POO5MK+1oIfRPXzwlTKxT4jRKVWJXVgY1nKySikCf6tan7qqAlZc+Dq42ZeV/fPFZiiGxkWEmGb+rySRWj1pL14Vof5ow7z3jq6rDqGLwcy9dc+7W/nP+/jzrk0z23d1Lhc1EcYR1MiawmI8+OgoUJpMiSG8rPIVtaDsAUdy7z+yftRfzV/VzW09+/d4fnnX2Rra4v5XKksKZqeek0UTXn46AFZlrK1tcX+/i5pGnPhwjaNZoP9/UMeP36sFYzARlMvtdANlnZyKSgKNT8tbMJmh7XtTVY2N7Fdm3v37zMdj0HTkhy/idfqsXHhCnmec/D4EXbQYOvqNaIsY3x8RtcLeP/RAZblUFYNd828r1Gk9Xyr/sWADUooo5QCISTNZqio7klEo9kgDEIGg+ESkDWPZ1iWjR/0q0yGySiYYLqO/teDDQvTxFO9zmQf0jRVtTz6uZVCgGXj+wGGkgm6+WytF01eFNiWalwahCGgsivCUqJGnu3g2A55kSNsQennZFGM3WozHoxUyYMUONjIXDKbzRCWYJ7OKXJVKrCoGVZrvyyV7SqLZ6P/PXOg8fDeXaSUqsFLI1BdO7OCaD6rdIMbjQZbW1usr6/jeR77B/scnxxVEaNBQGzdKbKuMKOsm7Z/QjAcj+l0OjTbLVqdNmEYkuc5k9lMOYm6q6dtWwihZOnyIiVOI9IsBlFyfHyoozTF4RUC1Z1cqqJFmeWMhmpz7Pb6NBtN9vYPmI9GtHxf8SpLXbArbNxGA0vAbDYBWeqipuVD6f8vnIhCcxSFZTOZzfmjf/fHfOObf8r6+jp//+//fXZ3d2m1GmxsbOK6Dpa9jNQsjH+t0KxcaGibxaQWif7S7rNKtQtdcFoLNLRzXy4Zn7qBU4ZAA2q1TQu9gS8jxvXjvIFdoMqSsqBqgGiuQVEWFpKJUkos3dzKBFuy9tn2UrpeLI+LlMrBFTaOJVTRu5QMhwMMCilZ1JxI1OuXj+VNpJ5eFdowmd/VlUvqKdnF8zOfYcaqrP5gjEkVZRsERpa8/MrLXLl6Bc/zefhwl+Fwwrvv/gTfa9Dr9Yjncwox47nnNmivrjMazxkc7ZHPJuxcvsL1m9dpBj5JNON49zZHB48Zj4bESVypWhjFi26ny9rGOisba7z44i2uX7vKo0cH3L+/y2QW0Ws3GQyGzGYjtra3CIImP/zBWzhuwK1bNxgPh3z/zTf5/Oc/z3Aw4NXXXuP45ITpZFrFbudRVPXs6/0nFK3NDIUQSpVE6maGZp2VNRUaM95LY17NO+WsU1o6C7JAYyzb4u69ezRbAZ7n4Xlu1enVXKfnefh+QKvd0P0VqKgWpiguDJrqOoXDZBIzHk8ZDKdEccTW9pfw/VDRA2wbpMCyHJxamlzZQhVyqayhTZGXCxRLr4U0SSoqV6EpCFmeLXohZEqBxCidmI7KcRyT6wyNkWOs90nIM0mSLLq6mrT9+QyhGbfzyO95m7SMXivAA72uqQWAytSYTKxeWBiHl0rm2UIFn8IgLHoeWUikJaA0c8BISEtM13KhnbdFxsCAQSWLT6s7jLIKgJ961DIHxh5WKLSwERjaKzVbprInjutqsKTENqIDxs5p9LAslJCEZdlIaas+VEIAts6aKNts2xa+E5LnWlffsSuql8qAQ54XVVBSp4gZ2/pE5kE8Cf4g9foxAVi1NutZhfo+tTRQwHLR+uKcAtexuXLlEt1ul3feeYeiAGm7SghAFpVNrStOfdzxrEHI07IgH5UZWL72Zznv+ax3ba3Uxms5m7GQIF78zQBw9c821LynX895wKUs5BN/q31U9Y3ZUw8PD9ja2qbbW2NnZ4cHDx4wm82wtUT8B7d/wuGhqoEYj0f8zM/8DIPBKdPpmAs7l7l56xZr6+ucnp5ydnbGZDJRdJ5SCQGVhQrApRDYrkur1Watv053ZRWvETKLI+7eu02ZKgq+Y1n0un1wAq5efw7XC3lw7zZlUXLh8hVW1tZ5/OARFDmTkyHJbIZtlUv7udlzDWhp9l/TYkG9xhSJGqBD6gJniR/4uimoosDHcYzrOrRabTY3NxkORySJUpmTpaxoVLJUdXmWvajfMM9GZVPsKkthsitmf0nSDKTqR2JpAE5Itf+ohpMFQmqgSQc9ji6ud2wlfuE6DhaQxAl5liNsBXTlWUZZlKSxytp7rsd8Ptd1fXbVdNPIlBvg2GRyDLBhAiQpF7UmH3c8e2fw6RQhYH9/H9/3aDSatNttfN+n2+1WHQPb7Tanp6cMBmeqQ6g2/ob+YJwc40TX04zmKIqco6Mjdnd3sW2VsjMIQCFlxWcrywWn1rYsStumlJI4TvXmmpOlOWmqO4nrB2vSl1Kq4sM0k4RhiO+5tJsNZmFAmqVLxVqqOBTdadVGBXfLi/48R9xoIptJb3jNs1lKlh3xB3/wRzQaPpICx7PptFuqOZRYRM7aH9cok9Yvf1rwIaXeEMS5vy8XtRmjJzWiZYIAqG/Ii/+j9sVqkZr31v9bSgYYrjCKEmE+u5RK8caMTVXoK0138xoiIxxsTIbABTTf3LJA1IqrqXVuRvPXa49ESa9JJpOxdjbVpmsoOdXnLBniD9m0xPLr6oHF+b1ogSguLqceeD3989Vnr62t8cILL9Bud3h47xFZVvDuuz8BYdPu9hhOphw82gUnYOvGy1hhl4ODQwIbPvvG62ytrzCdjvnRm9/n/t3bRNOJQktlWWWNBFAIQTwcMNh/zIP3BXbgsXlhh+dfeInnn7vK9vYmP3r7XY7O9llZX2U8HjI4G3P5yiWyrOAHb/6AdqvBjRs3+P73v8/du3e5dOkScRzz2muv8Wd/+mdPjIkZt/NjUE8Jm/FXCj2mYFw/t9ocLmpzaeFMyaVnYdZPUSz40M1miyAItdqJh+PYau37PnEcL/G3FUKlHHNFTVTBspSQ53MVCJWK87p94QJnpwNAcHx0hhCOVllRWRNVc6W6tBvFIrVJRVpuENJEZVSjeVQZ+zRRBetlTammDkAYYYO66ECFnllW1WHezNPKcZeWzj4s01Tq39czPMtjvVgDy3N+4Ygu/Q0Lk5WsxQ3qGnWsfT54kbKW5TTnqxUKl5bOklY1KP/hiPezHQaIMV/6nNIG6aKcNomg0JmSHMdWndR91yEMAlrNkMBzSdKU2TRSwEspsSwPKSEMm7RabVzPZWW1T7vdZnW1z8rqinZwmly/dov7Dx7yu7/7uzx69Eh1J9Z7WV4oGq/q2q16HNT3ArOOFsisQpeLfLHuqv0Y1ffBsuoOrvkMlsbBzKkFv5ulmhZY1CZ0ek3+u//uf8Xq2jr/+//d/4EHD3Y1HduiJMVQ1OoCBv8pj58qk6LX5fkas2q9whNrRGrAr8KzpPzIc9bXnwFQzGfVvz4sIDl/1FWs3n//fT79mRV6vS5pus3jx4+ZzSJUfxAlW1sUBa1Wh263Rxg2OT4+4ic/+Qm93ipra0r+9sKFC1XfiSRRTJMSgbAVOu/5AX4Q4tlKUvXRg9uMx2OlIidsxmcDkiSntGxuXL9Os6XArqOTM3rdFW5ev8XwbMBoOKAVutx+7y5Yqo3CcgB8jg4neMKGod9igA7btllfX2MymdBohkgpdTE1NMJQ0WvjmJM0I0sz5vOIXCtBZalucKlHvyhLAt9H6L5zpn7iPHVQSqkDiQLXWjSgLsuSQhY4wkJmBZSaZaIfb1kWS9LYlmWRxUnld2a6RmSSTyqfWWUoFFCxf3gALGSk64ILzWaTVqtFr9vD871KWrfX69HpdAjDkEajQafTeaZ59syBhqKICOJYNWupK/eYhRSGYVV4opQPFrJqZiDrKT5jTExBDJgFY5EkJrWfV4UxlqV4js1mczFwWgLWdGGVpWQ0HCGlRbvVIY5UJ3KlMDKp5MnMdedZjh3nPJZw6fJlneqn6vtQof+aPuXYDq7jktTu5WkbrDHYJqhaGBsBOOSF4Dvfe5Nut8lkPsENHG7euE4jCJT8rj4U13jxvRk7dQ6D1i4b/PrEgUXaTl0r1I3Q+Z/PG8EnUq5iUZ9Qd3jq713MmZrzI1XWSRMeKKVWaWLBs1eXrxS3JLq4V7/GEhaWVGNnOO4qZLKqwmLbdhBAmmWUMse2BfNorrniVE5XdV215/ZhAcB5hHc5IF4gvcvvMe8TtazQk5+/5FghkULw2muv0Wy1GI3GzKOI92/fZjqP6K9t4Ld6HJ6OkJaLEDZpHLG3+4D+So/XX3uZwIU7773Fj3/4A8bjkSZtqO7MZaHECQyP07ZsLFvPz7Ikn0+5//577D64z41bz/Piq6/x6ddf5CfvvQfxKZ4fEgYqo1cUkvlsxA++/33Wfv7nuHHjBm+99Rabm5tsb28jhODehXs83n38off8YeO8ODTqXbMX9QyJ6fS7CPaKKtAwiKChS/l+gOd6dDpdgkB1VY3jTP8LaVriuolqdIjUCiQleZ6C0IpEWl4200XheV6QZ7qIOVFgBgjiJOLf/tvDKkCq98pQDh4LBx/TZVkh80ppSFZgwnlkVAihOcJqKFQtWKGds7pjo8ZPN5zXY3IeiVafYja+CgjRR/389cNwgKFO01lw7+vPuFo7ep0uzIzObKHricWy/THntG1bd5BWcIVt1Wq3LMVNPn8Nli7qLstFxswSi8/4qHn3cQ7e4tr0/aCy6RY5UIDIQeQ0mx4XdrZ54cXnuHJlh2azwbWrV9je2iRNInZ3d7GEq75sBR41ww7d7hqtZq8qMjUUn1gryxyfnDAYnNDttvjN3/w1wjBkOpuSJorOfHR8wqNHu+zt73F2dkYcx2RpRl4o2fY8L5Zogpal+kTJ0qqAJz2zqLJDwtw7aNK9HjOdidYOkWkAWc8yng8cm80m/+gf/QM+98brgM1//V//V/z3//3/idFwhiVsbMshl9kT8+fjsg9/UQ7jpNWFKcCspQJDnapnwWE5RH7Cp6hs2odnXp6WRTl/XefneX2MzRqaz2d88MF73Lr1HGtrK2RZxuHhIdPpjDAM2Lmwg+t5bG9vM5vOCcOQra1tJpM5xyennJyc0GiorHu73abVaoEosWzVcDnNFD0py0uGozGTwSlJNCfNE4ZnZ6z0VphEOdE8Jskll6/eoL+6xnw+5/6Dh/hhk1vPv0SZFxw8fkwz9Hhw7yfkeYygAMuqOs7X71XVfy0aq9bHo14YblmCdruNZVmkaURRKuEYW7iqRk0omzObzGt1E7WT6WbLKgvk6CydztKilJo67bbKJAsqupSpDXRdlzLVPpJYKCymKGUnE1CYzLS5D/O6qsGofq55nuO4Dpah6yJxfZ+m5+HYNo1mA8dxuHBhhzAMyLMcV6teXblyhfX1dRqNBqYO2XWVQAhC4Niq9iZJU57leOZAQzV4Uz0IdJPvxSZclmRZWhVrKv/AQnXtfFJdxgQcRhf4/KZmGkvVF4FxnkFUkoLWEwWgArAYjSbM5xFplnP79h0OD4/Vz2lcPRRzrizLEJlK2Z4cHxKGDfI8RcpcbVjSxhJG1lRWTYWWnYQnZQXN7+rFZCbroN9NKUvGkwnv/eR9xYnOStZWV2m1WopGZTjmllVtoKYAte4UGOfRBB0G4XVsp3pGFcoiNYFILBwhYZ6Xno71z/6wo+78lOVCsae+cJcCHLSujk5lupalqQIGVVWvU5kvtwoOERLL0ipg0kIWBTY1nioCsDWCoCa9optkZFnKbDZhPB7rZ6muokJxeRrCvuy0meO8Ma9zbdW/tQ1iCYY1n7ms4V3fhEupOLob6+usra3hex73Hz9kOBzx+PEejXYHN2zS6q3yyc0LnO4fEIQNELC13uPV116lyGK+/fVv8vD9dyHPEIUqrFSdxstqvdhCdbNOskxnmMDzfFzPxhEWRRzxzo9+wOHBPl/40pd4+cVbhC48uPuIZthGSMjTnDxPGZwNeeedd3nttVfpdDr84Ac/4Itf/CKDwYDXXnuNvcd7HxpYnJ8jiwxeieoavuAaF4XqXyA416iOuiJHUY2zcbSFzmZMp2N8PwAKBoOiWh/qtecD6lIb9HNFuHpuLIKZOrK9QHAXgXgV/qvPEYIyf7KmS/3fUnKgtXljuh0jTX2W+Xnhr5vC8MW9qPuqFyQbxORpz+B8gHzeTj8R5NT+dj4L/bT3Vr+TBjEUuriw5mRZquHpso1XFFQbgWvbi/E0dRmWQFqGWrXYVM1cKPMFj3khGKADEnEOAKl9X0eizXgaRxrqnZ4hz1Msy6a/0uLihRXKMqPTbeD5Fj/75Tfo9dt4nk0QOsq+ygHHx2da/eqUnQvXKKXFdDrRm/kcyRDLckH6IBXlyrFLwtAhTSTra32arVbV3dw4h1KiVXxchLAq9UNFQSo5OTlmOlUI82w25exsQBRFjEZDfvSjH3N4cKppGWqfyIsCy9FzqgTLrmXOtQ23dAdsBcwpWpeyM2q+G4BMCIHjKPnM3/jN3+Bv/q1fpSxLPN/na1/7Bb7/5g/5Z7/zu+RZgY1FWSz2TWBpTvxFP+py1Eo4Ylk1iFpNxRNsjg/LaDwlOq78JD2/6wF+9XexLJF8ft+CRdO/+jkPDvdptZtc2N5hY2MdEJycnDGbzikbPpblMBqOyTPVF6PVaqk6rijSVCubg4MDdnd3AbDtEoWbWsRJTilt8kIiLJvAtrAteHz/HlE0g7ygKB2kcLl0/RbbF3ZI4piHDx8iBVy9eYtGp8fevbvkScRoPuf09ADbkghslR2sD91TQYQnB9TYKMuyuH7jBlEUEQQuSRprcQn1WYYm5GjJbs/3oW63bMhAgeROWWUBiiJWQHhRMJ9MyYqcpFYjlKZp5RvY2JUwRRzHWLqGw3Wcyt45+nsjP2vsVqfTYWNzk3a7xcbGJkEQsLG5AfaiPwYoGparG62abL4QopKqFUJUqlSG1Bf4KhmgcH1JVhaUBbj+nzN1qip8Fia7AY6jFD/U5C2QlFim6r3MlfNV47Q/beMyDkZdAlLRcZbRjOp9KCWUKIrIs3yxeFALJ2w0+MY3vsnXv66oG0mSUxZUnOa6HrGtozLbcsizlOlkgue6OJZFVjmFoJwFWSFjRo3JOENPQ7uf9r26Nz2epdDOMURRyrvv3eHx7iG+62juuFcFVKZ5i+M4OK4q7EFzdk3Rkbkf3/er16r3aeTJVuk723F0AbWim1Xoi2VVqd86Olm/v/phis8r6oa6QfWMLKuq4zCHBCXrpp+947gVCiZNAFBrJGSKb4VQXdjrgdsisLL1tZhIXs2B4XBIGudMJmOOj49I0wTTBC4vjKa/tXB+niHLbFAGg9rV0QP1PEvNs7aQ5bl3ngtS6mNaFAW241Aief755+l0OownE9Ik5f79+1i2Q7Pdpd3t0+6tcOnKNa5ev8mDB/exHY/XP/UqaTTnG//+jzjae4QoUiV4APh+oFQvZMnKyiq262pHQSI1MjIcDhkNRzAvlDZ2EOJagsHRIf/u3/wbfuZnv8St554jy2D3/gHdVodud4U8i8gzj/ff/wkXL+5w9epVvvvd7zIej1ldXWU2nbGzs8Pjx48/FB3/sGMRrIuqVsGyVJPQonh6dkic22BMTw3lhKbYtmA4TGqfb3Z2heijNxuTXq/Fm7XnXHdC60HqMtptJoCs/m+ydVrcgEVWUEMD+mtp2lRHuXzmZWeYZTtTHwcFjSyDBufnoRmPerD1cc/pPIhSB1fOK4FJKavibgFIuSxD7Aa6SZW2ZWYT9DyP9f4K7VYbW2exm60WrrZtQatJf3WFIAjI85zDw0MePXrEYDDkvbd/wvHhMZ7jaq175RhIISjFAnmuz0uzFuvB19K4SFUCrjIXBY4LV69d4r/97X/AC5+4zN7eLt1ek7xIOBsc8ejRfR4+vE8YeFy7dg3HEiRJRLvVxLUdGoFPUdo4lmQyHTEaTun3tiiSAiFcJNDr9QmCBpSSfq+NY7uUtoNlVBr1uJuahiw3lGLXpCKwbJvNzbVqgRRFTiNsgL7n+/fu8+Mfv8ODBw+q/ihRHNFutblz5y5nZ4Mqc2jbtlZ/U+IXvudXbIQgCAiCgF6vR9gIcWyHldUV2u02Fy5c4MUXX2R7e5v5bMxgOkEIQZYW/Mqv/jLfe/O7PHz4CFmAKJd7RZwHFv7nOv48Pt/MoXrPHePQSYRC3Gu+wIcpWpk9xqwd8/onr3HBKli+DyV9bT7nPLD1tH1ICBXA50XGgwf3aIRN2u0uW5tbuE7Ayekx0+mILMtI04zZbE6z2WQymfLgwUP2Dw+wLIubN29y69atiu8vi4hG6BA22uQFnJyMsCyXsrRIk4iHDx6SRDG9bpckz7GDBpeufoLuygbTKOHe7dsUecaNm7fY2LzA3tEJs9kI20q4f/cDhFBMGyp1ynJpXOqB1RLAUQvyhAaDbNumEYaEYYhtg8RDFpIykeRZgSxV01AlBwuT8RSF9SwEBuIkIdWsmcqeCGX/K6aJ3ofNemq3VQ1yq9Wi0+4SRzGj8QjLsul2u1y9eoWLFy9VzY1brRalZicUZYHruARhUPl8pl+T53kgBKPxSANhEt8PtMQ5nJ0NcFyHeTTHcRyarSZpmhHHEUEYUkRz+v0VkiTGdlTJgOXYqrdIWRA2wmdeN88caMAidVMUqiW7bS8QnjAMKiNtpAWpcc3OBxOwWFAmDVShk6WsigLrkb9KgUmVDhKCPM8oclVwbQkLx/VpNpokSUySRJpKY5EXC2Ncn3iWpbTQfdcHIElizk5PVGdL43ygVBMsHWjE8bxKy5sI8+OcqHoqWUpFIVJF34pPq+qRLKaTmKkO6ARPBlmWbavNo74ZoiURa8iwQerNggPlWDqOWzX6WzgB1pJTY36nCpvMb8XS966rGm6ZgEUY9OQpRqxCEPRrjcEzBlgIgePauK5dceNNca7rutiOpRE1rWlt23i+j21ZWsFnUeyrEBqbyWSC7wXsPnrMnTt3kdLoTosq2HScoIZWLh9PM/51FLkeaCzes3ivrKVvF6j28jwxQacxSI1Wk0uXLxOGDe7du8doMubw6Ihuf5Ww0aDd6bKxfQHH89k7OmSe5Xz585+nzFO++80/43D3IeQp0/kYz3NphA0syyaKY9IsQwqL7uoqfhDgaA6nbTusbTVw/JDpcIgsCmbTGa1mC8eySaZzvv7H/54v/uLP89wnnmc8iJmOpnRbbcZDD9fxmM0jPvjgAz772c+yvr7Oj370I9544w38wOfqtas83tv76YKM2ndKRc1s1prSWJ4TkTg30rAIAFTRtagCYNs2oMjieaEzZ2ajpayn1uuf+fSA2yBhCwhhkS0RgKxoTaJa1ybLtcismCDmyQDniaMGfqj/C+qa+RWvSqh+R7IWQNWvWSxDfwuwAC0kcc45qTvddTqnATrUmnVwPY9Ou83169cJghDP8+i0G/TaLVZW+riuWylXNRohzW6b/kof13WqfUL13rD41CuvKsQwVxt0US5oKTi2Ak0sQaY3PiEs0jTlnbd+wrtvv8vdu/e4d+8uo9FIdfOOY0phnAxRzQXzfI1drTIjpdSvU2IgjiVUQOQI3vj86/zWb/1d1lY7PHp0n93dh6zNV9jZ2cbC4guf/xKzSUSRF5wcjvmZL7wBUrL78CHzeUoyEzQaLY5PT5Q9Eh73bz+k1Vrjws4FhJA8vH8Xzw+Io5SjoxOuX79Js79Ct7+K6zq6Qzs0Gk1ljywL13OXgj3LWsgdO45DqSnHeVFwcnzExsY6X/nKF0mSz1RFvM994hMEvs/h4RGPHu4DqpdAs9lkdXVVdXIuMiU92mhUNEDTk0Iide2I6t5u2Tanp0dMpyMCP+Ds9IzpdMpkPKak5Atf+CxngyNG4zmO7VCng9SzG88aCP+nPKrMvq3YCAbVFraS9D8P4JleB08LBFzHAbnIup3fl+rCJOZQn7MIZOrnqv9b9y0W7zViFBnvvPsOL7/0Gr4XquJoAc1mwOnpKePxhCRJmc8j5Rx3O5wOTjE2bjAY6D1SNeX7zKdeIS8EBwfHHOwekuUxcZyTxDGu7dHv9YmzhO5an60rz+G3VpnMEx4/fADA9Rs32Nja5mQw4OzsjK5vcecntymLBCFKVJ2UDVggMhZiCItAw7IM+wGDEi0Fb0IopkySJMwOxtg2ZHlKFmegG8XWwQlF1S+QsqgA616vh1WjEjmOw+XLl2m127iOQ6PZJPB9bE/1Gup0Oly5coWLFy/i+z5SSvwgxA/DCgxEGJqSEkzI8ryqs5BSEkdxJYteFgqsTRNFmUzLgkYY0mg2qxKEOIlxChWQNFtNsjwnbDSwbZtMK0wNRyOEZRE2Gpgq2yhWdYOLBsUFzOeVWMrHHc8caBj1lixTu5Zt5Glru5gQli6mXDRFqvcZUGpPJshY6A4rhE9tFFKWSq5LLBalKSQ3jkDFdZZKrUOgVFssIWi1GsymkmgWkUQxnhcoGsS5xbYwWha246nu3KVkHsfMkhGO6+H7HpZEyYDagul0QhTHel9Xnc4/1IlaYuMsnAIh9EYN1QZQXY8EgULEzaav/XP1MZp2XJaGG6vuP63L7EqWumzLok6zqqehF7Spuv0yTowUJk1eczbK8glKiaV7AFSOs56ai6Jx/bn6q7rPWr2JWuSOknEzBcDaQTLXYNA5x3HwXFd9r7nMts5oSKTOUKmAdjQas7a2rrIE48fVmNg2qKLy+kOq00ieLGy1LZUBsY2TWxQVUmFZDrbt6LkoKORCYs981T+v+t4g57bNxctXCJttkrQgTQoe7T7C9gTNhk8r8NhY7dHrNhlMJxwenfLp1z5FOwh563vfYvf++yBzZvGUZqfH+voG49GQ6WjEZDJClgVZHDGPYpqtFpawCHyfTBcax/M5sihotVrK0M5ntFtthCWI5lO+92f/nq/8/C/xiRdv8e1vfYc4L9l//Igsm7O2ucnuo0Nu3phy6eJ1vve97/GpT0lWVjYYjseEzQbz2aya/2oel9W8P4+KG9qZ0BVvVa2UBCElthDkuiGbkkQ1KiKOtjU6KFA60OrJWg55buht1mIN1gAPKZUwgahm8LmAoaLpLSvqCI0yVbOoBKewKCzIdf2BlFpdXqDmhjyHUFpUNkWp6aHXkM4uWgag0QLLwsISLmUJtpBYjlmQ6kqVpLXihZumfLajQAozT7OspMjLqtGToiaq51KaZ2UADLGIU4QWY7AdG8e2aLVaPP/CC3z5y1/i6rUrBEFAp9Oh2+1qmyFVVqVcUAlMtrIoCsaTMQeHhxwc7NPRyF7g+3R7PQbjEZ7rUZQlcRSR54Xeh2wkqveR5/mUZaFR1hllWbK+ucKtT/xyxWeez+ecnp5y7949dh/vcnh4yGQyYTqdMR6PSZOELFd9Rgzq2Ol08IOAJI4p84yLWxt8/gtv0Os1cT2LF198jnk0IZqe4QUO/ZU+SDg+PGF1ZZPH9w/4mTe+CkJREvb2h+RpyqWLz/HDt95iPEvwAjg7U3STzc1ttrdbUFrkEs4GI3yvQbfXx7KmbGw5hM0Grhdi2R5SCtqdvla7UXPfcVTWej6fE3hKMWf3/kMi7RAkiepkru45ZXNrk2gyZX9/n/F4gud5zGcz/p//4/+DbrfLq6+8xv3bd9jZuUB3bY3AdZlPJtgtRdk6O1aSpuvr69y6dYujg4OKjpEkKd/73ndZW1vj3t17dHtdZrMZ08mMXq9fZeqFgF67x6/8lb/GP/8X/4rJNFLzzYJM5uAocMEEm3+RD7V2tM9jpH9N8IAKUl3XVY1SHZs4zsnyVFkPoXwDAEuUeJ7HG298jvv3H/Fod0+vQb2L6u28FE+K6VQ2RStznge3VMJ1we1fsAOMPLjaB/M05523f8yNGzeIopgkSfEDn62tbabTSaUqFccxruexvr5RFSGfnJxUvYGKXpuTsymDwYgP3r/NcDQhz0vyrCAtJGlREDY6XLt2gbXNbUrhcnx2xv7uPkHY4PL1m/RXVjg5O2F0dkzLLrn7/tskkdpTFsGUBDTdvRZg1IM3W2MuUkq9lxj5c/1eMvb2d1F9eCxFkcpLHBQY6zgOoR/QCBv0+32yIqfd7dDpdHBdl69+9auMx2MePnxIp9NhZWWFjY0NpFSSsUEQqOdl25Xin2VZTGZzZrolRKfTxZlMFDgoJY1GA8e2SdKUPFM1hM1mkzzLNEtDiYxkOoNkRJmEL8izrMosmeCg3W4/UeNh+mH4vo9lWWxubpIkSUW5z/Tn1KmARqXxWUUbnjnQEEJFuvWHWz9JnQO2rGZS58MuULFl/tziM8zkMBGpQcusqhBQFZ5JvayFpf5WFkpVp6GLWizLJgg8bMshjqMlDnU9FZvnOVmRE3ounu3h+AFpllGUkjjNcIA4ipCyUB0sC1VkbKQXPyzQeAooXt2scTJl7d6NI2HSeB93GKqOGa+ycqosXWEpawZsQQ1YjMH5VKxBONBB3OLnJeqLWLjn6jPrhW2yKs6n9prqe/1mKaXSUtfBhBCK+5dnRaXoJcSCj2/QhCcyAqI2nrXz1RHts7PBEh2sLEtFP6tJ05qA7jxitOQMigXlwsxfRflQDpzQCvdL987TJ0G1KehAXQKXr1whCBvs7+2T5yXD0wHNRghlye2fvEeU5GxdvMjg7Jhep8WlnQsc7N7jnR//kLLImc/ndHp9trcvYtsWJyfHDEdDijxDAI6bM5/NCMMGpSyJsoIkjsnSVKGPUvFst7e3SdOUyXRCt9vFsx1Ojw956wdv8unPf5mLly7w8M4HRPGcJJqysr5Jmubcu/eAT3/604Rhkwf3H/GJ52/ROm1z6fIl3nv3XfP0q/t/atZIzz0TlJq5YdTUZKEymsqOqP4kwlLoIWWBJZQMn++7NJoh/V6HnYuXONgbcOfOPU2Z01K5NRtQvx4TYBiE22RCLctCaJGGKmCue+DVvRVIq0AKF4GSthWUOKLEkgIp3QXarOutbNScV70LVPBpsUDZhVXguEKn2JuEfohr+4Rhg163RavVwnZsRY20Ha2o5eL5CpAJwoBWs0UYhvT7fXw/4PRkxP37D7j/4D737t1jf2+PwWBImqVkWppVOUeLrveOY+O4CmG7cuUqn3vjc3z+jTe4cOECrucSxVGVcSjLvErtl2WJY9uKUqPrMSzLwg98Ot0Oly5dQkpJFEWkacp4PCbLMvYPDhiNxoASDFFOmqFLWtUmap6R7/uKSlVknJ4d47ouZ2dnBEHA5SsXuXHzGiabClTvNRu0kaIsy7LqQJ/nOUWaIvOIy5d2yIuU+XzKH/7BH/Llr3yZQuaMR3NWVze5euUK9+/eo8xthmcz1td2GI7HWJbFJ557GT8I+P733mRv/5Rbz0GclVy+dotms40sodVq02y0kMKhvzql1Woxm81ptPoAtNsdbL+B7Xh6zysUmatQIF2WKlUZV3cPPj0+4ezkhOFgyGQyIdVNNbMkpSwK0ljJIPc6PVqNFkGgEOsH7kMO9w/5w8M/4Mc/fod+v8/Ozg6PHj1SNWS+j21brK2tsrm5ycnRMUmkmto+fqwAnS9+8Yv0uz2OD4+4euUKg8GA0A8YDUbkWUYQBIxHI9rtNkkcs762zmde/xR/+vVvKKTecpEIClkiy1w74c+m2f+f6ljaT2vfKxaD6tVgqNtVlqYstSCAWnOWANdx+fwbn+XFF55nc2ubk9/7faJZhEYiNaC32Afr4i+G1lY/loEclvbMZV9MATEmK5JlKR988D6XL1/GcW2m05nKUHa6tFptZrOZVpeKnzi/yeiMxmP2Do6U8meinGMFGLgE7Q6bGxusrq7juB6TecLJ6RHjyZTVlVUu7FzCD0MODvaJJkMcmfLg9k9I5tNaDZsed7EA9JboUuefkb5/A04qAFOwtq5kfYMgoNVqce3aNba3txkOBvTaHZqNZgU+eJp5USDxAqVWWJYl/X6fsNmg0+tWdHcAz/XwAr8mLe8SNpoIDUIIIbQ8ecpsNqt6cQghGA4GBEFApOlNIDk5Pq4YIf1+H99xKFDBqSkul1JWwYAJAB1Nf1r2A5WPPZ1OsSwlwmRsuFFhdHTPqvF4XH1GGIZLkvAfdzxzoGFu3ETBpureFOGZTdxsJObn+qQ3wYi5EXPDZnIYZ9KqRelmgEx0hea2tVpNTo9P8T0Hy1YKLMKycF2HIPBoNEKKwqS/rSXu59LEE1AWik7juR4rq6tKVSdOiOZzijTFcx2dPRAkaayzLx8daLBkc8TS7+s/PuuDUkogVOc06CWaWrK6tsrNmzc5Pj7i/v0HmkeonLAKLZXGiRIIUauJkSXG567uy1AKTBpe/03WArVFZ+Eqp7XU52KR8TIB1LLxNWNXD1zrv6/Twc6jNobqUTeU9SDWvNYsIOOIeJ6H5ShuZF0i9eOPp9da6D/9Bx0mcAuDkFazRZ6rgGFwNiDLMrqdNsPhkJOTU86GU67euMloPOH1z3yWLJ3w47feJIkjsiQjCFpsbV6i1+txdnbCZDKtajIc28GyXRzfxwsCQt9HIGhkDYaDIWeDAaXMK3GGzc1N9vb3mc/ntFpNHNvj7t27XLv5AteuXObg0T02trbY232o6BG2zcOHD3nuuedYXV3l/v37vPDS81qVZIt333m3CuTMPFo46x81PmbcQUpBia3mqSr2wbJLHEfQbPlc2F7n0qUddi5ss7q2yspqn8D3GY8n/N//ye8uzatCy/sZVNUc56kZdXWl8wDFkzQGDVyIEmkXCFwsbGxRYpUxLU8qiqZUJtexHeWEF4I0y2j0BMKOKXKpHWoVHLiuT9jq8rd+7TdUGr7ZptVuo+ygRegHWEJUYMzx8TGTyQTXdcnyFNd1aTQaineswZosy9i6sM0nX39FbS5pyvHREfsHB7z77ruMJmNFT9QbyurKCrbjEIYBjYbi4vd7PcJGQ4+fyto0Go1qrRpVMNd1K+fKbKzGqYcFb9mgbgZBS5KEvCirQkWzritFQ6ik1c1nmPo0S8hqo+/1etX7T05OGAwGzOdz1tbWaLVaFT/a9/3q88zrDcg1n01IoolS0QFGowHdlYdkhculy9e5ePk5GkGIbdt0WjOElHz2Mz9LmqU8fnzCc594DgubRtDhU5/6HNNJwo0bL7GxsakAHSlwHU8DdJJ5FLG6voVtO4wmEe+/f4c0TfnsZz6LZxdkaURZFlVt0Xw+ZzqdECeqILff67GxtkaZ56yurLK5scna2loF3Jj9dG1tTReiL9TELl66xEsvv8xsOuV73/se3W6Po6Nj1tfXuH79GrbtcO3aNb773W/T6XS4fv06d+7cYTAY0Gw2uXbtGpZlMRqNKunL2WxGnueMRiMcx2Zv77FeVzanp6e4rsve3h6Nhsf1azvcf/iIMi7xXJssF5SUSMti0RfkP/+jbmvUTq6AUs+1uXHtKteuXiEMfDbX17h66SK3b98h01mdp41ARSnkSfn7J/wPlns+Ldu0ZQCyKAru3bvH+sYGvV6f0UjVaZh6nJWVFVUMniS62WdKluUUib5Wy2I0T/A8H8cLaQYhnU6PVquF44dYtss0SRgdnTGZzvCDkKs3brDSWyGOIg72HlFkMXk85uGD2+TpvPI1njamdXr8E36ZHuvzYyKE4Nd+7dd58cUXEELoGg3lyxZ5znQyZW1tjSAIiOOY6XRKFmc0W03G4zGNRmOpuNrYKMuyCIKA6XQKQBiGGuBUvk4cx7oLe0QQBBV1y/jUZn9SsrimJ9SiJ0eWZYzHY+JYMXeCIKDRaFQJAPV79X7zfVmWDIdDgiBASmUnoyjCdd0KaKmCRUtlrOfzeVU/Z5RlKxXYZzx+qhoN27ZJkoRms7nk9J0vjDVRlK2RFfN7E1nVI06zedQ390KWuLaoBtpo2ydpQilhMp2ogCL0cB2bssy17JZF2AgVj63IsG1TUKzqKWzsCpE21+u6Lral0mpZllJkGd1+XzVbmU31hFGcXte1sR2LKJp9+EKGOpusOhaveRqSW0MbEE9fJEikzLFs1e06CAIuXb7Mc889x81bN9jc3lITVU/e+/fv893vfo/jwxNVHCQliq67GPd6RsK2TXSrnxW1YmkT04BCOnVgYTojGx6pontQ0WKoHMXlwKE6v+ZN1oOIekFmfWyfij5rpOhpY1l3EhfZNU2t0hmN88jPhx0mW2PqjJaEC+SiYO9p12FZizF46iYpod1pEycxH3zwAbJUDpGNje+FjIoZQiiOdBpFhI7NhY0V7t39gL3d+1AWlEXJ5uY23d4qUuYMzs6wbZuV1XVV9C4Eruvx3IsvcPPmTTqdDp7tkCQJjx894htf/zrv/+Q9pXDheXS6XaI4VmhwGOA4LvM040dv/ZCvfPWrXLq4QxZN2N7eYjQaM5lMiKKIyWRCu93mwYMHlZpOo9HQhfcqI/GxR23tmMDaBBtCWDiuA0Jxv11X8rNf+hx/5a9+jVbbp9HwyfOialyX5zl//L3vsPvwEfUuupUAwrnNpv7cnvY8n7Yu6xlYgFLaSMvFkha2SHGZ88LzfX7z179KsyUppSpI932/CqxPT0/p9Dukec5wMKYsLLqdVWRpc+XKTXorr7Bz8RWieYzt+qqrsi1Uk9IyxbEdJrM5x8dHSAkrKytVQ0bVQFRnk/X69G0bpa6VU5aCvEhYWeuzsb3O8y88h+Op+qjpdMpoNCLQkttJEuM4i+LS4fCMRqOB7/uqUZTnVw2gwlAVCqpA+YSsFtiZdW0ylQZ9C4KgVh9R0mw2CbQD32q16Ha7lQMwn8/Z29tT1L84JkkSJpMJvV5XqdZpBZU4jqvg4cKFC2xvb1fr1zjXxj6oRl1UoIQ5HM+j2d7ENLXauniNX/2bl1RQlKZ4joNtWSqgFyqgK3OHIi+4c+cRL7zwGv1+H1mW3H7/XR49PGA+S/G8JlGccHJ8ShTFtFsd5SgUgn/7L/8VQgg++9nPEjRafPNbf0TYbJPnGVIjmaenpxwfH3Pr1i0dmCkedjSd4SBotzvMNdBiGurO53PW19eVYEaa6uDM5e7duypQ6nTI85zd3V1u3LiBlJJr167ieR5vvvkm7XYbKXN+4Rd+nocPH/Dt73wLpGQ8GbO2ulYJpTze3WU2m+E4Du12m9l8TjSfk+cFWZZrlDbG933SVDUSLdOMnZ0Ner0O7773AZNpTFlINZ6leML214+ngn1/gY7zINtSRhW1h7iOzSdffZUb169RFgXDwRmz2Zw3PvM6R/v7TKYzCqlonOg96XyWv75PngfyFvuvXHrN4m+ChbDK8ngeHhwwm0Vsbm6QZRlRNCdNEzzPxfUDGu0OvZVVLFt3lC8V/7u0bITj4vuBtrl25WgPpxGjyTFpmtJoNrl67TqdThsp4fT4kCSaY1EwPDng5GAXigSLAsSTGZv6uJ73capnwLKdN3vAlatX+dznPlsBKybLaYKEZqtFo9nE81yiOAYhaDSbuK5Lp9utnPM8zyvH3yD+URRVmYzZbKbtUY+yVDav3+/T7XYrhoVx7E1G1dgoldG1GY1GVQG5yfAqQQwV2I1GI6bTaQXACKF66jSbqo7rfNADC1EkKeVSZ/OTk5PKbpi93VCdDeW20Wg80/z/KahTamNotVpLi9ykYswkXmpWU1tMZsDqxeEmS2EcviookSzd0ELnXVFz+v0u/8Xf+00GZwNkUfLtb3+H995+l6IsaTTCqgeHksUsyPJ0IcvLIvo3fOF+t6cq6aUkTWOGZ2eMJ1PKIkdI44wrorgKfLKqIdLTAo2nxBlLf+OptBFdvCWXnemFsRB0ex12dnZ45ZVXuHnzJqurq7oIUJ0wy3KC0OPipW02Nld5+ZUXmU9jDg+OePTwEWeDM2azGUVeKJ5ulpKlKshLs1TJpaGLL0u1CItyoeusnrGFtM41nxNoFS5Quv5Py/As1MUqgydVA8T6fZ7fQOqBofnZBJ6ObVGUiwClPpbnHceniQDUaVD11z4toyKl4srXFXPq7zHfP81RVYj8UzYbTU9pNBrEUcx0rtReJtMJnh/gOB4vvPQy8zThytXrlCVsrG9AnvPw3j2KLCNLItrtLv1+D4Rkf2+P0WhIs9lUqlNhyIWdi3zhC19gZXNVUfZK1W+mJSVr6+t84sUX+eM//Ld859vfoShLkjRlZW2V0Vj18ui0Org2HDx+xOjslJ2LOzx8cA838GkZBbg85+zsjGvXFD3l8PCI9c0VXNdV9zSeLKfynhgjPZ5oeWC5oDGZ4j6lZlbgejYr3TZ/52/9Cp/5zCuEgUOJqjeRRYElwbZdfMfjU699kj/8w+8TJ8ty0AbROT9XnhZ81IPKp/28fDgI6eJaCS13ytd+7mX+2i+/QruVUJYJpVRqbcJSzTvLsqTT7JCWJcdnQ4SIWV1ZI4pG5BkcHd5jNLbo9bfJM4ssigiaDZrtBkKAZ3sIqbKWjVYLx3Ho9Lr6Pu3K1qVpWlG1TB8aRys9+WFQFQueDQcMh0Mcx6nRZJRqU6vVQgil4KccJYtHj3bZ2dkhilKENefhw4esrq5W4+w4jgqkasoqJnttxs/Qos53mR2OxlU20mQojBNg2zbb29vVGjWbrpSqaZZ5jHXVHWN/6rK3Zr8y+5uxw0mSaLRfZQSn06i61tlMddVVP/vIoiSKUlyn5ML2Rf717/8rVvorxEnMiy+8wo/eeoft7W1GoxHf//73abV6pEnGnTt3mc+UaMl8FvHtb36Hq9eu0WiEXLt6jXv37vHHf/THKlNw9Rp3b9+hLHKazQZHBwekaUq73ebb3/ympuUotsHm+gZFmnH50iWKPOfx48cqI9VoMJvN2NzcZGdnh8FgwNtvv83W1nY1Vm+//XaVmcqyjJdeepHvfOc7Gt1s8slPvoaUkrfe+iH7B/vM5zMsy9J9O6LqmZ+cHpNlGSsrKwxHA13royg57XaL0Wik15dHWRaEoY9leRRFDlLw2qsv88Hte+wfHiMsB5mWSNuq6G7/uR8mAJBSgixxHYvnbt7g5o3rCAGuY5ElCTYloWvzqdde5k+//i3twFuqZsx60g5VfgRP+iYV4FYbvmUbpkHZp4EplsV0OmY2m7C+vk4Q+EynU4oiYx4n2F64pEpWHZ6gzDOSXPmIaVJUmTvHD9jY3KLVVGBFnqWcnRyRRDGuBXk04eDxA+LZGEsUKrPFMjuivr8vavSW/2YEEeqHsQW9Xo9f+Pmf14GQyrgan3Q2m9FfWQEgzhJG0zECQW+1rzKyllVlAnzfZzJRamqrq6u6CasChOu+rMomLsAV44Mam2iyC91ul1AXhZtu3SBpt9uVnTKgv7KlVIGDoTSZtXj58mUmk0kFwPm+X9FDzTw02WYTcMznc7rdLmVZEsdxFajUqX/mHp/l+Cka9qkHs7KygpSS0Wi0FDgYpKqe2j7frM5MALN5mAd6XlWhTs2qT9pOu0233+Pg8JB2u0W/20UIuHLlItFf/UXu39/l8pVr/Jt/828pypyiKCkLVZxlikvN55lz53mOazv83d/4TaIk5o/+6N8xHI/J0lQ1i6voP6aw3apSzybQ+PM4VApVBRQG7bctm9XVVS5evMhLLz3H5as7NBuqf4KiXuRIWYAlKMpFpqgoS7I0VRmgIufmzRs899wtoiiqgjZTODkejzk7O6s4eQq1y4gmMRPNyTs9PdN86JTpdLZkJM051bMukdQd+oU6jUQxXgyH0HVd4iSu3ns+yDALxff9asNXPMakuocsyzFFWmaOfljmoF50bFAAMwfrkoTnHU3zeaJm2D+KQnP+kJLKUX7i/vTIrKysVKhIURTEUUyr1cJvNFjd3uRLr7xKnud87zvf5bVXX2U2mbD7YBdV7yzp9dpKInN/j+HpkVL/cRXSdOnyNb76c39JGSSrIM9SPVaqGZGiHAr+8l/5K7Q7Hd566y2kpWp0mp02Z6enBH4Dx3WIp1Me3r/Ly6+8StBskunnaOSUB4MB165do9FocHp6ypVrF2k2m+xcvMi777yzxCuuO+3nVgImg2FmjnoGIGUOVsnFi9v8t//NP+TShQ0oUzzbJkpyirzEwmM6mqEaJkl6rXUuXbzM7bsPlmqNzNdPo9P/YRnMZRpEjmulbK4Ifv1v/iyf/8wOthgjdTbWcgKQOTJfKOElUURphcwmAtfukmcesrSZTqa0GjCdH/Dd7/x7+isXGY1Tdi5f4YK/Q0GOtAWe4ynlEP0MoiiukCYppcrwlkoZyNXOfJ4rgCGKYmbzGbu7u+zsXKTb67GxsYFl2ZW++wIckiRxguO6eJ6PJRysdYdud0VTtTKef/75yu6bjPEbn/tcpUhkVN+CIFiixJoN12yunuexvrGJlDUAimVOurHhZvyN/bK0TVDd15MqqDEBi6EWmD3N0LkAWq2WygpEUQVYGX5oURTMxlNcz2FveKaV8jziuWq4lacZg7MBH3zwPu1Wiw/u3CZJE77yla9yenrC0dExd+7c4ebNG9y7d4e9vcfEccJLL71CkRe0WwEnR3ukWcZwNKLZaCCLnIO9x6ytrdHvtBUQVOSErSbzaI5Asr62qlDmOKbfX2E2mfLeu+8ym0zodrrcvHmT73z3u8zmcyaTiZYlnfDgwQO++93v0e2qwPRnf/Zneemll6qM1GQypihzXv/0p7h9+zYXL+1wcLDHYDDg6PgI27YoipzZLKbZDIki5biEYcjzz39CNyKLK8dqPp/jtXx8P6CUhfrZdwGF/DaCANd3FX8/bHDx4kXev/0Bb/3obUoc0mxBvT5vR/5zOxaBr0UYBLz4wie4dvUqOl9BmsREsxmuLZiMzrhy6SIPLu5y78GeIkyXJXbFH1gOKs6PSX2/Ur0mrKe+zvzuqfunAIXpSY6ODkEoh7bVbOGGHnGaYts2UZIq6rtt4Xk+YRAQhg1ASdp7ro9tuziOajqbZRnRfM50eEaRp3iOjSgTHj+4TzwdQpHiC0mBpABK4WCzAHINIPhh+3f9e5PRhQXY/Df+xt/gl3/5lxmNz7B1sX79/qezKaX2RTJtu6bzGRsbGwwHg2oPNLSjZrNJGIYAVV8RY+NMtsD3gyqDamhN5j6iKMJxHAU+xjGTyQTLMtelsrcmG26k/FX2xK/88UajUdkzy7LY29tboj4Z6rAJHBzHUZmbZhMpZVVzYvwy46+bLyEUXbOh1aqe5XjmQMPUV5ydnQELWUMziQ3PzDh9eZ4vFQ3DInVXVzkwEZIx+gptDFntr3JyclL9zch/nZ6eKq6xRkjSNMW2LK5dv8ZLL79KnquiqvX1dd7+8dvs7j7GstAZDbEkoWocTtuB4+ND/pvf/m1+4Wtf45/8k3/KH/3xH5MXpUrTycV9lHKhFLU0ic2GpBcj9VJgg5TWnG79TpRhEdVCcF2PtbU1Xn75JW7dvMXa2hrb29sUMuFscKxlGqNqvJRD6REnqhgvSzPSLKXIc07PzkjnOZub2whgqHmzeZ5XkXaWZbiuS6/Xq/jUcRxTdArcq1cByHRwEEWR4hTGEa6jxhEhSPQGb9s2YTNQyGWzSRCGrK6u0um0cT2f9Y0N3nzzTf7pP/2nfPaznyXPc771rW9Vk9nMD8/z6PW6rKysqoJkz0NKydHREffv38f3fU5PTyu6lnkGJph4GgJd/3Idm1aziUDgOi6mQP2jDonOQMhl2U8AacnqVU9957kAY4Heq4BxfX2diU6VqpSpWlOFgGangxf4TM5mSAHNdoOH9x4RzyOKrCAMAsqiYDodcTYYkMYxjbCni/Y6/MwXf4Zms6XVUEqEbamGQEIghZKKztOUeTTnc59/g5PTEwaDIVIWdHtdzk7PKIoS11GbzcH+Pq998jVWVld5+OABXd+vuoQOBoNqbp2enmJZNrbj0ul0Fvd9bpyXA0Oj0AKmzrr+cklBkacEgcvZ2Snjs2Pi+ZQ4mjEcjkjTnMl4ysnJGXGcUBZK0OFwNMVQ34Qlqmf4Yc/8fGbj/HXWk/FSKJ0qIcC2wLVzblxp8V/8+he5ftnBkieIUpJnNsKxyaXabMy8nc6mlIUkLVUjqNHwjFIOCIMmaRZxdLzL9s5LDIfH/MwXf45Od5sCh1JIpCixpEWRlWRZgeeFrKyojrTD0ZjpdAJQpdlns5l2NFsVwKM2uoS1tU1sW8lW25aL7ThkaY5tCfwgqOw1baU4CCoA6PW0QIKWBTaZB5MpKMuSJI5ZW1lFWKKqTTHOf0U70KCBCbalyXoXBXlR4Hsecy17m+c5rqdoualWTpNoZyDNmE7GlGVR2bMsywiDkJlG3x3HqbJwoIILg/h5nsfe3h6+7xNFESsrKwgE09EUx7HwfBcpc+Jkxt7eY5qtFlIKdR15QTSbcXy8j+ftEEUzZvOY73//TTqdDoPBgHZbIYPz2YRuK2S112F0dsRKf5ULVy7y8OEjjs5OGI7HHO4/ptls0mq1SeM5J+MxCCjKkrOzU23z1DgrGlTIfDpXSHOeM5tM+dxnP8vB3j4bm5tMJhNOTk74vd/7PV599VXeffddwjDk5s0bNJstjo4OkRK2t7coCqVONZtPGAzOyLKUb33rG6Rpqil5QtVB5nmlumM6Q4/HY6W9r52sLM0q8ZQsU8+r3+8hhGpu1u12MHtmHKd4vqea5uYJt25eY22tx3fe/DF7e0dY1qKo1ohCKE3qxcJ8cpX+pz/q+1I9U9rpdHjjc6/TaTWJojll4RB4Ho7r0Ot1GZ6eUdiS4fiQTruN67mUWVn1qTqP0zwtS7vEpZfyIwdkuS5SgT4mz6z211JtBFKSZSmnZ6c4fsTK2ha9fo8iL0jShCROSNMEObVotds4jgsIyiJTwIqU5GmOlODaFjKLiaZjHh4dEs1neDLFKjOENCJDAolNqSQ2zM1UykvVtUG1dyzNActCSNO5XtmlTqfNreduMhiekWUxo9GoYom4rqNAc9si0T7SbDrTAZTHyckJrrOQ5DZg+3AwJMtylQ3p97Qj7+J5blXjIYTF6elZ5Ts7jjqXAesty6rWkm3bVe2kaoqt7ON4PK7qonzfJ0kSTWtUSYDZbKbkdrW9O9/bxcwJA/IYoKde39FoNJhOp4uu5Xq/MD1zjMLVsxw/hbztgpd+nqYiSyhy1Z1RvabEsT0EVsWhN9K1YJHnRn61oCgkQiwyG0IoidDT09PqZk3hTJqmVc2GZVnqnMIiywts16Og4HRwQrvb4Atf/Ayvf+ZVJpMxBwcHnA3OuHbtasUzA6oGJ1JmnByf8P/6Z/8jv/xXf5Xf+i//Lt/6zjeYz2Nyg5IjWMjU2ugKdG3VVDZCCk35kFQOnclU2LaNJZX8ne04uJ6LY9vYtuJSC0uw2uty+eI2mxubdLvKOTs9PiSajcnKnGmkkNrpbIrU0W8QhjTDEMtSBfFmnGzHphm0aPmCNI5odzpcu3JZp7AF3W6XRrNVdfcEqkIfy7LwLJs4UipbSZIQ6e/H4zGTyZT5fF5L8QXYts3a+hpBK6DdbivVG8+veJFpkpFGGYOTY7Y31vnNX/s7pGnG3fffJ2w1sDUnfGV1VRdoBriOq1LFKE5+2AjwfIew4eNObNIio8gX2QgT+dcNuslaGEfJti1826LXbOAKGwebnBzdJx3TQq0+v0H3CZGoTFMtihdCWbWyzBZZnXN1I0+j5qhAxUJaNlGakUuQUhDNE2ShOhv7tksgLHwEZRzTboQgJKPBCRQZZZnj+22yLOf09IxoNtOStDPCMOSlF59jdaUFVgZliWNZSGkhbUFWlhSotL3j2JoqB6998pP8wR/8Aa7rK3qN45Ekc4JASQqPJ6qh1+pqn4d370DhkKUZtmUzjyKyIscNfA6OD8lKQSlsojSnKFWGC9OhXSyPsRoPAAUgLOoyBGWpnfxS4Fk+D+495v/yf/4foCyxhU2RK7Tetm0ajQbNZotud53NzQ1c1yPohuzuP+ZP/uRPSbMYyw80DUtisch01QPI8zS3+s8WEiEKMulTSh/bBk9ENL2IL7y+za/8lRdoNTOKaEYhM9XVVUhknlMWOdIqKShIspzxLCJJStIkZzhImc9z4iTFdUvCRgu8JrLs8dKLnyKalwRhjuM5CGxsy0OUJba3UGEyRXoqSO8tFf8KYdPvryClqq+SpaJE5HlWzWnLsrAE5JqiY5poOo6lNnUBJWrO2I7afGypgJ8gVNkAAZS1LIRnu8SzBNexyUWKY9uURU6aJsqa2kq5LaqhdZZlMRlPyIuC2UzJ0F68eJE8V6IFiUWF2k2n08qhOjs7q75XdShqPZ5J9frh8IyiKJhOp9WGqzZbm+HZkPX1NXq9Pnt7j5XDHs8Jg4But4fnucymU8qyoN/u4e7YnJyqOpXt9W2yPGf30SMczycvJa+//hnGkwnr62vMZjOyLCHLMnzfxrYEeSkZjgZE85g7d+6wtbVNluU8ePgQUPtot9shzxNtX2AyneoC/R6z2YzRaFQBTsiCk+NDhLAYj0c0m02+8+Z3+MIXfoYXXnwRx3VZ21jnT/7kT+iv9fnaL/0CrWaL2XjCdDLi4OCAvb09XnnlFfI85+Bgj1k0IdWUCkuUNBs+8/mUdruN41g0wpaiOyHpdBQtbqXXJ0ty5llEf2WF+UyhvXmQI4SF5/oMh0O67R6lLHEdhzTOWF3tgigrKdDpdEI8G9NuBPzcz36B2/ce8NZbbzOXJVluKIAlyBgl52qdCzIWiP9fhKNu+13Xpd1u88Lzz9MIAtJ4ThrHTMcpWZqSF8q3SLKSNCsoUf1+mq02mWaTmLozeBIoe1qwYds2wl6MiWEcmIw7UiBlpj9XUBS1onFpQWlh4WjQTe2UjgCZ5ZzuP2J4tEcYavsbNlTmIgyINaXIth3QAWKapRRxQjSd6MA00tdRYEuQQlDggDDKmha2AEuCEAtkvSjyc/tHhQpjsuFqDEosLH1vEtuBT3/mVZ577jLjyZiiyOl02sznUx48eEC326XX62vkvonlWoR+CAKm4ymbm5sUeg8WAqIoZjSc4ro+vi+wbY8sy3XPmRIpFShQFBIoCMOwEiQRQlTBgnHuNzc3q+yv8Wfm85j5fM7W1haeZ9PvrxKGYRXcz+dzZlpKfn19nTzPGQwGVYBggH0TJKg17FQZlSiKaLeVAI25HqBqimoyJuPxmMDXGel00QD7o46fOqNx/qssVOGPQbIU0kD1kOsos0G4TArdLIA6hcGkbqSWXzUDXefT1xWqVETocnh4RH+lR3+lx3gyQiIJGz69/kU2NterSLDORRNC6OI62FjbYD6P+ee/8zu8+sqn+PSnPs03vvFNFf1KEzDYlFKSFaoAECkqrr9xZj3PU1GeUP03mo0GvU5XRafCwvU8LE85Z47rVNdfFDmdZoMsjimLnOFwWDU7ynOXQpY0tATh9vaFSo3FcRyajYBGGColiH4fr9ZdVwih0m1BsNQJXI21Ml71Z2KoBp5lsbLSV1G9XqyqgZ6jxz/HdVxKKYnmcyRgu06l6W/Sc6YoFJETJwkrq6sEYcitW7dY39jgzt07fPmrX6Hd7fCP//E/ZjweV9edazWwNE3pdru6UaCojKZKAS/qg4AqQ2Yi9fqcE0KpYjUbPu1mE99rVP0xKipN+XSOfr1w3WTt6gi3AutNkPG0Yv7FsTB+qglZFEV0V1aI45TZRKGutqUaIgoJZZ4z013ry7JkNptCjaI2HAwZDYdqLUllMPIs5fr1a1TNVzCNMC1KIPA88txSTcyKAksI0jhmZ3sb3/WYzWa02x0c2yJL4kXKVFNKmprH/cHt2xwdHbG9c4EyUfciLIv5PCIrShzHo9vtaWdycf9VDug84lZlgOoUKv3shIPjWLRbDT7/uddVkGQ5NEKlHvTSSy9y4+ZNxSH2fWzHYTabkciEhw8f8sMf/oCzgeqS6liKz5/lOZYllmxVvXiyTrmrnp0QyMJC9U8BIeas9kv+6i+8zhuf2sTimDRXaKsSWbARQtHU8jynkJDlFtO5ZDCU7O2PmU0k41GC6wW4XkCr3WN94ypf+MIXuXz1JZLM1g7kBMuJsV2PIGggNJUGFNDg+V517ZVyirZPvq8Cf8uysTACDiBshWhlea7q6hwbT6NbJsNU5AuFNsdeiGoYecY0SXBdu3qd53kMhkqasUgyitSoSyk6kmUv1pzjuDSbTcoiZzpJdMFwxv7eHsJSXacHZ6cgSxqNhqbowHw+YzAY0O12mc8jwjCoaFBKclNJ5kopabc7xHGE57nMZ1OyNMGxVYO7JE2YTmJW+j1sCybjIVubG0SddqUEs/f4EWVZ0u12SdOU0WhEFEWcnJzSbLeJ5qrPh+JpK7nINM25f/8Bh4eH3Lx5vdKvPzk9Ic8Sut12ZcuSJOHNN98kzwtKbO2kOEwmYy5c2AahqLtSShqNkCxTtKT19TWNYE5phIsO3Z7nMhwOOTg44M/+7E/JS0meF1y6dJG//bf/Fu9/8BP294cMzs5Io4T5PGI6neL7Pj/60Vt4nstkMqbZCtQeqYMeFdhY6nyNJtPJpApuhRDMpsrZmk0Vw2Hv8V5lz43ijZQlqXZQXNel2VTUmv39x/T6PSxLOZC9Xk/TfR0m0ymvPH8Tm4J793c5PR0yjxJsW1AUaDVESSn5yFqw/1SHuX/jVK6urhIEAUfHx5we7yuUXmj1TJORR1GFSkRV02rZSmbatBr4sH3mwwCT+t/P/4xQVNxKzltoyX3ttC/q5hRgRwXQFFiWeu98OmU6nlRBkLQEpc5U27alM9S6yXJp9iY0qKQ+S+f6kRU4bYBeiaGxK6VMk9F6lgegBTGKAtsWfOmLX+Sv//VfIUkUmH06H9BuhzrDd1OBMZbA9wOKotT8lJLAD7CtNqqWRZLrOuBer6vYNCWcnZ3oJsMtjo9PKqZPo9HAcRwmk0nlx8ZxXLFLTD2clJLxeFz5v2maVgp+Ozs7mtY4qWrapFTdwk32ttfrVbdtCrkNDbbT6VAURVWHZYJeI75h/HLf96uidqCqj4vjmHa7XQlnnK+r+7DjpyoGr2+80+m0ulig0iZfopSUqqmScW4NP950wzwffJijKFQBsioQylSaLcs0ug2FpmV1Oh3W1tY4OjoiDAKKPOfR4QFhGLK+tsZ8PudEU2zSRPFoW+22UmEqZYV+9ZptRuMxw+GY09Mhv/v//j+ytbVNr9lhFs8wbHrHsVlbW6fVbCKBsBlUk8c4KsPhkF63QyP0SBOF3gWeT6MR4toOzU6bZq9Lt9cl8AMCnQ2whEUzbOA57pLWvOEsO56LFAs03aB+lkplYNuqxsLUyJgAQw901ZQljiKKsiAIQlzHqya3OYwxnE4Vl9dy7FpQloNUdCXLcUhypTwgdDMwyzYKXRa27ZCmShdaFZd6NFttclly7eYNDk9PWN/e4u/85q8TzVX/hm63y3Q6XQocDG/RBHAmoPN9n3kULwrqWPBezZyqF5yaTJzrevT7fTY2VpnHud7UFPXivGGuBxqqsY9YGqPK+bQ+QlXqY9eVRb/fx3Zd4ijRhlsFSkdHR9y9e5cvfvlnCZuN6r7ieHHfJrByXXeJT+95HmGouKCl3hCKPK9oemmuEOU0zSjLgmg20QGBxerKCg8fPCBN0goTVJkwtdGkaUqj1UIimUynJFlKqos04ygGAblWOnNrCl+y1nSr2kzPIW8fPk7CkAzp9/v86t/4FS7tbLG2ukojaGC5LkjBPJqT5zmTeUyWK8M7nU1oNhr8pa98hf/v7/wLykIibQsLi7xU0oHnqXv1rG19jqkN2cayHN0luqDbtvnbf/0LvHirQymHSOFq594l11xqI7Iwm6UMhzHzucV87vPgwYjTkwTb8XH9NnFm0XXXuHj5U9y69SLt7k2CxhoBkiwvcD2PopRYtoORxCz1dXm+p4Nllb3Sk1VlL6Qk15uN67pYUlFw0jTF9zykEFpTQjA4PSUMw6VaBsuylB0uSqLoSHHqm02kno9JEpOnCXGccHJywvr6GtPpDNu2CPyQwPWJIlVjlaSx+n2gbI8pgDSSuIv0/7RC64Mg4O7dU0CSJClSFpXi1ePHu5peoIoTjURkp9Mhy1IdOJbkeUaaRUq8RBbkRUqSquDb8xzeeuuHbG5uVjLYRqXF7FmdTofDw/2q8PzRoweMJ1MuuErfXtHQImxb0Ot1OTo64eLFi4RhwNtvv4NlQX+lX+2fk8mINE1pNTsamQyZzSIohbZ1qnfKfD6n2WpUtRNHR0f0+33tvKmC1kajQZGD7wdVMf94PK6acP7z3/kdpFSF2G98/nPcvv0+SRIBqrGX67gIIfF9V2dKBvT63aWGX8b5MaDUaDSq9v35fE6WZUwmE1qtDmmSV5Kapp5T7UcleZHj6OBWypwoUv0ZXP3aBbVD0Ol0iaOI9ZUe89mMW9evsL2xzmwe88Htuzx8+IgotckKA/L8xQsyYOHrtNtt2u02oMYsz3MoVENLQwU2+1hZluSl1Grey7WuyiZ9/HmNz/Wk8tST9G8DANVfs7DJJYh6Fbl+r1DZUSGkBqNU9sHQf1XWWXM+8oXdtw2YJFTmrtQ9REzgIEVZZSX0CauxUVmMcun6P2zMl+w26toajQa/+qt/nevXb3F6ekwQ+IRhEyFUM0Xfh7OzgaJNCgGUlc96cnJSqTjF8Rw/8MiyjEaYISWsrq4xjyaVah8s6kEeP35cMUiM82/s1HA4ZDQaVXQnU3thlPlMfyvT26LX61UgkqklM8/Z9OIIgqACN4IgqAIKy1Ly04aa5bpuVTsrhGBra4vpdEq/369EG+oF4Y7rMtc+2dnBwcdPQn7KQMNQjU5OTphOp5qftaAUwWJTqtNZzKIxjpLhzppNwTiRZlCzLMN3Pd0NVm0+s9mMVqtFAVX6vN1qUeQ5qysrtNttDg/32drcUghRnDAZTyi12oHr+kzGU1I35fDgqNIPnk6m7MWPmU8j0jRDYNEMQxpByKd//nXm6Zw4igjCgJX+Cp1uB0tY5EVOKSTrGxvs7OzgeV6lqPLwwT2imeL7WQilApLnNMMGtu+R22hOnEeaqqZJruviOT62cLA0PUelq3QBu6X09k3AUK9xKbIUUCoGrVariopHoxHNjtqo4jgGSxA0F5GsKMVS0Y/Rki/Lkkaoei3ESUyaKRlE23E0j1pxChHQarf0c1U1DIbCoaTiGjooCCmlet/x2SlpkTOL5jieS7vbpd3pLPEAzbwx//q+z8HBAevr63iex4svvsgHH3zAaDLF1s0hzdwzh5k3QMVBBLXRrq+vsLaxwnye4/kuYkoNMVmknet8VYWoL4qijPF4mrE77zg/4ahWf1OIfVmUFElaPWtDN3z8+DFRHPH7v//7/Nwv/DyBzg7Zjr2UDTRSdkmSIIXqJtrr9UCqMUmylOPjY8o8p6E/I80yJXggFL+7yBJWej0cS+B7LqPBgHgeKTqduUepKDEAvudh2TZrm+ukeVbdX67500ipO9AqGo5lWZRC0QHqGY36ZnB+jMzv6uOY5wWNRsjzn3iOwLeJ4xnDwSm26yunXhtOKSWFLAgaAUHgIxH8nb/9a/zhH/4Jo/Fc0dNsQ51c2KdWq0Wv16tQazOX61kxhMR2wRKS0LfptRp8889+yN13HFZXGnRWFOIThL5G8ZTSShRJphOPk+OIs7OZLpBu4Hkr2L6F4wlKaTNLJN/49g958607tJodLl3Z5pd/+S+zs7ODFELTmNTcLvQ9q3mkAv9cP6MkSUCjXWmmmrmNx2N8P8DRdtkUAVaKKEVBmiQMBwMePnzI1tZ25QDZtk2SJlVR4+HBHnlR0O12GQ2HuI6tnVFJkWd4nkMSJ5xOplBCEPicnp3SajUYDseV6kmaprRarQo9M4CJ6zo0mqFu8CUIG0oT/sLalmpWJ6XOdnZUFm02I4qjKqtycLCv1LSyVDvSkKSJooSVi67hSRLTaXe0TK9bzR9zn8b5GY/H7O3t6ZoG1ZvE9Tx1jVnO6dkJjbBBoxHSaje5c+cuRaGCbVWgGWMJwepqnzxNKcuc05NT5rOYCxd2WF/fII53GY3HOK5Hu60kNcMwwA88yjKoghzTHyVNUzY2NhSldawKSXd2dtjd3WVlZYU4jivqcZalpGnEj3/0QzxfScMD2JbaS4+Pj4mTCNu26HY7lEVBUZT0ej2Ojo6qWjnTRTjXe6sBNoxwB1i4Tl6pURqHqNfrsb//mDSLtXJRUFHljMyuUQhq6MLUJE5xHBebEtcShM0maRTRXO1zcednODg85ie373Pv4S5TLf+qe17+VKypjwOJPs6pfZbPtywlM2ykS83vRamouWYfNecTAkohK/ri+esQwv7Q666zSM73KzP7xtPuqa5Y9eRnq0BOxQ/1ruNllQGQEoSlaK5lWWKJEkvIhY8oQUhVWyKFjZSKyqSyGVJ/bwKOJ/cBcw8my/3EPdR+PJ+xMRS/69ev869//1/z4MEDzk5P6XQ6vPDCS+T5hHa7o6/bYT5TGTPHVZTsMAh59GhXS9L2CEMFFI+GQ23HEs7OTlBNpcsqW+B5KhgxtH2zFg4ODqrMgakXPj09xXEcrly5UgX0k8mE4XBY1doJIdjb26PT6bC6uqoYEd0uWZZx8eJFTk9PaTabFaXUZDuMZLfJVIRhSBwrOpZplmpEcubzeRWgmNeZ8c/zvKI/d/v9p86/88dPFWgAleHY3t7WKHdRaeqeV+MxTmeapjQajQUyVi5kTuvV+MaB6/f6dJotXQ8wptPv0223CcMG7Xab8WRMt9NV/E7XpdPusLe/x2Q8wXMckiRlMpkoBZ8kJk0Sdnf32X38mMe7j3Fdl5WVFW7cvMHqyirrK+tsrG8qdLTRwHEUf9L1XFWKUXM4zb0JzbGVUCmZGKRhbW0Fi4LjoyNaWp2n0+1Q5oWSi9UZC4O2VR1vLUGinb/JZKIeLiqDk6YpiR5H1fnXqzh2jm2RxBFHR0dcuHBBOdV6kqdJStho6KJ3Xaivo9wiL6rnZjaRqtu7pZ6fFwSqN0mWkWUKBS/zrOJNR1GEbdk0W01VIC5s0jTBdb0KdYiiGEUjcRidqYLl9bU15tOZGmPLwm00WF1d5e7du0u0OLOxGRWGMAz57d/+bX7v936Pg6NjJpPpEn/w/Hw1c9ZkNxTya+F5FhJPEXQsgajoOk/O+SrzJsvKUa4fKs39pKb5hx31v0mp0q95LgkbIbPJrAp4PM+rjIVBFRzbJgzCpSBnY2MDx3E4ODggbCrOplLJyPAJdGbBRQrwtHPRDDtLDRJtUeK6Dp7nkCaqC60s1e8MYmICIMdxNLc/59KVK7iux2g41MW5ioduQdUVej5T+vmWzqYgnt4r5mkb3xPcYxRd5/HeHvF8iu+5tJptnNwibDSxbYs0Tiv+a5bkZHHOaDzh8PCYZqPFeDSlzFOFtIkFPcDYtnqhnLkGY7fUuEsaDYtXXn6Z1V4fIQt8G7J4xnSekBQOJ6eqO3YpMyWTbYEsbWTZw7bX6a84JGmmqYs5WAWZzBEl5LqOKk5nTOcT/IZNp7dCmhe89+Mf02m1WF1RFEnHcYn1JqF4vIumSwZhdl236jVRFAW+7ndhRjuKIprNZmXHxuNJdf/37t6t0vfT6ZTJbFKl2M1GajKgvudWhcEPHijaTq/XI/BDiqwwACZCNOj1umxsrOmA4FD1SUrimga9Q5YnHB0p3fjJRIEH/X6fk5NDiqLUFKmIra1NynJBNzDASaerQBbbsSogSHHBJWGoHOV2u8lsNsN1HS7sbBH4AVGsAuw4ivED011XKbbMoyl7e7u0Ws/R6bYYjScMBqe02x02NzcoikJv4gGdTofRaMrKSl/vjUoGXErY2NzEtmBra4ujwxOyLGc0Gleg0PDwiH6/S57nbGysEUVzXM+ptPhNE0bf99nf36/EOEzB98nJScXF/uD9DxBAEITksmA+nZBEKqOU5zleEHB6dkLYCCpVKoTU748rPrcJSlWQllcBx3kqdJFL+v0+g8GgcqwMmPjCCy8ym09wHZe8KAjDoKqzC/yw8gOODo+rzJQQAldF0kymM2zX4fjkHrbjkuaqUPfChQuMRmPG0xlplpFmSoWOJ836n/vxrEHI0v5a/z3GHgKVEmu5FC19mG38qHPXbafxYRaO+pP7G1DRg81rl2mjy/ZyQXGVIEx0J1TwIFD0IbloFLx0lFLL1epAXhf1m71UBSZPp32ZsXqC+lV9v3idAfmUb6n+8M4773L79m2+/vVvIqXE831u3vgBvV6XTqdLEChlNNd1WF1dJU0VvSkvCgLfpywE9+/v4nse3Z7A85rYliCKEmaziEB3C8+yfKnhnRCC2WyG7/vs7u7SbreXfJzV1dWqdsP05DDKVQb8GA6HNBoN1aXc9yuQZjKZMBgMKoBaMRpC5vM5o9GIru73YVguBuQxPrtRlDVCC0EQVAGxoXeZruFSShzXBUsQ6zqOjzueOdAwFyClrHhZSmrUUahlnlWRs6FKGAUjWChNLSgsynCbjEaapjSbTeVIhw2mozEr/T6XdnZIs4zj42NOT05U90zHxdfvmY4nHB0ccnh4iO97PJpOq2ZO0+lURZNphrAcXnvlNX7pF3+JV199lX6/TxAoaonn+eSFoh/lRYbQnMiyzEFKhFB8wLwoVKMwz1XpwWKh3+y6TjXxbdtBYrF96bJS+NGZG+HYtBohUuvXW5ZFqXt0mHGUDTXGjWZzqbjZTEgTzBi0yFCnGmFQbTpXrlypnoO0ROWIz2rKRkII8kSpsZhMQh2ZktYCMS/LEtfzcFyX2XxWNfIqigKEICtyRuMxlrAosqLagGDBFW8329jCouEHFEnKWm+F+XjC6uoqrutRyJL1jY1akdeimNRkNYxMXBRFfOlLX+L/889+hzhOKufqo9AdsxFmmaJduK6lCs10jYcEpUzxFBjM1kX7spAYZRzzuaCM80dtZnU06mnofbPR5HQ0JAwtXMfRRWMFFy5cYH19nU9++nWa7RYHh4eKPtEIl5w827ZZX19XQgBZWtEUxuMJzVYL3/dVozJZUmrKXT31LKVU8oVlgePYHOzv4zo2zWaIbS26hApZ4jhulX3MNfUmL5UykBCC8WjMfDrViucKmVJqQWqcykI50fWMxrMfshJQ6LR79Ns9JpMpnfY6jq2yFkkUMzib8ujRLvfu3ePevXvs7x8yHA4ZDAdESYTvexRlgefb5KUqNjdUxCRJmM1m1Zwx6804757nsbbS58rOFp7jMJ1NyLMcKQVZqiSDJRFIRRERSGxH9aEwGvjNZhvX8cnzFCEKLFv1rbGFT6mRW8txiJMY33f55V/5a7h+yDyacefOHfqdNo3gBU5nU1QTQ5fjk2POTs9otprYOvOT5xmWZTOZKAEHY7td1yGeR0ynirLSarc4PTlWvRjSHMfxiHTn7izL6K/0q7nWaSt0rNttE0cxQejT6/YY+q7qYYJkPlPB/9rqCkVeMJ9NEcLG06DC6ekJrqfW0Gw210GM4RwLpTgEBIFC9VUzKqmuK5rpuZ4wGg0rmUcpJdvbWxWC39T2MwiUHZpOZ7r4XGJZqi4kDG3ttIe4joOjbUuaJsxmqui62WxWzsFwpIrF0zStmsbeunWDooT5POLx48d4nkuW2UipMmmj0ZRHjx5RliqoUdLBqrFWmqi6iEsXr2DbDgcHhwyHI3r9Pv2VVcbjEVKWiuJLSa/Xrey3KdpU9LBM1zUuFGmKoqgUIi3bokgzkAVCOKpBrWUxHo1Is5RAU6Adx66opKbIFmSlLNNsNjk6OmJ9fR3TpdvYXmN/R6MRlrDJc+XMGsTU8zyGGowwXHLjuJqaliiKlpxgBU7ZyFJCocQLSinBgiiJsbTzlhQ5SVZUttAuJVZRKmW2Z0xr/MdmLD7u+FharVjUpanvP/5znvWS68GC+ddkaOvqcFKCbS3TqZaDjUXRtVE7U6/T46y8f1SdhW7uBfr789fDIshAfwmQOhugyVb69dTOreaFCXaWgiRRp1otrt8Ed6avkPFl1e8ssqzg9gd3lP3R96AUp5TTXmjKr+3Y2JZdZRKklFy+fJGrV6+ysblOu91CWALfD0nTKWdnZ1WW1gDuk8mkosMbtU8jTqHEKoaKSm1UPHXtrelzZMBl27YrWwcKhHn06BGbm5tVUGCCSlO3JYSoel/4vl/5x51Oh263y/6+ooUagQmT2ZBSsSTa7bayDWVJLhf1Rs9y/BSBRo5j20pBQqOqcZwQayUk09+g0WhUvPE4ThBarWc2m9MIG2Rpxmw2J4nTKmVqHr7vB4yGY04Pj7EkJFFMPI949913SZKUZrPBcDCsJkiFWqYZSZrgOCq173ke6+vrPP+J5+n1ely4cIFGs83a6rpC+TOl9WyKJJM8AQFJklNKZWQ9z8N2LGQpsIWNKEscz8Wy1f1ICabrshpwj0oFQlVcmlWFLQRBo6kKMHXKyTRrc5zFgq3TzQwqp4IyB6MWpSbPAp0vy0I5x/qhNxoNdh8/ZufCBSzbpkRqhZmFfHDFv87VYjM/J0nCYDBQ/S2QeL7KmqysrGBbNoUs6Ha6tNtttra2KPICx3W08whJnBDNoorXd3x8zKNHjxRKN5tjlYrjOBtP+aM/+ENWV1eUiIDv4zdCRsMh6MUhixJhWVj2Mu3I930GgwFvfO4NXnz+Bb79ne9UsnGVDT7n99fTyFVvANvGszwcRynO5Dog1KVm1XuNo2nbiqNufnf+36VsV20H+Dg6kCxVwaox9n7gY9mKmud6Hp94/hPcuHGDs+GgQq57vV6VgTJG03EcOp0Oewd72I4qLr1/7x4bG2tYmvKmgiQ1OKbjbl4UCpPS435yckKaJWxubuK4LoOzEY7tAKpxpRf4tFotTs/OQBdTqyBOceDv3rujisovX8GxVXYxms8oy0IV73/M2Jw/llP4JnwRqvFTXjAexbz79je5/cFdHj58yMnxMaPxSBnhLCMvVDMjtYkVBL5Ht9/lxq1rfO6NN/in/+P/xMmJkswuypI8yxiPxkoEosjxXIfnn3+er3z1K7z7zjv87M9+mS98/g3GZ2e8/c5b/Nmf/nvibE6Spbh+oAruy1IXmFPRQYWQZDJFCMk0zmkELU0Fy3AtgZAOUip6T14oWo0jbLa3trCF4J23f4xAcvXyZd76wQ+wANexORsMCMMG82jOeDSm1WoSm2BJq7sYW2Ia3ZVFWQlDxHHEo0cPuXnjBoHnEQYBs2lEq9XUtChVAHw2GOC6DoVUSFtZlIzHIzxNtQw8jySJaDZbrK+vMxoOSdKU1ZUVpU5VKB6241iEjRCJW1FGm81GFRAkcVw18ZxMRjSbjQpRM7xk17VpNlaqDsS+7xHpuiUjPmFAkkbY4NHuI0VrLQoQJXGsMnZxEtHpdlQtneNgGWQZ2Nvf15mbrLIR3W5HgzGKfz0YDDk9O6PZ6hBFEXEc0em0q+yX66pmhUmiKE39lS5npyeUsiTPUhq6hupsMKDVVAFcrgOEIAwB1e/I81yEBXGsiojXVteUlHSWMxwMiaKI8XiMLC1arTa9bo9up0McJxwfHyl1INciy1PW1lc1Tc6m3e4gLEiyjFarxXikFOWiKFoCfLqdLpPJmFJKwiDk/r37ugt5RpKkCxGRPKfT7TIeT7U9lbqbvALRVK2HjSyp9r+iLGrURCNg4JLrupDJdKLoRKWj+uTYFnlZMJmOycuCsihI8pRCswtyI90tQWD9VMmMZ8mo/s9zGMqvQfFNUADnT/+0bPqHHYvXyif2JXPUmy3rly4775aolPmUD6KM6YLaZGoAdYCI0H6QKeKuBxxU+2tZZW0MLazUL1u0AjifxVjOrnzIniuefJ8BOwHdT0jovVxQZCVCSCaTafV3x7Y16AhCqK70hrZbFCnD4ZT9/WOEELz73gd4rhIpWVtb5fqNazSbDS5eukC/362yxY1Go6JlKkDC00p0ig3UbrcXDUJ1fRUs9g8TrBsQxfgxrVaL4XBYKYCaNhMGHE7iGFt/nslIGBvpBwHj8bjy/zqdjrKZmoVjRBx6vZ4WmFCCT1hKpEgBQ8+2Pp6dOiVt8lTiOkplqddZIYlzKCwGgzOmU1X0u7q6Wun+zudzHNevCo7HQqEWRV5otKmBa4UUsiRNC959+L7S4fdc+u0WJ/kJjmMzn6h08nQ8RVoCKayKT9ZsNmm2O1zo9en1u6ys9Nna3KLdaeN7PqDkZEejMWmZk2ey0khWqa0mQqOVrruo4rf0YNoVUr5opldo6TlLaiRc1GXgTD9jXTcgJXmpf1MtDG0ExMLgGjqWmtzo8tESSUGhNeoXxchUD7goF82rsC06/R7vvfce9x7c5+qVK1zcuagWZUDlmKrOnBlREgOCw8NDokh1vjU0LtuysbFJ5glDOVSopuPi+DXtaFt32rW0Lr4jcTs2Yai6ZD7//Ce4fPkiJycnHB8ccrp/RJElvP7aq5wcHvDiJ55jZ2eHAjgZDfEsB9dSyjVqjiieP5ZSXxISVSeR5VhC8Eu/9Iu8/faPSZOE3HHI8kKPreLFnw82LMsizTKEcJAFWK6Fqws51WYoKGS+ZNDMe9U9L4rxlhrVCHXOuuEzxu9pG0E9NW0cjSs3rpMWBUma4TVCkiInlzlRmhCnMZ7nApJoNqPT6+I1AuIsoZAFo/GQjfUNWq2m6qpqOyTRnPfffYfrVy+ysbEOpU3pKO6KJSywJJnMQKgiYxvVQ+G73/s+EouVtXXGowlJmtFqdhCWQ0HGaq9HEIZMhyMCYdNyXQZIBCWeZ+N6LrlMCdpNhOWRxAnNMECgC+iFnsXnNoyP29ClVDUXlJIHjx7xv/7f/G8p84IsycjSjLwsyYpcc/fLav0JIbl4cYtPf/pTDEcjfvM3f4Pr16/Tbrfw/YDtrU3SJOOf/+6/4Mc/eoeiKFVHdd+j1XZ56aWX+If/6B+ws7NDrhuGlWVJr7vD1RuXSNKI737vuzCZqixhrgpdFSXPxfNdTfOJsfGUoxr6OJYK3hxXF+MlGdLSzet0MaVtO7SbLc6Oj2g2mwottgTvvP0O0/GEl15+Gc/xGOqGmmWWUaQZDoLVbh/XtSsHMcsyus0e48mYNInwm03GkxG2ZdEIfQ4P9qtMWJqk9Pq9qpljlmXkScJsogoiZSnxHIf1lTUePnyowB7PAUqyJGY2Uf164mjGyXFW0TwBLDwsWVJmGVkcK5U9XbcXBIEqis0y+v0+B48fkye65490EKWFa/l4TkAY+Ny8cY0szxlPJri+ouJkaUYn7CCwNJiUcePqVR7v7SpE0oYwcHUBpCSNZkocw2vhWD55VrDS79NohBwe7hEGPWSp+tS02x1ms5mWC045Pj5gPm8rBDNJK/Q0iWP6vX5VhD6bTdna3sCyJJ7vkBcZtu1TImi2e8xnc+7ee0gcq1q4VrtJHEe6A7tPmiqVRM/1Cdw5kVDZSjPfpJSUqSSKpszGE3ydgbAti9APKoA8zVJOTwc4to0fBDiOYh14vsPB3gFZmiKlqmOxLd0UNc/YF/sgVS+qQtNQs7xEYlXgjAlKRqM5BaVqrqad2ErDX0rKQoC0KUupnSWlLnV6eorjeUr+XaO1QMUNx1BwKn9SVMXBGDQdUPL4VFLz/7HHn1fw8VEBggEoy3I5a6Bf+RGf+lGKSypgWZym/v2itqPOHlCCDwVCCr2n6ayC9lUsW1T1WujaXGnuRQoNrljV+dC1Fyb7ZZx3BY5CJatbu9XKNzp370v7MapNgsmIqRsxlKunByWWpRkMxj+rqXtZQoMvto2wbOWn6dPJstRy85aSRJfq7Jmm+VOquZdkOfPdAx49VrbatnJW19qsr68ThiFf/epX2dzcrMQbVGbZrWip5loMu8RQPU3WwoCRhjZ/dnbGzs4O8/lcqVp5Hj3t39haoMHTdbVGNMMUfZuAp/L1TOZGA+9G4MHU8Bl6pLBtSlBCI2XBfDpVNWKbmx8xD9XxzIFGr6uq4afTKcPhiB/+8K1KDch1XV544QWuX79e8cWVkVQT0tCojIKFok01VFFirSv0w4cPOT4+Js9SXEdU6R/XcQlCpfA0GI5otTtaL79ZVc6ryLyoJFCllKRZxt7eHmdnZ3zy9U8tFQWbCViPhuvRfbXwyoXSllkwIBTnutDJC51uAxWBIgQlWhFIqDQ1aAdTmGChrKJZwwu3bXvJOTZOmKEMGQe/jtDX05vmHJcvX+bRo0cgBHt7jzk5PmF9fb1C9BcKYErpxXSO3NzcrAr+60XZSZIwm6reDJ7nVe9XKF5cIWBFUeA4iyxPmqos18WLF7l14yZCS+k6tqKFVNr9EtbW1vjFr32N+3fvcef2bWw9pnmaKlUrYxQsq0otfv6NN7h27SpR9K7axGRayfVasJTWMM+4SjUWBc2Gg+3YZFlKKZV8KNayYT9vsEzQUaexSZa7hYvaM/5oxEmN1cnpCbdefB5bwmwyJwhDJuMRaZIyn82I50rfuhGEHOzvc/PWLXr9PjOtiHN6ekavqwqYjZJJkgSUsuTrf/Zn/MIv/LxCWgtrMSZSKlqflBqkkvzkJ7fZ3X1Ms9nGtmztVKn0babn3sWLl1Tm4+hYSWBOhyALsjxlZWWFi5eucOfOXdbXt8iLgsl0Qhon1Vgipcr2fUh26Px41deAeftsGhHNYiilqvtAUFBUiJjtqO7QnueyfWGLv/y1n+Mf/Vf/kGg+x3XV/M2LnPFowOuvv4ZA8InnbvHw0S5xpOignU6b9c2eQtzKguPDQyyt7DafzWg2WyRpwiuvvMLq6irf/e53eLS7i6WzaUqeWDsQRYZjO6SpQnR9z6csShqNUCNmJX7goTooF7iuKpIMgpCrV64QzWdKZjhNmEcRw+GAF154gbOzU8o8QxYFcTRXRX9pytlgQJaltNutahNT1MMUR8tjpmmCY9tVAad6JKoXguHl2rajayYCpFRKTULYNDTlVQiB5yppbmSJsKhosYafL3xf142ptW4ADXNNSZLg+35FDzCd5rMs4+WXXybNUh49fMjBwT7Xr1/XNt6mKGziuFQbq+PgWC6tdlt10i0tPMcl0qowZZlz/fpVpUJ4crRQkJNUNSyH40OuXrnB7HiKLFWgeWH7AqPxCBB4XsDZ2UCpmE2nrK6u8qlPva7oTmeqQeTGxjrJfK7EHbKM1ZUVti9s02w2WFnt4TguJyenFGVOlhXEUUIYhuzvHVCUij5blBKBpip0OsRRrIO9nL39fc5OBpXkbhRF9Ht9pjMV5LquR1koGXEjGlKWirpo2bYCpfT+pWhSynlCKkqSUhWUFaqaF8UCIZaaJqydwyTNSNKiEhkoy3JRr1kqVcglAQVjS0uBEM7SvjWZKXqGjGO1d9ZqOM/Tdiq7bFB/NZsqEK7+G/WrP39K1H8Izepp+8BHf44KFOogTB3Ff4YzspRJWDr/k01tzWvMszdj/zQhk6VL1KdS+yIIsawGtTQHdA+lSlnqYwK2D2MJCKHELxYSvMuBRf3nSsGsliGpZzzrtZul+beoB3C610hZKmpozZfr9ptcurRJq9XiypUrRJESOfD9ANex6HU7usYjrfzUPM9ZWVlZqrE0KoeO41SUdKPiZvwN4/MYv3FnZwcpVS1Ur9cDXTMZBEFl84UQFfPB0D+N2I+p4yiKoqINR1q63tRyOFoeXohF3Vscx9X+VmU4nuF45kBjPp+rDsaTCdvb27RaLba3t3Fdt6JZRLqJWz0qsizTgdbBdRW3zPM9vQlbFU1ISslzz93i5s0bFEWGYlnoXgK1OoM8U6i1cWyBpUVhnHJzHaurqwAMBwPW19cVQq4Xoe0ouoTpk2EJlSpUUa8pUpJaaUeq1xZlNcktqeo2TORn0KUgDPECvyrE6XQ6le6wlFJxS2EhTxbHlFLi6wdnFoCJbA2KWl9A5qsKUMRCE7nb7dLpdNTYZDntVruSTzNt5s37AK5cuVJNdBO9mgloHGgT9Ekpq2DDqCkYbWZVvJdWi8M0EDMcYguBsJSj43s+hVQFx7nWdQ66Hf4Xv/X3+Ff/8vfUgkpTclmS6qaB0+mUbrfL5cuXFIc68Pnql7/MwwcPyPOCJEkpP4TiWvE1M+WwGqfG930VxJisk55TZjxNcGdSyucVO84XoNeDV8PxNz8bNTBzSH3/o9GIIi8INL2j02lzdnKiaAHasW23WvT7fY6OjvjEC8+ztbXJ/mMlbDCdTBkMlAPS7/eZTlU338lkxHg8JIrm/NzP/SW2L2zrYs2yUgiTek6//e57vPnm9wmCkDQtiONE0R0bDbWGNUBw69Ytkjjm7OyMhw/vc3S4y+bWFlKWtDt9grCFFC6bWxfJ0kzXNqkMlGFMWwvA6JmOxUZjYXpelJnq+WAS+LZn0W63cD2HNE34rd/6e7z62qv0+106rQbDs1Nms1lVmGoU74pCzfHBYIRjC3wPptMRrlNy+/1DVldXGI0UFcto308mE05Pjul0OopHG3jkWUoaK2EEy6KiN5p1ZdseRvrZnLMojMJRgaezr+r3ud5EulgW5EXG8clRVYi+urZCUWYMRwNsKZUyUSNAUjKPZjQaAb7fZT6fYlmwublRSU2ruoNGtbYHg0HVPMysccXpVRtSs6nS7FE017UNNnmhMmHCEnS6LW7cuMH29hZnZ6fcu3ePk5OTap77vs9sNq1snbFRphmVOafh7o9GowrsCEJPUYXWV+j22pSywPVsonhOXuTaVoHtKfGLNMvwg4AizkjzhLzIKFFBUDSaU5YF6+sb3LlzB9P917JsQCib7bnYtmA0Gio5SM9hb2+f+XyOHzQIwwaz2Yxms0kUJUoe3AuQeYElJY4QuFqhZXByzGA84+j4WNV95BkXL+4gpWA8iUBKxuMJ01mEHzZJ0wzP9ShLTQvOCvJIbfpFprJ0CJs4y5lFieqy7gUcnw0wtFVQCm91ZynVgiOilkU1NRVq71RIt6UDXsMFF5aSSY4z1TzO1G0YW5gXJWDr9bxQNoKFqy+lWrPmt1KabGYNgBEqQ6YAG5UFMfv4s9iF807on/fx0wcIf/7Hf+z5nryHJ0Ees2cbcNW872kA2hMBj6iFeU8JXsxhPr9+jmc96uez7CeZA/X7qF5Xn+eyBLkMzi6CoOV7Xbo3HUCZuog6AOv7Di+9/By/9Et/Gdu2mc/nhGHIdDoljlJaDeV3TadT3YR4IXZg6pIBDcovMiwm+2Bso6E2mezC1tYW/X5/4W8GAYWUNJtNLaA0qXpmmIBlMBhUAeT5TuTGz4FFHzIjamH8QNM5XDXuFGSpahdRtVD4mOOZA40vf/nLBEFQRbyGzw/qIaS6yMQ8/EWDvUw7pQ6+72rakXI5DMBf6KYnJnUjUShrrnXRjQFUTb8E08m0qjeoBxWqwNWunLqyVA2WbFuhszNd/Fh34pURrqcx6yjA8kLxPbd6r5SykmR1HIder1dFoJPJhLxUzrOJZM3nGmfTPFjHtpVUaGX4F8o+pnCn3kL+PG3n/MKoO7RFoXT3Te3MysoKZamKC0ejEfP5oW4AuF1lO0yjPWDpnObZAJWDEEVRJYvZarVoNhsL2U39ejNRPd8j15H6eDJhpDWl79y5w3Qyodvu8Pxzz7G+vsYv/uWvKSk4hOperWthzBxQ6jQRsiz53Gc/zb/8l/8/VdjkOshUBannjasxcmb+AdiW4hlqs/XUOWAOVZS4+NxFFm0hF1h//3k0SM2nJ9F6CZWCV6PdwXYcOt0utm2RxDFZmvKNr3+dOI65desWlm0zHAy4cvkK9+7e4+jgAM/32N/fZ3t7uypSUzKnOfP5nHfeeYc4jnjuuU9w+fIVer1ulWW8f/8+b731I45PBly6dInZLMISFkdHx7iuR7PZhlIF2RcuXaDX67H78AGz+UxlH3WRs+N6rK6tU0rVFXVza5t5NMd1HKbT2cKYfchG9FGb6VKBKLqrtQDbEdiWqj/q95r8l//gf0lZFMyjGZ/+9GtcurTDcDjk9OSYyWSiM285k8mU8Vhp+8/nM62JHunNI8BzPaRM2drcIvA93NUV8ixXtDskqyt9JuMJJ8fH5LmS6R6PRvieq9kMCqRQz980qpLYtq9T1LkuopPa9uWk6UI4AZSaX6fTZjgcgBBMZ1PCMKDZbOH7Hiv/f+b+rNmW5DoTxD73mPe8z3znm3kzEwliTAwsDCQBAiS72F1dspKZzFotKz2Vfk29qKXXlkylp26xpW6pRXVNXW3NIggSJAACyETOmTfvdMY9DzG762H58vC9zzk3b7KgKoVZ5rnn7B0RHh4+fGutb31rh6g5y9kU/X4PWmt0u12kKXHsoyhCv9+1G2lZFtjZoUq3JKNMBs9wODTrUW3X4cGgb+Z2YdTjNPb39ww1hir5KqXQ6XTw8ssvYbVa4unTJ7hz5w5effVVvPXWW/jlL39pa1FkWQ7D5kFd16SOZgA5J9iz/GK328X5+TlefvllLJZzPHv21CoWuRHZVtKBgEScxIhapNSieF31JIoig/AkpC8hhIe6UFgtF1jMlnj99c/jgw8+wHpNmvSrFUk53jy6gfF4hCzLqNCjidrMZnMovUC/T4paj8fPkGc5Ot0O1qsVdF2RDOxshgcPXsF4NEYQBJivM0wmM5RViXa7g48fPia5ZOnhjTfegNYKP/3pzxAEIYQgqeYoSlBVuRGt0CZCWxtVMQAQtqiaEERrKYsCBi1BOU4inl8UiSAjn99xA9DIINBKsxPd1KuiaykzdpmWIgSvb8Ls40Tz5dOpHTyvXYBqorw2+ZcXAEpWV5qv3yjhbK+Z/75A/1Xr9It8b/u77ufb19iOlF/1nd+8gdH8fbud7n+s/gk0MrZsHFz1Xiy96op7XvdMrlHwaXvAdluva4f7bG777Z5tEthdJ23zb3Fl24SUEM67Itok5SWOLib4H/4//yMuzmf4j//jP0ZRZPAPQsRxgjhswZO+pU4lSWKdvVJKyzDhdgCcwyRtm9khw/s5r5kPHz7E8fExjo6ObEQ4ZbVHw0DheWQLqhpjhg2JKIqsGpab78y4jZ+TBYm4SnhoZO07nY6lc73I8cKGBktmMsD2PA83b960BUFOTk6Qpinu3r2Ls7MzLJdL7O/vIWklgNCoVWWtXs+naIe2hgnx9eq6NMaHQFmUKPKi8SgDmE2maHe6tk3cmZQwR3KqeZ5ZKzBNUwu8pBBUrM4kREIIZByB8YUFAAweOSLAVrGAQF1SSMoDpaVy9IHbwobPcGcIOBOTJ68QBIoobE9t8myiZkWRFcfid6utb1vr3Db3uMrC94zXWghhlVj42VarFB9++CFOTk6sZOVqtbJazgApjbCBslqtLE2KK7YzYD05OTERq6ZuCk+QyWRCXtEsxcnJKe7du4s7d+4gSRIqUAMCQvk6xQcfvo9svcZ0OoZWGpVWyIrcqh0AsNGTuizx4KWX8d1vfwunZ2dmYgBZXqCuYRc/oFlwClNcjr12gfMOzaja6E97rtlSbWTEeITdmibbEQ130XCv14xful9Vlji/OMfe0RFaSYIyy4jjvk6RrVN8/NHHKIoCo/ML/L1vfQvvvvMOvvWtb+PBgweYjEYQECiyHGdnZ9jb2zORmhBZVlNV+CjAeDzGT//mp3jzl2/aNl6MLoxCjcLRjdtQimiKT548RVnWpjK4j7zMEQQ+vva1r0EphXfffRftdhvdbg9FGUCD5I073R7OL8bo9LroD3r46OFHqJXCdDqhZzfY47oN8HkHbTAlAAHf8xFGxF1styLsDPvY3dvFhx++iz/8wz+A70vcONrDJw8/QFXVSKIYngS6nbbJofBwdHgAIQQ+/vghdnd38OTJY8znM6TrFW7duoWiSPHJJx9DSqIKFYbmyPxxliDkhZyVlgI/AFeI58q1ZVlsPIdvVKiqiivYk/EcGBoSzdUWPI805quqtHUbfN9Dp9MGoNFut1Bm68bYmc+MChFFaiBMQT+toXSN5XIOIQXm8yVV91YKSRJDehRh9H0Kn59fnAEAwtBHqx0jzwvESQQhJNrtDo6ODu363+31MLq4wPHxsVU5+p3f+R3cu3cPP/7xjzGbzbC7u2MdP1JKdLtUcbvdbmM6naIsS8RxjE6ng16vh6OjIyo65/kQPstk+3jy+BleeimG1gpRSGuZ5weINKgmkaNkJL0QWimk6xTL1QLLJUn2ilrh6dNnuHHjJn79619jNptjuVzixo1DJK0Iq/USuzu7GA6HePvtdxAEIXw/RpoVmE4XRslL4uDgAM+ePTPUK4qQKUiU732IXq+H0WSC+WqNqqbo4MVoAq2ATqeL73znu5jNpvjLv/oxlssVoAU8z0er1cbZ2djuhVXlRhJMxF4p1PWmsb5NUdpev4BGRoE+ALRd5xS4dsOlOQdT14EpSCYSqfl/2l6uuZ8233edwu69r6AzKa03Pr7KafOix3VA/7Mcf1eA7zr9nmeE/IeMktCtn+/scY2gq366ex1dDRsOpOuexd0PXWPBbcd1RtdGn2k4+Tl0uKyW7ffg7stXPS8frhFi/60oV46drK5jsa4FVssKf/njn+PWzXv46htfQZbWCEPy+i+Xyw0ZWnaouAyUNE3R6VAtstVqZelPSil0u11Lt2JMxSyMMAxNTaQIvu9jORpZulNd19aQAIA4jm3NHYCwPEdUGMP1ej1bYJDzOLiiORshSpGClQCQGuW7Fz1e2NDgysNcWIRfDHf6vXv3DAf2wsrUpVmGNFtb6dpOp+NssjWkKdhS17Xl7uZ5jsDzSMPf81BrIC1ynJ+f46OPPsRvffFLePXV1zCeTPDJJ5+g1+tZGsz+/h7KsuGpSylxcnJCnsowhOdYbswLJn6xhi8FoClZ6dHTp8izDLs7O8iNZ4jlVReLOah6ZAzfD6wBwZ59qjqrsFitNowzpVQjBaY1qqKkxNmCpdckhZA9UznTDOxtq/eqCXEVj5J/Mi3MnSh8eJ6He/fuIYwiAh7Gk1FWFdL12koXugYVe8PcBKIoirCzs4O6rlCWhTU+fN+nwmVxjNl0Bk9I3Dq6AQ8S09EYU9Ak2N3bQau1h9PjE/z1X/8EQpO+/M5giN2DfShjfLLRxROgLgoIDfT6Pbz73nv49dvvYp1m1vp2D9drUJYlsjSFEBJJq3XtmOf+5YiaxDZv+GpvlPvZpVCscyilITzyCJ2enOLBq6+h3+9jMhrh8OAQH7z3HtI0xY6hTCmtcLC/j7PxCOPxGK+88grOTk7wwfsfWMN6sVig2+1CqQpxHCEIfZLvDHzoWiDP6dmV1lgvU6gakMJDHCdI1xnOz8+xXqfo9fpotdrIM/KUvP7FL+Do6AiPnzzGbDbFwc4u7r/0AJPpFJPJBHfu3UYYRZjMxrhz9y5qRepNyyVVQPUEbQ6UxElzwOXYPu8dcF96PqmdDIYd/Of/2f8Kf/u3P8Xvf+93cbC/B9/zEZuw8nq9xGw6QhQRLen8/AyelKSAla4BCIxGF4jjBBfnU6wWa8xmU6zTFZJWTPVvul3jYZVI1zSX57MZTs9OMegPEMURyiJHul5htVqTvooEgJqUWgTMWkdgTRhvMcx8DXzfOBYAjRqeLyA9wPepnsSdOy8jaRE1KPRJQ325nJtqtRppuoLnkdqd70QaF4u5zZ1TmuSKPY+ME94kuf7C2dmZncdZbiLHdQVpEsDzPENe5Oh0OqZORoReb4C7d++i1WrhzTffwk9/+jekTNTvI89p7Z3P53jttdfwwx/+ED/5yU+osnVb2khrURRUf8fz7KZZFAUuLi7Q6XQwmUzMmudhMqE6GtXZGFVV4Ze/fMsW6QNIEeXW3TuQnoed3R3sHxwiCCJAA91eB1VV4vj4CR49+gSL+Ry9Xhc7wyF2dnbxn/6nr1haXJLEUHWOP/qjP0C/P8T+3gH+xb/4V3j48BFGowlmc6IgBH6A3/u975AsZfU3aLVWKJXC8fExLibHUOopbt26Bd/38f6HHyMvC5RVjel8CQEPSbLCn/zf/5+YL6ZQdQlFZd3pp74gnC4v1wlQSpmog2eNBHcdkkZIhE+hvxtgRRPoWrqidrmm+gpB2GtOdN1cm8AVbg3fy8d1n72gXfCiEYff1HHd/T7tvs/7/N+XYXHdcRXQ58MdV/y7y24AsAnotTZr3PXX28YovBY8L+riHq4Dr67rDUODr+3iUfe8JnLXKFBtPkdDsXLxlhCU+yOEKWzpGAhUS0ogCDzcvXsLw+EAUgJllSKMWhDCw8HBgW0jM2m4EB/XoxFCWFDPlF42TDgSwRQnrjHENHx+J6PRyApuMEZnWVxybPn2udlJy5+xAePiem4vO9k5UsJUcGhtqf8vSoF7YUODX4r7k6k9nJzGoDQMQ+LcxzGULkFa4CP4vmfDLUnchu8HtrOXy6WlN7TjBL1OF51OG34QIFuv8eTxY9RlhcVsjoXR3N7b20UYRqYDqYJinmeW/8va71pr4pTV5Gmsqhp5mJvQVAmBElEYIopCxFGEl+/dAaBRlzkmoxF5Kc3AUGWJxXSCJG6hZ4qgrLIMn3zyGLfv3CVOcpoijEILMMKQBk6eFyjyAmWWo6pKLOZznJ+d4ezsBL/1+c/jwWuvQamaPHmWN1hbsAvQIk6FZ0x0RJLC0lUTVmsNmORCjotrE/6WktShWq0E63UKpWqjSFWDQ4ksOUl9SPeta1O7wwH+Qgis09SAR9hwn5ucLD2JOIoJ5NY1VEXyrQJAWZRAK0F/2Mc/+l/+I5yfnuH4+Bi7B3sQUiCOKaenVjWk9JBnGVKlMJ/OMB1PkOY5vvylL+Ojjx5itU7N4rC5bzWLIrUvzTJUZUWJrtRbzn9XRzVcw9INa2pNnHwb8UCjELbpJYKz6BmWgVIQQuL87Azz6RxHhzfR6vQgIZHECdJ1imF/gOFwiDt37+DWvdvI6xI///nP8b3vfQ9f/vKXMZvPcHpyiiCi+gdZmkJKgZu3bmE47KPVSoi7rT2slkuqoFsp+F6I2XxmxmeJR48eQyltqp62oGqFqlbYPTrCl994A3lR4K1fvYl2q40szZFnBbK0QBDEODq6geVyiaIs8frnP4/VegUhNM5OTsGLPL+QFxeEcUCPoKhnEof4wz/4Pvr9Nr73ve9A6wInJ48BRR6XZ88eww98E2EosU5TVEVtC0iu16nlpxJw7hEVSCvcvHkTcRyi0yGFpzCMTI6Fh6LIcHh4gMlkjCDwqLK27+PG0REePX5s9OclQlNYCaKRlA4CyjVTStkom5ACvvCNlyqEFALS8wCt0DIF3zjPzbbXeKkoSjglb5YQKOqaCmkqjXv376M+O0cSxwgijySRywJS0ZpNlYlXEEKiKiu7WYVBBE+S8liSRJjPK1vkCTCbrBSYTiaoyhJ+4KOqSvT75AlL16ktNvrRRx+ZCGeIg4MDvPfee1QfYjBAZgxXIQTG4wkKI0eepqlNWAyCwHj3gOFwD6PRGa2lkjZbKSRWqxR+4KMoS9y+dw8//OEPMdgZEtWoIuM9L3J4nsTRwRFeffAaAKDKchwcHGA8pnX99q37KMsSp6cnUKrAm2++hbKUKAvg85//Es7Pp8hzhVf7e/B8H9PJBD/6y5/gvffeQytJsExzrJxnUqrG8fmIkq9rivZLQ/nVWiDNS6JgooYURm5TSBMlEOAaOhtGhF1DyHFkldsEz5LGq2zcvVuziOaOsxo2K5zQxtBwjJKNCMOW1xdu0MINaTjA9Mq57FzBWiHb37yeOqM3DCC22pvjarxq9jz3Vi+C7696HrMtuMYct01svAde5Oh/7pM2a5m4tinX9h1fVnzK9/gWfNoVX3yeQcBXb+osbSaNb0cKCOQbYwKO40hwOzZzAD7NwHKjDi6mcZ2ryo5l19nqUbkBOyrphTWUKKJ38b7bGDuMZxvhn22cyyptnXYb3V6PmDpxglu3b+Dll+9hf38XQeih3Y5JcCOQEAhsvTJ+fqa2Uh5ebQqT0lrHBVddIR52qgJErwZgqaaMQ/I8x2AwQLfft9ewuadgDKmswcD9xdiNP+Nru0nonJcCNEZNWZZoJQl8jwptcxHoTzte2NDgl6x1o93PjXMXxn6/b38nr5qPnWGMfn8HdVWh3e4Rx1o3VcY5FH10dESd4HlmcSZKTX9vF1/75jfsvbJsjSSJTZHACnVdbrSLDQzuKA77KF0gSTpW5kvVNdrdDnxdYnRxhrPVClA16qrE6OIcO8Md/NVP/gar9Rq///3fx+7uLsIoRD+OsVzOMF1PESUt5KXGTreLMisRhR10uwmC0EdZVZBCIi9qSBEQNcyL0e61ka1XCIMQrSjE448/wDu/+jnS9QJf+vo3UFc5fD+A0CQJx+o1ZaVtnoqZfqRJDuLUblN3tCbZUZo8nv07DxzqyxTzOSUPxXEMKYkfzgso/6TJQYVyai2xWJCnmgvSEIcwBkzhJB7EbKkLIaDqGrfu3EIYRpSjI4SRFiapuggUkvOiEMODfUhT4MsTno1KCSGxKOaYTWeolcL+jZuYTWf4/g/+AG+9/R7SX/wKRV5DFxkqp96IXaQkUJQ1ilohL0sI36OogtlNxJYrjr0bda2gvcbTATShYCGoSryUkpKB3eiG0hZksJeWOQgapOHtQULnNS6enWM4OER/5wBZWuLG0R08/PADlGGB/t4AfhKg9GrsH+3hyceP8Itf/Bxf/8bX8eU3voK//MlfEfjUIeqyRFkUOHl2jOVygcFOH1EcQWkBSIG410OR12jLEGF7iCzLTVVliV6vi1a7g7IqkeU54k4bX/2d7yLodvCzH/8IVZ5jdzDEaDQlalZZ4cHLL6PT6ePd99/H/sFNDPeO8NEH78OHwrMnT+j5jf9TOJLQVx28J5jhDQGg1kRn9AC0kxi9ToL55AztdoIoDBFGialrMMZqOcOtW7cArRGGEc0/j9TIfD9Au00SgbxGtTshev3YOkl44SWQT7kJnNekVI0vfOG3cH5+joPdPcxmM1qQhUBkIr6AAYZCkFyns5DzzyAMAbNOlWUJ3/NQmXHGnqlet0tiAEWOvCioZkUYUo5GEKLICqyXKeJIYr1aYnd3H1//+jfhhxF+64tfxeNHj/Ds9BNkleHWBj4W0xklcxclRWXDAIBEWVaYzxaAFuh021C1QhxHpgaCB5L8jTCbTVEXNbL1imrX5DmSOEY7jiE9H+vTFNmakqRHF2MopXD87ITGlvRwfj6BUgpFSXkKFHUWqNUCUkhoCJJ4jRPcvnMXx6cXOBtdIGklWC+WqFVtI2wc1bx99z5+6wtfQhy3MTqbUJuFh+V8gfPzc6xWS+wfHGAxX+Dx48coS43pZIrBYIBPHn6CpUlUL8oST09OcH5+TkpWnmdoV0toAKVo6Bo2qjlZNIPWYm4D9OsaEJQfUtXaOB8oWdvSObQZ5AyihUbNidIWY3HNATqUri0nniVeaZ1qQOWnO8s3ow92svH/ty6wESmB4w236+rW5V/UW38VWhbO5N/4qgPVBTZCJteD7mYx4X7aNJz01nevvLW1rJo1y7FaxDXXu3QN9w+f1j+X26Xde175PffYjHhtU7Zco3ObZkSOzc2/N9e8TD/aiHRITfN4Y/xujSUjnQvAEea5ogc0tVMpnjvCYAajIIXG0HFV5GpTLsCuuRvRiABVVSM0ZQyUVlY2XpgIdBCE6Pf7SJIEt27dwnDYw42b+1Yp6uDgwArmsNO0LDK0kj6qQiEIEuhaGdXbBieUZWkLVrISFLN4iqKwebTssGCqE+dg8JzrdBolwU6ng52dHWLmGKcWs3vcg3GKm9TNBhU7SwFY5zwbOxzlcCNajH+KooA02P1Fjhc2NLIss+A9iiLbifyy3QHHSSeuJGsAQMRNlV23E9wJ4V5XSIFAhBgYbWGW/Vqv1zbh0RoRhr/GHcbJcL7v22x/0W4jyygBMAgCJL0eKddUAlGri/F0gSSOMZ3MUdTAw8fP8ODVVzGbzfGjH/8YN2/exOc+9zmSatQay+USe1GCvMhRw0foeUizFColkEFUqhLL5cImVfq+D9nyAd9HGJIS1z/4h/8LjC7O8W//4keIOz3cvHULSq3Q7/cBRRa80o0R4Sbz0YJPE9YNZ1pLX5Bsa12rS/3s+yE67RBh2MLp6SmOj4njv1pR9d31eo0ooomnFPG9a6VQKUqydwexEAJ1VcH3hB2slr7l8DK1Zq35HHmem9BgAKVqkwsD9Pp9dHs9a4SWxqAhr6pEEIUY7OzA9wmwLXdXePbsGP/4H/9j/Bfj/yPK6iEUFGqTr+N6Y5Qi6c48z5FmKYFR6QGocJWnzHpoHEPbDTkC2OhTd/xeHRbe3Eg1YLXoP3j/Pdx96WUk3R4UBHo7O0jOupgtl/AiH8HFBY4ftfHS3ZdQHBzg8ZMneOutt/C5118HBPDTn/4Mk7MpAr8FWVeo6gKT8RzTyQzSk/AC3/h5qPiV1h6Uokr2cZIgikJ4QYBVnqGqa3QGXXzr29/Bwf4O3nv7V3jy6CFiz8NyMcN8NsE6zRDGbdx/5XOoAEwWK3z3ja9hnRaUcD0aIV2vSdFGV9bbxCDlemOj+Tv3M1ESqdr07Vs3oXWByPdRVxXimMbGrVs38cknn0AIgV6vZzmxeU6LPFdVddeGpdECJ+pfbcF/p9MBV6F3JajjmJLFqTp2/5JEdWPUwiY40zgQ4CRYVjYDYNfIxvDPce/ePSQm+bmtO1BQWCyXKIqS8tGiGOdnIxwd3UCWpliu1uh2K9y8dRvPTk6xHo9x+/ZtDPd6+PnPf4ZsnaLQJaTnI89Lk1NQIcsLhEEEltSN4xaqqkRVkHhDFPmoSqL3TCYzqnqugPH0HFT0SqGVtLBaLVFWClleoqpKxHECaMqHIp4wGRE8d7gWhTDrSW2LGhIt4tnpBbrdLvb2DvDgweegtcYoHOHhxw+xWq1I3aWVIAxC/PJXb+PJ0xOEQUiGRFXCl+RtS9epBWiUV1MC2iQbS0qGFyYPQUOjNPSP2qxFdr4DqMVVwM28RGeeb3hhnbwGx/9vv/dcr7S49I+Ne2/fi+bNC1zuyr9/umEgROMdtc9v/tsIr9jrfvo1Lz+/Yxg8d+18oSbT15xO2V5vtiMTn3aNbcDufKFp0rWXEZcf+Kp72rXi6ja8KG3suu9dR1VyzsR17+C6sefiEld97LpneF47tz+znzOW0CxK02BJ1/nnmX2FaU5ujq3vRwgCyoWK4xj7+3vY2dnBcDhEHIfoD/q4f/++VWsaDAZI0zWEIGfRcrm01H8AxBQw0WbOrWBsxoCeaVAAbA6vm68mhLA0Kl4DmYLPSdhMn2KKKecGlmWJvb09ojSZ5+UoCQv7MAWK8wtZcaplKOO8v26/Q74v06UY0/F74eKCnxah4uOFDY04jm1EwQVV2xnyzPPnjYRDL9uhNxek8UtwD8uL3zJEuMIiJ6zwPVlKlcNNvGlZaVXjpfRNARPu3DCOIWQLYauH3YMbgNK4fe8lTEYjFEWOMs+xd1jgxu276HY7qJUGtIQnAS9KcDGZwgsihHGAdZrCDzUACeEFyLMUEEAYtmyFRiF9LNcpRW2CAF4YwZfAUauN/6g/xF//zV8jihPcuHEDzIKlcB9Xqmz6lCcSRKNNLQQltrOsGhRQVzU6nbZJJvWp8mwcA5oUYZhqVhYKF+cTRHGE42dnFpAt5muilSQtQGhUqrLvy11Y8jyHrktbMyVJEvv+OKzHNDmefJ7n2YTV1XJJVacvLuB5Hvr9PqI4RhjHJHNbkPJC0mmjyHMICKyWK2it8MorDyClhzT93+Gf/tN/ilrXKKrSjoPGAKtRFCXW6wzrVWoS5D1ofXmBdI0FNp65oI6rxsHj2N2IX2gCCjJslKGjrVdLPHn8EC+/9jncvHUDjx89wc379/Der9/CcrVCOAtw+vgZEi9Cu91Bp93Gxx9+BKUUvvDFL6LVauOXv3wbjx8+hpASURghUjW0yRtSdQ2taghPwROkuy89osuIgOqBrIsMWggc3ryBN77xNezt7uLj997B+2/+Ck8efoh0tcL9ew+wXqdYZym+8MY30ert4Bdv/QrdnX3cuHUXx8+eARB47913ybtjPGQb0Eo3ymvXeUXcee95HgIBfO61BxgOehCihlAkWaiNilKaprh//75dyKliamjrufCYY2+4EFTLYWnqkfC7tZuWiYayI4V1xQ8OD5CvqaAa1wbiOcmbYOMlquzizpufTeytauu14sJLVJ1VYrFY2s2i1WkjNblH0+kcVVljOp3i3Xffx/7+EFHUwnyxxH/9X/1X+NrXv4FXX3sd777zNu6/ch9/9Ed/H//jv/pXyNaUjwNNzodS5RACSLO1mQu0PnHtn7pWtv1ZnkHVNaIoRpblZk5RkrtSGnmRo6oUojiBqhUuRqS0xO+vqmrj5K/tmkHOjwp1rcGVerWm5EsSFxnjgw+eoKoUfFMbab2i5EalFVargvJJnp5emquQzZznyDk7RExcgqLpHhWOI9CvoUUzDitVO47ry1FO9+engb3tPe8q0Pc8A+L/Xw4GSqyI+FmAxlXHi4D7f9fDdbptr8suv/x5a/aL8tAB4LrklKaux6e397q/f5Zx4e5Lz7vuFXcy0QQyOJrTnhd9uMJktCc252134/Pa1LSbfve8hqbFY5CBOoN3BtmDwcB6+2/evInxeIx2u43Pf/7ziGPKJ60qKhRZFAWiKEReZMjSDJ7vIS9WCCMP09kFWkkLMJQwKaU9pygKRGGIJI6Nkp8y7SRq03K5tBQnt14Fs204qrFYLGwkQymFJEksW4TrxDHG5rwWZu6kaYrz83N0ul0qzmdy3lwDzaWD8Rji/YjnMwC793Hfuzm4LCLEERh+d59lTH4m6pRLmWLLjTPiAdhNl60vV3d4e1Ax6N9eYNn6mk6nG54vIYRVeOn1erZ4nPuw7svg37c7gsNOHP0QQqKGBwUN6UfwpEArjNDpDWiQKwLbTB0qitxq0k+nI+wf7iNO2qhqIAhiKA1I6QOm0rJrkEkpoYVGDbqmJwUVpgNRyHoDD9/+9nfQarUs7Yv6x3iADZ/QrdxIz6A3FjEewHVdI/RCTBdTw0M+s0nDURRhucgsXYPoCIkJRXpYZ02l8Pl8gdnsHZN3E0H4DVjjQUgWuA8lmgHO44MHNPdDr9fbAOsCGmWeUWBGafQ6XXS7XQtS/NAHNFDkRLnwfY+8q5ruSXrPZIh861u/jT/+47+P//pP/sQKGGwncBNPvEaaZpAygICEgAR5HTcNDh5fSquNsCc/jzu+2NBwE98a0NlMTElFYqA1ybSSg5/IRR+88zZu376FznAP3WEfwhM4unMHx48/QTBbwhcS76Xv4K1f/xpKa9y9fw9CCqRZhq9+9av45t/7Jm7dvYN3334Xk/MRlBbwvQCBT/UdtKk8oc2G6EkqzJWXBSpVYzAc4sHnXsUrr70GL/Dx1ptv4vG778DTCrPJGF/58pexziqsshRHt27jwaufx2S5wMV0jt/7vd9FUdcYXYywnk4xPruAlJybYMaoMJ5ddTXIst5B5yeNEyCMfNy+dQPLxQyDfofUyAqFMIxRqQrz+dzWASDhCaqp0WpRDYT5fI4gCHB2RtVb2+223UDYGJ5Op+h0OtZ5kmWZdbKwKkdZFGgnLazXa6xWq433XRQlKHlQQwguiEfJvlSHwkdZVlZJaLGgAqiUGwXs7R1ACA9aC0RRjMlkgsVqhTiJMR5NcXx8guFwB7PZAkdHNzGbm/urGm//+tf4+c9+gR98//v4vR/8AD/6sz/HjVu38PnXv4Af/8Vf4PT4BOl6TfkckkLmeV5AQ6AqyQCva1PxWTc1gpTxctEjknwiHI88SSnXqOsJzX2tURZsaBCNoFLazFmqNq0UGRUNJYOoErQHsHw30SRUltu9gRWSarMuV4qoEuRo0YAQqLSy9ZDY2NB1bSi7ys7H2tRE4jGpoYxTR5B3xxR80VpdWZvnquNFvbbbf3uRDfs3Bb5f9LiqjezI2m7PdUbHi3rgrztvO5pwOSrxYv121feucnBsR0CaMdS053qjsInIbLb5aiziXt+91otEeq86nveM7mfbztvNi0g7J5Rq6kdhqw/dBOztPW/7uZr2N7Q7+g+AoBou9NkmK4MLLJMDpouuKdRMBZ+pvk+SJHj11VfRMXWmuJAzR5nXa6oFtV6vICUJx6RpijLLsE4XRs2yQBD46PWpEne73TF4hgsoS7v3M11WCIGyqhAaxzX3CUtjd7vdjTpiHA1wAbqUVHyYowdJkkAZtgjncrCSFEdNVkZkiM+v6xqL+RytTmfDUbZarSwWZuYPHyzg4/bxeDw2daUaw0gpUhrlfY//xkI/HFB4+ZUHzx2XwGcwNJbLpe2g7QHFv7OlyYMPgClIxYWoCMRtP7j7EBwS4lAUX5cjFSzntT353evwse3FYPDgDnalFWoFaOEkMmnCQVTrw3SRB/i+gPBD+FGNdn+I/RtHxPkLI5QlVc2tlYIUPrSWRiWEtjBWlxEC8AyFwjNeNiqCQi+83+vSHueEA4UAyqq2LgFWTmIgr6EQBL5VxmKDLMsylKgg4CGKEsRRAq0B36sQ+BH29miChGGI6XQKQJPEZbZClpO2fOAHxlNANLA0rSADb2MSuXVMAq8JDzZexUbtgT2LbmhTaA0ZRogjet/bCUr07oDI9yGURpGSgcS8XY6gFHkJ3w/wv/7P/zO898EH+NGPf2yjWWwYSymwWq2R57nNTSFgaMbQFZFrAh641CY33MjPvH1IIaCloWewp8hcnyqRSipAVJN863oxxwfvvYPXvvhVHO4fYTFfYO/oCHmeYnJ6CgmKHKVrks58/OgRvvjFL2J0foH/6d/8G3z+S1/Ca689wNHRPk6fneHpk6c4Pz1HludURZrnjOV3l0haLRzuHuDO3bu4d+8e2m1Khv6bv/oJZpMx9gcDVEWOe/fuI4gSnD39BDJO8KU3vg7fD/H22+/i7v37OLhxgJPHj+BB4a2//VtICMNVpTtCbOhObcxRnp98bK8zStXodrp46f5ttFoRsnSFKIigPYF0nWOxXlha1Hq9ttHMKIqQphmqqrZ8VH4+kv6NrPHNmxqvY0yb0lpjMpnYuVoUBdKIqhm/++77GAx6ltbpjgkey7z2VVWFLKOE7CzLDNDPrTE+nc4Qx+dUBEkDQRjQd/McChqe9DGfL3FwcANVVeH09Ayr9Rpf+sqXcH56hjTN8cqDV3Fxfo5sscAf//E/wHy5gITA974X45OPP8af/N/+BPPFDGmRQnpkXHvSx+HhEbrdXXz88cdYrlNT2JLmFwtZUI0GcriouqkSrY3RoZx/b4AeU5yVD9dDvJmkTAevGxKwc0ZrvUE5c6k5CkaRyQwziMaOddtBtRoceg60WVK1pb0IOskYw047cRnofVbg96KRkN/E8Twv898V/Lsg6bOc86KfbwyZK/ZuvXXei7TjRSNF7rNtX9dty6cbOs3nmw4npxaQvlpyla/9vAjvdc97qc1XtM81Oq4y3NigsL9L917aob02Tl1b+0w3Tl7XeSOERhAwFpCQnkS71TKqnT56vR4Ggz46nQ46nQ7CMLRFlvv9gf28Z6jUVVVbxTqiXLvJzlyUNMJyOUen00G32zG0IYk4IUGQNF0jjiOk6drkP9QocmXrs82qGTptclQJSGRZbsF+lmU2xw8G16zXa6O6l1uDgNe4NE2tXK2tfWMOBvthGFqc7EbP3THEDnJ24HNlb+vkz3NbdoLfA9f7WC6XFiOx85WvU9e17W+i7mY2QsNRDKZfudF73gtfpLAm8BkMDd4wOQzjWvr8b96g+W/bkmEM9NkrzIaFW5uBVayYysC0Hu4IpkVdNen5Xtu0LPfffF9ur5QSUpnQdk1VZFVdIQpNTQhIJxpq+H8+0308yIAscUhCqL7vw5MeGR6eMFr4bm4KGRtUMV2biq0GnFQKWZZbIM6ApSgKwPRlVVWYzWaWilQUBZJWjL09Gizz+RxJkuDo6AjpOoWqgOlkinSdoVGWUobSQXkwqzW13fMkwshDq93HwcGuqZTrG+POs94+5Symbj0JmMgEJzQBsO9aiKbaOdAselmWQVc1Qo8reGrkRsatqitKGi0rk5gaoEKOPKPKuDUUtNTwPB++H6KqS1vY6p/8k3+C0/NzfPjhhxsTHwAW8wXSdYrZdI6i0oY69WJzwBaOBKyx524olzYJIUxyOBsawurG28Werm79YR+8+zaObtxD4Ldx+9ZtPH76CDfu3IGqSpvQe//efYynYwwGQ+zu7GIwGODx48f4m5/8JXb2dvHqq5/D/Qd3ce/BPazTDLPpHKvFytZ7oFyrEN1uB71+H0lvQAoYyyV+9Ytf4tHHHyP0AxwOdqHrAuPxFBA+3vvwY1QiwBtvfBOt3gBv/epNxGGAN974CpaLGabjEU4fPsRyNgGbb9y1GoTztr3Dm+sI7HzgSBRtXB4+97lXEIUBpAA6rRak8FBXQOnXqKvaqpFwngXXajg/H1m+62QyQa/Xs16oPKf6I/w39hq1221oTYIWp6en0FrbJOQ4jiEFGdRf+9pX8Z6RIV4sFqgqhbqiMZkXOWpDj2qS7rSl69DzcVgcEL5EXWlcnI/teK2qCkk7wWq9QprmACSePTvGfLbAepVikaZI8wL3797BH/zwD3H/7l385V/8CP/n//K/xLe//wN853d+B77vI8ue4umTY7z26ut4+MlDFKqC5/vI8wKL+QLzRYaT0wk+fviUqFJmved3wIISRa223pt5s4LrIbhAjUHiJulCO+sH0T4312maLgISypzIRoQDGrF1bEw7DUdIaWuwSdsuYxE55zgG8MbVtv7wGY4X8bj/hz6uoxA9D8T/uxhJ15972ZB7HrD/u7bhOuxw3XVdvLNpPGyfJ8FSqHxes4ZtPoPbhm3Wx/MiGs8zNDa+i03M4173umgRfei2343QkBS362xTSlmVOC7aG8cxdnZ2LPXn4GAP7XaLREkGA+zt7eHw8NB65bmmjvscSZLg6dOnG2qmnFAthMBiQZHrvb095Hluveue52E4HMLzPCPxrqzx0W63kec5er2ezUFotVomYiPheQE8LzSiIR7IpyFQlrnBHr6JjCfWuZqlKTyHEcLP1O/3Nypmu6UheO/l9Z/xGOc+s8HmpiFEUWSLm/L74ugHt2dpShEAsEYKGx1crG8wGFiVKxeHzWYzO7YYa7MjmAVS2Jkcx7GNwLg479MOoV9wJXz8ySN7UX4QBo6XcgZw2VPJAyHLMmtYuJ+zgcCDrq5rZIYH2jYAQAiBOI5trgG/FD54EWDvNbCZ7OK2kz8DBGpFFXpVXSMKAwQBFVwRAlCSaAx286QZTO0W5m+aPGMSTRiRrX6KjhgDTUhUZY46T6FBmvkKRA9aLEh2dDFf2KKDda2glUIYhVgbmUqO6rSSFjrdDpRS6HTapCsvBIo8N5K/lABeFYokdU1hxSAIEIQh6fwHJN2mtaZkYSlRbVndLMuptKE+0DA03ngBqgRO36/KAqPzMxRFgW63a95XgixLAUGebCFo4lB7KkjpwfckKiOVTNQTs5BpU2/E800YkTzMUkikWYqk08I6XxuZZTLeiFoVQEHg8eOn+N//H/4LPHnyDFlREFdcaySxh9defQ1HN27CDyL82Z/9W8zmCwOKVfPusL0IC8vBpHdOkpueUUhzeZpu1M3SsjRTygRYOUaT1iXVmahrSF9CAegNb+B3fvBHiNoJ5qslzk6OIesKTz7+EOlijl63g7iVoGekbw8OjxBFIWbzMS4mYyzXa3R6fRwe3cTe4QHanS5CGVKynOW7Kgusx5MZHj96jOlohOVsjk67jaPDQyyWS0xGF5gvFliuUyjh4/UvfRW37j/AyckZHn38CX7/D3+AOAnw4QfvoFzM8dd/9j9DFQW0qsnbDCOhKTQMMQeoG8OMjWqaOwJCAqpugLgAEPge/rf/m3+EL3/xNQSBB08KpOsUnggALXF8doykFQOC8rgmkwlqVSOJE5ydXdiQc9/IALKsLSUJeggcqW0ON2d5gcVigfPzMyyWS7upSpMvlRdkuKyWK6zTFFQwtESRVfCDAHVV01hyxolgI0qbdcn8Lj0JDSAKQ2gNVBXlSoRBAD/woQWQpRm0Bl566SWk6wxPnj7DdLFCWVUQWqHXaeP20RHqqkSarrBzeBNHN26g0+7gww8+wPvvvQ8Y50Rel6gMHUqAjAg2hhQMrWnLQ2pis+YPolkHNVWRhmxkSDeU17DBlNviq1MxQfAeYFRjIASp7jl7kHRyKDaME2xaMkJQtE5rYHMbFBDw7HNd2vr0Nm2yab92//CChxuVo9O3PdWugbX1kdj6yhW/XzKGrjjYlbEtDrtxtmh+NO01b9zet/lSI919ud2b66bjBbdXvd54cINS248NY7i6DgnCGJe99ByWZsNeY3McUd0EF0Tzu3LeuW6eAc7zCiGhr+ltejZpryOEtGsY0LR5O4/vOnr5Vg9sfW7GsLpM7eIHsBES48SDmaeewWjSo7ZKJ7riOnE5wuAHPnrdLpJWbPMeOPLbarWwszNEGEYQAhgMhhv1w6qqwHK5oPpoQWABfxAE2Nvbw3K5JOaFYbH0+32sVisIQUnSDMQ5QswSrFEUWXqSEKSC1Gq1LIMhyzILrrmwnYtPOZrNRVaFMNEZ3wcMrlwul1C6NtF0wlqxoex7xtsvhdhQeuL8YSmlzbtjwwBolJ1cBy07jPM8t0X6OALOmJdlZxn8ex4JdcRxTLRVRVGQNMuIOmYcbUKQiujFxQWCMMCgP7BrrBtBq801rNGnQRgrobw77n/GCxy9ieMYP/jDH145H9zjhSMaHDLhYmj8wtzCHgAs52t7QlUVcag5P4DPcwcQnxMnJJ2oBawecKtDHsayKK0V61Js3MiKe00OSXGbXSvf/l6XkABFH8w92CipVGkHVl1XNhyVpimENHkjTsSCIzbzxQx1XdkXRxZrjDLLsZqvDDhZ2wRV824BQVVioYEkCdFutdDr9bBaL5GmKzt5OoaTZyePqUKcRBSmg9LwpYQfS8QxvWbqX1rwqqoCrz+cF1MYLjb3GUdTeJKyZcx0g6qqAWj4no9a1YDSiH0fi+kUSRhivVrhvCio1oeikGWrRVx5lkFeLpekduRLaziu12sUeQE/8FFXNVZLqkI5Go2sZ4AWphKjESWOe76HLM3gBwGKvICARpwk+O2vfhlFluH0fAwN4pKnucajJ6dodQZIEkqM9rQCJIxQ8NWHBvHNIQwwrGuzYWmbPAs0xu0mlUpf2nA00ziEua+UlBwrJSbTC/zylz/FF776NfQHeygqjdnoHPc/91s4fvgRxudnSEqFsgayrMQ6pcJqrSjC04+eYr5c4M69u8iXGd5/+12iBYWhMcRMNfqKhBKKvICEQCdpIR+P8cGv30aJGp//yhdRa4VsscZ8lUOEbXzhja/j8OgWjk9P8dGjT/Dl3/4aom4Lx48eQq1T/OInfwVVZLSpmegEjT0zB+1AbxwTLiAj0Ej9IjQgFCBEjZ1+D/t7O5iMp1ivqd5CGIVoJxLz+QShWUTLqiLZwjhGVVfIq9LkPAWYTMZI0wyDQR/j8RhlUSJdrVFXpLLEnrl0vcY6zaC1h/F4TLS8skRZjgGtEcUxFuuV8f5oG86H1saM8qAqBYDokwICQgvCsbZPjBKTGQLKREiKmmqyED1aIy8zKF0jjELkxkumoDGajrHOVlhnKZSJyBbTJS5mH9gRJ47H8N98GwAJQtSKHBdEcVLNQBcaUNXGe4AxpiigsAXqnb9tgHXlvuPtsJX7ozEMNoCtMXr4K9gg2QG1ZtB3PV3FntrcaQOka2xnpDqeXrV5bb113c9+CBNBadrVYMVNkMuFVZtPuf1643e3SS6I3zQSnH8zcNxu2TXebSnF5ly0OWtmTgr3J0foGirsJeNq6378Tl3GA62JAtLZw8HXscDXiUQ54F87/UbXZLCvAShaQLSZg0wF0hqU4NtQfYTYlOmVhkrN92/6/OpcC/qQmRRcG0VZgwPGyUZ9vEmLFsJz7tEYSUIIeDIwlD/aFwQaB6nQAvCaInW2aJ4wBAhN7SUnpzDOQcD3JcIwgG9o0VJK7O7u4ubNI+wfDHF4eGAKtibW+et7PsIohGdqfOV5YTCcwHy+wNOnT3Dnzh3k+RplmVmAzN5wjl4wmF4sSG6aef5A44FnFSYuUDefz22tHcY9bIxUVWXzMjiCdH5+jm63u6EKyN5/3/exWCwsaC+KAkE3QF0R7UjXhHGkCNDvtTdYOmVZEo5ZrcDRbvb0s0CClNLmj7g4mNkzPHYYZ7HKE6cKMINHSmn7iqlUYRDZsSGlRJGToiJhZI21qUMEpeAZzEXeckBoAVUqQAESckOZqtPpYJkZme+0MdyEEAi9EPPV3NKulFII/RBxGG8oan3a8cKGBlWkFZbutFwubRVYNhqYJpPnuZUjZdBfFAWyLMPBwYG1VJkrxodSCrPZDNKE5ZiHxskp9HIDeLLhiDWTTFm+GA8uNmia0D8rjzQeECklAhOGIs+ih4pfdFFgNp/b0vB8jziObZ4EZ+LzYAsCiohEMQ3CxWJh27lcLlHmJXStELVidAc9c45vF6OG6y8az75S2NnpO9EDV7GnWSy1VkaOkqhRYRgYTnWNZkOgQlugIYuyKBCEgZ1M0MAqI836dE0JScfHz+AHATqmvgInE83ncxR5jnanYxSuKALRarXw9MkTLBYLHB4e4v3338fR0SGkJ3B6Robak6ePIYTAaDTCarU0FDNQZezJBGmaUl96gUn0LuzEZgMLoPHQ7XZt7g5z7nvdDoqyxjf/3rfx+S98Ef+nf/Z/xbOTM6iMonDj8Qjvv/8+XnrpPnl20WwIl92LdPA4c6mCvABBi42/NUbwZe3xZjOWV3g5zeeqwicfvotOp4PbL72Cw4N9SACzyQh3HryGuNXDk8ePkBZTkgrOUqxaLYwuzvHxxx9DCdrwvv+DHxBgzXNk6zWqssL5CXH779y+g2G3CzHwoAIPqijx9FcnKKoSg14PaplhmaaY5yWGBzfw+hffQHuwg9OLER4+/ARf/sqXcffOLTz66COsp2O8/9abWMxnCECeaQhSRKM3JZq+deae2y9X9YOqa0BXuHF0hIuzM/hSYblcot/vQ2tQxXMN7Ax2MD4fYzqbISty5GWB3FKWQH1UFKirCh999HHjTaxqq6DDa1AQBJjNF1BKmCTn2ngOQZu98bzzHFRaGwlfZRKMfcphMDKI2nke91npusoCL2XmqFbaRovZOy9AbZFC4M/+7Y8tsChrAkius6c5arsm8r23x6L55dI7eFHKzzaVZRvw8vNvA1v3cGHwi0H7K771fGfwtb9fjjr8uxoXm9e/Tub1KrC67VXe/px/um3eME5cQHzF51dd76q/uQZA4+JnmpwL+slxwopAjRHYeOhdbzsdzHhoPncjwbx2uk4a+k4T0dJOqMqTPjRIuU+Y/iaxDWq/Ru1EKthYI9AvKLba9MVGl8gr3wP1T/NvN5JCxVfp+aWUl949G41SCnjSqYztGrvQm+MAwhQDpWfT0Ag8LkSsbJ+ERk5fGguj02kjiiK0223s7e1hOBxSNfu6wp27t6GNw7LVbqOuKwyHO8jzDKvV3GI5pvbUdY3ZaobhcGhLC3ieh06nY95NTUXjul1LGSJ2QmFLC0RRZIE45c2l9nyttQXqnKOrlLIJ0ez0ZGpRr9fbSGZmo0QIYVWn2JvvGjuUv0GRBbewtABQGAdyt9vFdDq1NCmmqHPUodfrYTabWTWoJElsMT12VHGOrJtY/ezZM/T7fWtUAdhIqmZMw/3F17AYoyiRFTmSpAUhhE3cZmqU9JromBsUICPTt1Sy5XJpjTuXVcT9zvcsy9LmLrJRxf3NuYjX5aVedbwwdWq1oMzz9XqN6XSK6XRqrR724LpauxxKcqkRPKD4b656Ek8s5kYzV1+DVF4qk3wDwHLX+LzBYGCvwzy5NE0tp5qtdj7HXay11qiryobC2GtfliXW6dpIOFLhGAGq5Or7PnzPgx/46LQ7hirVZPCTVwU2r8H1wFCBqib863l+ExITErUxaITxQkjPQ7pekyFgFiFKfM4RxbENwxEPO4PvETWADaCSZWWNhQzQ4uhJicLUFFkuF0bhi8OZCyilMBqNcH5+DoA2gX5/gDzPIAQVnup0OlguqAIz0UpCSEPDePz4EZ48eYq6rvDVr37VFMaS6HQ6OD09xdwYcEmSII6J6qWUspQrHty7O3sI/MByBwFYo6iqCsvd5EHPxgjlUvjIiwrC8/HW2+/gv/l//Ld4/PhJY5QKiZ3dXSyXK6RZZiIOTLvY3KgbY05veC04rCvhbRi9PJmllFD1toHB15MQYtPWtwakIADqRS188avfxNHd++j0hphOZ5iMRoiDAIvZBE8++RjL+RTtOEQSRxDQmE6nSLMUt+/cwauvvmoXXEDjyeNH+OnPfgatNe7fu4/XXnsNeVFiXZbI8wLTixHKojSenxVkEOLu61/E7ZdeAfwQj58e4+L8HF/58hdw9/ZNPHv2CLPRCA8/fB+PP3gfqHJ4xrOotAAXJYQxfJSqAE1CCFdKXwsqGlVXpMKlawXPU/jud34bt/YHCDzgS1/6EpRSODs7w+PHj7FYLNBOugiCCEVZQAGYLxeYzWcoq9qoJ2kqoCmbCrDactMbo57/qyplohic36ONp8njU6w3ys2n0Jo848pEGGmN4md0l1q6JwMrBdjkaikleR/5m8IHIOA5ntCiLMA0jutA5XXgfvt3d/11gd/2dbaP6zy7l+4nro8Sut//u4D8q+bppx3bgPxF7/9Z26dNFOBTv+fc3wWuV93/eUbR887bzsO47nvbn/OaaL5hATrN58vCK1f1JY8vAOCCpZsRDWysl+675HNVDecajRec56ArRc2RcWIf1DZK0/zH7eP+vtwnjVF1uY+3IxwUgaHfWGWviapo57xGXYl+b/p4e59prl/D90lp0fNI5ZEBbbfTwt7eHuIowv3793Hj5k30ul3UqsbuzhC1YsZADM+T8H2q67BeL+wzllVpc9oowZmqUJMjRxsVpralPM1mM+vs436fTqcWZ9G+TFEGXt8ZnK7Xa0u3YaYEC260220URWHaG1kc2Ii4SOtMXCwWloblJkmzOhKzYPh3xoeuyBAza6qqQlkU8KS0dZYWi8UGG4dVQNM0teOLxxrTTVngKAhIwIPbxA5qbj/PQzc3Qxi85hbacyMhXF+pLEpbM4qNvSAIoLTCer20/cP4hIwKD4HfqEgxrasoCtsvPEf52ZimxXjWjejEBnNyTnVZlvjBf/Tp1KnPZGiwVff06VNrDbGFyCCWLR8eZPwAvICwseHSflxvIr9cKrSV2xfJ12cLE4BNzNzd3bXWrJugwlKXQGNt8j3YOCqKArmxnKWUllNnlRSEMZZ8z3oY+DmU8UYKEPCWkgr5aWhUdWHzG+q6hpASVVkhCAOUhoIlBIEHC34goEpTTCwIMJlMoLW2liWrcDEHMU1ThKbKo9Ia08kEg8EAs/ncGiS+5xm+urKDQwiBvd1dnBwfI03X8HwPSZxgsZgjLwoEZvA/e3aMe/fu4ktf+jKePn2CxWJJXtuqhNIKuzs7FtzPZnOkWYpXHryGn/3sZ/jpT38KIYB7d+/h5QcPsFwuEIYBiiI3FnlhlSNoEq8RhgGEoZAsFiRFqhXJ2nK9C6oiTsZFGAUQAhiNLrC/f4Ag8BGGpCIhBRleGkBRVhDSw/HJKf7b/+6/w8cPH6IoShQlvZdaC2hhPHa6iXjxhOff3Y00iiKbayKEJGqMbkL/vBnSJtSMF74Wfc+DGzZ3wZ7QNXnjhA8viPFbX/k69m/dQZR0UdYaZ6enCD2B0BMYnT3DydPHSNdLhH6AxFCFuG8jQ5kSoOjU02dP4Xkebt+6TYl7eQGVK2RlibSusSpLKClxcOsmXnr5FfQGh1iuM3z48BE0gK+/8RXs9Do4P36M+eQMjx8+xPvvvA2hahj5BON9a2RHhWTQQF55KRoPvAsgNBTVV6iUFR3u9Vo4OtjF0f4Af/8Pf4g333wLLRMG393dxYcffYTz0zG++93fxdHNG2i121isV/hv/uRPMJvNsc4z40Bo7mMBgyBaUVmWqOqKaIAmP6yqNwtNNusUGREam0CVfgpHthWNk5dXCtd5uuXwUNgEkRb4wQNzrDi6YceL3IxUPM8ouG6pvw6sX3Wt7YjIdR5191AN4Wrj3O3r/IcwNPic5wH868779EM8l351XZs3xic2lRRdkPNp7/SzRDP4767B0OQOcHskoJvIhSsFzmse3du2wn7OlF3KZOR7NN+h4mYxeZgFXZ89sgz6q4pAN9dLKMsS5+cXoDzFjhWRAYDZbObULiC1Ia0ZY1w27phyxTiAnmfTULT1mJwn21i7DFWKf7cGvCTc4Ps+pCdRV0SbabVauHXrFpSqMZmO0OkQ3efg4AD9Xg9CSngesLe3ZxkTL730kkkOTrFczEzicWpp6ORxn0MIs3ZpAqu+51OxW59ozuxUXS6XiOPYSMLWiMJ4Q82IwfVgMLDUZZfi44r/sPhGURTY3d3F48ePAcAWQHXZJVNi9kAAAQAASURBVOws5nHGtJyTkxPs7e1Z8Q7GF/xOGM8xRrOFP831XAo/g2NWFHQLq/LzhWFogl/agmgWKOISA5xMDsDSudzxwI5zBvBslHA/bhoMmQXvDPq1pgTy+XxuIw2c5M3GCuWm+pbhopSy0ZqyLJEXqY1E8Rz2fR/L5QpRGFujho1ANrS4/7l/Obrv4vYoiqyhwjQu/v5qtfrNGhrL+cIOGjeawQOEXyIvYtyx/OIZeLmL+javkztRAKgMIE6zDHmWITde/OHODjrdru1UN9zKA4s5gdzhvFC7HiO7kBvPIV/DtsEsdgK0eNSVGVTG855nueVO+r5vPIxUPKwoSZeZ+4uKiWWmXwSUeVlsCLECwnq1svy8brdLlmVRoiwLpGmOygAi36eKyFVdmeQnMiYa1QJpvPrk7YnCEAtTlExKiclkjFarhW6njTiKEBkDhsN8XPXY8zw8e/YUaZoiXadIWi30+z1oXSFLM1Q1JUFdXFwYIy1Bp9NDmmY4PT2FlNLWPImiEL1eF6vVErPZDBcXI8urjOPNKNhqtQQv8GEQQitYDnOn00GRE18wjKiiOE/QrhkXRZFDSB8CAus0RavVshPkgw8+wJ/92x/hF796E8tVCi0kiLpoNlBdvxB9w41qQJN94hbB4QXV86gdPL42vZKN7Of2uCRvoSYpfyGhhI8Hr38Re0e3IYIE6yyDqgoEnkC33YLQCmcnJ7gYXWA2mwFKIfADBCb65gkJiBoSTgEz06a6rKBzUxu908Lg6Ai3X34F7V4PgMDZ8TnORhPcOLqB1155AA8VLo6fIF2M8eij9/Dh+++beaQh2LCAACCtoQEoowpF/FHLgUYD9KhNtY1oCK0R+gF2d3v4ypd+C7/znW/hf/h//ynOzs4wGAzw3e9+F48ePcI3vvENhGGCOE5wdnGBKI4gfR//7J/9XzCZTKk+hKEkkZIZgRdtqCFlVcKTFAkkKpNRCEPjCFFa2ToQADbGiNYOkN4Cfxt0JrFJpdkwXhiMC+fL7onXjEqhKe+C+2/bW/9Zj6vOuS4C4H72vHuRjfTp33tRIH8VwP40Gt5nvcdnOa437rBhaFymtl1/PdfQ2I5GbINkPty98NPa+Lx+cPdkYeepSaQ385pG7HbyvEO52vyEZL6hoWr3mnROE93gz4ySI9ioBZqaNO796DOOXjDGcCU36VpcXNVNHud8OWH3fO67MAqhVOW0kTCEJz2LGVwvO39PeiRVHoYhjo5uGCBYYzgcYm9vD+12B1EUQgiJnZ0hWq22ofqGWK8bpTsAmM5miKMIabaG73kITFVogOS58yyH7+S1CiFsgvTTp09snRl2nvq+j5OTE5Rlif39A2hNtbaiMCRvvOfh2bNjQMNSk8jhR7iP1Zq0AeRMG+LPuS84SsCyqrT3Ey7hhG12JLMRwbmgDKB5X2XgzlEIxogMdFmJiZOxXcPFVYdkChfXrJjP55eoeZ55hyz4wfd1HdLcXsaJWZah2+0C2KTr87NKKa1UrFu0j2lbbEgw/uNn4yTyPM9tFIQiL1R7KU1Ti3WsAmaVW+OFo/KsVlWVyooIsYPbjcYwLncZL0x142txxIVTJ5h2prXG3/udb127ltg+/iyGhgvUq6rCo0ePbK7G/v6+TQ7h3IggCCix10Qh2ELiiIZ06ErcaaxPXBvqi9YKcRQjiiN02m0Iz0NlQKO7OHC7lCIgUzod6i7A/J2NKIpzbmNkgNSfqgJhEKCqyHNNHmxSjCrKAlFIXu3FYkHWpCRDgr3t4zGp36yWS4pqFIVVWJpMp/A8uuZsNjceXVrEkiTBgwcPcHFxYWpcCKzXKXoG/AGbeSccutvb37ec8qoqURSl4RrSIMqyzA761XKBwPeR5Tn1mQHKRVHANyHALM0wnU4ofNrpwPckklZkJxX1m6lwXJRIko5dSI6Pj3Hjxk14nkSSxKhr8oJMJhMsFktIKUwdENpUkiTB3Tt3bTiaojzGc2dAohtepM1FWK9DkiRmkxHwTJh4Ppuh02nbCTSbTlHWNX7xyzfxr/+nP8NstUatJUpTCFiomqQxN/ZhniKbgIs9IABQl8pOYleAwJOepdtse4MBCSn9K/4OaDbYhYIUGrUGlAhx485LuPPgcyhqKkpWlTWgaSFrtVvwPIF0vcZiNsd8OsVyvkC+JpUzKWq7IQNN8cdWq4327j52Dg7RGe4iaXVQZBWm5xOcnpwh7id48Oqr2N0ZYrWY4fjxRxB5ird/9XOMz0/Yv44GVpkO1BKcBE5caTLapZCmeNplz/ZlQ8NHkgS4dfMQ4/EEWZqbSCGPf4FWq00GeVXRnaVAXprftYaumxfq5jl5nkcJxsZF6QIsDQ3hULs23pGGYXdz2zfHyotiWXKqUJRDiyba4Xp6AQae7pkOeAU2DKB/1+MqQ+I3aWj8+2jj847fhKHx4tfYjGh8ljZe1cfuZ1f1+7Yhcx1d6kUiNxxxoJ9OZM3Jsdg2KDYNlMuGDQs98HVdloP7LG5UZXPsbd7Hsg68pmaTiwvIyKgs7dizEXEBCGGpt/1+31xTmeJwPfT7XSs6s7u7a6979+5daJP32G63bJ6B5/uIk8hGLAbDAZIksWIxWZZhvphjMBhguVxuqA0NBl14nrBiDYURUPE9H4vFEklCUtzsZef8VyiN9TpFGDa5oP3+ANPpBFVVoj/oG6oT12TwUNcKSdxCYQpqnp6eIggC3L59G0opPHnyCN1uF71ez75LzjVQigq49Xo9mwTNgJ4pzIzrhBC25oTLSuG2M62JjTw2JJjCxVQt/izLMgvs2RjhPmGDw6pIOXmcy+US8/kc+/v7G2OKPffdbpeoTmYcuU5qfn4u8soSt61WixSpmOZsnrcpAt2MWX5OVshyqVbcV5yL7DqLoijCYkGUdjYSirwxoNlI4T4rigxRHNn2c66IJz2kaY52u22NIH43HJ3i5+S+43ZyFIflcDkSw7R8zrX+/T/6wXPXE+CzGBqLBTXSWRCyPEeWpiiLAqUJpSkDgNg4SEyyDecdMM/YLjCa6hi4IUxdUy2L0WiEv/iLv8BLL72MGzeOaEEwCkNlUUIaIFDXxI2u6xJA46Ggl0jVbj1nkLlF3NI0Q9sM2qLIQQVgakRRDKVrLKZUqIuLu5DVR7KT09kMUpIOcRTFWC6X2N/bw3gyRpanKIw8Zl7kSGICwQLaSr434bEA63WKnd1dhFGI1XpNXEuTAMVScnVdIy8KxGbA1EqhZZKRyqoCQItCuk5pYMUR5jOiUQ2GA0wnUxQmwkIJzCYXZb3GcDBAXhDdq1YK08nEWuNaaQRhgDAIEYQBDg727OLlWvdpmsEPI4RhjI8/fogoirAzHODi4hy+7yGKI2RZjiDwMZ8vzALBfMIFoig2FZ09dLs9RHEErTTKokKR56iVwujiAr7vo9PtotVKAFBymMvzJC4oGb3tThur5RJRGKLIC8zmU9RaIYoSPH12in/zP/85Pn74FKt1Yag+tYmemLoAdkPlzbbZ4NlbRGoVm5t+s4EKClubCJlSuuHVa4HLiiN0Fw3K+5FCkddaa0AGqCGR9HfwhS9/Fa12B5UGAA9ZUSDNC3hSIIpCtFttREEAoQ2FMM8p/4dD6YEPz3hWwjhGHURQGphO55iMplhNlhi2+7h//z76RwPUdYmnTz7B6dNHmJ4f4+LpI6gyIzIPF10TgAZHNKTbW+DiGWRoNIiaMXVjaBgvUm1kf6WE7wEU4ZGAaEAFNAwtAWYs1hAm4kjvzhirDJSEBCVoN/2tDT1C6+2K7uaBmGZhIiC8BsrnxL2uA3/bAHkDSDmGBpz8DfpO492FM/6EMImvelMx5/rjkgX9qe137+lex3Qv3L689nrbpzvnOW+iAZLuFa9oioCwOSyC+23D0+2AU4dq5t7bPYXHIwHhres4X6T2sPqPsNcTzmdmytunu97QEOZ1CBdBO31K3n3f8ygeqGozHtQGQGfnhnv9q95fU23djaq5Hd5ED9iA11pYw4DGmwdXMMPVsWhUjYT97uZYV2jqFWnTJmmfZ3MOkmhJXVcG4DcGiHs0FBxiCgRBaOm4t2/fwc7OEICC59M6ffPmTezu7mK5XKLb7dK+EEXodDrI8swaFLQuKbTbbZsDUquakoDjBKEf2IKbrJJY1zUUNPzQRxLHiGPyyi8WC7TaLZRFgXWaWlyUrlOs0zUC38fh0T4uLs7h+T6U8e4zMPS9EEmS2L2PQaiUHuqqxnqdASDAPJlMsLOzA6UUhsMBhBB488030el00G63rQNwuVwbYB4jikKQE3OFVisxAjK1TVy+uLiwLAfeZxusJi2dZjgcWizA4J+BKQBrmEwmE+t1Z4c0M06CIEAcx1aOlmVd+bOVUXsiml1kAXue51aulrEdQNR6rpnBf+t2u9bZ5tbX2t/dhdbavkuOdHEUwpWa5XHN1+R7c59wdIPzlbkmxu7urn02KaVVzmKDgb/LfS1EU+Gb6G/hJWe51sSgqarS5OeYukxSIstz9LpdUlBUivCy1gijCFIIS5NnJ3yaZTY4AA0cHBwgyzJbrLvT6Vha2WAwsJS332hE4+L81FquSinM53OcnZ1RaMZInSVGp77b6dB3PY90850NnF9GVZbwmGtv9X6bolZVWdjBMJvNcHJygv39AwwGfZRlhdLUlAAaq1hIYXWNG34phT2LNIMEvbg0TRFGERIzqKUA1uuVMSjIWpvOZgj8wCQ/CzvYfMNxnE1nmM+XNpLDE6Hdbm9k6LOmNLdltVqiKHIbDWD6lNbaegs4yWo2m9nkaCE0gpBCa8+ePbNRJPI8wHpj8jzHarWykSOOUiilMB6PbciNJg7J1FHSurb8xLIssZov7ASN4wS+79nEsIODA7twMLBvt9sYj8cIkwiqBhaLFJPJBCSgRYZaEISW78feHFb04onLC+Lrr78O3/dxdnaObreH42fHVueZ73f79i1w+JvHlRsKdClz7sYwnV1Q2E9JzGZrvPmrd/GjH/0VptM5SqFRqcoaGcrKYTJ9YHMzD4IAraRFOQXOwsv3dfOTNjzmBrxu68BbsAAJDYlG4NMBT54PIX3cffkB7r/8Kvy4hUoBRaUQhuQJsSocfoAgDBCFETwvMoBWQEiJoipRlCXVaMkK1GWJOGlhZ3cHe3v76LQ6yNI15tNzpMsFTp98gk8+eAfZagapK0hBZQaVMjK/goCQEM272PZSCuEYH87RRCZZd77xyLIkq6VackTyGs/sNqC/DoVf9VcXtF0VcbnqXtvnXnU9tx+edz3+jsvx3r4299U2Vep5x+Z1+JxPP/fTEsOve56N+wlYQ/Oq715/yCtf0ra3+yoAelWUkD5rhEncMQkArBLG19ykY13fV+685t+5nxuQ3lB3yFj1EASRpT4wbYKptABs5J9rDlHEvSIxN8ERutraKpvPwpRFAaqTEjjPoO0zUR5CI+rdGBr87JcNJWtsS2z0c9PvAkrDMRJcarS7TntGpQ0Iwwhlldlreh7VJorixgtbVzVa7TZ2dnbQShJIz8Pe3i729/rY39/FzZs34Xm0P965c8fKs8ZxjMViYUEdU32ZIrxYLKxca13XWK0o4rC/v2/XUd4XWX6VjQFO6mVuPtO52WPOfx8MBkRpBQHgs7Mz7OzsWGcVUaoIq6RZhtLy92HFbJaG/uz7vq1lwBSnzIBEd993cQjvh71ezzoQyTCTVjm0rmscHh7aa/FY5H1+28sPNG1z1UX5/mmamtyPylLdz8/PraQq94t7P85R4IgER61WqxVWqxVCQ/VyyyTwXB2Px7YPuKYGY0o2YjjqwkZQWZYIfKqbtk294utylKXJyRQWx/D77/V6tnI4RwvYEAoN7Y3HMSejM/1rb28Pi8ViI4eWjREWNRJCoJV0bD+z+A/P1clkYmV+eV1YrVaGYu5v0J7c3BaOFvFew9EhpTTCoMFqfCRJYmnojF3/4I//8Nq10a4dL2pojC7ONhJRrKdOExwiydnadiZ73IXv2UHv5lEsF0v0Oh37EG5pd9+TqMsC0+kMg8EAn3zyCf75v/jn8D0f3/jmNzAcDC3vLk5ilEWBTqeLxXKB0egCT588gef56HTaCIIQJycnEKZU/XQ6teXiWT6t22nZwcmyYVEUWSNBKWXDncPhEADw4YcfYjab44033oDve6iq2ig3+TbESaFXKiDHk1Zrkp5jwMzULv43t4O9Dzw4ut02lK7sgv/nf/7nODw8xN27d6GUsoPODf1JKW34lycZe3PCMLS5GgAsT5ALsqBWNqGOjSIhKPl/d3fXhtL4HtZoqivkeYnxaIbJZIKDw32sVnOUZYHFYol+v4ckadlQb1kW5v6F8WKQepUQwljNLPMpzaIcWRUNMjQF8jwDIDCbzbC7u4MkaZlcFs9S2oIgwOPHj03Sb4EwCE1CegABH6en5/j53/4Cb733rpE2JRBN22STANk44xt6V7vdhoRn+8BNEnP/czdq6yV36ADuT+3kb1yetSZ5XUiESRsvPXgVRzdvQwsPnh+h1SZDP0tTrNPU0hPrGqhNNXoFWgSjJEa720XU6ZMXLfRRFjnS9QqT8Qh1lqFeTDG5OMPHH36AuszhC426MrVmhECTBEnFDpku5Rb03AR1zoOjcQbQpsDa85vVwfl726DuuuNFjAS3v93ft8G967R40Xte9dll8Hr1uRsR3612usDuOqD9vLZ9VkNju50vathsXWVjKL/QlqMBlhg1d94YQw2Q5s82Wun8zvEG+oOUzR62bWi4Y4/63+23F8uv2DwoYun7PmJD62DAEQQRfD9wALiy6wcDC35ON9cRgvK2hDBrE0fvuJ1S2kghgyeqY9S0393DSVb88vtw3/N2vwthjBHB16uxkftg5jNHjyjHIEBZklJhFIXYMUIiQRBid2cH88UCN28e4Natmxt89b39PZQlOfhGFxfk2Itj5FmGjnHC5enKsBGUUVVaWwVMdmIVRYGiKDAejzEcDu33WGaVefG8p/X7fSvtSRGCITklZaM2FEURptOpBfe+71MRUDN3y7K0QJr3dCGIzjMYDBBFEcbjMTiXMYoiLJckusMAmdvPa2gQBBaLsJHBKk4M1OM4th5zNmQ4D4IB/GKx2MgnYKcog+ztnITZbGZzJ9jLzvkJrVYL5+fnG/3GEqlhGGK1WlmHKb8LBv+8P7AhwgaHEE3dLnZIsvjPer22ggDMZGCKEudDcN/M53M7nzqdjq1ozXLAbCD7Zn5VFY1Rvi/Q0JRYurfX62E6ndq9n52bTK8bj8eWXsbOaTZ4+dndfdE1WNhQ5b+zk5RyU6kWHWM5dlK4UREXf8RxDA2NViu2RbJdiiGPR86zYXZGWZam3lZoE9h53LMBBMA6fL/zve9++kr4oobGs8ePiPYkWZFBWh14VW2qMXBxvuHOEAoKdVUBoqmgXJQFHj16hDwr8PLLL+P4+Bh7e3tWnUBVJdaLJdYpDaizszOcnp7irbfewve//31T7K2yncAWFlf/resak8mEqvauVrh37x6gtJ3sXL4dIHWKQb9rATdPdB5U7KUAgIuLCztAOYx0cnJiOYO84LC8Gi9UbnEUdwF8+PAh0jTFgwcPmmIoZmK7ocI4jjAaXaCscsufPDk5wbvvvouDgwMcHh7apCH6fmwXzsViYRcFXiRcK1ZKYY2JIAgwn8+JtymJr8jfa7VaCIIAOzs76PV6G94Ca9AEPoqqxsnxGYqixnK5QqsVYbGcQkqBKIrtouYCJ14sWZOaVRfa7TYGgz7yPEW/P7CTS0qJ6XSKwWDH3N+DEMCzZ89wdHRkPRVlQepYJMs3N3kyAhcX5+h0utjdJY8SR2WyLMfpxRgnJ2f421+8icUqRVlqE10QgKht/og7baSUiMPE3pcnv51kZuxv02igWcFIXzJEAA8Qm6CUwGVTVEtIDxoStQbCOMFgZwdekKDX30G327E8VvJmKaQZUQuV1tAC6PZ6uHnrJqQfYFVTVC9bLVEXKQKhsV7OcfLkESZPH5HSmJMLsOkRZoDBqlr1Bji/BFrQBCPYaGBARTkU29zsF/WAX318lvO37/tZgPVV97lqrLjfdR0z17Xjqvtse/U/7dyrDA33lted81me/9r7isvzofl8+xruuVffe9M4uJpWsz3umoNVjK4y4mg9dD2bdB15qZ3XtatpuzbKaiRNzB81Tgjy5vN5riHKc2J7bJB3t0li5nVj26B3+6Xpi00Zbf6c1p3NZ+B7e56E77lREJiojFFQkgJVRTmArVbLesXDMMDO7hCHh4fo9nrodbs4ODhAWZbY2aE1m6VEXeeMH5BzjZKKyRFHuXxNrYgkiTGZTFBVNXq9LqqqxnKxtPl5jAUWi4X1anseVbBmOhADJP5uEARWFYnVHcfjsaXv8L6zWq3Q6XQwn8+R5zn29vZM/mQjBMKOPN772+025vM5zs/Pcfv2bVxcXGC1WmHf5FJKB0/xfsuAUEppQfV0OsX+/v5GQjW/x9QInhRFYUVkOp2ONXCIIp7aNrpSrC71jrHHeDy2Rg05RjtYGOo84xJOCA6CAP1+H2dnZ/Z5R6ORNQRY6rXT6aDb7dqxdXJyYqVu2dHKmIoNPzZ8GGxzBIlxzO7uLkmbO5K/z549Q7vdttEUjkYkpqJ3mqa2MjmvEaWhEHEuSpIkVl2KDQTezzj6su3lZ5DPjmpWrOJoExtEbMSx8cGHGxXiiAYbKUzDUjWssc8RHSHERl+xWBC/Aykpp5bXM1eWeDsSxYqrvEcUeWmfg/vcVZll4+rbv/edT18bX9TQ+Oidd4y6EoWaXI92XVbQSmE6m6LX7RHwLApEcYhKlRiNRtBaY29vz15PKY2PPv7EhvJarRbOzs5w584d+ELg2ZMn9j43bt7ExcUFJuMxzs/PcOv2DRwcHKIsCxM+JHWH9Sq1PM2iKOD5HpYLStrhezBnrwHIGZIkRmgGDy80PBg54sChRw6lUYjKyFxqmDwEWsyjKDYDqbb8Um248VRNmyY2vzhecJWiIjpM32IvLw2iCrWqkKZraK3xuddfx1tvvonpdGrl79jqZmODFxCOyvBmxNZ6nmd24XETmyaTCU6Pj7FcLHHr1i30+30bbeLvcl9wIj9ANUaKssLZ2RhpWuCdt9/Bnbu3ID1t7uXBkx7iODLjJ0Ack2eP+KEhyrKy3qBWq4UoCtDtdZCma+NZiOyiWlUKgR8CgpKuOXlsPp9jbSo3ex5NulrVyDMy1JbLFZRWCAJSMlks5jg6OoTneRiPZ4CQWK1ynJxe4P0PPsb5xQRZUaAWJL16lcEQ+OEGf5M3bHdSX4paaFAuArABMuhdeBByEzg016ZYS60YmElAekaq14Pn0xw4OjrCrVu3jKEsUBQ1pOchy3PUWkF4ElEcI4piaARIl0uMzk8xG1+gSBfIVguSrBWlqSYN1FqYm5KWvnAiPUpV0FAbkU32umwCQm158Twum2dUxtjAxnnXgXj3e27/boPkv4uxcR2Ive54kXtc1abPer9tAHoVyOafV/efG9VoznHbwWvGdZEVtx1XtXeTOucQAEUTHdh+R+57o59uNWi3f4Dt9l//LLQ+N44waXuA4xz2uxtVsA3tiO+lpWN4sBQzqJCjFNhMKGnO0/pyMj2vBduRMv7M/c/lsDOFisDCpnAJwF5v+rdSm3LaJA3ubfRv47igdodRiG6nUXQENHrdDu7duwsAePDyA/iBb/apPsqqQJ4Ts+Cll+7D9wNMJmPEUQQ/IK9/VVKEPAjJSbVYLKFNBN4PyIse+AGqmtaOgaEyzWZTeJ6HXr+PuqqwXK7s3rSzu9Oo8oQR5vOlpf0yCyHPc+zv79tK0gyU2FHo1oTgfY33nd3dXazXa5uQOxgMNrzw7OFVSmEyoRzObreLnZ0dUmhMUyRJgvF4bJO/T09PLbWa6x0w84GTnz3Pw/n5uc1B4Hdb17U1mljqfrtEgEvVYWPNrbUwn8+xXC5RVRUODg6sY3VlqknzM1l6uAHdDJY5n4DzD7rdrv03jzGmjXNBN0pSpn47OjqyjmE+h52Y7Ljl/dJVVWq1WlQY2BhRnJDOuRyM6Tjngw08dlrzewJgn9M1FPj+2owBNkrcBHaer65j1aVe8fPzfRgb8Zjk5HR2OHMSPfd5URTomHQDjpSxgdQ4KEneuSxKu2fy82itjUgQLH51jZCqbsSWAGz8220PG1V1XUPVCp4XWLzIkQ5WmmL2jud5+NbvfvvatZiPFzY0/vWf/imCIESWZ1CGYxcnCVWLNpJhi8UCw+EQBwcHlMNxfoogopfxzrvv4Pbt29jd3UW/38dqlWKdUiXIO3fu4Ne//jXm8zm+/e1vI1utMZ9QSHEwGOBP//RPcfv2bXzxC19AUeZIs7VRgRJYLWkRa7fakNK36k2e52FhZE/jJMHp6elGghEvMFVVIYkjtNutjQqP/BKa4m+encjsBfB9iaquwLrgbMBorREnsUnsMolBUQgpmD9Zo9vtYjgcYjKZYDab2Ym5t7dnrdiqqozRoVEUOfyg4R5ziJSTl3jy8kAAYKMEADCfz21EhStwrtcrGx7kewZBACkE4jCynGFeyLY3PW4zt2OdpjgfTTCfreDJAO+++y5u37mF4bAHITTyvLAhwiiK7eTnqAp7XLIst5um1hqtVkJJ7FKaMdc23FlpvStSejZ83mq1sF5Tv7GhRxQtrtFSm0WbitgtFgus1itUZQlfUiRBej76g12kaY7jk1MsVissixwLozYhRFMUERoQkDYqxAsYL0wudcj1YAHCVJBuPBs8zrSWgNg0Tixf0tCUtG6SchvPK9GZCFg1RSSDIESctBBG5J2RgQ8NoDBcWl3UyNMUdVlC6BrQRGHUdQ3tU4UHZakkbGww/1sQh1zzptN4XV2jrDk2JaUbDyoZfnme2XEGNEbWdV7rbSODz3meZ3/7Or+p4+8Sfbnu/ld5p6/6jgust3Mq+Pxtg2Cbe79tnLh9/rz+eV7bbbvF9YaN+5VmLEs7tl/kXptUqeZ8ayPYsSBwVWY6Gw9Kb8u1GgeAkOBu5WgIzdMmF2Kznxqv4PXPreHOEdeRwAcDSVeutZnzV78X1yl23Zzh79H1aviBwiuvPMB/8g/+Ae7fv0+GRkBUp8gj51mWZRiNLhDHMQ4ODilPxBM4PT3BarXC3t6+ccw1svHQGkVZIjR0n1abhDna7bbNI+M9iud+HMc4PjlBYPaepvo0JbNysjSzAvK8QBhT/Y2LiwsLuu7du2crVadpivl8bqPkDM4mkwmABmy6Cb9ZluHw8BBPnz5FHMfodrsW1LKACnvOWcmRjRAG4Mx00JpqTDx9+hTD4RCe52E0GiHPc2tgcOQkz3OrgsW0o9FoZFWg4ji2eaZHR0cWTHKkg6MbnEfC0rAMiNkQ4toZ3BcANpgGLrjUuqnlxZQ2Btmz2QxFUeDg4MAaEoyZeA9stVrWSOA+Z2n76XSKw8NDTKdTi5/YCGKqkwvI2XPPEQR+HwA2ZOwZQHOVcKaBk/My2lBSEubZteOM5egOK2Wx4hVHifgd8xxjTLBcLjeKBnPfcrvcPZH7l9ksbMRwBIONFFZyDfwQRVHa9YOjSjyG5vO5HXNMjaQ6aYQjWC2LHQlcQJEdtwAreUqURYkgiOxYYIc4pwBwrocQAr/3w+9dWoe2D/9Tv2GO8cXIhpA6nQ7iMIKuakApLBcLzKZT8hgEAdJOB3VVIQwCRJGP4aCH8WgXnVYCXwo8/OhDaOEhjBLMZjPM53PMZjOcn58br0SCh++PMBwO8d477+K3v/FN/PrXv8bTJ0+xWi/QakUABJIkxnDQJ6BdFhBCodvp0KBVCqenp9jf30eSJDg6OsJ8PreqDIeHh1gsFoZrR1b07u6unYxskTK/kDmPHJoCNGpVgRJfCWgJqZEYnmdRFOh0NydyVVXIixztVtfKvPKiyQob4/EYcRybQjy0gB0fH6MoMhwe7Vsjir0BbjiMFyOeLFmWWSoSy7Jx1cfxeIwkiW3Ysa5rLBYLytFYLqEqsqaHwyHiODbJ+Pt2MnGYkL0fAJClGcajMQR8dAcDaA2cnpxBSiCKAopABKHR2F4ZzuLSGjHkiaD+SlP2Gmmk6wKpUbGAnkCYJCohtF1MuX95ArNXgzfULM9tJeiyJInTqqoN0CeEU1cVAikQJzEOb+zgxuEBBsMhyqrEyfkFnp6PsVqvcXZ2BiEEHj582Hh9VTNJ3cV6mxLl8q25loQLBvh6UnLBuytAppAAPDRZJCBetlYUKdCAJ8jjWhclVClQZhLr5QK1aVOtyRPLSe9SKwPMNCApmTPXNYQHCOkb3KAAwWo/xu+rm6iEMH/kZ77WQDAKMwyGXJBVVcoanK43yp57BbjaBsp8XOeJ///l8SLRiO3vfhqgf9FrboJWYBsAN/cWl/rMNQwaY/f51KnnGUKbBpCrtbd5MDCluVGZzcvUVNgC6s97t5ciI3CiPcL5+xV0LBulwGakkvuT+nSzHhP95ErXz3/2qz639EchNsY55TsYI95cI4xCNLV4GqrhVX1yuY2b73j79yiO8L3vfxM//OEPECcxFouJkWVVgAL8hLzUvV4bqi6RFzlm0zH2Dvbw6OljlEWBg4N9dHs9HB8fU9TZDwCt0UpMzt9iifliAXaseNJD4AcovQphGEEIiel0Bk96WMg1em2iySLwUOQ1pJDIcuKpl4WCqgUW83Xj1GtJ62HlIrdPnjyxuQq8j6Zpag0EpZSNQHABOt5LpZQWrDHXv6oqnJ2dWWqPUgrPnj2z3uPpdGrp27z3MhjkqAIDb468dLtddLtdTKdTTCYTiy1ms5nNH2AHDACbVOxGP+q6ts5GplBrrS39qdfrWYaHKx3LBpFLoWGaOOMfcqaS15qfjyk2DIgHgwF5zR1jmCMRALBYLGzyMwDb1wyke72e9ZRzPgkbFRxxYizGlHSaJzT+2bjg+5ZlicPDQ9uPRVFY2hgnSnMS/cbzl6VNdGYHKuek8Dzl/KnpdGrbIkSjTuXuVfwumVnCogJunrKbn8KYgI0KIYSlg/F9Vqu1HUucZM4GslvDi3/n/q5Vo4DFKl28hvD4dPdsWj8bLMJjh+cNU/vc4tmfdrywoXGwf4AoDBGYQiNlTqEpoQFd19jb2UEcBYCu8fTZI5JdBLBeL7CO1tgd7iLPcuhawxMN/5xDdUzJefr0KV598AC9YR/z1QJFWeCvfvJXiKII7U4b7U4LWld2Mc6yAvP53BSY00YxwkNVaUwmYxwc7GM8HiFOEhR5hqokPl6WpaRcFYWQHnlweJECYC3JdjuB1qbwXRzCkxJplkLVClFEnmJKzgpQ5IUBehpCA/PZHGEYIDc80bquEQYhBBR532uqzVFXVJSvVtpIAidYrZcoK7KaDw73UVUFqqqwhgmphWhT/TnAZDI1FDKFbqdLRl8UAigpEpXlEELC90lKt9ftwfelXWQC30en3cb5+TnmsznqiibOdEq0ok6niw8++AhRFCKMqTBPfzCgnBwz8NIsgy98rFYpsnCFIs+QZ2toRRXRkziBMt6dLMswGVHF8qLIEUcRalWDq39rDRR5jkoBaZoDZvKzp76qK+sodQGP71HyfV3TGBGyhqprKN0YJUFIE7mogKKosF6nKIoKVVmSJz/w8eR0hJ/+8k3keY6iLFArhVIJVPVmdW8e5zDAgaNgPOm3DQ03uVlzJEI2+U1EpWJSRzOJGThKKUyNDbnhOWwO8x1DGQEaYKJBSZt1TQaDVgbKaQEhTGRFCNiyE2bBodQLk2BqvcdMG+SIjAP8+Cc/AruqbTSmMUKU1tYApJoqygF3DVD+tEgER642wLW95ybY0xttFbh+qdykGwn3r7r5t3Tv5XaAcxadswXcbQcJe01x6VpisynCbUnzuwXUGmQM2tOvMjSw0ScWfKIRfOBILNGC2BikqJnYOo/HmJ2PgDUW6DdTUdq0NQh8OzYhAM+T8IwaVMXzFgJlXZvh7bSbox7PjXaw8lxTCdomc0tpr2mHh5E4lmCJVc9+FscsR7pCJbgAJVsuzTuTUqCqqdinlJ75irayr3aM2Hei4Pseoih0PIYBev0eirzA4eEBDg+PEMcRhsMh7t69i+l0hjfffBf/8l/+a2ctbIYGJX83RmITNSE5Xk9KaJAqnIbC7ds38Q//4X+CL3/lNazWK5R5jigI0GklRHHSJFwyHo8gpQfpCQS+h6LMsVwuEIchup02yrLAxdkZWkmMoNelujWaksCLvIDWwN7uHqqqwmKxpLo9rTbSNENVVlYivxYS7U4XeZ6hqmpEcYTVcoUwJNoJtEa71UJZUdHN3ICyTqsFISWOj4/R7/VI0cgwGuI4xtLkKXL+hDaAnylW49HIAjFLC/ZICtQ67TwPM+Mx5uJlnNvHEf3d3V30ej1rvLAyI0ci+DPOGXEBInveeZ7yGsg5DmwssEd5MBhgtVpjNpvj6OjIAsyqqpGmS+R5jsPDQ4xGY6uUNZlQAnPge2i129DGox8EAQqzd1YGoJaGqpQkCSaTCXyTX5vE5NlOogTSqIa2khZarcSCd07e5imSGs+5lBKRUYlarddoGYoS37NvJF2FEE6NLoX9/X1LmSrL0snjoe8wU4MV2riumas0FoahrTdUqxrLbIkojijq7/mA9FGW7CiUgFbWGVrXNaTwkOcFuKBknhcoiwJCig1lKTacyrLEerVGnhXoD/p2OY/jBKvlEv3eAOvUiAFJz9RkC+FJH1VdIV2nJrKWI45ieL4H6KbIHo8bzglhJgVHGRh7sHOiLCpkKkenTQJJVUlGvta6YZAYpoKUJH2cZ42RzJEjV/qX87Je5HhhQ+Pw8AZKM9DrSuH8/Bzn5xfY3RnCk8B8TpEBCI1VuiL1ID+AJzxUBb3AdkIW0SpfIYwTeJ5vZcHyPLdhtaIs0O53ESUxsjxDWZXY2Rmi02mbcGvHPrBZYiEEVWEOAgbIE5RlgXa7ZdUc4jgCVdleIQg8QCt4HiVcTbLMys2xihKFo2YIo8CGwhhIBoGPPM0ApREFNMg6Ri1DK/L6xsZL305adiCsVit4Egh8SVx0IaBVibLIoCFQVx6qsgAVFqKaHkWeo9WKkOkKfhwjCAPr4YIBakmUQGgBCYl0nVIl8wDoJG2s0xRQwGJGEZxHjx4BAG7ePIIA1Q+ZzeYIAvICVBWriAhUlcLJyZn1rEync6zSNeIkNslGHkYXF5Q8rwXKrKmDoKoKw+EAu3t7GI/HGI9pocuyDFEcw5MSSSvBjaNb2NkZIk5i3Lx5C22zcaRpikppRDElUXGIeD6f48mTJ/jFm78ir70xdNi4YGubPO2s3GHAPQAFzwBuQy/gvxsjQFQ1kBW00XAfg734LkDbKsRn/l3VNZW2cvITGOy7nn6t6w1QDZD9zZ9ZAGnvZ0CycsEjAHBCNgxwd7y5DihiyGuvqLXtFW3oX9AUK2mwnQYMpYRAVMMvV0pBK1aKYhAqNvqoqT3h0ntq1MaoEQBgPLq1oggNPcsmknyet18znnVAfXO6sAto8zxXA+7NQwPi0l+aazr0HGG8Ua4Bc+n6Vxg8rme8ef9N/zZGFqwIgTtW+BrCefbmPbuUoSue4KrnNsZlUbK8s8mREM14Es6W0RgTgBAm2rVl+AOAVpQUzWO/qnTzXJqKswrR5EdQd1ItBhs222qzfI4jjbqa8xWUM2ZripMIlnWlaypNXnZpjA0pJYSpQl2VFdV10jUCnyIbVEfDJHbLprJ1HIWojdHgeRKDQR/tDtUGCvwASZKg2+ti0B+g1+9gd3eIbreDyWSC/X2KVrO6D6kipZbTnyQxRqM2/uqv/gae9FBqAhq2f9iwNHWoyENqpGSVBmoNTxDNcXd/gK9/7Sv4zne/hU6njTIvURfk6V6v15iN59aDOZ1Nqb6DUsgMpZFzF/I8h5c19RAEBFSlbH7DaHxhnpn490HoI4wCFGWOdbpCEProdIl+tE7X6O/0rfJjGJEsd1nlODoiydXZbIayJo96KALkZQ6N2kYtojC08vDkNNIoTd2psiwxNApQ08lkwwNfVRVWAPr9vlVdZBBVVhVgxmhoaNgzkwzOLAGmZ7G6H4NgptckSYKLiwvrAaa6UUubkM4RLc5B4cLHTJ3jSAJHOfr9vnGCdmxEiP1NjIM6nRCTydQYKCWSpIVOh4rGxWFABZHDkMoBlCWkEIjCEPP5nPqkLOF7HlbLJaA19nf3LOVYaIH5bG7XqMPDA0CYaL0gA1MrEraJzdhgTFUbKlfHULyloGKHeZ5jZKhvWmvESQLfePQnkwm63a4dZwx40zTdqFUBwPYtJ18z9ouiCElIBRS10giDELrWUFCYrWY2mpPna5ug7kkfVVnbvAlSw5L2vVBOJmEGFhRgGeQ4TuC3TbmAokKWEs0prTNoLbBYLK2joNYKnvShtREFEBLQAkoBvhdAKY3ldH5pXLHxxtEyd99gmhYlvxcmVynEZDIzuSsetKJ8YhcvtdttunfdSAzzu3Pv0ay1v+GIxqu/9br1PC5WK/ztz36GyWSCrC4hKwUtBDzzwL4fgFU1fC+0CVN7e3vWMlqlGXbNQGy3iLt54+gI/W4Pvk9FX+qS8hQmZmF48OABut0OqEAfl3n3kCQxWC0kz4li8/rrrwOANRxY0YgPt7NYTo//zh73oiiQZit0ZRdKwSQyEz9vPl8iW1OIsd/vgaqG1/C8AEpVBlDncOVZmSKVZRS6oqQm4j7OZjNAA61WG6okqpMHiSSgnJDZaIZ2K0ZVlQiMLnKeEcczy3PURYFZuoaqyUvh+R5GZ2e4uBhDSurPvMhR5AUeP36E8/NztFoJ9vb30Ov2rHUNDazWKwS+j7IqLQ/Q90wORxgiCCIcHdzAF7/4RSilMJ5MUBYFJpMZfv7zX5DKVRzjS1/5Cm7euoWqLHHr7n3cu38ft27egvRIzq/VaiMvcrTiBPP5ApPJBFJKjEYjTKdTrNcpLsZjjKcTnJ+fYzqboSorzGZTpGmKVZYaD4WCcsKnDNDczYQnhTYASouG7sMGwjYNwU4isyC4XOpLnmlnwrn5BTZR3hg1buK/e2xTHa5zs5NRRObSdtSDm7JxnU85BK5eLDYNmeZwjaZGDvRqydYGhDYhWaUUKifM7Er0CXH5eV70IVyazactfts0m+sv6kaU3CrLsB7459OLGkPiKnnUDQNhqz1MKaJfr4/uPP89kwXW9OvV5wknFwiAiXT5kIKjbwRQBUcnNtorm+ewtDp+3+bvnokYOGIHNtkc2BA94Gekz0y8SciNz9x34T6PNJEJwZ2rndorpv98j3MI6Cu1UvDJtIZvCr9xPQ3Pk4iDEErViL3Qqu6RGt7AbvZ3797F7u4uDo8OUVeUv1iWJTxfIow8xEZtjz2VRJsg1SQpJYbDIfI8x+npKW7evGn7Zzabot1uYTqdYDxWmM8XODl5Bs8XCCPfetv5+amoZQXPo3ETRRGiOEan3UYSxLh//x4+97lXce/+bcRxgNl8gulsbOkdnB9wcnJi8w/Ye89UmN3dXXieZxUYGQBui6cw7Zi9yXx9pqNw/qFbh4BFSrjmgZQSi8UC77zzjk1gZooK77vseOI8B070ZQ4+MyWYN89RDXbw8JhiGVTP87Czs2NzJK3Hn2s8mL9lWYbpdGrVnTgHgT3bAGz0gsEg5zewAAt7o4UgidHlcomdnR0AsLmULqXJ87ytOlmUM8nvjyP2rGg0GAxs/ibL5ydJgsATKAqaD5ygzvsSJyBzjofv+2YsUE4k53vw+7E1PYrMJrh7nod+vw8ppc0NLYoCw+HQ1otwIxEuxWg8Jsl9hUaJiaMKnEPjeuy5vezA5H7qdDpWBphzV/J1vvHO2Uhh6jbTxPj7Wmv79/V6bXNTuK8htGHPVLZcAky7fa8RTOI1aL1e27WbVbD4Wq4YAY9hm0MihMlrXl3K6WA87dZ0cfONeCwQHT3dyE3mNdjm5pr+dPcZlx7F6x0fHFV9keOFDY1CVcZalmh123jjt7+B995/H+vlErKqDDWFKhB6MoBvMtazNMfZ2Rk4Sbfb7eLevXvwggBZWaJWNYLQw3DQx3g8RqfTgm+UDoosx+7urh2Ab775Jj7/+dcRhoHtVK6JUVUlKCG4sF4CN5THL5S5iZwsxBw1zmXgxXuxWJhQZYbhcIhWq0W5KXFMCTSDFiZqDCGA9TpFHCfI8wzr9RrL5ZKMqdXK8ts8jyp5+kGAsiQDqTK1CFi6bblYQmqJZyZpvWOK183nc6i6QhD6iMIIvX4PMLSA1WqFoiownU2xWq5ocxeN3nZVAkVRIkszFGWBIAjR6/RRZCW6vR7m0yUmozk0gITlzaRAoSpEUYwkbsPzPUghSZ0rivHt7/wufvf7v4/ZaIzR6AKvv97CYDjERx9+hJt37kNrYH9/31je1Nfn5yO88+6H+NWbb2N0QYaE0gqLxQLpmqqKM6+Q363SGkrXUFAbYJb5/ZBG+UULaFNhu9aKspYF/zB8bd348rVq6sC4EYZtILcNfvj+2wfDuMZjv6kIw1PRlbjlCe16rjfAnv0frrivdn42tT2EIArRtsF03fG8RcI9zzW6XCoYIDaAnE1Wd9rp3sPlsbp9vsEr15vGxva7uPI5zP8tu+h5373is6v+ph0vMX3H24zUPBfsf9o9tozKK4wrBvAcKVKqMXakcPICbMDkqn5yIhFbho5wQh9N5IsME604v6iJyDXfuWwYNfdsxrKbQ0BVomGjom4yJA1hsRm904AnKNIAKWwuk72nvHrb4oiPL6X1NNoxYaJaGhX8gMCeABWEa7Xa6Hba2Nsjxb9bN28iThIcHBxACoHDI0p+hgbu3r2L9XqFqqptoi2DiLqu4SUBosiDRonHjz/G7t4QH41GSOIYSmubTHp4cNREUB2Q+OTJE+zs7NikTZZZj6IIg4HED//g93Fyco7pdEK0XSPjun+wjyAQiKMIQgrsDHdszYowiNDrdAFokrDO17Q2Cg2gtsBZKYUnT54AIMrYxcWFzUHodruYzWaWm1/XVD06CAJbq4gjGdPp1AK5TqdjufYMQhk8s0qgK1nOxgL3DUu5cmSAwTpTiDjCwgDYJs4aKjS/GwaMt27dMoVkad3iGgwMtl1VSlf8hHn9tVJWppevy4aly+WfTCbWuGHsw5KrLGDi5jrwvBmNRlZql+eLS59icE790bKgkSMl/JOpNUqRXC33ZRAEKPPUPhvnTHBfshwve/EbKXwNAWlxE9DUlwCaIrm8nvO45WgGACuqw+/czUFgI4WT/7Vilc7K0tm4rQxweSxwAjrTyziPxnUMhkEIGTRqSzynGBuyIezmdvA74/HBBiz3fxgFVmGMKe1sKLOjmaMCLG3LBgSL9HCfsJHCERu+hjLjjY0hHhec88Fzh/uJn4MPHgMuA4jHBkc8WOCI5xz3EdP73HvzPdgwetGIxgurTq3TtOHrotnQsnWKdLHExdkpTo6fQVUlpJBotxIIAOPJBD/72c9wdHSEL33pS3YwLFcr9AZ9TCYTDHd2SLVqPkev3yceZJ4hDiNUZYl/+c//BRbzOXZ3d/GFL3we/X7XJhjxAFyv15jPl9YK8zwPZ2dnVs+ZF8IbN25gPB5bS265XFpun6uvzIOCLTrmA3KSdpZlyFZrO1GyLMPFxQWGwwGSFhlLSjXgi192GFKF1lrV4KTYPKewlRQSuqZwIlvPtVI4PztDHIVOHRPyqAqzGddaYZ2l4CqrNMA8+L6HJO4gz0u7QEVRRHSm3T2USiGMIvieh/29fVudtNVqQfq0afGkWi6XpM6UZvjg/Y+Rphlmc0rgz9IMnW4H0+kMeVlgtVrbxYt4+Ipka7GprqJBNB+tTNhXSkjXYysEIBS0qVxrC1MxmNEayhgRjJvYQKEbNEC34fDDcLAvhwCvmzjbIG77O3prTmyD0MAswny4ChPuf/x99rgyOLvUHoiGruM8I9FQNiseb3/uHld5yLkPrlaL2j4UpEOr2VS60RtAlse/1qZgIFOveCzweboZw9ttv8rgawCobMwvp/1XRRy2r3n9cfV5LoDf/DtHgJq+cz1obsKdu/A3RtfmvZuxYDz1NnKw0YwNA/fqxzFREk9aOWVu22YfK3OfpoDcdv9c15/uf7y5NeOq+f6lpEOlILQx+NEY/iSGQP3kB838aQxd+pzXC60B36dNt9tJoA0NoNPtYm9vj3LK+n3ESYgbN2+Q51OSil0QBNjf20VZplCaBEXOjDBJHMfodCiJlNUBez3ao6geDyUGB0FgZT37/T7KskKep5jNphbkMjVBCIEkbmOxWFmwzQBjuVzi5s2bG17609NT7O7uYrlcYrXOcXhItYJ6vR4eP35M+YvtNlbLKQaDnvWuzuZz3L59G0WeQ5qoFKCRZSnCMLBezaKoEYaRdbrx3sqUCRYR2d3dtWCLo/7c7m63i8lkYvdH3nuHw6FVQuI9iMExg5idnR1kWWYThwFgOBxaEBgEAUajUbM3yUZulOopDSx4m8/n1tBg8OZ6ld11hGlqnBRbVZWVw3UTqIUQth7HYDjE0tS3csGlC54ZIDPo5Hs8fvwYBwcHWK/XuLi4QK/Xs++VhXY4kkQJ+STB2+v1bH0vNniI2hVvKFcBsIYZf5+Bs1vDodtONkRcmILDHm13D+B+StMMeVZgf3/fAk52klLkV9t+ZkUwN9rA9CJeV7hfeQ/ma/I+AdkoXfKawliME9ZZvYyjaGx0urQqBsRCCER+ZI16/h4zXkj2nor+sQOa28VYxjV4wzCEkLTmcDSF53hZlojCGEXRFKrm/uV5w/3CAJ9/5z7jgtQcAePk9CzLLPODo3VsKLARws/HbeHIE889Xkv5357XSF+7/9mos3lujjTydXlu/UYL9s0W843kVivdKSU8s7F+8tGHeProEco8QxQGWC2W+PDjj6yELb+gwWCAi9EFUuNFWa5WmE4muHv3Ls7Oz7C3f4Ck3UK/28NqucTPf/ozfPDBB/A9D6+++jKE0GaBb5RKqopqVqzXFPLiRCDeBNj4YOuTXyjrSFsvulJ24C4WC6tvLE2dBhr0AuvVGoHhP/Z6PWvsZFlqsLBAlqU27NYoIIktC18abwh7MYnnLqWE53tIYuqzPEvRM8lSURhhMOjDDwJ4UmJnbx+J0aGO4xj9Xs+ESVugHAWqbK6VQpzE9t3N0xSj8RhFnmM+m2G9TpHnGc7PL7BcLDBfLLBaLU0kKLfnaTgLkuX3G8oQgxYDLyywMspOEJsecs414T4Tgjn15lyhLPf9co7DZVb8pie1qS69cWwYIGrroy3gi6vB/vY51xka7JlxVUQYZLoGBp9nDQ/Dj7/e0OB72S4HKdKwkdKAYRfcbT/ndcbIVSBz43k1bS5SNP230ZeCIyyNfK9Ll9LAhvyf+3Rccdhd7LYNjY1DMBDfVPzafjb3efna7v3daA31G1eR1s1tbB9cDcSpDa7HvaEvMaVHa8qrEu57uWqMMXB3xoLW2BgzzUzjf7unbz735tzh67gGNj0zP/fVxt3l/nTueKlPhGiM/G3DBiDz0GMDCpS4aI1EoQCpEYURWi2i3PhBgMD34QWBjY4zfWdvdxfdXhedJEaWrpG0Wuh02uh1SXlnMpkgK3PrvQVgNlkCAHlBHtXplIyD0WiEbrdrDQ6mu7hRSQbQDG7Ye0nnXwCgSsKqVqgNjTYMI5RFBaWaugxMeWBhlPNzqsu0t7eH0WhkwcTK0B92dnZQ1zWm0yl2dnbomUxNqCRJcH5+jt3dXUwmE/R6PSuRyqCXPfBE64ksMGR6DXP1ef6x8XLr1i0bmXQZAwwIuW4Eg2fGDCzYwpQgXgf5d5fmyvQMViPqdDpWjZGxB3/O7WVqC9ehcA0GlzpSVRV2dnZsbQnP8zAej9Hv920UiZ2KDBw54qCUQrfXQ14UlgJEUSOK4rBaE6897Nxst9sb40Zrjd3dXShFEX2mja1WK1sMl6lOUkpraDDFiI2NqlJWfp6jJ4xr3HWMnakEWAtIaFvziR1ETNdhYK21tsYOGUwhoMUGjYmxTRAGyLK1pfCwUcBgmes9ALDAmQsTctVr1xBpt9tYmFoZLPnPuQ+uxK6bEM0OYgbkPLfZGO33+/BMVNqNEjFg5nnIgJ1raVjRBbFZfZsAdw0NZbEf08joHfgIg8i+C26va3zxuGRamdsv7EDfNsz44KiH53kWu7LRz2OGqYlMdeP+cJkFbpSMMZ1bV43vw+OEcQxj4TiO8bs/+D182vHChsZ0RuFQz6PCYNCavNRaIQxisIDhbDzC008+wfHTp1guFtg/OsAnnzzEjaMbOD05AcxiNBqPcDE6R1VVeOutt7Ber/GFL3wBrRbRcOJ2B1EQYjqZQCuF//7/9d/j7p07OLqxj3Y7thsFJ/tUVYW6IqDFnc6VPHmD5ZfFYdWmwnWNKAqxWq1tIT7qaGHVN7I0g+c3L7UsS3gQ1mjhKoy8QHD7ePPQWsPzfUhBknPD4dBuLlyxtNPtYv/wCK12G0mSIEliBL6PqqwADZRVheVqhcqE2YWg0Nd8lWK5TrGYLzCdTjC6GBHntCpt0l6WpjbsCwBVVaPUFFVowJS2XpC6oqRmA2vtplMrojO432flIGnUGtwF1QU2FiBbVgrLcDZa9HweL5IAQxB9JS1oK7ZggXczqq8Y3lseb/debJhc5eXfPuw5zveuuhePPxYE4A3dDe26Hls2NFzgvNEewDE0mmdRSgG6oalwG9kT7l7D9UCzwegaKJsUqY0HAktskpyuuqZ/tB1b/BkvmlJKikY5RqF7nsBm5ettD9tm97Jbf7O4G1/306IWnNjrnsM/pZX13R4jClo3XNbNozE0rOKU86zbRp9rNFwXKdiWZL2uD7ajUNcZBNvG7ran13bplfdpxht9rp3vX5aHtdfQTSSSr6E14KFGFPoUPQ0D3LhxE71uFxoan/v8K5CexN7envHgBhDCUGJVjU6nDd8P8PjxY7ueQmsEHikw1VWF1XqFOCIjYblaYzQe4eat21gsFpa6kWUp4iiG9H2URQEIgcAPzJrtwZMSCwOcF/M5sizHnTu3SeYyjikvLvAxnUwRhGQI+QGpEHIycbvdwd7+Hj768CMMBgMIISxAZs86860ZKDC3Po5j68Xc29/FdDZFlmW4e/eurYCttUa6WCKOYgsKYABKVZbYP9i3xgWBDVKjKvIcZUWA3vVyu0XDmI7S7XYtaGLwuF6vsb+/j9FohNVqhRs3bgBoaDW877LXls/nBGmmQ7l5EK78JtDQSTjSwkYOj0OOAHQ6HYxGI5Rlif39fVRVhdPTU8xmM+zs7FAeJGAjKC4VhaNRriOSue5s4ChF9YRy87lLh2HwHUURZrMZWq2WxRfsvHQlX13MMJvNjNQ7GQ3dbte+BwaTTI9Zr9dOrQ1a8zzPs++DgfZ8PrdjiA0oz/OQxDHCwEdR5LbNbLgAsICUjQj+d57l8P3QtoOjGeQ81fB8aYsib66hzXPzeAIaCW2gifC73vWiLJGZaB/nJ7Ax5FKe+HwG8G5ODT9fURRot9ooixLQl6MnzNrgfdlVbOL9mIE4/1RKoShzG0XlsWr3+Kqhe8dxjOVyacfUdh6EG/EAmppm/H0eFwz4GfcBsDUw2DBkfNeok0q7HvDz8vXYgGEDk5k9rtHKc5Lbxv0zNzXqgiB4IUPjhXM0tKoNOKhIocOT8CSgtYRSNcmfAdjZP0R/uIt7D17Fu++9i48/fAdVXeLdt9+C0MqgxhzHx8eYzRaoqhqhH0AkLRR5DlXVyIuclGgMXzLwfFSqxHQ+QRwH0KoHIQWqssJ8vkKv2wXgocwz1JUZLNJHv9tHXhQWpFO11BopCvheiCdPjlEWJXQtoGp64UVxagYhXUeDrFoNVkcxtQcMoI2i0FrVSZLgxo0bOLp5E3fu3YXSGt1u11YobbfbSKIEviRPyWw+x3w2x2h0QZ6HdYqz8wlWD5/i6dOn1pswnUwwmkywNNxOTjarmY4iJMqaakIwyGaOMk0Y8p7WVQ1tDAetNUmyYstzrBTKWhn0TCBVsVQqg0YtDE2JKA5CCAijNEF0hxINzDKARNAYYo+7lAxoFHGxNZseaKwEIeAJKlxnMM4lSgdd2iw47HGFIVQTIjcD2AHCUmy5p+lZDdw2haGcqshCQ7PsLN+bDQSgST7FZiRkG+i50TJ3keFn4sVXKcWFt210a6Ox2kjTSqM2pcy8goYQiigS1phzIzYNGN/uQ4DnJvd9EyrZMAP4RRjjsDH2mr7g91CzV7zpBDrTobddBurCfs88EVHq+DVBbPQ1X1wKaceyC4bpu8py9JtxTRvkdnkH11zSerOfmsfwoOBtnCOMEe0JD9CbeT50HW2/6XmbxgVHEzYjExzNECbt39U4p899z4MG829haJxEx+RNniQbG+oVPUuT9yANXVE5sq08f0lmunE00DWMAWH6lqQgifbl+dJ6Ttkz3G63EIaR1fgPAh/7+/t2rN+8cYhOKyGVGb8xkuuqQqsTQ3hUe6Ew1NayyuD5AnVVo8g86KDCS/fuYDKZYrVcEshPYgRRCGgNz/MBQdKzvV4Xda0gIRB4Pm4cHpEH3AtIXaqiubhcLnH37l0kSYIPP/wQw+EQR4c3cHp6ijhuYWdnD6tVijwv0esNTAQkgu8HCHwjk1prBEGIulYoygLL5dJSGvI8x3q1wmAwgNYa+3t7mE6nRHEwYGkyHhvBjwyelLh18ybRe7Mcw/4A7ZvkQCvDEsv5kvL5IG3kOYpitNsJOu0uRuMRhKDPqMp1iaIo7UhjQ4CLjTFIAWiuct4Ee5hXqxXOzs4saFoul5Yyw57fLMuskAjvLcfHx1gsFrhz545N0mXn32QywcCoQrmF7zhCovUmS8H18DIwHI1GNqrw+PFj69DwgwDL1QqQbFhV8IMAs/kCy+UK7TaJwczmc9wwRfCyvEQiPazTDGlGRtb5+Tm63S7SLLXUrrOzMwv6uK289nDEpNPp2CJ7WpNqFImdrK2Bx3sC7w/sGR8MBijLppDgfL5Au91FHCe2eJtbv4mjT0WWo05KhEGIwPORJDHJuOcF8ixDv9fDdDaDgEAradMaK2ldrMoaraSNaT5DrTK0khaCIISUnjXQeC8jRyr9PYpihGGMdL2GkGSsKw1keWENMlKD6iDNUjtWak1UcKUUyqpGXhgJ25jZF7z2SGQZSdFTYVcyuNbrzJHMFjTHpQffD1EUc0RRjNV6jWyVWjECLpzICdb9wQAQZLQyo6IsS7vfcw4VM1PIqAlsRJQ9/FqTsSEF0cU5+sagnIE9APs7GwFMQWSjgvsLaBLj3YR1V27WTQCXsqlHws4LV0mVHd9MNePx6j4bR/LYsHSNOq699qLStsBniGicnR4bEKvtg3m+DwmJIi9RVyV5f3zKQYjiCIDG6ckzvPvLX+EnP/oReu0EWmikRYbleo3VgpKzWX+crSk/8CE9qvScpZT0MhqN4Hkednd2oOrSbFr0oBRFENA1WXp1VRvjAKirChCAUmRsAI2qSM1VmTVv4hIee5oBo2AA+J6Pbq+LMAzRbrXR6XRwcHiA/cN99Pp9xBEVvusPBmi1W5Cej4vZBJPJBIvFEuPJGGma4unTpzg7PsN6kdqK4EVe2HAZuMiaqi3iqWqKZigBVLrxDvMgquuaJA35hYKpSo117oZIXaDO73NjQBjgI7HpbXcHmvXEo6kjwb9rvcm7d73Q25EC/s5VR+PFpkT0ba85GXybSlN8ngum+L4btB65CRxdz7rbds6/ab6zGX1wwaTbr3w9216n/7bb6uZruP3L3+OFg+9zVdRnu1+u61+tPTCy3gDQJin0yugP+M+XvU9XRTJ4nLFB7nryt9vjnnNV5Gb7c47w8HfdJPKr+qU5yLtLBij9J0DSqVo0NUC2oznSMSbc5GkAUE6Uwb4rKamukPPMbh8JU4eB6zRQhI6uznex3wVFrSgh21CdhLQ0QhgjSIPUv1y6RENRYrtRWzoU38+TwmwaLbuZNYZuieFwSPKUhirR7fUgBXCwt4tutwchaP28ffsWoIFevwshFXHOVyu0EqItsRe53x8Y+kwPk8nEej4ZbPB6eHBwYHMFKlUhjEJbfZmivAnOzs7QilsGAAU2OXcymWA6neL27Vt48uSp9c6yrv9gMABA+XS9Xs9uvuwtF15Tq4ATIReLha0oDcB6+NgLP5/PbbHXxWJhE2jdNZfBO3u70zRF4PuWWsoAwB3L7gbPFbSFEDZBlfX6mX4TRZFtV1VVVp51Op3a98vn8j2YEsYGhJQS5+fnGA6H8H0f8/nc5p4sl0u89tprlgbMbd3b28PFxYVNFmduPBsrSZJgOp3i1VdftZ9zQrTrceWIBydKs4QuKyfN53NbPHYymWA+n+PGjRsQQlg5Wk7I5zoLNIY2qU+utzoMY+vlZTrzer22Re5Go5GN3rChRZWs963cLlNz9vb2bGJ5p9OxeSnr9Ro7Ozt2P+H7n56eoq5rHBwc2CT4TqdjqV+cT7lYLFHXaqNmAQNBN7eAvdoMMk+eHSMMAhvZYTUmNtDcd8hSvdt5AowxGPRy4jDLzDI1hyMc3O+r1cpGjdI8g/SaauIctSDDpCmGCMAmszMThfMXOCLCxQJ53+R9hnNp+Pk5L4PfdxiGKPLcqphyXzCgz7IMNRr5eTdqIYWEZ4w5/ozzi7gtboTY3bM46sLKUUCj3MRROs7R4r5x936moPH4YyU1nq8c2WHczO8KgBUDctuitd7IR+bIBUfiuM8558jdS/jfTOkCYOlsP/z7f4BPO17Y0Hj2yUNQMTXP3tQzyYWz+RxB4JlQtkReZqirEknSgRAxdFnjr//iR3jn7V/D8wTyssB4PEVdUGirrCqsliuUVdmEazNa0MMoBDSwu0sbyTpdIi+yxpqTwhTPiyAgbTEez6Pq3VqTR97zfPI4BQH6/T6SVgthEKLX70IGjaXX7nTQ6XTQShLsDHeRJF1ACwyGQ3i+hzzLUORUqfpiOsF0MsXZ+TkuLi4wm82oyudsiqlJoKrrGlVdkceMN5+q0cSvjLeCIgwStSaenBRNgSsCJQpV3VwDcECVbBJhidai7GRiKWDeuBicubQU9nQK4dR0uKICrQsu3QHoGhIQm0B8m0bltt3921Xef/amcs0C917szRZiM+GWj7qqwQDuknGz5UR3wb718hpvjWs4sGHGXEY29Nz+2W6jVpvUoqs85Nvt2AYdfLiL0MbzPMfQcH/XDnBmD7dzd1xnaOhrjIurDA1+DgLBuGRIbRtG221kI3H7c/672ydMpWtOdyM0LlXIGIGQoPoKVA8BAITUYBlbN5dACAGh3cjD5jXh0IQuUZa2/s7G48YYQdPb7jPYiIwxKqiPqd6P50kbzSEPYA22fzyfn0sjjiJEcYQookTmIAgwHO5QsTJtkqRbCe7eu4ddA4LKqkISx1SMVNXY3dnBYrkwWv20eWmloOtmvSoMOF0uFojiyAJXgJw0s9nMGkAulYZB13Q6tdVmuTCYCxKSdoLVemW9xL1eD1prkhVtdeBJzwIATrh2JT45+su0FKbpcN4eJ3YycFCApQnduHHDJjezGg3LU3IV6rqusbu7a9WW3J8HBwfWo835fvv7+zg9PaWCcgYQMgBgkMCAgZNVGUhTJKKw6wN7w5mCw7UVWMI9DENrgDC1mBWimLLlRhAYRFxcXGBvb88CQSEaaU2KkJUbvHA2rObzuZ2XLqDmfuY+7Ha7NirC1+Hn5edhBxm3n9cTrrFR17X1RHPtD07GZWOAQWvMtLI0tQpFURRhZ2cXs9ncqgnNZjML/hgIsxea8yJIGpfmw8XFBU5PT/Hqq6/aJHZWbOLcHebHM2AcDAYbyfDsweYIQZqmdpyw8eH7AYqC2sR5JK7nmUErGwEM3Ku8UVNy930A1nDg/ncjFAzumdbFCe3L5ZJkZ5WyeRVskPCYYtDLhnsQBNCCmBe8zrHYAJ/H44jzatipzOOEQTCPCQBWpZNzItjod6k+vO7yuVpreGicrdzW4XBIRooUG9LHnK/hex6igNYtNgpcqWLOGWGDwnUQuPNl+3deo/g9uJiC3xlTIvl9uY4Rdgq5OUiMD1zaHwC7tvC74fHgqrjxHGPjgfcpHhsArGHF7eFr/UYNjeOPPrGLgB/4RDnSGtKTmC/naLcThIFEUaQIAomqyiGlj3Z7D3GUQKkaH77/Hj788ENoAOlqjZOnx1itVhiPyeNfmsmXp1TFWpuXure3h7t37+Ld994jj78BmfyiAKpcvru7i4PdPUjfR2y8KbXhVQpJeuatdht+EEBphelkgtV6jeVqjvlijizLsFqtbAhW1QpFoXFxfkHh96pCajiSZV0jNWG92iZJ06Zf15vAkgGDYb1seGbZs0Bo39B02LqG46lVVUMvMgPMAnXpWQBCX6Afnk9ghGlgDJobPqIHlszk9lC7BYRzr21PP3sKeDIzoKpVbY2i68DwBvC9wtDYBuXcZ/zZhmdcNA/rRhT4Gdxoi9s125kd7nls5bttone0mS/AHhVeuDbe97bBsRXJcZ/VBaBugtZGmx0DDdg0OK4yWq4zZCBIjMC9btMrl2sT2O+pTYUoPnf7XbleXCEMBWqr7Ve1+XJ7Gw9/U0+CcxXcnBNWSWLY7tCDnFestLA5LzR+mvdIhTE35VjtT44iaG3pRzzuPLOZbY9fIQzdaXv+ormfUrWlerFqkjA1HOI4RtJKEAahnWM7u33EcWgpSGEYoNfvw/d8tDtts/4wjdPDYDBAHEeGJiDtnCRAFyPLUgCGb57l6HTaRl6aQHqvT5t8u9XCw08+weHhIb1TALPJGEHgI4pi825ojlVVjSCILJ3h/8van/3asmXpfdg3Z0Ssfu3+tDcrm2oIyw+WKIgskmJr2vK/4Re/+s+xLcCmXmwJIEg/GKABWbYlgRSpIlkki4TYuViZlZn33tPtbvXRTj/M+M0Yse5J3lNALuDec87ea8WKmHM03/hGM23z6na7laTR2EXKYryPY00JMAC1h8NBXV9W6b3Xfr/X27dv9Ytf/EJZlunq4kqL+SLV+bMH1P4zVx6GT1ICSJSertfrBEyqqlLWTyoqyzhWnd6Joij04cOHVAbz8PCQwHpZlnrx4oV2u51ev36tw+GQwBEHssHQPz8/JxCXZ5kKUz7EKHSmKsWTn/cJVNA4C9PNNVerlT59+jSqs7+5udF+v9cvf/lLXV5ephGjZHGYXmP7E9q2TcD+5uamn6B4rcPhkLISMMuw02RHmNaEPbSH1jGNShqavCeTiR760jB7roSdAkRdOyNZ9/u9nHPpLACyJnb8Jmw96z+dTlX390SwA/h6/fqNNpttArdV3+BtyQECMD4TgX+mU1/203Xx/A/ArhTLpWi4h33GRsCC234DWz4GWGVP4tlfB1VV7Dlxzunp6Sn5J4I5Go2R9RCC2ioGMeyRNIwXp7SNYIJ+VkrcCGLodSBIZMwr/7bNxTSRc+YH+u8yr6oPJiEYiqJIGUNJIxLU/ozvsGCe50Nu8Es0kn+u0TmEoElRaG4Op7O+N8tzdRqC/RBMyZKL5dvszXa7HQFzsr6sE1kPAL+tpoBEIMvKe+zUqKZpUpBjhx/w7ASXdriA7aUhu0RgMfTRDHiZAQzoP88CNjwcDlqv1ylgI9gkqOHn7Nn/8n/z1/V9ry/PaPzRH6c6O++8qjqmmKezqRbrleSCFrOJ2vqozfOj6urYp3xm8eyIPoKCWezaTqfDSZNJobbrdDwc+lRco+OplHeFZstlrHlSrPv2zmuxWKtueja5abTfH+JBdFWtzfOzToeDmrbV08ODHh4e9OnTJ223Wz1v99ofDmrbJk3KiEro1Tmvpm3jid7enS2+LSlxA+p1Xk0YGiF5JfAVYMCVehcU+pObAV9uOEMg817yUttFAR+D707qWnmnkdAkYQ5OnIRLo24Cfj4y1Qg2UXNU5EmvDK3adlzu4zTU1p+z0BY8WhY+grBxo+nnGn7Pwaf9Xht8DGs+vM+Wbskp1ZGfN1iRtmCNxsx+bGC3hovPnoPiAVB/fjrV5+/ZruPnmX8L0D8HvL8TcJnP2CDjHOT+qiDDhDnpTwBovPfzYNN8thtG09rn/dwzjH7ux70In/v7eWYsAtfPB1HurMfEvmxWwQbh/W/FmRDx+VplmVfbcq7DOJBOWduglJXJs6wHvVksZ3RD5isa3yzWMTunrHfeXdfp9es3qaTizdtXyjKn25tbSfEMh9evXveT4GodDju9efNGFxcX6Tli6UauoDjViDMWKC86HI467GN5hnpn6F2czvTp40ctFsuUibVOaraIpSk00i7mC5VVdJSAujimtU6NjEVRqOjXKp3g3Afmp1OpLJskhrSu6zRwwzZe4oxhX6fTqd6/f5/GvgKOyrJUWZdy3qVGX+ecPn36pKurK10sL/Ttt98m523HZQIEqCf++uuv01jOm5sb/exnP0uH5AFmJOmpH40qKWVYyAzzurq60rt37xJTStlXCCFNOuJgMpomKUV48eJFWrOqLOV7oAIgATAy1vLp6SmVhTnnElvOGQ7e+9TETGYBtt+SIExOJNCjfhtACIsM0wxwZjoTmSFKxAh47Nrb6VPILuCMiTySUpkOn8VPcL+UG1lbZP8D1AIUE1Gn8bhOQNC+z2Swr2S6osxWuugnNOLvAbshhBTQbTYbrdfrVNqU5+PGXQLQ3W6n+/t7dV2n6+trffwYxx9TskcwANi0k4MsEw3QjadcxyDQMvisC9OOrCwmAN0N/X8EbgBcsjpXV/HcGDJ0rDlBFrbAZgj4/eFwSDLApCkyG9iH2HPRKDhpt9sl302gin2zvQTIgx2favVD0qiMib3GfhMgWIa/ruPJ5/PpLI09zrIsZTO7EGJA1Gc/WR8CFHUhZRDZG1tCTG8S92UbscFayDcZnbIsU7AAIYPuUnKFnydwZi0IFmxvB8EhWRfkAd/I5yw2JKiyusQ9kg3Cz5KZZI/INJZl+UUZjS9uBp/3o2Z58Hw6U9HPyT5UlQ6HvdYXC00nCy1mV/r261/qsD1ov/9GV3d3Wl9fq2pjc2J1Oqo8lnp8etZ+v9duv49Bwumky4tLNZ3Tdl+mTYL9OBwPUpfpcBhKp7abrf7Nv/030dCVJzV1le7ZppTaAFBzohG5bfvTVJ2TFIG6GvoNYm20xTMYuqhwIY2ntJF1KtdRbHwOoW921lAi4bo+gaE+sOliIJGmy/SXCelk4j4465qR4EYhytS0QSE06foyTGq8Lj0pbVoPSb3CwAT3pS39DcQqje8Cb5yuNQw2MPscg/25zIV9/SrQarMU59fjXi345ves2QCiz4Ia873sHy9rQHgNLPjnT/P+3Cv97ixY+JKXNQbsl30WC4rt+39VsHT+3P1v0k9DYFrXONBIfS1hPCL4fH3s/tugx77X9ruc39c4cDJ9JJLGB83Z5xqyOuO9cn2mLoyuGQ1o35ekTlnmlIfYvB37o3rjOykU+4LigdZZnmm9XkshxDMZbm8l53Rzd6u2bfWbv/Wbenp80mq90u/8zu9IXdBiPldd1aqbWq9fv07OcDIpdDzGMhbKKP7Vv/7Xur661mw+k/cxwxBn0zvVZavFcqnTsdTl5YUy5/R4f68QgsrTSd57rZdr5T5T1wOkT/20mel0qvVqFfegbXXoWdQ8yzSbTVWeon1ldGQkayLTt1yu5Z3XN19/q7aNB7Pd3r5QVZbabzc9I1712QoagQcG++npKbHRgMnLy8s06YmpQnd3d2kiEPJAAAXzenV9lcDNp0+f9OLFi+Rwb25uUtmIcy6Be0uqOOf05s2bdE5Dnuf9wbCrBDo5HbnrujQGlp4LgNxv//Zv62c/+5l++tOfpmZIiLP9fq8XL14kcMozc8YBdhMQsN1u4zTBPkuR53kqu5GUwK5zQ5kEgARgAVAA0FOvTQAynU51PB51dXWVSr44bNZ7nzJBMNTUgTdNkwJMRr9777VarfTq1asky8/Pz8kHUA7GeQ4w8vzbjjwFnLCndV0nUAqAxbdh82DJbfacfQE0EjBdXl4mIOi9149+9KN0CB4j7gnmttt9YpAZ5cr4fYIrm5GKzHutqmoTQN5sNqMAMk6DirJ8e3ubenjsKFLWiHW18ggrTfaJDAPZG/aPUb3cvz0vQiFoNpkm8A+7TfkY/SDU8M/n8zTRi2ALsEsWi3Ije7YKU474HfcPM348HpXludrQjUr4LIAOIYwOSJSUmushI/B/BBHYddazrutUFlcURTpfg6wAmQLuFR2T+hHJWRwehLwhjwD/xSyOy7Xjj8neYGuQX9h/rg9wt9kVez4Lts6eGm5LQNfrdQpM+L2teOB+eD/4zPpdAh+mm5H5InizwRc9GnwHtob7BHsiK+ek5K96fXFGY789qe3axJg1Td/wqaA6dGqbTmqDmlOl6njUL372c/3X/8+/o/uP7zW/WGuyXOlQVtpt99o/77Q/HHUoa213OzV109f1TfWbv/mbevPVj3WsI3g5HobUX2Qh9mrrMjXn7fd7ffPNN3q4v1fb1epM45dzrs9QALJig2qeDRF617VSaOSdUvPqmBm3ZTcGLIcghaGkZMzc9yVQYWAVzILLmdry+J6+cVNeXThj/FPw0KoLg6JZkNV2Xt4PzIAVyCyPk8KiAbFjZPvgSi5FtsOz96VaGp6L57Agk98NgLdLWPCcfbeBxLnI2cDivOzKnY0FsvcZ13kcnCSA3nH69md6Glz4zv18Litxfn+/KtD4HPA3Nzx6/78vu3F+bXuPNtCwWYDPBWifDea+85Pvvs5ZxPTZs4DN/t7ey/l1ZO7nvI8BtgkjNgo0wmBIbcp8OB2eaw5BflyjWBhHYDi8x/WNqVPJBS2Xc8kFrVZLrReXynymu7s7tW2rn/zkJ7q8vJQUdLFaqKwqvX79OrF1lxeXet48qemaHlwtEjsV5S4o70ElLCSlOtNpoc3mKRrsLOrqarnSbr/T5nmrH/7wR6rrSpJLJThSUJ4Xmk5nury86CcfzVXXlSaTqbIs13y+0L/9t/9W19dX5kTbUyrfCSGkUpnYrLlTNonDPKaTib7++mtdXFzo4fFBi/lCy+VlajDFUTrnlGdes2mhsjwpBCWGz3uvd+/epUkuWZbp+fk5AUSyIZykTN06tfCcuQDQAMDMl/NURko9MM75sDtoOpmm3gv+pIafkpb5fJ5AMWdhwDx/9dVXCViFEJT1/Xs0nwNAabw+nU7JCdOwSuB0cXExAtJRhpSAIvtJUND2jG0IIR1yV1VVOrDN9ibAosJsU5rDn0ysAnxyL5ST2PIJC9JCCKlOvq5rvXnzJu05hNpyuUwZubZtdX9/n7JBsbRnn7IMgEf6BjgF/RyskPWCXSdgI6ND0GPXm3IvdAm5rqoqBRFt2+rFixfpYMX5fK66v2ealDljIQayMSMgDX0LnzutO4SQGs7btlFVRSaazBM9CfRPMJLY9304kIM08SJL2AiCBFv+Q0BxOJySnaSm3vbh8Cyp2sTHaZ1FFvHAYrHQdrtNcoje2RIqy7JbYC8pybQtbyPbAGDlufgOXmVZqphOlPXBE4GAzQSwzzwHGR2Ig8vLy/RcAGZkjMyU7RninggE8J1N08iHMSGZMJv3qpo6ZVgs0CcTcjgcRuQEPU/YD2mY2jSZTLTZbEaBA8EmsnB9fZ3k1N5L13VpUMJisUhEBYE0AQvZMMZQY+PZX3SRzzJ8g3u2ezwqw+8JEuTQZuHIrGB3vPdaLpf63b/45/R9ry8ONP67/+bva3c8qa47HctK++1B281Gu+1exzr2LlRVqcNur8f7ez0/Peuw3ylTUNW28nku5+I5DF5x3CBTlAASbdupKHLdvXyrtz/8iZzzfRR9UjGZKM8y1dVB1Sl23zuTOr6/v9f2+VHeOakL4iDouOg+1fuysUPE2ci7Tk7D+QCxbtv3p9b2rLLj5FoJdrutq1RqFUFtBEHxEEGfyqXoCRgaskL6v3MuTR+RaVLtui59pyR1oVVsxfDpHqOwBDmXKy8mycjgoHyWKZ203GdJui6OsGUGtwWs47/X6romlpQF8xwhAm6AXQg92O/bWzHMrLV3fnRWQRDgeLw2oj02/YwrDmuUvk9D0Me1hoCCqLJfG7l+DGyfbem7Z7uu64O44XtimVw/1jiYfeoZ//NA4/x1HhjYl31+hfiEFsB/HzuAzNqAwr7//PPn70u/I0tmA9oogCMDNNy/6+M5N/yz60vPJBVZrjQKOpgeGjl5P/S6jLMWsVTQZz6WKzqnPI/9Iz7L0l6ffzbPXd/LkKex0ozJnEyiAby9uVGWZwk0/OhHP9JiMdft7Z2m0wiGgloteqddHmHxI/v69PwshaBXr16pqk46Ho/68OGDrvpzGpa9wa7qMgFiwHNdN7q8uNDHTx+j0Xexn+14OOrq+qp37nmac9/UjRbLpYo8126/1+XlVepnWC1jqdB2t5WCVBQTFZOhZpoyi+lkqrZn4tfrtcp+QpE9UIkxjd45LfqJP7PZVK53SgCMtmfE3r+Pz5v5oaG3LEs1baOqPCWACWiOJR675IwBdQTHOKrVaqXNZpOc6Ha71fX1td69e5euR3+BFBnN/WGv9XqdDv5KYyb7U3d3u13qK3h6ehpN/CFIenp6kqRUk27r7i0pJQPAYQCdc6Pg6PHxUSv6P3owmIJi75X1QCTr142JO6nBMgTtDwcVfVbmxYsX6SwNmFmyPYAaAhkpAj+YSQAW5R53d3fa7XYpS8KLAOa84RSwTI03NgTGH13mLAiuy/NIEbgBvADHkhKgob8CEizLcrXNkPFhyuRsOkuyCKjuuk5N2+p4OKhuGq16HSWoAgiRMTmd4oSjti+HWcznCn5g6Ifm/1ZNU2sxm6cJXrFcLFcInY7Hk3yeJcDftvFgxCzL9Pr1a1VVGZ+jbVVVsRzt4uJSWRZHCMfTooOKIk+gMWZEsl7OpcPhqNlsKk5kD6HTbDZXCMNZV/QQZVk+6sGxmY7TKU7lJBt5d3eX/FzoiVBrSyNxkfdnoBy1XEIW9OO+u6G0er1epz3uPbb2+10q4yEgjwH8TFVVJhkC9OZ5nCBqAwOyGtg6MhfScCYKQF5SavhnGhfsv5VBghYA8qwfjUtAW9d1HAceQhykEbq0ZpGs7RIxwj2iO1UZMWgsgYtr6H2m+XwmL6f3798nYoEeBwhRyj4Jpuq61mq1Gk3rkgbSFlKGYJD1pLcHWSYzRbBIwBhCPFJhs9mk9Sezs9lsRnbAZqA4hwW/AgYgG8bZMIvFItkbKeLrX+uBff+7/+3/Xj/7xTdqlasLmbzL5bq4aXKZjmWc992FpmcaTmqbRt6FOPO8judZ4NzqplbT1Skymk2jw/TeazpbKiuG0XM4gzzPVZUHNXVULjYLwJQ5Jy832qDIfnp1atI41AHwx2hzkvu0aAgLEXJo4iEv0Q/1k2A6TquOoyW73oF0ZinTUQ0uAjVG1rZdq+Bgnc+nzThlPjf/Hhj8LM/MuMthdnj8fATVCCvAzHsfg67eKMGMpUDEj0fP8p/3Tl2o1HVDXd/5f/ZzFpT/Ktae39n32OeMf4/XOa+xPwfw8fPDd1IOx7ke3ns5xTMF7Ou8vOf8+duuUdfVomb/PAizmYLvBBJu3FD8q9bAviIDbrJd5vrnn/1cr8n52sCow+YT+KZMnMyauSHZEkJIBwCmD/Gmz3wXv/PO9XOs4pkLo6YzeWXZRES5WZYnRibzsWwQQzmfzTWZTjSbzlRMcr169VLT6TSVyVRVpbdv36ooMq0vIqjglGOYG2rEGZ15Op2S8YcxpN6YsgBOUEY/bm9v4+GWBlBRS7zb7bTf73V3d5cAC4YfppER3KvVKgFVHNbLly8TK0fTaV3XaZQm7CQjRXE4lNosl3Gs9na7TSUPHOxFMyLAA9YYdssemGVHSVqGreu61Mi63+/16tUrbTabVA6Ag4RVt/0W7ANBBGNJAZJ1XevTp0/6yU9+ks5LeHh4SONsr66u9P79+8TAWd0hKGFPbBkC+gtr/v79e719+zYFKrz34eEhySZZjxcvXiQGkp6Xq6urBExsuQxOmwZzABN6xyFyTBEio/Pq1Ss9Pz+nQNZmNWw5DCcj8xzIrG2Qvb+/1+3tbVrnxWKRANpms9FsNtPFxUUaJ8zze+8TG5r6c2azpAeAdcAdz8T6wiADmMnY0PBKGZt9Jgvy0EuJqTWSd+MyEkpdGLFKIGPBpg0AbbkU4NuWy8Hyri8uVNZV2hvA0WwWD8ItsqH+32Yx5OJkTK4FSGNqF/YEwA3IYy8IsghSWCdJKVPIWGHWsuu6dAI41+C8DWuf7BQr2++B77FBLQEI9sVmM7CFkAiQJoUfypEsQy8Xq1fYZ2koxbZZBX7vXBzLTCYL3MHakXFIhEk/MpeyHK7L88Csk1k5HA4pU4EfsROVsCF2whb2HF9GsELwQiBj75lyM9h8AHqWZQpd0ObpSSGEZPPJkJEx4mWrP7JsOGAR+4pcZlmWAh3Wj33jNcK8Ri/ANjaDaCtceA7W2wY3rM9Qku9HumYHeViivuu6X+/Uqf/2//0P9V/9zf+7Pj7uVFZSWTZq60reOdXJWbWRMXVSeTpqOp2o6g/RgxFr6qYHNSH1LuRZplmf0vTOqe2kthmaeRCK2GjUqCyPUi/IXRcPe/Pea5IX6jiwL/NquyYJW9NUatsmTVKwm5+5IeLHkPKdOee9dTHq7bq2Z3TJOPSlH3Jx/GwHaBtnT9q2P++iC5J3iS2MNfI9iANAm2wMwplP+oOw+mk1rs8ikDn4HDCX4okBlqkmcDkHrJJMECLJdWrbRozHhdEnIBqYeA33r/NyovDZ39lAw/UZIt7Lc9vn4b6H9P/wnc4EbZTNeB8PTTsHytwXARXOYQigOrVdPWyA+cx54HCuNuNAQ1JilL77vuEiitmNzwQyZI+GD6oPIvoPmgCVz8a/M8Z1nPWIsmbPjDh7DnO2SMqypXKnmNGTowE69vTkWabcuf6gpkkCSz/+8Y8jA3mx1nwWQfjF5UVyQOvlUqvlQj/84Q9jOrrIh7R3CFpfrBS6oP0hgpvDvi8j6jNR19fXCdwwytKm3dE3Js2QYvbeJweLU7PNkTgK6qaLotB6vU51q0wY2W63adTqZrNJ5zIAOlh7OyEHdguGnXIf+gyoh6cBeb/fp1IkyqF4RqY08bxM+ZGkx8fHJAscBkZJDdN+3r59K1hHwDHAydZL89yUwACqAeKUfdhJLZRoAYY4nXi73eru7i6VaZGVoTQA5myxWKSzFAgGsPMABerOHx8f1batXr9+nSa0EORYR02Gg+Zvsjwwd4xHvb291cXFhT58+JDKRCjRBXQRTCGvsID8PTWY9uCW6VpkcGgA5XwI9kCSrq+vFUJIh7ldX18nHWUfWDtADCDBNmq+evUqTaJiXwHJAC0ar7GH2AGAH8GHpBSEXl1dJZtJlsVOxrIlG9hrZAYgE4I0ny0ScGGPbMArKfXA4Ktgf8nyTCaTUfAFION+syyOTw3epf4b9iplCjToKcwwgC2fxvW1wa/NKBMckA20oNaCRxpq0WP8BPIXM7VxTwgM2W9AIWvJMwCI5/O57u/vRywz9fZgJ8gHxh9zf/Z0bWyPJM2Kyeg+EzBXUFkPY0/t80CC5XmephU9Pz+nwIBSQJ6NTBHBop3ixGnqVufIfhGIEhwgE5Qq2UlYlpGXlPwTe8raUh7IfdjAjWw1+8/PKcEsTydVpzLtM4E6fsQCdOwCBDbvJ2PMeGXIg6EX+Lu9jPzZtm26b4IXq3us90Ag+xQAIZP8/Bxr4QOwCZD+3Ju1I7/WjMY3Xz/p//pf/W39w9//l2o1U9PGBuYsc5rMpgqhU1XFFKDPvO7vP6lrW3EIbtPUYrKRetHtujYdSIdQSkF12WqSDxvMAjjnlOVebVvHz/bNzICGxWyhPIsnVdZ1pS60yvNMTVOrrkpV5SltBv/FBskIrLbbbQIpCEieDTWyIzAYItiLjmuupqnTNeNmdcq8j+d8dADBLhkXDHPTmPGzPv67mPS1f02b2ObMF6I8qOuGk8tjU2zoGerhPhOQD0O2AgfJc2AQuR+i37jWndrubHRrkprh9OHQhdQnMaLJJQ2nP6ctT6VSA761tfwxeDofPxtC6LNK49p/hdiQH0JQ1wdy4HPvxuPw4vXdSJGk7x5I03W1wtmo1xCQ1++WToWU7Tovl+qD6e687yOM/urM9fnTrg/BlL2e3DhzYjN4CrFUMP5+KCeL1xned260zv/DmRVFruVqrtlsrtVqqaura+V5pjdv3uirt1/FnqMe3CCPP/7xj3Q8HdWERpOir9GfFMp81jOuQV5DkzslA9FhNSkAmM/natumB6WdmqaLJUQ9KAVA4bhgTwEaOHEcDg1ssOQwhxw4xlSXi4sLtW2bwJ5zTl9//fUIFIcQ69sB6ew9aW0AM9eikZnvW61Wo7pfWHAYZ4DvbDbTw8ND0m1JWq1W6X2TSTyUjbnzx+Mx1ayTVUD/m6bR27dv9fHjxzSulIwEjpyfc7Aa4JX+ClhS1pum2KZp0uFt8/lc6/U6Ar0w9FhQzkQggu4RiACuCBoAmoyZxU4BDG026+7uLjH1bRsPeIOFBGACRPm7ZWL5+bm8AFTYI7JRA4E1NIUSnMDowzoD9mFNbY05E40eHh4SyIDtxpYzVhRwgdwC9sqy1OPjo169epX2krG2nz59kqS0DrCZ6A/PDSClp4B1gbkE0DBlaCD+hhIW7hV7Z08nRichgAic8jxPQbftAeDfZJbYS9toa0lI7pEA3LlYdlw1Q2YE9p6Snav1RfJ5yHAIQWVVKZ8UiRhA5w+HQ9pT9gIdJ/gFoBHIWfDJtcgOcU2bnbM9DOiXDTjIpoKXbI8a7Dslf8glgyeQFRuQ2cxpXdfK5BLJAKhumkZBQac+UGFfuYbFRXYSFPfOxCbW7Hg8jqZgAZIBrwRvrAcEgZ18BJaxa9e2bco64B/JdFHKhVxa2AvgRu95Fmw6U/AIdJL+57lcGMZ2s+bcy3nAg78lK0WgD5kCIYYNw18RMGKTCAAItLCxyI7tq7M2zJaW8TP2wmZAuE5ZlmnMMs+HzBI4Ouf05/7Sn9f3vb586tQs03/wP/sd/f4f/Bs1jaQsk8ti78D+cJRcTCk1daOubVT0kfxsEms0mWGMcpTlSfP5VBwr37adJpNCoQuaz6UsDI2ikgZjpnh2h80UhBCUOa+qCTpVpdqmVhyzWqtuysiA15W63khbB9c0jTIX2Xo2kJrTEIKauksz86Whrj24WMZUN626/tj6tu2kfm69c76ve/fKsv6AwzxLDHaW5YoHIHp1XZweJef7Z+uVbDKksgjM4ubSONYq9PPw22ZghDDsXddpkhdp/VgvhAZlsilNgr22lUIXAbsF/jY74r1X57rRz0Zladn4sD6ldoBxo/N5hsOZTETXdUo4WxyqRjbFR8cVJKn/e/9W7o9rnL9sEMJzk62RzhuXx4yZfdn7tkFLlBOvPB9nVUbBTxjOUbDX+k52wxgP753atpHPxus29EhkCl2clhS6oLzvV8jzQt4rlt85r8l0kpoZZ7OZbm9udXV1qTwv9Pr1K00nU/3mb/1mD/imms9nKopYT93UdX8ew0nTolCWx0k+TtGYffj4QXnutVgvdCrjFJzjJtbgz2YzzaZTPd7H0dNv3rxRnmfabg99GdJMh8Ne8/lCeZ5pv9/1DqPUdLpIQI5afIAw2QsbJD33k+zovwAsPj4+JlBLyQJg2jawkuV4fn7W7e1tAj82g2hB393dnbyPfWMAc4L5m5ubBL4BkzZA+eabb3R1daXlcjm6h48fP8bS0tksMbGc1AxDiSNkXWBEy7JMTdmUv7Rtq+vr6wR2np+fEwhdrVbpO+y0JKaf4LS5f2qNrRMkA9A0TWpsBhQ5F8ucWHv786urq9RfMJlM9PHjxz7QbEcTZQCalAdQXgdgo5YeBhMgAxEwm82SvXt+fk5Tt9BNbBi+4eHhQXd3d6kX0N4T+27LUJBxyjhoPl+tVqmxlXsFlJKxwsGT0SEjAgDn+e7u7r7TfHt3d5eCTQAGoJAAjxI79EUaMhuUUvA8fO96vU6ZFMD4ph8DzFrxzAQN9lwJG+TGfYz9DQBtppRxVsd8Pk/MLk3lNhgEmKHnBEjIFn8vy1LOe7WhS8QFJINzTtM+0OO8DTIQqaH+KpZdIvPomqRRmQrgkOfExgAWCTC5DhkSbNV58ItNsEAaeeZgQAA0B17aiVkAQ0A89gc7xT1yVgPfeTqdpB5HHY9HXV9fnzVwDz1O2FpbhkRAwnOwXwB8QDMyVlWVbm9vU8COHUBn0FmuzZqyZnbSliVO0XkbMBAcWBY/+sR4PQ4WXa1Wo6oPsCrjmLGjYEd7xgbkC0QKGQ1sAWtPcA9Zhu+mLBW9573sH0GWzVrwfGA7GwRht5FVK3vYAWwUgQPkN/qFXNlAye4PGbYveX1xRmPz8Kiff/2g//z/8rf07tNeVRfUdaXK8qg8m/aCONXhsFeWxTFwZVVq0S+s805N3SjL42LUVSWnoMmk0G6312RS9MZXUghq6zY1upVlOYzTcgOzV9W1ut4AZ3kuhdhQmudxFGxQbKAuy6NUV8qcH0WWGK3DbpOEgQ0aUlchGQ2UdACUYyBNZB5fw4FuNqKsekbB1txjsHyWqzxrUkzC3TWaTYsRQOramHVQ35cC2B9lIcIAVC1QRkg/x3DH54llNiGMew6IoO01rKLb1/l7bXaKz/EaGq1/dV+A/XvKbrDany0HC6Pf/6rXKIhwZ9/XP/+4dMk8+3mJE59z43sMIQwHCNLPohhU8R67R+yF3dNofCaKI5mH4Mga4izzevv2jfIs13QW+xx+8IMf9E260Vit1mtdX13p6elJzjutlitd9OMpj8dTz8jPVZWV9oeDNpvnNAoTkIcROy8hYARgUNByvUysHyz2dDrVfDqXgvTx40dtNxvleaGLywhkhkBjPNEmAteV6joaOgA4pTL2BGcc4Pv37zWdTnV3d5fAjy1ruLi40Gq10i9+8YsUJNzf3/f3MU/AFHBPPwblNjgTzjWYTqepHwJwTiBA6UpRFMnpU1dvwS3rCGD55S9/mUojsHvX19fa7XaJwaQ0hLpa2GdbA02PQGr8NmD56ekpvYe6/aurq+RIAOswmdhi3kuTYFVVaTysFDMvyLCk1CC+Wq30+PiYrklpBQ3hOEVAuHWMT09Pur29TeAVew67bvtJPn78mMgjSkdg5yijQx6w69K4zAKHb3szLLC0JIstW0BP2AfA3B//8R/rT/2pP5WyIwAcmsEtkFytVglMImuAhdVqpffv3ycwztQjmultppLMADaY5yWoSzXnvS2h50RS+k4CB8AuNoryLymCSr7fniyNny2KQpNiqqYZMhLoGlknGyTBsvMe9Jo1IMtlp1GROauqKma28yw10lpG+e2bt9r2Da74S9ataVutLy9GTbbYAoAYP7PgjzXFn5CtBPAT8JB1PM8i0xOADLJ+6DX7RLAPicD3Mb0NuwDusIcE8nkAv51UVFdVmlZF5pBs0/riQm0YejvsyGSb2bMEAs9OwIy+EFBDGtgJawTgyBh6Zl+2PJMXYNiWB7E/NqtGMECQCa5hPdBTAlxb5cH7syxOkZsWk0hLGh9tiRayvudlS3wP9txiCtaBz2BTyEhZ0oT15u+8z/aQcS/ojsVp2AEyleBE/Aa+3Zauorc2SPqLf+0v6fteXx5ofHqnQ5np7/zXv6f/9u/9E1VNp8fnT8pzp2mxlhR6JWtVFFEZq7rStOgVrR2mPu33ezV1ra6pFSQVed5P/ek0KeIc+7qulOdFX44VS0Ymk0LBOU2mMROSF3kSrqZplfmJvM/lfKcskw6Hrar6qMfHB4WqkuuGY9YlqWvbCPm6oQ6TBkscRTHtp2xUtZzvU2M9NR+CV1Fg/FqFrlNe5H3Womdy+r4Qhbjhp+MxRsLZ+Aj5ruvk80JNF6ch+d7wBEl1ValrK+WZ1JCREE28kckPv6JPIutn7MPWR6M2boS2n8GhwMiH0A2Tksz1UVjn+mlcGmr57DVtxiKJmlOUhxQQDY30MePhhx4EM9nKAvpxUDR+7vj3IbiwQU5/1ZFs20AjBFuZZfsbvtuXYX9mnxUjcZ65CSGkjE48g2WcvSHAg/FrmiY1md3c3Oj5+UnX1zf6yU9+Q69ev9TV1aUeHh71gx/8QLPZrC+V2WuxnKe9ocFwOploMp3ow/v3Wq3XKstTAk8X67WO+4Nm06nyHgBLSgdirlYX8j6C36fHR3X9XPQ8LzSdTdNptTioqqp0eXWp580msS0XlxeaTWd63mw0zSfabQfG3zKj02muU3lKdeI8/3a71c3NTepB4HdM7Lm+vlae59psNulcBhwxTuTy8lK//OUvEwPPHjEF6vLyMpUqZVmWSh8wwpy3QPoalhSwvV6v9dOf/jTdC88gKZUjAZ5wKDBrMOWAbuSO4IBRquieLWniNG0ckz1LABBkSxwsICYwIjtDBggmnlGmAAiyH3yeAI7sBswejo/3nwcS0lCyYHspKPeiAXe9Xo9KBrbb7YgkAWC3bavb29tREESmgD2TlMouAF+wjzB/MP8Ez0UR5/Lf398nWbIBHOCBa7Of7MXQ9+b6aV+zVKLH4XRW18kIE8wCxgkW6J1g3QA/lGVROhNPh5+l5mX6JAiaKFEDULDm2Ex00mY6AEYA6raNk8QAyHbIAoCSdQTsrdcXKk/DXH9JSdasvYaVlzRMDTLZAgIY9oKeIds4nOe59qdjukfbb1Hkubom9uCQ8Ulll3muqhnOXLCH1tk+JgI+qwP0R8D6Mh3LOZdswvv370dBDz4DRv3p6SnZHLIt2CtGFwP+YKGt77Ml0oD2w+GQgjBLDNJbxHNdrtbpvgGuh8NBznt1GjIX1s8jv2R7sSfIclEUiTRiDdI+9Mw+uIzme2wctge7SXBCEOac0+3t7eg9ljSw+mF9NOWtrDUBXZrSp6GfU9IoKE8Av8d83D9BBDqDfNrJV5aQxjdaohfCCd3Bn+JDKLnkviC4kA9sBgGlDcZs0ETGHJ2wdgxd5U/WYjKZxjaEejjbxzmnP/+X/8J3cNH564sDjfff/kzOr/Rv/u03+j//F39Tz5ujqqZW2zWqy1ptOzDxse8iqCyPaupTBKvU54cQGY0QD4WjCavI4wnh3jlVVV+baOp5FfqRoCHT5dWNVpeXmq/XUpGpWMzUhqCs88pdptPpqOfnp/7gq05t0yiUOz0/fFJ5PCnzTj4EtXW871Zdn2kh5d6pbWOfxaTINZtOVTfNaAxqFIouBR1tG5vEfdanFk+lnFx6jiyLY/fquk6VObDhWd6n8zqlwa4+82JKVZ7lqrtaTd/c7vwAsl1/0oTrAwICkH57FUKsm3cuNo4rEEwEZT6kpt/EpPf/79rYC9G2capWPpmobltJnXI3GDHAQpFHg9F2kbmPhjSeWxINodS29ShFGoU4qG3jgIBRJwMA3WfyyhUU1LVdCjq89/Lh35epcHFtUOB+6tfQqD+O7kelR/1BiyhqSs+GIJ8Nhy0RUET57tKoY+9cPKiI1HTXxSknfWnger3WYrnQ7c2VfCYt5gtNZ1OFLuhHP/5RPK/h8lLL5VKz6UzTWTzFlQlJ64u1TuXJTOk4SX3PQ2bOjUAfQxcUFLTd7RRC0NX1lbabbWomnM/nWi4W2u12yUmV5Umr1VpN3ag8nSKj1cuxJE37SSSw2hhSSake93Q6qawqzaZTLXq2nDKA0+EUg/C+tC/vR0GG0Gm326WTeGHpLGtk08QfPnyINcu9Y26aRpPeuRS9Q5j3TCRGHOD5+Pg4ctYAEkAKTdmSRo2+tsSFBl6CAHv+xOXlpfI8T/PgWSNbQsA+4ax5Nq5nAaSVOds4jXOuqir9G2dum6Tticw8V3Qg43n8OHPbx2abgwn0ABM4c+fiyd0AN/60zD4TbhiHSyYCsMQIRu6TsqNzJpTMmaRUdoPzJNNlJ2tZPZciWH54eEiMrM10834LPgAayV/1jh3AS0AKCKnrWsvlSlVZ9300j3LOazqd9HK1UzEZ+kAIgOJnmxjET2KQWFYljiEGcn1gMJlM5X0EaFmea90D3balfLbVcrmSc9Lz8yYFwMfjQVVVq+hJwMVy2RNFsc8SuTz2ALSpa81mc7m+BW8yieCTMqPZbKYCsNnrzHp90dvsVm3Xab/babWOB0HacxPshDdbTw4gBFTxHluikki63uK3bRwXnWeZDsejQhd0sY5Z0NB18n1gfHV1qbZtdTielOXD6NVZf16Cc1LuM7VdqyKPsqGetHn37p3a0KWMJTpry+bs6E9Kmo7HYzovpa7rUU8HpXEEyExAY7KSzWTwPvyaJVLiGrSj9bJAkRLOT58+pUAIMiQF2GCV/sytvCjkJB36MtU8z3V3d5dKFC2pRtaJzCyBjK02sL6T9SKjSvYO/0HgZzP+DHUgc8t98/w2E4pdx49bggVgTdCPvUT2+F72l7Wmp2E6naptWmX9Z7g+f0dGkXPsEM+MzSA4wMbbM1h4HjKKZKMhGvC31nYl0roPNmI2cShnR0+m05nK8iTvhzOs8JGUisfjJcq+zJ8emJliv3UrRjj/hb/y/YHGF/dotEEKTanpNFPuO1XlQVXTqgudytMw0sumoI6HvZrqMDLeCJr3Xk3VqKn7EXv9POq4OU5VFcFeeTokJ+ac16SYabuJvQHZfBrH4DatXJ4py+NZHS7Ptby41PLisq9N3qlsa8nnKptWWQjyISh0MeBpQqc2BEmNTmXZ9wREwNY0tfbHo4YJQiFFgbHHIhvAvXMKZd+n0PUO+VT2Ahz/m8xmfbtzPDgQwY9rHBRC7JFgLebFRM5JWXWShzHvZ22TIcokOTfU93d9loD/ex8ne8mRrYj/jt/73XRdnGbVxolaeR7XxklFkcem6xCHFAUnZT6TUxfHHOfxtGXnfJqwNe0nCsUG4BhAdV2Qd70R814htKqbKnVA24MFc19EHxskl8WJWxlROr0tin0U0tAcjTGRogLlbjikMZ6UPvQvkA1CxuKGDiVMzsWJakU/otVnWfo+752KItfd3a1ubq4VT0ie6O7FC+22W/3wh7+hi9UqGaeuazWfx1KT65sr1XWpto0Gh7pZOx0l1vd2evdu34Mbp6enB02mkV2IvQiPg5HvAfak6Fn4wz7V97f9jPSnx+fewB31G7/xw2iwuyA5r+lsnvoEonPaqgshMYUYyWNfVkBTGBOOYCnJEACCT6eTVn2JD8HD1E+SPWjbVi9fvtDj42NipqkVZ234Lu99yk4w8lGSlquVfvazn6lpGv3Wb/2WHh8fdXd3p1MPaCkfeHx81A9/+MNkpwiUYKTo/aAkiXpiehBg75Annuf6+joxfjc3N6k59fr6OrH10jA+W9IoILy4uEhTZHA4l5eXI9AvaVSSwQFzlGNcXV2ltaIvg8Ct6zp9+PBh1M8CkJb0nclVMNOwW5RDnIOGx8fHlLkgWCAIovSJ4AQAQXmWzYJRQmMdMWsznU51f3+fPmfLJPgszC9Ay5YRcMAeTGKe57q8vBzKRvpsjO2VsEEDclKWZSpfZaIUrDE/Z133u9hrFJlcMmhedR2D4Xhuz1DagI/suqDT8aTQDQfSoX+L3nZ0XZcyRC9evNT9/b32+0OaBvX09NSDrrjmBMR2uk383kLe+cQIX1/fpLM75rN5/9xD8N+2jZ6fOWF6PgRxQZpNZ/1aDAd6SU51VasoJtrv9il4pnKATBI2+zwLDilA4I/cEXju93v5IoLq6WyagtkhY+nV9nvSNvGcm6bugXDoNMmGkb3IZde2muRFKlkkE/X48BBPUu9H33LfQ5m1S71OgEeyl2SouH8OgUSnhpLrYTAOGVVskiUgYNDPsZVdO+QK/UIn0WH0gIlo6pHHvmfFkRMCa9af7AA2yjmXAgB01gb2BJC2vwmig34fdIlMKDpky4vquk7DBrBBjPx2zo3sdcKgfSbTZljxUxA/2D9IA0A338P9oef4ocm8kLqQKmRsQGPLFZmwx7XJJGA/yZad92cQgEpKWRBbnmYHKBBwYauHSpkBSw6kUp4yFDbLQimpDYqinFFuF0afi8H+l4UQXxxofPvNN+q6Qvtdo9/4jdf6wz/6qYIiUPRZpqqPYLnx6Bjr7xxKhkLE38WRsSHE03Qlab5YqGPCTF7Ecyf6syDatlHVHNUeKp3ag0rVev2DH2k+n0k+TgBIzpPRfL1gH9SqPJ0UXKbDZhOzHKGT5L9T5jK8vFpF1j+fzNKZBz4bzjPgIMGufwauENrIjvczf/qND3GKaIgNzgQYXKtTDDbOGQAyBj4M/SC1i+d71E0tp055Hr+L7EnoYqla6Ic0+SxTkQ9g23mvps4U1B+cFuJUoq4vHcqKmJ3pQpDaNmZtujhJS32A7BSkzsm7TAq+/85+ulHoszl1kxxO5ieKh+hJs8lUzqnPeHh5V6qp+4xNFlI/ROYzOTcek+v7IIZG9CzL+jNc4rkUnY8N83mWpyzD0C/SB30uNmLnRaGubTVfLHrQNdVyGcHGzc2trq+vlPk4nnXVnwL96uXLIY1aFMoyr+vrS7VtlyYlFUWhx6cnTYtCq2V0vJtNPA9hOplou9vp+flhxI5aBsQ2V2KoYXPlnOoeLHof5/szuaZt4sFWeZ7r8fFR0nBuDMYGpw17iAGijAYAV9fxoLfLy8vkpGBeYKZJ63Lf/B72G5aZemBrVDHmMFhd1yUmD7B6eXmZDPOi36OmaVKN/3w+j4eO9UHazc1NAmbz+Vx1z/JL0YG/evUqTZ7hXi0IgAWH3YkHdFXJbnFYGsDMe68XL16MUtQ4VEqY+O5zogUAIQ1TgTgLwdbGs1+UFgB4LaN/PB612+3S5DwChLqu05hUgDigdj6fa7vdarPZpDG07AklBDYDySSnCDIH1g2QLSllXuitu7291Xa7TSVhZDAeHx/TfjrnUnBH1gjHaXviCPJgYUOIk4/evXuXwDeyxnuQuTdv3uh4POrh4UE3NzdpLSzA+frrr9OEHMsIPj4+pqALGee7+Q6yBd77dP6I5KS+pIj+JoLSohhGmwI6WO+nx0fd3b1IQYt9H82b+FiyaKw5srter9O6Id+r1WqUlSIjYcHJ8/NzOqgtnkIfg10GKACMkGf0G1sCCLXlPgAgggnAKesIPkCv0EnLSlPWBcDmM4vFQi7L1PTT6gDMtjyu7gNR7MhqtdLheFSWZwnojiaFmVp0gnb+3TSRIMA+nOskvoZAg+yjvWcCLPv8XdclOw8LD6AECAPkCchtn0FufLvtu8D2MU6Z69mg2Q5/CCGkckkyn5SxWaLATqDL81zffPNNCoQgNbB3NPgjdzabeo6BbNM9gB79IEBCBmazWbLHrDN2AVtjS4PwfwB0ZAubwffyd+996vtjbUIISSaKPFdVVyM55dr8DJ3m9wQFlthlrciYQmLY7BSyiX22fULIFdkw5I7+oqYZro++Yz+4PjaG32FDsSG2Bwc9RK6/5PXFgcbl+lJVHXR9vdZf/St/QX/37/19bfdb1U2numrSJnETRK7ZJJY9ESUNdacRMJG2LstqYImzoOksbmLT1H0kFVOkrmtUlUf5ttJ0uVBTlppeT6Rs0pcaNQqGpWq7Tk3oVMwXunnxWrcvgp4fHvTp/Tt5JxVZlrIBbRubbTF03ns1XRNZ9x6cZz6y6rndZB9H0WZ9wOGd6yNJsiKtsswntiS0bQ/i+8Xt+zfqtlVIqTUabHMFOQUndX3fQVBQlxeaTmdSXcUG+V4ofTFR6/qzDoL6iDPeR3DxfJHQRoO/XKyVF9GIzuczFXnRl6eF+Nk8l/NSnmd6enpU17WqjgftPn3Uoa8JT8oS4sGM/eP0axeS8SiKiVxeKLQcihT7WpjOVWRTFdlQ2wiL6/q1jkoenTffmWd9NkYxAMqcl3f9dAoftFot+4DhRsvlMk3+mc9nyotcv/mTn/SlYZ3yLNdkWmgyyVOtbNe1vbGLGYztbqPddqvbuzt5F89w6PoMwtPzfV/zPlFeOO32z3Ku0+PjR1XlQtvtpjeSrZpmoixzKXUKG81acYgbaVVYsrQm2TBL/Pr6OoGAly9fquynh8Au06/AoWTexxNf9/t9mjhkwS0GnZGq69VKmz7dT1kOh+LBIAFiuBcCIhqNu65LZx1YEI1z4Tlvbm70i1/8QnaEpi0t4PkJ8u7u7pRlmb799lvlPdBhWg0gJAa7g7E/Ho/pYDr6G06nk7766qtUBgSApgyKf19dXSVHxj3akgWeeTKZpHptSjzIQKAzIcS64TyPs+cp07LZRZ53NpuNTrUGJMK24VBoWgcYca8AShwH42J5DsrAYPix37CHAFQyFxxEiHMCqMDIAWQITJ+entL6E2De3t7qw4cPur29TWUY3LctE0NeXvbBPetmAzdKregz2PUlgkVRjMa83t3dSVICD6wxjdi2B8Z7n/pebm5uEoDD9rDfllW005BiNmuW9Gk+n6dniY3KnYpiYLIJNEIIKVAmw4aO8G9bD08vC0GGLe0CMFDrTjBISQ5ZBcAXoHC/36cSQwColQ1kC6ADg29BFuUrdpIPAQxEBcEk2TPbi2GfmX2RhvMbsAtk+LuuS+fbAIYOh4MmWZ7sHTIYS24anaoyBcQ8J+Oo26pO8kRJC+UyJ5NBWywWyZYQuKZysh7zQDwQpGI3WXfuyxJOeZ7r6upK+/0+6RF6ZVl3WwrENQn6sEesOQEI77Glougosog+2dIegLLNJtKjwrWQLwI7QCp6QBYKGw2DT0M5bH7ydW6YSIdttOCX5msAL9c4J+/sc/M+MhS2fJMgwE4yQ3/RfwvKya7bHhHbN2GzKKwjvSW2FNDaFvp8bFDO3tgAhWcAe/Mn74nPHfGt7S0haLL9JNyT7bOBHESG2XPWCHLnS15f3KPxr/75H0g+U1CuU9nqb/6t/4f+X//Nf6+6dXIuluAAEIfUl+RCPYraLDBt0vkSQ1QvSd7Fka+8FwPXdZ3k4shanxWaLtaaL6/0O//B/1yXl7fyRa7gZOr/B6eirlNdViqPBx33O+2en3U6HDTJc4UunuWBkaNHI8u8OvWZARPtElT4LEvpb9hy56gAcglwt22b+i66to1N8P1a4eBIjWZFlgSUk67zvIiVPFmcKsR3Zf34WOcj0JlMJ5pOpsp7B3Y8HBW6XPPZItVFdyHE+npJs+W0PzQxZgzS97ZBde2UZ4WcD3LqdP/po6RWoS716Y//UA0srzTUjbpYFBbBVUxbS31PS585yXx0lPG06tjfENcmSwaTvY7yEM9qCVJq7MzzXMvFQpMi03w+1atXr/XVV28VgrRYzPXjH/9Y292mZ6fz9JkiL3Q4HpLTdy7K2uXVZZrU8/T0kIwyza80U07nU3348F4vX77UZrORFFO/r1690na7U5b5BDBhMHbbrRazmaqq7MdIzrTbbfva1I2qKrLIgBkOHkJnKCNBD4qi0Ha3S70iNoVdlqVe3N4mVpExqc/Pz3GiUA82//iP/1h3d3d97fhTOoPg6elJ2+1WL1++TIzKYrHQQ3/OBI7l66+/1suXL5Puzudz/fznP9f19XUCHYBfDouCraah1/ZLFEWRQAL6gPMm84BjGnpIyiQvRVGoaVtV9XB6taR0+FPXtrq8uEjsHyUuMPPsvS05gpG1TGzbtukMC8A7Tsr2aOB0AV6WfSY7QHkaBh6gji3EKcPS8R/gknWg5pusEECHOl6uz2hVygaQp9VqlQ6ow7HRqwMgAIRxvza7kGVZCtzYb9hhe7+AFu7hPIAkwLOBEvuMDuCYse+2h4Lvvr6+1vPzsw6Hgy4uLkQzK8E8Acput0uNseyNLaEgI4JtBwwsl0u9e/dOq74cEtsHaYDchBA0KaaqqjrpIQFBBBmZ6mY4yR59l+KBdnXdpGyBBaQAMfwa3wtZYIM8gsQ8z9OUMjIdlCUul8v0OdhShiPw3OiENDDPAB0AECCX37GuktI9SUpsNuBFUupfgJQ4Z6MJLrgG99C2cdrkdrfVtAeMfGa73cZ7z4sUmAOW67rWdDZT23WaTAeQRwDQNo1COx5Xy7M671T1ZIe1DewJzDo2nDWwMmR7l2zJGAw62T8wEfafbMzxeEw9Y3wvAJDAzDYTs8YWpBMQ2qCCnxP04ocJepFrngn9p0SR6wP6CUrIxBHAo9P4LoJWbAD3boEt2RxkyR4mCSmHvjB0g7XGdrAvBI8QHPR8sKc2QLFBMJiAn8+m01Q6hR+gjIoAjClgNuMBUYAdtPrDntsGdWsPuT+75tgr5IRG+gGXDnsiKU2wQ75tgGJlnT3khT+0dt17rz/7n/4Zfd/riwONf/YP/5EuLtcxOMim+ge/90/1f/g//g3t9pWyfD4KInB43gW1TZnSxLwnyzLVTaM29GDceXOQW1CRM7rMaTKJ5Vld2+l4PGg+n/WTnCbKiqk653V1c6c3X32l6Woll8dGJkAv4+QyX6ipanVNo+p40NPjg077vbwUeza8Od+gzwB0XVDoD8OjHq1tmjQRKToBehe61KScZbGvAaHMfJaiv6ZtYqlQn+G4WF/EJuEQm42r8tSnpxHoPrKsa3WKYN75/lTmnpWr+8bg0+movI+Yj4eD5Jx2m52mxWQ0rWC5XKppG51OOx2PwyQY55zajgxV0Z+L4HU67HQ6buWd1DWVsr4pnelZbddqOpn2hxM2vVINtadFMVE8Z6UfH1lM+hKllcqqVJ4V2m738llUiPls3kfMcy2Xc93e3ejq6kovXrzQi7sXct5pv9uryOPxfk3TaDanfIOmpUkqaxjKP2pJTkX//ZvNVlVV9gZ7JpqgOCkUcEVQmE2ypNgA7Fi2lanrlECX95mqquxrwic6Hfb9VJZaeZ4lYHU6lVoslqPyCE6kRukBoIB655yW/ex5HBTfe3l5qcw5ffvttym4AlBOJhOdemc9m810f3+vN2/epAa8u7s7bbfbNMZ10TeH397e6tAfGAYDb4NBHAnAH6B5dXWlzWaTDGNd12kCFg4He0EDMHO7SfmvVqvRoUZZlun6+npUgsVaNV2XHF/XDWMnvfcqTye9f/dOb9++TTbIsnSweSGEUX8EqWjWWVJyKJZQoRwJ4GAZ17Zt08Qk7AGgl7R6bJ5dpyALlhFHjOEviiJNr8Kxwgw/Pj6mCU3SGOwB3ilN896nLBiMLGcYUKZFIA0woGSGtbAOaLlcJiAE6OZ+pMimcngfzwhTiI6S9UEPsEns9XmAWBTFqOkWGSMQ5Gf8HTBhgasNKukjgvnjsEaAMQwtYN2uKezmOfCezxfyLks6ZZvivXeqm6Hs4qGv/4/ZuolOx1MCMMgEtgzdIdi0ckOwAyMLUYK/IqBk/whm+S7knL3nRcBqS/os8GF6F6U2fB/3iC0iQJSUZJ595nopE9kMB+uiy4A3gFnTNGpD0HwxH2VKQoiDZ6bFMBGM56mqSj7L1Pa9jpRfordFniu0321gjn5mrk6DbtsAjEwEWUwAGc/GOR9kO3heO+HJBgzosM3GksUAuLMWNjCwGMxmUwkubL8BtpuyGkvsoOt2/9hDbB/Blu0zIivEPUFa8NwE7LZ0B5uG7kNO8LvLy8v0PXw3tsWWsVo7lILKXv7JKLIm56OArQ6z9nat7GCCyWSiIstjyXbvU3gvBCHXZXIgQSE+GHvgnBudS4L9IPCAjKOEF3lg/bG5rIeVdyparGyiY7ZMDTnHp0tDqbWkRMIQwLDfeZ5/UaDxxaVTeRZZEXknl7f6wdvXurm+0nb7bWwQduc9GI2koDzzquroOMuqUpblKrJMt1c3cqaRhM9GRYoHs4UuNiPz4LFMxinzudSDizZIXd3qw7ffqlitNFkuErsnxd6EtutrAV0n54OyYqr1xZWKfKKuaeRDp7pXwOl01i92LjmpDr3C5F5tCJr2qToFaTILms9m8pnXbDpLBwlmWa6qqmPDd16MJhU0baP5cp6iys1mo2NvkNuqlFdstC2rUm3TJiVxnVSXlWh+jgY+MqhtVUnd0JzW9Sd613Utp0p5Pgikd173CvHU8n5SUZ5l8kWccjKZTJSt4xQf76TXr16oLg+aTjJdXvQHn00XkouHHs1ms8iOT6e6uFgr9Nmf1SqyQ3HSk1eRZ3LZMNoTkB5nyecq8onqmqkNlJ4FVXUpRhzf3lypaY/ywev5+aMuL1bKM6+yOkku9iacTidN5zHa985rOY9s6P5wSD003gVVp6OcOhVZFgcRdF3fb1OoqVt5l8k7r8U8AmynoMzHfoz97qhXr17qcDyqa0PfBzRV03SaThfpcLOyLLXbHbR5etLl5aWur2/1i1/8Quv1WrPZXEUxTY4Y5uT5+Vk/+MEPEsg89OyWTcufeodDk/LhcEhnSTRVpR/96Ef68OFDKsvBQTvndHd3N0ohX15eJjYUppgMDpOS0E/OWeDzm81G1IPTrMvzAOowcDhRzrtgHCwlX9iMV69eJV3PsiyxgOcpcIw1jrIyqWscO8a8rqp0QBdlCDBFBDQAKK4LC2azGDBFBCEhhBSIwirR0A8AoOyNdeF9GG0YRYx3VVWpVABwhWPMsnjY4MXFRS9bu+RMAak4HQC7pLQ/j4+PKehBpiijsaWttlcH+4ODB1gwSYd1AuhT5orccXYMzw9jig2TlBw3tgEnxnttUMr3EXgDGGDgT6dSXdemyT309kwmU7Vtk+yzBUuULXI6/G63iyU4dRMbpfthDdwTn+HzyCBMa1M3cfpg3ejp6T5ll2Ah67rWcrUYsYacPQKRkWVZOiQPuz6bzVLGydrPqhoOZFuv16mh3Qa6ZAkJRKQBWNjg63Q6ab1e67k/YwKCgX2iX4Ugz+oJ30kgezqdUrkazwWIQw8BRPgEMnR2ahHyQ7YIsIqMF3mWsri8v67rWLLdjwq3NfLoTCen9Xqd9ItT37u21Xq5SsTKdDo1Y5Uj+KNPxpaZ8IwEC2QdsGG8H4wE6CMwO+97oASJ57Slh+gFukltPgE6+4p85Xk+OkjRgloyLGQ47XhZS3LYwMUGWmSb7N4SKGGLGWrBd1swS28acsj6EERQMmkzCpAIbdum/ifkGlIXXwZxQwkdhMV55s1mKwjs7DoxmCDhy745mrVBb9EHbBnyYWUdvMyzoLM2eB/Koob+YWTYEj/2/i0JFte3UQgukSL4LmwtL+uTkCmCRNv7YmUe4uNLXl+c0fhH//B/7EsUOnlf6LCv9V/+3/62fv+f/As1Xew36Lqg4Lx8lvfA3skXLpUh4YjyfqScd6GfcNSpbeKUo6ZpNJvOlWc9UGk65fmkH/3qVJYnzZezeBJ2NjTwzJdLlepULBZ6+/atiiLXgXF5QaqOjWaTue7vP6oqT5pMChVFrs12o87H8qjlatlnTHoAUBTK5VNzWNk3ipVVGScvtVEAtpuNJtM4bejp8UmH/V4ZTd99mvxw3KvrGnVtkLq+EaftdCpPaQ3UNZr0QUGWR6Ab+w2cprlX5uNkD5zFbD7TcrFQ6FpNZ/GkZyLV9SoeFjadeV1erDTvjcnl5aUy7zVfLDQphgkWIQTd3t4mRQsK/ZkmTvvdTkzgWq3X2mx3ms1iI2nmvVzPaEUhjOd+eFPPObAi/cSVXnijYgfVdQR4nJyMgcGY1nXs8ZjP5z3jnyuEqETH46G/f/XZHtef5HuS70/BzouiH8kYU6qH/V7T1DgZ76ltmjg/va83j+Btpe12o7qqtVwNxqysKt3e3Kisqn4cc7y/sqw0mw3z0yMYOyQnhxEF9E0mk1S/ayfxzGYzbbZb7Xp2ECdc9wYy9HsE0ycpOW7AM4w6aeqiKDSbDGefVD2bAsM2m8/14cOHJCM4vMVioU0/ftCyThhF/o6jfXx8TP0wxXSayqhmfe9EMZnE2sIwTNwgo7Db7SQN7AmgjGwAYAqnAyMaQhg5egtI9/t9H+jmqfkZhgqnS6kIDhwHQX05ARNG/Hx8os1U8D6bebA11BhyW6plS2N4dv5u09zRcbTp2TH6thmX9xCoMZHJzqMn8GmaJrGkthSEwBWHDNgk8Hh4eEhAAmd0PJ6U+UxZf1BkXUVQ0rRxvPDhcOz3pZNzjNMOmk4n2u62KXiygYzNEMCOSjEIrcq+6XM2S2c0zaYztW2j1Wodg7A8U10NgeFsNlXbxnKZ/W6fgFFR5GqadlTf3TR1so3OeVNS4FSWlep6CAb2+4MWi7nKspJ6cglGF3ABe4lNDCFmyp1zqWyXfj7b92LBOWWQZCrIdALM6A2RhvMDbPMmNtrWwgMEkfnZbJZKUHh+7gE9sMQfwPf5+TkF7KfTKQU3gEtkkOCfgMEy5Mgb4N8GSrbBFlkkK9h1QcdjBPVk15s2+tc8j9llwDJgiYAjKPYWOufUtG309c4l+4SNoGl6No+j9Ok/4Zlsrw7rbWvisRusH0CPwMCWW1F+YzMq1k9TlQDwpySPYFyK/WWsMTbSe5/8DfIMfsInA2SRD5tdxs6il9giS1wgW5FsXOn+/j7ZPDKfZMeww2R0AdlkmbgeNs0GmrbkTBoYdoINgiv8IwEs94k9ZfiBJcixwfhXvssGCJHElTLnEzF3f3+fyoRXq7Umk6mqqtTpNBygR7Dq/ZC5taW6k8nM9AWGnhRp+sqZbNTHxCTEqL/DePJ4+PX4nvk7MsjeW0yC/UXm+PlgB8e2AHn5T//qr/EcjV/+8ucmWvJSmOin/+6X+j/95/+FnveN2k59lqHVfDGXz/I4panrdDj20b9cBOmKoDV0bWo+JuqsylKtOrkik3eZJpOpsixX10nlqVI+yTSZFpFlcl7T2Uyn41E3N7daX99pMltotVzFWso+g9J1rXxWKMj1m9ZqNpvqVPZj84pYL1fVVQwOvNQ0tZq6UrWPTW51Vatu6jTtoWsaNcd9OrDFKm1oW6mNc8pjmZRTlkVDX+ReXVPr6vJSX331VWLzYp3+paRWi0UMeK6vrnXZO/y2rnR3faOqrlJ5x9Xllep+CsZ0NlFd1an2ODYwzfTw8ElVHZvdvvnmG7148SIBKoSWk2lfv36dFJ3Sg/Pm0rqO3/Hy5cs04QPDBYMLk/j+/Xu9evUqpY8xvhhojCyGDSP08PCgV69eqW1joybfZWsnUQTKUChPoGSIaBsWkBIUy96yZ0VR6OLiIgFD7of5/QA2+ha4d8opcDAYUEnpYCVKhXDeNFTjZJ1zev/+fWKRMcixfnia0qqUOwES2QeugRMGAM5m8eA5m8Ze9H0Yr1+/1s9//vPUlzFfLPSbv/VbqXaf3o3NZqM3b96o6bMOKcA1jY7nZSfU3rZdp6b/XoD/8XjUdrtVXVUKhqEl6MrzXB8/ftSLFy8SM8jP+S7bFE1KGhDFOtzc3Kiu6zRhiEZYGv+6rkt9Gdgeu18ED3w/qX5OcibjgczjnDH6/B42zdZdU+4E+0rgR2BCqZh1xjhUavltKQU9KYARHAF9L4ALHCv7QR08gRdMG8+CrSd4JVBhLxj5mDJgh6OqqklOuyzLFAiir4A2njnalaCgLjVFwtYxDciy3OhMfF/ox6YWI8ANIITBt8wpZX88K89LeQ4ZQt5rSzseHh4S+CeTZntopAGsWfYZVhe7goMmi2H1F9tGFgZmG1kpyzIx9+g6wTjML5+nrCaEkPq+IH2w7wAf1t7KCgwtekbWh5p6dJ1nsUBaGibnUTJC7xKECBkufKat/+Y5AEkDsxtflNoNE3qGwNpeNwaC8b7tgYDII9+FvAPWKcGyZVGp1j7P5fOhbIw9hpHn2siY/T5b2oO+IjMhhHSoHUAXIoOggZIXmtc59PHx8THJNr6fz9ObYbOP3A/+CxYe2bEEITYfebLPbO1xCCHZVPv9BLfYToI9bNq5/Wbf2VvkkywXZUSQVLZkCrtjAzdJya9jU8kekGVA30OIPRbYVKoKWHfbb9G2rTLvNenPD5OGSYpR1teazxcJO9jsUhxLPz7QFZmTfOrfsGVysbRxyEoglwMhOxxiyfUgC+zeYrsG3RkmbtmgVBoOp2SdybLx/WC6v/zXf40ngz883KttafDLFLpc335zr7/xN/5L/es/eq+mP6zOZfHAvtliqq5plQen8hTPCuDGsixT23U69ulXhAQGp3WtslkhqZ//3Q0NLbPFTIvFrDeK/XhEpj65qXbbo+bzeVIK6sIbJzVdq7qudDoddTjsdDjsYjquzdQ1rY6ng7quVdvWkoLaplHupK4d0kin00k+y+RCq8JXyotcNzc3evnihZyLp1ROJxPlmdN6tdIPfuOrfmKV9Pbtax33O3VtTClbBuDy6jLW9+cRyDw+ParrlXoymWgxXaqp4rSq4yECtvXFRRyxVtWKpzYOJQORqWrlXDyMEIFcr9f69OlTAhCWoZA0GvMHoCmKQg8PDwlk4PStIbVp4BDiGFA7qQRjhTLY8aiwX/v9Xre3t8lBLRYL/fKXv0yThDAMGGTKRWwt5na7TWD38vIyga2PHz/q5uZGi8VCX3/9dc9ERqbm8vJSnz59Ej0A+/0+lZDg6DB6pLnJGli2FxBHmZEFmVmWpRp42AFbD48hjCeAP2vSl0jc3d2l2nAA6M3NTQLepNcBsZRIUe4Ac9/Utao+vQ6oIPiZzWa66Cec0OAF0xlC0ObpKYEKggPmkPNcyAAG6OOnT1Jv1HFO8bCsK52OR637II71sMynZZcIgAkWKEXASPKsVu7Yt+l0qs1mkwJGQDHMadfFEp/7+/ukGxhaZKcsy3QmBs3FHDAlKTF3XdelMwos4LCTthKT3b9SD5cpiSBItqUKgGLKrGxvAbLUdV0CcTc3N/r48WMCJwTROGVkmnXEiQCG+c8GNTaVzmf4LwK0oLoaWEXsCOtOMIdTJ5DsulbFZCiFYj1whsg9pUIEQOWp6rPj+ahHAVCa53nSTdbd1jlb24X/YU34HkkJdCNb0+k0AZHZbKYPHz6ormvd3Nyk5wKIQLDYcjAAEvuPrlEeyN4C0AAikpKuwKDaMgbuEXmAZQfYSho1vLIe2BRsLnrM51hfW+YFUGRUrw0uuCbrS9Bggy0bVNg9RTZtIIXcWrsAKBy+z41sL/cS12xoKOY7yfYQHElD6bYNdtHhUTmS9wpu6A1gv5EdGHUCO76PQQq2DBJ5bJomlTWxb5TtAPa4NmdrkPlgvWwQY0vF8D0EsnwnvowGeIIRSDk7Shx7in8g8Kc0zO4fcksmACBPJgWZwpYgI7ZXBHlmYIHNTDCJi4wz60RmhKl4BDFkZrfbrdbr9UhfWCee3wao4BNe6DC2KISgzMVMOTpqy5i6Lp43cZ5Bi/awTnpOwA9x8fy80WIxTDO0cjadRn9hh0QMejmeOGX1nmdGhvmdtXs8I7Ji7aDNmKITyECWZfpr/9lf1fe9vrhHo2kiSO+6VnnuleVOcq3kWx3LUk/PG82X8ziStm0kL8WTteOBQMWk0PxqrcViqTzPdCpLvbm8lBQP+Im9Dll/gvJEXYMDPimEKIxlVUrqdDjsdTrW6tqoRNvtNk4Uet4qNPHU58PxqKZulOfx/Ir9fqu6rtS0tbxzato4TjfzTvNpoeVirrc3K4WQ6fLyTre316qqUvNJHJF4fXWt65trzaZTzeZzZZlT7oeUtPdOs+ksjoSVpND169WpmMTTyou8UZt3urx5oaI/yM6FTk1V6vnhIU5e8pmOh6PautVhf9DV1aXqptHxdFDmvPbb+MyXV2t5LxUTrxDyvryo0Gy2VjyBW7HnwXWq+kMRMdwYQA5hWq/XifXabrfJcU+n03TwE4IKgH94eEjOFvYfh4PjJc2JgWrbWAMOO878fgwl4BLj9+nTp6SANGcWRZGCtMfHx8Rck41hBrj3Xvf39+n+CD632206V+B0Ounly5cpM3B5eZlKD0gbck/WYZLep6+BYJbGbUmjtWZtcDAECSiqdaIYW/ownp6e0mFbm80mGU6Mrw1cAM4hBL169UpVVaUmuq7r1PSMfdM0o4kldV2nGvf9fp9AD0HSqmfZ0TXeg6FifzFKKRtk0ut5nuvVq1cRqC2X/QjooUynruvEHl1cXKSm+Nvb25RpAby2bZsYytVqlc4LkaQXL16keujNZpPYLFv6wb7A+tvSJIAMwSMlPWT4Pnz4kCb5UMMNq23BESwQzhVGjHu/vLxMzoQyO9bKggdYPDvClr3mP7ILvCAF7FQl2EtJI7AAA5kAfM9gsWb8nOs9Pz8nB8ea7Pd7eec1n8esjwWEODTrMCnXO51OmkyLBMogBXCOtlwK9haHnefj0j1pXPsN20fZnQ0ueDbKAsg2se52QpYtFWL6FutG0E+fi6SU3aT8AxkAyBNQAfhCCAk4kEnFfhAAkF0gyLAkALYAssWCJkpSeGZpfCiZzQ5bQG3BCnpgMw82w2Jrvi14AVR571NPCZ8n2LMAnXvAPlo7CoCzn0EG4xoMLKy1sfGeulTWZa/H51m/6+vrJCMEQugCMud9PMy1Nhl8Au2qGs7r4b0EZbDxBBmsFX0o9mRoADXXsQEYcksmC7JttVqlrIcFrjwjJBSE1WazSb084IJ0NkRRpPIf9NaW0ZGhIpAhQ0AJFXtCD0+eD2cqIfcAbBsIo2tkWAmKLRmLbSXIgcjg2gQDXPPFixdJn66urpJco6chxF4bsuZkUdHJ5+fn5HshS5Hh6XQqF8ZnE6HbUSZiJQ4BAb1L8TmHCYIWyOOXwB/YbgLQeJ4YZ9Q1JgCtledFIjAgPa0dsRllmy235BJ6hv3nWlbXsOMMmbDy+u97fXFG4w//8N9J6npwO1FTd9o8H/S3/vbf0R/8q1+oaYLWV5daLJaqm0Z126iYTpVNC/nMp/6B3W4nhTglQpm02+4SgGm7GCSEU9Dmw7O6EIOK3W7bO4voOB6fHof0FeUL3ss1pXIfhXmxGJrCp5OJXl5d6XK11HQ21Xw+03K5UJZ5vXn7WqurmTq1WixiGVY+iVOTvHOa9w4o81mv8Jz/4NQ0XWIkrq6uFJvAK52ORxV5rtPpqNVqqaat1TTUdBcqT0P9XAjxFNiu6+SzTMcqNoMqBD1vNuraVovlUpkPatvhwCSizggYWhX5RHmRK88yVXUcd1meSm22zyndjzNDkC3TEUI8rZQ6eBTn48ePKstSX331VVJg69RgLbIsS9mShQGm1mB8/PgxGTDYaWlossIwIfCbzSYxxJSvcL4C5WOsAyUFZDQAppEleE6gBMMKEMCQ4qBtCRinjnKuBU7BOjOcB7WeNhtwfX09cgAYRv7O51Fg6/g2263u+hIi28fBGFwMBaUlGClAJ0zgtO+TOBwOmk2n8bwR44hT03JZKjMlHzjktm016UGzfYbD4ZACwuPxqKenpxTorVarOFXOMOUAmzzPU4+GpBQknDsXDL9lX3Fs7Nn9/X0K5JBJzBnZMgJEAC7XtoGFpJGRtTWzXLNpGl1fXydng9PDaQE2KdtKBtaUqpBB67pOt7e3yTHf39+noJJSBIIDG3zAUFLrjJNk7y0rJw0ljQAhnLUNWGz6PMuGKWdkVvg5z0zgxP0wFnNSxGlJdlzler1OpYOWrGBd4v3ksb+il8Ou69LaA3YhK8gANE2jxXyp06lMjLHNvlLSaTOHZKKwDew/98XLgliyg6wtNg02FJBw7A/ls+VWZA7Zd1vmRGbMlpqwrtYe2ACAgMWWYPB97As6DbjDN2G7sFvYf9YTeUXWeU7be8QkPjscANBLIAEYQ5ewn+w5LwtcWRfuiUwwz4httgytZVbj2mgEjgCt8RmzJM/4I2QFcEfZJHLBfuMbyZjOZnHi5a4nRKysYJPiCPPI5iNvWZYlIM8a2/4NS7Tx3AQRTdMkQhC7DAHB3y0DzfriI8gmIG8E0eyv3U/L7nNv2F72ABtkR9E+PT2lMkBbwsQ+oEM2cCcDLCmNA7dBepZlo3vDZiMD9lBC/uRFCSq6ZScH2pJH3oudvLu7SyAeW8X+si6jzFfTqDoNfUd8XyQIFiO5A29AnjunJPfYkVj2F8f+o1/IYMQ9wwng+DRwhOSTD+UZrU+wZVY2u2JtAfuGLBGk2JJGSC+bPf3dv/hn9X2vP0HpVDywLculyaRQ6JzqOugP//Dn+rv/4J9qsz1ofyxVla3qViqKqb7+5hsdymGqy36/12636x1nkFytpm50Kkt1basTStBKM18oHtDW6eIisvdy8QCxdT8ZYTqd6Ic//JFevnwZnUkelPlodF68eKFXr15FcLjfazlh5vFRXYjnPITQSS6oDa2attZyMVdZnVRMCtV1pdl0ptAOJ4TOZlPVdaNYkpSprAfhy7J4WF/TK8ng2HNJXd9LETSdznXYlwl81f3J2W3TaNIbKN+fj9G1neaL/jCgPFdZRkAZJK2WS1V1rdl0qlN5SrWbGALY+9PppDdv3iTQghMG8HOq8OXlZfo5oB3ABcMxmQyz9S3LQ98K/0Y5LXDPskyr1Ur/4l/8C93e3ibgxnkJlK1QSsRnvfd6eHhIJTsYx67r9PDwkFKQGBQc9NXVVQIAtgyM/cIAU5OP8Sdw4HoENZYhtecu4GQooyDrYtlEjAHA3h5mhCLDqqDwznste+bc1pHCTrBPrK8FBazhbDZL2aq6rnXRZ1aouca4OedUVlVq6kd2YZOcyeqQnrZzzDFQGOe6rhWkNDELRwNwratKc9PnYEttWLs8z9OhgACXm5ubVGbC73EwZKoA9pbtss4N1jDN2Z8Oc+Nhna1zads4pODx8TGVT1kn3bZtaiQnCIY4oUwLGXjx4sWIIQYEc8Bc13WpNAJ9tUZ+MolnkFDW8PT0NAIZ/Idu2+dFzm1pAg26tmfJlnOxN8yjh6VEpmBE43plyrOhbwcHx3dYVpZsRgS6TsfTIQExejwsYEUmYd/yLFdRTJPcofM4VsYlwyTHKW+xF4jeDdYb0GvLUAgaeA/2gj+RdXpcLIjnHpODNSALcGl/x3+2fJXP8zzsB3uIfHANaTgvivtk/5BhZAJwDFDk98AAfs9/trTRlgti/8kYIkNt26YJQ5AFfAY9IJgmEwhhQj8BZTqAJe6bvULvKDWDt2BtJCW7g5+3gQHAEFBJqS1MPFkAdBWbOp/P1YWguh2aoSHByPBcXV2lvUOn2FP8MjrH2vNZZA4QbAMY1os95swhfocts1kx/AZkAz6NPSLTc17Cwx4QGFm7wrOh06wzvZw2ICT7YUkqst8pQyQlO37O/rNe+BnuEdnCZpOVhqTiOZA5wDP9OxBwZNu4H0gapm4x7p2DLW1Z4+l0Uls3KvKhLxH5jOsfh0hgS7C3cX3jeV+2nJXPNs2QlbFlXhFjDEN0kNdBdwcCx2a/LDlsZcsSDdZPDrh06HGxpAL7xGeqqvr1NoO/f/dBckFleVDTNnLyahtpNl/pp3/8C/3sZ7/UL79+r0+fnvXp07M+fnrUbrtVaKLTKXrwtt/vVUwmmhRe02kEum9ev9Z6vdbHT5/09s0b3d5eabmYaDaf6XDY6sc//pFCiJOVLlYrladSoRs65QGg6fA5xaMuADyTolDTxEUsq8gOTopMm+0mOq18pjwrtNttleeZvFc0UJJ8KPoD+mJ5knNeedGnE/OBeecwKOec6iYGT5eXF/1UqaAs9zoeDprNZ+q6VnHKyTBK7HQ66fXLl2rbWk4usSflqYw9IcpV12FkLAbFKFRWZQJpUjS6lPQwAhXDxTkLgFvLFGFoAe+wWLZMCgW1qW9S+hghlNq52Lfy7t27UT0ooMaOrKPEhPISshaAiP1+r673KpQjYaiJ5AmELi8vUy8H7O/d3d2odMieDYEB8T7ue9WvMcrImqKopJ8JFvg+6vnJbtBbAKjkeTEU0gDOMaB5nseT3kl3hqC8KNJeUMMrDaU+GG6MAiMD2cOid2KTHvTAUAIk9uash6ZpRmP8Jj1gwAhx75RLEbxeX1+nw6RCCMoNOJ5Np/p0fy/fy0PohhPFCSwWi0ViAQm6AI7ee7148UJPT0+JiWQccNVnAQHkZKRgTHGGrDNBDSBjNpvr+ekp6TUB+DfffKO7u7vkENCRtm37s2CijqaSgkn8nqqOE2nevXsn55yWi6XyIj4PJYrcx2Qy1eGw7zM2uZqmTlmK0/GkLM90dXWtpqnT6NZ44nSXSi9gO+MpsMOBc3kez/fJ8iyBhgiQ4vhuMizxNBr6kLzKcjgBl7GwvOyUrCFQ7Wt/3TBpjpp0mjft3mRZPHsndEHTWSw7ZU97t5T2K4KxppfLVs7FPdhu9iMQiv7iBMnMEMTbEgtsDxkGywRjIy3YliKDyinNjGyFlb24uEh6iF4RdFpHjy2yfRy26dUGn+cZF5sdsllpm8UCWOAbbHmLRFDC9wxN1awZwH5gSceH4xGksj7okAUkdp1pHAXg2EwD98pBhmQsbQM9907JIfJAMM+fXRfLp9D3PM9NT8Mw5Yo95k9rOwH+A0B1qusqDrhpGk1739B2nep2OITPTv8iq81ZK5S80feAH7MAnD23E7l4zWfzNJlsOp0qdCHqaR3Z/7qpkx0MXUiZwel0qqZu1LRD+RS21LnYz4r8TGfTdA8DaTDYSd8HUpKUGxLC9ghE+fHijCj0KeKAqUJ/XonN3DG05f4+TpEkmGOvLPnXtp1CGMrxnPMpI0CJE717XB/dsM36mc+SX5AUzzTzcfIYe4lehi6oaZuBiOuDQ0seTfJ41hj2FDzCPdqxtMOzxNaDiA0qTafD+WbxnuPnbEDEXnVdq/l8ltbGBoVtOxzWB7mKfkCy2gy/DdzsCzuEHbHkBzrC58BN//Hv/unvXOc71/3SQOOf/ePf1/5wUOyWL1SWJzV1o6vra4UQhXC1Wqs8VfrYNxu3TavHh4eUTnTO6f7+Xl3odHN9rayPiLvQJXCzXC77iRunXvCisvt+s6kFhGFACWC3Li4uRowYRruqhsO34rkX0/6sChYuTsLKs3jSKAx/VdYpso4GtlNZ9nV5BanyVt7HzT/s95rPF+pC6BVoKLWhBnC5WsYAwjsdTyf5XnHs5CE2Ms/imOC27ZRnuVzvuJ6e4hjdqmayQJZYalsfbicYMPrUpsARpE+fPqVgicAC5g5wRenQ7e3tqLmP9cfosNYoP4KOw8U54qgIeihDAEAcDgd1vXNiApMtDVqvVip7eYDxtE3H1A7zfTc3N8kIAVBOp3hyNQzoY8/yAFYSs1rXynrHyJrYDAfKiWPhQDTALGVadpIL5Qa2fMeWU7FGnObOhLaqZ92bto2nvLs4jtGCmQjmYknh8XhUWVVq+3IG7pH9gtWiV6Vp4ghdxtISrJCOxilgxAmsZrOZlstlKqOazWaazmZ6fnoaHHIP4nd9cMIzAtYOh4N2u913ztNo2ziBDGdIOSD7kOd5OmyK7KmkUT8F9eHsX13Xmk3nKoqJfOb1/BTLDBfLhY6Ho3b7nZaLZQKfOBLvvTabZzVNq8l0YrIz+age22b2OFdBTlrMF/295j0AnyrP42jYU3nSYr5IWcK2bdPhh4yYbJpa2+1OVVVqNptrtV7JO2ptG+V5zwRnXq4/fHRIx/ejoL1tCGxVFMP5J12IJ9TPeraYPXLO9axcLe8z1TVngri0prYPgXVz3sn5TEWRx+DZe3VdiESP93FKoBsOnbJjFrMs64kt9Ta6Ud4fkIpNs+UdAA1bL849sS+AHlvOJI0bfy3Q5jnu7++TY7eHvHFd+p7Oa/VZO8CDBecw+Xy/lTV+xrWwW+gA17dZOAvmKLuMICcGslVV9sNDJn2p0kLH4yHZUMAewQYBj2WLqfe3JA1Zk/NsDvdly0hsBscGXhAxAPCLi4tUHkhACEhHf2MgMkw+enp6TOcqFMVEIWiUafTea7vdmEzwJAWY2Pvj6ahOQ7a2KAp1faZusVhILox8GFnGiEFqhRCvG5/7JOe8ZrN4cC1DWrr+3KsQYlPxtNe7pm4SO++c02Q6iePvuy6N7j2VcZQ0gWFZlmq7CATzLFdQDNpXy1XycV3XjcoG2Y+iKFTVlYp0QHCUt6qOvaxZX5JWV5Wcjz2kp/KkPOvLafNYqt32sskkPGQiZnkuVRSFHh4ekz6uVqvkB9l7KxeQSOwrOAZ/1baNynLInKahJ00z8rN2NG9bcYhdnymdTpId6UKXDgpu21Z1U8exx95pPpunACjPo40O/TEN2FUCR3TWlmsh5/ZeYyAQMx8EBakaIAzyZYkPSVouF6qqITsZZTfadPr5IIIgGmxmw2YorZ0jeLABhs2O4De5N1u98qf/7H+k73t9caDxz//JP9Xz83MSbJt+wmCeG2suvd/vU32z9z7VzEtKLBBNrzArgFIaUjE2MAb8nSZWamYph6GchckIsCSUJ9DwilMiBepcbA68urpK0SlnO+BcOPQFxwywoayCunMCId7Hd9qxngQwTIZhczG2MIPOuTTKjoAC4E8JwJs3b5Kxdy4eRgRDg4OFQQbAobw4Duo5AaN8BwDeHgjFHjLVAZDHlKgQgj59+pSE+/HxMU2VAjweDgddXFykvg4AdhqH1wNsO92Dfo2ubVX2e1b1jc5kGTCqln3n80N6MyrY5eVlki9OdEcxqW3t2la5yWigrDga2KhzhT2dTmlcKyMTYXwJWtgD7s02lePA7RkpABP0kHIUAkgcdgghpYbZE4JIHDjfgQHe7XYpQOu6Lp3rYevm27ZNo3OZ7ARwyrIsTee5vb3VL3/5y2RcAWiTyUQfP37U9fV1OkEaeYY5sY6HccghhFQuh6OC7WSfkd35fD4am4tNggFEZtpmGOXHtBJJo6krlvHb7/ep4bxphoY8gvHz2muCY6YE4WSxYcioPYMAYGZBrS2JIZivqipdizMFbAofIIGjOn8e6zBsGcx5Wh5ZZh25tq31JahGHvEFs9lMwUXgQgkRTrlpGnnFs4GwB5aMaJpmlMJH3iWlLCbBn2XZbb/HwdTTcw1Ydu6HwMbWgSPX19fXquta19fXur+/TzYSAGCzD/gRS2RISuQY8mKzFgA/7ArZNltGx7XwCbzfloBhd/Az6As+QPLDmkPwpYz4kAUEhPIcgFnWB1khW8zvkWU7gnlgW8enolP6aPccWeSeLEEAKLbZB0pOWUubhYHUjPc/HZXNYDu5d5sNw9Yfj0e1GkbBErjEz8SR9YfDIU10Oh6Pfa/HpfI89giRyWOsOrgGXGJtxCQvNDXMOTYDuUIfbWkVeo4Nt/1UPBM9HnYSFtfZbDbJx+Nz4ueG0lzkMeIP3wdu4TsA2HmvUxX9FT1T+DnWyJZ1pYCtv28CVqoUWCcIPPaYdYBEQP/t8A3WBJ3nc5NiorYPoAmUsTXoDjgLH4CNQW5saSlEKsSnXROqR2yplzRMQrM9ZcgVumxJCeyftS3YrrIsU5AG3rCN2eyTDRasrx8y1pNRgGQziaydrVwB42Cjsiz79QYa//Qf/eNROhSgwoZjQGB5bLNvXcfGzevr61QffXV1lcA/LLZN/yKgGJemaVKKjEUEzKKMtl6fzbVpVJu+k5TKbLjPqqq0Xq9TkzF13w8PD6kUiSyBLc+gmZkgg5ITggo2m14IDLJlcihVIRjhuVFGhAyAWtdxapQNLHCuTFuws/9J59oJSaRzKf+yNYgYWWqQnYt1s5eXl6nHwKbhADCUO/EZjCJsOVOhbm9vE3CAWQQkPD4+6u7uLo6xa+NZK5L0/v17XV5e6vXr17HcrJfBtm1HBxjBdLMHgGzWiGej/hwwW9W1jv2/qbuXorE97PfK+2vjDJE/SmvYS0A/RswG1YC2tm0TkMDBEVgjrxYg2h4MvhPwApt2zjB2XWxI//TpUyph+o3f+I2UFv/06VPqI2G/kAcbODDFiPfu93sdj8dEINzc3Gi73erDhw/J+HJv6C5kAqN5KT2DsAAsQzLQQ0EG5v7+Xi9fvtRms0mN+tTOAr4x3tT7f/jwIU13ssMGkNWyLDWfLRP4xFkQoFiAzQtHQCBLcIxzAhRRiw0glAZDTnBkS1sAA4fDId2zBa22CZ2sia2ZxTagw8gj92lrjAlqISCQQVuWgr1CbrDL9rkpQcRpW/kepe3zPJWbsE7JDncxQ8ca2WwEIJT15N+2Thlwhp2xIIY6fwJd+ossyGBdIHSoo57NZinwAnBjZ9EXADYyRwCLYz8vMUGOWDubwTxn/3kfTp61o38Ov2vlDwLDBpDIa123CewB5ABPi8UsyRpyZW03WUsyiQShFthKGoE7W6rx8PCQdIZnZg3xAVwX3bZ7C1C1Z0GQ/SIbajMfgKqyrNJZBugEOgSZxL5jSxJG0PBMgPW4H16n0zHhHcmUU/ZnfpElpz/JBrXIDP1nXdfJS8r8cI+8j5cNqtFL9tf6Mu4XWbAlu7vdbgSi+R09DkVR9PszyAH+jJLKPB+GByB7WZbpeDopK/KRHSZYwbdj59FHiw+sXPK91i9Lw8AN/DHXw9ehN9gO8BnZka7r1FbDwYEE/8gy/pJngjiBdEAuqJix5AU2wPYBopdgW5tZQHcow8LXo7/IKOQeOIR7QybR7VRufYZ9LZFCcMs9Y5+wO2Al7gXdwg4igxZnIqf/0Z/5D/V9ry8ONP7g9//JdxgcInduiJIWgKqNqhBmolya8myzIYYPxhVDxhx92wyHwKHU1qizKZRr2JQrAQfAlPtESBBwNojvYjxlXddpJjOpKsAJwY5lgw+Hg7bbbTo4jBKQu7s7/fznP9cPfvCD9EwoMc6PzAzfD2CC4UW5hjRwkf5EmM4V+XSKB+p9/PgxrdPNzY2enp6S83737p3attXbt29TaRCCa+v8MCaW9bJBIIrAadGWNcZRIgMhhBTUMVaO8p+Hx8d0CCBlSJI072sqiyJOvgB4sWd8DxkbapwJ/u7v71MD33Q6VVXXynp5IPDC2YUQtDIMI2V+Xdel8y5s0EH2AQaiaZp08jmGBHYHwxhCSKCOz0+n0xQUWlaQ05n5PEacLAqGGeeO3tkAQlKaHiVpNPoYQ4NxYz8xaOg1oAKGEyaYgxopIwHosR6Aoevr65ThxLiv12s9PT2lgxjJXD49PenFixcJbBCUYFABkjgbGlGxEY+Pj6NJJsvlUm0zZMjYryyLzdyk7wme+Jxlz21KHCduQZbNfNq0tnWUNkiyZAvG3wY6OAZYM1gpOw2NPiCcm+3PICMGKYDTsJkIQA3yhhwh15Z5s84Hx2j3JITYM9d0AyOO7cjzPJaknMqUScVJ8j6uiQOFpLFZSeTRAm+bXbRZAGwYTpYMxTnDx7PbYABwhn3lfRBP57JAdhEQw3vO2VQ+x8sy/DyPzX6QlWOdacS1a8JzIy+z2SIBVJ7dOdfrSNDFxXrE9qOnkhIpho2xtp5hHjYDZsd141OzLEtlYl3XjaarMV3Q4gZk3QIkS4TwWQJT23vFmsWAzWk+XyS9Yl0pr8GeAY6LolDbtWq6YXQtk4nifQVdXV0qhKD7+/tU6SDFcfJtG9efDCX3iH4jM+Ak771C28o7P/IVyBd7TDCML7cyw74jqwB49hrMg41grfksez6ZFFJfdoWNYj/jd0RQDeGKnMo7dYb84tq2L3REPGRDb4DdUzDb8/Nzsu/om81c4ot4Vp4BfICvQw+LoogHK5dVskHoHy/sDn/ih7k/KmiQE3yq/Yy1n9gknsHiJMhk5JDgBJkkMOA9lrQA07A3fCc/O6+OIJgGKxIwcF0rb9becE2+12aNsWlgyl9rRuMf/4+/l5h7DAjGhc3MsmHuP+CM2mtu3I7G4jrT6TSdy8Bm4KSZs49B3W63icG+vb3VH/3RH+nNmzfJ2MC0rlar0WQBFonfEVDkeZ4chWUf2AyEwjYy4lRt0LLdxr4Oe+4BzsVeK8/zBG75N0rTtrEem+kopK5olgXYPT4+JvBHdgODbwELBlxSUhQAhHVw7F9RxBG0CBPgCgCNQUUpuDeAN0aAaJ2yts1mk8YDAnpgL7z3aQoVgs+16x74Z71gA15S2tw4QsAijJ8NuDBilKuUZak3b96k/WEO+WKx0LZ/Hhsok3nommHaiM1UPTw8aL1ejxgJADvZsRDiIXA0QJ/rDixmnudpYhH7zR6zj9boAMTYqyzL0gFxyRFICZhgwCWlUj0YGrJzZVmmkkXWgjMEWEuMOiDHZjDsuQSACoIRG6Ag87yfwB5dI7gGtJNRY29gstEhnMvnMgZ8hu8MIWakDvvTyJlVVRwhzLPDfPE9GHaYRdaSoMBmo+x/tswC9htmFcbPstoEF5ZAkAbgbdl1nh+9Q0ZgiAFseZ6nYIwsrXXigBiua+0zsm4dEXvDPrFW+AZsvvNe8sMe8Nm2bRXaTl3bjq5tQTdOE4dN+VFyYP26U35g9R2QRpCFfcHx0odn5V8aSrR4FoIne11sFPb2vJzHsqXYDHwkusta2H4SiA2uix4yfc2y+QyasE2sgCjYZOyCc8NIcu6VYLOqhn47C17wFfzO2pKiKJKdwncSyLLW2GtKWvG5+FBKiLlv5IXvRS/Zd0vkbbfblIECrEFY2iqBqqo1mw2ZBWTGBsuUHVLG671XE4ZzlCBA2rbVarUUwwvOp0dNpzPl+SAHlqAB1BJoQHx679XVTZquZDEQ+4jtQQchbNhDiAHW1QJYdNiCSZvtAqBG4mWRmpMtVot7OVFdDzpgy4vrtkn9gzyzzZoSQIB3bNDFPVlfxfqBb7g/G1iw9siMtXeUk9rJbG3bqj6VidwkqLYZYuuTsCOsO/cOnuI72VtLMqBzrCPvRQbQMxsoYvMhdS0hxzUA/NglAguCZ2wLGMjqE3tj75W9Ry7ZC/ywLVez9suS+ZPJRP/hf/K/0Pe9vjjQ+O//P/9fXVxcpHIi0n84KlhYFBDnjjOF9bCpJRbMe59KdADNlB5gXJqmSaBWUmrQ3u12qXRjOo0H0zw8PKSFAJhYwEeqlAyDFXRKuzgIB0OB4WTWPcoAe2gbrNlUDFSWZaOzJewBcwgRDoBMznlaj793XZfuzwoZ4NCy+uwJQmknRdHYy35579P+tm2bagAZ9QbDbpkG26+AMeBgHABv27a6ubnRZDpNo3+l4ewMHBMAippcniEvijhpSkOgyjN++vAhMf44O/bTGjgOSKMelOwKzCJ7UJal2l65z7MFzjk1dRwn/OHDB4UQdHd3lwJRlBC5hfFZLpeJFbf1j/bUcfQCnWEPOETKpjTps1ksFvr2229H7OPV1VUqXeNgPYLePI/NrDhPRrXy/QTAlMLYLJat5+bvVu4uLi7S2trSE4L6tm1TmSLPSKofwM7M/el0OgpoOYEdR4WRhDVF5pum0ddff516N3ifDQZYe/q85vO5DvvTKLtJiQjG3vZKnBMSBKDSUJts2TmcGk4XR2kNtaQEmM4ZadYHp3DOZgEC7bQagl2b2bOByjloYV0ITrDPfLe1Z9y/Dfp5VnvonGWH0eHZYj76fMpA94GGvRYyYoGS/axldNlT7g95se9h32xPjH02W/KF3HEfMHnoM8QJwJB9xjYVRZGy8+cMNfuHrPDneebFBp12LSz5YVlUPsNeY7+xY9F+1Jr2vTD4Lkl9aeIpyQ+AB3mAzLD29BygWHngMwQKrBsHX1LKO5/PU5aR9WMfISRWq5Wen59HE8RYG4JN9o11tAQZ4Nj6Kj4HuJzP56kklH42553KHodgc3gVRS7vXQqs0eHIQs+1Wq1TmRJraTMw1o+nYKGNQzv4N2toAT/Xwt6zHjYwxF8hk1bPrWxRjsp+gX3if+MT09lf7zM1Tfud4QVVVclnmaqmTsE5GQVG7pPZw4fZRnRk2wbJrBF6QWBsM8GQIpQ2oV+2CRsckPoKyirJGfd1HlgjSxA01paxRnYYCoEqcgCxBKYBA4OP0Amb2bXgHb2ypBPPAlGAXcR2YSfwr6yhvRY/t8EC2M+uAT+HRCQwAXexR+hh13X6y3/9L+n7Xn+iQOPu7k739/e6urpKDv7p6SkpwOXl5ahGuWkaffr0KTVGYdwokcK5Un5lwTKCaMtLYK0IOjCYAC8Mk3MupTVZVDu/GgBIKQ3CJA21gOeA+JxFLYpCy+Uyjd48nk5aLhbxoLJmXLvM82w2G718+VLb7S4x/m07pPvimL5hgkl0jJm8HyJlZudfXl6O2EGYDMo+SHPzO5rIMfqUlZDqJC2LsbYOhnGacepVdNz0ogDQMSqsL8aD3gzWCscH02ibrQi2yEI5F893mM3nWi2XsWSiz55Mp1Pt+j4KlP7y8lJVFU9oRbb4u90HCxap7Z1MJmq7Tk3byjsXD080I1+dc1I3jOb1ftybBHAHHOMcbZmCLTsia8Y0JOtEMeAEk3VdJyCfZbGUsK7rUd0+bHbXdaPeG5wpJTOAIFuqguMAhGBUAPQYTWa38xysO+Dpc8/K35mVDhMqaQTEaHimvKjrOlVlFcdDu/FcfZirKJexnAFD2XVd0m36rajDJojxfqiX3W1jMGbLGyhT4xmRAYwwpTv0ArDG3sezLSAVkBGAJk4MwgRdQ9ZtSaItz+FnFvDAOFm2mesjY3yG7Nt5EGOdGHtFBgonbpnYCM6dmGwVwnDGhF0fHHRqrsy8vM9UVmUa0emcU9d2qspSk5R1GEaxRhs0nofP785BLu+3WW2eC0DP+mPrz5k866S593PABShAr+0anpNMNpBhXXkOG9RgC9CXgSWPI2i5/7puJA3ZXnSVfaEfwIJN/F58lthfwJh31isEhjA0qfxoLB9xYlII6nvvxsEyOsL6ngdEAHKymmR8z+0I34eM24DlvKTTlkRH/LDqM05D4L3ZbHuAW4z2g0wlWWzn48G8yPrpdNLxdNSkLxWUlPoE4v1UCeDleZSB/f6gOIGtUNuOWWbn4mG/bdfKSfJZpvJUKs8zhX4dMg2gGPzEHkHGAZjX63UqwQU4Yh+RA4iLxPQryLtoo5n6ZgG4816T3t4E9XrRDmdVyDnlWRwzKyc5ObVdpyLP1bSNTqdSxXQYu4ws4GvRFUhk7De+ATCLHbIEKzafQUSWVOFzZH3wx/wcO5sC/LJSboJn772atk32J8tzTXtbv9lu5b2T60dtUy0xX8RRwtgSsCDYC9lAN5ABS36AmZBlnhvS3doK1tCS2wTj2Cxrn60Ns8QUwQK+9jwzYclMZJegBl/Ds1iyN4SgP/MX/hN93+uLA41/8Hf/Xkp/cpKtdcIsoI0EYX5QVJg9y8idbxJOgs0i2MB4AlwJOqwht7XZFnDg8O0LxprvBfjbxh4WEyGmQfX9+/e6ubmR/HAqpy0xmE4m2vQBz2az0cXFRdrcrgvyeaHj8SDvs3TN/X6v5XyhIs9VN7UZN+f6NYhzsTlngmDJpqKJ0E+n06hsimvgfKgXR4ARfJ4lz3NtnnfJ4GH0Hh8fJSdl2ZBCZ6oGAJKInzIpGtZhxtl/yhOsk93tdmk6GadC0wT41Q9+oIf7e0nRIRFITCYTPT8/J3YQ2cHoAbbs2FyYAdaHtQGwoXC2mZTJIwAK3rtYLJJsYOyloWHN1v0DYMiwsO9MhuEeaQg+Z1cIxCm7AeQhxzDz3DfPj4pb1shO+aJ2F+PHc1mjZa/FMwISMKR2fTH03BOO5LxsDlDPxDnJybtMVV2pbYaRmYvFIrHVUUYzTafDdCEybuz3druVXJxFDyHSdZ0uLy+TTrIuACyeq67rUbkaz25ZHGwNQcJ57wIOFlnCzmR9AGsNPbaIRnHsFTIMcykNDgWdZ0+Recuk2pS9ZbFsVoH9sk4HJwVYQA6iI/vu6cFNQynmeETtwI7HwAQ5sdkYbDs6iU2LgDVTHB0+OF9sNfdn18USJJa5xGag47aMzvoW1pyfW1m3JTKsE9+H7WWNbZmR7dmDhLH7yDogc9Gxx3ObmqZJ5N2Q2R7K/rhv2NmyjJMBIYDwkdgCssbo1ED4DO/DH1mbaMEfjG0c0To04XKOECw/wSo+BruCLlPeYXuZuA4yz76RIbXBH2RKDCYmoyASppk9IivN/lRVpS50Cv175vN5GmSB3iIX+JnBDgbRhyENQw3anqDKnE/g0Pt47kYIQd4Em+gotgb/DOEzBPUaNQwTaJwHmTaLX9e1JtNpyjDMZrN0GHBVlvFsMD/0dgE8sa/cD+tHaawNHrH9yJmt4T8PyJExbIXt/+Lf2Bxk4ZykAeMQnKJf4C7sPvuBnNvsAe9tm1Y+Gw6qBAMAnq2fQw4sYZb1wYkUz2fzGhrvLdll75O1sxlV9s4G6fZZF4tF6gW2Nof/bFZEGshmZIrgjr1E/232A7LV+jXr6212lfXMsmzUO5znuf7CX/nz+r7XFwca/9Mf/HPtdjs9PT3p9vY2PQQ3hDDZwIAHxtHC2MCeU3MNyCeChnGA/ZCGmrj9fp9ANkYTQ08vAAaIa6EYIQxpb5vqDyGkOk0Enuj7cym9siy1Wq9T7wBsvu1PaUxdJwbs4uJCh+NJddOOmk6lvtnbe7mg1O/BxkrSx4/v+8O7rhLoteUSMKM4CPaAiRyUQVHOhRJSu81BaNPpVG3TqiyHw6vsiN7NZqP5IpYr3d/fJ2WyJTPUCRLMIJRVVaV1pk4c2bAlWRgPC6is08exooCHw2HEmBdFkcrAeFaCRVtGg7y1bauXL1/qeDymEjjKh2wwV1VVGnvM9ei5YK8pbeJ5LZuHk2vbNh0+B4NI+R0BPMAd52MdAGwkgJXfo4cE67bWF1kDHPE7eq5swI5z5bqwbAA3SukGQDik9AE41JYTsNNY3TSNbm9vU8Dx8PCQnNZsNtPmeaurq+ukl5QBASCKokjsLY4Ix0RgwwhnO6yh67qU6cPwA5JszwP3T1BMKQb7QHYTYMdz4PhtKptrYbusQccBe+9H9c7YVZylDQxslsICbIAnNpZrIkvSGLgRYACQuFd0xYJwy5LF+xieDdmIshIzS+dZjShr8VA/q4sAVgAE+sPP4j3Hcz943nNwxvtYB9bO1nNzL6wX5U2sMTbP1sSflzYMDHY+ArH0LfECaNkMnc1SWkAFYTGy/2kt4gQjbDV6FddhCGKQfRtEct/oKmQbZcZkDIfeh1gWg7xht2z5Cd/VNE2aCBXvMz6HHblpWVfsPvIHKWL727hXgBZ9GwyPOZ1OqdyKbJ3tNYzr65Vl+Qh8nmdXsJvsb1EU6twgNzRv01eIvbekp9U9/o7taPpKhklejNh6G8AjpzwHemb7mrh31t+y1hZAo68ERqzv09OT5JyyPNO8DwQIOCxTbtceEGzJiXNSAr20vgA5sIQt94cPQqfAc2AlfIYdsmH3iMyUxR42kMGWsYbImJU5a4Mggawuc9+WbGAt8MlcxwaH2PtJXsgb2cWe4FvBZRarIQP8nLXkGWxm3dpentf2QNngKs+Hs6LA3ciwzXBIGvlO/BHkr61c4F4h0iCHz9f3r/6v/4q+7/XFgcbv/Q9/P5UKPDw8JJYAY4RRsxNPbIRmozpuksCDmjuAD8EKm7BcLtPEGBh0DDMsOqU5V1dXqeQFo38ebLDINpUHCH9+fk4gik1FSWi2xnnP+7IqSppgpS4uLnTqDx57+fJlCqouLi5UN42KyWzktDAsRZ5LfVqOwMA519eNt5rOpukwOg6PIvhCMAF21qgChghGmDzFz969eydJiUWvqkr73TGtJc2+IYR4WE1o0+hQmkEJuAC7P/3pT0eNuzis0+mku7u7VLplI2XuGcVi3Zxzo/IPeh4oL2LiF1OK6rqOp0+HoYkJYIRy4dRtapcSMgwurALGiPHEZBkAWrYskLHNTdOksh3WhwyQZQlSWZYGpsmWkWF8mYJlP+OcS+cEpHr4fDigEtbTMiJMUeHfGCQcEg4H44O+AiYwjgQTGNY8z3V1dZV6HAiCWF+bQrZriTEbWPJWeTYMQsA82TpnDDH3Yg0x32PXwhpla69gu+29YRtgWXFctlb7c/0YrCXfxb7hzNAf1t2ylsg+wRrfhcyeOzpAFEbfBhrS4HisQ07gqhtPmLL1vDbYtIE9/44ncw/lLZbti3XrQ1kS3xlBcqYQfnXpk2VQAXAEL85ptIfnz2SzlzYbwf4jC/gT1tT2bQyBzcDK2kyi1Te7NgAiCyy6bihdREZtwMhzYuvsOhNcTyZTlWWVAhKbvei6ZhQsWf0BwFr/it20wRPPy7oeDkfF05bd6J4hmiAQ7SQi56SmqUekHf11bdumIMxmrQCNrLHNLEkanVElKU3Ds8DzXI/fvXun5XKd5IimeTCAJUewl6xn3Q3AFJtl5cae98F6sIcWHCYsc4wHnFrZtPuKrAJg7e/QBQJC1gMAz32xXtjdIWtYJ3nK81ydG+w7GIzSQpsJZS0AkdZWW7LJsudWVySNJt6dkxd2nSixtj7YlgxxPZ4ZmwYAtntgAwhsJZUU9vlYL+7D+hRspcWs9n2WuLEBdyKq5JT5IYNv7Sx+FGxgfRA4+DwAtP7Y2mT0m89BlvHM+BJ0DTzJcQnoG99tyaSo/4e0HsgJxD/rzKAj/JF9/1/7z/6qvu/1JzoZHANAWhxASyRlWQBb84rTRZh5AEo8bFR3nuYk+n337p1ev36d2Blq1FAO2/TM/cBaUeKFUEvj6PDu7k7v3r1LwkUPQlEUKT2IAj8/PyfWpaxrPT096e3bt8nxkBrM3JAOJZCKCtopmPRqWZb6+PGjPn36pLdv3qg6lclIA4QiQzZV3dQjJ2kNCACbIMiy2iijBe5FESdMUdqyXq9VVZVevHihjx8/alLEmeCAJdZrvV7rVB4S8AVsAvRppqe2lIMI2cu7uztJQ+Na0zTpFG8UxPaToIDr9ToxcpJG08tg+JG92Jg3S/fMM9qyPJQTA4bcINM4bYIT2wxl2XPLsqdmQjdMgaAcBtByPB5VlvEcEQwT7z03BmRECOhw4EODZzVy0oAsroFqAxLIrNmzcAAPjO7DAAJYEnvTZ4MwvOgaoJh1tjYAx4kDsulcC8jJeMTPedXV0BRsgcr5dUMIIyYWXbGBHwYf8HFeYmT1CNuUegvcUIZEZoX7IGAjs4aTR0ZsqRTPjG5aWbdgwNZc2x4NC1bZW1vLbZ00a4JM2UCF9TlnynjZunlJI+ca7c5MWTZeP5459mtoJL8wlm3byfuh5he5IlDnuyyYj989lGjZ0lcbkNlyJByxZSQBRKwDe4y9ADgAlrkez4DeIiNMSQJscB+W6eXZ7PfhM20AwnPiQwHH8eyHYT/xi3Hdo15jH9kHy5gi15YBZl8BzXzX8XhSlg0ZPt5vdR35RobiPTVpzCsBDeWfrA26ABloR/IiQ2R08jxP9hQ5t/phgRbyzgCZm5tbxf7GYbwywfbpdEp7CFHjvZeck8+HoMoOErFEFCVe6IKt0LB6m+e5MucFBONe2T/skR2mgSzzfgtorR3/XJBtcQBVAkyjattWwTn5/mBBsMdut0slcud2we4j8m4zNp+7J0AoWXvIJfop8FP0myLHdhKe9VE2mCGYsvJsS5us/bIBMv4HP46OYMd4HosdeHauzR6ATyxhwdrnea75bKauGcb82mfhGc73l99hY/j7kP0dqjrsWliMAAFmMTS/s/aOn9kSevARmPT+/n6QX5MwwH7Y84Vs8GXJvD//l/+cvu/1xYHG7//ePxwxhzZgAAhWVZUALyMibTQPowEgAZjZFDhOFCCKkeY9bFie5ykafH5+Tuke3mfrdK2DxqHgCHEyOGeyCQBaDDMpzl/84hf6yU9+Esu6/JBex3ing576e8ABYLiqulaQ19XVlf7dv/t3ury8TFMgvHOqy2oEpBDWLPMqq1O6LxgeskK2bA1hIBCwhp8AYTab6f7+fgSKALfz+VynY5UMBVM5KHVyPqS6dk4YxZgtl0s9PDzo6uoqgVYia4zS69ev04FtsH9MD6NW9/r6eqRIfBeywEQQ28RuWV+Ui+DSZh4smMAwc13S9bxgHaxiEzgxyQoQ2XVdOn+BqWY2o2NBOi+Arb0vFNim5a3xsU7TGnA+j8GxTs1mF5Fla0Tbtk2MnhRZKvo0ANiWQbYsi021c9/IKJ+1WSMICwvCBz11aptu9KzoPMDF1pqyhvYeWDPLEtmgjGwR62QdmmWTbDBkWTLrbGyzMbYAwIqtOZ1O6XBCZJKSOT6LnJw7ElsewX/YhHMW7ByQcL/YIZsNIyCxgRRZF4D9eRYkyskAAtG5OGjjpCzz39GvKO9BlE7ZayJr1tnDzEfdyZTnw3hi1ncIfCKzBwvOGpMpPgdUBCb2OSUlooD3ch8QA+w5GXzAEr0GNgOO/Nm9enx81Gw208XFRfJNPLMFe4Ovy/ssUBjpcnz+2LtiAQWA1tp//o0MsIecSQPLH/coTzXb2E3Or6Gc08p43H+v6+urpE+MTbYZM4IrC1p5v53uZjPh2GLsEvbcsuN23SKptEjraidfWt3Glmy321j+5b2yIk++wzL9rB/fy5/sj70ezxNCiI3GYSjpQQ4hqmzwR+8FcgAoZqoX92AJWqouzr9fGibkse7Khl4AKws26LZEhMVy7BOybG2h9R/8eX5CNcEg9pZAGjJsKHlzKWNns6PcMzYfm8Za8r02SLJYD9mwGenP4UhLbFg/g95ZO2Gzr3y2yHMV2aDH/MkaWcLCfp9dm3P4bbNw1u+iR/gyPmu/k/VHh+yenQfQrB0VRBD+2BOLP84zpTaIXiwW+o9/90/r+175976jf2FwAWYwbIAVNoPyEGosESb7kCwIB79g4OzIP1inc6aGzbdGByNME61ltDFYgCiYHEqvcOyUQtjZ3pbZxlGRUi/LUqd+w3l2Sseauk4jGxFaGJ2yqpT1juLt27eJ7fHeS93AkHnv9enTp1G5TF4M92vTggQmsNxkOUirWSdN8zeHpBENoxyc78GaYhxgwb33ms0nycAQBPB9kvTVV18lgAWzxPSnohhGAWNwWWv6HSyYYj8xtuxDXcfzSxjTyxQslIiJYsipNXqz2Swd8EegYE+HRw4xaDDYBHO2Yc0GaJPJJJ3KjrOwwM7KCgw7Yx9x8BgX2+xNzwfO05b1WEPqvU/jZDHcGBD2HyNCUM694WAA87YOGh2wjC5rahlV3oNRlGLtM89bFHE8tC0HsCxW3N9MXTswvcg2AMam2Vl/vg+nwXtsyt+CLcuSWmBZFEWSU7smvI894ZlxkDarYTNAgJaLi4tUdy6Nhw98LqCg1I732j8tCEZmrE0lcLXTxrDL3OM5E06wYPuizjNCg711oxIG+leappZzA6hAp2LWIPYcWLbQrr8tleVnMYs3ZJG4L56Hdcbhca82UEI3WRebzcFvsF74NxvMZlmWSkwJErHNlBFb8CwN7KoNRu34bVtihfzYADTK0jAkwDKTVo+tTbO9Z4zGbpomZV2xHZISucSaxvscygwJmB4fH5O9xv5Z0JXn8dBQ5AaZu7i4SPITQhiNK0cn2GNrz3l/URRp0iP3Z2XFBqpDjxplfUNJky1tJNOPrGETgndJZrCF2CQAGzpWFEUqU+UFQLf9DeqGkhfq2pkeyBpZO2wJA2zUec8DZB3fjV1nD6Xh/A3eg91EDrEtrCkBlgXTPDdBEjLOvlmbj6+H5GGfyCoBju292eyszS6AAQnYsTcw7JakovSY++a+LNAGqOMfbTBOmRf4BluEXtn1sr6CZ0TXsyxTkRfqzrIZ1k5YXGX11RL1NpiwftsGNtgN9maz2SQiFkxt19raV2wMWTvu1cotMnROOrNHXA+7Yu/lS19fnNH4F//0n2mz2ejy8nJk3ONG5L1zLeTktD/s+9TMTHVdaT5fpEU7HDgLI9b0dl3olTkozwvVPSuU5UNqchDeTpNJkcpyJsVEq/WqB3p1nPqQ573Tc5pNZyomhbq2U1BQUzfqQpCTlOUR0NRNo912q9V6rdPxqC6EODVqu9F00pc7dRyOEhd7Np0py3N9+PgxClOeqaljo1zd1FKQjoe9FoulqmpIBXvnVVaVnM9SiVFdN/rBD77Sbr/XxXqt02Fo/gWIRAN10sXFWl3o4nqXpWbzmYqCec442sg2WQDH+09lqfl8pv3+oBAoT3CaTIphFKD32my3Oh3j+FDGui0WC93f36sock1nk3RfpG0te7XsR9HCnkXFi1mX9ZpRgV7H40GrZZxBXTe1ui4q9Wq11Ltv32kymejqOo5Svrq60vPz8+hQQlu+gGMCGKMIpI5twGoZY7IjNpWJwtZ1PTKcAF4UG6eGoToeI8sZgwup6Q84ms1naa2bJu6RhHPz6tpWdQ/MbYYEg+BcXC90JLGDIeh4OsrJKS9yxabITE0zBEllOZQWRUM2MIIYRevwJSU2FX3uQifJqetrmuuqVjEpjGPv5ONNilGzm81WRZ4rL3KdTqVm06m6nkW3wZFzAwNYVbUmxUSxeXhgtnC41iDyOxwnQNECGBt4YDi5FhlIa4ABW8hWl/R+6PUA6GK8pYGFsuwTusDzYstsVshmHAABNhvEe/lunC/XZQ2RPxySBd6MMrakA7YYAgBQBiCXlEoorB2RqO0dgrm4F20PwF3K1FigEMcJD46atbE9DshBVXH6LWfz1D1xNO91eJicx3NYGeaeAFMQXtEODuVbOH+GV3BNm13h2haQty2N5l7L5UKHw1H0piAbdvodgQngEoIFwEXGgPLO+LuQRp7zbMhHXVfJvrdtXJ/JZNrLTq4sy3U6HVOGivdstzutVstUchRtS6HJpFDXDY3s2EkIF5hNQDNymWXDsJdIBJ20XK7658rVNK3quhqV57HXIcTMTNSBrg804mSyOMWv6IPTiZhkNrDUTK6Mk7minZsmMoS1tuQI2QT0KxGMbaOi14csi+Nmu66Td15ySqWR55mnxGgXQ+Oz916Zz+QAcQ3TxVqFLoyyyXLjnqSubePI596OK0jOu4SNDr2OYs+QhbZtleXRr0TdClKQyqqSz7MRULRBGiBcGkp4xlmz8YGc2EmGcFgCyAZjg48ZerTQK6oPuC5EIc+D7NGXgc9FJ6y/5d75DojFYbLncPgc6ww5yxrYjCL7YjMbvM8Ccxt4tG2r0HVyPY5VGOxaVddpyhj3YP2SzzK1TSPnnYAcTpLzsfTOe6+qruV6Gy4XJ5nynFVVJQKEZ4IwshgGGwlWG4iMocro/DM2u2fXkHW1Pga/82sdb/s//cE/T4rHJsf/MjV1mzaSyBUjhLDyAAg0TEmc3z2cccDnHx8flOdFmhrDSE+CDJhvnLdNRdlolujQpuOsItkJRqTaERCi3ygosb8CVgOGwW60Pc2xruOkBUqVYAtJX0tR+TebzXdAlB21lk5NrkotF8veIQ+GBmNF+dSvimK5T5h7XswTJ0Cw6T7LshZFnBB0cXGhU3lIASeMpi09Ilrm/rpeIff7YWKPFI3carVKJ50XRTH6XV3XWq2XimMuu9FMccDAdDpNY5dZP76T/+q6TsGErT/HEFvlY/0A/OwTqVfklmukNHIzODfLkJJlQDaRQxTZGmTeYydCIGPOKQXs6BXyDdC2TK00jOAFQAbFf9OnQyYlPmsWA4iiMLo9Ph/j3BmkmuCulZMbMfrs0c3NTWJ30AEAp82K2lQ4vweI2vT5eW0ra0bZBAGk98Oscgy9ZdXQURuMWLYzgQ+TMbEZG66DIbfBiQURXMfqK+DWBjNx/n6Rgl/uAXAdA9TB4bGnFnCT8ZKGMhJbQoasABTQFcvaoce2fMTaIkpTLKtoS6Kso0ZenPOaTIaT65GFaD8mKoohsY5exL3PEwOMbR1KPQYZtYGzcz6VH1n7L9EkP8g0smWzpdgCq39dF0H58XgcBSWsj834sC5NA7ExHieMjFmHboPguL9DUybBos18sX62pIFMGL7A9psgo6wf12A0NzZ+Npvp48ePyabbAQN8tm3bVKbMnvOdgOGiKFK5GM/G2rLvESvkUm83LCDDNoMJbFBu2XELHgFT8/k81Z/DuhPsE0RZGeXf2OXJZKKyqtRpHHhbthd5Y91tFhVG2j4LQf58PlfmM3WhGx3oyPriY9gT7+MUyu6MpWbNOzdkHNFJuz7WFqEndj8lJaLBVoEgZxZ826Ae4o7rsl/slcUflHZjo22mOs/z0VlVjE2FrLOEgMVsklK1hCUAsX9kawZdHEgDi0vZL/7j5zZgxV9ZfwE5ZEmhc8KjOpXqDOlk7UMxjWd2cf/ci5VJu+7Yqa4e8AtkpLWZfI/NTGNXrC+zARZ6Y3UA+4DsYNet3mBfsiz79QYa/79/9a/Tpls29HQ6aTZdjMASRgLhs6yYNcYohwUhBAjWCOBQ6Y5n0WCQECSEC7COclPKgMADqrlX7vO84c2mAGE22rZNU564PxR/MpmkiRG2dIIXDVtFUejq6iqBZxR7NpulyRsIO2lr20hflmVq3rVAk2dcrVapVAx2H6YN8IjBv7q6SjXOlIzYmklAFEaiqiodT3u1bSzpsSUh3BP3Wte1OQFbqso6TXKiBA1htSUcs9lMDw8PPZM216k8jso9rFPAkNuI27KDHFJD82Se52kMMoCP61oQRAkIe2uZDTuNJAakR9XVMJ3i+fl5FExiAPg9DvJ8eoxVfowsBsdOIAFAs++2Nloapg7Z4F+SqvqU5Ay5TyyzG0YQc13L6KGTPBclEZTkIJe8F53BiWGocT7nGSG7DjYw5J6Qk3N2in3AGfEd1nDbGna7l6wt+s6asiZ8RtLIqRBo2iwZ9oq/28DG/hy7w2soDYhniNgAhnuTxlOa2GPWyDo59M8Gw+wJawOAPQ9qbPCNPNpAhetZWwuAtLazKIo0BCHajVxd9/n1pbcDGbDp/cjUDqV4dl2lyGpbpnkICMcZIGvbnQvp7JPzUcchBJMJaEfjHItimuSLzzCsgUlz7C+/i1OZhpIx51yyKef7wBrHM14uFfta4vpjy9Gd0+mUyo4lpSwSfWzoDyRWCCH1QXAf7JPVGYJVnpl1Yd9tPxF22AbXljW3YNu+j//AB2TLLWBn39hTXuf+2WIH7tmWtwLQsD2wujaAsExzkhHvUv8lJVOU3NqAx+q8BWbcv+2FsKQDukTQZ0sgCdZ4DmdKsfhe8EDdjZuaz8kD7OeQSRr300GUJf/Q97FZMgObw36ynjaDiH7hW5hYZIfPsGfoL2sHCUXWjHXD7jCgBf/N9xJM8/6iKEYTnGxgxfPyb54NUs4SkDy7lX/r29AB5NeuISXN0+lUTVUrdENztrV5bejk/DBIA0yGTPFzZCL5uGYgkcgwnfsFsh5gOBsg2GAD2eaFfFrCCL/AOlkSyAbcX9IM/sU9GrysQQHAozgwqURoOHn+bZkyFobNQjABtDYr0nWdnp6ekhNl85+fn5ORAaAy/QahsCAJJwcQ5R64PxtB2uiQe0axMDj2vne7XXI03Bf1qhg4Sbq5uUnjcDEmgF82EWfC+1FGDuuB5eK5P/cn7NZ5BG9TjygQ7FmKxvtn/pzzzfM8ZRDoJ+HAOeSBdbRgtqkbHY9lWldAPw7DHsiGTDRNo7Iq0xpZVg6ZQx6QyzwfzhNBSW5vb/X8/JyMAgEX+48yS8PJ0gRuKCTg1gYmrB/fzXMDJq1B43tg+3nBANnmYO4T2WQPLFtv2X4cAAaIPg2CrTRGuRtq28+NUxe6tF/njLUNpp+entL6EPRw79w3Boksm2Xt2C8LKiSlAQywalbPMf7sP4YQx4OuWFYQ+WavYNbsGuLk+TdA1hpnCxRsEIBdsoCFZwZAxszsYxrjK2lERGAX4vN4zefDAVgcnBbvcTDT9tmpo+ceuC+GbbBW1IZzn9Yu81x2Xyyzz2ewdeiaBc8AGVvzC8ETX9/NgCAv8WcDe2fBW1FME3DAHvGcXTceZAD4iLXey8/qd/zZcGCkDaA4xBE7xjPH+5N2u326D4AVJaLYssfHx7S3kvo+p+FZ7dpKSvuPzDvn+omDXl1Xp+fCn7F2BPDIAcx413VpFHsIcUAL+0NQir2x4Il1sr6RPjYbkKPXNliw2WDkk3+jr1ZOWAd0i5Hkdr3RZeyZ1Uk+y3sAZawNhAS2wfpYuzdku/hO7GvTNPIuk8+yER4JYRjZbUEZL+ubzsHseZBh/aPNgljMgS3xik3H1o/Y9bLN6ZA72EQyzvasJr6Le2JdWD9kg5I/Mke8zwJf1oDr2xfrBg6hRPA8KMVnQ25ZGW3b8YGTTBrF3thJcdyLlVHrJ88JDkvQkgmn93Nsg8ZVLjw7OsCesOYpOOrJBNvvkUbvNkOAjL9g7y3xYUubnIttAfjiSHAeRpkZSzzzd0t0Wx3Gn9tKEOsHz4M29ot+Kt5rg5V/3+uLAw3Lotp0dFRMjRYEYWExKTOybBzCDkOYZVk6swBDgdIBvhFIBGI+n6fpQ5PJJDU6Y+iY/GMXxKb4WHwUw9Yhsik4Ae6J56DMi2dmbXCyfJ60N8wNI0UpBSObQBMxhp0xsFyTe/Xep4ZVjKMVFJyozag4NzSyS0N5jjQewUZZDI6JpnfLfDnntFgOa8L7URCc8Gq1GrEI8/lC83k7ypLYtD6ZGO7DKnBdd8kw2oDPTs3BqPB8zrl0CJytjbbsCt+DwcZgWSNrlc0q/ul0SunvLPPyvVOCZTgej6m/hWtjjGwAY5kd7gsWx6Yw2WdesPas51Di51L2DzDLMxOkAoS5zyIvlOeDE4HVQBZxcjja/X4vSSlFDYPJ3y2zzl5Y8M56Zr0zDyGkgQI8RzJQeT4ykOw77JtN/yL/BOasJ+AbEHmeCubfBMrcG3aH7zsP8NBJykawXTb9HfuahkMLceYQBWQDFotZ2nvsUJZlSb5cf57EYrFIjOH5qbHsq03HA0TJdi4WCz0/P4/YK4AqZYQEVKyDBTmAA4Is1s3u8/k9dF1ITve8fMs5pal/gEK+m34MW+4TbclcTTMcJmllJ5IIg7O2IJr9AqRZ/QNsAkqRf8o18Qur1SpNYyqKIp0VlOe5Li4uUpaEjKD33x0xzjoSBCKvPCOBH/fFPTNGFBnEDgKw+Bm2wQagVt5tDTb2LYSQgkPLYGPHsKME7EwLwr7Y77BBoS1DgTBgXbFJNlg4zxbYjBoAFF+HnNogxeqxBe/4dGxnCCHJHTaB4KmshsoH1hUZ4l6sPea6XTf0bWGnLKlk1wA7TdBtezDozwkhqD4NBMHIB3qvphofrMh3YschOllT8AK6CEgn64C95z/rTy1RYEF3CCGRpGTzuSdrP9Fdm23GniH3NgDANrZtm/rMKLEC0wHUIffQnfv7+3SoMXvBmqBv6/VaRVGksm9kxwasPLvFjxbr2cMHAf74s67t1AalqgtsYlyXRgcz7AB9xvZii20AHz87jMNnb7gma8a9dd1QzYMP5HmszbOEl81+24MS7Wes77bf+X2vP1EzOArLjRMdTyfzZGSen591c3MziuwtqLdRZJbFkzgBmygei0mEiCLywHZDrENFIFASFAxjacEJAM2OjLMH5OV5PmIEMAgoCE4N5tuyLDBCHNIHg4jyYWxgpmhkCiGkWeLn62fTz6zXuSDyfQQZKLWN0jHcTJToui45Tcvm4TAJFnF03ntNpsO0I5yRZT25H2kY3+qcV9t0IwW2M+pZez5PA1qWe4UwlEpxzzgUSrBsitdmOOyYN+TnPKWNEbTXPg9KkE/2Xxr6PDKfqW3Hde42BcpzWqBvMyK2B4F7hCWyzBMOgjXDIOEQbWrUpnWRI7kurSvrnIysslGAx55K47ngAGVLCHBP1omcAzscqXXK6Cv3i54DXCzzaTMg9nd8lj3iPmwQyz7YRkauaQExpZncJ89igR3faf9jHZANy1hCqlgAzTPB2sasRGySZT2Rx2hjDpJCcrSWMUYvz7NnNkOH7LTtcMgiwTnyZRk1dAqba4NwXuyHXX8b9LKmAALnhkyAZRe7rtV0OrDY7GvUjaFZfL+P5ZrDifRRXrgehFCU72kCj2PGzmk2m6Zg34Ir1gaAR+DIq6qGpmZ+h62xGWDWJgbPU1VVObI16Aq+iKlsVk6ci4fo2TItu2bWLpP9tucOWYBg7QO6jN20+4g+c1+WXWcdCKBYH9bV2kJrs2zAbsE6fz+XJX5vQRRZc5slQL+sr7FBDDLDqH0YYO7HklXnBKkk+cyr6YYpYra8zbK5lojBZtCfB0tuSQcIDYsVLKgDr9hgysup7Flk51zCIiEEnapS6gk1a7d4Hpt9w982TSwbB7BfXFykw38JfixZi051Xfcd8E5ACEjebrejDBtAlHVCb7AVNkuPnFv/AEELLrLnb1jcSIk2wbDFoOzTv/yX/1JZlun169dJB9Aj7Or5AZ0WtzKin2E0kE3sh/V3dV1LISj3w1hZ7GTXdeoUUqBh8QA6yPWtrLVtqyLLVfd2jTW0Npl1s5+VBszH9VlD5OH8nBP8gH0ui3uw88jLl/RofHFGwzocFJI/ESYiS9gQnJNVLmnoX2ABrABa8Ezq1wYVbKZ9YBYAZ0MPgHXIAAppODSHlDSg/DxTc3V1lcAggJVzP86BLyd6sviAK+7Bvh+gh6AAIEOIKUYLdrk/W0dowTLrQr08gIln5XMIMMEV34dhwDFbo8n3W0YCxaWW19Z+ngPekQJqYHn4LM6QfglYY4ySc06TItduv0uAne8CbFKKYgGuTfWieBYQcX/IEutvAw7uw74XPbDKLElVXak81SPwZsuTSAFjWAlEbUDC+9lTewYNQTflbRhh9tAOW8BI2D1jrZwfai1tCjsGS0NNJo7aGn2uxZ7b5+C+kHsCdOv8LeuJU7Hsle13sJkk9tSCc5yoDaww5tagW+PI+2xW7Dw4xfHY7/hcNgwdhmghALesENkIwJ4FgLBMkCaRWTuJaVvsAb0WhZn3Dxi0gROAgnWAhac/yvaUWABigxDuB6CJE7SybsEAa4wOFEWRym4s4IwyNnweUDzOeIzrqikxnE5j/89ut0uggZ62eL0sTbazI7PbdtxIbINLSWnaDXsjDUDZ+5gxJxspUUc+THsjeAEgoIMw/djdtm10OOy1WCzSvSGj7Jv1ZUzIms+XI6aafcF/ALwtm4/ttIDZ+lRerLv1jeieDfLQp/Msrx23ji5jx7ChZJm4FgERtoN1gMyjfwT94VktIYj+ASrtM/BzS9oQsEPY2MmDVvctOYKceJ+p6P0AOkCvpNV7u77o0Gw2S2tE4Nh1XcqAk8W1RJjNjhIYcU+Zc6NnsjjmYjZVVQ+HbFqfauUAm4Jdmk6no2mM6C3Pc26zAcF27cCCyX9ksUwK4pV9JVuCTed3ZE9Zd2kYjU05HVlbyBGbCQLrgR8Y1ECG1mIP771++7d/O10PgE2wwPNShWF1HP2gXA17aSdb4l8t4VXkuUI7TLjDzqGjZATx4ZYk4jOQSLPZTE1dy/V9W2Q7rRxabMI62aws2VDsynnW0/ol1oO1s7aD9bf250teXxxonE6lPMpxis3IVaiUGcbQApKyLNMZEbBktp6e+kfrDK3wsCCcBn0erPAeAovVaqWHh4fRz+0UFkCSNWT39/eaTCZar9ej9HwCuX1AhIMGPMG0bLfbVBaGkeFeLMsCiLQRZdu26RAbWzOJceB7iKB5fluDh8LjnO05EnwvDg2haJpmdFgS0T0vPmuzKYMB7tP0PfOaea/TCYPjNZlkCl0cd9y2rfIsV1n2J8XPJjoejskh4qRpxmK9UR7uY7cr1YV+NHHXKUhq2zizv64bhS6mkfO8UOg6dSEohD6jEqQQJGasS66f+hHUNo2kvl46xKkyCkF5fwBP28VJQN5nYtRi2xAEOx0Ox95oHUXDKvcO6IOdy/p1CEGKI3y9mqZVVdWSk/aHg2Lzp5JyhwQOnJqGSRq5nOtUFHHMo3Nx5CbvA6jGMbhD9isBy9DKSTqejgmIZVlfxtgNbDT6Yp04MrBYLEZBGEAH3YAxI+CzGUibTSSIsCUNtlnTgqwsy0aZMNaIsgcybpZBtOQC+oEOWN20RheQbssPWRPIC+s0zzNNAClbpoljsJklZMOWJMZ7gfnM5b3TcrlQ23bKsqGvwtopuzfch2WgYUd5wexKQxkWTpRT49kHGwwSbPFMOFbv/WhIAetpD7/juQgUCATidSsTGNpT5ONnHh8fU4BlmxGxU5TxEBAC7CaToYcOUDNM1BsY99Dr/cePH/v9yHVzcyPvM223O5XlSYyMRj4IaJAVm9HgwMDUENo0fY9dqaqq+7rnIdMFgG+atiex5qqqOCq2bQcSR1IirdhzG2Cwt865dN4R/sj25qCzNqNns/zIhc0u2CyKDWYsGAWIouu2XMbqIPIfwpBR52e2FIlrANpgtC3LzWclqaprZXmmvCvkMy/G7c/mc7X9vVgCDSxiATm/i/+uFQxRCCgEmNnAGJm2ZGjTNMlv7/f7FFxTHQGxYplpdMbuufdxZG7oBnm1LHvQEEDha86nhSEfthyI057PMzXo8Dn5YH2JLfdi31lf5J59e35+lqRUsinFHjV0EvKNag70FOL2vOyHoMj2ylD+RhmU9UkWz5GtINi0pZy2dAm9tHtjSTbuFftqMamVr7qq4phixbG1ck5yUtM28tkwTMHeK/dnnxmdxPfZQAIfwr0Q/Fl85X08E4tzN9ArgnCbQYdAxC/z/OffxVr8SV5fXDr1B//4nyVWg3QP4BPwgfG1TClGmeDDMqncMP9mIVEmBJ30MswOt0xkS40gwQVGy2ZeACIIN99FipPFtg7RGl+aVWGoAUdWqbNsmIDEGmFUUF6e024mn4WVQPmtwLHu/B1jbJ0E+2FBlGUI+R7W1c5q57vW67Umk4keHh7SfrG3Vkkt+4th4X4sG8Ie2CACxbXKxDpQNsb62lStNLAzlsWxzq9pmlQqxzqy/wAGrnmexQCw8qwYbTJZthQGgIrTYo0BfXxPZHPH9dB8Z9O1ms5m6SyS2WymT58+RedWTARXgLxZveHF9wyM88DQ27QrLKVlK+z+YegtgLbMP/dhsyXSUG5oWRi7p1Y2caS2WRrGkSYzmBVbumeDE9bRspOWQbfmrGmaZDusXvFe9MQCBwuGWF/rcHBE/AySxWacWDeeHwdg5d6yjNwP10HXAYpcy7JLVsdoyrUOmKAnhDCa7AIosPofwtCsycuy2+wtf9rBE7D5tqHW2j97DUuoYHekeA4L9gm7CGhHrywTRwM5PRznh8llWTHqh6NEBFBmgb4tz+De6auz76nrOoEMK49VVeny8nLUN4ffs+BBUmJn7bUOh0MCgaxrURSJDKL2nOvYUgsIOnTS2gYAC+Neq6oalX3wHHZ0LoDCyjrBPwEr41DpFYKAA1STnWBN8f/I3MXFRZJBSzhYO4MusE7sGeclgT2Sze9aZfkwznjEztbNqKnbZjvRia4bqhv43P50HFVaIB+sK/aRYOpzVQboA1jCNuFb/8ba8+yW/fZy3/ED2LZsMvSVWP/DNW0Qwp52Xafn5+eEhT59+qTLy8uEEyAUyFSz9jYbxb1QLWEHDSA3WZYlGeZ3+C8rg/wdLIc9DyGMynxZZ57PBorcD3bP4kqexfq3/X6fcBL3YHuELEawuIt/W+KX9UHfeS6+n/3BplrCnM9TuoWugVUJ4sAtDAagv4m1soG+NEzOggS3+mfXRxqmHhKgWNtvdfNcPrE9TdPor/yv/rK+7/XFgcY///0/SA9IVAsYsJuKALI4OAsapMlqpBtwQykFn/d+qAvEkaDgVhhYAAQP5gFnbY25SL3hAAEAAElEQVSXpFFWxaaMc2OkLAjHIfE7AgVSoZZN41l42f4IKzhstjQ4A1umghECfPJzvscCIcsq48htmtMaFxsJnwu7BQPWqWG4YHgxoBjLLMvSeFP2HSfCs3N9m8I+D7Z4Pvae+8J4WLbYBhpc3zZc8Xuuwb/tAIFz487+2DS9NZB2yAB7xzphzHE0yNYQeMXD7qyi8vx5UUh+PAmC/c99FtkQN6TTaYqzjtkGEfEeIzuMjtqD1wAOkkbGlLXGIFoWzAZelqnn+SQlY2obXVlfC6Zhy9AFprdZ5sqSA6wzL2sI+Q4MPeDLBlnOuWTE+QxlXZASAH8Lqs71wgJ3m5mwZELqKTKBK7Jr9QEZ5n22HNCCehsEw/phM+xIVcvWog8EKWQXbGOx3RvbxA1baLMvPAOMoM1u2CwQ5A7lIt77BGqRTTLWliGNjHqttu3ShDJYTZyoBdKTyUSbzUZv3rxRWZ40mURATvlUnHATs5jex0w3wGQ6nY76wGxQSmaddWevsTHnmW0CHvQAmbc2CPtgg3Ib9FubSZkW8moDX+tT+B5r+7guPTX8HT/A/fJM7CHBxWazSXrP+RisPawy49yRUZh+5BlQCetpySxLNhD0YgOQPfw977N9W9y79WO2JxLCRgaA84zOOU3zYR/BI03TpPHyMN12vfM819N2k2wK944usq7S0C9jmXF8Cuto329toQ1i2AMbfLVtK3XxAGH2FVDYNI18kQ/v61/WxrA+rLs0nMuFjHC/2DaCq91ul3DXdrtNNhOfOJlMtN1uU19oWZZ9NnB4fuScjIMlJdq2TdkL7pV/UzZs9wV/NplM0oRP2/CPLjrn0gQ57gF9Qjbxt8fjMU1p44U9417sXiFb+EFs7+cwWNd1KbuD7pRlOdJNAjgL5JEpKx9ZFrFAnmXKs8FH2KDWYhmL8azc0AvEfYG/uD8IVZtVsUEieokesh+/+xf/rL7v9cWlUw8PD8lAAOqpH2Ojednok7/bFIxtBgfQWfBplfOchWDjMew2anTOpQDFRteWUVutVokxwhBMJpPE7Fi2xI7JvLq6Sotuwbxlkqjtw2hYlgwls9kPBMGCZYyIVVAM/vksYxwX1z0PHnB8KJgtL7AsmDVu7AUv1l5SWifAB8bJKgvKbw0IChqBxRCh23QsBsSyFNZBcm9WcW12ge/DgaIsKD7MHgpj115SMma8bK0sxslmRvjT1slbQzP82SYjZ8H9ZDJRG7oRYCCYK4pCZV3Lu/FELbveyJAN2ieTiQ6HceMlYJ+95h6QOdtjQwYLxvmcnWYvpWFqjgX5Foihz+d/B7TDzloAZ50U+251BeOLnnBN9JY9sPpuM6CAd8A070OPbe+U1SXuF7uAzFr7ZbOVNkCzGUNbtw2wxGhjOyy7xn5T1hRCSEw9a8aUFwI9wMJ6vU7v4ztx4OyVtZ+cb0PgAzNNL4jVQ5sdQwYJgLhfC7StHsHg4zdOpzKNla3r2MiJrcTp2fLSq6urntiJ+sv4b0pw4/1Wo6wYjDb23I4/R7/OM6026LeZWcATOmAZZUCfJd9sQG71D706JzjOWUebXbR+8nA4qOvi4a82E2ttGaDODiyBFEP/r66ukt2xY1P5TvpLLJi1thjbYfcYH29BkGWh8eGWCabk0IJZ61cAxeiBzXK0Gk9+JPgrikJtNRARrMdqtUrXtEERJc4+G6bU2WwEem+JHu7V7i/3gu/mftlzu5bIpgW1NgDLs6G0ibVlbbo+m3Be5mJl0z6DzS5ZgoHsiQWQ4B9kCVtkezuYBGV7ByUlXeTf4BdkC3tmA1DnXOrF4v75Xl7W32MjANLoGviCIBLy2eqcDcTQe56V/UHnWW/8FP1btjfR2gabkUdHbA8fOoXNQG4A/ZCX+Ff2IRZsuxFesISVzfBY34hcWL/I+qBTlJHZe2Q/+b0NXLmWLfP7vtcXZzT+h//u740E1S4uDzCdTtOJoDbFzibjdKzDZiNZYA4ZIsCwPQQ2gEEYrcPjO6TxITXW4KO0NrCxbAmLz7X4ToCpTX/hSFl0W/PIc1oWi++zBvj8HqxTsgw/a8198PwWmPN3FNimWjE8GFtbRmAZTD5jjZot2bLgwjK71HtbBeOzNmMFu3QeoHXdkNKUxvPYLy4u1HVdYiil8dkXlmW262OVTRpneABMrD8/w3hYQ2uNsA1OuAbAC4cGWIvAMp4sbGWS65/Kk7K+/Aonn0Cs99pvd8kwW/ALCLIMwyBDcWQooPncgdng1JaC2Pp9dM+uJQ4cR9o0zWjaF7pgmRSuxc+433Mm/TzIwPkD6myWwNoL9oN7IWsKaGWNbFZC0qgf4TyLxovfW+CAgT3P6AAirFPnuqwFZZfU0OP07JrZckibOieQQ385Y+Pm5iYFTZSQ0tjJ+gJ0LKgAOLF2NjO12Wx0e3ubHB1A2oJtnou94ecEN5S4sGc4P/QihKDLy0s9Pz+raVo1zdD7czgc0qGQlDUR7FgnGs+nGBpJrXx0XVDbjsdxMoPfAjLkETlDx5FBG2BDoNjn5jN2Upp10tgQgOXnSk7RC2TBBvm2lEVSIvYAFWTdLWhizwiwsCvsGbJbVVXKHJVlmTJyrAcgyxIkBMrYDMi5tm1TRgh5sqAbO7rf75XneSIZbWYL+0PvAGvAVEar99bnTSYTlc0wydFii8zHk7UBxZaFRWZYd543kRpuYOUtLrBZQ2tjWRf6ESxrbXGDJWTsftvg39qa0HbyblzV0LatmrZVPhkf9moDBktoUCJJppPfW6CLHUJHwD78nLI/i8msP+N+WT+ug47Y9bCBiQ0s8GvIjSVekTNLENrsAjpmswDIgsWI52SQ9Z+sBfJls+qsCeQFWNbeG+NkeU5sIGNweWVZlvaB76Sk0k6bRObYA3UhHQIIBrO21ZYk8zsbfJzLiSV7LZmHrbIva+/YG/T913pgH84RJo9pPyniMiCXEg/LhiMIvM+CcIx4WlB9dzoGxgjHwsadNzvxfdZh87LG6jwAQMloNLMHqEljkG/TZTa7YQESUaxlU60A2HIGgCqfxQhjiAAEKIRVAO6Bteu6LjWyEonbYMbWc0vjcWisHetvGXj2hb8D2CWNMgUoMKCUTJN1wPa+CXZYJxu8cI3D4ZDuwzpxu+aWUWGdCFZsoGSdh3X2GCRrGC0TY1lL5MxeD+OKTFVVlRiVLBs/J8Y2aMjO8fP0/GflRDghGxBQBmZr47138n4YE2yDI5uRoXnbXtMCQ+QNPbaHgpE1ZM2Qu3Pwj26wd+eMGywbIBLjCbg+308bkMPccz+sgw2aKZexdah2z22Qwb5ZOQthGKvIenJvAHdb22rtG688z1NpAUwftgC5urq60vPzc/od/1GyRxCy2WwUQjyAEntZFMOZG7BpVl7t/tuGYrIUANaqqtKBoFwbOwK4YX/YGwAH5QcAYwI8mEbKMaztZc+dc+nQQe6VIPicPUUmuYe2HUiSEGI/QmzanysEA9b63yHbluA5lwlrUwjGYJzttCDkO4Ha7Ls9Z/yHvtd1rcfHxyQHADULQrhPGxxynzajhK+y7DQMML7H2jxABXsHiLSgEhm3vtwGJ6wfz8XPqHIoimKUWbP9HKwt/tPqGYysJbe47mazScGmtVUhhKTvnfFPBOv4jtAM5UCUyJyPG/fep3ISSQoaRuTiD+j7s/tkSTnL5rPmFkiybtgc5Jg1sQEJtuh4PGpaTNJkKWuvZtOpOoXkQyw45znJejHJKYSQSqLASwBUfDG4B7KYAM2WVFo7ji+3RJy17+ifJZPtOlAZQ6mSlWfsE8E2/b/4IqtvtuLD+hh01RIi6JLNLrHm1q9ZXGZ/znpgX/jT6ptzsfzd/pwg/jzYQda5D+4RPUsBcNspN0Soze6QIeZeLI7hfvAPrKuVX4t9bE+JDXx5nROvX/L6E423tacCWlDk/VAHZsE9RhRm6hzksWm2hIdI7xzcofgwJnw3AnoOvqWxUeR3PAvOym4mjtteB4cqDUGNBbX8nE2yYMgqIEJkwRx/t+UoCCTreR6M2SjeMikYCgsk+A7LuNvP8N2W5beCT6Bi2RabYeJekAcco/0u9tzWPp8zwzaotAGO3Vd7vxaAW2NujeA562GNtDUYNvhkDyxIsHvEftg1vLq6GgEoq8x8d1nWoyka/L1rO01MvSRgxXsvl+dazhcpyOD33C9AAQD7/6ftX3slSbb0TGyZu0fEvu/MqjoXgGgdsjEkIFFQEyI5Q4ISBQH61YJASdOUpiloRhAlgJ+mQeGgwcPuqszc9x3hF9MHi8fscc/qrjwAJ4CsXTt2hLvZsnV517uWmXO0oPWUOQ/DUPvTkSXO2tUB26aTQAIS14xo+yXQSTs21gQHzXgAldxrm6hxbYK/QR0BFBnBphhscz87QvTGveFmI2GdzOIaDHDMom0m51zfNwBn7NgEciS4w9qRlNMfbzvyEZ0ppfq03M+fP9cAgExybg8lRW8BEYyPo0YfHh7qU3ZJCrAPgKyP1kbO+O3r6+u6B8DtIpz6Yn9rHx5RTpoBLHqD7X6/j6urcmIdgY7xUS0DFNjPFX+WI6KvjCGJpgEKINqJH8AFHSSpI97wvm2IF76F9eMkMrfNOZZYF/Bj3333XdV3QDH7XwDv6Dbfx/YfHx/j/v5+lXwBvrbkCXNyBwE6araZ9bL/xDaxJeIKeoLfhalFH0kM0WfAHGQa+phza82DCLLN2M91XVdbnVxVY24ppYiunMC0jb3TNEWXW/sv18WfIG/0Gdm9vr3FnJd6ShRrhT90guI453vM81y7HYgFAG1+3wJhfKhbpcfjMYa+tbAy94iIaW5HkaOrPMuCyhE+ifY5P6LA5C26gw9gzcZNkkM7I8mxj5U2qQOGYE2pGnE/V+7QTcYNjsAGONjF1QcTPQbKEe1EKewYPUY3TEKDSxjPbrernRXc+/Lysp6UZXBOlfp4PNaTRre41sk987Su4W9MImyrM/gtvs/1kbvJV5Mg6BPENw8k3Sb0XM/kHmMxht2OxYneL72+uXXq3/3bv1gFT/8/TtiDY8GXZVklCxY0yklJ2EHAysBzLCIawOFeZgEIKpzD/PHjxwq6t6zsFlD9XODxP2e1OGm3pkSsN3jhWB3szNDa6RssOylC6VhUnDIgAKDF/QxumeM4LxHzFFfDLuZY4pSnWJaIw7CPtCwxLkvMHKtaqKGYI583Hq1baO7v7yMi6pngMBLWgbqZWUCygLHh7Hj7OB5PK2fX9p7kOJ1aS1R5UF/EboccWpBojqW1MqAf6Cb6xfraUFiDbSsD6w3LxzjRWYAha0cAKLrRTj3LeTn/bYrTqTG9dsiHi4s4jafY7fYROUeOVrrsUheh+7kNiESUuRTAdnWeU2uT27ZW2RGZITVQNMhqjEYDKc3WyyZ3bCWiHQRRxpFWjDDAYKurODiCMnMCjEBwYHNcw4HJzCCVAbdvMkeffc66Pz62jY4lmBa9ur6+iXE8VWfMdX284X5PhSAiJU6KW1b+j6QE/SmtTW1Ph0HJ9fX1OcileHp6rr4Rm4LtPh7fI+c4VzJaBYCEi6dSX1+Xh7jxMLfT6Xi2p10NhCTH0zTF4+NjCZjLUs5lzLnMcSlHRR8Oh+iHvhzdGI2FG4bzXp1d22yM3WBbb29vdU36vhxHXWS0r8kifnqapnrkOPEEkNASyTmWBaC1P2/ovqzHSBvw4DPtA/ycBwM9J3EmpqigYR8mXyDSAH3EPL6LDEx0sO58Hp8UETVJNJnCdx38DfT9zySR70fiajbejKYZXscc9Nn7PFgz4iaycvUBG3U7qasXxLltjCVumrhj3RiPgdecW99537XTnnLO0QlE8Rk/AJB54+/m+dyWtDvLeV6Kzo9TrRi9vb+tCEnG5FYwYjVxirYaE6boBGvpFq6aoJ7GmM7JGs/HqjIb2vOVWFvwAIfJUOl0JdjxAcxjIs9AFqICXcafG8i6IoOPwjcDzllzV0i3hxc4jrAe3mdBHAYsGwuA24gb2DVyZr7emE5MMknN+oEXTawA2OlcuLi4iPGcTAzDEO9v7xEp4uLifLJptE3+rFFErOLhlpgzJnXMzTnHfreLvutqFWuZ1UUgEpG1NOHOujrpISFzooG/5LWtdhBnWae+7+Of/ct/Gr/0+uaKhllcDNyA1z1ngDR66pmIgYFZZRRu69iYCD2dVA6cmbIwKBObq37zm9/EspQSF6wcAcNMhMG/e6RZLIAri4jQzWw5iGyTMBScRQOMecwuSxOkkKsXdcueOLtlbGaqI6WYuiX2yxI3MUcfS8RhFzmniDniNEc8LnMcuxwpp+jTEBFd5DNYHc5KhnLSk5tSqk/odUBAHgBqO4K+L0nDNBWAymlMfT/EsuSYpvkMlHYq/3Zn4JcjJQJDFym1nlczicgJ2bCOOFPmwpinaapPFIVZRBdIUEjmvEGLFo2UUg2g7+/ttK3392N9kigHJwAeCFan0ynmaYqUIyZAdi5PEwWMsebMgZeDAfNprXpLDENLfgjoZpCQrx+6hN26wtMCegGG/L2A6jgHrZZor4+vHurvTuRs5+gvYAkGCN2n+gFrDGvKfiAAk0vm7BMgmXJfMvbJPHLOcXt7d17DiIgUyxKx31/ENLVWz2VZanvS6XSK02mMruvjdJpW8ypBtCTTBrkEmcJylz07y5LjeHyvOpFzxOfPX+LHH3+MP/mTP4n7+w9n1uymnrLSdPOqApu+b3pASyTg7OXl9fwerSK7sz72cTqNwXNXxrEkB/f3H4oddX0Mu7J+w35fg0RKKcZpjtSfwf9ZdwhMkASXl7tzMO2i6/oq5yL/RtCgCyRCrLP7nB1jWLPyLyKlPnhGTWHKW4UNmycRQI8I4E5qnVAAQk2YMQbiyXb/ifebob/Yzzbp5zsAcJ9cY6YQoA44w+4BbgAp9MA+AvKB+zhus49pS6yYGXesxGbMwHpMZpojGvlCQkIywj3cOsK6mrgzO881GYdbW9xBcHl5GePpTGbuUvRdIWkuzkAZO3TlBB9n4AiAHV9e4v21VIpubm7i6empzH2a4jXniK5VrwGpHjfvgSXQO4gDPmewPo5jPR7Y1fxlbF0IrDk6Gbm12xorQM5C9LC2xEj0GF1y5cUJCPF865tNGHEiFYmNk3rus01GGKc/44oWMmSjObgH/eczOed4eXmpG/exA+MPxk6Cg+4ZxFvP0AMfXGAilViT8/lZXEuOlCNO5+fMzfMceZ5jv9/FeJ6viTsnpN6/mvPXh4hw/7o+3DPUHZMicopVq779VkTU1rMtcY5+uiK/lQ+2hn7bD5uY+KXXNycaOBOMkmDvDXMoBINH4QAU3vDHNc16sbhmcMaxnWZihhzQaCBG2T3nHH/4wx8qoCFwwcJvM9UGEN9Xjpf7OTFydrh1kAQzC59F3zJnDgwobtd11TGi9Dm3Y9lQdBjuLSMf0YARYzocp8g/fYlfpUPc9fvohhz95VUcn17jfxyPcfP9XUzzMQ6Hi+hzF8d5jv1hiIthiDy3PkvujSypQpH8AXy93g7GZT2/3ijsCg6GZ8fEnJxUtQpZC0Lcw7pAVYmAzX19uMDpdKotR3ZgHgvJRtd1ddOkgx/H4b29vdWjNpEJbQkkBFsHx3u0ipjJ/DmDt30gM3r5y5jbsa58HkBup4Zeom84ZMZl0JLS+hkg2+oCskGmwzCce29fV4DJusp88AMQEzc3N3UuBC2CmZNden0vLy/r0abY5M3NTWXjXNZ3smGgN89zrYKy3ux1gY3zKXmHw0XwoESuhYwjdnE6HSs7iT8scx9Wdkob0cvLSy29f/fdd1XOlLoJ9vYzrNNu105AM9lSfG/bPwXA4dQ9gGhKKT59+hR3d3fND46n1b4KM2Qkf/h4KhXjaYy+a6fBPD8/1+TH7Utm0Al2+Lt10tKeq0HCT+sHbR18z8A6oj2xG2BJXMHOAVEETYM4fAZjZa4Orvhj/hnEbwMvSSpz4T2DDscWYqzXByLvy5cv9ToGhvg+V79hkH0NfKjt1euCHRps+HQcZG2whI5g++g8L+a0vdeytJZKV5LQK5MdyN57jAC8yID1JTbib/B56Jlth2viZ3gWCvYG4OdeJAunqekV4yWhY6yu6gDI0AX8kQkixoOt1HvNS1zs18/ncQxhLZwssRboCT6eQxpMhqLP28q/fQr/j36zPuM4rqrO2InxHGuOzJ1IowOulPGTceCrjA3dau/WU0gK5o088ensIUPn0HX7VPtm+wLrKbhmGIaIrlzDp3HO8xy7wz4WJQrI3PfkXvwzVjE54HYzvmO7Iy4gd366SmS/y+8+iMR+yevOdcCje+kiMv6W1ze3Tv0//m//7qskAuP1YF0WRMB+DsGa5W7PhsCAcFQWrJ2wnQtOYlmWlcGSuRpYYejuCTTYMePi373Qrtg4eKIg2/IfY0TRI9ab1FNKNXC6bxbZchIBZ1+jhC79ORu3IuVcTigY3p7jf/w3/zZ++ov/d3y/pDjs9nH94T7uf/2bWP7sfx4X//B/Fs8xxcXFVeQ5x+vpGIe727ja7+L5vPmUwMX6opROLlB8ZI5ccWRlzC2bdnmO9bXiogesH2vjRCOibQxlbKwpjoJx4QjNZFnvCFSwWDhSxsMau0+2BdghdrvmLJmj9dbAnEBCwCDxvr6+ro4X52nAzHicHPt4RICnA4kZPLdhEJhIWHGQ6DAyL2uwTpTQBdsaDnxdxZhXwWm7yRubQA4wW+iYx951Za+D/8Z1sCH0zaCL91l79KGdF55qewBl9RYwW+WQqlRrEbiuv9vmSitTkU95cvz7KsE5HC7j+fm57nmgH5hrAGiKXvUrkD0M5Wm79/f3Mc9z3N7eRkq5PoALEqfv+7O+NF+N7i7LEvf399UG0AkC/263iyk3MIYNcn8zsd4AvMxzzGN7hoHbahi/wbl9IkAM32YQDMiwr0CWZhxdBQasYy9cA6CBH/XGfgIvwAwwASNJoro9Ahb7oS3MSRnrQeLj9g8TTQaFZo6d4Di2cX37e7dhWH9sZ3zP4AG/AnBzfOQzrggD9hzv8Wkm0rgnc7cuoR+l3a3sLXt6eordbld9IHpCG9Q0TbUn3gAJkEVFmljFsby8X1uRVCV7enqqtklbsPcomOipLHwuFQ1XyNFh5GeWGP9vuRmMb4GsE6xlWaKLFPtdO4HRiUBO5WnTEFWsGf7KZJWTO+Mv4lJKqZ4KxvhdQYLEZS2cGJFkIWP7Q7ATMvIzHMA/6Cn+x6DWFQaSHWz69fV1FS9MUE9TO/UJ2ZHYklhxfcdFJ+5gn4iobVMG2Yf9PlJuD2pmzuM4xrDfxfGsp8RG9MrrS/wgxqM34A/rHtdnjetY+j6WeY4U6xOljEPsX7xxfquH6B9ysq07sbGt/9f/6p/HL73+qNYpFMBHkCGUGqSm9aZsZ5UImOuhzC5BbidMUMLIABL7/T5eXl7qtVAiL4grADZCO2kfwUvA2DoGgoMzZ4IajpbefINAGHCClbNIy4mgx8IhYxbbBk+WjaI6eFIGZm5v7+/xMuzjp+ubGP/0d/HX7++RLvbxp//L/0Vc/1f/VUypi+M0xtznOJ5O0eUUXeri+P4e0/tbpA3z7F52mHTWw3J1NQAAtCzNuVg3zHjs9/v40z/90/irv/qr+PTp0yprt95grOV0pb6eXIEeAZpxgARLn+JVHfkZOHuT8vZQAJyOvwvIKIbfrsX3cWLoOWO38+V6tIyYqb+6uoqPHz/G1dVVfPr0qT4vwdUY1saAyzImoDF/5OgWPJfXGSuJEAxNzm1TqQMsFUDGTs+4E8Ft8gdgNZOFXPykap4BYRaQpAr9532Sl9bG9r5qk7FfwUfhw/AdBlSAj/f312pvtL7Ri//+vmYeWddxLE9g5vkE2MJut4uXl9c4HsfVUYTMH0IGVtW2wfHOBKxhKJvYC0Af64mAJmu2DLBZZx+5ynv43Egpclr3C+OneWFT6NzxeIxYzj3Em2QBMGli6HQ61epVRGiPVvPdJohIvrAZyywiVr3wBhr4aK7hth4CvMkEJwsmB2hJSymtjqp0gu6qCN9HFugcSaWrgnyOSqmBqefP/5uRRJ7IwP6JNfNeLoAT9o5/xIYdi5ZlWREKTk5ccTBRyJps1wFgeHFxsXqwHzq83+/r8yBIXpEv7ZLoqQHtspTjmDkOmROujsdjPDw8VJ9DTHJrNC2syAb921azeI9Yu9vvohOBhY9x2yl6ho+zXLf4yESFbaHal3QU3STeTecN6y8vLxU/8HR69m0ZP9mn2A6IN042uT/VNO9b9fcc7/EjAOec8+rkPHyeMZ7XwoQ1umfC0ASmSQzu6zWwPvuwBa9xI+dau7cTMj5nfGo5LnM5HdIJP9hhmuevbMY4wEQGeJb5udIH+fq3keNlDjnykiN1LcHbJkzYKn4DH2Fcg3wY99an2Cd5Lb7l9c0Vjf/r/+n/snJ0ZspQGBYGIMD7OBYcLmwGjgTF5vuHw6GydM7I7RAiGovgIGNQ7+8xVqoHLh+7fYuxAF6YH8Zl8AYbQ6brIGAmm3tgHFY0jIh5MVaUk55alwANfBmzFYa2pmmaY067GI5zXM9zjNMx3oYccXGIlFMMp1PkfR/HPiJPOebXYxwuLmN3cxXz6RR5aQGD9XZFgn0aDjKucqAHjaVfV3asOwCt3/3udzEMffzH//j/q0DNAME6sN+3wE7AJSib+WENtoHaToD1c5LkZJfA7b5E1qMEhwbinWjC5tLy42ogcyKQmBFCduM4rhhdHBL3IVFHJrvd+iQIkkHkaNvYOi7342KX5anFa7BCYIDRhzE2Q1ZK2PNKfwGdV1dX8fLyUpNwM5NOkgAYBE/kAbijIkDSU1lHJZD7fXlAF+Aa+1iWJe7u7uJ0mlbfdTDO+evndfC3eW5HphKYip52UZ5aXZ6cyxoVwHoRp9NY5fD4+BgRUffzsGGU8eKvsA0SKQfXlCKmaawyo3Wg3LexydvEAtBlouDp6Slu7+5izku9P8fKOql1SyE6HDniYr9f6SXjwVcDvL1HBtbMlW78ovc+YKe2L16EMK5Lu6IrZ65UmfXnbxGthQ92ksQYPTTBY9DlBIjWSfQCedNasT54oI2FvUf2sciRfSEkBLe3tysyzDHOMjGbyf8bQPFCxvhIV1QMVjwf7uv1NqtuIMpPANuXL1/i5uamytaAD/tE9qwp1UwfYMAzNlzVACBtq1JeX/wt/8Am2ALssjcu1+ukiH7XNtE65vFZCAF8Iy/+DjHD4Qf4SHSG6/V9H12kiNz2oT48PLQOga61DzVCr7UWmVzAnzsuIhdsy23wJmKQET4KgO+knM3sfk4Ha8H3rddb/UWe2Ok0lUMssB0wmW2QJBp5oo8vLy8rggc9NknpGE9SjY4aZA/DUAkI5FWPk++68pyT7usW9kgpTtPXVUDjSuujCSAnbE4U0EFkCym5LEvEkiM2WIJ1cmJnOzA2xb/ZV2wxt8djXPwtTwb/ox7YxwuBohgoJZOwI7UyO0nBuZh5I7jYQbIIMMRMztUOgJQBHsqCoqHQd3d3q98ZF8zVsiw1KFig/EPgOAwU2I6VMdrxO0FiEb1J1MkWRsP8YLo5TcYvMxawhRHR2K60jzROsYxvsQw54mKILobYTRFLnmPa9zENXQxzxGHuou+HeJvGWKYxLi4am+CWte0mXyuvQfCaeUyRc9T1dSDj+xgIc0He3m9g9jmlcjKVATNMBqwKckcnWFM/yArjJ9jh6Dw/t05ZL9jIWza0txIyjg79B/TiAAiqrg6ix8gMOaGbKaV4fX2trQAke257mucpLi8v6gkkrlhwve1c0EEHJuZc9K9VHgw4TQK40sDaQNQB/GArT6dTnbcfFIZt0C5m+8FGCQ5PT0/1b/M816dDA+a8gZ/xAR5g/ArLXU5U4WjOeZ5rcvb6+ryaIzY7TeUUtZRSTSBbct3HPE91bUksD4dDHA4X8fbWTmyjzQngYIAOECE4oteQKyQW7+9vMc9NV9HLkgi+xX5/qJUfA2MqDK+vr7ViUnWgX1ernWAgB+SKbR72+xiP67Yfgyf0z5UJXgAPdM9VDMsev821XLFED+xH6Le33uJP8KvuB0fHiQOAH9tMRAvM9ove/8H1thUCAz5AGS/HDzO7+Dy+76TGCRh677ZhYgEAAtvh99PptDoeHnl7rQ0m8Y+MD4JhC5hcJXIi51hJFQ77QXdtbySqsPUkIYB59MH2w9+R05bJRkbERxhkxvj09BQfPnyo1UUTXCmdW5WG9jR51oiOBpIGAzFXupxc20a2rDoJ/ng8RX++F5XBiHMc7XxgR6q+lfkbdFJ5ZbwQk6zHluTC7k1q8P9cD99EfHl/f69txwb31lNsgGuR8DsJsLzdkcDY+QnZa2I357ZfhO8SD2zD+B1kz5g4EtjYZVsRquu25FjOPoXqUbX/iIiuVazs40xqIXNkYTtn/MaCyIo4yfX7lGIa24EAXMdVfXwL13JrHffctshHxArz+P740//iD+zDeFyiIojauaD0DMqO0aAYI359ff1qEbeZE07TgQeBwPJyfxwgwaIYSorTaYy3t/dzC8T7GQwhsLdqCD65ZRgay/ZzSo8DtgJhrG7DaUzounLjVh9AvZMtZ/tk8LzvIMs68N1pmmLY7WJKOcaYI3ZDpKGL0zxGfz7i9uJwEdGnmKc5xtMUXRQ5xbLEbr8PjmZFpsy5rE3E+3t7yBJH0BbFXJ9bnnNjyuyA7Ii4tsvEDdi1DX6A7iL7OTiNihOs3t+P52SlnSRmJrTIbIn9/lDXeJrmyp6dTjBVfXRdc5BFf9rpHGtWtZURuQ6OmwSBNb66uqptQQDVi4uLuLq6qjIuydy7WmX6OB4LC18e+HVdKxkEqMYWtYQFsICTo6oGqGSMJTAsMQyAMtrjphVQcosSQYETP5AFbXwliXg9g7Ayl8tL5j7FMJQTmna79oAvAjB2jQMsMhjOupjieDzVxK4k4e28e9hf2iien5/j06dP8eHDhwrwG/A/xPPza237gh0sCeQuuu6mzpvWKRKEw6Ht5yJAIXNYvS9fHuL29jbKaUy7+PzlS6TUlT7vnOPu/j6Op2NcXV3H68tLZc5gdEkuSCwjovYlM9YcEcN+H/vdPvqhj3TW0xw5+t0urs4978xvWZZIfRd5WWJayqbFeVniNJ5bT9N68zBJj4GSATbJY2Xjur60DUSOLlLMy7nldDi3u0SObujLcw+iHD/KmLctVNguPm3L9hEcsS8D/C0pwXeKXq/tw0maCSv0CbbR93RMqsG+b/tPDJjsM7gWNmnCihgR0U5u5Ho8Md1zoK3EyRv6415wdJeXP8/zVVwFcCxak0Wt7YRKBKB/2x7dSJi88vX4QIAgcQ2SAPujTZFqNqDeD2vDBpwQ4n+Q+/F0jOM5qeu7oktd30fX97FLKfplid1hH9PZ193e3UU39JG6Li6vi03vh13V45RSLNMcqY/oIkXqUvRdH7Hk6Ie28dzVWXwvJ1iBT+qaLDlO78dyCmFK0Q1dvDw/xzROJYEf2zM7nDDOczs+lfhJ5QH98ZrwPRO02Ay6zD4Y1sckH8kEOoSd+OABfLLxIfoD2YQtIieu7e6WbdJJHCM+LstS/aXxJjKAMMTG/fBd1oV5oav4FvBsjcfzHF3qYslnLHsmKSLnSOfkzjbf9+fToHLEtORIfYoUEX3XxTzNMefmxxjzlpRmrbcxkc/jd/DTy9LaLF2RQdb4FmMrdML3xHZNktkfmuh38vRLrz96j4aZn4io5XyCEZ9lUDgBJgzwQiAsEt/btq3AynqDm4MHGbUzPwcSrl3+vxyjejqNK+fUdTiDArjKsYwpcl5vniJQu/rBvDAIFMJMvxkfszBmswHcJCl8n88jZ9+Hz/EALoKDlazvukjRxbJETK9T7NL5HO+Y4vXtDN67LpboCgDpUnS5i2Ve4ng8VSPNOWpQK0BxiP2+MR2vr29VFsg554i+j5imOV5fXysAQyboi40A3WEu6BwG56SE5CKitSFw9CpBp8isj66DweGUq6F+vrQbpShH57ZEuTjC/Xn9yj/0FX0vzmW9t4gnyNJehOOz0/DG5nEc68O4uE7fl6NqS5L1Xp3I7e1NHA6XVU/GcYybm5t4eHiI/X5fnzxMS9Hd3d2KSXTVx8xlzk3vCkDDgbQ+bHrM0UnkSzJslrNcv8h5nud4e3uP9/djBQ/TxAlX5ajXlNqpZA7MBL1i/+h+iuvrG21mzrHfD7VXmT0OtHZxopIrqTjQjx8/nvX3dWVbxRbbmefX19c1iby8vIqLi3baFQEVH/X09HwGHHN0XR8fP94V5na3i67v4+LqsgaIq911LDnH9c1NpGi69/z8XPWeBJwxAsL6vo8cKQ4XpQ+67u9IRZdvz2t/uLyInOJ8LGcB+f1uiBwR87LE21G+pW9g2+1PtlGDSVebp3mOJUqv8EnVjffjMbqzPkRKMU7adHwGbtyLOeMbqAQCLAw2IHL4rllk+1FXIpxcoLfe62D2nbGQWJFsoI/b6gIB3t/HVkhYmdduA1AM5hk/hEBE1ONDiXmc4Oi44SqQe/2JudyLNidXT47HY/Uj7HkwQNlWaLH9aZri6empJvf2LezHQEeI48gDVpuKWiNL2joamHItV56QMTaM7UZEDLshIqXYHw6x5BzH9/bQupcvn+uYuq6LcZ6iG/rYHfaro81TSmed7mK330eKiGVqFbSYI6LPsRuGSF0XvZJa9AtiloTPOpdSipQj8rJEXpbohyGuLsqzcPrU2PSIdugBdjcM7TlP+G3iJokm629mm7GD5VwR8eEVLZ639ULnAfJu6yVZ9F4kruEDbYhx3rNCcmFiCfyHrUO6YL/4RvaDMC5etn/uiY9HDyF6iV1gu2obyxLT0hK6eZ4jlhzT2BIqOk5MrpOYHM6+Ky/nWNtHTMLH6KsPGLL/dRKCDSJzZJJSishNT1inRrK3DdzojnGpcZfXvcXddceJiW4nSH/X65sTDZQCQO+Fw4j894h1aYifLr+hQK4EWPHNunLNbRuAfyIYEgIzrThygsUWzEdEfZiRKxHjeFyxeMyXtizu64CG4nh/AaVplIP5mq3BiThImZ0z400Qwtk7kPi6pdpQZA1bAfhOqbXBeS5OzpA7a2vGgs+5JIvC0m/uJy+zTls2gcSLvyMbGA8zf+63Zly8KMebEYBBxLiYr42bBIh7WfYuq97d3Ubf9/Hly5faX1tOr9hFSv2qfQj9paSK0TMXZHN7ext3d3fx6dOn4JkvJVh3cX9/F4+Pj1+daDNNY/z617+Jz58/V/3F4XLK08ePH2O329Wz262LONRxHL96INI2+fNGPZwXm7bNnlLBw/66bv3wJgArFUhOOOF97I7qjQMZDrzvu1qRjGiBrYy36NzNzU1NMuh5R1epvvCd0+kUd3dXX5EZzUG3Y/8IcoUBvqq+iwDJfFNKtW+cBAeQ3O+GGHbtacn87f39PVJXADcAFNmgS2ZHGdM4jnF7exs5cnz+/Ln8f84rVhJ/05iv9f4C9MAAm+/hYyAbkB1/Q/6MCd3LuT2h3L6OyhFgAV+Z56WOne+3hLvY7+3tbfVBToLoDUcefuI0cQdbJi70ff/VA/scPPGpjkXYxfPzc9VXM6beb2RSgc/gO53c47O2ya/jFnJk7Xa7XfWpfIdqEPbF3NEzZMomYoMy5Mb3SBScjODrrq+vawUEPGAmnPnyk3WyXLn3MLT+eSdZyJlkirkS38zCAxLxOwaewzBEXnKMy3p/Dn/Dp3ne7kJwEl2qsuej8Q+H2pfvPW/l1dqG7W/RtYjWJoiunL9W5/n29rZKCGHbkSkPe+26QgpWGxJBMwxD3efFeiIz5u1nizEPtypit2zQh7iLaM9lQP7YlfdUocvYhuM7J4wh7237MP7BCTz4yWQZ6+SWP5PAVFyty+iZK3ROIgop9tZwZZwrV6m1ZtHWxjoSu0gqSSTxP/bX+/0+lmmMeWl7nHxoAPqP3ZjgB/MwfvutoVv7DsdxExhbMpf3GCO/s/7ENuutY8v/JBUNBmBw2/d9ZRJYMCs+ysSkt8wF4M9CRVBWDL5jZgWnE9H6yHAQKbV2lSbM7mcDX0rlaLe6aEPbL9F1X58uQlDesmiMD4cP0MLx+6xqDAtHi3HaWWIcEVEBI8Bwy4Txk/FxPcZgcF7mGbWSY/DgYIHsYV5YMwIUIPz5+Xm1Vi/nNpDD4VBPxTBTZdCJAWwrF9x3WwY1S1Gz+WjtC8gbWVjfXPVC/jARyMY9yziv4hCWeHh4qNdZn/RT2FqfimQm+vn5eQXuYMgNlKk8fPjw4bxH4b2CA/SjAYfCFr6+vla27Pb2Nv7zf/7Psd+XDdzM8w9/+ENdM9aL71RGLaV4eXmtQQpn7cCDHFk7Xk7WDMzoWbcd46CwtYioGy/Zt0Elh8/TflFOpWnPDHFSWtY1VvbkCqt1jPGXsZYnfvvUL69T15Wjjg1CP378GOVJ2HNtz3I7AWwY8uAJ14yFvTPDMKwe/LZMcz3GkuD9+PhY9X1LjBCYXt9e4/LyMj58+FDlb3vDzsxwGVACFvDxZvqZB+DL7KZ9BX8HoGI7FxcXNTagC14Tkrf90B4GtY0PACNYy21LDy1bJMRs1GR8fId2EgiAiHUVEvs3KYGP429c00CGGOAHluG/SfS9ORed5XM55xXw8rzRcbPgxFnPjXW+vr6u3zU7zJoD4ByX7dsNuPy5w+GwqoyihxAUJJZeCxNF9jNOzqjy8FmDFxIig1rGiA547wo/8TeAwd15jd/e3uL+/n6VWJgQZR2Yp32JE/3T6RR9WrPiFTMsS+RolQX3tnNf7o2eFXm2hyC6kmIW2sCyxuDN6XB8H31gDNZV4uz2eTjonpNRfH8jgdbP/XKilXOuLZ5ULpy8mAxGJ7Bfrvfhw4dqc4yB+RKTib0mJLeb6dFPk8P4NT6HbJk3MuJ7Eed9p10fKbc9PqyZE1KSIGSCT8APGLiXz06RukbWk+yYVGJszNHdQq0LoVUw+qEdiGSd4EAd72Ux+YH+cx8nJbz4nIkvV2e/5fXNm8H/z//Hf7NyfHayZik8IDM3GKRLzIBh/r4NdM6WUAgbG4uMIqLUGDUMQXGGaRVEWAiDI4+TV993sd+vQTpztIIaoGwZC7MZZuPo1feYWFgzpb6+qxwOTFzHGfrPfe/p6UkZcjMAQDcOHVn6Gvy7vr6uG+VgMljrLWNkWRqg4BhxDBgTCmxjYXxOVAgoXM/JJ46FMTJHnAD3QS58D6cAK46+UqqcplMFgi7TFqdaQNTt7W09JcNlZZdZ3YaBQ2YTGuDz4uIQEbnqcs65lt53u328vr6tHjDVdd15Y2Uffb9+IN39/X1dF3TH7XXFIa1P7WLeXN8VIgISNmr9NbMF2DRT8tNPP9WWBa8fLFLZG5EqwLFfiOhWDtgBclnmGMdW4QPos9n0dCqnORFci0wjeMo810NPi320o6OxBXxKSuuNdqwtz+TwnLGNcZrqBkFskTXxpk+eJcDcHVhdbo+IuLi6jIOebE/SAzkCWwjzTyKPrzJ7CzvHtWhVMsCjpQuA6YqAKyfoNQkk3zd4oP996Nf7GtBB+1FX0lljB1oTNJeXl7W1zIknCTYxAbBLYs5eQSphXDsizieUlbng7xir4yDVXRNXzM3tVugVMcwAA4IFn+EDE15fX2tFgXWgQgoYdKWD+OMKGbpghtTAGiD6/PwcFxcXq2qWK8n2BwbtJqiwJ3TDAIkkwsAY3fZYHIcaadgITYNYx4uUUkRXTqXYnorn+O+Ywv/zk3WoSXCkyPO8mgf6nCPHSfpv38g1rQ/44V1f+v0ZnxMNYwLWkTXYHfYBeHNy7oSWWMg9fX38Hr4S+3DcYt3QK5OmrJsJNONCdIT7YtOMi8+7erT1T1sMhS37fXcpcD/+YXPc2ziP+5q4cDKWUoqhH2Ie24lY6Bc6YQIGWfIy+e0k5PW835I5e73s47kmY2WdkRE6FhHRx/oUMdbO+sl7JHPWG+6zXUvswCdcORnpui7+yT//s/il1zcnGv/df/t/r4ZBcGQCnOSyzYgYNAtpA8ZoXNKOWJcWLTiEQ5DBCW0rGgjTbRyAlK3D8uKi1HaChYEbK3DbOiDG5A3fnr9lQN84c4QBhO1h/Bi7nRMOG7aUJ6BGtCyb9hqzJSR/ZLXO2stY2qkLjIu1Gcexsh5eAxIBtxltGSAnnJYFzsdJJwoOMEaeEa1C5sDOepoljli3b9HagC543d1HiQ6/vr5WMOQ9OaxJcTApXl6eV6w/Abis+1D1AQbVoAzgDEDgczgZ2F6StcvLixjHVlK1M0upi9fXdtwlYy5PfR4i56Xu0WAe6ArzPh6P8fLyUhmolNrxk+iNj0DFjtEnEiC3MrIerLXL1awdoGm/L0f+3tzc1HuUxKJUJ9Av5F0cZGn54z1vBpznxsy63YLN9ugucmAfSjkYoIyF518gh4uL/YpxwyY+ffocu13bPAi4JaiQ2JkByjnH+/EYu8P6Scvo4mG3i+en58o+4dz5ud2zATEw5yXGqfSn89TvrV0iR7OAyBAfs2X83L5jX4nu+AjZLaiglce278Bo4JuXcjSjgaiJIOxyCy75f9YYP7bth+d6XMukDPZOK2BLMJs80E1XmgxobX+8ByvMWnFNmFe3A9oXcR0AzDCU9jta8QyGx3GM6+vrVZsJesja2mezFrC8rop9+fJlFaMjWhXbts2aogvYt0EQ32fdXImAhDDrvSXniA/4Sq6PHbjKsCUMIYoKYVHu/XZqsRCChPugF6yVYx06zprTItqlLrKq68x9HMcYpylyirrO2ySSNeb/idUX+30MfXsuE4AWvfBaM9eUUiyp6Q+JiatnrvgjN9bJtkuMNUnkRAedZJ22yQCxDPLMSTOfQSfxD8Rs+wQTsZCZjscV/A9fH9vqKuaWkDRz73Yh26wTH2S+LEvshiHy3B7g6MTUyYsxBmtif+UxzjnHdD6Z0AQqc8I/Wf/xNfgN7Leuw9Q2glNJQs+8zsQ/xoZeOA44Cfm5WLLVo3/6L/7X8Uuvb26dchkWQ+ZmOFGCPu1DLKo3dMGORjS2aLtQBAOujcB4aqczQDNkXAPhINTiVNbPSEAJvRDOudommKbg9KXSf0crixeGMeGEWDyuOQxD3c8CGHZChByZB9emVYce4YioDtsG4GwWg7DSmvWK6FZK5MSLFw5gG7hcdiSguvTO+vl3Su1OEp3xU1VwEPb4MIYtQ8A4+JtBnx9YhTNEPjg6Agl65uBBUB7HEvx4giwODxY456Ifnz59qmyg29xg7ZkDiZHL3ciyJJQpTqciiy9fvkRE2RD6/v4e19c3tQLCXLjH4+NjdF0DiySnrENEVLDPSUQFhDWQ44dYOqDYMQI6IqLOk2tXELlhGyOignAnZOhJuUYOnqwNcwbrwyEE6DVrW/Roif1+V5ls1u7u7q5eG6ePDRWbKt/nmODW1vQax+Pbypb7vrT6lER+qMz3NJWN64+Pj5Vx9vwBFJeXlzHs1y0x6MLx/T2+//772juN7yJJcELH/p7dbhfTXHzo9fX1qqILGeFNu8uy1LERgA3USNJpqyJJo92L+eInAe4w6gZQ24CLL/O9CzAaYzcMq+DFKV/YuBN/V3vt5/EZ+DfkZDaXGHF5eRmHw6G2zRFvuCbjJAZsx22WOKJVt9m/ZBIDueL3zCyb+TWjDyBOqZ006FYY/AatSug3cRH7dBsnvoe1AEw7Jroy5ZOkkDFJHD7Dc8IXM3au4VPJXMHwvSKiJoZOBPDBtJji602cbElK1oixujKC/e73++qXqaQiN2I8pwAyxtvb2yLfSDHNcz3Uguvy/dQ3W0JOTn6QCaDt8vIy+lQSbvQFHXCcIebzmXmeI/V95Pjaxzo2g7mwB/tkdNgkkvGZ7YHEwWQs1QBXtlkf7NDAHPnmnCuZQkwhjrCGHoO7PtDfrf8ivqFPxoXGZ8zJ1Tz7CCdCfCf9zH0ZG2OHjHPngu0R2R2Px0h9S24cY7ckjPeB8UL2btEq42yJEt/3HBoOXj8Tx2tqn8VnjcGN2fgs/umXXt+caByPY6SEcM5PI8xs2mstON4RX5R5iJTKCQnle+VkJwI0SuxylRUXp+EAYAdtwwRcmMFoga+LnFnMJfp+iGnKMY6n8F6F6jAkWJwkzhUG1GyFQTXjIWjTc+he1YhyZjeg2AAXhTS7hDLguLdtRq+vr7WigXxIhAC1AEvLi5Olzmocw0B1o/y+262PgCxr21p/bMQ2LpwoMsRImYv3zwC2kDu6BHPiaoXLnDi13a6c0oM+sS4ue5PM0ZqyLEs8PT1VJwNQLMeRnuLLly/xww8/rE6TmOcpbm/v4vLyMh4fn+L19SVOp7HYQirPsEh9H6dpjJu727i+vY3xdIoUawBkR0CQJhGj53/JpS2m6/u4vb+Lp6eneHp5iS9fPkfOKe7v76vz/fLlS9XXYdjFbsc5/ezP2TdgOk1nfc9xOFzG9XV/BkIX1Sn/HAuDDZq1JPiYbbWzNHBygDN7fH19XQMU9nNxwZN2y9HD0/Qe+/2uVhE4Sna329WH4hVmeYz9nv0G7TSr4k/e43C4iK5L5+dL7OP9/fQViLKuApaKDxpjnt+j69o58gDfy8vLeHh4iOvr669OH+Go7Kurq3h9e43307E6aPbpYLf4FJIjbN/sM9VK2sCW3J5CTdB/enpaPV8FkOMg63YDA4JlWcqDn46nchrOPMd+2MXb62vkeYlht4/L61KFmscpTmKbX19fI4Ycc0SM0U7uSilFyjnG0yl2wxC7vuxpent5jcfHx8iycc7iR7fRFVdEImIFRKh4cZACNsU6obvEpW0Vgs+TML+8vNT2SfTXraAEYbc5sYb4pW2lAXCM3RBP/BwJ/Cb3MBFgm+MeVG6zdAD75Hr4eQCZ20W2YyK+GYjwkyTTbXDIZpv00ZrmuIUf3ravkvBgNwYy7mBw4mgQvizl1LTI5431kaOLvsZt9AaZAoy2vgoAzHve0+NOgYvDRQxdtyJAalzc7SKnAgIfHx9XJCR+khhlfLLMS4zTGP3QRxflVLhIKZacY15KcgN4d8IRsW5F4ppgD2OKZVlWeoBeIk8nck5mSBpti/hpJxAmf5mfdQvdZJ2Rq69HrDH5aODrioNBPv7BHRIel6sLVA6Yryup2wSrjGOJQUSM/8Y4sSf8y/F4jHKEYBexLNEPfeQU56O9h8iRY1Cln7Vy3HD7sefEffkdjLPkOeYMibGUo3SXhifdMYEcnWRYT7EN5mWfhCxNAn3L6494Mvh/WydqIF+cfAFZOefqZACO47juN2NCxUG3M8n5DI6VYICz3W5qYtFxWtsyNcKxY+L79KhyncvL65rgGHAUduO0cu44bsZxd3en6kdXP4fx4LxJwHiqKwmUg4kVmLYWxu5rMT9v1jUjTtYNKLMTiCiO8Pn5uZ4mQisLisZaEcTM4JVxlhYW1pE2BAAUYJW/GyDYWHmhRy4Zu8rB+B0MXakwaCD58DnQMI2w3dtEFLb58+fPlenn2vM81zVifJbJ6XSKaZ4j9a1Cxpy7rivnZ6fuvJn5uEqUCZ4EoIjWhnMaT/W87YeHh/jy5Uv8+te/LsesDvuYz0eC4hhor4Fl5B7M1XtX3BYDy2g74TPYIwyz+0kNjNw/jny8ORwmy5/n/81gYkfb5N1JPDLHEXJSHPaLznHqCmtoRt6tPQASkoEff/wxfvjhhwosmK+dMnLHlunbd8uTWSHmnCPiOLbWyNbCNdcnu3rekAVvb291H4FbRHe7XXTDEPNSdOEPf/hDfPz4caV/yJdN0vhE/Jyf3TFN5XkXV+eWQHyMg5D9nKtaXJeWPbeO2X9ERHz58qXKlWfI/PTTT7Xi6TnCAJsBhcBxksB+EJMYzBdwYdtFzk7AbYeAJe5NIohP5l74PkBNRNQ1xV64tqvM6IjBFePycxCurq7qyT8+oMEMJXs28Cfcg3WBvecexACAuJM4A1d0ZGuPEetTcfgu+kr1HWKN903mYVOsD2RTZX3T1w8D5rMkx8xzXNpD97guft56jt+gOkj1ghfX3Z5QRFztui7ykqNXlYA5LcsS/W6ITlUCfJY/ix8xKHYM5DskoV2k6M/2Y6AZETHnJealPTgXX+3kwT5x2+IE+Ee2HjMkplltEnf8NWPCvyI/4gXf4/Mm2lhzy9DJh8dl/8HvXMN4iHVyooIuW3edhDjRYB2Za0SsTp1ivZB1bYWaW6sxY+mHIY7j12SG9dvzNCZBhxmX1wIdgNxjHh4zdlwrKnm9zwP94/omDdx+Z/zJfbF92/2/+N/+N/FLr2+uaLBYDJgFLorUwADHC+L4u25YnVPcHN0ucl4qOLFCG9QT0CxoAi6Tp8qAU7dxs7hWeoQI4292gzmxCDBt9AEbeBBYHTD4LgtudomAz7yYhzdyc20rF8HDQZO5oSiUxvksgY22B5cU+Yz7ZVF21iciauK13+9XGxCHYR/7/WHl+Ox4CCre94AMkEtKqRoca/T8/FwdIoHebTj85F6tpaZtyuWEJ4KdgTwPvDKjgfxgpM0ac1LDlgnASVdwch4Djpt1vbq6ii6luNi3U42stzg6QDOAdBzHuLy6jHlpx8jd3NzUE5DsoGgBOp1ONZGy80Zv7DRwFi73ppTqcyHMbLGO6I4TQZwja+TWOe7roEcQsi34qE78Cs4TnWFTP2uBj+AIW8Y4TVPc399H13W13YLxcSKPWVGDU3QJQM+avLy8VKAJ+WF7Yd8GPtKVAwDs29tbPD4+xrTM8fT8HN99911N4hsoTzXRcBCjekGfNjIhmM85R6SSBPzwww8REbWf2/rI+mMn/HQbCmCKs/TR6W1yw/rShhIRlRhh7cwicj9sm/aiYSiby6+vr+PXv/51TWZ9H44vxQejl+g+gZuECl1yqyfjZSwkL+g094XUKPGpMftvb29VFibMuCZzNtCDvIGJ5rWVEf4LIgK/zXxcWXD8QscZn9lnJ1oR66PCmZ+BP/GaF3HDByEAfNxm5T0rBpHe17Rt12ANkJsTHwCSiT3HUK7rCtDpdIpuN9QkBTslKXOFluuy54X1YDz4KxNK+H6Sw2kcI+Wo/ob40vd9zO/vcXF1uZIj8952aaAD/HSSEaGHQHbl5CP+5uRgyRGD1od1Nf4hBnJNM+dOdoxRwEP4O4PZbeLugwqIieAGJ37IwPHLSSwx2gkGPs4VQsc3sBlz5rqO1fgG/gZW8hoTC5GDZXw6nqJPbasAvgy9MulhMmqcWpsne33Aep4nOuIE2vdAH7yeTtC3Bxy5imVZ+v/xJWBrYzPbtTHtNhHDd37r65srGn/+b/7tirlAUYoQ1iDJLGbObYJumynXai0uTNQs9jAMtUTJKR44GwIkC+VrwHbj9FH+7YlGbdH61aIRCMscYwUOq+C0eCgzBm4QRquTHSng0IGERbWsbMw42Gkq/dps+kMxHLic3KCUAC/WzVUC1oCgBfuJsntT9jTNsdu1Iwa5B44XwMba2IGi5GYd0KeIlqQyfhgnHIpZMjOLtKEgD5yHmSFaSfiMe4bROxwTwRqHHBHx+9//ftVKxee7rotpnqPfrffkoCv73T6SAhYBedv3bTYp5xzDfojTeTM4gBgQe3o/xfvbe2Wv0TWzkXbkBFz0zwwnesX3cLoELmwEezF4QG5bB2gAgjwApVQaGBM6Y2BrdnTLohMot22IbilkfnwHHSKJfH9/j9/+9rfx8vISv//97+Pjx4+1J555EkTYsO5n7OCbkCc+y32zrCM6vCzlCcTj1PZ4MaaXl5eIZYmhbyy1gyXjplKMP3h5eYnr29u4ui4VOLdrsBa05DG3iPXJevhpJ/Qxr8vqfAf/CXg+Ho81CXI/Oz7YeseLE7XMcAKAkL3BOWMwKUOCxpxyzrVyy1gIoLSUEiMAFPhPkkNs32wt75PA06qEndifUskxaWDwhK64NQWdzznX67qNAl9kggaZbO3SjCh2y/oydidb6BN25IoiSRb+0cDSQJn7euO7QRsvy5mqApUi7NTML74FHYmIWqV2ElKTzi5F15f9jfv9vlbMGBeJt8Eya+gNtcjJpKTHlHN5kn2f1oe01FbY81hMirImJsqcLJkIYszM+XQ6xb4f6nps8Vfuio9gbugdemkcERGrhMBk0TZegFFM8IE7DMidPOac69jxj8wNTLBNZh0DwRhb22dc3Nd40VjHsvS8mDs2hNxZM9aHexi073a788P5xlWcJGnnuugpY8g5Rzf0McveuZerSfgEbJI1Qj6Mn3W0bNFVEjBjCmy2ynBZ7+Fx3GSu24dUWl+xNdbPMaHv+/iX//pfxC+9vjnR+Is//3dfMR8t+KfKPAG2OWpxWdpJJd5EXZzwqbIwDqxWemfTOF4ECagxU0bFgOBpds6MB4ZWgk9T0HmeK0NZXmtFgEVBFjhLnPbWEXusfB/gTDbMJigMGDBBMDCrhAJsmTQUlE2U4zjG3d1dNSgAGMa7HaOTFDteJ02s0/v7qQJH1oySuTN171HB4FFa1olx4/BdDUJ2sMg4GLe38QLMGQCfTqdapfBamMk3c2ZA7KzfDCrG7NJl3/expK9P5DkPJHb9UFk0A3MHMGRPoN5f7GPJ7QnyAIrj8RjjcYxlbhuDkSvrTBkXGzVYMzAB1LFWAMeIVsEzK8V8zaL4muivbYU19pO3nfzASl9fX1dQiB5sN7yhV8gclhM218y7gyTjYxxbhhO2EvunymAADMlhGVNBMemBrZDQ8v44jrHkHMO+HVvqRCIvS6QcFWhOU3k+DXuGsBOz/F++fInUd/Hd999H3/fx448/1nUisQaEIDN0neTcAAd/0kcjKAz2AOrosYGGiRjmxTq4FQV9MqPrTf3bGOCgT+KAvuNHCaAASwN87H47dnwp17J9befC30liWB98E3oKGLK/c6KFT8H3XF9f1z1GBjEkUlzTibuTep5dwXwANfh3+0lkxV4a5gU4/NuAPj/RE9acayNXz9MJia/HNQywsEsDHNbbLWjYIt/1faIrR0czfr6HncCKG/ATz9AX7o3t4g9Yt6oDp1N9OBr6yzHA3dDHcdNR4CqVdcB2BYB3BYeq0q7rVyy+rzMtcz261w9+JHlEp/m87Yl1YA3QOXyoK6IGsMQGfBifN6lpUoh7OR5YdowZQtN2j20zd9v0FvRyTXTJFQvLwL7F+oC++m8REX3XRxdt7zEyMXbCJvh7zjlyKo97dQUYGzae9P3tp/gbcnLLmvGZcZL9lYn7mNftjVuymTH5esarW9vBFiPKvqg/+2f/q/il1ze3TjFBQLUXbBjaQjqDK8GhDPjm5mYFAnlIjRfKbC9BA8dLZgxjx8PKpmmqDzxyPz9A5fb2tgIjNrHhqItRTrHbdat7OhjmPK+ecmtlMZhjQQiALKTBKf9gAwGVBk9m9q6urur1cB4YOAmUHQJlupxzfPfdd6uqiI8kJTjCLLmVgf0bnhcGVJzHus+bJ/a6LQlDt4FzHYyIpGfLwvizgDs//8DMupMFElbvl7m5uVkBeNaUa8PaEWzNqBuckhw+Pz+vWmgM2LtzRYP2FsDOPM8RfXuYnxNEAxfLJKUUlxeXsURLpGituLy8jNP7KZa5BFSOh2XMrHNbrxbsIhpj4iocG3CRt09osjPCWRFclqXsd/rw4cPqRDjvx3DQ4VqsGdVJ9NLAxfM4nU41EG8ZXicuTsjtcNEb5OeAg1+APHAC23Vd9TcEGoAff3N1x0nSNiG6ubkpT4Pt23uwkdM0RSzlKbRO6L777rvqlzyPaWrHbQ6HYsc//vhjBX+sD/6RNhizZbvdrpIZTtj7rouUo84Z5h8QgN1A8nBPxo3ts672Zw5wr6+vqyM70QdXnQ+HQx07PiuiVEWwYdYPcIdu81lkbH0gmRiG4atKOddHlyHPWE++a+BGDMOXbv0m4+i6Vl3NuTwgjhc2Q6zFVnMu+/VIFkxUMGaujZzQRfwh31uWpRII2CPyRt9NXuEfSOLxs9gxz1oxa+3xIyPv/+PekCQc7ADQ3foQbxLf+vJ5niNHA2tmrfHbEHf2h8jb8Wk7XuIIr3YEbo7TdFqRGOCPHG1TM+MhwXOFnd8dj7ZArlZsu26VzBoElx+t0sHaNCJ3qutsxp352XcR/2gjdPJtn4i9oS+WYY2FXbdKdrZ/t4yImd5btAXSTgB97Yj1JnKuD4Y0aVOrTucXugpmY28x86nfSSli0R4dxUQnTR5PRNSWVtaVe2FvxAr0wvO0j02pHd/d1r0lV/x0+/h2fBBZ286hv60Kxnf8WeNX9IAY8y2vb040fAygjWSaxui69VnACJtEA9aSiZXvR/BAMl5OPMx2AlqoiDizxcmhwCzs4XBYsZywGwAKwFRx4iUQ8HRd73OIaOeFs8B+EiWGC8BwYsQCYfQ4Wm9gimiOjn0QDt4RET/99FMNlA4KBJGXl5cVwz6O46p1AeBLVYgeyqurq9VRu3zPxm9HwvcuLkqgJBFi7lSDGAdyA5x3XRcPDw81iJjVcaIJAAegudUq4mum3CeAAJBoT3PrVkR78i/gieTCm4NxVMgZnbq5uamVMtY85xxLXmKZvj6xwkwYm25dJeGeKaUqNzbETssUkVrLCvr2/v4ey7RE5AZEzPoCkugrp6qFzMwMsb8IphgZGbQjOz7X9621EBk8PDxU/UZ2OeeVnTiIoo/jWDY6Pzw8xM3NTa1qmDEh+TDYs5PGb2AbyBZZMx6CMHoKUO/7vgIFwIRfnEyG/UB2oMMApYjWA709ahTAPU5jzLm1hro6No9j9F1LXElqHx4e4vLyMi4uLuL6+jo+ffq0ut/N3V0cT8e67uiAx0OFCxDC+gBesNMKLqI9PdbtTdik2XWzZNgP/tXPJyBuoFMQT9giDD0yMbnDWmND6JLtGp+Nr2GtrI+W2/bJ7Vz750iMLVvLfHmP17oS3qqnBhLoL/O+ubmp5M7PMfbI0bI2kGdM/J17AGjcYmawWo7B7mr85JoGdBHtFB0n4YzLiY2JAAN65sl9sTXb6RbU8DvjNkGD37Hfm6O1krHW/N2tPtyX+IoPYh1JfpwQYFPEDiqP+PRxHOM3v/lNifl9F9f7Znvbth18EmvB3jrri8Fg0YP1Q3XR9WVZypPBl3UF110fBoeQTYwZOYOBwDb4RMd0fidWYlNeY/TGwB4bMR4kcUXGjAG7R4/RBcaFLtovoRtuCUP2JrSc8DCX7Zr4vshuGIaYpzlmdUvwWcdTY9QK/lPEpDhj0onPW/edBHFd9JXEGV02wca1TKBzj1op6odaQYXEI8azluBt673ltB3n1vf90uubE41tjyOKxKI/PDzEbjeslHuaWi+fGZSiIMfouj7KsbMAD55KfYqIVr4DEFL25T0YLwK/MzECaGstKS1Sy5Kj78tzA06nMQ6HfQwDJVcYzz6GoYvdrpXgGTcMHIkOzoqFdybO5/i+AfQWAKNgyNSMDspmZ2IwiyMxc4XDKXM8xPX11VkeU1xcXEbOS3RdHx8+fIybm9vzHKIyaC8vr3E4XJyBxXJe23LcKGvu4A4DVmQ9rI5BNCvu8dqAXPVBFgQ0l2fNygBokC3GAxhED5y4sjZu9QOEAIxhEZCxe5edSHjt+q6cZZ3nOZZpLv2zuZxYMU3T6vkIXm8HSJi84/EYh4v2wLN5nmM37CLlFCmnyEvrUSdQ4OiovOAoOYmKdUF/3ZePnLxvImIdqHA8nDtvncdBM56IqEkrAMHMje2UcQA8sWvuuW0Fc5uSgZXBL36B+6Kr7vNGL3Debi2MWB+ZSNUOXwZwcuUHUgQdwy7GcYzn5+eyyf7MMB/2+4iUo4sUOVIMXRdL18VpPo9hWeLi6jJySrG/OMT1ZTl56PHxsdoBTD8PdaTnHZ+SUopy5lmK/eEQfT9EHyl2/XnNz7pVjq8dIqUuplMBi+O0bgGirQF58CyRbQIL6+w2JewzogQn/DFyYr14TgEsPHrFZvGua3vV8G8cQetrEatc3bT94odoqYGEciUKm8RP2G/A5JOsoGOuODBH5mC5AVbY78GRxrRBmVgwq46tofvWRcaJjaMD2BH6zHeIQ2415ntmLLEpV5WYL2PCThnTFuwbDELWADLNuDJmz9+Ak3swHoPJSZXucW5PtZ4jxZxbF4YBNvpocMj1bEPMqbajdF2kdF7zyOVZFul8aNw01VOn+K6Ze3z81mZcLVzFlL70+Y/jFLvIEXOJMdM8Rzo/K4kkEVDPum2TN/avGD8hf6rwrujj4xwjXK0gLrnSZLLZpLGfIm48+HPkIXgKu/TeDOsK+MgJg4kiYyM+83M/bb9OkJnnyJ6dZY6Ul4iU4vqqPYtoiYjcpThNU6QUMU3nZ5ltxmuCz7rndk/GTfKLPFxBMsYkYTWpbYyyLOWYW/AW1/Bn8bn2K6yhZc548CN/7Oub92j893/xP6zAIaADJ+2TL8jm7ShQUgCemS+zCIVdfYn0M2wuAsVBw6q8vLys2DqOgwSglxLvZXRnxvB4PNbe/WIUqQYBM0jck+x5u8mcoAMD6fYEHJQftMUJNgQQPst1rETIkMoCykbLFHPz2OzUeFJwSk15YEtg/QFKBO6UUjw9Pa2AOnPB0RL42TeBkzbwsNMwE2YgwovAxH1IEPm+S87bwAMYskEACpwI2SnC9nJvOz3Lr+vKca3u1cVgSRxxrugda+qz8Z1kMz87QBwr4wfsXl5e1iejmm0HaHIvAxKc+TiO8dd//derRI+HlHGyF8CR5IrA4sAbsT7KDtl7LtiB36NvnDHyGXwCv5t52Z7kxDoAotEbvs81cMqAWiqC9jcRbe8S8/SYzUixP8qMOnJg7k7O/DvVETPIVNZIdEmu/GyYaZpiWuaYzutEe049VrnvIy9N5yOiPm9lXNoeKvwn63V5uIhRmzqRK7bBenu83AO9NYGCXjvZQ+eQs4EcCT6+etsuYIDrlkp8iWWLHycJoWWHdWQt3DaFPgKgOEUOH+eHTeGHqILSvuKWIBIUgyNebt1lnd2m515tPnNxcVEfyrUFVMiX9eSFb2PMft/fdSXG18UuidO+tuU1TVM9Bh45b8GQ/ZrZY9hv7BWdcPupr7f1x8zHyY59iH0d62Cf6MMGqHb4uujKdt4mDrcvYovliPwg1ngOC9dznOB+EHmM2yDSschVfCeIW6BpYojxo3O2HWQF4eW4G9ESVPwcfpY54yOxbVeIve7IZUu4IlMnqeAF+3a3A/IPHaCS7ljl9WBtmRefc/cIemIfyDgYK7bsKp39pyuS3vflJBy9oIKED0APWUvjGrdUuZ3dmMoxYEv0IAPHqpRSDGl9HLFJGPt78LZ1jfkTg+0DwEv/7F/+06/sZfv65oqGSymAWpwVGSiOwi0LgEsrBwbCBKiWkL31/RCHQ8nyOP7SbKxPO/EpEQR2TmWiClL6rPfRdX19z+1Dx+NbdWxk3WZzCX4wmywCYBw5mPmzIeGQnZDAIgCMkAtjI5h2XVeZOzNZJHbciz5U3iPwT9MYV1fXNXtGQRwkaC3JOcf9/f3qXs7ImevxeIy7u7sVo+GTuswEOVC7b9p6gpI7WDhgwtr4MwaaAEzAG0ZrYIWBeW+K9zLgwEiWbeR83y0XODfmgH778AHaBDBe93k6IBic4JQeHx+rHjg42nGbyUU+T09PFZBxhCrywEEwJgczBwCu5yQZ52P94Xde2AvXxBk7MJq9RJ/8cCySFLfAoAOAQ+TF3AGdDw8PjWla2rHY6CdAwMGCueec4/Pnz3FxcRF3d3e1Usp8uN/r62vc3d2tEhU7edgpwC9jIFCTqGJHLdkdIlJ7KjM6t9vtYjmX75HF1dVVBWzVkQ/teQwkMylHOY5T5MXWP7gFwbrpPmj+ZuaM+VI5BZTj49GtZWnPKwBUAzS5HtUnVzO8P4TEi3+MOSJWSTO2SwD3oQVd19Vjkn0ddAE9wnbxxeibfZIZcOyDwJ1zrq2cyM6fZc04wcxJufWGdQLIcA2THry4BnqFDfAZ4rCJGmSDLF1N2SbVBmz4XjPf+HqDMreL2Obxn7xPzLWfQX+3/oIY4rGSFEEMAKhqMneu5LvV1QkvOrz1kdg2a+V9Z45zrtqhr9iXdRRd2CZt2/2BW5+ITlp+6LpbA4kH3JO183zwA/h/4urj42PFXsZo6A5z4PtgQOsh6wY+2cY6+3x8FUk3uoQvJgbaP/EZd3aY6NriAr7P97aEn1/o8LaShs/DbvFDxl3cl3tsfQu+z+uC3iMrvm//YQJgm1QZO5iMdTyulahI0W2usU3MnURhx+A2t1SiO7aDb319c6LBQnBTmFYCI4YCk4FS4vjZLOpWBVhWM4MlwFzE7e1NPamG7xF453lendZhAeMocUDtHOUcORdnfXNzEy8vL/V+0zQHrVpeTBaM6xM0DBIwWjI+nk7rSgFBnXI1oJ85m6m1/AwgkRHg/cOHD9V5coY9DpgAUsYxBHY1DEPtI8a5b0v28zzHx48f46efflq1M3F9FBumkoQLQ3MbFEGFNWdNSGzs0HCiGBYBlgqQ2TpkgTzsSAEpboMw8+jKEePBaTuAbispZk9dQmYOOBkHeKoFrB9J9TiOq4cCWmboUURzgDhUxuIgyQsZXV1dVcDMNVz6p3UBe7KuMw8cK6e1EGywWwKak1zrpvcwIAs7Z8BF13Wrp7Ojo+gIwcfJA+0zp9Mp7u/vV+MxE+gjdAES3ltSHaCSbo659eERj4+PNZEB0CA7NtETvNBZdMqn5tBu4+rZOI71TPeLq8vKTlLJqE+6nuZYzvZhG99WoUi4mWOK+Mr3oBMQMq6EcFIgzD9r7oQNYEVfN/JGB6ybW2bYCY8DvxNRE1l/8zd/U+ND3/erdjiCOD4W34RMzHg7KOLzOI6WuRtkYefoKP/QO/y9Kw8kI97Hgl7br1veBibcD2DlijJ2bhCIzyM25dz2kDkZMfjDjny9bUKCzeKLkD3xz1V4vuPKioEj9mvG1tUmA3D0xkSdfQUJJUkDuoK8nLxHRO1H97wM8AxskRPjNrlD3CJ2cK2cc9Uh+2pszckc8iIRQQ+wAeIrhwRg91dXV6t9m35GGckFcQudcXsOZAnzQZdYc9bAe59Mhljn8JWuzLjVir/jiwzW0QH+5jhju+f3bSLLNcy245+dEDM2E72MA9mAVW3TyAT7Y36sG2tNjGX9bENOhhyXeZ813CaArk5aJ5xYQHIhN7e94QMYp/0FYzwM7Thg7mW/aDLSduHE3JUakz22/b/r9c2JBkoL0ESxbEg4U0CClYykg7PeSUDYhGoHdzqd6okcZq+WZYm/+Zu/qWAZQVnhMBocZCux9yuwQvCMiLi6Wj+1GXDKPI/HY935j8KiYGZ55rmdk0ySYzYJthMHBDAwIOPe/I5MUSyXqM26elMUTE9x+ruIaMqCwdKi4fXDYNxG5nIhLRLzPNeTUHwvgpCTADNA29MzmA9M5DzPq71AAA7rFAZn9on1sDPdtnKYibWjYFysHzrngIlDcgWG+aFvBAefHMXctwAC9on5myX4uYRq6zhIcuZ5ruBrnue4ubmJvu/jT/7kT+qYvnz5Evf399UWdrtdPD8/10Do8uu2bYA1cpLtxAFdI5ABEgxYPC/WEAIBOWNrdsLooJk0bAM5A1wM5hzwmRv6A7lhRgcHzBr7Cdo+KjuitZsAMLinHTNAhzFuGTa3MeAP9vt9pL6L4WznVMWQRUrrB96h1znn6LsU+8NFnbeZ4WHYxTy1vSXoLIH1+fm5Vq0Yv+WDX3Hy2fdtTxA+2C19yBA7dOsFvtHrDtCKaFVINipjt7S98Z6THiqabndF77quq4cLoKuuvgBaAWdUBrZMOb7ER8kanKJvBhXIxvtNsDETFW6/YYwkpfgqJ0nI2a1WrO/j42PVaTPKBnC8rLP2q/yN97ZsMX7Sft0gyP6WWMPYvVeDOVnXzOzzQn4clsH6MyZXuvkc8sw5R/Rd9EPb8+h2GJNAyNGtWayT9Z+xzvMcd3d3FQxjz/hPgKsTMzZ/kzy7UujE+OrqKvq+Xz2g08D97u6u6gZJLzLmWuiPgbOrrXyeuMvYrWP4xu2T0j12x1YnK+iF15fv4wfQpa7rKlm6JTienp5q3HIFl5fjum3EGIm1MRllvccvcw3vX2R90Tl+bkE9czVmQDf5jBMsg3vHSHQUnbGNI2P8n2OYddnkW4qItHzdfmm/Ad7a6j3XIjn2vZjPt76+OdEAsHuB3JuGozboY8CnUzkGFWViQhi2laA4qm4ViFzK/wf/4B/Ely9fVtUVLzqBwgtVxpFWGTHfLSzC+gnNZjVxnNfX1/U9/sEG7Ha7+PTpU3VwAKmIdqSZlQq52VFj6LByW5DrrJ4NXYDcn2uhaPJPsSyt5AxwAuDSguHnYgAUcHw4AxI8lO/6+noFXgDFDrxbhsiZsa8Ng+sgZOeC3hnwMyazKuiWAYkNywbDtUigcSRmNRkHAdAgyddwgmpwYce93dTlRN37LDB+dNqBBh0DSCBvessJqHz3hx9+qEwOskDH+JwTK9aWwGpw6LlHtOqh924RdN0D7haVbULqxApbAbw7+YyI+tRut3Z8+fKlAnquiW0Q2AG5VFqopmFX+/2+VueQNevtYG87AHziK7Z7B/q+7NcwI+9gwstscaTWSgSwmuc55mmOw379UMOczyfp7XfxdpaPK2DIM8X6GTnIgNY5/C/rzpjcygEAAZQjD9pV0Ev8N3M0+2uga99u/xFR4gxHkhvEmoH1qV7ogavqObd9fC8vL6sT5fABVHRMljD3vu/rHhjLbgugANxUmtBbM37YKfZrMIuMsEXWm58AIn9+639432y+9dwgDP9iJtTxhbhgUOWj2s0U23YZn+PaNqEycYaO+F4ppdpm0nWt7Y01Zi7b+AF49nUYb0opTudkru/7SsxFxFcb+rFPZIVcmDM+wqCLa+JTrT+M2SQh4Jw54hfxk8gFH24iy3tf0TNX46+urur4kAv+3P6W95gvesD9WS+fXOdxYm/ojMe8JZi3MjWpafxo3WT8kAI+GARSjTXeJq9OjvCVzN9kIWPYVuL4Pn6MNQUHbXGG9ZP3Iay3mNYkmmXBy7qLneAv+Ps2OeG6/u62RbBc5Hxs+SYZcQLjJBn7sm/Y+gB04b94RYNJ40RwFGya8QPYUCC3SUW0bHwcx5qUYOgoUWHVbiOltuGI7DainShCcLDC830L++bmJp6fn+N0av36GCGLPU2tZGVAjODdz8r9GJsV9/r6Oi4vL1eni/DEWrNcXdeOlMTJwKTSOsN47LBZAyvFFkjbuZe/tSNjSYxg3egBnaYp7u7u6jo7iDv7Z00BGcgcFr8ldY29QC8Arigq+oCsdrtdfV6GDbrv28MeuRb3vbq6qkHewZ3rmg1CX/l922ZhIzNjFxEVrBLAcRoGaDhbxmxQAqhjrajmcR8DcRycwShzxga4FokA32FcOBJ0c57n+PHHH2u7lvcYUXnj+lScSExd2jWwcYsIzBEBcrfbrY5MPBwOXzHljMt7ewjQ1i/k443e19fXNRC6wscasf7eq8L7zS7aAwexv8PhUDeD4wsIyvgD7MesEcEeu7LPYu28B8IVLmRSdLiPl9eXCprRm5TXYBL9Oh6PMefWgmRfuNvtokspptz650na3NrpZJk1eXt7q7aOns/zXE+2Y4231Vg/gdlBDT11dQ57wV8DxABVMJl939cWL67rQyy8pw1dmKap2v/19fVKdwEf+FrskGu6SgZYcHsYQI/3eBaJwQ56AcChPY77M398BaDRCaLHaj8bESsdx9Yhq7AT7M1sKr7KfpC1d7KHfpn0sM90JYQT1XwvxuxkZxiG+Pjx44owwV4dH1kPk1bWQx9i4sMV0AtatGH77Uvv7+9XYMmkp2VPiyv+wkQPSbiBN3Pnuqwx64Tum2BCP8BGNzc3lRjp+762dpN8gTfQBfQ0pUYM2pa9RgadgEQOvLAPsL/1fpItSCfemKDid+S0FzGCbO1HsR3kAslqgEsStG3ndGLKe8jTckan0X0nedvk30kyawm+5BrIytfhhR9yyy/XZszcE53B39ofmOS0r+SzTt64Zkrl6YDI1ARtinLyZdf3EXldDTUuYszGktwbPUP//NM45e96ffOpU3/+b/48drvmyMvNu+g6bpSCM58LaFrOf0uRM+whWVwphxO4WUxOg+q6Pua5GTGBEYMCoBiYwWYxNgyy7/vz6UEXMY6t5G0BARTcjsP1395equOgx3LLRGMQXmBAHQ7Um1ft7OwUWFiUgaBOIABouIpTQGofw0CP/3sMwy76HmNojCAgA7mY5TVQAcSaRcGRex52xDhdkh0D0WoMEauA1nWlZHp/f1+BHkmDWQA7cn43y0xwaPJobBRjx1nYAZjtYOwkcTCnZsi2rD96gHxtqKwna4UDMjvL+CMaw+FEjGtbrui7A4iTUPSHIIAzZnM54Or777+vVSwADAcsAOBcqUL/WDNAAnIy6+p5oEuM+fX1NZalbGh+eHiI29vb1d4CAtPWufP0XdbUz+jg5eC9bdHgd3SQ/2d8Tja3zCzfgb22n7B+kkC4+uVgjw9zCwayilR86Hg6xf5wiHmaInXlOUVLLu51v9+XYNG1FtOUc5xOYwx9H6mjBaM8P+VFJ4zZBp2YOiCTdLIvyr6eubjVDn1zwmk7MGHi+xPUbG/IxtUHJ9T4WNYB+7MP5x8Jo5lhAwTbCuMFyJrUckVmS/QwB9uKQQrjZ0/NthrIvfEFrmh6w68ZSMvbPgybZ67Ym3WZE8PsQ0mmDTa8odisq3UVHSBu2L/aj/3cGju+8f9moN0SRiJDVZFDVLh/TV53Q6Su4wl25zh4Tuwjr+Jrznn1UDr8muOYmXuTVRAwxBjv0/E+LgNFrsF1XNWOiDrnbRLil3UAvULmtD9C9hCnLR/00lUEyBR8ePGbc3SpW9lJY7RTLHn5yh5sI8RiV0dNmKBfNcbliOPxdL73GMPAKYqnc+LcDpIpB2SU4/qdJHd92fBcHlzYxzRP5Sh41qJLscwtiTKBWPQvzji2i2WZUaFI3bm6PWsDdZeiS+eEdDfENJ4PquhbN8M0TefPtD3BETlS6iKlqO+N0xi7ge6K8p8yziXS+ZSo1KXz8bR9XZNh6CPnKJha69B3faQUUfbknqsoCy1yc6RosW6a53NissSubyd/8UJXsGHvmyq6u37Q5b/81/9N/NLrmysa+33bwNv6YUsE3BpWeeUoG7DbzvrX15fqXAEtTAxHZHbl/v6+VjoIGhiHM0Su0ZRnzeQUR5W+EhD33TLfDTy2J5MCzAFBLtMTBBnb+/t7bUmCAcPYDURIorinA76d1JatZ54EqN2unTHfgHJ7+jMygaU2O0JgYZMrcmGdaLOAIfe4tqDD7LKZMgA5QdCOExnhoJgTAMdzbUnsvFovxoZztWNnjYqBtITCbJl7+AGcMLbe84O+sW7oF0CI+xM0uB9zNfgxS8n1sR3L0VUSPmPwinwAAE4mIwqLRzLH+Kdpqgci/OEPf4icc/zud787V/7K08ZpM8DeCawwT+gAa4SOEAyRDRuHsSHLzicyuZ3Jz+qAFd32z5Mgsy+FeRnMYWfIzrJkTw0ydjsE9m2Wz9UC7md/58QWOycpB8RYL1iLyoRGW0OOpI2co0tdDLshTmN7kGfY3/RD7M7rfnV1Fcu8xH63i9fzCUtO2Bg7doff9rhub2/rZ3POlUnkfqwNlVu3ihlUmZnE/vEHJpC2QIx7s3EdmVIBBiDd3t6ubBjQjV54fUwG4H+ZP3ZJQjDP8+qhcq5EYuscEYpPdiWPeXsPlpMPs5m2R1pu8Tu80LmI1jvuJIk4in834eNEyv352N22ys06ukLjViVAOnsIkCkEwjzPNSmIiK9ACmvEi/fwd6wJhCL693Mtz6xxSSYi8tLa4nLOBRT2rUpsOfO7T0zb+lNiOb+boGLtkTtVB7P8jNkAjWTKD7J1jMBnOcabdDGxge66VZrEtvqJ88vteU4CnExERKQoYBofyj1rUp/WpyM5OXO8Y3yOD95ozRoWgpTkt+2HgTTFXyHr06nth2Otju/tZLmUuuhS28eQUoqY21PJkR2/m6iyXtYEO2/IvjlHnMU6T62S488uiS6IhiHK57pYFiWtqXXflDVvhD2EluMYYyZRyTnFck4YUkrR79qjG5zkp5Riye0AiknkRZda8sqam6RnHa2jjiX2Zb/0+iOeo/H/LAur3tmIWG3qhvG3suGECQAuY0esnyT78vJSe6tx3GzcdiBhsSIayKrKkNv57wab49gchbPwiKhJAWDIDmeaxnOmuz6yE7BA0uXTpQxEnBDgrHjGx36/j5eXl3h7e4uPHz9Wo7VyR0R9ToiTKH4WcNlOAJumqT5hGeeNnA06tqwxjCzvMwdAnZkRszvMi+uQmHisbnuIaJvJcIw/x6oRoJC5AyV6QMCxEbilw8e7GlQ5cUDenhNAYruZbwtcHPSpqDjAozOsq5MKn2jjIMs/b9Q2I2cAZTsz4PUmZOx1G/QAj9M0xb//9/8+uq6L+/v7OB6PcX9/H8MwxK9//esK9K0nBA/kxtxJQiJi1ZYX0Xp9mQ9BCuDj73pufvhg3/er51tsXZeDI2vplh0HZwMf2zZsvkHyOI7x8PBQQY8DloMs9sLvrJsfjGaA6zWxTfI3SINpWWK3362cf60yDY01p03IJ9HgBzxn7AmWe6tv7GtwYmL54h9IOqgoMleAVtd1FZiyrtt14vokmtgEyYMJGnQM2Zqg4fkw+LGIWJ2yha6YZMAXeP2xD47XNRscsT56236a6jBriz5sfSSAx/fn3vY3DXQN9ah2V37mea6nFFnnDZio0jAm3vN10JVtPPULvTMR4iN18Uf8P9/3KUnEeR8IQlujOwKMB1hbE0isK/455xxpKGtDsg1JYh/Dqyb2Zxs1vjCZSKyhYssc8dXI5PX1tfpMdHybzKN3JkIsJ2TseG1CyUk5ibHxgRM5x2h0H3mxMRpfu8VKhdxoz/QywTlNUyy5rT96jM6QwLCPju/8HEgFr52O64NuAL0QDchuW7WHxHECARh354CTZicnrA2yMy6wL7ftb9dtayd/GwjHpzF2YyDLhc8a3xlXOWlz7EGnWSvec6fEPE/1AY/Gf13qYpFvh5DwPCEztq3lJDx93/+XrWgAjLgpQmYDb0Q7/s0DZ3Iohp2t+/IQJE+Bnaapbm6yAuAkURJn7ig4jAhKXAJPiv2+7aswcPdGwi0oK5/7+WPMuCcC533m4oQEQ2TPBkF5y67h2ACIsLrb4Ho6nSqz9P5+WoEv1mQ7DjsUVxnstCJaYF6WpR61CaDAkaLoyO3nQDsyYvzoA/N3kugkjXUAeDlZA3RY8dE9f8anaXh/DGvGT4MwrsMYAYg4dnTGgWvLNDFm7mfngSN1mx/7DwwskKMBLYCctXdbBTLhfhz3yQZGNu1HlMoDbUjoyz/+x/+42knO5Si/h4eHeHl5OT/0MZ1L143dJKhYx7EFO0XskGcLcJABegKQ6vv2jBlkAEEB6DNxgYzwIf488np5eal7wdxHTpJqAIuOAg4B4Q7uJgtciXMCSnJgIG2GFnDH/RgLvhX5EuzHcYwlcuxi91VAjGgnIQGqvUbus+Yf9uZrEFAjoo4J+Ua0k++wOXwF88Z+3CrDHOw3WTeOYbX/ZTyARMsEf2W7dEwhueJz+E8/n8nAAN3jd+IBNkR8Y96V4YxY6SKy7LpudVgK409p/bwB5A5D61gWEStwhR/2HAwkXRFD7yBIXAVhDlQ78THoMJ+BGDCAtIwMTDkREpvnb9uY42OHGa/jEJUVxsE93TNuPeYaJLXIqs9dnM5rxkNOveeDOUPwpNSO5IYcNdERsT4GHTu0rtqGuAb3QmcAxLDaPogCPTRpwHzwPQa8PtoZW4JoQ4fcfYCtVR+ytEoEMQO/DWkwTXOkKOvJ4TcNiKfYDYea9KCL7McjqXUXBvJBz50Q9X0fl5d9pNT2GhkzbPcyETtNDhDjXC23Hm7jo/0w6+lklHGxNtwXe7Bd2T96bE4A7LOIh8ZazA2d8OE7yAoShnk7kbIeEQshv9GfaRqj679urS5znmq7oW3l52yGuFf8VjvRzP7r73p9c6IBs0hpBfYGFmabfWGI7hd19hjR2CECBQL14m5ZAQMmFoxFMLtqAFg+s+6XZkFtbDVzFxuw25Vy1ZaZ3CoK7BJzpiRNRQAwgHHCHLLonHCSUoovX76sGBQAD4EFR8TcLy4OcW7yXjH7OCaeh+AEyU91d7BgnpV1OJ1WDIh7fUl0nITa4boEy9o7sTQ4taF6vvwdvUCf+C5z4Xs8lIvTwAARABEzQ9vk1fpEgIZxA1Sia14f5hgRqwTI90APXcHZnnbF2gHMts7XTBPz4MUDnjB8nKnH4oTXJ9Twnf2+PAPj7u6uApzPnz/XZ7YAoJCXQb7X1baKnN7f3+uGcbepDcNQ1w85ACYJasjBAQl9JFGxzBw8Pnz4UAEY9uPrIA+SVwNFdArdNrHhxMLA+3A4rHr2GQc6uWXH0DcSBnwYQXAYhpjPe9x4mCCyjChnpLvCB2iy/dHS4c3P/J05bn0f34uImlAS0B14+N2glOQcMLMFJgRUAyl08v39vT7MjjUx0WEixe0YgH3mwcEG3BO/BZjAT2Ab/ESH0HfkZGC/PUrXrCQEAu+hoySpjMlJDp8BUNrGnQjbHtwu5nUDiJhR9xxYW2TnPU0ppcoAY8P2H/x0UmWCguuzXvYH+FfHA8Zu2VoufqaQ29I8n5xz5HNuxj0ZfwNb7UF++Ctsk9On+J4rK9itfaVtx3phgMmhCcRYKmNm7M2229aJdxFtn5KTPdbOtgXmwC86aUIWxlTbPWSMa+iH2vLDEeh8zgAZH817PvQCXUUu+BgDVeSXl7KvwpXOrc/0OjEOYzZXJ7EL77XDlnxAg/UT2RkTmjjGDoxtHc/RA9uqSQ10kOuYsLWPdTxwUu33nIxYh7e+m3vN8xxLzrHIH/l+KaU4XDSSx3q3vYeJzSKLvNL5X3r9Ucfbmq1lMpz+QvbLgtGKBKBiUWoPZWrsuheUidqR8F2DU4NYmB8AnDPMCErIrV2Fe5h5NrjFwMr4WwkQp3Rzc1OZUo58dbDgmhg+jrzruppc2DC4PmCGoy0BZSm1Bx5yrjvOsyQ0l/H+fqwGZKUkySDbtcETbN2X5wzWAM6gw4kkzpK2N+sHDxsCzAIoDYow/oi2ZwZm9/n5uSjpOSB6Ix7zv729XZ1aQzLIiUPoAxtN0RsHUwc/jI2yvzN7652TJMrt7M/hdz7r5ALZe2MzlQo/KIn14xrWK+yJJBb2FTAFIKSf/e3trQYXA1p0YBzHuL29rbYR0Y7I/Ku/+qv41a9+VYMJawmgYj4GlDj1rX2zlvyOTrF3hd/ZF8V76BH3ofWQ9Xl+fl5VgUheIlrLVs559fwdTjXi7zh6klVA6+fPn1fH57qlh6CFHrEOTlpZPxMjTkqZk0EtFShOD3o7vtdxf/r0aZVgpuXcq3z2R8uy1KoQa70FctiegRO/I0fGg//id/ST8fE7baBXV1cV/NhWI9b7yrBBZIDsvcl/W5GpgGhoJ9xgh+gDn90y2q5iAY7w9/hYkyGsD76TVhxkhR7jE7gXOuEWBgMox4ht9Xee53ogwxZgsAYmEwzG6h4dzQHZ+Ihq/A3JPM9DmqapMu5cl9eWaeZaJMiuppMsoYPojfdYOaFzhcAA0HZBfGR8tjl+8v/EUFfst//Pw/xSSvUYZPQEu7+6ulpV4llrdILrsfauqiIXqox+7gxEzXYOyMuVC66P//D+PtYFP0lXhhNK9Bh7cdUE7EGcSSnFNK/79UvV4bLtYYn1g5PxByYXsWPrJutpPFO+u255cuzDTtA1sAjrYDCOjzFxjH5h48QY1h0fYVkai/j62/F4Xug0Y3BShXxYD2K144Nxqv2FdQOcZ9k0fNrwnpMb5tCnPk7jcXXNis3jfCKViDvjbtZmW10r4237d77l9c2JxsePH6vyMACDiC3748+iIARsB2srF8CHhS9/KyUeg/OcI5YlBw+is5K08vAu9vvd+Uz208rZIjzui7EAzJyB9j17PMqOf76DwpcN7+v+1mVpIGOrQFsDxWjHcaz91IyBOTvR4T4APjJq2B/aBu7v72vbiVlLHGRKqQJ6ronDsSMFdNiwzJpGxOqpme7RdFB0sum2ETOIy9JatQiE203qXkcSMDtf9AD5YiS0ztiBEAxwggYWMElUppAFG0epQMF8mg2cpqk+uT6iOXoSDq7N707S+Z3+ZRyX2VHsgPFxHWRPkMTp856ZIdus90Bt2daIiE+fPsVut4sPHz5U3dkmSk5u0S0HIN4zKGIO3BdZn06nVUL08PBQS98+JYWx4vixbbdzMlc/QyYiagujk0eenQADTivn6XRatTLhn9A1gjZzdesE/gg7Zb6s9bb1IWL95G5kkbr10d014HZdZIFLPs+13C5jn2JQvixL3NzcVHk7kbV/ggSAMGItkP/d3d2KhXQV1YDbwNXjMYES0Z6RgPwctL3eZhyRu1lDB8xtRZp/W6KIMXmdtgwuPok1Yy8KQdrzM7PM9/kMz01BngZNJngMYAwo8dWvr6/1nibbiAsGLoBaJ5LEGeK61wx/ZXmxTsQc5Idt0qLJeuFT+BzjhligayLnHIuSw5xzvL69Rd91lTgDPNoet2AeP8XfnJCgnxGx2stnlh//iK/Ykj7b/TQ3Nzd1rsjPts61XYE4jWN9Rg6JDt9jjZE5CS/rjj/kmqw1fgZZuNLBAT2JeHpaE099v27dxV9Hiuj7Rtwau9n/uWpDbEfnaHOqJEA0dr/IzKc/rbsL+H8nF/gG7ufxOPY6KQRXoHfYE2tk3Gof4VjDmvp7BvmuABnLZdkB9zIR5CTFvqn8XiRW55kidvtdRI4Yx1Ms8xK7sz7Pugd+DTvHtmtin2O1Brz4LGsGvmlJaEtmvuX1zYmGFct9gCgCzhRB0eNH6wnsJBMon+tinnN0XeuRPxwuFXy/fmCTN/EUh9nHsswxDLuI6GK/v4i+p3KyxMvLa6TUBadjkUwABhgfAMxKVMaZY57pAU6RM21YnNhQkpri/HP0/S66ro++30VKfXDkb1H0HDmX5KkcX9BV5n0c2/GZEV2MI0/HZgN9Y00wEEDmzc1QAQKBH2fFdyIacGR+dmYR7SE/BmQ4NuRvsExvL2viE7pgtqw/BOW7u7tV9cjON+fWGjEMw1dPu3WCZOaF+b6/v8ft7W1ENGM22DUgRIYEP4I/1+E9Xj/++GN8//338fnz57i7u6sn7+Ds/SDFu7u7uL6+joeHh1rpwInh8AAMtJ6YxSLBRJY8BBK9J6mIiFoBYywRRVeQM7JCpk50SJKQE3bK7//kn/yTyDnHf/gP/yHe39/j7u6uEgYwlzx3gbWx7hhQuS1j60i9d8nAEr0EKDM2gA2nJHHQhJm0aZpq/3BKqR7La11kPageOWhumSX7C/wYsgNIAEjxKR6Lk2p00ISN7RUiYRzHOOz2Mc1TdLlUMNKSI+c5UtfFxdV1TONYSQizWQ7MTlTtE4ah7GnwXgLWymw4rCm6anbSbB5+iITB80ZHTA65dxkbJzgzZogVdNj2y1oC3PAlZtxd0fEaEIfQG2LcNimy/0CfzVZiYz6a24ms1zoiaiWZa7iyhs1bb5gnQM5x2C03rDtEBTGZOcEMm0xgPbke/29iiZZm/oZ+e12td64WMzbmRczC10PAvL29xbTMMZzHu+tLAp2GPoauiykXf3XY7+PqtnQULCkiDeUEudPpVJ/TYTKGOGeASkI2nsaYpnm1FuNpin7oV7btmMHaOGY4RmzjEv4K/TieTtGddWKiwhax8v8GnF06H7jxforIKSKnOB1bl8C2FbitW5QT6Pa76Ich8lI2X6OviaNWo4u+72JJjVnHBomNJTFJscw5xnGKyGefN/SRzhhtPE0x7IbYDbs4Hk+Rl1KxWObSHhUpRV6izOOsJ9HlWPISXV/I5H7Yx5JLu0/k8gyw/WFXSZ7dsItlyZFy+somt6Af/46uOhkxJjAm5e/GQPZFvCB5TGQaW/V9H+M0RY4ceZljmc7t80uOSHHemJ3LvKc5ur7owpKXiMT5uhHzMkff9eVY4SiJSteniFTm+v72FtM8R15KkrEsc9GtfCbS81L+1g/lhKp5iYgUp/G9zhnCD/xgOfL/bnWNaFX9Iptv26PxzadO/X//X/+fVfC344GNZLOne3mdeTK4iDgDg6LclCt5EcScQboK8XNKZhCJEeLceMG20KNNoMA5c22EjqM2k2hl2yqws2KSIgeAeW4PwwLQ8F0cNBl3SuXZByjyft+ejYFSNzZ1iuPZ+cBc4OBg6/0d5mNmgiAJO82LtihABmMFRMLso7hu3TGYdSYNe+WydmVOoj3Ij78hV4wCkGt9ZH2djLoSYmbi6empXhu9nee5njhkXUD+brVAt6aptMTxoDL01PrpMqt/Z57IHsAHQHBPKbpINYU52aFGNCb848ePK2bJOkOwzbnst7m7u1u9Z8aZdT2dTvHTTz/VufIU8ojGhngDL2uEPvZ92UBqwIWecg3G64qn242QOXZDpcEJtffqMA4HlmEYamsd/sJVOycG3pNi0BuxfkhmRANoJEDo2lam7jM3cHSCsx03n6Pa41aTLUPLT+sZSQBgFhmb7UbfXCJ3gMEPICO3MBCIGSstHk5oSVKoFNVgvPFT2ATg2sEO4gKd2ibl9hWAQ2SzbeWwzcCwGlibSebabitC1k5s7dvQEWTMi/Fg74BwkuTdblfJOcbBnh/7BeItPsEEGWvC71ShrH+8TzzEXiEz0AHiqeWFnrqtx3Pr+35FNvB9J4e+Fp/JOcc4TxEilHx9fLd9sBMdJ5dmjUm6vE51s3Vq1Tfug8/b7Yc6DjO+rgwakJlM4N6QZ7Wydo4Z7B98fn6OYRhiv1ufvhjR2gbHU0s8wVOVLBnWFQb85TRNMY3txCz8s9fSWAV9deJsH0XliFgPPvF+WPwgLZSuALg6wpqVe04RqY2fuM/9HH/d9l6So77GCHCD4xjjMsYzVnSCbDvdMv68j+5BUtg348ftB6d5rs818vXL5yOGfn26oA9LMmaOaJVly3OFKbouDru/PVbZhrAVV5j4mwkW7mHSzfqDfvZ9H/+7/8O/jl96fXNFg+DGYrCQvAe4pP+RE6N8og4LXIJA+743D1kpmTj3BnwBcgzSWSQCnbNbWJmIdloADABC3zKUGJRZcd63YvAdZLANUtyTcbv33w+Gur6+jufn53oeOX9vTF17cA3rEUFLUnuoi/85UPId5G+w7LYr5DoMw6pf+Hg8xsvLS3z//fer+VLVcDkcp+bEDrm7z5b30AMCrxkVswvb/smIluRigLTVYEiAdOsY1/emRthq1pDqgEERjg/AQwKFI3BA8t/sxHEQrKvBGs+bmKZptT+GE5ucOP9cEMbhfvr0aXWUbkRUkEqVabfb1aSSsT4/P6+OrXRA/+6772pCtSxL/P73v49lWeJXv/rVV4CBnwB3dAzdcP+/5UHbJPKmpYSKA38D+Pm7EW3jHcALvXeyui3Dsy5mlAFkBBDugU+yzjrgUGEhWJAM8x3uHdH2tDkJ3lZLXPnY6iqBnnuja8iWQMlcXfbGl3l9uLZb/MyWQ5J4H5mrFgRGAhD+Cd3Gf2CzXdfVTd/I0DJHnrz3+PhYdZoxOAB7s7T9v32GSYCIVs0EXHB9fBTMO2uBb3RSgezRJccrkxl+3/s4DAx4iK0PrnDLlckt5GNbMFBEB0lEAMIkGIyVtTZgp32QNUV2lh9+iLV0u5rthetiR5AlxGqDmCENMcuPcR8ndo7ffN+VHe4DDoiIalfYL62lrBHyZx0vLi5i2DWfQeLCGjrJph0PWzOh6rXFD6DfXG8cx4jc2sjdTtz3fUROK7/D+4Vtb+CYuRfb6WqMQxds28jbRDDyRX9SStUGqAozZtaAxJh5OxlB9109NR4bhiHej++x37fDPlg35GviiuS767pY5iWOx3Xl3RU8YwTLDj9lksXrg04zThPmJjy8dwf7cFJSr7usr119RVofpUsiiE/aJhrGlbyQYdWX5ESmJc4mtm2Plg1y5B6ukPnv6J79MrbxS69vTjTcV2rGwCwQAvfmXDNEBl38Y/BMzgJ1tu0s0k4XgW+rIhiVe/CdSMAqRXz9QBfu6+DkTYuM3aziNmB7EfxZnD3XMvNPbzXfx+mX/vocZ92p3yPgRbSgR3CkRO79NAQ4gsgwDKsHLTF/gitrAtDh9Bk+A6g3yCHQOyOOaEyBKyrIFUaY9WMz9/b7rBMBmDWOKO0ItDNt22gAZFun6mDT9318+vRplcVzDZghb2TzZj+cthO7lNLqaee2FYKUg7J1Awdh1sEADkbfOjeOZUP3dq8Avf7Ilbk/PT2t2BPaOQyyn5+f4+bmZsXS0kN8d3cXf/7nfx7/8B/+w/jtb39bj8FFF5D3NoBib+M41gqSK0929mYt8Qlm9lg37sPaOnDZD5lx5rvMGfl60yBgyIk542CNzZLZWRu4A3oYFz7QQZXEhKN+DaKt+waGXdetHmaIHiFz2419Fjpj0sIgEgYdG/G5/QB97JPxAdBcOaP6QEJj0oZrYX9+PyKqjc1zOZSCdkgnM2YfnaDhkxxDWG/G5rVkbRmPWxG55zbJM5Dnuxx8gU+IaEfH8j0nGJza571dkFskzfhH1tLteZALjB/CB930mnKP0+m02u9hX75t/UP29h3Ig4okPhGZm2hwVwJJhmMBIKZiiLxEUsJmFpnvMVb0gH2IBvDe98QacE2TR0Pfxsc67Pf7ehwo+kAFxPsiuY83YXve+Hhi0ziOpfXlbCuuYPCEZ9YT2btFGgwEAL28vIwc7Tk+6GOxnyWWvN4bh97zE7lzypuBNDGJiozbi227zNFrbpDLNdEz5FZjelpXWGxnvPClbiGM3Cod2C9+yMnrlgji+8Z7vi9zoYXI5AJzR+/RTY91u68jR5s/92j/vz51D73xYSv229ZHJ981Xsa6e4L18jxdvfeeRfAL620cvSWsuRb+6r94omGQz80wdDtVgF9ErP7G4O00cm4ZsgPrVrG5Pw4YgcJUbPt3UQYWgVYJDMwsHILCuD1XFsEsg42MEh+KgoLgSOxkDbANMl32xoFUpiOa8pY9KO04Qyoj5drt1AOSDeQX0RyMe6xRRpyon9LM57eGiyHyOZzhV0rfrzeAsy5mqCNakONJvIBbghay8abobTULwzHz5yBnIESAMhjZAm0CNRUPdBN2g3VnbXCgJDgAAxI6AGZLCtfncaMLlglVE3SEoMS4vK9i+7A7rsF1DDiYC04b8uDx8TGurq7qZlbm6Sqgr388HuP19TV+9atfVVlz5Orl5WVtTyIhBAT6WRj4CfsUJxRuK2E+yMOyY25mstA97uu2GloEWVNIh21ijF4DvFJKtXWPnnDu54SNdTSQMCCLiHrSDUmHmTsSSRIcM9xm5lhPy8ysJzKxD8J++LxBBQCGz6Hn+Azr7pa9NluLH+f/SZZNIpmI4Htc2ySUwbO/syxLXR/GbB11UmC/YNbf/sfBkkDr6pDtEv/iZNb6ie7ap9uncA9/Fzmz0ZlTkBgroACw7wTR7Tp+yJ1JEZJHE0gGRZYr+sA6cg+6E4izrhCve7bXCZ4TWz+jaNuiOwxDxDLHLEII+zOpSHKNTaIfPmwEQsxr5/Wa59L7ntL6CN/aHjyluLg81NOi0CPWD9snZrp1EtmiD1VHBWi3GKTvWlsRuluTw2G3qn6zbvM81159g9mq25Fi2LUKj9cC2912FNiXOaHmu+ik197Jt21qWzH4ucR+mqfYLa11L2J9qhm2aDLicDhEipZ8GPib0LHNewzoKX/je8QB/r4lX9BH9IH5Gfs5Qe76PualESnMu3y/q1Usy9VEtTGMyRuwg7sBUkrsFq+xHT0Fk5o8ZQ78xF/YX3Jt4oXliH3iK77l9c17NP6Hf/ff1wXt+74CHAaFkjkQAX5Pp1NlmTHAEjymerIQZXUbDAqD0FwONJNpB2kFcsIAM8sYyeBYAMCnqysWNAvmjbsYh5nyKtjUqjvbKo2/h4JHtPYzWk1cBRjHU4xje+ItjrsYQNnsjsKbQcPAzIpFtAQGFs3gliQGQ96yDJ4fgRCnAOsdEbVVh7Wk5QjQgfMAKAMaqFQ4ICND7w9g/Aak6AUg3+yWK1xbFt1GbCaE9TcQZK4kdG2NGjvvZJyN21Q4fFoKn3H7idmYnHM9kx3GA/k7QPB3/uZrWNfch01CQIC8vr6u64PNGagSRDjCd7fbxcPDQ9W59/f3+N3vfrdiWGFEsbMtm0SQxnGZiXT5mL1fJh8IEoAdt07Yj6An2AR+wraL/7HcCO5OZLesHFUZ64+ZScCfdRu/6OQTe+OYS9/HydLFxUV8+fJldbIY8scuCL4G3/g15EXSyTz9TB38IXNC55GtWS9XDp0kuF3H/hQdts2aCbeM+Xzft2dXuBrA+rqVwbbIdQ1UWWMHcPs4Vx7MtnMvkw74MJ7TQuLqteZ9kjXADuy09RB58ruBvvdp2LebyHO8ZU0NMpwQGaCabMPnkuxAcGBfXOvq6mr1YFgni25fwoa4vgE2vg09zKmAY+YHUHd7jpNo3rN/Yj2Jn1wHuVvf+q59zvK7vLyIrl+3xiBTCAASJYNc1n2bsEdETPPXnRoVxIrVN5k5TVOkaIkV3+N17pap111/JkXkdogAuuw2GftJZI5/cJWPa25BZQXVXavSuq3GxAPE7/qzfewP66ddm4k3qW0skpdWASEOe+3neX30trGiMaOfF4YcGRt64uTEBCy2YLxg31o2fa+f/l3je5QTvLBNxsd8mQO+m/kRL9zKVFukc4sV2/k4uSKpwAfvdruK0VgDdNtkATqGHVgX/ut/9c/jl17fXNEoJzWk6LrWelRAXhfD0Jy7nXbp2TvG6XyEGovYdeW4WN7zmfcEToOMiKjP62jOJiKlBgxZBLNsZvJxeq4IEFC230HofugTDo8ki/sybxT38fEx9vt9BbS+JwrlRcMQnBwBRjAUFAjlcuCY5yW6rhitGTsrLkpFYuKgi7FZcRkT8o5oDsunzTDvLfDw048xEj6HY7dzxOG6BM01+ZuTDmSCY4tooNTOHnBkVsI66mBulhOHbCaEvUawHrwPa+9KAXNgzbey9cMZHejMiHgTPf/MDLG+3A/9sT3wO7oEQCOxofcWEJNzrgADB2gmB4aFRHS/38cPP/xQ9fv+/j4Oh0P89NNP8eHDh5jnuZbmvQZOMFwpYg7oBYRFRDtZi82d2LpbiSAPDDyQRURUh8rcCAr7/X7VqmbQ5KSEz7tSgx/kfYAT1TD+mbVDv5gnekKL0nbDtcfC57aMMUELHQcgYEc+UQQbQf4GC2Y4qTb2fWkr8THG6J2TK9sTiY99OhUh1o4kDRs1EMMP2h+jv7wAGQZ1rJVBBj9NPLh6CRjyMc/YB9Vexuw9Q9ivkxninvdomUggTmBr4zjFbgc7maPv234Qg+eS2KaV/Fty1PyBEwjuuSWLbGcmzcymwih7DLs9D+yc4v1MsrRqazmsBF3Y7QBd8zk+DRVsd10XXd+Vk4xyOyQj9X2k7rwval7q6U8+iKVUAMqpPuPpFF3fkslSMUkR8X6+5hAR7QnyBoJd1w4GoDLRfEeO1DUmeksCDWefgN8pOtxOCpznObq+Dx6i+3a2PZMYtMgtyxLLGXzmsqjRCcB33fowHOt3XiKmib0J+xqnil6eVlVbbGNZylHW4zTFu/zhOJ19Yl5iXtbsPuuDbeIjHEPBBvYLyM62ZtDa912tfJsUwLYdZyHkyn2L7jh53+93EbE+fpxrDbshlvkc0yPHYVfInCUv0ee+kp3WdWKBK56cOhrRAHdEOUUKWfCzH8ppYrTDQyyQZJhw9h4MP1PLGJDP8XLSWOTU5myiyA8x5RpbDOoEA99rMnAY2tHyrCGJlcf3d72+OdHIOVXFL449x/s7PaHrJx3ThlKM+xApUWI9Rd8PkVLEbtd6nwEy7Ri9ltWO46k6evpRcWYpxfneDVx6T4ZPn4JxJXlgsYrzmYpzSV7AXQxDOarWjBas6jRNX51y43P+zVimlCo4wBmZ+WM+2/KiDa0saBfH4xgRGFFjXA2+UEiDgMqQiAkj2cKQLi8vV4Gb61JBmRUoImI1dvq23e/pp4hHxGpsTnZw5Ch6xLqkb0bCDBrXY1zDMNSTulhfjBl5c08YKByMW0ocVOzkzLq7emBmDxBqgM99ubf3ZLjShNPnMzg+9qzgQNzbj2wZE5/3w9pIHAg8Nzc3tS0AnTGodaUS+bGxnrFjky8vL/Hb3/62Ps3+8+fPcXl5WTeW46y3gBZb5f8B6vwdfQXUoSMkG9jU9kFgAFGCnttp8C/jOH6lJymlWtHZMmIASqo4TkaxFdZ2fdb4+uQnfrpqg54hH5IM93lb39lT5UBgvWUusFbWd+u/7RKg5TY8g30nAABqZIOOuAKELbql1QkbL2zLzHPXdfGrX/0qHh8f69/M9PE5rw/XcguL7Y4qnpM0+5aIWJ0aZ7BdKu/taF98qAM9xADrAUuIHfs6XLuMiY2VOea5kRvzvNQkzyTM4bCPAkfbcxmKvUCSRfUNzNdJJbrs1hkSCu7DXPq+j+eXl0hdOY3qcDjEaXwsAPX9PQ6nfeTzgS5LLJHTHOM8n6vuKU7TvNLNfY7o+yH6vovUd9ErwctLe7p3nnMscwFO42mKpW+tM62VJiIvOaZpjj5HzLHEmKbou9ZWvSzL+TNTLHOO/f5QjsuN8rCxvmuVbA45oAI5TeXUpog55uUMmnPEfn+IiBTTVNbx/cixnynezoeOFBl3MU2N/Om6dRvSbrc/a22q+KKOey4nFkXkSF0f03lMaV5iiRzRtare0PURqYt5yRFnX3lxxmd5aWROw0tne3h7LcfNpojTNJ6TvqJZ49geEjsMjRgdTyXRtc1jawa3JpFI6NFDJytFb9vz1YxztoSh22dbMhUxTufjZ/uyH4JEN+eIYdfXRHaez1WJro+USyVo2PXx/j4Fh+z0Q6tSpFQeZFc+HO3IWV4px5LnGNkT1Q8x7Iv/Hnp8cNGzw34Xu6HIIMXX+zPBfU4Gma8xAp/HF2w7aFxtIaabrMfutwTXNokmPrJerN3WbxKnt+P4217fnGh44gikZOUto41YP+22MDQNEBkEuCXFAJkKx9XVZfDgFlp6ItrJCG1c7ils+z4QMGMCiHEPFqU4r9a3ymI0B76ItZhqWfbl5aX+zougSkAEVNzc3FRFcLC1AiFjkh/YWSchh8Oh7gVAcfb7cqTwy8tLfPjwIV5fX+P5+bmyhxgoABWAzDUAoCjwly9f6slSAEUHTebJ/OxgYGnMwpslYBOiT4LiezYErstGVAKfk1LGQd9v37cnYfMi0NlZsT5cEz1xNYi5MQf3iafU9poAel3Gj4i4v7+Ph4eH+rsZT+uJkwv3HcOIksTQX418GKuTRoCD9zcxdrPjDbS0VhmCAkkm+2RINr2vCMZ+HMsDJtEPA7fPnz/XJPzq6io+fvxYSQjG4yoY+mTQGtGeu2FWeltqdkJIsu/WCYATLXck5t5/wn3xQyRS/B2ZoWP4HyoC6C5gGCdsf+LqmoM+duUN076mAaCDBJWUruvqw/a4L20t+BCe7oscTRZA4DAfiBqCIPfk8/bX6LWrf8yfIMb76Ix1wEdGMybsHRmx7w/CaFtpi2gblU1EIWeCM/MDHDk5NJBxCyY+2baKTpAUk7wwNhMjxJeI9YPgyvdbUuSfyBgigMpt0Z85ykNj28Z/7xValqgtlFyz7fFrvdbbKhLrM01TZWDL+1HameT7kA1Airlis4dDY1B3u91q30hKKY6nU1xcHKqcXPWa5yV2w27ll5Gp9Z51AtAuy1JP8iGW8Xlk6GSPZLAlAutnhAzDUGMeJFo6d3JM8xRvm0MCDKx9OMOWkLKuI+sk+a7XpBz/Whn1FLEbduvY0fex79pegZSa/2NNIFhcuZvmdTutCRMeNmy7TSnF0A/hDhJ8rvUbIOqKMmSHiQljEipYzIk1MZj1/jbLkEo5120k1hLnKda2Rd+zVaLXRDfXsv5wXeSFz/c8sOk1AdUqP/gK5ARuNLDHJ1HVYK7N3lq8Bwswxnma4vJwUY8Vjlgf1ERcwr9zL8bjyogxrUlBE0H4fx9+8Uuvb040EAys/bonsS2KFWG/31XFRwA4RgwNBpwH1wEs6MukBG0mDcH470U528PzEI6fzWCjQAkKCLiIaRq/AnERLWDxXQMdxsH3xnFc9aS7NG9wAZjlO7xvQEti4CQDRhnm1u0ZJHF2bMjQwd+ZKsGfoHo6lWcwwOCxRgAagsa2VQojojXKgdZMo8FUSqnKar/fx/Pz8yoBJQhZJ2h/gM1GBzBugw/kyzqR3JiB9lowP8AqCS+6EtF6YJ2s+n0C5pcvX6qR+xQjM8VutzKzwXvsbzHLwz0dAJA1jsD3gUFlLZzMmEVDP2Ftr66u4vr6esVuRkRNTvhHAs0mVgAF476+vo7Hx8d4enqKm5ubFYuKLluOTvSYj6+LvrJGDgBmhQz20CPk6woS17dcPY5hGOrDvawHrpKY9cGP+fQfBy3bje+Db3QCDIlAhaSxue0BiG6/4J74PPyHg5mDBWMiqTIYd4KAPRlAbPXQwZg1Rr9YAyf2+JAtMcDn3AeMbQNquJ8TfNYbX+b9bfa7zIVKLWw2axERNSlr7HTbkO01YAxeI4MBV2ENNNDVsuYN3OBLmTN+HZ/b/Fwf0zQGLcsptQpgWcuL2ibne27HZxKGZA6f4f0g3VnXeR/7xAacKNmWOFGLpKBuoL5YV76d1PVK4LEXfOqyLHUflYkskn9Xwg0q0R/HaezMxBNtvvgH63pLDncxTutDBwxi+R39YO3Rx2EYVgeJoAsRscIXjB0bw2adVBpIci/sO6UUs5hq9KkSAgKgrGH5vTzFz9VUZDRNc3nCX7TYasCLvgOat/JZ46qzfPMSMbf2Krdie/5+ujz3c1KP7XBdr4ft33gBX4FsGbt9lAkx1sQtU1TA8E/c3/aKjuKXuB+EMr4FGXDfiKh66THYV1USJbXWJ/SKz4AHjNvsn0jESXSJG2AH7sPL8nJ8+6XXNycaZuu2i9517ahB9y4ej8d4fz/G999/H9M01U1zOEIDU4Lk29tbXFyU0hjsKU7ePWE4ZAuvU3Yc0Tazmk3NOdcecz4TkWMc28ZXO/y+X598gNHC7uJ0actCEfq+r+0c3pcAKPDCk6Aw7qenp8oswgpMUzu1BxaZJ1EzBtgckg6zNFYQ5sn3SHIISBjPblceKgR7jx5w3S2ow6mhkHb26A8n7pA9u81s208Kk84LJ2DghBMxk2XHknOuzDt/v7q6qjroCgr7a7gurWQ4hKenp5imKW5ubup4zBwiA5Jxbw7FiNGl0+lUWzr2+33thb+5uanlU+5BZQFGDzl7TpT/mb8dKWuNbTj5o4cTeaL7diIE6iSHhp3c3NzUMTHev/f3/l68vr5W3efp7j4O2KylEzknfw4wBFE+46NxSWDRl0aA5NUpeHzXyY73UhlEOslG781SW/eQK8A/Yn3iHp9jLmbdue/V1VUFltiPT48zk0QSwnrgi5izwYpZNfwtY3E7G6DOdsvYDRbwI1yXcfBd1s+EAjoFkGUu+DKDYLeARrQ2PmyGwIkfNdGEvmDXBproGWtiP8ZPQBIVPz+vA6baAMbkAHYcEdV/mr3GnteAq7Xz+dpUNHnOiEHrOI5xfX17rgZNtX2579sDXSEJTNwQg4g5Tg59jCqfT6k8YA5b9f4c+2Qz5ciLuMRc3eWA7GkFJUma5zmGfohx9F6Jti6tP7890G/bV299tE654mwmGX31tbnWly9f4vLysibh+MAupdip7ZZE06y8/ZT1DsDnE9S4rpN75GFf5m6JiPURvsjAhFsseaXj+Pzjea72ZcTmkkg0EIoelNiyj2Vet2a3Ssp6jd3aYzkYlC7LUnq1UiMsnCSYcGXuYAd0m3sTW+1Pbdd+rz0uYN16zTpxP5PA9hcmHbAJrm9yZ0syoavgAvwaFVF+Z61MnhHHqcqjI/hKMIxbnpxQOO45IeQ++M6Hh4dqHyR+JuWJGfhC7PlbXt+caLj9yEZcnMtUFZ9A5JaE5+fnaiz7/b4+1CoiausPyl4mWnoFEQRA1yermJVH2cZxisOhtXYAVlBM2gqmaaqsX1GcLnJufYckIl3X1zakl5eXei0rGoqHg2YzbT0qT9nn8XiMjx8/VhC2ZV5IxHyMoJUVp46cUUrAAH9DaQ0IDSAAMRFfs7IE/4g4J30XNYC4D5kMHYNlLBip2QAzCXyGe9Aq8fHjxxWYd1LhOZJ0MQYcHE6WoGHmgxfz48FYERHPz89xe3tb2zUeHh4qG+c2N9YFJ7VtP6ByUVjFw2pcvLzBi+94neyQXAVEbn6ZGTmdTnF3d7dKznA+Zq6wRWzANrVNQNFFiAEDJByqgSf27nk9Pj7GDz/8sEpmvMHOFUqvtdeLygef81NjCZJbtsnstoEVOroFs+gsYK6RDH0F4AApAh06EBF1XAQnJwXWRd8PUGR7hjnlvnbkJCs4fpIKM11UCJAJwYW5+FCIvu9re44rLQY1vMc4XF3DjglMTjDQJYA7CY6JDzPLgD2vFde0X5rn9lwHJxCsgRNjV+EiopJNkByOYZaxk1rLjrni+5kbPp+HWXINWjaoDEe0jZit9artJ0COjAt5mhiwnhTwPUbO54Rrt4/39ylSWh9Fz71JqL1vDnmaefUapVifaIVvc9cC8yKm8D7zABDW9oxY6wCvUrneR+SGNdBxdNQMfkSs8AAYgPEAkqyrbnlhnN7HwOchL1z5Ink8nk6Rz1iCdXZFyYmw9Qf/5FZACADGzmc9Roi/bTzBT4N18OnLssR4OsV4as9+MtnVd13sD/tVIlCT57m05iEPQG4lDaJV6C1P/K7XE5+8JQWxy6ILpYrFtez/DfKxd/QLHGDixTrlJAk/2yp+JYb7+HGTHdgYcnfMc6LNfE2O4R/cWeHPu0NlW8WhrZw4Q9whVjlZdtytPiw3uSM//r6txiMXJ37EZlf0iHvbygU2bcLhl17fnGjQEuEFZFF2uwJsnp+fV9WMkjE3RpYsLKXS1uPKAgIti7pWSLPOOGMfeYexlhNByvXIXFFQAo0Ng6fbLsv6AYBs7kWRSKJQOIDZtmWErPP9/b326BMknp+fq5OmSkAGyRxQWIMPlB8Qy7g48hTlQhG2BsNYMR5n8tvA7wTCwQ154LQMfAmUrJ3XCbnQjsD7Bmk4i//0n/5Tfejb1dVV7TUmKHM/+hBtPKy1AyuyYE44YbOzBpJ87u7ubpWkPjw81GTEbDVyZR5bsEC1C73Hhpysb23FbAqJLPKhdY7gmnPbbA9DaLbO4AD7Q2/sIFkDGFfm93PB1ocoOElAvugAcyc5//HHH+O3v/1t1QnkhjOkNc4gDTluj+i0nrHGZpbsM3gBVMZxXJ0uBfBCBswPW2v+bd2OyVqzRoA/39MJgIMCgdDBxIyeT8Bp/rABTge+nHNNFlzNimhHZbvS9/z8XAFnRKtUMTcHTXTWCSifZy04IMCBFtkhR2wfH8w8Ilqr1JbooF3SbCL3q6DobMvec4YtuKWU77D2XhN+YnPEGdYW2XgNYSCxR/yb2eV5nlf7l3xtg61t1YG/E+BJXNDNx8fHOB3HsrE555jnKYbdrmzUzSnGqVXvkJlJGsbgxNMPJwPksk6n01u8nYETQBDbNevOnNE7sAK+A7tKKcU8zfWkKMbFWI/v75HSuq3PuoFd478MvtBn+whezHWbuEA4WmbYBsfhA/or3ogcS27xh3GQWGNzjJVxO9kyuWhiacvKuxKCvCEqfXADgBT5l2u0+3AN7rnEel/isrRDKC4vDtV3oPdFF8ZIkVZ+mL2K6DT3M0nIy/G2sfntdE+TKBGx8nW8kN3t7e1q3K5EsN62gXme6xHzrnIgF7/wb04kuCa6R0zfVqZNxqGPxlVUyYkrlrH1nISU8U7TVMm6Ld4ahiHykqPv1lU6/DHXRQfxRyZ6WDvWwSQK/xx33S5oIvfvev0Rp04t8fLyfmbxUxwOF1GOjjvGOEZlAh1MI1LN8MZxrMb7+fPnahzO/AAdbIJCSWCPUZDyzIjGHjqDJGs1C29GEYUxwIuIc5bOGIaIOJ/zfHaSzupodYpoTIoZTC+ES8ssdM45jsf3es3397dIqTyUz4CTBY6IGrR438nQ3d1d5NxOBiCYkDRhVM5A7fgoTTvZMSjAefh5H2adMDCMyaeEIRMDl23iwbMluN7Ly8tK4VlXfifI51zKqW6fsAMy+MSh8x1YeuZskGfAToD1pifrJfNnjHZQ1RGIhTPThU6if76WGVf2L+EQnDRaJtiIwSb3Zo3RLVcD5nl9DK3X0U6mBbFmOwBZy57N5D/88EN0XRcfPnyIn376qdoizo1gj0wAF8gVeblVYmu/fMbBjvXeti+xngZOzA3fwLqaheL72CIJIwCEdYfBxqk74XFyxjob+BJIsFHAtnWFtYP4IJDwPjLlHk74uT/3BGD5M65i4Y9pMQM4+m/YNv4A4sXld/sc/Ajkwevr63neEeWI1xzTNNZYgi3hi8ygu3XEPs2VmohYJWLltJ98JhAe6/vbI4rr2fRdH33fnX3jPspG7PWxsbxM4jSQ1EXX0WJXWoyLbyjxlGcfuW3KSbd9JP4upVSOIu3aU4zZCL0sSwy7XQyqfFycybTj+/v5XP/2sFwIu64rR8PmiLi8uCinXXVloy5riT55HKwlfo6f2xPOkFfOOVKXYlHCxZr2fR/LvKxs8udOSnOcR3+pKMJ4e+8A/gkfRbskcdQ+1z4IIuB4PMa8tIp8ihT7i9aexefdxtp1XfRdVzqDAKHzGvjbLjnOdjcMcXkmR7HFvu9We4DeXl9jOMfioe9jDh9ZWnQOm8FPOjYNQzni1cl+qVbEecN5qxA50ePUqeF8bGs6/z++dMnnGLgssSxfV+b6vhwOxImkXV/28G59tRNt1gOd4ndXUyEETFQD2Bk/13JLKfqE/jrumjjiQBrHAq+7kw3Gg+82JuEzPEwSnOfOAx9U8HOVzS6VB/1xrXReh67vYuja8e6sP2tngtW4wZUpXsYwJNBusUJvrFvf8vqjEo39fohhQHE5UrSdlGJne319HacT5d3GVHl/BhP0zwJw9lEeUNfYECb9/n6MlLqz4h2j63KkxBnl7ZQmC45yn4EXLEdRqH3sds1xlPJhjmlqPbYoM4GIe6C4rvTgkFF6gHcJjl10XWn/uL29PSchcQ5ujRmKiMpcsPhc3y0xMNRmEUggzLqY3WfcZrecsXNKj0Eahro9wx9DZt43NzcrYEMLmSsrPAsBORr8RsSqPcZ9w/wtoj21HBBNUoPsaXNBPpx/33XdqmXEJUIDVgcQ5IBTenl5WSWpABSXcJG5EzKAqati2IsTbY6Gvb6+jt1uV5NamPDtfgz3v1P9IihfX1+vemYNChz02CMEAPb6ojswxBGNNUKHfE1ernR8//338eXLl5Wdc28noYBR5OGkDTBuYI3jM/NkgMZ1t04yom2mg5VhLiYP/P+M3SSCbcEleCcF2GEFHUsr//M3J+WsISwjgZbxYFvIiLExds/XrTMmQDxub4xFjw2YXV2hKrYlD9BT1g5ZmZwhefXaXFxcxul0jNOJzbGAhnJ0OWSJgRxrZRaztd/1wZGhXK+0xc7yDz4SeY5yAlSOrivfL3qQz38rLU4kXACfnCOOx9PKt5JssobbPR34BV6uCm4JBPtqM4u7farEitnEYRji9f1s030fkSMurs7kQ+ri8rocxrDfqcK6LJH6oT5VOHKOOUe8n87Ar+tj6NbtNV47j524QdwZhqESQswJv4qunqbmGyOXo15tQ5B0kCjoFQQIeh7RnpHDGhgDGMD6EBsTZW5XHscxllji7Viq6nkSMB/6mM9EQ9+lojdne0Xfy1ouBQimFLuhjzEvkSJH5HI6VAr2fLaKVUREXso+kKvLi3O8WCK6FONpOreQl+Rjtzs/KXu/i2VZt/L0Qx9D3x5uCn5ZliUOF+WY34hcx9OlvuzBUGXKazVNU0kQz0nyPM1xeVXIwmkeV8RMl7ro+hRdTjHP5enfxKCUUhwuiu5Gbvu/XM12BQDfRvzDVzmWEv/QSRMvrtLb/3s/mpl/V9fQk7u7uxW+ASs5SUWfAPeu6lB5en5+XlVYPU58CBjX2NIxZznrXZfLdpqUUkxn+b0IJzFWxzjWEYLJsR0i3P7be1fwQVyL+Om4+Euvb040Pn78uAIVGHNz6C2I1BMmDodYlq+f4EigcoDDmTB5erNxpijE1dV1TV4ARwBkFNasqA0GQAWD5VYqn7ySc9tsxZwJ6g7SDh7cE2dDq40/UxR8jGWZ44cffqgLfHd3p+pCOy/ZVRPmZjmb4TZA6LrWSsNaGewaDFipMU6YHDPEy7LUhyYSTBwMrq+vV2f8m4kyC2WH4mM1+UmC4/IdAdil8b7vaxmQ1zagXV1drU4ti2hHplYmZmkPcnLSQ+DcVhGQqQMmBg7IhblHFtvTn9BDTmNhLLAbV1dXq7KngXdEY7CwG0CNDyewvBkfp0lYLwGmtjWDCWyP75NoAZK9V4UExRVE/vbw8BC///3vo+u6uL+/j4jWR7osS33Ss5MVM1A4YwM4fIzXgqTT+4OsFwbh3L+V8puv8DqTCKB7rLnXxjrOtU1KEBCpaPJZfB16zPddtUA/sR3k4+SS61vP2IeGb2L8rrgwb/QXvcUejsfj6jkxVANphTIgwN8SyJ+enuL6+jr6vo/7+/s6Rp+KRbstRAzJdESr8g3DUPefYGPuHzYDeTy25KyBvnnF3qE/bt9EZkVW7ahJCDH8EfHi53yg2UB+GiTbV9lncS0fZsC6YH8+7ZG5c5Ib92YcbtlxEsQa8v9cn++imyaqnFwYHLma45MdsTWSAd43ecP1fZAAOs542MvF97c+hdiIDiMH1pvYbnzBOABITtRZo64rD1vzOjjRwz8iR8aLT2b+Xl/8FODYLV/YC3qNntiuIkorF7/75CPGYQICUgE7MK4aT2OMU8Nu2CqdD2w4Rk6vr691bl5z7zNB33LOMS2tUrLb7WKYh3pvJ9HzPEeaUvWtxC50wPsZHCeZL/d2GxPysBzdNYP9s9YG0/x0MsE/fEFEO92qVhm6dpCDK9TGoyY1bQ+OE9Zb42sT+LthOFeMml6b6OBa+HHjlv1+vzq1zQSNMQPjdxLhhJDPeY/vt7z+qOdo4ORQpG1Q5ubsH9jvG2PNSRTsm+j7vrLTtB/g/Pf7XU0iUHCfK+6TS0hytomBwQUK6mP2fBKVwTaLjjNH+c2C8necmVlOlHm7gYvrFGC0bp3AAe33jamhPQAZoyyANN6zg2kVmTZft6EQiJC5nSfydAkTAyMB2M4TY56mKZ6fn+u4YB1wcN6nAHCkP5iKz5cvX+o6YzBUtFwRsvHZEThg7Xa7uLq6ioeHh1XplF5H5stPJz60Dxls07JGksc9ve8H3YDJw5h9Ek1EY3aPx2PVe0qzP/dEaDM8Bt5m88yqYFsRzVkgGz6LLjAOO2L3DPMeYNqOjO8iR1hn9JH1wjfc3d3Fn/3Zn8WyLPHp06fqbK+vr+vY0eGLi4vVsbJOFF9fX2t1Crlgq4yX1kkzWPghkwsEM9/Duu3KCHrhRJ/9Qq5W2C/ZRgz88Z8Ea3ySA5eTZP6Ob2MPE/4EcGld8UZzgn5K7SAEbBr5sGfGyTwAwG2U+Bf0wHKlWonfvbm5qetgPeSknhIol+i63UqGbuvCf8NYO0GmigI5grx5urbbPn2KG7rPT3QJfTNZwXi2rRnoFnJm/bgHPgJ5GFzwO2MwiWQGEv9hG3SPtZPcnHNM81yfRmx9MXMKkYGeGIRbBsTT7d5KKtQQNKzjth2EMaErriY6NuPvwA+AcJN5ADK+j0+2D0Tm2JgTJRJNZIX8nTA4YYz0dbXTOpP0u/2GmWTHF689a7fb7Wo7NCQRL/wh83drsEkK+363sJ1OY0ReP1fGsuD+VE2Nc8pJoe9Vt/Advje/8//gDBJhfD+xz/ewrnjfoBMX1pvvu/2dOGjs4qTSABkgbtKT9s7tOJGzyXRIqy1+cRWCn7TakXCgg2C57dq5GoP/dRzntSJb8zqGG6PZX5iU4+WqRcOhjWxAn3lvi4FNAGK/Tgx/6fXNiQbtGl++fKmb4RgEAIHNfwCz19eXiGjZ0+Xl5YodopRP2ZJM3E+g9HcjIk6nsQYOlA8naOADMOB393A6qF1eXtYnGTuoY5gwAygbc+a6DqSATB9RaaddHE55ImZKKe7u7s4PJ7w6Kxj/lppk0KqEIvDCQdNKgzw9B8aKjMy48TJrE7FmEjBmK9a2VYW2IcZjh8gRpIwfo98GWtar67p4eHioTohretO7kwYcK/M0AAUcULaFKWV+OBAcCo6GuWGAOAMYF+aw3VMR0RhIqhMEF5964fVwAOFzBEzWAz1Cb7GH7dp6v9K2osI1zEgiP2TM5ywHdAD7QlcBCVyXnyTZ/I2kb1mWao+vr6/x/fffx/v7e3z69Cnu7u4iYs2QAJD5nXHZVwCgDM628kYufI8kj9Y6xnx1dbUCm+gfMkXurlzYNwGOtjJnHlQ1fAod30sp1USz79s+Ca7PTxM72IMrm4yNBMbyBEw7MBrw4S84FtuVipRSPWjBLCsBn/uZbfT3jsdjrUaQpGN7y7LE99//UHXg5eWltiexd2BZWsuqwSs+HJaOdStr19pgPB7sjO9j6+g8wANZm4mtLOyGhPDBGXzWPsHrYr/qSpVBKOPkHoyJdWEdzFJXdjPWQN5EHe9TPXMCGsEexbmCEGLSNg5A+OEH2v6AdmgAOosdGfD9XFzhu9gra+OExv5oSywYQHNt5IM+mWjhd9bZz7ZAHkt8vem3xppobWNux7Zfxu9Yjr6GiUoTgI716ME4jtVHmehxVYWqI3OM3E7cNNlBkoFvQ4/xUcjblW8ICO9Bs347KWJsHMiwTRIMXg3iLSPGCmb5uUqEfSQ+yXZGAm3gzBzxY+gneJIx2w4ZA7q4lamBPmNmjU08MQ5slp/YXd/3qxP1mLfxXEptLyTytD92DMJeXJXws7HwffzNNml/iuxsk9tE/Vtef1RF43Q61VK4szMMh4VKKekBXW2HOyDIgqdCsc5GGztLUEDo5V7N4ZMQ+P4w2hYaR8oCfs3QppTi/v6+7h3gngRPfjegYWzOOJkX1zkej18lV2yAsmMGOOccwRNjcWIoottaWHCXtnNu5VucBcmX5YSSGNTCpCMn2kSur69Xm+KcrLB23GsLAN1S48DJupIU+oGO642bu3pSRNd18fj4WKsqVIKcjDEOHPw0tfPkWT+cBRtA0T3vCTGzZf0xq+hgZiN3m982geNzJKNe+77vV0lZBQ65nawCWIQd2rZ9YJNm+pCzA7WTVb5DoIARATiRCLGu2INtM2LtGAkKyAmQadCNjd7c3KzYaGyN65sBAzAsyxLfffddbbnp+3YOORVLgnXXdbVNk6pn13X12R8EDvTIAdOBhEADw49+IOeXl5cKxt0+aXBrEAYwwn4clPg7c2F9SYptq07U/buTcVcHnRxxL3SVQI4csHX0D10h6LkyyndcVWCsAFvWkPVFnyPKBtG3t7c4nU7x+PhY9SDntkkXIgrbdiLPRvXGGDfZGwSYtWPevO8EEJ33epmgcbKwnY/BpwEnOsP62D9wb/wPAAKQajmzfswdwq/sK4jVWtp+rBv4PyedjHcb+9BFJ+Su2La1aicmOqH2aVeMGx2y7psE+7lYx3e35Ilxgf0310FvDQgBT8zV+wgjziz91NqTtpW+FOsnVFuOzAt9tR8hRtF+iH1b97AlgD3+yzoLUcRauGpUk7/UQK2JkJxzLHmuPtN7pkgk3YqHvvN91sbkBHbhZMHPFnFs5XMmh/kJUejnJ7n1yf7IvnqeS+Xw5uZmpY/GHsge2+Tv+ErWh7+hX47F2D32Dt7ErrwHzsTCtjLoJBm/CfllPL1NYPOyPoUQPSZxKOR+e1QE5BZ64Ofb2F62a8S9vS8QGeIbkA3r8UuvP+qBfVwcB2cgxkIAdgkwyxKVTQR8OhNnIgT8IoTWr8a1MCoYf7M0zlIROEGHQMtZ506S5nmu7KABJwqDo2DuGK17Qc2mEIiRRUopnp6eNq0NS1xclIrH6+trfYZDMdjWboLi4gyGYah7IHgxP5yvWQqzPrDnLvcaQG5bNAhEGIeDI44GneB9M2VUgQyucfqsJ8yMmYXj8bgyDEAkwNX7UOgnHsfxK/DnnnbWBDb9/f09fvjhh3o0bEqpVoRs2BFR9QaZWOfQIcAu9+DegFocmxlZdIY1RLcYv3twI9qRvmYcAMqMCb3me5z8hJ7bRn1tMxXojitUXhPk5WQgYn0iE5VDdOn9/T3u7u5W4yeRHccx/vIv/zJ+/etf15PTvFfDoJd7kjSRXDW7yisHik1dXFzUo6WxBSeErrjxO84YNo6AwVwte94jyd0CHCcTfhmcG1xBABhQcn90jL87CCAjAAx+OKK1FhicmxE0+EMPzWZ6zfFv7qnHL9KW0HXtoVa0RHidXJH88ccfI6VuVRlo7atjTcztj7B/xsj48UX4UAMHxx1iF99xtfry8rLGAXzmy8tLBUAGMWYoAXvIGyLF7YQG1ozd+xCcmJpRxV+Y4UcP0Yu+76MTiLA8rKvu+bateYOsq73IzO11gEPHXlcyuCbz2JJO2CFzd9LO50zCAK63yaN9mitwBmF8xskHa+Wx2Dcfj8fod83u0J1pmuLy4iIOZ/3YEjWsPYSmx0PigE9EfsQTdGYcx5qIYM/4LhM81j2DeOLq6diSWuwQ2UZq1SLIE/y39wkhK2zw+fm5thoBsN16i8/kbyadWGPW3Q/XtBxtV4yJBAR98/6T29vbikf5CV5E19EPqsXICX2yj0Dnkavbquw7Gf/PkW/YkGOH8SI6ZXIGP4r/5X7oy263i7Ss98HZdokVXkvICkgrz491xb7xf8b3jutOlvkcvuxbXt+caJhJwCkgmFJhiLPDLidDlWShnLDw+PgYd3d3K6Mw82LwgTISDAxqyqRyRAwrxdwyUiyeARbZJwqIASJEG40VHcGjVCiMy0oYpZkHFphFO51OtZWgjLuL7777PpZljmXJ8eOPP0XXlb5mDJZAQZaKAXiDKfMjsOBczCzyGQNkZ/wRrcyGo/TzFpz8EFBYf5fekY+DBkwm14sowIz1jmh7enLO9dkmzMU6g25gIBcXF5XlNHg1KwzIcR88+mjwZnaMNUwp1aeAmxVDJ5EHOuRgi/6479glb5ckrcsOrnx/y7Y6sOJwqGQgX38OG/GJE9Z7s30G1fTqYi/oOWtl+1uW1j9ugEM5GBmk1A5kWJZSnbi/v6/fOxwO8fnz57i+vo7Pnz/Xliv+TpWPOeI7LDMYWG9ktqzdRuFK3zap5n3u5WdfEOzRSZ7sbjmSxHz8+LEm4mY5XXFgHXihI36WyhY8OSAQYFkTyB30GttmPbGLiHb0Mz7OLLeDq4Ez+uzk2AkEL0CKgS9yahXGXeS8O8ueBwgukXM7jcYPytySPrar5u+oPnfRdVTSl7i8vK0+BXACcMBmLI/j8ViP3+Y0wtPpGNM0n313ez6BbRyg4NaaclLQUisCfMebSLERkinrbc7lhKOcUxyPp0hdF+NYTpXKkSLSup2Ee6Dj01T2rzRgHZFSeVgtfs0+rJGFbcywp24HNggBwFEpd6xkDvYR2yTQCcOWXHH84j1X5ne7IXLE+eSjcqQsJ4xFxHmTdzkev8bTpY27JfBLdGmIfI7t6B7xG3/Wdd3qAZ7ES5MEPvCEcTJ+bN8AkGqrD0zAVyJL66wxCK2Jy7JEjhxd38Vp5GS0KXa7y0hdisvLEm+fn59XhAH38P5NEounp6eIaK3iTnZMKPJd9AbSA7+BX7XfQFYmLtELOmOMfy5+JtHD90A6uBUSebNGrt6i99zPPtiEj19giy0WiIivZOrEm/thk+gl2NEEGPfFJqZpipRz7Ia2cdwYlnuhg67eRkTd8+zklO9sSURjc8dG+ybHum95fXOi4ReDx6l0HVlgjog5TicysmFVNgJAmqUjgCFwJks53Kx7mfT6qbBm4zBMAJoZS4TkIOzxRLQnyvIdHqoHy2BACsvAwrm/zlkmyogjM5O4LEVmw7CLw+Eibm9vV8bH8yRQUth9M9gGegbnzMdGADuHHFYBTIHGZT4rNAbERt2I+Gp9eHF9KkVXV1fx/PxckwlXHvi+QTrrE1GMF9lT1bm+vq46QNXB4zTjSUZvlnAbHNAJmGmuDaBhPlzPezbYRE5VhfVmDj55ZgsUzUaxDqwJ1RpeOHafF8/3SaawJ/b/2KEAplgHszHoiMElc0ePIqKCj2EYahUChtvXRI7oD+vrqhNtBIfDIR4fH+Ph4SE+f/4cHz58qAmaiQkICEC9E1v03uVegx/WmUTHJIKfH+HguWXLU2rVr9vb21Wy5SoaOo0sX15eVi0kfI77+yhpAqgBiQkBO31v/EP/Yf6RCe8T8Ai+Pq2Lz3JAgxMb/CN+z8kO62gbdIUNBtytJ/YPWxatzDPF6XSs18dHOzYYjDIen3LU2FlOldtFOSq3bYaEzTUp1SrqrTJCnOr7LqbJJ5e1DfrD0PwDNlj0K2KaYHI5dKQ8QynnFiscv5zkbRn3lFKMU47nl6e4vLyIPEfk3Kma0SpCAFVA4TQ1xhn7fH8fY56nyJkjgNvzO7B/2mJpXV3H4rZZH9DN+GnTcAUHQIVOs67YieOjE1LWnf83C8w652it2EueYzm3V19eXawSx15V6UhdDKlfzbvru+j6XfWzF+dKNro79OsjtYnrJFWAXWSAnCwz1oQYYaLS7b0R66ecs3eCe7NnDjvH/grQ3sX7e7HJ92OJhcfT+zlhaselu9rkNTUY9SE/Xu+I9R4N1p7PwOr3fdl/8PT0tEoiTVyzrvg/7IIxYCtOdrcdMrT2bckhY0TbGfHFlQTIHfw0dsjnnSzjGxg/49zGbd7H721jCmPdxmATY1dXVxHLUp+Zw/e2yS066QqQEyLrFp/HzhmnSUHHCD5P7OQz3/L6oxINB/AmhDl48BBBin/X19d1c7jZ1YjWzsPk3IPc911cXt6smEoU7+3tPa6urr86oQJlc8+cx4JQfKSugxzJA6BkGIZ4eHioD5hhDmz2hkE3U4HykCxgYA4oNkYMEcePMqLQrozgrClNGoygHCilTzrZVkdwmoBmAAeO0ptgkVlKqfZbew3NLiN3HCbryU+zxa542BBwIg5KyIT9FrCjZoJwMD4SmWTkdDrF8/NzPd3IiS2A3UcfukoAMwJAZN7oLeNw9Ydrc70tI+xkwIHWoM2gEJDBdQjmES3J9QZt5IWOMBbWH92gFQzGDrkCUBiPA45ZDDMpOEb0ACYKp8uczEyllOI3v/lN/PTTTxERcXt7GxcXF/Ef/+N/rH363333XUSUo7WxD3SF8UcUtsbJL0GFxOrl5aUSAfgTt/K5JcZrRcAB0OOn+Bzfn+e5PgXdLBoAacvI5lyqam6v4OVjOwkUDnJmH71/h4DnfVoRawbSpXL+7iDvAMd3mIdbLJ6ennSAxVKfOM66UN3CVgxE8EUkwfM8x/Pzc/VLzNeEBMEQvwKJwFxcEdqSR9zXB3SYiLEdWweQQ9GrUkUHjGITxVc2QO4qcrGl1p7phLmMr4vjca7EDnrBOPnd442IWDIPk1ufADkMfczzUtsF8SvEDwMarl+A2hgp5bpuZWzlOSGXl1fBQwbxyZ4DpAv2bIbecmRN8VFmQrER+0TwhRMV7meGl1g9TeU5D/4OsuP/sQv0iDERs7Ajz8XXcfsm3wFQepM+pOTDw0OVFQkCjL/3M0ZE3d/FPj1wEPZNXEgp1ec6ECcZNzLyA3ojWpsWejJNU3z69GkVe7ELfDj6bCDslhsIFycNvgeEhffs4hOJpcYKzJm14RpgF/4fHLfdvG/g7UqB9Z3rGxshY9bdpDT41OQS90CvkJN9MqfgOfaavOaz/A0CkFjJ97mHSc/IEfPSOovQfdsRv7Om9vusH/bP/bGlbfISEat4svXPf8zrmxMNszUILiLO7FNjkllYsl8/zZoHqCEYB04cEu0w7++vq6oHDg02kgDqlhHG6J5PgzGAPQ5iW30gQPI+hsdYfRqHXyyA+6JxBs6atywNCUvOuW5k2j4bgp5rA38nJC5jbltlfH0nQc5K+Yn8PXcUHWNBVqw/a8J8MSSfkIGTNiAwY2LmdhiGWjn67rvv6oPx3GrgBMtrE9HYVOQLO8SDaKxnJEHoJgkHiRpOBN0wqGFOsH0EYJIcP6QKmdASZqfMvH1/HI5bVwBnu92u6pNb1thL4FO37DBcXbm8vIzb29sqb7eOGZBYB8dxjI8fP9b72PkC1O0fnJjZgW8TMezQZd6///f/ft0/85d/+Zd14zdjJNgDAJgb40XXvb+C960vTuoqW3meG0DAzFdE25Qc0fqGnQS6t9bJP+SEdeL29rbagxlaAiJA2qDLbFpEO2kG548sDf55Ei0ygw10wJ/nuW7GHoZhlThjRwaI/B3d/+6772Ke5yqTt7e32hduwEngdpUGAgB5EwiJL8yHZAG2FH9kmdj/4nNYl2Lb8+ra9uv4RfSQWHR7e3uOMWk1RgPWiFjJFX9gEGdAW+ZyUf23SQ6z+twPf9n3feRYYti1h2Ziw8fjFBFLfP78OXIu7bbEvHKa2Pppzfj64p/mGAZ6vnPkHDFNcwxDOX7YrDE+c/symHfsdGLD77Y3EzhmZpkf/tOkJL6sgqhohw0QPyASDBi3LDV+yRUKdBLCzdW4LbBkbE9PT5VoMAjn8xzdDqAD5PKZ19fXurcNYuPm5qZ+x0DP8dtknD+DrElgwWWOC8QQVw2wUbcuuzppphzQDpnDP98f+2fdGKNjIHtzsXPGhHzRCSdprCF/M7DHvh2nkAU25PV2koY9ghs4st12bLxjTEa89v+jo8jBRCDXYdwG/ryMm6+urmIe28mSjqmM0UkXWAmdc+y1f+q6UuUlGfbfqO4Yozspt33/0uubEw0CIotM1lWAfwveZtbNEDJYn+7AApDBoyBd15QVhbSS9P2wCvrOeHFyOBD/9IKizCQD28yYwA7DiME50zNDaQNm3iwIBujsFscMQMRxAB64FzLiM1zTDmaapsr+GrB++fIl+r70CfPEbubt/QsvLy8VMMIAA7C2TJhbziIa6CBo3d7eVidGogNT49OiuNa2Z501en9/j8fHx1plstzQB4PExjA2ELGV+5ZZdCBD1iSvDhrMh2shd6+zHSjVAZwO77tqY101qwmTDvCgikZ1BWdstoIASkLC39B71gZ9N9PoZAgdJtheXFzE58+fY57nmvAydzNeZqfN/ptB4e/oNafAkZi6MsT8/9E/+kdVBoyftp+uK3u/eDAmfgCWyq1tDp6QDbvdbnUSHfZHYmfbtp4ZnGDDBDEfHoGuGLT7yG3shz0WZpe4lwO3gS0BgRNftsk+OuT2Nc9hWZZVCyXAjHY25u0TrvD9rOU0TatWiGEY4vHxscrIifd2YzG/o8t+jsDWRnnP7RSuEhDI8R/MC9vmhc5DjgCc0A3u5eSBo3MLKGw+gL+XmLB+jg499dzLmzo5PhgdsY7BZqJ7Hr91L3U77fNrVfKLC8iYVCs0vs/xONeEi/hXfM8h5nmKeV7O/yBtdjHPS+x26+qD4yw6t/07MYf1MZFg/2/wYx+KzTt2Ml90z0k448DP2ddzTXTbVRmDKGTNGgEy3TcPyHt6eqptnyTWgDWTiZBZJBEkf8Y9bLCmWrgF5Ojf7e1tlZljF9chMcberAM+Thr/e3NzU+eI7EkekCmYx/9vAtK6yTUiorYqs47IiZhp0jKiVcrpHsGGto8jyDnHw8ND1S1sl3tjC2AXk6mWm/8fDLStCHNNCNXtHlOPyYQN141o8WibMLGOThx5j8RgW5l9f3uLLrUknWvix4xb8anYDvHdJKsTfuaJzrqtCxIPuSArV1W+5fXNiYZLTgYaw7CLx8enFaNpxpF/ZtsBcnYSZoGPx1Ms5ydM4hBhkft+F8vSsiqMm9MZDPYxPiuzTwOIiApIbGAsuvva+Pzz8/Nqg/DWGb68vKxKg13X1ad64ngjiiMDREesT8PBGAAUtIm8vLysyv04iYioSYWNzGzgune4/QTI8lmUyRm2GQtKsx431RPWmjUlaLpCgF4gG47T67qutjgxZhwlG9dc2iUxeHx8rEGExI3reZyMyxUJjMgsBNdCNiQ5TrDtsPzEYgzUCZFbUFhf1phxmTEhiBKMDfAYN2NFtjh0s11uq7ADpKWFp7zjrPgsDvPl5aW2MHmPVUQDmgBz7MNJ9zZxj4jVSXUkor5vzrkGy2ma4uPHj9H37fhlEhDGcn9/X/2DWVLGxX14pdQ2/ZLQoOfojJ8/gXyYL06WU2FINEjMzGaiD15T9IzrbdlhnLkZMOS4TWQ5QQ/bAmjbtjmtzOvC3PEPPm4cdpHxb9srsBkHKQANDx7bBjGDQ8cPM/XIwOwec0WOMIxOvvgbvfCspxlTJzzlvl8/wIyAiq173dlEnvP6qc+AqaK3UZNKdLCAikZg4f/4e0SKvm9r5jYgfLt9aV3HOSJSazFiLsWXTTEMfU2gWNvys//Kp7U2E1qN5yh7NnL0XR+RcqTUmHT3zxusE1NZG5hQ5o3PdDwi/hsj4DO5j/XCLbn2QdM0xbBr1TYfOmD/azLL48S3Ml6TT7zP3/DLzJUkHl2izYeKLP4aX357e1v1NaI9Z4huBp5Pht2ZhTdIRSdSSrXVBhuxX8d2SYKYPzrmJOLn1vDn9jXY19ovOuaYtPH3DKgBtLZVk9Ss4bYaYBs1yGV98Cuuptj/2AdzXXCAkwDLGJIWfbIPZA7osP0Ih6aYmGVdnIzy/a2/RSb4qV3fR9+1PWne4+P4x1zQIcg3J4hOvpAPuN6x2/aCvFxV+tZEI2Wk+guvv/jz/64ycpww0gBV2+tAwAUsYOAo2rIscXNzUw2QxUdBysKM0fetFIQilUDRQLAVDIXlfQyf4IODJVt0mRelNYPEAhnYYjRmLqzMX758qRUJHkKF43CA9QLyQh6AdpyBKwtmkzAc5A0wwMB96pVbb6apbT4FyGx7CgGwrvQwboANeoDS/1yZ8OXlpSqlz3s3K3V5eRmPj49VNiRxzJsgZdDqZInPkSB4fAYTOH6+Z92DBWLOODRebsczcEeGOA0CIfcgOWScW2bACYzXletgX+iJmRZsypUzxk6A8N9xPtuExBvDIA/ck8r55AQoMyIR69YWy9psYsSawYF0wH6cHLu9xoklcwSkGHwzJtbSJX9sC5kbLDKuiFZd9f4fghD7zJDV9fV1HROycGB0uRo5MDYn8vzEztFH7M0bzLdBHFls925QPXSbjhk4V66Yhxl69Mrn2rNuBpX4VP6OXrs6EBH1gAuqH05kzJqZHPA9WTPWmLY4bAz9ubi4qPvhkD96XwP1bhcpdat9Bfbj9uWADti+lKIeXEDVpCUpLQHfArXdrtkHc5nn0jqFb3F7DPfkeGZ0ofqKVE6usk0V+cxR2p6WFShCH9hj4jiMrJe5VSPsGyItcXHREmO+hyz5LGvDGqJLtg/iBWvHvWyLXI/7GaBuZQtLv9/vzwlRi6luZ2VNkTNjp9qA3B3juBdrxslRJDne5Iy/3bLhtHGhmyQf1nXW0D7VIJ37mRzjc6fTqXZbMFds3A9VNAtPHCMuIB8n9RAgWxtCJ9yzzzW4P6QoxIPXmfW1TwdLEVfsr+2rfS9fx8kYRBQ+hCQQ34T8nNC5JZ35mahinfb7fT3cgHE4dnMPyOotrmRdPR+wlwl6PsPBMtyLitkyzZGXtpeDe0N2us2N9SeGO/mwDLEJ2z26jI93uyB2Rtyd5zn+N//7fxW/9PojNoOneH8/ro6APZ2KA+66oU4egzZbwAANXszGMzmyqaIQfgprFymNkXNEShHL0gSCYiIUgo0dHAGLz8KMwsC5nQhg7MBv0Pf+/l5bjRgzrRj09NrpGXhFtBK+gaGV10laRGutiGhPhkURADsos5mciKhtWWaHXGbLOVcDYn44aa7pDN7sO++79er9/b0mNXd3d5Xhcx8n8mc8VGnMVAE47QhwAG75Arhb+dELQB+JrVkDBy4CgBlm5opsAR7bFgt+sqbIizlQPWBeANVtUEfenCoGEPKmc3+O8bjdMCJqnz06S4LnPlyzQ9ZfVyVYq4j1cxy2pXR/h5aDp6enr0AbciFBd0XG98I+DcoMWEgC+JzBmcFTROufRuftRD0nbBGdxPk/PT2t2N+rq6uvEh9IAewBZh2G0rbjZJJAwwETTiRMSOCXuq6L5Ty/9+N7DH1fTtkZhpjmdhpURETq+uj6HPPxeC61d3F9fXWuCsEQ0/JWWoKKHMvBHuOoey5LFOYdlr/8awRT8+kRKTiqu8SE8mDVef4SZePyHPN8qte5urqOy8vyjJN27abj6K8TS9bSuukA3lhMn48fZ5Z+qWMbx7b5kXXxJn+D35TaKWVmopf68Kw+hqGBDABwOZ2tPJAQGz6dqLSdZX06J+85x27oY1nOJErXRz/sY5pyTNMSXRcxTefDS7oIjmcdT6fo+j5S6mK3GyLnMaaptRjhs4qtRkSUY06HgTa0Y5FVzpGX5Syrc+UhL9F3rcXKIMkEgiuB7ihIqTyvYVnmCnCH3RCXV5fx8vwSw3A+cOBsz3nJMc1T7He7mKY5Updi3+/LmJcldsMu9vtdvJ0PJBmGPrruPIf0dYwxoML3okfEWuwd/4FN397extPTU/VT2Lyrcujo1t8AxvHdl5eXtRqPL+Ma+CPiGNfALx8Oh1rNx0dhE07AAKsQd8QQ3uNerjqaoEBHDDCRJXEVP2ibMdDuuq6exEfL4ePjY30Q8ipZzq29yH7TyRv2ZABv3eI6+AVIAORLnLHesp4kEvxuGRF/8DMmnZyIGlduY5j9uCuykMLgkohYjQsZOKEiiTgcDpF3S4ynU/X9JJSR2r5p7uU9gW6FAsPUeJHWhC0ENzZhmTh5QgZc55de35xoEKRyZtP0ewWysPhm7DA+SqQEUibnHvaIdYtHyRAPZyM4xTB0MU3t4UW0+hhcYogkKgaKfI6N5ma+XcXglBMU9Hg81oWOiGr8GPqWNXXZ3aDTjA4KxHe9SdjlM2RBUoRcAOo2OAMnsmGSJjP3LmVayVyWdvtbSuUhd24JwjEyBgwN4MQJGhHF+fN9mGpaY3DwMKdbA57nufazstGO+zJ2jNsMCeyCDYb+2Ii2YRyDo2rjBNnsHHN0y5IZC9bFOoATcdUKWVsWr6+vKzYJgwew2Nmb9WQtPBafZGIHh+OCXbN+Ihv0FLl47MgZYMbacS0eMoWMmBtzRt+xcTtrn/phGXIfM0jYBfrpsZlt4Xcn+2aU+DtyccDw+fH39/crdoikAd/j0jLXAQjQfoVDZw2ZT8457u/v4/LyMv76r/+6+in8mJPniIhpmWPR+I/nMXUpR44U+0N7sv3D42PRwRzRdSmWeY7X1/Y8hkY60PpSbI82KwB0RGlhLbrQnT/zutIVfEdExOHQCI8SK4p+vL9PwclMzBGfQbWvrVkB7eX/uxiGPi4vLxpQFeu71VFXyJYlR9f1K3uc5xwXF+ylGVYyxjezXtgqdthAa3mOxjyXdYGkiGh7D11xKjEQtrKQZOjvNEYsS4qUhpinMboUMQxn5rBLMaQz4OupgEUcDvs4Hk/Rd7RpDpGXkkx1fRdzbq2CbtkqutiqgrvdZUSUpKvvS7KEzZX16WPIXZSjefuVTPAt9kUmDuZ5jt1+F+/HtxUDHikHic7V9WUlJLr+fL2hq8nJsOvPbPe5An/WgdN4imEoLV2Hi0P1OfNcTi6DZETHTEqZuOFZB7DcZZ1a0oFte78PvpF47Cq2n1njdhYD5pTKw3sBxPM81/2LrmITe6dpqq03Tq5Zh0IUvK26CZgvOkYM8RyMWbYAm3jJOAww6YxwZwIJCBWCt7e3atPEamzVQNyJq6sarlI4ftCqaqLSHRjo5NPTU8UYxputRbC1IvOPubkKzbXBJdyHcXsuxiv4cdabDglsg/uxJvZP7AMBR6FXyCvnHNM8x/vZz8x5idP56OxOsRPZgP0gxyFL0B3G5+q1Y6or6CbWjLOsS7/0+qNOnfLiUNZlQQyO+ExE28TddV0FO85mCe6n06kygSWRKWyfNzIhKIAjlQaSCBwPygo4sWKO41jBEQvIGFBw3veeAgORjx8/xjCUZ3245I8yYqBmZg1UKb3O87wKVhj46XSqLQfIEKPmFBkrDWOEdfMGVbeAeMOZN+WP41jP4z6dTlXRHx8fq/yGYYgPHz7UJ51HRGXgcXQkA7TasC44FI7HRZFxfCRWx+OxPkXaCQ/6BTiglM34nZFzbRx0zrk+JdtOHB3BKaAvzIN54TgMdMzOb9cBUORN0bAy6LBZ+Hme4+bmpuoecsK2uBZ/wxkwLrcMOVkmyXcy6AQAh2tGCvlt2QvmyJjQNfSTFhw/VM3VlwYA109CdXXtcDisqqV8h4SWa22rEt5QSKDcsnPcgzIxtowOMFdeTlhgLQFUy9KO7PW+LpMpTjB4hgafQX6Pj4+r5NYnngFQWiVk/XR3XsWXtjGZpd/tdpFyjv6s44zZfu/nGK4VIx1t39B2vfw+PgsbNGjjs+gKa+BKD9fGxplr17UHcZrocHA3M8s6zXPx3Yf9+bkPuzNzO8+lQpBSpDiPP0WkSDEvSyzzHKc8lhpEzjHshlLpGefqG16eX2N3tsfxdIpTas/3yEtEl/pY5iV4OF6pakT1M8h4vysPjyvrUZ4PNY6n6Psuci4sZZwfujbPc/RDH8fTMaZ5iiENkVKOfujODGfUB88VML8+3MEMOL6krF3Tpe3D34qf62uMcoKOD+26roI671VDL1qSV8Dky8tLbVsy+cWGaSeUBqjohSux2CPrz/4dvmPbhSTAt9K67TjqQxmcdFJtBzQiI4Nt9A/bYl4+dQ0S9HQ61eqoNzOzVsQQt8NAAOJT0H3G4Ko2vhu5bSv9JmYYqwkXxzOSK+MQtzJzTWS5PcjAyZl1n/UnIQQ3Igc+y/i3JBtra1+BD/UmcnTdxI+TYmIo/66vr2vVx756i2vtg42LTVSAW41zvMbYETEAbMb86Q7imq6ooVOuqDEXkl5O/qPL4ebmZoVXLXc/Gwvd3eoJsnAXgvX3l17fnGgYvAACMRgUwT3FOAFnixgxi0BwhIkHiAI6+Ty9iFZA7gFD7FYsBzcMnqAE0+8KjBmDnFvLi7M3B8atMuNMmRdjsGNw7x/jw5Fs2QqUyHtEcNSckGOQCXB6eHhYgTAqEZRL3T/O9TldCEdJewr3YD0p30ZEZS/MCmE4P5dwEuS2PZ+8z5obNCJ/5OInf5slQEciGohy8hcRq70mTkj9GQKBW+nQNwISa2bQCthF3qy552G9BNjidBiDEyuCt0vaZkK4NvM3+PbTeAkGAAP0iDm4kuNKIMEGGzZwcXCKiJXdOSmhN9zMH/9c9SHJAAShA4wfvUIO66pnS4xs7/yO/Enmkff7+3s9kMIsJnbKPM1mG4S5+mjGa1uRIAAxTwKynbuP2XYCy/cKgJ2jj36lb3w+pRQp2uk+zCWldG5DmVa6huxMsnhu+EA+z7qSyAF6WOPKYu92K1mZBcO+AFnoFjqOPElY0PuIdvgE1zGpczqd4uXlpeoNgHAc55gn7UFY1m0W76d2Ig86aZayMPBdzNMioMVejFTOs5/nWn0pMi6VnMoe90NpD5pbcoiMS8Wp9FuXvRUl0djtykPe9hfr5LokG9NZnn3kvETqUkSUn11K59apXGXsh8WZzGEM9se0r7CmyNUkh8GU7dMseCXXUmPM0XnIIes5sQMfQCzGD6Hr+MZtyzV+hOvZZl5eXuL6+rrG/oi2twKd459bOrkvVQniydPTU93MTYxgre0L2N+22+1qRZ51RP4QKiaMuAb2iU9ETxnjxcVFPfbdCQfrS4tYRIl7VPKJPeAU7IkTJvEf3v9k3+tkAp9ONQM7jojaocH7yJF1Z674ZpNcxlOuBliHObI551xtH7mbDCTBJBEyGw/mRK+naaoH9lAVYxz4FZNIVK7xkczBB3MQR/j7lpQhSaADhbZzZOrDkYjdJKeQOhGtrbpPKbrU1dMhwYd938fd3V2NU9Z/Dt5x+7T9FC+PnaQfn7kl6f621zcnGjgVgBoAhEFx1j3CYFHYFIRzQ/GpMlDGPB6Pq03JKBCGjuLD/BEM/YArA1qAJOUvyqD0cu52u/ogLzMoGAMOgeDswOu2FcA8SYYzbJfSMWwDNAKowYsTIZwT/0hwqGoAhgguVIwIGii0kxucG0cpMm8Yz21my/s4TZwM59+TReOseJnpRTZk2FRJ7IAj2gMAt8w5wMp7FQyOLi8va5L0c1k5c0Z/cDoN0MSqTI3uslZbgMg6Wue6rqtlcE5AQz6MBXDM2pghtJ754XIG6Vt79E/WDkeO08DpYhMuzyNzdJD5mzkxa+dSqZMNQJzb6ByEzUYxTr+/ZdTMXvuYPq7NZ9APXiYPCA6Af3SHJ8r7WFy+Aynh6ogBAXaPfD0nj4P3uT46hr4ROFkX7sFaEgQIMrtuHzlaW5nnnc79+p4vcpiHofS6xvoI8C0jZ8YRP4mueH4mRvBJ3HebMNmXREQFiQ7yXku3nDg53hJYrCf26TbEcRyLT7+4ibf3Y71maRPi+Ez88LLyh/v9cNbJFDywrnw3RUp9OJ7mHFFOP1yi74foOki1so9wWcq/aZpimudI5z0rkDjzPJfksR+i7wEAJZm5ubmK6Lo4jae4uCh7QbxeXUdVsuxRyHk5JzmniGjtN8Q5bBzd8yZYt25g5z6FDPvEXzoWm0RzFaMmJNHW1ZUI26eJHvwLbRzoAOtM1d0tlW77xI7YAE0VGR3Fv+P3AZze20H1xs9tYhzoEoQSssRnnJS8Gu+QHOBL7PsAw/YRkCcppXh8fKxxnu+/vr7W77POp9OpHp0b0Ta+O5GBVMD/EH+Y47ZLgj2WPm6fWGU/Qjx3jGM+xBXWhjnjw5AX82OM+/2+HnnuyviyLJU0sk/AZ4MNAcPonGXK+PAdrJ9j/JbwRL+K/XU1nkSsuwyI+74HcdaVebdkIeNlWeoRxlT2SNrw925lg7Bn3pEjltzIQFejTOjyuxMhE90QZSZ5mafXKWL9UOBfen1zosHCoGwoJ4rgPQpWdgAliu8SUdeVXmhAtI928/GvKCzlpMfHx1V7C2DYJTknHNyXe3J6Ctcmo0R4AAEDJsYFUDQQxVjMFBoAGgChXGZFKE37msyr7/u6ic3ZJIa62+1qa5ErFhHtadooZkTUa+AcI2Jl/CingwvfMzjcvrYZPjrDd1F8BzESVCcNOBHmyP3RFYNPAw4M2NUKghnHo7KOfgiiS72+llkys0Fm6d2qEtGAIHt5kKXZUphs1pHStxMSM4fI1IyDDd57cLg/skMfSYD8YDL01JvuucfPJfjcz2vFGjBnJw3WI4N4rkVSbHC9dWoQEAZa3JuAzbgc4HnPDAw+ydc0s+kg6nYDs8Fcw0GUsXt8zBdbQFZ+H//E2JEJLaErprTvI3WN4UZuOefaMoONM66+7yMvrW2FRNAAEruyjv1cQkv1OaIdc856MgdsEh+Mj3VQRqdYE+6NHQEMIbKOx/aAVYK9mb6tn+W74zRFzhGn0xjL0qp+l5dXK72tydpZXy8vr6JsXvaR5dhVF/s9VZDS2bTb7WNZ1gx4RGl5IuFI0frTIR8uLi5iN+zPsmETctnUvSxLHC4vojummOclLi8v/v/t3dmSHUmSJmY9W+wbMlFZ1SPdMvMIpJBC4dzw6SmkkBw+Qd90X01WdSaA2BFnceeFx2f+uydYiRSpy+MiEAAR57ibqeny669q5tX33XsrxEkNR+1W2WNxeXnxPp5Fdd3o49g3/WJP1sc7T9hngrmTk5O6vLxsPe98cpIOgNx8n0D6qPSR/DMfmgnn4XBo71D4ViV0t9vV5eXl5MhcOsRG5uCJ/Se4rKpmWwgt8ZIPyOSaT+Xz3F8bMmI0n5/6TJb8ScrDfOl6MtHsiJzEM7gokzx6TDYwQB6kkoB3Xt1KAjSJumx/NR4xPBMV68eWtO5+CxPCFEk4zWOHuM0f2NSOIMoxZ6eL8ebx5El+0pl51SZJjZSFeWYSag55aEx2tNzd3U3iOf9qPio/p6en9fj42Nbd3gqJfupwjuvx8bHOzs7ayZzr9fiC4zqMMcqYELqJPdlx6kQ+j64nkTev5idOTdv6e9cf2qORzKCgRGETYPz6668NqGtryv5pQYuzAXgEsFTUX3/9tW2cpPAfPnyYABP3pbzJVGUGx8G8vr7Wy8tLe0MyNjxLiKn4uQ8kDdLzOEOKC2TZLyFIcmYyVsmESlECda0dGeid6Z09jQkeOGpluNVqVV++fKnFYvGbEyGqBjDmpXiUSNn56uqqOauu6xpbkiCSAmbZ0pgoMWXHGgAYPo+BSoc0T1YyAcrkgM4l43I4HCatYGRPH/xJfa0aQQrAbzzZe55Bw7xcSuQCvCDtTzqODIQc1jxJT+Cf7EI6Rsx6BpWLi4uWUNgElsyDdWC7udfK3z6fCQ3dMIZ0thmE6bCxCQJ55RqMgG56kk3+jr7wGXSEPMk8Qb6Lszw9Pa2rq6vJkZD8Gl1LxtP8c06qYX7H9umlwJ/vkxCQM7haUyAniZH0MZ6zOT2pRbDB3h+y3W5r+zYGKWNridO7LZCbF4f5HIaMvLUpsScy0rY4Dy7+zrWQzCWpkNXAw+EwOQAjfVHGFUFZEpOMHH1MH2TtlstVVa/dEugYqgeDL/BizKEqMBIkw0bv3W48jGFY71Xt90OisVgA712tVo6xxu4OG+hHfTrUYtHV8v2Y9qyQdV1XL6/jsddnZ2e1XC1qONbd+yuqFou+DgebjNd1OOxrux11azzpSwveegJM+AV+TjyqGl8mxr/5nATXePO6vLysm5ubSVXAWtnk3GRSYwK9Wq0a871YjFWHTIL8kWiLsZ7x8vLSTihMv+T55svXW4dkzdNfpg1YE3G+qtqhMWlP9D1jOftP8sH4+NPcW6RCYM2+fv3aEnJdA8uwdbZ3fn7eOhmy6iTZ8h1Am45kBT51gjzYNZmkvMT+eXKBRSfPJCozlrPn9O90MZ/ts65MzOz7c/H1xgYfJWGmapdEFr+RpAjZZSUqq1rul6SVKg4b4ycaKfSeOCHUrV/KInELeaWcs8qtsn04HOrm5qYl9WyttaPXvuGsJIeTTJkTQmzc3xmPfD5lnzJMnfqe67vfo/Hf/s//t2VqFgCgoEgcw+vra93d3bUNTRmQGEl+PlnHZJazdEQhKFkKIgMfQ6uqxozPQSvBUmZ/m1e+TCiZHhloZocvLy9t0TimBCwSJIp2OBxa/yxZqkyoNGQmu1gM7ODDw8NECbJ3lVxl2w8PD7Xb7erDhw9tU1CC98ycKbdx3d7etp+v1+u2cW7OPmQguL+/b0bBiaXDTWaAc5gzBZIQQDBLu1mZcmUlwvjnDMBqtWqGakN4OnHPrKq2VnQTkDN24DMDTDqMbDcCvP3MlQ4U05GnmCVbkMk2XfF993RgwunpaevDlJCSaTrydPTWIdumrIt/Z3DNQJpVF21xfk/vlX7nrLN1sYZk5p7myRnmGNlcMnbGkYCTrdF1vseaZxXB980x9TztP6sAGTxTDwDj7G3PZ9CHZJvnSRa9cb29vdXqfS77w76ur65bBRZ/vlqt38HwcLrR0MffV/U20w77B05OhvdIjIzyrpEemWzaYG6M80TK/FerVSMw6II19fZka526S8fmf6eujj7Ifp4xhpyfnzXCZL3elON6Bzb3UJvNWfV91WE/nlg2VAvGPT/L5XBkcPV99fV+StN+fE9M1/e1XIwn2wnCu93u/bjVscpHP5MNfl/5Wm/GpDT1M9dduxb5L1fL2u321fVdrVerqlrU7e1tPT8/19PTU1uLIQ4MbV5ZAZSkZeKwXE3flI68Gux2+N3pe1LadcPG+FoMJJKWjteX11quliNIfo8t5oYw2+33tVwuWpwy/wSmdImu88OZZGfCwZ8lYZgn66Qu5brorBjfJzLu1Uhf4bMAeq5VdgkkuconwAR8UFYLsqWXT8lqeSZ45phxUywS+8lyHkdzDAkw+dskqDLu6+rIij8bR3RmZ4r7GfODU+7edcIa06OMi7nOSY5aUzgv/Uyy7sjorILzCT7DhpJgyuqwNSHjtMs5STYH6uzf9+mGeJtxZLVatRO4yDdxpdicVbiMgVU1wR+Hw6G6w6FOT8ZOif1hX+vVu76GHJJQzYpLJsL0Kkk6vs9ckmhLG/PHevyP/8v/UL93/aHN4AlgTAp4MzBGJGNMdjHLkMnSpgCAZiWfr1+/1vX19aQ3kSAscjIZy+VycswqsMZpaa9R9s/2i1SCLBsyGEkMhVO6AooTaDJcDj1boUZGagROmZD5P0CQjEwq5LeUgMEL8sku2hyGnU9FNxaGSFGzJzcdb4KnTDCqRiCZJTxgzNjnznKz2bS3mibQyveAcDwAdgYXTgSYFLAkqynbZKHIDFBKIEWHkvWYJ0iZuOTv0hkKhuZro2DqctUIvNMZC4C+mw5gvx/ejn15efmbZCwBUMouqwQ5JjInl9TnBAZV0/ahBBKS5ATTnBc9Mmd/z/1J3/dtI6EEjJ/gX/yc3tAlcsQ6mYtx5+/JJSupCYaz4kFWyZRZW+NOfybBoqOSZT+bA5KUlfVNh59gavv2Vof9vqrvW3Dpu8M7IH0H9Iea6ODIMHbvyfx4/COb4R/HMY9tBXxeAixr6GS6bMt5eXlp7aE+S57sku9xn6yA5Pput7tJ9exwONTz80sdDmNLB3sZ3guyrNVq0NGvb8OBFX11dTi8+9BukGXfvVfMGvnxVl3f2ev9viaH6us9GVgtqut3td4s6mSJFMIOL+pw6Gu57OvQ7ev0TJvouCeL/BA8A7gfyYuuG33EYv9+8tpyTFJenp9qUVWXF+cTW8m4t98PeiAB2O/3tbXxeJKcbFqb3n6/r+1uIAefnp8m1Qb2vNm8A/39tvqdzeCL2u131fVxCtRmXfvDvvb7XWPnVebFar7A/sgkz/g3/ioBHQIFwcbviIGq/X3f16+//tpsIROwJOkwwpLjrJQk4ZJ2TE8zxjhJy3dgpKwOZt++Z4szmcyzATFCm634l3Z4enra2o6Ru+fn53Vzc1ObzaadnuTz6WvEVX4+Y0VVtf2X7A0Wm8fazWbTTjMiJzaeAJ0tHw6HdkIh/YIV+V76nsk5IjqTrtwjAesA83xMxj324t9JsCbQV/XNDoWMGdbA+MQB+pP6kpWJ1FXkceJFMjJ2Y2zkxuEwtEctV0NzZtfVoh/ol83s2a7E6JmAkr/fJ1GS+CwJVslX4oI5kfr3ru9ONHKBvAshL0JkhHOl8XmKMPa0jmdYZ8+yZEAATHDj+5IPSuieuTPf85QsXUqKVdM3rKaCnZ6e1snJST09PTWGVnCU4XMc2NdkJiUZmXFnQpPlXRu6zs/Pm7JznF5qlSXmTGJUjgRcz0/DT2WXFKRM5wwCgE82EkCKyqHaiJ2yZRzZh5oKnnLP5AjgzUMB8lQcDnO1Gk+2svZ01L+rxhfeMFyBK8u2DImBZdKY4IjMsuJG55Oxy+CYPbdV0wpbMg1swN90mMyzqmGdW3CPFoAsu2cCl0CWTdFroBDwA7wTzOQ65dw9x+dTv5OhSpkBpTZo0utkadkROSQI5dg8E/iX+GfATuedPoruC3bJ0FuDZHv83Iky1tJzsqUsgYPvCcrJKmXiAegbH132vbTdDCSpv8mCzYNXkiXube3o09vb27tPnB5ykJ/PwJuM33K5nPhXQBZ4MEd643MSjkwmk+CZ6x1dSd/59evXVlVmBz5PdtmCqNKU67Vej/FprNotarsdE/v8nrU7Oxs2YR66vtarZa03m1r1NuO/tYRusRgr7eaVVdX0V8bA/pNgQuKlXZpHxh42pH1jtVrVIuyx67r69ddf23psd+Om6dT9q6urFicd6mLtrXcmqtbSO1nELxuVD4fxiPM88CSBJtC4Wq1aVSw3eGesppeXl5ctYch9Zf6fR35nwgzIZ4fD3DbFujyIJAlDxFfG1NPT07Y/8urqqmGKZPclgsYhplWNJ7SxA7o+Z76zEnF5eVknJyf15cuXSTwHwFWetWvRM2ubL8Wkq9rYssKcujqvUoo39Di7HsQ8z6D3SYgk+ZQEDJ30Gd0j1k5SJ77meyjgKCdVAfhpV55hPNZHrPR7/juxXvopdsnXwUhJZueV86ML5JgH7zRCuJvul6SH/HreJxPHJOjTr8MGKdu8MrlMMo7uWNfvub470fjWplOGnCwpxaMMuYmWkSdYYSgER/CSCI5V4Mq9HmlwlPrp6ak5EG/lPBwOk53+KhxYEuPZbrf14cOHptgSlMxAczPXzc3NBKAnwMhAAEh/C5yl8lHMzGgFVdkt40r22zMdO2t+aQAUSWLgeRxnBvSUlUDFeWcLTY7P/zl/30+HxEgyAbK+CZDIZt4uJZAul8vJ0WzuD0zQMayYe+YL2XL/Rm7qs4aS1QR3memnkwA05wA9E0k/myddWanwmbQrcsnEMCtH+/2+Hh4emvzpYjJmPptA2GEIt7e3LSkyr2TqE/yywUxiMwgmkKRL7CaTtgS96bwBDGCRM88qWwLEqmotNGxDcpJjABbImS9Kx562mxswc/7mlyeIVNVkf1UmeAAEJ53HIiahkYlv/szclf+BmmTZsuJi7sbPt+X9VR74YnPgM80vn59zn9vjvJKUhEELkBE3rFWOVwzIdTQG/o0+zHU6yRNg1Ofcg565V85JopnALwO8z2cQpjOHw2E47aV7PxK6G9+nUL1T8rrf6M+gf9N50JlM1OdJvrYW7S5A1VgB308qS2LgYrms3XvsTGBoDb9FPFm7s7Oz1ifPT4jp6b/noCZbSuhJAtP02/aU5QZt8koiIZOC5XLZ3v2EiNMPnxVMhKV/A6HZ0uRar9cNkJJxrsk84Rd/xAtzS/0XI5MEcYlVbPbp6anZhHXounF/pMMSANEkdsjYHs3Up77v6+bmps318vKyEZRkqcthvtk8cUQmSvQwSWK/A+5tmOfTkGZ8vaQSSZYnpZETX5bks3dtPT8/Twiuvh/2Rj49PbV3YqSNqWzRvazym1va6tnZWUvC0v6TyadX9DzJKb7Hmog/7DkJWv6PHxMrEmPwJekbkmCaV974G0mxMbLjm5ubFvfmpE7GI/IQE7Ka8w9PNAwk24Y4gaoxm8pMkqJlvz1jkAAwRhmS4EgA6ZgyAK9Ww2lMjoC7v79vp1qoRAgiyvhd1zVnpE/TIiQ7l/sX8iQsigI0MISsbAgGHDWwOmcEBd1UtKwoSI6yNSQBEeVzP/c0vnkJzXweHx8nLHtWATi0ZFnTGDJwOy0h2VTj8zNKmxWDBHTmkeXobIWoGpnjZKoEIHK27gx0XpaeGzPH6L6CgACcrX/Gm0yStUqHQ88TmHAmAonvCNYcgmRHEDkcDu1ktUxKAc50YpnQzVuePJM+JSvo8wngfS4vss7EzDrPDybgmMgUWOfkk+HKs+Q9N5MU+sOnmKNE3eZugMFnrGky29mGYX3ZniTz7u6utc49Pz9Pjif+8ccf28/tlfJMembsaVOpMwkScq3IJ32b9UiWi3wAEFcmT6nv7p+VGWPRPsmnsYnRT41JhkCXc5m3m2X11nisL71If2Pd6TcW2GfTf/g5X56ANnUO4ZG257NA4Hw/VAZY9p590QmUU+8k6sP8FrVen7wnau9vct8PR85W/9tN7vwQuyeDPBVxzrYCdkBu+lE2ab1yze13e315qdevX2sRSZZ7nJ2dVdfn/pzBVlUlxEP/fnl5aaCVD81z/+l2EjgOXckEJfUVSLJ2knS/yxMS81ASOsk/VVXzB8B6tn6Il0kGnZ6eTjojgMIknzIBOzk5aa2qi8WwF4l/IdesTiZBmhhGFS6TlGyv4+v3+/3ks+Jl+gyfZxNze6cHdC5Z7MPhMDkWF16ab5i3Lunf2cEcJ/h8dj0gclPP6HdWKIwRsJVciPu5hxPhIy6IHfPOkyS5c9M735bPtY7WxVjTr/uZ2Oj5mWTknplmZ+/fR0BJfMnEmBPfJam/Xo14OPGdBFm8z3icMs8kWMUwn5n+NJNY/854neTH91x/qHUKgMe4UqhklGWnVTVxUGn0jtbLyfk/x0bBGRRmYLfbtU01hCzpODs7a/3RlIvDAHCctoENyQ1GSrTY8kwMOCXAJ0uiCSL8LYNPQxaoMkter9et9JcsbjK080Dtb/Ok+JId8js/P6/7+/sJC/ItUMRYsqfVOgINOb/MluetRwkMPStZW1dm99Y9306bLxWaZ93+nYxrApN8A3oGZI4lKwKenW0cAvvcCBP8+rn1qBqCYG7yox+eyegzkTK23M9yfn5enz59qr7vJ4GVDtP7b42B/IDpPI0jGRBzMV+fp5vzKoVnrFardsBA13VN1ph2TordpUytezqyXJ9kjTKpMU/j9x1gJEGl9REYyT7tMitxnuEs85yv5/3tb39r8xdck3Grmr4jY7vdtjcQYy3z3uzeZ9NOzC8rc4I5Bo/PSpImg122dGUFOdnarFDTu9E3TCsYbGSeeKedZ/tIguSs+OWaJAFAhtnr7jNZJc22l0yAUk/4qkymJZ9pcz5r3tYzEyZ7CzKZdO9xjos67J0Q9FbDJujlb3R7XqXabM5rOElqrL4YW1ZWMsmm60Bx6vxYnRrfZZUvdeur6sP7AS1e/DoAuqq37TCm6+vrpg/ktlwum95tNpv6+PFj2wOQepAkzGIxbF5/fX2th4eHSXLjc+xJwpaMP7Dufrk5PN+YLLm5urpq63d1dTXBB8Y3bzm0ntmiYt7+sBfj4/vEdvY632fJt3hunvzEd3RdV/f39+10R2MlrzzSPmO9+WSHBNtQfbDmAHz2+YsHYqWEP2NE6m12mdBJc6mq9poBCaFYkuSxeyKmnIQHi2Vlgz/xDFgodchY6bjEhy3l8/mVJBmtNf9gL4u1S/ZenEu9rBqTKb7BfbVcueDDjGMZy5PkTF8sXqRPPD05ncSS9A902Lok7sj7JbmVVZwklua4LH1SdgKIo99zfXeiAcTqiWNgCRiyaiA4rFarBsA4/MPh0PqdHTlJ6QgJI3F2dtZKilXVgDSgQVF/+OGH2m6Hd2xst9u6u7tr90plnYP8DNC5eFiaPJc5A9rnz58by8lpWigARgLknk6+oGicH6dByXOvir+z7C9h6bqubXxnqByesQHw+/2+GbS1oXC5xoJLOkyyYxg5BuvKUBIEUWpXMt6ZSCXDm1Uja5Os+7ecOQPOSkUG5gQTKWeOyhyNj25nm4rxZ3KSoIpcPMf43AsgrxrBUFarcgx937dqlnWhX7mx0DzJLZnnBGzGnW0lbMN9017JzVoqQWfCVlXNjquGoCFhXa1W9fPPP9fj42P99NNPDSzk+qQjdC9BPXWTrvl92g2wnC0QuT6CaYIO7CiZsCMVOmyYzwpCnpGBoKomjBTWCotmw2tWpTJBFnyxkubMfpK1RLBkQpYBDhDir5LZ1v7pSnKAvNMugNVcH8nEnDjwbzFAyxZf6xkjwN5M9D4Tuqpq86T3kgG2ASixq6yw8XGeBxSwXYlZ7nkC6MSsZBmNL5NBzxlB37KWi/HEseVyXYvFsob3XPTV16G81TttOdeBHS2Xy3bGPr1Ie0vQy44RP8NYhvd70CdyXq1WdfGeHGT1mH8Wb5L1TT1NMMyWn56eJif68B35RvLlctnepp326g9bzmSZHvOPq9WqPn782L6bVaWs1mX74no9vhk8iQkseILV3DC9WCxaG9bcl0iWvcOAP6MLKtQZww6HQ6uAdl1Xj4+PzWfQU/aiA0RMTd/sohNOUhSf8nQ/yZPkgc5X1WTjtoSNH0qikT6KN8CydfP2bCBz3sufuAU5K2Fl/7DV3A/QmznDL5lIzJCEd+qPtc3kkb5ba+tVVU1+np2JqGfyT7pckpzzWTFU7M0Ym/GUD8jf8W/uZ60z4T500yptJkXGZm1V0dK3JrYTS617rmHKItfFHI0z5/l713cnGjYLJovMcLPFg2JYpKqRPTUpg1OFIEyKnc7LxCmQ184LgldXV3V5edky6tVqVT/88EMLJPr5LGqC5r7v29ncnu//2VOXSiNJAYIoNMFTQPfKrI/jdOJQKruFtRGcTPq+n2yITuNzD4HC5zxT4EoQKjBh0CQomVWbC1nNKyFKzO6b4Cj7awWDBN+pHxmQ/N6c9ZHOHa57mYtn+bfz2pNly/knU5flbgYkIfjy5UubK/0QEOdgliNIBpaOJQuUAJ6zSWbXWI1LEMxELoN1JiAAgzXV18z2BB/raJz0WJDhiI2drACCZFDIIaskbODy8rI9L+2IrgjoyIt0smRMl82HbAT9n3/+ubbbbV1fX0/aEnKMfJNgAyxnUgccIQWSnMi1mR8hSWcTrCYDWzUQEhnI0ulny8vckft7zmj7f17WMu0p1yx1c/BB63fb3AV7DNRWWwc2lsc+C6Zz9oseen4SKuSzXHrvQ19VgMnyffPsRX35cl9nZ6dtvSSCyb5ZV8/KhMr+M+urekwn2BUdrBpBEv14fn5qyc52+1aHw7jvZwAw2vu0CletV4c6HLrabNbVdeOm8q4/1GIxtpKenGxatYvv9yb2ZF3pW1bJkoHmUzMRHPRyeNbj42Mtl8PL/Z6fh+Nwvzw8DEBH7Fqs6vnluTbrda0P01P2+FrEFZ8ukU3b+Bb5kwlvbgBOG7ce+UwxL3XHOPI5QP6cBHIfOueo36urq0nSnjbEhwNb4mISn1j7u7u7enp6qs+fP7f5fousWS6X9fj4OPG11g42qKp2ymLu/7Svle2J6V4ZwO7YpT2pNzc3bX+mmJX7TfkZ9p7xLxP/THCTEKSHqXdZ1ZW0AN+ZbLBdNiRBSsIkExy+3GXdk9AWz7KjJZNuRISYISaJYfTX2IzBmKumb/3OigcsS0Z5P7owB+5JpGabqvH3fd/eySG5E5cl0dWNvtZcs0KcY5KQzxP5jOlJnNDVzWY4mTTXJZ+Z8/sj1x/ao5H9qYTw888/txfqcVZVNXkbM6UGFtbrdd3d3dXl5WXrufNiuTwNarlc1tPTUy0Wi7q/v29Gxii+fv1at7e3rZQrm+M8OKj53gUAgZLpEdXqwHgSvJlDbqBKBRLkLy4uGvuXAMLcGCIFmpcsKTdZZQaZm+Wur68nfX+Uab/fTyon1s5YJGzYP3ORcPjsyclJO6IQaKbUvpNAyJx8P0E3J2PtOIY8ySQDAGNQZk0GlQNLJz9n46rGBCpZMN+lx7n3IB2BJBODnPPNPTdZMchqibVM/cJYc34J9D2XzpKBteWMqsYe9wyamF8nhd3f3zd5+H7qImZZAJozWSqWCYCMO53Z2dlZvby8TFodM9nkkOhJ13X16dOn6rquVTH1F9/d3dXj42MbU+oTAJ/Bd7FY1J///OdmP7vdrvUyp4NHjmQVSgIs4OeJK8kAkQGCIcmK7XY7Sdzy5Z/8D1CZldBMGukrn5nPz1Y6+u4+WXnKtXD/b9kpnRv7qRfNJoaAt2njz/EaE3lmJcTP6GHqCR2uqnp8fJgkLnQ+9Xi/39XhsK/9nu3sarlcNfaULmQr4dvbW11dXf2mkmiNvHNis9k0AiltyBqNJJg9Yuvabt8mYGe7fZskOyN7PrzQbzgWd1Fd/0461KGGg3KHzeJVfb2+TkGO9amqlsQaG7CQSVdufuVT2brKclXV9fV18ynW6+R08L/Vd7Vcrqvru3p9fanN+wv48vNJqFijJCSyimR92GTul0jf6Pt8I/3xmUyOMb98+c3NTb28vLRKTwI28Vwlkmwk/IvF8BZ0epBEAGbd98w3mXA+ervd1pcvX5rfBsq7rmsn94lZKikSXXHb3hbVBGuZbcJ8c5Ilu934Tiy2zI87Wp4Ptg5vb2+TFvAkdzzv/v6+fvzxxza+bN/LtlP3v7i4aKRu7oNhQ4jBJKLpTB5MAU+YLz1nG/OEJqtz7p9jSGLMmCTJEmNj8vzEsJ53fn7e2oIlymmnSSrf3Nw0/XS5T+Is3/dZcqA/dE5VbB6/2OHr62sta1GrIOsTz0ok5i1dYpb7JQnE91bVpBPFXMYq7ejnM+Hzve+5vjvRsChuDCD89NNP7f/Z+3t9fd2SDQpEyFVDP7u+aMAu215yUXOxOFWKybg5mgRkVSP7RcEy4KegMBoSH/PJRMMYGDwjn7PYHF8CpqoxefE54IjSbbfbVqYmi3R2FFiglv1ntWg+91TKNO45A1RVE0dDBtYvEwfPSyPPjZMSJc7cWKqmb/rO+wIR5+fn7YWDwKj7UnKO2HddKgWMaL1eT95abmyZeCWo8pnT09N20krKNBn/TAiqxhcOcoiuBCYMPxkIzlCSJyhrQ/I9ATCdgfuyOa0RghowSg/oqMChP9p4OT4Jt2dhdFN2y+WyPn/+3JJGRIKKn7GyJ+NIAJPJa77cyOeBGmvOB2lzqqrJXikgmp1k4koG/IcqXf6ekyZ3PdpZss8gSWcEtuyHXi6HthGspfkAEtrnrDOdyEpUsssu/iPBet8PVZlMHHIu7jeOfVGLxcgs0xPgNhk7fitP0Mrg5EpQTtc8u+9rosfJxs19ZCbbgJIkndzYgvbYOSvJpn0Owy1+bbfbVv2QoA3rP4ABc3WfTJyzQjjIbzwwAaBCUry8PNfp6VmzH35O1ZU9pj+jwylXvoqOqCg8PT01gJAJ7GKxmOyrOHSHSQJoXbJ7AAlm7Q6HQ9v0zIfO7XG/HzdKszljBhAzwUg/kPphDFqL6B19fXh4aG8ez0q2ewHW5Jntgz6TNssWxbC8l83g9FtrNBImiQ+2Qg5V1U7xE4eWy2Xd3t7WxcVFs22EjTWQAFlHWIntITezupen7VnbJGRSR+GyTOIOh0P95S9/aT5bHBe7EZZ0ln1//fq1np6eJrjEmicJRI+yIs7Wk7ChH2KweGZdxIgkYSUU4kCC4UyS5mSL1xRkzM/n5p5Kutb3/WTPBf1KUtP8xJFMEpOwSVKPDfsu25mTqYlN1stVbd6TJLrLl5Fvdreoes1f5SAufMsu5/JOYiHJsVzz77m+O9HILDr7xLNMKrPnhDIjS6AqqFVVY/5lbSZFONiZZF0zMfFZwF92zelo8bEIXdc1UMN5VI39ayoSOe48P3+5XLZWAvcgm6pqbU9V1ZgLTqRqPN0FSMiKSLKYHHC2V1WNR/MKfrmh0Wky5sMBAiBYogxeWc2guGSRgY38kgVIpjgzZPKYMzcZnPLZyRzbGF81rWxkkEmWRmUik6eq6aYx+x2yJEj2CSLmCVRuTks2vKqaHDkja0v27sdGrJ2e3Txxx/NTP/q+n7QeuScASReTFayqJguMzZztqap2qop7+C4GhuNP20oGuu/7enh4qLe3t7q+vm5nt3OMefyrP9aTEyRrTtOc0sb5Cc4fCOOczT2BfrLuyQwCcWTOBjJJT0CXa5eJKZnxiRlAV6uxRz0rAOwogRx5YoDpl/vmOtAFYHmeIJADmam+kFcCV58f2peqrXtVTTYQZ/97ztc9gISc/zzJlrQfDvva7abHcM5bDeYJ0UA8DL3oQBodphPzZJ/MMs5kiw2dBLwy+er76cZjdnJ7e9tY52QgteQOBNUI8skByDa/rOTQw2z3+xbbj/yay9/YMoF2fz729PR08v4ldp6gsapaFRAh4DPzd9yIefxUEjxp49l6lHE4E9Rke/kDPosc1+t1G9vFxUU7QGa32002cNMhLdzmnb7MmmTFq2p8XwS7ent7q/v7+0b0kPnDw0P7v8TKz9mlcVhXc7++vm57MIxHzMo11EaWiUzal2SK7iDhVFrYgz1hko0ka2GwjH3e+p4JZibMSYRaNzqC1GEHed9cF7bddeOJUJIUcQROg7usbSZJQK/YhiSAzzIZpyvsiW6fnJw0cipB+WKxaO8x00mRLb2uJPVS/zO2JTGVSZB7SfhUvDKBF9fYSfr6ZU0PMeDbksRhs9ZGtSTtP7F46oY4LA6Ym+Qsv59V5O+5/lBFI0FCspwmaIAWitJhQ6rGsl0GbgaEDSX0zLrmoBN7LOnAPux2u7q+vm6l8hQMhU9AlBuJBEoLkwxp1Vh2Y8SUl4MHkikpkJ4sKfkB//ZraMtKx8DYc2EZtp+nES2Xy8ZG7/f7dgpXAhnKlxv5JSCMKB2B+8xZQwA2Wc1kq3zXz8mPUZJ3GkAC5gS78w29ZJrBe36yg+dl0M6An4bGQWUiUTVuvvNHgCOzZCwymJMf4LtYLCasEeNPp2gcxs+IOS62Y+6cfq59BpZMFPO0NHow3xvhnvSDbakWYurNB8NoPVXwlsvlZGNzysoY0k7y6EVV0qqa2GKuYeqPkr/1S3/R9+Nm0UxUssKWVaZM2oyFnLKcTe5IgPV6aDNMtgxIyFNr5klQJn5+Z1zJTLNNc8hyfAJbIBmbRx+SmedHhntMgavPe6ZxJDixVvxgkg+5LvSV/9xsNu1EI0xbxpSs1gJPw3OHaogk8urqqukOAGKPg020NvunjxaDsPRkxw7pS9UIbHwW8NE7v16v28lAubdHFTsZwZeX5yZ3vt4BAfy0tXe4iHm+vr42MJpJWBI/6Xe0Z5L5yclJa6U8dF2tV+vqq5+sb754N8m/TALn90zSJ9tn8oSrBGl5KhDgSN88L/co0OO+79vLayV6OR76kq1PkgSxg52Ss+8kUyzuGIfvvry8TFquc+8Pf+PvjNGpb0k2SCBsjldJyAqMRIG9IV4lKjBQErdJBtL5ZP611GYFSUwXU9wzKzP0is8UCySl9/f3reJBFlndyLimc0N1JlvjEAkw4f39fYtNfIn1YZfGbj2TWSd745HoZkXv+fm5YU3xkT/i59hJJv/0hZ7n/JCqWTHJik+ST3xoHgrD/uw9sR5Z0e6rJvHw7e2tnp6eJgeYVE1Pd5M0sr/8XY4L/uGLxQ36lNjM91Muv3d9d6JhISx4PiRB8PPzc93e3k4M1hsmLy4u6u7ubpLtmYx7UQzBLIMnp87BAB7X19dtPwGWgEPLU3EIlxO2sXy1WrWTHDjFeWmwalCy6+vr2u/3LSnIJMg9ctP8HETLzCksxUrgkQ4rZQ5w+JyxSfrS6LJVLZMEz52DzDz5igz8Ltfa7ykmw7JeCfjNKRO8qvGULXLhmLLyk78H+NNxZ7LCKXnut3Qqs/p07gBx9hVnBSCTTmDbvTl5xpzOxbPoOpuhh5noJGtpTPMEMpOqnJv1T5bfdxKschhz5tQzzM13XVdXV+13T09PdXt7O0lSOGrOG1CwHuQElAHvdAZYFUh9FnhjR9nDyjaM8+bmV7LK5gAAQYhJREFUpt7e3trbirOMDyymHPw9T8qy3K8qQC844WTsfT7fS8G2PIdf8AxykXgKMNnCkbaWCXnVWCUlk9RhdpHsmPagbMmyDnTK2Oh9Jslp/+mXc335i5QvImhoEzrUp08vrRpuPsY5ByZj1XQEg103nNpDP7Xz5HoD5cAaAOtZgme2GJrnINNRNvb6ZULV9/032nvGNri57wT0yDxJK3uh+JYkZ/Lko2wFTfCQP7c+mchiTPm25WaMI3PCh39Nv3t3d9fAYOqFZIrd8wVpH9lGcnNzM9lvgp22xmxDUp66TC5JqonV9DtjrOR+tRraPxEs5JrkBHkDrlmtS5tK3JDdF8mw05H5H7ZHLmJVVgtOT0+b/5Akk+HhcGhtdofDoT58+NA+9/r6OqleqHIksTEHy9bcyVkqITDW/f1922sGmyXJKJbPSb1MptkZOfI7WSEyL7LLJJXOJu6yDvzm4+NjqyLlSaVZZbX2aSNkyo4yWad7YlD6nYyfSbLk/LMTZE4UZaXIuJOMk8jRSWNA1Prcoe9qtx19Xu4zNB5+il9jc8aVsVsMMR9JaPp3v3MPfjYLBd9zfXeikaxKlqMzoz0cht7w+Xsj8hSFDHQclIBxdXXVFsG9ObuqoWf3/v6+VUyMp2o8MjRZa0Ify+NjOU9JlqB3u117AVgGVWM7Pz9v79kQoPwOyJgro3lm64IgrgKSwT+V1KJnRkrGHFcCBrJSYpakZSbKoFJuxuSesupkKDjrbD2yvpSZESVITiA0Zz1yXO6ZLAR50K85C5U96OnsVb0mTEBUhDJ5oTOceQLQOSglJ0CPE3Avc8TIVtXEmM2FwdIZzizHm9/NpNK/n5+fW8BKR0bWAqf7SmyzVGrsxuWZ2V6QSZLg3XXjSy99JoMXRlFAVsHz2ZHtfWlJvvK/AwLs9+As3TvH7fmCd7aCAVsJlI1rXhEwvznjR0/TgQuyua+L/dNXMsvk2XwSjGUw5WvYN9lVjS0ydJ1fS+Dqd+kbRpZ+fMst+xjkOtq+xCDtLO+DrU9yJIGDoJ7g7e3trZ26B3Dm2vE1Sch0Xdf2/bD11eq3L0MTI1QZjDOrVdZmtVq1PXVOIhJo8/NDr/vmN7JOn0l3yOr09LS+fLlv40igMtjRfrIPAqDL5DWTz0waVED2++GFbeJAVU1Oz8mYAXiJudk21y8XzU/SN7oNpJ6fn7cjnXe7XXvfRpIsjo19fX1tSUSCPDYE8CeI9zebzerffr9vrUNzneYDJCb0IGNtVrr4dLZvvef2lRX39COZvNBrgJZ/9C6ujGkZu1PW1s/v2Lz70y/PVSm2huZiY7m+fDrMhlUvVLeMy5wAUHp/fX3d/KJj//f76SldFxcX7bmAdJI9SE2y9tyM93y+udFhMmML/q8y6fvkpvU0D+Hw5/b2to0v/W8mfp6TxBKdsj7mVTVWz5LIy/XLroJswyJj60of2bP7uHcmGV03nvyVp9MtFovab8dKTRKrSbqRu7nTd9dIkIyJAv+ZpIjPZjeMGJkdSdnR8veuP/QeDQtFMFjzqmoZKlYJwMAM+b2JZMlKUNQ7zolQoqqx149g9eVhLHOD1k8//dTK6l3XtU1zFoKTwTgI5vMAkAkHh0fYyZT497igfQ1HI45ABAA9PT2pil67rAZ5DgfG4W6328b8ANTzti8AGoNivbIfnlMDUHMTspIoEJMlZoqYL0ISeDKIc3pkUjUAP29eHZnKcf7JNuV3ssSahp+sPCNO5lKQziBKthyz9W1GsB6PDLTGGfTpTFVNZO75yfSmvOm2oDOvBBhHliiTQaOLwJi/tVYkU58Bz5ySdcmkT2DKU1OyipFOuqomuuhzWI5sWckkbrPZ1MPDw4Q1dTTk09NT3d3dTdjku7u7ur6+rs+fPze214lym82mtSbZs5UMVVW1pCXXRhWVT5J48wVkkvYrwGflIQO2xMha0Gm6gw231tmaMq9ekGMmDZJRQSkT90yKnEmfLZCAViaW5nF7e9uY40F+Vcvlorbbfa1WwzGzfd/Vej1W41QU8AH04PT05B2Y2Tw57FNwNO1+j7nv6+JiAERfv77VcELTod7e7B1Y1uHQNYJpsahaLJbvib8Tjca3nosrI1myrKp19b29VYM+f/nypW5vb9saZYLHNtih9UhiAbnl7wGobdom2N3OHpCuqpAX+1qtTuv09KReX7+WPR/sg+3RW0Gab7m7u2v60nXd5Mh4uo0cSZ9FF7D8c+JAjNtvd7VeDn3em82mulVXT0+PtaiaVO/YyPn5eZMhOdrbSIfyhZmLxWKyyZ1uW6uzs7O21wZxx/cvFkP7TFZEkVpiDRu1TjZmA4nAbso4E3KxgLyTiOFz+Zocu2Q9iUNxlt2lLdO1bB3LFtpvkVh+v9ls6vLyslVm+QNjNP+Li4t6enpqLeJZ3UoQCI/QI/ghq+niukQuY584npWMjAl5AljiBJ0imfjypeIL7JE+C/nkGfnsTPCzMiFh5c8zkchkWgyipz6TBKB1Rk5khQF2SJI9400mAHSP/HJfT1XVarmqftnVoq/qD8NLNpc1+NX9dleLvmqzWtfV+UWt3+/T7caX0NILf9N9sjG+JNj4P/HDXH0u2yUTK/IpSeQilub7h//etejTUv7O9f/8H/+tGa2yj3dgcGxAp4kRBFA8Z1QXi0VTSoZpsSgn5WMonsUAk03OqosTkzBJaeSLxaJtpsJg5riylMaAbNzxs3QW2dYxsl4jM5+ZctcNJ5XYO0FhGG0yqxRIbyenMrJ9o0LlPDgvwJxjp+jAc9UInm5vb1vmTcE48qenp8aozxOy7NvMsmI6S4p6ejq8jIo8OWrOLpO+7LNOIEfODN+apUNPVtDv/ZxxJcBI8JiMMx3w/WThMjHh0IyPAToVI6uAAjlmJk8KyvVLloiup45aX/pI7uZuXGwp25mwRe6HOTE2QP8//af/1BzbnH3L51onOsK5YrW32207jcXasaHUZWDbsySyt7e37RSdZNK1BHVd1w6CuLu7m1QQMqA7254f4cOAJWuRVRF/OyIzg3X+zb7zpB33tmbWFxvJPjPxngcB60QX/HEEMbllApjMOuBhjQTQJCfoSSaUaTMCUQK03MtAzoDbbrebHEP78vLa9vq4nwSbn0vyB8M6JA8nbcyA9tC+umvPYXfG9/w8HkqS+jhnm+1/sq6vry+TymlWH5bLkUhKv3JyMrYcqghgI7G2SYYkwZGMO9BuLgmsfCcJIgkIuSBnsl0ngVcyzUBQVVXX97U7DJuC2b1qSvrurJhmy1qyuMmoj+9OGRnwrCxUDQlOnjaXR/xmKyF5mE+SNDkO8YOsrC8btWZnZ2ftAIuM8ebnfvNYSC+QYH4uMUxG2O+yumpcWXFP/3B5edliZMazp6endpyqmPX169dG3rJF65RHh1sDe4OsD38tlgDa1oI/yHdesOG0dWvNBsTu3BeYMoEN7a1l45kMWVdxgezFMc8G5DNe871pN3zrnMDWfkaec/+eODVJm8Rzqr1ZCebDMhnKBPVkva7t23gCmbF5dmIXGDrjuvZPvjCJvhyrOJIYKH1QxhgJo/sn8U3nDofxxZyZ4PzP//V/qt+7vruiIcsDAixs9lwCAQDHcjkcgZm5TLZaZSadAHoOZhMwWGRvw85gmQJ1n6qxjy7LQhKQdITpGAiWI6+qSXZNEfSp+v6YXU6PXata1MmJF6gcWnKRG/IYXZZvGSwAnm9ZF5itQzILyUwZK2Vn7IJuVdX9/f0kQ/X34TAeleqZZEjGgLLPM/wMSJl9W0djAfzu7+/bPfMZqmLZusBpASTpaKzPvPpDPhk45kAtmaB5MlE1nrCSpeHVatWC5m63a6eR6HHNigkZ0lnz1B4HAKSzzyR0zp77fm66tFZ9P+wpyopS6n+ydsr7VVUPDw91e3vbPpdJdz43E13yeXp6mujAhw8f6vPnz+0dGX/5y19ai2ImXNZN8NL2keyN1ryq8SVa9EOg/OWXXxo4yUTLBl57Oa6urlrSqtWDQ1W6Tnmnb+Pv6IngyO6qagIMrCsQWDWW2lVmBaZ5qdoazME/dsuc2Dudl9ymv01WyvMzweD70odWVQOfWbUF3vP0Fb4sqzyA6dvbW2u9w4ymHwAyVHKur69bP7rWOf6KLkguJOlZ4bQW/CkQDOj5PBswTr5GAmW+b2+jT06glqw8+0mSiI2ouKtIuDcgyc6055JtkmGSbmuZ1dr0IXzLer2uz58/183NTQPCCUDo6snJeJAK2abeZU93+nYgM/eC2KslviZ5s1wu24tYgd9k1zNhSiJCS2VWHqyrMbN3SRJ/ZU34itQ3Ms/q73a7baReJkrmkJuIE0An+eh+SS5ljKHjmdywJ/EhCZmcj7Vlw9avatyPyp9LVFXD6Co50NPcB8KvGZvxpa6rwCexk6Sg7wPgZJHgXxziAxLckyWsaX3T96Uu880DqfHSyDMJa3afZBcA35zkXRLlfEOCePqAGMjqRuqUZIuvS7D+duiqQu8S92U7bJJAPkeey+WyVQWNDVbUApfdI3y2cbBv/i0ToSRH2T/5Jj7MePF713cnGk73ELjnm7hSOQk6FZQTNzmK57u5GVl2KRgCWZmtCdIZ+Dglwp6XzgQDVRaKlE4oA0+2VGQQpxQUgHJawAF0L99ZVmcwL957gJe137825fDcdH4ZgLNFJgN4MtKAlfklmHAfa+B5WR5VKUkgROkTnHCi+Zx8dgY5v9dGg5Gi9OmYE7TTHcmqtfedrKiR09w4rZsgZyzJHEuc6aWf5+/opnFnssEoyTYdsEMB8k8G3kxYOX73NcZ0KKlbWUWa64s/yYbkRrC0E2yf9X14eKiLi4sWBNk3kJGb2BMIswvAIwEYW7i5uWnj2Ww2k029AmwmRwCi77HXqvEIbUDFOJKtwm6uVqv68uVLq15la2aW2Kuq7u7uWgUq77NaDS9K+/jxY1ujBLBkzS7z/TmSpcNh2Phpo+XT01OrwLDJrBhg25LZJbvFYjFhkPmvrDJpwch2BEFWsp46xY/NiRqJCrCbtvFv//Zv9e///u+1XC7rn//5n+vu7q5Wq1XbY+GdOIOcF5P9bfTJszz/5eWltdAgBwDkrGLmeOesJNu3t+Pp6WnCvqafEOAx4UML2WIiH9+t+u2bgtMPJOueLHgGcwE7gXzf9+0Fb6lL5q1CutkMLx0EJi8uLlqr8nxs5pgHLPiTL409HA61OTmpt/ckCDBSuc1xZkJHbnwzIMk/ZRcC3bSW5JGgB6nCvpJ4sK4JDgEqchJ3Hh8fWyWGDl9fX7c12e12k83rCaYBq8+fP7fqZR7p68WbmewuFotJtUEsZPsIiyRm+FT4I4kGss33JFSNADirOMZA7lmZTYDNTxhPrpnPZCzgh8QimO1wOLT2PLoupiXbzm/oclCty6qRNU5b4bcySTb3JE6z4lJVbU4Zb3Lu4is7zUqDZyS2SNI746jvSeLyRLgk4YyFn/vWy5P7qjrZbH7jH3zGPdIXZSWHXzDGbAFOTJA+hYzdXzKVnQRJuhoDvJ8EiXtm4vh713e3Tv1f//v/3QAG5Uqg4fSEvu9bCTmzfy+YYRAUw+8F78y4c8MuAWWmm84MmH18fGz/pyAqBHkmNGd8eXnZ2juAuwyIFgSLYgwJYAUlDNmwoIsGCi3QAJhO2hnI/mRFhjFSNPdPJryq2nftQzFGxpZOxs/z7emUniPPpNDPAPoEO/OSouANVJAPpZYwVI2l82QQ6cC3QHJWrOZZOLlx2uZoHTPIMdbcKEdOmBd6kuxH1Xj0KFCTjo7OzcebYFuiqtSdG9nyEoByjxJnQpclnZ6RlQZ6y4HO2Z9M/ucJaNVQiVABcZ8EJVVjqdh6sQeOWwKUSd7z83NdXV21t64aU7KjWRr2p+q3pd20OeMRAOjD3OlXDRWarLJm6wldTTZM8M/kgi533XQzfDJdNs8CI5KjrJyaazLreteznZDD5yux1RLtBJbmRAZZkcv3P9AJv8u2r3kLEzs2/2zbyP1vxqFa8fj4WL/++mv9/PPP9V/+y39pLyvr+2l1bH7kpjGN/nMEGXQOUB5saCQfAAg6MbyQcEqGsIm0F88UYA+H/cTXZRK0WGivem3rVFV1enoyIWPmLSs+l22OCc7pLrmzR3J2byyj9c8jOCXsyWCnzOig/UoJQhaLRe378YWxWV0CBpNQoyviwnK5bC/UU8l1ZZWAn00dPzk5aftekulOltjczU2iQcZJMjw+PjaCJMlJIJp888QfxJQ5b7fbSYIhLliLnFsmF9nZYc2urq4mlREkqLkhApbLZXsvSx6rLWnjB9hK+qxcF3ORiLB1n8lkMMHsHFzyGXnUrgMg+Dv6Zv+ctQbo+b9sYWfXdDNJxyTyxKe0l/RJ2WafiQO/mdXsXFvrjVwkq6y4iQHklBhitVq1xIsMyJfO8Cl01XytX9/3tej76rvx5CmYINc0Cc6MszlmY8m2NdgkKyHWJnFqJh2+l/4+iUpyy6SPjnVdV//1f/tf6/eu765ocG4YOqAN68VAks10MkOW+aqqsVCEkhv8lMoBI0oJVGMjMT2CFLCcjHuCEHOQbVtYoILA5y+MY0yp0HMF5qDS2J6fX2u33dX+sK/qq7q+q0Ut6tDt6/r66jeKlQkUxc+khwJkq1EqhPklwy2p8nkgkHyAw0wKGXEyMRyF5zHwNAQXZZwG8PEIW8YocMqazZNczs7OmtFbf8afiU62VWHj8mcurFruA0hArQUuQQOglmVXYzYGAYyuZPAyxizvN8Nbj0ciArfOKk+GzBpUjccC+x5mwzxSjp7LFnMTm2fnvbCqmMenp6fa7/d1c3NT+/145OZ6vW6A03OzqoABybaMBE3JmpDr4+NjnZ6etnct+G7qt+SX7tHtDDK+IyHDihuPNfQzz8+jsbUDaCVxDz6Bg/UsP68aAqbTT3Jc86qo+7B/n2eH1lr1IHUqwWeC1HybO9YrdW7+3Ew6zSOTVcFKNcn47Yswzl9++WXy/cViUf/0T/9UFxcX9fHjx/c1HMv2gF7Gk0xe+bq+H1qKjNF4xY3BvvoGavj9vq/qukPzNfxlgpyU3+iHlrVYTDdaVtU7KTMeU+tZadt8frKD8/vkMxP0GCffDuyrLlp/wBE4AeDyjdmZbBpfJvZY+WSiT09P6+V5JOD4CFUe8UAFzu8lAPwmTIDIQkqcn5/X09PTxLceDuOR5alzxisOSurpIOJCqxmdU4nky/P7VdVeSkfOfJzWPBfbVikS37RtpU1bDzZCxjkPe1ZhoKpqgP1wGE8iMu70c2wpWXwV3GzHzOQ040/aTfpT88gX5/G5CGG/Y5v8cDLZ9FzspO9s3DMlpOMhFL99cacEJ0m0eeLNtswB3stEER5LMtjP6FEmm2JY6rP47jkZxy8uLtox7WTNHn0/Eyo+i063BGmxrOWM6Ep/PScSyTLJAXjZHPJe9N+LCY0pK/VZ3TV++kAXkihJfJqxMJPvv3d9d6KB0Uqln5eZsnwl45orFwEYaC4+493vx02BWe7SDyhrFrgZBaXPdhEKiQnLdqyqaZ8awEWoVeNeEMZzf3/fnud4OGPf7/f15cuX+vz5S/X9our9ZVOHw77W601dXV3VzfVN9TWWu7LlzMILOAJSgjrKzwmlcc5BQoL3TEh8P9cm1zCDjqBEuTi6dDqp9OQ4Z5uy2pPrnC1HdALIMDYgMdclGWJALYGVeRiPi0wZGn3iKHI96FAyP1laJuecfx7tPE9o8lCEBB1Z6vzw4UPTBc41K1XWyHfmfdBzZ+vfyUSxT21IEn+fe3l5aac8aX2qGgiCq6urdk/nuX/48KE9j176zLz9whqlzd/c3EycHr3KQJSJQcqAPgBZyey+vLxMADUgkOxT13Wt2iqpwlrnM7Qf0GkgJfdJaA9yb+soichkWZK8WCx+0yOtNYR/YOMSjapxP0SebkUH2I7kca6H5GczvU2l9Jdt5EEFWblhM4L8n/70pzo5OWl7e/b7ff30008tMT49PWusZyYU1jJJqDzRhD+hP9keN4x33DOV1bK3t2kQzZZFgAZo9rwhQRvb6RIg7HbbJv95LEx9TaY1AZD/i5WYU0CcXfqTlZcErAkK6KBDSsRelTGHBTw+PtZut6vLy8tG6CEoTk9Pa7vbNjt0b+tO95K44pMlKdkWk+0ugL92uPSzSbiIaUm6YaXpRpKHqccAkT/2VhgD/CDeiNuewf6Tqc8knF/PA2fM//X1tZ6fnxsmcQ+/Nze+QNVDIuPIWLLNRIwum3OuVxJG/Kvk2fjdU4JIn/gNcv7y5UuzqaqaJKFsLgmjbMWbV8AyMQBWraP4TTbkOY9T/BR/KYkkS77asz5+/Nha+q0Zuzw5Oandfl99NyVqE4znemmHEitGnzAmj/x5JgDp99On8TH8GGw6xKqvdXlx2fSJL6JvdMa4kxzlp7uYV/qe7OTx+6rxwKDERWJzJi+ZgCGo02eyI5/hE3/v+kPH22L/OK7FYtE2mmLaBCqtSgxDsJwfg5lZJUEJZpQrW0q+fv3awA7HzBAlJckyr9frVrXw/GRVr66uJkya/9uQlgJerYaXBR0OQ78i43t8fGxg/e7u7r2NYDjycDCS1TvLNrBtq9VJAxRYc+N2cSBAGTBgzowvS/QZ4ATGNGLKaf4UMBURGwWMML68fzIwjsTNRCGDYiYAaaTYgKpqLTrzAJ3VGwGGITEw7SoAFeec/fOZcHgGWWSiINHI6sucCbYXgfzpH7tQVUlwSCbzQERnyCMZmmRPJQQZoBM80p0Ef3Ql13cETrvW6w0AJwDYbrfthVcC82KxqA8fPkwA+nI5tlewXWObr1kCZhf7Vp4WiI1zuVy21gM6ZXyCDf+y2Wxay6bvCsTzigS7S0fNB2Rrm/W0Zlr2ks2UHKS+J3t+cjIcscvujIlfcj8+zHgEw0ze+GHstGNJVV9UhO7u7iYntLhyPee+I8EcUJiVG99JYmKxWNSf/vSnBtZTRpl8D/MYjtMd5n8aAMybold1ejr4Okz6brevkxMV6K7e3lStT6tqUZvNuh4eHpsurVbriY9YLpctiXOIRlY2s10gE/vhZEAvkty2lkcnArm/z6/XYwXcn2FuY7KUAPBb4Frizo/xQew/k4BMYKwde1d5BCjv7u4aC7vfD3uvgO/FYlGbk0114R+sN5tJUkulxf8fHx9rvV63vRH86qdPnxrzud/vm//K+Jbxg86nX2Pb5EO3JPyIzPTrZJIAny2mD0QOGiMbtw7WyPPZ8dXV1eRUxBwf/fd8Y2NLmbCpKHgfibmL83BH2vu8mi45GXV/PGnT8/MI2bRN/o6P5pczVtAZFSIkxPPzc3tOEsj25Yh9EhixmHzyO3y59nUJmDXLPRMITm8RJ1PtafRrGTZRVdUdDvX17a3O41CWbD9jwxL+HOOc8MpqZMa2y8vL1p4rtvDRSTi2WH961vzCPE5nLLKWiFH34KOzemQ8XvcgSWMXcA68IJFLIjCTMFiHTdDfJFMSu//e9YcSjbmQBauqaudkG4CfcVDAKcEm08bhJvuUTCPjZXDKVc/Pz03ZKEUCBM7CH4J1L4mCAM9xZIuGkp95GivAn0xuGugQSDYT5zqw0+dtru7LKBm7tgLOB6hIJSAnCgGsZW83oO2Pz3NK2ceZzARlVt4lx2TGycF6JjtB0Z3vXjVWFZLxTQW2Mdv4c4MlJ5vfFQDpXJYIrb01lqxKMub61Pd9Y0pSTpKsDD65D8HzzSFLmVmt0OaHLUhAnoGQjnEgWbYlz2QTMiEX0ACoZNl8r6qaDQo6uV7ZGkEumfzTf+sAMKUdWxvrZUxV0xOTzIE8MaMuY0+gw84+fPjQfEMmEEiPXDN2TbbWF1Agb/Znrn3ft5Oq6DhdoicJdPipxWLxm2Qnk5Kq8XjMOfAUTAXSTJTpPV+WNugUryQG6A0ZYMpy/GxB+0smFK7UM7LFVkrigIuPHz+2yoVjS/NZ5JXsJSCRa5SbhC8vLxureXFxUY+Pj+86ta+vX6t9v2o4LckLSwFtPi2Da7Yb+v9IIkwPwAC0JHXG/vLy0k5Q2myGRPPp6anFIrajHc547u/vJwSDMbJb/i6PoNa2RAcw6oBmJnfX19fNt728DG9jv7u7q6qxYpeExeCzxo3qWXXLk7KsCQB0dnZW5+fn7eh14IcNWec8+jMPbyF7IIv+2Zic9iNup00ne50YI9cU0altJtuF+BV6rBLEn3pOEiaAe+IXGICvTpLOnFPWYit982+2eHNz02RgnT3biWN0Y35iZYK+L1++TOIT/fF593l+fm6H+5ClgwiqhkMyxOmsAOa/k3BJ0gIxjPH/VuWF3rNxfmC1mraDkum8U0Hybb20Tvt9/y6b/WG6/2NeRUgb4v8zWQWwR5sZ9/6YG2yVrZ7uh8Cqet/A/i5n8ssWskxi+D1xiZ5tNptGnCCH+eKsiqa/FcsTEyaWZPfzNbVu7DR1+B+eaMz77PRd5uasBKIWQiDQb5utPn/729+awWy321buzQUBOE9OhvPUbTyjYAmqU0j2kKicJNjmoF5fX5tjSMCdxitIWSQGSjmrBueitzENLYEC40mgnJl13/cTpjydHeNK55hONZmnH374oU5OTur+/r452qpxg1KC6OylN1efMcb8rudmObVqeoxwJooJiJfLZXsJU7IJWeHK72kXwNwcDocGShmQNa+qiaFmm0z+nkNPIyODZJm/xYZZSwE3y78cSyaQ5GZdk+1M1hWAU7kCMtmRk5eyfS03dEoqVPw4mc1mON0pyYD9fmhbFLTtgSF3Sa7jX/PEsEwOyDkDLGeapVdyAlAEck6ePecRwJIi4+ZDyLPruslJQj6TlYdsBcne57QVz8CW0eGXl5ff+BfMKx/lZ1kRML5kMLNKZVzJJiYzxCclS5T2au0zSUaKqIwA0FXV5Gzt+c2s5rgnvae/2V6KbMjkJ9lqc9F+kP3lKROgJMeevo8s2HhuGu77vlWQAej9fkwM2cvDw0Nbt6qxRzptN4Px4+Pj5G33GTTFm6rpASa5DuyaPfBTWj98DrDJVgZJpQpJ13WtKiC5Ilf7tiQ+2dpEpzxPRwGbEafoLdBHT0/PTmvx/j2XitJqtaqnp6eWJM1JJUkR/TRufoje+9uV+srXZiIlAc0ThehekjzGSHf4r9Vq1fZzSlJ8VkKRBFACLr6e7qW+2zND56+vrycby30n9xPlHim6QxfoL3nYW+j5wDZ/lVWYbN8zxt1u16oOcxn4A5h2XVc3Nzf18ePHVlWBXcyVXJBA8Irj7qvGKinCL20jKyhVI/FBb+i8+CteSFiROdaUnmdSkVW91WpVh3dbJnck7Ha7rUXE8QTTCPGqESeYqxg9xxrpd/gnrVTsga9NHGge+2jdYx8S+7nNJHmcscr//Z5MyZ3N+8O++DQxPOOPe87bd/nOJF3TH/7e9d2JRrb6dN1QoknBEf7T01P7t6Mlz8/PJ5sbE4w9Pj62l3FRGEoi0SAk/6asHHSyhsmSC8QYGAyP4Jc9a+aQTozgfceiGlsurEXETFIii+NKJaEADw8PrawtEUpHwrjyJVgcnuclW5LMrjkJ5sCBKxWqGUEAMfIV5FPW7uu5qbgJUs1XkDMH9yev3CiXpTmOB4NAtp6XDIN18m8OxZwFTI5FYkSnOPZkwDkk4CCBpjU3xmS6BAWOyxzsEZCca7+yBpmAAL4JyLTa2DNhDkrI2bqSgM1aeyEU8EieAuN6va6//e1v9ec//3kSnDw7HR8nniA71y/L8mSWSZOTcLqua++2yGSX3dNHcuXk/E2mmGVAhj5nyxOdJBfVNPaXyVkC7NVq1fZlJRlBTzNRpG9ZYaEDyd5iZjNw+Q4CJ22I/SUjCpQYoyBPn6qqMd3GmCRJJoLzJCcToyRAkoAhyzx22X0BKXaSrY/Wb87qJjOa5Iq1GwDvqGMZhPkdepKtCwgicum68QWGyUCyB/7A/FTRMpHc7XaNja2qpsvktN/vJwlQ9sEbS5IE1sW8qqpt6pQsISr4gc1m08BS6uXNzU29vLzUw8ND05nPnz+3KrMEc30yHgfquWLw3d3dJGb5HmDDh1nHXPescAA/KoliU1a+EmzZO2aN810uabtJtuVLPdmKmGUt6HRVtZY49pZgns6JkdbaXBI8qxrwgfTPXJB97qf1yNg2m03d3d1N/Bs5V9XEZqqqHUVuLtne5KV64sB8bpJwY/fH59MWkwU/Pz9va5U+ANhPsjaJIXPPg0vgLnOUVCYhhzBDPBmXt9Vrp8+qijHAMWlfeX8vj/XzBMuZzNCb7KjI+bEVn8lEKv1MymO329X28Fab9XqSKNGDjFm+Qz5ia/q89G9pR2Sf/3evHIu1Ntck5fgRP5uvM537nusPbQZP0Azkc7oWy6CUvWXajI7xV41vyK2qur29nQQ6i20hACvsDsXJtg/BkuAstrJgOgTgRB/dvL3FMXlz1pRTq5q+vM3JElm1yExWIpFGBCzYqGf8AIaTfzKpyVMOslfY+NwnZSDYk7U5UD6fBaI59AQMfpZAJtltRgo8MORkcRkRo8ygY31Sx+iOewt+yfgk28DhZsKYTgG4Fhwkm5yh4MHhJ+vLmJOJEjjJLg05k8B5a5znZqD0rOwd52A9w2cSOH/+/LmN+Zdffqk///nPVTXuRcg2LWuXbIm9TWTz9evX1ndPjzFo9Cx7l6vGgJhzz37bDPLYuyQPMI7ZhpVsabbCYbc4SLqlOgYM5/zorSN28+24bE65Pasu2TJmXBkUrCEZ5CbO3G8BIKYtYeskmdYd4MW0eYZkK32ARNJcM2BmAMlWhiQRsiSuMp3EggQ+ZZt6RSb5krlsCaMXkhyBkH76m0zSjvjMrJ6mfUoKU0+SvAGq+I9sUcg1rKrJSTJ0Ubx6enpq9/rhhx/K5nnjMA8McrK6ABw9y7aabPsxbnEvD8Kgk9Yh/avELdl0/gVgdZoafQH29vt9q6BkO2X610z07IVL4i2T4IzpxpEJOx3KDf2JH5I8tF5JZN7c3DTmPUEfu1mv163f3L+RjMnkmp8xqo5apzxFKSszSAqyT+LFmngp6WKxaLbNpuiyDo0kH5NARDh1XVf/8R//0dpEtYPDBP/0T/9Unz59asSVmCZGpE4lQZD+0u+MKStubJjtfav7gh/Ikxnpizmaj2fTrQS5nmW85C5eWN/cd0kPs3LbkqDltEOEnyGDfA2D7yWpkzqD3E7Mxg7T9rMilwluJlXk/bbd1XIxvs8nAfwcg7Bz+DuJrcQnuWZwKL9A7qlznpXH9WbSnn4gkxq//1aV5O9d351oYFZz8pRrtVo1sJytUV3Xtd38Aiiw73sA33K5bOdg+2yW26sGB3J9fd2M16JkBiiwSBySPaUgmW3qA5T9ZyCuqkkrRwJ6SmITE6CRzFWWuRKMZbBNNjxbhJJBp3ipjO779evX1nImwJCDz+jFxFozWoGHA81TJSgYI2c0cxbZnDPYZzKVG16/xY6Sg3vPKx4CjT8JPAUnl0CT7VgcUpaf/e7/L5PPoG0dsqQ5Nzoym7dQ+cNBZgXI9+ZMtrmnI02Zkxdm6scff6zn5+f6+vVr/fTTT5O3buccsSWeC9xqH8wgTZ+Soc7AZb2Sma6q1h6ZDE/KarFYtIqAoLTfD2+El9hIJNLm9LLa6Apc0JcM5ggCoIadCl5ZjWCfmDxrTl5JJFjjTMaBorQBPfnpn/jPTJyQE5mAArwCFz1JQMzven4GUPdiY0kGWOMMUoIqEEQOrgTtydaxgzkLJ1HAjvOnfDGdIZdkdrMNk49mN0BxVm/6vpp98BnmcDiMe8tSVqryPgsIGTMdzHYavvn+/v43LROjXY7VHLaQ+p0soPnngQtaLrIVSmU6iR9+DPss9vB3kt9kg/u+b5uY6Ybkerfb1cXlZdXX14nsAbT0g0mauA8yIQE4e9ROk61eYsj5+XmrUJBxgmI/zxZYybaXfVaNTL+ES3WHjWfiRR/FELENaWM93PPm5qYlDvOq23yPi/VVPeq6rh3M4HQxLc1sTnKDdMLQe59GyoSfuLi4qOvr62bXd3d3k5cgp75WjQlqxgIHl4hru92u+Ss+2nzMFxlnbehXxuF5ouj/+UoC60ovJUd8g/FZd74DsZnk0nwzfsOcfV/9fvqiZX4y41LV+C4UupO+if7ld5P4FgfpF/llVWxOxFqX8/Pz6g5jOzObT1vn08QCupbkl/vDCvkMY2Y7mWjAdNZ2uVxOcKj1S4LQPTLeZyz9veu7E41k1bHuHCLnxAEnO2CgylWY9VwQzMtiMWyWc7LFly9fWsZOqTBMCbw5wHkpL51zBoGqEYzOe88yIci5ZHUA2Li/v58wO5iMdLqCYfavJ9gGxDhL5V/KYk6bzaYeHh4mvXRVNekbdSrKdrttPZPJCua8GSDDM2bKk+W3VGhzoujmxxA4qGzPSCNgzH5WVZOqkvXKBMJYcxNnsvAqHwz6xx9/bEyeZ2Hrs6yOraIbGVg5GQCkaqwKpBNJJ+s5fu8dJVXVGGPzB4pzk5kyuyCQwNezzdFzMS6Y7VyrTKx3u109PDy0+WYbouCcjv3x8bHpl8QZIKNDnsGWM5HLQJkAhR5km4gjUdOpCVjWHziiZ8nIA4wpf3JOXVSRTH3HmuXa08ls25wno3QdiOWPktwAZpOgydaYTDSrxlYiepcMdAZBiY8AObcvATST12xbNEZrBoRmUqcdSI80355M6DxwWwt+JltnJFHJYvIhbDFZ1ZxjMrRsYLebvm9oALzdRF6qb/x7JiKCLPvmt8UY8SPBd1a5POfp6bH9PvV/sRhOfGILmUjM/bsY5MrNs4McltX30xcPqrJIGvPf1iRly2fSGWC4+vHAhfRF1su6np+fV/XTFhgkRcbl9HHL5bIl/pj4xWJsZ6ZHCWD4GHP3Wd0A2POq8b0RCYLYL/0UV1O/sur06dOnVnGzwT5JR0BTIrnbDae7HQ6HScvz/f19nZ2dtTeRO2nLiVxJPGQFPUk3z6W3ni+Jp4/kz7YyHsNlZMJ2+NyszGSszUrHPH58y5/6f/oo9p/3y72MSfwlscpG5lUB4zkcDo2wFuezqk42y+WyKsgvNrHb7arvutpEpSTxYSbf9CLJJbaZrWhJOiJQyFm86fu+VQF9Zrfb1cl6XP85mE8cgoBhB1UjLhVDrDHZZaWZHOf6k0Snz0n00ndYa/MkV/fNhOj3rj906lSyAU9PT815JjuOGedIGHUyLT6vumHSStLALSds0arG1gbGxXhzcdNAnPCSAcC9OVaBRz9utkAA6SovjIhjEMBeX1/b0bfJDLjHfr9v58xjQK+urtpicbC5iEAARy4Ykh0FzXaD29vbCTPGQH3GPZOtTLkwDqyB8VBQTierTZkUWAuODSjEZPgdh5mACgOSzKNnCvCZNFlnp79IDLEEHJnPYk/m7RiC8fzUovV6PK45GZGqESQkQ5ytJu4/fxM4eX3rxKJMzNyLHKx1MsgZpNfrdf388891fX3dApn1pIOObpYECWj03gkhdK2qGttK1gmQM3Ho+76BCvqeYFtgyVItGZ+dndWnT5+aPPf7/eSkLCApE9UMogn8VBSAqfnnktnhW3IjufkBHBg2Po9DVpngd9iHF5TxD37Or7BXAJidZiXA8zMZpyPp9PNYzmTv2Rbfwf7oEV1KskGvunsLMEkMJfhKn5zgUyIAxNCPJFisBVBKvkm80DXrn4EPk7rfDyc+DWBiVVXLquqrano8MdlojU2dVG3h75ATnsUGMtEz92H9N9X3XV1eXr37leHY3cMh3x/V12p1qK7ra78f92McDl3tdiOIW62GM/bPzy9qOAq4r9VqPQESfHu2pQJ46SczfvKHSZ6xd+uTQBez//b1rQ67Xa0Wi6pD19j5T6+/VC0XtQ7GN1uHrbv9KlqG8qANPtK4yfRwOLR3I2TC7fhQerTb7erq6qrp5Xa7bWx/4ouqqr/+9a8t2RUH3F/lS++/BFnyLf6oBp6cnNRf//rXuri4aNVjvs16XF9f11/+8pfG2NPr/X58wWK2kyf7fnp62l4WKJnzmdRN4+KHMnlwJYnG19KPTIoztiXpmtVNhGXGgGxrppuJfdbrdZ2enNZ+f6jDvqvlclWLGl6quVwsa7FY1mq9rEPX16Hra705qcNhX30tard/f0fYoau+FrVcrqrrq7a7fW3ebXC1WtV2t6vFe4JB/vQrCeDFcjyxiS/kuxMsZ+WCrBHLrtPT08kLXZNA8bz+0NX+bVurevdv6/fE8tDV9jBW7TOBy5eR8uXfahWGl8xFvMhELXGuWOfn1hOZ6kpima7D6/QkE/iMpb93fXeikdnzajUeu1Y1gqVMJgjP+eMmyMlrAwAGOSqflUwkg+yZq9XYD5vZfTKpwBSHk79LJoQgs21gDBBdPTw8NGeaiRWl4EBUeRaLoVzquavVqvWEc+AWv6p+w7K7fzJvCcAomjlxNhZdFnx/f19d17WjDedVmVw3iudnjohMBsZckz1ZLBatApPBLct1xs4Is7rEWWL2rU/updhsNu3FY1h2TjcBVpYgATinXOUxnDlvxoilJ++qas6FnnA0WQFIIJu64MoTbTjyrDBwagmqmqPqxz5Y/55vXGdrvitxr6oWrOmpU3uwPIvFoskTwFWlExDTMecmW2uaiSub5aSzrSf9hARA0GMrEgQy9mLM1Wp4iSF/Ys5AwmYzvj9DOwb/oncZW5mtVFk2TpY9WUZ+AKPp2dfX1w08sQ/rm4GBrrLh29vbdiyqe5ElOQ8s+VNrt0hmit8zPgRCstfklFXAZPHIhn1ZY+vpOdYvSYH0yZngzFnS9GXiQvYXkz1f5T6ZQCZg8bu0rd8mJcO7OIbY9HVSVc+qLf/DzjMZz+q3vQb8se8vl9NTeHKN6dLZ2XkD2H0/VirnTCp7T7Lh9PSsPTNZ4iS1UmfJYrlc/qa9jG/L1qFMPIy7223b/fn9Ye6rOn230ae3p0nlZ73Z1GozAkvJPdsyBvEvq925b4Y+8NFwQcbZxAl8hfGqpCwWQwcE0m+9Xtd//s//udmev73narfb1ePjYzuaV0Kd7+JJlld71cnJSYvn9BTJQn/5hWS6+WHvfUh/R05VNdlcn34hk+b8PV9A7nNixVqKIWyZ76yqCSFBp6xNVinEq8QGSah+6+/Dfkiwkwg57A+1eE9q1tH6N8hg2o5r/JLJwV8cWgJmfVyey7bcdxsVxcSUnsXe0r8k+ZF+sKqa/6e3mQDs9/vq3pNGn9EudvoO3hFNkh1rZw4pg7Qdtsa+skWQX0liOG0xfc3c34utfpfJcRLJvkOf0if/veu7Ew0KjEnZbDYti5LZOVZMXx5B930/OSoQGE+QnS0AHI83+wJ3DEM1xekZgiAH9vnz50npLoFdGl+ymZyyDDYZCEDUQiYINvbc3JcMBAbTd77VcpGBKsue7kOG7p2b6KtGZj973RMoZnkxWfjsNSV396OsnjMGznEzaG6E9p31etwUq50AEHNCktYMhtR145ufky3JUve85J0MX7JXDDr7woGcZJAkTxgtxm8zaDI0eTJSsjjGBOy5rF+2E2YSIoiRzZwZMBaBJMvF6XDokOdJKrF7nBmmjPx8XiBRNTFfugoIGosgaP7mhPkWbMnTfcxfG1kmDGwZgCFvlaeUXbaYpPPLhCGrCMmMz1lgiYrgw9mnjJyCZg34G4Atk03jnQNa43RymD1hWaJOHWFf2FkgIJO8XBMAKRP89BNs2jiwuXnKWfqIXDukRBI/CZY9i+wAGDbsT+qB+7N7c2ArfHZWhq2bIO5+WUnJMRqnsbk3m7dHQEzII1lzf521dhwoRtm9u65rDLX/exY/l7ZsfekLUiUr5ZJJ8sxkdzjIYAQZ9G+73bY9eGxrs9m0F+q5nKhnPNa9agRoqjrs7HQ9JpHWZ5Dxqrq+b5vEM9YBxsbt3j/88EMtFot2pDW9/o//+I9JnLDmp6enbZ/KycnwXoxffvllwphLDn799dc6PT2t29vbury8bMcBIxxy3401UoE1RkkGXZIckKkEZbFYNLJBXKE3aXPwinHm4QRs2OcyWcm3xhs3Xfe9vu8n7ylLktY6sgs+1/1hMeM3RxWuTHKtoXvQY//3N/2FoficvuuHSsZiMfExuc7ul3glqxPi2IhXFhN/Jj7MSb8k4fr3+4oLsF/akuQqOwboctqvWISYoB+ZGO93u1r0I05IctW8E0PyH7mxHq5IDJTVqUwgkqCEC1KGGS/5/bTN9P1j0lfNf7oH38c3Jm75e9cfqmjMNwunoiYoyBMZnp6eWksGQ3diiOCZZUCgAUAUQHPTnnYPn8uya7L7kh37GFQJlGG13Ag+5kXZzdWiyk69NMrvM1FKdloidjiMm5zSsQHixsBQyS8BUjKSgm7VmO0yyCzHuSdDyRJ7Al3jpaieK5kASoDWfJFTgnNrDDxryaA3et5fXl7aZzl1c8TCkmkmcdnznW8INQeBP4GGdaJLStYfP36cGN0cbAML6VgkGtmTKpDTUd+ZB+YEIQk8PCevdBT+z86Ai0w2ct3Yj89xCJkA59rl+ufY6D/dMhfBIFmWrhv6va0R+dGNbKXM94L0/bBR9fb2tvmYZHokzeakJ5wNCYzWQRB2xGPqdNeNJ5hIilL/rVkmv57Jl/ELydrPg28m66mvfGXqDh+X/iqZez4gSRbVzvQhQEpWIdhPBo1krYzVfb4VtOgFIgmTlUHI/cw3AYo5p11llZBOZVKZBEaW940lS/YZe1SU5yxdki7pN+l3VhOSQTwchiq7Ay+czJTgzhqRayZg2H/zTLBINvxX+gh2wP/6rrh5crJp/iHtlm9J8kwCQGaPj48TJhzY57uqqs11t9vVxfl59Senk7hmrJvN8EZx5EaCIXNcLoej2/klPlZ8I8fD4VBfvnxplW33QUZ++PChqob4JlkBjPnjf/mXf2nPlSAjEIwl/RcQlxuNrX0mzNZEXGXDxp9gWyxgH8k2z49M5dfS9tiPPSCqM/aopnznhI9klz1YX75KRSQ/n1W1xFpJBMEKSJxc6wSZGbMmfiE6ILIdeLvdVr8YD0dIXyN+tCShHw+4GPzBuqr6hi+cIpXgW0XftV6vqwviiZ/Kiqd1FNOyHYkv4RvoauoODPn169daLaab5N07cQiynh6lD5mTdeaQeihOJpYwf7LMNU19zoQhMZ9E2D212iZ2zaqpuf/e9d2JBsURyDnUBDUcpAETRLYKMEglS5NK9hE7AnRgF4CFZAZUDrAKVdWUh5H9+uuvE2YMqyjhAH6THWZU5mRjL2WgcBjdVhY8jBt5KQSmg7FQPACTwVM8cyP3OXh3n6x+eBZlA7Yyq82kw4t9MutnKHmspvXNMrLnJ+NDjj7HIap4uQ6HQ9srkD272GrJJwBiDbDLVdXOHLee80ze+uT7WcjZejpC0l4Ae3AS3PR938CfNZLsAhFsIUvbHBVnb95ZKSNbesaZS0rNe84s0WsOMEuhyZwlwAGS2KgrncZ+v68///nP9fj4OEkyFotFS0pysy5ASFcSUCprPz8/t3cPYA/pbdW436rrugaO2D7gmBWHdJbkR8/5D8mHNSAbDGASEQJHsuBZYcDYeLZxYqMwoNlCBViQBT1IAkOiZc0EBL8DBOgiX5H2bjzJztMPPjjZuOz9no819TvZSTrD/837eck3A1q2uCSjyickWOGzyC/nnqDb6UrJNO52u7a3SAte2kG2i9HvBE3IhTzYgE/hb5Lkoe98hLUBIOleVltUWRP0kanYxu8mueEeyJlpsrKt1Wo5IXtOT0/r48ePjf33nKrfJlD0UWK7Xq9r1fe13qzb/+1zWy6Wdf7O1Od3jXcftsJvZ/sjf0mnVFgkfev1up6enurk5OQ3if/NzU1by6pqrZTml8ksPwEM8RHuLQbmiWPGcHNz08i0ruvaOmWrXyb2bFuMEWORYj5LBkmiZgWUX2FHWUXIfUWY8ux+oId8mITRlcd1J5nFPjOppWfIPvLNxNFaJYnBv2ULqLmYBxvvDuPhGRmn94dDdf1IONNX92JjiSkHe55WROCGrKTkPlNJxsn7YQjsJIlpV44DsZUxOxOi9LNspsXXxfi+M+vHD8EIkmn6ZE7in3XKZCxlOE9SE+fAReThGS5rnXNiy1nFsv5JMmS1Vyz/vesPbQZP4MMBeJAsPxOABDX5ndzUZJJ6avXhVY2nUAhcq9WqVRUYtufkkX9KiJxEsiy//PJLu6fM1LiSSfP8XGgKnc5hXs7MDTQuQQyb7nNVY5IFPPo/I8sSe44rGazMSDPQAB6CmADjZAytbRK1OYNWNQZBTK79Gzc3N+3exujfnz59akrJiQu6jCJbFOabjRltsn3WGKP4yy+/tP0/9EQbgh5YffkMmj4CnBJeOpjAgaNMp0CPJCn0mJMTyCRYQIvnM1JOgQ5la57qH/ZVsEnGW/KdbHwyG/QjQbO1BZ7JWjKm5TH3tdApcs21xvgJyNolOaqLi4ums7lhDjBgC+mMzUPbA7m6P51k25lcA3DuT9cymbP+7MrcUi5ZHQM80n5Sfqkj6fSNKcfKVpJt9XsgNoODMRwOQ6sDsE0vzBnx4jnGZ76Z4LTA303bn4AhCRsZ8jvukQlOVhX8zjMzWGdCkQGKD2ATWG2VLMHWM56fn1vrj7kghzKhGOzlMAGL9JEd8dsSD/5tv99PXigr4U/QrkVpnqT1fd/2kpH74+NjI5gkBOKAMYglmbCQkQoE8Dvo6b4OhzFuGFeO8+Liovl/lREk3W63m5ADi8WiTk7Hl8xWjQRALcfj3SVm2+1wIt2nz59rtVn/ppK5WCzaoQn5kkhk3ocPHyaxT2fCzc1Na6kC4Oi+5I6ek/HV1VXzbXx+br5ORn61WrX7ZysMefPZYk8ebEGHU48l70g7uiXmJGNMz7OtMDFOJgLsU2UlKzJTsD19x1hW65L4TRY7SbAEyuZP3/kkpGHa4Zx4oWOpj74/2Om+DvsR8Itn5rQ/jO3q1iVtyPPod5JMdEvXynq9bm2HiR3eBzVJFPkgLa1wa8omKxFk5N5sP1s5jScBfiYP80pAJi9JTuZ3Eo+l/0y5J9mdSUX6bXHBOtK1JJkQV9YodSwJYDKZE5d/7/ruRAOz4nQYjtoCUGYZOOFxeIKWQc6ZcZOvGk8xIQjC8Lf7pjJhJDiIZNk5kf1+346ak/E+PT1Njga1yBSFoOe96lo1kmGjKBxdgkOAhsElsHBfTkpr0FyRGb+ABYi5VzJh5C6JEGCTSfOZbLnCmMxLdBQcCATSTk5O2n4LPYo//PBDVY3n/ms52O12bd/N5eXl5GSprhv6E/XBChASDAZJ3k6DYiSCd27qypODJClV1UrRnBgQl0mDNfZcuv76+jrZDJygirEmI012ZJZJoUDiM0A+efks3ZeQcJiAMfZKJcH8Ly4u6vPnz20+QAedWi6X9d//+39vTNzb21t9/Phxwm5JxNmecnPuAVIlzOqZsbG91FNOTyDbbDbtOXSO/XJ62epAJyVD7iMxMCY6n8kIgsJ4fN+6m6c58knmxO6TjWb7bFDSlOtkDkle8IP8hDWScGLW6UCSHCqP+q7JPRljege0SHaNo6omfkggImtgKq++71s7B1vjixIEsGv/TwBR9Vu2N8mgDGCqiyoGmcRla0m29X5Ld+a+nY6Tp88mc5jJfFaAc4zWTxLofnx0tqrxZ+afDHa2yySoZSdZZUzd9fJaJ52x7Tzas+u6dlACX9+IneWyuu5Q6/eK17/+67/W9fV1ay/80w8/thhvvkPr63kd+vGkw+fn59ZCa70Rbuzpw4cPzT4kRXTu4eFhEr/yZMSsZNCrtDHJQB4jnb+3Ngm+M5nh38UotoMsBLbzs0m40n1+hR1az6wU8BGJDcQz8ZG90jW+PxNR+uP34nBisUyEEwQnAM6f8z8JJo01SYu8t7H4XZK2/PCiRowzISG68UAOz5vbXiZPbPTr19cWNzNpST+dBJBnWqM52TfvGCB3fticyCbXmP/L7pzlcjmcOtWN5BQ9sq6uxA2J2+ixeSTJaE65rpkszBO0rIyYH5ueV2IyviSRl8kOfUnC7PeuRf+9KcnxOl7H63gdr+N1vI7X8Tpex+t4fef1fTs5jtfxOl7H63gdr+N1vI7X8Tpex+sPXMdE43gdr+N1vI7X8Tpex+t4Ha/j9Q+/jonG8Tpex+t4Ha/jdbyO1/E6XsfrH34dE43jdbyO1/E6XsfreB2v43W8jtc//DomGsfreB2v43W8jtfxOl7H63gdr3/4dUw0jtfxOl7H63gdr+N1vI7X8Tpe//DrmGgcr+N1vI7X8Tpex+t4Ha/jdbz+4dcx0Thex+t4Ha/jdbyO1/E6XsfreP3Dr2OicbyO1/E6XsfreB2v43W8jtfx+odf/x9oNP6G6C3eDwAAAABJRU5ErkJggg==\n",
+ "text/plain": [
+ ""
+ ]
+ },
+ "metadata": {},
+ "output_type": "display_data"
+ },
+ {
+ "data": {
+ "image/png": "iVBORw0KGgoAAAANSUhEUgAAAxoAAAIzCAYAAACHlG8YAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjcuMSwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/bCgiHAAAACXBIWXMAAA9hAAAPYQGoP6dpAAEAAElEQVR4nOz9ebxtR1ngD3+raq29z3Sn3MwDYUqYghgSIAKaEAYZ2qlFUURRu1ts2m4cabVpQGkcUIGP2N2igEO3MjU4+6pEiK0yQwiBhCSEhMw3ufMZ9rBW1fP+UcOqtfba554Lofmp+8nn5J6z91o1PFX1zM9TSkSEBSxgAQtYwAIWsIAFLGABC3gAQX+1B7CABSxgAQtYwAIWsIAFLOCfHywUjQUsYAELWMACFrCABSxgAQ84LBSNBSxgAQtYwAIWsIAFLGABDzgsFI0FLGABC1jAAhawgAUsYAEPOCwUjQUsYAELWMACFrCABSxgAQ84LBSNBSxgAQtYwAIWsIAFLGABDzgsFI0FLGABC1jAAhawgAUsYAEPOCwUjQUsYAELWMACFrCABSxgAQ84LBSNBSxgAQtYwAIWsIAFLGABDzgsFI0FLGAB/+LgiiuuQCnFq1/96q/2UBawgAUsYAEL+GcLC0VjAQtYwI7h1a9+NUqp9POOd7zjhO8873nPa71z2223feUH+lWCqqr47d/+bV7ykpfwpCc9ifPOO4/l5WVWVlZ42MMexgtf+EKuuuqqr/g4rr/+ev7Tf/pPPO5xj2PPnj0MBgPOPvtsLr74Yr7ne76H3/zN3+Smm276io/jnyOsr6/z6le/msc+9rGsra2xZ88envCEJ/Brv/ZrTKfTL7v9v/iLv+BbvuVbOPPMMxkMBpx55pk873nP40/+5E/mvnP11Ve3ztiJfn7u536ut53RaMQb3vAGvv7rv579+/dTliV79uzhkksu4b/8l//Cvffe+2XPbwELWMC/MJAFLGABC9ghvOpVrxIg/TzrWc/a9vm77rpLjDGtd2699db/N4PdBi6//HIB5FWvetUD2u7999/fmqtSSvbt2zeDgxe/+MVSVdUD2neE173udVIURau/vXv3yvLycuuzyy+//CvS/z9nuO222+TBD35wwuHKyooMh8P098UXXyyHDx/+ktqu61pe/OIXz+ydfC1/8Ad/UJxzM+/+4z/+o5xxxhnb/qytraV2/uIv/qJ3bhdccEFrj+zZs0e01q2//+7v/u5Lmt8CFrCAf5mw8GgsYAELOGk49dRTWV1d5aqrruKOO+6Y+9zv//7vY63lwQ9+8P+7wX0VYTgc8h//43/kne98J7fddhuTyYTDhw8znU657rrr+K7v+i4Afu/3fo9f/dVffcD7f+9738vLX/5y6rrmG77hG/ibv/kbRqMRR44cYWtrizvvvJO3v/3tPP/5z2cwGDzg/f9zBmst3/RN38Rtt93GWWedxfve9z42NzfZ2triHe94B7t27eKaa67he77ne76k9l/1qlfxe7/3ewC87GUv47777uPw4cMcPXqUN77xjZRlydve9jZ+8Rd/cebdJz/5ydx7773b/lxxxRUAnHPOOXzjN37jTBvf933fx80338xgMOA3fuM3WF9f5+jRo4xGI/7kT/6Ec845h2PHjvGd3/mdjEajL2mOC1jAAv4Fwldb01nAAhbwTweiR+P8889P1tfXvOY1c5+/8MILBZBXv/rV/yI8GicC55w8+clPFkAe/vCHP+Dtx7YvuuiiE3pMtra2HvD+/znDW97ylrSHP/jBD858/4d/+Ifp+6uuuuqk2j548KAsLS0JIN/6rd/a+0w8eysrK3LgwIGTaj/3LL7iFa+Y+f62225LY593Jq666qr0zF/91V+dVP8LWMAC/uXCwqOxgAUs4EuCH/iBHwDgd3/3dxGRme//4R/+gZtuuomHPvShfMM3fMO2bd144438yq/8Cs94xjN42MMexvLyMrt37+biiy/mFa94BQcPHpz7bl3X/NZv/RZXXHEFp556KmVZsn//fh7xiEfwghe8gLe97W0nPbff+73foyxLlFL87M/+7Em/Pw+UUjzpSU8C4M4773zA2o3wqU99CoDnPve5FEWx7bPLy8tzv9vc3OT1r389l19+OaeeeirD4ZBzzz2Xyy+/nF/7tV/jwIEDve9dffXVfMd3fAfnnHMOw+GQU089lac//en8zu/8Dtba3ndi3k+0uL/nPe/hWc96Fqeffjpa65mE/WPHjvHa176WJz3pSezbt4/hcMh5553Hd3/3d/PhD3942zl/ORC9DU972tP4uq/7upnvv+u7vouHPOQhgPfknQxcddVVjMdjAH7qp36q95mf/MmfRGvN1tYW73rXu06q/d/93d/FWotSih/8wR+c+f6ee+5Jv1966aW9bTzxiU9Mv29sbJxU/wtYwAL+BcNXW9NZwAIW8E8Hco+Gc04e9rCHCdAbt/2DP/iDAsjP//zPywc+8IFtPRrnn39+KzZ97969opRKn51zzjnyuc99bua9uq7lmc985kxceR4330fmtvNo/NIv/ZIAorWWN73pTV8SnuaBtVae9KQnCSCPecxjHtC2RURWVlYEkBe+8IVfchuf+MQn5Lzzzku401rLvn37Wuvxhje8Yea9H/uxH5tZwzw35corr5Tjx4/PvBf31OWXXy4//uM/PpPbkq/Rhz/8YTnjjDNSm8YY2bVrV6vfX/iFX+idV55fdLJetc3NzZSr8LrXvW7uc//+3/97AeTMM888qfZ/+Zd/OY3tyJEjc5970IMeJIA873nP23Hb+Tl9xjOe0fvMgQMHduzR0FrLLbfcsuP+F7CABfzLhoVHYwELWMCXBEopvv/7vx9gxmuwubnJu971LrTW6Znt4LLLLuNNb3oTn//85xmPxxw5coTxeMxVV13FE5/4RO666y5e+MIXzrz39re/nfe9730sLS3xlre8pRVXfuDAAd773vfy7d/+7Tuaj4jwspe9jJ/+6Z9mOBzyjne8gx/5kR/Z0bsngsOHD/MP//APfNu3fRsf+chHAPiJn/iJB6TtHKLV+V3vehd/+Id/iHPupN6/4447+MZv/EbuuOMOzjvvPN7xjnewvr7O4cOHGY1GXHfddbz61a/mtNNOa733G7/xG7zhDW8A4Id+6Ie4++67OXLkCMeOHeMNb3gDRVHw/ve/n3/37/7d3L4/8YlP8PrXv56Xv/zlHDhwgMOHD7O5uZk8Z7fddhvPfvazOXDgAM9//vP5xCc+wXg85vjx4xw4cID/+l//K8YYfvZnf5Y//uM/Pql5nwhuuOGGhMuLLrpo7nPxu3vvvZfDhw9/SX3N8/zk31133XU7bu/qq6/mlltuAeDf/tt/2/vM6aefzr/+1/8agF/8xV/kv//3/568FlVV8ad/+qe8+MUvBvy+fehDH7rj/hewgAX8C4evtqazgAUs4J8O5B4NEZHbb79dtNayuroq6+vr6bm3ve1tAsgzn/lMEZETejS2g/X19WTF/vu///vWd9GC/EM/9EMn1WbXozGZTOQFL3hB8oh84AMfOKn2+uAXf/EXW16V+LO2ttbrEXgg4Oqrr25VKTrzzDPlO7/zO+V1r3udvP/975eNjY1t33/Ri14kgOzfv19uv/32HfW5tbUlp5xyigDy3d/93b3P/Pqv/3oa08c+9rHWd7mn4cd//Mfn9vP85z9fAPne7/3euc+8/vWvF0Ae97jHzXz35Xg0/vRP/zS9e+2118597o//+I/Tc9ddd92O23/nO9+Z3rv66qt7nzl8+HDyKhVFseO2v+d7viet6Xg8nvvc4cOH5Ru/8RvnVp167GMfK7/927+9434XsIAFLEBk4dFYwAIW8GXAeeedxzOe8YzkwYjwO7/zOwC98eAnC2tra1x++eWAz/vIYe/evQBfVn3/48eP8+xnP5t3vvOdnHXWWfzd3/1dyhf4cmBtbY0zzjiD0047DaUUACsrK7zmNa/h3/ybf/Nlt98Hl19+OX/1V3/FIx7xCMDj5V3vehcvf/nLufLKK9m3bx/Pe97z+L//9//OvLu5uck73/lOAH76p3+a8847b0d9vu9970vW+3kXIL70pS/lrLPOArwXqg+01vzn//yfe787fPgw733ve9PY5sH3fd/3AXDttdfO5JG8+tWvRkQQkZOugra+vp5+X1lZmftc/l3+zong6U9/OktLSwC89rWv7X3mF37hF1IuVF3XO6r8dPToUd7znvcA8KIXvYjhcDj32X379vHe976Xn/iJn0j79dixY8mTs7GxwcGDB7f1uCxgAQtYQBcWisYCFrCALwtiaEsMn/r85z/P3//937N3716+9Vu/dcft/Pmf/zkveMELeOhDH8rq6mrrgrGoxHQTqJ/73OeilOJP//RPec5znsPb3/527r777h33ec8993D55ZfzgQ98gAsvvJAPfvCDPO5xj9vx+9vBj/zIj3Dvvfdy3333MRqN+NCHPsRTn/pUfuzHfoxLLrmEG2+88QHppwtPf/rTuf7667n66qv5mZ/5Ga688kpOOeUUwIfB/OVf/iWXX345r3zlK1vvffzjH6eqKgC+6Zu+acf9ffzjHwe80nnhhRf2PmOM4corr2w934WHP/zhnH766b3ffehDH0oC75VXXsmZZ57Z+/OYxzwmvfPFL35xx3P4asP+/fv50R/9UcArbi960Yu44YYbqKqKO+64g1e84hX82q/9GmVZpne0PjH7/oM/+IOUZD4vbCrCNddcwyMf+Uje8IY38NKXvpTrrruOzc1NbrnlFt74xjdy+PBhfuZnfoZv+qZvOumQvAUsYAH/guGr7FFZwAIW8E8IuqFTIiLj8Vj27dsngNx4443ysz/7swLIS1/60vTMdqFT1lr57u/+7lbIRlEUsm/fvnTZWCz9+f3f//0zY3rd614ng8Gg9f65554r3//93y/vf//7e+cRQ6fiz9LS0o5Dhb4ccM7JN3/zNwsgl156ae/la18puOGGG+SVr3ylrK6upnn/2Z/9Wfr+He94R/p8NBrtuN2XvOQlAshll1227XP/+T//ZwHkkY98ZOvzuKee+tSnzn33t37rt3rD0Lb7eSDC3yJ8pUOnRESqqkqha30/F154YUq4X15e3lGbF198sQDypCc9advnjh8/nsITX/nKV/Y+c9VVV6XQrbe85S0nNbcFLGAB/3Jh4dFYwAIW8GXBcDjku7/7uwF461vfmkp7Rk/HieCtb30rb3/72zHG8MpXvpKbb745XXQXLxt7/vOfD9BbRvenfuqnuPXWW3nDG97At37rt3L66adz55138ru/+7tceeWVfMd3fEey1HfhX/2rf8WePXsYj8f8wA/8AFtbW18KCnYMSqlkuf74xz/ONddc8xXtL4dHPvKR/NzP/Rx/+qd/mkJj3vKWtzxg7cc2v9TnjDFz34nhOsvLyyn86UQ/D0T4W4Szzz47/X7XXXfNfS7/Ln9nJ1AUBf/rf/0v/vqv/5oXvvCFPPrRj+ZBD3oQl112Gb/wC7/ANddcw+bmJsBcz1EOn/zkJ9P+OpE343//7/+dQs3mFSl4+tOfzsUXXwyQwrEWsIAFLOBEsFA0FrCABXzZEJWKN77xjdx5551cdNFFc+vxd+Ed73gH4IWhn/u5n+PhD3/4TFjIiXIwzj77bH70R3+UP/qjP+LAgQN8+tOfTsLV//k//4f/+T//Z+97l1xyCVdddRX79u3jb//2b3ne856XhLmvFJxzzjnp989//vNf0b764Morr+ThD384QCt8K+ZQwMmFHcVwp+1uiIcm7K1bsWoncOaZZwIwGo2+Kjh71KMelfbkZz7zmbnPxe/OPPPMFK52svCsZz2LP/iDP+Czn/0sX/ziF/nQhz7Ez/zMz7CyspJya57ylKecsJ23vvWtAKyurqYb6efB9ddfD/i12b1799znLrjgAgBuvfXWHc1lAQtYwAIWisYCFrCALxsuvfRSHvvYxzKdToGTSwKPAmq0lnZhY2MjlYTdKTz2sY/lt3/7t5NA9r73vW/us5deeil/+7d/yymnnMLVV1/Nc57znK/ohWRf+MIX0u+7du36ivWzHaytrQG0koMvvfRSBoMBAH/2Z3+247aiQnnnnXdy00039T5jreUDH/gAAE94whNOerxPfvKTkyckKqb/L2FlZSXtpb/6q7/qfUZE+Ou//mvAKwsPNPzjP/4jn/vc5wBSqdl5MBqN+MM//EMAXvCCF6T1ngdRiTp48OC2inb0eny19u0CFrCAf3qwUDQWsIAFPCDwy7/8y/zET/wEP/ETP8GLXvSiHb+3Z88ewFcK6oPXvOY1cyv4TCaTbduOt19vF5YDXsl5//vfz6mnnsrf//3f8+xnP/ukqgZFqOv6hN//yq/8CgCDwaD3hukvB/7mb/6mN7wsh2uvvTbh+vGPf3z6fGVlJVm+f+mXfumEHooIz3zmM9m/fz8wv+rUm9/85pSkH8PsTgZOP/10vuVbvgWAX/mVX5mr0ET4Uu+w2A6icP+BD3ygV/F997vfnZTIWP3qgYL19XX+w3/4D4BXYvJbuvvgPe95D0ePHgVOHDYFzT4QEd785jf3PvOZz3wmVX17oPftAhawgH/G8NVIDFnAAhbwTxP6ksF3Atslg7/iFa9ICeBvfvObZTKZiIjIPffcIz/6oz+a7gAA5MUvfnHr3Wc/+9nyAz/wA/KXf/mXrRuVDx06JK95zWtS8uqb3/zm1nvzbga/7rrr5PTTT0/JzceOHTupef7wD/+w/PAP/7B84AMfaN0rMh6P5W//9m9bSeg/+7M/29tGfOZkcSwisn//frnwwgvl53/+5+WjH/1owqWIx+frX/96OfXUUxO+P/WpT7Xev+OOO9L35513nrzzne+Ura2tNIdrr71WfvInf1J+//d/v/Xem970pjSvl7zkJXLvvfeKiL9R+9d//delLEsB5AUveMHMmPObwbeDW265Je2D0047Td761rfK0aNH0/f333+/vOc975Fv+7Zvk2c961lz++nbgzuBqqrksY99rIC/qf6qq64SEV/M4F3vepfs3r1bAHnOc57T+/6J+v/whz8sr33ta+Wzn/2sTKdTEfE4//M//3O56KKLBJAzzjhjR0UL4h569KMfvaO5bWxsyFlnnSWADIdD+W//7b/JwYMH03dvf/vb0/eDwUBuuummHbW7gAUsYAELRWMBC1jAjuEroWgcOXJEHvnIR6bvtdayd+/epCS85CUvkRe/+MW9ika3etTu3buTwBd/nv/854u1tve9rqIhIvLZz342VeB54hOf2FJgTgRxnIAopWT37t2yf/9+Mca0Pn/Zy142M6bu2L4URePMM89szV1rLfv27ZPhcNj6fNeuXfLud7+7t41PfOITcs4556RnjTGyb9++tB5A74WDsSJSnOO+fftalwc+7WlPk+PHj8+8t1NFQ0Tkk5/8pDz4wQ+e6Wdtba01v2c84xlz+/lSFQ0RkVtvvbXV/8rKSqqIBsjFF18shw8f7n33RP3/0R/90cy65fvmEY94hNx4440nHOPNN9+c1ur1r3/9juf2kY98RE477bSZfZKv+8rKytx9s4AFLGABfbAInVrAAhbwVYW9e/fywQ9+kB/90R/lwQ9+MMYYiqLgiiuu4O1vfzu/+Zu/OffdN73pTfzyL/8yz33uc7ngggsQEUajEWeffTbf/M3fzHve8x7e/e537+jOgQiPfvSjufrqqznrrLP46Ec/yjOe8QyOHDmyo3d/+qd/mte97nU873nP4+EPfzhKKY4dO8bu3bu55JJLeNnLXsY111zDG9/4xrljipWLLrvssh2POcJNN93Eu9/9bl760pdy2WWXsX//ftbX1xERzjjjDK644gpe+9rXcvPNN6dKXl14/OMfzw033MAv/dIvcdlll7Fr1y42Nzc599xzueKKK3j961/PC1/4wpn3Xv/61/P+97+fb//2b+eMM85gY2ODXbt28bSnPY23ve1tvO997/uyY/svvvhirr/+en7jN36DZzzjGZx66qmsr6/jnOOCCy7ghS98Ie94xzvS5X4PNDz4wQ/m05/+NK985Su56KKLUEpRliWXXHIJv/qrv8qHP/xh9u3b9yW1fckll/Dyl7+cyy67jNNOO42NjQ3279/PlVdeyf/4H/+DT3/60zuqNvW2t70NEWEwGPC93/u9O+7/iU98IjfccAOvec1ruOyyy9i3bx9bW1usrq7yNV/zNfzYj/0Y11133dx9s4AFLGABfaBEThDQu4AFLGABC/h/AnfeeSfnnXcexhg++9nPphu+F7CABSxgAQv4pwgLj8YCFrCABfx/BN7//vcDPvF4oWQsYAELWMAC/qnDQtFYwAIWsID/j8AHPvABhsMhr3rVq77aQ1nAAhawgAUs4MuGRejUAhawgAUsYAELWMACFrCABxwWHo0FLGABC1jAAhawgAUsYAEPOCwUjQUsYAELWMACFrCABSxgAQ84LBSNBSxgAQtYwAIWsIAFLGABDzgUO33w67/mEp76Td/IvgedgzgoMYDCatBKYUJNeOcc1lpEhMIUiICI4JzDOQeA1hqlFFVVATAcDrHWAv7Z+H38WymV2oi/a60xxgBQVVX6O/bvnEvtKKWobE1tLdZayrIEYDQaoZRiMBgwnU4BKMsSYwx1Xfv+nW9zOp1SVRVKKeq6Zm1tjcFgQFVV1HXNsWPHWF1dpSgKrKtRymGMYTqdsrW1hVIKYwxGa+pplXBkjEk1zyf1hFOGy1z5pMsY7lnG3XeQ4/94LUuVRUoYlGXCQ13XaK0TXrs4KooC51zCX8RlTMkpyzLV8Y9j0Vq3/s3XQmvtn1cKJy61rbVO+HbOoVEJt8vLy609FPvLx5GPLa5ZPg8dfnKIcypFMRooBqI4/ZyzuPYv389AYGnXCmVZ+GcApWBCzbQQ9p57Bo998sUcPHIIU5SoYohZXsYNSqxS4DSmhgOf/TwHP30TuyqFRZgYQStQIogS6oFi90PP4aKnXMqRzWMoJShd4FCgClRR4tBsmQHnfe2lLC/twlqhFmFSjTl07DBDrdiztge1uoxylo1bb+fgTdezrGpQUGuHGIcSh1jDuhtw+iMu4tyHPgSnxI8XjbFCaTW3Xn8j9dH7+chb/ze7jmxyXEZY51i2GluYcP5k5jyiFVb8+VkaDhgOSkRA6QKjNc5OMYWm2r3EN3z/t3PrkXtZEcWyGOxwgBkOQGlc7aBy3PPFO1lfX6fGIfG8o0CB0RozUDz0woeglMI5QBeg/N4SAakdiDDWwsruXdx69UfZ+sjnWLaOkbbUCoa6gGkNRrNlhMc9/1nYtQFFUaALgwOss9TWUk2n2PGUzbvv5wsf/CR7awPWUStBFwUKzXg8pq4t1grWWuq6ppra9Ltz/jzv3buXpaUhSivitow0Ju7NLsTvnAguO4/58zWKcV1zxx13MBwOGQwG6cwNihINlEaxa9caBgVicc5iFFSl4ZRHPJg9DzsPvWuVohxgtEEXBQNTopzDWsf44FGu+cv3s3cMWgljI6AVQytYHPWpq3zd85/HCOVvZwvnO9F1cahpzX0f+Qz3febziILaKIwDYx0Ov78qDbsfdBZP/rbncsBt4VAMxaAzGmWtZTwacd3/72qW79+itIIVy7Tw53VXOWBaWbYmVeITRVE0uKRNn3IaaK1tjTvnFWjD2NRceNnjMKesUq6tMRisYIoBqlSo2lGWJaI1alrz8b/6AOO7D6ItGGOoCoXatYxohT26iZuOedSTH8/jv/7ruH+ywZbzPMKIwmDCCXC42rK1ucVf/eXfcOzIJrffe4BRXTEZT6mrmrPPPJXl5YLLLruEpz/9aWxubmCtxRiT0Xmhqh3Owe23fZG/+eursFUNDgamZPdUOG24ymkru6jHE8bK4XYv83XPvpKLvu5JqML4/SdQimJ8dJ1bP/s5bvjIJ7nzjjsYDoZMqymENRIRNKrFj+NY8r0bv490Pa5xTvPnQWyjj+/HMYgIzDlj/neV+Gh8p+9c5vwwjjd+l/NJJ651TrtnOr6bt++fUyC69Vlrv/bMN+7bfBxd3OTt5HPJef7MM+hWGznvzdtsyVl4XuvplPNjznDS925832byQD7Ovn4jdMedr4slW4/Oc/laRdlDxOMXVC/e8j0R34/tRrkxH0cfruN6pfa1QmX0p4ubnM/me0x6+EazNw1ateUv35/glEM5QVsNKFzhePhjLuSCR19ApTSbkxGHjx7h6P2HuOfzt1EdOs6+pVU2xxOOjbfYchWVswy1Yc9gmdVyiKE5uy18eVT27pnueXnz5z82s7Zd2LGiAV6gd+IQB05AUDg0Sgm2Q2BEhMl0QmHKFkK7mydf5L5Dli9aXOz4L5CIcRdyQlBVFdO6YjyZJCG8LEsGgwHj8RgRoao8QxMR9u7dC4DWBitQ13VSCiKTrKoq9RuViKiMmEJjDEF4qSmKgslkEhQc339RFEm5ioK+iGemeLoaxqARarQ2LUJkjEnzy5WNiJeoFDUbtcFlzrC7xDJXMvJDltZEqbQB42dRIBIR6mnV2oTd9ncC2xGnlpISDomzjnoy8TidTBsiGJ+3FpRDa8Whew9w7NgxRqMRKyuGogjrqzXOaBCFQqikxiqoxYH2BFg5h0IQBGcd9999D1vrGzixGKMR56idhOe1f1I7Cq0Yj7YQDFNrGU02GW1t8oU77uDRj76IvbtXMEqztDL0Sow4NGCtQ7C+X9GItayuLKPxe0UpEoGtqoqq9grKoBzgZN1jSEWBK17u20CzriBYcIKuNaUpQIE46xUoY8AJ1daY2z/3edQpK0x1OJfOYuoatMFZ30a5vMTQ1uiqwoW9rZTvXpxQV5ajR4+yZ/deaico599HKawTqB1KoKJmdXWV0WSCMhqxjiBX+HMPWIRaOY4cP87ycB+CQgtBIQZnwdWCoFBlidMGh/L/Kc84tGozs66Q01XW/QGI/5485Ewyrp/rEXzS/hdASRBkAI0XCrQG8eM+dOgQxVn7WV5dwtZTtDYoZ3HGYZTGOYstFLbUOKeQqk7zr8UhRrE+2uLY+jq2LFFh3+Rnd2prjMDxasxUe6UbJygLyglK41UNpTh46CDHjh1FVoqg9Akuw6ENRh+zNKQ2WxSiwCkQhyjPX2ygazkNSiC0lIl8jdIjHfrlES1g4Itf/CL7zbksacXAKXRRU1iDQSFK4ZSgrMMZhfUbDSWCdYJ2Dl2UoBVOwW1fvI2HPu7RHJts4kqdFA2tIl9yiHOMRiNv0FJ+btZav5OcIwpI1113HY961CMZDodhbiBSN/RYFM4Jx4+vE3Y12miUVtTKURcwKYCVAY+46FE84enfwPJp+wCFsmCUxk4rbv/CbVz3kU9w6403IVtTcMJ4NGr4q9KIuJZA2RWuc548T8Hu8vW+Z+L33XXeCd/IeWC3vXwftBSJTCjOn20LtLO0Mh9PVGy2m1su14giCaXW2hlFpyvTdOffFfC2U+C6I9ox/1VtuYseAXOmrx6hPhpluspnVwbsUwKaoczOfSfQt9b5d324yNe921fffm9AtfZAV/Hr4icZcpVqBLzOHOft/6j4auWVG+cEYwo0CrHOG5w2RoyPbeAmFcZ5WlxPK+qqpppMqF2NFUetHE4P0AMNQsswk/ZkD1674zrR/s/hpBSN0WjkhWCtEAtRh8wJRCRU3gooWJpJRIE8vhM3Yxx0/lzOPOLCFUXRInb5AsdF7B7CqPFGgR9Ivyul2L17d0J0URTUdZ2Y4HDotcuiKDDGYK1lOp2m36MCEi1mdV0nZSR6FLqCut9jzeaNYynLknE18c8HIa4wfrwKhThvSY/t5Yc1J5jbWUXi+sTDkFuicm09197zNY2w3e+RkHYP4MlA1/KUQ5p3+J8E/NSV9xIVkcCIF1YN3ipXBMGprmqm4zHg94adTPz8jaGyNTjt31teYqoctVZoEcSBdkHJ0JIO4nQ0whrxvSiDl+ctojQOwcqErfXj7Nt/BoePrHN0Y5NJNUKh2LdvP7UICqFUsDkZIWKxCLZ2WLxVCSeYoDBJPUEFAUNJQxB0YTCFQbRmeXmZOp5TcUSy3SUJcV2tOBQOpbwdrJBohbOIEzCFx7N1uPUxxe5ltlSFW1pCW4tSoI0kvO85/VQmVYWdVoiAVo3VR6z1gqSF0Wjima/WBO0AQSF1DYF2bBw/jnMeE0Zcy8oiGioclVEoY3BBidEiaO2tyVVV4ZxjXFXo4QC9PGQ6nTCIhF0rtI5WYws0+y7/SX2GMzxvf24HSnnPb9daJSLYbHFmhetM8RfnBXtvH0UbTe0sg7JEF4XfO7amSMq43/uiQK8sceqDz+XYTbezYlSQYr2iMQV2nXoak6k3xqAa40Giy1ozqSvOeNiDOXzXAfRoSuH80inw+1GBVcLyrjWqqqbaqsEYnClb1r3oJTrtvLO55/5jqLqmQLzHUFTyWMxjZEq316SrnPUpi/lcrHNM6gqNw9qKQitq6xiIRgCrQaqasy94CJ+99z4G4pV7Ec/oBbA4Krxivb65wdROwRlEe0VDKY0T7wlFBFMUDJaWGI3qsBcMqlBMxhMIypeIsLm5mXkzTAsH1nkk796zm8IYqtoFvqYYq4oN5Xj4Qx/EZU95Cuc89HzqQiGDgrIGV1vuvv0OPvvJT3H3F27j6IGDqKqJJIjCpdIarRTWfzFXQNzOIDTvbPQpgycCpdQM7Wq3MSu05u3PE3RT29135vSW762+uXSh5emB5NHo0pVuH/Pw1qecdP8OE0hzONEY87lEwxxxbNJ+t2/tWs9n4+gzDnTn1uo7fzbYMl0HzyfcK9IxRM6RLfPvc6Wzq3Dk8873UNpHWnnDijSRHd25dXGnMiWjb/5dOha/1yoYYcIc0WDrGjutqLdG2Mpx7O4DjDc2qLa20JWlRGOrino6xSjNQBcYcZTae5ed80aovvXqUzT6zspO+d+OFQ2lgiVcq2hEw2iDVWRW08atlJQIaQT//HuRJmwoPp8LwLHPPmYf2+rbyLlwHP92zrtCTVAI4k9UMPJwo6WlJZRSIZyrRpxuWRi01gwGA0S8EBNDHIbDYRpnVU8ZDAxVVSWFJj4XGcrS0lLL6xBDt7yVSwGN0O6FQcFk84z/dglofCcPRcu1+1yxyBl+ro1HxakbxpTw7RpXajd0obZ1YpJdIphr7X3KUN5W+ts/kOaX9xlOOSCUgwEizgsB4qjrIDQHJuXd4Yrh8pK33C0NvMAY96WzaFMgyls01047BbW2RL1eUVQO4t7VIFpRSc2pp52FdQ6M96oo7QU08RQPQdACh+66k9XlVYpCs7q2wumrp2FtzaHDhyjKgkKDmkxZP3g/rqqotHilRoEL7nijNIXWHL3/Pk4962xQBT560ftYtDGY4YBq3TMZ55y3fMdzQ5twtQgpPpRGGc3UaMZGU3iXCgrvwayNplbOn4uphaFmYi1DpVHBSmwFTFEydbC6axf11oiyLL0A5WJgDdjaopTBWocShSESNoVo0Dp4qWzNfffdx7iaemUsbZhgFQfqAvaedTrLa6u4cJa0Mn5bZAxTFwVuCOdd+HAOXHsjdlwjzguBUYH3ez2cqcxa1RVShe2V7T5hJ+G8h6FIEGL72vLtBUE+bFhRzb6fWEu5tsLqnl0sra1Qa0WhDWVRILpABcHY+UXmwsd/DXdScP+Nt2Bqr4RPFdilgjPOPxdRJME1pwVKKZQ41NKQ4oxTeMxTnsDnPvhxZH3snxXx4XxGMcZy/vnnMamm6HLQomMtA4kx7D/3bIqp4+5rrkdNMiVBgQ20Mg+p7BpV+vZz9ztoaF9lLWrJsGffXlZ3raGKwnvLtPKeyBBy4hAq5dh71uk8+gkXc+M/fpJCeQVIGY3TYJXCGcXp557N+tYmauh3qISza50NlkcvwOvC8OjHPIYPffBjoEAbjbWe1o3HY5ZX1ti//1S0NkynFcY4tPZ0vKHFXgDbs2cPX/O4x3HtJz+VaPSpp5/Gc57zXC55/CUMisJ7kDQoC+Nj63zmk5/iEx/+KKOjx9GVpagdWnz4swQc5kalqBR3hdx8PPOUwXkCSN/Z6O737vmAWcGn20ZXGOzyxr5xdftIfTtJimy3n1z+6Cpa3kPYY50PNLrv/RMZK/qUmlyBzpX3+JzWGutm22jNsQfvEuUAIj2Sht70jCGnaV3c93m5un1316K1x1Q7NHUexPl6HMyGWM0T3PN9nRt2ugrTPPxHvuJCn7mS0XdeWm0yew5SH9L/XXxfB6ORt7IK1XjCtR/7JG5i2djc8OkBtUU7YVCUgGNlxbCkvPdflDcMaT8IrLMthTiNn+bMzVNuT7R3czgpj0baxNYFC77FSpvx5gqECFTTKYPBIDGr/IB14zij4B8nFLXE2GZ8Prd4i0gKQ1JKteJ583yNpaWlJDznhCh6JowxLC0ttZSP7uaM3oe6rmdyJMDnPfg2FVVVp3nTwg+p3ziOycR7MsSEB5QXjAeFV4jEVj5WPiMquWKQt5+Pt3to+lyE+UGNa5ETifydJPjrGHrSsagASPNs3zhypWIeoe8S8DxHY4YpiLdOeiVY42qLCBjlrblWBLRi6izOFJx3/nksr65AEayF2oDRoA26MCCGibUs7VnjUY9/HDde/ZGk7Fhbg9LUWlHuWuWch56PLgsfO2m0twIrjdIFGIPGWz43Dh3ks+sbnPmQC5ByyHgyZliUlLpgabiEEWF05DCjw4dY0oZa+3AelEaX2oen1DAwmvvvugMzXOZBFzwSpYOIHpR/a31OQg5xvyl0K862jXcwKKwucLvW2HXWWawfOsjSRFHWNUoUWzjOfvSFlLvX0KVmZWiQ0lA4jS4KKMpAvEBbGO7ew2hjHVvVOLFYEaauxlrHOeedzXA49OfRFChlEOXx57T3RihqbKmplHDhox/FzbfdTz2pkhDnnGDKAjUseMijLmS4vIyL5ztYmlCgtMHpGiWWqqxYO+8c1LExB67/PAWeUcQcBgnC+3bMpbGAzSeyXeE2nTdmDSQNY23enSXgjZroxFuhJGofw4LTzj8Hc+peBstLlIMSYwrvxdCGAo3RmolYagRRjgc95hHcdfPnWcZ7ISrteNSlX0tx6h6KwYDhcOg9QhmtBn/OahyyYth93pk8+BEX8IWPXot2fg/VCFu25sGPexT7zj0TNSwph0OUNsRQrDjfqIC6ZeHsRz2MjbsOsHH7Pb4f8eGDkYnn7yV8nUB46q6fiN83UhbsP+sM9p5+Gkv79sLSEHSJMSW60JQ25BYODBaBSc1DHnEhh2+9m/vvvAddFgH3mqmznHX+uayesofB0hKqNOhBmZQ6xO9DpcR7jxyc/+DzOXZskzvuuRcb1zvQwuFwyKMf/WhvlFImfRd5iA6eFK019bTmosdcxMpwmU9+/JM85SlP4Yorr2TXrl0o75/0a3t8iy/e8gVuvPY6vnDDjdjJlIHoYIBRaKOCYcQLyp7WBnyqRgHpnoOuEDdP8e5bh77ft3unb23bz57o+9lz2jV6zQhPnXdyo1u3nXTOs77ycJT82T48dfHXx5fz53PDbS4nxXe7c56ndOWfKRX2avZdF/o+i3uy+10352He+vTJBtAoN909lo+5u2ZxDbrj7cNtPrauvJK/N29t+vAxb5/nuILZfJfWGmfPtcHnVoVNRm0thVbItKba2MJOLMYKykGB9oRdBIymCAHfJrAMhwuGUPy/PXsjR+Q8Ptc9C9vBjhUNCV4Bay1OhGk1xZjCn0dpW7ZjWJSI9cmZmfLg5+aRnFu5RLyHoCzL1gHqc89G5SBHQi54x++jkjIYDDBFkYhH7DMPpTLGpDyKOBbft38nfp4rCQCTyYSlpaX0TFVVDIZDRGqKYpiej/8SlC9rLYOBT16dTqfUtsbVAsNldCD4cf5aabQxWFuneeYadMRX10MUcTfJclOgvZG7il9XCYzP53jOFcKcCORKV47n7RhKl4jE/nLC0yUyzbNe707raQof3688kwXB4ZjWFjs0nHbe2ew790xc6b0PZTmkRvuEN+WVJ7SmKA1VVbPr1FNY2r2GHNnwfRqN1cIEx2MedxHF6jJ1ERK4dEhkBh/6pjUOjXbCklEc3dqktlOm1jGZTlnatx+tNKsrK9jRiIO3305R195rpQx+6ymsKREVPByuZqnQ3HX7FznzQQ9hMFjz+ULTCl0ue6XHOWJ4Y4sQKFBowLXwDJ4mlargmDGsPOgcnvx938PH/uZvOPqZ6zHrI1St2Hf+uTzsKZdy5NgRBsBQFM5pDAbv5vEhSCnED+s9LM5y6mlnceTQIfaeup+trS32nHIK02oS8GZaioYKIVjaGYba4KRmuLzE0q5V6vVRIIxe+aydZWXPPga7VrECOuRegA8Zc06oqhqpLbVyTJwDsVQ+IwVlQ86NEh+e5QTQmZez2aP5vvUe3PlWp3mWnkif+hhJn3Ke6KWfUSrC4HxjKKVY3reH084/l+Pa+gTlusbYYF01PgxJtEaUIMYr3OvHDzN1liXnsVUuL3H6+eexZSzTysf0atMTe2wtgjDCMrE1RydbiFE4HQpEKDBry1zwtRcxXSqwyivBTpoiEV0DzlQJUiiq4ClUziHOJ4bH8Knco5EE3Uz56hMY+9ZEBFZP3cd5Fz6MDe3z9kpXohFsPUWsZskM0Fa8EU177E/FzzcKPz7xVeEMPOprHovZu+xD8AKPkaKxOnoDt0t5Tg7FGWee0dDYYFlEwZOf/GTOOefskNfYeJKgiRCIOClNiRs4HnvRY7n86y/nnHPP9WNy3nPvJhUH77ibWz71GW7+zPUc3ziOtpbSeZ+N1opag9MKFSRMDYFupk1JHrffzff7SkJ37/V9lw20pRf0Ck7b9NNNyvae6X5FpzuetlxD65n2GZ4VivsUlz7hdUbJps0juwnYzXMNz+7Ot9tn3IsS//NENoUo52MRkdbeRPppXo6DPlmgO898Ti6EKZ9IAe1+1/12u/7mKTBdmKcc+4b8P/kemqfYNY20/2ytx3x92SsJES9ao3CUxlAQPMbWoYMM4vApb+D5IqLQSFA0NA5vyJmnNO0EtlvPLuw8dEprJuOxFyScoywGPtnSOUyHyEdB3Qu77Q3Y9QJEwdVam5Kn67pmOBym6lBdwTd3HeYVk/Jk7RgeFQVwz5zChlbe1e+tOLA0HDKeTDDGUBSFF9y0xtY1Ii6EPSmf7Fg7ytIrB5OJz9cYj8dJyC+KApRQB4F3PB4zDV6doihwwXKaC+tJOFQez6IVRVEiSjGqpxQIrnJoo1sHo2/hi8L4cJ6MiEUFI+IpJ3C5hyc/JPHZXNFLa6Aaghnx7dd1viDVVRq6+yHvP29DK5USivPxxKBXDRjjFbPKWQpArMNp7/pXKIwumGJZ3r2GKzTj6RZlUaJNiXWCmALnQDlQOKz48IRKKabiKJXC2RpbeC8JAuXqKk57LxcmWi+Vz6rQglK+SoRzvj1jNHvWdjFVBlOUaCXs27cXLUI1GjHd2kTqyid9FYMQnyreQxHCJQSopmP0sAz5Ox6ng6WhT0SvJpRaUbs6mJgFZXwoWGIigYjP0EAHThkmg4Ly9P089Tu/nX8cjRjdcAvaWioDrC2zcegAa6IxgYpZFUYheCUhUDkRn7CqC0MxHLC2by8ijv2rp1KHCnAojSjvgRAk+nMRW6Ocz3NBhArLxnjEQEmTm2MdojSVs0xshZIBBQZCsQqCrGC0DuuBr7pTOCrthccyeQa8EGqdw2QhEzGMLlrsEo3r4K5Pke4ynb5nc9AoYtddAcQE2oMTxPmwIh2yNI6uH+fA4YOwa4VlpTD4n0L5nCETChMUGq8PFsLe/ftZWlvFHtyg0Jqt0RYHDh1AVoeUZUERBQutA0MjKHfaJ+AXft2K4YBKHCFGD6dg4ixjsWxOpihjGKoBWpR32SvtBVoVPNUIVoETS7GyhBVhoDQah/IYaQxXQYj3OQ8xQ6W1CEnRj/sx+8rjVMHmZItjG+tMh7C85g1Bynkvhi48DbfOghjPoLUGA3p54PHuBFc7iuUlVFFAoalsjdSCcQ4rgioMosG6uN5CYTTiQInmyJEjVFVNXbfDXk477VRAGI22MJ0iKiJCURY+pA8oiwFnnHEG+/ftpzClTwjV3oe6cegI99x6O7dcdz13fu7z2K0xKOuNV4QzEZQ1wmf+WEVFvdmHuRAt/n8pMVWlL4JXoXdnz8KJhLo+gZVwTmFWwPlSdZ6c7+XJyzA7lz5Fo6t0NTTC03uSd7RR2LrKQXe+uUA+r/0IueKXJ6f799s8tsvbuzjwf8R1Tn+SE7s8/Ksl7/W11YPrPsjn34SvOsiMm/mzfW21lAX/QOv5Pujmo0Y5sqswzZNXlFJJEc+/z43kfeuW+qD/vHjaNd9r4vmPBHOaL+6A+NxTHcN9GxQk3qUEVNzrga+1XFh9A9mGz3lcq/nvd2DHioZRmunW2JdWVH5Hutqiy8JX3Mk2QY4kFZhK/KxbejYfePQaQH+iWb5gcaPE3IcYKhV/j8J1shQKlEXhq33UvuSlMYaiLEEJy8Mlb+WZVr5KkXO++o7RVNWEQhUUhV/euq5R2i9aDNWKSoZzDqVJIVbOuTSWKDwYY1JZ3Lqum40Z7B6VUuAMZmmZ6a4l7NFNltApBj0XYpRSocqVDjiFQoecDxWrDs2zeNBSeiK+Iv6jItG1tqI67r5EYKT1fmw/JsrnRDGfR/dwJ8uSauI9888bhUdROlLC9ET5hGbjnK8Uo6B0vpJMIbC5vs4ut897uLRBOUVhBqBLlFlCFSWFiFc2jE8m18tD3JEtjCimyrFnqlHDgvXjG+xb2scSBme0t+6HykmYEorsaNWWejJmdOQwemmZrapiUxymHLK0vMyyqhFXUQ+gUAUSPWlKUSqgUFjtE8EKXfqqb9UE5QZM6gpb16xozXTzKMtbm9RuSi2WIaUPQ9GS4m+9xb69F5QItbIUTliymuXBEmpthYuf92w+cOfvMpxscnxjHVtVLGvNqiqoS6gGGo0PWctLZyqEQhR2s2Kipux59Cl88Y5rueBhD+XwPfdxyqmnYMuCYlB6ZUJrlPI/xtVMC6hLQ1l7d69bMqyetoet4xtIbTFR3BJYXVlGxFEMDE67MD8vMDlxFEbhMAxCPK0elCzv202FQ8SLtIIPnXO1t6aL+PKKtXiF1WlfAWygTLZf6YWugNBm5CqVeI3PRtAotPP7WAq8dT96MxEKFarzeXt0YiArSysMtMY6oRC8qzyUSHR4RdAZQo6XAqUxwwFFOcSaLSzC8tKAU/fu4mC96T09pvBVwAClTLB2i89fsI6BKKyD1V27kaLATX3ZRVMWFFphbUUtFWXpaWqhCkKprIYSKZ/zsaR8Zbfdp53G/TffTlEptGiMlEydD821IQwoChE24reXy0VvR1wDL/B5o5gwUMLWxjrDlX1oXXjlyfjSwRjj8xoCzTH4dZAC9p65n4O3343UilIGFGZIubLKqK5x4wmDwRKF1pRao0yBUhpXgjLG8xPxa+ys5bTT93mvpzQ8yxjNgQN3IbKXtdW9rSIkOoZOFYbCGVbXdrH/jNMpl4ZRm/HC0njCnTffwqc/9DHu/+KdTLfGVLbGKZ/fp8TPxwb5oIg5BUFYEo++xrJsnfd2BAHOez5UCkttPEtBeA7ClxMJZX17VifjKScSTPtCM/oF1n5BfR7k38/zUPSdUegPF2med1luRzRKeFqRly3tm08u5OZCL9CKVOjyzTy/oKt8xT+7hot8rnnFzlZCdDCooUhFHqKhNl+bxmMzH7Zb49zg2hpH59k8KmaesiRh4n2Gn3lzzxWOLvR5m9pzkRaO87HMm3vqSylP63uVivZ+Th5dXxPPKxgi4Cwb6+sIGlHGF4pAgbgQQhXaVV6tEdq5JCae+T78dP5uyYJKMWdJ58KOFQ1nrf9xzsfv1o6iKAPRigvdMAAVmD2SxTeGxY0Z765zmOKEck9G36HPS+LmIU3eol/MWAzie7EsbS78R29KLEGbW/qdiBdsgrXDK0m+8hTi7/8YjUYAIa65sc5b2+RxRCFbxAt8cTzT6bSV6wHCNIRVeUFBse/M05kev5Ulo1vttywfzoctRK9OnL9SCnHtpM6cMMW55ockJ2Jdj0b6iXsi4DEpJbTXMm+za8HJD1gfsY0Q80L6CL8TvxcRx2hrC+tsqMqCL2MZxmuVt2bu3X8K07pipSwpdAokwgQByAsyYf+Gkp3DomRqHYUVhjUYUdjSsP+8c5hsbbCiFNQObfxdEH6+gSlrhVIaUY4STSEwNCUFimo6YToeM6mmTEbHqDY3GIil0DpYSkxgUt4abFHUVgDDtKq57867Gezbx2BtjY2jR1haXUXGFdXmiHpaea+Fc8HLIqFCVX/+gQIKKxSVZbUYoMSgyyGnPOjBnPrwC1hfv561tV1oDKoWVOHxq5xP0PZWGP8TW9WArhxbhw9z499/lOMHD/LxW+/knAedhzn1FAoUZRBfY7iVQvz9A9q7dk3tq21ppRmYgpGLzNOT28paBoMlnzDvGq9ACgWRkBchAtahaoeuHKpyFA5U7fOirHXhx2ZnpG1BVTkzFMl5QQv69mnOjLtMJZ2HEDIkoXnnBIxKStOMABSes84nSFR1zdTWKK2xOAwhJjfsSY3fzxKUGWI1PgTRJdb6MDOjDK6uUcYX+0Akra1T/t6MaQg1KwYD3z5+f1M5VotVdg2W2Nga4XSFUyXOeEE6514KmvBGEcqlIZU4pjZ4GGyJdY4q5B0pYzCZUJzThHnCRFqTbG2WiwGqFphYqEMNyKD9GAnhj+JTLGK7BcJQ+ftqjBVfex7FoCwZlCXjukIVvvCDEoUOFacMPpTJ1i5UjQnKnnWYsFeLcAZU7ThldTdqWuMGNapsjFMqCO/Ly8ucdcY5rKyu4sQr82IFNak5ev8hPvOpa7nhmmsZHz5OYSUoA3he3BNOnaybHTzmBrHufs6t3CcS5k/0zNz16hHU/FbpF+ByntHkUOneZ7vji+/MPKt2NvYuD2u1o/zIJch/+VjzUK0Yat4SKucI1Xlf2+3//JWdtNH9PT3H9krEdtA3rj5vQa9yF5lxNv74XDcKIxmvlecLuWI1jzb09Xui8XYh0vOucbzrHelTNrwXsGm7SSPQLXo1gzP/hS89Dz5ChqhGSOAVtHyTkX60ZEeiArKz+bYUIv/gXLz0wc4VjeC+9gutKIzxTDyETpmMEfu7Njyj9jHYwcodJiJxo9Au5RgPWlQWgJlEJxFJlp4+S3h3A8WfPBE8btYoWMSStV1FZTQaYWLcexhrI4z4ProKhnOO2lZAc9HXJJRQVSrgLTw3Ho/TnKuqoix0UmIEfInUosQOB9TWC11xnnkIlCl8UnCurcbnonInIs0lhNmBjX/n7/QR6S6eYdZdq5T/LCp/0Vsj2Rj6rCERf91cnhzyfvJ367rGlCWD4dALWc5fgKW88R6Hogam1oYyrr4snCl9DLtVDqtq/JVpCou/oM86C1MvuNV4gVpXjqosqXYto/bvZrK1ztD52HcJEorDKy8qxBOI9mUiJVjGy6UhyhWY0mCsxU0nPl7STRFxYDRa+bAgabgT2mi0KtDUyNQxHC6h0YzWtzh+6ChqfYtqPKHa2KAajdHhXFm8LBWjmrpnIxIdn6vr7/xAwdHJhOMb65z9+K/lU5+7maIwSAgDq/B3Imh0iulOxBFv/apFqOqa4/ceZI/VFOtbHJluUp95BlVdUTvrc7x0RvBUEO61V5CjgFtbb9nGCcFp4ZUHrRlNJqxaS5HtqeQtDT9O+ZwM5wRqm6peoaNFVlHVPj9huSgCUZbWPQ5aK0/TOmege37yvdp9DpFUsjF/zz+PX3+JwrQPGxQnfu9Egw1N2UefWyJUlWVcTakmFaDQpa88FS3MNu3JgMu6pjC+6IEL8v/WeMJoMmGIwS55hb0oBKMaz7Aov/aVOJytvXIUShHHu5VKgWo89ZeSKo1Wlb/Ur4QiWueDscKF+RFopMOfkQIdlIyaqa2oa4suDKUXyRsm2kJtvziUr4UgPtyurmE6pawtWAvRyOWCgSbegyMx589BFfYNvuIURuNCQvhoPPEeIGMoCoVRglYeJ6JJ3qGUN2Stv59DWR9eGcY3mUxRKKaTipISowvPawcFZ55xJrt370YXA1DeQ6smNVsHj/DZj3+Smz9zA4fvP0ghCl1Z730KVefEuWCcbtPV7Qw8MBte0ofXEyl5Jwvzzs5OFZa+ecz7Lg/Bjt97IXf+nLpj6uIg508tGcQJqNnE4j5ht8uP8+9yOSlXVnqF2Z7fu5AbAfP2eueeYi4eOMiVq3mKVRfadLMt0LtQAnYn/UY572T2Vj4GyT7vGkdzg3WfXNZd56TURyUgk39zxckrGaFtpTBG45zxMmMw3OSQK+gnd1ZlBo9denEysPPQqZZgH1xeJrgDg3dCh3hrE+P1rQW0Lx8oQWxyIcZWN7HPcRJ5nGRE/HQ6nVE8YlnYWKJWqcYLki9w3wbq5nHEm8KjEJ63ubyywng6SWOJYVI+/0OhKNImiP/G8RWFSmPMxzUoB76sp2oq2MTvrfWJfFopbwUrStxgwLgoMJMxS6rZpHEDK+UtZdq0E7YjaD1bIzm3WPUxkW5SaldjV9DE6So1U9othpBFb0eu4cexRLxEvPVp/mkMnTklgotCl4Y6xnCHPSiIr7wgJEFSPJ3HTSsqMd5hYKBWQi01hbIgiooozDnqaspYaqZa0NpbMkfaYc48hcmwYFTXDEXAFCjlpWILoIJ3T7xXYVAL43FNUQlmXPtL7kQwZYldgdqWmMJgpxVGHE4sogxONRZcAcQoaqeolbCxtcG+tTUGAuecfjqmrjnsLMcPHqLaGlPWtRdeszXzjc0yoVocVvsbndc3jlFNRxRruzk6nXDeoy6gOOc0Ku0rbk2tZVz45O9CQSU+4R6lsYGRutrhlMJpOL5+nM1ySDWdgBZG1ZQtW2GdRaxBiQsKR1B6lWKCj923eIVlbC1TJdTWYZzvT5ygTcHG5iZ7pxVbozHl0hJF6UsUu6jo4ZU/0d5DOJ5MOba1xViJX2lRbGxssL61hTjHcFlRO0mu+4bxeTYbvR3aNGetzyKaCwVpn0sT395lqCL4/AsRdOjPWusriynj56Ggcj7pO3pclbUcP3KMutDIuAYxiKuh1LhSEPElhG24V2ZSTZHRmGFZsCXOezytsHl0k43NddwuKMsxSmuKsmSoFcqYdCeLOMFNK9x4iprW3ktiHVYX2EJT25qN0YjN0dhXO9E+5LSAoJw2CpMVoR5PmR7bZLS+kXBkRZC6ZlRN2RiPEOcYDAcNc09lrPuFkpzO5HzAiWA1VM4xGY1wm1uUCIU4hgBlKG2glD+DeFpZ1xWjakqtBSuOcligSoVIwdhZNicTrNY4YzBOMdQxdM2hjfH5KXijz2Q85uj6OrWrmbgpglDjGDvLxmTC1ClWzQRjvWJ8/nnncdaZZzIcDIMVUiOVY7o54vPXfoYbPvEpjt13iGprxMD5MEgTLgoUpXxcNo2S0d2X8bM+63KjZOteRSP/t/tZn+i2neU4Fxi7vCDKDvPFwROHsHR5Yz7WGd7if5n5rrvfusbMHK+zc2zfMN0dVz6mCF2+3eXD+fhnjXDzFY/cwNcdfw7p7AR6JKq95l36lrd9orXOYR7vz/vYTnHK1zIagE+kQMzbv11cbidUR2NWLsN016urZOTf9e0bIRqdZvdlUoKVD8HUWqcqk74tz5t8LkaTX+eyfvpwkq9VnubQuUal2V9atQxmO4GdV50CxMVqUk0Mv60qlDHpcjkIgqyIj4PHP+OcT2ZrShaqcFlWIyDnhC0/1LlikVtZ8nso8sVqwpeaJOKIxFzgjc/Gg5u7iqdTzwSUUq2bwePf/ihLCo3K3419xfHF8Cj/e4U410ssFKC1UFcVVW1ZWV1isHsPu886C3fnXahp1fIiRAYQQ/rjJolJ7XloVB9TznHd/byPYCTtmtkEqVzhyC0FcZ55lTCtm7tIotLXDQnL+86hdZBjSJAEBU1rnPjcF6MN6FCGFDDWIZtjjhxaxxQl+884A7MiMBxiihK3OaUswRQDamuZTqa4rQl2NPE48doOlVY88jGPZmAVHB9RB6FkYJy3jGqNndQMVg11VTG2FRvTCVvisGtDNozD+bB3NDCQwsdqT2qY1tSVwgwMUlifxKxDMjxQO587VNia9QP3Mjm+znRaszZcYvfSkNF993Hk7nuxkykmKrPRLxLwJKq9plG4q5QgynH03nsY3XsPy8sFu7WiUIpHX/YEbvzUNUwOr1NvThhNK4bLA6wVZDDEoSicCVVrHDKtcRPHymCJelqxsblJVU3ZUpWPG98cUTuLtv7eDUpBaa9wWBRSgrKCqgRX1UzrKUb74gi1hHwDFcJGxhX1xpjh0gpIBVahB8qXG9Y+KVJbhx3XjI9vcuTe+zh25Bi1wESEAn9x4Pr6JoNBKA6Axjkf+hitR576Bxol3ijQZSx9+zQ/e93d3K88A5lYFelMHEMdzooxxuegTAyH7riXCmHIgHJlGTMcUgxK1vbsYnXPLsolX4J4fX2d8eEjTI5tMNrYTPOhEg7edYAjx49S7xrhNi268F63wfIye/afwvLKMqUpGK2POHzwfqZH11GHNjA25JXhqASGynD04BGOHT/M0u417EqFMQOKsqQsS9bW1jCDAYUpOHrsOOOjxxkdPMKRuw9AbREULtDJzfGI45sbaBSrq2vB0jybmZHTmZzpw2yVq/Foysha7HGFVgXV1oRiZQm1WjNcViyvrqLCrdjWWiZbW2ytr3P82LEQ0mooTLgDxlq2Dh9l48gR3OoUJoIpxrjlmuHSEsWg9HlgWuHqmvHGJhvH15keH2FqRxHas06YjiccX99AUWOd5mEPP4dHXHAha8sr/v4nNGIdTCoO3H4nH/27f+D+O+5i6+i6v5VdoIw4yAoaaKUolWlZNefR2JaiINvv7y60+cisIJn30VK+s7XqKjqdRtK6zyoTTc5ULvx3jVndOXYhV0jFzi8bP2/eXSE1F9pi+31Cdh/0CqHhs+6e7n7u32kqZnb72Yky0FWipEfT6xPGt+Pd0C6S0Z1v7tWwnfn1CfLd+csO+u8b/06fm1UySTLiifZJ+71ZRa15px+PUWYVkZTUHc9EUZThb43PLqR5t0dRTfPojDHfc/m76VwkudUb8JTWia6cCHZ+j4ZEq5x3JRunvdBTlpQoxGYuOOvzDYwJyW4oihBzingXug8pyTXRtlcgT1DOw24ixO/jTxeJUdHID0x+GHLXY1QUcmRGBWJqqxQKlLvEUKTE0W6ysu+7uQgvluz1FYoKn3zbvYdDhDr+HhA1XF6hWFlmujRksLqKseutDZcEfFcnq3/u6WiI8CxBiM/lxKlVso7ZwxrXXymVEhS7BCm2HXGZf55/H3ETw+C6hLLLHPJ20hgl5FgY3QrT8p6nsD+UwymN6Jojd97Lsc3jjI9NuKX+HKeffy4PuuDhOK0YjSesrayyvLLC1vpxRqMx041NqvuOoremaAkJag7WbMHGzXdx9LpbGBeag3aTwsL+005j9ymnUK4sw6b3XBw6fD/H7ZSRhfVz72NpZVcoGyho0SCG6ZFjjO86gh1tMigGLK/sZrBrF4OlgVcgA97r6ZS6mmKmllJKTh2s4qxCjm4wHd/H8Ztu4fiB+9JNzRLi35XgKzGZdlnWhrHizRfjCnXkGJ/+q6s4/9KvRemCAxu3MFQad2iDg9d9nvvvu4e1vWsYDWt7d7N0+imsrK1hNyaUxjDdHLF1/yG2jm1y8La70eOKaTFGKdi/exenmCGbd9zHZDqhXlv1SbTDIeVgiBkusby6grY+v2Jy4Cj33Xcv0wLG9x0BB9aoUHVJY6sa2Zpw+K4DlIeO+zyrumZ5bYXVPbvZu/8UhsMhxw4c4fZbvsCxY8c4dvgI1fFNlqwCUUyCN7YoS0xZMq39RX51yN1Kwk22Dwnnqg/6mFJDM2ZDO+dBZJqCF3x0CGmzznoPnvNGm+q4pQ65Gbcd+Sxo4+96UApjFMsrSwzXVkEpRpubTEdjpK6R8ZglZ8A6puub3HHDLVgnbNT3UZa34fCKrR4OKIYlw5VlTtl3CpvH1zl07CgyrViuYWD9c7V1GF0wPnSMGz98DbWy6KLEuuBNDGd+eWmJU07ZjzGGu+++C6kqX8lpUqFqy9RGWmhBK3bv20uhDcPhsMFxB79dpt7Fa1VVSRCpDhzygrhSjO45jB6WSOG97kYV7Nq1i7179yIirK+vs7W1RWE0o+NHWLKesW8dOIReHQKWgxtfYGPjOOtFwa49e3GiMEVBYbyit7ZnN1U15cihwxy6/yDV1Id2nqmWOCaCMSWTJYOTis17j3DGOafxdU/6Os4+70EYpSmVRgvUk4qt9Q1u/MSnuOnaz3D43vuRqkY5H24pWlGLJGt8hJgt5/T2VuN5e3eeZXenQlr+bpcPw3zvebePPgF9OyE9/z3nQ33hwn3z6TujJzqz88batD/fe9CFeePsji3/vlUoZpu2+3h2/DwX9rteLNcZf2qHedTwxAL/TvZR3lceZjUPtqMN273TtwdP8BYn4gPzxjV/HPPfiYYohZc9nbVY59Jl0dHj5JWO7H3VPgedgbb6SnKX6jPphGfwxmYdQ8x3ACfl0RiNJoTYkGApVRDiwJX4+F+logWuSfhOl+2FSde2xtZe94oHMAq+ZVk0zFX5fqfRC2BDuVytG/wkBhzq3ov4mFqJ1ZQaG6HKBGkdvCmFKRhb661UzlEHL4QKZXl96LovHTidTkOiarjdOCTuxgM+mU5DLLtgtL9d1y+sH1NdW0BRaJ0sBBJw628uV2hd4qygRPtNpzVSaMygBKOw1vkDj9dshYaARuUq92w453A2Hk6CZdYncyarqQqx6uKIt5t2k7chJM6HmyTjdo1KWU7Mq6ry+TzaXyzjcoUPLywJMUTBl/aNlcKscz4Uz4VbwKKSkoKggjYdFtWvlcFZf2uur85TU03rMG6LUpqaigO33YXSiqEdUFjD+q0HuO6O+8FobO3xoVRI3seHShnrKCxYbXBaYScT/u5/vRsRYXVjgmAZD6EQWL/jPp8QXxQoY3AKZFIxcP5OjY9++BYwpbe2I4yVYlpqSjdFttYpxIdvYQr0wAtAKJXKGk/rimpaoYClwTJlMfBlaasaN50wGW35/BTrvDVfBQsSYMXHandDpyJo68M71KTmxg/8X2740EfAFFRTC6bATKYcFX927yvA2RozKHFrQ047/XSOHjniq9hMKqabW0jl0Mpw6upuxFrvmdkcc9s111Nhw3lVWOctI8oUlGWwfO9apZ5Omd5/lFE1ZaqFtSmULlQT0wrnLEYU4/VN1m+6FZzyKR7aJ0MrY1jZtcbq6irr9x+hqiqquqIUGFiDsf7meKsUw+GS96ZY689XuCvImCIlaENzs3k8MydiTHGPhxcaRSN7Jp09LA4bEvdjKEigP+HveA5NLMAgyt8Yb7znWCtNbZ2/wVtrzNQh4002D62HUCNH6cJZKkrq2u8lJRodKnwVYihGvnpOLUBVIaMatz7l0H3HQcFQecXV2GCJLAyq9gn2A11Qb1UUWhAqnzMQEsaV1sjWiI1jd+OcsEzkB37fK10gymGdrw+/NvT5CEp81a3k2Ak48fhpC8daeY9I5AcmVPupXI0AZioBXyBTh4wnXnEtfPGF9cMbHL/tHl8aO6zt1NUYIwxUgbNCvTnCTSco59h0NQqhFjh2eAvnglIlwr1KYcoCW9U+F8R5umWU4iFrp1CtCs4YXGHYtX8P33DF5Tzm4seiVoa+cpV12KpmtL7FrTfdzOeu+yz33HQLaupr5hvw1dJUuF8jKgWEXBaJwokCJb3VLJPALmS0Naex/WErfZb29FxH/uoTatPez76bF1KkIh/I1lgH3tttNxcY81zAEykNrbGppqBJ9NLnylj3vT6BHdoREtC9aV0n3q1oC4ZdL888nOQhmzPz3Eb57hoFT7QukW/nvGOe4jgjKTO7Z+YpSt1x5pCHnfUJ8SrQidya/6Uqil08d+eYr2FLoJ/zbhc8zoEs5C+0kvhNVCqIaxnPiNJICOtUSjGtagYDL5d5w7eXmyTl0whR2IyyaHuyvo8McyThinh+0oNezlPKhzg7x/Hx1gnxCSehaFhR7FrZ5avxDApf2UR82TwdypeCr1TiApGP+Zx1pvXE70FCsY+4QBALyVsEZXQTo46/DKnRtsEEgV7Ex5h7xhvDRLzQG2vi19U0EDGfSK4LQ1V5gbaWiuXlJUSE8XiCtf72b1v7MKtC+zKDdVWB83dq4FxQDoK6pTXT6SQRP2stpSm8SxuoqhqsotQDyqLAKYuzvn68rxojvva6cyhlwrOFT1ytphRGoweGWkGNoywNrqpDaIiEHJaG6OReHoWAWBDJ7g9xnpkoPwcTGG+4Mw2tSMmQXYuW0SYIyo0FJH6vtcYqm5S/GC+pTPDcRA9WwJ02zY3utbP+QhmlwryCwuoLQCdN2vpil4gQLqIBcYalpV0oSpSyeG04lkwNOKLAuAIt/hItpaBwgkwtUFPGfe5cOBQ+Jj0y2wqXFLCljZFnCOG5wdQLFzhfxcVVNUpZioQf7YW/agK1D8lDYAlfzUYpwdagtc8zcZXDjUYpRtKFMMMhimHgSTIeYWXLWzaCcqbFUYiPhZ9m3kIBaq0QXKIzimgpD6VS0dTik62LqaDqKcI0JFl7YcXnF4AOVmqco5yMOXrodq9sgg+vDOdDFwLO7z2xXvoQ51DWMQiettr6ulgo399UhOm9h4OSr1gSYRjOUS3iFQp/bTpV9BhaaeJJlRfAlHW4IxscP7yOQTMQFwRjPIMo/LoasaB8OUAXznx0h2tnqKT2O04bkDoIPG1G1o11jndvKBVuKA9nRBtPH0xYF3IDgVjE+BwC5wkuBZaB1oFpNFXgcgZmbbRg+bKvSoXkX+eoVcNWdGJAXrBxtU03U4OA9YfCKvEJzIkDiq+iZF1S4hItUeB8rVNMoVOOicKAa2TNJP4GL65kniJEws21/kEnKuUzFLYRLH2DgWb5HuJbzf50DlE+7MJGC74TlMOHKJUaRGOVSjYMrYNA7gDlN4hSPqwx3hmlELQqoVCIdpShcIIo8d5S50uKex7thfw4VmUdQ3S4SEtwSnBaYVwoqbs65DFPvIQnXvFUVvbsxhTan1VrcaMpG/cd4jMf/SQ3feo6phtbvsBlED7iumuJeRhRuIl7gnRmifQyYCvRAZVtEol3lPg5BH9yS6nYDppnGtqTfz7P0r9djl56jmaYqT03r4hunE4wEcyJn4+fdS8OjntpO49K3zy67bbfcWl94lqlMtVBzonv5mHPkcd2FZC8327kQHfMfZ/nikafQpYrMt2Z52sGUVZteHukba2/e6APV43M0c630C0lrWNcyDw583bpiTwM3Ta7ezf3qKQxz2njxN6MPJeHztylUapz/BKUUwFf5cGAJoQSB28TDtEgOGqai4tjGGCjVOQjkXR5HyhfnCU+0a1Ul8ZjqEUYGcUXjh+ZmWsf7FjRqJ1jaWkZcUI18Qna/gInTR1u0VbKx5O72obkZJ2s1q1E8RCy40vg6oRsFZipONtJYlah4kujeSnnyaYOydsSLwBzXuuzzgsFRUgSHg797d3+IkGNCbFmKgjVVT1NhFahKIsy3MStfY5JUB7qyocp6UCgY6z0IIxjOh5j65pS+z5iToafkxfoDV77JiTuACAOozRae8/KZDqFLaHUhto6puMpYi2DsgTnSx0iUE+nITRg9k4Kb+2nqfKVabTpQPdYFnSwfsYD0U0KbJHPLNypG0LWTYTPLU0t4pAd8rwtEaGupx7fediabyyxTV8lqMkPievTPvCBoQYi5g0KXQJMi1DllpxoGEhWhtaBDUJ4jtdIPJwgyiUBNlYuikQxWicQXwYzx1O0YnjhUKeboXMc58QvXojmq1i1a9VLtu6kXRDXzyu9sV0RQUI+k0ijMAreeKBU44lShBvnXVZSMLPQRWgxy/hMEH66lrmI92ihjRc2JnxbC+HczqxXmJ8xpsG1pvW+pGddqDDm0oWIKEJlJHDWr5e/CdphQlWsLi5b+5dZaM6lbgkUOcM22lCEdvzFgTExOlbrC9WmpDGgpHmH7xsBzDPpHKs23yfB4i5hw+f1/UUEJ53GRYJxQlrx/17X9PtGK91+L59/whdNzkvCTUPXxeui4Ww31r4oLHvyFfLK3MwW88+6kAgZwt/CBLziGy4OjKTAV6iJSqLvMzZqJTuz0lwiFn9Pey0w/hx/aQ86X+0tCsm1ElypqRVQDjj7Iefz9c96BqefexbOhDNlBVMp1g8d5ubrP8dnPn4NW4ePoqbW37Oi2snADY47eyKjbX3hJl2aGz/baa5cF1rPxHXM+unSo/y9bp5D/Hc7AXUn4+nOY147Od/MwxxjG90wpnnt9eG09X3qF2L0gGS4itBdg64Am7efh8N0FQg4cZnXneK4q+R159z3d3cNtsuzmPdZvg/69k7ez3Ztbfd+9/mu8Sh/r5Vbu42ae6I9Oq/v7hltzSv126yv4CMCKucjOiJJUuEFb6Jp2nSZLOAfDkbdbuZ3B3KDhCZUbRTCPW0nhh0rGuXQx4sbpRhof8O1E7C4cOOoCuEn3kVotEmLUqhG4LRV7RURpSDkz6pwmVO09BbBglfowqNS+XAbQyOcmqB82LpKCoK1Fa72d2LoIDWoEE6TrGjWJ51W9dQn0eAt0HZa+4uuBiVlUVBVNUoZptMJRVGiNSH0yd8iq7RCmxIRqGtHqTV2MmEQEoIV+NAEEQaFYepsSGC1KA2lNuE21+byuqXBIF2GsjUacXT9CKtGQe2YjkYMIMxDUVcVpfHhRkrBdOpL6M4kiyuVAnVzy43WmqmtW/ko6eC6GKrRHxpFDzGJmzFXIKB5P89HycO84pi7buZcOBNnZ9zJiQgli74kIc5r5u1yedtZp7rCN7QtLOEjoiW7CyLB5dlhCl5Q8fVYu8K0S16xNtPQWichOSdkcR5dfLf6yoSgLkGPeInkKu8zKvPQhArkeEuhdF3CF5SbuI75WIJ22BpXGrO0GeQ8C1COs6jo5EzZBs+cV1pmGU08AxHHSaSNYxJH7Rx1yKfKVRFfSU9BKHVaVbW3cqsoKLQFOZgtP5uDPxuNDb6PkRfaX2wnKKx4a1WNUKqYgBcF5LzdYBWjvY+VVsnzGvvPhb4kXIcLPRVRcFYp3DS86cPegmfLC/thHhJoNyR60QdxbN4IMLuHVIZTEa8sNGc2PC+SlCknJMNT7CC240L4gCDgoC68h09ZR2kdzuig7Eiag+9XN+XXRVLZ5si8rY3e8kxTISidPfRFoVChJLnTGmt8IYmJEXaftp/LnvV0LnzMI703Wnv8KydMNkfcfcMtXPPBD3P/PQdQ1qGF4BFpbkbPz3yOy+bMNspFnyLfFay7dDK9o1Xrnb52Yt/NjpEWregT1vPf++ZyIujSrfjPvDa2szLP0Eqkpbh16dSJFI74TLfgS/ZtIFeeJve1nxvucrrfxVVXGep+v90Yu7CdchcPeG54zGWJ+G7X69LHg/sUvC6OREjh693czS5O2/jpv4Nk3rs5vvMxzzOO5gYzFDPvzY5nVrGKdG67ddgOVDCQR6NNWQ4Y1y4YxBpNI51laFUMy/lEs9cbA1p/n83/DQ6o2KrB7kzP2Lmisby25gdmHWJ9cqI4X09fhQl4C78OFinSbcRRA4tlb4twp0W3Ukh+mV1BqKpiDHWozmGUwinfTqELnFgfnqWEuqoxkMrcChqjoCxKz4DEKwhLg2FIzl5qEeWBCXeEGI2zjmE58PNbWmJaVdSVYml54G/rDTF24/GEaTWlDhf9GYGy8B4JYwzR9l9XNbr0JUzH4zFaF9TOu6f9beVe8fIXZPk4+K3RiM3RccxwgBpP/C2P1oVypX4nWalx1t/bETdQXdfpMkIRXwLU6CbZOk+sN6LT2hThjpSmvK9uHTLIDmuUvTPFIj9cfRWvogCdx77mRKSPkam4j2gT30RInAuCBaxvrPtcFLy1yNkYYtMmSLlQnPrIGLcTZsYTFQmfhEyrzQiSn4OsbY9322orZ/yu83caY4aK7YjsdvPLCZ3vt62oNGOM1l1pEVLPNHQjBJJLk37tLLOXY4qIL4ea7ZuWAkRbmOl7P+EnWRijkO0Fu/iExgvLKtuT8b1klSKUlrWNGVzE+XMtrtVmrvh5OUZhaz9vG56N+yqeJ+dcOj+x3GA+lvi7Uv7W8pic3NrPEvJVQp6FNqH6khO0E7T21f7EkTw98Z6MuI+StyBI7t2CDXENotIQ/3M2hNeE3d3yTKjQp3eVNXiRJmwsrp3L92y+p8mECyIjTAuBksjoSMxSBL+mKtIbFcbsB+g9yg1tih7mVMpRFMoYRlqYiGMoisIqHDZVXvNKi6Tx+jK0xitfUVAJAZ/O+hBdj8u4l+O4ZCaW34nzOUtKUWlhpBxm9ypPfPKTuPQpX4dZXQr373gloh5NOXLwEB/9xw9y7w234DbGDEJ7tqp9CWjjQxa6tDI35OTKRtcwkz/fd9baezXOPy5TvzDcD7OXwe4E+p7N59InsHkts/Fsdr09OS3Mxx9pUjyDeXGZnN729d1ts88jE7+fURqC4hqeAAKPzehvfDevVplD31p2f49nbruwsS5eWuue8QJ/GLNw5g6eu/jqw0MXZvhr5xml+t/r23Np3BDOZg9/7uzXbZUqmJlHzldayss27XVx3CdX9M0pNxI0a+r5t/cihHdDn5tbW0xs5Y0ivuFGaVCqRZdnxqP8HWzp722UjWZegtWOiRNqdeLn4SQUjVe8+pWsrK56Ymx0st4WZZEsitEjEQcdBVcVs7qVZxVCqDyVW6VoGJfXZP2NvaOtkfdmROVEKQbDIVtbW4h4a3hd15RlmSzBZVkky1YUbLU2dO+UmE4njEYTtFaMRmNcuETMBMFbEEajEc4JS8OhvxRONcKZ0pq6qsMFhU0VJaWNrw5jbbj9u0IFy691NVujMXfffXciBF6R8jgcGp8MX9na3w3hhHpzzMAG6634PJcYh00mvMXNnqqsiCDatg5JXJtYAtfz/IYQJgET1WJIkB0I1Vgy4ns2hdr4u0/iQekjvMlqL20PTOyjyyC7HpE4Tp32uGJ5aZlyUFJvbPo8BXEoN3vQ83/T2y0lQPqfUwo1S+PSd/H+jijsJ4YBoOZYtpRqzSl+n4hmduhzPPWNL8dtXsY53ZqqfYUrL2Xl/YW50+yNeNGkb6OxEkXm5ZPB/LvREr6d4JGPN+0tZi1wfUJBUlKcpMvlWoxQBd1BRcWz556WoCBY13j0XBAhBR/f6pPp2jHfSnzYVO0sIo4ieFdjYnV3blHJl45ilWHCM4tsnfO94D0EKnmLHcrfJxKEWwSKQqdwJaVUULQCDmNoTQhTrW3dogttpT56FX3XsViEC/jytDbeRdNUwvOhbv53pUjV3pT2Cdg5xNmJ+BCrNq0J9yyp6FXx4DpKYYMj1SgpkG66TkprwI8Th0VRiGBFcceRg9x28F4efeaDWCrWqMS2mLDqeM2MbsYoiM/VczGs1SvejbIR9aXMg5yFeFaFZqwcbljyiIu/lide8fXsO+NUf35C3hrTmmMHj3Ddxz7J9Z++jslojBlXDAmFS5xXGD1v9d4ml+27nG7PE/Ty/ZYbEnLBOn+u2a3SK7R1n+0TZvuErHkwT+CKOO16ZHK6kAt7O4FuW3l7+RjzOW0n6MdxxnZzupPviVwB8G10xqT6aWG33z46Gde2pdzNEdTz9/I55zS8+5mIpLzLebwnVzxaEQs9fbcF6P75iWp/3re/Zww5NN7QeXuqu87bnRno3y/5u5GmdXFC5/N5PK6L6+6ce/uloa0eLw7r6mS0jDxGR49Qd1xB1rYi5OVwoxw5b64RrHb+7i0llOzMpbFjReMLt92aBP14uVYdDkhfWEjcTH0HzxN0f3NtbC9dCIhn5EZrTFGwurLC1tZWumCvKEuWl5dx1nLs+HEfMhUEbhMs+Vvh8q0cvbauM9dSIN7SKCq50FuWZbLKV1WFtZbBYMBwMKAcDJJ3Jm7a1dVVJtMptq7RxjAYDHwlFhSurlgeDFlbW0ulgY+tr7M0GIYqQJkrEp+4qBxMbU1dg64qiqIMybQ0YSKRWYSNEa0fwMyhj8JAt4wspplDflmiX7eCJqygWTc/iHZMa1IoM4EmepaisJu30SeUdg9/HkYUQ49yxuOcoywK6tpXOtsajaiqmmht1MEq2e2jj3HkTGAeg/RW8TntRCGcHoKS/7+HAOZMKifYKpTgjM/nilz+fj6HXgYBaS9nZCwOO40NSHfctJmOTWiUYNRWSvlL41TTVhfHIk2YzMz+kfZ4u/juiysWfHUiCbhJlwY5X6+poG1VbBF5FbQRiVbzzKvlDdJB+SC970OnSB4M5/zca2u9IE6bKbfCCTohK0lZVhor7Tt00opITNbVyVNrRZIXOIYo5dUElQbn6pk9m7cp2TibfRbXPh8/6eworX2xiplsQMIdOu13lfJKGWp2PfP1ixCt/845kEaBF8nCunxn2Zs9oSiqOeISrH1WnK8Q54QK4cDGce7ePMZ5rmZqLaKbohSzZ0hhdZ8V21f7E9EolXs1CIp4M6bcGjnGcs6FD+Prn3klZzz0fO/BCHMwSuPGYz5/7We57sMf5/Dd96KsUATlq1Yx1yzkm0X8+E5nQpFi33307UsHRXvlOt+qxhA0T6jdjs53BecT0bT881w4zLue2Xc9QvU8aGhCe97z2oTmAuDt8N6ixzH0rgPx/XkXvHXb6cNLS6Hp4TPdvvoE4T7joP+3PeycnnfxE2WRpNR28NWl/XMmmw63yvZ73zrm4889Dvn8u9CnFOft5f10la98iF2FaB50lZl505+neEBm6JRwzQCCc4qyLBiUJni1VZJztdYhskgaA02Q4T2uBEejqGs1v2xwS9EAXwQDWBnsmjvnHHasaPjbYX18q609MbTOturoeubahIrEG729kOQH68N6GiG5LMtG+TCm1ZYIrK+vN5pWsLwdO3Yse6a59C1HSNNvc1CsrdPzyaLf2UzOOkb1KIy3if33RMBhNzZYWlryydj48Rw6fDiFmYBXeBQ+qdQYzWhrxPrx46nqjNaG0hgsnunW02kQzL0AVRQFUmuMEuzGFoW1Pp8jlLJMAgN+o/uiFcEiGjmSSNDwG69OrhTkORoRXzmT9AqfJ4pKZQJzaF/IDrjzTLe2TQK+1j4EDWnK+kV85Zf3JUE09onHeyy/G2l+7j2J79lAjMQ5tC8b5OdgjB9fx1OAUiG0ag5jcw7J4s/DTgxCZwgNCYTTC46kdbBB4FMBWRISqB15YmlsMRB7L8mG0BFJoSzNwrYZAcHCCJkHISfkEko7o8i9KPEzz+haLJToLK0JSWOJ6mhUIm6+MgUSElaVCjcfR1yFRZIMt8Zggujs8dMwAKPijaUuH0yYZwzd8Xu4YRwZPlxMYPNjUUCtvEKkAgGsQ06W+A2Icx4PcV/4/eNviU4hYWHOMVzIig2hVX79Nd5rYa1DmWbvxHBDY0wqIRpvZVWQ8lv8Xp0VtOKmcOK9xVZ8KWwjYJww0QpvQ/F7RoVLKJXzVn6jCJcn+fm6aHgxJuDQtgUF8cn/fr8ShH2XcGqrOo05L6rgaWrdeDviPlaBmelsZ7lmXvHd9IGE8DNRwfrWKBPQhBNGZSK1aevm94xxRytcsC+mcLjKCWiNdcLWeMLWcInChFvjk0yZCRwCmLZQEPekwns/Yv6KZ9Eq5BqGAgeFVxAcwt4zTuWZz30WFz7+sVgFFJ7mqtqyfvgo13/iU9z7xTs4cu/91BsjTO0Lg2hUKFcbvcomzEr5ioDZIkaa7GlBW0DqCko5r8yVg24segsn+ZplxpK0Bj3C1wy0ienMu9spAF2j1Ny+pa+H2ba67+aQhwD7ylv9ycBKtdvKvcfdtnNDXPNZk9MUN3fynmUGuRxyXOXKROSjXbz4H9V4euP7oV/J1rKrWCTVOu6FmFeWsYY+QT/NPx9H1tY8BWjePOmZU9+zrTk7hzFZqG/2Xp8BsW//bvfcds/0QXfP9T3Xp6DmRqtm/0ThDmJEQuTNhTHsXV1r2peMvvlHSB8EPhBxlJuS2qNoFOKGOkuzf6LMOdyZUWPHioYJMchOKUwRCLCvj5i55MOzpmgJhibkP0TExcogTjwjUEHwta6d1OvfN1lZ1rbg7A9AIEbxzghpNNvoyo8L4CKejUEZg+BjqiUI5pI9GxmYC6VVHd4VNR5NKYfDVErSOZdKWKa+ax+6NN2c4pwvibu8vEwR0K11HsIAg4G/2VHpAqMMBgNaMbUVdlpRb/pEcBXGl8KHwu9GKwZF4S0JIdxBK00fEZds3EBrQ6dNETxDStFKEldBEEsVX1wjDCoVwjhQ1FOfqB69PqAQ5fGb35bahPR4959XarwQo8LdEa0qTZliEsdY2wpra7Y2jjEcGCZGhcvDmrtWwvL65NigDHo8RKUqWt8hHB+E4Ikh2xsqCrteSE3x3dAofCpaY0N+QwgzdLi28OV8eWcdsoslKDQ6CGGSjzvRDZX+H89H9ELEcTjxCp42Kgme4rxg6Y1pUbjMPBgoKoJyRif+W0BRp9tIxb+YzoNt6JHHnW72ma1sUFx1K19GEJQ4X+ozlK6N3iAnChGf/OyCApuU/TDGNFl8WKbW2sfeS7hDQvzYEm0IRovaqcYwEnIibGZh9EpmxJfCaoVzOuVmiHPh5nCPR6FRInT0yGqf5xV3klJN7LDRJnmX4pmL+9kF/0GxVGI3N9DisNYnhQsGV4db7hVBAFXgQBMukrRxZ4TFUMrfnRLw1OAsKnMOUa41zogXwRDJQWRmaYWVCYnqknifitW4Mq7lor6blNWU3YRE1xhRngj0OdADT1YaAScq+w0p83RCAj+Iintsy4aqW1MlLJkllqxhc3PExmA3Ze27EwkeA6NBvOeoUApc4/mVUAc7VvBSwcsg4vC3R/lCI8Z5D/10alnat8YTrngKF3/9k1g7ZQ+igufPCdONTW6/4Wau+YcPsX7fIahsQlYSzJTCKK+Mg6+MnAvBLcFEopmgMUR08zSAmX/j79FAl6IFih5xQDKqIx1hUM+2G5fMdJS/tC+SmJs93yOkx89zHtb1aKUfVHtcGeRe/Ph9/nfeXvOu3wcKHSIj/J5twgttUuy6Am+3/67nKQmNGbacNFjpW6scuopL37PRk5wbvSAYI3KBNRtzfNZ/6NeJcEzjnWnzhGXijGK7KgtnUyqdz9bz0lXgsjBZaXbNXKNgj/Llaa2nN91Qq3yefW3mSkNfX3kf8XutaN1gfiJo5J7mTPQpNLnBvb1/guFVkyJ2lBKWl4YM8AZ8HdbbcwKPe+tspmc0SogoQDdGijZoVJBXRUXZwkcPxM+6CuF2sHOPBk252shQjfbCrVMuJB5KYII65WaIa+IUlfK3cI8n4xDP7Jlzyr/ICGpEbp4Q1bI6ZK657ibobrL4ftQU06JqWu0455r7QILgYGjGqJTyYVvOMR6P07hjTH6MhweoqmnqezQaUVUVy8vLDIdDL4RlFaCaA+AQZXDiczbqusLWU0pceL6JwYesipTzt2PnjKLPjZq7LZVWaKdTElru/o2MJ74bcZmqROkiacRJictwPh6P023qw+GwUWpoH/a4plb8JWlxzFG5iesX51sUzb0bRVCslPLK4tbmJtV06gmb9l6EqHS5bIwQLpwRQet4GBXhyqsWA0mHKrLzjA9FYQ1prD4qk/M8Xqy/GE40msYbkazAWlGbePO3oI0KlZR0CnvpWmaAoCxpqnA3RYq3d16ZcPEeoUAMfNy7r9ZD/PG7hGQgiIKjSKYsNPOJk0vVwZy/m6BrDWoIu/KKmQvKh2v6rnE45TJlSrK5Nh4l50hGiaj+ZbJmGq9PDvYfRmVYi7cGp5AzBOtIAnRsX+K44l7PvqsFrAPrlL/fQcLFhyGBLp7//Iz5hO+2RTI/O11hL62EMhitWRosgTLUDlSwrg+VRonGWY9ArfH3eihFlcKVghKSlxtMimqDt4iLJsk67JOcYYinRapTPtjT9/wvaaKlpB0iET4iLXr2ldI+DyV6TPMiICq0I8EooCRUJHRtnFa19Qqhs6n4hvf2SvC8KybOsjRc47xzHsJANONKfGnZOGka9UcLlBoKo3G1DedaU00r76myFq3i+rmAa4UoR6U1ZqB4+EUX8fRvejann30GalCgnM/rqaZTjtx/iM996tN89mPXoCc1ys0Kuw2CVIqv3gnktDTGqPeF5/U93y3OkQs5+fPx3xYPYWfjazc2a8yYJ0xuN/4WTewRDCMO8kiHXAaY11fiSa75O56tpHzq9vN5+/Pm1Ai4mcdBtdvovtv3XU5ju4JzI2xDVDrzNk8mtE5BKnDS93RubW/6/PKgNe/O530KXFe+icaGrvISn0nGuY58eCI4kfLXfa47l77nfChmE1K8k7HEORit0YbAvIJhK8gkyZhI4/2MZe9n2qORcRJDJZ+DVzER0p14+f7KvVwngp2Xty0HaB2UCdVot2U58MNU7eTg+JkfcEMYiqJkWXkB15iGAedx6nkFj7iZ/a3hZav9PNQnF4hjdaPJZJJ+zwWCPitJtO5EATlXfGIfcax1XaeEWaVUEqan02lSOpTyxHs69QrHZDJhMpmwtLREWZapjdXVVZ/TEazTdVUz2tiitjVaKpYKk25CFVe3wsEaBar2lvEM13GOuQehruukMPmEU0nCaBevXWWuIdgx4aohYunm9/B7WZZsbW0xGAyS8qWCe7jlkcra7eaP5MQgKh55iF1eGndQluxd3c1d+os4a6mtkHMDazOGrnwctheSxHszJFdQbaMs0FjbHWBtO7bVBuFcBzUlhbARLHcOjHgvRWSwSEzS0lgRJmKTVRYJZZzDvPz9etIinuAvtETrcDu9SmfSiZfofWhIkKCD0OicIKpREFXAhSQ8N0qVv5Ot2UfJx6OIN8R5j1EyO0XcQmI5ipBLATrG/xMVOCCsd+P+98pJThCdeIHar41AfgscDT4JeBdARy8Z4m8yQoLw7ZUF61QSvJ0Dm8WvJisTPjCmFpUuRBJRKOs/i5pTFNRy+mZttn8i/jLaOI8BKXx58GG5hNSeAcQKc876PZGYkbUURdiH0fsVQm3iOvrlzemi70UiyvJxqI7QKN6wlB7OnstVDycRv82ez9uI6x3Hkr6qg6BnPab9RX/BMKAk/d3aD20eSO0JFxahshZcjQnbQ1nQLlSQU7AyWEVVlmllqVRTbMTrWy4wb6EWTaF0KGMO1k79d85hVPTYCmIt2vjLOSkU5zz0QTzjm57DQy56BGbg92shfn6H772Pm6+/gRuv+ywbBw8zsApdO0Q3FyzOCDLi0mR3IoRHPuUNDnXvM337rmvk266P5G2KngGtZtrckbDUEU26RpTt2uoKkOnczXkmjjnnhzlvy/turM3R89wWGpOcIJau+p0/1xX8Y9v5Z+leIokYkWTw6857NvSq/XtX2Yifa61aRUmaddNJ0eulRSKN4tY5/t255jLVdgLnjhSb7nhOoIjm65V/prLP+p7vVp3cyVi7ikBay22mNU95jPPMz1tueD3R2HJ67kvqx72aG+IkeMLDWuakPRl/YhGUzmWZOb0N9N1FJbvZFv49rWODJ4QdKxpeyYij0BRFIyw2k/CTbgSj7kH21iCtCzQOpSUjku1axX0HKnfv5tV0uhp9/FlZWWlpsvnC5gc4CayDQStUKB9bTpziO1FIimPx8duxTJ5KbUT3dHymLH2o1Hg8xlrLrl27UEoxrSuqSRUUjYpCOZa1Dhe+ueRN6lpqjG5fjNes2Wzt8victeEGbxqc5DkQ0FSUiW14j0KjUORKQa7wRTxNp1OUUmG+kO/4vF3nbCrZ1k0y67NKxLFGha0oCobDYcK/EU1ta2rnomiQ8OTEhbh8AJuIU9i6aT6qGWgzThrLQMv7Zr0nojkHTcWHiYPoIhDxDMVIsCKK90I4kXCBpO9vamsK1+RgoJowB6UUogtfchVQEq3+hFAPn9sSE3sFssIIIanZReXOu1tra3HaJaWhIVdRQfIW3YxGpTycnGG3SKsCXRjvFojTCPNTKIxVSWGNIVLpxURQ83AJb8lvcNyxCEuw4SiAxtKmtUKkbikDznqlxzrHVElaU0+3/Fi08p7Cuq6pbI0WQUuwtgcrUhxb/LeqqoSgrjGgexZzI4BzvkR1bX3YpRZJFeVqsTixGF2E+GMvqBT4/WxEYZROyqQOeRkzrD8I7UmIz/Ip2knXCiWqdYlfS/mjyYuJ81BKJcEzrltiZpH+J2U1rm/ARcBpNJgk/AA4leahUO39qT1/MRoogkEIX5bb1ZUPgRJhoH19MS3CQMBig77q23NVaL8wiFhq13hTB4VBG4MmCNrGG4NUUYCGtX17ueJZT+fxT34ixeoQVyqUUci0pp7U3PzJT3PdJ67h8IH7oLIMnPIV8ZzzF7GbWet0bh3eiZKRf597gru0tA/yvbhdsm0+vuZleq2kfX20eHlcx+y7eQp4rgh0BbWuQS1+lxu8ci9in5LSN0aP/xDa3YmuiN/H8ce2unJIjrOuItWuOhcwEmhiPqcuHrp8Mf/JxxefdU5mcjOBVMY5F9TT2uZGI4KMKtkZzubbXR9OsEdznMR3ux6W9ryb+eQ46fNSzVN4++S82EZ3LF2hv2++s2Nsh/P1KZnd3/Nn+8bXfTYfm2T4UormQlvXzunwYbWxHG5QEKQJR2v4qyCxWqYfVVp/hQ8z1v6iO0+jCcZiEd93z7zmwY4VjYaq5IhXDWPWkdi57IDGnRsvgWqQpJRBad9O7jmYR3zyz7oHrOsO7WrbeRv5hlVKMZ36PIqyLFvW9fy5fIPm4T35nRQikrwhSrUPd1VVSVCM9fad87X3q6ri8OHD6e4Esc5XnlJe6EEpxMUbbtsHLxELcSn0IfcM5IQuKgY58cyh77DGilz5/Rdxfn1EPF+7SBCisjIYDtL44jgiThHxTD6rnAWwtNTcdTKZTFJIV1cRUlpz9OgRrK2p6ho7tT7WP4R+aK29kBBKbMY6+l3FTCmFEz8GgeD1aYLVLU1YQXzfBqG1a92IzMMpcLnXzYViAYqkGMX9akyoVCZCrUPhgrjeREVSBeLgBba412xtA4MkXXQU+3MxHEv7vKWkSKmpT2bViomt/ElVzTlvmJFPJlaqwUkdLKdJ5FTRRduYRJRr9lW8OV0pH9aEJcvhyaoNqag4edri94gvqmBtVAa8kNmsRRxHsFQHQVhrf4+BhOL1Eh5OuVvOC9wzp0EcdeXC3TUW7Sw+6VooFRhNS7lvlTPOlKMo+LVyMfLQTeJ5dtSuRmlYHhbsXV3h+HiEFu1DN7UP7dNBiFcBtyp4bVS4VVwpfMZGD8/3hS1IDEqAVpWotOqRTjYfthlh80w8G0HFQ3TMWcsMD+HiSZM8Uy7sR9W6VNO311FWRdEcrFzgUGBcuoRKqSLl8XnlWlNYhXKOWkFtvF4ycD6nKCoNMY8teqCVjoqoTfcuec+coRaFLjVWgV4qeOTXPIYrnnEle0/ZB4MCo31uhRtNufe22/nkhz/MvV+8C7s59uGTzheicBpcqZNyFfHbElg6a9dHp/J/mzYUVdVEA/QJ2X3taN0U6OgKtN31by1Pp622QH1y4SndMc37vE+47hqwohI/TwbothPHm56Zq0F5WcZXi2zkiW7EQ4s35+FF2XfBjhD4/Gz+QD7G7jrPE0bbfJgWr+/iNRo58rBxNTPztubRlb1SmyexxtvtiXmKVv53F799skz3HWhHafS9G/GXy235nuhTWLrznoef7vi7v7d5QXv+Xc9bFw8Ao9FWMpz5wjjaFw2hodlkY4vnwrpQckIpr0SIZHxAUmSESPRWh/+Lm+WZJ4CTUDQay2LUyj3xjxOPG12FZzuJMy3FISgonRjCnNh2FY3cYg5tgpHHmuYL0HfI47v5Yh47doz9+/fPdWf1aeHdvJD4TPRcGNMsbFRikjAZiFJMDG3Kz2rQGqMMzvk4Xo9l0iaIfeeel5iF2SWceQ5L/Gzewex7PwmJnXWKIVDdg9vFOXglq6oqirJIF4jFeadSfspfajgYDJo+ArOIrv24vjnu079KY4xieXmFen2ETxfKhPGQGOxCUnGIhQHxISM5w8j3FlnFF2MKH66Rg/IWgFiJKYLNmKxSGpcl5kclVUQoiwJXtNc4EQftw7F0Rhzi7/7vuK8B4xOXQdC6ICa5dxmN97qYJJBp3ZRpXnGDpLSpfH5hfaI1PJ2LEGcvc7yQKG98SN6RbBw+j6EpK53/OHyCri9bnJ93UHivavwsGiiiFaetfMfKYAoTqzR57QpJF69FhTDs3VBlzit4IZcnhH8VWlHiLdJavOLlnErnN1lQwxmo65qqqlBKzZzzHB9pfj6Lj2FZ8JBzz2J9a+SrJylhoHSoTMYMjXLW5wtorRsxQdHyAOR7Oq6Ho00Lkk0reDMS7rvkIpRzbeijjseA6LkSpNVGUixUYwRr+EJT593PJROquopH2loKbfoVKoAK8SFKDioc1vj8GmObMAAVlYuwH73XzxeRiPgzRQEiOG2odEmthbMfdj5PetrXc8aDzsFqB4PCK0O1cOSLd/H5z1zPpz7+Mba2NhmYAdp645HWxutNRlMpBbVNoZYzgohqT207wSw3KFnrWn/3CSh9bXSFnz6emcYWf+/8PbNGOxQ+83Hu9J2uIJaXHY/f54rOdoJ8/nxqO9C6vnmooPt2c2DmCYIzSoLLn83OpMwKpF2lqre9HnnIf9bIYK1xtWS2ttHSOZeKEHQh31N5Xx5fJ7fWM3y2Z76qIdi9gviJ9nVsP+8jlxFzeTKPFujbg93IljTvyPuz53Jc5XPrjqvND9ty6TzFKvck+UcCHwwVYevJBES8EVD8DlDQuncHgERno0w0u9e9rOkNIo4m/y6Z+E7OfrBzRaPZYP0JYxH6FqsvZg4USvkysNbFUoEmMCNBqdnFydvv0wahrZB0y+XOjgGGwyFnnH56mpcPjAgXIzkf2pIrFfl82nih1X9uIdLaJNzFR41u8hqGg5gwHeagNE60L185maLxMfGE5/M7FaJwqnVzaLpjU8EKI6k0ZtRXVfvg44fghd2QFK5NsD6GGt9Bl4zKUsy5mHfxXjrM1oW7OSQlJzn8ZVh1VdPcfOy9BMb45FfnKrTWqRRxC9cCDl+da8/uPZx71lkcqhzaircY0ay5ddZXY9JN2dYkqCPJ6yF0ktFVI8D73GsvLbmIy1wYxwtSeRyoF/A7xFkvec9F8IT48YX2dAiDEVoW31hiV4I1IYZa+UvodBLixIVqPFlpZr+nFCiHKUxjhQ+KBYIvRatiyF8ntj8IXjGOuK7rZKmOYQa5pyniIxkLlN/TOlP4ameBATEm2uMr5MJkzCQpXwnJbQ9jQ1viudKJcWvj19rooGwolQljAS8uE4BzwVwrnCZdZ6QQyqDsaRSuzmJbxQvJOhTLmE4mjSEgPOPvDMosrHHfBQRrrdD48MilsmSpMEyrKRZhgEZJ8CYEBhxDLVxp0nmERhn05WMzGpoxRomTjcneYd7RuR4VlnR5pfKfNDkZQfcM95n478K9EibS8RCyGM6hn7NAOjNhPpKFeWmaBfAjaOgNKq2rIBTSlN5VaYV8S0NtfOK2FYwo6rBmWgm1PwwhmtG/G8vmarxyorT3zBXa84NKa/aetZ8nPPXJnP+oC1CDAjEKpQyTrS2O3ns/N37y0xy/616O3HMfMpmw5N3TGOUrCDoktBuUZq1Sxbl4xpDIxuNmjDSlLWz65ZwV0ryxyszQ3vh8VyjNIRV56OlzJ9bg/LNcBpjhSZ0V7ptLd45JodI60MeGz3jP0Oylg7nQN0+B6fLt9HnPGOM3XcNJHx765uKX1iu1ae9Hhhv2tFKzURu5YN3lr9uCCmc1nguXThlCm3bme6epGJJR3Y4wnM+34X8ZA8xxkA+pZ8yzilynvayftObOzcV1t4u+9+bhM283n5sPlyWtfRAe/BmmjZd5SkZbUYz0L/7E9/v3VvNe025jLCwQNFNnmdR10BkkHTSlVLheICrcTc6ql7kij2qUDwU+9y/MxUY5QkW2pXwtkc5abwc7L2+bVVjKiVKupXYPXS6Y51phfqidc6maR5qodijV3M+RW7DjQvYRtz5BNx9P/Dd3F0ogVM07WR+ZVybfQHnyc2ynK2hHCyfBYlWWgyZkRUJsfqj1r7W3nkXhTwClDcYITKbJ89O66Ip8U7cZU+42JhA0a0MZyETg4hyBEM8ZhcmIh8KUDZMIFXq0bjwL+U98LlqYcyUveXFCPkVdVf5ZG8LJTPBw1HlIXvAyqMbymBhOEJqwPvG5EocuDFJNWRsOQpx7FmOrggBuGkUw3wdpjwGVE1/hJ6yVt7gCIUk8Moii6Iq/Ya8jONUojU7hrdU0oXdxYZo7WsAqz0h1AYIGK0l5RCSEe4FSJrTpQ87CFktrHYPslGrWM62DVqC8QkMqYRwUi0Qwm/Mi4oVN53yOkcTE/qAs6lC6VwHa9IgQsW8BhQMbCJ94T41Sypc9jiErzitYUdlXCfdR4NWgmlKzGo0E2uErjIlX38QLdSYwcqXEC3xKQGp0FIqJhDWKqjRleHEYKxgyT2uMDfamiEYAUzqFqDnbDh0inbmGCaqM/iRaI9FrIShqjDgKsQFPjTLlz2zYNAgmjj+iPv5qZ5mAiLTucZWA2y59I+47ZwOGQpnyFj0kKABN+BTap32psMfEiS8P3gqj8UwwFjFIzDbuxZxJE89H82xSnAm3yycmnVhkKPnrvUEKhQlNSlCqJcwpoUzpoIiYkOpjkEIxUYrh2hqXXHYpFzzpYgary6jC35ViBDaPHOPmT1/Hfbffyb133oUdTbDVBCNQSFj/eA8BYfsilEHoU7q54yZVhpGEzQQ5r+sK4g0/1Bgz67XuExC7e2KesNynMKS/I2PpeafbbkuRmCfCd5SN7u8u0Iz4WZ4jF3POcloe2+yTTfpkhjZ+ZoXYFIbFNlV8sra68olWRfC8dK3xQRFTtJ6P8+iOOy/u0sXbzDkGmly9fM5zFNAwv0YJCue8s0dyfCThfRYdvZDjZZ6SkRSinDfvYE/7ebbxnr9zIiUtl2dSm5AqOUHGHzr7O1cIu/11551oGQ0u8+I6s+NrDHFpTOHMO6U4ur6BrRwqVGxMRkwEJVA7SbwOQJmQ5wze6IKKNuykeJCdK/95CI+FFPZ3EnrGySSDK4rCoDOLVCNg5sJmvpiB8GvvxGkIQNNu1PDjO3HwfYJsVziMbeeur65LM76ffx8XUuvm5sSuQpH6kXZbOfQRr+7vfWMhy1HoVsTylmeFiA1WU1oXm0VlI7d8+FK47fyGthLS/iyNT80ekqQwIGhtUj+pWlXGyCLuq6pKQnRUMHKPTqyqJSJMJpOUy1JVFWVZzlTuaVnOmF2D+J0xhtpF5cznPgwGAyY25G5IRjSMVwe6jCBfU+dCuVqa/IG0Jn6BUr5D3LVJSIp3J2RrGHFchMoQWquoBQTrfnhfKX8BXFSglE+kVgJV95bVLL9AqZjs3BAgbUhKGnhPRRi8t20FIXw2eTHHQ6PQdr0zcY3jmsWbrpVSWdJ5s1Y5bvvO8KxxIIj+8YySydDhMiZ6whfJ9mR3rwQDNUopCmOQYDBpxtDeVx4bCm36jRrduXXPlTb9oZw5LevmasRnZsIbJbNEZjiLkOeJpbH0hEjmZyv1F9ruG0cbvw1WuqFbDQ7aOI9Ci1YKFbyRjbAadltGb1P/HSNUDnl/3VC97YSI+Ek4WighKR+IFxx9NR4FhWZqFG6p4MKvuYhLv+Ep7DplL1b7/aeB8foWN3zyU1z/yU/BtGZrfT2WMPNnAgHtPXgmnPl8r/YJUPMElK4gPI+3eIG1vcbRwJfzv+4+z587EbTPViyp2RaYGjmgGf8MzJFK87l3cZDvkza9UGne8bP4TjeMN+d1XWjhOdDrvj5PBF05ois8d8eYxpcNKe9z3prlckqfcrkdrfKCpWvRAqUUc3dWZw/mskKfctPqM6Nffe12YZ4S0PdMd475HWrbKjI9/eZ7LH/O64bzx9Q3953slT4a2m0vx+28+cT84nI4oCgLknJIYIlKMSWWpfa8vXsmnPP5f/HyVK21D6GzvgiRpx+RlvjLfS1eVp+/um3YsaJRFCZ0GhdkVgNUuRbc+jcS1B4moGI7maVXSGEp+YHalrlnluoI8bvcwt79Xvwv6e9IlOPzOdGe12/c3LnCMHO4o+Ckog2QVH2qxUBV0EZrr5sr5S9gs87SDVnrbkilmpCtxHC2OVSKJsQsZ0rO+fs8cjxE4SgXkLq47wpArb6y72MZ4FhBrAoeju5c/N9tISbNITBWrTVKfGz11uYmbjRq3f7dZe4tItIVrgCFv2kZFdbCxYvxBERhVPsCKK3axKu79j68g6TUJZaTnZ9IzJT2d4rgBC+uzDIkrTW1szNMNOEqWS5klhCo5u6HfA1zYTM/MxE3McegL2/HhDsuYnx99Mgh0grdUgJFTAjuCBGtOUoTD9o9Q11ctAQAP4lmXQIDzvdvK/GxI6Rsd3a73kqkja98P8R3u4aN/Jm8rb7+ukLpdoyxKac9K4zk0N33XaEh9RfWLkIuDPedo2773fHlbfQJP11hqktD5s3f39TeZsa5Z7kXB/h9qKOi4ZlYysWptcKWmjMe/mAufdrXc+aDz6PWMDU6FAZwHLrnPq798Me499YvUh3bgNriphNf4AGF0ganvaJBdn7zfdm3NtsJJzsTZJq7N1rr2TnXfXukyBTBGUFLZMa4lebREY6hCRudNWScaPyz/Cz/zHToRpp1pK/M8ua8nW64TeRzsY/2nEPxDNU2rKXvo2t7G4jjaAyWs/JPs/ebUJj252rms/zdblTFvPPfpje0FHxo8++8hSbMsv/s5/um7/xDo2DNm0ffWFGNoSKfX1/oXo4rMqN3PuZ8LSJ0z1wSuLPIm/Rc1s9252iezNGF7rjyvuI4tuN3+Ri01uw9ZR9PvPypDJeXGAwGHncBj9oYiuESOkTYxPvdQOFCdZW8DxuVCxFcXTOZTkIBG+MNJkZjygHKFOEIPMCKhnNNfW6RuCBNDXw/8XwBMpMRGqViLNocq1MrIUXjZDZ0yvc1aznJN0fedlez7RP+RbybP8ZPR0IZrfTRVdbN0+hujrzcbhTcoxegdViz/uN8RCRVo4p1+EUkxNA394LkLCq/a6RvfOlw0tyGHHEXcRUv0Ms3bxSq45pGHOcCTR7y0cVn1wLeJWh5m/kzfbklfixNPkqrPcnwoGE8maS/Vbg1OXcz9xGKXEBpBC0XQhwUvhSzQLigS8crMgk5EoF35IJ67Cv1kZyZKt007AkBzcEhtuN9kn7cTTJf9Gi0qpp0+iG16VrNtghB2Fd5jk9UDmrXVG+Ln+dKSZf5JyE6NN1iqEIKwYulU1uhdJmQku+Z1EcPwfZ95+wnL7yQAohmGFnEZTzTXYUgFrbozyPrw3HzfO6hSXtYaHlII+TP521392C33748s66lP38+X4s+S/U8waDVfgf/LS9Ip6/uXLrfd+nEvP2UP5v/ndO51nPW4TLcz6xD1l/7bxXCzUCUwhWa2ihqJew+/VSe9IwrOf9RD4dhCQODEqFQmumxDT736c9w86c/y5E772WIpqz92Z5ah1LesuhTyr3X0F8kqWfm1q28l++peYpI/Hcna7DT8Kkuf5y3L7oC2rz++/ro0ncVSm/m32/H29OcegTtiMu+sXbP7U5w1zyvkiGoL0LCCzK902+NudtXvgfabTee6T4vTA7dPZLz1pye5Lw+H08egZLjMc0/F9SZVRRmcEGbjuXzzNvI17aLoxm8iYCKpcrbuOvbXzmts3OS+HMa1qUJ3Tn0nYH4TB897eKnS/Pyz/qUnT7FIm8zX9MunyqKgtPPPpPnfNe34UJeXlQyVJh3LFrq2xMfJaF8IRgT5AwXqlQl+USJN5j4kSCSydmCvwNJYkjWieEkksHbCV24Jgyj82D7b6UQZ8OFTFFY6HPfRhf9LCOed2i7TKU9jFmrRheSkB6qjuTCVV3XM96OfFPFZ/usvN0D1RWUu4wg9lcURSo3qrUOaQEKZXQSLnOPRWpD+XyHuJHjhuyzCMb3AR8KkBHmNL8QQ9x1wedW2j7hozvP7gHJiWfsKxckuozEuea27u4+cM6hrA/dsa3+HdaCoX2zeXfNu/ugGaO0D6vypNLn1jVJ814pkRCT35yD2Xl7RVYZf/FitmR+p8e9g/ibjtNnQSsP0IrnVyrcguw6Cqcfu5o731ki7dcgv3ditopYH778fmyUAkWzb0QkhVGlcDrJBNkUxNIeh49Vnt0H84hwS5EM/eVtxX3axHK7JJz4c+A9qfnN813BB0jVo9J30jDkOI603taBnmU2XaEy/z0/O11FoE9gmhce2m1/HswTYvqem6cQ9L0/75x1hacuHd3uTObftYTGDv3Zjkd0xyhK+TLKRjMuQO1e4uKnfh1f8/jHM9y9C2fw7deOQe244/Of55Mf+gj333UPdnNMKQqUoE2BtTXD4TC7mFT5wgohDj56FHPDU3e8uRCWG3T6cLwd5OdXRFI4bS6Mbydk97XX5Vdp3DTGqPh53k7u2WitPWrm+e5azxtPzmdj23ke5HbvdPHdnWcEbywQlGo8Y91Q3lhWuftu9+y25iJNzPuMINqRe6AxkuUCai4gd3lq/nySX3oEVdjGKi8kftunSXXXJ79NvkszkxzSkQfiM33nII1Hkc5OPqcuv+u+2901LZpNW1Ho0p6558wz+5M6N32Q0/a+NnL5qovn/Pzl+cFAuqOt1kKtJJg5YqSOL3YiVlp3sCltGI3HGKcZhmgFlSl2Eff+QmdJfFUrhVOSDDUoULN2kV7YeXnbvAqUNBqn1p16zR2NLQqJWtqCWI5IAN0JlYr107sECdqWmIg8actlrcOVb7DWFKIAK+1x5x6U2tnOIRfy8qHdWOu+2OucKJhABHJBKBfciQKcgryqijjxcfvZwdhOeOkenAZPbc09J1YtT4VqJ3PneMnb7oZuxLnGOcW7IiJBAhID7HNTdq0weQ5Pdz5KK7CeMZRlmcKpYFapywl2Fz+NAKoRidZ10g++xSwsqU3EOgXS2vtaKS+YRktLWOPOC4g4lDEYDUp8mWORNvNK+KHtgSLqJU0Hqa/WPHtw2HwTz/Ps3RZ9uI8dSGadNMEbpiCVMgayfJJwrpzfXvHNFgPtwWM6yzTntBsfbIzHQ+5liD8i7dvn28J65w6DlnAa1iXrJyoa+UDz9fGljvvP5zxmlp/HrrXyZJjZTqGLV8jCm9jeSpXjdzuYJzT20cbthOkubUr7KCjVsc3WeezSPprlUtorGVYEW8DDHv9YLnnWFew6fT/oUHoWKKxw7J77uPEj13Db525ia3MLmVSUAoOiAKOZuhpTGrRrvECRSrgsZ64r4HSFjjjeE+H0RNCnCKYQx46yEfGYSozPga6wln3TQ8YyWpAZuVo8Ubf5f3et+vam741EN3O6Hnn/PHzME/z7+BhE+ufD3nK+kcaiaPGkeQLoTCiTCHnRmRwcmXGLfpzHNrvtR4VSRFIosqeHTRn9vI04t74IEC92qGTsCTOcmV8XJ7mVvftdrmR0eXK3zdacgw0rH2d8t8+jo5RqXZeQf9/F43b0Zvb9poRt/zloxt8dU98zffjJz0jeTn5O+kJ7I6+uplOoakwRIieiMhl4pjMqKfhVcG8MloZeNom1fsSX4IZg9BfBZHvHGO3D+Z3DaINoQgGUneFxx4rGQJdNbXkJl3kor9KURTjsXmEOBz8qGQ0jc66puqSVQWsTtCaQmPCsNDpULwmPYm1jxXeBWOko9CkNFEHQsKG/xpok4qvAEG+7JTKexvoax9glEJ4YD0K+iC+R6IWWLHRENbX046bJw4fyZ0QEp3UK4XDOsbKykuHH35CttMboAmUduKm/NEyR8hq6N8CqoHXnByHXfJ2PZSGWF5Uwf1tbXys+CqbpAEsiUrmSoVSTA5ITqZYQoHxcYBLqIJT2nLUUR8gtzV0mHPHSxyCsAm2hqP2GF1GU1oFyIeQt1kmQkPfQWEmiFT/iKN507XrCXuJ8neAvT1QqEEF/n4LRxlfXiQpDUBRTO2F/p1hHbzryJDwki4ollHNo8j6i6O3xmJVtTRYfwlhc8r55QtN4ZJLMKE1lrLDCiYcU2Tn0+1qlkCKUIqZ4i0ioXBUV4FlBL1cL68yCF1ciDiFV3JIQb69U5tVscC7hO8ETQE04o+JzaeKeIwpPwftnTCy5C9DkmERV0QTBOlZ6c87iLChMyyqcjyNVT8oYdSrUkCknqeQhYU3jeWF2brmAkUP8Lr6jsp8WdMbZHXf+b/y9V8hIHUeBVxrcx/XNTFgR541gMGsdzGlUmlNnPI2XO3SeNghJkYh4UOFzZ10o9+vLIaMary/4c6PEV5vS8QOtsSIYUzDGsu8h5/KEZz6N8x55AVaH+RmvNFTHNrnvi3fysav/gcN3H0A7wY7HzQV/Rvs+onKWhd+Ji+W+i1aeYXdt+0Llcrzlf3fb6N8vUZgPeM08JK0qhBk0yn0j3KEIhc+DQJ02nsqf9L9nw5gZYzB4xPPRUhoyQSmfT59wnf5VSbCYETr7aHX+ex/f6eK6HdYb/s54pX/Wz0mH8x5MgJ0z1zG8xv2tMgE+2zO+iQavOe/Lx9YV7BP9yRTJHC/x/a4S0Myxn15Y5c+kjxJuCXRz92vX+JDoaoeObrcm3eeca3h1/tx2hhj/e1uY78oS27XT7SuNN/xPx/3se2ntjTiH/N8unvLxdBWonIfOU1QijyT2G+7AmIzGOKcwzlBPpxTGMK0qBoOBl6mUog4y5yAkhSvdKBfGFF5msI7a1hRFiQR5KvEhXSC1ZePohjeIDkrWdu3axiTVhp0ngyuFQ4PROPE3DLcOv5A0okjwRAS0Ty5pGHEQCqKqEJmRjpsj3GwIyRJa6Jg3IBRlKEEo/hI1MCCBeebTDgKbaIOtHIJFGT/GKABLDOdKi+8t7y64Y3UI+fDCI8mt6C8wsd7yzCwB6264PKRKq0ZByS36SimioUTAl5atKlxt0dZ6hhksUF0CW5YFNngOYj9pU8dxBLkyCmLOKUS88KzztfEDb4WbJJRKOzQrzSl+liV4TyeTBhcdwhmVitb+KtpbMXlJOm7x/DBaJZRoClFMKgtas6wLKplQuRpF26oGDRFt2mqYS15Luh98BHZinMp74iAqCH6qzXCzuMfQb/wuEvGgBmVCdSjBaV2LmUUFJj6jlEo3geY4jmVvUwUoCfPUbQY3YzmJgrqOVmNwtAm2VtmcJNi+dQg71DrNJc7HhGRBn3ckLcUk38Ma8C4Om/ZpwniYi1coYhWqoHCIoJWkO0UknwOhvyh4KZUvDFFxUDSKjNG+j2j/Uapxx0ehOwr2ooKiRNwujaABgXbR9D0jDGVr3lqHDCKdyhlS/LzZYc27eenxXHjK286F/76QJpFYAjcwv8yyi/JJufkZTIJC+t986DJgCXtIp4+7glszhjhZSYw+K6yhCKGNCRveSy3hPBYFUxxOG4ZrqzzhGy7jEU++FLNrmVophspgUEy3Jtx1863c8qnPcM/NtzLZ2EIUTOMFjwiqKKjjGNLZaGihtZYyht+GkLvcw9sVKPr2QE5zu2ue85aukBWNJPmz3fDXGc9KwGtUJtJ+93+my0els79pc9vuQiejTvy9e/Z2AjMKQrb38v3XpzDn+I3zj5+35p+10fzotu0gWohVxHM0IMViISo9k8YiPhwl3Z0DxBQ/gWS8UTTVkiJ0ee48BSkPT8u/m4ebSM/yQi0tfCu8pTqGfkZjUCa8x/e665CPtaV0ZH33eXh750bTb7e/7ri769v9rNtXd190v++eM8gKvmQ0vRETmufiGZtVfmj9vZ1Cknuq8rV1LpOLE1/wcsLRw0d47+/+AdO6YnV1lTPOOCPlGO/evZvaWW8ID7x6c3OT0WhEXVs0TYRNWZZU06lXWgsDhQ/3LrRmZbgMQfaobM2kmrJr926q6ZRve+wjORHsWNGoVZ2YvUEoC+NLRf7/WfuzXtuSJD0Q+8x9rb3PcOcbY0bOc2VVVlbOWVlDZtZEUITY6CY0QISgR6n1oIZagAAB0pME6He0xOaDAEmACEjUQ0MNNtnFJllVWZWZlVPM4417I+50pr33Wu6mB3fzZW7L1z4nivTAjXPO3mv5YG5u9pm5uXlegMVbSATqPcApfp6JAMo3rCoieyIQh+RpFsdJBjkxjMXrSJTeO+i66cKofPhTLh4BALfqSl9kYgQ0MgeM4w4hjgB1ClwCznegmC/hykbIGGICSWFAn/HwEAJWqzWGfGNxZCBm0G+FgTCHxIJrgG4NBct46UBTDrGKOQ49iyftvdALYhxD2TbUCsXGM2pwIYBVLwNt/HT5Xg/xTOhzGsB0u7fErwPAbhiw3WxKHyWrli56QVlhqJWxlKiUeFMo5QXvfE63KEqNp+e04AshIIap3b7vy26GnUdbLEibUv7W2+IzIMg8U/Lp2eS5saknixdB+ALZg5LBE2HCBpjxkMJbqAWbpltFQ6OQbSicI1fikm19+rbwSmhjMkyt4tP8bpXVNLqpaAEuz9k4dr2WdP81wNCfC82lPs2v8pnm0abSbgBFXa7KS62yRCf5W4o4fIQn5fuluHztfdSGhgU3QuNWvz5q0X3XJQHYCH27R0vRN2lFBCYqt9/q8MWOk1EUCQg94YIi4nqFL/72b+G7f/xDHD97BzufdpfX5MEXA9596x28+stf4eW/+Vucf/AIa7mHJ+/g6bVbX8ZKAOow06D0gqaBHpudz6vwkAYeLZ5Muxo0A58iqzV4uSrY/yjzXc/P1evYtwYKLy6Eftn3W/pmqQ+tZzljDNv/lq7WMlM/Y+cZQDHULhuz7dc+2lgcsG+sLcA7N9JoArJGLuuoA3uPmG5TnmmFwgJz/XGVYuVH6/0CyLneadv3ji1tmly9VGd5uDZk92XQ0+0vfa51qvwt2Mwx8PTtewjjiKch4q2/+Xl6NkZ0fQ93uAaQMsd2fY/VaoXjo2McrNZ4eO/9jL0d3nr/fTx+9KgYwmN2vIPzPVTMOFivMY4j/KrH0eEhfNfhP/7f/a8upc3VD4NTis1CDECM6Loea5/CWqLzoK4DwNgN2+TpJwZixDhGdH1XDq9OhAtwDumyrgyl0uVbDucnJzjoOhweHiLdmItkKIQRq36FDg7eO2zHEcNuRGTG4eEhIhyGIWC322Gbb+edhHrAGAaEEHDt2jUMw5AOfg8Oq24F8h59n8hxcNCDKAV7cNhiu9uh88B2e46LzQ5utS6LyWZ/AmqG00LdWvzyb1rU+fZTTOnuZDueMnhuMWNLoVmQZy1lZgbTPLMQgBkI0zH0YmxsNhsMQ6Jn3/dpoatFpYFMAeQKDIkho9vVYElKtZUNJfTTC6W/Xd9jDCHvjAExMAj1YTkxDurdoL5sRWt67lNYGvgUhUeu2X8xCTT96jmrAUeJ1XSuPhYFtXUe5JB8K1RmAupWYVlBqt/ft3MVaZqbyhvGksShreT0mC0/WeU9CdO5B0/SKFqvlZ0jXa/eNbRzaIFKa24swLNjbCmNJWOkpYz3vaffb/W7kjVZDgmddJt2LrRR0TozcBWFbukyPTx7tPmubsdZHr8iYBTZ5ZDCGVzSwMn4yJ8FEAYPbDvCnU9/Et/5sx/iE5/7LEJH2OULHHsmxMenePWnv8Df/Ju/wMMPPgCGgD4AErgYcqhkR/XZJe04sLnpi5PLTR7IVrha5fQxu08tWlg9MqcvIGvfvq8zXVVzjOzJNnK4BZiW5mTWR+XpXQbzl5dqZ968U9db3C6LRdPU/tTPEFF2V8/7rOWX/l30mOg50X1aZulL3+Q9afMqOxj7jFH93JIMsqVtpAElvn+hWANa87C+1FnaFm3UwkBLgJ4aziY7Ril6bmKUoL82D7dosY+3l+T19NDcgFzq87567PkLrZ+qdxRvaKfSsNvh7PETfPjggRpT7iBR0t8yT5icbikxfUpNv16vsNsNxXHsu5RxD5xGOMR0hcDFdgMQYbchXDx5cuW1fGVD49HjR7h+7Tpu3byJdb9C79K2ysX5BtvdiL7vsd1e4PziHM4BZ2en2O622G4HHB4c4vr16wns5dtzGQHeA6dn59gOOxweHAOuw/HxdVw7OsLhqsfBwUG+vyOl5EohJQEnT08AMDabTW53g6dPHwLUIXDyKg27HU7PTtWuR0CIAevVCmenJ1itVjg7O8Ph4RHW6yMcH13DwUFW1vB5y5PB3sGvVnj88BEePTlB369xbbUu2/YtJqnCQtTCKyAXU1YOYNodiJx2LxhdicUDUECnbGzPvJJAYSAJQdKLRIN6ed85X91QrAWfcym+fZtTxooQAVIGnt1uB+dc2QmQC/gi1XcOWANiNAfTdNEgdjIOVWx/LtVBcmYwAb7vcHh0CBQA40ExgJhKX6WfLof4ON8+/C+eAj2nZR6U0J+lHW0okRhjEUZtATfNm1VmxWRQf6M8nxZ/K/5W92lRkBuQr8emeWQSeHNv7FTXVKcFVLIGtMGp6aqBr67DtqHpImBJX3Spad56R+q2wMXyqWw3t5Si/Uz/021bQLk0B1JXyxDSfW6tk4q2ql+6XTu2fX2yc6+ftXS1hkw1Twvj1XSa7RwqTLGPVro451ICOCY4JnSOMMaYLtsLKYQydg4Hz9zC9374e/jCN74GXjmw9+go3aGxe3KGD96+h1//1U/w3qtvYHN6ho4j4pizDmXHiTC47PJazy7AkAxFIjsKbdS86F1mOzcW9LX4tAU8rNygDPBFfkudUr+0b0O5BCxpYLy0g6x/b8m00i/12WXv2nVgCxEVwGPXYX6isg2uAiwtnWdysPH8VXSBfXYJsLbWUUW/RpvAXOZbXWXHbNuXMFEiqjNQGjmhncKWD3UbmndboZhLQHuJrqU/GQlZerRkpJSEh2o+sfO6L7zJ9t3qAmmj1MW1U9HKXl2/xoBLY7J0mIXCq/e0vo0csRk2GHicORIQAccMT9MZZY4RHEYMzAjZ0bk935V3+67HyCFRnxJ+iS79SyKGC66xNFgqVzY0CB02mwFvPHkH3nus+hV858ExHZgexzMwAvreY7Pb4NHJUzx+/Ah3b97G5uIMHEccHBxgu93i5OQEBwcrkE/nWTrfY7MZQA7ouxEnvMHp+TmG3QOM44hhHME5xARjxLDZIh2AjRiGHbwHnnvuOfQrxrWj43Rgeu3Rd8B2u8PR0RFCiNhtd8nQiQwHhzBEbGmHk7MdHnz4BEACsmn7O+2UXAznYACrrsfR0RG6/gBxHMDGwyWM0doi0wvXOwdWHg/ZPUi7IwPQe3Rdh2HYQWJ/EzOlWdCCoOw0xADv69ujRTEBbe8WUQ49cK6Adxm7CDB9D8gwDCUMbLVaVQtBK08opSiFmRFyumC7GJeA1AREqALc1U8S5RmxGwcM45iTuyEZNXlr0d6+LgdHrZLR7es+Ct1aJX2f/mmlo7eOZU5mIBao4nOtV5OqNlJlBEYIjKi6Uyuy+c5MKyzGKhIrwOwYhV9llzD1tVYoFVDxdeYW3aYV/tVPnpCnVex2V0v+1qEsFb3Uu0tKTtdnv1v6Ke/Y9Na2Xf3sUn9ascWXtS3vEVExrvVnS/SVeizvL/W7tT4tUNNjIAPc9gHMqc8Sb1yPYy8tCUjx78kRESODPeECAfGwAw4O8Jvf/Ta+9rvfwfHtGyke3iXvnd8MeHrvAf7yX/453n/tLcTzDcbdADDgO0q3xnMs2UgklXxl9Fdjme4rGIahBs1E4GwY613jltzRdLUpbpfAqKZn+mye1ai1roV3mWugoJ0Lsr501qLZbojp/8QPXGXGs8825/Sy54w8XDJ2rIxp8a8dr3a0AZOR0epTqz1rPOu1PfF1kmst4GrBvK1f6hBZvqgvFuRMLaNEJ9Xp0if+yCDS8Kf0Wcv4li7XBuw+WrbWgC37jJS2jnYA5pdL6np0tMWSjNlXWnpDt6Np0ZqPqxQttzWea8lxomQwUp8T0uRD3sjPOkwOTVnruo957ynNnU/O25DvDZORRqQw1MjpjjLnHCjnQGF3tTFd2dD4P/0f/8/4zGc+g6Pr13B4dIjD42P06xUOD46w6o4QwoiuI4Sww/G1A9y8eR3dagXvHW5cv54OlfQ9mCNu3byB1brHZrcFyGMcE4M+PTnHL3/5CoY4YjdsUgjUbocwpsMsJydPMZxvsTk7x8X5GUAM54DPf+Gz+B/9D/8HOMw7IOM4ZgPE4cb1Y/T9CjE49P4geS29x9nZGYZtwE/+5q8xdj18typGCMBYr9fYDQMGnw/fcsBzd+/ga195Bt45OEQwuWrxLYG1lnATQT5tZycLMWVDStmMiExcP9VeLb1Fqeu1zG77phepGAlaiUi9Aio3mw289yVfvIxDh1RJP5aEHSMBEWtI6MVq60qCaw4+Sv+R0lRGZjjvQd5hGEagS95HBs92eNLvdSiPFVzW2MgvVeOqhclcgZRnAMHj85AVJM8NWmAvRgBUDiCn3ZE8ryq3dfmX6SGhTLo9AcQTTeeAUBupFb0I5fyPVaYJfNVKswW8mxdXKgVYGxCpTssH2mAqQlLdo6HbaylIO9+6niXQp9eSrbdlvC213yrWONDvy/ctBWO/a5UWELNzvjSuy8axT6la+WLH2qYDCrCx63EmR+Ud2ydHGB3A6x4vffHz+Naf/Ame/8THMXBA8C5lKIvAo/sPcP/V1/Hqz36Bd199HV3KRIzgUkyyYyClMvPgvKPhsyEk4UWz3QBOyU4kjTfzJHM0Xy/RRtNUFwswNV3mNMxGNyeJ0tpllzqBWm9wTLvCOqRV91kXbfzo+rQuS78T7JBaY7S8JL+3yj7jycqLJXrptaBlR2usVwkFlGLl0pIxoJ/R619/boumuRiINtRXj82Ox9YbYgBR7VUvRgzHInwt7WSOlww43Uft6Cw6UD2zJHuqOqn8b5E2drxFpy70sdDgkpTO+0qt31HOLl7Gw9op81ENjknOzmmR9DDhoPM4I4AhiZGmEinvWvLkqJF9TJ8xBucBTbLBwefPHTHGmDN5MgNjLGdFr1qufjP4wHj91Tfx3Isv4JkXnkd0Oxy6DoF26EM+PMwentJlRR9/7nmM2xvwfkqzd/3mdawP1wCn2OLN/Q/Q+w59Rzg4OMZ2O+Cd994FQBi2O2w2G5yfn+Pi/AIXFxfYbDaAZxwcH+DmC8/hxo0buHH9GB97/lmsDg5B3uNis8XFxQbr1QrOO9x55hmsVms8fnqKuN3hfHsOj4Bu3WEHxtY5wHfY5DMbDKDreuwYCM5hDAGO0u2ww3ZE361AGcDGYX4+Q6cSlM+rBWqAhQDB6VyEhIY4xBGAcyVbBaH2oBRlxMlDIelv9aKX9qWtSbCl/8Uce0ecYyzzxXKnOTPBer3GwcFB7b2NiR7C5EDun/OQNIvIgNfnC9EYDN91Ja0oZ+AM5uKtovx7zLToui6nFEa6ACvm9rKMJY4Iw4iRk4G2Io+V8xh9FqDOoXMpvIGzEiaXM9VIXZWSmgsMWdhpMdZep/Jsnpwpa1UWCDlFn2TQkOwkAghK/TInIW2DeufB5FXkMZedGhCKJzfRgMpYfG4jmcrZMCXJJOXMgXJKhp/MgeHjIszy8+CU8YmcV8ZA2pLlbHEQAd4BHNPfYiRKBhaUA+Vhmo9MN+EtzilunaJ9MaMyQUSZWVBkQbUFEi0FrP+2XucYpgxHIMo8m+nEeS3nOaWsGGWHStb8PgVp+6CBpVUoc6UzN5Bse6R/cgLMzvD3EnC1QEiKVpT2O4qo8pIzlAECKtnedPau5E1rb7+7LEsCUEKlKIdL+eBAjjAQMKw8jl96Fn/wZz/Cx7/4OdCqxw4RjgEfAi4ePsGbL7+KX//sb/HonfcwbrZwAghTtYicUt+mjGVOKeTaydF1EhKbBjMMoWSX6rxHiBEx5OQcKqRGh1wl+mnZk/kUImt84SOCZAYUHpg0vDVwreq369k6k7SekrAwXZaMA6tf5s9SkaW2Tvve0mfWWBZHih2z8JD+TDsytM6zBkj6OaVyBrsyN7otW7f8PQP3SI4vAXFEibdKOkL1rAWegpHsurbGd6s/dp6WZA5RCp+RnUdgHiInz9m2WrLG6spWn4F63nQYX8uAEDqWNWFktq7Dzk8C2FRwheClqc6aRq1dD9ueNaDqfrb1Zs1fNc1a9Gl93zZ+09j098ycjccDpI2MJL+q16px53owrZ00P3I+icFMYEcIgmtiWhOeUmrcGENyyFM7YUirXP0ejW6NYRzx9lvvYDcGPP/xj6XDxNsB/UGP9eEhfIxwIQLjkA7kDemehgjg6Np1HBwe4fDoGpxzWK8PQG6F89MThHHA6ckTjMMW9x+8j9OTC2zONjg/vwAR4fDwADdv3MKnP30H6xtr0MqB4dD1PTwzXN9jCAG3b9/BbrvD6dl7IN/h8OgI77x7Dy+8+AJc1yPutnj+xefgHOH9+x/g8Po1+PUBdpEB7xCQJs1R8obDOXgkADzutiUXsSeZdwciuVdD+CChMkmjq71fOv5Ve3OLEcDJix1ixBhEuDJCjAiR0fl6cU5hWvOFr2OFpT0rdJ2bjJJiwGRFGULAer2uDovLe72fzs2kMydUmDdyvbAqTxlJ6uDE7PN4bSqgKNWLKd84C1jP6V8FODmXADAh3TsyBkRK2Vd8Dq/IKjyHmeWuZhBe+prbQAYDVaw15XsW1Lgq4ZtB51RR6ne5HVty/LM0MhmNnHlHBEjKtJb5SAEKLnWL0mJInGQRegQQfHkkgSEuxq0Adi3oZqFqpnAW2ukf8vvqAVLdKrsuMcVEkiQ7wAxM1kJXPMNcjBi56b4SujS9OwvNMzfj6jZse9qLaMc6M24UDQR8aoUTg8o+ltNgU0MRLtFWewB1P7XibinxMkYzNgvYJJ32pIintQMlM7QcsIaErXMfyJD6U4cw/aTpu8RGbZChxxhcDu1hgocHx4iVy+cknMPYe/hb1/D13/sOvvLdb8AdruFW6XsXI3ZPT3Hvtbfwys9+jjd//Sp4N6ALES7XHzGdpfDOwbspZFSfaRP5Loo5eZSTjNztdiW9stCbXH0Ja7k1XNGaMIEfKq0ovkCWW2LYyu9Gr+u5kU0NLXdlPcj60P3KD1TrqsWLS+3Z+QJymC+Sk8fyiX5Wy1C902sBnwartg75XnZQtIFh27R8Psn1JM8cdaIYspHQBu9LYL/8LcIwO3pA4vhZBuP7oiGWin7OKVrrOjWNSr+pppP8LjtiS4ZDy/hZKvbMWuHzPXxVl8kxKGPTO2Yto7TVJ3mv4qXG/Onn9dg1/7aMcFHp1nC4bN1UesbgoH20aRlaROkwN0dJb418aa6up9YlIoOdI0SmCVtQckjKpbtMlJJhlPekTQfqchTNFfc1PlLWqa53iGPE40cPMcYRd559BtduXEegYwR26PtVAv6RENjh4Pgaut7j/v37uHHjBo6Pr2G9XuP8/BxEHnfuPIM7t27h7PQpzs4vcHox4L137yHA4dat23jxU5/ErVs3q0vjAgbAMcbA8K7D4arH5mJTBOm1a9fw0ksvAQCOjo4wDAPev/c+outweLjKh4MJq9UqM08+6JyFnWRSksN+yVpMBJbD0V3XJcBspL5lUM3oBbjmcfR9PzvINQlOMVyy0vIOPEyXFhbBgOyZotbN51x2OFp9lHEQUZWdK8aI3W4HIiqHvO17EhO/yzmXS9apRiGasgaFGOcKV41bAJtkgtJj0UqpfJaBQrrMMPX7yDkkH2h7YSderg9qaqEdG58BGfiqC7jmsfW1ECbK29yqPmtcimKy9ACS1wAqdM4qeKsE0u8AWM7ztBRCrUiqUCdeBt72syVlq3m+zI1zM3qBajGoBbWEC9qDcPp33feWx9TSqAZjtREw441LhL0ttp4W71xFQcuY5PelZ6+q7IGJXho0F17kZRWx1A8LhOx8tJ5p9V2DGw2ILY/vsiJcBaCPhM6tsYsBtF5jOPD4xFe/jG/88Q9w9OwtUOfTBX0jg863uP/ue/j53/wU7772Bs4fPUUXGDyGnNlwLp+1TNRjk37qEFPmlIiEKO1i1LK7PhwrY7H3Bu0DzhaMV3TBtLO6RF/9u+6zzrjXAvC2P1ctM3nQkCX76rc8relZ1d1oz77f4tlWG9Nn2slFYHVGrNXfVrhneYaQDtw25nBJrui105JnLQPkKjJKA/OlMp+H5BSCAdmt9az5fZ/My+Bptr73lzQHYoDOdHFjXGm84rSq+1DmqBrr5fNidazuhwBv0d+6vn3rV9dt6dXSt7pwrJ2CzuVztcdH6Pq+fGadcEtzR+qcse6HPOM6D+ddwYeWpjO9vqdc2dC4dfsWzs7OMcaAi4tzbHebxA4hotsErI+OsFqN8MQYHHB6scHHnruLMA549pnncPL0DJ/59DGc9+i7gNXqABvs0Ps1jg4PcX27w8WO8Ru/8RWsr18Hucm4mLa4CZ1fIcaAvkuGDUDYbrfgCIxDOjSuwc3t27fhvcfpZgsg3ZB4fnGOW3fuYrVaI8nFxAySqnW1WhXlIltE05Z3ngTvwKEGbXoidNECRNrRzCZteeeBfMtzjBFQXnXpo4xLFpv3HjGn7bVgwh5M10IyhFDdUC7gfrvdptS/mXE1M1mB3lpc8r0dqxgGosglvXBrEcjYbOpgC+YA2R5NO1F93wO4mHZYeHqnOsMSuQIcum3dRgVmG+C6CBFCdTtwLZAmHpjTB9Nco35O+yRaitTOdVLwuf8LfKjbl/ckZCLwxFMy50tgRrdpzxiUvinaauPQjsXSJCmXWojJT08OpA7b6zmdeWrRBuy6j5ZnrYLQCtKCySWALRcj6nqWlIdWRFaQ637pcwEWcGg62va0I6Oqm2i65dyMrTmXqi+tvrYUpx3n0vhaz6QPAM8EHwhdTIkFto5xcdDhmU+/hD/84x/ghc99EuGwx+ABH4F+x3j4xjv44K138ZO//DHOT04xnF+gD+msBUeAuyQbdDirvlVZxtx1XUl+Yde7zIV4gSWZhtC8JVf0+GOMKbwQ1KSdXn+Wv3SdtjC3503a0Ouj8B7mAMzOS0u2L82f9yktZlCJTCzPWr1h+VN4vupDNU7N/83u7O2vfj+tZZRLetP5BQl+mp5v6T5NqzRfEVHV33L+tfqwtMOqS4tH9o1Rf1+9y2x26/Q7OSrZfKexhK6vpYMsn+6TL61SPs/hZloHWB6yc0AELBmKIs9Bbfmj69U7bBr7WANHdK0UG7Fii6Wb5cPLaGO/l35enF+Ar1+v9Mk++pYd7jIftZ5O7zeyXjXwxz6e1eXKhsbvfv97OD09xZ//+Z9jPBswbLe4987bePzwIZ7/+KdwcXaOfr0GEHHgE5McHx+DMzFWqxW6boVxHLHbDfB+hb5fg+II7zocrD2uX7uOo6NjBDj4vkvnBdSkjcMAUL4QBg4cgYAIH4GuW6HrugrIPvvsswCAzXaLAyZ0ncOzd5/Dw4cfAuRw9+7dBBIzA8oug4DwRFggjAEr7+C9xLF6EKWtdjvxlTGiJqhMTEOxyPdikUsMnJybCDHFhqezG9NBrmEYAKT+eUdly1+UYIl7N8xgs0XFGMu4mRn9alW2BPU4gClrg/wufdF00OMqz7h0rkAbEBZECQ2BeezozMtKacswpmizcnGc9qZLfRaYSWiR7bcoXg2Si5ImQkBdjxWodmt3CWSW9jAtdv0uUT6DsUco6r6VtsSbswTqCNWWqsy77lOhQ2MMliZaIOv3iKa+C8/quYYBGhaI6jmrQJJ6xh5wt/Ng0ywvrTk7l8KLLcA4A8NmLoDJabGkTOw7SyBmyTibtce150+PraVw5Dtr5F8GImy7tu/CSxrQ2jnV87APwFJCDFhFAgeHQIR4tALduYHv/PD38IVvfg3rviv3u/QjsHtyildffgM/+9f/DvfffCcd7A7pnIZkjkrABSA3B/+alvKdTQkO1ODROYeQvX0WHNti2yM3hSK0lLYNKy1tMADUz1veW6Sp6UuLT3VpyTcr9yz9lj6Xf+IdtanMbb9a7+tkIvPv9wO0feMTfZJ2NBig9nO2v/b7KIdpUK9LKS36aLraLHb6nct2J2yxa9PyVusOK3I+h98tz6Ouw2Kbq/ar9bulq6adbXefnrUyp6xJpZOkft0PawzN1paR3zNMgRqjtNZhS3a25K12cGoeIXLVnOn6BQuK7rP1tuYgzWGt9yYHXkSOmqrC1/R8Wf7eV65saHz7O9/G5uICN2/ewD/7Z/8MngghjAjbLR7dfx83b9/BuNtit9vgadyBEHCwTsaEDH63G/ICZIxjulPDgxGJAXJYrw9xcHiE4FwyIFw+KA2dQjVPBnkwEtjuOoeu63F8fA1d53F0dFQYIxEkwHcen/jEx+ER8dprr+LsfAPqD1L4z+qgXCZXLex8iLbvHTyxyb4TAfIVw2nm9b4WOJWgxnyxJ695TIY8JkbxzmM7TpmepFQpZTPA1MpeM5RmDn1bOdHEWMMwYLvdwmWaw8Y25hJjLAeRtcWrDQNppxLwDDBN/dbMq2kk74uX0CrDlsInENbrVQMsTX0uQpeTcaLDD+qFOxfmRAS7XOsQiTS4JrhjTMbsQmmDOYkVXlZsM0HLze6nZyIjso63bIMV+z1QGwv6HStkdEaUdCajvpSq0Ex2KA2YtUpIGxnye1CeXus50iBGPtfJEVq7NBoEa34jmu8oNelq60PNK0vval5uzWfrM/l7ybhoPddaX/LckhKy86CdAEuKuGVIXIVmtZw2wIwIYe0Rrh3i09/8bXz9B7+Hg1s34PLFql2IoLMN7r/2Fu69+gZ+/ld/g+H8AtiN+bK85N0MHNMh+LwOvatvN9ayWe/AWk+zdt4UpbwHbGm+sjTR4PijALWlkvj1378eKdrgBtoGr+a/eV9qL6nID717tARUmsaMWzrU/XcfYwV0y2cp3l2fp7Xzo/ssYdZSSQugLrXdoqldG9bp0qJXaw5a9dl3LHCWXR0rV5bWtHb0aHmti86aaMH9zNDR7+6Rm1rmLBXdHuU+LBlQtrSMfN2+7qP+rgbqc0NiX39t32fzx0jZJjXPqnk5OjzE/cyLLYdAix+TdKz1b+ELaVb1Xe/cyudXlV1XNjROz05wfnqGF154Hp/77Gfw8q9fxsH6COMwIGzO8eC9C+xCQAprYjiK8E5ugI6ZAOLVCPB+hO96eOfhKJ0dXa8PcLA+wNlui77rABDG3XR/gwOhcx2Y8qHpELKX3GEcRmw2G9y+fQvAJNjSmQyP2zduJKIQcHFxgRAinjz9EOMwYAjAbhywWq2QYsQzU0bA+ewpQsolnASlS/94LlgAWYDT7oMIVLslpxeMGBrkHLxzCGMAeNqWZ4z5sCkVgc2cLFmHaRFpT6/0aw7AJwNFnhvHEev1unwnAgKYZ83SAtCCmCVPbAtYyrOVsFZlqd+yGDylbXrmRNfdbocQY4orjJOhUQnvnM6xnqu2ANfzWg57yyG/6hmAeRLe1QJUn2n6pH7V7dSemvRPCwG7hannWN4PBmxogVWy6ahyWSwv0XTGpqVUrEAWGkTmcihaA8lxHOHzRY/1Vq1eR21Pl23Xjt0qOmuItISijK/Vjs7QtE9h26KNWD0+K/jtfQm23hYQkWIN+da86DVm21gCOvLskvzQ79rQzEWFDFQGsK0f0OsrPRtBGHqP57/0OXzjT3+IW5/6GMh36KmDHyOGsMP546d4/S9/il/+d38FbHboIyOO6eLQJHMybQjlHg3CJL+EPhowWS+qHTNg1rACFlaGWVlfy7F6/bfWYIvv0VjfS9/Z0pqnpaLluzbEWjSx604HlFhnkV0Dlk8s0Na/axrbPu0br25Pf1fxfjH6cuz9Qj8s7fQ5xxgimGr+tg6BVv+uCtisrrVja9HS1p3GNt/hAGTe6vmxsmRJHug+VFgoM7qVo02+0XR287Vgx2N1QWpqWpta707JWua6Y06j+i6yJR0guKaMdUHW6u+X5s62LZ8XPAXhzTlfeu9BjmbOk/JT8XPd/oQv9Hoq8kmds9RjaMnJy8qVDY1/+k//S7z/3vu4uDhHGEfstjtcv3E9py/dYhgiQoy4dv0ann3uDrq+B3UOKQwoIEU+pFRyR0eH6DoPULoJ25FPqSQpAjTC9x7wHbbbbRIsPmUc8T5l1BEg0zmHcbsD0OPw8AjXrl3HarWqGOXg4ADP3L0DJmDYXYBWK9x55lk8eXKK+x8+QdjtEMH5FvNdAUGO0kE/xwBiEiCePQgE530STJEBlV0oz046IOjqw6pFsYVQMsUIE0vYkhNlSJTG2XlwCCC3zlkCMnNHTmFknNKLgtNBa2AS7BJGZYv2MBGly+705XxFWDCmfiIdcksevFroC+NZa30G2hwhhil0CSQHr5PXQwtke1mgpp/UHUKAiynrQSCg2wasfYfRpXnoyJcsUc75Un/KxFR7ZrXHMcRQ9LU1GhyhpJBD3kXKl2SCvEx/SjAgkU/aKz5TQAQwJmFityiT2BdBLTFiaSfKCllpw5dpSI1zGm11bsP+LIYB1LtGeZSRSHtGwLS8jWjMXdd1ZW5l3kUJ6FtrtXEic5TCpxJhIidvshjZySgovYcjBzkVz/nEi9QfMn8jKyYq3u9i3s2UZqU81Xy1vN4elM5waYUm8k/JeS2wrResNb+2LK05rTikaMDHea5LCmEA1sx2qaI0N/k5yatOqcL0U/dPeEhol/sSwYgU4UFAzgYXkdNMg9HDwXOi+wDgogOufew5/P6f/BE+9eUvIfTpVm9PDjQEDGcXeO3Hf4N7r7+B9998G2GzRRhGhBjKDoOeoy4rYklXrPUDK37WfWagZJMitfssn5OinaZ5Cxy3DIgkL/QFl4kWmftSGlKg3PwurgcuDgjki7nSG1lMIKmDGlTYvlmwLxd5LfGbBYdL39txLwFoC+5aYG9m7GJ+lm16PtGjVa9ex6x4I8mnHI7J9Vokt7w3pHdXdd2SGl+cdxx5ms0EDgAzJi0rNXDTz7RCU1sGRz3H044SiKudLnJA4DryQdpxRAgNINvq1xIvWOCaIkPa5w8sb1Q3rGMy/qjUm/BjpLkDJfWpvWNd+BeV+G06ofTYWuunql9I3NCrlgelDcuLtn5r3FSRIunhqt9St4T1zxyHzCV0NAr2QnK+pMv3CjUSb+REP0QEL1RTkRCOUqr9qX1cqVzZ0BiHdAleyZZEwMnJCY6Pj+GdR+TkET88OETf9Tg7O8fjJ0/hkWL60xmNLoPEESHuAAR48ujcCiESTk9Psd3tsI0MphEgwna3m0AictZMEEDJOEAcEQKhz/VvNhsAKBmXvPdYrdcYxi1CCNhsNrh16w6uXb+Dn/7tr7DqVzg736GcgciC1+WcwcNuBDgpsJ7WkEUsKqYwUUxbrpPinrI2iWCIMaf/jLFkatL5zDmEDJxFqSWvcNet0fURwIgwBDHds6KvY+2lT8zp0kG50Vt77ibLl0vqxSo7FZf/AUhCcwzp8LaOSdaAULcrxlMFmkCzBSnpZQscNAtcex21MVDaj4wBEfCEzek5ep/jtscAl+97EKtddqmYGRHzON+ifJQnxSq+TI4EAGI9/6O5PG6qI2WQsgInxljm14ZWlJ+qDwI00vkk+cv0DWKYYNq1Iaqe1s8ugQFKkr3wM9T7AiJFCcgNwK06ZA22dhZmwAKolLulV/nJE/2mzibDIiBkGy8BZBbDTWWHKwZOAcNUNJCmt1ZkrbDAfdvglNDeJLcoZU8SQ0kbT0uGhKaPVlAtXrF81/I+NxqYgI/tQ/5Odi+d5ksDzO24m2sgG96IDOLEj/laDIDSGQx2hIEjutvX8O0//F186bvfwOroGIx0Fw6HiPHiAvfeegd//W/+HU7eeBvY7bDL+kE7dLQ30rkUOotYG7CaNszprJSk3pbnWjHz4OTUkbNqznuMC0B8HwDXf2v6AUj36WD+OZCdW6Xf5YFFPtL90CDHglT5uQ9Eaj60INgWkduttq4CVG2bUO/pMe1rX9NXn7cp8xBTiHN9kWycIdIWv7Ta8yLnOI9DvkMt23RdrTascWSf2Wf4ybzEnKjGkSs7rIWXqQ5zLTosO1RjjDXoV++2+MaWis55/Etj0u/osMVmiBiQXUbz96c13959u6y0eNIC+jn9MdvB0t/b8dl29BppvWdlhegxy9uRI8ZxKLrB0i6dTHCQiCiGyF5pc4o4mfrQ3rUoWOKKBoaUKxsab7/1FmJMWZxu37kD7z3u3bsHIsIQAkCEYQh4+PARvAcefvAQN77+9RIPKwQq/1zGdBEgdICjdC/HagU/BsQc5tF1XcmOxKwuPCJC3yNdLBIZHz5+hFs3r+H2rRsAptApAPAsl4URnO/huoDz8y3u3Xsfb7/9NoYRcKsVDq8fw+WdhRjT7YesbpF2jtK5DefSFjzVYyrx0GrCNFNwNhB0vJtmNkmNhxgBUjcnS/3kkrHGKdQpjmMBsVqBSiYhC9ytBU2U06N5XytVw0RaCLYEkH1Gt7ekcMTIKoKR65Ar23e7uOR35x2GGHBwsE47YDGWcCrxgExiPu8MFGM/tVHmwniyZNEuxbkvFb0w069zRQugOm+gaajHq/tZ3t2vY1XJnr4Jm8z62RJyFtS2AGV5z4RJ6LbFE6LrtL/rz5bAgwXkLbrouuT3JTB0lTlsKVSr9HWf9TMieywfJ6w9r8PW3QKiLRBv/9bPLhl3rbI0v/sUZqv9Vt/k+XQom9IFk0lwgsghOmDrGHS0wue//lV844e/j+O7NxEdAZHQMRC3W5w/OcHP//Kv8cpP/hanHz7Cihl950vSDqG5PbsjAFMnsdD01EaK5jObmadlJFQ3bDd4YYkm++hbnuN6LpaKreejznPM4BKYh3i1+tXiw8uKDR1tgbKW/LF91zxVn5OYA0I9X/rZCTzVur0eaHsOlwymJbpdlU5LHmw9dqlPj0nPhY4GSPys7mNC7TDhxudFZpDaPTZttwB8SyZpY6EKidxTrs5bKZJgX4hjC/O02rN/LzmPWn0TnGTDmW39l/G3xhaWd1p16DbEIOTIODw8mtVPJEllzM6N1rlmrHqH/T9kufoZjdNTHBwc4Gu/8zu4fuM6zi8ucLo5R9/1OH16ivF8gzgmL/vp0zN8+OBDhDHA9fNFnhg7GRrkHQAP1/V4+bXX8fTsHIEIYYxYrVbVYbT0nkMMAbthB/IOvfdwnvDOvffxza9/DcR12I33HpvNBrvtLnmfxgDvOpyePsQvfvFLPHr0BE9Pz3D7mWdwPRspzOnMhsvCqPMElxVLzKFGaShtr6Je9JoJZeFpBSefe+9ziFIKKUjGWLJCnc/pFJG88ZFjCZ1yziOE6e4PvUuiF48VwOlMQ1LS+lbYwqSoF5WMp7UwdFhGK+5cnrfxumK0MNqgS/hFnzspCyAvGAllcyod8uRDmjwPQArTKv1SwrDqfwyVEFgqlaDjOovPXGC0Ux8LnmgBb/ndCs4Yp0tyrEJl5snjoKggv1gRvqTwtYBrCcBWHVbREk3zq/n8MrC15PnTylz30wJ8+V3mVc+T5quWILXzoPlNKxQLOnVfZXfRrgGiehdUz207DIBn81uUhwIGrbnR9bX6uG/eNT2tYrN9uiroJABgSnxL6aZrdg7REULv8exnPo7v/f0/xu1Pv4TREzYAOhBWIAyn53jjVy/jx3/+b3H2wUPw2RYHkcGOsQ314UTdT228y78QQnYSTc/ZWGxND8v7Vt7Zzy2d7Pq1PNOaQ/l8yWBIooyrvrf6q+dmH2iX8cjn+4wa/YzdWWsZB7oflrZWVl4GCO08XBYPL99ZPp7aA5IzyiQtSW/O3t9Hi9bamc39Fb1DLX6zYFqPT/dDfy6JXvbJKc1/RITOO4yxnWRCnp3t8DX6VclHnrzlH7Xovhc6xuW1ZtfDZTSz8tnOtwX1M5lMiVOsPNB1tvRqq98tx3BVl3FWyrOC9y4uLuCcqxzYUz1ppy7mcL4Us51DJk06dk27pXkWXHEV2S/lyoaGI8LNmzfx8ZdewrVbN/HrV16GX/XoDw5wq1+D3FM8efgEDoTNxQb/6l/8K/zohz/A7bu3S9pZZp5itAGAUz5x8g6np+f4yd/+DCNSvFnfueKtEmImL34AkQM5BybCEBnkCL985RU8+OABXnjmLna7XTnYHGPKqJRu254y4fz4x3+NcQwl5nW1XiUP8zDA+RRnHWPawg5jwFqAZPYGOEoHjoXYEp5UgHgGG5qBJHRKSozzg2Ip5IcQISltU4gQVROdY0JzfV3fF0GmjYHdbjcDRXYhWaYsTGyUjxgxdjtRexCJpnsZxNreZyGXfjgNj+egVegn3poEKAmQg18MeJ+zZbHcsp6/QAK9tSct/bQpPi040HMk32salc+yIpHPa/Az7ZLId614fE0jDVSXFrMWepqW+nvZuNZKTrerPbJLdWnDstQr31P6nxXYQnnnqKrH9ru1QyQ00/RqFUs7S6vLQLDwrv1M98PSWH++pMgsYK14phEe2OIDGbf8beOpa1q1x7Zv3LpYR8Ssz2buNd00H7c8jLI2IkeQ84hMIO8xgjB6wtGdW/juH3wfX/zW18ByH4Zz8AGI5xs8uPcAv/7JT/Hqz3+J4ekZaBeAMV1kGdVdOLqvdixWhrTmjZnLoe4WL9uxtuq/jO66D63+VGPgtoeWiCr90Zq3pR1mPYd2LRYaNPpi6acNo8vAo5UzVnfo9lv8remmf2+trdb3QHuHID0XwVzrszLHqdKqz9oZpWWDXgtE9d1V+jlELuu/NT691qyXfB8A1vVpw4IwXxeCXxBrwFzGZsap9Z6VW3rcLWxQ+oPcZJyHK+siPGq/s2u2zCdN3+uxt2grz+1bn5pGrR30Vr/IUeET+4yVS1KflZPyng5ls/UVXRDm2CuEgL7z2G7zBaIqmgVAPu+VnDveO4QYEXJoJoNBqLGNPtvbWp9lLJfIOluubGik9LQ7/Df/8r/BwIyTizMcHB/C9x181+GZ7gCOepw8egzEgPvv38d/9+f/Gv/wP/6H5UZoYcYYU+paYgLlsxA/+/nP8cGjxxizMB2HHXbbLbouHQqXCTjo14iRMXDA6nCFYRwQ+xU4RvzVj3+MP/vRDyvhVkAbkkctRuDi4hy//OWvcHpyBo75rooxYNjtQPmsggh85zt03QouCwmXb88MIYJ5DtJkwdgbpsvkKwazW66RGewinO/TeQ11Kzk5B+Q0jUMY4eTwGXNOwztnbGEUK+BjjNngcxjHlCJYDtFrppLf9WLeJzD0mOzuhQZNNsZd4o5bSscK+AIOaWpzGAcAKUYWlfKWnyl2cxrHwiKhKcOSFQTye+u7NDfLXgGnws00aBBBZYW4pudCR5sAUMiSjFJMio1SCJVKyDEb176ilUjVT0JlkNpiPxHes0B6X2kpCgvQlt5rGfItYHiZErLv6Xdb37W87Pq9FjhszX0LUF2FZvp9uw41cGqB5xZQXarbKuOl553zGGPOBuUdcLjCb373W/ja7/0uDm9eQ8gGxkEEaBuwfXyCN3/1Cn7905/i/TffBIYAl+8Vig4YXWMnzCj6JaBgeX7i5fbBWzveq4CVFpjY924TSIstr+acOTmw5HCtBbn639yBtf88xRKQlfo1sNYeWF3HNAgUnaRDnu1YW/34D1EuW+8FkGNyb+n1EmKs4uGBiX42XO4q/Uht1Q4UXfbxRgvk2zHq/pfvOIUYaSMmPacGbWlCAMwakGfseG00BjA57mY7KRakNsas+Vn/zTxdMFjk5B42WZJJRDQlVmjM3WVGkKVjebYxNkszPWYbzqqftTTQcoOodTJFngN2u/p4wWS0UDq+QJQSGnmf+hwDguIPbeC22tbjEVpqB9hl5cqGxqpf4fDwEBfbLajzuH3nTo7tJMSQsqzcvn0bGANOnjxCCIx//s//v/j9H/4Bbt++Ded8ORwdY8Q4jAi7ESCHXWD8y3/136aD4MzoQ0yeK0BdnKe9Mpm4QzoAM4YIDgE/+9uf4xtf/Spu374FMTa4ECSFXDnq8G/+7b/DkydPESPnW8VjBqwjEANWqzV65yFnNS62F1h1HscHq9wXlw/d1p6NMZ/Y994DOYRCJqzkIGYu223yjoR6+RwaBqStzxAiYiSE3RbbcUDfTYwdQ8h1pUxWeiFYwSQCVD6XG9Cl37JbpLOptJRXa7HZoheKFka6fa2QOQvESd/XoEovRr0QpsXH6DoPBmMMAY4TIMmyNtcni52yPbCkdFnshQp46cVn6Rlj1OfHF0GnXZBEKexLFqwFAvtBzfwyqPJNTFmCJJNS4DgpUzU+3Q8rJG0/mHl27ifV1wbg5TPRajTRQvhNnm3Hgk4GoqaF5uerGAYyT63vZn29pC47xnTmfplmVwmvkbqWwn+0bJHdPL0OWuBD12HDveQZC7btrtU+OlgZU+hRHpK1nGgEQkq53HcIjvDJL38e3/mTH+HuJz+GXe+wcQxPDt02Ij4+xYdvvIuf/Nu/xL2330bYbUDDAJ/TOgZisCcEB9CYM+5dobQMTk0jOzY7By1gbUG55jc9b5fRc/F3nssM5uS0sHyl+Y2ovsNoyXgo7RDKIfjW2Cw4n+5gmuuGUmhujO4L52vR4LJnr/L+vnfz0Ktnyzmfhpyp761a7t+SAVA9pxXeQlkyMOS7ffIvfSfnE1F+chLYFWi1er44L0XGLfTBjk8D1YpvDL32zWnLmNHvFYfXzIPVsj3q9RS51hkto6EC9Y313Zpbeaa1c9aSu1Ze7Ktb/pXEOli2sSSiRjCocw591yc6ROQLQpVOydEfjCliSLeZRPjl+vY/uKFx87kXsT44wHq9TsJOvCmcLtwbOYA6h1vPPYNAjJMnj/HeB4/x//h//r/wj/7RPwIz48aNG9lz7jCMI7a7HQJ1+P/9yz/HvUdPUtqyMOJiO6DzfQY3AczJ0CZKMYQMoOtSStxxNyC6lNnlweMz/Ff/4r/FP/wHfx+73QWcI4QIRCIQB3AY8PD0BH/1Nz/BLjDWhwc4vzgHxxFht0HcbYCuQ3QOIwI4RDA8OufRwSMMYxbKHabDxg1rFqK8Y047FrIQyxa5WUwlvW3fpcsLOaRUjZmznPegcQDFiekikjc5xJgMKFDaEkXiLdkejTFdsBfHUHZumBlhHNPNjwx0ziejre+TcRUivDq30QIUeuEIUJ4OotVxixqg6kObUz3IXvd6y1bqaQGb9C+C4wjXe6xWHZwDHInnbErTVgNkBihADqROhxgI6dK9lFHNjtkCiVpxqolXhYiquqznWoCq9NGOb6loUGTnBF19WJ9DzGd9KGeransqbGmBrpnCQy3ztZBOqWuTwQdGThOdgS1RtROiaekqYy8lYGAW8MUVn7TmqKKF6veSIF8ES413y3pyDhyUwpP+YmKnJYUqqS5JQtoYRaFL+J3eQdqn4PQ4bWkBZ/udvN9aW0ugOrtYcnpEV8kzyhvxHnnNeofoCcPa4fBjL+D7P/xDfPrLX0DXd2kXgxldZIxnp3j41j28+ZNf4M1fvoynj59ATiIxGCM4pQd26XwFh8Rf9p4i3d9FQ06DCcDc37E8dkvrJeWrd+5t4gwbimINydJ3pLEWMCoAcIGPdf+0DNVyZZFnLjGY7dopazUJ27R+8/m3shxUnUvGjvTR9k+Hblg6SWnt5GjQptuy4HGiOcHRtHs9C6PMISfiDCwp7IGyW9MCxro9bZw6KAIpIxxAyY6nxya/N2XIwnireSVGSnwi8pRBOWc9uemQdtUGc+mnZOImOHBIdWl+bRkEUvRzhMmI08/u42M9H3ruJ/piIl7uNyBps1mla1b0yf8XsJ50M03rTc1ZS1/YtSt1suq77uuS/NR8sSRn5NnZ7n9Muly3J7+v+h4H6wMMtEu7TI5AnOQG+dr557LMJhDGmHgkXVORAWFMSXZ0j6p1xcmZe1VHD/ARDI3D69fhnQe7dDbCSWwXGDEOiMgDcIRbt28jxIiL81P8xV/8Ff6T/+QfZcDN6a6KfHkfKOVYf+uddwDyKQwqpNSkUpzz+Xr1BJYGOewSCLvdLk1IyBPnCW+/+y62ux2SjzsiRIDJo+MARx5Pnp5is9mBGViv1livVjg7HzLDpcxOwzACrgOYMPK067KOPuXuJwLIIfJccBaQQCjGRfpetmvTpGpLVc5S9F19oFivp3EYAVd72IC8cA0okbqth0HXvd1ska60z8rYLACpf3bDN2ojQ/+TBaFv/9b0aS3E9Hf9mQYOGnDptoGC0RI9ELE6WGP39Lykc9OX98i7RalSpoWAvgbIXFJeMyFp2qhLPbaqHaVs5DuhtxXetYEy92QvAc4isCOXHRT9XkuRLbU764cRlq3zLBKmp3e1WMCq4pE6vG+qv7oLhuZzZQ1BzYtNmjf+XnpmCcRcVvYZiQXwiJGZ/4UsM+yu3RJA3Gcctvq7pNjterRzat8viln+5UWov48OCJ3D6Ak4XuN3fv97+Mr3v4eD4yPAZeAfImgc8eF79/DOy6/iF3/x1xifnCFutmkcNLU1xQKmfnUWFOq2G0aHLnUab57R2oJSC0RrB8l+o8zKrBZojgbwMRuhkI2Mpfm2lybaflyFZ/XY7fOt2Pv0XARHS4NJplpatPq2tIN2pfVjAP1l71raa/kk45TPrYwrz2d+3Lc+7BpsOcrKO5A+cLn1uQXEWzJXj10D0um5lL4+vY8ZaGzJBio9wixTIZFD56ZUubosyQ5Nk9ZcWz1f6XbDv1Zv2r6JRI3ivEE9F+VcJxp8qda4xi+t9V3RMB/5Xeqz5Qld7PxaI1XPZ5lztPEQc47GyZiTMo2Q3wlxfp+azLR3vuI7oB36q/tm+3+VcvUzGhkslAWaZ1OsR+fSTdnOpRz1t2/fhvfAdrtBjBHXr1+Hc+mA93a7Red98hT4Pu1siGcDyYPPLLd6z7MnhRCqtIYTsIgYx7Q7cHx8CAA432wRmJF2lAgEjzBGhCFgc3aB7fkm3ZmRL5EKY4prc11i5ugZI8WS9z3EgDFEdG6ukPT2tT5DID+995NRpCautqZTKt6WetALWWdiYqJymFGKPU+hFcYUW8four48K/GW+g6MluCTenUaT7sA5He9CFuCZAkotgwL/XfaqcnGnGPscgiccwRE8Yy1ABtlzJJpyUoxgrObYu6hkHqWPDL7ypICWXqu4qNGoUmWNuuonpU6BKjx3AOzpDjsXM36QVQuNQNQGwWYG6Tymebuy9qq+ADtVMm6PXumZ4nvSl8WwJDtt3wWlZzSn5e6s3egBThbY5U+d4ourTMbf5eyNDb93b7vLW+IAZCDO+G4zl4DIkRH2Hlg1xM+/du/ge/96R/h6Jm7QNeBCPBMwC7g7MNHeO/1t/C3P/4xnj74ANgMwHaAg8PIOfyPqOyatOaqNT4xaHWxcdFaJi7RxJYW8GvRbborKsye0etbfrdjS0k+igi6Utm3Pv99i03zO/Wdi6d0CYgtgUcg0ckeOm0B9PIuKvNrNj5NR9tf3bb0K0YGeApHbMmUJQPByq8WoFwyFNqlHp1de0u8t49fdThMJX/TywBcc2zLPazT9i8V2y/OXvhWqO8+4GpxhH7nP0SxxhGZz/R3S30Wo1PjAnnmMlnSwha2ftvf1r0+ok+dSxeTbofpnjPBNhZLVfxFqMCEnKFN52bbNPu7lCsbGl3Xlfg9PQEF0OZehcjlQO2142vofcr6tNvtyufDMODo8BAxBgyYjA8nHn1O5yB0KI7PhokQTBMmUwHrfrLOttsd0h0TKSPCEHeIcUQY06VePIZ082EIOLx2jM53KdzIU/4dIE9IZ2dSStndsEWMIcdwUklFa7d/Y0xpwwS0y+eSHpcwhRaJQE0/U6wdOYcxjFUYifMu3w8xMXYBU3FaKBq86J0PonRfhDBbopsD85TZC7kOUZaW+W39Uk/LWLBCRY93DrrrhaMXgxWsVmml3QzGOOZDki4dmtfvVcokfZgwN4t3lko3KKcttkLHjm/Wf7uA1fetha7r1GPX/L6sCJaBlq2z0N5RMbxaY9N9uGphcJVuUDsFLB9UwhsAXBs8LtGPiGZCUZeWV1Pmy+6yLAEj3VaLDmXNqbDE2Zzy8rxYT3s9vglc6sxtrf5aI6ZlEFnwtrR+WvXLsy2gyEDa+c1KiglgB0RPiM4h9h63P/Eivv3HP8BLX/wsYu/SLjgADAHb03O88/Lr+NWPf4J7b76d7kza7tDlm9yZkqxjMfh56qP0w8oPCwiWwKaeJ8uXLWOmtas6kyeGb23GON1H59LFtdvtdtYfeSbpUjmrN83HUlkyvC0NdFuaZ/RzS+tCy/qpPszesUaVbkv3dxZC2uDLVt/tnAq9WPHIVdb2RDeUQ9/6TqeleWHmFIbq5+fu7FrTf7d22Oq+0mxsLdpJP+yup01gottpzvFHkPHl/Zw1S4eF2jmyPFZ+Gpross9xZMtSKFmRy+Zzy1dWVhb8pJ7Xz7R2Yco7zDn6ep5l0OIETZ8WjaysaBVd74wGyiYomEZEJ88dI6Vvqj493lJHg78tLa5armxoaGtWJlwfIvbO5zjGaeF3fYejg77ylDNzvhU7AV+/PsSq79PNhjnWM3K6ZVt7dzebzex+DFnEZfswToRMN2Lv4Ls1IBmaKO24cBzhXYTDiN4F8LiFCweIww5dfsYD4HGEozB5vDtfgGraeWgr9xBSmJYYShKvG0JIQirfuCwHxGWyo5z7qAQnSlgTgYvBVcf0ckEpVshZpTgxVk4RyVz1oaWQ9OKzDKc/1zsh8p1+DpgUTd/31RglbKT1vl3EAHLWMgYPEYEjur4TF0OmbX3Ph7SdBK0N6YqQtMLW6FlSfFUxnoNaYMm9Hg3lmbd5l4SQpcNEj6qbZixtY8zTdGlmywhsCRFNd/35UqkUMk0x9Lq90jfVtvbS2PqXAJKUVnzwvv7ZOpfatMq0ogEm5WnfT8J9bnBfBvD1YUUbwmjpZ9ejrq+19pbWtn2uNf5KMefvnMQ6dx4REaF3GDvC8d07+Or3voOvfOvrWB2tEQWUjBG8GfD+m2/j53/xYzx44x1cPHmKdbcCdiP6fFs4E4G8Q8g0zNeiFpoIPVv8ao0E+bvacVHP7ivWa6iLlSlWRsq7+nyGtJkcYNtZXdKfMi6er7cWQLJjsUDJ/t4CW1cpVq6kn1SiEGx41T5AYp9f0hf2ezu/tl6tx1p90G2n30MKfVkgg16LhhrNNrSercPg5jtqdqyiw/V3rXfsHOrdu6UwNKsPiAigOsvQPpk59XNy9si6ss9ZvKHHbzFJiwZL+s7SwH6nHmqGCU3jq+WrHaOl71I7Zc2Dq/Xe0istmWtp3pJlliacQZI9IwqgODCYI3CxSe8JY9NUp8WBRFTOTVpdJePTvLbEY1cpVzY0QhFQgET/BU6efopIihcE5zxikO0bIMYwu1p+s9kghHQhH6u7FhLgcxiHscShC6iWxSfCWt/RkAAqsN3p3YMR3nfo+g5jZKQtCuDwaIWDtQdFwq0bh1jRTbDrcHzjGmi1AjoP7ztgTCnufJezeIBwsD5AzMaD89Ple60JjDFWuxnl8xDLe/Vuhng1uXmbZowRjuaMGmMsOx1S9Pd2YcpP79MOCvM8DleHRtmFYn/fB8j0c1ooVnHSyPaaUSitMeiFF0KECyGdOSDg9PSsCEG9SPQ7pa5YX3pHJOClFvrau0U0N6SWypIA1yCFiGZC0fb1stJSuPL5TAkaoKXbsc/b8KOrChip13qAhZa6zP1P9Zh0mfozf3ZJSe5TFHbsV+kDYADenvblOZvS09Jd8xMtgIxWsbTU7dq+txREa13o72y8sC4JYhIoZ38KvUc8WuM3vvV1fOOHf4jD4+NiLHgGsIu4+OAh3vjly3jlZ7/AB2+/h/Fig953CGGHLoOXiOQhjDlsqmuA0ZYsWwJKSwAdmIem2XnUcyCArEXDJT5pASSgnot9QMP2v/X3vj7YHfbL5ErLWLGfz99B09nRGs8SkNpXNPDZV+c+GaCfsz+dcwDPsxhKsc6py+Za66zW+m3K5PLZcv9tHbJ70QoRvawUrGHosKTTNeZK7aMyUlr1y08LljV9P4qOa9V/WWmteas/NICWMen3gSk8fak4Sjuvmh4tx4au86pzpfu5T8doR3xJ4X/JeihyMH1S6egp5HP+rp6/j2p0XN3QyJmTAEoZi3LaTHIuhQPlNAUhBsQYwJExDDsQE/q+RwgpbezFxYUaBZV0ecMwwCOl45oMDVeMjxgZMY4qhazDONa3hgfEKaYXlEKzhgGu6+G9w3a3xd07t/Cf/+f/GU4eP8ZwfoKVdzg8uoFdiLj3wQPcvHsXq36FVbdCHEeAA5jzZX/O4eTkJBlZ4JxGta2whPlk8oQB084EZs+k72XnKJbDluJ0IRBCGCsDpgiEXF9qemIyHX4jYV4a9Ald9bNW0Cwp9ZYi02BcPreLZGn7s6Wcy3PMgGrf5cNf5AiePMY4pjManLe2I2OMnHcpHGIMENPeOYcgh8TzohTPBIB8eaDqB0+gWIS8HrNQfJ+CbvHFUtmnOEvbkZFyKTSAoBICWoDEmC6n1HPc8sLotpY8u2Xsycky65/+u02vZaBr69EKj0HN5+bAmTPLWMU2PS8ZsYjmYOZSRcBp4Eu0E9peBgJasoORdjBZP2Ne1/3UGbycVqY01SmY0K5T3a68SDK+3Bc915SCpgBHCN5hXDm88IXP4Ft/+kM8+5lPYusIwXl0RHBDxO7JKe699iYevXsPv/7Zz/Hhvfvg7YBV1wOIQOcRmOEdITCnG2up9iSL0rYGrAUwWvGFkMJjnZ8D+yXwWuFmxTstD62dg9Y8Cn21vLMx83attuZYy2Lb56WdyJYs3bejY22GS+VPlsdVHY3+LY2n9WxLHuj1w4Bas1onAQKWWsXSaOrH/J4n6wTQ45IS1Vppjc/ybWss+m9rREtpgfKmvNhTx3JR2RO5ThdrjYKJ/kmmSgr8Zq0GO8i8kfrejnFfn6/K27o4cikiRvWhVar5VvVaui7pKcEEpHYZNLZq9XtJF+wbk+YXiSrSa1pkyMVmg+Ojw+k9QnJecZ5DUvTQgi6PAcq5WvSjwkIfJcStVa4eOhXTJXthDOnSoNxPEuAcI8YQsNlssdtucbG5QBh3ePbuTYBcutRwZER26Lo1njw9Bzji4PgId27eAMKIAMYQ8uUvJDH9KcSGirc6wBcFkhb1OIZkzXmPw+Pj/HwEYgA47bAwOnjHiIFx8vRDXD8+wJYOcHF+js9+8iUcHB7i5N89xeMP7iegkDNfjTEmzzOnHZy+73F0dJTnKE2K976ANhEwMU5ecGGO1Gcu4H7GlIycbQVYj4zRAZs1oeeAQxA4Px/yLoYAAiijLDGCCImcoi8zh0uNqoWVGgvjmHYZmAGO6TC+o8oQst4TvYVn452lCFPq+NemwmZAbpMj51KKvUwPEeqO0lY9c0qn7J1DlCSYkdD3B4hdh9FFrGIAsQdROtSU+otirDj2IPipbcoeZW24FQMj0Y8wgaDZGGOcGyhQnlj9eyUsqFKc+0I26rrlmdw/JwJRxHrLU13PicyL3mmqgJfq72JoHbgC6kulpbh0soSWEWvfl3FLJjHh9+l5RghjCdNMn6P8FEDSAv/MNQhfEqblOyXApRSPVvbIt9ZGS1AXOkeGxNqmLCoAY6qrWhN5UPIs5XUi9xpNg1JeuvLN1I6Tc2ZqLA4Ex0myBgfA5ZZDRO87MDtseofuxbv4zp/9EJ//7d+E7zqMiHCe4MYRNESc3PsA77/6Jt595XW88/obGHYpLDWuXFJ6ngCX+IcJ0DfUilKV7HyUz6ClsFKlaGXenFzIKnTOY44MP4066ykuDEFCfxPayJzeIyJQ15W54Uxncqm3lOm0FL7XAostsGFlg4CXiudMaTkUtFFm15vdxak7rCQGQxLy5XC2ebtJpmWHD88dEkvG0WUgxT5v12havxpsz9+ztKyGqcEjaro3wWQLyCpj2PZdZGXhYXOeYok2MTPnkgOqBUTtZWmtvloaFDlKAEqWq8l4I3JlTuX5Seah4BnhPcubrR271oy3zkfN+o6cSYsIlFPuyypOge1NQgHgcoZOj1n0bQHXWclr0D7xWMrGwJKenSa+ijEi8nSvBThhEU5uvOzsYZD3+VLneWREa55a69wawjrSRWMG5wi+S1dOsENK/63kHrPIOFGEStZnDA3nMQpWFRrJe0UeGB30EcrVDY0hYDemsB8w0k2D+V6HzcUFhmHAZrNJfXYOq9Uaq+Mj3Ll9GxcXG5yfb3DnzjNYrdYIgRFCxPnZCQ6OjkFMePzwMY5v3AQTo1/1KPmf80FsATTe+UnAZDDsSdJ6Ma4dH4MB+G6FXdjKmsI4BDiXMp8QCI8ePQaQ7qt49Y3X8YlPfBJ3n30WZxdvpvEib4F1HnHkcteFZMtY9Wl3RxaWjcUGphP88rv2aBW6VgdwMtgF0FFSyOzSQiNMXhZdJ5jz7o/UOFdqUYFFqIUFngwjWRByYBxuUtwtr5s2Qux3umhB27KKrbCx32uQOwO7lLxciR/zkqEUkkSYLrYiqFS3jNm8FaXNXI07V1eMDjFadEiM9MMqD0uPthE2gaL687oO3Vfn0sWT3jvUhhsv1pF+ym5Zc5qq9/S7LbBUFBDmISf698WdG6r7uGRkWMOmLnMQwcyVURvjdIbL9jPZ2zU97Pb30thyg1XbUmJkMOrQyMvKEiBaCsHTc+Jsv0yh1h8EdFkRJgWu5oMIO5eUjOME5j05UO8RHSEeHeE3vvcNfO2H38fq9nXAp0TnHXvwdsT5oyd499XX8davXsF7r74JDCN2m5Rl0HceTsJVihBHMZo0LVryRHZ6ZL0W2pj51WunzGNuUxv/8v0SwE3v1TRPX2CyXLjuT5kXxfslVDI00kwuzN8+UK5BizYiNHD+KGeXltpuAZ+qD+o7K6d1uzHGkuBAf9YyiFqGwrROydSbfm+FvUipD7Cr9oy90DKM9He6bl54RgPoJaea1W1pVHVGpzZIrss+HSo00TStX55AI5Gqm7nsBtgdsJzMsRqH7WcrWQ/28LHtezXOPD8sjhHR9QDEoTqfr9pAmo89GyqCt1Wx/NjS39KOYEC960U0Y6hmX2qenrDYpXKAudyhMZvX3EaI6WJqiRhAXjeRORkNVPMwWMcIKJmpxqz7Ub37EcuVDY0x33+ByOAQsN0NOD8/w3a7g+s81us1rl07Rt+vEGNAjAzvgOs3riNyxPVrN8r9GUQAOYeL7QbnZ+e4ef0GHn3wEA4d+tUhfM5PrAfJyODWi1WaPLli8BAAR4yDvkcMEcF1iHBY+RUiR2y2WxwfH8M5gvMd+tUaQAB2hMdPnuDk9OeIMeQwhFS/tAmgyoCV+lMHclSgwggwHaISMgNYxTCB5xQORHHarrQCVkrrQFYBzbl45xHCWDH1JCjqzFdSElhLvkArgOWfFUQzxW6K7VcrTlr+tnVroF2MpxgROCBkISSXKDEEpOVtbujQkfxPkc32Q5TITDCg9iLYubBzrmnUmmu9qLWw1TRY2q7Ul93Jz2mOappX76EuS0B6L8BWnzu4clhXvyfviKE970cSytbAaCnWCjRdAr4kXEne0/NnwxgkpNEqOj1Xi2CPeXYfiTXG7ftL62IfkJhCKmk2P3v7d6XSNgQjEQbH6GIyMgBKd2L0Dp/4ypfxjT/5EW6/9HzamXCEDg7Yjbj44BEevPkWXv7lr/DBu+/j7MlT+MjgMSTPv1pnf9d+W0NAfreK1+4i2Xfsu3a+ZT6X6G7nrAVQFwGUKlc5jGvrba1TWSMasFhjy36/VGqQWH9ejYWoEqT7dmNbAKulU8ZxnN0jVN7lWu7ZOWoB/yXjIb3DFWCy79u1W55pyClZq7Z93S873lq31G3ruaoMalX0xYa2v62/S79SJ5p1MosFPV9rqT6e8ZIFzB+Fl5cMMcFWWo9M8mOPc4XnDjqZm33rcKk/QF4C5l2NmZb4JO0+7NcBdi1fFlZt29Z9dM6j7/uGvEvRHGSce2AuRpzUS8gGeHMf6t+vXNnQOF73ODs/x7jboXMeHozDVYeb147g+i5n02Bszk+y94IROeDw8AhhDDmkwSGEIVmmBNy+cwfOOzz77DO4dniAsNkgbnbgdY/duMkUQPYkxwwUuVyaJ0JJdhqODle4dngAMIHJ49qN2/DO4+z0FM734JwpirwHoUMcI8h7eM5nRLxPh7y1IGjcxZCYoVaaFZBUDCbenFK4BjWVUpRD9WJMMbJXlgpDCENWSpsn8GsP4pZm1XuFqclVdQkAkwPmshMiY7Nxq1aY62L7aQWsDcexsdBW8es6C72zkREiY7fdVeAdYISY72EpgSNOohHbgke1NwMpNIVYzDzkZmu0BrtzwFPqL80ub6vq8UuRMDIrmKZ5qnfZAJQsboy5gLOgpIxZPdNSIiKchCa6D7ouvbMHTF6qtqJbBoC50pny3kc/u1a08Za+8zPAtw+M6T5rRSY7Kd776QyQGdPSOrF/Lyls67leVHKVMmuNARCvoKZzkgmEVUiXc8EBY+dw8NKz+L3//p/h41/4LLrVCkOOtekiI15c4NHb7+O9X7+Ke6++jnfffhsOhC6mUAJy6ZJTMUivCogKbzV4Vb9nPenz9demeQuw279nYLfxPLk6NNKCHC1LWu00wUcDD7X4wbbXKnZtfDSwNTludF2JR+sdzZbc1nM1C6kxMla+03qgog21gZrliZbBb8/2TL/Pdbjui/69ADzUuwX29ndL8xYtZv2gWodYetr+6D7NgWU9j7pdIqpuOLfPZzI3ZXjaBUH1mZalLcND6mNMck1Kawew1EUOjMmIqs+6BrgqgZAxIBVP6vOvLRq1ylx+1jxnZbC0Yfk/ZszQ0lW27A1r1H1DjS11f52jvNMywiPjXE5yeuqbM/yUQ59lvg0vWR7WPdHtX6Vc2dC4906Ks+27Hp33OU8vY7hATi/awzsHx4y43aWQJt/h5s0buHv3LmJM4VLTyXaHi+0OYWQ8/9wzOOwJMWzAIWCMScCFfGeFMOluu0XIB8+JHDZhzNtpDO87jBc97t66BZADuR6gPu9yE7zv4FxX4oIjA0xObGc471Pmk6xExbaXbSitfHTspfyzgEYmSbysVYYZNUmVgqJpUepJ7bq+tAFMylV7vW2fpvprhtBCUh8Ob3n29d/aq7Ak4IQ2AGa0aCl32ycZm96CtcpatzmGEYHTzsXZ+VklVIjyuQwBONBp4doKRlPd9jvdzzH/XgsW6+mJUWLs2/0X/mrRxAKXJUG0BEDku2lsywKhpQSt4WD7pgGA8JD1xuwDfTNwZT5vhVa0QGeLTpb39Ds1OLeCt57XVh+LQDZ9KYoPPJuTfXNnFZGljf1uqV/tutpzTpTGbteuz+FUznmMIKzv3sBXv/9tfOUPv4t4/QCjJ/hI6MhhuNjgyYePsXt0gl/85V/j8Xvv4+LJU/gIsGRTIyp8p+fJOiD095r2zFqRtjMEWSC5D3zZzxYPhpv5sjxk6bw0jy0ZaOsVWiwZCnrsto96x/Squzj6czvO1npp7dRKv7WBVckaWwfm/K3li9Yb8n3VtwwgLb1bAG1p7lr8Zse8tIu1RA87bl303LTmTn4SUTqXifbctebyKjsHVwGus3mLKXTKpmYWLGR13mVrbV9pramqDkNnoL5WoVWf7ZOm/dI82XdnfVN9INqf7OYyGrTWsu6XnteWvKiIYtrbbrfo+w7OeYDZnKcoQW+1k5S5yOd0T8o04Jas/fcpVzY0/tf/2f8yGxod1v0Kne9wfHSIo6Nj9F2H09NTrFYrrFarcj/E9Vu38WSzLcpXQqrSIAjb7Qi3drh75yb+D//7/y2euXUDhBEgB86HU7xPhDs5OcHjx0+wG0as+jXGELDdbDDkW8XHcUQYR3zshefTHQ2UQqcIBOc69GsPzoAQziN1IQFIJuQLoqYFT9QGZzXRJ2tehJQAcuYpZEoya5X3jbCTuzFmDOxSPKDstFCsPbITM7YVanpmuiDJKoMYQ2WsVMzPdUwgUF+SZBemfldAS6tYZSb1AknQ61TIdjz69xhjOsNCk+HmnSu7NFyCqJH4KQq9xcdyeZmBVrXV2BL2Frgw517QdKbD8s/S+62+lDoN7eeAfuFwPibgZ3nBCmorXFrb9DHvMsoasJ4d7elv9aPVjua1pbABO/YWv8hzdsenHm/63K6pfQCCOfGArrsywOPlfdJ1LSmnJcDaopWu67Kt96lOQNaHyCoAoM5ju+7x+a9/Fd/6ez/C8bO3ERzQg+ACwW1HbDdbPL3/Af7Nv/iXGJ6eYx2B4WyDkSNGTtnzXA49ddKWAid2ndjPdB/JrLMWGNB80l4PBtg16KQNIP2MBSnWACei6QCoATm2flv0/Fd8sQAorqLwW+t63/tX5UfdDyDTwYRqaZloQZNdD/YcVGudTg2j8sza/i/xh+WH+l2qZIw8s5TS1Nazby5aukvziz1TYp2Z9t2lz5fkjKb7Vfon/UhnXif9WoXaZV22hAfk72b9qp/WqWh5tLyitlBsCHFLJpS5bOycXnXdyM/qeaKqztbZKys3JpxR123pY8d9GV8tFcGdSdcCyI7N6YJncS4xpvMtQAQh5xtJ/2usI93f6bOEoT5KX69saHzypedwsF4nYD+O6LsOHCJ226cYLxjjZovrB7dx+uQBzs/P0fc9dtsLHD7zIrzvMOw2iJGxGwbEwOjXa5Dz8F0HgBHCFg8evIWjlYPveuxCsrIk40DXdbh5bYUYOxweHOHg4CCDGw/nPFarFVx/gF1Id3m4zpcLhRiEru8KSPD5Aj/K4TRJilHZ/RDLLtHXemJkYSADjmliEiN6OB+BUHtuNHNJjKEWPkCKs4MnEFw64BgZHg67YYfOMME+pVCD4Noi1eFPMdYXWtnQKgDwXYeQbysnqMXAKbSKQFXYiM/1xBCqVMMy9qU+D8NQ7UjokC1dKsHqGGGMCDFiM+yAYZdSEiNl5vI+hfAhz5f3HQCHGEdokF/1qQG2Y4zgEFL6TfPOBP5r72prTqyC0bbQRyl64c+VKVU8Ob2EScjIu4069ZhaRY9RlJMOYdSltcuWXkQhvwWOmhdb/YLhB44RwYApAT0tg0TX1QKtUz2V3NWEKrIjjS3tkMUYCy1S+5RlRXkRdrInxWPDShKRLKixhu+0FixYT+3KDCdHCk3ZhDj9T3rjug5DjGDv8NxnPoWv/tmP8NKXP49x7XABxgE81tuI4fFTvPPO23jjtddxcXqGzYdPcPboCXxgOO+wC0PpB8ck55zz2UBvh+eV34Wncp+SrMFsEqzsawFl+U5Ao+aHJWBjiwahU9jGxM9a6e4Ddpr3lnb8ZrHZTDO5sE+p79MH+nMZy0cpls4FXOa1SEhp5AvgMv2R8Wu5Lo430Rm27/N1ycnj2gD6Vt7OQGkDjNfgC4XWotdbAHBOmPQepQdmu+Gz/vPcAJiA8+QsI0rOikXDqvxMAko7A5eM2328LuGSyDv2k4id+l7EtYAeU6xx1yBTpVNbsncmb2lSEhonaUdkE5jrSngyjqS2pXU0o7P0T+1Qt4xj24+6T9PYRO+ycYpIWy2e22d4yPcuz9utW7dw9+4dnJ2cKn0ifZicj4I7YozgiBTlI/Rd4GPdphgpIveuamxc2dB4+v67eO/0FE+ePMYrr/wa47gDc8T5xTnGYcTR0TGOjo7w9OlTjMOIa9euwR/ewH/0j/8XWB92oC6dkfDdGsO4gYuMw3w4m7oON2/dwnj+ED12OFo7DAG4OD/H9aPr2O12OD8/wfnpKbbbU2zWHUJgPD05w8NHJ4iRQM5jdfNF/PBP/kHaKBrTmQtyDilIqCveb+e7ElATYoRjD8Dlu0EIgdP5hTGMacEjIjLlf2npSWz3FIojwIIBOMiN0AncBjCnOzDA9dkHfddFAOcDmIytS1GK3RDAAEaHSlnLxHvvEcd2zm8RqJpJ5PdJ6NVCQA7Irrt003Yc0gE9DkE9mxUjc2HqJPACkFNKMjN4DIDPB9diKIBQK37dZxt21VKMGoRGAKtI2AXGwe0bCdy9ex+RCIAHON1WDxJBFopyqXCvUlqyIC87QGbDpGw4m9QrQNCC3/K9Wtqt0DQpkopWTVpzzolqoamFWJfVVFBGIKseaJCv61gKdbHb2/qAog11qfqIlMhB6pZ6tSKSOmahJcK7ymAiInWhaJufZNfQ7rwAwhNUeFnWc6VUFT0cTeCK83851DXzmPSX0XVOGWDJUWGNzlR93gkoxkcoIDQ5C2RM2hBJfZzWtiSySDZxz8DAAaNzYJ+8V10kOGaAQwIrvsPWEYYb1/HNP/sRfuM738bB4RpjR3ArDzcG0PmI937+Kt7++a/w4P138eHDDxFDciaAcwhmjOiys6YjB3Z5F5tjOaOj135ZP8BkABEhIhbAs6zA20aXTrrhnMPdu3fx5MkT7Ha7wg/7FPc+wKS9l+ZFECe5XfS6cA+hhFQWIE7zkCcNZFI7U/X6GQtM5Hf7mTZudLvaqNlH11L3NJwZeM/qCAQuN8VPz+YLGM24LC2l3qX5mBkfRi62Qp2W6mkZHzEOadctg7XEowCRB/NYtV21IzIryo51Gn9kBuWsmOlMabq/yblUp6S8Z8UTSbdORjaxOACoODSUhJ7WC02GV2v8FrxqmYo4ndPochp/lhuis9+VCCCnnSMZsCKNLTkpC3zHZWnOLUgHgMih8iwUxw3JWqv5uYxVyQs79s55iCHM2ck4mQz7DXahz9KOlv5pv5vvAMUpfAkpUVEWarmOuf5u6tiFftjnh3x2GpIKPD2AtLuR5LMYp6C04xzlkCuj3IsnF6WOMQK+TSupR6cRvqxc2dC4/+BdMDMODnv81m//Jk5OTjCOI9brAxwdHqXdAxDGkO5kcEQ4HwnXr18vMfcajDHnm8FjSjEL8jg5Pceda6vEJGBshy38xmO73eFic4H3H7yPGLY4XK+w2e4ApAvZLjYXGEfGpz52HSjbeQFd52VGpgWe89zLDeaACBGAOO1+SC5pATQytxqcxwxgW6AOiilt+AdllKuBZ23J5kXuU5Zjl1c9g6tsC5VV7wgddTNQlphgLmAL4FJZeqTIQtMAsKUo5HMdMqYFgl2YYwjJgHP1AS0LGKR+oA6lapVxHNFzCpeCk0PQEvZWlpuZu7k3tLTrXeEX/ezk3ajfL2Mw3tKqTcV7YhgWw6b1PGqgoL8r36cPqnemMgHmWQx3JUAnXs5SqTlmTR/9tyh+5yfhqvlBF0vvWY/V+/K37UcrVE2DOEsvqUNCgqyiawEdyw8TVVCBHA0U7LzKhV7W+63XkDWogHy4tqFo5mFG9e927KKcZYcFROiigPm0JtgRggdi5xH6Dp/86lfx3T/7Y9x47lmwd+gB+BDB5wMevncfr/3kb/HWz1/G9ukJwm6DGKdsXTGvz67rCuCyc6DHrz8r4IeW07+2Sj3e+eVc0t79+/f3vmuLlRFLsmkJHAtjl3ezQW3rWHpfywWosej7boT39G7N3Ghtr+HWGrHtW4OrRZ/yPGperuYE9d96PbT6qdu0jo7cucrYn3DEHJTZ/rfWeD2mlBQC3DYydR3S1/ka1nIsredkuMTiwKw8M7kU+TX7Rg29ocdqA2RelnaELb+4War2ui0tb3R7Ex2zTFGYRheOMRlgVD9DRDnipHo6tzntANkzj2nOF+ik513Pi1BMtbW0BlufL60Hi1fsd1Z/2zpaNGk59Vp9tN89fvwERwcH9djz+eWpQanA1NeI7nDOzXihNcarlqunt8WAECO2myGltHUdnjy9ALktgCcAUirVrutwdHSEg8MD3Lh5B33fYxi3lZBk5nxjd/IkDEMEk8db77yPp4cdnIuAQ7rwBB9Atnq69RoUVyACDo4OcXR0Hf7pGXbhEeJ2wAsvvjATeESUmJ0yw2fPhfceMQwpgw9RpbRle1cIbMFpYQjX9iKViTKTJALFMoq0WcUCeocwJutzNwzoF+aFmbOHNRavoU7z6ciVsATpUxHQNGceMQJEuemYVRn3bKtffWcZsoAHQgX6dNH1twwaTVtpP92VITdGJzqcn59DQoRANT31PNq50tv6S/HRoLrftUKOIJWPWSsj7bm4bGFaD12L5wCA99Qj2dmA5dtt04OodzNQAzddLECYDI16fQgPtoDVvrG32tTj1bTQf2vAT0QlZtyCKg3W7FrW9c2AZQNEaEFs+SrREZOXFPVaPzw8TDyK+RmUmUfM0NrKDA20mkaTdxiI0bFDH/KZCeex88DgCYMnPPvZT+Kbf/YnePGLnwV1HSI5+EjAMGL78Ane/vmv8eavXsHJkyc4PzkBMWO32xXwLOtV/tm+S8iRNbD0+Fs8sgjkzfxrGlnaWMPmKqUFHnV9l5UWj+/r52LbxSis51nzbate/XkL2EjRa+ajhFItgY0mAFPt27TT+jm7BpfGqN9t7bq2SgvozWRp6dfkgU7PTLtu9tklnmWg4Ij07HL/WmvisjHozwqWWGijZVAtGVHCB+Lg1e+oP0prbbov6Deqd56r+TePLumBiu4WJJt5BZZ3JbTRZNto6YLLyhJNW+8u7aZa+X5Z2802ix7OujqHMOa4vkvHYesHkKJDLnnW6uh95cqGxo9/8jOA08Hq3W7Em2++g83FFuMQ8Pzzz+P2nTuI+QZt5uRl/70//CO0vMpEpABw8rqtVkd46537eOX0MUAjduM2L6YEaMRbzWNMoTkg+K4HE+GDDx+i61f4e//RM5VnvVjOIaITZ7VLZyD6vsew26abqCMQcjo1OZRdsix5Y6HLJFNbaLaEEVB76fXzFYjIpHL5ZuACeoRmzmcgadtAFZ4glyMlI6QOjdGAinK4mBXumtHnAnnuuZDndeiMnQPphY53tqC69bs8o1OkijKOnOIMmYCzs7MUjpN1nFM3DLXqbioyTOdO9JjTHMwPD8p4mLnyOmqBybK30jAgYpTLKNsARNNc04PNMzWonb9bwtTyWiOavFfOu5I+OsZ5nbY/mkeccwiKPyx/7QP1oLbQXQJKM6Vu2wFSSFAurR0E25YdV4v2UONqtmsArqxby2/MXC40XRqfDq1p9c+C81Zd5TsC2KVQzxQW6hC9w7YjrO/cxPd+8Hv40ne+gXh9jS0xOkfgzYDd03O8++tX8ODVNxEfn4FOz3Hx4CHgCSNNuyhCQ8ndLp9Zp4RV4nqeRQ8QaiN+31zN5gcN3gIqel1W7Bzqeq3D6arAXK9/+btpEKq+F5o1dKatYyle3BYNrC1P2otHZ6C/ATpte03QBlQ3TLfG2RqbDZ3VbYgDZUmuWPpqx6bVtXp3KNGGE6JwDigOo1rfWT6285CcVOJkyOEqmjQ06RApekdK6tBtzmlgjDVHMzpL32ZySY3BZk6Szx0wO+82UQLFaJjLyyl0yupHXbQsBJDDrdXuiuJhrSP1WNLukK/6Z8et36nx1Vxma1mk5aztd+v3q+ht+86+0pIvZZ0jheyC5uA+reUUclmtZaKSBMe5+W6lxjRaPohe1ynJ7dxcdUxSrp7e9v4pwDkEJkT4/hBd7HC+PcF761PpGQABAABJREFUDx7i/sOn+br4pCSPjg7x7PMfwzAO+fAX4MjnBZhimmNMaW6ZCew7RPT465/+CjHuEEnHKE/b6zwGuHyqPsSIIQSsDw/wmc99Dv1qXS79qSbCGQHBQN/3RSBoISIe/KKo1CKvmMyJETD3yOxjPmC+1TZ9x3CUdhEGDiWlatlFUDdi6vo676dQR8UsMcbKswRoIJDq1opIig1haS2oJWGl29ICHwvP6roFHLZ2g2Z/i/JwQBgHPHPrFs6enoOdA3O+FbqhfFrgowgsnoBBC8zJnFtgl+FlU+BrGuu+pD5wFQIh77Ro0/rdgunUH9fmNTUHWvhSBhRpu3+uXK1w0cJQmrFhEfrZmXBrgELdp6pvC4Jct1HorNqo+zifT8unrXaSIK77aZ0ES8ocpi07Lk0LPdf7Ytf3gYmWUZLikwF2HtvOI3iHsfP4zd/9Dr7xB9/Htbu3ETwA57AGQJsBZ+99gHd++Qrefe01vP/GWzhgh/Fii5EjIjsEMLzaFV0yCPTnrTMB0m/t6RZQb+mq6affX/pMA8sWv+nPltpq0VR/JvzV4hvd7nT563wOW+u80ApJflmebfFcNeeNvuv3rbOLeUq7Lo6Sy2iiDRzr8S/tEorc2wdK7HdL85XClAnAfN3a8dt/0j87NktbZhSZnB6JFS/pshTiJ/UwT7+32tLgriUTWrSQdyv6NOhpf5/JScyNF/2sLVrfynVerRA46Y3VR025KnOF9nqw62vGRzThLosfWjrS0qqppxfLFHJlw7iX5kj/3nrGln1zUMmTJNIX60uYdsKsYHEMLRhFVM9TC8OVi5BN/1qyfl+5sqGx3a1Sx2IEkEKb2AEjA96tcLbZ4ebNG+i6DsMw4NrNu3j2+RcRxun+CGYl7BlIBx6B7W4EDg7w4oufxMXmX8B5j92Ybh93zqHLhsMYRqzJwxOBPGE77jCMEdENePa5FxAjEGmKXy2hIxJiQ0ghLpQ8cWl7NB34tkK/CLmcHlb/SyCkJrD1npL5rgJ8S4ISBpBDeQgUSNYCyvZXK+zSp8izZ1BiaCcvjwVoVilLkflsgXYthFqAXurUh0NtW/YdoA67EtrI333fY31wAD4+wtMQAEg41X7Pb1MR0lSvfi/GiBjqflahSb4dr2v3h62BJjHu+p9u19KEefLM6M8mxTo1Wr3L6X/ynu983ioXoN4GtlZhVYKIFww2RbMWqN8fXXy10gIQxVxfADat0hTAuVhvqD7zUo1H81FjviwQ1N9ZZbQUlrhUzz5Bv6IOoyNc9MALX/osvvOjH+Clz34G8A6h7xFDgLsI2D5+gvdfeQOP3noX77zyOp4+eYSu77ANI0aXnS4+nfFpec71TouVF60+VyGRyE4PTIZHS6Y1AYcpWq5YGl+l2OeWdo+uyl9EBK886/scKPodyuesLO1aQFl7xS/ri7wjF8jaNW4dBjBzuK/ufTSx49Y01ICwBbJkTvPRoyYt7FpcalfrLDseV5x6Mux6ve8bj+oxBNJWNCMgOVTb825l/5K82FeaesJ8b3nHFgti7TqKtGSMpLetnHIuyYyo2q3xAVfv6feXQo0Aifi4XB7osRKwGApk+bEau8GGVy2L9V3hvdZcLs0fM6f7T2jSheV7lmfbYYaEGo9VmMc++xH50ZYrGxqvvvYOIkd0ncNq1WG16uG9Q7c6RGSH9cEhHj85wfXr1+Gcx9HRNfSrNWJkcAS8d5BMM6nTKezFdx6dT8T67Gc/h4Pj69hcnMH3a/gIxBBxcnaRYoPJ4SxGHK0PcHTtCCEwQmD4CHziE5/CMAxgmnYFhFrJypNbNSZvmvcO41jcLwAyeJR5JJRLbOTgqWbAlCBl7lmLXF9mpBdNjLHkXbfAFznOUTIASB3ee4Aks046wBVziBgzl9h02c2RNr33yTsGHU6WszJEAbjTHI/jOO2eiHFEeagKVBITus6XsKtJULR5pxhRnD34IZaUfgmw1he+LSmcFBYnW+gAh2Q8jiFgc3aOYTciAPBIrhdtOOn5SaBUhUiZtnQfJhA7v7FZBKLvOsjHkxGDMqfMc2GVQBZVuyRW2VT048ljFJmbz6W/220l+mfhnm/1BceSNjJvypi65gag3i0kJF7VYQi2X5o/imebc/vSKE30sCZIS8BZxWTH6qhNU1taYMWO367tliLQHmKOsRywbNW1pMhlzQ7DgMPDw3rOs0KImVysJ0ueoRRTSzkxQmTG0HkcP/8MvvsnP8Tnfuc30R8eYIwRvvMYtjucP3qCs/sf4K2f/xrD4xM8ePMd7C4u4F0ax8gR3E1hCl1OrcXpAy0mIeeUnOq3dw6QlNecsklFoITYwqX60uFyAXDiUS5UKutdDrrXPGGBK9RPTd/y22xudLHz3QL6S3w3r6z+c0lRa2CV2q0vPtXry/LRPrDVkgOttoF8l1MIZZ7SOk2E33e3hCQWqcbMNa2Wz7bVO1F6PHNS0l45bdel6D+RO6LXrCEqRSJtiVo8Nu976zMiTHItKW/FApNsk/nTzhJd3z5Dw8qMYtpkPQpMXL9oUCzpGlloC+Nf4qOk6yaj1+WQKGYUA1GK8BdySDGjffbRylrd9pSMosYvut+6j4W3chg85aHq9Wn50o5Tz9e+chUwXtpXfyN/Ro2kIGX9LWCCRMuEn3znEcYRjiRqKB24b/dL48DJSJbvQPU6ver4WuXKhsbh8WHJLALkOEQAXdcnwBECvO+x3W5xfHyEZ559Bqt+hWFMUY+ePDw5OMcIBGyHDAmZsHIOjoC7zzyDa9dv4uz8FBhHEBjDsEMYB2w3FwCA3nvcvXsLIY4YwwCAceP6DXz8xZew8itE8uDASSEHRr/qweMW3qXUK4R0wZIjh9Vqje12m+LRckwaUzoPIsbFCE5xi8jCMDI4JKMloj6oVwEOzIFu9b0RrommPp+vEACWJp+IkiR0BJBD5zy2WUB55xJwVwpBhPs4jqmfAeCcelI83hwJker+HB4eposPw5hS28n3QMWsjCRAiAjOJ6Mx7aLItv88xIsobf1RZHiikhqNATC5HGbQAPjqDIn13nXMiB4YYwQNaSGO3sEPKc0uqfRs1QJxlC5vzPNdipJaVmCVGFwlkNKumBgTk0BM4SUqLpjqMJHCFzS1uS+kyxo35FzJx62fFQMeqD3ihd+Yi5STWHBJp2jFhxUsLcUkxmdLCNmsOE1DQKxYpNTOnJW9UKEGkAs7UHWn6/Mw8pxRmhWIpwTKJaGCVW6WH8scGA2n+0dAScCQRqf6V8aOQgfpAxn+k3ccJwATCKWvKawywiGlmaaY5EfsPDZgdNeP8aU//D5+5/e/j/W1I5BLMgAjsHn0BMOjR3jnlVfx5IOH+ODde9g8OUHcDgnkMoCB4THxMxHllLURjqqlAnBMz2bwkAzHBCg6R+AYQELH7GiJHEGRRSAh3TsyKtoyvE/rSBsREwARKgo41MDf8iNBEHCaozk/7zNIdV2aN1qgM42lfTB+n0Fg75OoEnqo3WatOzRgba1Xece2bflMLqx1XurJ+gsJKVpZLrKEXYrNl1CNpFepULxqwwBoqVNkng2j0zRNsmSiRavs2z3X+kO+k7OciScAzmmu4ZJhG0LDWbMwd6WfRIAy1CYcmOScPhMjc24BfSVHGvyoP3OkgTMXD7WAxJYcs3XMwt7U5/PdLa5kaU2bFHYmhn/VFqX1TTTt6FO+RHfyutdz1uJpG/qXOJQVs1FVn50zERPEk+yNIScJ8nXdFW7j/VEXuo9WprRorrdWZLVMq65dv5ZrIl80zwuGBSJAk0MWxV+wtKMVEm4jApHoa+nH5DBrjW9e13K5sqGhQWxaIBOTJ3mUCDsM6UzGM888I12s/iVmG/PiBsgB3uVL4Rg4Pj7CdrvFMFxgu92W9q9du4ZhGHDr5g0473F+cZHuwHAO6/Ua129cx+pghRCnBeZ0fFmMcD4JQvl+tVoBqEO6hHgCVKK66VsE/HR4ZkrLqA+hi3dIT4ieMP2clNQmCjiiTKAY43TxnUseQ+cd+q4rfZM+LCm+1WoFZq4ONrbCM3a7XY7V9XBu3lcNxLQCm2Kro3BEURD1+OrMVIXOhGrh1MB6fkjUWvPee5yfnKDnpCTkMFNL+Vb0mSpGq+j+OnLl4LYWgqn/KRHxtBM0eYFFkcvvVXyvkistJbakHKyRoZ9nTh5ioA7nW6pbjD29jWoBvQUJUx1T/3WdLaDVGpMFAHqsrecuU7y2HaknZK/rzFgAivG4BCJ07HqrTctjVnEvAVj9SVkTlEI67RZ2oJQuVPqcZG7yYoWY02x7h9h5jKsOn/rtr+C7f/RDXH/hOZD3IEdwTBjOzrF5fIJ7r7+JB2+/hScffoiL0zPsLjbYbDfonM9nBIxBqGlmhkKVPbd8jkDPiaXhUojKkkFp25DPao/qPDxnX19kXU8AdF40wLfAuNWny8BHq35mzoJpDgble8tzM3mqntW6S/pcne1qdUT6yPU4dF9I6Q+7rlrj0s+2wqSWSpm7Rp26TdFts/OZRp7pOVji09aYluZY85A2/qzTwhZ5tnXYWx9kb41FnFJXpfk+Wlc88xHe0+vM0qFuAMU40XxHNDd49c995+Hk/dSP2YigjR091zqcXvoh8k4OPuu5LrqR98/lVcqs/2iPPVyBJ9vzHbHdqgRKqZGFBV7rfWmrrvdq6/Oq5cqGBoBigVeKFkDfdSBH2G5HeN/lXY1jFM9WNjBiFGAM+OwWY47FYOAYcfPmDZydnaLvXaoDkyK+ceMG1qsVzs9PEWK6EXi73SJwRLda5efSJXld1+X+prh1ch7e1wLHnidoGRNiKZZJoFoByMKXC8GANHn7mKLQzgi9dFOjNENlF8WDpsPwzIhhSukaQoB3U7iUrTcsCHULQvVCTLsq0/kDq1iB6Sbvmhb1vQH6Ge290T+dc4ihFqp1fyfBMfPiBU5e3AzS5HOJJQfVi2gfAF4qRfDxZGzMAMYCTct4muPCtOXd+q7xt+17Swg7RwiBm7xHhneFJtpTtaT8WkohNupfpMGCkp8poBxioNuugNEla0q3p2mk16NWrI7mW+Ja4Wtwpse5pMgsj8p3+wwiAVJO9TOosztRPM6cwqgcU5YVHqMnBAeMvcfdT34c3/7TP8KLX/ocqO9A5OCJEHYDnjx4iO3jp3jw5jt485XX4GLA9uwM24sLXJyfA0QYOKJzrly4aemXezyjZ2vuWx58u/Yvm089XxZEt55rzb2l/xKQ0vKl1YbUZx0uFoTO1olZn/sA7dRn5Q3H3BBvjb1FUz2evUZcgzdtfTa0KcaYQjAbvKD70Oqn1hH75kjkdQghBbou9FPL9iXe0LJNaLrMM7UjQbfb2lHRYW+td1plHy9bZ5z9Xp8NtGskPQSAYxMq7tUzzMXpp+tf6v/SfGs9O4YAcvOMUvvW7D4+avXDfDKTS8JD0rfZOjX11AbR3Hj/D1HseCfaTOnp7fj2zQczcH5xnmUOBFzIm0udmMnXqf6/u1HVKlc2NLquWwQe4zgCJLGQ6TZMubQPAJgDYt5pGMcB4zjAr5JxMg5jyiTlCJ3v8MKLz+HGjetgTrsEcu7g+PgYq9UKZ2en2A0Dxhiw2W6SIcCM9cEaQExnNrwrBgaz5HFPccBSXy342ilcmVmZzJkhYpwJyJpR2p6I4oUAygFBqWMSXsmLOIwB0U2MJanLtJCfFkAtBIdhmABKjHCMYshZxWGNk0oBuHqR2a3Uug9CIUKINT10XKxd/PI9lzhsqvjMKjENCJ3LW/5IoURy23UaS0y7CsrwkR2YJHRG4ArKoFbgaZt2n+LW9C0Hs1ydTUjTXPOHVVS63ppHpnf0761QihYAkOcrIEg5TaI5LqcBo+0PkAW08a4BteK1OwJLAK6sI6o/s+Nr0bw1zkp4qjVrQZhOz2tpu1Snbtvy9dz4vlxgE6VtgaVwmI4Bx5TCoyIB7DAAiOSw6YDj5+7gm9//Hn7re9+BO1xh7BxGAmgXsHl6iu3jE7z32pv48K13cfrhI2xOz3B2fpruEOK8c+Hl/IWVSZrW0zkJvSbl+dZ8aPrZQ+P7AEULENbrsS4toNr6nRR/6e9b/bHv6yJyTRdrZJMx2Gy9S7yUwkrrrDtaTrcMiBYtrexYkiUMNPtpx6jnQjuWluakZXxpntFjtzLMfg8Viqo90zKeJZ7QdJuH3syNWQCzG4/1OFrzt28ubH/0c9Z4k7HYOvV8WppagFwiG1yLhvM+aBqwGavdlRHZ3HL6aHlgZbeUlpHWkrvyvuwwtpyiLRmin7Gpm7XsEVqVOSfKoZvz9OL2bpElmtoxt/RD6fcCiLd0997vdbAVHcEpY6Qjl87xImEje/p9aY1quk10RTVqiwOWsMVSubKhYYXMFCaSYtcRJ0ODKF1Otd1tEULNcCmlrBxsSTdosqd06Dp70UMYIQfiVqtVORx5dnaGi80FYgzYDTsMYYR3Dl3fIZQD2wEhjmDuCoG6Lp0pkB0VybohC1PvYOidDX0orxyUXiBuxfSUYv9ai0R+bwHLGCPGvHXvyJeL2RgptrFT77k8Nm+8sQLUp8JlN0SXlnKwW5vynF6kIrz19m5hOkMPoXWMsaRe07wg9BaaWcWQ6p1iJqs+5JXAzAg8IpAD3DTnib3mQkeP3woLWdx2AZV5Qq2QrDLSdWlFuDpYV3SenovQB1xte/rvipcWBEaieXs3Q9N0Nq4YwW76rPKmK2U46x+hGGwyL8MwlPtUtHEH1MB7yUsrxri0aQX2Zcq8Gpe8m/6YjWNfsQr9qkL1snW2pBhBVJ0v0crUxwjPADEhgLAjIKxXiAcrfOl3v4pv/egPcP3ObTARAgAXgLDd4fTBhzh58AHe+OXLeP/NtxEvdtheXAAMkFKs3vviACOgeDU1OJvGP/dA7zMcLOCwz9k1BLSNC00ru9Za9GwBtRaIXQLJrTZb45b+CkCpQGxkRMzrtzw1a78B8ojqMD4NSFp1yrstp0NFByr/20tDTUupF0Yf6HftDmCLrhaY7euD/lyPy5YWWNR6ZanU8zsP5VuSGy2+WuKnFu+0xrm0Pi6rnyg76jAPBVritQogN+ou/EQEbpBAA/nWu7Z/9u8lmaplSkuu6DomWgJA+/nL9EUMtUFaZYecnfmqHVnA3KlksVGR5d4jhMnIsQZzAM/qED0awpiSjSg5w5xcQxJS33GHcbeDnAuyY6/miDALnZqwDjUT1VxFB7bKlQ0Nm5ZT/sWYD0hzzB5RFp2eLxhJF635Lhkhq24FUGLcMYQUKkQOMQR03kFScRERVqtV2hlxDpvNBpvNBjEyxhDQ9X0KnwqheOx3wxbedzlUigFikOOU/znMPQlTPO5cSAhAiXkio5zDuERg5VoqYFyHVdWlVgzZ48IRFIFxyMZNCPk8y3QIeAwBjgi+86BQe8krzz9R5VlbKpXQR1voy3wvCVciuSBs6ocIoJZHvtpOVeFROkQvHbJu9CdyEYyOCKt+hZ5S1gWKIYeXUemHhDwMw4CAubJqKcDZzoOj2biXaLnZbOC9R5/Px9g2co0gqoGTBhBXWdRWWWtPaEuR6zUscxKiZJ+a6tTZyxaBMgORQ9V/rdAsMNRt2jGUenky6PaBkVa/7PqWNbxPqV+1LAHbj1rfEqACc7HuhU7O5YPeziFwQCQgrHrs1ivc+fxn8J2/9yd47nMvAo4xeg8EBnYBFx8+wdP7D/HhW2/irZdfwcnDxxguNuDICIjwfZ+zQ6W++3xiUIyNNKiPRo+lMJjWPNZhe22nh/6sFRazZCB8lDJfj1cr0q6+bb71PTMXo832eZEPgGZotaajpqXIeg08Wu+0QFt6AbOkGftoK/qMOCZt3+hTC1QurZslPWLLkhywRsQS6L+K3J5eQrkI7zLeaM2t7m/5G+mwvT1fYftqdU4L3O7ri5bZl83lZWXW3oIhYY2CiifMHF8F+EudNopCt9UCvUQAOQ+dzrWl9+RvkSvJaTk9P45jlQKaXNs5YvV2qw09J0DWTTXkrOgC1HpM1+GIEBvtpGMHKZKo6FfpF3SSh2W5aeeQQJUMWqLjVctH2tFInREFPnljAYBjxG7Y5oOXhA8//BBEhN77ZGhQ8iyv1ivEcUBgxuE6XbDnCIgk2aAYRIzVao2u6xBCwPn5Oc7Pz8uEed+BAPT9CkQjHj18hM3FBswOR4c+HWoEgBiAmMF5TNlOvEvZWhhADCOEKbXhVIBeBrPn5+cF4DPmjCSEL+EoeWdGPOlyWBxIqWkhKVrzORUBREBi8jAGgB1CDOl779GverhhhxDFCSXeJC6pbvt8TiXboykBAaXQEeFtzv/2AQlSqk4zZcvL1hIa2hCR9IfaUJW/5dko+RYaglK6WpSlKNTIxbr3jtBdO8K1u8/g8ZOniPcfwPEUkpWZFs57BDnTkzOoSf8noRMnD7jW+A3BoCkm3gMgnV85PT3F0dFRut/DKMay6FGDSz1mK9haoSzVnJm5sErGKuqqTzkMIobEby7TWYSb8HxLker1IEw2jmM51Gy9OhYUWMWjvUdLinKfkJvRBQvArUG7y8plwvqyQsn3UbJr5caTMZHpTJkXvfMpAx6SIUirHlsCrr3wHL7zoz/EZ7/+28DRGpFGEDPiMCKcbfDorXu49/IbePL+Azy8dw/jdovxYlM8V0TTDcbeeWTLLmWw4doDT9QKkaxpoMFAk7c4rUH5KNXTmpFU7G6G/im/aw/6jMZ7DJL0+7y+JSNnXz3lJ6FczBeUjswCYUo+UurK9Yr8ByqaEaXwU1nz+jvZKbRrHKidS62+2nms+L3B+y1gURkGPO02LxkXek4sXVvyKlGHyv+16UVTxeWnpJ5fMiYsXe04WvNbPlcscdWxXSYXNMaw71c0oDlf2Gdt0WFhMUawCp3Scy88mluslyHNx1b0Ihhjw5idry9jOLHsFtS7a1Dh0i3Za3fSa0xAah3n9VbYYm7stDCKxjKCQfTugfzuvU9ZKiXihbngL2vM2XmTOojmySNav8cYS+IYTcOpv3XWzbptYNjt4D1V7wEo96gtlVb/U1pRztcQJKdUCzNeRW8CH8HQGIYhvdCl+zDIASDGMA7F6z4OaWtn1fd45eWX8aM/+EP4zsET0OVO8jjgYJV3IxjoKN04SSsPAuPBvXdw/egQ2zEWD7Rkn5KDygKyV32HVb/Gdjvg5z//Jb7z7W+DxwAeR1DnwSGAspETOXtp+w6RA2Icsd2egjACmMeQy4QKs4SYQkqiEvQtgSBKRE9KWeQhFEMNuU9U0tYC7CiFRAWHyLleRxhdMsQQsueKs6cASLmS870EkZMVElPuWUS1OySRhsziuZ68vVpZ5VkqY9FCXI/F3mhdfqqsX3p3gnke71/ok4F609KG7IxNKQmTWicw9ejzPJ1wwJe+/TtYPfsMfvp/+7/jkJIiKhf95TH5vgOb3O+lv6z2cgQsmHnUY5Uib+mdiPV6jb7vq+e1wGkJP/ts6/f8QdUnq1AtfwImXV9DUAGMTsV8Fh7LtGfTXnnfhH555xM9eA4sdLFrpzyT144FDXY8LQWvPeUzvq2JXP1shVW0wIU9N6DbEEVovVC6/nSrTQpvYkcpC3FgEAOR8gplgo95bfc9Rg4IXQ8cHeBrv/8d/OYffBerm9fAjuARQLuA8ewcTx88xPuvv4VH77yPR+/dx/nTE3B2XETKGfhA6JAOlAOUUhvTtEUOEChGyF0CAszTMCaD3M7Z0jwLDVI430Ry2bmdZqUNqPRnGnjY7/Vnlj910X0T2WS/144mLd80H0hJ/JDnMe17Jzml6RYZEDDMgIQNS3p4qzusYWDp0VoDduwtg8+OcwngtWSJbceGUV9lnWra2Xc0gOREFF1b3rnWDo1sqAHw5HJK+lABY9u+prEOP1uiVWvudT12bK22tL5LoWb75fvSfFlgr9tr6kyq02VXcoi5nN9IZOSif0E0q5OLTqR8H057/KLbbHFQ73A6C5jWcjoTaOdA/73IRxEg58uuE5hm66W1blt12/XcCnUnUYdKZoqP0CZEkfbnIezLRlU1PqptP+mL4MolmgCE3bDDUXcAYIr2YEz4ZM4rykIDKrkHJnSUz2qUPlMJud3Hr63ykbJOxRhwenqOYdiBEeF9svgSmE+M5vse4zDgZz/9Kd59713cunOrgC7nHB7ce4A7d+4gxAjvU1jJw8eP4R3h3bffwi9+8QsAwMHBAc7OzrDZbKoFGTl5srWn3DmHf/pP/ymOj47whS98EZQvuFut19hsd2BmXGw2WK16RI7Y7bYYxx02my2smSbCKi2wFIrCxfLO5yjGgHEM6LrEOFXKUiCFOKkbxS3gs9vcOpQrMoDI6V6BmHLaM1KoVJ8FBTNPue0jo+vqWHq9g8BGQVchVtnYsMCJkRbXPoVuFWQZUzY0dLhD8QwYOreEu9DIhjXNwXOamzDsQB7lEP3FxUWiebKiKhpLvfrA+SwGXbSa9qJdoej+yW5J+onZOKqF21AWrfFWgta0XQOMq3sZbN/tYckimLNAatWrvcvF2JCY/0vabK0PIko7eao/Vqi1lMTSd3Yslu/sZy3+bhUb/rM0Rl3/yFwu1mMGKKZ15hgYwYieQHDYRaDzKcNZdA7Pf+UL+N4/+DPcfe4uwroDdQ7EwHixxfbhIzx873289utX8PYrr4OGgLjdgccACUOzZ2WYecbbNeip45WXFKQFJC3gm34Cmms1XaSKpfltASmhv5VHWra2zha1ijU+Jhos81vFWxm4lTBEcYY4B0+u6uO+NVwZNjx31rT6LO2IvBeetWO3dJzJl2zc76OPNeCY4wxkaQ9uC+jp/tm5AzKQ2zNfLaNFipZBtq9LTjGtD2sZ4GYHwi8rmk77zmXacdj+yHc6AmCfvLN9F8OA9jyfQl7tZQ5zY6fM5cJYbZ9aslzOAchzL774Iu7fv4/NZoO+93U/MF/X0oaW39HootbvLQNGvtc4Y8I8beeE5ttJx078aosOl6/W9J4ylwttvEVUt6j7450rTj9mkbmXlxaPCY64Sn+vWq5saJydnWXBBqzXK/SrrizgMcZ0WU2chMjDhw/xT/7JP8H//D/9T+G7iDHssFr1uH3nbgKAkXGxuwAz4/DgEKenJ/i//l/+CbbbAb7r8PT0NIUsZWEqZzVEuEnbsqg/+OAD/L//P/8c/5uv/Ca2u2RckPMpGxVz9i4TvOswDuc4v7hYHGsBXiTZq3wyLoYRUQkg7UXRnjBC7d1uCT/9M8gZDJq2jL0jjCEZd8mYGeEVANBWLjAJTZvGTRhmDtSnhSILQoMmBpcLgXT9uh59IHyK95/6pj0ELfpKiflQtDaGZCcEM3CuF0V+P0YcHB6gcx48jOgp+42NwrP9twBTCzEN3i8tWbLrRVvAAQPkph2g2qiTsJK2ILTj3dsFVaem8UcRCrJ2dRwxx4AISne4uHncsvYOAtOa4IapMRPUVJ+TyR8u7ny1AJPtRwtMtAyMqbk2ANunHLQiuaxowBAp/cutwZPPRjKj52yAOI/QeQy9x83nnsO3f/D7+MTXvgJ3vEbMmYi3ZxegXcCH793Duz/7Jd574y08ffIkXc45jCmznnP5Yqr5OYiWUaXpOAOiZsxyb45W5LN1VO2atWluZWMLmLVA2VL/dDjmZcZKi4+sjLFKuHLSqPNNkn3J1sGQy6+WL5qz40pjcCVl+RLf6j5q4NQ6q9H6W49LdiBbfbL1TbTgYsRqed+aRz0+qUOv18vkbEv223Es8QuAWbiZHluMU3KY6S6sxa7s7Z+VbeapDAD3yyJLS9GFV5HnpU7mEu5j+5V7UgF6TbvFEF3TrF0T+u+6j/U6GoYBm80mR4nEQmv9jH6/aSDCz+hyFZ7TfdXRKjCAfomu+pml+ZM1qGVRizevoDpKndO4598BOVyO0lmMhDuuVrmghb+L4fBR37myoXF0dISSMQoMRshpbfPhZU6w1bkpBvhXv34Zf/Xjv8Y3v/lNrFYrrFZrEDnshh0YhNXqAOfnZxjGEb/65a9xenqG1arH06cnuLjYVHFyekHoyRPhHELA3/7t3+LnP/8Fvvzl38AYIoYxoAuMrvM4PDzGdrvBbrfFwcFBPlg+gjlpb63A9OSmcCnO2bMIKWUqYbPZpUPnlC7Zqi7tc3MBOsUYovythUkMAfmSXzhHs2wl+ndpp8uHRVnBOjsOSy/N8DFMOyS6nZalbusDUA65T+MkEM0P5gkIKMYDTLgK1wKmEqymH2U8SOFQ3qdLDMMwonM+hackFq28FLpua3DIHJBrLx4rVHRfmbl0UuqqPPw09zjpPrGaM3nPKmzbfoyxEo6lrUwx2U2b9dM8q3ljn3Fjb23XpQVMpX+L4XANgV36ZJ7R4MmOV8sE6znSY6wMaK5DJ3QfNA2scrBAutUfTVPbTyIqNzBTDqECkpwcwDjwPZiBDRHczWP81ve/g6/9wffRXT8Ce0q7IQxsnp7i9P5D3HvtTZw/eoIHr7yOi6cnoFjyzKT2XH0fRmtMdi7S723FKPTR9NNzqJ0Ktv5WaNrUpxS/bYGPrndfHXZerJyaz1UbSOj3LC+1jBq91rnxDIDsoZ/TIcmMWjaW8DrvoZ28OqmIpqnut+U3/Y7oR70GKqPc8Ksdr9DFhszZvlwFAGsZrOsvz3AO5FmoS/OGPecn47JGi23D6nfZfZ7tpmPuRJP6WhjE6sYZTQgzmb1EK01rux4sPezvhbcw6VF774Yehy2tULhULyqMoX9K0Q6ioueZlaedcf/+/WntNIwX27blvfRhLa+XsI7Wa1pP1OOSMMd6zbT0pqVdS4doGaLHUNN2Wf7KOQzbJlD8mVV90n9mTkcXOD1F2SkVxlDoL3Mk9TLzLBTOjt+KS0uby/hZypUNDecUIFcJejkyOu9zLKqAK2GyiL/+m7/Bl7/yG1it19iNI8DAGEaMY0AYd4iR4X2HP//zf41xjHAuHZQexgFd16Hv+4ppmLlkm2Jm7PLuRfoceP/+B/jCFyJ8l279HsaAzXYL77p8oJvQ9132NKUDsEzpAOu7776L5557riKkeKRiTMbGOAaEnLp2GMay01IxXay3iNP7U2YQzfyVx5O5xAOCpmxJq34F53xa7PmcBiEfKOXMNGgLI6tEK0EIlLmyQkJ7uVqKTD5vARcL3DQN7MFR3U8dIjAJswjCfOFPCy6dTTl7+hRxGJInMOa7Adzcy6IXkhbgLJLULByrpKSOCsgSIfB8fGJc2TrKnDiq2ltSUhZY6OftwtfT33q+NTbbXtVmerAAksXnrBJMXy4orYkempdijM2tdGB+4ZNue/Hsj5IbNhyvBaKXaGGfk35bxd16v15vlHcZ0veBI6jzCN7hwgGuW+FTv/VlfO1Hf4hbn3gRu46w8w59ZPjdiCcfPMTuySle/ekv8MavX0G82IJyaGiiQ3KEOEkygTkv2/nSQLI1Tp19rMV7Qv/FMRsgOp+n6UC5lpHyjm5H9/8qCq7dp/ozPQb902ZZ1Gt+JguUnKlADmIJQZ2Ny4ANfXYrOarmtLysiMFiaWN3HS19Sow+aj21b16dm4dpLs/xvLTkKhTHWgPB9qMGnvMQk6uAoAK2jIPhMrmpxwrgUn0IoOhn+UyHuy0aDKpYOdnSl2UtE1VpUitdS3PwrPvdlNfqNyuD99Foqn/6u2qD6tqX6pnxINd0askFuxZ13fO+YzGbqO6vXlsyrhorzs/nLRBlNs/aoTZ/vJh4AOZrONuwJatZ2argvDun1oMNJcYCvbn+YJE2Vy0fMevU9LcYHiGH9rSaJBBu3LgF5zpst0P2EqQD3nGMCGOEc4QxBnz969/AK7/+dZksvZ0p7Y/jiGEcy50WovC99+j7HnefeR5f/NKXsdkNWB0cYhgDtsOYBPAYcHiwhvcOwzAWoosVuV6v8eyzz8I5h3EccX5+jq5fgchjGLYIIRlA4y4ATOi6Hs716Do/U8J6Iiwo1d8BNfPHGFPIg0s5k2P2UiZjqxAVvutAeYGVrEBxQWA4gMME/GVhOucK4BHBVxsG8xndt4jSu+33pFgBLkUbsU1jyNRR+oJkEHGMePbuMyl0bxjTYfEG6NbjbylIR64cGl/qd1PpYVqvdr6lfxr0FkMzolyMqMfWGq/uh37K0kuHoC0pzKXzLwuqAtH0U5ePImxafbZKQsfztp61pbXbMRuBUaa6rss8xh+pKHBo5wVIjjgC4MWg7TqMnjB64OanPo5v/9EP8MkvfRHoPAIRPDv4TcD45ASnH3yIe2++jfdeexOnHz6C3wwIFzu4kmVj7vHSvK5B42XGnx1Dy5jSzwDzszrWCNPro35/3g8tZ3Qd9ixcq//7xwbIQXcpLWNGf76vvul3mvEWEVVx/vP+1aChmjPT3nId9RzYnbuSUj1/b1NWu7wjLjH6tj07VtMraJnd4o1WadF5moP28y0ZaAGT5vUleSFjL4B8Iaw3OfKSLrN8cBk/SH+m/skzmIH8j1L2yUDdbvojYS9NIw2EI7d3f/99yr76WmdWkjziRUebLUt9rHRHhenma6V1his3jMjLyWp03+r66nT+S+OwMkUb1PYZRwSm2rFT9JexMzRv6vqo1DftuLZ2cpYiDq5aNJ9fVq5saJRdDEoarTAxkkAV8omg9M7j+Np1fP1b38QQGS4EbM/PsFqtsBtGbM438OSx2W3Rdx0+/6Uv45nnX8CThw+xWq9xROlcyHa7TXcfaCVDCeh3nS/Cc7Ve47/3D/4ButUKu3HE4ydPsF6vsVqvASL4foUIhzAEhDDAOY8YQ/JGBcKwG7BaraabtbPHQTI4MYAhjBjGASlbAkr7rS236eeUmmyK152HbIjRAFbAFJRy5wOgyKAQUngaUUmzlrbF5p5h+V0OJFqvjW5X/6uAHebCQ9evf5bFVP6nrXDMrGLdHgB4IkyX12XOygJTIv7T83nHAK4YWztmjCcncGHAB+++nVLqcQTzPANJJbDzApXtw7iw+DTATzs9KS47u/vBTFMWDGBKJ0yTMaHp1SotI4zVd/ozZhTwOLkvJmOnZVxY8Fk9p8BP2Wad8CtkqzpPyBTbiZrX636ymvplZW3758mh5D5jgDmWez500eCqBUrtc8vrc34mpPBmISpB9gcqcJKIA1a7MJ4BD4dIhOAYgTmnLAS6CPScHAmjdxg6grtzA9/5wffxuW//Dvy1AwwgeCasIrB9fIKTBx/i/mtv4o2XX8b777wHChEelG4JF+CShAIoKxcg8x1poJMyHRHVAF+emQyGGjhbkDJpOlZ/c54r66SQuuq51r/LO60QldTuNKfOiQc3KlA6eWBaxp30o6wN9SlluS63/xLygoUQThn2+wAiJ17nLLshoQugkq5yGq/oUTdRqQGmZW1Z3lweo57DyQmnZbqlsbSVEXCiMWXwdAUQsg98T3W3v28Zk1cMLa/qnvh6vkO+bxdUPpN/NV0kaiPzLgGErC8KL+ddBZecpxCgT+KqimpIBNDcA86MHKkw1wtaXrVAvDVqK9rEJBOcOOKyWBB5ltRrkd55/c+zYtnd5MjITjyUO5f28SNnocBoy93IcZasZqlU47VtYNptkDBBHSJtDVHd70mucaFNhgYpvJVRUijrNSS6l6jun92Vbc/ZdBi/vMdTamyRz0WyUc42W2LNFBZRf4WYdWX+zGn+NfoxySpOeqNN8fT//H1UtP67lKuHTkn6RUxAMP3uEHJIVJ4XeN/Bdx3+x//4f4LPf+FL5fAPBCA6D+c7xAgcHB2n8CMP/OP/6f8M/+V/8V/g4cMHBUBcXFyAiEqIklBuElJpIfzohz/C7/7u99H1B9UuB5hwcbHBMEYcHR7A50NSznu46BDGITGTimMMMcJ1HiHf7BpBBYRGRDACQhywIn0TdWLCcvDMiTByCmPLRLXj+1xe/N65tO3uUnakgQf05NB3XaJhwRaULqaLdf5nveiY50ZQEcA8xe9aEDaputzzPUw2UzgFuKu+wQHkZ4rPe5+NqxyCB1S0ER7Laj8t4oxhPSIGjgi+x0HfYx0Dnty/B+8AjlTVVWVlUYbZknFR6CB0ocz4WQpVGVdkIRMKvSfvSjoLs+Tx0YqwilNX3KL7krBtuhF+el+EdNtDrH9quhYhSwR2SZhFEtUoEhTq52SEKBFQ8Y4GDfrMixbELUPArgPhT0ICPp1zCDzfb7Lztk9haRroNavpUgGSUIdJkQg4eT4HwLS8WkTq/Ao43xHkAOcxeIfx8ACf/dbX8Dt//AOsn7mJQAEuBnQM0GaH00dP8eE79/DWK6/iwZvv4OTh45S227l0XiPLOJ/nIgEB67VC4QsxiGXS5nNGmS40A0SatpMO1WueQCR1aGNBZ0ua+LA1P0Irfft1jCj1aeAofRD5n+Z8nzdS/a6aDpJcQ/SaI5CEMEVGUBOrjYKpbc5y2JURyhmD4nRAOks2yZipAy1AkvhsbpDJ9/rzpoFveVjRTrdRvccSsuWmsfKUVlwAqAZuMH3RNAHmZ7daY9Blem4uG6x+0u0tAXK7u9OiidWLNX1kzdTdSn8LOAdAEc6LASkyTjlF1VpKWD6nW88pn2O546CmU4uXbYhWq5T34rSrxvlyX5ZdDkIVzVCGx9noNvwiP536XsLtGHNjo+q7obf8nkIT2+OYdGetG6Znaxlv9Zml3Qzb8JShTp71xXGYsRWmkKQIatIk5nvO7PkyKVbX1f2SMUmdmYcytqP8YZFxNvKBxZzITh7KxgtN0kPfdaz1W6UjiwiwO4IEkAMxTYaiq41RTYvLykfY0agBS2F6Iywl1vTFF1/EV3/rt7DuexwfHRXFOAzp3o1wHOB9j5A9lsNug0996pP45je/if/6v/6vwMQ4yJedaUYKxjPvvcdqtcLXv/ENdF2P1WqVdjJWq3K+w3uPk5MzgNI17eR6gEfstmmXYRxDofk4juXyFsmsIQsDWQCNIWA08bB6Ap13GMNY+m2f0XS0QtCJomIHonRYu++7/D0AUKH5BJJq0KQP20EpCG2NhxBAkWd9mgDtJPzswtULzioTy9D1tun0ud51sUJ/H/OW9jitSE8OLgLbkzOcfPAQ26enuM7TFqR+pwD1PaUlpIQeLaG61F95Ru/EtRQEm+fLT/XdHExP/Wh5KfeNyR7q5ITUsgGzP+OTntPEWyjG9UwxuVrAWoFrgYAW1NUOmYAvolpyNvrXAl62//ZwsW7bCvKynhte4CVhGwgYHKEHoQ+ENScDNBIwdA7bdYcXvvhZfOOPf4S7n/w4giMQA30EVuRx/uQEH7zzHu699ibuvfk2Prx3H3E7wOd+dF1X5I73Hg7ihWuvVWB+AFDzgD1XpGPHRRlPYVdizM6V6pIh2aKR/Vxf/GbPBegyiy8287FEA/3s0j0A8vdVQgGWYrFnPNh4RhcLkGt9sewp1u/rtWTXjD5vsiRb9wEjW64WR95eH0tzswT0W4BR96M87+ZrvmVE7KvL6qT6s1DmY6obELBrdfxiUV+L/Jb37PpcAqcz7HUJjS0/SON2B6XUk7GLbqfI4+zgEyOFkVQwX+L8EdpJH7QxwDVZZphI06jaSVhYFppvLA/aYvFJC6MtlaV1Yj8XLNxac5fhnKuU+v1kcHgv+i2HgxnnmLT/UUvRB5jz6FXKR7pHwyom+X29SvdkCMAHUpaqB/cf4O4zDuv1Gs579H2HzndYHR7gAtu0YxAjQhgxhhEYx3TXhVJuoviKN0X5e/Rgz8/OquwKAIpiDiHg4OAQXZc2E50DQiAMQ2o3xoiLiw2AfEBT50COycgKIRTQLmdEtHLVf9tFr5neeiWsoaGNDGES33WIAsLCdMCQcywpERVv/7Stl+lAE5PYLB26/zPmo+WFqseqM6ZI2y06pHbn3uyWMLH9WwJ1MeZMU2PE2vV4/F4CZS4wmGO65FDNQf6jlm6NYuemGChU02wK23Gz3Qc5TGr5omoni9qWYBRDY9YPFqO7TSPhWzse5imfvH4v8QhNbV4inDV9BCQKkKnz/be3q5fmVPd7CUSmrrbv1rC00EBDh1dpkK2faQn+fWyyJGwlyMpHQhdTCObOA5sOOP7Y8/idP/oBPv21r2A48NhQCqXyQwSfnOHhBx/i3Tffwmu/fgWP3n+A8WKbQqUcVZc/2hAj6YU1iDR4kt9tBho9dm00Sha9qh3D/3aupH9L9NpnAOjPpucsFGlnZFsyMoRWV1Ww09paNjZa4FLzmeatCC7nNKwstH0S+icDZQJTLSDeCgmxh9mZeZbW1RogdlzN9Tfb256cRvpSuBbQvwoYkXUvcnTfe5Z+IQQ4pFBEHYrSAqotB4rue8tp2JKjFsxaei0PFJBtA2b7fO1AWQLJtn1b9Oc6uUD9Lgpm0KWskwZQr3+mOkLeGUGWP/vWlp3Tspuwx2lk+VqPQfdp6V1LD1uWwpuaYbRI9Jzfl0bFOSd1LvHvEu8t4UZLhxYmkXdcbjMlOZoMP44RnGVJS/dqfGJlDLPRiSJ3yMiHS2SqlCsbGuv1Guv1GgcHB/DeY71epwq6Dr3vSpo4IcjR0VFOaZsMj912CwLQ+w7jOGIcBmyHEbtxACOl5gKlUKmTkxMcXTsuB8KLB56SkaHDRsSYODg4wObiAs73Vaaf3W6Xtwt9OkSNCA6xTMwwbgAQXn/9dTw9eYovfPGL6NcrIWMyhkK+HTwwhny4XAtsbXglxV8LNvkp45DdnSYI40m4J8GbDLGUMUuYD9CqIsQw3YBtvX4OkKh3HbeYFNF8e1LelaKFdLV1jnqxyFkZGxc81T9t10qxTN5SqPr3maAnwhACiAm78wucPn4Cn9sZA4MzkXR/pFhl2BJKVXvgEqc4V9ZJAGsvOVDfs9ICJ3asi+B1BubqPto+LxUrYKrvFKhbEuZWIMlun4yxDs9IRoEAVmuASv0t48Aq2mluqOqH0Ne+p+fSKlo77pYRUoS1qc/yp6UtEaFjgg8uxUevPE4pIN48wm/+wXfx1e9/H/3hIcaVA/cEjAHxYoOLx6d45a9+grdfeRVPPnyI7cUm8XFMZ6xcXtvS1wo0qtBIDSy1bNI7nS1eszytaVuHrcxjku1ctXaMloBT6ncNEDU9JQ7afq5/t/NuleDM2w/kC1XnnuMWQGFmlHAGQ3vNey26XqaQW+uBmRHDCAHdrWJBWwsgt8D2Uh80yKrGbgy9mt4oQNEavprnWnNgS2k3zp1gul29ziu6oZ4TLRfkOR07r+etVTTdLE00rWd6v8ETpU4xOkEginA5LDpGcSlN9Gvttupx2/Wmz+S0ZJnW0/KqHVMC1Aziei51ScBaOaQYIL9/185+auW6Hrt8r8di37HPan7TuyVCR+lbK2RX2hHnsU6/P7WZxizvawdjeqRtlM1op961Y23x42xuGrqYp8lEjAG73VDLFFeH09uLP62MqHcsFR3yUGJMBwNb2PaycmVD4/Of/3yliDSDc6gXBpAMkBdeeAExEFarFWh9gGEY0Pl01mLwHuebLZz3GMcBq/UKYbvFxz/+8XSmo3Po+x4HBwdFcOx2u3LtvFaM6/Uazz//PI6vXcf68CiFFOTvuq7D0dERiDoQMZjTAfDdLpTFEmPASy+9hLvbZ7Ber1MsOEsq2yn2OaUrnWIwI8fqUjs9gfKzNRE2Lly/Jx5RUDKo0s0QA4ZxxIqT15gldpwIUMJEt1eMraW+cO4/Wl6kicll8ekzDnYR2a3fq3g7nXPlDg4pdpFb2lnDJLp8/gEO675H5zsQgDGEZXc0TWDJ9q01V3X/2lWK4G3F+y8J4KU29pUW0NXttuq0c9tSoNGMvdXv1lwy1zxSKXKmkl5YnBC2Puudbin/qi9UqyULJCxdrMLR71kgY3f1yPBJax5b/SUAznXYeGB31OH5L38J3/7TH+D2Sy+AyQOuR8cMOh+wOTvHuy+/gkfv3MP9197C4wcfpjNNoHRewCHxa+cXQQ0n5quAmKWbXVf7QKddB/X8TAaHBp26PRt+ouvSgKieo+l7q3RbAE/+1jRpeShtbP80Q/WcLq3RYRjArNK3Y37Xim2zphuqMyFLa1HTL30+H3dZq43wMSsDLHjRdGjxxKL8yXbGEq+I8WX7b8u+kKyqH9Km7sKCTK7oo2jTllO1Q0TzqdTR0jXyvo4UWKLjZeGr8qz0LtWveb3Wjbrt6n3DP80dakO3Che4dHjdOu5yjXvmMclDMUGb2KVF+1RrcwxiIOrvWvLHjkeo2OpnC0/MRmJ4v9WeqlEgVNF1Ux1LezLzftu7Y5bkmg5dlfldWp92fOM4JOcxytItbLWkZ1tGjow7xnyW2TlEIDm8qK7vKvgG+AiGxvHxMUII6Pu0YyA7BensQlq8XZdCo0DprEMIAd6tKi/+OI44PDzEGAKGYcDq4AB932PYbdH3PT72sZdwfHyM3bAr5yzquwhQUpGJ0Oj7Ph8on7zqIR+AChnQOicLc8S42+DJ44cYhi1cttAODw9xeHSEN99+C7/81S/xzW99C+UgdeS8CzPCMSaDJzLYtRlGimYUDchEeLXChSgvapdivMrBdhfGdO+HZRizuLTQ5VgvpCLEiOHQLXh5anAgn2uAo9uTuHEZv11Euuj3dQyxvZRR5lF75zRzExEGRDClS/uAtOwDp1syaTqb1yxLCsjOYQUGliuDpJVtAaylBUlEk3dogV5L/VlS8C2AZues1Y+cZOVKwkO3EWNNw1axcfe6jb1AZ97TCoTpIjKipZi1gtgntKv5F0ndAPHTvKE4BeTz4D3OXMS1T30Mv/v3/wgvfemz8KsexEBHHcIQgO2AJ++8h9d//gu8//ZbCLsddhfb1M++T8koiMrOLWF5xyut8Xaqz0UqNnhCG5427G96dr/xqT+TPujQ15Z3OJ0vi9VuzPT+tIhb49a/t0JjWp/Z7wFU8th6AIXHyazBJVlRAYMrKmHhW2u4tcZt39vHz3b8dh1eVr+0YecMmGShlcktsLnv7+pz3u/Z1X3WugJ5DcrnrTTIWi7rObpMLur5sHN9FaA9vYDSV4lWSF8LH7Xb1G23+G4JbOv+2Drl79Zu31V51jlXzjtZnV/JoAa/lT7vEftafuj3krxbBsgtMG2/k+91O0t0TaqgXkNFFrv9a0m313Ki2LG2dPtV+NR+Ty7FsFAegMY6djdCGzhLdTJPe5uM+VGBq5QrGxo3bt6BxHqlhdylCWBgGHdwIByuD+Cdw6OHD/OBamC7u8D5+TlijLhz5w4iGN2qx8XmIp+UD3kHIoFp3/X45Kc+gyHssLm4wNnZGYjTod9nn3seq4MDvPXWW4nJOW337YYthjDg5qpDGAcQR5ydnWG3G3D79i2cnp4C5HBwcICu67C52OH07AJ9n4g7xpD+hQAmwvrwCENkcATG7Q677Q7bXcAQEqnPLgbEmE/5C89QZkiaUpVJEQUm50Ukv7kViBwB6pK97olSWlsiwHv41Qq83YJIebyI0tmNSugaz2F6eCa8YoyIYUg7MpmDpP/23oeWYLICQNfbWrhpuqb87VrgSTt6a89u/1sBRkRAACjFhiVDMgQQpywRlFNgih4qMp1rAT4zDlwGkeCcRSq3JauMJ5A5lezdYN4rUMo8l/moQarujz20Wve5Bs2VAJVndPV5bgk0CU35jCTMicqZkGpke4VJGrcOnSvfOEqx03t27+TdqxgdlXLSUg9IY3W1UtU/Lf9omrkc5ihGVsrilmRLOiMlY2IEcFprLtGugwONDILDQJQOgd+9hW/+6A/wpW/9DtzxGpEAzx5+iIgXF7h4+hSv//JXOPvgEd57/Q2cPH6MvuvgvcOqS/Pqna/6HEOAZINKfZcQCIKk2SzeQUcTj6vxW89nyDxS1lRMOwuF7ynRlAkTPVyiGFS2GIYAionvygFdYApDo5SprRwkhfRPTamXXC9Ixnv+gij1o4TgCR/znK9Q2oo5VDPd00SUdoksTSwwaYVrAmlDQ9ZsekYZ18Qle12I2uhr8O/C39rYSfRrr4PLwhYsmGoB7zm9pl+yukg/qX5e9/lSYK36oIGO/bz+e9IttSExb6OmQyxzA2IUk5jr96z+aPXJ/s4sKWiR+S1V3DI0ban6LzKrCK0kZ5L8a4fT7JvfFh1030ukPlHOJsbgwJVjS9cpYdUOtdwsz5Ief97N2uPRl34wMyKHksFMojDAsoO1sBPSAN7ld5UBVa5bIJdkeYj5DhTicjt2MgoSvhKaWYeUlHmYM5cp0/IhfYBpvaBe7+KAs1hoieeWPrOhVkslMqPzTiUOopKKeJ8O1w6ggj2yfGMEAEm/KeVT6tyHcWy5sqHh/bpkXiLnsD5IrzIYNHbAGBHHiO12gw/uf4j10SE+/PARHp8+LdmjVhfnGJ4O+PjhAajz6L0va8+RRwwA+R43bt7BbrfB9Ws30fkPcPLkCVZdj5MnT/Dpu3fx2U9/Br/49S+xGwaMYQR5wmZzgRhGPHj/Q8QYcXR0hJOTE6z6Do8fP0LkiDt3noHveoQQcXh8HcwDtttzhBiwCyNCjLjz7DOgrsd2N8I5j5B3MobAGEJSkpvtkPMV1yklC1DnBOoEOOvdFyCFkmiAXRjSTx5MB2A3jnAxYggjVl2PwASKhJ48QIyRAwK4xBwL45T+ZEUOI1Sn3xnDuEtpMnOa2TKOIqfacc9aIVhvnAY2Mn75XEpr69r23RoE8rv89EhZEEIMcI6xci6l4BMBlaX71O4kOJqGC5CApLo3InKc9EM59CF1TUpZC8WWkpyDbA0Y7edtOk51Fq01X/BRjIwsAdWOlvMOOpNaeS/noW/tAC2NQxsoOjSqUqyYC1I9hvTRXPC2wmDSmkL5mU1J6VRBRZqXtMJsjUUUXvqXhi9AGJQMfZezQnHWKuwAEMOH3CffYUvAcLDCl775dXz9T3+Ao+fuprtcYsSaPMLJBicPn+De66/jrVdfxumTE5w8fgwKER0IPgCElFJbxudo2qnweW4kO17q+nRmS89NkTMyfmBG32SYkDBucdro6WegyBUBnOVmAE7ta9oWg5FyenCXEySI4aPTeGbWDLK2kgIoy0oMFwGfEB4PoRgpntuAiCjfikxTffK7vu27bfhOoEuXyMKrVAwWiXdP9M4Ho0GTDBeeM/Hzuth+23N7raK/0zsyLeNaZw+zB/urea4togzkJnFgQV8BTKZvFhAKcAmNXfiWXGEwHLnZ3MgY28YJV6E0zJPuEoNY5IG0Z8GkDcmd2lQgEpTQLCKYB8RY7+AsycgyNhJ4zsXIZkRF6/nZCDuftv7ZjgSV1TQZ8/lnZJ7SLINmdRfj26wDK7+1LK4cV6rU+jpOcoWT86C0p6aqRbtFgJyEWnGuyAWEzksOvjRqokxtnmSTGPQtbNGaSzG+7dgqPV++nJ4Th0grrLnUvIAZLK3tO/rz8n3+uVqvAc4XaWcdIrKlJX/s2epiaBAhpSw3uxfM+X6WOabbV65saEg8vQ5Xcs4hxADyhMNrK4wXW3z44ANsdzucXpzj/oMHgHO4ON9kAnlsLjZ47tkXwEjhSv9/2v6sWZIkSw/EvqNqZu5+14jIjMil9qyq7q5e0Oi1Gg00qtHAyAiFIpxnivCJzxTyF/CJv4XzwgdSyAdwBIMBBhhwMAC6gQa60dXVtXRWZkZkxnr36+5mqocPR4/qMXX1GzcBjFVFXndzM12OHj36nUWPjuMWIZV9vb5BjIxhuUSMASFMODl5gNubG8QYMHHEy1ev8Df+5q/j8ftP8I/++/8ezncAeVzdrPHJ02e4vd7g4OAATA6BgYvra4QIXK83WG62WLIXzwUIL169wuHhqqS3jcBms4Hvemw2W8QwYtrKYYHjdsQ0BRAc1uuAMIWdid73PUIIWK/XeZ9IjDFvnK8vFYAqjL1zwhi+E0WGi+ZPyTtRAAhnawCDU3hYWcyslT4LkYZC0GJyK4itkmCtfRrupFctkIDdjAq6ILTcbnW4gp1IORFALRhZlbWA9e0aODotfbiD/21b6w1a9mpt3GqVldsKoBYWNU1m5QEzcH+fDXD2Nzt2ZayRlQyGOScEgsXZpXA6Y5lT1eWuq+0qlXMXLC3yMwkotjYl1rSZjyt2+tSiR92W2r2tZdSgsW4/0Xzx0HoiAVsHOJZD+BQIEBgUCCv2uHXA7eGAR9/+Bn73H/whHn/9q/B9D4QJHTnEccL6/Axvnn2Bz37y13j26ae4ujrHuN6A08F7Li/Wu8YA/VvPU3vVoXp54SSBAa0YbitX9NLxqcubh08B9rwK+1flxk4YqKXpWxZ4faY1jq3vWs5di/kc9MxDCHZ4qOqPXiSN3GlHAdBzkG/Lqvt3V10qY60nZ9979bWvL8BuOt598sh+vovvlBdiVU4LuLYAY11+pkWMIp8q+lsQtI8Gtp5WXywdrIFsX/tSqVWZnOeAlVMtGmib9oU8zrxpO73ZVR5221bKqX9jzOd2PV9bfJUVucoIlWleHRaka52t6S5a1OPNui7tAdP1pff2hezY8uv2CA4rn7X+1l7SmkaUFcS3X/M5sju39/J9JZfuGidLDztv1KAUszHFFSxAbXxW022mzN9R93/KdW9F4/b2FovFIu/LYJZzLg4ODhARsbm+wfX1Nd68eYP17S0CGK9evcbjDz5E4BHDYoGb2w2c87i4usZ6s8HEQJgCtusNHAGvXr6GI8LR8QkAIIQJZ69v0Q9LjOME74Gz83Ocn5/jWx99hIePHuHlq9eITDg7u4BzSyxWB3jx+g2G1QHeefwEb968QQBhChFTYLy5vMIXXzzH5eUZHjw4Qp/ip8MUMW5l0/V2O2GaJBNBGMeczlZB77jdYr1eY7td5rzFOmgAMAwD1ut13mNiLU96KaNbIB05InI6nC5t2JJTkcXN6p1D5ClDHufkvA7nvKAhzIU4M+cMW9Y1rxfBwTlh7mmaZsK8Fup2Auj4Ky/UC30dPlQmzlxhye0gyl6VnUXeCI9aIdJ7zjk4L4oreL9g2Dfp53Qr9JmFMxA1hXcur7pf19VUPu5Y5Fi+7BE61Gj3PsFgBEkW8GqloQyi0Fgw3laHLrqWRjUNau9XDQxtuZZvalBq/7ZAIrgseZbmdwnrrJ6YgZ2NKycrNQMdeYAh4YzO4cYRDr/6Pn7jj34f3/z1X4YbOoAcKDBoM0kWtFdn+A//5o/x5tkL3JxfYJxGoJMw0OgARDnVeJ+WV4dFWNro97rds7lyB81EtdkFZfsuoanIpVZb7H6rGnTb52sgRtQGleV5NMtIK/k9+H9utbZ81fK0NulAcgCfZlDLMicbhtoAvgW06t9tW9TrIBt27x6Pup0tZQAooRF2/s3GoGqLVcxb4LD0Ydc8Uc+3lpyv14aZzDDyYV/4lP7eomVL4bTA0ho97Hyo16nSXulnGQv77+5rH7Cc8772fS4D6vXtbXygz+XPla9B62opahYTqIegLg/pV6VFKmRHyXhbW9s81O7HvnL2zbH6zIrWeO4LO7S8vxuKNvdo3PfSyIHW2naXrJqNR0O+1TKV0zhIeBxhs9lorzJPteZdTZMWve+Uq/R2+WSveysa19fXICJcX1/j0aNHsoF7HLE8WCVr/4RXr15hs9lgvdng+PQEm80Wzz5/ga7r4bt1TiH2+uwS4zSKqysKoEeIuL66AseIJ++9jxADNus1Hr37GOMUZE9HDAgx4uOf/xzf+va38Xf/8A/xD/+//wgxAp9+9jmev7yE63p45/HqzUUW3s45dEOHl68vcH19i3GcsN3e4ur2CofH35YTpscJm82I7SR1TFPAzc0Nrs/O4PyAiR2mKWDkAIQRt+tbrNcLHBwcZBrpIjaOI66vr2dKRkvA6ASZAYf0PlPSxKcxl00akqBneqTDcqwQ1cHP+zQqIVqELEBcMlCo96VO3avtUqZThrXpdPWd2no8n2Qua9at1L7MxStTg0QimnlsagCrolW9bkRqgZ4Lk33udwuSrOvYtk0+7x7cBihc3RUEtZCw40xEOQ93oZHpM9oWwlJHe3FkSIgUOCmZToFZUivIQASGeDlSEJJ3HrUSoJfl49yvVJjdaF3Gbxd41le9AAt/8Uyw10CtFpa5TiHYztjZtu+UCcxia2c8ycDA4tEgFp6dSMK13NEBfvHvfh+//Ld/F8OjY4wIcBFYBEI4v8bZq1f4qz//Czz765/j/OVrDOSBcURHeqp1lM16SRnQ0LUaDNTjq3P0rRv3GoDT0ktxek0jC6B1LmmYZ6IQNOnBvoXPGlXsxsl6PpXxlHAUO6/1CmE3i5u+p/vP3rbY1aCttmjWdKtBJ5F4kOtzGuqF2x5aaZUZ+32f59S2NcdHV8BTr/soL3YcyryahxK2+r2vzLr9NaC3tNoHsO1z9r2ZB4vaip+l8T66tehUIit3671rjrTkldwTRZtIQfeuQaauY8ZPDZAoaz7tqC6tdaT+vWVwALTbbUVwH6AE1PtdcIImeSntxAzYUijKRi0HbBtbQDmPPe0qqMBuJstWe1s0qvGDPpv3dvFumv76810Au+bnFqZo0bc1N/aVrf24c4xnNEh+8ZQ8w4YrxhjheK5gtfqq77QiD2rsaqbWva8v5dHw3ueYruvra3Rdh3G7Rd/3eHF5iYuLC2lsCPjoo4/w5s0bXI9vwCxZq7quw9HhIYjW2E5bdEOH7WaLq8tLrG9vsV3LWRvf+PpX8bWvfx0//elP0XUdHjx8hBgDnn/xOfqhx+uz17i8vsYv/tIv4/ziFv/+P/w5zi+ucXQyINyM6LoOF5cXiCHg8OgIR0dHGFi0zEmQGCJ5XN9s8PrsAg+PVgghKRvjiBAZU4j4/NkX+PRnP8NH3/kuumElno0wYuhciiWVAby5ucFqtQIz54Ndbm5u8ODBg1nGrHpw9Te7+On/IkMsZemdKUwYEuNRCOL9QJydjGqZKS98hkl2w0h4JlBaC1o9ierwhZbSoNdMi8c8ZWAteOxi0hLce71CISKCMTnkELzIjK4BTt62gMXG4lTeuUswAM7vCr164arb0Fo88me5sVOnvAfACHiikjsehOw656THWGAN6KLGpkui4NrxsWXva2O9SNi/LoHyFh3ssy0rkxW2NZ1an+u/FrTXC+COgOdil5uBD2a4GEHOI3YOt8TAwQpf/+Xv4Tf+6Ac4/PBdBMdgJgwB8OsR28tbvHn6DH/+p3+Kzz/5DGG9wQCHGLbwncMUIihKuJlzlPdxdF2XYmh322H7Wve9tRDlZxrz0ZQ246F5+UVprmmrvA7shjC0gVn78EjApnsEgF3wXsq4A2w05GppwPxZVXzqeWjpt9fqaDBbrYhoH6ysbM2ZfYt3izaWzq33WvKxfr/lEdx3EWi213Bfu0rbhE/q/tYgbF9f67Vqvs60w07fBuRa7QSQszS22mOft/y8w7MxmSTIgciDUcJ89wHpmh53t3nuSW89p5/rNbkp0/aETt33aq/F6RwsStOu4a36z73uWg+t57TFj3etBfq7Hktw11xslROxqyjY91rGH12La6NDSyFr/V4fPt26LLaZifMky5wpf/as+ayX1me9fvuv/TJo33VvRePx48foOo/lciUH9i0XOc3t0stBfh9++AHWtw9xdHSEr3/zG4DvceQWAFSIA1Oa0P0wAMTwncfR0RFWq6XsPYiMfljA+w4fvP8BLi8vsFws8OjhA5yenmK9uUaII96cvcH7mw1+87d+CycP3sFyeQjfL+C7Dt53ODo+BgHo+nTSeOcwhojBD0LkzgGY8PrsDeL6Bp33mKYIggNHCSN67733cLhYYLk6APkeB4dHAAd0jtH1JaXrarXKYA8Alsslvva1r8E5N8ufbBc1KzTKb2IlduQQNGwHkvUiBDn/g0HwXYfeEbbTFpEYPMXZoqsgC5hnxrJMJudxJIBtYldtDud6s7edWK0JA1Tp3ywz0jygaddFiR1FyE6IGpDWWrlLB5sVpSbMyrF11hM714NdTb08ywC3LcmE3QWhnti2/iy0VCGohCW0HXuAnJxnMPcwOOekNAX4YLHyVwJyn+JkD1O0yvFdikYNzrSdMc4VYH22FmaZfpXQsvTa52EBMAOPsfF7Pc65LqK8vyelE9odeyJMDuCOEHqPR9/6Jn7j7/8h3v/ud4BOstB0zMBmQrhd4+WzZ/jRn/1HXL16hYvPX8AFgCKBOMJ7h+AIjnzO9ESgssk6RsSkgFh61Nb3eqGw49+iz12XLWs+dgU418BGvBn761LwVYPNehHOPEIErjZ1747f3Do6S2PM3FRU63lT7/uwba/3o9VALhU4o9Gcl1LGuz0gpF7Q9122TOY2YLLP1vf0u86ZFnButoPkn55gXl/725+U5djeg3DXxva9Hp40L7St+95vXa1nmXm2j8TyfAtI7QK+9I8AOc07WY1pV5bX4P9t7d4B1faz6XvNq/P2oc2vXKsabTBdXwSIp6IJoBM/aghibk/b22LrqWlz32tXNu2uNUB7n1q99sq9e1d9Z3+sAayt6LUVoLZsade1rx/171kmxgjdLzlb4Wm+prTwHCBjPU1TMXo52T/YajOR/uf+170VjT/6e38glWi8p+m0HJkGgBkxbZKWDCoOAZQtxdq5KUy5nZrVJyY3edd1QMoi8OTdB3COEKYJzskO+WkaEeIkG7OdB+DwO7/1N4SJksWBSMC5MmZQ0EkC4mNkgBjTNIKI4ZGAOidPgnNYbzbAgyP4D5+IxV/DJ6YRIUw4OjyA9xJisFgs8kCoFUAPGqyZTUKfYjo2vkxUpzEtoJSqU8JIvBQKTCMoBjCPiOTgXQdiRpwmeNmiCuYI4rL5KUY94wS5fpsjHxUgrmPkWwt/E+Snxa0ldO3ViuMHRISRkxWb1GKSlC4FgnUbYhS+8YlOnXMYuj4NswOhndVKgb215lNOCbprzZpfBfhkl3HiK0ubGsDF/CzvgNla+s2EV1NBUNppSJIsgETSh8hzd3YLBLSA/V2b0KygUhADoISvaCrh5C0hl+hIBb7rwi1lSbdr4deyzrcWsSb4SvUXIiErEI6Fv0S5Q87mBGZwSofpmeBSHv8AxkSEa+dx9N5j/M4f/QDf+hu/ArcYMFGEA4NigBsjbl+8xrOffYwf//CH+PzZM8kQtZ3gQOg6mYe+9yWBA5Dlke98Ui7QvKyHaR+IaSnP5XMJyUhcIrwehX/sO6WuCCKfZYjsQVMZwmCev9dSpFuLqx1f20ZRNHQsNdyxhD1a/rXhkjHEolSr5VDnAc3fa/F7DRBquabv5UW5AsCl3P0e09bz2v5dEGT+YdcjV1sa20pZG3jeJZc5cvN0Z5krIkk0XbsaVIo8m5db/61ll/618fSzPiXlmzntR9Q5w0V21ApYixa2fufnBpnaq94C4OV9CflVA46dS7WMmr8rfK2hOhouX2AgZXnQOgHerse1rLNrbk2H1ne9ag9Xy9CXcQGwS5vUcueSEVTHz2AL2859c2s2H9LvioXKK8XDZnHIPiVlJv/Y1quKK0PNb631o7W+MpusW0ae1PJtp0+5nDZ/ttbzFiaycvOuMlQGWdmrnrZMN7Rlk5arvKFKRq7D1LdPtu0rt77urWg8fHiSJ2otKG3na8LYxkh2JwbQmwnT57I0RoyZ4Jw3A9thHEXBAAF9P6DrOB/U1xJ0GmssC1w5yA8o2huwMBO2pD3r+x4hHmC72cgZHiY1WIzSlr5zoOQB2G63YOa8AdwuiLrJ2tImx1qTgOTCk8VyqHnsiZJQigJw1KoSUm54DweXMgmFmJhVzLs55rUWHi0hU4/lPiZvLdrap1aYWK4Xu4w5E57SM6jylcUylUPh9J1cd9pM68kB/PYDumw9+piC3hqstRZliwjn/pk2qGdBUOU7kPdM6ALUqq+1OM/pXuhTCpG9DWTaZueEllEDDv27b15nulWgSD+7pBRLX9UzUlKm1rSxcslaX0ufd+m6D1zZ/uyIO0oCVsGQKq0EDUOWPkRO78rZJdE7jAT4o0P8xu//Ln7t938Pi6MlghdGWTJhe32L88s3OPv0GV7+5BN88pc/xvr6RlK0Kg0JCATAk5xZAaMEpoVrHEcQUdoHIV6NlvBuLW41HWpgRwkY5cfNvcBzBcZaZ+V5QgjReDDaC416qHRxq63p+xZkC551sLSdMTKc2wXvlgZWqYi6IGr7Gu+0QGmLnjWYrwGk1m3HRavdXfzL/Vb7W16e0gYxGlga1iEY9r5tf93Pus81YCKiLDt3LkaCZ6UcNvsTuGrTvrV/H4Dala9SqRlKFAWjACY7RpYeLQDXsj7XY9mSsYVO+oyhAd8NvlStZ1ASzy5lebbrjgJDQ2zs8tk+wF73vW6/rjPNdQxo8pIdr6asBWXcYfd+vu39FkjO9bMYmYns+OyOBTAP227xljxv/xUe0axTNS1nNKtkVq7blTG5C7DP6GrWupaSd9e41m2alVv1wTnZj6ln7/RDj947XF9fJpPNrgeohS0sjmZOhpVGVxV93IWzWte9FQ0VjrXVyg6WTuyQTv1mlsxU2knmAmbU5aMd1EEcx3EnHq8FvJg5u3r0O9FuvmAdjNYmSy1/HLd50cwboFLsNBLR9f2u6yRdLQFTUoy22+1O+do/OyGYOY9dvQBq3xQKEzm4pKk6IowxglnaFRXYJQbm2J44LaA5W4zQZurWvbrNdX11WNhdgrgW+IgxW8lagmNfWzwRpimASU5rv7g4T0CHk1LWuJizpa517et7+nFWf00Xy7f53Tym8/f2LXL2uTvbUrU3f0eRD/sW+V0a74YAtMCSllFvDG+BY9K+NxY0y4NKtzJH94c2tGixD5jPvqeD2hDTXLa2RXYg7zA5wrjwuO0IX/veL+D7f/gDPHjyGOyASIyOAd5O2Fxc4fLNGZ4+/QT/9v/3v6DbBoSbTQkVS4vwPqC9byysTFIa1+PfBGfm3Vou28XVhkfaBBStMbH12FBK+zxzsfjpAaQ1ALjLUGH/tni0Dpur+2rlTP3dPnuXh7KWzZZ287J3vX31s7b/++qydbb6Vc8927d9IGfnzI8qxK5uA3PZv5efoV3DSavdrcu2sSX76/7Wa0iLBq29NLVRps6OZftn67Ce9tY8sfW2+l7zZl3nndeMZ+Z9bob8YZcPavmg795l6ebsBZq3tVXWvLkMUNsQabtEpKoUUC+k9dyvr5YssDyb536leOnnFl/vK3/f/db79bqmc0RD2FvrYo235s8UJbLm5Zof73u9DXMBwPn5OTwB3ncFA8XyPoCZAdz2fTZmtN/TLkrInh/3XPdWNCxBWpNXFy+bJlWVDbt42tjNejGS0KS5B0AHXdOf2jqsC7a1EFrmKfSbu69t6lq7cHZdJ4pGLADAbtDRQ2KsBU+VFAC575otKXtRRB3coSmzqOExREzMYO/zwXF6cFaMku7WgeCNd4YqwVALJEubmcu1MVFq2tXl7oKZeYjS3qv6bdYu7F8YUcWA2rEOKXyKU/Gr1UEKTZua2njuh+lP3c+9guyOvtXvzEDKnv616A4Y5XoPvfa5vPNnKbS5WM1osGcBbcVv3meB3amnApxW6W6BtX11Kc+2QHYtvFuAA5ROpAbQseQi04yy+bRn57D2hP7JQ/ztv/d38NGv/yrYEwIneo8TNjdrrF+f49Wnz/DxT36Cj3/2U9AUMY0TOucRCTm+ue6ftsnGNNdx9LXyZt9vyd67xkPB5FztnNPUfq7lufVuKd3rsSISo5COq+Ub+069QNfjVF+uomE91vss+7M5Z/jsLpm0D/DadqryG8Lc0FbLvZqu+y47j+v69HdwOS26Bict/qjbcVe99btEtGOhzDQjDXPcX58d31Yb9/FrE9w0+jH/e7eyY/sKlHVzn7xs8aS9b2m2j59b5RalYt5GDUGbtbEhK5Tvan6u+7x3LjEwc9tid3wVSNcG0txWIxO0TE6GT0nDL1EX5CgrqXZe7FvrbF2tcct9Mt1pyQL7uR6bu8Z83/ywa40tl6iEDDa9flUZGd9ibtBuzd2WotAq036usYJi4yy3iXCwWuFss8nhZ5p1yq6jdX31us9RQ5/n9AMzmHbff9v1JU4G9ztuSP2sl97XWC+rYFiQrvc17MgOrr4PYOat0GcsYe3g1Yyi79kFXYmpioQqPn3f5b0LNlVrDQyYJdyhTxvMQcXiNwxDrleVCv2tjkm9yzPUdQ5hG8AoGx71Ged88rKkSVnRwJav35X2BXyYVJZwiHT3fgzbtnpRseNa80XtxtfJWi8sPp0Or7G5tQCWOHE/a79th/MuH1Kj/KIpM2slRX6cW+/qSW55fNZW5nnYU3UpPewC65zb8Z3Ui269iLRAVM3n2s76nuBKlzaG7Z7BUNPO9tmWWwvrfUCh/s0CqJBo97b85nbhlT61PZj7Fpu3gS+lC3HyNDDARBgRETwQ4OAOBvzCb/w6fv3v/j6GhyfYegJ5B5oCxpsb3F5c4vXTL/DxX/wIL37+FBdv3sA7B2KWbHUxgjovaXDNHLTtkjlPiHH3oM+6L5bWLUDTilvelYU6trtj1wLJ+tlaiusMcPW41Atd6eeuxVXrqUOP7L2W11nfbYE+24f689ueuQsIaX22na1yidSy1zbC1WXqWnAXuJbfpch9ckGft3K+Lqf2bLToUYPZFpi6C+jUfbNzsObH1vrSKnMexmfrntt6agNaXTYRydp5pxFr93NL5rXmYF2W/pOxVUUNQEp2cBcsa8n3erx0TBWj1GNZy/XIkubcjr0d4/qkeCIxyOgaV8so5xzySZLy0vzdCkPsG/ta3uszOydXJ72yHpsWL9UgeR82ba1pdZktLPQ2XqjldrqL+pZtwz4+33fVc3l2L8a0F8kaiQANiYyTJASqeSBjKCOvM30czXg21y0FZVzztrmh15fyaNQuLvubegaiARgK/IIBgvWiFEKYuXG08Zq/3TmHvu9n5bQA3T6BWg+sehhsajrmUq8yvPY3ThIGtt1uZ+865zCGaTYIWp+2qxbmdmDs9wzQSNLxOe/kYDCS/2TB4FJ5QSwKdYhGXW5tMVKBkMMyOO4IlNZl37nL5Wv7o/Sz9LQ8ObccxNkY2LI0fE15y2rvnSuHaG02Aev1LYg009Y853oWQiB4R5iqk82Vr1sCswjv/YuVlmHHPZdXhcHse39HUDbaoLSbtWsGXObj8DaPk96rQ3XqPtV0arXXvuuI0iFCd1uR9K89l4V5t/2ttresT632y8GUDhw4pYUGth4YO8Lj734bv/uHP8Djr35FlAXnsIiEuJlw/eYVXj77HM8/fYqf/9VPcf3mHGGzTSd6AwGMIFt3MSSZ4BL4rBUNK4e0zfbzfehkx1vnlT2/YR8/Zjo05LbObdumu1Ir1gCiNhLV3mcrDy24aF21rLT1tNrSkj+tvr6NrnX/2p/LOzNwwsV6Wb9TrwF2ka/lnKWTbn7ed2noQ21Ua7W9VUeLT7TcikI7z++j874wN9ueu+itZdRKdOudnTFo9HdfO+77jK2/7n9rHtl2aVbAusi3yvs966lerfFuKRIAiqESu2uynbdWMSa6Y8yq+452PZdvu2x/6/PDdvi06ps1YNyFO2y46L41sB7ru+TcXc/c1U/WDABVeZZWb41OoLkC2XpWaSUeV8I4ThjHESo/YojZaGHneS1nG72A7UCmM0j2Hn3J60uHTtlFLjepscjMwLpZzFrC1wK+YRgkRMhkbGqB9dZiop8VfLZcXZbJrfeCiLLCo39jlHS7Wp7WoV4NADvelZpmu8KQs3a5b/J452TDpjIkuaKIpHAhyrQE9plL6thpvXQMHfk7gZylWf29pVjoZwUrM+bekyc8xoiQDh60AnA29qFhGcFcSE7TiHE7ZnkofxuLQvrb931zAaqFi7aJiIC4b1LO265lyf35CbQtnmzVWZddz7carChRAooQq8to1aX36kWr9W7dlhbPzCyNDaXNllFbXYtyVtqxY2nZA3oIyKESGlKnG9JzKlsiROcwemD1+BG+/4Pfxzf+5q/CL5eYUuYybAM2Z1e4evUGL559hp/86EdYX13j+uwCcZRsUkxAlArh+qK8d97DOT8Lq7TKhV51jPzbFr4W8G8pEa1yWnUo7et5y1y8hna+1XNd76nsagGmFvjZdxWg0wYFyu+1wms/2/pavN/iny8DHuq2FlAMwKT8ba1HLUBcW+R3DQK7CosFBjY7TE0Hux7PDEtv6dMuqMaOR8B6n/aNbYve+8JE7lI8W+BsTqP94N2Wr/W3jEjSz/37iVpyU8ut5Zde0mZJla/DeNcMuCuMqlW2Gjvts3YOMDPgaIdv6vXVXpnOlZer/F448q6+tJQAW3/NB3Wf8/vU6FODHpZuMsb71wigGLfvuuq5hj3lfRn5Uc8HncPtub/bt5rP9L5zmgFW/nVdwd6OKM9ffadeD+w42PsMzGwdeawImrPhS133VjRsZSrErGVVQ5HmwEBaUxQP8QlnwkYhhncuW4vjNAFm4akHAsCO67AltGtrp4JufV8vItEC52DQQ0GqZFqkHIsY0yQGEbzroBlSvC8M7F1RxKZplJ3/uT4Jp1EgbkEjOWAaGRz1rEfAeY/gOaUQdhL6weK40n57cjk0Sftn+2+tB6rcAAATITIQUyy6xvQxkMKy2sKvLqsWfkprK6hj4gcisXZHMjozUd6YvjMJAIRM88QnBLBzmbY+Qg5ZJEYgRs8AyKUD66yCmwQmu7wI6LjkvlNyfVMZLyLJMGY3mE+Tjl8ScJBQOkrpFMGcsqRAth/nviWaMGfDJSf6zkQMlU3Fllf1N3aUhHFKpqQCwwEeLs817wW4a3YovewcqgXz7gJhwEAaEx07FWhOs6ikTXDaR0BBoi5eAJQuDXBTt6MGw/Y3bZMjhy4lANjEgOgSQHKSstZPDtE7bFc9tqsOv/r938Kv/u5v4/DhKUZEcIjwEZjOLnD76gxXL97gZz/6K7x69QKXlxdiGAgBvvMzkKd7P1ySfUgyzi6o1sOLNO/rhTz3w7sSL89RlHMidP2QZE9E5AkpyZrQEZRlCoNA5AFiUfJQFqZWSJy2QQ0P2UKJanO45YdYUkSzlfVcziwgiJKpfJJlkWVvlPmdeTLGWV2WLzQUL68Nph/AnJdsv1Q2Wb7Rz7UXr36/tAPgQnSxVlJZa/Oir6u9vFg+m/u5xUQAnIwVy8GQYoASD6gao7SdtTeoBkN2jtQyVMewyA/5T1QZD9tXmsl3xrwdLdCiz9p22fr30di2z7a/lnm2/pqfW8CzVoBtWfvA4dsMQPZebTS15cszABCTDLbeRkq/qTdMXyxl75Nxlha2/1bhmGEgaoP+feMhN9oGndxGIjm8UNuAIofsXGh5TVpjVdNuphDvaW8LF+ZyWc60SWBId8qkCmQ9boU2WmN43UbJrjUnRV6rXaJJPddyuwpN83pEsjZnOW/6uM+Q0vqu9/RfRESXzluTNRkJK5o2V3NT+27n9KwuzX4KwYrJT5ONwjV/3nXdW9FQK79a8oG5d8KCS+2ACukCyMr9mM6S4BhTJ+baYx3nS9V9/ddaOLRNdrFXTwvz3EOhYNkqUMp0w7BAjEE2PnkPl8LBdNO3d5Z8acFn2bDtDfPXVqAWU8uiTHLoHGTBYWLEMMGlsAwO8w3oINpZlJROWekxAMIeHsgJBJLzIMji5jSeNO6GHdlJoW1vuT/t2NiLIYpU7/sMFnRsWgu8jmkiLYgcENJY5Psk3g7J65sOgSRwkAPjIjMirDVYXZoSW08GAOQ83jwHEFldZsnkYAWctFEa2Fqo8sBCBWh6N3UxRhnjPMFn3LT/miko1Xe1bkhdhQdkcdtNf1kL7xpAZDobEDkXSEpXBTP1/gN5i6g8r59rb0Upb97Gt10Mxugpb/LGFNF5X0D4YkAYOjz53rfxm3/0B3j0wRNEjgjM6CNhvNng/M0Zzj9/gWc//RgvPnuGm8tLrLfrbCSxXty8iLY8DakHFuTOFh7sATw6cCwgNsYo528kmoagXl6k7wHeuwJizaKisggNsGLBpPbLzjsb7ma9klmupjm/Y4VLbZ8pVjWQMW3I8wpGSTCf9TnoHLSLebpfAya9WmACdRk1D92xYDJjtpFX21/mfNwd07fyroIzmT8ia6RfeqbU7OkKDLTaXs8n+3wdU82F+rNnZ3RMvNjin53yGzK8nuP6mwXJzbY2ALL9XIOles2w9BCj4S79LEhrgSar9NS8sS8KoA3sU/8jQY1MqmTo61HTbtOuR6/ulz5TYxcLGi3Atv3aBcJ7wulmbNxYj+VLKY95vnYZetZ017GvjcO70QCUadIa77vbzcYTZ+4xdmjYAsv199ZMVjxh+7sTPliJFAJlA0w9r2z0idKpNR9sfZm+uf6Ag8MHODo6wvXVhdaYloj2vkDb55kMq8YUlIw9Tg7q5F0Rdef1pUKnag219b0OA7JCP0bZJN33vVjvgnyXmDLp/DAMM0FuGdAu+roQah0K3q2Fvd6obEO0rHIRY8x7QrQdaqEnmtdry2oJ3JpmGZSgnDVhlaXcHhVsQLLEOkSodTQgxjkjzIC6nm58j0lt/9r+6nPOyQnbHIsHyD5T98kKdSuc69/VG1QvFq1JXru7s3Jq/gIyj50uXBPj5uYG0xSwSO1VwFePT13nPHMOdp6TvnFetLSNuW9OwmlaUIWIQEyzMSmTGSWzWGNB23fd1ZedusnWTVnYeu/fGoufPs1AXf3svnbXC7j9rI9bXpqDEwM+70MXAqZO0ta6QFjAgwPDDR22nrD48BF+7w9/gK/90ndAix4cGb33COstbl5f4PWLl/j5T3+GZ598hjcvXsJpGJVpo36uFQ77twYaLV4nmvNApqcBNcpb4zjmfW6tMLPWAqR8HEJo7uGy81Pvq1zL8rKSH7Y+Lbu2Wtryd4wMDTDYum/bX8umFo/WddhFuv58b15qXETipW4ZUFrtsO229/T+2y6rbrfKu0vZsLxm5ZeeyaTP1KDTts8qIxac3XXVssa2xYJh/azGvrlcmIMsu3a1+l/Pzbotbxuruv3197r+mj53xdjXoX7yXnsvlb3uQ+t97814ALueafvsf0759SVgd/7dAvnWeOlz9RqQ6c5lU309b+8a1/3zvBif30b/um+1DMltqgxHNlSt5keLW8gV5cA+Q0SzyJu7LktTmVfibbq8uEDYbgEkb8yevUJ3yZJZHVnv4Iy3CG2sc9d1b0XDWvLriayNtWEBdmG1lgsbMgSeu2MzqISEDGkHWyDHZsHSdmjIkF0QdBHVdLN2k3ot2DRTVAkD4tx3m7Fp38KRF+4UN1dbC7WNteUpK1QO4IkFJHmf7O+cTjWWjT2WtmWR3xUC2h+iophZT4pzLit4ti1ZuDLvpOvcByCsx6amS24XSZhHHdZVL056f59lp2W101zXqhhmpYR2wWBrwVChGEJAKyRC+zmGIOOAFOaSsnCQc+C8OwJNS0aLzlY414pa3e+5gJsLqruUAABmQS/9rcFubeHJoMAVq1CL1y2N7OJq50k9B0Rpnsc51+2+D7Ap7SD46PImbRBj6h3cwyP86t/5Pr77W7+BfrVEIIIHg6eAm7MLnD9/ibNPPsenH/8cn3zySfKypjby3DBh0/Pua2srpNCCq0S5/N40TWWhrc5DsHOL0vOzU1u5eBxsO1o8Uc83beO+MYdZNG177GJbW6Ntm/VspPq3u0DUXXxv68n9a5ayC6JbPFvX8fZrTst5eyREsVWeBVK7bdid2/os0dywU5dZ98XW1brH4Lx26L3aKGdpn6MTnMte0VadrXt3KXT2fiuUr+7b7LeqnJYyqp/3epcx549aRtmrJY/rcvbR421AVmleQDblkME6K1nhibmcrcMBZ+tiGnO96n7uk7uymjHE2zLn3daY5jIxX/Js+6yBxNK1jujYkRcoY37XGLztnq2j5UGvZcvbQPjb5NdMoWjIz67rZO02Hiddj+07+/pby4XMo8lFNk7TXFkRQLTT/hpD7qObKhXz5EPzNt3nureioSFTNcMpE5dTvUv4DLNYvxTYKwPmBS7MLe0xyuF3w2IBb45Dt51vgS+1zlohWoDnbsygzYJlmU/bpwcOWuBq+1vaOx/sVihRzUBal9Y/c3+C4fWU4MSIjhxC2M4Yy3p0tG6Nwa3BjtZn227DJuxinNsOkwK3UubshNL3W8/a/jOLhSLE3YlUC/56omu5djN+FhQp7t+TeMJWBysgfd6O2xwGsu+yAicLRFdCTmbPAuBo032WfR0OJT7djj0zizfDKIKzRZCQD3qztKgVNm0fCQIBeH5aeg2gdoHLfN60FMJ6LPK9GAFqnw9xFyC0v+8K7/n47gqrXTBV98Xyo09hfwSH0DuMg8NXf+2X8Gs/+Fs4ev9dcEgLV4hYn1/h9vwSrz9/jk9/8jM8+8nH2KzXiMzovAcobeBM/+q5YOWd9W7YjHg1DfR5u1GvBkpqLLB9Ux7y1byw4zjzrFVjV4ORvaC9GifbDwsGWyDR8rq223qH63a1QEMNgOu50uKzmsetx8Uu3PVYtOjUmptzEDsHKWrA0XFzrr23wH6vAVdd7xz4cTJi7Bpz2vMFTb6a9buSFfW6a9tbxjfu9KHujy2rBdRqPtjHi/uAbAFSEtpqjYhWHlgD48w63qBRTf/WdRfge9vVklO2vrrM2GjT2+hRKyCzdZET9G/I1zpsbTb2MeaQo7o9+y6rbLTaUYN5O1YWH2Va3DFPbJmt+b1P5qQf09rZ7sc+mWFxlj5ni4RrzynbjhoHakiipUdrPrZo18JHgKzTzBEuakrbgMgmQsXIRr1qD0+L34BEMqVfuqMy8b7z40udDG6t0Vbw2pPAbSNlE6qbAWK14rk06NZSaBfuGqxaC9rORK3cdBYU2MxSLYtjnW5XyxnHMb0331RtXb/72mPbVAsDLUe/z8KVOIIdAz7tifEJ6bAoIDROc9CZ6nE8F271wtmaCLZdVnCXsaosSjS3qNqr1T9tY6bDWxxudV2ttteClomBKWbrQJgkXKSVVeKuCTGjj+mbFT6SSYhS3H/S6qlo++IsSJ4nnaBp7CTd7tsXrX0KwEwQxAh4RcJv71t5F6jpv0+w6Ht5Trm523kfULyrLfO69vOCttOO811WFyBlmfMeoXM4/uoT/P7f/7t4/M2vwS178UyMEbzZ4Pr8Ejfnl3j280/w2c8/wZsXrxC2Irf6rsuuYYbIVO9oxgMtcKtt1LlhF1G7qKosUlCqfSnKPe3sf6kXKEuDuZdkTuN6PKz11NKuVh5se+x413XNAKC5v0/ezAHQvL11W1uAugleGn1uydu6za122TXDKkwzepl218oQ0V1Kc7nm9bfnkHiwkhxpgK6aPsoj1nikYUnaPu983udi22fLsut5VhRpPk9r+ujzLf6yV+0d2Ecj26cZPfbIwhZfafus8W7ftU+e3OdqPavtr0E0MwM83yM3ey9ZNFpKUAtYtsD2ztySmzvtbeGk/H5a/1p4qFVGumlrnP1e/2vRq5ap+i+aQytt3TU9alq17hd6tGm17537XK33WnJnX5376mvxZmssWlff99jGCcRJjgduypJ6XFrziJyTRDxs6yttqZ0B+657KxqbzSa7ZGKMO5mFbCPtAlwvuLKYusyf9hkF8iIUI6aJd7wSNUGs5d4uiMWrUqxt9R6N+rLARuvV8rfbbbZihhDAce7y0jq0j66xALfCSqZpKofWqRMy0WIiltS23mfrvRUwSlPwXBDVYV6tyaxXbrN9Jpe/6+quw6dqBaB2iSvACkFOHKjHvAUUapBTW6ryZAOlLFEACAhhQoyS3tT4XUV47ox2uqrJG7G70AkBktcIWnSyGAHZ+0RJ8eDUHmXTGFPPSRU4lXn5w4xPKG8UzV0rdEV5nw0ov6N79ltpfUvwVb8RKO8/iUrTDD4Sx87oV9VEZNrK2cJGO/VbS1NpY81PhTbyDLmU6QkMenCEX/1bv4uPfutXgdWA0Tl0mwl+O2F7doOzF69w9uoVPvnZx3j9/IXIr3QYZCRCYC4byE27vGaUyvQsm+sojScwB2pElOZszP323mOaYgalejmnZ+iQ0MdJ2GWImoKadCRABITApt5MqkyvDFrAeaFhoLQlDZSV29Ybo89bZU/nXg0C61PBs5xVPjby1oKAetGsZZTQxZVMU0AO4SvsR5JVlmR+MTjTgiDeZh0nM9uyXG4BA1u3/U60Ozds34GyFhTuxexzbhlRbhfz3EiWy7dzpQEwaiOWNerYOaOXNdrVClXLgJDPtSKAqcgipZ3OX6qMeSDkMdlRpPB2C6hdW2x77W/1eqGfa5CZ1+b76w73vvYpVS3gpjIw3Wi+p+tG+S6LRGw8b8f9LlBs19e7lBV9FjDjmhpUK4j12q/v3Oeq+dEaUCwv5rkIXW7m2K/mh5o+NW1KP6XEDKArGiDXenfPZuNLyCncFevU+Kp+x9yc15G+3jW2+8agtFjKy/iQNJR5d5tDzQ+tdmYahRSGnmWglNnC0PuueysaLu0232y2iDGYE2F3BbT0KaWU9ZKS1aeFt3MePqVjnLgoAzb8CSQHkCwWQ65DLiXObkiAEqvlepeNkWLZQQbqlBdfAdbpHZKUg5KyUyZcWubBkTElrwIYkrY2IT4i2Yyqi6EdBDthLVgnkjCfMukka5VzAqccAQ49Ou/hXYfI447yIMzN4KQUSOhP2gvReYk7d5Jgl1nSRxILEHEok9ZOFGYGNKNN5GTNB5glHS4AeHKIEjSU+kwgTv13XUbCMQTAeTi4nA5zzlfp9GxKgBacLMliZSYieHSYdEM8BHSAARcY7BzgCQ4Rvesk7WU61TLZiFN40h7BkZFLEhwswFVjVZFAP0MOaLOmEU8u7/mZwoQphKRkpvHUlLkdZcHJTierLMoZ2hLg2PBMMiJkwartZZZ0tlnBSOnyWMF3AhIKvuxF2nYuihCLG5QCoaO08VhGNQENIJJ414TvTG52ZlBU0KuSstB1SilvHVEBnc7JKd3cgUBwNFe2mIJkCmOlvBhUIgNwHWIAOiI4Twi9w2Zw+Nr3voPf/IPfx/HDB5jCJJ6/7Yiw3uDV85d49dkZnn36DK9fvsK02UiWsphkBjE8fJ6/yF6piMgBnjrAwYQacGq3AYVgOEoyjBlBJ4mTeea9zEPfq5yRf8Im0gYR5GWhEiUheXuZRb1ioPPGY+KAgIAIzp427ZMgBZfHPToCwxgOUnJKsXjJnixEkfGglAEl0YPhEEMBQLohULUd4UI5FT3q3HQup1cU+VCMS8LHMbOMS3yuBhdRapM8SMkSwIWbI8eUBCJxiCNwVEOAhNmIsqXKMKA+VZf1ETm4E6lPzJIi0oaOEIksEKVFsvs5yR89B2BgSRWe1q6Y5JkDwxOLTEl8D+eFpgSZZamOvFnbKBrMDMopjxMZGmFDFjBZWd4C4/aflmPLY2azn9GJXCMCdx7AhI4jOg7w0YFoiYkDghNedIjwURKxc8p6ZrOYqcJr1+hZ+wx/whgfLP6pFcR9YFr4t4BLC/4ssLIGMfvMPhBfA/g24KWEUZIA1TWjNgro+6wgktMcKfMKXIPh+fu2LzMDBt2tZFlwPwuFhIgPXRa1SJY8+IWP8lgVpVjbZelq26r1qiytsdBO+xv9qse4BuV1GKJth/MpIMCV9Suvf3PiosjpXeyQ20MKcyqFraEsqEI+V6YFo8QEBjx5OT/N9Fv7o9jYGhMsTSiFDjNHTEHC1PMEqhT8mp/28Zf8ZvZ2oSijzs2TIb3tureioYAqxojNpnRaf5sLtuSqQRKMkbEJGxmyDnAOWbC2NDRmhvPFWrJYLErIlZundKvdxFZw2LZNPCaQajYqUQLkwGxAgblyIYuhy+CTo8ZcdwaAzMG6/bcvu4+dfDFKZpAYY64zt4OSlbEScl3XZboABa8RUT54R8vXBTTTKBYPjE3pW8LUYMrUycbQMxXKBKO8zyDEKGd9JGGp2jSReB60bhsKx2lR7TqfPUeabWeWOAC7E9mnE9TZIbsHoUpSnAtA7JkUWaRw2jBp+VDrynQt5SiNfdfh4PAQ5GVz/eZ2jWkcZaxYxVUp1ZMpOy1EAg4xG0dmUS7I8k2a7OC5AJydURFhvDLzvjpYUKLCMC0s3oGT0BMlJ/WTgSUvTOrj1P50wramE9CWK+B1IHTqwdO2AfAMTASMPs7mlB0Pl5Q9EOXySFUtD0wOmFzEw6++hz/4O7+HJx9+gADGeH0NhIhxM2J9dY3PP3uGLz7/As+eP8d6vZG05x1AXmgBRwgcEiAC2LkEXgnEDgOXgxo718sYudSXfO6KNCtwgGNCR5ItToETQMAEeN9jGyZEV4CU9Vt17NCRh0tnvDDFpAyQ8Heaw8wRjnxWKDsOydsZ57xEApxVhvnEuqpEB47S58jiFSQCp+dVThKLwYecF+tYCKkNMk5eF/XE2HLwZuItn9Zx5Wcy/SYgZo00Ag4giqktjEjyax+j8GbmBbkiE3h0mf+Vu2UuROSqMlKl/EfOJEpjJowsYIOACJcMMZR05gKmeiTPGSGDR52blBQHkNBNP3swumTiDxNjigyKohYinYNDTtcYUVLIUbEq2Eu7Ws3pfcDbZgYjRwk8tsFZfek6HwFET3jyra/jybe/if/wwz/H0cEST46OcPn5a3zxySuR20ygkM4pgheQTSXL4AzkV94U7QNl2Vb61fKe5zE2a9lM6au9JpVSUANgS4+alvuu+8amU5q/oj/uJlLZubJc58RfJYxz99H9ypOse7vPtz5bT1G+T8gRIJpqeR9QzbMyNd3Sdp+ye1f7bR13jce+MbDevvr9Onqj/FaXUrXNKMBsebrCJi2lHjAehirSp9U3ovneNKts1DSz9bo8v13BjBwzvmnRvebBJj5Ne0xjel6ieQDn9oeEta4vld52Sjvay0ZpmmladoD1X+BykAiSxowuWdQqQA6UEI0YkVPhWiWjZs59QFT/Zs2ZGRwC+r6fAWztQ+22LWDWzxio9pjUYQP6vmp8tcZu22jppaA8hCj5+Z0DdSX0QLOG5O/W/Ve5OGuhO5scMBv5kuVVT8nW+7XL1NK05gnbJxsiVtPM9rnQaB6OEdL4aBk2vaeOha07cqorhSyM0yTejMAzgH7XomDrry/bf8WM2m7b/vV6LVZVpQPZBeKOsC0gnzKtALHULV5E2/6av2378/1qPPJvEGsumBA5w8msNIJSqAlzAnZJQLEDoU/PpP5w8odFYFFpZgps4BnRJ+BJyGEA3AlwJGbAWVAol48EF8tBYeqNcmnT3UQR7niF3/j+b+Nbv/I9eGaEm2uMIWDaRmzXI85en+H89QWefvIUN9c3COMtFsnA1/lO9l0lPg/JKu7IwXe6EACOPDyWYE6eQCRPjHMgTxg5ZRlTHmMJ2XPk4cnMB2ZsxxHOD+gHh8lJ/LGGQlYcB/JqSElKDwOTR3bTK5AAJNzLBxnXGkgwBZDbyqAEhmeGhxOPHxhbN4piICtU8uZxAr+d8EZEMsx4UWZJvCxlTpdzNUIMiCR98t6BvQ0/olkoqZwbkBZjFto5EmPDNIWsYArDFo+kGGGSUuSKosGKUFmMR65mqtnFZZoZYEUkVniXJi4h7csCwZNY65X3VRPIimTSDZgB4hIe7NIcJnKIYYJ3OqfVE7MbwiQsRaVtmM97Nh7AGvxYGa/yST9HDrPfZxSp+DBHAsSIbuhwHUZ853d/A9/6we/g6vIMfrPGi5/8HB+//Gc4YKDfMlwAIjkEL54yqrz4etl1T/ublQ6jDLVAUL2ua1RFTaO6by3loqbf22hyH8Vi9z0tX9u/O0/rMLf6kmrbIL9Vdw5xvec7LXCpmKjmp3pscni6OTzWlrMPUNdgvw5VrJ/ftz6/jRb/Kb+1rrovma/veL61Rtd4pKUItdDCfqUklSdPpXoM3kxr19v61qqn/C41ZBhEsu7chZta15cInSqCUJUMe8hI1qxMTD0zY9xssWVxxx4eHiYgUs5YtsKohAQ4ODJ7HqpFSrUpSxwbglVrlMwFeFotc583oskAFaPpAYDqZra0kX/z8C5LRy3DfndONt30nbh8ApfTPRUMknOzmMD8XlqYrPC142E3rs+UCLcbymVp19RwG22vN9xbXqn3Wmh9m80GwzAIjYwl3E5Ktaw552aZbJQvPDmwSyEX3qEbBBBHTr/xfq3b8kZWMhMdm/0nMUKC5hNd+CMgRqNIUTrVO4uNXcue3FU1JI2fKT6yWJtbylJdzkzxwdyikukJgNJx7EobMIv1nAUoECGdFs8lhS4Y7EbkxqX3AAAeCClEQsFZCT2JKXRIrb0kpx97BxeBFZfnEwWk/OTyj2CwE54XEOvRdYRf/IWP8J3f/nXQasDt7TV4M4K3E26niOevznD2+gyvX5xhfTNisx7RuQ6r/hRD57Js8QnIA4yRQp5bTkMoGYjO4cZ14GzJptnCyskD55wrZ7kwY0sunZsiJ9oTkrzrO7DzYC97PlTZoEQbBiM4gLoOXd+jT8+RoNUccqc8m0+sDaldQQ4KVWVkHLeYNpdAmCRhwhgQpgBMAZ4J3XgDHsekwEm5IQZpqxM5G0nAtXg/CI68GELAYCrnAQVmONfBxQnMET3EMyPKqnhBdU8CgBKiBMkYxiEAgdF7B0+Anle36TtEX5+xYi2wRRZa44aDz2Cc9FkAxMAwkSi5jOyJdUheCC5eAO994k0xAIm+JGG1WbaSnPRLrnhbXOdTyKPwmUtyNkaHOE7iyS8TeUcuOOdS7PE+a+HcWt1aq+rfRIbKfN4nD/V5a6AavMM0RVy+eIV/+6//Db79238Ty9NTXJ1FnH7rQ/zgv/kH+Lf/w78Av16DgoRuRHZwHnAmLLqWYRbM2nHVNUDbrM/aNdR+3tm/VclIHfcZtqhwQw0C99HEPj/bS7DnXSIymcPKvX3jZuminzWE8L5XLpPfZt4ybTT9sm2wyS0Ac8YOGpv7CZjMGrdPWbT1tta12fiAM/1sO1u81FJk67prPqmfqcvfV59tv/DX7nM1DfYpXHW/LL/ua3vdXkCMeB7K54101MwzPmrNlxZWUiyjh1ATEcjTvY249rq3omEVCw1HssBSQW4WGkS4ub7Gdr3F+cU5Dg8PMY4jjk9OMIYJR0dH+aRrvXIIFO1aO2ohYRcWOzGmaUKMEcMwlE1tSECCiivKLlBWuNbxo9oOmwrXgmDNGa+06fs+1bm7wckyaD3ZvPfJnS4LL3MEeQcPBrYlU9dUgUgrmC3Ir5UN7c88exeAuCv0mqC4MVFsKJR9puu6nLXL0toqaNpm3d8QjXWqrm9X2ZRxGKOclBymEY4g5SjwwXxBai0MO8LF9K/uoyzSyIYi5XcisWxEcI5LT6gkge9igbSX8ghQFD5O7+lvLUWvJSTrcL29l0+hOLXgY6BTEJhBmAM5h4kjNn7SBgiwUoEUARfEguYMEHaeQJNHhwVAJHtbiOB9UqKJk+W5WIVijLKBGh5TqosJEpITGacPH+CXfuWXcPzOKc7GDS5v3si5N9sRl6/e4PnlFa43Iy7OrxADYXlwgP70AbphgXHoEbsO/dCj63vAe9xsNwjMQAd0fYd+GNB3HbzvsFws0HUe2wSwiRw+u9jgOnRwjuA6Dz90YOckLt97gc0EOSDJE9bR42N8LXsnvume4aSL8OQBIvx0fIytWwpZAfEoCMvgPXqFJ4tt4iF1hpfLJWc2c1JIEz/qqbMcI8ZpRNyuEbYjvjps0IcJ4foW6/NL3J5fwF9eIa7XiOOEME7AFOBcn/iCwQhw3gGcEn/ohgsQfOfhnBdrvXMAOXgAYCf7WtAhjiW9ODmfFM6U3KIzB4mCEVjm7RQJ4u4WpWSAAweVHYCGA8TIIDchcgBB04wnxSYyED0Uo+khmyIzxEgFlYua5ZAIRAzP26QYynfxwnjxnMrGDKGB64CYAtPSPHEEKS8Zfsg79N2Q5gswxRs4GuFVcYq7a1+euxUQmcXQEzI3tOR0Db6z3Ki8x/aq5UaW5zFi6Tx4An78P/0xXnz2An/03/xv8O7Dx7g4f4nu/YDv/1c/wB//d/8c2ze38CQeqrKvbxd8Kuq2bS9rVVEMtV02LFr/7uujlqvrnN5vnWdVK2W2DL1qEF4/awF39auhuY7jPC2v/rXtqkPBmOcbwve1p17bmLkYf/as5/uUgWmaMrazz7XC0vX9yJzmTBv01/SsAW4TRNN+JcSWW4/hvvW9pp2+1/Io3aV02PaqEaX1rr32YY86ooN0/tBcQdnH57OxkU10cM6j73tsNmtwTJjKYJa6rLvmAFEKpY5pHdSojQq73ue6t6KheyF04tu4fp0Ymv52miZsNhsQCP/jP/kn+OzpZ/jGt76F3/md38HV9RWOT0+wHUcMfn7qrRIvxgBHfsYUlsnthLLP2L0Qt7e3WSip9dtmkrKXCgw910LLtWVqWXrZNiiwB4q3R9FlPUH0GcvoGfxz0TwdOURQ9mA45yQkyCw+qki5qk+2PhUcti1ZOJoNw/qbfdZOzpZwq59ROtozVawCqM9573MIm3NOTkE379chcjoONq5XL+89tnFCiAHjNKWdwwTene/Nds/oBbHo1+MVQkibmXcXosx/STGQ0zgpKxdaTUtoiZKSNpOmECPSPQIJZLYWhLoM+892e2eRdx3YWLtYlSIibGOyvHLqS7KAOgZOgx6Elzw1auXywLYXyjnvcsgIETCBsPU9qPOIBMARRi9eu9ERQif7W3TeDcOAvu/hug7dMMD3HeAd3qzXWB0d4fjRQ3wMxrvHBxj6BzhM8+zTV68xPXyM19cLbPwhnO+ywsDk8K1HEccnBzJ+BPz5iwlr9ngW38UNHWZvBSmtGTjBORwYF3hQePC9HjHtA2Dz3zQQM++M5RPdi/BX+KpGnsm1ZICc8XolhQHANZ7gJ1pKApa5Np63YLbOebOoLgAcCDD9MU9wHPH49DlOPrjA19xrjK9f4/zzZ+jXW9DNGuFmjbAZge0Et93A04QQJzkMk2PaXCq8CXKyb8OnlL3eJa+Nw+ubddpDEvHOYgEG4TpMuGLA+Q5jZHzi3wMnpYbBWGzP8UE4K/vKNL44OiASPl2+D+4XZg4Itd20wde2X6QNxpTop5Y3Q1NmIO1rWXjGohOlIei4MXC13aJDj75P3kGvCTRYzs9J67HKItcRvEsGt6SsuORZdclo1PULLBcH8J1D9GcYx43MsTCJpylMTRnLaYzrRb9mu/teXArNa3RL/u28R8BEEX4knIwOt3/1FBc/fYbjb3+A5eERrjbX6B6d4Bf+9m/if/7v/hmGkTGwT2CpeF5msiu1pSXPrCXergF2Xa8t7DV42wfC7e+6frYUlta7tbyt+1S/w5w2dmM+nrYddwG0Ofjc/a3VPstH9wV/pb2lTHvcQE2beqN1XQY3ytvXv3otnylXGv7V6EdLea29X/Vztv36fK0w3dHYHe9QpoujGQ/t48Pay2jbWfehghg7WKSlfDki3Y2X9+455xAqxaxVZz0PZ1iCea7okyjMtrx70RBfMnSq1UhOLnYL4vu+xziOGMcRP/3JT/CNb34Tr1+9gnMOR4dHuVMK0FsaKrPEvi8Wix2ruEVx9jRyJVDf9+Bk4Q9mAGtBo/2xB+fpPTsR6v0blia2XTFyDpkCirJiBaR1zVtFCBArsliDEuCMssFOBhmmHqONJyBQMjpJDLjuv9CQo9Z+DcqbGmmnjSL1DVquZAdjV0BnL1QIkoFJlaakTIXEMyEyKAR436U92w45bMERHFy2iDlycOQlrzYoZw+TDB2SHYm8Q9iO2jDJgJMyjKlVmMEpM0Nqa07RVs/sMtdjCiUREBNBkIxe9rksYFM8vWyITw+kP8ULoO77ktBAIWpMYVIK8GFS4oIUxmqRlMsAlf0PIpxLWKIqB4BYb0dyQAJGCmqlKsLkuwTGKQeMgAiT97jyHVxKfNDpeRPO4w0zroYeX3t0jKPDQ3Rdh8Vigb7v0S8G+MWASA5Pr9Zg57EB4SfTe3C+wzcXl3jvyGeQ7rsOL9eETzbH0keScJbX7hFuaZXaBbzLz7HkANpK8M0XJ7+LLXnQu6SUmUH3nzHDnSk0lfFgAthRioRRd3UiFQFneCzjj0J3VUKgHioyPGDHhs1fSsDXWKAzmxEAiknZS8NcWqm+rqwYGrab8V+C/tL+9GZO++pkC/2WBhADn7mv4zMw/oIZ/ARYvHOL0+0XmG7WeP/6rxFePQe/fo7T62tgGrFe34KDB8cJ2v2O+hzm6ZJs8c7j9XbEvzv6ZZx999cA38PzhOPzn4LjhM3qEW6PPiy9IlFWHAiSaI3xGYr8VqsZnCs9ZJ1LqujK/H5BRUypzGIOM5DLWX4xDq6foV+/lvE1C+16+RjdZgu/ucxg+P3Ln2DgCRQn+JTMBGAEzeSXhuvERTxYLEXBNZ6zxbDCcnEI7wkYVthsbhCj0BXbW2BKUDR54VURZV1TjDDKlkRlGHux4e/mJW3WdacFLiwIyWDNE9YIWFCHYWJwnPAn//x/xvef/NdY9EscHh/j+vwStx3ARz3G8w0WTKAIMFyzHq0j98n8rtPL8kFt/KoVDF0P9ykBds2v37G/13W2Ptf0svXZZ2RNV17U33dBYuuq12iunq/rzeGLiS7FaIkd0HofBaCmYSuEbcfgp7yZPttqbY112TXd6nG7SxFseTJaf+t3LCaxWKx19larfPudAwPUTvRTg/DZmO7pb6sce9XYM4+FCiIqBn9O9zlqShnMeL+lkNo2RE4ZQy1+ISTHdnnubXTT6/4H9gXJ6NM5n8+UkMojyMui2HcuHVUOOGIsFz2++53v4tnTZ/juL3wXR8sDLH0vgDGS2UArwElBWNcncBwC4iS7HX3aFMxBkm9mpQBAZ/daxIg4TRkcKLF1kSgKgDKIDT2xDKEELSe/2sGSgZlrjF0n/QAiQrJWWUGlWapiRCkz1escIQYJCwjMoMgYHMHxBLfwsvnUd4ghgCCHsHTkMTIDCIgsQJucSwwi8c8S618YiVUCMYMDgdgl8F4Yl4OkZdQMSUQun4LNCSQwSzo2vRgKjCX23EFCOQJHdMOQUj/2iAiSNQYefliIPhS2cDwiJelATHHzOmIOHoQSciFhKgzvGJtpCz9I+BXIYUEdliFKOlYw2BE2BETn0QdgGSTjkfJQBuhpAvkEhGLe1GncwuSzNT+GWA6yA8Q6WilrAhZYIpbAYHRpo4cwnk//g5NNrJzOrNBUmBQh4U4upc70lMJKPOAcYteBOycbmh2BPSG6XuL8k1W/7zt0XQ/Xd1geHcAtBnTLBfzQZ6/BJgR8fnmLy7iQ/QF9B+88fO9BzqP3YsH2XqzCZ9sen8YnWLsjjG7ADV/AYzeemIgRuMPVw+PEc2XheUMETObhFCmEAVUZyrvy7iv3HhCRsxpl/SpxSwbeyjxJQM6UAeUsoxTkLJTmcmW2yMKBpL+rXIcBuUZBJfOe1qVKjl6sjWTVXVXNIFNGKdzbuqo+apajefspZWwyfdeXElE3/gDPV98CrYA373wP/FXGsD3H8PynePjpv8TB7ZWEcRLLfhtP6FbHODhYoh88oiPQYoFPbjv8df8t4OibeEiSDU5Cq74Hcg6HKgOBrFyLomWs3kqvrDhQDiUD27YL8TKWUppyPb5FZbOvAt+dl5docwrk6DCGKO+3zLjhBBhDBFLqSGYJDYohIESG216hH6/w3tWP8R4u8HjZY+kH9MMJVoeP0HsCX7zG+uYcYXsDujrH9uYKYX0LXq/RjRPcZg1Ke2gCT7JPJcYUUicrPCcDkMJPyrwiRi7W1GKRk7U1ec4Z+WyT2vqq99qW/wRcHWHyEdEB5y+e4emf/jne+doj3GzP0HUDThYL/MHf+dv4i3/973H+9CWW1APGwGZBofX+2/VRQ8lqEGZlqlUqMpdTwhGArPNOPFGanttMmjsVnZYSUAND+1wNtu2zYvWFmmuSkuGbew7qcnfAp2mzpWMz7MbKX6ug7rnyet94v6aHBeYt2jnMx0yvtKOrWa6Wo/+s4ZUx50v1xFlFoaZLCzzbttZgvzYk1wpkurm7MJirblfmYSrZHyWpRKJHwlESsWIKNrhADx3Wcm3/bJ8ytgTK8QaQM+9cwqF10+uxLgYsEYgxYV9NPmQxDieBSySZEe0B3m+77q1odN6j8x2mFE+r8fXWqi/0kknuvUeYAv7eP/j7CQzIShxS3FiIARQYzAryy3kA0zgPubGEmTTcpvpnte1sCSFCPwwzjV+embIAqyeO9qXWmPWaM5QMkdBalQzsMLHW5RLwdxorj7S46qRJscFI6T1jssxR59GtBmwvLpOCJJ4k7yQDToxy6JiAIQd2SSkjh4HFEhVSLL1YSWU75uSFniGkMyhU23XCohMFqLdD01MSkPc/sGaOAc0OFIwpzaVOqpAUNo9JsuGQw7LzGHzEFAMQIoh6qYPSAgnJ4sOeEEj3DoSkUEg/huixxAKRPbDoMDx8hM27D7DejFherTEw4QYRi6+8Bz5aYWRCXAesLy5we3Odx0XHixjojddDJpooYZGAbScpQwsfJOUChJ4LL1mruoNDTCEW5L0ozMlrwX2HcTGIJ6GTLGO+79AtFvDLJfwwZM/AsFpiWC7QLRdwywFuISFGbuhEeVgM6IcBA3e4ubzC5c0Wf/F8jSv2+PUPlwIYJsafPt1iRPFaXMUBT/E+4mGHCX5HrpYDuJKgiQC6AqIdgOscYkTljwrFDOhmT8zvUQGN9bpoiyF9L33R52f3TflWSbFKkFVi53XPPRNs3rfPJb2gAF2e04zN7zX6ZSr8BWJTRkm72qxb6ZAq56rcGZ2rtXYvzauy4QjbxQOMX/stXL//Kzi5+Cm+4l7jN7/xAO8/eRd+WIC6AU+ff4F/+SzgY/4QkTy2bgEPwkNTFzPAMWCjZzIMfTpLiWd1S7NkgdSESlSac8dFO/S3CsZcPylWVjEiIJ2D0iBZepHM+FF6z9Kv8I54jRwIt/wb+IQnPOMJX41PseQRRB6nfsJH33iE5y9f4M8+X+N6uAavLvB4fIUjB4xXNxgvr2Uv3jiBbq+A7RY8jknBYRAzPDvATRnASripeHThXfbiUzIy1VZpGZc5kJ9RtAEidS1KGX8xgPAf/9Ufo//3DtvtBRgO3nU4Wpxgc3GDIXqEICGsaimuw0usVVXrbWE5C0CBEq6t+yKtB0FxQlMRafRxnzeidb+lFMzAtAGqu8BrJm3yXRvJ0bJs28/7+rOvb8CO2G3Woziuvmy7rOW8xkhUJjAEk8wT1QDIiUBsvZYHam9UTmnfoEFt7L1Librr2qeQ2K0AX6bsFo+w0oTLPhuNAlHsxNiv4NUGgR261nWSGtV1vkVsN9POyd31HM9/Ufhdt0h4ckX2VcaNL3vdW9HQFLM1CK8npk60YRjgfYcb3OZMSIPGXsuLAGTRcU72ZWgZNhxKGX2z2eRUp6EKy6k3cNdKRK0Z1hkVrFDRga8tCLav+k5hBMlWYxdPfd5aQKRMACl1pa1TFCHxAERiOYwriBIyEcEPQz5IzXsn7vh8foKHxhODdZEBAELsIiYERA0B4qLIAAziiK4DfCchT0QMuKSwgKGeprLqE7Lxmgvw8inMIcYpZVmJEuecFmhPBDjJeETOoXdIOeZZLPjoJL+Lo7QfghMQm2SjaQqFCuhy3nnvlgAIE0cEF+EevYvjv/kruOUJl3/8QxyMwG3v8ehXfhnbd04wdh02l7d49/AIJ8fHuL29he98VoIRGdM4ynkBXMI0pnHEZrPGiZNYcOfS/gKQWP+7LsV7E6YwYb1ewzuHxWKJYVhg6A+wWC4wLBcYlkv4vsNmO+LZ+Q2c9/jWV97F6ekJnp9d4PX1WuiRyqMU/nK+CfiLi0PhsRsG3RgErvZvHgEaccUnuKTTfBbGv32KBFZETETtL4ByRmBBsnqgo64RESiHOKUnM4jOyhWyJceurQq6zR8zQdIzPGtB/bM2a66EVCDRLuf5EaOU7FzNupNM0vrSo+kMugrMki3GVMHzflDVj/QwW8JUzWrV3ey3pYlF13ddb6M5pXTLiyXO3/0enq83+JMvAh58+hSeLuH7AefDVwHfZ4Cop8ZSLH2fwoTNRkJfvRdgCJJEAVluJgWr9JtmfbPd2ul3PtxMiEQVkSxl3ewbQc/vtKwxGyNnAQ6S4YByQ5SvZAglxCkipWWHx8Qef+W/JXMptf1fXDGw+A7cN9N6wIyLGPBo+xT97Rm+gRe4fH0GvrxAf/EK61cvMV1do5sYcbNF3IxAiOgdAZjkUEiKgNc9VUjyeA5UarDa2vx61yXKtzBanOSgPowMt2YccPKYI2KLS7gADDRgJHtezG5MvF07rWegBkH1fft9rgzthmX951w1oG79XuOF/5y671KG9DDOuj37FKTcxqq99j2rDLXCe2yf9+3JuE8/tCGVRJyVV49p/s3N9wq06Py2drVAe2tOvK1f+y4iKhukd64SNmfbUCsQ9bt1AqEW/eu2zsYWJqFLrRCaZ7PXCLtyIo9JWidy9rP/jKl1/9Ap02G7mTmEAG8yMmm2ISKScxB6D+fTPgjvxAXPcvozooRZgSX7iCodYM4WCs1SFGOcZb1SS4lzJfWpjVOsrShWyNUbyut+tlxqNZOXv1YAqItRPA6yyBS3I1iFhsQRx5CUKe+SpyIihDFvLA5hBKgDuw4ODj4QKBJ6pIxfPCEGhqMITwGS7d+lk5TTxmwQJkimnMDiZZB9EIQhiDfDew8fvYQ0xaSA6C5TVUoYyTXtgU7SR6oiwRDFUGL5ZCzIlT0WlLJpBaW1dwh9B/ge7DnRweWTsDkxNQOgIDGGSm/PjCkEhBDxpvcYBwJCxDYGfH5zi9VXvgI/EOgmYv3iDdxiien0Ad5ERoTH0TuPsY4bbLc3YMe4uryE9x0Wix7e9+BlB3IdPn2zBbsBH717gHcensA7j01kfH5Nec+Jcw5b53AbPH66fWKyKFkIjHJnDWAjn7fc4dodA8w4/PklOppwiydYu5V4CmKOJANA5YTkxHTW0zADWQnsO0AUwqIygCEpk0ltogmpMlRVTv9hBXEFTJdK8o6Dgogz6Jr3d36eQZkv+TxK1tetBsOWbAU/51gjQ8+k6GTMbh4pYJ3zc9rvGrgycz5MG6Z9traZUsOMZMZOoN0sYsRJZzWqCFmloHROWlSs65l86Wa1DGZwnFs1YzPpsDTJFoSdfu8QuKpGe0tJ6/n08xf46eQwDEusFgucnkaslhISWCz984LGcZQN/l2XvThCH9N/LuNbGqMLsGnijBAF6Bc6MOy2ep0bEjxQdzU9U7a07ZCiXtcjqoYaXmNmeAulSNqrgQvZM5Vk2KS85gD2Di/9V+FWX8NzEPCQMEzXGLbnWN9cY/PmBY6f/gnii8+wurlEHxjd+hZu2gI8wSPmNLLCQA7syr7FGmDss9ADbfCmY6b975xDmAKWvpP6uAelqRAiy6GUUbIlAmHHWl0bJeu2AfM9mroW23VclRNbLqeyW8lCbP9afW8ZD+392uLcotfbnsmNNNddnpf5GLSfubMuonLmjrlafWvVqb/V9Kgt6oUGJdTJKjK0Yx1q19W6xzEJs6p/tTfDgneL8Vpt3tc3vZpKOBcsVGNGxUU1PVIt8kR1v1YObT/0snxsD96s6VWXwyFC2V/vWSxbhzDqIbCKsfX5rKDMiIZkpNQFv62s7bvurWgsl0s457Ber2dAXTttlQ+d9BIfLmFS3knWF68HcClx4pR/ky4wfOfhu36e8i+Vq0JUCaheDv2+7wAfbaO1pFglhJNyo65Ze/aELcNqnC57pSK6Lm1gRgSntItIC6CEOBPiNAnTknpsZMOxRw9KikaXlK3tVFI3Bmb4fgHnezgIkN9uZHNy5zpEbAX0e5vKDwAYw9RhEfp0eAsKkCPCmregrodPKXkplk3l5OWEVzmTIh3MFeQMgY2nvEmayOV3YlKyJJSq7OlgABMcNhBvhm4kFaXHgYhBxLLhuPPwvWymHEPA2RSBlJXo9dThnI6F/s7hcJjwnXd69CzAvD88xA9ve0z9APza1+Hh0RHhfHmAj+kDOER8073AepA9HJGBj6f3MGGRgYNP5BlPl2A4vMIG7kY0+gkdRi9ndVAkKHojBsjNVQyN5yfiAoF0fqqCAImfvqWUIIEAH1O62DQfMvjR1whgOASk+HYLUPM8sfWogOY89FmkKX+n/2YclRUm+6w+qB9KzP38rgHNWREx6gSbZ2wTUwEi5LSfpgEkBErnKhf5k4SllMeaAwEApwPnSl0cY/bO5EWCMLOOx5nwBmDia7VfokCXfoNTsjONyVEwjGLVMl0Es3jLlB/kI+XD+kAEhOJE5DSoZP+m+7ktSTnhxBSU2qH15br0Tcsb2jbly8gpkQCwGHqEKWJ9s8U4MqZxQt95dM6Beo/eOYRUvp6O4Qi5L7InNsmUzAsw6m+S1VT6Y5o2U6aKkSbdMjgm5EXdsBwje1u0MNVXSRXPvLWovWDmOWgnDkFOr09j51o0LqwwKymfOs4xx0MDGgpH2PZLbPoV+ADoHn8H1x/9Lnhzg9fnr8E//zdwn/0E7774MU76AGw26GJE7xhxGhHc7uJff64VihagnL0DCWEFyQZRBxLPt3OYnJOQ2RgRCQg8gX0a/1jK0jrqhCQ7ll2eW3T3ATRbFgCz13PXImwVARs+DcwjGiwNasBq6fg267K9ZiCyAqx125plVcXuq7seQxEFTsJzGsrGzvkle3ik/r4PuKtgs1mp7lIk7fe67PzdHoBbKY/7FNd9SmOr/B3eq+7VfW0pOjEtvjZiprRDI1zaY2txaP3bvqulbOh9kbWyFq7Xayy6EgqvBvq6D5QEWLPcLGNJs8pkc0rh5/uHmH2prFPOOSwWCxARNptNqoRn3gW7aajzPYhjrkYWl9Kxfpky1PT9LG3udgzYThGLxSJPBisMtD5tSy2YrPfFCrSWtcMKKP2ufdP+1ExcBGacMV0WckAOa4KpP4QIRwEIIygdzkcdYTE4UNpYPcWAm+0GY4hAOonYwWH18F1cvjqXEKUoC34Mk9DIrcBONs9L3vgUGBUjaPJw5OHI5dhWAJg44tYx/GIB7jpMYcQ4poP3OgfnS778s/UGW+pBTg5Ne//xKZ5f3mKCQ991cN5Lil3fwbsOk3P4y+27eOBu8e3jlMvZeXx26/AsPpCFNo2F63w62AoJcUlqSeccrukQb/w7ZaMu6V4e4aZXzPhEeUpugQcBwPFQvDYugYsA2Vvyl/wIkH2dAkoUrKQy1ymxgQKLEYsM6J3Zv5GhOCMfLpeBZPqryp6GmmVlAwAc0qnIlBeU8o6Er1iAM8M5XM69yOBXq9J2OAVuxbKb2z4DQNqNXTt4rpsyZJ09oYHbCuzyxrJ0T1M8KtjOv7EBkFXdszbpYpEUAzFMFMVC+Vx/Lwg0gX6WBUu1D85KCSmrGeWhELP+zulwPa1RvZUxdSQyJwuiJHOYppjbUuLK03kOIQhgc4S+67E6WIEjY4ohh0kcHB5gGIbkCVCiqiWfcjtUYYqqdEYgQFMQpz4C+WTtvYCo+p7BevpycHCAs4sbTFHCKa9vb3GwWqDzDhNi8qCmvQoko3l5foGDgxUODg5kfNI8JOOe4DyCPGtEzP+xvADYQBLt/+x3w1uZVJzGKdEiRqN85XbMhMAufRgidzJNRJ7ojBiRFMecHKQGBWbMqNxzqBZqDTdiZOAA7+AOj3BweAx+72sYf22Dj794iuVP/xkO//qP8e72Bkchhc/GDZiLF6De5Lpv3+Fdl5d4VwQkJT4JkwA5r4iY4RjoCAgcEKGHYZarNhhmCtA8PJkj78SU598q4Dgrg3fPJNDf7rr2lVnfu6/VttW2XNZ/WhE7Vwv8Np/D3INVP2uVQGAXzO8DkDVYBVS+IJezj6b1v7sUmNq63sJztSJry2r1udX/ff0tv1MWC61nZJ3b9ThYWtTeBI2IAObRQVpmXUYdYaPPWVo7kj2gFEPCEQnnmeMNdhR36dWsPptKuvyU1vkcilAUpf/iisai77BayCF467XHcugRQ8B2HHO4ACB7MzbbLVaHhwKKpxGr1So3nFlSbcYYsTxYIUwTpkk2+S4XSzDLQnZ5fYvOO6xWK4QQcHl5mU4nFEvR0HdYLhfofGc6qxDJkFBP4DWDnhlUiYiyj8M5h3Ecs9Ig+yHkDIUYw+w8h8VSQgOyIE+r3LSVE3IVYMkJsoTjw0N0jrHoKosoZFOfMITHNI642o4AyaFY280W67DF9OAIve+wXC6xSmeQMDPcMAApw4juhWFmbKYJfLRA9ITVcgXnHN5cb/B66/EUj/HB4gYHQwfXd3i57vEFPS4KWUpZQwSs6QhbL2cOeA74OV/g+iunCNRZI99cgyfgnIGP8+oM4MiGGBjgmhG1eTbddhpWl4c45v0C4i2xceIooJwoZQgiMMWkbEQ4SesEIGGZ/LxU3qW0Qna6q1XUZhFRbESAbNTM/TfzM31Q66feUrDCXNqv5XJSZlwWrIYkufwUomOVFxblwjOqeHUzK3RPzJ5nItvvcf6jflSBDhNipJ2a40UB4QqIad6PXEhjBRagGIEowlUOYgziUQPP6rbl6OI6t8gacAnI5lqo4oJMj5gUhRA5f1Z5FdLBkN7pgXGQLDkAwBGRgTBNAvoDI4aIKQSM44gQ5UTuqIdwpkbpPDs9fYCjo0MwAf0wgMG4uZG9Q4eHhzg8OJD+UAk/yjMnCf8cMgQAJICfkmbpiERBJsnGoxnUDCfmz2YYQcQpzSpwcHSIyC8gWZcYt9sttmFCzx2IXeYUhngWiAmBI87OL7BcHRQQzzrPakYpc6fwEWd+tzxD4JT6u8hO/ZOCLDM9OM55TT9GHfdMgfmSq+GGpTmEnLrPzFGVO9p29ULKyfBpTxTpvCt1Cs/pXigCSBdt8WZ60ZQzGMiKVQf4oxUeHHyE23ee4PNv/T18/vG/w7s/+af4en+DbnRw0wSEIAd4gcXTA8mmF5Kyp0SlJAfYcMOOJRgAO0p7B5NcRZojYLjI8El49J5SNi5AMxMCBZTAlN8C+URlA7kdkbz/0IyUTbIih9v6Wfk1kL5LoahBUxNQ3hNQ1eXn9igx9zzXsirL+N+v3lqR1DDk+rca4FvjLLCrcNhrnwchB9M2wKeGae+j336AP19rQJQTzkTMvVa2rL3GlKpt1vBc80xLUU1QomxWT8KK1PU7r23eH7S9MvvSMtdzZV8/7XMhhJRjhuRICNrNjFaXAWCHji1vHmwb+O0KVuu6t6Jx0osHIcYO20E25k5hwmY7Ykoa23azxWLosXIOw9Dj8PAQN1eX8AQcHKwQY5QNuMS43qwxdg63t2sQyYnay6VkiJrGLXjRoe88DlcDYohYOunYm/NzDMsVFssFekfgKG6hvBdA6CJnLXAUy5N3IOoBEAICYpTc74V2aaVITOaGAdvtFgDDEYMQ82Z4ArAYJE2tJ8k42veibIzjiO12C8di7emGDts4IXLE4GW780HnMIhkzvVGBEyQLFyeBgxguBgxpr50bsBXfvUX8eDkCGMkLFerxFQOn7y6xtNry0zC2CMcfhY+SCfall+nBz0CegDAmR3go/l4q2C0gI4BBOpwhncSzVMDoQtmWUr1HQ1dUUSay7KTioww5nndtux540y52AXOjhMQV4ASgRL0aZQJBQezfpuYdmONzHeYc5pTAXxmn4D2wQAbPcCvxGsj9137XNBzse8XeFIJXUEzRXmJSSiBgVgAqdLZAmoDdQQgRc4eI1b1YgdskAF9xRtQhAwVZcf0W9rGRTEzqJHBcOzk1TSQukxGZmy3I7abDcIkgt3NqFGeUyE421tExZPAnDwMiRbTJNCLWM48kZTSkrY0hgkxisFgmkZMU7JERTmPR8sEZPaGEHIqaTDnceKMS+cAFmwpI2P54s05nPPwRDhYrfDw0UM8fPgAjhzOz85wcfYGR0cnODg8RJcSaeh+HQ3zckkhYDOPFChH1hA+yfbm0wnaIj8qsM2qrEnrHBMiExZ9L6PDE8AeMQSM44S4AFhtEjrukcAEHB8d4+c//znee++9tHhXDD2jS5It45TO2ongEDBNI8DFY6TAi5kRJi68TcKjuQ1ZUSk8T6BEL5HxgXnOqIknidJmcVQWX537WWhIp1VxIxB814l3Nv3zyVvrU6hnftVMkpg8Qgy1RDImBuBcNkGoUkOQueIdcHx6jKOjQ6yfPMbZd38b8Uf/H3zlxc+xuLpFd3WNLqwReI2tC5gwot+KsWvNEYFEae4igSJj4wTYB5gQFwUzqd+dhv2ktJedkxkZOaSQWQ2PIxH6sNZyPZ29yHxVdtVyrYpL4CihUBpik2huDRUxySxK6cA1YcnbPBkKImtL9j7LesvKXpd3H6u5eGVpp/z7XFZxdpWxdF9dnGSRBcX7FLC7vAp1v+v3a5q3vSNzzxoR5XbZftiwOrsuqpKhfBCYZ1b+mga192PHil+BdEtX+9yM/kkbJwKcS/LESQZVRJNkB4WWLs0BMTS7vKFa+2Ov1p7hHYW/GqdaOXGc9nSmSJ9pGsXD7Obv5X2kae2v2zG/zO9RjBWKy5ju5v36urei4QkYOo+uW4BXEgcWQoejw0MEFkvE7foWADCNE7rOY7lc4nC5wPPnz3F5cQFmcY0erFbohwE36w2ury6xWCww9OIhOT+/wHazwenxMaYQMHQdXE/wjjBut3hwfIzlwUFqVQrvIYeuk3Rxm80G3nclVCHKhucIJ6FLoezP4HRIGqezH5T5RfghbTTv02FHwlDDMKDreuGVMAEsZ4uA0rEAyevS9x0CRzgwxnGLwBHc9fBuAY0LIP0XCRzEqxEdYzOO2G4nLI6O8dG3v42Hjx7gJ589x//wsyUuD75VQB6XkixWdZSse6ptGyF9XzmXmREZR+XFPAMF1W7ZLIbpWTbPaF8LgDZWWfP7XXWjUbaQgHbrrvo690/sXvlXBYnmflEK5n1SrGDPVsikpbKXQPtjwWYpPwElFS5pALV8iW8vexJiepaoeM9EEdTvCiwT6E6fdeGhqh0zgjuzPwHI7zgAYAEVMicop/wlInQpH7haZ2eeC1R0yXXq+LPi2wwox3HC1fW1ZO4iyiClcz57FMMkWXc4BrG6Jy9EiKIIhGlEiIztdpvc1sA4jdmzIM/J/I9JDgjPyaYOVkIm0lBmSGd4xNBU4+6VbqRsQHMeQuFFpS8CYwojHAib7Yjzyys8+/xzPH78Lt59/C76vsf5xQXOLy9xcnSMg6NDdL2feeN047nWxUprQ1tZXGNRzJy2j2ahD9n4wgXc9n0PRwJEkYDOZjtiCpKFzRuhoKQahh6RIzabDYZhKHxmJ32iyvp2g9dnZ0imcIAIhwcH6HyHMQTxQlE6g4gZMOcUEMpm+qgWz+xtSvIKEm4ZOYpFPirwE0kU5ccZ/8u+sbTFXI0hqROyHogxy5N4JrbbMTWdSrgCA8xxdiCs8x5D38N3Ht0gZ9b0XTpZHTpOAugdZEF3CWgr+pLdeZJ98OD4EKvDQ4yP/4948cVf4Be++BeYnr3A+Oo16PoabrOGGx22LmTvC8eA4II4drPBogC+GeA0DKyWzBpc2k3vpaS3XzUwbF3ztlDmX1VOLEAF2qE7LcBm+9Cq/y5lZJ+npKWI5M8uzTWDMVpAzfYj8zGV3/a9R0Q5DCfEKKfZG1rYdluwf9e1r307e1vQ9k5J03f7vK/cVvKd9GPxYAn4yc+2DqDUyyoyLWXrbcppNt7JN/lcrW/z14rxL8vD2TqbFvb0nI6B7cO+vrQU4pniFxScADc3N6IUpZTXM0XGNrfq8848qH4v7395pfneioakq/WZyZbLJW5vb1O1IvyHtDH7YLnM711fX6NPm403mw02mw2Oj48lrCptND4+PMTR0RGICKvFgKPVEgcHB2Bm3Nzc4PDwEEPfARzR9T2GYbGzmdunuDdtgzJ3ADB0PSYGtqO4k73XvNsyAGEKac9ED+fEMzFNohRtNyM634HSSbRgOViPIK5i5xzCJJm2wjhi3I7gGLEcllgMA7bTFhgB4oDOD4paygnCESA49OixRcQYgQjC4vQh6Og9/NmLgJ9+Rrjqvod+WKGjdHqzonsYAAzjvreDVxDR7m/3WBbquWLftHVT9Xt+boZwC9i6z4LEBphkwOboP7nuOy+at0ut+9pqrUgVOtZngOxViAaAIgkDm8WIk4Kgwll/ixDAmxWRLN+4HO6WgHmEAUWcRGD6vVhLWf9vuqcMAyNA0xXK3gRVHADZK4Iop89vN+Kdiyynji76HkO/QD8MZfOxahoJ5GYLTO5CGsui3aUQF8b1zQ1evT4DQUBcIMZmM+Lq6go319fYbLaYpkm8iyEaJYrntE0CvQjvMqoK5oTOlMFoFqD5fWkwKchThZ10T1bWJnLoaPbmUUmoWjx8Wj/KglMBODAwBcZ0u8Htp0/x/OVLvP/e+3j38TsgAK/Pz3B+eYGTk2McHBzC9+Vk9WrJyP8lLp+VLnAEF1J4j3MQI7IqReW/SaLkmOIwTXJmDST2V0LKXObPqBa71N/T4xOcnZ3hyZMnu0AklR4j47PPniWZm877AeOs67E6OAAzYRpHjOMWHGVjcuSIcUzp1mOQ+7qPhiBeqvQ98zmLQqYHccLJyd5qs5eTcGMZ97yvJTVY9wCgLO6OCF7p41z2aABy0n3f9ZKRkR04edLDNOXBIggY6HtJdrFaLbBcDBgWA3znRbFFTIedIomg5Kkl2TeBtP4NywXiN/4mPn7/6/jgm/8OD15/jJc/+ik2n78GXd0C2ADjiG5k9GBEihhdkANVY980xtSW1lbmmhZYUwNC62oB0hpEad36fEtxsIBc7808CHfUN2vrHkWnBp4tK/J93qnruuv91ruWltrWOhlPXaZzYvxppe/Xd/dt3N53tcD5Xc/qc5qy3u5FaNV9X5rIWkJ5rbZ9AhqKsn1P562x3Nt9IHX7bfmtPqrSo/XnQ6yZYSdA3U/FB/toWrfFen00HKq9iV/IIoYNwrhZ7/BA3YcvoyyU90Ru3ocX9PrSm8EtwyqBe+9EYHZpI3Ii+vn5OciVPQPee1xcXGRN3XsCc8B2u0aYBhwcHmKzESJeXJzBOYflYokYJnAM6DrZNC31lGPjGZLNyssRzFiv19LoTAiWBXyaMKYDpIgIfS+hWhyTVS8GTMnq2XvZH9ENsuG887IfQRc8hqRZncKUGB/YbrZ5gZumDRwFHC0WeHj4CJvNWmIVYzpwiQiElCkgAmBCiISrMOEz9wF+vPgb2IQeDEakgM6cSm2VhR3gv2f8FGzpacdZT2nImLdj8xmsyv/NVtaqTG2jxj7Pfku9oYRMNTsSyLxXUFt5iwEwpVSSlFMwEs1ponJ6XoSxU6jgYlnABbzWgi+10tzK1g4F7VwEmoLJvNAgWQIB8VhAlYOqDlMW8pum/fkwR3lO+o0MliW1flHjmHl+MFk07UsjEYKccKxXqBaAEKKEjVAyKEDAURwnnF3dIMSI1XKJo5MTLBeLnI0ssrhaFUAXBFq0Y+YSVnVzc4vnX7zEcrXCNAZsNyPenL3B69evsdmsy3irMqAART9bpiXKOcBBZc7IT2LRzhtWXdnkG/MipozHSYlIoUkMEEewLjxc5oByMQj5PAmGARm524XfVHmRjwlJJst5DBFX12v87OOf4/mLl/jKVz/Ew5NjTDHi5cs3GIYrnJye4PDgQCxi0oyc3lZ0ijKXwJz76Nil074lRMWRHEjpXOIl0Ey5JeI8pqqIaYrpyAwXAXZpL1KmNePk9BSfPX2Kx0+eKIvn+akqwLidcLveoPMel5fXOD+/yDLU+ZTJLyRrfFbEZb+cHQMCZrxd+m0W2RSWk57IbSqXg+4NgloKrcxKilpWULJhQu+7DD5AKZyXHBbDIul3LiW/8PC+w3K5wjD02G5vcX19g9dvGJ4cus5htVpitVzi4OgQi2FAr2FzkLEIKRuady6dWSGAZ7N8Bz9b/hG6R1fYvHeJiy9eovuP/xjvfv4fcMiMJRP8uEWYRnDnJDsYXBqbolDoVVtRW8Bev2fgkeV324K9D0gB83Cflldhn1Jgk7bUba7rrNti+7DPU3GXEmGBrN2UbumnRhB72X0mNT0ykLR0bdRt+7gvg1E9dvZdratFk320qQFuTYfc3tT+GhRre60lvwbUdVKAfEQAkPne0rHur3Nulhq2bp8NQ2spZJbmrQylqaL8nqWPPLPL55YXa/6+C/TrszZb2A6fmvenEHBycIT1zXXmubcpGa3wsZpeyo8R++fTvuv+oVPGm6GN6PseUXe5M7J7cIoTps0Wi34AnMOwWGC73eL8/BzDMCCEkHOsv/PoUc4gxTGi8x7Dcok4Bdzc3KB3ku7Rey/ZqdKiLH0mbDZrhBAweY++H+C9eBhCmJJmp3AngtLuN3Erekxhi67rcTCs0oRggMVKqMwrKW+BMZ2IHkJI6cIYPtmvxU3OiDGg8x1832GxGLDsBwzJfdVBrGnTlDa0+y6ngwwgjGHCwekD/OjFAX6y/CVEUA7rEC3VZ61VVoXEEMAsXCUfCIa5DqGATxfNvUYM2sdExeJdHiyVZCB+R91SgHknoaO8+ZJS+2xnuISDZUAWFeAjpyzN1kzm6jTruTuTCyFmSofCj1xu/qqpPikpCSneG8Xqn5UOJKEAs4kvKUP5zACSTZ8EsSIHg8TJKCwAMrADUZ7cHGP2ZqiFQ3JiJ0UuyDMKdJBpxGUzXQo7CpHBLKmWwxQlvCgEgIHNdlNAVkTuN3nCcjHgnXfewcFyBSbCzfoWV88+x9HxEY5PjrFYLGUB40RJFVqFcxSzAZBsbG/enOHo6Ag3N7fYbLZ4/eoVzs7OxWoOmmW8QJZDgA2ds9ok6wOkPKa/MXJ4FIryVNiz0BzmCQ1rA7nC52Q9a9YTpbG4hs/1RzK8UaqQ9wkgXUQoHVAZgMurK/zVj/4Kjx49xIcffIAHDx5gvV7j1cvXuFld4+j4CAcHB3IKPYplK3N4Il1UNkYEsezB0OhKmSeU25h5G5x1IE4FCS/GLPs1WYINFwSAxWKBME6YRvEKq2yYoXsCfOexWq1weXWN69ubpFAAkWLe1KxKWb500c5NLjyWZUV+zmihO6JNB2d+6gazCB4iV8YEu8Uob6iVtTaKOOexnda5PQQFDh4EMc75rscwDHKoZ98jcodpusbl5TXo5SvZ73h8hKODAyyXCwxDn+dUYAalsF+aZA1mR5j6Y7hHx3j44H1svvoRnn3+BaYf/0usfv7v8OjNJ3gYvJyDEvWQ1l3AVIPpllJhwaoCRJUVNWBtgSk1QLYs0ffJkjUHdyV1a0vZqOutgZX9XIMwS4/WJmIFrS1gDiDJ3rf3pwa4mua13qxdKzi2DzGWRBa23fv62QLBetkQpVpZKO/uZkSaKxy797UM6wWwymLdHvub7o+zz7ZC5lpHLmj9tXeuxS+tz3UdLaVLP7cUZSBhAdO/Wimt6ViXadsiWU4TNmE5JHm1XOLk5ARnr17utOU+PFFfrXkf+X+l0CnZ++BnsZGipQPkgBgnOPYSFzYGjNMGq4NDwMlG6YODA4zjmFPSEkGySp0cASB0XjYpHh0eCABzI26u0wF2MWIYFimFqkOIssEGnnEzyTHrYRTPQucWiGHCckipcUPAZrvBJgow6Lp04Fwi3DhuwSNy2d6LxWkKssANncua92azAYYOSKdTcwhyWGACcV3fpYwzk6Sv9OJBENpElOTu8jdCUiPGzuPh+1/Fv/pki590v4iU2TYtgSxpadPmwJhz/svCm7EUClhKv0pV1fqM9Mw+HjFLcr5kGdY9AumeYjGz8BKQk7MwA0xl85FahaGAV9uXUdh8AjAbYWbaxPpj+hK5/KL8yMy53xnfYQ5G9DfdLFUUjzkxiFMqS9nwMFtENW81cr+QQosU7GvYkC4AacFgUTpV4JXDlaiEfBBl6KMCMUTJyxuCnGCutJB9CRPGccLEAeBkcZ6CEkkO1QoBMWVQIhJvhZwTUQC5AmYHyqmHlZiaNvV6fYOXZ2/AMeL4+Bjvvfc+Dg4OcHFxgevrazx89AhHR4eiHCN5ibR0/ZDqY0io4uHhIbbjiOura1xdXOHy8ip5Pqk8nxA0pzeVRwow5jIhuFTGBTWnMeXyxSyEzChKhvLhrLlU+M8Epef5qDyTGqBWbyu7rbqVa+AE6O3BH6lgfSpGxsuXr3F+fo7333sPH7z/AU6OjnGzucWrl69wtbzGyckJloslOu+yoqXKa+43lzFgTqlxOXmfDHDICoYUhOXBCle3N7pKglksZxGcz0SaLaxpvq0ODnB9dYXTBw9mNNXLe4/OO3RDj6PjQ/GcJFp6OLB3uUAdFiLSWZgFnvBWkjR2POoaa3lp2KCMDiOpYJnXShtmqumsDs5tKOVFMDg5X4qsAsABFCO2vmyc1hCsYRiwWq6wOjjAcjFgM45Yv3yF1/QGi6HH0eEKB4dHODhYoRtK9kFGFO9SJAmPc3Jm0fL4EAcH38L6/fdx9vLv4EcvvsCTP/lv8dHNBfy4ReQrZPmJXcVC7+Wmm+ea/6oxrq8axOvhvLU3wD6bZeWehaulYNxlJa779F/62gG+WS7I1eqj/Z6VjUnCAFvAtR4je2W9uFKOWoDTKhstAFpnJqqfK/uR5vssWiCjVpCIyh6FfamNa69ETduZUlPRs+WFae3daH1uvVeX3VISWuMye9bN51XNu/q5DpFrzcdMlynktenq+lo8oLQbELlPqWzxoH1n3n4niUL+18g6ZbO4tLTCyAwOE0IScoeHR/Bdh8DF4tEPfd4YF8KEznsB0Un6M7Ok6HQugTvC1dUVANkTQmnFH8ct+n4AEbBcLsBADpuKHHCwWuVUuJ332I4beOrk4DsnYV6UQZ0D4gRxnIhSQMQ4Olwly1EZ1Gla4uzsLCkjHcIk8cEHh7I5PYaI2/UtBtdjMXSyAE+ThBvECHgZePGSMKLrMByd4N0Pv4L/8Ydn+Lfxe5iCuPcJ4gkhEPoE2GQhk62ArlYgdMFMn5VWTQA9k3+zRKYFw2uGEMgSGpA2W+r7giRyeYJFjccAMM9yBh7gsnFZF+LyjBEeSauZWaxBO0t7mSycMSMDxQpvgRPmiokqTllp4GR1YqGzepRy/HeMRcGCvBdUUUhjwyx8wJxCUnSuhJAUBen1mEL0CCVt8nY7JkUkYkreM8XLrCcAKz00LVZqkPcSphGgYY2+nKXgHLq+Q19MS3BOMmMwRMCHpACpIqbPGVQq9aSECL7rMG23uDg7xw9/+EN88OGHeOedd3F9fYWXL14hhIDT0xN0JsxI3TqcoLuMHbIh4YtnX+Dm5gbbcZt4TUeTNCYo867lzqwRMqVxL2M0Z0SC6Vzuov5eQKR232WLv8HrKGmWzCIAFdgobTFKR/EkmsUi8V5JD248YzMg7fL8GLcTPv3sKV69fIWvfOUrePfJu+AYcX19jfXtGoeHBzg+OsZytSzKtdZOVA4s5DTHKAJwiIm+WZ8rRAaB8t630kpRZmOMYCoepkIEuR4+fIA3b97g9PTB7CwXqUv2y/VDh2masDo8xGK5wrgdk/clUyGPn1qFZa5Tlj2i7MQ0LlqB3Sszr1vHO2saqcMmCA7WGmuYIvevBCmmfwq4oJvREx2Si4VjzHNZ/EoRU5xm8tiRw3qzxdXVDZx/I2ncVyscHKxwcnyMyIyzswucnUsSlYOjAxwfHWGxWsK75C1jCWeLLgEYT+LxPz7Ak8Ov4cGTx7h65/+MV3/83+LJ2QvgmsHjBo4DCCnNM8k4I29bqbw6hqAZNIKKjHI14XavfeCw/t6y/tbguGUJv0/9et0FmPalIS18AmgA717wxSVL3o7SkYRLDSiV79WwZS/FVJpooU5fW+QOEu9xlgX76KDhRpa2tQW9pkfGgFTq1vYVI+J+2lolxtbRUm4y8IbMNTXSEfIglPXBfFecUPe39tIoPsnGqyRLIs/3luRnibJRkZzK6FLHLhsor7qsPKoCGEz4suU12776fJxMs0QD76Tc7XaL29tbGQOlj7GwFDy1q0TMlC5pcdrXRvOzpGo6v+W6t6IBCDE6c+JgzvggZECIkoWEiNAPnYB9lwAYIkKYcBumfMr40K1yp/IARrGk9v0Cx8cnCCFguVxis9kgxC2mELHebnF4KIzouz4TSjZta4xfsfQsBgnlmELIB8wBAvjJE8aknXnn4AlYLgccrAYZWJQN4x4em5sNur7H6ckKPp370fd97sdyuUCYRnQQBphYNmYFQE77dQ7Be6wDcHh6iu7wIf6ffzbhY/5e2qyeNhlxAGnZpHHvuvjKcEe2Sx2M0JMwCCJli3Sl93XPY0RSHC3YT/zIKYuB7IGYp4MURs2rDPIJt4wUO1+EngJlMoxcelAt/lp3EoyqvOjhWAq29KCoqGFE6XMI6mnTf+rlkLqnEFJj5FwUTmcgcIhpr0NRLiIiEKWuGGSTqkw6BqKkdhY5Ku+EKWBMJ8urlWKcpoRjCJxynjKQszYxJLNMSWUpcd6+c3Bdh74fwCy87IiykqSKBJKiQ0lxiFkQUAI/0scQIziksXRO2hpjpnHvHcYxZIUpRlFwiIuHRvkbzDg+PUWYJqxWSzx49Ai3Nzf4+OefYJwi3nvvCS4vr/D61RnIOUn8APEqxLwoiLyQ8Za9XuvbDS6ubzCOW1Dn4Donsfmabkf5nsQCX4B7ivN1JY1zPvmbBKZmr1pGnZnRpClaBWMOkNTbUyZPAv8+31NVWDdCZ5xLRkG2bkVtG8RqTorqWQC77IFQBYQMyCj9jzHiZr3BT372Mzx/8RwffuUrePTwITabDS4vr3B7u8bx8RGOjo9TSlwxughoLOBd561HRGSXN4TvXMRYLRfi5UoUYRaPWIiAlzPdIDJp1lWsVis8ffpM9vp4l/O7Q5oDB8bBwQFevT7H6uAYR8eneHX+WmibU+eplkeQVEmczqiQwVP+Iu6QFQhtA5cxyYYQsuPvsqKgsEjeY/EKZLFnw4HKGGtYpXivVHalsdcwclL5J2BEtpBHsO/QzcI5ZM2IMSCSpDufRsJ6fYvLC4dXr17gYHWAo+MTHJ8cYztOuHnxGq9enuP46AjHJ4dy2GPfIUj+ZsABPhYegnNYHq4wfPNbmN7/v+CLH/9THP/4X6F/fYb+4hJ+fQvmLSKNiISUfETaJIzp4bhPvD9l5ULo7DJIE7LMuUn3dWoIsoImC2Trzbn2GQtuM2s2FQDMfr/L8t8qwwJte80twIpbRAY5IjAFaChq/Y4cpiZzRkNrnXNFOdVMghXd1CsKzC3qNS1qK72H7sfSUsq8DFU96kmoFYydPpjna6+G/T4rg9u0tW1vKYe2rPrAOi4WwkIL7aOb00qxjRoNLLCeHTQt0rgk+QBUeM/emY8N8voN0/YsS1RWqAxKB/sQzfdESRFlk35N29aBfXb8smhEijogyRS4vb2Z4SqLu9J2vL20Z6KUlU4iKQgS8SP031VQ3nZ9aUVDtUAdqK7rZoyqBLFuFh2ag8NDycE+TVgOA8ZxFO+A2f+hbjgiOXjk9vYWi8UCi8UC6/UaTBN6SIYaZtng3XWdpAn0XY7Lk812C4zjhOOT4wQERwGMzOi8R79cggF0FPM+gM47DJ03GnUaIieM3afsW74TpUZCpwzhAVFkYsDEApLHGNEvlilvf8B6jHj05H1c8gL/70/exxkfYFxvhVYEXF9d4ejoEJTS9moKVQVpM40SAJEyCzJjSyiGPlHeC0GmgYCZZHlL1n+kySjKgyzMYAkdEgZj5HSIZgGeKTpULDdqfSgTh7IGrn3QQ9iUZ0SBZQHwesZD1EMXSzyoTKyUEljPQGBdmORwNOmHnJUwhpDToMphahJfLkqCeJiYZS9DTPsU1AJbCwRZIES0OUfwzsup6F2HDoSuE8CjsbKUlF4VFH3fg2PEGCYQVLinfRY68dW6EoGRRxmHlFZT09zOLHxAtpiq4iXCtQA1rnjB/tXx0zEEAErnKsAIWWbG9oXEfp69YZycHuPk9BQPHz7C06efYRh6PDg9xdX1Nd68OcNiscRyMSSFzwJotUwBi+UCL1+8wvrmFuQIh0cHmMaQzr9I+yl0k4uYzoxSnXDNPHU75rZpo9CmLxksgnJIEVI2szzHsjKjigpBFdSi/KRn0txhU1sGrYbGpQmqfOieIpcWKO1rUhw1S10eGAVmwg8XF1e4uvpLPHz4EF/76ldxcnqKq6srvHlzhpv1Gg8ePsBB8vqSGVztHUH2CXmS+c0emc4qVwA5I0K9qMk/KXM1RFBX5E7poNzwzqPrO2w3GywPVmn8U873RJaTk2N8+unnAHkcn57ien2LyDJfFdy3rKyZ0nbx13mj5afvRS4ic4Z6QvI82HPIHJhz+tmZ1TbRT+owWa5isbrKfI0S2uAIlA4cZfISKuckQNKBUl77JPtY5JAcVBkwhgAaR9yu1zi/OEf/vMfR4ZGcsbI6wNn5Gc4vzrE6WOH05BhHx4dYDD0QIXuxSIyAjhmB0jq7OkL81f8tzj76A4wf/yncn/1jjC+e48nNGQ5DB88RkwsyWM4lZUNAMaLwi4I1Cwz3KRo1PtgBbo3nFWjW3gfLA2+7as9HXU5tJb6rnPpSfmKe8yNz+RWgtEcDuf82TEgt5jPvQaP9wO5ZBzO6V88qOJytE+b5KRnGWkC29uLs6z8lWZ7xSKUIOZdOuCfM7tfeD/vuvnv13LQKmK2v2UaSBApK93o/DYhm+z5ynY2ybHt26C9fTLuLAQJICkVVamvs9inH+5Rgu8JxZGw3G4AIzpNqPTtlFSw574P+WM4odWa/pxpFQlaM7nPdW9EgL5u8KRSXVeAowjKWRuqO+8jGOm4mjrq8bm5vwZFxdHSYwJ0Azo46hMlMPC9xptM0ySbrzmOg5UzzG0fZxLpZb8CbTRZ+m+0GzIzlcikpdp1YDL336PpelCZHYO8yOF4OkkZXwZoAi8Iop6enuZ8xxpylxzmHkNrS9z3GKIf2bZIyxSBstjL4h8cPQMMB/sknj3BJhwjjCO87eO/w9OlTHJ8cwXpKstCyGmz6JCFgJsikYEkDLDkrH5ySqTMjbaoWq3hmIhRGt+/pPd1srR6tKfFC3pQMUSSCWszzZCwWOwbS5qVksSZRYkOy5oEcOJ2uHDmB/iDAHCk8KWf4MotXdvElGKUb6e3ily0YTkKNAKDrBzjvJbwtxTYTCCGGZCEQ6zurIEpQhTnCOW8sPMhtCWHK/AGMxcUK4EaVBCDTTqms7kkdQwFNGvaVAG21sOtzRLuxq6CYwTDMOxlRZ0BpFjjWcjkdslcUPvLz1Hrn5xcpTOoBFsslnj59ioODA/RDj+12m9KbPk4ygnNbBZSLUPfkcXt7ixjlzIHFYomuW0vo5WRTBlKeB2qhsrQi8xkJOIsyUD3BiaKps6qQ6PNIADWHLnGpk5QfUOSa5a+6XWnQkPO9JdBaVubynvIWVBHzlOaLsaSzS8ppKZ4D49WrNzg/v8D7H7yPDz/8EOM0Yn17ixfjC7zz6BGOjg/TIljGVxU/JD4EOUROB9al59RDuRiGBJwL3UICmvUSJvO78MjD0we4uLzE6iB5sGEXSsYw9Dg6OsL17QZd16PrPKbAZQyVxuYvDM1znRD55DKPufyI/k7mUAr7W1ZACMmz5fJdEOUUx0Q0M56pR4vhQU4syORKiCUxSxhjn9arnPmNAfbimZUBkPFN4+A4iNcSxVgS45Rl5DhNWK83ODuTBCtHR0c4PjpBuJxwfnaOw6MDPHxwiqPjI6yWixS+ywgUQZ4RooROkneg41MMv/J3sf3mb+P88+d49vFf4p0f/mN89eopFm4DcJDUv4n+lE4w10O7Wl6FfQC1BTBnvFMBVXuvfm4f+LbXXXHkCkztQZyt/tSW+Fl5jKLEg1AsHlYi6Zyusicx5zNX7mMdbgH/uwBp/W6+l4CvpZuNUHmbAmfBsBqQ7Ds7yhDmz9Tl31VfzQN2HFr00v0+dXtVLu8YKojyHrOWovOfetm1oealmNYZm+a35vuWp0G/t9Lb2it7ymCWoha9Ut/r8tOPGfcqplfvmq5FX4ZG9/dopAPsIEmZEAlicSGXXSmO0sJIKd1osv5RAm6d78HMOPBy+JZYqVMce7IQR0iGJUYBn5uUktanZ51PjUjAcvByroaGZOkcD+kU4KurKxx5iVMPMXk20kAtV0s479B1nYS7hCCnECfhDiDH1ocYJC96KkOt4dvtiK4XD8c4jljEBTa3a4CAv/iLv8ByucTJ8Qm6rsN6s8XvfP97+Ed/eY43/j2EcUqgWE5NH9PmdiKX953MFAwFqFAMlECQZRSzgjJ0cUOyIEqIUQgBYUz7AjgpjkEzvIj1KsdfMhBYvDH5dN3knZlM1ohpmiSkKC2mgSPCKN4FSnTU9MKcFJwQQlaS1MshQEpDayALbwbHlE7fFRqp1caRbk5KJ3WSy4qTWo/zZFb3KhfaTJo6booAheRVMcqAfMiCVWmt1ihrzdRD0vQ+snJSCbIyiEYQGACatUdVbBJjl9O7ihIK6W9MQKm8i1Kr4SP5j1pcU6iHkhgK4hJoTiE9eQ2llE5VthLj5uYWi2GBw8NDvHrxAmdnb/DOO+8g+A7X19eYxofoOp/c0mql1jNfpO4pHaQ3UC97qAygzGcfZJWLS/us7Mz9lg9WiNpQvyzIsxKSqmLKRcgQiIxJzDNbMKy1eya+q4WfCbnNZMdR6zbaEbNQg3SsklJC0EUq5mGV9hY+0tPUP/n0M5xfXOCjjz7C6uAQ6/Uaz1+8RNd1WK0WeZx1mIVzDCxKSlhWChON9WBUIO2HSPNjmlLInZmvWflPi/vB4SFevf4E7733BHridFZ0GYBzePDwFK/PPwXI57TjOrfqK/fByDrnjBU5KUj6mVRZVmJTIXtOmJloUeaYgjI2z6VHuWwEcrBjSWKoQAKTMZbwhAxSlT8o71WThCEsGba8FzkTKPVfyu56D46a7jemDIajJIGYRqzXa5y9Ocfq4ADHx8eIF1e4urqWvR2nJ3hwfISDg5QNLgBMETEZITrqAEfoDg/w5KNvYPv4MV5/5Rfwp5/+CO/86B/i0dUznDqPHoyOI2IcJazCxLhbw5+CkH3ArfZStMDjfUCftcbfdbWs4vp5FnNflW3btk/ZASi1w4BoBqzMKCF3VL1b+lfTsX7GPjezjlcgtfXX9gOU8qs1aG4Vqda/ul16P1Zt0Lpk7wbNlKu7lMyWZb/+Puezdln1pu1sICXKPDOvg/YCZ7LCwpT3NoWnNRYzxZDmhxjuo4+dK7YMe7xEMVLJZ9fJkRKbW0k/r3K7Rdt9imqhi8gqZtmjW9qDGe+97bq3ovHDv/whpmnC48eP0XUduq7DdrtNYU0ryRHuHDabDaYQsFwsMnjs+h5nb97grz/+GMdHR3jw4AEODw8Rxgk3Nzd4/fo1pmnCgwcPMjGGhWTecE72fqjLa1gt06JQmEetArODW8zhS845fPH8ubR96MGRcX19jYuLC2y2WwwHyxTuJClwHYnVhmPEdox49fIVvvnNb4IhylXf97N4Uz0Bd5rkEKnnL16g8x2244hnXzzHwwcP8OrNGR4/foyPvv0LcP0Kr8KE4GUx32w2uL64whfPv8BH3/4WDg4OjQBVhitfM1sU7SKDx6x8JCVDBiGFvIxBDk1cr7Ed5aTkaZowjbJYTdOE7WZjPBOcDtGaMuCepqkockEAuSqSuoFaQonKJmBnQuMAgu+75CkQwOK8A8jlkCoVziF5NCiF/4QQc/x9PuAOsik1Z25K5apyqJiBUyhWUmdS25LCIfk6AUI6dVcVnwIyRVHT8qUfRUwZwUeQsAIFQVnJwEzZyJu5o52ohIICo6IpzPSPxAv5LTvRM3BOhTtXFI6ad9INAsSIAKsMqXdkvvEtL7pIQiam9kXg5vYWJ/0xvHe4uLjAg4ePQN4hjBO24yjZ3iq2TU1OZ3noJvzEP2kDrapU6ncodDJ36n5RpTDo2Oh04LJPSBuU+62jrwplAsREzrQ7jTdcPiVc9+JAnyv/KeE5rFxgxrIMJGaDVTB0oj2lvLJlSzVTKUvaJzx+dnaBH//4J/j2d76Nrh8wbke8fnOOD5bvJW+FEiK97JSOdsLYj+LFcZ4yL2QZnDx3Me3Ns4OrusTQ9wAD0zjJ3hvWwDapkzni9PQYBCBME4Z+wM3tbaaG0Ml4nvIPnD+n8GepNCsZws95bxCRTvMiA4gso+joGmXQ8hqVoWLdq1Hu6UGilGK+xRgX8ziq51nfdSm0ipnReQJzOvk8RgQQYgqt1H2CcB6OHUARHoToxbuhcjikENGb6xsMywFHR8eYpoCrq2ucHazw6MFDHB8fYnUoCgccA4HBPAGdk/NhiDCcHuH9owNs338Xbz78Fr54+QLLv/5f8EvP/g0eMMN7IMQpM++uUjCXMneBGQVZ+oyCQHuv9c4+D0MNuut39gGjlhW89fsOuCQdzxqNqiIjnvucBQzz9Lg1gK//1e23n+sUrzWI1jbtbN7GnEZ3KXVvs7SrN7622ud2NspoXbXSVys4rTKs8lHX3aghA2WriMQo+5ioek15saVk2M+WZ+2Gbi2j/Z2ycN/Hw/Z7vSdpTvtK5LEcdrtcLnHxRj1O5f2ZcrpPvwDAlTFz3saE9e4RbqjXvRUNRsRf/tUPAWJ845vfwOGhWMsODg7hqGyG7lLIhA5oNwySaarvsBm3+OD0BJ8+e4rVYon333sPgSNWhwe4urrCGETxWCwWcJ1HN0i5t+t1Fv7DNGJYLlMcPPIeDQYwhgl65Ppmu0WYApyTMyr80OPnn32KcbvFdhwxjiPeffddPHznEQ6OjzCFgKGXOGTEiPPzNzh78wYPHz3G4dERrte32G63kv2q86DAcGCM2xEgacfFxQWurq7QdR0ODg7x9PNnODo9wSZM6Psepw8f4KPvfhdPn1/gOX2AyGINBoDFconT01OslgeIMaawqQRq04I/A41QpaKslWrl08cIjBhFUdus17i4uMwKxs3tLc7PznB1dYkp772RzZo+pdPVMV0sVxKjGwIOOg9HZSOyKhIAZ4+HAvuMAFnBcgnFmmIszDpKmFVJ+ZpgfqUsxBzSFhKzq9CL2XOgXgFS9GSUsBm4AHB4KCFqMYSklFEBN5y8KpBJJ2ewCAi1FLZ/7UbYLEiQbdSqYqTfFbgUoKNjKUDMZxDlCCnkw6BPXUxQ6EOEZMk1qQxVAGEuV5QmZOpWRYVZEw/48hCLt6i0O31PCG+z2SBMB+j6HpvNLaZxC99LQoXtOGK1Ws4UM4IC2ASo0oFwIWhgqEsKg9GSUieLbbqEq2XLk1n/05AWAWnnj+13gbO6BM8LSYI1h6YpT+p7qmRgvkDM1q5UN5niC2+X0ckqkK1bz0lwLnld0t6IBEI1zEcVcmLg4vIKTz97hq9+7WtwPmK7kXnv+uK/yJgw0Ul2Z+t4m25B0o87cnnfgS5sIc1jwM3CNq0MAkl685vbGxyfHOckBACyl7XrBpyenuD8/Bpd36PzHcI0ZqVAx0nPpMlzRxV1Q8Oc3YySMUL5IPOJGilKawV4U94jlYFuekd1KCody3MTmC/EomwQZJu6VCz7zAxnqMEizTnSv0zZa9+lZ5h187QYH5hk26pzyYDjOoS0p2Uct5gcYQwjNusNhmHAweEBttuA66tbHB0d4MGDU5ycHGJ1sBJFHxFuYoAivHdpP4fD6vQYy+NDHD95D68ePsZfHj7Ar332P6FfM3x0oGnbBKs6L9u/macq0FZbimtwXV81OKuBuP2s5d0HlLZA/r427F72GZlr3vcpD8Cu8mSt7F/GQqzvljDgomzUZdQgXb3/b6uvBYLtVfYB7v7GXLyxuGefWueT1N/vtsC3+wDIvAKVOjQZQaogr/W2Pk54xe6hafYz3dcQ6rcBcIkgKe2rjeRfpl/WiJbbBEmwIXKHy0HPlUJrsUfdd9GF2umGtf593pzWdW9F48Gjd/H3/ui/wunpCZiBcQoIkRBZ0l2qm8x7YNn15cyLRIh3Hz/B33rwCOO4xcuXrxEBLA9WIO9wRGKlur66xoNHD/H4yXv5gD4g5WsPEev1LW42G8B3iCD0fZfBDJDAWEopOkWG6zoMwwKrwyPEGPHw0TtCSIjlzDknhw6SWLL7YSngPEx498n7WB4c43B1iM12i9XhEZ4/f47tdswCPoaAxWKBzvuUU55AzuPs7Azr9Wt88fw53rw5w2q5xDe+8U18+OHX8OOf/Az//NUT3MBjGjdYrlbwIHzy4hOcHB9L1i4nJ50LVqY8T1tAsTAHQMRyAJx5PnDExeUVLi4uwTHkw9BevX4DJsaD01OsVgepPxGaNSMCOSVrYAanjWPjOCIy0uZrs1BEzdiEvKFaPSqifKTUjlH2ZbCq39KBpBCkiUAkpysz5wOLQJSzDRHK5Mmb1jUVqSsHbHEigqYopXSDSfo29Assl0ucX1zISblMZvOodVNSBuJKWQWdlKwTxMZ7YOZ9jpTMzzrz2SC9PKambqtlqdKgoAgERxrahaQDmX4rRGMF9s7QXBdOHby0WLB4Hw+PDnNo4eZ2jc04QmGaNpREahfvTdqPIt4kws3tLY77AeQ0hBElrapSkdUqLMkZwGV/i+yR1f0liRZGuWIFw4R0OnjheztLsjfJAlHtsxJBQSclYlqa58uE5hhlD7HQXEMktCh9RpXurHBmxElVm3XRKGA/odA07nLDwUuqp5QVS080L3ql0O31mzM8fPgQq+UKAYztdkLfLyTzUwKCM72LZqOc+lz6E5nRQWL7lQwhRkwhwnvZU0KEnESADGsdHx/h4uIcxyfHuR5OZUooI+OdRw/w6tUb9H6RQlmnsiFc9SOdS4lvLM2BCERCdEkmmP1olBZd9QfJdDZlsRonpHHe9clLMAEQ/Qs6x1yRLfqHYGRBYhNHJEYpaRmCMHjmSgnNTUpPBgUpNhrlHAyPDr5jcEjei6BlpL0gDui4B3sJZw1BrN2S+W7EerNG3y9wsFxhmiZcXV3h+OgQDx8+wMnJCfqDIctg3VujKXEjEVbvnOIbp8e4fPcBLv/kNR68/GuE8wt0Nw7YjnCIiBwwISD6JDMzBwk9XBqiyJhZ1OuQEQXdmtSlpTTY5y24Flm9P5Sq5T3YB5ZqoNvymkANDSQjbFZD4RlPOfmMkyC7/K4916IG9PbvfTwwuv7PDAimNcUrgLRulXMb9tVR06rlWch/CfMzYrQMQDw5kQRD3ENprK319l7dnpYyattp22i9QI7KKdcqy219M4UHvHOvRaear7J8gV3hU/kJg5SLSyp8Y8UQ40NRrgJn/2kOJY+hGEO0rbqv0TmXcVlqXH4m12yX9dRuzt+N9xwle6OEiafQ1nvqRvdWNB6//zVstyPYyYnePYBhJXsUbrYhH3QHltSgTF5OwXZeYQ1c5zC4Hr/267+Bi4sznF1dYZomjNstxhjx0S9+FyfHJ+Ii9pLaM0bGABno1clpyrwjh3y5LqUpTW1UmsUYcXiyNKFNnCa9TDBPhG4opxc7kskQmWQDnvMYI6NbHCGwQz8cwMeIDz/8OmKMEm61GGTypHCfrhvgp4iHj48wLA9we32JDz/8Cr71zW+jHxZ4953H+Mf/7F/jzXu/h7OjDyQmtpf88eM0IcQpZWWJ6PyQBz9yiv9kyhyg7DLneUaZK8KoIQJXVze4vLpGZMm1/+r1a1xdXaFfDHj46BEACd26Xa8xjVPJdJK8DTn3e1oQ9X+q6Sg4no2AmcAz4UslFGFu1XF5YmawpGBBp1GmRxEyYIZXBWAGmucATq2qgrMljIKchCm4voPve0n5S5LHnrPig2ylJfWicgFluOtv7rZREkp3ikKiSlTqD2eRYSSAUR6yfETMYLs0zABgKKivKjQClrU+UhoBUxix3WxyuBt5klMljZKhdWi2JHDawM8QKwgHjFsJsXMgcDpBGqYlimvSf5CzLkUAkbEYOsn0Fh04ehCFTBWY9u4qBBVNteXa70QY1nfy+/pbTUMyxRfBKz/G/FxmP6PcZI+TzglVmk0ZRhWajXf5LVnNs2Ik/xFLumQ3CzOghbxHIE4BFxfnOFgtQASM2wl8sMxpbS3pVCFly4ck9CCS/XFDOgjQExLYTvuw0hxUpaKcl6LlM1YHK3zx/DnKQZbFS8DMIA44PT5G33nEKcC7DtnDqOUqfXLmlhQalfbqEZGceh4p84YAIU5lSTJb7auQWnI4iscyjZ/3ADl05OBjj3E7SmKIzHKc+69pjXU/kNORI8g+Mm2/J3AcMUU5qymYLEUp87X0TnaGI8vWIPtfnCO4rsfQ9whhSgpHSCm7Ux8h6d6dK1mrQmREntI5PRvc3vZYrQ6w3QRcnN/i5PQKpw+P8eD0FMOikz1eCODgROlwBHiP2Dkcv/8E4e//n7D4+B+Cf/xnCJ98AXd5je52DaIRhAnRSxgr5QQxBZTbLIg6N+uNrWrZ1XDoltejld7WAvV9yoRVZu4CjBmk7VFA5t9FJkQWWonnWa3gBDhRQAJ72FSvrdSuLQ9QDWTnF0H22dlQrERrSkn12aX9Iw4lpfguGFclbZ+3wCpxOgZzZSfu0Dn3hWimWOn9emytkmj3ddispvuyYVnlQ99vUQsJy6TFMa0FmL07Kxsknk6i7AXRumrlxCqRMUYxpM3qlu/RyHMiSkloAOhexDRtVFYqNshSL61/YoRJWIVLaK/vOjlHA0VWpcrAEJWYdf1MCSF0P25RgDLKLGNEShsC2GWsfZ/r/lmnnBerCpAykQgD9YsFxnHE1fU1Dg8PE1OIZch1HXKO7WT9nOKI8/NzfPH8cxCJxeg73/lO3sg9ThMG388sHUVjdVD+6bp5060Wad2ImfHSBnK9pxaTmDJU9b2ex6EWePkXWMKYCHIgyrhei0vQeVAMsxzKlPapHJ+cYjn0ePjwEYg8bm83uLxd40+G7+Ph8S+BXDrLYLtFBOPVy1c5xMy6d4ECzARHljCg3G+dNEKEBBDEehGmCdfX1+i7Dmdnb3B2do71eo1hGPDg9AFu17f5HjND0TaRlquVUbZOEBdvAsr6VoCAKhMWu2lHyp88VvrZRU4JAdJzpu4MoiMnTb5YkDNIzFitVGTFhYIVPW+bGRhjMLwMsSwm01u2kKcOqpcEZMhP8/7YMSv9tmA3DRXNH+IykpZsGfjlus0VQXLWmkrPQlVDjiLUNWQkQ6wk9IiMoBY8huvbWxDEnSxzz9nSEz1SGwkS253CArxz2LJkX0Ma4xi0/ZRzuDtAQltYnuny/GSEOMm+ndQmorQ9QbtpHAI6Z2cXUWEFLsqpgug7L0pzKCsrhgv13Jo8FLuLMpl7RWVMPKvalW7wRsbkqdnzulVtscNb6i9LmHdejDI8B1AxxnQA4oiuG2R/VVZ6S+hU0oFkHmqjVHHIc83MtzTHXZJ9spcK4mHjVHbJqgxADk71XsLo5JCxsozJ2RqMoe9wenKEV68v5LwjcgjiMpsTmcWiZrhRbqdQy4iiAGaAm2hr51gZDxLGdyndbFpDAoulcVgsMMUJ0yhppokZ3igKpMoGVGmnvMZsNxvxAkcBnA4kqXJjmt9A9qgxBKAqcNSpHTlANlLJ+QhdTuPO8MnTHKYpPQdZe9O/mOgSghiROAaM44Shv5HDEacNLq8ucHF+gQcPT3FyfIxhkY72JM4b38mxLOv9gBff+d+h++D3QD/6p/j8r/4Kpy/+Gg83HfrNFgfbLWIHrGkr3swYwS77quHYySkiab9fC+ja/RktK3adrWffidJIY/Nlw5JalveWElC+J7kaKY+99NYoDGlcvkz993gy/bN+unI/j2E+N4pmbbJ11UcUSHPnCkPLy6Cedx2bnU3N2K0TmCt7+5S+mjf0PT1i4S5lI3sWqnHP7zTGtu5b6oDIsUYb6/dqhVfLqr0vut/MvtfKIsXV+0WR3OWjYoQTxYWIcpbA/QkPGKAIDsULUzwy+0PUbH/+y6e3dXKQnjZCgWLgiGGxwM36Fp89e4rFYoGT4xP0Q9m3wcx4/fo1btKBXF3f4/Hjx7i4PMc7jz7EYrHK2ae6bgCRm+1wB8pAq9CwwkUngd63WqcSus6RbK0j+u5iscj16Pkgt7dr+K6HWvj6YYGwXmO92eQNrlpm34uC5JICFqYI5zo8ffYJ/l9/GfDh938ARw7jOGGaxpQ5JOD65hrvPXkCcpqvXhdzWGNVZs4ILplf0mrOZjeTMsz1zQ2WqxW++Pxz2QOz3YKZcXx0hPVmjZcvX+U9Jp4c0JkQNBlgQEGPInWYe9q+jJoq0JdWStHIKX9HWsBlHMpGzTL7FGAXUCR1Jetvrp6KIEhFzzCg0s20SYEfOSCmzfvee2y3U+qHPaTNdD+DVJopDFlxKH/S6ctceRyK0MifFbipkizUQraI672kbJS6KPMDz1qrdNA+lMUnIgo9dRHK9E9jBAgAysKsZJnQirPcybc405xJwgS8kzZpykhR1qc8CJTGUw5Yk2cdOXRDD+d8nhOLxYCCVgvgN/haWcl0vtCcwfm3LDDN+ReFhRXcF5oqPxbqMTQNs04DM6wKM8ydBDLIgGDY8U7N4IrPzXiDTTIAQ/uslFR1E6VsRxxKFUSYkqzpuwFj4ndzsPnOvooIwEP53jI3YbFa4nYzziyfxClMMhSQrvQilHoYsifq+voai6HPJ5QTRI45kjDPd995hBcv36DretkvEOUwxF2AJ+NJKeQzh1iirDnaMWHx5LWwKkoCSYiQ0KwoIF8PO5NU7EIs6jr0ziGMsvePdP6awVBe9iSWbY4BNzc35awpToeNQj0x1vtV9rTpCed5brJsKnfk0rkbZd51fQcwMDknno50sJ4q1p4BePGAhRgRYkDgIJ7LacRmM2C1WmEaJ1xeXeHk5ASP3nmI48MjdL0DQvIYpdS4feexAWF79AHwm/979L9wjS9+/MeY/vT/gccXt1hcrtHxiI4kLMw5YOIJ0TGinACagY2OU509x2bZkbEu46r3sqEw7j+Nuwad+4CT1rEPlO5TMnaeqZ6fAzy7vt193QV8d5Ugs3KQfSeXBk3TX9IGzuuytHxbG+7yHtnyMiZzhS71OMyNyAWr1UZi68VotWsfL9lnZjKh6mPrt/qqPVD73qsVA723A8j3vFdfd/HevAAgLy8NRXkms/OciDsZw3JbqvdbinqtfN513VvRiDCHquVVulh5h2HAV77yFYQQcHFxAbqlnJ1pu91isVziUQrVeXP2BudnZ3j46B08ePgwdUAzIoS0sBYNNrfBZFWwzFcfGKS/67vq8tKDAa2CoQwwjiO22y2AIsSkTbIwab5tkMNiuUz7FTYAipuu7yV9L5gxbmWhGhZL3NIKR9/7PSyXBxinUfa3TJJKlqOk5T04PBTA5X3aRFUhAPORUDEelZASBQ9jSjs5hYCLy8ucVnaxWICcZAYK4yieocTk2fJbAXkBeGppRQKAGT3n56Bty8BIQKICQspPWIUkbbBOAJf1mXy+gJRDs/dT0Rk8690M54pQl1V8NskojVGIUWLsnYN6gbROMv3ON6h4A6QB1vNUwKgqDlAhCJf7xbYsBr7x7hL/t//Dr+P/+n//U/z85TqD5EzN3HbKqND2WzupoSiZ/rnzWpKFxwWMt6yGnJChVSDtpawBRt43Mz/1lJN1OSnzIebxpZlCKW10SbF1jhAmGZeu81Ktdso0oyytc3BflINKaGeGLjyrljhbYOY9ozpk2lHqm7aFVcUz4VGGhsWzwakES3NDSDupQWbPB5mupTLM9zLeWv7/n7Y/j7Vuye7DsN+q2nuf4c73ft+bu/l6IrubEimyKYqURImkqIFtGQggOYHGQI7tCLAiIIkRyQ4SSVEQMP/EABEIMGQ7SixHUyjJoWlKJi0OYkumODXZze5mT29+75vvfM7ZQ9XKH2utqtr7nvu9rwVld7/v3nvO3ruqVq1a9Vur1iC99Xq6ZIA1qgV7PiuLON7EPGkz1O+kOB+N2q68B6EHyOXjeOeSH3oxEZl37D8wdneWePzkMY6Pj1IaaDuxcbpo9/b3UNcVQhxQVxVC3xfKbiaa7DsiO1zBU9kiN0mFCau8rMR2JfE5iSoHTjETMCXDwL33qN0cwfcIXa/1OiJq51JF3nQSBmjGIR71qwQENt85ZgdJdlD5t+BzOGY4lT1GDqdyu6rkxIhZUg5HTRedZI5zqNRnO0T5jns56ej7Aet6jcVyia7rcH11rQrHIfaWCzivPuUU0bG4IXtiOKow393B7Nt+L1Yf+Dge/crfx95bX8Tieg23ZlAMoBjgovBjz0OSheXJBJDBTwkYy8/tvnL/B8YKR6moGM1L/rafZeyHWcina6H8fapwlPeMPxPMYHW8Ji9Ns3pbvYqpMXXajvU3v9u+GwPM9CEoBR3LOLLVumxzip3ss9viEqbAnSHzYK7pI/DJOZh6+twUqNv309TC5X3b+jQ9wShpWL5rqtBuo/HNv7fzZdn2tI+lkrRN6SjxSPmebe8taXPb/eX4AXGVMmVvSuMp/Z2jERYu5xST+Sj7NVVM3+96dkXDNijmZFE3IRw4Su57LwD54PAw1TZgAEtepoAUjoyTkxPUTSPab92g7zupe0C22Y2JPk3bxjxO7TbV1IZhGD1rILvUkO19pY+oaeNCYwEEQ4i4vl5jb29P43jFHw4khZgsk0RZcVJ83SSN6/7BIX7tYYWjjx+nyuRRj8ol0Dpid3cPdaX1A9ztDKgYNvUPxd9yr3wQwBjCgNl8hndffzvRgxxh1swkjW3XqQ8xmS6gAEcbyt7GMIGW/NpLzQfZ5znb1o3pb4Il5Lelv6lsewtMLt1Rpm/LkJBS+0/T/tM3ulgY4u6TQaOMpHxFUhrKNi0moWg7Z/0qwPGUXOV8Afif/4GP4Pt/2/P4sz/wYfyf//4XMIbPxe8ECbJNIDlTwUApg1PYwJSWN+lQvEGBHOXpy3y35fHphkYEBS0RdS0Z4MyNh4iU5yN85dWv1F4sdHbOoWlq+KrSbHGD8GYaSLkZ5XVgozNeu6HD4Obf1uexEjEd6hQAQIWrbNb5ex61PX2Upx8l8J4/sD5PTxbG3S35WvtbKMZZKbb354rUIQZ0epJpsrGqfOLTEXzn4vh9unwBzGYzXK/bZEQwvgka08VcbsI0+pWZ0aibbbTg5ySTdRVxRF1V2N/fxcNHZ6I0gWBVmZTiqe/luJWahrhkn+KYDBScOpL7k4+LlfLMkIrkSIViuQgA10WIejbHfD7HZrVGHAZIFjyr36PAyhLmFQDa2pESJCyB4YxiHln52njKXNGMXhFWgdpkUkyptJEU4ap2YO/hrAhq4DR+cpQVjhCkplLsMMQBbd9j1jTolj3avsPV1RWODg9xdHSAnZ2Fti2pd5kYNSAKm/fYvfMc4g/+eTx872vY/dW/h9333oZbr1F1LVwPIAZUzIguM1W5305Tg5ZXuc9vA5Xl+iiBpH1WPle67Lzfu+wazx9Gn5fPTN95474tzxt4nfZlW3vAGGh7S77gVOGMlk6X4StZO3E01ix9bjtVsHdvM97epiBMx158MPrutme3gezpPdPEAFPwvO25shDjNEZk+vtUAR0rUjfncqqwTJXRktcsq9S2MW/joW3XNr4s56V0UTPDHnh7LFC5JraFKOiNKF3ipmvKkk38G3edApCMU6lByGT2fY+6aVJQorlgRBuYdVw76KsZlsulgIooWUsq3WwkUn58DEhEqUaFxWbcdlxaulAZEWezWSIQkE8ezKUKkBMZUzxKEL+/f4DVaoWzc6nAWleVbmaUMqMYQ+f+SFD5Yr7AvfsPMRx/DAvy2XWBoEJB0rIuFnMAjNpbEbpbAAfG4NusowkAGxjWjWzoAy4vL9Kxu7gjeKzWKwF4WvAuGrAuF561w8huQ/a9oT0FHPlZrYWQOsrZ8k5Amc95pEro8wb10z32ri3UGPfUoKspO9qXW0A2kboiabA7aRoecXehyWvL99MEfLGCMl0Z5o6k4xYQNIGWI55l/PB3vggA+OFPvYi//vd/czTu5KtfytxCiSgBr3xBJdFG8zmlmj1DifZjADye7/GjI8Ga7iNYMJsBWFHopcJ6CEFOKXSASZlkSBAlSawBgJSi2hVuItPugSdtoxg3JsqQNmTAOK2RrcK9aMzAdiJnyQsWKmJgNfMIletkG82JRos5F1gsNpEJyh+BD57MfVqsuoJU+SMtWhnUj5+I0Hc9mrkvsgJlsM7FuykBcLmDmZJrqSkH0ly2bjHnzCSY0p8kOqqqanStpF0liELjAD0hEvB9cnKE+/cfwWmV8L6PyYiSxqkbaVqTSYHIrqWJPsW8J/oxENV9z9ZYakMz77EHCJW8PCqfeqnxUlcaVL1eY315iRgDvHdwJAH6ZUIWjlwefsIBCPa5wYNCFEoXixgUoqIWERf3motDwRKmhFnmphDR62m8FAiU94o9T2rlxGDxEpIIpOs7zNs52sUSm02Hi4srHB8d4uh4H82sln2fIoBBFDkOksCl8lh+8FvQ3f3f4tHXfhH1r/8THJw/gb+6Ag0tQA4UNdPWBEyXpxt5mrLi+7RA5cxiN5WLG++j8YnHNkBt302fnf49HUPKRLgNTE/6OS3CVvb/aePLCokp35oO3hIkkI2lLKpma7gYB+V3lrS/zUh3m4XerhL/bFOUnqYovt81fe5pdLptPm+b17KNKQhPhukt49wG+G8bbwnU32+Ov5FrpPhNlKHNen1DkZoqC4xxtrDRuCb02lYccpsCddv1DdTRQEpVC6IEPmNkNLN5UiIAOX4mIkn5yixH4DGiazsRilHy7qcMQlBrQ4iI3lLjuQSmY2Q4V2EYenRdj7qWoOlS6ZgyYEkg+RuwugDMlP6mBAQt+4gv8LTUe1gsFogccXFxDgJhubODykt6W+8dqsolZcOlwjwRi8US//Anfw7Vh/+EBvlZ+k4J3gMBIQxS6dq7nKUEhuOVgWwTtflnqINZ2jNHjGbVIM/PH2NQrTMyY1Y3iMxoN51mNPD6bAGsyl+IUl9ylWSMilbLfUj9pNHjlHqme3UK8h6BvBEW4wTQ81e5NR6L7NTbdF/CR8UCsL151DalzFrC0wo6CkFsgMo+sxOL1J6BqvxlAuhcjNtgdUFNAMC3v3qIl0+WAIBXTnbwba8e4Ddev5C2FfnI3VKnYDzLNxUDTh0v5iHdtg2tT2heqlC6vm3uR+LR+ELHZsGsMc2dWFXEomwBw5rilUq3OeFwp5tkXVeJp7P6oP+zD4vvR8HdJQjfMu7SCIA02gyms15VagAFPcrf2J6JmUeKry0e5qYLV56bbC0TwC6C3AKfU2eKNVZYFBNl5HPTRRNoNsrGAFCFIcRUn2QYBjiMXQWNV1S0oySgvFJ+r6tajBaFkpiP3rWOjOH6gtqAyHznCLs7O7i6vsLx7E4yKMk4VIoR42B/H01TYxgiqqrC0PcgmHVW6W/pblOsj7Y9BSJlZxScmbtWZpGU1H4M5PR9HpDYCDsFrypUTYWm8thdNIgHu3h0/wHazRoxDKirRopOEsGTQ4gBZAkRyPhXlA8OuW2G7leMFPBauoXZ2DNt5TST9H2j/S9mHkuB9VqPA3b6REJIVzk4ZvTBMiDKSVi72WA+W0q2qtU1Li4vcHLnGLt7u+Le5qPUk9LitnIi7+DmS/hv/UG0H/ydeOuLP4vj3/xJ7Kw3wKaF71u4vkuyOLIqYd7chcWlzhKHEQsSKMHe1CBYWq1vA5LbLNBTwDh9X/n5yNKtay9Lc/nNlFu7dwzCCFY419ooTzPK67a/xwDaq7I4VXZUHrDVoypkDav7oBu/y35Oszxto8E2jGWY5AYANxoVz5QKzdMUjamCsM19Z/q7GY/LvpkL0ftdhgPsZ8KNNpAJDUrF5Bu5THlmjOdlm3L0vu8paFPsCGAA67ZFJEIslF+gcG1WXM0FdhD5L4JVDDguuZGWaIyhmMD50R75tOvZ1BFtwpMBJhHATjd6hwqIhKHrJYsTAI4B3hHmsxnqqpK4gbbF6vIKl2fn4D5gXjcIXS/WrBClM0ELY0UgREYIDEdWTM6nhVlmrCiJX07AODuBgIm+DxiGoMBCilCxCgGA9OhR8UpkVI7hXcTucobjw31UnnF1carH/A28q+GoQl03qKpac5hHNM0Mm02LJ9WLaGYzhKAB4GGAFD9jXF1dgTmgbry471AGkmwWcaTdP31nLsRkzMG2fUaAJKc5iPDk9FzucQ7eVxJnMkQNAJf0rmLlyu5TiqBF6NvGDkZ2TMogw6QtW+dMAU30VjcBIH3OBLBzKN8sdUwUUBKKKliyeKJuSGoLG/UpzT00M5GTTcruEhRn9BMUZH0CJMMR6XF+TASlBOyYS6vjzXYN2JAFvZHBMBvC1BEsJqL98KdeAgD8jV/6GwCAT3/qZYyvKThmWXc6/+bwRTZOm7fp48WWmIRIcY+NKJ0+FtgmjgA8J4CWMDmxZCNz2RVNNuOIIWpFeTiEJNQKahAgoVAkCnutbhS6p/harMmJ12NuMg0vKYO5MrwpiZlfDTimmSwHMKJVWn+Jkgmajh5jYvXdN5rn9+bTxkxzAFbWIa9rVTJACpISt2jmIxtr0eV0GlLM93izs/f6BGpjYK1xAgxDRIweXJ7+lONWVknLoOD5qlZXUW3H600Rtn5ljEVSMGlf/47MWC53sNl02UDCsJWv8ihgVnsc7u+CQ4AnVwA4wHYgWwP2Eom70oyCE/CW5BpJKtB04oPyHSSnr1H5PDIQAtD3iF0Ljr0obiyA0jtg1jjUM4fFssErH3wRR3eOEEJA27YYelFUmqYWA5MqLzFK4T0HUQBmljQFhMoRdpdLNFWFedNg5r2kYveSbZEKfskanM4eWSCtpiQnO6GVW7yX+L+6lsB0ck5ksvOAq0DOo6mkUCLACEOHfmhxvb7C6cUZzq+u8PjJE7z+2lt49+0HuDy/RujFlUtC3dQVqx/AcQAjYL6/g73v+jSufvh/hwcf+hTWu0fgZhfwc1TVHI49HESxCjHo2CLgOPcfIu9gsnjLf9sA8NRqXp5mPM3SXFppp+AvGVnzMhvvmzS5t+hLIYxvXLednkyt4uX7nmZBB7IL99TqTMWONKVLWfzv9nEg0S0H42dFbET3gr5lW9tOA7YpU9MAZpufrW0V75/yw230m463fL/95yY8Y7S9TTEo+3YbX06vcqxPO+25cUo2wiiKK4C0rvvICCAMLFkqI3kMkdEzMDAhslOcKamPxRCff4YgySsiA5HF9U6K+RKYHCLlLJLvdz3zicZ7772HO3fujIhwdnaGneUOopcc3SEKaO46ycjEABAlsl1ANePo8AjeSbVqphyobdpkXpQkBZY0WEuEI6HytYL2QWppOLd14lMNjRQ8ZScunIQ9kE80IgdQzBkYrF9iNaD07N7eHu7fv4+Hjx7g5OQ5FfRIsRVOgyMPDw5x7959xJd+pwhfCOAHM9brNa6vr9EPPQ4PX4JzXqxBZNYIZSTkjZ85i6oSviRymbKgfprrTYvVaiWnQSQuZ8ySdrQfhgTSJuoD+MZxhfwu7Sv6mOAayx4k1kxK2nECLQmMUbaOF7EoZqFNFl99kBQEU2aJG+1aV61dhgWymlJivxdA2zYLFss71Zw6XLosyNhLYIrJd9p2sY8kaqbJM//J1NNEn09/6kWcb87xl3/6L+NP//Y/jR/+zhfxI/+fL2SwWiziBFxp3HbZJQFNxT2YEq4Ez/rWRHOlkSkb9gQbpr1to7QRy3q1LtsJJWqZ3WEYRvoOQd1LnIBYR0598gGOEV3fK+QmBEJ+cItck665tE6Ml0qaj6+Mpglaf6ZIHZ2eyP/omHI3nkbzRIOJUkdK0DJwP2qyphAseH4y1IKVtvLaqG0bOiWlRIrOBQXhUBfUCOfSQVQxi8VrJqBCNl0ndRsgPuGsi40gQJENsCt6Vx0y6UWRgaquMfR9qnaeJpTzfwGMu3fv4P69RyDyqKoKXdubWjVaY5TWiFr3VdnnOKQJI52TxMIpg5gCgoJ4xgPmgsgAECJCN6iiS+DKasY41JXEuUUi3L17B3u7e7h/7wHa9RohVqjrCsvFMs0jJopQu9kguIjlcoFea0dA1wM8aRxHctIrZqqULchAHOMVb7LG5J4n2UurKPtgP1iFZKGbrwiOHWJQsMpSQ2ToerSbBsvlDtquxeXlGU7uHOPw8ACL5VwySVGEdwTuIyrv0MOhqjx2X3wVw/G/jydvv4azz/44dt/+IhbtBp4JPg5woUcdnRYgVcDloPJE6nLl06AMKqdWeft9+jcwBqj2/NNA4tQlpDzNuM3ivK0/6buY42umJzDTIOXyXeX95bvLrWB6P5F4e/T9UCgEuhbMxaq4bvXTn7x/CuRTALjy3Q0F6TZabJm7p9HO3jeNtyjn8v2upwH4abuj+0wWP6V/0+tpJ2vfyPV+7xjxMsZ0IZJC2maQj5x3Q0Bp6iaB3kW8siiJMe1loUxYgZs8+n7XMysas1mNe/few8nJMdbroEC/hfO7aNsNTPB1XYvV6gr379/HG2++ifWmw6e+4zuwmC1wcLAvwXYapJaMagSEIYoAdg6BB9GSFWyFYYCPcgTWDYwwBEQw2r7TEwk5XSHnNN0iS7YL75VA6oJELAGprMpGiEkhEYsKAYOgFZuE2Eu9ixADYmQMQ49Nu8aDBw+wWl1jd3cPVVVhNlukI8emkcq2X7l3gdh8JC2S1dUKq+trDEOPvu+lCvNygcr5JDVK68e0TIIV2kqaq2oaTIQUSKiC6/zsLNEQynghRLSbdXomAT4D/5QgP5hcjpMEScE6kvuzJ76BoQyoTMAwS+XqtLvbQk3t8AgUTfFSzjIFO2xK9JE2CFapNzG+3QPJ0AIDQ9ByJ5HVXUp4laHHjurPLFXRxzjdXFvs/rETUeYto3Pe6IsTKVXCcrA48IkPHODV53bxt3/jb+Oyu8SPf/nH8ae+7U/h46/s40tvX+TxGkgY9clGOSZaocakecvIedwPswyb3ihpVkscnxEuK+KdzpMBSAM4Uf2vKW2cMc1PUOVWD7bTGORZO9GoAQg4HkJAXVVgtDBXlzTubcK+1Mg1ViUL1gmvFZ+JgSCWA0+AJgE7hqaPZhDc02muLnSmHGS/nky1tCSA5BrDVuXZeK3c5wqgOBrytG39NNW2YQHiFpgvLpVi3PHqolP2BcjZn4zmiQ0gsW2WpjVzkMQbhMGMNy6vgcRrNlahQ9006LoW8/lC4xSQG4LIuYN9SZHe972exg6iGNkaYx71O80xA4KSbXClsmFqSiGLCj6PNk+MtF8QtJ5LjOB+QBcYxBGzymEYKkTn4TTtK3PEcmeGb/rgK3j85AxPHj9GbGOmGwiUWE0s9nXToK7lVINZ9zEiDfCVAPMQSAx2FJMsL0Y1FgVJtnPBa3J/RS7FTZIjNLMG1Lbi4hyCLAMVq66SOMZBg90jIngTMAw9ZvO5FOpdr3FxcYU7d0+wb+5ULIatIQbARfRgRM/wTYWDD30M3fP/Id555130X/x5HH/15/BCv0YDQsUEx1HdDk0mqaWWlNMKYHNrTMcWoG57Yqk0WyDr1Ipse3W51kqlg5PMuAm0bjttsGv6eQghYYbSMLrNEm73jI1PhYZLcFEAAQAASURBVCxOCkgG5VJPISepARwqRyLLePzcbTGv2wB2GZPqnGURG7sf5T5OTtD1XdOsUO93lUrOOG3wTbo8TWG67QTl9oaL3eoZgHVJp2k/i1f+G7nGChGNxk2Tv7cpdsyWiU/fF0KOr2aGOZre6C9n/nlWZeOZFY3XXnsNb775pgp+j6ryWCyWmM/nIHg4T7i6usT5+RkiB4QwYLncAcOhbVtU3uPs7EyUBqs6XHkRt8ySBYmsRoa4Ijmn/q0QolnbzAznPVhPOyw2pMxcYUWSAEjWFeQAcY6icGzWG7Rdi67rUsFAjiJc5URDrUmEVPchckQYJMj6tde+JkpGM8fx8R0sl7uYz+f4jt/xnTg9PcVvhW/CwMB6fYX1aoWu6yQgPMrmc3R0DBDBeUrvH2mdPP6AiolN80uUUm2SgogQgYuLi4QE7bB0CAO6Xq1mzhV4zQR5zLETVtzHqvPq/xz5ovES4pRij7UWh24OqiHDwCwBuRSuvKX0rSYUwpDslKf83rhc+10CPy14JQCn9AEvTovYQISeqAU79bIK1nnntrFTAbzyNR59Cf1gQWMGCRTA2SM//CkJAv+xL/5Y+vmnvu1P4dOfelEUjfR6ATsGDjJU2tJ2uSEXwLbs89iKPBYiXAww0TzDscmIy7aRaWsGAiDFaAFIJ4Jkc8HZDxsKBAxkMWST9FWFrOBkPk/dT376ALOAMTP1JShsiN/oj1Kh4lRaIw8ExTybhXzMf+VF2rYFpifjSZnRaKQHcOJFUzDSCiUR8I7cSIEbz+e4j9Z2VmzHAFpOliwQGAis9U0iaRa9PI70WjtxoRvkGFn6GOJO68ip25MkuXA+81Dqclr3jOViidVqhfl8kegLyEkPM+AooGpqHB4e4v79h3CkdTKG7B7HPFY2jK+NZ41+WePjcvklSol8yOckpUGEVX4RQTVksd5264grjvAAGl/BO6DyBPIelSMMCLjz3DH293fx4N5DrNdrRPaofaN7jK41X7JehmO2F6SZdE7jHn0CkACQndjGc0SZORIAQWQElsg+kyXkHOqmgQ9iIOi6TuRh4knA1wQXxeVrCAGhC1plvMdstkCv9TeOjw5x584xdnZ3ctV0FndeZkb04qZc7Szw0kc+jKs7J3j06nfi0Zc+g+ff+AxeIIcKUYLF4yDqKjHYUeLdG4BtCwieAk77aaC2dJuZ3mfXtjSo2UWFQeoJcZv//zZLO5lsxvgko3z/bWO51eqv/F0C8FGwcqFYSV/HQHTa7jbFafr3thiLvMfdjHkZnehOlKHbTpemYHk7Lcfvsb5tKzxY9mfb6dH0nqmiN23X3jNVCkc0mdChfL6U59vo/n6nJtv4lSbz2LbtCA9vWztlTCVN5J9h3m088q9zWvPMisZms8Jzz93BkydPcHJykvokFhcDeMDV1SVm8wbL5QI7O0v4qsHXv/5VJQZweXmJr/zWl9GHAR//bZ/EMlUTB7zz8JVHXTeo6wZd12kaVtVYWbKWELmUOUrSNcowKq1EnjpHZbYqUVqMQTabDdpNi6qWZ2abmViQvChGXdehquToe7GYg526ghDAToS2cwzmgBB7XF1dAnA4PDjCbLbAT/zqO3i3+wiuVqfYrDcYNDtVU9eYLxdw5LG7syNuU84XwIIS7pdx2AatG5L+LeHmY8YIgTEMks53s96IkkCyoYQoJzPkCLN6DsDcka2iMOA0bgNAtnAnXEcpk9IYerJuXjC9ZmxtKxm8HEPhYgFAlIPJjVwuTFaBpspHOcdl26nWga0ggxAJQKj7liLjIYQEVNLYOANGQl6EY8v1eGxltU9pI/9O5ef696c/9RKuu2v806/+UwDAP/nqP8F1d41Pf+ol/N/+v1/OtEh9KSeDISgRkGBYHp8IbRNUjMRbWTmY3kfl7Wkckrs/jzsVIoTZr6E8ELTmjICDEFQQg9APQYug6ZgK1SxyRFM3KeV10ODlqq6hCcEyzQtAnb8wZSQD9DyQou/Ic3SD125QYPKs8l3SWRJqzVbjG//aeqHxZjxqP8VHSSdMBsUhZIyMzOdAdlFMF404c7RGGRaIn+kyDANmjUPJNEUzWSfD+KWOCLO6TsCdQIiQXOyWwU0qNpIeKJQbEiVy7uwscf/eA/CxvKcEJN7mmxl375zgvXv3EdnBO48AOYlJMqrsIudJjDahbFycxaQ9aAVORWGBeN6xngorjRO/qBJj1eo5BHTrFufDKXgI2N3bQeU8PMR32VXiklnNarz8wZdxfn6BJ4+foA8dGDUciYENkZEqJmmaKkv/bJmqiAiOWeLaWEBuVFBp47X+moQztUnAJwMUC7nGySJPAHzlk696qmSuNZjM0GR7VEBAjAOGGBC7FmEI6NoK826Orm1xdX2NO3dOcHR0hMW8TvpdCJo61DGiF9ex3aMDLPc+ifM7z+GdD3wbHn3ux/Hq6dewGFjiHuMAYjmBg7M0vhjxsRkZp8rDbVbyKQjcBgqn7y+Vk2T9fwrQmsrUDC7H77cTlW1pV7f1pfzb+lJ6d5X3pdOaotlncfl5msL1fgBzm9LwNNC97V23uS9NgX+ZsWv6fI4bGQd1l9/fpkhYe2X5g2m5gW0Kz7a/b1OKb7t/Ou6n1YKZ3guM963yxKh8rjwNSnOa9qMs8+xfU0ynclaw+O28sO16ZkVjd3cXXd9hf38Ps9lspM0TeYQwgIgxX0gq2b29XVRVDZCDpwo7yx2tkCo58130mM1nOD45kXgO1UgrX2kK3EoD6fZ0s1SBAg0K9w5916Nu6pQWE0QIYZAMG8osTdOAAYTYo3ENQhgAquC8w2zWiNWUxa2grmuEELCsllgsF+qHHJMQJpePXOeLORaaOaWq5FRnsVjgox/9GH7tN7+M//HRIa7DKfpOKoDXdYO9vT09Yoe6W81k8wKB4MD5XH0EfgwFCJhCyuA0ll6EGAOcdzh/fJlytTsNUo5BUhdWvkrwm1OCTslAYkCGGepmUlgTDFjLzpsAHWXNAjCAPY4s3zKgwipRWjxsSETp9/JkYyqss5Uog11Kf2Y7ZQIyCfHLZuwKwWOKsA2Fpm2j+DlSMhT8av/+9O9/FS8fL8bjHsNXzBuPb35pH//gN/8B1sMaALAe1vjJr/4k/vgn/zj+j/+zb8WmC1uftevdx2v87Z9/XVq4dROZPK+0KRWhW58zHuBM17SJ2LuQv8uKlloB1R3DAE8IIfnlM5ACfM0P21deqtMrgA0qC8RnL0z4j5PCOBpb0X/aVgVXgdaN21HONyU62XiyZVxvLBTGm1Ok77D33kLzlIXN3mF8BNZMH1rlG8hKZbEJID8ybns03xrnprIzRsmvL8VCafRImlMjAd14lbSrQN9F6O6RXVFiiOBq3I3x6gTABF9VouBrRe982iHxGSJ3Aw4O9zBrZuj7TgxMziVrPggjpY95LEsw/Vtpzi7TvBBbkt6aSBSOmKmcVjlB26Z0/xAZZ4/PsNlscHR8iJ2dOVwl2RKd92DH4CFg73AXOzsLnJ2e4+LsEnUFiWXQk40MGNTdUOWS170ByWLJ0MSJ0ifLjFVyBktck9EzgZn0Q8CDM8NOtIQgotgTObiuxzD0UoMjWkpdOWGU+I2AGCTWJ8QBQ+jRdg2GIWCz7nB2cYm7d45xcLCPClU2KEVG5E5SsXoPqjyOXnoBO0eHePDcS/jqlz6DF7/4k3iOB6DXIHCUcZslM06L173/NQVq75fWdasCQvn04GlW72ftzxQwZyViDPKn73cuz/q0/WfNtPQsfSvB6m3A3ziwBMjZyp/9/MvPt/09jRWZugLd9o5pn6TsQEiY0a6nFWa8rU9T1nvWa6p4/etc07kvaXLbac90C7Dsj0CBufRZ46CSDxPmQ455Lb+XLbBMH/5s1zMrGr6qMCMSd6O2laJ8SWsi9AOh4Yjjkzs4O3uCZjbHcrkDkMOD+w/QzObY299HVVX48Mc+ivPLS+ztH2I2nydCzaoKHBnNXFK9GggRBrYjMYgwtA3PmbuVTwqKk+jKUdYCBwHi3tWqLHi4RixLMTLIC3CpG0kBaynDvKvy7wp8YoiYL5YgBBB5OFRofIPDgzsAE/7Br1/htDpADBtUdY39nT0sFvPkwx5DxM7OjhZP8sni6UYnBnZxGrfscTT6LAFjktMMIoeLi0sJvnXqF0yEIUi9EiqEK9Q/Wt6RYwqMmcplaK5I+TI0In1MVn9OkzQKXJUNs3hcKwPfgAMl6MkNS9sFuC1BP5kLjRIk04RQPJaoaTn7DTzkRcTiNuJUwCWL7/Zxl0KEAOzOPf7an/jtaKpn2/z+68/91zf+/uOf/OP49/7gR9732W6I+G/+1Tu43PRJmeJtNC+7nZDZFIJNL6OtOGeIbawYd8zjZuI8l8pMSViZZck78DCI/zVyCmeZK3Ff8s5Lmk3nxAUnBFBVgyybhoKLG703q0wStgQqUhszF7w8xtZZbzD6GPPpZ4m9k1CebB4Tmqc1RHYvJZpPndAKncVILToVyykpVOgzqcgfKbfY0jZG32eDhJgTegWODh5dyrqXCcFOVDPZhMZ0Kmm1s1yg3bSgpslrS33/o6WPLZa6KVORzU0JcHBoZg3avpPaHMabkDgOBiNEoJnNcHCwi4cPH6n8dRgssxmb4qLzQ0jWN2f2GptOA+OU59vmr5zyaMQ0K2YRLZ/WGOxESZSeSISry2v0fYf9gz0cHOyhnsmphSdG9JCYkdrj5M4Jdvd28ejBQ3T9IMoTGAicAJm5cMUQwFp3JgF1sjmRLFRmcUyxUaYgkcxldjfESJkDA1SZxVuqirMqHF7dmckT3BBUgQyIGqsCclIZvPJSfTwExCDK7BAGbPoWbb/BZrPB1dUKJyfH2F0sAceA09MNDvAIkh7TeTTLOV7+yIexOjnGo+c/hNmv/Vc43KzhNhtQt0YVRAGNsIyCQi8HyT4GM6YVKWOfZjkvgRptkeXGH6X1O4E+ZinkaPy6xYWmfF8yZBEXn4/T7k/BdJ7T28Fw2U/7z8C1cAHBXItZpZF4At4sWHjbe+1dWVmlJBByX3Vv1n3TwGh6D/KYgHEsyLYA/fKyuSzpP03+M6X3dA7Kn6bAbVMSp25RxZsxRWTb2rjBJ1vGM+lwQaP8Xud93us4G0rTfUkhyM+kUwl1W3YgIEqCkciAY4kfM1wT1AUUmunQPFLYNmUAjIiYsqDyyEjGIFDMXgnPcj2zouHIA46wv3+I9XoNMOlnwBAHVLWcEhzTCS6vrrDedHC+wWKxxM7uHpr5Aq5uUDmPD37owxhCRN3kkxEic4vKjBdJYiRM0JZHo+VkjtPYZoYqF6BMlLZVTJIjQlTCk6ukIBMzQJp5KjAcVeBICEwgquCc3SsWw4oqeNfg1Q9+GD/5S2/gjfYI1K1x584JFkuxbsdgQIvSiYizOAmdYMbNIz3bKDPwLllfdk4iqWDOzOiHHtfXawUVjOg09XAIBSNRfjuXfF2qHARogGpSGpQ5wVGtrjkGwbLaZERnQXzF38kp33q/bawGCkugT7kfal3TCQQ7SgtyPLrsqpGUEHDRonwh2X4giQh03UgQcwZcIkfVGczaMgRgSkqMuFhH/Lkf/Zf4T/8X34nnDhb42pOv4S/+k7+Ih9cPMb2u+2t84eEXRp/94y/9Y3zr3/hW7NQ7N+6/u3MXP/pHfhQfOf4IHpyv8b/+Lz6Ly3WPfBKlAj8BKIuxsWko52J8Zf1Dae5Ka70C6rFZKq1Zmy9rIsYoPvrMGoyogJkFZFQ+u8pk8SmWdkcEXzl0XY8wMPxOrUtD64joWCyDRlIIbLwKBLP8mwQiJjrdQgllYGaNh2F7B9LmWo7baG4AVngxg4ncLpXTMqG91RdBAWQKn1ubnAIYJ37kPN/Wtj6UlZgIABF9P2gtH8IwRCGpT8h1RCLKr0ng1mlTTVVjFVeZ5jo1hCyXbd2xEmZczRpgkiKl6/UazaxBCaKFJnZ3xMndI9y79x4Gpwok5RwQluN9OrcjcWlyjawZvnGTyTJb3+n+5LenYyjoIacCJClvQeg2HZ70p+jWLQ6ODrDYWUh9JGf1KmRPaWYVXv7Ayzg7v8DZkzNUzmnBULklBdUbP5AYP1L/rICI8gireyJbWt4CAMK0CuNizptHOs0tXGw4RrB3chqjdCJHCJ6AYLE9ClBiVJdfdXWMATxATjj6Dn0/YOgHXF+ucPfuCQ4P96ROjofEB4GBGECeVeR47B4fYvEd34Nmv8fySz+D9t0HwNUFCCv4GAAOYIoIaa/StSaVTkb7/xTYbstUVPqwbzsZKcFneq5cHxNgW56QTBUYUY56SdsfWI0hGeARjfu9rV/TExDxssCoHQBaONmrzMquXqmvW/DhdKxTt6MtYrRQvkz+qwxWZSPC1tXNPpoyVSoIZdulovW0k6Ntpz43Cyjn9m/LsDVVeEpesjVVPjuNh9l2wrDtFCYZOIo+3RgXFzhjy0W4uXdFrY0kokZcV13TANUGEKdOCSMgo3uUTNJUaZtxHBgOYJSRp/icFeNFvtn/265vqDK49x5N09xIOUs8zjRQVRX29vbADJyfn2O9XuPk5CT5JMYYUdUOdTMblYmfljSfTlR5nGjvsr+rqhrV1iiZd9tVMsbUejASTENI927zDXSuAthhd3cPdVPjl58sEYaIxXKGnd1dGHBhcqhIUt8uFovk95qsBLgJQgDdICgDq+wOVG7cMgbvHB49PlU3Nlsg8jMEza9uAFxaVHcRTu0Lhs87sWZbFLyi4EaARKEk2QIDgUZmWiRBw0rXhIXK329Mjv5D6a0F0JfvSBvPOIMy0Fb6gIp3W3vEgFbEFdghLmXO0iqOhmQvGbed+zWeIwD4+S88wh/6qz+H//Tf/Q78wG//CP7mH/3P8af/0Z/Cz7z+Mzcnd8s1VT4A4Ac/9IP4m3/0P8dL+y/iZz93H/+b//JX8fjSTjKs7YKKtgaAFI8P2i6wS3ID6pNqINLmW+/Ks5zHTUXtF8A2fqEvJ5pJPyTTnM9W5QRIpSAnWUA4JMbDG/M5UiXVepLne+w+ZYOVjTytEWPHEugzYCcGufPmGkOK7c1/Pv2DgrIZHBvDpLZl3THGNE88VQYA8YiaAiCRaT7SqNJnUz6n5F8rMg/q/uSEv5kRgiXHkJNdkySETBNGNuaXtLIeBgbm8xmGJ6HoEcNrbYqgaTS9LyBuAULsIWapp/Hw4UMcHh6mtkm/s99jjDg6PEBdS9HBpvI6PqW/yzxpIMc6PKJYYRAwvD3KSlas79JamCZNgWI0hVAVHGYuXO7EJe3i8hLrboPDw0Ps7e1gNpMK6JV3CBFwLHETR0eH2Nvdw8P7D9Cu1qJggDCEARwD6qZOSptsRcJTRHm+mRkOThRHqHI84rUJ6yjv2MkVqFSA88Q7ciBfIVJEpACKDnVVox8G7V9McW4cCa5yiJEk09TAKWtc33VYz9dYr69xeSnB4ru7O/CVR2CGd1IQl1wPRxHOe/iqAn/zD2L93KvY+9I/w/orX0B7fgasLuD7DlWIaKKY7ILjlPraEtzlbEZQl+cMMKeW6KcBxBFwL+JAhDfHWKTEEdNTkOm7QTSaT2vvaVhlxMfp/vT4KINTMlYUY9ymvExBt91/m0uYYY+SfiOaFasmxkJRvtHvmycYUyOx9XHaVvnsFBuWf2eDx/jebcURt7Uxrd/BtGW8kz5va6+k/7SPt13vxwNbFS8VtF4zsAYwWor49u/6LrRDj4dnp7g4P0fXbrC+vkbsW/EwCIzYmxM9JxerfPkkP0q+kFpEFRAHVFuKO267nlnRWK1WqKoKbduOrQMq8EIIqT5Eennlsdkwlstl0gKJCPP5XKyWalHIpxo3LQ+2KFLV8UmaOqlbUQgCHmcfKBUEe699ZgxZV1Vyw7J77D2uYKKR4AAw9AFec+C//NIr+NxX3sS75+LSdXB4qK4Q0HSw8oz3Hrs7u6i8Vz9L/a8A+3av/Z2zReTN0b43o/8wDPCuwpPTJxhCSBsmkWTrCrHIf0+kftsYN2ZaNJVeA6aM6I3JLSWfwPDkRQYYDJCZcLbvRuOzZkqQUALC9Fwh5misuFACMfpQzMC7hOBGjzJbC6JYEX1lvrflHNONt5T9Sm0nwChC/tHFBn/2R/8l/r0f+gj+4z/2Sfz0n/lp/MhnfgR/5Wf/CoY44FmvylX4a9//1/CXf89fxhAZ/6e/93n8Fz/99ST0pzRKG0wJlkocPQHa6cvppliA5hLg2DwmYKLMYq49BORMFgxwsBSLAphEoWsK+sXULzMcVHWDtu3AUS2oMGHPmcbF/NgL2AZnoJuN5wrlNGnMRieMGCQBbxY+t9WWlZEMNqaMPOLnBPonE6qfs41hFLThtvJaTONAMXlZXiRacpYN9p5kFYvA0A+SwhSs6bxZklkQAM1AZW7fDAVDhayzl1dVhb7rUoavUvG3TH2J5qyrRBVWexezpModNM25c9kYYXMQWSpOz+Yz7B/s4/HjsyTXyrHfkD2k1v0R3ceyJd1n81TSHMr/JrcoSzBnSkaax4L+MSZZ3W16PH74GO16g4ODfcznc1R1BSmiGOFITlKdJ7z4wgv4ype/ijiIa4PzDr6upNZRTXqCnD2meQRQRZEk+92AYx54MriM1r6TzIGyR4hzoqN8Om2nGVLpm+Q0I0RUlcRGxhAQUi0U4U/SzIkhDqluyzpIOlzL7Hh9vcKdu3dwdHiIxaJRMS1ucOwYARGBI2pX4eLwQ7j67j+H5z/wz3H45q/h0W/9Fuj0AnS9QTX0UiyMIgYXUUWC1RrRmPqUMadcgzcs1ch7/bQGQXndFi8xvX8b2JyCa0dScyXPx3aXq/LvbeBW+JEgJ4bjvjEDdvDFk7VSjvWGElT8Xn73tBOF3CCS8MljHz/zNDBevncK6qeKxjQGZTqObfME3HTb2nZtUxqYbiozUwXitjbL+7bRcvr3VCkZpQqe0KN4CxzbziLKd0TER3/bJ/Btv+t3oj7aw2Z1jX7T4vryEu++8zYevv0WHrz3ABenV3jy+AkuLi4QQkDf92jbDZgdADvtkD3Ra5rCwAxfz+C39P+265kVja9+9avY2dmRehCrFT74wQ9iPp9jsVxgtVmBmbHZbOSlVYWHDx+CSCpSz2YzXF5eYmdnB7PZLPsRKsHKKP+SqHbaUSobRJROL6ADtewQpfJQ5sm2+6YLcgRUtU9TbTiyuDvZ+y2zFZFDVTWIQ8TB3gH29w/wW1/+RWy6D6OZz7C7uxQAVGyMHCVvumT6oCKgRjfjvIdkcGxrWAV6UgaQt52ox+Zd12Kz3sim5xycr6QeSBcQhiEBBgFxAVIcCaYZpOxGaYO1HPcZPY02eQMHIjWLT+wFNjYFL+lkRp/OwIiLBDi6OVjD+Q9M9Z3Udtkb2TX1Xmtb+pfJyzBvBYAROKJSa0CRvgVUtC10HwuLGzEPjFSUkZnxN//7r+EXf+sR/u//wXfhP/m+/wQ/8OoP4E/+wz+J189ex/tdrx6+ir/zx/4OvueV78HX713iL/xnv4LPv3mega4CegNF22huZJlgYhgxS/BBygMxARBk0I4sAHn0prJtFcbMSTmPYAGwjhCDWgbJslIVXXF5bpxVGGdoBWaPGAZtlceHNwaup7ym82JjEtLYeAtXL+THRn9QCdx5TMDSnyjRN7upGX2SwaCITRhnYRqvJ+tTNsgocCQF38Zr5BKaSlZlnrx3BHLEhUFAvcld9ek3kiVXq0KyJH8weYeDHCo1swZSVwGoTGZBg4s55DmAxVsYdC1Wvv5aWVydq0pdIPFl5IiaHI6PD3F6epZoRsmCE8dThxJMmVtKuVEjrWPTF/IZwHR9m9zW8WRhpTSPSdZwuk/duxAxhICLi0t0XYf9/X3s7u+irmsB5U4CsWMIeHx6hr4fxD0KES46NLM5+r5P7CZKtip2I/ko37HWZbdTDbvkAMs6Xci1NA9U0Nz4kJWF8neV8wjGZyHA+QqenNTY0HS4YAK8JH5xJAokYgAPLBkXtXZU1/VYXV3j5I7U3vCVRd9L+4EjwBJD2VQe917+vfj4Cyf43m/+KL74C/8KZ6+9Cb66AsKAAC0CypTmLqpmJZ4WrDw53v+nIHebdXwbgLoNdG8DxrfdG6PdI9QVjHIToE7fvQ34J+MjZY+LqIr7NEHIWBEp8M8WTLQtaxc58f3fbnEvcJu1VcihdNeWv8v3lcH92wD8VGkr52mb4iFFC/uJNf7mO6bPjZQG3d+n4y4N2FN6Tu+7bdzb+nyb0jpVhsf8xUmxjmAEiOz9sX/8j/Bzv/qv8Pv/7T+CVz7wCh4/vo/LJ08ABLz0kW/Ct3/Pd+Pg7nOIIWC1WuHi4hJ9GPDa17+OBw+eYAge9997D1eXV+g3La4uL8VVE4BfLOCcSzj8/a5nVjT29vawXC5xeXmJuq4xm83EKtUPaaM1AuzsiI/5fD7HZtPh8ePHuHfvHnZ3d/H888/j+PhYC+dlopZuSeWRnhHTgr1N2bDP7e9Saywnx+6dKjfpYh5ZsaeKBiIjxJC06EGrtzrvEOHgvcMHPvBBdG2Pf/HVc8QD4Pj4eAymBA2BY8RisVS/3eyqY2ty+rs+JuMouq3bWnp5DFKb5NHjU3R9L/cQpU2wPA2KMSKGvLmO4yAK0GPogmF+Uwl8TpUN6MaZQFOpHMDBXEgyxJs8P4Z9+kU+T0ibflpYGkOh/TG6ARBfdRhwpUnbmLxPnre0xU59j9naNvClbU8BqgGG/EHpDiZtfv7NC3z6r/8s/vqf/Hb8O7/ne/HZ/+Vn8Qf/qz+IX3r3l26OWa/f+dLvxE/9mZ/GwXwff/8X3sRf+bufw/UmpMZt3LYdGNhOYNVoTGrF17/H8q74QxmOS5pPxj0CKdNNLIFqy2BjYJy1roLQOgyhUBYzBOXIQCXW3MpL7QyOEaSumcILOZ0viv6kcSs45GixQQxwYdVM7EM3PM0SgORMF5rMpQ0+fUYJqqd7xq4F9kUG62l2yvVtfWdOdCn5anqaYQpQOQdJ7hUKEghqjS5lgJzYMVTpq3zqrLlUGsbOQ5OeGq9VvhrxvAELcg6hl+N4rrMLV1a4ChmnTy6XS6xXa1T7ewoUi6xODDAkY8rR8THo62/oSYUT+TIK1C5on+hQ0qZou1zHKTZDaJXqNeh7LeGIlSgtPd5AlnJdv7c0xTHfG8FYrzr0/Sk2rQSLz+YNCA7eOTx88BBPHj5B0rRZAqWjFnJzuuc5QKyI6rps+9B4hgA4SumRZbBB3SEoKyxTfrJx6diTIqVfmnx3XJ4aiAGtJofoQ8pQRZLbGkRO9eGAEHowMbpe8voP/YC+67C6XuH45AQnd46wXM6EjhEYhoABAa4aEL2H9zV+030Ch89X+GP/4e/AP//xn8Tnf+EzwPUV0EeJp0y4mDI11AvgtuJ6dj1LGtEyKLoUfbdZc6cgeZs13DnJPikGUXnvbaAUyNb4XODP5Mi22hbWNra2v62/22qMjEEvRkrs+H1TgZo/2kb325SD0guljMN9P6v5NnAPIGUR3RY8fls/7POslNlgtl/TeS1xqX3/fice5TumSt6znhjYvY4IlSPsLHews7ePd954E7/wsz+L5194Hufnp1hdXoBjQOUc7jz/PA5feBHf/M3fjF/65V/GcrlE0zT4xHd+O37P3edRzXZwdXGJq4tLDG2H++++h0cPHsBVFQKL11Dbts/Ut2dWNF599VV473F0dISHDx9KLnZVNngQAs5mM7RtC2bGfD6H9x7LZcBsNsPFxQXatsXrr7+Oi4sLvPjiS2hmUs/BJsBOIMrMAGWA1dQFqswyYZ/Z71Ptr1xE5ksJ6MQWWSRGE2ubPjP6vh8FmJu1f3dnF8fHx/jqb30Nj/oGVVVhd2dXMVGGfgwpMtg04rNLadyUNnaGxGdq06pQMKZLegTTOZ/enJ+fS6E45+F1Mw4hoOt7BYGheLhEO7ZNm3KgvxeCCjGD+FFnbJOi7ByVs/xk9yr9Jj2Xyaz33FjMlL4BkCw0BHVFs34VbSfLb/G2dCpRIDvbjuzZGMX9wJHDgKyQJl4o2h4JVGubtX8xZqW7GPdqE/Ef/T8+i00X8Gd+4EP45N1PPlXR+OTdT+Jgvo//5z97Df+H//fnUqv8tLZZqahgIvNxpjmmNJ+A9hHNBQEXCi9N3oEJzeVrqUuSN/gYItjFpOwXU5bWXNTgVyLJZgOWLDNDGCRInxxK99HUGuX5Nl7LyLYEn8iTTqOX5F+5VLLKR8pxK22V5onXRqmfIKBz2rZS1ikvlrw1Ajnl/GrbFjdTFi0sA+BxA8gU06Rthxg1cFkt+noaIKcOMtIIzTxVdoQySCftS+0rlRmc7rMj9qinLZTaTqyULhMZ88Ucp0/OsL+/r3JN13FSIiRocWdniZ3lEheX13AgeCJYlEgyKCVlo3R3vNn2iM7lHKTOlXRUkK5EoFTFXDd1RzreUnnJwJ1JCu0N/YCL83Ns2g0Ojg4wX8wxnzdYLhZ4lOjn4CqPO5oW9u233gYRoa4qcS9jUci7vpNTU11Hjhx8yk6V4xYjs+wloQBSCpqIjEol7USRSDJV75dsZKo4kq5FF2VdI59+UgiIlBUbQPZOchWGocegGSTXm4i+67DZtKl47Gpd4+ToEJdXK9x75x6GOIAQQVpzw7sab1Qt3nvt8/je3/e9qHbn+KV/+t/DnQ+Y9ax7a6VGtDyHwt+3g7xiJ0hzKvM+Bn9VVRV4Yzs/lc9v+zm2wqdVZpyW/t5mFQe2ZWjS05Eim9UYpG5XiqYnItP2tv2dKFU8OzLu2hBuubbR4bb7pics73eVipTRwOiw2Wy2zsW2fkzHbMqOyLFvDOxP6TpVYqeK3/vR5X0vFqOGrGhxo9pcXWO5t4u9Zo6rh4/RX13h4GAfsevx4ssv4vDgAG3foSbC17/8FXTXK9x/5x0sl0u8+fWvo1oscfLiy9is1jjc28fzJ3fRd2tUHjg42MXLH3gFl1dX6o77/tczKxrNfI4YAnb391E3DYYwoKprrNuN5MC3Y3Avr3TOi+vOELHc2cHO7i66rsPl5SXOz8/x2uuv49VXPySVxWl8XDfNdwxkJYIBDBp0aLUy4JwKPq2qqpsnm7ADaY5+uygtVClEZDm5kSwNrJmVwtDpeFwSEDHKIg4Y8OILL4AD45/+D7+A/uBTeO5gD7724DikDZwgVvPlzjKdhgjwcMm9oMAVIxE03fTtd0uIIlufQ9sNWF2vwETwBEkdCDmNCWHAYjHH/t4+Tk/PtLaHWbgp0cronJAFSkDEhTBRSGCIoQCbgGyw5UjGYzJJbQpBCYjHiy2faBiIhgJCvV0QMCQNa6FsUO5ugh4ktBKFJY6ATVT/6lFxngKUm+KS/y1UI207WVJHYMcADQBEfMvL+wgx4Ce+8hN42vXffeW/Q4gBH39lT8fE6b2JlqQ90J9ZEdsmFJ+N5lT8O5o122BGeyOnAP30GCl4gRRtk0Jxkt6WYKktCaMoGdWoOUbUdSVrX1PmxhBRVx6bNgNDBgvgowy+Ub4L5Z88HuItrHbruEs+L9ooSm0UoC3zU34kN8Tpni3rm8ZtZ3BcKCymZBCBOGd0M4u9YuHcprrwpHnnqNloIpyrEKJwcdRscVNFoPxFAK24TjmIbImsv0Py8pqPv4HcHHdhPHFz3HXdoOtFvqaTqHIO2SFGoK48Dg4PcXFxBXaF62gat3XUhl8oGbaCCoSYni+m1k4nrHecOJRTvyz2KclKbdupAE/SgZFS9tquxgFoNx2ePHyCvb090P4udpZL7O/v4fTxGeAYla/R9R0iGLsH+xj6HsMwoKk9uiFid28Xi+Ui7Zd910kGyF75I9GE4Ozkh/T0KmZulLVUnozJXpAKRyYeyortSE44B09ibIsxAK5C7QghegxBTrUE4ItrU107hKFHCIMUvo0DhlWPtlshhg7PvfACwhBxeXGFetbgwx94VepdwYrJMtquxy+sKrzxC7+OeL3B/ec+juXwZRxdnaEh2QxrchLrQUDLA4JjEDuAU3lbOFLlmiVodhhiyg6WPTMkfobT/qry192UrqOTC8uKaVjFXHYKhTZGU2CREq9YONRUwQFu1pYAzIhq7VJaCBwJYBlHiaksjnX6HrtKl3OGKqneVnfpBjqO78juRVmiyx4rn5VA+1YFZqIITkH5VDEq+1zeV75vm4vRtvffRo8pbcoMhFKENvc/SYyJAjON65n2aUqHsSK63TPntn7aCo2KiSgywqrFxdk5eGcGGiL2Z0vcvfMcIgc8uH8fm80KzhHu33+AyEAfAjZtj+vrFtfrDb79O78DHpLg4qd/6p9hf28PHBhxkFpsd++cSEzHMOAH/u0/eiv97HpmRYO0wFDkiLbvEGPE4dERfC0B4rOZ1ImYMrQU+ZFj37quUVUVmqbB/fsP8N577+HVV18dt0P52Gy6yFiF3qCZoOTIWfLus1oKSBcVkSgNMhFaIIxtQlWIMMszzEnJSBZwrdxUpUq40q5IY0JkQjOrcXJyB1/5yhv4pfbDqHZmODg+hFiKs69+UEvRYjYv4jIKRrUNs/h9TBTtQmFpEgFAyvgOFxdX6PuQADAREKLQcLmc4+jwCMudJQDg/r2Hck/yBTBhirTHlKCeFUBmWm4LpCLdm0pAdRNgZNBB5ZPF75REli2h8iSkfJJZTokceS1CVgjsCeQWHsobqLlNAEiVk5Oekb9KvRtDlLwhj9y7ipHLJp1ByZ39Ob7ro8f42Td+Bo9Wj0bj/djJx/Dlx19Onz1cPcTPv/Hz+P0f/X7c2W/w8KIdt80GJBPcLQBQMeqslWwZy7arQOTlPNK4bbFikSog+YUJbidGkkxEIQ7wrlH/5HSel/ha+h1R11JgE3CIHDGEHs573TiRKtiXG/dkoImmI1c5mtxSyusSQ5Ft+/bRzfkuNQyizKHpbobGPNCE9hO6b1ljSTaw8avR3Ips2Bqzk111aUib1WT8Cj6jWFUQh1zAalDDjLStSpJ+UGDyRAuJoZd+zBdzDCGgQiV5b/UB0qx6kbnE7DrYTGYLPvaasrbvh1S0tRRzAswYITKOj4/x1ltvpbZk44759GNE3Amfc/FzAuhMObD2xu7ySsfCxSoZGRLfqO+6ASybCOUDtjpARBKU3wVcnF2gbSVQnMhOu+X9dVXLmkHE8Z0TIEQ8evQQvnKYL+fouhYXl5eonENV19jd2wVHxuX1FTiqayJnPiEX4eERSRR3pMxExUlc2mCKObeJKPlcaZDksCf9jMHOAUMQFzQ78YiWp1+L/ZFkporM8JERugGPT5+gGwLuPvcCrq8vsVjMMF+Kp0PlXRJzMTDWmyO8cfYczvwpum9agZ77fZi98S/x6vWXsNNeY6eL8F0Hx0BjtX2CjCNalkRI9jurDuQSaHRKAplY2x4IxakhxtcUIBtLsH1X3qtEtVPXpIyCYBkBn+bek9ogKtZ7dpGSyxXrNr/rtpSu9k4gG3cjWNzCmZNCZOCdijGX3iURSIrG9N3T2Nun1bCY9nF6WjFVxLa5FW0D7rdd06xb0/ekU6Synpu9X+vOWO2QbScl05OLbdc2hWJbH5+uqMgzURenZzECOe9wul5hPm8w27TYhICBGVR5bLpNwkRdHxBAaOZLPHpyjodnF/js574A72VNXF6vUc8WeP75F6WdbsDZ+TWYGRcXF08dn13PrGgY0xij1HWNGGNyn0qKhcYymKLgNFDbCDifz5VJgYcPH+Htt9/GnTt3UFUVKi22VzJVqZmLm5P5KGbC2/vL1HJPqxg6/d45sQBtqxwZ+y4JBu89wCSnIDHi1W96Fe16g3/4ZYd+5wXs7e9jMZ9DnFUFzJqbQ93UqJs6M+YtOarLjZ5tw5LOGJaH6UIEi1GpcPrkNAeCFf0nADu7e3Ce0LYbEZiO4IK9Szf3SeCgYKQS4BdYTfsyAlGiudg2DBPYIxugAbQtvAUTugniFeMohFgGdrq4ohRuMqt+dlfLP61tS7tvwBUkAiOEkKxQCXiNgFIG0duu3Oub47YJ/CPf+SKcI/zYF38sPXd3eRd/63/yt/Dpj30aP/Hln8Cf+2/+HB6upObGj33xx/ADH/oB/OHveBF/++deL1CkCjSlOZvLEG7SvgTFN67RHE4GO/2kbHsC4qQfnFIWSQplTvm6QwgpG2vQY201yFl8a5pPX9WaSUXe7oikoBtfqUGgVCAm85ysPlE2velt25SM6Wu0hoitm5t0MQXCzhEBLvtgYJOLtTIiuVkHXbopKRQJhOT1PW1fFNcI1vgk1sBwMiOKAfoSMOu7QohibY6MqpJAZI6M6FRXUBpR2jzHfSftawRjuVjg/Got4ynqzTgzfGylsYHfTJcYgcVigfVmjV2N6zOWNPaMUVyGDg/3MZvP0a5bqWGUlAMFWuV8j4muc6LzU9Lcph1G8zGfMxvNjTbQvaB01UJSfgsHrJHMTjyjbkUhRKyu1+j7Hn3Xo/IVnCpwR8dHAEkBy6vLS+zt7uClD7yC+/fu4+rqCkdHh5odpgPAuLq6gvceB3t7GEKPq6tr5S2SRAwsma5MLgQbcwLYyLxoG0yhdIJMghYMYduCblReOpzdtoJ5AwwYQocYCM5ViCA03ks+/2g1XXps2g3eu/ceECPOzxn7e2+jqjxm8zkqjZ0JYcBq0+L8/BJX1yug7+FjxOqF78LJJ/4E6s2bmP/6jyE8eoLqYo3FqkfVBXRVj0ARgbXgHwjR9uDINyzjwsdmrDTeNncnTQ4zYfBsuQYM7IshMysxqVDKiM0kpiZHQN28bgPW7+tixFl52QZgy/ek0wB1k5ieMtjf5qI9DYJm8GjZ3Qaarb1nuba5F932+a2Wfh7Hr0wx4dOeu63MQolLR+t9othMizi+37hLbF3GyyRlrsDQ07ac4kkzdMipM8H7CjwIfo3M2LQdnK9h9YQHNQxUzQzEBFc1khLa0agv+/t7uL6+ThlT29UG3ItL/jTB363je7bbZHBVVY2AfPm7/W3F80wI2XdGGDvZODg4wIsvvogYI955550U27GtdHzZB6sRse1YrWQO89Wz/8rXle1YEaJtWrTk4dZK41Agqm3MmhnuntzFz3/xCV6/rAEGjg4PEeJQ5CPOoHA+nydgkRgk3TXGQYo70t8JNKLARBBrX2RG27ZYXa9S/733iCwBg5QUMvGfH/q+UHJEGhIM2xm8kh4xjKl50rYJUv282IdK0H3jSdLPtcaCtVTuYXYWYVbuItKveFde4lT2w2he/JU+JdJ0wjxqL/EqQ32fS+GY+5haKFKS3kwWktscWbSI8MPf+RIA4B998R8BAH7owz+E3/jzn8OnP/ZpvPtkjX/rm/8t/Pqf/w380Id/SO77ktz3w596Kb2jfP+NgObUXwNRVDyHzFAJoI3fd4MDlS+UNGm+DcyONQ1zGXLJmp19xQsgHGNGkEZOiPtOhBzX+8pS6rFk47ENPt6AO2Oa0+il8o5SUS7X/+RnflUed9ZEi+1kwufmFzuieQHQkOSTrTFD88gZo4oOyqOUFI4pn48GrzRP/t7p3TckCYznzQ0lQuezAP1pvmGnvRMK69p1ECNT17Yp2x0APVzW+iklACrkqrll5LXBWC4XWK1WWY4DGv+m8p0lLXLTVNjb3ZFnY36P0ZO2jhuZHmQ0o/xx+ipROX/ISHEwRCUN5GFTLmTsZN3Ie0c5f8RW9y+tiRgjuq4HM7BYLnFy5w7mswUuLi5wdnoKcISvPIYQcL26xgsvvYC6qXF2eoad3V3UdZMASdf3uLy8hPeSocunkwBKPGfxGyYDWSfZTjesbxwjwjAghAGDxvYlwG3TzQVALXjS6f5eVRXqpsZsPsN8vpA4Tu0DkUNd15olR/fpIO69Xd9jfb3GG2+8ibfffhfvvH0Pb719H2+++R5ef+0dvP3We3j06BRX1yusuh6byOjJ4dHpGeqPfg/8H/rz+ND3fS+aV15C2NlFqGrAE8ixVObmCEZEIKBPhTJvgkGjFSCuTiFwln8FcL2Bf4r5n6yerRcV8/O075+mbNhPA9UJ70zuBd7/NMH+tvuqqhoVQ54qIDlu5PbxTft12z3lOKZKxba/p9/dBuSfRrttSlPZjxs0Leb8/QLMS4VjimenSlw5jmkG1hJPT+me2tH9Nb1fQwu6rkVV1YB3uFyt8NWvv4a3372Pq1WPSB4BDl0A2j7g9PwCb7z1Fs7Pz9E0M5C2LQcJDebzOR4+fABfeTSzGV56+WW88sor4vHzDNczKxqlYlEykBHAiFkerRHGzF0WtHHOYXd3F3fv3kXTNHj06NENwk+ZZNvx0bbjtam2X2rk3vub70lYTO4vGcM5EyY+ASBmxvPPP48njy/wudULuLxaYbFYYr5cYIhBKqUOmR6OHJrZLG1QN1LWTnayydrPigePP7B0lRfnF1JISUGeWKZYspckRY8RhiAKnQmiEi2W9OZiI5r05Ca25YSvbgrM8mnK6GW0MIoFWLzfIH6qyMvb2i5/3N62zRugygQX44S4lkQWX910WmI8mOBXHsYIUE5GmUeSHzjaqfG933KCz7z5GTxaPcKP/NCP4Kf+zE/haH4Hf/XvfA7f+5f+Kf7a3/08ThZ38VN/5qfwIz/0I3hw/QD/4q1/ge/9lhMc7tRF20g8Ox53IXBLc/b70Pxm7/PGp9hMVL8EvPMPA2H5LfJv5CjudSojhpgzwynZR63Zo957eOdQ6aloCEGqCZuFXYGfzcF4nWSa23xncJ/bSEuIeawoEqHwfSnolj/K7yo2LP1f1ndECaT0ztye0czW1qhtaGX6BACLlt5njY02vAQAXTFYecUwDJL4gPUktHidcTrR5L3FGrNVMJvP1UVW+6X3+ZFfcn73RArochZ61HWDru2K7pfyGKqcSJDx8fFh4gUB98anNKqdkclR2Fp1vkf8ysjF66ZUtX4okWKUDGoGOEulI5n1dL7T/qVB/DGyplqNiVbM4ooMBvqux/X1CpvNGhcX5zg/P8P6+hrzxRxVU8N5j4urSykCuL+Hx48fYbFcYLncEWDvPXxdSbwGgOOjYxA5xCjKegziYkrOwVUVrBZS1Dke4oCBB3FxrByOjg9xfOcYoEke/5LPTbaUtEh0y/uYdxXm8wXmszm8qyCOZpImnnQOhjCo8hUQOODq+hoXFxd4+PARHj58hCdPTnF2fo6rq2tsulaCy4cebd+h54jL80u06xarg49h88k/gE/88A/h4Du+BesXD7GaN2jrGrFpACcnRx7QfXE7kBX8UsH7SvGCV0bQjFpb+AXQvSWlU5C9i1mUldF9ZDJK6VsA7KedPlgfgZwdcwqA7SoT6yTDZhGLUb5riqemn03pY+8qPytpN32m7PuU3k8bp/X/tn7Y+A34b+vPdJzl2ErlZ4ppp/Ur7B1l1XEzgpX3TZWWbbQo+1cqElOMWz5vSpH9Z89pyyMesPf1/YDlcgk4hzYEdCFiYMKDx6c4vVjhatPjat3h9PwKbSfZY3d2dzCfzVDXVRHqUKOua2w2rSSBms8xWyyxs7ePu889f+scltc3VBm8TJPaWxrVyYTZ32WWBCNa+bn3DiGI9X0+n+Pi4gJ93yc3rJIJreJ3An4F45Tad3lcVSpA3vtcvbZQIkzpYDcORi8X55QRTen4wCsfwD/7/GO892QNjhH7Bwfo2g1848HqGiaFi4DFYjkCPeIhOsIwsulljwpMQX1RDw7GWJL6kKRI3zAkrMRgWL7uqq7E11XbHoaQMTKZ2wZQOqXIWC3jSompRz0CirkY32d/FK48+rf8lM0oj1CrLBVpHjNgyu/S3mUr+bRtzn8kpRAFwFWzIlHuCyEmMFB5DwKPSiWYmpFxLo948MY1GTcz8Ie+40VU3uHX7v0afuHf/QV898vfja/du8T/6j/7ZXz+zXOAHP7Ln/46/tWXH+FH/4NP4S/9nr+E7/+m78cvv/fL+N0f+N34w7/jRfy9z7yVejIqLD0av4HwYtOwjsP4rxRO8hZKz4zHVLoBCd0oBV+nAl8FmBWilQGIA4Z+gFdQyArW6ko334z6wTHK6WElMRmx4ME0WrLZuKkeWdu2lrKlrUDsxufWVxu3uf9Q8S4jGxnNS+VizOdEE+4vNwDtcaKxtY2Cx2/QGpO+j/l83JH8KRfjpoSqpagbWIwfQVM5y+lSucKzXCqpYCxVtt00zU3rJBuQEQNIhZy+fCTn7F0KSM1dNcSo/s9b5lhB6PHJMSr/BoZe9pHkkGLr1XSDEtzcmG/kqZrQvPySLEtHInPmiTJpBE/kmpxUCeGkHqvEGyXuYEArzIhVX+XTer3B7q64FS+Xu3qyB5B38IpfV6trNM0Mz929i3fefReL+QIHBwcYhgH90CFGwnrd4vBgB5v1Bpu1xFLWlUczb9DUjRzaVeLOLE7dDBCjaWocHR4lC+XQ95gtZujaPilHZNkZdS0nVz2Ix4C5LBI4ZYkj5XNHDnUtSWRYg8KJRJb3fQfnK3G35CDuVhxA1AmYYwVx4GwLsBMHFpfA07Mz1PM5vu4/grdOPogXfvcH8fzLv4h7v/br6B6fIVyvUXMPFwIcxSLGRvtZyvORMDCwG/V3D+bhBrgnXWtl/BQVGQDlNnlHUlaNHwrWBIrvpv0qvrvNgv+vc1/6b/JdjDEB2mmK/GkBZZN1036XIL3EayVGKwFyabxm5rGHzKRv2xSf28B++Z31r+zXNB1tef8Uxz6Nlk9Ly3tb2+W9tylo29of0a+kDUucTTcMqAiYL3fSZ8558GaD9UaUe9Ki0QwH5wV7z2upfQenYQ+q3FQV4ezsDCfHd3UdMO7cvftUmtj17MHgBUivqgrX19foui4pBnZti42YMoW8z4Eox3ssFotEvLG2Junl7DuJicxabqnQbNOQjXm9+pCW+cftmBc+f16+h6QBOQFICxd4/vnn0W5avLHaxZMnjzCbzeArj9VmA7SMpvFoqpn4yHHEYrmAGYOkv9J+ud/ZRqlGsPQ9CKMTkHK3jjGia6Xias6zrZVbNUi88mKZiTGoltshaReGQxOiMH/nEr4KGLmJewolAhmE82hQyL9kpJ4Gl37lPEgT0paWEKWyYW0buNJNXiF92vRp2nZGmUXbKhyVqDEGoKo0U4tV2C1HmMd9E5TnvoiCwpL1RTfxT3+nBFH9he/+CwCAv/fP38Bf/bufx2ozJFoxMz735hn+6F//Ofy1P/Hb8T/9vb8Lv+uV3wUA+COfegl//zNv5bZ1ZzIgnMZtQGCKDu1n2W0mpPicNM8lFMzPpHHb5Gp/yYAGybMGEcUiqGmpSeIDvIsJ1CZAjOKonMTK2NQ1qrrCetOl522u0jCUGZnLORjPc1KyiqB/Y/ab47bBjgFkOd8myt+Xz8cPj/gcRgFdCzmmRnmtABzWdqlsJeWDkQAtpRfKuJIQ0XckD3CWuIyowiWkbFO6iRVyZsracFl5IZBmB7PaOUg8n9hE3VElyBVbL1O8mKUI4Ga90T1gG0AAmCOWizkWOwtcnF3nl7C0UWRVHXde6c+jrwrZMZGpUz6XJZzdQEmz0MQQU1wLR9aMRLZvqCyFVFgnWNyiFkpUxTYWfOy8GKbqymM+W6jiwCCoXK+8BFP3PRw5fPCDH8Tbb7+Nt99+G8udHSwXczT1DBwZr732GlZXGx2GQz8EcCt7ddM04LYFVR6L+RJVU8H7IvU6idGu61vM5g0263ZkSR36IbvgxZjGn4CTjs8IzyyubiK2nQS7O0IcxunqY1Q3SWIwS4X5pMQB4GjuajLfIRKo8nAk+/e63SByAA8EVBXe2v1WNJ/4GDZ3/gDOf/EnUH391/Hc6gwL9ODYiYsYijpIJPMmy6lc2JounyyxjBWVM4u0U6OeyQjLuKh8yaxYp1gsUJyUGWjMnRNwLqw+/vv9rilAvu30ILm46slKGTtagtvyvumJgoDR7e8vFYnS0FwacqcgeqqY2GelwXpqvS9jHMq2n+WaniTcpqS93/u2GdfL/mxzHbM+M4uru8UpT5+9bf7S50XXvPfCgTFKog2VTaSZYJvZHASSNVcRmtlM5Ypwb1XlEhFEBNY6ct7LSQpHRh+iFhV9NqeoZ1Y0hmFACCHllK6qCqvVCru7uyDnIUe1UQNTfJp8Cc6NCnTL4zAxShBRKgS42Wwwm80wPVIyqxcza9aMDBK4sJiYD6hp55aWjJnhXSaeaa+AFHWp6xqrsFLxYBNvYIVUhDidnIAXn3sZX3rzCV6/vIOua3Fy5w60ugOICH0XELoNyDnMmjmcq1IGLFKBhnLxFxjHMAorZkhY0f6hvNgAwqm6TdnLiRxCFCYgSIxJVVXYbAL6boCBFxlnca6SUJxWJbZ+FWCMkX3ODVqSdjqNpczXOwIs+gzfjMswSzubxcdEfgmUi+OKpAAYoRTomEtACQINpAhfRFD5ufaDNPjPjtOHMMam+beYX1xOlk1s+igDjr15hd/7SdH6L9Yd/uP/12/gv/2ldwuaj5HOqo34j/7WZ/Hzv/kQ/5c/+23YXzT4vk/ewd7C43IdYP77zDFb2bdtQmxvNCUc48vaphLuFg/a74nGlIOMFVjlsSpYKhUdCC/GIWgtDOGLOGJqSIB3ZHCQRA+OAO8lA1MMEbUfBzwbr6Vm2KaCR11P4y6SIwiYzw8ajyWrflqHmc+d85ATwpgCostTpZs6ZwZYI7xSUrc8qWHje4zWVsH4ic/TKU0Rd5VeqkDWKtMnvAxATjXUVUfHwWCEwOkUNSkt9lN5Qlz65QaTAY7EWu8Ykj5UOyMZwjSrT1rkBW8q8DJRZsrNcrHAZr3CUg0ybPcn+io9PeFgfx8XpyvVH/O7kyywZifKQ2GOSPM3Dngu5o6yXLNnrDAkmDXJB6daSrIZR5DTFypNCFL80zuH/f0DXF5do+86sSQygZx6ARAhBkbXMWL06E4fY29vD5v1GjOeo6preOfF6FVFhBjQdS0+8IFX8M7b7+D89BztqgWIcXl5Bd0SlcBymhJCRN/1ODg8QIwRd+6eYG9vB+Q9QujAzFgsl2kud3aWuLi4wPXlWsfHYJivelQliFWhJNiCGClbOi8DAkIfUNUeO8sdqRCu8zUMK+GZENA0TmSL51QU0AQ16STlfZCASPCVQz0TGBODFDXlXmqL9G6G+vlXsfuDfw6PP/4evvbZ/xYff+tXMFuv4YceXRzQEaNDQFXXoCHCB8jJa13wE6PIFmnuUbKGo2UVU3BnS9gqNZcGC6IqYRoroMnpJA9JBoyMtcp3DDuZM9xT8reeJlH+vAS6U+BbnhZMFZHSBTGJI5WHti6n686+A8beIECRzUqVjBLE32b536YsTOkyVbxKj5rpScQ2DxX7PcaYDNnWf/tuesoyHVvekrZX7S6VIwukn54O3WaknxrmtxnrRzTSudJlgSFK0hDedKhA6MHwtUfV1KAgxVWrWIG8QwwMokqwgPdwleDVuhbDwzpu4JzwS9+3qGoP5x36da8Z3N7/emZFo9QYiQiLxQLX19fqvmMgLvutiWIBAGUBPvnb1m+puTVNgydPnmCxWODw8BBN0yTGLCeIAFSVR4zCAGahc8UkEEmUvSOXNO3yXZZRovR1s40q2pGwTm5U66UBoqODY3iq8dnLO3j48Am8d9jdWaAPUnwo4eMY4QDs7u6B4FSrUqZQBSvthQXvpM0M5ULP3xrjDsMABnB2di4nTWRgwQEsLivDEMB8hNV6gzAMWG9a2InBqC3SzXTaPiBFmhgChpJiZADVBuDS52T9NOxGttcX4C6PpoAA+RJsI6k0ZTEzLB1hfk5HQLkhKkDRaJQkR+wmUIYwIM+yXFFP6xwRrDZAVrTKsH2jTeFOU7gsJQGoQOal4wWayuNXvvYEf/Fv/ireerRKdDCXGi7pov3/8V96F7/22il+9N//FD71kWO8cLTExTqnkhu1DRSoqfxxk+YjZEyZ7glYUUllo3mhIAJFHmD9VsEjc96MjObWpCly0HtHyoatW0eafc5noASJk8ryrFg3bP0saU6aNay04pVKhE5MwqQ0GvdoLkAIWswx83BJwZJe9ojSnG6h+ehWa9sZMsR4RjjNS1qXxRqDKR4GmieWMFOqSIFgZAm8TRTjCJacQbDXl11yplzY50qryjssZs0IaAuRRLkSuQwpGmqjKkAQpX/k28VigfPzixEJSCc4aoxWDAJAT06O8fbb9yE1kDCiv40zSzdTLDj9NZ2FkXhN9+e55MTbnJR70ROzux0D8JVHVXssFUhfX29AxJg3lQpmqQdC3KAdelGsY+YX25v2dvew2qxxcXkNBjBr1tjf20fbbTCEgOPjI/iqAsBo+w4vvvwyvHuAsyfnUiwzGkhRXiZGXTUwZXk+n4NjwPXqCjt7S1TKI227wWKx1PXo4CuH/f1DLJcXWK2vZQ9ngLwDIsE5rclCPu+bbGtH9tb9/T2sVtfo+w4x9ti0vZyo2z5leIEADgEcLA5S5yUaxBbZki4nM+e8nNAs5nMQFLw7AjuAA+CZER1jtrPAcx9+FeHOn0b/L9aYvfs6wvklqvUGYehQq+GTCUClOABDDuUDEHTdect+FxnkpZCoiCpbr5yV9mItiqKh66EAoiHtMWPOTApJUtrtXYZxDGTnNWY/pycYJeAt+7TNwj66b9Tn8X1lbMh4nDeViCnonp4MlMrPFGxP25iOpWzTMF5JZ3OPH4bs7la2ta3/5d/ZMH4zDmbqbDZ9Vzne8tltCkXZ7zKl7XSOyrFnbwAznKiUI/OKZMR+ALF4BQ0xIg69nOaFQUoC6Jpr2xZ936NpGskutbuL/YNDDZMYUr8uLi7wysvfBBChbhq0V1c35mLb9Q3FaJQEMaFlkzUNnplqdiXRyu/Nfenw8BCz2Qxd1+H6+hpElN4/dXkqmWSbhj3tx7aFluIzmFPGK/uuvA+IcM5L1egY8fLLL+Nr7z7CO+3LuFq9ib29fUm5m9yrZLJtzDs7O1nw2Gar8oEZmg2jQHzFZV0ueqQbvyg/6/UGV1fXGIIE33onVhUpZEgIw4C2a7FYLHD/8WMR4MyqnGmhKVN4REKNFQGiBCJRfqNIIYk51kVnwCRpGJzum44EzMjBVAYEikAoKlWQMVTOFnguiFS+O/2T/jQ/W/HoMKCfAWdSWJ0qhbdsAEmwEyXLpo173AFZ8L/13hW+73//03j74QqDBoXauIstKHe7GPdbj9f4d/6vn8HLJwu8+XCVxm1jz3S62Xb+rfh9pEiMx5NpaEjPZdrChGHxeFIS7N0Q5ZBRZF2zQHtGpdqFGRzSUjGlBKzHth7eV6nXzjt456Sopo08dYSLac40z58oBRKfc7q13EDLkwSznBpZzDKJYr5vWpWeneYlWNAGipTM08tO7pDWPShBr4JH3Xjcxhcm+/TdMUT0tuGCEJhRF8/YWrZJFQAF0yGULeS7xWIuPsBc2cBAIElnziy5a1lhO4235KQc6d+SNpyTscq6URjqEh/t7+9hVjdYt5v0kqQsjmhuz+vmP6INct90bCm9L8bKW6loyAsoZdiy7H4gUTR29/ewt7eDwICfXeH66gpDZOwsF1itNrLPJH50ad1YB4ch4uJyBSapJi6ZqQZsNp1a68XY9sJLL8pJia8QI3B4fIzHj8+AwHDk0xrz3mFnZ4nZbIbVag3miJ3FHN4R3n7nLewsl1gsFwhg7Ozu27laSnfcD9KHoQ9gHsS9qq5RzWtRdpys+RAiPLT47TCgbVsM/QDnHV790Dehrmqcn5+DoyR36IYOXdth6Hq89fZbwoshJuvo2AWG075la9gldyZCM5OMOInvgsjFGBnsGY4JwUkBvmG+hP+BP4sP3vtnePNXfg3xnSfw6w3QteAYEBjoKyBwgI9BVxkhgjQjYSX0CQX4M/lLY4A9vaaW/BKAO1072y3WXMio8XUTq4zbua0f03tve+fkQaH9xJhBac8ftzEF2dvG/n7pZm/ty1Ou8sQAwI1Tm6kLmNfyC/bsjROeLRjyG+nXlCdue/ezjAu4JXPYCGPl+2MMGNoWm80Gzd4uuq7Fkwen6LoO/aZFu2nRzBfw3qPrOo3DEHl+cnKC3d3dFI9dHjJcX1/B+w6z2QxN82xZp55Z0TAN1qLuAaT6AxXRCPhPNbhtWqk9b99ZrEdd11itVri+vk4KhQ1yGAYMw5CUhLquJ8dPY1+7aZaF6YSHENB13db+xULoOQ0kXy4l+O5zb13gwcNHAAgHhwcYhl5gq/nlkliU5vNFig1xSfmgpHBQAdiBHJ9h2KTEdPKLLGlTFB48eIigGirr5iea6oCgBbnuvfseQFT4/okbmAHkkkFH8zWxlKQuFFDKfPSzpAXYaoikGTFlg4u/MAZ+qphwQjr5ae3QCEjZ0kqgAVlhGQM2ea8F5ZlPNEaKJ6cNPHKRxCBtcAVONKHKMdWwyJM5bjuBR2K8+XCtrgZAckszqhRAo7SkMxiIQCDgjYfX6d0jJyeatJ26YL9kbeCmklH2t/w9KxU3Z8Pmm8bMaoCP1ZqHXHzOij6FGODUvUC/SEASDHAQJbCqK9S1bOh104jS4T0Y/XhYE77L/VP3qEzWMZ/zmFYlpxYkSFdksVKmIiwwhWsLr70PzUd3s9CStGjd1DqW38ijSdjadumKZcYXQE+eKN3DMWLopYYBFNwDwsfEN8dv+hepO3mKFQPgfYXuepXTdtsKJ5FBMRkoWICr8TqNmlCyq6tLP6DWjYvSYCFzypbmtsHO7gLrzQpgr4pBNmChmN7UWyNhOQE2L0Wf0lKk/AxDN3dA4zO0eooCRFGqZf7mixkiCa12D3fhPeH64gpDjOKiMPLlF3qYukMg9H3AMEjmKIv54MDoYw9oe+vVGpv1GvP5Ih26vv3WWwhDDwefeAocsbO7g8VsBucItZdYjcp7LOYzxCDWycPDQwRHWK3W2NvdgVM+uL68wte+8nVsVms1zgDOE/q2lfS18xmWe7uYz+ail4aAru9QVzWWuwuEIaLre7x77z00VY0Pf/hD2N3dAxDQ9WI9HXop2Le6XgHE4n6WJlCpn2RRljXMEQQH5z0Wi4UEsDuX+E1cQfR5lr2XnewvD3GA4UN/HCc7r2L43Gdw70tfBp/2OAoMDylkSUzwiKAIRLb9MkLc0LI7zihVsyaUKUMVpoBwCjJTfAIos2MJZsmCz8e4Zfr+qcG1/K58X4mDtmU3uu39NsbS+p7eJTeglJ/bLPvbgqSnKWLLcWw7uZgake2zKdY05WFbatoy66l95r1PuLZ077Jrakwvx26Gp5Im295xGw2MDtMxlZ9Pr6mhPRvebt7XDwO6rgO6FlfXV3j0+DFC34MH8Thq+wFN06T4LVPMVqsVzs7OsFwuUxvWvy9/5csYesbR8ZEW2H3/6xsKBje3o7LhZPErBgdMA73GWalKbdaIb5qUuTJZZoNtDGBZqEzpsFMROb4dkgKybQzGiDbx9rnVCOn7PrXlvUdAxKyZwaPCi8+/iL4f8PmLPZydn2E2n6lVq6ibIS8EMWNvb1+qoFpVX0La0EnbHUHyjGXsI4z4VTfdECKGYRArEZMepWdeM5cyEVYWyGcCy9CC9SP7LZvFmBT93Qy2nbrhGPqgUb8zoCiBjvxqVXRLBJ8E+WicUMXNminv39I2cjNpEOWeVUAPInXHCVAUVaS5c4VATo3JiyR5kmRLGylcauVNrlAJGwpAZYq5YWTAJi/PLmnlO/P9dnPRJ/3OpWdKcpYA1GjJkw+QCENpXeXv0riZQYXLWgliSxUlk1tPBAqap/SNiIm2wh9iGRZpbXBLrKLOexABfddhGHo0dYVuM6SMakZEpV6iWyJp2veKzbZEtjBhzpgqiFM62b9MaXQ3by9X8S00J+PHclNIj5WLfNI2GZC2ft/edvqkANFZgckurZEjKrV8cyZW4h8yPtb2UpdtLbDDcmeJx6dn4qKaZx7eOQx9FOWHs2+30CCvZ3uncfVisUDbbtA0dQI2TGNacIxgzzg+OcTjx08ggF/nB/mUMoEuAsSdj0fjyXzOI/KNZHHqdTFdGgieFBBmcVXyts8FuCiB25GBnZ0d1L5C3/Wwp0gNH5FVeRFBB4vxS+ONBp6MSARopqbri0vMZw0oOtx/7x4211fwUH8hA13OYeg7DJ5wsL+HGAZ0Wg2YiCQlLhE26zWa5QLr1QoLTWsZ+4DXvvo1XF9dyn6lRiALBYxhwDB06PsWOzs7ODw6RNVUmM1qbNoNuk6snbOFgBBmxlvvvgtHhN3dJU6OD1B7DwfC8fERri4vQVA3RZKdyLQoSyrAnHkIDJAH6tqjaTQFZ10r5UTpYwAhMkhPWZ1nNHWNs9NTNPURuhe+D/2d78HpJx7g9M3X8cZrn8Xx6/8KL/XXqF0ARYIjlpi9PsC77GLoLMMlCOQIQYPjCWNlYromp1Zx3iqX8/pNsqfg6akR9+a78vPb28LW/j3tO5OVPLmHCl6LVADwoo+G77Zlj5qm5r1NkZhe204CypOWEmMadizfOS25YM9sO60p27yh/BT7ytNove2kZNv8TRWUbfNY1v3IRlGoC17RF5K103Wi1Fcx4vDgAH0YBOOySPqqbqQwZlVhsVikebLA9OmJT13XaNse680V3DlGnkZPu76hEw0D/1GDjbuu02wV86QoWEo0+326uEqlY5oS1whZZqAygpYKzjQFWowRm80GRAKmey00ZP1YLBY3+lIGmJtrVvleY5DGN6LpocLB4SHevfcQr1/sYegGHJ+cYOh7TRMmAWLyHOB8hdmsuQlhCAmoMRd/jwDqyDkISrwEyDgyrq+vMXQdzPpeVV4tlj0GDTwSkCLWRxClyr0JgEPFmM0P1G04SZTcAdv00kJI6MMlq5y8zeIqcLP/5SfFIkrvRnE2McViheJQtm12BXm+OMYtUBKN2jZXkgxPiShZp3wZUJ7al/dKgbJBwfm2/uXCXNZdsXwJiKiqWngsCMAT0GGWuJj6nGeDi7HkcUsWoRKYZItYeWUhZ6XlinMqDerJ8wmU5jjBY24LzZNkTWpRApD6mmEYxJ3BamnYekpt59eU+J+ZUdeVpOFUXo3qFmjK66heQoKWN8dtdySlyTpXUCH1iPKYJr1K4x47CND4nnHjRduZ5iWfp9v0dXHCa6npGJUfSEcr30/VfXth8aTcRxInEVhSN/uqkm8YNyg3Wl7IJxzGFmZpjvq3+PrHQmbJS5wC8RCLjVUbLeEUFzICzJjPFzg7PRVX1InFxUY/xIAKEYdHB7InWLajFHOTeVSUFU4nybbyhfWLcY9JlvmcxPUgTY53qXaHGWUiWBVQMaDUVYWubdFddaiqGt5V8I6wCT1C18HbOmTAq8VdTmGs/1GTLOTFYfJB9k4CAmF1cYmmqsAx4MmD++AhAJpByXmPb3r1VfT9gPfeexd9t0G7ugaYMIQBXdui7VqEYQBHxuOHj/HiB18CYkDfblC5Bd575x1cnD7RaaBMKZaT5QiZ59i3iO0a15fnuHP3Lg6ODtHMGoQYsV6vEIkxbxqACSFGXJyf45133gIFycR4dHCIyvl0EiokUBDojACqZHCGuhZ3OWt0b65qEEk6z7qqrasAGIHNLTPAOcLuzi5OT89wcucOXF3h+Vdewv7BIR6evID3Pvgp3H/vyzh+91cQ2wvcaZ9g1zm4SooYEkdJFY8MjAM0FlSzPRLdVDRKAF4CyZSBaQswNZYs37HNbcbeU963zSIvpI0jt6Lyu6nVuuyPtW1y3Ay16blJH4HssmSY7mnK1/Szsl373XCj9bd0iZoqEqWSY673pSfOtD9lP6d0LsH/9OSCtGr99L5yHGUb28a57d1PU0a2KWMZLxR01U/7XhSLOQN10+Cll14Sb4MoOJlclbxdFosF+r7XxAxNouNsNhspWoeHB3KiSlIu4VmuZ1Y0DOiL32iX/qvrGt7XaUKBm5H9JWGmBJ1qciUzlZ+bYjAiMOdCgYAEvIQQk7JhzGmBQBZgbgQs25kuQED8bh0Yfddj/+gAdV3ji++u8OBxj6ryWC4WaLtW9zjOc83A7s4umJEAPzmziGdoDBSgHlnZMJGaeNM+YwBqPTk7O0fe/gHvPELUarPq5uGdh6c8voTRyFyfMJJmZdtbgZRJfFACxCP4ygqJSuA2Aqn23gxuE+AhUm+cDHfGyKQAHwmMF+TRe3ImplFLRdtFl9JoKKUwJuWzEejTm4nKtjMQyxM1wkcCsgv6DMOQt21LJww7BRmD/HJMCaBSoYyVitpknFw8Z4JwIs7TZkyU/0b5rsyM2Ebz3FhWM8t5BZAqrccY4Z26iow963QtaLwQyzqv6yqdwIWoGWGcA0JhLND5u3G4rINiTMZcDGWyVKUHPKa53OBGisOUijfoYTINec4z10/XU9HHcn0kDZYm4xjzx/hVClZcDt5PC5wls15Ta4rwKOeWEaq0sakW2iNzGyLpc17bJbUYtSot2Y1QeVMzEJbF6WydlEu5WHyymTU1Qsqed5OfbUpCCFgul5gv5lhdr1P6XgPjpONKcmkiU4mmc1+8vORzlU2WzcdR5gVrJxVmhCga3VoCwHeaGVbrNXreIEaIO2uQOkdD1xVul1Hnw2zw2ks291vKrEFSd8NBAP7jboNNuxHrJBxiHECe8PxLz+HOnWP4usLu3g5e/9rXsFqJO5bzHpv1CterFbq2xerqCr6u0K7XWC7m6LoWHoTHDx9ITIjRIClCtrZYeYgxtA6urnGv67FZb/Dciy9gPp9jNm+wXq/Qdp0UFmTg6OgYm6sVTh89xtXFFR7dfyhukjbIaAY7dRsrjFpJMnG+fTafo6orzShJePzosSgQTk5EIwMBEY4JLgIeBpKBzXqN5bwBO4f5/g5eWn4IO8dHeG9nF2/e/Rhiv8EZrfHR1RfAX/5FLFDBc4Bjgg8eju0kWtKSiqubSwUgTXym4rhpPsdgnkizt5Hxa5a7BCCA4Z1P6d5TVs0EsLm4n2AK2TZAClj2rJsA3xoc+VjoPaZgpJTz+t1IScEWdx7cdAkbNXcDbI8TvpT9tz2wxJP5+S1D2aI4mIvUjfFNDN8lbaZxxeW17XRp+v22a9uJVNnW9PnbFJBRu0VTJp+qqgJ1QNu22AfQthsMzGIc78TzZwgRp6enmM1m+PCHPzyigc1nWSG+73tUXuShxAL//+FEwybNUnXNZjMA5q6dq35L2kSXmG3bkVU5SdNjqSlRS9cp1o1TBj3AUuZWlVTvNMXCjs3s6MfS85rGBgB7e3syGSygPIGUyPBVhdpVCFEqJh4dHOPs9Aq/fH6MzeYRjo6PEGGZtPKOY8Bvb3dPhIiTXOpONwthAtvtMsBglsA1g/LpK8MCkEf6IaLrIy4vr9U6JkAMurlboT5oulFboLb5JwTCYp1KNTQ4W0xHO/FIcJQQqkBu6RskFxM20CKTmPiIkwKRwa1t9NmymwGKwlClQW6b8p2pF6WlUjan3D8DgCaIpU8OFCVTCSLLvHsqhs/FXBVnTHn3LwDUGBKasB+BmhEoRxr3CM+nFyRiWC/SuG0WGEiZHvP60V5S0X+Mj+2t7ZGwQ3lxer+NipISMj41YrKMxlwsA6GRHZAIyKpkjm0T1PkxVjDw67xDVVd6mCKuKU1dJ+c6U8wsRWvqZaJh7l/Gj8Zr+cM0hjIZQ0FzWyd51qcUUtnEUTdgJBAGMKL2w0q1ETNcoYik9cbWtMrKyRorlUqbt/JsgKyPpG4lKOZC3Sp3d3bQd20qHFfXtbw3CqMY/SXLk+ShGp1AJT7n1JW6riX1sPrVOxufE2e7EGKKbylDiBJ9Of+MiS5yiuBSdrIs+FJGFSY0dYWjwwOsrlYa40IgVgDBmsVI59NqPLDSxaFsuwB8CutSL3VPkzkgeK8++lF42xRTAoAhIqJCt15hvV7h8PAAw2adArhjiKAYQdyDQ6s8oWtMAavwQlQ5JvyUHBcVYGpKKXAENitJk+sLV67do33ceel5WWMh4PjkCHt734bXv/4aHj14AHLA1fUlVqtrxDig7Teo0OCdt98BW3pvclhdXWtfCFY3IsmWdDqq65MjYt8jMuP89BShH/DiKy9hvlxgb7mPMIu4vrrCYr6ArwizuoZVSY+REcIA5gDPJsNUphgfK5M440XKdS3qZgbvagAE7ys8eXwG72ocHR8lN00ikgBxpzF6jrGzt4fTs1PMZ3cBzSrnK8Kd54+xd7iH00ePcf/dezi/bPDlV/4gDj74+/DC6WfxynyNuzOPYdWKV0focHl5iZ2dHezt7eC9r76G7tGZyEoGKDJI+cUKHNqqEgOpWthVCXIaZ2JJNQCgdpnOU0OtN+nO4nYGAB4eIGCgojCvWngq58HOizE2QE7mVUZZKmGyNP1mfHViJCUWBU3P4sVdylYOAZ4soYr2Na2zbKwA5MTfe6eeE6z4TU6FnO0LkUEUMbCdjlRaF4wAeEuuV+BHNeeRA6scKMF5iTvL05jy1AIYZ3sqr+n99hmR07TWIreTEjcWLTeeL/fi6WnMbQrZVDm5eWplGdt01ThReivngVUHtJLs4Atf+TLOT89F8d87xKyucHl9JQWnn9+IUY8kkVAfBrQAmvk8y28ieDjEIcopuXs2FeIbyjrV9z2qqkoKRoqVCAM8squSAWzApbR3llJ2dPRUgOwyl3FJzJJJsuYnzGzalikgMBADpGBxe89sNhspS5vN5ubkqrADieYfo2wsi8USTT3Dl19/B++eSias/b09dFrkBBhr903doKpnyIV4GDFq9kkNVrWiTQnnpIVKCRyVzg2yaRNiZFyv1uj6HHDpnAQBdp1UaycnViJmToF8llaFE/rilAO9hFAGftgQrE0oZ3CjI745X+kNhbJxwwcKOmhDyEj3WNso2y4AVQa+Y9CXJaoutMmzozkGa1iEAizKbXOIgEehlNlbJm2bBpgHLXQ0sMl8gz6mljAbKARGMTA2bmynubXN03ah7m7JzUZ7bIokbN0UNLf+ZnMTDNakzZCTyMzagI2DBGBC6ZcAAbFaV83/XGcqBnC0yqslVcvBKxAkJwXhKp+SP8xn8/Gz2iVxbc+8RoYwqaCaKZwFzdP6KuZu7Nhjn2c785TorMq515PcMrDTUtCS8X/J50mx0PdNrGGJ1xK4LNYQMBpf5gcNUEaxgWl/T46PREb3HTgw5s0MTVWj7zt4X7oQMMwX39S3rIyWtNGxOfHXHTSYUPdYEAiVd8nFjdJgKTWjnU9zLvc5KdzXtljM5wU9kGQWQwvlVYyjo0O8+859cFRZnThf94Y0tbZyocqKzmFR2RqsblAKssT2oUY1s4aigqc8N6lvOhcxAhx69JsNnjzqsbvcQXBZaem6FqHvIYd8ZdrKwliSstEpVUx4EyVrf2TZO8r4GiaG84Sj42PEyKLgRMbpkydolZ62v15fX+neF3H35A7mywWenJ1jvdmgch6LxXwkKyUGR2s+iPYjwLc4jXUksrNrO6zoGm+/+TaOTo4lpWbXY71e4b3rd9D1HTbXq3R6LOslZiImNGPrm3T4mj4/7SUkNapmszTPkcUA+uD+Q+zs7GAxn43SK3NkBAKsppLzHhdXV9jZWcIhanpoQlU7vPDi8zi5c4LV9Qpnp5fouhbv7v9hfPXiMZaPP4e7YY35fI4Xv+U7sTr4OHaHdxD6U3zrh1/F6skphq5H7HvUcKiiWJC7rscw9BiGoLGn4tKyWq3hh4iZEyBv95jhtmJRUpnF5XYIqgzzuLYCBy9ui5E1qL5KtEEUF1SQU4OHqgsGsI2TmEFR9y8mVK5SERoRmBGg1cS4NJYCTBHstJ8aNE/k1PDndV+R9QtisHO6P5m8Eo4fbF05UYwyPozIVdYF/1liGy5ly5arxJDl71PD222/C7tlnFr+7ohkLGapUZluv5qx8bbg8Knr17aTkbK9qevX6KRK40SjAU0lS12LrL+6uIDf3wGznHS4gdFuNnAkcVnD0GPTtdiZ1YgccHlxgYfv3Mdms4GvK1R1jdliDpCccC6XS9w5ORFXxWe4vqFgcPPbKutQlMdTZYYo+dsnob2NiGUwUEn46bFS6e4ktB1PfMlApmC836Q55yTtV9OIi1UIo++S4gDC4eERHDn81junuLjax3K5QOWd+H/GmComgiUl4N7uHlgtnURWnFBtjwR4FHxpGIQLbIm8Aae+66KKzLi8ONcgW7EOkHNyHBZCAgdp251qyKZcCUFy28gL3qwQaQNEuQjECiG0N3hj6oW+I619l4CGWMGKExVrGwIGUq+IRiC97L3Bydy2AX8RRgkMJz4pCFsiHCpfnjfPEANqkiPi6YGgWGYLBSNZgOx1pVpYNkAFbTNIzNh9TPNtF0GFchEAYuCLihYytM/9GDm42REDp3/AaQxu9ITcwfl5+9BpL51Lm4FURjZAzCmzWqKNWs6Mj0odSp5H6ovzqmg4j3YQK3zd1KoU5r5bd6K9p+BC+2lWciOrlC0QWhpNbX0CBd4pxi/rydQYTk14mwP9j1g3eAOLalnXvVX7a8fwSunMxOP5ViUxB/y4gjeKMyWyTR/pvVRsbs89d4Kjw0M8ePAQHAW8HB4epvTXkjFkrGLl0ylK0z7S+1MnxXVldb2S9a00ISKQpjkVQClFMG/QODWaZfJyscB6vcZysRgLRKWh3RdixP7+Hurao+8CnCe4mNcxIQi4igypMl0qB9mla3zmCcTEmCqvogS6OxAqB42ZyXwtioZL9UZCjHBe3Jv6YQDHAc5XMAsvE5JlO8k1IhDnbEZU0BzGA6pvRmSacIy6FpX2TY3rqys4EJpmhvv33sVm0+Kll15E30kmwspXaDetViCv8bGPfQzn5+d48613UFcVdnaWaOomyQROe7nJGl1XSh9xE3LJ3QnM6NoBznV45623EIYBlm3P9qtyjzd6wvZvdf0jZeaxraVYT6TZG0HoY0BFgGOHYQjo2hUuLi7QNMdw5m5tIkyNDswBuzs7ePLkcVZqdc/wlYC0uq5xeHiA/YNDNThGhPACQvw4OEZsALw7awACLuIJ5FRvAxzYbgDcjQ9w5FZJZu36Hh+9UyMG2WvE06KHHxh1JBztLSUTZt+j73oMfQfqA0LXod2Im1yv6YO7tkXfy8/N9QrdZgOKjKHt0K5buEiIQ8DQS1ZKxIjIGnfEIZ2UIcpJJKsMc4CewLGs55h37q5wA8sbLBCJi1M6hnekW67UCWGo27hJL5b9JnJAUGMskwN54awIAEM+EZdCpASwGav8jeDvba5NhkNh/Afbf7Zjw9vc28rL8OHUE6dUGKbvfb9rmzF921i2KUuAiQmGhyb9oXy65IjQLGYIPID7FotZhfWVnCSuhw4DesyXCywPdnHdruAaj/Vmg9XlFWpXoVrsygmpc+jWLYgc5rtL+HmDx5fnODo6et/xAd9gZXArcJfAuVpRy/iJknhATs+27STDrukElUqDMUueyPxOq1Ru7zDiT/3M7N6p5mguVMk/v5w8IjjvEIPD3u4B1qs1fuOBSPzDwwN0g8RCOCJUdY268ghB8nfv7OxKbvGqUotPTnmruDZv3AkoAQI+ALG6jn3viSTwJoaAq8urBDpns8XINUw0zpgASHKA4HHDKt9z27rDJdjCCq30xkI9yc+PgKy8g2F+oEm6p/fl+/SdRo8RUMxEGWOwMSjIbVvTLr/HlCku+2vnrfZ1VpRUFCYrrPNeTgjS4xl6my98AmilwlSO09pOGVN4BKzSv4RsqbsxbsI4ygOwqsXpESqpoIqcNZ0GjHyNkHThLmdtl0AwKUr5WQekI36QbBY2n46cKN1OgLH3Xlw7oqVkxmjWRpWZI+vxOFA3cmp6dXWFMAyYzxpUdY2+3WTSGgZVn+WRgpVRnFjAmNO45c6Cq+xZtfbZDNi7jU8JhvGyai1H/TG7IMEh5wIz1yg7uRyvnZLqSRe2iJMC1IkCGpL1MZ2IMcTK53KmYV8RZrMF9vf3cefuHXhyePjwAfp2ja7vcHJygrt3TnB1fY07d07gvNO2OI2v0FHFQJKRH0reJDD293ZxfXWVaaLj8N6j7/o051npL+ReemNucjGf4+zsDATJouIK1mW7nwFwxGIxx3Ixx3l7CUcV+hARgwBbjkOawyxbofMQk9KahqWKgNVnYAIcM2I6eZV7nCrXUQfFACiKw5WLEWGQTEqHhweoqgqPnzxGiH1SSDmBnrwPptS8hSRCNKMJpfV9Q64lHhF5u5wvQJGxurzCvYt30fcd5rM5rk4vMMSQwHzfd1I803t84Tc/j/OLC7AgE7Rth3a9LvbpLFOzCyES7xM5jV1x8g7tUde2GMJQyBCkFMe6QYCCueER7OTQlXuEus+RTlI6WdO9tKolO9kwDOr2Cuzt7uDe9RXOzs5weHCAJq2ZLMmivZOByte4vLzCzu6uNOccuFdFnSzoW+73lUNVN+CSEraJ6s9Ija16gIH7tI/7JQ8y41dPsxxI9CDhn7un78FRoQgTAxUL8ea248i7P7Y8w0mtbkpDBA8DMESEfkDfdhKf0g/oux5938OHHkeLBt2mxfr6AlcXlwhdL4rJZo12LQkCwtAjDgNcVMPaEIAgnh0c8kkhB80qx4BHDccBEXLy4jXWggEMHBCJ4cmLzBKNWfYQchhs/yBJGBBsr8gpCdU90lQQAtiPMOJonzcDUPG3JfsholGQuq2lqXvVFJ9Ojd/T049tbk8pbfkE+5Y4s+zDttONkVLO2YC07SJQwrEgcddHZIShx+b6Eg0FLCuHg2aGrvJo20EqgHuHF567i+eefx6enKzBTqqJN8sF6lmTXOws+P1bPvkJHN09wT//zGfw2ptvbO3P9HpmRcMGbQqHKR1TYk01vTLLVJmaKx3xK+HslARA4YKV3w2Y8iJ+eGV2q/I90z6UbVtQtLlc7e7uous6yXITQjoJSSl2Gdg/2Ae5Cr/0m1/BvUGsaLP5DJu2BRHQNDVmTaXCNmA+X6KuGgxDr/tE4TNcMKsZBZKmX2zmtonEyAoiKClLl1fX2GiBQe8rEDmEKFaQaMCR1Rfe5o7GR/5CJ4UNXPSLbDMvLLicgZmB3NRN7Vt5mXJCnC31+TttG1vaLj7PbSNtdNm7FQq+UIwwgwbbCAtkWHYujXtkMdDxRMl3q9ayskcGxxnJQVRB7Ogd9hnjZiajtE8WSM4epZs0NwAu5kwkWlFuqmjX/rZ5pDxYIwNUyHPx/RaaG1AetT0Ch4Vrj/4Ulyd5y97BAbpWfJhnsxkYkqFuPqu1wFadnzXeB2mWYUmLWtcV9g/2cXp6inbTAUS4e+cEb737DrJylEnr0qaUN/k832KVTuMuaOgSzc3HV4U7QZP6epibnynFI9wNBWM6IXKiG8S4oFlzCCELf2tZi/QxCM7JCaHEcfkEpJz3qQZPVXnUjZzy+Mqra2YN5yRN6Ww+h3OEWTODc0DbdVhdr/D49AJnp2fouhYnJ8f48Idexd7BLg6P9uTUIfQ5QQRyqRBLypBORkdgicBK7uVyrlmIzKImN1mQKicDESUuA/K7S01DFCVJUW7uSlzwvD3HJBmtfA3sHe3h7PxC9pkwIIZBZKpF81iwrLGDGUw4FsqdyatiqaZ+qRsWO7HyusxHpKc0KY04GBwZTVNhMZ9hvV4jDLKZRxYAZj7kIyBDcuprnxA5sLo+5M8VIBuoIkqxJuQIO3u72N3bA4FwdnoqLkO+QhgGrNYrVE5SchNFhEHo2Ice9x88AMHB1zWGMIA6YL2SEypRIHR9+HxiU/K9GPecyAnKTBKCxZpkuhrvEAm/k8ZEpvUP218IcFqjBPZKVbbstNCL5TZqnAcjIkJOj5xzuL6+kpoejYdlQcydyHy+XO7gyekTzBYL0RZJPTWU5kZ/Mm3b+of8rmR1TyLbni6xSF4/pvCg+BkBBOdxz33Q2C7fXzJHch1j3GOABuVhB1DNguZmDNolBO2EGc+q2GIZLhJPxxDVxUpOMGIIYLDwbHeND/RvIGw2aNcb7A6XWHDE6uIalxcXqCLQty02bQfPDBoA9LLeYwgIrZQIEPfEHoRBkhgMQRQTdb0lx6hI3RMZQAhwrAWaSdzzYhyUZ3RNJ2PmuA6GYcpoKZIL7DjFinaNXY+2uIKn/ZPSz9Jrp7ynxJYANOnJdgVoiplLXFx+f9vvUyWJTYFjjROhLNOIgfXZOWLbYhYJu3WDvZPnMOwHtH2Plgc0XcDm4RPM6gZ1VaFat2jXK2A2w8HhHvowYNO26DY97j7/HD7+oQ+hj8Dv/z3fh5/6mf/hBt22Xc+saJhiUZ4uWEal8rSgvBJ+pZsnDeXn9nuZBapMZ2Z/r9drzGZzEPnRs9MUbaVyU/Z/quRUVYW+79G2LWZNk9LiWuESEOHw+ASr1Qa/cG+OYYg4PjnEMAiYqKsa87kURBLwBRzs7aLvB/V/nlR/tXHqHusoyw67ElzSZ7JVUHxQT0+fwI7YfeUR1f89p+YVgUz6LHN+2YjZJ0pAspTqOGwTLu4ofGRRjCuLTi7uM2tNiSdSTzgWcRSGot1IyIqktTdmOHyTUMV7YZsSFx/Q9rZ1gcpY5R6bV9Lv06Y6bYOnNBjfZ78z7F2FcpUUkDyuRDsav4XLHQe5vSlN87gnfRs9x9l1qiAfQYWipZPcQuPRuRWbr6iuJfNrB2NvZxfLxRybzRqL2QyLxQKr9TU4RjjvMV8u4M2VhCnFN5Ge+jAzhjBguZhjudzBcrmDi8szXF1d4aWXXsDF5QXOzi9sB1YgUARQlpOhfXZAoRyWY9K7yFw0WAPeGWCXNjfxs83ETrzgLFBbVZLKa0BeBeckCNurwkBEUohQ0wjWvgKpi2ddSzrOyjvUVQVzN/S+kgKHISCwGHfsZIiIpFq6WhlBQDcMODs7Q9u2uLq6xNXlFdq2h3MeL7zwAl555WUcHB1guZiBOWLTdelEOrGdeTay2A6dblRmOBCGoZQ1aTabYdbUKZbNXlSpO2dIcQQTGVAaNgplAyD1Fw5Ci8mWYi4bUX3Bj48O8fYb7yCGAZV3aEOU7GXOuDiO5FpMgi3La4O5rPtJNmjoGQNRMtRYOEEKltejJHMvIo5wTipVn52dScAvmWXewZknjyk8JICpqnxKMUkQtysjSgIvTBjigNj3o1W6nC2xu7sHArDSjFLmpksQed+pXAOy/GeWUwBXZYNgGAL6rkOVQJnyASQGpoxpSkqG0pbI651mgNEMQub2AiQ/x8pJqt6osQfJIGRKFEmF4n6QRCyj9eod5rMZDg4P0MxmkscDltJe3LW7rtfYlBmocqMxI40MkrjAV1ivW8xmTUpDLkPUik+ElAFM1mbeh0S2kPKQyccw0gtS/7loV3nZ5DWnh5VPCy40ek/3UMeclJDUZ1NgiBHyoyAQhmqGc3fXlnCKf0lyrTCMBWa8ju+AnaI9iS08DwDLCdxL/ZvY6Vu8xi/i8Orr8JtLdG2Pk8190HqNKgSEtkPfdmjbDdquRRzEBYwCSzrmyBhiB0aUv0MEhiAukOrOBWIQBsBFMA9gttT52Xtlevrg/U2cB2RMWWLVqXE68cYE/JeG6+lz5WX3e+9TvZ3yu6kCNFUiphi6/Gx6ijJ285J90HiBVGZ577Gcz1FVWuz68Sl6Jkl8BDF8eURcX6xxzYzKV6jVAMAEcOPx4OFjiZfUxAAPHj/B/3jV4uC5F/Hd3/978ds+/gk8y/UNBYNPU4ul0wKffebKIy2Z3KxV3uaHNvWPK5WZcnJns5kW6KtG8R23HSeVk1OmzS3bapoG6+sV1mtJAei9R9/3WK/XaGZz9P2An/nyBu9sliBaY293F10Ujd0qKoIldawnh8ViKcFcNuvMkKqhrIGAAuyEEQskCGRXotEgcv+lmutlAqBEhBgC+mEQi5sMLgv/aL6TpkDcBGLl5pGMUpPFmzpF01+zA9O23zPAtoEYqHETwZmP5g1Ep74W6V0SeEcG6SN0XRIsjRIJzaS2CSmLks0RKY0ZqkQD2XeDZFGO4trzP8pPEPefISTVKYma5Ec/oTkoJ+ayu7kc3xby8xQK5Y3PaG4ULcedLB+4ed3mRzpSVAyMGygoQH1dVzg8PMTx8THeffcdhGHA8ugQ4o4WERhYLJbY3dlNYCKBpWRlljkZhgHzZo75Yoa7d+9is1nhvXvvYW9vD9/6yU/gjTfewpMnTxAjo++DBDmCxO2BxvMtyhBGG725emdXS7EC1XUNpznynXeoq0Zjr0SOWXHOdMrQeNRVBTuxrCqvAhzgKB0xF7OQ3Bo5ZYiJmpUJLMpD17ZYX6/hKo84SHY8U+batpcgXxZAP4RBUyWLXOn6AVCrOUdRKKuqwp07z+HOnTs4OjzAYmcmsQ8Q9xnjdQuCzeZnW0H6uyVqKEWs0tl5h8VyiXbTi8GDJQkFFcYhRNYTkHwqVEw+0hrWeZvN59hsNqj3dmVNJt0gg3qhccDu3i6apka3Xgsw7fR1hCxMJ3ItGgQnXWMpbVrhFuakZobjIWW7SbVzmEE+81qhM2EYAnwV4Z3XHPXC/6ZACFCTbkWtm+O8fH5wcIj9vT288847Gmg/g/NOYl10FYfrK3HJgE6VgprNeo0IxvVqpfuidMqTS+Iz9UG4SpSJpLiJX/2m3YB1zTjKgIoAOCZEL+N3VgSWDD6ktIp6uigndiDO8VmqAJITnuvDAB8sx5EZxWQteu+wXC6xWq91rXpR1Jsai8UCy+USy+WO1tuR9dVuWpUFQBgCNps14v5eGRINM0AZq0cAe7u7ODs7w527d/J3ID31kNPOaPLJjA4qw6Kuz7TzmPwp90kTuqUMSrJZdwSGuDo7e67Yr4r+p2UD5EKlJpwn+2PUPU7WLuVtlAFrKDl4Fnt+ao0NozCIapBvEk2+Vn9Sh0Q4PXwRUWXDOQJ8DHh+eBccetxxl3hpzug3AaEXN63Nao32+hr73mG9Osf16hLDpsPm7BLDugX3A4ZND247lYMtgAFAQAg9mANi4JRq1www4j3B2bBAufaGyU7y4nZv8j9qRjDLcldeduJqborbXPDN9d5OSyor5JgsUzfdqra5dtnP6XelojO9xthZmc9aZTFAOUdoNCU2XIXKeVSuAlGFqArlANaEKoIXPVuMIYPaAeQimDsw6Umz93j3C1/C6qoFf893Y17/G64MPgzDKItTeezjqRKQFaOkiwUkGDKWSyNfZTC5EatUGqbuV/Z70zRgxsh9a6Rtam5fqMZmtlY5WYiSilIBfoAEZDki1I1sDDvLXS1EKNmbDg8O8YXXz/Cl7kO4XH0J+7u7gHfwgTCfNVjOZyAHxCDtSOyKZHqyoGJDzmY1B1BsUnKMXPoLW+VTO7Uw//IYI9p+QNcOIO9Q1SqYIulRtZOYkpjBS3KL0A0yXbrJ06TtjDJMahVONYUQzQJNLYEsd03hvm2I8ioD2azvKDV+3X0TCOURqDegMuo+7Htb1MV7AJCaNVMmqLT5IYEecg4UzDoPTVUqoHFvfxd3T07gKwnyd4SU+i3GgNdef0PAnpPgZSLGMMTCvYAV9MnYqQiojOBUNMdwO9Io9F8V9DYsu08Sl5l1Ud2WMjEK5YIT6KLyJNHuMfAluwycpiWGWkOdl9ztssbEraX2HuQkqWJVV6gqj6b2mM9mWG02eOetN9G2HULfY9bMcH5xjqEfcHB4iJOjfczmVVJYBIzkblvxs9AzQs042N/BMHR4rruLe/fu46tf+Spe/cir+OZv/hAQX0XXtjg/O8f55QXaIAXLiDyaWvxOnau0bg2hqaVYnXMERx7eE2ot8uU1Jzh5p+yvaT0VgA0xgCKDdbMOIaAPQYtjBjBLBplh0EQMAPpB6iUETREaWNzHQh/SwVEIESGogcCLa04I+aQIQFIqyef88klG6idNXWGuSlDT1PBVheV8jvligfm8QTObYWdngaquEULQgp5RLFas2ZoGJBQkcsklcMmsFnybK1LFjoRPdpY72KweJ+s0kbibOecwhEGKu3HhYlKsVuNz0wkiRywXC5yenUk1axQgzvhX6RIjYdHMsbuzxOPVCiA9DXJi1ZYq0y4DXuk8KuW95JJJBgiK4oMhIkZZQ173GNEHhCdi7OUdurcAXoEco/YN+oEx9Iw4AHB2AmgnqLre9H6KADvGwcGhZCYKcvoX+h6hz3tFPwyy0cOnRVNVEqretR0ODg4QBsbQhWTFtqyHohRILAVIzhqc8ruAByDoiTk5r/MlctXONrKiJa6lUtuhTumXiUR2ONj61rlzwg9RZW4IQ1JwCQFRAbtU2BaBVVc1ljtLDSAnwMmadZoFKQYxn1VquWuHDptNK2tqCBgGiUsQwB7zfDPBCiyK7GOV71HrA/iCR9X4xFQoCBKAz7ATBeVb42nxuZQ5JYtLofToTSSEzEccVTtAUmoiZUXEISdfNprHpDkwEEndTznpHmyKUygVFyAHVauyov2Vd0sfGAAFZOOUfQbrYgFskcIW0cPhTfcymIA3CfjVjsT1riLQAsAh4MDYj6cyZgW6L/F7eGXR4bm9BULf4+rRGS6fnGN1eYXV2SWuzs7RrTcIbYdhfY2+bRH7AdwHuBARh6Bn2xJjxDEgMAPswCAMBKx90HlRV0hyEpfFDIcBdi5FcHDsdG5JYrWQZa/JoNIwXn6fXE6La9vpB5AVmMwNSIwiv3PCb8mYv+VeUMZMMp48Q841iJCkRRaEDwDeAWRpg9O+rNicCMya+Mk5YX04IDCIB4RwjVhFVMsZnuX6hmI0nHPoui5pbqbheRcnCqFuCMWmWVbiLifI3LHKE5Gpm1P5t52QlJtO8ptzXmPIWP3ti2dhfuGULH92hF1XVbKCeF/j+voaR0fHmDVzvDfs49579+AI2NvfR4wDfFWpexUEjBMBEZjN5uhVCTKriGMGe5eLLitoVH4AgBFQFCGR7dnJzco5bNZrDCGi9l5Lwbfiq6oAxR7iiBw0nGdizPxm4S404wkEQCEm9R35nUnLNmtC0kBUWSil0uiNpZJh4MZ8cAsBpoI88ZUdddgb8uD0I1NUkNomyve7yfhFvMeizRyw7NVq+MorL8NXTnlcrNzChxEXlxfYrNcAERbLOUIYcH3dot0MyQfYUgTLWDgBWDv3oWK+1WyrGWigPuDq2kICwgx1kJKjtHS4yqvlQgBg5Z3E8Ki1xnkvea99jq8yZQJEavVS5URNfjGakBMQzFGt8BpU2m56XPQ9+jCga3u11AccHh5i07ZYr9eoqwof/ehHUTc1pOyCjIONIRKfy9bOMaBvO8znc+wsF6DnnwORx4P79/GVL34Fl4/O8NEPfRh3Du/gePcIPUcEMJgCYhiQlEZ1BWEAISiw1yw4m37AOrYC3sRpPQHNEENKumCuSjHo34wkM1L2IFtznPPPgy2LDgEkWZdsfTnkjDm+qlB5VvcqUXDtdNh7h8pLti1nyqyT7yrv4a1QmaaZrSovc+q0sJu6bBGAIQSsVhspXAoDfZSU1WjrSjcYR2qF14KfZjEza7pF8oAIOztLPHr0OBVONQuv8w4Y1LeafFrf5VVaUW1tNsmFteAPXR6EAtRBwM3R0QGePH4kiUHqGszillFxjvOz2DWGebrYpFHqHyDF0Uy2iLVYLaEqmIUepdYk69h5OaHyVYXlTgOOGwA9nNc6BEqzVKSPVUFhAsOBmHD/vfvougGeKiBkazYRwCGCo0eNmbxPUWRdNQqICDF40OCw9POsaICSbCG15ApNNGlDVcm8spe+zMTtx0Fc8+SEj4WHVVEhUtc47+U/En52zkn2L9uXVUljdaHruw5DDBg4gDwQ+4B+s8EQAvoYsGk3uFpfgnlAM6tQ1x51U2OIEGMaGDH0CG3AwFFjEMT4WNVy/+NHj2TNM6cYSfE0kLmagj875d3d3cP15RWOjg4T3yVeM7CujGoWblsyiaeMh9lwiQF3VVtKfrYrb9n6TD6JjqkDlPpibdh6HS8RwUbG50lBMBGe9tpiHy4ArfWPtW078Ulrs+h71HHa/jVt23b07JWQuDnd1NJ+2seYCA/dMT7fDlisr/Ch6j78/Hm4V14ERVHY9oeIvu2x6K/wwqzD4/sP0V1dgTctrk/PcXV2gc1qBe5axEEC4jEEhH4AhwDiiJ0gSkgEYwgR8KSxQkFSHxuxCFLDw0sJRo5PL0q37dSBOVdSNwXktlONqSsU0vsI2MI3eR2X6KzEldqOTqph7xgZMTnVqUplxvw4RojB8DcAnoRGMAccHh2gmtU31tRt1zMrGovFAgBSxqlyQMY904AbghyDWvn3qatUeVoxzTBVuk4RUTqmIsruVKVSAmTFxv7Oz+gmSVnrTJXOVXmpa9ngiBxOTu6gqWfYdD3ebXdwfn4PTdNgPm/AiFjMZ2gacZsQwSNmDF9L6jpbfOZHab7oYDviy+4sxV5aLPZMVdsyvPdo2xYcY7K8DH2PqtEMQBpV7i2TQ4gFj47VBRMo6VNTOkYCM1t27RWEsbrBSVpRtsybBlAuvOLl5uNKxj920lFqJUbTxF+MfLpS+HCkJrhognMf7F06xgQgKGv74PwaW+TeeazWK7z55psAqTtUFGttGAYB1CypLMlJlpW6aXSec1o+66LIDKc8rZYBp1Zjkrkl78TVgaT4VFX5lO7Re4+qqqWfGihJzmUhwQpgCuYRC7lYcFh9U5mjgk21CqowFEGjCQrtp9LCaJuBNWeXHz29iWFIPqGHR4dYzOZ48vgRmlmDj3zko9jd3UlGifLkq+TzJElITuXarsPR0SEIF6DnHJbLBR4/eIKz00t87uqL2FvuShKEocfAERzVfSdmGWAp/iLUhdN4d6KkjRSe5K7J5nEOX3t4XxsbCVCrKlXMRLZUvkKlvrlEnCqcW9AwNAuJd15OXDQtqq9krp0Ti6QpGeaGBbOiFZu1ZT9iGPDgNO4hBgFkMYrBwZQlFkoAOWsuCrrbjiZNOVTe6e4gALMqDBElfzdNg6qSirsxxLSjVJVH10JTzCZX9vF8T3YpkfVC9SEEsdiXApLsRI9kLA44OTnCa6+J9KjrGdp2o3KXk1zz5VRzEatEeZYZnDJ72RWtNgCpywVBTrYMyMuxI8g5iTsIAXFwiIOHdwsp/unU/cs5hL5PgfSVBi4LbUSprGesyr+chLqJXDb6OCfZ3Oq6QdXUiaefu3OY4hu8q1KNF5CDh9e90/hXlVInRCVVPEkNFV5lDFwOMDVk6Z3X4ncm2vPeCthneR+MMWLTdrAMW5UTDYCDKPdDiLjarPBrn/01bLoNri6vcH291rVQoaoa2AZk8UD9MKBrW9x9/i6aqsZ6tcZmsxZV3kFqbDhLv1DsgnnqkxyaL+Y4vzhHYA2CR1YgRjhvjOzFY0x/L9eRAHN5OCrPlc+lvbLkNd0BU6hTufWN1sh47SQwWOzBSb6WDZjvFLKLLlPqrXUCxtZqo89DLrEJQeSP2r7Kftlaj6MB5sEU5alSf62vgRx62sdnhz1NBCA8GaPGpc09qh0HTxHuIw6LcIU7/Agv0zk+QhucPz7H5ZMLnD5+gsuzC6zOTrEcIlaXl+D1Bsv1DDEMouxyr1my5AybnZfxKDUjkQgOBqjosxm1pzEg00syso3xbomBb7tK1+ipQvKs1yhmGYZBSJNzyBq3E8sYw63vKcc4UozAaDTr27Ne31BlcGvQFAo7jdhWOr1UBqbgfhpbUSodT0tbluNCspZon2VCjhnAUvlld4gcYF6Oi8ihrmfgKFlb7pw8h68/avH2oyuE0OP45BCRI2bzBnXdwLLzWKVMR5UKjyxsGWNAE0mPJotFWySSyEIExSI0pBqhhXxkM1qvV2LlltYUtIqbBper1xQbFbpJ+bJ+UgbDWajwWAoU8yrdL4on3UQsmJ5YWPAnl/dqo5SoaJt8oSik50yf0dS9JOcTCRaoXmKCVP7Pib5lFh3bbFIXUFiGlHazeYOua/Hg4QOhK2xfESAJJ9WJpVgNo2pqTa+4h729AyvgK1WuvRcwAgGDznyjo2TUkJMKTWBQAHhRzsUiLMGNK3XLYyCKi5YUYVIKlopCIWDkVEIBpioKxEhVosGAWfNT1V/jHZvvOA4kN6WQSRTbupmhbmo0dY2u7dC2LfZ29/Dyyy/jueefg3NSfC+oqxgZL9n0kaymIhYZ3Ads0OHg8ACz+UyyxO3sYr3a/P9Y+5NmW5JrPRD7lnvE3vu0t8mbmQASeAAe8EhVFVnsilRVqVqJk9JQpn+g36SpBhrITBOZZjIro2RlJItFIynqPYpFio/o8ZDd7U+7945wXxqsNuKcC2SavQ3kPbuJCHdfvnz1DW6vrqWqTxNFQ0LTKohG0EDe4bgO5rGZPW9hqMWCo6Sy0ziiqucBgAv54hmQ8yvCX/FQMhTCOAxanU7gQeYlSkquhJO4vgav4pPxGsuiDcLkgxb23sGT5IAtlUH1TKjVE/p9T+F4S6EjRIqYDrviB1PCOkDU0LmiccfYK0YegArUUegXd5IG3Kpsn5ye4Pb2DnObMfbRaTWIBHf86TG3bEdY/u3YbKTJ1DCc+DleehEA81pfPL3ET//kJyCQlLt9+x5v377F8XAEWEMXEZZ2OLjIaZ3zojRvU+a5dTEKmIXfjESlqNV/wDCMGBRHNtsNail4/vy5XF8llLiU6nRMlHINQaKioX4SsmFLld4cRueE5si+B9Wyvi2kEjFriBIxuYeQYB59gb/lnMh1ihOsBgMGMAs9mBkgkiZxRlsAyX8AMbhBQsOEgCBHDXg1KKUzncWb2Ng86yz5g5ZfBcJhnnE+PAWmG8xtxjQf0TDjiANqlXzJUgfhAWigY8F8OGI+HDFsNnj77q2Edw8Dxs0WH734SJRlLVrck1HPXm6oAXB6eorbmxtcnF/EeeKML+mVJPmsVCz4t545gtE1vWalOAQfyq+gD/EsvT4TyaR0hPISnDdRIojnShVwVvq7khPT7Xr/w2ctlA6E3GIlmwEsPSFQOqj3ZKkhpV/GeEmuECVAwu06qxGmVZRKoNJxxyd4V/4IP1NprLwooBdaCKc19MMd+tXvcHd9jc3Lf4er3/0Cu5tXmG9vQIcDapvR9nsMEHwvzNrJHUAhtCYwzoJ7zh/OYVO+c2YQsjOZ5F2H8+rzItpH+cOH8ibX4/jza/Y48OI3b3wJjeZpqkila9e5IvY+zzXWJnlYvXfc3t7+3nna61s17MsDEwnjPhykLvc4jgslQW9yQm7fr7U6A4Z1+F4AiJfN8/JccriV36PvjUEvgIdIOFsDkxBlegWxgN3uBD/bX+D1q1copeDs7BREjLEWryjgm9CBWkfXvC1xkhV57VSZZmnWHrflrw4uG9wS3C2URoQLiSntrYE3rBWzpE50n3owc+5gKwNXNCmoKlGgCHNIQDRxA1ECMiGk83p26iCE1JAxqReuJfHqflKBK5Qd6HgoFs7R85PEClmrCs4A0CR5zi1tplw6WYVN0BK96iBVUjIBrKWANxuwlsSrteD87AyXl0+w2+2ko26VeG+R2iqIpMJJ6xMYQGcJteFuXdgZc2vuxbPYdU5Ep2ulIGsEBSdKzZWHhTvTGANiDMs/guI9swJHK+E8xqRMwMo/2L5JqK/F/wvsWZOj2erkOcwBS4KuRT17rWOiGSenJ3j+/BmeP3+O58+e4+Rkh+Px6EYGj19VnkKw9cTLmHM/Sg7DbrvF9sUWx+MRt6f3uHh6qsqYVqYzoUrxwTxDtsaqDgH7rqgVuqoAaaEkpjSAzN0cSYdAVoT0cxcx3ax3M8+gBvUghABmny3UyumfG0XI/zO64sKbKiFJn3AlQqz78PvWlW0YQWs9ydXPCDlO2XkNZUBwr3cxx7sAQ4MAswClQ700wOXlBa6vrj20rgAwz0RXmjWUyJNyO4LPBBpWJJ9OT0+x3x9wenqqyeBJIqLcqUT4xuXlJQ6HAzabE3z2/Sf40R//MXprmJt476q4B5z8JFIm+TeAe6+K4qeHCaoUx1DvAuy8WahdhA0bvebOGIcRc4vSxvM823FVekIgy5FRob8UybfrkxTh6RrGZ3vKrWFmy90D+txcEOLeQQ2win+9q6+GJFlWhD3LK4E22ZTQkNIjnM8FQgIIBZWLGk4YVpaZapHw0pFQh4pByy6bYl5tT9U7Au5omiM5oWNqMxqk27MZpYaRcPriFIfpiHe37/Dm/WvM/YDWG3g64sgMaLVJayTIAG4AwUmZHsbtiP/gf/FXcHl5GZ47Tl4tk2V102y/Ly8u8OVXX+Py8tJRzfBkbRiwM+PcK/NvGzLxVv+7lKODPZqSkAVx+92fhwf4m8SoRXgg+Xf2QfCr6RwWY8CzWAxUsDOZuXCWUfxL+8ORs5Kf7esCp1oT2fPC/lmMEnKthG/a3LUhcTMeLLhN3eRAObudCERaeVBlsHKyQzv9KTafAvTTvy2es/u3mN9+je2v/ynal7/C9vUXmK+vgJlQpobCHQMgXdipoRcJI8qC/zoaZ/1ilrPHq+vzayFX5ftomfeRDe4fUmpsfyzi4LFrAIRnMo33ofcud6Z5Gn8lkg72vTftVP+HX9+66lT2QgBScaa3cClJPPGoYRUPuyVmReQxbcqrlayuXSoX9OA+QJA4nz4DlJSqVW1VX4uxrb4cyzpOT8/x7voOv3j3BPf7PZ4+fYJaC3a7LYaxqlwYQkDrwDBqqIPX3PZHwixlblF2Ic/mGQc2C4V26MUb1LHTjrmH4xHDMOL97S3G7Q5n5+d4++YNWmOvm22HG6TJf6Vo/WqgFJK68yaE6D85kIsB9wszhyDga8vzT0TG0ZhCkNG73Bvh8q5S05B/zQKZn2UID4CKwL9oojIVj1MnqMVj0B4o3i9lFPcgSUgSt4ZpnrzkKpjVyyP4enNzg+vrG5gHAugOJ/FCdBf+O3dPWGWtbBECYnc3uFsEXcGLDTZBZKEcGCU2uCTzr1uHmN2yYJdQibh8I+yuFHDX98lakhgRehAWDyWxB+t+WplHs/5aaMNmu8HJbovTs1NcnJ9id3KCi/NznJyeYDo2zMfZXbS9p93Vtx2ZMZMLAgxgmifM8yzhIEPFk4szt96Yhd+EajmXkcAufWgIYAuHEA9AKMoc3gRlYKxereNxktwP8xBZkQVY+JUJnoBZLmWPDVXkesszcoXBtASKvaeE7UAwYUMI81x6ucws6Kil0kIv/GzKwdQ5w3EtiiykhEUTBjie3HrDYLDx82lzFGWDFG4nJyegIuFOvUlQNVXxDrmS7qhcfB6GeqCYT2fGbneCm5sbG8k9oq6k6tMsX+/i4gKvXr3GV1+8RpuaVAMcpGywWc1NC7OCu2TCQDdltTgNtOM3z5MLjZ1DWMihhhKSJ+ewODKGNV9dRCBAPXqG+xWANg9DePp8hVqGO4RGM2IpPyxhNLETWyHx7GTFAoglDKsKDfA+FEmIoEJAFY9l1ZC+WgpoqKiwUD8N7YOUYS5DRd0U0FaKRAyliCFHcVTARL4mgZPCzkKmkHCLbf3i/X31/h1+9qtf4v3VO9zf36C3o+61VNQyOJHytHG7xenJDs+ePsEf/dEP8PTpUxEOuyn2CYULfE8N9wsBKBXjUHGcJmw3G7/B4O90VxmfC+y6wAX/zgK3jWv0PfH4IEO0+N7u83O8+DI9Kwu5fnbjUhNAwZHjEYnrcSul6+U/8zwmj0yIFTAUtjlTer6tWBQfinmxnWO2I6FXKu3iMEL53HVym3GDzQaaJxjGN9vY7udHAJ+VuVKDf3EF6sVzbC5fgH7wH6JMR9xfv8HFn/6fMf3632N69x7jYUI/znCtDIFAjykYWSjPv7WkFKw7eduz8v32nRuLOLzaa5nbIe04zMEj1opLKaDVXmcFZam6xNw+5M0wWFxfX+N4nBae4t/3+saKhnXhzp6LsMbJ4PM8e4K3LTIETvj3j9Uyzs1O8ibY90vXTtxjSkmtVQ8BeQhDJiiPamwwgJsdX4SHi/NLvHx3h89fXYFIOr3WobpbnAEX6EVQkbGKWo/cW8DwWus5McgIq8wFwXSdQAURZqVopRScnZ5hs93gcDjg7PwEh+MR0/GI7WaLy8sLvH33Tq1dcTgYDMkPkDJ9nIQpYwYAuxcF/n1YOOwQh8xBKTbTBJwopejiSCHPJbDF1WJx7KEESgUUEdLrMEhSp85TlAqputKZ1WqmYXhdtPTOUUJUmnZ1NPMx850fWrMUdyV+FjrAvYHdg1PBkMZFRBDlQokNYSlAGvH0hHpdtyhUCWcd8RAwZwa0wot7ZpB+Vzi7JVaArZ4c2xfyfSkArEGZ5TEZXbcbSqXAMdLQIBVKpBOulvW0/A9TLHR+Q60eIjWMIzabLTbbDbabDYaxog7WG0LIymF/xOFwlNwJBJ4bg3H8h8EywnfgAgvQ0dGPR+CgDSypuJW6+DmJ54DgDIkQ1Vr8HOpm6FFVlDfmFczWw4rSs0ywM4rBcrz8sy3Kcc7OIMccTMHw0rEI76uvm5M3y86onS/FObEGSnqfCHnkdMnmZrTZrZa6XlJFKQAWOG1K2tS7KIhcNWRPzuSWB2CQXAJmSfo9OzvFdJxhITQSblfAXp4VC8FoLcBZSEchgMaqOUSm7AYD9p55pXjo2Ha3w/e+9xm++uIl9vcH7G8mHPmA1qQ8reUGmI5r+FcQ3mQFintV3SOmZ04KClH6XvuklO4FGAqx8yY7W7VK2BTcm6peExOM1Cs0FDMGkYZowQXp7H2DnkX5Q6oYSSI2DSQKXhFvY4FdLmc7sWrnj9B5eNlcXYsXE6GUk0MhhAoqG09WXCflG5xpoc5B6RZxAbgmhZfRubmyxMyYrg84f3aO4XyH+XDAPB3RufnZLcXCGws244jtZounTy7x2Xc/1TPW4/wYrBaHy/hyQkQAT589xdt37/Dpx5961Sg4LTD0jXMqMGCnqdmiv37lo7b4nm0PjOeLkUcpedozVSN6PGYRZZAevZB70jgh5ySlR4cw2FoiuM3LFZNEj6Eyj++9cSF+6PVFHkeVj+CdClulw5bz0hngajKaBp6ZN11tbp2Ef5sxz8a0EGubdBMrOIgYAzEaz2CSQhdlM4Cef4L7v/2/x//2v/4lvvzzn+PP/8Wf4varr0HqhUdTuKjRcb2FWWlfGK/X4cYmX1HkatjW5vsMajk0y+TVD4ZpLeSH5fPM4286k3luFZXiNg7jFa2eDwhNMYMpMWM+TjjsD8jb/Pte3yp0KjfssxKz0zSB6iBR9kPFWDderg4ltLzsxcj9MVwABB5slllPTaEw4JdCKY69YxxHUWKalI9svXnjFj1GUooS0IosWtYMIhTO3FCJJYEOAy5PL/A//Mvf4ub9JU5OxVq73Yyo2v/BGKLVAC9DDeFBXe4depAIHoNu8jbnsB/bZ4MzUllaYyQAQOJR+ej5R/jiiy/RJ+Dy7BK3tzeohXBxcYnPPvse3r59h7u7ezSWtqGaHRAVB9TU7Z4mUyxAQTRJXI+h1aoFm4QhiVBLsORC39c6SNKkEzDr2ikCizE9CwHzsBfuKswB8zRjnmbUUnE8HqUZIbpbwUxYNK8BGOmzCkOkh42NkAV1FmxIHBfwHARXmhJcjGB5LodwOg8PMUYNkJc1rKvQQQvVIahU6vitzy7OBuWzUXblXhHyQ4tngiwxWMPsqiSJVq06VGv2/gF1kDyCcSPKQPHrtGFYLdo4rKY8LDkvMMWw2LlNzDOd4z533B3vpXpTEhbZJDwEc5LbYx9I91IkXf1CxzCiKBbkhlkryYNDIYgty9YlSIlKZ5R2D0Ig8j1cM+nErE2AjoPqYY6lp7OThAXk6+02kn9MyAvFBq4YhtAS3h1bQLbECrOFGyss3NHxPAl8sgQKYcgZNOlekoYjxLo7GGjAvjcMzZit5ABUAAMqKkQouLg4x1dfvkQdpB9J0Zr1vU8i+EnfcBVUA99FQJXxUo426ljQ+oxxGHVNSwHPhJbWZoxDwZOnFzg53eL9u/eY9sB23OJwOOL6+maR8CihuKFkS6Ukcc+Q0kVS/mRhu6UUcJEEaav65L0kVEEQZSAEdOdfphg4wsALBCwZu0nktNqzkJvW+xk4Le8bpWfBcIsT2ChgnvEx4yyZVTmuERFLJwCbJiXp1hib8jYb23iDegOFLlsBCiDPzioAHg4T3l3dAqgYa0XdVdTtBtb5mIp5ssWzPY4VhTsuzs/QWKtNJoNCpqmGaxYcat5zW8dut9W8uSZ8DBzx7UnC9DOW8dJ+TsJ7QtfYqBU9MMEtYJ1omh9urDbe6NTyeby6znDH8UAG85AoRQb3KCvzl3sTnfDZKY1b0Ei23UNSHtM1HF9kGud5K0a7E4wYQOkdhcVQySnrQ/4nkRnd16UlaB2IKZSbCGjyQ1O8bUWe35Wp7Dcf4//57gZ//2+d46/8Z/8F/vH/47/HL//f/wz13StsqaOrR3xWgAptMCCF4mDyqfDJFJmTNo7AIkey0bzEFxVmJnc57ckKzOrlsjXnEeI3AQEt8cfGATDouTcDCAzKWujFb+tdZElm1A6cj6cYyrDA/9/3+laKRs62z66VrG3lylNrzWoNqHUMmG9SSo55GC8m8a45lKp3qaajD/W5mRcmNtwoRT48Mk7rjFqlLvxuu8O//OUbcDnHk6dPAbAkgJeKoUqC3jxJLfXeGzabrc632yMzB/Hv3CrnkTD8YKN6ukEIP4NZGOK4qXjxyUd4+/Yt7vf3uLy4BHPDzfU1wIzLyyf48Y9+iP1+j+vrGxznCX3u4kZGxN+7kJ5gEoRBLQyDCjY9XPhs1M0ITjfBR5SFuR8BhOWfAG9OxsquZCsivtkoJvtfeS/xys2ly8wQFjhk/zqRIydoBvPiCpFcV11ocTsaxDJoopfxT4sPke+if4HsmwgRxemzKVJZUCx+gDUOmkRBq3XZZZYglsxatGrMMMicStVa/tCyyuOyTO0weFfhosJO1RKpJvAwNFzOETOYhJV6nln2x/rhNJZyrlObHyVSJqxQAB4mwGcphnlh64/77TB0CwEzJkOwpHSLn7cDYaGRku/Q7WFJWIFGiMX6fDqJ2TrvM96a4ET5+kCT+C4xQ2PEYlhgrU5itBGBc+mVQxeET/FibjH7xJ4owZV8dc6wY5EhfIb1Mp6zEB4y77H3lB5GNoqc92mOIgXzhjHygC0YTBUVFSe7HWZtnAZmbHaC52bk8DOWlR0d03efY/6nJzsc9geM5xvYqVwopSpISJjbjM1mxGYz4tPvfAKwlqVkBvOnaa84VQFU/LXI3u4bFs+PLVGPdNAUF4xoiUtrxdL2xPBUhFteePdi/xPS4RGlNq3fFmVjm27+6CvhvI1JtiZ+cOnyhgX+Bh4SYq+SrBRX8uouF0y7ry3WZzSb8O79NfrMAEnSrxgFo+jCoigDy2kpJF3qW8pn8RBShIdYcC1kAIOrkzAiXJyd4/rmCk+fPl/IKx/KrTB+mq/zMwYbI6zFLgcksrkEfpg3gn7JQfftsO95cbecMcbifGdZvzv9ewRJ/SHJ2xFfLcem1bzz/rMaQPSa1Bok2Y34wfPj8aK29CY8wpob53DiddUnf16ahBlyA/bkEyArZqGIu92d4A1+jP/TP/+f8Lcuf43P/vrfQN3s8Mt/8g+xf/8WW5ZeSlKESoDRla9bdM5aGeAVIUiURc7/71Ee1vd/6Jmc4LEYyww5Sb7+fWOY0XMR+bGeG8Pll947jvs9tt+wWR/wLRQN8yxY0ra5dbL2BWChUOSJ9i7N/Ox9/n0d47ZWLrJXxIRQC9HKWmSeCzN7mFfThl4G3HXSughlFdwZp6en+Nkvf4HftWcYtgOeXF6K0KdlN4GG3WaDeZpEaNZEiELRObZQCJdAEGU7kJ0N3dYimBEE+OlkBjpJg62Tky329wf84I++j1/84pe4vr7Gxy8+wfXVO7y/eofD/R1ur69RB+uerjHTqkhpl4FEqLqP4ZYUUq9PFxgeDwdNeORU+hQeTmKCFrElxYob3OpIuafHcMGplgoPKmiEJi4wsXhmhoYeMEDVgMip0krU9CfzvwqWwcIYTKHI5ZJNuHQvhoV4KRcuqj1YKVELWyBAQ/PCiklEkidbB4zjgHGwpnFVy2IKPgwaFuY16inyHGJu8JBDY+ggWlSxEK6j+5X6OXRVIKfe0Odk/Ta8T7HArlTqe+VPinbsYzOgYXVL3DHrBxG7UmXCnCs0zKnU4UOJxnCpLHItDDk1jhvBLJyZOCE02cy8frrzmespThmMwriTiKvPh5U5YWGdc2W8ANXmsGCu7MKywTPc4HndlGAajDVnHrgSj5gnYEYduKATK1uulP1LuyiEHEq/L5QnOw96tQgFRoBIrcCqgB4Zx6lhPFbMu1FKfY8S8ljHAYfDXvOFCuowAlAjFEPjiZaCV0BmCdPd7gRXVzc4v7gU+LB4so18kK9WEs6neVZPogiyfSENcaKpcg7EWg2gGXYAzNX3kfJf22+271xiWgig+U3e18VPBtbVngjMEy5q8RBbb8ZfQxP/bgHE2NcFlmQhxc6LDLpUjhgLYTkUzoRrNv+1wLmCXUwrJ8PKak3htPMGInQmvL++UfwkP0OV1NgCDTe05Si8zk9PhOdD9sbuy3Ne4xqvJ64/PHlyib/43ed4/uwjn7PhHbN5ZWIf1uvOZ8wmsYCF49KKHqZbwuyS4IdQFGLohF8mdNpPPf1qhg+jrivklqOZc85iHjaxyJNKk81zNHq3MsSUfCkJzjqb9kIMKzy3J3SgURdtxcbWBYQxJUEijV38DCnNpZQMTxFiVdWgOYwj6LO/jX90fYvN+w2e/vHfxNO7irs//YcY3n8NnhsqSI2rEtCVS/iu2zP8PiF/oSQxL657UEmVl3ka+RlrI3/+zfbk973+0O+PzRsQfLy/u5f59Q+aNxavb+XRMMtpBhKzlF1dl7rNCoDdb8DLyTFZW8uN+fL9uTlgTmqz59rf7OUAQqEZxxFt7ssSbAlARBXQ0oK7kx3+4T//RzjST/Dx5SWoFIzDiK++/hq1Vjx/+hR9I+Bu84xSJZ+AhoT8SRJwYYGN1yYRIu+zCRB24DiuE3hJF+DtboMnTy/w4x/9EL/69a/x6tVrfPzRE3z/s+/i9es3ePv2LaZ5BrN4GRhwiyL3vuBUAY0QugqRHLpapMuqJo2T1JcThk+qGpC6ArU0YwUAHoIBUYSUiBITyqDdby68IEaGDzKc5H6wxOObtkYIy5aVGNUkxlKsJg1JeFCpXg40LP3amKxUDIN0kS9E0nF9KKosjEAhDJpT4o3SBmmOZngnYUYlkuFVYhIB1uIwEzk0GSUJCiL8KH6yKQ7s1ZjsmYEroSA8FHAUv2ECkbIXltkYwwyhQUm7wpYoLJ0R+rDE0wXTM4E84bULY8qYH4ojmbEAs8FBdw5sCczLsCsXftKLzGolyRuJTWUBigP0KimYoOnymHkNek+lMMkXSC5whXRF/tzA81xtZLlguIC0AInOa+Ep0QfYHhI5ZBR2trZgtaKwx+eFMpIkLstxiHXbqsgLGxR/XhYZSWdTtKrahON+j8PugNPTHc5PT7EZRtxe32re1QCLTRHPZYRxRqECPfvKuI1uMKxx32FJR3iFSWqlKID38fC+EFnM1/v8LDkMOHkK5AoTWLTVQyw/byrnP0lpUgJu+0kq0ZpgK+PR4p60NQtI2/4mkhGCYix9hWv5/Nk3FoKzFFBtTutKZQlkD9adwx2zYp3HBqfnKg6aQCZ4rMmpNYw54nUouLm5weEwoZTBn2g0n1l4jsX6O/x6x8XFRQg9mhNpKRh5Tg7bDOcVDy6lYrPZ4O7uHicnu9gLlgVYPt4DRYFXz4XRsiUQVx9X18vLxJTI20DyAsYKHpuDGTDz01kNIYszlni0/TWpaiGX6A3VR6XF71nRJQBcSlp3Xh/79U5Tqxq/nKkIFATmykPJM+VWELMzZlBR/qbP6qpAezEJVhlU73YJUhO3qEg0C1BwdXWDl1eM7Y/+M/ywHvGbf/IPQHe32HTpPt4goaCdsAiDygpEgG+Vu6F/LV95LexnQ3u+nx/Bu8cM8+tr1vL2A7il+dnndZRRnrtBfzpOksPU13vz+OsbKxrzPLuHIIc4WV+GpRvmIfDWQFiHVeVwLCuFOWpTkKWn4vExTMFYuDtXCLAGqDxbFJfWGCe7E7y/usE/e/cMw3aHZ8+egUC4u7/H+3fv8fHHH6EOg1anIUxzw/nuDG2S8CJJXlYSTHogXdOHCDNsFnhoVRyoAA63lMg082kGuM3oZcTFxQW4X+P5R09Rh4rPf/c7vH77VrqZP3+O88tLtLnjcNjjOM9oc5OkSPXsWBWdJhKnCp4pB4JIS1tKjsdYBjnCg9Z0txwDF65oRdYCgQGJVZRwBY3vVwVSrPpRJakU0hwPcqI+Vkkw7krNquYOiCeA1IMg3ZNFIRSPApFUSRmGweOtB/USdGYNPSKdrXm2dA+k1pASuxD+2D0sArcoXzpjmoOZuhC4UuR4RSwVHUQASV4JE1YtPiMLhCEYFf0tiSv6tifBxq05rvikEDRd49JKFgyig6FRDjq2MtmkCK50nzjnmalzhNEthReFMkfpV/OSdb8krJOeoLt6uZDWwrUrC+AkRDzkjHk3LNla3sf6liFLdi4Xi1g+x0azfQVi3SogZcufoAnDGnoZzZbrTXDLSgV830Ow9S+9MAETaendwJEsUNocQfC8DJufXVWI1CqoWKRM3xrlSSWvjv1+j+PhgOPhCLO+TXPD0BqoCA1pUwOfaOJmsTmy00H37HKcMes/43Q95TGZUGb40NmEi47eSUIjDPkSnpoQsvCSAQ5f68xFDMxrVOPAZ17gs85+vd/Qx60Ab8qcfSVDk2+lCYSw1WbcRFid7VtTqOQ9h+fY5kKr6/08Q+94sMzF61GhcsHTHsNz0qRd4/HGMyD0vwP393vc3t1jnpt4v5lwPx1BRRRU5/Fkd5LTC5s5gzWcdBtnhhHHYgVGC2lEorUMs34Hfjx9+hRv3rzF2dkJrB+IrJ9jHUlAc3bNS0rv8E/K5frl+JwBisCvrDRkvFuGDVno75IqGT6ZoSrMs3LOChJykHn5H8Evgx/yPwFDg+1KZFmgvsHW5Rxdgxk+wIyuSY7MljdCQKreyPnp+WhQhDYuNDOksunGuvRBvcQaiIDCUuzk9GSH4zTj/v6I11fX+G//zn+K/buX+OLf/s8oN1fYlWiEm8O5ssC/Npo/9vtayVi/f0xBeezaD927HtM+5+sfU4z+0MtDElvDnCu0/YHXN1Y0wo0Y2fBWyz438PtD7pj1ZtjzchdvUxis2d7ynsgBWW/IWnlZe0gEsZYbzNzRJolff/r0Gf7s51/j7vT7ON+d4OR0ByLCF198jt1uh4uLJ9IhnUSjI/tfFH22Uwf3atjcSYWlYgRHNszCjox4W4MrnZ0KgwBxwTQ1DAPhydNLXF/f4AnOcXb2U7z8+hXevHmNr75+qbkqJMlyanlvSgmJxPJuZVgJRYWpAgzVp48U32/VUsyqn8OOaq1ebnGoFeM4AuquHEaz/KuwQNIt2KqFWAJyVQXAPluNdnu2KQI596fUsiI80NKr6XAr0XGG4l4dgb8oBtpYak5EGwwrTZszB5wPOJAU33wSJrwYAVMiVjJDSoIPJ8GSg2GUQuLidSTIkpJYnbtVyNLfO/eUmKgWQifA8mwnKBZylaZuhJ4okvRMRWH/DGWu8i3pfEAp1CgTLornShWwAJ2VChULkwKCNORqoaAFew7GlRTbBRwt/ycUDtJJCGhS2BKHcAjuC3l9EbTuEoAJKKt5ZUGDoRXn9NSaQKPjGA80oVh+kXC/rgxrMcTi2Yud8rcL740Kte7J4hBYC8V+2z5aeVevwsWxHrCESUneDpukAAZjbpPkHdXqHedvbm5xc3OFWgs++ugFuDflC5L31jTxUqpJq9eEVOhWgcAMEzo9MIlX43A84mS3w/qV5J0QhijBxXlCEmwQIqvQ2iW4XbdLIM9Clz1gGSZiYaFyCLJn0x6fxzZPSZLv/KJVEF0amaKi35LNuCBqhQnsG7Y7mTxOnoBkybZFxficvop1x7lJaC3vE3Dy3Ay2HvpKRksItzf3ePv+Gvv9Xu8p/leaH2RhaR1YaNZtASAx4+z0RI1TEabp+01huXZalNfHD8HAkL5Uc2uYjrPy0CVpWFyf8KZzNv3IVcb71xvL+VkLkSkJpz5T9uQuN0hB+Y/CI6ovBQ56ue/QBvSJyQLu38k/Fuq0nnPwI3kWs0ZCUvbAkK/FFGbvs5kXmWijwZUhyqaEfIkhlDuUpidDse+vPC+qXAU8iLT3ha9MqSIbN4u9LLYWBnqbsRkqzk92GOqI4+EMv/r6C/z1/+a/w9W7Gxx/8wvw4RaVuifQ/yFhfS3nBjwf90A8dv+HFIsP3ZevzxVeH3ve2kPy2DMejMUi/75/9x6bb5in8Y0VjUX3wjSJOlSYm2sNTJvwWgGwl+VP1BpVbh6rObx+lik6poyEIoEHQFwe2uxqCuRkSL+F7XaHX0wf49PvnOB0d4rtZoOr6ys8ffYcTy8v0HvHu/fvcXd7j/v9PT568YlWU5IKFR7upWOZ0OaHyZhMEjycwHtFj6ixAETxHavffzzOGMeK8/Mz7LYb3N/v8f3vfxcff/wCNze3uLu7xeFwxOF4dE8At645E0EIwOJhkIpdgxIXGcOreIHkpKugX2vFUCuoAEOpGMYR1kFXkpIrQF2TmiUkSXQVKdtowqx5RQIvjIAG7njeh5BM3zMA0QPEZKAkyMuSs8ch8CcL+sYwpXGVbI4IB2o1ZKlSARgzURwnUmWQ1IuVw5BCiFFOmAggkhAEZ3pLoZTR1GDcS+AISTkmH4PRvTeCMUER2uDWQ+dBq3WnHGrHBQux8r4fMOuQzSGEF1uf1Un3Mod5CNtXBOO1zfLt0D23HizM5KFiIQnJfbmgCBBnQfAkwxzxnT439oYXzwxhlNF46WK39QYlScLWg3mEEGOPdEXMYI90sxcXkKsem78t30Qtc/JZxWbfI8YyP0Vxfu499Spg7xXRe5dqYNOE+TgJTLR88zzP0njSOtW3pgYJZYoglCr9aRjW4V5CKWf1lNaBsLm5xvnZuVZ6kk7UgPblQPXGaabIO43ktG49l+dnp9jv9zg9OYXTbocrVngReyeCkP0YtN52Q8Y2rAe4h2gYeO7HNAQ8pB/zpjqM9B5BjoUF1c5Tts7SYk/pwdgJG5ZJtY/gIlxmpDj7Or6ZZfxeyvgcZwkJpowkQK/h4nQx4bbDeCVw6kMaE968fo1313dgLmBN8AZpSKwalWwNZrDK++xzcMAxLs5P9byyep0TzNMeUoZhAl5el8GOAVycn+Pm7haXFxcLYTave/E54a9b72E0LvYrxk47rL/3nuQS+0GTLQynFpOG8bdEA2CpUMKfKsjLL0Nhp/VL5D4TWv12zZejtW/G6BpDeCX5esgRPPCcAadblAYQ5YbBrEUZNNzVDLO9iJeDmMGVwT2qVEqlqIC9txJIe0JEYbDSTTNlUHCJJcKC4SGbpUiPDjHIzNjttqDSMD/9Pv7Z19fYDLf4T/7bv4//6f/2f0Gf9xgg53hKNDbLrBEtQ4v3GXeAh7nK/vJr2N8vIwUMBkuu4XKlRl/4UcjP8CEeUJDVFB7+HnIWoVZC7zN2279kRcMAZgK+xbsfpwmS4/BwQR9SPPLz1s37svZnikROkAE054B5MaestZnysVRaWARpLY5tHhSFHE42J7i+vsHh5Af4o2dPwL3j7v4eZ+fn+Oy738P1zRXevnmHq+srFCo43Z1gs926l0EYnHbf7kVKQFoug6wYTo0phBlWzWPB2DiLKomwK5dqcwNRR60DLi4vAGa0uePJs0v0WcKkuHUc2ywCh+YoFCoYxmGxB0WVByMUlrtAKSuSSEtAgt0CZYKyzds6ljtRD6lLumwilIBMGPRRC2HWLBc6ySS8yYhZZnSYGX7BkpHZCV7Erab7fet5kRCablpwB3s7M7TWPKuQnYg9pbAHu4e1lZoBRtdqgstCKFUYdA2S9zAsWwtDcFiJJQBP+iOI5ZLVu2EWqYVblY30IKo+cTRMMnjbnjiEzNtgQiDY98REthyyIYsIvFboIDd99DWrOGECTFmb0jh2j3R9BisYPhk+67rZwqaMHiVGs1AEzKMC6bVhUwdZmEGEWiRo+EcCew+L9PVSgVZkNQYLVdCsr47TtCZd0Hvv6NpZvvUu/Vy07003BaCzXA/ZX2Kx4LU2o3dGU4WBNea59ebhqQYThtZipqWg6fujldqkfGtV6+SAcbMV2GiFNGYpVLHdbND7LN4Mbj5f6XfRMXHHRiEv3hSArXmnHo2wDMuH3W6Hd++vwOhugXRBN8iL/8AhAcfZFMlP9y2IRk/0AyVRWzsWRg3ydXqGyQQhP2NINKI4DhnqLPBDp2HXJPnBlaRYaTx3KRCHoLjUAFYwyuO6sJiekaRTTvc6KPLz0vcmDJvHcI0+jDhzMj7h5as3uLrZw7p7F124CZgm5NqaFsoFKVSzxAhgO1TsNiNghhcEmfWJINGFhC8Gv26eAjZOIXt7enqKly+/xsXFRcK1RHPyABneac6GM6tUXf8bie3ynsFOzz1HSAcPupVgnmh0lF1OvJ3iHNvG+Tkzep6KARCR96ZyOCnPyTzXAJ1xwulKLA+G3E4P7QcO+AOyWBunQjwyFfJdLwyw0BDuQo/F28HoJYwPRCkENxcMSPOTZav6quQPajgEGFwIDAntE2PrHvdPfoJ/+urn+Ps/qvjRf/538Yt/8A+w2RdgaqooiUfc5EwP51ylA+QiSWslxPGGCMQN5mq140nQPAuj1Aq2CnaDH9HgcCcOo633k1uAgn08rL5fzzFfb/fMbcbcOr786nOcfPc7+Cavb6VoZKVgmfSNBYDz9TlOzJmdvtb9NOxv9kQ8thlySAMQ9uz8155t1bIeA5g3F2xSbeKXr454eX3A8dVfgJmxGUd877PvwsokvPj4Y7UKMs7OzkAo6DxJuEvP4St6xsjmH6FTcqisDG4Qtge5+ytB3A6iuefFN908oQ4AxlpBw6CE6mEoFiNK6xrRJZI9Cw8AY+6zCt/hUQnRGIlpsh9o1sMvxMyUCRVkeInovhdrDpaevRCmbeTEJexWA9MCX5TYuDWJAEp2Oa9kuZhXot68+ARnQbaetrTVr8U0F8r90eZGSKthTz1NcwipxnJposFcwNIsNkiEwp7JOs0FE7J52Tr0eQuBRDfSXc4LpkJpPUslWL4JIcYRwvFgJSIZw7RzDDhCZsupK56CDDL/VOnMlDXSRTgNckZnNCQpMkhTceYKZb7Rsd6ZF8Iq1DkShbkbFNRCrmt2iztLSKl5EZi750rx3DC1CdxYCPZxQifW7umzn8PeGEYVWLtEy6M1xI0tHAAuQDjAKAW/6bkQGig4tdtusd3tNLxywCblOQ11wFAHoEhOlBUAgcKolsEbP9peztOEq+v3YhSqumepWRVDCmcwtomuBT4kmVp+sSaVNUqT+x2BFE5Ts1IJJK9BUlIBx3gQgGlubhE1nOXOqa+G4lOXin0g0sIRKkQQSfllemwRCpzFvth19vYR4reAA/t7UiTMdNROT9AYhHdr+bjF50wz16/19Y+9FnR49Xlta7DLrm9ucHtzC2j1KAOKC7z+1bKyDqVnGp674qXKgPAvZP3jwRkHll7OB+tY0UrmKBwyT5OGa69pHq93D0aqLO9toTAZr9QLja6RMZjEd3y9MO+w/ua4BjEakeG0KRlI/aAiNCrz/wfkOCuy5i2AKjYmjOcQQ5vcgj8YAvhUlWZmXqLzSF5ZQig5Gc+N6Xp+S4F07NHKYoWheaRdFRAWb1XXSAY1jJlh1kdjMTQzS/guVNgXIwq5Ykca5XB+do6bm1fYP/sT/Mtf/2P8r/7qf4x3v/oc7//nf4PNwEBrSCrBo8rEOgLogTLSOywnyWjTYwrAspBPVKbMJ8Z2Om0vjOMb6jBH2HDAJ/jEetzHXpVIcjSOE5q1lfgDr2+do/Egxqt3gOqDEKasjCyZXbweA+i6VFe+33pmGBHIHov1/OYEgGw5zNcBlkQ+oPWOn+FHODkZMc8zuDGePH2KaZpdYSm14vTsHJ0Z42YjygXIw3g8ztwq1OiBKcXmZYTIcCYTl6X1LcT1xBhYhI4AjF6bBH5KyLhwHYLd0mtQN4EYHNYAUmRcUCeKsCEA8C7iDl8kGJCvyeORheosK3/k05AI7OKUpPm6wGmmKZceKNZn9wMgWBIZA10b+tiPpqzBGG+IygkkThDZ4ExQncHtZzFdJ+DkFj+DfSbKPnX9Z2nFtGviosVPprCSfxQwdWNEbGATAsRhuV2Dl8ErZsz+50F8ruNlLNSUAsuxMKtjVwHcLEYWiuOChTKXUPTCqBChDyFQ2PcBl4iPZ5jQr2E4FOtmJ+ZNcVp67XjlOTYPwSzhQ90qf4VywMoIOnftVK2NJpt2nrfNTQpG77mhpJ45dG+ABD1jCgm1IrI0RdSXNYFjJv2+ggYpWiFFEyrQ2ZstUq2oxsA8r0n2bG4zjocDbq6upfQsgNOzUzz7+FOMmzFKNROSYEKOKGZ5Nr9HMYt9IdQCUKloQ8XV+3eYW8dgVVisdKXixXGaBQZDXTC+pXTKKyGDsRkHHI9H7LabON9E5hxyeFqVMsNQIOGYMtdpmrDf7yV0zIpktIbepLqehUQSAeMwYrPdeDGJxpIzcnZ2hmGscUaNbtqAbDRL3luIo03M50TZAGQHGf5MJxIUfCFOX3qfSWES+LJHAIjz4DBDeoidb72PSOPrYfQRnu9g3y9oto2Rz7XCoHfGu6trlCEqO5pxbCFYJr7EIFghBtvRQup5VY8uFcLp6YmXTuY0iTCO5clFuKEjBxv/TcIXjFd2nJ6e4er6Gk+fPHX+bc+x+zJsZfhlKK0J8gxE+KvSQBe6df2LMErnpd1hvgiV1M+kneWLKnBFzzEbsvlexPxkLsuxm/FK/c1w2mXRhB8Zrtlgl0WG9e++kwSgk+S1doY1by02Fsv+F5WloomcCukQvOJq5a6tIbCFhqoxu/GK97EK19CIT10fDK8Z1AtQupfbL4Xw/OklXr+7wecf/Vf4R7/9/+Bv/M3/FFdffA1++yVqtyL+D1/rlIGFrKswzTQsfmKX8dYKyofGeOy3xXXpfe4jYzmSa4/LAmrMD8dQg8yrr77GD77z6e8d217fWtGwxVluBQAX/tehTut4tHWvDXuOhWJlT8SHEmBMacgKyWPKgyk99vysaa5dV9vtFn/6869x/eJv4uKcsdvupFV7rSBtXGYVsE7OTjHNTcMT2LuCOwFFEg8p5sf2lyQ+UL4HDMkYQK6jbgigV4oWDnaB3oRFCyHJTa/8dCdzUITh6PNsfkYwjYC4hcPgbcKSCq2U5qlr0IJ2vh4jtc0ZsDIhT2izi7PFkXyczASNSAeh7DArDXd1g1Kav9+8hJO/N+7sxDH+5bgNVq7VvhdDSVJE0l9Wgo80tPyJREAP8fG8jXxhzMIYK2C5EuT5KsZkhADDn2PrNoFgEWfNphDIE8GQ8q3rtSSJJckrsVc2dqpmZOMtzpThF5vgkzxI+rxieLzYWwtHC7IrQoQJ7h1t6kBvLuxzwnHuHW2aRHBkRptntHnGYZrQ5qYhR30xooUSmShgY/u5Yymn7euJHfO/JpxDFXHpzl4i7nwAiEYxVBChDgWlDNqwsWDQxoulVlCNTtTWUbpooYniTauMNsTYREmo1TAA85m2qWE6mQAAh9dH8Z4ysN3tpM+Ldn2PvVC6rfjcdUwreEGqEElulpaJHjfi1ekAN3Zly/CmEoly1jqGUqMDOFHAkxMOKN52Bk5PTnHY7726idNRw8JEi4IGRPUaYeiE29tbvHz5Cvc3N3j37h2O00G8TNnLbtZFxasCiJUIQKkjnjx9ghcff4xPPv0Y2+02CW162sxDr3tREtI/oBsJzxeimZ09o8uAC90GJ1KiGvR+Sfaz8hFn2Z61GntBh5Y0g1eXmIEs0xYAD4xXxebHhJu7e7SmGYIEOU9+PaUFubivSrJT7sVzheYQNsOIcRj8Gk7CMRSHE1T91W08Tp52pWFBN+XOzXaLd+/f4/LySfCrBLjgGUnZZNcn4LyU+FGYG1yNNwZFjOc6PSXhJ1a5DhQCLDmdiD3PIgDbuhcXAOjhddACT4nnxoRJ6Qklx/xjCob/ptgjBkggDy2oQSAWY0EhAEUVHV0jSPPmyOBEPhAD2keXIteICVykOmW1fLQiRp+m4dwmJ8m6XAgJvNYqVKVrnkhrQCnYnWyxu99j6sAXT/+XOF7/O/z0r/81/MU//hrbUiTy4xGB/0PeAIM/KV20YjoA1GC3CqXWZ+YKr1j97lEzHDLjWtHx72xuLPTKmg4+FlmU781jFirgecK7129w/ur1h9eZXt8qGXwdeuQTZPFWjOOIYRgWAMnAyK+sjKw1tw9qgvItgLgnKxK5clUO9ZrnWSoarZ5nyggz45/+7B2enB3w0UcfoZaKu9tb3N3foxLh6v2VjMXSSM6IROOuzeSUCCGYf7xHWDaMCRlCBH1HCDOOZuElgBw8F3YJUeGCQ+BLCxM4cBJKEIQ4rH/kl3uoio/uPzixKG5lkquE8Iu3IIioSRGq2NjYhAcKCiVCQi7wJeLFNteUrGsQWtDNpeAoOJQYrhLlnmHuhDLgbf9aA6E8D/j4sBvjRVDvFtQaSMt1L2AeCl/aAaicptbCZAlV7ifNhowIxP4DEcsruThLDqCnRRlDnCubT3d46WYxw0IYHB84PvXOHn7XNXeAVEDsDHQ9g603cJvRWleGw5hnjT/Vc8A6HinBkz2SZ8zThKP+13sHtybhN62pW7zBKqJZvxhWRJU5p0KibDDPXhKdR7IIyjykcEGpRQR/khLNVKoqBeJNLcPowjaVqtdV/Uy+JgW4zEGvzzTRMYoc2sHFEbki+XgbjrjlUl8W0dSZUWEMVNZ5/uQJ3r+/QpsnMAPDZquwlzOV8RXpnDGAUiMvSnCUFjHv4mmpqhCTen/MoyFzZO6YW8NmHPzsZ+FL9nEZQsrM2Gy3ePv2LS6fXOrxSYzQhAcKXA2PLzvUpmnCb3/zF3j39i1ub64xTxO8EprS1Aj1Sh44mxgAxhHHwx53tzfofcZHL16Il4VUkCTrIxTCW3sgfKR5pnUjf6ZEmg3mnPCEEz0nwYXG6Tm8fJ6PbWMFS/H1LfcgTWoxQ31OTkjOwrLPP+U1EeP27g5MNR5DochIlW5a3EfpOvi62XkqIF6Ns7OT4CkcCoCFh/q8OE5IlPIOegvALcsGe1HsWJV7YJqOGKqU9heDC7syEXsZPNc+s47lzkz73RUP7W/BcdaCP9hq5SWGC4UTSf4nJWV/yU/hY9sZW3hafOJ5LEpjIxS1vCcOX4Twnl52XUQxIOai9M9GMhI3FIrcQYWtyE2mbFB405x4L1BEFVjhQuLlKFpoiEGtS95YD1kI6QzFnEkMYGA1iAoyEIBnzy7xxVevUGvF15vv4ccvvoOT7/4Rjr/9DQoO+FAkzocUD0rXL1IMdFUZ3lkWNhl87WUgo9f0MB8EWIZ0kV6fZvNAycjzf8zLUQAMTOC54fzs/MHvj72+saJhEzHhvNaK4/EIgLzkbF7QOsQph1XlRX1oMR/SqNZzsXHsu3z9PM8+1+WmhNej1orD8YgXf+1/g7tpAveGOg643+9RqOBkt8M4Dji2Jkx8nqXyihK53AjHGCsQjNOIu/zO7paMmnDJwk2JKKggZ0IqcwirC4bFJlwkoZjMUxBJvEY0sluZPc5bFR9jcq65ROM01jGEqRuhFoLAXb9Tc3pmaplh6nJhAIpwK7jwnL1BTngh/caNLdl5sPe+46a4Js4XjNDc5gRQdyXoMbtXNxzKihGAwmHFyhYfIAlJuiYjfMDKmoTYbyLb27DEdd05n0KLrtk9zTffk7+LOcU+qN9n8a9DlxH9VdI90SSzo6vCYB7I1sVDIHGyLc5is/CkJuGH3CJkaCVYxt7YnFLJ3qSQS7Jd8TV6LgWghR20pwoV0CY8Ag59Cm+ArfX29gbHSRjQ6e4MLz5+ge12i81mI0IzieV+M44YRgmlnI6TnxlC0cT7JD8ZsYYfA98F0upM7vXSvbcwHQuUBNleaZiGKQDGURGhPb3r81IYINl4+l50iIrSGJsN4ez8AldXVyCqLg1wgpMuxMMpAFKmKD+Jp0IMO6VrsyoCxmHAbrvF7fUtoDjSNZQW0PhnIkzTDN5sXMmPSkphgXYhRqc0jCPm1tCbnzqdTPpk9ExpaueG1hjcOqbjhJdfvcT11TXubu6kbwOnM6awZWhgjxqKHBb6/KHIeIfDHlfv3+Hi4gybzYDdbifJ7ocJs5V7HwatuveQecfJW773nDpbkv2gpmQT8DzRVRedcc2xkVdvM51aj515iX2fLiJa7ku+efHsxDsMfIdpwuE4wYrMMlhoqDFLDpokYwV/ssMVvCR5DSAKqIU1Si5OHEijkx6aYs/1NXMGka87VzQS40jHyckp7m7vcHZ2Lmc1MXtGzNEFdo4xDECh/MXvpgRktdgVZ6cF0PAoAGrMkFwMNY4oAmfFxMYwkpF7GJknsKTPgFwjRsOlITHzWccHW1qWFZxWxcGltM/ukVfGJ+uXnJIZpAVAyA2zhDiGXd90guelBL7RYg9N4bCbS5F+Xb0XUJfwV/NgsuKNz6dIaJ6EqHGqi9xABfj4yQW+fv0azz/+GP/m5jP81//Jf45/9fVr1HZ89Iz/vpeFVQLqGc6HL71MnjW52Yzq6wJK+bWuvmqypJ2bYqGtrIbCEgrKYo5mCHtE/ibuqCBcnJ3j8vwvWdGYJ/EK6FDKAIsrENn9sg5V+n0xZNmzEYuN60V5yY34ooeHaYWtNfdY2Pj2Mi9HKUUPYLqGgVoHcD3FOFzi8OYKb9++A1HBm9evcfnkCXa7DRozNpsNQAXj2PH+6j2GYcRB/GZCHNTSS2XZ42GxJiUI1qeB9LMnj+l1Zl3OVgVOAmLGCaFlSjYJGhqxxNxI65DrLKxBCDvr70uC9FiiFuuzGAhLgg4V4ThhnXH6x7GjwTCXjC5kBiN+K+aWksrjK/ZnWox+Hsuu0yJOalmRCXQNCXNMMeHHyOD6WSwdrBdEVd8Sq9CU9suus34BzpSZY56ZUBMt8MZw1b1QqZKSVffqmkfgfgw2uLIKXdK/oLNWL9JKRvM8h8JgVY560w7ONkYo8mL9tY02LLT1KnP0jQpLnglEEvdNQtTYBP8UJqQN2QqJV0F6rURlu2oJyQQxapSCQZs/mhUL+kwBYCrR6BVFCnrrOBwOKOOIV69eSuWkccD55RNstxtXDoexakKw9onpDKZZno/iQnqWSR2XSekiQlCwmI+sRDuNIng/C8OFog0ZQYa3pooYbSAVqMjhHfioAqvOUYLFCKCC5x99jJPTc5yenmC2/Da25n6qEJmEokyfNQ+t9a4KA7wJ2ECEcTMABFxenuP66hpza5jnjjYLU+8s4VJEhHmaBMcsH4XFGp2oZdg4/AzIq7VZclNc+Q+P6fF4xKSeL9sTJmnSOQ4VZ+enONntcP3kEq9ev8L+sNeSv9Y4lFC0yScpPtZSvK/PAMLJ6Q4np6c4OT3Fd77zKcpQca8hXcyEUkb0uWF/f433Vzd4/uxZWCYT+xP6R44r9mopMTO/SPcvaLMp7hHXHrhmNCILfYkO/76XoyP5fYToR2DzdkHWjAE+NqXwHvn97u7OhWa7r/s8I3yTF0nR8XmhHEDoGBjYjLI/rXdQbwBqVDk0vMpr4wx7JxERQWMXKe4JvRV8H8cN3t68xe7kVOBDFIajxH+CUTt2yt8elxICDpz5OMcdsn0Bw6q8IbEJmA9Znmu8hcGUVxN9ifIYYDHaKVX0nMymDK89gihuSEyclfxf6DllX7Mbtlg+eU6OfJS5GQ/rwouleWdxA4xJx2ZYyVb7AvYcoJDnAHN9MCQsiVmjMLigtI6ZGKR8joCUSweX35hVNmAJRyo67+1uxMl2xPu3b7D76D/A23ev8fyHP8b1n1+jtAYiRlOlXPqBLOFohgTh003XKJ7/YoY05mUFPIM2G1x1v3vAxhCa2eof5p1RpCkZhoajrPRXQxUpDKJr/YUWOCFetN47TnZbfPz8+QN8eez1LTwaBUQVvTdhhFAUKuH6qbVinmdXNHKIgCkGj+VLrMOybEGGWOESCreRX5WUlEUsWtIGSynhEYcKH0plTrYn+Pp2AG02eP7sKQ7HI063G3z0QgBIpWDuDfu7g+cQgBncmvZU6EEcipXtI93ECOMRxqj/daCrBVdecURhJKBnXJXv+gpGC6s2sVRLQBBPQUxDxjR3G4/TZ+NzFERxAWNjMEBqMMY69jK0Y0GSfO3xg1u00jrsDo8RXD+Dg9hlNmJravmG+AFEJbqg61qiGGK+Vu5vqlXZkTX3vdrcF4yEDT+VccJml4Sn2cZWoGZrQm8dME9Bb25x6b2JcKv7KRV72D0IFrLUml7nz414VE9q7knx7B3grr3PGaxWYsNfVvhbn5PCatEeBALFwoKooNaieUwSNlOrhB15voEpAiRhSEXDkkSQEyHJlIjqYUsiEM/K5A0Rax1E2WldhWJ1kYNdSJaxZBt72u8yGE0oaCNh5oLTC2B4+w7oQpyHYQCI3BJt9KM1yfuQeVRVLgQTSjYTI5ioCGBKml14EygbrgZN0Eeb1bNUuPvAGj0azYIJBpn+idFicW5070Ek5SABxSlGLwXj+TkaEQ5HwamS6KslhUMVNvfAkNFUEppPQIEI9eenO7x48REKGE8vL/Gzn/8Kx7ljaoxtlypmYyVQk/4eU2ugGv2GFkyMQxAzgY6oSOO+wwG7kxO/z8B0fXWD169e4/mzZ7g4P8NmM6IMhOgSz7jf3+IHP/0Reus4Ho447A9ercbOeq3eqsxJgnklJAxP8G+aZrx+9RbTPON+v8f9/QGEQZ4H1rCYjs1mh7OzU0S1O7gga68Q0kMOJDLasqR/QruU/Cg9bw4zhFBmMEz3G4jtGX6PCppuRaIsuNqEzOjDgcO2b5x3z57FMGV8fzgo3liYYigyIRLBE9BNSab8vPQyAXS33SpdU967OgMu0MPO4jIs2GfsTDD9pjyRiDA3Ri0D5lnCPqkU35vF6WerDsie6yZ7FiGqeUxXsBKj5QwTZdklCc0mDJoLq+saTflzT5DJGYE9yz01BNIvcj4JkIxiCU8drm7MiD+Ga97hW+91A4kaLLzQv/X0KFXCZJVWWw4hMTmeuy3GhWp7VvdQsgChwscqE5pMUiKkiipQGqH0hlYANv7ZFFoORNLCOYzeRVFqxLh89gxffPElNpstftYu8ff+zn+MP/3tn2N3dYvKHVPtaKVg1yTp5IF9XfOUO4TfgaRkb4f0HAKZSSHkWLmtK0/WUNqVnCOgUF7AEb9A+juT8gPbMUpY3BlEFYW7n+61EpzPDhGhVcLMwHR/Dzoe8U1e31jRWPfE8HwIRJjFo27iJPTYc+wVDD28IY+9iMjDoDJDtfc5dq3W+iBGTRh2KDw2j947ain4xfQx+tBRC+H0ZIfepYs1Q5jtqA3tQAXz8YiZg0hEvDtcM+7UnRmY1mjUPYfYCCO1w6LEw62UabORvRRGhtPaDE6gzDNcOFEcDoKjh9JEdrnPLCDQi4Oa5K96GtOEJMPZEHh9mjDXHQC31LAziIwnwPpLhtmml0wBi8uCS3sICgA/siyd0uOQWfJ6crumse1w2n5KjK3hcPPKFlYSmJtYba3qmgm4vXcJs9OEZvdOdalY1JsoFr113V9N1GZ2j0UqkaFLZIcJW7YsLcANI7hG2IVpqCWoEogGVF1cL8A8HTUUkLDd7XBydoZhGDFqp/ehjpDKgsU7tQu/KM5EKCQkqJih8wxiaddwl7ymOgwYxyFKiYI832Fj1UNUmCi1QniC+G7Mu8GMlPNQXNEfKPJxTCkzxltrwWa7w+npGW6ur8BEaB3S66VPIExwTkvRz8cTDz0W18svQMpcW2vJCHm0fbEcGpmP7cryfDMXUPMvpGqK0zjDS3ZhLJ4Hhz2BNF6/oqm3q9SqcKooXZqklUIYtIJV5IqYEknwgA4CLBnePFHCwLUnjzbmLCxVmj759BPUYcS/+f/9e03Gb5K8CkatA1o7YG4zhl4X3aKDNhk8yekd947ddoe7+3tsT04AhWdnofFffPEFXn39El9/+RXGoaDUgs12i+3uBNvNiEIF76+vcXt7AFi8RRECKOFzAGmon8Cs2dnWcAtjJeIBDANDbw37+wNo0PVUEpjUivPTE5yd7tATnfFtozDseAStXrQwhBpNRXiYmUNQB4LOhYiwuB2LLxB006CfHSmZHpvSYDSQ06MIrEps4j0UcwF3HCZpAGk/ZtuSCUtZmFxM03E60XtdZAFjM24wtxnWw8BotUPhA2tmnbtJ8n19PbmcKbSTxftcBwmv3oyj4IU1mdLrXRFjNXjpaBlmAk52pdGvSTYvMkDCKjyS50yF0AhXJgV/jFnBe/rkswTf49xfSmWI1dgM9WiE8OCv4mPJfCzUKuR7ct4Q6QoMLqKEWJi1JZQ7QihA7C1FKSbnY2z36n1ErBEUZviR7wzPHJ8z3EBS14EqqCsvo4LeZszoakRW47AJ+jCPr5gE6jDg2dOnePf+CuX8J3i9/wov/spP8PpP/zVOjwXbTphYZT810ixk1gAnohrjH36ZoZcQ/HQta+fec4uS4H4+VhtqvyN4WpaZyWTblPbg8k0X/Hz//j2mv2xFI+c05HApc+WsvQp54o/Ff+V+F2slxYRsF5BSv411c761RyMDO98jjHJY3G8lJA/1IoiRCZUswDwcDjjQ0Q/e3HoId6SMVxMh5JB3EVxggmoiNlkQ5bBY66+eT+GIYbQ2ESgis0DHdZFUukxSW+wfEK51wKt0xOhBpEDRyAw9lKBgZ3GTEe+QpSxPQiYfXaKhnxM+ZA7nyk0WwGJu3kV0lWRekIR4e68a02xCvpYj7WrZZe163FWQEMt498Nv30PxwOpde6hRN+tB90od3XDWGIwBpHMwWdvLxLLBnAQ88r2UKiLVQ4rKUD33gAlSvYjEe1CSR8ATkYt6HPzsyG9mrei9Yz4ccPX+Pd6/fQcGY7Pb4cXHn6AO0vXZ80wWklIol7aKSBBm/WzCaIT6mGejzU3WUitA1eOIAQamDuaGqUnpUVFCCJianwEisdDrbvuzzXMjqBTSk7wlV5KBglIY55dPRHjYnaIBaDMrs1KrfmexBCEYe6ElIOJcJ47NbRH6Awp8N5qW1Vw3BEBwqRQVAKyXhOKJDE0IihIlaa1ySQFhtJuo6HrgoZUW212pwEBbKDxRw1C0eScrrxT8qsXmClU+CONQsRmlPC5YQ/vAePL0Cc7OznB7e4em5YR7F2GNpiI5POMG1jZYEjBVQGBTwRC0hSVs9f3VexBDE7hZzyzj6uYa9/f3ICLUQhg3I969v5bPQwWYME1HfP31S1iomCCp0Iqe9s7PZRLkoEqsiqhxle4rtwaayD37UynYbDe4399ruKPQtcwHTGAyARDI4Thw4Y3T56C5iXoIgARm3Z7rlz0wOtnz/bPGJy3wFb41cY/NJzG0EH1iDMBonfBNTjgrawk4BCYvNQ1KSR+WtGpPYJLQSSKoAceiJIrvma+bA3AORx9E95iWv1GeXGwyNuMG+/1BCkEQxAKdeJCcYTUWAM7HVXSFC9O6X5l2Gm0oCjdSGg6zYKsgLfkD5Psvz4qQy+B/sBnF8+0sUVZsgs+GYG78O/bTuTezexZ61+I0FpWh/7mMAZWN2PgYxKtNFv7qgg1MUzNcsfnLXjCaUUqyZ1K8N7qhcphFk9g8i8o75C3KtUoeCS0fCmGeCUQz2ixRBVkOlfSoDqpV5to6zk5PcXt7i/sO/Nn8Xfy9v3KNr3/+S/D7W2zaDCJgrgQuQO0hk65fvTNA3asKfujlET2PRAMtn9cX1+dXUdPqh/IwADyQw7NM/WBclamIxfjyTV7fyqMRnbn7YmJmyc6KRlYG1q3W84Jyoz17sR5ye940Ta7krIGTE2PypmZNUgS0aOCX7399s8fd+Bx+8JJgzDo/E55NASolCtnaqXRBHySJR7AEUKQ4TWn2B+YQ5GPBC2YgAgKcgIJMlQniKLK3fJfzPDLhd40EStQZLhB63wIjgEbInHoso/Oy5kRQATMRTcASv4xEcVqbWnI53NgOQyfUBijLQWCgS5fzOTVBs7Kl0JKlzf6qEmFwZgsf4lCUAQ6r9IpAi/BiVjgslFgjVMbJhKal0nQkB5pK+ktSucjKyNWhwnshJOXB/pPwIytzmognZOwCzXOACs/GdGBeI2P+zrUXAq2UEBQcqGAMwwjuhOvrW3CbUYvkLIgEGufEcx9kSikRmW0mCgIVHZKZ0t7KXgJEFa0Dc2+gY3OBzUIAjIESFS8OwA7zdVUiU+7Z8cmf4fhKaW8lBIZbx+7kDN/9/gnKUHDUechDUq6ZMwCKM54NKXFkAJjVR+dlAkNHgqMwWdFnSGEJVSbjbEBxy6dEDNKuZm5MgbyvFM8rGvZVq4SyoUAqZWmo2ziM6omgSDWpUmVLcIVts5Yx8gnPzPNGBLRJGg4CFPkYw4iT0x3evX8vXgJNIhCvaUGbtaeIAtQpn9EuzjkBuoWlSN6H5RCZQAmT28S7MNQRz549xavXr3HY3wNHIaLz3LSLuYVrFS8djSSomXCzDgUVXmTfdccBa+JYWcpcavY9pjbhs/GzwA02QSrRVF1AfGPnWelnwjNXIlavxK6WOAnfxkRoOQmc8QCDsbEKAtCy3mzPDNK3/EF/y7l3nYDDdISFuyhV8PcJrKFwkOA5L0aO32VtjLEOaI0h5gxR5HjuMZfF7SY02do41pPWnerTLe63dddSMR1u0Dcb9FKCpRLUkETOU1i9myo9wEtssK6m91iZ4oVXDiPNFaJkNILkJIA1rBdKlwiYtdyYC5ALEKyMenHAIv8xf+9XqbIERm+M3qUQSJtnOe/ae2ZuavzpQRPW0RWGT6YMmEGsEqEMA4ZaMIwDxmFEHaQ56FAHEEmTTNIz2tmEYtk885SHF1b3tqinBQVUup9j6pHVYrg2VELvFTSoPEkNmNmLWBjWNtYMICbwIJ7cZ0+f4MuvvsbV2Y/xr+6O+O5P/hg3f/ZvUI/CQ+dRQ/bn7nLHOp3AQuGyTvCYUrKuGJVl58eM+uvPzByKFmKPHlMsctXWLL/bPOw+qOf39OREC0L94de3Dp2yUKiqzaKs0VtWHD60kMcA9Ji2t/4+N9vLCk1OJM9eChM+gag/PNSyUHj8Hk18zF6ZECaTCz8d4sWmrogb2+HoXRhPJ7ewW1Mwp/1G+lKirzMZI+qch/EZIAuVLtwnJpBjgTNRyYTW1hWPDouIsIYYz5kBB+GvBsuuZeFsHpZDoB6FZgnHbZZwIVUA/DM3h13vXZppzZMQM1PMVHFwgVFDa9AtFE3TFZXwWrKhB7pQcYgtDyV7cpV3GgVjs9k6MSzDgGrWXUtQrjX6JqhgXi2xOVkBmAA23FTrVLZELvi2YYUqGSYgi7AtkZxZCM6ucLcI2XOSggJA2QclLABan7A52WEYN5LoruvqKugb7niSsN3LCIs7x7i2Hps3cw4wSpY+5fxhXDPWptY0TuMgWUwUkU04M1z1s5kEO1MK5cxXZbANjC5WXIVHmxm1xHm30JqFsqFM38q6EiwhWuhDKeFdMCMJkVkj4XkQAGtjvegpUDVcrA6xe5KgnD1KLF6IKtezMt6quGdNutzK57AQYcxCsIriERjKyIE2MWbfN90p18ND2IvCyex7GYqeXGvx3bvdDnOTrrF23gW9NFRhbqBBAelYHy/HH/2VFCbTcUatRUU4oU/bk53QDwIOxwNutPxs63PQT+7oTh8IHbMaMuI0UJbSTGjioMumXzAgYWhFw+mIouogM6gUnF9c4tmLF+rlWT5zoXh/8GVqt8myyXxAyzP1e19uSMncxuCO4DFpjjEW+RlzfQxqJc4HEYAfCv3sYaSuIZhNVeeymrx/JOkxxVpf3MeGKBlEUJmjeU6ErTNlZDv0OAGfE0PkBM+M4/YEo2u2bpDmOTGSosAu8HMzY2kDFBfZzp1a/TNtzKuWs2VnlqLKsuJTV0OCriLWiwh1Zv0ur8m+Y+OBWRZLG2CKrXjuG+apY5onL64QESsdeSHMiNBdZqeH8L/sPN3yZLo2UZ4A4HDQROigkaVUDEPFuNlgs93gZLvBMI6pkA+HcM7CJ4nhnm9iqW5XSpPmexReDmkcavKP0HHrdWRe4FqAaQbm2cKYZSzDNSm8Auy2O5ydneD67h4vT36CH/3gF3jzs19gN3cMvbk8kV+LYkkw5YbS+VvKxx+Si+31Ie/GOqooX//Y7/n73OcOeCjD+/UN2NQhZLBv8PpWDftMgDZhyhvvra7L2tBaMzJFZX3d+pUFNlush2olYNmzckiUXZNLfbXWFome7iFptqk5DyJ1OO/K1BiK4fKfVwDS+Vq+BXVoYztJJiNSywA3eLMz0oRb4iAKZvk0+VC/82GDGjuDDgQgt7IQweMDjSUYtaaMMACiDwHACOs/wCgsVmf2eGXGNE04HA+YDkepib/ZSHnH3jAdJwmLYFEg5rl53PPcOlhjaqVManNriyVk2gKtHCoTebUos8J7cxsSy7DhyKCWi2IeL6tqpAmelQhUtUJR1c7KCHm0tYZpmvDm9Rv0SfIinj57htPzc4zjiDoMEoJUyBmw7UOU3FOizhm+gg/ZzSuENTNpE6cMN1KVDsNxZ+7w/RQ3u1pLUldpskUBbpETIY80NEUtXXLIUIYB29MTTO8OKHVwRigCuSkwzecPOyEzw8TBpJvrkiK0yRsxJQbFtmwkpu/300JZsLo2EbbEfh+IHGbCgzKBFRyQxnja2ItrbA5VwQeQhp1BGZLCstg+YP1U+bmwz1e2RP5WAkjPd63FvVhDHTAMBWONalpDsQRzKG5BkxCT3GbAtTUnAYoV1s2EMmXszrAc1kvPXf4tLSzJjiGUx9g6on5nH73ACrMrw2enOxCkf8U8zeiNwaOcX56lmSJR8Yo6SM+KddvX8mYYBhyOB+x2Oz1njNZmPH32DF9/+RUmFWLevX0HUHiXQNC2MDJvExhVFHXaqJ1YYod1Wr0JjIvtD0hCZakAVLAdN9jsdthuNjg9O8PZ+SXOL85BZZDu8Q7zELwiFDWvW00KhtMrOmKzQ2d0Svub6P5Chk37SYsqTkvjUob5QjxJvCXwIjxbVvnHlSeL+2dgmme5TmkZKdyKzTcLQrT4g2Us/vIyo3K9iQcjciOSwOWwhOf+dIbP19btFGot0OleUQYoA0QFc2ui6DvA2IXGYRjQ+ozWZjAHjbdcMVOcTYl2kdPOPwWcfI8IiSeT75OcP123jeF0Ea4kWyiTdzI3Y4DKIlCZam7WgFgt95nAUIR6WvhrIUKpAwajbWOV/XGvvAr5gFc8snBjU8bbNEvZ8GkWOjFP6Mw4HI/YHw7AtZYtrwO244DdyQl2u51WglO5UPOnipbBK/pfZ0LV/kFdeQe7B2FJZKRPR8E4Al2VE/DshVQUedTIKXS6c8OTJ09we7/H1Aj//uLv4Ol3/jX2N7/CaSdU5WGPdfgGsMh1BFibXEfTxWycz0qHn8hHFIkFCn9A2VjfmxWbtcclG/XXZ0TOImE6HnF+dvZ752Kvb17eVmOmjZH13lHq0ntgXobsaXhMqVgnlq+rUWUgZLfTY9f54lWYswZhQ5XGgY37Aoj5uZZUageVjGlmtblEeBAr0pFyAiPOjTmYOmAXh2CASKph5VGdzfWrgksSDq3ai2vdgFebYbbEJUhCMfPCS8BdYg3neYYRUtb8A6vQY8SqW1JyF8G/zaFYgDuaJvM1TXiem/YQ4bR+EiupCy5LqSyJ5SIYW58CKSlpmn1xj4GVmBTvQBVClcI/RHisqcmbMIFlSJ1aG2215opR+HbbW2VC3DumacLd4YCb91coRNienGC727mCQSQhUEumzCbFqNAiIUk5T8ZCqBTpDBJJgDWJwmJjlaxblIj+awIux+VwYTAODdxjAsVllfT7HJa4roIaa7fmp0+f4fzsHJvtBofDpNVVgCgfHEyfkqKkdNLFD6Ag8hWsuldikCpEdK1eZA91VziJMmSKslxreQMEiyGxMCKbjwkmRcvK2rbI8+y3YMak0icD6hEQ2uEldE1p0BA2hlrEStHQBt92qZhlXi0i1AL9nbzPhO8Qd5DRBeoSPqbYxBy5LbKVITj4FruFPBjErNDl+Nph5wqbwti9Y4AkUtotSbmJ/eBANlcsCFYhy1VAo3tqNOjcUesIAJjnCXObPCHfqopNjVGqhTawCpUmmMEVpsACYLPZ4nA4YLPZCg0kwtw6trsdfvSTn+KrLz/HNB21GZ/M3fsEESs9JE/yHoYB4hXshsRwxTWtq5SIG3eWVSS/6KOPXuBHP/4x6qh9mjpjZsYwboQew+YRu0aZPoSssTib4sF0scIvWigLaZ/t4XkPWRWrjBCZNPv9/szsFAgK9+jL+eTiSaqDsudQmTfQn6bnMZdhzfRh6RfNVwixKaWCwQsDp1jju9PSJHPLN7qeBiwNd9AQUIprFstxWiH/lFpxPE7YjINPrxJwdnmBs5MTnJ5scTiKwNy6NIt7f3ODeb+XFbixiAPdwDEfpR+B83oeEOchzmE8wyNJTAYx2o6Ed90UDOuW3RbFSwznjCaTK2uMQY13VfNTDKjiJW0oBZiOM3qfRVwqpAY/+F7YPEn3sGqlwu1ui7PzM4zDCPOat3nG4XDA7d09Dvt7HKcJt3cT7jQPaxwGbE93ODs/0+R88SQVKuBC6EUMi838fiT8hLRpT3g4FDfV+yDeZQCDiNHzNIMxG+F0Bc6s/eMw4PzsDFfXt3i3/RRnP/kvMf7mC7R5jwYJK6uJWVeTHVhzQQAUYlfeLFzcUU/56wIfkL5zg0TwgoVSYgqDnSebShqCEr1DepZFXuiiHYyGx4DkZpxtNtidbPFNXt/coyEzcKGpWTWXpAj4tWxaWngU1qFT2WWz9kCsjQzZJbd2Ky3dQMWFOXa9Sw6Ja3kcsWjDOOKMOsaba0zDuZNvSRyVg0sKbIJ4KgobQTRCqmtQJlGLlAAmC03oUXHLLPpdkaq5kB+eDRP0m/Y6sDwDe9+sURr31V8GtD8HJ+uBBIErUMn2UolW74GIhMUeyVlhsR4UK8cmMC4FKnCRexGKWTuG0ffJXKEFhDJUf46V6yta+UEprTNDb8pG0PAEJGlrjZehyjA7BdcDuQxBYGXGbuDsIlCVMqCDcH5xiburaxQCxnHw+YonxZ64ZOZEWAj3xnBNgLDB7GAHcqt3wSiKKyFAJNllkSK9uu6NMtbgjWkve1eLI7zHh0kSFtKRXePQMo6tN4Csy7kQ425WRl8fOeT9OkTSeSWCd7o2oh7SBgbfbyOW5DHJtmt2O6wyEuDMuPh7+OKlXC5i//V5lQrGAoyjebtyUz+5z0OV0lise1cQIXWWDJoZPIC8Af6vwNgqi7AfP07IaCEHUa5y+UhPrFywm8WGy1t7nt7I+drFXEkq4jHQe4RpdJNo9Fkm3Ni9Ifq51OACj8X/mkLPnbEdB4x1wNxmtVSKIFKKCfeQrr1FFJyKyJ+wMI98jtE7NuMW1ze3En4KoXHzLPh7+fQS508uPFQTLRQ4kPSA+vyLL/D61SsUZqAU/PGPf4zrmxtcXV15k0k2SdQ5qxwgokHzewTrQYTTszP8+I//GDTUoN8sIW4Mxqy5XsyqxBkcDVZKM7JsYYJDp7yHSNdxKJ7s0/OXVfQxWrOgHBxn+BGKsngxgKIhvkkS9zkRoF7EjBuBL71r67P1gBLnslIjkgDlz8uLsgOn58qKseSxOzuts7Np57j7ulNugj5eeHxMkhFsxmVEMIjFyDUdjuBx8E0ppWI3Dri7eY82bbxx8N3tDUoZcLrb4nB/70nWRjVjLHI8i3BKSiAPb5gohOxzY2ZYHyPxoERvJYMXWHjA3MMQ6ZXsOOSpAgJ6Fz6nQJUQzQ7JD+sYCmGog5QArxWbYVDyLB6N/fGA3hvGYcAwjF6VqnWgNyl13FtHHQfMxyMOWmbacj2oiEFp3IzYbrZ4/vwpxvEFCgj3+3vc3Nzg5vYO0/GIw/sjbm5uMAwjzs7PcLI7wTAOoEagBsnVKB1UqhIyga0l/5cC9CJwNSOT4UEtFahafh0sFalYjRZcULxxqJTzvr27Q2fG/Sd/A2cX/z14eoXej6gFi+pbLtAUEnxVOiD4FpXtuMV5MAXB55jOmvHdXAzgMUO9D61P4HS/DZqVk/g1lPYYXeguqYyLwug84Zu8vlXVKas4ZYI6EKFR6xK3y8pOCryVxvXYGKyc2LqNP3ZtBmj2cnSNlVyHVz02luWYPD89xfb9DaZyJoKHusgLi5IwadLxcZ5xOBwxHY6omrS03+/Fa9KaxDwTScOqaYZVLJpbkwRlmTjIQoNMOSANjWGbO2AN/VwZMJkqZfcJw0kIq3Yp68JZag2kKtLcqABq6dWI/aFqOJkDFsSMaZ4xtSMAxjBscfn0CcZhQB0q6jCi1gGDEpxiYScQ4dLixUOuDCHJyoXmFzsxXWrXUAYNW3E8MGnXFq8sF4obNBi6zYm0jrsdGBPAqDCKuoorEU5PT1GGQQnfgFIGlVVMcU0HWb/1LRE5K+Zua+mxX3Zqe2OX5OTrVBqgszb0M7gZIzEmucxFEQuwSB+ybg0KUJzxpFpYGAO5AOeNgoaqiXQU4WmAW6CrKhEuaNi5guISkcNJ4CrEtK5K15oQZ8pl7KntnQg4Ra3MVjHLCzhwXCcGBFEQ6jBgrMIcyaokkdroLPnatmmBfwyYN447erP16VSbhkHCQiCal3dOW+QhaSEchnBm8+YsVabYfT3mxlMezlNhVpSpOB4Z/BF2YFcA/NmsApo+WctLRihFyCTmvUo+T+gj4aWvfbxYKzUNJemqsLIosrvdDtc31yLEaynZUoQWWSU3w4GGpl5eLNfXZU/nThhqxXQ8ihcWcOstJSPSoBWwUOsCT8fNDj/+458ARHj99Veg3nF/OOCnf/In6K1JFZn7e/HYauWZ3jrmNoGoYJ4brq/eY3+Uzye7E/zkp38CGqrvqZ1W6RECRHAOIo9Mv5Dz3ReJ26xES+VDEC10vyVdVNwrFtqYUCXZGvIGgtEXis2D566+b3prWQSVYfE+LSm9TwAxrUhv9PuY3UCTHyaeQ/bvF54bfV4nRInUNDYrUhg/DDqaYLOYhPJTL4yieG5zUlrNUJpEBVObsXW8ZXBhvHnzBsf7e+z3d6hDxe5kh3lu2OxOsNmdQsK2xQMnRSLi8dkDpVKH7J/OyztXGxw1R8C/g9IJgkc5sFnGVQBtvKymZOeCShhUChjQtgClsBaWIGzHLTabEcM4YlOFH5rw2VkMnnObMd03tMbgDhz3R3Tea0lb5VcusRZtrlxxdnoquWlKq1tj9DbhOE14f3WFrobqzW6L3XaLp8+e48WLTzDNM25ub/D+3XscpwPevZ3wvlzh9OQEZ+fn2I4DwITOReQgsqI8aiwk8/qL97mrEF+URzHUS02DymySDM9K37gKfUMRefjy4gLvrt5jXxif/Yd/FX/xT99gcxR5q2k+GSC8drMZcXJygv3VLebDUcLEO0t1Q0tqf0xZgPGRh6fVje/JGP8hB4A/J70ek43/0MucAp05NfH+/a9vrGisQ5fsv1ljY9eVqOwec9E9lo+RgZGBI0oGLZ6z9oLk72NMudfmkpPI12uZpglv3rzB97//fZxM7/AOH+Hm5ga3tze4v7vH4XjwakY5X4OKNJAaLFwCwO3tHQ7TEa2psN86csdmUgXAmM668Y1Xh1ABOgtfIaiQxNQXSDIiRZhaqRJqVIfBS4qK+1oPVYnDZsoUyPJgqocgiSLQsd/f49XXX4MZ2Ow2eP78OeooMZkWm2wHOFfgIBVKzHpjazQFyhLvfe22ZJ/n8jBlxpY2b0Go849ClxVmkUEHTl0lTEi1MDYo7Bliofroo0+E5A+jlMelAiv2mxMKhbhrKE8SNBXhdF9DoItVGv9VKxSMychDw1Jnik3gulurqjJiPxcCl2LPhgralBL2VfD232xEM2tbwrdZ9EGuQJLtmzHHLGlQCBdu9dDHGQ5nmNt35ESfXRapVYTF7bjFZqiaCGjKbISW+WanOYA1VFAte7b9Es5tdMMMSpyO2ZI2uOXRJRhbkJ3hEFb8yJpg7PdwwCEpBQsArqQ1Vjy0rwKX5H3zimxYFHoAknCVZTyKZ8p3Qo28OWB+AsdcOc9L6Q5ZHhUDTJHHFaJLWruGZmw2G6GfjTEdJwzDBuOgxh/1EEk4g8ysdDNCGHABJhbljxgk3V+k94WN6vM0w4uhhZQtzyS11Iof//gnOD89xddffomvvv4ar1691jwug4Mm7uoYvTU5VySe2/PLUzx58gSffPIpNtud0Fg3RRrgGU279AZpTIql0RyIoSkndvtva5niERmDWasQcey3R7ul/SGKB+dHfEi8EDpnDxVBLBRWuLXdUMLG9mNpyOT7oycqHddwyQBLhM/499CXy7rwx2QjTrDwuzlwO84J1BMQPICg3o0cCwgsfyuqMOhYVQca6oCZCoYyYjoccDPP0liyN6WfQfM5A1G/DLnGzpGNgbgvKxNZwch/U5K63eP9ERTm3p3a5CiVEawL+nYz4uR0i+1mi3EYYWXeD8cj9tMBbRbDqzSXbZhn6QUlXkszFEeup8xNoiZKMkaVWlCpogzV5ZaqfZs22y0uzy9AtWBuM+73B7x99x5v377HZrPB9mSL09NTPHv6FMfjEW/evMXNzS1ub+W/k90OFxcX2GykhDYVRuUC6oyBJFfDmgL2rjIQSDLB1VgsvLN46W7JKY1GuR0MNEYhxuXFBW7ub3HHBYdPvwecnWA4HkE8Y3Y+J8pLrQM24wb38xWKGZsIXlSiVE1NUKtONuL33j08N45RlkeWLR3WZ+NDisdjrz+sfAgf3GxGjOP4B58HfEtFwxQGjwvsfbG4RSmutKh1uJN9l38jInc9AgTrAp7vpRUwSyneyA+AC3DyfpVIwxHbafP+sz/7M7x8+RJ4c4OXpyOu72dcX70HWJIPN5sNxtMNRhV47ACZFleYcZyO2O42SogaUAqOh0nyG7h7xYSi863DIHRGA71LlfAiskpGZUQdBCmrfVct7Cisu1U1dCohCAoRlXyaaZI5tDaDPTxLDo3Fahoz8ZAQdcFuTwrqMGKajmAqoGEQy2GpasEuGsetbLJ48JLDPV4qXhNE+nRGQaGUJF7tn5n9s8odihlJIGM4w7DvjYnbPMy1aAjiCp9bRqWUXm9S8//k/AJgxv44u6XeuKR5NnJYhgk46askXMTEJV9AYnGsr4H7WEoI6cYUnGUarq8JhFvtDS523qoqfHG9eOmKuot1LhnWQNbLHFb2TQgUQQTBKgByg5fsLSlHy1bE5rkjB2Vh8epQIWkKOA7YjIPk6JBHMus43S15OQ+KHDRKe1KTPKRrWAVWww+3mlMQ+sVyXXJLP8oAcOFtOcPFK1tpHTeQBYeO1QLhXgRePimvYfFLqrATuJbHSc/M9/nYsS6X66AiAa/0oG7WWD1zfSkCkmqd0TisY55nnJycYr/f4+JSikNYXPLCWORnFQBlQSnOd4OEjbQu+V3TNGMYBxeOmu5LhJyQ4zWvdopqxXe/9xk++eQT3N7d4XA44Hic4F5CiDFmVMGHSJp0bbfboMNELvCVYjlBKggi9cYgY/AJ3EkBNYHaunvn/RYrZ8K9dDbjvCcBWnFivd7V7qc7H/s9zdFQmB4ROpyePfJoxDmPc7K8LBSBFT3zmx4XhOTIGs7YLertzTSD3ZyzmJudXqPheV12h5/ZNCW/t4tAnXlT74zt6Qkuzs4wzzPafAS0WlxnybnKeheCc4RAW7KimwwZoLQe8RbAfw8PIxBVJ3PzvhiSwrAD0lBrzatlxm6zxcWzS+x2W4AZx+OEw/6Im+MdpsMR0zTheJwwTUf/b56bKhsWxWJhgmbY1bmaVmrQTOzUQvALhVwzDIP+V1GGESenJzg5OcHTJ5cAgP1hj9vrG9xe34h34PQUn3zyMT755BNcXb3H27dvsd/vcdjvMW63uLi8xGazQS9qBCeRlcRIq1Ew0PyOFhWwrDhIIQKNgxjMCzDPmd6yKJN1wJOLC1zfXONX5/8Rnn7nX+D49j2GXhIfZqADVIH9zb08oRCAosZV6QzuMqudbI6ckA8pCf4d0cK4/vsKLdmz/9Ary+h2j+Ft6RqZ8A1f31jRAJZhUNawbz0ZKU8qgu5ms3kAnFyxyibvyV1JgTGl4UOeDAvhMm3N3Og2hj3H/tq4NudSCv7W3/pbYGZcXl7i6tVv8NWnfwMASyxm77i7vQPu73BycoLOwN3tHYZxxOW5xAPv729xd3ePp8+e4cUnn3hIkZCz4ptvHYtlkwq4mBASVkF2AhnUzoROFzhc2MUi7p3ZLPbyqmVAHcXiNk9HaVDXrfmcCNSwKlNKsdxiqj0gxs0WU+sSV61KBmvkojMEEndwEPMIJ1orl1IKk2PdTtA15tq5b+zzQmhkW39YbMzK6kpJmKzQO8McJLLEDjP7ubDpRNysXeRVsApZXgYWIUUWjsPsMwthHeF+zbKFWaxotX+29xF65DxmoXjkDqeGIkifTRgVohUErrfuiqik2HCadygXRNCmkzFpXwMBpLkGBHhC/lArNpsR25GkP4N+bw6SrIA5qqb5Cr/s/llk5ybvOfY7S9lZnrFwHYN8ZIwYbsQcrKRr3J8wy2gLAv6POByW967m1RHN/CQ+3QIhELht7CM92FiKnRvXh1fCQl73cu95+VUa5wPZPR5iYmvN+BD0hB3Gprgs5mGvJEjY+bPqdNvtiOPhiP39PU5OTyR8am6R49cETnYOmGE+F5hXL+PK3CSurTVp+BjeMaCL9o7O1o+EdGtlQWW1NqoDzi8ucXFpZ4zCQeYGDjbpNA4CNMwVpM82oiR0Q2xKyzO2FvyCzi/pmtMxIqdzMWeDNzzPYL0flHZ+ISivL/J7OdHUBB/fzHz+KH5zIUhg4EUDAYAfGi5A6fwvJ7AmksiGExdSGQs8y4DrtscrmC418zB0mec50z2LhLBrbauzwgGYFzbTc7n++vbaC5WAGZhnzE0rwYEANVASgh76M5GEONsPFTjzkQRMxkFsDK2uE6YYMEfwLPOatWkWw+h2g6dPn+L07BS9dRyPR7x/8w6H4wGH/RGH/R7H4wGH4xHz8ShKVGvoPMM8JcvyzJZjwEvDHokcJKFK8OI2IqsVk5J8zmCVD4sUXqlVDK3DuMF2u8HFxSUuLy9QSsX+fo/3b9/h7uYWu90OZ6dnePrkKa6urvD6zWvsD0ccX73GbrfD+cUFxnGQ8OAGdJXJqiaJMwmQWJUesvA4RdxSK5iBWqN0s3vFesPFySn2d/d4TR9j/tF/gc3Pf4GzWsEtQqJLKeBSsDk5xd1hD9YmgIUlBwhgVGjo+8JImPpZYfn6fekB+RlrA/066ihflw3zZvzPvUDkNzgtLTVSHH7f61spGnnC6wnlxQ/D4Nd8SHPKYU9ZmbDOyxmsEVL1MB8kezcAWiSh29heYWH1rNaa9EbYjPjxyWu8roTbu1sUlhCi+/s7lFpxenqKaX/ANE34wQ9+gN3uBNN0xG9vb3Dx7Bm+873v4fLJE9fwOgNM1YV7J/wZbsi0NrEIp/wEy9t4IGAASeAMCdXcdEaQirrrIo+kofZR4pw7o/QZgFTIkDqOonD0xtidnGFujM32BK1Dq/YEYUdJtdFVGDHLp7PYNfIn4mnNAgNpXRSLQ6DWqhiETCRTBSlLtYkJqJRiMC5mPSDAlEC/zAm34iSs4hJgeeoL5kep1OpqXksO7zclZhKwip3P11NSlvwBAbckDC2FF4BIrRk8eZ6GNdojnd8GQiyhHgjDnQJKfRvgRNb/0zlaB2n5z2BgBgNxm1vQiORbyCWmDxQCuJOGVXUprkDFz7uHjVHAIULJFuAWELjUtcSzdQiSx0Zz4NxqBxDyIKfB8ktudLxZCGbLRoL25Ka/EWlNBo8hXw0RslzMKJ0jGJ30eZhAIlfT8jECc4WDpsu40s26IWSK7goWFhe+AI2BJGlgYRsOMmS4fJwmDFpn/e72DheX52htpxWpBj/D6Ixe7NmCh+y00AwKIii13jCOI+Y2o/ZhJczAAWjzKiRZa0aj7Ey7dxXkTfsEtkYvdGd4aUwQOqVQSrGDTCJ0SNlLmZPk08Qa8gY5/ackjOs4WcFwHMl4mHEUttbYbyu1HfALpIozxU5HePHM2O8Fgue9zS+FYWZP/l4/5KU/wNFEI9cNEoMcLk7o4gL3YOkFdq5Jn5dHMxKRx6a0trif0j0cy08LZK22SWR9gASYc+vi3YXsi3i31OBQpIlfQV/sh03avGSeo5NIkHkwnD/KARa8UM9mwFnpuSltBHBj7I8HtHnGxcUFPv3kE1Al7Pd7vHn9Bof9Hvv7A/Z78fAd9ntpyjerF7LPTosirIuXMDd4Oo3VRXaW4hOIdTY949RlB5rRMBOmlb8wAdNk1aHucFcrrt69w9ebEbvdGZ4+e4qzs3MQAfd3d7i7v8PJboezs3P88Ic/wps3b/Hu/Tvcqefy4uICJ6c7EZ6ZQUzoXZQNLiJPlMoaVkVgDdc13i5h40pDvaGweFkHIpztdnh3/R6HH/7n+OLHv8Cnv/vn+KgWzPMkqQBEOJaCYVdBl6dAm8HzBJ4bqAMDAxWkyecCR5O1TdhfEoOgJWtF4rHX75XF8fCMPWbcXz4Qgi+HwwfHzK9vrGi4JpcUhLVGtVYeSq0aV25uFq1qA6s7zSpMRww2U1iFmcXKZVWjrGye5YWYBVmeLyxCxlO3mJU31O+ZoXFwAl0p4yn3zccjru6v0FtH4442TQ7QgoLDYY+PX7zAR8+fo9SK1jvOn1zi5PQUpVQcNYSroKiLV+YgibTF8zWCeIXQItb3IMkmtHufC+cXRvwiVAmsGnmKvZbzYa5J0pJyM+a5oPUG6h2ldDBLbXCChZQBpBmxu9ML7E7PMYwjjsdZq/JIiUhr1GWVMmRMedM1tCJbaCmouxMoXY18LiTwSkIAyeQlQiizK6PPXX5XLHAlItZvv8WAEV6kTJrI4WY9Eyy5wCw0wbIYHlHdZc5r9/vaCpYFBSPI9hyCMQ7yaiseAgb26mZmcYv9BopmQ1YvJaiWn6FiGEhyHUqRHAeS/J2hVhG6WBmRzr8AriAi75nOtFsRE1bPj87Jmyf6Pobb35nkQkkm76kBox0AOqxc8koIYSxgYviyIIgLIU6Y4CLNx6RLFK8A8uCZCR/9CuPnROmM9cXg9tYFPY7znYUfcFihmZD2ePUAwx0OXEK6Jluyl0tnf0wWGA3XZlu30lf3onQTFOJ+uTUBb1Gb14BnU7IqPuJF8DwzFkPQsN0K7TgcMB1ntLkDrYOrerFcUQ0Bygo5qGzlZVDFcthBtWK/v8d2twVRWezjEpycGgzK/cXhH9dQXjcrJ0hClJUYY6XHtIK1+TjtC7PWdtWsU0EjHSNmuGbuWcHJCmkGPaW71ygrNE+VCyCSQ5nT+Y7prqb2CBCNsIdV3OZJYDfoSAiZrS+MEsI3E3bquRe+sRyb0of1mvN0bO/inMDn4vtKFMUfKCmLGZVZrjMF8wEgM/zs+ZCSpvM8ow7bdNYYU4cXH3GvBChCRsmyBBMMXVYCbMK2RW7VVsLoBT98TDe3yd7YXJ2FiRF1fziAe8fl5SWeXF6it4ar62vc3d5if3+P/f0d9gfJR52nSRvoNq2w1p2mSzGVEkYwhZMnqxt/0vVa2eAghqkwgh5uU/gX3lsGwA2lW5XLUNTm3tCIcDzucXd7h3fv3mIzbnB5eYmnz55ht9ngsN/j7m6P3ckOF5cXuLi8wNu3b3B9c4P3799jfzjg4uIcXCuoWmRCEa8COgq0rL6VSXfDooSWD7WAuGKalUBBm+Z2xtnpKa6ur4Ey4OTv/O/w8if/FYZ/+3/Fj04YbZIQNADolXDy9BNst6egzmj3B1y9fInp5hpDKSjzEb01x3HDEUGFZYighy6Rnk9jpCDHFzcW1vIwx4fMuBN86QFd6tJDKGiYSC8FhOP9Pe6urvFNXt+66pSFT2UFw2LDHsR09e5lcGsNlxmgB1kFTCu5ZsIhyAi/CSPxXkKStOEaxAUvuR3yHOtwSUSYLXldezOArf5z13yJinme8d1PPsUf/9EP8S/+hy9wc7vHZhzRphmdpVTjPE1gMD7+5GNcPLmUEK1CIO6YG+PYNE6dZAsKJBG8MMkBRRKiOYQ9s3aZ15WNAScGmhNvg9WZQEXh3iYTouMGe4acWYkvHnpF7+Le7QCGUiWJvUuN/94KmCRXxKg3F7XYWjw0LIwKMHe5CfGlmPXYFkDKry1kSFfiZQ4FLtmavlg3WUgMOSE1AmSKmE7DoOzjghLMVLGDhRGZcA84bhlOGQizZYlQ3CLKxZQK8rEd3plhpoQvh4kKLBbCAuKUtKfWUSJUAja1YBglR8hjV2vFpkjidC4fHe7VSJZd4gq7cGRKhSuJ+l7BY6RKBDSNO+EOcFWc1TPdWOOQuzXNZMF8fR8W1phNCFCLYIdVRZygLUTqIbQr7Qzpuv0QsQiXBWFZjlGb3bYUXuz96nvHCRuXl/esn7HwujDAJd5njWGhPNiTrCyYYlMorMHAoaWyF3H7aR55bEC8jz2X3AEWMPH7NZrQ4Onw8OcuNkV/JJ+bXdPtXLgyV4BC2O12uHn/HtPxqKEX3Xj3olEns1rZ2SBg85JLul5Thqqx5XDaECElS68NJfqaYaW2BX9+NhZ4iJhXpglhjpCvWz7TaODSsJLwFXBiYl2J83X5YvN05N/cxMFBzxb7lcbLyobhlfxLCYfsRBplTRSQbcT18zNPCcUlwkiDJ2XtPfiY+6sfHTvg/BDl/PNyisiUe81z7EpawRy29zD6AWmAyEluSfP04B6VXaQYATmcZW/CexQVA3U9VjCAYmDndbomV/qR8ZGdrsQ3dn+MZ7zX9oHAuLu7w3E64sVHH+H8/AKH/R5vXr/Czc0d9vf3OO732O/vcZyOmOejhkT1iBLgvEe6S2zwNYIVRjyDlzNAMtqd+iqpAmiHd2GYI8U4pUUd0MR8OVe9qREbrHKWGKz30xGHwx1ev36J05NTfPTRC5yen+O43+NwOODkZIfnz5/j8skTXF9f4+bmBlfX1zg7O8OGJIm5o7kXo6Kj9yI9Q8AiX1ABUZMkcpCEDkPwwBoztyI5s6cnJ2jTjPHkBF9/3XHz5O+g/fz/jg0gFfEKwJsR28tnuP70r2I8fYbKBV9PT1B//j/ik1d/juHqCrUdAVhzSGk6yGQKkcDIjxgLD3FDgG6h4ZcZP6rSlp6IlBgMRVYenJayPp8DT5OCQpAohJEKpuOE490e3+T1rZLBc4JJ19KvmVDnnAhAYtvyd6asyOcGomUJ27WbZh1TlhUccxeZ4pPDqUz5sXvXz8hzZK2s8N3vfg+fnr0Roa4O6I21++GEtpPGUGUYABIFpZSK4/Ho1nMqBWzN2yyGUpN8s4BhLl/ADfILQk1ANEgz5pS4TmZy1uRYZR+UAAEAAElEQVQKRO5+dgYL+IPt+1IrUAHuFePImLt07a61i7eoN8ylYhzhyWWiHMqIxazgWqkKNk/TmqEMzSXYUEKApfCQlUq7lxleGtUECaVCcWOCgTHmQKL0liw5mKMjLTNMg/HYeYpQB3tIJuzGykzVJSf35rnOgzrJdcuWWRmMCVhfFlZY1SoJp8NQsBlGbDajFCEYC2rNuRwhSOWymGHZSmMjQCb5KsGQcox4WKXlt67AzSFMNoqVfZa5V5g3pDMB1kiLWZoAcgc3ywliSH8XUVa8FhrnsU3OWu6vQdzgBygjNwE4771e1+1AJVwDW5iDjZ3kexOAVlIf56euJR8bPz7F+yTdmthi5YlF0AylxB9Dy6fYutcW9EcmspyDPtjDtHQAHxtRLShQc7nW9JgH66PF56DVMTej0fLzbrvD+/4Wx+OE3mYp+2nRI45aBisTPngBjjw2QT3rq999Xg+PotKrUDqyUrnY49UaocqPPz/hx8IrFbKZ0GPg4X5zerbT+N8z9gKvw+puwigWzyPF89VGIwR/Snhndy5w1qEfdNuEzUcmtIJTrMC9KZBCKZz4mJ0xo1SERGeQPCSLWeY5BqzIh6UEn5hHXsvD/TZqHkstTI+OGwqBqBvDOGKeJgUPLfZ7PUcfKdHQvCBG9vhkXqIQ4YfP8euZQNpF2MJZAWA+7nF9fYsnTy7xve9+F4fDEa9evsTV1ZWERu33OBz2mI8T2jwp3vaUi6OwTIoasPTIhoYe+2kwtygOL7G73gePAQ7NyuHjdNN4lOa68VKhKaUrDROeQw3g1nE9X+Pm9habzQbPX7zAkydPcHd/h/v9HtvtBicnJ9idnODu9haHwwGFCHXUnF6QGqgKUDq4AwOL/DYUgAuBewGqGUprMi6avEW4OD/H27dvcH52jg7gcPopfnd7wEU/YgLh7jv/Eaaf/q+x/ej7OP3oOxg2JzjZbLGpBdP3/ybe/vz/hc/+1f8IvHsH8HuA7zG3I8AFA7TsPkKGFbAlmms4uzJI5dcfysnI338o1Ip7BzFj2h/wu9/89oNj5de3ytGY59kVhRwmNQxSBeR4PPp7QBQNq95h91huhLjXQjnISoxdn0vjhoa19Kb44h9RKGx+VqY2Azav493bt/iL3/wWYwW+/9n3cXNzixcnO7x8+RK9NZydnWN3cgJ0xrv37x0WxIQ6DtjuTrS6VFhtQFCLoRySB1V9sGSSCya/YsL2eyZkC7d9vpmdT+i4KmxQPIVUOx9LxTAEvLqGsomSnCwQTnvk4cWT/kLRAJZatVu6XPVGOpyPCC/pixyx4UTdWIEzdl7QbqGBnG7WtVOGOcXYcVn0wrDwM4XZ8rjy4nlupNLvrRCQKyIujMjfWgs244BxqNgMVRobjaP0c9HENwAeUid23KikVBDhATZdBGgfCGb2e+S7AMZgLQTLhG3W0VyAcYEmCcX63UJpBi3PNhhMhIqKrvXGu1qyxYPWgbm75zELIKTKuVSysjWEkGV7loW2xJfljSYjLK3Uy5ejJNY/rNXK2F+bY37mggY7Luj1hj8hjTlsU9GuxaTy+Y7Vp73OY6+mvvjOnr++KAkurHgRdorlyPbxMTaTc4gM7LYv7jUhQusdJ2cnapA6YpqkJCZz1wxuE+FsHPbPAZTlLhWSAgf2++PzzAjycK88N4I9MipoSILR+rkPc6fk7WO5OYYPaTaxFj2H5qHwuzjfnoVmpXxmwfaFLQ1Y7BuS9i/huYcxMhAlyAPPYxJGskmLGSzXbaFYhgCL5FUVFgOX+cEaA+bpjJJiOyWg2zgZ17DEdR9traymOUSi/fLxiZ25Nzx7VWwAhgqXLCVK960n3cpoH0L5XOxJ4N8CldN6FgNSCr3qSDDHgt/aCoVnyEZfXb0HUcEf/eAH6Nzx9dcvcX11hfv7Wxz24uGYjge0Jj2+DN6kAOisBjnjCmlsN3YtDFAU6wNcofV1OCwMP5xAOv+OCAyDl2ElXG6R2jNxf1PvRiHNBiT1ckCs8/f7Pb78/HO8fvkSLz5+gYsnT3C4v8fxeNTEagk5Ph6P2Jat5BNzIIfkjrJ6d7pwYIV5ZSn3LMV9KsCM3iOqYtztMAwbMIDLp09xBeD67/4fcLx7CX76A9DJU7TecOCCYWZwbRhUft5eXKD/tf8Oh93H+Mkv/wxXr/8cN1e/QTkewU3C97lWmPz7WOuGtWH+9ykc61eWsXMaRH62OQsKII1J546rN2+/0fO/saJRa9VmK4M37DMlwrtOatk0uyYLofaSMKoqQkgq3ZUXY+/XyodYzwThbLz1PNYKBxEtlJ/s0ZAkLKkT/erlG/yovsPP6vdwnCfwPUCl4HS3Qx2lvOxhmnCYpPJCZ2kGMwwDTnenUuOYScVDCekqmljcOIRw8n+M4acf1gQImdE8AKX8vqS6CV7yHZtErJxTh0F3Cwm5VaFWBnjQx5mAxy4ExpwycwwmaL+5dYgAqHWPKO5z5qbXmNJgr5LXmcIS7DkGl/W6LZnU7rOKWJH/wipomF0dCpOQCopeAwSDELwLj5E/KzGbhaBEkmRWSsE4DtgMUr61loJKnPqWGKEH1EEa8NCn2bp7GjPT52Z7mnk9lhZTE4gsbtN/o8zuYw/WwjDroI676XeTOeQzpXYchFoYGAqm1lAro7WOuTaU1tH0P8v3EK99ATi6pILCqu+8IOM5L2YvU1t0VjVlihfrWbK3eAkfXD4zQJM9XWl8Y1D5N72+M2W0lss/ZCXS9RovXv4Q0la2XrGd7yzQKcx6nJC0bta5huXSRLTlPNK6U5gG2zPCfKbfy8YUnUtnOB8gEq+w1Nq3EEHxkFnJ7RAQ9XxlgZUh+VCdPSzTp7cWHKFzofzlkmim0+t0y63HLjWlM+brjpuXe8QuCFq1vXi+k8DluIv79fkWMuswz2PHAzrSuaWY1+JYpO2JdbNfx6sF5bAiUnoeyw/az4ozGZCyR8n7oc/1GPE0D7eSKj3N8PSx7XunN0qzDJaI38L45JgJw6bFvqfxke6khLt+iA2WSTG0M1e1rL3AxGqk2Rhm4IgxIuJAIZnprQvvDln/voA0iVp/LmmvmKW0PUmi9PGwx/urKzx/9hwX5+d4/+4drq6ucHd7g/v9vVaQ2ouCz6ZgRMKazFkbspLRJ6MTZBsDmUYocoka6KOk9EJYf9avkAN8NbYftt96L6V/3TKgiMtEUh7deRKJ4lSsH5jQiv1hxu/+4i9w8uY1Pv7kE1xcXopHdbuRfDEw2nFCYdtX62gPdOrSyI8KamkoVcu3d8nVKMWqxJCWwRWFr5aKs4sz3N7d4fTiAr/57W/R5w14+C7GPeNy2zGMI7ZjBaYDUAm9D+iNUDcDttsd7v7Kf4nfFMYLvMHZuMfdu5co9xPa1L3AR478yTKzycH5d/ttsRNJIVlf/5gXY+3tID0khQjn5+eP7PXD17cKnbLO4OsavfbdOI6uhIjS0VGGh+FRwzAIo+nLBdpvjwEzngGPac+lvx4LrSKShoLLXhvsCpH1uKg0YJpm/PYX/w4X3/k++JNPQQV4Mj8BYJ0itTqOEmKLdR9LwfHuDi+//hrzNGMcBlw+e4azi0vMekbMalKApdXMzllicEKQEIzXOUoQT7Os2yN0h1Sg5IXsT+k3oal6jBmSbK1AdSKdGRoy47ax06j6Pfu19l94E7Cah43tq8lVbtKaMuPyn/MPfkGQPTeCLACMZXxwlwvWNdlNiBGCYY0QqxAY7X5tQnV4zRDCr86tkj5L+0oMiqNDOjNmIVt73tjmyuxwNzBawz0bl5Uxe5Iw+S47QZIVh6WNySo/IX57BOaZ1DgucXhtjPcwWCq0+R4HHpW0TyMquAJD7aitoNeONjfMpWFuHVOTxMPetcllJnbKgBwPfew8NxlnTVJtCp0QcdRYluRciSQLQckSgNkUANb8B5DjcOH4fYlrNl3OqLpgtkkG0S9CONOlu1VXxAHbg/C9ZKYc6yCHTTFmbQ9EBADSg8XDwwwF5+RqG5tBrnSIbLAMm8qnvPWOzSh5XtIdvEslm3lG0SZPBJJ8CF23j521CaS5sJWalHj54BH+NBgWrpblryQGIpSBFJaiA7I+eI0bGWaLOOYMShe8l/vS0/cpv9IFpyCzWZDW/deEYusQH5eGUC/7lBaSJm/7bbA0SDykqYnXws5Y0POe1uy47DjBTq+El8hEOgjFibiln9rpgBEzLKFmNEvupdUZ8y1xXpLF/oC7knvw4smxbjnfNt80J6Tzg7Dytjb7GPY0IBR9KF0GltkMpiGTLmxtcc481ABrZyz/Xk3mYeD6+grT8YhPP/kU3Dq+/PwL3NxcS6Wl4z2O+3tM8+xKhhkCvHSw7XcwlDhFbCHTaU/0d6MfkqsXNMXlCGeK0H3VUNCFlcwwHE7fXaHm5NmAGDrlrDohlLPPSgGJ0PusPEJLrBMBpeDu7ha//c1vcHZ6iu3uVJ5dRJabJqmotTs9wXa3E/6tzxNZ1PqGxZw7ujZjrNq+oaC1GcNQUccRm2EACLh88gTf+d73MB2O6NOE/WGPd+/egUvB9vYOn37nM4x9APWGSozdbsRuqOAN4e2P/zb+ZPcV3vzrPejqDpVuAD5ItVDuDwz0coSiStU6JOqxa/Mrl7D9ULhUboLdtM9PL4QnHz179Pr161tVneq9Y7vdPtCIiKTTdmsN2+3W3VS9d3eR22LzYvKiTBEwRWV9j73MKmFKRg6Nsuvz9zl/Y/kMzdNQ3P3iiy9x+b0/wduP/yo2ZaPMhlH1WXPrWisoiFElgDrwu1/9Gldv3+J4OALM+Przz3H50Qt8/4c/Am13QfidqBvjzwJVnE2TDXJowJIhUFxoj7Xr9LB6XkKSpjMjA7NTQjtHi2mqZZkzgXgEBxnwCjLGaKySES0uWopftkavWBO/YLE6XsLowStNi8iMP4RCmngKUxCK4wa0KkZR5ibvtba2wqPbuhO8rR+DSeouD5E2qyPS+tzwz9VyGyzmFBEnLyFbRvQtZMiYb1Q5sn01ZUQEvgxSeZglzcpc+cGWEUsDNCAshAZDkxd49b08LgmUWUoGYNWYus0xMXxpJJW8NqVgLFL9opeCoVfp1TI3zPOM49w9gd4xm3MghO1DWpTh7QdwU0DZ0UjYhIt9fsYocMjXrnNICqq9vCEb4MK8T8inyA/hpfA0fpmXFGRhtc68DjuLCh07Y0Dar8W6ZXLSdTaL3rpH67Ht3uX2rsZGikxMBIsfmXNnrYgG76vU5o65d2wMRzP8OTyJWYgjCz3VcSpJWNZAxfHMFNxQuMiFyM4BI1OY7exlT4HRAd8aR6q0bg74mNBDaxg6MXZTkXMMX5Wds9iSxAooaDJEASItmWX7XYjCgGUwN9ph6zHS9QgvWQy+Qh5O3xmr8HAp4/cLtKZEZ8L7LDCkWNsCV7N/EFifkQwKU+T93ocoFxcj8NxpEUMrBCIJujKmPSMf4Vi3GcRM6VPPuCnVDqOEX2w0lMP4Yn2VPG+H0126lrT+PLbhvbFPC69lZrx6+Qq77RYff/wJbq+vcX19g7u7O9zd3uI4HTAdb1UpMn5nJVCLwj/jqNI0DoWXnUHZvirsiLyQA5WiYVi0xL/e3UhixU3EqEV5lYnGBNW1JHCHPAOM7mOLQUrpAjOiCTApvszujUDvoFIw9wlX11coN7eyUi/vLcrN7e0tylixGUbUQcL9h1Kx2Wyx3W2x2Z1i3IwY1GNQqkiCRas5yh6y9q2y+RPGcYPbm1tUKrg4v8Tp6Rlev3mD6+tbUH2Jz37wRw7/QZt/9oFBl2c4XJ+jnj0D6DUK9gDu0cjyd9cUHw+M/x96PaZImMy9fu46LMuVlkKYuoSVbXa7bzTut/BoSBx57xzx5CRxgnNvGMYNmGYwyeDTNAGdUbQ0rU1UNCMVhJQImPSVBRK2mJAeC84JYzkXw4Wr3oNgEGDat2monAhlrRWtSwOpqU1gYrz66O8B404s4mTjiWY/lgqPxqM4/Pfv3uNwewvMM0a1uvA04/2XX2N/d48/+ulPsb24kAY+ioCPu6f80TH3BdElF46AzJjgAqqvO1kdM+OIweBELBNZ0kXlsU1wD7fzYjpuofHvH0h85OsxC6IN6swIS77nxDWe4E91S5ReWKCVrkqR8DXrEUHs12Q3uCga8P4Cy+eL/ZZNmDT8MrCxiZDssCGN+xwLgWpRZcNqmeORe6FEP20Gscfk2nXGVB2ayQWaQR4k2sXL+IfTZwVBIbgn0bfH+K/R7oWkEYNxem94WtIcA8zxZYSywXt3SNG2goqC2jvGSphqQS0zDtrwys8rW0iN4Up45/K6MtaZOJ5/KVnopHQrhWJjcoSdMcuLCTjoHztb+YzpnDi9sY7FwrOVeeaz6Ahui0ieN3uyM1ibY3hbFiukR4QXxeNuCcE2ZwtH9HFWL0MaF/DTupml4h5SBRMI42cmV0zBXUM8inYRnjD3OboJQ55V6yDeDiizS9V0BCS2DtmcUqp4tGuCX0YCAxuse3J4CjJtSQiaPifEIMM0pSUmXC0Yru6HAkcruINIqn5ZPLVZ43NIjwuoSruMzkYIcEqoTVaBlpVahQlpw0IpedCXgnkOR9Lx/awveEmMEbiG8GiYEGnDJnDbWIITcJwP5FiIs0ZknH8s+BzHA21suwXxU1zrx4SVROpu+ro5y8uxbjfIpGGNpq7CDkKmEMTkxfOWBp1MFwI2xgOVwxArbUlnLK3HzoB9xdAoEgLmacLLr1/i2bNn2I5bvH39Gjc3t1Kydn+Hw3GPNs/gPsM91nrWQQF/96joGhh2huFKpdOHPF8gEm1U0F/kLgL+3gDCiky+XZyUjgd7s6BiCcwJAZh97MBBSx7XqA7D7cagKkDo6jk3j4aAX3qcUJvR6oQ6DB7BUu/vMdxtUEdJMt9ut/J3M2IYR4xjkagd5WtDrWrYIUyt4+mzj3CcZ7x/+w5n5+cYuePp06f4+tVrXF29x+7VK2y2G4BPcH19i7OTE5SxoFPBL09/hD/54Tt88fN/j5EbmBqYKtBWsIDQIM+xyNDrXfu+VP9tTe2zXOxKpsE4bY9da69KQJuO2A5/yQ37pBeDdWQNrcrCPEqV8ltdEdCs1IW1C2zSZomKZK6DPe6PdHEEaDlHRQySMWqtIBCals+0Dt8ZaZlNSNbYNIIDuBhC6XiSOS8HkLmjDSP2J59CWtQHilvsLKcdcsZVCu7v7oG5SeKcB+vKug83N/j5v/23+P5P/hhPnj/H7CdtZR30gxEWjKXgFG8WvNUJIxZ80gi70VpzVstP7IfTD2NiLGFdoCz/AOmzXuBEzCxknJDThCFv6mfzQYwlT+VF9a1Md2RtltMgHoKieCA0X+uTF1KCTb7u7nECOqI+2GzaLf0sdMtEgSVB657PETG1RCI0W4iVhElpyBR0LokZS76IKieUrEauILM/295kkuEH3PaYo+OoMw7bR4M5x286BRBpL4uEA847kF9JIJFNWFo3QJ4QaZVERMgwoS4JqH5GoQUg5N5Sda/qgKFWDGPHMBQMU8V+mrUb7eyVz3yUFFdv1YRsH610MpAs9onBL5J/8/v0187gwxenCx9Vpx/5gtLcjG0HLtm/cabXY1N+VMyEaDH3RdhPvpsC59ieoYJWhJ/kMIXl3ONBcTYe0CwXloymmeWWUMcRwyjV+eZ5EoWiK+5qzsXJbovrm9vgAws6q5ZUG6ZInfs+N9AoM/JYbcd3+D12DkJJhdPQ4BlQA4V8x0kJJ6KwSJfAlzhzDMolth2eBbUsz0Pebwn9lblTB9A7ZhWeYvQwaTiYAQ3nMXqiUHdDnvA8Dx2BNkRLSE8LeqAPTrtve+tzdqXF/q6vRVpbwjUscZL8yc5ZV3ud7sj4atOBYeAjY9tZptghoesrxd7HSmYZvSWx0Ad/87p7ayI7UFBMkzHWlYjSDsnZYbjiCQ7Y+nP8QCs0VGvb1ApQwWG/x1dffolPPvkEzIxXr15KFaX9PfaHe8xHabbn/r1kvTP8ccmGADMqymfdwaJ47UAQC1hXC4zJKQZjAns5ROtts6Jqi13jxV/bXJsn+VeyJ4/jmuCHUi2DcykpH4/Ci8Md1LSkvTdUNqM2Q3Jt5G2fNcJFPRa9FDGY0z2gwrzlXY7jiM1mi912g3GzwWa7xWbcaFqAJiqWghcff4zTszOc7rZ4en6OP/93/w6X56d4e3WF4/Ee8zQJfSQCNykYc+wN5fJH6Iefo1ycYLphNHT0SZopr9MXLM/RjfmrqCArP29r8HvMYJIFPcre5NjFrMQQxNNIrePdy1f4Jq9vlQy+jikHgLk1MBjH4/FBMnbRjcp5ExZSJchB2iPDrJ22KgBEbh0JBsQOgPyyeUlseneL3dybs/aiTfOszn7vkqPBrQEduMfWiZYQtjiWi9GWMh+m6YChVjRmrYigv5Nae/cH/Obf/wyf/ejHePrpx5Fo67tGoHyYjBEiCZjpRbDE3uW1FqGWCaS976v7168FQU1nPf8V8HOERFHc7WTEhEok+C21lWXohT87rEZOazWZuhbCYLhhsNKFuWFF4eHx3oxFGBHYfte/nMdGEmTZ8xcymwymAVUqCoZKIKqotWiCGDnzZKSEak6MjaOOlE+N47f8Nx/whfChng/Pb0KO/Zaxm83etI3HNn31Mo+1X87BfHKManCB8BvYfpv6sxBOKJhwVhCbXUcycLXGg0PHMAw4ThMOU8E8Ncxdq9SlNdpMAsi0yL1YCwrr+2j1fnEGFFc4azEU4z2mICyEKsO1B2OHi9/OwGIOvFqXj/f4d/b9QyqxZM+LsYHIeUl32pUheqz3Gy5A+flOMDEvliugAIZhQB1G4HhQxbGh94bWmlQtYcnfCOAvN09sNvLBZmLWuSXMabHvRsTznlpYY945gznAkSqW6FX3vkHk1ZeIGbxoYKWNzShgbgoQwc67jpHRSd/0zg4zIrhwyYm+Z3w170Ml6Va8GUaMG8mFaTpniaPuwps1fNj3SXGOdC3RxkU2LxublufCsGhFO4F0tX2/PB8PeEnC+/iFltesvuXF2HG48l3uB3Sv2BIHFsPlYY1uuJyiI+p+oVDau+QJgIm7yUBlwnjCZ5lOkfmw4UHa3BVsVDNWg5Z4Bff39/ji8y/wnU+/g+NhwtXVFQ77O+z39zgc7jEd92pcjQBCO4c+HcVdM7BK35ru888GRzceJoFA8DnlQBrMmOF1MH3deWGkCdtYjR10aLHfYlV4FNcebKM2fA4jp6zPVlU0tKr1FkZJIGiIT5PlOszoLA1wXUAHiRdX5ff9ntXwKWFopcr1tVaMo3g+tjvxfmzGAXWs6K3hOE3YbXe4u73FQCJ79jZj7ozD/QHzlrDddnApOPYBv96f4/l3f4Avv/wcBQN6k6Z/uZ+dydzz3DCO40JmXOcsm6IEwO/LyeJrJWSd7/HY6+ovu2GfvfLA3hadIlnE8iUs2TrnUtjLe2voogCgIprwiTejOeLVR6pGrV8ZaJYwYwnskdAjD6RCGEieSbWCe8NnTzf4HXcw1XTo07rTmzhn2i+gzSBI+AxIOzDWApKQc/Bxxue//CUad3z0nU9TycDsaaAQbrAitIlic5pHnk/U2I6fOuGR2Fw8PLH2VSa6AB6A+jHzEAgRAx5KaLinw1rv9Hl1PyB7UkAejlA0BMoUTJulEQQ1AD5cjgmJqTygW7Y4BIs8E7E2qUDx4GHsQlYpEidrJWllftn1LczehTBjKgYThjObdEsiksqkWXMpbJ3p4sgy4KTM8IKpOMTin8Ur84nFTuQvFgwTC+XeWANZmJ1cjoKiuKZCGUlHONKHGwPLQiFZAQ9ojkuVMBLpL1JxrBP2xwnT3DR8rCdhXZmpWdTT2QxZ5KFIY3Bf47ntQgabzR1YWmsznJdnDM7sXWJM1nOHDYDMSO1ejRRa7E2ShxZfZi/rck0PxauFRy59T6tP+b3R4oUCajAzWpHmbkIGO14UbHdb3N7dYNKiHF37q1Q9H/M0L/EuKQlZAFGMw1Aq7vb3OD07U2GyhLVuQSzDG7LcHDtv2WsYSsCSxppir4YBNbTYwWO/2M4fuTAWo0U+l3wyZIty6Kw5Y9aAlSjhGpugSMq3CJtxxG63wW67w263AcBoc8NharjfHzAzY9YmW6T0pz9YHCLEiuwcscMtIM+u9MCMjPGEdMbSc+3fFdL4E50/ZKzmkFtj1/x8PyRjH6Bii4O5xu/1LUGIjPZGbqHiIYkXiBROtQ4IdVw2i/QwcnpWXjCl9/kwOQhgnevNE6xW62FAZWB/f48vv/gCH7/4BPd3d7i+vsF+v8fxeIvDcY95OgrD07wFrwC1Xn2J9YYXU9ZnzQcdF1QhwRr0C8MX0h5zJG2bQVBxymmd09QwYJnRw/gvEGPnbecP7jcFgK0/BxkoVF4gGav1htIJpQ6LtViIIyDGaGpdeZN13u6QVETyfWQGGqQXXG8NMx0hiej3uCmEoQ6gUjAMFeN2xG6zwe3JCeogZXHPT3a4v7nBzdU1mAe0Rpi5YmbCZjOiE+Or4bt48eQZpjpggwqiWZe8Om/K/3OUzzox3O5Zt3p4LAwrpyR4dFC+potXFZ2XFUJ/z+tbdQY3L4VUX2j+l1XgyhrRMAxirUJoYNbgz36f5gCcNPSS5J1aB4i2KZ+lo6zUPj7dnQjDSlnwnnhOghxtnkUDLQVTm0EkJW6ZgKbPsjAA5o7j4YCLJ8/TzsE1X0PxcLUJ9hdI8k+fZ6A1DCCFQ/E4WhFcJWmmTzO+/NWvQWC8+M6nUgK3M7S0w4K4PSbPB5EOAmWEeEmuTfBJhNLYxmOCiV2KtLwHlAQw7d/pJYJVLwU0jrucCPsCEZeYxix7JoJ8EMJiT2ELX1rOOVsQ43tl7ZbkngRI1vhds1p6zDHHumWvjKeyEyBiaaxXqpSwq5b4DYR1OCkFTOxJzTa3vqjQkeQT3bDwBAYMOwNZCTHFDYA3eHIBSOcc1DmseeHOXr1WXxq9zoyBbB+VWJswafG8hUL46CkB3zx6wfiFKMn3ySumFl2yfAaId2hARRmLKpwV++MB8zSjdetJnz1rlISFJIIshKLlgh89Y/kc6DPJf1vGNwsM7BSE9dP21XeA7bkxEx86HTQiETSyAkSLi20v4wNzeILd+6I/+hwBZInB9scgGHhFC/gRggEvaIsN4jRScV8FDRChW7wOAeN2AwDuzegcxilioPW22hkVfgpW34shYhgGtLl5gm9oiXb+jPbGA93tz3kX4iwZ6PqD++S63mNuBmdSsKbRVLBa71t4WxjiUVdi44KlVZISr8syXwPQkNESle8qSYjX3f0dDod7AMDxeMRxEi9Gd3qgo7oQCZ9tzs+I/V7vctzACTHjjMUdDz4xXLjhtZhIjwTF0HIu+eDS6suFBzcZ5vJZNQ/NksSx50lajxBCzDP2irA+iG4IsftTR/TF5J2lr2EeSmrMxyhtwJwZ4K4Vj0DYH+7xxeef49mz57i7u8HtzQ0O+wOOhwMO0x3aPImcpDeTbm6c2RS2tOLfmbdb4ns+7DnXZB0WZvsi0o0GZ69iOF0+0H/M7+NjOy8GAipB15e0O85YHiHkkqBemS5Yby3fZwZ6m1FK9XX7fuucWPN6iqGAjrnOSQM0BaBAlSzFqEaY+ySG93nGPE3Y0x2O9/f4wWef4fzsHDe3t9iWgndv3uD2/ojT82doNAClgIkwDhXvtp/h/3v2VzGe/hOUm3eKH+yNr7NSQITF97kiq7280irwQHmw7+yeXJzJ5P5QShhDqSgArt5dPXjOY69vpWiYcpH/k4z1sgAAABwOB5+4NfozBcFDnZidYbRZLFsDCg7HA2odnQMUFEzzjLfv3mL7yWYxrwzs1jq4NcxtBoEwjKMoGGAtDcZyGHXMrsngdRhwPwHY5oMmiGcMyKxOVkXBkLr3yNg3WjjqXyaJQ56ZMUCqr3z5y1+DQPjok4+BIoqPtZmnFHtvijpDJuCHfiUgBbuML0J4gHM9zr8hnp0FI7stiU/pt0wg49489qLsoD4r3a6ha2pYUeVC9hcuaMa10qHzMVHR17kaL79MOHDC5sCMEJK8djusTMHIiEhCFKoUQrAYcUpqvOBUqmbkhE6FHibJF+kMUCpWwKvx9QvLSQBCmQCW3gsTqMxiae8Fbnmp8X2SihxiwZjTftv+mCIFaB+8QECzcps3g9TQAKIQkgCwMlxrqtR1M8Tepoy4yN7n0Cpj5ATChrQnCQF7KtgfjkL4KFawYl8euqR8KC2b/Du7JfGRuMqFmsSwXeFLfxfSU+Ca/aX0WwgVyvbJaMuSoxbLSaBYT1b8rdO0bUfuL7DIv/K77U+MLWeOHL8i1C0AkJl/Ppf5tcg1shAgLbTQmDH3ju1mCzDQ5oY2S3y7K8gIITKMAgp3T75O0FPaDbDnUth6raz3Qh5JBMrkicVvtty0pgV90U/5d1rAR/mBlkmnqCLi1yYZFoPRYgbKWJbP1g7ProxAwyJ0g43hN25ePWkJO0ZTmphIjI9Nq8/ghN1pkpy+MhoOcJwj2w8O2C/FeRPa8nPWVDxywixhX/6fLfCP0H3dkxwGm72MiwvTGryZaqJpMtO0j0kpMg+GA8B4u8OkA1wWvJgXgrQl5+fQnDWoS6w7ESlWGaqUguPxiC9+9wWeXD6RZO87SfaeDgccj3u0NsE9AcazEjDCa2TrTQSLlt8szmBGAoNPgjk5EYWPHRUGBWasYUUxVF/QMYCc5huoHVKcAWUTQOwtOefB8pXvJVcsAO0mrv0vGHDFPiG580xZYUdXyz1VOd9WIVO5pId/Ba+HNPSDGJxVcgRYcksPxwOub25w8eQJ3l9f4+z0FNPccHd7DdQRddzg2CpoknYMJ7sd+Ed/F7/58jV+9OX/EdskG8zzDPM4VI3KAbDwZOTcZXs9pmA49PR5ayUj/waILNC0YuvFX3YfjTxo792b8tVh0Bjq6G0BknK3pRRv9GfeDMv16MyY2oyBBlVSmrgllTqbF6P1jplFwXn67BmOx0mFm6LKhcWgijJBtYBY43+bxNtlIDEztMCJEHKSTXt32IF3RfM3RFxb5I08ZgLtklxOnbEZR/FuKK6bxaSXInXSO2PTgbnP+OJXvwYx8Py7n0g1Kj1FcvBsY5eClMuJyewaREKJHMfBIdX0A8cC2fQsrQ5+erSPbzG8uu8wxmKsJVvNE41fBakvhAUbK0kAnZS48zLELq5NrGzBSLN4Hy8n7lnI4zhw+f48mFgsbO8lP6RW8sRvF8iM4clN8vhcNco0DR3D9oHZwv/gCoMwI5mJhSIa/D3PRAFr91j8ae/xvQhfi13Oxt4Eu8RsYMEeHN+QKREKeWNAiXAVJ+TKzEkJq78XxcBKFYol0GKbye8H5BrzDAjvLQt8qUUYd9kMoCIM+P7+ANbmU7IvNe1mWotJ5PmV+FPWxT1GH0sBKjPiAgq8Zmj1PPWOxmNDeIGs33GW8smBCnsmEKzP2BKnvQ+IP8O3eUE3fFf9YKQdT5K4GxQSfOzXkt4HLEMYy7/aGZSqbxpXXQDqhHk6YtiMQJGwhcaaDK4HIp9Pe04uXOECQBxY9V6HIGTGjeKCyxJuLuj4IxXnc3ibwzid2rTf5l0xA5NYqsn315TjHKog82xekUbCsDQUIVlgmilpaAtLLPn5lbwL83pYLp6rKT3tCQUmJpDln4O2kwHnYQ8R6xGly5PnrXhF0I7gUz5elhH9xkTDTf7j1RlLPGFxiDjeR24ixXPyq2R+JHNUsrLkFaxKPcXBJzuM2Siz1CbEM90ZXJfrtgIs4zgAIMzzBFdkyHhY0AmreuhGS8WPqkat1ho+/93n2G13uL/b4+7uGtN0wDQdpLJUm316WdkwC7+DjvIeLHfCQcwOVNmTtOdGm+wOYQWr/dZ3jr4MlJKJm2CLLLMjK+pYjW0zj/w4Ow82dtqO9C68s1g9G35GuXdAy9gToNbIQJjATTOyNnQUFCZYMGjOV5SlBQ+1/Rb86QBXye8BAO7gTri/v8ezp8+kj1xrePb8KY4v36AURuszeJ5QqGCcZhwro9MEfOenOIwjxuNhoSgYvem9oS48DnCZd610ZK/Fh7waWV4OMCavhu6xRHd8s7K631jRmGdJyLS6wfMkwj+KWsaogEm6AIOl2kXvjArCzADVQfIuEvOQ+DYovavgDkzHJhbPIqtxL4ndRwRwQeGCuXV01oZqpQA8SQIck1pQRfia5oZaBtQijUksTKvWAa0z9ocD3l5+Is/vHcfpiAKJEe9dnjdUyd0YhsEPdess+RkMbErBrB1srRJPAbkATURo3IUZH2d8/utfg4nx9FPN2TDiKXsKTzhbMXjF7UACICxc9iOla1esIA5rEtKNgKeX0V8tKBHsgKHJkGFZNeYi080cAc5ZbAnRrA7wI80aQ5wEdFs3AxE6laSfxdgI1hqMNYeFJI7FUHdqwC4n7lo+z1ALhqqN+zw8RcYxK1yz59mUu67fEzxVgdCb2ZRK7Xkhnir2BpRmGQJrYidC0TCvBfeAkYyrjE8Fk+7Khs3NIBLWkDUfl3WznpuAO6A4rN8RSEubkoR4uFJCIOpJkQicrbV47W/zfDARGsWzvext1/UULZnI8FKqpVTsNoxaNuA+43DQaiEgdXGrgKuWQi91aYK2PSsJIFTIQ988ld0ESObAaY4TlIy/jsPuQTFIc1wXHiV4VTB9EqzhonSjN+ZK/nzbBEJi1IuxF5f5vX7G8npWL1JBx4TKfPwXCaBKh8L4F1jjoChFEyPlutbZy0duxp3k7jCjz7PyAIG17FTg9wPLt4GihEIh59PgEAARL5cAJicbExA5cVBcY6j3IIARsiV7qDcy3sNoLAltsdhzhnu7hSd07dtCkkyKEJQAtfw6TdWdjekp7gQUbL8blrgRtE33yOlQCZiSjV2UVpI3oHPYBnbJJyKnYUYzOM/Fx004kD8b7iVGZXyhpG9yTH7MQ+9JeG4f4rPdD4d57CPieWQrh8gIiT8EzZNN5vSvj+MwjuudDnB4ZDLXMXxobRY8hdDUqLxIDp/lmmWOVCByRu/46osvwb2htRk3tzeYp3vM8xHH48E9GT5JhbWfWzM8Au7l9BfDGaffGsQqA2+lbwXM3duoDxTFvfh7kOC5tn9ZjR0xkcnehKjCEnjFCU55bMfRBRNzc23IFrYOMLgbD+8eCi2P7+qlKQ/CCQ2Pe2OUalMMYp5xMqARMG/cULjoc0QePRwmUAE2uw2m6YhxGPDDH/4R3t8clFhJZM5cGXxo4OM9CAWHecIZN5ixUOidyr1gzNyc13iYpTAA7QWndJ4EBszQFiSx557T0oUaC38gFCbUYRT5hghcpWlhZeBwe4dv8voWfTQqirq/LMyECgHdNHM5yswSLzqMIw7HI/rhAAAYxxEoRfMyhAiPdUBrWj7ULFPqEckhJE09KESEuck188wuQ7be0PukrutlKh70sPdOKKWidWvwF0Ld7uQE53yNW2YpqTlNbtk9Ho+y/s0GDGAYRkTJN61TTAD1pkoFe9Uf+WwETRjyxIyBCNM84/Nf/wbjbouzJ09U0Oga106LJUSpOUqHU5mqIn34RdLy/RDEb4vKEplAUjpgFH/jgkwYBPBZJgpEgQtpRoyy9yJ4EocCQ4JHYUEJ5gSkexLF53ikChPrdcticlfw/JMBgwEPTRPrnpWtrd4jA0ShOBiSp+dZKefcbC46fIunxPGZEeu2a0zx8HV1vUfeO5HoFv6X75fzIdO0cBg4o3GGYgJAXjcreU4ApPQbSEL7iu5RMTigeAk/aUpo5sJQMjy0UnOoChVQF+G+2JAk3qLetZurhVppmU6zztm2VwJoqKDTEzCA/WECaaw7yARNqUIyaO10LwWchPiM516S0aqgxGV6XygeHebNWeEawcNdePUTDPaKeCXB3BS7fIKyUONIbnN11E0CkU8hRSnbGhZyA6XnLeFqgkde2oKQpLMWsFziedNE1GaMUOnrbrdDLRXcZrRJwqd6Y2C056WQC194HHdSrzhYPekaWw1SF78xR6uoZWF8aT2VhVZDcbOUglLN+4CogghEPinFWq1oiVWYyoGSKxDFhyS8CVNPZ18J+gOajeR5x2N0LW1E2otcbW2Bk2zKfcGDrc0IGmCHdHtmmNEjqwP5FlEcwsLN+SGEpZXc+UA8x8+RCkTBx8hxeDXFhVDscCtxPjldF+cwPLS27qWAywibbOA1gxLf5cBHIp+7Li0dK/Jr5dHL8+25k3YPq+dLHzAUMeK+ffsW1+/f4/T0BDc34slobcJxOmpOhimrC6yLfAMdM9j30pskczNcY6cFdvIymjn82UEROOp0gGNtPiJWz7WHhWcvK6is8Ht0bKzGJjO46W8dYCoLWPs9+rD/P21/8nPLkuQHYj/ziDjTN93hDZn5sqoyq9hVRVIkmy2IELrRgARooZXQC2mjTW/0H+if0kI7Adq1QKkhNUQQIsWxq1VZJLMqh/feHb7xDBHhblrY4OZxzn15U6Di4d3vnDgRPpib22zmbshgCdzNeRb+zoAefFXXrfF2KpUqmpdTGbjITBbWHvd7wC83YxXpd9LDSzebNQ77PfaHA/7gqx/jcHwHToRZ8zVzLkiU8Pz4jKtEeEpr3PEL3NOpdKQofyuAK1YW0pqSKtq5KicC5ro+JnAJbAJj1OWU4x4InAvSsEKGhMQa7Xr32+/wOdfnh04p93LXi4Z5dH2v3o6CThOY8ixVn7rUSywXgHGcME2TJqtAjn8vYqmcptlDqnKWRD/q6rkd8nx2AFmJxBiuVcK5GIYkrK76PGdIxv4JOWf0WsUq54zxdMTt1QYDHxUxRHFJKmRKkjnpWSBqGTKLly+MLa5s8o5dzAuES1auQFxkPXWYpwm/+su/ws///M+wvr7CDNtgJsQ6traCBZtw1W7sIIJUTq3IFYlw3YHUCDDxcxRUdej+vm2sKAfZW3Z4z/IXIFbGCmSEQwnIynsqU2i+czOQZSjUWYeojJrCqy6XRJmA7JyOhNR1IhgjbshWuYmTd0GV7HPd1KZgFFUoWCfGHPIx4u9KyGQrK9MvVsmmMoWY6NjZwUWklruALAZzZkZCZybsSE+kZTILGCqDtT6pVKFn4YVhsHi4KGmyN3m1DkuetIINRGIdydBzRyhpKiGjEKFjEV0svLejVHM37DA0AH3X4/rqCvP0hLkUgLMo6JmwWq/VmmP0ykIJuMWfUs9IKXF9Q1JnlI7q2rsTfYHnLpVcFI5MrOSzHys+Ufh7VpK6khrEGOnYe/M9zME9BYu+L+1vww2K7TRXnXcjRJgwpvQRECFqvVqh6zpMeZbwKfMo64Ri2AGMrsU5FatSpbXt9SykrFUJm/EGGNkwmypyDEhp5eKlKqUJw43UPuzzr4TCFXabKy6jgaxh4AGBALvg5/TcQuaC0NXAdtkJ3IiRGgJe+zZ+A6rcxOdpv7PwktIupAtmcbugGUIVw6wzw3NA+UOKT9ewFkAMAiacGt2KdnfnRWHeTe4BAl8IX9yoZIJUnNKSj7FEndX5UdN607f9EoTJRliL+9vhHnlpy7+9FzsNWqMrQMBBy9heXe3w8vKCaZowz/V/O9meNeGtFqSo+7JSoopTlZwz7FA5hzV0D5DtwbBuXMOwTfCReymcMbbom8MYorax6Ns1PlN6wsDrrIJwb30jtfNOOIMBOHhBdN5IhEQd2LAtIDiVIonYLaF1GoQEOYRzqdE7HEMoYcQ1o3WkKQOl4Hg44frqFh8/3IOYMJ9GlDLh7u4Wj8csORDzhDxmHA97bLc9Pv7sf44v/uX/ESvUvS+FBWpIckUuVSw0sdy2vSlqXk3LZRWhi5HWE4lvlIzPJ2CcTqCh1wMPpd2HDx/xOddnKxrjOKHrJaF7tVph0sTuAZL43fe9VIXxw/kkTyMza4UGxjTJO/M8o+8GPcCLPd+DSMqBMYBxmkTzTRa3TxrXWFBKdgEGqNn01jYR/ERye2aa5kYTN+FHgEpYo1bEmueMvpcwqGmekFKHoR8EjdwSIAvt1gXT0o1C6spW97gm7iSWyoZ5xkAJ+XTCX//lX+KP/vRP0W026trSzWfnvgBK/HVz+e7BgrgsqJs+UG1n4X6g3L7fKl8UgmB7aWE5aaQanaNZtZYWuRpqpFo3AzVa1eZVqgAtC1IZPFqhyS0ZvokXUz7bcO24RfhgXyJjUuLJ6PwQPmdWXNspZt3WNoyoWBCPGDw1V4jt0Eq1UEgJqeqRYGglKsOV+qyMtXjolDFUY67EJEQz1C5nB4p5CCuYLFwDxU/xWMotDmSrbOOX5iFU4aV5CYCGKVGuTMQP5qshU7nUgxcpEVIhdJq3UfQ+J03y1lwEThb/D6RiI4cn5d/cXOHh6cmrczFYcrjcyulIAai7uAofilsGW1oE7kS/P7UMO26vuA0d1wIfdQvtOcTPLmeMuqBxPHHLLYUEP/V82YXLRcakG7JQeaXCzxlno0S3bTU5JtaM7U3DO4U5sZzkPaxWOJ2OyFkTwjlUMIxCiQsSdXysgsgMrYNPFtJavOqVWUfZoUK+x+R1PlsvDmMXQUBpLuwdg3VNuI/vW1iMCSYMWzsTtCoM67uMmkgSDBc+1zjvuq/J+tAxJtLiIfp7lRFNeA8e2KyUgYyPBuul9m0ORBP8XPEzdqZrA1juYX3KJ2joFwjyZVzTfbRMqFl+jn9Ds37b1oiaLuVZ9iHVy/G8wtyU28pLbD5R2F6w09C3e6aMsFDlR3ZA8A9dEpkxe1Wxkmf8+le/wjD0OB2PmKZRz5+ZME+TA5U1920JKLbJI+BU3KAQBaG54r7/BMwrDXBGE2Civlzmc5iH9pdx/wC80IHjudGrMCvfRS4ThCcM5s6X2dfGDQIsBmdKpLlOthc0OV0Nb4UYKcgLFLoBkYeCmVzgodlYKElx3rbnjD6xnOex3+/x9u1bgAnTOOlYC3bbFR6Pe3DJeHp4wtPDeyAf8Wr7JcqP/hyHf6nKtFurhIZ0iUAaVkGAKx5yRFyp3nbWSemBfuaZ8+wSjrBnkCoyRQkTDx1ef/kWr+5e4Rf/w/8HuSQM+I98MnhhII+zLhJhniV3Yp6k6tQ0VRMRswj80zxLXoLmdUiYFCGlXkKXAFdCiDqpEKUL0qXBPR1WGleSUbK2kVzZiAqFIDU0RpiRNdSKNaG8lgkkVVCkHNjP3iT84ihVUTabNYZhQCkF11dXcjqkso6q4bPvDGYAdtJxgVp7bXGLCpXsxI6IQcpsu0QYX57x17/4S/z8z/8c6DSx1ZgovCnU+ubh3nKhAietuE+Xnwt0qlpo2RmWsRM4U6uYWPdgbZmW7cLZmsKJm3fjWBpmXCrx8ZjmYDlQ+bYyHHvXlbsLcEFlyiZ8wARfkspG1FnZWrUqs4MZ7pUAYFVeomXWnjn3ZoQqa1Ypxxiev18tFAYhhlV6Ih+nCEJ2XoARd42tJPOO6H5Q5dsENQDoTJAPB/eYUOSnnJPE2LNWaSu5YJ6L9wVwcFNHJq/rU+DGgcIsGdOzlra1MA6Wz17eE6nSAZBU+DJ8I0bKCZwseRMwgXA1DNhtt3je793qxqUgMTUhJ0veCgTm1uBeZW0ckYjh3hrr2y11sL1zZju88K3ek77ZbzSMNuyTM5lrsd9kSK1yaPyEFi/HZ9p5t+OIfdOlCcgg69gcF5TAueAqAtd6tcILkXqi5SwNP6E6UgilQ0Z/PD8kTMzob84z+j7Ww+cw7zofwEJdzulC06fNP9AWoxeN90o7MabdtOf1cVthyefJAdaIcpt47DgIC5HMxysKdfEhR0cKv1AQFEvNoTLF2scYvIXyfYFM2o5heHteSZisIh0tGVNsm+B4xqEZP8BtuUCfgEMFhk15KcgyLgyjKmdh4NECzfXHCtflYto8HC8qn4xzlP0jH2Kojyk5OWcQIAUtwPj44QMO+z1Ww6CK+QwuM/I8Q/z+yjhUozUaSaj83fYBBR2HbU9Q9RwFW0I7L6PjdTYt6hMAy/kxA5bN2fiY8Qqja2A/LNPHAwddHcLZei88U74o+jDVzz5vjiNWzuTnYcDHB1sbhuZsqoEw8DYfAYdxmwxAFMCmMDWBwZWiovRMPjMSSpYc4K6X0OynpyfM4wQuGb3xvVLw8nyP0+EZfSo4jScUJGQmTKEAjMmhOUvuL1CjCKJy4/uV0Bz02yKB4ocpjDoOIgL1AzD0wHqNv/2P/ie4vb7BX//mWzxP7z335Xddn39gHyUcjwes1yucxkni21KH0+mIOWctcyuXCPaiWGQuomCwuAhnyn5K7Ha9xTAMTiDyLIsAtVo9PT1jvZYTFuWEcYConooYvRo6SORc6sF97rVIfmpiDmO1jH1mliRyJfQlEAVBUrPj1UX0TZII/WbAerXGdDwhz6NuJCmpZqFX5nYkVqCnhJkLCs9IlLC//4DvfvlL/Phnf4xZbUaFVBt1KWSxqMbUwuZ0Aw1qIncrsuhMiJq7QBCeAhOyho3+LgWPICs5UWEmJFOKAjJHohHkNB8WG9EO7zLgIUXOSC8wc08+i3PiCpuogMQxyxJKuBShWgIzG6OqVsuMqmw6sYPlTRb/a2MuQclgHwO5wOR/Axe2vZBIHfFuQWHP4ym56KmltUJWooT1egUiwkrDVfqhR5+6ej4A3Ccmli2lzEkVrRjDabNTUo1SCqZpwvF4wvEkSYmz5VepogBKLphxeJ8Ifpo9mcBVGEWreRUUpKIWcJAql+L9E08HwEzIWsmkV29DImC3XmMaTxin7EzBT3G25PMoEBrTWOydiKfGSPwi1MRCiknUYVsuN1Ns68K92ne7ef1575/rCwAs6dmEh5pDaRPi2JzM35gL1R8cJxZtX2QbioPNvC89FyQI+1hKxnq9lj2VZT9kPa/GnUayqVyscIEvAExQVVay08pTde+4RFMVyDCmZVhJbXYpwgRBzO/EfdDSj3M4Xfzod2puxoVn2XCutapGb8rimII6IbLlj+JZbSSiGdAKSf5bgz62SWqLAWtxdtfbDpsqxjqFvq35s31BLT13PvZJXKvjNt5cO4Dvh0a9VI9D0zcByzm5mfBC35/ay/KF9XwGDUfpUoWnCX7eBotRJElC7zie8Nvf/gapSzgc9kLfsyjmeZ5qmBLX2TbzBtrfqIZRXzQWVALhY/cVNWURC0+ECgAVNrQAgJuiashraD7CnJmrQqt7lHz8bd8irBc08z6bFDkMHP2ohl6ZMlb3QvXwSR32AkIHSsIb47yLwcmKd6QIjxYErsDrQAsYnRGlJFEMp/mEjIwvvnyLjx8f8Zvf/gbdMMgcCZKLmSckzuhJKpBRnjAXxqRWymWeDiGjS1I0yRRvKJ+PSq5F/sRICb8cv2T8lMTw33U9fvKzn+Pnf+fPQW9eg7ZX+E//8/8c/7f/5r/Bfv+Cz7k+W9F4fnnBOI44jaMkdgMuRImnoPOJWOLcerVGN8h5GNM0YbVe4+rqSvI0GADLGRvTNGEYhnqEOhGG9UrDoMjb9IP5gMYzYZpdyQXDagXW/gBJQk9EWK1XnteRUpLqWUTgkpHKjPVqjfU0YR4GMIAu9UhSBkfCuagmCAuhFKLRrQb86IsvcHx+Rp5n5FlqGjNr5cEUGYsKQH7ADWld9ILEBe9++2vcvHmL3d2tVjQiTyxqyeZiky0Q3v868Yh3F0zGf2XUXVyZWlGBJnLqmLAdhwCgDeuq9FU7NNdfnYuNxAWOKlW4cN5MVb9HpmujCwbFlptYG7punpxPEq+YuuQPm1WisPFK9iFlMm+PzIFtFlxzLAD9jdXKYi5aGwJXQUZ0VnFsUnMSK4E0VKQULVCgMbnrVY/1do3VMGBY9ei6XkIpNOeoZAktLPOMg55lY/O2SkBWOtpwgQhIbPW39cwQSuiHHqthAPXA0A9Y7za43u3AIMx5xjhOeBlPOB5PmMYJ81wWQo7NKVj7dY6FCyiTCpgGjCQJ4ro2woySuLQ1ftbKk3cQvxMR4eZqh4/3LxUPDTGK8ZCFpRSo4zKYX+DGrONyhwgBtTLXuaDU/DUB8EKbNSQxtYyK6p+4WxtGFp5jJSy02Cs+lKWy5JNqq+ZYf3WftlNplPRGsEGwyrPv72a+DGw2G6ElagTiXFzysBAaXzIOFlqlX9a+/e0tdMoEBu8b5zAn3fNc51qVkUVuAC8Fovrrgh8jnp7tAtcFgS7eNuFnqc65NdbnDYeJezV18ayqmq9aoBtLnOPQVuJW+V+OEYg4sRRQA6WORii+OOVz4eusFZt1/XU57/Pn230R53a23oF2G99seMOi/QRyOTuC8tIlZEMVb0R/vbzYDR3yJB4IyROoQne8sh8wLL19+9vfehiV0GzZK/M022RgArMRkTP8jWMPuHY2b67wbAYf97Ibnazt1mMU6VDoru5pUEAgrvxP/1n2TQCWh6LEvn1/4xPrGBDbDHT+Lhu2JTBpQY5mIxj9lDVL3L5LNi6DKaN6quDLU4G7MNR60jyLYWieJozTCadpxMf7j8jMuL65wZzVWAbzQhSvcnr1/l+DM+OkZY0FPuTtU0pyojlRU02qS6jltAlgOyQb1bAYx1nsvLjUgQvhR998gz/9O38Hb7/5CbqbKzzPI7rCeDqdsJ8mCQn/jOuzFY2//+d/1w+ngw7SqnVwQKiu7/UAkZrY3SVJwDEhP5Fm/et/RmiVb7YLhErcCFBAtEpGjT9Fo4nGe0xSalMOjJPllHH2QB7w1Rdf4u3773Aafg5mOabetL5cpGYwkVbFAiGxJLKWwvj2wwdcbdYoK0kyL8MgCoTVGWbpex5H5GnErPkixIyOxfPDiYB5xre//Pf4+f/o74I5IUGrIliSxhnJNoZQLQJRh687Lwp0YZPFTR2/hq4slMjZAqFW7VGGa43Gvv1QPK9qoOvgOL/kiGEk7umsA/Ehh81Reav0mVCZvzPz5WZC3aBkyiNMeZQxxeRgNpwC1ItgXg2N+S+aS+HEyt7lxcitb/naufU/+bpQEuaS5xmcxdO1Wq1wc32HXvdVUSvXPGeMzwctp5k13ElLiBbxzpU867kwOuYczjHQEVnYTyIJWZIDLDvB9yQlfhlA6jr0XY++l5j7VT+gWw14fT0At7eYpxmHwxGnacTpeBTPIkRhMeJsPQImVJGf4i6Hd6oSBxWoFG+LKhsEYzZSAjcRAykhdT1WqwHHcXSsZyJVFg33UJUDE9wYTeJjXCtPsjNcM5wJ6+hQNKF5gZeXPjeyGwVRi2u7BLSCsT/OnjvVMDJUAf+SgAfHd+0nWDLjmG3rcWg/yLhgimcuEGJMeg0/qoApkBjhYb2W76oAlzz7wX2Gf0ZLOt3FlY4HJYGqdXGaJveKGBSiGeYizPXGJdZoVCOCzJZIqo2FBH2KeNzyrabvM5ygur7NGCOlIA3TO++7CrXUwLzNCWrxxslgGN/Z3Lm+B+IaxuT0vF5Limxzb+azBHDgz/W5qlSx9Ub1/Uqh2r9nV2SL+j3usTjvJV4Yz4r72dbJStJSmGMcf8U0OKC9D7M6Kwm72u1w2B/0GIDKw6wc8+l4xPv374GSkZlB0CI2ZQJzrvsD5DzqElSavZzC/g7CL9meaykLJORW8LNNFg+egAArD1UFa5ly650r/3YvjiAzAWr0udC30zXyZgxBIszjPJt5++TDrzZvtpFbdpF1kNwIRSjIKEDRkGLNgay7oI5H8EqNahyoDsGNirbPHbehkRosh5fO44ztdoMpT8hlQi4Zz8979GmNQrMX+8lZS2YjY88FvRvtKp+Qs0E6zFnC6zokbLZbfPPNNzjsj3j8cI9JDwE0oz6YcTgdkaFFljSHxQhkooS/9ad/G1fX13g5Trg5TMD0jGk84Vf3v8S//if/BHl/EqPRZ1yfX94W0nnMTyCIZt6pd4AAeAy2bjZL/uKsiaiZwUkqRKHIhqKu01OEq1xIgFbpqbGlAKQ9hYec9l3jx63kpuFRFEpLKo4IJbQvKw/AKxlIX/Oc5UTIYmQHQrWU6zKkPCeGHikBtNng6vZGclaYsdnt0PU91ps1pnHC0Pc4HPYgZnz4/h3Glxec9kcQIIxXRonnx3s8Pz5g8/qNW9eYK+NpNpVtGecs0f0IZ6oLOtxaCi6ssyfI+pQJrqiE56SNyuWavrHom42ACbFrCIJN0j/D22yYZniejIkEC2hNCqPq8lAirfnFIR6XXOF0QQrwMjWOO+aBIcFFgD2Uy8ojQxXZ1kLAqB1L38m8F0ROeADJp5hnicVdDR2udltsVmskiOdgmiYcDnuNb88Skpgz5mnCdBoxzTlUJxlR5lyVDQQhn6uS4YqewoiguRFaRMFyNkTpEEF+GFZYrVdYrdYY+h7D0CN1CcPQ6/0VrnYb5OsdDocTXo6SzAgoA8N5HLUZERhWUQjgTEiJPRekOr+lEpjQiiJeRsiZBevNCtM8+WGbEc8NHeKNmO9E4R+3KhPVZMWw56swUVcZ4T54Wc3mwv6D4W5Ad+vHk7rDfgtM1MrjJuEG1QJ/wSOzvOX78dLguFYwIoVPBaIIgda3wavuNo6oLjQNFhpFWG82foBdtphzU3jDfq/KYLTCkq5fxWMJbbBadewTO7O46uUnmBsQFvOGrQeqIuACbiQlC7hSJCx6v/WILMYnPQQ2Uo0/LpxwHQsI4s0LdJ8WTVf8bMfmF7dTPsPX0K6udA17CXw+dNfypNBVO29yxVjGH81Vi/fiwAwHmVuYxzks2VZgJxxuNnuMbPxG8/WbwdzmRxRgTm4Yqrim9JNqK9ZHLS6jvA5y/tacsxcgARGK1lkkLT/661//GnmeJSSnFDCJkSjn2Rc6hrR88lLgeDEJwzOTzergFETsCgmQAv92BNfufeO5Ym+wMUNisxCLvsECY0qymTzXREPsieyQisqPzQsZN8/FqTtyxk7tN/K1iRaTmqBdHNdgcitJyHPHCaDqoT/DL0bFZ2aPAzV88f0dZFcptU5g9DgcT3j16k5CzFlkgPE0ottu3GNSitCueRqRMIl7gtlDodqS6ozUqVkgAfvjHh8fPuLV7SuMmzVyzthsVug6Qtf1csjfnJA5o3ARo3aXKg8mwm+//xb5t79GKQW7v/jvxdBZCk77Z5TxgM3NbsHPP319tqIxxQpL7inQJPG51Prleuy2u2G4oIPkTkgIlE7KKtlYLUuQnzdgCyTdpKAlGrVgV0KsLxmXn1am8l/VtphZTw0HtEwNMknZxDxOzQnjXepEOUiEPGdBHCvrydJ40bGvrna4vbkW9ysx+szYH494erzHZrPG1zdXIpT2Pfq0w9B3uOMCvr3FX/+7fw/iBJ7hHKrkGe+//x4/e/0WM1diGbdZZDyuZOgPsWKNexXCOjYH+HDbtAvhtok+1XfcdIHZGeuPUfFGuhh2hoAKK3EcqPPxdiOTqF/rOFBxIiod9YHKHl1YMEHJcEmFXBR1gofDFovjONuLYD0Upwl/YikPGRWTOAZXaLQ/P/mYGfN8Qp6kqtnN1U5CByGVk56fnjDrAWfjOGKaRhyPB5zGE+bThDnPyFrVreghYXYQpUHKLEpFiXjLrMgFHdk/QmhMuPYxQw7ETElzQVKH1HfoiDCs11iv1thtt1htNlitVxiGFdarFTbbLb7YXeE0jnh52WPOS09KXWSyMrZsXiRLnLfKRFmt6erpYLHsJa04Ikwooet78DRVuq9tmaBhPVLAyiUHq+vY4lokp16RzedCdS8BXr3Eeqkwr3ssnTWqvxuJu6Q42DwUf1VuCZBcHCTG4cXYN+m4KKAr1RdI8SOqYsSsB3We70W4cKp7JwgMUK9cShJrzBo+Vd355FBq2gwmZg9zI4CYvGiI4zTpWlJVvCLZ6hoIURAE/Ksz64buaN9LpbAKHzJvX29erre9XPuqi4M6b64/2TrVqkEB5i3QjRW6wONLuOjHvVA2n/DYxWHpvWIKVPjN/6rQKTyTfLnqHBRSfAbkOv6ApLaH7LnFo82cl2N22BCau8n4IVr4Wt/NvAOutaFjBDMkEah60Yx/LecNKb8ttEsiOaZxqnNSGtclKQf+/PSCh/t76StLFiAXxpznGoqLQK3aDdt+XMJ8AbeIax6hYHsLDO40b48lFCcWTDFDItueNRx1GAkNBkd6Lj0zVYMSKWB9HyVIxSQLSWfzctrCUICb7fUlErCv0w/hmvE6208+J7MQAL7xRDEk56HSJVV8MXpTJIHcKi0CdQ4xVYkVATiRFliZ0Xc9UicieM4Zh8MJm15kkZR6UCfVFcv4jB/n3+LhZodercAlFyTADYKZJy3fK2kMXd8BXcHDyz1oxbhe7dB1HbZpA/MW33Z3XnRotVpJ1ISmJGQw0HfoNLJns9ngy6++xNVuh931DrurLa6vr3Fzc43PuT5b0TjawXVUhTBbuFLYBRET8E27B6gKbcpkLPfB4nPLPDuxzCwnHZu12RDd3ZEgyIniuY4j/G6hVPFiQBKrC6lHRASyBDmEZR5HccVrPDsRyVkaJdXTvMH1XUW1lDpsN1fouh6USBLKOyD1giQv+70kt2uibSYJDaHNGsNqDRo6scwRXFkiMJ7u75GnCeh6R+6kXKVJIA0fHVZoharKjFCJg/6lyL0CA7J1Ntg1EYfhftzty7KOTswCQWjyMICwGTm0aYvGTtDqbOuXyNhcp1gKDRzg4DgRiKd1quO2A/KciSjhM1buJ3ijbZdgjKgOLNl49PRO2ytcxHJRmLHbbnB19wrznHE8HnHYnyR+c5wwjSfs988Yx5MoGvOkuRpZ3ZWsJw/XMQojjAFsFSDmPSEEhcOZBQFUULK46amouYDqTM2CZTlTIEJ3OIBSh0SEfhgwrFbYbXfYXm1xtbvGerPCerPB7e2N4PXTCw7jqFWASPmTBgToWFxBUMQtepKrWdhJPR0JJERSTyoHyam68zQC5oHUvdJax4xhRKbFLUJR80c+BMsuXXomcHLH88U+jNdlUaAys+UV+27CYMK4DI/9WRtolDCCAI/ws33h5tFIZz5NWxrhMM5bP/ddh9UwYD9nse6qYlwB0QQthbmFMZpRAKJ8ysGvXOOno8ZF7bjcoABqoEsXP6jRCuR7uD4T9pbPl2peGhkxOafPzRXHt3ikWR5buk/APM4xkrflVfdCeO/ysByUDd+Ivy2+RwSKz0SKbvzNx24P+3ttGxc3TBznBZi24YTGk6j2X4eDBVNpYN7s3diP3ksa0smMEOKrbISLHD6qQnotBlL8ucxm5QZQgO9++1upENiRGjBEyShasKbCsw0z9D19AaOr4scG3eUjMNXex7Lc33bfcE0BZd1zwPNotdfNKpyIyA3KLb2x3/V2otCVjDqJ60OMZGxtGp1YZtwsiNmSnjdPhg3gfP7CBmIpRdtppUS/FJHMWOrKBekqhXtgAqcqD0VFZBqlaNBqtQKR5B4fjwekzYhEnU5FDhIc7n+B/91//b/FvN9r6L8qdCongxiUxMzb9z02242ER6kilEBe+dXW2fIxQRKNJBEKkiOdkkQYsVZSTXrOQj8MSCDkMgMkVdPmkDPyQ9dnKxqncfLFMKtuUm2qZJFMch4xDL1o7J0AXjwZsmv9sD8DvKKOJUZJXLUuVuh76eUg9YIQwS2fnjOiGrXkgtjJxBpuMUobXUpy0qECvEzm0TDEhhMILhnU9SALm3FE1IP5NO9kvVkDLOd/IBekYY3H4wmnwxHb3Q7QesZMDHQduj5hGFZyvkeqVrFEwHw64vSyx/r2RmohMOChHsaY3ZILX5N4XRDdLzMb3eHGYJSf+n5tLKSo9y8R4Spo1B9ttT1h1fsmJzRGYP15ApgpKC4VZypm1HVwsCCMAYpfNmCzhnA45ArsyadmXZPzL/R5GEGt44iCXByTW6gN/yBwsAoV8zTjdDyKJeHuFqt+wH5/wP2HB5zGE6bTiOPxiNPxhOPhgHE8YC6TH05ZK2SUBtjGSigSeg03ZC3X19DWKmbDC09B9xdIDicC3KUuCrwI9aRHEHtVt1TQUcbEwDiOoOMBL89P6O97rNcb7HY7XF9fY7vbYbPZYrvb4erqCs8vLzgeTxqWVYXbFJFQ6YAxNasLQhlInZxLkpgAlvCqlIoYJ5JV2ag4o5zL552CN0C6onY/RAwzyy2wgLk24PuwhvbYxnSYB57dcv3QZSPU4xPtYtH3cn/XMMK4T32P2fuhq4v7W7tvKkxV0nMmgERoM3GYN2nJZpYiHcdjU+JW9kq7o5Zet0jfzKpr3jZbRxfC7LWlRBzu+3i9n0BbuK7V2WWAY2PSbfsCLzqnjeFy/Avw/F1XhHlTZQtw72tFrkXfS5Tieqt6ac55SUNT+UI7i0lR+9r5vIy2O14YrZdcPveGOYOA02rnT7SAg3W/3GNLnGSZX1VTyXp2Q+dy3nUTsMO8ej+Vj8R10FZFjNHahGYYZYMznBclkoiOw/4FT4+P0pbKMYXF4NOiEAfL+oKYGP5F3HY+FGgEhQebSUdgVeOu/KnvR0VHQrgJxfIuvC1yiBA6EIrDq+lb+wiv+R9W74BatJHMyEsUKrCluvBN/6EP9VxEBcIUsAZRA/J6uVuI7CdVw4orGmdyi8HImzEeqr1ZWT2lccyMjrTAy6xnvqknpxRgPI1Y5YJVr4WKdI437/45/taf/q9AaqARI7wWTWEjSzOA4ue3mDxjVQoFNCGUy3BTOUDOGcNqpfyzuAGSS0HqkmE4MrPkj5aCgQgUqs3+0PX5ioaHEMmGIJITDS2hqet72URFgD/q4XxelUpP+UbQ7g2pWd1XU5ZKUdUbIletNCVvWRiWLFDxfvq+1xj2LO7yTg7/O40T4rkinantqoQMbMRL4rLnWXImchb7sG22uRSsuIpqlOQUcUpS1WrWc0b6lFC6DlwKTscTdlcSPiWKD8TCzYT1doPpcABBT35WQQFzxuH5GevbWyfacbvLpmC/76EbZ4y/JfquuIeNZpbkpZWLF58FzeSqxoKWHIpln2DCmBG0RnjgOqOY8Hqp7xoSYDCni/Pypq0tHR/7g8pQFM+MX7iSYeNlRkFpXdYKH5/ORTgZBdRQHz0lmyBJq6fTEYkS3rx5g5wzTvsDPuzf43Q84ng44nQ6Yjyd5ICmqdZNZ45euwh3hyCglqMobLkGYQN0Cw/5GtEZEKM0oYTIYN5wMKPhQnBY4+VBBGTCnIB57nE6nXB4ecH9h/fYXl3j5voG1zfXWG9F2djttnh8fMLpdMJqtdZSzKxDJXWl1wHKNAxnZN9KCW/9rHQnUYfC+SI/jnhVWUOA5+K5i3sIrUDjjN5hprTN8CYKAIs2DJYEeKlH78vaNdz191pxrsYbL/iqN9NgxsXr0v6+PO8goCgCuYfUbjfzZmSI8r5erwBUep2LnFnEXWr6Ev5G7uFtx6l7QUMEqvW57mnvm4Pdk2IbcKHi8rzbTuv+rpbZJU1d4te5OaLt+xJOtv3V6xKuLZH0Eq5d7Ns+U5w3XV7vilatHBf+Gg+vMA24RtVzuiQz9k7E10v74wfnHZ4BLuTReFstXassiBr8avtuQ658rABKrgePel4P2GVjZgar0bLuGmnPhFaihI6A9+/eiVKhvzG0gEfJi4ka0hmwwuKYAS2uDde5+vs+fzNFhPuI8GhnTEqHXUewcv2UQg4PIZZlCERRx1lgyc20fMbHrW0x19wz+6vwJqgMqvOO+WLnsLL5ncsOS8JSwzBrNUYRshklAVZQxA0NXPHD4O/yjtI956E+52ooYYhsOWn4lATKFE1DyCj9ICfF22YpR7x79x3Wk4Sfl5xlz5eC8XTCfr8Xz0cidJQwl4JpPGE1CM3NrAdlT5Mcol0kuJUI+Oabb7DZbPCP//E/BgDsrq6Q5xkddehTp/mgM6ZpdmP+3c0VfvTlWzw9PeHf/bt/j//6H/4D/K7rsxWNmTPAKnxzETdLArphQJlmjOMIK7PVdZ1MRi2MeZ7dUxFWV+LJ1KXjB+9BAGmudSudKwxqhiH0OI6ukNi7FWlQcy6YtaytipMsia49SWJpKYxxnjDNE5gHCaWaJvGuZJnzKZ/c6jKXFcxaQMTIKMJMu4RCBRZGk0sGdR2O41HK2OaC1HUo86xVtzI2my1e6B5OjAS1kADsn5/wWueTAfSm0RuNCAJwE7uIxb5Dy8TdBs7wnBN/3il1bdxiUi+VB4wvUdj4bX/hA9eQJLvndEHvxZK89bFIoAIT12HWvG867yMMyA/go3C+CdiNHxZ7C4hXw4UZvS/MJfTtIxGCkKhzDwYXxsvLM4iBu7tb5Lng4/sP2B/2OOz3fvKrnAExgssk+UAqJYnjolPBSxmYwcUZjY/aMUhtdSppVayqoQVRerDJaSlGF6gWwqkRTIbucfFukOZcCQyl9ZKlQEQCoaQJXddjmma8PD9jc7/F3as7jLd32GyvcH19DYBxf/8AEKEbeqGrSti9jKRLaEH503s5A8xJCjKQhXfJ2hRlUoCcXi5nfSjcSGGmuHFJSTdYkyJNVMgv7jFjlPbdcDo+s+zAhJqgpMQ1aODfCLAVsWNFH8S1I2B5mN/yurS/afHdsIwXg4/72+iRWXDlPU3fp4TtZgcC5FwADaHNOD/7plGm9YeGpqgAK+FXLd1z+C7Gj7BmHH4/mzfV3yMunMVmowkmhVMCRU52CXkxB8e1KnScwfLCvJfLx4sX7IwaWB8/2Pd5u5fWW7OgwqjaMRtECqrn4QzXFvvhsxR5CqoBL39r5938dqG9Bm5BGDfDCdn4Ad1j9s75HjPCYoeYtXtZKuCxH7gqbdtayPoIPeoSQAk4HU/4+PGjWMv17CXYmWM2jyjE2h7jSs8d5ksgRB7qCjL5NKKQbvTcDnUz74FXWgxQlt+qQlE/B77v1kzruwRh2+Bc+5byzNaLvlsKvACPzRsM6jrJhUgFhVOlSRx3JdX14oZDo8GSwEOXipcYKTSUvUjqfg09cvYhOK2IUPumEE5dDXo2V7CU+c4lI88zhmHAPFuUghz3MBhcANDhPdZ5j//2//qP8d2/+AvcDBucjifkeQLnWkjGctdO46lBWUBk0a6TkD8PyWNG1yV8/dUX+Ef/6B/h4y9+ib/5m7/xKKXECSknj0JiLfqUUsJ2t8a/34rq8N133+Fzrs8/GVzLbXLJKDnLwSFgvJxGJD3xcLvZ4HQc8fr1a6xXK0lO6RIeHh/w8vLi5W2JTEsuoJLD2RsqvBSAufNYbnEriZspEXsyoVTHEU/JPIvIX7VJYDqd9GyNAQRB6GmcUVJCt9mIl6UUcOpwnGdk7sAMTGVWFgj0qijJKctAN09ybDwYm1WPTiUhKlBr6gSGKAer9QqpG/TQPcZACVMpoD5h4oJhu0EaeuCo7i49QTkx4fDyDJRJNhcnEbaIwj4Om7vhEDWcJpAbqKzkexkqEMhGCCS54VTyjJflgzE09+nUHpzJNiKQt3kpvME3qr9URSVrU6YdCThQTymzdjSMjhlVYAtzICPQSkpjZSklYsziCnYwolpVfCbRIhZgmBLAidCRsOfxeMTxcMLdzQ0YjA/vPuLl5QXj6YjTeMB4OmKaZqkQlWf12AXqwEqkPScnTLaxXrXikP915s6VIaG9bL0MTsVYrhF9almMjQnOhMwKZ5TXVBzSkr/SSdZkuZSlItbh+IKHj/d48+YL3N7dYbvb4u2bV9gfD3h52WNYrdX9Gxm8iTnGR1mrs4jnqFip1NQ14w0cyGFglZDq5qj0wvZS3AE1kbZCI75efXfGXNEAu5G79B9S7mnWOvvVjQh+RxllVETcasx1PjYWY8rU9sdNm+eX7aZL817CpIBdQK9ihvVdmbcZADIJwDZXO4BZjUizGI10/9V5s4Zl2L5vx1WFEUhIq8MIoAI04WE2tgU5i4JwkIn8hoU8ukXa5AMVmk0Esu9Nzpt3EmhlGJD31SxQGNsC3uDlM616ssS1ps0lWQj3fxDPF43LM/UvIa6FNhjkNJt3FebjVmN/Dtqezzt2HgZmykCChUCdT615LRgGRHzQkdu8jYYa2bK7hmsMEGmmW1D+TegvXA8GBdjn6UVDbNP5H9utRXh7Ekjf33/ANI7orVImS0hNKXPllHpmisEurreDi+K89IYjf1zkFlLkcJBVdXw34dvyACKNjPwb/ijEY2F9G922kvFhvP6lehkkzMgoi+K3ektcTiR2WVByHhLIqJaGKRnBMEVJbtU5NzhIYvxocdhwqwVyoSIhvYgKlj5hVQlbatmwnbjvPVwziTw3zyr7IsMjffII4Bri+SroP/wCBVvwYcTTd7/FkYNxzIzzWtxI5OJSDzhWI71Vim94DCXkGfjVL1/wf/rNr+SMo2mS86pIIwRKVTRSSsizyNzj9IyPj9kNPp9zfbaiMax2cqI2E4CEST0GferBSEgD4TQLsrz7+AAwY7VegZPEnjGArhswWxJ21wEsyd+gziuJ5DzjcJKEzr7vVcEtQBok/0EPMel6OTQwQ5Kv+zRgyqPnbBARTrPWCC5AKepJQMKcGRhn9APpwX0Z4zSh8AqMguk0gfU8gULwk8TFtVnLMnrMW7ZD2RjzPGGcpmqBZikxKnhpcY5ycMywWaHrJNN/ngUBiQFKhPEkicFSI7mVi9wyZIScKlJHeh0ZQiVMgQgWIxbsNOKSoMTWafjdGE9xQggfpG1W9yDoWDkK8prg6zG6+ruTBq6fObRd3zcBif0ZF42D1aQ2EAiENcDBRhzK4bqAUE3nLhAaM7P69nKyq/w2lxlPD0/YrNd4dXeHp8dHPD4+4Hg6SlL36ShnqeTJw0fcFW3QNilAJ+yhbfa71yFX3AsiZEMoDUFiGGKUXownUHw7PriQRAiw0+0NmLaaVqEkWtsZUo1LrAYFpZAYK2aJzz8dT3h8vMebt29wdXOL3W6HV3ev8Pj0qFUzBmTWMtiJHF/ccm7suwhPywCSJV9CcSFIqmTrbXsHanGMmybw6EaYiWtwtscqHPz7BVDGvxwzV71vdgEmrnfjpm9Wilo5wqDe4GlArfNh+L14nQ/XaFagN3DyEdpajFNxjQBQSthutiAtcVtK1hyNH4C5jc+WsG5tEEFDC9jhEQX9H8ojaeYdOvaiCN4ZaaIlnLYbzTPvRd1rMYQjmHgCTfW++TIexflfCvmyr2dhcA09rtte+jag8Hlniz4iTY3ja5SBBQzjX6dEdlOJf337MsxNOU3QstDhGROOTNxuSFHsmwOoqOJDpGPSFDufupyLw0rXqiLvU4p0j+rYEPqOpbp9pL5pNAoCEhXy/t17yR31nDsJUYH3TUAchWtGur8ZbvSTxSZUxeDC2CLMAYDs/KbWJGm/RVi6cSkmResghN6FeYZ5N/SDL8ElYlVq1zd6YqLxk2rbRAncMTgXX2+vTAr4vBrbaTCE1B9qz0s8J1V07JDbJq8nOXGIUK6z1D7c66dJbwzWUt96mncZVYFiUWQTeagdv/8FJjDm0yjnrJQareMRPc735L/MltMJJGSpGmmnnesYucwgAD11KGPxwjJkxkOQ5iWLobDkycE1ToypTIof57vo0vXZisaHhxeAxLVjkyQCjmqZ6rpeBCcW4atwAQ4nUFeTR4kkU92FMwaOxyM2G8mSn6YJp/GE03FC18lJ4QTgcDjg+vpaSoAdj1gNA7q+E0QrtcJV5uyW7TxndJ0oMC+HF3Rdj17rAAPitZhfjuCcsU6M9dDjsfs5EiW8ev0Kc86Y5oyOgMP0gr7fgjNLsnvOiFxcKqnI+QYSyyZz7foe69VKGUx1R9reGXo5hyD1PXganXkNfY9TkXMSVms5VVf8rvCFNXSom+jCgvsQIxExQiWIaAc7RiXjjCepcOT91dsNgY9XlKVI1759QBk1KWl1S4gJ+nGcQkCZ2rjfSOzlUwwfagfYEBDt263RbtkJA4Y8GMVnaVPe6hLpuTLy/v6wx+Flj7vbW0zThG9/+2s5wO6wx2kSRWO2w8qg3jtmJ1aNYgQREpx2Gyy5inYXN/iZiXZxLfBE1ttibuMkwzP2PRCps7459O1rUbHO5jtnmTMzo3Qz5scJ++MBNzdPeP3mLa5vbnB3fYvnwx7T6YRhvRZl0ixHVFuMSMq5SD5WacOP7I9iUAUk2R4KZeR1HheiXi7JaO3cF9xpoRc4SCu6mvhFEdSO23WY7NC+OIYIc38oPElu92vauBQGGfdywefMezFR7TtWoLFQT4J4dymRHyCZS0ZBaTp2kecCPWsVJq1wWCRkdRnItIT5UjCOY7683m0IkMs6gEYkVk/hMgRKoVA/68el8sDWNxs9atHo4rV4yHPcFvCLuHZx3heajc3/YN+wvs4v83zLnGSgLY/AOcyJPmve5HzBHq57Jc4hfvawqEjPCUJ3+VKf5yMghDNhWA5aJWr3pMDckI1RLfbQPANWm4+8d9jv8bLfSzQEyC3TWXMz3KNfWA79Wy4QA64cUFxks+gnLDUpe9UUA3k/+V7jJZIU402o+LS4YhixsAjhJeYtYR9TfH9JJMMvus/Y+j57ovJvGxSB9DyOQLXiesfxwkL52r6b8S2tKX67eDWo5jIlLKWzn6ruxS47uKDPko/R9R3c6MUabcHQNQTmt3+G46//OwnFJ/JDsy0KSNqqocvmfXBPg9Et54fNpJyw+Yn0zeAtpE4Ujq6TaCTJJuoDBH/39fk5GuiR5wxmzZeY66DE4j/Xz65dixWy73uIFmcAmauwQh3244wu2wnGHbqVhENN6p3oN1sc54yUCOvdDtM0Y5oyuk42VZkF+CUX9KqA5MKYs7iSQCscTxNYxyjhWZMCipHHI55e9siv7pCIMFCPoe+x3YhWuVmtAYi3Yr0a5LRkZnS2QFz8FPSkWfszNI6YVIBQrdhkAaIkJzFrrWQqLDWWFRmJC07HI1ZXN1WeKOyWWRPGJTymCuq2R8zb4rGWziyDkEaBiCFuDLtRn2vkl8XPrIQ/VufhOpBKdBbMm6yRaHmGKFG1v2oJaqhhIODG2m0zm3hWxxntUxfmoYSbUPMDbIzGvmslNItpJWEipXgd9JvrGzw+PmD//IzT8SjJ3qcjxumoVggN8QHX9eM6b17M24hYe8ns6tKEUDkDqAuBQVm5IDnae80N+xBcWzX86jxOu+KaJfUawbe51U4JAOeCuch+6XuJ1Z+mCfv9Aa9evcar13e4ur4GrVZ4fH7GdrOF1XtzXKlZwOFrce8YN8OP/ZOiP6PveuQcwhRQ0dDG6mNeUNPYtO27WAFJgdU4D5v3L5hTI2/zrcIV5vUyyYrgFkfHifNFXr5Jyz7O/kYJLCjgHPI0Qt+OA4bBcd4OPCmZuF6tcToeND45u/fZ91gzU6NftS3P37LwWaW5haGGK/PyVZnvBzkh+TQrfaEaVuPPcB2LLZ2N95yqtDC0/ef6YJhPM4alYLNYm+bZ8Iy12VS/8b65NhJQw8cSxxS2lfXdVFujthkv7LbA81icYEFd5LvxKWp/N9q1nHdV8Ni/x/1x6TLLreNMmHcTvrt8z+hdGMMShRqPoT1nVvJmni05TZ31y/jw7h1SYVCn9J2qldryNUSAbvGSQ6PN+Bve3CpBzWhJYeA8VyIK6rtKvZhqyHDgJYYczdopjeKw3i3ZlU0Tow0c1kuh1+imKRmquNRAbRlHoujpAZBIKoCynhnlm7fKQMZjnY9FJSQSGd/8xn91CoXBKVCoZn8v19/6DgGJCh9OprQy5pJDERR1zSsOeEjbj/8+nv/Df4dECfOc0QcDrM8NOAthisc8mCISDf5SOEXKxCdVTtB1MJqfAHRspZqFp/e9/J65II2jR/p8zvXZisb9/aNoVHa6cMBkRjtp81wAjC4RJvWCWGKlCYiSWzGrd4S8jfpd4hbjfQB+5kVKEl5llUwS5EAx1u9EhPGU0A895iw13G3s3gcYhSf8+rAG3nQgSJ6Ex/BxBwyy49erNVjDOax8bupEsSHY4SkE6sWtX1jCn/Kc3bIhREniNUES9lW4eIUFQWpRmI77F9y8fSvGBbU+eEI4ARSxPZCeutltU+NcYApCQGSI/lMr7dRuQnv2bOUKgcf4xlYCa/tzyQStQdTfnbbpw4z2eYoPhjak7yAoaGynE+4w8Hg6eWRebq1iJcIKc7NR9ZYslRKmacKH9+9xvbtCYcb3330reRjHI06nA6bTCVOekcuMWEu9+aCA5wDndj2rdFFZZCDWNm9DHlB16Z4JJq0oV3uInqKoTERJwlzguh9j376IGvvqli2nrwiP6J8icIGUdj4eXvD9eMI4HnF3PIl34/YWT0/PWG+DV0/XN+JMcmYEcBGDRIm4Yesf5k0R/s5U0QDMP/Ji/wQeacvFy+W6JMmcNby4GfZFMxQXoC9JWeSwjh23s/+BbvVZ+9/ga/NdVlkzhZbCO03fDWsgDxMjIgzDgONhL9VcSj29njqla825BC3d8DUIeFggRTIaeWWB47/X1VjXa+irNFxDyARpyQtgXGio7tmIRGFRI65x85y3EH4MP0Qa5gaYxWNGT2JDugaxDaOR+qc+voQ51TWp4U4Xh9S8F8HnsGBq7rcBl+HZZp4tjV4M8exqPYWkeCUNLA030Qe+HKuvi/YtieCh4xQmQhXrPMLIGaHSrUSYxhlPDyJLubGpFKk0aNWmfG10ppH++njq2rcTouaj59M5XIx+2oZTbOd6hlhFKAsLXhA8m16EF1r6WAlH5BXtXLxaocuTERfJf2tDhG1dFpzNhycf/PwNG53xKTd8cu3b51P9v47nthhEMF0gwmGpK7Uwr3CrhgAzkHLIH5YCKl0iNU6TnksHoFth6ta1jQBzk3uXV5TDG4Nz+Nv3PXpKWEFkmS51HqWUOqk4lRpZXCJ0CMA8zziOI06nkyeX/67rsxWNw8uzf85F4r6kDn4niaRq3QWAYRiQSMppZU327vSQL1YAcRFPh4RWaXvUAUnyJo6no1uRs8axM0n2/9ARMiTvIk9yAFTXdVpJSk8p73oQEVarAQAhdwmnsd2VUkmA0WMF8CSehWBi9spMMFmEUbJ4NpjlrJCkm7WwCqEgcJeQSkFKHeY8Y5xGbDebkMFfEU/cUeSMjLUiFRJwOhxq3rP6busBVYBvq2jFC/Nz23Llnn4tPM+VaUZKbhvHBI4F4/D3oyAW9+ZFTOLmGemKG4HUiL4rCZXXV0IbONlZ3zpnI1CR2ZPChRGZTiDOaAkGwjz6LonrPCUcj0fcf7zHzfU1Dvs9np+kVOvxdMB4PGAaZRNqRKaPUy6LlwwEPMyxDtcGUucdJYEYYmaPWQnYSzCPpJpgYTVLxlvXoC7+5/TN8IQ2itZ9sx61i15Aci4HZ4AZcyngMuP+4wccj0ccj0fcvX6F27s7vDy/oF8NYLP4gMRd7vktFNY7iXHCNvAFODDE+OHTWUz1HCqX8dzpftxXC1yKbS33J5r7lRlHRZsW+BEZPts6+c8Rw877jmFUNpZl1Sefz5I+LMZe/VbLiy/QFhn3SkvcMliMPnp+kk9rQaPiXrD5EUnfEjpr71gj3Mz7Upt2fWot6gNU90zYg8xhjg3j5yYRv/ZBbZMMNzLFfuzJ0Fw7UGqnejbcC/S9mV+Vl5y3NQJt6MPxPLwu611DxuL4WphTGzZr6Kts1em5w7Iyi0/xEgtdaqauHdhRBfF+DEWLMI/nNUU4m0DoNm6qHngxokpbmUXOiPs1diyRBTHctiovpKG2z/tHjMeTVMBT70VWodNxDQYPqnwiAjOuA0J/ZjgL87b7hJC/cImegzxUqj52YYc4z2SYwB7xvFlSMgCzH+bcIIEpW0ATplU4eP0v9q1rpG0bhAiiVJZccYhLkRK9WOBP3Ei+KUI/YbNJNE5Yn0YZo7MmGyNWhLlDSO5xKX5InlW0tMImyc+KI4w/+oco5akeYo1QpVVlbg68wgzynR4pwVTPvLPf+75Hnzqs1WtBKlsnrRqbCO7JdUWjk9+GocNq3WHe9nLq/Wdcn61o/NFPf4LT6SQTP530IDx1rZDVghZqklInSkYv8bOdngybdJMCNcE6q6ehSwnDMOhEeoyTHIBnv1t5re12i9V6DS4Fx+MJp9NJXTqQcp56yEvqpGrVerPGNM0oKJhmcw0BRAJsOTkxYzswnqCCvIYOm4DtFlwwQPIMQbwtXd9h1rM7VqsB1CXdgwl9P/ihgaAEZpmnJQAXZjkhHEKEMhfJ/+jtDI4DmKUqlgneBmdeIvmFNTM60jKvSkKcQCnuk29a9ndjvHbtozqZLzE/I3D1nfA2OZmu7VFljM4gsIhrdiZZuZwLRZf69om1fxi1OtUSdnG8ucQQKtuEMrKn52fsX15wtdvh48eP2O/3mE8nzS86iCKaxYth4YOkJZptWG47NWuJQpP8XwRuUWHXsskwsSj1kgCCIuAC0TOXbmJ43ouA1rx4UOaEi337Xlj23TA66dMO4bQZ+2IGRl6KnsdBCWWSfTVPE6ZZ3LOv377F8/Mz+mHloYkuRUAINuJ5DDr/c+wzCUukEauMFPdIxL+IM44nAd9qWGJ15cfQhQtseimjXXguKBdUWf3ZHvP3YzBb/YVxHopkSbUMaPFIWpS1bWFWDQGhRw59nzHPOg7HI22AQNhtd3iveMWlYJpz2wc5BPym7OcQuqT7O2mN92GIbyhtCfTEUN/WeFEfJrwVxo36boRupWsVUqYQGr+ok2CdNzejc5rqxqEgjMSL2nEBOC+YESdgY44w5yXuxhymdvLL9ap9ksOtxNGQeXTCvK2RuM1Qw+2bKTpZi0aJT/OSuCEv7U0s5m23knZk+RqNxd7mEehjQ2G5rgER6vld7TSq8kLsnvIaaqvpDvrt48cPsF1rIaE5z8Hz12wjn7wrHErgmGpIMcVFdOAYHbE8Qq3g5Buh3e0STmR9LfY3s+O5zc2UhMjH/Gwa4zU6mWRncWh/Hr1RkQAREa0AiHQdVBhXwqiBka2rUb7UEZh7FbLR8IIfoqnLH/wtZgm3V5i4kcGKxSzmHfm3hR3JFtc97zIMe0RMKXJgrWfo6Lucsxd0KcxAEaXUk9Odp0PkXlUUJIy/QykZU57Qd53LxMaluBSpglrkew9Gh04jfwpSAHIyJaMfMPQJfSIM6xV2mw0+5/psReN2lTElAFyAzSrgs8zSlI6sB9B03VrXoCaQF43NTilh2AzawiB1gMkUjYRSJqSVWKy6XtxGJWc9+wBAOWG1XWPqe0xrQfA8Z2y32wp82FkbE4bdAC4ZXerRa4L5rKdvStWoGadxBnFBIVkMg3Hcu2DUeDaWw1y6rkNWRSNnRup6VUAIlBKmScr1dimhkJ4xwgVDn1DGGate+uu7HpQLSpJF5kKYxxHIMyh1iqQEPzGbDPZSDtcZl3MbZbptTpAzDYR5KYl3IuvENRA+vwe0VrtQBrF92TZpEByMiBsRDPzVyU2gl7KPJZTNa8Ubc6tPBc+EEd/K2doQmkrMGyWNa63zyPAMVtQl9J2s+cPDA6Zxxqpf4/vv3mOaThhPB8zTAcfjSZhGkXQpECmsYsUHDvCrooQJMJXwE2K50IYqRmAHWDeh/w0Bt2eV6XK10smjVJ9zqYzBdihTlBQ+0XccH1sz/mRlELEfdtwxoaWgkNIKFPBHPYyzFLx++wYvLweshpUmrqlRAGpF1DK6Qz+AEmGeZvUoLUDH2peOu3BrBU/KEGgJc9g+sLlEyLY41ghUzS9hfRD3hUM0MKxPvVvxJf7l5jfD83rXcNnEXhe89E5CW0b0vFX4oi77tt8YC5gElCKSA0qLVjUpuYD1PI2+6yRcAC16neEa6pIQhOZ7KA5MELMxk6N8pBaytgC04p2XCw7r7ST0bJ7t/F3uC5cl8EOVT+vL5R17X/egrfcC0mhWNgC8XZnYXt1eS5rqczIYGFlZzHMxTd3XtZ1k+9X+BhqvUqfTYguxs3j0OB7H8wIsz81o5lSFDNguiyjhitSCxLf9qEBMFgqreUSMRpC2d40G162v9KLAvQ5eGAXsyhLsu7bn6MsWig2UPOHp6cnbMDo35xm2gBwnCKM3QCMg2/2GuFXfZKUj9qnufAqLX3Wu6Fm4QFuC4cPhGqzw5PRbZQtPjGYvCgAiEVxNOUoAODXgNwXElQMiNOd26L8xEsFxmEhpdyeGXLArVwUkZ3PIKbp1L3KcZfvR2yfFZajHquRQRn3xajQe2DoYDzVYBhmmlFpUSZCUfTnFm0XIWq2nTwUJLOdXAV4gJYHQJUIPUTR6NeinvkdKHcZ5AvWEn/zkJ/ju22+RpwkEcsX3RAFjzDvBWjFUPR0WqdSlDl3XYZMSrldrL+L0OddnKxrrFbBZCRO3w0vEfSNxi6VIlafUrUGQOK+ShYVN8ySMnwsSrV3jinkZWRWJvk9IaYVek6es7jSwwpxncJGKUolmrDYd0tUKko0vZW8t6bYUlqpORGDOGFadaHWarV+6Tg4xAUDcKTC5WtbNIkUVKQ3p+q53hD3MUmlrvVoBEMTJnDHpgSzTNKLXygJIgrhZsAJTkaR4KsAAgcWcklfvytMEOxCtbiopG5ocncPFylK5Cj/hTd3vlSgaihk5iucLyCapjMgZtW08BYrTOuuC4aGf8lv4Qa8YX0nxgz7S1JGh0Lc9r/No+IsS/EDiWgbWUM9AMO1dDgJisNalThToAuDx40dMoyjF33/3PaZ5xDQeVdE4Yp7n5SDbvp26o3L7MEE/abWphwlHwoYuNgCxW9Wqw6jvUCOJ6Ge16Nf1ZmUaqa4jDAdaBnapb4ce/455uxRD/jhQlDnJyEvJ4Bk4gsEP90JnwPjiiy/x+PiE9XrjTNkMZ2K7ZEzzJCUDl4sfJJI2vKW1/BvIa2WWdt5L3lTbMbph8Lx8RZx1mAehp+6xCrag+3nDcbxnZyAsxricGwA/CwJMzXLVePVKm+1dcqZk7bXhPhfnbAIJM9brjYQEaCnFMteyjNWTF5WC83G3hCHinAGs7gORWtr3vP2ADwLzcFYDydwY7ErSJfBaOxGfOLTrnxjtnBbr6L+FrbMgmWd9/9DNJU01o8KyDKmRQgNdg2MBbhF/lvxm0ZW3xWA7B7SdY/zsDwccXExOxmj0mqrl35nUBSCF8Tu51z7svpfSjY8baV7A0WhBKVl4v40pGLjsT7O/mVGIPb9yfzhgPJ0k6sHPgeB2DoE/+eV7KNxCDa9xPDZPAUFLMysv8ZAoJZZc/ZhOt4Plqd1vFo0RHjFjnvINItVOtFnz0hHXM0JcKXGlkRf91zWoY+a6j3XxxEtRDXJNCWqS8ZKWQzcPXEqEbFQhWuOoXbMWt+tmNPlADmQ2JUMD+hqEZcgZIOZR5rr3W7YHgNXgJ2fNxQOmZV51bGn/HuvtFbhT4zsReJ49Kij1YqjJRJgSI607dOsVSiLMI4PHjP/w699I7vKsYdy6r+VAVfJQLIO3nOlSMUEil+S3ngjP/YDdbovr6xt8zvXZisZm0wrq8n+CaF4ZKa2Qs1WCInQdIScGsygAZZ0wjRN6Pf1XTsoOsYPo5Uh2DbdKID9lWVyWkoyS84T10EM02OSKiBS7ykid5kFoFQIbL0GTt83KbBWASDxTHk9OgCWtN1cjPNhmAVarAS/PLxj0HJBEysTzhHmUEJr1do08z0ApKJBaySiM48se6TQCOcPy1QDZlAUMLox5nDCstw2BXgZLyJDqHae/TuTPWQVhMUHjgEvLOZ0/0wpLddzCAALnDRaM5Xibe2ETRtkg/mwhLvFdF6vJ4HJhSst+nZMHph8hZOsPS+6XE0g/vP+A6SSJ/U9Pj5imEfM8YhyPGE9HTeQjNDEbsLYCZYvScYR5sKrVxyMFrVzARWMfdCW+cXWLCxVmGYrqJbSKWXWFNwJQHFM1s8AEuQrshQW/USIp3Kt9V+bB1bvFANsJ5YmAklFmYOQJj48P7pl6dfcaL/s9trsrAIwcLKgGi5obU+fBqtQ1BN/65RqLKm2ZCB3nEpYEdY9F0EQgXWRei8vxrwVvfSeCb9FYZPxnAmB4/NK+u9S3rYxGRy/6Jn83JkCfDauhFdoaWcgTY71e1dKLDBSt986Ae5GXOQ1xAkGWcd7Q4GkzscvzXl7mzakCRyVAYeoNTY1tXiggthjLovML6+2PErV8JwzAtygv6G9Dr8+9aQ1+xnnZ+G0cl3BtQZIaXhJphX4/o+lne+PS1eJaxSXdt4HmRNoVW17KenFfNoxTx3+Be15Yw6p0knYyTzMGlV+8X17M2XmoipoFoF6g9/D4qB68FMh99aJHeh7h0ljKg9JV0UPpmHt5w+X7pJoj2LwEbDJPCl3bwXkVMs0+Nzq5NJQBei6ITex8/FiM3+hD7Vz7PnvP0MGUxdo3m2U/deg6wpwNfCJDlk48HB2Jz7ZeFcZudFiMWbqqURIWboTUVUYQlKDYrO2YGk4V92IVmCws+8Szj4NQz/AhELrv/i2G1X+B1A9IRTwXTAmpk4OrcykoJMrzCMaf/e0/xc//9p9j6gjvfvsd/of/9p/geNhrpb8i4VdFZNCeQu6GjpMZmoYg4ZKsYXaZWSpOoeA5T+jzCZv5hM+5Pv/Avg6gVGAucYke0ljDIi5oUWx1p3NGl6zsFqEDgwYCJdGcuo5V0TZiQdIHFSSbtHomOnMvQbQ3QA47E0ZFGpcmi20lE1MywUEWs0zi9iSStru+cySShGzb8C3ixCoVlV5REE4Sjoc9Pr57h/V6jXkeJSfkMALThM2qB+9POB1OKCyVBfIk2ujDh4/g/RFlnt2KZhvIzhs4HU8YrnGJ7tg3/2ubkMNtF4oUxhXFF4whctVwRV7Ji0/+DNdcriqEVGhdYjStcFr7JlrCm1piro8a0bPkZ2PUNiCRsVUA1w0bp9fMO7Tvy00kigYIHz98xOHlgDIXPD49Is8T5vmEaTxhmiXpO+YoNczwUp+NINPCqKGj9vsCgFVZMmlTGZt5HmydL/Ud5rz0CkkbgOMSBZc6Ag5xZXqxPKIxJXklWs3avuva2TzJBSgCxOKtyZJZzx15enyUdS3A27dv8LzfY7PdwW1HXK14nsRP8PlwA3MDXw0h875dKVnOG24M9jlWdKvLdL6Fzq4oYMblvfRq3KfL07qXfdPivfg3sPrwnHyLuSbnnVOUD8ChpabvsIebkBJl+oAIA33fq9LIyLn4wX3LwgwG6+W8rXcLXzUOEst9+6XCAiJuLQwfNWxpMW20O9lgHt+N71HzXjOV5mq285KuwYSklgZ8Dl5dorHL3yN0GhjEvv0e+7/WAn/C89DO2wTFVtG/NMYWX6s3q5aKRgPz5b5b0nS5Wb1stJygf2x5WFyPBs9tHixjyyVj7SHhF2ButCx0mZIAi0vB89NTSIqWtqPVuDFCAZWeX5iDwyd271UGKqcOjfvbXlIVFBR8pedY9K1tUijt6vRCJyJ01851UA9H02N7RXrd8BJTeBorKVd6bfjrfMuM1KJgrdcbDFxwOp2Qs4TZd6Tlr4lRWBUTLHgo1JtKtW/P+SDUeevYCsRLdS4zKR8OWHamBYNcpvF9oYCSKnxFZelKS8e5YMoMzAXIcl5cyRmncfSXZxSUvgNvVvj6Jz/F3Zdf4kiM9eYK+1/8Fv/yn/1zSPlfIToWVlwoS1EmK9jEEDtxT8iUkPoOaT2Ahh6rzRqZGZtNh7evb0FE+NnPfobPuT5b0egINYNfE8Et1lu0RUafqiuP1a1jArMBvtfz0HPOEu8GwJOa1F+UNK5NFpoh5WCrICelbO09CZcx66whhSe96EJ3XfLf7NATUmGSuaDvgC6/oKRXjipGA9wqbbive1noAoFzxre//g22qwF91+Hh4z0wzr7TSLPLS5HSuJ26lAsXdMxIzMgErXBFKuwIvMfjEYnl5GMzICgGOiG0gdkmjMzzHM0vM6UaboPqIdDNeM6KF+8GIavWXlePlL0afIHGTGRMpijYSCtjcobRMGeuQpaO0V2QVBOP06Icibkxz6ASPAmxGl5Hgi9PDw94vL8HmPD0+Iw5jyhZFI15Pnn8ohMoG7U21locK9G61Kk96gzygtm6smNWoUkU8oocHBjZ+WpXoqklaD8pNQR2aX07g68c2ZS5Jg5LJo7oeaFFaZgqWIQxepxFAVjDDVFQMpDBeHl+QaJ3GIYem+0O83hCt1o7Tjl/CozImm8MZwb6Bi4cR9+yD2r/NqtgoOD6cNNP047CbLGnluE3DczDeHwrQSun+USoAd/FPg3mHFlhbbTBFAPE2bzDXtT8hiVGexOOP7bnJcxhtV6Hc4+yholW5r4kUp5PVpsCM9B3HcbTGKNAKt0IA16Gpzk8l3QtvuPtKGSU7yjmX5xvaCj8zhc+oRnLOY5UmldbrPOuNHkxEF62pO0s+wp4tVzvqhNUDIm4Zt5qM0JEOt38JTiu+Q2gxb2oRVGFOVDPMhJeS5Hk/87LPR/mKYvgoQBf1DAjIXeMUMopzFvw3HI0+t5Epogj9VZF32CMBDDOM/YvLw1/ZkQc5AAT+xxo6gIpSGlui2vkMKtRBdZMIFS8NESxr2f05kYhe4Eg7TxYsrukj5BTIYwetklNwBYDbezbPCwtH5P51T3nhztyeJZFJk1EmLUgz2oY5LDccYTzAEg4lR8MbJvBcTMSvcpDa76IgUu9Gp0RwnOO4Wla8fZie1Y/lsLcPB/qcSAi9zTMpeD5cMBhHJGPE0jl5zzP4s0oBUwJOQFlnPBv/sW/wTEzRgL+4t/8W7z/7/8Kp2lGZo26SCTKSiLwqgMRY72WKq2n04ivvvoSf/gnf4K33/wY3/zBH+Dt119is9uCOgkh321XGLqK359zfbai4aWziMCW2V7sePKqIVm4UkpJQTlXzdeWilRjdK8A+bkYNSO/rY/fuHU4+SmF8Rh2Qg23sn44MI2kCN5Bqk9ZoikT4+Z6h9v3v8TH4Q7Olqkl7pE4RyLVUYd8GvH09AwqBfNpRFLqbDSZSJIdEwDiBCaJdUNmDacS11fJpfGW7Pd7GXOoidhYuyIhQUT3esWY74jvjRu+SpE+zxTfNZITOC2Hf5s/oZPI3KPiZlaUCscq6C2ZOYd3wlR9vCakGAQ8CZbQ5Ji0YTp1oEYQCFqbX/H3uD/gN7/+DdarNR4fHjSPaMacJ0zTiKzJgZLXsADuD+w//uS3pAS1EvPmEbbKL8pUWJ9dmtfqUjbWsyCTAmR9LWBO4QO3a1HlBqo/UBAoEGGu+5XO33c8Nn4S+vBEbT2ATzTGglwAmic8PT+h+77Dl19/jdT1wDyLlVxJt7LIBaOWf0ugBU2fenOJcxf3Uth7zsMW82xned4m12H5g03fzf6OHbY0yMZ9aY2aToGQ0FlRlRbfm0Eum4hodtbJpavSKpGRCNR1uNpd4fHxoakmaFSolCqYLYfRJi3Lc1OeXejlgEhxPi6cUBUe47ylcfI/zPWd2nm1/Fr/jd/StusnYGCfqpBdb7ocE+h5m0NU+7iEaz+0FJWu6Rx0DPG9y54Tavqz6kIW5pNMsY19RZgvBh+LfzSi8bLvMNcmTym0G/G/wVn76IOuxoCgP5zx7/b16mV1nLdxJtLTmau13i3T3ncFAkGj+FXmOB4OmHJGT9VAyww5CI5DW4rPUd5gveVzd+NBpe+eNE16mrMrBWbsCftRqyV5WyaLAcIXbB8pCXX4B8WpIkvYC753AxA4rJbzevMWBOMCYh6K0nKfZ52vTaIaRWWehRnIM47HjM1mg6urHSiRVEoNa0hFQ/9RZYEI84gPpHOOu93HyDbfoAhxmHf4u8TziIPMQbFmPV+ISy3nTAn567+LmQkfJi02o+tQqKBQATr4YdB5HPH/+n//C/yLv/gLTAUi0cwjVrsBqVtjd3WFP/jZH+Jnf/zH+OKrL3H75jVSSri9vUVKCQ/39/jDP/ojrHdX6DYbIwWi3JSCcTzh+ekRx+OE1WoVFO8fvj5b0RD3YZJE7K5DKQBrRpWU58qo1WtUpOaCRD1ANaG5ZIaR+y5pCTJtiwF3GRU9f8M4nMQOMih1WHU9mOXgvmGwA0VSowXGPAv/TIKQ9t09MtpetE7HPWLIT5pAG0tiEoD1asCYOqDrcX29wYd37+HbzdoqWUukJRQtbCfePfk9KWEhEMi8RWDkaYb9wmgTP0kRAOF7u2gtght7sG3bVA2xiSpXJhKh1sYUhSTfm5AbTBCrz2KjQg8BipGRlWmwjQIcCXwgsAjPNsxGx22KSxOWSoarCnc9WMs8LEZoraKVUVMiyfNJnZSFm+cZf/PXfw2A8Pj4oJXTCvI8Iqsnw2GAQE/9u7MiH3llfRWmkXuyQ7zCgJazd80sYkGFlynkjQJwbnavsFz8XfbteMJLvAkYpS8YsWzyRczKZaUfbd4X+jYm5dZTEhpCIKAAmWUvPD0+InUJX//4xxjHI7ruyverMHdjDC3hP0u61vFW4VN+TIaTqGVgo0XUr4CvcQ5ecOEcKbBckkuwMNqSgFqJBedJ306LbOzREuzzrsJPlFAbWqHzqAniTaaEzruy23bM7Rwde4OGb3ieUsJms8HD/T2macJ6U7SaIKNLgZYxI7UjCEORGVporR+EqnA3WzEZsdK+Df0F5roHXZCp603hOwJ9ZK7rKfQ/7O/ILOL62BMO3wA7atfbxwn2dXJYa9sM4RO17Rb3YscNnrPNyfo2mLEPwPeq7u/muCZbP2r7WeJaa9SRmH0r6d3SPa7PKlxsTEbf42TqXAMfcmzEwkodaWW7x+q42/1tc5C+66yNH9UQbwmzbuCitCbKCpGPmWD6/PykeFTPPVDBp65D1H4aXhjHpPyMUoVp8CKYEG4KeFi+RSU9hR8rLPW3SAfN0t4o3n5qnQ9O5K5Ocnj7YZAiPFpERXJiJeojF8kpmMcR4zhiNqNq6BMEoFjfYsh2msJymJ3TYUu6ZjV0s/R3OByw213hancFZsZ4Oik8TQmTwlTuV1oozs6HUCNkbGEFVgXQpPBYLKOBtS0n7D2ows6+sMn2uH43GsOcUQQM2K3XOP7h/xQfDv8UeHWFH3/9NdbrNX7yk5/oaeEzxnHEu3fvMZ5GpK7HZrPFerPD27dvsd5tcPvFLW5e3+H169fY7Hbohh6ZayUpkOa4pIT121s8zxP2hyesixRWMeyaZynGdLPZgViKMu2f9vic67MVDZC4pgBZVKlnL7FkfSIwz7CazZKXIZ/nPDWMV/IzLHOffeOtVjV2FyqQs3s4TCmw8Cd5TrwXxZUMedQODavL7kqF81xC14kCJN4UqMZWGVAxwYJbViqhYPJZvBPAsN2iS4RhWKHfrEWhUM0TzBJ7SOJF8Q1qY0zJrdQ9JyBpmUkSAp3HEQRxjRFX4mkMvFoAA3WuHKoZtzETI6iupYd6t6wSDTHXU8gDY2gYo8IXVqZw6b4IlpdmzPYeKFTKYCfSKbwuP1XC7/seVfAlguOi5WxIlQutYOUCWAKoVHquG19wVupvD10CCuPXf/0rlFlC18o8AZzBPCOXqRGuLoeVRQAp8zZKc+l3U9aqecoFDF487kwkMuz4u3FqjmOLCNf27TG5cWVMUrBXgrDkApwjgu0oYXju0WA/4ssP0I0KSD0LBgibLaBtZXqszyeSwzKBgqfHJ/TDgLdvv8B4PGC13VW8cqbg6pz8m8gtRUX3YYKWyo2QCXhfhTPUNQz8muoS1jaczpxfBjExJFYFG6jo0Vp5bQ4VNk3fjg/BShraCA9WY4AzOMMiHbsxwuaq9M5C5ogQaKlcep5oUELrOBKzK6PbzRasschcZjBnEBdl3lbqMYSfhb0qcG6CLCFKCTveR/rkMFjMO65vJcfthAxnKxi5DoiqAOICfEAeh6f9HvdoQ9cWpNTnVWlh431a/G0V4tA3GfmvY0mIxhz2vlnhU9uuNIXiRJp5mHAejAYUx8mVJut8POQqwDwsK+ym9xnWIq4BLb7HNfD2EYQ8W6cGoYwy1ZZallYXxvaJGCgLEgHZSUygLcZPyOh9EZ6rTR2eX1SpqZ4hEZJD/Xlqp24YlmL+Qxi5eSqWOXvy3faTtthYAa0znWQJr4P9nDAYzhjsNTTeBOOu77DZbLDdbDH0kiBNyWpGpqCYMsCd0iYGdnL2QinAeBqxP+wlDNLWMxHAyRXVqnClupYOL/nCLA1KqF3CYb/HZrPBbrtDmbPLrkKfEkBZ520brMKn7mczStfjIkn5CsOMIQwToIyVKQnzfJBKEIInhytf42IH+hKYehBk3jn1uL69w/PTPb78w5/iv/pf/y/x6s0rlGJ5KBm73U74LuoJ3pYHRxAvRC5ZlASFr3n2mQWX+67HnGcUhuQXl4IuAePLM0rOGMcRfd9jtVqBKOFud4thGNAzsHn9H7nqlJ2B4VYgIglXKoRZXd45zxJSRagbSN+tuRK1BrFVICkswOi6rkmOchdROHF8HidhLknCp2JolJ3RYe/a5zhmIyjTNPlYhGhYP9FFrjKQa62V+pNSSKKEfugV2dTt1SXkSd6wDpalRGVT6/ZhRk6VSdomBwjTOAr8ukrY3TJmChwWAkIk0ia0+J6ghphbjkOTvBsrT8S94mOre5NJrQSIP7Lfj8JIJBBG2Rrbqbbj81n03UwvMGBjgLaxZWxysygVJQoMHHBiCRJBk8HoqAOB8OHDB9x/+AgCME8zEkmlsHkekYvU/3drSBiYC2+Kt5V9GzslmLXYqiBFZayVDuP3ynqiTe9yfGSEQYR1YDhVAoudnfetE6pCXAy8oNp/5eehO/NGAJYwXvNB6tgZ7DH0DZKRMRCxoBHMgMHImTCOJzw+PGDoB1xdX2ud9GRONJhQYoMizYvy4TpDZu0yzD/MteK5fKiKXp1rPIfD+4tIy0DUwRuMiHhtU3cYUovnYZnqVuLKHG1ejGop9HGRo1sgaYGJ17abTRtu+wtAXHJ/ihI3gjGxmn2c7jLWm7UKAxJbXHLRfRtw28YWZCGnV9p315nVVh4kRSAfl62ZNRaXdzHHs3wJDrB1auyLaqJNhR+1MIltRbjGsUWYV2NWoOfL8eJ8TNZ3zMMgrqVb+ezdC30vfm/DsvgMT9A8X+dtNsKmbKxsr3BGETVtyzav1t643pXi6V/loUb7TWEyOpGYmr4bOqgf3FtKzS9n6+0ekjBP1lPBQ5dwnFV+5wD0d0UhLTljv99LfxplW0pZlBCNZpHQdwN4pZ0AXCnXabhBqGnNFkZ/M3pu9FthYl6ZyE9Y361ePz2ysTDWGpq0WW9AXSc5tSTRJNnKpJaCnLVtIrWYa8QJkVTUzNkPVS6l4Hg44vnlGfOc0RNpYnRddJM3wOyecxkcOe/NzOiSHJcwjROwIlxd3+D5+QlzluMEmo2OBmna+wC8Whfr2iqis5Xu9ZC1BU1sNnHFLjN8Mqw6ai1zC0piAGc5xBFMUoU1Af1qhQzg3//ylwARvvjiC+yurwFIDsfpdMKHjx8xa9nb4/GI0+kEZsYXX3yBt2/fYpombDYbXF9fSwI4JRQWmfx4POJwOGCz2bhMParsCSKM04Td1RUA4OHx0RWPKM//0PV75WjEfAr73060NkVEFA0jhOy1fnst/2oH99lzlpcxDIPft5rCpmCYoiJt1TaY2WPE3IUVNkcMXXDBQq94wqcpPF3RLP7AeWz/mjICVCFBPjO6oUfXJeR5xm63w0MizKQW55QgcY8FIWq0hjzYGIvUMuDCYCvPrNpByQWdr1S05dfrElOpYU6LDRV2A8MsoaYY2GZqGWsjEBULRfsEQ1Oi69Up7DcTHlFhaX0tiWx8senbmIwObxFYBONCchorzLDjUACRKyHOrFi8bF1KmE4n/PUvfykMshQQFeQya0x5gYXwnQ0szMXqhbfKxmJuLlTxoh3Gp1c29Ok4Hp4jgh1IJ9YRE5D+f+u75rQsYnCp/s7KaA0halIdhAgz1zVq+i5N27wMRbG3uFprbQLMBfM04Xg84vHhAav1GtOccXd7JwYHVRxbJa5Ff2OksH3NCNM3SzE377aCUqANi/uxj2XfzVZcLm14JL4bLdPQdWjAiXafta2FeQfStrwiT1xi4KeuKhqR4sQilEjxL1apGfoeHSU/g8lovMGcKiqd0xZCDb9j8ay7ErhMjK3AaULmKnFsJlK/EvzdKqpGFCf3jttTvOhjud28SxPsXIipcMQn3qlDln/9UEUQzELaIFeD57Rs5Adp6iWYx0sEpYqfcd6fwnMbB51p43UQ7R6D85s4ZHbagjrv2E3Td+jElbh23kZbWppAZ/M23lhmEYrhoXoB28hbdOWnKgGMcZwwTbOH+0lvYpiUPsjhGcdtwqd5EkEB5oq0lY6QzpWC4aTFNR+byzfVMyVRIQo6QwjjlSTl9oduwO2rW2x2Gy/9nnPGPE3VWNeZPKYhrwwUFIzjqIcay1EFw7CSA9/08OdpGgEAm80ah+MR++cXcJ4FFlqpq/pZbB3MesTOm0opyGB0qcM4TRrCNWCz2eBwPHpOGBHJ2U0KS1Y62vAxWsgkMEVVlCBOXQ1HCw865MlAaeOXH21dAfYDTCl1chCg8cw5I3XJ7W43t7f4T/70z3CaTpimyXOau67TMFTG7d1dLR8O6AHYncvhJkfbWvQ9oe/lwL2u6zAMAyziqOs6bLdbTNPk96D4nVLy+ybf/67r9/Zo2LkU9XNbntAmFKFuyklM/o6eCmsfgCsedpq4/W9XTTKHKyumhBBJTeJ5nj0h3RYkKiCm0NR25e8fb97jn89HcLdZ0ipHxsaKoL91nZQHm3PGYX+UGMNgURSLR3WvGUFyIurEz4TFChcujNPxiJ1qmsbak1MdYUKxOkckvJWQhMU0JmmEvj4IuxFYgL9i1kpXSKB9w+WK5ryL+isaJc2tni2Vby9lYD6kyNCM36DGaPq87RO1fXgyuRFT66MITJPO+Vd/8yuUOTvhKerBmOYJrAUPtMEKP1QAOF8nCmNyeRAmMvgVFsaUyzZZuMI5tsYInjetwEHeSFy9+l6dvzGxBVIw3JpHqMqf/StCY/H3KDbqvZ2LKPUARt3LyggbnUTn3a43a4KcVodT64qcmJqRpgmHwwse7j/i9Zu32B9esN1u5SR5F0qSr2VcB0ZFGmO8dW3tPhrcrIyjFrZAeKTBNZtTvG/PWvvh/rItC0WytWgE1IUkWIUL+66rxos+OPRt3wOC2kcTJlvbvWEAXCkUOLZ9+9r54AKdYyB1HbpejElWAz678BXoVGDMkbbYKha3mFofVI1NRqS5hYXBt96vfYFqeJGvQ1z7aLQK4/A2vd3l2oQubH9X0IQ2FyYTrjt+aa5YmlZspUK06mVca9Y7zmeJ/Bf2gr7vfXB4OtDzmJu2xLVIEJOqS2d0/2yP1QesVHmV7WIAm3RSe2/7jsahSFtaCk0+H8c9hdU4TXIKMpv1396qqhdr+9C16HSs+8Pe6Z7lFUixC23DrWJhbRpUOCcUVnADBnMzpHKg78ZLHLSVnnO1FmlIlD7BZQESsdzfXl/j6voawzAgEWGaZhznA3IuztMLMwqPFX5JS8R3CX3qMQwrgCXWfzxNeHl+Ruo6bDdbXO12WK/WOI0npNTharvF09Ozw86G1HhMQaJw1BRg8WqznfeQcDqN4MIY1iushwGH49FQQ3mJYVHMJNV1pCUtM5AorYnEnSreLIucNKZhhhqdZZnnuUieRJfA6ND3A4gSxukkYdzMWGHCerXCOM84HI+Oh8zA8STnWJQsMq14KiQJ3ozwKUkux6Q4vNls3LOUUnUMABLpY/L34XBQUIhyYnL1MAzo+x593//HPxncBuAwN6IOOdgsKg3mlQDBhfx5lrAq8yRM09QAwtq0fmyziBacXaEYur49GEYBYUqFtWvvW9vWhj1XQ65Em0+J8KO3t/h79/9P/Jvdf4kZnXgXHIHqZjdiZESXuiQuxNTh6elRtV2JFQSrhyIShcqndQLyTyNwGFNgxjROmnwckN+JP/tzZNRxSdxDN9x0ghCyYrCEC30UTXQafEhBuLCNRkZpEAKwvM0qcC/7Nrg2vEbnQ9ZkZJAc8kbMUqV9c4SNjtWtPgryWDnG4iABKX3cpYTHh0d8eP9BLFcs1gZwxpRHgIvPrS3rpqTblbPlpayPamwrWPDO8xmUIbV674IxInhgKgeEbrJKyJqufcSNBHJ5pPKcW8sATaSHv+tKhj1DYd7MPqz6veZYGQV20SG8V9eOa9+OV1Yrh2s+T8lASpjmGXQivDw/Y7vdApSw3W5qbXhneDBZIOA5VbwKELB7iePjBj8J0bnofWugePk3++63dAyyTSrjcuZmm8b24lLecNxhx6l2T4UJxj9GP2DbNsAcaHKzlnOxOuxq+qyC2Zn1T/uJQyATHhWq6iGU2GpbpkpbgrFS6G0QTHMWix/ruUkl0PMWSGj2XcVXWwtyWLC/H2nL4j2gWWRC+zni0wJ0/iHusYphYd6+m9n/1YlUGm/96UBr6E7bYYRlpKlxrTg+txh3Y9wJuNsYbBqYVAAs+67wZJQFWWrgZEtobYZ1cLgED1b1bteHzuYNVdYLXwgtM2NZ9dQr1VaYS36qCHjLMZsno935JAwHBMJh/4JSspxTQADJcQiwvIs67MBLAnxq0FkgYABqXuoC5vE7h/eJPITN2YIdSWAuOq2skkByqnmX8PrVK2y3W1AS6/k4npBLwTROmKZJ8h/ifvNltmgJBnUJQ9djtV5js9lgvV5jGHq87Pf4+PEDHp8ecX19jbvbO6xWwHg64vrmGuvNGg8f75GLhRr5JGHFH2oRCPieRmFwKshzwdwlpDmL5zvPmKfJaW89zjz5mCsi6myMttr9OIZwz1GVa9Oc4DzUQ3VTJzIiM47HI7rVAEKPUoD1Vio9TacjEgruP7zD8K/+D/jD/83/HvvjCYfThOf9EeM4YrPZYLPZ6PkXUxPdQ0SYpgkAXO6OBvzVauXJ5GZ4typSZoRfrVauoMzzjPv7ezw8POCrr77yZ88Knnzi+j2qTok18lMxWRfjxbnGIMYJWDseo6YTtX6AqqDEsrfLScVwKQCuaCzdPEvPSVRspK9Kin7+1QZ/ef+IqXslSKwSvXtWfI9SJUpEWG1WmJ+eawIcEaAlx8DJA7nZNoXhM0vVm0LSpgcSGHFW7dRoeIJZox3wiKwp/l268t2KC+k+KSGOdNzei1ZTs9C23oowRpuMEkaLE4avjz4bhLuG4Tk4+ELfqAyOAn2wD24WYmcMpiRVmYMbQpFY4nAZrC5gwcu/+dXfuOBluDHNkrBaWOv9k8W1wZmQg4X5zJPRACzC5CLriBcp/a84L8yMfHxGuFjhwMukGF8b9eYorhGlCrfYY4R5Cn0roazCVoAnw+M44bCz4Ye66Kb8UTvfKiTY1Oq82QdDmqAmifq1JI4c6Hc6HfH4cI/rm2s8Pz7h5u4WZuEuxOiMCSwEjCWuITyDkHRcZbcaTkOIeB52geI5Kx4udZzmb+zb5t3sUUN4bWGxZNaGN2GWTe0hhZiWwIql5Xj+hOKaUfZyJuDKI6bAm5If8bzGy3uLjdBtJRyRxHuYtZ9S9LzewiDNu1jIq6FNmVcBHB9qrpX+brijYPPwobp1wgBbfKwoHR+sv1WvqoYCcczk0eccMLZuF64AnIV5KQjX1YCE0HckGBFODP496Dngin54ls+nXcFm5DMYGqJOt/T+/VDfwntY27+goNqlD3sb2nD00C/7/sH9rXS/pc91vanegBdZ0b/zNGGr5T7DYzV0xmiL8STDE4Kc56CeAagxhc0Mb3jCla6Rzd0MBxH2zcp4vECdt+3/YPgJVskwzxTKiLHyhBbPV/0Kb968xmq1RmHG8XDAaTzheDphHicxxEEK66SU6oGBgS+yy0ASEfPy/IKXlz36vsd6Ld6RnAvG8YBpnHDcH3D76hWudzt04wkEwtsvv8D9/QPG01h5Hi3mrX8TZI2Lyp4pSUh7ToSuI2w2G+wLA1nyaWFFjQjuMUfANd98BnJVYCwW0Pm45e3GbW8VLwO+mfeoU+Pg8XTC9e0dTscZmYFhWInBfZzQ0wz+q/8LftQf8fbNGwzDCt0gIvsydSCBPeUAaFMDxnHENE3Iqix7yFvOKAWaG13TE0xuNqVkGAYQEb766it8/fXX3ra99znX5ysahT352g7H89+4hkSZOxyAIC+xam/APGc9sVuTwMvc9BHbtByQJdByyWIVM0TWZ3yTkbh5VqtVMzZTPsyzEUOyci6ywcyzMf07/KL7hzD08BAuJ1iKWLZliZD6Hmm9wioB+2kEz7PjaSEGlco4auy3MU5St2MlHYBs9lIy1utVDQdRgc8CsSJzJJiQY/AI66fPV6uY9hWtzLYOUcLgZRs2h2blvF3vu96O0kig0+K+rfs6cCgYTQ55DmxEn9tnbDMT6iZDZZp13qghHyrgEKSsGwh4//07vDw/o0fyKhC5TMhl1rhONH2ch7lZhww/JTWYCYmiuBdCC2B8JlK3oIw6wwlrocAVwljnacIjL+IbXKThusdiEYU6DoUPAZxVgKKEjuo4LORKEvXiuS+AKeTyg64FETqztBgEIvOsYk4jl7ENTmHPRWuOaB36hAIUQmYg5RnHwwHr9RrvDu9wdXMNq1DHppgEnFp0grMr4hpM2NJd6wpewPMLm6Ter8KCycSVd3HFgwtCWlRslgKVged87Bx+U4mBQgwy7N3wsn4sQYGwQRHB6ZZMW0aWqFr9XaBrnpHfKurISidK6Poe4zQCRQ9PNeFrsRrCwEO7qhUkMnhyqJCzhEN9xtvigG91ogHmhDD61qMS1kUs43WnCjsK+2oB6zoffbtus3bGEScIrZBsz5OPQFfCEKKlNY2O09DU0KauncOrfbwZn8GSuV2nBvaLKZ/pWTbvqJifd3hx3DZ4dgPT4hWnYYuNFMYSg9NC6ZNPrHcTrCiFbjxSwvquA6Zl3zB5BDgdj2rMrIPmojmoZkQwmhnphPMYbgytbX6jenyXFhw1dDo9V94kuRjy2fppSlqz0IH1ao03KtzO84yX/R6n00nOpSApI9v3a8ktoM5lp1IyXp6fUThjNayx3W1h5W1FdpQKSPM0YR6PgAq9zOLdnOYJH96/w3i6xqu7O6Suw2F/wKu7V3h6esTheNI1azP3DK/ibha4SI5rLhIts16vsRoGjCyVPOWMAW7pROB3lsNZkdBW3tal0vi6JhT2N4z5e/siL4o8utvtcHt7h+9PH7Fer+XoiHlCzhNofsIfjn+F1199gZvbHWZowaSc0WvUUM5CP4lFjgWA1WqF4/GIp6cnnEZRzjbrNQB4yKqBqBS5Z94PK0FuqQ3DMGDWs6q2263nZFj6xH90jwZ0wUxgTyQu/qQlLUsuEpOnv4swAPSpx5QnIczMyHPBatU544sJ3zFvwojaMq8il4JCdaGTuiNLKcjqBrJElfV63YRrxb6i8kKUYTGLOU+ayCtIUdiswNWa60IsiVUuMQHrFdavb7HtB6mmMByx3++RFcmdUKsQaoQvK+EuirTGjImSWP36Dlc3VwprG4e5Qg3/UxXgFnhvV61UpXPWf51ZWoz8guGYvEpByjnnYeEl4rDNA5PmOibjFfUEXgr7U+4Vfc6SQ906HOgya8POdJMm1ZkyR41c5iOWAxIL+q5DSrLmv/n1r/SwT1aLbsacR6iTuwLPLCo+RxVIo+JNCIyBsHQgMCAlPgM1Ih03bH19UhbuZe1whZPuQTZBWpWy1ClcqGYSkC2CjdrqsJOVn2WY+xisJ3qQxbsGIpyqQYGKwiFpBRQVTAkMTnXSTqwdhK1EEVqvYzXBzZMUWSuKCEMXIVPmkHPGaRyx3x+QS8HDwyNevXrteVJt6AGq1Zdq/xFOdpYP/F4Vudg21xLPEZVm76oKxKGP5iFW/CkVLo28YDBTFEwcoolDH+08KiMxAYPDhMnuLy9FR9//fqJv23YTbmZ7jCIM2X8DbJ+zKwb9agAOGk6oSeEAn42Lw1+BQxD+SGhSQqXPOmhfFJ9Hs97c0LVm/0WhM8JFaX1DV0mSsquTh2ND56A1fIaFxVyGf1g6mBhZaUB9sCaEw3kXLNTRBFSfa5gdwQ0z8jUASwFTh8fafsiG8N+rSCfN6S4IvFGGpPN2utXC/FMwM5zSraatp0qK9bI1i8YLppjRpgYtG+yyb58F4IYgDn3r2JmBXk9GDpiF2nCdW4GEWCIxZi6Yp9H3QB3scrZw3iLr5TvZ1w9EYR0q8M3IEwlM5SVh3vqd3LhYnzHMZ5IKR6/fvsWwWuN0GvH89ITD6ahexB7rYQWiAkaHrt8AaQXqE/pO5JDjOGE+HjBOI676VxhWG5EPOeNweMFp3KPvgL4bFM+SG0432x0A4OnlBdM0483bN9hdX+Pl5Rk3t7dgesJh/wIG66HjyzBmpfbuJhd6JVWcOvS9nO4+zzPKPAPqyeHGxcsX12K5VMIrbA0qja0wr/ghy6HYmnqsVltsd1v8+Ec/wmHK6Ldb9MMWHSWcTk8gZGze/yvsNmt889OvMJdnHE8ZpQjdzFp21oR9y5dYpzXef7jXKIMOfb/SimcJp9MJV1dXmOYDVqsV1us15PwwOeTQCjJZSFdMMTCPiHkxLM2BmfHNH+F3Xp+vaBiczaq5uCzMyfIgYugTANeE7D6YkUt7zyYQy9LGvpbWWFNG5nmWRBWQH2ACwBNVomLRJoHbuBkp9TDr9F1/gJVPs8PfKlmFb9yitbILA8Nqhf3TE1Zdj9J1mItozKzIVlTwA4BCCZyAKWdkZZTGVIhIysBRQr/Z4Mc/+hr74wl32x0akecTQtIyXMrnqf86QQ4E2y0xti9IGWJD1Cvljds69sP1yeY3Y+yx7+qpYJgLxWmnwsKUDduzcZMvL2urFaDkwRSsQW0InMDz++++x+l0rAqPWlYKB43duS9VYmI9hAOTXDgI/Vv4oMesnomoxojJ8a7F+wptt+CSMAyPAdUHOxMqmJp5yzDtIEhz95oyoK7zIGqRKjFGKMXCwepBbJlgVDL0aRDMqWH7q0kpdyXI8j7IDmMyJS70DRDspCUbfyFCUkZQ1AhyPB6Rug7ff/cdbm9fCQyLnDAeXdt1ZcLSxnsLxLZiz8ZyCsHP4zjDcwQZklHxsfKuyuSBSluozdm5dFnfteLRp/ei3XOYEzfKgOHpQr5bdBhwoRnzeX/Lvn1/u5Gl7tv1eoNnPIrRqBTxgDNfaLUOo6Ut9Zuf/M1V4LSFMrqzvJZGl7Yzl0/a75fGxG37/j3gWMztiLv+01fY98obYoWr2hb5GOLlYw8e90pxuJl3zK0DEPDD9mjwki/7sOcM6Cbc1wE09Keh9xeupUG+lgc4x3PjY/YjExpvRH3eTAymZAXGF9apYaY2FjPiQMOcqF0/Cgvp/cV1l0mDpxmTFhHxcGq20KnwUgOH2hCFD/VJ2b1mWIujaHiJvmvRFz7Gop4h+x/wMNC+6/D29RsMqxWOhyOenp5xPB0BghzG1w3Ic8bh+IzMjO3mBm++vAE6TVAuM169+QLHw4t4ofsBmVmMp13CZrvD8bjHNI9IiTH0KwhdV+F1HLG7usJ6vcLz8zO+//4dvvjiLXbbHfaHPW5vbsBccDgeUbgewmswIC2rXgBP2ubCyMjgwnImxDBgGFZaUELKoldjiIFeaIsvclx4BSSjwA4JZJVpbB28qIoih/D+hPV6jaubO3zxxZe4u7vBervFy4d7bDcbcOpBc8HLyxMIjC+2BdP9hH/4D/8z5DxL4ngnMi0RYbWSMCtTNnLOeH5+BgCs12v3eLx69UqgowrEbrdD13U4HA7uwYiXtWdejbV6QywEK+aCzHMblfSp6/cqbwtUpSBaNOx+zIeI4Ukxx8IVjdBmbNu+x3ZsUpfajkCZp7lJ+m6IXLSuLuaVUjuOuyEDnMHoGkLXEhQR6iQGsSClDqfTiPl0Qtf3oGFATwmUc4jL6yXEapATNKnrpERan5BUI+37Hh116FKHfrUCiHCcJhAlF2CFmFTKyrggRDEQ64FHxWLJ6cxb4IRK2zCPg4eRUNvOJ4W1hbzgIY5BCnMrHEVFro4hth9DoWLbS5ZFOhlumGy75kRAzizWlySK6XfffivjL1Iur+QsVqhkAgx5rX/nZghSo42GucHNRtCEzp26hinVcdVZt0K2dWnsssb6whiicVtKYa6kQ6phjSZAmIBgQjqz5imxtWu4bYRXz8yJ83ZBRPqmZIIPN+tdzDVNfVBEAM9fAuqYOIYXwjVNCwUTps+a/BaAx0XOOZlGpNJjHCc8Pz/i9vZO51iccTTyRVg6WxP5y037Ni/7jAa7ggjkcfc2S6oo4nuTm7fss+/BZo8Z06rv2dp9ao9FgcQEvyhXXXj1wnhcNKvwWaI7As5eIAhOb894NWOlZRTBmsRtcb4LQhvHbVWqKx1X8wy38CQwyllI5nl4KDjgr8/5khzsu66Zqu8zHSQBjUJUYYmKz5d+i+1GOLpRQtd+uWimkAdtw0PMyQNqFvRcX62y0jmea3+NwN4IWAGn7FY4nV1gYXgRc7nc91vxk+PzSwNDBExYywbPCVWIq+9FPK/vMFz4rkPyFwS323nbqpVcNKbePKkVro4PzbArUOd5BufoFYfzEsdh/ez5Fb73AtYFmNvg3QsBBAt+BK7OwRQcIgmv9f1tyqHMNCVJ/F6vVzgeT3h4fMTpeELf9Uh9hzQM6LsVZhoxH2Qwp3lEgchheZ5R8gzmgn7Y6JgJXCQXgGcGuGB3dY1xOkphH1WYROifcTyIwe/6+ho3Nzd4enzCu3fv8OWXX+L66grPz8+4vb1DKQWjWtTbxbT9bEREeXEmcJeQ56zW/x4lD+BycmW+MUBHvGn+mJGuhXNcJ2MonuNYANJStJakvd+/4OpmB9IiST3kDJBxPOJ4eMHN1Rp/cHzAV3/8c3z19df47bff4fHxgNtbScy/1jM0ohxMRB7qFFMGrAzuZrPx8LGUkp+F8fHjR9zf3+P6+rqebRdyNsxw/+bNG+z3ez9vw+T6z7k+W9GwicTD90zw71fCOCwR25WDYmEocOHf2mKW8wmsdu8l5cL6MEHJXDf2jJWyte9933t95zhW+99jTFXhicqIaMbS7zQegI//Gvz1P6gIBG6SAc2CAwBPD0/YbjZ4/fYt+r6XsLKvvkDWZKRBS5Z5HosKJUxAJgJR8vAXiYlX+CkfXa2rjRwAvNwdgmATGQNsI7ScpLl1JgBUouU/m1BlFO4T1ih7z98PBP/8ucrc471mnFFSsj9KDI1JisWJm/ESka9PpQMV/8CVKSWS9f/2229xOp1EeIVYVTJntYYo5y6o1qMIg4U5kxEYLozRB65O7H/snllBI3Mzz4qNWSMGQKhKseGfMEgCdZ22l2GsmzwUKoxXXSDisSJ4rR8ydc/6NO4r46dCPi55xFzE7HAwpcSYuuSQJNjZI83J8QvscDe+MdAo1S4QqXifBnMApaBQAbO4wz+8f4/bm9tqxGQOYRwtzBsBGXB8j8I2BZibCGKfWwHDrIphrg2vqozK4QdqFIJlCGPbt7Z1aXM1AlRdF1OOOCxvu+Pg+9uFMyzosD5DCKFbi8tDbKjCsQrfGppZVNGwbtlOXeb6niKt7eKzebO0w7757WYdYwXHhTZsLoGuXYQnWrr4qavJbUJdN9h+ARbwVdqOKvIpS6kEGIQSei2XaCobJraGINL9yY5E8kPRfV6jYINviKhpv55uYrhmHiOzjsc9zw7PKtiasLag6wHPHV8dQ5YTjLxkCdxwBZ5mNBEkfNK8NtVLQPWBYIjzPabzYRfkGXOePUnX6Q6rlxBUj4O2AYRrnCYPI/8UPTP6GzHWrOluGglKWzUExIbkuch7a26HwYIl+dlf0RaS8IDr62vsrq5wOk14eHjE6STW/77r0PVrpGGDod9gd9WjX+9wOu7RDyuMU8ZUZqyGAdv1TkKSlceyYVKxBO0Z43jEMA/I0wQC0NMGpRTM4wlTzjgeRzCecHd3h9u7Wzw+POL9+/f48osvsdvt8PT8grvbO7z/8N5pQORfAkrFQbeQyH4oenZP3w9YrVfIJaPoeR1WGrfxICr/qkjGTqDZTgyPFgYKe8x4qPLsUoqe0H3C09MT+tUKX3wl1ZtmnoFxxv3HdyAUvN0Rvihb/K2f/QlevXqNqexxezt42Nc8z64wyHx6l71Nprb/7TwNixgyuXi9XoOZ8erVKwzDgPfv33v1qdVKPEo25i+//BLDMODNmzd+hEVMbfhd1+9VdcpcJoKbNdwphkXF54nEOhwVEwPMPE/oh655PoZNRQExKgR2z9qMpWwtIdFcOszcVLqKHpRq6ZWERBPqAcLd3Su8+u0v8a78vZbBK6OEWrqTHiRTcsZ2u8XV1RVmO2wQBX2pwrHUBbBGovNf5iLl5FCFNt0wTJoDEokKBdrK1ooBMggxCGLQQugBt9auSsPjJ2NgxjgI9V801if7XqiWBm0FB3nISWmQpOIzwQAWxlIJqFfxcfyoc7ITaI2JNCKgCTPMSBAlA6Xgu+++83K2gju5SU4DgGJMQAmWWbagh+24oGImRV3HRGGC8a8xeTKPQBDqHDc1tEgnHNsityBK6FMB0F2oIhStVvYPKfFz+DaKUbWsOZGGCOhFKz6Z0GpjkXAfOWzSCbz+njQPhKHVojqzswLUAEPf0xAF0r5VjYgTg80qKaGnopVDIEzEQsceHx5wOp2wWq2cMfu7P0QbGS2zRsVzFwp93nUKHntva2R/w9atvIdrQiyd710HB6gpeBIe87H598WcBEdt3LXvxVTbvi/AoiE73IZuXdrfzfx93po8XiTMtOt7Z+oW9mYCoiuAi7ET0IQRFaMfxsxDfxU2zQ4AbN9GOLGFSFySYVthLsI83vQy4It5W6Ut2e6LfrWxmNwcn2izDIR7NIpi3Ov+iQKe1vWOgmWciCcBE12G+QU8b/4GxujvchiffzajCAfa0sK0rUxVaZLn5YV91AAqrP2n8fwSH4NjBgGwalTRApH02XmSRPAlfXW+u+BjLltAzvthLpI4p3yinvFDTpcrb0FVCiDhOUTJ88ZMXmjWhM1wpEI9qawR5JxKzzWU2BApiUGoWw24ub7FNGU8PYgno+s7DP0gguqwRjdcYVjtwFyw2SV0wxplzuj7FXbrAUPfqcw3Y54nzCWjqDeHkkRpDH2P1XCNUmZM04jT4Yg5z+hSwpwSppe9JDMfjgAIr1+/xs3tLR4fHvDhwwd88fYttpsNDscD7m5v8fH+PqAluTJt8oXs7+Q8p7BY/+d5Qt936DoR3I2XRGXZDX2RMrDgimk4Z/zbcEsjBDisG2DnzJ1QLCmbCHd3r0FzxtPHjxiPe7y6u8FX/Tv85Ms3+E/+1p/g9evXSMMrEHX47rvv8f79e9ze3nqSdt0K3DgCjOYsFYyu6/zUcJOP1+s1fvrTn9bTwAHc3t5iu90KDyUpsmQeGQDuKfmc67MVDUkcEcQ1z4JpUadpPCtXa8pArLVbvQdJD/yo3on47tKzEYF3SYOqB/IBxkxsES7lfVibcZzyTM3feDsc8B6BYdk5EoFAGpFerVd4fnnBzfWNxsEXJE4oejS1CI2avkekyexKXO1/EDpUlDY60qHe5NrzOc2DEUzjvcp0GqUGroREe6HRvShXVLoeiOGFvn0NYLHrVSkwTtO46hfXknFXflx/qXbk2HdkwhpaQZqI14zbWhNAFzBWXYeUCB8+3ON0PPlagqF5Q0XfYF8bwGLNa81+wTVNmDXFgSyEaDFvs2wYA4maVVSiQeEAJV2l1MbTy+OaJJ1Ik7Jtf6RqLeU6b2hytoQQdQ5Ns5sac6dUC7LasG2Ozu+VEbpSGXJU7CGqLcDiZquFtcI0fqsWxXpq+DmGWN+EpEqG7SXOclorWAwZHz++x49/8g1KFkNCKeyeqQuoKK2r6bGRrXz/qcoShbEocMR2qrzS7r+z2Zy/09yPQgzO27Qfm2TsRd+Mto1Lff+uwTltQc2dWvZtDN77MUFn0bQd+gUYE9SKNBDIu8C3mG/TN8vpvz80BTcC+G/LCQJm7b5AYWDrehHmi479dxZrd/xN9leA2YX3luGjLnTCaHhd4PNm2lwE9tbIYWVzqYKwwigqusY/oYoNUUi2jw/pyJrxt7i2HKGr+i6EL3CdqnxQFR9u5bwLGzfuxYt47mAz+ghjS816mLJ4tr81vHa321V4Up11zeVsabgsobxLobQtFAZY7gtt05QMM1xEr16lRZ/gJU7jI+gr8KoXSpHRYJ4Ir+7uQF3Cy8MT9ocjur7HerUCs5Rg3Q0rrLcrFGaMU8Y4HpAI2F3fiBzHBafDHsfjAfN00lO92bGamUBJIk5WqwGb7Qar1RrrzQbjQQrnyDkjcur0sB60ctIj7m7vcHV9hafHRzysBrx69QpzFrhut1scD4eW73D0YEU+xsI7StEKqB36LmHqOiDPyEQOp4v8O+wVl8UoGthQcUSfSqkqORbV0mmxn3kc8XD/gM2wxtPTC54f73F9tcXbt6+xevkPuL7a4U/+5I/R9QM4zZjGCbvdDt999x3u7+9xdXXl8muMCIrGdfNIxPSEeJq3RQRZeNTV1ZV7P06nU3P+neFzPLxvu93ic67fO0cjxoAtfwMqIfHPptlx611g1HJcRISuryXScs4gAF3qmhjynAtWq6Fm2nemPKhwZFpsSpIDQYSsXpQ2+EiumiReCYWUCyNcXV2JIqJjJtTkVvvXEkLXqw2+/fZbXF1dg7qENMtp3uv1RoQ6tSAkriExBEhNeYZzT4/FTdXq0TLJaIO5LCxVYaMS6ZiqAVTLmHHBc4tku6lqYl4MGWkvB40TdoshDi9EIm8c2Agnx0d8G1fLpfdTvzhr0ERfe7SJF2afjv6uIXxM+P67b3VeYjliNiVXCxM4vHXey3I/IMU9+ezVm4zR+GOkOFCtSw4n56RxXqzWRiUiob66e2aCJZTIKawzOGeFZMwR/o4zMI73KrtmNsZow2qFFGduhSWRDlAPkDyfGgSxiSZUIYMaJGI1g1bhIKpVEcuNZMtc3S0OuAekK3WxP77/gK+//pFbAMXvEucFF9F89obILbeG4aiLB9QKKgBqkRFtJ5YOraFSQA1nqCu/DEf65B679NtijxtKxT2J5edAQ7i518J9QTpUmY7KBNB6OJRKuNU1bHr9bNXCzGtYDPAujVPssqUtgaF3fde0+ynadAYuxf8C41cIfbdXOYNbC48679i3UjgH5yLEYKE4oKJx0579wBc7j82Rw77SlrDHzOgU1rlylyXMXCzyMbhSgrpXbV9zhI3uDwOnv6MfnJqeMwt9lgw84XsY3eJrs+ahORuTj82E+mgl5EVT7gFv6bN5r4fV0GLlcvMu9gEp3LLlZ+gCMFtd5NBa5Le2xwBEWarZYywzT+HsC98/YMcHB6TyH6Nz7mFSCG7XO2y2O4ynES/7PVISA3FhxtPzC4iB43HEsLkCc4/TNGHoB1xt1yACxsML9s/PmOdRWy2QCppWtU6Nj1xQcsHhZcTxsEc3DLi+vsFmu0Xf9TjsX7zU6jAMmMuMw/6A9WqN7XaHeZrx+PiI7WaL7WaLx+cnXF9d43Q8gbnUcKXCYOhZF84jBC4mfAMzpgmgJMncRekaUEMOW7kpbtYK1mT8tdlTumapKgEEQtdJJMVue4Xd1TVW6w2G1QpPj0+4//gB17sdXr95hc1mhbfv/wp/7x/8z5B6wpxngDNKyTidTvjqqy9xPJ7w8vLsygWzlLU9nU7IOWO322G1WmHSvGXrW46WsOpRdYJ2HMTxeERKkrS+3W5RSsHj46Pf6/sem83mzHnwu67fS9GIiaWvXr3C4XC4mHXumyNRFRRJbacELcOXXBCSDSh/pcxrJ8lXVN2BBHG7ERK6VEOnmBmczf2rpzkDSL0qCKpRTvOscfho3D3FqtIwCwNlYYCbgXF6+DVO/Q026y36NChzKgAKUueB8+j7DvM04t/+63+Fq80OLy9POB5P+PFPvsFX3/wUs3lOoMSgGBEtUga0A5zyKbJXOa/GjVY6eb64Db0PAk/k28yooUXal8u9Zj1icz2HTYfAU6ntx39jVo9C5Qedv1fbruwmDtheWrA8Dn+drp8zRwuZ0wAeOGs2OOiAcinoux6UCMf9Hs9Pzzo2Ub5mjT3MmVH06FpWtxMZhaeAe/Dl8k5M6bUnDDa2pojroUJxolo6yvMzOFUle7EArtywwoPUM0FkxZkqEihTi30zUOOK2QgsQNSFSelacxWhmkASx5POIU7QMEmu3qAKq4osXmkqcHyjLz5VDh1hAbgKfUi4VfVE5pKl3n0pOB2PeH58xNXdnXgyco0rbeXKhTXZ16yOP/ZtYLWVtl8ar1OUoSLQANj5MYuZNHt46f5e9m3yjau5tq5mDT3rG0GGqhTEYM0XXojPGJ57UraOhOPyuPCmilSck9J2JKAbxBtecpZwQ8vhCWNzoRnOPjw0knX9kh+aBTRaXZizwSvCGCA5s8hwwSccCYa+H/Y3LdoRmHOd99IowuYFbQ1EdUfF+dXfpD1yYbXoPtdgyTN8ccE0zt22B9dx+lr5eld7eYVNXW+BeZy3/ut91JArqWKk/FNz2sB1/DYD68HCAlvsrgOo8444t5h3xL0wbvhv7G2x8Qh9NlHdBYYT1DTiEAVz0Zw+qoae8JjI++QD5yxRokkHIm2wt2fQsKvBwchBTY5yek6Oa0Y9zYAVNhok1xCwQ/gWhKWGZSkNvrq+Bgrw8vyCPGcMqxW6Ya1DOAKcwUTI04xxnrFebbDbbcBlwvPTRxxfnoUOM6nxoNJYaURzYknlID2PLY8j7t+/w9XVFW5ubmQckAMOKQE0J0wnOQ9i6AfsdjucxhH3D/f4+usfYb3e4HQ4YHe1w/PTSy3eovJkXeE2eqMwg3MBUUEPCXGmlOQQSfUKSUinVAszPk1G9EOb5gEnX7Lk3/tOzgxKqfMw+69/9CN8/eOf4Hg64fD8gu+//x4vz89YDys5gX3dg16+w4/e3OH67jXeP3wAkVSYGoYBt7fXOJ1Onnex3+/x8rIHQBiGFe7u7rTsLHA4HDV6aHAjv40PSDrVNuLHooDs5HEiCV8D4EqMhU/9/+XAPmtwnme8evUKu90ORISnpydf3JggYod9VI2Lz0KilpfneCyoj70b3T4x6dzDobgNiYrvdqHPWB/YnmGWWsH23s3VFlf7PT48J9x/fECHhOvrG1xdXwFJhFZRhISK3d7d4dvf/BYfywdVjhJ+8+13uPvyK1DqwSh+xAxDPD0dpSAUUDg8VJPoOZAmp4J25oZLDYHohEfDX6NRUfN296w9g0jLgms7Ckzh2UjbVF4969vb9C0fGVMriEUFxW+TwaB1tTuj1A7qONoggmhtM29Cl2Q09x8/oJQsypGYVP2gyVyKiztORFAJd+wvrssZ5IkAzXlgWTjnekQkRG0hyDJQq6BpMXcXis29T+16W3ldh6dKQaSCnfetUJRxk69vJcRwa28UYqRN86QI8I2EJxMgdZAuRHMNU4LWOreTV+V+FXHq2i7huPzcXo7PZlBgE6iUBnHBhw/vcfP6NXJzkjRVwfWs0QZKrZJvwptDMlwuvIV2uM5L2ZLj/aW+z8ZyUQqrP8U91ggS4bczARJ177VBQ1SVFZuPPt+UOQ6zaQlOwO3QVzM/knXvuk4E0SyGoZyzWiGNtlDbdENbyHGxJtByIHZGc4ze1FE0cIiD83Wii7TJ4Rzb8fXWhV7CXH+zsKMa0mmwuLCG3mVVwlvr/vl6m/h6Vq2J6jwjbW3oRpyL007AuU7A99i3k4RGqg+Nkrbg74bwNedZWjaaKyzpwsAqjJb0XPaS5QNSgIevGbfeFfvsdI3rO0t+al45MCSc1I2gzm3tqYArSde7QrKUUHFKB+Ce7bA7fV0cD4IiwWiMt7IQBUydyBpq/fN5NJC8QFOJYEriahiwWW8wThP2hwO6vkfXr9EPa6w3W2x2N5imEf3QIzNhtR5wtd0g5wmPH99hPL0AQT5LKaFPSemx5QaI0J4h/KLreqQuoSfJ4d3v95jnGbe3t7i+uQG9PON4OiGlDl2/wjyPOBz22N1cY7fb4vn5BS/Pz9hdXWEaR2y3O+z3B8+JAsx4JpQqke1D46dCz0vOQN9JUaGSQanDer3CT37yDf7yF78ASMpuJ/XAksoyzEXoYkqSe9KJ8G6ldj23k4E8jnZ2LXbbK1xdX2OeZ9x/+Ij3775HyTNub+Vwws16QJof8c39/wP/4L/8+7i/f2jk5mEY8Pr1a63IJbklV1fXyPm3eH7eI6XsHglLb7CcaKOXJj/v93scj0cQsadFSDpD77j28PCA3W7nHiYLnTqdTn6u3adk+eX1e3k0SilYrVYeG9b3vSMXgLNJxdgwayNmwy+z1k1JSHpyuAEqJoPHvznn5jC+UuawieUy5SGlrlEwonfGYmqjgpJSwtf5l3i3/R9jHB/x+PyC7759h/VmjZ/+4TdYbdeuLBARrq+vsN3t5FRMTRj48quv0fcrObBPxyP0UzYfoyCxJdUoa9RYHyd2qC9aeEs9bM1+qpY5QuwokOogQYgrMxJWuPC19CrEtmQRw1++8NgFhic/BtEmcL0zoWvJTPx+eIHCvUZgWIhW8TcTdpW4vX//rskjzUXC9YoSISHVqRIsJeDOOBe4G4FRLQe6ZpobgEQNzOr7IUiLoXG6Zr2sgWs1IRBBUlps9CgJUJ33UrKqSagKM7UGOcNnwZ20EM6tApdYG5PjqHs8O4NdO28XmFhd2gZDhLEZY+coYnxibqhtinxrFa60XQaQGE9PT5jGCd3QC5On6Bqnsy5iQmy9idqRwu/sal5Y4LnB3BHb5h1aY5cXoqzRdHWh13ZY8RWzwMF8p83wmj3mpMQV+/pc/HzOVNr1sAVZkosSvhDbOUsdMmaxMM6LE2YXxGA5b2GYM/qhh5tLFHcrDaIl+IKwF8Q7VpobhbMgrXJzL0x1McwgLsJaK+HFWMksNuy0e0lKAm1aTiHijXuadF5VCai4Boa3b1veBFuODaLuDZvDxTE4kKVDK0ltZOYM5k410TzgdIIi5IJoTOkTeGEfa9++3stKUjAPtHzrjLYIm9UqRMpzSUKtRVCUEKdxGnUs5Hu25puQA1PwvG6YpH0WN/Dos7oeZ3wrVBM8A/Zijwk9DyW+tSiJ0OCq0jYoG5ElwHK33QEk3gwGIfUrpGGFfr1FGtZYbQdsmXE47EGZcX21wzxPePz4AafjC1BmUCKVYazCJjl8mBmJxJNUGGAtY1tYEom7vgfUgv7w8IC7uzvsdleY5hl5tpOwE/b7PTa7HdabLQ77Ax6fHrG72mG1lsTx3W6nZ0gs+KLC3GhBQ8KtFJiOv5SC4+mE+4d7Vxacf1PlkSklrIYBg4YbTeMo8pyXbJcNJ96EDsNqjWG1Qt8PuH94wPjtdzieDhhWPV6/eosuMb5MH/GHwyO+5P+A//R/8Y/w6tUrdF092w0wQ7wY1HJmDIOERn399Y8xDB/xcP+A56c9jqcjEiXc3Fx7SVsiqUaVug7r1QpXu4Sbmxv0fQreDtJwqwnzPONwOODp6Qk5Z6zXa+x2O2y3W5cJ5nlu8j1+6PpsRcOE/tPphF/96le4vr6WRPBxVPznRuEwRUCE/Fpv1xQQX0S9YmK2CSHWZkxAN8JjrhvTtizvIyoesU+zZkYFo3pHajmweHr4n74h/PLpiOfUo1dF5fHpEU9Pd9iVjGG9AvoBHRFS1+HtF28l9nC9xtc//jF+9JMfO+yspnJhhoXAg/WwviLEQc4yaF1RS8e1kv/IFhvawYu/AGAnwUbLiFug0QpXJtxTeF9ZirbVdsvNqBgmUNm7KfJVEyQBj6k/Y0TWpwqLDLgAQWC3mBMgAiyqYFqFOxmZnYvNCudOD7t7ObzgcDpVTq65GWYN7/xUa7VAq6XWHk/KUSsPrJAg2PPhQCZlIqw5De5tsFU1d6tBXw97FGVFEqmjq1z6ClBulIuFhLLs25iVYYlbYfT1wmG91JNp+wjkHpJEEfbKgINw6+ETEE8Gq5JHpTizdmudws08PkXXcCkoUjQ4ABJ2k2yVyeFWqEgCHYBpmvH0/IRXb974Svnziy1kuAbUn4jit/aKeO6lXLnCvAp45PtguceAUKUN5zJIvGyMy4P2qDbs+7FNTg3zdmOPjUSeqKE0jXmjnS9XpaWyc9/QZ7hnoU6RjgCSezcMPcbDQQQPLqLgnwlhEceqgGcCMAX4Vw8nKl0LrfhPdq+hLRTCweJ8A8yp5s15v1znGefHqDQ3Cn2VgtehWt/wXyoO1n0XQ27IB0YgpK7mPnnuVgkjuiS4hj4CuWz6hPGpgJs+QiI9hLNaequSJ336HDl4AwPPaXGt5ThGG8CRynHlJSxrUdxyrHy7CF20g8qgioBUGZpdcZnmKZSQlxEktcJ3SSo8iZGasH/ZS/QGc6VncR2ThbqaXAGdo8yv5OzvGg+MVbGIUJXCsEZeWKQybqcdcDnGeEnlUWZsIeMxzscU01gPEoZUE9zutsg543SSw077Ts746vsB/bASme94wjQV3N3dAsx4eviA0/EZzBlD1wEEzNOMqQit7/te6bNGCehcvIwsheiXlNB3HTKAaRrx8PiI169e4fr6Gk8Pj5hKxjhO6Icex8MRV9dXcsjdywsOL6J8nA5HbDcbvLy8CIwirun+RpQHHc9F5qKUwKXDqGN6/+69nqllRFvXXN2ThRmn0wnHcQSX7HLNeiPwIkDCpboeqZPQ4mmSBGrcM9brFe7ubrDbbLArj/iz8Z/hD+4Yb9+8wY9/9Pfw5Zdfuzw6z+xeCpGFRzw+Pun20NDqRDgeR3SdeCOudlcAgHnOeHp6dhn6cDiKzL6SkrrrzQqlMPpevMyWUmCFnna7HZgZ+/0e7969w7fffgtm9vM3ttstpmnCz/G7r89WNKZpqh6HlPDu3TtxpyQCUfVkLD0G9tn+LoX95bVUMGIMWFQCUkqe+X7pcD+7VquVE57l2OxdUzhimJd5Qb46/gXeDX8HBzqoclI0iV03fCmqrRO++vprXF1f4+pqh9Vmq6Ju57K0VG1hV4rsVHERDyRXJLMJkeGi8FcFuwugq/Imx1erQCX7QVl1eN9r03vPC1Ej3DKLVx2W/FiYlwZ7gFvm3DAOFxhZYaO/EQcGH0QDEzbiuNn3eD3Uzx4OY7XQHoYwlPuPH8FFlGCL2xclwxL3FnM0YTp07KEmrKznTEKscHePQMgtMorI/qhZ+Ov6eCxwrK7D7e/Wd7uXat/OpGixskKNm/V2AtxIhguAG+6EeZswbp5Be034nnpiioyRU/K9YJ00ng2CKy9VCJG/fiCZ9Y0q0Mm4yAXpnDNS14FLwcP9A16/eSPKTmA4AVrt1eBaDchrnj9b7wCuyp/qb4vPFidNFwZgAlv1uBqcmmIzMpZoQiZoOcfzMZoCKPu0Kng+IcW1wnXcS0pwgTIEvaJKpAEEdUKWQK5w6bwksVYazJIUnsLzsQ9qBhtoNepcW/pAzcv1Nw6CRh1f430APNSiKMxLYYer4ysqjXJRmZaekaok8IX19kqZYdQFFshUK21Z+xzgDDB4tnGJcu9WWhXwvXdfG/K96a0avlZZSsdGAdd0nlznWbUVqt5Low1Gn4KyZOelmJEvGndKzpizhKQULphV3rANP89aJlXXsuhBuJ0muBJJcYAudfoKYRj0XC393SoAmbchkXI8hgr20PtqqNTynYfDwXEo7gAhVyLEI+xD6cMExblBReclUSYymHPbfosV5LAw41dFdXLssKc9Odpu+FXD01erAX3X42X/glIYq5WEPQ2JMPQJQ5cw54JpGrHZrNEnwvPTA8bDM4hn9H2HvuulOlGewdDDbucZXWfGZfk/zxnTJJWoRJDtkAtjniak1UqNex3GcdRD+W6x2Yggm0tBVxiH4xHbqy02qzUO+xc871+wvbrCsBowjhNWq0GqSAYe5vu0qYzIMNNDzhmDeliHARhPIzLrcQcOy8pDDXZFC9DYupLmu65XkgPad72EiCUR4HsNUdvttprfW7AZCD97+Gf4yW3BNBbc3b7Ber3Fw/0TAElTMIO50bvNZgMuknNcNIQrpQ6Jeg/dMu8KQGqcB/b7A06nE66vr8AMHA4nPDw+AMjYbjfY7XbuPBCUIpc/ttstvvnmG8fXGElk1ap+1/V752iYAmDehU6rKsWwKBtoLCkb79vfJcN3BSFwwdhvDH0yL0nbDumZGJWYWXkuOx3YFi0qFyn1jWJjwM5zBjLQD31TnYqLvDsoEk3zLEhYGG+/+tLorhChItUhOBARS1i2qlOV8BQ8Pz3j+ubKCeoy9tbo2SUhwAma/riUhdzqf5GYWQNcBcHQkZPZyktgRU+bGuiu7AWGBNTGgnAdBaSalOzsFGatESGyjt6TEM8kH303CCZu3QAkJ4YL7u/vYUzTBeIWkouGgweAqkBtwmAcTCMUcYU5/L4KmFQZPitT8/haAsjOpQAHQTAKkcFSmOKCk/dtc2BT1tsyGnXyZ5JuJaqu8JiEaEDVeVs53CpUqLTCUi4afK6ECXOXZ8lqvhusXCAyWLsIp/ONIWsqdBQgJWUGJsyk3rt8fnl2o0QMMfTcmSBoGVgacKAKS/Y55h4vUcbXfNGONe5zazuBvXK2v21scX+HoTpttXFWkNUttsRzx1tW3FwIKqH/s23WTuf8xzhv3xd1fxdAKvKZoSYXodswtZddKHPQ+vy1reg1CuM2UPqgTOBtfqufLi2RbCNqaS95oM/FyRr9tbGbjGVl0W0OzToG8C1hbvMti3tpMZHGs5lCK4utbYfXxbNIIs8Q4UlxiNVaHhCGC1A466nWJnAU8Sqo8DFNs5OIeZoxl6yFLjQ8DlKSWNZODGtdJwY9kBR56VRAW69WgCsJyu9xLjO4MUDR2ZRAC0kzibEaQ/hMkTa4ktEYwOnxZr3Bfr+vMozBKMCOvF1TxNjJsShIsb9qUIqGjMZqFml4nK73Ub3M7WWLXgdn54OIYhJgQoRhtQYIOO4PIAL6rgOXCR8/fI/h+QVvv/qR8No8Y7vboUwTDs+PAM8Yhg6UOhSocZQBUEFhMcZSGtClhL4bxGPQSeWjaRrF2NH16HrCNI6YpgkrDevpABz2B6zWa2w2G4ynE45pD0LCPM04nUZsNxupsHSU8qur1Rqj5mocj6fKq01BiDxU+bd4mwpy0kOglU4od3a+3noLK2gJ4gmhQshlBiBy5Zs3bzCsJAJmNQwY+kHODSLxcqW+BziD5wlf/s3/GT96DazXX+Bnf/THWK03OB4mVxJKySBKLtgTAYfDwU/5FqUiq6Kdggwu903GtTSHYVjh6mrnbff9Bl3PKCU3ToR4PobJxCaHW5vGc6xa1e+6Pj90qu/A6grLpaDrErgwpnkWy6GWtzTrqgj0QvRijkUMpZINWvzcABeIuHotYkiWuW1IS93abu66TsK0FkmmMhZREOa5KLGSjW6ndqeuF4QLikfX93ooSUKeC4Ztj37oNedW3kURTZILg3NGgZzyPU4TdpstOl1M7pLAgUxQsdHp8KmGQjAD26ttsAIpOEzOQ0t7Ghrk/ziJgQliCJ9aG/aS7eqnIDxUJlh7tk3n43ZGahY7edoqjrUMm50GIEAj0k0PVSL7TdmpD9LKlFahkbnOzRqzUowWNpWIcDqdcDjsbeS6MYt/bgDeQACQ+MgQ2kYV1xzugcFbXLavSmgzpU7eKyyEh83SBjTxt8bwjXka3ILCjnDPY0sBzcOotlq2WOSUKsMM5lS33KASWB97Y3Zd3q9MVowOWglKJ2FhykbAW0WXW26vc6n1/ReSrBkWuPZtw2BoyemUUJCd4YynI06HPXZX10EoNYFKeojhQL7i4no4E2AZAGkInw1DH21i4an2BGsu7lqCvFOUNphgafgMHytc8V8mkReuO3OZchIx15MhW2giRnQbL63rheZ5X1+jLVEQtfmQ0V52WOmy1dEwY7PeQBieWH2neRZamsLaB9QGBH8N9bq+R4HZJXkx2wgD4zvhHgeB++yVoOwERbQZD8K4fCsE2gh2YwSFOBnCOa7pkZ8NzBs0YcUgtZqzuljIhaZaLtVppAm8VA11UMVgLpZ4z1JlTw8OY3C1oELCQ/I8IyUN6SVCycVDXawwRtd1Eh5CCavVSg9jFFqb9KA5DzVLSbd4oDPOG+vauJAX1rVRJo122TvUrpHAkDQRu4a6Cp2KaxG90nGVoMfr6v8cODeH8bLhQeXrgEZhqOd2nkfYwaccMNaVivhd+/dd6jQ10AAYXabqGSVTrAwxjYaEdpnBqqyx/rbdrFFyxpSrEea432McJxyPI1arNXbX11gPK/R9h6fne8zzhJR69HrMwTxPDhOjWZQsvjZhvdlIbsV6A4JExjw9PWEcT0hEGFYrzNOEmQj9MKBLhCkXvLy84PXr19hstxjnGVwy5jzjdDxhs9litdrgeByxPxxxe3MDog7DQH4Qb+UfDJCbditFUlpdSvFcEFJcyURapVDnJe74usa2fEGmBYmXdrNaYXd9hcRA1xEo2XlzPeY8Yzzu0T39NX789E/xpz+6wjc/+Sl+9OOfYjxljKcRAGk1p+xrslqtsVqtmgqv45g1B2SlClw9csLC6vo+uRy9Xq8B1Pw4ogF9n5C6jOMxN3MppXieRjT0Vw87N319zvX5Hg0lRiCEeEOIwsGohJVSE+IAtPkV5k1IKaEzgapUQcUEEfNgmIblORcUSuYqQ8ulYM4Zog/rwLgmHw2pk6K0uQ29GqfZFZ9JPR/DSg6lsXj21+kJ35ePeO57GDWzmEhSNy2VATnP4Lng8LLHdr2V6gqpF+1ew4GWnoSoZNgi913n87J7SRfUhJnIHN1qpcKaCRt2y4R0w4fKv+TE8Uq82jYrMwjk3uBOhhNweMh8qponY6/LgXC/ZR1wwcVHthR02OBU4efvGrEn8rwH69JwVJTZHokIT/ePwCzliS3xW/AyiBDKyGU2weVKgEVUG4848w5xFSVqnC3cWmKbo4RTtimF8wBMiABVZuSMtHpypM2i9b9tMGycGu79oSr0mZJRPUcWKlgc4Fb73DYwm/SIuj99PsboKsfVd1NYuyLjVcbj44T/0bZIDx5EYKBxNQOIgwdIlCdhBoTkYSS1b0LKM54fHnCj5RMtXNFCYxiQk8ZdyAjIBRU9GzwP4zImi7Aw2o5FslTVdLEhlNmR9RHFlZCYLfAjp7+OEoozNYep0g1e9t1Irwh7jM0B5eOo9ApB2YxCS91/VQqCj62ibPJ3zTMlOWmM9XbnTCvngnmaJYxK269VYjjAXKkLM1arFcZxQvGRBFHRjBQRJ/UqQbDlMG8QFsn7rbAWaRH5ntD3mEPOVQw/Mwu3dFiUz0V651WujKYqQhrkihlC9LyRwsVP5uXCmLMJAwQUbnia8F4xCiaL5wdr/Lh5C6RqTuoS1hv1HpCcLUCdhBe5khiYDzOQQqJHAoW1aK9qKLP3yXPBBJYV0Y1/GEzI6U7bZgxkSkan6ugAwMvRyoGnFqaM8AQcYWsiN3uIMzS0h8vkSksUMJs9ZnSgFM2HI0zzjNM0wRQR82ZE3h4Vq2aPIdwzXLG/ZPOGP19JktJtrp+dr9gykqh+XT9gmjPyrBWEtIoSYwKB0PdJDyu8Rs4Tjiep7NQPKyTqwCyW8L7rQHpCNQMSctYPePP6NW7uXsGUVAajW61xdXeH00lK286nETmJEmF42hEwnU4YxxHDZo3ueETJhMQF0ziBC2NYbUDpBcfjiNvbhK5fSYGIrsfEk887Qs9QuPIYkQXnkkHdpeOSGxOiykDw3FAjkuZ161OPvuvRgwAeMTx/L94CBtLxPd7u/wodZfz8yyv8+X/xn+EnP/kGzIz7+3vs9wfc3t7gsD8ipQ7r9Vpla8nvEPwjD8UyPMx5Rs7QSlPFn5NzMzo9MNsOrM04nQ4YhgHffvsdvvzyC9zeXeH169cumx+PR0Tjvv2NqQcxusgrxf6O67MVDRvIechTJf7LXAynxVSTf+wSYV8ekHKitvHYn7e2LJ4zJTk10jashzjp79ZXfC+lhIeHB+xf9vji7Vsff0oJx+PRE8qtbyPiklFf8NMvbnD7+E/xf99/hffDK/DeTo8GQCTl4HJBwgDuhBmcTiP+v6z9WZCtWXbfh/32/oYzn8y8mffeujV0TT2gu9GNQQ1iIgYRhEVbNETAIZKyLTkcjrBlSX5Q+MWvfpUjHHaEwg6HIywrHLYkhkzLNAXSFCmLpIixARCNbnSj0VVd851yPuM37e2Htdfe+2QV2CVbp7tuZp5zvu/bw9pr/dc8m06DkmFCWTR/IPhysJCLyhxj6gc+fhiXO1NOiAwpVh5RBhutLxmACTexgfnoAyN4jPfNQZGPTCp/2WxMChDUohndlWnKGXg5vJmGu0RQlT1D5mdS48c4Kn8YUO7vLpFkyLiMtpyXkm2mSNWSlFZz+jT64E+Wm7Ie+QZkAB9dzQzIQRbiVxRJade8BUK4lAL0aD1Ja+U0lCksYrhDsPLKs31ATgnkHPRJj+V0PZ5Y9zxCQ6UCRWFp/+KxzYkzEuuhIEzj14skHjWGBvsAzDK+oQA5UqnPQpqyNU84RZ/nD8pUJgXGBcNHShRfrVY8IghZr+EtiU7vZEXpE2UGGWHlsj9XMu8maHt0b9NLeIAyxZxSycBW+rYAuHyJTXbGwrcy4ZkDlYx9iEDIaCY+IjtPfzZv8dm8VR3KaCoqaJlyQs5rDj22BPA4Go+wRRmq0Ay0XSuWxVBGMYaTkNY8p9bRaMxms8uKDuhQfVS88pfyXg0RSyF56f7a6OzgjBmDdo3OOGUYTzgvuJT7QlAOnJQzd45QyWhAqvA4urYNZ1fCkbQBrgmhnX5wMTlZByfJmmXgg17iv8uCcVVJic3gdYjhxAg/yWlEebDJfgLRcxOVJaNV5cAal+23P6D/KE2CscOGc5zLNWUViWZ9SpTP34u09nGjmPxUPECkxyRPE4/S/CP5O3h7nDRkI577MO/I94IMIii6ThQ6YyxtuxfLbyhYEKx+MczMRXKQM9YPg8h9PNvNli4UHTHWJiEZX0rnHC6S8eRe7dx7ZUIYtiq78awe0HOUwCR+TuTZ3khxHGsN7V5CdWxRY2zB8ekZS+cpy1qqaG621GXBbr+la1uMNVSleKsVKxkM1gTPljUURcW9e/eYLxZi4HUaiieqaN8PVGXJwwcPOX/+FMdAu2/Eg1ZJNU/fS6Wr49EpdV3R7iVEyLuewTmqqsYWBW3b4AZHUZR0XUNd1fR9d4AL7gIKo3QhQhE3eJztM4klpdFtwIQuEZR8p4+3ikqiW39EcXnFveYfc39RUVg4W4zpe2m0N55MeeVLr/Dqq6/y6OVXKOs6AvXT09OU7O3g4uKSx48fBy+ErF3XtUgn9CnD0B9gasWzWhSJKGc8mndaFDaEU8k5euGFhyyPFtR1KO/bSzPE7XZL0zQsl0uWy2Xsq+G9pw1hbm3bSgUra9ntdrz65mf5Qa//SjkaeRJIil2LGWgHoE0mn0I5ZGNMvJcxhkE/8x6sjSVGy6qm73qVdEGYeXw/hFJqJk5cF1wUEXHhqrYnCySlwNabNfPFXMbvYddIJr/D03SycOJLS9YH+axjNB7xk0dPOb+65sbcC9qdDL1QN7J14K20tO86CcVScOnE3hMb5XAHywWm5ZXJBHI/iKm/g2Iivk2rmxSKyH2ILOfwe+G6GD/sDzB7xCt3gIOCfqKXxMdDnF2aPTtcaw6FhgICtWCJxVjHnuU9hH3IJ5t03OymZEIwDkTFU7DiWxHi2802DswYUgiewogY2qVc/oBLh5/mYN45aIkbSrYJKO2nOFlZFwUEIbxAeaMKfBtAuiIENDTwkBhSEraCFY+E/JiDfVchps+GHCzpbYMwjspqhBPZXPONTILM5/sX9znsb0Yrci6C4AlnO1JpBmL02bHJUC4wgsAMyxrIQ+5UIEBJG0Z6L5aavu+xZZkATmYM+aRXAszp8XH1M1Lwd66L1BK8Vvp3nmh7kOxEWlNd1viuMXfG6NP51rXVAgq6XtkY9IwdhIZl5zs+V0GI8nV8PEPxe8pvwlmNYV53npkDwPx7cZwGqrJiMh6x3WwOhFg1qjFF0EpN7o1L62cMOGOZLxZcXd9wfHwUQbWED8VdI8uuEqXkExJxDMH7rWvrPd5J7DJGvGaajOwJhq3A3wHxZoez4jQJ01pMETwDIX66DFbjqqpDyJGN50OahkVVPcmOO8P1B2/IeFNyvwtV5FIsfk6/eGIkZmya7DJIGh/txaLvAZ/TXzilRn/6qAhreIl6ng+TlcOzc26UhNDBuVZIICwgnXkJqw6cItJ5bkJL+5hupvlxPuaWRF7lAYZIH3Fldf8RvrHdrhmNx/RDC8ZiBuUyEnaI5kt4T++JzdJcP3B+/jxW3hwGyVFJBi0NYb0jQPUUZUYdVd70XCpWSI1PkywhX7cwFzDYQjm93NsWhZSYDjReaEL0ZMZ4PMEgc7GFhL/1bSuJ06Xk3bVtg89bEMQQuoLFYsF8vpDxaySK92i5eJUHzntOz+7z7NkT2qaRhrr4qGQ3TcvgBkb1SIzC1tD1nq7tqOsRVVmx2+2kilhZ4B1Uowq26Zyk3DOVQQYtrx533Tu8L2KZXvEJeKqiwDVbmm/9Lbr3f09C4V3iR8qviwLOTpb8zE//JG9+5jVm0yllNWY2XTCfz1keLaUSlIHxaMxms2VYr9F+FxcXF3gv/SxOT09ZLuc8ePhVNpsN5+fPJf9kOqUqa0ajEVdX13gvitgwDEwmk5A+IMn2dT2iLAuslQqvEiJVUJSGxXzBdDbNcpL7WHHq/v37eC8l4dfrNev1mnmIAtBiUNodvKqq2CX807w+taIRaThIOQ2HkpATF5MtD8Ok9AwmEBmVgqJIngHABoBvrZU40lLyLtpGlAnNwyiNpW/T4VWNS8G/dwP1qBZ3fD9QVZIIc+/sjN5L3woD9N5ReCPVhwpRONzQR8FijLAhN/QURcl8MeNzxdtcj16mHktdZLwkGI/H49DszVMYi/PQ9j11XceYVy3Lqvc2gR9E5uxT4IZXRk8KfTiQ3ZE3pXAPOASQ8YtR2By6AQ9/PbSs5ErGIYhSxq+hRQd467CyTvgnH48x8ZMDBp9AcIin9cQOrmTfin/54OqOMFkt255sGonZhO91bUvbt3HeqVKaXuNC5ZawCP5wDDmzikA1TCw9M6yHJjnremgpVisdSL13WAKYUMHtw70MmPyZYQ7O5UI5xWYnbKJjPgRRUVnTtcusr8L+w7ppW/EoiNXTImcizcdLjkJqQ56FnSSqlPGEcrZG81s8VhPdjQU3BDo5HLfSmgnrrONXT2lOzR4VwkkZMsGqTGGxpqDvO/b7PbP5nASL45IcrBf/jL8hkUbab/PJ12Tfi+/HM+az85Guz0cVPQFxzdPfcQa51kF2FlURU6XVp/vqj3hvf3eePtbdz8ePSec2ne/8Ms/haPL1kM20hLNgYDqbsdls8KFpX9u2TPw0YaScA+UA0Ui4QjUaMQGub24Yj8dUZRnD4vAuuvtVidXGgGjFq1DlKA1UQbqNXpIihNDawlKWZZyNlsVUZdUaE3mdjYSb7qv89W6OTdwSQ1YmVvmWbEy0B5mP76PVJq82vR9Pdji70UOj9JizN00WzhT36HE0er+7ZyTIMM3/Uv7j0yYZQliuV1Ce3ReisclndB3lEKr4kWj+Ttl3XYH8PMQQJn0v/p6Z2nyiaen4LdfFZm8BAHukGMzt6paHkzG73Q6NpAjaKIMLnvhQPcuFipTGWvbbHRfn53HlvCHmoEbeeBDLpXSeyxLhs4n35TLUBN6dFkNZv8GrwzpWBY339sKrtbxvPwyRHiR8KjVhi03ZcPR9i3gCDE3b0IeQMN0vayT/Y1SXHC2PolzSMxL5iEl7irFY61gsFmy3G6kOGgzGID1NpF9OhTVGcjWQcEEdr/diBBiPK4yRhHaHKrp3KNeYGLqslGEJ1Ue9p0APhmc2m/HVr3yFR+/9Jxy9/BU++uiU8/Nznj9/zmq1knLJ3oMfuHd6j3/j3/o3+cpXvszb33+bsiw5u/eQoqxjJE5VlvSDNNTbtnswRLAuPTOKaMRv2gbnHWVZ8OKLL9I0jRive+k3Mp2Occ4zmYzi3qoiINVYO0ajmrqupbJYVUj+VNbAT3KSA5cNtKdhU3Vdc+/evfg9bb6tColGCw3DIAb6T/H61IrGYZWm1KFbvBomakh5WJW1JlMCfPb9oNkHRuicwwWC7IcevKWwVbg2MPJCgIQbhCFookpRSEm0uq5pmh6xwAQFxhvapsd7F0G9JDCJ78uXnqGXhaxHI2FWwyCeFSPJ7taXON+z6xpee+k+31mNOVoeUddVBKg2uLXVNaUhWLqxCo408TNnjpFvoH/k7Db8fWBFTkIiD/eI65746YEl9BObk2W/ayMzfS8OKYChHA4JkzBRiOTfF4Z3B/xEQBIlCod/eqJlJnz4yeMIENYEcBcxk4YN5QAlUwYKC9awXov1VEIaspCdIDx89uAYOw3i5YpcMq1zWnMFZh+DyiTLZPDKxRA/7ZOReXXiXI1KwnRduHk0ymgb+T/rFYCDPCuPVc2uvaMoZRg0Cl0O5u0P5i3WVPBJywgS3welRdbYxMvDeKxOzYX55NZPXdOs4GgAPzqXgzmmQxPHrGBNgQrG453UxJ8t5mGNszMYDtQnwuT8XKXtPhBhXkGdgqh8rbN/84sOQrWyC0z2+SGmDPBRn20OPky3zg/+nwH8D3lLBhSzocbj9c+Y98fuocq+7ufhBAL4lM+dc8xnc56b51JkpB9oO6kiY0M9eAVbH3u2B4eLVsB6VNN2LftWOtZaJBFZlQFDiFkeJQuyJgjLMQjhukZ5b6JzPYYJFwaatiabmU/88cAL4eOA9a1oSInX+LDWJsu1idwL75Nn7mD3dM2V54WYn3SO0rhzusnD2HQGuTrpnQFcDEk0+JTn4xHg6tWrloUzHVB9SrZX3uXxMblWlib9Hh1naswwREeBi0vo4hPSeHykubth23oWNHw5KhDeSfEWVRC0yZonVt/xSHhP0zQU1nJ7c0tOCMrHFcc0+yYCMi0tKtb4AJpVdoUKa7LbRUg4zugm3967vD2e67RrKSzWkLNgZYYHMtsnmjJGLNyQwprUE27RnDqPdwNlKMU6DH289dBrnxLP0ENZWzyOsigZjccUZSEBGZhYBlZPs/NIdAGimFlbMJ3NsEVBH+5rwtl1g1Qvq+sRxlp2+z11VUo+l9PQecFak8k4hKcFJcN/bPJh/EnWxXDmTNzO53O2G1F6ZpXjF37sTR6eHlGUooC1Tcvt6lYa2m02GO+ZzWe88eabTBdzfuRHf5Tvfve7fO/7b/Ho4YscHR9RhepTNVBVJftmz+CG2I9iv9+L98hahqGnbfdhqIbZbBaa5U0wxh6UvNWQqTyPQq9LOFsUimHoGIYuXqPKgoZbdV3HTTDYaEPuoiiiIiFOhaR4aK+N/9pzNLRMrE5CS2xNJhOur2/p2i4y3zIkBsmC+Hj4NXNdvRqmFCHQDz2+T7kZbjAURfJ2lEVJ03aBUDyFlfq9GlsGQaMbfKxiIh4POTRFWeKtNOoZhiEmaw0hxMkFBtcHF7j3XnqEYHF+kIPmPHVdceYeU05eZ/CeglQOt+97UZIIsXM4dvu9EAg+HpwDfqJMNDCJ3GKpbycAeygW5PNczHH4vsk/4QCU+js/yZ4T7xEEVQ6eU5BLuvfHQMcdBqmgKN0jG0c+7z8DNKt9PFagis82UZh6/Z7mMegaBOGjTXRW61US0Abc4PFD5iWIYFUHHgTLAQI7BLxpPimEUAGvAhkDoRh/sqzJ3nqxrh4okgF4ZEINNIzp416pHNpKyAKBrgJQyACjzhvvMeEMHIKO7HMTEqW91ISPQVtG4Z96YZRw0rPzhioHtKZWJj8cvhddBOl+eg50LU3Y9cPk3BS+6VWYRYAUPDfZxq43Gx4g4XEuIKGosGZnLH/FXc/OrShPd/eAjPj9wbx1XdRqTFxzf3eBDrGC170kXpNN55PHakzak4w603nJTuDHzne6TySVj837k9dG6VK9cap84UPsvjnkbdosrAi9DZz3dJ3kK1SVS+FTkQNkUzLEnvQeASZ1VVHXEv6qxTriEPTiCL5UmRBaskZLILjIqxU85wquVoWT26VzrDSZEAxxv+/yVD1sh2ue8SoCnw1g/i7rSfkjOoS48vF/sub6wLDe2bZnmCsM2SdajPQTxhoCSfShfsjpMSkaxiSPgtJh9GL4OMt4sfbUUKoI7A0fkt61YZrP9kCATurXFRv16VgCM9NmflplTxXuA9rP1kHn7YJFfb/fs91uWSyXjEYjhr47zJnx4L2hb3vWmzWbzSY2nDSF8oYArdWCHtcg8HWvJXU/6ZW8cGoiyquXAckYFe6Vqk8lnuNz5qO8JTcQ6qKHxbAAroehCwrlEErzB+9fmJfrNVTQ0ffBm4PIk9F4BMZRFbVEHWg5ZAu9AtVhkKpTRUU1k6IQk1DKNu2RzKQfegzqWRTFyEUvuclCHFPysgnMU4uBKO/Seyp9Rtp14K3Iin1oIlpWNeP1+xy9OGEY9gy9p6wqqspydnokmK/p6NqO6WwqndPLgno85nM/9AVefa3l8UcfsduvqeolXci7KirDyNShSIOEOx0dHWUKg3gyyrKM3grByz1gP+aV0Dzj/D31XiRjvDbkSwql946qKpMiDpydnR20r9D7SUK5j+8TztJut6PrOl78zKufSMX569MrGt4w9Ao4PPdO7rFcLBi6nmHiuGquYBAg4lzwPvgBSYITzbXvBzzSFMVhKIYyeTsiqtDa011oxmOkkgbiOei9w+Bouo6K0HHXqxIh+RjDMFAWZTiHBvoWrJNIDc0PaUVBEcUD2maIIMt5T9s6ClvgjVTH6rqBahg4mpywK4JHxyJNZ4ZUWswFl5Qwy579bk9dVRQhd+TQkqrMIB2teBDil+4AAGMib9DrcoYpwiNBJh8RJgdA4y64yG+Zj+nwZUhW5EMgozdxJusTovcCsehEnnb4gLtKRoIWmcU6G+ddjw+RiadRRUHtoTByz+1mjTEullR0wdOllZGEDMNdghD3mTDPLZ13hZYPJfTi7DIruQ+TNIRu5dHikC8QwvFMtlex/0X4Qg50dH7GxJjpyEyNiYLnYPRhLncBudxOc0GIn0WA6JVRZ5sQfhFwka7VspdxCX1YkVhGxuN9AaHZULxrRtcpnE3nSP7NRKDGpGfnD40/VJCKEtjst7FhXwT/lgP+k3sl8p+HoISDCnBpryOVCIBVAKVLmhF6Arx62/zM3j1d/uC6A8Uwf2VKRh4ad/e7cd2DNS+3dnq4E355d9466rtnQGnNHM5NeZx+Iw7IUIV4377r6LuWvpfuuVEZ13FoKh/5OE1aNVVyESUybGRSNrKFNSa7OjMWaJ87ecNnBOCzNde99XFMUXnQeztdo0+4XukyOz+JR+QUwAFfiDkReqDi7NOQlVv6CLKyfdO9C9frdS4mJyf+Fp/h9dlZ4FHGc8DHHhrk59VpBb9kYPQhkdq71LQvdu8OGyy4VUvkB4+BymMF61moUWTLWnErlNTNPfv6bO2BlQs3McoYFNB7J+HfNze3tG3LeDLGWkOz32OMlBi1+IghnHOhf4KsR4z690nR0B4HcqaU/vRcCvOJ+VBxUsRznIPkjymdWaUuAm/JaQGfRZcoPYZxhdN1R4ZC2+65fP+csii4/+BhahRr0nmyNqxXBPGhCajz9G0nypZQB25wtF2Lcy7m0wKRDuoiddEui5LkGdfDYvCDD40TS0b1CO/y6keigDnnUzll4xKtq/yLyhZEd/rB1IV+rReP1OAc8/mcs6MRk6ll6Bv2+z1t3zOfz6WDeuieXk8cXdczdB12v6coy9BVe8LLL7/Mer1mMpkExSFF82izSQ1FSgWQpMGeKNQC8vf7PU0jyeCz2SwCf5BmeqIcDBhTxtQFgKoq8N6yWt3Q7PccHR8Lpg5KCR7KcgRI7ojIxZB4Xsh6ejxd21KWFV3X0rYdTbOPfGC73fJpXp++j4aVyfVdx0svPGI6mlCZgqIwHM/mLKYzumFgtd1yu97ShwZMHmkhLx6GPoE0U9D0Ka5MNVGp4SuWJVfo8AaGIXhUrGHQGsPeMHSDxAsCXe/og6JRl1CaEH83OLwZKEvdVFBx65zkckiFiTbkVXiM8XS+h0JdiobN7YaryZcYe3ErDkiMY1GUgVES690V1uKGgc1mA9MZVdAoVagp/0/MT85F5KV3UYf+6dObyloc6s4nCTyfmJvy2BQfnJiMPP4w7j3/cTf4Ih3ZFHubuymj3P0YkE3X5sqD2m70LWWCCbjlzw6CNMzRxTtkgj4iUwGh0RA0DLTNjmhpJRz4IDCTFTi5Ag/UnISC06LGSXliGJTJhAKh6GpcHy0xSbY5d8csV6URSPnGRBwJOSXQZJJyGD7W9YmgUK/xOi+fCTRJBIxAJFgAY4Wmg7VQoUN0Uys9iEUtgI+s4lNKPJd/82crKIsh2CYBBMLnaBJvVkVHD1tSisOKSxmiGNju9QLvaXZ7XN9RVHUsgXpwuHQecSlFeRQ6DwDaZFeENyQMT15O1wbuzJtsrUhjy86nvg5LXocd1ul/0vnW8RqicNBZ5M3ZdE/jmHLAG0Zg0QCcT5p3FpYSeZDOlSzsi0OjSlxnf5CnWpQVZVXRtXv2u5bCGvrlUvLirAFTpq3NgXe2/HH9lHbDgxPYSvzGRE0gbUrOidQwkTMthWaqeyiYJLzvAkAROg/3vLPmcVFi2JHP3kxnNPcqx9+dlG12wQBmVEE3wvfVY+eyB2rH4PzZclyVI8hkNHQITMozcHKGUu6BAmuffZ84FlUwXCjrCiEESa8Pn+PlXIerJYcAJ3qC155ZRF6ohhJjSICXUE7fGApjQiO4kIwc+KdVgjEpJMgaVSxCTk0o9Tp4Wb/BDXT9wGg0oum62AnbGksxKmNOWVkWFFVF17YMA7Sdp6or6r5it9tHBUPpRD2wRg+n7rcqAUFJS4dT6VylR+CiqswF+pHQo6RUSchzQBaZgemTGIyWbR8Gl74bxrDbbunbltZ5zs/PuX//YQCkPhYmMUZ6aKj3KidlY1O1UIOJ3d2HrsMCVVmGfAthZLYoYBAPotWKi/5w7EoSIJXm+r4Tv6MP/cx0u23gQVo4RF+BCen65F44/dx4aaosDxNcdXNzw/HmXerRF2i8oyhDCgAW5w3XNytGoxGz+ZzlyTRG+4j3R9x+4/GEyWR6UEhJwLzKTR/z1cCHKqzSHiLvW2FtSd/vKAqix6Kqqvg7QNcNMfQPpLhGWVaURcHR4ojLbuD50+ccHx8zHo+5OL9gOp1Rlo7b21uOjo7Y7yVkazKRMK2L8+dst9vgZa5oMo+ThlDpNT/o9enL23YtVVnx2quvcv/sjMvzC4ZOkrKrwmKcw9qK+viY1WrN6uaK0XSCx9B2KaZPD0FZWaQtvHg6jE3tzJWNKwCMbdgBM8DgTcz/6IeBZi/X2VA61DnkvapCKgo4rIVukLJn6kVxwxAbpw19K6Xpuj02VI7yXsrY1XVNWRScX+/YLu5RO8dyuaRpO4a+jwSsAlXPSt8PXF5cMqpGMb9YwFgCislNTRLCkdfkUk8PRxDzPhP3Jn1NmTpkgp70d1pdZYbqniYpgdnz0l96WMmuD1Zbk97U592FbweCjwBR7jBW/V7Gku/c53DsFmJpxhx+JIurlAM0QNt2DH1q4qauX7WkH47nTtKmT9BNxKORRMjMYiQ/gmdBLWsmlBEO949AM1paNUlP+WoAcubw2ckihZyZMC8y+olWmyA4jLWMqkriQ6uKqq4S8wrCvx8GurajH3q6pqXrBSDEIWoPjDDAlFwchFOo1X/gwYqCRpFxosOU+CLzsaYIexFCn6yuH5Ee07wUfqc1T8qPUGKkAefxNlubcJkwxoZ5VUe6OADKGX3pL8bLef54JOqhByK7hAM0HckjE6CZ7M+vPXg2h3SeDvHhGctYQoInGRK/e7/4u0/X5vOOz7s7b0Nc47tnW+8Xf9cxZgBKT2kK4ZFfxuMRu82KsrChxG2H73tcUVDa2M5OrvA+WUw92ftpdtFCnK25slKlpWx57vz0aEW9yNd8fkUI2fIx+Ap8yrdQa3yuWOmlHi8hGgc81ccj6wIYErNBKinr8RJyGYquCBhPln8tvemNl1BQfASHCez7aMEcvIvvKV/z+NDngHgW0wg92uAvr7gzRCVMNzp8P1NO8F76dVgB/I6Un1aUMueyFEXAlmWoFufROHJQwIUAQGuitfaQijI5ERVpIyDSSOnVwbsI0kHCbUoMZVFKudRSwrJGdU0/nUleAFI9yodeIkVRQNdTliW77Y6hH+iHIdK6xvvjo5QRqoo0EYk1vYxFEjUOZUmSY+GaeJZMpJmcj6R/P27MiBEEgXdLyJHQWBFLQzvKqmLX7MAY6dRtTSiQM5IQRwfeefE+OC8GXyOh8vrffr+P/YpGoxEjwI8lTAg1WoUSl4WVHA7nHK2WytWS+8GgZzNDlIlyI5txoJXChnyBLLcvo8q03KgcC2csGLPS9wMqcgN1SNTO6xCoF24+n0uJ15jrktovCP3K05Re9ad6hTRkX8KZco5q0bQHPQez2YzJZBLTBPb7fSxkoxVOpZ+GhEpJvnLD7e1TJpMJ0/GEpml5/PgJm82W4+NjhsFxcXHBdruP99OQQX3GaCRVvbT89m63Y7lc0rYtz58/5/LykrIs+St/9a/yg16fWtF44zOfkTg0N3B9eYHBMbiBuh4xdCk3wVYV09mUy+sr9k2LMyXGlGI9sDa4zRyu9/RDi7Js56Q+rw3uRCkOYkJylQ/VD8TzEMOfBlEiNBfDE2pCWysx6BquYmwAmlJ6rmmbuElCPJ7NZoMxJi5q3MihYzweMYxOWb/0S+AM19c3TCZTyqJk1+5xXsrAHYAJoOlaMIama7GljYmJsbiP8o87gF4lo/ep1UUyeCujCUwjCrxDBpb/dVCvI2Nad4FOrmS4nJlFKJ8fXfkwv7cK9ISzDkTqwUvB5N0xRziZ+CLKrOP37mC2/IZ5jLgzWgo5VFTI2YnP/wr3dMEarpaa+BzZoOj5cS4qIqm6RVg/tTKFzwgg6CAhO7c6GRCXsTA+H6x9MSY3KCz6uzBKm4WbmTj+siip6xGz2YzxZExVSrUOW1gKW0QGpt4E5zSkYZCww75nv2/Y7jZstzsGN0RySc9OSDfuN9keWRvfz5+lseUHiD0Qv1Rk07wbG62SURGPlrtsbfXZRkFFos+crpzz+MLHi7a7HfPlMlzscT6cx6yM5126uAumNDhIFR0bGzjlO6JHTQeZI/F07hOdZ8Aye/bd+eSfmXBZpIVwIDLSim/nrzDd0GQtKQEHwln3Wz/x6Wdckzt8y2RzTP0/MnDjPdZIaII1YmGvKgEIRSiZOPQd/dBR+hJ8iLcOEzMuBgcl/uLTQsZnRK5kPraP3lusEZrL2Fl4RqoKpDw1/owHQV4ufobGIBGw7WGlwMDHteGeITUHjYoC4AYX8wp88Lr4oBRoXLoq8ao05O+J3eSwChTeB49z8MhkCdVyHH2UBx5iSWu1zMuJknUygY9o5TvrDVVZRrlXlVmzXKNJxsGzr/MOtKlx4MIuslCWjHBjyd7g1ZAcUQk/cc7FEBDvk+80D1mLCpgDWxlwReCtoSN6TJKVEJ/BOckRCuVCd9sdHkLYiMAkY3fRSNm0jeCOEG6jho+I6Z3GGSh/43CO4XcT+f8dUjRpLdO8MvkblD7xdGZeeOWp4dtq4ErPlt9jlcyywvktw+AYj8fcnzykLEvmiwUA7b4BY2LfBM3P9d7hO1Eki6KIYWvNfifNj8uCohRlRZVegpHLVOlUGzx920bL+AHoNjb0vCJ6SgScJ5kLhrKsRHa67OQdMrNsfczBT+Ub+FQZTT1vNzfXbLZbLDbSgCrA4/E45u0kgxgpOsfofyYqITo/wZZiCJVomrBTBoyRsPyu6xiNRrHs9263y7wXXVQK2rbFeyk3fHNzG3pvQBMaHm43G0b1iK7rOD8/x3vP6ek9Vqs1AK+++iqTyYR/+A//YSiFW8b7lWURMbJ0Ny+4vLxkNpvFTuWTyYRP8/r0ORrtgB9CAm3ITWh7h6PDDZIUVFQlXe+ox1NMWbPZ7rC1Wi0LNCSz6zz9bodWOfLBstJ3oWmKsWAKaZpiLX0/YE0vB2qQhMG6rmmbJjAb0QzxWnKrlLClbksbFrwPG2YAG8Kh+r6n6zq6Ttxas+lMlIu+Z1McMVQL+nuv4BafgXpOYSvY7ShswdXlFcujJf0w0O9bKXdrbfBcyEHYbfcUZRXcWLJRhTZXQ6EKSbJ5n2xZyrDC5wlopwMWS/KZw3Ol8l3tYwdwIPvu3U6uOYDTZwaYEPYwWWYihvgkZeIOADmYIiE84wA9JWbsfSYok8TnY68DRhK+blKoj8Zuy/uw2+/Cs0Mn5HCxuPmdRFSE8qvxER7uFqR0PmFGj4/WFfFekCHHsF7YmHStHpiEHHWkmWITQHcENwpolWY8sZeTWmjr0Yij5RHjyViUjaoKwE0SymR+LoROEBmjyUIOPFLhYzrrORrEarHd7litbkPZOyKIdUHAHe5RJiQU/Ic1yvNFUICTCVkTrD8KInNaP1RIfXxk3PO4bhxY0pXWxBwVur56z363PRx0GnB6fQJtZd8Ms8phbBi9SaAHDnLiD26YnzFVFiJ0vqvwhH9ynJvOt9BUpA2TvIsfqyblEzdIIv7wDOY+Gq8gJhPWJjwjZxQJMGTrkvMun97XvbdBCzFewgXKSgBkWUruTt+1uKqUuPsQNiN9GtSqTtrvuIYBeDkfQpR0EWQuUkKceA8NRwMNi/IQKlklmaQXCc370N0YT0pE9kkRUAOFGM5EgU/KhQuN+1KYUfIky+o6L88IT4v74byPle+Mz3mnj9bh6M8zhC7gAlpi3kJhsabE4ylsEWhPeIMpQvUauSjyh6hcZWQizd2KAGBt2G8xIqphQiMIbLCoKQy2XhPtw+kJtDUExQkQWgjLPoR4fO8Fd6jEGvq7OZEhlCbkfTgv0QpSLlXMN4MTpawfeikaEyIdMCaE8txhy3GfXVS2gLguuifO6BrpudBzTDzcJt7ukGvE3LB4wsL7Yc11vw8MB5GnaLiuDlf/VqU47OUBHzahYIoRT8zgI4D2YT3q8ZTpeCIKyDCIwuQco1Eliqb3jKuKuq5Zr9dB8QrAOYST395eU9f3KTLOoCGd6vXRkTkGKRerngAjoXFK49LfzEcl2TsXvAgmhplbW+CGcNZMWns1VH3M9+wP+Zb3PnlSEGVhMal549VXmE4n7LcN2+2WqqpiRSZjpFmzyc6LhhN57ylL2Rs1XGsxpevr6wjeq0pDoPqQ+yDKqyoJWtRoOp1yeXkZK5k2TcN6LUUIIs078VAUtuB2tWK9XknPMAOzySwoJhvatqOqSh4+fMjnPvc53n333dgzo67r2JNjNpsyHo9YLpeoUV7ncnFxIT2PqorLy0s+zetTKxrGFBhTsVrvMEVDURb0ztFt9gh8M7hmYL3d8u7779MNDmcMhRdvxzAMdH0XLTTBDxddUVGhCIXBnbJ+Jy3nrbWUVUm73+OHnraTsKUi9NEQ15zcc7vZ0XedNFwJyd4mCJZ1GFkH6gABAABJREFUM2DpGFelWEjKgqqAfdtztW7ZmSnDa7+MPX6FnAt453Ch8lVPx9XlFVVdYzxst1uKtotNa2xhKI1hs9sxGY/Y7/axHBilxuhpLPUdgZIdgAMwl/3qCdYhFYbhIp99Nxt5+k2ZVnbdAdyKD06x2h8Ll4qWCX/nkwMseYe5cjjOj40xs08YDphABJHZeHOGK7gnWb99HJsPYEQmtN/vRXCYxFQxYoxMIQEizBK4D16qMGcPCciEcSegQBTScW4KchT4GhOFW5TfMclFLbZpozSONxfomWlM6l2fnDCZSozoeDSmKCx96Emw2+8iqLE2dDstighE/OCi5c8aw3gyYTyuMXZM3/eMRjWLxZz9bs/V5ZW41eOaZoJZ9z6szV0aiNa+tMtZInUiBDU4KNhDqe9g3unP5FxJByUP/3ODo6iKKEg8sNuHTr3R+i3Pz8OTZEjqt0ggI2GJJMDj+COgMNm4Pv7Kz1ju5DioYkQA5NlZyfB+pkwT1xqIhoektKYQnGw1Qe+t5/sOmIQsT+TO+xEueRKdpo+yp0V7bpieAowQDOVDs6hg4OnahiIkmvbtnr0VgFiVVVosNRxkx1U8I2R9Xjz0ZDMVJdsbF24hsd2xhw4+yqTBDRivBQ58BLkQFIXgQVAjjnrbhY8oTblImKqs6XPQZGiy8MrsrPuQJKrw3BikiZgHU2nibLKiAtEaK+fBZPsRqmQZ4n37QRriFnm4R1EcKLFt14nyF+Sqycbmvafte6wtsEWZ8ipQOpDN8D7Iy6AADSG8SL0BwzDgeqnw5Lyn79qooHkIYVw+gEfZ6KEXhSJWq9K9CfPLD5uPSe7yBZ1DVVV0/SAJxaQz5gqIhzL+pgFsiWfJmoVxKh88EADkhy/8HqoKhnKvUZbE86NyNZ11fZzR+5mED5KcVEVQDQBZxUOliXgoRSk86MoblC61wGvFzmEYGLwP+a0m5F30VFUt+Kvt6IY+lJUesdvtJBnbD5Kf5j2b1ZpRPWKxWFCPRrHqIwdyTOhhdbvi6uoq0qJ61VShKEP/iX6QwjrGIDmxQNf1eC/NP3ttohnOpSxBOGPR40TM3dOl8Wgolpxx7QY+7m/4yhd+WPiKl7Ch1WoFEBvWDc6x2+1Yr9fs93tub2+ZTCY8fPiQ7XaH97Ber2nbNoY/rdfrUMbX8eTJk+ipUQ+G3r8sS5qmAQhhULdcX1/T9z3r9Vr6unipjrrf7zEUMWyrqirKoqYse66urvADQWkpaNstfT+w37f80R99i/1+y3K5jKVux+NxPPdVJeVtF4tF/Pz29paiKFiv15RlGdMdftDrUysa601LURYMFDS7Fmc6mq6l63qqckzb99ysVjx+9oym66nqkTDsfU9RqDuoz6pMeRGECnSCa6ksSwbvaHvJv9Bs/bK0DG24vu/EtVOVuL6j7zpx+QwDs9mU2WzG6uaWPngSRAhZbtoR66/+VXy74Wb9NB1MDH56ih8dRfCRu9OMprBFi5Nnu93w3nvvMp3OsEVN3zTYqqLCY51csd/vgofDwnZHVZbiSjah0VI8BD4yhijXTRKkQAxZiYIbghYe3jN3rodMTfARXB28lO8EJpcDiwTwgsAMD9V75pb5ZIlWEEZ8P94sDk456mFycQ5a076Eb+XDzr5oIMaR+/y6wMjV42CtkQOhwN0TmnVp7DNJ2IsEOACYETlC3JBcqH/CssZ1iCURwwLdBZcJzIRrwqZrHHh0iwcwixHX9dHJMUeLBdWolmoc3tM0DbvdnqoqY6w0QO8GQjGOIPsMRVlQ1lWwToL3wjRX61tsUTCfL5jN5/T9QFlWTCZT1us1l5eXtF2rqtjhtuje54w923YN91MIENcRwOUJrCZ6HfW++SuPqD0A28pXMhNg2M4otNumifsTG6zpGcs0DbGWq0ZA3EObqDo8JluJiMAzcK9gKN93PRY6rlBuN52x8PkB8MhzE9J3BHz4w8fGaXgO4v1zYEN6ns9viJxxw+HaRuXGpF3Pc2DuVqoyIdkXBWQorct9LF7KhhaW6WzKFuWDUrN/v3N0+0ZKSgYZ0HZi9evalq530do6hNKmg3Niye59fB5GEnYn03EIWQ1x3CZhDgHSd/w7akjJqpolS7wSzKHBplCvAMFbqOES1kTPYdxja2LJzpzEo1EhgPsIGoOyLh3J5dnKG7wX74ENPK/rQjWk0IlcSlrKZUMooiANBtN5iwYHbZbWD/R9CDEK69P1EgfunXgFnfP0zolXuB9i6NfgBpxLSemaoKoTTYYEUuhjWMvEVQ7DZZOZX8934COxhG3GS8IiW5MUIRG1Sn8hTCWcXc1BUZ7tjYY4m5RfjQ9l8cF7afCbPBLhNKnCEWS+PltCK/UznV0A/+oxN/ncch6gBgwdX84gwnk8CAMM9BkFcnbW8xK51tK0DdPJVBSwto1Jy0Mo5IORRnNtaHQ6nUxp2xu6tqMwlqos2HtwrqfDYEMlqn7oef78GYPrWS6PGY1G4kULgGMIz7m9XfH8/Jxmv49yTY6cyK66KqmKkqZt2e32tF3DuKqpS/F6DaFJdBGUEe8lQiH2kY2MLp93xoxFWOGxoYqHzBkMN29/nYuLR5zeO6FpGsZjadp4dXVF3/csl0u22y2Dczx//pzJZMLR0RGXl5dB6VjhPcxCU9Lvfe97gIRcHR/f4/3338d7z9XVFa+88grr9TqcZc/NzU0sUTsajbi9veXi4oLVaoUxRgoMkXrJWWvZbaXZnoReueCdmMaKXG3TUY+k0JEUKdqy220pS2k4rfeVniQThqGn62S8qlQAcS2qSvrcPXz4kE/z+tSKxje+/w6jWjpiS/JOqNDkPcNuQ9u2bHY7Wk3W9sSSdsMgzEisGaKF9n2PsSUmMDVjZAGqUuL+6qpkPKpDsjaUZS2EMaqwhcc76QJpTRGaM2nVCsfRcsZyuWR1c81mvaFrOgYPzcmb2LLCFUf48SI05jNyUH0IC1KwGQ69WDytCPphkA7imvDWe25XKwor8YgTJuLcDZnfXdcx1COMGdhte0a1NGixVhi3CU0IVfDlkZgfw1ce/AFK1QpVyuyIlUfysAll30rE4Zf4I4EGDp59gDx8UkQOvu8PvhKZW95ISoGUvmIoCMp3fbzWHN4yAe8cuJHuG3/6/HoFsy5aBI0JioZOnwCCUJesJ/Y4yAeREHKctFdmH4SPMUX6LFsrIYNUVjGGWxkTLSg+rIUmponhK1jLciGRAeHpZMLZ2Rnj8Yh6NKawluvrK5quD8wc9vuG/XYXwgLbSOdemxkZqX5lbUFVWkajEePphMl4zGQiXUdXt7dcD47FfM5sPqFre2xhGI9HXF5eCtOzIuhV6Yw5KSYI5iCcrdWcEh9mkVu2wtlKk0TjBcQLORAd3QpQonLipRLLJxGP3l+JJmgbfcgBqIs6CNM7hyxOIanp5kAxVhkWIJEeBH2UApuwDnrG8mDJCC8ivvChMlk6uIewPYEvo2csTjL91CVIVc6CEpJxAev9wXqGu5JOTgrli7jHp/FKuAhRuVDrfkyYVMAYFCCtdKQKUeqmLLX0C2MoqpLJdMJeEw8Bi6NjoF+v6IeB3X7PbruXvLygIaS1EGCYKwfGCMAbjccYU+H6XizsJYGOklfReU+Z1YeP1V6CYi8WWR9BnylCyGEQ7ArE1fAj4DLlGkrpyVCVLgBUF8Ct857SFuFa8Yg0jcRHF6Hqoiq9xoEtyljVxkXjgXAzibqSMJZhGGha6V48eE/TtvIZnmHwUnpeq0QNIfzLuZjErfTih5CorPJHNjecW+JeJMCdzg9aAS7QTZRx3gcwH8aLzkMTeQ1aDSjlhB0w5XhPQ+5599kZyWSSE0VeehEkIRArbqU3AtAM+TRF3pPBh5/J4h7PTKbA58qD0RA+SOA/O7a6Tt67yB/0DCW+lAnzcJ+DQjAQ+afSfqLuXF676PXQ8bVNw2w6Y1zXtE3L0PfBcNvSeI8pLEVh2DUteMdkMmG1WtH1HU0rFm/pR2jouhbfy34bDGVR8LRrWa82HB8fSyM/W+D8wHa7Z7Nes93tQvO/UO7VhJAoZ/CmYDyZYwpL0+ylEp2x2LKgGI2iJ6wsS2xZ0GwbMDaEJSXv8kFulRpLwpkRRpPW3NiCyWRC0+4xV2+x3zc8e3ZOs2/o2i4UqxjYbreMwhjunZ7ymc+8StdJjvHFxSWXl5fsdjt2uz1vvPFGUKqkyZ8qCaN6xNnZfV5/9VVG4xGT8Zim2XN9fcPTx49FSTeWi4tzhhChYK1ULh2NRoKhuxbvCqwtGI9H7PcNZSV8bDyuGY3HQdaV9H1H17ZUVRnC1OCFFx7S9S22MFR1TTnIvbq+ld4extA00kRVw7PKsmS9XjOdTum6Lnp5ftDrUysa71/cyEDLMmiz4j7abXeUdUU9GgkDw1KURcDOhQhWa+MBtAH4FYW4Xw1Sqg7kUFZlCX4IoQ4SB+eAPjQ88abCluB6B95Iok5RxiRyGBj6lt12hbVwdnrK9cUNzzY39I8+iwoBjxCZ84Nw6EB0eVSji4c8AMvCQp+qalhbUARG0XcNG9dztFxSlCO6rqfvWkAYejsMbNZrRnVNYafi0SgkjEqZorKPaB0+API+CkHggCcpOBJ0YA5A94GdLudZGa7Tn8r8ksww5Jd/7GV0pTKQryAzA9fypXzcGjPtAwy6g/d0HD5CiOyZh4PVazU8QcchWFWqPrkhNHFE7Lvo2NQ78UkL+rFXWnvBH4EuhNNnDZWykBtvEJ952t0kPoIyRGJ+xBmobPdxM6wtWC6XnNy7R1WLi3O32bLd7kSJHxybZs9+v5OYZyfXmEJyNTCeEvGUeGMDAHK07UCzX3Nzc0NRlsxnM+bzOYv5Au9hs1mx3txycnTCcjlnu9tjrIRZnZ+f48xADL8hJ0Z5iSvaReGPUYhu4qYLKNeKIQkI5MqLfOWOL8PmQj6rwhXAbwxl8YlQhmGgaxuqupRd8IQu5kRQkSBoUDCM7g0JWGNivk/ceR+HFc+dObiVRxOmxQuRgYm4HD6R4QH1BdoORu48fErPvlpNva6d9icI7xmy8+9TIrIuZ8pPIK4h+GgwUgttyj0Iz3YCzFz0LPRhnbsQL++whXoNZC+MMUwmU4oyGIrGY+qqFMtl2yK9FyS8Zrfdsds1gDRV816quqTwLXA4TKhGWFSWorCMJxPqesRoJFXGbGFjIyxNNo7J6okqZQ+NvRMimXrtKGDW/AATQkx8DO+Ssz/4FAKiYTbaidkWmtTtgidG1l6Tk3ddj3OafKz5BS4kjfsQ+hIaX3rxIvjBR8Xfa/hIpvgJPapClug88ntVBCKNBNDuApVHcjEZfdwlVg2LzMCyyw0JWTiS5j/olRkYF7oN+5ILB58TnszDZrwlCjCTfz87Z8rHVUnUNYnTUKXZQz8cioM89Chb0+x4I7nxha5S8Drp4da19nGs6hmHjOscMI1s6AQ6D9RqM5mTAHW2gNlYzZ33DZ62a/E4qlGN3UqOjRt6dusVT25v8d5zdHTE0WLBfrdjOp0xm025vb2lbRu8K+XOyseDsdc7hy8EA26329hUTgv3NE0TzmJFOwxyZotSZMMgOKcajWKhoaHrGI9q2q7HBsWi2zV4J3kOGBPxYde0aT1ymavzTuAmhfl6xAM1DGy3G5EZXcd3/+RPmIwnbNZbNpsNu90ulnntOgmVny/mPHr0KK7z9fUNxliOj0+YTBo+/PBD9nup7LTZbFitVnjnePHRi1xeXEQvklZ+0kZ73mfGCs2VQfwvXWhWXZXSN6OqR3hjqEdlTBjf7jaUVcF0MuL2dkVVFdT1lK6XfkVd1+DclKPjJbvdDvCSDhFySZpmT13VMTdjPB4jSeLSD2W73WKM4eLigk/z+vR9NIoJ1WwmXVT7nqoeU5Ulk3tLTGFj7exRPaMoi2QZ8VK61hhJKCnL4ELzjspAVRYCJo1hXI9k8Zwkll9d3SCpcYZRVYGx1JWhabeUo1Iy9kN8YFVaptOaYWjEMzKp2ay3XD9/ztP6TdZf/Ms4H5LgYqiSwVJgS6IgNXicFYCa4pQlJ0Jz1lJ8bQD12sFxcNxc34KRahXeO26ub5iMRzg3sLOG3XZNWYAZj6F3EFzVROCShx5xh/kEC2IWapUYlHz7bjGVqDYZyEuiqEDJLa6xktKdZ8fBxLEcfpizMwU8eWBNFC3xpsltb0Lyc4qJT/d0Pnt+PqdM5kUlRL1PYb9EABmwhqHr6TsJOTA+CJWDMno6LhUAOZM2cdJR0QsM/SD5Of9+XF+Js07l8Uwae3h28hSFZ4bKV/me28JycnLC0dEx48kEjOf6+gqLpe97dtstzX6Pc1BUUuvd2hJrSrCWsrBst2t2zS6Uy1tSllVoyyGhKrgW53pubm+5vr1hNptx7/iExWLJ4Hour64YTyacHJ9Q2pLClpRVeRBn6jUMMFeSM3SbkhvDfivTV0ARKUDDpkRYRJGRE0NWnuxAJKvyGwB2pLW48JI8Z5BGjh5DEdZbH2Eikfv0E5KHBJ1DIhMTz55PN9GBxVv5A7rNAQrofA9f6S2f7Ag+AcgcA+l30DF4TV4OVvSoSIQa9N6HEJAAmvI11/fC96XSmmfoOgG4JlQisTaWUXXhnkPosLzZ7GibDu8HlkdLKRNeSrOrUVVhrABwYw3WeZwpmc4m2EI8kL53lCH3yNqStmnZ9+EcK9czBmMcpS2pg8d4NK6o6hprxLIaK8PY0C/GOYqqEsHtXCKlMO+8hr3mCRSxqqCs7RArx/hgydXKUSHkKACotu/FUqxJ42FtvA9KRS9hKrGqTs6TvNaiOwTKOcsKTO2QezrdbyKojmfM6O0TPzP4w7Cag4OA8CPvP/GMpTFk1+UHNfLS3IiiZzGpd5Hf6XGzStT5uJJXyYMYd1L5v8CWk2fO67w0BE3XKFivvU+g3Shv9l7kaxZKF3lZqGCYe73yE2uU98WxaIVJi0qq6Kn2Lt4v7WX+OuRr3mYy1CK9PVLMp65I2oRQzesgRyueZ/EgqDGgqmuqspRQ+F54Y9/3YAyr1ZrjkxOatmU0mrBYLMRjvt/R9j1l6A+mnaRF0S9DwQGZQxe8Fl3XhZK40itC8VtRVmKc9qFscsjbKgrLbrsRWV4U2MExHkmPh33b4oHJZEzX9/R9R+Gh6/sgcjIU433Mj8zNlomew5oZCetiaPj8SyesVitub27pWqnGdO/ePVarFbOZFA3aN9LI7/nz58zn8wjEt9stTdNwc3MTFRPNqQDhE2+//TZlWYaeFQlLaFsFTSCvQuL90dFRwM9lLEW7WCwoy5LtdhfDzrqui1XdLi4upFxz17HZbCSvJpS+daE4jLU23me/31PXNepx1R4akj8tiemz2YzZbMb19TWQ8r1+0OtTKxrL5bEQYNdTjKSroTUhacz3EsJkDY6BoXdS+i4gv6HvwMNkVNE0e8BTF/D5V1/hs5/9LIvZnHHIeB+PxmAsrXP8k3/yG7z/wYdSY7sURWNUWfBTTk7usZgtaLYN3nlefPSIR4/OqEcFzvVs1ht+8zd/h3/4jcdcHf8oza5l19yyWB6hjFFK66WYRq3KY51WowjCxjtJ1PXSzt0h5dwYRCioZc15j2PAmKBA2TF+6KPrDzybtaUoJNZzVEvoSwL9QbkxCfwfYF8C7ArPOzgsxGmhwjD1mUiCK3bODW8EzHwgV8ienazOmWXJZ8/NLKkxPCS3WuUDPABniRnfxWWQyxj5IK1JHHpURkx8to/rlLNpqS/dJ4HntHzkHQtTNFlmr0zpiPf1cSfC4kniIxiskXAqTwgHDeUqtSKILrbXvw4sfCqosmdbw/37D5jP50wmY/ZNS993DL3jdiPVIsSrVzGqDK6wmLLGFjXGlKHEoKVbb+l6Udsn84Lp4kg8PcNAMfTsbp/TtT31qMYA2/WW3XbPYjHn9PQep/dOubm55cnjx5ye3We+mGMLw6NHj3jy5ClDqKShlckicM+qKOXViKTzbxDK6u43BHDnPkZrAoQ1FEP3KdCa91AkAEYcg0lEHZ9twA1xn0trMvoxophIsPsBTWW3QMNfVA/RvVRainSle6hEr2A++ywqGRCSlsNHLnu28hbNaSPE72cCVL/nM2VDE92jUhIVCx/nQ0Z7Ut7RfSzsS8N8pBxjT9f1GEK+gN4iKigSmuc93N6sAmCRJlDT6Sz0JLKAjYDMAj0+8t/xaERZFLRtQd87fGno+iGeUU3YNkBRWsqiYL6YUZVlKJlbUVqRR6YoRJE04qUobMGAicnbJoAb51ysZiTNzByD8yHUbgieBjGcDYOsgypYOYjOFTavtBLh+CFPlYb1STkgAF0FSocQm6QAB7eWj4xT+FHyxRPXCf1dd1uJOPAWDTlL8sSEcxnAcChxp7w6KqMKmMnGGRFcIh6TX6MJ0Xr284nFM5bCA00A4tqwNFZT8pk1X90ZYW3SOTLp2WFYVQCL5xcXQpfhGVo5UJ5tsE4Sm0NVgCwfMSgpd6Z7wFsyWaKhtVrWXv1IYtQM83cZT8iQr55Xovw2WZiaCbkigQdl9fI1bCrRWqAP70VZMSYqogCbzZrj+h6T6ZTmWsKnqlry/pz3zGZT+b13rDcrlssjjo6XDJe9hKQPA2VVUpUVg3cUtgg5VUXcMzcMOMQwYYZUch7vKasqdsd2wTM6nUwYjWpJAN/vwAVjmLGMJ2OGvqfdN9ItfDKNoT2SszVwEE7hPN6mfdJwubhtehYynDN8+PsM5oqmaaiqmrZtWa/X3N7e0jQNms8wmU5wXgD5s2fPomKwXq/jfHa7XQTwasBo901UBrQiqSZbl6UUWRCjTOoADtKXRBWJsizZbDahC/lUDNRajTUkn+92O9q2izkVOr6jo6PQ4dzSdk1UhnKFoqor/FDE96qqCkdbjEDOuViF69O8PrWiMSpCkzxbRg/EZDQKFh+DDYkr1hjRKo2h3W/xbmA8H4fkN8Pk4T2OjhYsZxNM39Kub/CVpRsaPnr3bdq25eVXXuHRy6/w+ddfYWh37JqGuh4zmU5ZLmbgB/bbHf/J3/iPePt7b+MGz72Te/zyL//z/OzP/jm2zZ7BlHzzvOK71ZdZXVyy20upr67tODm5R1mVmhoh2MVabLCkOlLimLJSYz2FM/QGGJzyIEpTUBYSkmLcQK+lC72T5Lm+w/UD1sLQlzT7PetQTqZcipCMrsd8wb1P0UaRl6bQhkMrTJ4QHf6NOF/jWFVRScIsf2As9ajf0zEFsCxWsyhJomDyXoVpHHi8rckH4iO01lHE9xW2q1tfFT9zZx3iVXEyPhq+DoSyFyArh9nR7PZ477Bojwx/WKnE5GPM/872IkBMg1ofgqCwmnSoVWxCdZiDzczudRgPly2nI7nR01LdPztjsVwyHo3Y7fZ0ofjB5eUlTe8oi5q6qjF4NusVrRuYzhbce3BGWU4kIdR7HljL5XOxVCxO7jEaz1Cg7vqWm8untF1PNwwsF0uK0K/m5nbNbrfnwf37HB0dsd1uefrkCQ8ePmQ+n+O854VHL/Dko8eSOOrvbHW+rjrZ6FXL9tdk9GIAjSkOgMEipSxdMAKkqitE0GXC77jgn/PEqiE6FhMGaLwLIUCOoqzSWPDRmikVi2TsTstkKunFngupzLQmw4KP1n1vvIQDGAn39FFzSnk5CpS8llfVWGodT/hOpPNMCdCRqodIwZhFE3/VSp6RtpGwHomn1mf7SNcYtZjKdwvnYnPGYejZN3u6tmWxWHB8dCR5R2H+sk4mgvU8pjx2/xWGG/QuH/fee/EUGC+VZYrC44ZOOogXPa3pIq8EqOuK8WQiRutmi/ujv0n32i8zzB+EMplp/2Oisg+KU+DT3ZAU5DgeEnhXYJcd1fB9CWUSy60E0kU+mLE5r17NUJ7z7vkm8Dsf8jsOlPIsxl+OhirFNn4x+YIPcGrY0+Tt9tkH6n3T62NjTb3cq6fIZs/gzsHObcPqlfABYJs0CIT2jS0SWNeznln/text9ArEL4XvCQWl53sB6yrEffxb5YpL8w5K1xCqF6mCrKGYqWSyKkCBv5g8MFKHkhvuDqWelO+18XlGf4/XIWFkQTFw+nvUanTt0ryz7TyUi3nsYhYPrSwwKbQ+YxZh5Fb5paFpWvFqVBWjkeRq2MExXywY1SPm81nIAZiw3qzYbjZMp1OGZc/11bV4E7RtgLWhv4lEaYic9RFzeAQnalif9kXxEKq+OerRmMl8hjGwXa0BE0q4OkbjmXgz9juGvme+WFIUFdv9Hmtgv5P8BzLF4mDemZxISqjJercJvfYf/lPKV6eh7G4ohxzxhOz5YrGg6wX0b7dbmXtRcHt7Gyva6TXj8TjmWSg/1BAnVZL087quhU5DCJMCei2JC6lXhyoywzBQ1iOMMTHUScvjOudo9vs4bq0S1XWdYGDk/mdnZ5yfn8cCFl3oaafeFe1srq/RaMRoNIqVsX7Q61MrGnXRiYJRISBkGJhUFaYKAmLoqIChHzieTjHGsHjwAifLGUfHS46OlpyenkgLeTdwc3VJYQxvv/UWl+fPqIqSKmhwV8+fsbq5Zr5c8IU3X+Pi8pKqHrHZbCmMp7QVf/Nv/8f81m/8Fv3oBE/Bk3uf57v/+Ir//Pwd7r/+RbrRMfMvfIl75Vu45xfYIjQKco7V7Q2z2Zy6HmUMOxAgRvphhJg4H6pkhTNOgQgNTY7pvWO7Eav5EJLpfBC44COot9Ywqivqes7Dhy9wcX4ulruqwlhNKiTJNh9PCeqiT6cnsfrI85RBZRYc+WKwqcU3M2dqwB8HOX4KXbIyjWTXH6gLyvPz52UAU0cqsjpZWvVLORYNUj4Aq8yqn30nH2MMx+HjfAUUuBcUxjC4PgjKMC9ECKQGP3rjO5NRRq731ZtEZSOqG6SOnoFQTCxXcrhPCTcGgSAW/QPlJdzmaHnE0XLJqK7Z7nb0fcduu+P66hqHparGlPWIoqzY7zbsQ+dQ5w11PaYboNs30qjSdcyPjvHesNu37BpJELdGmm3NF0fcDLIe9XgqtB1c0n3f8dHjx5y1p5zcO8FYy7OnT3nw8AHz+QIwPHz4gCdPnoYktgzV5kApgOFsMaOgyectkM0QrZjI+SjKEt/38e9ET+qVTGEgBpslKOuzw2fWMHStlCv1MAoHIPVC8LE3gnOSY5X6JmhpVFUsZJ2G4CVRD1ICZaAJkikfAA4IPFKvPwQy5OBX1ycTlkr5xlLq/MOaG61ql+VGGSP5cN5IiID2OQAfz4JiLmslXtoYE7oqi8LS907c5iK5Obl3SmkNfdczDD4IbelVZAtLP3RgJMeuDS77ckj9FJRfariVVCdsGfrwe99Hw4Ekige+6iR0oeskJnu4/pD+D/4xZflZ7P0KtewObsAQOiAbg8+UuIOfCiK8I+b7BHpNXqLsZSylRlPdgfN5RT4BhWSJ4onOxchywN1AlQDlNRl2jjxMgWycS6QWlCH77Bl3AWv6yGd0mJSAA2/DwZgDjwphP7GhT7Ym2dGOg1CDWLIaB94dvuxDbo/HR7kJmbzw8Z1YHCRXwOVfkwA1JG9AEHDy1YHz5+doLxCMYej7KG98uM5nk4hTUd6SKQNp6iYKIk/ywChfigqC506emU9yIFMw7pJa5F0mf3a2yXHeKRAs46hJ4SCngbSOu/2Oo6NjJpMpbfBSdJ2UMd43rQDbomQynkRQvVgs8N5wc3PDMHTCLzWxu3MRS3mIfDMqlkY6shsr1Tl98HjUozHzxYKyqtisVmy2G0wW9jabzXAetusNxhbMpnP6wdG0LbU14v2IK2RS8QLIcJGPfPOgwWNQ3NztY+zV2yy/8jPRA1GWRQT2GtLUtq14Y8pkKNbwKG1mp5Z/Y0z8WZZlNICo58IYE5v06XfV00FYPwX86v1QhUEVl1zBMEZK3Op3tGO5fr9t2+jFKCor5XHDc/OS1uplUUVDFSfFBp8U6vtnvT61ovHqi6fScC6U6+zalrIoWc7nFNZTlqL16oAmkzFd2zKqCl598QG7/ZYP3vlTbm9vqMoCYwsuLq5xg5TPVNJ3znN9c8ViPqWwjq53LOdTiRGsClY3tzx7ds6f/Mmf4sYn2J/6N/FG4tY653i/OWJqFtjBcXl9xbiucX6gKKzEBhpD33Rs1huGiWM6nQYm5A6E+r6Vpik+lOR1ob27hi+k5m5qU0rgOVlIEuPDSWOZz775JqORJNasbm+pRiNGI+FC3iVrkzKjFCcdGLNP1qPEOkwcQZQX2ffj25nyEoZ0IHwk1EqZnw+g0YTvZoJTZ270nhx8modB6bjFlWuitIxyXq8KVrTIAONkUvy8yCplohpyk55twrxduE0qbdvInApCGTsJ1hDOD3n/hzRBXci0GfH5JnlefKzyQQB4NlMsDBHt5pW38t98stDHdfSe6WTCyekpo/FEKj90HdvtlqvrawpTUJcjitEEW4+pRzXT2QxbFgxNy2J+xGq1CSlABXVdMBnNpf69LfBI8pwfBikV2jYUZcXxyRlVXTEdT+m9o9ntsF2D6wx930nIwdDz4MEDPJ5nz59x/8FD5rMpzg2cnZ6G7qNhJhm53Q0FSXkQCUAloKWgT3ZXDOo+WqI8KrcyAZz9pw3ZBGAkunLeUyBKRlOYYPEZGPo6gF1Jqu07ed9pAzKlTx/COZwCDvlMKqcMsZqcJv8aI7HgRZintUWsZJStRHAWhEK0RsqeJo9NZhFNGkaoLBXWT5UMn+Zt0Go8ssAueAqUzrV1gJxRI6F/HtTd5Ibk3XGqaA1C69PRFFsWUl+9Hehw9F2Hdrwehp7NdkvXt1Hfvr25kYoruSEknLHkPdb3FUgFhZLk7cS51M3cgaOQdV68QPWL/wvM5ESghGI/U8h3TRHvGXlh8HpEglIQmwH0OCqDhM/GWHmflcqMC5nANsK7o2UbkuHZe9ztE/zu8uC7upfK08zsPmbxID0bj7t+D7t8BOUorVlkmzb8msJ5E41k5y6+kRs2TKTzPPdAeWrA0WEe4lnIvQ4JPHNnfdK2yhkyB5V+tKKT0EAoURoMe/JxJhe87k2SS5CB9Gx9U+fn7D0dZ1D8nZ5jDUPKZWigFZ1D4lT5TLOF1T+9h5jjk30zyAYvICesnQWjHcPSOup9YpUzfU52/kNg1h2eGgxomVTMPj38LRv3brdjPl8wGtWMJ2P22x29sRRFT9u0FLZgPJZwnfFkzGazxnnPYjGnKCy3q1vafRPDh9ORklLKKhONSflPgpOksIM3MJ5MmM3nVGXFarths16xXUlCc1kUTKZzbFGw3W7phoH5dE49HrPebfHOsW+baFyUhZQ1dhA9KDJvGxvOJjoPYZRDR/9Hf5NXXnzE8fGxVHoyFu986i8Rwg0vLy8ZnKPyYlgahiGC8/1+H70fo9Eo5l9piJgNMkq9BAruJ5NJ9GBoMrh6JfIwKpvJBxOMRqq4qBckVxLqsmI0Gh0oE1VVMZ/POTpeUpRF7AWizTw14VxLbOt5k/xGMVDu9/uoDP2g16dWNH75538K72UA19fXotl12vBFXDJlYZlM5+xDXNpLjx6Ccfzxd74ZtD1Z8K5rsUV5gOUAqSJrDVVZ8dqbb1LXNZvNlvPLy1Dvd8rZgzMeP/6QUV1RLM9wRR2UANGwbtc37PZbZvMZzb5h3zTRNeYJ3ce9w/ueZr/B+456PI1JNs47Vqs1+90uCn0180n4wxBtBtF2oNJcaDbwhMA+Aoh1eFarNd/+zp9wcrJksViy3+/YbtYUdk6pVRdMOAQ+MNCUSZxCWfOwHx3YnTEoY04KiMLxNPqUPE1iTV4v9Qf5A3pdXrUhNxhkMDndVFnO4FUOYry98710Aw3jUKAUH6Jf8FEURCXBqlKSSTkTAKqWPG73bQK8maVZ9cAkyEgMXSelzD0Cu1x4+syYZO4IAcUuPhiUBPrlO4Bep98N21iUJaf374uL2jmh472UvittEZonjbCjCfVsQV2PMG7g6EiUKodhMh4xm80Yj2tJevapQZa8CqwdYc0M7xxN17LdbNhsttxuN4zqMePJgrKoud1v8E6qUlxdXWGt5d7pKcPgeP70GS+++EhiNb1nt9+zul0Rxf8nlGuNyxGqIqnFLVaA8mm/VQuJHj4FhIUCcM2HMVmiawIGKqjVODA4uLi6oq5KNKQm38t4qp0AH+FPWuLUHCQWq2VscI7zyytG9ZjlcsZsVFNWFWVhQ3OzkExrVOiSWZP1NCa6MpA394ivHIzbYKFPNBtGbgjCNlR2C0naCuBwYtDoQ3Mr7Y/QhdKNQ98zDI7B9THsqB+0p0KyZPmmZbvZ8YRnMVwMVXRiSWIJKdTiBn3o7yDLnLx4GkYmYCyHKkTAIGqTrIsN2l9etMvaAman6bpwjrV6oQLjZBUHj0sKb24U0uvDvWN+WKxO5rPIqjQPBcF+d037x7/O8OxPICTt2sBLrILHvsH3QwgrkjXDOBwDnhpPKV2nyxH2hR/GrZ/hV4+xXcNQzyk/90sUr/2MeDXyhismeQ19PFcmrnlGTBycsTwnKCVyZIWWMqVLtyYLJMwXT49v1NLD/VUGS9NTe+dK2XyfjxGSwqBKzcEgDJ/4yvZO+UfUo8MctVHw4YA/fp8Do20krT/72cmgojLAx7Oqz4/KnM/CFVF/VPg3NzxFAe0xRqptCtnqd9RAmRigynzliwf7nU3XIMay9eo2VEqaxjysrKgVfd+y3qxxg2M6nbDbbnBuYDadUlYlm+2O7WbD0A9xHtJ0Msj7jEepQcJgKMqK8XTCaDrFWMPtekXXdoJxrMEUFbasmMzmOOfYbtbYomS6WDI4R7tvqGzJzeYKo12OVMYbk9WAzmjhY9vt8X1L81v/R+zVO8wefpa6LmmaHdPZlMl4wtXVdaoC5Rzb/QZrC0bjk+jJUI+C916qqmbW/1zZsJjYT64oiuh9aNtWihSEvXXGgC3EMK00gFSTVMUGkDxLaxmck2IxiPIoJYMNdVFSFiX90GMKgxv1dLs9xXzB7dWNpDx4Q0mB7z2bzQZjDdt2y9D3ch3iHVYZ7FwqgPFpXp9a0Xjv+2/jveeFF15gPh1Lu/RuYLfdxLrB0+mUF154gfv371PXNY+fPOb5+bMAupNlpyirKLx9HLSJzXG8MVzf3rJcLpkt5syXCyaTCX3fs9pskOotDmvLaP33SNJRP0gFLINnv9uGRZIKH3LeHITrnfO0zV606lFNVVZstzuGpqGyRYhl9AFsWCpjsUDXd3Log3AR+hXCtpk1SC2CUo7R0vU9Hz1+zNNnT5iMJ3z+859jvd5QVVJ9wFqbwLvI30RgKuzCmcGF2NcDwW4OeaxXAJMEc5Ijd8MBfPq+8ZhAP9GiS7qvMoz4hfylMvsOEPDGi/Fe1z9Um0qQUEJ+MF5yKSIaTUJPvpfWXJ+hiYEpFtwE+hKlo+2aNHZSOM7Bfx+THWFcBww/W2PvMaYghgnJlzPXO4HXmTBQBWJKGWrxUit0Ejf37t1jvlhQ2ILN+pam7YTRFVJVZ+g6OtNzdDyhGo1pu55mt8V3LdP5guXRkqqwDH3PbnPLfrOh7RrpnhoYnjWSH1TXNePJhNFkzMnJEcvFgvVmx3q1put66qqi2bd0fct0OqGwJRcXFxhbcHS0pGsbnp+f88KDB7RVzenpKc1+L9UzIg0mwokhZwou0TWIiEbWFc2DSu97N8Q90bNAqFgU8/8CcPQGaVKoIClYzY034kmsSqlkYi1W82zCPW1hJIm4KGNVjSKEimicqpZjtBi6bqBre9pmzTD0TGYTiqBgpBKaEkpk0CI4SlcCQiRJUwbgnA8N70ilDYPVF+9TiKaThGUXYnqHUCHJDYMUQBg8g+tDnwQX8unkqc4RBYiHaLlK+VvJcq/81ZD4oRpQovcu8pb8IGl4jzkoDaqwPx1kE8+y8SbxNTx59y3vHb7d4tstFDV2vExeLLzwlgPAqrTmA9BLZzXCwcgvszHkdBenIn8b5zMwKRf43Q1uc8Hw3m/juwZ7+RaF1p2vKvE+OScKfyxEYbBFGYT1IFXiCpFPQ0ioB4+lgye/DziK0jIaL+j7gebbf5v+yTegXqJGDvvaz0I9k30ox1BO4/gV9B7MkQRYD/l57mGV6lo2nM8E0pJF3UegnlV3uuPpCXfFWsNyLkUBLq+ukbwIiyF0XbcG60M4lV6VWffTs+9C/cy+f2fvEu9O+/6x6302PxLsz/mPEoxemysvypFUcdXPJOzORJ4FPngPswDJGB6kMjPkp7nDMcmzD4Kn4uyALC+EFK5wV46pbA7jV6Vnt9synU6p6xHT6YzNakUbcm2tMdze7tjuNhgPXdfw4OELNM2OrmuZzeYcL5dMxmP2TUOzb6R0bjDcRtylM7GWuqoZ1yPq8QRbFvShgZ93jsJDb2BU12AKFkfH2KJkfXuL9zCdzhmNR2xWG/COftfguj6TxTlmUE4SZLAJ8iMjTzz4dou7eBtrfUhw9ozGI9pWwjidE09FVZXM5wsePnzI9fUNTdOy3++jIU496kM/YIuUvyHTtmhbBPVSaDhSVYlnpGkFW1ojETjai6WqKjEADQPGE3N7nXOUoRliWZRUlVQQs0Czb+i7HlPUEnradbhBlLPdbkdd1Wy321hWt23b0Huri7gzhn1ZKdKiCrJ6ZzTX5Ae9Pn1n8PUaY+Dx48eMRjXT6YzFYsFoNOLo6Ch2DFwsFlxcXHB1dcm+aaRPBZL0oqWz1A2kLiPVFPU1DD3Pnj3jgw8+oCgKptNpdE8NXlxOTdPgX/+paDG2mFiBQjfEOY8PiTwuuKly97nEnnmc31OWBUOomNCHOLjECgKp+gRi80RxfQkzCcLXSKympoyqh8MCfe/ZbHd88OFHUu7XiOWtrqp4/yib9eaB3yn4ErwQRXYCz4ppFcaF2AWfH6ooHQ4Znj7oru6gACLm6ep7GQSJa+DjXeJ94vVx3AK81IIcv0NI1LShf4YRUWsxMREy7QeBaaRx2uyPwPbxRrxwxii7SWEacXejJSgoiSazqQYhl6FYvSjQgc4nMa9oVTKB+euTo9zNRZw5uO94POHk5ISqqtjcrhmcD6XkpKlO23Vs12uwe6bLE0xRs9vuKAzcf3DGZDym61ourq5Z397Q913oWZKFG3gkTt9Ds92wurnGlJbJZMbJyQnHRwtmkwkX19fs9htGk5r2tqFpOubzKa7zXJxfUFcly8WS84sLbm9XzOZzhr7n3ukpT588jucgaRopvyAX4hGo5GEpxqCJngcW7rCWEveuirn8HcMJFdSq0qF9PDChyol0m7ZBMBRFSVla+n6QsAZbBGOYSuUQ12tc3G/n+ngQ3DAwnU7Zh8S4/a7BYCmHIiQe+2i97ActdyoKwxDyO7yXZHHJg+iCQmhCjkgW1ulJNHyguJKtp3wWkxdzuauMBBMMGS6dz/i1TKmIAMykLQg/81h7Ldup+xmt/BHRHIK2qHCGoxXLTetnfYO7fIfi+DNQT2Su599j+P3/AJoNzlr87D7Voy9jT9/A3nsthBPp1pvkpDCHz04IIzvfkdsfwtc03zR//Ya7eUz3x79OcfE+xjvJ2WAIa9pTFh5rHaOqZDIeM59NGNcVTduyWe9wg9CYtTXew2QyYz5fUNUV905PWCwWnJ6ecO/0XgA4M954/XO88+57/K2/9bd4//332a6eRuto+/QbwXvl6byF2amAg+WLVC//WKSVYv4QMzsNfaJc4EcpIdxnioZVnpiOcOT9UfZFvmYjeUUDl36z3dKff4/Js9/hr/1r/138/CF/4+t71sMonHmLJoKDC0f/kJ+nIeRwO6kQ8fdsvz+2p59mvzl8drzUHDzl48+OZyiTE1qhUM9ruIcYVsjZWpyg5lndeTveVz+ygacJncdN+K9E57n0vrm+4ez+A0Z1jZ9OJfyx69F8p8KWeO8oq5rRaERZVux2O66vr8UDPh6zmC+YTqchZ6sXz6mTqozGiIHGqhHHiGV/s5aGzwbJIWubJoRuWpbLJVVV0jRtKAo04mh5RLtvaZuGqrRcblaIQMh2T5fQO1JIdorKuGt06B9/E4sA6Pv3z1itVkxnE7z3IZlaqmG1bUuz33PednRtx3a7ow+VoLpW+Lnu1+Ac49FIjNRlGfMnikxJ0PwLUSQGKpsaUDvnGPxAaSy+k3W0PvWNcW4IRqWUP9Htm9iLQ7u9r/pVzAERD4XkeDx++gRI3j2VF8MwMAv9tI6PjqlHdSyte3x8zHK5DFUEpyyXy4+dk096fWpFQ7pqGvb7LTc310jCc6ifH5QGtcprCS511arGlrt71KUExIQYCIDNWFEkfJZ4E8p+YS2z2UwW19YHqgAaKtNKgmBV1VL9BIkDHtqW3gXQEcDIEKyC3sN8nikQmXVPk3eMEXBjjWXQ7wRijol5GX8yiEv/MJE7gHsPz87PGdUVXd9hCsPRcin5K7GDp3w9VmozyR2rDFXaICah7SF24fVY8EOyQkJK/Cbnc8nSlYN4sX7ItTE6IqOJqDhoGaGMFXoFKko/CNhNTNAlnpjhQhnUgEMsWxgYAqPzPpQkDgPxYXNisl2IUR6CJUUroLV9F8fEAbPVB6Zx5QqGMRy47vU5MvDMzR+tZ/p+tsCYrMLVHeEVgF+0Nhk4PT2lLEu6tqUfBm5ubui6gfFkQlHV7HYN3gijGvqB7WbFaDTi7PSEwsLN9SVXF+e0XSu4z3tcqGYULWRGK20QvIwe33esbq/ZrFccHR1zfHrK2dkxN1ewGRpsUcUOxt4b+r7l/OKcl198iaPlgovLS8aB+WAMq9lMLE4KMnPKOQC82Us16xgDrjHMZPWOfaS9IYT/5Jb4uOwq9L0N1U0so1EVOkB7eucowuWD8wy9MH4P0t/GS6iVB4klhiAYfPQmOOeCsuDjtW4Y+PD9D4m1vTOjRuwITxqvC3tkjM34CXEmeaijClBdRFU+ok6FiSUwfQD8egRTz5JD3iKNHQ3aK0EhluYXHFpziRXWUpnhtJcR5IWfeUWpyEiDV0r3Kd4+rMfw+Fv49VOGd36Detgz2BG+KMF7ymHPyBioK0noby4w7/5j/Dv/iK6cYl79KYrFQ8wLX5Ih6eTtIU9NuW7K85KCo2f/7ryzjcHdfkT/rV/HXL5DiRNvFwOYHkzPbFbz4kuP+OKXPs+rr77EbDbl9dde5dELD2mbHR988AHWVPJfIfxiNllydHTGfHYck0w1KXQfKss8Pz/n6uqco6M5f/2v/8tMJhPWmzVtI+HMz56f8/77H/DR44+4vLxkv5cuzt3Fczj/p9K3wBp6U+DsCPA4U1F85mdiknz54Icolg8DjynugNd0hjW8UPmBKr9agMB7B66j/+APcO//Lmb9hPmo4t/4N/5H/LVf+wW8t0xv/1P+9//FY9zZV4XDmwKtFpevufbAOTA0xTEl0E82uj+Ln+cgPP/sY7wou0+mNvwzny3nzeEpcvYv2MG6cCY1PE08NZ9Ia0JlqReGJz3vzrPJppQMOPkU7oZmZiA8L2OHVGC7ub3maHkkZWSdZ7fb0nUdVVkym0hu1mQ6pev6aATuul6a0jUSs1/XtVjWQ6NYreg0DOH8eE/bSG6glJ4Xw/GoHtGFIhC98ywWS+lu3Q+sVyuKouTo5B7eezbbDWVZsF5d43wflVSTrHnCO4MskSUM+xUL3WSy90aM2ovFAmstbbuL4aOFqXDDQBPw4ma1zfImsrV2gkukr0jJMPQYTwyXHI1GLBcLmkZCuTVcqm3bUEq3wrUB7RgT8XGLGLBUoei6LhoXFCND6mmh2LXve8qqxIY8Co80QpzVNWVRMJ1JysCLL77EZDKm76S08TAMvPrqq9wP4dvaVb6qKlGkjPQnKsuSJiSc/6DXp1Y0rBVmMgw9ock3GGL8Wde1knAdXHdSRUmrkCQLiS6YMSbWBc4z3YFYwUUTYhKokEMRaxJnnbydAe/kHqm018DtzW1qdR8IJ0e2Lng+rDE0+y1FUYXEtFAez4XEwqA4qWVcLg+WFe3+KbtJ/ouOUd/ygpbl7yBIrq9vGIYe76SGfF1VmELLpJpYci+NO1nlA2WhLk5IioiJj3EByKiSISEkQU0U622IqzJ4NKgliM88j/ngpXHm3hOr1kR5ZA4VjbgiUfibCLxcZk113lNYjcr2QZgpSDCBaZtYXhgIZWthMBJzLfQTmmd1nTRPNGG83qXQlTg+czC+qGCoguZ1DMlbFT1UBwI4WVFTKW8fk0b9kNd3DyEDYVO8gclozGQ8whYF69uVWD43G6p6hC1LqnrM2cMZ++2WopSwi8l4xL3Te+AGnj19yvrmWqzyQdnKAVLqiBxCagKd2KLAmkBrw8DlxTnb3ZaHL7zAvZMjygJWtxuqsgpnxuH9QLtvuby64uz0HnVdcXl5wcOHL9A0Laf3TtlutmGJc1HtI3XFPQ4MPwEKnymlJuylj1eLENFwmfSez56gCNdH3iThWI3PaDCAAAj7HYwJakDJ9cK4w9lz8oR2vaVGKMdeHeHcgWeI+qw/oLVYvUdpLYC1w0GkwcTzHXlm8momr1UA+ZHOdS2JCoYxSCtjlxQC2QITk1pjkrIQkPDEbg/9HnxP/71/hO/3d8aY9lvp22Bgd4m//iDyq3DL0KwrJEf6QSqhhcTGqvB4L5WrTF3JCbQGr/w/E6ruvX8kBqx/GvZCm4NNT7HLR4H3Eedkzz6L21zgt9Ld1lqLXb5I8eKP0L//dfzmOeq1LD7z5zDlmP47v469fAszSFWee/fmvPziPZzrWB5NqUeWn/v5n+T4ZEFdF4wnpSj0/ornzy/FqMYFL734Os5b1utVEOZbPNdYW4Efga+wBsrCMZmUtI3n/tkJs/mc6Xwe5aJ0MhYQIyHJlq5ro1wdBsf5+XPWa+lsvNmsuby8YrfbcXNzzR/90Td5+u4/CFEAPf6tv8veQbE4wxy9At5BOaZ88xcwtjwA5sOz7zKcvxWBbi5nTLfBX7yN9QPjqubswRl/7a//NX71134F5xz1aMR//6/9Gu9979/hb/7G/xn7pb+CmR5noV0hnEsjbhRMK31ldJ6HsuW85ZP4uZ6/GDqnRHjnpbwlKsqf6tnhqAXDqzWhL5Y1cW3Uk+EDDzPWElNdwu01TzN/cHp2yvFS3JIf+TQ+H89yXAM1emiORCi/qzjGANvthqosmc5mTKZjjBEPrTZbNs7S7hv84EP/jFJyvvqBvu/AGPrtFu83gQt46UnsjRh0UWOIpQjz2qxWUp3OObwzYAsWyyOmsxlDUDK8MSyPjijLms1qJYVMuj27/S6sjc2MI7KneVGeqIx90n6HP621vPHmm+x2O8bjiqbdg1ODTQoTKssC5wbq0QhybFpAB2IkL130AgyDdEYfhoHtak039DQhlwNE4VBMXFAITvBekspDDkdVlpHfleF3LT+rHpLlcsmDhw9ZLOY8ePCQ8XjMg4cPoEj9MUDCsKqqis4BTRTXUrXGmFiVSksVjEfiDBA7kadzA26AavRfc+iU88EbYdS7AWVpsbYM7h9xGVvNend9tJTl3ooYKx2EjbqQdLE0n0Mlt89++qClukE6I/aPv4l54378TmEkkfbpk2c8ffoUkLKKOKkm40OtZj20xhqsTW6sru2woxA24VPSUCwnqNVDfC7Ag+U1U16EMWi1JHlDwGemQSsYR5Itr69XbNc7bGEkvtta6UZrLIWxmKDEaagZhAqDUYGQtdQkJPk9xYhjCNVsbFQGlHAFPMub6tGJMeueGLaUjC+BURtRvpTBhjtkypC+RxyDgh4NY4uNyTKYqAxY1szEMpwmACcFG8l1r3HwBEWzYeg9bdex2+9iVYY0v1SzXGhO/w5CgBQXrAOPwiRYn21082f7GZI+FXSqwNQIaAHT6OLL/JwLvS4cxyfHVPWIvmsZnGO9WmFMQVnVlFVNXY+YLZYslktW4bOzs3u4vufJk4/YbdYYHxqPQejaKtV2RvUIUyT6xcuZ6NqWtmkBhy3KQHuGZrfjo/c/4IVHL7A8OsINsFnvqMuKupZO97boub25YTaXMMpnz59zr2sZTUb0fcdsNmOz2aDhuUJimVg2RhJDdY19sEB54n5rErfGOHtibQY0NC42xNFX3BqlaRFgTaOqdfBAKog2SZHFZLSsPCDSmVhv9c9UnUi/op43H7+v4Mco/ereeycJvrubqBDkMJ16ihkt8KunDJvnuA++Lh/WC8o3fg739I/xV+9GHmMffFHCh4Dhg9/Hr59ij17BvvDDaVl217j3fgtTlNjXfg5TjuT7j/8Qd/2hGHZO38Q++EJ4/4/w1+/H683Ri/ibj/DbC2zfSG5LZkzQ+u7K3/MqKyb4Xf0o8TFjDNU4NKkK3YVVCNZ1zf2TeyzmC4rgxZaqNKVUv5nPODm9x3g8pu97nj59yvvvv8/V1TXf+daf8Pzpc0xZSK37/SVu+1xox6Ta9d07vx35qSq6zvwBw7d/nRigEnhZ//7vh/Pt8GagrOC111/hf/qv/w/54hc+w0cffcDR8Yx+aLi8esb777/De++9w2Rc8/rrr1NaQ9PsWMxnVEXJdDxicAWl9azWN9xcrzk5foGhGTBGupYfH58wHk/BeU6OF5RFhStKrFZpDGuvVWa6fggKRhXHbYuChw/PIrgahp7pZBqVvXe+/w7f/OYf8+6773J+fs7t7S27/Y7FfMFbb73N5eWVlMZ8/Luhgl0V8o8KxvWI8VhAyngsoTPHx0sm0wllUXLv9KdYLBa8+OKLfOlLX+LRo0dsN7dcrVcYY+jagV/9tV/hD7/xv+Tt3/zfMLz6c3D/h2D+Qsh19DgbcjdiT4/EjWV78oOvPEK/9Wfzc+LJJH03/pvxllx+f5pnh1A0gxfjXVFghkG8GVHuEM+Fj+qvSYIyr65FVknsY89Wg4X+HvBFUEB0HIdyLPfmE6uvJVL3rNYrirKkrkdMJlOMLULeXRuV12EYKPuKrpCKRZvtBmMtR8slR0dHInOHAecHqtJSFELTu10jXjwsbuhZr1f0/cBoVEtX8LJiPj+iHk/o+oHb2xu8cyyXR4wnU7a7Pf3QYs3AzfqWUFcqDN6QKiG4aFyMOEb3O/BaY7KKloFfTScTJpMJRQGeWkLvG0/fDXgnpX6lHCysbteSB2pSSdp909CGpn6x90R4XgxRqio8oiDUdc1iITnI8/mc5eKI/W7Pze0N1hYcHR3x2muv8vLLr0R6mc/nuEFCpQY3UJUV48k4epO6VnIs6roGY7i5vUHLRo9GYwnXBy4vryirku1uS1mWzOYz2rZjv98xnkwYdltOTu7RNHuKUvIVbVnEqoyT6eTOGfizX59a0YDkuhkGacleFIlAJ5NxlvSibvMUa3ZXmQBiXJm6gWK94Kipp/rD8T5eNOnCWobLdyhe9yFCy2ALKx0qXR81RONDaJH3aBdX7QqLI94LxAK2byThx2tTHeQexgrAGEKH7+R2M+H/8nuex6DMzWYoPXb3JLveCzNs+wE6jzGhOUvGESITyQwqiTFmVlZ9z/sU9xwBVRqcAP2Ij9L1QQGK+Q6fQEexAk/UWJQ1680OLfdRAbPJIxEBSVAarDWZIiXauiTTZqFRKEOQRj+xIyr6mVjsm76jtAXb9Yab1SqGuahlQmixTKVKdXwRQZIx5zClIBjUQh2TXHV/PIfCzCemH7UPk4sKDeWS8nllVTGfLyiLktXqlq7r2O521IEx1HXNeDrDWst619I7zwuPzvDO8ezpE3YrqfTU9a1YhCtpQtcPUkXIY6jHI2EWRpPSDOOywhQSqkUIZ5RrDa7vefrRY1545SWOjo9p24Gu6UL30T3WFHRDy+31DfcfPGAynnB5ccGDhw+xhWW+WLBerwOoydYyJ6yDdU7rE/UxUvihkY3BhPi/mJekdJg0YXlGSGIjGC+stcEzYg/228e98fEgqPKZIpjzZFMdYyb+g8IRlQwdy51iAX6/ov/O38U9/Ta0a0ww4FirYSq6RgZvC2ww6hT5vC7/JDZNjfxj9QTekj+LwK/s5hn+w98lHXSk34YH/4f/tzisMhhxvPf41WP8O/9YxuT9QSlFt/oobplUKTUxob4sS6qqpKprlosFb7zxBuPxhLquWS6mHC/m3LsnuUe73Z6+75lOJ8yOFpzcO6Gqyigndrsdxlh+7CtfFYW4FwE9uCEqM5QFRVliraELgs8YS9u2/PE3/oRvf+vbvP329/n+99/m5uaG/X7Pbr+X6taBxxSF5onJnFR+pYZbElYmBXAKqsJiCyhKw0/+1I/zr/6r/wpnp0vef/8dPvjgPc6293jppUdYLD/9U3+ezUo86edPb/mZn/5J8J4P3nuP7bal2Rim0znPL87F8mlq3vnee8znZ7z40osY43nvnbepR2P2u5Znz855443PMju5x9HJKVVVst1uAZhOZxI2YS1VXR0oe9rTxSOdmV2I1e6HgfPnz3jw4D6/8As/S9N8jcvLS1arFZ//whcYj0Y8ffqM9997DEgvgdlsxunpKXU9Yhg6ZrMJk6n03DEgSbHhrG23W4bBUViLLQouLp6xXt8wHo25vLhkvV6zur3F4fjpn/4JLn/9P+X6e3+X7rt/j66aY9/8JcpXvhbKkB5WatO5HXjw4inNeEtuJrjLW7hjRLjzyuW3nm/zg55tQmU3DRE3JtKQ8EAJBfHthuHxN/C2YDj7EtgyndH4U6oLBYIMvEXKt8ZnRyPhXZ4auFUQ7nHeUQyZSPe5eqWhk94NXF1fc3pyGjp9VzASS/4+FPqQ0PfQFbyusE2BGiybpolyvSoL7p+d4h1sdzu26y1dDDntscaKkjE46vGI6WKJrUTJ2KxWACwWS6bTKbt9Q9M01BZubm6QSm26YCEJnhD2aoysm/e6mR/b72gUDZaruq5pmobNk1uKArq+pdt30JlUbCPg0aIoQm7dQBHCiI6Pj7FZKFFZlnzmM59hvlhEL9F4NKKoK4yV/JNXX32Vl19+mdFIylWPxhNGk0nAwYKdJEypYhj60ARa8iy89+x3e2k6WxRS9MM72mZP13bSvHcyYTqbxRSEfbOnHEQhmc1ndH3PZDqlKAppvjj0XN/cYKxlMp2iJuDdfkfXddGQPQwDbLeMx+NPPD93X59a0ZCwKEPXycYWWp42k2LG2FC/t4xJac5JILQQ+RBLm4lgMEHLM3gvgkI6rg4UpogxZ5pILl00tY4wuO05pdd0awG/VVVA5xk6CZWSMrohFMKaLC5RFCGPl06WxmA9sol9iy2lZ4hBPAFYKY3bh/JtMl9zh01lykBASdFGot81YIxabvWzMJyoE9y9a/CaBK1csLuNa+YiwNIcjmA9HHJABl6tiqJfHzI35Hs5eAd/wNTIiD+ytgNLk/52+Fe4eXp2eI6Sj0GAkRYJOAz/CGqUVzAgFvfcEmmsAkcfcmhkDm3bMR6PqetKavgH+pKPfWJCGUBNw03jUAUnB6M+W3NVikWxlVLGB0g5WFeSsJK7aoI8hWU+n1OUVWha5lhv1phCGHVVWCbjMaNRSdN17HZ7zk5PqYuSy+fP2K6vwXj6rqOsaiYhaa0LDc084IY+xGxKwYEilMgTINeDk9rafWiSVpUVxkDfdzx/8pgXX3qF45Mjnj19xuA8280aP/SMpxM2my1HTct8tuD8/JxhkKT2tuso64q+6yJtpqUXBSyuh1qe8niFcD5MaKQHCu6VbH121mz8W7+XQEkhsroIYtdnYQxhmzRUy+QHAkj5RySlOZ7KDMpktGI9uHj/IMDbDe75d+i+/bcp2lVSRIOMTOfXhchKh6XHGy+5MQEkWCzWFFhT4RwUxmPLHEKJN1J64AwxP6UopTNzUZRYW9B1jqF3sdGTJ3TPNsR+HhhiGUODhgkK6C/KgjLQ7Q998Yv8/M//eV57/VXG4zHLYNU0wbAiHdZTKEFVVZH3365uefL0KU+ePGYZLHvj0Yij42Oubm+oq5rBOfa7HX0f+iFZ8dJ1fRe9a23bsdlscM5x/+E9PveFfzHGM2+3Wy4uLvj+97/PBx9+wNOnT1mtVqzXG25vb2mbRvLkMNHquFxKfHiz3+P6jpdfeMBP/fRPcnw8o6otX/rS59nuVuzWl9TjkpN7J+Dh+dNzTu895MN3nvAzP/mLEXh99Piavm155eXP84ff+Aa3m4Z6DJeXG4qi4OHDRzx6NAdn6T1cXt0wqqccHZ9g7ZoHL5RMZlOqeoItarw3LJYnodpNiXMDZSlJp9vtlnEtFXM+eOc9dgEQNE1DXddhzi0PX3jIbrXm8ePH3N6uqOua7WbD3/i//gccHR3x1a/8CO987y1eeulFjs7OGFcV29WKYi4hW5fPn/Lhhx9y//59Pve5z/HsyZMYjtE0Lb/3e1/n7OyM77/9fY6Oj9hsNqxXG46PT0jNyuB4ccx/+7/5l/l//r/+Dqv1Drtf0f3h36C9eo/6R34Nq3LxwPiVZIPJeQs5b86Obm4oiK+7Zz0/0R+X3z/o2SqfY7U8fQ3iBccY3OM/ZPjDv0FlHU0/wE//W9ijl+Kz5dhJZMiDB2es1luRXXGIia/piK1yrcBTZZyqQtxRiOKwQggxJjZfNNls/DBwdXXJcrmkD32CikLyM/qupeukQXEfQggnYzE0e+eCxV+iPMajmv2+o2lbbq+vado+ltx2HgbvKEoxRownU7yx7Js9282WoiiZL46oRyP2zZ622VMaz+3NFUPfh/3OwFO219qRnEg2JoYNJ1miRkwHz76Br+Gjxx/g/RCMJwWud5RBiSnLkslozHQy5eTkhG7oWRwtQ8J6xS/+4i9ye3vLe++9x3K55N69e9JzykvJ2PF4LLilKCRPA8Gyq82WTWgJsVweUa5WtF2H957pdEpZFDRtS9+1eKQqVt91YkD0DmOt9MPquliUyYwMfdfFSlKqHCwWi4/leGg/jNFohLWWhw8fSu+u0J28C/fJGwhqjw7ND/lBr0+taBhjJQaPZPnJH5LHgGnCZApLIb4fLWfZQdRzoDXaowUteDw0ETyoKFKJBU+xv8LvbzDjk3hdWRQMQZkoygqDpff9wbmPBxAJ73HeUdgyWl801KYfJF54cEEQO83uJ5TkA/1HYbVYqT34LOkycCIfJhuH8jGref65j/c9sKQatWAIgPJ46BuGmw8x0xPs9F485D5TeAQ1qBbv073yQRoTr0mFkSSRK9Vm14ZUJo05A3XyZ6Y8mTSTGBIXn5OzeYMb8sRWogfCDy41DDSpAEG8gVEVRplsUIqQ7sHKXIx1Qb8UZWRQoGdUiXNxXkZrAeseqyU4m7OFkAwp1qfobj8oF5bc43lcerxxmMNsPqcoS3ZbyWto9w1VIeDw5uaG3nkmsxlNs6eua+azGZvNistLaZDXdwPVaMxsMsNYw26/D3GgWpBBrDJlWUpOTCjBJ6VRO7yRetzT6VSAV9dRj2psYdnvd1xcnHP24BGz+UyqWQ09ru8Y+SlugNvVmvtn9ynKktVqzfHxEVW1YzabcXN9k4lw/cUk2tF1OKDzfKG0AIBWfQrNJCMCJpZNxkjvm7IUS9lsNme3bbm5vc2URxsLJuh5ihWU1DNhTKy4o7HQGZKJY80bESbRHhpVGYvbXtF99+9jP/o6pesZUeK9eOTUs1RQ4IbguQkJhap7SC7aQFmZ4GKfMRlNqAoJazg+mgclVSrmFUXJfD6nrivqkRhkxpMx89mcyUQqmo1GYy7Ob3jnnXd55913+P73v8/jjz7i6uqatmvpfBBgGAnlLCSZuiwLykp47Kuvvsaf+8k/x0/95E/y4osvUtUVu/0uehyc66Nr3zkXmm5NojHBWstoPGJ5tOSVV17Be89ut6NtW25vxaP3+MkTbm5uAUKCaRWNT5KwmeciDIxGIwmlGjouLp9TVRWXl5eMx2M+8+rLvPnZ19H4YyBeqwJaS1E659hut1GQDm2L73d85pWX6IeW7XbNP/j7/4Cf/4WfZ/A9tzdbTk8f8tqrr/LO29/H9QXXlxvun73E9e0t1lq+8PkfZjQe8we/9/t89PiCz30e9p3jM69/jtlsgXcwny+YTed4U3JyumY+n7PZbJnOTwCx7BajKUUpOYpuEKOXeO8tXStVZapQNfHi+TmX5+dcX12zWq1o25Yf/dEfpWta3DDQhv48x8tj5tM54/GYi4sL3q3e4+njp/yDp3+fb37zjzk5OeGll17i/fff5+zsTPJBCsvZ2SkPHz7k/Nlzmt2etm358MMPMcbwsz/7s5wcHfP86TNee/VVrq6umIzG3Fzd0HdiALq9uWGxWNDs99w/u8/XfvzH+C9/4zfFg2Frmvd+m9YY6q/8ai5BDnlqkkbp9c+SofGspiuz0xz+TZ/mfOsHPVtExMefrTIU59m+87v0t5eYsqZ6/WcZL16IeEd5XP/Of8lrj+6xOP7vMJnOeO/9PX2XJXIoRgrP0fy1aOTMPf3RaHcwSMgNhLmmpN5eI7l4Nzc3zENOUNd3WFtQ1yOqSrpfd8HSL5cM0fCnCdBd17HZ7mLIlUasYCxlXTMfjxmNQxGhXkrINn3HuB4zm6cmfUPXYLxjvbph6Ls7eqQaGl0mn++8TFoPgQxq6PXQ7Tk7mfHaKy8xHo+Zz+e8/vrrPHr0iOurK44XS2bTWTQ+1KEU7YCnHo/Y7/c45zg5OWEym7I8PqKu6wjM66qmHks+sveesqyYTGdoXoQxhu12S9NITqb24jDGcH11xXg8ZhfCm8Bz/vx5zLE4OTlhVJYMuBBp0MbrVRnQKlRlCH9SY4pGDFlrWa/XUl63aSIP3+/3EiJXiry6vb2N95hMJvH+n+b1qRUNnXjf95EZl2UZk8FV41VBon+rYICkjOhEdMKqVGi4k82s1bpAql2BLNx8PuPi+QXmt/5d+hf+OcyDL1GcfkYUkxBCFZOMncY8ZtgUk6o5OYdhwFaWyUhKJPa9WHYJMfQexxCIe7h4i/6b/wnl5/4C5Ys/EoC/ATfgnn0b++CLKXGOxL4MAZiE0yAJarnFNDGGQ/tLuEPkeB5217Tf+Tv4i7corOP+yZyXP/M6zz5c8fjxYwGZTmI8WTyi+tK/iJk9gDD32BgtjkOfqMArjD4HgIS4eQ1JORi3fp4rKWne8tTgOg5zUMUr8kLnpPOu1ytD+IrJlS15mOC9sH5hU73+LzpdPL1r0fCkopDa9TYAOFGgPp6LcRcAHwqiUIYxU0TinqXbJG53sN933g+7XBQlVVmLctv1NPtGuo7WNU3bstvv2e9b5ssj2rbl7OwBbmi5ujgPxQwcRVkyncyoRiOaZkffttjCCoA1BmMKEQC2kHrfiIWmbRr2bQOBIblhYDKZsNlu49kzWG5vVyyWxyzmc3brW6aTKZvNOlrR1us1R0fHjEYj1qsVJ/eOKQupVHJ9fYMq9XHemWcnkXhQQk2iuEgneFyoooaXNTXWY4yXsI5JxdH+XY7mY6bTKdPZBFMVXI/u8yfffVeEm7ZnQTxzHkL4jI/7HVs7EKz51kTZnJ+RPA4810e9IfIaf/OY7jf/d5TtFYsJjKoReGG5ZVEKCB8MbdcxPTaYYs/Q+wCoRTmoqhGT+RG/9i//NXHDzxbMFwuED1omozHWmGiMef78OavViqqq6PqWqqqYTqcSdxyMNV3X8cKLj/jRH/+KCJe25fmzZzx+8oRvf/vb3KxuqUejKFBO792jKEsmkzHTqcTinxwfM5lOQ4Kk7O10Oo38ve/7GIbXdV08J03TRFAPKW5ZrW5qQWuahn5wMVFRjVOxoiHE0up6Dym5WWKNj4L++Pg4Xn9+fs7V1RXb7ZazszPm83mMjx6NRvF++n01cm03K5rdivl8DsDNzRVH996jGype+cwbvPyZzzMdTyiKguV8g/Gen/jaz9F2LR9+eM7nv/B5LAXT8ZIf+7E/x3rV8OabX+bBg4ehN4qhKutgoPNsdztO779AUZTcrHZ897tv0bYtP/G1n6AuBrp2h3MiXwkgZb1esW92bDYbTo6PeXB2hut7Tu+d8vDBQ87OzmJomsrTs7OzkIhO7Cj88iuv8OUf/mE26zW/93u/x9HRMc+ePef+/TPeeON1iqLk9ddf5+tf/x2WyyVvvPEGb731FldXV8xmM15//XWstdzc3MTSl5vNhr7vubm5oSwLPvroQ0AU64uLC6qq4qOPPmI6rXnj9Zd45733cXvHqC5p3/ttGgf1V/9KOmMEz6PyVJLhTHkq8XuRkaBKRWItKriCapHJsciS4k////ezc1Y3+qG/xOgLv5wZU8SY559/m5dXX+fHv/g1Lp//l1w+/HkWsxm3N7cMXhWBT5IlSdEQdpZXVrIH806jiya9oGck5qfL4JxjdXvLeDplVI9om5Y2GA6qqg4J0Y5+cCG8yOEHRx94qrcWzxAiEUrKwlLXY6qqxNgSawz94Gh3DW3XUZQli+WSUT1i6HuardC67zvWq5vQLsFLny+r80trrj2HQv3zQ958x9Olv7kn3+Bf+av/Ml/+8pcwxoQcDcGyQ9+zXq05OztjPB6z3+9Zr9d0+47ZfMbt7S3T6fQguVp5lLWW8Xgs4cPAZDIJvTMEC+/3e54/fx6Sz8cxdEsxtXr9pCyuTcWWEPzSdR23t7fs93vqUF54Op1GB4C8L9fr7845rq+vGY/HaIL7brejqqpoaFHcbq14rLfbbcyf08qysQrsp3z9V8rRKIqCpmmYzWaZddYclNUibGhRSAxtXtJWNSsXiYEoPJI3xDF4R1WYuNDaTr1pG5yH1XpFVZWMJzVV6dl/+E/Yf+8/hwdvUv7c/4ChPJLkdVtIFSIUnIaKWH7At2u8LbHVUoCYNTGWfzQagQmN+aK1XKykxhja934bs36C+97fhxd/JDEUI5py7k5NgETrlOsBFMbm+5Zh/ZT+27+OGc2pv/xXoJ4JwHUOWnGbehzeDbj3fhP/+I8Yuw1vvvoKn//az/HZz73Jw0cvCKEG4n3nnXf4+td/j+dPz+lu3mL4jf+t1FY/+zx2/oDitZ+VZ3gfOeqBJcdYbD2TuSjSCgfVmYwpq4fFS9hHaNgd1kNQl37POxctwGJUUa9QeM/4kNOgMcZ6D60mYQ5yJ2IiXTY2Bazep2fLvTwem3JBrMU6l93PxxVIooWD+eieinU7ajcyboLdPbq079jQrM0ah0V7EwBVXTK4npvbGwiuTIOlsJIDYUCUhr6ntIbpZMR6dcN2s0Ks/J7JRJotgafZN5gQ+2qNKLeFtRydnLBcLqVqmxGL6Gaz5umTJxKXaaQCVVXXjPpBksCKAmsLeue4vLjg0YsvMZ/PcEPPZDqhbTvoOvq+o+taqqoOzf46yX+qquDNt3F179oIc/U/Gkg0DCAqwUEG2gJJkvSY9pbX3bf5y197gcVixEsvHOM9NM2OYViz273P/+W/+Ads7NcwtoxPTO723PqYDynQkjUHo1Oay3M61DqnLxdG2n3zb2Pe+UeMzYYvfvGEv/5Xf5HZ3OO8VPYYjUbRg3txccHyZEnb91xf3eIGy9HyFO8KXn31sxzf+wovvfwVdts9RTXCFOJpcH6gd63k9Wy2PH/+DO/h3r174uafTEKxi+BNDus/Kgq8d6G0pKEfGu6dnfDg0X1+6Iufp6wlIXu9XnNzc8N4PKYoSppmH3mg957r60um0ymjkVg4q3oUG0BNJpIoeH19zfn5OV3bZuEyJhqR1IVfVRXj8TjLj3Chs/0kGJbmHB0dRQCw3W756KOPGIZgBW0aVqsVx8dH1HWF154m+31UHl588UUePXoUcwUVXKv3XRp1Eb0j+irrmtniYWxq9cLLr/Mrv/qKKEVtS12KN7wsSqwRhc71JUM/8NZb7/PFL/4IJycneOf43ne/zfvvPWG7aanrGbt9w/nzC3a7PYu5xKL3g+E/+0//DsYYfuInfoLxdM5v/fb/h8lsId7HYMm8uLjg+fPnfO5znwuKmcRh79YbSgyLxZJtsFRqQ93tdsv9+/e5vr6mbdvYD+Htt98WRWm5pO97PvjgA958802897z++mvUdc3v//7vs1gs8L7nL/7FX+K9997ld373t8F7ble3nJ2eSQJsUfDhBx+w2Wwoy5LFYsFmu2W33YoBr+uDlXbPaDSibUPcf9vx0ksPOD5e8u3v/Cmr9V6aTr7zG2yffpPJz/6bmOm9wB5y0GgiOE4QOufDh6f8riyJ5zsqAjmXUG6dc/MsdyMzTvyznq0vCdO21G/8eeEbrsd1W8AxvP+7fN5+ny/92I9ggfubP6b9/X/K6ydf5FvdMc4ZqOdScS3TBg5EWLJ+yQiix5YoI2N1P4jGMc2tMRQH8lt/32639FUXc3KkiqeLoYxlUDqipyXgCmdsBMlaudF7wTZt19MGr6IqGHUlSePNfsfQ9Rg8bbNlv10HL6uPmEPHqDgg/ZuiHlQpDJpYVMaS7me4Z9f85E/+t6JhRb2cqiTM5nOmsxl1XbHb78EYprMZVVWxPDqK4Lzv+wj81eK/2+2iJ2Oz2QR+dIxzwvNOTk44OjqKzfsU2KtHVXmUeHQLbm5uYgK5enjHoQQwSO6KGP2OIvbuOinMUoTEfUhKD3DgIMg7m5+fn0e+sVqtYulfxeySZzfl07yM/5S+j7/5//gbB0pC3mRPm4Fovwy9ZXLvJYuJJtSoW1rf1/uAKON1Vcf7qIa1bxrJsq9rtpstV5dX+MHxO7/zu3znW99mcI4f/uqP8PRqw3vnO0BcQ03T4lyPMYSwqAFz+yFFWTF94XPMFscML/0UfrykPH4JawvaVuLYEijRFYP+5jHNH/869Zd/BTM5Itk1M4t4xpf8foXfnGPKGhaPwA+4x9+gf/c38evn0G4whEoR1Rymp3K/bo8NJRaNGZjNx7zy8kt89atf5bOf/Synp6chCVCe13V9IASpgLDd7tiu9zx98oz333ufy6tLsS51Pdc3t7R9S9+Kl6nt2lBpKpRr8yUcvRxK3Qqj1TAc78EePaJ46cc/TiijKXbxEDX25OsgnqMshMpKT5LEM02oMKLsOliOIPX5COEzsWqVKkYxYS5u08FLwuOK2BG6qir6rmez28Zn6MaJUmLi+LVhoIRKHTaXFL4nHoP4VnakTFiIVFY5jC4KBcN8uWCxWNL1A3VV8vz8AuORjt31iM4NLBcLvDeMJxOWywUfPf6Im6srXC+1rxdL6Z6626zZ7jaxq7UtJInzhYcPGU3HMfQozRdcP/DRhx/w/Pkz6noUFG3poG2soS4rnBdf1CuvvAIYnj55LGGKfc9uv6NpWs5OT1ksl1ycn3P/4X0mkxE3V9d89NFHdF37sV3RsUSlLZrTcntbEB9JH8YMDeX3/ja/8uP3+YU//+PMpjWOlsENUmax69G+FN/903f4X//7/xD71X+FcvEwViuT+WvtzEMFM1kJEpjxkTbS55G8s+8P1x/S/vHfobr6Exb1hl/+Cz/MX/4Xv8Ji3uBcg/Oh8lvwKGq1ktY5nl9eslrtOV6esdv19B2cHN9nNHmTH/mxv0jfWbrBMJ5NmS2meOOoixrjJYzo6uqKsiw5OTkBNJ/JxjCjvLiGnmUF3Zos+OTJE66vrynLkrOzs+DqL6MBxhgpx6hJ2+fn57z00kuAAIn33nuP09NTTk5Oovv9W9/6FsvFIjaBUjmg50TDou52mb2+uaUsxVJ4//59FotFlBXah0n/VqHrQ9U1PaIHyeyhIIlWg1Evfa745J4TsfZ7uq5lt9/FsTrnqatawBMGP0jFwqoscf3A//vv/h3undxj3+yZzCZsNhsePXrEzc0Nf/AHf8BsNuMv/NJfYDKbsd3sKIqS7WbHd77zJ7z2+utMpxMGP/D973+f7XbLbDaTPgX7PW7omc2mkW4WiwWPHz+WCnKB/z+8/4AXHj7kM6+8wtD3fPjhh+KRmk7ZbDY8fPiQl156iaurK9577z1eeOER2+2Wqqp49913o2dqOp0yn8/43d/9Xay1XF5e8mM/9mN473ny5DGPnzxmu93EzxSIlGUZznzHvXv3oswXgOoYjcbc3NzEZwzDQF1XWCvl87e7hq53/On3vs/jp88ZBs++bXGjBaOf/Z9hpvc+FrLxiUnh0dqdTGjJAKi8JZzvTH7n97grR/S7MSXA8LFv/bOe7dZP2f/x36V64Yt03/8NXLfHrz6gKgyfe/MNfuxHv4oxUk60axr6ruNoecy3v/s9fut3fo/+6DXGX/vXsNMz7bF4MNBUMEZxSyhpHsaEIfZT4mBFwvV5oRefK02g4ZST8ZiiLITejBWlq0jhoDbmiQC2SDIacL1GNIAprIRhhXAcoelGmisDQ9+x3a4Yug5N8g6TxGi4c9gIUV60BYKPBiqRJaoGJqOQd5IHU/dr/qWzt/grv/KXYnixGs7btuU48NK2a2OS+3gylvNSViwXC7bbLaPRiNtbCfPUfChVAhS8a66D98KPNJFavSHKE1UBmISkcO3WbYyPfG86nXJ7eyv5Gn3PMPhovMqNNfP5nGWoUtk0EiqpnpY8wmg0GsVcDVU4YtPAwC9z77TKlLqu+aV/4b/xCafk8PWpFY3/+P/+H2KM4ejoCO8lblzdO+qqUe1JXSoxHjxTTPS7uqjqKoeU8yHt14sYD6avuq45OjnmydOn4FOSZNe27DYb3nnnAz7z6uv8vb/3n/E7v/O7DIPDDbJo2tn5rvJSVRUvPniBv/Krv8r16pZ/8Jvf4Ob0R+nvfyVa5BWGOK8l6VIHyCjRfBY3mVtbnKP9L/5Xkk+CgS/8Jey91xl+898N2CQbU9bnAAOFLTg9PeXll1/my1/+PJ957SVm0ykYCb3wBOu6lTwSJbDBOVmTfUO36zk6OolWLS05qYmTt7e3XF5eRlAgVruO3WrPKsTkXVxchnjolvV6EwWzErMeDu8dAzDUs0gPEbs9+iosH8GDLzN4sbD3gXEVxkZelwzaWnlMEhy9IXQbTR3bY/8Vq0mnCTbGVwbosYaqCNVxRiP6rme9Xh/sARmPjNtoJFTHWpvCerwq0j50pS8ju/YBGMt9fFCARLkSK1IQBuFLpw/uMxqN6YaBwhY8e/qMqqqYTWfMlnOOT05x3vH8+XMePXwB7zzvvPMOfd8ydB2zxZyiqGi7jrbZS2J9IcBrvjzi0YsvUpXSPGkIwAwX8h2C0met5emTJ1xeXlCWUrFqHxjTuB5JwlnfcXrvlHunp3z05DE+JJPvdzuaVjydZ2diLZ3NJpzdP+X65oaL5+dcX13FM6EpQgfHJ665eP8khNbH9cR7AccGZu/+Hf7tX/sar73yCFzLqC7YNTu6vsdguby8Cg2TPH3v+T/8n/5D/vTdx1Q/9C8w/vxfjFY+4JBucho4ABKEhp3JOpiHB3rncNfv0/3x38Zfvk1lB144tfzVX/0aP/W1lyjMCkPD4MGWY1RxUia+2+1wdsL7H11RFDWjekbbDtxcr3nh4Ys0/Yzl0Wc4ufcyN7ctL33mVV585SUGesbFmLqsqeoqKhuT8SSCRWNM6DYuyZNVAPN9L17kZt+w2W744IMPeOmllykKy6iug7GljUJGz3mzbygrKUnbdx273Y6z+/dDqFYXw+3yXDtNEFXjUtd1MbRJBbsmiatwldKMUhUqhtSGcNs8xlh5hcoeqarm473zxEcBtHWUM6p4aDgXwHw+F6/Absd8Pk8e33B917VUdcn19SVVJeEj+62AkL7tuLq84g9+7/dYzOf86Vvfo2kbfuEXfpG2bXj27DlvvfUWn/3sm3zlqz/MRx99yH7f8OUvf4WhH9jvJZ+s7Tqub26YTae0Xcd6LaEbVVkGQ1DPZDJhu9uK1zMAkd1+z8nJPTarNevVildefpmj5RGvvf4av/v1r7PZblmtVvzET/wEL774Im+99RZf//rvcXR0BMDP/dzPRa/SZDJhtbplcBIC973vfY/j42OeP3vG1dUVz54/oygsw9DHsIymEWV2MplwenoaGpHtpYCKl0pUYsgYxxA2Da/a7XZMx2OKwtL1PePJFFuUfPd7f8o3/uhbbHYdbdfT2QnTf/5/jp2coEm/kaem43rwOlQuPv5ZIKIovw+qTd35XkyW1mv+f3h2f/0+67//72AQj8BkXPGlL36B1197jaqSnkYGz26zoSqEl48mc/7RP/ktvv/uR7gHX2TyM/8TMYAFg4XR82CSupRCULM8Mp+dG1QmmVQZ1hap4uTBNUmqxubFhVSkKoqSwRONJ1o4pbCWoqql5xMB11kJ4TXWSuEUHwwGfRd7aA1Dz269ou9a8A6LRB4Map+E0MwwyXsXiwJlZqNo18sybjK8ZnH8zOz7/Nv/vb/Ean1NURwaytu2pawlBD/PCfPe8+DBA66vriitYEgF5rPZTEKPNxs2m01oaCh8abPZ4L1nNJpED6qGNakRaLfbUZYl0+lUEsVXq8yAL97b0WgUQ6J2u13wniQPrCo6QCz+oFhX+aDyPi3QoR5kTQ5XXqnYSOWARh/t9/sYMvaLf/GXPoHyD1+fOnRKtZ/Ly0uAGMOlYE/jzFQb60Mtf9ln2Vy1PuW9HlTJ0ImLtjXh9OSU8/Pz+JmW/7q4uJBYYyfJn23bUljL62+8zpd/+Kv0vSQy3r9/n29981t88MGHWEtoNCiJgGp1UY2zKOHq8pz/8b/+r/Mv/co5/96/9+/z9771NzFf+MuYahw1e8GHjuHpt+nO36J87Wcw9RxjLX7Y47s9/Ye/T/HSPyeafLuj+/q/R7G7DAcLhu/8Op0psJ5oyVULgsdTVTVnZ2f88A9/mc999nOcnZ3x6NGj/y9zfxpzW3bm92G/teczn3e87x1qriKrODbJVrPZ7CbZ7FFqWbIGK4otJZHtJIiNIDCcT/kQIEA+JDYQBQZiIPAQG7AdJ2ooGluSJUYDm2QPbLLJJqvIYo331p3e8cx7XisfnrXW2e9b91YVu9tyNli8955hnz2svdbz/J//8//TmpLzixMr05j76xXHMXGaiCpDVYmsWV3RNg1n5+dUm4Zr166jgJnlzTaNlK7dwInjmOl06jPWoihoxy3x008Dksi5QX1yckJe5MSRXEeUorQJShiG9AaZaEIPBmR2wRmPR8RJyu7eHl/5zd/mH57e4vC5T2CM4eHxMUbXqNYa2IQxYdIjSRPhTSepT1zzzYZlp2kJbPIntuPe5VpADls5sYiTlFAlKVFBIKaIqG1TpbrcAGjspLRdIKyNoVOzUKozkXUWGVfN6z48HSTG+MlRFoIAtS192kDMKWNpBVGcEEYBdVkDhjiOWC3XNK2YT0a2YbxuZFFvm1Yk9MKAOEk4unaNOIoxytZ/xPrE84uVUphWfvfg2iFFkVNWFdrIJCXyeYbQCCKU5xtQe2S2FyOxEqOBUlSF9AVFYejpX4EKSNLEV4TceV92pXWXyaqzuHkD44303KqijSZtLpjPZ3x/fk6xWVHka2azOVXVsFysOD09pyhKdGsoqpqH8xWqLale/g3im58kHOzbyKHz236sbF/xqBh4lTTlj80eoTHo4x9QffO/IFaaOGl57qkh//pf+jzPPhkRmFOUNjR1iIpCGiPj3C3bq/VKwBAt8pHz2TnaXNDLBlR1zvHJO1y/+VFmsxN+5vNfZjy5TkuEVgajNIEJaGtNXbckSY/dXXGknc0XrFZOHlLK7Ov1muVyyWAw7CCIFUVRsr9/batQFcSEUURdNYSBIrVzhVIKRtJTBJIATKeyCIkw2LY3wlVKtNaURcH+7p5NgKU3xQX/nnZQNwKu2IqDo7E2bUvTtqRJwsbK3jZNI3TDtqUqKw8+BIE0RK+WC7Ru/XxW1zW9rMfaou9RFJHnuU84hsOhR/ySJOHevXukaUqe5+zu7qJQrOYroiggSWOMaSjKNffu3WUwHGKMkuNoWvL1mpOT+yTJTfJ8zXpT8O1vf4vxeMzFxQWjkVAYNuslk2GPvemY+fkxuzt73HjqFrdv3+H4/JTZYsHD+3dtFWhEVWw4XSxASVX+/PzMJl9ynYUG1WOz2rBarWibhvVyxU/9iT/Bg3v3Obx2jeVyyenpKb/xG7/BJz7xCV555RV6vR7PP/8cg8GQ4+OHGAPXrx/RthKgrDdLLi7OqeuK3/7tb1BVlaXkKam8NI1X3Tk9PfVIq6NdNk1DXdXWswnqWu7Xzs4UpcTcbDIZ40LxoqhI0oSmqTBNyQvPP8P+/pTf/db3uHfvmMCU5P/8/0Ly0T9LdOszl+ZoO0twaWLuPN9dSrNHkcyWovvu5xt/XOrSv9yHbMKhW0y96cJb8tliQfXmNwDd/Tna41fAtF7i9LM/9WnGwwF5vkG3EVmSEMUR0+mE2dk5bWiYLR4yHo2Ik5ji+IfUb36d5Jmf8UmCmz87k+cWJFUuykAmfxXaBOPqGifXxcE7bi52SYYDDlx/ptGasixQYUSW9kiS1IKP8sy2rQFVe8lliaM0bd34JNEYC5bqlrapWec5TVMTGo2YC9i7agACjJ2HA6SaoQ3SR/uuLO/yWuLmc2WP39QF0Q//P/zi//zPM1/MqOuC+XzuWSJxHAloHgaUNkZar9YEodA/T09PpYJp5ylHb5pdzKjrRnqldqY2kI9Jktj3eCgVcHZ27mPnKIo8+OIAFfcshWHoja2d8WzbtiwWC98XlaYpZVlaWqMUAdbrtcjt2vnOgTNOMcrFVA7kcUBPt7+j3++zWq22ruV2vXCeOU7h6oNsH7ii8Td+/f/pB5o3IsEi8hrW6w3D4dCX5Y0RXrlDULuomEOgHKLnNhc8Z2mK0cbzw1zZ35VqLpe+ZcF78sknieKI05NT4RM2DWVZsVwuePDgAecX5zzzzNO+vAt4gxNjak5PTtFa8Wt/6s+wXG34d/+d/zXzQtPc/BzB/vNyrsUcffu3COZvU5eloMKDA1QygMV9lK5Qxkh2H0oAG9oEIwwludCIHGGcxNZQTbjUKlDsTSc8ees61w6vMZmMbQmrpt/vUeuGlaXErNYrjM1+s16PQa9HEOCNDKuqIoxsMmcE7R+NxwwsvxJbmeoPhrY8Lk2OrtEnCAKSIKTIC9q2oSxLcvv3xWLBcrnypfbJZEKvlxGGIfsH+2TDjNFoJKo3SeqRlqqsqfKar371q/xH//l/y5/9y/8Tmrrl13/91+mpNZkSecrB7iE8/SV46vNslcZkmnSKNFEUsclz6qYVlNvNlMpKzTrECVsiVQrnfxEnMWkcMRpJwnV6ekajNRjngdlBe3ALkVRWfEm5M6ltk8StWZ9PsDsJhtun6q44ACrk6MZ162auhNZ2cUGaZQwGA3Z2dxlPJqw3a9arNdeuH3F+csbDBw8wbSuTuA3sm7oGKxOcpRlH14/YPzi0i4nxgb571iTxtxiQ9SFYr9e8c/euVJlQgqggAWRt+ddPPfUURVFwdnpCHEas1yuaVqSrb966SVWWbPKcZ559luVSKmZnx8d2sbH9Wd5IUsoDshjKEqKuLBKGbeUsUFB/7T+it74LWhOqkLaRzogwDOn3+wwGQyaTKdeuHRLHCdmkxzv37/LVr/4mVdBn9OV/n2B0bWsEZpA5yy5E23L79vd9KGNc64ZBm4Dm4avUv/dfkakNgyTnc5++zr/yJ19iOIhQVGCEUiP69wJ4mEDT0lLWDfN1TllqqjJhdlGx2RQUZUUc9+j1h/T7Q45u/ARPP/MpDq9dZ2fvGlGSoZUo5KnO/FpVlU8glFIeuXLoflVV4hFkF3fxtBE1wa6aU6DEf8XJ5LqKpfNjCYJQXIKROVwbMVWL49DP1dBBThtNXTbEUQhKkmPpJygB2+NnDLlF65zgyHKxpGlb1muRob116xZN01gZRjzY4KqSjsLj/i59KNqvR2VZMpud07Ytq9XKL7iy2IbMzmccHOwzne5w795dVqsVO7u79LKMyWQqMtmrFVq3or62WnJ6dk6vP2AynlA3De/cucObb77J3t4ek/GUxXLJwcE+6/Wak5OH1HXNrVs3uHXzBk1TimP3piDPC46OrlPXDW+8dRtJYjVHR9eI7FxuTMtytfI88vV6zXw+94BTFKVs1huUClgs5gwGA6bTKZ/73M/w4Zc+QhTHvPrqD/nqV7/Kpz/zKQaDPsPBkPVCpH4fPHjAvXv3+PjHP05jTUDX+ZKqLEU4wo6vzWbDaDQiimORH24bQEkPpdYEhNS10Kl3dnfYrKXJtGmF0pjEKbPZTIIXo4mtUt3e3gSU9lKgq5UoZUVxDCrmtTff5rvf/T6bTUnVaMzOMzKrmQqVDEhe+EVMGBGOb4g3RSdJ6Io3XK09dAMgdem1y2VNZQy6XqNXp2AM1Rv/Ap3PMNUGvbh/ZU9YbMTuyY9J44PL0WjESy++yOH+BN2Ufu2uq4qmFfn5stZUdYsG2lYzmy2YzefUTUv89OdIP/prBOloe5weynfroF2/wBsOXz1bV233FWf/f1Y+vrNW+YTOyYGbLX1ZvGkiOxYjUAFBFMp1d3QnJLlodStN47WAo61u7HHYyoRThXJiObaxW+6e9tdaa0vutue9pdC5a9C5fwBGo09/iP79/5ovf+Gz/Dv/q/8Fi+WCuhKZ3rquePvtt5lMJkynOxgjPjVplomxrYLVcsW1a9do2xqtG6IoZjZbUJUNcZwyne7QtBW9XmLjVe3nGdcj0a0WK6V8suCCe0eJcglIWZYsFgs2mw1HR0c4elOv1/PJfRRFXgp5d3fXxsClTxAGg4HvPXGJiatOuGLBaDRiNpuRpqmvxjgmkutdKYqCLJWiQpok/Pyv/BLvt/3YFY2r/+lWzFcckiUZrdxol511ubDd/owupaqrQFUUhacquBPt6v52FarkoY15+PCYnd0pO7tTFss5BkOvnzLducXhtQOfCTrlEyfZJc11cLh/yGZT8Lf/1t/iEx//FD/56Z/kG9/4Ldq7X6N956v2YZUBW6MI4hhMSxpsaMslYT8iCGRgZVkGCpI4ZtDvMx1PJDtVgjIHSURdSbOsO/62bRgP+tSWhzubzbzcbtPEtEbTtxKE16/f8GosURQx6Gf0ez1xZt3ZIem467qBlGaZ7C8IOkmiTF7de1KWpZTNgoDd3R3J6u3DG8ex1WyXRlKn7JVvBM0J48hr+rdt6x8ECc4birJkd2+P3bTlL37xkxwcHtLP7/KFL32R0WTMX//rf53FYoFafZvjsx2a/Y9itAQLSRp76hJu/NnxYiw6LaQ2cKpGSgUQBjagdAuNIo4i4YUGkU0gWmlwZ+s67ReoLlSi5D+P9Hikxc3RUn/2yYRD490utNsJvroB2gdPTasxdY0zHnSNbEZb1/ogsMpUtT1XW+ItSx/gKVcaNZrxyCGFxoNCjh4QKKEnNZb+BPKM9Xt9IiX0hdh6bsj+JNlrmgbdioQmKBbzOZtcZGy1acRczaLOgjKH1gOn677tlivlETlXB/IqTl6+Vvl3lE3mer0+X/zJL4DRREFEvyfqQR/96Ed47vnnOTg4kKqOnXhLU3L79m2+853f5/xiTv6b/zGDX/7fgwrR9v5YwtalMMQt0lYYH48LKqmO0da0f/DrxMGavR3Nn/rFT/PZT10j4ISqEapXGCq0DlHKoJ0yi4G6CVhtDBczw737C9ZLw2JeEicZcZIxHE05OHyaz33u8zz59Ecp69AGkEuCqCCME7Ksj8LYQE+AhiQVapQDbRya5ZAxhe3dwC3SoEJBtOpGNO5VFJJYdMs9Z23TeqApclUHY7w8Y1WWxHHoP5ckCRczkWZsy5q2cupSQg8S66Lt/D0YiMDAalnahuGa+/fuoQKp+F2cn4HRYtyVb1AKNps1FxcXTCYTNpucXi/zNKg8LwABq4wxjEZjiiInSWI26xV1VYo6YSIiI6tlwe7OlDCA5WLG0bVD8vHIL/L37t5Ba81kIspv8/nc9qicMRiNyDfi87FcLlFK5CKrquGtt97m4cOHPP/8s57GdXp2SlOXTCYjH4CUZcm3vvUtmqZFI/z3JBHzzhs3roMSpNgYI8BTLRXMg4N9i2Cu6Pe2Dt1JEjObzXjw4AFf+9pv0mhD07Q88cQt/sJf+PO8+qMfcv/+jIvzc6q8ZLPJWa1WpGnKH/zBd0mSmOVywWCYyRppNJPJ2CY2gfxef8BqufQKNEop1qsVcZyyXgnD4d7de34dcoo30kNY+zVlMOgDivv37zLdmRJY+sx0OrV034jlasXHX3yekJY333qHs7MZm4vXMUbRtgUaw+but4We2N8jfvJPkH7oF1FxrxP+dzsOoDl5FZPPZX5Jh0TXXvKfre/+PuUr/wDarQEbgKk2mDq3/+hIlvPeW7c/Kk1T9vb2yLKM45MTzk7uE9qd6Fb758wAWkVom9A3TUMQisx009Q0b32D9t7vk7z4qyTPf8nPqbZEY//nnMXt8bo5ziUkbJOh7SyHqPq5/gdZ1rZXzsj6Ie8pmauVwZjAB8cWORKszh6B9HPY/Wi7TtqFSXrnTIeSaqvZVmWrcxLu0nfup5MT356JrJ1u/TYeFKn/4G8SvvPbfOGLn+fP/at/hrIU5P5sc8Fo1LMVvucFjAkUaZrRtq6yosnSjDAYoZQIzIghbst0OhE2jYbz81OCUKHUkJOTU8/06ff7RFHEcrn0cWxRFJ5dklqlP2OMxEE2/q2qyiv43bx509Ial76nzRhxC3fV2+l06u+na+R2ic14PJZ1vkOtddUKl9wIvSv1Te2Ap1cVRcHI9tsB7+qre9z2Y/hobDV3jTGsVit/sIDXJncH7waTaC8H/ntOuaP72a4KFeCbsNM0pamFu9fUta+OtJaWNR6P2d/f5/j4mF6W0TYNdx4+oNfrcbC/z2az4fTsTDK6Uni0w9FILNq18ejXdDBivlgwmy04O5vxd379/8jR0XWmgzHrYo2RaYAoCtnfP2A4GGCA3iDzg8clVbPZjOlkTL+XUJUVURiSJSn9fo84jBiMRwymEybTCVmakdlqQKACBr0+SRRf0pp3nOUoiUU9KNyaGPqkQYuRlXPtdJN+URTu5vlGnyLPaXVLlvWIo8QPbre5yXC1WjIYDAiisJOUNR75D6KI0nKylTUDC8KtqlMYCgK2Xq9tc2nCYDiiMZpnnn+Oh2enHFw/4i/+5b9Evsm5fv06k8nE6jkrxnf/GeeD65h0Qts2NE3gr5Oy16FpW9DKz2nb/+swaTsN7BjhxKZpSq+X0bTa5wIWfuogIj6v8AF6t4CucL00Fs3BTnvGz6+XJ0hXovfD3HGCA2+UQ6s7iYsiL3IWtxccXb9uk1L5ngssgUsVw63LubH82ND91PbeWvSn1duEBGNo6ookSWVyzVJWp6tL1UZ3Lsomp1ESYzDei0CQ7U7Qq7WfrD3tRm+Ddd8g6NbG7S9tEUi1rU117/FoOOTP/Kv/Ck/cPGJ/b49+1reJv2KTSzVzuSmoG5l4V+slg36fn//iF/mbf+vvotcX1G//DvHTn0ebxrtsO/pUYCd7fy8s99hIhiZn0DY03/hPSPWS6TTkL/zZz/GRF8ZoM8Oo2Ab3MY3WhDZ9apuW9bpiNivYbAI2m5S3355zdloSRilxOqKoAybxPree/BQvvPARRpPnyfr7ZBhBMZOEVhsxIkWqddqOlySVgK7VmsgldraiZ4yhsYtNHMdiTmqRrjTZUtsUiouzM3q93qVeBicH3bSaPD+WavNg4PsvyrKgqUqKouT09JSDg31WqzVhGJClPbI4Jc83kghUhbxuneqdvKKTxN2W/1cerc+yjDfeOAMMZVlhTOsVr+7efcfSC0or/iESkePxmLquLLCiaZqaqs7tuG9p2oqykgAoSSK++93vcO3aNc+BdgikW7PG4zEPH973jed37rzNYrniRizoudDQcsJQMZ1OOD4+5datW/R6Gd///ssEAezs7vj1c7mcU1UVw8HYIpM91usctLJKX+KdstlsGAz7vnfi+PiYnZ0dPw9Op1Npqm4gTTPfzL9YLBgOh5Rlyd/+W38LY2A0GvLZn/4pXnvtVcpSBFOaurYGnYY0jW2l5ILpzuSS4ZcLfhwoNZ/P/bq/2Wyo65rlcslwOKYqt70brp9T1iMxeYtscmtMQ56vRRDAfnZL7VCMxxOKPOdgd8pmveaFZ5/i+uEB603Bj157g9u375BXIXUrppAKhckvKH/w31G99s8Jprcw+cyrN3Y305Q+2EYpVJReeu9xyYN/XT3uE4/4jo11RqMRo9HIX7OmaWTet3OoU7Vzc2qjjfWG2L6+BXAVqimpvve3wWiSF778iF+WeTSw64LvtOhoiBuN996Q/rltOuaqGdtERfbXTU26PR9eFcoYP6c6XoJyRsKu0qOU1+PQRltGgOt7ceuAvrKGun5M41cRc+VOeczPwVZ2nTbLB3DndxgMB/yZP/NnefbZFzg7OyHLUnq9AUpJv0mawvn5hdAmlQK0j1lPT0+9ilNRbEizRIQjejXGwN7ePpt86VX7AB+n3b171zNIXPDv5qnZbMZ8Pvd0p9ls5ufgtm25fv267+eQxGbqQaTSeoW51gPnxZFlmQc3sizzCYWTn3bULNdj4sDKo6Mjqebu7HjRhqIovHJVFMds8pwkSTh/8OADjf8fK9FwVKPT01NWq5XlZ1l0z27uRFyQ4ihT7gFxHDEXoDherOuCdwpWaZxYN1hZfNbrNcPhkBY8AjwaDmmbhr3dXUajEQ8f3ufo2pEgREXJcrFEN639zZTlYkUVVzx8cOz1g1fLFfeKu2xWOVVVowgY9Hr0sx6f+YVPs6k2FHlO1svY3dllPBkTKCkDa2U4ODzk5s2bYqJmFVVuv/0m+Vr4fgGKaweHtE3DoNcnTBOaEMuJS6gqKZnGcUwSpYQqsiVIJwVsrLKU6O27hKHb49LWFSByacPh0GfF8/mcwVgWqqIoIBDFGl+R0spTKxzSkqYpWmv6vRSFkt6PWmQQwygCBWEYWdQChqOhva/SkNWlcPR6fZup99BGvndyfkbVitpTlMSMJhNG4/ElHiDAKI3g1f+G+e5PoAdPkK9CejvXCYOAnZ0p89mcynIotU1MjUdspAmhcZW0QKRlje3RSXspWS+laYx3f/ezWWfhMd2/d5IL8REJfMXBT6xsS9WXTfuM1/zuNui5ORkjTdqO/+om+vV6TdO23Llzh5u3bgqHHqQ6oCRhUCjiWDw4WtVglBiqib657LsxmjIvhKYQRh45Exqd+7ulpCgIbQ+M99FwC6rZNmSHgagnZb1se+zIvuTs3MKGL7N3u6i3CRw+YbvMNHOLl/tdkZg2GNI04cUPf4gsDSmKNbOLM8I4laC+2/RmWrJ+RpalGBR/8S/8a3zlK19lvthQ/+AfEz/5U9vqnr3mUgl0btOVnI8HCF0VTaPv/DbJ+i79XsR0OOC3vvYd3ng5Ym+3z3hXEJ+sJ70yxgitLM8Nq2XC6UnO+fnaNkj3SZJdwjQgShTahKxLwzd+5zt867uvMxyMeeKp6/zar/0KN2/elPsbBT6ha+05KwW6lcS/sXNvWUogNRwOqWoxc1ssFqRpRmTnZVemd02BTdtSlSWzjiKRC4DCMKSsSq+i8vDBPZq2ZTKZMJ/NiKPQBqOGtqlJkoiyKDlbrkBDlqWcnZ8xHPaZzYQG4Cixw+HQo2cOMInjiP6ghziCK3p9aYC8sX8kfVWWPjCZjFFBwGa9Ji9yX1V58OC+UMbqyjvdi2hB39MAxCirYDwaW5ne2I8fd55OoWuxWHDv3j3b0yDeJHGSyDHWDWfnp/R7ffr9HsPRgNdff4O2lb6qfr9PWRYESrG3t0NTiRLi2ekZm3XBjRs3OTg4pCjeYb5YEMUJo5FIavZ6GWmWoHXmkxznj1JVFYeHh0JpXUgj6c2bN3nnnXfY3d0VSqXV7K/riqrK+d4ffIckTYTKBoSBrKUnJycUZU4YBkwmY3Tb0raa6XTK8fGxbw51LsJNs1WTSpLE0y0gII6aS9Q9Fxzdv3+Xqi6k6phlnirnZHaFXmkkiTWGsqiIopgQTRwoeoMBVZ4z2Nvh1s2f4cHDE3742lu8efsdVqs1rbF4hgLaGn32xnsnDC5INgZTF5feN93P/hhJxaM2Bxzmee6lS93rSuMBNK0dsCLzu1bG0xevHofQMeX18nt/B2MMyQtflp5RG8F3asTbZOESmKacLnsH2LHfMp31DKlcmGC7x8sz+Xa580mETUw8SOSqF7g5P7CGtzYBsU3mHizU2kuMG+2/aLsl3bp7tZq0PTKfVMlCSfkHf4dQtzz77LP8o3/4j3j77bc5PztjPB7z0ksfpWmWjEZjiWFVxGZdEoaKKJZm7F7W486dd6wk7ZReT4Di+Wxm57GS8/NTxFRa+2pBkkgy4mj77ll48OCBrxy4fuGzszOiKOKpp57yCf1yuWQ2m/leO6UU9+7dYzwes7e3R57nTCYTS8u8xdnZGYPBwFNKXbXDSXa7SkWv16MoCjabjTdLzbKMtm3FJNEmKO5zLtltmkb8f5RiYlW53m/7sRINwE8c169ftyh36zV13cWF7YPlMqW+7Q9wiYfjEju0qNv7sTPdYTwY2n6ABeOdHSajEb1en9FoxGK5YDKeSOAUx4xHY+7dv8dyIc2p0puxFI31sqAqS9555z7v3L3L3XfuEscxu7u7PPf8c+zt7nGwe8DhwTVBR/t9oiiWm5rEBOG2ib17bipQgjaAVzJxSMP+/i4BLSfHxwwHA+qqYjwZo5uWVrcoW7FwaJt3vA0Upc0ql8ul3FykglNVFaW9juL8K1rKUSQmOGWRc3x8zI0bNyw/UgZ5VVb0+n3b9G4b9W2W2zatv29uEfFu74HcvyTL6PV7tiwnvGrd1J43nec5YRAyGA6kQVyFVFUpwa9xQgGFpZFEzM8vqIpCKk6rtW8Ui/t99vb2eOONNzzFbRAr0otv0pz8NvN1zvrDf4mwf51ferrlrd/7bf7ZeQw7z2Osw/LWRFD5cqwdtOLN0crEE4aKMFCYsNNI51ETi6a4iU0p75yq3eR9adGxAXU3YXHItzG2+SywFZUO+uPnQ01rk5coDGkIfMO5a5J1C17TNqggILKNtm6S7/V7qDCwknuRVD/cRB1FspAFCmWs9KARbwDHXVeJuFyoQJRCfMXEJT6t9scAeLRR65bBaEQQhiIhbRG3VmvL3TWgRS3MJSLbS9ZdjLYol1uyfO2oe81tkaGua+7eu0exWZEmMcPBiKgJ6PUHhGFAVVReBaQuG+qiYb5Y8vDhCYP+kMV8hVmfU37jPyH+5J9DDQ7kt7DKKOA84nGSjn5ra+pv/heM8tt88qc+wd50B2Va0hDqYs1qU1K2Eadn4o6tTY1uG9uEH2L0lDA8YGc3oqxqS11sIGipTYPSSM+QUhTVmtVmSdoPGU93qZqWH3zve4yHQ/Z2hSIZRTGFXSScso+j4ziEOY5j7zXRti2p9btwZ5Vb6pubxxaLpX1OQt584w1fvl+tVizXS19idwupq4CmSewbg99+W2g70+mULO3R1q2tGIJSfabTCYeH+zYheCg+SWXR0aCPqJuS42PRjV8uBWDa2dnh9PQhbastRSrn6OgaWm/pBi45Hk8EZAmjwANBZSlUql5PAuXRaMB6vSaOI27cPCJLM/JClFyKvCDNnLtubJWeVty79w7D4YcYT4bMF0suLs4YjcZcu3ZIaw0ve72M8XjMfL5id3fHro2uWgaH164RBnB0dMTxw1PqumE+X3hQaPbwmJ2dCU3TcHi4T55viJPIa/E7E8Y0Tbl//74X43AN36enp56L/aNXf4QCsqxHY1o2qyVlLhWlpmlIsoyz81N6/cyKBQxAGfv9wvO5XVIqSVrjE46rVOi2Mezs7HBxceEDKwcmvvTSR1hvlsRRTNO29HqZeDK0LVna83HA8cMTD3YopYglk2a5WhPGESenbxJGMVUjjbo3btxgPl+wWK1Ffa9uaBvdjTv/e9s+aBJyaX3tvu5AMoVnComcq7z7uN8wnfVEAdXLf5/41qegv9tR9tsmHApXVNaYILBU0S0d1EgJett3YWTPjg2gbBIold/AJy5uHfPrLtu6tatzuHXVA3P2+N2kbtAOr7Prhv23pViJKIi/Wrif9osH27XEvebmc9egzlKMIl9++RVee+01vv7135LkLE15/rnfZzqdMB5PyDJRRovjyKqnCb2paUVoRbeKt956hzRJmEwVSTIgDBR5XrJe52TWLbyum0uGd0op1us1aZryzjvv+B4Jl7zv7e3R6/V8pWOxWLBery+BZ7PZjH6/Ly7laepBmuVyycXFhQeokySR+WqzYT6fM7F+H47l4kAeF7OHYcju7q5X1cqyzCfEjt7lXMONMdI3FSgK2yf3ftsHTjTcAThlEcBqBUtzYdPUvorhVEdc4whslabcROKkDF1FwzWr9Pt9hr0+q/mC3Z0dnrh5k6quOTk54ez0lECJrn9qv7NaLDl+8JCHDx+Spgl3Vitv5rRarSSbrGpUEPHJj3+SX/3lX+UTn/gEOzs7ZFkmlIMkpWmFftS0Nb7JUTc2ONRobeQzgfB6lQowrWuqbW2TpQtkIwwB1594UoI0W7lRUciw38OEwVa1q5XGJncdTV+ucX8w8EmIq0C4icVN3i5xQ7f0e5lfdJ566il/H0ywbeRZ24HjBllTihqLqyR0kSkTbPtntBaX6iiOWW/W3sirbVtQirptmC8WBCqgrVu/AMGWKz4ajAhVQD/NaMuK/ekum8WSvb094jihNZqDw0OfZHR7cOI4YjLIiF/7G6zyis/9yv+On/m1n+O3/71/n+Xzfw6z8wLOV8PPQJ2J2aPqBouEaoIAItVBYwwyeboeC+ecDuIobQN7h4L5INQ2ibvtstM427+7gok7PnkTpQLiMKKsK/EVsapYGEO/3yfLUvb2D4iS2PPNRdnN3h8bhDvqYOuoUG1DWdVimBeG9PsDOQA7scj070zsXLAviUW+yQkCJU2o2EZ4pQRJskGs641xlCnnY1JVldAd/flfWVyNxjjjFwOeV+sQNb9AbtXDfPXD/hcEIePRlJ3RlOVyxXh0QBRK1aLMCy7OV9y58w5vvvkmb775JvfvP2Q2m3ExuyAvc9I0Efrg+jbVb/5fMfsfJvzwnyRIRzSmQr/5bUwlNJ/m/C2C5X3fY5JEIbd2Rjz97MdIoojVemkTKUVdNbasnyNuuWI4FUYhWovBFSZgMBgRRylNU6FUSxC2oANClaItchtEEUVZkKYxv/av/GnitMcmX/P666+zMx7Rz17ibL1CqYAojjk5PeH87JzBcCDS0U1L09QEQchyKQIObu6O44hik7NaCWVlOBpydnoiXgxVQxQl5Na52zX0unloPBJ0bDIZUeQFWS9lOpkyS2NM2xJg2KxXNE3D/t4ubdOyWa9QKrReCQFnZ6fEiaDp6/XGJjGOc6xEcQjIMkH1xYzKyHHlaw4ODiiKkvl8dklO9/r1I4/gD+z8mWUyD61Wa9t8buzYjun1Qhu09yRBtzSuqipZr6XpejAY+OBgNpdm8aqqvGnsCy88R6ths8m5e/cuSRJT1yHGSCVtPl9x584dtJak5vDwkCAQY62qlL6IJ249RRhGPHjwkNlsznRnh53dPRaLOcZoofiimU4nfv52TZtCD6ttX+NWkaZtW68QGYQBbVWDaVEqIrSAwmI+p6orMkuBlqZzZSWEGx8IOmWZwWDA8fExBwcHaG0uJbZubZ/P5wQqpGlkBnCIaZIkzGYzz1iQ3kuH3EtPS57nl0A9AadCQbNbocxoYyCAvCxEDEEpyrahrFsfMIXaELRalNkuQSSP3/6oFYv3295Xc0d1Zjj1+M9293P1kJXR1G//DulH/uTloN7IPCwBhsEoSSa0saIQXb1xVznBeBl2XxFxoIsxEDjqUgfcs3/IfO7ENXxawLaEjf+mqxbaT9jPOSNdC27bc5P1wXiq8zZNUn799mihX0ukItSevYGq1gQ2LnXXUZQ3W1770etWUlvOTxSnJGhvrRleGIWEQegrCcYYnnzyFk8//TSH1w4YjYaoQJGmPapqxfn5ua/SOsB9uVx6OrxT+3TiFCJWMWNnZ2er4ml7b52YhwOXQycAY9fWpmm4c+cO165d80mBo9q5vi3Xn+xUXF18PB6PmUwm3L8vtFAnMOEqG8bGIqPRSOYGrcWawLJgPsj2YyQaDVEYioJEGNLLehRFSWGVkJxBietUByisQzFGFpR+r09d1azXG8qi6iiIBLa0kzGfLTh7eEJgoMwLik3OK6+8QllWDAZ9ZhczP0A8alnVlFVJFElpP0kSDg4OePHDLzKdTrlx4wb9wYj9PdF7F3M65Zsky6aU0lrZoI1MskkisqJGK0Il6i5REhOETqUGwjDwwXCaJnilHImG7NNjCJUi6w8EKbUPv7YPbRSFfpLr0s0cKidJWeTVolx27pIOrVtfRnSl63fu3uXmjRsEYYjGen/orXyw51838rC5f5dlycXFBUVZYDAkqVRNdnd3CYOQ1rRMxhNGoxFHR0e0TUsUR55eUhYl+Tr3vL6TkxPu3LkjKN16Q6CF47herPin/+Qr7O3tiohAmpL2e8xnMymNao1pBUEJwsBPCmkcESqhFH32pz7Lxz7yEb7+rV9HfebfxgwOtpOlq9V20A53X7QxoCWgDkxovTpsEO0TgC0SIw3IovttfFnb/YxrVOsg8J3fvqQwJauqRYvwnzFIUgCApckpe5yx5V9PJmOKUiSLXcNvEIRoIz0WgtxIA+56s0ErhW5aVqslvX6GZEpspf0665hmW1HAGMqioNUt/V4PFQRUZbUd11qC5iiOqYoCrIGQN0tstGjv1w2D8QilJCFu2gZ0a6/BtjnReJjL3iGbpPlX3N99NcQAGqVbqrJFNy2LecEr3/8tXvvRG9y+fZvTkxPmi7lX4Wra1g8BQ0uWJkx2Jjz3wjP81Gc/y3/1X/+3nJ7+kOY3f0Blf0cZI5SntiGNIl588UW++KUv8srLL/NzP/cFPvfTn2Vxfs73X/4uX/vNf0FRbyjrijjNMNoQaC0Jo8LTQZUy1KZCKcOqaOhnQ1HiaWriQKFMhDFC72laodVEKuT60RGhUrz8/e+hMDz95JN89/d/nwCIo5Dziwt6vT6bfMNivmA4HFCUpWi2a0NVV34ucXruutVeGKIocu7cuc3zzz1HliT0soz1Kmc4HFhalDQAn19cEMcRrRGkTbeaxWJOYqmWWZJQljmDwZCDgwPmsxllVbG3u0sYxULPM5ooCuj1exhiTxkdDPo+ISiLgiiWZWm5nDMY9D2i5njJcRwy6O+KUITWpGlCbo2onPiEA0n6vT533rkjtNa2BaUpihwwFGXOeDKWXrooEoTXjoF79+/byk1NFIkq1WQytmCM8K8vLmacnZ8zGI7J85yiyBmPR75qH8cRZ2dnlKVQmnZ2J5yfnYp3QF3R78nif35xwXAgCVxjE4Ss1wPE7yhJYlQARSFNxPt7+1xcXFiFuhl5nrNYLDA6YDgcMZ1MmYzHFEXJyckxCojigLqp2D/YszS5kNFojAqgrGuGwyGL+YK8yMnz/BLgMxlPWC4XaGPoZT3eevMtqxpWU5bVVkSkaRhPJiwWKxG20Ma6yQuIJr0eIUbj179Wt57d4BKLKIppbF/IcrUUOpGOaBtNEAY0umW5WtDoFt22lE1Fa6vATStBqgDtgZ+XP8j2uKrBf/+bC7a3VWr5bbj681eP8erxla9+heiJzxAMD22+Yjrr4eXvOnDJ0F2r5B1XQVYu7wlcg7qlI1sKreuScIexrerbc3AJg9rO4E5ExaeBrirSOV5/7JdYAKbDDGAL+Lnv+IsCHj7TmuqNr9H+8B8RI1RThXgLgaKtpZF9uZR+itYyC5RlKCgVoLWyc3VL21bMZivu3xcj5Vd+8COSOCKKAvb393j2uWcYDPrceuIGOzsTXy12nhNxHFtAImG9Xns20Gg08gahrr8KtuuHS9YdiOKau4fDoVdwm0wm3mbCgcNlURDa/bmKhJsj0yxjsVj4+G88HsucaVk4TsRhOp1agQkRfMKKFAkw9MGejw9OnTIhTWWIo1Q4ZuNdyqKBNuDi4pzVSpp+9/b2vO7vZrMhilPfcLxQglq0TWvRpj5x0KM1mqpqeeX2q+LxkMTsjIacNqdEUchmKeXk1WIlOsoq8HyywWDAYDTmxnSH6c6E3d0djq4dMRqPSJMUEDnZ+XxBpRua2niNZCltDTxKG8fbLv7AXswwcIGuIgi28r4YCGyQ5xY2+2UbRFkHW2NobBOs7tBmlFI28LUNbDYItM+PzdY1hlZ6hM0WPXCqXvJg2Gw7DCEMGO9M+cEPfsCbb7/F0089xa2bt2RiyGQf0htj0LomLwtA8fDhQ/JclDQcjSsMQkJCyk3JzMwE1YxiorSjHR1ap93A6uJHhngc0uulLJdLXnzxwzz55C1OT085efCQs/vHtHXJpz/5CU4fPuAjH/4QN2/epAVO5zOSICIORLlGxohobRPIxKOMmBq2dUOgFL/6q7/M97//PU6/8R8T/PS/ixrs24lPoRC5WBu14yZPSYokgVShvW8KAqO2dCfUNuDVxqNBbpLbem50EgnDlqrlZt0gkJvlJ3C2k6NyTW9imjacjC31qCWIIlqjLQounHs3vpqmJo4Ti5JrK3RQ0uv3iOIY3TRopWiDlvn5OaPRgF7WA6MwARgrJQug0V6O2dZGOD45A0Rto7ICDFFozdOQXqc4DFlVNaEJiFWAFE/FbCkIA1oTEEai6KUbTRyG9ryV/Ka7Hq5yZIez6SwoytXAO7mfMRpTzDl56/v8b/69/y26aanLmrqqabSmbhtfsXLPn1KGW7eO+MxnPsVsPucv/+X/Ec8++yyj0ZA0zbh+dI2qrPnbf+fv8r0/eJm2FefiNE0YjmI++tGP8m/+W3+NmzdvWsdxqfBNJzd5+rknKKucb/7eN2G5wgkmRL6XJiZJY0vzKQhJJFDtpUSBqHZFsW3GK2tMYM3rVICjGo4GQ85PjhkMBoIWB4qXv/8yq8WSj37sYyRRwswaauq6pq1qIhR7kx3iOPQBYl3XTAZTFssFVZmTDgYslnPCIKDfS3n44L5v2K3KiunOVBRwAklQmrJkvZSGSKMNSRRxsLvP7du3BexJIkBTlwXrpfj1FPma05Pa0zwBAhICo9F1TV0UorJn+/ayLJOm2LpmZ2eHB3fv0pTW88dEKB0QBylJlNHLUp5/7hnqpmGxXBKnQsWpq5pxb4x4uCjatua5p5/m7r13BJEMoZfFtgHSUOVrqW4lQ6Igpalbdnd26Pd7PHx4j142xeiW1WrOaDRmvV5bueCKk5MHbDYjQTDLylNjyqJgZ7rjm9DX6xVH1w8JAkOSRjRtTRimaBSD0ZTNesMbb96mKKQXbjgaUBS5dWBPqSpRSUzilCzekKuCxWLpx5sxBl0Z8nzFerEktRWIMAjopZkHyKu64uzsgigMSbOMKBJ0N0kjHtx7QF1VGCN9LGEgVcu6qbmv7oMRaeZWi+Jj3Uhl0ujtGti2LfP5hhYxbtW26u41/I1BtwqMqL1JsCTqUmdnZ0RJIvLvFq0FPDcc48Q37DRqV0hPv7Fzh3ISrF2U/o+w/XElH++VIDggRzuxDLWdo9/7JPS7X2pyNr/5f6P3U3+NcOdJe12MX6P8jl2VwwbjHiAz2q6D2IrAFiBTbq3D9hoahVGW4uW4xz4OwqFH0tNo35Ol1CVSnXvn1gMXANm/O8nxSw3fnQRHdcCoS4pV2qDndym//3fQJz8SlUQ7pg0IkGmB20BZ8CUMUUEocZpbd7TGtJY9YGNBDSL1HgTeZb2sGzbvPODOXZmrw6Bhb3/EwcEBvV6PL33pS1y7ds2LN0hlOfa0VHcsjl3iqJ6uapHnOUopT5s/Pz/n5s2bbDYbUbVKEqZBQFULiwEgsX21TjTDNX27hMfHeq5yY4F3J/DgevgcPVKFIRpEaES3bFYr6RG7du09xqhsHzjRmE6kG361WjGbzfnOd75LbjvP4zjmpZde4tlnn+Xw8NBrbmsb4DkalVOwENpUX5oSLdpmjOH27ducnJzQ1BVxpHz5J45isp4oPF3M5gxHY6uXP/Cd80IlEvTf7a+qa+7du8f5+Tk/8elPeWMSP17Vlo4EeDqSe88hU64s7MrFoIRz3drihX8Arbu5RcidzFtoHz5ncOduostmXXN3GIaXEBhXLXHuuS6wdMfcpVR1S4FPPvkkd+7cAaW4d+8upyenHBwc4BovtwpgovRy7949wjDk2rVrvuHfXQdnjrderen1eiRJ4r8vKF7hEbC2bYmibZWnqqTKdevWLV547nmUbUCOQqGFeO1+A/v7+/zyL/0Sb73xJq+/9hqhvaZNVYmqlZsUgsCXFn/6s5/lmWeeJn/5FdYv/23Cn/q37OzgSgr2nx20ozXbBDCy3hq6be28aJONzqLgjO3kfriKiM1hcJMvSGuFnQ5d4/cWSsebHm335ufVoiyYhFMCxEej+/w0tZRu41h8V/L1hvF0InS/piHQol8vyHJLbaVoW1v1enD/Abdu3RRZZYsiOY0stFswZLKcWaMfockEIqOrJBjW9nwGwwHaiBu4uPiKEIHWmjRLGQ6Ft571+rTaWIMuq/zl8KxulckV0a9WhTrXHKwyHTLxb9Y5dzcFaOMTpJbWL2xhJO66SRJz/cYRv/JLX+bf+rf/TfLNhjiW8du0DYv5BZ/+9CdRKD78oRe4fecdilzooOPxiINrUzAao1tOHj4ksMpum/WawWBIWZV8/OMfZ29vj29+83e588471tVXgjwnAanbmiiMqCpBdNMkRbeafr9nETNNmiWIg3JLHIcYI8alTz/1FPlmTRQG1JX4k8xmF7z00kucn5+hmxrTthS5+BjVVcX5xQV1XTEaDf0iJk23FZGVx6yqkigMLXhijXaNYTwWN2xpUIxsz0SGMaLUpFRI31JelVIksUhzC4cbT4t1/HyVprZvTJ51B2i4YyrLkjRNPT3AafDXdc3HPvYxqrrizu3bPHhwn2effdbO8SFtG1IUWhbWKCIKYoajkfi+6IAkismtKozWDc8++7SoEJ4eS4XSPpeuh+Xh4iFPP/Uc65MVRkuieeP6DeaLOaBIkozz8wtRMVut2Nvb41Of+rTQnc7FIPLw8IBysxHJ97pmb3eX6zeuMxj02d2bEkUxp6dntLqhrluKvKTX63H/3gNaLfTZVgslpN/vMxqPKfLCJnsN9+7f5/z0wkvu5nnOznSH1VqS3DhO0K3IiDvREK01mzwnCEPr1SPPnvPmcDRN5x7v5i0nDCDgtASp3jPFGMqqpqxaLzIg8qu2X1NLX1l3rZJp2QjAo6JL69ZyLfQMUxSydnZ6OLdr2+Um5stCta4D4fIrOLDij3n7w9CsHpWcvPd+toF0txH8/X5bKQWbMzb//K8T3fgE4eQG8dOfA2ssfGn/bj1wlQvcumbrBO61btWDbQ5h3PX1ySZWSt5/8epFcH/Z7sQ1w0EH6MMDUJcKHZ3jk9/bdpmIKaJTpWoof/hPqH/435FEIXGS2Fxrex27tgqeHeL+bLsJnMyPknBsAb8gCJjsDHjiiWsMh0Oeeuop8lxEDtI0I44CppOx7fGofJzaNA27u7tbJUbw3nBRFHlKulNxc/QnF/O4uPHmzZsYI71Q0+kUApEWzrJsK3WvlO+9dfRPJ/bj+jjatvUKpnme+6qHmz/W6zXdvjcx4pX1zVc4PsD2gRONzWbDwcEBy+WS69evMxwOuX79OnEcS4Aax3Yhjy9lRUHgHGgj4li4ZUma2EU48DQhYwwf+tALPP/8c7RtjQpkIAVKSeO1m8xqoUK4wBa2E1pgL7b7/TAM2dvbA2B2ccHBwYGlv9gEKBJDQW35ZoHCUkuMRUuE765b4Qi3WludaytZZow1KpPMz6FLWa9HkqW+EWc8HnvdYWOMcEthK09WiPtyam+cewBcZutQVDfpdv/zCYpy/QxSQhuPx3Jt6obRcOTl05zNvPsewFNPPeUHuste3QB0zUIu6XM878AOtLquvTazNO9V/uGoqsoHDUVRSFAYSKCTJqlvgm6srnM2GfNX/uq/wT/4+78hD1RV0RhNZU0DV6sVk8mEJ598QjjUWcqXvvAFbr/9NuXiDvYC49rFfDkYl1Rqy6EXdDwIHPKuvDSso0f5yU87Tit+PxIXK/uhLcfV9Uv46dRNbFiAxiZobvJUNjCuqwqjIYwFcYkToZVg0UCpYkQkaUpe5EzUlP6gL702FnF27uxpmlBXFWXZUNeVSH62DTdu3qTX70sOpAWuctcEI3J+p6enhFEo47xpaBoZE1JxEyrbZDLxjbjL1YI8X9Pv9cAY4iQlCCMgoNcfWrRzq1Rlb48Et17M6QrSd+W+uddk0Q0QpZIQXYvng1unwiRgNBoSJxFVVfJX/+q/wSc++Ql2diaMh31m52es12vfmOoU79pWxvjFxZwoVKQJrFZz4kjz2qsP2dvbZT4XKpbTvl8ul5ydnjAej4VHmyU0dUVViDCCFLJa/xwJpzbBSf2632xbp3DUktjqq/OokUVkQhBA09acnB7bxcmwt79Lq2tm8wtCY0SZqJ9h0GzyNf1+RppO2GxWBAFcu3bopaal76Dvn+2LiwviWMQv3DMunF5ZkAYDKbPn+cb37TRtLeMnUIwnQ5577jmuXz/i/PyMN998k9PTUz/20zRlvV75uc7NUU5v3/2m4+7P53MPdmS9RKhCB7tMpiO0aYmTkLzY0LSNnasgTET8oqpr0iyjLWqqpqRpazSSBOXzDVq3HBwc8vrrr+Pcf4NADMWyXo8kiQlDxXw+EznIJOLevftsNhvSrE+v1xdT0cGAPC9FHjzJME1LYAyRUsRWoeXi9ISLxZrjkxPp+2hqbt26iTGKxTIHY1gslqzWOWlvQFXVJHFidSsCqrqlyWXRb2trTKpCirphnZfisp5knJxfgBLaKljBiE6wVFnBERdk+mp9sEXRpbAY+ACkqipUIDLJRV1Zl+fWj1uMUJQgFNhCbX2wts+rwhiFgBryqjEOfe7I2dv5SHrsBPRx6/j7bW49+u+zv+LHTxD++Lc/zO8p06Lv/T7t3W9TvvIPCMbXCfq7hAcfIrr2ksRWgz1UEPkKhjGtXxPcOmZcBVoOBPz13vbOuUqFi6u6l8zgmrmD7XfdumOBPfdJX9VwSeKl9Vs+40ApEcrqJEOAMprm5HWq7/0d9OyOp4eCFXIxl8HZbSKM//e7kjkjvnCuL6ILwKZpxEc/9iF+9Vd/BWdk2ev1WK1WFHnFsC9x12q1YjQa+d4MtwY5yVwBFbcVFld9cHOjoza56sLR0RE7OzvbeDPLaI1hMBhYAaWl98xwCcvFxYUHHq46kbv4EvBtD07UwsWBzjk8iiICpWyMUW4tFN5n+8CJxhe+8AWyLPNoh+Pzg9yEyjaZuId/a7BX26A0Ik1jSzuSQN4B/K01PXGlGxmc0FhddDcBioOsYrVc+X6DblIhD4gE3W5QTCYTwjBkvRZnZZfFuSBeJuFuGbMT4JjLE02axP67xhgvyRpFEdPp1Gegy+WSRkvw7DJZt1/XSOtubBSGpPY4YKtw5a5xVx7QHV/X9+Lqg+Hed/cgtnrw/X6f3d1dtJbmwvl8zmbz0BoAXvfVDme0B1z6TXdvAB8g5HnuZTGHwyGDQX8ru2k/7wZqkiY0NlNfLJfMrab066+/zmq5ZDIa8+KHPsTBwT6//Cu/JFJwKFoM2F4YNwZEnSbHaM1P/YnP8Pf//t9jsVxRz95GTZ/Bqxd1Ji5tG7eNsaiekQXSVZu6CLv7twJPd/NeCra/wyNN3YXOITmdPRqLGkk/h1NB6fQhAHUjSYGIDCjiJEEpLAdZ8/DhQ9qmZTIWGc+yLBkNhyw7ql95ntsSaSbPl62I1HXD+cWMpm2YTKYMhyPbTyTByHK55PzinDwvGQ4H1LVIBW8s5z2MY3/eg+GAJE3ZLKUBWhpQrXJVGHi5a8eNbxoxH6zr2qJhFovyNe5t9uHQMUGtLqcfDiXzd0aJWlgYWfUwrdmZDvif/bX/Kbpt2eRrPvOZT/LEEzeZzWacnZ6wXC5t5a1huVyxWIi2/2aztprouV08MpI4wZiKo2tHZGlCvLdLUzdU1ihxb3eH5WLJ6ckJTSMy3Yv5nDSJvTKKS2SNUVbi1hCGqS1RN7aJzti5r6GqtsIJIGp+4/GI2ewClGK1XtHrZQwGQ9I0YXdXqDmr+YzJZIwxhtFoRJ4Lxz5NUyaTkV9I67pid3eHzWaDSGZLwrOzs4Pr+3Lz8HQ6sc92ZdXjDAcH+5Yas5QeDa0ZDoc8++wzrNcr7t59hyeeeIIXXniB73//+3z3u9/1XhRFUWLZPLRty4MHD7xkYmi5vk5+cTQacXJywrPPPstyteDevbtesahbke33hihEXjnti1KLUz0jDKiqAhUGBFGAUiFtpVmvliznK1588SVee+01NhvRpF+vRcrxxtF1zs/PKIpCjB5t1WY+X6DNkslEFLXunN8TuuNoyGa9xrSNyMDO5zz33POcn50TxzGLTcHFxZy6qRkMhrz51h2R/g5CPvWpT2GM5vd+71vEcYJSItWcpj2apqSunRKjUCgrS2sCAUNc0oZd9F0QqDsgkTxaZivYwHat3QbokhBs5UOdN4/sS9uxewn5VjaJcEg3ZqvmbSu83arlFpRxyn0dxNhIs7o2bv9bJRx3/P6j/5KC/qu/87jfeL/juUyPugKo+ErN9r2rn/mjnpvfv9GY+V3a+V2a+39A6QDepz5L9qm/jPKmeKob27uduKOxyW7gjfaMTQi6DeHdOpOvNLl7iR0FRtbDS+It9gO+GtL5/W1KI1REYwzt/C7ohnD3aYzRtKevUX3/76JndwgsAg9bEBogDMJLlTTHzJC/q0v3wV+7wKpw2X8LbVIsF85OL/gHv/EVTk/m/Kk/9SepqoLoMCHLemRJnzCIPHWq1+t5sDcIAs8wcccBrocp8MfsABlHyXRz5ltvvcX9+/c5OjryFeG8LP333bzlwDQ3b7pqCAgA5NSwuv3OLm5z5+kEiUqrLpUkCUEYMhwOPZ3rg2wfONHo9/v+xrjG7xs3bnhDkAcPHpDnOU8++STHx8esVisODvbp9XugDK1u/PgJI6l2GJ+YCMLctrVNPhR1VVOVlU80AOYXMwbDkT8mdzGlYU7kOsuy8FlgnudeHSBQSszqbEMkSlG4CkykfADgEglXEXDoj0LR1lKSCmW4X/IYcOW4MAzZ2d0BO2DcYHILg9Fb5YZAKY+o13UjwbD9PZcIuWpPd/C7zfeF2O0qwqNsIO0CNafE4s5tvc55/fXXefDggZesXK/XXssZRGnEJSjr9drTpJxju6PFPXjwwFastr4p7gG5uLgQVLTIefDgIU899SRPPPEEvV5PDGqQQKjc5Lz2+o8oNhtms3NxwTaaoiq92gHgqydtXfPcM8/y+c/9NA8ePqTNzwj2n7Nu12zRELDomqHVzgyptYCKSxL8qPIL7rZ0LOgd4PswjHbXGpzggVL+1zq76iLz22RmK/8n1ysvcrJenziKMI0gHq2d0JaLJVq3FEXBtcND5rMZ1w6vMbb+I9oYdGP3kWXbJnpLJ1QYirKiOjnl4uzcByVFWVLVFUYb+v2hBMUqYLVZo7VMdKEKaHVLEAbs7++DEYm9KA5J4oRWyoBEYUgUJ9LgmyQkacxyKWhHWVVyvqbT/Ifaeop0EgtflnfolX1fkjq3aGiSVLiLg37K7s6Evf09Xn/9h/zSL/0iURRw/Wift996jaZp6aUZYQCj4cD2UIQcXTtEKcWbb77F3t4u77xzh8ViTr5Zc/PmTaoq5+233yQIhCpUWZqj4487CUI3kTulpTiKEdlgbdFiTV1v3YUFqBEVqqbBTuqSPMeWhiTPap8wFIpb09TetyGKQoZDURAbDPrUxWab7CzmVoVIKjUoa+hnDNq0rFYLVKBYLFbi7q01vV5GEEqFMYqkfH5yegxAkkT0BxllWZH1UpQKGAyGHB1d8/P/aDzm7PSU+/fve5Wjn/3Zn+Wpp57iG9/4BvP5nL29XQ/8BEHAaCSO24PBgNlsRl3XZFnGcDhkPB5zdHQkYyyMUJGTyY545849nnkmwxhNmgxsRTImNYgnUUfJKAgTjNbkm5zVeslqJZK9qtXcvXuP69dv8PLLLzOfL1itVly/fo1eP2W9WbG3u8fOzg6vvPID4jghijLyomI2W1olr4DDw0Pu3btnqVdSIdME1K++zng85uzigsV6Q9O2YmJ4doHRMByO+Jmf+Tzz+Yzf+u1vsFqtwSjCMKLfH3B8fO7XwqbpVhJsxV5r2tZcWguuUpS6Y81/hs7aYbpzkcZ5N1zdDNbXwc1rqoPd2MTAPbP+94xxpcrOfjr793PkdtPdgJzLAfaj1r332h4X6P842x82wO+Cfu+VhPwPWiVxCJwxNG/9FuuT14ie+mnip36KIOlDEHXv1na+Dhw9rStBLovkNt10o+pR52JFadywcd5Kbiwp59kRvPurbsy0DaatKL75X2FOfiDrctyT75ZriamC4F33oVvFcK/BoxO7bgwlVD/plXMgq5vDBHxVrFcNv/WNb3PzxlP8xKc+SZG3JImg/qvV6pIMrQNUugyUPM8ZDsWLbL1ee/qT1prRaOTpVi6miuPYG4qKJ1JKFEWszs483altW59IAGRZ5j13QGJ5V1FxMdx4PPYGg66PwzmauyTEKVgpILfKdx90U+YDPo2rhZRj3A8CvsTpDlY4sKc+GB1PxjhXxcFgwHA4tNzQkKZpCVTosyjH3QWIw9CrJLWtlsXv5IQ33nidj3zs47zwwoc4v7jg7bffZjwee26vuNEuL2Vq7pjTJLGyj41FLoWv1rYNYYg8eDbJuH37Njs7O+zt7lJbZMgZCy2XC8Q9MiOKYj8oHbJvjMipLdfrS8mZkxRTgDJQVzWxrZD4a9m2hFZxxSURboF+1OTrBms3M+9+RmvrZ9BZSLqfKUupTCRpKoGHvVZ105BvNl66sJtQdWlbXbt6MXoRZL57PVxlZj6bU9kqiPs8yEOwt78rzZf3H/DP/uk/RRnRl9+d7rB3eIC2yae7vu4BaKsKZeD49JT/83/wH/LtkwT9sX/NewpcOmdXUQoCnnjiiMl4zHS6y6s/eo0H9x/i3BKkoOtwGduUZ5zCmPXDwE5GOK4nFqFx06/poDRbudt3B9P2VaXoD/pcu36DUAUs5wvqpmYxm3thhdyiv08//RR5Ufh+mof37zO3ChWul0O8aUoJ0EK5f2EQWLTSSMM4UNskRQGD8Vh47XlO3bYkcUIU2Qpe2zLZ2eHa0TVW6yUnx8f00ox8s6asaoqyZDKZMBwNubg4ZzgccXB4jbPzC+oq5/j+PZvb2IVJIY7VgfNTd4vWu6sZKEdnE3GE5s7vMb79G/yV//Ff4vd///f4+S/+HIcH+0RhRGbLypvNiqatqRuh7M0vFtaEsCLPN4Di7OyULOtxejKTvpL5BZt8Ta+fMej3GI5GNnmUxL/f7zOfz3l4/JDpZEqapVRW3Wm93vDgwQNR0LGLkKv8ygJh/DhCCZ00jiJrcCkqY45iFUXiJ/GhFz7EZDqRNdjSOeu6Znd3lx/96EccHR3JAqVFJQXwi5hTKNGmJYrCrZS23hpqpmnqTdjcnOiawd2+3LzqDZ+SlPF4ypNPPkm/3+d73/s+d+7cFmWiyYSylP2Ox2M+9KEPkec5v/M7v8Nms2E6nfjr4tA1N7e5YwAYDodcXFxYpC/k4mLu33cNi86kD0QR5eaTTxCEIbt7uxwcXiOOxaxyNB7SNDX377/D7dtvs1wsmAwH7O7ssLu7x3g88rS4Xi9Dt6Wtgu9wsH/IP/pH/5i33rrN2dkFDx6KI3AcxXzhCz/HdDrld3/3myxXa2qtuX//vq0WaW7evEkURfzo9dco64q6EWEKRUivNyAMIxbLGbqt0WLrji0i2Pu9pXO4TdTdDKjQh3PdOT/wVdbuPN/BlzsVwcubpTZuJ8vLn3uP+DfoGPVemm/pFC0ftT3uPfPot66GKI+qODwqUP/DJhrvt5/3Sgr+/z3RcFWxdx1PEKJUQLj/LOkn/xLR2DX4du/rtkndg5l2tXQmti5p8P0cnc91ahr2d12yYbbvKSU9H8Ucnc9o3vgqRlsFtLM3UfWGthaV0O3YD3w81GWPuM1X7iw42A30ja2uBEHcOa5OwoJCKWts2fleFEWoQBHHIU8+eZMvf/lLPPPsUxgEFApVyGg49sB8l0ljjPF+NA4kz7LMyzt3ExPXS6GU7Y+wgDFsGSdixhzYeLa9JIvbXYccw6QsS/+eS2C6tDDAs32cImw31scI3dvt98WPffR9x90Hrmi4G9r901F7XHOaC0qTJLEeABna1IgW+BlRFPpySy8bEEWxD6JXq5WnNwyyHuPhiOFwQBTHFJsN79y5Q1s3LOcLllZze39/jyRJ7QUUB8WyLDz/12m/G3thylaQxqZpKZPSlqZqFDVpkpCmCVma8uxTTwCGti65ODsTlNIODF3XLGcX9LI+Y2uCsi4K3n77DreeeFI4yXlOkiY+wEgSGThlWVGVFXVR0jQ1y8WCk+Njjo8f8JGXXuK5D30IrVtB8uyDpO1D5gaBMbKoyIOjLe+/feTkZYwRKdcuTmxj7iAQdah+v8dmk6N1axWpWl9KdJKTbgETjXXtm9q71ZZNnltEAZ+AVFXFZrORQCYMyNKMIs9FjaRphCKEJF30e0x2Jvy5P//nOHl4zP3799k73EcFiiyTnp5WtwRBSFkU5FqzmM2ZnV+QlyWf+PgnePnvfYWNcxntnLVsnWBWG9vAKJOOCZSv5m8LG6qD2nUqI3avTo3MNVf7hd1peXfKxYBXzvCV4a1FOAB5XlCXFXGvT2T1vCOLZkhSnDAcjRgMh7Rac3p6yvXrN9jZ26Osa/LNRqQfm4amFVWuXn8ofT+x1aJH0dQVdS0N44EKrGmkqG6s8hVGYZOMSIIOA2mvx97+Po1uOT8TrmfbtDStEcDABuJN3dBqw2S6Q12Lh0SxkcAeh3Zi9c39YuB4251r7q6/AixfWNvoJZi9zq/80s8zmQz44hd/BmMqHjy4A1oC5Xv37hDFka0w1GzynKZqvYHkZpN7fqoEzmOhAhnNjRs3yLKE4VAUnpIktQlASFUVXLt2yMXFOXEcirN2FHH96Ijbd+4QBgoISKyxEmorKR3H0mumtd5W2QJFpCKLUiUEShGEIRhN3xq+uT43f7wWpZIq4UzQLKWo2laMNLXhqaefpj0+oZdlxGkoZn51RaADO85yNps10uzf+MUqiVPCQJTCer2UxaLxJk9gF9lAMbu4oKlrojiiaWomE0HC8k3uzUbfeOMNW+FMODw85NVXXxV/iOmUoih9NfT8/ILKypHnee4bFuM4tuge7Ozsc3Z2LHNpIIttoALW65wojqjqmltPPcUv/MIvMN3dEapRI6OqrErCMODo8IgXnvsQAE1Rcnh4yPm5zOu3bj5NXdc8fPgArSu+973vU9cBdQUvvfRxTk5mlKXmhck+YRQxu7jga7/1O7z66qv0ez1Wecm6c05at9w/OZPm61aq/YGl/BqjyMvaMihbAmXlNh2AYRRBEHZoxzaQ8gGhUI98Mm4fIZ9SuDnoylIgoPHlBtftPGdV9bpJyaUKw5WgjW7RolvSuJxoPH5TnSzk6icfHWx7dPnyUVz6zKNzig4Cbzovvd/2qPNxcfCV35LAc/s5f5T2BnXP1Gy/9NhDeey160yL7/k59xPua4/44CMDcaPBaPTJj9j8s/+QcPdp0ue/iBocEIyueYDNzeF+0nbGfW7u7q579jXF9pY7PwwPsvnTU6Bbyj/4W+izNzDLh5JgdI5RQFzjaXYe8FPy3IRh4BMfd8O2lChJYtwhbinmLp7dAjFX41yn0jYcDBiNx8LUyXrcvHWdZ599ioODPeIkZDDIRHAjDlDE3q/MxW+O2uqU2MSYVOY6B452hXgcqAoi6Q94qqljyJRlyXQ6ZTSZ+H24qofbhzsvR+3vgrbuPbfvbhO660uBbVJT1zX9Xo8oFKNtZwL9ftsHTjS6SHbX8MRlSe49aRZttxfNROzuZEwmu7RNw2Aw9iU013/gStFHR0dyEcLQTs5CqZns7/HpP/GT/reKYkOvl1mTwIa2rS8dl0sw3IVyaJ02Fb3e0Mt86bZlMBoSmZqz02OO12vQLW1Tc3Z6wu7OLr/9O99kvdnw81/6efb29kjShEmWsVrNmW1mpL0+ZW3YHY2oi5o0GTIa9YiTiLppCFRAWbUEKhZqWJgxGA8oNmuSOKGfJtx58zV+8AffJt8s+fhnfpK2KYmi2LtKO/WaujG+T8U+fqJJjsBhl7N0p+DgHp7Qv+4GjlzLnIWtVmVZRhAIP9xNoO5PeTiEj9+agOVySVVV3pBGOIQZ1O12UrClNt/Q3rbcfOImSZJibClVpIWlKpAiJbkwTdg5PCCwBl+hrXyliXiVLKsF89mcVmsOrt9gPpvzpS//Ir/1+z/gVd2igwijt71ASjkpRDBKMvjW2EU+sDUIP4N3Z2ZXznUqdnYa215++/Guc7wNpv3f7G7dh1XA5ZqJkfupDcU6J0l6JGmPptH0+kNWiwU6bEmylCBUaCVO4KvlkrOzUw4O9tnb3+PhcUvlnDvtRJavNzR1RZKKHK6xwXyQxKANsQoIohTdtsLzRpRrImfg2LYEccTe0ZG48T58iGlbkjSlLEVNqtXGukEnzOZzer0Baa/HcrYgQPxztiipQ7w6AYv9i79WSl3OwWzADqB0S7Z8i/HwORYXxwwGPdIkIUl71tfgnPVqzs2bN8EYkiSV5y+UY42imMFAJALdHDUYJownmQdJ3MQrQb70Jri+Jq1bPvrRj3BycsLh3j7z+VwmZKVI4051Uh4ckevsTOTuT1FBMV7eMApDGouiOSnY8WgkHgFVSVlV4lmRJNKjESdURcVmlZOlAZv1ir29Az7zmT9BlKR85GM/wZ3bt7n38G2KxnJr44jlbC7N3FUtVdkkBgLqumExX4JRDEcDdKvJstR6IEhVOU1T5vMZbdVSbNZkWUZRlvSyjEGWEYQRm4c5xUaapM9Oz9Fac//eA3HsDkJOTi7QWlPV0qcglRRFq5fi4IsSidesx60nnuT+w1OOz07p9Xtslita3VLaoN5VNW89+TQf+ejHybIBZ8cXcswqZLVYcnJywnq94uDwkOViyZ07d6hrw+xixnQ65e233mZlG9WruubugwecnJyIklUYWtrVCgPUCpycqu9FvFj6MbqNuW0Q1LagpD+kaY2nlTS20V8p5Q0p/fOhDK2jB/ppyBmUyaaN9FBh0VavvmS2U9f7g+OdIHob/W7//2og2vmcgW2F3SUA78oXPiA6/6houQNAXP5oJ1TvRq6P2c32gy7wdaFtd7/mymcf+dPbOUttZ3P/QfWY/b1rH90X3u/6vPu4TPc3H/m57uYS08tU6i11aJt0XqUZad2idEP78BU2D1+RSkfcJ7z+cYLBAdHhCwTjm5eTpjCyAh6yjqMtAKfbd+W9l47YALqmvv27mLakeeu3YXNmEx/AaOuPYvxYDyxN2a3rgY2PnIpca+0C/Jx7qRoR0zRSrQdJ2pNE5nmlIIrE4mAymdDr9bh58yY7O2Ou3zjwSlGHh4deMMeBpnVV0O9NaCpNHPcwrfbxAuCDfGdY6ZSgHIunqirfR+sAC0d1cj0Y7pkbDrdKgsPhkN3dXWGTWFDLVaG7m4t/u03dLqFyoDDgwXmX7IRh6CsfXeaN6/kIbOz+QbYPnGi4so1TJrram9BtHHZNJ11J1hhQmbqUMboD7z4Q3f2qQBGrhKkNfJzs12az8RQcn0RY/pq7YK4UH0WR7/ZXgwFFIQ2AcRzTG49FuaZRpP0R57MlvSxjdrGgauGtO/d47oUXmM8XfO0b3+DGjRt8+MMfFqlGY1itVuynPcqqpCUiCUPyIkfnEmQIX65mtVr6psooigj6EUQRSSJKXH/6z/xZzk5P+OrXv0Y2HHPj5k20XjOZTEALFUubbRLRbeaTCV8m4S4/0Wf6SkqikiRcvs5RlDAcJCRJn4cPH3L//jH7+/us1+K+u9lsSFN58LQWvnerNY1tsu8OYqUUbdMQhcoPVncv3cLc7dsoi5KyLG2JMEbr1vbCwHgyYTQe+yS0tgmNoKoBcZow3d0liiRgW+2tuXfvPv/Lv/ZX+D/8N19ntveT0Fi5RmUnWIVHUroqKqEtGavuKm3XNF8TMQavact2wvbcYhsxO9Up+yLiG9HZHLLCdrkwKK/YMV+IdHOYyESYpClhLLKoSimKUBGtVoyGY1G3WK+5uLhgMp2CgZOzU6q8JAgiVCCLRlGKqZZyjuOAoKsgDZ2CrgdRRBTI9XXBUJxEHF47opelzGbnrFYLoiAQhaVKDLqCMGQ0nqKBsm442tunaUR2tLLVxcB6cGzjBCdP6A7najthp7Jh8EiWMg37o4xbN29gTEUaRbRNQ5bJ2Lh58wZvv/02SinG47HnxJalTPLOVbU7N6ysFvju7q6fF2prYBaGUoHtSlBnmTSLizv25F0S1VueL77B2TgU0HnrdBR63By5TfxLnnrqKXq2+Xlghmg0y9WKqqql1J5mnByfcXR0nSLPWa03jEYNN27e4t6Dh2zOz7l16xY7+2O+/e1vUWxyKlMThBFlWduegoairEjiFCepm2XSwN9UIt6QppG4vGu4uJgL9UDD+exExrbR9Ht91usVdaMpypqmqckyUSGr6sryhCWJcPOP86JQdj5pvamhiE7ce3jKaDRif/+Q5577MMYYzpIz3nrzLdbrtai79HskccJ3/+AV3rn7gCROJJFoaqJA0LZ8k/sATfpqajCWUhpIM7xC+hAMhlobe0ztpXXJAK16VODmHuJu4N7F3SVjdiHupYDrEkL/iE296y+Xfvvqb9F5nt5zd498/f0TA6W26Kg/fxxy/e59XK2EPGp79/l3EoNHlijeIxl4zHaVcnzp982jP/e4fTyW+tStUDx2N+rdJ/yo3/RzxaOP4YPSuB73ufenk135fd1iyiXNW99AqYDqZQXB1kRXRT3Cax965Hm0D18BvVUPe9SYENZF88jzuEQHd7GEcaI021iyKxUb2tjG0Zy6PbZRlBLH0guVZRkHB/vs7u6ys7NDliVMphOefvppr9Y0nU7J8w1KCVi0Wq18fx1Av9+jsdVm11vhYjMX0DsaFOB7eLv9ao4K5dYAF2O7tWgbIyW+r8L1BtZ1zf7+vlCa7Pm6KokT9nEUKNdf6BSn+v2+XE8bO3djS0evcr+l1Damc/fFmQt+UMrfB+7RWM4XvqLgAlWXVLgL6Di03eDz6gDvBp/dfz/qgB13uDvgXOXCNax0ebuuHOQGmWtadlWN2KKO/X7/EnKpAnF9RDegDWW54eLsjKoqqUtRANlsckajIUaLAWAYQNMIUhrGKUk2QBMRJeLEnGZCJUHh6T5hFJFmKbUWFLOXxoQKogDatmYxn/O73/xdXnrpJa5fv06aZh2AJ7yUJbtrJjSmLc9WKWlsd7JqaOHuD4cD20waifNsloERRRhHNXOa8mkmOv8uIBuNRuKu3u+DMjS68cliV9awLEuMrS4ZIw357v65sp5SyldD3BZHIU1T+8ao5XJJGIZMJhMxn7IVCa21TziqskShWK9WNHXLYDAkCEL+/m/8d/yf/t6PKPY/Jn0KWLm+Thn92sEug+GQ6c4O88WSN998k7btJA2XHxH/R2D5+hL8SjfHVZM+RyuTX7MVEeMCC+WrU9v1RKOMXWCVYu/ggPF0ijGwXq1pm5rZxQVxJNK1TpknimI2+Zqyqrx7+ybPOTufsVrYxlcX3GqNd7Iw24a7wCKu2KqVwdDa8+gPBuwd7JNlGav5jIuzM1aLBU1TMxpOqJuGomrY3d9nPJlydnGGMfDErVusNxvqMuf0wT3yzcbv31eYfL2nc4XdOmwTH9wn3LNvQNHyqc1X+Nf/9M+gVIvSkvwZLUhwXW/1yrXW1jE1YbPZUFr3Z8eHdYGu1iJNLdW8LWgB22qtE7wYDoc0TUO/36e0FKyqqnj55Zc9gOEWQTdPdeUEu/xhN2c61MoZL43HY1588UWvh962Lf3hgJVVQZrNFjR1y9nZOePxhIODHdIkJopi+r0en/7MT/LCh17khz94haeffxql4Cv/+B9TbHJq5y6vW8p6Awj1bbMp2KxlfnLeP877pK4birJAty1pmlEUpZ1b5XprbSirkqbRpFkP3UpPXt1s54GmaS3I3/o5Q8CPhra1CbkL6u2CK8l1SNNoIuuNtFlLc6M24sXTtNt5yC2UdmBvxTfMtoFT20YIN5dEYYjzRjIYkeC0Q9NXJmTnHrDoLpdX17Tua35sd9bAq2vepaTkPfbxqNc/6AL/x7l1+elOevOP9zi2icbV7QMFKY/aY2dcdO8FbO/Ho97rbu9137qvv/dR/tGu0xbA+GBXIrhyrO/1/e55vYti183tHtWo/R7HK9u2EvXu/Ozx1+TqcYZhYGMJfMDsAnUXvLsgezqderT/xo0bnJ+fMxgMeOmll8iylN3dXZpGjCKlXy2hrAqKvLCVf+Pn5n6v7491vV5z7do1qqqS7yVCeXW9WYPBwFObVquVV93rqm+6dccpgy6XS1lPbBtCr9fzVCrnE9dVoTJGPI7KUkw8syxjOBoJKBmGjEYjX3Fwa4+r1Hfvv4sd3VrpjAIdcObWJcCLCLl/u++7MfXs88+973j4sahTXcqUy9xcRzzgDflc9tVtMLk6qJws7NUJ1mVfs9nsEvLl+GgOrXTmcd2JxA2Q7r+vDlhXdnLVD6UCWkI0hiBKCQNFP0kZjqfykNmM3FGHqqr0mvSz2RkH1w7IegOaFuI4QxsIgggQvvPVhMwoQ4vsMwyUGNMhA2I8Dfnc536Gfr/vaV/KoeBKkO8traM7AZpL85gbwG3bkoQJs+XM8pCPvRpXmqasloWnawgdoWdLkSGbYusUvlgsmc9/YPtuUlSED9bcIJQMPEJbw4lu9cINaHcdxuPxpUxaYajLQpB9bRgPR4xGIx+kREkEBqpSKBdRFNrGLvlN0XvWVFXDl3/+C3z929/jK7Vw3rUx0HYbtBVNqyWgaVoCAhQBykgQJA6p3eqGzQi0wQTeGsg2viGBsK1mGLVFHR+lv+HCa3k38N/F2GZhFbC4uGAwGBCnGVEqvRr9wYDNeiU+L0oxn804tw2zw/EIhaJpW/b39jg8PGAwHDC7mFMVBUZLchMFNohyVC13TEqCvMYGeUmaMplOGU9FSvfi/Iz1fI4yhqoqrUCCoW4a+oMB4/EOZV1TFDXXb1ynNYayKGiqSszGbLAnTugdJSnj/w8TbCtKKnDXw8oB42QVpS+mf/QCq+Wc6WQoamSVJkkyGt2wWCz8JCnCE+Kp0e+LB8JisSCOY46Pxb11MBj4Cdclw7OZNIe7ib0oCrIsIwxDr8pRVxWDnviYrNdr/32ZXyRAlnK8M8STZl/xoYio68YrCS2XYoAqvVGwv3+IUiHGiDv7xcUFy/WarJdxfjbj/v0H7OzsMp8vOTq6wXxhf1+3vPLyy3z7W9/hy1/6El/48pf52r/4Ta7fvMlLL36Ub3z96zy8/4B8s5F+jkCqVmUpimBNLcF921rHZ7MVx9AW5ZJTtAtOB5GXvqCWtr2QZ98Y6solGkIjaLTxzZh1U0uAr50LiquwOT8kJ98tz5guSr82OIWk1s7LjRYQQQIkqSw2RvsGej/+2tZSdp1ymSRLqlPpNFipZvfcO0lro72Pzvttj0Nm3++1DxJA/stOLh51jA7Iuno8j0s6PigC/7jvXQUi312V+GDX7VGfexTt4yqQtx1Dj05WLu/3cqK0PeZHxyLd/Xf39bhr9H7X7r3OsfveVRbJ5Z0E/pnQWttHSuKPR+3jUmxzJam5um+ltrQ75cAn5QAv8XTpsjJckCwAzIiRNWoWw2fx9+n1erzwwgsMh0N2dna8kbML6jebDf1+n81mTRDAeDIWwZOiYJMvrZplRRxHjCfixD0YDG084wyUA18dcHRZpRR105BY5213TZw09mg0uuQj5qoB3QA9CMR82FUPer2eFaOY+F4OpyTlqiZrKzLkvt+2LcvFgv5w6JMFlxS5WNgxf9zmVKm61/j8/Nz6SrWXGtfX67Vf99xrTujH0Y3/WBON1Wr1rqz46r9dpukGH+CzMFcaAt514t2TcCUhV4py+zVGGmOcnNfVh7+7H7d1Ky+ADx66g10bTasRUza3TyOcfIOxSQMQQhQpVJQQpS2DyQ4H14+E85ek4j+gRDIyUBHGBN4YDYw4idOiFIQWXw4tyiYmKHLDJ+ORrHGdcqBSiHKJ3pqquKSvaRoMmjiOvDKWS8iKoqCmQRGSpj2ytIcxEIUNcZSyvy8PSJIkzGYzwIjEZbGmKEVbPo5iixQIDSzPG4I4vPQQdX1M4jC4lMW7a+o4fw5Z7JY2lTEESUqWyv2+2qAk9w7SKEJpQ5VLguR4uw5ZrsqaKIr5y3/+T/Odf1zy4PQc2obOiJCKTNPQajEEdAjOVmHKlRocoukqGnay7aA8Ssn3JLsUE6FLEJDseFvhMDbZUdvqCgZrywxGa2qjWcxnTHb26Wd9FtWcbNAXfvomBxQ6CmmbGm1gvVqxu7NLmefcvXePnd1dJhNJxPPNhvV6Q7EpaNtma1Zpj0GeHzt2sh6DwZDxaEgUSen15OyEqirJkgTTtgyHI4IwolgvUVHE7v4+KgiZXZwwHI+ES79eoYCL09POtdNbGsmlhbv7fFqimb3mxh+jvcbGEIcBnzwyjEcDinxNGqeYUJFvSpabpadFbTYbX4lI05Q8L2ia1vNRB4OBVxtK09Qn325Rc/OYo00ZY7i4uPDPalVV5Km4Gf/whz9iOh17Wme3BO3Gspv7mqahKKQhuygKG+iXPhmfzeZk2YmoiBiIE1EBK8oSjSEMIhaLFYeH12mahocPj1lvNnz8kx/n5OExeV7y/HMvcHpyQrFc8if/5J9msVoSoPjiFzPefvNN/sb/+2+wWM7Jq5wglH6hMIi4du2I0WiPN998k9Ump6kdd9d4IQvxaBDARbdbl2hjkw7d+fuloMeas7qtiyRfRlBlc/NGYB9H9xtdylmXhqHRl4027SPJleOQJtJtMCiVDff0y8uSi9tns3ucvDvQ+3EDvy4A9kG+/0fZ3g+5ftTr77d1g6Qf5zsf9P1LQ+YRa7e58r0PchwfpFLU/b1HBeDdY3n/RGf7fjf47vbxuf1fBUndvh/He3+v833XMT/i+LpJx6MSN5dQ+H8H3d8y22dAbUFd731mtiBvF7xRyhDHLhYQ2fWB9XuKoojxeMx0OmE4HDIcDkmSxJssTyZT//7YUqmbRhRKpXIQo3W32dmZkqasVguGwyGj0dDShgKyngiC5PmGLEvJ843tf2ipSu392ebNnOFAgCpFQFGUPtgvisL3+GHjms1mY1X3Sp8QuDkuz3MvV+u9b+zmgv0kSXyc7JIHZy/QBcHcZx17qNs4XpWlt51w98Ep9a1Wq0ssIJdMuPvnrrdQdwtfoQkCkTt39CtXSHAFhC4N+f22D5xouAXTcd66AYP7u1ug3WtXy9ou0HfNMC6x6HozOBUrZ8TnaD3uQjjjpkc99O63ul37/jHpPNAu0XCBb6BtabsVF1ndNqSJ9YQg6ADAlv8XhVafPiSIJRMnkMBJpERDSTxCZbXwu70pkmyIY7pFxm1g1Taaoih9IO4ClqqqJBhF0MP5fO6pSFVV0etn7O/LYFksFvR6PY6Ojsg3ObqB2cWMfFOwVZbS1HUjiVOgWG/k2MMwIElD+oMJh4d71ik3ssld6NE+3ZlM3UMlD4ZUJlxDE+DvtVJbt3PYTnpFUYhvROgcPAUR7/V6NLaHoqkb25ga01BSFuKM26IxgSEMI6IooWnlYdoZ9fjpZyL+adUwXyy26KkSRL2qJLgrKwnWA28E9KiRbxMDLQG6c02VxjNj0XdlE4ZOjxEuZt5WOxQd+cl3VduNG2HMZxf0+qKh3R8MWK9X9IdDMJq6dI1gY8qqJE1Sm4AnrFZrTo4fkmYZ48mU0XjEcDyibVqqUuRe27qmNdKIHwUBkas+JgmhCqibmrOzc9bLBSoI6McpBk1RiinYbL5Eq4D9vQOiOOXi/JwwDNjf36OuK6qiYLNcUldVF9uziQOi8GULcFclMF2O55vzLeLtErrpdMKoFxMoGPb7BCqkbaCOWtqmtWZg+D4L59VwcnLm+a4XFxeMx2OPQpVlyfHxsX/NoUaDwQBjRNDi4cOHuIquuGZnBEoS6k9/+id49dVXyfNcjDobTdvImCyrUq695bq6wN3RdaTqp+0iDSoKaBvD6cm5f06apqE36LHerMnzEgi4d+8+i/mSzTpnmefkZcXTTz7BL/7CL/H0k0/yW1//Gv/5f/qf8rkvfZmf+dmfJYoiiuIud9+5z4deeJG33n6LSjeEUURZViwXSxbLggcPL3jzrbtClbLzvatMOkGJqr1MNzEuW1auZ6kbqCl/X7uPlumMDKF9Xp6nlR0cgU88OxXGq4+N2y7FZoaOkNLlzYox+J343zbbPq3tJ7a/9YfMCT4I4v4/9PY4CtF7BfF/lCTp8d99dyL3XoH9H/YYHhc7PG6/3XjncvJw9XuWitr5nnt+urvsJhrwwWjk73fc70oeO69dTWwfVy2SN7vH363QaFTwbtl9pxLnTHuzLGN3d9dTfw4P9xkM+qxWS6bTKfv7+1y7ds2j8s5Tp3sevV6Pu3fvXlIzdQ3VSimWS6lc7+/vewqRY03s7Ox4CpHEOZWfz8uyZDwe+x6Efr9vl/eAMIwJw8SKhoQIpqGo69LGHpGtjPc8uFrkOWGHEeLOaTKZXHLMdsG9SxC6ik9deq3r57vahpCmqTc3dffLVT/c8aysFQHgkxSXdDga1XQ69SpX3ThsPp/7seVibQcEO9qVA5OzLPMVmG6c937bj0Wduqqe4gLH7gVwg/hyY6TxF7IoCk5OTi5ld90M21Ux2rZlvRHUcGADAMBqnvd8w0yXKtWdBNyfXYpO9+K599Cy8LdtIzzkJCZLhXunZKcY00EhHMzGVrscY9BhTMC2jBjF9rgMVi/fEChDU9c0ZY4Bkfe1POnlcsVqtWa5WHrTwdZSfJI0YWNlKl1Vp9/rMxyJS/BwOGDQ74NS9Hs9K/kbEEcxTaV986prMIqThEBBFIt0mzGGIAzEZ+RK1u1kObVxgTYohJKklNCenClgU1ecnZxQ2b4BpRRt1qMochtwCyXGeUO0bUMQhERhwHIjCZZQT6AocqH0VDVxGNky4rlvLs6LnN6wz6bcWH6jJG9CrYr5ycE5xbWYf54Hwn7z6DhUVUNZVIRhjArCK+ubTSyuulcHzsDHoEJliyMGFdqeDCOBlvLO4WwTEPDJhktoBEHdBjwSWItSjTFwdnrC0Y1bhLbaUOQb+oMRa72wev4y8cVJymq5JOv1GQ5HVHVBWRacPHxAFCf0ewOyfkbaz+irvgC+AULdsmZdddOQr1esV2vKohCPlyiil6XUNskT3n0LQcDOzh5Zf8ByvaaoCq7fvAnasFotMU3Ncn4hrJN3LcgSADo02qHIrsLiqh4g19MKI6KMcHQP1RnDXuz2xGq9JlQxUWj9VZJUnoF+n4uLC6q6snKuG19ydrzcfl+oVArFZDwmjmKqoiRQiixJiYKQoqyYXcw5OTlmuVr5RVVUTqCsJHFZr9Zs8hwxDK2pioYojmkbMYV0bvJhGMp1V0ZoOkqhlMgIEwTU2nB6fo4x0DTSK5HEMbVuMUpU0ozRpFnCtaNrvHP3Hqt1zsWrr/HDH77KeDjg1tERbVOT52t+ePse//Aff4XhYMjrr73Gj179EVhwomxrGkuHUkgS4ZIhjUvMXaAh6naNbrdJglK+imCMlZwMthWooPNQGcQw0G3b+yybRvuEXbueJYf8br/k+5u687vbfzepUMqqzHHpZ/y4upTnqM5z3jnG7uMpv/FH397Nce8mWFc/fOUjj/j3u5Khyz/W+dr2eshb3QDS5l5cDk49VOJ/V/nf8c+v2h73o4PYDgru9/r45OHKL9scc5tk+j67S8nGu1F6d5QusXeKX+5tSRguXwNj17bA9YcZF9jbM7Zgv1Ly/G7Ph87fXZXCfVb56wCBf+1q/+r2XB4VtKnHvG+PU29VFS99xhhfkQjCwL+mjazX7nV5bC9Xqtx/rsIQxRHj0YheP/N9D67y2+/32d3dIUlSlILpdOeSf1jTVKxWS8pS7ARcwB/HMfv7+6xWK2FeWBbLZDLh5OSENE0ZDAZecakbAA+HQ9+r6JB+N6c70SIXm45Go04jdJ/1KidQEQphdTiTVaVCMC1xloIN9lerlZ+3ellG2zTE1uVbfKkEsHNKTy6+WiwWvhqQZZmPWd396fYWu6SjqiqWy6WPm1yS6s6jaRpvDSFxrwh1ONp05Krwlurb1LV4OiFy9afzU6qqYjqZSlIWXO4XbNuWpm28LC4GibF60ndXV/JbRS7UMFe9cfH6+20fONFwJRPXEOKSja6xB+A5X1cfqKYRDrXrD3DfcxSDLoc/64l0olH4E+8PBWGsq9pnsV2KTbey0t2nK0m5Y+4mIv7fbU2ABDPY33DJU6MFGQ2tSokrR+V5jgps30inYuEqNovlnLZtfLYuiVZGXZSsF2sbnGwuNUU7BDwMpSeh10sY9PuMx2PWmxV5vvaZ6dBy8tygxLoQ99LMJ1BREBBlAVkW+UHuvD2apsHNP64vprJcbHfNXDXFlfhcZuzoBk3TAoYojGh1C9qQRRHL2YxekrBZrzmpKvH60FKydAGek0FerVakaUIYBT6b32w2VGVFFItfw3olLpRnZ2c+uZSJqebs7FQy9yikyAuiOKYqKxSG59OU5cUb/O7FhPzos7RK7m+rYbUpiJKMKJTJInCorKdVdKZ4t3IAGtvXoSzqbhF4b6BrFyytLPWDS8uZjaNdMqOBwH/AOD19pSirgvOzU3b29kjSDK2hLHNGkx02q4Wcq5FCS9tqmlYT276e1WJDVdcMR0NWdctsPpMKRhjKYhgEcsza0OrWPi+KJIxoy5LFxQyNYbo7lQC3aqiaFhXE7Ozv0+sN2Gxylqsluwf7REnEZrmEpuHs5NhSXOxz5hKH7mTiShfdoMN0AsMO0iwJhyYNQ17Qr7BZ9Tg9PpY5JE0Y9AIWiwuSJGY6mVI3jcgWZhlN21A2te15irm4OCfPC6bTCefn59RVTb7e0DaisuSQuXyzYZMXGBNyfn4utLy6pq7PwRjSLGO5WdvFz/hyvpxDgCFEN3JvjZYqmjJK4lifXVklJhvvaFshqVrQukXo0YayLtCmJUkTSouSaQxns3M2xZpNkaNtRbaarTidv+Yvs7p/TvS9VwARhGi1ABfaVua2kZ0B3fg5VF4LtlW5q0F957VLyaRNPIIr38Gdsv9jmxhcCmyNS4DdD19Wamr9uHlcVN75auc57gbphitULQcIAEZf3re5st8ff1PbKN7ueRsrXg5ytdGXAknlj99c+nf3kLpB/OUkofN3FzhePbLHoNtB0KHzYMATT7vPazeA3tJiu8Di1bPsJnSGy8Al2GpBZw3H7ccHvp1KVGdWNZ3rJvuUz8oxaFA2ieWqcIdUH7bB9WWZ3sBSqd3vb6/5o3st5E3HpHDeKHqbnNAR4bhCi1aqazK3TZKUUoRB7EE+ZQNH7Sq9RkGo/P60TTpQlgBh5Hil71JZcBCiKCCxAhJOsGVvb48bN444ONzh2rVDxuMJ/X7PM0yiMBKZdOvxVZaVjeEUi8WSu3ff4YknnqAsN9S1BPuOMuTiidFoRFmWjEYjlkuRm3Y8f9gi8E6FyQXoi8XCe+24uGe9Xvu40vVluOD85OSE0Wh0SRXQof9RFLFcLj0aX1UV8SimbYR2ZFqJcQIVMxkPLrF06rqWOGa9xlW7HdLvBBKCIPD9I9042LFn3NhxcZZTeXKtAo7B45qvR6ORT0iSOPVjIwgCqlIUFSVGNmysDxFae/AXpeQxMApda9DC4OgqUw2HQ1aFlfnOt4mbUookTFisF552pbUmiRKyJLukqPV+2wdWnZqdX/iLVpYlq9XKm0e5pMHRZMqy9OpALuivqoqiKDg8PGQwGHiEvfsQay169ZPplKZtKIrC26W7EmQUCmrtBuX2IduqJDmqgkto3I3pNqd3y5UB2+blIAwlGwxDyqpivlh4a3j3G1mW+T4Jp4XsBlscx5bznni6hivtGWOoyxrTiklXYiVw4zjyk5E7L4eiuGNWCtq2wS2029LXdrJ0smuOGpUkseVUt2wXBDHaQoYsdVURJ7F/mDCSVLa6FeqV1ty/f48ojhkOhkK/sc1Ei8WCqiwZDIdW4UoqEA5RXi6XXLt2zToZXyMIlU/U3IN+dnbGer2yFDOYTCZcXFyQ57lcyzC2jd6Vf7BdggWGOI4YjUa+d8dx7sejIVXdEiUZv/vNb/N//5tfYXn959CTJ+UaGkPW6zEejTi/uKCpatd7Klv3qbgCHYZRaNWnNAbxB3EBknLUoED5heXdcOV2x+bq4tkJEECxu39AfzQmzTKKvLA+AYp8s2G1XqGMIYkjojAiiiPKvGCxWmCAQX/AjZs3MEjw6kwKy0JkZwfDIWEQChIdKNCakwfHAgbEsWh5tw11q0l7fSY7+8S2KrlcLtnd3WU4HrFeLKirksX5Ofl6eTnoUVsN9E50iYNkFd2wge0Ldh9Ga2hrjs6/zpefgywWc8/JZIIxEMcRxsDudBelAmbzOUVVUtYVpacsIXLKlagudUu+umm9go57duI4Zr5YorXyUsjGJujKzTdmq06lLbIlCJRBqUgCekfhpHM+nbEg+9U+8NL2GTXaeCTLoZUOuQrcv21gUbcOib0sG+4vZycI6/7+1Wn//f79uO1RVJZ37QuksfrH2O+/rO2xQeMfx76BK5yux/6um8Ov0moeRXPp3sf34vN3v3d1e9S9ejeVxmzRe+Noct2g3zXWu6TBHdt2be2yHLhyPdz7XRqHo5R0z0s+s61oORomYKWzDbrtrOedBMbQdnCi7XkpJSIgrnLx7i24dB+6W5fy2a2kGK1Ranv8V9O7btUhtOv2u2hNXBkHndKVm0ddEmSM9tfExRKBzTCGw4GvCuzv77Ozs8N0OqVtG5548hbGApb9wYC2bdjZ2aUsC9brhY/lXCWhbQVI2dnZkf402yMxHA5RSnpB8zznxo0bnjLk5i5vLaCUD8Qnkwmz2czT4B3jxSkvOTpRnueXGrtd8J6mqe9DvTp+3fE4g1MHXLrkZDKZ+IZul3gopMfBJUOz2cwLDlVV5cflZrNhPB4zn8+9GtR4PPaiRY5K5o7N9ULUdS0y9JOJT6pcXOz+7Y7fXS/Xu+foVGVRUlU1vV7fJwIuJlJKEYSKPN94jwxHv5IkM/LX1NGxHCNIKcV0OuXs7MzH0k7W3V0fl3S4Z2uz2XjbiKqq+Lkvf+ERz8/l7QMnGuuldJ5vNhtmsxmz2cwfgKMndbV2nTKSO+kuhcq91lVPcoPRcaMdV98gKi+Nbb5xN6nLf5xOp34/jieX57nnVLus3X2nO1kbIy7RoS11OdS+rms2+cZKOArFRCH0hSiKpFQVRwwHQ5ykqavmBJY64/oauqGUGFQ55AbCMPKBT6QCGwxqa9Qnykm5vbFuEpLG55I0y3wZTnjYBVEocqUuAaqdrGywlSczRsqnlZXkXK2W9mFx5cwlWmvOzs44OTkBsHKzU8qyQCkxnhoOh6yW4sAstJKEwNIw7ty5zTvv3KVtG37iJ37CGmMFDIdDHj58yMImcL1ejywTqpcrdbr7kyQJe7v7xFHsS6fu4XRlWcfddAmaS0akXBpRVg0qjPj+Kz/g//Xrf5MH408RPf9lH89nWUblHZLNpaBQ1ib1CADVWPd2K59ptO3zkM8Lrq1sstHpy7CJnKKzoHRIJlv0WBSaUAqCiL29Q3rDEXGSUFbSBxEGIXVVslouaepSEnBrfFiVFU0ricRkMpaKm63QbVYrjk9PUMBwOGI6nYhUqX2Gyzy3jvOhlEuDkMF0h+FoAkEgzeVFwe7eDsP+gM1mRVUULBdzVos5mNa1K4FPMPBnaCysL1XADupsz91dbt0a2wysqX//v+VztzRPXtslDuHjH/84WmuOj4+5c+cOy+WSQW9EHKdUdYUGFqsl88WcummtepJQxNwcEDjER26aT+rdf84LpK5dY5+xSFPovuLRqG4/hTGCjGtbYZQ5ygV0l7NXAW4lMNHgm6uDIBD00X1SRYCobrmApKorQU15d7Dif+Fxgf+Vf3fn327gd3U/V7fHBenv+r1HPEKP2s8fJsh/V6D2AZazSwj1I4K9D/K9D3Rstgrwvp/r/P5lCtC7f/9RicH7Hd/Ve/p+ycfl6+OUwcAlGcpWYY15t/DKo66lG1+AfX62qKzbXPDTRfvds2GMEe+3TnLVDdhclbvbP+oCraZpfZVm+587Pne9331NtknVu6/x1QqH8muEVFQkxgguPfOuKqMUvvLgdnO1KnN5/y1RJEqLYSgqj67yOhr22d/fJ0tTnn76aa7fuMF4NKLVLXu7O7TaMQYywjAgisTXYbNZ+nOsm9r3tEmDMz4gN8ZYFaaBpzzN53MP9rnr7pIGFyS7KoNjhTj1p81m4+k2jinhBDcGgwFVVdnjTX0c6NRNXa+Cq0g4Gla3SdqpIzkWjPu3iw+7IkOOWdM0DXVVEQaB91laLpeX2DhOBTTPcz++3FhzdFMncBTHsac4dRvD3fG757Dbm6FsvNY12utWQpy/Ul3V3jPKJXtxHKONZrNZ+evjqiqr1YogCImjrYqUS5yqqvLXxT2j3YTKKUu5/1xFJ7Mxp+upruuaL//KL/B+24+VaBgjXLK7d+/6bMhxz1wQ6zIsN8i6DeTd7LVL++miie7mitFW6W+k279rggZ8Y+be3h5KKf/AuAfVSV3CVk7X/YZLjqqqorRSYkEQ+CzbKykomyxFoUcY3Hloi0YqsJruYuRnMDRt1UE5W/HqqBviJKa2FCxBNrYJUIBC19ZMLI65sBKmThXH8eGcjFqe5yQ2g9XGMLu4YDqdMl8sfEIShSEXFxdijGUHh1KK/b09Hty/T55vCKOQXtZjuVxQVhWxHfz37t3nqaee5OMf/wR3777DcrkSla6mRhvN3u6uD+7n8wV5kfP8cx/iW9/6Fr/3e7+HUvDUk0/x7HPPsVotSZKYqiotulF55Qh5iDckSYyyFJLlUqRIjZbAWUqjLpiW5CJJY5TCOmQfEscRSSIqEoGSxMsAVd2ggpD7Dx7y63/zb3I7+xjqic+ho54N1sAHxRb+8qCZwPPu6cexPsJwWyFTlvbhH6VAbRMNR/8wSGndJx4ycpSnTsmOnXldl2WugpCdvQN6gyFBFKONOKgHgSIEynzDZr0UBCMM7P2TnhsVBD5AVQo2mzXr9cYn9WkqzuCmFYnbVhsaW6npDXqMxhPipE/TtMyXskDt7++RJTHFek1V5qyWC+ZWtWx7NW2g5RKnYBvUKRtke861vbZbDrb211Wfv0n2nf8HN6/tcXQw5Vd/6Rf43ve+T9+iLXt7e7z+xhucPDzn85//OY5uXKc/GLDcrPn1v/E3mM8XbGyPiZNG7UooooRWVNc1TdsIDbBtKcpSZJA7wc52npJjdJWIy1UC1ZFt9RfC3+9LDJgrgIfuhOPdgEYR4jhWrrrhfk8FlysV75UUPG6qf1yw/kg099K5Xv7M435bX003O8fR3c//EImG+857BfiP+977b92K5eP3d/WYL41PLispdoOc97un75dQPOr1bsKwrfq74wnAuGqGVAu6393SmP1R+PcdZReZGTsAjHxGzM0y+v2+PT7jEXAX9DeNBN3OL6Gua05OTtFa+34CF3fM53NPSRGzXEn4HTvganLnKFe+GqHe3cfhPcQ6Z9ZNfhxVyv3bJ/B2HYiiiCAMaBuhzfT7fW7evInWLRezM4ZDofscHh4yGYu8eBjC/v6+Z0w888wzttc1Z7Wc28bj3NPQBXFfoJSdu4wEq1EYidltJDRnB6o6DyGpHLSkSXZJzcgF1w71doI8jpXQFf9x4htVVbG3t8edO3cAvAFql13iwGI3zhwt58GDB+zv73s2iIsv3D1x8ZyL0bzxp91fl8LvgmOnKNg1VnXnlySJXX6ND6KdQJGzGHDN5MClfguvjmeBcxfAu6TEXcfLCUPhg/dutWQymbBYLHylwTV5u2RFelMjH3NorT01ra5ryir3lSj3DIsh7Zo0yXxS45JAl2h1K4iu6tR9zSVILlFxNC73+fV6/cebaDgTMGel3vWjcJSiri+Gu7DdBvLuoHQDpVtd2AZuSKOLUuRFQVkUguSWJTu7uwxHI39RXULgHmqnCNBF6NxE3UWM/ERukUO3jy1VyYVKlrbU2EFlkfeyKD13MooiizBKg2RViy6zu15hGJDnhb0uQrVxN90Zo/T7fTbrtefnjUYjySyrmrquyPOSxgZEUSSOyI5eFgSSTGxVCwKL6gvakyYJy9XKPwwXF+f0+31GwwFZmoopnn3oXDIymUwIw5B79+6S5zn5JqfX7zOZjDGmocgLmlaaoE5PT22S1mM4HJPnBQ8fPiQIAl+CTNOE8XjEer1iPp9zenrmeZVZdrkKtl6vcBN8EicYjecwD4dDqlL4gkkqjuLuAR3ZcVFVJSqIUCg2eU6/3/cPyGuvvcY//edf5Tsv/5A8PSK89lGiD/8ywpk3djwoHhkfGF+Dlwc57Mh2GqEnSbOgD7P9It1dVLd/kwRF3ncKS+pKcuP/j/FUmrAJxKzMaE2gILGKX/kmpyjlWcFom8RKX0agFEJjwjfyO56+1hoaSXKII9J+j8F4QhTLfSk2omzU7/UZT8aECE+1rUtWixnz+dyfl3MkkL9bEMEmUg7hc4u1R0Bdtq6U/5zWBn36BuZ3/jMOdvp88uMf4Wd/5qf5B3/v73N8fMx0OuXzn/88t2/f5id/8idJkh5Z1uP49JQ0SwmiiP/yv/wvuLiYiT+EpSSJkpkEL8ZWjeqmFgqZUpbKZOz7WyBEG+19ILZ3xA2LTiB9Jfi7RG3xyVXney558QlX58PdLz4mYFVG+i7cAn4Vrf9xt0d953EVgO577/Vbxt/b9/7cBw3kHxVgd3v13mv7wyQz77c9PrnjUqLxOJrTo/bXTTSuViOuBslu666F73eM73Udumuym79k5Eo1AqfSx9Xm+S1l6coePeVPt919yne21Q33nlVyxCW1sPWk6f6evNeliVyV3JR9aZ84bJvHNW4ucmu+u3ZJmqA7btUuhvANtGarqun6F0Gaq4NQkOyjo+s2EGzZ2dlhf3+fwUDEW5QK2N3dod8fWKpvwmazVboDmM3nZGlKXmyIwpDYukKDyHOXhVSxHWiqlPIN0nfvvuN9Zhx4GkURDx48oK5rDg4OMUa8tlJLMQrCkHv37oOB8XjsaUdLCy45tSZjA3LX8+Ded9fCVQmcrKqs/akHqV0i6VgILubY9n9q3+PgAndXhXAxogt0nRKTa8buJi6uARzwHhXOs2KxWPj33P0N7T10gh/ud7uAtDteFycWRcFoNAK21ZLuuTqaketz6Zr2OUqVU9ZyFSBX/XHqTq4KIpUXoT7nee5jHXcedVP65MVV5Z34UlNrLyLkAO5uNcbF5V3Gi6OAuX25iotrnUiSxLOHPvuzP/3YucRf4x8n0egG6k3TcPv2bd+rcXBw4JtDXG9EHMfS2GurEC5DchWNoENXchfN6RO3lvpijCZLM9IsZTgYoMJQuuyj6NLk4I5Lawmw6s4F7U7A7jOXqiid726TDET9qalI4pimqXFIulKiGFXVFWmSelftJElQgSQSDm0/P7+g1S3r1UqqGlVFY7mIF7MZYSj7nM+FG+moEL1ej+eee47T01PrcaHYbHLG4zEOUerSwVzpbv/gwHPKm6a2vL4eVSWDyPEX27ZlvVoSRxFFWco1s0lOVVVEtgRY5AWzmZjIDYZDojCg10/9QyXXTSaKsqrp9YZ+Irl//z7Xr98gDAN6vYy2bTxfcblcEQTK+oDIotLr9XjyiSd9OVqqPBa5s0Fit7woi4vyqEOv17OLjCK0ZeLFfM5wOPAP0Hw2o25bvvPd7/FP/um/YLYpUTd+kvjFX0P1dmygbDGr7mLsXnZ/p9urIcenbZLi7iPGmY9J8uCas5SR4EsZ5U3B7AHiOxr8Imf85w0B/cGI4WQqC7FylAgjaluxJFdNW1NXFXVZUVW1VCyMaJob3U2WHAAQE6cZSa9HkmaEke2LKSryTU6UhIwnE5mo6orNagG6ZXZ2QlFsLgXPstkmd+OCAbNNnlywfTlSt5fX+CqBrivyr/wHpOWMXi/m5o1rnJ9fUOSlrRS68a/o9weSkDeN7CdQlLX9tzGYdnvzun1OYRhKg7G/3Z0KAwYVOg+XK1ULg6/c2MPvnsylYfNem6+GKbywwHZ/V6sb3W92gle4lAD9UbdHJRJ/nInGv4xjfK/tjyPR+OD7uFzR+HGO8VHXuPveo6771UTmcXSpD1K5ceCI/NmprLleNAsePOq4H1VNUcpVjLf77bIcuufSrapcHnuXf6fr3+DQ5W5cIElG42nHoa+IK1DKU28nk4kHXsQcbsxkMvL9lXt7e36/Tz75JMb2PQ4Gfd+nEEYRWS/1FYvpzpRer+fFYoqiYLFcMJ1OWa1Wl9SGptMRYai8WENlBVSiMGK5XNGz7tQOZXf9r2jDZpOTJDHLpfgITSZTZrMLmqZmMp1YqpPzZAhpW00v61NZQ82HDx8SxzG3bt1Ca80779xmNBoxHo/9vXS9BlqLgdt4PPZN0C6gdxRmF9cppbznRJeV4o7d0ZpckucSCUfhclQt915RFD6wd8mIuyYu4XCBdLePc7VasVgsODg4uDSmyk5PRp7nKDuOuiC1O39n8uokbvv9vihS6W1vkQPdrz5f7jydQlaXauWuletz7oJFaZqyXAql3SUJVblNoF2S4q5ZVRWkWeqP3/W8hEFInpeeveDOrbC0eXfdjTH+2rnjdFUcJ4frKjGOlu96rX/+l7/8nvMJ/DiJxnIpB9mZEIqypMhzCWpsKU234srqkoNeXyQ1Xd/Blsbh0EwJxrolTNOKl8XZ2Rlf//rXeeaZZ7l+/UgmBKswVFe15523rXCj27YGtgiF3ERxuw07g0yqAIFtcioY2EFbVaUgqbolTTO0aVnOxKjLmbtI1ieyk7P5nCAQHeI0zVitVhzs73N+cU5R5lSlSJaVVUkvkyBYWPmybctjMZtNzu7eHkmasN5shGtpm66dlFzbtpRVRWYHTKs1fWtZXzcNIJNCvpEmqjRLWcyFRjXdmTK7mFHZCktd12BsL8pmw850SlkJ3avVmtnFhc/GjTbESUwSJ8RJzOHhvp+8utl9nhdESUqSZLz55lukacruzpTT0xOiKCTNUoqiJI4jFoulnSAcn3BJmmbW0TlkNBqTZilGG+qqoSpLWq05Oz0Vze7RiH6/BxjG4/ElnqdwQSXpHQwHrFcr0iShKivmixmt0aRpj7v3HvL//ee/yZtv3WWVt6jhAcHB836RCvZfIL7+MRtwdqNAF5nS6dVQPpAGCabF0Vp6bSTCliDVBbKYLRXvUj0eg1GdBd1IImaMAhUQJik7e3vEUWw1dKw8naUFhEEoClSBdVY2MqYd8q0Cte0BCuR5MioUmpk1Z6uLmjROROe8L3S0zXpFvl5SFhuK9QpjxQcuJWEYfKKBC1CMTbRsomEvBVjVJR9Y20RDt9S3v0n1e/+NKKeFIHzwANQ2qMBgaQnYsdiibMVRm20iFrhASQWIYMI2YzSWHmHMZXdbdxdxiZKtgLg5sCvfenV7XPB3NUC+FEh1Eg3Y9m+4BHE7ONSl7wZWSe2DzeKXbtQHOv7ub3b3Y3y+eiX7ftT+rn69873OndgGkt09PuJQFMr3sLz72blSgelQzbq/3f1K4IJ2zLv30/mgHI9T//EP+vYj7j6o7dk9PtGwAIOD5eUDnWsq6H4UynMpzvHGj1O3XjqEsrv/R92/rds6nevRveDb6oFL4GVOs5LFxiDqSE7OyHQFtTqqRsp/9vJY14hwifstVy10jd/dZ1BES9q2sQH+NgHpblsKjjAF4jjxdNxbt55gd3cH0ISRoPo3btxgb2+P1WrFaDSSdSFNGQ6HFGXhEwoBPjSDwcD3gLS6lSbgrEcSxd5w0zUbt22LxhAlEb0sI8sElV8ul/QHfeqqYpPnPi7KNzmbfEMcRVw7OuD09IQwitAW3XeBYRQm9Ho9v/a5IDQIQtqmZbMpAAmYLy4u2N3dRWvNzs4UpRTf+973GA6HDAYDDwCuVhsbmIv/koCYa/r9nhWQaX3j8unpqWc5uHV2G6ttJVh3dnZ8LOCCfxeYAj4xubi48Ki7A6Qd4ySOY7IsY7FY+Lhns9n499ZW7UlodqkP2Muy9OarLrYDodY7zwz3mpO7dQG+SxYO9vYwxvh76SpdrgrhztsF5m78Af633TVx1Q3Xr+ykbPf29vy5BUHglbNcwuA+6661UluHb6G/Je8Cy40RBk3T1LY/x/oyBQFFWTIejURBUWuJl40hSVMCpTxN3oHweVH44gAGDg8PKYrCm3UPh0NPK5tOp57y9sda0Tg9eegzV601i8WC4+NjKc1YqTOh1kwYDYfy2TBEYy4t4O5mNHUtBmE2M3NVEmODqqau/GCYz+c8ePCAg4NDptMJdd1QW08J6CgzBcrrGm/5pVL2rPKCALlxeZ6TpCk9O6gDJdx1SSgkW5vN58RRbJuft2pJkeU4zmdzFouVr+S4B2EwGPjzcRmwG5AycFZUVemrAY4+ZYzxaIFrsprP5745WilDnEhp7d69e76KJMgDHo0py5L1eu0rR65KobUoermSmzw4IlMnTevG8xPruma9WPoHNMt6RFHoG8MODw/9xOEC+8FgwPn5OUkvRbewXOZcXFwgMbq2igiJ5/s5NMcperkH102IL774IlEUcXx8wmg05v69+7RakBX3e7du3cSVv9246pYCu5S57sIwm59K2U8HzOcbvvcHP+RrX/ttZrMFtTI0uhEJUAXB4YcZ/Oy/i5T4O8iyjUlCe50dB9kvyi4SUx15SZ80uGDAvb7tCTHKBUYuSHE1jk4AZulZo/GY0WiCiiK0waL8IXVd0bb6/0fbnwXNtmTnYdiXueea6x/PcO+5t7vRYIMADVMCB4AECRKSLVoMvskRfpMf/OQIv9p+dvjNDw4/yFKETYUjLDFEk3SEaMicwpKCICmAJCZi6G70cKcz/GPNVXvM9EPmt3ZWnXO6D2S4Iu49//9X1R5yZ678vrW+tRagXFWWSGvoKPIVShy4V0rBdAadNS5ZunUazDiKkeU58iJ3et62Q1UdXG+G3Rbb1RJtW0N5PbIjBsY3nrRgHopnSAGW6RGYy2k5jhhROmathanWKP/J/w5onR6XJVlFasmI5Hs8s6eA/n0o/F1/DUHbKSl437lOv/uu44Xe2h91PH4m1HifHpsbw6lU6ke9jo/D7/z47/64xPD33c/R+RQQ9h748OiLfudDOvV2vwuAnnrJ+/f6wiR0ePH7rNrHYx7Lsd4/VqH3k79znHuQ3kt3HFmNkCSZSB8om6CUFoBE/tlzyEXcW9cHx1+zA0VcTqdyK9oYDa2T4B6s3JPLQ+BnQ6LBe3+bKAnZ1jga537cFYxFQBJCaXRop52HXSkgTTM0bSnHjKIIsHDOJj9+XdthMBzi7OwMg6KAjiJcXJzj8mKKy8tzPHv2DFHk9sePP/5YyrPmeY7NZiOgjlJfSoQ3m42Ua+26DrudizhcXl5KXwbuiyy/SjLApF5q8ynnpsecf5/NZiIxzfMct7e3ODs7E2mTk1Q5rHIoSzSi34cUs9l6+XMcx9LLgBKn0oPEcN8PcQj3w8lkIg5ER8y0lI/tug7X19dyLM5F7vOnXn6gv7awuijPH1aNotSdPdScQ9GNS3g+5igwIsGo1W63w263k2pSYZsErtXHx0cZA/bUIKYkiWHUhSSIPam0CmSyXqrE4zLKwv5fJHthk+nJZCKdwxktIBFKveyN85jJ6JR/XVxcYLPZHOXQkoywqJFSCoNidFStiqTKyeEXUuaXdmG323mJeXwkewpzWxgt4l7D6JAxFmnSYzW+iqIQGTqx67/z1/7d99pGsR0fSjQe7m+PElHEU2dd3ZxIR+J14YTsjIGKI5n0YR7FdrPFZDSSmwhbu8eRRtfUWC5XmM1m+Pzzz/EP/uE/QBzF+Lk/83OYz+aiu8uLHE1dYzQaY7Pd4OHhHi+/+gpRFGM0GiJJUrx58wbKt6pfLpfSLv7gk8DHo4FMzqqqZFKRJBhjJNw5n88BAN///vexWq3xp//0n0YcR2jbTsqcMcTpQq+ugRwXrbWu9BwBM6Vd/JnXQe8DJ8d4PISxrRj8X/3VX8X19TVevHgBY4xMujD0p7WW8C8XGb05aZpKrgYA0QmyMzI6Iwl1JEVKueT/8/NzCaXxHEKauhZV1eDxYYXFYoGr60vsdms0TY3NZovpdIKiGEiot2lqf/7aezFc9SqllGfNLPOpvVHOpIqGI5oKVVUCUFitVjg/P0NRDHwuSySStiRJ8OWXX/qk3xppkvqE9AQKMW5u7vCbv/Xb+L3vfseXNnU9NQwUij/zHyL5+OeAQBZDnGv9hqqVa/zHRGFHIPomTSBdkAMce2xJRATSWPd9WU8IYIK18GgDOo4xmUxRDIa+AVzkyiVD+9KsjiB3poNEXTzZcM0SI8RpgihJEceJ5BB1rcv/gelg6hp1ecB6s4LpOt+MzxduQFhZyoLpyiRVDljAEa4QrJ0AdOntYAzq7/9/0P3+/wvAccWaMBL648zWh5AEHvP091NwHzotPvSc73rvbfD67u8eRXxPrjMEdu8D2j/q2v6oROP0Oj+U2Jwc5ajK6wdtORZgiVF/5iNi0ANpvnd0lcHvjDe4P2jd72GnRKPve9BLh/px+7D8iuOXW49xHCP3sg4CjiTJEMdJAMCN2FACC95nmOsIZaH9NZLkM1cQgCP81q1IgifXx6i//nAPd2XF334e4XM+HXelPBlRPF6Ho9wHD5hp1FyOQYKmaX2ztRRnvpBIkqQ4PzvDerPBs2dXeP782ZFe/eLyAk3jHHwP9/fOsZfnqMoSI++Eqw47r0YwvqrSXipghiXv67rG4+Mj5vO5fI69GaiL5542nU5xOBwEeM7nc2nERkddlmVYLpcC7uM4dk1A/dptmkaANPd0pZycZzabIcsyPD4+grmMWZZhu3VFdwiQef10siRJIliEJINVnAjU8zwXjzmJDPMgCOA3m81RPgGdogTZpzkJq9VKcifoZWd+wmAwwN3d3dG4RVGP+3a7nThM+SwI/hkFIREh4VCq79tFhySL/+z3eykIQCUDJUrMh+DYrNdrWU+j0Ug6WrMcMAly7NdX27o5yvMCvUyJpXsnkwmWyyWMMZJXw+dPhy7lZXROk/Dy3nnfJJfEeiSq/DudpC431fWiI5ajkyKMijB6ItEXWAwGjtgwOkfyyfnIPBsqZ5qm8Y2PU0lgDxPDaYvo8P2Fv/wXfrwl/FCi8erLL6SKDTdM1oE37XE1Bjbnm5/NYWDQtS3g2Zy+UtgAAQAASURBVCmsK834xRdfoCprfP3rX8fr169xcXEh1QlM22C/2WJ/cBPq9vYWNzc3+L3f+z380i/9km/21sogkGGx+2/XdVgsFq5r726HTz75BDBWFjvbtwOuOsVsOhbAzYXOSUUvBQDc39/LBGUY6c2bN6IZpMFheTUaqrA5SmgAP/vsMxwOB3zjG9/om6H4hR2GCvM8w8PDPZq2Ev3kmzdv8J3vfAdXV1e4vr6WpCH3+VwM52azEaNAIxGyWK2VkAl2tby5uUGinV6RnxsMBkiSBGdnZ5hMJkfeAiE0SYy67fDm9S3qusN2u8NgkGGzXUJrhSzLxaiFwInGsvAyMFZdGA6HmM2mqKoDptOZLC6tNZbLJWazM3/+CEoBr169wpMnT8RT0dSuOpYry7f2eTIK9/d3GI3GOD8/k5yU/X6Psqxwc/+IN29u8Vu//bvY7A5oGguDCIgzQLmU3SMQGMUY/tn/ObInf9KF+40R0nC00HwDNIlqKEUFgkQBwq9YBF5R/s0GBTMVPGlx3sMojl1IVMdI0sx7bZhjAO/RMkeQIvEJXUprtMZ1o+7axpMJl+Oz325R7bewXd+Mitcu0QlF4NuDYBmfo/s60W57QKT89Vk4idfuH//vofb3wcc+1AP+7tcf5funkYM/CrB+13lOCcMp0QgdM++7jned59Sr/+O++y6iEZ7yfd/5o9z/e8+rjt87HuPTY4Tfffe5j8nBu2U14WeOX6xi9C4S5+xh6Nl0x9FvXef7rqu/dtfvQGtXmphv9ZVqnDef3wuJKNfP6dxw3t0+iZm2lxVhCFDCcenH4rg3L993UbHje+C5o0gjjsIoCHxUxldQ0gpt63IA2e/K6fkTnJ3PcX19jfFkgsl4jKurKzRNg7MzZ7NZSpTkqus6xIlzrrmkYueIc7l8fa+IosixWCzQth0mkzHatsN2s5X8PGKBzWYjXu0och2sKQciQOJnkySRqkis7vj4+CjyHe47u90Oo9EI6/UaVVXh4uLC509ClAN05HHvHw6HWK/XuLu7w0cffYT7+3vsdjtc+lxKHeAp7rcEhEwmLooCy+USl5eXRwnVfI4HX/CkrmspIjMajYTgsA8GrzEsxRpK74g9Hh8fhdQ4x+gIGy+dJy5hQnCSJJhOp7i9vZX7fXh4ECLAUq+j0Qjj8Vjm1ps3b6TULR2txFQkfiQ+BNuMIBHHnJ+fu9LmQcnfV69eYTgcSjSF0YiiKOT5sjM5bUTjJUTMRSmKQqpLkSAQLzL6curlJ8ino5oVqxhtIiEiiSP54CuMCjGiQZJCGZbpIGSfER2l1NFYsVgQn4HWLqeW9iwsS3waiWLFVe4RddXIfXDMwyqzJFc//5d+4cfbxg8lGj/49rd9dSUXago92l3jKuAsV0tMxhMHPOsaWZ6iNQ0eHh5grcXFxYUczxiLH/zwcwnlDQYD3N7e4uOPP0asFF599ZWc5+mzZ7i/v8fi8RF3d7d4/tFTXF1do2lqHz7MvYb8IDrNuq4RxRG2G5e0w3NQs9cD5BJFkSP1k4eGhpMxTCbn4m+axoeofJlLC5+H4Ix5luV+InWiL7W+zJzrpu0WNh8cDa4xrokO5VvUB7pJ1KIzLQ6HPay1+BPf+hZ+73d/F8vlUsrfkXWTbNCAMCrDzYhsvapKMTxhYtNiscDN69fYbrZ4/vw5ptOpRJv4WY4FE/kB12Okblrc3j7icKjx7T/4Nj5+8Rw6sv5crtlinmd+/iTIc+fZc/rQFE3TijdoMBggyxKMJyMcDnvvWcjEqLatQRKngHJ5CUweW6/X2PvOzVHkFl1nOlSlI2rb7Q7GGiSJq2Sy2azx5Mk1oijC4+MKUBq7XYU3N/f4w+/9EHf3C5R1jU4ZdF3bexdBIBVj/Iv/S2RPfxq999RHDgJPY4DP/Zd7oHWCv0EPrlV9hMP6N5X/w5Gkg9Va4Orc60hjULjENR1HUABcMznloxvuq1Ecu+ZRUC6KcTigrkqYtvESKQtXKpFkQPWhHOUS23mBFpRA8foCYB3eN3/2BIVJ8rbrUP3O30H9/X8q4xEC8tPX+0jBu0D4fx+y8T4Q+77Xh5zjXdf0Rz3fKQB9F8jmv+8evzCq0X8nvA7ajPdFVsLreNf1hoA5JMtK9dGB02cUPjf3b9gNOhwf4PT6338vxk9VOsK0jADnpHz2qAu2lx3JRNUB8fD3B7hGjlLQ4TTC4vIc3iIgum8yG44p3wv/CzXslFA5sHBcuASg19v9bExffYrOGO5jIZlw9+KuO81SjEd9RUfAYjIe4ZNPXgAAvvH1byBOYr9PTdG0Lp+rKAp87WufIo4TLBaPyLMMceK8/m3jIuRJ6pxUm80W1kfg48R50ZM4cVX0YDDzUqbVaokockUourbFdruTvens/KyvypNmWK+3IvulCqGqKlxeXkonaQIlOgrDnhDc17jvnJ+fY7/fS0LubDY78sLTw2uMwWLhcjjH4zHOzs5chUbf7Ozx8VGSv29ubkRazX4HVD4w+TmKItzd3UkOAp9t13VCmljq/rRFQCjVIVkLey2s12tst1u0bYurqytxrO58N2nek8jDPegmWGY+AfMPxuOx/Mw5Rtn4fr+Xz3Lcnjx5Io5hfodOTDpuibHCqkqDwcA1BvYkignpzOUgpmPOBwkendZ8TgDkPkOiwPNbPwdISsIEdq7X0LEaSq94/zwPsRHnJJPT6XBmEj3HvK5rjHy6ASNlJEgkBIAr79zUjWA53o+11hcJguDXkIS0XV9sCcDRz+H1kFR1XQfTGURRIniRkQ5WmqJ6J4oi/Plf/Pn32mK+Ppho/JNf+RUkSYqyKmG8xi4vCtct2pcM22w2mM/nuLq6cjkcdzdIMvcwvv2db+Ojjz7C+fk5ptMpdrsD9ocKVVXh448/xu///u9jvV7j53/+51Hu9lgvXEhxNpvhV37lV/DRRx/hZ376p1E3FQ7l3leBUthtnREbDobQOpbqTVEUYePLnuZFgZubm6MEIxqYtm1R5BmGw4GTDKEvs8pQIysrcCHTCxDHGm3Xggm9JDDWWuRF7hO7fGJQlkIr6ic7jMdjzOdzLBYLrFYrWZgXFxfCYtu29aTDoq4rxEmvPWaIlMlLXLycCAAkSgAA6/VaIipV5cZ9v99JeJDnTJIEWinkaSaaYRqy002P18zr2B8OuHtYYL3aIdIJvvOd7+Cjj59jPp9AKeuSjH2IMMtyWfyMqtDjUpaVbJrWWgwGhUti19rPuaHXzmrxrmgdSfh8MBhgv3fjRqLnJFreg9F03mjnAFyZv91+h7ZpEOsIUBo6ijGdneNwqPD6zQ02ux22dYWNrzahVN8U0ekUUox+7n+G7NM/B6VdtTRj+zKIsAEAYiQA8LIHv8isAy0e4gAIiAZJCxtoqeMEYMEbVvfRDkuJgyMeURT7eQw5jzEuRwOtI1HG+vwSeBBjLawHIrBMSHfXA16ngpSF5c38KBAqLx/FgHHJl83v/D3gq19DXVcyz3isd3nXefxTkhGe/+1T/mjC8v/r679P9OV953+Xd/pdnwnH+TSngt8/fRan2vtTchKO+Y8anx917WFU633EJvyI565gHsPb0Y73XcexdKrPg0AQbfPX8I7MdJIHY0/LtbpzaqXBYWU0hOuIEq7jceq9gu+/byvfOyZl/YtAMizXynF533MJnWLvWzP8nDtehzgx+Imf+Ab+/b/+1/Hpp586opE4qVMWOedZWZZ4eLhHnue4urp2ys1I4ebmDXa7HS4uLr1jri8bD2tRNw1SL/cZDF1hjuFwiM3GFQPhHuUAlZN7vH7zBonfe1jVyfhkViZLUxVQVTXS3PXfuL+/F9D1ySefYDweS7+p9XotUXKCs8ViAaAHm2HCb1mWuL6+xsuXL5HnOcbjsYBaFlCh55yVHElCCMCpdLDW9Zh4+fIl5vM5oijCw8MDqqoSgsHISVVVUgWLsqOHhwepApXnueSZPnnyRMAkIx2MbjCPhKVhCYhJhNg7g2MB4EhpEIJLa/teXpS0EWSvVivUdY2rqyshEsRMlGENBgMhCRxzlrZfLpe4vr7GcrkU/EQSRKlTCMjpuWcEgc8DwFEZewLo2Wzm+3ythLBlWXZUSUn5e7eBM5bRHVbKYsUrRon4jLnGiAm22+1R02COLa+L651rkDkjvCeSPZa9JTnJsgxJnKKuG7EfjCpxDq3Xa5lzlEa6PmmOKLFaFh0JbKBIxy3ASp4aTd0gSTKZC2GXcOJHRjr+0i//5bfs0Okr/rGf8K/H+wcJIY1GI+RpBtt2gDHYbjZYLZfOY5AkOIxG6NoWaZIgy2LMZxM8PpxjNCgQa4XPfvB9WBUhzQqsVius12usVivc3d15r0SBz/7wAfP5HN/99nfwZ3/uz+D3f//38fKrl9jtNxgMMgAKRZFjPps6oN3UUMpgPBq5SWsMbm5ucHl5iaIo8OTJE6zXa6nKcH19jc1m47V2jkWfn5/LYiQjpb6QmkeGpgCLzrRQynqg3EJpi8LrPOu6xmh8vJDbtkVVVxgOxlLmlUaTFTYeHx+R57lvxOMM2OvXr1HXJa6fXAqJojcgDIfRGHGxlGUpUiSWZWPXx8fHRxRFLmHHruuw2bimb7vtFqZ1bHo+nyPPc5+MfymLiWFCej8AoDyUeHx4hEKM8WwGa4GbN7fQGsiyxEUgktTX2N55zeJWSIzzRLjxOhzoNbI47GscfBUL2AWUT6JSyoox5fhyAdOrwQ21rCrpBN00rsRp2zrmzlKxXdsi0Qp5keP66RmeXl9hNp+jaRu8ubvHy7tH7PZ73N7eQimFzz77rPf6mhaHf/Wfof3uP0L6rX8P8Ys/24Md/+qrFvkcCQSbMgCKnuU7dKweRS8I9ENttSMAvd+YXUFcOdsOHTqj0DZNXxmGhxcJlPcWw0ldHNXwciir+ovxIQxlWYKXPSd4zY4iOScvS1ke2xIVjAUAdPsHHH71P4I6PAKwQjhDb1R/+LfB1SlQlvF+jyf+/5+vD4lGnH72xwH6Dz3mMWgFTgFwf2711piFxIDr531k7V3X/673+nOEtfaOXwSmDhy3fvPyPRVOgPqPerZvRUbQj4kE/VRfqvXtawU0jiOVHE83psf9mNy/7HT9o+/9Xe+zWzXPwXnu8h3c93iMNEudzbDW54CFzfSOx+Ttazx+xqe/Z3mGv/xLfwa//Mt/FXmRY7NZ+LKsBjBAXDgv9WQyhOkaVHWF1fIRF1cX+OLll2jqGldXlxhPJnj9+rWLOscJYC0Ghc/522yx3mwAuAIUripegiZqkaYZlNJYLleIdISN3mMydDJZJBHqqoNWGmXldOpNbWA6hc163zv1Blo8rGxy+9VXX0muAvfRw+EgBMEYIxEINqDjXqq1FrBGrX/btri9vRVpjzEGr169Eu/xcrkU+Tb3XoJBRhUIvBl5GY/HGI/HWC6XWCwWgi1Wq5XkD1hrZQ9jUnEY/ei6TpyNlFBba0X+NJlMROERlo4lIQolNJSJE/84Z6pzTvH+KLEhIJ7NZs5rHpBhRiIAYLPZSPIzABlrAunJZCKecuaTkFQw4kQsRkm6Wydu/pNc8LxN0+D6+lrGsa5rkY0xUZpJ9Ef33zSS6EwHKnNSuE6ZP7VcLuValOqrU4V7FZ8llSUsKhDmKYf5KSQfJBVKKZGD8Ty73V7mEpPMSZC5Z3KuknzleY7O9BWwWKWLNoTzk89bIp7o+89w7nDdUNoXNs/+ca8PJhpXl1fI0hSJbzTSVC40pSxguw4XZ2fIswSwHV6++sJXuAH2+w322R7n83NUZQXbWUTKeY0BSKiOkpyXL1/im9/4BibzKda7Deqmxq/9+q8hyzIMR0MMRwNY24oxLssa6/XaN5izvmJEhLa1WCwecXV1icfHB+RFgboq0TZOj1eWB1e5KkuhI+fBoZECIExyOCxgrW98l6eItMahPMB0BlkWI0lSn5yVoK5ceVhY1/tgvVojTRNUXifadR3SJIWCcd73zvXm6FrXlK8z1pcELrDbb9G0jjVfXV+ibWu0bS3ExFULsb6zdoLFYuklZAbj0diRviwF0LhIVFlBKdczYb8/YDKeII61GJkkjjEaDnF3d4f1ao3OVyFaLp2saDQa43vf+wGyLEWau8Y809nM5eT4iXcoS8Qqxm53QJnuUFclqnIPa1xH9CIvYLx3pyxLLB5cx/K6rpBnGTrTgd2/rQXqqkJrgMOhAvziV8olFbddK47SEPDEkUu+7zo3R5TuYLoOxvakJEndQq5boK5b7PcH1HWLtmkA2yFOYnx184B//Tu/i6qqUDc1OmPQGIW26+UI1lqZ5yQJ7eYe+M3/At2r30Hys/8BVDHtvf4E5dYldFpB+u773snpvLuAky0F1ZoEzgdARJiCvE1pRP+7v2AY9ONET687HCNl7uRySJIJ66qeua+pIGLS9704ck3711sQK9RPGfeddneP/X/7f4SqNi4CBBOAux4o/7hIBCNXR+A6dJMfXUYAUo/o2bsuOPxk8Ffb/6zDc53cOL/lvnMC3BWZpJJjqreOFT5bIIyGhb8LoHYTR4o8vZto4Pg5EXyiL/jASKyTBTHC4fIV1Mn3SIRlPQJCFtxvWiJtCgpJEgsRggKiSDv5nrV+Xbs13nSdrJfwkSiFsIjVybW4Dzmg1neClmRureWYMj18iWMNlliN5L08ZznSHVrlSq/2zKV/ZlortF3n7lZHsl5Z9lXmiDwTgziOkGVp4DFMMJlOUFc1rq+vcH39BHmeYT6f48WLF1guV/jd3/0O/tE/+ieBLeynBstVhxEptx5cOd5Ia1gYt5Zh8NFHz/A3/sa/j//Bz/4kdvsdmqpCliQYDQoncbKucMnj4wO0jqAjhSSOUDcVttsN8jTFeDRE09S4v73FoMiRTMaub411SeB1VcNa4OL8Am3bYrPZYjAYYjgY4nAo0TatlMjvlMZwNEZVlWjbDlmeYbfdIU2d7ATWYjgYoGld083Kg7KRzzN7/fo1ppOJq2jkFQ15nmPr8xSZP2E94KfE6vHhQYCYyIJ9KVBx2kURVt5jzOZlzO1jRP/8/ByTyUTICyszMhLB95gzEgJEet65TmkDmeNAskCP8mw2w263x2q1xpMnTwRgtm2Hw2GLqqpwfX2Nh4dHqZS1WLgE5iSOMBgOYb1HP0kS1H7vbD1AbbxUqSgKLBYLxD6/tsidZ7vICmhfNdRJdAsB70ze5hI5eM+51hqZrxK12+8x8BIlnnPqS7oqpYIeXQaXl5cimWqaJsjjcZ+hUoMV2tjXLKw0lqap9BvqTIdtuUWWZ1BQiKMY0DGapvWAWwPWiDO06zpoFaGqarChZFXVaOoaSqujylIkTk3TYL/boyprTGdTMed5XmC33WI6mWF/8MWAdOR7sqWIfDPew/7gI2sV8ixHFEeA7Zvscd4wJ4QqHEYZSB7onGjqFqWpMBq6Aklt40i+tbZXkDgwBa1d6eOq7EkyI0dh6V/mZX3I64OJxvX1UzR+onetwd3dHe7u7nF+NkekgfXaRQagLHaHnaseFCeIVIS2dg9wWDhGtKt2SPMCURRLWbCqqiSsVjc1htMxsiJHWZVo2gZnZ3OMRkMfbh3JDXsTC6WcNCRJCJAXaJoaw+FAqjnkeQbXZXuHJIkAaxBFLuFqUZZSbo5VlFw4aoU0SyQURjlVksSoDiVgLLLETbKRr5ZhjfNk595LPywGMhF2ux0iDSSxRte5JHlrGjR16XXyEdqmhmss5JJj66rCYJChtC3iPEeSJuLhgnUa9yIroKyChsZhf3CdzBNgVAyxPxwAA2xWLoLzxRdfAACePXsCBdc/ZLVaI0mcF6BtWUVEoW0N3ry5Fc/KcrnG7rBHXuQ+2SjCw/29S563Ck3pyzB2BqZtMZ/PcH5xgcfHRzw+OkNXliWyPEekNYpBgadPnuPsbI68yPHs2XMM/cZxOBzQGossd0lUDBGv12t89dVX+O3f/TewgDBskguybRfxYeUOL+kBYOC8piIv4N+9t0G1HVDWbqPhGMMDnCMPa9/QjcemIbM3vw/zL/5jFH/1fw3qxN13+t7ZPLdSCjBWwGJ4POUJCqMA7osOyLioAm8tAKxGLtB9hj+jByXBTQCi9e7L7Pov8UIdSOa1wn3HndbAVevxFYKEKCkvwWK0BQK0KCmzhwXKf/p/gm52MIBPpCcAtCeX+X5vf8+1elDff12JAQXffQ/gPn5xII7+0h8zkOcoyUN5B2URovA24Qk940L6Av1+T7L8HFB9xCI8hgruXTgpeq/8O+/gXfftCWTdtL4Pic+RUH10QAVbRk8mAKWMIzgnxB8ArHFJ0SSMbduTYWtdc1al+vwIN5yuF0Mfdju+Zv2OoZa7tG5tuo/3ZYCN6cAiC5rRQ6VgrPOya082XKUmd31t07q+TrZDEvsS19qRra7rXEUnDwzzLEXnSUMUacxmUwxHrjdQEicoigLjyRiz6QyT6Qjn53OMxyMsFgtcXrpoNav7uKpIB9H0F0WOh4chfu3X/hUiHaGxDmjI+NC++D5UzkPqS8kaC3QWkXL9Mc4vZ/i3/62fxS/8hT+P0WiIpmrQ1c7Tvd/vsXpciwdzuVq6/g7GoKxKyWdwJWErRGXfD0FBwbRG8hseHu/9PTv9fZLGSLMEdVNhf9ghSWOMxk5+tD/sMT2bSuXHNEtcpaq2wpMnruTqarVC0zmPeqoSVE0Fi06iFlmaSnl45zSyaHzfqaZpMPcVoJaLxZEHvm1b7ABMp1OpukgQ1bQt4Odo6mXYK58MTpUA5VlsPkwQTHlNURS4v78XD7DrG7WVhHRGtJiDwsbHlM4xksAox3Q69U7QkUSE6OshDhqNUiwWS09QGhTFAKORaxqXp4lriJymrh1A00ArhSxNsV6v3Zg0DeIowm67BazF5fmFSI6VVViv1mKjrq+vAOVzWJUjmNYXtsn93CCm6ryUa+Ql3lq5ZodVVeHBS9+stciLArH36C8WC4zHY5lnBLyHw+GoVwUAGVsmXxP7ZVmGInUNFK2xSJMUtrMwMFjtVhLNqaq9JKhHOkbbdJI34aphaXkurqeGwwwsKMAyyHleIB76dgF1i/LgZE6HroS1CpvNVhwFnTWIdAxrfVEApQGrYAwQRwmMsdgu12/NK5I3RsvCfYMyLZf8XvtcpRSLxcrnrkSwxuUTh3hpOBy6c3d9iWE+u/Acva39Y45ofPNPfkukJ5vdDr/1G7+BxWKBsmugWwOrFCJ/w3GcgFU14iiVhKmLiwthRrtDiXM/EYcDp918+uQJpuMJ4tg1fekal6ew8IbhG9/4BsbjEVyDPrZ5j1AUOVgtpKqcxOZb3/oWAAhxYEUjvsLBYjk9/p0e97qucSh3GOsxjIFPZHb6vPV6i3LvQozT6QSua3iHKEpgTOsBdYWwPCslUmXpQlcuqclpH1erFWCBwWAI0zipUwSNInE5IauHFYaDHG3bIPF1kavSaTzLqkJX11gd9jCd81JEcYSH21vc3z9CazeeVV2hrmp8+eUXuLu7w2BQ4OLyApPxRNg1LLDb75DEMZq2ER1gHPkcjjRFkmR4cvUUP/MzPwNjDB4XCzR1jcVihd/8zd92Va7yHH/qZ38Wz54/R9s0eP7iU3zy6ad4/uw5dOTK+Q0GQ1R1hUFeYL3eYLFYQGuNh4cHLJdL7PcH3D8+4nG5wN3dHZarFdqmxWq1xOFwwK48eGBvYILwKQFauJlwUVgPoKzqkykF9AdA5kgz7Q1CqKV+yzMdLDjJL9jcoP6D/wrpT/1P3DFFniRFYCHkwANG6wHpqceW34Oy/XfFtRx+Br1X2wNsEgw2L+txOUnPCRgOMLGVgwb3SPLiwbjzhAfH5/iExMO6MthCMqzB4Xf+HnSz82V56Xn/MMN1MjAIZTY/zvidymzef9D+OH2Su7ufSH+IvKgnEu8qj3pEEE6uh5Ii9+v7ozvvPzdA8tmP67u/JySR3zKOUGjF0sIOoCpGJ46uV/f3oXoyKhEOKCDyEQPdV3OSZHMASvfVkniP7j0/W6V5Je//7TyUnjwEpNYGvVf8+MURI4HuI50xiBEBsIh94zf204gijTxJYUyHPEql6p6rhjeTzf7Fixc4Pz/H9ZNrdK3LX2yaBlGskWYRcl9tj55KJ5twVZO01pjP56iqCjc3N3j27JmMz2q1xHA4wHK5wOOjwXq9wZs3rxDFCmkWi7ed9++aWraIIjdvsixDlucYDYcokhyffvoJ/sSf+CY++fQj5HmC1XqB5epR5B3MD3jz5o3kH9B7TynM+fk5oiiSCowEgKfFUyg7pjeZx6cchfmHYR8CFilhzwOtNTabDb797W9LAjMlKtx36XhingMTfanBp1KCunlGNRgx4JxiGdQoinB2diY5kuLxZ48H/7eyLLFcLqW6E3MQ6NkGINELgkHmN7AAC73RSrkSo9vtFmdnZwAguZShpIn9Ofo+WS5nks+PEXtWNJrNZpK/yfL5RVEgiRTq2q0HJqgTmDIBmTkecRz7ueByIpnvwecjPT3qUhLcoyjCdDqF1lpyQ+u6xnw+l34RYSQilBg9PrqS+wZ9JSZGFZhDE3rseb10YHKcRqORlAFm7kq1r46eOUkKpduUifHzzK1hpTLmpnCsoaxXz7TSLgH+uuOoL5hEG7Tf78V2swoWjxUWI+AclhwSpXxe8+6tnA7i6bCnS5hvxLng5OiHo9xk2mDJzfXjGe4zoTwqbEII9Hm6H/L64GTw/W7n2bKW8OF3//APsd9uodvWRztKISNZ5hZWeajwgx/8AMYYfPrppxiPx44xJgnKpkFnnIdku9ni8fERX//61zEaDfHq9SscdnvAWvzD//c/QF3X+IlvfAM/9VPfQpomMqjsidG2DbSOpDzcZDLBw8NDwESVDFqoZ6NGjbkMNN6bzcaHKkvM53MMBgOXm5LnzmjFCRaPj3AOYYM8L3w/B1cit2ka7HY70bdFkevkGScJmsYRpLZtRM85HA6x3WyhrZak9ZFvXrder2G6FkkaI0szTKYTwMsCdrsd6rbGcrXEbrtzm7vq6223DVDXDcpDibqpkSQpRqMh7u/vMZ5MsN26HAkLoGB5M+2kMtSnRrFr9lYUOdIsx8//wi/iF3/pr2D18IiHh3sUgwFm8zl+8P0f4Hs//CGsBS4vLz3zdqHUu7sH3N0/omlqPNw7ImGswWazwWHvuopTV8hna6yFsR0MDMJKNda68Da0FpLQd6U1EgowphNQz2CA87D3+v8Q/ISe2PdpwLloT18mAJz0UlFvrq+/hfRn/6eIillAbJwEgx5gJWQlAPS8HjgpQh/F6DsTC2kIrwOMnATv8pJPSInciYQFjs/dkwr3M7251jrCo/18Y/RHiSe8JyEIPg8LmHqLw+/+fTQ//OeIvaRQXkH5Tn6Pz+BdrzCq+aMM2Y8yiO96T6Rk/YdOoln99UllLfuOQX7nOdTJ39515eHccMnI7F2iQ9Iij+ntcQr/dnqPIoGT7/DZK7h2JubovvrPvE2M+mP3UZgwh8B1iYZERU+lULDqHddoYawBtGs6+SHkkBGfWGvxNB49EaVg0SL2m6qCawg3GAwxHg1xceEq/j1/9gx5UeDq6gpaKVw/uZYp/eLFC+z3O7RtJ4m2BBFh9ZuyLPHll5/j/GLuSk3mOYy1kkx6ffUExvTjt9/vpRcBgS7BIj2mTdPgu3/4Gd68ucNyuXCyXV/G9fLqEkmikGcZlFY4m59Jz4o0yTAZjQFY7Pc7lNUeeZ5iu9346jxTKQNLZ9z19bXkOWRZJg3n5vM5uq7Dw8MDptPpEaGgpGW5XArImc/norUnCCV4ZuIwgdhyuRSywKIm9MoqpaQ8apiUSpBGAKyUEnKxWCyQJIn0UmJC92KxkHFnDwYCNEa5CTIJhtl3wliLQ1liOp1K5Ib3zuutqkqSgllhirkPo9HoqL8Fcx04ZsyBpbOT0RqC66qqJM9hPJ54SbSSSAn/JcYxxpWrtdZKifqmOgiY5f5HQM+kYnrxpQqRsVDQkmTN+cjqZFHsjkP9PxUcdPSyMhfJC585cxBIUiQfwj8P4jPKz8I+M21A+uh9Z1VRVrFiorPpDDT6aksABBsSXIcNA5l4bq2V6BNzR6huSTOH5ZzUtBaS6QrqRCjLSuY3AJE9USoZ/o3Yh7mqJE8Aq811Ug7YWiuVvUi4OF84BnyJND6otMXnHpIc2hueG4AQLt5b2Asv3Bf+wi/9xXfa4yPb/MFE43Do9brojX25P+Cw2eL+9gZvXr+CaRtopTEcFFAAHhcL/MZv/AaePHmCP/Wn/pRoDbe7HSazKRaLBeZnZ65q1XqNyXTqiExVIk8ztE2Df/QP/iE26zXOz8/x0z/9U5hOx5JgxAWy3++xXm+FhUVRhNvbW6nnzCz7p0+f4vHxUZjcdruVRRPWV+YEIDmhHpBJ2mVZotztZaGUZYn7+3vM5zMUgwHiyHVXpOGi9jNNXYfWjiDYGlSVC1tppWE7F04ke+6Mwd3tLfIsDfqYOI8qw/6dNdiXB7DLqptgEeI4QpGPUFWNTLYsy5yc6fwCjTFIswxxFOHy4lK6k7qSqG7T4qLabreuOtOhxPf+8Ic4HEqs1i6BvzyUGI1HWC5XqJoau91eWL4jAcaVrcVxdRUmK1vjnelaQ4ceW6Xgelc48CmNqQhmrIUhg/C4iQTFr4SAIPTTXHPsTkKApwQjfA/BnD/9jD1ZE6ckJY4i2OEFBr/8v/Ggy8jnCeD0CcgieO/jHkfvggnlfRTC/dURDRV8KxhLG8Y10JOJ8MDWRSff+f7xBThS4EMoSnmJRv8mKOugzMjUOxx+/f8Gu/oSptodzwU+K9vP4TBaEHr03/VMQqJxCv7fAtknx3z/693f45iGXngZGuuuha/QgxYm3IXSzz4ycnzunoB6T71EDo4u44gEv/t2fJQk0jDdce324zEm+e0byJ2Oz/vGM/yPAOddxOutpENjoCyJcR8N0doRZddfIZZj8fvwDgTaC2uBOHab7nhUwHoZwGg8xsXFhcspm06RFymePnvqPJ/aVbFLkgSXF+domgOMdQVFbn1hkjzPMRq5JFJWB5xM3B7l+vGMJImYm/90OkXTtKiqA1arpXhFKU1QSqHIh9hsdgLCCFa32y2ePXt25KW/ubnB+fk5ttstdvsK19euV9BkMsGXX37p8heHQ+y2S8xmE/GurtZrfPTRR6irCtpHpQCLsjwgTRPxatZ1hzTNBNRxb6VkgkVEzs/PJVpAYMPrHo/HWCwWsj9y753P51IJiXsQPaqsGnR2doayLCVxGADm87k4CJMkwcPDQ7836b7cqOunNBPwtl6vpScUPcwhsA3tCGVqTIplszaCQzoJlVJCxGbzOba+v1UILumg5HdDmTXP8eWXX+Lq6gr7/R739/eYTCbyXFloh5Ekl5DvSvBOvEOQQJ7NhNM0P6pcBUB6bPDzTIoOeziMh8VRERdKcAhKaY84zqvVCodDiaqscXl5KYCTTlIX+bUyzqwIFkYbSD5oVziu3IN5TOIk6L7SJW0KsRhJG6uX0alHWV8oq2KkQCmFLM6OwDUdgq4h8lia/pHQ8bqIZTjnJBqhnc1hNIVrvGkaZGmOuu4bVXN8uW44LgT4/J1jxobUjIAxOb0sS1F+kFCTKJCk8P54LYw8ce3RlvJnljAOMRCfP58Xox6cpyRGcRz/8TbsW23WR9npBOKR1oj8xvr5D76Pl198gaYqkaUJdpstvv/DH0gJWz6g2WyG+4d7HHzlpO1uh+VigRcvXuD27hYXl1cohgNMxxPstlv85r/+DXzve99DHEX45je/DqWsN/B9pZK2dax7v3esmIlA3ARIPsg++UBZR1q86MbIxN1sNlLfWPs+DW7SK+x3eyRe/ziZTITslOXBYz+FsjxI2K2vgKRkEruyudp7QyhDcN5qrTWiOEKRuzGrygMmPlkqSzPMZlPESYJIa5xdXKLwDD7Pc0wnEx8mHfgcBdfZ3BqDvMjl2a0PBzw8PqKuKqxXK+z3B1RVibu7e2w3G6w3G+x2W19irpLvWQQGCUwS9pIhghYPLwRY+cpOzmHfA0xKbThmSlFT77+rWDa1r4JwtCBO5umxJ5WVWk6kFkcExJy8dQJ8g7+97/WjiIb1RiSKIuif+KvIvvXXYIKO4SQMyvbRB6Updwp86NYKAbDWAlr7/AsCUN5Lny/QJwT3PTx6HhASkJPveblKAJ/lWqwQG4LSfrx4eMidMPndoLv/Hsrf+n/Abm6c1hi9N+dkNKXjcGjsTonG0UsRiOuj5xoCi/6j/fw5zXfoQSy94+wibfvTyON4NxB31xAqUnv5knjVrcurUgHoxrvmGIG7z5XgOiGJCo/f/xx+/fi+j9cOjxMSbHfPvO93k7u3xzM441tjolRP8k+JDeDoYUQCBXaS93NRGUBbZGmGwcBJbuIkQRLHiJIE4/FYyphmWYaL83OMJ2OMihzlYY9iMMBoNMRk7CrvLBYLlE0lkhQAfm06AFDVzuO8XDpy8PDwgPF4LISDchdeH6v5MUeMnnf2E3h4cE0nJ5MJTGfQeRltmmZo6hbG9H0Z6FFnYZS7O9eX6eLiQiLzbdti5+UPZ2dn6LoOy+USZ2dn7p58T6iiKHB3d4fz83MsFguJ7k8mEwG99MA7WU8mwJDyGmr1uf5IXp4/fy6R/zD5l4CQfSMInokZWLCFkiCSbf4eylwpz2A1otFoJNUYiT34Pq+X0hb2oQgJQygdadsWZ2dn0lsiiiI8Pj5iOp1K6U86FQkcKUMxxmA8maCqa5EAuaiRi+KwWhNtD52bw+HwaN5Ya3F+fg5jXESfsrHdbifNcCl10loL0aDEiGSjbY2Un6c0jLgmtGN0pjrAWkPDimecHnB6vAmsGRlh1ChJUsCqIxkTsU2SJijLvUh4SAoIlhnhAyDAmcoTdr0OichwOMTG98pgyX/mPoQldsOEaDqICci5tklGp9MpIuUSnqMokrVKwMx1SMDOXhpSdEEdd992gLuDhRHsRxmZewYx0iQ7ityEvTGINUkM5vP50bjQgX5KzPiihIolckNnBecMpYmUunE8wgpZJGghCQn7qvE8nCfMEyIWzvMcv/hX/xJ+3OuDicZy5UJ7URS55EdrnZfaGqRJDhYwXD0+4OXnn+P1y5fYbja4fHKFzz//DE+fPMXNmzeAN0YPjw+4f7hD27b4vd/7Pez3e/z0T/80Bl6Gkw9HyJIUy8UC1hj8/f/y7+PFxx/jydNLDIe5bBRM9mnbFl3rEk856OzkyQ2WDyvxFab6DtcdsizFbreXRnxuoJVU3ygPJaK4f6hN0yCCEtLCLow0ELw+bh7WWkRxDK1cybn5fC6bCzuWjsZjXF4/wWA4RFEUKIocSRyjbVrAAk3bYrvbofVaTKVcWHm9O2C7P2Cz3mC5XODh/sFpTttGkvbKw8FVTvILq207NNZByB5MWfGCdK11/RUCuKu1RmcMoNXR540HTtpXawgNaghsLJQ0t+plTADwo+UyDoI4EHLsPT4lGiQsIW57x/S2b8tdwnOfyqPeF+mQ7wSfe9e5OP/iOAaKOeJv/TWkL34O4p32DMACIotRjonI/YfEwPo/Kv/8oHSf9O3fPI2qhNENgaYKpA/00R+Ph3r73PKrtQK2GQU5Hnz/zLsG7avfQvUbfwvWJ+trrV00KiCFwYBBIWzadkwM3uVhdwc5bu7G4/64qAWlYMdjRaIRe6J0OkcMrO21rMevnmiEsjHea+jR5++n5w5/d599X2TleAyOCcjbRCP8PCMqpxEG9/OPOk+/dtz7Nvj82+Vh5Ri2j0TyGNYCETpkaeyip2mCp0+fYTIew8LiT/zUT0BHGhcXF96Dm0ApBwQb02E0GiKOE3z55ZdiT2EtkshVYOraFrv9DnnmSMJ2t8fD4wOePf8Im81G9OFleUCe5dBxjKauAaWQxIm32REirbHxwHmzXqMsK3z88UeuzGWeu7y4JMZysUSSOiIUJ64KIZOJh8MRLi4v8IPv/wCz2QxKKQHI9KxTb02gQG19nufixby4PMdytURZlnjx4oV0wLbW4rDZIs9yAQXwAKVtGlxeXQq5cGDDRRrrqkLTOkAfernDpmGUKY3HYwFNBI/7/R6Xl5d4eHjAbrfD06dPAUBkNdx36bXl95kgzR4aYR5EWH4TgAAoRlpIcjgPGQEYjUZ4eHhA0zS4vLxE27a4ubnBarXC2dmZy4MEJIIi1YhsL0UJHZHUupPgGOMi0ZV/n1ECrifKjVarFQaDgeALOi/Dkq8hZlitVr7UuyMN4/FYngPBJCVW+/0+6LXhbF4o1yPQXq/XModIoKIoQpHnSJNYehXRW89yrQSkJBH8uSorxHEq18FohnOeOukUmyIf29D+vjmfgL6ENtDLkUPvet00KH20j/kJJEOhHJ7fJ4APc2p4f3VdYzgYoqkbwL4dPaFqI5Q80ylCskcgzn+NMaibSqKonKuUjHVtL/fO81wk6lxjp45Qngfoe5rx85wXBPzEfQBEGkZiSHzXVyfVYg94vzweCQwJZiiH431yTfLaOD5r36MuSZIPIhofnAxuTefBQesqdEQakQas1TCmc+XPAJxdXmM6P8cn3/gmvvPd7+CH3/822q7Bd/7g96AotbAVXr9+jdVqg7btkMYJVDFAXVUwbYeqrgCtYbzeLolitKbBcr1AniewZgKlFdqmxXq9w2Q8BhChqUp0rZ8sOsZ0PEVV1wLSXbfUDgfUiKMUX331Gk3dwHYKpnMPvK5v/CR0x7FwrNaC1VGUNFlTCsiyVFh1URR4+vQpnjx7ho8/eQFjLcbjsXQoHQ6HKLICsXaektV6jfVqjYeHe+d52B9we7fA7rOXePnypXgTlosFHhYLbH1zOiabdX7iWKXRdK4nBHEeNcra65WV1ujaTnzTziveJ0KL59gYNJ0RwKoUYFg1iQDcVxFy3kfvxfSVJpzcoUEPs3rQak3nQJN1ya4kGYbaKRBz98A2UhrwVTVge091b8z6Mxl6XNljwgJMJD3yGOsexPcndVIMC/jGUEFXZGVhO0eGBCyRQIGgvQeVoaHli8fS5RLtb/0taNsi+fQX3Jj5CANLU7rPGn8fSnrw+XCQ+8W4+1Dh3/zFKAUo2/cScG+45+afqrtca6Udh/yu6LXW8hUlUi4SCjYNdMeWfhr8rD9jt73F4Tf/Nuz9HwYa+WN529tAXfVkCiSnOugaoo7GmpNMqz5fJwTD7rMGTIzv57XbIE/bO4RU0WHjd0UtIhhER99RnkRHKgLsMWFzx7HyySg6JheMJhxHJhjNUPCxo35u+PfjKIKF8RsXvIxTCQF0HswWkiStetLJvAft5YomKNvK9evKTIdxNRfBCqMzbp442VcUa/Gc0jM8HA6QppnU+E+SGJeXlwI0nj29xmhQuCozcZ/L0bUtBqMcKnK9F2ovbW3aElGs0LUd6jKCTVp87ZOPsVgssdtuHcgvciRZCliLKIoB5UrPTiZjdJ2BhkISxXh6/cR5wKPEVZdqHfjYbrd48eIFiqLA97//fcznczy5foqbmxvk+QBnZxfY7Q6oqgaTycxHQDLEcYIk9mVSO4skSdF1BnVTY7vdiqShqirsdzvJv7i8uMByuXQSBw+WFo+PvuBHiUhrPH/2zMl7ywrz6QzDZ86B1qQNtuuty+eDlshzluUYDguMhmM8PD5AKfee63LdoK4bmWkkAswrIEgBmH+Yi2yCuYe3t7cCmrbbrUhm6Pkty1IKiXBvef36NTabDT7++GNJ0qXzb7FYYOarQoWN7xghOVUphB5eAsOHhweJKnz55Zfi0IiTBNvdDtAkVi5PZ7XeYLvdYTh0xWBW6zWe+iZ4ZdWg0BH2hxKH0pGsu7s7jMdjHMqDSLtub28F9PFaaXsYMWFeBnMQptOpL3ayF4JHEkYgR8/4bDZD0/SNBNfrDYbDMfK8kOZtlMBxbKqqQl1W6IoGaZIiiWIURe7KuFc1qrLEdDLBcrWCgsKgGDobq51dbJsOg2KIZbVCZ0oMigGSJAVzYEM5kHOkur9nWY40zXHY76G0I+vGAmVVCyFz1aBGOJQHmSuddVJwYwyatkNV+xK2OdUXtD0aZelK0WvdFy/Y78ugZLZya1xHiOMUdb1GluXY7fcodwcpRsDGiUywns5mgHKklYqKpmlkv2eiPZUpjtQkEhGlh99a+BwNJxdn9I2gnMAegPxOEkAJIkkFxwvocy3ChPWw3GyYAB7m/9B5EVZSpeObUjPO1/DeGMkjsQxJHXuvfWhpW+CPENG4vXntQayVG4viGBoaddWgaxvn/YldDkKWZwAsbt68wnd+59/g1//ZP8NkWMAqi0NdYrvfY7dxXR9Zf5xsKk5i6Mh1ei4PLsHl4eEBURTh/OwMpmv8puVu1EURFGznmF7Xdp4cAF3bAgowxpENoK8q0nXGe8G4iWtEfpO0gK9gAMRRjPFkjDRNMRwMMRqNcHV9hcvrS0ymU+SZa3w3nc0wGA6goxj3qwUWiwU2my0eF484HA54+fIlbl/fYr85SEfwuqolXAYPljrTCeJpOxfNMApobe9p5yRyJRZ7YEZA0pmenYch0hCo83keTQgC4iCfIgTPYQK100gH0QtYITj8W+iFflci9fumX+/Fdonop1EFR/iOK03xeyGY4nmPJFL6GDiGnvXw2pl/03/mOI8jBJPhuPJ4cr3B+IkHOUpR/PL/FsjGDjZ6qRKJoFKUVMHX+e+fbxCcOP7ZWlit2FPP9aoIPdkBmGVEw9LTTDLiPijnFme6ZcUq6zlc/1k5twegpmtQ/Zv/J5rP/juYthbjdzQmwSsE8z/qfUqj+Fl6x971/WNy0Pl71ID/T8GVTrXKyE2Ea0spBR2QiTB5GgBMEGWQPAyt3ZgF0Ytwvijfh4F9GlyETp4GEEaU4J67awjnpU5KH427Ix2uvHAol+glSuTXVuRQPF+kld80BrKZ0VYY02A+n0vyYdd1GE8m0Aq4ujjHeDyBUs5+fvTRc8ACk+kYShunOd/tMCicbIle5Ol05uUzEywWC/F8EmzQHl5dXUmuQGtapFkq3ZddlLfA7e0tBvnAAyC3WZ+dnWGxWGC5XOKjj57jq69eineWdf1nsxkAl083mUxk86W3XEV9rwL2OdhsNtJRGsBRMivlN2z2yoThU1kKwTu93YfDAUnsOhJzDMLqUVwv3ODZQVspJQmarNdP+Q2TjimPYHnW5XIpz5ff5TkoCSOB0Frj7u4O8/kccRxjvV5L7sl2u8VP/uRPigyY13pxceEKi4zHcm8hWSmKAsvlEt/85jfl/eFwKHkeIUAm8KOHfbPZSOWk9XotzWMXiwXW6zWePn0KpZSUo2VCPpPS3Rw6lj6F3uo0zcXLSznzfr+XJncPDw8SvSHRcp2sL6XcLqU5FxcXklg+Go0kL2W/3+Ps7Ez2E57/5uYGXdfh6upKkuBHo5FIv5hPudls0XXmqGcBgWCYW0CvNkHmm1evkSaJRHZYjYkELXyGLNV7midAjEHQezgcpMQq8yRYapXHZtdtRo0OVQkd9d3EGbVwxKRvhghAktmpRGH+AiMibBbIKECYxB1KAZmXweedpinqqpIqphwLAvqyLNGhLwgTRi200og8meN7zC/itYQR4nDPYtSFlaOAvnITo3TM0eLY0ElDGyBdwX3RBRJ/jjXvPSxcAECKAYXXYm1fVIJOAN5PlmUy5sw5CvcS/kxJFwCRs/3yv/fv4Me9PphovPr8M7hmapGcNPLJhav1GkkS+VC2RtWU6NoGRTGCUjls0+Ff/vN/hm//we8jihSqpsbj4xJd7UJbTdtit92haZs+XFs6g55mKWCB83O3kewPW1R12bM5rXzzvAwKWprxRJHr3m2t88hHUew8TkmC6XSKYjBAmqSYTMfQSc/0hqMRRqMRBkWBs/k5imIMWIXZfI4ojlCVJerKdaq+Xy6wXCxxe3eH+/t7rFYr1+VztcTSJ1B1XYe2a53HjJtP29fEb723wkUYNDrrdHJa9Q2uHCgxaLv+GEAAqnSfCOs6xxpZTCwFzI2L4CyUpdDTqVTfKA3v6EAbEo9wAoZEAuoYiJ/KqMJrD/92ukhFI+49GW/LV6w4twXoBcfo2g4EcG+RmxMnOs8VLnB6a0LiQGJGLSOJXjg+p9dog7Aw35P3dYz0Z/4Gkk/+PFSUok/GPS5B2wcrrO/Z0PuYgziQgM/+07xmRiW0yKt6fsLohidi3ulPksFAB6MYoViNIFYuQQG23GD3X/8fgMMSCJ5jKLd5F7k9/vk0gtAnzYfjRyld/3VGknB0DMmngIbrr+D6IQCA0oziHOcSKKWgbBh5OD4mApnQW5Klk7+TnB/NkX7kju5BIjKeVLi54/r9RJEW4ug8gB3If6KY92WRZxmyPEOWuUTmJEkwn5/5qj0+SXpQ4MUnn+Dcg6CmbVHkuWtGajqcn51hs934Wv1u87LGiPzNWovag9PtZoMszwS4As5Js1qthACFUhqCruVyKd1m2RgsBAnFsMBuvxMv8WQygbXWlRUdjBDpSAAAE67DEp+M/lKWQpkO8/aY2EngYACRCT19+lSSm6uqEikJgRC9+efn51J9KPz36upKPNrM97u8vMTNzY1rKOcBIQEAQQIBA5NVCaRdJKIWoEZvOCU47K3AqlFpmgoBobSY1ZMo2QojCAQR9/f3uLi4ECCoVF9a00XImiNdOInVer2WdRkCao4zx3A8HktUhMfh/fJ+6CCTSk8eALLHRtd14olm7w8m45IMELTmlJUdDlKhKMsynJ2dY7VaYzgcwlqL1Wol4I9AmF5o5kW40rhuPdzf3+Pm5gbf/OY3JYl9OBxKOVd6nEng6rrGbDY7SoanB5sRgsPhIPOE5COOE9S1uybmkYSeZ4JWkgAC97aqxVaG+z4AIQ4c/zBCQXBPWRcT2rfbrSs7a4zkVZCQcE4R9JK4J0kCq5zygnaOxQb4Pc4j5tXQqcx5QhDMOQFAqnQyJ4KkP5T60O7yu9ZaROidrbzW+XzuSIpWR6WPma8RRxGyxNktkoKwVDFzRkgoQgdBuF5Of6eN4nMIMQWfGSWRfF6hY4ROoTAHibgllP0BENvCZ8P5QHvIXCSSzjDqwrkBQIgVr4fH+mMlGq9/8LkYgTiJneTIWuhIY71dYzgskCYadX1Akmi0bQWtYwyHF8izAsZ0+P4ffhff//73YQEcdnu8efkau90Oj4/O49/4xVcdXBdr6x/qxcUFXrx4ge9897vO4+9BJh8U4DqXn5+f4+r8AjqOkXtvSud1lUq7euaD4RBxksBYg+Vigd1+j+1ujfVmjbIssdvtJARrOoO6tri/u3fh97bFwWskm67DwYf1OkmSdpt+1x0DSwIGWMoxemBMz4JD+w70MG+Cnm23ybci/+EEE6CuoyPPNRFMFDswQhkYQXOvR4zAmvS8HnfdyicnHxMS/k5PARczAVVnOiFFxx7ld3ua30U0TkE5x4zvHXnGVX+zYUSB9xBGW8KhOc3sCL9Hlh9ek3tGx/kC9KjQcB0971PCcRLJOY6+aOizT5D+9F+Hnn8a9BQIOlYHBA2eMBD4yqdCsI7jMXZkxQIQDVYQlVDoO/z1Rzh6WS8qsydJ4ZzXyie12w7lb/4XqH/wz91zEiJ7TCRO58bp76GHv+8nwVwFJfceErNebtTPG76MpVSIOtj+ObrGmMflWOVfRhGsFfkR513kN7PT+auUlzudrl/05zOmE6kXqyYp38Mhz3MUgwJpksoaOzufIs9TkSClaYLJdIo4ijEcDb39oYwzwmw2Q55nXiagZU06QJejLA8AvN68rDAaDX15aQfSJ1O3yQ8HA3z2+ee4vr52GyCA1eIRSRIjy3L/bNwaa9sOSZKJnCFMXt1sNgAgXmMAIovRWrtcB08wCGr3+z2Ml1VqrbHb7fDs2TN8+eWXiKIIs8kMg2IgOn8+A2r/WVeeHj4AApAoPQ3LbdZ1jchXKqqqCufn55I7kSQJbm9vRQbz+PgoYL2qKlxeXmK73eLJkyfY7/cCjtiQjR761WolIC6OIiSBfIil0FlVyXV+3gmoYOIsPd085mg0wv39/ZHO/uzsDLvdDl999RWm0ynYMI1RHFavCfMTuq4TYH92duYrKM6x3+8lKkHPMr3TjI6wWhPtYdi0jtWogD7JO01TPHppWNhXIqwCRF07S7LudjsopaQXAKMm3MtIEng90tzMXxPJDsHXkydPsV5vBNzWPsE7dA6QgPE7DvhHKL3sxxjX/4NgF3ByKSbc0/tMG0EveJhvEMrHCFb5TFzvrz3q2uWcKOVKAHN/IpljojHnurUWXe1IDJ8RANmrKG0jmWA+KyVuJDHMdSBJZJlX/h4mFzOJnKV8uf5VpFF7MkkHA8sXh7IgHif8G88RgnneH+cN914mkr8r0dlaizRJUATN6ULHYhTHMOjJvrWBZEk5+TafzWazOQLmjPpynBj1IOAP1RR0IjDKys+EVaPathWSExY/4L2TXIbFBcJcGkaXSCz6PJoeL7MAA9c/74XYcL/fYzweC2Ej2SSp4d/5zP7q//iX8eNeHx7R+MHnorPTSqNuXIg5yzMMxiNAWQzyFF1zwHq1QFMffMgnd70jPIOiZ9F0BuW+RJom6IzBYb/3obgWh7KCVgny4dBpnuD091ppDAZjNK33Jrctdru9a0RXN1ivVij3e7Rdh+XjIx4fH3F/f4/NZoPVZofdfo+ua6VShluEGkZptF3nOnprdTL4LiHaD1ePepVGa/tESL4EKNvem8zcBdi+K7JyiKhPjtIa0EBn3AQ/Bt8GMB20wtGkkclsFdgJ15j++A7AOGkIJzZZs1vIqV8MHbruWO6jYHu4d+KFDsEjF7okd6njRNN3Jfyegs/wvKeRD3Gx+1co3YKC6MhPE6wYtuAYHZ0ffd+N8HreFVnpIy/vrk717msOx/GYPL31Pr+jFJAOET/5GejpU0TzT6FnH7m3SCSN7fMy/LGhGYJwf1HhYPVu8uBvfUdrqHdFF/rrc/fvR8z0Gn43viQfbly622+j+eJfoX35m3I+dsw+us+Tn08jYw64vh2hcnfXJ3yfvhdGFUIS7t/1EiQ+0w5RpNF11m/Wx0RaorZuyTrjGkUe9EZOzqj6yJczvpHTMSuFyG/exhg8efJUJBVPn10jihTOz84BuB4OT66f+EpwDfb7LZ4+fYrJZCL34aQbMSxcVaOzszNst1uRF+33B+x3Tp4BetWUq850f3eHwWAokdhwk8oHTprCRNpBMUBVu42SoM6VaW0kkTFJEiR+rKSDsyfmZVkhilLxkDZNIwU3wsRLbsb0vmZZhpubGyn7SnBUVRWqpoLSShJ9lVK4v7/HbDbDZDjB69evZfMOy2USCFBP/PLlSynLeXZ2hs8++0ya5BHMAMDSl0YFIBEWRob5ms1mePPmjXhKKfuy1kqlIzYmY9IkpQiXl5cyZnVVQXugQkBCwMiylsvlUmRhSinxlp+dnUnRESYxhz0PqO/ncVk5kUSP+m0CQnqR6WkmcGZ1JkaGKBEj4QnHPqw+xblLcMaKPABEpsPvcp/g9VJuFNry8D+CWgJFcdThuFwnQdDORzL4XBnpcnO2xsRXaOR+T7BrrRVCt16vMR6PRdoUx8eJuySg2+0WDw8PMMZgPp/j7s6VP6Zkj2SAYDOsHBR6ogl0XZdrRwJDDz7HhdWOwrkoANpYWQMkbgS4jOrMZq5vDCN0HHOSLNqCMELA9/f7vcwBVppiZIP2weVctLAK0qukz+uIxb6FuQSh55/jG64PAEcyJj5r2m8ShNDD3zSu83mR5VL2OIoiiWYaax0h8tFPjg8JCoyVCCKfTZjAztwkXleYiE2sxfnNiE5VVUIW6JDh2qXkikSIxJljQbIQ5naQHDLqwvnAvZHfC7EhSVW4lniNjAZxn2Vkks+Ikcaqqj4oovHByeCFLzXLG4+zHImvk72va+z3O4wnA2TpAIN8htcvv8J+s8du9wqziwuM53PUnUtOrMsDqkOFxXKF3W6H7W7nSEJZYjqZojUKm10lD4nej/1hD5gI+30vndqsN/jOd7/jDF1Vom1queYwpNRZgjsFJiJ3ne+mqhQAB9TRemDou8WGeIaGzi04K+UpQ2YtYAwu8dlan+yMXiKhjA9gwBMb44iEVJehDEU6E3tyZtqjiesmUYS2s7C2leMj8KS64zInpZPxAOAXDD3BXtriL8CpNN4G3tx0Q8MQErN3ebDfFbkIX6dRjJDEvA/881r5cyjN4ZiJ/OqU1ATn5fPjKzQgfPVe8GOy8a57eeu9U0Lxoz5b79B98WvoADRKwUDDQiF98W8j/dZfg8onvOs+X8IcRy2s6nNvFM/vGa9VCor5I/IepVLWE49e1GOEXDAGZGGrHUy9Q/29/wZmc4Pu4Yfunc4Zc6X6fggcY3qg3jd2ofTNJWn3c/G4o3Y4D3ot6/GzUgiT6nlMZ0D92MAgihRi65K3XX6UN75pApcX5BpaR3GE8XgMWOt6MpyfA0rh7OIcXdfh69/4OpaLJUbjEb75zW8CxmJQFGjqBk3b4MmTJ7IZpmmCw8HJWCij+INvfxvz2Rx5kUNrF2FwtekVmqrDYDhEeagwnU4QKYXFwwOstah8M6/xcIxYRzAeIN37ajNZlmE8Gvln02HvvahxFCHPM1Sls68sHemcNc7TNxyOoZXGq5ev0XUdptMpzs8vUVcVdpu194jXPlrBRODeg71cLsUbTTA5nU6l0hOrCl1cXEhFIM4HEih6XmfzmYCb+/t7XF5eyoZ7dnYmshGllID70KmilMLTp0+lT0Mcx3h8fHTyJQ862R3ZGCNlYJlzQSD3Ez/xE/jss8/wwx/+UJIh6Tjb7Xa4vLwUcMp7Zo8D2k2CgM1m46oJ+ihFHMciuwEgYFepXiZBQEJgQaBAQE+9NglIlmU4HA6YzWYi+WKzWa21RILooaYOvG1bIZgs/a61xmg0wvX1tczl1WolewDlYOznQI88fw9LnhKc8Jk2TSOglACWexttMb3kYfScz4WgkYRpOp0KENRa45NPPsHDw4NEsgjwi6LAZrMTDzJLubL8PslVGJFynvcGdd0JQF6v10cE0lWDcnP5/PxccnjCUqQcI45rOB/plWb0iREGRm/4/Fiql9cf9ouAtcjTTMA/vduUjzEfhBr+oiikohfJFsEuo1iUG4W9VVjliO/x+ukZPxwOiOIYnTVHEr4QQFvbN/kjMGZyPZ0RxFckEbTrHM+maUQWlySJ9NdgVICRAl4r1xjgSyRHrngQ5xvnI4H/IHflcsPyx4ze0NZw/tL7z+MTuIfRlbA/C21d2DU8lICywTXHCDiu2MXr4eeJz8J9l8SH1c0Y+SJ5C8kXczR4DtoaXiexJ+fKB8YpPjyisduU6EwnHrO2dcbUwKKxBl1rgM6iLWvUhwO+/OwL/MP/6lfwcHeDYjJGOhxhX9XYbnbYrbbY7Q/YVw022y3apvW6vgxf//rX8fT5pzg0Drwe9n3oz3khduiaSpLzdrsdXr16hceHB3SmgQkSv5RSPkLR69GNtYijnqEb0wG2hVaQkpvHnvFQdhOAZeu8uZycx557L4GyvVchGHCoQFvuPuMTN6Fh7InHX8hDB2P7hRaCrM5oaN17BsIJGcWuUpgzIGEZWU+uoITZ9vfupVro74v3EYJwvtd7g41gwXAhHJGDd0zOkFicyq7USVmg8Drhkw1CMiLExsBv+O8oiarsW9fzrqjE6fW9j2iE3vDwX//L0ed/VHTj9Njh342KkP0P/wPowRl0OoCePj8G4Sr88SiuEeQD2OMPkoSEh5CgnZVfutVLmP2jIxeLz2Hb2vWB8PPwXc9TKSXHPiVzAMTbRCN2RDRsdDSH+2dLKRyP2ZN8t+adnIvEsP+M8ompGaAshsMCUBaj0RDjwRSRjnBxcYGu6/C1r30N0+kUgMVkNEBV13jy5Il466aTKVbrJVrTenA1EO+Um3cWsQeV9EJSqpNlCdbrpTPYkVuro+EI290W69UGL158gqapASiR4AAWcZwgy3JMpxNf+ahA09RI0wxRFKMoBvjud7+L+Xwm8pvDoRT5jrVWpDIuWXOLKHXFPLI0xcuXLzGZTPC4eMSgGGA4nEqCKTdKpRTiSCPPElRVCWshHj6tNd68eSOVXKIowmq1EoDIaMh+vz+q9U4tPHsuEGgQwBTDQmSk1ANzc95v98jSTHIv+C81/JS0FEUhoJi9MOh5fv78uQAray0in7/H5HMCUCZel2UpmzATVkmcJpPJEZB2cwgCFPk8SQo677G11kqTu7qupWFbmJtALyo925Tm8F9WrCL45LVQThLKJ0KQZq0VnXzTNHj69Kk8czrUhsOhROS6znUEZzTISXt2EmUgeGTeALugn4IVRr3oXSdhY0SHpCccb8q9uJY4r+u6FhLRdR0uLy+lsWJRFGj8NTNJmT0WHJF1EQGgz1sIu3WHOIAJ513Xoq6dJ5qRJ+YkMH+CJYm1z8Ohc5BJvJxLtBEkCaH8h4Rivy/FTlJTH+bh8F5EbaJdtc4kcnhgMBhgs9nIPOS6CyVUoZc9BPYAZE6H8jZGGwhYeV+hpBpwToMkSxF58kQiEEYC+Jx5H4zo0HEwnU7lvgiYOccYmQpzhnhNJALEgm3bQttjh6RgNq1Rt41EWEKgz0jIfr8/ck4w54n2A+irNqVpivV6fUQcSDY5F+bzuczT8FqMMVIoYTAYiKOCRJqEhdEwlqGmjefzDSMsdPowChQ6x7nHhviHBDc8D50fWZaJ3dFaYzgc4s/9xT+PH/f6YKLx3/zjf47toUTTGByqGrvNHpv1GtvNDofG5S7UdYX9dofFwwNWyxX2uy0iWNRdBx3HUMr1YdBw5QZZRYlAousMkiTGxdUzPHvxNSilPYsukaQp4ihCU+9Rly77XgWh44eHB2xWC9dh2ViwEbQbdC16Xz7YnnG20MpAwYrsyOm2te9a60NL4qkF6N3umlqkVg7UOhDkmghqkUvRH9wnZAWwTympPoIgSdUYI+cEAGM7OAWNlmt0k8VCqRhxkoqR4QalowjSadnjRmOMB4m9Vh04jiq4nxsY0zpJmQ3uwzrATWBnvVecKcsS4WCJTaWPehVY9Pr+cGwEDsvfgiRoP0ZyPvSkj8fqCQVZpR8bOLIp0RafPWuM8SSuP4+TyfmyxgK2OR5vE43TV0heQnLJu5MjWneHzN04IrbveYWGQ+kIKh8ffZ7fj5//aUSzZ0g++regtM8jgJKoBmyH5vXvQidD6POv9zyD83rzCs3DD92cvv8+uocfwJYbIcdQgDVeegYgiWJIKWgb5NBAQes+1+U4auGkgjpy3cQdyHDNLHUUybM+/W4cK5/LEEtZaZbJTFNnAM/PzhDFkYCGTz75BINBgfPzC2SZA0MWHQZ+064O9OI77+tytQKsxfX1Neq6xOFwwO3tLWa+T8PQG+y6qQQQEzw3TYvpZIK7+ztn9JXLZzvsD5jNZ35zj6XOfdu0GAyHSOIY290O0+lM8hlGQycV2mw3gAWSJEWS9pppyiyyNEPnPfHj8RiVr1AUNlRimUatFAa+4k+eZ1B+UyLA6LxH7ObG3W+k+4TeqqrQdi3qqhSASdDsJB5b2YwJ6kL9dNe55mbr9Vo20c1mg/l8jjdv3sjxmF8AOI/mbr/DeDyWxl9SZtJ33d1ut5JXsFwujyr+kCQtl0sAEE16qLsPnVIIADg9gEqpI3K0WCwwYv6HB4NCirVG5IFI5MeNFXckwdJa7PZ7JD4qc3l5Kb006JlltIeghkQGcMCPnkkCLMo9Li4usN1uJUrCFwnMacIpwTI13rQh9PhzLbMXBI/L+wEccCPwIjgGIICG+RV0gkVRjK7tIz6sMplnucxFgmpjDNquw2G/R9O2GPk1SlJFIMSISVm6Ckedl8MMigJW9x76Pvm/Q9s2GOSFVPBycrEY1hocDiV0HAng7zrXGDGKIjx58gR1Xbn76DrUtZOjTSZTRJErIey6RVskSSyg0UVEIj/Pgf3+gDzPwI7s1hrkeQFr+15XzCGKovgoByeMdJSlq8rJaOTFxYXsc9Y7QkNb6hwXse+BcsBwSGeBL/dtemn1eDyWZ+x3bOx2W5HxkJA7Ap+jriuZQwS9cewqiIbEgFEN2jpGLoC+JwqBPABJ+Gc1Lnr/wzlI0kKAnPvSuCS0TdO4cuDWukIa1siYOWetEccIr5Frp64cBnUSODeGWkcoihwaCjc3N+JYYI4DHaKUfZJMNU2D0Wh0VK0L6J22dMqQDHI8mdvDuczIFMkiCaO1rqXCer2W8WdkZ71eH9mBMALFPizcV+j0ZTSMvWEGg4HYG8Dh6z/Whn3/i//wf4XPvnyFDjGMjaBVDGXcQ4OKcKhcvW9jW+9pKNG1LbSyruZ54/pZcHNr2gataYQZ5ZnbMLXWyPIhoqQvPcfNII5j1NUebeMWFx8WwVqkFDTU0QNy3k8Ng1bKofaA37HNNNYyaJwsZMi2dU1e3D7kK8EYdqt2pSWN30BMMJTSqkE5bQpL1namc9V8fFSBQM89BoVIx8HvvQc/iqOg3GVfO9x934FqTlYCM621I13eKNEzJkREH5ee5X9aKxhbw5he13f6X/i9EJS/z2vP98LPhPfpfnbHOdXYnwJ49/3+nJTDsa+H1hoKrqdA+DqVYp3ef2daGNOAmv1TEhZGO94iEuo4ofh9YxC+nAc8iHYFxz/97rtyTU7Hhh51awEVpxLNU5MniGfPYR4/h9ndAV3jCIPukwfluLZz/W78uL7rXHxPK+ULwLqeC0dJZ9CIohRkuVEUi0cm0oBCL+Uo8gJpliLPciRpjOvrK2RZJjKZuq7x7NkzJEmE8cSBCnY5JgGjRpylM8uyFONPjyH1xpQFsIMy18f5+blrbhkAKmqJt9stdrsdLi4uBLDQ8NPTyBLco9FIgCo3rKurK/HKMem0aRoppUnvJEuKcsOh1GY4dGW1N5uNSB7Y2IvJiAQe9BrTuxU2zApLSYYeNmOMJLLudjtcX19jvV6LHIAbJL3qYb4FnwNJBMuSEkg2TYP7+3t87Wtfk34Jj4+PUs52Npvh5uZGiHS4dkhK+ExCGQLXL73mNzc3ePbsmRAVfvbx8VHmJqMel5eX4oFkzstsNhNgEspluGkzwZyAieuOTeRYRYgRnevra6xWKyGyYVQjlMOwMzLvg3M2TJB9eHjA+fm5jPNgMBCAtl6vkec5JpOJlBPm/WutxRsq+Tl5LuuAYJ3gjvfE8aUHmYCZERsmvFLGFt5TCPK4LgFWrQG0OpaRUOrCEqskMiHYDAlgKJci+A7lcvTyjicTVE0tz4bgKM9dI9wk6vX/YRQDylXG5LEI0li1i/aEgJsgj8+CJIskheMEQCKFLCvMsTTGSAdwHoP9NkL7FFaxCvM9uPeEpJYEhPYljGbQFtKJQKdJons5Uuihh3LqFT5noJdih1EFvq+UK8vMSBZxB8eOEQdxmPiSuZTl8Li8H3rWGVnZ7/cSqeA+ElZUog0JK2zRnnMvI1kheSGRCa+ZcjN68wnQoyiCNRbr5RLWWrH5jJAxYsRXqP6Ior7BIu0r52UURUJ0OH58bnwdYd5gXRDbhBHEUOHC++B4h+SG49NL8vXRWgsLeYSOemPMH2/Vqf/6n/w6/tbf/nu4W2xR1UBVteiaGlopNLJZdXCVk4CqPCDLUtS+iR49Ym3T+r4AVnIX4ihC7kOaWil0BujaPpmHk8IlGrWoqgPgJ7Ixrtmb1hppnMCwYV+k0ZlWJlvb1ui6ViophA8/Uj3jpyHlOWP2ezOO9RrTeY8uIw5e+gHlys/6hHLgOHrSdb7fhU/opbcQoLfcep04BD+Hers49Y2wfLUa5aMIjBy8C5gDrmNAGCojcTkFrAACEgJAGXRdC5bHpUefhKj3xKO/fpzKiew73wuJhqJeB31i/SnR4HX34f/+nCogbZTNaO2app0CZV4XCRU3h55AGXSm6R9A8J1T4nC6bI6JBgDxKL39uf4gcNGNdxAZRo/6L7o5KF8MCCq/635mGddjWZeba2HPiJP7CHt1+ChPn8ztInpQTIB2OT1xFCFWyjdqSgUsffrpp84DORmjyB0In0wnsgGNh0OMhgO8ePHChaOTuA97W4vxZARrLHZ7B272Oy8j8pGo+Xwu4IalLMOwO9cbK80wxKy1lg2Wm1qYHMmNgrrpJEkwHo9Ft8oKI5vNRkqtrtdr6ctA0MGxDyvk0LtFDzvlPswzoB6eCci73U6kSJRD8R5ZpYn3yyo/ALBYLGQusBkYJTWs9vPs2TPQ60hwTOAU6qV535TAEFQTiFP2EVZqoUSLYIjdiTebDS4uLkSmxagMpQH0nA0GA+mlQDJAO0+gQN35YrFA13V48uSJVGghyQk3akY4mPzNKA89dyyPen5+jslkgtvbW5GJUKJL0EUyxflKLyB/lgRTD25ZXYsRHCaAsj8EnwEAzOdzWGulmdt8Ppc1yufAsSOIIUgIEzWvr6+lEhWfK0EygRYTr2kPaQcI/Eg+AAgJnc1mYjMZZQkrY4WSDdprzhkCGWuBIh8IcOEzCgkvAMmB4V5F7y+jPGmaHpEvAjJebxS58qlWK8m/4bOSSAH6dUrPMAFbnLnxDckvbQ7nK7EC95BQgtzLJbMjEsZ9gvPPRWrdMyEx5PMmKORY8h4IiIuiwMPDw5GXmXp7Yic6H1j+mNcXdtem7QGAPEmPrlOAOSyqpi97Gt4PnWBxHEu1otVqJcSAUkDeGyNFJIthFSd2Uw/XHKNfJKIkB5wTlCqFlbBCjzwA2Z/4TDm2lAfyOkLixmg1nz//TglmVZaoy0qeM4k695EQoNMu0IHNzzNizPLKdB70ucBv5zLy367r5LpJXsK1x/HuHchaCBDnJP9+irW4B9Am0OnPawvtyB9rROPVyyX+73/r7+LX//Xvo0OOtnMJzFGkkOYZrDWoaxcC1JHGw8M9TNeBTXDbtgErG8FPXWM6aUjHSQlYNFWHNO4fMAdAKYUo1ui6xn3XJzMTNAzyAeLIdapsmhrGdojjCG3boKkr1FUpD4P/uQRJB6w2m42AFE6QOOo1sseeXwf23MZVoG0bOaZ7WAaR1q7Ph+m7PdO40DC3bVB+Vrvfk9Rr/1rHRpVWiHQCyoOM6TuXu6RY6+X0/XUKkLd9tIIbJO+DBpHXQ/brxtqgMyelW2XWuHtRyhOnEOwH06nv/iyPvE8rFnwbavmZX/A20HdRpWPtP6xLyLfWwngiR3yu1XE5PHd8dbSQgLcb0hjTwJ6Ue7WW8/Vt6ZSVaNepXMqTaXNMII7Yg+cLPD7/DceHZCo8HtRx5CSM4ME6qaB7v5eTueP0nzs1Wqf/cTNLkhjDUYE8LzAaDTGbzRHHEZ4+fYrnz567nCMPbjgfP/30ExzKA1rbIk28Rj9NEOnIe1wtNPpu9JQMuA2rFQJQFAW6rvWg1KBtjZMQeVBKAMWNi95TAg1u4txwmMBGLzk9h2w4xqouk8kEXdcJ2FNK4eXLl0eg2FqnbydI57NnWJuAmcdiIjPPNxqNjnS/9ILT40zgm+c5Hh8fZW0DwGg0ks+lqWvKxrrzh8NBNOuMKnD9t22LZ8+e4e7uTsqVMiLBjZx/Z2M1glfmV9BLyvFmUmzbttK8rSgKjMdjB/Rsn2NBOROJCNceiQjBFUkDgSbLzNJOERiG0ayLiwvx1Heda/BGLyQBJoEofw49sfz76XwhUOEzYjSqd2D1SaEkJ/To0+tMsE+vaagxZ0Wjx8dHARn0dtOWs6wowQXnLcFeVVVYLBa4vr6WZ8mytvf39wAg40BvJtcP75uAlDkFHBd6LgloWGWod/z1EhZeK+1d2J2Ya5IOIBKnOI6FdIc5APydkSU+yzDRNnRC8hpJwJVysuO67SMj9N5TsjMbT2TP4xy21qKqa8RpIo4Brvn9fi/PlM+Ca5zklwCNRC4EnzwWo0M8ZhidC3MYuL5CwsFoKvFSmKNG7zslf5yXLDzBuRISsjBy2jQNIihxMhBUt20LC4vSExU+Vx4jxEVhJSheOys2ccwOh8NRFSyCZIJXkjeOBx0EYeUjYplw7Lquk6gD90dGuijl4rwMYS8BN9c974U2nVXwSHRk/ccxlO3LdnPMeS2nhIf7LaNSJPp0ptAhRhvG/YqEkTaJBIBEizaWcyfMqwttWCgt49/4LMIICI9TVZWUWeb9cc6SOCql8Od/8efx414fXnUqj/BT3/om/vVvfwdtCyCKoCKXO7DbHwDlQkpt08J0LRLP5PPUaTRZw5iLo6pKFEUGtpXvOoM0TWCNRVEAke0TRQH0xgyud0cYKbDWIlIadWtR1hW6toErs9qgaSvnAW9qGG+kww2ubVtEynnr+QCpObXWom2M1MwHepmJVU7G1LQdjG9b33UG7HGglPY5ABpR5BscxpF4sKMohmuAqGGMqx4Fpf29+UWW9qEsEjP3cJk41sH6evhd23uEaNiNMUjjRMaP48VJw8UUhjRJ9roOsMYB9hD4h9ERrTWMMkd/O5KlRcfN+nx6xBGBJLANIxxhHwhjjCQpu99dpET5sYVVkpPBkrYKx/093kUQQhLC+2a0BjhNXD72mIWv8LpD0uLmiUYcH0dVjsiP7fsohMd6K7oRGA+tFbquhY6Ox63PkYhgjauWZI1F7PMV4jiB1nDyO6WRZqkkM+Z5jvOzc8xmU8RxgidPrpGlGb7+ja97wJehKHIkidNTt03j+zGUyJIEUewq+Sg4Y3Z7d4s41hiMBygrVwXnsHYa/DzPkWcZFg+u9PTTp08RxxE2m72XIeXY73coigHiOMJut/UbRoUsGwiQoxafQJjRi5AkrXwlO+ZfECwuFgsBtZQsEEyHCayMcqxWK5yfnwv4CSOIIei7uLiA1i5vjMCcZP7s7EzAN8FkSFBevXqF2WyG4XB4dA13d3dOWprn4ollp2Z6KLkRclzoEa2qSpKyKX/pug7z+VzAzmq1EhA6Go3kHGG1JFY/4abN66fWONwEGQFo21YSmwmKlHIyJ459+PfZbCb5BWma4u7uzhPN7qiiDIEm5QGU1xGwUUtPDyaBDB0BeZ6LvVutVlJ1i2uTNox7w+PjIy4uLiQXMLwmPvdQhsI5ThkHk89Ho5EktvJaCUoZseIGz4gOIyIE4Ly/i4uLt5JvLy4uhGwSYBAUkuBRYsf1AvSRDUopeD8873g8lkgKwfjalwHmWPGeSRrCvhIhyXXP0eU3EGizShl7dRRFIZ5dJpWHZJDAjOucBIlziz9XVQWlNTprxHFBJ4NSCpkneuy3wQiEJNTPnOySc55rDcCRTIXgkPdJG0OwSILJ4zBCQlt1Sn5pE0IgzfnMxoAE0Gx4GVbMIjAkiKf9oZ3iNbJXA89ZliXgcdThcMB8PpeooJuXfY4TbW0oQyIh4X3weRHgEzRzjtV1jfPzcyHstANcM1yzPDbHlGMWVtoKHadc8yFhIDkIvfhuT3THY2PR0Wh0pPogVmU5ZtpRYsewxwadL3SkMKJBW8CxJ7mns4x7N2WpXPf8LJ8fSVYYteD9EduFJIh2m3M1nHu0A7RRJA50fnN9cV6FRCl8PoywfcjrgyMa68cFvnj5iP/k//p38OZ+h9pYGFOhqg6Io8xPxAz7/Q5R5MrAVXWFgR9YpRXapkUUu8Fo6hoKFmmaYLvdIU0Tb3wBWIuu6STRraqqvpyW6j17ddPAeAMcxTFgXUJpHLtSsBYugbqqDkBTI1L6iFnSaO23a5kMfEB96MqK0eAi7QHlMZAmM3evvqFbyChr71EINfc0WDqKUZ0kKcrkNi3yLDkCSKZzUQf4vBSC/aMohO2BagiUOUnf5eF29+NkNtYe5xyQQYfHCBd6+Dr9bBid4vf4sh+QFxD+LNENjvY75WD26P33vY5IhDo5n7//Y+lScO+nEid+Tx1fo7W2byDIfBY4UsXPhM+IzyJ8ps74pHAlmXtyFBriKNJ49uwp4ihGlrs8h48++sgn6TpjNRqPMZ/NsFwuobTCaDjCxJenPBxK75EvUFc1dvs91uuVlMIkyKMRO5UQsASghcVwPBSvH73YWZahyArAAnd3d9is14jjBJOpAzI90TiuaOOA6whN4wwdATilMmEHZ26ANzc3yLIMFxcXAn5CWcNkMsFoNMKXX34pJOHh4cFfRyHAlOCe+RiU23AzYV+DLMskH4LgnESA0pUkSWTTp64+BLccRwKWr776SqQRtHvz+Rzb7VY8mJSGUFdL73OogWaOgCR+B2B5uVzKZ6jbn81mspEQrNOTSVvMzzJJsK5rKQ8LuMgL5zAASRAfjUZYLBZyTEormBDOTZEgPNwYl8slzs/PBbzSntO7HuaT3N3difOI0hF65yij43ygXQeOZRbc8MPcjBBYhk6WULbAdcLnQDD3+eef4yd/8iclOkKAw2TwEEiORiMBk5xrBAuj0Qg3NzcCxln1iMn0YaSSkQHaYN4vSZ1ozr0tYc4JADkniQPBLm0U5V+AA5U8f9hZmvtskiRIkwxt20ckuNYYdQpJEr3s/AzXNceAUa6wGhUjZ3Vdu8h2HEkibehRfvb0GTY+wZX7Jcet7TqMp5OjJFvaAgIx/i0EfxxT7ieMVhLwk/Aw6ngaRWZOAOcgx4/rms+JZJ9OBJ6P1dtoF4g7wiaB/D4Bf1ipqKlrqVbFyCGjTePJBJ3tczvCkslhZC90IPDeSZi5Xkio6TQIK6yRgHOOcZ2Fr1CeyRfBcCgP4vMJo2okAySZxDUcD65TEtxQ5cHPR5GrIpclqXNLBnt06Ghh1PdUtsTz0J6HmILjwO/QpjAiFTpNON78mZ8Lc8h4LVw7IU6jHWCkkjiR+wb39lC6ynUbkqS/+Fd+ET/u9eFE4/4N9lWEX/mHv4b/+ld/A3VrsFjdI44VsmQMwPpF1iFJ3GKsmxpZ4hda11d92u12aJsGpm1gASRx7Kv+GKSJq2PfNDXiOPFyLCcZSdMEVimkmYuExEksk6ttO0Q6hdYxlDaIImC/36BuDlgsHmHrGsr0bdYBwHSdg3ym12EywZIbRZL5Kht1A6V9aMy75q3VSBIavw7WGMRJ7KMW3pPj80Jg3QMvDwfHhKPjFvLGGOg4QWtcNSTtDY8F0NQ1TFcjjoCWEQl4gK+dJ9++J08i8jX26a13Ru04ETr8DjcUeuStNX2lpOD4XLBKKRa0ksUcHjOMWMhUU3DzQQhRn0jvIh59B2sbVLYKAf0xKTq+b/dzTy5CkuOPejS3Q6JhbajMCvMb3s7LCP8W3iuNxGnkxlorER3Xg+U4ekOCR49f27aSZHZ2dobVaon5/Axf+9rHuH5yhdlsisfHBT766CPkee6lMjsMhoU8GyYYZmmKNEtxe3OD0XiMqioFPE3GYxx2e+RZhtgDYADSEHM0mkBrB36XiwWMr4sexwmyPJNutdyg6rrGdDbFar0Wb8tkOkGe5Vit18jiFNtN7/EPPaNZFqOsStGJ8/43mw3Ozs4kB4HvsWLPfD5HHMdYr9fSl4EbMTeR6XSKr776SjzwfEasAjWdTkWqFEWRSB9ohNlvgeFrekkJtsfjMX74wx/KtfAeAIgcieCJGwo9a/SUE3Rz3pEcsJQq114oaWI3bW5MYS8BgqBQ4hACYhIjRmcYAaInnqVMCSAY/eD3SeAY3aBnjxsfP39KJIBeshDmUlDuxQTc8Xh8JBnYbDZHThIC7K7rcH5+fkSCGCngMwMgsguCL3of6fmj55/kOUlcXf6HhweZSyGBI3jgsfk8+Sz6vDflq33lItFjc7pwrTMiTDJLME6ywNwJjhvBD2VZlM647vC5JC8zT4KkiRI1AgqOOW0m12QY6SAwIqDuOldJjAA5LLJAQMlxJNgbjyeoyr6uPwCZa6G9plceQF81KIgWkMDwWTBnKEwcjuMYu/Ig1xjmWyRxDNO6HBxGfER2Gceo277nQti0LsxjIuEL1wDzI+j1ZXUspZTYhJubmyPSwz2DHvXlcik2h9EW2iuWLib4oxc63PtCiTRB+36/FxIWOgaZW8T7mo7Gct0Ervv9HkprGPSRi3Cf5/xltJf2hHM5SRJxGnEM5Dl4zz5xGZPvaeNoe2g3SU5IwpRSOD8/P/pM6DQI10e4R1PeyrEmoZMqfejzOQEckXIB+B7z8fpJIrhmOD/DylehQ5p7Y+jopcOJa4f7KfcQSi55XXRwcX7QZpBQhmQsJE2MmHNNhHaMa5X/cizSNHNpCE3f20cphZ//S7/wFi46fX0w0bh5/RmUHuE7332F/8t/+rexWh9Qtw0606KpGnRd74l3eRcWVXVA25QOrFKfb63zaFjXFI5JWEnsOoRrpVDXXpsY6HlhfUlQG2E6O8NoOkUxHgNJhGSQo7MWkdGIVYSyPGC1WvrGVwZd28JWW6we71EdSkRaQVuLrnHX3cH4SAtD7gZd5/Is0iRGnmVo2vaoDKqbFEZIR9e5JHEd+dBiWUFByX1EkSu71zSNKHPoDY9iH84zkMKuOtJglao4itGYBq1Pble6B9ku9RdQnhCQgPjHC2udbl4plzgOSzJhEWkrSb/iSff/N53Lheg6V1UrTlM0XQfAIFa9ESNYSGJnMDrjPPfOkLq+Jc4QAl3XHIVI3SS26DpXIOAok4EAXUfQiGFhYTojpENrDW1/VKTCddCWBeyrfvWJ+sfs/kh65BstcqFKeNZa6KhvtkRC4ea3kVLHWinXqIihaWNclRMvDRyPxxgMBzg/m0FHwKAYIMszWGPxyaefuH4N0ymGwyHyLEeWuy6urJA0noxRVmVQpaMEfM5DFPSN4Hq0xsLCYrPdwlqL2XyGzXojyYRFUWA4GGC73comVVUlRqMx2qZFVZbOo+XnMQBkvhIJvdo0pABEj1uWJaq6Rp5lGHhvOWUA5b50JNxL+2JfCtJag+12K5146aULvUZhmPj29tZplv3G3LYtUr+5JH5DKLwnkkacwHOxWBxt1gQkBClMygZwlOgbSlyYwEsSEPafmE6niONY6sFzjEIJAZ8TN2veG48XAshwzoWJ09yc67qW37mZh0nSYUdm3pfbQI7r8XMzD/PYwuRgEj2CCW7mSrnO3QRu/Df07LPCDcvhMhJBsMQSjLxOyo5OPaGMnAEQ2Q03T0a6wspa4ToHHFh+fHwUj2wY6ebnQ/BBoCH7ld/YCXhJSAlCmqbBcDhCXTU+j2YBpTSyLPXzaosk7fNASIDcd1tH4lNHEqu64sbgiJwnBmmaQWsH0KI4xtgD3a6jfLbDcDiCUsBqtRYCfDjsUdcNEu8EHAyH3lHk8iw5Lw8egLZNgzwvoHwKXpo68EmZUZ7nSAg2/ZoZjyfeZnfojMFuu8Vo7BpBhn0TwgpvoZ6cgJCgip8JJSripPMWv+tcueg4irA/HGCNxWTsoqDWGGhPjGezKbquw/5QIor70qu575egFBDrCJ3pkMRubsA7bd68eYPOGolYcs2Gsrmw9CclTYfDQfqlNE1zlNNBaRwJMiugsbJSGMng57ivhY4UNwbd0XiFQJESzvv7eyFCdIYIwSZW8T234iSBArD3MtU4jnFxcSESxdCpxqgTI7MkMqHaINw7OV6MqDJ6x/2DxC+M+LOoAyO3vG7efxgJpV3nPh46WAisSfppLzn3eF4+X441cxqyLEPXdoj8d3h8/sw5ynlOO8R7ps0gOaCND3uw8H4YUWQ0mo4G7reh7RKntScbLprYy9m5TrIsR1WV0LrvYcU9klJx116i8jJ/5sDkcPnWHVjC+Rf+8o8nGh+co9FZwLYVsixCrA3qao+67WCsQVX2Jb3CENRhv0Nb74+MNyea1hpt3aJtfIk9X4/aPRyFunZgryr3sokppZEmOTZrlxsQFZkrg9t2UHGEKHa9OlQcYziZYjiZem3yFlXXADpG1XaIrIW2FtY4wtNag85aAC3KqvI5AQ6wtW2D3eGAvoKQFRbociyiHtwrBVv5PAXjN+Sy8hPY/ZfmuU93do0DOfHdGFtY63IkOBZFkkIpIKpL6bxsfK1tRogiAEr1+n7jowT8v9aushcUoxXud3fet8N1rppV5ypqxbEbGwUkSeySrq0rUmQVEOkICsaVOY5dt2WltFTYynxFIZcA7AiUMRZaeSOmNazt0LS1ZECHjQVjnbg91gIqchW3IrJ05rbA5VEAfXI0jQngFlCs+iaNrlN6n7/AaBDnmHugvYRJKVdRLfElWnUUyfm0VkiSGBcX5zg7m8N1SE5xcXmJ7WaDFy8+xmQ0EuNkTIeicFKT+dkMTVOh65zBoW42rI7i9L0Gb97sPLhRWC4fkWbOu+ByERa9kfcAO028F36/E31/52ukLxcrb+AO+PjjF85gGwsojSwvJE/AbU4bGGvFU0gjefCyAiaFscIRvZSMEBAEl2WJkZf4kDxkOhV70HUdrq4usVgsxDNNrTjHhufSWkt0giUfAWA4GuGzzz5D27b4xje+gcVigYuLC5Qe0FI+sFgs8OLFC7FTJEr0SDH3g5Ik6omZg0DvHecT72c+n4vH7+zsTJJT5/O5eOuBvnw2gCNCOJlMpIoMN5zpdHoE+gEcSTLYYI5yjNlsJmPFvAwSN2MMbm9vj/JZCKQBvFW5ip5percohzgFDYvFQiIXJAskQZQ+kZwQQFCeFUbBKKEJN2KOTZZleHh4kO+FMgl+l55fAq1QRsAGe/QkxnGM6XTay0Z8NCbMlQhJA+dJVVUiX2VFKXqN+XeO627rco2cJ5cRNI2mcWTY9e3ppQ3cI42xKA8lrOkb0nH9DbztMMZIhOjy8goPDw/Y7fZSDWq5XHrQ5cachDisbuPOm0ArLR7h+fxMencUeeHvuyf/XdditWKH6aIncRbIs9yPRd/QC1Bo6gZJkmK33Ql5pnKAkSTa7NMoOJ0CJP6cdySeu90OOnGgOsszIbN9xFKj88+ka12fm7bxQNgapFFfspfz0nQd0jgRySIjUYvHR9dJ3Ze+5XX3MmsluU4Ej4xeMkLF62cTSK6pXnLdF8ZhRJU2KXRA0IN+iq3CseO84vrimuQa5jpgRTR45LHzXnHOExJrjj+jA7RRSikhAFyzIbEngQzzm+joYL4P1xIjoVxDobyoaRopNkAbxJLfSqkjey0Y1Ecywwgr9yk6fmj/6DQg6OZ5eH1c59yH0iIBjBWFTEhoQrkiK+zx2Iwk0H4yWnaan0ECCkCiIKE8LSygQMJFW90rZXos2TuVYolQhFEWSklDUuTmGeV29uh7jux/GIX4YKLx+tUrGJNgt23x8cdP8L0f/BAWDijqKELtGSwv3G2MzVtNybgg3HuuZKy1rpsuABSDAQwrzMSJ6zvhe0F0XYu6PaDb1yi7PSo0ePLRJyiKHNCuAoBsnizN5yf2Hh2qsoRVEfbrtYtyWANAvyVz6V8aHZzXP05z6Xmgo76fARsJGn8PPILtnHfc1/zxD966KqLWJTiTYPBYBo5snHoAGDHQts8HaZTr79G0DRQM4tidi9ETa5xUzfoiTTqKkMQ92FZao20iWPjGadZVJTJeOhQlLjpjrAW6zkVtjKukBU+QFSxgFLSKAKv9OX11I+ujOU0rG06kU7gmekCeZlAKPuKhoVWFtvERm8hKPkSkIyh1XCZXexLDRPQoinwPF9eXwmiXMB9HsUQZ+nwRT/qUS8SOkwSm61AMBh50ZRgOHdg4OzvHfD5DpF151pHvAn19ddWHUZMEUaQxn0/RdUYqJSVJgsVyiSxJMBq6jXe9dv0QsjTFZrvFavV45B0NPSBhciUNNb25UAqNB4tau/r+rFzTta6xVRzHWCwWAPq+MTQ23LTpPaQBooyGAK5pXKO36XQqmxQ9L/RMM6zL6+b79H7Ty0w9cGhUaczpwTLGiCePYHU6nYphHvhn1LataPyLonBNxzxJOzs7E2BWFAUa7+UH3AZ+fX0tlWd4rSEIoBec3h3XoKsWu8VmaQRmWmtcXl4ehai5oVLCxHOfOloIIIC+KhB7IYTaeD4vSgsIeEOP/uFwwHa7lcp5JAhN00iZVAJxgtqiKLDZbLBer6UMLZ8JJQRhBJKVnBzI7L1uBNkAJPLC3Lrz83NsNhuRhDGCsVgs5HkqpYTcMWrEjTPMiSPJoxfWWlf56M2bNwK+Odf4Gc65p0+f4nA44PHxEWdnZzIWIcB5+fKlVMgJPYKLxUJIF+c4z81zMFqgtZb+I4ACvKSI+U0kpUnSlzYl6OB4LxcLXFxcCmkJP8fkTe6xjKJxzDl3x+OxjBvn92g0OopKMSIRgpPVaiWN2lwXekd2WUCBwIjzmeubtoQgNJT7EACRTBCcchyJD7iuuCZDrzRlXQTY/M5gMICKIrS+Wh0BcyiPazwRpR0ZjUbYHw6I4kiA7lGlsECLTtLO39vWOQhoH07XJPcaEg1GH8NrJsEK798YI3aeXngCSgJhAnkS8jDPIA729jDvgraP5ZR5vJA0h8UfrLUil2TkkzK20FEQVqCL4xivXr0SIkSnBu0dE/w578Jo6ikGCpPuCei5PkiQOAfyPBd7zHGmXaCtCaVB3P8I0Dm3aDN4Xv6stZa8P46NtVbmRBLHqJv6aJ7y2Pwb1zTfJykIHbscK0ZM6cQIo1Ocm7TPYZ4Q5xWjYZx3zC9q2/74XO+0Hzw+bQzfow2lDQlzcLgOOa8/5PXBRGM6nqJuLObzMX7pL/8C/umv/nNsdhs0rUFTt/KQeBFkrlHqZE9kSb3u1AEmhq2rqu69xJFFlruH2LaNZ1IuRKpMi7o6QHc1suEAbVUhm6dAlHqpUQsbeKk6Y9Bag6QY4OzyCc4vLVaPj7i/eQOtgCSKJBrQdS7ZloZOa43WtM7r7sF5pJ1XPQ4fsnalaCNPOLRSnkkyKtIhirR4S2zXeRDvB9fnbzRdByuhNSbYxrBQsAowPu/AwsLECbIsB5raJcj7SamTFJ3yvQ4sPON012GV6y9iO2fwh4Mx4sQZ0aLIkcSJl6dZ9904htJAHEdYLhcwpkN92GN7f4e914TLYrGuMaO/HT92VoxHkqRQcQLbsSmSy2thda4kypBEvbaRXlzlx9otcrd585xx5KMxcAQoUhpa+eoU2mI0GnrCcIbhcCiVf4oiR5zE+PrXvualYQZxFCPNEqRpLFpZYzpv7FwEY7NdY7vZ4PziAlq5Hg7GRxCWqweveU8RJwrb3QpKGSwWd6irATabtTeSHdo2RRQpCZ3SG82xYhM3hlXpJZMxifpa4vP5XEDA1dUVKl89hN5l5iuwKZnWruPrbreTikMhuKVBZ0nV8WiEtQ/3U5bDpnj0IBHE8FpIiJhobIyRXgchiObmwvs8OzvDl19+ibCEZigt4P2T5F1cXCCKIrx+/RqxBzqsVkMQ4shub+wPh4M0pmN+Q1mWeP78uciACKApg+Lvs9lMNjJeYyhZ4D2naSp6bUo8GIHgmrHW6Ybj2NWep0wrjC7yfvM8P+pqTZBIbxs3FCatExjxWgkouXGwXCzvgzIwevhpv+k9JEBl5IKNCLk5EajQI0cgQ2K6XC5l/Ekwz8/PcXt7i/Pzc5Fh8LpDmRjny5Un9xy3kLhRasU8g62XCCZJclTm9eLiAgAEPHCMmYgd5sBorSXv5ezsTAAcbQ+fd+hVDKshuWhWLuupKAq5F5eobJAkvSebRMNaK0SZETauEf4e6uGZy0KSEUq7CBiodScZpCSHUQWCL4LC3W4nEkMC0HBucG4R6NCDH4IsylfCSj4kMHRUkEwyehbmYoT3zOcC9P0baBcY4TfGSH8bgqH9fo80isXecQ46yU2Lsq6EEPM+WY66qxuZT5S0UC5TBhG0wWAgtoTEVeRkHvPQ8UCSSrvJced1hQ6nOI4xm82w2+1kHXFdhV73UArEY5L00R5xzElA+JlQKso1yrnI9RRKewiUw2gic1R4LM4vEjuCVK4DRqFoo+nBZ0I5vfmy16m+Ih1tYwh+mXxNwMtjnDrvwvvm5xihCOWbJAFhJTOuX67/EJQzuh7miIR5E2EUhePI3JJQChjaFub5hKSczyYkKLwHYm/+y8+4+3b4NswtIWkK80l4TWGeDZ2DnMN85hwjOnc+5PXBORp/8Du/DegIFjHKqsPf/jv/Jf7RP/5v0XQKSjkJDgFiH/oClG2OWFsITFvpL9GzegDQypV85Wdp4IwxgHIla3WUIBuMUQxn+OZP/UlMp+fQSQyrEOj/+00FxqCpalSHPQ67LbarFcr9HmkcwxrXy4NGjjkaUaRh4CMDAdslqdBRJOFvesuVogJICeDuuk7yLkzXuSR4P1bc4BgajZJIJig7Xcdx4pQ8kasqxHNFvnys0g7opFmKLM0Q+w3ssD/AmhhFPhBdtLHW6esB5MPMN010EQM5b2fRNApxlEBpCwWDh/s7AB1sU+H+8++hpZcX6HWjyonCHLhyYWvA57T4yEmk3UZp0Sebu7GJxGDyWbv54Hq1WEASO+M4xnAwQJpEKIoM19dP8Pz5M1gLDAYFPv30U2y2a++djuU7SZxgf9jLpq+Um2vT2VQq9SyXj2KUmfzKZMqsyHB7e4Orqyus12sALvR7fX2NzWaLKNICMOnB2G42GOQ56rryZSRzbLcbr01do66dF5lgho2HuGYoI+E6SJIEm+1WckXCEHZVVbg8PxevIsukrlYrV1HIg83PP/8cFxcXXju+lB4Ey+USm80GV1dX4lEZDAZ49H0muLG8fPkSV1dXsnaLosAXX3yB+XwuoIPgl82i6K1mQm+YL5EkiYAErgdu3ow8cGPqc0gqmS9JkqDtOtRN370agDR/Ml2H6WQi3j9KXOiZ57MPJUf0yIae2K7rpIcFwTs3qTBHg5sugVfofWZ0gPI0GngCddpCbsr00vE/gkuOAzXfjAoR6FDHy+OztCplA5xPo9FIGtRxY2OuDgEBQRivN4wuRFEkxI3Pm97h8HoJWngNpwSSBC8kSnzOXAPcmGnfwxwKnns+n2O1WmG/32MymYDJrCTzJCjb7VYSY/lsQgkFIyK07QQDw+EQb968wcjLIWn76DTgvLHWIk0y1HUj65CEwIGMCE3bd7LnegdcQ7umaSVaEAJSAjHuazwvnQUhySNJjONYqpQx0kFZ4nA4lO/RW8riCLxvrgmg9zwT6BAAEeTyPY4rALkmAOLNJngBIPkLdEqceqNJLngMXkPXuWqTm+0GmQeM/M5ms3HXHidCzAmWm6ZBlufojEGa9SCPBKBrW9juuFwt71Vphdo7O0LbwGdCzzptOMcgnENh7lIoGaMHndE/YiLaf0ZjDoeD5IzxvASAJGZhMjHHOATpJIQhqeDfSXq5D5P0cl7znrj+KVHk8Qn6SUoYiSOB55rm3kXSShvAaw+BLaM5nEthM0k65bheWHSDY03bwedC8kgHB3M++ExDghKSYGIC/j3PMpFOcR+gjIoEjFXAwogHHQW0g+H64TMPE9RDe8jrC8ec9orzhIn0PS7tnwkAqWDH+R0SlHCu8xnyxf0wtOtaa/zZv/Bn8ONeH0w0fuvX/yUm07EjB1GGf/Frv4n/6P/8N7Hd1Yji4ohEcMPTyqJrKwkT8zNRFKFpW3TWg3Glg0ZuFknM0mUKaerkWaYzOBz2KIrcV3JKESUZjNKYnV3g6fPnyEYjqNglMhH0spxcpBO0dQPTtqgPeywXjyh3O2jA5WzooL+BjwAYY2F9Mzzq0bq2lYpIbhNg7oKRJOUocnkNnJSRjoT9tV3rpEI+wjEZT1ySsHXJxnVV+vA0J7Rnlk0DAwfmlfZdmb1XrvGJwWV5QOwZ82G/B5TCdr1FlqRH1QqGwyHarkVZbnE49JVglFLoDCNUie+LoFHutygPG2gFmLZG5JPSWT2rMx2yNPPNCVu/qHrtaZKkcH1WfPnIJPUSpRGqukIcJdhsdtCRWxBFXnjGXGA4LHB+cYbZbIbLy0tcXlxCaYXddockdu392rZFXlC+waSlVGQNvfyjAaCQ+POv1xvUdeUNdg4mQbFTKMEVSWGURrKwCbCdbCuCMRDQpXWEuq68JjxFud/5qiwN4jgSYFWWFQaD4ZE8gh2puegJQAnqlVIY+trz3KB43ul0ikgpvH79WsgVAWWapij9Zp3nOR4eHvD06VNJwLu4uMBms5EyrgOfHH5+fo69bxhGD3xIBrmREPgTaM5mM6zXazGMTdNIBSxuOLQXTABm3W6G/Eej0VFToyiKMJ/PjyRYHKvWGNn4jOnLTmqtUZUlbt68wbNnz8QGhV46evOstUf5EQxFc5wByIYSOlQoRyJwCD2uXddJxSTaA4JehtVd8uxYSBa9jNyIafiTJJHqVdxY6RleLBZSoQk4BnsE75Smaa0lCkaPLHsYUKZFIk1gQMkMxyLcgIbDoQAhgm5eD+C8qWzex3ukp5BrlFEfrgPaJD7rU4KYJMlR0i3nGIkg/8afCSZC4BqSSuYR0fPHZo0ExvTQEqyHY0rv5inwLooBtIpkTYVJ8VorNG0vu3j0+n8XrUtRHkoBMJwTtGVcOySb4bwh2aFHlo4S7lcklHx+JLM8F+c5nz1fJKyhpC8EPqzeRakNz8drpC0iQQQgc57PmceTSGTbN9blWiZ4IzBr2xadtSgGxVGkxFpXeCZL+opgvJ+6rqGjCJ3PdaT8kus2iWPY7u0EZrfPFDDo13ZIwBiJYBSTgIz3xj4fjHbwfsMKTyFh4BoOo7GMYhC4cyxCYhBisDCaSnIR5hvQdlNWEzp2uNbD58dnSNtHshXmGTEqxGui04L3TcIeSndo07j26Zzge9PpVM7Dc9O2hDLW0A4JqfTznxFFjslpKeBwDXPsw7EKCxOkaYokip1k2+8p/CwdhDwuKweSFHIPpj1QSh31JaH9IPGgM44SXs4Hjj9tLscjnO9UtIRzk2sslKlxnnNPB3qpNQBxwpDA8HnHcfxBROODpVNx5Lwi0Aoq7vDRsyc4m8+w2bx2CcLqNAejBWARRxp14zbOqq4RRTGSKML57AwqSCThd91Cco3ZrHHJyLxxJ5NRiHQMeHDRWcA0HW5fv0YyGiEdDsS7B7jchM54LaAyUNoiSjKMJzMkcQrTttDWoPELMMtyP9gxoIDG+gUTa3TWIvOhOlggzS2KPIeONPIsl0aCURSjrhuX8B0nR5UK2q5FMSyEVa7Xaxy8Qe7qChou0baqK3RtJ4tEGaCpajD52Rl450Ht6howfXKa8R29m6aBQo047iekVhoPsK5rua9UFEcRdOKqnKRpimjsqvhoBTy5vkRT7ZGlEaYT3/gsGwDKNT3K89x5x7MMk8kY1kd/RiPnHXKVnjSSOIKK+tKeBOmulnyMJE7RNKzaQOmZRd1UYInj87MZ2u4AbTVWqztMJyPEkUZVl4ByuQllWSIrHNvXSmNYOG/obr+XHBqtLOryAAWDJIpcIQJjfL5NgrbpoFUErTQGhQPYChaRdvkYu+0B19dX2B8OMJ31eUAZ2tYgywbS3KyqKmy3e6yXS0ynU8zn5/jyyy8xHo+R5wWSJJONmJ6T1WqFjz76SEDm3nu3wrB86TccJinv93vpJdHWNT755BPc3t6KLIcbtFIKFxcXRyHk6XQq3lB6ihnBYaUkrk/2WeD31+s1qAdnsi7vh6COBo6bKPtdsBwsJV+0GdfX17LWoygSL+BpCJzGmhtlHYSuubHTmDd1LQ26KEOgp4iEhgCKx6UXLIxi0FNEEmKtFSJKrxIT+gkAKHvjuPBzNNr0KNJ413UtUgGCK26MUeSaDU4mEz+3trKZEqRy0yFgByDPZ7FYCOnhnKKMJpS2hrk6tD/c4AksWEmH40SgT5kr5x17x/D+6TGlDQMgGzdtAzcxfjYkpTwfiTcBAz3wZVnBmE4q9zC3J00zdF0r9jkES5Qtsjv8drt1EpymdYnSvlgDr4nf4fc5B+lpbZvWVR9sWiyXDxJdoheyaRoMR4MjryF7j9CREUWRNMmjXc/zXCJOof2s674h23g8loT2kOgySkgiAvTAIiRfZVliPB5j5XtM0MHA58R8FZK8cJ3wnCSyZVmKXI33RRDHdUhAxD2BEbqwahHnD6NFBKuc40kcSRSXn2+axkm2fanwUCPPNWOgMB6PZX2x67vpOoyHI3GsZFkWlFV24I95MqHMhPdIssCoA20YP0+MRNBHYnaa90AJEu8zlB5yXXBtUptPgs7nyvkVx/FRI8UQ1DLCwghnWF42dHKExCUkWow2hc+WRIm2mEUteO4QzDI3jfOQ40MSQclkGFGgE6HrOsl/4rymU5d7GR03lNDRYXEaeQujFSR24TixMIHgS58czbHhuuV6oC3j/AjnOvEy74VrNiTvvSyqzx/mHA4dP+H1h04wN74trFXiFOHeRVvLV7gncU6RJIa5L+Gcp+PjQ14fHNH4l7/+33mJgoHWCfa7Bv/5f/Z38a9/49+gNS7fwBgLqzR0FHtgr6ATJTIkbkSxLymnlfUVjgy61lU5atsWeVYgjjxQaQ3iOPWlXxWqqkQxzF0n7KhP4CmGQ1QwSAYDPHv2DEkSY89yeRaoDy3ytMDDwx3qqkSaJkiSGOvNGkY7edRwNPQREw8AkgQxtCSHVT5RrKorV3mpcxNgs14jzVy1oeViif1uh4hJ3z5Mvj/sYEwL01nA+ESczqCsShkDmBapJwVR7ICuyzdQyGKNSLvKHtws8iLHcDCANR2y3HV6JlMdj1yzsCzXmE5GKLwxmU6niLRGMRggTfoKFtZanJ+fy0KzsL6nicJuuwUrcI3GY6w3W+S5SySNtIbyHi03CV3fDx3oOXuviK+44ievW9gWTeMAHjsn08DQmDaNy/EoisJ7/GNY6xbR4bD31w8f7VG+k28J7btgx0niSzK6kOp+t0MmiZPumrq2dfXTvd7cgbcRNps1mrrBcNQbs6qucX52hqqufTlmd31VVSPP+/rpDoztZZOjESXoS9NU9LthJZ48z7HebLD13kFuwo03kNY/I3r6AMjGTfBMjzrD1EmSIE/73ie196bQw5YXBW5vb2WOcMMbDAZY+/KDodeJRpE/c6NdLBaSD5Nkmciocp87kaSp0xbavuIGIwrb7RZA7z0hKGM0gGCKmw49otbao40+BKS73c4T3ViSn+mh4qZLqQg3cG4Q1JeTMNGIn5ZPDCMV/FwYeQg11DTkoVQrlMbw3vlzGOZ2G0cn906jHybj8jMkaqzIFNajJ/Fp21a8pKEUhMSVGzLBJonH4+OjAAluRodDiUhHiHyjyKZ2oKTtXHnh/f7gn4uBUiynbZFlKTbbjZCnkMiEEQJ6RwFHQuvKJ33mufRoyrMcXddiNBo7EhZHaOqeGOZ5hq5zcpnddifAKElitG13pO9u20Zso1I6kBQoVFWNpunJwG63x2BQoKpqwDuX6NEluKD3kjbRWhcpV0qJbJf5fGHeSwjOKYNkpIKRTgIz5oYAff+AMHmTNjrUwhMIcs7neS4SFN4/r4HrIHT8EfiuVish7GVZCrkhuOQcJPknYQg95JxvBP8hUQoTbDkXGRU0xuJwcKCe0fW2c/trHLvoMsEywRIJh4XLLVRKoe06t9crJfaJNoJJ03nhSukz/4T3FObqcLxDTTztBsePQI/EIJRbUX4TRlTCfZqqBAJ/SvJIxgGXX8Yxpo3UWst+w/lM/MQ9mUCW8yOMLtPOcl3SFoWOC84t52wc4eHhQWweI5+MjtEOM6JLkM0oE49HmxYSzVByBvQedpINkivujySwvE7aUxY/CB3ktMHcX3mukCA4Jy4QKS2OuYeHB5EJj0ZjpGmGuq5Qln0DPZJVrfvIbSjVTdM8yAu03inSeuVMdJTHxEqIbv325cld8+vja+bPnIN89iEmof3lnOPfezt4bAs4X/7CL/0x9tH46qsvArakAZvih9//Cv/xf/KfYrVr0Rn4KEOHYlBAR7Gr0mQM9gfP/qEcSIcDrdZ0knxM1llXFToYqCSCVhHSNEMUxTAGqMoacRohzRLnZVIaWZ6jPBxwdnaO8fwCaT7AaDhyWkofQTGmg44SWCj/0DrkeYay8mXzEqeXq5vakQMNtG2DtqlR71ySW1M3aNpGqj2YtkV72EnDlnDR2q4DOlen3MmkFKLIGfok1jBtg9l0iufPn4s3z+n0pwA6DAaO8Mxnc0z9ht81NS7mZ6ibWuQds+kMja+CkeUpmroR7bFLYMrx+HiPunHJbq9evcLl5aUAKk5adqZ98uSJLHRKD06TS5vGnePq6koqfNBw0YNLT+LNzQ2ur68lfEzjSwNNI0vDRiP0+PiI6+trdJ1L1OS5Qu0kFwJlKJQnUDJEtk0vICUoofeWzyxJEkwmEwGGvB7W7ydgY94Cr51yCm4wNKAApLESpULcvJlQzU1WKYWbmxvxItMgO/1wJmFVyp0IEvkceAxuwgSAee4az4Vh7IHPw3jy5Am++OILycsoBgN8/RvfEO0+czfW6zWePn2K1kcdhOAGiY6nshNqbztj0PrzEvgfDgdsNhs0dQ0beGhJuuI4xt3dHS4vL8UzyL/zXGFSNEPSBFEch7OzMzRNIxWGmAjLxD9jjORl0PaEz4vkgednqJ+dnBnx4Jzn5kyjz/fpTQt115Q70ftK4kdiQqlYuBlzQ6WWP5RSMCeFYIQbAfNeCC64sfJ5UAdP4kVPG++Ftp7klUSFz4IlHyUCtj+grlvZtKuqEiLI9UrQxnt2dsXCwkhSJL11rAYUerm5ZtznrC+bmhwBbgJCevBDzyllf7xX3i/lOYwQ8rOhtOPx8VHAPyNpYQ4N0IO10PtMry7tCjdoRjHC9UvbxigMPducK1VVieeea51knJ5ffp+yGmut5H3R6UP7TuDDsQ/nCj20XGeM+lBTz7XOewmBNNBXzqNkhLlLdIgwwsU9M9R/8z4IknrPrntRatdX6OmJdXhcRwTddYcNATkfeS7Od4J1SrBCWZRo7eMYOu5lY3zG9Mjz2Jxj4flCaQ/XK+eMtVaa2hHo0pFB0kDJC5PX2fRxsVjI3Obez+8zNyOMPvJ6uH/RC8+5EzoIafM5n8J7Du2xtVZsanh+klvaTpI92rRT+83nzmfL+ckoF2VEdFKFkinanZC4AZB9nTaV0QNGGbjerXU5FrSpVBVw3MN8i67rEGmN1PcPA/pKim6uj1EUA8EOYXTJlaU/bujKOQdoyd8IZXJO2thHJTgve4ds38SSx6OzIHy2tF392ukrboWkFOibU3KcGWXj+Ynp/tIv/zF2Bn98fEDXMcEvgjUxXr96wN/8m/85vv2DG7S+WZ2KXMO+fJDBtB1iq1CVrlcALyyKInTG4ODDr5wk9OB0qkOUJwB8/W/TJ7TkgxyDQe6Noi+PyKpPKsN2c0BRFLIoqAtvFdCaDk1ToywP2O+32O+3LhzXRTBth0O5hzEduq4BYNG1LWIFmK4PI5VlCR1FULZDomvESYyzszNcXV5CKdelMktTxJHCeDTCRx8/9xWrgGfPnuCw28J0LqQcegCms6nT98cOyCyWCxi/qNM0xSAboq1dtarD3gG28WTiSqzVDVzXxl4y4DxVHZRyzQg5IcfjMe7v7wVAhB4KAEdl/ghokiTB4+OjgAxu+qEhDcPA1royoGGlEhorLoawPCq9X7vdDufn57JBDQYDfPXVV1JJiIaBBplykVCLudlsBOxOp1MBW3d3dzg7O8NgMMDLly+9J9J5aqbTKe7v78EcgN1uJxISbnQ0egxzM2oQensJ4igzCkFmFEWigad3INTD0xC6DuArpF4icXFxIdpwAtCzszMB3gyvE8RSIkW5Az33bdOg9uF1ggqSnzzPMfEVTpjgRU+ntRbr5VJABckB65DzvjgHaIDu7u8Bb9S5OblmWTOUhwPGnsRxPELPZ+hdIgEmWaAUgUaS9xrOOz63LMuwXq+FMBIU03NqjJP4PDw8yNqgoeXcqapKemIwuZgNpgCI584YIz0KQsARVtoST7Z/SQ5XIIkgSQ6lCgTFlFmFuQWcS8YYAXFnZ2e4u7sTcEISzU2Zc5rjyE2EYJj/haQmDKXzO/zPATSLpu69irQjHHeSOW7qJJLGdEjSXgrF8eBmyHlPqRAJUFXWPjoeH+UoEJTGcSxrk+Me6pxD28X9h2PC8wAQ0M25lWWZAJE8z3F7e4umaXB2dib3RSBCB0soByNA4vPnWqM8kM+WAI1ABICsFXpQQxkDr5HzgV52AlsARwmvHA/aFNpcrmN+j+MbyrwIFFmqNyQXPCbHl6QhJFshqQifKedmSKQ4b0O7QFDYn08d2V5eixuzPqGY52S0h+QI6KXbIdnlGj6SI2kNq/rcAD5vzh161EnseD4WUghlkJyPbduKrInPjbIdgj0em701GPngeIUkJpSKce8hkeU5uZcxAZ5khE65sJQ47Sn3BxJ/SsPC58d5y0gAgTwjKZxTtCWcI2GuCOczCxaEkQlW4mLEmePEyAir4pHEMDK72WwwHo+P1gvHifcfElTiE764hmmLrLWIlIuUc42GMiZjXL+J0wias4eNrHMSfjouVqs1BoO+mmE4z7LM7RdhkYh+XR5XnArXPe+Zc5jvhXaP98i5EtrBMGLKNcE5EEUR/sr/6Jfw414fnKPRtg6kG9MhjjWiWAGqA3SHQ1VhuVqjGBauJG3XAhpwnbVdQ6AkTVDMxhgMhojjCGVV4el0CsA1+HG5DpHvoJzCtNyAS1jrJmNVVwAM9vsdykMD07lFtNlsXEWh1Qa2dV2f94cD2qZFHLv+FbvdBk1To+0aaKXQdq6cbqQViizBcFDg2dkI1kaYTi9wfj5HXVcoUlcicT6bY342R55lyIsCUaQQ6z4krbVCnuWuJCwAWOPHyyBJXbfyJG7RxQbTs0skvpGdsgZtXWH1+OgqL+kIh/0BXdNhv9tjNpuiaVscyj0ipbHbuHuezsbQGkhSDWtjLy9KkOdjuA7ccDkPyqD2TRFpuGkA2YRpPB6L12uz2cjGnWWZNH7iRCWAf3x8lM2W3n9uONx4Geakgeo6pwGnd5z1+2koCS5p/O7v72UBMjkzSRIhaYvFQjzXjMawBrjWGg8PD3J9JJ+bzUb6CpRliaurK4kMTKdTkR4wbMhrCjdMhveZ10Ayy8RtAEdjzbHhBkOSwIUabqI0tszDWC6X0mxrvV6L4aTxDYkLgbO1FtfX16jrWpLojDFovce+bdujiiVN04jGfbfbCeghSRp5LzvXGj9DQ8XnS6Mk0aAgvB7HMa6vrx1QGw59CeheptM0jXiPJpOJJMWfn59LpIXgtes68VCORiPpFwIAl5eXooder9fizQqlH3wu9PqH0iQCGZJHSnoY4bu9vZVKPtRw06sdgiN6gbi50iPGa59Op7KZUGbHsQrBA714YQlbPmv+x+gCX3QKhFWV6L0EcAQW6IEUAO89WBwz/p3HW61WssFxTHa7HbTSKAoX9QkBITe0cMOkXK8sS6RZIqCMTgFujqFcit5bbthxfCzdA4613/T2UXYXkgveG2UBjDZx3MMKWaFUiNW3OG4k/cxzASDRTco/OAcI5EmoCPistQIcGEml/SABYHSBJCN0AtAW0NkSgiZKUnjPwHFTsjA6HALqEKxwHYSRhzDCEmq+Q/BCUKW1lpwSfp9kLwTovAbax9COEsCF3+EcdGPQe2FDG+uuyYisKzwev8/xm8/nMkdIhLgWOOe0ds1cmyCCT6Jd132/Hn6WpIzeeJIMjhXzUMLO0ATUPE5IwDhvGcmis200GknUIwSuvEc6oeiwWq/XkstDXCC9IZJE5D9ct6GMjhEqEhlGCCih4jNhDk8c9z2VOO8JsEMizLXGCCtJceiMpW0lyaEjg8cmGeAxLy8vZT3NZjOZ11yn1rpcG0bNGUXlmlytVrL30lnKOZxlGZQ97k3Ete3mhFPikBAwd8ndZ19BMATy3JeIP2i7SUBdPzH2qGsDAtogjhNxYNDpGdqRMKIcRstD5xLXGe0/jxWuNdpxFpkI5+uPen1wRON73/s+AOPBbYq2MViv9vg7f/dX8Nt/8CXa1mI8m2IwGKJpWzRdiyTLEGUJdKQlf2C73QLWVYlABGw3WwEwnXEkwZYW69sVjHWkYrvd+M3CbRyL5aIPX1G+oDVUWyHWbjIPBn1SeJamuJrNMB0NkeUZiiLHcDhAFGk8ffYEo1kOgw6DgZNhxamrmqSVQuE3oEhHfsGz/4NC2xrxSMxmM7gk8Brl4YAkjlGWB4xGQ7Rdg7alpjtBVfb6OWtdF1hjDHQU4VC7ZFBYi9V6DdN1GAyHiLRF1/UNk8g6HWDokMQp4iRGHEWoG1fusiorrDcrCfdzM+NEDj0d1rpupdTBc+Hc3d2hqio8f/5cFnC4qdFrEUWRREsGATANDcbd3Z0YMHqngT7JioaJE369XouHmPIV9legfIzjQEkBIxoEps5LsBJQQsNKIEBDyg06lICx6yj7WnBTCDczbh7UeobRgPl8frQB0DDyZ36fCzjc+NabDS68hCjM42AZXBoKSktopAg66QnMfJ7Efr9HnmWu30iwEUvSclUhCiQf3JC7rkPqQXN4D/v9Xgjh4XDAcrkUojcajVxVucBTTmATx7HkaAAQknC6udDwh95Xbmx8Zg8PD0LkOCdpzhgtI0EkwOWxQ2IB4MjIhppZHrNtW8znc9lsuOlx0yLYpGxLDGwgVWEEzRiD8/Nz2ZgfHh6EVFKKQHIQkg96KKl15ibJZx965YBe0kggxM06JCxh+DyK+ipnjKzw77xnEideD8tipomrlhSWqxyPxyIdDJ0VHBd3PbHLr/Dz0BgjY0+wS2cFIwBt22JQDFGWlXiMw+grJZ1h5JCRKNoGPn9eF18hiGV0kGNLm0ZvKEHCwTflC+VWjBzyuYcyJ0bGQqkJxzW0ByEBIGEJJRg8H58L1zTBHfcm2i7aLdp/jifnK+c67zPMPWIlvrA4AEEviQTBGNcS7SefOV8hcOW48JoYCeY90jaHHtrQs+rGBkfgiKDV3WMk85n7EecKwR1lk5wXfN7cGxkxzXNX8XLrHSLhXKFNciXMnTef8y2KIgHyHOMwfyN0tPG+SSLathWHIO0yHRD8OfRAc3y5RzCawPlGEs3nGz7P0LvPa6Pt5TOgDQpL0S6XS5EBhhImPgeuoZC4MwIMQMqBhyQ9iqKja6PN5hwImxLyX74oQeXaCisHhpJHfpZ28uLiQkA8bRWfL8flKPLVtqjLPu+I53MOgsHRvCPeoPNcKci8px1xsj9X9p/ri3PQ4Z6+Azj3NOIIQMseynsM94RQZhVGV0JbwOfGuUSSEkoa6fQKo6d/7i/+Wfy41x9BOuUatkUxkKYJrFFoGovvfe8L/NN/8ZtYb/bYHSrUVYemA5Ikw8tXr/D/pe1PnyVLtutObPkZYrpjZtarNwAgGjDog0RZAyRBgmipwZZp+KNlEnoA2A20AJIArUmZyUCy+fDIeq9yuFPEjTiT64Ofn/s6JwuofGboMKvKzHsjTviwh7XX3r79dCldXY7Ho15eXmbHGaXQa+gHnS8XTeOoM0owSruqVbqgbdLtbWLvFdIFYjdzZ4TtdqO/9/d+XV9//XVyJk1UXSWj84Mf/EA//OEPEzg8HnW1oefxq6aY7nmIcZJC1BhHDWOvq8Nel+6sdtOq7zvttjvFsdwQuttt1feDUklSrUtfhK+u02V9w6wkxbE3kqb5LEXUdrvX6XjJ4Kufb84eh0Gb2UBV8/0Y0zhpf5gvA2oaXS4JUEZJ11dX6vpeu+1W58s5125iCGDvz+ezfvzjH2fQghMG8HOr8N3dXf45oB3ABcOx2ZTe+s7ycG6Ff6OcDtzrutb19bX+9b/+13r37l0GbtyXQNkKpUR8tqoqffz4MZfsYBynadLHjx9zChKDgoO+v7/PAMDLwNgvDDA1+Rh/AgeeR1DjDKnfu4CToYyCrIuziRgDgL1fZoQiw6qg8KGqdDUz515HCjvBPrG+DgpYw91ul7NVfd/rds6sUHONcQsh6NJ1+VA/sgubFCyrQ3ra+5hjoDDOfd8rSrljFo4G4Np3nfZ2zsFLbVi7pmnypYAAl7dv3+YyE36PgyFTBbB3tsudG6xh7rO/LX3jYZ3duYxjalLw6dOnXD7lTnocx3yQnCAY4oQyLWTgBz/4wYIhBgRzwdw0Tbk0An11I7/ZpDtIKGt4eHhYgAz+Q7d9vsi5lyZwQNfPLHk5F3tDP3pYSmQKRjStV62mLud2cHB8h7OyZDMS0A16PZ8yEOOMhwNWZBL2rakbte02yx06j2OlXTJMcuryls4CcXaD9Qb0ehkKQQPvwV7wJ7LOGRcH8YwxO1gDWYBL/x3/efkqn2c+7Ad7iHzwDKncF8U42T9kGJkAHAMU+T0wgN/zn5c2erkg9p+MITI0jmPuMARZwGfQA4JpMoEQJpwnoEwHsMS42Sv0jlIzeAvWRlK2O/h5DwwAhoBKSm1h4skCoKvY1P1+rylG9WM5DA0JRobn/v4+7x06xZ7il9E51p7PInOAYA9gWC/2mDuH+B22zLNi+A3IBnwae0SmZ13Cwx4QGLldYW7oNOvMWU4PCMl+OElF9jtniKRsx9fsP+uFn2GMyBY2m6w0JBXzQOYAz5zfgYAj28Z4IGnoukW7dy629LLG8/mssR/UNuVcIvKZ1j81kcCWYG/T+qb7vryclc8OQ8nKeJlXwhiliQ7yWnS3EDie/XJy2GXLiQb3kwWXljMuTiqwT3ym67q/28PgP//mF1KIulxOGsZBQZXGQdrtr/Xv/9ef6j/8h7/WX//s53r//lHv3z/q2/ef9PL8rDgkp9PO4O14PKrdbLRpK223Cej++Ec/0s3Njb59/14/+fGP9e7dva4OG+32O51Oz/ov/otfV4yps9Lt9bUu54viVE7KA0Dz5XNKV10AeDZtq2FIi3jpEju4aWs9PT8lp9Xs1NStXl6e1TS1qkrJQEmqYjtf0JfKk0Ko1LRzOrEpzDuXQYUQ1A8peLq7u527SkXVTaXX00m7/U7TNCp1OSmtxM7ns3709dcax15BIbMnl/MlnQlRo76PC2NRFKPVpbtkkCYlo0tJDy1QMVzcswC4daYIQwt4h8XyMikU1FPfpPQxQih1COncyjfffLOoBwXUeMs6SkwoLyFrAYg4Ho+aZq9CORKGmkieQOju7i6f5YD9/eqrrxalQ343BAakqtK+d/Mao4ysKYpK+plgge+jnp/sBmcLAJXMF0MhFXCOAW2aJt30TrozRjVtm/eCGl6plPpguDEKtAxkD9vZiW1m0ANDCZA42l0PwzAs2vhtZsCAEWLslEsRvL558yZfJhVjVGPgeLfd6v2HD6pmeYhTuVGcwOJwOGQWkKAL4FhVlX7wgx/o4eEhM5G0A+7mLCCAnIwUjCnOkHUmqAFk7HZ7PT48ZL0mAP9P/+k/6auvvsoOAR0Zx3G+CybpaC4p2KTv6frUkeabb75RCEFXhys1bZoPJYqMY7PZ6nQ6zhmbRsPQ5yzF+fWsuql1f/9Gw9Dn1q3pxukpl17AdqZbYMuFc02T7vepmzqDhgSQUvtuMizpNhrOIVW6XMoNuLSF5eVdskqgOtf+htJpjpp0Dm/63tR1unsnTlHbXSo7ZU9nt5T3K4GxYZbLUSGkPXh+Oi5AKPqLEyQzQxDvJRbYHjIMzgRjIx1sS4lB5ZZmWrbCyt7e3mY9RK8IOt3RY4v8HIcfevXgc51x8eyQZ6U9iwWwwDd4eYtEUML3lEPVrBnAvrCky8vxCFJZH3TIAYmvMwdHATieaWCsXGRIxtIP0DN2Sg6RB4J5/pymVD6FvjdNY2caSpcr9pg/3XYC/AtADer7LjW4GQZtZ98wTpP6sVzC592/yGpz1wolb5x7wI85AGfPvSMXr/1unzuTbbdbxSkmPe0T+98PfbaDcYo5M7jdbjX0g4axlE9hS0NI51mRn+1um8dQSINiJ6s5kJKkxkgIPyOQ5KcSd0ShTwkHbBXn+0o8c0fTlg8fUhdJgjn2ysm/cZwUYynHC6HKGQFKnDi7x/PRDT+sX1d19guS0p1mVeo8xl6il3GKGsahEHFzcOjk0aZJd41hT8EjjNHb0pa5pKMHCRt02m7L/WZpzOlzHhCxV9M0ar/f5bXxoHAcy2V9kKvoBySrZ/g9cPMXdgg74uQHOsLnwE3/8Pf+wWfP+ey5Xxpo/Ks/+3MdTyel0/KtLpezhn7Q/Zs3ijEJ4fX1jS7nTt/Oh43HYdSnjx9zOjGEoA8fPmiKk96+eaN6joinOGVwc3V1NXfcOM+Cl5S9mjebWkAYBpQAduv29nbBiGG0u65cvpXuvdjOd1WwcKkTVlOnm0Zh+LtLnyPrZGAnXS5zXV5LqnxUVaXNPx2P2u8PmmKcFaiU2lADeHV9lQKIKuj1fFY1K453HmIjmzq1CR7HSU3dKMyO6+EhtdHtejoL1Jml9vpw72BA61NPgSNI79+/z8ESgQXMHeCK0qF3794tDvex/hgd1hrlR9BxuDhHHBVBD2UIAIjT6aRpdk50YPLSoJvra11meYDx9EPH1A7zfW/fvs1GCIByPqebq2FAP80sD2AlM6t9r3p2jKyJZzhQThwLF6IBZinT8k4ulBt4+Y6XU7FG3OZOh7ZuZt2HcUy3vIfUjtHBTAJzqaTw9fVVl67TOJczMEb2C1aLsyrDkFro0paWYIV0NE4BI05gtdvtdHV1lcuodrudtrudHh8eikOeQfzLHJwwR8Da6XTSy8vLZ/dpjGPqQIYzpByQfWiaJl82RfZU0uI8BfXh7F/f99pt92rbjaq60uNDKjM8XB30enrVy/FFV4erDD5xJFVV6enpUcMwarPdWHamWdRje2aPexUUpMP+MI+1mQH4Vk2TWsOeL2cd9oecJRzHMV9+SIvJYej1/Pyirrtot9vr+uZaVaDWdlDTzExwXSnMl4+WdPzcCrryA4Gj2rbcfzLFdEP9bmaL2aMQwszK9aqqWn3PnSAhr6mfQ2DdQhUUqlpt26Tguao0TTERPVWVugSGcumUt1ms63omtjTb6EHNfEEqNs3LOwAaXi/OmNgXQI+XM0nLg78OtJnHhw8fsmP3S954Luee1rX6rB3gwcE5TD7f77LGz3gWdgsd4PmehXMwR9llAjkpkO26y9w8ZDOXKh30+nrKNhSwR7BBwONsMfX+TtKQNVlncxiXl5F4BscDL4gYAPjt7W0uDyQgBKSjvykQKZ2PHh4+5XsV2najGLXINFZVpefnJ8sEb3KAib1/Pb9qUsnWtm2rac7UHQ4HKcSFDyPLmDBIrxjTc9O8zwqh0m6XLq6lScs033sVYzpUvJ31buiHzM6HELTZblL7+2nKrXvPl9RKmsDwcrlonBIQbOpGUSlov766zj5umqZF2SD70batur5Tmy8ITvLW9eksaz2XpPVdp1ClM6Tny1lNPZfTNqlUe5xlk054yETK8typbVt9/Pgp6+P19XX2g+y9ywUkEvsKjsFfjeOgy6VkTnPTk2FY+FlvzTt2XGI3Z0q3m2xHpjjli4LHcVQ/9KntcRW03+1zANQ0yUbH+ZoG7CqBIzrr5VrIuY81BQIp80FQkKsBYpEvJz4k6erqoK4r2ckku8mmc54PIgiiwTMbnqF0O0fw4AGGZ0fwm4zNq1f+wT/5HX3f64sDjb/8F/9Sj4+PWbA9/YTBXBtrHn08HnN9c1VVuWZeUmaBOPQKswIo5UAqxgbGgL9ziJWaWcphKGehMwIsCeUJHHjFKZECDSEdDry/v8/RKXc74Fy49AXHDLChrIK6cwIh3sd3eltPAhg6w7C5GFuYwRBCbmVHQAHwpwTgxz/+cTb2IaTLiGBocLAwyAA4lBfHQT0nYJTvAMD7hVDsIV0dAHl0iYox6v3791m4P336lLtKAR5Pp5Nub2/zuQ4Adm6HNwNs7+7BeY1pHHWZ96ybDzqTZcCoOvvO50t6MynY3d1dli9udEcxqW2dxlGNZTRQVhwNbNRaYc/nc27XSstEGF+CFvaAsfmhchy435ECMEEPKUchgMRhxxhzapg9IYjEgfMdGOCXl5ccoE3TlO/18Lr5cRxz61w6OwGc6rrO3XnevXunv/7rv87GFYC22Wz07bff6s2bN/kGaeQZ5sQdD+2QY4y5XA5HBdvJPiO7+/1+0TYXmwQDiMyMQ2nlR7cSSYuuK874HY/HfOB8GMqBPILxde01wTFdgnCy2DBk1O8gAJg5qPWSGIL5ruvys7hTwFP4AAkc1Xo+7jC8DGadlkeWWUee7bW+BNXII75gt9sphgRcKCHCKQ/DoErpbiDsgZMRwzAsUvjIu6ScxST4c5bdz3ucrJ6eZ8CyMx4CG68DR67fvHmjvu/15s0bffjwIdtIAIBnH/AjTmRIyuQY8uJZC4AfdoVsm5fR8Sx8Au/3EjDsDn4GfcEHSFVZcwi+nBEvWUBAKPMAzLI+yArZYn6PLHsL5sK2Lm9Fp/TR9xxZZExOEACKPftAySlr6VkYSM00/u2ibAbbydg9G4atf3191ajSCpbAJX0mtaw/nU65o9Pr6+t81uNOTZPOCJHJo606uAZc4jZi07TaGnOOzUCu0EcvrULPseF+noo5ccbDO2HxnKenp+zj8Tnpc6U0F3lM+KOaA7f4GQAOVaVzl/wVZ6bwc6yRl3XlgG0eNwErVQqsEwQee8w6QCKg/958gzVB5/ncpt1onANoAmVsDboDzsIHYGOQGy8thUiF+PQ1oXrES72k0gnNz5QhV+iykxLYP7ct2K7L5ZKDNPCGH8xmnzxYcF9fMtabRYDkmUTWzitXwDjYqLqu/24DjX/5//mzRToUoMKGY0Bgefywb9+ng5tv3rzJ9dH39/cZ/MNie/oXAcW4DMOQU2QsImAWZfR6fTbX06ievpOUy2wYZ9d1urm5yYeMqfv++PFjLkUiS+DlGRxmJsig5ISggs3mLAQG2ZkcSlUIRpg3yoiQAVD7PnWN8sAC50q3Be/9TzrXOySRzqX8y2sQMbLUIIeQ6mbv7u7yGQNPwwFgKHfiMxhF2HK6Qr179y4DB5hFQMKnT5/01VdfpTZ2Y7prRZJ+/vOf6+7uTj/60Y9Sudksg+M4Li4wgulmDwDZrBFzo/4cMNv1vV7nf1N3LyVjezoe1czPxhkif5TWsJeAfoyYB9WAtnEcM5DAwRFYI68OEP0MBt8JeIFNWzOM05QOpL9//z6XMP3ar/1aTou/f/8+nyNhv5AHDxzoYsR7j8ejXl9fM4Hw9u1bPT8/6xe/+EU2vowN3YVMoDUvpWcQFoBlSAbOUJCB+fDhg77++ms9PT3lg/rUzgK+Md7U+//iF7/I3Z282QCyerlctN9dZfCJsyBAcYDNC0dAIEtwjHMCFFGLDSCUiiEnOPLSFsDA6XTKY3bQ6ofQyZp4zSy2AR1GHhmn1xgT1EJAIINeloK9Qm6wyz5vShBx2i7fi7R90+RyE9Yp2+EpZehYI89GAEJZT/7tdcqAM+yMgxjq/Al0OV/kIIN1gdChjnq32+XAC8CNnUVfANjIHAEsjn1dYoIcsXaewVyz/7wPJ8/acX4Ov+vyB4HhASTy2vdjBnsAOcDT4bDLsoZcue0ma0kmkSDUga2kBbjzUo2PHz9mnWHOrCE+gOei2763AFW/C4LsF9lQz3wAqi6XLt9lgE6gQ5BJ7Du2JGMElTkB1tN+VDqfXzPekayccr7ziyw555M8qEVmOH82TZMqSXVVxsj7eHlQjV6yv+7LGC+y4CW7Ly8vCxDN7zjj0LbtvD9FDvBnlFQ2TWkegOzVda3X81l12yzsMMEKvh07jz46PnC55HvdL0ul4Qb+mOfh69AbbAf4jOzINE0au3JxIME/soy/ZE4QJ5AOyAUVM05eYAP8HCB6Cbb1zAK6QxkWvh79RUYh98AhjA2ZRLdzufUK+zqRQnDLmLFP2B2wEmNBt7CDyKDjTOT0d/7xb+v7Xl8caPzFn/+LzxgcIncGREkLQNWjKoSZKJdDeX7YEMMH44oho4++H4ZD4FBqN+psCuUannIl4ACYMk6EBAFng/gu2lP2fZ97MpOqApwQ7DgbfDqd9Pz8nC8OowTkq6++0n/8j/9Rv/qrv5rnhBLj/MjM8P0AJhhelKukgdv8J8K0VuTzOV2o9+233+Z1evv2rR4eHrLz/uabbzSOo37yk5/k0iAE1+v8MCbOenkQiCJwW7SzxjhKZCDGmIM62spR/vPx06d8CSBlSJK0n2sq2zZ1vgB4sWd8DxkbapwJ/j58+JAP8G23W3V9r3qWBwIvnF2MUdfGMFLmN01Tvu/Cgw6yDzAQwzDkm88xJLA7GMYYYwZ1fH673eag0FlBbmfm8xhxsigYZpw7eucBhKTcPUrSovUxhgbjxn5i0NBrQAUMJ0wwFzVSRgLQYz0AQ2/evMkZToz7zc2NHh4e8kWMZC4fHh70gx/8IIMNghIMKkASZ8NBVGzEp0+fFp1Mrq6uNA4lQ8Z+1XU6zE36nuCJzzl77ilxnLiDLM98elrbHaUHSU62YPw90MExwJrBSnk3NM4B4dz8fAYZMUgBnIZnIgA1yBtyhFw78+bOB8foexJjOjM3TIURx3Y0TZNKUs6XnEnFSfI+nokDhaTxrCTy6MDbs4ueBcCG4WTJUKwZPubuwQDgDPvK+yCe1rJAdhEQw3vWbCqf4+UMP/Px7AdZOdaZg7i+JswbedntDhmgMvcQwqwjUbe3Nwu2Hz2VlEkxbIzbepp5eAbM23XjU+u6zmVi0zQtuqvRXdBxA7LuAMmJED5LYOpnr1izFLAF7feHrFesK+U12DPAcdu2GqdRw1Ra19KZKI0r6v7+TjFGffjwIVc6SKmd/Dim9SdDyRjRb2QGnFRVleI4qgrVwlcgX+wxwTC+3GWGfUdWAfDsNZgHG8Fa81n2fLNppbnsChvFfqbvSKAawhU5VRU0GfnFs/1c6IJ4qMvZAN9TMNvj42O27+ibZy7xRcyVOYAP8HXoYdu26WLlS5dtEPrHC7vDn/hhxkcFDXKCT/XPuP3EJjEHx0mQycghwQkySWDAe5y0ANOwN3wnP1tXRxBMgxUJGHiuy5vbG57J93rWGJsGpvw7zWj82Z/8aWbuMSAYFzazrkvff8AZtdcM3Ftj8ZztdpvvZWAzcNL02cegPj8/Zwb73bt3+nf/7t/pxz/+cTY2MK3X19eLzgIsEr8joGiaJjsKZx/YDITCDzLiVD1oeX5O5zr83gOciz+raZoMbvk3SjOOqR6b7iikrjgsC7D79OlTBn9kNzD4Dlgw4JKyogAg3MGxf22bWtAiTIArADQGFaVgbABvjADROmVtT09PuT0goAf2oqqq3IUKwefZ/Qz861mwAS85bW6OELAI4+cBF0aMcpXL5aIf//jHeX/oQ344HPQ8z8cDZTIP01C6jXim6uPHj7q5uVkwEgB2smMxpkvgOAC91h1YzKZpcsci9ps9Zh/d6ADE2Ku6rvMFcdkRSBmYYMAl5VI9GBqyc5fLJZcsshbcIcBaYtQBOZ7B8HsJABUEIx6gIPO8n8AeXSO4BrSTUWNvYLLRIZzLd2UM+AzfGWPKSJ2O54Uz67rUQpi5w3zxPRh2mEXWkqDAs1H+n5dZwH7DrML4OatNcOEEglSAt7PrzB+9Q0ZgiAFsTdPkYIwsrTtxQAzPdfuMrLsjYm/YJ9YK34DND1UlVWUP+Ow4jorjpGkcF8920I3TxGFTfpQd2LzulB+4vgPSCLKwLzhezuG5/EulRIu5EDz5c7FR2Nt1OY+zpdgMfCS6y1r4eRKIDZ6LHtJ9zdl8Gk34IVZAFGwydiGE0pKcsRJsdl05b+fgBV/B79yWtG2b7RS+k0CWtcZeU9KKz8WHUkLMuJEXvhe9ZN+dyHt+fs4ZKMAahKVXCXRdr92uZBaQGQ+WKTukjLeqKg2x3KMEATKOo66vr0TzgnX3qO12p6YpcuAEDaCWQAPis6oqTf2Quys5BmIfsT3oIIQNewgxwLo6gEWHHUx6tguAmoiXQz6c7Fgt7eVGfV90wMuL+3HI5weZs2dNCSDAOx50MSb3Vawf+IbxeWDB2iMzbu8oJ/XObOM4qj9fMrlJUO0ZYvdJ2BHWnbGDp/hO9tZJBnSOdeS9yAB65oEiNh9S1wk5ngHgxy4RWBA8Y1vAQK5P7I2Plb1HLtkL/LCXq7n9cjJ/s9not3/3v9T3vb440Pjv/99/qNvb21xORPoPRwULiwLi3HGmsB6eWmLBqqrKJTqAZkoPMC7DMGRQKykf0H55ecmlG9ttupjm48ePeSEAJg74SJWSYXBBp7SLi3AwFBhOet2jDLCHfsCaTcVA1XW9uFvCL5hDiHAAZHLWaT3+Pk1THp8LGeDQWX32BKH0TlEc7GW/qqrK+zuOY64BpNUbDLszDX5eAWPAxTgA3nEc9fbtW22229z6Vyp3Z+CYAFDU5DKHpm1TpymVQJU5vv/FLzLjj7NjP93AcUEa9aBkV2AW2YPL5aJxVu51tiCEoKFP7YR/8YtfKMaor776KgeiKCFyC+NzdXWVWXGvf/Rbx9ELdIY94BIpT2lyzuZwOOg//+f/vGAf7+/vc+kaF+sR9DZNOsyK86RVK99PAEwpjGexvJ6bv7vc3d7e5rX10hOC+nEcc5kicyTVD2Cn5/52u10EtNzAjqPCSMKaIvPDMOhnP/tZPrvB+zwYYO0557Xf73U6nhfZTUpEMPZ+VmJNSBCASqU22dk5nBpOF0fphlpSBkxrRpr1wSms2SxAoHerIdj1zJ4HKmvQwroQnGCf+W63Z4zfg37m6pfOOTuMDu8O+8XncwZ6DjT8WciIAyX/rDO67CnjQ178Peybn4nxuXnJF3LHOGDy0GeIE4Ah+4xtats2Z+fXDDX7h6zw5zrz4kGnr4WTH86i8hn2GvuNHUv2o9d2PguD75I0lyaes/wAeJAHyAy3p2uA4vLAZwgUWDcuvqSUd7/f5ywj68c+QkhcX1/r8fFx0UGMtSHYZN9YRyfIAMfuq/gc4HK/3+eSUM6zhSroMuMQbA6vtm1UVSEH1uhwYqH3ur6+yWVKrKVnYNyP52BhTE07+Ddr6ICfZ2HvWQ8PDPFXyKTrucsW5ajsF9gn/be8MZ39rapawzB+1ryg6zpVda1u6HNwTkaBlvtk9vBhfhAd2fYgmTVCLwiMPRMMKUJpE/rlh7DBAflcwaXLcsa41oE1sgRB47aMNfJmKASqyAHEEpgGDAw+Qic8s+vgHb1y0om5QBRgF7Fd2An8K2voz+LnHiyA/XwN+DkkIoEJuIs9Qg+nadIf/F//a33f65cKNL766it9+PBB9/f32cE/PDxkBbi7u1vUKA/DoPfv3+eDURg3SqRwrpRfOVhGEL28BNaKoAODCfDCMIUQclqTRfX+1QBASmkQJqnUAq4B8ZpFbdtWV1dXufXm6/msq8MhXVQ2LGuXmc/T05O+/vprPT+/ZMZ/HEu6L7XpKx1MkmOsVVUlUqZ3/t3d3YIdhMmg7IM0N7/jEDlGn7ISUp2kZTHW7mBop5m6XiXHzVkUADpGhfXFeHA2g7XC8cE0+mErgi2yUCGk+x12+72ur65SycScPdlut3qZz1Gg9Hd3d+q6dEMrssXffR8cLFLbu9lsNE6ThnFUFUK6PNFavoYQpKm05q2q5dkkgDvgGOfoZQpedkTWjG5I7kQx4ASTfd9nIF/XqZSw7/tF3T5s9jRNi7M3OFNKZgBBXqqC4wCEYFQA9BhNerczD9Yd8PRdc+Xv9EqHCZW0AGIceKa8aJomdZcutYcOy776MFdJLlM5A4Zymqas25y3og6bIKaqSr3sy3MKxry8gTI15ogMYIQp3eEsAGtcVeluC0gFZASgiRODMEHXkHUvSfTyHH7mgAfGydlmno+M8Rmyb+sgxp0Ye0UGCifuTGwC50F0toqx3DHh64ODzocr60pVVevSXXKLzhCCpnFSd7lok7MOpRVrskHLfvj8bg1yeb9ntZkXgJ71x9avmTx30ox9DbgABei1r+GaZPJAhnVlHh7UYAvQl8KSpxa0jL/vB0kl24uusi+cB3Cwid9Lc0nnC2jzznrFSBOGIZcfLeUjdUyKUfPZu2WwjI6wvuuACEBOVpOM79qO8H3IuAcs65JOL4lO+OF6zjiVwPvp6XkGuO1iP8hUksUOVbqYF1k/n896Pb9qM5cKSsrnBNJ4ugzwmibJwPF4UurA1moclyxzCOmy33EaFSRVda3L+aKmqRXndahVQDH4iT2CjAMw39zc5BJcgCP2ETmAuMhMv6KqkGw0Xd8cgIeq0ma2N1GzXozlrgqFoKZObWYVpKCgcZrUNo2GcdD5fFG7LW2XkQV8LboCiYz9xjcAZrFDTrBi82lE5KQKnyPrgz/m59jZHOBfOjUWPFdVpWEcs/2pm0bb2dY/PT+rqoLC3Gqbaon9IbUSxpaABcFeyAa6gQw4+QFmQpaZN6S72wrW0MltgnFslttnt2FOTBEs4GvXmQknM5Fdghp8DXNxsjfGqH/8X/2uvu/1xYHG//RHf5zTn9xk606YBfRIEOYHRYXZc0ZuvUk4CTaLYAPjCXAl6HBD7rXZDjhw+P6CseZ7Af5+sIfFRIg5oPrzn/9cb9++lapyK6eXGGw3Gz3NAc/T05Nub2/z5k5TVNW0en09qarq/Mzj8air/UFt06gfems3F+Y1SH2xuWeCYMlT0UTo5/N5UTbFM3A+1IsjwAg+c2maRk+PL9ngYfQ+ffokBamuSwqdrhoASCJ+yqQ4sA4zzv5TnuBO9uXlJXcn41ZoDgH+yq/+qj5++CApOSQCic1mo8fHx8wOIjsYPcCWt82FGWB9WBsAGwrnh0npPAKg4L2HwyHLBsZeKgfWvO4fAEOGhX2nMwxj5EDwml0hEKfsBpCHHMPMM27mj4o7a+RdvqjdxfgxLzda/izmCEjAkPr6YugZE45kXTYHqKfjnBRUhVpd32kcSsvMw+GQ2eoko7W229JdiIwb+/38/CyF1IseQmSaJt3d3WWdZF0AWMyr7/tFuRpzdxYHW0OQsD67gINFlrAz9RzAuqHHFnFQHHuFDMNcSsWhoPPsKTLvTKqn7J3F8qwC++VOBycFWEAOkiP7/PbgYaAUc9mitrDjKTBBTjwbg21HJ7FpCbDWSq3Di/PFVjM+XxcnSJy5xGag415G576FNefnLuteIsM68X3YXtbYy4z8zB4kjO8j64DMJcee7m0ahiGTdyWzXcr+GDfs7OWSOgNCAOEjsQVkjdGpQviU9+GP3CY6+IOxTS1ayyFc7hGC5SdYxcdgV9Blyjv8LBPPQebZNzKkHvxBpqRgYrMIImGa2SOy0uxP13Wa4qQ4v2e/3+dGFugtcoGfKXYwinMYUmlqMM4EVR2qDA6rKt27EWNUZcEmOoqtwT9D+JSgXosDwwQa6yDTs/h932uz3eYMw263y5cBd5dLuhusKme7AJ7YV8bD+lEa68Ejth858xr+dUCOjGEr/PwX/8bmIAtrkgaMQ3CKfoG7sPvsB3Lu2QPeOw6jqrpcVAkGADy7n0MOnDCr5+BESvezVSoH753s8nGydp5RZe88SPe5Hg6HfBbYbQ7/eVZEKmQzMkVwx16i/579gGx1v+a+3rOrrGdd14uzw03T6L/6Z7+v73t9caDxv/zFX+rl5UUPDw969+5dngQDQpg8MGDCOFoYG9hzaq4B+UTQMA6wH1KpiTsejxlkYzQx9JwFwADxLBQjxpL29lR/jDHXaSLwRN/fldK7XC66vrnJZwdg8/18ymB1nRiw29tbnV7P6odxcehUmg97V5VCVD7vwcZK0rff/ny+vOs+g14vl4AZxUGwB3TkoAyKci6UkNptLkLbbrcah1GXS7m8ylv0Pj09aX9I5UofPnzIyuQlM9QJEswglF3X5XWmThzZ8JIsjIcDKnf6OFYU8HQ6LRjztm1zGRhzJVj0MhrkbRxHff3113p9fc0lcJQPeTDXdV1ue8zzOHPBXlPaxHydzcPJjeOYL5+DQaT8jgAe4I7zcQcAGwlg5ffoIcG61/oia4AjfseZKw/Yca48F5YN4EYpXQGEJaUPwKG2nICdg9XDMOjdu3c54Pj48WN2WrvdTk+Pz7q/f5P1kjIgAETbtpm9xRHhmAhsaOHszRqmacqZPgw/IMnPPDB+gmJKMdgHspsAO+aB4/dUNs/CdrlBxwFXVbWod8au4iw9MPAshQNsgCc2lmciS9ISuBFgAJAYK7riINxZsjSOMjdkI8lKyiytsxpJ1tKlfq6LAFYABPrDz9KY070fzHcNzngf68DaeT03Y2G9KG9ijbF5XhO/Lm0oDHazALGcW+IF0PIMnWcpHVBBWCzsf16L1MEIW41epXUoQQyy70Ek40ZXIdsoMyZjWM4+pLIY5A275eUnfNcwDLkjVBpnmoe33HTWFbuP/EGK+Pk2xgrQ4twGzWPO53MutyJb52cN0/pWqutmAT7X2RXsJvvbtq2mUOSGw9ucK8TeO+npusffsR3DXMmwadoFW+8BPHLKPNAzP9fE2Fl/Z60dQKOvBEas78PDgxSC6qbWfg4ECDicKfe1BwQ7ObEmJdBL9wXIgRO2jA8fhE6B58BK+AxvsuF7RGbKsYcHMtgy1hAZc5lzGwQJ5LrMuJ1sYC3wyTzHg0Ps/aZpVZnsYk/wreAyx2rIAD9nLZmDZ9bd9jJfPwPlwVXTlLuiwN3IsGc4JC18J/4I8tcrFxgrRBrk8Hp9/5v/+z/T972+OND403/+P+ZSgY8fP2aWAGOEUfOOJx6heVTHIAk8qLkD+BCssAlXV1e5YwwMOoYZFp3SnPv7+1zygtFfBxsssqfyAOGPj48ZRLGpKAmHrXHe+7msipImWKnb21ud54vHvv766xxU3d7eqh8GtZvdwmlhWNqmkea0HIFBCGGuGx+13W3zZXRcHkXwhWAC7NyoAoYIRug8xc+++eYbScosetd1Or685rXksG+MMV1WE8fcOpTDoARcgN1//+///eLgLg7rfD7rq6++yqVbHikzZhSLdQshLMo/OPNAeREdv+hS1Pd9un06lkNMACOUC6fuqV1KyDC4sAoYI9oTk2UAaHlZIG2bh2HIZTusDxkgZwlyWZYK0+RlZBhfumD5Z0II+Z6AXA/flAsqYT2dEaGLCv/GIOGQcDgYH/QVMIFxJJjAsDZNo/v7+3zGgSCI9fUUsq8lxqyw5KOaujRCwDx5nTOGmLG4IeZ7fC3cKLu9gu32sWEbYFlxXF6r/V3nMVhLvot9w5mhP6y7s5bIPsEa34XMrh0dIAqj74GGVByPO+QMrqZlhymv5/Vg0wN7/p1u5i7lLc72pbr1UpbEdyaQXCvGv7n0yRlUABzBSwha7OF6Tp699GwE+48s4E9YUz+3UQKbwsp6JtH1zdcGQOTAYppK6SIy6gEj88TW+ToTXG82W10uXQ5IPHsxTcMiWHL9AcC6f8VuevDEfFnX0+lV6bblsBgzRBMEonciCkEahn5B2nG+bhzHHIR51grQyBp7ZknS4o4qSbkbngPPtR5/8803urq6yXLEoXkwgJMj2EvWs58KMMVmudz4fR+sB3vo4DBjmdd0wanLpu8rsgqA9d+hCwSErAcAnnGxXtjdkjXsszw1TaMpFPsOBqO00DOhrAUg0m21k03OnruuSFp0vFuTF75OlFi7D/aSIZ7HnLFpAGDfAw8gsJVUUvj8WC/G4T4FW+mY1d/nxI0H3JmoUlBdlQy+21n8KNjAfRA4eB0Auj92m4x+8znIMuaML0HXwJNcl4C+8d1OJiX9P+X1QE4g/llnGh3hj/z9/5f/x3+j73v9UjeDYwBIiwNoiaScBfCaV5wuwswEKPHwqG6d5iT6/eabb/SjH/0oszPUqKEcfuiZ8cBaUeKFUEvL6PCrr77SN998k4WLMwht2+b0IAr8+PiYWZdL3+vh4UE/+clPsuMhNViHkg4lkEoKOilaevVyuejbb7/V+/fv9ZMf/1jd+ZKNNEAoMWRb9UO/cJJuQADYBEHOaqOMDtzbNnWYorTl5uZGXdfpBz/4gb799ltt2tQTHLDEet3c3Oh8OWXgC9gE6HOYntpSLiJkL7/66itJ5eDaMAz5Fm8UxM+ToIA3NzeZkZO06F4Gw4/spYN5uzxm5uhleSgnBgy5QaZx2gQnfhjK2XNn2fNhwlC6QFAOA2h5fX3V5ZLuEcEw8d61MSAjQkCHAy8HPLuFkwZk8QxUG5BAZs3vwgE80LoPAwhgyezNnA3C8KJrgGLW2W0AjhMH5OlcB+RkPNLnKvVdORTsQGX93BjjgolFVzzww+ADPtYlRq5H2KZ8tiCUMiQyK4yDgI3MGk4eGfFSKeaMbrqsOxjwmms/o+Fglb31Wm530qwJMuWBCuuzZsp4ed28pIVzTXZnp7perh9zTuc1tJBfGMtxnFRVpeYXuSJQ57sczKfvLiVaXvrqAZmXI+GInZEEELEO7DH2AuAAWOZ5zAG9RUbokgTYYBzO9DI3/z58pgcgzBMfCjhOdz+U/cQvpnVPeo19ZB+cMUWunQFmXwHNfNfr61l1XTJ8vN91HflGhtKYhtzmlYCG8k/WBl2ADPSWvMgQGZ2mabI9Rc5dPxxoIe80kHn79p3S+cbSXplg+3w+5z2EqKmqSgpBVVOCKm8k4kQUJV7ogldouN42TaM6VAKCMVb2D3vkzTSQZd7vgNbt+HcF2Y4DqBKgG9U4joohqJovFgR7vLy85BK5tV3wfUTePWPzXWMChJK1h1ziPAV+ivOmyLF3wnMf5cEMwZTLs5c2uf3yABn/gx9HR7BjzMexA3Pn2ewB+MQJC9a+aRrtdztNQ2nz63NhDuv95XfYGP5esr+lqsPXwjECBJhjaH7n9o6feQk9+AhM+uHDhyK/ljDAfvj9Qh58OZn3+3/wT/V9ry8ONP78T//nBXPoAQNAsOu6DHhpEenRPIwGgARg5ilwnChAFCPNe9iwpmlyNPj4+JjTPbzP63TdQeNQcIQ4GZwz2QQALYaZFOdPf/pT/cZv/EYq66pKeh3jnS96mseAA8BwdX2vqEr39/f6q7/6K93d3eUuEFUI6i/dAkghrHVd6dKd87hgeMgKedkawkAg4IafAGG32+nDhw8LUAS43e/3Or922VDQlYNSp1DFXNfODaMYs6urK338+FH39/cZtBJZY5R+9KMf5QvbYP/oHkat7ps3bxaKxHchC3QE8UPszvqiXASXnnlwMIFh5rmk63nBOrhiEzjRyQoQOU1Tvn+Brmae0XGQzgtg6+NCgT0t78bHnaYbcD6PwXGn5tlFZNmN6DiOmdGTEkvFOQ0AtjPIzrJ4qp1xI6N81rNGEBYOwoueBo3DtJgrOg9w8VpT1tDHwJo5S+RBGdki1skdmrNJHgw5S+bOxg8bYwsArNia8/mcLydEJimZ47PIydqReHkE/2ET1izYGpAwXuyQZ8MISDyQIusCsF9nQZKcFBCIzqVGG2fVdfWZfiV5j6J0yp+JrLmzh5lPulOraUp7Yta3BD6J2YMFZ43JFK8BFYGJz1NSJgp4L+OAGGDPyeADljhr4Blw5M/36tOnT9rtdrq9vc2+iTk72Cu+rpmzQHGhy2n+6eyKAwoArdt//o0MsIfcSQPLn/aoyTXb2E3ur6Gc02U87X+lN2/usz7RNtkzZgRXDlp5v3d380w4thi7hD13dtzXLZFKh7yu3vnSdRtb8vz8nMq/qkp122Tf4Uw/68f38if7489jPjHGdNA4lpIe5BCiyoM/zl4gB4BiunoxBidoqbpYf79UOuSx7qrLWQCXBQ+6nYhwLMc+IctuC91/8Of6hmqCQewtgTRkWCl5Czlj59lRxozNx6axlnyvB0mO9ZANz0h/F450YsP9DHrndsKzr3y2bRq1ddFj/mSNnLDw7/O1WcNvz8K530WP8GV81r+T9UeHfM/WATRrRwURhD/2xPHHOlPqQfThcNA//L1/oO97Nd/7jvmFwQWYwbABVtgMykOosUSYfJIsCBe/YOC85R+s05qpYfPd6GCEOUTrjDYGCxAFk0PpFY6dUgjv7e3MNo6KlPrlctF53nDmTunY0Pe5ZSNCC6Nz6TrVs6P4yU9+ktmeqqqkqTBkVVXp/fv3i3KZpi3j9bQggQksN1kO0mrupDn8zSVpRMMoB/d7sKYYB1jwqqq022+ygSEI4Psk6Vd+5VcywIJZovtT25ZWwBhc1przDg6m2E+MLfvQ9+n+Etr00gULJaKjGHLqRm+32+UL/ggU/HZ45BCDBoNNMOcH1jxA22w2+VZ2nIUDO5cVGHbaPuLgMS5+2JszHzhPL+txQ1pVVW4ni+HGgLD/GBGCcsaGgwHMex00OuCMLmvqjCrvwShKqfaZ+bZtag/t5QDOYqX9rTWNhelFtgEwnmZn/fk+nAbv8ZS/gy1nSR1Ytm2b5dTXhPexJ8wZB+lZDc8AAVpub29z3bm0bD7wXQEFpXa81/90EIzMuE0lcPVuY9hlxrhmwgkW/FzUOiNU7G1YlDBwfmUYeoVQQAU6lbIG6cyBs4W+/l4qy89SFq9kkRgX82GdcXiM1QMldJN18WwOfoP1wr95MFvXdS4xJUjENlNG7OBZKuyqB6PefttLrJAfD0CTLJUmAc5Muh67TfOzZ7TGHoYhZ12xHZIyucSapnGWMkMCpk+fPmV7jf1z0NU06dJQ5AaZu729zfITY1y0K0cn2GO357y/bdvc6ZHxuax4oFrOqFHWV0qavLSRTD+yhk2IVcgygy3EJgHY0LG2bXOZKi8Aup9v0FRKXqhrp3sga+R22AkDbNT6zANkHd+NXWcPpXL/Bu/BbiKH2BbWlADLwTTzJkhCxtk3t/n4ekge9omsEuDYx+bZWc8ugAEJ2LE3MOxOUlF6zLgZlwNtgDr+0YNxyrzAN9gi9MrXy30Fc0TX67pW27SaVtkMtxOOq1xfnaj3YML9tgc22A325unpKROxYGpfa7ev2BiydozV5RYZWpPO7BHPw674WL709cUZjX/9L/+Vnp6edHd3tzDuaSOa2bm2Cgo6no5zamanvu+03x/yop1O3IWRanqnKc7KHNU0rfqZFaqbkposwjtps2lzWc6m3ej65noGen3q+tA0s9ML2m13ajetpnFSVNTQD5piVJBUNwnQ9MOgl+dnXd/c6Pz6qinG1DXq+UnbzVzuNHE5Slrs3Xanumn0i2+/TcLU1Br6dFCuH3opSq+now6HK3VdSQVXodKl6xSqOpcY9f2gX/3VX9HL8ajbmxudT+XwL0AkGaizbm9vNMUprfflot1+p7alnzOONrFNDuB4//ly0X6/0/F4UoyUJwRtNm1pBVhVenp+1vk1tQ+lrdvhcNCHDx/Uto22u00eF2lbZ6+u5la0sGdJ8VLW5eaGVoGVXl9Pur5KPaj7odc0JaW+vr7SN//5G202G92/Sa2U7+/v9fj4uLiU0MsXcEwAYxSB1LEHrM4Ykx3xVCYK2/f9wnACeFFsnBqG6vU1sZwpuJCG+YKj3X6X13oY0h5JOLdK0ziqn4G5Z0gwCCGk9UJHMjsYo17PrwoKatpG6VBkrWEoQdLlUkqLkiErjCBG0R2+pMymos9TnCQFTXNNc9/1ajetOfZJVRqkaDX79PSstmnUtI3O54t2262mmUX34CiEwgB2Xa9Nu1E6PFyYLRyuG0R+h+MEKDqA8cADw8mzyEC6AQZsIVtT1vty1gOgi/GWCgvl7BO6wHyxZZ4V8owDIMCzQbyX78b58lzWEPnDITnwppWxkw7YYggAQBmAXFIuoXA7IlHbW4K5tBfjDMBDztQ4UEjthIujZm38jANy0HXcfsvdPP1MHO1nHS6d85iHyzBjAkxBeCU7WMq3cP40r+CZnl3h2Q7Ix5GD5pWurg46nV7F2RRkw7vfEZgALiFYAFxkDCjvTL+LueU5c0M++r7L9n0c0/psNttZdhrVdaPz+TVnqHjP8/OLrq+vcslRsi2tNptW01QOsmMnIVxgNgHNyGVdl2YviQg66+rqep5Xo2EY1ffdojyPvY4xZWaSDkxzoJE6k6Uufu0cnG5EJ7PCUtO5MnXmSnZum8kQ1trJEbIJ6FcmGMdB7awPdZ3azU7TpCpUUlAujVxnnjKj3ZaDz1VVqa5qBUDcQHexUXGKi2yywvJM0jSOqeXzbMcVpVCFjI1Os45iz5CFcRxVN8mvJN2KUpQuXaeqqRdA0YM0QLhUSniWWbPlhZzYSZpwOAHkwVjxMeWMFnpF9QHPhShkPsge5zLwueiE+1vGzndALJbOnuXyOdYZcpY18Iwi++KZDd7nwNwDj3EcFadJYcaxisWudX2fu4wxBvdLVV1rHAaFKgjIESSFKpXeVVWlru8VZhuukDqZMs+u6zIBwpwgjBzDYCPBaoXIKFVG6894ds/XkHV1H4Pf+Tttb/u//MVfZsVjk9N/tYZ+zBtJ5IoRQliZAAINU5L6d5c7Dvj8p08f1TRt7hpDS0+CDJhvnLenojyaJTr0dJwrkncwItWOgBD9JkFJ5ytgNWAYfKP9Nse+T50WKFWCLSR9LSXlf3p6+gxEeau1fGtyd9HV4Wp2yMXQYKwon/qboljGCXPPi37iBAie7nOWtW1Th6Db21udL6cccMJoeukR0TLjm2aFPB5Lxx4pGbnr6+t803nbtovf9X2v65srpTaX06KnOGBgu93mtsusH9/Jf33f52DC688xxK58rB+An30i9Yrc8oycRh6Kc3OGlCwDsokcoshukHmPd4RAxkJQDtjRK+QboO1MrVRa8AIgo9K/OadDJiXNtU4BRNuabi/vx1g7g1wTPI0KCgtGnz16+/ZtZnfQAQCnZ0U9Fc7vAaKePl/XtrJmlE0QQFZV6VWOoXdWDR31YMTZzgw+LGPiGRuegyH34MRBBM9xfQXcejCT+u+3OfhlDIDrFKAWh8eeOuAm4yWVMhIvIUNWAAroirN26LGXj7gtojTFWUUviXJHjbyEUGmzKTfXIwvJfmzUtiWxjl6kvW8yA4xtLaUeRUY9cA6hyuVHbv8lDskXmUa2PFuKLXD9m6YEyl9fXxdBCevjGR/WZRggNpbthJExd+geBKf9LYcyCRY988X6eUkDmTB8gZ83QUZZP55Ba25s/G6307fffpttujcY4LPjOOYyZfac7wQMt22by8WYG2vLvies0Eiz3XBAhm0GE3hQ7uy4g0fA1H6/z/XnsO4E+wRRLqP8G7u82Wx06TpNWgbezvYib6y7Z1FhpH0uBPn7/V51VWuK0+JCR9YXH8OeVFXqQjmtWGrWfAol44hO+vq4LUJPfD8lZaLBq0CQMwffHtRD3PFc9ou9cvxBaTc22jPVTdMs7qqibSpknRMCjtkk5WoJJwCxf2Rrii4W0sBxKfvFf/zcA1b8lfsLyCEnhdaER3e+aDLSye1Du013djF+xuIy6euOnZr6gl8gI91m8j2emcauuC/zAAu9cR3APiA72HXXG+xLXdd/t4HG/+/f/n/zpjsbej6ftdseFmAJI4HwOSvmxhjlcBBCgOBGAIfK6XgWDQYJQUK4AOsoN6UMCDygmrEyzvWBN08BwmyM45i7PDE+FH+z2eSOEV46wYsDW23b6v7+PoNnFHu32+XOGwg7aWs/SH+5XPLhXQeazPH6+jqXisHuw7QBHjH49/f3ucaZkhGvmQREYSS6rtPr+ahxTCU9XhLCmBhr3/d2A7bUXfrcyYkSNITVSzh2u50+fvw4M2l7nS+vi3IPdwoYco+4nR3kkhoOTzZNk9sgA/h4roMgSkDYW2c2vBtJCkhf1XelO8Xj4+MimMQA8Hsc5Lp7jCs/RhaD4x1IANDsu9dGS6XrkAf/ktT15yxnyH1mmUNpQcxzndFDJ5kXJRGU5CCXvBedwYlhqHE+64yQr4MHhowJOVmzU+wDzojvcMPtNey+l6wt+s6asiZ8RtLCqRBoepYMe8XfPbDxn2N3eJXSgHSHiAcwjE1admlij1kjd3LonwfD7AlrA4BdBzUefCOPHqjwPLe1AEi3nW3b5iYIyW40mqbvXl/OdiADnt5PTG0pxfN1lRKr7UxzCQiXGSC37SHEfPfJutVxjNEyAeOinWPbbrN88RmaNdBpjv3ld6krUykZCyFkm7LeB9Y43fFyp3SuJa0/thzdOZ/PuexYUs4icY4N/YHEijHmcxCMg31ynSFYZc6sC/vu54mwwx5cO2vuYNvfx3/gA7LlDtjZN/aU19o/O3ZgzF7eCkDD9sDqegDhTHOWkSrk85eUTFFy6wGP67wDM8bvZyGcdECXCPq8BJJgjXkEK8Xie8ED/bQ81LwmD7CfJZO0PE8HUZb9w3yOzckMbA77yXp6BhH9wrfQscibz7Bn6C9rBwlF1ox1w+7QoAX/zfcSTPP+tm0XHZw8sGK+/Ju5Qco5AcncXf7dt6EDyK+vISXN2+1WQ9crTuVwttu8MU4KVWmkASZDpvg5MpF93FBIJDJMa79A1gMM5wGCBxvINi/k0wkj/ALr5CSQB9xfchj8i89o8HKDAoBHcWBSidBw8vzbmTIWhs1CMAG0nhWZpkkPDw/ZibL5j4+P2cgAUOl+g1A4SMLJAUQZA+PzCNKjQ8aMYmFwfNwvLy/Z0TAu6lUxcJL09u3b3A4XYwL4ZRNxJrwfZeSyHlgu5v1df8JurSN4Tz2iQLBnORqf5/xdzrdpmpxB4DwJF84hD6yjg9mhH/T6esnrCujHYfiFbMjEMAy6dJe8Rs7KIXPIA3LZNOU+EZTk3bt3enx8zEaBgIv9R5mlcrM0gRsKCbj1wIT147uZN2DSDRrfA9vPCwbIDwczTmSTPXC23tl+HAAGiHMaBFu5jfJUatvXxmmKU96vNWPtwfTDw0NeH4Iexs64MUhk2Zy1Y78cVEjKDRhg1VzPMf7sP4YQx4OuOCuIfLNXMGu+hjh5/g2QdePsQMGDAOySAxbmDIBMmdlPuY2vpAURgV1I86m035cLsLg4LY2xmGmfO3X0jIFx0WyDtaI2nHG6XWZevi/O7PMZbB265uAZIOM1vxA86fV5BgR5ST8r7J2Dt7bdZuCAPWKe07RsZAD4SLXeV9+p3+ln5cJID6C4xBE7xpzT+KSXl2MeB8CKElFs2adPn/LeSprPOZW5+tpKyvuPzIcQ5o6Dlaapz/PCn7F2BPDIAcz4NE25FXuMqUEL+0NQir1x8MQ6uW/kHJsH5Oi1BwueDUY++Tf66nLCOqBbtCT39UaXsWeuk3yW9wDKWBsICWyD+1jfG7JdfCf2dRgGVaFWVdcLPBJjadntoIyX+6Y1mF0HGe4fPQvimANbUikdOnY/4uvlh9Mhd7CJZJz9ria+izGxLqwfskHJH5kj3ufAlzXg+f5i3cAhlAiug1J8NuSWy+g4Li+cpNMo9sY7xTEWl1H3k2uCwwlaMuGc/VzaoGWVC3NHB9gT1jwHRzOZ4Oc9cuvdoQTI+Av23okPL20KIR0LwBcngvO0yMw48czfneh2HcafeyWI+8F10MZ+cZ6K93qw8re9vjjQcBbV09FJMbVYEISFxaTMyNk4hB2GsK7rfGcBhgKlA3wjkAjEfr/P3Yc2m00+6Iyho/OPL4in+Fh8FMPrENkUnABjYh6UeTFn1gYny+dJe8Pc0FKUUjCyCRwixrDTBpZnMtaqqvKBVYyjCwpO1DMqIZSD7FIpz5GWLdgoi8Excejdma8Qgg5XZU14PwqCE76+vl6wCPv9Qfv9uMiSeFqfTAzjcAXu+ykbRg/4vGsORoX5hRDyJXBeG+3sCt+DwcZguZF1ZXPFP5/POf1d15Wq2SnBMry+vubzLTwbY+QBjDM7jAsWx1OY7DMvWHvWs5T4hZz9A8wyZ4JUgDDjbJtWTVOcCKwGsoiTw9Eej0dJyilqGEz+7sw6e+HgnfWsZ2ceY8wNBZhHNlBNszCQ7Dvsm6d/kX8Cc9YT8A2IXKeC+TeBMmPD7vB96wAPnaRsBNvl6e90rqlcWogzhyggG3A47PLeY4fqus7yFeb7JA6HQ2YM17fGsq+ejgeIku08HA56fHxcsFcAVcoICahYBwc5gAOCLNbN93k9hmmK2emuy7dCUO76ByjkuzmP4eU+yZbsNQzlMkmXnUQiFGftIJr9AqS5/gE2AaXIP+Wa+IXr6+vcjalt23xXUNM0ur29zVkSMoJV9XmLcdaRIBB5ZY4EfoyLMdNGFBnEDgKw+Bm2wQNQl3evwca+xRhzcOgMNnYMO0rATrcg7It/hweFXoYCYcC6YpM8WFhnCzyjBgDF1yGnHqS4Hjt4x6djO2OMWe6wCQRPl65UPrCuyBBjcXvMc6epnNvCTjmp5GuAnSbo9jMYnM+JMao/F4Jg4QOrSkO3vFiR78SOQ3SypuAFdBGQTtYBe89/7k+dKHDQHWPMJCnZfMbk9hPd9Wwz9gy59wAA2ziOYz5nRokVmA6gDrmH7nz48CFfasxesCbo283Njdq2zWXfyI4HrMzd8aNjPb98EOCPP5vGSWNUrrrAJqZ1GXSyZgfoM7YXW+wBfPpsaYfP3vBM1oyxTVOp5sEHMh+3eU54efbbL0r0z7jv9u/8vtcvdRgchWXgRMfbzT4bmcfHR719+3YR2Tuo9yiyrtNNnIBNFI/FJEJEEZmwb4g7VAQCJUHBMJYOTgBo3jLOL8hrmmbBCGAQUBCcGsy3sywwQlzSB4OI8mFsYKY4yBRjzL3E1+vn6WfWay2IfB9BBkrtUTqGm44S0zRlp+lsHg6TYBFHV1WVNtvS7Qhn5Kwn45FK+9YQKo3DtFBg71HP2vN5DqDVTaUYS6kUY8ahUILlKV7PcHibN+RnndLGCPqz10EJ8sn+S+WcR13VGsdlnbunQJmnA33PiPgZBMYIS+TMEw6CNcMg4RA9NeppXeRIYcrryjpnI6t6EeCxp9KyLzhA2QkBxuROZA3scKTulNFXxoueA1yc+fQMiP+Oz7JHjMODWPbBDzLyTAfElGYyTubiwI7v9P9YB2TDGUtIFQfQzAnWNmUl0iFZ1hN5TDbmJClmR+uMMXq5zp55hg7ZGcdyySLBOfLljBo6hc31IJwX++Hr70EvawogCKFkApxdnKZR221hsdnXpBvlsPjxmMo1y430SV54HoRQku9tBo9Lxi5ot9vmYN/BFWsDwCNw5NV15VAzv8PWeAaYtUnB81Zdd1nYGnQFX0RXNpeTENIlel6m5Wvmdpnst9875ADB7QO6jN30fUSfGZez66wDARTrw7q6LXSb5QG7g3X+vpYlfu8giqy5ZwnQL/c1HsQgM7TahwFmPE5WrQlSSarqSsNUuoh5eZuzuU7EYDM4nwdL7qQDhIZjBQd14BUPpioFXWYWOYSQsUiMUefuIs2Emtst5uPZN/ztMKSycQD77e1tvvyX4MfJWnRqmqbPwDsBISD5+fl5kWEDiLJO6A22wrP0yLn7BwhacJHfv+G4kRJtgmHHoOzTv/k3/0Z1XetHP/pR1gH0CLu6vqDTcSst+mlGA9nEfri/6/teilFNVdrKYienadKkmAMNxwPoIM93WRvHUW3dqJ/tGmvoNpl1889KBfPxfNYQeVjfc4If8Hk57sHOIy9fckbjizMa7nBQSP5EmIgsYUNwTq5cUjm/wAK4ADp4JvXrQQWb6RNmAXA2nAFwhwygkMqlOaSkAeXrTM39/X0GgwBW7v1YA19u9GTxAVeMwd8P0ENQAJAxphSjg13G53WEDpZZF+rlAUzMlc8hwARXfB+GAcfsRpPvd0YCxaWW12s/14B3oYAqLA+fxRlyXgLWGKMUQtCmbfRyfMmAne8CbFKK4gDXU70ongMixocssf4ecDAOfy964MosSV3f6XLuF+DNy5NIAWNYCUQ9IOH97KnfQUPQTXkbRpg99GYLGAnfM9YqVKXW0lPYKVgqNZk4ajf6PIs993kwLuSeAN2dv7OeOBVnr/y8g2eS2FMH5zhRD6ww5m7Q3TjyPs+KrYNTHI9/x3dlw9BhiBYCcGeFyEYA9hwAwjJBmiRm7Sy6bbEHnLVord8/YNADJwAF6wALz/koP1PiAMSDEMYD0MQJuqw7GGCN0YG2bXPZjQPOJGPl84DiZcZjWVdNieF2m87/vLy8ZNDAmbb0vDp3tvOW2eO4PEjswaWk3O2GvZEKUK6qlDEnGylRR166vRG8ABDQQZh+7O44DjqdjjocDnlsyCj75r6MDln7/dWCqWZf8B8Ab2fzsZ0OmN2n8mLd3Teiex7koU/rLK+3W0eXsWPYULJMPIuACNvBOkDmcX4E/WGuTgiif4BKnwM/d9KGgB3CxjsPuu47OYKcVFWtdvYD6ABnJV3vfX3Rod1ul9eIwHGappwBJ4vrRJhnRwmMGFMdwmJOjmNud1t1fblk032qywE2Bbu03W4X3RjRW+azttmAYF87sGD2H3Uqk4J4ZV/JlmDT+R3ZU9ZdKq2xKacjaws54pkgsB74gUYNZGgde1RVpd/6rd/KzwNgEywwX6owXMfRD8rVsJfe2RL/6oRX2zSKY+lwh51DR8kI4sOdJOIzkEi73U5D3yvM57bIdrocOjZhnTwrSzYUu7LOerpfYj1YO7cdrL/bny95fXGgcT5fVKEc53QYuYudamMMHZBcLpd8RwQsmdfTU//oztCFhwXhNuh1sMJ7CCyur6/18ePHxc+9CwsgyQ3Zhw8ftNlsdHNzs0jPZ5A7B0Q4aMATTMvz83MuC8PIMBZnWQCRHlGO45gvsfGaSYwD30MEzfy9Bg+Fxzn7PRJ8Lw4NoRiGYXFZEtE9Lz7r2ZRigOc0/cy81lWl8xmDU2mzqRWn1O54HEc1daPLZb4pfrfR6+k1O0ScNIexWG+Uh3G8vFw0xbk18TQpShrH1LO/7wfFKaWRm6ZVnCZNMSrGOaMSpRgleqxLYe76ETUOg6S5XjqmrjKKUc18Ac84pU5AVVWLVovjQBAcdDq9zkbrVRxYZeyAPti5el6HGKXUwrfSMIzqul4K0vF0Ujr8qazcMYODoGGgk0ajECa1bWrzGEJqucn7AKqpDW7JfmVgGUcFSa/n1wzE6nouY5wKG42+uBNHBg6HwyIIA+igGzBmBHyegfRsIkGElzT4YU0HWXVdLzJhrBFlD2TcnEF0cgH9QAdcN93oAtK9/JA1gbxwp7nONAGkvEwTx+CZJWTDSxLTWGA+G1VV0NXVQeM4qa7LuQq3U743jMMZaNhRXjC7UinDwolyazz74MEgwRZzwrFWVbVoUsB6+uV3zItAgUAgPbezwNBvkU+f+fTpUw6w/DAidooyHgJCgN1mU87QAWpKR73CuMdZ77/99tt5Pxq9fftWVVXr+flFl8tZtIxGPghokBXPaHBhYD4QOgzzGbuLuq6f655LpgsAPwzjTGLt1XWpVew4FhJHUiat2HMPMNjbEEK+7wh/5Gdz0FnP6HmWH7nw7IJnUTyYcTAKEEXXvVzGdRD5j7Fk1PmZlyLxDEAbjLaz3HxWkrq+V93UaqZWVV2Jdvu7/V7jPBYn0MAiDsj5Xfp3r2hEIaAQYOaBMTLtZOgwDNlvH4/HHFxTHQGx4sw0OuN7XlWpZW6cirw6yx5VAih8zbpbGPLh5UDc9rzO1KDDa/LBfYmXe7HvrC9yz749Pj5KUi7ZlNIZNXQS8o1qDvQU4nZd9kNQ5GdlKH+jDMp9kuM5shUEm17K6aVL6KXvjZNsjBX76pjU5avvutSmWKltrUKQgjSMg6q6NFPwsTI+nzM6ie/zQAIfwlgI/hxfVVW6E4t7N9ArgnDPoEMg4peZ//q7WItf5vXFpVN/8Wf/KrMapHsAn4APjK8zpRhlgg9nUhkw/2YhUSYEnfQyzA5DJrKlRpDgAqPlmReACMLNd5HiZLHdIbrx5bAqDDXgyJW6rksHJNYIo4LyMk/fTD4LK4Hyu8Cx7vwdY+xOgv1wEOUMId/Dunqvdr7r5uZGm81GHz9+zPvF3rqSOvuLYWE8zoawBx5EoLiuTKwDZWOsr6dqpcLOOIvjzm8Yhlwqxzqy/wAGnrnOYgBYmStGm0yWl8IAUHFarDGgj+9JbO6yHprvHKZR290u30Wy2+30/v375NzajeAKkDfXG158T2GcC0PvaVdYSmcrfP8w9A6gnflnHJ4tkUq5obMwvqcumzhSPywN48ghM5gVL93z4IR1dHbSGXQ3Z8MwZNvhesV70RMHDg6GWF93ODgifgbJ4hkn1o354wBc7p1lZDw8B10HKPIsZ5dcxziU6w6YoCfGuOjsAihw/Y+xHNbk5ew2e8uf3ngCNt8P1Lr982c4oYLdkdI9LNgn7CKgHb1yJo4D5JzhWF8mV9ft4jwcJSKAMgf6Xp7B2DlX5+/p+z6DDJfHrut0d3e3ODeH33PwICmzs/6s0+mUQSDr2rZtJoOoPec5XmoBQYdOum0AsNDuteu6RdkH8/DWuQAKl3WCfwJW2qFyVggCDlBNdoI1xf8jc7e3t1kGnXBwO4MusE7sGfclgT2yzZ9G1U1pZ7xgZ/thcajbs53oxDSV6gY+dzy/LiotkA/WFftIMPVdVQboA1jCD+G7f2Ptmbuz35XCZ34A21ZvyrkS9z8804MQ9nSaJj0+PmYs9P79e93d3WWcAKFAppq192wUY6FawhsNIDd1XWcZ5nf4L5dB/g6Ww57HGBdlvqwz8/NAkfFg9xxXMhf3b8fjMeMkxuBnhBwjOO7i3078sj7oO/Pi+9kfbKoT5nye0i10DaxKEAduoTEA55tYKw/0pdI5CxLc9c/XRypdDwlQ3Pa7bq7lE9szDIP+2f/tD/R9ry8ONP7yz/8iT5CoFjDgm4oAsjg4Cw5Ik9XIAwillILPV1WpC8SRoOAuDCwAggfzgLN24yVpkVXxlHFjRspBOA6J3xEokAp1No258PLzES44bLZUnIGXqWCEAJ/8nO9xIOSsMo7c05xuXDwSXgu7gwF3ahguGF4MKMayruvc3pR9x4kwd57vKex1sMX82HvGhfFwttgDDZ7vB674Pc/g395AYG3c2R9P07uB9CYD7B3rhDHH0SBbJfBKl925ojL/pm2latkJgv1vqjqxIaGk0zkU547Zg4g0xsQOo6N+8RrAQdLCmLLWGERnwTzwcqae+UnKxtQPurK+DqZhy9AFurc5c+XkAOvMyw0h34GhB3x5kBVCyEacz1DWBSkB8HdQtdYLB+6emXAyIZ8pssAV2XV9QIZ5n5cDOqj3IBjWD5vhLVWdrUUfCFLILvjBYt8bP8QNW+jZF+YAI+jZDc8CQe5QLlJVVQa1yCYZa2dIE6Peaxyn3KEMVhMn6kB6s9no6elJP/7xj3W5nLXZJEBO+VTqcJOymFWVMt0Ak+12uzgH5kEpmXXWnb3Gxqwz2wQ86AEy7zYI++BBuQf9bjMp00JePfB1n8L3uO3juZyp4e/4AcbLnNhDgounp6es99yPwdrDKtPOHRmF6UeeAZWwnk5mOdlA0IsNQPbw97zPz20xdvdjfiYSwkYGwJljCEHbpuwjeGQYhtxeHqbb17tpGj08P2WbwtjRRdZVKudlnBnHp7CO/n63hR7EsAcefI3jKE3pAmH2FVA4DIOqtinvm19uY1gf1l0q93IhI4wX20Zw9fLyknHX8/Nztpn4xM1mo+fn53wu9HK5zNnAMn/knIyDkxLjOObsBWPl35QN+77gzzabTe7w6Qf+0cUQQu4gxxjQJ2QTf/v6+pq7tPHCnjEW3ytkCz+I7f0uDDZNU87uoDuXy2WhmwRwDuSRKZePuk5YoKlrNXXxER7UOpZxjOdyw1kgxgX+YnwQqp5V8SARvUQP2Y/f+z//E33f64tLpz5+/JgNBKCe+jE2mpdHn/zdUzB+GBxA5+DTlXPNQrDxGHaPGkMIOUDx6NoZtevr68wYYQg2m01mdpwt8TaZ9/f3edEdzDuTRG0fRsNZMpTMsx8IgoNljIgrKAZ/3csYx8Vz18EDjg8F8/ICZ8HcuLEXvFh7SXmdAB8YJ1cWlN8NCAqagEWJ0D0diwFxlsIdJGNzxfXsAt+HA0VZUHyYPRTG115SNma8vFYW4+SZEf70Onk3NOXPMRs5B/ebzUZjnBaAgWCubVtd+l5VWHbU8vVGhjxo32w2Op2WBy8B++w1Y0Dm/IwNGSwY5zU7zV5KpWuOg3wHYujz+u+AdthZB3DupNh31xWML3rCM9Fb9sD13TOggHfANO9Dj/3slOsS48UuILNuvzxb6QGaZwy9bhtgidHGdji7xn5T1hRjzEw9a0aXFwI9wMLNzU1+H9+JA2ev3H5yvw2BD8w0Z0FcDz07hgwSADFeB9quRzD4+I3z+ZLbyvZ9OsiJrcTpeXnp/f39TOwk/aX9NyW4abzdIisGo4099/bn6Nc60+pBv2dmAU/ogDPKgD4n3zwgd/1Dr9YEx5p19Oyi+8nT6aRpSpe/eibWbRmgzhuWQIqh//f399nueNtUvpPzJQ5m3RZjO3yP8fEOgpyFxoc7E0zJoYNZ9yuAYvTAsxyjlp0fCf7attXYFSKC9bi+vs7P9KCIEueqLl3qPBuB3jvRw1h9fxkLvpvxsue+lsimg1oPwJq6lDaxtqzNNGcT1mUuLps+B88uOcFA9sQBJPgHWcIW+dkOOkH52UFJWRf5N/gF2cKeeQAaQshnsRg/38vL/T02AiCNroEvCCIhn13nPBBD75kr+4POs974Kc5v+dlEtw2ekUdH/AwfOoXNQG4A/ZCX+Ff2IRVshwVecMLKMzzuG5EL94usDzpFGZmPkf3k9x648iwv8/u+1xdnNP75f/fHC0H1xWUC2+023wjqKXY2GafjDpuNZIG5ZIgAw88QeACDMLrD4zuk5SU1bvBRWg9snC1h8XkW3wkw9fQXjpRF95pH5uksFt/nBng9BndKzvCz1oyD+Tsw5+8osKdaMTwYWy8jcAaTz7hR85ItBxfO7FLv7QrGZz1jBbu0DtCmqaQ0pWU/9tvbW03TlBlKaXn3hbPMvj6ubNIywwNgYv35GcbDDa0bYQ9OeAbAC4cGWEvAMt0s7DLJ88+Xs+q5/Aonn0FsVen4/JINs4NfQJAzDEWGUstQQPPagXlw6qUgXr+P7vla4sBxpMMwLLp9oQvOpPAsfsZ410z6OsjA+QPqPEvg9oL9YCxkTQGtrJFnJSQtziOss2i8+L0DBwzsOqMDiHCnznNZC8ouqaHH6fmaeTmkp84J5NBf7th4+/ZtDpooIeVgJ+sL0HFQAXBi7Twz9fT0pHfv3mVHB5B2sM282Bt+TnBDiQt7hvNDL2KMuru70+Pjo4Zh1DCUsz+n0ylfCklZE8GOO9F0P0U5SOryMU1R47hsx0kPfgdkyCNyho4jgx5gQ6D4vPmMd0pzJ40NAVh+V8kpeoEseJDvpSySMrEHqCDr7qCJPSPAwq6wZ8hu13U5c3S5XHJGjvUAZDlBQqCMzYCcG8cxZ4SQJwfd2NHj8aimaTLJ6Jkt7A9nB1gDujK63rvP22w2ugylk6Nji7pKN2sDip2FRWZYd+abSY1QWHnHBZ41dBvLunAewVlrxw1OyPh+e/DvtiaOk6qwrGoYx1HDOKrZLC979YDBCQ1KJMl08nsHutghdATsw88p+3NM5v6M8bJ+PAcd8fXwwMQDC/wacuPEK3LmBKFnF9AxzwIgC44R12SQ+0/WAvnyrDprAnkBlvWx0U6WeWIDaYPLq67rvA98JyWV3m0SmWMPNMV8CSAYzG2rlyTzOw8+1nLiZK+Tedgqf7m9Y2/Q97/TC/twjjB5dPvJEZeBXEo8nA1HEHifg3CMeF5Qfd4dA2OEY2Hj1oed+D532LzcWK0DAJSMg2Z+gZq0BPmeLvPshgMkolhnU10AvJwBoMpnMcIYIgABCuEKwBhYu2ma8kFWInEPZryeW1q2Q2PtWH9n4NkX/g5gl7TIFKDAgFIyTe6AfdwEO6yTBy8843Q65XG4E/c1d0aFdSJY8UDJnYc7ewySG0ZnYpy1RM78eRhXZKrrusyo1PVynhjbqJKd4+d5/qtyIpyQBwSUgXltfFUFVVVpE+zBkWdkOLztz3RgiLyhx34pGFlD1gy5W4N/dIO9WzNusGyASIwn4Hq9nx6Qw9wzHtbBg2bKZbwO1ffcgwz2zeUsxtJWkfVkbAB3r211+8araZpcWgDThy1Aru7v7/X4+Jh/x3+U7BGEPD09KcZ0ASX2sm3LnRuwaS6vvv9+oJgsBYC167p8ISjPxo4Abtgf9gbAQfkBwJgAD6aRcgy3vex5CCFfOshYCYLX7CkyyRjGsZAkMabzCOnQ/l4xGlibf4dsO8Gzlgm3KQRjMM7eLQj5zqC2/vzMGf+h733f69OnT1kOAGoOQhinB4eM0zNK+Cpnp2GA8T1u8wAV7B0g0kElMu6+3IMT1o958TOqHNq2XWTW/DwHa4v/dD2DkXVyi+c+PT3lYNNtVYwx6/tk/olgHd8Rh1IORInMut14VVW5nESSokqLXPwB5/58n5yUczafNXcgybphc5Bj1sQDEmzR6+urtu0md5Zye7XbbjUpZh/i4Jx5kvWik1OMMZdEgZcAqPhicA9kMQGal1S6HceXOxHn9h39czLZ14HKGEqVXJ6xTwTbnP/FF7m+ecWH+xh01QkRdMmzS6y5+zXHZf5z1gP7wp+ubyGk8nf/OUH8OthB1hkHY0TPcgA8TmqMCPXsDhlixuI4hvHgH1hXl1/HPn6mxANfXmvi9Utev1R7W78V0EFRVZU6MAf3GFGYqTXIY9O8hIdIbw3uUHwYE74bAV2Db2lpFPkdc8FZ+WbiuP05OFSpBDUOavk5m+RgyBUQIXIwx9+9HAWBZD3XwZhH8c6kYCgcSPAdzrj7Z/huZ/ld8AlUnG3xDBNjQR5wjP5d7LnXPq+ZYQ8qPcDxffXxOgB3Y+5GcM16uJF2g+HBJ3vgIMH3iP3wNby/v18AKFdmvvty6RddNPj7NE7aWL0kYKWqKoWm0dX+kIMMfs94AQoAWFoLupwy56Zpcn06a4mx9uyA66YHgTgknimV8xLIpBs29gQDzXgAlXzXOlDj2Th/B3U4UNYINsXBNt/nhhC58dpwZyNhnZzFdTBAm0XXmRhj/rkDcMaOTrCOOHdYO4Jy6uNdj7xFZwgh35b76dOn7ABYkxjLpaTILSCC8dFq9PHxMd+yS1CAfgBkvbU264zdvrq6ymcAvFyEri9ub92GS6nTDGDRD9huNhsdDqljHY6O8ZEtAxS4nUv2LEqqM2NIoOkABRDtgR/ABRkkqMPf8HPXIV7YFvaPTmReNue+xGUBO/b27dss74Bizr8A3pFtPo/uPz096e7ubhF8Ab7W5Alz8goCZNTZZvbL7Se6iS7hV5AT7C5MLfJIYIg8A+Yg05DHGEtpHkSQ64zbuaqqcqmTZ9WYWwhBqlIHprXvHYZBVSzlvzwXe8J6I8+s3en1VWOccpco9gp76AGK+zn/jnEcc7UDvgCgzb/XQBgb6qXS/eWipi4lrMxdkoaxtCJHVrnLgswRNonyOb+iwMlbZAcbwJ71qyCHckaCY28r7aQOGII9JWvE93nmDtlk3OAIdIDGLp59cKLHgbJUOkqhx8gxsuEkNLiE8bRtmysr+O79fp87ZTk4J0t9uVxyp9E1rvXgnnm6rGFvnERYZ2ewW3ye57PuTr46CYI8QXxzIek6oOd5Tu4xFsew67F4oPd9ry8unfrTP/6ThfP0v2OEfXBs+DRNi2DBFxrhJCXsTsCFgXsspAJw+C5nAXAq9GF+8+ZNBt1rVnYNqL7L8fh/HtVipL00RVoe8MKwurNzhtaNvoNlD4oQOjYVowwIAGjxfQ5umWM/TtI46NC0GjWpi4OmSdo2G4VpUj9NGmmrmqghjYrzwaNlCc3d3Z0k5Z7gMBIuA/kwswHJBMaa2fDWuly6hbErZ0+iuq6URKWL+qS2ZR2KkyiGpZQyIB/IJvLF/rqisAfrUgb2G5aPcSKzAEP2DgeQZKN0PYtxmn83qOsK0+sGebvbqes7te1GilFRJXVZhUqy7/MyIAJR5pIA22GeUymTW5dWuSFyhtSBooOswmgUkFJ0PR1yR1ek0ggijSMsGGGAwVpWMXA4ZeYEGIHgQOd4hjsmZwbJDHj5JnP03ufs+9NTOeiYnGmSq6ura/V9l40xz/X2hpsNGQIpBDrFTQv7R1CC/KTSpnKmw0HJ1dXV7OSCnp9fsm1Ep2C7L5ezYtScySgZAAIubqW+ukqXuHGZW9ddZn1qsyMkOB6GQU9PT8lhTlPqyxhjmuOUWkVvt1vVTZ1aN6qwcE0zn9Vpy2Fj9Abden19zXtS16kddVqjTQ4WsdPDMOSW4/gTQEIJJEdNE0BrMx/o3uc20g54sJluA/yeBwd6HsQ5MUUGDf1w8gUiDdCHz+OzrIETHew778cmScpBopMpfNadvwN9/89JIv8+Aldn453RdIbXfQ7y7Oc82DP8Jmvl2Qd01MtJPXuBn1v7WPymE3fsG+Nx4DXGUndeV6XbU4xRlYEo3uMXADJv7N04zmVJ7bzO45Rkvh9yxuj1/LogJBmTl4Lhq/FTlNU4YYpMsJdewpUD1K7XMAdr3I+V16wp9yuxt+ABmsmQ6fRMsPsHMI8TeQ5kISqQZey5A1nPyGCjsM2Ac/bcM6Tr5gXuR9gPP2eBHwYsOxYAt+E30GvWmfn6wXR8kpPU7B940YkVADuVC7vdTv0cTDRNo/PrWQrSbjd3NlU55M8eSVr4wzUx55jUfW6MUZu2VV1VOYs1jVZFYCQie+mEO/vqQQ8BmQca2Ete62wHfpZ9qutav/v7/0jf9/rijIazuCi4A16vOQOkUVPPRBwYOKuMwK0NGxOhppPMgUembAzCxOGqH/7wh5qmlOKClcNhOBPh4N9rpNksgCubyKI7s+VOZB2EIeBsGmDMx+xpaZwU6+qbumZPPLplbM5UKwQN1aTNNOlao2pN0rZVjEEapW6UnqZRlyoqxKA6NJIqxRmsNrOQIZzU5IYQ8g297hBYDwC1G4K6TkHDMCSASjemum40TVHDMM5AqbX0bzUDv6gQcAyVQig1r84ksk6sDfuIMWUujHkYhnyjKMwiskCAQjDnB7Qo0QghZAd6PpduW+fzJd8kSuMEwAPOqus6jcOgEKUBkB3TbaKAMfacOfByZ8B8SqnepKYpwQ8O3Rkk1tcvXUJvPcNTHHoChvw+gWrNTqsE2sv21U3+twdyrufIL2AJBgjZJ/sBawxrynkgAJOnzDknQDDldcnoJ/OIMerm5nbeQ0kKmiZps9lpGEqp5zRNuTyp6zp1Xa+qqtV1w2JeyYmmYNpBLk4msdzpzM40RV0u5ywTMUqfPj3o/fv3+rVf+zXd3d3PrNl17rJSZPOQgU1dFzmgJBJwdjye5p9RKtLO8lir63px70rfp+Dg7u4+6VFVq2nT/jWbTXYSIQT1w6hQz+B/lh0cEyTBft/OzrRSVdV5ndP6F4IGWSAQYp+9ztl9DHuW/pNCqMUdNYkpLxk2dJ5AADnCgXtQ6wEFINQJM8aAP1mfP/HzZsgv+rMO+vkMANw71zhTCFAHnKH3ADeAFHLgNgLyge9xv805pjWx4sy4+0p0xhlYH5MzzVIhXwhICEb4Di8dYV+duHN2nmcyDi9t8QqC/X6vvpvJzDaorhJJs5uBMnromRNsnANHAGx/POp8Spmi6+trPT8/p7kPg04xSlXJXgNSfdz8DCyB3EEc8D6LjMN4AAEAAElEQVQH633f5/bAns2f+lKFwJ4jk4ql3NaxAuQsRA97i49EjpElz7x4AII/X9tmJ4zoSEVg40E937MORhinv8czWqwhB83BPcg/74kx6ng85oP76IHjD8ZOgIPsOYh3OUMOvHGBE6n4mhjnu7imqBClbr5nbhxHxXHUZtOqn+frxJ0HpH5+NcbPm4jw/Xl/+E5ZdUyQYtCiVN/tlqRcerYmzpFPz8iv1wddQ77dDjsx8X2vLw40MCYoJc7eD8whEAwegQNQ+IE/numsF5vrDE7fl24mzpADGh2IkXaPMeqbb77JgAbHBQu/jlQLQDwvDC/f54GRR4drA4kz88Vn09fMmTsGBLeqqmwYEfoYS1s2BB2Ge83ISwUYMabtZVD88KAfhK1u642qJqreH3R5Pumv+ouu391qGC/abneqY6XLOGqzbbRrGsWx1Fny3awlWSiCP4Cv77c747Sfnx8U9gwOiueGiTl5UFUyZMUJ8R0uC2SVcNh8rzcX6Loulxy5AfOxEGxUVZUPTbrzox3e6+trbrXJmlCWQECwNnD8jFIRZzK/S+FdP1gzavnTmEtbV94PIHejhlwibxhkxuWgJYTlHSDr7AJrw5o2TTPX3p4WgMlllflgByAmrq+v81xwWjgzD3ap9d3v97m1KTp5fX2d2ThP63uw4UBvHMecBWW/OesCG+dd8rbbnbgokWexxlKrrrtkdhJ7mObeLPSUMqLj8ZhT72/fvs3rTKobZ+92hn1q29IBzcmWZHvL+SkADl33AKIhBH38+FG3t7fFDvbd4lyFM2QEf9h4MhV916uuSjeYl5eXHPx4+ZIz6Dg77N0yaCn3ahDwU/pBWQefc2AtlRu7AZb4FfQcEIXTdBCHzWCszNWdK/aY/xzErx0vQSpz4WcOOty34GN9fyDyHh4e8nMcGGL7PPsNg+zPwIa6vvq+oIcONrw7DmvtYAkZQfeReV7Maf1d01RKKj2ThFw52cHa+xkjAC9rwP7iG7E32DzkzHWHZ2JnuAsFfQPw810EC91Q5IrxEtAxVs/qAMiQBeyRE0SMB13J3zVO2m2W9/O4D2EvPFhiL5ATbDxNGpwMRZ7XmX+3Kfwd+WZ/+r5fZJ3RE8dz7Dlr7oE0MuCZMv5kHNgqx4Zeau+lp5AUzJv1xKZzhgyZQ9bdprptdlvgcgquaZpGqtIzvBvnOI5qtxtNFiiw5v6dfBf/OVZxcsDLzfiM6x1+gXXnT88Sud3l396IxO2S7zvPAY9uTBZZ4y95fXHp1P/8z//0syAC5fXBelqQBfZ7CJYsd7kbAgXCUPnCuhF244KRmKZpobBErg6sUHSvCXSw44yL/9s32jM27jwRkHX6jzEi6NLykHoIITtOr5tlbelEQO9rhNBTfx6NuyDFmDoUNK8v+qs//GN9+JO/0LspaNtudHV/p7uvf6jpt//32v3v/p5eNGi3OyiOUafuou3tjQ6bVi/z4VMcF/uLUHpwgeCz5qwrhiyNuUTTnp5jf11wkQP2j73xQEMqB0MZG3uKoWBcGEJnslzucFSwWBhSxsMee51scbCN2rYYS+bocuvAHEeCwyDwvrq6yoYX4+mAmfF4cOztEQGe7kicwfMyDBwTASsGEhlmzdMeLAMlZMF1DQO+zGKMC+e0PuSNTrAOMFvImI+9qtJZB/8dz0GHkDcHXfycvUceSr/wkMsDSKsXh1kyh2SlSonAVf6361wqZUrrk26OPy8CnO12r5eXl3zmgXpgngGgSXJVL0B206Tbdu/u7jSOo25ubhRCzBdwQeLUdT3LS7HVyO40Tbq7u8s6gEzg+Nu21RALGEMH+X5nYv0A8DSOGvtyh4GX1TB+B+duEwFi2DYHwYAMtxWspTOOngUGrKMvPAOggR31g/04XoAZYAJGkkB13QIW/aEszIMy9oPAx8s/nGhyUOjMsQc47tt4vtt7L8Nw+XE943MOHrArADf3j7zHM8KAPff32DQn0vhO5u6yhHykcrd0tuz5+Vlt22YbiJxQBjUMQ66Jd4AEyCIjja+iLS8/z6VIliV7fn7OuklZsJ9RcKIns/AxZTQ8Q44Ms37OEmP/fd0cjK+BrAdY0zSpUtCmLR0YPRCIId02DVHFnmGvnKzy4M7xF34phJC7gjF+zyBB4rIXHhgRZLHGbg/BTqyR3+EA/kFOsT8Oaj3DQLCDTp9Op4W/cIJ6GErXJ9aOwJbAiue7X/TAHewjKZdNOcjebjYKsVzUzJz7vlezaXWZ5RTfiFz5/uI/8PHIDfjDZY/ns8d5LHWtaRwVtOwo5TjE7YsfnF/LIfLHOrmue2Djuv5P/k//WN/3+qVKpxAAb0HGomQnNSwPZXtUyQLzPITZU5DrCeOUUDKAxGaz0fF4zM9CiHxDPAPgSuhG2lvw4jDWhgHn4JEzTg1DS22+g0AYcJyVR5G+Tjg9No41ZrNd4YmyEVR3nqSBmdvr+axjs9GHq2v1v/nr+sX5rLDb6Df/j/8HXf3Wb2kIlS5Dr7GOunSdqhhUhUqX81nD+VVhxTx7LTtMOvvh6+rZAADQNBXj4rLhjMdms9Fv/uZv6mc/+5k+fvy4iNpdblDW1F2pzp0rkCNAMwYQZ+ldvLIhn4GzH1JeNwXA6PhnARlJ8cuz+DxGDDln7G58eR4lI87UHw4HvXnzRofDQR8/fsz3JXg2hr1xwOVrjENj/qyjl+B5ep2xEgjB0MRYDpW6gyUDyNipGfdAcB38AVidyWJd/KZq7oBwFpCgCvnn5wQvpYztvCiTcbuCjcKGYTscUAE+zudT1jdK36jFP5+XzCP72vfpBmbuJ0AX2rbV8XjS5dIvWhEyfwgZWFXXDdo747CaJh1iTwC9zx0BnaxZM8DOOnvLVX6GzVUIimFZL4yd5oVOIXOXy0Wa5hriVbAAmHRiqOu6nL2SZGe0iu12gojgC53xNZO0qIV3oIGN5hle1oODdzLBgwUnByhJCyEsWlV6gO5ZET7PWiBzBJWeFeR9ZEodmPr8+bszkqwna+D2iT3zs1wAJ/Qd+4gOuy+apmlBKHhw4hkHJwrZk/U+AAx3u93iYj9keLPZ5PsgCF5ZX8olkVMHtNOU2jHTDpkOV5fLRY+Pj9nm4JO8NJoSVtYG+Vtns/gZvrbdtKqMwMLGeNkpcoaN83Vd4yMnKlwXsn6ZjCKb+LthPrB+PB4zfuB2es5tOX5ym+J6gL/xYJPvJ5vm51b9c+7vsSMA5xjjonMeNs8xnu+FE9bInhOGTmA6icH3+h64PHuzBd/jQs6Vcm8PyHif41Nfx2lM3SE94Ac7DOP4mc44DnAiAzzL/DzTB/n6N5HjaQ5RcYoKVQnw1gETuordwEY4rmF9GPfaprhN8r34ktcXZzT++//Xf7cwdM6UITBsDECAn2NYMLiwGRgSBJvPb7fbzNJ5RO4GQSosgjsZB/X+OcZK9sDTx16+xVgAL8wP5XLwBhtDpOtOwJlsvgPlcEFDiZgXY0U4qan1FKADX8bsAkNZ0zCMGkOr5jLqahzVDxe9NlHabRViUNN1iptal1qKQ9R4umi726u9PmjsOsWpOAz22zMSnNNwJ+NZDuSgsPTLzI7LDkDr13/919U0tf7Df/hfM1BzgOAysNkUx47DxSk788MerB21GwH2z4MkD3Zx3F6XyH4k51BAvAeasLmU/Hg2kDnhSJwRYu36vl8wuhgkvodAnTVp22UnCIJB1tF1Y224vB4XvUy3Fi/BCo4BRh/G2BmylMIeF/IL6DwcDjoejzkId2bSgyQABs6T9QDckREg6MmsowWQm026oAtwjX5M06Tb21t13bD4rDvjGD+/r4PfjWNpmYpjSnJaKd1anW7OZY8SYN2p6/q8Dk9PT5KUz/NwYJTxYq/QDQIpd64hSMPQ5zWjdCB9b2GT14EFoMuJgufnZ93c3mqMU/5+2sp6UOslhciworTbbBZyyXiw1QBvPyMDa+aZbuyin31AT12/eOHCeC7lip4580yVs/78TiolfLCTBMbIoRM8Dro8AKJ0ErlgvSmtWDYeKGPh7JHbWNaRcyEEBDc3NwsyzH2cr4mzmfzdARQv1hgb6RkVBys+H77X99tZdQei/Alge3h40PX1dV5bB3zoJ2vPnpLN9AYG3LHhWQ0A0jor5fuLveU/sAm6ALvsB5fzc4JUt+UQrfs83gshgG3kxe8hZmh+gI1EZnheXdeqFKRYzqE+Pj6WCoGqlA8VQq+UFjm5gD13v8i6oFteBu9EDGuEjQLge1DOYXa/p4O94PMu12v5ZT3R02FITSzQHTCZ6yBBNOuJPB6PxwXBgxw7Sek+nqAaGXWQ3TRNJiBYr9xOvqrSPSfV5yXsCkHd8HkW0HGly6MTQB6weaCADLK2kJLTNElTlFZYgn3ywM71wLEp9s1txRpz+3gcF3/JzeC/1IV9vFhQBAOhZBJuSF2YPUjBuDjzhnNxA8kmwBAzOc92AKQc4CEsCBoCfXt7u/g344K5mqYpOwVfUP5jwTEYCLAbVsboht8DJDbRD4l6sIXSMD+YbrrJ+MsZC9hCSYXtChuFftDUv2pqorRrVKlRO0hTHDVsag1NpWaUtmOlum70OvSahl67XWETvGRtfcjXhddB8JJ5DIpReX/dkfF5FIS5sN5+3sDZ5xBSZyoHzDAZsCqsOzLBnvpFVig/zg5D5/Pz0imXCw7ypgPtJYWMoUP+Ab0YAJyqZweRY9aMdUI2Qwg6nU65FIBgz8uexnHQfr/LHUg8Y8Hz1nNBBt0xMeckfyXz4IDTSQDPNLA3EHUAP9jKruvyvP2iMHSDcjHXH3QU5/D8/Jx/N45jvh0aMOcH+Bkf4AHGL7HcqaMKrTnHcczB2en0spgjOjsMqYtaCCEHkCW4rjWOQ95bAsvtdqvtdqfX19KxjTIngIMDdIAIzhG5hlwhsDifXzWORVaRyxQIvmqz2ebMjwNjMgyn0ylnTLIM1MtstQcYrAPrim5uNxv1l2XZj4Mn5M8zE7wAHsieZzF87bHbPMszlsiB2xHq7V1usSfYVa8HR8bxA4Af1xmpOGa3i37+g+etMwQO+ABlvNx/OLOLzePzHtR4AIbce9kwvgAAge7w767rFu3hWW/faweT2EfGB8GwBkyeJfJAzn0lWTj0B9l1fSNQha0nCAHMIw+uP/yedVoz2awR/hEGmTE+Pz/r/v4+Zxed4AphLlVqym3y7BEVDQQNDsQ80+XBtevImlUnwO8vner5u8gMSrMfrbxhR8i2lfk76CTzynghJtmPNcmF3jupwd95HrYJ/3I+n3PZsYN7l1N0gGcR8HsQ4OvtFQmMnT8he53YjbGcF+Gz+APXYewOa8+YaAns2GWdEcr7NkVNs00he5T1X5KqkrFyG+ekFmvOWrieM37HgqwVfpLn1yFo6EtDAJ7jWX1sC8/y0jq+c10iL2mBefz7sad/5xf2oTyeosKJunFB6BmUG0YHxSjx6XT6bBPXkRNG0x0PCwLLy/djAHEWSVGCuq7X6+t5LoE4z2CIBXvNiuCdW5qmsGzfJfQYYBcglNXLcAoTuszceKkPoN6DLY/2ieD5uTtZ9oHPDsOgpm01hKheo9Q2Ck2lbuxVzy1ud9udVAeNw6i+G1QprZOmSe1mI1qzsqbMOe2NdD6XS5ZoQZsEc9m3PMbClLkBckPEsz1NXIBdOeAH6E5rP4puVHSwOp8vc7BSOok5E5rWbNJms817PAxjZs+6DqaqVlUVA5nkp3TnWLKqJY3IczDcBAjs8eFwyGVBANXdbqfD4ZDXOAVzZyuVqXW5JBY+Xfh1lTMZOKjCFpWABbCAkSOrBqhkjMkxTGoaQBnlccMCKHmJEk6Bjh+sBWV8KYg4zSAszWW/Z+6DmiZ1aGrbcsEXDhi9xgCmNWhmWQy6XLoc2KUgvPS7h/2ljOLl5UUfP37U/f19BvgF+G/18nLKZV+wgymAbFVV13nelE4RIGy35TwXDoo1h9V7eHjUzc2NUjemVp8eHhRCleq8Y9Tt3Z0u3UWHw5VOx2NmzmB0CS4ILCXlumTGGiU1m4027UZ1UyvMchoVVbetDnPNO/ObpkmhrhSnScOUDi2O06Sun0tPw/LwMEGPAyUH2ASPmY2r6lQ2oKhKQeM0l5w2c7mLoqqmTvceKLUfZczrEip0F5u2ZvtwjuiXA/w1KcFnklwv9cODNCeskCfYRv9O90nZ2dfl/IkDJrcZPAuddMIKHyGVzo08jxvTfQ6UlXjwhvx4LTiyy8vfz/0qngVwX7Qki0rZCZkIQP+6PLqQMHFh67GBAEH8GiQB+keZItlsQL1f1oYOeECI/WHdL91Flzmoq6skS1Vdq6prtSGonia1242G2dbd3N6qamqFqtL+Kun0pmmzHIcQNA2jQi1VCgpVUF3V0hRVN+XguWdnsb10sAKf5D2ZorrzJXUhDEFVU+n48qKhH1IA35c7OzxgHMfSPhX/SeYB+fE94XNO0KIzyDLnYNgfJ/kIJpAh9MQbD2CTHR8iP5BN6CLrxLO9umUddOLH8I/TNGV76XiTNYAwRMf98l32hXkhq9gW8Gz2x+OoKlSa4oxlZ5JCMSrMwZ3rfF3P3aCiNExRoQ4Kkuqq0jiMGmOxY4x5TUqz12ufyPuxO9jpaSpllp6RYa2xLY6tkAn/TnTXSTK3h070e/D0fa9f+oyGMz+ScjofZ8R7GRRGgAkDvFgQNonPrctWYGX9gJs7DyJqj/zckfDs9PfURrXr+oVxqiqMQQJcqS1jUIzLw1M4as9+MC8UAoFwpt8ZH2dhnM0GcBOk8Hnezzr79/A+LuDCObiQ1VWloErTJA2nQW2Y+3hr0Ol1Bu9VpUlVAiBVUBUrTeOky6XLShqjslNLQLHRZlOYjtPpNa8F6xyjVNfSMIw6nU4ZgLEmyIsrAbLDXJA5FM6DEoILqZQh0HoVp5PWrFZVweDQ5arJ70/lRkGpdW4JlJMh3Mz7l/5DXpH3ZFyWZ4u4QZbyIgyfGw0/2Nz3fb6Mi+fUdWpVm4KsczYiNzfX2m73WU76vtf19bUeHx+12WzyzcOUFN3e3i6YRM/6OHMZY5G7BNAwIKUOmxpzZJL1JRh2ljM9P63zOI56fT3rfL5k8DAMdLhKrV5DKF3J3DHj9JL+I/tBV1fXdpg5arNpcq0yZxwo7aKjkmdSMaBv3ryZ5fe00K2ki6Xn+dXVVQ4i9/uDdrvS7QqHio16fn6ZAceoqqr15s1tYm7bVlVda3fYZwdxaK80xair62sFFdl7eXnJck8AzhgBYXVdKypou0t10Pl8R0iyfDPv/Xa/Uwya23ImkF+3jaKkcZr0ejHbUhew7eVPrqMOJj3bPIyjJqVa4c6yG+fLRdUsDwpB/WCHjmfgxncxZ2wDmUCAhYMNiBw+6yyy21HPRHhwgdz6WQdn3xkLgRXBBvK4zi7g4P3z6AoBK/NqVwDFwTzjhxCQlNuH4vPo4Oh+w7NAXuuPz+W7KHPy7Mnlcsl2hDMPDlDWGVp0fxgGPT8/5+DebQvnMZAR/DjrAatNRq2QJWUfHZjyLM88scboMLorSU3bSCFos91qilGXc7m07vjwKY+pqir146CqqdVuN4vW5iGEWaYrtZuNgqRpKBk0jZLqqLZpFKpKtQW1yBfELAGfy1wIQSFKcZoUp0l10+iwS3fh1KGw6VJpeoDeNU255wm7jd8k0GT/ndlm7GA5z4h484riz8t+IfMAeS/rJVj0s0g8wxva4OP8zArBhRNL4D90HdIF/cU2ch6EcfFy/ec7sfHIIUQvvgtsl3VjmjRMJaAbx1Gaooa+BFRUnDi5TmCynW1XnGZfW0uD4WPk1RsMuf31IAQdZM1ZkxCCFIucsE+FZC8HuJEdx6WOu3zfi99dVpw40e0B0t/2+uJAA6EA0PvGoUT+e2mZGuJPT78hQJ4JcMF31pVnrssA/E8WhoDAmVYMOc5iDeYl5cuMPBPR95cFi8d8Kcvie92hITh+voDUNMLBfJ2twYi4k3J2zhlvnBDG3h2JPzdlG9Jaw1YAvkMoZXA+Fw/OWHf21hkL3ucpWQSWenO/eZl9WrMJBF78nrWB8XDmz+utGRcv0vHOCMAgolzM15WbAIjv8rX3tOrt7Y3qutbDw0Our03dK1qFUC/Kh5BfUqooPXNhbW5ubnR7e6uPHz+KO1+Ss650d3erp6enzzraDEOvr7/+oT59+pTlF4NLl6c3b96obdvcu91lEYPa9/1nFyKtgz8/qIfx4tC2s6dk8NC/qlpe3gRgJQNJhxN+jt6RvXFHhgGv6ypnJKXi2NJ4k8xdX1/nIIOad2SV7Auf6bpOt7eHz8iMYqBL2z+cXGKAD9l24SCZbwgh140T4ACS67ZR05bbkvnd+XxWqBLgBoCyNsiSs6OMqe973dzcKCrq06dP6e8xLlhJ7E1hvpbnC5ADB9h8DhsD2cDa8TvWnzEhezGWG8rd1pE5AixgK+M45bHz+RJwJ/29ubnJNsiDIGrDWQ+/cRq/gy7jF+q6/uzCPnee2FT3RejFy8tLlldnTP28kZMKvAfb6cE9Nmsd/LrfYh3Zu7Zts03lM2SD0C/mjpyxphwidlDGuvE5AgUPRrB1V1dXOQMCHnAmnPnyJ/vk68p3N02pn/cgi3UmmGKu+Ddn4QGJ2B0Hnk3TKE5R/bQ8n8PvsGk+b69C8CA6ZWXn1vjbba7L9zNv6VXKht3eImtSKRNEVuaP5Xm+vr4uAkLYdtaUy16rKpGCWYeMoGmaJp/zYj9ZM+btd4sxDy9VRG85oA9xJ5V7GVh/9MrPVCHL6Ib7dzqMsd7r8mHsgwfw4Ccny9gnL/lzEpiMq8sycuYZOg8iEin2WnCl5sxVKKVZlLWxj/gugkoCSeyP2+vNZqNp6DVO5YyTNw1A/tEbJ/jBPIzf7VZTLW2H+3EnMNZkLj9jjPyb/ce3udy6b/nfJKPBABzc1nWdmQQ2zAUfYWLSa+YC8OeLykK5YPAZZ1YwOlKpI8NAhFDKVcpiVt/p+EJIrd3ypjXlvERVfd5dBKe8ZtEYHwYfoIXh917VKBaGFuV0Y4lySMqAEWC4ZsL4k/HxPMbg4DzNUzmT4+DBnQVrD/PCnuGgAOEvLy+LvTrOZSDb7TZ3xXCmykEnCrDOXPC96zSosxQ5mlcpX2C9WQuXN896sf4wEayN1yxjvJJBmPT4+Jifs+z0k9ha74rkTPTLy8sC3MGQO1Am83B/fz+fUThncIB8FOCQ2MLT6ZTZspubG/385z/XZpMOcDPPb775Ju8Z+8VnMqMWgo7HU3ZSGGt3PKwje8fLgzUHZtSsux5joNA1SfngJec2yOTwfsovUleacmeIB6VpX7XQJ8+wuowx/jTWdOO3d/3yfaqq1OrYQeibN2+UbsIec3mWlxPAhrEe3HDNWDg70zTN4uK3aRhzG0uc99PTU5b3NTGCYzq9nrTf73V/f5/X3/UNPXOGywElYAEb70w/8wB8ObvptoLfA1DRnd1ul30DsuB7QvC2acplUGv/ADCCtVyX9FCyRUDMQU3Gx2coJ4EAkJZZSPTfSQlsHL/jmQ5k8AF+YRn2m0DfD+cis7wvxrgAXj5vZNxZcPysz419vrq6yp91dpg9B8C5X3bb7oDL37fdbheZUeQQgoLA0vfCiSK3Mx6ckeXhvQ5eCIgc1DJGZMDPrvAn9gYw2M57/Pr6qru7u0Vg4YQo+8A83ZZ4oN91neqwZMUzZpgmRZXMgte28718N3KW1rNcguiZFGehHVhmH7zqDsfnkQfG4LKKn13fh4PseTCK7S8k0PLeLw+0Yoy5xJPMhQcvTgYjE+gvz7u/v886xxiYLz4Z3+uE5PowPfLp5DB2jfextsybNeJz0nzutKoVYjnjw555QEoQxJpgE7ADDtzTeweFqpD1BDtOKjE25ujVQqUKoWQw6qY0RHKZoKGOn2Vx8gP553s8KOHF+5z48uzsl7y++DD4f/v//MOF4XMj6yyFD8iZGxTSU8yAYX6/dnQeLSEQrmxsMoKIUKPUMATJGIaFE2EjHBz5OHnVdaXNZgnSmaMLqAOUNWPhbIazcdTq+5jYWGdK/fme5XDHxHM8Qv+uzz0/P1uEXBQA0I1BZy39Gfx3dXWVD8rBZLDXa8bI19IBCoYRw4AyIcCuLIzPAxUcCs/z4BPDwhiZI0aA72Fd+BxGAVYceSVVOQxdBoKepk1GNYGom5ub3CXD08qeZvUyDAwyh9AAn7vdVlLMshxjzKn3tt3odHpdXDBVVdV8sLJWXS8vpLu7u8v7gux4eV0ySMuuXcyb53uGCIeEjrr8OrMF2HSm5MOHD7lkwfcPFimdjQgZ4LhdkKqFAXYHOU2j+r5k+AD6HDbtutTNCeea1lTilnmeh5wm/Sito9EFbEoIy4N27C13cvic0Y1+GPIBQXSRPfFDn9wlwNzdsXq6XZJ2h722drM9QQ/kCGwhzD+BPLbK2VvYOZ5FqZIDPEq6AJieEfDMCXJNAMnnHTxQ/97Uy3MNyKDbUc+ks8fuaJ2g2e/3ubTMA08CbHwCYJfAnLOCZMJ4tqS5Q1maC/aOsbofJLvrxBVz83Ir5Aof5gADggWb4Q0TTqdTziiwD2RIAYOe6cD/eIYMWXCG1IE1QPTl5UW73W6RzfJMstsDB+1OUKFPyIYDJIIIB8bIto/F/VAhDQuh6SDW/UUIQapSV4p1Vzz3/+5T+Dt/sg85CFZQHMfFPJDnqKjO5N9tI890ecAOt3Wq92d8Hmg4JmAf2YN2uxHgzYNzD2jxhXynPx+7h61EP9xvsW/IlZOm7JsTaI4LkRG+F51mXLzfs0dr+7TGUOiy/9yrFPg+/kPn+G7HeXyvExcejIUQ1NSNxr50xEK+kAknYFhLXk5+exByms9bMmffL7fxPJOxss+sETImSbWWXcTYO5dPfkYw53LD96z3Ej3wDlcejFRVpd/5x7+t73t9caDxP/0P/2NWDJwjE6CTyzoiYtBspCswSuMpbWmZWvSFY3FwMhihdUaDxfQyDkDK2mD55iLUbgQTA9dn4LY2QIzJD3z7/H0NqBtnjjCAsD2MH2V344TBhi3lBlSpRNmU1zhbQvBHVOtRexpL6brAuNibvu8z6+F7QCDgZUZrBsgDTl8LjI8HnQg4wJj1lEqGzB07++kssbQs36K0AVnwffc6SmT4dDplMORnctiTZGCCjseXBeuPA0773mR5gEF1UAZwBiDwPowMbC/B2n6/U9+XlKobsxAqnU6l3SVjTrc+N4pxymc0mAeywrwvl4uOx2NmoEIo7SeRG2+Bih4jTwRAXsrIfrDXnq5m7wBNm01q+Xt9fZ2/IwUWKTuBfLHeyUCmkj9+5ocBx7Ews15uwWF7ZJd14BxKagyQxsL9F6zDbrdZMG7oxMePn9S25fAg4BanQmDnDFCMUefLRe12edMysrhtW708v2T2CePOn+szGxADY5zUD6k+nVu/13rJOjoLyBpiY9aMn5fvuK1EdryF7BpUUMrjuu+O0YFvnFJrRgeiTgShl2twyd/ZY+zYuh6e5/EsJ2XQd0oBS4BZ1gPZ9EyTA1rXP34GK8xe8UyYVy8HdFvEcwAwTZPK7yjFczDc972urq4WZSbIIXvrNpu9gOX1rNjDw8PCR0sli+26zZ4iC+i3gyA+z755JgISwlnvNTmHf8BW8nz0wLMMa8IQoigRFum7X7viCyFI+B7kgr1yX4eMs+eUiFahUrTsOnPv+179MCgG5X1eB5HsMX/HV+82GzV1uZcJQItc+F4z1xCCplDkh8DEs2ee8Wfd2CfXXXysk0Qe6CCT7NM6GMCXQZ550Mx7kEnsAz7bbYITsZCZ7o8z+G8+b9vqWcw1IenMvZcLuc564MOaT9OktmkUx3KBowemHrw4xmBP3F75GMcYNcydCZ1AZU7YJ5d/bA12A/3N+zCUg+BkkpAz32f8H2NDLtwPeBDyXb5kLUf/6J/+Q33f64tLpzwNiyLzZRhRnD7lQ2yqH+iCHZUKW7TeKJwBz2bBuLXTI0BnyHgGi8OiJqOyvCMBIfSN8JirHIIpAk5dKvV3lLL4xjAmjBCbxzObpsnnWQDDHhCxjsyDZ1OqQ42wpGywXQE8mkUhXGid9ZKqhRB54MULA7B2XJ52xKF66p3983+Tavcg0SN+sgruhH18KMOaIWAc/M5Bn19YhTFkfTB0OBLkzJ0HTrnvk/PjBlkMHixwjEk+Pn78mNlAL3ODtWcOBEae7mYtU0AZ1HVpLR4eHiSlA6Hn81lXV9c5A8Jc+I6npydVVQGLBKfsg6QM9ulElEBYATl+iaU7FDeMgA5JeZ48O4PIFdsoKYNwD8iQk/SMKG7WhjmD9aEJAXLN3iY5mrTZtJnJZu9ub2/zszH66FDSqfR52gSXsqaTLpfXhS7XdSr1SYF8k5nvYUgH15+enjLj7PMHUOz3ezWbZUkMsnA5n/Xu3btcO43tIkjwgI7zPW3bahiTDb26ulpkdCEj/NDuNE15bDhgB2oE6ZRVEaRR7sV8sZMAdxh1B1Brh4st8+9OwKhX2zQL50WXL3TcA3/P9rqdx2Zg31gnZ3PxEfv9XtvtNpfN4W94JuPEB6zH7SyxVLLbnF9yEoN1xe45s+zMrzP6AOIQSqdBL4XBblCqhHzjF9FPL+PE9rAXgGn3iZ6Z8k5SrDFBHDbD54QtZuw8w7uSeQbDv0tSDgw9EMAGU2KKrXfiZE1SskeM1TMj6O9ms8l2mUwq64aPpwsgY7y5uUnrq6BhHHNTC57L50NddIl18uCHNQG07fd71SEF3MgLMuB+Bp/Pe8ZxVKhrRX1uY903g7nQB7fJyLCTSI7PXB8IHJyMJRvgmW32Bz10YM76xhgzmYJPwY+whz4Gr/pAftf2C/+GPDkudHzGnDyb5zbCAyE+E77jexkbY4eM88oF10fW7nK5KNQluHEfuyZh/BwYL9beS7TSOEugxOd9DgUHL+/E8T11m8V7HYM7ZuO92Kfve31xoHG59AqBxZlvI4wc2islOH4iPglzoxBSh4T0udTZCQeNEHu6ygUXo+EOwA20KybgwhmM4vgqxchmTqrrRsMQ1fed/KxCNhi2sBhJjCsMqLMVDqoZD06bmkOvVZVSz25AsQNcBNLZJYQBw70uMzqdTjmjwfoQCAFqAZa+XnSWmsVYTUN2I/27bZctINPeltIfV2JXLowoa4iSMhc/PwPYYt2RJZgTz1Z4mhOj1rapSw/yxL542ptgjtKUaZr0/PycjQxAMbUj7fTw8KCvvvpq0U1iHAfd3Nxqv9/r6elZp9NRXdcnXQjpDotQ1+qGXte3N7q6uVHfdQpaAiA3BDhpAjFq/qeYymKqutbN3a2en5/1fDzq4eGTYgy6u7vLxvfh4SHLa9O0alv69HM+Z1OA6TDM8h613e51dVXPQGiXjfJ3sTDooLOWOB9nW91YOnByB+fs8dXVVXZQ6M9ux027qfXwMJy12bQ5i0Ar2bZt86V4iVnutdlw3qB0s0r25KztdqeqCvP9Ehudz91nIMplFbCUbFCvcTyrqkofeYDvfr/X4+Ojrq6uPus+Qqvsw+Gg0+tJ5+6SDTTndNBbbArBEbrv7DPZSsrAplhuocbpPz8/L+5XAeS4k/VyAwcE0zSli58uXeqGM47aNK1eTyfFcVLTbrS/SlmosR/UGdt8Op2kJmqU1Kt07gohKMSovuvUNo3aOp1pej2e9PT0pGg6Ti9+ZBtZ8YyIpAUQIeNFIwV0in1CdvFL6ywE7ydgPh6PuXwS+fVSUJywlzmxh9ildaYBcIze4E/8HgnsJt/hRIDrHN9B5jaaDKCfPA87DyDzcpH1mPBvDkT4kyDTy+BYm3XQR2ma+y3s8Lp8lYAHvXEg4xUMHjg6CJ+m1DVNcT5Yr6hKdfbbyA1rCjBa2yoAMD/zMz1eKbDb7tRU1YIAyX6xbRVDAoFPT08LEhI7iY9yfDKNk/qhV93UqpS6wikETTFqnFJwA3j3gENaliLxTLCHY4ppmhZygFyynh7IeTBD0Oi6iJ32AMLJX+bnsoVsss+sqz8PX+PkowNfzzg4yMc+eIWEj8uzC2QOmK9nUtcBVhrHpMaIGP8d40SfsC+Xy0WphWAlTZPqplYMmlt7N4qKaizTz1653/DyY58T38u/wThTHDVGSIwptdKdCp70ignW0YMMl1N0g3m5TWItnQT6ktcvcTP4/5An6kA+GfkEsmKM2cgAHPt+WW/GhJKBLj3JeQ+GFWeAsV0famLTMVrrNDWL44aJz1OjynP2+6sc4DjgSOxGtzDuGG7GcXt7a9mPKr8P5cF4E4BxqysBlDsTF2DKWhi7P4v5+WFdZ8SJugFlbgSkZAhfXl5yNxFKWRA09gon5gxeGmcqYWEfKUMAQAFW+b0DBFdWXsiRp4w9y8H43Rl6psJBA8GH94GGaYTtXgeisM2fPn3KTD/PHscx7xHj8zXpuk7DOCrUJUPGnKuqSv2zQzUfZr4sAmWcJw5IKmU4Xd/lftuPj496eHjQ119/ndqsNhuNc0tQDAPlNbCMfAdz9bMrXhYDy+h6wnvQRxhmryd1YOT146yPHw6HyfL383dnMNGjdfDuQTxrjiGkUxz6i8zRdYU9dEbeS3sAJAQD79+/11dffZWBBfN1o8y6o8vU7XvJk7NCzDlKuvSlNLKUcI35ZlefN2TB6+trPkfgJaJt26pqGo1TkoVvvvlGb968Wcgf68shaWwids7v7hiGdN/FYS4JxMa4E3I751ktnkvJnpeOuf2QpIeHh7yu3CHz4cOHnPH0OcIAOwMKgeNBAudBnMRgvoAL113W2QNw10PAEt9NIIhN5ruwfYAaSXlP0Ree7VlmZMTBFePyexAOh0Pu/OMNGpyh5MwG9oTvYF9g7/kOfABA3IM4B67IyFofpWVXHD6LvJJ9h1jj507moVPsD2RTZn3D55cB816CY+bZT+XSPZ6LnXc5x26QHSR7wYvnrjsU4VerqlKcomrLEjCnaZpUt40qyxJgs/y92BEHxe4D+QxBaKWgetYfB5qSNMZJ41QuzsVWe/DgNnFd4gT4Z219zJCYzmoTuGOvGRP2lfXDX/A53u9EG3vua+jBh4/L7Qf/5hmOh9gnD1SQZZddD0I80GAfmaukRdcp9ou1zqVQYyk1Zix10+jSf05muHz7PB2TIMOMy/cCGYDcYx4+ZvQ4Z1Ti8pwH8sfznTTw8jvHn3wvuu96/0//69/T972+OKPBZjFgNjgJUgEDtBfE8FdVs+hTXAxdqxinDE5coB3U49B8oXG4TJ4sA0bdlZvNdaFnEWH8nd1gTmwCTBt1wA48cKzuMPgsG+7sEg6feTEPP8jNs124cB7uNJkbgkJqnPfi2Ch78JQi7/F6WYSd/ZGUA6/NZrM4gNg0G20224Xhc8ODU/FzD6wB6xJCyArHHr28vGSDiKP3Mhz+5LtKSU05lEuHJ5ydA3kuvHJGg/WDkXbWmE4NayYAI53ByTwGDDf7ejgcVIWg3aZ0NXK5xdABmgGkfd9rf9hrnEobuevr69wByQ0UJUBd1+VAyo03cuNGA2Ph6d4QQr4Xwpkt9hHZ8UAQ48geeekc3+tODyfkuuCtOrErGE9khkP97AU2gha2jHEYBt3d3amqqlxuwfjoyOOsqINTZAlAz54cj8cMNCE/XF84t4GN9MwBAPb19VVPT08aplHPLy96+/ZtDuILKA850HAnRvaCOm3WBGc+xiiFFAR89dVXkpTruV0e2X/0hD+9DAUwRS99ZHod3LC/lKFIysQIe+csIt+HblNe1DTpcPnV1ZW+/vrrHMz699C+FBuMXCL7OG4CKmTJSz0ZL2MheEGm+V5IjeSfCrP/+vqa18IJM57JnB3oQd7ARPNarxH2CyICu818PLPg/gsZZ3zOPnugJS1bhTM/B/74a174DW+EAPDxMis/s+Ig0s81rcs12APWzQMfAJITe+5Dea5ngLquU9U2OUhBTwnKPEPLcznzwn4wHuyVE0rYfoLDoe8VorK9wb/Uda3xfNbusF+sI/NeV2kgA/zpQYZkl0BWqfMRv/PgYIpSY/vDvjr+wQfyTGfOPdhxjAIewt45mF0H7t6oAJ8IbvDAjzVw/+VBLD7aAwxsnGcI3b+BzZgzz3VfjW3gd2Al32N8Ievga9xdOtWhHBXAliFXTno4GdUPpcyTsz5gPZ8nMuIBtH8H8uD76QH6usGRZ7F8Lf3v2BKwtWMz12vHtOtADNv5pa8vzmj80R/+8YK5QFDSIixBkrOYMZYJetlMelYpcWGizmI3TZNTlHTxwNjgINkofwZsN0Yf4V93NCqbVi82DUeY5qgFOMwLZ5uHMKPgDsIodXJDCjh0R8Km+lq5MmNghyHVa3PoD8Fwx+XBDUIJ8GLfPEvAHuC0YD8Rdj+UPQyj2ra0GOQ7MLwANvbGDShC7qwD8iSVIJXxwzhhUJwlc2aRMhTWA+PhzBClJLzHa4aROwwTzhqDLEk//elPF6VUvL+qKg3jqLpdnslBVjbtRsEcFg55XfftbFKMUc2mUTcfBgcQA2K7c6fz6zmz18ias5FuyHG4yJ8znMgVn8Po4rjQEfTFwQPrtjaADkBYD0ApmQbGhMw4sHV2dM2i4yjXZYheUsj8+AwyRBB5Pp/1ox/9SMfjUT/96U/15s2bXBPPPHEiHFj3O3awTawnNsvrZtlHZHia0g3E/VDOeDGm4/EoTZOaurDU7iwZN5li7MHxeNTVzY0OVykD5+Ua7AUlecxNWnbWw057QK9xmVbnM9hPwPPlcslBkNezY4Nd7njRUcsZTgAQa+/gnDE4KUOAxpxijDlzy1hwoJSU4iMAFNhPgkN039lafk4AT6kSeuL2lEyOkwYOnpAVL01B5mOM+bleRoEtcoKGNVnrpTOi6C37y9g92EKe0CPPKBJkYR8dWDpQ5nv94LuDNl6+zmQVyBShp878YluQEUk5S+1BSA46q6CqTucbN5tNzpgxLgJvB8vsoR+oZZ2clPQxxZhusq/DsklLLoWdx+KkKHviRJkHS04EMWbm3HWdNnWT92ONv2KVbARzQ+6QS8cRkhYBgZNFa38BRnGCD9zhgNyDxxhjHjv2kbmBCdbBrPtAMMZa9xkX3+t40bGOr6XPi7mjQ6w7e8b+8B0O2tu2nS/n6xd+kqCd5yKnjCHGqKqpNZq+812eTcImoJPsEevD+NlHX1tklQDMMQU6m9dwWp7hcb/JXNeXVLq8omvsn/uEuq71+3/wT/V9ry8ONP7kj/70M+ajOP+QmSfANq0Wp6l0KvFD1MkId5mFccfqQu/RNIaXhQTUOFNGxgDn6eycMx4oWnI+RUDHccwMZXotBQEWhbXAWGK014bYx8rnAc5EwxyCQoEBEzgDZ5UQgDWThoByiLLve93e3maFAoChvOsxepDihteDJvbpfO4ycGTPSJl7pO5nVFB4hJZ9YtwYfM8GsXawyBgYL2/jBZhzANx1Xc5S+F44k+/MmQNij/qdQUWZPXVZ17Wm8HlHnnkgausms2gOzN2BsfY46s1uoymWG+QBFJfLRf2l1zSWg8GsK/tMGhcddbDmwARQx14BHKWSwXNWivk6i+LPRH5dV9hjv3nbgx9Y6aurqwwKkYP1gTfkijWH5YTNdebdnSTjYxxrhhO2Ev0ny+AAGJLD15gMipMe6AoBLT/v+15TjGo2pW2pBxJxmhSiMtAchnQ/DWeG0BNn+R8eHhTqSm/fvVNd13r//n3eJwJrQAhrhqwTnDvAwZ7UKgSFgz2AOnLsQMOJGObFPngpCvLkjK4f6l/7AHf6BA7IO3YUBwqwdICP3q/Hji3lWa5f67nwe4IY9gfbhJwChtzeeaCFTcH2XF1d5TNGDmIIpHimB+4e1HN3BfMB1GDf3U6yVpylYV6Aw78J6PMncsKe82zW1efpAYk/j2c4wEIvHeCw316Chi7yWf8eVal1NOPnc+gJrLgDfvwZ8sJ3o7vYA/Yty0DX5cvRkF/aAFdNrcuqosCzVC4DrlcAeM/gkFVqq3rB4vtzhmnMrXv94keCR2Sa97s+sQ/sATKHDfWMqANYfAM2jPc7qemkEN/l/sDXjjFDaLreo9vM3XV6DXp5JrLkGQtfA7ctLg/Iq/9OkuqqVqVy9pg1ceyETvD7GKNiSNe9egYYHXY86d/vdorfsU5esub4zHGS2ysn7jUuyxvXZDNj8uc5Xl3rDroopXNRv/27/6W+7/XFpVNMEFDtG9Y0ZSM9gkvOIQ34+vp6AQK5pMY3ytlenAaGl8gYxo7LyoZhyBceeT0/QOXm5iYDIw6xYaiTUg5q22rxne4MYxwXt9y6sDiYY0NwgGykg1P+gw0EVDp4cmbvcDjk52E8UHACKDcIpOlijHr79u0iK+ItSXGOMEteysD5DZ8XCpSMx7LOmxt7vSwJRXcF5zkoEUHPmoXx9wLu/P4DZ9Y9WCBg9fMy19fXCwDPnvJsWDucrTPqDk4JDl9eXhYlNA7YqzmjQXkLYGccR6kul/l5gOjAxdckhKD9bq9JJZCitGK/36s7d5rG5FBpD8uY2eeyX8XZSYUx8SwcB3BZb+/Q5MYIY4VzmaZ03un+/n7REc7PY7jT4VnsGdlJ5NKBi8+j67rsiNcMrwcuHpC7wUVuWD93ONgFyAMPYKuqyvYGRwPw43ee3fEgaR0QXV9fp9tg6/Iz2MhhGKQp3ULrAd3bt2+zXfJ5DENpt9lskx6/f/8+gz/2B/tIGYyzZW3bZjLDA/a6qhSi8pxh/gEB6A0kD9/JuNF99tXtmTu40+m0aNmJPHjWebvd5rFjs6SUFUGH2T/AHbLNe1ljlweCiaZpPsuU83xkGfKM/eSzDtzwYdjStd1kHFVVsqsxpgvieKEz+Fp0NcZ0Xo9gwYkKxsyzWSdkEXvI56ZpygQC+sh6I+9OXmEfCOKxs+gxd604a+3jZ438/B/fDUlCYweA7tqG+CHxtS0fx1FRBaw5a43dhrhze8h6u39ajxc/wqu0wI3qhm5BYoA/osqhZsZDgOcZdv7t/mgN5HLGtqoWwayD4PRHyXSwN4XIHfI+O+PO/Nx24f8oI/Tg220i+oa8+BpmX1hVi2Bn/XtfI3ymny1aA2kPAP3Z0vIQOc8HQzppk7NO8wtZBbNxtpj55M+EIE12Rsd8ogdNPh5JuaSVfeW70Dd8BXLh83QbG0Jp3132vQRX/Onl4+vxQWStK4f+piwYn/H3On5FDvAxX/L64kDD2wC6kgxDr6pa9gJmsQk0YC2ZWPq8xIVkvDzwcLYT0EJGxCNbjBwCzMZut9sFywm7AaAATCUjnhwBt+v6OQep9Atng/0mShQXgOGBERuE0mNo/QCTVAwd5yDceUvShw8fsqN0p4ATOR6PC4a97/tF6QLAl6wQNZSHw2HRapfPufK7IeFzu11ylARCzJ1sEONg3QDnVVXp8fExOxFndTzQBIAD0LzUSvqcKfcOIAAkytO8dEsqN/8Cnggu/HAwhop1Rqaur69zpow9jzFqipOm4fOOFc6EcejWsyR8ZwghrxsHYodpkEIpWUHezuezpmGSYgEizvoCkqgrJ6vFmjkzxPkimGLWyEE7a8f76rqUFrIGj4+PWb5ZuxjjQk/ciSKPfZ8OOj8+Pur6+jpnNZwxIfhwsOdGGruBbrC2rDXjwQkjpwD1uq4zUABM+IvOZOgPZAcyDFCSSg30utUogLsfeo2xlIZ6dmzse9VVCVwJah8fH7Xf77Xb7XR1daWPHz8uvu/69laX7pL3HRnw8ZDhAoSwP4AX9DSDC5XbY728CZ10dt1ZMvQH++r3E+A3kCmIJ3QRhp41cXKHvUaHkCXXa2w2toa9cnn0dVvf3M6zv4vEWLO1zJef8Vpmwkv21IEE8su8r6+vM7nzXYw96+hr7UCeMfF7vgNA4yVmDlZTG+wq+0+e6YBOKl10PAhnXB7YOBHggJ558r3omuvpGtTwb8btBA12x+3eqFJKxl7zey/14Xvxr9gg9pHgxwMCdArfQeYRm973vX74wx8mn19XutoU3VuX7WCT2AvO1rm8OBhMcrC8VBdZn6Yp3Qw+LTO4XvXh4BCyiTGzzmAgsA020X06/8ZXolO+x8iNA3t0xPEggStrzBjQe+QYWWBcyKLbJWTDS8JYeye0POBhLus98e9l7Zqm0TiMGq1agve6P3WMmsF/kAbzM0468X6XfQ+CeC7ySuCMLDvBxrOcQOc7cqaobnIGFRIPH89egrdd7n2d1uNc277ve31xoLGucUSQ2PTHx0e1bbMQ7mEotXzOoCQBuaiqaqW2swAPbqXuJJX0HYCQtC8/g/HC8XskhgMtpSWpRGqaouo63RvQdb22242ahpQrjGetpqnUtiUFz7hh4Ah0MFZsvEfivI/PO4BeA2AEjDV1Rgdhc2PiYBZD4swVBifNcaurq8O8HoN2u71inFRVte7v3+j6+maegzKDdjyetN3uZmAxzXub2o2y5+7cYcDSWjeLNojOivt4XYE868Na4NA8PeusDICGtUV5AIPIgQeu7I2X+gFCAMawCKyx1y57IOF7V1epl3UcR03DmOpnY+pYMQzD4n4E3293kDB5l8tF21258GwcR7VNqxCDQgyKU6lRx1Fg6Mi8YCjpRMW+IL9el886+bkJaemoMDz0nXeZx0AzHkk5aAUgOHPjeso4AJ7oNd+5LgXzMiUHVg5+sQt8L7Lqdd7IBcbbSwulZctEsnbYMoCTZ34gRZAx9KLve728vKRD9jPDvN1spBBVKSgqqKkqTVWlbpzHME3aHfaKIWiz2+pqnzoPPT09ZT2A6edSR2resSkhBKWeZ0Gb7VZ13ahWUFvPez7LVmpf2yiESkOXwGI/LEuAKGtgPbhLZB3Awjp7mRL6KSXnhD1mndgv7imAhUeuOCxeVeWsGvaNFrT+LHyVZzddf7FDlNRAQnkmCp3ETrjdgMknWEHGPOPAHJmDrxtghfMetDSmDMqJBWfV0TVk32WRcaLjyAB6hDzzGfyQlxrzOWcs0SnPKjFfxoSeMqY12HcwCFkDyHTGlTH7/B1w8h2Mx8HkYJnufiy3Wo8KGmOpwnCAjTw6OOR5rkPMKZejVJVCmPdcMd1lEeamccOQu07xWWfusfFrnfFs4cKn1KnOv+8HtYrSmHzMMI4K811JBImAevZtHbxxfsXxE+tPFt4z+tg49xGercAveabJyWYnjf0WcceD30UegqfQSz+b4bICPvKAwYkix0a857v+dP31AJl59pzZmUaFOEkh6OpQ7iKaJMUqqBsGhSANw3yX2Wq8TvC57Hm5J+Mm+GU9PIPkGJOA1UltxyjTlNrcgrd4hr8Xm+t2hT30NWc82JFf9vXFZzT+/E/+xQIcAjow0t75gmjeDQVCCsBz5stZhMSuHhW+g81lQTHQsCrH43HB1tEOEoCeUrx7VTNjeLlccu1+UoqQnYAzSHwn0fP6kDlOBwbSyxMwUH7RFh1scCC8l+e4ELGGZBYQNkqmmJuPzY0aNwWHUIQHtgTWH6CE4w4h6Pn5eQHUmQuGFsfPuQmMtAMPNxrOhDkQ4YVj4nsIEPm8p5zXjgcw5AoBKPBAyI0ibC/f7UbP16+qUrtWr9VFYQkcMa7IHXvqvfE9yGZ+bgAxrIwfsLvf7/PNqM62AzT5LgckGPO+7/WLX/xiEehxSRmdvQCOBFc4Fne80rKVHWvvc0EP/GfUjTNG3oNN4N/OvKw7ObEPgGjkhs/zDIwyoJaMoNsbqZxdYp4+ZmekOB/ljDrrwNw9OPN/kx1xBpnMGoEuwZXfDTMMg4Zp1DDvE+U5ua1yXStOReYl5ftW+qmcocJ+sl/77U69HepkXdEN9tvHy3cgt06gINce7CFzrLMDOQJ8bPW6XMABrpdUYkt8bbHjBCGU7LCP7IWXTSGPACi6yGHj/LIp7BBZUMpXvCSIAMXBES8v3WWfvUzPa7V5z263y5dyrQEV68t+8sK2MWb/uX/WMzH+XPQSP+3P9vUahiG3gWed12DI7Zqzx7Df6Csy4eWn/ry1PWY+Huy4DXFbxz64TfRmA2Q7/LnIynreThyuX/gWX0fWD2KNe1h4nvsJvg8ij3E7iHRf5Fl8DxDXQNOJIcaPzLnusFYQXu53pRKgYuews8wZG4lue4bY9511WROurKkHqeAFt+1eDsh/yACZdPdVvh/sLfPifV49gpy4DWQcjBVd9iyd20/PSPq5Lw/CkQsySNgA5JC9dFzjJVVezu6Yyn3AmuhhDdxXhRDUhGU7Yidh3N6Dt13WmD8+2G0AeOl3f/8ffaYv69cXZzQ8lQKoxVgRgWIovGQBcOnCgYIwAbIlRG913Wi7TVEe7S+djfVuJ94lAsdOVyayIKnOeqOqqvPPvHzocnnNho2o29lcnB/MJpsAGGcdnPlzRcIge0ACiwAwYl0YG860qqrM3DmTRWDHd1GHys9w/MPQ63C4ytEzAuJOgtKSGKPu7u4W3+UROXO9XC66vb1dMBreqcuZIHfUXjftcoKQu7Nwhwlr4+9xoAnABLyhtA6sUDA/m+JnGTBgBMuu5HzeSy4wbswB+fbmA5QJoLxe5+kOwcEJRunp6SnLgTtHN9zO5LI+z8/PGZDRQpX1wEAwJndm7gB4ngfJGB+XH/7NC33hmRhjd4zOXiJPfjkWQYqXwCADgEPWi7kDOh8fHwvTNJW22MgnQMCdBXOPMerTp0/a7Xa6vb3NmVLmw/edTifd3t4uAhU38rBTgF/GgKMmUEWPSrDbSKHcyozMtW2raU7fsxaHwyEDtmzIm3IfA8FMiErtOI28WNsHL0Fw2fQ6aH7nzBnzJXMKKMfGI1vTVO4rAFQDNHke2SfPZvj5EAIv/mPMkhZBM7qLA/emBVVV5TbJ/hxkATlCd7HFyJvbJGfA0Q8cd4wxl3Kydv5e9owOZh6Uu9ywTwAZnuGkBy+egVyhA7wHP+xEDWvDWno2ZR1UO2DD9jrzja13UOblIq7z2E9+js91O4P8ru0FPsTHSlAEMQCgysHcnMn3UlcPeJHhtY1Et9krP3fmfs6zdsgr+uUyiiysg7b1+cC1TUQmff2QdS8NxB/wneydzwc7gP3Hrz49PWXs5RgN2WEOfB4M6HLIvoFP1r7ObT62iqAbWcIW4wPdPvEer+xwomuNC/g8n1sTfv5ChteZNGweeosdctzF9/Ida9uC7fN9Qe5ZKz7v9sMJgHVQ5djByVj3xzkTpaBq9Yx1YO5BFHoMbvOSSmTH9eBLX18caLARfClMK44RRYHJQCgx/BwW9VIFWFZnBpOD2enm5jp3quFzON5xHBfdOnyBMZQYoNJHOSrGZKyvr691PB7z9w3DKEq1fDPZMJ6P03CQgNIS8XE7rWcKcOqkqwH9zNmZWl8/B5CsEeD9/v4+G0962GOAcSBpHI3Qq6Zpch0xxn2dsh/HUW/evNGHDx8W5Uw8H8GGqSTgQtG8DAqnwp6zJwQ2btAwoigWDpYMkLN1rAXr4YYUkOJlEM48euaI8WC03YGuMynOnnoKmTlgZNzBky1g/wiq+75fXAroa4YcScUAYlAZiztJXqzR4XDIgJlneOqf0gX0yWWdeWBY6daCs0FvcWge5Lps+hkG1sKNM+CiqqrF7ezIKDKC8/HggfKZrut0d3e3GI8zgd5CFyDhZ0uyAbSgmza33jzi6ekpBzIAGtaOQ/Q4L2QWmfKuOZTbePas7/vc03132Gd2kkxGvul6GDXN+uE6vs5CEXAzxyB9ZnuQCQgZz4TQKRDmnz33gA1gRV03640MuGyumWEPeNzxeyDqRNa3336b/UNd14tyOJw4NhbbxJo44+1OEZtHO1rm7iALPUdG+Q+5w9575oFgxM+xINdu1329HZjwfQArzyij5w4CsXn4phjLGTIPRhz8oUf+vHVAgs5ii1h7/J9n4fmMZ1YcOKK/zth6tskBOHLjRJ3bCgJKggZkhfXy4F1Srkf3eTnAc2DLOjFuJ3fwW/gOnhVjzDLkthpd82CO9SIQQQ7QAfwrTQLQ+8PhsDi36XeUEVzgt5AZL8+BLGE+yBJ7zh742ScnQ1zmsJWemfFSK36PLXKwjgzwO/czrvf8ex3I8gxn27HPHhAzNid6GQdrA1Z1nWZN0D/mx76x1/hY9s91yIMh98v8nD1cB4CenXSZ8MACkot187I3bADjdHvBGLdNaQfMd7lddDLS9cIDc8/UONnjuv+3vb440EBoAZoIlisSxhSQ4EJG0EGvdwIQDqG6geu6LnfkcPZqmiZ9++23GSyzUC5wKA0GsqTY6wVYwXlK0uGwvLUZcMo8L5dLPvmPwCJgzvKMY+mTTJDjbBJsJwYIYOCAjO/m36wpguUpamdd/VAUTE8y+q2kIiwoLCUavn8ojJeRebqQEolxHHMnFP8unJAHAc4ArbtnMB+YyHEcF2eBABwuUyics0/shxvTdSmHM7FuKBgX+4fMucPEIHkGhvkhbzgH7xzF3NcAAvaJ+TtL8F0B1dpwEOSM45jB1ziOur6+Vl3X+rVf+7U8poeHB93d3WVdaNtWLy8v2RF6+nVdNsAeeZDtgQOyhiMDJDhg8XmxhxAIrDO65kYYGXQmDd1gnQEuDubc4TM35AdywxkdDDB77Ddoe6tsqZSbADD4TjfMAB3GuGbYvIwBe7DZbBTqSs2s52TFWIsQlhfeIdcxRtVV0Ga7y/N2ZrhpWo1DOVuCzOJYX15ectaK8fv6YFc8+KzrciYIG+wlfawheuilF9hG33eAllSykBxURm8pe+NnHvSQ0fRyV+SuqqrcXABZ9ewLoBVwRmZgzZRjS7yVrINT5M1BBWvj503QMScqvPyGMRKUYqs8SGKdvdSK/X16esoy7YyyAzheLrNuV/kdP1uzxdhJt+sOgtze4msYu5/VYE4ua87s82L9aJbB/jMmz3TzPtYzxijVleqmnHn0chgngVhHL81in1z+Ges4jrq9vc1gGH3GfgJcPTDj8DfBs2cKPTA+HA6q63pxQacD99vb2ywbBL2sMc9Cfhw4e7aV9+N3GbvLGLZxfVO6j919qwcryIXvL5/HDiBLVVVlsnRNcDw/P2e/5RlcXu7XXUccI7E3Tka53GOXeYafX2R/kTn+XIN65uqYAdnkPR5gObh3H4mMIjOu46wx9s99mMuyk29BUpg+L790uwHeWss9zyI49u9iPl/6+uJAA8DuG+S1aRhqB30MuOtSG1SEiQmh2C4EyVBVC0fkqfzf+I3f0MPDwyK74puOo/CNSuMIi4iYzyYWYXlDs7OaGM6rq6v8M/6DDWjbVh8/fswGDiAllZZmLlSsmxtqFB1Wbg1yParnQBcg97tKKMr6B01TSTkDnAC4lGD4vRgABQwfxoAAD+G7urpagBdAsTveNUPkkbE/GwbXnZAbF+TOAT9jclYF2XJA4orlCsOzCKAxJM5qMg4coIMkf4YHqA4u3HCvD3V5oO7nLFB+ZNodDTIGkGC9qS3HofLZr776KjM5rAUyxvs8sGJvcawODn3uUske+tktnK7XgHuJyjog9cAKXQG8e/ApKd/a7aUdDw8PGdDzTHQDxw7IJdNCNg292mw2OTvHWrPf7uxdDwCf2Ir12YG6Tuc1nJF3Z8LL2WKFUkoEsBrHUeMwartZXmoY49xJb9PqdV4fz4CxnkHLO3JYA0rnsL/sO2PyUg4ACKCc9aBcBbnEfjNHZ38d6Lptd/shJT9DS3IHsc7Aelcv5MCz6jGWc3zH43HRUQ4bQEbHyRLmXtd1PgPja7cGUABuMk3IrTN+6Cn662CWNUIX2W/+BBD5+9f2h587m+9y7iAM++JMqPsX/IKDKm/V7kyx6y7jc7+2DqicOENG/LtCCLnMpKpK2Rt7zFzW/gPw7M9hvCEEdXMwV9d1JuYkfXagH/1krVgX5oyNcNDFM7GpLj+M2UlCwDlzxC5iJ1kXbLgTWX72FTnzbPzhcMjjY12w525v+RnzRQ74fvbLO9f5ONE3ZMbHvCaY12vqpKbjR5dNxg8p4I1BINXY43Xw6sERtpL5O1nIGNaZOD6PHWNPwUFrnOHyyc8hrNeY1kk0XwteLrvoCfaC36+DE57rn12XCKaHzG3LV8GIBzAeJKNfbhvWNgBZ+DvPaDBpjAiGgkMzfgEbAuRlUlKJxvu+z0EJio4QJVbtRiGUA0dEt1LpKIJzcIHn877Y19fXenl5UdeVen2UkM0ehpKyckDMwns9K9/H2Fxwr66utN/vF91FuLHWWa6qKi0lMTIwqZTOMB432OyBC8UaSLtxT78rLWMJjGDdqAEdhkG3t7d5n92Je/TPngIyWHNY/BLUFfYCuQC4IqjIA2vVtm2+L8MVuq7LZY88i+89HA7Zybtz57nOBiGv/HtdZuFK5oydpAxWceAYDQdoGFvG7KAEUMdekc3jexyIY+AcjDJndIBnEQjwGcaFIUE2x3HU+/fvc7mWnzEi88bzyTgRmHpq14GNl4jAHOEg27ZdtEzcbrefMeWMy8/24KBdvlgfP+h9dXWVHaFn+Ngj9t/PqvDzohflwkH0b7vd5sPg2AKcMvYA/XHWCGePXrnNYu/8DIRnuFiTJMO1jqdjBs3ITYhLMIl8XS4XjbGUILktbNtWVQgaYqmfJ2jz0k4PltmT19fXrOvI+TiOubMde7zOxvoNzO7UkFPPzqEv2GuAGKAKJrOu61zixXO9iYWfaUMWhmHI+n91dbWQXcAHthY95JmeJQMseHkYQI+fcReJgx3kAoBDeRzfz/yxFYBGDxB9rG5nJS1kHF2HrEJP0DdnU7FVbgfZew/2kC8nPdxmeiaEjmr+XYzZg52mafTmzZsFYYK+un9kP5y0cjn0JibeXAG5oEQbtt9t6d3d3QIsOenpa0+JK/bCiR6CcAfezJ3nssfsE7LvBBPyATa6vr7OxEhd17m0m+ALvIEsIKchFGLQddn3yEEnIJGGF24D3N76eZI1SMffOEHFv1mnjREjrK3bUXSHdYFkdYBLELQu5/TAlJ+xnr7OyDSy70HeOvj3IJm9BF/yDNbKn8MLO+QlvzybMfOdyAz21u2Bk5xuK3mvB288M4R0OyBr6gRtUOp8WdW1FJfZUMdFjNmxJN+NnCF//qfjlL/t9cVdp/7oD/9IbVsMefrySlXFFwXR8zmBpmn+XVCMsIdEcSkdjuNmM+kGVVW1xrEoMY4RhQKgODCDzWJsKGRd13P3oJ36vqS8fYEACl6Ow/NfX4/ZcFBjuWaiUQjfYEAdBtQPr7qxc6PAxiIMOHUcAUDDszgJpNZqGmr8z2qaVnWNMhRGEJDBujjL60AFEOssCobc5+GGGKNLsONANCuDtHBoVZVSpnd3dxnoETQ4C+CGnH87y4xzKOtR2CjGjrFwA+BsB2MniIM5dYZszfojB6yvKyr7yV5hgJydZfxSYTg8EOPZvq7IuzsQD0KRH5wAxpjD5YCrd+/e5SwWAIYGCwA4z1Qhf+wZIIF1ctbV54EsMebT6aRpSgeaHx8fdXNzszhbgGNaG3du32VP/Y4OXu681yUa/BsZ5O+Mz4PNNTPLZ2Cv3U64fBJAePbLnT02zEswWCuFZEP7rtNmu9U4DApVuqdoism8bjab5CyqUmIaYlTX9WrqWqGiBCPdn3K0DmOugx6YukMm6ORclNt65uKldsibB5yuB06Y+Pfj1FzfWBvPPnhAjY1lH9A/t+H8R8DozLADBNcVxguQdVLLMzJrooc5uK44SGH8nKlZZwP5bmyBZzT9wK8zkL7ebsPQeeaKvrks0zHMbSjBtIMNP1DsrKvLKjKA33D76nbsu/bY/Rt/dwbaS8IIZMgq0kSF78/Ba9soVBU32M1+cA7sFRf+Nca4uJQOu+Z+zJl7J6sgYPAxfk7Hz3E5UOQZPMez2pLynNdBiL9cBpAr1pzyR8ge/LSvD3LpWQTIFGx4spujqlAt9KQw2kFTnD7TB9cRfLFnR50wQb6yj4vS5dLN392raeii2M2Bc2kkkxpkpHb9HiRXdTrwnC4urDWMQ2oFz15UQdNYgignEJP8acaxlaZpRIQUqjm7PdoB6iqoCnNA2jYa+rlRRV2qGYZhmN9TzgRLUSFUCkH5Z/3Qq22orkj/S+OcFOYuUaEKc3vaOu9J09SKUQlT2z7UVa0QpHQmd86iTJTIjQoqvm4YxzkwmdTWpfMXL2QFHfZzU0l2lxdd/v4f/J6+7/XFGY3NphzgLfWwyQOuFSu9otIB7HKy/nQ6ZuMKaGFiGCJnV+7u7nKmA6eBcniEyDOK8CyZnGSowmcLxPeume8CHsvNpABzQJCn6XGCjO18PueSJBgwlN2BCEEU3+kO343Umq1nnjioti095gtQLrc/syaw1M6O4Fg45Mq6sE+UWcCQ+7jWoMPZZWfKAOQ4QTecrBEGijkBcHyuJYgdF/vF2DCubtjZo6QgJaBwtsxr+AGcMLZ+5gd5Y9+QL4AQ34/T4PuYq4MfZyl5Prrj6+hZEt7j4JX1AQB4MCklFo9gjvEPw5AbInzzzTeKMerXf/3X58xfum2cMgP0HccK84QMsEfICM6QteHgMDrka+cdmbycye/qgBVd188TIHMuhXk5mEPPWDtfS87UsMZeDoF+O8vn2QK+z+2dB7boOUE5IMblgr3ITKjKHtKSVjGqCpWatlHXl4s85fambtTO+344HDSNkzZtq9PcYckDNsaO3mG3fVw3Nzf5vTHGzCTyfewNmVsvFXNQ5cwk+o89cAJpDcT4bg6us6ZkgAFINzc3Cx0GdCMXvj9OBmB/mT96SUAwjuPiUjnPRKLrtAjFJnsmj3n7GSwPPpzNdH2k5Ba7wwuZk0rtuAdJ+FHsuxM+Hkh5fT56t85ys4+eofFSJUA6ZwhYUwiEcRxzUCDpM5DCHvHiZ9g79gRCEfn7rpJn9jgFE1KcSllcjDGBwrpkiX2d+bd3TFvbU3w5/3aCir1n3ck6OMvPmB2gEUz5RbbuI7BZ7uOddHFiA9n1UmkC22wn5peX53kQ4MGEJAUlMI0N5TtzUB+W3ZE8OHN/x/jcP/hBa/YwEaQEv+U8DKQp9oq17rpyHo69upxLZ7kQKlWhnGMIIUhjuZWctePfTlS5XOYAO67IvjFK87KOQ8nk+HunQBVEwRDpfZWmyYLWUKpv0p4Xwh5Cy/0YYyZQiTFomgOGEILqtlzd4EF+CEFTLA0oBiMvqlCCV/bcSXr20WXUfYnbsu97/RL3aPxZ2lirnZW0ONQN4+/ChhHGAXgaW1reJHs8HnNtNYabg9vuSNgsqYCsLAyx9H93sNn3xVB4FC4pBwWAITc4w9DPke6yZSdggaDLu0s5EPGAAGPFHR+bzUbH41Gvr6968+ZNVloXbkn5nhAPovgzgcvSAWwYhnzDMsabdXbQsWaNYWT5OXMA1Dkz4uwO8+I5BCY+Vi97kMphMgzjd7FqOCjW3B0lcoDDcSXwkg5v7+qgygMH1tvnBJBYH+ZbAxd3+mRU3MEjM+yrBxXe0cadLP/5QW1n5BxAuZ454PVDyOjr2ukBHodh0F/+5V+qqird3d3pcrno7u5OTdPo66+/zkDf5QTnwboxd4IQSYuyPKnU+jIfnBTAxz/rc/PLB+u6XtxvsTZd7hzZSy/ZcefswMd1GzbfQXLf93p8fMygxx2WO1n0hX+zb34xmgNc3xPXSX4HaTBMk9pNuzD+OcvUFNacMiHvRIMd8DmjT7Dca3njXIMHJr6+2AeCDjKKzBWgVVVVBqbs63qfeD6BJjpB8OAEDTLG2jpBw/0w2DFJiy5byIqTDNgC33/0g/a6zgZLy9bbbqfJDrO3yMPaRgJ4/Pv5brc3BXQ1uVW7Z37GccxdilzmHTCRpWFM/Myfg6ys/am/kDsnQrylLvaIv/N575KEn/eGIJQ1ekWA4wH21gkk9hX7HGNUaNLeEGxDkriN4ZUD+1lHHV84mYivIWPLHLHVrMnpdMo2ExlfB/PInRMhvk6ssftrJ5Q8KCcwdnzggZz7aGSf9eJgNLZ2jZUSuVHu9HKCcxgGTbHsP3KMzBDAcI6Oz3wXSAWvdZdloxtAL0QDa7fO2kPieAABGPfKAQ+aPThhb1g7xwVuy1331/u21pO/CYRj0xi7YyBfF97r+M5xlQdt7nuQafaKn3mlxDgO+YJHx39VqDSZbYeQ8HlCZqxLywl46rr+u81oAIz4UhaZA7xSaf/mA2dyCIYbW6/LYyG5BXYYhny4yQUAI4mQeOSOgMOIIMTJ8QRtNuVchQN3P0i4BmXpfd/dxozvZMH5OXPxgARF5MwGTnnNrmHYAIiwumvn2nVdZpbO524BvtiT9TjcoHiWwY2WVBzzNE251SaAAkOKoLNu3wXaWSPGjzwwfw8SPUhjHwBeHqwBOlzwkT1/j3fT8PMx7Bl/OgjjOYwRgIhhR2bcca2ZJsbM97nxwJB6mR/nDxxYsI4OaAHk7L2XVbAmfB/tPjnAyKF9KWUeKENCXv7+3//7WU9iTK38Hh8fdTwe50sfw5y6LuwmTsVlHF1wo4gecrcAjQyQE4BUXZc7ZlgDCApAnxMXrBE2xN/Peh2Px3wWzOvICVIdwCKjgENAuDt3Jws8E+cBKMGBA2lnaAF3fB9jwbayvjj7vu81KapV+5lDlEonJEC175HXWfMf+ubPwKFKymNifaXS+Q6dw1Ywb/THS2WYg9tN9o02rG5/GQ8g0dcEe+V66T6F4Ir3YT/9fiYHBsge/8YfoEP4N+adGU5pIYusZVVVi2YpjD+E5X0DrDsMrfsySQtwhR32OTiQ9IwYcgdB4lkQ5kC2ExuDDPMeiAEHkL5GDkzpCInO87u1z/G2w4zX/RCZFcbBd3rNuMsxzyCoZa3qWKmb94xLTv3MB3OG4AmhtOSGHHWiQ1q2QUcPXVZdh3gG34XMAIhhtb0RBXLopAHzwfY44PXWzugSRBsy5NUH6Fq2IVPJROAzsNuQBsMwKijtJ81vChAPapttDnqQRc7jEdR6FQbrg5x7QFTXtfb7WiGUs0aOGdZnmfCdTg7g4zxb7nK49o9uh9lPD0YZF3vD96IPrlduH31sHgC4zcIfOtZibsiEN99hrSBhmLcHUi5H+ELIb+RnGHpV9eel1WnOQy43dF35Lp3B7yW7VTqauf36215fHGjALJJagb2BhVlHXyii14t69CgVdghHwYL65q5ZAQdMbBib4OyqA8D0nmW9NBvqypYjd2MD2jalq9bM5FpQYJeYMylpMgKAAZQT5pBNp8NJCEEPDw8LBgXAg2PBEDH33W6ruch7wexjmLgPwQMkv9XdnQXzzKxD1y0YEK/1JdDxINQNrqdg2XsPLB2cuqL6fPk9coE88Vnmwue4lItuYIAIgIgzQ+vg1eUJBw3jBqhE1nx/mKOkRQDk34EcegZn3e2KvQOYrY2vM03MgxcXPKH4GFMfiwe83qGGz2w26Q6M29vbDHA+ffqU72wBQLFeDvJ9X11XWafz+ZwPjHuZWtM0ef9YB8AkTo11cIeEPBKo+Jq587i/v88ADP3x57AeBK8OFJEpZNuJDQ8sHHhvt9tFzT7jQCbX7BjyRsCADcMJNk2jcT7jxmWCrKWUeqR7hg/Q5PpHSYcffub3zHFt+/icpBxQ4tDd8fBvB6UE54CZNTDBoTqQQibP53O+zI49caLDiRQvxwDsMw8aG/Cd2C3ABHYC3eBPZAh5Z50c2K9b6TorCYHAz5BRglTG5EEO7wFQuo57IOz64OVivm8AEWfUfQ7sLWvnZ5pCCJkBRofdfvCnB1VOUPB89svtAfbV/QFj97X1dfE7hbwszecTY1ScYzO+k/EXsFUu8sNeoZt0n+JznllBb91Wuu64XDjApGkCPpbMmDP2zra7ruPvpHJOyYM99s51C8yBXfSgibVwTLU+Q8a4mrrJJT+0QOd9DpCx0fzMm14gq6wLNsaBKusXp3SuwjOda5vp+8Q4HLN5dhK98LN26JI3aHD5ZO0cEzpxjB44tnV/jhy4rjqpgQzyHCds3ca6P/Cg2n/mwYjL8Np2813jOGqKUZPZI/++EIK2u0LyuNytv8OJzbQWcSHz3/f6pdrbOlvLZOj+QvTLhlGKBKBiU3INZSjsum8oE3VDwmcdnDqIhfkBwHmEKZFCLuUqfIczzw5uUbA0/pICxChdX19nppSWr+4seCaKjyGvqioHF64YPB8wQ2tLQFkI5cJD+rpjPFNAs9f5fMkK5EJJkEG06wqPs/W6PI9gHcA56PBAEmNJ2ZvLB5cNAWYBlA6KUH6pnJmB2X15eUlCOjtEP4jH/G9ubhZdawgG6TiEPHDQFLlxZ+rOD2Uj7e+RvcudB0mk2zmfw795rwcXrL0fbCZT4RclsX88w+UKfSKIhX0FTAEIqWd/fX3NzsUBLTLQ971ubm6ybkilRebPfvYz/eAHP8jOhL0EUDEfB5QY9bV+s5f8G5ni7Ar/5lwUP0OO+B5KD9mfl5eXRRaI4EUqJVsxxsX9O3Q14vcYeoJVQOunT58W7XO9pAenhRyxDx60sn9OjHhQypwc1JKBonvQ6+Wcx/3x48dFgBmmuVZ5tkfTNOWsEHu9BnLongMn/s06Mh7sF/9GPhkf/6YM9HA4ZPDjuiotz5Whg6wBa++H/NcZmQyImtLhBj1EHnjvmtH2LBbgCHuPjXUyhP3BdlKKw1ohx9gEvguZ8BIGB1DuI9bZ33Ecc0OGNcBgD5xMcDCWz+jYHFgbb1GNvSGY5z6kYRgy485zea2ZZp5FgOzZdIIlZBC58TNWHtB5hsABoOsF/pHxuc7xJ3/Hh3rGfv13LvMLIeQ2yMgJen84HBaZePYameB57L1nVVkXsox+7wxEzXoOrJdnLng+9sPP97Ev2EmqMjygRI7RF8+agD3wMyEEDeOyXj9lHfblDIuWFydjD5xcRI9dNtlPxzPps8uSJ/d96AmyBhZhHxyMY2OcOEa+0HF8DPuOjfC1dCziz1+Px+eFTDMGD6pYH/YDX+3+wXGq2wuXDXCer03BpwXveXDDHOpQq+svi2dmbK65I5URd4672Zt1di2Nt5zf+ZLXFwcab968ycLDABxErNkffy8CgsN2Z+3CBfBh49PvUorHwXmM0jRFcRGdC0lJD7fabNq5J3u3MLYsHt+LsgDMPAKta854pBP/fAaBTwfel/Wt01RAxlqA1gqK0vZ9n+upGQNz9kCH7wHwEVHD/lA2cHd3l8tOnLXEQIYQMqDnmRgcN6SADlcsZ00lLW7N9BpNd4oebHrZiDOI01RKtXCE60Pqvo8EYG58kQPWFyWhdMYNCM4AI+jAAiaJzBRrwcFRMlAwn84GDsOQb66XiqEn4ODZ/NuDdP5N/TKGy9lR9IDx8RzWHieJ0ednzgy5zvoZqDXbKkkfP35U27a6v7/PsrMOlDy4RbbcAfEzB0XMge9lrbuuWwREj4+POfXtXVIYK4Yf3fZyTubqd8hIyiWMHjxydwIMOKWcXdctSpmwT8gaTpu5eukE9gg9Zb7s9br0QVre3M1ahGrZujs73KpSNHDJ+3mWl8u4TXFQPk2Trq+v83p7IOv2CRIAwoi9YP1vb28XLKRnUR1wO3D18TiBIpU7Elg/d9q+3844su7OGrrDXGek+W9NFDEm36c1g4tNYs84i4KT9vk5s8zneQ/3prCeDpqc4HEA44ASW306nfJ3OtmGX3DgAqj1QBI/g1/3PcNe+XqxT/gc1g/dpEST/cKm8D7GDbFA1USMUZMFhzFGnV5fVVdVJs4Aj66PazCPneJ3HpAgn5IWZ/mc5cc+YivWpM/6PM319XWeK+vnus6zPQPR9X2+I4dAh8+xx6w5AS/7jj3kmew1doa18EwHDXoC/rRbEk91vSzdxV4rSHVdiFvHbm7/PGuDb0fmKHPKJIAKu5/WzLs/LasL+LsHF9gGvs/H477Xg0JwBXKHPrFHjlvdRrivYU/9cw7yPQPkWC6aHvBdTgR5kOK2Kf07rVieZ5DaTStFqe87TeOkdpbn0b4Du4aeo9s5sI9a7AEv3suegW9KEFqCmS95fXGg4YLldYAIAsaUhaLGj9IT2EkmkN5XaRyjqqrUyG+3e3O+n1/Y5Id4ksGsNU2jmqaVVGmz2amuyZxMOh5PCqES3bEIJgADjA8A5kKUxhk1jtQAB8VIGRYdG1JQk4x/VF23qqpadd0qhFq0/E2CHhVjCp5S+4IqM+99X9pnSpX6ntuxOUBfWBMUBJB5fd1kgIDjx1jxGakAR+bnxkwql/w4IMOwsf4OlqntZU+8QxfMlssPTvn29naRPXLjG2MpjWia5rPbbj1AcuaF+Z7PZ93c3Egqyuxg1wEha4jzw/nzHH7G6/3793r37p0+ffqk29vb3HkHY+8XKd7e3urq6kqPj48504ERw+ABGCg9cRaLAJO15BJI5J6gQlLOgDEWKckK68xasaYe6BAksU7oKf/+nd/5HcUY9W//7b/V+XzW7e1tJgxgLrl3gb1x2XFA5WUZa0PqZ5ccWCKXAGXGBrChSxKNJpxJG4Yh1w+HEHJbXpdF9oPskTvNNbPk9gI7xtoBJACk2BQfiwfVyKATNq6vEAl932vbbjSMg6qYMhhhiopxVKgq7Q5XGvo+kxDOZrlj9kDVbULTpDMNfpaAvXI2HNYUWf3/t/cnP5IkS54mSLKoqqntHuEvXmQtyLxUXWsGvaAbPejBAPOf12B6eqaXQ/etgEQW8pAvX0a4u5mpLaqyzYH1Y/6E3euFB/COJoDD3c1URZiJafnRj4hZzE6azcMPkTB43uiIySH3LmPjBGfGDLGCDtt+WUuAG77EjLsrOl4D4hB6Q4yrkyL7D/TZbCU25qO5nch6rSMiV5K5hytr2Lz1hnkC5ByH3XLDukNUEJOZE8ywyQTWk/vxbxNLtDTzO/Tb62q9c7WYsTEvYha+HgLm9fU1xnmK/jzeTZcS6Kbvom/bGJfkr3bbbVzepI6CuYlo+nSC3Ol0yu/pMBlDnDNAJSEbTkOM47Rai+E0Rtd3K9t2zGBtHDMcI+q4hL9CP46nU7RnnRipsEWs/L8BZ9ucD9x4O0UsTcTSxOlYugTqVuCybpFOoNtuouv7WOa0+Rp9bThqNdroujbmpjDr2CCxMSUmTczTEsMwRixnn9d30Zwx2nAao9/0sek3cTyeYplTxWKeUntUNE0sc6R5nPUk2iXmZY62S2Ry129jXlK7TyzpHWDb3SaTPJt+E/O8RLM0X9lkDfrx7+iqkxFjAmNSfm8MZF/EBcljItPYquu6GMYxllhimaeYx3P7/LxENHHemL2keY9TtF3ShXmZIxrO142Y5im6tkvHCkdKVNquiWjSXN9eX2OcpljmlGTM85R0azkT6cucftf16YSqaY6IJk7DW54zhB/4wXLk3251jShV/SSb79uj8d2nTv2f//v/sQr+djywkWz2dC+vM08GFxFnYJCUm3IlF0HMGaSrEN9SMoNIjBDnxgXbQo82gQLnzL0ROo7aTKKVrVZgZ8UkRQ4A01RehgWg4bs4aDLupknvPkCRt9vybgyUurCpYxzPzgfmAgcHW+/vMB8zEwRJ2Gku2qIAGYwVEAmzj+K6dcdg1pk07JXL2pk5ifIiP36HXDEKQK71kfV1MupKiJmJp6enfG/0dpqmfOKQdQH5u9UC3RrH1BLHi8rQU+uny6z+P/NE9gA+AIJ7StFFqinMyQ41ojDhHz58WDFL1hmC7bKk/Ta3t7ern5lxZl1Pp1P8+uuvea68hTyisCHewMsaoY9dlzaQGnChp9yD8bri6XYjZI7dUGlwQu29OozDgaXv+9xah79w1c6JgfekGPRGrF+SGVEAGgkQulbL1H3mBo5OcOpx8zmqPW41qRla/raekQQAZpGx2W70zSVyBxj8ADJyCwOBmLHS4uGEliSFSlEOxpWfwiYA1w52EBfoVJ2U21cADpFN3cphm4FhNbA2k8y93VaErJ3Y2rehI8iYi/Fg74BwkuTNZpPJOcbBnh/7BeItPsEEGWvC/6lCWf/4OfEQe4XMQAeIp5YXeuq2Hs+t67oV2cD3nRz6XnxmWZYYpjFChJLvj++2D3ai4+TSrDFJl9cpb7ZuSvWN5+DzNts+j8OMryuDBmQmE3g25FmurJ1jBvsHD4dD9H0f28369MWI0jY4nEriCZ7KZEm/rjDgL8dxjHEoJ2bhn72WxiroqxNn+ygqR8R68In3w+IHaaF0BcDVEdYsPXOMaMr4ifs8z/HXbe8pOepyjAA3OI4xLmM8Y0UnyLbTmvHn5+geJIV9M37cfnCcpvxeI98/fT6i79anC/qwJGPmiFJZtjxXmKJtY7f5L8cq2xC24goTvzPBwjNMull/0M+u6+L//v/8H+O3ru+uaBDcWAwWkp8BLul/5MQon6jDAqcgUL7vzUNWSibOswFfgByDdBaJQOfsFlYmopwWAAOA0GuGEoMyK87PrRh8BxnUQYpnMm73/vvFUFdXV3E4HPJ55Py+MHXlxTWsRwQtSeWlLv7jQMl3kL/BstuukGvf96t+4ePxGM/Pz/Hjjz+u5ktVw+VwnJoTO+TuPlt+hh4QeM2omF2o+ycjSpKLAdJWgyEB0q1j3N+bGmGrWUOqAwZFOD4ADwkUjsAByb+zE8dBsK4Ga7xvYhzH1f4YTmxy4vytIIzD/fTp0+oo3YjIIJUq02azyUklYz0cDqtjKx3Qf/jhh5xQzfMc//iP/xjzPMcf/vCHrwADfwPc0TF0w/3/lgdtk8iblhIqDvwO4OfvRpSNdwAv9N7Jal2GZ13MKAPICCA8A59knXXAocJCsCAZ5js8O6LsaXMSXFdLXPmodZVAz7PRNWRLoGSuLnvjy7w+3NstfmbLIUm8j8xVCwIjAQj/hG7jP7DZtm3zpm9kaJkjT372+PiYdZoxOAB7s7T9v32GSYCIUs0EXHB/fBTMO2uBb3RSgezRJccrkxn+ufdxGBjwElsfXOGWK5NbyMe2YKCIDpKIAIRJMBgra23ATvsga4rsLD/8EGvpdjXbC/fFjiBLiNUGMX3TxyQ/xnOc2Dl+831XdngOOCAisl1hv7SWskbIn3W8uLiIflN8BokLa+gkm3Y8bM2EqtcWP4B+c79hGCKW0kbuduKu6yKWZuV3+Hli2ws4Zu7Jdtoc49AF2zbyNhGMfNGfpmmyDVAVZsysAYkx83Yygu67emo81vd9vB3fYrsth32wbsjXxBXJd9u2MU9zHI/ryrsreMYIlh1+yiSL1wedZpwmzE14eO8O9uGkJN93Xt87+4pmfZQuiSA+qU40jCu5kGHWl8aJTEmcTWzbHi0b5MgzXCHz79E9+2Vs47eu70403FdqxsAsEAL35lwzRAZd/GHwTM4CdbbtLNJOF4HXVRGMyj34TiRglSK+fqELz3Vw8qZFxm5WsQ7YXgR/FmfPvcz801vN93H6qb9+ibPu5O8R8CJK0CM4UiL3fhoCHEGk7/vVi5aYP8GVNQHocPoMnwHUG+QQ6J0RRxSmwBUV5AojzPqxmbv+PutEAGaNI1I7Au1MdRsNgKx2qg42XdfFp0+fVlk894AZ8kY2b/bDaTuxa5pm9bZz2wpBykHZuoGDMOtgAAejb50bhrShu94rQK8/cmXuT09PK/aEdg6D7MPhENfX1yuWlh7i29vb+I//8T/Gv/t3/y5+/vnnfAwuuoC86wCKvQ3DkCtIrjzZ2Zu1xCeY2WPdeA5r68BlP2TGme8yZ+TrTYOAISfmjIM1NktmZ23gDuhhXPhAB1USE476NYi27hsYtm27epkheoTMbTf2WeiMSQuDSBh0bMTn9gP0sU/GB0Bz5YzqAwmNSRvuhf355xGRbWya0qEUtEM6mTH76AQNn+QYwnozNq8la8t43IrIM+skz0Ce73LwBT4hohwdy/ecYHBqn/d2QW6RNOMfWUu350EuMH4IH3TTa8ozTqfTar+HfXnd+ofs7TuQBxVJfCIyN9HgrgSSDMcCQEzGEMscjRI2s8h8j7GiB+xDNID3vifWgHuaPOq7Mj7WYbvd5uNA0QcqIN4XyXO8CdvzxscTm4ZhSK0vZ1txBYM3PLOeyN4t0mAgAOh+v48lynt80MdkP3PMy3pvHHrP38idU94MpIlJVGTcXmzbZY5ec4Nc7omeIbcc05t1hcV2xoUvdQthLKXSgf3ih5y81kQQ3zfe83OZCy1EJheYO3qPbnqs9b6OJcr8eUb59/rUPfTGh63Yb1sfnXzneBnr7gnWy/N09d57FsEvrLdxdE1Ycy/81V890TDI52EYup0qwC8iVr9j8HYay1IyZAfWWrF5Pg4YgcJU1P27KAOLQKsEBmYWDkFh3J4ri2CWwUZGiQ9FQUFwJHayBtgGmS5740Ay0xFFedMelHKcIZWRdO9y6gHJBvKLKA7GPdYoI07Ub2nm87XhYoh8Dmf4ldJ36w3grIsZ6ogS5HgTL+CWoIVsvCm6rmZhOGb+HOQMhAhQBiM10CZQU/FAN2E3WHfWBgdKggMwIKEDYJakcH0eN7pgmVA1QUcISozL+yrql91xD+5jwMFccNqQB4+Pj3F5eZk3szJPVwF9/+PxGC8vL/GHP/why5ojV/f7fW5PIiEEBPpdGPgJ+xQnFG4rYT7Iw7Jjbmay0D2e67YaWgRZU0iHOjFGrwFeTdPk1j16wnmeEzbW0UDCgCwi8kk3JB1m7kgkSXDMcJuZYz0tM7OeyMQ+CPvh8wYVABg+h57jM6y7NXttthY/zr9Jlk0imYjge9zbJJTBs78zz3NeH8ZsHXVSYL9g1t/+x8GSQOvqkO0S/+Jk1vqJ7tqn26fwDH8XObPRmVOQGCugALDvBNHtOn7JnUkRkkcTSAZFliv6wDryDLoTiLOuEK97ttcJnhNbv6OobtHt+z5inmISIYT9mVQkucYm0Q8fNgIh5rXzek1T6n1vmvURvrk9eGziYr/Lp0WhR6wftk/MdOskskUfso4K0NYYpGtLWxG6m5PDfrOqfrNu0zTlXn2D2azb0US/KRUerwW2W3cU2Jc5oea76KTX3sm3baquGHwrsR+nMTZzad2LWJ9qhi2ajNjtdtFEST4M/E3o2OY9BvSU3/E94gC/r8kX9BF9YH7Gfk6Q266LaS5ECvNO329zFctyNVFtDGPyBuzgboCmadgtnmM7egomNXnKHPgbf2F/yb2JF5Yj9omv+J7ru/do/G//8/+aF7TrugxwGBRK5kAE+D2dTpllxgBT8BjzyUKU1W0wKAxCcznQTKYdpBXICQPMLGMkg2MBAJ+urljQLJg37mIcZsqzYJtS3amrNP4eCh5R2s9oNXEVYBhOMQzljbc47mQAabM7Cm8GDQMzKxZREhhYNINbkhgMuWYZPD8CIU4B1jsicqsOa0nLEaAD5wFQBjRQqXBARobeH8D4DUjRC0C+2S1XuGoW3UZsJoT1NxBkriR0ZY0KO+9knI3bVDh8WgqfcfuJ2ZhlWfKZ7DAeyN8Bgt/zO9/DuuY+bBICAuTV1VVeH2zOQJUgwhG+m80mHh4ess69vb3F3/7t364YVhhR7KxmkwjSOC4zkS4fs/fL5ANBArDj1gn7EfQEm8BP2HbxP5Ybwd2JbM3KUZWx/piZBPxZt/GLTj6xN4659HOcLF1cXMSXL19WJ4shf+yC4GvwjV9DXiSdzNPv1MEfMid0Htma9XLl0EmC23XsT9Fh26yZcMuYz3ddeXeFqwGsr1sZbIvc10CVNXYAt49z5cFsO88y6YAP4z0tJK5ea35OsgbYgZ22HiJP/m+g730a9u0m8hxvWVODDCdEBqgm2/C5JDsQHNgX97q8vFy9GNbJotuXsCHub4CNb0MPlyaBY+YHUHd7jpNofmb/xHoSP7kPcre+dW35nOW3319E261bY5ApBACJkkEu614n7BER4/R1p0YGsWL1TWaO4xhNlMSK73Gdu2XyfdefaSKWcogAuuw2GftJZI5/cJWPe9agMoPqtlRp3VZj4gHid/3ZLra79duuzcSb1DYWWeZSASEOe+2naX30trGiMaPfF4YcGRt64uTEBCy2YLxg35o2fa/f/p3je6QTvLBNxsd8mQO+m/kRL9zKlFuklxIr6vk4uSKpwAdvNpuM0VgDdNtkATqGHVgX/tv/4b+J37q+u6KRTmpoom1L61ECeW30fXHudtqpZ+8Yp/MRaixi26bjYvmZz7wncBpkRER+X0dxNhFNU4Ahi2CWzUw+Ts8VAQJK/R2E7pc+4fBIsngu80ZxHx8fY7vdZkDrZ6JQXjQMwckRYARDQYFQLgeOaZqjbZPRmrGz4qJUJCYOuhibFZcxIe+I4rB82gzzroGH336MkfA5HLudIw7XJWjuye+cdCATHFtEAaV29oAjsxLWUQdzs5w4ZDMh7DWC9eDnsPauFDAH1ryWrV/O6EBnRsSb6PljZoj15Xnoj+2B/6NLADQSG3pvATHLsmSAgQM0kwPDQiK63W7j48ePWb/v7u5it9vFr7/+Gvf39zFNUy7New2cYLhSxBzQCwiLiHKyFps7sXW3EkEeGHggi4jIDpW5ERS22+2qVc2gyUkJn3elBj/IzwFOVMP4Y9YO/WKe6AktSvWGa4+Fz9WMMUELHQcgYEc+UQQbQf4GC2Y4qTZ2XWor8THG6J2TK9sTiY99OhUh1o4kDRs1EMMP2h+jv1yADIM61sogg79NPLh6CRjyMc/YB9Vexuw9Q9ivkxninvdomUggTmBrwzDGZgM7uUTXlf0gBs8psW1W8i/JUfEHTiB4Zk0W2c5MmplNhVH2GDZbXtg5xtuZZCnV1nRYCbqw2QC6pnN86jPYbts22q5NJxkt5ZCMpuuiac/7oqY5n/7kg1hSBSCd6jOcTtF2JZlMFZMmIt7O9+wjorxB3kCwbcvBAFQmiu9YomkLE12TQP3ZJ+B3kg6XkwKnaYq264KX6L6ebc8kBi1y8zzHfAafS1rUaAXg23Z9GI71e5kjxpG9Cdscp5JenlZVW2xjntNR1sM4xpv84TCefeIyxzSv2X3WB9vERziGgg3sF5Cdbc2gtevaXPk2KYBtO85CyKXnJt1x8r7dbiJiffw49+o3fczTOabHErtNInPmZY5u6TLZaV0nFrjiyamjEQVwR6RTpJAFf3d9Ok2MdniIBZIME87eg+F3ahkD8jkuJ41JTmXOJor8ElPuUWNQJxj4XpOBfV+OlmcNSaw8vr90fXeisSxNVvzk2Jd4e6MndP2mY9pQknHvomkosZ6i6/pomojNpvQ+A2TKMXolqx2GU3b09KPizJomzs8u4NJ7Mnz6FIwryQOLlZzPmJxL4wXcRN+no2rNaMGqjuP41Sk3PuffjGXTNBkc4IzM/DGfurxoQ0sL2sbxOEQERlQYV4MvFNIgIDMkYsJItjCk/X6/CtzclwrKpEAREaux07ftfk+/RTwiVmNzsoMjR9Ej1iV9MxJm0Lgf4+r7Pp/UxfpizMibZ8JA4WDcUuKgYidn1t3VAzN7gFADfJ7Ls70nw5UmnD6fwfGxZwUH4t5+ZMuY+Lxf1kbiQOC5vr7ObQHojEGtK5XIj431jB2bfH5+jp9//jm/zf7z58+x3+/zxnKcdQ1osVX+DVDn9+groA4dIdnApuoXgQFECXpup8G/DMPwlZ40TZMrOjUjBqCkiuNkFFthbddnja9PfuJvV23QM+RDkuE+b+s7e6ocCKy3zAXWyvpu/bddArTchmew7wQAQI1s0BFXgLBFt7Q6YePCtsw8t20bf/jDH+Lx8TH/zkwfn/P6cC+3sNjuqOI5SbNviYjVqXEG26nyXo72xYc60EMMsB6whNix78O905jYWLnENBVyY5rmnOSZhNnttpHgaHkvQ7IXSLLIvoH5OqlEl906Q0LBc5hL13VxeH6Opk2nUe12uzgNjwmgvr3F7rSN5XygyxxzLM0UwzSdq+5NnMZppZvbJaLr+ui6NpqujU4J3jKXt3sv0xLzlIDTcBpj7krrTGmliVjmJcZxim6JmGKOoRmja0tb9TzP58+MMU9LbLe7dFxupJeNdW2pZHPIARXIcUynNkVMMc1n0LxEbLe7iGhiHNM6vh059rOJ1/OhI0nGbYxjIX/adt2GtNlsz1rbZHyRxz2lE4silmjaLsbzmJppjjmWiLZU9fq2i2jamOYl4uwrL874bJkLmVPw0tkeXl/ScbNNxGkczklf0qxhKC+J7ftCjA6nlOja5rE1g1uTSCT06KGTlaS35f1qxjk1Yej22ZJMRQzj+fjZLu2HINFdloh+0+VEdprOVYm2i2ZJlaB+08Xb2xgcstP1pUrRNOlFdunDUY6c5WqWmJcpBvZEdX302+S/+w4fnPRst93Epk8yaOLr/ZngPieDzNcYgc/jC+oOGldbiOkm67H7muCqk2jiI+vF2tV+kzhdj+O/dH13ouGJI5CUlZeMNmL9ttvE0BRAZBDglhQDZCocl5f74MUttPRElJMRyrjcU1j2fSBgxgQQ4xksSnJepW+VxSgOfBZrMeay7PPzc/4/F0GVgAiouL6+zorgYGsFQsYkP7CzTkJ2u13eC4DibLfpSOHn5+e4v7+Pl5eXOBwOmT3EQAGoAGTuAQBFgb98+ZJPlgIoOmgyT+ZnBwNLYxbeLAGbEH0SFN+zIXBfNqIS+JyUMg76fruuvAmbi0BnZ8X6cE/0xNUg5sYc3CfeNGWvCaDXZfyIiLu7u3h4eMj/N+NpPXFy4b5jGFGSGPqrkQ9jddIIcPD+JsZudryAltIqQ1AgyWSfDMmm9xXB2A9DesEk+mHg9vnz55yEX15exocPHzIJwXhcBUOfDFojyns3zErXpWYnhCT7bp0AONFyR2Lu/Sc8Fz9EIsXvkRk6hv+hIoDuAoZxwvYnrq456GNX3jDtexoAOkhQSWnbNr9sj+fS1oIP4e2+yNFkAQQO84GoIQjyTD5vf41eu/rH/Ali/BydsQ74yGjGhL0jI/b9QRjVlbaIslHZRBRyJjgzP8CRk0MDGbdg4pNtq+gESTHJC2MzMUJ8iVi/CC59vyRF/hsZQwRQuU36M0V6aWzZ+O+9QvMcuYWSe5Y9fqXXuq4isT7jOGYGNv08UjuTfB+yAUgxV2x2tysM6mazWe0baZomjqdTXFzsspxc9ZqmOTb9ZuWXkan1nnUC0M7znE/yIZbxeWToZI9ksCQC63eE9H2fYx4kWnPu5BinMV6rQwIMrH04Q01IWdeRdSP5rtckHf+aGfUmYtNv1rGj62Lblr0CTVP8H2sCweLK3Tit22lNmPCyYdtt0zTRd324gwSfa/0GiLqiDNlhYsKYhAoWc2JNDGa9v80ypFLOfQuJNcd5irlt0c8sleg10c29rD/cF3nh8z0PbHpNQJXKD74COYEbDezxSVQ1mGuxtxLvwQKMcRrH2O8u8rHCEeuDmohL+HeexXhcGTGmNSloIgj/78Mvfuv67kQDwcDar3sSy6JYEbbbTVZ8BIBjxNBgwHlxHcCCvkxK0GbSEIx/n5SzvDwP4fjdDDYKlCCBgIsYx+ErEBdRAhbfNdBhHHxvGIZVT7pL8wYXgFm+w88NaEkMnGTAKMPcuj2DJM6ODRk6+DtTJfgTVE+n9A4GGDzWCEBD0KhbpTAiWqMcaM00Gkw1TZNltd1u43A4rBJQgpB1gvYH2Gx0AOM2+EC+rBPJjRlorwXzA6yS8KIrEaUH1smqf07A/PLlSzZyn2JkptjtVmY2+Bn7W8zy8EwHAGSNI/BzYFBZCyczZtHQT1jby8vLuLq6WrGbEZGTE/6QQLOJFUDBuK+uruLx8TGenp7i+vp6xaKiy5ajEz3m4/uir6yRA4BZIYM99Aj5uoLE/S1Xj6Pv+/xyL+uBqyRmffBjPv3HQct24+fgG50AQyJQISlsbnkBotsveCY+D//hYOZgwZhIqgzGnSBgTwYQtR46GLPG6Bdr4MQeH1ITA3zOfcDYNqCG5znBZ73xZd7fZr/LXKjUwmazFhGRk7LCTpcN2V4DxuA1MhhwFdZAA11Na17ADb6UOePX8bnFz3UxjkPQstw0pQKY1vIit8n5mfX4TMKQzOEzvB+kPes6P8c+sQEnSrYlTtQiKcgbqC/WlW8ndZ0SeOwFnzrPc95HZSKL5N+VcINK9MdxGjsz8USbL/7Bul6Sw00M4/rQAYNY/o9+sPboY9/3q4NE0IWIWOELxo6NYbNOKg0keRb23TRNTGKq0adMCAiAsobp/+ktfq6mIqNxnNIb/qLEVgNe9B3QXMtnjavO8l3miKm0V7kV2/P32+V5npN6bIf7ej1s/8YL+Apky9jto0yIsSZumaIChn/i+bZXdBS/xPMglPEtyIDnRkTWS4/BviqTKE1pfUKv+Ax4wLjN/olEnESXuAF24Dlclpfj229d351omK2rF71ty1GD7l08Ho/x9naMH3/8McZxzJvmcIQGpgTJ19fXuLhIpTHYU5y8e8JwyBZeq+w4omxmNZu6LEvuMeczEUsMQ9n4aoffdeuTDzBa2F2cLm1ZKELXdbmdw/sSAAVeeBIUxv309JSZRViBcSyn9sAi8yZqxgCbQ9JhlsYKwjz5HkkOAQnj2WzSS4Vg79ED7luDOpwaCmlnj/5w4g7Zs9vM6n5SmHQunICBE07ETJYdy7IsmXnn95eXl1kHXUFhfw33pZUMh/D09BTjOMb19XUej5lDZEAy7s2hGDG6dDqdckvHdrvNvfDX19e5fMozqCzA6CFnz4nyP/O3I2WtsQ0nf/RwIk90306EQN3IoWEn19fXeUyM91//638dLy8vWfd5u7uPAzZr6UTOyZ8DDEGUz/hoXBJY9KUQIMvqFDy+62THe6kMIp1ko/dmqa17yBXgH7E+cY/PMRez7jz38vIyA0vsx6fHmUkiCWE98EXM2WDFrBr+lrG4nQ1QZ7tl7AYL+BHuyzj4LutnQgGdAsgyF3yZQbBbQCNKGx82Q+DEj5poQl+wawNN9Iw1sR/jb0ASFT+/rwOm2gDG5AB2HBHZf5q9xp7XgKu08/neVDR5z4hB6zAMcXV1c64Gjbl9uevKC10hCUzcEIOIOU4OfYwqn2+a9II5bNX7c+yTzZQjL+ISc3WXA7KnFZQkaZqm6Ls+hsF7Jcq6lP788kK/uq/e+midcsXZTDL66ntzry9fvsR+v89JOD6wbZrYqO2WRNOsvP2U9Q7A5xPUuK+Te+RhX+ZuiYj1Eb7IwIRbzMtKx/H5x/Nc7cuIzSmRKCAUPUixZRvztG7NLpWU9Rq7tcdyMCid5zn1ajWFsHCSYMKVuYMd0G2eTWy1P7Vd+2fldQHr1mvWieeZBLa/MOmATXB/kzs1yYSuggvwa1RE+T9rZfKMOE5VHh3BV4Jh3PLkhMJxzwkhz8F3Pjw8ZPsg8TMpT8zAF2LP33N9d6Lh9iMbcXIuY1Z8ApFbEg6HQzaW7XabX2oVEbn1B2VPE029gggCoOuTVczKo2zDMMZuV1o7ACsoJm0F4zhm1i8pThvLUvoOSUTatsttSM/Pz/leVjQUDwfNZtp8VJ6yz+PxGB8+fMggrGZeSMR8jKCVFaeOnFFKwAC/Q2kNCA0gADERX7OyBP+IOCd9FzmAuA+ZDB2DZSwYqdkAMwl8hmfQKvHhw4cVmHdS4TmSdDEGHBxOlqBh5oOL+fFirIiIw+EQNzc3uV3j4eEhs3Fuc2NdcFJ1+wGVi8Qq7lbj4vIGL77jdbJDchUQufkyM3I6neL29naVnOF8zFxhi9iAbapOQNFFiAEDJByqgSf27nk9Pj7Gx48fV8mMN9i5Qum19npR+eBzfmssQbJmm8xuG1ihozWYRWcBc4Vk6DIAB0gR6NCBiMjjIjg5KbAu+nmAItszzCnPtSMnWcHxk1SY6aJCgEwILszFh0J0XZfbc1xpMajhZ4zD1TXsmMDkBANdAriT4Jj4MLMM2PNacU/7pWkq73VwAsEaODF2FS4iMtkEyeEYZhk7qbXsmCu+n7nh83mZJfegZYPKcETZiFlar8p+AuTIuJCniQHrSQLfQyzLOeHabOPtbYymWR9Fz7NJqL1vDnmaefUaNbE+0Qrf5q4F5kVM4efMA0CY2zNirQNcqXK9jVgK1kDH0VEz+BGxwgNgAMYDSLKuuuWFcXofA5+HvHDli+TxeDrFcsYSrLMrSk6ErT/4J7cCQgAwdj7rMUL81fEEPw3WwafP8xzD6RTDqbz7yWRX17ax3W1XiUBOnqfUmoc8ALmZNIhSobc88bteT3xyTQpil0kXUhWLe9n/G+Rj7+gXOMDEi3XKSRJ+tlT8Ugz38eMmO7Ax5O6Y50Sb+Zocwz+4s8Kfd4dKXcWhrZw4Q9whVjlZdtzNPmwpckd+/L6uxiMXJ37EZlf0iHt15QKbNuHwW9d3Jxq0RHgBWZTNJgGbw+GwqmakjLkwsmRhTZPaelxZQKBpUdcKadYZZ+wj7zDWdCJIuh+ZKwpKoLFh8HbbeV6/AJDNvSgSSRQKBzCrW0bIOt/e3nKPPkHicDhkJ02VgAySOaCwBh8oPyCWcXHkKcqFItQGw1gxHmfydeB3AuHghjxwWga+BErWzuuEXGhH4OcGaTiLf/qnf8ovfbu8vMy9xgRlnkcfoo2HtXZgRRbMCSdsdtZAks/d3t6uktSHh4ecjJitRq7MowYLVLvQe2zIyXptK2ZTSGSRD61zBNdlKZvtYQjN1hkcYH/ojR0kawDjyvy+FWx9iIKTBOSLDjB3kvNffvklfv7556wTyA1nSGucQRpyrI/otJ6xxmaW7DO4ACrDMKxOlwJ4IQPmh60V/7Zux2StWSPAn5/pBMBBgUDoYGJGzyfgFH9YAKcD37IsOVlwNSuiHJXtSt/hcMiAM6JUqpibgyY66wSUz7MWHBDgQIvskCO2jw9mHhGlVaomOmiXNJvI8zIoOtuy95xhC24p5TusvdeEv7E54gxri2y8hjCQ2CP+zezyNE2r/Uu+t8FWXXXg9wR4Ehd08/HxMU7HIW1sXpaYpjH6zSZt1F2aGMZSvUNmJmkYgxNPv5wMkMs6nU6v8XoGTgBBbNesO3NG78AK+A7sqmmamMYpnxTFuBjr8e0tmmbd1mfdwK7xXwZf6LN9BBdzrRMXCEfLDNvgOHxAf8YbscS8lPjDOEissTnGyridbJlcNLFUs/KuhCBviEof3AAgRf7pHuU53INnzrHelzjP5RCK/cUu+w70PunCEE00Kz/MXkV0mueZJORyvC1sfjnd0yRKRKx8HReyu7m5WY3blQjW2zYwTVM+Yt5VDuTiC//mRIJ7onvE9LoybTIOfTSuokpOXLGMreckpIx3HMdM1tV4q+/7WOYlunZdpcMfc190EH9kooe1Yx1MovDHcdftgiZy/9L1O06dmuP5+e3M4jex211EOjruGMMQmQl0MI1ocoY3DEM23s+fP2fjcOYH6GATFEoCe4yCpHdGFPbQGSRZq1l4M4oojAFeRJyzdMbQR8T5nOezk3RWR6tTRGFSzGB6IVxaZqGXZYnj8S3f8+3tNZomvZTPgJMFjogctPi5k6Hb29tYlnIyAMGEpAmjcgZqx0dp2smOQQHOw+/7MOuEgWFMPiUMmRi41IkH75bgfs/PzyuFZ135P0F+WVI51e0TdkAGnzh0vgNLz5wN8gzYCbDe9GS9ZP6M0Q4qOwKxcGa60En0z/cy48r+JRyCk0bLBBsx2OTZrDG65WrANK2PofU62smUIFZsByBr2bOZ/OPHj9G2bdzf38evv/6abRHnRrBHJoAL5Iq83CpR2y+fcbBjvev2JdbTwIm54RtYV7NQfB9bJGEEgLDuMNg4dSc8Ts5YZwNfAgk2Cti2rrB2EB8EEn6OTHmGE36ezzMBWP6Mq1j4Y1rMAI7+HbaNP4B4cfndPgc/Annw8vJynndEOuJ1iXEccizBlvBFZtDdOmKf5kpNRKwSsXTaz3ImEB7zz+sjivPZ9G0XXdeefeM20kbs9bGxXCZxCkhqo21psUstxsk3pHjKu4/cNuWk2z4Sf9c0TTqKtC1vMWYj9DzP0W820avycXEm045vb+dz/cvLciHs2jYdDbtExP7iIp121aaNuqwl+uRxsJb4Of6uTzhDXsuyRNM2MSvhYk27rot5mlc2+a2T0hzn0V8qijDe3juAf8JH0S5JHLXPtQ+CCDgejzHNpSLfRBPbi9Kexefdxtq2bXRtmzqDAKHTGvjbLjnOdtP3sT+To9hi17WrPUCvLy/Rn2Nx33UxhY8sTTqHzeAnHZv6Ph3x6mQ/VSvivOG8VIic6HHqVH8+trU5/xtfOi/nGDjPMc9fV+a6Lh0OxImkbZf28Na+2ok264FO8X9XUyEETFQD2Bk/93JLKfqE/jrumjjiQBrHAq+7kw3Gg+82JuEzvEwSnOfOAx9U8K3KZtukF/1xr+a8Dm3XRt+W491Zf9bOBKtxgytTXMYwJNBusUJvrFvfc/2uRGO77aPvUVyOFC0npdjZXl1dxelEebcwVd6fwQT9dwI420gvqCtsCJN+eztG07RnxTtG2y7RNJxRXk5psuAo9xl4wXIkhdrGZlMcRyofLjGOpccWZSYQ8QwU15UeHDJKD/BOwbGNtk3tHzc3N+ckJM7BrTBDEZGZCxaf+7slBobaLAIJhFkXs/uM2+yWM3ZO6TFIw1DrM/wxZOZ9fX29Aja0kLmywrsQkKPBb0Ss2mPcN8zvIspbywHRJDXInjYX5MP5923brlpGXCI0YHUAQQ44pefn51WSCkBxCReZOyEDmLoqhr040eZo2Kurq9hsNjmphQmv92O4/53qF0H56upq1TNrUOCgxx4hALDXF92BIY4orBE65HtyudLx448/xpcvX1Z2zrOdhAJGkYeTNsC4gTWOz8yTARr3rZ1kRNlMByvDXEwe+N+M3SSCbcEleCcF2GEGHXMp//M7J+WsISwjgZbxYFvIiLExds/XrTMmQDxub4xFjw2YXV2hKlaTB+gpa4esTM6QvHptLi72cTod43RicyygIR1dDlliIMdamcUs7XddcGQo90ttsZP8g49EniKdALVE26bvJz1Yzr9LLU4kXACfZYk4Hk8r30qyyRrWezrwC1yuCtYEgn21mcXNtsnEitnEvu/j5e1s010XsURcXJ7Jh6aN/VU6jGG7UYV1nqPp+vxW4ViWmJaIt9MZ+LVd9O26vcZr57ETN4g7fd9nQog54VfR1dNYfGMs6ahX2xAkHSQKegUBgp5HlHfksAbGAAawPsTGRJnblYdhiDnmeD2mqvoyCpj3XUxnoqFrm6Q3Z3tF39NazgkINk1s+i6GZY4mloglnQ7VBHs+S8UqImKZ0z6Qy/3FOV7MEW0Tw2k8t5Cn5GOzOb8pe7uJeV638nR9F31XXm4KfpnnOXYX6ZjfiCWPp226tAdDlSmv1TiOKUE8J8nTOMX+MpGF4zSsiJm2aaPtmmiXJqYpvf2bGNQ0Tewuku7GUvZ/uZrtCgC+jfiHr3IsJf6hkyZeXKW3//d+NDP/rq6hJ7e3tyt8A1Zykoo+Ae5d1aHydDgcVhVWjxMfAsY1tnTMmc961y5pO03TNDGe5fcsnMRYHeNYRwgmx3aIcPtv713BB3Ev4qfj4m9d351ofPjwYQUqMObi0EsQySdM7HYxz1+/wZFA5QCHM2Hy9GbjTFGIy8urnLwAjgDIKKxZURsMgAoGy61UPnllWcpmK+ZMUHeQdvDgmTgbWm38maTgQ8zzFB8/fswLfHt7q+pCOS/ZVRPmZjmb4TZAaNvSSsNaGewaDFipMU6YHDPE8zznlyYSTBwMrq6uVmf8m4kyC2WH4mM1+ZsEx+U7ArBL413X5TIgVx3QLi8vV6eWRZQjUzMTM5cXOTnpIXDWVQRk6oCJgQNyYe6RRX36E3rIaSyMBXbj8vJyVfY08I4oDBZ2A6jx4QSWN+PjNAnrJcDUtmYwge3xfRItQLL3qpCguILI7x4eHuIf//Efo23buLu7i4jSRzrPc37Ts5MVM1A4YwM4fIzXgqTT+4OsFwbhPL+U8ouv8DqTCKB7rLnXxjrOvU1KEBCpaPJZfB16zPddtUA/sR3k4+SS+1vP2IeGb2L8rrgwb/QXvcUejsfj6j0xVANphTIgwN8SyJ+enuLq6iq6rou7u7s8Rp+KRbstRAzJdESp8vV9n/efYGPuHzYDeTyW5KyAvmnF3qE/bt9EZklW5ahJCDH8EfHiWz7QbCB/GyTbV9lncS8fZsC6YH8+7ZG5c5Ibz2YcbtlxEsQa8m/uz3fRTRNVTi4MjlzN8cmO2BrJAD83ecP9fZAAOs542MvF92ufQmxEh5ED601sN75gHAAkJ+qsUduml615HZzo4R+RI+PFJzN/ry9+CnDsli/sBb1GT2xXEamVi//75CPGYQICUgE7MK4aTkMMY8Fu2CqdD2w4Rk4vLy95bl5z7zNB35ZliXEulZLNZhP91OdnO4mepimascm+ldiFDng/g+Mk8+XZbmNCHpaju2awf9baYJq/nUzwB18QUU63ylWGthzk4Aq18ahJTduD44T11vjaBP6m788Vo6LXJjq4F37cuGW73a5ObTNBY8zA+J1EOCHkc97j+z3X73qPBk4ORaqDMg9n/8B2WxhrTqJg30TXdZmdpv0A57/dbnISgYL7XHGfXEKSUycGBhcoqI/Z80lUBtssOs4c5TcLyu9xZmY5UeZ6Axf3ScBo3TqBA9puC1NDewAyRlkAafzMDqZUZMp83YZCIELmdp7I0yVMDIwEoJ4nxjyOYxwOhzwuWAccnPcpABzpD6bi8+XLl7zOGAwVLVeEbHx2BA5Ym80mLi8v4+HhYVU6pdeR+fK3Ex/ahwy2aVkjyeOZ3veDbsDkYcw+iSaiMLvH4zHrPaXZb70R2gyPgbfZPLMq2FZEcRbIhs+iC4zDjtg9w/wMMG1HxneRI6wz+sh64Rtub2/jP/yH/xDzPMenT5+ys726uspjR4cvLi5Wx8o6UXx5ecnVKeSCrTJeWifNYOGHTC4QzPwM67YrI+iFE332C7laYb9kGzHwx38SrPFJDlxOkvk9vo09TPgTwKV1xRvNCfpNUw5CwKaRD3tmnMwDANxGiX9BDyxXqpX43evr67wO1kNO6kmBco623axk6LYu/DeMtRNkqiiQI8ibt2u77dOnuKH7/I0uoW8mKxhP3ZqBbiFn1o9n4COQh8EF/2cMJpHMQOI/bIPusXaSuyxLjNOU30ZsfTFzCpGBnhiEWwbE03pvJRVqCBrWsW4HYUzoiquJjs34O/ADINxkHoCM7+OT7QOROTbmRIlEE1khfycMThij+braaZ1p9H/7DTPJji9ee9Zus9nkdmhIIi78IfN3a7BJCvt+t7CdTkPEsn6vjGXB86maGuekk0Lfsm7hO/xs/s+/wRkkwvh+Yp+fYV3xvkEnLqw333f7O3HQ2MVJpQEyQNykJ+2d9TiRs8l0SKsav7gKwd+02pFwoINguXrtXI3B/zqOc63I1mUdw43R7C9MynG5alFwaCEb0Gd+VmNgE4DYrxPD37q+O9GgXePLly95MxyDACCw+Q9g9vLyHBEle9rv9yt2iFI+ZUsycb+B0t+NiDidhhw4UD6coIEPwID/u4fTQW2/3+c3GTuoY5gwAygbc+a+DqSATB9RaaedHE56I2bTNHF7e3t+OeHlWcH4M+ckg1YlFIELB00rDfL0HBgrMjLjxmXWJmLNJGDMVqy6VYW2IcZjh8gRpIwfo68DLevVtm08PDxkJ8Q9vendSQOOlXkagAIOKNvClDI/HAgOBUfD3DBAnAGMC3Oo91REFAaS6gTBxadeeD0cQPgcAZP1QI/QW+yhXlvvV6orKtzDjCTyQ8Z8znJAB7AvdBWQwH35mySb35H0zfOc7fHl5SV+/PHHeHt7i0+fPsXt7W1ErBkSADL/Z1z2FQAog7Na3siF75Hk0VrHmC8vL1dgE/1DpsjdlQv7JsBRLXPmQVXDp9DxvaZpcqLZdWWfBPfnbxM72IMrm4yNBMbyBEw7MBrw4S84FtuViqZp8kELZlkJ+DzPbKO/dzweczWCJB3bm+c5fvzxY9aB5+fn3J7E3oF5Li2rBq/4cFg61i2tXWmD8XiwM76PraPzAA9kbSY2s7AVCeGDM/isfYLXxX7VlSqDUMbJMxgT68I6mKXO7GasgbyJOn5O9cwJaAR7FKcMQohJdRyA8MMPlP0B5dAAdBY7MuD7Vlzhu9gra+OExv6oJhYMoLk38kGfTLTwf9bZ77ZAHnN8vek3x5oobWNux7Zfxu9Yjr6HiUoTgI716MEwDNlHmehxVYWqI3OMpZy4abKDJAPfhh7jo5C3K98QEN6DZv12UsTYOJChThIMXg3iLSPGCmb5ViXCPhKfZDsjgTZwZo74MfQTPMmYbYeMAV2sZWqgz5hZYxNPjAOb5W/sruu61Yl6zNt4rmnKXkjkaX/sGIS9uCrhd2Ph+/idbdL+FNnZJutE/Xuu31XROJ1OuRTu7AzDYaGaptELusoOd0CQBU+FYp2NFnaWoIDQ07OKwych8PNhtC00jpQF/JqhbZom7u7u8t4Bnknw5P8GNIzNGSfz4j7H4/Gr5IoNUHbMAOdlieCNsTgxFNFtLSy4S9vLUsq3OAuSL8sJJTGohUlHTrSJXF1drTbFOVlh7XhWDQDdUuPAybqSFPqFjuuNm5t8UkTbtvH4+JirKlSCnIwxDhz8OJbz5Fk/nAUbQNE97wkxs2X9MavoYGYjd5tfncDxOZJRr33XdaukLAOHpZysAliEHarbPrBJM33I2YHaySrfIVDAiACcSIRYV+zBthmxdowEBeQEyDToxkavr69XbDS2xv3NgAEY5nmOH374IbfcdF05h5yKJcG6bdvcpknVs23b/O4PAgd65IDpQEKggeFHP5Dz8/NzBuNunzS4NQgDGGE/Dkr8nrmwviTFtlUn6v6/k3FXB50c8Sx0lUCOHLB19A9dIei5Msp3XFVgrABb1pD1RZ8j0gbR19fXOJ1O8fj4mPVgWcomXYgobNuJPBvVC2NcZG8QYNaOefNzJ4DovNfLBI2ThXo+Bp8GnOgM62P/wLPxPwAIQKrlzPoxdwi/tK8gVmtp+7Fu4P+cdDLeOvahi07IXbEta1VOTHRC7dOuGDc6ZN03CfatWMd3a/LEuMD+m/ugtwaEgCfm6n2EEWeWfiztSXWlr4n1G6otR+aFvtqPEKNoP8S+rXvYEsAe/2WdhShiLVw1yslfU0CtiZBlWWJepuwzvWeKRNKteOg732dtTE5gF04W/G4Rx1Y+Z3KYvyEK/f4ktz7ZH9lXT1OqHF5fX6/00dgD2WOb/B5fyfrwO/TLsRi7x97Bm9iV98CZWKgrg06S8ZuQX8bTdQK7zOtTCNFjEodE7pdXRUBuoQd+v43tpV4jnu19gcgQ34BsWI/fun7XC/u4OQ7OQIyFAOwSYOY5MpsI+HQmzkQI+EkIpV+Ne2FUMP5maZylInCCDoGWs86dJE3TlNlBA04UBkfB3DFa94KaTSEQI4umaeLp6alqbZjj4iJVPF5eXvI7HJLBlnYTFBdn0Pd93gPBxfxwvmYpzPrAnrvcawBZt2gQiDAOB0ccDTrBz82UUQUyuMbps54wM2YWjsfjyjAAkQBX70Ohn3gYhq/An3vaWRPY9Le3t/j48WM+GrZpmlwRsmFHRNYbZGKdQ4cAuzyDZwNqcWxmZNEZ1hDdYvzuwY0oR/qacQAoMyb0mu9x8hN6bhv1vc1UoDuuUHlNkJeTgYj1iUxUDtGlt7e3uL29XY2fRHYYhvj7v//7+Omnn/LJad6rYdDLM0maSK6KXS0rB4pNXVxc5KOlsQUnhK648X+cMWwcAYO5Wvb8jCS3BjhOJnwZnBtcQQAYUPJ8dIzfOwggIwAMfjiitBYYnJsRNPhDD81mes3xb+6pxy/SltC25aVWtER4nVyR/OWXX6Jp2lVloLSvDjkxtz/C/hkj48cX4UMNHBx3iF18x9Xq/X6f4wA+8/n5OQMggxgzlIA95A2R4nZCA2vG7n0ITkzNqOIvzPCjh+hF13XRCkRYHtZV93zb1rxB1tVeZOb2OsChY68rGdyTedSkE3bI3J208zmTMIDrOnm0T3MFziCMzzj5YK08Fvvm4/EY3abYHbozjmPsLy5id9aPmqhh7SE0PR4SB3wi8iOeoDPDMOREBHvGd5ngse4ZxBNXT8eS1GKHyDaaUi2CPMF/e58QssIGD4dDbjUCYLv1Fp/J70w6scasu1+uaTnarhgTCQj65v0nNzc3GY/yN3gRXUc/qBYjJ/TJPgKdR65uq7LvZPzfIt+wIccO40V0yuQMfhT/y/PQl81mE8283gdn2yVWeC0hKyCtPD/WFfvG/xnfO647WeZz+LLvub470TCTgFNAMKnCEGeHnU6GSslCOmHh8fExbm9vV0Zh5sXgA2UkGBjUpEktEdGvFLNmpFg8AyyyTxQQA0SINhorOoJHqVAYl5UwSjMPLDCLdjqdcitBGncbP/zwY8zzFPO8xC+//Bptm/qaMVgCBVkqBuANpsyPwIJzMbPIZwyQnfFHlDIbjtLvW3DyQ0Bh/V16Rz4OGjCZ3C8iATPWO6Ls6VmWJb/bhLlYZ9ANDOTi4iKznAavZoUBOe6DRx8N3syOsYZN0+S3gJsVQyeRBzrkYIv+uO/YJW+XJK3LDq58v2ZbHVhxOFQykK8/h434xAnrvdk+g2p6dbEX9Jy1sv3Nc+kfN8ChHIwMmqYcyDDPqTpxd3eXv7fb7eLz589xdXUVnz9/zi1X/J4qH3PEd1hmMLDeyGxZu43Clb46qebnPMvvviDYo5O82d1yJIn58OFDTsTNcrriwDpwoSN+l0oNnhwQCLCsCeQOeo1ts57YRUQ5+hkfZ5bbwdXAGX12cuwEgguQYuCLnEqFcRPLsjnLnhcIzrEs5TQavyizJn1sV8XfUX1uo22ppM+x399knwI4AThgM5bH8XjMx29zGuHpdIxxnM6+u7yfwDYOUHBrTTopaM4VAb7jTaTYCMmU9XZZ0glHy9LE8XiKpm1jGNKpUks0Ec26nYRnoOPjmPavFGAd0TTpZbX4NfuwQhaWMcOeuh3YIAQAR6XcsZI52EfUSaAThppccfziZ67MbzZ9LBHnk4/SkbKcMBYR503e6Xj8HE/nMu6SwM/RNn0s59iO7hG/8Wdt265e4Em8NEngA08YJ+PH9g0Aqbb6wAR8JbK0zhqD0Jo4z3MssUTbtXEaOBltjM1mH03bxH6f4u3hcFgRBjzD+zdJLJ6eniKitIo72TGhyHfRG0gP/AZ+1X4DWZm4RC/ojDH+ufhGoofvgXRwKyTyZo1cvUXveZ59sAkfX2CLGgtExFcydeLN87BJ9BLsaAKM52IT4zhGsyyx6cvGcWNYnoUOunobEXnPs5NTvlOTiMbmjo32TY5133N9d6Lhi8HjVNqWLHCJiClOJzKyflU2AkCapSOAIXAmSzncrHua9PqtsGbjMEwAmhlLhOQg7PFElDfK8h1eqgfLYEAKy8DCub/OWSbKiCMzkzjPSWZ9v4nd7iJubm5Wxsf7JFBS2H0z2AZ6BufMx0YAO4ccVgFMgcZlPis0BsRG3Yj4an24uD+VosvLyzgcDjmZcOWB7xuksz4RyXiRPVWdq6urrANUHTxOM55k9GYJ6+CATsBMc28ADfPhft6zwSZyqiqsN3PwyTM1UDQbxTqwJlRruHDsPi+e75NMYU/s/7FDAUyxDmZj0BGDS+aOHkVEBh993+cqBAy374kc0R/W11Un2gh2u108Pj7Gw8NDfP78Oe7v73OCZmICAgJQ78QWvXe51+CHdSbRMYng90c4eNZsedOU6tfNzc0q2XIVDZ1Gls/Pz6sWEj7H832UNAHUgMSEgJ2+N/6h/zD/yISfE/AIvj6ti89yQIMTG/wjfs/JDutoG3SFDQbcrSf2DzWLlubZxOl0zPfHRzs2GIwyHp9yVNhZTpXbRDoqt2yGhM01KVUq6qUyQpzqujbG0SeXlQ36fV/8AzaY9CtiHGFyOXQkvUNpWUqscPxyklcz7k3TxDAucXh+iv3+IpYpYllaVTNKRQigCigcx8I4Y59vb0NM0xjLwhHA5f0d2D9tsbSurmNx2awP6Gb8tGm4ggOgQqdZV+zE8dEJKevOv80Cs85LlFbseZliPrdX7y8vVoljp6p0NG30Tbead9u10Xab7GcvzpVsdLfv1kdqE9dJqgC7yAA5WWasCTHCRKXbeyPWbzln7wTPZs8cdo79JaC9ibe3ZJNvxxQLj6e3c8JUjkt3tclrajDqQ3683hHrPRqsPZ+B1e+6tP/g6elplUSauGZd8X/YBWPAVpzs1h0ytPbV5JAxou2M+OJKAuQOfho75PNOlvENjJ9x1nGbn+P36pjCWOsYbGLs8vIyYp7zO3P4Xp3copOuADkhsm7xeeyccZoUdIzg88ROPvM91+9KNBzAixCm4MVDBCn+XF1d5c3hZlcjSjsPk3MPcte1sd9fr5hKFO/19S0uL6++OqECZXPPnMeCUHykroMcyQOgpO/7eHh4yC+YYQ5s9oZBN1OB8pAsYGAOKDZGDBHHjzKi0K6M4KwpTRqMoBwopU86qasjOE1AM4ADR+lNsMisaZrcb+01NLuM3HGYrCd/my12xcOGgBNxUEIm7LeAHTUThIPxkcgkI6fTKQ6HQz7dyIktgN1HH7pKADMCQGTe6C3jcPWHe3O/mhF2MuBAa9BmUAjI4D4E84iS5HqDNvJCRxgL649u0AoGY4dcASiMxwHHLIaZFBwjegAThdNlTmammqaJP/7xj/Hrr79GRMTNzU1cXFzEP/zDP+Q+/R9++CEi0tHa2Ae6wvgjElvj5JegQmL1/PyciQD8iVv53BLjtSLgAOjxU3yO70/TlN+CbhYNgFQzssuSqmpur+DysZ0ECgc5s4/ev0PA8z6tiDUD6VI5v3eQd4DjO8zDLRZPT086wGLObxxnXahuYSsGIvgikuBpmuJwOGS/xHxNSBAM8SuQCMzFFaGaPOK5PqDDRIzt2DqAHJJepSo6YBSbSL6yAHJXkZMtlfZMJ8xpfG0cj1MmdtALxsn/Pd6IiHnhZXLrEyD7votpmnO7IH6F+GFAw/0TUBuiaZa8bmls6T0h+/1l8JJBfLLnAOmCPZuhtxxZU3yUmVBsxD4RfOFEheeZ4SVWj2N6z4O/g+z4N3aBHjEmYhZ25Ln4Pm7f5DsASm/Sh5R8eHjIsiJBgPH3fsaIyPu72KcHDsK+iQtN0+T3OhAnGTcy8gt6I0qbFnoyjmN8+vRpFXuxC3w4+mwg7JYbCBcnDX4GhIX37OITiaXGCsyZteEeYBf+DY6rN+8beLtSYH3n/sZGyJh1NykNPjW5xDPQK+Rkn8wpeI69Jq/5LL+DACRW8n2eYdIzlohpLp1F6L7tiP+zpvb7rB/2z/OxpTp5iYhVPKn98++5vjvRMFuD4CLizD4VJpmFJfv126x5gRqCceDEIdEO8/b2sqp64NBgIwmgbhlhjO75NBgD2OMg6uoDAZKfY3iM1adx+GIB3BeNM3DWXLM0JCzLsuSNTPW7Iei5NvB3QuIyZt0q4/s7CXJWyt/I33NH0TEWZMX6sybMF0PyCRk4aQMCMyZmbvu+z5WjH374Ib8Yz60GTrC8NhGFTUW+sEO8iMZ6RhKEbpJwkKjhRNANgxrmBNtHACbJ8UuqkAktYXbKzNvPx+G4dQVwttlssj65ZY29BD51yw7D1ZX9fh83NzdZ3m4dMyCxDg7DEB8+fMjPsfMFqNs/ODGzA68TMezQZd6/+7u/y/tn/v7v/z5v/GaMBHsAAHNjvOi691fwc+uLk7rMVp7nBhAw8xVRNiVHlL5hJ4HurXXyDzlhnbi5ucn2YIaWgAiQNugymxZRTprB+SNLg3/eRIvMYAMd8Kdpypux+75fJc7YkQEiv0f3f/jhh5imKcvk9fU194UbcBK4XaWBAEDeBELiC/MhWYAtxR9ZJva/+BzWJdn2tLq3/Tp+ET0kFt3c3JxjTLMaowFrRKzkij8wiDOgTXO5yP7bJIdZfZ6Hv+y6LpaYo9+Ul2Ziw8fjGBFzfP78OZYltdsS89JpYuu3NePrk3+aou/p+V5iWSLGcYq+T8cPmzXGZ9aXwbxjpxMb/m97M4FjZpb54T9NSuLLMoiKctgA8QMiwYCxZqnxS65QoJMQbq7G1cCSsT09PWWiwSCcz3N0O4AOkMtnXl5e8t42iI3r6+v8HQM9x2+Tcf4MsiaBBZc5LhBDXDXARt267OqkmXJAO2QOf/x87J91Y4yOgezNxc4ZE/JFJ5yksYb8zsAe+3acQhbYkNfbSRr2CG7gyHbbsfGOMRnx2v9GR5GDiUDuw7gN/LmMmy8vL2MaysmSjqmM0UkXWAmdc+y1f2rbVOUlGfbvqO4Yozspt33/1vXdiQYBkUUm60rAvwRvM+tmCBmsT3dgAcjgUZC2LcqKQlpJuq5fBX1nvDg5HIj/9oKizCQDdWZMYIdhxOCc6ZmhtAEzbxYEA3R2i2MGIOI4AA88CxnxGe5pBzOOY2Z/DVi/fPkSXZf6hHljN/P2/oXn5+cMGGGAAVg1E+aWs4gCOghaNzc32YmR6MDU+LQo7lX3rLNGb29v8fj4mKtMlhv6YJBYGMYCImq518yiAxmyJnl10GA+3Au5e53tQKkO4HT4uas21lWzmjDpAA+qaFRXcMZmKwigJCT8Dr1nbdB3M41OhtBhgu3FxUV8/vw5pmnKCS9zN+NldtrsvxkUfo9ecwociakrQ8z/3//7f59lwPhp+2nbtPeLF2PiB2Cp3Nrm4AnZsNlsVifRYX8kdrZt65nBCTZMEPPhEeiKQbuP3MZ+2GNhdolnOXAb2BIQOPGlTvbRIbeveQ7zPK9aKAFmtLMxb59whe9nLcdxXLVC9H0fj4+PWUZOvOuNxfwfXfZ7BGob5Wdup3CVgECO/2Be2DYXOg85AnBCN3iWkweOzk2gsPgAfp9iwvo9OvTU8yxv6uT4YHTEOgabie55/Na9pt1on1+pkl9cQMY0uULj5xyPU064iH/J9+ximsaYpvn8B9JmE9M0x2azrj44zqJz9e+JOayPiQT7f4Mf+1Bs3rGT+aJ7TsIZB37Ovp57otuuyhhEIWvWCJDpvnlA3tPTU277JLEGrJlMhMwiiSD5M+5hgzXVwhqQo383NzdZZo5d3IfEGHuzDvg4afzv9fV1niOyJ3lApmAe/9sEpHWTe0REblVmHZETMdOkZUSplNM9gg3VryNYliUeHh6ybmG7PBtbALuYTLXc/G8wUF0R5p4QqvUeU4/JhA33jSjxqE6YWEcnjvyMxKCuzL69vkbblCSde+LHjFvxqdgO8d0kqxN+5onOuq0LEg+5ICtXVb7n+u5EwyUnA42+38Tj49OK0TTjyB+z7QA5OwmzwMfjKebzGyZxiLDIXbeJeS5ZFcbN6QwG+xifldmnAUREBiQ2MBbdfW18/nA4rDYI187w+fl5VRps2za/1RPHG5EcGSA6Yn0aDsYAoKBN5Pn5eVXux0lERE4qbGRmA9e9w+VvgCyfRZmcYZuxoDTrcVM9Ya1ZU4KmKwToBbLhOL22bXOLE2PGUbJxzaVdEoPHx8ccREjcuJ/HybhckcCIzEJwL2RDkuME2w7LbyzGQJ0QuQWF9WWNGZcZE4IowdgAj3EzVmSLQzfb5bYKO0BaWnjLO86Kz+Iwn5+fcwuT91hFFKAJMMc+nHTXiXtErE6qIxH1c5dlycFyHMf48OFDdF05fpkEhLHc3d1l/2CWlHHxHK6mKZt+SWjQc3TG759APswXJ8upMCQaJGZmM9EHryl6xv1qdhhnbgYMOdaJLCfoYVsAbds2p5V5XZg7/sHHjcMuMv66vQKbcZAC0PDisTqIGRw6fpipRwZm95grcoRhdPLF7+iFZz3NmDrhSc/9+gVmBFRs3evOJvJlWb/1GTCV9DZyUokOJlBRCCz8H7+PaKLrypq5DQjfbl+a13GKiKa0GDGX5MvG6PsuJ1Csbfq7+8qnlTYTWo2nSHs2lujaLqJZomkKk+7+eYN1YiprAxPKvPGZjkfEf2MEfCbPsV64Jdc+aBzH6Del2uZDB+x/TWZ5nPhWxmvyiZ/zO/wycyWJR5do86Eii7/Gl9/c3GR9jSjvGaKbgfeTYXdm4Q1S0YmmaXKrDTZiv47tkgQxf3TMScS31vBb+xrsa+0XHXNM2vh7BtQAWtuqSWrWsK4G2EYNclkf/IqrKfY/9sHcFxzgJMAyhqRFn+wDmQM6bD/CoSkmZlkXJ6N8v/a3yAQ/tem66NqyJ817fBz/mAs6BPnmBNHJF/IB1zt2216Ql6tK35toNAtS/Y3r//Mf/6fMyHHCSAFUZa8DARewgIGjaPM8x/X1dTZAFh8FSQszRNeVUhCKlAJFAcFWMBSWn2P4BB8cLNmiy7worRkkFsjAFqMxc2Fl/vLlS65I8BIqHIcDrBeQC3kA2nEGriyYTcJwkDfAAAP3qVduvRnHsvkUIFP3FAJgXelh3AAb9ACl/1aZ8Pn5OSulz3s3K7Xf7+Px8THLhiSOeROkDFqdLPE5EgSPz2ACx8/3rHuwQMwZh8bldjwDd2SI0yAQ8gySQ8ZZMwNOYLyu3Af7Qk/MtGBTrpwxdgKEf4/zqRMSbwyDPHBPKueTE6DMiESsW1ssa7OJEWsGB9IB+3Fy7PYaJ5bMEZBi8M2YWEuX/LEtZG6wyLgiSnXV+38IQuwzQ1ZXV1d5TMjCgdHlauTA2JzI8zd2jj5ib95gXgdxZFHv3aB66DYdM3CuXDEPM/Tolc+1Z90MKvGp/B69dnUgIvIBF1Q/nMiYNTM54GeyZqwxbXHYGPpzcXGR98Mhf/Q+B+rNJpqmXe0rsB+3Lwd0wPY1TeSDC6ialCSlJOA1UNtsin0wl2lKrVP4FrfH8EyOZ0YXsq9o0slVtqkknylS29O8AkXoA3tMHIeR9TyVaoR9QzRzXFyUxJjvIUs+y9qwhuiS7YN4wdrxLNsi9+N5Bqi1bGHpt9vtOSEqMdXtrKwpcmbsVBuQu2Mcz2LNODmKJMebnPG3NRtOGxe6SfJhXWcN7VMN0nmeyTE+dzqdcrcFc8XG/VJFs/DEMeIC8nFSDwFS2xA64Z597sHzIUUhHrzOrK99OliKuGJ/bV/tZ/k+TsYgovAhJIH4JuTnhM4t6czPRBXrtN1u8+EGjMOxm2dAVte4knX1fMBeJuj5DAfL8CwqZvM4xTKXvRw8G7LTbW6sPzHcyYdliE3Y7tFlfLzbBbEz4u40TfF/+3/8D/Fb1+/YDN7E29txdQTs6ZQccNv2efIYtNkCBmjwYjaeyZFNJYXwW1jbaJohliWiaSLmuQgExUQoBBs7OAIWn4UZhYFzOxHA2IHfoO/t7S23GjFmWjHo6bXTM/CKKCV8A0Mrr5O0iNJaEVHeDIsiAHZQZjM5EZHbsswOucy2LEs2IOaHk+aezuDNvvNzt169vb3lpOb29jYzfO7jRP6MhyqNmSoApx0BDsAtXwB3Kz96AegjsTVr4MBFADDDzFyRLcCjbrHgb9YUeTEHqgfMC6BaB3XkzaliACFvOvfnGI/bDSMi99mjsyR47sM1O2T9dVWCtYpYv8ehLqX7O7QcPD09fQXakAsJuisyfhb2aVBmwEISwOcMzgyeIkr/NDpvJ+o5YYvoJM7/6elpxf5eXl5+lfhACmAPMOswlLYdJ5MEGg6YcCJhQgK/1LZtzOf5vR3fou+6dMpO38c4ldOgIiKatou2W2I6Hs+l9jauri7PVSEYYlreUktQkmM62GMY9Mx5jsS8w/KnP4VgKj49ogmO6k4xIb1YdZq+RNq4PMU0nfJ9Li+vYr9P7zgp9y46jv46sWQtrZsO4IXF9Pn4cWbp5zy2YSibH1kXb/I3+G2ackqZmeg5vzyri74vIAMAnE5nSy8kxIZPJyptZ1mfzsn7ssSm72KezyRK20XXb2MclxjHOdo2YhzPh5e0ERzPOpxO0XZdNE0bm00fyzLEOJYWI3xWstWIiHTMad/ThnZMslqWWOb5LKtz5WGZo2tLi5VBkgkEVwLdUdA06X0N8zxlgNtv+thf7uP58Bx9fz5w4GzPy7zEOI2x3WxiHKdo2ia23TaNeZ5j029iu93E6/lAkr7vom3Pc2i+jjEGVPhe9IhYi73jP7Dpm5ubeHp6yn4Km3dVDh2t/Q1gHN+93+9zNR5fxj3wR8Qx7oFf3u12uZqPj8ImnIABViHuiCH8jGe56miCAh0xwESWxFX8oG3GQLtt23wSHy2Hj4+P+UXIq2R5Ke1F9ptO3rAnA3jrFvfBL0ACIF/ijPWW9SSR4P+WEfEHP2PSyYmocWUdw+zHXZGFFAaXRMRqXMjACRVJxG63i2Uzx3A6Zd9PQhlN2TfNs7wn0K1QYJgcL5o1YQvBjU1YJk6ekAH3+a3ruxMNgtSysGn6LQNZWHwzdhgfJVICKZNzD3vEusUjZYi7sxGcou/bGMfy8iJafQwuMUQSFQNFPsdGczPfrmJwygkKejwe80JHRDZ+DL1mTV12N+g0o4MC8V1vEnb5DFmQFCEXgLoNzsCJbJikycy9S5lWMpel3f7WNOkld24JwjEyBgwN4MQJGhHJ+fN9mGpaY3DwMKe1AU/TlPtZ2WjHcxk7xm2GBHbBBkN/bETZMI7BUbVxgmx2jjm6ZcmMBetiHcCJuGqFrC2Ll5eXFZuEwQNY7OzNerIWHotPMrGDw3HBrlk/kQ16ilw8duQMMGPtuBcvmUJGzI05o+/YuJ21T/2wDHmOGSTsAv302My28H8n+2aU+D1yccDw+fF3d3crdoikAd/j0jL3AQjQfoVDZw2Zz7IscXd3F/v9Pv785z9nP4Ufc/IcETHOU8wa//E8prZZYokmtrvyZvuHx8ekg0tE2zYxT1O8vJT3MRTSgdaXZHu0WQGgI1ILa9KF9vyZl5Wu4DsiIna7QnikWJH04+1tDE5mYo74DKp9Zc0SaE//bqPvu9jvLwpQFetb66grZPO8RNt2K3ucpiUuLthL069kjG9mvbBV7LCA1vQejWlK6wJJEVH2HrrilGIgbGUiydDfcYiY5yaapo9pHKJtIvr+zBy2TfTNGfB1VMAidrttHI+n6FraNPtY5pRMtV0b01JaBd2ylXSxVAU3m31EpKSr61KyhM2l9emiX9pIR/N2K5ngW+yLTBxM0xSb7Sbejq8rBjyaJUh0Lq/2mZBou/P9+jYnJ/2mO7Pd5wr8WQdOwyn6PrV07S522edMUzq5DJIRHTMpZeKGdx3Acqd1KkkHtu39PvhG4rGr2H5njdtZDJibJr28F0A8TVPev+gqNrF3HMfceuPkmnVIRMHrqpuA+aJjxBDPwZilBtjES8ZhgElnhDsTSECoELy+vmabJlZjqwbiTlxd1XCVwvGDVlUTle7AQCefnp4yxjDeLC2CpRWZP8zNVWjuDS7hOYzbczFewY+z3nRIYBs8jzWxf2IfCDgKvUJey7LEOE3xdvYz0zLH6Xx0dqvYiWzAfpDjkCXoDuNz9dox1RV0E2vGWdal37p+16lTXhzKuiyIwRGfiSibuNu2zWDH2SzB/XQ6ZSYwJTKJ7fNGJgQFcKTSQBKB40FZASdWzGEYMjhiARkDCs7PvafAQOTDhw/R9+ldHy75o4wYqJlZA1VKr9M0rYIVBn46nXLLATLEqDlFxkrDGGHdvEHVLSDecOZN+cMw5PO4T6dTVvTHx8csv77v4/7+Pr/pPCIyA4+jIxmg1YZ1waFwPC6KjOMjsToej/kt0k540C/AAaVsxu+MnHvjoJdlyW/JthNHR3AK6AvzYF44DgMds/P1OgCKvCkaVgYdNgs/TVNcX19n3UNO2Bb34nc4A8blliEnyyT5TgadAOBwzUghv5q9YI6MCV1DP2nB8UvVXH0pAHD9JlRX13a73apayndIaLlXXZXwhkICZc3O8QzKxNgyOsBcuZywwFoCqOa5HNnrfV0mU5xg8A4NPoP8Hh8fV8mtTzwDoJRKyPrt7lzJl5YxmaXfbDbRLEt0Zx1nzPZ732K4Vox0lH1D9Xr55/gsbNCgjc+iK6yBKz3cGxtnrm1bXsRposPB3cws6zRNyXfvtuf3PmzOzO00pQpB00QT5/E3EU00Mc1zzNMUp2VINYhliX7Tp0rPMGXf8Hx4ic3ZHofTKU5Neb/HMke0TRfzNAcvx0tVjch+BhlvN+nlcWk90vuhhuEUXdfGsiSWMs4vXZumKbq+i+PpGOM0Rt/00TRLdH17Zjgjv3gugfn14Q5mwPElae2KLtUvf0t+rssxygk6PrRt2wzqvFcNvShJXgKTz8/PuW3J5Bcbpp1QGqCiF67EYo+sP/t3+I5tF5IA30rrtuOoD2Vw0km1HdCIjAy20T9si3n51DVI0NPplKuj3szMWhFD3A4DAYhPQfcZg6va+G7kVlf6TcwwVhMujmckV8YhbmXmnsiyPsjAyZl1n/UnIQQ3Igc+y/hrko21ta/Ah3oTObpu4sdJMTGUP1dXV7nqY19d41r7YONiExXgVuMcrzF2RAwAmzF/uoO4pytq6JQrasyFpJeT/+hyuL6+XuFVy93vxkJ3az1BFu5CsP7+1vXdiYbBCyAQg0ER3FOME3C2iBGzCARHmHiAKKCTz9OLaAXkGTDEbsVycMPgCUow/a7AmDFYltLy4uzNgbFWZpwp82IMdgzu/WN8OJKarUCJvEcER80JOQaZAKeHh4cVCKMSQbnU/ePcn9OFcJS0p/AM1pPybURk9sKsEIbzrYSTIFf3fPJz1tygEfkjF7/52ywBOhJRQJSTv4hY7TVxQurPEAjcSoe+EZBYM4NWwC7yZs09D+slwBanwxicWBG8XdI2E8K9mb/Bt9/GSzAAGKBHzMGVHFcCCTbYsIGLg1NErOzOSQm94Wb++OOqD0kGIAgdYPzoFXJYVz1LYmR75//In2Qeeb+9veUDKcxiYqfM02y2QZirj2a86ooEAYh5EpDt3H3MthNYvpcA7BRddCt94/NN00QT5XQf5tI0zbkNZVzpGrIzyeK54QP5POtKIgfoYY0zi73ZrGRlFgz7AmShW+g48iRhQe8jyuET3Mekzul0iufn56w3AMJhmGIatQdhXrdZvJ3KiTzopFnKxMC3MY2zgBZ7MZp0nv005epLknGq5GT2uOtTe9BUkkNknCpOqd867a1IicZmk17ytr1YJ9cp2RjP8uxiWeZo2iYi0t9t05xbp5YsY78szmQOY7A/pn2FNUWuJjkMpmyfZsEzudYUxhydhxyynhM78AHEYvwQuo5vrFuu8SPczzbz/PwcV1dXOfZHlL0V6Bx/3NLJc6lKEE+enp7yZm5iBGttX8D+ts1mkyvyrCPyh1AxYcQ9sE98InrKGC8uLvKx7044WF9axCJS3KOST+wBp2BPnDCJ//D+J/teJxP4dKoZ2HFE5A4Nfo4cWXfmim82yWU85WqAdZgjm5dlybaP3E0GkmCSCJmNB3Oi1+M45gN7qIoxDvyKSSQq1/hI5uCDOYgj/L4mZUgS6ECh7RyZ+nAkYjfJKaRORGmr7pom2qbNp0OCD7uui9vb2xynrP8cvOP2afspLo+dpB+fWZN0/6XruxMNnApADQDCoDjrHmGwKGwKwrmh+FQZKGMej8fVpmQUCENH8WH+CIZ+wZUBLUCS8hdlUHo5N5tNfpGXGRSMAYdAcHbgddsKYJ4kwxm2S+kYtgEaAdTgxYkQzok/JDhUNQBDBBcqRgQNFNrJDc6NoxSZN4xnndnyc5wmTobz78micVZcZnqRDRk2VRI74IjyAsCaOQdYea+CwdF+v89J0reycuaM/uB0CqCJVZka3WWtaoDIOlrn2rbNZXBOQEM+jAVwzNqYIbSe+eVyBum1Pfpv1g5HjtPA6WITLs8jc3SQ+Zs5MWvnUqmTDUCc2+gchM1GMU7/vGbUzF77mD7uzWfQDy6TBwQHwD+6wxvlfSwu34GUcHXEgAC7R76ek8fBz7k/Ooa+EThZF57BWhIECDKbdhtLlLYyz7s59+t7vshh6vvU6xrrI8BrRs6MI34SXfH8TIzgk3hunTDZl0REBokO8l5Lt5w4Oa4JLNYT+3Qb4jAMyadfXMfr2zHfM7UJcXwmfnhe+cPttj/rZBO8sC59t4mm6cLxdFki0umHc3RdH20LqZb2Ec5z+jOOY4zTFM15zwokzjRNKXns+ug6AEBKZq6vLyPaNk7DKS4u0l4Qr1fbUpVMexSWZT4nOaeIKO03xDlsHN3zJli3bmDnPoUM+8RfOhabRHMVIyckUdbVlQjbp4ke/AttHOgA60zV3S2VbvvEjtgATRUZHcW/4/cBnN7bQfXG721iHOgShBKyxGeclLwa75Ac4Evs+wDD9hGQJ03TxOPjY47zfP/l5SV/n3U+nU756NyIsvHdiQykAv6H+MMc6y4J9lj6uH1ilf0I8dwxjvkQV1gb5owPQ17MjzFut9t85Lkr4/M8Z9LIPgGfDTYEDKNzlinjw3ewfo7xNeGJfiX7a3M8iVh3GRD3/QzirCvzbslCxvM85yOMqeyRtOHv3coGYc+8Y4mYl0IGuhplQpf/OxEy0Q1RZpKXeXqdItYvBf6t67sTDRYGZUM5UQTvUbCyAyhRfJeI2jb1QgOifbSbj39FYSknPT4+rtpbAMMuyTnh4Lk8k9NTuDcZJcIDCBgwMS6AooEoxmKm0ADQAAjlMitCadr3ZF5d1+VNbM4mMdTNZpNbi1yxiChv00YxIyLfA+cYESvjRzkdXPiewWF91Rk+OsN3UXwHMRJUJw04EebI89EVg08DDgzY1QqCGcejso5+CaJLvb6XWTKzQWbp3aoSUYAge3mQpdlSmGzWkdK3ExIzh8jUjIMN3ntweD6yQx9JgPxiMvTUm+55xrcSfJ7ntWINmLOTBuuRQTz3Iik2uK6dGgSEgRbPJmAzLgd4fmYGBp/ke5rZdBB1u4HZYO7hIMrYPT7miy0gK/8c/8TYkQktoSumtOuiaQvDjdyWZcktM9g44+q6Lpa5tK2QCBpAYlfWsW8ltFSfI8ox56wnc8Am8cH4WAdldIo14dnYEcAQIut4LC9YJdib6av9LN8dxjGWJeJ0GmKeS9Vvv79c6W1O1s76ut9fRtq87CPLsas2tluqIKmzabPZxjyvGfCI1PJEwtFE6U+HfLi4uIhNvz3Lhk3IaVP3PM+x219Ee2ximubY7y9iWeZzK8Q20lG7EeyxuLq6PI+niXkuPg77Rr+wJ9aHd55gnwZz2+02rq6ucs87PtmkA0Cu3idgH2UfiX/GhzrhnKYpv0PhW5XQYRji6upqdWQuOoSN1OAJ+ze4jIhsWxBaxEt8gJNrfCo+j/vThgwx6udbn5El/sTyYL7ouplo7Ag5Ec/ARU7y0GNkAwbwQSoGvHV1ywSoiTq3vzIeYrgTFdYPW6J191uYEExhwqmOHcRt/AGb2iGIPGZ3ujBeH09u8hOdqas2JjUsC+bpJJQ5+NAYd7Tc39+v4jn+lflQ+dntdvH09JTXnb0VJPrWYY/r6ekpLi4u8smcfV9ecBxTiVGMCULX2BM7tk74eei6iby6mm+catv6S9fv2qNhZpCghMIaYPz6668ZqNPW5P5pghbOBsBDALOi/vrrr3njJAr/4cOHFTDhviivmSpncDiY19fXeHl5yW9Ihg13CdGK730gNkiehzNEcQFZ7JcgSOLMyFhJJqgUGajT2uFAz5ne7mk0eMBRU4brui6+fPkSTdN8dSJERAJjvBQPJaLsfH19nZ3VPM+ZLTGIRAFdtmRMKDHKDmsAwODzMFB2SHWy4gTIyQE6Z8ZlmqZVKxiyRx/4Y32NKCAFwM943HvuoMG8uCiRE+AJ0vyx43AgxGHVSbqBv9kFO0aYdQeVy8vLnFCwCczMA+uA7XqvFX/zeSc06AZjsLN1EEaHGRtBwJfXoAC69Uk2/h36gs9AR5AnMjfI58JZ7na7uL6+Xh0JiV9D18x4Mn/PiWoYv8P20UsCv98nQUB2cGVNATkmRuxjeM5mt41GbDDvDzmdTnE6liDF2HLidLYF5MaLw/gcDBnypk0Je0JGtC3WwYW/vRYkcyYVXA2cpml1AIZ9keMKQZkkxowc+mgfxNq1bRex0G4J6EjVg+QLeDFmqgoUgiRt9B6GchhDWu8uxjElGk0DeJ+j6zjGGnY3baAv+jRF08zRno9pd4Vsnud4eS3HXl9cXETbNZGOdef9FRFNs8Q0scm4j2ka43QqulVO+qIFr18BE/wCfo54FFFeJoZ/43MkuIzX19XVVdze3q6qAqwVm5yzTKIk0F3XZea7aUrVwUkQf0i0ibE84+XlJZ9QaL/E85kvvp51MGtuf2kbYE2I8xGRD42xPaHvjuXYv8kHxoc/9d4iKgSs2dvbW07I6RpoZevY3n6/z50MrjqRbPEdgDY64gq8dQJ5YNfIxPIi9tfJBSw68jRR6ViOPdu/o4t+Np/lcmLGvj8ufD1jAx+ZMKNqZyILv2FSBNm5EuWqFvczaUUVBxvDT2RS6Jw4QaizfpaFcQvyspxd5aayPU1T3N7e5qQeW8vt6DFmnGVy2GRKTQhh4/zteMTnLXvL0Dr1Pdd3v0fjf/mf/tecqbEAAAoUCcfw+voa9/f3eUOTAxJG4s+bdTSz7NIRCoGSWRAOfBhaRGRmvAatCBZl5m/m5ZcJmekhA3V2+PLykhcNx2TAQoKEok3TlPtnkSWVCSoNzmSbJrGDj4+PKyVw7ypyJdt+fHyMYRjiw4cPeVOQwbszZ5Sbcd3d3eWf932fN87V7IMDwcPDQzYKnJgdrpkBnEPNFJCEAARd2nVlisuVCMZfMwBd12VDZUO4nTjPjIi8VugmQI6xAz4dYOww3G4E8OZnXHagMB0+xcxsgZNtdIXvc08OTNjtdrkPk4QUmdqR29GzDm6bYl34t4OrA6mrLrTF8Xv0ntJvzTqzLqwhMuOezBNn6DFic2bsGIcBJ7aGruN7WHNXEfg+c7Se2/5dBXDwtB4AjN3b7megD2ab6yQLveE6Ho/RnecyTmPcXN/kCiz8edf1ZzCcTjdKffxLxMJm2rR/YLtN75EojPKQSQ8nm2wwZ4x1IsX8u67LBAa6wJry9mTW2rqLjtV/W1eLD2I/T4kh+/1FJkz6fhMc15vY3Ck2m4tYlohpLCeWpWpB2fPTtunI4FiWWOJ8StNY3hMzL0u0TTnZjiA8DMP5uNVS5UM/zQafVz76TUlKrZ9ed9q1kH/btTEMY8zLHH3XRUQTd3d38fz8HIfDIa9FigOpzcsVQJI0Jw5tt35TOuRVstv0u905KZ3ntDE+mkQi0dLx+vIabdcWkHyOLcwNwmwYx2jbJscp5m9gii6h6/hhJ9lOOPBnJgx9so51yetCZ0V5n0jZq2FfwWcB6F4rdwmYXMUngAnwQa4WuKUXn+JquRM85ui4SSwi9iPLOo56DAaY+FsTVI77dHW44o+NQ3S6M4X7MeZHTrk76wRrjB45LnqdTY6ypuA8+xmz7pDRroLjE/gMNmSCydVh1gQZ2y5rkqwG6tg/30c3iLeOI13X5RO4kK9xJbHZVTjHwIhY4Y9pmmKepthtS6fEOI3Rd2d9lRxMqLri4kQYvTJJh+9jLibabGP8YT3+r//t/yV+6/pdm8ENYJgU4I2BYURkjGYXXYY0S2sBAJop+by9vcXNzc2qNxFBsMhmMtq2XR2zCljDadFeQ9nf7RdWApcNMRiSGBSO0hWg2EATw8WhuxWqMFIFODkh4/8AAjMyVshvKQEGT5A3u8jmMNh5KzpjwRBRVPfk2vEaPDnBiChA0iU8wBhjr53lZrPJbzU10PJ7QHA8AGwHF5wIYJKARbJq2ZqFQmYAJQMpdMisR50gOXHx7+wMCYbMl42C1uWIArztjAmAfNcOYBzT27Gvrq6+SsYMgCw7Vwk8JmSOXKzPBgYR6/YhAwmSZINpnBd6xJz5u/Yny7LkjYQkYPgJ/As/R2/QJeQI68RcGLd/j1xcSTUYdsUDWZkpY20Zt/0ZCRY6SrLMz2pAYlmxvnb4BlOn4zGmcYxYlhxclnk6A9IzoJ9ipYOFYZzPyXw5/hGbwT+WMZe2AnyeARZryMl0bst5eXnJ7aF8Fnlil/ge7uMKiNf3dBpW1bNpmuL5+SWmqbR0YC/pvSBtdF3S0bdjOrBiiTmm6exD5yTLZT5XzDL5cYx5mdnrfV6TKZY4JwNdE/MyRL9pYttCCsEONzFNS7TtEtM8xu6CNtGyJwv5QfAkcF/Ii3kuPqIZzyevtSVJeXk+RBMRV5f7la047o1j0gMSgHEc48TG41VysslteuM4xmlI5ODh+bCqNmDPm80Z6I+nWAY2gzcxjEPMi06B2vQxTmOM45DZeSrzxGp8AfsjTZ7h3/BXBnQQKBBs+B1iINX+ZVni119/zbbgBMwkHYwwybErJSZcbMfoqWMMJ2nxHTCSq4Pu2+fZxBkn89gAMYI2W+Kf7XC32+W2Y8jd/X4ft7e3sdls8ulJfN6+hriKn3esiIi8/xJ7A4vVsXaz2eTTjJATNm6Aji1P05RPKES/wIr4XvTdyTlEtJMu75EA6wDm8TGOe9gL/zbBaqBP1dcdCo4ZrAHjIw6gP9YXVyasq5DHxovIiLEzxkxuTFNqj2q71Jw5z9EsiX7ZVM/mMkZ3Aor8+b2JEuMzE6wkX8YFNZH6l67vTjS8QLwLwRdCxAhrpeHzKELpaS1nWLtnmWSAAGhww/dJPlBC7umd+TyPkiUXJcWI9RtWrWC73S62220cDofM0BIcyfBxHLCvZiZJMpxxO6FxeZcNXfv9Pis7jpOXWrnE7CSGyhEBl+fb8K3sJAWWac0gAPCRDQkgiopDZSO2ZYtxuA/VCm65OzkC8PpQAJ+Kg8PsunKyFWuPjvLviPLCGwyXwOWyLYaEgTlpNDhCZq64ofNm7Bwc3XMbsa6wmWnABvgbHUbmrmqwzjm4qwXAZXcncAay2BR6DSgE+AG8DWa8Tp47z+Hz1m8zVJYZoJQNmui1WVrsCDkYhOLYeCbgn8TfAdvO2z4K3SfYmaFnDcz28HNOlGEteY5bygwc+B5B2aySEw+APuNDl/mebdeBxPprFqwOXiZLuDdrhz4dj8ezT1wfcuDPO/Ca8WvbduVfAbKAB+aI3vA5Eg4nkyZ4ar1DV+w7397eclUZO+DzyM4tiFSavF59X+JTqdo1cTqVxN7fY+0uLtImzGleou/a6Deb6BY24x9zQtc0pdLOvFxVtb9iDNi/CSZIPNsl83DswYZo3+i6LhrZ4zzP8euvv+b1OA1l07R1//r6OsdJDnVh7VlvJ6qsJe9kIX6xUXmayhHnPvDEQBPQ2HVdrop5g7djNXp5dXWVEwbvK+P/PvLbCTNA3h0OtW0S63wQiQlDiC/H1N1ul/dHXl9fZ0xhdp9EkHEQ0yLKCW3YAbpeM9+uRFxdXcV2u40vX76s4jkAnMoz7VroGWvrl2Kiq7SxucJsXa2rlMQb9NhdD8Q8noHemxAx+WQCBp3kM3SPsHYkdcRXv4cCHMVJVQB82xXPYDysD7GS3+O/jfXsp7BLfB0YyWS2L88PXUCOPngnE8Lzer8keohf932cOJqgt18HG1i2vpxcmoxDd1jX77m+O9H41qZTDNksKYqHMngTLUZusIKhIDgETxKBYyVwea+HDQ6lPhwO2YHwVs5pmlY7/alwwJIwntPpFB8+fMiKTYLiDNSbuW5vb1cA3QDDgQAg/S1wZuVDMZ3RElTJbjEus988k2NnmZ8NAEUiMeB5OE4HdMuKQIXzdguNx8f/cf583w4JI3ECxPoaICGbul2KQNq27epoNu4PmEDHYMW4p1/I5v0b3tTHGpKsGtw507eTAGjWAN2JJD+rky5XKviM7Qq5ODF05Wgcx3h8fMzyRxfNmPFZA2EOQ7i7u8tJEfMyU2/wiw06iXUQNJBEl7AbJ20GvXbeAAzAIs7cVTYDxIjILTTYBsmJxwBYQM74Ijt22643YHr+zM8niETEan+VEzwABE7axyKa0HDi658xd8r/gBqzbK64MHfGj2/z/ak84IuZAz6T+fn5nnttj3UlyYRBDpCKG6yVx0sM8DoyBvwb+lDrtMkTwCif4x7oGffynEg0Dfwc4Pm8gzA6M01TOu1lPh8JPZf3KcTCKXnzV/qT9G89D3TGiXqd5NPWQrsLoKpUwMdVZYkY2LRtDOfYaWDIGn6LeGLtLi4ucp88foKYbv9dgxq3lKAnBqb22+wp8wZt5GUiwUlB27b53U8QcfTDu4IJYcm/AaFuaeLq+z4DUmTsNakTfuIP8YK5Wf+JkSZBuIhV2OzhcMg2wTrMc9kfyWEJAFETO8iYPZrWp2VZ4vb2Ns/16uoqE5TIki6HerO5cYQTJfTQJDG/A9yzYR6fBmmGryephCTzSWnICV9m8pl3bT0/P68IrmVJeyMPh0N+J4ZtjMoWuucqP3OzrV5cXOQkzPZvJh+9Qs9NTuF7WBPiD/Zsghb/hx8jVhhj4EvsG0ww1ZU3/A1JMWPEjm9vb3Pcq0kdxyPkQUxwNeevnmgwELcN4QQiSjblTBJFc789xkACgDGSIREcEYAdkwNw16XTmDgC7uHhIZ9qQSWCIEIZf57n7Izo02QRzM55/4JPwkJRAA0YgisbBAMcNWC1ZgQJulY0VxRIjtwaYkCE8nE/7sn46hIa83l6elqx7K4C4NDMstoYHLg5LcFsKuPjZyitKwYGdMzD5Wi3QkQU5thMFQEIObPuGGhdlq6NGcfIfQkCBGC3/jFeM0mslR0Oem5ggjMhkPAdgjUOgWSHIDJNUz5ZzUkpgNNOzAld3fLEM9Ens4J83gCez/lC1k7MWOf6YAIcEzIFrOPkzXD5LHme6yQF/cGnMEcSdTZ3Axj4DGtqZtttGKwvtkeSeX9/n1vnnp+fV8cT//jjj/nn7JXimegZY7dNWWcMErxWyMe+jfUwy4V8ACBcTp6s79zflRnGQvskPg2bKH6qJBkEOs+lbjdz9ZbxsL7ohf0N645+wwLzWfsPfo4vN6C1zkF42Pb4LCCw3g/lAIu9uy/aQNl6R6Ke5tdE32/Pidr5Te5jOnI2lq83ueOHsHtk4FMRa7YVYAfItR/FJlkvrzn73V5fXuL17S0aJVnc4+LiIubF+3OSrVKVIB7y75eXlwxa8aE+9x/dNoHDoStOUKyvgCTWjiSd3/mERB9Kgk7inyIi+wPAuls/iJcmg3a73aozAlBo8skJ2Ha7za2qTZP2IuFfkKurkyZIjWGowjlJcXsdvn4cx9VniZf2GXwem6jtHT1A58xiT9O0OhYXvFRvmGdd7N+xgxon8Hl3PUDkWs/Qb1coGCPAluSCuO89nBA+xAViR915YpLbm97xbX4u68i6MFb7dX5GbOT5TjK8Zybb2fn7EFAkvsiEMRvfmdTvu4KHje9IkIn3jseWuZNgKoZ+pv2pk1j+7Xht8uN7rt/VOgWAh3FFocwok51GxMpB2eg5Ws+T4/84NhQcg4IZGIYhb6pByCQdFxcXuT8a5cJhAHA4bQM2xBuMKNHCljsxwCkBfFwSNYjgbzJ4GzKBylly3/e59GcW1wxtHaj5m3mi+CQ7yG+/38fDw8OKBfkWKMJY3NPKOgIaPD9ny3XrkYEhzzJry+XsnnX322n9UqE66+bfZlwNTPwGdAdkHIsrAjzbbRwE9toIDX75OesRkYKgN/mhHzwTo3cixdi8n2W/38enT59iWZZVYEWH0ftvjQH5AaZ9GocZEObCfPk8ullXKXhG13X5gIF5nrOsYdpxUtidZcq625F5fcwaOalhnoyf7wBGDCpZHwIjsrdduhLHMzjL3PPleX/+85/z/AmuZtwi1u/IOJ1O+Q3EsJa+N3bPZ20nzM+VOYI5DB4+yySNg51bulxBNlvrCjV6V3zDuoKBjdSJt+3c7SMGya74eU1MACBD97rzGVdJ3fbiBMh6gq9yMk3yaZvjs8yb9XTCxN4CJ5Pcu8yxiWnkhKBjpE3Q7Ve6XVepNpt9pJOkSvWFsbmy4iQbXQcUW+dLdaq8y8ovdVsi4sP5gBZe/JoAXcTxlMZ0c3OT9QG5tW2b9W6z2cTHjx/zHgDrgUmYpkmb119fX+Px8XGV3PA57ImEzYw/YJ37eXO435hMcnN9fZ3X7/r6eoUPGF/dcsh6ukWFefMHe2F8+D5iO/Za77PEt/Bcn/yE75jnOR4eHvLpjowVeflIe8d65uMOCWyD6gNrDoB3nz/xgFhJwu8YYb11lwk6yVwiIr9mgISQWGLymHtCTHESHljMlQ38Cc8AC1mHGCs6TuKDLfn5+BWTjKw1/oG9LKyd2XvinPUyoiRT+AbuS8sVF/jQccyx3CSnfTHxwj5xt92tYon9AzrMuhh3+H4mt1zFMbFU4zL7JHcCEEe/5/ruRAMQS08cBmbA4KoBwaHrugzAcPjTNOV+Z46cROkQEozExcVFLilGRAbSAA0U9YcffojTKb1j43Q6xf39fb6XlbUG+Q7QXjxYGp/L7ID2+fPnzHLiNFkoAAwJEPfk5AsUDeeH00DJvVeFv132J2GZ5zlvfMdQcXiMDQA/jmM2aNYGhfMaE1zsMJEdhuExsK4YikEQSs1lxtuJlBleV41YG7Pu33LmGLArFQ7MBhOWM46KOTI+dNttKozfyYlBFXLhOYyPewHIIwoYcrXKY1iWJVezWBf0yxsLmSdyM/NswMa43VaCbXBf2ytyYy0pQTthi4hsxxEpaJCwdl0Xf/rTn+Lp6Sl++umnDBa8PnaE3Iugbt1E1/i97Qaw7BYIrw/B1KADdhSZYEdU6GDD+CxBiGc4EETEipGCtYJFY8Orq1JOkAm+sJLMGfsxawnB4oTMAQ4ghL8ys037J5fJAeRtuwCsen1IJmrigH8TA2jZwtfyjAKwNyu9d0IXEXme6D3JALYBUMKuXGHDx/E8QAG2S2LmPU8AOmKWWUbG52SQ5xTQ10bblBPH2raPpmkjvediiSWm4K3etmWvA3bUtm0+Yx+9sL0Z9GLHED9pLOn9HugTcu66Li7PyYGrx/hn4o1ZX+upwTC2fDgcVif64Dv8RvK2bfPbtG2v/MGWnSyjx/jHruvi48eP+buuKrla5/bFvi9vBjcxAQtusOoN003T5Das2peQLPMOA/wZukCF2jFsmqZcAZ3nOZ6enrLPQE+xFzpAiKn2zVzoBCcpEp98uh/JE8kDOh8Rq43bJGz4IRON6CPxBrDMuvH2bEBm3ctv3AI5S8KK/YOtaj+A3tQMP8mEMYMJb+sPa+vkEX1nrVmviMjy49lORHkm/okuF5NzfJYYSux1jHU8xQf4d/g37sdaO+Ge5nWV1kkRY2NtqaLZtxrbEUtZd6+hZeF1YY6M0/P8reu7Ew02C5pFxnDd4oFisEgRhT1lUgyOKgTCRLHtvJg4CsRr5wmC19fXcXV1lTPqruvihx9+yIGEfj4W1aB5WZZ8NjfP5//uqbPSkKQAglBoBI8Cci9nfThOThyysrOwbARHJsuyrDZE2/i4B4GCz/FMApdBKIEJBo0ExVk1c0FWdSWEEjP3NThyfy3BwODb+uGAxO+ZM32ktcPlXsyFZ/Fvzms3y+b5m6lzuRsDIiH48uVLniv6QUCswSyOwAwsOmYWyAAeZ2Nml7EyLoKgEzkHaycgAAbWlL5mbI/gwzoyTvSYIIMjZuzICkBgBgU5uEqCDVxdXeXn2Y7QFQI65IWdLDJGl5kPsiHo/+lPf4rT6RQ3NzertgSPEd9EsAEsO6kDHEEKmJzw2tRHSKKzBqtmYCMSIeFAZqfvlpfakfN3zWjzf1+spe3Ja2bdTD6oP9vmIPYYUBt5HbAxH/tMMK3ZL/SQ55tQQT5ty3sflogAmLTnzbOX8eXLQ1xc7PJ6kQiafWNdeZYTKvafsb5Uj9EJ7AodjCggCf14fj7kZOd0OsY0lX0/CcDQ3kercETfTTFNc2w2fcxz2VQ+L1M0TWkl3W43udqF7+dN7GZd0TdXycxA41OdCCa9TM96enqKtk0v93t+Tsfhfnl8TECH2NV08fzyHJu+j35an7KHr4W4wqeTyNo2vkX+OOH1BmDbOOvhZxLzrDuMw88B5NckEPdB5zjq9/r6epW024bw4YAt4qKJT1j7+/v7OBwO8fnz5zzfb5E1bdvG09PTyteydmCDiMinLHr/J/tasT1iOq8MwO6wS/ak3t7e5v2ZxCzvN8XPYO+Of078neCaEEQPrXeu6pK0AL6dbGC72BAJkgkTJzj4ci7W3YQ28cwdLU66ISKIGcQkYhj6y9gYA2OOWL/12xUPsCwy8v3QhRq4m0h1myrjX5Ylv5OD5I64TBIdc/G1zNUVYo+JhLxO5B3TTZygq5tNOpnU6+Jnen6/5/pdezTcn4oQ/vSnP+UX6uGsImL1NmaUGrDQ933c39/H1dVV7rnjxXI+Dapt2zgcDtE0TTw8PGQjwyje3t7i7u4ul3LJ5nAeOKh67wIAASWjR5RWB4zH4I05eAOVFYggf3l5mdk/AwjmhiGiQHXJEuVGVs4gvVnu5uZm1feHMo3juKqcsHaMhYQN9o+5kHDw2e12m48oBDSj1HzHQIg58X2DbpwMa4dj8EkmDgAYA2VWM6g4MDv5mo2LKAmUWTC+ix5774EdAUkmDLLn6z03rhi4WsJaWr9grHF+Bvo8F51FBqwtziii9Lg7aML8clLYw8NDlgffty7CLBOAaiaLiqUBEOO2M7u4uIiXl5dVq6OTTRwSejLPc3z69Cnmec5VTPqL7+/v4+npKY/J+gSAd/Btmib++Mc/ZvsZhiH3MtvBQ464CkUCTMD3iStmgJABBIPJitPptErc/PJP/A+g0pVQJ43oKz7Tz3crHfrOfVx58lpw/2/ZKTpX+qmbbBMp4G3y+D1exoQ8XQnhZ+ih9QQdjoh4enpcJS7ovPV4HIeYpjHGEdsZom27zJ6iC24lPB6PcX19/VUlkTXinRObzSYTSLYh1qiQYOwR6+N0Oq7Azul0XCU7hT1PL/RLx+I2MS9n0iGmSAflps3iEUu8vq5BDusTETmJZWyABSdd3vyKT8XWqSxHRNzc3GSfwnptd8n/xjJH2/YxL3O8vr7E5vwCPn/ehAprZELCVSTWB5v0fgn7Rr6Pb0R/+IyTY5hffPnt7W28vLzkSo8BG/GcSiSyIeFvmvQWdPTARADMOt9jvmbC8dGn0ym+fPmS/TagfJ7nfHIfMYtKCokucZu9LVQTWEu3CeObTZYMQ3knFraMH+doeXww63A8Hlct4CZ3eN7Dw0P8+OOPeXxu33PbKfe/vLzMpK73wWBDEIMmotEZH0wBnmC+6Dm2USc0rs5xf4/BxBhjIkkmMWZMPN8Yluft9/vcFkyibDs1qXx7e5v1k4v7GGfxfT6LHNAfdI6qWB2/sMPX19doo4lOZL3xLIlE3dJFzOJ+JoHwvRGx6kRhLqVKW/y8Ez6+9z3XdycaLAo3BiD89NNP+f/u/b25ucnJBgqEkCNSPzt90QA7t714Ub1YOFUUE+PG0RiQRRT2CwVzwLegYDRIfJiPEw3GgMFj5DWLjeMzYIooyQufAxyhdKfTKZepkYWdHQpMoCb7d7WonruV0sZdM0ARsXI0yID1c+LA82zk3jhJooQzZywR6zd9+76AiP1+n184CBjlvig5jpjvclEpwIj6vl+9tZyxOfEyqOIzu90un7RimZrxd0IQUV44iEPkMjDB8M1A4AxJ8gjKtCHxPQKgnQH3xeZojSCoAUbRA3SUwEF/NOPF8ZFw8ywYXcuubdv4/PlzThohEqj4MVbsiXEYwDh59cuN+DyghjXHB9HmFBGrvVKAaOzEiSsywH9QpfPvcdLInR5tl+wdJNEZApv7ods2tY3AWjIfgATtc6wzOuFKlNllLvyHwfqypKqMEwfPhfuVsTfRNIVZRk8At2bs8Fs+QcvBicugHF3j2csSKz02G1f7SCfbACWSdOSGLdAeW7OS2DSfg+Emfp1Op1z9IEFL65/AAHPlPk6cXSFM8isHJgCoICleXp5jt7vI9oOfo+qKPdqfocOWK74KHaGicDgcMkBwAts0zWpfxTRPqwSQdXH3ACQYazdNU970jA+t7XEcy0ZpbI4xAxCdYNgPWD8YA61F6B36+vj4mN887ko29wJYI0+3D/IZ2yy2SAzzvdgMjn7TGg0JY+IDW0EOEZFP8SMOtW0bd3d3cXl5mW0bwoY1IAFiHcFK2B7kpqt7Pm2PtTUhYx0FlzmJm6Ypfv755+yziePEbghLdBb7fnt7i8PhsMIlrLlJIPTIFXFs3YQN+kEMJp6xLsQIk7AkFMQBg2EnSTXZwmsKHPP9XO+pRNeWZVntuUC/TGoyP+KIk0QTNib1sGG+i+3UZKqxSd92sTknSeguvgz5uruFqlf9Kgfiwrfsspa3iQWTY17z77m+O9FwFu0+cZdJyexxQs7IDFQJahGRmX+yNiaFcGBnzLo6MeGzAH+ya5wOLT4swjzPGdTgPCJK/xoVCY/b5+e3bZtbCbgHsomI3PYUEZm5wIlElNNdAAmuiJjFxAG7vSqiHM1L8POGRk6TYT44QAAILJGDl6sZKC6ycGBDfmYBzBQ7Q0YeNXPj4ORnmzlmY3zEurLhIGOWhsqEk6eI9aYx9ju4JIjsDSLqBMqb08yGR0SWI86ItUX23A8bYe3o2fWJOzzf+rEsy6r1iHsCINFFs4IRkWUBY1OzPRGRT1XhHnwXBgbHb9syA70sSzw+PsbxeIybm5t8djuO0ce/8of1xAkia5wmc7KN4ydw/oAwnDNzN9A3625mEBCHzLEBJ+kGdF47J6bIDJ/oANp1pUfdFQDsyEAOecIAo1/c1+uALgCW6wQBOSAzqi/Iy8CVz6f2pcjrHhGrDcTuf/d8uQcgwfOvk2yS9mkaYxjWx3DWrQZ1QpSIh9SLDkhDh9GJOtlHZo4zbrFBJwFeTr6WZb3xGDu5u7vLrLMZSFpyE0FVQD5yAGQzP1dy0EO3+32L7Yf8quXP2JxAc3987G63W71/CTs3aIyIXAWEEOAz9TtuiHn4KRM8tnG3HjkOO0E124s/wGchx77v89guLy/zATLDMKw2cKNDtHAzb/sy1sQVr4jyvgjs6ng8xsPDQyZ6kPnj42P+P4kVP8cuGQfrytxvbm7yHgzGQ8zyGtJG5kTG9kUyhe5AwlFpwR7YE0ayYbIWDObYx1vfnWA6YTYRyrqhI5A62IHv63XBtue5nAhFkkIcAaeBu1hbJ0mAXmIbJAH4zMk4uoI9odvb7TaTUwblTdPk95jRSeGWXi6TetZ/xzYTU06CuBcJHxUvJ/DENezEvr6N9SEG+DaTONgsa0O1xPZvLG7dIA4TB5gbyZm/7yry91y/q6JhkGCWkwkyQBYKpYMNiShlOwduDAg2FKE766pBJ+wxSQfswzAMcXNzk0vlFgwKb0DkjUQEShbGDGlEKbthxCgvDh6QjJIC0s2SIj/AP/s1aMuyY8DYvbAYNj+3EbVtm9nocRzzKVwGMiifN/KTgGBEdgTcp2YNAbBmNc1W8V1+jvwwSuRtAzBgNtitN/QiUwfv+mQHnueg7YBvQ8NBOZGIKJvv+EOAQ2ZmLBzMkR/At2maFWuE8dspMg7GjxHjuLAd5o7T99o7sDhR9Glp6EG9N4J7oh/YFtVCmHrmA8PIelLBa9t2tbHZsmIMthMfvUiVNCJWtug1tP5Q8mf97C+WpWwWdaLiCpurTE7aGAtycjkbuUMC9H1qMzRbBkjwqTV1EuTEj98xLjPT2CZzcDnewBaQDJuHPpiZx4+ke6yBK5/nmYzD4IS1wg+afPC6oK/4z81mk080gmlzTHG1FvCUnpuqISSR19fXWXcAIOxxYBMtm/3to4lBsPTIDjtEXyIKsOGzAB965/u+zycDeW8PVWwzgi8vz1nu+HoOCMBPs/YcLsI8X19fMxh1Embix36H9kxkvt1ucyvlNM/Rd30ssazW1y/eNfnnJLC+p0kft8/4hCuDNJ8KBHBE33ie9yigx8uy5JfXkuh5POiLW59IEogd2Cly5jtmiok7jIPvvry8rFquvfcHf8PfjtHWN5MNJBBsjqeS4AoMiQL2BvFKogIGMnFrMhCdN/NPS60rSMR0Ygr3dGUGvcJnEgtISh8eHnLFA1m4uuG4RucG1Rm3xkEkgAkfHh5ybMKXsD7YJWNnPc2sI3vGQ6Lrit7z83PGmsRH/BF+Djtx8o++oOeeH6SqKyau+Jh8wof6UBjsj70nrIcr2kvEKh4ej8c4HA6rA0wi1qe7kTRif/6dxwX+wRcTN9AnYzO+b7n81vXdiQYLwYL7IQbBz8/PcXd3tzJY3jB5eXkZ9/f3q2yPyXAvFINg5uCJU8fBADxubm7yfgJYAhyaT8VBuDhhNpZ3XZdPcsAp1qXBiKRkNzc3MY5jTgqcBHEPb5qvQTSZOQqLYhl42GFZ5gAOPsfYSPpsdG5Vc5LAc2uQ6ZOvkAG/81rzexQTw2K9DPiZkxO8iHLKFnLBMbny498D+O24nazglHjut3TKWb2dO4DYfcWuADjpBGxzb5w8xmznwrPQdWwGPXSiY9aSMdUJpJMqz431N8vPdwxWcRg1c8ozmBvf5bq+vs6/OxwOcXd3t0pScNQ4b4AC64GcAGWAd3QGsEog5bOAN+zIPazYBuO8vb2N4/GY31bsMj5g0XLg7zopc7mfqgB6gRM2Y8/n/V4KbIvn4Bd4BnIh8STAuIXDtuaEPKJUSZGJdRi7MDtGe5BbslgHdIqxofdOkm3/9steX/yF5QsRlNqEpvj06SVXw5kP46yBSamaFjA4z+nUHvSTdh6vN6AcsAaA5VkET7cYMs8k0yIb9vo5oVqW5RvtPaUNrvadAD1kbtKKvVD4FpMzPvnIraAGD/456+NEFsYU39ZuShypCR/8q/3u/f19BoPWC5Ip7B5fYPtwG8nt7e1qvwnsNGuMbZCUW5eRi0k1YjX67RhLct91qf0TggW5mpxA3gBXV+tsU8YN7r4ww46O1H+wPeRCrHK1YLfbZf9BkowMp2nKbXbTNMWHDx/y515fX1fVC6ocJjZqsMyac3IWlRAw1sPDQ95rBjYzyUgsr0k9J9PYGXLE77hCxLyQnZNUdNa4i3XAbz49PeUqkk8qdZWVtbeNIFPsyMk6ukcMst9x/DTJ4vm7E6QmilwpYtwm40jk0EnGAFHL56ZljuFUfJ73GTIe/BR+DZtjXI7dxBDmQxJq/87vuAd+1oWC77m+O9Ewq+JytDPaaUq94fV7I3yKggMdDoqAcX19nReBe+PsIlLP7sPDQ66YMJ6IcmSoWWuEXsrjpZxHSRZBD8OQXwDmoMrY9vt9fs8GAYrfATJqZWSebl0giFMBcfC3krLozkiRMY7LgAFZUWImSXMmikFZboyJe5JVm6HAWbv1iPVFmTEig2QDoZr18Li4p1kI5IF+1SyUe9Dt7Kl6rZgAVYScvKAzOHMD0BqUIieAHk6AezFHGNmIWBkzc8Fg0Rmcmcfr7zqp5N/Pz885YNmRIWsCJ/clsXWplLEzLp7p9gInSQTveS4vveQzDl4wigRkKnh8trC9LznJp/zPAQHs98BZcm+Pm+cTvN0KBtgyUGZcdUWA+dWMH3pqB06Q9b4u7B99RWZOnpmPwZiDKb4G+0Z2EaVFBl3Hrxm48jv7hsLSl7fcYh9JrsX2SQxsZ74PbL3JEQMHgrrB2/F4zKfuATi9dvgaEzLzPOd9P9h61339MjRiBFUGxulqFWvTdV3eU8dJRARafz71um++krV9JrqDrHa7XXz58pDHYaCS7Ghc7YMA0Dl5dfLppIEKyDimF7YRByJidXqOYwbAi5jrtrmlbbKfRN/QbUDqfr/PRzoPw5Dft2GShWNjX19fcxJhkIcNAfgN4vkbm3X1bxzH3DpU6zQ+gMQEPXCsdaULn47ts961fbnibj/i5AW9BtDiH3kXl2OaY7dlzfrxO2ye+6NfPJdKMWvIXNhYTl8+OowNU72gusW4mBMAFL2/ubnJfpFj/8dxfUrX5eVlfi5A2mQPpCay5rmO9/h85oYOIzNsgf9TmeT7yI3WUx/CwZ+7u7s8PvtfJ348x8QSOsX6MK+IUj0zkef1c1eB27CQMeuKPmLP3Id7O8mY53Lyl0+na5omxlOp1JhYNemG3Jk7+s5VCJKSKOA/TYrwWXfDECPdkeSOlr90/a73aLBQCAbWPCJyhgqrBMCAGeL3TMQlK4IiveM4EZQoovT6IVj68mAsvUHrp59+ymX1eZ7zpjkWAicD40AwrwOAEw4cHsI2U8K/y4IukY5GLEAEALrbbSPUa+dqEM/BgeFwT6dTZn4A1HXbFwAaBoX1cj88Tg2A6k3IlEQBMS4xo4h+ERKBx0Ecp4dMIhLw482rhaks8zfb5O+4xGrDNyuPEZu5JEg7iCJbHDPrm42gL0cGssYO+uhMRKxkzvPN9Fre6DZBp64EMA6XKM2goYuAMf6mtcJMvQMeczLr4qSPwORTU1zFsJOOiJUu8jlYDresOInbbDbx+Pi4Yk05GvJwOMT9/f2KTb6/v4+bm5v4/PlzZns5UW6z2eTWJPZsmaGKiJy0eG2oouKTSLzxBcjE9kuAd+XBAZvEiLVAp9Ed2HDW2q0pdfUCOTppIBklKDlxd1LEmfRugQRoObFkHnd3d5k5TvKLaNsmTqcxui4dM7ssc/R9qcZRUYAPQA92u+0ZmLF5Mu1T4GjacYS5X+LyMgGit7djpBOapjge2TvQxjTNmWBqmoimac+JPycalbeeE1cKWdJGRB/Lwt6qpM9fvnyJu7u7vEZO8LAN7JD1MLEAucXfCaht8ibYYWAPyBwRkBdjdN0udrttvL6+BXs+sA9sD70lSONb7u/vs77M87w6Mh7dhhyxz0IXYPlr4oAYN56G6NvU573ZbGLu5jgcnqKJWFXvsJH9fp9liBzZ24gO+YWZTdOsNrmj26zVxcVF3msDcYfvb5rUPuOKKKQWsQYbZZ3YmA1IBOxaxk7IiQXI20QMPhdf47GTrJs4JM5id7ZldM2tY26h/RaJxe83m01cXV3lyiz+gDEy/8vLyzgcDrlF3NUtg0DwCHoEfnA1nbhOIufYRxx3JcMxwSeAGSfQKeLEF19KfAF72GdBPvEMP9sJvisTJKz4cycSTqaJQegpnzEByDpDTrjCAHYwye544wQA3UN+3tcTEdG1XSztHM0SsUzpJZttJL86noZolohN18f1/jL6833mobyEFr3gb3Qf2TA+E2z4P+IHc+Vzbpc0VsSnmMiFWKr3D/+lq1lsKX/h+v/9v/+XbLSUfXgHBo4N0MnEEASguGZUm6bJSolhslgoJ8qHofAsDNBssqsunJgEk2Qjb5omb6aCwfS4XErDgNi4w8/sLNzWUVivwsw7U57ndFIJeydQGIzWzCoKRG8nTqWwfUWhPA+cF8Acx46iA54jCni6u7vLmTcKhiM/HA6ZUa8TMvdtuqxoZ4mi7nbpZVTIE0eNs3PS5z5rAznkjOGzZnboZgX5PT/HuAwwDB7NOKMDfN8snBMTHBrjwwA5FcNVQAI5zIxPCvL6mSVC162jrC/6iNyZO+PCltzOBFvE/WBOGBtA/1/9q3+VHVvNvvm5rBM6gnOF1T6dTvk0FtYOG7IuA7Z5Fons3d1dPkXHTDotQfM854Mg7u/vVxUEB3TOtseP4MMAS6yFqyL8zRGZDtb+G/v2STvcmzVjfWEjsU8n3nUQYJ3QBf5wBDFycwJoZh3gwRoRQE1OoCdOKG0zBCIDNO9lQM4At2EYVsfQvry85r0+3I8EGz9n8geGNSUP2zxmgHZqXx3yc7A7xvf8XA4lsT7WbDP7n1jX19eXVeXU1Ye2LUSS/cp2W1oOqQjARsLamgwxwWHGHdDOXAys+I4JIhIQ5AI543YdAy8zzYCgiIh5WWKY0qZg7J5qin23K6ZuWTOLa0a9vDulMOCuLESkBMenzfmIX7cSIg/mY5LG4yB+ICvWFxtlzS4uLvIBFo7xzI/71bEQvYAE4+ckhmaE+Z2rq4zLFXf7h6urqxwjHc8Oh0M+TpWY9fb2lslbbJF18tHhrAF7g1gf/DWxBKDNWuAP/M4LbNi2zlpjA8Ru7wu0TMCG7K3Fxp0Msa7EBWRPHOPZAHnHa3yv7QbfWhPYtJ8hz9q/G6eatDGeo9rrSjA+zMmQE9Rt38fpWE4gY2w829gFDO24TvsnvtBEn8dKHDEGsg9yjCFh5P4mvtG5aSov5nSC81//9/9V/Nb13RUNsjxAAAvrnktAAICjbdMRmM5l3GrlTNoAugazBgwsMm/DdrC0QLlPROmjc1mIBMSO0I4BweLII2KVXaMI9Kny/ZJdro9di2hiu+UFKlNOLrwhD6Nz+RaDBYD7LesEZtbBzIKZKcaKsmPsBN2IiIeHh1WGyt/TVI5K5ZnIEBkDlPk8hu+A5OybdWQsAL+Hh4d8Tz+DqphbF3BaABI7Gtanrv4gHweOGqiZCaqTiYhywopLw13X5aA5DEM+jYQeV1dMkCE6yzxpjwMA2Nk7Ca3Zc77vTZes1bKkPUWuKFn/zdpR3o+IeHx8jLu7u/w5J91+rhNd5HM4HFY68OHDh/j8+XN+R8bPP/+cWxSdcLFuBC/aPsze0JoXUV6ihX4QKH/55ZcMTpxosYGXvRzX19c5aaXVA4dK6drytm/D36EnBEfsLiJWwIB1BQRGlFI7lVkCU12qZg1q8A+7xZywd3Se5Nb+1qwUz3eCge+zD42IDD5dtQW8+/QVfJmrPADT4/GYW+9gRu0HABlUcm5ubnI/Oq1z+Ct0geSCJN0VTtYCfwoIBujxeWyAceJrSKCY7/FYfLKBmll57MckETZCxZ2KBPcGSGJntOciW5NhJN2spau19iH4lr7v4/Pnz3F7e5uBsAEIurrdloNUkK31zj3d9u2ATO8FYa8W8dXkTdu2+UWsgF+z606YTETQUunKA+vKmLF3kiT8FWuCr7C+IXNXf0+nUyb1nCgxB28iNoA2+cj9TC45xqDjTm6wJ+KDCRnPh7XFhlm/iLIfFX9Ooko1DF1FDuip94Hg1xgb47OuU4E3sWNSkO8DwJGFwT9xCB9gcI8swZqsr32fdRnfnEiNl0yekbC6+8RdAPhmk3cmyvENBvHoA8SAqxvWKZItfJ3B+nGaI6R3xn1uhzUJxOeQZ9u2uSrI2MCKtMC5ewSfzTiwb/ybEyGTo9g/8jU+dLz4reu7Ew1O9yBw15u4rJwI2gqKE2dyKB7f9WZkskuCISDL2RpB2oEPp4Sw69IZwYAqC4pkJ+TA45YKB3GUAgVAOVnABLrbM8vKGczNuQe4jXF8zcrBc+38HIDdIuMAbkYaYMX8DCa4D2vA81wepVJiIITSG5zgRP0cP9tBjt/TRgMjhdLbMRu0ozskq6w933FFDTnVxsm6EeQYi5ljEmf0kp/7d+gm43aygVEiWztgDgXwHwdeJ6w4fu7LGO1QrFuuItX6wh+zId4IZjuB7WN9Hx8f4/LyMgdB7BuQ4U3sBsLYBcDDAAxbuL29zePZbDarTb0EWCdHAES+h71GlCO0ASqMw2wV7GbXdfHly5dcvXJrpkvsERH39/e5AuX7dF16UdrHjx/zGhnAImvs0u/PIVmaprTxk42Wh8MhV2CwSVcMYNvM7CK7pmlWDDL+y1UmWjDcjkCQJVm3TuHHaqKGRAWwa9v4h3/4h/jP//k/R9u28W/+zb+J+/v76Lou77HgnThJzs1qfxv6xLN4/svLS26hgRwAILuK6fHWrCS2z96Ow+GwYl/tJwjwMOGphaxZyYfvRnz9pmD7AbPuZsEdzAnYBvLLsuQXvFmXmDcV0s0mvXQQMHl5eZlbleuxMUcfsMAfvzR2mqbYbLdxPCdBACMqtx6nEzrkhm8GSOKf3IWAbrKWyMOgB1IF+zLxwLoaHAKokBNx5+npKVdi0OGbm5u8JsMwrDavG0wDrD5//pyrlz7SlxdvOtltmmZVbSAWYvsQFiZm8KngDxMNyNbvSYgoANhVHMaA3F2ZNcDGTzAerxmfcSzADxGLwGzTNOX2PHSdmGa2Hb9BlwPVOleNWGPbCn7LSTJzN3HqiktE5Dk53njuxFfs1JUGnmFsYdLbcZTvkcT5RDiTcIwFP/etlycvEbHdbL7yD3yGe9gXuZKDX2CMbgE2JrBPQcbcn2TKnQQmXRkDeN8ECfd04vhb13e3Tv3P/6//bwYYKJeBBqcnLMuSS8jO/nnBDAaBYvB7grczbm/YRUDOdO3MALNPT0/5/ygIFQKfCY0zvrq6yu0dgDsHRBYEFoUxGMASlGDI0oI2GRSyQAkwbfMZyPxxRQZjRNG4v5nwiMjfZR8KY8TY7GT4ud+ejtLjyJ0U8jMAvcFOXVIkeAMqkA9KTcIQUUrnZhDRgW+BZFes6iwcueG0mSPr6CCHsXqjHHKCeUFPzH5ElKNHATV2dOhcPV6DbRJVSt3eyOaLAOQ9SjgTdJmkk2e40oDe4kBr9sfJf52ARqRKBBUQ7mNQElFKxawX9oDjJgFykvf8/BzX19f5rauMyeyoS8P8ifi6tGubYzwEAPShdvoRqULjKqtbT9BVs2EEfycX6PI8rzfDm+li8yxghOTIlVPmamad3nW3E+Lw8ZWw1STaBpbMCRm4Iuf3P6AT/M5tX3ULE3bM/N224f1vjINqxdPTU/z666/xpz/9Kf7u7/4uv6xsWdbVsfrITcZU/GcBGegcQDnZUCEfABDoRHoh4ZoMwSZsLzyTADtN48rXOQlqGtqrXvM6RUTsdtsVGVO3rPA5tzkanKO7yB17RM7cG5aR9fcRnCTsZrAtM3SQ/UoGIU3TxLiUF8a6ugQYNKGGrhAX2rbNL9SjksvlKgF+1jq+3W7zvhcz3WaJmTtzI9FAxiYZnp6eMkFichIQjXx94g/EFHM+nU6rBIO4wFp4bk4u3NnBml1fX68qI5CgzA0ioG3b/F4WH6tN0oYfwFbss7wuzIVEBFvnM04GDWZrcInP8FG7HACBv0Pf2D/HWgPo8X9uYceu0U2TjibyiE+2F/skt9k7ccBvuprttWW9IReRlStuxADkZAzRdV1OvJAB8kVn8CnoKvNl/ZZliWZZYpnLyVNgAq+pCU7HWY+ZsbhtDWziSghrY5zqpIPv2d+bqERuTvrQsXme47//H/+7+K3ruysaODcYOkAbrBcGYjaTkxlc5ouIzEIhFG/wo1QOMEIpAdWwkTA9BCnAshl3gxDmQLbNwgIqEHj9wjiMyQpdKzAOysb2/Pwaw2mIcRojloh5maOJJqZ5jJub668UywkUiu+kBwVwq5EVgvmZ4Sap4vOAQOQDOHRSiBGbicFR8DwM3IbAhTKuA3g5whZjJHCSNTNP5HJxcZGNnvXH+J3ouK0KNs4/44JV8z4AA2pa4AwaAGouuzJmxkAAQ1ccvBijy/vZ8PpyJCLglrPKzZCxBhHlWGC+B7PBPCxHnostehMbz/a9YFVhHg+HQ4zjGLe3tzGO5cjNvu8z4OS5rirAgLgtw6DJrAlyfXp6it1ul9+1wHet3yS/6B667SDDd0jIYMUZD2vIz3i+j8amHYBWEu6BT8DB8ix+HpECJqefeFx1VZT7YP98q1fPgAAALXhJREFUHjtkrakeWKcMPg1S/TZ3WC/rXP1cJ53Mw8kqwYpqEuNnXwTj/OWXX1bfb5om/uZv/iYuLy/j48eP5zUsZXuAnuOJk1d83bKkliLGyHiJG8m+lgxq8PvLEjHPU/Y1+EuDHMuv+KE2mma90TIizqRMOaaWZ9m28flmB+v7+JkGPYwT3w7Yp7rI+gMcAScAOL8x28km43NiDytvJnq328XLcyHg8BFUeYgHVOD4PQkAfhNMAJEFKbHf7+NwOKx86zSVI8utc4yXOEhSjw5CXNBqhs5RicSX+/sRkV9Kh5zxcbTmcWHbVIqIb7Rt2aZZD2wEGXse7FkFA0VEBuzTVE4iYtz2c9iSWXwquG7HdHLq+GO7sT9lHn5xHj4XQpjfYZv4YTPZ6DmxE33HxnkmCWk5hOLrF3eS4JhEqxNvbIs5gPecKILHTAbzM/TIySYxzPpMfOc5juOXl5f5mHZkjT3yfSdU+Cx0OidITRttRXTZX9dEIrI0OQBeZg6+F/rPiwkZkyv1ru4yfvQBXTBRYnzqWOjk+y9d351owGhZ6esyk8tXZFy1ciEABurFx3jHsWwKdLmLfkCyZgI3RoHSu10EhYQJcztWxLpPDcCFUCPKXhCM5+HhIT+P4+EY+ziO8eXLl/j8+UssSxNxftnUNI3R95u4vr6O25vbWKKUu9xyxsITcAhIBnUoP07IxlmDBIN3JyR832vjNXTQISihXDg6Ox0rPXKs2SZXe7zObjlCJwAZjA2Q6HUxQwxQM7BiHoyHC5liaOgTjsLrgQ6Z+XFpGTl7/j7auU5ofCiCQYdLnR8+fMi6gHN1pYo14jt1H3TtbPm3mSjskzYkEn8+9/Lykk95ovUpIhEE19fX+Z6c5/7hw4f8PPSSz9TtF6yRbf729nbl9NArByInBpYB+gDIMrP78vKyAtQAAbNP8zznaitJFay1n0H7AToNSPE+CdqDuDfrSBLhZJkkuWmar3qkaQ3BP2DjJBoRZT+ET7dCB7AdksdaD5Efm+nZVIr+Yhs+qMCVG2yGIP+HP/whtttt3tszjmP89NNPOTHe7S4y6+mEgrU0CeUTTfAn6I/b49J4y54pV8uOx3UQdcsigAbQzPNSglba6QwQhuGU5V/HQuurmVYDIP5PrIQ5BYhjl/xx5cWA1aAAHeSQEmIvlTEOC3h6eophGOLq6ioTehAUu90uTsMp2yH3Zt3RPRNX+GSSFLfFuN0F4E87nP2sCRdimkk3WGl0w+Sh9RhAxB/2VjAG8APxhrjNM7B/M/VOwvHrPnCG+b++vsbz83PGJNyD3zM3fAFVDxIZjoxFtk7E0GXm7PUyYYR/JXlm/NyTBBF9wm8g5y9fvmSbiohVEorNmTByK15dAXNiAFhlHYnfyAZ51nEKP4W/JIlElvhqnvXx48fc0s+aYZfb7TaGcYxlXhO1BuNeL9qhiBXFJ5TkEX/uBMB+3z4NH4MfA5umWPUWV5dXWZ/wRegbOsO4TY7ip2fNy77HnTz8PqIcGGRcRGx28uIEDILaPhM74jP4xN+6ftfxtrB/OK6mafJGU5g2AhWtShgGwbI+BtNZJYIimKFcbil5e3vLYAfHjCGSlJhl7vs+Vy14vlnV6+vrFZPG/9mQZgF3XXpZ0DSlfkWM7+npKYP1+/v7cxtBOvIwGUl3ZtkS29Z12wwoYM0ZNxcOBFAGGGDOGJ9L9A5wBEYbMcrJ/FFAKyJsFGAE4/P9zcBwJK4TBQdFJwA2UtiAiMgtOnWAdvWGAIMhYWC0qwCocM7un3fCwTOQhRMFEg1XX2ommL0IyB/9wy6oqhgcIpM6EKEzyMMMjdlTEgIHaINHdMfgD13x+hbgNORebwCwAcDpdMovvCIwN00THz58WAH0ti3tFdguY6vXzICZC/umPE0gZpxt2+bWA3SK8RFs8C+bzSa3bPJdAnFdkcDu7KjxAW5tYz1ZM1r2zGaSHFjfzZ5vt+mIXeyOMeGXuB8+jPEQDJ284YdhpzmWlOoLFaH7+/vVCS1cXs/adxjMAQpdueE7Jiaapok//OEPGaxbRk6+0zzScbpp/jsBMN4U3cVul3wdTPowjLHdUoGe43ikar2LiCY2mz4eH5+yLnVdv/IRbdvmJI5DNFzZdLuAE/t0MiAvkjzllkdOBOL+fL7vSwWcP2luJVkyAPwWuCZxx4/hg7B/JwFOYFg77J3KI4Dy/v4+s7DjmPZeAb6bponNdhOz/APrjc2Y1KLSwv+fnp6i7/u8NwK/+unTp8x8juOY/Zfjm+MHOm+/hm0jH3SLhB8i034dmRjgY4v2gZCDjBEbZx1YI56PHV9fX69ORfT40H+ez9iwJSdsVBR4HwlzJ86DO2zvdTWd5KTofjlpk+f7CFnbJv4OH41fdqxAZ6gQQUI8Pz/n55hAZl8OsY8EhliMfPwdfDnt6yRgrJn3TEBw8hZxZEp7GvrVyiYiIuZpirfjMfY6lMXtZ9gwCb/HWBNerkY6tl1dXeX2XGILPtqEY471u4vsF+o47VjEWkKMcg98tKtHjIfXPZCkYRfgHPACiZyJQCdhYB1sAv01mWLs/lvX70o0aiETrCIin5PNAPgZDgpwimDNtOFwzT6ZacR4MTjKVc/Pz1nZUAoDBJwFfxAs9yJRIMDjONyiQcmPeTJWAL+ZXBtoCiSblXNN7PQ+z5X7YpQYO20FOB9AhZUAOaEQgDX3dgO0+cPncUru4zQzgTJT3kWOZsaRA+tpdgJF53z3iFJVMONrBWZjNuP3BkucrL9LAETnXCJk7VljklWSjFqflmXJTInlRJLl4ON9CDyfObiU6WoFbX6wBQbkDoToGA7EZVvkaTbBCTkBDQBllo3vRUS2QYKO18utEcjFyT/6zzoAmGzHrA3rxZgi1icmMQfkCTPKxdgNdLCzDx8+ZN/gBALSw2uGXSNb1heggLyxP+a6LEs+qQodR5fQEwMd/FTTNF8lO05KIsrxmDXwJJgSSJ0oo/f4Mtsgp3iZGEBvkAFMmcePLdD+4oSCy3qGbGErSeIAFx8/fsyVC44t9bOQl9lLgITXyJuEr66uMqt5eXkZT09PZ50a4+0t8vcj0mlJvLAUoI1Pc3B1uyH/LyTC+gAMgBZJHWN/eXnJJyhtNinRPBwOORZhO7TDMZ6Hh4cVwcAYsVv8nY+gpm0JHYBRB2g6ubu5ucm+7eUlvY39/v4+IkrFzoRF8lllo7qrbj4pizUBAF1cXMR+v89HrwN+sCHW2Ud/+vAWZA/IQv/YmGz7IW7bps1eG2N4TSE6aZtxuxB+BT2mEoQ/5TkmTADuxi9gAHy1STrmbFkTW9E3/o0t3t7eZhmwzjybE8fQjfrESoO+L1++rOIT+sPnuc/z83M+3AdZchBBRDokgzjtCqD/bcLFpAXEMIz/tyov6D02jh/ounU7KDKtOxVIvlkvWqf5/XKWzTit93/UVQTbEP7fySoAu9hM2fvD3MBWbvXkfhBYEecN7Gc5Iz+3kDmJwe8Rl9CzzWaTiRPIYXyxq6L2t8RyY0JjSey+XlPWDTu1Dv/VE426z46+S2/OMhBlIQgE9Nu61efPf/5zNpjT6ZTLvV4QAOd2m85TZ+MZCmZQbSGxh4TKicE2Dur19TU7BgNuGy9BikXCQFHOiORc6G20oRkoYDwGys6sl2VZMeV2dhiXnaOdqpmnH374IbbbbTw8PGRHG1E2KBlEu5eeufIZxujv8lyXUyPWxwg7UTQgbts2v4TJbIIrXP4e7QIwN9M0ZVCKAbHmEbEyVLfJ+Pc4dBsZMjDL/C02jLUk4Lr8i2NxAoncWFeznWZdAXBUrgCZ2BEnL7l9zRs6SSqo+OFkNpt0upPJgHFMbYsEbfbAIHeSXI5/9YlhTg6QswMsztSlV+QEQCGQ4+SxZx8BTFLEuPEhyHOe59VJQnzGlQe3grj32bbCM2DL0OGXl5ev/AvMKz6Kn7kiwPjMYLpKxbjMJpoZwieZJbK9svZOkiFFqIwAoCMiy5m1x2+6msM90Xv01+2lkA1OfsxWMxfaD9xfbpkASjx2+z5kgY170/CyLLmCDIAex5IYYi+Pj4953SJKj7Rt18H46elp9bZ7B03iTcT6ABOvA3aNPeCnaP3gcwAbtzKQVFIhmec5VwVIrpAr+7ZIfNzahE7xPDoKsBniFHoL6ENPdxe7aM7f46Ki1HVdHA6HnCTVpBJJEfrJuPFD6D1/c1lf8bVOpEhAfaIQumeShzGiO/ivruvyfk6SFD5LQmECyIALX4/uWd/ZM4PO39zcrDaW8x3vJ/IeKXQHXUB/kQd7C3k+YBt/5SqM2/cY4zAMuepQy4A/ANN5nuP29jY+fvyYqypgF+aKXCCBwCscdx9RqqQQfrYNV1AiCvGB3qDzxF/iBQkrZA5rip47qXBVr+u6mM62jNwhYU+nUzSK4wbTEOIRBScwV2J0jTXsd/BPtFJhD/ha40DmMap1D/sgsa9txuSxYxX/5/fIFLlj8/zBvvBpxHDHH+5Zt+/iO0262h/+1vXdiYZbfeY5lWgsOIR/OBzyvzlacr/frzY3Gow9PT3ll3GhMCgJiQZC4t8oKw7arKFZcgIxDAwMD8HPPWvMwU4MwfMdFpWxeWFZRJhJlIjF4bKSoACPj4+5rE0iZEeCcfklWDg8nme2xMwucyKYAw64rFDZCATEkC9B3rLmvjzXimuQynwJcsyB+yMvb5RzaQ7HA4OAbHmeGQbWiX/jUJgzARPHQmKETuHYzYDjkAAHBpqsOWM000VQwHExB/YIkJzTfsUaOAEB+BqQ0WrDngnmQAnZrSsGbKw1L4QCPCJPAmPf9/HnP/85/vjHP66CE8+248OJG2R7/VyWR2ZOmjgJZ57n/G4LJ7vYPfqIXHFy/I1MYZYBMuizW57QSeRCNQ37c3JmgN11Xd6XZTICPXWiiL65woIOmL2FmXXg4jsQOLYh7M+MKKCEMRLk0aeIyEw3YzRJ4kSwTnKcGJkAMQGDLH3sMvcFSGEnbn1k/WpW18yoyRXWLgHeomMOwvgd9MStCxBEyGWeywsMzUBiD/gD5kcVzYnkMAyZjY2IrMvIaRzHVQLkPnjGYpKAdWFeEZE3dZIsQVTgBzabTQZL1svb29t4eXmJx8fHrDOfP3/OVWYSzH5bjgPlucTg+/v7VcziewAbfBjr6HV3hQPwQyWR2OTKl8EWe8dYY7/LxbZrss0v9cRWiFmsBTodEbklDnszmEfniJGsNXMxeKZqgA9E/5gLZB/3o/WIsW02m7i/v1/5N+QcESubiYh8FDlzcXsTL9UjDtRzIwln7Pzh87ZFs+D7/T6vlX0AYN9krYkh5u6DS8BdzJGk0oQchBnEE+PibfW007uqwhjAMbYv35+Xx/Jzg2UnM+iNOyo8P2yFzziRsp+xPIZhiNN0jE3frxIl9MAxi+8gH2KrfZ79m+0I2fv/3MtjYa2Zq0k5/Ag/q9cZnfue63dtBjdoBuTjdFksBkXZm0wbo8P4I8obciMi7u7uVoGOxWYhAFawOyiO2z4IlgiOxaYsaIcAOKGPrm5v4Zi8mjXFqUWsX97GyRKuWjiTJZGwEQEW2KjH+AEYnPzjpManHLhXmPFxH8uAYI+smQPKx2cB0Th0AwZ+ZiBjdhsjBTxgyGZxMSKM0kGH9bGOoTvcm+BnxsdsAw7XCaOdAuCa4ECyiTMkeODwzfpizGaiCJzIzobsJLBujeO5DpQ8y73jOFiewWcMnD9//pzH/Msvv8Qf//jHiCh7EdymxdqZLWFvE7J5e3vLfffoMQwaeube5YgSED1399s6yMPemTyAcXQbltlSt8LBbuEg0S2qY4Bhzw+95Yhdvx0Xm6Pc7qqLW8YYl4MCa4gMvInT+y0AiLYl2DqSTNYdwAvTxjNItuwDSCSZqwOmA4hbGUwiuCROZdrEAgm8ZWu9QiZ+yZxbwtALkhwCIfrJ38jEdoTPdPXU9klSaD0xeQOown+4RcFrGBGrk2TQReLV4XDI9/rhhx+CzfOMg3nAIJvVBcChZ26rcdsP4ybu+SAMdJJ1sH8lcTObjn8BsHKaGvoC2BvHMVdQ3E5p/+pEj71wJt6cBDumMw4n7OiQN/QbP5g8ZL1MZN7e3mbm3aAPu+n7Pveb829IRjO5zI8xUh1lnXyKkiszkBTI3sQLa8JLSZumybaNTaHLdGiYfDSBCOE0z3P8y7/8S24TpR0cTPA3f/M38enTp0xcEdOIEdYpEwT2l/yOMbnihg1je9/qvsAP+GRG9IU5Mh+ejW4Z5PIsxovciResr/ddooeu3OYkqF13iOBnkIFfw8D3TOpYZyC3jdmwQ9u+K3JOcJ1UIe/jaYi2Ke/zMYCvMQh2Dv42sWV84jUDh+IXkLt1jmf5uF4n7fYDTmr4/beqJH/p+u5EA2bVk0e5uq7LYNmtUfM85938BFDAPt8D8LVtm8/B5rMut0ckB3Jzc5ONl0VxBkhgIXEwe4qCONukD5Ds34E4IlatHAb0KAmbmAAaZq5c5jIYc7A1G+4WITPoKJ6Vkfu+vb3lljMCDHLgM/RiwlpjtAQeHKhPlUDBMHKMpmaRmbODvZMpb3j9FjuKHLh3XfEg0PDHwJPgxEWgcTsWDsnlZ373X8rkHbRZB5c0a6NDZnULFX9wkK4A8b2ayWbudqSWOfKCmfrxxx/j+fk53t7e4qefflq9ddtzhC3huYBb2gcdpNEnM9QOXKyXmemIyO2RZngsq6ZpckWAoDSO6Y3wJDYkErY5elnZ6Aq4QF8czCEIADXYKcHL1QjsEyaPNUdeJhJYYyfjgCLbAD359k/4TydOkBNOQAG8BC70xIAYv8vzHUC5FzZmMoA1dpAiqAKCkAOXQbvZOuygZuFIFGDH8af4YnQGuZjZdRsmPhq7ARS7erMske0Dn8EcpqnsLbOsqMrzWYAQY0YH3U6Db354ePiqZaLYZanmYAvWb7OAzN8HLtBy4VYoKtMmfvBjsM/EHvwdya/Z4GVZ8iZmdIPkehiGuLy6inh7XckegGY/aNKE+0AmGIBjj7TTuNWLGLLf73OFAhkbFPNzt8CSbPOyz4jC9JNwUd3Bxp14oY/EEGIbpA3rwT1vb29z4lBX3eo9Lqwv1aN5nvPBDJwuRkszNkdyA+kEQ8/7NCwT/MTl5WXc3Nxku76/v1+9BNn6GlESVMcCDi4hrg3DkP0VPpr5MF/IONYG/XIcrhNF/u9XErCu6CXJEb6B8bHu+A6ITZNL9Wb8jDmXJZZx/aJl/KTjUkR5Fwq6Y9+E/vm7Jr6Jg+gX8nNVrCZiWZf9fh/zVNqZsXnbOj6NWICumfzi/mAFP4MxYztONMB0rG3btiscyvqZIOQejveOpb91fXeiYVYd1h2HiHPCAZsdYKCUq2DWvSAwL02TNstxssWXL19yxo5SwTAZeOMA61KenbODQEQBo3XvmRMCz8XVAcDGw8PDitmBybDTJRi6f91gGyCGs6T8i7Iwp81mE4+Pj6teuohY9Y1yKsrpdMo9k2YFPW8MEMNjzCiPy29WaOaEojM/DAEH5fYMGwHGzM8iYlVVYr2cQDBWb+I0C0/lA4P+8ccfM5PHs2DrXVaHrUI3HFhxMgCQiFIVsBOxk+U5/J53lEREZoyZP6DYm8wosxMEDHx5NnPkuTAuMNteKyfWwzDE4+Njnq/bEAnOduxPT09Zv0icAWToEM/Alp3IOVAaoKAHbhPhSFQ7NQIW6w84Qs/MyAMYLX/kbF2kIml9hzXz2qOTbtusk1F0HRCLPzK5AZg1QePWGCeaEaWVCL0zA+0gSOJDgKztiwDq5NVti4yRNQOEOqmjHYgeaXy7mdA6cLMW+Bm3zpBEmcXEh2CLZlU9RzO02MAwrN83lADvvJIX1Tf8uxMRgiz2jd8mxhA/DL5d5eI5h8NT/r31v2nSiU/YghOJ2r8Tg7i8eTbJoY1lWb94kCoLSaP/zZpYtvhMdAYwHEs5cMG+iPViXff7fcSyboGBpHBcto9r2zYn/jDxTVPamdEjAxh8DHPns3QDwJ5HlPdGGARhv+gncdX65arTp0+fcsWNDfYmHQGaJJLDkE53m6Zp1fL88PAQFxcX+U3knLTFiVwmHlxBN+nGc9Fbnk8Sjz4if2zL8RhchkywHXyuKzOOta501PHjW/6U/9tHYf++n/cymvgzsYqN1FUBxjNNUyasifOuqiObtm0jRH5hE8MwxDLPsVGlxPjQyTd6YXIJ23QrmklHCBTkTLxZliVXAfnMMAyx7cv612DeOAQCBjuIKLiUGMIaIztXmpFjrT8mOvkciZ59B2vNPJEr93VC9FvX7zp1ymzA4XDIztPsOMw4jgSjNtPC56luMGlK0oBbnDCLFlFaGzAujNeLawPhhBcHAO6NYyXw0I/rFghAOpUXjAjHQAB7fX3NR9+aGeAe4zjmc+ZhQK+vr/Ni4WC9iIAAHDnBENmhoG43uLu7WzFjGCif4Z5mKy0XjAPWgPGgoDgdV5ucFLAWODZAIUwGv8NhGlDBgJh55JkEeCdNrDOnv5AYwhLgyPgs7EndjkEwrk8t6vtyXLMZkYgCEswQu9WE+9dvAkde3zqxyIkZ90IOrLUZZAfpvu/jT3/6U9zc3ORAxnqigxzdTBJEQEPvOSEEXYuIzLYiawNkJw7LsmRQgb4bbBNYXKpFxhcXF/Hp06csz3EcVydlAZKcqDqIGvhRUQBM1Z8zs4Nv8UZy5gfggGHD5+GQqUzgd7APXlCGf+Dn+BXsFQCMnboSwPOdjKMjdvo+ltPsPbaF78D+0CN0yWQDvercmwBjYsjgyz7Z4JNEABCDfphgYS0ApcjXxAu6xvo78MGkjmM68SmBiS4i2ohYImJ9PDGyoTXWOkm1BX8HOcGzsAEnesw9rf8mlmWOq6vrs19Jx+5Ok98ftUTXTTHPS4xj2Y8xTXMMQwFxXZfO2N/vLyMdBbxE1/UrIIFvd1sqAM9+0vETf2jyDHtnfQx0YfaPb8eYhiG6pomY5szOf3r9JaJtohfj69Zh1p39KrQM+aANfCTjRqbTNOV3Izjh5vhQ9GgYhri+vs56eTqdMttvfBER8c///M852SUOcH8qX/T+kyCTfBN/qAZut9v453/+57i8vMzVY3wb63FzcxM///xzZuzR63EsL1h0O7nZ991ul18WSDLHZ6ybjAs/5OSByyQavhb9cFLs2GbS1dVNCEvHALc1o5vGPn3fx267i3GcYhrnaNsumkgv1WybNpqmja5vY5qXmOYl+s02pmmMJZoYxvM7wqY5lmiibbuYl4jTMMbmbINd18VpGKI5JxjIH/0yAdy05cQmfCG+22DZlQtkDbHMtdvtVi90NYHC85ZpjvF4ii7O/q0/J5bTHKepVO2dwPllpPjyb7UKg5eYC/HCiZpxLrGOn7OekKlcJpbRdfA6euIE3rH0t67vTjScPXddOXYtooAlJxMIj/PHmSBOnjYAwCCOis+STJhB5pldV/phnd2bSQVM4XD8OzMhCNJtAyVAzPH4+JidqRMrlAIHQpWnaVK5lOd2XZd7wnHgLH5EfMWyc38zbwZgKBpzwtmw6GTBDw8PMc9zPtqwrsp43VA8fsYRkWZgmKvZk6ZpcgXGwc3lOsaOEbq6hLOE2Wd9vJdis9nkF4/BsuN0DbBcggTAccqVj+H0vDFGWHrkHRHZuaAnOBpXAAxkrQtcPtEGR+4KA07NoCo7qqX0wfLveuM6tsZ3SdwjIgdr9JRTe2B5mqbJ8gTgUqUjINoxe5Mta+rEFZvFSbutx36CBICgh62QICBjXozZdeklhvgT5gxI2GzK+zNox8C/0LsMW+lWKpeNzbKbZcQPwGjy7JubmwyesA/W14EBXcWG7+7u8rGo3AtZIufEkh9yu4WZKfwe44NAMHuNnFwFNIuHbLAv1pj15Dmsn0kB+2QnODVLal9GXHB/MbLHV3EfJ5AGLPzOtvV1UpLexZFi09uqqu6qLf4HO3cy7uo3ew3wx3y/bden8HiN0aWLi30G2MtSKpU1k4q9m2zY7S7yM80Sm9SyziKLtm2/ai/Dt7l1yIkH456HU74/fj/NvYvd2UYPx8Oq8tNvNtFtCrAkuce2GAPxz9Vu75tBH/DR4ALHWeMEfAXjpZLSNKkDAtKv7/v427/922x7/M17roZhiKenp3w0Lwm138Vjlpf2qu12m+M5egrJgv7iF8x044d574P9HXKKiNXmevsFJ83+Pb4AudfECmtJDMGW8Z0RsSIk0CnWxlUK4pWxgQnVb/09jSnBNhEyjVM056SmV+tfksG6HZfxk0wmfzHlBIz14eK52Bb3PamiaEzJs7A3+xeTH/aDEZH9P3rrBGAcx5jPSSOfoV1sdwbvEE0kO6wdc7AMbDvYGvblFkH8iolh26J9Te3via38zsmxiWS+gz7ZJ/+l67sTDRQYJmWz2eQsisyOY8Xoy0PQy7KsjgoEjBtkuwUAx8ObfQF3GAbVFE7PIAjiwD5//rwq3RnY2fjMZuKUyWDNQABEWUiDYMbuzX1mIGAw+c63Wi4cqFz25D7IkHt7E31EYfbd626g6PKiWXj3miJ37oey8pwSOMtmUG+E5jt9XzbF0k4AEOOEJFozMKR5Lm9+NlviUndd8jbDZ/YKg3ZfOCDHDBLJE4wWxs9mUDM0PhnJLA5jAuxxsX5uJ3QSQhBDNjUzwFgIJC4X2+GgQzyPpBJ2D2cGU4b8+DyBhKoJ80VXAYKMhSDI/JkTzDfBFnlyH+ZPG5kTBmwZAIO8qTxZdm4xsfNzwuAqgpnxmgUmUSH44OwtI05BYw3wNwA2J5uMtwa0jJOTw9gT5hK1dQT7gp0FBDjJ85oAkJzg209g04wDNtennNlHeO0gJUz8GCzzLGQHgMGG+WM94P7YPXPAVvDZrgyzbgRx7udKisfIOBkb98bm2SNATPCRrN5fx1pzHCiMMvee5zkz1PyfZ+HnbMusL/oCqeJKOckk8nSymw4yKCAD/TudTnkPHra12WzyC/W4OFGP8bDuEQWgUdXBznZ9SSJZnyTjLuZlyZvEHesAxoybe//www/RNE0+0hq9/pd/+ZdVnGDNd7td3qey3ab3Yvzyyy8rxpzk4Ndff43dbhd3d3dxdXWVjwOGcPC+G9aICixjJMlAl0gOkCkJStM0mWwgrqA3tjnwCuP04QTYMJ9zsuK3xjNudJ3vLcuyek+ZSVrWEbvA53J/sBjjZ45UuJzksobcAz3m//yN/oKh8DnLvKRKRtOsfIzXmfsZr7g6QRwreKVZ+TPiQ036mYRbzvclLoD9bEskV+4YQJdtv8QiiAn0w4nxOAzRLAUnmFxl3saQ+A9vrAdXGAO5OuUEwgQluMAydLzE79s27ftL0hfZf3IPfB++0bjlL12/q6JRbxa2ohoU+ESGw+GQWzIwdE4MIXi6DAhoACASQL1pj3YPPueyq9l9kh32MVAloAxLyw3Bh3mh7MyVRSU75aVR/N6JktlpErFpKpuc7NgA4owBQ0V+BkhmJAm6ESXbxSBdjuOeGIpL7Aa6jBdF5bkkE4ASQKtf5GRwzhoDnmnJQG/oeX95ecmfxakzR1hYZOokzj3ffkMocyDwG2iwTugSJeuPHz+ujK4G24AFOxYSDfekEsjRUb5TB2aDEAMPnuPLjoL/Y2eACycbXjfsh8/hEJwAe+28/h4b+o9uMReCgVmWeU793qwR8kM33Erp94IsS9qoend3l32MmR6SZuZETzg2RGBkHQjCHPFonZ7ncoIJSZH1nzVz8ssz8WX4BbP2dfB1sm59xVdad/Bx9ldm7vEBJlmodtqHAFJchcB+HDTMWjFW7vOtoIVeQCTBZDkIcT/ma4DCnG1XrhKiU04qTWC4vM9YXLJ37KGiXLN0Jl3sN9FvVxPMIE5TqrJz4AUnMxncsUbI1QkY7D/zNFhENvgv+wjsAP/Ld4mb2+0m+wfbLb7F5BkJADJ7enpaMeGAfXxXROS5DsMQl/t9LNvdKq4x1s0mvVEccsNgiDm2bTq6Hb+EjyW+IcdpmuLLly+5ss19ICM/fPgQESm+kawAjPHH//bf/tv8XBJkCATGYv8FiPNGY9beCTNrQlzFhhm/wTaxAPsw21wfmYpfs+1hP+wBoTrDHlXLtyZ8SHaxB9YXX0VFxJ93Vc1Yy0QQWAESx2ttkOmYtfIL6oBwO/DpdIqlKYcj2NcQP3KSsJQDLpI/6CNiyfiCU6QMvqnoc/V9H7OIJ/yUK56sIzHN7Uj4EnwDumrdAUO+vb1F16w3yXNv4xDIevTIPqQm65iD9ZA4aSzB/JGl19T67ITBmI9EmHvSamvs6qopc/+t67sTDRSHQI5DNajBQTJgBOFWAQySkiWTMvsIOwLogF0ALJgZoHIAqxARWXkwsl9//XXFjMEqknAAfs0OY1TMiY29KAMKB6Oby4JT2ciLQsB0YCwoHgATg0fxmBtyr8E793H1g2ehbIAtZ7VOOnixj7N+DMXHarK+LiPzfDM+yJHP4RCpeHFN05T3CrhnF7aa5BMAwhrALkdEPnOc9awzedbH72dBzqwnR0iyF4A9OAY3y7Jk8McakewCIrAFl7ZxVDh75u1KGbJFz3DmJKXMu2aW0GscoEuhZs4McABJ2CiXncY4jvHHP/4xnp6eVklG0zQ5KfFmXQAhumJASVn7+fk5v3sA9hC9jSj7reZ5zuAI2wc4uuJgZ4n80HP8B8kHa4BsYABNRBA4zIK7wgBjw7MZJ2wUDKhbqAAWyAI9MIFBosWaERD4HUAAXcRX2N4Zj9l59AMfbDbOvd/1WK3fZifRGfxf3c+LfB3Q3OJiRhWfYLCCz0J+nrtBN6crmWkchiHvLaIFz3bgdjH026AJcsEHG+BT8DcmedB3fARrA4BE91xtocpq0IdMiW34XZMb3ANyZp2snKLr2hXZs9vt4uPHj5n95zkRXydQ6COJbd/30S1L9Js+/599bm3Txv7M1Pu7jHeUreC33f6Iv0SnqLCQ9PV9H4fDIbbb7VeJ/+3tbV7LiMitlMzPySx+AjCEj+DexECfOMYYbm9vM5k2z3NeJ7f6ObHHtokxxFhIMT6LDEyiugKKX8GOXEXwviKYcnc/oIf4MBJGLh/XbTIL+3RSi55B9iFfJ46slUkM/JtbQJkL88DG56kcnuE4PU5TzEshnNFX7oWNGVMme15XRMANrqR4nylJxvZ8GAJ2YmKay+OA2HLMdkJkP4vN5PjalPedsX74ITACyTT6xJyIf6yTkzHLsE5SjXPARciDZ3Cx1p4TtuwqFutvksHVXmL5b12/azO4gQ8OgAeR5TsBMKjxd7ypiUnSU0sfXkQ5hYLA1XVdripg2DzHR/5RQsRJmGX55Zdf8j3JTBmXmTSe74VGoe0c6nKmN9BwEcRg0/lcREmyAI/8HyNzid3jMoPljNSBBuBBECPAcDIGrW0kajWDFlGCIEwu+zdub2/zvRkj//706VNWSpw4QRejcItCvdkYozXbxxrDKP7yyy95/w96QhsCPbD05WPQ6COAk4QXHTRwwFHaKaBHJCnoMU6OQEaCBWjh+RgpTgEdcmse1T/YV4KNGW+Sb7PxZjbQD4Nm1hbwjKxJxmh59L4WdAq5eq1h/AjItEviqC4vL7POesMcwABbsDNmHrQ9IFfuj05i206uAXDcH11zMsf6Y1fMzXJxdQzgYfux/KwjdvqMyWPFVsy28ntArIMDY5im1OoA2EYvmDPEC89hfMzXCU4O/PO6/QkwRMKGDPE73MMJjqsK/I5nOlg7oXCAwgdgE7DaVLIItjzj+fk5t/4wF8ghJxTJXqYVWEQfsSP8NokH/m0cx9ULZUn4DdppUaqTtGVZ8l4y5P709JQJJhIC4gBjIJY4YUFGVCAAv0lPx5imEjcYl8d5eXmZ/T+VEUi6YRhW5EDTNLHdlZfMRhQCINpyvDuJ2emUTqT79PlzdJv+q0pm0zT50AS/JBIy78OHD6vYR2fC7e1tbqkCwKH7JHfoOTK+vr7Ovg2f783XZuS7rsv3dysM8sZnE3t8sAU6bD0meYe0Q7eIOWaM0XO3FRrjOBHAPqmsuCKzBtvrd4y5Wmfi1yy2STADZeaPvuOTIA1thzXxgo5ZH/l+stMxprEAfuIZcxqn0q7OutiGeB76bZIJ3aJrpe/73HZo7HAe1CpRxAfR0gputWxciUBG3Bvbdysn4zHAd/JQVwKcvJic9HeMx+w/LXeT3U4q7LeJC6wjumaSCeKKNbKOmQBGJjVx+Zeu7040YFY4HQZHzQKgzGTgCA+HR9BikDUzzuQjyikmCAJh8Df3tTLBSOAgzLLjRMZxzEfNkfEeDofV0aAsMoqCoOtedVo1zLChKDg6g0MADQZnYMF9cVK0BtWKjPETsABi3MtMGHIniSDAmknjM265gjGpS3QoOCAQkLbdbvN+C3oUf/jhh4go5/7TcjAMQ953c3V1tTpZap5TfyJ9sAQIEgwMEnlzGhRGQvD2pi6fHESSEhG5FI0TA8Q5aWCNeS66/vr6utoMbFCFsZqRRnbIzEkhgYTPAPKRF59F90lIcJgAY9grKgnM//LyMj5//pznA+hAp9q2jX/6p3/KTNzxeIyPHz+u2C0ScWyPcrP3AFEldPWMsWF71lOcHoFss9nk56Bz2C9Oz60O6CTJEPchMWBM6LyTEQgKxsP3WXfmyRzxScwJuzcbje1jgyRNXifmYPICP4ifYI1IOGHW0QGTHFQe6btG7maM0TtAC8ku44iIlR8iECFrwJSvZVlyOwe2hi8yCMCu+b8BRMTXbK/JIAcwqotUDJzEubXEbb3f0p3at6PjyJPPmjl0Mu8KsMfI+pEEcj98tFvV8GfM3wy222UMarETVxmtu7y8lpPOsG0f7TnPcz4oAV+fiZ22jXmeoj9XvP7Tf/pPcXNzk9sL//DDjznGM9/U+rqPaSknHT4/P+cWWtYbwg17+vDhQ7YPkiJ07vHxcRW/fDKiKxnolW2MZMDHSPv3rI3Bt5MZ/DsxCtuBLARs+7MmXNF9/Ap2yHq6UoCPMDYgnhEfsVd0Dd/vRBT94ffEYWMxJ8IGwQbA/jn+x2CSsZq08L0ZC78zaYsfbqJgnBUJMZcDOXhebXtOnrDRt7fXHDedtNhPmwDimaxRTfbVHQPIHT/MnJCN1xj/5+6ctm3TqVNzIafQI9aVy7jBuA09Zh4mGZmT19XJQp2guTLC/LDpuhLj+GIiz8kO+mLC7LeuZvnelOT9er/er/fr/Xq/3q/36/16v96v9+s7r+/byfF+vV/v1/v1fr1f79f79X69X+/X+/U7rvdE4/16v96v9+v9er/er/fr/Xq/3q+/+vWeaLxf79f79X69X+/X+/V+vV/v1/v1V7/eE4336/16v96v9+v9er/er/fr/Xq//urXe6Lxfr1f79f79X69X+/X+/V+vV/v11/9ek803q/36/16v96v9+v9er/er/fr/fqrX++Jxvv1fr1f79f79X69X+/X+/V+vV9/9es90Xi/3q/36/16v96v9+v9er/er/frr369Jxrv1/v1fr1f79f79X69X+/X+/V+/dWv/z/Q8GF9ukQKugAAAABJRU5ErkJggg==\n",
+ "text/plain": [
+ ""
+ ]
+ },
+ "metadata": {},
+ "output_type": "display_data"
+ }
+ ],
+ "source": [
+ "for i, (mask, score) in enumerate(zip(masks, scores)):\n",
+ " plt.figure(figsize=(10,10))\n",
+ " plt.imshow(image)\n",
+ " show_mask(mask, plt.gca())\n",
+ " show_points(input_point, input_label, plt.gca())\n",
+ " plt.title(f\"Mask {i+1}, Score: {score:.3f}\", fontsize=18)\n",
+ " plt.axis('off')\n",
+ " plt.show() \n",
+ " "
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "3fa31f7c",
+ "metadata": {},
+ "source": [
+ "## Specifying a specific object with additional points"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "88d6d29a",
+ "metadata": {},
+ "source": [
+ "The single input point is ambiguous, and the model has returned multiple objects consistent with it. To obtain a single object, multiple points can be provided. If available, a mask from a previous iteration can also be supplied to the model to aid in prediction. When specifying a single object with multiple prompts, a single mask can be requested by setting `multimask_output=False`."
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 13,
+ "id": "f6923b94",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "input_point = np.array([[500, 375], [1125, 625]])\n",
+ "input_label = np.array([1, 1])\n",
+ "\n",
+ "mask_input = logits[np.argmax(scores), :, :] # Choose the model's best mask"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 14,
+ "id": "d98f96a1",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "masks, _, _ = predictor.predict(\n",
+ " point_coords=input_point,\n",
+ " point_labels=input_label,\n",
+ " mask_input=mask_input[None, :, :],\n",
+ " multimask_output=False,\n",
+ ")"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 15,
+ "id": "0ce8b82f",
+ "metadata": {},
+ "outputs": [
+ {
+ "data": {
+ "text/plain": [
+ "(1, 1200, 1800)"
+ ]
+ },
+ "execution_count": 15,
+ "metadata": {},
+ "output_type": "execute_result"
+ }
+ ],
+ "source": [
+ "masks.shape"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 16,
+ "id": "e06d5c8d",
+ "metadata": {},
+ "outputs": [
+ {
+ "data": {
+ "image/png": "iVBORw0KGgoAAAANSUhEUgAAAxoAAAIYCAYAAADq/5rtAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjcuMSwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/bCgiHAAAACXBIWXMAAA9hAAAPYQGoP6dpAAEAAElEQVR4nOz9Wa8lS3agiX3LzH3vM0TEjTtn5s2RZCaZySRZTM5ksYpFVrO7utEPhW61BAgQ9Av0LkAQBEiAfoMeBDQg6UmAHlutQqO7WqqBYzLngTnnzTsPMZxpb3c3W3pYZubmtn2fiGxRECCEXcQ95+ztbsOyZWtey0RVlWftWXvWnrVn7Vl71p61Z+1Ze9aetX/A5v5/PYFn7Vl71p61Z+1Ze9aetWftWXvW/v+vPVM0nrVn7Vl71p61Z+1Ze9aetWftWfsHb88UjWftWXvWnrVn7Vl71p61Z+1Ze9b+wdszReNZe9aetWftWXvWnrVn7Vl71p61f/D2TNF41p61Z+1Ze9aetWftWXvWnrVn7R+8PVM0nrVn7Vl71p61Z+1Ze9aetWftWfsHb88UjWftWXvWnrVn7Vl71p61Z+1Ze9b+wdszReNZe9aetWftWXvWnrVn7Vl71p61f/DWPe2Df/zrv8U//k//Q57/5GtohB4PCMGBE8E701lijIQQUFU636EKqkqMkRgjAM45RIRxHAHYbreEEAB7Nn+f/xaR0kf+3TmH9x6AcRzL33n8GGPpR0QYw8QUAiEE+r4H4ObmBhFhs9kwDAMAfd/jvWeaJhs/Wp/DMDCOIyLCNE3cuXOHzWbDOI5M08SjR484Pz+n6zpCnBCJeO8ZhoHr62tEBO893jmmYSww8t6jqmw2G/bTnhe2p/zp7/0+2+dOie++z+N/+1VOxoD2sOn7AodpmnDOFbi2MOq6jhhjgV+GZb6fse97XNqzPBfn3OJnvRfOOXtehKix9O2cK/COMeKQAtvT09MFDuXx6nnUc8t7Vq/DpX91y2vqVbjZCBsVXnnto3z1v/pv2Sic3D2j7zt7BhCBPRNDp9z/+Kv82h/+Ju8/+ADf9Ui3xZ+eEjc9QQSiw0/wzje/z/tf+3vujkJA2XvFCYgqKsq0Ee79wmt88Y9+mwdXjxBRxHVEBKRDup6I49pv+MQ/+m1OT+4SgjKpsh93fPDoQ7ZOeO7Oc8j5KRIDlz/6Ke///bc4lQkEJhdRHxGNaPBcxA2v/PIX+fgvfIYoavPF4YPSB8ePvvVdpofv8Zf/x/8zdx9c8VhvCDFyGhyh8+n86cF5xAlB7fycbDdsNz2qIK7DO0cMA75zjPdO+Cf/8/+MHz14mzMVTtUTthv8dgPiiFOEMfLWT37GxcUFExHN5x0BAe8cfiP8wuc+g4gQI+A6EMMtVdApgio7p5zdu8uP/vVfcf2X3+E0RG5cYBLYug6GCbzj2iu/8Z//OeHOhq7rcJ0nAiEGphAYh4GwG7h68z1++O++zP3JQ4hMoriuQ3DsdjumKRCCEkJgmibGIZTfY7TzfP/+fU5OtogTMlpmGpNxs235u6hKrM5j/fyEsJsmXn/9dbbbLZvNppy5TdfjgN4Ld+/ewSOggRgDXmDsPS/88qd57hc/gbt7Ttdv8M7juo6N75EYCSGye/8hf/df/bfc34ETZecVnLANSiAyvXTOH/zn/wk3CFrR4kLXNSLDxLt/+Q3e/cb3UYHJCz6CD5GI4dfo4N4nP8of/sv/mHfiNRFhqx5X0agQArubG77+f//XnL53TR+UoIGhs/N6t98wjIHr/Vj4RNd1MyxZ0qeaBoYQFvOueQXOs/MTn/v938C/cE5/5w6bzRm+2yC9IFOk73vUOWSY+Jv/+r9j9+b7uADee8ZOkLunqBPCwyvisOPzf/glvvTHf8B7+0uuo/EIr4LHpxMQiVPg+uqa//q/+lc8enDFT99+h5tpZL8bmMaJj33kJU5PO37/93+LP/uzf8bV1SUhBLz3FZ1XxikSI/z0xz/hX/0//hvCOEGEje+5Nygvb895+ewu027PTiLx3il/8B/9KV/8g99DOm/4p9CrsHt4wY+++R2+/Zdf5mevv852s2UYB0h7pKo4ZMGP81xq3M3fZ7qe97im+cda7mON7+c5qCocOWP2uxQ+mt9ZO5c1P8zzzd/VfDJqXJzT9kznd+v+7TkBdYvPFvi6st6Mt/U8WtjU/dRrqXn+wTO4RR817637XMhZGK81OhVtzhVM1t7N74dKHqjnuTZubu28630JVPvRPFfvVZY9VA2+IKtwq3Eiv5/7zXJjPY81WOf9Kv07QSr608Km5rM1jukK35hx0+NkKX/ZeEqUiETFBQcIsYv80q9+js9+4bOM4rja3/Dhwwc8fO8D3vr+jxk/eMzzJ+dc7fY82l1zHUfGGNg6z3ObU877LZ757C7gZaBcxZn2vPwfvv/XB3vbtqdWNMAE+qgRjRAVFCHiEFFCQ2BUlf2wp/P9AqAt8tSbvHbI6k3Lm51/AoUYt60mBOM4Mkwju/2+COF937PZbNjtdqgq42gMTVW5f/8+AM55gsI0TUUpyExyHMcyblYisjLiO4f3JOFlous69vt9UnBs/K7rinKVBX1VY6YYXU1zcCgTzvkFIfLel/XVykaGS1aKZkSdYVkz7JZY1kpGfcjKnogUBMyfZYFIVZmGcYGEbf9P024jTgslJR2SGCLTfm8w3Q8zEczPhwAScU744O13ePToETc3N5ydebou7a9zRO9ABUEZdSIITBrBGQGWGBEURYkh8t6bb3F9cUnUgPcOjZEpanre2ZMu0jlhd3ON4hlC4GZ/xc31FT98/XW+8IUvcv/eGV4cJ2dbU2I04oAQIkqwcdWhIXB+dorDcEWEQmDHcWScTEHZ9BuiXhiEJAtcRqzqNu8rKAGi4iZH7zsQ0BhMgfIeojJe7/jpd76PvHDG4NK5jAE/TeA8MVgf/ekJ2zDhxpGYcFvEhteoTGPg4cOHPHfvPlNUJNr7iBCiwhQRhZGJ8/NzbvZ7xDs0RJJcYeceCCiTRB48fszp9nkUwSlJIYYYIE6KIkjfE50nIvafGONwsmRmrZDTKut2APLPn7/VTDLvX1wRfAr+KyCaBBnAYUKBc6A27w8++IDuoy9yen5CmAac80gMRB/x4ogxEDoh9I4YBR2nsv5JI+qFi5trHl1cEPoeSXhTn90hTHiFx+OOwZnSTVQkgERFHKZqiPD+B+/z6NFD9KxLSp8SKxiGZPTxJ1smf02nAlFAIyrGX0KiazUNKk1ZKBP1HpVHGvplgFbw8JOf/IQX/cc5ccImCq6b6ILHI6gIURQJkeiFYIiGqBKi4mLEdT04IQr8+Cc/5hd+4ws82l8Re1cUDSeZL0U0Rm5ubsygJba2EIJhUoxkAenrX/86n//8r7DdbtPaQHWa6bEKMSqPH1+QsBrnHeKESSJTB/sOONvwy1/8PL/zZ/+E05efBwQJ4MURhpGf/vDHfP0v/5Yffffv0esBorK7uZn5qzhU40KgbIXrmicfU7Bbvr72TP6+3een4Rs1D2z7q/FgoUhUQnH97FKgPaSV9XyyYnPb2mq5RoUilIYQDhSdVqZp198KeLcpcO2Mnpr/ylLuYkXAPBhrRajPRplW+WxlwDUlYJ7K4dqfpq3tdf3dGizqfW/HWsP3uckCB1rFr4VPMeSKzAJes8Zj+J8VXyem3MSoeN/hEDREMzhd3rB7dEncj/hotHgaRqZxYtzvmeJE0Mgkkeg2uI0DZWGYKTi5Atd2Xk/C/7r9XIrGzc2NCcFO0ABZh6wJRCZUZgVUAvMiskCe38nImCddP1czj7xxXdctiF29wXkT20OYNd4s8APldxHh3r17BdBd1zFNU2GC261pl13X4b0nhMAwDOX3rIBki9k0TUUZyR6FVlA3HJuRN8+l73t2496eT0Jc522+gqDRLOm5v/qw1gTzNqtI3p98GGpLVK2t19p7vae53fZ7JqTtAfx5Wmt5qltZd/qfJvhMo3mJukxg1IRVj1nluiQ4TePEsNsBhhthv7f1e88YJojO3js9YZDI5ASnikZwMSkZTstBHG5uCF5tFPGYPB9QcUSUoHuuLx7z/Iuv8uGDCx5eXrEfbxCE559/kUkVQekFrvY3qAYCSpgiAbMqERWfFCad9kgSMERnguA6j+886hynp6dM+ZxqJJPtliTkfQ0aESIiZgfrNFvhAhoVfGdwDpF4saO7d8q1jMSTE1wIiIDzWuD+3CsvsR9HwjCiCk5mq4+GYIJkgJubvTFf50jaAYqg0wSJdlw+fkyMBgmvcWFlUQcjkdEL4j0xKTFOFefMmjyOIzFGduOI225wp1uGYc8mE3YnOJetxgGY8a7+V8ZMZ/gYft7WRMzz21qrVJVQbc6hcF0p/hpNsDf7KM47phjY9D2u6wx3wkRXlHHDfRVwZye89OmP8+jvf8qZlyTFmqIxAHdfepn9YMYYZDYeFLrsHPtp5NVf/DQfvvEO7magi7Z1AoaPAkGU07t3GMeJ8XoC74m+X1j3spfo5U98jLfee4RMEx1qHkOV4rE4xsjELfekVc7WlMV6LSFG9tOIIxLCSOeEKUQ26lAgONBx4mOf/QzffPtdNmrKvaoxegUCkRFTrC+uLhnCANGjzhQNEUdU84Siiu86Nicn3NxMCRc80gn73R6S8qWqXF1dVd4Mv4BBiAbke8/do/OecYqJrwk7GbmUyC/9wif5/T/6I177hU8xdYJuOvoJ4hR486ev880vf4U3f/hjHr7zPjLOkQRZuBTncCIE++KogHibQejY2VhTBp/UROSAdi37OBRa6/6PCbql7/adI6PVuLW2lrYtPD1QPBotXWnHOAa3NeWk/TstoKzhSXOs15INc+S56fLdtb1bPF/NY8040K5tMXb9bLJlxgbOT8QVbQyRR2TL+vta6WwVjnrdNQ4VPHJihhWdIzvatbWwk0rJWFt/S8fy906SESatEQdhmgjDyHR9Qxgjj958h93lJeP1NW4M9DjCODINA14cG9fhNdI78y7HaEaotf1aUzTWzsrT8r+nVjREkiXcSTai4Z0nCJXVdHYrFSVCZ8G//l51DhvKz9cCcB5zjdnnvtYQuRaO898xmivUJ4Ug/8sKRh1udHJygoikcK4JjW5hYXDOsdlsUDUhJoc4bLfbMs9xGthsPOM4FoUmP5cZysnJycLrkEO3zMolwCy0mzCo+Gqd+WdLQPM7dShard3XikXN8GttPCtObRhTgXecXalt6MIUpsIkWyJYa+1rylDdV/nbHijrq8dMpxxQ+s0G1WhCgEamKQnNiUmZO1zYnp6Y5e5kYwJjxssYcL5DxSyad15+AblzwnQx0o0RMu46UCeMOvHSyx8lxAjevCriTEBTo3goilP44I2fcX56Ttc5zu+c8cr5y4Qw8cGHH9D1HZ0D2Q9cvP8ecRwZnZpSIxCTO96Lo3OOh++9y0sf/RhIh0Uvmo/FeY/fbhgvjMnEGM3ync8NS8K1IKRYKI14x+AdO+/ozKWCYB7MyTsmiXYuhgBbxz4EtuKQZCUOCr7rGSKc373LdH1D3/cmQMUcWANhCoh4QoiICp5M2AR14FzyUoWJd999l904mDJWECZZxYGpg/sffYXTO+fEdJaceEOLimG6riNu4ROf+yXe+ep3CbsJjSYEZgXecD2dqcpa1Qqpyu3K9pqwU2C+wlA0CbFrfVl/SZBPCKsy4/0+BPo7Z5w/d5eTO2dMTuicp+861HVIEoyjbTKf+9Kv8zM63vvuD/CTKeGDQDjpePVTH0eFIrjWtEBEEI3IyZbu1Rf41T/6Hb7z7/4GvdjZs6oWzueFHYFPfeoT7McB128WdGxhIPGeFz/+Mboh8ubffQvZV0qCQEi0sg6pbI0qa/jcfgcz7RtDQE48zz1/n/O7d5CuM2+ZE/NEppCTiDJK5P5HX+ELv/ObfPfffplOTAES74gOggjRC698/GNcXF8hW8NQTWc3xJAsjybAu87zhV/9Vf79v/trEHDeEYLRut1ux+nZHV588SWc8wzDiPcR54yOz7TYBLDnnnuOX/+N3+CrX/5KodEvvfIy/+Jf/Mf81pd+i03XmQfJgQTYPbrgG1/+Cn/7F3/FzcPHuDHQTRGnFv6sCYa1USkrxa2QW8/nmDJ4TABZOxstvrfnAw4Fn7aPVhhseePavNoxythRiyLbjlPLH62iZR7CFet8otFr7z/JWLGm1NQKdK285+ecc4R42MdijStw1ywHkOmRzvRmZQ41TWthv+blasdu92KBY7IMTT3W8noNBochVscE9xqva8NOqzAdg3/mKzGNWSsZa+dl0SeH56CMoevf5fddMhqZlVUZd3u++tdfJu4Dl1eXlh4wBVxUNl0PRM7OPCdi3n8VMww5mwQhhoVCXObPfOaOKbdPwt26/VwejYLEISYLfiDokvHWCoQqjMPAZrMpzKo+YG0cZxb884Kylpj7zM/XFm9VLWFIIrKI563zNU5OTorwXBOi7Jnw3nNycrJQPlrkzN6HaZoOciTA8h6sT2Ecp7JuFvChjJvnsd+bJ0N9ekBMMN50phBpGC1WviIqtWJQ91/Ptz00ay7C+qDmvaiJRP1OEfxdDj1pLCoAOj+7No9aqThG6FsCXudoHDAFNeukKcGOOAVUwYtZc4MqOGGIgeg7PvGpT3B6fgZdshY6D96B87jOg3r2IXDy3B0+/6Xf4Lv/+i+LshPCBOKYnNDfPee1X/gUru8sdtI7swKLQ1wH3uMwy+flB+/zzYtLPvKZz6L9lt1+x7br6V3HyfYEr8rNgw+5+fADTpxnchbOgzhc7yw8ZYKNd7z3xuv47Smf/OyvIC6J6En5D8FyEuqW8U1wizjbJdzBIwTXEe/e4e5HP8rFB+9zshf6aUJUuCbysS98jv7eHVzvONt6tPd00eG6Dro+ES9wAbb3nuPm8oIwTkQNBFWGOBFC5LVPfIztdmvn0XeIeFQMftGZN0KYCL1jFOVzX/g83/vxe0z7sQhxMSq+75Btx2c+/zm2p6fEfL6TpQkBcZ7oJkQDYz9y5xOvIY92vPOt79NhjCLnMGgS3m9jLrMF7DiRbYXbct44NJDMjHV+95CAz2piVLNCadY+th0vf+o1/Ev32Zye0G96vO/Mi+E8HQ7vHHsNTCgqkU/+6i/zxve+zynmhRhd5PO//Y/oXnqObrNhu92aR6ii1WDnbCKiZ557n/gIn/7lz/LDv/oqLhoOTSjXYeLTv/F5nv/4R5BtT7/dIs6TQ7HyerMCGk+Vj33+F7l84x0uf/qWjaMWPpiZeP1egdcThKd2/1QNb7TvePGjr3L/lZc5ef4+nGzB9Xjf4zpHH1Ju4cYTUNhPfOaXP8eHP3qT9372Fq7vEuwdQwx89FMf5/yF59icnCC9x236otShhociat6jCJ/69Kd49OiK1996m5D3O9HC7XbLF77wBTNKiS/fZR7ikifFOcc0THzxV7/I2faUL//Nl/mjP/oj/uRP/5S7d+8i5p+0vX18zU9+8EO++9Wv88Nvf5ewH9ioSwYYwXlJhhETlI3WJnjKrIC056AV4o4p3mv7sPb7be+s7e3y2Sd9f3hOW6PXgfDUvFMb3dp+yjmvxqrDUepn1+DUwm+NL9fP14bbWk7K77ZrPqZ01Z+JJFytvmvb2mcZJ9vv2pyHY/uzJhvArNy0OFbPud2zvAftfNdgW8+tlVfq947tzRo8juF5DSs4zHdZ7HH13LJZblVCMqYQ6Jygw8R4eU3YB3xQJEKHM8KuCt7RpYBvn1hGJCZDKPZzBTdqQB7jc+1ZuK09taKhySsQQiCqMowD3nd2HnVp2c5hUarBkjMr5cHWZkCurVyq5iHo+35xgNbcs1k5qIFQC975+6ykbDYbfNcV4pHHrEOpvPcljyLPxca2d/LntZIAsN/vOTk5Kc+M48hmu0V1ouu25fn8k6R8hRDYbCx5dRgGpjARJ4XtKS4R/Lx+Jw7nPSFMZZ21Bp3h1XqIMuz2VW4KLBG5VfxaJTA/X8O5VghrIlArXTWcb2MoLRHJ49WEpyUy87Omd5f99J3F94sxWVAikWEKhK3n5U98jOc//hFib96Hvt8y4SzhTUx5wjm63jOOE3dfeoGTe3fQB5c2pncEp+yJ/OpvfJHu/JSpSwlcLiUyg4W+OUfE4aJy4oWH11dMYWAIkf0wcPL8izhxnJ+dEW5ueP+nP6WbJvNaicdQTwi+RyV5OOLESed446c/4SOf/AybzR3LFxpGXH9qSk+M5PDGBSEQEBwQF3AGo0m9dDzynrNPvsYf/s/+p/z1v/pXPPzGt/AXN8gkPP+pj/OLf/TbPHj0gA2wVSFGh8djbh4LQSohfgTzsMTASy9/lAcffMD9l17k+vqa5154gWHcJ7j5haIhKQTLRc/WeaJObE9POLl7znRxkwijKZ9TDJw99zybu+cEBZdyL8BCxmJUxnFCp8AkkX2MoIHRMlKQkHJuRC08KyrgKi/njKM13poH97jV6ZilJ9OnNUayppwXemkrKkUYonWGiHD6/HO8/KmP89gFS1CeJnxI1lVvYUjqHCqKelO4Lx5/yBADJ9Gg1Z+e8MqnPsG1DwyjxfQ6vxJ7HAKKckNgHyYe7q9RL0SXCkQI+DunfPYffZHhpCOIKcFR5yIRrQFnEEU7YUyeQokRjZYYnsOnao9GEXQr5WtNYFzbE1U4f+l5PvG5X+TSWd5eH3scSpgGNDhO/AYX1IxozqA/qK03Cz+W+CpED5//9V/D3z+1ELzEY7SbrY5m4I4lzykivPqRV2camyyLCPzhH/4hr732sZTXOHuSYI4QyDDpfU/cRH7ti7/GP/3jf8prH/+4zSma5z7uR95//U1+8JVv8L1vfIvHl49xIdBH89k4J0wOohMkSZgOEt0sSEkdt9/m+/1/s7W4t/ZdNdGFXrAqON0yTpuUbZ7pdUWnnc9SrmHxzPIMHwrFa4rLmvB6oGSz5JFtAvb83Myz2/W2Y2Zc1PyfEdkSolzPRVUXuImu07waBmuyQLvOek0xhSk/SQFtv2u/vW28YwpM244px9aR/ahx6JhiN3ey/HOxH8f1ZVMSMlycQ4j03tORPMYh4pIMErGUNzC+iAoOTYqGI2KGnGNK09O02/azbU8fOuUc+93OBIkY6buNJVvGiG+IfBbUTdhdImDrBciCawihJE9P08R2uy3VoVrBt3Yd1hWT6mTtHB6VBXBjTgmhxVz9ZsWBk+2W3X6P956u60xwc44wTajGFPYkluw4RfrelIP93vI1drtdEfK7rgNRpiTw7nY7huTV6bqOmCyntbBehEMxOKsTuq5HRbiZBjqUOEacd4uDsbbxXectnKciYlnByHCqCVzt4akPSX62VvTKHshMMDO8bV+PC1Kt0tDiQz1+3YcTKQnF9Xxy0KsDvDfFbIyBDtAQic5c/4LgXcdA4PTeHWLn2A3X9F2P8z0hKuo7YgSJIESCWnjCKMKgkV6EGCZCZ14SFPrzc6IzLxc+Wy/FsiqcImJVImK0/rx3PHfnLoN4fNfjRHn++fs4VcabG4brK3QaLemr26T4VDUPRQqXUGAcdrhtn/J3DKabk60loo97eidMcUomZkW8hYIVJpKI+AENjBDFs9909K+8yD/+L/4z/u3NDTff/gEuBEYP3Dnl8oN3uKMOn6hYkDQLxZSEROVULWHVdZ5uu+HO8/dRjbx4/hJTqgCHOFTMA6Fo9ueiYUKi5bmgykjgcnfDRnTOzQkRFccYA/swIrqhw0MqVkGSFbxzaT+wqjtdZHQmPPbFM2BCaIgRX4VM5DC6bLErNK6B3Zoi3TKdtWfr5hDy0K0A4hPtISoaLazIpSyNhxePeefD9+HuGacieOxfJ5Yz5FNhgs5h+mCn3H/xRU7unBPev6Rzjuuba9754B30fEvfd3RZsHAuMTSScucsAb+zfeu2G0aNpBg9osA+BnYauNoPiPdsZYNTMZe9OBNoJXmqUYJA1EB3dkJQZSMOR0QMIrPhKgnxlvOQM1QWm1AU/YyP1VcGU4Gr/TWPLi8YtnB6xwxBEs2L4Tqj4SEGUG8M2jnw4E43BveoxCnSnZ4gXQedYwwTOik+RoIq0nnUQYh5v5XOOzSCqOPBgweM48Q0LcNeXn75JUC5ubnGN0VUVJWu7yykD+i7Da+++iovPv8ine8tIdSZD/Xygwe89aOf8oOvf4uffef7hOsdSDDjFelMJGWN9Jkdq6yoz3hYC9Fq/yuJqVK+SF6FVcw+bE8S6tYEVtI5hUMB53+ozlPzvTp5GQ7XsqZotErXTCOM3lO8o7PC1ioH7XprgfxY/7nVil+dnG7vL3lsy9tbGNgfeZ/Ln9TErg7/Wsh7a32twHqt1eufw1cjVMbN+tm1vhbKgj2weH6ttfmoWY5sFaZj8oqIFEW8/r42kq/tWxmD9fNitOu418T4jyZzmhV3QC331OVw3xkEhXeJgmRcT3xt4cJam8gtfM5gLcffb9pTKxpeHMP1zkorimFknAKu76ziToUENZAkMZX8WVt6tp549hrAeqJZvWEZUXLuQw6Vyr9n4bpYChX6rrNqH5OVvPTe0/U9iHK6PTErzzBalaIYrfqOd4zjnk46us62d5omxNmm5VCtrGTEGBFHCbGKMZa5ZOHBe1/K4k7TNCNmsnuMIhA9/uSU4e4J4eEVJ7gSg14LMSKSqly5BFPoXMr5kFx16JjFg4XSk+GV4Z8VidbaijTuvkJgdPF+7j8nytdEsV5He7iLZUnmeM/681nhEfpISZjeiyU0+xitUoxAH62STKdwdXHB3fi8ebicR6LQ+Q24HvEnSNfTqZqy4S2Z3J1uiQ+u8SoMEnlucMi24+LxJc+fPM8JnuidWfdT5SR8D111tKbAtN9x8+BD3Mkp1+PIlUZ8v+Xk9JRTmdA4Mm2gkw7NnjQRegE6IThLBOtcb1Xfxj0SN+ynkTBNnDnHcPWQ0+srpjgwaWBLb2EoTkv8rVnsl7ggqkwS6KJyEhynmxPkzhm/+Z/8R/x3P/sv2e6veHx5QRhHTp3jXDqmHsaNw2Eha3XpTEHpVAhXI3sZeO4LL/CT17/KZ3/xF/jwrXd54aUXCH1Ht+lNmXAOEfvn48TQwdR7+sncvfHEc/7yc1w/vkSngM/ilsL52SmqkW7jiS6m9ZnAFDXSeSHi2aR4WrfpOX3+HiMRVRNpFQudi5NZ01WtvOKkprBGZxXANuIrfGW1tQLCkpFLKfGan83NIbhoeKwdZt3P3kyUTlJ1PrNHFwZydnLGxjlCVDrFXOWpRGLEFMHoSTleAuLw2w1dvyX4awLK6cmGl+7f5f3pyjw9vrMqYICIT9ZutfyFENmoECKc372Hdh1xsLKLvu/onBDCyKQjfW80tZOOVCprpkRiOR8nYpXd7r38Mu9976d0o+DU4bVniBaaG1IYUBYiQobvKpfL3o68BybwmVFM2YhyfXnB9ux5nOtMefJWOhjvLa8h0RyP7YN2cP8jL/L+T99EJ6HXDZ3f0p+dczNNxN2ezeaEzjl65xDfIeKIPYj3xk/U9jiGwMuvPG9eT515lveOd955A9X73Dm/vyhC4nLoVOfpouf8zl1efPUV+pNt1mZMWNrt+dn3fsDX/v1f895PfsZwvWMME1Esv0/U1hOSfNDlnIIkLKmBb7Ysh2jejiTAmedDSljq7FlKwnMSvqJqKuu7sjsVT3mSYLoWmrEusK4L6sda/f0xD8XaGYX1cJH5+VjldmSjhNGKumzp2npqIbcWeoFFpELLN+v8glb5yn+2hot6rXXFzkVCdDKoIZQiD9lQW+/N7LE53m7b49rguphH82wdFXNMWdK08DXDz7G11wpH29a8Tcu16ALG9VyOrb2MJWK0flWpWOJz8ehaTTxTMFQhBi4vLlAcKt4KRSCgMYVQpX7F1BplmUvi85lfg0/z90IWFOHIlh5tT61oxBDsX4wWvztFuq5PRCtv9MwAJDF7tIpvTJubM95jc5jygmpPxtqhr0vi1iFNZtHvDiwG+b1clrYW/rM3JZegrS39UdUEm2TtMCXJKk+hdv/Hzc0NQIprnq3zIcx5HFnIVjWBL89nGIZFrgcoQwqrMkFBeP4jrzA8/hEn3i36X1g+ooUtZK9OXr+IoHGZ1FkTprzW+pDURKz1aJR/GScSHItSwnIv6z5bC059wNaIbW45L2SN8Ec1XEQjN9fXhBhSVRasjGWabxCzZt5/8QWGaeSs7+lcCSTCJwHIBJmEv6lk57brGUKkC8p2Aq9C6D0vfuI19teXnInAFHHe7oKw9Sam7AQRh0qkx9EpbH1PhzAOe4bdjv04sL95xHh1yUYDnXPJUuITkzJrcECYggKeYZx492dvsnn+eTZ37nD58AEn5+fobmS8umEaRvNaxJi8LJoqVK3nHwjQBaUbA+fdBlGP67e88MlP89IvfZaLi29x585dHB6ZFOkMvhItQdusMPYv9+oAN0auP/yQ7/6//orH77/P3/zoZ7z2yU/gX3qBDqFP4msOtxLU7h9w5tr1k1XbcuLY+I6bmJmnkdsxBDabE0uYj7NXoISCaMqLUIUQkSnixoiMkS6CTJYXFUJM/0J1RpYWVKmZoWrNCxZtDU9rZtwylXIeUsiQpu5jVPBSlKYDASg9F6IlSIzTxBAmxDkCEU+KyU046TB81qTMkKvxoajrCcHCzLx44jQh3op9oFr2NordmzGkULNus7H+MfxmjJx359zdnHB5fUN0I1F6ojdBuuZeAnN4oyr9yZZRI0NIHobQE2JkTHlH4j2+EoprmnBMmCh7Uu3NabdBJoV9gCnVgEzaj9cU/qiWYpH77VC2YvfV+KBWex5h0/ds+p7dNCKdFX4QFVyqOOWxUKYwxVQ1Jil7IeITrnbpDMgUeeH8HjJMxM2E9LNxSpLwfnp6ykdffY2z83OimjKvQZH9xMP3PuAbX/kq3/67r7L78DFd0KQMYLx4JZy6WDcbONYGsRafayv3k4T5Jz1zdL9WBDVDlXUBruYZcw6VW322nV9+5+BZebq5tzxs0Y/YzDXJf/Vc61CtHGq+ECqPCNX1WLfhf/3K0/TR/l6e43Yl4ra2Nq81b8GqcpeZcTX//FwbhVGM12J8oVasjtGGtXGfNN+2ZXreGsdb78iasmFewLnvOY3ALejVAczsCys9DxYhQ1YjNPEKFr7JTD8WsiNZAXm69S4UInvwKFzW2tMrGsl9bRstdN4bE0+hU75ixHbXhjFqi8FOVu60EM2IwrKUYz5oWVkADhKdVLVYetYs4S0C5X91InhG1ixY5JK1raJyc3ODz3Hvaa6zMGJjtApGjJEpjMB80dc+lVAVSXBLz+12u7LmcRzpO1eUGAUrkdr1hO2GKZjQlddZh0D5zpKCa201P5eVO1WdLyGsDmz+u35njUi3cIZDd62IfZaVv+yt0WoOa9aQDL82l6du9Tj1u9M04fuezXZrQla0C7DEjPdEhAkYQkhlXK0snO8thj1IJMiEXZkmBOyCvhADDCa4TZhA7cbI2PeMd0+RF++xv75gGy32XZOEEjHlRVI8gTorE6nJMt6fbJHY4XuPD4E47C1eMg6oRvAOJxYWpDN3wnmHkw7HhA6R7fYEh+Pm4prHHzxELq4Zd3vGy0vGmx0unauAyVI5qqk9G5noWK6u3fmBwMP9nseXF3zsS/+Ir3zne3SdR1MY2IjdieBwJaa7EEfM+jWpMk4Tj99+n+eCo7u45sFwxfSRVxmnkSkGy/FyFcGTJNw7U5CzgDsFs2wTleS0MOXBOW72e85DoKtwqnhL078olpMRo8IUStUrXLbICuNk+QmnXZeIsi7ucXBOjKY1Z6A9PzWuts+hWko21u/Z89j+axamLWxQoxruZIMNc9lHyy1RxjGwGwfG/QgIrrfKU9nCHApOJlhOE523ogcxyf/Xuz03+z1bPOHEFPauU7zMnmEV2/tRIzFMphylUsT5bqVeYdwNdimpOJyMdqlfD122zidjRUzrI9HIiJ2RDpeUjIkhjExTwHWe3kTymYkuQLsuDtV7oaiF200TDAP9FCAEyEaumAw0+R4czTl/EcaEN1jFKbwjpoTwm93ePEDe03WCF8WJwUQdxTtU8oZCsPs5JFh4ZZrffj8gCMN+pKfHu8547abjI69+hHv37uG6DYh5aGU/cf3+A775N1/me9/4Nh++9z6dCm4M5n1KVec0xmScXtLV2ww8cBhesgbXJyl5P287dnaeVmFZW8ex7+oQ7Py9CbnH19TOqYVBzZ8WMkhUkMPE4jVht+XH9Xe1nFQrK6vC7MrvbauNgHV/q2svMRf/cK1Wro4pVm1b0s2lQB9TCdinGTfLeT8PbtVz0Orz1jhaG6zX5LJ2n4tSn5WASv6tFSdTMlLfInjviNGbzJgMN3WrFfSf76zqARxbevHztKcPnVoI9snl5ZM7MHknXIq39jlePwTAWflATWJTTDG2bo59zouo4yQz4IdhOFA8clnYXKJWZPaC1Bu8hkBtHke+KTwL4XWfp2dn7IZ9mUsOk7L8D0HoChLkn3l+XSdljvW8Nv3GynrKXMEmfx+CJfI5EbOCdT1xs2HXdfj9jhOZkTQjsIhZypxfJmzn5txhjeTaYrXGRNqk1FZjF5jjdEUOSrvlELLs7ag1/DyXDJcMtzXNv8yhWVMhuAiu90w5hjvhoKJWeUEpgqQanScOI6N6cxh4mESZdKKTACqMZGEuMo0DO50YnOKcWTJvXMR/5AX2246baWKrCr5DxKTiACDJu6fmVdhMym430Y2K3012yZ0qvu8JZzCFHt95wjDiNRI1oOKJMltwFVAvTFGYRLm8vuT5O3fYKLz2yiv4aeLDGHj8/geM1zv6aTLhtdoz6+yQCU0aCc5udL64fMQ43NDducfDYc8nPv9ZutdeZnRWcWsIgV1nyd+dwKiWcI84QmKkcYpEEaKDxxePueq3jMMenHIzDlyHkRADGjyiMSkcSekVYY/F7gdMYdmFwCDKFCI+2ngaFec7Lq+uuD+MXN/s6E9O6HorURyzoocpf+rMQ7jbDzy6vmYnajutwuXlJRfX12iMbE+FKWpx3c+Mz9hs9nY4P5+1NYtoLRQUPNc5vr1lqKpY/oUqLo0XQrDKYuJtHQJjtKTv7HGVEHj84BFT59DdBOrROEHviL2iaiWEQ7pXZj8O6M2Obd9xrdE8nkG5enjF5dUF8S70/Q5xjq7v2TpBvC93smhU4jASdwMyTOYlCZHgOkLnmMLE5c0NVzc7q3biLOS0g6SczgpTUGXaDQyPrri5uCwwCqroNHEzDlzubtAY2Ww3M3MvZazXhZKaztR8IKoSHIwxsr+5IV5d06N0GtkC9Km0gYidQYxWTtPIzTgwOSVopN92SC+oduxi4Gq/JzhH9B4fha3LoWsR573lp2BGn/1ux8OLC6Y4sY8DijIR2cXA5X7PEIVzv8cHU4w/9YlP8NGPfITtZpuskA4dI8PVDd//6jf49t9+hUfvfsB4fcMmWhikTxcFqojFZTMrGS1e5s/WrMuzku1WFY36Z/vZmuh2m+W4FhhbXpBlh+Pi4JNDWFreWM/1gLfYLwfftfjWGjNruB6ucXnDdDuvek65tXy75cP1/A+NcMcVj9rA186/buXsJHqkstzzlr7VfT9pr+t2jPfXY9ymONV7mQ3AT1IgjuFvC8vbhOpszKplmHa/WiWj/m4Nb5RsdDrEy6IEi4VgOudKlUnry3iT5WLM+XWxGmcNJvVe1WkOzTUqM345WRjMnqY9fdUpQGOuJjXH8IdxRLwvl8tBEmRVLQ4eeyZGS2abSxZKuixrFpBrwlYf6lqxqK0s9T0U9WbN4UtzEnEGYi3w5mfzwa1dxcNgTEBEFjeD57/tKGsJjarfzWPl+eXwKPt9RGNcJRYCOKdM48g4Bc7OT9jce457H/0o8WdvIMO48CJkBpBD+jOS5KT2OjRqjSnXsG4/XyMYRbvmMEGqVjhqS0FeZ10lzLn5LpKs9LUhYfXYdVsc5BwSpElBc46olvvinQeXypACPkT0aseDDy7wXc+Lr76KP1PYbvFdT7wa6Hvw3YYpBIb9QLzeE272BhPTdhid8Cu/+gU2QeDxDVMSSjY+mmXUOcJ+YnPumcaRXRi5HPZcayTc2XLpI9HC3nHARjuL1d5PMExMo+A3Hu2CJTG7lAwPTNFyh7owcfHO2+wfXzAME3e2J9w72XLz7rs8ePNtwn7AZ2U2+0USnFSWe5qFu1EUlcjDt9/i5u23OD3tuOeEToQv/P7v8N2v/B37Dy+YrvbcDCPb0w0hKLrZEhG66FPVmogOE3EfOducMA0jl1dXjOPAtYwWN351wxQDLti9G/SKOFM4AoL2IEGRUYnjxDANeGfFESZN+QaSwkZ2I9Plju3JGegIQXAbsXLDzpIiXYiE3cTu8RUP3n6XRw8eMSnsVemwiwMvLq7YbFJxABwxWuhjth4Z9U80Ss0o0DKWNTytz16LzevKM1CJVZnO5DlM6ax47y0HZe/54PW3GVG2bOjPTvHbLd2m585zdzl/7i79iZUgvri4YPfhA/aPLrm5vCrrYVTef+MdHjx+yHT3hngVcJ153Tanpzz34gucnp3S+46bixs+fP89hocXyAeX+JDyyoiMClvxPHz/AY8ef8jJvTuEsxHvN3R9T9/33LlzB7/Z0PmOh48es3v4mJv3H/DgzXdgCihCTHTyanfD46tLHML5+Z1kaT7MzKjpTM304bDK1e5m4CYEwmPBScd4vac7O0HOJ7anwun5OZJuxQ4hsL++5vrigsePHqWQVk/n0x0wIXD94UMuHzwgng+wV3y3I55ObE9O6Da95YE5IU4Tu8srLh9fMDy+wU+RLvUXojLs9jy+uESYCNHxi7/0Gr/82c9x5/TM7n/CoSHCfuSdn/6Mv/rv/w3vvf4G1w8v7FZ2hT7DoCpo4EToxS+smsdo7EJR0Nvxu21LPnIoSNZjLJTvaq9aRafppOz7oTIx50zVwn9rzGrX2LZaIdVwvGz8sXW3QmottOX+14TstbYqhKbPWpxuP7d35oqZ7ThPowy0SpSuaHprwvhtvBuWRTLa9dZejdCsb02Qb9evTzH+2vyf9rlDJZMiIz4JT5bvHSpq8zvrcMwyq6qWpO58JrquT387LLuQ+d0VRbWso5ljjXP1u+VcFLnVDHjiXKErT2pPf4+GZqucuZJ9dCb09D09gobKBRcs38D7lOyG0KWYU9Rc6BZSUmuiS69AnaBch93klr/P/1ogZkWjPjD1Yahdj1lRqIGZFYghjCUUqHaJIZTE0TZZ2caeL8LLJXutQlFnybftPRyqTPn3BKjt6Rnd2SnDyZbN+Tk+XCwQrgj4cSpW/9rTMRPhQ4KQn6uJ06JkHYeHNe+/iJQExZYg5b4zLOvP6+8zbHIYXEsoW+ZQ91PmqCnHwrtFmJZ5nhJ+SCSKQ93Eg5+9zaOrx+we7fnB9B1e+dTH+eRnf4nohJvdnjtn55yenXF98Zibmx3D5RXjuw9x1wNOU4JahDuh4/J7b/Dw6z9g1zneD1d0AV58+WXuvfAC/dkpXJnn4oMP3+NxGLgJcPHxdzk5u5vKBipOHahnePCI3RsPCDdXbLoNp2f32Ny9y+ZkYwpkgvs0DEzjgB8Cvfa8tDknBkEfXjLs3uXx3/+Ax++8W25q1hT/LopVYvLLsqwzY8XMF7sRefCIr/3X/w2f+u1/hLiOdy5/wFYc8YNL3v/693nv3be4c/8O3sGd+/c4eeUFzu7cIVzu6b1nuLrh+r0PuH50xfs/fhO3Gxm6HSLw4r27vOC3XL3+Lvthz3Tn3JJot1v6zRa/PeH0/AwXLL9i/85D3n33bYYOdu8+gAjBS6q65AjjhF7v+fCNd+g/eGx5VtPE6Z0zzp+7x/0XX2C73fLonQf89Ac/5NGjRzz68AHj4ytOgoAK++SN7foe3/cMk13kN6XcrSLcVHhIOldrbY0pzTTjMLTzWMtMUzHBx6WQthCDefCiGW3Gx4Ep5Wb8+ME3wXm760EE74XTsxO2d85BhJurK4abHTpN6G7HSfQQIsPFFa9/+weEqFxO79L3PyZiiq3bbui2PduzU154/gWuHl/wwaOH6DByOsEm2HNTiHjXsfvgEd/9i79jkoDrekJM3sR05k9PTnjhhRfx3vPmm2+g42iVnPYjMgWGkGlhACfce/4+nfNst9sZxg18W6bewnUcxyKIjO98YIK4CDdvfYjb9mhnXncvHXfv3uX+/fuoKhcXF1xfX9N5x83jB5wEY+zX73yAO98Cgfcvf8jl5WMuuo67z90nquC7js6bonfnuXuM48CDDz7kg/feZxwstPMjcsIjVbzv2Z94oo5cvf2AV197mT/4vT/gY5/4JF4cvTicwrQfub645Lt/+xX+/qvf4MO330PHCYkWbqlOmFSLNT63nC0X3e1W42O4e8yy+7RCWv1uy4fhuPe8HWNNQL9NSK9/r/nQWrjw2nrWzuiTzuyxuc79H/cetO3YPNu51d8vCsXc0vcaz86f18J+68WKzfxLPxyjhk8W+J8Gj+qx6jCrY+022nDbO2s4+IS3eBIfODav4/M4/k42RAkme8YQCDGWy6Kzx8mUjup9WZ6DZqKLsYrcJWsmnfQMZmx2OcT8KdrP5dG4udmTYkOSpVQgxYGLWvyvSLbAzQnf5bK9tOgpTITJdK98ALPg2/fdzFzFxh2yFyCkcrnOzfApDDjVvVe1mFrN1ZRmG6FUgrRL3pTOd+xCMCtVjEzJCyGpLK+FrlvpwGEYUqJqut04Je7mA74fhhTLrnhnt+vaxtqcpikAQudcsRBogq3dXC441xODIuoM6ZxDO4ff9OCFEKIdeEyzVWYCmpWr2rMRYySGfDhJlllL5ixWU0mx6hrJt5u2yduQEufTTZIZXbNSVhPzcRwtn8fZxTKxVvgwYUnJIQpW2jdXCgsxWiheTLeAZSWlBEElbTptqu2VJwa7Ndeq80yMw5TmHRBxTIy88+M3ECdsw4YueC5+9A5ff/098I4wGTxEUvI+FirlQ6QLEJwnOiHs9/z3/6f/K6rK+eUeJbDbQqdw8fq7lhDfdYj3RAHdj2yi3anxV3/xA/C9WdtRdiIMvaOPA3p9QacWvoXvcBsTgBApZY2HaWQcRgQ42ZzSdxsrSztOxGHP/uba8lNCNGu+JAsSENRitdvQqdxcsPAO2U9897/7f/Ltf/+X4DvGIYDv8PuBh2pn990OYpjwm554Z8vLr7zCwwcPrIrNfmS4ukbHiBPPS+f30BDMM3O148d/9y1GQjqvQohmGRHf0ffJ8n33nGkYGN57yM04MDjlzgB9TNXEnBBjwKuwu7ji4u9/BFEsxcNZMrR4z9ndO5yfn3Px3gPGcWScRnqFTfD4YDfHBxG22xPzpoRg5yvdFeR9VxK0Yb7ZPJ+ZJzGmjOPphVnRqJ4pZ49AJKTE/RwKkuhP+jufQ58LMKjYjfHePMdOHFOIdoO3c/ghorsrrj64SKFGkT6ms9T1TJPhkqjDpQpfnXq6G6ueMykwjujNRLwY+ODdxyCwFVNcfUiWyM4jkyXYb1zHdD3SOUUZLWcgJYyLc+j1DZeP3iRG5ZTMDwzvxXWoREK0+vB3tpaPIGpVt4pjJ8HE4LMUjp2YRyTzA5+q/YxxQgE/aIIX6BDR3d4U186KL1x8eMnjH79lpbHT3g5xwntlIx0xKNPVDXHYIzFyFScEZVJ49OE1MSalSpW3RfB9RxgnywWJRre8CJ+58wLjuRK9J3aeuy8+xz/5k3/Kr/7mryFnW6tcFSJhnLi5uOZHf/89vvP1b/LW3/8AGaxmvgerlibpfo2sFJByWTQLJwKiq9Usi8CuVLS1prHrYStrlvbyXCN/rQm1Bfer746FFEnmA9Ueu8R7235rgbHOBXyS0rCYm8wFTbKXvlbG2vfWBHZYRkhAe9O6K7xbWAqGrZfnGEzqkM2Ddd6ifLdGwSftS+bbNe84pjgeSMoc4swxRamdZ93qsLM1IV4Snait+f9DFcUWzu0a6z1cCPRH3m2bwRyoQv5SL4XfZKWCvJf5jIhDU1iniDCME5uNyWVm+Da5SUs+jZKFzSyLLhdrY1SQowhX5PNTHjQ5T8RCnGPk8e76ifCEn0PRCCrcPbtr1Xg2nVU2USub51L5UrBKJTER+ZzPOVVaT/4eNBX7yBsEuZB8QBHv5hh17DKkWdsGnwR6VYsxN8abw0RM6M018adxSETMEsld5xlHE2gnHTk9PUFV2e32hGC3f4fJwqw6Z2UGp3GEaHdqEGNSDpK65RzDsC/EL4RA7ztzaQPjOEEQereh7zqiBGKw+vFWNUat9nqMiPj0bGeJq+NA5x1u45kEJiJ974njlEJDNOWwzESn9vIIChpAtbo/JBozEVuDT4w33ZmGE0oyZGvR8s4nQXm2gOTvnXMECUX5y/GS4pPnJnuwEuycn290n2KwC2VE0rqSwmoFoIsmHazYJaqki2hAo+fk5C5Cj0jAtOFcMjXBiA4fO5zaJVoi0EVFhwBM9BnPY0yHwmLSM7MdiUUBO7m8MYaQntsMJlwQrYpLHCdEAl2BjzPhb9zDZCF5KJxg1WxElDCBc5ZnEsdIvLkpMZIxhRluEbaJJ+nuhqDXZtlIypnTSKcWCz9U3kIFJicosdAZIVvKU6lUHJNasnU3KDINKENKsjZhxfILwCUrNTHS73c8/OCnpmyChVem8+E6hWi4p8GkD40RCZFN8rRNwepiITbeoMrw9odJyRdOVNmmczSpmkJh16YzZo9h0DmeVEwAkxCJDy55/OEFHsdGYxKMMQbR2b56DSBWDjCmM5/d4S56Rp0M45wHnZLAs2RkbaxzvntDJN1Qns6I80YffNoXagOBBtRbDkE0gktHYONcYhpzFbiagYWQLVhW9lUkJf/GyCQzW3GFAZlgE6dQbqYGhWCHIohaAnPhgGpVlEIsSlyhJQLRap3iO1dyTAQPcZY1i/ibvLhaeYpQTTfX2oNRpeQzdGEWLK3DRLNshPzWjJ8xomJhFyFb8KMiEQtR6h2oI4gUG4ZzSSCPgBiCiFhYY74zSlCc9NAJ6iJ9KpygouYtjVZS3Hi0Cfl5rhIiW1y6SEuJokQn+JhK6p5v+dXf/S1+90/+MWfP3cN3zs5qCMSbgct3P+Abf/Vl/v4rX2e4vLYCl0n4yPvuNOdhZOEm4wTlzJLpZYJWoQNSIYnmO0psDcmfvFAqbmvzMzPtqT8/Zum/LUevPMc8zdJfPFZENy8nmQiOxM/nz9qLgzMu3eZRWVtH2+/ynVj2J+9VKVOd5Jz8bh32nHlsq4DU47aRA+2c1z6vFY01haxWZNqV13sGWVadeXumbYu/V9oarGaZY5lv4RZKWmNcqDw5x7D0SR6Gts8Wd2uPSpnzkT6e7M2oc3lo1q6zUl3Dl6ScKliVBw+OFEqcvE1E1IESmZgvLs5hgLNSUc9Ey+V9IFacJT/RVqor8/FMqtx44YePHxysda09taIxxcjJySkalXFvCdp2gZNjSrdoi1g8eZxCSk52xWq9SBRPITtWAtcVYEtiphpDk8QsqeLLrHlJNLLpUvK25gvAoml9IZpQ0KUk4e3Wbu+2iwQdPsWaSRKqx2kohFYQ+q5PN3E7yzFJysM0WpiSSwQ6x0pv0jyG3Y4wTfTOxsg5GbYmE+g9pn2TEncA0IgXh3PmWdkPA1wrvfNMITLsBjQENn0P0UodojANQwoNOLyTwqz9zFW+Ko22HOgVy4JL1s98INqkwAX5rMKd2hCyNhG+tjQtiEN1yOu+VJVpGgzeddiadVbYplUJmvND8v4sD3xiqImImUGhJcAsCFVtycmGgWJlWBzYJITXcM3EIyoqsQiwuXJRJorZOoFaGcwaTtmKYcKhKzdD1zCuiV++EM2qWC1r1Wu17xQsyPtnSm/uV1XRlM+kOiuMihkPRGZPlJBunI9VScHKQpfbglnmZ5Lw01rmMtyzhTZf2FjgHQKkc3uwX2l93vsZ1o7F+1qejanCWCwXIiKkykgQg+2X3QQd8akqVgvLBf5y2OZz6RYCRc2wvfN0qR+7ODAnRudqfanalM4GlLLu9P0sgBmTrqEaajxJFndNCF/X91dVojadqybjhC7i/03XNLxx4pbv1esv8GLOeSmwmem6mi6azvZs7cvCspGvlFcWD1DMno0pETKFv6UFmOKbLg7MpMAq1GQl0cbMnQatzqzOl4jl3wuuJcZfw6/gYLRqb1lInkSJvWMSoN/wsc98ij/+83/OKx//KNGnMxUUPwoXH3zI9771Hb7xN3/H9YcPkSHYPSuyTAaeYdzgREXb1sJNWpqbP3vaXLm2LZ7J+1iN09Kj+r02zyH/vE1AfZr5tOs41k/NN+swx9xHG8Z0rL81mC6+L+NCjh7QCla5tXvQCrB1/3U4TKtAwJPLvD4tjFslr13z2t/tHtyWZ3HssxoP1nCnHue2vm57v32+NR7V7y1ya29Rc5+Eo8fGbs/oYl1l3Hl/FYsIGKNFdGSSJOkFM9HMfcZKFrCHk1G3zfxuWm2QcKSqjUq6p+3J7akVjX5r8eJehI2zG66jQiCmG0clhZ+Yi9A7Xzalk1ngDONkiogIpPxZSZc5ZUtvlyx4nesMlGLhNp5ZOPVJ+QjTWBSEEEbiZHdiuCQ1SAqnKVa0YEmn4zRYEg1mgQ7DZBddbXr6rmMcJ0Q8w7Cn63qcI4U+2S2y4gTne1RhmiK9c4T9nk1KCBaw0ARVNp1niCElsAbEQe98us11vrzuZLMpl6Fc39zw8OIB515gigw3N2wgrUOYxpHeW7iRCAyDldA9SBYXKYG6teXGOccQpkU+Sjm4MYdqrIdGsUJMMjLWCgTM79f5KHWYV55z62auhTON4cCdXIhQsehrEeJMM1+Wy7vNOtUK37C0sKSPyJbstqkml2fDFExQsXqsrTAdi1dsyTScc0VIrglZXkcL78VYlRDUEvQMl0yu6jGzMg9zqEANtxJK1xK+pNzkfaznkrTDxbzKnHXJII9ZgGqYZUWnZsoheeZMaTlkNPkMZBgXkTbPSSNTjEwpn6pWRaySnkAqdTqOk1m5JQsKS0EODsvP1s3OxmyDX2PknbOL7RQhqFmrJpRecgJeFpDrfpNVjCUei5Piec3j10JfEa7ThZ5CFpylhJumNy3sLXm2TNhP69BEu6HQi7WW52ZGgEMckgqmqqYszGc2Pa9alKmoFMNTHiD3E1P4gKIQYerMwych0odI9C4pO1rWYOO6ufy6ainbnJl3CNlbXmkqJKVzhb4IgqSS5NE5grdCEnuv3Hv5RX7/z/+Mz/3qr5g32hn8JSr7qxve/PYP+Lt/9xe899Y7SIg4JXlE5pvR6zNfw3I+s7NysabIt4J1SyfLO04W76z1k8eeMUYXtGJNWK9/X1vLk1pLt/KPY33cZmU+oJXoQnFr6dSTFI78TFvwpfo2kSujyWv914a7mu63sGqVofb72+bYttuUu3zAa8NjLUvkd1uvyxoPXlPwWhipUsLX29zNFqZL+KzfQXLs3Rre9ZyPGUdrgxnCwXuH8zlUrDKdu20fbmuSDOTZaNP3G3ZTTAaxWdMoZxkWFcNqPjHj+mxAWx9z/r8nAiPXE4Sn0zOeXtE4vXPHJhYiGiw5UaPV05e0ALPwu2SRotxGnDWwXPa2S3datJVC6svsOlJVFe+ZUnUOL0IU66dzHVGDhWeJMo0THkqZW8XhBfquNwakpiCcbLYpOftkQZQ3Pt0R4h0xRLb9xtZ3csIwjkyjcHK6sdt6U4zdbrdnGAemdNGfV+g780h478m2/2mccL2VMN3tdjjXMUVzT9tt5aZ42QVZFgd/fXPD1c1j/HaD7PZ2y2OIqVypYVLQiRjs3o6MQNM0lcsIVa0EqHdzsnWdWO/Vlb3p0h0pc3lftzhkUB3WLHtXikV9uNYqXmUBuo59rYnIGiOTjEcsiW8hJDEmwQIuLi8sFwWzFsWQQ2yWBKkWissYFeOOysF8siJhScgs+sxN63NQ9W1wD4u+asYfm7/LHCtQ3EZkb1tfTehs3KWiMs8xW3d1QUiNabhZCKSWJm3vAoeXY6qqlUOt8GahALEUZtbeL/ApFsYsZJtgl59wmLAsFU7m94pVilRaNsxmcNVo51rjos9a8TM5RgiTrTukZzNe5fMUYyznJ5cbrOeSfxexW8tzcvICnzXlq6Q8C+dT9aWouKg4Z9X+NFI8PfmejIxHxVuQJPe2YEPeg6w05P9iSOE1CbsXnglJY5qrbIaLzmFjee9ijbM1TlMJF2RGWDYC0czoKMxSFdtTyfRG0pxtguZRnmlT9jCXUo4qiPfcOGWvka0KXRAioVReM6VFy3ytDK035SsLKingMwYL0TVYZlzO89KDWP6o0XKWRBidciMRf++c3/3D3+O3/+gP8Ocn6f4dUyKmm4EH73/AX/3bf8fb3/4B8XLHJvUXxslKQHsLWWhpZW3IqZWN1jBTP7921pa4mteft2ldGF5vh5fBPk1be7Zey5rAZlrm7NlsvT01Laznn2lSPoN1cZma3q6N3fa55pHJ3x8oDUlxTU8AicdW9De/W1errNvaXra/5zN3W9hYC5fFvle8wA5jFc7cwLmF1xoc2nbAX5tnRNbfW8O5Mm9IZ3OFPzf4eqtSBQfrqPnKQnm5pb8WxmtyxdqaaiPBvKfGv82LkN5NY15dX7MPoxlFrONZaRBZ0OWD+YjdwVb+vkXZmNelBBfZR2WSJz8PP4ei8b/63/yvOTs/N2LsXbHedn1XLIrZI5EnnQVXyVndYqxCSZWnaqsUM+MyTdZu7L25vjFvRlZORNhst1xfX6Nq1vBpmuj7vliC+74rlq0s2Drnae+UGIY9Nzd7nBNubnbEdImYT4K3otzc3BCjcrLd2qVwMgtn4hzTOKULCucqSuK8VYcJId3+PSLJ8hvixPXNjjfffLMQAlOkDIZbb8nwY5jsboioTFc7NiFZb9XyXHIcNpXwlpG9VFlRRV1YHJK8N7kErvH8mRAWARNZMCSoDoTMloz8XiihNnb3ST4oa4S3WO116YHJY7QMsvWI5Hm6guPC6ckp/aZnuryyPAWNSDw86PXP8vZCCdD150SQQxpXvsv3d2RhvzAMADli2RJZrCl/X4hmdehrOK3Nr4ZtXca53JrqrMKVSVn1eGntzLiRL5q0PmYrUWZelgxm72ZL+G2CRz3fglscWuDWhIKipEQtl8stGKEk3UGy4rlyT0tSEEKcPXoxiZCKxbdaMt0y5lvUwqamGFCNdMm7mhOr27VlJV8bxaqChDGLap9rXDAPgRRvcUTsPpEk3KLQda6EK4lIUrQSDHNoTQpTncK0oAtLpT57FW3oXCwiJngZrc130cyV8CzUzX4XoVR7E2cJ2HXLq1O1EKslrUn3LEn2qliLjVI4w0hmJQXKTddFaU3wiRoJCJ0qQYXXH7zPj99/my985JOcdHcYNSyYsDReM+/mOSpquXoxh7Wa4j0rG1lfqjzIVYjn2Dl2Eonbnl/+zX/E7/7JH/P8qy/Z+Ul5awwTj95/wNf/+st862tfZ3+zw+9GtqTCJdEURuOt5m2KFd7VdPuYoFfjW21IqAXr+rkZW3VVaGufXRNm14SsY+2YwJVh2npkarpQC3tP09q+6v7qOdZruk3Qz/PM/dZ0p8aJWgGwPpo5yTotbMddo5N5bxfK3RFBvX6vXnNNw9vPVLXkXR7jPbXisYhYWBl7KUCvr09l+fkafh8Ycpi9ocdwqt3n284MrONL/W6maS1MaD4/xuNaWLdrXh2XmbYaXCIhTsVomXmMyx6hdl5J1g6q1OVwsxx5bK25BRft7i1Rep7OpfHUisYPf/yjIujny7WmdEDWwkIyMq0dPCPodnNt7q9cCIgxcu8cvus4Pzvj+vq6XLDX9T2np6fEEHj0+LGFTCWB2ydL/nW6fKsGb5imyrWUiLfOikot9PZ9X6zy4zgSQmCz2bDdbOg3m+KdyUh7fn7OfhgI04Tzns1mY5VYEOI0crrZcufOnVIa+NHFBSebbaoCVLkiscRFiTCEiWkCN450XZ+SaZnDRDKzSIiRrR/AwaHPwkBbRhY/r6G+LNH2rWMOK5j3zSaxjGktCmUl0GTPUhZ26z7WhNL28NdhRDn0qGY8MUb6rmOarNLZ9c0N4ziRrY0uWSXbMdYYR80EjjFIs4of6ScL4awQlPr/KwSwZlI1wZZUgjM/Xyty9fv1GlYZBBRcrshYnnaZG1DuuFkynVDAqMmoLSJ2aZzMfbUwVp3DZA7wR5fzbeG9FlesWHUiTbAplwZFq9fUsbQqLoi8JG1Es9W88mqZQTopH5T3LXSK4sGI0dY+hWCCOEumvAgnaEJWirIsjqDLO3TKjmhO1nXFUxtUixc4hyjV1QTFQYzTAc7WfWo1zxnP8t7X86ecHXHOilUcZAOS7tBZvitiShlyuJ/1/uWWrf8xRtBZgVetwrpssOrNlVAUmY+4Jmtf0GgV4qIyorxz+Zg3rx7xiTgxhIC6uSjF4RkSgluzYlu1P1WHSO3VICni85xqa+SOwGuf+0X++D/4U179hU+ZByOtwYsj7nZ8/6vf5Ot/8Td8+ObbSFC6pHxNknPNUr5Zho8NehCKlMdeo2//w5uw3LnmW5kNQceE2tvofCs4P4mm1Z/XwmE99AHerQjVx9pME5brPtYnzBcA3wb3BT3OoXdNy+8fu+Ct7WcNLguFZoXPtGOtCcJrxkH7uZx2Tc9b+GRZpCi1Dbxa2n9kseVwS4Xva/tYz7/2ONTrb9uaUlz3V4/TKl/1FFuF6FhrlZljyz+meEBl6NR0zQBKjELfd2x6n7zaUuRc51yKLNLZQJNkeIOVEpkVdSfHywYvFA2wIhjA2ebu0TXX7akVDbsd1uJbw2TEMMSwqKNrzHUOFck3epuQZJO1sJ5ZSO77flY+vF/0pQoXFxezppUsb48ePaqemS99qwEyjzsflBCm8nyx6DfIFEPkZrpJ851j/40IRMLlJScnJ5aMjc3ngw8/LGEmYAqPYEml3jturm+4ePy4VJ1xztN7T8CY7jQMSTA3AarrOnRyeFHC5TVdCJbPkUpZFoEBQ3QrWpEsopkjqSYNf/bq1EpBnaOR4VUzSVP4jCiKVAJz6l+pDng0pjuFOQHfOQtBQ+eyfhle9eV9RRDNY2Jwz+V3M82vvSf5vZCIkcaIs7JBtgbvbX6NpwCRFFp1hLHFiFbx5wkTk9CZQkMS4TTBkbIPIQl8koClKYE6UieW5h4TsTdJNoWOaAllmTd2yQhIFkaoPAg1IddU2hmh9qLkz4zRLVgo2Vk6kZLGCtVxSCFuVpkCTQmrIunm4wyrtElawdZ7fBKdDT4zA/CSbyyN9WTSOnPojuHwzDgqeMScwGZzEWASU4gkEcAp5WSpISAxGhwyXhj+2C3RJSQsrTmHCwUNKbTK9t9hXosQIuJn3Mnhht77UkI038oqUPJbDFcPBa2MFFHNWxzUSmF7BR+VvRPMhmI4I+kSSolm5fdCujzJ1huz4cX7BMOwFBTUkv8NX0nCfiwwDeNU5lwXVTCaOs3ejozHkpiZqzArzuvK75YPNIWfqSTr26xMwBxOmJWJ0meY5t8rxp2tcMm+WMLhxqjgHCEq17s919sTOp9ujS8yZSVwKOCXQkHGScG8Hzl/xVi0pFzDVOCgMwUhotx/9SX+g//4z/ncl36NIEBnNFemwMWHD/nW336Ft3/yOg/efo/p8gY/WWEQh6Rytdmr7NOqxCoCVpuYabLRgqWA1ApKNa+slYM2Fn0Bk3rPKmNJ2YMV4eugLYnpwbu3KQCtUero2Lo2wmFf7bt1q0OArfLWejKwyLKv2nvc9l0b4ubP5pymjNzFe1YZ5OpWw6pWJjIfbeFi/2T29Ob307ha7WWrWBTVOuNCziurWMOaoF/WX8+j6uuYAnRsnaysae3ZxZpjxPsq1Ld6b82AuIa/tz132zNrrcW5tefWFNTaaDXjTxbuIEckZN7cec/98ztz/1rRN3uE8kHiAxlGtSlpOYtZIZ6ps874k2XO7dMZNZ5a0fApBjmK4LtEgK0+YuWST8/6biEY+pT/kAGXK4NENUYgSfANcZnUa+/7qizrUnC2A5CIUb4zQmfNNrvy8wbEDGfvEe9RLKZak2Cu1bOZgcVUWjVirqjdzUC/3ZZSkjHGUsKyjD1Z6NJwNRCjlcQ9PT2lS+B2rg5hgM3GbnYU1+HF4/HghCGMhGFkurJEcEnzK+FD6XfvhE3XmSUhhTs4cawRca3mDSwQuiBF8gyJsEgSlySIlYovcRYGRVIYB8I0WKJ69vqAoGLwrW9LnUN6zP1nSo0JMZLujlhUaaoUkzzHKYyEMHF9+YjtxrP3ki4Pm+9aSdtrybFJGTQ4ZKUqW98hHR+U5Imhwg3Jwq4JqSW+G2aFT7I1NuU3pDDDSFwKX9HKO7uUXaxJoXFJCNN63oVuSPl/Ph/ZC5HnEdUUPOelCJ4aTbA0Y1oWLisPBsJIUs5o4r8VhKncRqr2YjkPYaZHBjs341kYQ1Jc3SJfRlFEo5X6TKVrszcoqqBqyc8xKbBF2U9zLIvFwjKdcxZ7r+kOCbW5FdqQjBZTlNkwknIiQmVhNCUzw0sITojRldwMjTHdHG5wVGYlwmWPrLM8r4xJInPssHe+eJfymcv4HJP/oDvpCVeXOI2EYEnhiidO6ZZ7IQmgAhEc6SLJkDEjbYaI3Z2S4DTDLCtzEZW4mGeGi+LJ5CAzs7LD4lOiuhbeJ7kaV8W1YtZ3i7JaspvQ7BojyxOJPid6YGRlFnCysj+TMqMTmvhBVtxzXyFV3RpEOfEnnATP1dUNl5t79JMNp5o8Bt6BmueoE4E4e3411cHOFbwkeRlUI3Z7lBUa8dE89MMQOHn+Dr/zJ3/Eb/7x73HnhedQSZ6/qAyXV/z029/j7/7Nv+fi3Q9gDAVYRTATwYsp42CVkWsheCGYaDYTzIaINk8DOPiZf88GuhIt0K2IA1pRHW2EQXfYb94y3yh/BS+KmFs9vyKk589rHtZ6tMo/ZDmvqtVe/Px9/Xfd3/yu4YHgUmSE4ewcXhiKYtcKvO34reepCI0VtKLOUFnbq7q1isvas9mTXBu9IBkjaoG1mnN+1j60fSId03xn2jFhmbyi3K9U4Wwi5XwuntdWgavCZHXGmqNGwRXly2it0Zs21Kpe51qftdKwNlY9Rv7eCYsbzJ/UZrlnPhNrCk1tcF/iTzK8OkrEjohyerJlgxnwXdpv4wQG+xBDpWfMSogK4GYjxbI5JMmrKlm2sOiB/FmrEN7Wnt6jwVyuNjNU70y4jRJT4qEmJuhKbobGOU5RxG7h3u13KZ7ZmHPJv6gIagZunRC1sDpUrrkWCVoky+9nTbFsqmPRT4xxvg8kCQ6eeY4iYmFbMbLb7cq8c0x+jocHGMehjH1zc8M4jpyenrLdbk0IqypAzQcgouKJajkb0zQSpoGemJ6fY/ChqiIV7XbsmlGsuVFrt6U4wUVXktBq929mPPndDMtSJcp1RSMuSlwF891uV25T3263s1LD8rDnPQ1ql6TlOWflJu9fXm/XzfdudEmxEjFl8frqinEYjLA58yJkpStWc4R04YwqzuXDKKQrrxYMpByqzM4rPpSFNXS2+kgl5xlcgl0Mpw7H7I0oVmAnTD7f/K04L6mSkithL61lBkjKkmNMd1OUePtoykTM9wglYmBx71ath/zPsIRiIMiCo2qlLMzryYsr1cGi3U3QWoNmwi6mmMWkfMR57IlIlFgpU1qtdfYoxUgxSmT1r5I1y3wtOdg+zMqwU7MGl5AzlBApAnTuX/O8Mq5X300KIUKIYvc7aLr4MCXQ5fNfnzFL+F5aJOuz0wp7ZSfE453jZHMC4pkiSLKub8Uh6ojBAOgcdq+HCGMJV0pKSF1usCiqM9wyLOYk64QnNcNQo0XSlA82+l7/pXO0lC5DJNJHlE2vvhJneSjZY1oXAZHUjyajgGiqSBiXMB2nYAphDKX4hnl7NXnehX0MnGzv8InXPsNGHbtRrbRsXjSz+uMUegedd8QppHPtGIfRPFUh4CTvX0ywFlQio3P4jfBLX/wif/af/ke88rFXkU2HRMvrGYeBB+99wHe+8jW++dd/h9tPSDwUdmcASYmvfppW09Ico74Wnrf2fFucoxZy6ufzzwUP4enmt+zs0JhxTJi8bf4LmrgiGGYY1JEOtQxwbKzCk+L8dz5bRfl0y+fr/o+taRZwK4+DLPto3137rqaxreA8C9uQlc66z58ntE6gFDhZe7q2ts9j/n/WFutuPl9T4Fr5JhsbWuUlP1OMc418+KT2JOWvfa5dy9pzFoo5hxQ/zVzyGrxzOE9iXsmwlWSSYkxk9n7msvcH/THLOIWhUq/BVEyUcidejV+1l+tJ7enL2/YbnEvKhMzabd9vbJqyTA7On9mEZ8LQdT2nYgKu9zMDruPU6woeGZnt1vB+0X8d6lMLxLm60X6/L7/XAsGalSRbd7KAXCs+eYw812maSsKsiBRhehiGonSIGPEeBlM49vs9+/2ek5MT+r4vfZyfn1tOR7JOT+PEzeU1U5hwOnLS+XITqsZpEQ42K1CTWcYrWOc11h6EaZqKwmQJp1qE0RaurTI3E+yccDUTsXLze/q973uur6/ZbDZF+ZLkHl54pKp+2/yRmhhkxaMOsatL4276nvvn93jD/YQYAlNQam4QQsXQxeKwTUhS82ZoraCGWVlgtrZHIIRlbGtIwrlLakoJYSNZ7iJ4NS9FZrBoTtJyBFX2GopVFk1lnNO67H49XRBPsAstcS7dTi/lTEY1id5CQ5IEnYTGGBWVWUGUBAstcJ6VKruTbcaj4uMR8g1x5jEqZqcMWygsR0i5FOBy/D9ZgQPSfs/uf1NOaoIY1QRq2xuF+hY4ZniS4K6Ay14y1G4yQpPwbcpCiFIE7xghVPGrxcqEBcZMKuVCJFVBgn2WNacsqNX0LYQKfzL8Ktp4jAEJVh5825+gkzGAXGEuBsOJwoxCoOsSHmbvVwq1yfto21vTRRtFM8jqeUgjNKoZlsrD1XO16hE1w3fG+bqPvN95LuWrKQl6wSBtF/0lw4Bo+XuBD0seyGSEi4AyhgBxwif0kAAupgpyAmebc2QMDGNglLnYiOlbMTFvZVJHJy6VMYcQBvsuRrxkj62iIeC8Xc5JJ7z2C5/kn/+n/4LPfPGX8RvD105tfR++/S7f+9a3+e7Xv8nl+x+yCYKbIurmCxYPBBmNZbFPI4RnPmUGh2n1mTW8a418t41RvE3ZM+DkoM+nEpYa0aQ1otzWVytAlnN35Jk855of1rytHnu2NmfP81JoLHKCBlr1u36uFfxz3/Vn5V4izRDRYvBr130YerX8vVU28ufOyaIoybxvrih6q7RIdVbcmuPfrrWWqW4TOJ9KsWnn8wRFtN6v+jOpPlt7vq06+TRzbRWBspe3LOuY8pjXWZ+32vD6pLnV9NxK6mdcrQ1xmjzhaS9r0l6MP7kISnNZZk1vE32PWcme0cLecy53+MT21IqGKRl5Fo6um4XFeRG26Fkwag+yWYOc63BExGlFJJe1itcOVO3eravptBp9/nd2drbQZOuNrQ9wEVg3m0WoUD23mjjld7KQlOdi8du5TJ6UPrJ7Oj/T9xYqtdvtCCFw9+5dRIRhGhn3Y1I0RjqJnDqXLnyLxZvUWmq8W16MN+/ZYe3y/FwI6QZvZpjUORAwV5TJfZhHYVYoaqWgVvgynIZhQETSeqHG+LrfGEMp2dYmma1ZJfJcs8LWdR3b7bbA36tjChNTjFk0KHCKGlNcPkAoxCmhblmPzBOd58lsGVh434J5IuZzMFd82EfILgJVYyhekxVRzQsRVdMFkjbeECa6OOdgIHOYg4igrrOSq4BotvqTQj0styUn9ipUhRFSUnPMyp25W6cQiC4WpWEmV1lBMotuRaNKHk7NsBekVcB13twCeRlpfYLggxSFNYdIlRcLQa3DJcySP8O4sQhrsuEIwGxpc05QnRbKQAym9IQYGUTLnhrdsrk4MU/hNE2MYcKp4jRZ25MVKc8t/xzHsQCoNQa0Z7E2AsRoJaqnYGGXTrVUlJs0EDXgXZfij01Q6TB89ip4cUWZdCkv44D1J6G9CPFVPsUy6VoQlcUlfgvljzkvJq9DRIrgmfetMLNM/4uymvc3wSLBNBtMCnwAopR1CLLET2f8xTugSwYhrCx3nEYLgVJl46y+mFNloxAISV+1/uKY+u88qoEpzt7UTedx3uNIgrY3Y5B0HTi48/x9/uTP/4wv/eHv0p1vib0gXtBhYtpPfO/LX+Prf/t3fPjOuzAGNlGsIl6MdhG7P7RO19bhp1Ey6u9rT3BLS9dajYu3JdvW85tfZtVKujbGgpfnfay+O6aA14pAK6i1BrX8XW3wqr2Ia0rK2hwN/im0u4muyN/n+ee+WjmkhlmrSC2rziWIJJpYr6mFQ8sX63/1/PKzMepBbiZQyjjXgnrZ29poRJJRtTrD1Xrb/eEJOFrDJL/beliW657XU8NkzUt1TOFdk/NyH+1cWqF/bb2Hc1yG860pme3v9bNr82ufreemFbxEmC+0jcucDgurzeVwk4KgczjazF8VzdUybVZl/wULM3Z20Z3RaJKxWNXGXlnXsfbUisZMVWrAy8yYXSZ2sTqgGXPzJVAzkEQ84qyf2nNwjPjUn7UHrHWHttp23UeNsCLCMFgeRd/3C+t6/VyNoHV4T30nhaoWb4jI8nCP41gExVxvP0arvT+OIx9++GG5O0FDtMpTYkIPImjMN9wuD14hFhpL6EPtGagJXVYMauJZt7XDmity1fdf5PWtEfF67zJByMrKZrsp88vzyDBF1Zh8VTkL4ORkvutkv9+XkK5WERLnePjwASFMjNNEGILF+qfQD+ecCQmpxGauo98qZiJCVJuDQvL6zMHqgTmsIL8fktDaWjcy84gCsfa6xVQsQCiKUcZX71OlMlUmlwoX5P0mK5KSiIMJbBnXwhQSg6RcdJTHizkcy1neUlGkZLBkVifsw2gnVeZzPjMjSyYWmWEyJctpETklu2hnk4jEGa/yzekiFtZEoMrhqaoNSVacjLYYjlhRhRCyMmBC5rwXeR7JUp0EYefsHgNNxes1PVxyt6IJ3AenQSPTGNPdNQEXA5Z0rfQC3rFQ7hfljCvlKAt+i1yMOnSTfJ4jU5wQB6fbjvvnZzze3eDUWeims9A+l4R4SbCV5LWRdKu4CJaxscLzrbAFhUEpsKgSVXY908n5wyUjnJ/JZyOpeKjLOWuV4SFdPOmLZyomfJTFpZrWX6OsqjAfrFrgEPCxXEIl0pU8PlOuHV0QJEYmgcmbXrKJllOUlYacx5Y90OKyIhrKvUvmmfNMKrjeEQTcScev/Pqv8if//E+5/8LzsOnwznIr4s3A2z/+KV/+i7/g7Z+8QbjaWfhktEIU0UHsXVGuMnwXAkuzd2t0qv459yGM4xwNsCZkr/Xj3FygoxVo2/1fbE/T11Kg/vnCU9o5Hft8TbhuDVhZiT8mA7T95PmWZ45qUCbLWLXIWZ5oIx4WvLkOL6q+S3aExOcP8wfqObb7fEwYXfJhFry+hWs2ctRh43Kw8qXm0cpepc+fY49vw4ljilb9dwvfNVmmfQeWURpr72b41XJbjRNrCku77mPwaeff/r7kBcv1t563Fg4ANzfXxXBmhXGcFQ1hptlUc8vnIsRUckLElAjVig9oiYxQzd7q9H+NhzzzCe3nUDRmy2LWyo3454VnRJf0bJM4s1AckoLSxBDWxLZVNGqLOSwJRh1rWm/A2iHP79ab+ejRI1588cWj7qw1LbzNC8nPZM+F9/PGZiWmCJOJKOXE0Ln8rAPn8OKJ0eJ4DcoUJMhj156XnIXZEs46hyV/duxgrr1fhMRmn3IIVHtwW5iDKVnjONL1XblALK+7lPITu9Rws9nMYyRmkV37eX9r2Jef4vBeOD09Y7q4wdKFKmE8JQbHlFScYmFALWSkZhg1blFVfPG+s3CNuolZAHIlptxCxWRFHLFKzM9KqqrSdx2xW+5xIQ7OwrFcRRzy7/Z3xmvAW+IyKM515CT3ltGY18UXgcy5uUzzWdwUpU3q9aX9ydbwci5SnL0e8UIiZnwo3pFqHpbHMJeVrv9FLEHXyhbX5x0E86rmz7KBIltxlsp3rgwm+FylybQrtFy8lhXChLupypwpeCmXJ4V/dU7oMYu0U1O8YpRyfosFNZ2BaZoYxxEROTjnNTzK+iyLj23f8ZmPf5SL6xurniTKRlyqTMYBjYrB8gWcc7OYICw8ADVO5/2ILGlBsWklb0aBfUsuUjnXmT66fAzInitFF30UxUJmI9jMF+Y677aWSqhqFY+CWoLz6woVwIhaiFKEkUjwll/jwxwGIFm5SPhoXj8rIpHh57sOVInOM7qeySkf+8VP8Xv/7I959ZOvEVyETWfK0KQ8+MkbfP8b3+Irf/PXXF9fsfEbXDDjkXPe9CbvGEVgCiXU8kAQkeXSbhPMaoNSCHHx95qAstZHK/ys8cwyt/x78/fBHj2l8FnP82nfaQWxuux4/r5WdG4T5OvnS9+J1q2tQ5Lu2+bAHBMED5SEWD9bnUk9FEhbpWq1vxV5yD6bZbDFvBYy29JoGWMsRQjaVuNUPZbB6+fb6wM+u7JemQn2qiD+JLzO/ddj1DJiLU/W0QJrONhGtpR1Z95fPVfDql5bO68lP1zKpccUq9qTZI8kPpgqwk77PaiaEVANAwQW9+4AUOhslokOcd1kTTOIROb8u2Li+/nsB0+vaMwItp4wltvaZq3FzIEgYmVgQ8ylAn1iRorI4ebU/a9pg7BUSNpyuYdzgO12y6uvvFLWZYER6WKkaKEttVJRr2cJFxbj1xYi53yBXX7UuzmvYbvJCdNpDeKI6qx85X7AYTHxpOfrOxWycOrcfGjauUmywmgpjZn1VVkefGwKJuympHDnk/Ux1fhOumRWlnLOxbGL98phDjHdzaElOSlil2FN48R887F5Cby35NcYR5xzpRTxAtYKEavO9dy95/j4Rz/KB2PEBTWLEfOehxisGpOby7YWQR0tXg+lSUaXWYC33GuTlmKGZS2MY4JUHQdqAn5DnN2JeS6SJ8Tml/pzKQxGWVh8c4ldTdaEHGpll9C5IsRpTNV4qtLMhlMCEvGdn63wSbFAsVK0kkP+mtj+JHjlOOJpmoqlOocZ1J6mDI9iLBDDaVcpfFMMwIYcE23wSrkwFTMpylcB8tLDONOWfK5cYdzO2157l5QNkUoYS3CJlQBcC+ZOiI5ynZGg9EnZcwhxqmJb1YRkl4plDPv9bAhIz9idQZWFNeNdArBzgsPCI0/6npPOM4wDAWWDQzR5ExIDzqEWsfflPMKsDFr52IqGVoxR82Jzsndad3auZ4WlXF4p9smck5F0z3SfiX2X7pXwmY6nkMV0Dm3NCuXMpPVoFeblmDfAZjDTG6Tsq6J0OpfelbJD1tPWeUvcDopXYUp75kSZ7DCkaEZ7N5fNdZhyIs48c50zfjA6x/2Pvsjv/OM/5FOf/yyy6VAviHj219c8fPs9vvvlr/H4jbd58Na76H7Pibmn8WIVBCOa+k1Ks5NScS6fMTSz8YyMmaYshU3bzkMhzYxV/oD25udbobRupcjDyphPYw2uP6tlgAOe1Ozw2lraNRaFyrlEH2c+Y56hw0sHa6HvmALT8u3y+coc8zet4WQNDmtrsa01pbbgfma4CadFDqM2asG65a+3NklnNZ+LWE4ZypJ21rgzVwypqG4jDNfrnflfxQBrGNRTWpnzoSLX9FeNU/Y8xqOwbodYe+8YPOt+67VZuCxl75PwYGeYJVyOKRlLRTHTv/wvv7+OW/N7c7+zsbBDcQwxsJ+mpDNoOWgikq4XyAr3nLNqMlfmUbPyIWC5f2ktIcsRktmWWC2RZq9va09f3raqsFQTpVpLbQ9dLZjXWmF9qGOMpZpHWaiLiMz3c9QW7LyRa8RtTdCt55N/1u5CTYRqfqcao/LK1AhUJz/nflpBO1s4SRarvt/MISuaYvNTrX/nzHqWhT8FxHm8V9gPxfOzuOiKGqmXjKl2G5MIWgipDGQhcHmNQIrnzMJkhkPn+5lJpAo9zs2ehfpffi5bmGslr3hxUj7FNI72bEjhZD55OKY6JC95GWS2PBaGk4QmgiU+jxpxnUfHgTvbTYpzr2JsJQngflYEazwoOAaMUa3CT9ors7gCKUk8M4iua8XfhOsoUWalMQpmrWYOvcsbM9/RAkGMkboOFAdBi/KIagr3AhGf+rSQs4RiZa9zkJ3IvJ9lH5yAmEJDKWGcFItCMOfzomrCZoyWY6Q5sT8piy6V7hXA+RURIo+tIEQIifCpeWpExMoe55CVaApWVvalwD4LvA5kLjXrcGiiHVZhTE19UxPqfGLkImoCnyjohMtCMZmwZlGVuQwvER8UT+VpzbHBZoqYBTBxJUQthmXoEOXMzUxQKvpTaI1mr4UiTHiNdBoSnGZlys5sQhoUn+efQZ9/DYdMQFUX97hqgm1L38h4F0OCUCpTvqCHJAVgDp/CWdqXJBzTqFYefBFGY0wwFzEozDbjYs2kyedjfrYozqTb5QuTLiwylfw1b5Ag+NSlJqVa05oKyMQlRcSnVB+PdsJehO2dO/zW7/82n/2932Rzfop0dleKV7h68Ijvfe3rvPvTn/H2z94g3OwJ4x6v0Gna/3wPAQl9Ufok9Imb77gplWG0QLO0mte1gvjMDx3eH3qt1wTEFieOCctrCkP5OzOWlXfafheKxDERvlE22t9john5szpHLuec1bQ897kmm6zJDEv4HAqxJQyLW6r4VH218omTLnleWmt8UsSExfN5He286+IuLdwOzjEw5+rVaz6igKb1zUpQOucNjtTwKML7IThWWw2XY0pGUYhq3vwUOG3rXMK9fudJSlotz5Q+oVRygoo/NPhdK4TteO26Cy1jhmVdXOdwfrMhrswpnfkowsOLS8IYkVSxsRgxUURhilp4HYD4lOcMZnRBsg27KB5U58o+T+GxUML+fg494+dJBhe6zuMqi9QsYNbCZr2ZifA7c+LMBGDuN2v4+Z08+TVBthUOc9+166t1aeb36+/zRjo335zYKhRlHF32Vbc14tX+vjYXqhyFtiKWWZ4F1ZCspiwuNsvKRm35sFK4y/yGpRKy/KzMTw4PSVEYUJzzZZxSrapiZBn24zgWITorGLVHJ1fVUlX2+33JZRnHkb7vDyr3LCxnHO5B/s57zxSzcma5D5vNhn1IuRtaEQ1v6kDLCOo9jTGVq2XOHyh7YhtU8h0y1hYhKd+dUO1hhnGXKkM4J1kLSNb99L6IXQCXFSixRGpRGNtbVqv8ApGc7DwTIOcpShqYpyJN3mxbSQg/TF6s4TArtK13Ju9x3rN807WIVEnn817VsF07w4fGgST65zNKJUOny5hYCV+kwskWV5KBGhGh8x5NBpN5Dku8MmgIzq8bNdq1tefK+fVQzpqWtbka+ZmD8EatLJEVzHKr88TKXFZCJOuzVcZLfa/NYwnfGSpt6NYMgyXMs9DiRJDkjZyF1YRtFb0t4zdGqLrV47WhercJEfmTdLQQpSgfqAmOVo1HoHMMXognHZ/79S/y2//kj7j7wn2CM/xzwO7imm9/+St868tfgWHi+uIilzCzM4GCMw+eT2e+xtU1AeqYgNIKwsd4iwmsyz3OBr6a/7V4Xj/3pLY8W7mk5lJgmuWAef4H7YhUWq+9hUGNJ0t6IWXd+bP8ThvGW/O6ti3gnOj12phPaq0c0QrP7RzL/Kop1WMe27NaTllTLm+jVSZYxgUtEBGOYlaDg7WssKbcLMas6Ndav207pgSsPdOusb5D7VZFZmXcGsfq50w3PD6ntbU/Da6s0dC2vxq2x9aT84v77Yau7yjKIYklijCQy1Ibb2/PRIyW/5cvT3XOWQhdsCJERj8yLbHLfQMmqx/f3WV7akWj63waNG/IoQYotRa8+JkJ6goTkNxPZelVSlhKfaBuZe6VpTq3/F1tYW+/V/ul/J2Jcn6+JtrHxs3IXSsMB4c7C06SbYCU6lMLBipJG51MNxexC9hCDLQhay1CiswhW4Xh3HKohDnErGZKMdp9HjUcsnBUC0gt7FsBaDFW9X0uA5wriI3Jw9Guxf5eCjFlDYmxOucQtdjq66sr4s3N4vbvlrkviEgrXAGC3bSMpL2I+WI8BRW8LC+AcrIkXu3eW3gHRakrLKc6P5mYibM7RYiKiSuHDMk5xxTDARMtsCqWCz0kBDLf/VDvYS1s1mcmwybnGKzl7fh0x0WOr88eOVQXoVui0OWE4EaIWKxR53jQ9gy1sFgIALaIeV8SA67xd5H42Agpt53d1luJLuFV40N+tzVs1M/Ufa2N1wqltzHGuZz2oTBStxbvW6GhjJf2LrdaGF47R23/7fzqPtaEn1aYamnIsfXbTe1LZlx7lldhgOGhy4qGMbGSizM5IfSOV3/p0/z2P/tjPvLpTzA5GLxLhQEiH7z1Ll/9i7/m7R/9hPHRJUyBOOytwAOCOE90pmhQnd8aL9f25jbh5OkEmfnujcV+Nud6DUe6ShE8ELRUD4xbZR2NcAxz2OihIeNJ8z/kZ/VnvqEbZdWZvnLIm+t+2nCbzOfyGMs1p+IZsjSsle+za/uWlucxGywP5Z8Z9+dQmOXncvBZ/W4bVXHs/C/pDQsFH5b8u+5hDrNcP/s13qydf5gVrGPrWJsrMhsq6vWthe7VsKIyetdzrvcit/bMFYG7irwpz1Xj3HaOjskcbWvnVY+V53Ebv6vn4Jzj/gvP87v/9B+zPT1hs9kY7BIcnfd02xNcirDJ97uBEFN1lXqMkJULVeI0sR/2qYCNN4OJd/h+g/guHYF/YEUjxrk+t2rekLkGvi283oDKZIRDJMeiHbE6LRJSHFEPQ6dsrEPLSY0cdd+tZrsm/Kuamz/HT2dCma302VXW5mm0yFGX282Ce/YCLA5rNX5ej6qWalS5Dr+qphj6+V6QmkXVd42sza8cTubbkDPsMqzyBXo18mahOu9phnEt0NQhHy08Wwt4S9DqPutn1nJLbC5zPsqiP63g4GC335e/Jd2aXLuZ1whFLaDMglZMIQ6ClWJWSBd0uXxFJilHIvGOWlDPY5UxijNTyk3DRgiYDw65H/NJ2rznZL7s0VhUNWnGofQZF90uCEHCqzrHJysHU5yrt+XPa6WkZf5FiE5dLxiqUkLwcunURShdJaTUOFPGWCHYNnbNfurCCyWA6ICRZVjmM90qBLmwxXoe2RqM5+drD03BYWXhIc2tfr7uu8XBdty1PLPW0l8/X+/FmqX6mGCw6L+B/8IL0ozVrqX9vqUTx/Cpfrb+u6Zzi+dCJFawP9iHarzl35LCzUBFiJ1j8sIkyr1XXuL3/vmf8qnP/xJse9h4RJVOHMOjS77ztW/wva99kwc/e5stjn6ysz2EiIhZFi2l3LyGdpGkO1hbW3mvxqljikj++TR78LThUy1/PIYXrYB2bPy1MVr6Lqn0Zv39bby9rGlF0M6wXJtre26fBnbz81IMQWsREibIrC5/Med2rBoHln3Pnuk1L0zdWhypeWtNT2peX8+njkCp4VjWXwvqHCoKB7BgScfqddZ91HvbwugAbqoguVT5EnZr+FXTunAkib+mYS1NaNewdgbyM2v0tIVPS/Pqz9aUnTXFou6z3tOWT3Vdxysf+wj/4n/yL4kpLy8rGZLWnYuWWn9qURJihWB8kjNiqlJV5BNRM5jYTFCt5GzF7kDSHJL15PZzJIMvE7qIcxhG8+DybxE0hnQhUxYW1ty32UV/yIiPHdqWqSyncWjVaFsR0lPVkVq4mqbpwNtRI1V+ds3K2x6oVlBuGUEer+u6Um7UOZfSAgTxrgiXtcei9CGW75AROSPkmkUwvw9YKEBFmMv6Ugxx64KvrbRrwke7zvaA1MQzj1ULEi0jiXG+rbvFgxgjEix0JyzGj4QAnuXN5u2et3gwz1GXh1WMVFpu3Zw0b0qJppj8+RwcrtsUWfF28WK1ZYbpGXdQu+m4fJa08tQW8fwi6Rbk2CicNnc5ut5DIm17UN87cVhFbA1eho+zUiDMeKOqJYyqhNNpJciWIJblPCxW+RAPjhHhhSKZxqv7yng6x3LHIpzYOTBPan3zfCv4AKV6VPlOZ4ac51H2O0Rwh8ymFSrr3+uz0yoCawLTsfDQtv9j7ZgQs/bcMYVg7f1j56wVnlo6etuZrL9bCI0N/bmNR7RzVBEro+wduw7k3gm/+Y//gF//0pfY3rtL9Fj/U2QzRV7//vf58r//S9574y3C1Y5eBURxviOEie12W11MKlZYIcXBZ49ibXhq51sLYbVBZw3Gt7X6/KpqCaethfHbhOy1/lp+VebNbIzKn9f91J6Nxd4jB8+3e31sPjWfzX3XeZC3vdPCu11nbmYsUERmz1gbypvLKrfvtmd3sRadY94PBNFG7oHZSFYLqLWA3PLU+vkiv6wIqnCLVV4p/HZNk2r3p75NvqWZRQ5p5IH8zNo5KPMRytmp19Tyu/bdFmsWNJulotDSnqPnzJj9z3Vu1lpN29f6qOWrFs71+avzg4FyR9vklEk0mTlypI4VO9GgizvYxHludjt8dGxTtIJUil2GvV3orIWvOhGiaDHUICCHdpHV9vTlbesqUDprnM419ZobjS0LiU6XglgNSADXhErl+uktQYKlJSYDT5dy2eJw1Qi2WEIWYHU579qDMsXQHHKlLh/axlqvxV7XRMEnIlALQrXgThbgBOqqKhrV4varg3Gb8NIenBlOS829JlYLT4Usk7lruNR9t6Ebea15TfmuiEyQgMIA19yUrRWmzuFp1yNOIBhj6Pu+hFPBoVJXE+wWPrMA6lDN1nXKP6zHKixpScSaAmlLvBYxwTRbWtIeNy+gGhHv8Q5Ercyx6pJ5Ffiw9ECR9ZJ5gDLWYp0rMJy/yef58G6LNdjnAbSyTvrkDRMopYyBKp8knato6JXfXDDQFTiWs8x8Ttv4YO8NDrWXIf9TXd4+vxTWmzsMFsJp2pdqnKxo1BOt98dKHa+fz2PMrD6PrbXy52FmT9tauEIV3sTtVqoavre1Y0LjGm28TZhuaVPBo6RU5z4X57GlfczbJc6UjKBK6OAXv/Rr/Naf/wl3X3kRXCo9C3RBefTWu3z3L/+OH3/n77m+ukb3I73CpuvAO4Y44XuPi7MXKFOJWOXMtQJOK3Tk+T4Jpk9qa4pgCXFslI0Mx1Ji/EhrhbXqmxUyVtGCysi14Iluyf/bvVrDTRuNQjdrup55/zF4HBP81/gYZPpnYW813yhzERY86ZgAehDKpEpddKZukcq4xTrMc59t/1mhVNUSimz0cC6jX/eR17YWAWJihxRjT1rhwfpamNRW9va7WsloeXLb52LNyYZVzzO/u+bREZHFdQn19y0cb6M3h+/PJWzXz8E8/3ZOa8+swac+I3U/9TlZC+3NvHocBhgnfJciJ7IymXhm9FIU/DG5NzYnW5NNcq0ftRLckIz+qvgKd7x3Fs4fI9551JEKoDwdHJ9a0di4fq4tr+kyDzGVpu/SYTeFOR38rGTMjCzGueqSE49zPmlNoDnhWRwuVS9JjxLCbMWPiVi5LPSJA7okaIQ03mxNUrUqMOTbbsmMZ7a+5jm2BMKI8Sbli1iJRBNaqtARmWvpZ6Spw4fqZ1SV6FwJ4YgxcnZ2VsHHbsgW5/CuQ0KEONilYULJa2hvgJWkddcHodZ8o8WykMuLalp/mILVis+CaTnAWohUrWSIzDkgNZFaCAFicYFFqINU2vPQUpxbbWlumXCGyxqDCAIuQDcZwqsKfYggMYW85ToJmvIeZitJtuJnGOWbruNK2Eteb1Ts8kSRRATtPgXvvFXXyQpDUhRLPwm/S6yjmY6MhKdkUQ2kcg5z3kcWvQ2OVdnWYvEhzSUW75sRmtkjU2RGnStjpR0uPKSrzqHhtZSQIkTIKd6qmipXZQX4UNCr1cKpsuDlnchTKBW3NMXbi1RezRnmmr5TjAA60hlVy6XJOEcWnpL3z/tcchdgzjHJqqJPgnWu9BZjIAYQ/MIqXM+jVE+qGHUp1FApJ6XkIWlP83nhcG21gFG3/F1+R6p/i9bMs513/TP/vipklIGzwKsz7PP+ViasDPNZMDi0DtY0qqypmc/s5U6DFwShKBIZDpI+jyGmcr9WDhmZvb5g50bUqk25/IFzBFW879gReP4zH+d3/oN/xid+5bMEl9bnTWkYH13x7k9+xl//63/Dh2++g4tK2O3mC/68szGyclaF32nM5b67RZ5hu7droXI13Oq/2z7W8SUL8wmulYdkUYWwarNyPwt3CKnweRKoC+JJ/aT9Xk3jYI7J4JHPx0JpqASlej1rwnX5KUWwOBA612h1/fsa32lhvQzrTX9XvNKetTW5dN6TCbA5c43hNeO3VAJ8hTPWxQzXmvfVc2sF+0J/KkWyhkt+v1UC5jWu04sgdiYtSngh0B3F19b4UOhqQ0dv25P2uRhnXl0/d5shxn5fCvOtLHFbP+1YZb7pfy7js42ywI28hvpnC6d6Pq0CVfPQY4pK5pHkcdMdGPubHTEKPnqmYaDznmEc2Ww2JlOJMCWZc5OSwsXNyoX3nckMITKFia7r0SRPFT7kOnQKXD68NIPopufO3bu3mKSW7emTwUWIOPCOqHbD8OLwK0UjygRPVcFZcsnMiJNQkFWFzIxcRo50syEUS2jnct6A0vWpBKHaJWrgQRPzrJedBDZ1njBGlIB4m2MWgDWHc5XNN8t7TO5Yl0I+THikuBXtApNglmcOCViLcHVIlZNZQakt+iJCNpQoWGnZcSROAReCMcxkgWoJbN93hOQ5yOMUpM7zSHJlFsRiFFRNeHb13tjEF+EmBaS6DM0qa8qfVQnew34/w6IhnFmpWOBXt0TF4iVp3OL1YQyi9Dg6FfZjAOc4dR2j7hnjhLC0qsFMROe+ZuZS15JebxaBXRinmCcOsoJgS52nW8U9pnHzd5mIJzWoEqpTCc4QF8wsKzD5GREpN4HWMM5lb0sFKE3rdEsGd2A5yYK6y1ZjiCwJtpNqTZps3y6FHTpX1pLX41OyoOUd6UIxqXHYAebiCAVPC8TTWkyhyFWoksKhihMtd4povQbSeFnwEqk3hqw4CLMi452Nke0/IrM7PgvdWbBXSYoSGV1mQQMS7WIe+0AYqvZ8sQ9Vy3SqZkj58xnD5nfr0uO18FT3XQv/ayFNqrkEbmJ+lWUXsaTc+gwWQaH873hrGbAmHHLl41Zwm+eQF6uF0VeFNYQU2ligYV5qTeex6xiIROfZ3jnnd/7J7/PLf/jb+LunTCJsxeMRhus9b3zvR/zgK9/gre/9iP3lNSow5AseUaTrmPIcytmYaWEIgT6H36aQu9rD2woUazhQ09x2z2ve0gpZ2UhSP9uGvx54VhJcszJR8N3+LJePaoPfLLltu9HFqJN/b8/e07QDBaHCvRr/1hTmGr55/fnzxfqrPuZ/bmk7yBZiyXDOBqRcLETKM2UuauEo5e4cIKf4KRTjjTBXS8qt5bnHFKQ6PK3+7hhsMj2rC7Us4C2YpTqHfmZjUCW85/fafajnulA6qrHXPLyra2Metx2vnXe7v+1n7VgtXrTft+cMqoIvFU2fxYT5uXzGDpUfFn/fppDUnqp6b2Os5OLCF0xOePjhA/5v/+X/hWEaOT8/59VXXy05xvfu3WOKwQzhiVdfXV1xc3PDNAUcc4RN3/eMw2BKa+ehs3DvzjnOtqeQZI8xTOzHgbv37jEOA//y136FJ7WnVjQmmQqz9yh9561UZDqAxVoogvQe1OLnVQQk3bBaAdmLIBrM0pwNJ0nIiWEqVkcRe++k6+YLo1LyZ754BMBtujKXvDFZaFQNTNNAiBNIVwmX4HyHxHQJV1JCphBNSAojfZKHxxDYbLaM6cbiqBCT0N8Sg4wcORa8FtBbRaFFPEtoSiFWMcWhJ/JUWy/qAzFNobgNa4bSxjPWwkUWWOtjUCs/XbrXI1sm6jwNmG/3zvHrAMM4st/tyhxzVa261QeqJYY1M84tVkx8lSilA+98KreYmZrOz9WEL4RADPO4fd8Xb0a7j21rhbS55O/SLX4gCKoeMHl71iw3benJYkXIeEGyoCThSZhlAw5wqJK3WBK2Gm4LGDYMuQ2Fc+JKXHLbX31b+IJoMyumLeOr8b1lVvPq5lYT8PxcG8den6V6/rWAUX+eYZ77q/E1f1bj6CrTXhEU6/a0uLTWjsEp/51bNvhknMzfH4vLr62PtaLRCjcZxmvz+nlbPfe6mQAbqW/3WGP0q7ASQUXK7bd1+GKnphRFgdALNxKJ2w2f+/Uv8nt/9iecv/wCgzfv8lY8ejPy5utv8MPv/j3f/9q3uH7/Adt8D0/y4NVnd3kZqwDLMNNQ8YUaBvXa2v18GhyqBY81nDSvhhwIn5lW18LL0wr7P89+L/fn6fu47QwUXDwS+tW+v8Zvjs1h7VlNMkY7/zVeXdPM+pl2n4GiqD1pze28boNNKwfcttY1gfdQSZNZkG3och110N4jVo+Zn1kLhYVD/vE0raUfa+8XgVyXnrbb3mnbOkyevi1yeXSpyN5WQa8e/9jnNU/Nf2fZzCk8/tnbhGnicYi8/rVv27Mx0vU97nQLWOXYru/ZbDacn51zstny4dvvJNnb8fo77/DwwYOiCE/J8I6me6hUOdlumaYJv+k5Oz3Fdx3/8n/5v3gibJ4+GVwsNosYIEa6rmfrLawlOo90HaAM494s/aIQI9MU6fquJK/OgAs4h13WlUQpu3zLcX1xwUnXcXp6it2YiykKYWLTb+hweO/YTxPjMBFVOT09JeIYx8AwDOzT7bwzUQ9MYSSEwJ07dxjH0RK/R8em2yDe0/cGjpOTHhEL9tCwZz8MdB72+2tudgNusy2Hqa3+BEuEq4l6q/Hnf/OhTrefMpe7y+54ScLzGjKuMbRWyGs1ZVVF5bCyEHAghNUx9FnZ2O12jKPBs+97O+jVoaoFmSKQV8JQVmTqcWthKbeFK5uK6NsLZb5d3zOFkDxjEIMiLJPlsnKw9Ab1xRVdw/M2hlULPoXhiVudf1YJavgt92wpcJRYTeeWaVFUrvOQk+TXQmVmQb1lWC0hrd+/zXMVZd6bhTVMcxGHdSZXr7nFp5Z5z8T00IKXyyi2Vqt2j+p+a69hu4etoLK2N62A165xjWkcU0bWmPFt79Xvr817QWsSHcpwqsds96JWKtZyBp6GobdwmR8+eHT13Xoc1+L4UwqMmXY5LJzBGQc25SN9FhBGD/tOeOHTn+R3//xP+MQv/gKhE4Z0gWOvQnx4yQ+/8R2+9ld/y4fvvw9joA+QAxdDCpXsZJm7VBsO2tr0xcjlZgvkWrjawujTeJ/WYNHykUP4Qj777ft1pavFHpMs2Q0dXhOYju3JwRwrS+9xYf7JbeGZb95Z9lvMLkdbDdP2Z/2MiCRz9eGca/pV/575WOZzmffVNKu+9C2/l8d8Gg/Gbcpo/dwxGtS2dSUNSnz/kdYq0DUO15c657EzN1qTgY4J9LJibGrXmFu9NzHmoL91HF6DxW24fYxezw8dKpDH5nxbP23+Rc2fFu9UuFEblcZh4OrhIz54771qTWmCIsa/8z4xG92sML2Vpt9uNwzDWAzHvrOKe6itcIx2hcDNfgciDDvh5tGjpz7LT61oPHj4gLt37nL/uefY9ht6Z26Vm+sd+2Gi73v2+xuub65xDq6uLtkPe/b7kdOTU+7evWvCXro9Vwl4D5dX1+zHgdOTc3Ad5+d3uXN2xumm5+TkJN3fYSW5LKQkcPH4AlB2u10ad8fjxx+CdAQ1q9I4DFxeXVZej0CIge1mw9XlBZvNhqurK05Pz9huzzg/u8PJSWLW+OTyVNQ7/GbDww8f8ODRBX2/5c5mW9z2a0iyCAupDl4RcpmrcsDsHYhq3gulK7F4QBE6s2P7wCoJBYFyCFJ9SGqhPr/vnF/cUFwTPucsvn2fSsZmIgJWgWcYBpxzxROQL+CLsrxzoFUgpiYxrW61EDsrh1Vsf2qLRHJVVMD3Hadnp1AEGI/EgKiUueZ5uhTi4/x68n+2FNR7WvahIvoHZUdXmEiMsRCjdQI371vLzIrKUP1Ned4O/1r8bT2no4S8EfLrtdU4MhO8Q2vs3NfcZytQ5TNQK5w1XGvBt+6jHaOGSxaW6osua5ivvZP7bgWXFk+zu3mNKbaf1f/qsVuB8tge5L7WFKF6zmvnZAHbal71uO3abptTu/f1sy1cW0VmsU9H1lvD6cBzWMkUt8Gqbs45KwCnglOhc8IUo122FyyEMnaOk5fu8/t/8kd89ku/gW4c6j2d2B0aw6Mr3v/Z23zv777OWz/8CbvLKzqNxClVHUqGk4zg2cvbWnZByRWKMu0osKn2pfYyt3vTCn1reLomeLR0Q5KAn+l37jP3n8dvQ7mysFQLxsc8yPXvazStzKv67EnvtuegbSJSBJ72HKYnFrrB0wiWLZwP6ODK80/DC9pnjwmsa+doAb+VMeGQ5re8ql1zO34OExWRZQXKhk7URuEWD+sxatxdC8U8Jmgfg2uZT5KEWnis0cjcTB5a4km7r7eFN7Vzb3lBHqP0pUujYkt76/5rGfDYmlo4HITCV+/V/DZqZDfuGHU6MCQQwaniZc5R1hjRMDGqEpKhc389lHf7rmfSYNAXk1+is39GYrTINS0MjrWnVjSEjt1u5CeP3sB7z6bf4DuPRkuYnqYrlEDfe3bDjgcXj3n48AEvPvc8u5srNE6cnJyw3++5uLjg5GSDeMtn6XzPbjciDvpu4kJ3XF5fMw7vMU0T4zShKcSEKTLu9lgCbGQcB7yHV155hX6j3Dk7t4TprafvYL8fODs7I4TIsB9M0YmKwxHGyF4GLq4G3vvgEWCCrLm/zVNyM16jwKbrOTs7o+tPiNOINhaujBhrLrL64Hrn0Mrikb0H5h0Zofd0Xcc4DuTYX0Mm24WaEBRPQwx4v7w9OjMmWLduiaTQA+eK8J7XnglYfQ/IOI4lDGyz2SwOQs08qZhibqpKSOWC28N4TJCaBRFZCNyLn5KZZ2SYRsZpSsXdMKUmuRbb29dz4mjLZOrx6zlmuK01+97+1Uyndh3nPTkQYmERn9taNWUxhnUmKCEosZrOkpEdembWwmJaRtISsHaNGV+zl9DmumQoC0HFLyu31GO2xH/xU2fJs2XsrVcr/12HsizgVb17jMnV/bXfHfuZ32nLW7fj1s8em89abPGTxs7viUhRruvPjsE399Pi/rF5r53PVlCr1yCN4HabgDnPOccbL9dxKywFLP7dDBExKuqFGwLxtIOTE371936H3/iD3+X8+XsWD+/Meud3I4/ffo8v/5t/zzs/ep14vWMaRlDwndit8RpLNZJcSn6h9C/WMt9XMI7jUmgWQZNiXHuN1+hODde2xO0xYbSGp312WNVo7Vxn3FVdCgq1cSGfr7pq0YE3pJn/jA+6qIzXPru6p096rqGHx5Sdlsas4W+73trQBrOSsTantfFa5bk+2zNeG11bE1xbYb7tP/eRaflRfnGEzixpVOZJy3LpM34kIbLBzzznmsav8fJagb0NlmtnoG23KSnrPNoBh5dL1v3U0RbHaMxtbY1v1OPUsFjbj6dpNd2u5bk1Oi5iCqP0qSBNSvImPeuYDZr5rNdzTL4n2ztvxtuQ7g3LK41YGGpUu6PMOYekGijqnm5NT61o/O/+t/97PvOZz3B29w6nZ6ecnp/Tbzecnpyx6c4IYaLrhBAGzu+c8Nxzd+k2G7x33Lt715JK+h7VyP3n7rHZ9uyGPYhnmgxBH19c893v/oAxTgzjzkKghoEwWTLLxcVjxus9u6trbq6vQBTn4Jc++wv8j/+L/xGnyQMyTVNSQBz37p7T9xticPT+xKyW3nN1dcW4D3z9a19l6np8tylKCCjb7ZZhHBl9Sr7VwCsvvsBvfOElvHM4IipucfiOCWtrxC0T8tmdbRqiVUOyakYiTVy/LK1atYuy7rdF9nZu9SHNSkLNRHK/Wajc7XZ470u9+LyOOqQqz+MYsVNMEGkVifqwtn0Z4ToUPsr8sTKVURXnPeId4zhBZ9ZHRQ88PPb7MpSnJVytspFeWqxrSUwOGUh5BrI8fhiyglluWBP2YgSkJCCbdyTta1XbuvxL8MihTPV4WSCeYXooENZK6gJeQsn/aZmpCV9LprkmeK9eXFkxwKUCYX22eFArTIVIVvdo1OOtMch2v+t+jgl99Vlq+11T3o6Nv9Za5aB+P3+/xmDa79bamiDW7vmxdT1pHbcx1Za+tGtdhwNFsGnP4wEdze+0c3LC5EC3Pa997pf47X/+z3n1Ex9n1EDwziqURXjw7nu8+8Mf88Nvfoc3f/hjOqtETHAWk+wUrJSZR5NHwydFKIcXHXgD1Iqd5DLeqjPNqfH6GGxqmNatFTBruBzCMCndahRlzcue+4Ql39BoXuE6pLWec91q5afur+Zl9rvQLmltjS0u5d/X2m3KU0svjsGrPgs17Vhb69OEAubW0qVjykD9TH3+68/bVsM8K4htqG+9tnY9bb8hBkSWVvWixGgsxLeFXd7jYwpcPcfa0Fl4YPXMMdqz6FPK/47Cpl1v4alH5lhg8ISSzre1JX+n5C4+CYdro8zPq3DMdPYQFsaHhZPOcyWg5MJIc4uSvJY6G2qyH9MnGUPTgmba4PDpcyfKFFMlT1WYYskVfdr29DeDj8qPf/hTXvnoR3jpI68S3cCp6wgy0IeUPKweL3ZZ0cdfeZVpfw/v5zJ7d5+7y/Z0C2qxxbt336f3HX0nnJycs9+PvPHWm4Aw7gd2ux3X19fcXN9wc3PDbrcDr5ycn/DcR17h3r173Lt7zsdefZnNySniPTe7PTc3O7abDc47XnjpJTabLQ8fXxL3A9f7azyBbtsxoOydA9+xSzkbCnRdz6AQnGMKASd2O+y4n+i7DZIE2Dge5mfUpQTz54sD2ggWWRCc8yJyaIgjToBzpVqFsLSgFGakZqHI5W/rQ5/Hz2PNhM3+F1PsnWiKsUwXy12mygTb7ZaTk5Ol9TYaPDKSQ5qf8+QyiySB16cL0RTFd10pK6pJcEa1WKsk/R4TLLquSyWFsQuwYhov0VjRSBgnJjUFbSOejfNMPhFQ5+ichTdoYsLiUqWa3NeCSR0SjHyw7TAurU7l2bQ5c9WqRBBSib5cQSNXJ8kCQek/70kwN6h3HhVfRR5r8dQgFEuuwUDKWnwaw1TlpJhKriTlmoRyMcUv70GDx4WYpedRq/gkzlfKgLlkNWkcIuAdaLS/s5KYK7BQEsrDvB8Jbhm3NJW4dRXsixqVAJKZWSsUtUJ1K0isMeD679bqHMNc4QiRhLMJTprOctpTSYwxe6jymb+NQbZzqAXLlqEcMp1DBakdT+qfagKza/D7mODaCkK51Yyy/U4ii7rkSqWAIKXaW129y6xp6+53l2hJgBIqJSlcygeHOGEUGDee89de5o///J/x8c/9IrLpGYg4BR8CNx8+4qff/yHf++a3ePDGW0y7PS4LhNYtUa30rVUscxVDXho5ui6HxNpixjGU6lKd94QYiSEV56hCauqQK4NfTXsSnpJpjS94JOTKgBkHZg7fKrgt62/Pc2tMqvlUDgur2zHloOUvh89KoaVtn+17xz5rleVsSGnXnHGo/qw2ZNQ8r1VA7Odcyhl1ZW/qsdq+898Hwj1m+MpCnIjhVilHWD3bCp5ZRmrPdat8r82n3adjNEfEwmey5xEOQ+Tyc+1Ya7Sm5ZVrc4blvtVhfGsKRIZjORMNza77aPfHBGwpckWWl+Y+lzBa83q047UK1HKe63xziV9LmK3BZ+37deXX1lZ/r6pJeTzBHBlGvxavLdad+mE+O7Y/OT9JURXUCSHLNdHOhBcrjRtjMIO8rBcMWWtPf49Gt2WcJn72+hsMU+DVj3/Mkon3I/1Jz/b0FB8jLkSYRkvIG+2ehgic3bnLyekZp2d3cM6x3Z4gbsP15QVhGrm8eMQ07nn3vXe4vLhhd7Xj+voGEeH09ITn7t3n059+ge29LbJxKI6u7/GquL5nDIHnn3+BYT9wefUW4jtOz8544823+chHP4LreuKw59WPvoJzwjvvvs/p3Tv47QlDVPCOgG2aE7OG4xweE4CnYV9qEXvJ++4QyfdqZDwwqSyX0a2tX3X8a23NLUqAmhU7xMgUMnFVQoyEqHR+eTjnMK3Dg1/HCufxWqLr3KyUFAUmMcoQAtvtdpEsnt/r/Zw3YzknUpA36vJgLSxlkksHG7IfxmtLEYqsX+Z645qF9VT+NQtOzpkALNi9I1MgilVf8Sm8IrHwFGaWppqE8DLXNAZJGFjEWku6Z6Fa14L4JqFz7sjmXW7HzjX+NQ8yK42acCcTEKu0lvCoEii09J2ZlpLjJAvRExB8ecSEIS3KbRbYa0J3EKrWNE1E2/6R3q8ekGpaxesSLSZScrEDDoTJJdHNlmEtSky+6X5BdGV+9yA0r7kZtx6jHa+2IrZrPVBuKhhk4bNmODFU1cdSGWxZYYTHYFtbAOt51ox7jYmXNTZrawW2XE57ZsTz2aGiGTUdaBWJts/bhIzcv02I+afM3xkarQsZ9RqDS6E9Kng8GiMbl/IknGPqPf7+HX7zj36XL/zel3CnW9zGvncxMjy+5O0fvc4Pvvltfvq9H6LDSBciLvUfmXMpvHN4N4eM1jltmb5nxmwWZaORwzCU8soZ3uKWl7CWW8MrWAuz8CNllAovSHQrK7b594av13uTnRo13c3nIZ+Pel7pgcW5WsPFY+O1+wUpzBcz8rR4Uj9b09Da09sKfLWw2vaRv88elFrBaMds8Xym60bPnHSZMSQlYV14Pybsl78zMUyGHiQbfo4L47dFQxxr9XOugnXdZw2jMm9Zwin/nj1ixxSHNeXnWGtz1gqe34JXyzYbBvPaao/ZmlK6Nqf83gKXVvavfr5ee42/a0p4Zumt4vCkc7PgM40cdBts1hQtEUvm1pjLW5Muza37WfKSTIOdE6LKLFuIGSTzpbsqYsUwynt5TId0KYrmKf0aP1fVqa53xCny8MGHTHHihZdf4s69uwQ5J6ij7zcm+EchqOPk/A5d73n33Xe5d+8e5+d32G63XF9fI+J54YWXeOH+fa4uH3N1fcPlzchbb75NwHH//vN89FOf5P795xaXxgVGcMoUFO86Tjc9u5tdIaR37tzhtddeA+Ds7IxxHHnn7XeIruP0dJOSg4XNZpOQJyU6J2KXKynlZD/TFg3AOTm66zoTmBuq3yJojehFcE3r6Pv+IJFrJpxZcUlMyzt0nC8tLISBZJmStZvPtXg41uaY1yEii+pcMUaGYUBESpJ3+16OiR9SzeVSdWqlicxVg0KMhwy3WncW2HIlqHotNVMqnyVBwS4ztHmfOYfZQNcPtuHyMlGzJtpx5TNIgm91AddhbP2SCIskN3fVX6tcZsbUwgPMakAVOtcy+JYJ2O+A5nyeNYawZCSLUCc9Lni3nx1jtjXOl71x7gBeyJIM1oQ6hwu2iXD17/Xc1yymLYyWwthSCTjAjScQ+7a1/azhztMw6Lym/PuxZ5+W2cMMr1poLriox1nEsXm0glC7H2vPrM29Fm5qgbjF8SExwk2APgqd2zLEgGy3jCeeT/zar/ClP/unnL18H+m8XdA3KXK959033+LbX/sGb/7oJ1w/eEwXFJ1Cqmx4SJ9rmlivLc+zDjFVtUIkIubFWNLuZXJsXkt7b9BtgnMrjC/gwuxZPQbf+vd6znXFvTUBvp3P07YDerBCS27rv8XpGp6LvlfGa99fw9m1MebPaiOXoFWO2Np818I9yzOCJdyu7OExulKfnTV6tqaAPA2NqgXzY+1wH8woRCNkr53nGt9vo3lJeDo437c324OsgB7w4pV12Xqz0Wo5h7JHi7U+eV9aHlvPIwvemX/X/d12fuu+W3it8du6aVwaBZ1LebXnZ3R9Xz5rjXDH9k6qPON6HvkZ13mcd0U+bGF6wNdvaU+taNx//j5XV9dMMXBzc81+2Bk6hEi3C2zPzthsJrwoo4PLmx0fe+VFwjTy8kuvcPH4is98+hznPX0X2GxO2DHQ+y1np6fc3Q/cDMrnP/8FtnfvIm5WLmYXt9D5DTEG+s4UGxD+36z9V69tSZImiH3mvvbeR1x9Q6bOSFlZlZVaVFZVqhKNZoM94PQLwQbBR3L4MuAQ4BP5Y4bs6QcCJAE2wGliZsBBT3dXixJZlZmVKrS8EVeee8QWa7kbH9zNl7ktX/ucqGoP3Djn7L2WC3Nzs8/Mzc232y04AkOfDo1rcHP79m1473G22QJINyRerC9w685dLJcrJLmYmEFStS6Xy6JcZIto3PLOk+AdONSgTU+ELlqASDua2aQt7zyQb3mOMQLKqy59lHHJYvPeI+a0vRZM2IPpWkiGEKobygXcb7fblPo3M65mJivQW4tLvrdjFcNAFLmkF24tAhmbTR1swRwg26NpJ2qxWABYjzssPL5TnWGJXAEO3bZuowKzDXBdhAihuh24FkgjD0zpg3GuUT+nfRItRWrnOin43P8ZPtTty3sSMhF45CmZ8zkwo9u0ZwxK3xRttXFox2JpkpRLLcTkpycHUoft9ZxOPLVoA3bdR8uzVkFoBWnB5BzAlosRdT1zykMrIivIdb/0uQALODQdbXvakVHVTTTecm7G1pxL1ZdWX1uK045zbnytZ9IHgGeCD4QupsQCW8dYH3R45lMfxff/6Ad44TOfQDhcoPeAj8Bix3j0xjt48Na7+Olf/gQXp2foL9ZYhHTWgiPAXZINOpxV36osY+66riS/sOtd5kK8wJJMQ2jekit6/DHGFF4IatJOrz/LX7pOW5jb8yZt6PVReA9TAGbnpSXb5+bP+5QWM6hEJpZnrd6w/Ck8X/WhGqfm/2Z39vZXv5/WMsolven8ggQ/jc+3dJ+mVZqviKjqbzn/Wn2Y22HVpcUj+8aov6/eZTa7dfqdHJVsvtNYQtfX0kGWT/fJl1Ypn+dwM60DLA/ZOSAC5gxFkeegtvzR9eodNo19rIEjulaKjVixxdLN8uFltLHfSz/XF2vw9euVPtlH37LDXeaj1tPp/UbWqwb+2MezulzZ0Pi9730XZ2dn+LM/+zMM5z367Rb33nkbTx49wvMf+yTW5xdYrFYAIg58YpLj42NwJsZyuUTXLTEMA3a7Ht4vsVisQHGAdx0OVh7Xr13H0dExAhz8okvnBdSkDX0PUL4QBg4cgYAIH4GuW6LrugrIPvvsswCAzXaLAyZ0ncOzd5/Do0cPAXK4e/duAomZAWWXQUB4IiwQhoCld/Be4lg9iNJWu534yhhRE1QmpqFY5HuxyCUGTs5NhJhiw9PZjfEgV9/3AFL/vKOy5S9KsMS9G2aw2aJijGXczIzFclm2BPU4gDFrg/wufdF00OMqz7h0rkAbEBZECQ2BaezoxMtKacswpmizcnGc9qZLfRaYSWiR7bcoXg2Si5ImQkBdjxWodmt3DmSW9jAudv0uUT6DsUco6r6VtsSbMwfqCNWWqsy77lOhQ2MMliZaIOv3iMa+C8/quYYBGhaI6jmrQJJ6xh5wt/Ng0yzPrTk7l8KLLcA4AcNmLoDRaTGnTOw7cyBmzjibtMe150+PraVw5Dtr5F8GImy7tu/CSxrQ2jnV87APwFJCDFhGAgeHQIR4tATduYFv//D38blvfAWrRVfud1kMwO7kDK++/AZ+/u/+HB+8+U462B3SOQ3JHJWAC0BuCv41LeU7mxIcqMGjcw4he/ssOLbFtkduDEVoKW0bVlraYACon7e8N0tT05cWn+rSkm9W7ln6zX0u/8Q7alOZ23613tfJRKbf7wdo+8Yn+iTtaDBA7edsf+33UQ7ToF6XUlr00XS1Wez0O5ftTthi16blrdYdVuR8Dr+bn0ddh8U2V+1X63dLV0072+4+PWtlTlmTSidJ/bof1hiarC0jvyeYAjVGaa3DluxsyVvt4NQ8QuSqOdP1CxYU3Wfrbc1BmsNa740OvIgcNVWFr+n5svy9r1zZ0PjWt7+FzXqNmzdv4F/8i38BT4QQBoTtFo8/eB83b9/BsNtit9vgadyBEHCwSsaEDH636/MCZAxDulPDgxGJAXJYrQ5xcHiE4FwyIFw+KA2dQjVPBnkwEtjuOoeuW+D4+Bq6zuPo6KgwRiJIgO88Pv7xj8Ej4rXXXsX5xQa0OEjhP8uDcplctbDzIdrFwsETm+w7ESBfMZxmXu9rgVMJakwXe/Kax2TIY2QU7zy2w5jpSUqVUjYDTK3sNUNp5tC3lRONjNX3PbbbLVymOWxsYy4xxnIQWVu82jCQdioBzwDT2G/NvJpG8r54Ca0ybCl8AmG1WjbA0tjnInQ5GSc6/KBeuFNhTkSwy7UOkUiDa4I7xmjMzpQ2mJNY4XnFNhG03Ox+eiYyIut4yzZYsd8DtbGg37FCRmdESWcy6kupCs1kh9KAWauEtJEhvwfl6bWeIw1i5HOdHKG1S6NBsOY3oumOUpOutj7UvDL3rubl1ny2PpO/54yL1nOt9SXPzSkhOw/aCTCniFuGxFVoVstpA8yIEFYe4dohPvWN38XXfvD7OLh1Ay5frNqFCDrf4IPX3sK9V9/AL/7qb9BfrIHdkC/LS97NwDEdgs/r0Lv6dmMtm/UOrPU0a+dNUcp7wJbmK0sTDY4/DFCbK4lf//71SNEGN9A2eDX/TftSe0lFfujdozmg0jRm3Nyh7r/7GCugWz5L8e76PK2dH91nCbOWSloAda7tFk3t2rBOlxa9WnPQqs++Y4Gz7OpYuTK3prWjR8trXXTWRAvuJ4aOfneP3NQyZ67o9ij3Yc6AsqVl5Ov2dR/1dzVQnxoS+/pr+z6ZP0bKNql5Vs3L0eEhPsi82HIItPgxScda/xa+kGZV3/XOrXx+Vdl1ZUPj7PwUF2fneOGF5/GZlz6Nl3/zMg5WRxj6HmFzgfvvrbELASmsieEowju5ATpmAohXI8D7Ab5bwDsPR+ns6Gp1gIPVAc53Wyy6DgBh2I33NzgQOteBKR+aDiF7yR2GfsBms8Ht27cAjIItncnwuH3jRiIKAev1GiFEnDx9iKHv0QdgN/RYLpdIMeKZKSPgfPYUIeUSToLSpX88FSyALMBx90EEqt2S0wtGDA1yDt45hCEAPG7LM4Z82JSKwGZOlqzDuIi0p1f6NQXgo4Eizw3DgNVqVb4TAQFMs2ZpAWhBzJwntgUs5dlKWKsy129ZDJ7SNj1zoutut0OIMcUVxtHQqIR3TudYz1VbgOt5LYe95ZBf9QzAPArvagGqzzR9Ur/qdmpPTfqnhYDdwtRzLO8HAza0wCrZdFS5LJaXaDxj01IqViALDSJzORStgeQwDPD5osd6q1avo7any7Zrx24VnTVEWkJRxtdqR2do2qewbdFGrB6fFfz2vgRbbwuISLGGfGte9BqzbcwBHXl2Tn7od21o5qxCBioD2NYP6PWVno0g9AuP57/wGXz9T36IW5/8CMh3WFAHP0T0YYeLJ0/x+l/+DL/6938FbHZYREYc0sWhSeZk2hDKPRqEUX4JfTRgsl5UO2bArGEFLKwMs7K+lmP1+m+twRbfo7G+576zpTVPc0XLd22ItWhi150OKLHOIrsGLJ9YoK1/1zS2fdo3Xt2e/q7i/WL05dj7mX5Y2ulzjjFEMNX8bR0Crf5dFbBZXWvH1qKlrTuNbbrDAci81fNjZcmcPNB9qLBQZnQrR5t8o+nspmvBjsfqgtTUuDa13h2TtUx1x5RG9V1kczpAcE0Z64ys1d/PzZ1tWz4veArCm1O+9N6DHE2cJ+Wn4ue6/RFf6PVU5JM6Z6nH0JKTl5UrGxr//J//N3j/vfexXl8gDAN22x2u37ie05du0fcRIUZcu34Nzz53B91iAeocUhhQQIp8SKnkjo4O0XUeoHQTtiOfUklSBGiAX3jAd9hut0mw+JRxxPuUUUeATOcchu0OwAKHh0e4du06lstlxSgHBwd45u4dMAH9bg1aLnHnmWdxcnKGDx6eIOx2iOB8i/mugCBH6aCfYwAxCRDPHgSC8z4JpsiAyi6UZycdEHT1YdWi2EIomWKEiSVsyYkyJErj7Dw4BJBb5SwBmbkjpzAyTulFwemgNTAKdgmjskV7mIjSZXf6cr4iLBhjP5EOuSUPXi30hfGstT4BbY4Qwxi6BJKD18nroQWyvSxQ00/qDiHAxZT1IBDQbQNWvsPg0jx05EuWKOd8qT9lYqo9s9rjGGIo+toaDY5QUsgh7yLlSzJBXqY/JRiQyCftFZ8oIAIYozCxW5RJ7IuglhixtBNlhay04cs0pMY5jbY6t2F/FsMA6l2jPMpIpD0jYFreRjTmruu6Mrcy76IE9K212jiROUrhU4kwkZM3WYzsZBSU3sORg5yK53ziReoPmb+RFRMV73cx7yZKs1Kear5aXm8PSme4tEIT+afkvBbY1gvWml9b5tacVhxSNODjPNclhTAAa2a7VFGam/yc5FWnVGH6qfsnPCS0y32JYESK8CAgZ4OLyGmmwVjAwXOiew9g3QHXPvIc/uCPf4xPfvELCIt0q7cnB+oD+vM1XvvJ3+De62/g/TffRthsEfoBIYayw6DnqMuKWNIVa/3Aip91nxko2aRI7T7L56Rop2neAsctAyLJC33BZaJF5r6UhhQoN7+L64GLAwL5Yq70RhYTSOqgBhW2bxbsy0Vec/xmweHc93bccwDagrsW2JsYu5ieZRufT/Ro1avXMSveSPIph2NyvRbJze8N6d1VXbekxhfnHUceZzOBA8CMSctKDdz0M63Q1JbBUc/xuKME4mqnixwQuI58kHYcEUIDyLb6NccLFrimyJD2+QPLG9UN6xiNPyr1JvwYaepASX1q71gX/kUlfptOKD221vqp6hcSN/Sq5UFpw/Kird8aN1WkSHq46rfULWH9E8chcwkdjYK9kJwv6fK9Qo3EGznRDxHBC9VUJISjlGp/bB9XKlc2NIY+XYJXsiURcHp6iuPjY3jnETl5xA8PDrHoFjg/v8CTk6fwSDH96YxGl0HigBB3AAI8eXRuiRAJZ2dn2O522EYG0wAQYbvbjSAROWsmCKBkHCAOCIGwyPVvNhsAKBmXvPdYrlbohy1CCNhsNrh16w6uXb+Dn/3tr7FcLHF+sUM5A5EFr8s5g/vdAHBSYAtaQRaxqJjCRDFtuY6Ke8zaJIIhxpz+M8aSqUnnM+cQMnAWpZa8wl23QreIAAaEPojpnhV9HWsvfWJOlw7Kjd7aczdavlxSL1bZqbj8D0ASmkNIh7d1TLIGhLpdMZ4q0ASaLEhJL1vgoFng2uuojYHSfmT0iIAnbM4usPA5bnsIcPm+B7HaZZeKmRExjfMtykd5Uqziy+RIACDW8z+Yy+PGOlIGKStwYoxlfm1oRfmp+iBAI51Pkr9M3yCGCcZdG6Lqaf3sHBigJNkLP0O9LyBSlIDcANyqQ9Zga2dhAiyASrlbepWfPNJv7GwyLAJCtvESQGYx3FR2uGLgFDBMRQNpemtF1goL3LcNTgntjXKLUvYkMZS08TRnSGj6aAXV4hXLdy3vc6OBEfjYPuTvZPfSab40wNyOu7kGsuGNyCBO/JivxQAoncFgR+g5ort9Dd/6/u/hC9/5OpZHx2Cku3A4RAzrNe699Q7++j/8OU7feBvY7bDL+kE7dLQ30rkUOotYG7CaNszprJSk3pbnWjHz4OTUkbNqznsMM0B8HwDXf2v6AUj36WD6OZCdW6Xf5YFZPtL90CDHglT5uQ9Eaj60INgWkduttq4CVG2bUO/pMe1rX9NXn7cp8xBTiHN9kWycINIWv7Ta8yLnOI9DvkMt23RdrTascWSf2Wf4ybzEnKjGkSs7rIWXqQ5zLTosO1RjjDXoV++2+MaWis55/HNj0u/osMVmiBiQXUbT98c13959u6y0eNIC+in9MdnB0t/b8dl29BppvWdlhegxy9uRI4ahL7rB0i6dTHCQiCiGyF5pc4w4GfvQ3rUoWOKKBoaUKxsab7/1FmJMWZxu37kD7z3u3bsHIkIfAkCEvg949OgxvAcePXiEG1/7WomHFQKVfy5juggQOsBRupdjuYQfAmIO8+i6rmRHYlYXHhFhsUC6WCQyHj55jFs3r+H2rRsAxtApAPAsl4URnF/AdQEXF1vcu/c+3n77bfQD4JZLHF4/hss7CzGm2w9Z3SLtHKVzG86lLXiqx1TiodWEaabgbCDoeDfNbJIaDzECpG5OlvrJJWONU6hTHIYCYrUClUxCFrhbC5oop0fzvlaqhom0EGwJIPuMbm9O4YiRVQQj1yFXtu92ccnvzjv0MeDgYJV2wGIs4VTiARnFfN4ZKMZ+aqPMhfFkyaKdi3OfK3phpl+nihZAdd5A01CPV/ezvLtfx6qSPX0jNpn0syXkLKhtAcryngmT0G2LJ0TXaX/Xn82BBwvIW3TRdcnvc2DoKnPYUqhW6es+62dE9lg+Tlh7WoetuwVEWyDe/q2fnTPuWmVufvcpzFb7rb7J8+lQNqULJpPgBJFDdMDWMehoic9+7cv4+g//AMd3byI6AiKhYyBut7g4OcUv/vKv8cpP/xZnDx9jyYxF50vSDqG5PbsjAFMnsdD01EaK5jObmadlJFQ3bDd4YY4m++hbnuN6LuaKrefDznPM4BKYhni1+tXiw8uKDR1tgbKW/LF91zxVn5OYAkI9X/rZETzVur0eaHsO5wymObpdlU5zHmw9dqlPj0nPhY4GSPys7mNC7TDhxudFZpDaPTZttwB8SyZpY6EKidxTrs5bKZJgX4hjC/O02rN/zzmPWn0TnGTDmW39l/G3xhaWd1p16DbEIOTIODw8mtRPJEllzM6N1rlmrHqH/T9lufoZjbMzHBwc4Ctf/Squ37iOi/UaZ5sLLLoFzp6eYbjYIA7Jy3729BwP7z9EGALcYrrIE2MnQ4O8A+DhugVefu11PD2/QCBCGCKWy2V1GC295xBDwK7fgbzDwns4T3jn3vv4xte+AuI67MZ7j81mg912l7xPQ4B3Hc7OHuGXv/wVHj8+wdOzc9x+5hlcz0YKczqz4bIw6jzBZcUSc6hRGkrbq6gXvWZCWXhawcnn3vscopRCCpIxlqxQ53M6RSRvfORYQqec8whhvPtD75LoxWMFcDrTkJS0vhW2MCnqRSXjaS0MHZbRijuX5228rhgtjDboEn7R507KAsgLRkLZnEqHPPqQRs8DkMK0Sr+UMKz6H0MlBOZKJei4zuIzFRjt1MeCJ1rAW363gjPG8ZIcq1CZefQ4KCrIL1aEzyl8LeBaArBVh1W0ROP8aj6/DGzNef60Mtf9tABffpd51fOk+aolSO08aH7TCsWCTt1X2V20a4Co3gXVc9sOA+DJ/BbloYBBa250fa0+7pt3TU+r2Gyfrgo6CQCYEt9SuumanUN0hLDwePbTH8N3/+Ef4fanPorBEzYAOhCWIPRnF3jj1y/jJ3/2H3H+4BH4fIuDyGDH2Ib6cKLupzbe5V8IITuJxudsLLamh+V9K+/s55ZOdv1anmnNoXw+ZzAkUcZV31v91XOzD7TLeOTzfUaNfsburLWMA90PS1srKy8DhHYeLouHl+8sH4/tAckZZZKWpDcn7++jRWvtTOb+it6hFr9ZMK3Hp/uhP5dEL/vklOY/IkLnHYbYTjIhz052+Br9quQjj97yD1t03wsd4/xas+vhMppZ+Wzn24L6iUymxClWHug6W3q11e+WY7iqyzgr5VnBe+v1Gs65yoE91pN26mIO50sx2zlk0qRj17Sbm2fBFVeR/VKubGg4Ity8eRMf++hHce3WTfzmlZfhlwssDg5wa7ECuac4eXQCB8JmvcG/+Vf/Bj/64Q9w++7tknaWmccYbQDglE+cvMPZ2QV++rc/x4AUb7boXPFWCTGTFz+AyIGcAxOhjwxyhF+98gruP7iPF565i91uVw42x5gyKqXbtsdMOD/5yV9jGEKJeV2ulsnD3PdwPsVZx5i2sMMQsBIgmb0BjtKBYyG2hCcVIJ7BhmYgCZ2SEuP0oFgK+SFESErbFCJE1UTnmNBcX7dYFEGmjYHdbjcBRXYhWaYsTGyUjxgxdjtRexCJxnsZxNreZyGXfjgNj6egVegn3poEKAmQg18MeJ+zZbHcsp6/QAK9tSct/bQpPi040HMk32salc+yIpHPa/Az7pLId614fE0jDVTnFrMWepqW+nvZuNZKTrerPbJzdWnDstQr31P6nxXYQnnnqKrH9ru1QyQ00/RqFUs7S6vLQLDwrv1M98PSWH8+p8gsYK14phEe2OIDGbf8beOpa1q1x7Zv3LpYR8Skz2buNd00H7c8jLI2IkeQ84hMIO8xgDB4wtGdW/jOH34Pn//mV8ByH4Zz8AGIFxvcv3cfv/npz/DqL36F/uk5aBeAIV1kGdVdOLqvdixWhrTmjZnLoe4WL9uxtuq/jO66D63+VGPgtoeWiCr90Zq3uR1mPYd2LRYaNPpi6acNo8vAo5UzVnfo9lv8remmf2+trdb3QHuHID0XwVzrszLHqdKqz9oZpWWDXgtE9d1V+jlELuu/NT691qyXfB8A1vVpw4IwXReCXxBrwFzGZsap9Z6VW3rcLWxQ+oPcZJyGK+siPGq/s2u2zCeN3+uxt2grz+1bn5pGrR30Vr/IUeET+4yVS1KflZPyng5ls/UVXRCm2CuEgEXnsd3mC0RVNAuAfN4rOXe8dwgxIuTQTAaDUGMbfba3tT7LWC6RdbZc2dBI6Wl3+J/+9f+Enhmn63McHB/CLzr4rsMz3QEcLXD6+AkQAz54/wP8+z/7d/jH/4t/XG6EFmaMMaWuJSZQPgvx81/8Ag8eP8GQhenQ77DbbtF16VC4TMDBYoUYGT0HLA+X6IcecbEEx4i/+slP8Kc/+mEl3ApoQ/KoxQis1xf41a9+jbPTc3DMd1UMAf1uB8pnFUTgO9+h65ZwWUi4fHtmCBHMU5AmC8beMF0mXzGY3XKNzGAX4fwinddQt5KTc0BO09iHAU4OnzHnNLxTxhZGsQI+xpgNPodhSCmC5RC9Zir5XS/mfQJDj8nuXmjQZGPcJe64pXSsgC/gkMY2+6EHkGJkUSlv+ZliN8dxzCwSGjMsWUEgv7e+S3Mz7xVwKtxMgwYRVFaIa3rOdLQJAIUsySjFqNgohVCphByTce0rWolU/SRUBqkt9hPhPQuk95WWorAAbe69liHfAoaXKSH7nn639V3Ly67fa4HD1ty3ANVVaKbft+tQA6cWeG4B1bm6rTKee945jyHmbFDeAYdL/PZ3vomv/P7v4fDmNYRsYBxEgLYB2yenePPXr+A3P/sZ3n/zTaAPcPleoeiAwTV2woyinwMKludHXm4fvLXjvQpYaYGJfe82gbTY8mrOmZMDSw7XWpCr/00dWPvPU8wBWalfA2vtgdV1jINA0Uk65NmOtdWP/xTlsvVeADlG95ZeLyHGKh4eGOlnw+Wu0o/UVu1A0WUfb7RAvh2j7n/5jlOIkTZi0nNq0JYmBMCsAXnGjtdGYwCj426yk2JBamPMmp/138zjBYNFTu5hkzmZRERjYoXG3F1mBFk6lmcbY7M002O24az6WUsDLTeIWidT5Dlgt6uPF4xGC6XjC0QpoZH3qc8xICj+0AZuq209HqGldoBdVq5saCwXSxweHmK93YI6j9t37uTYTkIMKcvK7du3gSHg9OQxQmD8y3/5/8Uf/PAPcfv2bTjny+HoGCOGfkDYDQA57ALjX/+bf5sOgjNjEWLyXAHq4jztlcnE7dMBmCFEcAj4+d/+Al//8pdx+/YtiLHBhSAp5MpRh//wH/8cJydPESPnW8VjBqwDEAOWyxUWzkPOaqy3ayw7j+ODZe6Ly4dua8/GkE/se++BHEIhE1ZyEDOX7TZ5R0K9fA4NA9LWZwgRMRLCbovt0GPRjYwdQ8h1pUxWeiFYwSQCVD6XG9Cl37JbpLOptJRXa7HZoheKFka6fa2QOQvEUd/XoEovRr0QxsXH6DoPBmMIAY4TIMmyNtcni52yPTCndFnshQp46cVn6Rlj1OfHZ0GnXZBEKexLFqwFAvtBzfQyqPJNTFmCJJNS4DgqUzU+3Q8rJG0/mHly7ifV1wbg5TPRajTSQvhNnm3Hgo4GoqaF5uerGAYyT63vJn29pC47xnTmfp5mVwmvkbrmwn+0bJHdPL0OWuBD12HDveQZC7btrtU+OlgZU+hRHpK1nGgEQkq5vOgQHOETX/wsvv3HP8LdT3wEu4XDxjE8OXTbiPjkDA/feBc//Y9/iXtvv42w24D6Hj6ndQzEYE8IDqAhZ9y7QmkZnJpGdmx2DlrA2oJyzW963i6j5+zvPJUZzMlpYflK8xtRfYfRnPFQ2iGUQ/CtsVlwPt7BNNUNpdDUGN0XzteiwWXPXuX9fe/moVfPlnM+DTlT31s13785A6B6Tiu8mTJnYMh3++Rf+k7OJ6L85CSwK9Bq9XxxXoqMm+mDHZ8GqhXfGHrtm9OWMaPfKw6viQerZXvU6ylyrTNaRkMF6hvruzW38kxr56wld6282Fe3/CuJdTBvY0lEjWBQ5xwW3SLRISJfEKp0So7+YIwRQ7rNJMIv17f/yQ2Nm8+9iNXBAVarVRJ24k3hdOHewAHUOdx67hkEYpyePMF7D57g//n/+n/jn/yTfwJmxo0bN7Ln3KEfBmx3OwTq8P/713+Ge49PUtqyMGC97dH5RQY3AczJ0CZKMYQMoOtSStxh1yO6lNnl/pNz/A//6t/iH/+jf4jdbg3nCCECkQjEARx6PDo7xV/9zU+xC4zV4QEu1hfgOCDsNoi7DdB1iM5hQACHCIZH5zw6eIR+yEK5w3jYuGHNQpR3zGnHQhZi2SI3i6mkt1106fJCDilVY+Ys5z1o6EFxZLqI5E0OMSYDCpS2RJF4S7ZHY0wX7MUhlJ0bZkYYhnTzIwOd88loWyyScRUivDq30QIUeuEIUB4PotVxixqg6kObYz3IXvd6y1bqaQGb9C+C4wC38FguOzgHOBLP2ZimrQbIDFCAHEgdDzEQ0qV7KaOaHbMFErXiVBOvChFVdVnPtQBV6aMd31zRoMjOCbr6sD6HmM/6UM5W1fZU2NICXROFh1rmayGdUtcmgw+MnCY6A1uiaidE09JVxl5KwMAs4IsrPmnNUUUL1e85QT4LlhrvlvXkHDgohSf9xchOcwpVUl2ShLQxikKX8Du9g7RPwelx2tICzvY7eb+1tuZAdXax5PSIrpJnlDfiPfKa9Q7RE/qVw+FHXsD3fvh9fOqLn0O36NIuBjO6yBjOz/DorXt486e/xJu/ehlPn5xATiIxGAM4pQd26XwFh8Rf9p4i3d9ZQ06DCcDc3zE/dkvrOeWrd+5t4gwbimINydJ3pLEWMCoAcIaPdf+0DNVyZZZnLjGY7dopazUJ27R+8/m3shxUnXPGjvTR9k+Hblg6SWnt5GjQptuy4HGkOcHRuHs9CaPMISfiDCwp7IGyW9MCxro9bZw6KAIpIxxAyY6nxya/N2XIzHireSVGSnwi8pRBOWc9ufGQdtUGc+mnZOImOHBIdWl+bRkEUvRzhNGI08/u42M9H3ruR/piJF7uNyBps1mla1b0yf8XsJ50M43rTc1ZS1/YtSt1suq77uuc/NR8MSdn5NnJ7n9Muly3J78vFwscrA7Q0y7tMjkCcZIb5Gvnn8sym0AYYuKRdE1FBoQxJdnRParWFSdn7lUdPcCHMDQOr1+Hdx7s0tkIJ7FdYMTYIyIPwBFu3b6NECPWF2f4i7/4K/zn//k/yYCb010V+fI+UMqx/tY77wDkUxhUSKlJpTjn8/XqCSz1ctglEHa7XZqQkCfOE95+911sdzskH3dEiACTR8cBjjxOnp5hs9mBGVgtV1gtlzi/6DPDpcxOfT8ArgOYMPC467KKPuXuJwLIIfJUcBaQQCjGRfpetmvTpGpLVc5SLLr6QLFeT0M/AK72sAF54RpQInVbD4Oue7vZIl1pn5WxWQBS/+SGb9RGhv4nC0Lf/q3p01qI6e/6Mw0cNODSbQMFoyV6IGJ5sMLu6UVJ56Yv75F3i1KlTAsBfQ2QOae8JkLStFGXemxVO0rZyHdCbyu8awNl6smeA5xFYEcuOyj6vZYim2t30g8jLFvnWSRMT+9qsYBVxSN1eN9Yf3UXDE3nyhqCmhebNG/8PffMHIi5rOwzEgvgESMz/wtZZthduzmAuM84bPV3TrHb9Wjn1L5fFLP8y4tQfx8dEDqHwRNwvMJX/+C7+NL3vouD4yPAZeAfImgY8PC9e3jn5Vfxy7/4awwn54ibbRoHjW2NsYCpX50FhbrthtGhS53Gmye0tqDUAtHaQbLfKLMyqwWaowF8zEYoZCNjbr7tpYm2H1fhWT12+3wr9j49F8HR0mCUqZYWrb7N7aBdaf0YQH/Zu5b2Wj7JOOVzK+PK85kf960PuwZbjrLyDqQPXG59bgHxlszVY9eAdHwupa9P72MCGluygUqPMMlUSOTQuTFVri5zskPTpDXXVs9Xut3wr9Wbtm8iUaM4b1DPRTnXiQZfqjWu8UtrfVc0zEd+5/pseUIXO7/WSNXzWeYcbTzEnKNxMuakTCPkd0Kc3qcmM+2dr/gOaIf+6r7Z/l+lXP2MRgYLZYHm2RTr0bl0U7ZzKUf97du34T2w3W4QY8T169fhXDrgvd1u0XmfPAV+kXY2xLOB5MFnllu9p9mTQghVWsMRWEQMQ9odOD4+BABcbLYIzEg7SgSCRxgiQh+wOV9je7FJd2bkS6TCkOLaXJeYOXrGQLHkfQ8xYAgRnZsqJL19rc8QyE/v/WgUqYmrremUirelHvRC1pmYmKgcZpRiz1NohTHG1jG6blGelXhLfQdGS/BJvTqNp10A8rtehC1BMgcUW4aF/jvt1GRjzjF2OQTOOQKieMZagI0yZsm0ZKUYwdlNMfVQSD1zHpl9ZU6BzD1X8VGj0ChLm3VUz0odAtR46oGZUxx2rib9ICqXmgGojQJMDVL5THP3ZW1VfIB2qmTdnj3TM8d3pS8zYMj2Wz6LSk7pz0vd2TvQApytsUqfO0WX1pmNv0uZG5v+bt/3ljfEAMjBnXBcZ68BEaIj7DywWxA+9bu/he/+yY9x9MxdoOtABHgmYBdw/vAx3nv9LfztT36Cp/cfAJse2PZwcBg4h/8RlV2T1ly1xicGrS42LlrLxDma2NICfi26jXdFhckzen3L73ZsKclHEUFXKvvW59+32DS/Y9+5eErngNgceAQSneyh0xZAL++iMr8m49N0tP3VbUu/YmSAx3DElkyZMxCs/GoByjlDoV3q0dm1N8d7+/hVh8NU8je9DMA1xzbfwzpt/1yx/eLshW+F+u4DrhZH6Hf+UxRrHJH5TH8312cxOjUukGcukyUtbGHrt/1t3esj+tS5dDHpth/vORNsY7FUxV+ECkzIGdp0brZNs79LubKh0XVdid/TE1AAbe5ViFwO1F47voaFT1mfdrtd+bzvexwdHiLGgB6j8eHEo8/pHIQOxfHZMBGCacJkKmC1GK2z7XaHdMdEyojQxx1iHBCGdKkXDyHdfBgCDq8do/NdCjfylH8HyBPS2ZmUUnbXbxFjyDGcVFLR2u3fGFPaMAHt8rmkxyWMoUUiUNPPFGtHzmEIQxVG4rzL90OMjF3AVBwXigYveueDKN0XIcyW6ObAPGb2Qq5DlKVlflu/1NMyFqxQ0eOdgu564ejFYAWrVVppN4MxDPmQpEuH5vV7lTJJHybMzeKdpdINymmLrdCx45v03y5g9X1roes69dg1v88rgnmgZesstHdUDK/W2HQfrloYXKUb1E4ByweV8AYA1waPc/QjoolQ1KXl1ZT5srssc8BIt9WiQ1lzKixxMqc8Py/W016PbwSXOnNbq7/WiGkZRBa8za2fVv3ybAsoMpB2frOSYgLYAdETonOIC4/bH38R3/qjH+Cjn38JceHSLjgA9AHbswu88/Lr+PVPfop7b76d7kza7tDlm9yZkqxjMfh57KP0w8oPCwjmwKaeJ8uXLWOmtas6kSeGb23GON1H59LFtdvtdtIfeSbpUjmrN87HXJkzvC0NdFuaZ/Rzc+tCy/qxPkzesUaVbkv3dxJC2uDLVt/tnAq9WPHIVdb2SDeUQ9/6Tqe5eWHmFIbqp+fu7FrTf7d22Oq+0mRsLdpJP+yup01gottpzvGHkPHl/Zw1S4eF2jmyPFZ+Gpross9xZMtcKFmRy+Zzy1dWVhb8pJ7Xz7R2Yco7zDn6eppl0OIETZ8WjaysaBVd74QGyiYomEZEJ08dI6Vvqj493lJHg78tLa5armxoaGtWJlwfIvbO5zjGceF3iw5HB4vKU87M+VbsBHz96hDLxSLdbJhjPSOnW7a1d3ez2Uzux5BFXLYP40jIdCP2Dr5bAZKhidKOC8cB3kU4DFi4AB62cOEAsd+hy894ADwMcBRGj3fnC1BNOw9t5R5CCtMSQ0nidUMISUjlG5flgLhMdpRzH5XgRAlrInAxuOqYXi4oxQo5qxRHxsopIpmrPrQUkl58luH053onRL7TzwGjolksFtUYJWyk9b5dxABy1jIG9xGBI7pFJy6GTNv6ng9pOwlaG9IVIWmFrdEzp/iqYjwHtcCSez0ayjNv884JIUuHkR5VN81Y2saYp/HSzJYR2BIimu7687lSKWQaY+h1e6Vvqm3tpbH1zwEkKa344H39s3XOtWmVaUUDjMrTvp+E+9Tgvgzg68OKNoTR0s+uR11fa+3NrW37XGv8lWLO3zmJde48IiLCwmHoCMd37+DL3/02vvTNr2F5tEIUUDJE8KbH+2++jV/8xU9w/413sD55ilW3BHYDFvm2cCYCeYeQaZivRS00EXq2+NUaCfJ3teOint1XrNdQFytTrIyUd/X5DGkzOcC2k7qkP2VcPF1vLYBkx2KBkv29BbauUqxcST+pRCHY8Kp9gMQ+P6cv7Pd2fm29Wo+1+qDbTr+HFPoyQwa9Fg01mm1oPVuHwU131OxYRYfr71rv2DnUu3dzYWhWHxARQHWWoX0yc+zn6OyRdWWfs3hDj99ikhYN5vSdpYH9Tj3UDBMax1fLVztGS9+5dsqaB1frvaVXWjLX0rwlyyxNOIMke0YUQHFgMEdgvUnvCWPTWKfFgURUzk1aXSXj07w2x2NXKVc2NEIRUIBE/wVOnn6KSIoXBOc8YpDtGyDGMLlafrPZIIR0IR+ruxYS4HMY+qHEoQuolsUnwlrf0ZAAKrDd6d2DAd536BYdhshIWxTA4dESBysPioRbNw6xpJtg1+H4xjXQcgl0Ht53wJBS3PkuZ/EA4WB1gJiNB+fHy/daExhjrHYzyuchlvfq3QzxanLzNs0YIxxNGTXGWHY6pOjv7cKUn96nHRTmaRyuDo2yC8X+vg+Q6ee0UKzipJHtNaNQWmPQCy+ECBdCOnNAwNnZeRGCepHod0pdsb70jkjASy30tXeLaGpIzZU5Aa5BChFNhKLt62WlpXDl84kSNEBLt2Oft+FHVxUwUq/1AAstdZn6n+ox6TL2Z/rsnJLcpyjs2K/SB8AAvD3ty3M2paelu+YnmgEZrWJpqdu1fW8piNa60N/ZeGFdEsQkUM7+FBYe8WiF3/rm1/D1H34fh8fHxVjwDGAXsX7wCG/86mW88vNf4sHb72FYb7DwHULYocvgJSJ5CGMOm+oaYLQly+aA0hxAB6ahaXYe9RwIIGvRcI5PWgAJqOdiH9Cw/W/9va8Pdof9MrnSMlbs59N30HR2tMYzB6T2FQ189tW5Twbo5+xP5xzA0yyGUqxz6rK51jqrtX6bMrl8Nt9/W4fsXrRCRC8rBWsYOszpdI25UvuojJRW/fLTgmVN3w+j41r1X1Zaa97qDw2gZUz6fWAMT58rjtLOq6ZHy7Gh67zqXOl+7tMx2hFfUvhfsh6KHEyfVDp6DPmcvqvn78MaHVc3NHLmJIBSxqKcNpOcS+FAOU1BiAExBnBk9P0OxITFYoEQUtrY9XqtRkElXV7f9/BI6bhGQ8MV4yNGRoyDSiHrMAz1reEBcYzpBaXQrL6H6xbw3mG72+LunVv4r/6r/xKnT56gvzjF0jscHt3ALkTce3AfN+/exXKxxLJbIg4DwAHM+bI/53B6epqMLHBOo9pWWMJ8MnnCgGlnApNn0veycxTLYUtxuhAIIQyVAVMEQq4vNT0ymQ6/kTAvDfqErvpZK2jmlHpLkWkwLp/bRTK3/dlSzuU5ZkC17/LhL3IETx5DHNIZDc5b25ExRM67FA4xBohp75xDkEPieVGKZwJAvjxQ9YNHUCxCXo9ZKL5PQbf4Yq7sU5yl7chIuRQaQFAJAS1AYkyXU+o5bnlhdFtznt0y9uRkmfRP/92m1zzQtfVohceg5nNT4MyZZaxiG5+XjFhEUzBzqSLgNPA52gltLwMBLdnBSDuYrJ8xr+t+6gxeTitTGusUTGjXqW5XXiQZX+6LnmtKQVOAIwTvMCwdXvjcp/HNP/khnv30J7B1hOA8OiK4PmJ3coZ7r72Jx+/ew29+/gs8vPcBeNtj2S0ARKDzCMzwjhCY0421VHuSRWlbA9YCGK34Qkjhsc5Pgf0ceK1ws+KdlofWzkFrHoW+Wt7ZmHm7VltzrGWx7fPcTmRLlu7b0bE2w6XyJ8vjqo5G/+bG03q2JQ/0+mFArVmtkwABS61iaTT2Y3rPk3UC6HFJiWqttMZn+bY1Fv23NaKltEB5U17sqWO+qOyJXKeLtUbBSP8kUyUFfrNWgx1k3kh9b8e4r89X5W1dHLkUEaP60CrVfKt6LV3n9JRgAlK7DBpbtfo9pwv2jUnzi0QV6TUtMmS92eD46HB8j5CcV5znkBQ9tKDLY4Byrhb9qLDQhwlxa5Wrh07FdMleGEK6NCj3kwQ4x4ghBGw2W+y2W6w3a4Rhh2fv3gTIpUsNB0Zkh65b4eTpBcARB8dHuHPzBhAGBDD6kC9/IYnpTyE2VLzVAb4okLSohyEka857HB4f5+cjEAPAaYeF0cE7RgyM06cPcf34AFs6wPriAi994qM4ODzE6Z8/xZMHHySgkDNfDTEmzzOnHZzFYoGjo6M8R2lSvPcFtImAiXH0ggtzpD5zAfcTpmTkbCvAamAMDtisCAsOOASB8/Mh72IIIIAyyhIjiJDIKfoyc7jUqFpYqbEwDGmXgRngmA7jO6oMIes90Vt4Nt5ZijCljn9tKmwG5DY5ci6l2Mv0EKHuKG3VM6d0yt45REmCGQmLxQFi12FwEcsYQOxBlA41pf6iGCuOPQh+bJuyR1kbbsXASPQjjCBoMsYYpwYKlCdW/14JC6oU576QjbpueSb3z4lAFLHe8lTXcyLzoneaKuCl+jsbWgeugPpcaSkunSyhZcTa92XckklM+H18nhHCUMI00+coPwWQtMA/cw3C54Rp+U4JcCnFo5U98q210RLUhc6RIbG2KYsKwBjrqtZEHpQ8S3mdyL1G46CUl658M7bj5JyZGosDwXGSrMEBcLnlELHwHZgdNguH7sW7+Paf/hCf/d3fhu86DIhwnuCGAdRHnN57gPdffRPvvvI63nn9DfS7FJYaly4pPU+AS/zDBOgbakWpSnY+ymfQUlipUrQyb04uZBU65zFHhh9HnfUUF4Ygob8JbWRO7xERqOvK3HCmM7nUW8p0mgvfa4HFFtiwskHAS8VzprQcCtoos+vN7uLUHVYSgyEJ+XI427TdJNOyw4enDok54+gykGKft2s0rV8NtqfvWVpWw9TgETXdm2CyBWSVMWz7LrKy8LA5TzFHm5iZc84B1QKi9rK0Vl8tDYocJQAly9VovBG5Mqfy/CjzUPCM8J7lzdaOXWvGW+ejJn1HzqRFBMop92UVp8D2JqEAcDlDp8cs+raA66zkNWgfeSxlY2BJz04jX8UYEXm81wKcsAgnN1529jDI+3yp8zQyojVPrXVuDWEd6aIxg3ME36UrJ9ghpf9Wco9ZZJwoQiXrM4aG8xgEqwqN5L0iD4wO+hDl6oZGH7AbUtgPGOmmwXyvw2a9Rt/32Gw2qc/OYblcYXl8hDu3b2O93uDiYoM7d57BcrlCCIwQIi7OT3FwdAxiwpNHT3B84yaYGIvlAiX/cz6ILYDGOz8KmAyGPUlaL8a142MwAN8tsQtbWVMY+gDnUuYTAuHx4ycA0n0Vr77xOj7+8U/g7rPP4nz9Zhov8hZY5xEHLnddSLaM5SLt7sjCsrHYwHiCX37XHq1C1+oATga7ADpKCpldWmiE0cui6wRz3v2RGqdKLSqwCLWwwKNhJAtCDozDjYq75XXTRoj9ThctaFtWsRU29nsNcidgl5KXK/FjXjKUQpII48VWBJXqljGZt6K0matx5+qK0SFGiw6JkX5Y5WHp0TbCRlBUf17XofvqXLp40nuH2nDj2TrST9kta05T9Z5+twWWigLCNORE/z67c0N1H+eMDGvY1GUKIpi5MmpjHM9w2X4me7umh93+nhtbbrBqW0qMDEYdGnlZmQNEcyF4ek6c7Zcp1PqDgC4rwqTA1XwQYeeSknGcwLwnB1p4REeIR0f4re9+HV/54fewvH0d8CnReccevB1w8fgE7776Ot769St479U3gX7AbpOyDPrOw0m4ShHiKEaTpkVLnshOj6zXQhszv3rtlHnMbWrjX76fA7jpvZrm6QuMlgvX/Snzoni/hEqGRprJmfnbB8o1aNFGhAbOH+bs0lzbLeBT9UF9Z+W0bjfGWBIc6M9aBlHLUBjXKZl60++tsBcp9QF21Z6xF1qGkf5O180zz2gAPedUs7otjarO6NQGyXXZp0OFJpqm9csjaCRSdTOX3QC7A5aTOVbjsP1sJevBHj62fa/GmeeHxTEiuh6AOFSn81UbSNOxZ0NF8LYqlh9b+lvaEQyod72IJgzV7EvN0yMWu1QOMJc7NCbzmtsIMV1MLREDyOsmMiejgWoeBusYASUz1Zh1P6p3P2S5sqEx5PsvEBkcAra7HhcX59hud3Cdx2q1wrVrx1gslogxIEaGd8D1G9cROeL6tRvl/gwigJzDervBxfkFbl6/gccPHsGhw2J5CJ/zE+tBMjK49WKVJk+uGDwEwBHjYLFADBHBdYhwWPolIkdstlscHx/DOYLzHRbLFYAA7AhPTk5wevYLxBhyGEKqX9oEUGXASv2pAzkqUGEEmA5RCZkBrGIYwXMKB6I4bldaASuldSCrgOZcvPMIYaiYehQUdeYrKQmsJV+gFcDyzwqiiWI3xfarFSctf9u6NdAuxlOMCBwQshCSS5QYAtLyNjd06Ej+p8hm+yFKZCIYUHsR7FzYOdc0as21XtRa2GoazG1X6svu5Oc4RzXNq/dQlzkgvRdgq88dXDmsq9+Td8TQnvYjCWVrYLQUawWaLgFfEq4k7+n5s2EMEtJoFZ2eq1mwxzy5j8Qa4/b9uXWxD0iMIZU0mZ+9/btSaRuCkQi9Y3QxGRkApTsxFg4f/9IX8fU//hFuf/T5tDPhCB0csBuwfvAY9998Cy//6td48O77OD95Ch8ZPITk+Vfr7O/ab2sIyO9W8dpdJPuOfdfOt8znHN3tnLUA6iyAUuUqh3Ftva11KmtEAxZrbNnv50oNEuvPq7EQVYJ0325sC2C1dMowDJN7hMq7XMs9O0ct4D9nPKR3uAJM9n27dsszDTkla9W2r/tlx1vrlrptPVeVQa2KvtjQ9rf1d+lX6kSzTmaxoKdrLdXHE16ygPnD8PKcISbYSuuRUX7sca7w1EEnc7NvHc71B8hLwLyrMdMcn6Tdh/06wK7ly8Kqbdu6j855LBaLhrxL0RxknHtgLkac1EvIBnhzH+rvV65saByvFji/uMCw26FzHh6Mw2WHm9eO4BZdzqbB2FycZu8FI3LA4eERwhBySINDCH2yTAm4fecOnHd49tlncO3wAGGzQdzswKsFdsMmUwDZkxwzUORyaZ4IJdlpODpc4trhAcAEJo9rN27DO4/zszM4vwDnTFHkPQgd4hBB3sNzPiPifTrkrQVB4y6GxAy10qyApGIw8eaUwjWoqZSiHKoXY4qRvbJUGEIYslLaPIJfexC3NKveK0xNrqpLAJgcMJedEBmbjVu1wlwX208rYG04jo2Ftopf11nonY2MEBm77a4C7wAjxHwPSwkccRKN2BY8qr0JSKExxGLiITdbozXYnQKeUn9pdn5bVY9fioSRWcE0zlO9ywagZHFjTAWcBSVlzOqZlhIR4SQ00X3QdemdPWD0UrUV3TwAzJVOlPc++tm1oo239J2fAL59YEz3WSsy2Unx3o9ngMyY5taJ/XtOYVvP9aySq5RZawyAeAU1nZNMICxDupwLDhg6h4OPPovf/5//KT72uZfQLZfoc6xNFxlxvcbjt9/He795FfdefR3vvv02HAhdTKEE5NIlp2KQXhUQFd5q8Kp+z3rSp+uvTfMWYLd/T8Bu43lydWikBTlalrTaaYKPBh5q8YNtr1Xs2vhwYGt03Oi6Eo/WO5otua3nahJSY2SsfKf1QEUbagM1yxMtg9+e7Rl/n+pw3Rf9ewF4qHcL7O3vluYtWkz6QbUOsfS0/dF9mgLLeh51u0RU3XBun89kbsrwtAuC6jMtS1uGh9THGOWalNYOYKmLHBijEVWfdQ1wVQIhY0AqntTnX1s0apWp/Kx5zspgacPyf8yYoaWrbNkb1qj7hhpb6v46R3mnZYBHxrmc5PTYN2f4KYc+y3wbXrI8rHui279KubKhce+dFGe76BbovM95ehn9Gjm96ALeOThmxO0uhTT5Djdv3sDdu3cRYwqXGk+2O6y3O4SB8fxzz+BwQYhhAw4BQ0wCLuQ7K4RJd9stQj54TuSwCUPeTmN432FYL3D31i2AHMgtAFrkXW6C9x2c60pccGSAyYntDOd9ynySlajY9rINpZWPjr2UfxbQyCSJl7XKMKMmqVJQNC5KPaldtyhtAKNy1V5v26ex/pohtJDUh8Nbnn39t/YqzAk4oQ2ACS1ayt32Scamt2CtstZtDmFA4LRzcX5xXgkVonwuQwAOdFq4toLRVLf9TvdzTL/XgsV6emKUGPt2/4W/WjSxwGVOEM0BEPluHNu8QGgpQWs42L5pACA8ZL0x+0DfBFyZz1uhFS3Q2aKT5T39Tg3OreCt57XVxyKQTV+K4gNP5mTf3FlFZGljv5vrV7uu9pwTpbHbtetzOJVzHgMIq7s38OXvfQtf+v53EK8fYPAEHwkdOfTrDU4ePsHu8Sl++Zd/jSfvvY/1yVP4CLBkUyMqfKfnyTog9Pea9sxakbYzBFkguQ982c9mD4ab+bI8ZOk8N48tGWjrFVrMGQp67LaPesf0qrs4+nM7ztZ6ae3USr+1gVXJGlsHpvyt5YvWG/J91bcMIC29WwBtbu5a/GbHPLeLNUcPO25d9Ny05k5+ElE6l4n23LXm8io7B1cBrpN5iyl0yqZmFixkdd5la21faa2pqg5DZ6C+VqFVn+2Tpv3cPNl3J31TfSDan+zmMhq01rLul57XlryoiGLa2263WCw6OOcBZnOeogS91U5S5iKf0z0p44BbsvbvU65saPwf/sv/fTY0OqwWS3S+w/HRIY6OjrHoOpydnWG5XGK5XJb7Ia7fuo2TzbYoXwmpSoMgbLcD3Mrh7p2b+L/8n/9PeObWDRAGgBw4H07xPhHu9PQUT56cYNcPWC5WGELAdrNBn28VH4YBYRjwkReeT3c0UAqdIhCc67BYeXAGhHAeqQsJQDIhXxA1LniiNjiriT5a8yKkBJAzjyFTklmrvG+EndyNMWFgl+IBZaeFYu2RHZmxrVDTM+MFSVYZxBgqY6Vifq5jAoH6kiS7MPW7AlpaxSozqRdIgl6nQrbj0b/HGNMZFhoNN+9c2aXhEkSNxE9R6C0+lsvLBLSqrcaWsLfAhTn3gsYzHZZ/5t5v9aXUaWg/BfQzh/MxAj/LC1ZQW+HS2qaPeZdR1oD17GhPf6sfrXY0r82FDdixt/hFnrM7PvV40+d2Te0DEMyJB3TdlQEeL++TrmtOOc0B1hatdF2Xbb2PdQKyPkRWAQB1HtvVAp/92pfxzX/wIxw/exvBAQsQXCC47YDtZounHzzAf/hX/xr90wusItCfbzBwxMApe57LoadO2lLgxK4T+5nuI5l11gIDmk/a68EAuwadtAGkn7EgxRrgRDQeADUgx9Zvi57/ii9mAMVVFH5rXe97/6r8qPsBZDqYUC0tEy1osuvBnoNqrdOxYVSeWdv/Of6w/FC/S5WMkWfmUpraevbNRUt3aX6xZ0qsM9O+O/f5nJzRdL9K/6Qf6czrqF+rULusy+bwgPzdrF/10zoVLY+WV9QWig0hbsmEMpeNndOrrhv5WT1PVNXZOntl5caIM+q6LX3suC/jq7kiuDPpWgDZsTle8CzOJcZ4vgWIIOR8I+l/jXWk+zt+ljDUh+nrlQ2NT3z0ORysVgnYDwMWXQcOEbvtUwxrxrDZ4vrBbZyd3MfFxQUWiwV22zUOn3kR3nfodxvEyNj1PWJgLFYrkPPwXQeAEcIW9++/haOlg+8W2IVkZUnGga7rcPPaEjF2ODw4wsHBQQY3Hs55LJdLuMUBdiHd5eE6Xy4UYhC6RVdAgs8X+FEOp0lSjMruh1h2ib7WEyMLAxlwjBOTGNHD+QiE2nOjmUtiDLXwAVKcHTyB4NIBx8jwcNj1O3SGCfYphRoE1xapDn+Ksb7QyoZWAYDvOoR8WzlBLQZOoVUEqsJGfK4nhlClGpaxz/W57/tqR0KHbOlSCVbHCENEiBGbfgf0u5SSGCkzl/cphA95vrzvADjEOECD/KpPDbAdYwSHkNJvmndG8F97V1tzYhWMtoU+TNELf6pMqeLJ8SWMQkbebdSpx9QqeoyinHQIoy6tXbb0Igr5LXDUvNjqFww/cIwIBkwJ6GkZJLquFmgd66nkriZUkR1pbGmHLMZYaJHapywryouwkz0qHhtWkohkQY01fMe1YMF6aldmODlSaMwmxOl/0hvXdehjBHuH5z79SXz5T3+Ej37xsxhWDmswDuCx2kb0T57inXfexhuvvY712Tk2D09w/vgEPjCcd9iFvvSDY5JzzvlsoLfD88rvwlO5T0nWYDIJVva1gLJ8J6BR88McsLFFg9AxbGPkZ6109wE7zXtzO36T2GymiVzYp9T36QP9uYzlwxRL5wIu81okpDTyBXCZ/sj4tVwXx5voDNv36brk5HFtAH0rbyegtAHGa/CFQmvR6y0AOCVMeo/SA5Pd8En/eWoAjMB5dJYRJWfFrGFVfiYBpZ2Bc8btPl6XcEnkHftRxI59L+JaQI8p1rhrkKnSqS3ZO5G3NCoJjZO0I7IJzHUlPBpHUtvcOprQWfqndqhbxrHtR92ncWyid9k4RaStFs/tMzzke5fn7datW7h79w7OT8+UPpE+jM5HwR0xRnBEivIR+s7wsW5TjBSRe1c1Nq5saDx9/128d3aGk5MneOWV32AYdmCOuFhfYOgHHB0d4+joCE+fPsXQD7h27Rr84Q38Z//0f4fVYQfq0hkJ363QDxu4yDjMh7Op63Dz1i0MF4+wwA5HK4c+AOuLC1w/uo7dboeLi1NcnJ1huz3DZtUhBMbT03M8enyKGAnkPJY3X8QP//gfpY2iIZ25IOeQgoS64v12visBNSFGOPYAXL4bhBA4nV8YwpAWPCIiU/6Xlp7Edo+hOAIsGICD3AidwG0Ac7oDA1yffdB3XQRwPoDJ2LoUpdj1AQxgcKiUtUy89x5xaOf8FoGqmUR+H4VeLQTkgOyqSzdtxz4d0OMQ1LNZMTIXpk4CLwA5pSQzg4cA+HxwLYYCCLXi1322YVctxahBaASwjIRdYBzcvpHA3bsfIBIB8ACn2+pBIshCUS4V7lVKSxbkZQfIbJiUDWeTegUIWvBbvldLuxWaJkVS0apJa845US00tRDrspoKyghk1QMN8nUdc6EudntbH1C0oS5VH5ESOUjdUq9WRFLHJLREeFcZTESkLhRt85PsGtqdF0B4ggovy3qulKqih6MRXHH+L4e6Zh6T/jK6zikDLDkqrNGZqs87AcX4CAWEJmeBjEkbIqmP49qWRBbJJl4w0HPA4BzYJ+9VFwmOGeCQwIrvsHWE/sZ1fONPf4Tf+va3cHC4wtAR3NLDDQF0MeC9X7yKt3/xa9x//108fPQQMSRnAjiHYMaILjtrOnJgl3exOZYzOnrtl/UDjAYQESJiATzzCrxtdOmkG8453L17FycnJ9jtdoUf9inufYBJey/NiyBOcrvodeEeQgmpLECcpiFPGsikdsbq9TMWmMjv9jNt3Oh2tVGzj66l7nE4E/Ce1REIXG6KH5/NFzCacVlaSr1z8zExPoxcbIU6zdXTMj5i7NOuWwZriUcBIg/moWq7akdkVpQd6zT+yAzKWTHTmdJ0f5NzqU5Jec+KJ5JuHY1sYnEAUHFoKAk9rhcaDa/W+C141TIVcTyn0eU0/iw3RGe/KxFATjtHMmBFGltyUhb4jsvSnFuQDgCRQ+VZKI4bkrVW83MZq5IXduyd8xBDmLOTcTQZ9hvsQp+5HS3903433QGKY/gSUqKiLNRyHVP93dSxM/2wz/f57DQkFXh6AGl3I8lnMU5Bacc5yiFXRrkXTy5KHWIEfJtWUo9OI3xZubKh8cH9d8HMODhc4Hd+97dxenqKYRiwWh3g6PAo7R6AMIR0J4MjwsVAuH79eom512CMOd8MHlOKWZDH6dkF7lxbJiYBY9tv4Tce2+0O680a799/HzFscbhaYrPdAUgXsq03awwD45MfuQ6U7byArvMyI+MCz3nu5QZzQIQIQJx2PySXtAAamVsNzmMGsC1QB8WUNvyDMsrVwLO2ZPMi9ynLscurnsFVtoXKqneEjroJKEtMMBWwBXCpLD1SZKFpANhSFPK5DhnTAsEuzCGEZMC5+oCWBQxSP1CHUrXKMAxYcAqXgpND0BL2VpabmbupN7S0613hF/3s6N2o3y9jMN7Sqk3Fe2IYFsOm9TxqoKC/K9+nD6p3xjIC5kkMdyVAR17OUqk5Zk0f/bcofudH4ar5QRdL70mP1fvyt+1HK1RNgzhLL6lDQoKsomsBHcsPI1VQgRwNFOy8yoVe1vut15A1qIB8uLahaKZhRvXvduyinGWHBUToooD5tCbYEYIHYucRFh0+8eUv4zt/+ke48dyzYO+wAOBDBF/0ePTeB3jtp3+Lt37xMrZPTxF2G8Q4ZuuKeX12XVcAl50DPX79WQE/NJ/+tVXq8U4v55L2Pvjgg73v2mJlxJxsmgPHwtjl3WxQ2zrm3tdyAWos+r4b4T29WzM1WttruLVGbPvW4GrRpzyPmperOUH9t14PrX7qNq2jI3euMvZHHDEFZbb/rTVejyklhQC3jUxdh/R1uoa1HEvrORkusTgwK89MLkV+Tb5RQ2/osdoAmZa5HWHLL26Sqr1uS8sb3d5IxyxTFKbRhWNMBhjVzxBRjjipns5tjjtA9sxjmvMZOul51/MiFFNtza3B1udz68HiFfud1d+2jhZNWk69Vh/td0+enODo4KAeez6/PDYoFZj6GtEdzrkJL7TGeNVy9fS26BFixHbTp5S2rsPJ0zXIbQGcAEipVLuuw9HREQ4OD3Dj5h0sFgv0w7YSksycb+xOnoS+j2DyeOud9/H0sINzEXBIF57gAWSrp1utQHEJIuDg6BBHR9fhn55jFx4jbnu88OILE4FHRInZKTN89lx47xFDnzL4EFVKW7Z3hcAWnBaGcG0vUpkoM0kiUCyjSJtVLKB3CEOyPnd9j8XMvDBz9rDG4jXUaT4duRKWIH0qApqmzCNGgCg3HbMq455s9avvLEMW8ECoQJ8uuv6WQaNpK+2nuzLkxuhEh4uLC0iIEKimp55HO1d6W38uPhpU97tWyBGk8jFrZaQ9F5ctTOuha/EcAPCeeiQ7GzB/u216EPVuBmrgposFCKOhUa8P4cEWsNo39laberyaFvpvDfiJqMSMW1ClwZpdy7q+CbBsgAgtiC1fJTpi9JKiXuuHh4eJRzE9gzLxiBlaW5mhgVbTaPIOPTE6dliEfGbCeew80HtC7wnPvvQJfONP/xgvfv4lUNchkoOPBPQDto9O8PYvfoM3f/0KTk9OcHF6CmLGbrcr4FnWq/yzfZeQI2tg6fG3eGQWyJv51zSytLGGzVVKCzzq+i4rLR7f18/ZtotRWM+z5ttWvfrzFrCRotfMhwmlmgMbTQCm2rdpp/Vzdg3OjVG/29p1bZUW0JvI0tKv0QOdnhl33eyzczzLQMER6dn5/rXWxGVj0J8VLDHTRsugmjOihA/EwavfUX+U1tp0n9FvVO88V/NvHp3TAxXdLUg28wrM70poo8m20dIFl5U5mrbendtNtfL9srabbRY9nHV1DmHMcX2XjsPWDyBFh1zyrNXR+8qVDY2f/PTnAKeD1bvdgDfffAeb9RZDH/D888/j9p07iPkGbebkZf/97/8YLa8yESkAnLxuy+UR3nrnA7xy9gSgAbthmxdTAjTireYhptAcEHy3ABPhwcNH6BZL/IP/7JnKs14s5xDRibPapTMQi8UC/W6bbqKOQMjp1ORQdsmy5I2FLpNMbaHZEkZA7aXXz1cgIpPK5ZuBC+gRmjmfgaRtA1V4glyOlIyQOjRGAyrK4WJWuGtGnwrkqedCntehM3YOpBc63tmC6tbv8oxOkSrKOHKKM2QCzs/PUzhO1nFO3TDUqrupyDCeO9FjTnMwPTwo42HmyuuoBSbL3krDgIhRLqNsAxBNc00PNs/UoHb6bglTy2uNaPReOe9K+ugYp3Xa/mgecc4hKP6w/LUP1IPaQncOKE2Uum0HSCFBubR2EGxbdlwt2kONq9muAbiybi2/MXO50HRufDq0ptU/C85bdZXvCGCXQj1TWKhD9A7bjrC6cxPf/cHv4wvf/jri9RW2xOgcgTc9dk8v8O5vXsH9V99EfHIOOrvA+v4jwBMGGndRhIaSu10+s04Jq8T1PIseINRG/L65mswPGrwFVPS6rNg51PVah9NVgble//J30yBUfS80a+hMW8dcvLgtGlhbnrQXj05AfwN02vaaoA2obphujbM1Nhs6q9sQB8qcXLH01Y5Nq2v17lCiDSdE4RxQHEa1vrN8bOchOanEyZDDVTRpaNQhUvSOlNSh25zSwBhrjiZ0lr5N5JIag82cJJ87YHLebaQEitEwlZdj6JTVj7poWQggh1ur3RXFw1pH6rGk3SFf9c+OW79T46upzNaySMtZ2+/W71fR2/adfaUlX8o6RwrZBU3BfVrLKeSyWstEJQmOc9PdSo1ptHwQva5Tktu5ueqYpFw9ve0HZwDnEJgQ4ReH6GKHi+0p3rv/CB88epqvi09K8ujoEM8+/xH0Q58PfwGOfF6AKaY5xpTmlpnAvkPEAn/9s18jxh0i6RjlcXudhwCXT9WHGNGHgNXhAT79mc9gsVyVS3+qiXBGQDCwWCyKQNBCRDz4RVGpRV4xmRMjYOqR2cd8wHSrbfyO4SjtIvQcSkrVsougbsTU9XXej6GOillijJVnCdBAINWtFZEUG8LSWlBzwkq3pQU+Zp7VdQs4bO0GTf4W5eGAMPR45tYtnD+9ADsH5nwrdEP5tMBHEVg8AoMWmJM5t8Auw8umwNc01n1JfeAqBELeadGm9bsF06k/rs1rag608KUMKNJ2/1S5WuGihaE0Y8Mi9LMT4dYAhbpPVd9mBLluo9BZtVH3cTqflk9b7SRBXPfTOgnmlDlMW3ZcmhZ6rvfFru8DEy2jJMUnA+w8tp1H8A5D5/Hbv/dtfP0Pv4drd28jeADOYQWANj3O33uAd371Ct597TW8/8ZbOGCHYb3FwBGRHQIYXu2KzhkE+vPWmQDpt/Z0C6i3dNX00+/PfaaBZYvf9GdzbbVoqj8T/mrxjW53vPx1OoetdV5ohSS/LM+2eK6a80bf9fvW2cU8pl0XR8llNNEGjvX4l3YJRe7tAyX2u7n5SmHKBGC6bu347T/pnx2bpS0zikxOj8SKl3SZC/GTepjH31ttaXDXkgktWsi7FX0a9LS/T+QkpsaLftYWrW/lOq9WCJz0xuqjplyVuUJ7Pdj1NeEjGnGXxQ8tHWlp1dTTs2UMubJh3HNzpH9vPWPLvjmo5EkS6bP1JUw7YlawOIZmjCKq56mF4cpFyKZ/LVm/r1zZ0NjulqljMQJIoU3sgIEB75Y43+xw8+YNdF2Hvu9x7eZdPPv8iwjDeH8EsxL2DKQDj8B2NwAHB3jxxU9gvflXcN5jN6Tbx51z6LLhMIQBK/LwRCBP2A479ENEdD2efe4FxAhEGuNXS+iIhNgQUogLJU9c2h5NB76t0C9CLqeH1f8SCKkJbL2nZL6rAN+coIQB5FAeAgWStYCy/dUKu/Qp8uQZlBja0ctjAZpVylJkPlugXQuhFqCXOvXhUNuWfQeow66ENvL3YrHA6uAAfHyEpyEAkHCq/Z7fpiKksV79XowRMdT9rEKTfDte1+4PWwNNYtz1P92upQnz6JnRn42KdWy0epfT/+Q93/m8VS5AvQ1srcKqBBHPGGyKZi1Qvz+6+GqlBSCKuT4DbFqlKYBzsd5QfealGo/mo8Z8WSCov7PKaC4sca6efYJ+SR0GR1gvgBe+8BK+/aMf4KMvfRrwDmGxQAwBbh2wfXKC9195A4/fehfvvPI6np48RrfosA0DBpedLj6d8Wl5zvVOi5UXrT5XIZHITg+MhkdLpjUBhylarlgaX6XY5+Z2j67KX0QErzzr+xwo+h3K56ws7VpAWXvFL+uLvCMXyNo1bh0GMHO4r+59NLHj1jTUgLAFsmRO89GjJi3sWpxrV+ssOx5XnHoy7Hq97xuP6jEE0lY0IyA5VNvzbmX/nLzYV5p6wnxveccWC2LtOoo0Z4ykt62cci7JjKjarfEBV+/p9+dCjQCJ+LhcHuixEjAbCmT5sRq7wYZXLbP1XeG91lzOzR8zp/tPaNSF5XuWZ9thhoQaj1WYxz77IfnRlisbGq++9g4iR3Sdw3LZYblcwHuHbnmIyA6rg0M8OTnF9evX4ZzH0dE1LJYrxMjgCHjvIJlmUqdT2IvvPDqfiPXSS5/BwfF1bNbn8IsVfARiiDg9X6fYYHI4jxFHqwMcXTtCCIwQGD4CH//4J9H3PZjGXQGhVrLy5FaN0ZvmvcMwFPcLgAweZR4J5RIbOXiqGTAlSJl61iLXlxnpRRNjLHnXLfBFjnOUDABSh/ceIMmskw5wxRwixswlNl12c6RN733yjkGHk+WsDFEA7jjHwzCMuydiHFEeqgKVxISu8yXsahQUbd4pRhRnD36IJaVfAqz1hW9zCieFxckWOsAhGY9DCNicX6DfDQgAPJLrRRtOen4SKFUhUqYt3YcRxE5vbBaB6LsO8vFoxKDMKfNUWCWQRdUuiVU2Ff149BhF5uZz6e92W4n+WbjnW33BsaSNzJsypq6pAah3CwmJV3UYgu2X5o/i2ebcvjRKIz2sCdIScFYx2bE6atPUlhZYseO3a7ulCLSHmGMsByxbdc0pclmzfd/j8PCwnvOsEGImF+vJkmcoxdRSTowQmdF3HsfPP4Pv/PEP8Zmv/jYWhwcYYoTvPPrtDhePT3D+wQO89YvfoH9yivtvvoPdeg3v0jgGjuBuDFPocmotTh9oMQk5p+RUv71zgKS85pRNKgIlxBYu1ZcOlwuAE49yoVJZ73LQveYJC1yhfmr6lt8mc6OLne8W0J/ju2ll9Z9ziloDq9RuffGpXl+Wj/aBrZYcaLUN5LucQijzlNZpIvy+uyUksUg1Zq5pNX+2rd6J0uOZkpL2ymm7LkX/idwRvWYNUSkSaUvU4rFp31ufEWGUa0l5KxYYZZvMn3aW6Pr2GRpWZhTTJutRYOT6WYNiTtfIQpsZ/xwfJV03Gr0uh0QxoxiIUoS/kEOKGe2zj1bW6rbHZBQ1ftH91n0svJXD4CkPVa9Py5d2nHq+9pWrgPHSvvob+TNqJAUp628GEyRaJvzkO48wDHAkUUPpwH27XxoHjkayfAeq1+lVx9cqVzY0Do8PS2YRIMchAui6RQIcIcD7BbbbLY6Pj/DMs89guViiH1LUoycPTw7OMQIB2z5DQiYsnYMj4O4zz+Da9Zs4vzgDhgEERt/vEIYe280aALDwHnfv3kKIA4bQA2DcuH4DH3vxo1j6JSJ5cOCkkANjsVyAhy28S6lXCOmCJUcOy+UK2+02xaPlmDSmdB5EjIsBnOIWkYVhZHBIRktEfVCvAhyYAt3qeyNcE019Pl8hACxNPhElSegIIIfOeWyzgPLOJeCuFIII92EYUj8DwDn1pHi8ORIi1f05PDxMFx+GIaW2k++BilkZSYAQEZxPRmPaRZFt/2mIF1Ha+qPI8EQlNRoDYHI5zKAB8NUZEuu965gRPTDECOrTQhy8g+9Tml1S6dmqBeIoXd6Y57sUJbWswCoxuEogpV0xMSZGgZjCS1RcMNVhIoUvaGxzX0iXNW7IuZKPWz8rBjxQe8QLvzEXKSex4JJO0YoPK1haikmMz5YQsllxmoaAWLFIqZ05K3uhQg0gZ3ag6k7X52HkOaM0KxBPCZRLQgWr3Cw/ljkwGk73j4CSgCGNTvWvjB2FDtIHMvwn7zhOACYQSl9TWGWEQ0ozTTHJj9h5bMDorh/jC9//Hr76B9/D6toRyCUZgAHYPD5B//gx3nnlVZw8eIQH797D5uQUcdsnkMsAeobHyM9ElFPWRjiqlgrAMT2bwUMyHBOg6ByBYwAJHbOjJXIERRaBhHTvyKBoy/A+rSNtRIwARKgo4FADf8uPBEHAaY6m/LzPINV1ad5ogc40lvbB+H0Ggb1PokrooXabte7QgLW1XuUd27blM7mw1nmpJ+svJKRoZbnIEnYpNl9CNZJepULxqg0DoKVOkXk2jE7TNMmSkRatsm/3XOsP+U7OciaeADinuYZLhm0IDWfNzNyVfhIBylAbcWCSc/pMjMy5BfSVHGnwo/7MkQbOXDzUAhJbcszWMQl7U59Pd7e4kqU1bVLYmRj+VVuU1jfRuKNP+RLd0etez1mLp23oX+JQVsxGVX12zkRMEI+yN4acJMjXdVe4jfdHXeg+WpnSorneWpHVMq66dv1arol80TwvGBaIAI0OWRR/wdyOVki4jQhEoq+lH6PDrDW+aV3z5cqGhgaxaYGMTJ7kUSJs36czGc8884x0sfqXmG3IixsgB3iXL4Vj4Pj4CNvtFn2/xna7Le1fu3YNfd/j1s0bcN7jYr1Od2A4h9Vqhes3rmN5sESI4wJzOr4sRjifBKF8v1wuAdQhXUI8ASpR3fQtAn48PDOmZdSH0MU7pCdET5h+TkpqEwUcUSZQjHG8+M4lj6HzDouuK32TPswpvuVyCWauDja2wjN2u12O1fVwbtpXDcS0Ahtjq6NwRFEQ9fjqzFSFzoRq4dTAenpI1Frz3ntcnJ5iwUlJyGGmlvKt6DNWjFbR/XXkysFtLQRT/1Mi4nEnaPQCiyKX36v4XiVXWkpsTjlYI0M/z5w8xEAdzjdXtxh7ehvVAnoLEsY6xv7rOltAqzUmCwD0WFvPXaZ4bTtST8he14mxABTjcQ5E6Nj1VpuWx6zingOw+pOyJiiFdNot7EApXaj0Ocnc5MUKMafZ9g6x8xiWHT75u1/Cd378Q1x/4TmQ9yBHcEzozy+weXKKe6+/iftvv4WThw+xPjvHbr3BZrtB53w+I2AMQk0zMxSq7Ln5cwR6TiwN50JU5gxK24Z8VntUp+E5+/oi63oEoNOiAb4Fxq0+XQY+WvUzcxZMUzAo31uem8hT9azWXdLn6mxXqyPSR67HoftCSn/YddUal362FSY1V8rcNerUbYpum5zPNPJMz8Ecn7bGNDfHmoe08WedFrbIs63D3voge2ss4pS6Ks330brimQ/xnl5nlg51AyjGieY7oqnBq3/uOw8n76d+TEYEbezoudbh9NIPkXdy8FnPddGNvH8ur1Im/Ud77OEKPNme74jtViVQSo3MLPBa70tbdb1XW59XLVc2NAAUC7xStAAWXQdyhO12gPdd3tU4RvFsZQMjRgHGgM9uMeZYDAaOETdv3sD5+RkWC5fqwKiIb9y4gdVyiYuLM4SYbgTebrcIHNEtl/m5dEle13W5vylunZyH97XAsecJWsaEWIplEqhWALLw5UIwIE3ePqYotDNCL93UKM1Q2UXxoPEwPDNiGFO6hhDg3RguZesNM0LdglC9ENOuynj+wCpWYLzJu6ZFfW+AfkZ7b/RP5xxiqIVq3d9RcEy8eIGTFzeDNPlcYslB9SLaB4DnShF8PBobE4AxQ9Mynua4MG55t75r/G373hLCzhFC4CbvkeFdoYn2VM0pv5ZSiI36Z2kwo+QnCiiHGOi2K2B0yZrS7Wka6fWoFauj6Za4VvganOlxzikyy6Py3T6DSICUU/0M6uxOFI8zpzAqx5RlhcfgCcEBw8Lj7ic+hm/9yY/x4hc+A1p0IHLwRAi7Hif3H2H75Cnuv/kO3nzlNbgYsD0/x3a9xvriAiBCzxGdc+XCTUu/3OMJPVtz3/Lg27V/2Xzq+bIguvVca+4t/eeAlJYvrTakPutwsSB0sk7M+twHaMc+K284poZ4a+wtmurx7DXiGrxp67OhTTHGFILZ4AXdh1Y/tY7YN0cir0MIKdB1pp9ats/xhpZtQtN5nqkdCbrd1o6KDntrvdMq+3jZOuPs9/psoF0j6SEAHJtQca+eYS5OP13/XP/n5lvr2SEEkJtmlNq3ZvfxUasf5pOJXBIekr5N1qmppzaIpsb7f4pixzvSZkxPb8e3bz6YgYv1RZY5EHAhb851YiJfx/r/7kZVq1zZ0Oi6bhZ4DMMAkMRCptsw5dI+AGAOiHmnYRh6DEMPv0zGydAPKZOUI3S+wwsvPocbN66DOe0SyLmD4+NjLJdLnJ+fYdf3GGLAZrtJhgAzVgcrADGd2fCuGBjMksc9xQFLfbXga6dwZWZlMmeGiHEiIGtGaXsiihcCKAcEpY5ReCUvYj8ERDcylqQu00J+XAC1EOz7fgQoMcIxiiFnFYc1TioF4OpFZrdS6z4IhQgh1vTQcbF28cv3XOKwqeIzq8Q0IHQub/kjhRLJbddpLDHtKijDR3ZgktAZgCsog1qBp23afYpb07cczHJ1NiFNc80fVlHpemseGd/Rv7dCKVoAQJ6vgCDlNInmuJwGjLY/QBbQxrsG1IrX7gjMAbiyjqj+zI6vRfPWOCvhqdasBWE6Pa+l7Vydum3L11Pj+3KBTZS2BebCYToGHFMKj4oEsEMPIJLDpgOOn7uDb3zvu/id734b7nCJoXMYCKBdwObpGbZPTvHea2/i4Vvv4uzhY2zOznF+cZbuEOK8c+Hl/IWVSZrW4zkJvSbl+dZ8aPrZQ+P7AEULENbrsS4toNr6nRR/6e9b/bHv6yJyTRdrZJMx2Gy9c7yUwkrrrDtaTrcMiBYtreyYkyUMNPtpx6jnQjuW5uakZXxpntFjtzLMfg8Viqo90zKeOZ7QdJuG3kyNWQCTG4/1OFrzt28ubH/0c9Z4k7HYOvV8WppagFwiG1yLhtM+aBqwGavdlRHZ3HL6aHlgZbeUlpHWkrvyvuwwtpyiLRmin7Gpm7XsEVqVOSfKoZvT9OL2bpE5mtoxt/RD6fcMiLd0997vdbAVHcEpY6Qjl87xImEje/p9bo1quo10RTVqiwPmsMVcubKhYYXMGCaSYtcRR0ODKF1Otd1tEULNcCmlrBxsSTdosqd06Dp70UMYIAfilstlORx5fn6O9WaNGAN2/Q59GOCdQ7foEMqB7YAQBzB3hUBdl84UyI6KZN2Qhal3MPTOhj6UVw5KzxC3YnpKsX+tRSK/t4BljBFD3rp35MvFbIwU29ip91wemzfeWAHqY+GyG6JLSznYrU15Ti9SEd56e7cwnaGH0DrGWFKvaV4QegvNrGJI9Y4xk1Uf8kpgZgQeEMgBbpzzxF5ToaPHb4WFLG67gMo8oVZIVhnpurQiXB6sKjqPz0XoA662Pf13xUszAiPRvL2boWk6GVeMYDd+VnnTlTKc9I9QDDaZl77vy30q2rgDauA956UVY1zatAL7MmVejUveTX9MxrGvWIV+VaF62TqbU4wgqs6XaGXqY4RngJgQQNgREFZLxIMlvvB7X8Y3f/SHuH7nNpgIAYALQNjucHb/IU7vP8Abv3oZ77/5NuJ6h+16DTBASrF674sDjIDi1dTgbBz/1AO9z3CwgMM+Z9cQ0DYuNK3sWmvRswXUWiB2DiS32myNW/orAKUCsZERMa3f8tSk/QbII6rD+DQgadUp77acDhUdqPxvLw01LaVeGH2g37U7gC26WmC2rw/6cz0uW1pgUeuVuVLP7zSUb05utPhqjp9avNMa59z6uKx+ouyowzQUaI7XKoDcqLvwExG4QQIN5Fvv2v7Zv+dkqpYpLbmi6xhpCQDt5y/TFzHUBmmVHXJy5qt2ZAFTp5LFRkWWe48QRiPHGswBPKlD9GgIQ0o2ouQMc3INSUh9xx2G3Q5yLsiOvZojwiR0asQ61ExUcxUd2CpXNjRsWk75F2M+IM0xe0RZdHq+YCRdtOa7ZIQsuyVAiXGHEFKoEDnEENB5B0nFRURYLpdpZ8Q5bDYbbDYbxMgYQkC3WKTwqRCKx37Xb+F9l0OlGCAGOU75n8PUkzDG406FhACUmCcyyjmMSwRWrqUCxnVYVV1qxZA9LhxBERj6bNyEkM+zjIeAhxDgiOA7Dwq1l7zy/BNVnrW5Ugl9tIW+zPeccCWSC8LGfogAannkq+1UFR6lQ/TSIetGfyIXweiIsFwssaCUdYFiyOFlVPohIQ993yNgqqxaCnCy8+BoMu45Wm42G3jvscjnY2wbuUYQ1cBJA4irLGqrrLUntKXI9RqWOQlRsk+NdersZbNAmYHIoeq/VmgWGOo27RhKvTwadPvASKtfdn3LGt6n1K9a5oDth61vDlCBuVj3Qifn8kFv5xA4IBIQlgvsVkvc+eyn8e1/8Md47jMvAo4xeA8EBnYB64cnePrBIzx860289fIrOH30BP16A46MgAi/WOTsUKnvPp8YFGMjDerD0WMuDKY1j3XYXtvpoT9rhcXMGQgfpkzX49WKtKtvm299z8zFaLN9nuUDoBlaremoaSmyXgOP1jst0JZewCRpxj7aij4jjknbN/rUApVz62ZOj9gyJwesETEH+q8it8eXUC7Cu4w3WnOr+1v+Rjpsb89X2L5andMCt/v6omX2ZXN5WZm0N2NIWKOg4gkzx1cB/lKnjaLQbbVALxFAzkOnc23pPflb5EpyWo7PD8NQpYAm13aOWL3dakPPCZB1Uw05K7oAtR7TdTgixEY76dhBiiQq+lX6BZ3kYV5u2jkkUCWD5uh41fKhdjRSZ0SBj95YAOAYseu3+eAl4eHDhyAiLLxPhgYlz/JytUQcegRmHK7SBXuOgEiSDYpBxFguV+i6DiEEXFxc4OLiokyY9x0IwGKxBNGAx48eY7PegNnh6NCnQ40AEAMQMziPKduJdylbCwOIYYAwpTacCtDLYPbi4qIAfMaUkYTwJRwl78yIJ10OiwMpNS0kRWs+pyKACEhMHoYAsEOIIX3vPRbLBVy/Q4jihBJvEpdUt4t8TiXboykBAaXQEeFtzv/2AQlSwYNtfgABAABJREFUqk4zZcvL1hIa2hCR9IfaUJW/5dko+RYaglK6WpSlKNTIxbr3jtBdO8K1u8/gyclTxA/uw/EYkpWZFs57BDnTkzOoSf9HoRNHD7jW+A3BoCkm3gMgnV85OzvD0dFRut/DKMay6FGDSz1mK9haoSzVnJm5sErGKuqqTzkMIobEby7TWYSb8HxLker1IEw2DEM51Gy9OhYUWMWjvUdzinKfkJvQBTPArUG7y8plwvqyQsn3UbJr5caTMZHpTJkXvfMpAx6SIUjLBbYEXHvhOXz7R9/HS1/7XeBohUgDiBmxHxDON3j81j3ce/kNnLx/H4/u3cOw3WJYb4rnimi8wdg7j2zZpQw2XHvgiVohkjUNNBho8hanNSgfpXpaM5KK3c3QP+V37UGf0HiPQZJ+n9Y3Z+Tsq6f8JJSL+YLSkVkgjMlHSl25XpH/QEUzohR+Kmtefyc7hXaNA7VzqdVXO48Vvzd4vwUsKsOAx93mOeNCz4mla0teJepQ+b82vWisuPyU1PNzxoSlqx1Ha37L54olrjq2y+SCxhj2/YoGNOUL+6wtOiwsxghWoVN67oVHc4v1MqTp2IpeBGNoGLPT9WUMJ5bdgnp3DSpcuiV77U56jQlIreO83gpbTI2dFkbRWEYwiN49kN+99ylLpUS8MBf8ZY05O29SB9E0eUTr9xhjSRyjaTj2t866WbcN9LsdvKfqPQDlHrW50up/SivK+RqC5JRqYcar6E3gQxgafd+nF7p0HwY5AMToh7543Yc+be0sFwu88vLL+NEffh++c/AEdLmTPPQ4WObdCAY6SjdO0tKDwLh/7x1cPzrEdojFAy3Zp+SgsoDs5aLDcrHCdtvjF7/4Fb79rW+BhwAeBlDnwSGAspETOXtpFx0iB8Q4YLs9A2EAMI0hlwkVZgkxhZREJehbAkGUiJ6UsshDKIYacp+opK0F2FEKiQoOkXO9jjC4ZIghZM8VZ08BkHIl53sJIicrJKbcs4hqd0giDZnFcz16e7WyyrNUxqKFuB6LvdG6/FRZv/TuBPM03r/QJwP1pqUN2RkbUxImtU5gWmCR5+mUA77wra9i+ewz+Nn//f+BQ0qKqFz0l8fkFx3Y5H4v/WW1lyNgwcyjHqsUeUvvRKxWKywWi+p5LXBaws8+2/o9f1D1ySpUy5+ASdfXEFQAo1Mxn4XHMu3ZtFfeN6Ff3vlED54CC13s2inP5LVjQYMdT0vBa0/5hG9rIlc/W2EVLXBhzw3oNkQRWi+Urj/dapPCm9hRykIcGMRApLxCmeBjXtuLBQYOCN0CODrAV/7g2/jtP/wOljevgR3BI4B2AcP5BZ7ef4T3X38Lj995H4/f+wAXT0/B2XERKWfgA6FDOlAOUEptTOMWOUCgGCF3CQgwT8MYDXI7Z3PzLDRI4XwjyWXndpyVNqDSn2ngYb/Xn1n+1EX3TWST/V47mrR803wgJfFDnse0753klKZbZEDAMAMSNizp4a3usIaBpUdrDdixtww+O845gNeSJbYdG0Z9lXWqaWff0QCSE1F0bXnnWjs0sqEGwJPLKelDBYxt+5rGOvxsjlatudf12LG12tL6LoWa7Zfvc/Nlgb1ur6kzqU6XXckh5nJ+I5GRi/4F0aROLjqR8n047fGLbrPFQb3D6SxgWsvpTKCdA/33LB9FgJwvu05gmqyX1rpt1W3XcyvUnUQdKpkpPkKbEEXan4awzxtV1fiotv2kL4Ir52gCEHb9DkfdAYAx2oMx4pMprygLDajkHpjQUT6rUfpMJeR2H7+2yofKOhVjwNnZBfp+B0aE98niS2A+MZpfLDD0PX7+s5/h3ffexa07twrocs7h/r37uHPnDkKM8D6FlTx68gTeEd59+y388pe/BAAcHBzg/Pwcm82mWpCRkydbe8qdc/jn//yf4/joCJ/73OdB+YK75WqFzXYHZsZ6s8FyuUDkiN1ui2HYYbPZwpppIqzSAkuhKFws73yOYggYhoCuS4xTpSwFUoiTulHcAj67za1DuSIDiJzuFYgppz0jhUotsqBg5jG3fWR0XR1Lr3cQ2CjoKsQqGxsWODHS4tqn0K2CLGPKhoYOdyieAUPnlnAXGtmwpil4TnMT+h3IoxyiX6/XiebJiqpoLPXqA+eTGHTRatqLdoWi+ye7JeknJuOoFm5DWbTGWwla03YNMK7uZbB9t4cli2DOAqlVr/YuF2NDYv4vabO1Pogo7eSp/lih1lISc9/ZsVi+s5+1+LtVbPjP3Bh1/QNzuViPGaCY1pljYAAjegLBYReBzqcMZ9E5PP+lz+G7/+hPcfe5uwirDtQ5EAPDeovto8d49N77eO03r+DtV14H9QFxuwMPARKGZs/KMPOEt2vQU8crzylIC0hawDf9BDTXarpIFXPz2wJSQn8rj7RsbZ0tahVrfIw0mOe3ircycCthiOIMcQ6eXNXHfWu4Mmx46qxp9VnaEXkvPGvHbuk4kS/ZuN9HH2vAMccJyNIe3BbQ0/2zcwdkILdnvlpGixQtg2xf55xiWh/WMsBNDoRfVjSd9p3LtOOw/ZHvdATAPnln+y6GAe15PoW82sscpsZOmcuZsdo+tWS5nAOQ51588UV88MEH2Gw2WCx83Q9M17W0oeV3NLqo9XvLgJHvNc4YMU/bOaH5dtSxI7/aosPlqzW9p0zlQhtvEdUt6v5454rTj1lk7uWlxWOCI67S36uWKxsa5+fnWbABq9USi2VXFvAQY7qsJo5C5NGjR/hn/+yf4X/7X/wX8F3EEHZYLhe4feduAoCRsd6twcw4PDjE2dkp/m//13+G7baH7zo8PTtLIUtZmMpZDRFu0rYs6gcPHuD/89/+S/wfv/Tb2O6ScUHOp2xUzNm7TPCuw9Bf4GK9nh1rAV4k2at8Mi76AVEJIO1F0Z4wQu3dbgk//TPIGQwat4y9IwwhGXfJmBngFQDQVi4wCk2bxk0YZgrUx4UiC0KDJgaXC4F0/boefSB8jPcf+6Y9BC36Son5ULQ2hmQnBBNwrhdFfj9GHBweoHMe3A9YUPYbG4Vn+28BphZiGrxfWrJk14u2gAMGyI07QLVRJ2ElbUFox7u3C6pOTeMPIxRk7eo4Yo4BEZTucHHTuGXtHQTGNcENU2MiqKk+J5M/nN35agEm248WmGgZGGNzbQC2TzloRXJZ0YAhUvqXW4Mnn41kxoKzAeI8QufRLzxuPvccvvWDP8DHv/IluOMVYs5EvD1fg3YBD9+7h3d//iu898ZbeHpyki7n7IeUWc+5fDHV9BxEy6jSdJwAUTNmuTdHK/LJOqp2zdo0t7KxBcxaoGyufzoc8zJjpcVHVsZYJVw5adT5Jsm+ZOtgyOVX8xfN2XGlMbiSsnyOb3UfNXBqndVo/a3HJTuQrT7Z+kZacDFitbxvzaMen9Sh1+tlcrYl++045vgFwCTcTI8txjE5zHgX1mxX9vbPyjbzVAaA+2WRpaXowqvI81Incwn3sf3KPakAvabdbIiuadauCf133cd6HfV9j81mk6NEYqG1fka/3zQQ4Sd0uQrP6b7qaBUYQD9HV/3M3PzJGtSyqMWbV1Adpc5x3NPvgBwuR+ksRsIdV6tc0MLfxXD4sO9c2dA4OjpCyRgFBiPktLb58DIn2OrcGAP869+8jL/6yV/jG9/4BpbLJZbLFYgcdv0ODMJyeYCLi3P0w4Bf/+o3ODs7x3K5wNOnp1ivN1WcnF4QevJEOIcQ8Ld/+7f4xS9+iS9+8bcwhIh+COgCo+s8Dg+Psd1usNttcXBwkA+WD2BO2lsrMD25KVyKc/YsQkqZSthsdunQOaVLtqpL+9xUgI4xhih/a2ESQ0C+5BfO0SRbif5d2unyYVFWsM6Ow9JLM3wM4w6Jbqdlqdv6AJRD7uM4CUTTg3kCAorxABOuwrWAqQSr6UcZD1I4lPfpEsPQD+icT+EpiUUrL4Wu2xocMgfk2ovHChXdV2YunZS6Kg8/TT1Ouk+s5kzeswrbth9jrIRjaStTTHbTJv00z2re2Gfc2FvbdWkBU+nfbDhcQ2CXPplnNHiy49UywXqO9BgrA5rr0AndB00DqxwskG71R9PU9pOIyg3MlEOogCQnezAO/ALMwIYI7uYxfud738ZX/vB76K4fgT2l3RAGNk/PcPbBI9x77U1cPD7B/Vdex/rpKSiWPDOpPVffh9Eak52L9HtbMQp9NP30HGqngq2/FZo29inFb1vgo+vdV4edFyunpnPVBhL6PctLLaNGr3VuPAMge+indEgyo5aNJbzOe2gnr04qommq+235Tb8j+lGvgcooN/xqxyt0sSFzti9XAcBaBuv6yzOcA3lm6tK8Yc/5ybis0WLbsPpddp8nu+mYOtGkvhYGsbpxQhPCRGbP0UrT2q4HSw/7e+EtjHrU3ruhx2FLKxQu1YsKY+ifUrSDqOh5ZuVpZ3zwwQfj2mkYL7Zty3vpw1pez2Edrde0nqjHJWGO9Zpp6U1Lu5YO0TJEj6Gm7bz8lXMYtk2g+DOr+qT/zJyOLnB6irJTKgyh0F/mSOpl5kkonB2/FZeWNpfxs5QrGxrOKUCuEvRyZHTe51hUAVfCZBF//Td/gy9+6bewXK2wGwaAgSEMGIaAMOwQI8P7Dn/2Z/8OwxDhXDoo3Q89uq7DYrGomIaZS7YpZsYu716kz4H3P3iAz30uwnfp1u9+CNhst/Cuywe6CYtFlz1N6QAsUzrA+u677+K5556rCCkeqRiTsTEMASGnru37oey0VEwX6y3i9P6YGUQzf+XxZC7xgKAxW9JysYRzPi32fE6DkA+UcmYatIWRVaKVIATKXFkhob1cLUUmn7eAiwVumgb24Kjupw4RGIVZBGG68McFl86mnD99itj3yRMY890Abupl0QtJC3AWSWoWjlVSUkcFZIkQeDo+Ma5sHWVOHFXtzSkpCyz083bh6+lvPd8am22vajM9WADJ7HNWCaYvZ5TWSA/NSzHG5lY6ML3wSbc9e/ZHyQ0bjtcC0XO0sM9Jv63ibr1frzfKuwzp+8AR1HkE77B2gOuW+OTvfBFf+dH3cevjL2LXEXbeYREZfjfg5MEj7E7O8OrPfok3fvMK4noLyqGhiQ7JEeIkyQSmvGznSwPJ1jh19rEW7wn9Z8dsgOh0nsYD5VpGyju6Hd3/qyi4dp/qz/QY9E+bZVGv+YksUHKmAjmIJQR1Mi4DNvTZreSomtLysiIGi6WN3XW09Ckx+qj11L55dW4apjk/x9PSkqtQHGsNBNuPGnhOQ0yuAoIK2DIOhsvkph4rgEv1IYCin+UzHe42azCoYuVkS1+WtUxUpUmtdC1NwbPud1Neq9+sDN5Ho7H+8e+qDaprn6tnwoNc06klF+xa1HVP+47ZbKK6v3ptybhqrDg9nzdDlMk8a4fa9PFi4gGYruFsw5asZmWrgvPunFoPNpQYM/Tm+oNZ2ly1fMisU+PfYniEHNrTapJAuHHjFpzrsN322UuQDnjHISIMEc4Rhhjwta99Ha/85jdlsvR2prQ/DAP6YSh3WojC995jsVjg7jPP4/Nf+CI2ux7Lg0P0Q8C2H5IAHgIOD1bw3qHvh0J0sSJXqxWeffZZOOcwDAMuLi7QLZYg8uj7LUJIBtCwCwATum4B5xboOj9RwnoiLCjV3wE188cYU8iDSzmTY/ZSJmOrEBW+60B5gZWsQHFGYDiAwwj8ZWE65wrgEcFXGwbTGd23iNK77fekWAEuRRuxTWPI1FH6gmQQcYx49u4zKXSvH9Jh8Qbo1uNvKUhHrhwan+t3U+lhXK92vqV/GvQWQzOiXIyox9Yar+6HfsrSS4egzSnMufMvM6oC0fRTlw8jbFp9tkpCx/O2nrWltdsxGYFRprquyzzGH6oocGjnBUiOOALgxaDtOgyeMHjg5ic/hm/9+Af4xBc+D3QegQieHfwmYDg5xdmDh7j35tt477U3cfbwMfymR1jv4EqWjanHS/O6Bo2XGX92DC1jSj8DTM/qWCNMr4/6/Wk/tJzRddizcK3+7x8bIAfdpbSMGf35vvrG32nCW0RUxflP+1eDhmrOTHvzddRzYHfuSkr1/L1NWe3yjrjE6Nv27FhNr6Bldos3WqVF53EO2s+3ZKAFTJrX5+SFjL0A8pmw3uTIS7rM8sFl/CD9Gfsnz2AC8j9M2ScDdbvpj4S9NI00EI7c3v39+5R99bXOrCR5xLOONlvm+ljpjgrTTddK6wxXbhiR55PV6L7V9dXp/OfGYWWKNqjtM44ITLVjp+gvY2do3tT1Ualv3HFt7eTMRRxctWg+v6xc2dAouxiUNFphYiSBKuQTQemdx/G16/jaN7+BPjJcCNhenGO5XGLXD9hcbODJY7PbYtF1+OwXvohnnn8BJ48eYbla4YjSuZDtdpvuPtBKhhLQ7zpfhOdytcL/7B/9I3TLJXbDgCcnJ1itVliuVgAR/GKJCIfQB4TQwzmPGEPyRgVCv+uxXC7Hm7Wzx0EyODGAPgzohx4pWwJK+60tt/HnmJpsjNedhmyI0QBWwBSUcucDoMigEFJ4GlFJs5a2xaaeYfldDiRar41uV/+rgB2mwkPXr3+WxVT+p61wTKxi3R4AeCKMl9dlzsoCUyL+0/N5xwCuGFs7Zgynp3Chx4N3304p9TiCeZqBpBLYeYHK9mGcWXwa4KednhSXnd39YKYxCwYwphOm0ZjQ9GqVlhHG6jv9GTMKeBzdF6Ox0zIuLPisnlPgp2yzjvgVslWdJ2SM7UTN63U/WU39vLK2/fPkUHKfMcAcyz0fumhw1QKl9rn59Tk9E1J4sxCVIPsDFThJxAGrXRjPgIdDJEJwjMCcUxYCXQQWnBwJg3foO4K7cwPf/sH38JlvfRX+2gF6EDwTlhHYPjnF6f2H+OC1N/HGyy/j/XfeA4UID0q3hAtwSUIBlJULkPmONNBJmY6IaoAvz4wGQw2cLUgZNR2rvznPlXVSSF31XOvf5Z1WiEpqd5xT58SDGxUoHT0wLeNO+lHWhvqUslyX238JecFCCKcM+30AkROvc5bdkNAFUElXOY5X9KgbqdQA07K2LG/Oj1HP4eiE0zLd0ljaygg40ZgyeLoCCNkHvse629+3jMkrhpZXdY98Pd0h37cLKp/Jv5ouErWReZcAQtYXhZfzroJLzlMI0CdxVUU1JAJo6gFnRo5UmOoFLa9aIN4atRVtYpIJThxxWSyIPEvqtUjvvP6nWbHsbnJkZCceyp1L+/iRs1BgtOVu5DhJVjNXqvHaNjDuNkiYoA6Rtoao7vco17jQJkODFN7KKCmU9RoS3UtU98/uyrbnbDyMX97jMTW2yOci2Shnmy2xZgqLqL9CzLoyf+Y0/xr9mGQVJ73Rpnj6f/4+Klr/XcrVQ6ck/SJGIJh+dwg5JCrPC7zv4LsO/8t/+r/CZz/3hXL4BwIQnYfzHWIEDo6OU/iRB/7p//p/g//mv/6v8ejR/QIg1us1iKiEKAnlRiGVFsKPfvgj/N7vfQ/d4qDa5QAT1usN+iHi6PAAPh+Sct7DRYcw9ImZVBxjiBGu8wj5ZtcIKiA0IoIREGKPJembqBMTloNnToSRUxhbJqod3+fy4vfOpW13l7Ij9dxjQQ6Lrks0LNiC0sV0sc7/rBcd89QIKgKYx/hdC8JGVZd7vofJJgqnAHfVNziA/ETxee+zcZVD8ICKNsJjWe2nRZwxrEdEzxHBL3CwWGAVA04+uAfvAI5U1VVlZVGG2ZxxUeggdKHM+FkKVRlXZCETCr1H70o6CzPn8dGKsIpTV9yi+5KwbboRfnxfhHTbQ6x/aroWIUsEdkmYRRLVKBIU6udohCgRUPGOBg36zIsWxC1DwK4D4U9CAj6dcwg83W+y87ZPYWka6DWr6VIBklCHSZEIOHk+B8C0vFpE6vwKON8R5ADn0XuH4fAAL33zK/jqH/0Aq2duIlCAiwEdA7TZ4ezxUzx85x7eeuVV3H/zHZw+epLSdjuXzmtkGefzXCQgYL1WKHwhBrFM2nTOKNOFJoBI03bUoXrNE4ikDm0s6GxJIx+25kdopW+/jhGlPg0cpQ8i/9Oc7/NGqt9V00GSa4hecwSSEKbICGpitVEwts1ZDrsyQjljUJwOSGfJRhkzdqAFSBKfTQ0y+V5/3jTwLQ8r2uk2qvdYQrbcOFYe04oLANXADaYvmibA9OxWawy6jM9NZYPVT7q9OUBud3daNLF6saaPrJm6W+lvAecAKMJ5MSBFximnqFpLCcvndOs55XMsdxzUdGrxsg3RapXyXhx31Thf7suyy0GoohnK8Dgb3YZf5KdT30u4HWNqbFR9N/SW31NoYnsco+6sdcP4bC3jrT6ztJtgGx4z1MmzvjgOM7bCGJIUQU2axHzPmT1fJsXqurpfMiapM/NQxnaUPywyzkY+sJgT2clD2XihUXrou461fqt0ZBEBdkeQAHIgptFQdLUxqmlxWfkQOxo1YClMb4SlxJq++OKL+PLv/A5WiwWOj46KYuz7dO9GOA7wfoGQPZb9boNPfvIT+MY3voH/8X/8H8DEOMiXnWlGCsYz773HcrnE177+dXTdAsvlMu1kLJflfIf3Hqen5wCla9rJLQAesNumXYZhCIXmwzCUy1sks4YsDGQBNISAwcTD6gl03mEIQ+m3fUbT0QpBJ4qKHYjSYe3FosvfAwAVmo8gqQZN+rAdlILQ1ngIARR50qcR0I7Czy5cveCsMrEMXW+bjp/rXRcr9Pcxb2mP04r05OAisD09x+mDR9g+PcN1Hrcg9TsFqO8pLSEl9GgJ1bn+yjN6J66lINg8X36q76ZgeuxHy0u5b0z2UCcnpJYNmP0Zn/ScJt5CMa4nisnVAtYKXAsEtKCudsgEfBHVkrPRvxbwsv23h4t121aQl/Xc8ALPCdtAQO8ICxAWgbDiZIBGAvrOYbvq8MLnX8LX/+hHuPuJjyE4AjGwiMCSPC5OTvHgnfdw77U3ce/Nt/Hw3geI2x4+96PruiJ3vPdwEC9ce60C0wOAmgfsuSIdOy7KeAy7EmN2qlTnDMkWjezn+uI3ey5Al0l8sZmPORroZ+fuAZC/rxIKMBeLPeHBxjO6WIBc64t5T7F+X68lu2b0eZM52boPGNlytTjy9vqYm5s5oN8CjLof5Xk3XfMtI2JfXVYn1Z+FMh9j3YCAXavjZ4v6WuS3vGfX5xw4nWCvS2hs+UEatzsopZ6MXXQ7RR5nB58YKYykgvkS54/QTvqgjQGuyTLBRJpG1U7CzLLQfGN50BaLT1oYba7MrRP7uWDh1pq7DOdcpdTvJ4PDe9FvORzMOMek/Q9bij7AlEevUj7UPRpWMcnvq2W6J0MAPpCyVN3/4D7uPuOwWq3gvMdi0aHzHZaHB1hjm3YMYkQIA4YwAMOQ7rpQyk0UX/GmKH+PHuzF+XmVXQFAUcwhBBwcHKLr0maic0AIhL5P7cYYsV5vAOQDmjoHckxGVgihgHY5I6KVq/7bLnrN9NYrYQ0NbWQIk/iuQxQQFsYDhpxjSYmoePvHbb1MBxqZxGbp0P2fMB/NL1Q9Vp0xRdpu0SG1O/Vmt4SJ7d8cqIsxZ5oaIlZugSfvJVDmAoM5pksO1RzkP2rp1ih2boqBQjXNxrAdN9l9kMOkli+qdrKobQlGMTQm/WAxuts0Er6142Ee88nr9xKP0NjmJcJZ00dAogCZOt9/e7t6bk51v+dAZOpq+24NSwsNNHR4lQbZ+pmW4N/HJnPCVoKsfCR0MYVg7jyw6YDjjzyPr/74B/jUV76E/sBjQymUyvcRfHqORw8e4t0338Jrv3kFj9+/j2G9TaFSjqrLH22IkfTCGkQaPMnvNgONHrs2GiWLXtWO4X87V9K/OXrtMwD0Z+NzFoq0M7LNGRlCq6sq2HFtzRsbLXCp+UzzVgSXcxpWFto+Cf2TgTKCqRYQb4WE2MPszDxJ62oNEDuu5vqb7G2PTiN9KVwL6F8FjMi6Fzm67z1LvxACHFIoog5FaQHVlgNF973lNGzJUQtmLb3mBwrItgGzfb52oMyBZNu+LfpznVygfhcFM+hS1kkDqNc/Ux0h74wgy599a8vOadlN2OM0snytx6D7NPeupYctc+FNzTBaJHpO70uj4pyTOuf4d4735nCjpUMLk8g7LreZkhyNhh/HCM6ypKV7NT6xMobZ6ESRO2TkwyUyVcqVDY3VaoXVaoWDgwN477FarVIFXYeF70qaOCHI0dFRTmmbDI/ddgsCsPAdhmHA0PfY9gN2Qw9GSs0FSqFSp6enOLp2XA6EFw88JSNDh42IMXFwcIDNeg3nF1Wmn91ul7cLfTpEjQgOsUxMP2wAEF5//XU8PX2Kz33+81islkLGZAyFfDt4YPT5cLkW2NrwSoq/FmzyU8YhuztNEMajcE+CNxliKWOWMB+gVUWIYbwB23r9HCBR7zpuMSmi6fakvCtFC+lq6xz1YpGzMjYueKx/3K6VYpm8pVD17xNBT4Q+BBATdhdrnD05gc/tDIHBmUi6P1KsMmwJpao9cIlTnCrrJIC1lxyo71lpgRM71lnwOgFzdR9tn+eKFTDVdwrUzQlzK5Bkt0/GWIdnJKNAAKs1QKX+lnFgFe04N1T1Q+hr39NzaRWtHXfLCCnC2tRn+dPSlojQMcEHl+Kjlx5nFBBvHuG3//A7+PL3vofF4SGGpQMvCBgC4nqD9ZMzvPJXP8Xbr7yKk4ePsF1vEh/HdMbK5bUtfa1AowqN1MBSyya909niNcvTmrZ12Mo0JtnOVWvHaA44pX7XAFHTU+Kg7ef6dzvvVglOvP1AvlB16jluARRmRglnMLTXvNei62UKubUemBkxDBDQ3SoWtLUAcgtsz/VBg6xq7MbQq+mNAhSt4at5rjUHtpR249QJptvV67yiG+o50XJBntOx83reWkXTzdJE03qi9xs8UeoUoxMEogiXw6JjFJfSSL/Wbqset11v+kxOS5ZpPS2v2jElQM0grudSlwSslUOKAfL7d+3sp1au67HL93os9h37rOY3vVsidJS+tUJ2pR1xHuv0+2ObaczyvnYwpkfaRtmEdupdO9YWP07mpqGLeZxMxBiw2/W1THF1OL29+NPKiHrHUtEhDyXGdDCwhW0vK1c2ND772c9WikgzOId6YQDJAHnhhRcQA2G5XIJWB+j7Hp1PZy1673Gx2cJ5j2HosVwtEbZbfOxjH0tnOjqHxWKBg4ODIjh2u125dl4rxtVqheeffx7H165jdXiUQgryd13X4ejoCEQdiBjM6QD4bhfKYokx4KMf/Sjubp/BarVKseAsqWzH2OeUrnSMwYwcq0vt9ATKz9ZE2Lhw/Z54REHJoEo3Q/TohwFLTl5jlthxIkAJE91eMbbm+sK5/2h5kUYml8WnzzjYRWS3fq/i7XTOlTs4pNhFbmlnDZPo8vkHOKwWC3S+AwEYQph3R9MIlmzfWnNV969dpQjeVrz/nACea2NfaQFd3W6rTju3LQUazdhb/W7NJXPNI5UiZyrphcUJYeuz3umW8q/6QrVaskDC0sUqHP2eBTJ2V48Mn7TmsdVfAuBch40Hdkcdnv/iF/CtP/kBbn/0BTB5wC3QMYMuemzOL/Duy6/g8Tv38MFrb+HJ/YfpTBMonRdwSPza+VlQw4n5KiBm6WbX1T7QaddBPT+jwaFBp27Php/oujQgqudo/N4q3RbAk781TVoeShvbP85QPadza7TvezCr9O2Y3rVi26zphupMyNxa1PRLn0/HXdZqI3zMygALXjQdWjwxK3+ynTHHK2J82f7bsi8kq+qHtKm7MCOTK/oo2rTlVO0Q0XwqdbR0jbyvIwXm6HhZ+Ko8K71L9Wter3Wjbrt63/BPc4fa0K3CBS4dXreOu1zjnnlM8lBM0CZ2adE+1docgxiI+ruW/LHjESq2+tnCE5ORGN5vtadqFAhVdN1Yx9yezLTf9u6YObmmQ1dlfufWpx3fMPTJeYyydAtbzenZlpEj444xn2V2DhFIDi+q67sKvgE+hKFxfHyMEAIWi7RjIDsF6exCWrxdl0KjQOmsQwgB3i0rL/4wDDg8PMQQAvq+x/LgAIvFAv1ui8VigY985KM4Pj7Grt+Vcxb1XQQoqchEaCwWi3ygfPSqh3wAKmRA65wszAHDboOTJ4/Q91u4bKEdHh7i8OgIb779Fn7161/hG9/8JspB6sh5F2aAY4wGT2SwazOMFM0oGpCJ8GqFC1Fe1C7FeJWD7S4M6d4PyzBmcWmhy7FeSEWIEcOhm/Hy1OBAPtcAR7cnceMyfruIdNHv6xhieymjzKP2zmnmJiL0iGBKl/YBadkHTrdk0ng2r1nmFJCdwwoMzFcGSSvbAlhzC5KIRu/QDL3m+jOn4FsAzc5Zqx85ycqVhIduI8aahq1i4+51G3uBzrSnFQjTRWRESzFrBbFPaFfzL5K6AeLHeUNxCsjnwXucu4hrn/wIfu8f/hgf/cJL8MsFiIGOOoQ+ANseJ++8h9d/8Uu8//ZbCLsddutt6udikZJREJWdW8L8jlda4+1Un7NUbPCENjxt2N/47H7jU38mfdChry3vcDpfFqvdmPH9cRG3xq1/b4XGtD6z3wOo5LH1AAqPk1mDc7KiAgZXVMLCt9Zwa43bvrePn+347Tq8rH5pw84ZMMpCK5NbYHPf39XnvN+zq/usdQXyGpTPW2mQtVzWc3SZXNTzYef6KkB7fAGlrxKtkL4WPmq3qdtu8d0c2Nb9sXXK363dvqvyrHOunHeyOr+SQQ1+K33eI/a1/NDvJXk3D5BbYNp+J9/rdubomlRBvYaKLHb715Jur+VEsWNt6far8Kn9nlyKYaE8AI117G6ENnDm6mQe9zYZ06MCVylXNjRu3LwDifVKC7lLE8BAP+zgQDhcHcA7h8ePHuUD1cB2t8bFxQVijLhz5w4iGN1ygfVmnU/Kh7wDkcC07xb4xCc/jT7ssFmvcX5+DuJ06PfZ557H8uAAb731VmJyTtt9u36LPvS4uewQhh7EEefn59jtety+fQtnZ2cAORwcHKDrOmzWO5ydr7FYJOIOMaR/IYCJsDo8Qh8ZHIFhu8Nuu8N2F9CHROrzdY8Y8yl/4RnKDEljqjIposDkvIjkN7cCkSNAXbLXPVFKa0sEeA+/XIK3WxApjxdROrtRCV3jOUwPT4RXjBEx9GlHJnOQ9N/e+9ASTFYA6HpbCzdN15i/XQs8aUdv7dntfyvAiAgIAKXYsGRIhgDilCWCcgpM0UNFpnMtwCfGgcsgEpyzSOW2ZJXxCDLHkr0bzHsFSpnnMh81SNX9sYdW6z7XoLkSoPKMrj7PLYFGoSmfkYQ5UTkTUo1srzBJ49ahc+UbRyl2es/unbx7FaOjUk5a6gFprK5Wqvqn5R9NM5fDHMXISlnckmxJZ6RkTIwATmvNJdp1cKCBQXDoidIh8Lu38I0f/SG+8M2vwh2vEAnw7OH7iLheY/30KV7/1a9x/uAx3nv9DZw+eYJF18F7h2WX5tU7X/U5hgDJBpX6LiEQBEmzWbyDjkYeV+O3ns+QeaSsqZh2FgrfU6IpE0Z6uEQxqGwxDAEUI9+VA7rAGIZGKVNbOUgK6Z+aUi+5XpCM9/wFUepHCcETPuYpX6G0FXOoZrqniSjtElmaWGDSCtcE0oaGrNn0jDKuiUv2uhC10dfg35m/tbGT6NdeB5eFLVgw1QLeU3qNv2R1kX5S/bzu86XAWvVBAx37ef33qFtqQ2LaRk2HWOYGxCgmMdfvWf3R6pP9nVlS0CLzW6q4ZWjaUvVfZFYRWknOJPnXDqfZN78tOui+l0h9opxNjMGBK8eWrlPCqh1quVmeJT3+vJu1x6Mv/WBmRA4lg5lEYYBlB2tmJ6QBvMvvKgOqXLdALsnyEPMdKMTlduxkFCR8JTSzDikp0zBnLlOm5UP6AON6Qb3exQFnsdAcz819ZkOt5kpkRuedShxEJRXxPh2uHUAFe2T5xggAkn5TyqfUuQ/j2HJlQ8P7Vcm8RM5hdZBeZTBo6IAhIg4R2+0GDz54iNXRIR4+fIwnZ09L9qjl+gL90x4fOzwAdR4L78vac+QRA0B+gRs372C32+D6tZvo/AOcnpxg2S1wenKCT929i5c+9Wn88je/wq7vMYQB5AmbzRoxDLj//kPEGHF0dITT01MsFx2ePHmMyBF37jwD3y0QQsTh8XUw99huLxBiwC4MCDHizrPPgLoFtrsBznmEvJPRB0YfkpLcbPucr7hOKVmAOidQJ8BZ774AKZREA+zCkH70YDoAu2GAixF9GLDsFghMoEhYkAeIMXBAAJeYY2Gc0p+syGGE6vg7ox92KU1mTjNbxlHkVDvuWSsE643TwEbGL59LaW1d275bg0B+l58eKQtCiAHOMZbOpRR8IqCydB/bHQVH03ABEpBU90ZEjqN+KIc+pK5RKWuh2FKSU5CtAaP9vE3Hsc6itaYLPoqRkSWg2tFy3kFnUivv5Tz0rR2guXFoA0WHRlWKFVNBqseQPpoK3lYYTFpTKD+zKSmdKqhI85JWmK2xiMJL/9LwBQiDkqHvclYozlqFHQBi+JD75DtsCegPlvjCN76Gr/3JD3D03N10l0uMWJFHON3g9NEJ7r3+Ot569WWcnZzi9MkTUIjoQPABIKSU2jI+R+NOhc9zI9nxUtfHM1t6boqckfEDE/omw4SEcYvTRk8/A0WuCOAsNwNwal/TthiMlNODu5wgQQwfncYzs2aQtZUUQFlWYrgI+ITweAjFSPHcBkRE+VZkGuuT3/Vt323DdwRdukQWXqVisEi8e6J3PhgNGmW48JyJn9fF9tue22sV/Z3ekWkZ1zp7mD3YX81zbRFlIDeKAwv6CmAyfbOAUIBLaOzCt+QKg+HITeZGxtg2TrgKpWEedZcYxCIPpD0LJm1I7timApGghGYRwdwjxnoHZ05GlrGRwHMuRjYjKlpPz0bY+bT1T3YkqKym0ZjPPyPzmGYZNKm7GN9mHVj5rWVx5bhSpdbXcZQrnJwHpT01VS3azQLkJNSKc0UuIHRecvClURNlavMom8Sgb2GL1lyK8W3HVun58uX4nDhEWmHNpeYZzGBpbd/Rn5fv88/lagVwvkg76xCRLS35Y89WF0ODCClludm9YM73s0wx3b5yZUND4ul1uJJzDiEGkCccXltiWG/x8P4DbHc7nK0v8MH9+4BzWF9sMoE8NusNnnv2BTBSuFLf7xBy3eebC8TIWB4cIMaAEAbcuHEL64sLxBgwcMSDhw/xu1/9Cp594Tn8d//9fw/nO4A8zi42eOvd97A+3+Lo6AhMDoGBp+fnCBE432xxsN3hgH3auQDh/sOHOD4+HNPbRmC73cJ3C2y3O8TQY9ilywL7XY9hCCA4bDYBYQiThb5YLBBCwGazKedEYozl4LwtIgBFGHvnEmP4LhkyPFr+lHcnRgDCxRvA4BweNioz7aUvQqRhELSYXAtibSRob5+EO0mxAgmYZlQQhdDadrPhCnohlUQAVjCyGGsBm/UGuHZzHMMe/td9tQe0dGkd3GrVVfoKwAoLS5OqPqAC91c5AKe/03M3zjWKkcFQ94QgYXF2OZxOeebEdNlX2lul6d4FTYvyTAaKrUOJljb1vGIyphY9bF/s9rbUYUGj7T9RrTyknUjAzgGO0yV8AgQIDAqEQ/ZYO2B9vMSdz3wS3/7jH+LZT3wMfrEAwoCOHGI/YHPyBI/fex/vvPI63nv7bZydnaDfbMH54j1XlPXUGSA/7TrVxYbqFcVJCQa0Yri1XJEi82Prq8OnAH1fhf4pcmMSBqppeomCl2da89j6W+rZp8xr0FOHEEx4yIxHCqVOTvoxAuga5Ou67Pj2tSUyVu/kzL1ny9xYgGk63jl5pH/fx3fCC9HU0wKuLcBo6y+0iDHJJ0N/DYLmaKDbaY1F00E7yOb6l2s1dXJZA1pOtWggfZoLeax20yajmRoP076N9djvGPXatuu1xVfFkDNOqEJzc1mQ6Drd0j5a2Plm0UszYNoW+WwuZEfXb/uTcNj4u7TfOktqaUTFQLy81GtkurZn+d7IpX3zpOmh1404lGJxprgRC1Abn1m6Vcb8nrb/LuXKhsZ6vcZqtSrnMpjTPRdHR0eIiNieX+D8/ByPHz/GZr1GAOPhw0d49sWPIHCP5WqFi/UWznk8PTvHZrvFwEAYAnabLRwBDx88giPCtes3AAAhDHjyaI3F8gB9P8B74MnJCU5OTvDpl17C7Tt38ODhI0QmPHnyFM4dYHV4hPuPHmN5eIS7zz6Hx48fI4AwhIghMB6fnuH99z/A6ekT3Lp1DYscPx2GiH6XDl3vdgOGIWUiCH1f0tkK6O13O2w2G+x2ByVvsUwaACyXS2w2m3LGRHuepAijayAdOSJyvpwuH9hKtyKnbVbvHCIPBfI4l+7rcM4nNIRaiDNzybClt+alEBycS8w9DEMlzK1Q1wtA5l94wSp6Gz40LpzaYCn9ICq7KhMlr4SHNYjkM+ccnE+GK3heMMwt+ppuI32qcAaipvAu9ZnPbVtN42OPkuP0x4zQoUa/5wSDEiRFwIuXhgqIQkNhXNaGKF1NI0sDu/tlgaGuV/ONBaX6ZwskgkeVp2m+T1gX80RNbDWvnL3UDHTkAUYKZ3QOF45w/LEX8LUffw+f+sqX4JYdQA4UGLQdUha0h0/w0z//Czx+7z4uTp6iH3qgS2Gg0QGI6VbjOSvPhkVo2sjftt/VWtlDs2TaTEHZXEk0TXKp1Rd93sqCbv28BWJEbVA5Po9mHVmTX4H/a6+15qvWTmuTDpQu4JMMakXmFMdQG8C3gJb9XvdFdh3Sgd3982H72TIGgDE0Qq+/ag5MX7Rh3gKH4xim7gm73lpy3uqGSmYo+TAXPiXft2jZMjg1sNROD70erJ4a+5vGOc6F/re/zAHLmvdl7LUMsPrtMj6Q58rvZq9B2moZahoTyA6BrQ/5W6FFrmRiZFzW1zYPtccxV8/cGrN3VrTmcy7sUPP+NBSt3tG4apHIgZZu2yerqvloyDcrUznPQwqPI2y3WxlV4anWurM0adF7r1yly+WTLlc2NM7Pz0FEOD8/x507d9IB7r7HwdFh9vYPePjwIbbbLTbbLa7fvIHtdof37t1H1y3gu01JIfboySn6oU9bXTEBeoSI87MzcIx47vkXEGLAdrPBnWeeRT+EdKYjBoQY8cabb+LTn/kMvv/DH+K//Zf/HWIE3n7nHj54cArXLeCdx8PHT4vwds6hW3Z48Ogpzs/X6PsBu90aZ+szHF//TLphuh+w3fbYDamNYQi4uLjA+ZMncH6JgR2GIaDnAIQe680am80KR0dHhUaixPq+x/n5eWVktASMLJAKOOT3mbIlPvSlbpKQBLnTI1+Wo4WoTH45p2GE6ChkAeIxA4XsvtjUvdIvYTphWJ1OV96x3uN6kbliWbdS+zKPuzIWJBJRtWNjAayIVtl1IxIPdC1M5rbfNUjSW8e6b+n36cVtgMDVqSCwQkLPMxGVPNwjjdSY0fYQjm20lSMjhUiBs5HpBJhls4IURGCkXY4chOSdhzUCpGg+LuPKlemD1uP8TYGnLVYBJ/7iSrBboGaFZWkzEWwyd7rvkzqBKra24kkGlpx2NIgTzw6UwrXctSN84fvfwZd+/9tY3rmOHgEuAqtACCfnePLwIX7z81/gvdffxMmDR1iSB/oeHcmt1jEd1svGgISuWTBg51fW6KUH9xqAU9NLcLqlkQbQspYkzDNTCJL0YE7xaaeKPjhp19M4nykcRa9rKSFMs7jJe3L+7DJlZ0Gb9WhaulnQSZR2kO09DVZx60srtTGj/57bOdV9LfHRBnhKuYrxoudhXFd1KGFr3HN12v5bQK9pNQew9XP6vWoHi9qGn6bxHN1adBojK6ft7lsjLXmVPkuGNpGA7qlDxrZR8VMDJCadTxPTpaVH7PcthwMgw24bgnOAEpDd7xEnSJKXsZ+ogC2F0diwckD3sQWUy9zT1EAFppksW/1t0cjiB3m2nO3iaZp++/s+gG35uYUpWvRtrY25umUce+e4okHeF8/JM3S4YowRjmsDqzVWeacVeWCxq1paVy4fakfDe19ius7Pz9F1HfrdDovFAvdPT/H06dPU2RDw0ksv4fHjxzjvH4M5Za3qug7Xjo9BtMFu2KFbdthtdzg7PcVmvcZuk+7a+OQnPoaPf+ITePXVV9F1HW7dvoMYAz54/x4WywUePXmE0/NzfOGLX8LJ0zX+5qc/x8nTc1y7sUS46NF1HZ6ePkUMAcfXruHatWtYcrIyh4TEEMnj/GKLR0+e4va1Q4SQjY2+R4iMIUTce+99vP3aa3jps59DtzxMOxuhx7JzOZY0TeDFxQUODw/BzOVil4uLC9y6davKmGUnV77Tyk/+i4zkKcvvDGHAMjMehZB2PxCrm1E1MxXFp5hkGkbClUBpKTS7iGz4QstokFJZ8ahTBlrBo5VJS3DP7gqFiAjG4FBC8CIzugY4uUyBxYZyGt/ZJxgA56dCzyou24eW8ii/pw8mbab3ACgBTzTmjgehbJ1ztmM0sAZEqbEaUjJw9fzouuf6aJWE/ukyKG/RQT/b8jJpYWvp1Prd/tSg3SrAiYDn0S9XgQ9muBhBziN2Dmti4OgQn/jSb+FrP/4Bjj/yDIJjMBOWAfCbHrvTNR6/+x5+/td/jXtvvYOw2WIJhxh28J3DECIopnAz56ic4+i6LsfQTvuhx2rH3lJE5ZnGelS1VTxU1z8azZa2wuvANIShDczal0cCOt0jAEzB+1jHHrDRkKtjB+pnxfCx61DTb9brqDCbNURkDFpWttbMnPJu0UbTufVeSz7a91s7gnOFQNVZw7l+jX1LfGLHa0HY3Fitrqr1TDvs9DIg1+ongJKlsdUf/bzm5wnPxuySIAciD8YY5jsHpC099ve53klvPSe/W53clGkzoVNXLW1dnO/BorzsGrtVf9+yTx/qndMWP+7TBfK9XEuwby226omYGgr6vZbzR3SxdTq0DLLW9/by6VbR2KYS51mWOVV/9az6XYq0p3f95su8DJorVzY0nn32WXSdx8HBYbqw72BV0twe+HSR30c+8iI269u4du0aPvGpTwJ+gWtuBUCEODDkBb1YLgFi+M7j2rVrODw8SGcPImOxXMH7Di++8CJOT5/iYLXCndu3cPPmTWy25wixx+Mnj/HCdouvf+MbuHHrLg4OjuEXK/iug/cdrl2/DgLQLfJN451DHyKWfpmI3DkAAx49eYy4uUDnPYYhguDAMYURPf/88zherXBweATyCxwdXwM4oHOMbjGmdD08PCxgDwAODg7w8Y9/HM65Kn+yVmpaaIzfJS+xI4cgYTtIWS9CSPd/MAi+67BwhN2wQyQGD7FSugKygDozlmaydB9HBtgqdlXncLaHvfXCai0YwKR/08xIdUDTdIsSE0NILwgLSK1V7vLFZqNRE6p6dJt2YZd2MLXUx2cZ4LYnmTBVCHZh6/aL0BKDwAhLSD9mgFy6z6DeYXDOpdoE4IOTl98IyDnDSV+mqI3jfYaGBWfSzxhrA1ietcKs0M8ILU2vuR0WABV4jI3v7TyXtojK+Z6cTmg690QYHMAdISw87nz6U/jaH/0QL3zus0CXstB0zMB2QFhv8OC99/Drn/0tzh4+xNN79+ECQJFAHOG9Q3AER75keiLQeMg6RsRsgGh6WO+7VRR6/lv02Vd0XfXcjcDZApu0mzHfloAvCzatEi48QgQ2h7qn81d7R6s0xsxNQ9WuG3vuQ/fdnkezQC5XWNGo5qWc8W4GhFiFPld0ncxtwKSftZ/J37JmWsC52Q9K/+QGc1vm+5+N5dg+g7DvYPvsDk9eF9LXufdbpfUsM1fnSDTPt4DUFPDlfwSk27yz15imstyC/8v6PQHV+nc1dsurdf/Q5le2pkYbTNtCQNqpaALozI8Sglj6095t0e1Y2ly1TGXTVNcA7XNqVvemz67c9N7xaAdY29BrG0Bt2dJua24c9vsiE2OEnJesNDzVOqWF54A018MwjE4vl84PtvpMJP+7ermyofHjH/1hakTiPdWg05VpAJgR8yHplEHFIYCKp1gGN4Sh9FOy+sS8Td51HZCzCDz3zC04RwjDAOfSCflh6BHikA5mOw/A4Vvf+N3ERNnjQJTAuTBmENBJCcTHyAAxhqEHEcMjA3XOOwnOYbPdAreuwX/kueTxl/CJoUcIA64dH8H7FGKwWq3KRIgXQC4atMyWQp9ivjZ+XKhOYlpAOVVnCiPxqVJg6EExgLlHJAfvOhAz4jDApyOqYI4gHg8/xSh3nKC0r3PkwwBiGyPfUvxNkJ+VW0vo6tKK4weSCCOXNDaJxyQbXQIEbR9iTHzjM50657DsFnmaHQjtrFYC7LU3n0pK0Kk3qy4j8ClbxpmvNG0sgIvlWZ6AWSv9KuHVNBCEdhKSlBQgURpD5Ho7uwUCWsB+3yE0LagExAAYw1cklXDeLSGX6UgjfBfFnepKw7bCr+WdbymxJvjK7Y9EQjEgHCf+SsYdSjYnMINzOkzPBJfz+AcwBiKcO49rzz+Lb/34B/j07/423GqJgSIcGBQDXB+xvv8I7732Bl7+5S9x7733Uoao3QAHQteldegXfkzgABR55DufjQs0i95hmgMxLeN5/H0Mychckng9Jv7R74xtRRD5IkPSGTSRIQzm+r2WId1Srnp+dR+ToSFzKeGOY9ij5l8dLhlDHI1q8RzKOqD6vRa/W4Bg5Zq8V5SyAcBjvfM7pq3npf9TEKT+YbojZz2NbaOsDTz3yWWO3LzdOa2VJEkkXbs4VEZ5Vtdrf1rZJT91PH01pmx8M+fziLJmeJQd1gBr0UK373ztkLG76i0APr6fQn7FgaPXkpVR9buJryVUR8LlRxhIRR60boDX+tjKOq1zLR1af0uxO1wtR1/BBcCUNrnnzmUnqMyfwha6n3Nrq1oP+XvBQuMr4w6bxiFzRkol/1i3K4YrQ9xvLf3R0q/MKuuWkidWvk3GVOpp82dLn7cwkZab++oQGaRlr+y0FbqhLZukXuENMTJKG6q9Odk2V68tVzY0bt++URaqFZR68JYwujMpuxMDWKgFsyh1SYwYM8E5rya2Q98nAwMELBZLdB2Xi/pagk5ijZOCGy/yA0brDVipBTumPVssFgjxCLvtNt3hoVKDxZj6sugcKO8A7HY7MHM5AK4Vohyy1rQpsdaUQPLIk6PnUPLYE2WhFBPAEa9KyLnhPRxcziQUYmbW5N4tMa9WeLSEjJ3LOSZvKW0ZUytMrLSLKWNWwjONDGJ8FbFM46Vw8k5pOx+m9eQAvvyCLt2OPCag14K1llLWiLDen2mDek4IavwbKGcmRAG12msp55ruI33GStLZBlJ902tC6rCAQ37OretCNwOK5HeXjeI0VtkZGVOmWtpouaS9r+OYp3SdA1d6PBNxR1nAChgSo5UgYchpDJHzu+nukugdegL8tWN87Xvfxpe/912srh0g+MQoB0zYna9xcvoYT95+Dw9eeQtv/eplbM4vUopWoSEBgQB4SndWQBmBWXH1fQ8iyucg0q5GS3i3lJulgwV2lIFReVx9Frg2YLR3Nj1PCCGqHYy2opEdKlFu1ps+p5A1eJbJkn7GyHBuCt41DbRREUUhSv8a77RAaYueFsxbAClt63mRZqfKf/y81f/WLs/Yh+Q00DS0IRj6c91/O047ZguYiKjIzklhZHg21sPqfAKbPs3p/jkANZWvqVE1lRgNjBEw6TnS9GgBuJb32c5lS8aOdJJnFA14P/gSs55BWTy7nOVZ6x0BhorYmPLZHGC3Y7f9Fz3T1GNAk5f0fDVlLajgDn3287L3WyC5tM/JyUyk52c6F0Adtt3irfS8/jfyiGSdsrSsaGZkVmnbjXOyD7BXdFW6rmXk7ZtX26eqXjMG59J5TLl7Z7FcYOEdzs9Ps8tmugPUwhYaRzNnx0pjqII+9uGsVrmyoSHC0Xqt9GTJwg751m/mlJlKBsk8ghnZ8pEByiT2fT+Jx2sBL2YuWz3yN9E0X7BMRuuQpdTf97uiNMsBqBw7jUx0eb/rupSuloAhG0a73W5Sv4xPLwhmLnNnFaCMTaAwkYPLlqojQh8jmFO/ogC7zMAc2wunBTQrZYQ2U7c+s3227dmwsH2C2Ap8xFi8ZC3BMdcXT4RhCGBKt7U/fXqSgQ5no6xRmIunrlXmxp6/rNq3dNF8W94tc1q/N6fk9HN7+2L6W/7GKB/mlPyUxtMQgBZYkjrswfAWOCYZe0OhaR4Uuo1rdD60oUWLOWBe/Z0vakPMa1n7FtmBvMPgCP3KY90RPv5bn8d3fvgD3HruWbADIjE6Bng3YPv0DKePn+Ddd9/CX/3bf49uFxAutmOoWFbCc0B7bi60TBIa2/lvgjP1rpXLWrnq8EidgKI1J7odHUqpn2cePX5yAakFAPscFfpni0dt2Jwdq5Yz9m/97L4dSiubNe3quqe7ffZZPf65tnSbrXHZtafHNgdyJnd+mBA72wfm8fxeeYamjpNWv1tF97El++14rQ5p0aB1lsY6ZWx2LD0+3YbeaW+tE91ua+yWN22be0vFM/WYmyF/mPKBlQ/y7j5PN5ddoLqvrbrq7jJAbUekHhKRmFKAVaR27dvSkgWaZ8vaN4aX/N7i67n65z5vvW/1mqwRCWFv6UWLt+pnRiPS8rLlx6uWyzAXAJycnMAT4H03YqA4vg+gcoDrsVdzRvM77ckImflyplzZ0NAEaS1eUV46TaoYG1p56thNq4xSaFK9AyCTLulPdRt6C7alCDXzjPSrt6916lqtOLuuS4ZGHAGAPqAjl8RoD54YKQDK2CVbUtlFSebghKbMyQyPIWJgBntfLo6Ti7NiTOluHQhe7c6QEQxWIGnaVFuujYViaWfrnYKZOkRptpjvqn5hXjHCxIDquQ45fIpz9YeHRzk0bWha42Ucajx2nLOCbM/Y7DsVSJkZX4vugDKuZ+g1t+Vdfk+VNpVVRYMZBdqK37yKgp20YwCnNrpbYG2uLeHZFsi2wrsFOED5RmoAHadcZJJRttz27Bw2nrB47jZ+/0d/gJe+8jtgTwic6d0P2F5ssHl0godvv4c3XnkFb7z2KmiIGPoBnfOIhBLfbMcnfdIxzTaO3hpv+v2W7N03HwIma7Ozpqn+3cpzvbsldLdzRZScQjKvmm/0O1ZB23myxRka2rme8+xXa07x2T6ZNAd4dT/F+A2hdrRZuWfpOlf0Orbtyffg8bZoC05a/GH7sa9d+y4RTTyUhWYkYY7z7en5bfVxjl+b4KYxjvrnfmNHjxUY9eacvGzxpP5c02yOn1v1jkZF3UcJQav62JAVwneWn+2YZ9cSA9W2LabzK0DaOkhLX5VMkDo5Oz5TGv4UdUGOipGq18WcrtNtteatjEkNpyUL9O92bvbN+dz60LpG10s0hgw2d/1MHQXfonZot9Zuy1Bo1al/t1hBsHGR20Q4OjzEk+22hJ9J1imtR217Vu9zlNDnmn5gBtP0/cvKh7gZ3E+2IeV3KfK5xHppA0ODdPlcwo705Mr7AKrdCnlGE1ZPnmUUeU8rdCGmGBJi+CwWXTm7oFO1WmDAnMIdFvmAOWj0+C2Xy9KuGBXynY1J3bcz1HUOYRfAGA88yjPO+bzLkheloYGuX/4W2o/gQ6WyhEOk/ecxdN+sUtHzavnCbuPLYrWKxefb4SU21wrgFCfuq/7rfjjvyiU1wi+SMtMaKenL2ntnF7nm8aqvzHXYkylCD61gnXOTvROrdK0SaYEoy+fST/tZwpUuHwyb3sFgaafHrOu1wnoOKNjvNIAKmXaX5TfXijeNqb2DOadsLgNfQhfivNPAABOhR0TwQICDO1ri81/7Cr7y/e9hefsGdp5A3oGGgP7iAuunp3j07vt44xe/xv0338XTx4/hnQMxp2x1MYI6n9LgqjWo+5XWPCHG6UWfdiya1i1A04pbnspCmdvp3LVAsvyuPcU2A5ydF6voxnFOPa7Sjg090p+1dp3l3Rbo02Owv1/2zD4gJO3pfrbqJRLPXtsJZ+sUXbAPXKfvU5VzckGe13Le1mN3Nlr0sGC2Bab2AR07Nr0GLT+29EurzjqMT7dd+3qsA83WTURJd+51Yk1/b8m81hq0dcm/NLdiqAH4/9P2J822LFl6GPYt94jdneY277738r3sm2oSlVVAIYEqtCo0pNEKE5jGgEkTTfQPONGIGugXcC4zakITRzQOaJKRYiMVAagIoVBNVmVl+/rbnnPuafbeEe5Lg7WW+wrfsc+9DwQj876zd+wIb5a7L/9W65rs4D5YNsff2/GyMTWM0o5ly9czS5pzP/Z+jNuT4olEIWN7XMujQggoJ0nKS9N3GwxxbOxbfm/PHJxcrXJlOzZzc6kFycew6dye1pY5h4XeNBdavq130d7ybTg2z49d7Vqe3MtZY5G8kggwl8g8SkKgdg4UDOX4daFPoMmcLXVLQQXXvGlt2PWlLBqticv/ZpaB7ACGAb/kgGC7KaWUJmYca7zlbw8hoO/7STlzgO4YQ20H1iwMPjUdc63XJrz1N4/iBrbf7yfvhhAwpHEyCFaftatl5n5g/PcC0EjS8YUY5GAwkv8UxhC0vCQahdZFoy231RgZQyhuGZwPGMrc5d+5z+Tr+2P08/T0c3KqOciTMfBlmfuazS0vvXehHqK12yVst3cgskxb05zrhQmBEANhbE42t3k9xzAr8z6+WVkZftxLeY0bzLH3DxjlTBuMdpN2TYDLdBzeZHGye62rTtunlk5z7fXvBiI9ROh+LZL99eeyMB+2f67tc9qnufbLwZQBnFjTQgP7CAwd4d1f+S5+5x/8Ht792ldFWAgBy0zIuxE3r17g+Wef4+nHn+KXP/4pbl5dIu32eqI3kMBIErqLhfKEoOCzFTQ8H7I2+89vQyc/3rau/PkNx+ZjocMM37a17dt0X2rFFkC0SqLW+uz5oQcXc1fLK309c22Z4z9zfX0TXdv+zX+u70zACVftZftOuwf4Tb7lc55OFvx87DLXh1apNtf2uTrm5omV21Do4PljdD7m5ubbcx+9rYxWiJ5752AMZvp7rB1v+4yvv+3/3Dry7bKsgG2Rb+T3R/ZTu+bGe06QAFAVlTjck/269YIx0T1j1twPdGi5fNPl+9ueH3YwT5u+eQXGfbjDu4se2wPbsb6Pz933zH39ZMsA0JTnafVG7wSaCpBzzxqtxOJKGIYRwzDA+EdOuSgt/Dpv+exML+A7UOgMktijL3l9adcpv8mVJs1sMhOw7jazOebrAd9isRAXIZexaQ6sz20m9tnA55ypy09yb70goiLw2N+cJd2ulWd1mFUDwIF1paXZITPkIl0eWzwxBAnYtAlJoQoi6i5EhZbAMXVJ6zttl41hoHgvkPM0a7/PCRb22cDKZHIfyROec0bSgwc9A5yMfZrRjGDKJMdxwLAfCj+UvzObgv7t+352A2qZi7WJiIB8bFFO225lyf3pCbRzc3Kuzrbsdr21YMWIklCZWFvGXF12r9205t5t2zI3ZyaaxhmhzZfRal2rcFbbcaBpOQJ6CCiuEuZSZwHpJZUtEXIIGCKwfvcxfvf3/g6++dd+gLhaYdTMZdgn7C6ucf3iFZ599gl+8hd/ge31DW4urpAHySbFBGSpEKGvwnsXI0KIE7dKL1zY1frIv2njmwP+c0LEXDlzdRjt23XLXK2Gfr21a93uGe+aA0xz4OfYVYHOPCiw+d4KvP6zr29u7s/Nny8DHtq2VlAMwKX8nduP5gBxq5E/VAgcCiweGPjsMC0d/H48USy9oU+HoBoHFgFvfTo2tnP0PuYmcp/gOQfOpjQ6Dt59+Vb/nBJJ+nk8nmiOb1q5Lf+yS9osqfJtGO9bAfe5Uc2VbcpO/6xfA8wMBDqYN+3+6q9C58bKVX+vM/K+vswJAb7+dh60fS7v00yfZujh6SZjfHyPAKpy+76rXWs4Ut6X4R/terA1PL/2D/vWzjO7H4JlgJV/XVexdyAq69feafcDPw7+PgMTXUcZK4LlbPhS11sLGr4yY2Jes2quSFNgIK2pgofYhAthsxAjhlC0xXkcAbfxtAMB4MB0OMe0W22ngW573y4ikQKnYDDCQKpkWqTii5h1EYMIMXSwDCkx1gkcQxXExnGQyP9Sn7jTGBD3oJECMA4MznbWIxBiRIqsKYSDuH6wGK6s35FCcU2y/vn+e+2BCTcAwETIDGT1RTefPgbULWue+bVltczPaO0Zddb5QCTa7kxOZiYqgekHiwBAKjTXeUIAh1BoGzPkkEViJGL0DICCHljnBVxlmBzKJmDjUvpOavqmOl5EkmHMB5iPo42fMjiIKx1pOkUwa5YUSPhx6ZvShLkoLlnpO2ExVIOK/Vy13ziQMmNNpmQMIwARoay1GAW4W3You/waahnz4QbhwICOiY2dMbRgWVQ0CM76CBhItM0LgNFlBty07WjBsP/N2hQooNMEALuckIMCpCApa+MYkGPAft1jv+7wg9/9IX7wO38DJ48eYEAGp4yYgfHiCncvLnD97BV+9hc/xosXz/D69ZUoBlJC7OIE5FnsR1DeB+VxfkP1Fl7oum838tKPGKq/PGcRzonQ9QvlPRmZR2iSNaEjqPAUBoEoAsQi5KFuTHMucdYGUzwUDSWa4HA/H3JNEc2e13M9s4AgQqbNk8KL/PRGXd9lTuY8qcvPC3PFK3uD6wcwnUu+X8ab/Lyxz60Vr32/tgPgSnTRVlLda8umb7u9vFg/u/ulxUQAgowVy8GQooASC6gpo6ydrTWoBUN+jbQ81Maw8g/5TzYeD99XmvB3xrQdc6DFnvXt8vUfo7Fvn29/y/N8/e18ngOerQDsyzoGDt+kAPL3WqWpL1+eAYCsPNhbG0l/M2uYvVjLPsbjPC18/73AMcFANA/6j42H3JhX6JQ2EsnhhdYGVD7k18Kc1WRurFraTQTiI+2dw4WlXJYzbRQMWaSMViD78Zxro1eGt22U7FpTUpS9OihN2rVW2lVpWvYjkr258HnXx2OKlLnvds/+ZWR0et6a7MlQrOja3KxN67tf05O6LPspBCuqnaYohdv5ed/11oKGaflNkw9MrRMeXFoHjElXQFbvZz1LgnPWTkylx9bPl5r79m9u47A2+c3eLC3MUwuFgWUvQNmkWyyWyDlJ4FOMCOoOZkHfMXjy6YbPErAd3eRvtUBzk1o2ZZJD5yAbDhMjpxFB3TI4TQPQQXSwKRmditDjAIQ/PJAVBFKIIMjmFsyfNB+6HflFYW2fM3/6sfEXQwSpPvYFLNjYzG3wNqZKWhAFIOlYlPsk1g7J66uHQBI4yYFxmRkZXhtsJk3xrScHAEoeb54CiCIus2Ry8AxO2igNnNuoysDCGKi+q13MWca4LPDJbDp+TQSU5rtpN6SuOgdkcztMf9ky7xZAFDo7EDllSEZXAzNt/IG8RVSft8+ttaKWN23jmy4GY4hUgrwxZnQxVhC+XCAtOrz3/e/ir/+jv4/HH7yHzBmJGX0mDLc7XL66wOXnz/DZT3+BZ598htvXr7Hdb4uSxFtxyyY6Z2nQHniQO9l4cATw2MCxgNics5y/oTRNyay80O8JMYYKYt2mYrwIM2DFg0nrl1933t3NWyULX9U1f6CF07ZPBKsWyLg2lHUFJyS4z/YcbA36zVzvt4DJrjkwgbaMdg7ds2EyYxLIa+2vaz4fjukb566BM1k/wmukX3am1OTpBgzMtb1dT/751qeaK/Unz07oqHNxbv4clD/Dw9s1br95kDzb1hmA7D+3YKndMzw9RGl4SD8P0uZAkxd62rlxzAtgHthr/zPBlEwmZNjr2dJu06FFr+2XPdNiFw8aPcD2/ToEwkfc6SbTeGY/li+1PObp3uXo2dLdxr5VDh96A1Chydx4399udpY4d49xQMM5sNx+n1vJhid8fw/cBxuWQqCigGnXlfc+MTrNrQdfX6FvqT9hc/IQp6enuLm+shp1i5iPC/R9nvCwZkxBquwJclAnH7Koe68v5TrVSqhz31s3IM/0c5Yg6b7vRXuX5Lv4lEnnF4vFhJH7Ceg3fdsIrQ4D717D3gYqexctL1zknEtMiLXDNPRE03p9WXMMt6VZASWoZ014Yam0xxgboJrYgAzTjibkPJ0IE6Bupxu/xaL2f31/7bkQ5IRtztUC5J9p++SZumfO7e9mDWo3i7lF3pq7i3Dq/gKyjoNtXCPj9vYW45iw1PYa4GvHp61zmjkHB89J37hsWtbG0rcg7jRzUIWIQEyTMamLGTWz2MyGduy6ry8HdZOvmwqzjTG+0RdfP01AXfvssXa3G7j/bI/7uTQFJw58vg1dCBg7SVsbEmGJCE6MsOiwj4Tlh4/xt/7B7+Hrv/490LIHZ0YfI9J2j9uXV3j57Dl++dOf4bOPPsGrZ88RzI3KtdE+twKH/9sCjbm5TjSdA4WeDtTY3BqGocS5zbmZzW1ANo9TSrMxXH592n3ja4VfNvzD12dlt1pLX/6BkmEGDM7d9+1vedPcHG3r8Jt0+/mt59LMRSRW6jkFylw7fLv9Pbv/psuL23Pl3Sds+Lnm+ZedyWTPtKDTt88LIx6c3Xe1vMa3xYNh+2zKvilfmIIsv3fN9b9dm21b3jRWbfvb7239LX3u87FvXf3kvflYKn+9Da2PvTeZAzi0TPtn/5eU314CdqffPZCfGy97rt0DCt25BtW36/a+cT2+zqvy+U30b/vW8pDSpkZx5F3V2vnocQuFKhz4Z4ho4nlz3+VpKutKrE2vr66Q9nsAao05Eit0Hy+Z1FHkDi54izCPde673lrQ8Jr8diFbY71bgN9YvebCuwyBp+bYAiohLkPWwTmQ47NgWTvMZchvCLaJWrpZH6TeMjbLFFXdgLj03WdsOrZxlI1b/eZabaG1sdU8FYEqADyygKQYVf/OeqqxBPZ42tZN/pAJWH+IqmDmLSkhhCLg+bYU5sp8kK7zGIDwFpuWLqVdJG4erVtXuznZ/WOanTmtneW6NsGwCCV0CAbnNgxjiiklzLlEWD+HlGQcoG4umoWDQgCX6AjMajLm6OyZcyuotf2eMrgpo7pPCADgNvTa3xbsthqeAgpC1QrNzXVPI7+5+nXSrgERmqd+zm273wbY1HYQYg4lSBvEGPuA8OgUP/h7v4tf+eFvo1+vkIgQweAx4fbiCpdPn+Pio8/x8S9+iY8++kitrNpGniomfHreY22dcyn04EopV94bx7FutM15CH5tkT4/ObWVq8XBt2NuTrTrzdp4bMzhNk3fHr/Zttpo32Y7G6n97T4Qdd+89/WU/s2Wcgii5+ZsW8ebryktp+0RF8W58jyQOmzD4dq2Z4mmip22zLYvvq65ewwue4fda5VynvbFOyGEYhWdq3Pu3n0Cnb8/58rX9m3yW1POnDBqn49alzGdHy2P8tccP27LOUaPNwFZo3kF2VRcBtusZHVOTPls6w442Rd1zO1q+3mM78puxhBry3Tuzo1pKRPTLc+3zytIPF1bj44DfoE65veNwZvu+TrmLOgtb3kTCH8T/5oIFDP8s+s62budxcn2Y//Osf62fKHMUTWRDeM4FVYEEB20v8WQx+hmQsU0+dC0TW9zvbWgYS5T7YSzSVxP9a7uM8yi/TJgbxOwbHBpqmnPWQ6/WyyXiO44dN/5OfBl2lnPRCvwPPQZ9Fmw/OSz9tmBgx64+v7W9k4He86VqJ1AVpfVPzF/ghHtlGCdiIECUtpPJpa36Fjd5oPbgh2rz7fdu034zbi0HS4FbiPM+QVl78896/vPLBqKlA8XUsv424Vu5fpg/MIo1O8/kljC1ps1oJ/3w764gRy7PMMpDDFUl5PJswA4+3SfNa4joPqn+7FnZrFmOEFwsgkSykFvnhatwGbtI0EgAE9PS28B1CFwma6bOYGwHYtyL2eA5s+HuA8Q+t8Pmfd0fA+Z1SGYavvi52NUtz9CQOoDhkXA137z1/Gbv/e3cfqVJ+CkG1fK2F5e4+7yNV5+/hQf/+Rn+Ownv8Buu0VmRhcjQBrAqf/ateD5nbdu+Ix4LQ3seR+o1wIlUxb4vtkcis268OM4saw1Y9eCkaOgvRkn3w8PBudAop/r1m5vHW7bNQcaWgDcrpW5edbOcW9x8Rt3OxZzdJpbm1MQOwUppsCxcQthPrbAf28BV1vvFPixKjEOlTnz6wWz82rS74ZXtPuub28d33zQh7Y/vqw5oNbOg2Nz8RiQrUBKXFu9EtHzA69gnGjHZ2jU0n/uug/wvema41O+vrbMPNOmN9GjFUAm+yIr9J/hr63b2mTscy4uR217jl1e2JhrRwvm/Vh5fFRocc868WXOre9jPEd/1L1zvh/HeIbHWfacLxJhfk35drQ40FwSPT3m1uMc7ebwESD7NHNGyJbSNiGz81BxvNGu1sIzN98AJZnRT+8YT3zb9fGlTgb32mjPeP1J4L6REoQaJoDYtHhBB91rCv3G3YJVr0E7WKiNmc6DAp9Zak7j2KbbtXKGYdD3pkHV3vR7rD2+TS0zsHLs+8RdiTM4MBA1JiYq0mERQGgYp6BT6wk8ZW7txjm3EHy7POOuY9VolGiqUfXXXP+sjYUObzC4tXXNtb1ltEwMjLloB9Io7iJzWSXuWxAT+ri+eeYjmYRI/f5Vqqcq7YuxQC1PtkB17CTd7ps3rWMCwIQR5AxEQ8Jv7lt9F2jpf4yx2HtlTYWp2fkYULyvLdO6js8Fa6cf5/u0LoBmmYsRqQs4+9p7+Dv/+H+Dd7/1dYRVL5aJIYN3O9xcvsbt5Wt89suP8MkvP8KrZy+Q9sK3+q4rpmGG8NQYaDIH5sCttdHWht9E/aZqvMhAqfWlCvd0EP/SblCeBlMryZTG7Xh47amnXSs8+Pb48W7rmgBAd/8Yv5kCoGl727bOAepZ8DLT5zl+27Z5rl1+z/AC04Rert2tMER0n9Bcr2n982tILFjKR2ZAV0sfmyNeeWRuSda+GGKJc/Ht82X5/bwIijRdpy197Pm5+eWv1jpwjEa+TxN6HOGFc/PK2ueVd8euY/zkba65Z639LYhmZoCnMXKT91SjMScEzQHLObB9sLbk5kF753BSeV/3vzk8NFeG3vQ1Tn5v/83Rq+Wp9i+7Qyt93S09WlrN3a/0mKfVsXfe5pp7b47vHKvzWH1zc3NuLOauvu+xzyOIlY8nnuUl7bjMrSMKQRLxsK+vtqU1Bhy73lrQ2O12xSSTcz7ILOQb6TfgdsOVzTSU+emfMSAvTDFjHPnAKtESxGvu/YZYrSpV29bGaLSXBzZWr5W/3++LFjOlBM5Tk5fVYX0MMxvwnFvJOI710DozQiotRmJJbRtj0d57BmM0BU8ZUevmNbeY7Spt9s+U8g9N3a37VCsAtCZxA1gpyYkD7ZjPAYUW5LSaqrLYQJolCgABKY3IWdKbOrurMM+D0darWbwZhxudEECtRrCiVWMEFOsTqeDB2h6bpjlrz8kEOON55cNknlAJFC1dq3RFfZ8dKL+ne/5bbf0c42t+I1CJP8lG0wI+dMZO6NfUROTaykXDRgf1e01TbWM7nypt5BkKmukJDHp4ih/87d/Bd374A2C9wBACut2IuB+xv7jFxbMXuHjxAh/97Bd4+fSZ8C89DDITITHXAHLXrmgZpQo9a3Ad6XgCU6BGRLpmc+l3jBHjmAsotSsEO0OHhD5B3C5TthTUZCMBIiAldvUWUhV6FdACLhsNA7UtOlCeb3trjD3vhT1bey0IbE8FL3zW5rHjtx4EtJtmy6OELqFmmgKKC1+dfiRZZUnWF4MLLQhibbZxcqut8OU5YODr9t+JDteG7ztQ94I6ezH5XFpGVNrFPFWSlfL9WpkBGK0Syyt1/JqxyyvtWoFqToFQzrUigKnyIqOdrV9qlHkglDE5EKTwZg2o31t8e/1v7X5hn1uQWfbmt5cd3vo6JlTNATfjgXpj9j3bN+p32STyzPN+3O8DxX5/vU9YsWcBN67aoFZAbPd+e+dtrnY+egWKn4tlLcK2myn2a+dDS5+WNrWfUmIB0A0NUGq9v2eT8SWUFO6GdVp81b7jbk7r0K/3je2xMagtlvIKPiRzZT4Mc2jnw1w7C42SuqEXHihlzmHoY9dbCxpBo813uz1yTu5E2EMGLX3SlLJRUrJG3Xi7EBE1HePIVRjw7k8gOYBkuVyUOuQy4hy6BBix5kzvEhgpmh0UoE5l8xVgre+QpByUlJ2y4HSbB2fGqFYFMCRtrSI+IglGtc3QD4JfsB6sE4mbT110krUqBIFTgYCAHl2MiKFD5uFAeJDJzWAVCsT1R2Mhuih+50ES7DJL+khiASIBddH6hcLMgGW0yazafIBZ0uECQKSALE5D2mcCsfY/dAUJ55SAEBEQSjrM6bzS07NJAS1YNcmiZSYiRHQYLSAeAjrAQEgMDgGIhICMPnSS9lJPtVQdsbonHWEcBbko42ABruarCgX9DDmgzatGIoUS8zOmEWNKKmTqeFrK3I4K4+Rgi1U25QJtCQjs5owqEQpjtfYySzrbImBoujw28K1AwsCXv8jazlUQYjGDUiJ0pIHHMqoKNIBMYl2TeedyszODsoFe45SVrqOmvA1EFXSGIKd0cwcCIdBU2GJKkimMjfKiUMkMIHTICeiIECIh9QG7RcDXv/89/PW//3dw9ughxjSK5W8/IG13ePH0OV58coHPPv4ML5+/wLjbSZayrDyDGBGxrF8Uq1RG5oRIHRDgXA1Y2+1AIRiBlIcxI9kiCbLOYpR1GHvjM/JPpom0QRh53ahESFBrL7OIVwx00VlMApCQkMHF0mZ9EqQQyrjnQGA4xYEmpxSNl8RkIQuPB2kGFKUHIyCnCoAsINCkHZmFcip6trUZQkmvKPyhKpdkHucyZYLOc1O4iFCr/ECTJYDrbM6cNQmEzpBA4GyKAHGzEWHLhGHAbKqhyCNycCe0T8ySItK7jhAJLxChRbL7BckfPQVgYEkVrntXVn4WwIjEwlN03iNEoSlBVpnWUYK1naDBzKCS8ljJMOM25AGT5+VzYNz/s3J8eczs4hmD8DUicBcBjOg4o+OEmAOIVhg5IQWZiwEZMUsidtasZz6LmQm8fo+etM/NTzjlg8c/rYB4DEzL/K3g0oM/D6y8Qsw/cwzEtwB+HvCSYhRloLZntEoBe58NRLKukbquwC0Ynr7v+zJRYND9QpYH9xNXSAj7sG3RimTJg1/nURmrKhRbuzxdfVutXuOlLRY6aP9Mv9oxbkF564bo2xGiOgSEun+V/W9KXFQ+fYgdSnvIYE4jsM0ICyaQT4VpwShZwUCkKOenuX5bfwwbe2WCpwmp6zBzxpjETb0soEbAb+fTsfklv7nYLlRhNIRpMqQ3XW8taBigyjljt6udtt+mjE1NNVDGmBm7tJMh64AQUBjrnITGzAixakuWy2V1uQrTlG6tmdgzDt+2kQcFqS5QiRSQA5MBBabChWyGoYBPzuZz3TkAMgXr/t+x7D5+8eUsmUFyzqXO0g5SLWPD5LquK3QBKl4jonLwjpVvG2ihUa4WGJ/St7qpwZVpi41hZyrUBUYlziDlLGd9KLM0aZpILA9Wt3eFY91Uuy4Wy5Fl25kkDsDhQo56gjoHFPMgTEjKUwaII4uisBTWgEk/D62uQtdajtE4dh02JyegKMH1u7stxmGQsWJjV7XUSK5s3YgEHGIyjswiXJCfN7rYwVMGODmjIsNZZaZ9DfCgxJihbiwxgJXpiZCj/WRgxUuX+ljbrydsWzoBa7kB3gBCZxY8axuAyMBIwBDzZE358Qgq7IGolEcmakVgDMAYMh597X38/b/3t/Dehx8ggTHc3AApY9gN2F7f4PNPPsMXn3+Bz54+xXa7k7TnHUBRaIFASJwUEAEcgoJXAnHAgutBjV3oZYyC9qWcuyLNSpwQmNCRZIsz4AQQMAIx9tinETlUIOXtVh0HdBQR9IwXpqzCAMn81jXMnBEoFoGy46TWzjydSyTA2XhY1KlrQnTiLH3OLFZBIrA+b3ySWBQ+FKJox1LSNsg4RdvUdWLLwZs6t6Lu4zafyfWbgFwk0gwEgChrWxiZ5Nc+Z5mbZS7IlZnAQyjz32a3rIWMUlVBqlT+yJlEOmYykQVsEJARVBFDKjNXMNVDLWeEAh5tbZIKDiChm32OYHSq4k8jY8wMyiIWQs/BoWB7jAgpFKhqFfxlXW3W9DHg7TODUSAFj/PgrL1sn88AciS89+1v4L3vfgv/9kd/gtPNCu+dnuL15y/xxUcvhG8zgZKeU4QoIJtqlsEJyG+sKdYHKryt9mvOel7G2O1lE6GvtZo0QkELgD09Wloeu97WN510/Yr8eJhI5eAqfJ11flU3zsNHjwtPsu8dPj/32VuKyn1C8QCxVMvHgGpZldp0T9tjwu597fd13Dcex8bAW/va91vvjfpbW0rTNicAs5/TDTaZE+oBZ2FoPH3m+kY0jU3zwkZLM19vKOs7VMzIueCbObq3c3AWn2qMadbnxZsHCOG4S9jc9aXS244a0V4DpWkiafkBtn+J60EiUIkZnWrUGkAOVBeNnFFS4Xoho52cx4Co/S2SMzM4JfR9PwHY1ofWbFvBbJxMoNZi0roN2Psm8bUSu2+jp5eB8pSy5OcPAdRV1wPLGlK+e/NfY+Jsme5kccAF8qnm1U7JtvutydTTtJ0Tvk/eRaylme9zpdHUHSPp+FgZPr2njYWvO7PWpS4LwziKNSPxBKDftyn4+tvL998wo7Xbt3+73YpW1ehAfoO4x20LKKdMG0CsdYsV0be/nd++/eV+Mx7lN4g2F0zIXOBkERpB6mrCrMBOGRQHEHp9RvvDag/LwLKRzAzYIDJyVOBJKG4A3AlwJGYgeFAoV8yEkOtBYWaNChp0N1JGOFvjt3/3b+Dbv/F9RGak2xsMKWHcZ+y3Ay5eXuDy5RU+/ehT3N7cIg13WKqCr4udxF3pPE+qFQ8UEDvbCIBAERErMKslEGqJCQEUCQNrljGbYywue4EiIrn1wIz9MCDEBfpFwBjE/9hcIZsZB4qmSFGhh4ExopjpDUgA4u4Vk4xrCySYEijsZVASIzIjIojFD4x9GEQwkB1KrXms4LeTuZGhipkowiyJlaWu6XquRsoJmaRPMQZw9O5HNHEllXMDdDNmoV0gUTaMYyoCpkzYapEUJYwKRaEKGmwIlUV5FNpJNbm4LjMHrIhECx904RI0LguESKKtt7lvkkARJFU2YAaIq3tw0DVMFJDTiBhsTZsl5tCFSaYU1bZhuu7ZWQBb8ON5vPEn+5w5TX6fUKSZh8UTIGd0iw43acD3fue38e3f+5u4fn2BuNvi2U9+iV88/++xYaDfM0ICMgWkKJYyaqz4dvl9z/pbhA4nDM2BoHZfN6+KlkZt3+aEi5Z+b6LJ2wgWh+9Z+db+w3Xaurm1l1Q7D/Ln6i4urm/5zhy4NEzUzqd2bIp7ujs81pdzDFC3YL91VWyfP7Y/v4kW/y6/zV1tX8q8vuf5uT26xSNzgtAcWjgulGh58pTW4/Cm7l1v6ttcPfV3qaHAIJJ95z7cNHd9CdepyghNyPCHjBTJyvnUMzOG3R57FnPsycmJApF6xrJnRtUlICCQi3loNimTpjxxvAtWK1EyV+Dppcxj1ojZCdBMNDsA0MzMnjbyb+re5eloZfjvIUjQTd+JySdxPd3TwCCFMPEJLO/pxuSZrx8PH7g+ESLCoSuXp92shDvT9jbg3s+VNtbC6tvtdlgsFkIjpwn3i9I0ayGESSYbmxeRAjioy0UM6BYCiDPrb3xc6vZzowiZSsfZ/pMoIUHThS7zIyFnJ0iRnupd2MahZk/umhii4+eKzyza5jlhqS1nIvhgqlEp9ARAehy70QbMoj1nAQpE0NPiuabQBYPDgNI4fQ8AEIGkLhIGzqrrSVbXIdP2kpx+HANCBtZcn1cKSPlq8s9gcJA5LyA2ousIv/ar38H3/sZfBa0XuLu7Ae8G8H7E3Zjx9MUFLl5e4OWzC2xvB+y2A7rQYd0/wKILhbdEBfIAY6BU1lYwF0oGcgi4DR24aLJpsrGyWuBCCPUsF2bsyQQSKi6LFAKGEJCIwLFmmkORGcTNJgSolTRIbFaQ9MIIobjc2ZwtJ9YmbVeSg0JNGBmGPcbdayCNkjBhSEhjAsaEyIRuuAUPgwpwUm7KSXhMED6bScC1WD8IgaIoQsBgqucBJWaE0CHkEcwZPcQyI8KqWEEtJgFAdVGCZAzjlIDE6GNAJMDOq9v1HXJsz1jxGtjKC71yIyAWME72LABiYDGSCLmMYokNUCsEVytAjFHnpiiARF4St9rCW0lO+qVQrS2hi+ryKPMsKJ/NOSAPo1jy60I+4AshBPU9PqYtnGqr5/aq9jfhobKej/FDe94rqBYxYBwzXj97gX/9r/6/+O7f+GtYPXiA64uMB9/+EL/3T/8D/Ov/5v8NfrkFJXHdyBwQIhCcW3TLwzyY9eNqe4C12Z71e6j/fBC/1fBIG/cJtmhwQwsCj9HEPz+JJTjyLhG5zGH13rFx83Sxz+ZC+LZXKZPfpN5ybXT98m3wyS0Ad8YOZoL7CRjdHndMWPT1zu1rk/EBF/r5ds7NpTlBtq27nSftM235x+rz7Zf5dfhcS4NjAlfbLz9fj7W9bS8gSrwIm+cz6aiZJ/Nobr3MYSXDMnYINRGBIr21Etdfby1oeMHC3JE8sDSQW5gGEW5vbrDf7nF5dYmTkxMMw4Cz83MMacTp6Wk56dqu4gJFh9qOlkn4jcUvjHEckXPGYrGoQW1QIEHVFOU3KM9cW/9Ra4dPhetBsOWMN9r0fa91HgY4+QnaLrYYo5rTZeNlzqAYEMHAvmbqGhsQ6RmzB/mtsGH9mWbvApAPmd4sKJ5ZKN4Vyj/TdV3J2uVp7QU0a7PFN2SnnWrrOxQ2ZRyGLCclp3FAIEg5Bnww3ZDmNoYD5uL61/ZRNmkURZHNdyLRbGRw8UtXVKLgmzHH822OAFXgY33PfpsT9OaYZOuud/SK6orTMj4GOgOBBYQFUAgYOWMXR2uAACtjSBkISTRowQHhEAk0RnRYAkQS20KEGFWIJlbNc9UK5ZwlgBoRo9bFBHHJyYwHjx7i13/j13H2zgNcDDu8vn0l597sB7x+8QpPX1/jZjfg6vIaORFWmw36Bw/RLZYYFj1y16Ff9Oj6HohRhRqg7wld32GxWGDR94hR3CFjF0Fd1DNsqrtmjAGh79CtF9gPA3bDKM8a7UPAwIw/f3qHPQNd8AJJQCT3LKG4HnBgjAQkqoBQH1BjeL2CGrOZVSAFsI6Mv/LhA5mLKWPY79DxgB7A7vU1dte3uH55gcvnL3F3eYX4+hp5u0UeRqRhBMaEEHqdFwxGQogBYE38YQEXIMQuIoQo2voQAAqI0gmJa0GHPNT04hSiCpya3KJzB4mCkVjW7ZgJYu4WoWSBAE7GOwS8M2fkzKAwInMCwdKMq2CTGcgRhtHskE3hGaKkgvFFy3JIBCJG5L0KhvJdrDBRLKeIVdAOHZDVMU3XSSBIear4oRjQdwtdL8CYbxFoQDTBKR/ufWXtNkBk4kPv58wMn27Bd+EbjfXYXy3fKPw8Z6xCBI/AX/6Pf4hnnzzDP/qnv48nj97F1eVzdF9J+N3/8Pfwh//1/4D9qztEEgtVjes7BJ+Gun3b615VBUNrl3eLtr/H+mjl2j5n9+fOs2qFMl+GXS0Ib5/1gLv51dHcxnGaltf++na1rmDM04DwY+1p9zZmrsqfI/v5MWFgHMeC7fxzc27p9n5m1jUzD/pberYAdxZE03EhxJfbjuGx/b2lnb03Z1G6T+jw7TUlyty7/jqGPVqPDrL1Q1MB5dg8n4yNBNEhhIi+77HbbcFZMZXDLG1Z960BInWlzqJoMpxS96f/FQQNi4Wwhe/9+m1hWPrbcRyx2+1AIPx3/+1/i08+/QTf/Pa38Tf/5t/E9c01zh6cYz8MWMTpqbdGvJwTAsXJpPCT3C8o/4yPhbi7uytMybTfPpOUv4xh2LkWVq4vs2gh9fJtMGAPVGuPoct2gdgzfqIX8M9V8gwUkEHFghFCEJcgt/mYIBWaPvn6jHH4thTm6AKG7Tf/rF+cc8ytfcbo6M9U8QKgPRdjLC5sIQQ5Bd2937rI2Th4v167YozY5xEpJwzjqJHDBD5c77PtntALotFvxyulpMHMhxtRmX8qGMhpnFSEC6tmjmmJkKLBpOpiRBYjoCBzbkNoy/D/fLcPNvnQgZ22i00oIsI+q+aVtS+qAQ0MPEh2EJ5aakzLFYF9L5QLMRSXESJgBGEfe1AXkQlAIAxRrHZDIKRO4lts3S0WC/R9j9B16BYLxL4TwaiLePD4Ed559wkGznjJCQDhxCyKOeEkjfigX4Jij+evbxG6HouuBwURFtB3oBhFAAom0Ku7EJKzCJHJftjtEv7081SSH1T7i147xovxFC/DYyA1ICoEjI8Wpuuy0TDPs/IdFJzVC2rh0nlobyqw9K8V3gLA9jnijP/x46ECCwAP+SWedNcI2CCsgW9+b49v/1aHq1cvsd5u8cVHH+Pq+UvQ7Rbpdou0G4D9iLDfIdKIlEc5DJOzBpfK3AQFiduImrI3KthedsCYQF1EyFkPfGOxAMWIECMG43u6yWXkch5Ndpt+zhkhBwSdlwUsQuNrwCDV3nESjT1DwDExlY2NdR1EyNoaIPnlQYREOqq2VvO68qBoCTRYzs/R/dh4UegIUYXIqMJKUMtqUKVR1y+xWm4Qu4AcLzAMO1ljaRRLUxpneSzrGLebfh3/L3dxLbTs0XP87+A9AkbKiAPhfAi4+/GnuPrpZzj77gdYnZzieneD7vE5fvXv/nX8wX/932MxMBYcFSxVy8uEd2lb5viZ18T7PcDv662GvQVvx0C4/932zzmBZe7dlt+2fWrfYdbAbkzH07fjPoA2BZ+Hv821z8+jtwV/tb21TH/cQEsb75UwVwbPlHesf+1ePhGuzP1rph9zwmtr/Wqf8+2351uB6Z7GHliHCl0CTebQsXnYWhl9O9s+NBDjAIvMCV+ByKLxSuxeUAu6p8tcne06nGAJ5qmgTyIw+/Leiob4kq5Tc41kNbF7EN/3PYZhwDAM+OlPfoJvfutbePniBUIIOD05LZ0ygD4noTKL7/tyuTzQinsU508jNwL1fQ9WDX9yA9gyGuuPPzjP7vmF0MZveJr4duXMxWUKqMKKZ5DeNO8FIQAC4LJmFQomZNggw9XjpHEFAjWjk/iAG0Iyl6O5eA0qQY100Ebh+g4tN7yDccigixUqJcnAZEKTClNJ50zKDEoJMXYasx1Q3BYCISAUjViggEBR8mqDSvYwydAh2ZEoBqT9YA2TDDiaYcy0wgzWzAza1pKirV3Zda1ndSUREJNBkIxe/rnCYNWfXgLi9QH9U60AZr6vGnIDsFndpAzgw6XEBU1BroxXKPOiaL0IgCUOAIpwAIj2dqAAKDAqoJYkuHaMAsYFTGrALBHGGHEdOwRNfNB1nfhudz3iZolxvUC/XGKxWqHrOiyXS/R9j365QFwukCng0+stOESELiD2PbquQxc70TYr2Itdp+llrRuEu8z4N1dnMpVTQIJkSosg0F75RdCg3h3AucPz7j0JNB61f3sumYYqoBfXMBm/XOlcJjcXUF3pZMKjWwvdtFwAGnNCJXOLBVgDLUgAQFmFPR1mVxrrOJtg6KbdZP4p9AczIWExmcdPwwf4wtY3A398y8AtI3DGk/gU4Rvfwztfe4UPcI3XL15hfPkCdHmB7tUFxt0W2+0dOEVwHmHd76gvbp5BeUsMESkE5K4HwKCuL25DKSdwDMhBXJGCs+D1MSJHiVGyLFJEQXPoE7jrVTieHlh5uU94//QhsgnHuY4sckbmLcwLzuJHREhhLFMS62mINZEGM8ABGBZIY5q4LzAzKA3oxruSaczAus0JE7BDECHDLGfLxRqr5QliJGCxxm53i5wHbLd3wP4OGBWKqhXeBFEuwmJlRkWTaBPGX3w4D9sHUnIuYTPgwoOQ0vdI2CJhSR0WI4PziP/5f/gD/O57/xGW/QonZ2e4uXyNuw7g0x7D5Q5LJlAGGO0J6vf7qBsflbUw1cR75VcrYNh+eEwI8Ht++47/va1z7nNLL1+ffyaogC0Clf1+CBLnrnaP5ub5tt7ivqh0qUpLHIDWtxEAWhrOubAdKPxsbupnX+2ENzZlt3Rrx+0+QXDOkjH3t33HYxKPxebO3por33/nxADNJ/ppQfhkTI/0d64cf7XYs4yFYWKqCn/W+5wtpQwmc39OIPVtyKwZQz1+Iahhuz73JrrZ9fYH9iXJ6NOFWM6UkMozKMpm1ndBjyoHAjFWyx6/8r1fwWeffoZf+dVfwelqg1XsBTDK7qKNlg3GQFjX6+aSEvIo0Y5Rg4I5SfLNIhQA6HysRc7I41jAgRFbpziqAGATxLue+AlhBK0nv/rBkoGZSoxdJ/0AMpJqqzyjsixVOaOWqfWGQMhJ3AISMygzFoEQeERYRgk+jR1ySiDIISwdRQzMABIyC9CmEHSCiP+z+PrXiVQ84pnBiUCsLh1u4nKStIyWIck2fwDqu6+HHZJzdTKNrWaPCWBwzpIMYLHQ1I89MpJkjUFEXCwVRO4ReIAm6UBWv3kbsYAIQnW5YKirQ2Dsxj3iQtyvQAFL6rBKWdKxQrSpOwJyiOgTsEqS8cjmUAHouoCiCl25BHU6szDFos3PKdeD7CAuL62wZuBGZE8Go9NAD5l4Uf+HIEGsrGdWWCpMyhCtftDUmZHUrSQCISB3HbgLEtAcCBwJOfSgrtO51qHvO3Rdj9B3WJ1usCeAu4jY94h9h27Zg4nwk4sBoVug63v0fYcYImIfQSGij6LBNqXAX24fY0trpQnBSDgB60q7xB2uH53pnKsbD4ljb732ONgYAUj2IlRZNxCAjJLViKhm50I08K37rEpSrIKmF9RqG8OkXTY2cM0xgTJA5Xfj66iyuBdQqa6ywnfYFwiVVxUzlsMeAVtFWkYtPPq6TLiAe5+aPpiwA9d3kooTRXxBHwAB+Axfw58AwAdA/94dTnfP8L3LPwGefoL86hLjfi8ByEGAZ7c+w2azwmrVY7VZo1uvMIBAXYeL3YgX+yjzJ/aIMYjwGEM9WwOEPTr8NH0AJk2wXQ9fmF5E09ssAcfbcIKn6bqCKSME7FYDCuy/CmLP+DW+tbpSd0FnUTI3UvZWdFHafPc8YBkj9uMeYIk53G332I8j9kMGp4wVRWBM4DEhJEYfT7A+eYw+EvjqJba3l0j7W9D1Jfa310jbO/B2i24YEXZbkMbQJB4lTiVL/nrhuaygoWrKqcwVEbbYUotlVm2rWs4Zhf6t9tXuzWv+FbgGwhgzcgAun32GT//Nn+Cdrz/G7f4CXbfA+XKJv//3/i7+7F/9ES4/fY4V9YBTsHlQ6K3/fn9Erl4L9ptMgSaovXGjJVIcAcg+H8QSZem53aK5V9CZEwJaYOifa8G2f1a0vjB1jQoZcTbmoC33AHy6Nns6zrrdeP7rBdQjV9nvZ95v6eGB+RztAqZjZpdGdM2Wa+XYP694NWHfnp8I98DBnAAO5/GEjpjOfS8IzMWouga3jHVyte0qc5hQsj9KUgmlB5tFNyD7gh0usEOHrVzfP9+ngi2BerwB5My7oDi0bXo71lWBJYw0K/a15EMe47Dup0SSGdEf4P2m660FjS5GdLHDqP605l/vtfpCL1nkMUakMeEf/gf/WPcL2TSS+o2lnECJwWwgv54HMA5TlxtPmNHcbZp/XtoumhAi9IvFROKXZ8bCwNqFY31pJWa7phNKhkhobUIGDiax1RUU+AfzlYeCEVs06hsMTe+ZOQntuig+4VevVUASS1IMkgEnZzl0TMBQAAcVyihgwaKJSupLL1pSCccco9AzJT2DwqTdIFN0pASzdlh6SgJK/ANb5hjQ5EDBrGkubVElFdgiRsmGQwGrLmIRM8acgJRB1EsdpBskJIsPR0Iiix1IKlBIPxY5YoUlMkdg2WHx6DF2Tx5iuxuwut5iwYRbZCy/+j74dI2BCXmbsL26wt3tTRkXGy9ioHdWD1loApIyAftOUobWeaDCBQg917lEBWpKoGlWFwuKUQRmc93pOwzLhVgSOskyJuB/ibhaIS4WxTKwWK+wWC3RrZa43G2xAyP2PcKiQ1j0iIsefb9ASAF/9sWILXfqVxlMCkBEwBfDOS7DQ1SrBQAiDA96MNMBX/UYsPC5pQfR/nmqf+xhmjxQcaO/p3WKcD9db74Ysvf0iz0/ue/KJ99uv3G6v9O6HbTnyoRtv7fnlJzleyuosPvdyQryGzkxh9iVUdOuztZtdNDKuSl3Qudmrz1K86bsfVzj5fob+MP11xAfXePd6x/jV062+PDdB/Jg7PBym/HL64i7yAAxBvT4GX+IzAF03mHULYUZ4Jyw01TPXd/rWUo8qVuaxbXfmLbx2HXbrQ/o7+cjTf5WLSsR4Ybfx1Ntw4Rkob5Ik/Fj/GkeQMnV0gE4hQqxMqZfw6fY0IAA4PsPGGfLFSj0WMWI76z/Ci4vXuD26hUuXr3A9dVrXL26wP72DneXVxhe30gs3jCC7q6B/R48DHLmCzOIGZEDEMYCYMXdVCy6iKFY8UmVTK1WWsZlCuT9NQcibS/SjL9YgPCn//IP0f9RwH5/BUZADB1Ol+fYXd1ikSNSEhdW0xS37iVeq2r1zmE5D0CB6q5tcZHegmA4YVYQmenjMWvE3P05oWACph1QPQReE25T7npPjjnNtv98rD/H+gYcsN3ZegzHtZdvl9ectxiJ6gKGYJJpohoAJRGIr9fPgdYaVVLaz9CgVfbeJ0Tddx0TSHwowJcpe26OsNGEa5yNeYEYdmIcF/BahcABXds6yZTqtt4y9rvx4OTudo2Xv6jz3UIkIpk7dJ1N1G4ub3m9taBhZuYWhLcL0xbaYrFAjB1ucVcyIS3M91peBCCbTggSl2FleHcom+i73a6kOk2NW473OfXt8M94ybDNqOCZig18q0HwfbV36kQQO73fPO15rwGRMgFo6kpfpwhCYgHIxHIYVxIhZCRCXCzKQWoxBjHHl/MTIsyfGGybDAAQcpcxIiGbCxBXQQZgEGd0HRA7cXkiYiCowAKGWZqKxC2ietngDXiJxoxEiNPzQEKs7gWRCAiS8YhCQB+gOeZZNPjoRDMdSOMhWIHYKIGm6gqV0JW88zGsABBGzkghIzx+grO/9hu44xGv//BH2AzAXR/x+Df+CvbvnGPoOuxe3+HJySnOz85wd3cngbymjs6McRjkvABGiUcYhwG73RbnQXzBQ9D4ApBYDHqxIhAI290Wd9stYghYLldYLJZY9BssV0s8u77FQB1iJy5IQf3WY98h9uKeBAI+v2X8ZHtW2uWBKzNw0T/AljYyHIP845s6PNyjfkFleoEJ1NXy5G6Z0UXosAMdbY/IQD3ESd8pIKwIVyiaHL+3+roOWJSBRG7bMvlZ11IjhDQg0W/n5REnlBxcs3UrT7L69FEL3ZiCWfLFuCoaj15q+qEPsydM06y5umf77Wni0fV915toTsBIEWn9AJ+sfoifbnfIT1kPlZJ533URnR08CUh2MBBCrn0f04jdTlxfYxRgCJJEAYVvqoBV+02TvvluHfS7HG4mRKKGSJ6yYfKNYOd3+qkxGaPgAQ5ACBiwKg1hbl5UxcJP8C25xcAfXdYZsuQ7vINXIO4Q6D1g/S7yGti8d4Pvne5x9/oWDyKwf32DZ589xf7pp9i/fIHh9TVon5B3e+TdAKSMPhCAUQ6FpAxEi6mC8uMpUGnB6lzw632XCN8y0fIoB/VhYIQtY8NqMUfGHq8RErCgBQby58Uc+sT7vdNbBloQ1N7336fC0KFb1v+SqwXUc7+3eOF/Sd33CUN2GGfbnmMCUmlj017/nheG5tx7fJ+PxWS8TT+sIQ1HnJTXjmn5LUxjBebo/KZ2zYH2uTXxpn4du4iqG+jhVd3mfBtaAaJ9t00gNEf/tq2TsYVL6NIKhO7ZYjXCIZ8oY6L7hMTM0Pw++pbX27tOuQ77YOaUEqLLyGTZhohIzkHoJQhTgFUQEzzL6c/I4mYFluwjJnSAuWgoLEtRznmS9co0JSHU1KfeT7HVongm1waUt/2cM6m1k7z+9QzATIxicZB9qZodwcY0GMwJOakwFYNaKjJSGkpgcUoDQB04dAgIiIlAmdBDM37xiJwYgTIiJUi2/6AnKWtgNggjCKGTU4uzpaoEYZHEmhFjRMxRXJqyCiAWZWpCCUNN0xHoxJ/FBAmGCIbiyydjQaHGWJBm00pG6xiQ+g6IPTiy0iGUk7CZKsCmJI4xRu/IjDElpJTxqo8YFgSkjH1O+Pz2DuuvfhVxQaDbjO2zVwjLFcYHD7FdLpH7BfrFKbZ5h/3+FkMecHe1Rdf1WC57xNiDVx0oiPZ1uVhguVpj2A14dcPoFwusVqsScxJCwF4tHgGEkQl/dvsOcslE4eEncH12ihEL1Q6qXpIhbkN7lENkCdBT4VHAysQIqsJAAfDsamL3hQ0CCaTymkmLwQDLNqA4pUgzRLX9ZJXotwIxqTaYrTzX3+l5BnW9lPMo2V73EozvjMPPxdeo3jdBp2B290gF61yeM5q3wJWZy2HacO3ztU2EGmYhoGXD9ZsYscqsThQhLxTUzkmLVJhgRz692WyDBRyXVvlG6SBIk3xBOOj3AYGbaoqFQaWeTz7/HPsxYbFYYb1c4sGDU6xXC8RymvVhQcMwSIB/17l4GC4HQQIoFozprLEN2DVxQogG6MM22GpFtLUhzgNtV/WZGtJ2QIp2X89oGurmGjMjeihFaNYY445X+BgfwpRBBMg+SIwf3QGhI5zkayxOR+TvML7+jY+wuH2Ozevn4JcvcPPsBa5fXID3A7rbG4RxD/CIiFzSyEIFQQ41brEFGMc09MA8eLMxs/53ISCNCavYSX3cg3QppMxyKGWWbIlAOtBWt0rJtm3ANEbT9mK/j3urRSlPy55LFuL7N9f3OeWhv99qnOfo9aZnSiPddZ/lZToG88/cWxdRPXPHXXN9m6vTfmvp0WrUKw2qq5MXZOhAOzRf19w9zsrMmv611gwP3j3Gm2vzsb7ZNSuEc8VCLWY0XNTSQ2uRJ5r7rXDo+2GXn8f+4M2WXm05khRjWo/Hsq0Lox0Caxjbni8CyoRoxtNsw58X1o5dby1oGMDabrcToG6d9sKHLXrxDxc3qRjEgTraAVxGnDyW36QLjNhFxK6fpvzTco2JGgHNymHfjx3gY230mhQvhLAKN2aa9WdP+DK8xBmKVSqj6zSAGRmsaRehG6C4OBPyOMqkJbPYSMBxRK8ZVDI6Fbb2Y03dmJgR+yVC7BEgQH6/k+DkLnTI2Avojz6VHwAwFmOHZer18BZUIEeELe8lcFNT8lKuQeUU5YRXOZNCD+ZKcobALlIJkiYK5Z2sQpa4UtWYDgYwImAHsWZYIKkIPQFEDCKWgGONH+g0aDh1HdD1yGDsEtD3HfoY8eGjh4ibBV5eX4PGjJCB1ekp4tkaP3s94uY3v4GIiI4Ir9drjHrydWRgu5AYjuu0wKf5KwWngeXkagevgcRIfYfx0QIZ6s9PLGdSKHqzQ8cAgHWhmz8/EVcIRADsoDcDllO5oAAar0V3t3WdBCRQfb9Z64W/e2GBuAx9YWk2v/W/BUcZeJ88aw/aByob/PSuA81FEHHiBLtnfBO1AGFy1k/XAALApuFzjF2ZpZTHJUsUwHrgXK2Lcy7WmbJJECba8Txh3gCcf631SwTo2m+wJjtT3/gChlG1Wq6LYBZrmfFr+UjlsD4QAakaEVkHlfxfvV/aosIJ66QgbYfVV+qyN/3csLZpwZRZEwkAy0WPNGZsb/cYBsY4jOi7iC4EUB/RhwDzKLLTMQKh9EViYpWnlLkAJ/4qr6baH9e0iTBVlTR6y+GYVDZ1N+XYQH8tzORVMsGzHFUwv2GWNegXDkFOr9exC3M0rlNhUlI5dZxz8YcGCDdhgxsmUA/8cf8IvAIWj0ecfPgK3+ef4vt0h89+/gu8/stf4Obpc4wW35Ez+sDI44AUDjf/9nMrUMwBysk7EBdWkASIBpBYvkPAGIK4zOaMTEDiERx1/HMty+poE5IcaHZ5qtE9BtB8WQBcrOehRtgLAt59Gph6NHgatIDV0/FN2mV/TUBkA1jbts2W1RR7rO52DIUVBHHPmRE2Ds4vOTJH2u/HgHvZs0KY4CpfZ6uhn1PcTu67MW2Fx2OC6zGhca78g7nX3Gv7OifoZN18vcdMbYd5uMyPrceh7W/Hrjlhw+4Lr5W9cLvdYtlVV3hT0Ld9IGVgs+UWHkuWVaaoU+p8fnsXsy+VdSqEgOVyCSLCbrfTSnhiXfBBQ13sQZxLNbK51I71K81Q0/eTtLn7IWE/ZiyXy7IYPDOw+qwtLWPy1hfP0Oa0HZ5B2Xfrm/WnncSVYebJpCtMDihuTXD1p5QRKAFpAOnhfNQRlosA0sDqMSfc7ncYUgb0JOKAgPWjJ3j94lJclLJs+DmNQqOwBgcJnpe88eoYlTNojAgUESgU31ZANuA7JMTlEtx1yDnVzCRdQIiSL58Z4BjQL1eStjESVn11+1mo7zWFIGcQhA6fXLxGgqZ/tHMzQhRNv07cECIYQFz06DpNERkCRmb8ydUpcugkDzlJ9tAbXuMyPlFwkvEef46OM55unmCkVcXAdwD3hPRIrDZBwUWCxJZInndAM1zqicgoiHGriQ08sDBAHypSQ4HijHK4XAGS+teEPXM1M8DCABCgAgq5MivYy+75As51/vlzLwr4taqsHcGAW9Xs2gwmX5itAxzqwUvdVCDr5AlT3RqwK4Fles9SPBrYLr+xA5BN3ZM22WahgoEoJqpgYfPcfq8IVEE/y4Zl0gcXoUQD2MnRz4hFdPCd9SRvq9GslVk7kplVgyjJHMYxl7ZUv3I9zyElAWyB0Hc91ps1ODPGnIqbxOZkg8VioZYAI6pp8qm0wwSmbEJnBhIsBbH2ESgnax8FRM33Atb1y2azwcXVLcYs7pQ3d3fYrJfoYsCIrBZUEiMPyWi+vrzCZrPGZrOR8dF1SM48wWUEedKIXP7j54Kse2cTnrhL+XG0fdLmedZ1S7A52c6/CRM4pA8DpNncTCZJqGtygAqOJTlICwrcmFG9F9Bs1OZuxLLfDtzhon8X/xPexUO8wvvf+xDf+bXfwO6zT/Hs57/As5/+HOPra4T9AKIIyjswVytAG+R6LO7wviuKvysSVIhXZpIg5xURS1a3joDECRl2GGa9WoVhoQBN3ZM584FPefmtAY6TMvjwTAL77b7rWJntvbfV2s61rZT171bEwTUHfmefw9SC1T7rhUDgEMwfA5AtWAWMv6CUc4ym7b/7BJhWuz6H51pB1pc11+e5/h/rb/2dCluYe0b2uUOLg6dFa00wjwhg6h1kZbZltB429pyndSCJAaWcFEdIOf54gwPBXXo1qc+nkq4/6T5fXBGqoPTvXdBY9h3WSzkEb7uNWC165JSwH4biLgBIbMZuv8f65ERA8ThgvV6XhjNLqs2cM1abNdI4YhwlyHe1XIFZNrLXN3foYsB6vUZKCa9fv9bTCUVTtOg7rFZLdLFznTWI5EioIIHcoJcJakREjeMIIWAYhiI0SDyEnKEgYLye57BciWtAYeS6y417OSHXAJacIEs4OzlBFxjLrtGIQoL6ZEJEjMOA6/0AkByKtd/tsU17jA9P0ccOq9UK62hBl4ywWOBuGIumqdcTt2PXAadL5EhYr9Y6MYFfXA0IcQF0PaAZiZi5Hi4WA0Bivfjzm4fY0Uo0JLrNc2EQ0w1bbka8fu8hsp0EXHZn6Weduw64jnUcQADWdTSDutWhznEwBzylD8GgGjRreN1AOZFmCCIwZRU2MoKkdQKA4rpEMIxA6DStkF/uphX1WUQMGxEggZpoQH8d3KL9tFsGVphJ+uBIwhqMHgpjnZBPy1cXHS+8sAgXGqM7ucqqsJiYI89k9t/z9MdC+yKGVBcj69QULwoIN0BM036UQmZ2YAGKGcjCXOUgxiQWNfCkbl+Oba5TjawDl4AE18IEFxR6ZBUUUuby2fhV0oMhY7AD4yBZcgCAMzIDaRwF9CdGThljShiGASnLidzZDuHURhmvefDgIU5PT8AE9IsFGIzbW4kdOjk5wclmI/2h6n5UVo4y/+IyBAAkgJ9UsgxEEptDdkp51bi5FQXjmuUXYk2zCmxOT5D5GcAZY2Lc7ffYpxE9dyAOZaYwxLJATEiccXF5hdV6U0E82zprJ0pdO3UecZnvfs4QWFN/V95pf9TJstCD83Su2cds414oMN1yzd2wNodQUve5NcpAUVTYvsQQYYqI9a+tu1qnzDmLhSKAbNOWhB1RJOUCBoiACzzCRXiIPwXh9N1XeBifYLk+RfzsE+yfvwRu70C7gDCOQEpygBdYLD2QbHpJhT0jKikf8Gz6QBMMgANp7KDyVegaASNkRlTm0UfJ1pcTYJkJYXPW9rsGbPqLqAaQ+xEp8YdupHySFTncNk7Kb4H0fQJFC5pmAeVbAqq2/NIeI+aR5+a0yjL+b1dvK0iaG3L7WwvwvXIWOBQ4/HXMglCcaWfAp7lpH6PfcYA/3WtAVBLOZEytVr6so8qUpm1e8dzOmTlB1dZhCVZXZkVm+p3WNu0P5q0yx9Iyt2vlWD/9cyklzTFDciQEHWZGa8sAcEDHOWsefBv4zQLW3PXWgsZ5LxaEnDvsFxKYO6YRu/2AUSW2/W6P5aLHOgQsFj1OTk5we/0akYDNRg5Duru7QyTGzW6LoQu4u9uCSE7UXq0kQ9Q47MHLDn0XcbJeIKeMVZCOvbq8xGK1xnK1RB8InMUsVGIBhC5y1gJn0TzFAKIeACEhIWfJ/V5ppzuFTrKwWGC/3wNgBGIQcgmGJwDLhZ4eTJJxtO9F2BiGAfv9HoFF29MtOuzziMwZiyjhzpsuYCGcudSbkTBCsnBFWmABRsgZg/alCwt89Qe/hr6LuNgBn+/WOoGpmLV+Mb6LrSF0uYWyANxcYBD2TySI+igLy/pKBvLCwxEDOSqckZ+Q0wlnpZvriiHSKiy4RUWOGXNtugFfNnXkpG+uXBwC58A8EYTEJ9sWnRMmDBz4osn5tDttZLnDXNKcCuBzcQLWBwds7AC/IhRZXSbsWtFZdn4uddbnJ0xX0EwVXjQtJ4OBXAGp0dkDagd1BCBlLrEhbOLFAdggB/qqNaAyGarCjuu3tI2rYOZQI4MRJIpY3c6oANbMjP1+wH63QxqFsYcJNepzxgQnsUVULQnMamFQWoyjQC9iOfNEUkpnjCkjpxE5i8JgHAeMo2qispzHY2UCsnqTnslgE83GiQsunQLYVionAM9eXSKEiEiEzXqNR48f4dGjhwgUcHlxgauLVzg9Pcfm5ASdJtLIOtnNzSuoQMBuHRlQzmwufJLtLeoJ2rIpNWCbTViT1gUmZCYs+15Gh0eAI3JKGIYReQkJBPfjnkX4Pzs9wy9/+Uu8//77unk3E3pCF/mchlHP2snglDCOkrHKLEYGvJgZaeQ6t0nmaGlDEVTqnCeQ0kt4fGKeTlSdk0QaLI5G42trvzAN6bQJbgRC7DqJ19J/sYuIGsNFZummyg9kHmUVUEwTyRgZQAiVh6KyCGLgrnuEu3f/LujR3wS+8QwPP/8XOHn1EfD5S+SXl+iub9ClLRJvsQ8JIwb0e1F2bTkjkQjNXSZQZuyCAPsE5+JiYEb73Znbj6a97IKsyMxJXWbNPY6E6cNry+109srzTdg1zbUJLomzuEKZi43S3CsqsvIs0nTglrDkTZYMA5GtJvuYZn1Oy96W9zZac7HK0kH5b3N5wTk0ytJjdbHyIg+Kjwlg91kV2n6377c0n7eOTC1rRFTa5fvh3er8vmhChs2DxDzR8rc0aK0fB1r8BqR7uvrnJvRXaZwICEH5SZAMqsguyQ4qLYOuAVE0hxJQbf3x11zM8IHA34xTK5wE1phO9fQZx0EszGH6XjCsont/247p5X7PoqwwXMZ0/9xvr7cWNCIBiy6i65bgtfiBpdTh9OQEiUUTcbe9AwCMw4iui1itVjhZLfH06VO8vroCs5hGN+s1+sUCt9sdbq5fY7lcYtGLheTy8gr73Q4Pzs4wpoRF1yH0hBgIw36Ph2dnWG004w7EvUfcgiRd3G63Q4xddVXIEvCcEcR1KdX4DNZD0ljPfrDJL8wPGmjeq0uRTKjFYoGu62WupBFgsQSAVDGvVpe+75A4I4AxDHskzuCuRwxLmF8A2b9M4CRWjRwYu2HAfj9ieXqGb33721iulvj01TX+4OU3kNZPyinVzIIiiACOFasGwhQoOyb9tnyuTEYUHFU28wIUTLpltxnqs+yesb5WAO20su73++rGTNmyX9Nh3U1fp/aJw6v8aiDR3a9CwbRPhhX82QqFtFRjCaw/HmzW8hUoGXPRAbTyxb+9xiRkfZaoWs9Es2/fDVgq6NbPtvFQ044JwYOLTwDKOwEAWECFrAkqKX+JCJ3mAzft7MRygYYupU4bfzZ8WwDlMIy4vrnBdruV2CAFKV2IxaKYRsm6wzmJ1l2tECmLIJDGASkz9vu9mq2BYRyKZUGek/WflQ/InJOgDjZCKmmoTMjg5oijqfndG93IpgFN5xDqXDT6IjHGNCCAsNsPuHx9jc8+/xzvvvsET959gr7vcXl1hcvXr3F+eobN6Qm6Pk6scRZ4bnWx0drRVjbXXAWzYO2jietDUb5wBbd93yOQAFEo0NntB4x6Ind0TMFItVj0yJyx2+2wUAura9xkgmzvdnh5cQFVhQNEONls0MUOQ0pihSI9g4gZcOcUEGowfTaNZ7E2Kb+CWFczZ9HIZwN+womy8lE//yVuTEPMTRminZD9QJRZkcQysd8P2nSq7goMMNc08GItVnfTLqJbyJk1fSeCSLXICaAPkA09KNA29CXReQzqFuBHX8XFw/8trm9f4L0P/hXOnv8Mu0+fYnjxEnRzg7DbIgwB+5CK9YVzQgpJDLtFYVEB3wRwuglsmswWXGbUOV9LevPVAsO5a9oWKvPXhBMPUIF51505wOb7MFf/fcLIMUvJnCBSPgddaw5jzAE1348yj6n+duw9IipuOClnOc3e0cK324P9+65j7TuIbcG8dUqaftjnY+XOJd/RH6sFi4Q/+Ayix8bACzJzwtabhNOivJNv8rnZ36avVeVf4YeTfVY3dn3OxsD34Vhf5gTiieCXDJwAt7e3IhRpyuuJIOOb2/T5YB3MCLPGIb+s0PzWgoakq41lkq1WK9zd3Wm1wvwXGpi9Wa3Kezc3N+g12Hi322G32+Hs7EzcqjTQ+OzkBKenpyAirJcLnK5X2Gw2YGbc3t7i5OQEi74DOKPreywWy4Ng7qh+b9YGm9wJwKLrMTKwH8ScHKPl3ZYBSGPSmIkeIYhlYhxFKNrvBnSxA0FPCGM5WI8gpuIQAtIombbSMGDYD+CcsVqssFws5ICnASBO6OLCUEvRwFMGCAE9euyRMWQgg/Dkg6/grnuI/+GLNZ7zI9zGb2O1WKAjETKE4cpk4DrHqvneD15FRIe/vcW20K4V/6avm5rfy3MThFvB1ttsSOyASQFsgf6d6773omm7TLtvrbaKTKBjewYoVoXsACiUGfgsRqwCgjFn+y1DAG8RRAp/43q4mwLzDAeKWFmg/l61pWz/d92zHQuOgeqVamyCCQ6AxIogy+nz+51Y5zLLqaPLvseiX6JfLGrwsUkaCnKLBqZ0QceySnfq4sK4ub3Fi5cXIAiIS8TY7QZcX1/j9uYGu90e4ziKdTFlJ0TxlLbK0CvzrqNqYE7oTAWMFgZa3pcGk4E8E9jJYrKKNFFcR42mZAfR+XulftQNpwFwYGBMjPFuh7uPP8XT58/xlfe/gifvvgMC8PLyApevr3B+fobN5gSxryerN1tG+W9JUmD0IZJkDEnde0KAKJFNKKr/VY5SfIrTOMqZNRDfX3EpC2V+ZtPYaX8fnJ3j4uIC77333iEQ0dJzZnzyyWfKc/W8HzAuuh7rzQbMhHEYMAx7cJbA5MwZw6Dp1nOS+xZHQxArlX4v85xFILODOBECiBQIQX/Ts4ZEplSx0DpkMQCom3sgOZum7D9q0QDEbbXvesnIyAGslvQ0jmWwCAIG+r7DYrHAer3EarnAYrlA7KIItsh62CmUBaliiSRuAiTa0/HkCT7+9u9j+eFLfPDN/x8evfolrn7yS4yfv0S+fI3MW2AY0A2MHoxMGUNIcqBq7meVMa2mdS5zzRxYMwXC3DUHSFsQZXXb83OCgwfkdm9iQbinvklbjwg6LfCc0yK/zTttXfe9P/eup6W1tU3G05YZgih/5tL327vHArePXXPg/L5n7TlLWe9jEebqfluayF5CZa/2fQJmBGX/nq1bp7n3cSBt+335c300ocfqL4dYM8MvgLafhg+O0bRti7f6mDvUfBC/kEUUG4Rhtz2YA20fvoywUN8Tvvk2c8GuLx0M7iesEbiP4tffdxqIrES/vLwEBTk/g1mA+9XVVZHUYyQwJ+z3W6Rxgc3JCXY7IeLV1QVCCFgtV8hpBOeErpOgaamnHhvPkGxWUY5gxna7lUYXQrBs4OOIYRgK0fteXLU4q1YvJ4yq9eyjxEd0Cwk472IHBsqGx5A0q2MadeID+92+bHDjuEOghNPlEo9OHmO324qvYtYDl4hA0EwBGQATUiaMXcSn4QP8lH8Dt8NSDs9LCR1ROdjPCwsHwP/I+BnYCgWUaRkzPObN2HwCq8p/i5a1KdPaaL7Pk9+0N6TI1LIjqSwl71XUVt9iACwa9AAqKRiJpjQxPj0twukpjHGp4CbgtWV82kp3q2g7DLRzZWgGJstGA9UEAmKxgAkHTR2uLJQ3XfvLYY7ynPQbBSxLav0qxjFz0faWuq19OhIpZXH/0Ss1G0BKWdxGSBUKEHCUhxEX17dIOWO9WuH0/Byr5bJkI8ssplYD0BWBmrBjzF9+v729w9MvnmO1XmMcEva7Aa8uXuHly5fY7bZ1vE0YMIBin/2kJSo5wEF1zchPotEuAauhBvnmsonZxGMVItQ1iQHiDLaNh+sasFkMgrijWbdtgyndrvPNhBf5qEhSNec5ZVzfbPGzX/wST589x1e/9iEenZ9hzBnPn7/CYnGN8wfnONlsRCMmzSjpbUWmqGsJzKWPgYOe9i0uKoHkQMoQdC6BJsItEZcxNUHMUkxnZoQMcNBYpEJrxvmDB/jk00/x7nvv2RQv69NEgGE/4m67QxcjXr++weXlVeGhIWomv6Ta+CKIS7ycHwMCJnO79tttsuqWo0+UNtUrwGKDYJpCz7NUUCsCSlFM2P1QwAdI3XkpYLlYqnwXELoolpDYYbVaY7Hosd/f4ebmFi9fMSIFdF3Aer3CerXC5vQEy8UCvbnNQcYiaTa0GIKeWSGAZ7d6Bz9b/SMsH13gG+/9W3zw/GO8/MkvcP3JL5GvXiMwIQ57pHEAd0Gyg2k2PS9Q2NVqUeeAvX0vwKPw73kN9jEgBUzdfeasCseEAp+0pW1zW2fbFt+HY5aK+4QID2R9ULqnnylB/OXjTFp6FCDp6TpTt+/jsQxG7dj5d62uOZoco00LcFs6lPZq+1tQbO31mvwWULdJAcoRAUCZ956ObX9DCJPUsG37vBvanEDmaT6XoVQrKu95+lgs7H3CSzu/7wP99qzPFnYwT937Y0o435xie3tT5tybhIw597GWXjYfM46vp2PX27tOOWuGNaLve2SLcmcU8+CYR4y7PZb9AggBi+US+/0el5eXWCwWSCmVHOvvPH5cMkhxzuhixGK1Qh4Tbm9v0QfJVBRjlOxUuilLnwm73RYpJYwxou8XiFEsDCmNKtkZ3MkgjX4Ts2LEmPbouh6bxVoXBEN8kOrik5S3wKAnoqeUNF0YI6r+WszkjJwTuiiHry2XC6z6BRZqvuog2rRx1ID22JV0kAmEIY3YnD/Aj171+NHqt5BA6t6RVUqNRWqVXUEnBDBxVykHgmEqQxjgs02zFQbKRccmUdV41wdrJQWI31O3FODeUXRUgi9J2+c7w9UdrACybAAfJWVp0WYyN6dZT82ZXAkxEToMfpRyy1dL9UkqJKi/N6rWvwgdUKYAF8SnwlA5M4AIFhQciGQ+T4StSn8DdiAqi5tzLtYM03BITmwV5JI8Y0AHhUZcg+nU7ShlBrOkWk5jFveilAAGdvtdBVkZpd8UCavlAu+88w42qzWYCLfbO1x/9jlOz05xdn6G5XIlGxgrJY1p1ZljmA2AZGN79eoCp6enuL29w263x8sXL3BxcSlac9Ak4wUKHwK865yXJtkeIJtj9hujuEehCk91elaawz1hbm2gUOc5ecuat0SZL66b5/YjublRq5D3CSDbREgPqEzA6+tr/PgvfozHjx/hww8+wMOHD7HdbvHi+Uvcrm9wenaKzWYjp9CjarbKDFfSZZvGyCCWGAyLZZR1QqWNZW7DLKc6L2U6QILik+M/U3dBAFgul0jDiHEQq7Dxhgm6JyB2Eev1Gq+vb3Bzd6sCBZApl6BmE8rKZZt2aXKdY4VXlOecFHrA2mxwpqduMLO6pYY6JjgsxuaGaVlbpUgIEftxW9pDMOAQQRDlXOx6LBYLLFfqQswdxvEGr1/fgJ6/kHjHs1OcbjZYrZZYLPqyphIzSN1+aZQ9mANht3iEHz/++9icX+FbX/lT/OoXP8GzP/9LXH/2BcbXr8HbLSKxZKmR/OsHgKkF03NChQerBhCNV7SAdQ5MmQJyThP9NlmypuCupm6dEzbaeltg5T+3IMzTYy6I2EDrHDAHoLz3zf1pAa6leW2DtVsBx/ch55rIwrf7WD/nQLBd3kWpFRbqu4cZkaYCx+F9K8NbAbyw2LbH/2bxcf7ZOZe5uSMXrP7WOjc3X+Y+t3XMCV32eU5QBhQLuP61QmlLx7ZM3xbJcqrYhOWQ5PVqhfPzc1y8eH7QlreZE+01t+4z/6/kOiWxD3HiGylSOkAByHlE4Ch+YUPCMO6w3pwAQQKlN5sNhmEoKWmJIFmlzk8BELooQYqnJxsBYGHA7Y0eYJczFoulZFCJASlLgA0i43aUY9bTIJaFLiyR04jVQlPjpoTdfoddFmDQdXrgnBJuGPbgAaXsGEXjNCbZ4BZdKJL3brcDFh2gp1NzSnJYoIK4ru8048wo6SujWBCENhk1ubv8zZDUiLmL4NU5/usX7+OL+FVoZlvdAlnS0mpwYC45/2XjLVgKFSzpr1JVsz9Dnzk2R9yWXC7Zhi1GQO8ZFnMbLwElOQszwFSDj0wrDAO81r6CwqYLgNkxM9cmth/1S+b6i81HZi79LvgOUzBiv1mwVBU8psQg1lSWEvAw2UQtbzVKv6CuRQb2zW3INgDdMFiETmN49XAlqi4fRAX6GENMWfLypiQnmBstJC5hxDCMGDkBrBrnMRmR5FCtlJA1gxKRWCvknIgKyA0wB5BqX0OZRJY29WZ7i+cXr8A54+zsDO+//xVsNhtcXV3h5uYGjx4/xunpiQjHUCuRlW4ftD6GuCqenJxgPwy4ub7B9dU1Xr++Vssn1ecVQbO+aXOkAmOuC4JrZVxRs44p1y9uI2RGFTJsHk6aS3X+Oaf0sh5tzmgDTOvtebcXt0oNrIDeH/yhBdtTOTOeP3+Jy8tLfOX99/HBVz7A+ekZbnd3ePH8Ba5XNzg/P8dquUIXQxG0THgt/eY6BsyaGpfV+uSAQxEwpCCsNmtc393aLglm0ZxlcDkTabKx6npbbza4ub7Gg4cPJzS1K8aILgZ0ix6nZydiOVFaRgRwDKVAGxYislVYGJ7MLeU0fjzaGlt+6aZBHR2GimBlrtU2TETTSR1c2lDLy2CwGl8qrwLACZQz9rEGTpsL1mKxwHq1xnqzwWq5wG4YsH3+Ai/pFZaLHqcna2xOTrHZrNEtavZBhpwnxJnEPS4E3HXn+LPzv4WzzV/Bt977U3z91c/w4ic/x+UvPgMubxH3O2S+RuGfOBQs7F5puntu9l8zxu3Vgng7nLe1BvhnC688snHNCRj3aYnbPv37vg6Ab+ELcs310X8vwsYoboBzwLUdI38VubgRjuYApxc25gBom5mofa7GI03jLOZARisgEdUYhWOpjVurREvbiVDT0HPOCjMXuzH3ee69tuw5IWFuXCbPhum6aueufW5d5ObWY6HLmMredH1zIxZQOnSIPCZUzs1B/860/UEShfyvkXXKZ3GZkwozMziNSMrkTk5OEbsOiavGo1/0JTAupRFdjAKilfszs6ToDEHBHeH6+hqAxISQ7vjDsEffL0AErFZLMFDcpjInbNbrkgq3ixH7YYdInRx8F8TNiwqoC0AeIYYTEQqIGKcna9Uc1UEdxxUuLi5UGOmQRvEP3pxIcHpOGXfbOyxCj+Wikw14HMXdIGcgysCLlYSRQ4duc4q82OC/efoBnsd3BRwGcavinEEg9ArYZCOTUMDQChC2Yepno9UsgJ7wv0ki04rhLUMIZAtN0GBLe1+QRCnPTrvm8gDcs1yAB7gGLttGXJ9xzEOlmonGGnSwtdfFwgUzMlC18B44YSqYmOBUhAZWrRMLnS1QuPh/51wFLMh7yQQFHRtmmQfM6pJiayUlFRSk14O66BFq2uT9flBBJGNU65nhZbYTgI0eFu2vDYpR3DQSzK0x1rMUQkDXd+iragkhUElZHGPUtnERxOw5h0qlHk2IELsO436Pq4tL/OhHP8IHH36Id955gpubazx/9gIpJTx4cI7OuRmZWYcVusvYoSgSvvjsC9ze3mI/7HWu2WiS+QSVuetnZ5EImXTc6xhNJyLBda500X6vINK6H4rG3+F11DRLbhOAMWzUtjiho1oS3Wahc6+mB3eWsQmQDmV9DPsRH3/yKV48f4GvfvWrePLeE3DOuLm5wfZui5OTDc5Oz7Bar6pwbbUT1QMLWdcYZQABWelb5LlKZBCoxL7VVoowm3MGU7UwVSLI9ejRQ7x69QoPHjycnOUidUm8XL/oMI4j1icnWK7WGPaDWl8KFcr4mVZY1joV3iPCTtZxsQp8rMy0bhvvImloh50THLw21k2K0r/qpKj/DHDBgtGVDmpi4ZzLWha7UsaYxwk/DhSw3e1xfX2LEF9JGvf1GpvNGudnZ8jMuLi4wsWlJFHZnG5wdnqK5XqFGNRaxuLOloMCmEi47M7wRw9+Fyen38d33v1z/Nr3PsKLP/0JLj7+DPmawcMOgRMImuaZZJwtA6Hx0kI/R9ACGkGVR4WWcIfXMXDYfp/T/rbgeE4T/jb123UfYDqWhrTOE8AceI+CL65Z8g6EDmUuLaC0eW+KLX8ZprJEC2362sp3oHOPCy84RgdzN/K0bTXoLT0KBqRat7WvKhGP09YLMb6OOeGmAG/IWjMlHaEMQt0f3HfDCW1/WyuN4ZOivFJeknkaW1KeJaoZ8YLx6FrH4TSwuRqK8GgCYHLuy36u+fa15+MUmikNYpBy9/s97u7uZAyMPk7DUvHUoRAxEbqkxRrXRtOzpFo6v+F6a0EDEGJ07sTBkvFByICUJQsJEaFfdAL2gwIwZKQ04i6N5ZTxRbcunSoDmEWT2vdLnJ2dI6WE1WqF3W6HlPcYU8Z2v8fJiUzE2PWFUBK0bT5+VdOzXIgrx5gS+k4OmwME8FMkDCqdxRAQCVitFtisFzKwqAHjERG72x26vseD8zWinvvR933px2q1RBoHdJAJMLIEZiVATvsNASlGbBOwPjvDR3cr/Iur38COA4b9AECDjDiBrGwyv3fbfGW4M/utDo7piRsEkU0LvfR9i3nMUMHRg32dj6xZDCQGYpoOUiZq2WVQTrhlqO98ZXoGlMlN5NqDZvO3upUxmvBih2MZ2LKDorK5EennlMzSZv/MyiF1jylpYyxrl7gcccoa61CFi4wMZKkrJwlSlUXHQJbUzsJH5Z00Jgx6srxpKYZxVBxDYM15ykDJ2sRy1rhLZSl+3rELCF2Hvl+AWeZyICpCkgkSUEGHVHDIhRGQgh/pY8oZnHQsQ5C25lxo3MeAYUhFYMpZBBziaqGx+Q1mnD14gDSOWK9XePj4Me5ub/GLX36EYcx4//338Pr1NV6+uACFIIkfIFaFXDYF4Rcy3hLrtb3b4ermFsOwB3UBoQvim2/pdmzek2jgK3BXP1/N/AaYPKObBZxVraDOMtGkKVYFYwqQzNpTF4+C/1jumShsgdAF55ITkL1Z0doG0ZqToXoWwC4xECaAkAMZtf85Z9xud/jJz36Gp8+e4sOvfhWPHz3CbrfD69fXuLvb4uzsFKdnZ5oSV5QuAhoreLd1G5GROZSA8IOLGOvVUqxcShFmsYilDEQ50w3CkyZdxXq9xqeffiaxPjGU/O6Q5iCAsdls8OLlJdabM5yePcCLy5dCW4kkNaIpcTUKpfA3KvOLuEMRIKwNXMekKELIj38ogoLBInmPxSpQ2J53B6pjbG6VYr0y3qVjb27kZPxPwIiEkGdw7NBN3Dlkz8g5IZOkOx8HwnZ7h9dXAS9ePMNmvcHp2TnOzs+wH0bcPnuJF88vcXZ6irPzEznsse+QJH8zEICY6xy6CWf4083vYPPhr+O7T76JD1/8Ai//9Md4/fFnCJdXiNs7MO+RaUAmSPIRkjbJxIwI3OvcH4twIXQOBaQJWaazyeI6zQXZQJMHsm1wrn/Gg9syNWcFAEx+v0/zP1eGB9r+mmqADbcIDwpEYEowV9T2HTlMTdaMudaGEKpwapkEG7qZVRSYatRbWrRa+giLx7JS6rpMTT1mSWgFjIM+uOdbq4b/PimD52nr2z4nHPqy2gPruGoIKy2sj2FKK8M2pjTwwHpy0LRw45rkAzDmPXlnOjYo+zdc2wsvMV5hPEgP9iGaxkRJETVIv6Xt3IF9fvwKa4R6HZBkCtzf3U5wlcddGo53lPZMpFnpxJOCIB4/Qv9DAeVN15cWNEwKtIHqum4yUY0g3sxiQ7M5OZEc7OOI1WKBYRjEOuDiP8wMRyQHj9zd3WG5XGK5XGK73YJpRA/JUMMsAd5d10mawNgVvzwJtltiGEacnZ8pEBwEMDKjixH9agUG0FEucQBdDFh00UnUOkRBJnav2bdiJ0KNuE45wgMiyOSEkQUkDzmjX640b3/Cdsh4+OQ9/Pxmgf9p+AHuEjBsd0IrAm6ur3F6egLStL2WQtVA2kSiBEBkkwVlYosrhj1R30tJloGAGdW8qfYfuhhFeJCNGSyuQzLBGCUdotuAJ4IOVc2NaR/qwqEigVsf7BA2mzMiwLIAeDvjIduhi9UfVBaWpgS2MxDYNiY5HE36IWclDCmVNKhymJr4l4uQIBYmZollyBqnYBrYliHIBiGsLQQ7Ab1D7Dp0IHSdAB7zlSUVeo1R9H0PzhlDGkEw5q5xFrbwTbuSgYEHGQdNq2lpbicaPqBoTE3wEuZagRo3c8H/tfGzMQQA0nMV4JgsM2P/THw/L14xzh+c4fzBAzx69BiffvoJFoseDx88wPXNDV69usByucJquVCBzwNo00wBy9USz5+9wPb2DhQIJ6cbjEPS8y80nsKCXER15oRqxTXT1O2Y6qadQKtfClgEFZciaDazssaKMGOCCsEE1Cr86DO6dtjVVkCro3FtggkfFlMUdIOyvqrgaFnqysAYMJP5cHV1jevrP8ejR4/w9a99DecPHuD6+hqvXl3gdrvFw0cPsVGrL7nBtd4RJE4okqxvjih0Nr4CyBkRZkVV+6Ss1ZRBXeU7tYNyI4aIru+w3+2w2qx1/DXnu5Ll/PwMH3/8OUARZw8e4GZ7h8xJT2Cfaq1b0GPCV61W142Vr98rX0SZGWYJKevgyCFzYC7pZydaW6Wf1OGyXOWqdZX1msW1IRCIs7YriqtcEAfJANK89sr7WPiQHFSZMKQEGgbcbbe4vLpE/7TH6cmpnLGy3uDi8gKXV5dYb9Z4cH6G07MTLBc9kCGxWCRKwMCMRMBNd44/ij/E5sNfwXff+Sbee/ZTfP7Hf4bbTz5DuLlFt9sh5oQxJBmsEFTYEFCMLPPFwJoHhscEjRYfHAC3mecNaLbWBz8H3nS1lo+2nFZLfF857WXziXk6H5nrrwBpjAZK/72bkGnMJ9aDmfYDh2cdTOjePGvgcLJPuOdHVYzNAdnWinOs/6S8vOCRRhAKQaz6xoDnQPucoDh3r12bXgDz9c22kSSBgtG9jacB0STuo9Q5U5ZvzwH95Ytrd1VAACpQNKXOjd0x4fiYEOx3OM6M/W4HECFEMqnnoKyKJad9sB/rGaXBxXuaUiQVwehtrrcWNChKkDelarJKnIVZ5tpIi7jP7LTjbuGYyev27g6cGaenJwruBHB21CGNbuHFAARZFLHvsOwiFrSaSH7DIEGsu+0OvNsV5rfb78DMWK1WkmI3iMYwxoiu70VoCgSOoYDj1ULS6BpYE2BRJ8qDBw9KP3POJUtPCAFJ29L3PYYsh/btVJhiEHZ7GfyTs4fY0xJ/sPs+9lnS4sbYIcaATz/9FGfnp/CWksK0vASrn8QFzDmZVCzpgCUX4YM1mTozNKhatOJlEqFOdP+e3bNga7NojToXSlAyRJBIpjEvi7Fq7BjQ4CXVWJMIsUm1eaAA1tOVMyvoTwLMoe5JJcOX27yKiU9hlB0W5ze/osEI4moEAF2/QIhR3NvUt5lASDmphkC072yMSKEKc0YI0Wl4UNqS0ljmBzBUEyuAWxMSgEI7o7KZJ20MBTSZ25cC2mZjt+eIDn1XQbmAYbh3CqIugNJtcGzlsh6yVwU+itPUepeXV+om9RDL1QqffvopNpsN+kWP/X6v6U3fVR7Bpa0CyoWpR4q4u7tDznLmwHK5QtdtxfVy9CkDqawD01B5WpH7DAXOIgw0T7BSVDtrAok9DwWoxXWJa51k8wGVr/n51bZLBw0l35uC1roz1/dsbsEEsUi6XpwmnYMKp7V4TowXL17h8vIKX/ngK/jwww8xjAO2d3d4NjzDO48f4/TsRDfBOr4m+EHnISggsx5Yp8+ZhXK5WChwrnRLCjTbLUzWd50jjx48xNXr11hv1IINv1EyFosep6enuLnboet6dF3EmLiOodHY/YWjeakTwp9CmWOhPGK/kzuUwv9WBBCCWrZCuQuikuKYiCbKM7NoMSIoiAaZQnWxJGZxY+x1vyqZ3xjgKJZZGQAZXx2HwEmslqjKkpzHwiOHccR2u8PFhSRYOT09xdnpOdLrEZcXlzg53eDRwwc4PTvFerVU911GogyKjJTFdfI6nuPfbH6I06//Kr75ztfxtZcf4aP/+Y+x++wFcHcL5GuAk6T+VfqTnmBuh3bNWRWOAdQ5gDmZOw1Q9ffa546Bb3/d50duwNQfxDnXn1YTPymPUYV4EKrGw3MkW9NN9iTmcubK22iH54D/fYC0fbfcU+Dr6eY9VN4kwHkwbAok/86BMITpM23599XXzgE/DnP0sniftr3Glw8UFUQlxmxO0Pl3vfze0M6lrPuMT/Pbzvs5S4N9n0tv669iKYPbiubopX1vy9cfC+41TG/WNduLvgyN3t6ioQfYQZIyIRNE40KhmFIC6cZImm5UtX+kwK2LPZgZmyiHb4mWWv3YVUOcIRmWGBV87jQlbdRnQ9RGKLBcRDlXw1yybI0nPQX4+voap1H81FNWy4YO1Gq9QogBXdeJu0tKcgqxMncAxbc+5SR50bUM04bv9wO6XiwcwzBgmZfY3W0BAv7sz/4Mq9UK52fn6LoO290ef/N3v4//x59fYaQeKY0KiuXU9EGD24lCiTuZCBgGUGEYSEGQnyhuB2XY5gbVIIqLUUoJadC4AFbBMVmGF9FeFf9LBhKLNaacrqvWmdFljRjHUVyKdDNNnJEGsS6Q0tHSC7MKOCmlIiSZlUOAlLnWQDbeAo5JT98VGpnWJpAFJ+lJnRSK4GTa47KYzbzKlTajpY4bM0BJrSpOGJAPhbEarU0b5bWZdkia3UcRThpGVgfRMQIHQIv0aIKNTux6elcVQiH9zQqU6ruotbp5JP8xjau6ehiJYSBOQbO69JQ9lDSdqoQS4/b2DsvFEicnJ3jx7BkuLl7hnXfeQYodbm5uMA6P0HVRzdKmpbYzX6TuUQ/SW1AvMVQOUJazD4rIxbV9nneWfssHz0S9q19h5EUI0aqYShEyBMJjdPJMNgyv7Z6w72bjZ0JpM/lxtLqddMQs1CAbKxVKCLZJ5TKs0t46j+w09Y8+/gSXV1f4zne+g/XmBNvtFk+fPUfXdVivl2WcbZhl5jhYpEJYEQqVxnYwKqDxELo+xlFd7tx6LcK/bu6bkxO8ePkR3n//PdiJ00XQZQAh4OGjB3h5+TFAsaQdt7XVXqUPjteF4LTIKiDZZzJh2YhNlewlYabSoq4xA2XsntNHuQYCBfixJFFUQMFkztU9oYBUmx9UYtUkYQhLhq0Yhc8k0v5L2V0fwdnS/WbNYDhIEohxwHa7xcWrS6w3G5ydnSFfXeP6+kZiOx6c4+HZKTYbzQaXAKaMrEqIjjpchzP8ydnfwlfWX8evvf9VvP6Lv8SLH/8l6NmnGLdbhH2HiIyOM3IexK3C+bh7xZ+BkGPArbVSzIHHtwF9Xht/3zWnFbfPE5/7pmzftmPCDkDaDgeiGfA8o7rcUfNu7V9Lx/YZ/9xEO96A1Lm/vh8gza82Q3MvSM39a9tl93PTBqtLYjdoIlzdJ2TOafbb79N5Nl9WG7RdFKREZc5M66CjwJk8s3DlvUngmRuLiWBI00MMj9HHrxVfhj9eoiqp5HPo5EiJ3Z2knze+PUfbY4JqpYvwKmaJ0a3twWTuvel6a0HjR3/+I4zjiHfffRdd16HrOuz3e3VrWkuO8BCw2+0wpoTVclnAY9f3uHj1Cj//xS9wdnqKhw8f4uTkBGkYcXt7i5cvX2IcRzx8+LAQY7GUzBshSOyHmbwW65VuCnXymFZgcnCLO3wphIAvnj6Vti96cGbc3Nzg6uoKu/0ei81K3Z0kBW4g0dpwztgPGS+ev8C3vvUtMES46vt+4m9qJ+COoxwi9fTZM3Sxw34Y8NkXT/Ho4UO8eHWBd999F9/57q9iRIef5Q+Qgmzmu90ON1fX+OLpF/jOd7+NzebEMVCbcPVrmRZVuijgsQgfKmTIIKjLy5Dk0MTtFvtBTkoexxHjIJvVOI7Y73bOMsF6iNZYAPc4jlWQSwLITZC0AGpxJapBwMG5xgGE2HdqKRDAEmIAKBSXKmPOSS0apO4/KeXif18OuIMEpZbMTVquCYeGGVhdsVSc0bapwCH5OgGCnrprgk8FmSKoWfnSj8qmHOMjiFuBgaAiZGAibJRg7uwXKqGiwGxoChP5Q+dCecsv9AKctfAQqsDRzh29QYAoEeCFIbOOTAPfyqYLZTJZ25eB27s7nPdniDHg6uoKDx89BsWANIzYD4Nke2umrTZZz/KwIHydPxpAayKV2R0qndydtl/UCAw2NrYcuMYJWYNKv230TaBUQEwUXLt1vBHKKeEWiwN7rv6nuuewzQI3lnUgMRmsiqGV9qR5ZWtINVMtS9onc/zi4gp/+Zc/wXe/9110/QLDfsDLV5f4YPW+WiuMEPpyMDr6BeM/ihUnRCpzofBgtdxljc3zg2uyxKLvAQbGYZTYGzbHNqmTOePBgzMQgDSOWPQL3N7dFWoInZzlqfzA5bO6P0ulRciQ+Vxig4hsmVceQOQnio2uEwb9XKM6VGyxGvWeHSRK6vMtyrhcxtEsz/ZuUNcqZkYXCcx68nnOkt5cXSstThAhInAAKCOCkKNYN4wPJ3URvb25xWK1wOnpGcYx4fr6BhebNR4/fISzsxOsT0TgQGAgMZhHoAvgEPBp/Co+776Gzfd/gM17f4nVj/8/CB//HPnyFunmFnHYI0Yg5bFM3kOhYMpl7gMzBrLsGQOB/t7cO8csDC3obt85BozmtOBzvx+AS7LxbNGoCTJiuTdLOTBNj9sC+PZf237/uU3x2oJoa9NB8DamNLpPqHuTpt2s8a3WvrRzpoy5qxX6WgFnrgwvfLR1z9RQgLIXRHKWOCZqXrO5OCdk+M9+zvqAbitj/jsV5n5sDvvvbUzSlPYNy2M57Ha1WuHqlVmc6vsT4fSYfAGAG2XmtI2K9d7C3dCutxY0GBl//uMfAcT45re+iZMT0ZZtNicIVIOhO3WZsAHtFgvJNNV32A17fPDgHB9/9inWyxW+8v77SJyxPtng+voaQxLBY7lcInQR3ULKvdtuC/NfjAMWq5X6waPEaDCAIY2wI9d3+z3SmBCCnFERFz1++cnHGPZ77IcBwzDgyZMnePTOY2zOTjGmhEUvfsjIGZeXr3Dx6hUePX4XJ6enuNneYb/fS/arLoISI4AlgJukHVdXV7i+vkbXddhsTvDp55/h9ME5dmlE3/d48OghvvMrv4I//NGnuA3fR2bRBgPAcrXCgwcPsF5tkHNWtykFtbrhT0AjTKioe6Vp+ewxAiNnEdR22y2url4XAeP27g6XFxe4vn6NscTeSLBm1HS6NqbL1Vp8dFPCposIVAORTZAAuFg8DNgXBMgGlqsr1phznayDuFnVlK8K8xthIReXtqST3ZheLpYDswqQoScnhE3ABYCTE3FRyympUEYV3LBaVSCLTs5gERDqKez/+kDYwkhQdNQmYujvBlwq0LGxFCAWC4gKBHX5cOjTNhNU+hBBNbkulaExIEz5itGEXN0mqDBb4oFYH2KxFtV263dFeLvdDmncoOt77HZ3GIc9Yi8JFfbDgPV6NRHMCAZgFVDpgXApmWNoUIHBSUnayaqbru5qRfPk9n8d0sog/frx/a5w1rbgaSHKWItrms1Je8+EDEw3iMnepXWTK77O7To6RQTydds5CSGo1UVjIxSEmpuPCeTEwNXra3z6yWf42te/jhAz9jtZ96Gv9ouCCZVOEp1t4+26BUk/HiiUuAPb2JKuYyBM3DY9DwJJevPbu1ucnZ+VJAQAipW16xZ48OAcl5c36PoeXeyQxqEIBTZOdiZNWTsmqDsaluxmpMoImwdlnpiSorZWgDeVGKkCdPUdk6GodqysTWC6EYuwQZAwdalY4szczDCFha45sr9MxWrf6TPMFjwtygcmCVsNQRU4oUPSmJZh2GMMhCEN2G13WCwW2JxssN8n3Fzf4fR0g4cPH+D8/ATrzVoEfWSEkQHKiDEgE+G2O8f2/R+Cn/w14NnP8O6P/ivETz/DePESfMOIOYDG/SxYtXU5/5t7qgFtraa4Bdft1YKzFoj7z1be24DSOZB/rA2Hl39G1lqMveYBOBSevJb9y2iI7d3qBlyFjbaMFqSb9f9N9c2BYH/VOMDD35irNRZv2ae580na7/dr4Of7AMi6AtU6LBmBVlD2el8fK17xMTSz/dT75kL9JgAuHiS1fa2S/Mv0yyvRSpsgCTaE73A96LkRaD32aPsustB8umGr/5g1Z+56a0Hj4eMn+If/6D/EgwfnYAaGMSFlQmZJd2lmshiBVdfXMy+UEE/efQ9/++FjDMMez5+/RAaw2qxBMeCUREt1c32Dh48f4d333i8H9AGarz1lbLd3uN3tgNghg9D3XQEzgIIxTSk6ZkboOiwWS6xPTpFzxqPH7wghIZqzEIIcOkiiye4XKwHnacST976C1eYMJ+sT7PZ7rE9O8fTpU+z3Q2HwOSUsl0t0MWpOeQKFiIuLC2y3L/HF06d49eoC69UK3/zmt/DBB1/D/+tf/Fv8Yfe3sEvAMOywWq8RQfjo2Uc4PzuTrF1BTjoXrExlnc4BxTo5ACKWA+Dc84kzrl5f4+rqNTinchjai5evwMR4+OAB1uuN9ifDsmZkoKRkTcxgDRwbhgGZocHXbqPIlrEJJaDaLCoifGhqxyxxGWzit3RABQJdCERyujJzObAIRCXbEKEunhK0bqlIQz1gi5UIlqKU9AaT9G3RL7FarXB5dSUn5TK54FFvpqQCxI2yBjpJtRPEznrg1n3xlCzPBvfZIb0ypq5uL2WZ0GCgCIRA5toFlYFcvw2isQH74GhuG6cNnm4WLNbHk9OT4lq4u9tiNwwwmGYNJeHa1Xqj8ShiTSLc3t3hrF+AgrkwoqZVNSqyaYUlOQO4xrdIjKzFlygtnHDFBoYJejp4nfd+lRRrkgei1mcjgoFOUmJ6mpfLueY4YQ+50txcJKwoe8aE7iJwFsRJTZtt06hgX1GojrvcCIiS6kmzYtmJ5lWuFLq9fHWBR48eYb1aI4Gx34/o+6VkflIgOJG7aDLK2ufan8yMDuLbb2RIOWNMGTFKTAkRShIBclPr7OwUV1eXODs/K/WwlimujIx3Hj/Eixev0MelurKONSDc5CNbSzpvPM2BDGRCDsoTXDwa6aZr9iBZzq4sNuWENC6GXq0EIwCRv2BrLFTeYn8IjhfoNAlEopSSliHJBC+zUlxzVegpoEB9o6GgOBAiOsSOwUmtF8nK0FiQAHTcg6O4s6Yk2m7JfDdgu9ui75fYrNYYxxHX19c4Oz3Bo0cPcX5+jn6zKDzYYmsoEsYYkQMhfOV7eP7k/4j3fvnf4eTn/xrXn3yE/cUlutsA7AcEZGROGJGQo/LMMoOEHkGHKDMmGvXWZcRAtyV1mRMa/PMeXAuvPu5KNWc9OAaWWqA7ZzWBKRpIRtjthjJnIpXkM0Gc7Mq7/lyLFtD7v29jgbH9f6JAcK2pVgHovlXPbThWR0urOctC+UuYnhFjZQBiyckkGOIthMZWW+/vte2ZE0Z9O30bvRUoUD3l2ni5r28i8IAP7s3RqZ1Xhb/A7/BavmKQenFNhe+0GKJ8qMJV4mI/La7kOVVliLXV4hpDCAWXaePKM6Vmv61ru7l8d9Zz1OyN4iaurq1vKRu9taDx7le+jv1+AAc50bsHsFhLjMLtPpWD7sCSGpQpyinYIRqsQegCFqHHb/7V38bV1QUurq8xjiOG/R5DzvjOr/0Kzs/OxUQcJbVnzowFZKDX5w80844c8hU6TVOqbTSa5Zxxcr5yrk2si14WWCRCt6inFweSxZCZJAAvRAyZ0S1PkTigX2wQc8aHH34DOWdxt1ouZPGou0/XLRDHjEfvnmKx2uDu5jU+/PCr+Pa3vot+scT52QP8X//bH2P89j8GI4II6HrJHz+MI1IeNStLRhcXZfAzq/8nU5kBNl2mc55R14pM1JSB6+tbvL6+QWbJtf/i5UtcX1+jXy7w6PFjAOK6dbfdYhzGmulErQ0l97tuiPY/k3QMHE9GwC3gCfOl6oow1eqEsjALWDKwYMuo0KMyGTAjmgAwAc1TAGdaVcHZ4kZBQdwUQt8h9r2k/CXJY89F8EHR0pJZUbmCMtz3t3TbCQm1O1UgMSFK+8OFZTgO4ISHwh+RC9iuDXMAGAbqmwodg2Wrj4xGwJgG7He74u5GkeRUSSdkWB2WLQmsAfwM0YJwwrAXF7sAAusJ0nAtMVyj/0HJupQBZMZy0UmmtxzAOYIoFarAtfdQIGhoai23fith2N4p79tvLQ3JFV8Zr/yYy3Nl+jnhplicbE2Y0OzKcKLQZLzrb6o1L4KR/Ec06ZLdLE2AFkqMQB4Trq4usVkvQQQM+xG8WZW0tp50JpCyn4ck9CCS+LiFHgQYCQq2NQ5L16AJFfW8FCufsd6s8cXTp6gHWVYrATODOOHB2Rn6LiKPCTF0KBZGK9foUzK3qGuUxuoRkZx6nqnMDQFCrGVJMlvrq5BacjiKxVLHL0aAAjoKiLnHsB8kMUSZclz6b2mNLR4o2MgRJI7M2h8JnAeMWc5qSi5LkWa+lt5JZDgKb00S/xICIXQ9Fr3E9YnAkTRlt/YRku49hJq1KmVG5lHP6dnh7q7Her3BfpdwdXmH8wfXePDoDA8fPMBi2UmMFxI4BRE6AgExInUdvvjOf4DzD3+Ar37+B7j6sz/D+NHnCFfX6O62IBpAGJGjuLFSSRBTQbnPgmhrsw1sNc2uuUPPWT3m0tt6oH5MmPDCzH2AsYC0IwLI9LvwhMxCK7E8mxacgCACSOIIn+p1LrXrnAWoBbLTiyBxdt4VS2lNmlSfg8aPBNSU4odg3IS0Y9YCL8TZGEyFnXxA59IXoolgZffbsfVCoo/r8FlNj2XD8sKHvT9HLSiW0c1R9wJM3p2UDRJLJ1GxglhdrXDihcicsyjSJnXL9+z4ORFpEhoAFouoy8Z4pWGDwvV0/xMljGIVrq69sevkHA1UXqWVgSEiMdv+SaEkeMkaU6YjYiizjhEZbQjgULD221xvn3UqRNGqAJqJRCZQv1xiGAZc39zg5OREJ4VohkLXoeTYVu3nmAdcXl7ii6efg0g0Rt/73vdKIPcwjljEfqLpqBJrgM2frps23UuR3oxYJp4GkNs905hkzVDV93Yeh2ng5V9icWMiyIEow3YrJsEQQTlNciiTxqmcnT/AatHj0aPHIIq4uHyNf/FsiU8f/ibeW56jnGWw3yOD8eL5i+Ji5s27QAVmgiOrG1Dpty0aIYICBNFepHHEzc0N+q7DxcUrXFxcYrvdYrFY4OGDh7jb3pV7zAxD20RWrlVGRTtBXK0JqPtbBQImTHjsZh2pf8pY2eeQWRMC6HOu7gKiM6skXzXIBSQWrFYr8uzCwIqdt80MDDm5uQzRLKrqrWjItYNmJQE58tO0P37Mar892NWhoulDXEfSk60Av1K3uzJIzloz7lmp6shRmbq5jBSIpUyPyDFqwWO4ubsDQczJsvaCL13poW0kgINq11kA6Z4l+xp0jHOy9lPJ4R4AcW1heaYr65OR8ihxO9omIg1PsG46g4Ct2clFVKcCV+HUQPS9F+kaKsKKm4V2bk0ZisNNmdy9KjLqnDXpygK8UTC5Nntat4ktfnhr/XULiyGKUoanACrnrAcgDui6hcRXFaG3uk6pDCTr0BplgkNZa2696RoPyvsklgpiYWMtu2ZVBiAHp8YobnRyyFjdxuRsDcai7/Dg/BQvXl7JeUcUkMRkNiUyi0bNzUa5ra6WGVUALABXaevXWB0PkokfNN2s7iGJRdO4WC4x5hHjIGmmiRnRCQpkwgZMaKeyx+x3O7ECZwGcASSpcrOub6BY1BgCUA042tLOnCCBVHI+QlfSuDOiWprTOOpzkL1X/2WlS0qiROKcMAwjFv2tHI447vD6+gpXl1d4+OgBzs/OsFjq0Z7EJfCdAgMh4nLxPu6+8U/x+PFv4IPP/yW++NGPcfPZU8TXN+h3e2z2e+QO2NJerJk5g0OxVSNwkFNENN5vDuj6+Iw5LXabrefYidLQsfmybklzmvc5IaB+V76aqYy99NYJDDouX6b+t3hS/3k7Xb1fxrCcG0WTNvm62iMKpLlTgWHOymCWdxubg6BmHNYJTIW9Y0JfOzfsPTti4T5ho1gWmnEv78yMbds37YDwsZk2tu+1Aq+V1VpfLN7MvzeXRYqb96sgeTiPqhJOBBciKlkCjyc8YIAyOFUrTLXIHHdR8/3595/eNshBetYIA4qJMxbLJW63d/jks0+xXC5xfnaOflHjNpgZL1++xK0eyNX1Pd59911cvb7EO48/xHK5Ltmnum4BojCJcAfqQBvT8MzFFoHd91KnEbrNkey1I/bucrks9dj5IHd3W8Suh2n4+sUSabvFdrcrAa5WZt+LgBRUAEtjRggd/s1Pn+NfpN/Gt7/zCIEChmHEOA6aOSTh5vYG77/3HihYvnrbzOGVVWVyZnDN/KK7ObtoJpswN7e3WK3X+OLzzyUGZr8HM+Ps9BTb3RbPn78oMSaRAtA5FzQZYMBAjyF1uHvWvoKaGtCnO6VI5FS+QzdwGYcaqFlXnwHsCoqkLtX+luqpMgIteoIBjW6uTQb8KABZg/djjNjvR+2HP6TNdb+AVJoIDEVwqH/09GVuLA6VaZTPBtxMSBZqoWjE7Z4KG7UuKvOBJ601Olgf6uaTkYWetgkV+usYAQKACjOrWSas4sJ3yi0uNGcSN4EYpE2WMlKE9bEMAul4ygFr8myggG7RI4RY1sRyuUBFqxXwO3xtU8l1vtKcweW3wjDd+Rd1Chu4rzS1+Vipx7A0zLYM3LAazHB3FGSQA8Hw463N4Gaeu/EGu2QAjvZFKGnqJtJsR5xqFUQYldf03QKDznd3sPlBXEUGEGHz3k9uwnK9wt1umGg+idVNMlWQbvQi1HoYEhN1c3OD5aIvJ5QThI8FEjfPJ+88xrPnr9B1PWIM4CyHIR4CPBlPUpfP4mKJuudYx2SKq9XCiygKkpAhrllZQL4ddiap2IVY1HXoQ0AaJPaPbP26wbC5HEk025wTbm9v61lTrIeNwiwx3vpVY9rshPOyNlmCygMFPXejrruu7wAGxhDE0qEH65lgHRlAFAtYyhkpJyROYrkcB+x2C6zXa4zDiNfX1zg/P8fjdx7h7OQUXR+ApBYjTY3bdxE7EL44+1VcnnwDX3nvj7D5+b/Gq7/4CdIXF+iv7tDxgI7ELSwEYOQROTCynABagI2NU5s9x2fZkbGu42r3iqIwHz+NuwWdx4CT1XEMlB4TMg6eaZ6fAjy/v91/3Qd8D4Ugt3OQf6eUBkvTX9MGTuvytHxTG+6zHvnyCiYLlS7tOEyVyBWrtUpib8WYa9exueSfmfCEpo9zv7VXa4E69l4rGNi9A0B+5L32um/uTQsAyvYyIyhPeHZZE/kgY1hpS/P+nKDeCp/3XW8taGS4Q9XKLl21vIvFAl/96leRUsLV1RXojkp2pv1+j+VqhcfqqvPq4hUuLy7w6PE7ePjokXbAMiIk3VirBFva4LIq+MnXHhhkv9u7ZvKygwG9gGETYBgG7Pd7AJWJSZtkY7J826CA5Wql8Qo7ANVM1/eSvhfMGPayUXX9AhcP/greie9itVpjGAeJbxkllSxnScu7OTkRwBWjBlE1CMB9JDQTj6pLiYGHQdNOjinh6vXrklZ2uVyCgmQGSsMgliGd5EXz2wB5AXimaYUCwIKey3OwthVgJCDRACGVJ7xAogHWCnDZninnC0g5NHlfiy7g2e4WOFeZuuzik0VGOkYpZ/GxDwFmBbI6yfW73KBqDZAGeMtTBaMmOMCYIELpF/uyGPjmkxX+k3/+V/F/+r/9G/zy+baA5ELN0nYqqND32zppriiF/qXzVpKHxxWMz2kNWZGhFyD9ZVMDjBI3Mz31lFW7rMJ8ymV8aSJQShuDCrYhENIo49J14l5YOuWaUbfWKbivwkHDtMuErnPWNHG+wDL3nOhQaEfaN2sLm4jn3KMcDatlg7UET3NHSL+oQS7mg1zXtAz3vY63lS+tjWpdMsCaVYO9WvpDHA8xT9kM9Tc5nI8mdXcxgjAAFKo5PoTih+4Gos4d+wfG6ckGL16+wOPHj0oaaLPYBF20Z+dn6PsOKY/ouw5pGJywW4km+47wjuDmVNXINakwYScvK7GDJz4XVhXAJWYCJmQYuI8RfVghxQFpP+h5HRl9COVE3mIJAzTjEE/a5QGBjXeN2UHhHeS/Cz5HYEZQ3mPkCMq3u04sRsyScjhruujCc0JApz7bKctvPIilYxhG3PV3WG822O/3uLm+UYHjIc42a4SoPuWUsWdxQ44UcUdr/OzB72L1G9/Hr33tDzD85V/gxV/8DHxxiXDLoJxAOSFkmY8Dj4UXessEUMGPB4z+vj3n939gKnB4QcVo7ue3/fWxH6Yhb9eC/9wKHP6Z6T3BDHaOV1NoGdVj51W0ytS2HmtvLdt+mwLMchNUgo6lH1Vr7etssZPdOxaX0AJ3hoyDuaZPwCfXYOr2vRao2+9tamH/3FybWguGp6EvqxVo52h8+H1+Xvq62zZ6IWlO6PB4xJczV66nzbHnff8BcZUyYa+lcUv/EGiChf2YohkP365WMH3T9faChm1QzEWjbkw4cZbc91EA8oOHD8vZBgxgw5sSkMKZ8c4776BfLET67RcYhr2ce0C22U2J3qZtY56mdmsltXEcJ+8ayPYSspXnfURNGhcaCyAYU8bNzR3Ozs40jlf84UByEJNlkvAnToqvm6Rx3Y2MT4ZHePLkUTmZPKupXAKtM05Pz9B3en5AOD4BFcOW9sF9l2flRgJjTCOWqyU+/fnHhR4UCMvFUtLY7vfqQ0wmCyjA0YqqtzGMoRW/di/5oPo8V926TfpDsIRaWvlOvu4ZmOzdUdrSKiSkUv990n/5RRcLQ9x9KmiUnvgiitDg67SYBFd3zfrlwHFLLj9eAP73//i7+Ac/eB//u3/4Hfyf//M/xRQ+u88ECbItILlSwUApg0vYQEvLQzq4EhTIUR2+Ou9mXm83NCIoaMnoe8kAZ248RKRzPiN2Uf1KrWChcwgBi0WP2HWaLW6UuVk64jejug6sdzbXDmQYHH63Nk+FiLarLQCAMlfZrOvvPKm7fZXbWwW81xvW5tayMG2un9faXicYV6HYyq8nUqecsFdLpvHGrotlnk7gOzvze7t8ASyXS9zc7YoSweZN0pguZr8J0+QjM2OhbrbZgp8LT9ZVxBl91+H8/BTPnl+I0ASCncqkFC9t9/1Wahrikn2Kc1FQcGlIbU81FyvlmSEnkqMcFMsuAFwXIfrlCqvVCtvbO+RxhGTBs/N7FFhZwjwHoK0eOYKEJTCc4caRdV7bnDJXNKNXhp1AbTwpl1TaKIJw1wdwjAh2CGri0n8KVAWOlORMpbzHmEfshgHLxQL7zYDdsMf19TUePXyIR48e4ORkrXVL6l0mRg8AgXDXnePfPvkP8d0H38B3v/cTfP5v/xiXP/4F8vU1uv0OYQCQEzpm5FAnld9v29Sg/vL7/Byo9OvDA0m759/zLjtvKsuu6fhhct+/05Z58NzM+wZe27bM1QdMgXa05AtBBc5s6XQZsZO1kyd9rdznmFXByp5T3h4TENq+uxuT3469Owey22faxAAteJ57zx/E2MaItJ9bAXQqSB2OZSuwtMKon2uWVWquz3NzaO6am5d+XLyLmin2wPOxQH5NzIUo6IPwLnHtmrJkE//eXacAFOVUqRAymMMwoF8sSlCiuWBk65g1XBsYuyU2m42AiixZSzrdbCRSfmoGJKJyRoXFZhwzl3oXKiPicrksBAKq5cFcqgCxyJjg4UH8+fkD3N7e4uJSTmDtu043MyqZUWxC1/ZIUPl6tcYf/+VzdKsPEShW1wWCMgVJy7perwAw+miH0B0BHJiCb9OOFgBsYFg3snFIeP36qpjdxR0h4vbuVgCeHniXDVj7hWf1MKrbkP1uaE8BR31Xz0IoDeWqeSfA53OeiBL6vkH98oyVNUONaUsNupqwo205ArKJ1BVJg91J0/CIuws1xfryqQFfrKBMV4a5I2m/BQQ10HIyZxm//9c/AAD8/g8/wH/yn//JpN/FV9/zXCdEeMArP5An2mQ8W6rZO1RoPwXA0/GevjphrOU5ggWzGYAVgV5OWE8piZVCO1iESYYEUZLEGgAoKaqDcxNpmwdu6obrNxphSCsyYFzWyCxzd5UZ2C7k9HPBQkUMrNY5Qn6dzNGcaLKY6wGLbhNpUP4EfHAz9mWx6gpS4Y/00MqkfvxEhGE/YLGKLitQBevsyqYCwOUJZiqupSYcSHVVu8VcM5OgpT9JdFTX9djvJO0qQQSaAKiFSMD3O+88whdfPEfQU8KHIRclSumnbqRlTRYBorqWFvq4cS/0YyCr+56tsVKHZt7jCBA6KTzrPI1yxkvfaVD13R3uXr9GzgkxBgSSAH2fkIUze+MnAoBk9w0eOFYoTXQxKETuLCJ2z5qLg5sSJoRZ5qaUMag1Xg4IlHJFnydn5eRk8RKSCGQ/7LHarbBbb7Dd7nF1dY3Hjx7i0eNzLJa97PuUAYwiyHECQsRfdr+OX7zzXXz4O1/DVz78Ezz94z9BfvYC6eoSNO4ACqCsmbYaMO2tG3WYquB7X6BynWKHwsVBeTS1eMwBavutfbf93vahZCKcA9NNO9tD2Hz77+tfFUhM+NZ08JYggawv/lA1W8OuH1TL9LQ/pqQ7pqG3y+OfOUHpPkHxTVf73n10Ojaex8bV19GC8KKYnunnHOA/1l8P1N80xl/mmgh+jTC0vbs7EKRaYYExzRY26VdDr7nDIecEqGPXlzhHAyVVLYgK+MyZsViuihABiPmZiCTlK7OYwHPGfrcXppgl737JIATVNqSMHC01XihgOmdGCB3GccB+P6DvJWjaCx3tBPQEku+AnQvATOU7FSBo2Ueiw9Ny3sN6vUbmjKurSxAIm5MTdFHS28YY0HWhCBuhHMyTkTLjv/9sg9X7Gw3ys/SdErwHAlIa5aTrGGqWEhiO1wlkm6iNP0MdzMqeOZlodhrk5eULjCp1ZmYs+wUyM3bbvWY0iPquA1b+A1FpSz0lGZNDq+U5lHbS5HUqLdO9ugR5T0DeBItxAej1p1obT1l2aW15ruAjtwBsb57UTSWzlsxpBR2OERugsntmsSj1GaiqPxaAzq7fBqsdNQEAf/VbD/HVdzYAgK+9c4Lf+tYD/NHPr6RuRT7ytJxTMB3lQ8GAS8PdOJTH5tB6Q3MvQun6trGfsEebF9o3C2bNZexEqyIaZQsY1hSv5N3mZIYH3ST7vitzuooP+j+76X6fBHd7ED7Tb68EQOltBdNVrvISgKOH/8T2Tq5zxP1s8TCHLlx1bKq2TAC7MHILfC6NcWvMaRQLZeS+yaIFNBtlcwKow5hyOZ9kHEcETF0Fba4oa4cnoBQpn/uuF6WFExKr6V3PkTFc76gNCM8PgXB6coLrm2s8Xj4pCiXph3IxYjw4P8di0WMcM7quwzgMIJh2Vulv6W5LrI/W3QIR3xgFZ+auVadISWo/BXJaXgQkNsKs4F2HbtFh0UWcrhfID07x/Iun2G3vkNOIvlvIoZNEiBSQcgJZQgSy+SvCB6daN0P3K0YJePVuYdb3SluxZpKWN9n/cp1jJbBez+OAWZ9ICBm6gMCMIVkGRLGE7bZbrJYbyVZ1e4Or11d458ljnJ6dintbzHKelB5uG2JACgE/P/kt4Fd/C5t3f4pHP/qvsP35z5EursB3W8RhhzDsCy/OrEJYNHdhcamzxGHEggQ82GsVgl5rfQxIzmmgW8DYlufvTzTduvYqN5dPJtzas1MQRrCDc60Ob83w17HvUwAdVVhshR3lB2znUTlew+o+GKZl2d82y9McDeYwlmGSAwBuNHLveIHmPkGjFRDm3Hfaz6Y89m0zF6I3XYYD7G/BjdaRhgZeMPkylwnPjOm4zAlHbyzH0cbtCGAAd7sdMhGyE34B59qsuJoddhD+L4xVFDihuJF6NMZQTBDiZI+873o7cUSriGSASRhw0I0+oAMyYdwPksUJAOeEGAir5RJ910ncwG6H29fXeH1xCR4SVv0CaT+INitlaUzSg7EykDIjJUYgO0wuloXpM1Z44vsBmGYnEDAxDAnjmBRYyCFUrEwAIDU9Kl7JjC4wYsg43Szx+OE5usi4vnqlZv4FYugRqEPfL9B1veYwz1gslvjo81dIq3ewXCyQkgaApxFy+Bnj+voazAn9Ior7DlUgyaYRR9n9y2/mQkw2Odi2zwyQ5DQHEV6+upRnQkCMnWa7yhoALuldRctV3acUQQvTt40djOqYVEGGcVu2xpkAWuitbgJAuc8EcAjwJcs5JgooCe4ULFk8WTck1YVN2lTGHpqZKMgmZU8JijP6CQqyNgGS4YjUnJ8LQakAO2avdTys14ANWdAbGQyzLrSOYLkQ7fd/+CEA4D/9V/8pAOCf/PCrmF4tOGZZdzr+5vBF1k8bt/Z1tyUWJuKesR4V66PDNnkC4LkAtILJiSUbWaiuaLIZZ4xZT5RHQCpMzVGDAAmFIhHYe3Wj0D0l9qJNLnM91ypL94owWE+GNyGxzlcDjmUkfQcmtCrrr1CyQNPJa0ysvvtG81putTZWmgOwYx3qulYhA6QgqcwWzXxkfXVNLtYQN97Tzc7KjQXU5sR6xgkwjhk5R7C3/vh+61Qpy8DN+a5XV1GtJ+pDGbZ+pY8uKZjUr98zMzabE2y3+6ogYdjKV36UsOwjHp6fglNCpOAAHGA7kK0BK0TirjSjYAPeCl8jSQVaLD7wZZBYX7PO88xASsAwIO934DyI4MYCKGMAlouAfhmw3izwtW98gEdPHiGlhN1uh3EQQWWx6EXBpMJLznLwXoAIAEtLmgJCFwinmw0WXYfVYoFljJKKPUq2RXLzpUpwOnpkgbSakpzMQiuPxCjxf30vgekUgvDkEIHQgULEopODEgFGGvcYxh1u7q7x6uoCl9fXePHyJX7+s4/w6cdP8fryBmkQVy4JdVNXLE2RzmDcPf4Onv3O/wH93/sneO8Hv4H+nQ+A5RkQV+i6FQJHBIhglXLSvmUgcG0/hN/BePHMvzkA3GrNvTXjPk2z19K24K8oWesym+6b1Dzr2uKY8cF1zHrSasV9efdp0IHqwt1qncntSC1d/OF/x/uBQrcajF8FsQndHX19XXPWgDlhqg1gtvGZrcuV386HY/Rr++vLt3+hmTNG22OCgW/bsXnZXr6v91l7DqxkE4yiuAIo63rIjATCyJKlMlPEmBkDAyMTMgfFmZL6WBTx9W9KkrwiM5BZXO/kMF8CkxzsmWbaOXe9tUXjs88+w5MnTyZEuLi4wMnmBDlKju6UBTTv95KRiQEgS2S7gGrGo4ePEIOcVs1UA7VNmqyLkuSAJQ3WEuZI6GKvoH2UszRCmB34coZGCZ4yiwsXZg9Ui0bmBMo1A4O1S7QGVN49OzvDF198gWfPn+Kdd95TRo8SWxE0OPLk5AR/fM04OX+McRDARUGkybu7O9zc3GAYBzx8+CFCiBKfQaaN0ImEuvEzV1bl4UshlwkL6qd5t93h9vZWrEEkLmfMknZ0GMcC0hrxAXxgrpDPUr+ijwbXWPYg0WZSkY4LaClgjKp23MWimIa2aHz1RVIQTHVKHNRrTbV6GRbIakKJfXZA2zYLFs079Vwa7F0WpO8emKL5Tet2+0ihZhk8858sLS30+Sc//ACX20v8x//P/xj//Df/OX7/r3+A/8v//U8rWHWLuABXmtbtmySgyT2DlnAePGupheZKIxM27A02THtso7Qey3q1JpuFEr2M7jiOE3mHoO4lQUBsoKA++QDnjP0wKOQmJEJ9cYavSdNCWSc2lzzNp1dF0wQ9f8alji5v1P9on2oz7qN5oUEj1JES1AfuZ03WlJIFzzdddVNpdq5N6rauUxFK5NC5pCAc6oKaEUIxRLlRdMU0oEI23SDnNkB8wlkXG0GAIhtgV/SuMmSRizIDXd9jHIZy2nkZUK7/EhjvvvsEX3z+HEQRXddhvxtMrJqsMSprRLX7KuxzHsuAkY5JmcIlg5gCAkc8mwPmgsgAkDLSflRBl8CdnRkT0HcS55aJ8O67T3B2eoYvPn+K3d0dUu7Q9x02600ZRzSC0G67RQoZm80ag54dAV0PiKRxHMVJz42U5y2oQBzTFW+8xvheJNlLuyz74DDaCclCt9gRAgfkpGCV5QyRcT9gt11gsznBbr/D69cXeOfJYzx8+ADrzUoySVFGDAQeMroYMCCAuxWef+MfY/3k6/jWh/8GF3/+F3j50acYrq/BTIh5REgD+hz0AFIFXAHKT+RcrmoNqqCy1crb5/Y7MAWo9v59ILF1CfHWjGMa57n2lN9yja9pLTBtkLIvyz/vy/ZbQfs8kXh7DMPoBAJdC+Zi5a6jfvpN+S2QLwHgOu8OBKRjtJgZu/toZ+W18RZ+LN903Qfg23onzxkvvqd97XWfZe3LXG8qYzKXMaULkRykbQr5zHU3BJSmoQn0dvHKIiTmspcln7ACh3P0TddbCxrLZY/PP/8M77zzGHd3SYH+DiGeYrfbwhjffr/D7e01vvjiC/zil7/E3XaPH/72b2O9XOPBg3MJttMgtaJUIyCNWRhwCEg8ipSsYCuNI2IWE9h+ZKQxIYOxG/ZqkRDrCoWg6RZZsl3EqARSFyRiCUhlFTZSLgKJaFQIGAWt2CDkQc67SDkhZ8Y4Dtju7vD06VPc3t7g9PQMXddhuVwXk+NiscTHX7zC0/67CKkebHJ7fYvbmxuM44BhGOQU5s0aXYiFa3jtR3tMgh20VSRXlTSYCCWQUBnX5cVFoSF04qWUsdvelXcK4DPwTwXygynUOEmQHFhH8nz1xDcwVAGVMRhmObm67O62UEs9PAFFLV6qWaZgxqZCH6mDYCf1lolvz0AytMDAEPS4k8zqLiVzlXVczJ9ZTkWf4nRzbbHnp05EdW4ZnetG7yxSKoTVYHHg+19/gG+9d4r/7I/+M7zev8Z/+Rf/Jf7Zb/0z/PrXzvGjj69qfw0kTNpkvZwSzYkxZdwqcp62wzTDJjdKmlWP4yvCZUW87TgZgDSAk9X/msrGmcv4JBVu1bBd+iDvmkWjByDgeEwJfdeBsYO5upR+zzF7L5FrrEplrM1cc/dEQZB9xwugKcCOoemjGYRwP83Vhc6Eg+rXU6lWlgRQXGPYTnm2ueb3OQcUJ11u69a75WwbFiBugfniUinKnaguOr4tQM3+ZDQv0wAS22ZpWusMkniDNJryJtQ1UOaa9VXo0C8W2O93WK3WGqeAWhGEzz04lxTpwzCoNXYUwcjWGPOk3WWMGRCUbJ3zwoaJKY4XuXmebZwYZb8g6HkuOYOHEfvEIM5YdgHj2CGHiKBpX5kzNidLfPMbX8OLlxd4+eIF8i5XuoFAZaqJxr5fLND3YtVg1n2MSAN8JcA8JRKFHeXCy12vpqyg8HZ2c02e7yiUuEkKhMVyAdrtxMU5JVkGylZDJ3GMowa7Z2TwNmEcByxXKzmo9+4OV1fXePLuOzg3dyoWxdaYExAyBjByjPj5+lfw8Xe+g/fe+Qu885N/gVc/+THuvngGurtF3BE6JgTO6nZoPEk1taQzzQGbozEdM0Dd9kQvNFsga6tFNkDr15oXOrjwjEOgdczaYFd7P6VUMINXjM5pwu2ZqfLJ8eIigFRQLucp1CQ1QEAXSHgZT987FvM6B7B9TGoIlkVs6n5U29hY0LWsNivUmy4v5EzTBh/S5T6B6ZgF5XjFbrd6C2Dt6dS20xX57+WaCkQ06Tc13+cEO2bLxKflpVTjq5lhjqYH7eU6f95W2HhrQeNnP/sZfvnLXyrjj+i6iPV6g9VqBUJEiITr69e4vLxA5oSURmw2J2AE7HY7dDHi4uJChAY7dbiLwm6ZJQsS2RkZ4ooUgvq3QohmdTMzQoxgtXZYbIjPXGGHJAGQrCuoAeKcReDY3m2x2++w3+/LgYGchbmKRUO1SYRy7kPmjDRKkPXPfvYTETIWKzx+/ASbzSlWqxV+8we/hX/5LCJ3C6T9Dnd3d7i7vcV+v5eA8Cybz6NHjwEihEil/LoNwgWJov5WJo49RCXVJimISBm4uroqSNCMpWMasR9UaxaCw2vGyHONnbDDfex0Xv1foOgq9xDHsz3Wszh0c1AJGQZmCahH4Uop3rea4JghmZXH/26zXNvtgZ8eeCUAx/uAO2sRG4hQi1oyq5edYF13bus7OeBVr2nvPfSDBY0ZJFAAZ6/8/g8lCPy/+LP/ovz9Z7/1z/BPfviBCBqleAE7Bg4qVJqp22/IDtj6Nk+1yFMmwq6DheYVjjU99nWj0tYUBECJ0QJQLIJkY8HVDxsKBAxkMWSTjF2HKuDUeV6aX/z0AWYBY6bqK1DYEL/RH16g4nK0Ru0I3Dibhnw6//xFWrcFphflic9oNJEDuMxFEzDKCiVh8IHCRICbjue0jVZ3FWynAFosSxYIDCTW800yaRa92o9SrFlc6IAcE00fQ9xpAwV1e5IkFyHWOVSaXNY9Y7Pe4Pb2FqvVutAXEEsPMxAooVv0ePjwIb744hkC6TkZY3WPY54KGzavbc4a/arEx/9/2v49Vpcluw/Dfququ7/Hfu99zn3fmTt3HpwZUqLFoShSFEHSoSyZkoEAkhxYMR3IURwHUAQkMCDbQSIpAgLmnxggggCGZEeJrejhKJKdSJZEWiQljiS+hxxqhpzHvXfu67zPfn3P7q5a+WOtVVXd+9vnnjGSnrln7/193V1Vq1at+q1HrVUuv0QpkQ/ZT1IaRFjlFxFUQxbrbbuOWHCEB9D4Ct4BlSeQ96gcoUfAnRdOcXi4j4f3H2G9XiOyR+0b3WN0rfmS9TIcs70gzaRzeu7RJwAJADmIbThHlJkjARBERmA52WeyhJxD3TTwQQwEbduKPEw8Cfia4KKEfPUhILRBq4x3mExm6LT+xunJMe7cOcXe/l6ums4SzsvMiN4hkMOHx9+F6rs/DX75Lbgv/33g3a8BixVotQE4yGHx2Iu6Sgx2lHj3BmDbAYLHgNN+Gqgtw2bG99m1Kw1qDlFhkEZC3Bb/v8vSTiabMfRklO+/bSy3Wv2Vv0sAPjisXChW0tchEB23u0txGv+964xF3uNunnkZeHRHytBt3qUxWN5Ny+F7rG+7Cg+W/dnlPRrfM1b0xu3ae8ZK4YAmIzqUz5fyfBfdP8prsotfaTSP2+12gId3rZ3yTCWN5J9h3l088t/HW/PcisZms8ILL9zB06dPcXZ2lvokFhcDeMBicY3JtMF8PsPe3hy+avDWW99QYgDX19f4+u98DV3o8dnv+jzmqZo44J2HrzzqukFdN2jbVtOwqsbKkrWEyKXMUZKuUYZRaSXy1Dkqs1WJ0mIMstlssN1sUdXyzGQzEQuSF8WobVtUlbi+Z7Mp2GkoCAHsRGg7x2AOCLHDYnENwOFg/xC//PYV7vnP4PrqCovlCpv1Br1mp2rqGtP5DI489vf2JGzK+QJYUML9Mg7boHVD0r/luPmQMUJg9L2k892sN6IkkGwoIYpnhhxhUk8BWDiyVRQGnJ7bAJAt3AnXUcqkNISerJsXTK8ZWttKBi/HUIRYABDlYHQjlwuTVaCp8lHOcdl2qnVgK8ggRAIQGr6lyLgPIQGVNDbOgJGQF+HQcj0cW1ntU9rIv1P5uf794194Bct2iX/4jX8IAPgH3/gHWLZL/PgXXsH/6b/5WqZF6ks5GQxBiYAchuWhR2iXoGIk3srKwfg+Km9P45Dc/XncqRAhzH4N5YGgNWcEHISgghiErg9aBE3HVKhmkSOaukkpr4MeXq7qGpoQLNO8ANT5C1NGMkDPAyn6jjxHN3jtBgVGzyrfJZ0lodZsNb7xr60XGm7Gg/bT+SjphMmg2IeMkZH5HMghiumiAWcO1ijDDuJnuvR9j0njUDJN0UzWyTB8qSPCpK4TcCcQIiQXu2Vwk4qNpA6FckOiRM69vTke3H8IPpX3lIDE23wz4+6dM9y7/wCRHbzzCBBPTJJRZRc5T2K0CWXj4iwm7UErcCoKCyTyjtUrrDRO/KJKjFWr5xDQrre47M/BfcD+wR4q5+EhscuukpDMalLj1Y+9isvLKzx98hRdaMGo4UgMbIiMVDFJ01RZ+mfLVEVEcMxyro0F5EYFlTZe669JOFObBHwyQLGQa5ws8gTAVz7FqqdK5lqDyQxNtkcFBMTYo48Bsd0i9AHttsK0naLdbrFYLnHnzhlOTk4wm9ZJvwtBU4c6RvSE6Bu4lz+L/s6bWL73FdCv/h00D9/FZL2B327l3GPsQSweODhL44sBH5uRcaw83GYlH4PAXaBw/P5SOUnW/2cArbFMzeBy+H7zqOxKu7qrL+Xf1pcyuqu8L3lrimafJ+TnWQrXRwHMXUrDs0D3rnfdFr40Bv5lxq7x8/ncyPBQd/n9bYqEtVeWPxiXG9il8Oz6+zal+Lb7x+N+Vi2Y8b3AcN8qPUblc6U3KM1p2o+yzLN/TTEdy1nB4rfzwq7ruRWN/f19tF2Lw8MDTCaTgTZP5BFCDyLGdCapZA8O9lFVNUAOnirszfe0QqrkzHfRYzKd4PTsTM5zqEZa+UpT4FZ6kO5AN0sVKNBD4d6hazvUTZ3SYoIIIfSSYUOZpWkaMIAQOzRODmWDKjjvMJk0YjVlCSuo6xohBMyrOWbzmcYhxySEyWWX63Q2xUwzp1SVeHUmkwke8Sm+Ej6LDx88wHazQddKBfC6bnBwcKAudmi41UQ2LxAIDpz96gPwYyhAwBRSBqeh9CLEGOC8w+WT65Sr3ekh5RgkdWHlqwS/OSXolAwkBmSYoWEmhTXBgLXsvAnQUdYsAAPYw5PlOwZUWCVKi4cNiSj9Xno2xsI6W4ky2KX0Z7ZTJiCTEL9sxq4QPKYI21Bo3DaKnwMlQ8Gv9u/f/uE38OrpbDjuIXzFtPH4zCuH+K/+5X+Fdb8GAKz7Nf7bb/y3+OOf/+P43/2PvhObNux81q4Pn6zxX/6Td6SFWzeR0fNKm1IRuvU54wHOdE2biL0L+busaKkVUMMxDPCEEFJcPgPpgK/FYfvKS3V6BbBBZYHE7IUR/3FSGAdjK/pPu6rgKtC6cTvK+aZEJxtPtozrjYXCeHOK9B323ltonrKw2TuMj8Ca6UOrfANZqSw2AeRHhm0P5lvPuansjFHy60uxUBo8kubUSEA3XiXtKtB3Ebp75FCUGCK4GnZjuDoBMMFXlSj4WtE7ezvkfIbI3YCj4wNMmgm6rhUDk3PJmg/CQOljHsoSjP9WmrPLNC/ElqS3JhKFI2Yqp1VO0LYp3d9HxsWTC2w2G5ycHmNvbwpXSbZE5z3YMbgPODjex97eDBfnl7i6uEZdQc4yqGcjAwYNN1S55HVvQLJYMjRxovTJMmOVnMFyrsnomcBM+iHgwZlhJ1pCEFHsiRxc26HvO6nBES2lrngY5fxGQAxy1ifEHn3osG0b9H3AZt3i4uoad++c4ujoEBWqbFCKjMitpGL1HlTXaN78V9C9/B148s1fx/xX/584vXgEblug00PgKM9tlsw4Ll730dcYqH1UWtedCghl78GzrN7P258xYM5KxBDkj9/vXJ71cfvPm2npefpWgtXbgL9xYAmQs5U/x/mXn+/6e3xWZBwKdNs7xn2SsgMhYUa7nlWY8bY+jVnvea+x4vXf5xrPfUmT27w94y3Asj8CBebSZ42DSj5MmA/5zGv5vWyBZfrw57ueW9HwVYUJkYQbbbdSlC9pTYSuJzQccXp2BxcXT9FMppjP9wByePjgIZrJFAeHh6iqCm9++lO4vL7GweExJtNpItSkqsCR0Uwl1auBEGFgc4lBhKFteM7CrXxSUJycrhxkLXAQIO5drcqCh2vEshQjg7wAl7qRFLCWMsy7Kv+uwCeGiOlsDkIAkYdDhcY36GONd6bfjfe+dR+L5QIxBFR1jcO9A8xm0xTDHvWwuBRP8sni6QYeA7s4jVv2OBp8loAxiTeDyOHq6loO3zqNCyZCH6ReCRXCFRofLe/IZwqMmcplaKFI+TI0In1MVn9OkzQ4uCobZvG4Vga+AQdK0JMblrYLcFuCfrIQGiVIpgmheCxR03L2G3jIi4glbMSpgEsW393jLoUIAdifevzFf+t3oameb/P7a1/+azf+/uOf/+P403/wkx/5bNtH/Ne/9AGuN11SpngXzctuJ2Q2hmDjy2grwRliGyvGHfO4mTjPpTJTElZmWfIO3PcSf42cwlnmSsKXvPOSZtM5CcEJAVTVIMumoeDiRu/NKpOELYGK1MbMBS8PsXXWG4w+xnz6WWLvJJRHm8eI5mkNkd1LiebjILRCZzFSi07F4iWFCn0mFfkD5RY72sbg+2yQEHNCp8DRwaNNWfcyIdiJaiab0JBOJa325jNsN1tQ0+S1pbH/0dLHFkvdlKnIFqYEODg0kwbbrpXaHMabkHMcDEaIQDOZ4OhoH48ePVb569BbZjM2xUXnh5Csb87sNTadBsYpz7fNXznl0YhpVszitHxaYzCPkig9kQiL6yW6rsXh0QGOjg5QT8Rr4YkRPeTMSO1xducM+wf7ePzwEdquF+UJDAROgMxCuGIIYK07k4A62ZxIFiqzOKazUaYgkcxlDjfEQJkDA1SZxVuqirMqHF7DmckTXB9UgQyIelYF5KQyeOWl+ngIiEGU2T702HRbbLsNNpsNFosVzs5OsT+bA44Bp94NDvAIkh7TedTzGU6+6wexfflTePAbfw8vvftLoOsV3GYDateogiigEZZRUOjlINnHYMa0ImXssyznJVCjHbLc+KO0fifQxyyFHI1fd4TQlO9Lhizi4vNh2v0xmM5zejsYLvtp/xm4Fi4gWGgxqzSSSMCbBQtve6+9KyurlARC7qvuzbpvGhhN70EeEzA8C7LrgH552VyW9B8n/xnTezwH5U9T4HYpieOwqOLNGCOyXW3c4JMd4xl1uKBRfq/zPu91nA2l6b6kEORnkldCw5YdCIiSYCQy4FjOjxmuCRoCCs10aBEpbJsyAEZETFlQeWAkYxAo5qiE57meW9Fw5AFHODw8xnq9Bpj0M6CPPapavASndIbrxQLrTQvnG8xmc+ztH6CZzuDqBpXz+Ngn3kQfIuome0aILCwqM14kOSNhgrZ0jZaTOUxjmxmqXIAyUdpWMUmOCFEJT66SgkzMAGnmqcBwVIEjITCBqIJzdq9YDCuq4F2DZvYCzleMRw8fAQTcuXOG2Vys2zEY0KLkEXF2TkInmHHTpWcbZQbeJevLzkkkFcyZGV3fYblcK6hgRKeph0MoGIny27nk61LlIEAPqCalQZkTHNXqms8gWFabjOjsEF/xdwrKt97vGquBwhLoU+6HWtd0AsGO0oIcji6HaiQlBFy0KF9Ith9IIgJdN3KIOQMukaMaDGZtGQIwJSVGXK0j/tRP/XP8J//T78ELRzN88+k38Wf/wZ/Fo+UjjK9lt8RXHn1l8Nnf/e2/i+/8v3wn9uq9G/ff3buLn/rDP4VPnn4SDy/X+F/9Z1/C9bpD9kSpwE8Ays7Y2DSUczG8sv6hNHeltV4B9dAsldaszZc1EWOUGH1mPYyogJkFZFQ+h8pk8SmWdkcEXzm0bYfQM/xerUtD64joWCyDRlIIbLwKBLP8Gx1ETHS6hRLKwMx6HobtHUibazluo7kBWOHFDCZyu1ROy4j2Vl8EBZApYm5tcgpgnPiR83xb2/pQVmIiAER0Xa+1fAh9H4WkPiHXAYkovyaBW6dNNVWNVVxlmuvUELJctnXHSphhNWuASYqUrtdrNJMGJYgWmtjdEWd3T3D//j30ThVIyjkgLMf7eG4H4tLkGlkzfOMmk2W2vtP9KW5Px1DQQ7wCJClvQWg3LZ5252jXWxydHGG2N5P6SM7qVcie0kwqvPr6q7i4vMLF0wtUzmnBULklHao3fiAxfqT+WQER5RHW8ES2tLwFAIRpFcbFnDeP5M0tQmw4RrB34o1ROpEjBE9AsLM9ClBi1JBfDXWMAdxDPBxdi67r0Xc9ltcr3L17huPjA6mT4yHng8BADCDPKnI8ZndfxOSHfwLdNz+Og9/+eWw/fAgsrkBYwccAcABTREh7la41qXQy2P/HwHZXpqIyhn2XZ6QEn+m5cn2MgG3pIRkrMKIcdZK2P7AaQzLAIxr2e1e/xh4QibLAoB0AWjjZq8zKoV6przvw4Xis47CjHWK0UL5M/qsMVmUjwtbVzT6aMlUqCGXbpaL1LM/RLq/PzQLKuf3bMmyNFZ6Sl2xNlc+Oz8Ps8jDs8sIkA0fRpxvj4gJn7LgIN/euqLWRRNRI6KprGqDaABLUKccIyOgeJZM0VdpmHB4MBzDIyFN8zorxIt/s/23Xt1UZ3HuPpmlupJwlHmYaqKoKBwcHYAYuLy+xXq9xdnaWYhJjjKhqh7qZDMrEj0uajyeqdCfau+zvqqoGtTVK5t11lYwxth4MBFMf0r27YgOdqwB22NvbxzvhDI8fPkLfB8zmE+zt78OAC5NDRZL6djabpbjXZCXATRAC6AZBGVjlcKBy45YxeOfw+Mm5hrHZApGfIWh+dQPg0qKGi3BqXzB83ok126LgFQU3AiQKJckWGAg0MNMiCRpWuiYsVP5+Y3L0H0pvLYC+fEfaeMYZlIG20gdUvNvaIwa0Iq7ADgkpc5ZWcTAke8mw7dyv4RwBwD/5ymP8a3/h5/Gf/Lu/Bz/6uz6Jv/xH/wr+7b/zP8bPvvOzNyd3xzVWPgDgX/3Ev4q//Ef/Cl45fBk/9+UH+F//57+GJ9fmybC2CyraGgDSeXzQboFdkhvQmFQDkTbfelee5TxuKmq/ALbxC3050Uz6IZnmfLYqJ0AqBTnJDoRDznh4Yz5HqqRaT/J8D8OnbLCykac1YuxYAn0GzGOQO2+hMaTY3uLn0z8oKJvBsTFMalvWHWNI88RT5QEgHlBTACQyzQcaVfpszOeU4mtF5kHDn5zwNzNCsOQY4tk1SULINGFkY35JK+thYGA6naB/GooeMbzWpgiaRtP7AuIWIMQeYpZ6Go8ePcLx8XFqm/Q7+z3GiJPjI9S1FB1sKq/jU/q7zJMGcqzDA4oVBgHD24OsZMX6Lq2FadIUKEZTCFXBYeYi5E5C0q6ur7FuNzg+PsbBwR4mE6mAXnmHEAHHcm7i5OQYB/sHePTgIbartSgYIPShB8eAuqmT0iZbkfAUUZ5vZoaDE8URqhwPeG3EOso75rkClQpwnnhHDuQrRIqIFEDRoa5qdH2v/YvpnBtHgqscYiTJNNVzyhrXtS3W0zXW6yWur+Ww+P7+HnzlEZjhnRTEJdfBUYTzHr6qET7zY3B3X8br7/wi7n3lK1ifPwVWV/BdiypENFFMdsFxSn1tCe5yNiNoyHMGmGNL9LMA4gC4F+dAhDeHWKTEEWMvyPjdIBrMp7X3LKwy4ON0f3p8kMEpGSuKMe5SXsag2+6/LSTMsEdJvwHNilUTY6Eo3+j3TQ/G2EhsfRy3VT47xobl39ngMbx3V3HEXW2M63cw7RjvqM+72ivpP+7jbddH8cBOxUsFrdcMrAGMLUV89/d+L7Z9h0cX57i6vES73WC9XCJ2W4kwCIzYWRA9pxCrfPkkP0q+kFpEFRB7VDuKO+66nlvRWK1WqKoK2+12aB1QgRdCSPUh0ssrj82GMZ/PkxZIRJhOp2K1VItC9mrctDzYokhVx0dp6qRuRSEIeJh9oFQQ7L32mTFkXVUpDMvusfe4gokGggNA3wV4zYH/6iuv4Ve+5vHw0SNEjjg6PtZQCGg6WHnGe4/9vX1U3mucpf5XgH271/7O2SLy5mjfm9G/73t4V+Hp+VP0IaQNk0iydYVY5L8n0rhtDBszLZrKqAFTRvTGFJaSPTA8epEBBgNkJpztu8H4rJkSJJSAMD1XiDkaKi6UQIw+FDPwLiG40aPM1oIoVkRfWextOcd04y1lv1LbCTCKkH98tcG/81P/HH/6xz6J/+iPfR4/8xM/g5/84k/iz//cn0cfezzvVbkKf/FH/iL+wx/8D9FHxv/+b/4W/rOfeSsJ/TGN0gZTgqUSR4+AdvpyvCkWoLkEODaPCZgos1hoDwE5kwUDHCzFogAmUeiagn4x9csMB1XdYLttwVEtqDBhz5nGxfzYC9gGZ6CbjecK5TRpzEYnDBgkAW8WPrfVlpWRDDbGjDzg5wT6RxOqn7ONYXBow+3ktZjGgWLysrxItOQsG+w9ySoWgV4LqQGs6bxZklkQAM1AZWHfDAVDhayzl1dVha5tU4avUvG3TH2J5qyrRBVWexezpMrtNc25c9kYYXMQWSpOT6YTHB4d4smTiyTXyrHfkD2k1v0B3YeyJd1n81TSHMr/JrcoSzBnSkaax4L+MSZZ3W46PHn0BNv1BlJltwAAAQAASURBVEdHh5hOp6jqClJEMcKReFKdJ7z80kv4+te+gdhLaIPzDr6upNZRTepBzhHTPACookiS/W7AMQ88GVwGa99J5kDZIyQ40VH2Tps3w3n1tuj5m6qSs5ExBIRUC0X4kzRzYoh9qtuyDpIO1zI7Lpcr3Ll7ByfHx5jNGhXTEgbHjhEQETiidhXunXweTw/fwJ0XfwmH3/oSHv/O74DOr0DLDaq+k2JhFNG7iCoSrNaInqlPGXPKNXjDUo28149rEJTXbeclxvfvAptjcO1Iaq7k+dgdclX+vQvcCj8SxGM47BszYI4vHq2Vcqw3lKDi9/K7Z3kUcoNIwiePffjMs8B4+d4xqB8rGuMzKONx7Jon4GbY1q5rl9LAdFOZGSsQt7VZ3reLluO/x0rJIFXwiB7FW+DYdhZRviMiPvVdn8Pv/n2/F/XJATarJbrNFsvra3z4wft49P57eHjvIa7OF3j65Cmurq4QQkDXddhuN2B2AMzbIXui1zSFgRm+nsDv6P9t13MrGt/4xjewt7cn9SBWK3zsYx/DdDrFbD7DarMCM2Oz2chLqwqPHj0CkVSknkwmuL6+xt7eHiaTSY4jVIKVp/xLopq3o1Q2iCh5L6ADtewQpfJQ5sm2+8YLcgBUtU9jbTiyhDvZ+y2zFZFDVTWIfcTRwRFmsznuPbqPzaZFM51gf38uAKjYGDlK3nTJ9EHFgRrdjPMeksGxrWEV6EkZQN52orrN23aLzXojm55zcL6SeiBtQOj7BBgExAVIcSSYZpCyG6UN1nLcZ/Q02OQNHIjULD6xF9jYFLwkz4w+nYERFwlwdHOwhvMfGOs7qe2yN7Jr6r3WtvQvk5dh0QoAI3BEpdaAIn0LqGhb6D4UFjfOPDBSUUZmxl/+R9/EL/7OY/yf/73vxX/8Q/8xfvSNH8Wf/H/9Sbxz8Q4+6nrj+A389T/21/H9r30/3rp/jT/zn/4qfuvdywx0FdAbKNpFcyPLCBPDiFmCD1IeiAmAIIN2ZAHIgzeVbaswZk7KeQQLgHWEGNQySJaVquiKy3PjrMI4Qyswe8TQa6s8dN4YuB7zms6LjUlIY+MtQr2QHxv8QSVw5yEBy3iiRN8cpmb0SQaD4mzCMAvTcD1Zn7JBRoEjKfg2XiOX0FSyKvPovQOQIyEMAupN7mpMv5EshVoVkiXFg8k7HMSp1EwaSF0FoDKZBT1czCHPAey8hUHXYuXrr5Wdq3NVqQskvowcUZPD6ekxzs8vEs0oWXDicOpQgikLSyk3aqR1bPpC9gGM17fJbR1PFlZK85hkDaf7NLwLEX0IuLq6Rtu2ODw8xP7hPuq6FlDu5CB2DAFPzi/Qdb2ERyHCRYdmMkXXdYndRMlWxW4gH+U71rrs5tWwSxxY1ulCrqV5oILmxoesLJS/q5xHMD4LAc5X8OSkxoamwwUT4CXxiyNRIBEDuGfJuKi1o9q2w2qxxNkdqb3hKzt9L+0HjgDLGUqqp/jwlR/CZ1+8gx/4zKfw1V/4JVy8/S54sQBCjwAtAsqU5i6qZiWRFqw8Odz/xyB3l3V8F4C6DXTvAsa33Ruj3SPUFYxyE6CO370L+CfjI+WIi6iK+zhByFARKfDPDky0K2sXOYn9321xL3CbtVXIoXTXjr/L95WH+3cB+LHSVs7TLsVDihZ2I2v8zXeMnxsoDbq/j8ddGrDH9Bzfd9u4d/X5NqV1rAwP+YuTYh3BCBDZ+7f/7t/Bz//aL+GH/40/jNdefw1PnjzA9dOnAAJe+eTH8d3f/304uvsCYghYrVa4urpGF3q8/dZbePjwKfrg8eDePSyuF+g2WyyuryVUE4CfzeCcSzj8o67nVjQODg4wn89xfX2Nuq4xmUzEKtX1aaM1AuztSYz5dDrFZtPiyZMnuH//Pvb39/Hiiy/i9PRUC+dlopZhSaVLz4hph71N2bDP7e9Saywnx+4dKzfpYh5YsceKBiIjxJC06F6rtzrvEOHgvcPrr38MH9x/jLeuGkRucXp6OgRTgobAMWI2m2vcbg7VsTU5/l0fk3EU3dZtLb08BqlN8vjJOdquk3uI0iZYeoNijIghb67DcxAF6DF0wbC4qQQ+x8oGdONMoKlUDuBgISQZ4o2eH8I+/SL7E9KmnxaWnqHQ/hjdAEisOgy40qhtjN4nz1vaYqexx2xtG/jStscA1QBD/qAMB5M2f+vdK/z4X/o5/KU/+d34Ez/4A/jS//xL+IP/xR/EL3/4yzfHrNfvfeX34qd/4mdwND3E3/qFd/Hn/8aXsdyE1LiN27YDA9sJrBqNSa34+vdQ3hV/KMNxSfPRuAcgZbyJJVBtGWwMjLPWVRBahz4UymKGoBwZqMSaW3mpncExgjQ0U3ghp/NF0Z80bgWHHO1sEANcWDUT+9CNSLMEIDnThUZzaYNPn1GC6umeYWiBfZHBepqdcn1b35kTXUq+GnszTAEq5yDJvUJBAkGt0aUMEI8dQ5W+yqfOWkilYew8NOmp8VrlqwHPG7Ag5xA6ccdznUO4ssJVyDh9cj6fY71aozo8UKBYZHVigCEZU05OT0FvfUs9FU7ky+CgdkH7RIeSNkXb5TpOZzOEVqleg77XEo5YidIy4g1kKdf1e0tTHPO9EYz1qkXXnWOzlcPik2kDgoN3Do8ePsLTR0+RNG2Wg9JRC7k53fMcIFZEDV22fWg4QwAcpfTIMtig4RCUFZYxP9m4dOxJkdIvTb47Lr0GYkCrySH6kDJUkeS2BpFTfTgghA5MjLaTvP5916NrW6yWK5yeneHszgnm84nQMQJ9H9AjwFU9ovfwvsa/dJ9Dfdbgj/zpz+GX/9E/xm/9wheB5QLoopynTLiYMjU0CuC24np2PU8a0fJQdCn6brPmjkHyLmu4c5J9Ugyi8t7bQCmQrfG5wJ/JkV21Laxt7Gx/V3931RgZgl4MlNjh+8YCNX+0i+63KQdlFEp5DvejrOa7wD2AlEV01+Hx2/phn2elzAaz+xrPa4lL7fuP8niU7xgrec/rMbB7HREqR9ib72Hv4BAffOtd/MLP/RxefOlFXF6eY3V9BY4BlXO48+KLOH7pZXzmM5/BL//Kr2A+n6NpGnzue74bP3j3RVSTPSyurrG4uka/bfHgw3t4/PAhXFUhsEQNbbfb5+rbcysab7zxBrz3ODk5waNHjyQXuyob3AsBJ5MJttstmBnT6RTee8znAZPJBFdXV9hut3jnnXdwdXWFl19+Bc1E6jnYBJgHoswMUB6wGodAlVkm7DP7faz9lYvIYikBndgii8RgYm3TZ0bXdYMD5mbt39/bx+npKf7Fb/wqrhfHqKoK+3v7ioky9GNIkcGmkZhdSuOmtLEz5HymNq0KBWO8pAcwnbP35vLyUgrFOQ+vm3EIAW3XKQgMxcMl2rFt2pQD/b0QVIgZxA86Y5sU5eConOUnh1fpN+m5TGa958ZipvQNgGShIWgomvWraDtZfou3Ja9EgexsO7JnY5TwA0cOPbJCmnihaHsgUK1t1v7FmJXuYtyrTcR/8H/9EjZtwE/86Cfw+buff6ai8fm7n8fR9BD/t3/8Nv63/48vp1b5WW2zUlHBRObjTHOMaT4C7QOaCwIuFF4avQMjmsvXUpckb/AxRLCLSdkvpiytuaiHX4kkmw1Yssz0oZdD+uRQho+m1ijPt/FaRrYl+ESedBq8JP/KpZJVPlKOW2mrNE+8Nkj9BAGd47aVsk55seStAcgp51fbtnMzZdHC8gA8bgCZYpq07RCjHlxWi756A8TrICON0MxTZUcog3TSvtS+UpnB6T5zsUf1tlBqO7FSukxkTGdTnD+9wOHhoco1XcdJiZBDi3t7c+zN57i6XsKB4Ilgp0SSQSkpG2W44822B3Qu5yB1rqSjgnQlAqUq5rqpO9LxlspLBu5MUmiv73pcXV5is93g6OQI09kU02mD+WyGx4l+Dq7yuKNpYd9/730QEeqqkvAyFoW87Vrxmuo6cuTgU3aqfG4xMsteEgogpaCJyKhU0k4UiSRT9X7JRqaKI+ladFHWNbL3k0JApKzYALJ3kqvQ9x16zSC53kR0bYvNZpuKx67WNc5OjnG9WOH+B/fRxx6ECPIE7xy8q/HNeYN/9s1H+PHPfhrfOfX40n/3s3CXPSYd695aqREtz6Hw9+0gr9gJ0pzKvA/BX1VVBd7YzU/l87t+Dq3waZUZp6W/d1nFgV0ZmtQ7UmSzGoLU3UrR2CMybm/X34lSxbMD464N4ZZrFx1uu2/sYfmoq1SkjAZGh81ms3MudvVjPGZTdkSOfXtgf0zXsRI7Vvw+ii4febEYNWRFSxjVZrHE/GAfB80Ui0dP0C0WODo6RGw7vPzqyzg+OsK2a1ET4a2vfR3tcoUHH3yA+XyOd996C9VsjrOXX8VmtcbxwSFePLuLrl2j8sDR0T5eff01XC8WGo770ddzKxrNdIoYAvYPD1E3DfrQo6prrLcbyYFvbnAvr3TOS+hOHzHf28Pe/j7atsX19TUuLy/x9jvv4I03PiGVxWnorhvnOwayEsEAej10aLUy4JwKPq2qqpsnm7ADaY5+uygtVClEZDm5kSwNrJmVQt/qeFwSEDHKIg7o8fJLL2F5vcQvfDhF3/c4vXsCX3tw7NMGThCr+XxvnrwhAjxcCi8ocMVABI03ffvdEqLI1uewbXusliswETxBUgdCvDEh9JjNpjg8OMT5+YXW9jALNyVaGZ0TskAJiLgQJgoJDDEUYBOQDbYcyXBMJqlNISgB8XCxZY+GgWgoINTbBQFD0rAWygbl7iboQUIrUVjiANhEja8eFOcpQLkpLvnfQjXStpMldQB2DNAAQMR3vHqIEAP+3tf/Hp51/f2v/32EGPDZ1w50TJzem2hJ2gP9mRWxXULx+WhOxb+DWbMNZrA3cjqgnx4jBS+Qom1SKE7S2xIstSVhcEpGNWqOEXVdydrXlLkxRNSVx2abgSGDBfBRBt8o34XyTx4O8RZWu3XcJZ8XbRSlNgrQlvkpP5Ib4nTPjvVNw7YzOC4UFlMyiECcM7qZxV6xcG5TQ3jSvHPUbDQRzlUIUbg4ara4sSJQ/iKAVkKnHES2RNbfIXl5LcbfQG4+d2E8cXPcdd2g7US+Jk9UOYfsECNQVx5Hx8e4ulqAXRE6msZtHbXhF0qGraACIabni6k174T1jhOHcuqXnX1KslLbdirAk3RgpJS9tqtxALabFk8fPcXBwQHocB978zkODw9w/uQCcIzK12i7FhGM/aND9F2Hvu/R1B5tH7F/sI/ZfJb2y65tJQNkp/yRaEJw5vkh9V7FzI2ylkrPmOwFqXBk4qGs2A7khHPwJMa2GAPgKtSOEKJHH8SrJQBfQpvq2iH0HULopfBt7NGvOmzbFWJo8cJLLyH0EddXC9STBm++/obUu4IVk2Vs2w4Pu1fwX3y4wmTVYv/sFczjh6DFAp5FXtTk5KwHAVvuERyD2AGcytvCkSrXLIdm+z6m7GA5MkPOz3DaX1X+upvSdeC5sKyYhlUsZKdQaGM0BRYp8YodhxorOMDN2hKAGVGtXUoLgSMBLOMoMZWdYx2/x64y5JyhSqq31V2GgQ7Pd+TwoizRZY+Vz0qgfasCM1IEx6B8rBiVfS7vK9+3K8Ro1/tvo8eYNmUGQilCm/ufJMZIgRmf6xn3aUyHoSK6OzLntn7aCo2KiSgywmqLq4tL8N4E1EccTua4e+cFRA54+OABNpsVnCM8ePAQkYEuBGy2HZbLLZbrDb77e34PPCTBxc/89D/G4cEBODBiL7XY7t45kzMdfY8f/Tf+6K30s+u5FQ3SAkORI7Zdixgjjk9O4Gs5ID6ZSJ2IMUNLkR9x+9Z1jaqq0DQNHjx4iHv37uGNN94YtkPZbTZeZKxCr9dMUOJylrz7rJYC0kVFJEqDTIQWCGObUBUizPIMc1IykgVcKzdVqRKutCvSmBCZ0ExqnJ3dwS/++lv4YDNDVTGOTo8hluIcqx/UUjSbTItzGQWj2oZZ/D4kinahsDSJACBlfIerqwW6LiQATASEKDScz6c4OT7BfG8OAHhw/5Hck2IBTJgi7TElqGcFkJmWuw5Ske5NJaC6CTAy6KDyyeJ3SiLLllDpCSmfZBYvkSOvRcgKgT2C3MJDeQO1sAkAqXJy0jPyV6l3Q4iSN+RBeFcxctmkMyi5czjF937qFD/3rZ/F49XjwXg/ffZpfO3J19Jnj1aP8E++9U/ww5/6Edw5bPDoajtsmw1IJrhbAKBi1Fkr2TGWXVeByMt5pGHbYsUiVUDyCxPcTowkmYhC7OFdo/HJyZ+X+Fr6HVHXUmATcIgc0YcOznvdOJEq2Jcb92igiaaDUDka3VLK6xJDkW379tHN+S41DKLMoeluhp55oBHtR3TfscaSbGDjV6O5FdmwNWaeXQ1pSJvVaPwKPqNYVRD7XMCqV8OMtK1Kkn5QYPJECzlDL/2YzqboQ0CFSvLe6gOkWfUic4nZdbCZzHb42GvK2q7rU9HWUswJMGOEyDg9PcV7772X2pKNO2bvx4C4Iz7n4ucI0JlyYO0Nw+WVjkWIVTIyJL7R2HUDWDYRygdsdYCI5FB+G3B1cYXtVg6KE5m3W95fV7WsGUSc3jkDQsTjx4/gK4fpfIq23eLq+hqVc6jqGvsH++DIuF4uwFFDEznzCbkID49IorgjZSYqPHFpgynm3Cai5HOlQZLDnvQzBjsH9EFC0MzjES1Pvxb7I8lMFZnhIyO0PZ6cP0XbB9x94SUsl9eYzSaYziXSofIuibkYGOtNi/OLazxcE95/40/An97Ha7/51/CJs310yxV41cK3LRwDjdX2CTKOaFkSIdnvrDqQS6DRKQlkYm17IBReQwyvMUA2lmD7rrxXiWpe16SMgmAZAZ8V3pPaICrWew6RkssV6za/67aUrvZOIBt3I1jCwpmTQmTgnYoxl9ElEUiKxvjd47O3z6phMe7j2FsxVsR2hRXtAu63XeOsW+P3JC9SWc/N3q91Z6x2yC5PydhzsevapVDs6uOzFRV5Juri9CxGIOcdztcrTKcNJpstNiGgZwZVHpt2kzBR2wUEEJrpHI+fXuLRxRW+9OWvwHtZE9fLNerJDC+++LK00/a4uFyCmXF1dfXM8dn13IqGMY0xSl3XiDGm8KmkWOhZBlMUnB7UNgJOp1NlUuDRo8d4//33cefOHVRVhUqL7ZVMVWrmEuZkMYqZ8Pb+MrXcsyqGjr93TixAuypHxq5NgsF7DzCJFyRGvPHxN3D/wWP8/IMD9OEaB4eHmE2nkGBVAbMW5lA3Neqmzox5S47qcqNn27CkM4blYboQwc6oVDh/ep4PghX9JwB7+wdwnrDdbkRgOoIL9i7d3EcHBwUjlQC/wGralwGIEs3FtmGYwB7YAA2g7eAtmNBNEK8YRyHEMrDTxRWlcJNZ9XO4Wv5pbVvafQOuIBEYIYRkhUrAawCUMojedeVe3xy3TeAf/p6X4Rzhb3/1b6fn7s7v4q/+D/8qfvzTP46/97W/hz/1X/8pPFpJzY2//dW/jR/9xI/iD/2el/Ff/vw7BYpUgaY0ZwsZwk3al6D4xjWYw9Fgx5+UbY9AnPSDU8oiSaHMKV93CCFlYw3q1laDnJ1vTfPpq1ozqcjbHZEUdOOFGgRKBWI0z8nqE2XTG9+2S8kYv0ZriNi6uUkXUyDMjwhw2QcDm1yslQHJzTro0k1JoUggJK/vcfuiuEawnk9iPRhOZkQxQF8CZn1XCFGszZFRVXIQmSMjOtUVlEaUNs9h30n7GsGYz2a4XKxlPEW9GWeGj500NvCb6RIjMJvNsN6ssa/n+owljT1jlJCh4+NDTKZTbNdbqWGUlAMFWuV8D4muc6LzU9Lcph1G8yGfMxvNjTbQvaAM1UJSfosArIHMTjyjYUUhRKyWa3Rdh67tUPkKThW4k9MTgKSA5eL6Ggf7e3jl9dfw4P4DLBYLnJwca3aYFgBjsVjAe4+jgwP0ocNisVTeIknEwJLpyuRCsDEngI3Mi7bBFEonyCRowRC2LehG5aXDOWwrWDRAjz60iIHgXIUIQuO95POPVtOlw2a7wb3794AYcXnJODx4H1XlMZlOUenZmRB6rDZbXF5eY7FcAV0H7w7wO5/+4/iBz6/wmVfv4hf/8c9j8f49VFdrzFYdqjagrToEigisBf9AiLYHR75hGRc+NmOl8baFO2lymBGDZ8s1YGBfDJlZiUmFUgZsJmdq8gmom9dtwPojQ4w4Ky+7AGz5nuQN0DCJsZfB/rYQ7fEhaAYPlt1toNnae55rV3jRbZ/faunn4fmVMSZ81nO3lVkocelgvY8Um3ERx48ad4mty/MySZkrMPS4Lad40gwd4nUmeF+Be8GvkRmbbQvna1g94V4NA1UzATHBVY2khHY06Mvh4QGWy2XKmLpdbcCdhOSPE/zdOr7nu00GV1XVAMiXv9vfVjzPhJB9Z4Qxz8bR0RFefvllxBjxwQcfpLMdu0rHl32wGhG73Golc1isnv1Xvq5sx4oQ7dKiJQ+3VhqHAlFtY9JMcHx4jJ/74ADvXsnhu5PjY4TYF/mIMyicTqcJWCQGSXcNcZDijvR3Ao0oMBHE2heZsd1usVquUv+994gsBwYpKWQSP993XaHkiDQkGLYzeCU9YhhT86htE6T6ebEPlaD7xpOkn2uNBWup3MPMF2FW7uKkX/GuvMSp7IfRvPgrfUqk6YR50F7iVYbGPpfCMfcxtVCkJL2ZLCS3ObBoEeFf/55XAAB/56t/BwDwY2/+GH7z3/8yfvzTP44Pn67xRz7zR/Ab//5v4sfe/DG577flvn/9C6+kd5Tvv3GgOfXXQBQVzyEzVAJow/fd4EDlCyVNmm8Ds0NNw0KGXLJm51jxAgjHmBGkkRMSvhMh7npfWUo9lmw8tsHHG3BnSHMavFTeUSrK5fof/cyvyuPOmmixnYz43OJiBzQvABqSfLI1ZmgeOWNU0UF5lJLCMebzweCV5ineO737hiSB8byFoUTofBagP803zNs7orCuXQcxMrXbbcp2B0Cdy1o/pQRAhVy1sIy8Nhjz+Qyr1SrLcUDPv6l8Z0mL3DQVDvb35NmY32P0pJ3jRqYHGc0of5y+SlTOHzLSORiikgbysCkXMnaybuS9o5w/Yqv7l9ZEjBFt24EZmM3nOLtzB9PJDFdXV7g4Pwc4wlcefQhYrpZ46ZWXUDc1Ls4vsLe/j7puEiBpuw7X19fwXjJ0+eQJoMRzdn7DZCDrJJt3w/rGMSL0PULo0evZvgS4bbq5AKgFTzrd36uqQt3UmEwnmE5nco5T+0DkUNe1ZsnRfTpIeG/bdVgv1/jWt97F++9/iA/ev4/33n+Ad9+9h3fe/gDvv3cPjx+fY7FcYdV22ERGOz/Df3PxBqYfewP/5p/9X+BzP/YjaF57BWFvH6GqAU8gx1KZmyMYEYGALhXKvAkGjVaAhDqFwFn+FcD1Bv4p5n+0enZeVMzPs75/lrJhPw1UJ7wzuhf4aG+C/W33VVU1KIY8VkDyuZHbxzfu1233lOMYKxW7/h5/dxuQfxbtdilNZT9u0LSY8486YF4qHGM8O1biynGMM7CWeHpM99SO7q/p/Xq0oG23qKoa8A7XqxW+8dbbeP/DB1isOkTyCHBoA7DtAs4vr/Ct997D5eUlmmYC0rbFkdBgOp3i0aOH8JVHM5nglVdfxWuvvSYRP89xPbeiUSoWJQMZAYyYpWuNMGTusqCNcw77+/u4e/cumqbB48ePbxB+zCS73Ee73Gtjbb/UyL33N9+TsJjcXzKGcyZMfAJAzOLK/4WvLfBue4zrq2vMZnNM5zP0MUil1D7Tw5FDM5mkDepGytrRTjZa+1nx4OEHlq7y6vJKCikpyBPLFEv2kqToMUIfRKEzQVSixZLeXGxEo57cxLac8NVNgVk+TRm9DBZGsQCL9xvETxV5eVfb5Y/b27Z5A1SZ4GKckNCSyBKrm7wlxoMJfuVhDADlaJR5JPmBk70aP/AdZ/jiu1/E49Vj/OSP/SR++id+GifTO/gLf/3L+IE/9w/xF//Gb+Fsdhc//RM/jZ/8sZ/Ew+VD/LP3/hl+4DvOcLxXF20j8exw3IXALc3ZH0Hzm73PG59iM1H9EvDOPwyE5bfIv5GjhNepjOhjzgynZB+0Zo967+GdQ6Ve0RCCVBM2C7sCP5uD4TrJNLf5zuA+t5GWEPNQUSRCEftS0C1/lN9VbFj6v6zviBJI6Z25PaOZra1B29DK9AkAFi19xBobbHgJALpisPKKvu8l8QGrJ7R4nXE60ei9xRqzVTCZTjVEVvul9/lBXHJ+90gK6HIWetR1g3bbFt0v5TFUOZFDxqenx4kXBNwbn9KgdkYmR2Fr1fke8CsjF68bU9X6oUSKUTKoGeAslY5k1tP5TvuXHuKPkTXVaky0YpZQZDDQtR2WyxU2mzWuri5xeXmB9XKJ6WyKqqnhvMfV4lqKAB4e4MmTx5jNZ5jP9wTYew9fV3JeA8DpySmIHGIUZT0GCTEl5+CqClYLKeoc97FHz72EOFYOJ6fHOL1zCtAoj3/J5yZbSlokuuV9zLsK0+kM08kU3lWQQDNJE086B33oVfkKCBywWC5xdXWFR48e49Gjx3j69BwXl5dYLJbYtFs5XN532HYtOo642Hj8rbdP8Yvvb/DZH/oD+P4/9kdx8j2fw/rlY6ymDbZ1jdg0gBPPkQd0X9wNZAW/VPC+UrzglRE0o9YOfgF0b0npFGTvYhZlZXAfmYxS+hYA+1neB+sjkLNjjgGwXWVinWTYLM5ilO8a46nxZ2P62LvKz0rajZ8p+z6m97PGaf2/rR82fgP+u/ozHmc5tlL5GWPacf0Ke0dZddyMYOV9Y6VlFy3K/pWKxBjjls+bUmT/2XPa8oAH7H1d12M+nwPOYRsC2hDRM+Hhk3OcX62w2HRYrFucXy6wbSV77N7+HqaTCeq6Ko461KjrGpvNVpJATaeYzObYOzjE3RdevHUOy+vbqgxepkntLI3qaMLs7zJLghGt/Nx7hxDE+j6dTnF1dYWu61IYVsmEVvE7Ab+CcUrtu3RXlQqQ9z5Xry2UCFM62A0Po5eLc8yIRISrxRrvrz6O8/p1PHr4DXCMODw6QrvdwDcerKFhUrgImM3mA9AjEaIDDCObXo6owBjUF/XgYIwlqQ9JivT1fcJKDIbl667qSmJdte2+Dxkjk4VtAGVQiozVMq6UmHrQI6CYi+F99kcRyqN/y0/ZjPIItcpSkeYxA6b8Lu1dtpKP2+b8R1IKUQBcNSsS5b4QYgIDlfcg8KBUgqkZGefygAdvXKNxMwP/2u95GZV3+PX7v45f+Hd/Ad/36vfhm/ev8b/8T38Fv/XuJUAO//nPvIVf+tpj/NS/9wX8uR/8c/iRj/8IfuXer+D3v/778Yf+lZfxN7/4XurJoLD0YPwGwotNwzoO479SOMlbKD0zHFMZBiR0o3T4OhX4KsCsEK08gNij73p4BYWsYK2udPPNqB8co3gPKzmTEQseTKMlm42b6pG1bWspW9oKxG58bn21cVv4DxXvMrKR0bxULoZ8TjTi/nID0B4nGlvbKHj8Bq0x6vuQz4cdyZ9yMW5KqFqKuoHF+BE0lbN4l8oVnuVSSQVjqbLtpmluWifZgIwYQCrk9OUDOWfvUkBq4aohRo1/3jHHCkJPz05R+W+h72QfSQEptl5NNyjBzY35Rp6qEc3LL8mydCQyZ54ok0bwSK6Jp0oIJ/VY5bxR4g4GtMKMWPVVPq3XG+zvS1jxfL6vnj2AvINX/LpaLdE0E7xw9y4++PBDzKYzHB0doe97dH2LGAnr9RbHR3vYrDfYrOUsZV15NNMGTd2I066ScGYJ6maAGE1T4+T4JFko+67DZDZBu+2SckSWnVHXcgrVg0QMWMgigVOWOFI+d+RQ15JEhvVQOJHI8q5r4Xwl4ZYcJNyKA4haAXOsIA6cbQHmcWAJCXx43eOX9z+JX7nvcDC5g+/4kQOcfvp1fONf/CpWD58gLFaouYMLAY5iccZG+1nK84EwMLAb9XcP5v4GuCdda+X5KSoyAMpt8o6krBo/FKwJFN+N+1V8d5sF/7/Pfem/0XcxxgRoxynyxwWUTdaN+12C9BKvlRitBMil8ZqZhxEyo77tUnxuA/vld9a/sl/jdLTl/WMc+yxaPist721tl/fepqDtan9Av5I2LOds2r5HRcB0vpc+c86DNxusN6LckxaNZjg4L9h7WkvtOzg99qDKTVURLi4ucHZ6V9cB487du8+kiV3Pfxi8AOlVVWG5XKJt26QY2LXrbMSYKeR9DkT5vMdsNkvEG2prkl7OvpMzkVnLLRWaXRqyMa/XGNIy/7i5eeHz5+V7SBoQD0BSlhhP61dx1Xwcm/UGT5+eYzKZwFceq80G2DKaxqOpJhIjxxGz+QxmDJL+SvvlfmcbpRrB0vcgDDwg5W4dY0S7lYqrOc+2Vm7VQ+KVF8tMjEG13BZJuzAcmhCFxTuX8FXAyE3cUygRyCCcB4NC/iUj9TS49CvnQZqQtrSEKJUNa9vAlW7yCunTpk/jtjPKLNpW4ahEjTEAVaWZWqzCbjnCPO6boDz3RRQUlqwvuon/+PfIIao/831/BgDwN//pt/AX/sZvYbXpE62YGV9+9wJ/9C/9PP7iv/W78G/+gd+H3/fa7wMA/OEvvIK/9cX3ctu6MxkQTuM2IDBGh/az7DYT0vmcNM8lFMzPpHHb5Gp/yYAGybMGEcUiqGmpSc4HeBcTqE2AGIWrnMTK2NQ1qrrCetOm522u0jCUGZnLORjOc1KyikP/xuw3x22DHQLIcr5NlH8knw8fHvA5jAK6FvKZGuW1AnBY26WylZQPRgK0lF4o40pCRN+RIsBZzmVEFS4hZZvSTayQM2PWhsvKC4E0O5jVzkHi+cQmGo4qh1yx8zLFi1mKAG7WG90DdgEEgDliPptitjfD1cUyv4SljSKr6rDzSn8efFXIjpFMHfO5LOEcBkqahSaGmM61cGTNSGT7hspSSIV1gp1b1EKJqtjGgo+dF8NUXXlMJzNVHBgEleuVl8PUXQdHDh/72Mfw/vvv4/3338d8bw/z2RRNPQFHxttvv43VYqPDcOj6AN7KXt00DXi7BVUes+kcVVPB+yL1OonRru22mEwbbNbbgSW17/ocghdjGn8CTjo+IzyzhLqJ2HZy2N0RYj9MVx+jhkkSg1kqzCclDgBHC1eT+Q6RQJWHI9m/19uN1vJgXFeH+NX6e/Hq6y/g8ycv4Z1//ku4fOsd0NUVqnYDjq2EiKGog0Qyb7KcyoWt6fLJEstYUTmzSDs16pmMsIyLypfMinWKxQLFSZmBhtw5AufC6sO/P+oaA+TbvAcpxFU9K+XZ0RLclveNPQoCRne/v1QkSkNzacgdg+ixYmKflQbrsfW+PONQtv0819iTcJuS9lHv22VcL/uzK3TM+swsoe52Tnn87G3zlz4vuua9Fw6MURJtqGwizQTbTKYgkKy5itBMJipXhHurKpeIICKw1pHzXjwpHBldiFpU9PmCop5b0ej7HiGElFO6qiqsVivs7++DnIe4aqMeTPFp8uVwblSgW7rDxChBRKkQ4GazwWQywdilZFYvZtasGRkkcGExsRhQ084tLRkzw7tMPNNeASnqUtc1VmGl4sEm3sAKqQiRsJo+dIiHnwIAPHn8GG27xdmdO9DqDiAidG1AaDcg5zBppnCuShmwSAUaysVfYBzDKKyYIWFF+4fyYgMI5xo2ZS8ncghRmIAgZ0yqqsJmE9C1PQy8yDgLv0pCcVqV2PpVgDFGjjk3aEna6TSWMl/vALDoM3zzXIZZ2tksPibyS6BcuCuSAmCEUqBjIQElCDSQInwRQeXn2g/Sw3/mTu/DEJvm32J+cTlZNrHpoww4DqYV/sDnReu/Wrf4j/7vv4n/zy9/WNB8iHRW24j/4K9+Cf/kXz7C/+Hf+d04nDX4oc/fwcHM43odYPH7zDFb2XdtQmxvNCUcw8vaphLuFg/a74nGlA8ZK7DKY1WwVCo6EF6MfdBaGMIXccDUkAPekcFBEj04AryXDEwxRNR+eODZeC01wzYVPOh6GneRHEHAfH7QeCxZ9dM6zHzunId4CGM6EF16lW7qnBlgDfBKSd3SU8PG9xisrYLxE58nL01x7iq9VIGsVaZPeBmAeDU0VEfHwWCEwMmLmpQW+6k8ISH9coPJAEdirXcMSR+qnZEMYZrVJy3ygjcVeJkoM+VmPpths15hrgYZtvsTfZWennB0eIir85Xqj/ndSRZYsyPloTBHpPkbHngu5o6yXLNnrDAkmDXJB6daSrIZR5DTFypNCFL80zuHw8MjXC+W6NpWLIlMIKdRAESIgdG2jBg92vMnODg4wGa9xoSnqOoa3nkxelURIQa07Ravv/4aPnj/A1yeX2K72gLEuL5eQLdEJbB4U0KI6NoOR8dHiDHizt0zHBzsgbxHCC2YGbP5PM3l3t4cV1dXWF6vdXwMhsWqR1WCWBVKgi2IgbKl89IjIHQBVe2xN9+TCuE6X32/Ep4JAU3jRLZ4TkUBTVCTTlLeBwmIBF851BOBMTFIUVPupLbIB/7jeHj0Go6/70W8/vIv4slXv4bthw9Qr5bwfYc29miJ0SKgqmtQH+EDxPNaF/zEKLJFWniUrOFoWcUU3NkStkrNpcGCqEqYxgpocvLkIcmAgbFW+Y5hnjnDPSV/qzeJ8ucl0B0D39JbMFZEyhDEJI5UHtq6HK87+w4YRoMARTYrVTJKEH+b5X+XsjCmy1jxKiNqxp6IXREq9nuMMRmyrf/23djLMh5b3pJ2V+0ulSM7SD/2Dt1mpB8b5ncZ6wc00rnSZYE+StIQ3rSoQOjA8LVH1dSgIMVVq1iBvEMMDKJKsID3cJXg1boWw8M6buCc8EvXbVHVHs47dOtOM7h99PXcikapMRIRZrMZlsulhu8YiMtxa6JYAEBZgE/+tvVbam5N0+Dp06eYzWY4Pj5G0zSJMcsJIgBV5RGjMIBZ6FwxCURyyt6RS5p2+S7LKFHGutlGFc0lrJMb1XppgOj48AQfVjN0bYdHDx/Be4f9vRm6IMWHEj6OEQ7A/v4BCE61KmUKVbDSXljwTtrMUC70/K0xbt/3YAAXF5fiaSIDCw5gCVnp+wDmE6zWG4S+x3qzhXkMBm2Rbqbj9gEp0sQQMJQUIwOoNgCXPifrp2E3sr2+AHd5NAUEyJdgG0mlKYuZYekI83M6AsoNUQGKBqMkcbGbQOlDjzzLckX11jkiWG2ArGiVx/aNNkU4TRGylASgAplXTmdoKo9f/eZT/Nm//Gt47/Eq0cFCariki/b///3LH+LX3z7HT/3PvoAvfPIUL53McbXOqeQGbQMFaip/3KT5ABlTpnsCVlRS2WheKIhAkQdYv1XwyJw3I6O5NWmKHPTegbJh69aRZp/zGShBzklleVasG7Z+ljQnzRpWWvFKJUInJmFSGox7MBcgBC3mmHm4pGBJL3tEaU630Hxwq7XtDBliOCOc5iWty2KNwRQPA80jS5gpVaRAMLIcvE0U4wiWnEGw15ddcqZc2OdKq8o7zCbNAGgLkUS5ErkMKRpqoypAEKV/5NvZbIbLy6sBCUgnOOoZrRgEgJ6dneL99x9AaiBhQH8bZ5Zuplhw+ms8CwPxmu7Pc8mJtzkp96In5nA7BuArj6r2mCuQXi43IGJMm0oFs9QDIW6w7TtRrGPmF9ubDvYPsNqscXW9BAOYNGscHhxi227Qh4DT0xP4qgLA2HYtXn71VXj3EBdPL6VYZjSQorxMjLpqYMrydDoFx4DlaoG9gzkq5ZHtdoPZbK7r0cFXDoeHx5jPr7BaL2UPZ4C8AyLBOa3JQj7vm2xrR/bWw8MDrFZLdF2LGDtstp141G2fMrxAAIcADnYOUuclGsQW2ZIuJzPnvHhoZtMpCAreHYEdwAHwzIiO8ejk87jefw1vvvIbwFd/DQ9/+3cQLq9RrTcIfYtaDZ9MACrFAejzUT4AQdedt+x3kUFeComKqLL1yllpL9aiKBq6HgogGtIeM+TMpJAkpd3eZRjHQHZeY/Zz7MEoAW/Zp10W9sF9gz4P7yvPhgzHeVOJGIPusWegVH7GYHvcxngsZZuG8Uo6W3h83+dwt7KtXf0v/86G8ZvnYMbBZuN3leMtn92lUJT9LlPajueoHHuOBjDDiUo5sqhIRux6EEtUUB8jYt+JNy/0UhJA19x2u0XXdWiaRrJL7e/j8OhYj0n0qV9XV1d47dWPA0SomwbbxeLGXOy6vq0zGiVBTGjZZI0Pz4w1u5Jo5fcWvnR8fIzJZIK2bbFcLkFE6f3jkKeSSXZp2ON+7Fpo6XwGc8p4Zd+V9wERznmpGh0j/GSOK3cXV48vsFgtcHBwKCl3U3iVTLaNeW9vLwse22xVPjBDs2EUiK+4rMtFj3TjF+Vnvd5gsViiD3L41juxqkghQ0Loe2zbLWazGR48eSICnFmVMy00ZQqPSKihIkCUQCTKbxQpJDHHuugMmCQNg9N945GAGfkwlQGB4iAUlSrIECpnCzwXRCrfnf5Jf1qcrUR0GNDPgDMprE6Vwls2gCTYiZJl08Y97IAs+N+5t8AP/W9+Bu8/WqHXQ6E27mILyt0uxv3ekzX+xP/xi3j1bIZ3H63SuG3smU43286/Fb8PFInheDINDem5TFuYMCweT0qCvRuiHDKKrGt20J5RqXZhBoe0VEwpAavb1sP7KvXaeQfvnBTVtJGnjnAxzZnm+ROlQOJzTreWG2jpSTDLqZHFLJMo5vumVen5aV6CBW2gSMk8vsxzh7TuQQl6FTzqhuM2vjDZp++OIaKzDReEwIy6eMbWsk2qACiYDqFsId/NZlOJAebKBgYCSTpzZsldywrbabglJ+VI/5a04ZyMVdaNwlCX+Ojw8ACTusF6u0kvScrigOb2vG7+A9og903HltL7Yqi8lYqGvIBShi3L7gcSRWP/8AAHB3sIDPjJAsvFAn1k7M1nWK02ss8kfnRp3VgH+z7i6noFJqkmLpmpemw2rVrrxdj20isvi6fEV4gROD49xZMnF0BgOPJpjXnvsLc3x2QywWq1BnPE3mwK7wjvf/Ae9uZzzOYzBDD29g/Nr5bSHXe99KHvAph7Ca+qa1TTWpQdJ2s+hAgPLX7b99hut+i7Hs47vPGJj6OualxeXoKjJHdo+xbttkXfdnjv/feEF0NM1tFhCAynfcvWsEvhTIRmIhlxEt8FkYsxMtgzHBOCY4T6EL+29wX8ru89xic/9hLe+uVfRXz/Cfx6A7RbcAwIDHQVEDjAx6CrjBBBmpGwEvqEAvyZ/KUhwB5fY0t+CcCdrp3dFmsuZNTwuolVhu3c1o/xvbe9c/Sg0H5kzKC05w/bGIPsXWP/qHSzt/blGVfpMQBww2szDgHzWn7Bnr3h4dmBIb+dfo154rZ3P8+4gFsyhw0wVr4/xoB+u8Vms0FzsI+23eLpw3O0bYtus8V2s0UzncF7j7Zt9RyGyPOzszPs7++n89ilk2G5XMD7FpPJBE3zfFmnnlvRMA3WTt0DSPUHKqIB8B9rcLu0UnvevrOzHnVdY7VaYblcJoXCBtn3Pfq+T0pCXdcj99Mw1m6cZWE84SEEtG27s3+xEHpOD5LP5zM87vfQecbDhw8AEI6Oj9D3ncBWi8slsShNp7N0NsQl5YOSwkEFYAfy+QzDJiWmk19kSZui8PDhIwTVUFk3P9FUewQtyHX/w3sAURH7J2FgBpBLBh3M18hSkrpQQCmL0c+SFmCrIZJmxJQNLv7CEPipYsIJ6eSntUMDIGVLK4EGZIVlCNjkvXYoz2KiMVA8OW3gkYskBmmDK3CiCVWOqYZFnsxh2wk8EuPdR2sNNQBSWJpRpQAapSWdwUAEAgHferRM7x4EOdGo7dQF+yVrAzeVjLK/5e9Zqbg5GzbfNGRWA3ys1jzk4nNW9CnEAKfhBfpFApJggIMogVVdoa5lQ6+bRpQO78HohsMa8V3un4ZHZbIO+ZyHtCo5tSBBuiKLlTIVYYEpXDt47SNoPribhZakRevG1rH8Rh5Mws62y1AsM74A6nmidA/HiL6TGgZQcA8IHxPfHL/pX6Th5OmsGADvK7TLVU7bbSucRAbFZKBgAa7G6zRoQskuoS5d16PWjYvSYCFzypbmtsHe/gzrzQpgr4pBNmChmN7UWyNhOQE2L0Wf0lKk/AxDN3dAz2do9RQFiKJUy/xNZxNEElrtH+/De8LyaoE+RglRGMTyCz1M3SEQui6g7yVzlJ354MDoYgdoe+vVGpv1GtPpLDld33/vPYS+g4NPPAWO2Nvfw2wygXOE2stZjcp7zKYTxCDWyePjYwRHWK3WONjfg1M+WF4v8M2vv4XNaq3GGcB5QrfdSvra6QTzg31MJ1PRS0NA27Woqxrz/RlCH9F2HT68fw9NVePNNz+B/f0DAAFtJ9bTvpOCfavlCiCW8LM0gUr9JIuyrGGOIDg47zGbzeQAu3OJ3yQURJ9n2XvZEQJ5/AZ/Cm+8/iJ+8JOfwDf/2a/i7d/4LfSPz1G1LTykkCUxwSOCIhDZ9ssICUPL4TiDVM2aUKY8qjAGhGOQmc4ngDI7lmCW7PD5ELeM3z82uJbfle8rcdCu7Ea3vd/GWFrf07vkBpTyc5dlf9ch6XGK2HIcuzwXYyOyfTbGmqY87EpNW2Y9tc+89wnXluFddo2N6eXYzfBU0mTXO26jgdFhPKby8/E1NrRnw9vN+7q+R9u2QLvFYrnA4ydPELoO3EvE0bbr0TRNOr9litlqtcLFxQXm83lqw/r3ta9/DX3HODk90QK7H319W4fBLeyobDhZ/IrBAeODXsOsVKU2a8Q3TcpCmSyzwS4GsCxUpnSYV0Tct31SQHaNwRjRJt4+txohXdeltrz3CIiYNBN4VHjphZfwzr0ZVts1Li4vMJlO1KpV1M2QF4KYcXBwKFVQraovIW3opO0OIHnGMvYRBvyqm24IEX3fi5WISV3pmdcspEyElR3kM4FlaMH6keOWzWJMiv5uHrYdh+EY+qBBvzOgKIGO/GpVdEsEnwT5YJxQxc2aKe/f0TZyM2kQ5Z5VQA8iDccJUBRVpLlzhUBOjcmLJHmSZEsbKFxq5U2hUAkbCkBlirlhZMAmL88haeU78/12c9En/c6lZ0pylgDUaMmjD5AIQ2ld5e/SuJlBRchaCWJLFSWTWz0CBc1T+kbERFvhD7EMi7Q2uCVWUec9iICubdH3HZq6QrvpU0Y1I6JSL9EtkTTte8VmWyJbmDBnjBXEMZ3sX6Y0upu3l6v4FpqT8WO5KaTHykU+apsMSFu/b287fVKA6KzA5JDWyBGVWr45EyvxDxkfa3upy7YW2GG+N8eT8wsJUc0zD+8c+i6K8sM5tltokNezvdO4ejabYbvdoGnqBGyYhrTgGMGecXp2jCdPnkIAv84PspcygS4CJJyPB+PJfM4D8g1kcep1MV16EDwpIMwSquRtnwtwUQ5uRwb29vZQ+wpd28GeIjV8RFblRQQd7IxfGm808GREIkAzNS2vrjGdNKDo8ODefWyWC3hovJCBLufQdy16Tzg6PEAMPVqtBkxEkhKXCJv1Gs18hvVqhZmmtYxdwNvf+CaWi2vZr9QIZEcBY+jR9y26bou9vT0cnxyjaipMJjU22w3aVqydk5mAEGbGex9+CEeE/f05zk6PUHsPB8Lp6QkW19cgaJgiyU5kWpQlFWDOPAQGyAN17dE0moKzrpVyovQxgBAZpF5W5xlNXePi/Bwf1nfwxc7hu390D/TyXdz/td/E+r37iFcrVDGCYwuKBEcsZ/a6AO9yiKGzDJcgkCMEPRxPGCoT4zU5torzTrmc12+SPQVPj424N9+Vn9/dFnb271nfmazk0T1U8FqkAoAXfTR8tyt71Dg1722KxPja5QkoPS0lxjTsWL5zXHLBntnlrSnbvKH8FPvKs2i9y1Oya/7GCsqueSzrfmSjKDQEr+gLydppW1HqqxhxfHSELvSCcVkkfVU3UhizqjCbzdI82cH0scenrmtstx3WmwXcJQaRRs+6vi2PhoH/qIeN27bVbBXTpChYSjT7fby4SqVjnBLXCFlmoDKClgrOOAVajBGbzQZEAqY7LTRk/ZjNZjf6Uh4wt9Cs8r3GII1vRNNDBTiHR9WreHT/Mfq2x+nZGfqu0zRhckBMngOcrzCZNDchDCEBNebi7wFAHQQHQYmXABlHxnK5RN+2MOt7VXm1WHbo9eCRgBSxPoIoVe5NABwqxmx+oGHDSaLkDtimlxZCQh8uWeXkbXauAjf7X35SLKL0bhS+iTEWKxSHsm2zK8jzhRu3QEk0aNtCSTI8JaJknfLlgfLUvrxXCpT1Cs539S8X5rLuiuVLQERV1cJjQQCegA6zxMXU5zwbXIwlj1uyCJXAJFvEyisLOSstV/ip9FBPnk+gNMcJHnM7aJ4ka1KLEoDU1/R9L+EMVkvD1lNqO7+mxP/MjLquJA2n8mrUsEBTXgf1EhK0vDluuyMpTda5ggqpR5THNOpVGvcwQICG9wwbL9rONC/5PN2mr4sjXktNx6j8QDpa+X6s7tsLiyflPpJzEoEldbOvKvmGcYNyg+WF7OEwtjBLc9S/JdY/FjJLXuIUiIdYbKzaaAmnrDyO0Xg6neHi/FxCUUcWFxt9HwMqRByfHMmeYNmO0pmbzKOirHDyJNvKF9Yvxj0kWeZzktCDNDnepdodZpSJYFVAxYBSVxXa7RbtokVV1fCugneETegQ2hbe1iEDXi3u4oWx/kdNspAXh8kH2TsJCITV1TWaqgLHgKcPH4D7AGgGJec9Pv7GG+i6HvfufYiu3WC7WgJM6EOPdrvFtt0i9D04Mp48eoKXP/YKEAO67QaVm+HeBx/g6vypTgNlSrF4liNknmO3Rdyusby+xJ27d3F0coxm0iDEiPV6hUiMadMATAgx4uryEh988B4oSCbGk6NjVM4nT6iQQEGgMwKoksEZ6tq5y0mje3NVg0jSedZVbV0FwAhsYZkBzhH29/Zxfn4Bd+cF/KP1C5i+/hn4/S9g+tWfwebrv4P+ao0q9Gi3V+AYQDHCVVLEkDhKqnhkYBygZ0E12yPRTUWjBOAlkEwZmHYAU2PJ8h27wmbsPeV9uyzyQto4CCsqvxtbrcv+WNsmx81Qm54b9RHIIUuG6Z6lfI0/K9u13w03Wn/LkKixIlEqORZ6X0bijPtT9nNM5xL8jz0XpFXrx/eV4yjb2DXOXe9+ljKySxnLeKGgq37adaJYTBmomwavvPKKRBtEwcnkqhTtMpvN0HWdJmZoEh0nk8lA0To+PhKPKkm5hOe5nlvRMKAvcaNt+q+ua3hfpwkFbp7sLwkzJuhYkyuZqfzcFIMBgTkXCgTkwEsIMSkbxpx2EMgOmBsBy3bGCxCQuFsHRtd2ODw5wofnW6yCx6OHD1FVHvPZDNt2q3sc57lmYH9vH8xIgJ+cWcQzNAYKUI+sbJhITbxpnzEAtZ5cXFwib/+Adx4harVZDfPwzsNTHl/CaGShTxhIs7LtnUDKJD4oAeIBfGWFRCVwG4BUe28GtwnwEGk0ToY7Q2RSgI8Exgvy6D05E9OgpaLtoktpNJRSGJPy2QD06c1EZdsZiOWJGuAjAdkFffq+z9u2pROGeUGGIL8cUwKoVChjpaI2GicXz5kgHInztBkT5b9RviszI3bRPDeW1cxyXgGkSusxRninoSLDyDpdC3peiGWd13WVPHAhakYY54BQGAt0/m44l3VQjNGYi6GMlqr0gIc0lxvcQHEYU/EGPUymIc955vrxeir6WK6PpMHSaBxD/hi+SsGKy4f30wJnyazX1JoiPIrfMkKVNjbVQntkYUMkfc5ru6QWo1alJYcRKm9qBsKyOJ2tk3IpF4tPNrOmRkjZ827ys01JCAHz+RzT2RSr5Tql7zUwTjquJJdGMpVoPPfFy0s+V9lk2XwcZV6wdlJhRoii0a7lAPheM8FqvUbHG8QICWcNUueob9si7DLqfJgNXnvJFn5LmTVI6m44CMB/0m6w2W7EOgmHGHuQJ7z4ygu4c+cUvq6wf7CHd775TaxWEo7lvMdmvcJytUK73WK1WMDXFbbrNeazKdp2Cw/Ck0cP5UyI0SApQra2WHmI0W8dXF3jftths97ghZdfwnQ6xWTaYL1eYdu2UliQgZOTU2wWK5w/foLF1QKPHzySMEkbZDSDnYaNFUatJJk43z6ZTlHVlWaUJDx5/ARnd+4oD4qOGBDhmOAi4GEgGdis15hPG7SuAc4+hdX3v4HFm/dw/ev/EPzWr2Haebz5sY/h1Rfv4He+/JvgbgvPAY4JPng4Nk+0pCWVUDeXCkCa+EzFcdN8DsE8kWZvI+PXLHcJQADDO5/Svaesmglgc3E/wRSyXYAUsOxZNwG+NTiIsdB7TMFIKef1u4GSgh3hPLgZEjZo7gbYHiZ8Kftve2CJJ/PzO4ayQ3GwEKkb4xsZvkvajM8Vl9cu79L4+13XLo9U2db4+dsUkEG7RVMmn6qqArXAdrvFIYDtdoOeWYzjrUT+9CHi/FxKNLz55psDGth8lhXiu65D5UUeylng/z94NGzSLFXXZDIBYOHaueq3pE10idl2uazKSRq7pcZELUOnWDdOGXQPS5lbVVK90xQLc5uZ68fS85rGBgAHBwcyGSygPIGUyPBVhdpVCFEqJh7uH+JLTxhPzy+x2WxwcnqCCMuklXccA34H+wciRJzkUne6WQgT2G6XAQazHFwzKJ++MiwAeaTrI9ou4vp6qdYxAWLQzd0K9UHTjdoCtc0/IRAW61SqocHZYjrYiQeCo4RQBXJL3yCFmLCBFpnExEecFIgMbm2jz5bdDFAUhioNctuU70y9KC2Vsjnl/hkANEEsfXKgKJlKEFnm3VMxfC7mqvAx5d2/AFBDSGjCfgBqBqAcadwDPJ9ekIhhvUjjtllgIGV6zOtHe0lF/zF021vbA2GH8uL0fhsVJSVk6DVisozGXCwDoZE5SARkVTLHtgnq/BgrGPh13qGqK3WmSGhKU9cpuM4UM0vRmnqZaJj7l/Gj8Vr+MI2hTMZQ0NzWSZ71MYVUNnHUDRgJhAGMqP2wUm3EDFcoImm9sTWtsnK0xkql0uat9A2Q9ZE0rATFXGhY5f7eHrp2mwrH1XUt743CKEZ/yfIkeagGHqjE55y6Ute1pB7WuHpn43MSbBdCTOdbyiNEib6cf8ZEF/EiuJSdLAu+lFGFCU1d4eT4CKvFSs+4EIgVQLBmMdL5tBoPrHRxKNsuAJ/CutRL3dNkDgjea4x+FN42xZQAoI+IqNCuV1ivVzg+PkK/WacD3DFEUIwg7sBhqzyha0wBq/BCVDkm/JQCFxVgakopcAQ2K0mT64tQrv2TQ9x55UVZYyHg9OwEBwe/G++89TYeP3wIcsBieY3VaokYe2y7DSo0+OD9D8CW3pscVoul9oVgdSOSbEneUV2fHBG7DpEZl+fnCF2Pl197BdP5DAfzQ4RJxHKxwGw6g68Ik7qGVUmPkRFCD+YAzybDVKYYHyuTOONFynUt6mYC72oABO8rPH1yAe9qnJyepDBNIpID4k7P6DnG3sEBzi/OMZ3cBSyrXOVx9OrrmN75n+D88R/Bg29+Be9+69fxu64X+M4f/h+g9oSmIYTNBttrqVsVYo/lcoHZbIa9/TnufeNttI8vRFYyQJFByi9W4NBWlRhI1cKuSpDTcyaWVAMAapfpPDbUepPuLGFnAODhAQJ6KgrzqoWnch7svBhjA8QzrzLKUgmTpek346sTIymxKGjqi5dwKVs5BHiyhCra17TOsrECEI+/904jJ1jxm3iFnO0LkUEU0bN5RyqtC0YAvCXXK/CjmvPIgVUOlOC8xJ2lN6b0WgDDbE/lNb7fPiNymtZa5HZS4oai5cbz5V489sbcppCNlZObXivL2KarxonSWzkPrFpgK8kOvvL1r+Hy/FIU/4NjTOoK18uFFJx+cSNGPZJEQl3osQXQTKdZfhPBwyH2Ubzk7vlUiG8r61TXdaiqKikY6axE6OGRQ5UMYAMupb2zlLID11MBsstcxiUxSybJmp8ws2lbpoDAQAyQDovbeyaTyUBZ2mw2NydXhR1INP8YZWOZzeboO8aH/AoePngXzjkcHhyg1SInwFC7b+oGVT1BLsTDiFGzT+phVSvalHBOWqiUwFEZ3CCbNiFGxnK1RtvlA5fOySHAtpVq7eTESsTM6SCfpVXhhL445UAvIZSBHzYEaxPKGdzoiG/OV3pDoWzciIGCDtoQMtI91jbKtgtAlYHvEPRliaoLbfTsYI7BeixCARbltjlEwKNQyuwto7ZNA8yDFjoa2GS+QR9TS5gNFAKDMzA2buymubXN43ah4W4pzEZ7bIokbN0UNLf+ZnMTDNakzZCTyMzagI2DBGBC6ZcAAbFaVy3+XGcqBnC0yqslVcvBKxAkJwXhKp+SP0wn0+Gz2iUJbc+8RoYwqaCaKZwFzdP6KuZuGNhjn2c785jorMq5V09uebDTUtCS8X/J50mx0PeNrGGJ1xK4LNYQMBhf5gc9oIxiA9P+np2eiIzuWnBgTJsJmqpG17XwvgwhYFgsvqlvWRktaaNjcxKv2+thQt1jQSBU3qUQN0qDpdSMdj7NudznpHDfdovZdFrQA0lmMbRQXsU4OTnGhx88AEeV1YnzdW9IU2srF6qs6BwWla3BGgalIEtsH2pUM2soKnjKc5P6pnMRI8ChQ7fZ4OnjDvvzPQSXlZa23SJ0HcTJV6atLIwlKRudUsWEN1Gy9keWvaM8X8PEcJ5wcnqKGFkUnMg4f/oUW6Wn7a/L5UL3voi7Z3cwnc/w9OIS680GlfOYzaYDWSlncLTmg2g/AnwLb6wjkZ3ttsWKlnj/3fdxcnYqKTXbDuv1CveWH6DtWmyWq+Q9lvUSMxETmrH1TTp8TZ+f9hKSGlWTSZrnyGIAffjgEfb29jCbTgbplTkyAgFWU8l5j6vFAnt7czhETQ9NqGqHl15+CWd37mD1Xd+Lh08e4+Hlh3ht+w4uP7yHul/hlaMp5vtzfOEL34+XXnoJbbvFZr3Ep7/nd+P8/kP0206Ury6A2w5916FtO/R9h74PevZUQlpWqzV8HzFxAuTtHjPcVixKKrOE3PZBlWEe1lbg4CVsMbIeqq8SbRAlBBXk1OCh6oIBbOMkZlDU/YsJlatUhEYEZgRoNTEujaUAUwQ77acemidyavjzuq/I+gUx2Dndn0xeCcf3tq6cKEYZH0bkKuuC/yyxDZeyZcdVYsjy97Hh7bbfhd0yTi1/d0QyFrPUqEy3X83YeNvh8HHo1y7PSNneOPRr4KnSc6LRgKaSpa5F1i+uruAP98Asng7XM7abDRzJuay+77Bpt9ib1IgccH11hUcfPMBms4GvK1R1jclsCpB4OOfzOe6cnUmo4nNc39ZhcIvbKutQlO6pMkOU/O2T0N5FxPIwUEn4sVupDHcS2g4nvmQgUzA+atKcc5L2q2kkxCqEwXdJcQBhOpvjF95nnG8ZV9dXmM9nqLyT+M8YU8VEsKQEPNg/AKulk8iKE6rtkQCPgi8Ng3CBLZE34NR3XVSRGddXl3rIVqwD5Jy4w0JI4CBtu2MN2ZQrIUhuG3nBmxUibYAoF4FYIYT2Bm9MvdB3pLXvEtAQK1jhUbG2IWAg9YpoANLL3huczG0b8BdhlMBw4pOCsCXCofLlefMMMaAmcRGPHYJimS0UjGQBsteVamHZABW0zSAxY/chzXddBBXKxQEQA19UtJChfe7HIMDNXAyc/gGnMbjBE3IH5+ftQ6e9dC5tBlIZ2QAxp8xqiTZqOTM+KnUoeR6pL86rouE8tr1Y4eumVqUw9926E+09BRfaT7OSG1mlbIHQ0mhq6xMo8E4xfllPpsZwasLbHOh/xLrBG1hUy7rurdpfc8MrpTMTD+dblcR84McVvFH4lMg2faT3UrG5vfDCGU6Oj/Hw4SNwFPByfHyc0l9LxpChipW9U5SmfaD3p05K6MpquZL1rTQhIpCmORVAKUUwb9A4NZpl8nw2w3q9xnw2GwpEpaHdF2LE4eEB6tqjawOcJ7iY1zEhCLiKDKkyXSoHOaRr6PMEYmJMlVdRDro7ECoHPTOT+VoUDZfqjYQY4byEN3V9D449nK9gFl4mJMt2kmtEIM7ZjKigOYwHVN+MyDThGHUtKu2bGsvFAg6Eppngwf0Psdls8corL6NrJRNh5StsN1utQF7j05/+NC4vL/Huex+grirs7c3R1E2SCZz2cpM1uq6UPhIm5FK4E5jRbns41+KD995D6HtYtj3br8o93ugJ27819I+UmYe2lmI9kWZvBKGLARUBjh36PqDdrnB1dYWmOYWzcGsTYWp0YA7Y39vD06dPslKre4avBKTVdY3j4yMcHh0jxjfRx9+PaejBocWDsAaBcK9tQO+JF24vXuGuq8AvnwEqDtOqVZm17zt86k6NGGSvkUiLDr5nHNQN9mdTCUnvOnRth75rQV1AaFtsNxIm12n64Ha7RdfJz81yhXazAUVGv22xXW/hIiH2AX0nWSkRIyLruSMOyVOGKJ5IVhnmAPXAsaznmHfutggDyxssEIkLLx3DO9ItV+qEMDRs3KQXy34TOSCoMZbJgbxwVgSAPnvEpRApAWzGKn/j8Peu0CbDoTD+g+0/u7HhbeFt5WX4cByJUyoM4/d+1LXLmL5rLLuUJcDEBMNDk/5Q9i45IjSzCQL34G6L2aTCeiGexHXfokeH6XyG+dE+ltsVXOOx3mywul6gdhWq2b54SJ1Du96CyGG6P4efNnhyfYmTk5OPHB/wbVYGtwJ3CZyrFbU8P1ESD8jp2XZ5MuwaT1CpNBiz5InM77RK5fYOI/44zszuHWuOFkLFhcJTTrjzDo+fLPCNdo5708/i0XtvAyyHYdpezkI4IlR1jbryCEHyd+/t7Utu8apSi09Oeau4Nm/cCSgBAj4AsboOY++J5OBNDAGL60UCnZPJbBAaJhpnTAAkBUDwsGGV77lt3eESbGGFVnpjoZ7k5wdAVt7BsDjQJN3T+/J9+k6jxwAoZqIMMdgQFOS2rWmX32PKFJf9NX+rfZ0VJRWFyQrrvBcPQXo8Q2+LhU8ArVSYynFa2yljCg+AVfqXkC11N8ZNGJ7yAKxqcXqESiqoImdNpwEjXwMkXYTLWdslEEyKUn7WAcnFD5LNwubTkROl28kW672X0I5oKZkxmLVBZebI6h4H6ka8povFAqHvMZ00qOoa3XaTSWsYVGOWBwpWRnFiAWNO45Y7C66yZ9XaZzNg7zY+JRjGy6q1uPpjDkGCQ84FZqFR5rkcrp2S6kkXthMnBagTBTQk62PyiDHEyudypmFfESaTGQ4PD3Hn7h14cnj06CG67Rpt1+Ls7Ax375xhsVzizp0zOO+0LU7jK3RUMZBk5IeSNwmMw4N9LBeLTBMdh/ceXdulOc9KfyH30htzk7PpFBcXFyBIFhVXsC7b/QyAI2azKeazKS6313BUoQsRMQiw5dinOcyyFToPMSmtaViqCFh9BibAMSMmz6vc41S5jjooBkBRAq5cjAi9ZFI6Pj5CVVV48vQJQuySQsoJ9OR9MKXmLSQRohlNKK3vG3It8YjI2/l0BoqM1fUC968+RNe1mE6mWJxfoY8hgfmua6V4pvf4yr/8LVxeXYEFmWC7bbFdr4t9OsvUHEKIxPtETs+uOHmH9qjdbtGHvpAhSCmOdYMABQvDI5jn0JV7hIbPkU5S8qzpXlrVkp2s73sNewUO9vdwf7nAxcUFjo+O0KQ1kyVZtHcyUPka19cL7O3vS3POgTtV1MkOfcv9vnKo6gaMCRgHAMRDYvxxzYe4pNds1WdeL3mQGb92nuVAogcB89UCR8tzXXes+yIDlWotU7m/Ro/vPFqL8UONB9xHcN+jAePV40O02xYxAn3bodtKzZJ2s0HbSVKC9fIKi6tr9G2niskaWy3qG/oO3PfgPsi+1AcgSGQHh+wp5KBZ5RjwqOE4IEI8L17PWjCAngMiMTx5kVmiMcseQg697R8kCQOC7RU5JaGGR5oKQgD7AUYc7PNmACr+tmQ/RDQ4pG5raRxeNcanY+P32PuxK+wppS0fYd8SZ5Z92OXdGCjlnA1Iuy4CJRwLknB9REboO2yW12goYF45HDUTtJXHdttLBXDv8NILd/HCiy/Ck5M12Eo18WY+Qz1pUoidHX7/js9/Did3z/BPv/hFvP3ut3b2Z3w9t6JhgzaFw5SOMbHGml6ZZapMzZVc/Eo485IAKEKw8rsBU14kDq/MblW+Z9yHsm07FG0hV/v7+2jbVrLchJA8ITautuvxzfAG1vPPY7Pc4PzpE9R1jcl0gs12CyKgaWpMmkqFbcB0OkddNej7TveJIma4YFYzCiRNv9jMbROJkRVEUFKWrhdLbLTAoPcViBxCDGg1TtZekyNpkQ5qDheIwgYu+kW2mRcWXM7AzEBu6qb2rbxMOSHOlvr8nbaNHW0Xn+e2kTa6HN0KBV8oRphBg22EBTIsO5fGPbAY6Hii5LtVa1nZI4PjpmToSMuhc/EZ42Ymo7RPFkjOHqWbNDcALuZMJFpRbqpo1/62eaQ8WCMDVMhz8f0OmhtQHrQ9AIdFaI/+lJAnecvB0RHa7RYxRslWAclQN53UWmCrzs8a74M0y7CkRa3rCodHhzg/P8d20wJEuHvnDO99+AGycpRJ69KmlDf5PN9ilU7jLmjoEs0txleFO0GT+npYmJ8pxQPcDQVjOiHi0Q1iXNCsOYSQhb+1rEX6GATnxEMo57h8AlLO+1SDp6o86ka8PL7yGppZwzlJUzqZTuEcYdJM4BywbVuslis8Ob/CxfkF2naLs7NTvPmJN3BwtI/jkwPxOoQuJ4hALhViSRmSZ3QAlgis5J7Pp5qFyCxqcpMdUuVkIKLEZUB+d6lpiKIkKcotXIkLnrfnmCSjla+Bg5MDXFxeyT4TesTQi0y10zx2WNbYwQwmHAvlzuRVsVRTvzQMi51YeV3mI1IvTUojDgZHRtNUmE0nWK/XCL1s5pEFgFkM+QDIkHh97RMiB9bQh/y5AmQDVUTprAk5wt7BPvYPDkAgXJyfS8iQrxD6Hqv1CpWTlNxEEaEXOnahw4OHD0Fw8HWNPvSgFlivxEMlCoSuD589NiXfi3HPiZygzCQh2FmTTFfjHSLhd9IzkWn9w/YXApzWKIG9UpUt8xZ6sdxGPefBiIgQ75FzDsvlQmp6NB6WBTF3IvP5fL6Hp+dPMZnNRFskjdRQmhv9ybRt6x/yu5LVPYlse7rEInn9mMKD4mcEsPRHWOLI2C7fXzKH7rXv95yGQ6Tkrxk+9ti/uBB+0eXFDQM1gD3GGZ/jlckKFUcc9L3wNDNCHxD6HgDj9X2gioy+a7FZrLFeLtBttuBth+XVEteXlwhtj3azkdpHfY/YRqCT9R5DQNhKiQAJT+xA6CWJQR9EMdHQW3KMijQ8kQGEAMdaoJkkPC/GXnlG13QyZg7rYBimjJYiucCOY6xo1zD0aEcoeNo/Kf0so3bKe0psCUCTnuxWgMaYucTF5fe3/T5WktgUONZzIpRlGjGwvrhE3G4xiYT9usHB2QvoDwO2XYct92jagM2jp5jUDeqqQrXeYrteAZMJjo4P0IUem+0W7abD3RdfwGc/8Ql0EfjhH/wh/PTP/nc36Lbrem5FwxSL0rtgGZVKb0F5JfxKNz0N5ef2e5kFqkxnZn+v12tMJlMQ+cGz4xRtpXJT9n+s5FRVha7rsN1uMWmalBbXCpf0fYft0SfBDDx+8gRd2+L07BR9L2CirmpMp1IQScAXcHSwj67rNf55VP3VxqlCwFGSHelKcEmfyVZBiUE9P38Kc7H7yiNq/HtOzSsCmfRZ5vyyAbOPlIBkKdVx2CZc3FHEyKIYVxadXNxn1poST6SecCzOURiKdgMhK5LW3pjh8E1CFe+FbUpcfEC729YFKmOVe2xeSb9Pm+q4DR7TYHif/c6wdxXKVVJA8rgS7Wj4Fi53HOT2xjTN4x71bfAc59CpgnwEFYqWTnIHjQd+K7ZYUV1LFtcOxsHePuazKTabNWaTCWazGVbrJThGOO8xnc/gLZSEKZ1vIvX6MDP60GM+m2I+38N8voer6wssFgu88spLuLq+wsXlle3ACgSKA5TlZGifHVAoh+WY9C6yEA3WA+8MsEubm8TZZmInXnB2UFtVksrrgbwKzskhbK8KAxFJIUJNI1j7CqQhnnUt6Tgr71BXFSzc0PtKChyGgMBi3DHPEBFJtXS1MoKAtu9xcXGB7XaLxeIai+sFttsOznm89NJLeO21V3F0coT5bALmiE3bJo90YjuLbGSxHTrdqMxwYMjGsiZNJhNMmjqdZbMXVRrOGdI5gpEMKA0bhbIBkMYLB6HFaEuxkI2oseCnJ8d4/1sfIIYelXfYhijZy5xxcRzItZgEW5bXBnNZ95Ns0FAfA1Ey1NhxgnRYXl1JFl5EHOGcVKq+uLiQA79klnkHZ5E8pvCQAKaq8inFJEHCrowoCbwwoY89YtcNVul8Msf+/gEIwEozSlmYLkHkfatyDcjyn1m8AK7KBsHQB3RtiyqBMuUDyBmY8kxTUjKUtkQeFiwkbWkGIQt7AVKcY+UkVW/UswfJIGRKFEmF4q6XRCyD9eodppMJjo6P0EwmkscDltJewrXbttOzKRNQ5QZjRhoZJHGBr7BebzGZNCkNuQxRKz4RUgYwWZt5HxLZQspDJh/DQC9I/eeiXeVlk9ecHlY+LbjQ6D3eQx1zUkLs8x4OWzoFkehN9p3NyWW8g7eN3DVZoXNtQsbx1bgBcQRqwM2FN+6Gezh2G3gmHHFE6Hrc9Ru8OPNYXV9jvVxjs95ic70AdQHLq2t0mw26bYvtdoNtu0XsJQSMAks65sjoYwtGlL9DBPogIZAazgViEHrARTD3YLbU+Tl6Zex98P4mzgMypiyx6tg4nXhjBP5Lw/X4ufKy+733qd5O+d1YARorEWMMXX429qIMw7xkH0zzrTLLe4/5dIqq0mLXT87RMUniI4jhyyNiebXGkhmVr1CrAYAJ4Mbj4aMncl5SEwM8fPIU/2KxxdELL+P7fuQP4Ls++zk8z/VtHQYfpxZL3gKfY+ZKl5ZMbtYqb4tDG8fHlcpMObmTyUQL9FWD8x23uZPKySnT5pZtNU2D9XKF9VpSAHrv0XUd1us1FusWOKkR+ognjx6DiHCwv482isZuFRXBkjrWk5OD431Aig1nhlQNZT0IKMBOGLFAgkAOJRoMIvdfqrleJwBKRIghoDPrhAwuC/9osZOmQNwEYuXmkYxSo8WbOkXjX3MA067fM8C2gRiocSPBmV3zBqJTX4v0Lgm8I4P0AbouCZZGiYRmUtuElEXJ5oiUxgxVooEcu0GyKAfn2vM/yk+Q8J8+JNUpiZoURz+iOSgn5rK7uRzfDvLzGArljc9obhQtx50sH7h53RZHOlBUDIwbKChAfV1XOD4+xunpKT788AOEvsf85BgSjhYRGJjN5tjf209gIoGlZGWWOen7HtNmiulsgrt372KzWeHe/Xs4ODjAd37+c/jWt97D06dPESOj64IccgRJ2AMN51uUIQw2egv1zqGWYgWq6xpOc+Q771BXjZ69EjlmxTmTl6HxqKsK5rGsKq8CHOAoHbEQs5DCGjlliImalQksykO73WK9XMNVHrGX7HimzG23nRzyZQH0feg1VbLIlbbrAbWacxSFsqoq3LnzAu7cuYOT4yPM9iZy9gESPmO8bodgs/nZVpD+bokaShGrdHbeYTafY7vpxODBkoSCCuMQIqsHJHuFislHWsM6b5PpFJvNBvXBvqzJpBtkUC80Dtg/2EfT1GjXawGmrb6OkIXpSK5Fg+CkayylTSvCwpzUzHDcp2w3qXYOM8hnXit0JvR9gK8ivPOao1743xQIsFq3GYhaN8d5+fzo6BiHBwf44IMP9KD9BM47OeuiqzgsFxKSAZ0qBTWb9RoRjOVqpfuidMqTS+Iz9UG4SpSJpLhJXP1muwHrmnGUARUBcEyIXsbvrAgsGXxIaRXVuygeOxDn81mqAJITnutCDx8sx5EZxWQteu8wn8+xWq91rXpR1Jsas9kM8/kc8/me1tuR9bXdbFUWAKEP2GzWiIcH5ZFomAHKWD0CONjfx8XFBe7cvZO/A6nXQ7yd0eSTGR1UhkVdn2nnMflT7pMmdEsZlGSz7ggMCXV29lyxXxX9T8sGyIVKTTiP9seoe5ysXcrbKAPWUArwLPb8ziAhG0ZhLPwbGjajNKmk3y4Abg7wnox9Gpe4w0+AELGPBT53ENC1Ed0mIHQSprVZreHaDWbkcH39FMvVNfpNi+3lAt1qA+569JsOvG1VDm4B9AACQujAHBADp1S7ZoCR6AnOhgXKtTdMdpKXsHuT/1EzglmWu/Iyj6uFKe4KwbfQe/OWVFbIMVmmboZV7Qrtsp/j70pFZ3wNsbMyn7XKYoByjtBoSmy4CpXzqFwFogqRGYEZPVgTqghe9GxnDBm07UEugrkFk3qavceHX/ltrBZb8Pd/H6b1/48rg/d9P8jiVLp9PFUCsmKUdLGAHIaM5dLIV3mY3IhVKg3j8Cv7vWkaMGMQvjXQNjW3L1RjM1ureBaipKJUgB8gB7IcEepGNoa9+b4WIpTsTRvaA/sZrs7PJQXY/j7gHXwgTCcN5tMJyAFRgjX17IpkerJDxYaczWoOoNikxI1cxgtb5VPzWlh8eYwR265Hu+1B3qGqVTBFUle1g/N58UTmHBahG2S6dJOnUdsZZZjUKoJqCiGaBZpaAlnuGsN92xDlVQayWd9Ravy6+yYQygNQb0Bl0H3Y97aoi/cAIDVrpkxQafNDAj3kHCiYdR6aqlRA48HhPu6encFXcsjfEVLqtxgD3n7nWwL2nBxeJmL0fSzCC1hBn4ydigOVEZyK5hhuRxqF/quC3oZl90niMrMuathSJkahXHACXVR6Eu0eA1+yy8BpWmKoNdR5yd0ua0zCWmrvQU6SKlZ1haryaGqP6WSC1WaDD957F9tti9B1mDQTXF5dou96HB0f4+zkEJNplRQWASO521b8LHSMUDOODvfQ9y1eaO/i/v0H+MbXv4E3PvkGPvOZTwDxDbTbLS4vLnF5fYVtkIJlRB5NLXGnzlVat4bQ1FKszjmCIw/vCbUW+fKaE5y8U/bXtJ4KwPoYQJHBulmHENCFoMUxA5glg0zfayIGAF0v9RKCpggNLOFjoQvJcRRCRAhqIPASmhNC9hQBSEol+ZxfPslI/aSpK0xVCWqaGr6qMJ9OMZ3NMJ02aCYT7O3NUNU1Qgha0DOKxYo1W1OPhIJELrkELpnVgm9zRarYkfDJ3nwPm9WTZJ0mknAz5xz60EtxNy5CTIrVanxuOkHkiPlshvOLC6lmjQLEGf8qXWIkzJop9vfmeLJaQcyzDuTEqi1Vpl0GvNJ5VMp7KSSTDBAUxQdDRIyyhrzuMaIPCE/E2Mk7dG8BPCzdcu0bdD2j7xixB+DMA2geVF1vej9FgB3j6OhYMhMF8f6FrkPo8l7R9b1s9PBp0VSVHFVvty2Ojo4QekbfqlcWBMt6KEqBnKUAia/BKb8LeACCeszJeZ0vkavm28iKloSWSm2HOqVfJhLZ4WDrW+fOCT9Elbkh9EnBJQREBexSYVsEVl3VmO/N9QA5AU7WrNMsSDGI+axSy922b7HZbGVN9QF934mHAwxz06VwXsoGJgKrfI9aH8AXPKrGJ6ZCQZAD+AzzKCjfGk9LzKXMKdm5FEqP3kRCyHzEUbUDJKUmUlZEHHLyZaN5TJoDA5E0/JST7sGmOIVScQHyoWpVVrS/8m7pAwOggGycss9gXSyALcRp3PEU13gNpDWTvrwUmpAnUEWgGYBjYBI3mGOR9skmtnizeoDY9ziqeswcY/HkUs4XbbZor1dYXFyiXW8Qti369RLddovY9eAuwIWI2Af1ba/VWxcQmAF2YBB6AtY+6LxoKCQ5OZfFDIce5pciODh2OrckZ7WQZa/JoNIwXn6fQk6La5f3A8gKTOYGJEaR3znht2TM33EvKGMmGU+eIecaREjSIjuEDwDeAWRpg9O+rNicCMya+Mk5YX04IDCIe4SwRKwiqvkEz3N9W2c0nHNo2zZpbqbheRdHCqFuCMWmWVbiLifIwrFKj8g4zKn82zwk5aaT4uac1zNkrPH2xbOwuHBKlj9zYddVlawg3tdYLpc4OTnFzM3ADNy/dw+OgIPDQ8TYw1eVhldBwDgREIHJZIpOlSCzijhmsHe56LKCRuUHABgARRES2Z6dwqycw2a9Rh8iau+1FPxWYlUVoNhDHJEPDeeZGDK/WbgLzXgEAVCISX1HfmfSss2akDQQVRZKqTR4Y6lkGLixGNxCgKkgT3xlrg57Qx6cfmSKClLbRPl+Nxq/iPdYtJkPLHu1Gr722qvwlVMeFyu38GHE1fUVNus1QITZfIoQeiyXW2w3fYoBthTBMhZOANb8PlTMt5ptNQMNNAZcQ1tIQJihDlJylJYOV3m1XAgArLyTMzxqrXHeS95rn89XmTIBIrV6qXKiJr8YTcgJCOaoVng9VLrddLjqOnShR7vt1FIfcHx8jM12i/V6jbqq8KlPfQp1U0PKLsg42Bgi8bls7RwDum2L6XSKvfkM9OILIPJ4+OABvv7Vr+P68QU+9Yk3cef4Dk73T9BxRACDKSAGiTOWLsbkXQpBgb1mwdl0PdZxK+BNgtYT0AwxpKQLFqoUg/7NSDIjZQ+yNcc5/zzYsugQQJJ1ydaXQ86Y46sKlWcNrxIF17zD3jtUXrJtOVNmnXxXeQ9vhco0zWxVeZlTp4XdNGSLAPQhYLXaSOFSGOijpKxGW1e6wThSK7wW/DSLmVnT7SQPiLC3N8fjx09S4VSz8DrvgJ6Vh31a3+WVrHnFUm5SCGvBH7o8RCHNHzsHnJwc4emTx5IYpK7BLGEZFedzfnZ2jWGRLjZplPoHSHE0ky1iLVZLqApmoUepNck6dl48VL6qMN9rwHEDoIPzWodAaZaK9LEqKExgOBATHtx7gLbt4akCQrZmEwEcIjh61JjI+xRF1lWjgIgQgwf1DnM/zYoGKMkWUkuu0ESTNlSVzCt76ctEwn4cJDRPPHwsPKyKCpGGxnkv/5Hws3NOsn/ZvqxKGmsIXde26GNAzwHkgdgFdJsN+hDQxYDNdoPF+hrMPZpJhbr2qJsafYQY08CIoUPYBvQcNTRIjI9VLfc/efxY1jxzOiMpkQYyV2PwZ17e/f0DLK8XODk5TnyXeM3AujKqWbhtySSeMh5mwyUG3FVtKfnZrrxl6zPZEx1TByj1xdqw9TpcIoKNjM+TgmAiPO21xT5cAFrrH2vb5vFJa7Poe9Rx2v41btt29ByVkLgZIKBljwUdp32MifBBfBHkCD60qGMAHRPcMeGl+BBHboPDPuLVpsMeAlbLSzx58AjtYgHebLE8v8Ti4gqb1QrcbhH7Ht22BfqA0PXgEEAcsRdECYlg9CECnvSsUJDUx0YsgtTw8FKCkeOzi9Lt8jow50rqpoDc5tUYh0Ihva/Q7oorr+MSnZW4UtvRSTXsHSNDV06aD/MMJa+QXsHwNwAeHY1gDjg+OUI1qW+sqduu51Y0ZrMZAKSMU+WAjMXGB24I4ga18u/jUKnSWzHOMFWGThFRclMR5XCqUikBsmJjf+dndJOkrHWmSueqvNS1bHBEDmdnd1D5Gg/6F7BarHB5eYWmaTCdNmBEzKYTNI2ETYjgETOGryV1nS0+i6O0WHSwufhyOEuxlxaLPVPVtgzvPbbbLTjGZHnpuw5VoxmA9FS5t0wOIRY8OlQXTKCkT03pGAjMbNm1VxCG6gYnaUXZMm8aQLnwipdbjCsZ/5ino9RKjKaJvxjZu1LEcKQmuGiCcx/sXTrGBCCosMdwfo0tcu88VusV3n33XYA0HCqKtTb0vQBqllSW5CTLSt00Os85LZ91UWSGU55Wy4BTqzHJ3JJ3EupAUnyqqnxK9+i9R1XV0k89KEnOZSHBCmAK5hELuVhwWGNTmaOCTbUKqjAUQaMJCu2n0sJom4E155Af9d7E0KeY0OOTY8wmUzx98hjNpMEnP/kp7O/vJaNE6fkq+TxJEhKv3LZtcXJyDMIV6AWH+XyGJw+f4uL8Gl9efBUH831JgtB36DmCo4bvxCwDLMVfhIZwGu+OlLSBwpPCNdkizuFrD+9rYyMBalWlipnIlspXqDQ2l4hThXM7NAzNQuKdF4+LpkX1lcy1c2KRNCXDwrBgVrRis7bsRwwDHpzG3ccggCxGMTiYssRCCSBnzUVBd9vRpCmHyjvdHQRgVoUhouTvpmlQVVJxN4aYdpSq8mi30BSzKZR9ON+jXUpkvVC9D0Es9qWAJPPokYzFAWdnJ3j7bZEedT3BdrtRuctJrvlyqrk4q0R5lhl2eDxf0WoDkIZcEMSzZUBe3I4g5+TcQQiIvUPsPbybSfFPp+FfziF0XTpIX+nBZaGNKJX1hFX5F0+oG8llo49zks2trhtUTZ14+oU7x+l8g3dVqvECcvDwunca/6pS6oSopIonqaHCq4yBywdMDVl657X4nYn2vLcC9lneB2OM2GxbWIatyokGwEGU+z5ELDYr/PqXfh2bdoPF9QLL5VrXQoWqamAbkJ0H6voe7XaLuy/eRVPVWK/W2GzWIIhMnkwmSX6W1nfkqU9yaDqb4vLqEoH1EDyyAjHAeUNkLxFj+nu5jgSYy8NRea58Lu2VJa/pDpiOOpVb32CNDNdOAoPFHpzka9lAyrGdQ3SZUm+tEzC2Vht9HnKJTQgif9T2VfbL1nocDDAPpihPlfqb5oIIgTy2UYsBEuGCX0HsBSNWHaFyDm4OuE86zMICd/gxmm6N391c4erpJdaX16g3W1yeX+D6yTk2ixWWV9eI6zVmqwli6EXZ5U6zZIkPm52X8Sg1I5EIDgao6LMZtcdnQMaXZGQb4t0SA992laHRY4Xkea/BmWUYBiFNziFr3DyWMYZb31OOcaAYgdFo1rfnvb6tyuDWoCkU5o3YVTq9VAbG4H58tqJUOp6VtiyfC8laon2WCTlkAEvll8Mh8gHzclxEDnU9AUfJ2nLy0hnW20Pcv/cAIXQ4PTtG5IjJtEFdN7DsPFYp01GlwiMLW1s8iYakrsli0aaFyoUQQbEIDalGaCEf2YzW65VYuaU1Ba0SpsHl6jXFRoVuUr6sn5TBcBYqPJQCxbxK94viSTcRC8YeCzv8yeW92iglKtomXygK6TnTZzR1L4l/IsEC1UtMkMr/OdG3zKJjm03qAgrLkNJuMm3Qtls8fPRQ6ArbVwRIwkl1YilWw6iaWtMrHuDg4MgK+EqVa+8FjEDAoLPY6CgZNcRToQkMCgAvyrlYhOVw40rD8hiIEqIlRZiUgqWiUAgY8UoowFRFgRipSjQYMGt+qvprvGPzHYcHyU0pZBLFtm4mqJsaTV2j3bbYbrc42D/Aq6++ihdefAHOSfG9oKFiZLxk00eymoqzyOAuYIMWR8dHmEwnkiVubx/r1QbLq2vJ6hNE0ZDQNA+iGlRRqnDsK/PY9OncQuWdBUdJZqe6hlfPA4AE8sUzIOtXwJ9LoWRwhLqqNDud0IPMS1QouRJOkvQ1pCw+JV9jmLRBNvksC2OM4E7OgA2VQfVMqNUT+nkswvGGoCNDitwdToofTAmLAFFAZI/AEXX0qLkCPOBrkV8cSQpwq7I9m8+wXK7Qhx51rJOsBpHwTnp77ltpRxj+jGgaKTJVVbO0jodeBMC81gfHh/jUpz8JAkm62/NLnJ+fo922AGvoIrKlHYlclGRd2ouKfpsyzyGKUcAs/GYkck6t/hWqqkalPNJMGnjncHp6Kvd7CSV2zic5Jkq5hiCR01A/CdmwoUptDpNzInNk3rPUsrotpIiYNUSJmJKHkGAefaG/nTmR+5QnWA0GDKAXedAzQCRF4ky2AHL+AcTgAAkNEwGCMmogZYNSORNZvImBzbPOcn7QzleBsO177FfHQLdAH3p0fYuAHi228H6NZjKF85XsAQig1qHftui3LaqmwfnFuYR3VxXqZoKzO2eiLGvS4lgY9exKhhoA8/kcy8UCB/sHeT1xyS/FVSD5UqkY7N+65ggm1/SekeKQ96HyyvIhv0vvL4VkoXRk5SXvvIUkgniuVAFnlb8jnFg8rs/ffNdA6UDGLZayGcDQEwKVg/pMiRqK45e5vQJXiBIg4XaRgc6ZoYZALmLFM1y4jwEN4bcJcHcc6jsBB/05TuNTfDxeYHF5hYN+gcWTczx9530sLi4Ql0vQagkfeoTNBhWE3x2zVnIH4AghCI1L4F6eHy7DplCOFchrssC7ic6jvwfRPro/3HZuctxOer8vPQ48+C4VvoRG8wRVpIp7x2dF7Peyr3lscg4rxojlcvnMftr1bRXsKxsmko17u5W83HVdD5QEfSgJcvt8rNUZMazC94BAPCyeV/alDLdKz+jvtkEPiId84GxMTEJO0yuMBbR9xAJ7ePL4QzjnsLc3BxGj9i5lFEiTEAHva93kKR2cZGVeW1WmWZq1J9nyRwuXjW4F3S2URsCFxJTGEMANa8YsyRMdu5g3c45gSwPn9FCQV6FAOcyhIKLBDeQUkAVDpr2ek3QQQWrMWKgXSUvi0fOkgCsrO9D24CycI5ZvEiuk9wqcAUByfBsoSIfAsliFddAOevlKsqSUAtA7B24asKbE895hf28Ph4dHmE6nUlHXS7y3oDYPIslwEmIHBhBZQm04WhV2Rh9C8uJZ7DoXQidqpiCxzsVkOpODbqI8DNyZtjEgt2Hnj6B8z6zE0Uw4uzYpA1jlFzZvEupr8f9Ce9bD0Wx58hLNATsE7Z169kJERz1m8xlOT09wenqK05NTzLQIlRkZUvyq7ikEG0++bHOOrZxhmE4mmNyZoG1bLOdrHBzPVRnTzHQGqpQfzDNkY/TqELDPnFqhvQJICyUxpQFk7uZ86BAoFSH9OwpMN+tdzz0oQD0IGYDZ3xZqleRfMopQ+s/kSgJvqoQU+kRSIsS6j/TcOLMNI8vadMg1rRFKPGXrNSsDwnsxijk+ARiqhJgOcBHqpQEODw9wfXWdQuscAPNMRJVZlcvnpJIdIfUEGlYkf83nc2w2W8zncz0MXiAiKiuVyL5xeHiI7XaLppnh1deO8MabbyKGgD6I986LeyCJn0KUyfkbIHmvnPJnChNUFMdQ7wJsvVmoXQ4bNnnNkVFXNfqQUxv3fW/LVeUJgeyMjIJ+5+S8XewkCU/UMD6bUw4BPdvZPSD2IQEhjhEUAMv4F6P6akgOywrYs3Ml0CKbEhriYg7nS4CQAIKDZ6eGE4alZSbvJLy0JvjKo9K0y6aYe5tT9Y6AI4KekewQ0YUeAVLt2YxSVU2Y35lj27W4WF7g6eUT9HGLEAO4a9EyA5pt0goJMoAFIDwp3UM9qfG5z34Gh4eH2XPHhVfLsKxOms334cEB7j94iMPDw8Rqxidjw4CtmbR7lfu3NVnsrennEEfn7dGUhBKI2/fpfbjBvwWMGoQHUvrM/hD+CtqHQRtIp1iMVLA1We7CJUZJH9oPzmdWynencYGLXBOl54XT32KUkHslfNP6rgWJg+3BwtsUDQfK2o1EIIroiLFyx3joj/E1EOhFYBo2oJci+s8yJssPMX3yTRw8+Aaqi6e4fvAYV0+fAB3BdQGOIypAqrBTQHQSRlQC/3E0zvhilrXHo/vLa4CryudoeO6jNLjfptTY/FjEwa57AGTPZNHebb8n3Fn00/ZXIqlgH2PQSvUffX3bWadKLwQgGWdiyC4liSeuNaziZrXEUhHZpU2lbCWje4fKBd14DhAmLlefEcp7OZBG8SZhTQDbKnLOYT7fx6YH7p1vsN5scHx8BO8dptMJqtorLswgIESgqjXUIeXcRl6Y2o9kUU4gz/qZF2wJCm3RizcoYqoVc7dti6qqcblcop5Msbe/j/OnTxECp6JztrhBevjPOc1fDThHknfeQIj+UwZyMZD8wswZCKSxlf0vhExiY8pARp9K3oiEd1WaZvxrFsjyXcbwAMgJ/Z0eVCaX4tQJGnZSyWYUU72UWtyDJCFJHAK6vkspV8GsXh7h18VigevrBcwDAcREJ/FCxAT+I8d0YJU1s0UGiDG5wZNFMCl4eYINiAyUA5PERpfC/JusQ8zJsmC3kMtx+SbYk1LAUX8vrCXFRoSYBUsKJbEX63xamkez/lpoQzNpMJtOMN+b42B/julshoP9fczmM3RtQN/2yUUbYzG7+mtEuTFTAgIMoOs79H0v4SCVx9HBXrLemIXfQLWsy3yAXerQEMAWDiEegKwoc/Ym6AbG6tVq207OfpiHyJIswMKvDHgCZrmUOTZWkfvtnFFSGExLoDz3g7BB5E3YGMI8lyldZgl01FJpoRdpbcrC1D4j8VpOslAcWDQwwPnNIQZURpu0Pq2PomyQ0m02m4GchDvFEAHHIC/eoaSkJ1Z2qR/GeqDcn8iM6XSGxWJhLSWPaFJS9W12Xu/g4ACPHz/Bg3tPELog2QArSRtsVnPTwizhLhkYiKasuiQDbfn1fZdAY+QMFspQQwnJk3XoEjNma766iECAevSM9z0ALR6G7OlLI9Q03Bk0mhFL90OXjSa2Yj3kADJZsgBiCcPyIgNSHYoCRJAjwIvH0mtIn3cOVHl4mAVZQ/sgaZhd5eEbB5pIkojKOTHkKI8KmSiNSeiktLOQKRS8xTZ+8f4+vrzAN955G5dXF1ivF4ih1bmWjFpGJ9I9rZ5MMJ9NcXJ8hI997HUcHx8LOIym2Bcs7JDm1HjfEQDnUVcebddh0jTpAaN/kru68SXArgMc7N8l4LZ2Tb4Xe3wWQzT43J5L63jwYfGuEuSmtZtvNQAKzmc88sH1/CgV98t/5nksPDIZVsBY2PpMxfttxKL4UO4X2zpmWxJ6p8ouzkao1HftXFM3aBroOcFsfLOJjWn9COFLZc55hw6NyOsa2Jx8BovTz8J/MuDu+h18bPk2tu9+Bd/8jS+ju7hEve0Q2x5JK0NmoF0KRgnKy+9CoRSMK3nbu8rn7bNkLOLs1R5j7kTpxMOc94ix4uIcaDTXpYIyVF1y327zZhgtrq+v0bbdwFP8rOu5FQ2rwl16LrI1Thrv+z4d8LZBZsCJ9PmuXMZlsZNyEuzzoWsnP2NKifdeFwGlEIZSoOzU2GAENzu+gIeD/UP8i/cj7t+/DyKp9Oorn9ziDCRAL0BF2nJqPUreAkbKtV4eDDLBKn1B3nSTgMpCmFWiOeewN99DM2mw3W6xtz/Dtm3RtS0mzQSHhwc4v7hQa1deHAyGnA+QNH1cgCnbDABOXhSkz7OFwxZxxhxUxGYawMmpFBMccZTOEtjgvLM49qwESgYUAem+quRQp/ZTlArJuhKZ1WqmYXhRtPTIOYWoFO2KCOZj5lVatGYpjir8LHQgVVhlgMiDwQh9L7SxFMEmdAsAacIzHajXcYtCVfBsYjxkmjMDmuEleWZQfK90TpZYIbZ6cmxeKM2LA2AFyuwck8l1e8B5yjxGGhqkoEQq4WpaTzv/YYqF9q/yPoVIVXWNppmgmTSYNA2q2sNXVhtCxMp202K7beXsBDKf2waT+B9Gyxy+gwRYgIiI2LbAVgtYkktWapfWSX4PCGlDIuRsLWkd6mToUlWWt80rb7YprKh4lwE7kxgsyyv9bYNKPGdrkHMfTMFIqWORva9p3Fx4s2yN2vpSnhNroBzvE5BHSS5Z30w2J6uljpdUUcoEyzxtSloXoyiI7DVkT9bkhCugkrMEzHLod29vjq7tYSE0Em7npMowMs8lVk4sTWnuDfRR7fUMkSm7eQNONfOcS6Fjk+kUr7zyKh7ceyT5/BcdWt4iBElPa2cDTMc1/nPI3mQlSvKqJo+YrjlJKETF51onxcWUgMERp73J1pb3EjaF5E1Vr4kBI/UKVc6MQaQhWkhAuvS+Qdei/CBVjOQgNlUkCp4Tb6OD3a4V6/NWnfZHaD9S2lwdS0omQsWZHMogVFjZ9mTlddJ9g0tZqH1QuUXsAPaFwsuIHJKyxMzorrfYP9lHtT9Fv92i71pEDmntOguhcQ5NXWPSTHB8dIhXX35R11jM68doNVhcti8XjAjg+OQY5xcXePHuiylrFJIsMPbN61RowEmmlhb98VUutcHnbHNge74YeVSSF3OmakTMrxlEGRSvHuCeop2McwqlR5sw2tpBcOtXUkwKeQzFPGnubRfim15flO2o8pH3TqWtymE78xIZYG8YTQPPzJuuNrdIsn+bMc/atBBr63QQKziIGBUxAvdgcgjO4978E7g//Rg+5hv8oe/+Ltz72jfwtV/5EpYPHoLUC4+gdFGj43gKS6V9YLwehxsbvqJ8VsOmtnzOqFaGZhlevTVMa4Afhu8zj7/pTOa5VVbKj3E2XtHo/YDIFDOYEjP6tsN2s0U5zc+6vq3QqbJgn6WY7boO5CuJsq88at+kdHVwWcsrvRhlfYwEAIEbk2XWU1MojPjOURHHHlHXtSgxQdJHhhhS4RZdRpKKEtCMLJrWDAIKew7wxHKADhUcO7xzPcXi8gFmc7HWTpoaXus/2IZoOcBd5TN4UJd7hC4kQopBN7zNZdiPzbPRGUVaWttIAIDEo3J2eoZ79+4jdsDh3iGWywW8IxwcHOLVV1/B+fkFVqs1AvcCJpFd6RHBVnz2NJliAcpCk0gs5EmrVQs2yYYkoJZghwvTvPpKDk0mAWZVOwWw2KZnIWAp7IWjgjmg73r0XQ/vPNq2lWKEiMkKZmDRvAZgFH8rGCJdbGyCLEtn4YZixwXSGYSkNBV0MYGVznLITpfCQ2yjBiilNfSj0EEL1SEoKk38re92aRuUv02y6+6VQ35o8E6QHQzWMDsvh0S9Zh3yvvT+Ab6ScwR1I8qAS/dpwTDvtHCYL85hyXqBKYbO1m2xeRbrOPYRq3Yt2ZsKsMiG8JA3J3k8zwPpXArS1Q+0DROKYkEO6DWTPDgrBHnKSusSJEVl2ijtGWRAlOZwvEkXm7UB6LxQU5iji8XaKcACyvvtMZJ/DORlxQZJMcygJXt3bAClJVY2WyRjhYU7Jj4vAJ8MgTIYShs06VyShiPkcUcwEIBNDKiCbbZyBsADqODhIaDg4GAfD+4/gq+kHonTnPUxdgL8pG64AtXM7wJQpb3ijDZ87RBij7qqdUxDgGegJYQedeVwdHyA2XyCy4tLdBtgUk+w3ba4vl4MDjxKKG5WsiVTkrhnSOUi6f5kYbvOObCTA9KW9SnVklAFQZSBDNDT/mWKQWIYpAQBw43dEDmN5izjpvF8Zp6W3wMV74LxFhdko0zzkh9LniWzKud7BGJpB2DdpALd2same5u1bXuDegNFLlsCCqDsnWUA3G47XFwtAXjU3sNPPfykgVU+JmeebPFs17WH44iD/T0E1myThUGhlKnGaxYcat5zG8d0OtFzc0H2MXCOby8QZlpjJV/a1wV4L9g1T9RIHhhwy7QuZFpa3BhNvMmp4ft4dJ/xTuIDaSyFRCkzJI+ybv7ybCEnUu9Uxg1kJNvsoVAei3s4f1DKuHRuxWR3QSMG4GKEYzFUcnHqQ/4nkRkxjUtT0CYiFqHcRECQL4LybXDy/qibylcnvwcPLt7GD33XBH/k+38QX/wHP423f/WX4C8eY0IRUT3ivRJUZIMRKSsOhk9lnywic4qJI7DgSDaZV+yLSjPDXUn2lArM6ErYmssW8ndCAhryj7UDoNJ1bwYQGJU10Ut6LEbBkszwEdiv56hcNeD/Z13flqJRnrYvXSultlVmnhprVmNCjWPA0iQVh2NuxotJvGsZShWjZNPRl6a+mRcmT7hJinLxSDshMryXvPDX6w5vPxWl4ej4GADLAXDnUXk5oNd3kks9xoCmmWh/o72y3EHSZ8kqlyJh+MZExeIBEfwMZtkQ68bjzgtnOD8/x3qzxuHBIZgDFtfXADMOD4/wiTc+js1mg+vrBdq+Q+yjuJGR4+8TSC9okgWDWhgqBTYxu/DZpJsJnGjAR5SFPrYAsuWfgFScjHW7kqnI8c0mMTn9lN8lXjkkdFluCAMesn+TkKMk0IzmLilEcp9PoCXZ0SCWQYNetn9afIh8lusXyLwJiHBJPpsiVQJFlxawxkGTKGjeD6vMEsSS6Z1mjakq6ZPzmssfmla5HqaprapUVdgp2PGaItUAD0PD5RJj5k3CUj33LPNj9XACSzrXLvQ7hZSBFcqEhwH4EsUwD2z9+XlbDNFCwGyTIdihdIuftwVhoZFy3iHaywqwAo0Qy+NL3Sk227T32d5a0InK+zOb5M+KzdA2YjEssGYnMdmIzHPFVYYuyD7Fg77l3hfbExV0pTS6tGHnQWbwma2X+T0D8FDuPfY7FS8ja0XWe9fnJAV9w6i5wgQMJg8Pj9l0il4Lp4EZzVT43IwcaY2Vyo62mWafc//nsym2my3q/Qa2KgdKqQIJCXPr0TQ1mqbGiy+9ALCmpWQG84vFXHGRBVD51yJ7Y5qw/P48JeqRzjIlASMa8tJYsbQ5MT4VcMsD716e/4LpsEOpLcZvg7K2TTffeRU8b22SjYlv3Dp8YMC/mQ8Jea4KrJTv5NFTCZjGNLY8PpPZhIvLa8SeAZJDv2IUzEkXBkkZWFaLI6lSH4rzLCmEFNlDLLyWMYDRNYkwIhzs7eN6cYXj49MBXrntbIXtp+V9aY3B2sjW4oQDCrE5JH42b2T5JQs9TYd9zoOnZY0xBuu7xPoxyb8dTJpeUng78kfDtmnU73L+WQ0gek9RGqSwG/GN9+fXi9oSg+wRVty4DCceZ31K7ys6YYbcTHtKHSBLZqGMO5nO8BSfwF/5nW/hxXgfd9/4frzuJ3jnn/0ceHGFCUstJUlCJcSIuq9bdM5YGeCRICgki6z/ZygP4+dveycX9Bi0ZYacAl8/qw0zeg4iP8Z9YyT8EmNEu9lg8pzF+oBvQ9Ewz4Id2ja3Tql9ARgoFGVHY5RifvZ7+f04xm2sXJReEQOhFqJVapFlX5g5hXkFLehlxB0fWhdQ5sFRiu7907eBx08vUNUVjg4PBfRp2k0gYNo06LtOQLMehHCUK8c6yuASyELZFmRkY7cxBDOBgLQ6mYFIUmBrNptgs97i9Y+9hrfeehvX19e4e+cFXF9d4PLqAtv1Csvra/jKqqdrzLQqUlploBBUMbWRLCmkXp8oNGy3Wz3wyEXqU6RwEgNaxHYoVtzglkcqeXqMF5LUUvCgQCNr4kITi2dmaOgBA+SNiFxkWsk5/cn8r8JlsDAGUyjKdMkGLpMXw0K8dBd2qj1YKlELWyBAQ/OyFZOI5Jysr1DXFerKisZ5TYsp/FBpWFjKUU/5nEPuG1LIoW3oIBpksZBdR+erqOcQVYHsYkDsC+u38X0RC5yUSv1d9ydlO05tM6BhdUPeMesHESelysBcUmiYi1SHNxGN8ZIbnLUw5tQ4buTNIm0mSRAaNjOvn858uespTxmNsnGnEK6pP6ybEwbWuaSMO8BbHwabKyewbPTMbvBy3FTQNG+s5cmDpMQj9xMwow4S0MkjG46U04d2UwY5VHw/UJ5sPejdAgpMAJFagVUBbRltF1C3Hv20llTftYQ8+rrCdrvR80IOvqoBqBGKofFEQ+CVKTOk6XQ6w9XVAvsHh0IfFk+2iQ9Ko5UD513fqydRgGwcoCEuZKqsA7FWAwjGHQCzT/NI5U+bb7bPEmIaANDyl3JeB18ZWUdzIjQveFGTh9h4S/41NkmfDYiY53XAJSVIsfUijQ6VI8YALGeFs+A16/8YcI5ol7tVHoaV0ZrCaesNRIhMuLxeKH9SWkOe1NgCDTe04Si99ucz2fMhc2PPlX0e8xqPO65fHB0d4v0PPsTpyVnqs/Eds3ll8jyMx12uMevEgBaJl0bysHgkm10K+iErCrnpgr8MdNpXsfjWDB8mXUfMLUuTCl7L/bCO5XNSRWfLPpq8GxliXHkrCc+mbTolYhjxub0hAoGiaCvWtg4gG1MKShRtu7SGVOZScRiecoiVV4NmVdeYn76EDxaHeBxrHH7mO3HYTtD++s+iunwI7gM8SI2rEtBVpvAdl2d4FsgfKEnMg/tuZFLl4TmN/y9rf7pryZKlB2LfMnffe58xIu4QNzNvZmVmZVWxqjiJECkQFCBBDTTU0gPoh4D+oYfRI+iv3kAPIEAtQK0mukGppSbZVLFYVWTldMcYz7QHd7OlH2s0Pycy7wVqZ944e3B3M1u2bM1DfsbayJ9/sz35Xa/f9/tT8wYEH/cPe5lf+6B5o3t9L4+GWU4zkJil7Oq61G1WAOx+A15OjsnaWm7Ml+/PzQFzUps91/5mLwcQCs00TahL60uwJQARDYCWFpxbxX+4Ocfp+BqfvnwJKgXTOOHrb77BMAz46PlztI2Auy4LyiD5BDQm5E+SgAsLbLw2iRB5n02AsAPHcZ3AS7oAb3cbPHt+hZ//7Kf421/+Eq9evcanHz/Djz//IV6/foO3b99iXhYwi5eBAbcocmsdpwpohNBViKQD9lCky6omjVNjd8VIrXET0lkb3BXpIstjMCCKkBJRYkIZtPvNhRfEyPBBhpPcD5Z4fNPWCGHZshKjmsRYitWkIQkPKoOXAw1LvzYmKwPGUbrIFyLpuD4WVRYmoBBGzSnxRmmjNEczvJMwoxLJ8CoxiQBrcZiJHJqMkgQFEX4UP9kUB/ZqTPbMwJVQEB4LOIrfMIFI2QvLbIxhhtCgpF1hSxSWzgh96PG0Y3omkCe8dmFMGfNjcSQzFmAxOOjOgS2BuQ+7cuEnvcisVpK8kdhUFqA4QK+SggmaLo+Z16C1VAqTfIHkAldIV+TPDTzP1Ub6BcMFpA4kOq/OU6IPsD0kcsgo7GxtwWpFYY/PnTKSJC7LcYh126rICxsUf14WGUlnU7Sq2ozT4YDj7ojz8x0uz8+xGSfc395r3tUIi00Rz2WEcUahAj37yriNbjCscd+xpyO8wiS1UhTA+3h4X4gs5ut9fpYcBpw8BXKFCSza6iGWnzeV85+kNCkBt/0klWhNsJXxqLsnbU0HadvfRDJCUIylr3Atnz/7xkJwegHV5rSuVJZA9mjdOdwxK9Z5bHB6ruKgCWSCx5qcOoQxR7wOBXd3dzgeZ5Qy+hON5jMLz7FYf4dfa7i6ugqhR3MiLQUjz8lhm+G84sGlDNhsNnh42OPsbBd7wbIAy8d7pCjw6rkwWtYDcfVxdb28TEyJvA0kL2Cs4Kk5mAEzP53VENKdscSj7a9JVZ1cojcMPip1v2dFlwBwKWndeX3s1ztNHdT45UxFoCAwVx5Knim3gpidMYOK8jd9VlMF2otJsMqgerdLkJq4RUWiWYCCm5s7vH5/C/rFf44fn97i1f/nvwE93GPTpPt4hYSCNkIXBpUViADfKndD/1q+8lrYz4b2fD8/gXdPGebX16zl7UdwS/Ozz+soozx3g/58miWHqa335unXd1Y0lmVxD0EOcbK+DL0b5jHw1kBYh1XlcCwrhTlpU5DeU/H0GKZgdO7OFQKsASrPFsWlVsZuu8Nffbvgizf3GDcTXrx4AQLhYb/H+3fv8emnH2MYR61OQ5iXisvdBeos4UWSvKwkmPRAuqYPEWbYLPDQqjhQARxuKZFp5tMMcF3QyoSrqytwu8VHHz/HMA744re/xeu3b6Wb+Ucf4fL6GnVpOB4POC0L6lIlKVI9O1ZFp4rEqYJnyoEg0tKWkuMxlVGO8Kg13S3HwIUrWpG1QGBAYhUlXEHj+1WBFKt+VEkqhTTHg5yoT4MkGDelZoPmDogngNSDIN2TRSEUjwKRVEkZx9HjrUf1EjRmDT0ina15tnQPpNaQErsQ/tg9LAK3KF+6YF6CmboQuFLkeEUsFR1EAEleCRNWLT4jC4QhGBX9LYkr+rYlwcatOa74pBA0XWNvJQsG0cDQKAcdW5lsUgRXuk+c88zUOcLoeuFFocxR+tW8ZM0vCeukJ+iuXi6k1XDtygI4CRGPOWPeDUu2lvexvj5kyc5lt4j+OTaa7SsQ61YBKVv+BE0Y1tDLaLZcb4JbVirg+x6CrX/phQmYSEvvBo5kgdLmCILnZdj87KpCpFZBxSJl+tYoTyp5NRwOB5yOR5yOJ5j1bV4qxlpBRWhInSv4TBM3i82RnQ66Z5fjjFn/GafrKY/JhDLDh8YmXDS0RhIaYciX8NSEkM5LBjh8rTMXMbCsUY0Dn7nDZ539er+hj1sB3pQ5+0qGJt9KEwhhq824ibA627emUMl7Ds+xzYVW1/t5ht7xaJnd60mhsuNpT+E5adKu8XjjGRD634D9/oD7hz2WpYr3mwn7+QQqoqA6jye7k5xe2MwZrOGk2zgzjDgWKzBaSCMSrWWY9Tvw4/nz53jz5i0uLs5g/UBk/RzrSAKas2vuKb3DPymX65fjcwYoAr+y0pDxrg8bstDfnioZPpmhKsyzcs4KEnKQefmfwC+DH/I/AUOD7Upk6VDfYOtyjq7BDB9gRtMkR2bLGyEgVW/k/PR8NChCGzvNDKlsurEufVArsQYioLAUOzk/2+E0L9jvT/jmtMEPfvIP8fJwiy//4t+h3N1gV6IRbg7nygL/2mj+1O9rJWP9/ikF5alrP3Tvekz7nK9/SjH6fS8PSawVS67Q9nte31nRCDdiZMNbLfvcwO/3uWPWm2HPy128TWGwZnv9PZEDst6QtfKy9pAIYvUbzNxQZ4lfv75+hv/nu2scjl/i8uICZ+c7EBG+/PIL7HY7XF09kw7pJBod2f+i6LOdOrhXw+ZOKiwVIziyYRZ2ZMTbGlzp7FQYBIgL5rliHAnPnl/j9vYOz3CJi4s/wrffvMKbN6/x9Tffaq4KSbKcWt6rUkIisbxbGVZCUWGqAOPg00eK77dqKWbVz2FHwzB4ucVxGDBNE6DuynEyy78KCyTdgq1aiCUgD6oA2Ger0W7PNkUg5/6UoawID7T0ajrcSnScobhXR+AvioE2lloS0QbDStPmzAHnAw4kxTefhAkvRsCUiJXMkJLgw0mw5GAYpZC4eB0JsqQkVudmFbL098YtJSaqhdAJsDzbCYqFXKWpG6EniiQ9U1HYP0OZq3xLOh9QCjXKhIviuVIFLEBnpULFwqSAIA256hS0YM/BuJJi28HR8n9C4SCdhIAmhS1xCIfg1snrXdC6SwAmoKzmlQUNhlac01NrAo2OYzzQhGL5RcL9mjKsboju2d1O+dvOe6NCrXuyOATWQrHfto9W3tWrcHGsByxhUpK3wyYpgMFY6ix5R8PgHefv7u5xd3eDYSj4+ONPwK0qX5C8t6qJl1JNWr0mpEK3CgRmmNDpgUm8GsfTCWe7HdavJO+EMEQJLs4TkmCDEFmF1vbgdt0ugTwLXfaAPkzEwkLlEGTPpj0+j22ekiTf+UWrILo0MkVFv57NuCBqhQnsG7Y7mTxOnoBkybZFxficvop1x7lJaC3vE3Dy3Ay2HvpKRksI93d7vH1/i8PhoPcU/yvt0LOwtA4sNOu2AJCYcXF+psapCNP0/aawXDstyuvjx2BgSF+qpVbMp0V5aE8auusT3jTOph+5ynj/emM5P6sTmZJw6jNlT+5ygxSU/yg8ovpS4KCX+w5tQJ+YLOD+nfxjoU7rOQc/kmcxayQkZQ8M+VpMYfY+m3mRiTYaXBmibErIlxhCuUFpejIU+/7K86LKVcCDSHtf+MqUKrJxs9jLYmthoNUFm3HA5dkO4zDh9uGEvxx+gf/Fn59w8+4Op1/9R/DxHgM1T6D/fcL6Ws4NeD7tgXjq/g8pFh+6L1+fK7w+9by1h+SpZzwai0X+ff/uPTbfMU/jOysaXffCNIlhHGBurjUwbcJrBcBelj8xDFHl5qmaw+tnmaJjykgoEngExP7QZldTICdD+i2c5oq7tsVnn73E+e4c280GN7c3eP7iIzy/vkJrDe/ev8fD/R77wx4ff/JSqylJhQoP99KxTGjzw2RMJgkeTuC9okfUWACi+I7V7z+dFkzTgMvLC+y2G+z3B/z4xz/Ep59+gru7ezw83ON4POF4OrkngGvTnIkgBGDxMEjFrlGJi4zhVbxActJV0B+GAeMwgAowlgHjNME66EpS8gBQ06RmCUkSXUXKNpowa16RwAsjoIE7nvchJNP3DED0ADEZKAnysuTscQj8yYK+MUxpXCWbI8KBWg1ZqlQAxkwUx4lUGST1YuUwpBBilBMmAogkBMGZXi+UMqoajFsJHCEpx+RjMJr3RjAmKEIb3HroPGi17pRD7bhgIVbe9wNmHbI5hPBi67M66V7mMA9h+4pgvLZZvh2659aDhZk8VCwkIbkvFxQB4iwInmSYI77T58becPfMEEYZlXsXu603KEkSth7NI4QYe6QrYgZ7pJu9uIBc9dT8bfkmapmTzyo2+x4x+vwUxfmltdSrgL1XRGtNqoHNM5bTLDDR8s3LskjjSetUX6saJJQpglAG6U/DsA73Ekq5qKd0GAmbu1tcXlxqpSfpRA1oXw4M3jjNFHmnkZzWrefy8uIch8MB52fncNrtcMUKL2LvRBCyH4PW227I2Ib1ALcQDQPP/ZiGgIf0Y95Uh5HeI8jRWVDtPGXrLHV7So/GTtjQJ9U+gYtwmZHi7Ov4Zpbxeynjc5wlJJgykgC9hovTxYTbDuOVwKkPqUx48/o13t0+gLmANcEbpCGxalSyNZjBKu+zz8EBx7i6PNfzyup1TjBPe0gZhgl4eV0GOwZwdXmJu4d7XF9ddcJsXnf3OeGvW+9hNC72K8ZOO6y/t5bkEvtBky0Mp7pJw/hbogGwVCjhTwPIyy9DYaf1S+Q+E1r9ds2Xo7VvxugaQ3gl+XrIETzwnAGnW5QGEOWGwaxFGTTc1QyzrYiXg5jBA4NbVKmUSlEBe28lkPaEiMJgpZtmyqDgEkuEBcNDNkuRHh1ikFmw221BpWJuwH5/iX/Jfx//7B/e4Fdvv0FbDhgh53hONDbLrBEtQ937jDvA41xlf/k17O/7SAGDQc81XK7U6As/CvkZPsQjCrKawuPfQ84iDAOhtQW77d+xomEAMwHf4t1P8wzJcXi8oA8pHvl56+Z9WfszRSInyACac8DczSlrbaZ89EoLiyCtxbHNg6KQw9nmDG/uF7TdC/zBH7wEt4aH/R4Xl5f4/Ic/wu3dDd6+eYeb2xsUKjjfnWGz3bqXQRicdt9uRUpAWi6DrBhOjSmEGVbNo2NsnEWVRNiVS9WlgqhhGEZcXV8BzKhLw7MX12iLhElxbTjVRQQOzVEoVDBOY7cHRZUHIxSWu0ApK5JIS0CC3QJlgrLN2zqWO1EPqUu6bCKUgEwY9FGdMGuWC51kEt5kxCwzOswMv2DJyOwEL+JW0/2+9dwlhKabOu5gbxeG1ppnFbITsacU9mD3sLZSM8DoWk1w6YRShUHTIHkPw7K1MASHlVgC8KQ/glguWb0bZpHq3KpspAdR9YmjYZLB2/bEIWTeBhMCwb4nJrLlkA1ZROC1Qge56aOvWcUJE2DK2pTGsXuk6zNYwfDJ8FnXzRY2ZfQoMZpOETCPCqTXhk0dZGEGEWqRoOEfCew9LNLXvQKtyGoMFqqgWV8dp2lVuqC31tC0s3xtTfq5aN+bZgpAY7kesr/EYsGrdUFrjKoKA2vMc23Vw1MNJgytxUy9oOn7o5XapHzroNbJEdNmK7DRCmnMUqhiu9mgtUW8GVx9vtLvomHmho1CXrwpAFvzTj0aYRmWD7vdDu/e34DR3ALpgm6QF/+BQwKOsymSn+5bEI2W6AdKorZ2LIwa5Ov0DJMJQn7GkGhEcRwy1OnwQ6dh1yT5wZWkWGk8txeIQ1DsNYAVjPK4LiymZyTplNO9Dor8vPS9CcPmMVyjDyPOnIxP+PbVG9zcHWDdvYsu3ARME3JtTZ1yQQrVLDEC2I4DdpsJMMMLgsz6RJDoQsIXg18zTwEbp5C9PT8/x7fffoOrq6uEa4nm5AEyvNOcDWdWqbr+NxLb5T2DnZ57jpAOHnQrwTzR6Ci7nHg7xTm2jfNzZvQ8FQMgIu9N5XBSnpN5rgE644TTlVgeDLmdHtoPHPAHZLE2zgDxyAyQ71phgIWGcBN6LN4ORithfCBKIbi5YECanyxb1Vclf1DDIcDgQmBIaN80TRjLASMBD7jEf//sn+NHf/YrPPy//iWecwHmqoqSeMRNzvRwzlU6QC6StFZCHG+IQFxhrlY7ngTNszBKrWAbwG7wIxod7sRhtPV+ch0o2MfD6vv1HPP1ds9SFyy14auvv8DZD3+A7/L6XopGVgr6pG90AM7X5zgxZ3b6WvfTsL/ZE/HUZsghDUDYs/Nfe7ZVy3oKYN5csALX11f4t99c4+3btx5vvJkm/OjzH8LKJHzy6adqFWRcXFyAUNB4lnCXlsNX9IyRzT9Cp+RQWRncIGyPcvdXgrgdRHPPi2+6ekIdAEzDABpHJVSPQ7EYUVrXiC6R7Fl4ABhLW1T4Do9KiMZITJP9QLMefiFmpkyoIMM9ovterDlYenYnTNvIiUvYrQamDl+U2Lg1iQBKdjmvZNnNK1Fv7j7BWZCtp/a2+rWY5kK5P9rcCGk17KmnaQ4h1VguTTSYC1iaxQaJUNgzWafZMSGbl61Dn9cJJLqR7nLumAql9fRKsHwTQowjhOPBSkQyhmnnGHCEzJZTVzwFGWT+qdKZKWuki3Aa5IzOaEhSZJCm4swVynyjY70zL4RVqHEkCnMzKKiFXNfsFneWkFLzIjA3z5XipWKuM7iyEOzTjEas3dMXP4etMowqsHaJlkdriBtbOABcgHCAUQp+03MhNFBwarfdYrvbaXjliE3KcxqHEeMwAkVyoqwACBRGQxm98aPt5TLPuLl9L0ahQfcsNatiSOEMxjbRtcCHJFPLL9akcojS5H5HIIXT1KxUAslrkJRUwDEeBGBeqltEDWe5ceqrofjUpGIfiLRwhAoRRFJ+mZ5ahAKn2xe7zt4+Qfw6OLC/J0XCTEft9ASNQXi3+sd1nzPNXL/W1z/16ujw6vPa1mCX3d7d4f7uHtDqUQYUF3j9q76yDqVnGp674qXKgPAvZP3j0RkHei/no3WsaCVzFA5Z5lnDtdc0j9e7ByNVlvfWKUzGK/VCo2tkDCbxHV8vzDusvzmuQYxGZDhtSgZSP6gIjcr8/xE5zoqseQugio0J4znE0CbX8QdDAJ+q0szMS3QeyStLCCUn47kxXc9vKZCOPVpZrDA0j7SpAsLirWoayaCGMTPM+mgshmZmCd+FCvtiRCFX7EijHC4vLnF39wrTZoO7donf/Nn/AduvbrH5j/8jNiMDtSKpBE8qE+sIoEfKSGuwnCSjTU8pAH0hn6hMmU+M7XTaXhjHN9RhjrDhgE/wifW4T70GIsnROM2o1lbi97y+d47Goxiv1gAaHoUwZWWkZ3bxegqg61Jd+X7rmWFEIHss1vNbEgCy5TBfB1gS+Yj94YS3m5/g7GyPZVnAlfHs+XPM8+IKSxkGnF9cojFj2mxEuQB5GI/HmVuFGj0wpdi8jBAZzmTi0lvfQlxPjIFF6AjA6LVJ4KeEjJ3rEOyWXoO6CcTgsAaQImNHnSjChgDAu4g7fJFgQL4mj0cWqtNX/sinIRHY7pSk+brAaaYplx4o1mf3AyBYEhkDTRv62I+mrMEYb4jKCSROENngTFCdwe1nMV0n4OQWP4N9Jso+df2nt2LaNXFR95MprOQfBUzNGBEb2IQAcVhu1+Bl8IoZs/95FJ/reBkLNaXAcizM6thUADeLkYXiuGCBcGUb/vqZ9NCHECjs+4BLxMczTOjXMByKdbMT86o4Lb12vPIcm4dgkfChZpW/QjlgZQSNm3aq1kaTVTvP2+YmBaO13FBSzxyaN0CCnjGFhFoRWZoi6suawDGTfj+ARilaIUUTBqCxN1ukYcBgDMzzmmTPlrrgdDzi7uZWSs8COL84x4tPP8O0maJUMyEJJuSIYpZn83sUs9gXwlAAKgPqOODm/TsstWG0KixWulLx4jQvAoNx6BhfL53ySshgbKYRp9MJu+0mzjeROYccnlalzDAUSDimzHWeZxwOBwkdsyIZtaJVqa5nIZFEwDRO2Gw3XkyisuSMXFxcYJyGOKNGN21ANpol7y3E0Sbmc6JsALKDDH+mEwkKvhCnL73PpDAJfNkjAMR5cJghPcTOt95HpPH1MPoIz3ew7zuabWPkc60waI3x7uYWZYzKjmYc6wTLxJcYBCvEYDtaSD2v6tGlQjg/P/PSyZwmEcaxPLkIN3TkYOO/SfiC8cqG8/ML3Nze4vmz586/7Tl2X4atDN+H0pogz0CEvyoNdKFb19+FUTovbQ7zLlRSP5N2li+qwBU9x2zI5nsR85O59GNX45X6m+G0y6IJPzJcs8Euiwzr330nCUAjyWttDGveWmwslv0vKktFEzkV0iF4xYOVu7aGwBYaqsbsyivexypcQyM+dX0wvGZQK0BpXm6/FMJHz6/x+t0dNmc7nLhh8z/93+H06jeYbl9haFbE//FrnTLQyboK00zD4id2GW+toHxojKd+665L73MfGcuRXHtcOqgxPx5DDTKvvv4GP/nBZ79zbHt9b0XDFme5FQBc+F+HOq3j0da9Nuw5FoqVPREfSoAxpSErJE8pD6b02POzprl2XW23W/zFb95i/mTE1eUldtudtGofBpA2LrMKWGcX55iXquEJ7F3BnYAiiYcU82P7SxIfKN8DhmQMINdRNwTQK0ULB7tAb8KihZDkpld+upM5KMJw9Hk2PyOYRkDcwmHwNmFJhVZK89Q1aEE7X4+R2uoMWJmQJ7TZxdniSD5OZoJGpINQNpiVhpu6QSnN32/u4eTvjTs7cYx/OW6DlWu178VQkhSR9JeV4CMNLX8iEdBDfDxvI18YszDGCliuBHm+ijEZIcDw59i6TSDo4qzZFAJ5IhhSvnW9liSxJHkl9srGTtWMbLzuTBl+sQk+yYOkzyuGx93eWjhakF0RIkxwb6hzA1p1YZ8TjnNrqPMsgiMz6rKgLguO84y6VA05at2IFkpkooCN7eeOpZy2ryd2zP+acA5VxKU7e4m48xEgmsRQQYRhLChl1IaNBaM2XizDABqiE7V1lC5aaKJ40yqjDTE2URJqNQzAfKZ1rpjPZgDA8fVJvKcMbHc76fOiXd9jL5RuKz43HdMKXpAqRJKbpWWip414dRrAlV3ZMrwZiEQ5qw1jGaIDOFHAkxMOKN42Bs7PznE8HLy6idNRw8JEi4IGRPUaYeiE+/t7fPvtK+zv7vDu3Tuc5qN4mbKX3ayLilcFECsRgDJMePb8GT759FO8/OxTbLfbJLTpaTMPve5FSUj/iG4kPO9EMzt7RpcBF7oNTqRENeh9T/az8hFn2Z61GrujQz3N4NUlZiDLtAXAI+NVsfkx4e5hj1o1Q5Ag58mvp7QgF/dVSXbK3T1XaA5hM06YxtGv4SQcQ3E4QdVfzcbj5GlXGhZ0U+7cbLd49/49rq+fBb9KgAuekZRNdn0CzkuJn4S5wdV4Y1DEeK7TUxJ+YpXrQCHAktOJ2PMsArCtu7sAQAuvgxZ4Sjw3JkxKTyg55p9SMPw3xR4xQAJ5aEENArEYCwoBKKro6BpBmjdHBifygRjQProUuUZM4CLVKQfLRyti9Kkazm1ykqzLhZDAa61CVZrmidQKlILd2Ra7/UH69Ewb7J/9BB/98Z/j8D/8N9iWIpEfTwj8H/IGGPxJ6aIV0wGgBrtVKLU+M1d4xep3j5rhkBnXio5/Z3NjoVfWdPCpyKJ8bx6zUAEvM969foPLV68/vM70+l7J4OvQI58gi7dimiaM49gBJAMjv7IystbcPqgJyrcA4p6sSOTKVTnUa1kWqWi0ep4pI8yM/+6v3+HZxREff/wxhjLg4f4eD/s9BiLcvL+RsVgayRmRqNy0mZwSIQTzj/cIy4YxIUOIoO8IYcbRLLwEkIPnwi4hKlxwCHxpYQIHTkIJghCH9Y/8cg9V8dH9BycWxa1McpUQfvEWBBE1KUIVGxub8EhBoURIyAW+RLwYbhH0ZF2DUEc3e8FRcCgxXCXKLcPcCWXA2/61BkJ5HvDxYTfGi6DeLag1kPp1dzAPhS/tAFROU2thsoQq95NmQ0YEYv+BiOWVXJyeA+hpUcYQ58rm0xxeulnMsBAGxweOT62xh981zR0gFRAbA03PYG0VXBfU2pThMJZF40/1HLCOR0rwZI/kGcs846T/tdbAtUr4Ta3qFq+wimjWL4YVUWXOqZAoG8yzl0TnkSyCMg8pXFCGIoI/SYlmKoMqBeJNLePkwjaVQa8b9DP5mhTgMge9PtNExyhyaAcXR+SK5ONtOOKWS31ZRFNjxgBjoLLOy2fP8P79DeoygxkYN1uFvZypjK9I54wBlCHyogRHqYt5F0/LoAoxqffHPBoyR+aGpVZsptHPfha+ZB/7EFJmxma7xdu3b3H97FqPT2KEJjxQ4Gp4fNmhNs8zfv2r3+Dd27e4v7vFMs/wSmhKUyPUK3ngbGIAGCecjgc83N+htQUff/KJeFlIBUmyPkIhvNVHwkeaZ1o38mdKpNlgzglPONFzElyonJ7D/fN8bBsrWIqvr9+DNKluhvqcnJCchWWff8prIsb9wwOYhngMhSIjVbqpu4/SdfB1s/NUQLwaFxdnwVM4FAALD/V5cZyQKOUd9BaAW5YN9qLYsSr3wDyfMA5S2l8MLuzKROxl8Fz7zDqWOzPtd1c8tL8Fx1kL/mCrlZcYLhROJPmflJT9np/Cx7Yz1nlafOJ5LEpjIxS1vCcOX4Twnl52XUQxIOai9M9GMhI3ForcQYWtyE2mbFB405x4dyiiCqxwIfFyFC00xKDaJG+shSyEdIZiziQGMLAaRAUZCMCLF9f48utXGIYBx2XB/qf/FFdf/S2W3/wGBUd8KBLnQ4oHpeu7FANdVYZ3loVNBl97GcjoNT3OBwH6kC7S69NsHikZef5PeTkKgJEJvFRcXlw++v2p13dWNGwiJpwPw4DT6QSAvORsXtA6xCmHVeVFfWgxH9Ko1nOxcey7fP2yLD7XflPC6zEMA75+fYOP/tF/gcM8g1vFMI3YHw4oVHC222GaRpxqFSa+LFJ5RYlcboRjjBUIxmnEXX5nd0tGTbhk4aZEFFSQMyGVOYTVjmGxCRdJKCbzFEQSrxGN7FZmj/NWxceYnGsu0TiNdQxh6kaohSBw0+/UnJ6ZWmaYulwYgCLcCi48Z2+QE15Iv3FjS3Ye7L3vuCmuifMFIzS3OQHUXAl6yu7VDIeyYgSgcFixssUHSEKSrskIH7CyJiH2m8j2NixxTXfOp1Cja3ZL88335O9iTrEP6vfp/nXoMqK/SronmmQ2NFUYzANZm3gIJE62xlmsFp5UJfyQa4QMrQTL2BubUyrZmxRySbYrvkbPpQC0sIP2VKEC2oRHwKFP4Q2wtd7f3+E0CwM6313gk08/wXa7xWazEaGZxHK/mSaM04RlWTCfZj8zhKKJ90l+MmINPwa+C6TVmdzrpXtvYToWKAmyvdIwDVMAjKMiQnta0+elMECy8fS96BADSmVsNoSLyyvc3NyAaHBpgBOcdCEeTgGQMkX5STwVYtgpTZtVETCNI3bbLe5v7wHFkaahtIDGPxNhnhfwZuNKflRSCgu0CzE6pXGasNSKVv3U6WTSJ6NnSlMbV9TK4Nown2Z8+/W3uL25xcPdg/Rt4HTGFLYMDexRQ5HDQp8/FhnveDzg5v07XF1dYLMZsdvtJNn9OGOxcu/jqFX3HjPvOHn9e8+psyXZD2pKNgHPE1110RnXHBt59TbTqfXYmZfY9+kion5f8s3dsxPvMPAd5xnH0wwrMstgoaHGLDlokowV/MkOV/CS5DWAKKAW1ii5OHEgjU56aIo919fMGUS+7lzRSIwjDWdn53i4f8DFxaWc1cTsGTFHF9g5xjAAhfIXv5sSkNViV5ydFkDDowCoMUNyMdQ4ogicFRMbw0hG7mFknsCSPgNyjRgNe0Ni5rOOD7a0LCs4rYqDS2mf3SOvjE/WLzklC0gLgJAbZglxDJu+aQTPSwl8o24PTeGwm0uRfl2tFVCT8FfzYLLijc+nSGiehKhxqotcQQX49NkVvnn9Gh99+im+rX+Mn/7pP8GX377FUE9PnvHf9bKwSkA9w/nwpZfJsyY3m1F9XUApv9bVV02WtHNTLLSV1VBYQkHp5miGsCfkb+KGAYSri0tcX/4dKxrLLF4BHUoZYHEFIrtf1qFKvyuGLHs2YrFxvSgvuRFf9PAwrbDW6h4LG99e5uUopegBTNcwUMqAevFDjLsrHF+9wdu370BU8Ob1a1w/e4bdboPKjM1mA1DBNDW8v3mPcZxwFL+ZEAe19FLpezx0a1KCYH0aSD978pheZ9blbFXgJCBmnBBapmSToKERPeZGWodcZ2ENQthZf+8J0lOJWqzPYiAsCTpUhOOEdcbpH8eOBsPsGV3IDEb8VswtJZXHV+zPtBj9PJZdp0Wc1LIiE2gaEuaYYsKPkcH1s1g6WHdEVd8Sq9CU9suus34BzpSZY56ZUBN1eGO46l6oVEnJqns1zSNwPwYbXFmFLulf0FirF2klo2VZQmGwKketagdnGyMUebH+2kYbFtp6lTn6RoUlzwQiifsmIWpsgn8KE9KGbIXEqyC9VqKy3WAJySTnFaVg1OaPZsWCPlMAmEo0ekWRglYbjscjyjTh1atvpXLSNOLy+hm2240rh+M0aEKw9olpDKZFno/iQnqWSR2XSekiQlCwmI+sRDuNIng/C8OFog0ZQYa3pooYbSAVqMjhHfioAqvOUYLFCKCCjz7+FGfnlzg/P8Ni+W1szf1UITIJRZk+ax5abU0VBngTsJEI02YECLi+vsTtzS2WWrEsDXURpt5YwqWICMs8C45ZPgqLNTpRy7Bx+BmQV62L5Ka48h8e09PphFk9X7YnTNKkcxoHXFye42y3w+2za7x6/QqH40FL/lrjUELRJp+k+DiU4n19RhDOznc4Oz/H2fk5fvCDz1DGAXsN6WImlDKhLRWH/S3e39zhoxcvwjKZ2J/QP3JcsVdNiZn5Rbp/QZtNcY+49sA1oxFZ6Et0+He9HB3J7yNEPwKbtwuyZgzwsSmF98jvDw8PLjTbfc3nGeGb3CVFx+dOOYDQMTCwmWR/amugVgEMUeXQ8CqvjTPsnUREBI1dpLgn9FbwfZo2eHv3Fruzc4EPURiOEv8JRu3YKX9bXEoIOHDm4xx3yPYFDAflDYlNwHzI8lzjLQymvJroS5THAIvRTqmi52RWZXj1CURxQ2LirOT/Qs8p+5rdsMXyyXNy5KPMzXhYE14szTuLG2BMOjbDSrbaF7DnAIU8B5jrgyFhScwahcEFpTYsxCDlcwSkXDq4/MassgFLOFLReW93E862E96/fYPd7hy/ef5n+Ognf42Hv75FqRVEjKpKufQD6eFohgTh01XXKJ7/YoY05r4CnkGbDa663y1gYwjNbPUP884o0pQMQ8NRVvqroYoUBtG1/kIdTogXrbWGs90Wn3700SN8eer1PTwaBUQDWqvCCKEoVML1MwwDlmVxRSOHCJhi8FS+xDosyxZkiBUuoXAb+VVJSeli0ZI2WEoJjzhU+FAqsxk3+Lr+HGMp+OjFcxxPJ5xvN/j4EwEglYKlVRwejp5DAGZwrdpToQVxKFa2j3QTI4xHGKP+14CmFlx5xRGFkYCWcVW+aysYdVZtYqmWgCCegpiGjGnuNh6nz8bnKIhiB2NjMEBqMMY6dh/a0ZEkX3v84BattA67w2ME18/gIHaZjdiaar4hfgBRiS7oupYohpivlfuralV2ZM19rzb3jpGw4acyTtjskvC02NgK1GxNaLUB5ilo1S0urVURbnU/pWIPuwfBQpZq1ev8uRGP6knNLSmerQHctPc5g9VKbPjLCn/rc1JYLdqjQKBYWBAVDEPRPCYJmxkGCTvyfANTBEjCkIqGJYkgJ0KSKRGDhy2JQLwokzdEHIZRlJ3aVChWFznYhWQZS7axpf0uo9GEgjoRFi44vwLGt++AJsR5HEeAyC3RRj9qlbwPmcegyoVgQslmYgQTFQFMSbMLbwJlw9WgCfpos3qWAe4+sEaPRrNggkGmf2K06M6N7j2IpBwkoDjFaKVgurxEJcLxJDhVEn21pHCowuYeGDKaSkLzCSgQof7yfIdPPvkYBYzn19f467/5W5yWhrkytk2qmE0Dgar095hrBQ3Rb6hjYhyCmAl0REUa9x2P2J2d+X0GptubO7x+9RofvXiBq8sLbDYTykiILvGM/eEeP/mjn6HVhtPxhOPh6NVq7KwPg7cqc5JgXgkJwxP8m+cFr1+9xbws2B8O2O+PIIzyPLCGxTRsNjtcXJwjqt3BBVl7hZAeciCR0Zae/gntUvKj9Lw6zBBCmcEw3W8gtmf4PSpouhWJsuBqEzKjDwcO275x3j17FsOU8cPxqHhjYYqhyIRIBE9ANyWZ8vPSywTQ3XardE157+oMuEAPO4t9WLDP2Jlg+k15IhFhqYyhjFgWCfukUnxvutPPVh2QPddN9ixCVPOYrmAlRssZJsqySxKaTRg0F1bTNZry554gkzMCe/o9NQTSL3I+CZCMYglPHa5uzIg/hmve4VvvdQOJGiy80L/19CiDhMkqrbYcQmJyPHdbjAvV9qzmoWQBQoWPVSY0maRESBUNQKmE0ipqAdj4Z1VoORBJC+cwWhNFqRLj+sULfPnlV9hstvj66o8x/Owfov7mr3F++4CBG+ahoZaCXZWkk0f2dc1TbhB+B5KSvQ3ScwhkJoWQY+W2pjxZQ2lXco6AQnkBR/wC6e9Myg9sxyhhcWMQDSjc/HSvleB8dogIdSAsDMz7Peh0wnd5fWdFY90Tw/MhEGEWT7qJk9Bjz7FXMPTwhjz1IiIPg8oM1d7n2LVhGB7FqAnDDoXH5tFaw/E4Y89bCcEqhPOzHVqTLtYMYbaTNrQDFSynExYOIhHx7nDNuFFzZmBao1H3HGIjjNQOixIPt1KmzUb2UhgZTmszOIEyz3DhRHE4CI4eShPZ5T6zgEAvDmqSv2ppTBOSDGdD4PVpwlx3ANxSw84gMp4A6y8ZZpvumQK6y4JLewgKAD+yLJ3S45BZ8npyu6ax7XDafkqMreFw9coWVhKYq1htreqaCbitNQmz04Rm9041qVjUqigWrTbdX03UZnaPRSqRoUtkhwlbtix14IYRXCPswjTUEjQQiEYMurhWgGU+aSggYbvb4eziAuM4YdJO7+MwQSoLFu/ULvyiOBOhkJCgYobOM4ilXcNN8pqGccQ0jVFKFOT5DhurHqLCRBkGCE8Q3415N5iRch6KK/ojRT6OKWXGeIehYLPd4fz8Ane3N2Ai1Abp9dJmEGY4p6Xo5+OJhx6L6+UXIGWurbVkhDzavlgOjczHdqU/38wFVP0LqZriNM7wkl0Yi+fBYU8gjdcfUNXbVYZB4TSgNGmSVgph1ApWkStiSiTBAzoIsGR480QJA9eePNqYs7BUaXr52UsM44T/37//K03Gr5K8CsYwjKj1iKUuGNvQdYsO2mTwJKd33Bp22x0e9ntsz84AhWdjofFffvklXn3zLb756mtMY0EZCjbbLba7M2w3EwoVvL+9xf39EWDxFkUIoITPAaShfgKzamdbwy2MlYgHMAwMrVYc9kfQqOsZSGAyDLg8P8PF+Q4t0RnfNgrDjkfQ6kWdIdRoKsLDzByCOhB0LkSE7nZ0XyDopkE/O1IyPTalwWggp0cRWJXYxHso5gJuOM7SANJ+zLYlE5ayMNlN03E60XtdZAFjM22w1AXWw8BotUPhA2tmnbtJ8m19PbmcKbSTxfs8jAOOpxM20yR4YU2m9HpXxFgNXjpahpmAk11p9GuSzYsMkLAKj+Q5UyE0wpVJwR9jVvCePvkswfc495dSGWI1NkM9GiE8+Kv4WDIfC7UK+Z6cN0S6AoOLKCEWZm0J5Y4QChB7S1GKyfkY2716HxFrBIUZfuQ7wzPH5ww3kNR1oAHUlJdRQasLFjQ1Iqtx2AR9mMdXTALDOOLF8+d49/4G52dnePX5/xwf//j/jeNf/RXOTwXbRphZZT810nQya4ATUY3x97/M0EsIfrqWtXPvua4kuJ+P1Yba7wielmVmMtk2pT24fNMEP9+/f4/571rRyDkNOVzKXDlrr0Ke+FPxX7nfxVpJMSHbBaTUb2PdnG/t0cjAzvcIoxy7+0speFgIp+2170HUZxZgHo9HHOnkB2+pLYQ7UsariRByyJsILjBBNRGbLIhyWKz1V8+ncMQwWpsIFJFZoOO6SCrtk9S6/QPCtQ54lY4YPYgUKBqZoYUSFOwsbjLiHbKU5UnI5KNLNPRzwofM4Vy5yQJYzM27iK6SzAuSEG/vVWNaTMjXcqRNLbusXY+bChJiGW9++O17KB5YvWsPNWpmPWheqaMZzhqDMYA0DiZre5lYNpiTgEe+l1JFZPCQojIOnnvABKleROI9KMkj4InIRT0OfnbkN7NWtNawHI+4ef8e79++A4Ox2e3wyacvMYzS9dnzTDpJKZRLW0UkCLN+NmE0Qn3Ms1GXKmsZBoAGjyMGGJgbmCvmKqVHRQkhYK5+BojEQq+77c82z42gUkhP8pZcSQYKSmFcXj8T4WF3jgqgLqzMSq36jcUShGDshXpAxLlOHJtrF/oDCnw3mpbVXDcEQHCpFBUArJeE4okMTQiKEiVprXJJAWGym6joeuChlRbbPVCBgbZQeKLGsWjzTlZeKfg1FJsrVPkgTOOAzSTlccEa2gfGs+fPcHFxgfv7B1QtJ9yaCGs0F8nhmTawtsGSgKkCApsKhqAtLGGr72/egxiawM16Zhk3d7fY7/cgIgyFMG0mvHt/K5/HAWDCPJ/wzTffwkLFBEmFVrS0d34ukyAHVWJVRI2rdF+5VtBM7tmfS8Fmu8H+sNdwR6FrmQ+YwGQCIJDDceDCG6fPQXMT9RAACcyaPdcve2R0suf7Z41P6vAVvjVxj80nMbQQfWIMwGid8E1OOCtrCTgEJveaBqWkD0tatScwSegkEdSAY1ESxffM180BOIejD6J7TP1vlCcXm4zNtMHhcJRCEASxQCceJGdYjQWA83EVXeHCtO5Xpp1GG4rCjZSGwyzYKkhL/gD5/suzIuQy+B9sRvF8O0uUFZvgsyGYG/+O/XTuzeyehda0OI1FZeh/LmNAZSM2PgbxapOFv7pgA9PUDFds/rIXjGqUkuyZFO+NbqgcZtEkNs+i8g55i3KtkkdCy8dCWBYC0YK6SFRBlkMlPaqBhkHmWhsuzs9xf3+P4+mEU5lQ/8l/ibNf/x9x1oBNXUAELAOBCzC0kEnXr9YYoOZVBT/08oieJ6KB+ue17vr8Kmpa/VAeBoBHcniWqR+NqzIVsRhfvsvre3k0ojN36yZmluysaGRlYN1qPS8oN9qzF+sht+fN8+xKzho4OTEmb2rWJEVAiwZ++f6Bhv6QJsGYdX4mPJsCVEoUsrVT6YI+SBKPYAmgSHGa0uwPzCHIx4I7ZiACApyAgkyVCeIosrd8l/M8MuF3jQRK1BkuEHrfAiOARsicevTReVlzIqiAmYgmYIlfRqI4rU0tuRxubIehE2oDlOUgMNCky/mSmqBZ2VJoydJqf1WJMDizhQ9xKMoAh1V6RaBFeDErHDol1giVcTKhaak0HcmBppL+klQusjJywzjAeyEk5cH+k/AjK3OaiCdk7ALNc4AKz8Z0YF4jY/7OtTuBVkoICg4MYIzjBG6E29t7cF0wFMlZEAk0zonnPsiUUiIy20wUBCo6JDOlvZW9BIgG1AYsrYJO1QU2CwEwBkpUvDgAO8zXVYlMuWfHJ3+G4yulvZUQGK4Nu7ML/PDHZyhjwUnnIQ9JuWbOACjOeDakxJEBYFYfnZcJDA0JjsJkRZ8hhSVUmYyzAcUtnxIxSLuauTEF8n6geF7RsK9hkFA2FEilLA11m8ZJPREUqSaDVNkSXGHbrD5GPuGZed6IgDpLw0GAIh9jnHB2vsO79+/FS6BJBOI1LaiL9hRRgDrlM9rFOSdAt7AUyfuwHCITKGFym3gXxmHCixfP8er1axwPe+AkRHRZqnYxt3Ct4qWjkQQ1E27WoaDCi+y75jhgTRwHljKXmn2Puc74fPo8cINNkEo0VRcQ39h5VvqZ8MyViNUrsaseJ+HbmAgtJ4EzHmAwNlZBAGrWm+2ZQfr6H/S3nHvXCDjOJ1i4i1IFf5/AGgoHCZ5zN3L8LmtjTMOIWhlizhBFjpcWc+luN6HJ1saxnrTuVJ+uu9/WPZQB8/EObbNBKyVYKkENSeQ8hdW7qdIDvMQG62pai5UpXnjlMNJcIUpGI0hOAljDeqF0iYBFy425ANmBYGXUiwMW+Y/5e79KlSUwWmW0JoVA6rLIedfeM0tV408LmrCOrjB8MmXADGIDEco4YhwKxmnENE4YRmkOOg4jiKRJJukZbWxCsWyeecrDC6t7W9TTggIqzc8xtchqMVwbB0JrA2hUeZIqsLAXsTCsrawZQEzgUTy5L54/w1dff4NxO2G++gHqn/6vcPn//b/iugJDKVgmDdlfmssd63QCC4XLOsFTSsm6YlSWnZ8y6q8/M3MoWog9ekqxyFVbs/xu87D7oJ7f87MzLQj1+1/fO3TKQqEGbRZljd6y4vChhTwFoKe0vfX3udleVmhyInn2UpjwCUT94XEoncJj91glAzFmm1Bpgk1y4adD3G3qirixHY7WhPE0cgu7NQVz2m+kLyX6OpMxos55GJ8BslDpwn1iAjkWOBOVTGhtXfHosIgIa4jxnBlwEP7BYNm0LJzNw3II1KNQLeG4LhIupAqAf+bqsGutSTOtZRZiZoqZKg4uMGpoDZqFomm6ohJeSzb0QBcqDrH+ULInV3mnUTA2m60TwzKOGMy6awnKwxB9E1QwHyyxOVkBmAA23FTrVLZEdnzbsEKVDBOQRdiWSM4sBGdXuFuE7DlJQQGg7IMSFgC1zdic7TBOG0l013U1FfQNdzxJ2O5lhMWdY1xbj82bOQcYJUufcv4wrhlrU2sap3GQLCaKyCacGa762UyCnSmFcuYHZbAVjCZWXIVHXRhDifNuoTWdsqFM38q6EiwhWuhDKeFdMCMJkVkj4XkQAGtjvegpMGi42DDG7kmCcvYosXghBrmelfEOinvWpMutfA4LEcYsBKsoHoGhjByoM2PxfdOdcj08hL0onMy+l6HoybUW373b7bBU6Rpr513QS0MVlgoaFZCO9fFy/NFfSWEynxYMQ1ERTujT9mwn9IOA4+mIOy0/W9sS9JMbmtMHQsOihow4DZSlNBOaOOiy6RcMSBha0XA6oqg6yAwqBZdX13jxySfq5emf2SneH3yZ2m2ybDIfUH+mfufLDSmZ2xjcETwmzTHGIj9jro9BrcT5IALwQ6GfPYzUNQSzqepcVpP3jyQ9pljri/vYECWDCCpzVM+JsHWmjGyHHifgc2KInOCZcdyeYHTN1g3SPCdGUhTYBX6uZiytgOIi27lTq3+mjXnVcrbszFJUWVZ8ampI0FXEehGhzqzf5TXZd2w8MMtiaQNMsRXPfcUyN8zL7MUVImKlIS+EGRG6y+z0EP6XnadbnkzTJsozAByPmggdNLKUAeM4YNpssNlucLbdYJymVMiHQzhn4ZPEcM83sVS3K6VK8z0KL4c0DjX5R+i49ToyL/BQgHkBlsXCmGUswzUpvALstjtcXJzh9mEPgLD5B/9bfPWX/y0u6ntMnvvV43hXLAmm3FA6f718/CG52F4f8m6so4ry9U/9nr/Pfe6AxzK8X1+BzTCGDPYdXt+rYZ8J0CZMeeO91XVZG1prRqaorK9bv7LAZov1UK0ELHtWDomya3Kpr1prl+jpHpJqm5rzIFKH86ZMjaEYLv95BSCdr+VbUIM2tpNkMiK1DHCFNzsjTbglDqJglk+TD/U7HzaosTPoQAByKwsRPD7QWIJRa8oIAyD6EACMsP4DjMJidWaPV2bM84zj6Yj5eJKa+JuNlHdsFfNplrAIFgViWarHPS+1gTWmVsqkVre2WEKmLdDKoTKRV4syK7w3tyGxDBuOjGq5KObxsqpGmuA5EIEGrVA0aGdlhDxaa8U8z3jz+g3aLHkRz1+8wPnlJaZpwjCOEoJUyBmw7UOU3FOizhm+gg/ZzSuENTNpE6cMN1KVDsNxZ+7w/RQ3u1pLUldpskUBbpETIY80NEUtXXLIUMYR2/MzzO+OKMPojFAEclNgqs8fdkIWhomDSTfXJUVokzdiSgyKbdlITN/vp05ZsLo2EbbEfp9ZSF0x76i74IA0xtPGXjzE5tAg+ADSsDMoQ1JYFtsHrJ8qPxf2+cqWyN+BANLzPQzFvVjjMGIcC6YhqmmNxRLMobgFTUJMcpsB19acBChWWFcTypSxO8NyWPeeu/xbWliSHUMoj7F1RP3OPnqBFWZXhi/OdyBI/4plXtAqgyc5v7xIM0Wi4hV1kJ4V67av5c04jjiejtjtdnrOGLUueP7iBb756mvMKsS8e/sOoPAugaBtYWTeJjCqKOq0UTuxxA7rtFoVGBfbH5CEylIBqGA7bbDZ7bDdbHB+cYGLy2tcXl2Cyijd4x3mIXhFKGpet5oUDKdXdMRmh8ZolPY30f1Ohk37SV0Vp964lGHeiSeJtwRehGfLKv+48mRx/wzMyyLXKS0jhVux+WZBiLo/6GPx+8uMyrUqHozIjUgCl8MSnvvTGD5fW7dTqLVAp3tFGaAMEBUstYqi7wBjFxrHcURtC2pdwBw03nLFTHE2JdpFTjv/FHDyPSIknky+T3L+dN02htNFuJJsoUwW7eDGAJVFoDLVUq0BsVruM4GhCPW08NdChDKMGI22TYPsj3vlVcgHvOKRhRubMl7nRcqGz4vQiWVGY8bxdMLheARutWz5MGI7jdidnWG322klOJULNX+qaBm8ov81JgzaP6gp72D3IPRERvp0FEwT0FQ5AS9eSEWRR42cQqcbVzx79gz3+wOWWrHdnePun/7vcff/+D/hWSUMysOe6vANoMt1BFibXEfTxWycz0qHn8gnFIkOhT+gbKzvzYrN2uOSjfrrMyJnkTCfTri8uPidc7HXdy9vqzHTxshaayhD7z0wL0P2NDylVKwTy9fVqDIQstvpqet88SrMWYOwcZDGgZVbB8T8XEsqtYNKxjSz2lwiPIgV6Ug5gRHnyhxMHbCLQzBAJNWw8qjG5vpVwSUJh1btxbVuwKvNMFviEiShmLnzEnCTWMNlWWCElDX/wCr0GLFqlpTcRPCvSygW4IaqyXxVE56Xqj1EOK2fxErqgksvlSWxXARj61MgJSVNsy/uMbASk+IdGIRQpfAPER6H1ORNmEAfUqfWRlutuWIUvs32VpkQt4Z5nvFwPOLu/Q0KEbZnZ9judq5gEEkIVM+U2aQYFVokJCnnyVgIlSKdQSIJsCZRWGysknWLEtF/TcDluBwuDMahgXtMoLiskn5bwhLXVFBj7db8/PkLXF5cYrPd4HictboKEOWDg+lTUpSUTrr4ARREvoJV90oMUoWIptWL7KHuCidRhkxRlmstb4BgMSQWRmTzMcGkaFlZ2xZ5nv0WzJhU+mRAPQJCO7yErikNGsLGUItYKRra4NsuFbPMq0WEoUB/J+8z4TvEDWR0gZqEjyk2MUdui2xlCA6+xW4hDwaxKHQ5vnbYucKmMHbvGCCJlHZLUm5iPziQzRULglXIchXQ6J4aDRo3DMMEAFiWGUudPSHfqorNlVEGC21gFSpNMIMrTIEFwGazxfF4xGazFRpIhKU2bHc7/OwXf4Svv/oC83zSZnwyd+8TRKz0kDzJexxHiFewGRLDFde0rlIibtxZVpH8oo8//gQ/+/nPMUzap6kxFmaM00boMWwesWuU6UPIGt3ZFA+mixV+UacspH22h+c9ZFWsMkJk0uz3+zOzUyAo3JMv55Pdk1QHZc+hMm+gP03PYy7DmulD7xfNVwixKWUAgzsDp1jjm9PSJHPLN7qeCvSGO2gIKMU13XKcVsg/ZRhwOs3YTKNPbyDg4voKF2dnOD/b4ngSgbk2aRb3/u4Oy+EgK3BjEQe6gWM+Sj8C5/U8IM5DnMN4hkeSmAxitB0J75opGNYtu3bFSwznjCaTK2uMUY13g+anGFDFS1pRCjCfFrS2iLhUSA1+8L2weZLu4aCVCre7LS4uLzCNE8xrXpcFx+MR9w97HA97nOYZ9w8zHjQPaxpHbM93uLi80OR88SQVKuBCaEUMi9X8fiT8hLRpT3g4FDfV+yDeZQCjiNHLvICxGOF0Bc6s/dM44vLiAje39zjNC64+/2O831zi8vCACgkrGxKzHkx2YM0FAVCIXXmzcHFHPeWvHT4gfecGieAFnVJiCoOdJ5tKGoISvUN6lkVe6KIdjIbHgORmXGw22J1t8V1e392jITNwoalaNZekCPi1bFpaeBTWoVPZZbP2QKyNDNklt3Yr9W6g4sIcu94lh8S1PI5YtHGa0A4n2K46G6fwYpACmyCeisJGEI2Q6hqUSQxFSgCThSa0qLhlFv2mSFVdyA/Phgn6VXsdWJ6Bva/WKI3b6i8D2p+Dk/VAgsAVqGR7qUSrtUBEQrdHclZYrAfFyrEJjEuBClzkXoRi1o5x8n0yV2gBoYyDP8fK9RWt/KCU1pmhN2UjaHgCkrS1xstQZZidguuB7EMQWJmxGzibCFSljGggXF5d4+HmFoWAaRp9vuJJsSf2zJwInXBvDNcECBvMDnYgt3oXjKK4EgJEkl0WKdJLw/zM8hW8Me1la2pxhPf4MEnCQjqyaxxaxrG2CpB1ORdi3MzK6Osjh7xfh0g6H4jgna6NqIe0gdH324gleUyy7ZrdDquMBDgzLv4evngpl4vYf33eQAVTAabJvF25qZ/c56FKaSzWvSuIkDpLBs0MHkDeAP9XYGyVRdiPHydktJCDKFfZP9ITKzt20224vLXn6Y2cr+3mSlIRj4HWIkyjmUSjzzLhxu4N0c+lBhd4LP7XFHpujO00YhpGLHVRS6UIIqWYcA/p2ltEwRkQ+RMW5pHPMVrDZtri9u5ewk8hNG5ZBH+vn1/j8tmVh2qihgIHkh5QX3z5JV6/eoXCDJSCP/z5z3F7d4ebmxtvMskmiTpnlQNENGp+j2A9iHB+cYGf/+EfgsYh6DdLiBuDsWiuF7MqcQZHg5XSjCxbmODQKO8h0nUciif79PxlFX2M1nSUg+MMP0FRuhcDKBrimyRxnxMB6kXMuBH40pq2PlsPKHEu3fWdAOXPy4uyA6fnyoqx5LEbO62zs2nnuPm6U26CPl54fEySEWzGZUQwiMXINR9P4Gn0TSllwG4a8XD3HnXeeOPgh/s7lDLifLfFcb/3JGujmjEWOZ5FOCUlkIc3TBRC9rkxM6yPkXhQoreSwQssPGBpYYj0SnYc8lQBAa0Jn1OgSohmg+SHNYyFMA6jlAAfBmzGUcmzeDQOpyNaq5jGEeM4eVWq2oBWpdRxqw3DNGI5nXDUMtOW60FFDErTZsJ2s8VHHz3HNH2CAsL+sMfd3R3u7h8wn044vj/h7u4O4zjh4vICZ7szjNMIqgSqkFyN0kBlUEImsLXk/1KAVgSuZmQyPBjKAAxafh0sFalYjRZcULxxqJTzvn94QOOG6eIZ6NkPwPVXaO2EoaCrvuUCTSHBV6UDgm9R2Y5rnAdTEHyO6awZ383FAJ4y1PvQ+gRO99ugWTmJX0Npj9GF7pLKuCiMxjO+y+t7VZ2yilMmqAMRGrUucZtzJp6KPXsqBi0SdkVItdcj100CaPZyNI2VXIdXPTWW5Zh8dLnB7t0NDsOVCB7qIi8sSsKsScenZcHxeMJ8PGHQpKXD4SBek1ol5plIGlbNC6xi0VKrJCjLxEEWGmTKAWloDNvcAWvo58qAyVQpu08YTkJYtUtZF84yDIFURZobFUAtvRqxPw4aTuaABTFjXhbMVRSwcdzi+vkzTOOIYRwwjBOGYcSoBKdY2AlEuLR48ZArQ0iycqH5xU5Me+0ayqBhK44HJu3a4pXlQnGDBkO3OZHWcbcDYwIYFUZRV/FAhPPzc5RxVMI3opRRZRVTXNNB1m99S0TOirnbWlrsl53aVtklOfk6lQZorA39DG7GSIxJ9rkoYgEW6UPWrUEBijOeVAsLYyAX4LxR0DhoIh1FeBrgFuhBlQgXNOxcQXGJyOEkcBViOqxK15oQZ8pl7KntnQg4Ra3MVjHLCzhwXCcGBFEQhnHENAhzJKuSRGqjs+Rr26YO/xgwbxw3tGrr06lWDYOEhUBUL++ctshD0kI4DOHM5s1Zqkyx+3rMjac8nqfCrChTcTwy+CPswK4A+LNZBTR9spaXjFCKkEnMe5V8ntBHwktf+3ixVqoaStJUYWVRZHe7HW7vbkWI11KypQgtskpuhgMVVb286NfXZE+XRhiHAfPpJF5YwK23lIxIo1bAwjB0eDptdvj5H/4CIMLrb74GtYb98Yg/+uM/RqsV9/f32O/34rHVyjOtNix1BlHBslTc3rzH4SSfz3Zn+MUf/TFoHHxP7bRKjxAggnMQeWT6hZzv1iVusxItlQ9B1Ol+PV1U3CsW2phQJdka8gaC0TrF5tFzV99XvbV0QWXo3qclpfcJIKYV6Y1+H7MbaPLDxHPI/n3nudHnNUKUSE1jsyKF8cOgowk23SSUn3phFMVzm5PSaobSJCqY64Kt4y2DC+PNmzc47fc4HB4wjAN2ZzssS8Vmd4bN7hwSti0eOCkSEY/PHiiVOmT/dF7eudrgqDkC/h2UThA8yoHNMq4CaOW+mpKdCyphUClgQNsClMJaWIKwnbbYbCaM04TNIPzQhM/GYvBc6oJ5X1ErgxtwOpzQ+KAlbZVfucRatLnygIvzc8lNU1pdK6PVGad5xvubGzQ1VG92W+y2Wzx/8RE++eQl5mXB3f0d3r97j9N8xLu3M94XKTd7cXmJ7TQCTGhcRA4iK8qjxkIyr794n5sK8UV5FEO91DSqzCbJ8Kz0jQehbygiD19fXeHdzXschxEX//g/x/Jf/5+xaSJvVc0nA4TXbjYTzs7OcLi5x3I8SZi4VTe0pPanlAUYH3l8Wt34nozxH3IA+HPS6ynZ+Pe9zCnQmFMT79/9+s6Kxjp0yf5bNDZ2XYnK7jEX3VP5GBkYGTiiZFD3nLUXJH8fY8q9NpecRL5eyzzPePPmDX784x9jen2Hu3aGu7s73N/fYf+wx/F09GpGOV+DijSQGi1cAsD9/QOO8wm1qrBfG3LHZlIFwJjOuvGNV4dQAToLXyGokMTUF0gyIkWYWhkk1GgYRy8pKu5rPVQlDpspUyDLgxk8BEkUgYbDYY9X33wDZmCz2+Cjjz7CMElMpsUm2wHOFThIhRKz3tgaTYHShItYuy3Z59kfpszY0uZ1hDr/KHRZYRYZdODUVcKEVAtjg8KeIRaqjz9+KSR/nKQ8LhVYsd+cUCjEXUN5kqCpCKf7GgJdrNL4r1qhYExGHhqWOlNsAtfdWjUoI/ZzIXAp9myooE0pYV8Fb//NRjSztiV8m0Uf5Aok2b4Zc8ySBoVw4VYPfZzhcIa5fUdO9NllkWEQYXE7bbEZB00ENGU2Qst8s9McwBoqqJY9234J5za6YQYlTsespw1ueXQJxhZkZziEFT+yJhj7PRxwSEpBB8CVtMaKh/ZV4JK8r16RDV2hByAJV1nGo3imfCfUyJsD5idwzJXzvJTukOVRMcAUeVwhuqS1a2jGZrMR+lkZ82nGOG4wjWr8UQ+RhDPIzEozI4QBF2BiUf6IQdL9RXpf2Kg+TzO8GFoUUc4TSS3DgJ///Be4PD/HN199ha+/+QavXr3WPC6Dgybu6hitVjlXJJ7by+tzPHv2DC9ffobNdic01k2RBnhG1S69QRqTYmk0B2Joyond/ttapnhCxmDWKkQc++3Rbml/iOLB+REfEi+EztlDRRALhRVubTeUsLH9WBoy+f7oiUrHNVwyQI/wGf8e+3JZF/6UbMQJFn43B27HOYF6AoIHENS7kWMBgf63ogqDjjXoQOMwYqGCsUyYj0fcLYs0lmxV6WfQfM5A1C9DrrFzZGMg7svKRFYw8t+UpG73eH8Ehbl3pzY5SmUE64K+3Uw4O99iu9liGidYmffj6YTDfERdxPAqzWUrlkV6QYnX0gzFkespc5OoiZKMUWWQap9lHFxuGbRv02a7xfXlFWgoWOqC/eGIt+/e4+3b99hsNtiebXF+fo4Xz5/jdDrhzZu3uLu7x/29/He22+Hq6gqbjZTQpsIYuIAaYyTJ1bCmgK2pDASSTHA1FgvvLF66W3JKo1FuAwOVUYhxfXWFu/095jpj88M/wGm3wW6eQbxgcT4nysswjNhMG+yXGxQzNhG8qEQZNDVBrTrZiN9a8/DcOEZZHulbOqzPxocUj6dev1/5ED642UyYpun3Pg/4noqGKQweF9hat7iuFFda1Drcyb7LvxGRux4BgnUBz/fSCpilFG/kB8AFOHm/SqThiO20ef/rf/2v8e2332J5teCbZ/9L3N094PbmPcCSfLjZbDCdbzCpwGMHyLS4wozTfMJ2t1FCVIFScDrOkt/AzSsmFJ3vMI5CZzTQuwwSXkRWyahMGEZBysG+GyzsKKy7g2roVEIQFCIq+TTzLHOodQF7eJYcGovVNGbiISHqgt2eFQzjhHk+gamAxlEsh2VQC3bROG5lk8WDlxzu8VLxmiDSpzMKCqUk8Wr/zOyfVe5QzEgCGcMZhn1vTNzmYa5FQxBX+NwyKqX0WpWa/2eXVwAzDqfFLfXGJc2zkcMyTMBJXyXhIiYu+QISi2N9DdzHUkJIN6bgLNNwfU0g3GpvcLHzNqjCF9eLl66ou1jnkmENZL3MYWXfhEARRBCsAiBXeMneknK0bEVsnjtyUBYWrw4VkqaA04jNNEqODnkks47T3JKX86DIQaO0h1t3X5L7wBT44VZzCkLfLdclt/SjDAAX3voZdq9spXXcQBYcGlYLhHsRuH9SXkP3S6qwE7iWx0nPzPf52LEul+ugIgGv9KBm1lg9c60XAUm1zmgc1rAsC87OznE4HHB1LcUhLC65Mxb5WQVAWVCK810hYSO1SX7XPC8Yp9GFo6r7EiEn5HjNq52iYcAPf/Q5Xr58ifuHBxyPR5xOM9xLCDHGTCr4EEmTru12G3SYyAW+UiwnSAVBpN4YZAw+gTspoCZQW3fvvN9i5Uy4l85mnPckQCtOrNe72v1051O/pzkaCtMTQofTsycejTjncU76y0IRWNEzv+lpQUiOrOGM3aLe3kwz2M053dzs9BoNz+uyO/zMpin5vU0E6sybWmNsz89wdXGBZVlQlxOg1eIaS85V1rsQnCME2pIV3WTIAKX1iLcA/nt4GIGoOpmb98WQFIYdkIZaa14tM3abLa5eXGO32wLMOJ1mHA8n3J0eMB9PmOcZp9OMeT75f8tSVdmwKBYLEzTDrs7VtFKDZmKnFoJfKOSacRz1vwFlnHB2foazszM8f3YNADgcD7i/vcP97Z14B87P8fLlp3j58iVubt7j7du3OBwOOB4OmLZbXF1fY7PZoBU1gpPISmKk1SgYaH5HjQpYVhykEIGmUQzmBViWTG9ZlMlhxLOrK9ze3eJw8Tnwo19g95f/BmMriQ8z0AAagMOdVKriQgCKGlelM7jLrHayOXJCPqQk+HdEnXH9dxVasmf/vleW0e0ew9vSNDLhO76+s6IB9GFQ1rBvPRkpTyqC7mazeQScXLHKJu/JXUmBMaXhQ54MC+Eybc3c6DaGPcf+2rg251IK/sk/+SdgZux2D7iZT7i4eAmAJRazNTzcPwD7B5ydnaEx8HD/gHGacH0p8cCH/T0eHvZ4/uIFPnn50kOKhJwV33zrWCybVMDFhJCwCrITyKB2JnS6wOHCLrq4d2az2MtrKCOGSSxuy3ySBnXNms+JQA2rMqUUyy2m2gNi2mwx1yZx1apksEYuOkMgcQcHMY9worVyKaUwOdbtBF1jrp37xj53QiPb+sNiY1ZWV0rCZIXWGOYgkSU2mNnPhU0n4mbtIq+CVcjyMtCFFFk4DrPPLIR1hPs1yxZmsaLV/tneR+iR85hO8cgdTg1FkD6bMCpEKwhcq80VUUmx4TTvUC6IoE0nY9K+BgJIcw0I8IT8cRiw2UzYTiT9GfR7c5BkBcxRNc1X+GXzzyI7V3nPsd9Zys7yjIXrGOQjY8RwI+ZgJV3j/oRZRlsQ8H/C4dDfu5pXQzTzk/h0C4RA4Laxj/RgYyl2blwfXgkLed393nP/VRrnA9k9HmJia834EPSEHcamuHTzsFcSJOz8WXW67XbC6XjCYb/H2fmZhE8tNXL8qsDJzgEzzOcC8+plXFmqxLXVKg0fwzsGNNHe0dj6kZBurSyorNZGw4jLq2tcXdsZo3CQuYGDTTqNgwANcwXps40oCd0Qm1J/xtaCX9D5nq45HSNyOhdzNnjD8wzW+0Fp5ztBeX2R38uJpib4+Gbm80fxmwtBAgMvGggA/NhwAUrnv5/AmkgiG05cSGV0eJYB12yPVzDtNfMwdJnnOdM9i4Swa22rs8IBmBc203O5/vb+1guVgBlYFixVK8GBADVQEoIe+jORhDjbDxU485EETMZBbAytrhOmGDBH8CzzmtV5EcPodoPnz5/j/OIcrTacTie8f/MOx9MRx8MJx8MBp9MRx9MJy+kkSlStaLzAPCV9eWbLMeDesEciB0moEry4jchqxaQknzNY5cMihVeGQQyt47TBdrvB1dU1rq+vUMqAw/6A92/f4eHuHrvdDhfnF3j+7Dlubm7w+s1rHI4nnF69xm63w+XVFaZplPDgCjSVyQZNEmcSILEqPWThcYq4ZRjADAxDlG52r1iruDo7x0GjYPDn/xvc/M2/xbNhAtcIiS6lgEvB5uwcD8cDWJsAFpYcIIAxQEPfOyNh6meF/vW70gPyM9YG+nXUUb4uG+bN+J97gchvcFpahkhx+F2v76Vo5AmvJ5QXP46jX/MhzSmHPWVlwjovZ7BGSNXjfJDs3QCoS0K3sb3CwupZtVaUYcDZ5Tk+++2/wS9f/Ge4f7hHYQkh2u8fUIYB5+fnmA9HzPOMn/zkJ9jtzjDPJ/z6/g5XL17gBz/6Ea6fPXMNrzHANLhw74Q/ww2Z1iYW4ZSfYHkbjwQMIAmcIaGam84IUlF3XeSRVAxtkjjnxihtASAVMqSOoygcrTJ2ZxdYKmOzPUNt0Ko9QdhRUm10FUbM8uksdo38iXhas8BAWhfF4hCotSoGIRPJVEHKUm1iAiqlGIyLWQ8IMCXQL3PCrTgJq7gEWJ56x/wolVpdzavn8H5TYiYBq9j5fD0lZckfEHBLwlAvvABEas3g2fM0rNEe6fw2EGIJ9UAY7hRQ6tsAJ7L+n87ROkjLfwYDMxiI29yCRiTfQi4xfaAQwI00rKpJcQUqft49bIwCDhFK1oFbQOBSV49n6xAkj43mwLnVDiDkQU6D5Zfc6HjTCWZ9I0F7ctXfiLQmg8eQr4YIWS5mlM4RjE76PEwgkaupf4zAXOGg6TKudLNuCJmiu4KFxYV3oDGQJA0sbMNBhgyXT/OMUeusP9w/4Or6ErXutCLV6GcYjdGKPVvwkJ0WmkFBBKXaKqZpwlIXDG1cCTNwANq8CknWmtEoO9PuXQV50z6BrdEL3RnujQlCpxRKKXaQSYQOKXspc5J8mlhD3iCn/5SEcR0nKxiOIxkPM47C1hr77T2hHH6BVHGm2OkId8+M/e4QPO9tfikMM3vy9/ohL/0RjiYauW6QGOSwO6HdBe7B0gvsXJM+L49mJCKPTWltcT+leziWnxbIWm2TyPoACTCX2sS7C9kX8W6pwaFIE7+C1u2HTdq8ZJ6jk0iQeTCcP8oBFrxQz2bAWem5KW0EcGUcTkfUZcHV1RU+e/kSNBAOhwPevH6D4+GAw/6Iw0E8fMfDQZryLeqFbIvTogjr4h7mBk+nsbrIxlJ8ArHOqmecmuxANRpmwrTyFyZgnq061AMehgE3797hm82E3e4Cz188x8XFJYiA/cMDHvYPONvtcHFxiZ/+9Gd48+Yt3r1/hwf1XF5dXeHsfCfCMzOICa2JssFF5IkysIZVEVjDdY23S9i40lBvKCxe1pEIF7sd3t2+x+6zP8b7lz/B9f4NBibM80lSAYhwKgXjbgBdnwN1AS8zeKmgBowMDCBNPhc4mqxtwn5PDIKWrBWJp16/UxbH4zP2lHG/fyAEX47HD46ZX99Z0XBNLikIa41qrTyUYdC4cnOzaFUbWN1pVmE6YrCZwirMLFYuqxplZfMsL8QsyPJ8YREynrrFrLyhfs8MjYMT6EoZT7nvo3GP//HdO7TaULmhzrMDtKDgeDzg008+wccffYQyDKit4fLZNc7Oz1HKgJOGcBUUdfHKHCSRtni+RhCvEFrE+h4k2YR273Ph/MKIX4QqgVUjT7HXcj7MNUlaUm7BshTUVkGtoZQGZqkNTrCQMoA0I3Z3foXd+SXGacLptGhVHikRaY26rFKGjClvmoZWZAstBXV3AqWrkc+FBF5JCCCZvEQIZXZl9LnJ74oFrkTE+u23GDDCi5RJEzncrGeCJReYhSZYFsMjqpvMee1+X1vBsqBgBNmeQzDGQV5txUPAwF7dzCxusd9A0WzIwUsJquVnHDCOJLkOpUiOA0n+zjgMInSxMiKdfwFcQUTeM51psyImrJ4fnZM3T/R9DLe/M8lOSSbvqQGjHQAarFzySghhdDAxfOkIYifECRPs0nxMukTxCiCPnpnw0a8wfk6UzljrBre3LuhxnO8s/IDDCs2EtMerBxjucOAS0jXZkt0vnf0xWWA0XFts3Upf3YvSTFCI++XWBLyuNq8Bz6ZkVXzEi+B5ZiyGoHG7FdpxPGI+LahLA2oDD+rFckU1BCgr5KCylZdBFcthAw0DDoc9trstiEq3jz04OTUYlPuLwz+uobxuVk6QhCgrMcZKj2kFa/Nx2hdmrW2qWaeCRjpGzHDN3LOCkxXSDHpKd69RVmieKhdAJIcyp/Md011N7QkgGmEPq7jNk8Bu0JEQMltfGCWEbybs1HMvfKMfm9KH9ZrzdGzv4pzA5+L7ShTFHygpixmVWa4zBfMRIDP87PmQkqbLsmAYt+msMeYGLz7iXglQhIySZQkmGLqsBNiEbYvcqq2E0Qt++JhubpO9sbk6CxMj6uF4BLeG6+trPLu+RqsVN7e3eLi/x2G/x2H/gMNRLPHLPGsD3aoV1prTdCmmUsIIpnDyZHXjT7peKxscxDAVRtDDbQp/571lAFxRmlW5DEVtaRWVCKfTAQ/3D3j37i020wbX19d4/uIFdpsNjocDHh4O2J3tcHV9havrK7x9+wa3d3d4//49Dscjrq4uwcMAGiwyoYhXAQ0FWlbfyqS7YVFCy8ehgHjAvCiBgjbNbYyL83Pc3N4CZUD55/8lyl/+X3C+HLEZRtT55A0QD8QYXn6E7fYcIwg4znh4/QbL7XuMRCjLCa1Wx3HDEUGFPkTQQ5dIz6cxUpDjixsLh/I4x4fMuBN86RFdatJDKGiYSC8FhNN+j4ebW3yX1/euOmXhU1nBsNiwRzFdrXkZ3GEIlxmgB1kFTCu5ZsIhyAi/CSPxXkKStOEaxAUvuR3yHOtwSURYLHldezOArf5z03yJAcuy4IcvP8MPX/4Q/93/MOPu/h6baUKdFzSWUo3LPIPB+PTlp7h6di0hWoVA3LBUxqlqnDrJFhRIInhhkgOKJERzCHtm7TKvKxsDTgw0J94GqzOBisK9TSZExw32DDmzEl88tgGtiXu3ARjLIEnsTWr8t1rAJLkiRr25qMXW4qFhYVSAuctNiC/FrMe2AFJ+bSFDuhIvcyhwydb0bt1kITHkhNQIkCliOg2Dso8LSjBTxQ4WRmTCPeC4ZThlIMyWJUJxiygXUyrIx3Z4Z4aZEr4cJiqwWAgLiFPSnlpHiTAQsBkKxklyhDx2dRiwKZI4nctHh3s1kmV7XGEXjkypcCVR3yt4jFSJgKZxJ9wAHhRn9UxX1jjkZk0zWTBf34eFNWYTAlQX7LCqiBO0hUg9hHalnSFdtx8iFuGyICzLMWq123rhxd6vvnecsHG5v2f9jM7rwgCXeJ81hk55sCdZWTDFplBYg4FDS2V3cftpHnlsQLyPLZfcATqY+P0aTWjwdHj4c7tN0R/J52bXNDsXrswVoBB2ux3u3r/HfDpp6EUz3t016mRWKzsbBGxecknTa8o4aGw5nDZESEnvtaFEXzOs1Lbgz8/GAg8R88o0IcwR8nX9M40G9oaVhK+AExPrSpyvyxebpyP/5iYODnrW7VcaLysbhlfyLyUcshNplDVRQLYR18/PPCUUlwgjDZ6UtffgY+6vfnLsgPNjlPPP/RSRKfea59iVtII5bO9h9APSAJGT3JLm6cE9KrtIMQJyOMvehPcoKgbqeqxgAMXAzut0Ta70I+MjO12Jb+z+GM94r+0DgfHw8IDTfMInH3+My8srHA8HvHn9Cnd3Dzjs9zgdDjgc9jjNJyzLSUOiWkQJcN4j3SU2+BrBCiOewcsZIBntTn2VVAG0w9sZ5kgxTmlRAzQxX85Vq2rEBqucJQbrw3zC8fiA16+/xfnZOT7++BOcX17idDjgeDzi7GyHjz76CNfPnuH29hZ3d3e4ub3FxcUFNiRJzA3VvRgDGlor0jMELPIFFRBVSSIHSegwBA+sMXMtkjN7fnaGOi/Ai5/iX338v8bw+j/h7Ot/CzRgKFvMF59i+dE/wnh5jasXH+Njfos/K6/x4+WEb//m3+Puq9+C3r7BUE8ArDmkNB1kMoVIYORHjIWHuCFAt9Dwy4wfg9KWloiUGAxFVh6dlrI+nwNPk4JCkCiEiQrm04zTwwHf5fW9ksFzgknT0q+ZUOecCEBi2/J3pqzI5wqivoTt2k2zjinLCo65i0zxyeFUpvzYvetn5DmyVlb4oz/+BX70b/8d/sM0YRxGtMra/XBG3UljqDKOAImCUsqA0+nk1nMqBWzN2yyGUpN8s4BhLl/ADfIdoSYgGqQZc0pcJzM5a3IFInc/O4MF/MH2fRkGYAC4DZgmxtKka/cwNPEWtYqlDJgmeHKZKIcyYjEruFaqgs3TtGYoQ3MJNpQQoBceslJp9zLDS6OaIKFUKG5MMDDGHEiU3pIlB3N0pGWGaTAeO08R6mAPyYTdWJmpuuTk3jzXeVAnuW7ZMiuDMQHry8IKq2GQhNNxLNiMEzabSYoQTAXDkHM5QpDKZTHDspXGRoBM8lWCIeUY8bBKy29NgZtDmGwUK/sscx9g3pDGBFgjLWZpAsgNXC0niCH9XURZ8VponMc2OavfX4O4wQ9QRm4CcN57va7ZgUq4BrYwBxs7yfcmAK2kPs5PXUs+Nn58ivdJujWxxcoTi6AZSok/hvqn2LrXFvQnJtLPQR/sYVo6gI+NqBYUqNmvNT3m0fqo+xy0OuZmNFp+3m13eN/e4nSa0eoiZT8tesRRy2Blwgd34MhjE9Szvvrd5/X4KCq9CqUjK5XdHq/WCFV+/PkJPzqvVMhmQo+Bx/vN6dlO43/H2B1eh9XdhFF0zyPF89VGIwR/Snhnd3Y469APum3C5hMTWsEpVuDeFEihFE58zM6YUSpCojNIHpJulnmOASvyYSnBJ+aR1/J4v42ax1IL05PjhkIg6sY4TVjmWcFD3X6v5+gjJRqaF8TIHp/MSxQi/Pg5fj0TSLsIWzgrACynA25v7/Hs2TV+9MMf4ng84dW33+Lm5kZCow4HHI8HLKcZdZkVb1vKxVFYJkUN6D2yoaHHfhrMLYrDS+yu98FjgEOzcvg43TQepblu3Cs0pTSlYcJzqAJcG26XWzESbzb46JNP8OzZMzzsH7A/HLDdbnB2dobd2Rke7u9xPB5RiDBMmtMLUgNVAUoDN2Bkkd/GAnAhcCvAYIbSIRkXTd4iXF1e4u3bN7i8uMSyucT+xR/j9voXgIbAT+OAYZpAl5/gdPkJXm3+EP/9NOJPl7/E3/v8x7j77a/x5X/7b3B6/Qrg9wDvsdQTwAUjtOw+QoYVsCWaazi7Mkjl1+/LycjffyjUilsDMWM+HPHbX/36g2Pl1/fK0ViWxRWFHCY1jlIF5HQ6+XtAFA2r3mH3WG6EuNdCOchKjF2fS+OGhtV7U3zxTygUNj8rU5sBm9fx7u1b/OZXv8ZmYPz48x/j7u4en5zt8O2336LViouLS+zOzoDGePf+vcOCmDBMI7a7M60uFVYbENRiKIfkUVUf9EyyY/IrJmy/Z0LWue3zzex8QsdVYYPiKaTa+VQGjGPAq3mjP1V2jKs57ZGHF0/6C0UD6LVqt3S56o10OJ8QXtIXOWLDibqxAmfs3NFuoYGcbta1U4Y5xdhxWfTCsPAzhVl/XLl7nhup9HsrBOSKiAsj8ncYCjbTiGkcsBkHaWw0TdLPRRPfAHhIndhxo5JSQYQH2HQRoO0EL6TfI98FMAZrIVgmbLOO5gKMCzRJKNbvOqUZ1J9tMJgIAwY0rTfe1JItHrQGLM09j1kAIVXOpZKVrSGELNuzLLQlvixvNBmht1L3L0dJrH9Yq5WxvzbH/MyOBjsu6PWGPyGNOWxT0a5uUvl8x+rTXuexV1PvvrPnry9KggsrXoSdoh/ZPj7FZnIOkYHd9sW9JkSoreHs4kwNUifMs5TEZG6awW0inI3D/jmA0u9SISlwYL8/Pc+MII/3ynMj2COjgoYkGK2f+zh3St4+lZtj+JBmE2vRc2geCr+L8+1ZaFbKZxZsX1hvwGLfkLR/Cc89jJGBKEEeeB6TMJJNWsygX7eFYhkCdMmrKiwGLvOjNQbM0xklxXZKQLdxMq6hx3Ufba2spjlEon3/+MTO3BuevSo2AEOFS5YSpYfakm5ltA+hfHZ7EvjXoXJaTzcgpdCrhgRzdPzWVig8Qzb65uY9iAr+4Cc/QeOGb775Frc3N9jv73E8iIdjPh1Rq/T4MniTAqCxGuSMK6Sx3djVGaAo1ge4QuvrcFgYfjiBdP4dERgGL8NKuNwitWfi/qrejUKaDUjq5YBY5/eHA7764gu8/vZbfPLpJ7h69gzH/R6n00kTqyXk+HQ6YVu2kk/MgRySO8rq3WnCgRXmAwONSIv7DAAzWouoimm3wzhuwACunz/Hzfv3aPOCQRvHllFC1U91wbRUYKg4TRv81cU/xpf1PX7+2YQf/7PnqP/pV3j77V/g7uZXKKcTuEr4Pg8DTP59qnXD2jD/uxSO9SvL2DkNIj/bnAUFkMakS8PNm7ff6fnfWdEYhkGbrYzesM+UCO86qWXT7JoshNpLwqgGEUJS6a68GHu/Vj7EeiYIZ+Ot57FWOIioU36yR0OSsKRO9Ktv3+DH9A7/YfNTnJZ34D1ApeB8t8MwSXnZ4zzjOEvlhcbSDGYcR5zvzqXGMZOKhxLSVTSxuHII4eT/GMNPP6wJEDKjeQRK+b2nugle8h2bRKycU4dBcwsJuVVhGBjgUR9nAh67EBhzyswxmKD95tYhAqDWPaK4z5mbXsOZI8KsBrauCEuw5xhc1uu2ZFK7zypiRf4Lq6BhdnUoTEIqKHoNEAxC8C48Rv6sxGw6QYkkyayUgmkasRmlfOtQCgbi1LfECD2gDtKAhz7N1t3SmJk+V9vTzOvRW0xNILK4Tf+NMruPPVgLw6yDOu6m303mkM+U2nEQhsLAWDDXimFg1NqwDBWlNlT9z/I9xGtfAI4uqaCw6jsvyHjO3exlal1nVVOmuFtPz97iJXywf2aAJnu60vjGoPJven1jymgtl3/ISqTrNV7c/xDSVrZesZ3vLNApzFqckLRu1rmG5dJEtH4ead0pTIPtGWE+0+9lY4rOpTGcDxCJV1hq7VuIoHjIrOR2CIh6vrLAypB8qMYelunTWwuO0LlQ/rInmun0Ot1y67FLTemM+brj5n6P2AVBq7YXz3cS2I/b3a/Pt5BZh3keOx7QkM4txby6Y5G2J9bNfh2vFpTDikjpeSw/aD8rzmRAyh4l74c+12PE0zzcSqr0NMPTx7bvnd4ozTJYIn4L45NjJgybun1P4yPdSQl3/RAbLJNiaGdu0LL2AhOrkWZjmIEjxoiIA4VkprcuvDtk/fsC0iRq/bmkvWKW0vYkidKn4wHvb27w0YuPcHV5iffv3uHm5gYP93fYH/ZaQeogCj6bghEJazJnbchKRp+MTpBtDGQaocglaqCPktILYf1Zv0IO8NXYfth+672U/nXLgCIuE0l5dOdJJIpTsX5gQisOxwW//c1vcPbmNT59+RJX19fiUd1uJF8MjHqaUdj21TraA42aNPKjgqFUlEHLtzfJ1SjFqsSQlsEVhW8oAy6uLnD/8IDzqyv86te/RlsquDVM44DrZ88wThO20wDMR2AgtDaiNcK8vcYvL/45vtxVfN7+b9jwK1xMBzy8+xZlP6POzQt85MifLDObHJx/t9+6nUgKyfr6p7wYa28H6SEpRLi8vHxirx+/vlfolHUGX9fote+maXIlRJSOhjI+Do8ax1EYTesXaL89Bcx4BjymPZf+eiq0ikgaCva9NtgVIutxMdCIeV7w7//i32H3D/4FPnv5GagAz5ZnAKxTpFbHUUJsse5TKTg9PODbb77BMi+YxhHXL17g4uoai54Rs5oUoLea2TlLDE4IEoLxOkcJ4mmWdXuE7pAKlNzJ/pR+E5qqx5ghydYKVCfSmaEhM24bO42q37Nfa/+FNwGredjYvppc5SatKTMu/zn/4BcE2XMjSAdg9PHBTS5Y12Q3IUYIhjVCHITAaPdrE6rDa4YQfnVuA+mztK/EqDg6pjNjFrK1541trswOdwOjNdyzcVkZsycJk++yEyRZcVjamKzyE+K3J2CeSY3jEofXxngPg6VCm+9x4FFJ+zRhAA/AODQMtaANDXWpWErFUhvmKomHrWmTy0zslAE5HvrYeW4yzpqk2hQaIeKo0ZfkXIkknaBkCcBsCgBr/gPIcbhw/N7jmk2XM6p2zDbJIPpFCGe6dLfqijhgexC+l8yUYx3ksCnGrO2BiABAerR4eJih4JxcbWMzyJUOkQ36sKl8ymtr2EyS5yXdwZtUslkWFG3yRCDJh9B1+9hZm0CaC1upSYmXDx7hT4Nh4WpZ/kpiIEIZSGEpOiDrg9e4kWHWxTFnULrg3e9LS9+n/EoXnILMZkFa918Tiq1DfFwaQr3sU1pImrztt8HSIPGYpiZeCztjQc9bWrPjsuMEO70SXiITaSAUJ+KWfmqnA0bM0EPNaJbcS6sz5lvivCSL/QF3Jffg7smxbjnfNt80J6Tzg7Dy1rr4GPY0IBR9KF0G+mwG05BJF7a2OGceaoC1M5Z/H0zmYeD29gbz6YTPXn4Grg1fffEl7u5updLSaY/TYY95WVzJMEOAlw62/Q6GEqeILWQ67Yn+bvRDcvWCprgc4UwRuq8aCtpZyQzD4fTdFWpOng2IoVPOqhNCOfusFJAIrS3KI7TEOhFQCh4e7vHrX/0KF+fn2O7O5dlFZLl5lopau/MzbHc74d/6PJFFrW9YzLmhaTPGQds3FNS6YNSwqM04AgRcP3uGH/zoR5iPJ7R5xuF4wLt378ClYHv/gM9+8DmmNoJaxUCM3W7CbhzAG8Ivf/Ev8E8vbvHm3+5BNw8Y6A7go1QL5fbIQC9HKKpUrUOinro2v3IJ2w+FS+Um2FX7/LRCePbxiyevX7++V9Wp1hq22+0jjYhIOm3XWrHdbt1N1VpzF7ktNi8mL8oUAVNU1vfYy6wSpmTk0Ci7Pn+f8zf6Z2iehuLul19+hR/+4d/Hcv1MD4uQnEGftdSmtYKCGA0EUAN++7e/xM3btzgdTwAzvvniC1x//Al+/NOfgba7IPxO1I3xZ4EqzqbJBjk0oGcIFBfaY+06Payel5Ck6czIwOyU0M5RN021LHMmEE/gIANeQcYYjVUyou6iXvyyNXrFmvgF3eq4h9GjV5oWkRl/CIU08RSmIBTHDWhVjKLMTd5rbW2FR7N1J3hbPwaT1F0eIm1WR6T1ueGfB8ttsJhTRJy8hGwZ0beQIWO+UeXI9tWUERH4MkjlYZY0K3PlR1tGLA3QgLAQGgxNXuDV98y2s3BmFJsDWDWmZnNMDF8aSSWvTSmYilS/aKVgbIP0alkqlmXBaWmeQO+YzTkQwvYhLcrw9gO4KaBsqCRswsU+P2MUOORr1zkkBdVe3pANcGHeJ+RT5MfwUngav8xLCrKwWmdeh51FhY6dMSDtV7dumZx0nc2it+7Remy7t9/e1dhIkYmJYPETc26sFdHgfZXq0rC0ho3haIY/hycxC3Fkoac6zkASljVScTwzBTcULnIhsnHAyBRmO3vZU2B0wLfGkSqtmwM+JvTQGoZOjN1U5BzDV2XnLLYksQIKmgxRgEhLZtl+F6IwYBnMjXbYeox0PcFLusFXyMPpO2MVHi5l/L5Da0p0JrzPAkOKtXW4mv2DwPqMZFCYIu/3Pka5uBiB506LGFohEEnQlTHtGfkIx7rNIGZKn3rGTal2GCX8YqOhHMYX66vkeTuc7tK1pPXnsQ3vjX1aeC0z49W3r7DbbvHppy9xf3uL29s7PDw84OH+Hqf5iPl0r0qR8TsrgVoU/hlHlaZxKLzsDMr2VWFH5IUcqBQNw6Ie/1pzI4kVNxGjFuVVJhoTVNeSwB3yDDCajy0GKaULzIgmwKT4srg3Aq2BSsHSZtzc3qDc3ctKvby3KDf39/co04DNOGEYJdx/LAM2my22uy02u3NMmwmjegzKIJJg0WqOsoesfats/oRp2uD+7h4DFVxdXuP8/AKv37zB7e09aPgWn//kDxz+ozb/bCODr6/w7bvn2Fy8AOg1Cg4A9qhk+btrio9Hxv8PvZ5SJEzmXj93HZblSkshzE3Cyja73Xca93t4NCSOvDWOeHKSOMGlVYzTBkwLmGTweZ6BxihamtYmKpqRCkJKBEz6ygIJW0xIiwXnhLGci+HCVWtBMAgw7ds0VE6EchgG1CYNpOY6Y9yMeLj4Eyl/awTIiGsBpjLAo/EoDv/+3Xsc7++BZcGkVheeF7z/6hscHvb4gz/6I2yvrqSBjyLg0+4pf3TMvSO65MIRkBkTXED1dSerY2YcMRiciGUiS7qoPLYJ7uF27qbjFhr//pHER74esyDaoM6M0PM9J67xBH+qW6L0wgKtdFWKhK9Zjwhivya7wUXRgPcX6J8v9ls2YdLwy8DGJkKyw4Y07nMqBBqKKhtWyxxP3Asl+mkziD0m164zpurQTC7QDPIg0S5exj+cPisICsE9ib49xn+NdneSRgzG6b3haUlzDDDHlxHKBu/dIUXbCgYUDK1hGgjzUDCUBUdteOXnlS2kxnAlvHN5XRnrTBzPv5QsdFK6lUKxMTnCzpjlxQQc9I+drXzGdE6c3ljHYuHZyjzzWXQEt0Ukz5s92RmszTG8Ld0K6QnhRfG4WUKwzdnCEX2c1cuQxgX8tG5mqbiHVMEEwviZyRVTcNMQj6JdhGcsbYluwpBnDcMo3g4os0vVdAQktg7ZnFIG8WgPCX4ZCQxssO7J4SnItCUhaPqcEIMM05SWmHDVMVzdDwWOVnAHkVT9snhqs8bnkB4XUJV2GZ2NEOCUUJusAjUrtQoT0oaFUvKg9YJ5DkfS8f2sd7wkxghcQ3g0TIi0YRO4bSzBCTjOB3J04qwRGecfHZ/jeKCNbbcgfopr/ZiwkkjdTV83Z3k51u0GmTSs0dRV2EHIFIKY3D2vN+hkuhCwMR6oHIZYaUs6Y2k9dgbsK4ZGkRCwzDO+/eZbvHjxAttpi7evX+Pu7l5K1h4ecDwdUJcF3Ba4x1rPOijg7x4VXQPDzjBcqXT6kOcLRKKNCvpd7iLg7w0grMjk28VJ6Xi0Nx0VS2BOCMDsYwcOWvK4RnUYblcGDQKEpp5z82gI+KXHCdUFdZgxjKNHsAz7PcaHDYZJksy326383UwYpwnTVCRqR/naOAxq2CHMteH5i49xWha8f/sOF5eXmLjh+fPn+ObVa9zcvMfu1StsthuAz3B7e4+LszOUqaBRwVdXP8Of//QVvvybv8LEFUwVTANQV7CA0CDPscjQa037vgz+25raZ7nYlUyDcdoeu9ZeAwF1PmE7/h037JNeDNaRNbQqC/Mog5TfaoqAZqUurF1gkzZLVCRzHexxf6SLI0DLOSpikIwxDAMIhKrlM63Dd0ZaZhOSNTaN4AAuhlA6nmTOywFkbsBUcHvxhyBktzZ57CynHXLGVQr2D3tgqZI458G6su7j3R3+5i/+Aj/+xR/i2UcfYfGTtrIO+sEIC0YvOMWbjrc6YUTHJ42wG601Z7X8xH44/TAmxhLWBcryD5A+6wVOxMxCxgk5TRjypn42H8RY8lTuqm9luiNrs5wG8RAUxQOh+VqfvJASbPJ1N48T0BH1wWbTrulnoVsmCvQErXk+R8TUEonQbCFWEialIVPQuSRmLPkiqpxQshq5gsz+bHuTSYYfcNtjjo6jzjhsHw3mHL/pFECkvSwSDjjvQH4lgUQ2obdugDwh0iqJiJBhQl0SUP2MQgtAyL1l0L0aRozDgHFqGMeCcR5wmBftRrt45TMfJcXVWzUh20crnQwki31i8F3yb36f/toZfPzidOGT6vQTX1Cam7HtwCX7N870emzKj4qZEHVz78J+8t0UOMf2DBW0Ivwkhyn0c48Hxdl4RLNcWDKaZpZbwjBNGCepzrcssygUTXFXcy7Odlvc3t0HH+jorFpSbZgide7bUkGTzMhjtR3f4ffYOQglFU5Dg2dADRTyHSclnIjCIl0CX+LMMSiX2HZ4FgylPw95vyX0V+ZODUBrWFR4itHDpOFgBjScx+iJQt0NecLzPHQE2hAtIT119EAfnHbf9tbn7EqL/V1fi7S2hGvocZL8yc5ZV3ud7sj4atOBYeATY9tZptghoesrxd7HSmYZvSWx0Ed/87pblZh772Fg4yhMbW1hMAqPluBi8vCuJucyhkYImIK5GQaACo6HA77+6iu8fPkSzIxXr76VKkqHPQ7HPZaTNNtz/16y3hn+uGRDgBkV5bPuYFG8diCIBaypBcbkFIMxgb0covW2WVG1bte4+2uba/Mk/0r25GlcE/xQqmVwLiXl41F4cbiBqpa094bKZtRmSK6NvG2LRriox6KVIgZz2gMqzFve5TRN2Gy22G03mDYbbLZbbKaNpgVoomIp+OTTT3F+cYHz3RbPLy/xH/7yL3F9eY63Nzc4nfZY5lnoIxG4SsGYU6so1z9GO/4lytUZ5jtGRUObpZnyOn3B8hzdmL+KCrLy87YGv8cMJlnQo+xNjl3MSgxBPI1UG959+wrf5fW9ksHXMeUAsNQKBuN0Oj1Kxi66UTlvwkKqBDlIe2SYtdNWBYDIrSPBgNgBkF82L4lNb26xW1p11l60aZ7V2W9NcjS4VqlzPE5w4ZozYVwJEb3Mh3k+YhwGVGatiKC/k1p7D0f86q/+Gp//7Od4/tmnkWjru0agfJiMESIJmOlFsMTe/lqLUMsE0t631f3rV0dQ01nPfwX8HCFRFHc7GTGhEgl+vbbSh174s8Nq5LRWk6kYt8SQAAEAAElEQVSHQhgNNwxWujA3rCg8PN6b0YURge13/ct5bCRBlj1/IbPJYBpQpaJgHAhEA4ahaIIYOfNkpIRqToyNo46UT43jt/w3H/BO+FDPh+c3Icd+y9jVZm/axlObvnqZx9ov52A+OUY1uED4DWy/Tf3phBMKJpwVxGrXkQw8WOPBsWEcR5zmGce5YJkrlqZV6tIabSYBZOpyL9aCwvo+Wr3vzoDiCmcthmK8pxSETqgyXHs0drj47Qx0c+DVuny8p7+z7x9TiZ49d2MDkfOS7rQrQ/RY77es2OZo5zDohDJ9vYUBjOOIYZyA01EVx4rWKmqtUrWEJX8jgN9vnths5IPNxKxzPcyp23cj4nlPLawx75zBHOBIFUv0qnnfIPLqS8QM7hpYaWMzCpibAkSw865jZHTSN62xw4wILlxyou8ZX837MJB0K96ME6aN5MJUnbPEUTfhzRo+7PukOEe6lmjjIpuXjU39uTAsWtFOIF1t3/fn4xEvSXgfv1B/zepb7saOw5Xvcj+ge8V6HOiGy8Ma3XA5RUfU/UKhtHfJEwATd5OByoTxhM8ynSLzYcODtLkr2KhmrAYt8Qoe9nt8+cWX+MFnP8DpOOPm5gbHwwMOhz2Oxz3m00GNqxFAaOfQp6O4awZW6VvTfP7Z4OjGwyQQCD6nHEiDGTO8DqavOy+MNGEbq7GDDnX7LVaFJ3Ht0TZqw+cwcsr6bFVFQ6tqq2GUBIKG+DRZrsOCxtIA1wV0kHhxVX4/HFgNnxKGVga5fhgGTJN4PrY78X5sphHDNKDVitM8Y7fd4eH+HiOJ7NnqgqUxjvsjli1hu23gUnBqI27qFh/98Cf46qsvUDCiVWkinfvZmcy9LBXTNHUy4zpn2RQlAH5fThZfKyHrfI+nXjd/1w377JUH9rboFMkili9hydY5l8Je3ltDFwUAA6IJn3gzqiPe8ETVqPUrA80SZiyBPRJ65IFUCCPJM2kYwK3iq+M5+DrmIGtN605v4pxpv4C6gCDhMyDtwDgUkIScg08LvvhP/wmVGz7+wWepZGD2NFAIN1gR2kSxOc0jzydqbMdPjfBEbC4en1j7KhNdAI9A/ZR5CISIAQ8lNNzTYa13+ry6H5A9KSAPRygaAmUKps3SCIIaAB8vx4TEVB7QLVscgkWeiVibVKB49DB2IasUiZO1krQyv+z6FmbvQpgxFYMJw5lNuiURSWXSrLkUts50cWQZcFJmuGMqDrH4p3tlPtHtRP6iY5jolHtjDWRhdnI5CorimgplJB3hSB9uDCwLhWQFPKA5LoOEkUh/kQGnYcbhNGNeqoaPtSSsKzM1i3o6myGLPBZpDO5rPLddyGCzuQO9tTbDuT9jcGbvEmOynjtsAGRGavdqpFC3N0ke6r7MXtZ+TY/Fq84jl76n1af83mhxp4AazIxWpLmbkMGOFwXb3Rb3D3eYtShH0/4qg56PZV56vEtKQhZAFOMwlgEPhz3OLy5UmCxhreuIZXhD+s2x85a9hqEE9DTWFHs1DKihxQ4e+8V2/siFsRgt8rnkkyFblENnzRmzBqxECdfYBEVSvkXYTBN2uw122x12uw0ARl0qjnPF/nDEwoxFm2yR0p/2aHGIECuyc8QOt4A8u9IDMzLGE9IZS8+1f1dI4090/pCxmkNujV3z8/2YjH2AinUHc43f61uCEBntjdxCxUMSLxApnIZhRKjjslmkh5HTs/KCKb3Ph8lBAOtcb55gtVqPIwYGDvs9vvryS3z6yUvsHx5we3uHw+GA0+kex9MBy3wShqd5C14Bar36EusNL6asz5oPOi6oQoI16DvDF9IecyRtm0FQccppndPUMGCZ0cP4LxBj523nD+43BYCtPwcZKFReIBmrtorSCGUYu7VYiCMgxmiqTXmTdd5ukFRE8n1kBiqkF1yrFQudIInoe9wVwjiMoFIwjgOm7YTdZoP7szMMo5TFvTzbYX93h7ubWzCPqJWw8ICFCZvNhEaMf99+gn/88W8xDyM2GEC06JJX5035f47yWSeG2z3rVg9PhWHllASPDsrXNPGqonFfIfR3vL5XZ3DzUkj1hep/WQWurBGN4yjWKoQGZg3+7Pd5CcBJQy9J3hmGEaJtyuemDU9OpxPOd2fCsFIWvCeekyBHXRbRQEvBXBcQSYlbJqDqsywMgLnhdDxK0nbQVtd8DcXD1SbYXyDJP21ZgFoxghQOxeNoRXCVpJk2L/jqb38JAuOTH3wmJXAbQ0s7dMTtKXk+iHQQKCPEPbk2wScRSmMbTwkmdinS8h5REsC0f6eXCFbdC2gcdzkR9gUiLjGNWfZMBPkghMWewha+1M85WxDje2XtluSeBEjW+F2zWnrMMce6Za+Mp7ITIGJprFcGKWE3WOI3ENbhpBQwsSc129xaV6EjySe6YeEJDBg2BrISYoobAG/w5AKQzjmoc1jzwp29eq2+NHqdGQPZPiqxNmHS4nkLhfDRUgK+efSC8QtRku+TV0wtumT5DBDv0IgBZSqqcA44nI5Y5gW1WU/67FmjJCwkEaQTivoFP3nG8jnQZ5L/1sc3CwzsFIT10/bVd4DtuTETHzodNCIRNLICRN3FtpfxgTk8we590R99jgCyxGD7YxAMvKIOfoRgwB1tsUGcRiruq6ABIjSL1yFg2m4AwL0ZjcM4RQzUVlc7o8JPwep7MUSM44i6VE/wDS3Rzp/R3nigu/0570KcJQNde3SfXNdazM3gTArWNJoKVut9C28LQzzqSmxcsLRKUuJ16fM1AA0ZLVH5biAJ8XrYP+B43AMATqcTTrN4MZrTAx3VhUj4bHN+Ruz3epfjBk6IGWcs7nj0ieHCDa/FRHoiKIb6ueSDS6svOw9uMszls2oemp7EsedJWo8QQswz9oqwPohuCLH7U0f0bvLO0tcwDyU15mOUNmDODHDTikcgHI57fPnFF3jx4iM8PNzh/u4Ox8MRp+MRx/kBdZlFTtKbSTc3zmwKW1rx78zbLfE9H/aca7IOC7N9EelGg7NXMZwuH+g/5vfxsZ0XAwGVoOs97Y4zlkcIuSSoV6YL1lvL95mBVheUMvi6fb91Tqx5PcVQQMdc56QBmgJQoEqWYlQlLG0Ww/uyYJlnHOgBp/0eP/n8c1xeXOLu/h7bUvDuzRvc7084v3yBSiNQCpikud/73Y/w5XCJzbNnWO7eKX6wN77OSgERuu9zRVZ7eaVV4JHyYN/ZPbk4k8n9oZQwxjKgALh5d/PoOU+9vpeiYcpF/k8y1ksHAAA4Ho8+cWv0ZwqChzoxO8Ooi1i2RhQcT0cMw+QcoKBgXha8ffcW25ebbl4Z2LU2cK1Y6gICYZwmUTDAWhqM5TDqmE2TwYdx9Hl30qGifwPc6mRVFAypW4uMfaOFk/5lkjjkhRkjpPrKV//plyAQPn75KVBE8bE285Ri701RZ8gE/NCvBKRgl/FFCA9wrsf5N8Szs2BktyXxKf2WCWTcm8fuyg7qs9LtGrqmhhVVLmR/4YJmXCsdOp8SFX2dq/Hyy4QDJ2wOzAghyWu3w8oUjIyIJERhkEIIFiNOSY0XnErVjJzQqdDDJPkijQFKxQp4Nb5+YTkJQCgTQO+9MIHKLJb2XuCWlxrfJ6nIIRaMOe237Y8pUoD2wQsENCu3eTNIDQ0gCiEJACvDtaZKTTdD7G3KiIvsfQ6tMkZOIGxIe5IQcKCCw/EkhI9iBSv2FdWB2NaWsCQzj3zGMmRcqEkM2xW+9LeTngLX7C+l30KoULZPRlt6jlosJ4FiPVnxt07Tth25v0CXf+V3258YW84cOX5FqFsAIDP/fC7zq8s1shAgLbRQmbG0hu1mCzBQl4qqNeVdQUYIkWEUULh78nWCntJugD2XwtZrZb07eSQRKJMnut9suWlNHX3RT/l36uCj/EDLpJNp1gmeSYbFaLSYgTKV/tna4dmVEWhYhG6wMfzK1asn9bBjVKWJicT42LT6DE7YnSbJ6Suj4QDHObL94IB9L86b0Jafs6bikRNmCfvy/2yBf4Lu657kMNjsZewuTGvwZqqJpslM0z4mpcg8GA4A4+0OkwZw6Xgxd4K0Jefn0Jw1qEusOxEpVhmqlILT6YQvf/slnl0/k2TvB0n2no9HnE4H1DrDPQHGsxIwwmtk600Ei/pvujOYkcDgk2BOTkThY0eFQYEZa1hRDNU6OgaQ03wDtUOKM6BsAoi9Jec86F/5XnLFAtBu4tr/ggFX7BOSO8+UFTY0tdzTIOfbKmQql/Twr+D1kIZ+EIOzSo4AS27p8XTE7d0drp49w/vbW1ycn2NeKh7ub4FhwjBtcKoDaJZ2DGe7c7z++X+Gy7/4l3qsQjZYlgXmcRg0KgdA58nIucv2ekrBcOjp89ZKRv4NEFmgasXWq7/rPhp50NaaN+UbxlFjqKO3BUjK3ZZSvNGfeTMs16MxY64LRhpVSanillTqbF6M2hoWFgXn+YsXOJ1mFW6KKhcWgyrKBA0FxBr/WyXeLgOJmaEFToSQk2waVH9psBCsZGEHesS3V5PkcmqMzTSJd0Nx3SwmrRSpk94YmwYsbcGXf/tLEAMf/fClVKPSUyQHzza2F6RcTkxm1yASSuQ4Dg6pph84FsimZ2l18NOjfXyL4dV9hzEWYy3Zap5o/CpIvRMWbKwkATRS4s59iF1cm1hZx0izeB8vJ+5ZyOM4cPn+PJhYLGzvJT9kGMgTv10gM4YnN8njc9Uo0zR0DNsHZgv/M6Kha9M1WSiiwd/zTBSwdo/Fn7YW34vw1e1yNvYm2CVmAwv24PiGTIlQyBsDSoSrOCFXZk5KWP29KAZWqlAsgRbbTH4/INeYZ0B4b+nwZSjCuMtmBBVhwPv9EazNp2RfhrSbaS0mkedX4k9ZF/cYffQCVGbEBRR4zdDqeeodjceG8AJZv+Ms5ZMjF7kskJRLSs+wl/cB8Wf4Nnd0w3fVD0ba8SSJu0Ehwcd+Lel9wDKEsfyrnUGp+qZx1QWgRljmE8bNBBQJW6isyeB6IPL5tOfkwhUuAMSBVe91CEJm3CguuPRwc0HHH6k4n8PbHMbp1Kb9Nu+KGZjEUk2+v6Yc51AFmWf1ijQShqWhCMkCU01JQ+0sseTnV/IuzOthuXiuprS0JxSYmECWfw7aTgacxz1ErEeULk+et+IVQTuCT/l4WUb0GxMNN/mPV2cs8YTuEHG8j9xEiufkV8n8SOaoZKXnFaxKPcXBJzuM2SjTaxPimW4MHvp1WwGWaRoBEJZlhisyZDws6IRVPXSjpeLHoEatWiu++O0X2G132D8c8PBwi3k+Yp6PUlmqLj69rGyYhd9BR3kP+p1wELMDVfYk7bnRJrtDWMFqv/Wdoy8DpWTiJtgiy2zIijpWY9vMIz/OzoONnbYjvQvvLFbPhp9Rbg3QMvYEqDUyECZw04ysFQ0FhQkWDJrzFWVpwUNtvwV/GsCD5PcAADdwI+z3e7x4/kL6yNWKFx89x+nbNyiFUdsCXmYUKpjmBaeB8Z5GbJ+/xLT5K8z71ikKRm9aqxg6jwNc5l0rHdlr8SGvRpaXA4zJq6F7LNEd362s7ndWNJZFEjKtbvAyi/CPopYxKmCSLsBgqXbRGmMAYWGAhlHyLhLzkPg2KL0bwA2YT1UsnkVW414Su48I4ILCBUttaKwN1UoBeJYEOCa1oIrwNS8VQxkxFGlMYmFawzCiNhbtzISP1nCaTyiQGPHW5HnjMIAhCY52qGtjyc9gYFMKFu1ga5V4CsgFaCJC5SbM+LTgi1/+EkyM559pzoYRT9lTeMLZisErbgcSAGHhsh8pXbtiBXFYk5BuBDy9jP5qQYlgBwxNhgzLqjEXmW7mCHDOYkuIZnWAH2nWGOIkoNu6GYjQqST9dGMjWGsw1hwWkjgWQ92pAbucuGv5PONQMA7auM/DU2Qcs8JVe55Nuen6PcFTFQi9mU2p1J4X4qlib0BpliGwJnYiFA3zWnALGMm4yvhUMGmubNjcDCJhDVnzcVk367kJuAOKw/odgbS0KUmIhyslBKKWFInA2WEoXvvbPB9MhErxbC9723Q9RUsmMryUaikDdhvGUDbgtuB41GohIHVxq4CrlkIvdWmCtj0rCSBUyEPfPJXdBEjmwGmOE5SMv47D7kExSHNcFx4leFUwfRKs4aJ0ozfmSv582wRCYtTd2N1lfq+fsbye1YtU0DGhMh//LgFU6VAY/wJrHBSlaGKkXFcbe/nIzbST3B1mtGVRHiCwlp0K/H5k+TZQlFAo5HwaHAIg4uUSwORkYwIiJw6Kawz1HgQwQrZkD/VGxnsYjSWhLRZ7znBvt/CEpn1bSJJJEYISoJZfp6m6szE9xZ2Agu13RY8bQdt0j5wOlYAp2dhFaSV5AzqHbWCXfCJyGmY0g/NcfNyEA/mz4V5iVMYXSvomx+THPPSehOf2IT7b/XCYxz4inke2coiMkPhD0DzZZE7/+jgO47je6QCHRyZzHcOHWhfBUwhNjcqL5PDp1yxzpAKRM1rD119+BW4VtS64u7/DMu+xLCecTkf3ZPgkFdZ+bs3wCLiX018MZ5x+axCrDLyVvhUwd2+jPlAU9+LvQYLn2v5lNXbERCZ7E6IKS+AVJzjlsR1HOybm5tqQLWwdYHAzHt48FFoe39RLUx6FExoet8oog00xiHnGyYBGwLxyReGizxF59HicQQXY7DaY5xOmccRPf/oHeH93VGIlkTnLwOBjBZ/24Mu/h49P/3cMXGHGQqF3KveCsXB1XuNhlsIAtBec0nkSGDBDW5DEnntOSxNqLPyBUJikWFIT3sCDNC0cGDjeP+C7vL5HH40BRd1fFmZChYBmmrkcZWaJFx2nCcfTCe14BABM0wSUonkZQoSnYUStWj7ULFPqEckhJFU9KESEpco1y8IuQ9ZW0dqsrus+FQ962FsjlDKIYlFFaTKhbrPZ4FS0OkFd0ObZLbun00nWv9mAAYzjhCj5pnWKCaBWValgr/ojn42gCUOemTESYV4WfPHLX2HabXHx7JkKGk3j2qlbQpSao3Q4lakq0odfJC3fD0H81lWWyASS0gGj+BsXZMIggM8yUSAKXEgzYpS9F8GTOBQYEjwKC0owJyDdkyg+xyNVmFivWxaTu4LnnwwYDHhomlj3rGzt4D0yQBSKgyF5ep6Vcs7N5qLDt3hKHJ8ZsW67xhQPX1fTe+S9E4lm4X/5fjkfMk0Lh4EzGmcoJgDkdbOS5wRASr+BJLSv6B4VgwOKl/CTpoRmLgwlw0MrNYeqUAE1Ee6LDUniLWpNu7laqJWW6TTrnG37QACNA+j8DAzgcJxBGusOMkFTqpCMWjvdSwEnIT7juZdktCoocZneF4pHg3lzVrhG8HAXXv0Eg70iXkkwN8Uun6As1DiS21wddZNA5FNIUcq2hk5uoPS8Hq4meOSldYQknbWAZY/nVRNRqzFCpa+73Q5DGcB1QZ0lfKpVBiZ7Xgq58IXHcSf1ioPVk66x1SB18RtztIpaFsaX1jOw0GoobpZSUAbzPiCqIAKRT0qxVitaYhWmcqDkCkTxIQlvwtTT2VeC/ohmI3ne8RRdSxuR9iJXW+twkk25L3i0tRlBA+yQbs8MM3pkdSDfIopDWLg5P4TQW8mdD8Rz/BypQBR8jByHV1PshGKHW4nzyem6OIfhobV19wIuI2yygdcMSnyXAx+JfO66tHSsyK+VR/fn23Mn7R5Wz5c+YCxixH379i1u37/H+fkZ7u7Ek1HrjNN80pwMU1Y7rIt8Ax0z2HfvTZK5Ga6x0wI7eRnNHP7soAgcdTrAsTYfEavn2sPCs5cVVFb4PTk2VmOTGdz0twYwlQ7Wfo8+zA0ZLIG7tS7C3xnQxlexb523U6lU07ycYOAiM1lYez7vCb/cjNVk3Fmbl+52W+wfHvCw3+MnL3+I/eEVuBAWzdestaFQwd3NHS7KhJM2OnVPp9KRpvytAa5YWUhrKapo11BOBMyxPyZwCWwSY9TtJFa+XxvKtEGFhMQa7Xr11Tf4Lq/vHjql3MtdLxrmMYyjejsaBk1gqou4eIYyircAwOk0Y55nTVaBtH9vYqmc58VDqmqVRD8aom+HXF8dQFYiMYdrtdQXw5CE1VVflwrJ2D+i1opRq1jVWnE6HnB9sfPDzhDFpaiQKUnmpL1A1DJkFi/fGNtcOeQDu5iXCJfsXIO4yEYasMwzfvvX/xE//9O/h+3lBRbYATMh1rG1FyzYhKv+YCcRJDh1Wpc/wk8gdQJMfp8FVZ26328HK8tBdpc171n/AuTKWImMcCoBGbwnmEL3mbuJrEOhHg2IYNSUbnW5JMsEZH06CsowiGCMfCB75SYv3gVVsvdxqE3BaKpQsC6MOeVj5N+VkMlRVqbfrJJNMIWc6DhY4yJSy11CFoM5M6NgMBN2pifyZDILGILB2pjUQuhZeWEYLB4uKprsTV6tw5InrWADkVhHKrTvCBVNJWQ0IgwsoouF9w5UInfDmqEBGIcRlxcXWOZbLK0BXEVBr4TNdqvWHKNXFkrAPf606JHS8v6mpM4sHcXeuxN9heculTwpHJlYyY9+DHyi9PdRSeogNcgx0nn07nNag3sKVmM/db4NNyg/p3vFujshwoQxpY+ACFHbzQbDMGCui4RPmUdZF5TDDmB0La+pWZUqrW2vvZCqViXs5ptgZNPsqsgxIKWVm5eqlEcYbpT+Yl9/EApX2G2teBoNZA8TD0gE2AU/p+cWMpeErg6260HgRozSEfAY2/gNKLiJr9N+Z+Elrd9IF8zycUE3hRDDbDDDc0D5Q8lXR1gLIAYBE06NbmW7u/OitO4u9wCJL6QPblQyQSovac3HWKLOYn3UPb0b235JwmQnrOXz7XDPvLTn3z6KdYPW6AoQsNcythcX57i/v8c8z1iW+M8627MmvEVBijiXQYkCp4KcM6ypnMMaegbIzmDaN44wbBN85LuSeoytxuY0h6xtrMZ2jc+UnjTxWFUS7m1slH7dBY9gAE5eEF03CqHQADZsSwhOrUkidk9onQahQJpwrjV6h2MKJcy4ZrSONGWgNRz2R1xeXOPtm3cgJizHE1qb8ezZNW4OVXIglhn1VHHYP6C2Ci4jqspX7mVsgnEWSRDIpYqFJpbbsTdFzatpuawidDHTeiLxjZLx+QKc5iNoGrXhoTz3/Zu3+C6v76xonE4zhlESujebDWZN7J4gid/jOEpVGG/OJ3kalVkrNDDmWe5ZlgXjMGkDL/Z8DyIpB8YATvMsmm+xuH3SuMaG1qoLMEBk09uzieAdye2aeV46TdyEHwEquXDBLDWJx1HCoOZlRikDpnESNHJLgGy0WxdMSzcKqTsb7nH5fSgslQ3rgokK6vGIX//1X+Onf/InGHY7dW3p4bO+L9C52fHz04MVcVlRN70gbGfp+0S5/bwFXxSCYGdpZTnppBpdo1m11ha5CDVSrZuBiFa1dbUQoGVDgsGjF5rckuGHeLXkRweun7cIH+xbZExKPBmDN+FzZsXxnGbWbX2GERUL4hGDp+YKsTWtVAuFlJAKjwRDK1EZrsS1MtfmoVPGUI25EpMQzVS7nB0o5iEMMFm4Bpp38VjLLQ5kq2zjL81DCOGluwmAhilRDSbijfkiZKq2aLxIhVAaYdC8jabfc9Ekb81F4GLx/0BpNnN4Uv7V1QXe3956dS4GSw6XWzkdKQB1F4fwobhlsKVV4E72+1PPsPPxysfQcS3xUbfQPob4o5czRt3QPJ985NZCgnc9Xw/hcpEx6Y4sBK9U+Dnj7JTo/lldjok9xs6m4Z3CnFg6eU+bDY7HA2rVhHBOFQyzUOKCRMyPVRBZoHXwyUJam1e9MusoO1TIz5jczo/2i9PcRRBQmgu7x2AdCff5fguLMcGEYXtnglbAMO5lRCJJMlz4WvO641yTjaFzLKTFQ4xt+fRNeE8e2KqUgYyPJuuljm0ORBP8XPEzdqZ7A1juYVzlCzT0SwT5aVzTc7ROqFm/z3/TY/1r2yPqhpRr2acUL8fzgLkpt8FLbD1Z2F6x0zS2e6aMsFDwI2sQ/LteEpmxeFWxVhd88dvfYppGHA8HzPNJ+8/MWObZgcqa+7YGFNvikXAqH1CIgtC98rn/AMyDBjijSTBRXy7zY5in56/j/gF4oQPHc6NXaVV+ilwmSFcYzJ0vs++NGwRYDM5USHOd7Cxocroa3hoxSpIXKA0DIg8FM7nAQ7OxUpLyuu3MGX1i6efx8PCAjz/+GGDCfJp1rg3nZxvcHB7AreL2/S1u378G6gHH55+hnp2D7x8UhxNFYWAoBNKwCgJc8ZAWcS287ayL0oZ+5pnz7BLOsGeQKjJNCRNPA158+jGeP3uOv/kPf4XaCib8HXcGbwzU06KbRFgWyZ1YZqk6Nc9hImIWgX9eFslL0LwOCZMilDJK6BLgSgjRIBWidEOGMrmnw0rjSjJK1WcUVzayQiFIDY0RZlQNtWJNKI8ygaQKipUDU/G3Nex2W0zThNYaLi8upDukso7Q8NlPBjMA63TcoNZe29ymQiU7sSNikDLboRBO93f49d/8NX7+p38KDJrYakwU/ihEffP03XqjEicN3Kenr0t0Kiy07AzL2AmcqQUmxhmMJ9P6uXC2pnDi7t48l44ZtyA+HtOcLAeyEYnh2L2u3D0BFwRTNuEDJviSVDaiwcrWqlWZHcxwrwQAq/KSLbN2zWNvRqqyZpVyjOH5/WGhMAgxrNIT+TxFELJ+AUbcNbaSzDui50GVbxPUAGAwQT417jGhyLuck8TYs1Zpa7VhWZqPBXByU2cmr/vT4MaBxiwZ04uWtrUwDpb3Xt4TJegASCp8Gb4Ro9QCLpa8CZhAuJkmnJ+d4e7hwa1u3BoKUxdysuatQGJuHe4Fa+OMRAz31tjYbqmDnZ1HtsMnPsV3Mjb7Fx2jTefkkcy1Om8ypV45NH5Cq5vzNf26+3nksempBcgkY26OC0rgXHAVgWu72eCeSD3R0kvDO1RnCqF0yOiP54ekhRn9rXXBOOZ6+JzWHesBLNTlMV3oxrT1J9pi9KLzXukgxrS753l93F5Y8nVygjWy3CYeO07CQibz+ZWFunyRoyOlXygJii1yqEyx9jkmb6F8XiGTPscwvO9XkharSEdrxpSfTXA84/QYb+C23qAPwCGAYUteC7KMJ6YRylmaeLZAc/wYcF1vpq3D8SL4ZF6jnB95k0N9TMmptYIAKWgBxts3b7B/eMBmmlQxX8BtQV0WiN9fGYdqtEYjCcHf7RxQ0nHYzgSF5yjZEvp1GR2P1fSoTwAs58cMWLZm42PGK4yugb1Zps8HDrqYwqP9XnmmfFP0Yor3vm7OM1bO5P0w4POD7Q1DczbVQJh4m8+A07xNBiBKYFOYmsDgSlFTeibvGQWtSg7wMEpo9u3tLZbTDG4Vo/G91nB/9w7H/R3G0nCPK1xhxMQEcz9mObRWyf0FIoogKzd+Xgldo98eCRQ/TGHUeRARaJyAaQS2W/zZ/+yf4fryCr/+8mvcza899+X3vb57wz4qOBz22G43OJ5miW8rA47HA5ZatcytvESwF8WichMFg8VFuFD1LrFn2zNM0+QEoi6yCVCr1e3tHbZb6bAoHcYBouiKmL0aOknUGpn54bUo3jWxprlaxj4ze/1xmWdiBkXiOOQMxCb6ISmEcTdhu9liPhxRl5MeJCmpZqFX5nYkVqCXgoUbGi8oVPDw7g2++dWv8MOf/SEWtRk1Um3UpZDVphpTS4fTDTSIRO5eZNGVEHXfAkl4SkzIHmz0dy14JFnJiQozoZhSlJA5E40kp/m02Ih2upcBDylyRvoEM/fks7wmDthkBSTPWbZQwqUIYQmsbIwqrJYVoWw6sYPlTTb/a3NuSclgnwO5wOR/Exe2s1BIHfFuQWHP42m1adfSqJBVqGC73YCIsNFwlXEaMZYh+gPAfWJi2VLKXFTRyjGctjol1WitYZ5nHA5HHI6SlLhYfpUqCqDighmn+4ng3ezJBK7GaFrNq6GhNLWAg1S5FO+feDoAZkLVSiajehsKAefbLebTEae5OlPwLs6WfJ4FQmMaq7OT8dQYib8IkVhIOYk6Hcv1YcrPeuK7GLs/vH69j89xAwBLejbhIXIobUGcHyfrN+ZC8YPjxOrZT7INxcFu3U9dlyQIe9taxXa7lTNV5TxU7VfjTiM5VC5WuMCXACaoKjs5aOWpODsu0YQCmea0DiuJx65FmCSI+Tf5HPT04zGcnnzr30RuxhPXsuFcb1XN3pRVm4JYENn2Z/EsHpLRDOiFJP+tQx87JPHEhLV49K0/Ox2qHOuUxrbHPzoX1NNz52MfxLWYt/HmGAB+Hjr1Uj0O3dgErNfkZsInxv7QWZYPrP0ZNBxlKAFPE/z8GWLULEUSek+nI7766kuUoWC/fxD6XkUxr8scYUocq+3WDfS/UYRRP2ksCALhc/cdNWURK0+ECgABG1oBwE1REfKaHp9hzsyh0OoZJZ9/P7YI6w3duh8tihwGjn4UoVemjMVZCA+f1GFvIAygIrwxr7sZnKx4R8nw6EHgCrxOtIExGFEqEsVwXI6oqPjk04/x9u0NvvzqSwzTJGskSC5mnVG4YqQisimNmDUqwvDAlD0ZrmIoUjTJFG8on89KrkX+5EgJfzl+yfypiOF/GEb86Gc/x8///E9BH70AnV3gf/Iv/gX+6//qv8LDwz2+y+s7Kxp39/c4nU44nk6S2A24ECUegcEXYolz280WwyT9MOZ5xma7xcXFheRpMACWHhvzPGOapmihToRpu9EwKPJnemM+oPNMmGbXasO02YB1PECS0AsRNtuN53WUUqR6FhG4VZS24K/fbzAOA9o0ggEMZUSRMjgSzkWRICyEUojGsJnwg08+weHuDnVZUBepacysymfJjEUFIG9wQ1oXvaFww6uvvsDVRx/j/Nm1VjQiTyzqyebqkK0Q3v868cjfrpiM/8qIUxxMralAkzl1TtjOUwDQh3UFfdUBLcYw1mIzcYEjpAoXzrul6ufMdG12yaDYcxN7hu6bJ+eTxCuWofjFZpVobLySfUqVzNsja2BbBUeOBaC/sVpZzEVrU+AQZERnFccmdZ1YCaShIq1pgQKNyd1uRmzPtthME6bNiGEYJZRCc45aldDCtizYay8bW7dVArLS0YYLREBhq7+tPUOoYJxGbKYJNALTOGF7vsPl+TkYhKUuOJ1m3J+OOByOmE8zlqWthBxbU7L26xobN1AlFTANGEUSxHVvhBkVcWlr/KyVJx8gficiwtXFOd6+uw88NMRoxkNWllIg5mUwf4Ibs87LHSIERGWux4JS99cEwCeeGSGJpWdUFH/yae0YWbqOlbDQ6qz4VNbKki+qr5pj48U57ZfSKemdYINklWc/3916GdjtdkJL1AjEtbnkYSE0vmWcLLRKv+z59ne00CkTGHxsPIY56ZnnWGsoI6vcAF4LRPHrih8jd892gesJgS5/bcLPWp1za6yvGw4T92rq5llVNd+1RDfWOMfpWYV75X89RyDjxFpATZQ6G6H4ySU/Fr4ePcVWHb+u1/34+v5c5LU92u9Eu41vdrxh9fwCcjk7g/Kpl5ANVbyR/fVy4zANqLN4ICRPIITu/LJKl9YX5uuvvvIwKqHZclaWebHFwARmIyKP8DfPPeHao3VzwLObfD7LbnSyZ/ceo0yH0nBxpkEJgTj4n/6zHpsArJui5LH9fOMD+5gQ2wx0fi8bthUwaUGO7iAY/ZQ9K9zfSzYvgykjPFXw7Qngrgy1njTPYhha5hmn+YjjfMLbd29RmXF5dYWlqrEM5oWIIkjjbov90gBtci3wIX8+lSIdzYm6alJDQZTTJoCtSTbCsJjn2axfXBnAjfCDzz/Hn/z5n+Pjz3+E4eoCd8sJQ2PcHo94mGcJCf8Or++saPyjP/373pwOOkmr1sEJoaz5HbdI7B6KJOCYkF9Is/71f0ZolW/2G4QgbgQoIHolI+JP0Wmi+TsmKbUpDeNkO2WeI1An/OF1w2/qgDZuwCxt6k3rq01qBhNpVSwQCksia2uMr9+8wcVui7aRJPM2TaJAWJ1hlrGX0wl1PmHRfBFixsDi+eFCwLLg61/9LX7+D/4+mAsKtCqCJWk8ItnGEMIikHX4OHlZoEuHLB/q/DENZaFEzhYIUbVHGa49NI/tTfG8qoHug+P8miOmmbinMybiU06HI3irjFkQzN+Z+fowIQ4omfIIUx5lTjk5mA2nAPUimFdDY/6b5lI4sbJ7eTVzG1s+Dm79L74vVIS51GUBV/F0bTYbXF0+w6jnqqmVa1kqTnd7LadZNdxJS4i2Kh6Dukj4k1XDqqmPgc7Iwn4KSciSNLAcBN+LlPhlAGUYMA4jxlFi7jfjhGEz4cXlBFxfY5kX7PcHHOcTjoeDeBYhCosRZxsRMKGKvIu7NO9UJQ4qUCneNlU2CMZspARuIQZKQRlGbDYTDqeTYz0TqbJouIdQDkxwY3SJj3mvPMnOcM1wJu2jQ9GE5hVePvW+k90oiVoczyWgF4z9cvbcqY6RIQT8pwQ8OL7rOMmSmedsR4/T85OMC6bcc4GQY9Ij/CgA0yAxwtN2K59VAW518cZ9hn9GSwY9xUHHk5JAYV2c59m9IgaFbIZ5Eub6xVOs0ahGBpltkVQbSwn6lPG451vd2I9wgmJ/uzlmSkEapvd47BBqqYN5nxPU442TwTS/R2vnuA/EEcbk9Dxea4psa+/WswZw4s9xXShVbKNR3B8Uqv/76JXZon7OZyyve40XxrPyebZ9spK0lNaY5x+YBge0j2FWZyVhF+fn2D/stQ1A8DArx3w8HPD69WugVVRmELSITZvBXON8gJxHPQWV7iyXdL6T8Et25nrKAgm51XAsCs96vhoJVh6qCtYy5TY6B/92L44gMwFq9HlibKdr5I8xBMkwz+vs1u2LT7/autlmbtlFNkBxIxShoaIBTUOKNQcyTkHMR/BKjWqcqA7BjYp2zh23oZEaLM1Ll9OCs7Md5jqjthm1VdzdPWAsWzRavNhPrSI3t0K4bxWjG+2CT0hvkAFLlfC6AQW7szN8/vnn2D8ccPPmHWZtAmhGfTBjfzygQossaQ6LEchCBX/0J3+Gi8tL3B9mXO1nYL7DfDrit+9+hX/3r/4V6sNRjEbf4fXdy9tCBs/5CQTRzAf1DhAAj8HWw2bJX1w1EbUyuEiFKDQ5UDQM2kU45EICtEpPxJYCkOcpPKTbd8SPW8lNw6MslLbSHBFaer7sPHCx2wL3OjIRlqVKR8hmZAdCtZTrMqQ8J6YRpQC02+Hi+kpyVpixOz/HMI7Y7raYTzOmccR+/wBixptvX+F0f4/jwwEECOOVWeLu5h3ubt5j9+Ijt64xB+PpDpUdGecs2f0IZ6orOtxbCp7YZ0+Q9SUTXFFJ18kzgst1Y2M1NhsBE2LXEQRbpL+HP7Njmul6MiaSLKCRFEbh8lAirfnFKR6XXOF0QQrwMjWOO+aBIcFFgD2Uy8ojQxXZ3kLAiIFl7GLeCyInPIDkUyyLxOJupgEX52fYbbYoEM/BPM/Y7x80vr1KSGKtWOYZ8/GEeampOskJbamhbCAJ+RxKhit6CiOC5kZoEQXL2RClQwT5adpgs91gs9liGkdM04gyFEzTqN9vcHG+Q708x35/xP1BkhkBZWB4HEdtRgSGVRQCuBJKYc8FCee3VAITWtHEywjpWbDdbTAvszfbzHhu6JC/yPlOlP5xqzJRJCumMx/CROwy0vfgdTWbJ84fDHcTuts4ntSdzltiolYetwg3CAv8Ex6Z9Vd+Hp+aHEcFI1L4BBBFCLSxDV5x2jijutA0WGgUYbvbeQO7ajHnpvCm8x7KYLbCku5f4LGENlitOvaFPbK46ss7mBsQVuuG7QdCEXABN5OSFVwpExb9vveIrOYnIyQ2EsYfF0445gKCePMS3afVowM/+7n5i/slP8LX9Fzd6Qh7SXw+DdfzpDRUv25yxVjmn81Vq/vyxAwHmXuY5zWs2VZiJ5y+7M4Y2fyN5usng7mtjyjBnNwwFLim9JPiKTZGFJdRXgfpv2Vh2eZFbVpnkbT86BdffIG6LBKS0xqYxEhU6+IbnUNaPvhS4HgxCcMzk81icgoidoUEKIl/O4Lr8H7wXLE32JghsduI1dhggTEVOUyea6Ih9kTWpCL4sXkh8+F5cumOnHlQ+418b7LFJBK0m+MaTG4lCXkeuAAUHvpH+MUIfGb2OFDDFz/fSXaVUusExoj94Yjnz59JiDmLDHA6njCc7dxj0prQrnmepbb7oOW8VUbpS6ozyqBmgQI8HB7w9v1bPL9+jtNui1ordrsNhoEwDKM0+VsKKlc0bmLUHkrwYCJ89e3XqF99gdYazv/y34uhszUcH+7QTnvsrs5X/PzDr++saMy5wpJ7CjRJfGlRv1zbbrsbhhsGSO6EhEDpoqySjdWyBHm/AdsgGaYkLdGoBbsSYmPJvLxbmcp/oW0xs3YNB7RMDSpJ2cR6mlHGCRbuMpRBlINCqEsVxLGyniwPbzr3zcU5rq8uxf1KjLEyHg4H3N68w263xWf/f9r+LPi6bbsPwn5jrmY3/+5rTnPPuVe65+qqwRKS7YClCw6FRTkJtiFFEucFNwk8kJRDER6S2CFUUTzFvKQoylCpQBJVAUVSlDDguIsdSziyiY0L2zKWLFmdJd3mnPN1/243q5kjD6OZY669z7mfUs6693z/vddeazZjjjm6OZqrCxFK2xZt2qJrG9xwBl9f49d++VdAnMATnEPlecLLTz/FR0+fY+JCLOM2i4zHlQz9IWas8VOFsI5VAR+um3Yh3DbRZ/UdN11gdsb6o1e8kS6G1RBQYSWOA2U+3m5kEuVrGQcKTkSlozxQ2KMLCyYoGS6pkIush+Ch2KKnO3ZlAmAtilO5P7Gkh4yKSRyDKzTan1c+ZsY0HTGPktXs6mIrroOQzEkP9/eYtMDZMAwYxwGHwx7H4YjpOGKaJ8ya1S1rkTArRGmQMotSViJeMytyQUf2jxAaE659zJCCmClpLEhqkNoGDRG61QqrfoXtZoN+vUa/6tF1PVZ9j/Vmg3e2FzgOAx4fd5jm5UlKWWSyNLZsp0gWOG+ZiWa1putJB4tlL2nGEWFCCU3bgsex0H1tywQN65ECVi45WFnHGtciOfWMbD4XKnsJ8Owl1kuBedlj6aRR/d1I3DnFweah+KtyS4DkopAYhxdj36TjooCuVF4gxY+oihGzFuo83Ytw4VT3ThAYoKdyKUm1Y1b3qXKcTw6lqs1gYnY3NwKIyZOGOE6TriUVxSuSraaCEAVBwL86s67ojva9VAqL8CHz9vXm5Xrby6Wvsjgo8+byk61TyRoUYF4D3VihCzy+hIt+/BTK5hMeOzssvZdNgQq/+V8VOoVnki9XmYNCik+AXMYfkNT2kD23eLSa83LMDhtCdTcZP0QNX+u7mnfAtdp1jGCGJAKVUzTjX8t5Q9JvC+0ST45xGMuclMY1SdKBP9w/4vbNG+lrlihAzoxpnoorLgK1qjds/XEJ8wXcIq65h4LtLTC40bg9FlecmDDFDIlse9Zw1GEkNBgc6bn0zFQMSqSA9X2UIBmTzCWd7ZTTFoYC3GyvL5GAfZ0+D9eM19l+8jmZhQDwjSeKITkPlS6p4IvRmywB5JZpEShziKFKrAjAiTTByoS2aZEaEcHnecZ+f8S6FVkkpRbUSHbFPDxgve6xudqiVStwnjMS4AbBmUdN3ythDE3bAE3G7eMbUM+47LdomgabtIadFl83N550qO978ZrQkIQZDLQNGvXsWa/XePe9d3Gx3WJ7ucX2YoPLy0tcXV3iba63VjQOVriOihBmC5czuyBiAr5p9wAVoU2ZjMU+mH9uniYnljNLpWOzNhui+3EkCFJRfC7jCL+bK1W8GJDA6kx6IiICWYJkm5qGAU3XFyQkkloaOZVq3uDyrqJaSg026ws0TQtKJFXJGyC1giSPu50Et2ug7UziGkLrFbp+BeoascwRXFkiMO7fvME8jkDTOnIn5SpVAGn46LBCLVQVZoRCHPQvRe4VGJCts8Gu8jgM9+NuX6Z1dGIWCEIVhwGEzcihTVs0doJWZlu+RMbmOsVSaOAAB8eJQDytUx23FchzJqKEz1i5V/BG3S7BGFEZWLLxaPVO2yucxXKRmbHdrHFx8wTTNONwOGC/O4r/5jBiHI7Y7R4wDEdRNKZRYzVmPa5krTxcxiiMMDqwFYDY6QkhKBzOLAigjDzLMT1lNRdQmalZsCxmCkRo9ntQapCI0HYdur7HdrPF5mKDi+0lVuseq/Ua19dXgtf3j9gPg2YBIuVP6hCgY3EFQRE3ayVXs7CTnnQkkBBJrVQOkqq60zgAdgKpe6W2jhnDiEyLa4Si6o98CJZdOvdM4OSO54t9GK/zokBhZssr9l25wYRxGR77szbQKGEEAR7hZ/vC1aORznw2bamEwzhv/dw2Dfquw26axbqrinEBROW0FOYWxmhGAYjyKYVfufhPR42L6nG5QQFUQZfOflCjFcj3cHkm7C2fL5W4NDJickqfqyuOb/FItTy2dJ8B8zjHSN6WV9kL4b3zw3JQVnwj/rb4HhEoPhMpuvE3H7s97O/VbZzdMHGcZ2BauxMaT6LSfxkOFkylgnm1d2M/ei+pSyczgouvshHOUnxUhfSSDCT7czOblRtABj751rckQ2BDasAQJSNrwpoCz9rN0Pf0GYwuih8bdJePwFR7H8tyf9t9wzUFlHXPAc+j1V43q3AiIjco1/TGftfbiUJXMuokRx9iJGNr0+jEMuJmQcyW9Lx6MmwA5/NnNhBLKtpGMyX6pYhkxlJXLkhXKdwDEzgVeSgqIuMgSYP6vgeRxB4fDnuk9YBEjU7FCgnO+O//M/8UnnStuv6rQqdyMohBScy8bdtivVmLe5QqQgnkmV9tnS0eEyTeSOKhIMb2lMTDiDWTatI6C23XIYEw5wkgyZo2zSVm5POut1Y0jsPoi2FW3aTaVJ5FMpnnAV3XisbeCODlJEN2rRf7M8Ar6lhglPhV62KFvpenHKSnIERwy6fHjKhGLbEgVplY3S0GaaNJSSodKsDzOEomH7P+MpxAcJ5BTQsytxlHRC3Mp3Enq/UKYKn/gTkjdSvcHY447g/YbLeA5jNmYqBp0LQJXddLfY9UrGKJgOl4wPFxh9X1leRCYMBdPYwxuyUXvibxOiO6n2c2usONwSg/9f1aWUhR7p8jwkXQKD/aanvAqvdNTmiMwPrzBDBTUFwKzhTMKOvgYEEYAxS/bMBmDeFQ5ArswadmXZP6FybpGkEt44iCXByTW6gN/yBwsAwV0zjheDiIJeHmGn3bYbfb482rWxyHI8bjgMPhgOPhiMN+j2HYY8qjF6csGTJyBWxjJRQJvbobsqbrq2hrEbPhiaeg+wskxYkAP1IX5VuEetISxJ7VLWU0NGNkYBgG0GGPx4d7tG9arFZrbLdbXF5eYrPdYr3eYLPd4uLiAg+PjzgcjuqWVYTbFJFQ6YAxNcsLQjOQGqlLkpgAFveqlLIYJ5Jl2Sg4o5zL553CaYB0RfV+iBhmlltgAXNtwPdhce2xjekwDzy75vqhy0qox2e0i0Xfy/1d3AjjPvU9Zu+Hrs7ub+2+yjBVSM+JABKhzcRh3qQpm1mSdBwOVYpb2Sv1jlqeukX6ZlZdO22zdXQhzF5bSsThvo/X+wm0hctanVwGODYmXbcv8KJT2hgux78Az293RZhXWbYAP30tyLXoe4lSXG6VU5pTXlLRVD7TzmJSVL92Oi+j7Y4XRuslls9Pw5xBwGm18ydawMG6X+6xJU6yzK+oqWQ9u6FzOe+yCdhhXk4/lY/EddBWRYzR3IRmGGWDM5wXJRKPjv3uEfd3d9KWyjGZxeBToxAHy/qCmBj+Rdx2PhRoBIUHq0lHYBXjrvwp70dFR1y4CdniLrwtcogQGhCyw6vqW/sIr/kf1tMBtWgjmZGXKGRgS2Xhq/5DH2o0jgqEKWAVogbk9XS3ENlPsoZlVzRO5BaDkTdjPFR7s7R6SuOYGQ1pgpdJa77pSU7OwHAc0M8ZfauJisy7or/Eex9e4KsfvCvyJgmVTyjgZUwAstdvMXnGshQKaIIrl+GmcoB5ntH1vfLP7AZIzhmpSYbhmJklfjRndESgkG328663VzTchUg2BJFUNLSApqZtZRNlAf6gxfk8K5VW+UbQ7g2pWY+vxlkyRZXTELlKpil5y9ywZIGy99O2rfqwz3Jc3kjxv+MwItYVaUxtVyWkc0FS5jdNEjMxz2Ifts02aRl4E9UoSRVxSpLVatI6I21KyE0DzhnHwxHbC3GfEsUHYuFmwmqzxrjfg6CVn1VQwDRj//CA1fW1E+243WVTsN93140Txl8TfVfcw0YzS/LSysWLz4JmchVjQU0OxbJPKNCkmjEYt9NWY8Drub6LS4DBnM7Oy5u2tnR87A8qQ1E8M37hSoaNlxkZuT6yVvj4dM7CySiguvpolWyCBK0ejwckSnj27BnmecZxt8er3UscDwcc9gccjwcMx6MUaBpL3nTmeGoX4e4QBNRyFIUt1yBsgG7hIV8jOgFilCaUEBnMKw5mNFwIDqu/PIiAmTAlYJpaHI9H7B8f8ebVS2wuLnF1eYXLq0usNqJsbLcb3N3d43g8ou9XmoqZdaikR+llgDINwxnZt5LCWz8r3UnUIPN8lh9HvCqsIcBz8dzZPYRaoHFG7zBT2mZ4EwWARRsGSwI81aP3Ze0a7vp7tThX/I0XfNWbqTDj7HVuf5+fdxBQFIH8hNRuV/NmzBDlfbXqARR6PedZGFqTqr6Ev5Gf8Nbj1L2gLgLF+lz2tPfNwe5JsQ24UHF+3nWnZX8Xy+ySpi7x69QcUfd9Difr/sp1DteWSHoO1872bZ8pzpvOr3dBq1qOC3+NhxeYBlyjcnK6JDP2TsTXc/vjc+cdngHOxNF4WzVdKyyIKvyq+65drnysAPJcCo96XA/YZWNmBs+zC3r2u6Uml0Q2CQ0BL1+8EKVCf2NoAo88LyZqSGfACotjBrS4Nlzm6u/7/M0UEe4jwqOeMSkddh3B0vVTCjE8hJiWIRBFHWeGBTfT8hkft7bFXGLP7K/Cm6AyqM47xoudwsrmdyo7LAlLccMs2RhFyGbkBFhCETc0cMEPg7/LO0r3nIf6nIuhhCGy5ajuU+IokzUMYUZuO6kUr5uFkfH69UvcJTHG5XmWPZ8zhuMRu90OSIQuERpKmHLGOBzRd0JzZ9ZC2eMoRbSzOLcSAV/84hexXq/xkz/5kwCA7cUF5mlCQw3a1Gg86IRxnNyYf3N1gS+8+xz39/f45V/+FfxPfutvxre73lrRmHgGWIVvznLMkoCm65DHCcMwwNJsNU0jk1EL4zxNflIRVlf8yfRIxwvvQQBpR+uWOlcY1ARD6GEYXCGxdwvSwK3AzKxpbVWcZAl0bUkCS3NmDJMU5Oume4zpAtM4yunKLHM+zke3uky5h1kLiBgzsjDTJiFThrnRzHkGNQ0Ow0HS2M4ZqWmQp0mzbs1Yrzd4pDdwYiSohQRg93CPpzqfGUBrGr3RiCAAV76LWOw71EzcbeAMjznx551Sl8bNJ/VcesD4EoWNX/cXPnBxSbJ7Thf0XkzJWx6LBCowcR1mifum0z7CgLwAH4X6JmA3fpjvLSCnGi7M6H1hLqFvH4kQhESNn2BwZjw+PoAYuLm5xjxlvH75Crv9Dvvdziu/Sg2IAZxHiQdSKUkOLhoVvJSBGVyc0fioHYPUVqeSVsGq4loQpQebnKZidIFqIZwawWToHpfTDdKYK4GhtJ5nSRCRQMhpRNO0GMcJjw8PWL/Z4ObJDYbrG6w3F7i8vATAePPmFiBC07XCy5SwexpJl9CC8qf35hlgTpKQgcy9S9YmK5MCpHq51PpQuJHCTHHjnJJusCZFmqiQn91jxijtu+F0fGbZgQk1QUmJa1DBvxJgC2LHjD6Ia0fAspjf8jq3v2nx3bCMF4OP+9vokVlw5T0N36eEzXoLAqQugLrQzjitfVMp0/pDRVNUgBX3q5ruOXwX40dYMw6/n8ybyu8RF058s1E5k8IpgSInu4S8mIPjWhE6TmB5Zt7L5ePFC1ajBtbH5/Z92u659dYoqDCqeswGkYxy8nCCa4v98FaKPAXVgJe/1fOufjvTXgW3IIyb4YRs/IDuMXvndI8ZYbEiZvVelgx47AVXpW1bC1kfoUdNAigBx8MRr1+/Fmu51l6C1RyzeUQh1vYYF3ruMF8CIfJQV5DJpxGFdKPnVtTNTg8802KAsvxWFIryOfB9t2Za3zkI2wbn0rekZ3Yzr7ybMzwBj80bDGoaiYVIGZlToUkcdyWV9eKKQ6PCksBDl4qXGCnUlT1L6H5xPXL2ITitiFD6puBOXQx6NlewpPme84x5mtB1HabJvBSk3ENncNH+cmb8tb/6V/DX/t6v46pb43g4Yp5G8FwSyVjs2nE4VigLiCzaNOLy5y55zGiahPffewc//MM/jNe/+Kv49V//dfdSSpyQ5uReSKxJn1JK2GxX+JWNqA6ffPIJ3uZ6+8rgmm6T84w8zxiVozweBySteLhZr3E8DHj69ClWfS/BKU3C7d0tHh8fPb0tkWnJGZTnUHtDhZcMMDfuyy3HSnLMlIg9mFCy48hJyTSJyF+0SWA8HrW2RgeCIPQ4TMgpoVmv5ZQlZ3Bq0G/WuLj9Bh5X34MxT8oCgVYVJamyDDTTKGXjwVj3LRqVhChDrakjGKIc9Kseqem06B6jo4QxZ1CbMHJGt1kjdS1w0OMuraCcmLB/fADyKJuLkwhbRGEfh81dcYjiThPIDVRW8r0MFQhkIwSSXHEqecbT8sEYmp/plB6cyVYikLd5zr3BN6q/VEQla1OmHQk4UKqUWTvqRseMIrCFOZARaCWlMbOUEjFmOQp2MKJYVXwm0SIWYJgSwInQkLDn4XDAYX/EzdUVGIxXL17j8fERw/GA47DHcDxgHCfJEDVPemIXqAMrkfaYnDDZynpVi0P+15k7F4aE+rL1MjhlY7lG9KlmMTYmOBMyK5xRXlNxSFP+SiezBsulWTJi7Q+PuH39Bs+evYPrmxtsths8f/YEu8Mej487dP1Kj38jgzcxx/goa3YWOTnKlio1NdV4AwdyGFgmpLI5Cr2wvRR3QAmkLdCIr5ezO2OuqIBdyV36Dyn3NGud/epGBL+jjDIqIm415jIfG4sxZar746rN08t207l5L2GSwS6gFzHD+i7M2wwAMwnA1hdbgFmNSJMYjXT/lXmzumXYvq/HVYQRiEurwwigDFTuYTa2BTmLgnCQifyGuTy6RdrkAxWaTQSy71XMm3cSaGUYkPdVLVAY2wLe4OUztXqyxLWqzSVZCPc/F88Xjcsz5S8hroU2GOQ0m3cR5uNWY38O2p7PO3YeBmbKQFIafY7iVa8Fw4CIDzpym7fRUCNbdtdwjQEijXQLyr8J/ZlLYVCAfZ6eNMQ2nf+x3ZqFtyeB9Js3rzAOA1rLlMkiUOY8FU6pNVMMdnG9HVwU56U3HPnjIteQIoeDrKrjuwnfFgcQaWTk3/BHIScW1rfRbUsZH8brX8opg7gZGWVR/NbTEpcTiV0WlJiHBDKqpW5KRjBMUZJbZc4VDpIYP2ocNtyqgZwpi0svooKlT1hWwppaVmwn7nt310wiz02Tyr6Y4Z4+8wDgEnLylQG0mJnAxxEPn3wLBw7GMTPOa3IjkYtzKXCsRnrLFF/xGEqYJ+Drv/qIP/HNr0uNo3GUelWkHgK5KBopJcyTyNzD+IDXd7MbfN7memtFo+u3UlGbCUDCqCcGbWrBSEgd4TgJsrx4fQswo1/14CS+ZwygaTpMFoTdNABL8Deo8Uwi8zxhf5SATilWooJE6iT+QYuYNK0UDZwhwddt6jDOg8dsEBGOk+YIzkDOepKAhGlmYJjQdqSF+2YM44jMPRgZ43EEaz2BTPBK4nK0WdIyus/bbEXZGNM0YhjHYoFmSTEqeGl+jlI4plv3aBqJ9J8mQUBigBJhOEpgsORIruUitwwZIaeC1JFeR4ZQCFMggtmIBTuNOCcosXUafjfGk50Qwgdpm9VPEHSsHAV5DfB1H1393UkDl88c2i7vm4DE/oyLxsFqUhoIBMIa4GAjDulwXUAopnMXCI2ZWX57qewqv015wv3tPdarFZ7c3OD+7g53d7c4HA8S1H08SC2VeXT3ET+KNmibFKATdtc2+93zkCvuBRGyIpSGINENMUovxhMovh0fXEgiBFh1ewOmraZlKInWdoZk4xKrQUbOJMaKSfzzj4cj7u7e4NnzZ7i4usZ2u8WTmye4u7/TrBkdZtY02IkcX9xybuw7C0+bASQLvoTiQpBUydbb9g7U4hg3TeDRlTAT1+BkjxU4+PczoIx/OUauet/sAkxc7+qYvlopquUIg3qFpwG1Tofh9+J1OlyjWYHewMlHaGsxTsU1AkApYbPegDTFbc6zxmh8DsxtfLaEZWuDCOpawA6PKOh/XhxJNe/Qsfkkl85IAy3htN1onp1elL0WXTiCiSfQVO+bz+NRnP85ly/7euIGV9Hjsu2lbwMKn3a26CPS1Di+ShlYwDD+dUpkN5X4l7fPw9yU0wRNCx2eMeHIxO2KFMW+OYCKCj5EOiZNsfOp87E4rHStKPI+pUj3qIwNoe+YqttH6ptGvSAgXiEvX7yU2FGPuRMXFXjfBMRRuGak+5vhRj9ZbEJRDM6MLcIcAMjqN9UmSfstwtKNSzEoWgch9C7MM8y7oh98Di4Rq1K9vvEkJho/qbRNlMANg+fs6+2ZSQGfV2U7DYaQ8kPpeYnnpIqOFbmt4nqSE4cI5TJL7cNP/TTojcGa6lureedBFSgWRTaRu9rNWUw78zBKnZVcvHXco8f5nvxvZovpBBJmyRpp1c51jJwnEICWGuQhe2IZMuMhSOOSxVCY59HBNYyMMY+KH6e76Nz11orGq9tHgORoxyZJBBzUMtU0rQhOLMJX5gzsj6CmBI8SSaS6C2cMHA4HrNcSJT+OI47DEcfDiKaRSuEEYL/f4/LyUlKAHQ7ouw5N2wii5ZLhaubZLdvzNKNpRIF53D+iaVqp/K1jGfOE6fEAnmesEuP5kxs5caGEJ0+fYJpnjNOMhoD9+Ii23YBnlmD3eUbk4pJJReobiC+bzLVpW6z6XhlMOY60vdO1UocgtS14HJx5dW2LY5Y6Cf1KqurKuSt8YQ0dyiY6s+A+xEhEjFAJIlphx6hknPAkFY68v3K7IvDxirIU6drXDyijJiWtbgkxQT+OUwgoU+33G4m9fIruQ/UAKwKifbs12i07YcCQB6P4LG3KW00irSsj7+/2O+wfd7i5vsY4jvj4W9+QAnb7HY6jKBqTFSuDnt4xO7GqFCOIkOC022DJRbQ7u8FPTLSLa4Enst7mcxsnGZ6x74FInfTNoW9fi4J1Nt9pljkzM3IzYbobsTvscXV1j6fPnuPy6go3l9d42O8wHo/oVitRJs1yRKXFiKQ8Z4nHyrX7kf1RDCqAJNtDIY28zuOM18s5Ga2e+4I7LfQCB2lBVxO/KILacbsMkx3aZ8cQYe4PhSfJ7X5VG+fcIONeznibeS8mqn3HDDTm6kmQ011K5AUk5zwjI1cdu8hzhp7VCpNmOMzisrp0ZFrCfCkYxzGfX+/aBchlHUA9EstJ4dIFSqFQPuvHpfLA1jcbParR6Oy1eMhj3Bbwi7h2dt5nmo3Nf27fsL5OLzv5ljnJQGsegVOYE73VvMn5gj1c9kqcQ/zsblGRnhOE7vK5Pk9HQAg1YVgKrRLVe1JgbsjGKBZ7aJwBq81H3tvvdnjc7cQbAuSW6VljM/xEP7MU/VsuEAOuHFBcZLPoJyw1KXvVFAN5P/le4yWSZONNKPi0uKIbsbAI4SV2WsI+pvj+kkiGX3SfsfV98kTh3zYoAmk9jkC14nrH8cJc+eq+q/EtrSl+O3s2qOoyJSylk5+K7sUuO7igzxKP0bQN3OjF6m3B0DVU/FOlRGpriNHbvICkreK6bKcPftJgdMv5YTUpJ2xekb4avLnUicLRNOKNJNFEbYDgt7/ePkYDLeZpBrPGS0xlUGLxn8pn167FCtm2LUSLM4BMRVihBrthQjNbBeMGTS/uUKOeTrTrDQ7TjJQIq+0W4zhhHGc0jWyqPAnw85zRqgIyZ8Y0y1ESqMfhOIJ1jOKeNSqgGPNwwN39Pcb2ixIcTi26tsVmLVrlul8BkNOKVd9JtWRmNLZAnL0KetKo/QnqR0wqQKhWbLIAUZJKzJormTJLjmVFRuKM4+GA/uKqyBOZ3TJrwri4xxRB3faInba4r6UzyyCkUSBiiBvDbpTnKvll8TMr4Y/ZebgMpBCdBfMmayRaniFKVOmvWIIqahgIuLF228wmnpVxRvvUmXko4SaU+AAbo7HvkgnNfFpJmEjOngf96vIKd3e32D084Hg4SLD38YBhPKgVQl18wGX9uMybF/M2IlZfMruyNMFVzgDqQmBQVs5IjvZedcM+hKOt4n516qddcM2Ceo3g29xKpwSA54wpy35pW/HVH8cRu90eT548xZOnN7i4vAT1Pe4eHrBZb2D53hxXShRw+Jr9dIyr4cf+SdGf0TYt5jm4KaCgoY3Vx7ygprFp23cxA5ICqzo8rN4/Y06NvM23CheYl8skK4JbHB0nThd5+SYt+zj5GyWwoIBziNMIfTsOGAbHeTvwJGXiql/heNirf/Lsp8++x6qZGv0qbXn8lrnPKs3NDDVc2Slfkfk+lxOST7PQFypuNf4Ml7HY0tl4T6lKDUPbf64PhvlUY1gKNou1qZ4Nz1ibVfYb75tLIwE1fCxxTGFbWd9VtjWqm/HEbgs8j8kJFtRFvhufovp3o13LeRcFj/173B/nLrPcOs6EeVfuu8v3jN6FMSxRqDoxtOfMSl7NsyanqbF+Ga9evEDKDGqUvlOxUlu8hgjQNV5yaLQaf8WbayWoGi0pDJznikdBeVepF1NxGQ68xJCjWjulURzWuya7smmit4HDein0Gt00JUMVl+KoLeNIFE96ACSSDKBsWUPZ+y6lD8ped5mp6lth4pvf+K9OITM4BQpV7e/l+lvfwSFR4cPJlFbGlOeQBEWP5hUHzKUNKl8mSpgmqQxu6+JzA05cmGKZB1NEosFfEqdImvikygmaBkbzE4CGLVWz8PS2ld9nzkjD4J4+b3O9taLx5s2daFRWXThgMqOetJ1cAIwmEUY9BbHAShMQJbZi0tMR8jbKd/FbjPcBYBxHj/do29YzmSRIQTHW70SE4ZjQdi2mWXK429i9DzAyjziOI4aL5yDSglbmw8cN0MmOX/UrsLpzWPrc1IhiQ7DiKQRq5Vg/s7g/zdPslg0hSuKvCRK3r8zZMywIUovCdNg94ur5czEuqPXBA8IJoIjtgfSUzW6bGqcCUxACIkP0n2ppp3QT2rNnC1cIPMY3thJY259LJmgNovzutE0fZtTPU3wwtCF9B0FBfTudcIeBx+rkkXm5tYqVCCvMzUbVWrBUShjHEa9evsTl9gKZGZ9+8rHEYRwOOB73GI9HjPOEOU+IudSrDwp4DnCu17NIF4VFBmJt8zbkAZUj3RPBpBblSg/xpCgqE1GSsCNw3Y+xb19E9X11y5bTV4RH9E8WuEBSOx/2j/h0OGIYDrg5HOV04/oa9/cPWG3CqZ6ub8SZ5MwI4CwGiRxxw9Y/zJsi/J2pogKYf+TF/gk80paLl8t1TpI5aXhxM+yLaiguQJ+TsshhHTuuZ/853eqz9p/B1+a7zLJmCi2Fd6q+K9ZA7iZGROi6Dof9TrK55FK9nhqla1Vdgppu+BoEPMyQJBmVvLLA8d/QVVnXi+urNFxcyARpyRNgnGmo7NmIRGFRI65x9Zy3EH4MP0Qa5gaYxWNGT2JDugaxDaOR+qc8voQ5lTUp7k5nh1S9F8HnsGCq7tcOl+HZap41jV4M8eSqTwpJ8UoaWBpu4hn4cqy+Ltq3BIKHjlOYCBWscw8jZ4RKtxJhHCbc34os5camnCXToGWb8rXRmUb66+Mpa19PiKqPMS00Ga0wouWCsLpwOY4YsM0teEHwbHoRXqjpYyEckVfUc/FshS5PRlwk/612EbZ1WXA2H5588PobNjrjU2745NK3z6ec/zqe22IQwXSBCIelrlTDvMCtGALMQMohflgSqDSJ1DhNWpcOrsR6GwHmJvcuryiHVwbn8LdtW7SU0ENkmSY17qWUGsk4lSpZXDx0CMA0TTgMA47HoweXf7vrrRWN/eODf56z+H1JHvxGAknVugsAXdchkaTTmjXYu9EiX6wA4iwnHeJape1RAySJmzgcDzAr8qx+7EwS/d81hBkSdzGPUgCqaRrNJKVVypsWRIS+7wAQ5ibhONS7UjIJMFr0uLy4wPPp63jZfjdss3tmJpgswsiznGwwS62QpJs1swqhIHCTkHJGSg2mecIwDtis1yGCvyCeHEeRMzLWjFRIwHG/L3HPenZbClQBvq2CNSvO0G3LhXv6tTh5LkwzUnLbOCZwLBiHvx8Fsbg3z2ISV89IV1wJpEb0XUkovL4Q2sDJTvrWORuBisyeFC6MyHQCcUZNMBDm0TZJjs5TwuFwwJvXb3B1eYn9boeHe0nVejjuMRz2GAfZhOqR6eOUy/wlAwEPcyzDtYGUeUdJILqY2WOWAvYczCOpJphbzZLxljUoi/82fTM8oI2idd+sR/WiZ5DU5eAZYMaUMzhPePP6FQ6HAw6HA26ePsH1zQ0eHx7R9h3YLD4gOS73+BYK653EOGEb+AwcGGL88OkspnoKlfN47nQ/7qsFLsW2lvsT1f3CjKOiTQv8iAyfbZ3854hhp31HNyobyzLrk89nSR8WYy/nVsuLz9AWGXevKW4ZLEYfrZ/k01rQqLgXbH5E0re4zto71ghX8z7Xpl2ftRblASp7JuxB5jDHivFzFYhf+qC6SYYbmWI/9mRorh4o1VM9Ge4Z+l7Nr8hLztsqgTb04XgeXpf1Li5jcXw1zKl2mzX0FVJQ6LnDsjCLz+Il5rpUTV07sFIF8X50RYswj/WaIpxNIHQbN5UTeDGiSlszi5wR92vsWDwLorttUV5IXW0fdncYDkfJgKenF7MKnY5rMHhQ4RMRmHEdEPozw1mYt90nhPiFc/Qc5K5S5bEzO8R5JsME9ojn1ZKSAZi9mHOFBKZsAZWbVuZw6n+2b10jbdsgRBClMs8FhzhnSdGLBf7EjeSbIvQTNpt444T1qZQxOmmyMmJFmDuE5B7n7EXyLKOlJTZJXiuO3CjvRawRsrSqzM2BV5hBvtGSEkyl5p393rYt2tRgpacWpLJ10qyxieAnua5oNPJb1zXoVw2mTStV79/iemtF48tf+hDH4xFySnDUQnh6tEKWC1qoSUqNKBmt+M82Whk26SYFSoD1rCcNTUrouk4n0mIYpQCe/W7ptTabDfrVCpwzDocjjsejHulA0nlqkZfUSNaq1XqFcZyQkTFOdjQEEAmwpXLijDYRvtK/xOv0PTDXYROw3YILBkiEfYKctjRtg0lrd/R9B2rUt44S2rbzooGgBGaZpwUAZ2apEA4hQjNnif9orQbHHsySFcsEb4MzL5H8zJoZHamZVyEhTqAU98k3Lfu70V+79FEOmc8xPyNw5Z3wNjmZLu1RYYzOILDwa3YmWbicC0Xn+vaJ1X8YJTvVEnZxvHOOLlS2CWVk9w8P2D0+4mK7xevXr7Hb7TAdjxpftBdFdJZTDHMfJE3RbMNy26lZSxSa5P8icIsCu5pNholFqZcEEBQBF4ieHekmhse9CGjtFA/KnHC2b98Ly74rRid9WhFOm7EvZmDkOWs9DkrIo+yraRwxTnI8+/T5czw8PKDtendNdCkCQrAR6zHo/E+xzyQskUYsM1LcIxH/Is44ngR8K26J5Sg/ui6cYdNLGe3Mc0G5oMLqT/aYvx+d2covjFNXJAuqZUCTR9IirW0Ns2IICD1y6PuEeZZxOB5pAwTCdrPFS8UrzhnjNNd9kEPAb8p+Dq5Lur+T5njvuviG0pZATwz1bY0X+WHCW2HcKO9G6Ba6ViBlCqHxizIJ1nlzNTqnqW4cCsJIvKgeF4DThBlxAjbmCHNe4m6MYaonv1yv0ic53HIcDdmJTpi3NRK3GYq7fTVFJ2vRKPHZvCRuyHN7E4t5262kHVm8RmWxt3kE+lhRWC5rQIRSv6ueRlFeiP2kvLjaariDfnv9+hVs15pL6DxP4eSv2kY+eVc4lMAxFZdiiovowDE6YnGEmsHJN0K928WdyPpa7G9mx3ObmykJkY95bRrjNTqZZLU4tD/33ihIgIiIlgBEug4qjCthVMHI1tUoX2oIzK0K2ah4wefR1OUP/hazuNsrTNzIYMliFvOO/NvcjmSL6553GYbdIyZnqZHhETr6Ls+lpkpmBrIopR6c7jwdIveqoiBu/A1ynjHOI9qmcZnYuBTnLFlQs3xvwWjQqOdPRgpATqZktB26NqFNhG7VY7te422ut1Y0rvsZYwLAGVj3AZ9llqZ0zFqApmlWugYlgDyrb3ZKCd260xY6yQNMpmgk5Dwi9WKxatqVAHmetfYBgHxEv1lhbFuMK0HweZqx2WwK8GG1NkZ02w6cZzSpRasB5pNW35SsURMuOsbAWQNECyLHvQtG8WdjKebSNA1mVTTmmZGaVhUQAqWEcZR0vU1KyKQ1RjijaxPyMKFvZfHbpgXNGTnJInMmTMMAzBMoNYqkBK+YTQZ7SYfrjMu5jTLdOibImQbCvJTEO5F14hoIn98DaqtdSINYv2ybNAgORsSNCAb+6uQm0EvZx5Ly13PFG3MrT4WTCSO+hbPVLjSFmFdKGpdc55HhGayoSWgbWfPb21uMw4S+XeHTT15iHI8YjntM4x6Hw1GYRpZwKRAprGLGBw7wK6KECTCF8BNiutCKKkZgB1hXrv8VAbdnlelysdLJo1Sec6mMwVaUKUoKn9F3HB9bM/5kYRCxH3bcMaElI5PSCmTway3GmTOePn+Gx8c9+q7XwDU93YNaETWNbtd2oESYxklPlBagY+1Lx525toInZQi0hDlsH9hcImRrHKsEquqXsD6I+8IhGhjWZ71b8CX+5eo3w/Ny13DZxF4XvPROQp1G9LRV+KIu+7bfGAuYBJQikgKlWbOa5DmDtZ5G2zTiLoAavU5wDWVJCELz3RUHJojZmMlRPlILWVsAmvHO0wWH9XYSejLPev4u94XLAvihyqf15fKOva970NZ7AWlUKxsAXq9MbK9sryVN9TkZDIysLOa5mKbu69JOsv1qfwONV6nTabG52Jk/ehyP43kGlnUzqjkVIQO2yyJKuCK1IPF1PyoQk7nCahwRoxKk7V2jwWXrK73I8FMHT4wCdmUJ9l3bc/RV/kUE5HnE/f29t2F0bpon2AJynCCM3gCVgGz3K+JWziYLHbFPZedTWPyic8WThTO0JRg+HK7BCk9Ov1W28MBo9qQAIBLB1ZSjBIBTBX5TQFw5IEJVt0P/jZ4IjsNESrsbMeSCXbnKIKnNIVV0y17kOMv6o7dPisvQE6s8hzTqi1ej8cDWwXiowTLIMDmXpEqCpOzLKadZJAZPAtrESGCpXwV4gpQEQpMILUTRaNWgn9oWKTUYphHUEj788EN88vHHmMcRBHLF90gBY+x0gjVjqJ50mKdSkxo0TYN1SrjsV57E6W2ut1Y0Vj2w7oWJW/ESOb4Rv8WcJctTalYgiJ9XnoWFjdMojJ8zEq1c44pxGbMqEm2bkFKPVoOnLO800GOaJ3CWjFKJJvTrBumih0TjS9pbC7rNmSWrExGYZ3R9I1qdRuvnppEiJgCIG3RtwvV6hfXLVzh2z1yIdwsDw5GubVpH2P0kmbZWfQ9AEGfmGaMWZBnHAa1mFkASxJ0FKzBmCYqnDHQQWEwpefaueRxhBdHKppK0ocnROVysLJWL8BPe1P1eiKKhmJGjWF9ANklhRM6obeMpUJzWWRcMd/2U38IPekX/Soof9JEqjwyFvu15nUfFX5TgBxJXM7CKegaCae9yEBCDtS41okBnAHevX2McRCn+9JNPMU4DxuGgisYB0zQtB1n37dQdhduHCXql1SofJhwJK7pYAcRuFauO+ZcXXhT6VmSO7gmkTIGU00Srlvmq+pDO9O3Q428zb5diyB8HsjInGXnOM3gCDmDw7RuhM2C88867uLu7x2q1dqZshjOxXTLGaZSUgcvFDxJJ7d5SW/4N5CUzSz3vJW8q7Sguhf1z7oo46zAPQk/ZYwVsQffzhuN4T2ogLMa4nBsArwUBpmq5ir96oc32LjlTsvZqd5+zczaBhBmr1VpcAjSVYp5KWsZykheVgtNx14Qh4pwBrOwDkVrq97z9gA8C81CrgWRuDHYl6Rx4rZ2ITxza9U+Mek6LdfTfwtZZkMyTvt+/avAv/Pan+D/9pdf4+H4+Ly9p42ZUWKYhNVJooKtwLMAt4s+S35zAw+fLVge0nmP87A8HHFyAWsZo9JqK5d+Z1BkghfE7udc+7L6n0o2PG2lewNFoQc6z8H4bUzBw2Z9qfzMjE3t85W6/x3A8iteD14Hgeg6BP/nleyjcQnGvcTy2kwKCpmZWXuIuUUosuZxjOt0Olqd6v5k3RnjEjHnKN4hUO9Fm7ZSOuNQIcaXElUZe9F/WoIyZyz7WxZNTimKQq1JQk4yXNB26ncClRJiNKkRrHNVrVuN22YwmH0hBZlMy1KGvQliG1ACxE2Uue79mewBYDX5Say4WmJZ5lbExA/1qhYdGje9E4Glyr6DUiqFmJsKYGGnVoFn1yIkwDQweZvy9b3xTYpcndePWfS0FVcldsQzeUtOlYIJ4LslvLREe2g7b7QaXl1d4m+utFY31uhbU5b8E0bxmpNRjni0TFKFpCHNiMIsCkFcJ4zCi1eq/Uik7+A6ilZLs6m6VQF5lWY4sJRhlnkesuhaiwSZXRCTZ1YzUaByEZiGw8RI0eNuszJYBiKTUAIOx3a7RvzziCD4heLXwYJsF6PsOjw+P6LQOSCJl4vOIaRAXmtVmhXmagJyRIbmSkRmHxx3ScQDmGRavBsimzGBwZkzDiG61qQj00llChlTuOP11In/KKgiLCRoHXFrO6fSZWlgq4xYGEDhvsGAsx1vdC5swygbxZ3Nxie+6WE0GlzNTWvbrnDww/QghAuy4trHAbwCvXr7CeJTA/vv7O4zjgGkaMAwHDMeDBvIRKp8NWFuBskXpOMI8WNXK45GCFi7gorEPuhDfuLrZhQqzDEX1EprFrByFVwJQHFMxs8AEuQLshQW/UiIp3Ct9F+bB5XSLAbYK5YmAPCNPwMAj7u5u/WTqyc1TPO522GwvADDmYEE1WJTYmDIPVqWuIvjWLxdfVGnLROg4l7AkKHssgiYC6SzzWlyOfzV4yzsRfIvGIuM/EQDD4+f23bm+bWXUO3rRN/m7MQD6ZFgVrdDWyFyeGKtVX1IvMpA13zujnCIvYxriBIIs47yhwtNqYufnvbzsNKcIHIUAhalXNDW2eSaB2GIsi87PrLc/SlTznTAA36IKr9/9A1f4rd+xwe/+gQk/9lduYQ+drHfEzzgvFPwI5KrGtQVJqnhJpBX6/YSmn+yNc1eNawWXdN8GmhNpV2x5KevFfVkxTh3/Ge55Zg2L0knayTRO6FR+8X55MWfnoSpqZoBagd7t3Z2e4KVA7sspeqTnES6VpTwoXQU9lI75KW+4fJ8UcwTbKYEKtZbMRm5Z4bwCmWqfG51cGsoArQtiEzsdPxbjN/pQOte+T94zdDBlsfTNZtlPDZqGMM0GPpEhcyMnHA3JmW25Cozd6LAYs3RVvCTM3QipKYwgKEGxWdsxxZ0q7sUiMJlb9pEnHweh1PAhiAfCjtZIbYeU5eSCKSE1Urh6zhmZRHkewPi+3/S9+Mpv+gcwNoQX3/oEP////qs47Hea6S+L+1UWGbSlELuh42SGhiGIuySrm93MLBmnkPEwj2jnI9bTEW9zvX3BvgaglGFH4uI9pL6GWY6gRbHVnc4zmmRptwgNGNQRKInm1DSsirYRC5I+KCPZpPVkorHjJYj2BkixM2FUpH5pstiWMjElExxkMfMox55E0nbTNo5ETWPKUz5BnJilotArCsJJwmG/w+sXL7BarTBNg8SE7AdgHLHuW/DuiOP+iMySWWAeRRu9ffUavDsgT5Nb0WwDWb2B4+GI7hLn6I5987+2CTncdqFIYVxQfMEYIlcNV+SVvPjkz3CJ5SpCSIHWOUZTC6elb6IlvKkm5vqoET0LfjZGbQMSGVsFcN2wcXrVvEP7vtxEomiA8PrVa+wf98hTxt39HeZpxDQdMQ5HjJMEfccYpYoZnuuzEmRqGFV01H5fALAoSyZtKmOzkwdb53N9hzkvT4WkDcBxicKROgIOcWF6MT2iMSV5JVrN6r7L2tk8yQUoAsTircGSs9Ydub+7k3XNwPPnz/Cw22G92cJtR1yseB7ET/D5cAVzA19xIfO+XSlZzhtuDPY5FnQry3S6hU6uKGDG5T33atyny2rdy75p8V78G1h9eE6+xViT084pygdF0ATXfYc9XLmUKNMHRBho21aVRsY8Zy/ct0zMYLBeztt6N/dV4yAx3bdfKiwg4tbC8FHclhbTRr2TDebx3fgeVe9VU6muajsv6RpMSKppwDm8+tpXxDf6Rz5a48f+yu1ZGns6pzLXCgaxb7/H/q+1wJ9x8lDP2wTFWtH3eYSrxtdymlVSRaOC+XLfLWm63CynbLScoH+seVhcjwrPbR4sY5vzjJW7hJ/ha0bLQpcpCbA4Zzzc34egaGk7Wo0rIxRQ6PmZOTh8YveeZaBw6tC4v+0pVUFBwVd6jkXf2iaF1K5OL3QiQnetroOecFQ91lek1xUvMYWnspJyodeGv863zEgtCtZqtUbHGcfjEfMsbvYNafprYmRWxQQLHgo9TaXSt8d8EMq8dWxSQi/hZGEU9nVM1pIqk8s0vi8UUJKFL6ssXWjpzMA30/t4PmVglnpxeZ5xHAZ/eUJGbhvwusf7H34JN+++iwMxVusL7H7xW/hbf/1vQNL/CtExt+JMsyRlsoRNDLETt4SZElLbIK06UNeiX68wM2O9bvD86TWICB999BHe5nprRaMhlAh+DQQ3X2/RFhltKkd5rMc6JjAb4Futhz7Ps/i7AfCgJj0vSurXJgvNkHSwRZCTVLb2nrjLmHXWkMKDXnShmyb5b1b0hFSYtLRmmS3wRv2YFQHcKm24r3tZ6AKB5xkff+Ob2PQd2qbB7es3wDD5TiONLs9ZUuM2eqScOaNhRmLGTNAMV6TCjsB7OByQWCofmwFBBmWfy6a0TRiZ5ymanyGQMCZEjmi2LjAi9DlXFLJK7nU9kbJXw1mgMRMZkykKNtLCmJxhVMyZi5ClY/QjSCqBx2mRjsSOMU+gEk4SYja8hgRf7m9vcffmDcCE+7sHTPOAPIuiMU1H9190AmWj1sYqtwsuROtcp/aoM8gzZuvCjlmFJlHIC3JwYGSnq12Ipqag/UypIbBL69sZfOHIpsxVflgyccSTF1qkhimCRRij+1lkgNXdEBl5BmYwHh8ekegFuq7FerPFNBzR9CvHKedPgRFZ85XhzEBfwYXj6Gv2QfXfahUMFFwervqp2lGYLfbU0v2mgnkYj28laOY0nwhV4Dvbp8GcIyssjVaYYoA4mXfYixrfsMRob8Lxx/a8uDn0q1WoezSrm2hh7ksi5fFkpSkwA23TYDgO0Quk0I0w4KV7msNzSdfiO96OQkb5jmL+2fmGhsLvfOYTqrGc4kiheaXFMm8iwne/0+HdS/GNfu+qw1ff6fALnw4nI+FzfQW8Wq530QkKhkRcs9NqM0JEOl39JTiu+Q2gxr2oRVGBOVBqGQmvpUjyv+3lJx92UmZTjHO05yIsmBFSOYV5C55bjEbbmsgUcaTcKugbjJEAhmnC7vGx4s+MiIMcYGKfA01dIAUpza1xjRxmxavAmgmEipeGKPb1jKe5UcheIEg9D5boLukjxFQIo4dtUhOwxUAb+7YTlpqPyfzKnvPijhyeZZFJExEmTcjTd50Uyx0GOA8AIdYb883guBmJXuGhJV7EwKWnGo0RwlOO4WFa8fZio5dzLIW5nXzoiQMRhcrfjOM4YD8MmA8jSOXneZrkNCNnMCXMCcjDiJ/56Z/BYWYMBPzcz/wsXv6dX8JxnDCzel0kEmUlEbhvQMRYrSRL6/E44L333sV3fvWreP7FD/DF7/gOPH//Xay3G1AjLuTbTY+uKfj9NtdbKxqeOosIbJHt2cqTFw3J3JVSSgrKqWi+tlSkGqOfCpDXxSgR+XV+/OpYh5NXKYxl2AnF3cr64cA0kiJ4A8k+ZYGmhnzTNEJEeiWIVIh7kFnk94BMDTWYjwPu7x9AOWM6DkhKnY0mE0mwYwJAnMAkvm6YWd2p5Ogrz7k6LdntdjLmkBOxsnZFQoKI7uWKPt8R390nzwCEMicj0oU5k7cR5U9vcbF/T/pGrbiZFaXAsQh6S2bO4Z0wVR+vCSkGAQ+CJVQxJrWbThmoEQSC5uZX/D3s9vjmN76JVb/C3e2txhFNmOYR4zhg1uBAiWtYAPdz9h9/5rekBLUQ8+oRtswvylRYn12a18pSVtazIJMCZH0tYE7hA9drUeQGKj9QECgQYa77lU7fdzw2fhL68EBtLcAnGmPGnAGaRtw/3KP5tMG777+P1LTANImVXEm3ssgFo5Z/c6AFVZ96c4lzZ/dS2HvOwxbzrGd52iaXYfmDVd/V/o4d1jTIxn1ujapOgRDQWVCVFt+rQS6biGh20sm5q9AqkZEI1DS42F7g7u62yiZoVCjnIpgth1EHLctz4zy50MsBkeJ8XDihIjzGeUvj5H+Yyzul82L5tf6rc0vbrp8BA/tUhOxy0+WYQM/rGKLSh33+2le2AIB/57/6d/CHftsfwte+sjmraBS6pnPQMYQhf8bJCVX9WXYhc/NJptjGviLMF4OPyT8q0XjZd5hrFacU2q14MJYfIn0rxoCY+nfJv+vXyymr47yNM5FWZy7WerdMe98FCAR4Yhki4LDfY5xntFQMtMyQQnAc2lJ8jvIG6y2fuxsPCn33oGnSas6uFJixJ+xHzZbkbZksBghfsH2kJNThHxSngixhL/jeDUDgsFrO6+20IBgXEONQlJb7PMt8bRLFKCrzzMzAPOFwmLFer3FxsQUlkkypYQ0pq/cKiiwQYR7xgXTOcbf7GNnmGxQhDvMOf5d4HnGQOSjWrPWFOJd0znpStB5v8WrUZDO6DpkyMmWggReDnocB//Xf/Gn89M/9HMYMkWimAf22Q2pW2F5c4Ds++k589F3fhXfeexfXz54ipYTr62uklHD75g2+88tfxmp7gWa9NlIgyk3OGIYjHu7vcDiM6Ps+KN6ff721oiHHh0kCsZsGOQOsEVWSnmtGyV6jIjVnJGoBKgHNeWYYuW+SpiDTthjwI6Os9TeMw4nvIINSg75pwSyF+7rOCoqkSgtkDhH89pkEIe27n8hoewDwnfg1/G3+UrVHDPnpTEpMArDqOwypAZoWl5drvHrxEr7dFIkkW0ECIyFrYjs53ZPfkxIWAoHstAiMeZxgvzDqwE9SBED4Xi9ajeDGHmzbVllDbKLKlYlEqLUxRSHJ9ybkBhPE6rPYqNAiQNEzsjANtlGAI4EPBBbh2YrZ6LhNcancUslwVeGuhbXshMUIrWW0MmpKJHE+qZG0cNM04dd/7dcAEO7ubjVzWsY8DZj1JMNhgEBP/buzIh95YX0FppF7skO8wICWs3fNLGJBgZcp5JUCcGp2L7Bc/F327XjCS7wJGKUvGLGs4kXMymWpH23eZ/o2JuXWUxIaQiAgAzPLXri/u0NqEt7/4AMMwwFNc+H7VZi7MYaa8J8EXet4i/ApPybDSZQ0sNEi6lfA1zgHT7hwihRYLsk5WBhtSUDJxILToG+nRTb2aAn2eRfhJ2pDFa3QeZQA8SpSQudd2G095nqOjr1Bwzc8TylhvV7j9s0bjOOI1TprNkFGkwrcwIxUjyAMRWZorrVeCFXhbrZiMmKlfRv6C8x1D7ogU9abwncE+shc1lPof9jfkVnE9bEnHL4BdlSvt48T7OvksNa2GcInvvbRGreHO/yRP/9H8Pt/6Pfjax9t8B/+1duq4wrP2eZkfRvM2Afge1X3d1WuydYv4Ku1HXGtNuqIz76l9K7pHpdnFS42JqPvcTJlXQIfcmzEwkodaWW9x8q46/1tc5C+y6yNHxUXb3WzjnBRWhNlhcjHTDB9eLhXPCp1D1TwKesQtZ+KF8YxKT+jVGAaThFMCDcFPCzfIpOewo8VlvpbpINmaa8Ub69a54MTuauRGN626yQJjyZRkZhY8fqYs8QUTMOAYRgwmVE19AkCkK1vMWQ7TWEpZud02IKuWQ3dLP3t93tstxe42F6AmTEcjwpPU8IkMZWfKy0UZ+dDKB4ytrACqwxoUHhMllHB2pYT9h5UYWdf2GR7XL8bjWGekQUM2K5WOBwOeN7s8OtPLvDB++9jtVrhww8/1GrhE4ZhwIsXLzEcB6SmxXq9wWq9xfPnz7HarnH9zjWunt7g6dOnWG+3aLoWM5dMUiCNcUkJq+fXeJhG7Pb3WGVJrGLYNU2SjOlqvQWxJGXa3e/wNtdbKxogOZoCZFEln734krWJwDzBcjZLXIZ8nuaxYrwSn2GR++wbr++L7y5UIGc/4TClwNyf5Dk5vciuZMijVjSsLLsrFc5zCU0jCpCcpshmmaaMDnrPBAuuWam4gslnOZ0Aus0GTSJ0XY92vRKFQjVPMIvvIckpim9QG2NKbqVuOQFJ00ySEOh5GECQozHiQjyNgRcLYKDOhUNV4zZmYgTVtfSQ75ZVoiHmUoU8MIaKMSp8YWkKl8cXwfJSjdneA4VMGexEOoXX5adC+H3fowi+RHBctJgNyXKhGaxcAEsA5ULPdeMLzkr+7a5JQGZ849e+jjyJ61qeRoBnME+Y81gJV+fdyiKAlHkbpTn3uylrxTzlAgYvHncmEhl2/N04NcexRYSr+3af3LgyJinYK0FYcgGuSFjeA1EqJxrsJb68gG5UQEotGCBstoC2hemxPp+I9dQx4/7uHm3X4fnzdzAc9ug324JXzhRcnZN/E7mlKOs+TNBUuREyAe+LcIayhoFfU1nC0obTmdPLICaGxKJgAwU9aiuvzaHApurb8SFYSUMb4cFiDHAGZ1ikYzdGWF2F3pnLHBECLZVL64kGJbSMIzG7MrpZb8Dqi8x5AvMM4qzM21I9BvezsFcFzpWTJUQpYcf7SJ8cBot5x/Ut5LiekOFsASOXAVERQFyAD8jj8LTf4x6t6NqClPq8Ci2sTp8AfPSswwc3Hf6Dn/6/4364x5/4uT+B3/dDvw8fPevwq68Gh3mkHwSjg4bH7H2zwqdModAUihOp5mHCeTAaUBwnF5qs83GXqwDzsKywm95nWIu4BrT4HtfA20cQ8mydKoQyylRaqllaWRjbJ2KgzEgEzE5iAm0xfkJG77PwXG1q//CoSk05GRIhOeSfp3rqhmEpxj+EkdtJxTJmT77bftIWKyugdaaTzOF1sNcJg+GMwV5d400wbtoG6/Uam/UGXSsB0pQsZ2QKiikD3ChtYmAr8UU5A8NxwG6/EzdIW89EACdXVIvClcpaOrzkC7M0KK52CfvdDuv1GtvNFnmaXXYV+pQAmnXetsEKfMp+NqN0KRdJylcYZgxhmABlrExJmMeDFIIQTnK48DXOVtCXwNSCIPOeU4vL6xs83L/B+9/5JfwP/8f/JJ48e4KcLQ5lxna7Fb6LUsHb4uAIcgox51mUBIWvnewzCy63TYtpnpAZEl+cM5oEDI8PyPOMYRjQti36vgdRws32Gl3XoWVg/fTvc9Ypq4HhViAicVfKhEmPvOd5EpcqQtlA+m6JlSg5iC0DSWYBRtM0VXCUHxGFiuPTMApzScmDuKELazU67F37HMdsBGUcRx+LEA2p92Gby8fO8E3KxiXUIi5fE9quVWTTY68mYR7lDetgmUpUNrVuH2bMqTBJ2+QAYRwGgV9TCLtbxkyBw0JAiETahBbfE1QRc4txqIJ3Y+aJuFd8bGVvMqmVAPFH9vtRGIkEwihbZTvVdnw+i76r6QUGbAzQNraMTW5mpaJEgYEDTixBImgyGA01IBBevXqFN69egwBM44REkilsmgbMWfL/uzUkDMyFN8Xbwr6NnRLMWmxZkKIyVkuH8XthPdGmd94/MsIgwjownCKBxc5O+9YJFSEuOl5Q6b/w89CdnUYAFjBe4kHK2BnsPvQVkpExELGgEcyAwZhnwjAccXd7i67tcHF5qXnSkx2iwYQSGxRpXJQP1xkya5dh/mGuBc/lQ1H0ylxjHQ7vLyItA1EHrzAi4rVN3WFINZ6HZSpbiQtztHkxiqXQx0WOboGkBSZe2q42bbjtLwBxyf0pSlwJxsRq9nG6y1itVyoMiG9xnrPu24DbNrYgCzm90r6bxqy28iApAvm4bM2ssbi8izmexEtwgK1TY19UE20K/KiGSWwrwjWOLcK8GLMCPV+OV+9/7SsbAMCP/+yP+9/f90O/D1/7aINfezUIzMN8Knp9ru/F77WrI5/gCarny7zNRliljZXtFWoUUdW2bPNi7Y3rXSie/lUearTfFCajE4mp6ruig/rBT0up+uVkvf2EJMyTtSp46BKOs8rvHID+riikeZ6x2+2kP/WyzTkvUohGs0jouwK80k4ArpTrNNwgVLVmC6O/GT03+q0wsVOZyE9Y3y2nflqyMTNW6pq0Xq1BTSMxtSTeJLOlSc0Z86xtE6nFXD1OiCSj5jx7UeWcMw77Ax4eHzBNM1oiDYwui27yBpj95FwGR857Z2Y0ScoljMMI9ISLyys8PNxjmqWcQLXRUSFNfR+AZ+tiXVtFdLbUve6ytqCJ1SYu2GWGT4ZlRy1pbkFJDOAsRRzBJFlYE/DNfI0ZwK/86q8CRHjnnXewvbwEAEyqeLx6/RqTpr09HA44Ho9gZrzzzjt4/vw5xnHEer3G5eWlBIBTQmaRyQ+HA/b7PdbrtcvUg8qeIMIwjtheXAAAbu/uXPGI8vznXb+hGI0YT2H/WUVrU0RE0VCCyey5fltN/2qF++w5i8vous7vW05hUzBMUZm1SqL9xszuI+ZHWGFzRNcFFyz0ihU+TeFxy0Hg7LZ/TRkBipAgnxlN16JpEuZpwna7xW0iTKQW55REUFIXENvk3ruNMUsuA84MtvTMqh3kOaPxlYq2/HKdYyrFzWmxocJuYJgl1BQD20w1Y60EomyuaJ/B0JToenYK+82ERxRYWl9LIhtfrPo2JqPDW7pVGReSaqwww45DAUSuhDizYjlla1LCeDzi1371V4VB5gyijDlP6lOeYS58JwMLc7F84bWysZibC1W8aGcpwi2+B+LqXYZ5W0E6sY6YgPT/W98lpmXhg0vld1ZGawhRguogRJi5rFHVd67a5qUrir3FJsgXhsmcMY0jDocD7m5v0a9WGKcZN9c3YnBQxbFW4mr0N0YK29eMMH1zreDq3VpQCrRhcT/2sey72orLpQ2PxHejZRq6DhU4Ue+zurUwbxPmcHpFnrjEwM+6imhEihMLVyLFv5ilpmtbNJS8BpPReIM5FVQ6pS2E4n7HcrLuSuAyMLYAp3KZi7Q9Pu5fCf5uEVUjipOfjttTvOhjud28SxPsXIgpcMRnvFOGLP/+yFc2eBwe8Wd/4c8CAP7ML/wZPA6P+NpXNviP/+vbBZ7TspHPpannYB4vEZQKfsZ5fxae2zjoRBsvg6j3GJzfxCGz0xb5kUNzp32HTlyJq+dttKWmCXQyb+ONeRKhGO6qF7CNvEVXfooSwBiGEeM4ubuf9CaGSemDHJ5x3CZ82kkiKMBckbbQEdK5UjCc1LjmY3PNupxMiVeIgs4QwnglSbr9rulw/eQa6+3aU7/P84xpHIuxrjF5TF1eGcjIGIZBixpLqYKu66XgmxZ/HkeJMVqvV9gfDtg9PILnSWChmbrKOYutg1mP2HlTzhkzGE1qMIyjunB1WK/X2B8OHhNGRFK7SWHJSkcrPkYLmQSmqIoSxKkp7mjhQYc8GSht/PKjrSvAXsCUUiOFAI1nTjNSk9zu1m1v8D3f+304jkeM4+gxzU3TqBsq4/rmpqQPB7QAduNyuMnRthZtS2hbSSrRNA26roN5HDVNg81mg3Ec/R4Uv1NKft/k+293/YZPNKwuRflcpye0CUWom3ISg7/jSYW1D8AVD6smbv/ZVYLM4cqKKSFEkpN4miYPSLcFiQqIKTSl3cJSnq0ZadpjSqW0OgdkrKwI+lvTSHqwaZ6x3x3ExzBYFMXiUY7XjCA5EXXiZ8JigQtnxvFwwFY1TWPtyamOMKGYnSMS3kJIwmIakzRCXx6E3QgswF8xa6UrJNC+4XJFVe+i/IpKSXOrZ03l60sZmA8pMjTjNyg+mj5v+0R1Hx5MbsTU+sgC06Rz/vqvfx15mp3wZD3BGKcRrAkPtMECPxQAOF8nCmNyeRAmMvgVFsaUyzpYuMA5tsYIJ2+agYO8kbh65b0yf2NiC6RguDWPUJQ/+1eExuzvUWzUezsVUUoBRt3LyggrnUTnXa83a4CcZodT64pUTJ2RxhH7/SNu37zG02fPsds/YrPZSCV5F0qSr2VcB0ZBGmO8ZW3tPircLIyjJLZAeKTCNZtTvG/PWvvh/rItc0WytagE1IUkWIQL+66rxos+OPRt3wOC2kcTJmvbvWEAXCkUONZ9+9r54AKdYyA1DZpWjEmWA3524SvQqcCYI22xVcxuMbU+qBibjEhzDQuDb7lf+gIV9yJfh7j20WgVxuFtervLtQld2P4uoPHrv/ubLvD8ImY0OiXYfZvwHU97/Md/+z/DftoDAPbTHn/6F/40fu/3/178wa89wTAtCWl9vXic8f/82Yeq81Mr75m9oJN2j1gOTwd6HmPTlrgWCWLSSKgTun+yx8oDlqq8yHbRgU06Kb3XfUfjUKQtNYUmn4/jHmQiwzhKFWQ267+9VVQv1vYBgVOjY93td073LK5Akl1oG24Vs6FwNSw+Qygs4QYM5mZI5UDfjZc4aAs952ItUpcofYLzAiRiub++vMTF5SW6rkMiwjhOOEx7zHN2np6ZkXko8EuaIr5JaFOLrusBFl//4Tji8eEBqWmwWW9wsd1i1a9wHI5IqcHFZoP7+weHnYsKhmu2zokQahrLqTZbvYeE43EAZ0a36rHqOuwPB0MN5SWGRTGSVNeRlrTMQELBIF1wDWWJy7Mwbl0QivykH5imLHESTQKjQdt2IEoYxqO4cTOjazt89/UDhmnC/nBwPGQGDkepY5FnkWnlpEKC4M0In5LEcoyKw+v12k+WUioHA4B4+pj8vd/vFRSinJhc3XUd2rZF27Z//yuD2wAc5kbUIYXNotJgpxIguJA/TeJWZScJ4zhWgLA2rR/bLKIFz65QdE1bF4ZRQJhSYe3a+9a2tWHPFZcr0ebNH/Dp9QWuPnmBN6vvkNMFR6Cy2Y0YGdGlJskRYmpwf3+n2q74CoL1hCIShcKndQLyTyVwmBDAjHEYNfg4IL8Tf/bnyKjjkriHbrjqBMFlxWAJF/oomujU+ZCCcGEbjYzSIDhgeZtF4F72bXCteI3Oh6xJ27TaQGF07OtgLi0+Ph2rW30U5DFzjPlBApL6uEkJd7d3ePXylViuWKwN4BnjPACcfW51Wjcl3a6cLS9lfVR8W8GCdx7PoAyp1nsXjBHhBKZwQOgmK4Ss6tpHXAhixOXqkufcWgZoID38XVcy7BkK82b2YZXvJcbKKLCLDuG9snZc+na8slw5FoMDIM9AShinCXQkPD48YLPZAJSw2axLbnhneDBZIOA5FbwKELB7iePjBj9x0Tl7+lZB8fxv9t1v6RhkmxTG5czNNo3txaW84bjDjlP1ngoTjH+MfsC2bYA5UMVmLediedjV9FkEsxPrn/YTh0AmPCpU9YRQfKttmQptCcZKobdBMJ1nsfix1k3KgZ7XQEK17wq+2lqQw4L9/UhbFu8B1SIT6s8Rnxag8w9xjwGEbUf4n/4jT9E1n/Hy4voP/9Z/ePL9937/78U/9YPX3/bdcWb81C88YjcUAPkWZ5ysYWXcCbhbGWxsgo605ZmIawWejLwgS7EZx3NrM6yD/MxOS3yMSiPtoWXfrqxnPuNaZsayclKvVBtQWj/Nswp4yzHbSUa980kYDgiE/e4ROc9Sp4AAknIIsLiLMuzASwJ8itNZIGAASlzqAubxO4f3idyFzdmClSSwIzrNrJJAUtW8SXj65Ak2mw0oifV8GI6Yc8Y4jBjHUeIf4n7zZTZvCQY1CV3Tol+tsF6vsVqt0HUtHnc7vH79Cnf3d7i8vMTN9Q36HhiOB1xeXWK1XuH29RvM2VyNfJKw5A8lCQR8TyMzOGXMU8bUJKRplpPvecI0jk57Sznz5GMuiKizMdpq9+MYwj1HVS5Nc4LzUHfVTY3IiMw4HA5o+g6EFjkDq41kehqPByRkvHn1Enj58/jOL/xm7A5H7I8jHnYHDMOA9XqN9Xqt9S/GyruHiDCOIwC43B0N+H3fezC5Gd4ti5QZ4fu+dwVlmia8efMGt7e3eO+99/zZk4Qnn3H9BrJOiTXys3yyzvqLc/FBjBOwdtxHTSdq/QBFQYlpb5eTiu5SAFzRWB7zLE9OomIjfQl14czouhbv8id4zV8SJFaJ3k9WfI9SIUpE6Nc9pvuHEgBHBGjKMXByR262TWH4zJL1JpO06Y4ERpxVOzUanmDWaAc8jNjBRcjaxcUJsks10n1SQhzpuL0XraZmoa1PK8IYbTJKGM1PGL4++mwQ7oJRNDA4PtM3CoOjQB/sg5uF2BmDKUlF5uCKUCQWP1wG6xGw4OWvf/3XXfAy3BgnCVjNrPn+yfza4EzIwcJ8cpJRASzC5CzriBcp/Q8CAVvLHKxWeuzLrEXulu2oQMgF14hSgVvsMcI8hb6VUBZhK8CT4X6ccNjZ8ENedFP+qJ5vERJsamXe7IMhDVCTQP2SEkcK+h2PB9zdvsHl1SUe7u5xdXMNs3BnYjTGBBYCxhLXEJ5BCDouImFxpyFEPA+7QPGcFQ+XOk71N/btmYbiHjWE1xYWS2ZteBNm2dQeUvBpCaxYWo71JxTXjLJnE3iqjuAKvCn5Ec+Lv7y3WAndlsIRSU4PZ+0nZ63XmxmkcRcLeTW0KfPKgONDibXS3w13FGzuPlS2ThhgjY8FpeOD5bdyqqquQBwjefQ5B4yt25krAIfA2I+Mf+PPfor/xe94hqfbFr/46hfxL/2ZfwmfPn568urj+Iif+fRnqnv/6d/5T/ED/84P4KK7OHn+3Yt38W/9k/8Wvvrsq3i9m/DHfvKVKBlBcbLZ8um0C9iMfAZDQ9Tplqd/n81LjPewtn9GQbVLH/Y2tOF4Qr/s+3P3t9L9mj6X9aZyA55kRf9O44iNpvsMjxXXGaMtxpMMTwhSz0FPBqDGFDYzvOEJF7pmvMQNERH21cq4v0CZt+3/YPgJVskwzxTSiLHyhBrP+7bHs2dP0fcrZGYc9nschyMOxyOmYRRDHCSxTkqpFAwMfJFdBhKPmMeHRzw+7tC2LVYrOR2Z54xh2GMcRhx2e1w/eYLL7RbNcASB8Pzdd/DmzS2G41B4Hi3mrX8TZI2zyp4piUv7nAhNQ1iv19hlBmaJp4UlNSL4iTkCrilBKSBXBcZ8AZ2PW9xu3PaW8TLgm50eNWocPByPuLy+wfEwYWag63oxuA8jujRjzBkXb/4uvvjh70LX9Wg6EdmXoQMJ7CEHQB0aMAwDxnHErMqyu7zNM3KGxkaX8ASTm00p6boORIT33nsP77//vrdt773N9faKRuZSQTtzhfTRJcqOwwEVaIhVewOmadaK3RoEnqeqj9imxYAsgTbnWaxihsj6jG8ykmOevu+rsZnyYScb0SVrnrNsMEo4Dke8vx7xd/MMDinM2JEbSvzKwW0iQmpbpFWPPgG7cQBPk+NpJgb56Uj0WTfGSXrsWEgHIJs95xmrVV/cQVTgM0esyBwJJuS4bFja0ufLyYf2Fa3Mtg5RwuBlGzaHauW8Xe+73I7SSKDTcnxb9nXgUDCaHOIc2Ig+18/YZiaUTYbCNMu8UVw+VMAhSFo3EPDy0xd4fHhAi+RZIOY8Ys6T+nWi6uPUzc06ZHiV1GAmJIriXnAtgPGZSN2CMuoMJ6yFAlcIY5mnCY+88G9wkYbLHotJFMo4FD4E8KwCFCU0VMZhLlcSqBfrvgCmkMsPuhZEaMzSYhCIzLOIOZVcxjY4hT1nzTmieegTMpAJMwNpnnDY77FarfBi/wIXV5ewDHVsiknAqUUnOLkirsGELYsZMQUv4PmZTVLuF2HBZOLCu7jgwRkhLSo2S4HKwHM6dg6/qcRgWZeiQBxf1o85KBA2KCI43ZJpy8gSFau/C3TVM/JbQR1Z6UQJTdtiGAcga/FUE74WqyEMPLSrWkEigyeHDDlLOJRnvC0O+FYmGmBOCKOvT1TCuohlvOxUYUdhXy1gXeajb5dt5jP+6W8c8b/5Tz7GH/rHn+G3fsdX8e/+0/8efv9/8vvwE7/yE+dmd3ItlQ8A+Ce+8k/g3/2n/z18ePUB/vqv7vFv/xcvcbuvXWPOuc5VZMb+pcAHUZ6tYL+Y8omeZfOOivlphyft2Z4xQ46Si/oVp2GLjRTGwmFtQ+qTz1jvyllREt24p4T1XQZMy75h8ghwPBzUmFkGzVljUM2IYDQz0gnnMVwZWuv4Rj3xXVpw1NDp9Fx5k8RiyGfrp0ppzUIHVv0Kz549Q9eJVftxt8PxeJS6FCRpZNt2JbEF1KB4hcx4fHhA5hl9t8Jmu4GltxXZUTIgTeOIaTgAKvQyy+nmOI149fIFhuMlntzcIDUN9rs9ntw8wf39HfaHo65ZHblneBV3s8BFYlznLN4yq9UKfddhYMnkKTUGuKYTgd9ZDGdBQlt5W5dC48uaUNjfMObv7Yu8KLLldrvF9fUNPj2+xmq1ktIR04h5HkF5xsVmhXe7R1xdbzFBEybNM1r1GppnoZ/EIscCQN/3OBwOuL+/x3EQ5Wy9WgGAu6waiHKWe3b6YSnILbSh6zpMWqtqs9l4TIaFT/x9P9GALpgJ7InkiD9pSss8Z/HJ099FGADa1GKcRyHMzJinjL5vnPHFgO8YN2FEbRlXMeeMTGWhkx5H5pwx6zGQBaqsVqvKXSv2FZUXohnmszjPI55sG9Aja5pVswIXa64LsSRWucQErHqsnl5j03aSTaE7YLfbYVYkd0KtQqgRvlkJd1akNWZMlMTq1za4uLpQWNs47CjU8D8VAW6B93aVTFU6Z/3XmaX5yC8YjsmrFKSc2LZvbN+DHLZ5YNJcxmS8olTgpbA/5V7W5yw41K3DgS6zNuyCWdKgOlPmqJLLfMRSIDGjbRqkJGv+zW98XYt9slp0Z0zzAD3kLsAzi4rPUQXSqHgTAmMgLA8QGJAUn4EakY4btr4+KXP3sna4wEn3IJsgrUpZahQuVCIJyBbBRm152MnSzzLs+BisFT3I/F0DEU7FoEBZ4ZA0AwrMX5/BqUzaibWDsJYoQutlrCa4eZAia0YRYegiZMoc5nnGcRiw2+0x54zb2zs8efLU46Rq1wOUU7yFAGl9Wy0f+L0icrFtriWem1BeT6oIxKGP6iFW/MkFLpW8YDBTFEwcvIlDH/U8CiMxAYPDhMnuLy9FR9//XtG3brtyN7M9RhGG7L8Bts/ZFYO274C9uhNqUDjAJ+Pi8FfgEIQ/EpqUUOizDtoXxedRrTdXdK3af1HojHBRWl/RVSLp27oL+H0WtIbPMLeY04duDxn/+z/zKX7PD17hn/1t7+PP/8E/jz/6U38U/9pP/muYFka5z7va1OJf/x3/Ov7If/uPYM7Aj/2Xr/Gn/pt72AmZZzKisLqBYJfhmeAboiH89yLSSXO6CwJvBEROgD1PZe3Cn7MwM5zSraatp0KK9bI1i8YLphjRpgYtG+yyb58F4IYgDn3DZBGg1crIFYek+L78kyEulkiMiTOmcfA9UAa7nC2ctwiu+E6GufOBKKxDAb4ZeSKBKbwkzFu/kxsXyzOG+UxA2/d4+vw5un6F43HAw/099seDniK2WHU9iDIYDZp2DaQe1Ca0jcghh2HEdNhjGAdctE/Q9WuRD3nGfv+I47BD2wBt0ymeJTecrjdSjPL+8RHjOOHZ82fYXl7i8fEBV9fXYLrHfvcIBmvR8aUbs1J7PyYXeiVZnBq0rVR3n6YJeZoAPcnh6oiXz67FcqmEV9gaFBpbYF7wQ5ZDsTW16PsNNtsNPvjCF7AfZ7SbDdpug4YSjsd7EGa0XYv2+Abf86UbTPkBh+OMnIVuzpp21oR9i5dYpRVevnqjXgYN2rbXjGcJx+MRFxcXGKc9+r7HarWC1A+TIoeWkMlcumKIgZ2I2CmGhTkwM774ZXzb6+0VDYOzWTUXl7k5WRxEdH0C4JqQ3Qcz5lzfswnEtLSxr6U11pSRaZokUAXkBUwAeKBKVCzqIHAbNyOlFmadztESwNHtQN/TjZs1V3ZmoOt77O7v0TctctNgyqIxsyJbVsEPADIlcALGecasjJJRChc1SXJnt+s1PvjC+9gdjrjZbFGJPJ8hJC3dpXye+q8T5ECw3RJj+4KUIVZEvVDeuK1jP1yerH4zxh77LicVDDtCcdqpsDBlw/Zs3OTLy9qqBSh5MAVrUO0CJ/D89JNPcTweisKjlpXMQWN37kuFmFgPoWCSjT32b+6D7rN6IqIaI1Yf2hO8L9B2Cy4Jw3AfUH2wUQBLFrFFLJMXgrTjXlMG9Og8iFqkSowRSrFwsJ4g1kwwKhn6NAh2qGH7qwopdyXI4j7IijGZEhf6BghWacnGn4mQlBFkNYIcDgekpsGnn3yC6+snAsMsFcbj0XZZmbC08d4CsS3Zs7GcTPB6HCd4jiBDMgo+Ft5VmDxQaAvVMTvnLuu7ZDz67L1o9xzmxJUyYHh6RiYOHQZcqMZ82t+yb9/fbmQp+3a1WuMBd2I0yllOwJnPtFqGUdOW8s0rf3MROG2hjO4sr6XRpe7M5ZP6+7kxcd2+fw84FmM74q7/rItB+H/8rQf8zDeP+F/+6DP8K//Yv4If/ehH8c/+J/8sfuXNr3zOm3J99OQj/Ef/o/8IX/vS1/CNNwP+zb/wCr/8UutrOK7p+Hyjad+OH7ZHwyl5NUaHQlGaTLh34NX0p6L35+ZN9XKU9ACneG58zH5kQnUaUZ43E4PStcj4wjpVzNTGYkYcqJsT1etHYSG9v7juMmnwOGHUJCLuTs3mOhVequBQGqLwoTwpu9cMa3EUFS/Rd837wseY9WTI/gPcDbRtGjx/+gxd3+OwP+D+/gGH4wEgSDG+psM8zdgfHjAzY7O+wrN3r4BGA5TzhCfP3sFh/yin0G2HmVmMp03CerPF4bDDOA1IidG1PYSuq/A6DNheXGC16vHw8IBPP32Bd955ju1mi91+h+urKzBn7A8HZC5FeA0GpGnVM+BB25wZM2ZwZqkJ0XXoul4TSkha9GIMMdALbfFFjguvgGRkWJFAVpnG1sGTqihyCO9PWK1WuLi6wTvvvIubmyusNhs8vnqDzXoNTi1oynh8vAcRcHWxBf/iX8HXftcPY54nCRxvRKYlIvR9X50szPOMh4cHAMBqtfITjydPngh0VIHYbrdomgb7/d5PMOJl7dmpxkpPQ8wFK8aCSEmIb3/9htLbAkUpiBYNux/jIaJ7UoyxcEUjtBnbtu+xHZvUubYjUKZxqoK+KyIXrauLeaVUj4NyxuXxG7hbfakidDVBEaFOfBAzUmpwPA6Yjkc0bQvqOrSUQPMc/PJacbHqpIImNY2kSGsTkmqkbduioQZNatD2PUCEwziCKLkAK8SkUFbGGSGKgZgPPCoWS05npwVOqLQNO3FwNxKq2/lMYW0hL7iLY5DCPOsFRUWujCG2H12hYttLlkU6mejWJn2F1gmYZxbrSxLF9JOPP5bxZ0mXl+dZrFDJBBjyXP/OzRCkRhsNc4WblaAJnTs1FVMq4yqzroVs69LYZfH1hTFE47aUwlxJh1TcGk2AMAHBhHRmjVNia9dw2wiv1syJ83ZBRPqmpBZ95mq9sx1NUxsUEcDjl4AyJo7uhXBN01zBhOmzBr8F4HGWOifjgJRbDMOIh4c7XF/f6ByzM45KvghLZ2sif7lq3+Zln1FhVxCB3O/eZkkFRXxvcvWWffY9WO0xY1rlPVu7z9pjUSAxwS/KVWdePTMeF80KfJbojoCzZwiC09sTXs3oNY0iWIO4zc93QWjjuC1LdaHjap7hGp4ERj5xyTx1DwUH/PU5n5ODfddVU/V9poMkoFKICixR8Pncb7HdAMdfejHgD//xj/HP//an+NHv/UfwN/5nfxP/nX//d+K/+sZ/daYluX7bh78Nf+4P/HncrK/xEz/3gP/LX36N41Tg4wpqkZVO8RwCw0pgrwSsgFN2K1RnF1gYXsRYLj/7LfjJ8fmlgSECJqxlheeEIsSV9yKel3cYLnyXIfkLgtv1vG3V8pzVp95OUksUj+NDNewC1GmawHM8FYfzEsdh/ezxFb73AtYFmNvg/RQCCBb8CFydgyk4ROJe6/vblEOZaUoS+L1a9Tgcjri9u8PxcETbtEhtg9R1aJseEw2Y9jKY4zQgQ+SweZqQ5wnMGW231jETOEssAE8McMb24hLDeJDEPqowidA/4bAXg9/l5SWurq5wf3ePFy9e4N1338XlxQUeHh5wfX2DnDMGtajXi2n4bkREefFM4CZhnma1/rfIcwfOR63zUssJ7rpcIyBKTEYN57hOxlA8xjEDpKloLUh7t3vExdUWpEmSWkgNkGE44LB/xNXFCqsG+OrmFT748B/Dtz7+BHd3e1xfS2D+pdbQiHIwEbmrUwwZsDS46/Xa3cdSSl4L4/Xr13jz5g0uLy9LbbsQs2GG+2fPnmG323m9DZPr3+Z6a0XDJhKL75ng3/bCOCwQ25WDbG4ocOHf2mKW+gSWu/eccmF9mKBkRzf2jKWyte9t23p+5zhW+899TFXhicqIaMbS727/iOPLXwV/+B0FgcBVMKBZcADg/vYem/UaT58/R9u24lb23juYNRip05RlHseiQgkTMBOBKLn7i/jEK/yUj/arYiMHAE93hyDYRMYA2wg1J6lunQgAhWj5zyZUGYX7DGuUvefvB4J/+lxh7vFeNc4oKdkfJYaeRYTICaQLJGYVDoJgpdRyYUqJZP0//vhjHI9HEV4hVpWZZ7WGaHBYRrEeRRgszJmMwHBhIkrg6sT+x+6ZFTQyNztZsTGrxwAIRSk2/BMGSaCm0fZmGOsmd4UK49UjEDmxIniuHyrxI9KncV8ZP2XycckjdkTMDgdTSoypSwxJgtUeqSrHL7DDj/GNgUapdoFI2fs0mAPIGZkymOU4/NXLl7i+ui5GTObgxlHDvBKQAcf3KGxTgLmJIPa5FjDMqhjmWvGqwqgcfqBKIVi6MNZ9a1vnNlclQJV1MeWIw/LWOw6+v104w4IO6zOE4Lq1uNzFhgoci/CtrplZFQ3rlq3qMpf3FGltF5/Mm6Ud9s1vN8sYCzjOtGFzCXTtLDxR08XPuqrYJpR1g+0XYAFfpe0oIp+ylEKAQdhPjH/7v3iFYWL8977/Gt//7vd/rqLx/e9+P27W1/gzf/se/+e//KYI4LraWfd58YINZ0MUoVXWuNBzOzEy63jc8+zwLIKtCWsLuh7w3PHVMSQCT39zXrIEbrgCTzOaCBI+aac25ZSAygPBEOd7TOfDLsgzpnnyIF2nO6ynhKBSDtoGEK5hHN2N/LPomdHfiLFmTXfTSFDaiiEgNiTPRd5bYjsMFizBz/6KtpCEB1xeXmJ7cYHjccTt7R2OR7H+t02Dpl0hdWt07RrbixbtaovjYYe26zGMM8Y8oe86bFZbcUlWHsuGSdkCtCcMwwHd1GEeRxCAltbIOWMajhjnGYfDAMY9bm5ucH1zjbvbO7x8+RLvvvMuttst7h8ecXN9g5evXjoNiPxLQKk46BYS4c1Za/e0bYd+1WPOM7LW67DUuOXE2NyHQ/ZGld2EZljGrrDuFPaY8VDl2TlnrdB9xP39Pdq+xzvvSfamiSdgmPDm9QsQMp7cXOH9T/8i/uEf+gfw5MlTjHmH6+vO3b6maXKFQebTuuxtMrX9Z/U0zGPI5OLVagVmxpMnT9B1HV6+fOnZp/peTpRszO+++y66rsOzZ8+8hEUMbfh2128o65QdmQhuFnen6BYVnycS63BUTAww0zSi7Zrq+eg2FQXEqBDYPWszprK1gEQ70mHmKtNVPEEpll4JSDShHiBstxf4gL+OX7K8/d4xPOd1OZ2RwlGbzQYXFxeYrNggMtpchGPJC2CNxMN/mYukk0MR2nTDMGkMSCQqFGgrWysGyCDEIIhBC6EHXMT7+Lf+ZCcZxjgI5V9U1if7nqmkBq0FB3nISWmQpOIzwQAWxlIIqGfxcfwoc7IKtMZEKhHQhBlmJIiSgZzxySefeDpbwZ25Ck4DgGxMQAmWWbagxXZcULGsFbqOicIE419j8mQnAkGoc9xU1yKdcGyL3IIork8ZQHMmi1C0Wtk/pMTP4VspRsWy5kQaIqBnzfhUBBcUXGMpNukEXn9PGgfC0GxRjblnAVQBQ99TFwXSvlWNiBODzSopoaesmUMgTMRcx+5ub3E8HtH3vTNmf/fzaCOjZtYoeO5Coc+7TMF9722N7G/YuoX3cAmIpdO96+AAVQlPwmM+Nv++mJPgqI279L2Yat33GVhUZIdr161z+7uav89bg8ezuJk2betM3dzeTEB0BXAxdgLc8giYsonCzEN/BTbVDgBs30Y4sblInJNha2Euwjze9DTgi3lbpi3Z7ot+tbEY3ByfiHj/nc9EIPqTf/dPnowwXn/q7/4pzHnGdz4T94pUhhU6LRPxIGCi8zA/g+fV38AY/V0OOOGfzSjCgbZUQ1lkpio0yePyIguMgApr/9l4fo6PwTGDAFg2qmiBSPrsNEog+JK+Ot9d8DGXLSD1fpizBM4pnyg1fsjpcuEtKEoBxD2HKHncmMkL1ZqwGY5UqCeVNYKcU+i5uhLb5k1iEGr6DleX1xjHGfe3cpLRtA26thNBtVuh6S7Q9VswZ6y3CU23Qp5mtG2P7apD1zYq802YphFTnpH1NIeSeGl0bYu+u0TOE8ZxwHF/wDRPaFLClBLGx50EM+8PAAhPnz7F1fU17m5v8erVK7zz/Dk26zX2hz1urq/x+s2bgJbkyrTJF7K/k/OczGL9n6YRbdugaURwN14SlWU39EXKwIIrpuGc8G/DLfUQ4LBugNWZOyJbUDYRbm6egqYZ969fYzjs8OTmCs/6I37wyQ6/6fv+ITx9+hSpewKiBp988ilevnyJ6+trD9IuW4GrgwCjOUsFo2karxpu8vFqtcKXvvSlUg0cwPX1NTabjfBQkiRLdiIDwE9K3uZ6a0VDAkcEce1kwbSo4zicpKs1ZSDm2i2nB0kLfpTTifju8mQjAu+cBlUK8gHGTGwRzsV9WJtxnPJMid/owvEowJ7aMdJqI9L9qsfD4yOuLq/UDz4jcULW0tQiNIowREQazK7E1f4DoUFBaaMjDcpNLj2f0jwYwTTeS7rRolIDV0KivdDoXpQrCl0PxPBM374GMN/1ohQYp6mO6hfXknEXflx+KXbk2Df5PYvnSKSBeNW4rTUBdAajbxqkRHj16g2Oh6OvJRgaN5T1Dfa1AczXvOTsF1zTgFlTHMhciBbzNsuGMZCoWUUlGhQKKOkqpdN6TlDBnhNpULbtj1SspVzmDQ3OFheixqGp52vO3CmVhKw2bJuj83tlhK5UhhgVe4hKCzC/WbNa20zrNQaKRbFUDT/FEOubkFTJsL3Es1RrBYsh4/Xrl/jgwy8iz2JIyJn9ZOoMKkrranqsZCvff6qyRGEsChyxnSKv1PvvZDan71T3oxCD0zbtxyoYe9E3o27jXN/fbnBOW1Bip5Z9G4P3fkzQWTRtRb8AY4KakQYCeXt3Oe+qb5bqv583BTcC+G/LCQJm7T5DYWDrehbmi479dxZrd/xN9leA2Zn3lu6jJnTebBK+7/0eP/krP4EXuxfVyL7n+ffg51/+vN/7dPcp/uLf+4v4xz/6HbjZEG73BVY2lyIIK4yiomv8E2IWk+yGXK+3cwZejL/GteVEXdV3IXyB61Tkg6L41DEl5zZu3Itn8dz3hdFHGFuq1sOUxZP9re61263GSFJoJNB9XtBwWUJ5l0JqWygMsNwX2qYpGWa4iKd6hRZ9Bi9xGh9BX4BXTqEUGQ3mifDk5gbUJDze3mO3P6BpW6z6HsySgnXb9VhtemRmDOOMYdgjEbC9vBI5jjOO+x0Ohz2m8ahVvdmxmplASTxO+r7DerNG36+wWq8x7CVxjtQZkarT3arTzEl3uLm+wcXlBe7v7nDbd3jy5AmmWeC62Wxw2O9rvsPxBCvyMRbekbNmQG3QNglj0wDzhJnI4XSWf4e94rIYRQMbCo7oUykVJce8WhpN9jMNA27f3GLdrXB//4iHuze4vNjg+fOnuHr8G3j/nWf46le/C03bgdOEcRix3W7xySef4M2bN7i4uHD5NXoEReO6nUjE8IRYzds8gsw96uLiwk8/jsdjVf/O8DkW79tsNnib6zccoxF9wJa/AYWQ+GfT7Lg+XWCUdFxEhKYtKdLmeQYBaFJT+ZDPc0bfdyXSvjHlQYUj02JTkhgIIsx6ilI7H8lVgsQLoZB0YYTnT65A4yO4v3RmacGt9q8FhK76NT7++GNcXFyCmoQ0STXv1WotQp1aEBIXlxgCJKc8w7mnacdiAK5Znx8LnhP44zr5mhQiHUM1YIqFU/daaNCFqzZVCcyLLiP15aBxws6FmC8kLWd7Pg72Z6JAIDDnaqKRjDpr0EBfe7TyF2afjv6uLnxM+PSTj3VeYjliNiVXExM4vHXey3Q/IMU9+ezZm4zR+GOkOFCsSw4n56RxXqzWRiUiIb+6n8wESyiRU1hncM4KyZgj/B1nYBzvFXbNbIzRhlULKc7cMksgHaAnQPJ8qhDEJppQhAyqkIjVDFqEg6hWRSw3ki1z9WNxwE9AmlwW+/XLV3j//S+4BVDOXeK8ZGXNEcQEwnowNgbW/5P/vhQcKbxmjMqGXVylgOLOUFZ+6Y70mXvs3G+LPW4oFfcklp8DDeHqXg33BelQZToqE0B9wqFUwq2uYdPrZ8sWZqeG2QDv0jjFLmvaEhh60zZVu59Fm07ApfifYfwKoe/6yidwq+FR5h37Vgrn4Fy4GHBxl/L348B9exB++MsbJCL8+M/+uP/87vZd/Ng/82P43d/zu/Enf/5P4p/7z/45fLqTmhs//rM/jh/9yo/ihz/a4s/9zKP2Rwt8jYrVEmYuFvkYXClB2au2rznCRveHgdPf0Q9OTU+ZhT5rckP8Hka3+FqteWjOxuRjM6E+Wgl50ZSfgNf02U6vu76rsXK5eRf7gBRus8Vn6AIwW17k0Frkt7bHAERZqtpjLDNPofaF7x+wGxkdkMp/jM75CZNCcLPaYr3ZYjgOeNztkJIYiDMz7h8eQQwcDgO69QWYWxzHEV3b4WKzAhEw7B+xe3jANA3aaoZk0LSsdWp85Iw8Z+wfBxz2OzRdh8vLK6w3G7RNi/3u0VOtdl2HKU/Y7/ZY9StsNltM44S7uzts1hts1hvcPdzj8uISx8MRzLm4K2UGQ2tdOI8QuJjwDUwYR4CSBHNnpWvQ9V7S1HqzFrAm46/VntI1S0UJIBCaRjwptpsLbC8u0a/W6Poe93f3ePP6FS63Wzx99gSbVYfnL38JP/ibfwdSS5jmCeAZOc84Ho947713cTgc8fj44MoFs6S1PR6PmOcZ2+0Wfd9j1Lhl61tKS1j2qDJBKwdxOByQkgStbzYb5Jxxd3fn99q2xXq9Pjk8+HbXb0jRiIGlT548wX6/Pxt17psjUREUSW2nBC1kklwQkg0ofyXNayPBV1SOAwly7EZIaFJxnWJm8GzHv1rNGUBqG1V0pJ9xmtQPH9VxT7asNMzCQFkY4JPrDcZf/WU8bL8D69UGbeqUOWUAGalxx3m0bYNpHPCzf/u/wcV6i8fHexwOR3zw4Rfx3he/hMlOTqDEIBsRzZIGtAGc8imyFzmv+I0WOnm6uBW9DwJP5NvMKK5F2pfLvWY9Yjt6DpsOgadS3Y//xqwnCoUfNP5eabuwmzhge2nB8jj8dbp+yhzNZU4deOD2fYODDmjOGW3TghLhsNvh4f5BxybK16S+h/PMyFq6lvXYiYzCU8A9+HJ5J6b02hMGG1tTxPVQoThRSR3l8RmcipK9WABXbljhQXoyQWTJmQoSKFOLfTNQ/IrZCCxA1IRJ6VpzEaEqRxLHk8YhTlA3SS6nQQVWBVk801Tg+EZffKocOsICcAX6EHerchI551ny3eeM4+GAh7s7XNzcyEnGXPxKa7lyYU32NSvjj30bWG2l7Zfq1CnKUBFoAKx+zGIm1R5eHn8v+zb5xtVcW1ezhp70jSBDFQpisOYzL8RnDM89KFtHwnF5XHhTRSrOSWk7EtB0chqe51ncDS2GJ4zNXTvg7MNdI1nXL3nRLKDS6sKcDV4RxgBJzSLDBZ9wJBj6ftjftGhHYM5l3kujCNspaG0gKjsqzq/8Ju3J/viRr0i6zz/+s38cAPA7v+t34t//H/wH+MLl+3jxMOH3fO/vwd/8n/80/uB/+gfw53/pz+OP/50/jj/2u/8YvvbRFn/uZ3fFyBLXyte72MspjMnWW2Ae563/OqiLy5VkMVL+qTFtUDzPSvdDhArMLfCUk+kSUiFRBedq/K9wL4wb/ht7W2w8Qp9NVHaB4QRVjSh+Q+hVUiOoG3rCYyLvkw+cZ/ESTToQhu3j6F0QKE7EwchBTY5yek6Oa0Y9zYAVNhok1hCwInwLwlLcspQGX1xeAhl4fHjEPM3o+h5Nt9IhHACewUSYxwnDNGHVr7HdrsF5xMP9axweH4QOM6nxoNBYaURjYknlIK3HNg8D3rx8gYuLC1xdXck4IAUOKQE0JYxHqQfRtR222y2Ow4A3t2/w/vtfwGq1xnG/x/Zii4f7x5K8ReXJssK190ZmBs8ZRBktxMWZUpIiknoqJC6dki3M+DQZ0Q9t2gk4+ZIl/942UjMopcbd7N//whfw/gcf4nA8Yv/wiE8//RSPDw9Ydb1UYF+1aO5/Fd/9xXdxefMUL29fgUgyTHVdh+vrSxyPR4+72O12eHzcASB0XY+bmxtNOwvs9wf1HurcyG/jA5JOtfb4MS8gqzxOJO5rAFyJMfep/78U7LMGp2nCkydPsN1uQUS4v7/3xY0BIlbso2hcfOIStbw8xmNBfezdeOwTg87dHYprl6j4bhP6jPmB7RlmyRUcXasu2gkfPzzizetbNEi4vLzCxeUFkERoFUVIqNj1zQ0+/ua38Dq/UuUo4Zsff4Kbd98DpRaM7CVmGHLS01AKQgGF4qEaRM+BNDkVtJobLjUEohMeDX+NRkXN249n7RlEWhaOtqPAFJ6NtE3l1ZO+vU0URlsYUy2IRQXFb5PBoD5qd0apHZRxFJHXGaszIYFZk2Q0b16/Qs6zKEdiUvVCk3POLu44EUEh3LG/uC4nkCcRhJ2RBGs7EQlRWwiyDJQsaJrM3YViO96ner0tvW4lzxpDsQRNIWuWjJt8fQshhlt7/Wk3Z9pJigDfSHgyAVIH6UI0FzclaK5zq7wq94uIU9Z2Ccfl5/pyfDaDAptApTSIM169eomrp08x51hJmorgetJoBaVayVegRIHHLxfeQjtc5qVsyfH+XN8nYzkrhZWf4h6rBInw24kAibL3aqchKsqKzUefr9Ich9nUBCfgduirmh/JujdNI4LoLIaheZ7VCmm0heqmK9pCjoslgJYDsTOaY/SmjKKCQxycrxOdpU0O59iOr7cu9BLm+pu5HRWXToPFmTX0LuV/VyvCD3ywwl/61b+EF7sX+KO/84/iD//2P4xhzvi//uU3+NN/+wG/6x+8xO//4ffw5/7An8O/8Zf+Dfyrf+FfxV/+tb+MH/niP4KLVcLjMVe0taIbcS5OO+WG3Td8t69RQedKqg+Nkrbg7wb3NedZmjaaCyzpzMAKjJb0XPaSxQP6mOKacX26Yp+drnF5Z8lP7VQODHEndSOoc1t7KuBK0vUukMw5ZJzSAfjJdtidvi6OB0GRYFTGW1mIDKZGZA21/vk8KkieoalEMCWx7zqsV2sM44jdfo+mbdG0K7TdCqv1BuvtFcZxQNu1mJnQrzpcbNaY5xF3r19gOD4CQT5LKaFNSemxxQaI0D5D+EXTtEhNQksSw7vb7TBNE66vr3F5dQV6fMDheERKDZq2xzQN2O932F5dYrvd4OHhEY8PD9heXGAcBmw2W+x2e4+JEp7NMEqVyPah8VOh53megbaRpEJ5BqUGq1WPDz/8In7hF38RIEm7nfQEllSWYc5CF1OS2JNGhHdLtVvKJADzMFjtWmw3F7i4vMQ0TXjz6jVevvgUeZ5wfS3FCdd9i3736/jq7q/iq7/lH8KbN7eV3Nx1HZ4+faoZuSS25OLiEvP8LTw87JDS7CcSFt5gMdFGL01+3u12OBwOIGIPi5BwhtZx7fb2Ftvt1k+YzHXqeDx6XbvPkuWX12/oRCPnjL7v3TesbVtHLgAnk4q+YdZGjIZfRq2bkpC0crgBKgaDx7/zPFfF+HKewiaWy5SHlJpKwYinM+ZTGxWUpmnwJXwD39x8GcNwh7uHR3zy8Qus1it86Tu/iH6zcmWBiHB5eYHNditVMTVg4N333kfb9lKwT8cj9FM2HyMjsQXVKGtUXx8ndigvmntLKbZmPxXLHCF2FEh1kCDkKDMSVrjwtTxViG3JIoa/fOaxpYThEw+iTeB6J0LXkpn4/fAChXuVwLAQreJvJuwqcXv58kUVRzpncdfLSoSEVKdCsJSAO+Nc4G4ERrEc6JppbAASVTAr7wcnLYb66ZJa8YrjWgkIRJCUFhs9SgJU5r2UrEoQqsJMrUHO8FVoTwvh3DJwibUxOY76iWdjsKvnbXCW04xUYIgwNmPsHEWMz5gbSpsi31qGK22XASTG/f09xmFE07XC5CkejdNJFzEgttxE6Ujhd3JVLyzw3GDuiG3zDq2xywtR1qi6OtNrPaz4ilngYGen1fCqPeakxBX78lz8fMpU6vWwBVmSixy+EFudpQYzJrEwTosKswtisJy3MMwJbdfCzSWKu4UG0RJ8QdgL4h0rzY3CWZBWuboXproYZhAXYa3l8GLMZBYbdtq9JCUE/MMfrdEkwl//1l/HT/3zP4Uf/uIP4+tvBvybf+E1fuXlCAbwp7Tmxr/8TzzFH/7tfxi/48u/A3/tm38N/+h3/KP44Y82+Imfe3RB3pqOBzdsc9Xx296wOZxlBw5kWX9LSW1k5gTmTjVRPeB0giLkgmhM6TPwwj6Wvn29l5mkYCfQyteNtgib1SxEynNJXK1FUBQXp2EcdCzke7bEm5ADU/C8bJikfWY38OizzKc8krlEsC/32ILmuZHKTisAWFISocFFpa1Qlv2fCpbbzRYgOc1gEFLbI3U92tUGqVuh33TYMGO/34FmxuXFFtM04u71KxwPj0CeQIlUhrEMm+TwYWYkkpOkzABrGtvMEkjctC2gFvTb21vc3Nxgu73AOE2YJ6uEnbDb7bDebrFab7Df7XF3f4ftxRb9SgLHt9ut1pBY8EWFuYsckYRbKjAdf84Zh+MRb27fuLLg/JsKj0wpoe86dOpuNA6DyHOesl02nJwmNOj6Fbq+R9t2eHN7i+HjT3A47tH1LZ4+eY4mAe+m1/gtm2/ienOP7/vaP4br62s0TantBpghXgxq88zoOnGNev/9D9B1r3H75hYP9zscjgckSri6uvSUtkSSjSo1DVZ9j4ttwtXVFdo2hdMOUnerEdM0Yb/f4/7+HvM8Y7VaYbvdYrPZuEwwTVMV7/F511srGib0H49HfP3rX8fl5aUEgg+D4j9XCocpAiLkl3y7poD4IuoVA7NNCLE2YwC6ER47ujFty+I+ouIR+zRrZlQwyulISQcWq4d/6WmPv3N/wENq0aqicnd/h/v7G2zzjG7VA22HhgipafD8nefie7ha4f0PPsAXPvzAYWc5lTMzzAUerMX6shAHqWVQH0UtD66V/Ee2WNEOXvwFAKsEGy0jboFGLVyZcE/hfWUp2lbdLVejYphAZe+myFdNkATcp/6EEVmfKiwy4AIEgd1iToAIsCiCaRHuZGRWF5sVzo0Wu3vcP2J/PLpgBI3NMGt441Wt1QKtllp7PClHLTywQIJgz4eCTMpEWGMa/LTBVtWOWw36WuxRlBUJpI5H5dJXgHKlXBSBTwdb923MyrDErTD6euawXnqSafsI5CckiSLslQEH4dbdJyAnGaxKHuXszNqtdQo3O/HJuoZLQZGiwQEQt5tkq0wOt0xZAugAjOOE+4d7PHn2zFfKn19sIcM1oPxEFL/VV8RzT+XKBeZFwCPfB8s9BoQsbTiVQeJlY1wW2qPSsO/HOjg1zNuNPTYSeaK40lTmjXq+XJSWws59Q5/gnrk6RToCSOxd17UY9nsRPDiLgn8ihEUcKwKeCcAU4F9OOFHoWmjFf7J7FW2h4A4W5xtgTiVuzvvlMs84P0ahuVHoKxS8DNX6hv9ScPBr6jb1L/7wvwgA+H/93CN+7L+8xWHM3nZqEv7e6xn/2//8Ff65r13jR7/3R/AjX/oRef+jNX7i53fVnFwZjDwjbrTAH6wYaI1r8kzOtaW3KHmyEXyOHE4DA8+pca3mOEYbxPpfIOi8hGUtsluOlW9noYtWqAyqCEiWockVl3EaQwp5GUFSK3yTJMOTGKkJu8edeG8wF3oW1zGZq6vJFdA5yvzyPPu7xgNjViw5XFjseDWIlHi2CFPjRWrMUpprPMqMLWQ8xvmYYhprIWFINsHNdoN5nnE8SrHTtpEaX23boe16kfkOR4xjxs3NNcCM+9tXOB4ewDyjaxqAgGmcMGah9W3bKn1WLwGdi6eRpeD9khLapsEMYBwH3N7d4emTJ7i8vMT97R3GPGMYRrRdi8P+gIvLCyly9/iI/aMoH8f9AZv1Go+PjwKjiGu6vxHlQcdzkbkoJXBuMOiYXr54qTW1jGjrmuvxZGbG8XjEYRjAeXa5ZrUWeBEg7lJNi9SIa/E4SgA13jBWqx43N1fYrtfoWsKz49/DP9T9At6/eQcffOF78e6777s8Ok3spxQiCw+4u7vX7aGu1YlwOAxoGjmNuNheAACmacb9/YPL0Pv9QWT2XlLqrtY9cma0rZwyW0iBJXrabrdgZux2O7x48QIff/wxmNnrb2w2G4zjiK/g219vrWiM41hOHFLCixcv5DglEYjKScbyxMA+29+lsL+8lgpG9AGLSkBKySPfzxX3s6vveyc8y7HZu6ZwRDcvOwV57/BzeNF9P/a0V+UkaxC7bvicVVsnvPf++7i4vMTFxRb9eqOibuOytGRtYVeKrKq4iAcSKzKzCZHhovBXBbszoCvyZqUMFIFK9oOy6vC+56b3nheiRrhlFq8yLPkxMy8N9gDXzLliHC4wssJGfyMODD6IBiZsxHGz7/FS1M8eDmM11x6GMJQ3r1+DsyjB5rcvSoYF7i3maMJ06NhdTVhZz4mEWODuJwIhtsgoIvujZuEv6+O+wDG7Dte/W9/1XgpCtPVNi5UValyttxPgSjJcANxwJ8zbhHE7GbTXhO/pSUyWMXJKvhesk+pkg+DKSxFC5K/pPA5zFIFOxkUuSM/zjNQ04Jxx++YWT589E2UnMJwArfqqcK045FXPn6x3AFfhT+W3xWfzk6YzAzCBrZy4GpyqZDMylmhCJmg6x9MxmgIo+7QoeD4hN4SUcS8pwRnKEPSKIpEGEJQJWQC5wqXxlMSaaXCWoPAUno99UDXYQKtR5lrTB6peLr9xEDTK+KrTB8BdLbLCPGd2uDq+otAoF5VpeTJSFDc+s96eKTOMOoNx0QM/+KFYTB+PM/6PP/Uaf/mX9qFdbXuSce2OM/7YT7zE3/j1Pf6F3/4EF6sGP/jFFdYtYzfGtSHfmw49w9ciS+nYKOCazpPLPIu2QuX00miD0ScX7tjrpZiRLxp38jxjmsUlJXPGpPKGbfhp0jSpupZZC+E2GuBKJMkBmtToK4Su07pa+rtlALLThkTK8Rgq2EPvq6FS03fu93vHobgDhFyJEI+wD6UPExSnChWdl0SZyGDOdfs1VpDDwoxfBdX194C/Hhy9wDcPMmCg7zu0TYvH3SNyZvS9uD11idC1CV2TMM0Z4zhgvV6hTYSH+1sM+wcQT2jbBm3TSnaieQJDi91OE5rGjMvy3zzNGEfJRCWCbIM5M6ZxROp7Ne41GIZBi/JdY70WQXbOGU1m7A8HbC42WPcr7HePeNg9YnNxga7vMAwj+r6TLJKBh/k+rTIjMsz0MM8zOj1h7TpgOA6YWcsdOCwLDzXYZU1AY+tKGu+66iUGtG1acRFLIsC36qK23W40vjdj3RG+cvsX8aXNHpwb3Fw/w2q1we2bewASpmAGc6N36/UanCXmOKsLV0oNErXuumWnKwCpcR7Y7fY4Ho+4vLwAM7DfH3F7dwtgxmazxna79cMDQSly+WOz2eCLX/yi42v0JLJsVd/u+g3HaJgCYKcLjWZVim5RNtCYUjbet79Lhu8KQuCCsd/o+mSnJHU7pDUxCjGz9FxWHdgWLSoXKbWVYmPAnqcZmIG2a6vsVJzl3U6RaJwmQcLMeP7eu0Z3hQhlyQ7BgYhYwLJlnSqEJ+Ph/gGXVxdOUONpp8AtbIAAu8jAiuJQ0xi3+p8lZtYAF0EwdORktvASWNLTKge6K3uBIQGlsSBcRwGpBCUTnDmTWchVAdHRexDiieSj7wbBxK0bgMTEcMabN29gTNMF4hqSi4bDCQAVgdqEwTiYSijiAnP4fRUwqTB8Vqbm/rUEkNWlAAdBMAqRwVKY4oKT921zYFPW6zQaZfInkm4hqq7wmIRoQNV5WzrcIlSotMKSLhp8qoQJc5dnyXK+G6xcIDJYuwin840uayp0ZCAlZQYmzKTWu3x4fHCjRHQx9NiZIGgZWCpwoAhL9jnGHi9Rxtd80Y417nOrO4G9crK/bWxxf4ehOm21cRaQlS22xHPHW1bcXAgqof+TbVZP5/THOG/fF2V/Z0Ay8pmhZs5Ct2FqL7tQ5qD1+Wtb8dQojNtA6YMygbf6rXw6t0SyjaimveSOPmcna/TXxm4ylqVFtzlU6xjAt4T5822Lrkn4uY+P+D/8xEt8cj9DWUY1kepkMxF+6hd3+PlPjviXf/Q5vu/9FZ5fNti9nmDF62ItksgzRHhSHGK1lgeE4QxknrWqtQkcWU4VVPgYx8lJxDROmPKsiS7UPQ6SkljWTgxrTSMGPZAkeWlUQFv1PeBKgvJ7nMoMbgxQdDYl0FzSTGIsxhA+UaRNgSejMYDT4/Vqjd1uV2QYg1GAHXm7poixk2NRkGJ/xaAUDRmV1YwWCGKX91FOmevL6HkZnNUHEcUkwIQIXb8CCDjs9iAC2qYB5xGvX32K7uERz9/7gvDaecJmu0UeR+wf7gCe0HUNKDXIUOMoA6CMzGKMpdShSQlt08mJQSOZj8ZxEGNH06JpCeMwYBxH9OrW0wDY7/boVyus12sMxyMOaQdCwjROOB4HbNZrybB0kPSrfb/CoLEah8Ox8GpTECIPVf4tp00Zc9Ii0EonlDs7Xy/rGoiR4UpKoEyY8wRA5Mpnz56h68UDpu86dG0ndYNITrlS24LyiO2bn8UHu7+NL9xscXX5Dj768nehX61x2I+uJOQ8gyi5YE8E7Pd7r/ItSsWsinYKMrjcNxnXwhy6rsfFxdbbbts1mpaR81wdIsT6GCYTmxxubRrPsWxV3+56e9eptgHrUdicM5omgTNjnCaxHGp6S7OuikAvpDPGWERXKtmg2esGuEDE5dQiumTZsQ1pqlvbzU3TiJvWIshUxiIKwjRlJVay0a1qd2paQbigeDRtq0VJkhSk2TRou1ZjbuVdZNEkOTN4npEhVb6HccR2vUGji8lNEjiQCSo2Oh0+FVcIZmBzsQlWIAWHyXmoaU9Fg/wfJzEwQQzhU23DXrJd/RSEh8IES8+26XzczkjNYidPW8axmmGz0wAEaES66a5KZL8pO/VBWprSIjQyl7lZY5aK0dymEhGOxyP2+52NXDdm9s8VwCsIAOIfGVzbqOCaw91ovc87UqfSZkqNvJcZUAuKF+WL/rfG8I15GtyCwo5wz31LAY3DKLZaNl/klArDDOZUt9ygEFgfe2V2Xd4vTFaMDpoJSidhbspGwGtFl2tur3Mp+f0XkqwZFrj0bcNgaMrplJAxO8MZjgcc9ztsLy6DUGoClfQQ3YGKTCuLuBRgGQCpC58NQx+tfOGp9ARrLu5agryTlTaAQlKEsD/I3uV6nALbsjOXIScRcz0YsoYmoke38dKyXqie9/U12hIFUZsPGe1lh5UuWxkNM9arNYThidV3nCahpSmsfUBtQPDXUK9pW2SYXZIXs40wML4T7nEQuE9eCcpOUESr8SCMy7dCoI1gN0ZQ8JMhnOKalvysYE4Afu3NiD/0f/sGPr2fkdmyyZEWjFW3GNvvui5GIz+5Z/zv/vMXeO+qwTdvJ5/0PGdM2QLvWbLsaeEwBhcLKsQ9ZJ4mpKQuvUTIc3ZXF0uM0TSNuIdQQt/3WoxRaG3SQnPuapaSbvFAZ5w3lrVxIS+sa6VMGu2yd6heI4EhaSB2cXUVOhXXIp5Kx1WCltfV/zhwbg7jZcODwtcB9cLQk9tpGmCFTzlgrCsV8bv277vUaWqgATC6TOVklEyxMsQ0GhLaZQarssb622a9Qp5njHMxwhx2OwzDiMNhQN+vsL28xKrr0bYN7h/eYJpGpNSi1TIH0zQ6TIxmUTL/2oTVei2xFas1COIZc39/j2E4IhGh63tM44iJCG3XoUmEcc54fHzE06dPsd5sMEwTOM+Y5gnHwxHr9QZ9v8bhMGC3P+D66gpEDbqOvBBv4R8MkJt2C0VSWp1z9lgQUlyZiTRLoc5LjuPLGtvyReM5ySntuu+xvbxAYqBpCJSs3lyLPO7Rfvw38f7jT+P9Jyts37nGB1/4EF/44EsYjjOG4wCANJvT7GvS9yv0fV9leB2GWWNAelXgSskJc6tr2+Ry9Gq1AlDi44g6tG1CamYcDnM1l5yzx2lEQ385Yeeqr7e53v5EQ4kRCMHfEKJwMAphpVS5OAB1fIWdJqSU0JhAlYugYoKInWCYhuUxFxRS5ipDm3PGNM8QfVgHxiX4qEuNJKWda9erYZxc8Rn15KPrpSiN+bN/x2aPb9ERXavJWlWgIBIkIgIod5jnCTxl7B932Kwk93mTWtHu1R1oeZIQlQxb5LZpfF52L+mCmjATmaNb+lRYM2HDbpmQbvhQhAepOF6IV91mYQaB3BvcyXACDg+ZT1HzZOxlORDu16wDKOqCjmwp6LDBqcDP3zVir9Zsu5zmElSZbZGIcP/mDpgkPbEFfgteBhFCGbnMJhy5EmAe1cYjTk6HuIgSxc8Wbi2xzZFDlW1KoR6ACRGgwoyckZaTHGkza/5vGwwbp4af/lAR+kzJKCdH5ipoieABy31uG5hNekTZnz4fY3SF4+q7KaxdlvEq4/Fxwv9oW6SFBxEYaFzNAOJwAiTKkzADQlL859A3Ic0THm5vcaXpE81d0VxjGJBK4y5kBOSCip4VnodxGZNFWBhtx9JyFtV0sSGU2ZH1EcWVEJgt8COnv44SijMlhqnQDV72HcblsFdY6QGUj6PQKwRlMwotZf8VKQg+toKyyd+1kymJSWOsNltnWvOcMY2TuFFp+yVLDAeYK3VhRt/3GIYR2UcSREUzUkSc1CsHwZbDvEFYBO/XwlqkReR7Qt9jDjFX0f3MLNzSYVY+F+mdZ7kymqoImQB8640qASwpgDOLW5FV5uXMmGYTBgjIXPG0b31LYNs0SU8WpG/xH7fTAsmak5qE1VpPD0hqC1Aj7kWuJAbmwwykEOiRQGEt6qsYyux98lgwgWVBdOMfBhNyulO3GR2ZktGpMjoA8HS0UvDU3JQRnoAjbAnkZndxhrr2cB5daYkCZrXHjA7krPFwhHGacBxHmCJipxmRt0fFqtpjCPcMV+wv2bzhzxeSpHSby2fnK7aMJKpf03YYpxnzpBmENIsSYwSB0LZJixVeYp5HHI6S2anteiRqwCyW8LZpQFqhmgFxOWs7PHv6FFc3T2BKKoPR9Ctc3NzgeJTUttNxwJxEiTA8bQgYj0cMw4BuvUJzOCDPhMQZ4zCCM6Pr16D0iMNhwPV1QtP2kiCiaTHy6POO0DMULjxGZMEpz6DmXLnkyoSoMhA8NtSIpJ26talFxyPeffnXcDV+E0fa4uX2e0HTDjf3P4sNdnjvqsPVF97BR1/9bnz44RfBzHjz5g12uz2ur6+w3x2QUoPVaqWytcR3CP6Ru2IZHs7zhHmGZprK/pzUzWi0YLYVrJ1xPO7RdR0+/vgTvPvuO7i+ucDTp09dNj8cDojGffsbQw+id5Fniv0211srGjaQU5enQvyXsRhOi6kE/9glwr48IOlEbeOxP29tmT9nSlI10jasuzjp79ZXfC+lhNvbW+wed3jn+XMff0oJh8PBA8qtbyPiElGfcXO1xbNv/nXcbX8rur4D76x6NAAiSQc3ZyR04EaYwfE44GK7VSWDNC0aV4wvCguRVUYZ035g/9HBHZQTOEHKJpAagXXrSxBgtJGkxMc6dOHR241CETuRilcKYzIBwSyaflxZphyEl7oxc3dxoSr0IfOjUvjRR8W1QzkvQSQRMjngVmZJ2UZNyZZkuBrxk6zj83xT4BEXIAj4MGgGQQ4ILn5NU5R2i1uAukuZgO7WkwKrbK5MCkRtQa280jer5FSEnKpOuqfTZTA877mLhoYFJoWV9fNtG5HTkbVmhGX89pL4o7prMKtgFuiGCciOpRxcmgLMi5xi/XGVprIoMFkNHyVQ/P7+Hh9AmSybe0vB00VUlPUoMwiIFXl/VDKXAdoMW9tyCQ0wohgxFUHYKk+LABdBTGGP6VOBeUZBJZAPYQgBZ7yLsJ8+m7ZwmLepQwGnXEELygkiralPbKHC42q9QmpazUIzYxgHsSxqGkV3J0GBecTW1WqNx8d9SDpgQ2VXvOJltNdcxIpLXmnfCp1Ve4wIVjU6UEodj+4X5BL7AjXKZUlnnjM0k9EMycKTMQ6D7l1xR7ICuKSunTxnD062wUmwZqt0kMX/u22w7jpJsamnDu5ODKEnEUeMBlP4C8BPblxZIssqByTKYb25wn/nJmrsSLqPI18zUlFwlkugfLznuHZqFJO/Jg/A8bHw00KjLP5IvutpT5aCbPB9r/N2uqc8CKroZlHoiBKG4SCWX01YoFY/dzPLjg6yx6Z5Fr4Pxu5xh1GTjlBKhUn6ZXiOGkjEiKfa8fSK1A3blF3fqxU+OwdGoedwms0kyXFSIgwHcdVJTQ9KDZ48fwfXmdG2vWTRfNyhbxvsDzuMwwBKhK6V02qTlQiERHqylQhN0+HZs2e4vLoSA282VzxRRadpRte2eP+99/Hi04+RMWM4HOUErZNsnjxJpqsnq+fo+w7DQVyEOE+Yc0bX9UhNg2E4Is8ZTdNiHI/oux7TNFZywVKgIMMLYYrIMyOnKXAsSY2eyPhSUFgIAT/FuGXUrvnWf40vHT/FVz58B6lrQGnEB49/CTnPuLi5xIcffg++/OUv44MvfQfavndB/fnz5yXYOwMvX77CN7/5TT2FENiN4wCphL7FPE+VTG3yrCVFgvMZhsWdNk1SdyrZR1/4wvu4vrlC32t630mKIe52OxyPR1xfX+P6+trrajAzBnVzG4ZBMlilhP1+jy9/9bvx7a7fUIxGDAIpvmtmt6uFNpl8ceWQNSZvi4gw22/MQEqeYrTtekzjZJxOmRmDp1lTqZFP3AAuiogc4Zq2JwCSVGAPjw+4vLqU8TOwP0okfwbjOArg5CytWB/ktxHfczXicP8zuN18CXR7q9qdDL2xY+SUAU5S0n4cxRXLhMss9h4vlIOFLKdEi43IKLpXPvULKcbl2wJdJy0uGAahv35O33P/Ya5kdpdXFoKDCf3wUxL2TRxeDX3ru1QzDRMIzIIlFmMbe4h70HWIky06bmgUgQn6QIw9qRU/CRPfPe58YEQoLngmRrhrl1GTikrrX6rmHYUWX1CERYDhfvGTFbiYQKDuBUYbjeEnFdKduplrYI0MJQjbhBWGuPxQte7GxKxvIApL1qwyY1dWXZwIc40LWRgZx/Xzddb1Dbgi+0IZj+5tx9IgxFjfXmQoMgxlmApWRQ9pqYEISlYwklksNdM0iY9sFJxjm4urCMyle4d+QAVevOfYoqdW9j0G2lbBTigwNbD6XaLFGLnsb4OtJVAweIUx2B6rXMPC/vZ+TQgxug72PeTPGb3RvepuXos+owAYn/NxEtC1HTbrFXaPjxUT61Y9qFGtlOJpXIEfEZAp4fLqCq/f3OLJkxsXqsV9yFcNIbpKlJIzgTgEPf022DKDs/gug+TUzIKRGWrYUvoOQE6zda9kC8JMCdToyYD6T7dqNe66Xl2Oku8PKRrmqnrhHYvhcnVDxluC+7NmkSu++BF/wXBPTC+anINI6l2zWPQZAEf8011K9pddETb3Ejt5roOVte9IjQoTqva1iQRCAsqeF7dqpRSO59GEVtaxNGbxceyxJU6rGABmxw+HrK0/hG7sdg9YrdeY5gGgBJqNyojbISxeghkTw4ul5WnGixefeubNeZYYlWLQMhfWBQO1XRSMOqa82b40WaEUPi28BBFuOheAkBqj9NJ2ahpJMa043lhA9OYC6/UGBJlLasT9bRoGCZxuJe5uGI7gWILAXegaXF1d4fLySsZvnijMsHTxxg8yM56/8y4++eRbGI5HKagLdiX7eBww5xmrfiVG4UQYJ8Y4jOj7Fbq2w36/lyxibQPOQLfqgF3ZJyX2zHgQwdKr+6pzBnPjaXrlTIDRETB9/HcwfuNvqbGAy9pt30H35d+G6Rt/E7j7Om6Ov4Z/+Lf+g/iu7/xuXGy3aLs1LrZXuLy8xPXNtWSCImC9WuPxcYf54QFW7+Lly5dglnoWz58/x/X1Jd57/4fw+PiIFy8+lfiT7RZd22O1WuH16zdgFkVsnmdsNhsNH5Bg+75foW0bpCQZXsVFqkHTEq4ur7C92IaY5MkzTr377rtglpTwDw8PeHh4wKV6AVgyKKsO3nWdVwl/m+utFQ3HYeVy5g4lLifZgy1rNynbg0WIdKWgacrJAICkAn5KSfxIW4m7GI6iTFgcRksJ01A2r2lcJvxzntGvejmOn2Z0nQTCPHvnHUwsdSsIwMQZDZNkH2pE4cjz5IyFSMhQnie0qw7fj1f45uMHeLy+Rr+WvMhgCTBer9da7I3RUEJmYJgm9H3vPq+WltXaJqUHTpy5OG6wEXosUicumA45yZMfowDpDzqzqY8B64+1ZSUqGbUQZYTfXIsqeavOrKP/xPEQ+S8VgS9CsPrTMryCK8JT/o31qNvFZLNsM8I0CrHR58ZhwDANPu+SKc3eycLo1DpYJk/lr1mXAGVk8O9R2PIgZ4OHpWJNUoGUOSNBhQlj3KxtEUCxT51DzpEpF9/sIpvYmGshypU1g12wvgr5V7hZWXFnxHbSInuizIclRqGUIQ9uJwUrZTyaipMsvoWRLNCdEpBnxZN63IZrpHC28dtJacRmhjHhogyRWpXRJCRqME0jDocDLi4vUcRiB0kFL3zOd6CgRllvOv9OeM7v+x7jsD/K+3FUxVZmMC/ffQZR60DYi6aImdLKpV37423zcp7seffj+EFl35b9HV9j1KOJ8JDFTNC9QMD24gKPj49gLdo3DAM2vC0yUqRAUUAkcVfoVitsALy5vcV6vUbXtu4WB85+3G9KrBUGhGW80ixHZaAmpCc/JWnUhTY1CW3b+mwsLaYpq4nIaV1yxC3tGn1dxtj4khBCmlijW7Iwbg+i03VMVuQ1lfu+s3Xv+gmN4WMkbxYsHBR3P3Eka2+5R5SHWfyX0R8ui0RQt1w2oTy0C7ixiQNeOx+CKX4oOL9I+24QiPvBXZjsnn8OpjYuOC0Vv+U9L/amAjBDksHc3d/h/c0a+/0e5kmh2ijmrCfxmj0ra0ZKSgmH3R4vX7xwyDHBY1CdNla+XIbnkZcInS20L/JQUtpdgGGkn8B2YO1ZQb1tFlpt6X2neXZ8EPepUoTNi7IhY5oGyEkA4TgcMalLmK1XIon/WPUtbq5vnC/ZHnE6QmVNQQkpZVxdXWG3e5TsoGowBqSmidTL6ZCIJFYD4i5o42UWI8B63YFIAtozTNFdYC6Ruy4bZiRo9lFmNLCNwbi4uMDv/tI9vvR9T3F7+0P4+te/jhcvXuDTTz+V2kwvfxH84v8D4hnvvPMcf+h/9b/GD/7gD+CXfvmX0LYt3nn2Ppq2d0+crm0xzVJQbzccAIIL60+ePHGFDQCOwxGZM9q2wYcffojj8SjG60nqjWy3a+TM2GxWvramCEg21hGrVY++7yWzWNdI/FQo4CcxyUplFffMbarvezx79syfs+LbppCYt9A8z2Kgf4vrrRWNOktTqdAtpxrkGlJ0q0qJghLA4XnV7JUQ5pyRFSGneQI4oUmdvquEvBFBIs9CECxQpWkkJVrf9zgeJ4gFRhUYJgzHCczZhXoJYJKgGm4Z8ySA7FcrIVbzLCcrJMHuiVtknjCOI96fv467i49wc32Dvu9cQE16rG1HU+aCZQtrwpEFfkbi6HQD9iWSW/1eWZELk4juHg73Qk8rS+jZ4mThsxUys3s+JBWGojgkRIKcicTnheAthB8XSJyjoP7KcMuM/nh+HCrCkgp3LjOZ21AUUIIy0CQgER4exHoqLg3BZUeZB4eO3XcakFMup5IFzgXmJpidiMoolkk9lXMXP6uTEU51fK5knLC8p427UcbKyH/WpYKD9BV9VcO7C0UpyKDOdFHNm6t5izUV4KJlKMdnVVoExuSv63iSTS3rfKL102AaEo6q8GNzqeZYNo2P2YQ1E1RADM6SE//i6lJhHPagbqizYnLcV2W5KxbGJtSZEBVhHf6NL1WuWuEFCr/XMqWKj9Y3VT+WpuPG/wzBv6YtQVAMQ/Xt9TnzPmnDlH1bz3oCKnzK7zlnXF5c4lP6VJKMTDOGUbLIJM0Hb8LWSd8MZGS3AvarHsM44DBIxdoECUQ2ZYCgPsurYkG2AGHZBuquS0Z7C57bNixyoeJ0ojAzLvSxOoVgH7DdckOKv8MKawqxNk69wFxO5qrVM5gbzVOfn7KPyrgj3kQ3NptBVCc5E4DsLokELnE+DBFc2U7VgjtThfUl2N5oF4M9uFZAUz77wZkZMwh+UJAdhNl7KONhx7ml27btBXNfdgWCsyRvMQXBiqwxPPsOQ9x7jscjmpRwd3uHiAhGx02OOR6OLpBZalGxxqvQbLxLM6zJajcacBzwJi7vkrb7vi6rVtxiCZEEGzGseDYXnCISCzdQ3JrsJDzBYuoYnGe0mop11hoYIFHApE4JY56Atk9gZLRNi9V6jaZtxCED5GlgbTdnhngXQBSzlBpsLy6QmgaTtku6d/Ms2cv6fgVKCfvDAX3XSjxXNtd5kbU2m7W6p6mSwSeT1/EXXufuzIHdXl5eYvcoSs9HTwi/9Xv/W0jEaFpRwIbjgLv7Oylo9/gIYsbF5QW+66tfxfbqEr/5t/wW/PzP/zx+4Zd/ER+8/yFuntyg0+xTPYCua3E4HjDn2etRHA4HOT1KCfM8YRgOOlTCxcWFFsvbgChVKW/NZSrGUdh7Rc4WhWKeR8zz6O+YsmDuVuM44lYNNlaQu2kaVyTkUKEoHlZr4+97jIalibVJWIqtzWaDN2/uMA6jE99WA4MEIOyb3yLX7VSDWmEC0zyBJy6/zYSmKacdbdPiOIyKKIwmSf5e8y0DVKOb2bOYyImHbJqmbcFJCvXM8+zBWrO6OGUlcJMegTOz1AhBQuZZiBwR+ukNLm8usdqsMTOjQUmHO02TKElQ3zlk7A8HQRCwb5yKnhgRVSIRLZZ2uwiwNVuQ3yObQ32f4i+ohFJe/EXox9tQRhWF5+LkUto+EToWBNKEotJGGEec92cIzWYf9wxU3jc5M2V7zuIYDAbKfKyIzv3DfWHQBOSZwXM4JXBh1QaujKWSwGqBt8ynuBCawGuCDAGajL9Y1mRtWayrlSKpgkdgaoC5MZ2eSkXRVlwWoHilgkIQGG3eYAbpHqiFjvA7aaA0S054d9oiE//sFMYQp/QdC6pUuGZWJp7re35EUNqzfWCwJF31Oji3uG+yMTMXkPTkJizsw+Mj3oO4x2WVhFxhDXssXr7qYd+K8rRcAwTk52reBhezGsNhzksA1bIC21rC3wnTOT9WorImATvLfgk78GR/l3YcVU7mfR42hpd2GmfKF1h996mmbVYsrNHaBpkZ4yjxCl2Xi/uUU4AwJYLXpGeIYNJ3Hfpe3F8tWYcPwV524cuUCcGlRJYCITutNuE5KriWFU6aK/vYcLJIMPD1XtJU22w1zAOtgtJZFeaXpKfEj9gQHPL+P4G5dajwDsseZC4dMhdcdPzRsaojiXXKc8THomgQlRMFw0M/xWCfpb9sNTUMK5S8gTXo3QqmcVgDEXSKC4sX6rOxKDGzYn6WZc8U7gr3Axxs3lkt6ofDAbvdDlfX11itVpinsY6ZYYCZMA0THh4f8Pj46AUnqTHaoKK1WdAdBkrX2VLqnrvKKZyZiGL2MgDFGKVtlexTheZwJD5GW6KB0ICuwEgAkCdgHlWhnDU1v57+6bzyZK6CGdOkpzkQfrJarwDK6JpevA4sHXICJhNU51myTjUdugtJCrHRVLZljWQm0zyBYCeLohhlPyWn4OJYgpdJiaclAzHaZW0afjruZoCT8IqDFhFtu17dOQe0zYx5YrRdh65LeOf5jch8xxHjMGJ7sZXK6W2Dfr3G9/wD34cvfzTgm9/4BvaHB3T9NUaNu2o6wop6TdIg7k43NzdBYZCTjLZt/bRC5OUJQDo5lbA443jPTi+KMd4K8hWFkjmj69qiiAN45513qvIV1p4ElLPfh+6l/X6PcRzx4Xd++SwWx+vtFQ0mzJMJHIxnT5/h+uoK8zhh3mS8Pr4GZhFEctbTB54hQXCiuU7TDIYURckgNHNbTjtcqrDc06MW4yHJpAE5OZg4g5BxHEd00Iq7bEqExGPM84y2aXUfEjANQMriqWHxIYMoKKJ4AMNxdiErM2MYMprUgEmyY43jjMs8YLtqkRo90UmQojNzSS2W9UhKiOWEw/6AvuvQaOxIbUk1YlC2lm8Ef2ghABA5bbD3IsEU5lFEJnYJE5WgsRQuYpNxTPVFKFbkWpCxRjKFOiHWFiAWHadpdQdLJaOIFsFiHca5PPGBE/EyKmfUDDQkbe4eH0CUPaVi1pMuy4wkaKitKBPnwMyjpXPJtFhT6PnsgpWcdZIErVbuFocIIAjFo7BWXv9CH4iCjs2PyH2mnZgSOeOpRq9zWQrk0pzFgsB/cwGRjVCHRdAPIlyUdy3tpYOQFSKeRobB3ABabMhbDXhd3NlsjohPFgQlKn3HTv2PMVJRAo+HnRfsc+E/oaI/8VQi/q2FElQZ4MpaO5aIAGsClIE0IHoReK3ZuGeXu4ur9yrFMF5ByYiucctnHe5qzYvWTgYW7pfLeduol3vAcI3quRmNsyd8QIRO/X2nccT/l7U/C7ZlSe/7sF9mTWteezpnn3PnuecGGuxGozELHEyCpEKEOIAOiZIHhSU75Ac/OMIRfnGE7Rc/8MEhhcJWWKKCClkUJVGUCJgDLJIgiKEb3QC6Gz3deTjTntdUc6YfvsysXPteqC9tr+579t5rrarKysr8xv/3/7q2oeuke25wxv04BtbzaJxqmDXv5CJOpHuQg7MRTaxS0dFRsEAPt0B4aO73Yc79s7VhTMF58Oc2fo4+4ni/LqP9M8iIeAWwJxdCTYTfUOHuhyF7aWmDkRU9N//s3PH+OBOKkwf5Fq5h/bUj4FEkc8CGHhrE+9V4Br8hwGhdIbU1Q9O+0L3bPWCxWz1FvssYeH3sjfUIahTEsmfccpS6cWbfX9v3wIqVmwRlFN6gt0bg3zc3K5qmYTQeobWiriqUEopRjQ02hDHG9U+Q+Qiofzs4Gr7Hgewpv/78vhThE+qhwk0R9nFsJH/I6YyYunCyJV4L2Ahd4tejG5fbXbd0KDRNxeV756RJwp27p0OjWDXsJ63dfAUj3jUBNZauacXZktWB6Q1N22CMCfW0QFgHeTJ00U6TlCEz7jeLwvbWNU5MKfICa2L2I3HAjLEDnbIyw1r3+i84WxDS6Xu3LutXW8lI9cYwzwyfeOk+40lB11ZUVUXTdcxmM+mg7rqn52ND23b0bYuuKpI0dV21xzzzzDNsNhvG47FzHAY0j2826aFIAwGSNNgTh1qM/KqqqGspBp9Op8HwB2mmJ85Bj1JpKF0AyLIEazXr9Q11VbE8OBCb2jklWEjTApDaEdGLrvA8kfm0WNqmIU0z2rahaVrqugpyYLfb8XFeH7+Phpab69qWp+/dZ1KMyVRCkigOpjPmkylt37Pe7VhtdnSuAZNFWshLhqEbjDSVUHcDrsx7osLhK5Elk/jh9fS9y6hoRe85hq2ib3vBCwJtZ+ico5GnkCqHv+sNVvWkqX+o4NWtMVLLIQwTjaursChlaW0HiU8pKrQ2cP4deOaLWNPTIxjHJEmdoCTw3SVaY/qe7XYLkymZ8yi9UvPyfxB+si+CLL1tdfg/7fCmFy0Gn85nUHh2EG5exg744EHIyOX3ce/xj9vgi2HLDtjbOE0Z9O6HDNnh2Nh58LEb/5YXgoPhFl/bKVJ3jyacIVL0wTIVIzQEgvqepi4JkVbchncKc4gCD6nAPTdnsIKHSQ03ZQkwKBUpBRzpapgfTzFJ9HBuj1mOGkYg9I3D4hgsp8FoUoNz6D728xOMQn+M9fdlI4UmhYDBEHERwMDQtDcXXukQ0tR+PUhEzRkfEePTUHgu/8bX9kZZgGCrwUDAfY4v4o1YdPxmG5xiN+NCQxSA7dYfYC11WWG6liTLAwXq3uby9xGmUpxHWefOgFbREe4NgeHJy/i5gVv3TTRXDGOL9qd/7VNeuyfsb/+j9rcfryIoB38XcXM2/0zDmGKD141A4wE4H3XfESwlyCB/r0SwL/aDKmGe7V6dapJmpFlG21RUZUOiFd1igek7x6KUDo82Nryj6Q/z59euu/BgbA3yRgVPYHgosSTygYlYaHnTzPse3pjEvW+cgSLr3J3z1pyHSQmwIxu9OezROKscfjfCbGNcAEx5B12J3PcZOxNd0HcMjq8t29VLBLkZDx0CNdQZGNlDQ+2BN6xt9H3CWLyDYRytKzgIkj/efY6Vfe2OlhoCjPgJ1vfMIshCHyhRisHgxdHpK0WilGsE54qRnfzUfsGoARKklXcsXE2No3rtrcxfb3rarqcoCuq2DZ2wtdIkRRpqytI0Icky2qah76FpLVmekXcZZVkFB8OvE5+BVX5z+uftnQDnpA2b069zrz2cFPXOnFs/Aj0anCqBPDvLIgowfZSA8bTtfW+G77oxlLsdXdPQGMv5+Tl37pw6g9QGYhKlpIeGz17FS1npgS1UoUJ3975t0UCWpq7eQgSZThLoJYOoPeOi3R+7XxIgTHNd10re0bp+Zv5xayeDPHGIfzkh5OcnzsL5z5WVpspyMbGrrh69TVM+RXZnjjEZSepKANAYq7i+WVMUBdPZjMXhJKB9JPsjab/RaMx4PNkjUhJj3utNG+rVwDoWVmkPEfet0Dql60qShJCxyLIs/A7Qtn2A/oGQa6RpRpokLOdLLtues8dnHBwcMBqNuDi/YDKZkqaG1WrFcrmkqgSyNR4LTOvi/IzdbueyzBl1lHHyECp/zA97fXx627YhSzNeeP557pyccHl+Qd9KUXaWaJQxaJ2RHxywXm9Y31xRTMZYFE07YPr8JkgzjbSFl0yH0kM7cy/GvQEY2rADqofeqlD/0fU9dSXHaUcdagzyXpYhjAIGraHthfbMZ1FM34fGaX3XCDVdW6Edc5S1QmOX5zlpktA2HcvN71CdvMzi6GnqpqXvurCAvUL1e6Xrei4vLimyItQXizE2GIpDmppBCQdZE2s9vzmcmreRulfD17xQh0jRM/w9zK4Xhj49zeAERtcb/vKbleh4F7VVw5v+erfNtz3FhzNRbglW/71IJN86z/7YNWLMDTPhj3HGtaMDVEDTtPTd0MTNp359JH1/PLeKNu1guol6VFIIGUWM5IfLLPjImnI0wu78wdAMkVZfpOflqjPk1P61h4gUsmfcfRGtnxC1cYpDaU2RZYIPzTKyPBuEl1P+Xd/TNi1d39HWDW0nBkIYou+B4QY4FBc75eT6YuxlsIKi8ZbxsA6Hwhe5H60S9ywc9En7+SOsx+G+vPk9zPng/MhKDGvAWKyO5sYdJoKxZpblYV3sGcrR+vK/KCv7+cNI1P0MRHQIe9Z0WB6RAo10f3zs3rXZX+fDJt7fY5FIGMyTyBK/fb7wux2Oje87XO/2fSvCHN/e2/584Xc/xsiA8rt0gPDIL6NRQbldkybaUdy22K7DJAmpDu3s5Ahrh4ipJXp/uLsQIY7m3ItSv5ai6bn10+IZ9YJcs/ERDrJlA/gK7FBv4aPxsWPlD7VYgWjsyVQbtqxxxpCEDQZKWYsVyKUjXRFjfIj8G2+EKitQUGwwDgdj34YIZm9NeM/LNYt1fQ4Ie3EYocU3+LM+0GHFSA/7Rw0rInZOsFb6dWgx+A1DfVqSyj2nqTgCOk0dW5zF48jBG1yIAahViNbur6JITwRHWokRqYR6tbcmGOkgcJsURZqkQpeaCiyryHO6yVTqAhD2KOt6iSRJAm1HmqaUu5K+6+n6Pqx1j/fHBi0jqyqsibBYh5fSSKHGvi4Z9Jg7JuwlFdZMLEeGfz8czAgIAie7BXIkaywJ1NCGNMso6xKUkk7dWjmCnEIgjgassZJ9MFYCvkqg8v6/qqpCv6KiKCgAOxKYED5o5SguEy01HMYYGk+V6yn3XUBPR4EoFfRGdMdurSTa1QtEtX3RqhymG6/H3B5zwazh+3JdY2UtHBwcDEEwhjqI2WwmFK+h1mVovyDrV67m16v/6bNCHrIvcKZYomp82YPfB9PplPF4HMoEqqoKRDae4VT6aQhUSuqVa1arx4zHYyajMXXd8PDhI7bbHQcHB/S94eLigt2uCufzkEF/jaIQVi9Pv12WJYvFgqZpODs74/LykjRN+Vf+8l/mh70+tqPx0nPPCQ7N9FxfXqAw9KYnzwv6dqhN0FnGZDrh8vqKqm4wKkWpVKIHWru0mcF0lq5v8CLbGOHn1S6dKOQgyhVXWcd+IJmHAH/qxYnwtRgWxwmttWDQPVxFaWdoCvVc3dThIcnisWy3W5RSYVL9gzQYJpMx89mcNEkYJwnJd/9z+i/+L0iTCWVTYazQwO0ZE0DdNqAUddugUx0KEwO5j5cftwx6rxmtHVpdDAFvL2ic0AgKb1+AxX/t8XVEQuu2oRM7GSYWZsGUj7eufBif2yv0wc7aU6l7L29M3h5zMCcHuYgX1uF7t2y2+IQxRtwoT4XsGBVicWLjv9w5jYuG+0hNuI48oJD5MSY4IgO7hZs/H2Vyn+GMoL2C7DjqpEBSxiL4rIv2BUyuc1j87yIodQQ3U2H8aZKS5wXT6ZTReESWCluHTjSJToIA89kEYzykoRfYYddRVTW7cstuV9KbPiyX4dqDpRueN9Ez0jq8H1/LY8v3LHa3+IWRzdfd6BCVDI54iNxFc+uvrbxRMazPeF0ZY7GJDQftypLZYuEOtkPX5YjG8/a6uG1MeXCQd3R0aOAUPxG/1fwgY0t82PfDOo8My+jat+8n/ky5w8JacBsiWlrh7fjlbtc1WRucgD3l7J+3/8QOP8Oc3JJbKrrHof9HZNxYi1YCTdBKIuxZJgZC4igT+66l61tSm4J1eGt3Y8oEcNAgX+wwkeEaQSqpDz1HazVayZqLxJm7xsAK5GVq+Bk2grxM+AyPQcLZtvtMgU6O+4Z7iqE5aHAUANObUFdgXdbFOqfA49K9E++dhvg9iZvss0Bhrcs4u4xMVFAt29EGfWAhUFr7yLzsKJkn5eSIZ77TVpGladB70tDWT4IvMnaZfX/fbm16HLiIiwjKEi3cQNnrshpSIyrwE2NMgIBYO+ROY8hacMAM6EyBSZxsdR3RQ5GsQHx6Y6RGyNGFlrsSCw42ImaS0mUIUtZNLXaHg9v4wEew6Y3HGXj5xv49ut9VkP+3lqIa5nK4r0j/OqdPMp1RFt7LVPdtH+Aari2/B5bMNMPYHX1vGI1G3BmfkqYps/kcgKaqQanQN8HX51prsK04kkmSBNhaXZXS/DhNSFJxVrzTiwtyqWzY1QpL1zQhMr5ndCvtel4RMiVinA86FxRpmonuNNHO2xdm0fyovZ9ebmAHZjSvG88uznl29wwaHdaAd4BHo1Go2xkCYgzoHOX/U8EJ8fcntqUEQgVN456UAqUElt+2LUVRBNrvsiyj7EUbnIKmabBW6IZvblau9wbUruHhbrulyAvatuX8/BxrLcfHR6zXGwCef/55xuMx/+Sf/BNHhZuG86VpEmxk6W6ecHl5yXQ6DZ3Kx+MxH+f18Ws0mh7buwJaV5vQdAZDi+mlKCjJUtrOkI8mqDRnuyvRuY9aJnhIZttaurLEsxxZF1npWtc0RWlQiTRN0Zqu69Gqkw3VS8Fgnuc0de2EjXiGWE+5lQpsqd3RuAnv3ANTgHZwqK4TNqm2lbTWdDKNIsSSpWh7w9X1hpvrLVmSioLMZiQX18yPc7q+p6saobvV2mUuZCOUu4okzVwaSx5U4pur4U0VBs1m7RDL8gLLfT4Y2sMGC5R8an9fef3u42N75kD03dudXGMDzl/TmQnuGQ6RmWBDfJQzccsA2btFHDxjz3oahLG1kaIcND4feu0JEvd1NUB9PHZb3oeyKt21XSdkd7Ck+Y0gKhz9ariEhduElMYONqPFhuiKZC+ILEc3X+hQdO0zMIPl6EcaOTbO6A7GjTdo/ZqxhF5OPkKbFwXLxZLReCTORpY5w00KyuT+jINOEASjiiAHFmH4mEw7lr1ELXa7kvV65WjvCEascQpu/xlFSsIb/26O4noRvIETKVnloj/eiIzX+r5DasMlwzMP88ZeJN2vNQlHua6v1lKVu/1BDwMeXh+xtqJvuruKzVg3ejUYPbBXE793wniPeWchmM63HR73T2znDvtb1lRYG2rILn6ITcoO0mBQ8ft7MM7RWG/ERMpauWvEgmIwGKJ5iWWXHd73z147L0RZgQukmRiQaSq1O13bYLJUcPcONiN9GnxUneF5hzl0hpexDqLkJ0HuRSjECefwcDTwsCgLjslq0En+IFnz1nU3xjIUItvBEfABCgmciQM/OBcmcPF7mNGQSZbZNVau4a4WnoexNjDfKRvLThuiwyGfp3BdwEWHhbqFRKNVisWS6MStPZENKnHsNXJQkA/BuYqWiTR3S5wBq93zliCiD0x4BIF2ETVvBmvrC+3d7nFrq3eOEyBrwU177/D41ord4TVW392uiXRQGlf3YaygFYQuVcI3vRGnrOs7IY1xSAeUclCeW2I5PGcTnC0gzIt/Jkb5OfL7wu9jwuZW4XT7UiPUhoUd5t53c+6f917gIMgUD9f1w/V/e6fYPcs9OawcYYqSTExvgwFt3XzkowmT0VgckL4Xh8kYiiITR9NaRllGnudsNhvneDnD2cHJV6tr8vwOSSQZPKTTZ338yAw96/WazmcClEDj/BqX/mY2OMnWGJdFUAFmrnWC6d1eU8Pc+0DVh3LPdl9uWWuHTAriLBwsD3j5pZeZTMZUu5rdbkeWZYGRSSlp1qyi/eLhRNZa0lSejQ9cezKl6+vrYLxnmYdAda72QZxX7yR4UqPJZMLl5WVgMq3rms1GSAjCmjeSoUh0wmq9ZrNZS88wBdPx1DkmW5qmJctSTk9PefXVV3nnnXdCz4w8z0NPjul0wmhUsFgs8EF5fy8XFxfS8yjLuLy85OO8PrajoVSCUhnrTYlKapI0oTOGdlsh5pvC1D2b3Y533nuPtjcYpUisZDv6vqft2hChcXm4kIoKDoUjBjde9BtpOa+1Js1SmqrC9h1NK7ClxPXRkNScnHO3LenalixJ3GaRhZ2oJHA1K6XI0pxEZRSZeMpN3cnDtmBGB1THn8Le/TToNAg8sGiVMFqVpJMKZWG325E0bWhaoxNFqhTbsmQ8KqjKKtCBkXqMnsdS31Io0QbYM+aiXy0uOuSVoTvIRt+NzOXhNy+0ouP2zK1w4QGr/SG4VIhM2Fuf7NmSt4Qr++P80Bij+IRiTwgEIzIabyxwxe4Zot82jM06Y0RuqKoqURxqEKooCUYOkABRZoNx77JU7p4tDIaMG/dgKBCUdLg3b+R4w1epoNyC/g5FLj5iOzwoj+ONFXoUGhO+68NDxhPBiI6KEUmi6VxPgrIqg1Gjtet2miTBELG9CZE/rRSj8ZjRKEfpEV3XURQ58/mMqqy4uryStHqY00gx+2fv5ub2GgjRvuEpR4XUw0LwAQdv7OFX3959D38OyZVho8TwP9MbkiwJisQCZeU69Ybot1w/hifJkHzeYjAyBltiUOBh/MGgUNG4PvyK91ic5NhjMcIZ5NFeiez9yJkmzDUQAg+D0zpAcKLZBH9uv79vGZMQ1Yncej+YS5ZhnQ4fRVcL8Vx3e97AcGAo65pFuQBP29QkrtC0ayoqLQZilmbDZPnAQbRdJTNC1OfFQkd0p+JkW2XcKQTbHXroYINO6k2Psp7gwO7JfGNMgB35II7Ptosc8WvKhIXpnTV/HXwxNBG8Mtrr1hWJevNcKaSJmAWV+cLZIYoKhGis7AcVPQ/HkqUI5+16aYibxHCPJNlzYpu2FefP6VUVjc1aS9N1aJ2gk3Soq8CvA3kY1so1jXOAegcv8tmAvu8xnehhYy1d2wQHzYKDcVlnPMqD7jtxKAJblX827v7izWZDkbt8wd9DlmW0XS8FxQx7zCQQNmX4zQPYBpklc+bG6eXgngIg3nzud8cq6Ohegy4J+8fr1WGv+8spfz412AeDnvSOoA8ARIyHfk2ETSlO4V5XXud0+Qi8Z+zs+57eWlffqlzdRUeW5WJ/NS1t3zla6YKyLKUY2/ZSn2Yt2/WGIi+Yz+fkRRFYH9nTY7Ie1qs1V1dXYS36rJp3KFLXf6LrhVhHKaQmFmjbDmul+Wfnm2i6fSlT4PZYyDgRavf81Fg8FEv2uO8GXuQpR0eHIleswIbW6zVAaFjXG0NZlmw2G6qqYrVaMR6POT09ZbcrsRY2mw1N0wT402azcTS+hkePHoVMjc9g+POnaUpd1wAOBrXi+vqaruvYbDbS18UKO2pVVSiSANvKsow0yUnTjqurK2yPc1oSmmZH1/VUVcM3v/ltqmrHYrEIVLej0Sjs+ywTetv5fB4+X61WJEnCZrMhTdNQ7vDDXh/b0dhsG5I0oSehLhuMaqnbhrbtyNIRTddxs17z8MkT6rYjywsR2FVHkvh0UBexTFlRhN7QcamlNE3praHppP7CV+unqaZv3PFdK6mdLMV0LV3bSsqn75lOJ0ynU9Y3KzqXSRAlpEnoaUzDtq4p1QSASb8VPKIz/JtkRv3KL8L8NBjkjqhP/tcbDD273ZZ3332HyWSKTnK6ukZnGRkWbeSIqipdhkPDriRLU0klK9doKWwCGwRD0OtqUKRAgKwExQ3OC3fvqVvHQ+Qm2GBc7b283HFCLjYsBgPPKUx3UX/OODI/RKK9EUZ4P5wsDM5L1P3i4tho9feH/1Y87OiLCgKO3MbHOUHuMw5aK9kQ3nC3uGZdHvvMoOxFA+wZmMFyhPBAYqX+EdMa5iFQIroJum1cDsaMO8Y9dI8DD2lxZ8yiJHW9PDxgOZ+TFbmwcVhLXdeUZUWWpQErDdCZHkfG4XSfIkkT0jxz0UmwVoTmerNCJwmz2ZzpbEbX9aRpxng8YbPZcHl5SdM23hXbfyz+2ceCPXrsHu7nTYAwjwAmLmBVIevozxu/YkTtnrHt5UoUAnSPMyjtpq7D8wkN1vweizwNiZZ7j4DwDPWwqt1lopkIFnhk3HtjKH7uflv4cTm63WGPuc/3DI+4NmH4jhgfdv+y4TYse3j/2LBhuJ6NT4jsccX+3AbnRg1PPa6Buc1UpVyxL94gw691OY/GCm1ooplMJ+zwclA4+6vS0Fa1UEo6HdC0EvVrm4a2MyHa2jtq094YiWR3NlwPJQW748nIQVYdjlsNNocY0rfyOz6QErGaDZF4v2D2AzaJzwrgsoUeLqFVyByGZ6xVoOyMl3gIKjjjPhiNzlmXjuRybS8brJXsgXYyr20dG5LrRC7ZeTmsdyQK0mBw2G8h4OCbpXU9XecgRm5+2k5w4NZIVtAYS2eMZIW7PkC/etNjzFCU7gtU/Y0OgQQG6KOby0Gq7MNlhzC/399OjgQK20iWuEnWanCERNX69edgKm7v+hoUL7Ot8hBnNdRXYx0tPlgrDX6HjITbTd7hcDrfX1uglf4zf3fO+PcZcxXfWywDfADDjy8WEG4/7sEA3foMCjna6zFFrtbUTc1kPBEHrGlC0XLviHxQ0miucY1OJ+MJTXND27QkSpOlCZUFYzpaFNoxUXV9x9nZE3rTsVgcUBSFZNGcwdG766xWa87Oz6mrKug12XKiu/IsJUtS6qahLCuatmaU5eSpZL161yQ6cc6ItYJQCH1kg6CL7zsSxqKssGjH4iH3DIrVt36Fy8vnODxYUtc1o5E0bby6uqLrOhaLBbvdjt4Yzs7OGI/HLJdLLi8vndOxxlqYuqakr7/+OiCQq4ODI9577z2stVxdXfHss8+y2WzcXrbc3NwEitqiKFitVlxcXLBer1FKCcEQQy85rTXlTprtCfTKuOzEJDByNXVLXgjRkZAU7SjLHWkqDaf9eaUnyZi+72hbGa93KoAwF1kmfe5OT0/5OK+P7Wj8wVtvU+TSEVuKdxxDk7X05ZamadiWJY0v1rYESru+F2Ek0QzxQruuQ+kU5YSaUjIBWSq4vzxLGRW5K9aGNM1lYRQZOrFYI10gtUpccybPWmFYLqYsFgvWN9dsN1vauhXhkSratmP16X8Nk8/oTU9Z3zD9/n/HXNXUvaH51F/EFssQPZaIpxZF3/fSQdwXvHWW1XpNogWPOGYsyV1X+d22LX1eoFRPuesocmnQorUIbuWaEHrFFyMxP2RfWbB7VqpnqPLCjsA8EsMmvPj2i9j9En4MRgN7196zPOzgiOx93+59JQi3uJGUN6T8K0BB8HLXhmPV/ikHwzs23BjOG9nv0fHemDUhIqiUczT87eOMIHxK1hJ6HMSDGCzkcNPWC3unfJRKhs+iuZJlMNAqBriVUiGCYt1c+MI0CXy5aFmsJCJDeDIec3JywmhUkBcjEq25vr6ibjsnzKGqaqpd6WCBjWtA6dacj24pgaVkqaYoCkaTMePRiPFYuo6uVyuue8N8NmM6G9M2HTpRjEYFl5eXIvS0KHrvdIaaFOUUs1POWvuaEuvuIo5sub013CQeL6BQKNsTEt3eQAnOiRUmlo9aPP78ftE4b6NzNQB5kjtlemuThVsY3HS15xh7HeZMIr8R/KW8YePmwe+xGCwZzItgX1jHTDZs3H2zfTC+lN9j4SaHn34KBpYz54REUkBbuzef7qwMO2eA8gW7xw7jFbgIwbnw0f1QMOkNRucAeaYj7xAN3ZSFSz9RiiRLGU/GVL7wENAYWnq6zZqu7ymrinJXSV2e8xCGuRDDMHYOlBIDrxiNUCrDdJ1E2FPcOhqyisZa0ogfPrC9OMdeIrI2GH0qcZBDp9i9Ie4DP2JcDrWGQj3pWOmcgWqccWusJdWJO1YyInUt+OjEsS56p1cZ0EkaWG1MCB6INBPUlcBY+r6nbjqUtfTWUjeNfIal761Qz3uWqN7Bv4wJRdx+vdjeFSp7/SMP1+1bwrMYDO5h/+AZ4Ny6CTrOWmfMu/Hi72PgEfRsQENN2J5QDudUxJl3G+2RSCcZceSlF8GgBALj1vCGMzRdPU0S92Sw7ucQcQ97JnLgY+dBeQgfDMZ/tG39PFlrgnzwe2iQS5Eyd+fZI4KBID/92h9Wd6yvTch6+PE1dc10MmWU5zR1Q991LnDbUFuLSjRJoijrBqxhPB5LV+yupW4k4i39CBVt22A7ed4KRZokPG4bNustBwcH0shPJxjbs9tVbDcbdmXpmv85ulflIFFGYVXCaDxDJZq6roSJTml0mpAURciEpWmKThPqXQ1KO1jSkF3eq60KgWMGJ1EPc650wng8pm4qaHfsdiVt01JXNW3TOrKKnt1uR+HGcHR8zHPPPU/bSo3xxcUll5eXlGVJWVa89NJLzqmSJn/eSSjygpOTO7z4/PMUo4LxaERdV1xf3/D44UNx0pXm4uKc3iEUtBbm0qIoxIZuG6xJ0DphNCqoqpo0Ezk2GuUUo5HTdSld19I2DVmWOpga3Lt3Sts16ESR5TlpL+dqu0Z6eyhFXUsTVQ/PStOUzWbDZDKhbduQ5flhr4/taLx3cSMDTVPnzUr6qNyVpHlGXhQiwNAkaeJs50QUq9ZhA2pn+CWJpF8F0iSqWFmhQMP2DuogODgDdK7hiVUZOgXTGbBKCnWSNBSRQ0/fNZS7NVrDyfExN5crttsdFkuLhvFCHAitMMkBu0/9q7Q/+FX6l34OxodCJ4rUS+C7nDnBQzewamidkDhB0bU1W9OxXCxI0oK27ejaBhCB3vQ9282GIs9J9EQyGonAqLxQ9OIjRIf3DHkblCCwJ5O8cSTWgdozuvfidLHMiuw6/9MLv0FnKOLDP/RyYxmO9QLXfqj+9RZg3GGmrTODbtl7fhw2mBDRNfcH64/18AQ/DrFVhfXJ9K6JIxLfDYa/z0581IR+6DXMvdgfbl2IpI8aKkWQG6uQnPnwdAf14ZwhBuFHuAOv2214GFonLBYLDo+OyHJJcZZbEYbG9NjesK0rqqoUzLORY1QitRooS4pkSqzSzgAyNE1PXW24ubkhSVNm0ymz2Yz5bI61sN2u2WxXHC4PWSxm7MoKpQVmdX5+jlE9AX5DvBjlJaloE5Q/ypvoKjx0Mco9Y8hgCMTOi3zlVi5Dx0o+YuFyxm+AsthhofR9T9vUZHkqT8HiupgTjIrBBHUOhvLPhsGwRoV6n/DkbRhW2Hdq71QWXzAtWYjImAjTYYdluLf63Np2Qe4YPuX3vo+aWj93vj9B5PDsFQrHF3Fzp/y1rb8HGwJGPkI71B64axsxzEzILHRunluHlzfoxGcN5FkopRiPJySpCxSNRuRZKpHLpkF6Lwi8ptyVlGUNSFM1a4XVZYBvgcGgHBthkmmSRDMaj8nzgqIQljGd6NAIyxcbh2L1YVXKM1T6FkRy6LXjDWZfH6AcxMQGeJfs/d4OEBAPs/GdmHXii7qNy8TI3Pvi5LLtMMYXH/v6AuOKxq2DvrjGl1ayCLa3wfG3Hj4SOX6yHr1DNqzzIO+9IxDWiDPajVvlYbmoaH3cXqweFhkZyyYOJERwJF//4I+MjHFZt+65xMrBxgtP7kNHsiUoMBV/P9pnXo57J9HPSbgN7zRb6Pp9dRBDj6I5jbY3Uhuf+FlyWSe/uf1c2zBWnxmHSOrsCY1o6Lh17larjnTOYFBHExiNVd16X2Fp2gaLISty9E5qbEzfUW7WPFqtsNayXC5ZzudUZclkMmU6nbBarWiaGmtSObOX4y7Ya43BJmID7na70FTOE/fUde32YkbT97Jnk1R0Qy92TlYUgWiob1tGRU7TdmjnWLRljTVS54BSwT5s62aYj1jn+vsejJsB5muRDFQvSBVjOmgavv+97zEejdludmy3W8qyDDSvbStQ+dl8xv3798M8X1/foJTm4OCQ8bjmgw8+oKqE2Wm73bJer7HG8NT9p7i8uAhZJM/85BvtWRsFK3ytDJJ/aV2z6iyVvhlZXmCVIi/SUDC+K7ekWcJkXLBarcmyhDyf0HbSr6hta4yZsDxYUJYlIN3PfS1JXVfkWR5qM0ajEVIkLv1QdrsdSikuLi74OK+P30cjGZNNp9JFtevI8hFZmjI+WqASHbizi3xKkiZDZMQKda1SUlCSpi6FZg2ZgixNxJhUilFeyOQZKSy/urpBSuMURZaB0uSZom52pEUqFfsOH5ilmskkp+9ryYyMc1kg19eM8xHKGq5vbqjG94OwVSg0CXo0o//MX3QyzGK0GKgDTllqInzN2oCvdUa97+DYG26uV6CErcJaw831DeNRgTE9pVaUuw1pAmo0gs6AS1UTDJcYesQt4eMiiBHUahBQ8u3bZCr+bOIv2UCJ4hVKHHENTEq3rh0GE8ay/2EszrzBEwNrgmoJJx3S9soVPw+Y+OGcxkbXj+8p0nnBCfHZJ/e8RAEp0Iq+7ehagRwo65TKHo2eH5dXALGQVuGmg6PnBPpe8XP8/TC/grMe6PHUMHZ37SFT5K7pmK/iZ64TzeHhIcvlAaPxGJTl+voKjabrOsrdjrqqMAaSTLjetU7RKgWtSRPNbrehrEtHl7cgTTPXlkOgKpgGYzpuViuuVzdMp1OODg6Zzxf0puPy6orReMzhwSGpTkl0SpqlezhT62GAsZMcWbdDcaN73l7oe4MirAAPmxJlEVRGvBgierI9leydX2dgh7UWJl6K5xTSyNGiSNx8+0uosMjt8BOGDAn+HoZlosLes8NJ/MDCqezeuo0NFPD3u/8a3rJDHMEOBmRsA/nv4MdgffGyi6IHR8Jx0FvrICDOaIrn3L/nvi9Ma5a+bcXAVY6JROtAo2rcOX0d3HZb0tQt1vYslguhCU+l2VWRZSgtBrjSCm0sRqVMpmN0IhlI2xlSV3ukdUpTN1RdPxjEzghVypDqlNxljItRRpbnaCWR1cAMo12/GGNIskwUtzHDUnL3HXPY+zqBJLAKytz2gTnGukiuZ45ykCNnQDVdJ5FiXzTu5sZa51R0AlMJrDqxTLLcqhOw0TMeJM3gHA+GvbWe5WmQZz4AJMcP8kxh92E1exsBkUfWfuQeG8YQHRdv1CBL4yCK34uDexfknd9u2i/qeFxDVsmCBHcG+j8nlofMnPX35SFofo5c9NrawWhXXjZbK/o1gtIFWeYYDOOsV7xjlZd9YSyeYVLjNVXIVFsTzjc8y/i1L9esjnSoRnp7DJhPPyPDQ3BsXns1WmE/SwbBBwOyPCdLU4HCdyIbu64DpVivNxwcHlI3DUUxZj6fS8a8Kmm6jtT1B/OdpMXRTx3hgNxD67IWbds6SlzpFeHttyTNJDhtHW2yq9tKEk2524ouTxJ0bxgV0uOhahosMB6PaLuOrmtJLLRd51ROZMVYG+oj47DlsJ7dnCmBddlmx2efWbBer1ndrGgbYWM6OjpivV4znQppUFXXVFXF2sPSPgABAABJREFU2dkZs9ksGOK73Y66rrm5uQmOia+pAJETb775Jmmaup4Vgy3h2yr4AvLMFd4vl0tnP6eBinY+n5OmKbtdGWBnbdsGVreLiwuha25bttut1NU46lvjyGG01uE8VVWR5zk+4+p7aEj9tBSmT6dTptMp19fXwFDv9cNeH9vRWCwOZAG2HUkhXQ21ckVjthMIk1YYevrOCPWds/z6rgUL4yKjrivAkifw2vPP8sorrzCfzhi5ivdRMQKlaYzhN37jn/Pe+x8Ix3YqjkaRabATDg+PmE/n1LsaayxP3b/P/fsn5EWCMR3bzZbf+q2v8vab7/HWW+9ycXnJ2eU501dPhNlDeWq9AdPoWXm08WwUTtlYI4W6Vtq5G4TOjV6Ugo+sGWsx9CjvQOkRtu9C6g8s240mSQTrWeQCfRmMfufcqMH437N9cWaXu97eZnF/OBUgsgYcR/SguELnXPeGs5n39ArRtYeocxRZstF1o0hqgIfEUat4gHvG2SCMb9tlEOsY+WCYkzD04IyocG275zj5bwu/dDcoPOPpI29FmELIMnpFTkc4rw1Pwk2eFD6CQiuBU1kcHNTRVXpGED/Z1v+1F+Hziiq6tlbcuXOX2WzGeDyiqhu6rqXvDKutsEVIVi+jyBQm0ag0Ryc5SqWOYlDTbna0nbjt41nCZL6UTE/fk/Qd5eqMtunIixwF7DY7yl3FfD7j+PiI46Njbm5WPHr4kOOTO8zmM3SiuH//Po8ePaZ3TBqemSwY7hGLUsxGJJ1/nVL26X6FM+7Mh9aaGMIeiuGfk1tr1kIyGGCEMahhUYdrKzB9eM6pVtH6UeKYCNh9b01Fp8DDX7wf4p+lX0thXfln6Be9N+ajz4KTAa5o2X1komt72eJr2nD4/UiB+u/ZyNnwhe7BKQmOhQ33Q7T2hN7RfAj25WE+QsfY0bYdClcv4E8RHBSB5lkLq5u1M1ikCdRkMnU9iTSgg0GmgQ4b5O+oKEiThKZJ6DqDTRVt14c96gu2FZCkmjRJmM2nDjcsRYupFn2kkkQcSSVZikQn9KhQvK2ccWOMCWxG0szM0BvroHa9yzRI4KzvZR68gxUb0bHDZv1aCeb4vkyVhvWDc4AzdL2htG9iMzjALq1lg+AUeRSCShDmCf+7f9p+ETvZ4iFngz5Rbl86Y9hR3HlZHZxRbzATjTNYcMPiUfExviDa7/34xsIeG+CByhnivmFpYFOyUTTfpzPc3Az7SA3XdsPKnLF4fnEh69JdwzMHyrUV2khhs2MFiOoRnZNy63b3ZEukSzy01tPa+zySZAfd/ZtIJkSWr9+vBP2tIpiacrUiTgZFfPkeNjWsNbc+rBVnRangiAJstxsO8iPGkwn1tcCnslzq/oy1TKcT+b0zbLZrFosly4MF/WVHW0sPhzRLydKM3hoSnbiaqiQ8M9P3GCQwofqBch5rSbMsdMc2LjM6GY8pilwKwKsSjAuGKc1oPKLvOpqqlm7h40mA9kjNVs8enMJYrB6ek4fLhcfm90Jk5ygs282Kuq7JspymadhsNqxW8p6vZxhPxhgrBvmTJ0+CY7DZbML9lGUZDHgfwGiqOjgDnpHUF1unqZAsSFBm6AAO0pfEOxJpmrLdbl0X8okEqD0bqys+L8uSpmlDTYUf33K5dB3ONU1bB2codiiyPMP2SXgvyzK3tSUIZIwJLFwf5/WxHY0icU3ydBoyEOOicBEfhXaFK1op8SqVoql2WNMzmo1c8ZtifHrEcjlnMR2juoZmc4PNNG1f8+CdN2mahmeefZb7zzzLay8+S9+UlHVNno8YTyYs5lOwPdWu5O/8rf+cN19/E9Nbjo+O+VN/6hf46Z/+MsUo43A+J080v/97X+ftt97jydkj0Ipp8Sx3XpDN4UojxHbRGu0iqYahcMyLUqUtiVF0CuiNl0GkKiFNBJKiTE/nqQutkeK5rsV0PVpD36XUVcXG0cmkC1GSIfUYT7i1A9ooyNIB2rAfhYkLot2/wc73OFbvqAzKLL5goHr03/NjcsayRM2CJgmKyVqvTMPAw2lVPBAbTGs/ivC+N9tDpkl5x2V/HsJR4WZsCHztKWUrhqxsZkNdVlhr0PgeGXafqUTFY4z/jp6FMzEVPvrgFIX2RYeexcaxw+w9zOhc+3i4aDoNQxp9mKo7JyfMFwtGRUFZVrSO/ODy8pK6M6RJTp7lTjiuaUzPZDrn6O4JaTqWglBruas1l2cSqZgfHlGMpnhD3XQNN5ePadqOtu9ZzBckrl/NzWpDWVbcvXOH5XLJbrfj8aNH3D09ZTabYazl3v17PHrwUApH7a1HHc+rv9mQVYuer4rWiwI8ptgZDBqhsjQuCDCwrhCMLuV+x7j8nCWwhvixKDdAZY2DABmSNBvGgg3RTGEskrEbT5Ppl17ouTDQTPtiWLAhum+VFTiAErinDZ7TUJfjDSXr6VU9ltqPx30nrPPICfAj9Rkib4xpfOGvj5JHS1sJrEfw1P7aNqxrlI+YyncTY0Jzxr7vqOqKtmmYz+ccLJdSd+TuX+ZJBWM9xpSH7r8icJ3fZcOzt1YyBcoKs0ySWEzfSgfxpKNRbZCVAHmeMRqP0cp3qrVgevqudzSZw/MPhcrWOU5OTrf94CCH8TAY796wi7aq+75AmSRyK0C6IAcjMWd9VtPRc97e3zh5Z119x55THmH8ZWt4p1iHLw654D071T3TIdttow989s0fHxpr+sOtzxTp6Brc2thxbNhnJawzsNUwCGTtK50Mxrrf61H039PehqxA+JL7nqyg4fpWjHWvxG342+sVM9y3c7p6x17kHWQPxRwok70D5OSL2qc2l1PFgbt9rSf0vTpcT/nfw3EIjMw5Bsb/HrwaP3fDfUePc18vxtjFCA/tReDg0NpIWLiRay8vFXXdSFYjyygKqdXQvWE2n1PkBbPZ1NUAjNls1+y2WyaTCf2i4/rqWrIJvm2A1q6/iaA0RM/aYHNYxE70sD7fF8WCY30z5MWI8WyKUrBbbwDlKFwNxWgq2YyqpO86ZvMFSZKxqyq0gqqU+gcix2LvviM9MTihKurdZvFZTKWUo911dMjBnpBnPp/PaTsx+ne7ndx7krBarQKjnT9mNBqFOgsvDz3EyTtJ/vM8z2WdOgiTN+g9JS4MvTq8I9P3PWleoJQKUCdPj2uMoa6qMG7PEtW2rdjAyPlPTk44Pz8PBBat62nnsyu+s7l/FUVBURSBGeuHvT62o5EnrTgYGWKE9D3jLENlTkH0LRnQdz0HkwlKKeZ373G4mLI8WLBcLjg+PpQW8qbn5uqSRCnefOMNLs+fkCUpmfPgrs6esL65ZraY84mXX+Di8pIsL9hudyTKkuqM/+q/+9v8zm/+tizEznD25Jy3Xv8BH7z7HqevfAKrE+6e3ufOS5/iws7pPvsXJD03vc96dcN0OiPPi0hguwWIkn4YDhNnHUuW2+MkiNLwxTGdNey2EjXvXTGddQoXbDDqtVYUeUaezzg9vcfF+blE7rIMpX1RIYNus2GX4FP0w+4ZRH2QeV5ARREc+aKLqYU3o2Sqsz/2avy86RLRNBIdv+cueJkfXy8yMP1IRVcPkVb/pdgWdVreGVZRVD/6TjzGAMfhw3IFvOGekChFbzqnKN19IUpgaPDjT3zrZrwg9+f1JwnORnA3GDp6uoWiAl3J/nMa7EanECSiv+e8uNMsF0uWiwVFnrMrS7qupdyVXF9dY9Bk2Yg0L0jSjKrcUrnOocYq8nxE20Nb1dKo0rTMlgdYqyirhrIWYaqVNNuazZfc9DIf+Wgia9ulpLuu5cHDh5w0xxweHaK05snjx9w9vctsNgcUp6d3efTosStii6za2FByxnA0mUHRxPctJpsiRDGR/ZGkKbbrwt/DevJZyQEGotBRgbK/tvtMK/q2EbpSC4XbAEMvBBt6IxgjNVZD3wRPjeodC5mn3mVJfAZpMMrAF0gO9QCwt8DD6rX7hgyx8evnJ1KWfuUrTerv38258qx2UW2UUlIPZ5VABHyfA7BhL3ibS2vBSyulXFdlcVi6zkjaXDQ3h0fHpFrRtR19b53Sll5FOtF0fQtKauwal7JP+6GfgpeXHm4l7IQNfed+77oQOJBCcSdXjUAX2tZhssOe8tkEMdp606NwHZCVwkZO3N5Pb0RYQ6j3cet1yBJFL6VJPZrqljkfM/KJUUhUKD6scwmy7Ek3uRf/WJwyCPEPv5a9IRvuJawWvEC20TVuG6zDRzZah4MTsJdt2Buzk1EO9hMa+kRzEm3tMAgfEBuixk52uy9bV9tjsUFvQqQvbHgnkIPEDrj8qwaDGoZsgFNw8tWe87NzfC8QlKLvuqBvrDvORjcRbsXLlsgZGG5dBUVkGTIwXi4FB8Fyq87MDnogcjBuL7Ugu1R87eghh/segGCRRB0cDuI1MMxjWZUslweMxxMal6VoW6ExrupGDNskZTwaB6N6Pp9jreLm5oa+b0Ve+sLu1gRbykKQm8GxVNKRXWnH5+kyHnkxYjafk2YZ2/Wa7W6LimBv0+kUY2G32aJ0wnQyo+sNddOQayXZjzBDaiAvgMguskFu7jV49BlFoH/nn3P09EHIQKRpEgx7D2lqmkayMekQKPbwKN/Mzkf+lVLhZ5qmIQDiMxdKqdCkz3/XZzpw8+cNfp/98A6Dd1xiB0Mpobj13/Edy/33m6YJWYwk00KP664bU1r7LIt3NLzj5G2Dj4L6/lGvj+1oPP/UsTScc3SdbdOQJimL2YxEW9JUvF4/oPF4RNs0FFnC80/dpax2vP/2D1itbsjSBKUTLi6uMb3QZ/qlb4zl+uaK+WxCog1tZ1jMJoIRzBLWNyuePDnne9/7AaiEavosZnaKuvcjNNbyD3ZHfDL7CipNMVeG7av3qcbvk7WtYAOtpalbtpst/dgwmUycEDJ7Sr1qpGmKdZS8xrV39/CFobmbV2qD8TxESAbBh5HGMq+8/DJFIYU169WKrCgoCpFC1gzRJi+MBpy0E8x2iB4NokOFEQR9EX0/vB05L25Ie8pHoFZe+FlnNCr33Uhx+jtX/pzsfRrDoPy4JZWrgrYMet4f5aJoQQCGmxnw86KrvBD1kJvh2srdt3GnGahta7mnBEdjJ2ANkfwQ938YbtBP5PAwwvXVkHmxgeUDZ+DpyLFQBGs3Zt6Kf7NDhD7Mo7VMxmMOj48pRmNhfmhbdrsdV9fXJCohTwuSYozOR+RFzmQ6RacJfd0wny1Zr7euBCghzxPGxUz473WCRYrnbN8LVWhTk6QZB4cnZHnGZDShs4a6LNFtjWkVXdcK5KDvuHv3LhbLk7Mn3Ll7ymw6wZiek+Nj133U3Um03G5DQYY6iMGAGgwtb/TJ05WAug2RKIvXW5ECjv7zDdnEwBjWlbGWBHEy6kS5iE9P3+XO2JWi2q6V941vQObXp3VwDuMNDqeYut5FfOQzX/yrlGDBE3efWieBySiaCZcscES0SmhPh4xNFBEdPAzHLOXmzzsZdrhvhWfjkQk2LlPg17lvHSB7VAn0z4JPN5l+yO4Y72j1stYnxQSdJsKv3vS0GLq2xXe87vuO7W5H2zXB317d3AjjShwIcXtsyB77970h5RxKhmwnxgzdzA0YEufYDj1v/G3Kz0S+q5JwziALXdYjLChvxEYGehiVQuCzAStvI6rMMJGDsY3I7hDZhiHwHMmWIXDCrfNE8uDWtf3eCXMWxKZ2vw5w3mGNRPsuvBEHNlRY53HtgZepfoblPiSzEGcdghz3P8P8DI9V9pDaY/rxjE6yBhxFqQvsyceRXrD+2Qx6CSIjPZrfofNz9J4fp3P8jd/HHoYU61C3Vvw9DJIqvtNoYv2f1kKo8Ym+6XSDtSBU3k4PKd8xbJhHf57AcuavE+1/B8y6JVNdAC3SitGn+79F4y7LktlsTlHkjMYjql1JpzRJ0tHUDYlOGI0ErjMaj9huNxhrmc9nJIlmtV7RVHWADw9bSqiUvU5Uaqh/siD9TNwzHY3HTGczsjRjvduy3azZraWgOU0SxpMZOknY7Xa0fc9sMiMfjdiUO6wxVE0dgosykTLHBkIGRe5bh4azwzr3MEpxMpeTjMPDsTA9KY01dugv4eCGl5eX9MaQWQks9S4L4gu7ffajKIpQf+UhYtrpKJ8l8Mb9eDwOGQxfDO6zEjGMSkf6QbmgkXdcfBYkdhLyNKMoij1nIssyZrMZy4MFSZqEXiC+macvOPcU236/SX2jBCirqgrO0A97fWxH40/+7E9grQzg+vpaPLvWN3yRlEyaaMaTGZXDpT19/xSU4Q+/+y3n7cmEt22DTtI9Ww4QFlmtyNKMF15+mTzP2W53nF9eOr7fCSd3T3j48AOKPIP5XdIf+9cxFkeba1nZjF1dM81S6qqmquuQGrO47uPWYG1HXW2xtiUfTUKRjbGG9XpDVZZB6fswn8Af+hAzCLEDr81lzTqZ4MSHM2INlvV6w3e++z0ODxfM5wuqqmS33ZDoGalnXVBuE1gnQIdK4gHKGsN+/MBujcEL5sEB8eb4MPqheJpBNFl/qN2rH/DHxawNccAgUovDSb3I6a3Xgyirb31vOEFQuCqK78RVxV4p+/eVi37f0nLKGaie8ripmsHgtYMQ9n7goMgYBLq/KS/cg2EXK08bBZPULSXgbRfrAkpi+sVPAH+c/657jEmacnznjqSojZF1XAn1XaoT1zypQBdj8umcPC9Qpme5FKfKoBiPCqbTKaNRLkXPdmiQJa8ErQu0mmKNoW4bdtst2+2O1W5LkY8YjeekSc6q2mKNsFJcXV2htebo+Ji+N5w9fsJTT90XrKa1lFXFerUmqP+PoGsN0+FYkXzELTBAeesqPFdviKrBIEy8Ae7rYVRU6DoYBl5R++BAb+Di6oo8S/GQmvhZhl1txPAR+eQpTtVeYbGPjPXGcH55RZGPWCymTIucNMtIE+2am7liWuWVLlE02e/GYV0piJt7hFdsjGsXoR/WrBu5wilbx+zmirS9AYeRgEbnmlv5/gito27su46+N/SmC7Cjrvc9FYZIlq0bdtuSRzwJcDG8oxMoiQVS6MkNOtffQaZ5yOJ5GJkYY7GpQjAYxG2Se9R9h8XQXbyFrq/JnvuyZAxix9XtY89e6A3jISoOFjM4vHFQKNqXRPvSF98qbISsGu4jdiRs19C9+1VsJ9FCLt/Crh+TPPfjeKpbay3m6m3UzXsi55VBqmgyLAmegluGJ1FhT1OitTiDan6KvvsJkvufg8mhG7fAV2zYVyrMebSY9vdYXBM0FHJEREuR0+UfTQQkjCfPb9/gpbvz+8CMantwcMXhSHn4Nh4jDA6Dd2r2BqH4yFf07Lz8CH60u0ffKHh/wB8+T+z/hv2p/uhrDwEVrwNs2Kv++sGZsxFcEZ+Pcv/GjmZQ0BalhG1Tlq3/jg9QDgLQ63wvF/eed3S7Cnkmm/XKMSVNQh1WRGpF1zVsthtMb5hMxpS7Lcb0TCcT0ixluyvZbbf0XR/uQ5pOOn0fySgfkFAokjRjNBlTTCYorVht1rRNKzaOVqgkQ6cZ4+kMYwy77QadpEzmC3pjaKqaTKfcbK9QvsuR1/FKRRzQ0Vr40OOOAh3GMLZb8vyYui6ZTCeMR2Ourq4HFihj2FVbtE4oRochk+EzCtZaYVWNov+xs6FRoZ9ckiQh+9A0jexb92yNUqATCUz7NYCwSXrHBpA6S63pjRGyGMR5FMpgRZ6kpElK13eoRGGKjrasSGZzVlc3UvJgFSkJtrNst1uUVuyaHX3XyXFIdtjrYGMGAoyP8/rYjsa7b72JtZZ79+4xm4ykg3bbU+62gTd4Mplw79497ty5Q57nPHz0kLPzJ87oHiI7SZoF5W3DoFVojmOV4nq1YrFYMJ3PmC3mjMdjuq5jvd26aHsPJ59GJ6kU8SFFR10vDFgKS1Xu3CQJw4fsN4NEOkUBN3UlXnWRk6UZu11JX9dkOnFYRuuMDU2mNBpou9YJfTXY+M5w0FE0yEcEhY5R03YdDx4+5PGTR4xHY1577VU2my1ZJuwDWuvBeBf9Oywwr+zcnsE47OueYlf7MtZ6A8YGhTnokdtwADt8X1mUWz8hostwXi8wwhfil9fZlkjxItApg6TdlcxJLLBFF8m1NR5GFkuIQTgFxe+u4QsDByy4cutLnI6mrYexM8Bx9v77kO5w49oT+NEcW4tSPprqDxmiIv4gFUKC3hDzK8NHvHwUelA3R0dHzOZzEp1IUVrTiqBLhFWnb1ta1bE8GJMVI5q2oy532LZhMpuzWC7IEk3fdZTbFdV2S9PW0j3VCTytpD4oz3NG4zHFeMTh4ZLFfM5mW7JZb2jbjjzLqKuGtmuYTMYkOuXi4gKlE5bLBW1Tc3Z+zr27d2mynOPjY+qqEvaMsAaHhRMgZ964xM9BsGhkXvF1UMP71vThmfi9gGMsCvV/znC0CmlS6I0kFzVXVkkmMUuFyURraXbmmb4AnSgpIk7SwKqROKiIx6l6OkaNom172qajqTf0fcd4OiZxDsZAoSlQIoUnwfHrSowQKdKUARhjXcM7BmpDF/XF2gGiaaRg2ThMb+8YkkzfCwFCb+lN5/okGFdPJ1c1hqBALITI1VC/NUTu7bBigzz0AZSQvQuyJd5IHt6j9qhBvdk/bGQV9rIYxQZz/R7dm78O1pAcv4yaHovh3u4wZ687tihDnmU0P/hH6Jf/JdLnv4xK8shg9WvNOkNv2KvBHAzyMhpDvO4i5wGlJLOAxZZXIqDTEeRTKK+xpqV7459CeYm9eJuuax37FXIfCuwb/8jZmkLNnigCQ5WUMRh626OU0C9LnzMLGJJUU6Q5XeegEwrszbuo1Xv0r/9DjNUC90ty1PHL2GxC9tLPRgazM2ZVghofsNcccE+exxlW48ZqhzURHA8V/Am3KBiCMZHSskMWyXz3V7jfvUVy9zUeHX4ZRgdSx4Lruq4V2jo4lVtYcXR/uPZtUz+K7996doPsHp77h4630f0NM7Unf/yC8cfGzouXSN5x9Z8J7E4FmQXWZQ8jgGSABxECMHEnb7V37T3wVLg73PxKXQgDXOG2HvO62Y3fOz1luWMymZDnBZPJlO16TeNqbbVSrFYlu3KLstC2NXdP71HXJW3bMJ3OOFgsGI9GVHVNXdVCnesCt8Hu8neiNXmWM8oL8tEYnSZ0roGfNYbEQqegyHNQCfPlATpJ2axWWAuTyYxiVLBdb8EaurLGtF2ki2ObwYctnA5WTn9Ey1M+GpApB1wDRxSjgqYRGKcxkqnIspTZbM7p6SnX1zfUdUNVVSEQ5zPqfdejk6F+Q25b49si+CyFhyNlmWRG6kZsS620BMhdnVaWZRIA6nuUJdT2GmNIXTPENEnJMmEQ00Bd1XRth0pygZ62LaYX56wsS/IsZ7fbBVrdpmlc76022J0B9qWFpMU7yD4742tNftjr43cG32xQCh4+fEhR5EwmU+bzOUVRsFwO3RPn8zkXFxdcXV1S1bU4BEjRi6fO8mkgnzLynqJ/9X3HkydPeP/990mShMlkEtJTvbUDRu2Fz4aIsUYFBgr/QIyxWFfIY1yaKk6fC/bMYmxFmib0jjGhczi4QRS4pWoHIzYuFPcvESZO+SrBavqSUZ/h0EDXWba7kvc/eCB0v0oib9KhfMB07hU5O3nnjS/RG0FlD8azt2m9GeewCzbeVEE77As8f6HbvoNXEqFO178XmSBhDmw4SzhPOD6MWwwvr/zCd3CFmtr1z1AgbocKhZDD88AJjWGcOvrDiX2skiycUl7cDNGL8HRDJMg5iSqKqTolF1mx/iC3Dvz9DMIrRJWUE/7+ykHvxipO7Z13NBpzeHhIlmVsVxt6Yx2VnDTVadqW3WYDumKyOEQlOeWuJFFw5+4J49GItm24uLpms7qh61rXsySCG1gEp2+h3m1Z31yjUs14POXw8JCD5ZzpeMzF9TVltaUY5zSrmrpumc0mmNZycX5BnqUs5gvOLy5YrdZMZzP6ruPo+JjHjx6GfTB4GkN9QazEg6ESw1KUwhd67kW43VwK7t075vK39TvWG7Xe6XA9EEA5lhPpNq2dYkiSlDTVdF0vsAaduGCY18oO16tMeN7GdGEjmL5nMplQucK4qqxRaNI+cYXHNkQvu97TnYrD0Lv6DmulWFzqIFrnECpXIxLBOi3DGt5zXInmUz4LxYux3vWCBOUCGWbYn+FrkVMRDDA1PAL3M8bae9pO/zxDlD9YNPtGW3A43dYKdNNYuu/+fczr/73UnViwD7+FBTIPQdIa42WDTqAtsd/5ezRv/GM4fIHsU38aNT/1dgVDxsLvu30HwgbZ4PfjrZdfn24qux/8vzHf/wfyhy7Q4xPU7hyFJaFHAikdKrVoXVNkKePRiNl0zCjPqJuG7abE9LLGtM6xFsbjKbPZnCzPODo+ZD6fc3x8yNHxkTNwprz04qu8/c67/N2/+3d57733pDtx35NaK302DFhT0z74fbCW6s1/Ftaed7a1TlCLewOsZHRA9vLPoKd3SGYn8vTdXGkvE4ctHGR/0H1BrumwvEKAy3+z3lB99T/mSF3yv/s//h84PrnD/+Z//3/m4hP/BkpnYDW+EByM2/r78nwYQmxuDy5E+D163h96ph/nebN/7XCo2rvKh68d9lCkJzxDod+v7hwSWPFra3+t+TqrW2+H8/qPtJNpss7DQ/gXWuex9r65vuHkzl2KPMdOJgJ/bDt8vVOiU6w1pFlOURSkaUZZllxfX0sGfDRiPpszmUxczVYnmVMjrIxKSYBG+yCOksj+diMNnxVSQ9bUtYNuahaLBVmWUteNIwUqWC6WNFVDU9dkqeZyu0YUQvT0/BRawwDJHlAZt4MOIfDQVZwcH7Jer5lMx1hrXTG1sGE1TUNdVZw3LW3TstuVdI4Jqm1Envvn1RvDqCgkSJ2moX4iiZwEX38hjkRPpocG1MZI0CFVGtvKPGo79I0xpndBpaF+oq3q0IvDd3tfd+tQAyIZCrGfHz5+BAzZPa8v+r5n6vppHSwPyIs8UOseHBywWCwci+CExWLxoX3yUa+P7WhIV01FVe24ublGCp4df75zGnxU3lNw+VSt99jidI9PKQGhIAacwaY0dV2zV3jjaL/Qmul06uomTFguSi6Etb6yXpFlubCfIDjgvmnojDM6nDHSu6igtTCbRQ5EFN3zxTtKiXGjlab333GLORTmRfJJIbjs/UJuZ9xbeHJ+TpFntF2LShTLxULqV0IHT/l6YGpTQzrWC1RpgzgobQuhC69Fg+2HKCQMhd/Ecs5GGYhBeUj0Q44N6IhoTQTHwdMIRaLQekPFrx/E2B2EoBlkYmQXyqB6DBLZQkHvBIG1jpLYDcT3SQjFdg6j3LtIimdAa7o2jIk9YesvOIwrdjCUYi91768jA4/S/CF65t+PJhgVMVzdUl7O8AvRJgXHx8ekaUrbNHR9z83NDW3bMxqPSbKcsqyxSgRV3/XstmuKouDk+JBEw831JVcX5zRtI3aftRjHZhQiZMozbeCyjBbbtaxX12w3a5bLAw6Ojzk5OeDmCrZ9jU6y0MHYWkXXNZxfnPPMU0+zXMy5uLxk5IQPSrGeTiXi5I3MeOXsGbzRy3vWAQPuMcxEfMc2rL3ewX/iSHyY9hBF1Y7dRFMUmesAbemMIXGH98bSdyL4LUh/GytQKwuCJQanGGzIJhhjnLNgw7Gm7/ngvQ8I3N5RUCN0hGcYr3HPSCkdyRPCncRQR69A/SR65yP4VKhAgWmdwe+34NCzZF+2SGNHhe+V4E0sX1+wH80lMKwNNMPDswxGnvsZM0rJkE1YBv45hdO7+ei+949Qb/xj6RieJPiu7BZIdFSvpX1B+8CMorsSdf5dzK9/l/74NdJP/yJqfAx6KNgEQqDFy3Y/qGH+P3zfYa9ai3njH5OqFOmTY9DVE9A9qA5Ux2Sa89TT9/nUp1/j+eefZjqd8OILz3P/3ilNXfL++++jVSb/JSIvpuMFy+UJs+lBKDL1RaGVY5Y5Oz/n6uqc5XLGL//yX2I8HrPZbmhqgTM/OTvnvffe58HDB1xeXlJVFW3T0vVC5dp1rhGutZjdQxIr/VTM6hHN4++ATtFPfZ70+Hny574EWeFuXAfWsWH1qcCgZK0znb1DI94OWEP3/jeg3WHf+ecskp5/69/5n/LjX/4xIOF/9W/+Mv+nv/N7mNMvioRXDi5m9+fc98DZCzSFZzQY/USj+6PkeWyEx599SBZF54nchv/Ba8t+MwjsbRD50jXeuD3p4WmSqfnItQa4os5gK3zYWY9GpOKft5yUIBcHBRu2bUxjhzCw3ayuWS6WQiNrLGW5o21bsjRlOpbarPFkQtt2IQjctp00pasFs5/nuUTWXaNYz+jU985asJamltpAoZ7vqeuaIi9oHQlEZyzz+UK6W3c9m/WaJElZHh5hrWW725KmCZv1NcZ2wUlVQzRPZKfTJTKF7nkFoptB94qcsqTv/QbT53Oapgrw0URlmL6ndvbidr2L6iaiuTZil0hfkZS+71DWBacRpqbFfE5dSzbSw6WapnFUuhmmcdaOUsE+bpAAlnco2rYN0CtvI8PQ08Lbrl3XkWYp2tVRWKQR4jTPSZOEyVRKBp566mnG4xFdK9TGfd/z/PPPc8fBt31X+SzLxJFS0p8oTVNqV3D+w14f29HQWoRJ33e4Jt+gCPiztm1IEgctcEYfyrOQDBESP2FKqcALHFe6A4HBxRfEDEaFrAjPSczNu6jZPdGXCqyRcwzUXj2rm9XQ6t4tnNiyNS7zoZWirnYkSeYK0xw9npGmO9Y5Tj4yLoe7yIoO9CPRJnfKSw/eMs4wCEaIUyTX1zdSY2KEQz7PMlTiaVJVoNwbxh1hCmVl4VOcMDgiKlzGOEPGOxkCIXFuokRvHa5KgAseiIWgcPeleHh5nLm1BNaaEDxQ+45GmBH/XuAvd4WAeLvHkmiPyrZOmXnjSDmhrQK9MOBoa6FXgrmW9eOaZ7WtNE9UbrzWDNCVMD61N77gYHgHzfoxDNmqkKEKN+zG5w9RkXHnorW2j/ndjaO+lHm3CsbFiPGoQCcJm9VaIp/bLVleoNOULB9xcjql2u1I0hQUjEcFR8dHYHqePH7M5uZaovLO2YosV4aOyA5S49aJThK0cmut77m8OGdX7ji9d4+jwyVpAuvVlizN3J4xWNvTVA2XV1ecHB+R5xmXlxecnt6jrhuOj47ZbXduimNVbcPqCs/YGyjBoLCRU6rcs7ThaFEiHm8/vGejK3gL1wbZJHCs2kZr0BkB4J63Cyb4AErsF4YnHF0nLmj3p/QI5dCrw+07sPTBn7V7ay2w9/i1Jgtwb23Ggwn7O8jMIasZsq31GpIUlU3wkeVghMhGk2snOhgc3g6TqJ8dmJj81ZWD2FhcTYQfkJeJ0YS1JbQlSkF/9jrmg99HXb39oeJCpXDNulxxpO1RTo8kKLIkGR6Xk6VKK6x2sIJIqQZaya4nvfg+7T/+DjbJsSevotIC/fxPoEYL+tVD+g9+z83lgDHWWqMXT5E89SPhmcfZa5qS7ru/QkZLb3u0Tjg8mvHMU0cY07JYTsgLzc/87Jc5OJyT5wmjcSoOvb3i7OxSgmpc8PRTL2KsZrNZO2W+w3KN1hnYAmyGVpAmhvE4paktd04Omc5mTGazoBd3uy3WihEjkGRN2zZBr/a94fz8jM1GOhtvtxsuL68oy5Kbm2u++c1v8fjRhUMBdCQX36R9/A3aH/yKPG9j4eRVVDbeX39RnYl/7F7P2NUHJNUV1hq0NWRZzsnJCX/ll/8Kf+GX/mWMMeRFwS/+4p/mH//W7/HrymI815yThX5/73WRDT8i49xGsKpbsuWj5Lnff0MlxbCH45eXLbGj/MOv7baaC7xq5fpiaTXMjShZt4eV6JWeaC8R6jTjCw/XHmq8vN0SDScanw17OcyBD3r4GglHv+vtGAXsdluyNGUynTKejFBKMrS+2bIymqaqsb11/TNSqfnqerquBaXodjus3TpR4+F/SgK6+GCIwAYVsF2vhZ3OGKxRoBPmiyWT6ZTeORlWKRbLJWmas12vhcikrSir0s2NjoIjDGs3WgN/5PN28pBmw/PpE6pqxmiUUTcVGB+wGWBCaZpgTE9eFBDbpgm0IEHy1IQsQN9LZ/S+79mtN7R9R+1qOUAcDm8TJyRiJ1grReWuhiNL0yDvUve7p5/1GZLFYsHd01Pm8xl3754yGo24e3oXkqE/BggMS3oOSXLAF4p7qlqlVGCl8lQFo0KSAYJetrSmx/SQFf9/hk4Z24eIrmQ3IE01WqdOwPdYhDZOIn1diJTF2YqAlXbKxqeQ/GT5eg6vXWz00zov1bg29v2j76Ce+mL4TqKkkPbxoyc8fvwYEFpFjLDJWMfV7Det0krSyG4MbdOiCwebsEPRUKAT9Kl7GxuqLvIaOS8iGHz0Td4Q4zOKXntjHCm2vL5es9uU6EQJvltr6UarNInSQfl6qBk4hsHgQMhc+iIk+X3AiKNwbDY6OAN+4YrxLG96pRow65YAWxqCL05QK3G+vIB1Z4icIf8eYQze6PEwttCYLDITvQCWOVOBhlMpwnj3HLiAg8c5mjV9Z2nalrIqAyvDcH8DZ7kvUPSqjcjQ2stmuLF5JatDmj96nloNRDQMCtMjoMWYxk++3J8xrteF4eDwgCwv6NqG3hg26zVKJaRZTprl5HnBdL5gvpCupUolnJwcYbqOR48eUG43KOsaj4Hr2ipsO0VeoJJh/WJlT7RNQ1M3gEEnqVt7irosefDe+9y7f4/FconpYbspydOMPJdO9zrpWN3cMJ0JjPLJ2RlHbUMxLui6lul0yna7xcNzZYlFalkplFcGYc49ZaZfcxYP+/JryR/ioXGhIY5/hUfj17QosLr2rrXLQHojWg2OLCpay14GhHUm0Vv/58BO5L/iM282fN8bP8qvX//sPf8/Sigcte9lEFkc7hx7VJ1+HQF29ZD+0bewzYbk9NNyVFPSv/3rsHqA1hl2fMTey61J0hHJSz/nZBCQjdGLp+Xz6J6CYvaGT2/or96hf+e3ULvzIJchZpSxqPKazIoyLZRrZJmDtYMcU0qRjVyTKtdd2CvBPM+5c3jEfDYncVlsYaVJhf1mNuXw+IjRaETXdTx+/Jj33nuPq6trvvvt73H2+Iw8lWyxvvi+sIs9+Aa9QqBrt6gcvaNr1Dfov/Mrbp9EjptVKA1aGYzqSTN44cVn+Xf+7f8Jn/rEczx48D7LgyldX3N59YT33nubd999m/Eo58UXXyTViroumc+mZEnKZFTQm4RUW9abG26uNxwe3KOve5SSruUHB4eMRhMwlsODOWmSYZIU7Vka3bx7lpm2652DkQUZrJOE09OTYFz1fcdkPAnO3ttvvc23vvWHvPPOO5yfn7NarSirkvlszhtvvMnl5RXd1fcCo02e58I+mSQUeSENPpViNBLozMHBgvHklDRJOTo+Yj6f89RTT/HpT3+a+/fvs9uuuNqsUUrRNj1/7S//ef7g//I3uHn+FzGeBhpf62gx2tVuhJ4e8R5h37kNDob/1h8tzwk7k+G74d9ItsT6++Nc20pNi8JK8C5JUH0v2Yygd+TZ+XsMmyuowEGuKSImsQ9d2wcs/O/OvnAOiB/Hvh6Ls/l+rw/601rLerMmSVPyvGA8nqB04urumuC89n1P2mW0iTAWbXdblNYsFwuWy6Xo3L7H2J4s1SSJrOmyrCWLh8b0HZvNmq7rKYpcuoKnGbPZknw0pu16VqsbrDEsFktG4wm7sqLrG7TqudmscLxSbvCK4KFZE4KLwY7xz9vpEl+j5OfTvPVPOT6dMB6PSRKw5AK9ry1d22ONUP0KHSysVxupA1UDJW1V1zSuqV/oPeGuFyBKWYbFhv00n0sN8mw2YzFfUpUVN6sbtE5YLpe88MLzPPPMs2G9zGYzTC/Z3N70ZGnGaDwK2aS2kRqLPM9BKW5WN3ja6KIYCVwfuLy8Is1SduWONE2ZzqY0TUtVlYzGY/pyx+HhEXVdkaRSr6jTJLAyjifjW3vgj359bEcDhtRN30tL9iQZFuh4PIqKXnzafMCa3XYmgIAr82mgwBccPPWBfzicx4onrZX0R0iMdQgthU60dKg0XfAQlXXQImvxXVx9V1gMpFkqzFJIJLyqpeDH+qY6yDl8BK93Hb5D5NFpYy8g4zoGL9x0ZKWH7p5Ex1sRhk3XQ2tRyjVniSRCECJRQGUQjFGU1b9n7YB7DgbVMDith+LXWMb5KG2od/iIdRQYeILH4kWzP9l+5D4YKnrISPiInHcatFaRIyXeuhTTRtAodw++0U/oiIr/TCL2ddeS6oTdZsvNeh1gLj4yIWsxHahK/fiCBUkknN0tOcXgI9ShyNU/H8u+MrOD0A/eh4pVhYdyCX1emmXMZnPSJGW9XtG2LbuyJHeCIc9zRpMpWms2ZUNnLPfun2CN4cnjR5RrYXpqu0Z6Y2TC6tL1wiJkUeSjQoSF8kVpilGaoRKBauHgjHKswnQdjx885N6zT7M8OKBpetq6dd1HK7RKaPuG1fUNd+7eZTwac3lxwd3TU3Simc3nbDYbZ9REcxkvrL15HuYn+GMM8EOFM/gc/i9Emv06HDxhuYYrYsMFL7TWLjOi9563Dc/Gho3gnc8BwRwp+uDoROrfGefByfBjuUUWEJS938vYoTaF6NgwWT1md0n/+A/De0qBPfs+6uL10P2bd387XCJzmyWhx+4eD07CsPTk1F9/S46xAqFp8zn6pZ8leeEnQCWY8zew60dBZpjtGebB75O0UhTqgxq+U22mpRhxMZ/z0ktfZjQak+c5i/mEg/mMoyOpPSrLiq7rmEzGTJdzDo8OybI06ImyLFFK84XPfV4c4k4UdG/6cD3ShCRN0VrROsWnlKZpGv7wD77Hd779Hd588y3eeutNbm5uqKqKsqowClqtHWTDRM4bQX/FekhkhNDkZolGJ5Ckii//xI/xr//rf5WT4wXvvfc277//Lie7I55++j4azVd+4qfZriWTfv54xU9+5ctgLe+/+y67XUO9VUwmM84uziXyqXLefv1dZrMTnnr6KZSyvPv2m+TFiKpsePLknJdeeoXp4RHLw2OyLGW32wEwmUwFNqE1WZ4NstUHpZyxlaYpxmG1u77n/OwJd+/e4ed+7qeo6y9yeXnJer3mtU98glFR8PjxE9579yEgvQSm0ynHx8fkeUHft0ynY8YT6bmjQIpi3V6T2hFDojU6Sbi4eMJmc8OoGHF5cclms2G9WmEw/MnP3+W/+Ud/nfLpn0c99ccCTbQ3EFUUxUcpYgfwtqGzJ1si3fAh2cKtIMKtV6y//f5WP+zayjG7eYi4Uq4GRzkZ6IOCw7UDa4/fo+Gn1NK4Belki9C3hmurKMMe34ty0sop93DfQQ0NQYvYvfLQSWt6rq6vOT48dp2+Mygkkl85og+Bvruu4HmGrhN8wLKu66DXszThzskx1sCuLNltdrQBctqhlRYnozfko4LJfIHOxMnYrtcAzOcLJpMJZVVT1zW5hpubG7D94Fh4Ahkc7FUpmTdr/cP80PMegqKA6UmuXqc5POXRozVJAm3X0FYttGog23D2aJIkrrauJ3EwooODA3QEJUrTlOeee47ZfB6yRKOiIMkzlJb6k+eff55nnnmGoigkKDMaU4zHTv6I7SQwpYy+71wTaKmzsNZSlZU0nU0SIf2whqYWyGRjeibjMZPpNJQgVHVF2otDMp1NabuO8WRCkiTSfLHvuL65QWnNeDLBh4DLqqRt2yDz+76H3Y7RaPSR++f262M7GgKLUrStPNjE09NGWkwp7fh7U0epaDFGgNCyyPtAbSaKQTkvT2GtKArpuNqTqCRgznwhuXTR9JEz4OotaLeQjJ3nr8iyBFpL3wpUSmh03WbWKsIliiNksdLJUim0lWhX1zXoVHqGKCQTgBZq3M7Rt8n9xoYjBOfBGxBq2MRB0ClQykdu/WduOMEnuH1WlzVxXrnY7jrMmQkGlq/hcEwPfWyQgQ0UkQro94Ub8r3YeAe7J9SIFn8QbXuRJv/b/l/u5MO13XX88lGA0iqQBAxFy06xOANQjAGJuHslKg6HNxytq6GRe2ialtFoRJ5nwuHv1pd8bAchFBmow3CHcXgHJzZGbTTn3ikWx1aojPcsZRddGZSVnNUXyJNoZrMZSZq5pmWGzXaDSkRQZ4lmPBpRFCl121KWFSfHx+RJyuXZE3aba1CWrm1Js5yxK1prXUMzkaOdw2wK4UDiKPLEkOvACLd255qkZWmGUtB1LWePHvLU089ycLjkyeMn9May226wfcdoMma73bGsG2bTOefn5/S9FLU3bUuaZ3RtG9bmMPXOwPbz4SNPMV7B7Q/lqD3BG/d+2dpor+nwt//eYJQkoqsTp3ZtBGNwj8lDtVS8IYCh/ojBaQ67MjJlorWiLZhwfn/fyt23wZoW22yJ15x9/IeYm/fdGvF73mKbHfryB2SOJU6j0SpBqwyjchJl0UlsQlnXL8igVO+CO5oklc7MSZKidULbGvrOhEZPqbaYZoP5zt+j+96vilFkOlc/4u/NFzuDThNSt24/+alP8bM/+9O88OLzjEYjFi6qqZQ3GA2YAUqQZVmQ/av1ikePH/Po0UMWLrI3KgqWBwdcrW7Is5zeGKqypOt6p4ckS9d2bciuNU3LdrvFGMOd0yNe/cSfDXjm3W7HxcUFb731Fu9/8D6PHz9mvV6z2WxZrVY0dS11cqgQdVwsBB9eVxWma3nm3l1+4itf5uBgSpZrPv3p19iVa8rNJfko5fDoECycPT7n+OiUD95+xE9++eeD4fXg4TVd0/DsM6/x+3/wB6y2NfkILi+3JEnC6el97t+fgdF0Fi6vbijyCcuDQ7TecPdeyng6IcvH6CTHWsV8cejYblKM6UlTKTrd7XaMcmHMef/tdymdQVDXNXmeu3tuOL13Srne8PDhQ1arNXmes9tu+Vv/6X/Gcrnk85/7Ed5+/Q2efvoplicnjLKM3XpNMhPI1uXZYz744APu3LnDq6++ypNHjwIco64bfvd3v8bJyQlvvfkWy4Ml2+2WzXrLwcEhQ7MyOD444i/+qZ/nv/67v8Lq6gHJp/8cXltYLR23PQIgLHO/v/EwSidbiGVztHXjQEF43d7r8Y7+sP7+Ydf2+jmw5flX76BmTmcJ0ENj+y6gQ4ZrG8lSPv42L7/0IucXK7b3voIau6LbyNnyR/k8kJepMk4ve245RGFYDkKMCs0XVXQ3tu+5urpksVjQuT5BSSL1GV3b0LbSoLjrpbHfeCSBZmuMi/gLymNU5FRVS900rK6vqZsuUG4bC701JKkEI0bjCVZpqrpit92RJCmz+ZK8KKjqiqauSJVldXNF33XueUfGU/SsvaNKWDYqwIYHXeIRHRZTXZJWT3jwsMXa3gVPEkxnSJ0Tk6Yp42LEZDzh8PCQtu+YLxeuYD3j53/+51mtVrz77rssFguOjo6k55QVytjRaCR2S5JInQZiy663O7auJcRisSRdr2naFmstk8mENEmom4aubbBYptMpXdtKANEalNbSD6ttAymTKhRd2wYmKe8czOfzD9V4+H4YRVGgteb09FR6d7nu5K07T9xA0Pfo8PUhP+z1sR0NpbRg8BgiP/FFYgyYL5gcYCmE9/3Nxfh9vw88R7uPGPiMhy8Edy6KMLFg0bal/63/APvan0Xf/QTKeX+9cyaSNEOh6Wy3t+/DBkQEmLGGRKch+uKhNl3fh8yJRZwmGROOkg/8P96slii1BRsVXToZYt3NhqF8KGoef+7Nk+HseGHrDRHXhMqsH2ObLWpyiJ4chU1uI4cHVGDm2ee3iwapVDhmIEaSQq6QkQwNqdQw5siokz8j50kNdxIgceE6sZhXwguvBpHrMxC2N0PDQDUQEIQTKO/CeCHrnCKke7AXLkob51+KM9K7ufQYeZ/alkeohsEpwo3Y6J41hOJKrSWiI+0y/JwPay04oXvTPszTdDYjSVPKndQ1NFVNlohxeHNzQ2cs4+mUuq7I85zZdMp2u+byUhrkdW1PVoyYjqcorSiryuFAPSGDRGXSNJWaGEfBJ9SoLVYJH/dkMhHDq23JixydaKqq5OLinJO795nOpsJm1XeYrqWwE0wPq/WGOyd3SNKU9XrDwcGSLCuZTqfcXN9EKtz/ooa14+dhb53HE+UJADzrk2sm6Y/TBNpklPS+SVOJlE2nM8pdw81qFTmPOhAm+P0UGJR8ZkKpwLjjsdCRJRPGGjciHFS7AcchLyECK1C7vsc8/Cbdd34VXd0EhyDRCRhLnqQh4+lvX2uNSlLSTLkU+5RxMSZLBNZwsJw5J1UY85IkZTabkecZeSEBmdF4xGw6YzwWRrOiGHFxfsPbb7/D2++8zVtvvcXDBw+4urqmaRu0NVgrBBUoFZyVNE1IM5Gxzz//Aj/+5R/nJ778ZZ566imyPKOsypBxMKYLqX1jjGu6NQ7BBK01xahgsVzw7LPPYq2lLEuapmG1kozew0ePuLlZAbgC0ywEn7TWQYl66FBRFAKl6lsuLs/IsozLy0tGoxHPPf8ML7/yIh5/DIRjvYL2VJTGGHa7XVCkfdNgu5Lnnn2arm/Y7Tb82j/6NX72536W3nasbnYcH5/ywvPP8/abb2G6hOvLLXdOnuZ6tUJrzSde+yzFaMQ3fvfrPHh4wauvQdUannvxVabTOdbAbDZnOplhVcrh8YbZbMZ2u2MyOwQkspsUE5JUahRNL0Evyd5r2kZYZTLHmnhxds7l+TnXV9es12uapuFHf/RHaesG0/c0rj/PweKA2WTGaDTi4uKCd7J3efzwMb/2+B/xrW/9IYeHhzz99NO89957nJycSD1Iojk5Oeb09JTzJ2fUZUXTNHzwwQcopfipn/opDpcHnD1+wgvPP8/V1RXjYsTN1Q1dKwGg1c0N8/mcuqq4c3KHH/9jP8Y//Y1/Tnfvk6jjV1E2cXLc9xDxxmMkUwdtNLz+h3Ro2KvDkdFudv8On8Zy64ddW1TEh6/tdSjOLvLfDeNQhOxs9+D36L/+n/CTP/ElPv1izpNFyq9+8++TfPqXwGc4vI3kzuDr10KQM870DxeKBwlxgDD2lHy2V0kt3s3NDTNXE9R2LVon5HlBlkn369ZF+uWQPgT+fAF027Zsd2WAXPlMIUqT5jmz0Yhi5EiEOqGQrbuWUT5iOhua9PVtjbKGzfqGvmtv+ZE+0Ggi/XzrpYb5EJPBB3rFHpq+8Xd4+ZOvBQjTiy++yP3797m+uuJgvmA6mYbgQ+6oaHss+aigqiqMMRweHjKeTlgcLMnzPBjmeZaTj6Qe2VpLmmaMJ1N8XYRSit1uR11LTabvxaGU4vrqitFoROngTWA5PzsLNRaHh4cUaUqPcUiDJhzvnQHPQpU6+JMPpnjEkNaazWYj9Lp1HWR4VVUCkUsFQbJarcI5xuNxOP/HeX1sR8PfeNd1QRinaRqK8LzH6xWJ/9srBhicEX8j/oa9U+HhTjqKVvsJ8t4VyMTNZlMuzi4ouhXV7/2nmJ/8d0kWJ+KYOAhVKDI2HvMY2aaogc3JGBQ9OtOMi0IMt04iuzgMvcXQhz1rIzGkwzsCsSIY2v4ReIGgcIaJ2w0Cn4iYi/YE3D7MBndav4vM4+/QffdXod2R2YqTkyOeee5Fnnyw5uHDh2JkGoNSKfr5r5C9+DMyOCXmU2iMFsbhr+gNLzf62AD0QtFDUqLhhTStip2U4b5lxoVFQOxLGxyvIAuNke631h/p4CsqdrbkYjIVbv7cQ7X+fyHpYulMg4cnJYlCJ6kUPjsYzUfVYtw2gPcVkaNhjByRUHcznGaQdnvP+9b77iknSUqW5uLcth11VUvX0TynbhrKqqKqGmaLJU3TcHJyF9M3XF2cOzIDQ5KmTMZTsqKgrku6pkEnGtN7SuZEFIBOhO8bidA0dU3V1OAEkul7xuMx290u7D2FZrVaM18cMJ/NKDcrJuMJ2+0mRNE2mw3L5QFFUbBZrzk8OiBNhKnk+voG79SH+44yO8MSd06oGlZcWCdIwSi2BytzqrRkxtIsYToZM51OmE7GjEYFM7XFjo6pO8v3v/+WKDffngXJzFkkUxsgWAzXVriicK2Cbo73SIwDj/1RqwiyBjTK9lBfoZ/8Htn7/5y82qETRboYiRHeK5q2ZbJUqERqi8SgFucgywrGsyW/9Jf+iqThp3Nm8zkiBzXjYoRWKgRjzs7OWK/XZFlG2zVkWcZk4nDHLljTti33nrrPj/7Y50S5NA1nT57w8NEjvvOd73CzXpEXRVAox0dHJGnKeDxiMhEs/uHBAePJxBVIyrOdTCZBvnddF2B4bduGfVLXdTDqYcAt+6ibj6DVdU3Xm1Co6INTgdEQArW6P4dQbqZoZYOiPzg4CMefn59zdXXFbrfj5OSE2WwW8NFFUYTz+e/7INduu6Yu18xmMwBubq5YHr1L22c8+9xLPPPca0xGY5IkYTHboqzlS1/8GZq24YMPznntE6+hSZiMFnzhCz/OZl3z8suf4e7dU9cbRZGluQvQWXZlyfGdeyRJys265Pvff4OmafjSF79EnvS0TYkxol9xRspms6aqS7bbLYcHB9w9OcF0HcdHx5zePeXk5CRA07w+PTk5cYXohI7Czzz7LJ/57GfZbjb87u/+LsvlAU+enHHnzgkvvfQiSZLy4osv8rWv/Q6LxYKXXnqJN954g6urK6bTKS+++CJaa25ubgL15Xa7pes6bm5uSNOEBw8+ACQ7fXFxQZZlPHjwgMkk55WXnuH1b/5N+i/8W+jl0w66rCRuZ4aMvGQmva4ZAmdephK+FwQJ3qkYRItXXJH+jvTdR+rv/x+uHfs6AbIbtIvF3Dyk/8Z/wisvPseLLzzPeFRw//QOz37zm3xw/Tbq8EVQyR+hSwZHQ8RZzKyk9+57GN1wbbmVQfj5aTDGsF6tGE0mFHlBUzc0LnCQZbkriDZ0vXHwIoPtDZ2TqVZrLL1DIqSkiSbPR2RZitICge96Q1PWNG1LkqbMFwuKvKDvOuqdrHXbtWzWN65dgpU+X9rf3zDnvueQ4z/fl823Ml3+N/Pku/zyn/kZfvRHP49SytVoiC3bdx2b9YaTkxNGoxFVVbHZbGirlulsymq1YjKZ7BVXexmltWY0Ggl8GBiPx653htjCVVVxdnZGWZYOeZGHTIJ3ALzzoJQeyJYQ+6VtW1arFVVVkTt64clkEhIA8r4c7383xnB9fc1oNMIXuJdlSZZlIdDi7XatJWO92+1C/Zxnlg0ssB/z9S9Uo5EkCXVdM51Oo+is2qPVwj3QJBEMbUxp6z0rExYDQXkM2RBDbw1ZosJE+3bqdVNjLKw3a7IsZTTOydKEvm+p/tlfh2e/QPrH/hy9GtHXFbqYohDPUzajY8TyOD6tXYG0clhcEcRFUYByjfmCAyBRUqUUfdc6I9mdL17NclfRVvYGiS/29BtQhUJra/05hvnDRUewVugBTYtZP8K8/zV4/G3GmeLV55/ntdf+GK+8+jKn9+/JQnWL9+233+ZrX/tdzh6f07zxD+jf/DX6ZIy685q7BujD59B3Pxkk6kdHctw7OhXmESUdK4daaGeMu0ZbrmG3mw+xuvz3rDEhAixBFZ8Vcu8p62oaPMbYn8MOBbGRoPCRJe8wRRahc0KGaJFSFuHdd06s1mhjovPZMAODamHvfvycSHQ7eDcybpzLGVLat2JoWkeNw4a5BcjylN503KxuwKUyFZpESw2EAnEauo5UKybjgs36ht12jUT5LeOxNFsCS13VKId91UrWWKI1y8NDFouFsLYpiYhutxseP3okuEwlDFRZnlN0vRSBJQlaJ3TGcHlxwf2nnmY2m2L6jvFkTNO00LZ0XUvbNmRZ7pr9tVL/lGUum68jBz2eUf+3MwSCdree7cAZ+E4H6gSBPokheP/eXZ5/+oS5OeMOj8jMjnv5Nam2vH6Z88+2n2W33QXH2O/G4NTsjYOwfmQy1N7o/JqLazp8dM6/JM+SAArdbul/6//Kayc3/LW/+rPM5l/CWGH2KIoiZHAvLi5YHC5ouo7rqxWm1ywXx1iT8Pzzr3Bw9DmefuZzlLuKJCtQiUInSljVTCN1PdsdZ2dPsBaOjo4kzT8eO7ILl012818kCdYaV6eg6Pqao5ND7t6/wyc/9RppLgXZm82Gm5sbRqMRSZJS11WQgdZarq8vmUwmFIVEOLO8CA2gxmMpFLy+vub8/Jy2aSK4jApBJJ/Cz7KM0Wg0MEcZ4zrbj11gacZyuQwGwG6348GDB/S9i4LWNev1moODJXmeYX1Pk6oKzsNTTz3F/fv3Q62gN6599n06nQKE7Ih/pXnOdH4amlrde+ZF/uW/8Kw4RU1Dnko2PE1StBKHznQpfdfzxhvv8alP/QiHh4dYY3j9+9/hvXcfsds25PmUsqo5P7ugLCvmM8Gid73iH/69X0UpxZe+9CVGkxm/9dv/PePpXLKPLpJ5cXHB2dkZr776qnPMBIddbrakKObzBTsXqfQNdXe7HXfu3OH6+pqmaUI/hDfffFMcpcWCrut4//33efnll7HW8uKLL5DnOV//+teZz+dY2/En/sQf59133+F3vvrbYC2r9YqT4xMpgE0SPnj/fbbbLWmaMp/P2e52lLudBPDazkVpK4qioGkc7r9pefrpuxwcLPjmH/yHrI+/gH71T6O06yIeETjsG40qGMf7etf/vb/Lb+uSsL9DzCOWEl5ax9I8qt2IghP/Q9f2Lx/YivtagcFW17S/+zf40c9+mldefgnT91xfXbLd7vjJH/8if+e/+4/pfux/jjp4HuOJUJw3sKfChuiXjCBkbAk6cqgPIwTHfG2NItnT3/733W5Hl7WhJkdYPE2AMqbO6QiZFiu60SgdjGTP3GgtWGNo2o7GZRW9g5FnUjReVyV926GwNPWOardBIOE22Bx+jN4OGP4dUA/eKXSeWHDG/GO12wvunv8GP/3T/9sQWPFZTu8kTGczJtMpeZ5RVhUoxWQ6JcsyFstlMM67rguGv4/4l2UZMhnb7dbJowOMEZl3eHjIcrkMzfu8Ye8zql5GSUY34ebmJhSQ+wzvyFEAg9SuSNBvGWzvthVilsQV7sPg9AB7CYK4s/n5+XmQG+v1mvl8Huq/POR2MpnwcV7Kfszcx3/1X/+tPSchbrLnm4H4fhn+lEN6b4iY+IIan5b27/vzgDjjeZaH83gPq6prqbLPc3bbHVeXV9je8Du/81W+++3v0BvDZz//I1xd3fDGW+9i509hjKGuG4zpSI5foK829OvHglNPEsaTKZPX/iVMOoXZXZLxHK0TmkZwbINR4mdsYC3xi36IayroG8zNg0Egbi8w7/1OmMdgHANMjtH3Pkv35q9jTStUwJHR7y+r1g/QtMxmI5599hk+97nP8corr3B8fOyKAOXSbdu5hSAMCLtdyW5T8fjRE9579z0ury7Zbrf0XS8boqlpG8kyNW3jmKYcXZtxTpVxc5Bk2Pl9GZu36W+tHDWak770M/sy2b304j42KYa5suJQaO+syYJxWRgvruUi3uD3TBxyqGOt8o5RKJgLj2nv5SEqviN0lmV0bce23IVreEiMOCUqCCPfMFCgUvvNJWUJSMYgvBVNjHLaZKBVdqMLSkExW8yZzxe0XU+epZydX6As0rE7L2hNz2I+x1rFaDxmsZjz4OEDbq6uMJ1wX88X0j213G7YldvQ1VonUsR57/SUYjIK0KPhfsF0PQ8+eJ+zsyfkeeEcbemgrbQiTzOMlVzUs88+CygeP3ooMMWuo6xK6rrh5PiY+WLBxfk5d07vMB4X3Fxd8+DBA9q2+dBT8WPZj+ypwfEkcsxtZCgoS15f8Pl7ih99WvHs0nC40GRZIjSLbYdSmrJq+G/eucdvv2Ppe0JAIaj/0K1238EMQ4mMGRvWxvB5cBgHzxEQnLJ9+A3y1/9L/sxP3uPP/7nPM5/VGFNjrGN+cxlFz1bSGMPZ5SXrdcXB4oSy7OhaODy4QzF+mR/5wp+gazVtrxhNJ0znE6wy5EmOsgIjurq6Ik1TDg8PZSR6KNb2zaJuQ1q90e2LBR89esT19TVpmnJycuJS/WkIwCgldIy+aPv8/Jynn34aEEPi3Xff5fj4mMPDw5B+//a3v81iPg9NoLwe8PvEw6Jud5m9vlmRphIpvHPnDvP5POgK34fJ/+2VrnWsa36LBiYs60kgksAG47P0seMTZ04k2m9p24ayKsNYjbHkWS7GEwrbC2NhlqaYrufv/79+laPDI6q6Yjwds91uuX//Pjc3N3zjG99gOp3yC3/8FxhPp+y2JUmSstuWfPe73+OFF19kMhnT25633nqL3W7HdDqVPgVVhek7ptNJWDfz+ZyHDx8Kg5yT/6d37nLv9JTnnn2Wvuv44IMPJCM1mbDdbjk9PeXpp5/m6uqKd999l3v37rPb7ciyjHfeeSdkpiaTCbPZlK9+9atorbm8vOQLX/gC1loePXrIw0cP2e224TNviKRp6vZ8y9HRUdD5YqAaimLEzc1NuEbf9+R5htZCn78ra9rO8L0fvMmDyx3m4EXUq38SPb83FOrfUj4fWRQeot1x4I9bssUHIAbnIj7HR6gyOVscI7kt1z7GtbGSjTWbC+rv/D149HVee+l5fvRHPo9SQifa1jVd23KwPOQHb7zJP/2tr8OLP0f+qT8n+kZHF1TRPFjCtfGU5u6aKEI/JfZG5Y6PiV5s7DThDH3FeDQiSRNZb0qL0+UIWqTZnB8MoJNBRyNNSUMsJ9ECw3JwHFnTtTRXBvquZbdb07ctvsjb3STKw52VdzzBGt8CITJQnH0mbt8QFLLGoBVkv/8f89f+3M/wC3/85wK82AfOm6bhwMnSpm1CkftoPJL9kmYs5nN2ux1FUbBaCczT10N5J8Ab777WwVqRR76Q2mdDvEz0DsDYFYX7bt1K2SD3JpMJq9VK6jW6jr63IXgVB2tmsxkLx1JZ1wKV9JmWGGFUFEWo1fAOR2ga6ORlnJ32OiXPc/74/+hPfcQu2X99bEfjb/+X/0+UUiyXS6wV3LhP7/hUjfeefEol4MEjx8R/10+qT5XDUPMh7deTgAfzrzzPWR4e8OjxY7BWGogp6fxcbre8/fb7PPf8i/yDf/AP+Z3f+Sp9bzC9TBqOm98rF++8ZFnGvTt3+aW/8Es8vFrx6998j83yNbrD19xmHCKxxgrW2vQN3foMPbtDvEm7P/xvsY9+H93s9oKksRCMHY04swOQRH0OUJDohOPjY5555hk+85nXeO6Fp5lOJqAgTVIsLrqupY7En683RuakqmnLjuXyMES1fOt4Xzi5Wq24vLwMRoFE7VrKdcXaYfIuLi4dHrphs9mGxekX82CMCMWxvydhH5N7a5MRNpUOk106I3/xJzDzp0kW99zaGDCjIIaddgIlS1OpIWg9HnSYvyEbZSNBHk1+ZNCjFVmSkmUpWVHQtR2bzWZfcUUyMtiZStL3Wuu9SJRy0RTpSp+GlWCdYSznsc4BEudKokhOGbgvHd+9Q1GMaPueRCc8efyELMuYTqZMFzMODo8x1nB2dsb903tYY3n77bfpuoa+bZnOZyRJRtO2NHUlcKJEDK/ZYsn9p54iS6V5Uu8MMwLjjoxLa83jR4+4vLwgTSWCWDnBNMoLKTjrWo6Pjjk6PubBo4dYV0xelSV1I5nOkxOJlk6nY07uHHN9c8PF2TnXV1fBaPclQrI3hsckcy7ZPwle2jCfWNm/KJhu3+bf+mLKp155lkT1FHlCWZe0XYdCc3l55RomWS5vdvzffxdW4xeC0g3sa7C/buI1sGdI4Bp2DtHBfXig+3q1onvwB9i3/nvujS/55V/6Ej/xxadJ1BpFTW9BpyO84+SFeFmWGD3mvQdXJElOkU9pmp6b6w33Tp+i7qYsls9xePQMN6uGp597nqeefZqejlEyIk9zsjwLzsZ4NA7GolLKdRuX4snMGfNdJ1nkuqrZ7ra8//77PP30MySJpshzF2xpgpLx+7yuatJMKGm7tqUsS07u3HFQrTbA7eJaO18g6oNLbdsGaJNX7L5I3CtXoWaUZnYBUuvgtjHG2MsKr3uEVc2Gc8eFj2LQ5kHPeMfDw7kAZrOZZAXKktls5vatCAMJqDVkecr19SVZJvCRaidGSNe0XF1e8Y3f/V3msxk/eON16qbm537u52mamidPznjjjTd45ZWX+dznP8uDBx9QVTWf+czn6LueqpJ6sqZtub65YTqZ0LQtm41AN7I0dYGgjvF4zK7cSdbTGSJlVXF4eMR2vWGzXvPsM8+wXCx54cUX+OrXvsZ2t2O9XvOlL32Jp556ijfeeIOvfe13WS6XAPzMz/xMyCqNx2PW6xW9EQjc66+/zsHBAWdPnnB1dcWTsyckibB3eVhGXYszOx6POT4+do3IKiFQscJEJYGMUYCweXhVWZZMRiOSRNN2HaPxBJ2kfP/1H/D7f/AtNlVPf/QJkk/+GfTsLp7MwZpIphJr4/29+WGTOtq3sohCYHSPberW90KxtD/m/4triyowmKt3KH/j32Oc9nzm05/kxRdeIMukp5HCUm63ZInI8mI845/+xm/x5jsPUC/8NMWP/kUJgOkhOzGwM7p9EcSc2rv2ADXyOkkNzLA6GRgn944ZtGpoXpwII1WSpPSWEDzxxCmJ1iRZLj2fcHadFgiv0lqIU6wLGHRt6KHV9x3lZk3XNmANGkEe9D4+Ca6Z4aDvjQuc7IWNQlwvwmkEhWPh+h3+yos3/PJf+UvcrC5Jkv1AedM0pLlA8OOaMGstd+/e5frqilSLDekN8+l0KtDj7ZbtdusaGopc2m63WGspinHIoHpYkw8ClWVJmqZMJhMpFF+vowC+ZG+LogiQqLIsXfZkyMB6RwcI5A/e1vVy0Ms+T9DhM8i+ONzLSm8beT3g0UdVVQXI2M//iT/+ESt///WxoVPe+7m8vAQGakNv7HmcmffGOsflL89ZHq6PPsW9HryT4W9cvK0xx4fHnJ+fh888/dfFxYVgjY0UfzZNQ6I1L770Ip/57OfpOqnEv3PnDt/+1rd5//0P0BrXaFCUmY+6eI8zyzRXVxf8r//tf5tfPjvnP/qP/ga/9k/+Nu3BS5DPfehVFvTF97DNhr4q6Z2jEzC9fSdGr4tyxEZzSNkRG1mu82FktPrmRp/97Gd49ZVXOTk54f79+/S25vLqzNE0lmG+siwjK3JhZWgaoTVrG/qu4+LykmbXcXp6HwVcO9xs10nq2i+cLMs4ODgIHmtVVfSLnuyFFwBx5PyiPjs7o6xKslTmEaWonYOSJAnj6UgKqqZTRk7hLBZzsrzgzt27fP3rX+dv/s2/yRcn71FuX+drv/FNkvufQRezsKjTNGV8/Ayj134hMCEAlLsd66hoCZzzJ23HQ5drD0OzUQZBUqguoq21NEVEDUWVah82Zp1QGhSEa2Po2SyUigRZpGR8Ni/ePFEkxgbhKIpAo4bUpzPEPDOWUZBmOUmqaesWsGRZyma9peul+WTqCsbbTpR63/VCoZdosjzn3ukpWZphlcv/SOuTgC9WSmF7ue6d07tUVUndNBgrQkro8yyJlYhQWe5AHTNytRi5oxjVStFUUheUJkmAf2mlyYs8ZIT8fe93pY33yQBDElICBVE2yFhD8eif07df4rvf+S7VbkNVbrm+vqFpOtarDefnl1RVjektVdOyutnSfe6vktz7LEZpdEiP3AoA7D+0ISoGgSVNhbFFa8xa+g9+D/Odv0veXfLKC3P+x3/5T/HScynanqOMpWsTVJrQud4SXm1vthsJhhihj7y5vsTYK8ajKU1b8uTsfe4//Rmur8/4yZ/6BRbL+/SkGGWxyqCtpm8NbduT52OOjqQj7fXNis3G00NKmn273bJer5lOZ1EEsaGqak5OTvEd1BOdkaQpbdORaEXhZIVSCuZSUwTiABwciBISYrChNsJnSowx1FXFydGxc4BTetMH4z/ADtpOgisu4+BhrF3f0/U9RZ6zc7S3XdcJ3LDvaeomBB+0loLozXqFMX2QZ23bMh6N2broe5qmlGUZHI7ZbBYifnme8+DBA4qioCxLjo6OUCg2NxvSVJMXGdZ2VPWWBw8+YDqbYa2ScXQ95XbL2dlD8vxpynLLdlfxjW98ncViwdXVFfO5QBh22zXL2ZjjgwU3l084Ojzmqeef4d133+PJ5TnXqxWPH37gskBzmmrH+WoFCnpjuLy8cM6XzLPAoMbsNjs2mw1917Fdb/jxL32JRw8ecvf0lPV6zfn5Ob/yK7/C5z//eb7zne8wHo955ZWXmU5nPHnyGGvh/v179L0YKNvdmqurS9q24bd/+zdpmsZB8pRkXrousO6cn5+HSKuHXXZdR9u0rmcTtK08r8PDA5SS5mbL5QJvildVQ17kdF2D7WpefeVFTk4O+OrXv8WDB39I9xuvk33l30Etnw0bMTbm9yL3t/a3z2Sq8B3lHAxuyfr9I/cM9fiz6Jjb11a3ZUtkD4DBXL7J7p/9+xzMx3z5x3+MxWxKWe4wfcooz0mzlIODJdcXl/SJ5Xr1mMV8Tp5nVO/8FubFn0IdPO0cnUF+RsITrGedgqDdrKPfswMZxt49+Ww3gyz2Toa3cwIM1RjqukIlKaNiTJ4XLvgoe7bvLag2UC5jwWLo2y44ida6YKnp6buWbVnSdS2JNUhzATezFkBjnRyWUlhhrsKY4D8Mr31d4uW5cuO31pK982t89s//Na6uL2nbipubm4ASybJUguaJpnY20nazRScC/zw/P5cMppNTHt50fXVN23ZSK3V44Az5jDzPQo2HUpqLi8tgO6dpGoIvPqDi91KSJKGxtW882/eCSPF1UUVRUNe1gzVKEmC73QrdrpN3PjjjGaO8TeWDPD7QE9d3TCYTNpvN0LXc6QvfM8czXH2c178Ave3QA2Po0o2LWEHfOXyfS8unSY5CD56moxYFTdcZp4RkMSpHZSsTL+w9FxcX4WZ94YxP1Xjvqu9kMbVdT5Ll9PRcXJ0zX074yk99kR/74udZr1c8evSIy6tLXnzxhZDeBUKDE2tbzs/O+S/+6/+UP/uL/zL/5v/sX+NrX/8ddqsf0BnvBBDgBlYrTJKgTB94vuV97QPEqERje99ozDXSs2KuJqlwT0tDNcFSK604Pljy3DP3Ob17ynK5EMfq7DHldkVrOjYOErPZbrDO+x2Nx0zHY7QWlgg/T0maMB3NmBWKpiqZLxa8+Pxz4uy5zNRkOnPpcSly9IU+WmtynVCVFX3fUdc1pft9tVqxXm9Cqn25XDIej0iShJM7J4xmI+ZOIOZ5ESItTd3SlC1X52fcv3uHv/qX/xJN0/L+W28y1k9IuGKz3XB0fMx8PqdR73AzGQ9CDyWY/0Q2Ttu19F0vUAmPgPH9V4JQVy5FKhEW7xQmCjGQEYFllELbuMB3P9Ilp3IRFKVjLSTfVhKZCfX1/rM41YtXdv4a7s6UpjfWlcgroZp1RnCi5D+NwvY9eZphFdR1JRzhxpDkGcZIFKJrW9CKtpMIytHhkqLIkMo5S+JmEg3GOCYUF4nyXUGOT054/4MPSFyfEJ0kmL4jTSTCXLsIsRR9rwZ5oBRt39Fbg040u1Ii+BZF19tQe6NcVnFgPZH0gBI/0M2RyIkQidLKMdZJ1u/Jo3P+g3//P5T7Vwl9J0WiSZIwmUyYTmcsl3c4Pb1LluV8ZTnmW++9yQ/sp6SreeihIjS3nm7XN+YMqXn37OLC7yEoJg25LAn9O7+J+vZ/wUFR8pUv3+fP/5lPMZu29OWW3gqkRimL7TpM32G1oaenbjtW25K6NjR1x/VVw27XUdUNWWYYT2aQT7HmgM98+guUO8No3JHmKYqEROcoY0jyIZXti/SOjo4dFngo/lUq4fDwKCh36RMhbIIxm5NW0n9lOp1grM9Yain0VGAwpGlC4mBNiZXAz2gs2QAFmKg2L08yqm1NliZ0qiF1a6ppalnnzlkuXbTOE46sV2u6vme7FRraZ555hq7rRLFqQrDBZyU9hMf/LnUoEni6tPL96+tL+r5ns9kEhSvKNuH68po7d044ODjkwYMPxGCvdoxHI5bLA6HJ3mwwpudwfkD2dML5hdSp3L9zn7breP+990jzgs5YfuzHvshqvebOnRO22y1tK2xuRZGQaEVnLNc3V5S7ijfeeIN79+7Tth3vvPuuyC5rWC4XdF2NMS1pCuvNxhXoH7Ddbrm5uQkBJ2zP+dljlNKsVjdMp1O++vWv8pWv/CSf+vSnSbOMk7t3+PVf/3UOTw75k3/6TzCbztiu1mzWNzx69IgHDx7wuc99js41Ad2Wa5q6dkX2humkYLfbMJ/PSVPNZDwLvaUWC4HFHR0c0tYdu7bk8OiI3VaKTLuRQBrzrOD6+prl/ABjDVma0lQtx8dLUCZQgW42a6rtivlkxC/8zFd4/a13+IM/+Dab3/z34Mf+DakvVBpl9yk2bTAw9+X5YO6rENmO4d2DUP+I2i0nz71hP2QpbsvzWNbv6xKFxVRr6m//t9gPvsbRcs6nPvlJJqMRTbWjqSo2q4a2aeh6oZ+vW0PT9hig7w3T2Zz25ob6D/42k5/6X0KaDXrGB8pCA1rv5Lhxau2atnpHzM2Tz+grhQ98oobsh79vIdeObCEfPOoN1W5LUwklbZZlFGkKSqPThL5ppK4zYsPsTS9F460ER3vTueyhK/hXGqwO9+Ib3GoLKvSrxpF6eCfKQSGHBxYCQn4+lCPEME++xZdePea1155jtV7R9x2LxZzdbsM777zDcrnk4OCQ3W7HZDJ1REFjULBZbTg9PaXvW4wRmGZZVtxcb8iygqJQJElO23au54w0cdQ6EeeLPlDQ+wCOdxa8cX96ehoyst7u3u0qdrsd9+7dI88TDg+PGY/Hwbnf7XZC4w/cuXOHruu4uroKDoIP7HsnQfZwGjIqZVkyn8+5vr4O4wECzMojmFarFaNCkgpd097ePR/5+hfOaNz+z/TSfMVHssSjBR8tvY2FjeszYkhVzEBVVVWAKviJjnl/Y4Yq8QgzHj9+wuHRAYdHB6zWN1gs40nBweEz3D29EzxBz3ziKbukuA7untxlt6v4b/7O3+Hzn/sCf+wLf4zf/M3fQmvlOOmlyNNYS9tLASBWFohn2PLFjqPRCBTkWcZ0MuFgsRTvVEmUWecpbSPFsn78fd+xmE5oHQ73+vo60O12XUZvDRNHQXj//lOBjSVNU6aTEZPxWDqzHh6SR911fZqrGI3kfHpgLhBYgtl7JnVdS9pMa46ODsWrd0I5yzLH2S6FpJ7Zq9ztsECSpehUvtv3fYh+SSq1o6prjo6PGY3HvPrqq9y5e5c33nyDn/35n2O+XPDX//pfZ7VaSWRg8klHwyrGQl5kAbqEX39uvVhnmEs5ughV5QVbop1B6RWCIktTwYVqieAqehGEDF2ng6COQyUir4ZIT4i0eL0l+WdvrOKj8f4Uxp+EkN0AE4ynrjfYtsU3HvSFbNa4rvVaO2aq1t2rXLyp6yBIlE+NWsNi7iOFNgSFvGLVSuBJnYM/geyxyXhCqgS+kLmeG3I+EeedM5azNAUUq5sbdqXQ2BrbSXM1F3WWKHPieuDE3bcHNe3T9l4dBhanQF+rwicK6bw+Hk/4uS/+LFhDqlMmY2EP+sxnPs3Lr7zCnTt3JKuTpmy3W2pb84Mf/IB/9z/6OubwkyKPnJtpAp3sQGc7RC9dJtLJsxAXdF6RUgnm/AeYP/xb3Ds2/OKf+DG+/IVTNGc0nUC9kkRhTIJSFuOZWSy0nWazs1xdWx48XLFdW1Y3NVk+IstHzOYH3Ln7Al/5yk/x3AufoW4TZ0Cu0WlFkuWMRhMU1hl6EmjIC4FG+Yynj2b5yJjC1W6471gQ+tw0pe2E416lCbmLbvl91nd9UHipzzpYG+gZm7omy5LwvTzPuboWasa+bukbzy4l8CBpXTTI7+lUCAY269oVDLc8fPAApSXjd3V5AdZI465yh1Kw2225urpiuVyy25WMx6MAgyrLChDKXGst8/mCqirJ84zddkPb1MJOmAvJyGZdcXR4QKJhvbrm3uldysU8MME8+OA9jDEsl8L8dnNz42pULpjO55Q76fOxXq9RSugim6bj7bff4fHjx7zyyksBxnV+cU7X1iyX8+Do1HXN17/+dbqux5A4I0Wadz711H1QEim21jKZjGlbyWDeuXPiIpgbJuOhQ3eeZ1xfX/Po0SN+4zf+GZ2xdF3Ps88+w7/6r/4S3//B93j48Jqry0uasma3K9lsNhRFwTe/+QfkecZ6vWI6G4mOdE6PODZarjeZslmvg3OrlGK7EWNruxGEw4MPHgQ95BlvpIawDTplOp0AiocPP+Dg8ADt4DMHBwcO7puy3mz43CdfIaHnrbff5+wb/w/K/JjsM/8K6s7LzuFw8jvwtTrDO5bn4d8POxhqEJLRtwjn8IEIdeuo6GgvNW6dX4E1VD/4NZrv/H2KxHJy9y6j0YgnZ2dcnD0kcV8zvQn7zAJGpRhUwObrRGimy7Pvs/vN/xvjH/mL6PldYtfHpWjc/3X4JMCk8CLY7o18kHIIq5+vf1BEtaPyj/aBIiX3ppTFWh2MYzyCQw1zLvUc7jzG6UkfvNFO9g+pFad7dcgShYuHoQcQNcIGOdyJ6E6vv+W+jQVle8zjb/Ol/Pv8pb/4l6hrCWZf7K6Yz8cuw/eKBGO0oihG9L3PrBhGxYhEz1FKCGakIW7PwcFS0DQGLi/P0YlCqRlnZ+cB6TOZTEjTlPV6HezYqqoCuqRwTH/WWlarVbB/m6YJDH5PP/20gzWuQ02btdIt3GdvDw4OwvP0hdweBrtYLETPR9Ban63w9R4C7ypCUTsQ4FVVVTF39XbAh+rq/qjXv0AfjYFz11rLZrMJgwUCN/n/h7k/DbYsu84DsW+f+dx5eFPmy6GqsqpQBaAIggBJAAQBECQ4SGzLcktqWW21rVY7/MOzw3/8xx3h7nDY3a3+40kOR4da0Y6WLcrdlNQUJ5GSKBIESRAEwEJNqKqsyunN707nnnnv7R9rr33OvfmyKotkSH0qst57955xnz2stb5vfYtvnjsTaS879jhW7mjvu52rwEnYYRiiroi7V1eV5ZdLQ8saDAbY2dnB6ekp4iiCrGvcPzlGHMfY3dlBmqY4v7ggj64gHm2v36cS7Urb6Neo28diucR8vsTFxRz/6B/8hzg4uIZRd4B1voYGIyAudnZ20et2oQHE3ch2Hnaq5vM5RsMBOnGAsqDoXRSE6HRi+K6H7qCP7miI4WiIKIwQGTTAEQ66cQeB529ozTNn2Qt8Ug9ymyKG1mlQVMiKq3bypJ/nOb88m+iTZxmkkoiiGL4X2M7NG8N5SbJCt9ulwlzWKasBTdEEx/NQGE62MMXAHLdRdXJdD2VJutCUXBqg2+uj1grPPn8HJxfn2L12gL/0V/8KsjTDtWvXMBwOkSQJlFKI5t9HcfPLYE5yXTu2nTjHppYSUMLOac3/WkxaRqE0AE0qGWEYIo4j1FJZX4CjPO18Gl6q2EBvLzsCnEvDsR6Oztv5dXOCZIjednPmBDsNPUyqluMikOUZlveWOLh2zTildBwblgDsmGAnhBpDG34s66633i2ovaRqHBJojboqEQQhTa5RiOQ82UAuLSXAOKde4END21oESiko3TJ6lbKTtaXdqMZYtwmCvDY2V2oicaKFTbXecb/Xw3/nv/tv4ObhAXamU3SiDhzfB7RAmpEs7yrNUdU08SbrFSbjMT4TvY9v5NeAaEyOAgSUrqngFSMXgpS3LDcfsNxjTR4ayE1xoKsE+tW/j72xi3/zL3weH39hAKXn0MI3xr2PWim4xn2StcR6XWI+z5GmDtI0xPvvL3BxXsD1QvhhH3nlYOjv4MatT+OFFz6O/vB5RJ0dRNCoahLCkEpTIVIQWqdMfwlCMuikUvDYsTOIntYatVlsfN+n4qQm0hUGDbVNQGB2cYE4jjdyGVgOupYKWXZKnPpu1+ZfFEWOuiyQ5wXOz8+xu7uDJFnDdR1EYYzID5FlKTkCZU6fm0r1LK/IkrgN/J/YaH0URXj33QsAGkVRQmtpFa8ePnxg6AWFEf8gicjBYICqKk1gRaGuK5RVZvq9RC1LFCUZQEHg4bvf/Q729/ctB5pVWnjNGgwGODk5sonn9++/j+UqwXWf9O2JhpbBdQVGoyFOT89x48YNxHGE733vNTgOMJ6M7fq5Wi1QliV63YGJTMZYrzNACaP0RbVT0jRFt9exuROnp6cYj8d2HhyNRpRUXQNhGNlk/uVyiV6vh6Io8A9/8RehNdDv9/Cjn/sRvP32WyiKDAAV9qICnRph6BukZIbReLhR8IuNHw5KLRYLu+6naYqqqrBardDrDVAWTe4G53PSekRF3jzj3GpdI8vWJAhg9m2oHQKDwRB5lmF3MkK6XuOF527j2t4u1mmO77/9Lt775v8Defc6gh/5m9BuBPgxNmeTq+aWxz+3U5zYohKhNZ+3DOF2IUveqz2v2a3OocsM6Tf+X1Dz+xj0++j3+7bN6rqmed/Moaxqx3NqrbSpDdF8zu9dn72F9J//LcRf/J/CndzGY4ljfPeCqK1oUTbbGuJawdbeoPy5Bs9htKRxVOh8bdeknfNhVaG0tnMqi8wKRis0mvMYwMIyAh5DjRr5entOq6DXuI3tzcb8OGzFKDUAnc0RvP5f4a/8B/97PPfcC7i4OEMUhYjjLoSgfJMwBC4vZ0SbNCgP26zn5+dWxSnPU4QR5Z124gpaA9PpDtJsZVX7AFg77eHDh5ZBwsY/z1Pz+RyLxcLSnebzuZ2DpZS4du2azecgx2Zkg0iFqRXGwW6uxRFFkQ1uUIqAb+fyxWJhqVmcY8LByoODAyRJgvF4bEUb8jy3ylWe7yPNMgRBgMvj4yv63OPbR3I0mGp0fn6OJEkMP0tsdHB+EDZSOI+DBwhzxNhAYV4swzOsYBX6gakGS4vPer1Gr9eDBGwEuN/rQdY1ppMJ+v0+Tk6OcLB/QBGivMBquYKqpblmiNUyQemXODk+tfrBySrBo/wh0iRDWVYQcNCNY3SiGJ/5yR9CWqbIswxRHGEynmAwHMARDhUsExq7e3s4PDykImpGUeXe+3eRrYnv50Bgf3cPsq7RjTtwwwC1C8OJC1CWlHDr+z4CL4QriPPeSAFroyxFevvsMLRzXGRVAiC5tF6vZ73ixWKB7oAWqjzPAYcUaywipYSlVjB8F4YhlFLoxKQQlRc5yopkEF3PAwTgup6JWgC9fs+8V0rIYgoHScV1jKceQ2k67uzyAqUktScv8NEfDtEfDDZ4gADQ90rk7/wT5M/+jDVGYoPKjMcjLOYLlIZDqYxjqm3EhpIQakbSHJKW1Q5572EcIopD1LW21d/tbNaiO+n27y3nguqImHqsba4vmBO7hWRQCIgmeju/C14DAE1J2sx/5Yl+vV6jlhL379/H4Y1D4tADhA4IQwWDgO9TDQ4pamhBBdVI35zOXWuFIsuJpuB6NnJGNDr+ncaUIwDX5MDYOhq8oOomIds1CfxRHDX3DjoXPR0vbLAwezuLunHgYB22VnNjIxppFllhhBnCMMBLH3sRUegiz9eYzy7g+iEZ9e2kNy0RdSJEUQgNgb/51/4yfv9/959AfuIvwenvE3JkZW/p4oQEcrXpkp7HBghbVIh6Df3Wr2GABKPeAN/4ne/g3dc8TCcdDCYU8YliypXRWkIpjSzTSFYBzs8yXF6uTYJ0B0EwgRs68AIBpV2sC43f/f3v4FvffQe97gA3b1/Dn//zP4PDw0N6v55jHTppnlkIQEly/Gsz9xYF1Ufp9XooKyrmtlwuEYYRPDMvJ0mCbrdrkwJrKVEWBeYtRSI2gFzXRVEWVkXl5PgRaikxHA6xmM/he64xRjVkXSEIPBR5gYtVAiggikJcXF6g1+tgPieon/MLer2ejZ5xwMT3PXS6MagiuEDcoQTI6zsHlFelybgfDgcQjoN0vUaWZxZVOT4+IjWtqrSV7km0gIx2rhpeFDkG/YGR6fVt/+HnZMrscrnEo0ePTE4D1Sbxg4DusapxcXmOTtxBpxOj1+/inXfehZSUV9XpdFAUORwhMJ2OUZekhHhxfoF0neP69UPs7u4hzx9gsVzC8wP0+ySpGccRwiiAUpF1crg+SlmW2NvbI0rrkhJJDw8P8eDBA0wmE6JUGupxVZUoywyv/vF3EIQkDQ8ArkNr6dnZGfIig+s6GA4HUFJCSoXRaITT01ObHMpVhOu6UZMKAgpakdylA9+rbdIpG0Sj0QhHRw9RVjmhjlFkqXIss0tcfk1OrNYo8hKe58OFgu8IxN0uyixDdzrGjcMv4PjkDG98/y7e/e3/CGkugfFtuHsfh3f9FTjdXZ5ltq2Zjb+sHISd8xu6pM3Va9FyLM2ydXZdZVDrCzqfUii+/5tAtYa8eA9aliYYSOsYS5fCnEso2ACaUhxYofldCW3pi/y5fQrhAnWB9F/+XxC88FUEH/sZCBM0bOhTzXpinYWNYJpgXfZWYMccpVvrGQi50I5otU57Jt/CdrjNwDki5g449qY1YNT3NDsgJsncBguVshLjXMgUWptsSV53H3+bLbeQG4rWuWKN8hv/GT5+5xn86q/8Kt5//31cXlxgMBjg5Zc/gbpeod8fkA0rPKTrAq4r4PmUjB1HMe7ff2AkaUeIYwoUL+ZzM48VuLw8BxWVVhYtCAJyRpi2z2Ph+PjYIgecL3xxcQHP83D79m3r0K9WK8znc5trJ4TAo0ePMBgMMJ1OkWUZhsMhqqrCjRs3cHFxgW63aymljHawZDcjFXEcI8+JjsXFUqMogpSSiiQaB4X3Y2e3rmuiXQuBoVHl+rDtIzkaAOzEce3aNRPlllZTlxsXpiOx0VmWJTpGf5kdD87J4GhRO7N9PBpj0O2ZfIAlBuMxhv0+4riDfr+P5WqJ4WBIhpPvY9Af4NHRI6yWlJxaFCVWqxVprBc5yqLAgwdHePDwIR4+eAjf9zGZTHDn+TuYTqbYnexib3efoqOdDjzPp5ca+HDcJom9/WzCcGw1YJVMGNXY2ZnAgcTZ6Sl63S6qssRgOICqJcnFGsSCo2224q0jUBivcrVa0csFIThlWaIw7UiVfwPLsfNcB0We4fT0FNevX6eEfNPJy6JE3OlQhIwT9Y2XK2tp3xsvIrbau0PvL4gixJ3YwHLEq1Z1ZXnTWZbBdVx0e11KEBcuyrIg41ezUEBuaCQeFpczlHlOiFOytolifqeD6XSKd999l6pRCoFp/i5O7v0W1M0vwXOZS+7g5Zc/jvv37yN7+22UFaFTSrWLCJoJiP9WimpzSJp4XFfAdQS0Kxoo10ZNTDSFJzYhLBKvePLeiGQZg7rtsHDkW2uTfOYYRKUV/bHzoYI0zovnuqjh2IRzTpLl6FEtawjHgWfypXiSjzsxhOsYyT2P0A+eqD2PFjJHQGhjWGuqDaCNVLAISFtNOKQUYhETdnyksvcAwEYblZLo9vtwXJckpE3ETSpFjh00oEgtjB2Rpsnai1ET5eIli/fV7TY3IENVVXj46BHyNEEY+Oh1+/BqB3GnC9d1UOal5b9WRY0qr7FYrnB2coGhnOPRb/zH8J7/MqKP/RSEH5lFXJvX5piyks0S6pCXYe9F3vs6/Pf+KT7z8vPYfflLEFoidIEqXyNJCxTSw/kFVcdWuoKStUnCd6HVCK67i/HEQ1FWhrpYA45EpWsIBdQmjyov10jSFcKOi8FogrKWeOPVVzHo9TCdEEXS83zkZpFgZR+m43CE2fd9W2tCSonQ1LvgNs4M9Y3nseVyZcaJi7vvvmvh+yRJsFqvLMTOCykjoGHg28Tg998n2s5oNEIUxpCVZFsOQnQwGg2xt7djHIITqpNU5C0Neg9VXeD0lHTjVysKMI3HY5yfn0BKZShSGQ4O9qFUQzdg53gwpCCL6zk2EFQURKWKYzKU+/0u1us1fN/D9cMDRGGELCcllzzLEUZcXdc3Sk8JHj16gF7vRQyGPSyWK8xmF+j3B9jf34M0BS/jOMJgMMBikWAyGZu1kdEyYG9/H64DHBwc4PTkHFVVY7FY2qDQ/OQU4/EQdV1jb28HWZbCDzyrxc9FGMMwxNHRkRXj4ITv8/Nzy8X+/lvfhwAQRTFqLZEmKxQZIUp1XSOIIlxcniPuREYsoAsIbY7PLZ+bnVJy0mrrcGxToWWtMR6PMZvNrGHFwcSXX/441ukKvuejlhJxHFFNBikRhbG1A05PzmywQwgBnzxprJI1XN/D2flduJ6PsqYk2hvXr2GxWGKZPEDx1rtIX//HcHY/gegTP2+oRWYubwcLrFEtrDMJ+3nrZ8spgFaoj1+DrgvI+X3UR39MM0WVQpfr1ikax0TQpLm5vm5cjR0ZWKaQzZWwiO7jaIV1fmSF8o1fRf3ojxF//n8M0Rm3lP0ah0OAQWUF7XC+RUMH1QRBm7mbvQNh2QDCOIHkfDnWceF1zK67aPAdxjl4XbWBOW5PM6lrKI7XmXXD/G0oViQKYlureS2i+cWuMeYzns85Qb1689cgVkd4/fVLvPPOO/j6178BrTWCMMTzd76N0WiIwWCIKCJlNN/3jHoa0ZtqSUIrSgq8994DhEGA4UggCLpwHYEsK7BeZ4hMtfCqqjcK3gkhsF6vEYYhHjx4gH6/bxFCz6Nrce4G1+RYr9cbwbP5fI5Op0NVysPQBmlWqxVms5kNUAdBQPNVmmKxWGBo6n0wy4WDPG2EbDKZWFWtKIqsQ8z0Lq4arrWG5/uAI5CbPI4P257a0eAbYGURAEYr2IPWJJfIKAarjrCCEdAoTfFEwlKGjGiUZYlut0uGdNxBslhiMh7j5uEhyqrC2dkZLs7P4QjS9Q/NMclyhdPjE5ycnCAMA9xPElvMKUkS8ibLCsLx8KlXPoWf/emfxQ/8wA9gPB4jiiKiHAQhakn0o1pWEBAmUlObCUNBKU37OMTrFcKBljD7Sfi+Z6MOrutBw8G1m7fISDPIjfBc9DoxtOs0ql3SJOqadtQdauNOt2udEEYgeGLhyZsdNyiJThzZRef27dv2PWijDa2Uwtp0HO5kdUFqLIwktCNT2mnyZ5SiKtWe72Odrm0hr3YS8GK5hCMcyEraBQhouOL9bh+ucNAJI8iixM5ognS5wnQ6he8HkFphd2/P5tHwz8HldzCLJghOvg0vPcHSmcL99MdwsL+Pu3fvwqlr1GaB0+2FoTUx26i6homEKjgO4IlWNEaDJk/OseDMbsDkJdOSQRMZR7ZMMnErprJZaRzN7wyY8P3RlxDCge96KKqS6ooYVSxojU6ngygKMd3ZhRf4lm9Oym7m/RgjnKmDkqlQskZRVlQwz3XR6XTpBszEQtO/Z9qHjX1yLLI0g+MIeJ5raEWmH4CcJkbMtIalTHEdk7Isie5on39rcdUKmlPPNSxVwUbU7ALZqIe1I4cClGMw6I8w7o+wWiUY9HfhuYRaFFmO2WWC+/cf4O7du7h79y6Ojk4wn88xm8+QFRkiV6N++59CXr4B3PgM3NufpxovGqiVhDD5+Mo4P6gL6PQC9f0/gHf+Gg76IZ57+QUEgY9kvTKOlEBV1gbWz8ggkVRwyvVcEr5QCtAOut0+fC9EXZcQQsJxqW6NK0IoE7l1PA95kSMMffz5f+Pn4Ycx0myNd955B+NBH53oZVysEwjhwPN9nJ2f4fLiEt1eF67jUD2RuoLjuFitSMCB527f95CnGZKEKCu9fg8X52dUi6Gs4XkBMlO5u6oqjCdjOw8N+hQdGw77yLMcURxiNBxhHvrQUsKBRrpOUNc1dqYTyFoiXScQwjW1EhxcXJzDDyjyul6nxolhzrEgxSEAUURRfSpGpem+sjV2d3eR5wUWi/mGnO61awc2gt8182cU0TyUJGuTfK5N3/YRx64x2mNy0E3EuSwLrNeUdN3tdq1xMF9QsnhZlrZo7Asv3IFUQJpmePjwIYLAR1W50JqQtMUiwf3796EUOTV7e3twHCqsVRaUF3Hzxm24rofj4xPM5wuMxmOMJ1MslwtorYjiC4XRaGjnb07aJHpYZfIaG0UaKaVViHRcB7KsAC0hhAfXBBSWiwXKqkRkKNCe55r8CAkpa2sIsrJMt9vF6ekpdnd3jThD49jy2r5YLOAIF3VNMwBHTIMgwHw+t4wFyr3kyD3ltGRZthHUo+CUS9FsSZQZpTXgAFmRwzHGWyFrFJW0BpPn+ZCqRH30XayOvgvHCyA6U3gHH8cTN61R3f8mUOdP3gdmDq9zO4e3qeIbrsCWY7ChCHXV1s4rEU/et32e9iUEAL18hPSf/6fofOV/A3QnzTqoaR4mA0NDC3ImlDaiEG29cX4uaCvDbhERzpvTGnCYutQK7pkfNJ+b4ry6lViv0dwPmjXUPpvdjwvpmuA2AGFQcb5vdjg4H4bXbxsttGuJcTLe+S3g7r+EZ+xSbkdS3pR4+/vvGEltej5SnCKjXZpieK7nwnVciyRorXHr1g0888wz2NvfRb/fg3AEwjBGWSa4vLy0KC0H3FerlaXDs9oni1OQWMUc4/G4UfE0ubdc54iDy65RduS1ta5r3L9/H/v7+9YpYKod521xfjKruLJ9PBgMMBwOcXREtFAWmGBkQxtbpN/v09ygFGoTRG4XNv2g7SM4GjU81yUFCddFHMXI8wK5UULiAiWsGwwAualQDE0LSifuoCorrNcpiry0kCnLrIZhhMV8iYuTMzgaKLIceZrh9ddfR1GU6HY7mM/mtoPYqGVZoSgLeB5B+0EQYHd3Fy997CWMRiNcv34dnW4fO1PSe6fidMImSRZ1AQigKGooTZNsEJCsqFYCrnAhFPHSHbdRlnJdx040YRigUaoB6TwDgNZwhUDU6VKk1Ax+ZQat57l2omrTzTgqR06ZZ9Wi2Dtnp0MpaWFEhq4fPHyIw+vXSTEI2ijMNPLBln9d02Djv4uiwGw2Q17k0NAIQkJNJpMJXMeF1BLDwRD9fh8HBweQtYTne5ZeUuQFsnVmeX1nZ2e4f/8+RenWKRxFHMf1MsE/+6e/gel0QiICYYiwE2MxnwNmcGhJEZTId7B79JsANKQvENan+Jz6BjB5CW90ApxUNVxXQSrZTJaM1baiHfxelNaAIoPa0a6tq6CgLR8VNsLNCcik+60trM2X4US1VgS+dW2bFM4/zURpA1WCrlIzgmBocsLcp2/418PhAHlBksWc8Os4LpSmHAuK3FAC7jpNoYSAqiWSZIW4E4E8JbSk/ZpxrdAgCtAaRZ5DKolOHEM4DsqibPq1IqPZ832UeQ6YAkK2WGKtSHu/qtEd9CEEOcS1rAElTRs0yYmsOMVDBrqhJHD4mz9nMJxDVmUhoWqJ5SLH69/7Bt7+/ru4d+8ezs/OsFgurApXLaXtAhoSURhgOB7izgvP4kd+9EfxX/y//x5O3/3n0OM7cJ77cUgvBJfplKsj6AffxPNTDz/+xS/gPc/Dj/87/zN8/nM/iuXlJb732nfxO7/9W8irFEVVwg8jaKXhKEUOo4ClgwqhUekSQmgkeY1O1CMlnrqC7wgI7UFrovfUkmg1nnBx7eAArhB47XuvQkDjmVu38N1vfxsOAN9zcTmbIY47SLMUy8USvV4XeVGQZrvSKKvSziWs566kssIQeZ7h/v17eP7OHURBgDiKsE4y9HpdQ4uiBODL2Qy+70FqirQpqbBcLhAYqmUUBCiKDN1uD7u7u1jM5yjKEtPJhNSppILSCp7nIO7E0PAtZbTb7ViHoMhzeD4tS6vVAt1ux0bUmJfs+y66nQkJRSiFMAyQmUJULD7BQZJO3MH9B/eJ1iolIBTyPAOgkRcZBsMB5dJ5HkV4TV97dHRkkJsKnkeqVMPhwARjiH89m81xcXmJbm+ALMuQ5xkGg75F7X3fw8XFBYqCKE3jyRCXF+dUO6Aq0Ylp8b+czdDrkgNXGwchimMAVO8oCHwIB8jzENPpFDvTHcxmM9RVjflsjizLsFwuoZWDXq+P0XCE4WCAPC9wdnYKAcDzHVR1iZ3dqaHJuej3BxAOUFQVer0eloslsjxDlmUbAZ/hYIjVagmlNeIoxnt33zNVyCsURdmIiNQ1BsMhlsuEhC2UNtXkKYhGuR4utIJd/6ShFFFOl7KOQm3yQlbJiuhEyoOsSdGuVhKrZIlaSSgpUdQlpEGBa0lGKgXaHcoPqHLoxUNUi4ePGzat7UmowWP7tReBP5ONje0GpaZrA9uX377Hx+4vX2L9m/8xgpd/DsFzX+SDGiO/fS5zvEZ7raJvGEEW7Pc4nKBuUBRDoeUsCb6NBtU3z8AOg7AzODjp3maMMCrCCyOzCIyh1WaS8DpFp+Ug1OYazOfREECVo3j7X0C9+SvwhUNoO4ziIgRkRYnsqxXlU0jDLBCGoSCEA6WEmaslpCwxnyc4OjqDEAKvv/F9BL4Hz3OwszPFc3eeRbfbwY2b1zEeDy1azDUnfN83AYnAKNERG6jf79sCoZxfBTTrBzvrHETh5O5er4f5fG4VQLnMBAeHizyHa87HiATPkWEUYblcWvtvMBjQnGlYOCziMBqNjMAECT7BiBRRYOhDHGizPT11SruoSw3fI5Wl0WCCIq8B6WA2u0SSUNLvdDq1ur9pmsLzQ5twvBQUtZC1NNGmDnwnhtQKZSnx+r23qMZD4GPc7+G8PofnuUhXBCcny4R0lIVj+WTdbhfd/gDXR2OMxkNMJmMc7B+gP+gjDEIAJCe7WCxRqhp1pa1GMkFbXRul9f0mi98xjemaSA0g4JjBJo30nGOMPF7YzMHGiDIVbLVGbZJgVYs2I4Qwhq+CzS9wDNQqTEQBChqScoR1Ez1gVS8aGMbbdl3AdTAYj/DGG2/g7vvv4Znbt3Hj8AZNDBGdg3JjNJSqkBU5AIGTkxNkGVW+ZRqX67hw4aJIC8z1nKKang8vbGlHu6bSrmN08T0Nf+AijkOsViu89NLHcOvWDZyfn+Ps+AQXR6eQVYEf+tQP4PzkGB//2Is4PDyEBHC+mCNwPPgOKddQHyGtbdfImwpN8qa9KMKPfeoQb37n9/D/S65DSccUhmSzWUBAkhFLVjt48iSniBxI4Zr3JgBHi4buBNEYvErbaBBPck3NjZYjodFQtXjWdRx6WXYCRzM5Ck56o6JpveHAUI8kHM+D1MpEwYlzz/2rriv4fmCi5MoIHRSIOzE834eqayghIB2JxeUl+v0u4igGtIB2AG2kZAGSKRVaUyE541Sdnl0AILWN0ggwsLStBuU6+a6LpKzgage+cEDgKb0nx3UgtQPXI0UvVSv4rgumLSgou4iBkSPTnXVrQRGMgbd8P23QmtOzM/wv/9f/W6haoioqVGWFWilUsraIFY8/ITRu3DjAZz7zacwXC/zVv/pv4bnnnkO/30MYRrh2sI+yqPAP/9E/xnf/6O9ASqpcHAY+en0fr3zuFfy7f/Nv4PDw0FQcJ4RvNDzEM3duoigzfPMPvwmsErBggmdzaXwEoW9oPjlcBGSoxiE8h1S7PN8k4xUVtGOK1xkpcNf10O/2cHl2im63S9FiR+C1772GZLnCJz75SQRegLkpqKmqCrKs4EFgOhzD911rIFZVhWF3hOVqibLIEHa7WK4WcB0HnTjEyfGRTdgtixKj8YgUcBxyUOqiwHpFCZFaaQSeh93JDu7du0fBnsADoFAVOdYrqteTZ2ucn1WW5gkADgI4WkFVFao8J5U9k7cXRRElxVYVxuMxjh8+RF2Ymj/ag1AOfCdE4EWIoxDP33kWVV1juVrBD4mKU5UVBvGAjEwhIGWFO888g4ePHlBE0gXiyDcJkBpltiZxjKAHzwlRVxKT8RidToyTk0eIoxG0kkiSBfr9AdbrtZELLnF2dow07VMEsygtNabIc4xHY5uEvl4nOLi2B8fRCEIPtazguiEUBLr9EdJ1infv3kOeUy5cr99FnmemAnuIsiSVxMAPEfkpMpFjuVzZ/qa1hio1sizBerlCaBAI13EQh5ENkJdViYuLGTzXRRhF8DyK7gahh+NHx6jKElpTHovrEGpZ1RWOxBGgqRaVVKT4WNWETGrVrIFSSiwWKSQUJAg9ZoVIXguVFIB2oZQ2xhKpS11cXMALApJ/N9FaAJYbDs3iG2YaNSukpd8wqiBcO78+pQ30gdvTOh8f9TybyATN7YrFMkQzR3/wQ6irPy5XKL7zC6iPvoPOj/5NwIsedzYY5YCg4q12TlZmHYRBBJoAmeC1DibXUAtoYShezD22dhA4ekQ5jeY7lhJv2qDl4PD7tcE5WKWvjYTvloPD9DRal5s200oDdY7st/+vUHOiy0O41rHSLXUvR5jgi+tCOC7ZabzuKAUtDXvA2IIKQMVrshFgKaoa6YNj3H9Ic7Xr1Jju9LG7u4s4jvGVr3wF+/v7VryBkGXf0lL5XphdwlRPRi2yLIMQwtLmLy8vcXh4iDRNSdUqCDByHJQVsRgAIDB5tSyawUnf7PBYW4+RGxN4Z4EHzuFjeqRwXSiAhEaURJoklCO2v/8BfZS2p3Y0RkPKhk+SBPP5At/5zneRmcxz3/fx8ssv47nnnsPe3h48zzOTJPU2plGxggXRpjqUlGiibVpr3Lt3D2dnZ6irEr4nLPzjez6imBSeZvMFev2B0cvv2sx5ohJR9J/PV1YVHj16hMvLS/zgD33aFiax/VU0dCQAlo7E33FkimFhhosBQZxracALOwBNdXMTIWeZN9cMPi5wxy+RvVlO7nZddwN+ZbSEq+eyYWm5maKhVLWhwFu3buH+/fuAEHj06CHOz86xu7sLTrxsFMBI6eXRo0dwXRf7+/s24Z/bgYvjrZM14jhGEAT2eIri5TYCJqWE5zUoT1kSynXjxg28cOd5CJOA7LlEC7Ha/RrY2dnBT3/ta3jv3bt45+234Zo2rcuSVK14UnAcjMdjeJ6Hv/TTn8dv/Ke/iPP+K4B2UMNMXhzC5jm1Fe2QunEAPeGQHyKlmReNs9FaFLiwHb0PRkSMDwOefEG1KTjyzonfTSgdtuhRczY7r+ZFjqE7ggOB2nCfefzUFUG3vk91V7J1isFoSHS/uoajBKF4ISUwV0aKVhrU6/joGDduHJKssokisUYWFC8YNFnOTaEfosk4JKMryBhW5nm6vS6UpmrgVMWXhAiUUgijEL0e8dajuAOptCnQZZS/OJ7VRpkYRN9GhVptDhhlOgDQGkVW4OHyiOqmGAdJQtqFzfWoum4Q+Lh2/QA/87Wv4m/+e/8usjSF71P/rWWN5WKGH/qhT0FA4GMvvoB79x8gz4gOOhj0sbs/ArSCVhJnJydwjLJbul6j2+2hKAu88sormE6n+OY3/wD3HzwwVX3JyGMJSCUreK6HsqSIbhiEUFKh04lNxEwhjAJQBWUJ33ehNRUufeb2bWTpGp7roCoLpFmG+XyGl19+GZeXF1B1BS0l8iylpL+yxOVshqoq0e/37CJGSbclPCOPWZYFPNc1wRNTaFdTLQTm5bquZ3ImImhNSk1CuOgYyqsQAoFP0tzE4YalxTI/X4ShyRujsc4BDb6noigQhqGlB/im6nhVVfjkJz+Jsipx/949HB8f4bnnnjNzvAspXeS5ooXV8+A5Pnr9PlXSVQ4Cz0dmVGGUqvHcc8+QCuH5KSGUZlxyDsvJ8gTP3L6D9VkCrSKEYYDr165jsVwAEAiCCJeXM1IxSxJMp1N8+tM/RHSnSyoQube3iyJNSfK9qjCdTHDt+jV0ux1MpiN4no/z8wtIVaOqJPKsQBzHOHp0DKmIPisVUUI6nQ76gwHyLDfOXo1HR0e4PJ9Zyd0syzAejZGsycn1/QBKkow4i4YopZBmGRzXNagvjT2iSTmWpsnV43neYmEACk6T0U40SVMhvqxQlNKKDJD8qsnXVJRX1l6rYOZmrQSE8DbWrdWa6Bk6z2ntbOVwNmvbZhLzRoIzOANh8xNGP/+st6ucjw/brkRGPvA8jSHdTgR/2msLaKjTN5H8yr+P4PmvIHjhq4AbthwYYVEFi1yA1zWDE/BnbdQDjQ/BhYlhnU0YKXl74HYj8C/NSTgZDmgF+mADUBtAR+v+6HpNlgnQ9DWtNaqjP0bxh/8lfNTwjTBKux3bZRUsO4R/yrYDR/MjORxNwM9xHAzHXdy8uY9er4fbt28jy0jkIAwj+J6D0XBgcjxKa6fWdY3JZNIoMQK2NpzneZaSzipuTH9iOhXbjYeHh9CacqFGoxHgkLRwFEWN1L0QNveW6Z8s9sN5HFJKq2CaZZlFPXj+WK/XaOe9USFeWt8swvEU21M7GmmaYnd3F6vVCteuXUOv18O1a9fg+z4ZqL5vFnJ/wytyHK5A68H3iVsWhIFZhB1LE9Ja48UXX8Dzz9+BlBWEQx3JEYISr3kyq4gKwYYt0Exojmlsvr7ruphOpwCA+WyG3d1dQ38xDpBHUBrXyXAEbNVIipZQBFVJ4ghLpYzOtZEs05S3wZ4fR5eiOEYQhTYRZzAYWN1hrTVxS4FGniyn6suheXE8ANiz5SgqT7rtf9ZBMR2LIbTBYEBtU9Xo9/pWPo3LzPNxAHD79m3b0dl75Q7IyULs9DHPm2uGVFVltZkpea+0g4MLiDGH2AHlH3geGVucBF0bXedoOMD/4K//2/jlX/onNKDKErVWKE3RwCRJMBwOcevWTazXCSajIf7CyyH+86//C6ibXwKkttEPOzHaSBdxfrVqlJAchyPvwkrDMj3KTn6KOa2w5yG7WJidGo4r50vY6ZQnNpgAjXHQePIUxjCuyhJaAa5PERc/IFoJTDSQUAwPQRgiyzMMxQidbodybUzEmauzh2GAqixRFDWqqiTJT1nj+uEh4k6HfCASFLdtAk1yfufn53A9l/p5XaOuqU9wsqRwHAyHQ5uIu0qWyLI1OnEMaA0/COG4HgAHcadnop2NUhVMOzgOyRoy9tTett8bf0aLrgNdJMDqGKomyhavU27goN/vwQ88lGWBv/7X/238wKd+AOPxEINeB/PLC6zXa5uYyop3UlIfn80W8FyBMACSZAHfU3j7rRNMpxMsFkTFmk6niCJKmL04P8NgMCAebRSgrkqUOQkjEJAl7TgiTm0Alvrla0rJCkcSgUFfuUYNLSJDOA5Qywpn56dmcdKY7kwgVYX5YgZXa1Im6kTQUEizNTqdCGE4RJomcBxgf3/PSk1T3kHHju3ZbAbfJ/ELHuPE6aUFqdslmD3LUpu3U8uK+o8jMBj2cOfOHVy7doDLywvcvXsX5+fntu+HYYj1OrFzHc9RrLfP12Tu/mKxsMGOKA6IKrQ7wXDUh9ISfuAiy1PUsjZzFeAGJH5RVhXCKILMK5R1gVpWUCAnKFukUEpid3cP77zzDrj6r+O4AATN2YEP1xVYLOYkBxl4ePToCGmaIow6iOMO1us1ut0usqwgefAggq4lHK3hCQHfKLTMzs8wW65xenZGeR91hRs3DqG1wHKVAVpjuVwhWWcI4y7KskLgB0a3wkFZSdQZLfqykmYMucirGuusoCrrQYSzyxkgiLYKGMGIlrFUGsERrmNj0XqniaJrTUmzbICUZQnhkExyXpWmyrO0/RaaKEqAS2EL0dTBasargNYCtigcSMWIpryWnL2ZjyjHjoI+vI5/2Mbr0Z/E8H/a7aM7CH/225/0ekIIoM5RvPZPUL79z+Hf+TL8Wz8Cp7tjkQcbXNOA1tKuCbyOaUag6YSAbe9WUr3jNFQnbFJzNTiZ22mO5XXHXJv3tKgGO4kb6zftw0EpEspqOUPmeVW2QPnmr6N+7+twoW10n2TcN4OzjSMM+/djzpymunCcF9EOwIahh0988kX87M+SMmaapojjGEmSIM9K9DpkdyUJFbjk3Axeg1gyl4KKDcLC6APPjUxtYnTh4OAA4/G4sTejCFJrdLtdI6C0sjUz2GGZzWY28LBdiZztSwA27YFFLdgO5MrhVLhTGBujaEoofMj21I7Gl770JURRZKMdzOcH6CWUJsmEB39TYK8yRqmHMPQN7YgMeQ7wS1P0hKEb6pxAbXTReQKkCrICySqx+QZtp4IGCBnd3CmGwyFc18V6vcbaJD+2jXiahNswZsvA0ZsTTRj49littZVk9TwPo9HIeqCr1Qq1IuOZPVk+LyfS8ov1XBehuQ+gUbjiNm7LA/L9tetebA8M/p7fgW/04DudDiaTCZSi5MLFYoE0PTEFAK9ZtIML7QHYuCa/GwDWQMiyzMpi9no9dLudRnbT7M8dNQgD1MZTX65WWBhN6XfeeQfJaoVhf4CXXnwRu7s7+Omf+RpJwUFAQgMmF4b7AKnTZNBK4cd/7PP41V/59/H+2wXcZ78KqVqCfq2JS5nEba1NVE/TAsloUzvCzn8LwNLdbC0Fk99hI03thY4jOa0zahM1onwOrrraykMAUNXkFJDIgIAfBBAChoOscHJyAllLDAck41kUBfq9HlYt1a8sywxEGtH4MohIVdW4nM1RyxrD4Qi9Xt/kE5ExslqtcDm7RJYV6PW6qCrKUEgN5931ffvc3V4XQRgiXVECNCWgGuUq17Fy18yNr2sqPlhVlYmGmViUxbgb74OjYxS12nQ/OEqmAUBJcpYE4HpGPUwpjEdd/I/+xv8QSkqk2Rqf+cyncPPmIebzOS7Oz7BarQzyVmO1SrBckrZ/mq6NJnpmFo8IgR9A6xIH+weIwgD+dIK6qlGaQonTyRir5QrnZ2eoa5LpXi4WCAPfKqOwI6u1MBK3Gq4bGoi6Nkl02sx9NcqyEU4ASM1vMOhjPp8BQiBZJ4jjCN1uD2EYYDIhak6ymGM4HEBrjX6/jywjjn0YhhgO+3YhraoSkwlVuiXJbHJ4xuMxOO+L5+HRaGjGdmnU4zR2d3cMNWZFORpKodfr4bnnnsV6neDhwwe4efMmXnjhBXzve9/Dd7/7XVuLIs8LGDYPpJQ4Pj62komu4fqy/GK/38fZ2Rmee+45rJIlHj16aBWL2ohsJ+5BgOSVww4ptbDqGVwHZZlDuA4cz4EQLmSpsE5WWC0SvPTSy3j77beRpqRJv16TlOP1g2u4vLxAnudU6NGgNovFEkqvMBySotb9y0dEd+z3kK7X0LImGdjFAnfuPI/Li0v4vo9lmmM2W6CqK3S7Pdx97z5JfzsuPv3pT0NrhT/8w2/B9wMIQVLNYRijrgtUFSsxEoWyNLQmgIIh7LTBLPpsBKpWkIiGlm4EG9CstY2BTg5BIx/KtXnoXMr03Y3ItzBOBEe6oRs1b4PwtlHLJijDyn2tiLGmZHWl+fyNEg7fv931X5HRv32dJ13jw+5nkx61FVCxSE3z3fY+f9pn2zh/laF8/ZdRvvGrcPoHCO58CcEzn4N2A3ISjFG/FeNpoRDGOTCJ5GAkwSIgZh86yP7NjgF/Ksw5hdgSbzE7WDSkdf3GpSEqou1bdvnQ0PkK5Vu/jvr934NQlakjtFmjzXXcDSSNmRn0u9h4D7btHKPCZf4m2iSVXLg4n+GX/8lv4PxsgT/3534OZZnD2wsQRTGioAPX8Sx1Ko5jG+x1HMcyTPg+AM5hcuw9c0BGa0Ibec587733cHR0hIODA4sIZ0Vhj+d5i4NpPG8yGgJQAIjVsNr5zmy38XOyIBFXCQ+CAI7rotfrWTrX02xP7Wh0Oh37Yjjx+/r167YgyPHxMbIsw61bt3B6eookSbC7u4O4EwNCQ6ra9h/XIy9TW8eEIsxSVsb5EKjKCmVRWkcDABazObq9vr0nbkxKmCO5zqLIrReYZZlVB3CEoGJ1JiESQiBnBMYT1gBgR4IRAY7+CAjIiiApl7r7Ro0BhuNc18V4MgZMh+HOxAuDVo1ygyOEjahXVU3GsLkeO0KM9rQ7P282L8Rs2xEeYQxpNtRYiYWfbb3O8M477+D4+NhKVq7Xa6vlDJDSCDso6/Xa0qS4YjvT4o6Pjw1i1dRN4QEym80oKppnOD4+we3bt3Dz5k3EcUwFakCGUJFmePud7yNPU8znl1QFWyvkZWHVDgBY9ERWFe48+xy+9MUv4O//4j9Gef0zEPHYVLtGEw0BTHRNQyouhiRNQIWdBNur7ILbQMcUvQNg8zC04rYGWPBACHu11qnakfnGmWnk/6i9sjxDFHfgex50TREPaSa01XIFpSTyPMf+3h4W8zn29/YxMPVHlNZQtTlHFFEfch1oQycU0MiLEuXZOWYXl9YoyYsCZVVCK41Op0dGsXCQpGsoRROdKxxIJeG4DnZ2dgBNEnue7yLwA0iCAeG5Ljw/oATfIEAQ+litKNpRlCU9r24l/0E0NUVajoWF5Tl6Zb4np06hfO934UDCD4m72O2EmIyHmO5M8c47b+JrX/speJ6Dawc7eP+9t1HXEnEYwXWAfq9rcihcHOzvQQiBu3ffw3Q6wYMH97FcLpClaxweHqIsM7z//l04DlGFSkNzZP44SxDyRM5KS77ng2SDlYkWK1RVuTFGPaNCVdcwkzo5z76hIdFY7cB1ieJW15Wt2+B5Lno9UhDrdjuo8rRxdpYLo0JESA2EKeinNZSWSJIlhCOwXCZU3VspxHEExyWE0fMIPj87PwUABIGHTjdCUZSI4hBCOOh2ezg42Lfzf38wwMX5OY6OjqzK0Re/+EXcvn0bv/u7v4vFYoHpdGIDP47joN+nitvdbhfz+RxVVSGKIvR6PQwGAxwcHFAfcz0Ij2WyPTy4/wjPPhtBa4Uw6BpE0keoQTWJWkpGjhtAK4UszZCsV0gSkuwVUuHhw0e4du06XnvtNSwWSyRJgmvX9hF3QqzTBNPJFOPxGK+//gZ8P4DnRcjyEvP5yih5Odjb28OjR48M9YoQMgUH1VvvYDAY4GI2w3KdopaSihhezKAV0Ov18YUv/BgWizm+8Xu/iyRZA1rAdT10Ol2cnl7atbCu20iCQeyVgpR6Yy3Ypii1+5rdB621Q7fnIgWu3bC9aZi6DjyviVbsxjgGPGbt9bRmqLJ1ntb57RzZbKptkGPTwL5q3fug7UmG/kfZ/jQIwlUO0vZ5/3WhJDaSvzxG8e1fQPnmryH42E/Dv/2jgEM5dcDm+7LztcP0tLYEOS2SjbvJveqqZzGiNNxtuLZS28nhgNxjN96cU2sBqBrV0R9DrU7os3yJ+t4fQNeFNZzbbd1GMfgzbo+r2qdtb5GIjmeDrDyHUfBVYJ3U+Mbv/hEOr9/GD376U8gziSCgqH+SJBsytBxQaTNQsixDr0e1yNbrtaU/KaXQ7/ct3YptKt/3bUFRqokUwvM8JBcXlu4kpbSOBABEUWRr7gBkyzOiwjbcYDCwBQY5j4MrmrMTwgpWAkBmlO+edhP6KUdjsiQ4hi8IwEKcfLPEgT23xuhgOABXVex2u+j1eoYb6qKuJRzhWi+KubsA4LuuVUmSUtHid3aGd999Bx//5Ct44YUXcTmb4f3338dgMLDcXqpGu9rw1PiewyAwso+1iVwSX03KGq4LQDc0qHv37mE8HmM6maAykSEuLLRaLUHVIyN4nm87JUf2taYCO6v1esM5Y0kxAUBooCor+AYhsW0pJVyjuMJOBC/QV02+3Fnbnnl7H6VMPYPWQtLepygImQjCkAwP01ZVXSNLUytd2Hao2rStdrl6KvRCkfl2ezAys5gvUBoUhPcHaBBMdyaUfHl0jH/+z/4ZhCZ9+clojOneLpRxPrl9eQDIsoTQwOn5Of5P/+f/CN+unoO6+QVbU2DjmRlRchzcvHmA4WCA0WiCt77/No6PTqAYwUA7LmOS8jQrjJl6GDCTEZjrCROh4elXt6I0jdzt48a0+VQIdLod7F+7Dlc4WC2WqOoKy/nCCitkJvr7zDO3keW5zac5OTrCwihUcC4H1aYpyEBz6f25jmOilZoSxgFUxkkRALqDAfHaswyVlAj8gGQiJSm7DMdj7B/sI1mvcHZ6ijiMkKVrFGWFvCgwHA7R6/cwm12i1+tjd28fF5czVGWG06NHxrcxC5MAVax2uJ46L1qPoxkQTGcjcYTiW/8lpvm7+Gt/9S/j29/+Q/zEl38ce7s78FwPkYGV0zRBLStUNVH2FrOlKUJYIstSAAIXF+eIohjnZ3PKK1nMkGZrxJ0I3U6MXr9vnEdy/DudDhaLBU5OTzAajhBGIUqj7rRepzg+PiYFHbMIMfJLC4S2/QiC6KS+55kCl6QyxhQrz6N6Ei++8CKGoyGtwYbOWVUVJpMJvv/97+Pg4IAWKEUqKQDsIsYKJUpLeJ7bSGmrpqBmGIa2CBvPiZwMzufiedUWfApCDAYj3Lp1C51OB6+++j3cv3+PlImGQxQFnXcwGODFF19ElmX4/d//faRpitFoaNuFo2s8t/E9AECv18NsNjORPhez2cJ+zwmLXKQPIEWUw1s34bguJtMJdvf24fvEye4PeqjrCkdHD3Dv3vtYLZcY9rqYjMeYTKYYDPqWFhfHEZQsDAo+xu7OHn71V38d7713DxcXMxyfUEVg3/PxpS/9OEajEf7gD76JVbJGpRSOjo4MWqRweHgIz/Pw/XfeRlGVqGoSphBwEcdduK6H5WoOJSsoKusOAyKY993QOXgjdTcNCNeac+0537Eoa3ueb8WXGRF8bDPUxmay3NzvA+xfp1Wod2O+RQu0vGp70nf6CSbqlolyFeJwlaH+J3U0Puw8H+QU/LfZ0aBrA22kSUMDjg9353k4/T1EL30NiIZwNlYr/q1JUrfBTLNachFbdhpsPkdrvxamYe6FnQ3dfNduh3Y7CQHUFeqjP0b+2n8DvT6337P9w3bo1ciQsMHBtqGvDbriOH7rso20P9GhTWHL1nGe50E4Ar7v4tatQ3z1q1/Bs8/dhgYFhVzhot8b2MB8m0mjtbb1aDhIHkWRlXduOyacSyGEyY8wAWOgYZxQMWbH2LNyQxa3vQ4xw6QoCvsdOzBtWhgAy/ZhRdi2rQ9NdG8+70uf/MSH9runRjT4hbZ/MrWHk9PYKA2CwNQAiKB0BdICv4DnuRZuiaMuPM+3RnSSJJbe0I1iDHp99HpdeL6PPE3x4P59yKrGarHEymhu7+xMEQShaUCqoFgUueX/sva7Ng1TSIo01rVEERQGmqogUCEMAoRhgCgM8dztmwA0ZFVgdnFBUUrTMVRVYTWfIY46GJgiKOs8x/vv38eNm7eIk5xlCMLAGhhBQB2nKEqURYkqL1DXFVbLJc5OT3F6eoyPv/wy7rz4IpSSFMkzC41S0joNNAhoUaGBowzvX145eWmtScq1HSc2NrfjkDpUpxMjTTMoJY0ilbRQIktO8gJGGuvKJrW30ZY0I96x48A6IGVZIk1TMmRcB1EYIc8yUiOpa6IIgZwudGIMx0P8xf/eX8TZySmOjo4w3duBcASiiHJ6pJJwHBdFniNTCsv5AvPLGbKiwKd+4FN4/Zf+BdIbnzNPKramtZYxq7RJYKRJRzvCovkNsCFaUbsWMmLOympknFxtF3bW8m7BxQBs7ohFhpsS4QCALMtRFSX8uAPP6Hl7JppBTnGAXr+Pbq8HqRTOz89x7dp1jKdTFFWFLE1J+rGuUcsajhCIOz3K+/GNFj0E6qpEVVHCuCMcUzSSVDeSLIEWME6GR0aHBsI4xnRnB7WSuLwgrqesJWqpKWBgDPG6qiGVxnA0RlVRDYk8JcMeHO2E0Te3iwHztlttzu0vABi+MBea8lb38bWf+wqGwy6+/OUvQOsSx8f3AUWG8qNH9+H5nkEYKqRZhrqUtoBkmmaWn0qG84CoQFrh+vXriKIAvR4pPAVBaBwAF2WZY39/D7PZJXzfpcranodrBwe4d/8+XEcAcBCYwkoQjaS071OuGUtUA+Q8eMIzUaoAjhBwXBfQCh1T8I3z3Oz9migVoYRzimYJgVJKKqSpNG4/8wzk6RniKIIfulTMryrhKMf0swxpugYl+9d2sQr8EK6JasZxiOWytkWeALPIOgLz2Qx1VcHzPdR1heGQImFZmtlio++++65BOAPs7e3hrbfeovoQoxHyvLBo6OXlDKWRI8+yzCYs+r5vonvAeLyDi4tTmksdWmwd4WC9zuD5Hsqqwo3bt/GTP/mTGE3GRDWqqVcVZQHXdXCwd4AX7rwIAKjzAnt7e7i8pHn9xuEzqKoKJyfHUKrEq69+D1XloCqBl19+BWdncxSFwgvDHbieh/lsht/5xu/jrbfeQieOkWQF1q1nUkri6OyCkq8lof2OofxqLZAVlWFQEgVQKqZ00pzgOG6LdmwMKWugEvXIOuNmCFmXguegraWAgsabCa7NPGdU9dpOyQbCsGW0oQ1atCGNrSj4EzfR8kK297za2LbR5c272Njnap+iFYHXrY8+bLvqedgO3roWGZ7NfvYuzQtqP6luDnrirTyx7VrT4gfux5fgw67YcSNoCUII1OkbkCevo37/G/BufhbBrR+GO33OrmccYOM53E7aXLiP5+72umc+E2heOdfDsEE2+3j8YMq2mqpLyPN3IC/uQh2/ClXl0Ollqy836IPjuBQMbIUJAdGiRJETw7fYUMzZnm0CMdt2Lqu09bpd9AcDYupEMQ5vXMNzz93G7u4UfuCi241IcMN3IODbemVsvzG1lZXYqDApzXUcHG0L8XBQFQDWayoGyVRTZsgURYHRaIT+cGjPwagHn4Ofi6n97aAtf8fnbiehc14K0Dg1VVWhE8fwXCq0zUWgP2x7akejHcluFzxhL4m/o2RR2TSa9jAZRxgOJ5B1jW53YCE0zj9gKPrg4IAawXXN5EyUmuHOFD/0w5+118rzFHEcmSKBNaSsNu6LHQxuKI7WKV0ijntW5ktJiW6/B09XuDg/xel6DSgJWVe4OD/DZDzB7/3+N7FOU/zEV34C0+kUQRhgGEVIkgXm6Rxh3EFRaUz6fVR5hTDood+P4QceqrqGIxwUpYQjfKKGuRG6gy7ydI3AD9AJA9y/+zbe+OM/Qpau8MpnPgtZF/A831aVZvWaqtY2T4U2SqqllNhNiND+BA8e137OHYfaMsPSoFVRFMFxiB/OEyj/pMFBfHypHaxWK5RlaQvSEIcwAippr81Qm01olxKHNw8RBCG0gVJJWphQgRAEyblhgPHeLhxT4Ms1yFcYUK2SVbnEYr6AVAq7165jMV/gK1/9KXzru6/h1fQCKpxCqyYXiCM3FFAnD15qs8g7BoOwM3h7ZmY4l1XszDTWNL/ZvV053hjT9jdzWt5ZONjETCjKD6WRrzMEQYwgjFHXCnGnh2S5hHIlgiiE4wooQZXAk9UKFxfn2N3dwXRnipNTiZIrd5qJLFunqKsSQUhyuNoY807gA0rDFw4cL4SSknjeIOUajws4SgnH9zA9OKBqvCcn0FIiCEMUBalJSaVNNegA88UCcdxFGMdYzZdwQPVzmigpR7xaBov5xbaVEJs+mDHYAUAoja4oMOjFWM5O0e3GCIMAQRibugaXWCcLHB4eAlojCEIafy7dq+f56HZJIpDnqG4vwGAY2SAJT7xk5FNuAuc1KSXxiU98HGdnZ9ib7mCxWNCELARCv4VO0sAhuc7WRM4//SAAzDxVVRU5lCaKxlKwg36fagSUBYqypJoVQUA5Gn6AMi+RJhmi0EG6TjCd7uIzn/lheEGIj3/yB3H/3j08OnkfeW24tb6H1XxBydxlRahs4ANwUFU1losVoAV6/S6UVIii0NRAIFQ5DEMsFnPIUiJP14iiCHlRII4idKMIjushPcmQp5QkfXF+CaUUjh4dU8Vux8XZ2QxKKZQV5SkQkiIg1Yoq+EKQxGsU48bNWzg6OcfpxTniTox0lUAqicIY9Yxq3rj1DD7+iVcQRV1cnM7onoWLZLnC2dkZ1usEu3t7WC1XuH//PqpKYz6bYzQa4f333kdiEtXLqsLD42OcnZ2RkpXrGtpVAg2gEgDLqdpcxNnK9tHG5jaGvpSAoPyQWpp5CJSsbdFoDmLw+BAakhOl7TTEBcpoU9pUeTHRVqu+pJup68OD4y0jurF+m/9vR4Rb+2mgQdjZAXjMX3jK6PxV1nIrALG5a8tUb1uuTzhNsyMbvmzats+rt/a98tLNnCWa2dzuKJ5wvsfO0f7gw9rn8fvS7WteuV97Y8d0k0rdUIcap3MbDVJlhvKd30J197fhRAN4t34YTm8f/s3P0trlULFYzpNQRtVDmLVNCJCAChp3UAOWNku/N7Spppsrsr3O30H96NuoH/0xtKyhitTYCo79Scexg+FsqMhJ46jYOXcDjfBR14TWA+S0BwHN80IAnkclDobDIeI4xuHhIcbjAa5d37VKUXt7e1Ywh4OmVZmjEw9Rlwq+H0NLZe0FANbI54KVrATFLJ6yLG0eLQcsmOrEORg85nq9Rkmw1+thMpkQm8QEtRiFbm9s/7aTutmh4qAwABucZ2fHdV2LfLSZN5zz4Rjb/Wm2p6ZOnZ2cbhjv27kJ7cRhTjppS7K2923fXJv20+70/EA8qbMXmBpKD0d6Adjv+FiG/bmhuBAKw098D3Eck3JNXWC1XODo0SPEUYjz01NkaYI8y010c4mjoyNcv34dH/vYx0iqUWvkWYKd3X2sswISHrqDCRzXh9JkZDBfLklWNqnS8zxEnQhlkcN3AF2XcLTExfkZ/uXXfwef/ZEfxfXDQ5vIbj1iTf/abWLby0Sk2m1ro2FoFEW225lzC8qqwsnJCWazGXZ2drBeU/XdNE1NUumQDCZBSiR1K8GKO7EQArKu4bnCdlZ+H+13yJSrPM9RFIWBCH0oJU0uDOk/c1s5joPKODQUVXVIpUspeB4ZbEmyxqNHR7i4mOH/8Lf/AS5u/7ylWrC8t40wCeBgf4p+v4/xeIKTk1Pcu//A8pQ3g1nNdEn5Lm7rU2G5xcIgGI5o922eiNtRP8ByUGnGNT/Isvb8AIeHN+EGAZLVClAKi/kMsq4RhgHCTohev49+b4AsS5Gs1+j3ehiORkhWCc4uzlFmhanGSmgYUaNMAjvfm2aVEWGCUqTs5jnUvgqcjOZhb/8AcaeDxWKG2cUFPDOxZ3lBOVRC4Nq164AAzs7PcXBg9p/NUBYpTo6PjZgu662z47cZndswG9rIhqYFQWkNoSocvv638Tf+nb8MrUuEngdZ14jjLqqqRK/Xxfvvv4/d3d2NJOOioEmeq6oyTcfzPCRGC3wymVjYeTv/iCk7rB53cnyCrolGVVWFV199FfP5fCMnS2uqecKLEiDsAs99hBcQDpIAgJQKr7zySezt7VkkUUFhlSQoy8qMnRJnpxd44YXnUZcZlqs5rh0c4t/8S38Zj45PqA7GaIR1vsQf/dG3kKcZfNdFVZZUc6SuoBQhX4EfmlwAhSiiBP5akngDAFv0kBL/NbQCVsnK9H+FTtzBep2gqhXygs4dRaRCVlal4QmTE8HzD9eiEGY+kbaooalKrST6/T52dvawu3sArTUuLi/w3t33sF6vSd2lEyPwAwxHI0wmYwR+QI5EXcFzKNqWpZk10CivpgK0oZQ6lAwvQHkIGhqV0uae5Ma6pAFI8WTDrb1t01evyjH4k1J6ts/9r3rjOby99j/pWZ7m/h4/1nli2/7JWgwb59u+p4/ank+6tw0H5AlVvXmuvfq4q+/p6vM86dqP7Wj3b/fDD6Kd0fdy4zN7KteDE0/gTG4huPUjEL3d5hxPBRPhCucLKN7+F9DlipyE0zeAKmuhMY8nzANoZPGNvdPOyeB7Zxu1nWPreSF8n3KhoijC7u4OJpMJxuMxoijAcDTEM888Y9WaRqMRsiyFEBQsSpLEFrsDiIZdG7SZg6p834wYMA2KaelM3WImEM957bWDj+XEbj6OHRTODez1etjZ2SFKvjknOxJ8TaZA8RrGilOdTgcArH3O1+YANCkyStu2bNNtP58QAvvXDj781T+to7FaLC2i0Biqwkbs2kU/2sbn9uBsG5/tv68aMMwdbnc4XpQ5YaXN2+WH507GScuMavgm6tjpdDYil8Khqo9QNaA0iiLF7OICZVmgKkgBJE0z9Ps9KiDneXAdoK4pUur6IYKoCwUPXkCVmMOIqCQQsHQf1/MQRiEqRVHMOPThCsBzACkrLBcL/ME3/wAvv/wyrl27hjCMWgEed8NL5jYjGlPDsxWCEttZVg2KuPu9Xtckk3pUeTaKAE2KMEw1Y035MCKdfzbI+v0+VVfvdAChUavaGkttWcOiKKANuqQ1JeTz+2NYTwhh0RDefM9FXVc2MWq1WsF1XQyHQyo+JdhwVtbhKIsCAgLrJEFdSXS7PTiOi3/4j38Zf+vrJTJ/RHkKxsBrJ7Lt707Q7fUwGo+xWK5w9+5dSMmG7WPhOfvDOhKao0LisSJ9TCsz7glYQY0MFmHRKW2ta0WOhomOTXd3MRiNoDWwTtaQdYX5bAbfI+laVubxPB9ptkZRlrZ6e5pluLicI1maxFcIAIqKoNFVwZxUgJ5HCFNMz0RspXmOTreL6e4OoihCsphjdnGBZLlEXVfo94ao6hp5WWOys4PBcISL2QW0Bm7euIF1mqIqMpwfP0KWpvb8FmHaoj4YH9A6eTbh3jQUR3j12Rv4av8N/Pk/91MQQkIokizUiiLBVdXolSulTMXUAGmaojDVn5kPy4auUiRNTWheI2QANGgtC170ej3UdY1Op4PCULDKssRrr72GPM9bymxNTkVbTrAdoOE5k6NWXHhpMBjgpZdesnroUkp0el0kRgVpPl+iriQuLi4xGAyxuztGGPjwPB+dOMYPfeazeOHFl/DmG6/jmeefgRDAb/z6ryNPM1RcXV5JFFUKgKhvaZojXdP8xLV/uPZJVdXIixxKSoRhhDwvzNxK7a2URlEWqGuFMIqhJOXkVXUzD9S1NEF+aecMqhpfQ0ptnXattUXjyrIiNKBW8ExtpHRNyY1KUy2eWjbz0IbR64hGfEM3CZzKJELwXOK5Lrg2koYmCU7TNS0yQSc3wMOmoXaVEfRBhtz2mvckQ/dJS/K/bkeDn4Xz7q4y3v+UV8CTov1/Gkej/Z42ovfqyZH99vZB7639+Qff5Z+unZ7kKDxpc7bu9YOO33Q0tih2baDHJos/3f3C7t2gbo/t84Q+tH2frusYW4IFNDxrBHPROaYijUYjG+2/fv06Li8v0e128fLLLyOKQkwmE9Q1FYqkfLUARZkjz3KD/Gs7N3fijr3X9XqN/f19lGVJxwVEeeXcrG63awNcSZJY1b22+iavO6wMulqtaD0xaQhxHFsqFdeJa6tQaa1tkNbzPBLR6PepOJ/rot/vgxEHXnsYqd923HgN4iRzBghY4pqVplhEiP/m47lPPff8nQ/tDx+JOtWmTDH1gDPiAdiCfEEQ2EbeHqS8sSzs9gTL3td8Pt+IfAkhrMLLYDCwxePaEwl3kPbf2x2WYSeGl4RwIOFCQcPxQriOQCcI0RuMaJApMraZOlSWhdWkn88vsLu/iyjuopaA70dQGnAcDwDxnbcdMi00JOicriOoMB2oQwxGLj7/+S+g0+lsIUcGKtdo0TraE6DemMe4A0spEbgB5qu54SGfWjWuMAyRrHJL1yA6QmygSBdp3lQKXy5XWCzeMHk3IYQHa6xxJ6RCXR6Uiei00Qvu0NwOg8Fgw5MW0KiKnIJBSmPQ66Pf71sjxQs8Ql4Kolx4nmsSu+iapPesUJY1fvqnfgK/953/O36z/gwclwrNQbYTtAVqSTUYZC3hwIGAA6HJCNLtaLr9XRAc7NjSQCbxDWQIC0NjEE0E6Sr9jQZc0RCGRqTtZAtAOFjOZuh2u/DDCF5IuRqdbhfpOqE6L0JgMZ/j0iTM9gZ9CAjUUmJnOsXe3i66vS7mswXKPIdW5Nx4jjGioNGG8Qkt06iNkReEIYajEQYjktKdXV5gvVhAaI2yLIxAgkZV1+h0uxgMxiiqCnle4dr1a5Bao8hz1GVJxcaMsUeV0FtKUi3oSDuOTR4UDreHkQNmJEAIiPQYz71yE8lqgdGwR2pkpUIQRKhVjeVyaSdJEp6gmhqdDtVAWC6X8H0fp6dUvbXb7doJl53h+ZySw3liz/McURTBdV2rylGVJbox1TFZr9f2eJpfyEAmFIwL4lGyL9Wh8FBVtVUSWq2oACrlRgE7O3sQwoXWVJ19NpthtV4jiiNcXsxxdHSM8XiCxWKFg4PrWCzN9ZXE66+9hj/61nfw1a98BV/66lfxO7/127h2eIiXX/oEfvfrX8fJ0TGyNKV8Docg86IgRbC6IuNeSlPxWTfiGMpEuegRzYKjGzIH5QVJSDmjsa81qpIdDaIR1ErbZMyqrsjAV1wFhRE2rofE8t00xlRe2LWBkUdp5uVaURCBDCRCw2qtbAK97X9SGspuI48pTU0kCmQQ6qZ1YwCBJa21elKg+rHtaaPUfxKU41+1c3HVPXIga/t+nuR0PHUE/gnHbQciPwiVeNL2JOTlKtrHdiCv6UNXOyub5910lJp7vtoWaZ+/fa4ntdGHtd0HPWP7u20WyeZJHDsmlFJmSJH9cdU5NmybLadm+9xCNLQ7wcEnR5iAF9V0sUnYxqFlY3ow6KNvCjVTwWdCFuI4xgsvvIBer4fxeGwLObNRn6YpOp0O0nQNxwEGwwEJnuQ50mxlENQSvu9hMKRK3N1uz9gzXEDZsegA02WFEKjqGoGpvM1twtLY/X5/o44YowFtA91xqPgwMzviOLZMFs7lYCUpTgxfG5EhPl5KidVyiU6vZ50FdorYFg7DcKOvsypVu40vLy8titFOXF+v13bd489Y6Ifpxn+mjkaSJI95xdt/s6fJnQ+A9cKY3gTgsQdvP0Rh9IBZ5ovPqzUlxrCc1/bgb5+HtzbyAsAaD+3OrrSCVKCibHxOTZx8DW2cBgAu4HkCwgvghRLd4Ri71w6I8xeEVH9AkGSkIzxo7djCaICmSuKQEAJwTXzZNVE2KoJCL3w46NMatwEHgpRLVFNUhZ2+uq6hoeD7nlXGYocsz3NUqCHgIgxjRGEMrQHPreF7IXZ2aIAEQYD5fA5Ak8RlvkZekLa87/kmUuBBygpZVsPx3Y1B1K5j4rvOhhfPbcqcP44stqFNoTWcIEQU0vveTlCidweEngehNMqMHCRmfXJkuSwqeJ6P//m/99fw5n/y/8X7nR8EZI1WjyBEpq4hFRUE5AhOozDFUANHNBnRMJNtK8ojBB1H3iUVEdoIAdGJG4RDG2dHNOgKNExZZkArhUorLBdzDMc76EQdLMsFom6H+OlpBkBAeS5kXUFpYJ0kmIwnKLIMDx89wngywXBIjniWplivU+RpDinrpliluQcaP6bvRDG63R4G/R48j6DXs4szlGWBKAigpUSv14fjesjXKwjPw2RnB8JxMZ+doTfoE5d+nUAAmJ2ft9rOIEptR8y0czM+BQTTqwwiADYS6UDEZ9/Gs8/899HphMizNUI/hHYFsrTAKl1ZWlSaphaJCMMQWZajrqXlo3a7Xas2FIahdb55UeN5LMsye8xsNrNjtSxLZCFVM37zze9jNBpYWmcbgua+zHMf0Z4oITvPc2PoF9YZn88XiKIzUhHRgB+QClheFFDQcB0Py2WCvb1rqOsaJyenWKcpXvnUKzg7OUWWFXj+zgs4PztDvlrh537u57FMVnAg8OUvR3j/7l38wt//BSxXC2RlBselfCHX8bC/f4B+f4q7d+8iSTPUFXN3tRWyoBoNFHBRsqkSrY3ToVq/bxg9pjgrb+1I8mYElTaeNxwzHPkaqj23tww6BbVZaNMMSWzdB9VqaIxBQjZ49NPH5Iubsdm+Tzxu6H1Uw68dAHua4/8024dFrq/6/MO2tpH0UY552u83uswVa7feOu5p7uNpkKL29a4ywNv38uGOTvN92/hu5/Hx+beDpHzuJ/HeP+h5H7vnK+6v7XRc5bixQ2H/dtrX0s0YEE1Q19Y+002Qtx28EULD99kWINn1rqn35HkeBoMBRqMher0eer0egiCwRZaHw5H9fjAYmPmdFEoJOfChVDvZmYuShkiSJXq9Hvr9nqHRO4hiEgTJshRRFCLLUkNflSgLZeuzLeoFel0KVAk4yPPCGvt5ntscPxi7Jk1To7pXWIeA57gsy6xcbZveD8Aa+0EQWDuZnQcuL9AOgvG+zB5qJ46XRWHLTvB7YPp4kiQbLCB2Jvj9cXtLQ5FlhMZxSO6c6VcMJDCA0KYhf9j21NSpB/fub2TlNxGmJjLNHg4P1nbOAFOc2Btl47Oqqo3aDMxd48g903p4IAyHQ+totGFzoBlU7YXMDpPWgOb7Zc5/rczxSgJaQckaYeBRISE4jWIC84yhjT49RfmU0pC1pMi4IC5/VUkAwmjht3NTJISoQBXTTWTcnFfWNVRVW0OcDZayLG0lz7qusVgsLBWpLEvEnQg7O1PEcYzlcmkpS1maQdXAfDYnQ0HJDTqH5zH1R9t7jeOOkcT0TKVczzh3ro32qdZkyoOKBgYhE+2JrF19ktse2BxAupYIXFOwUFNEPI5j1LKmpNGqNomplLhV5FQZV0JBOxqu68HziCKjJPHjv/fWu/g//voFFmJon5kNiijyMR6PEcddKA08uPcApR0wuvXTtI0gy4VrnFDEkw2XVs5Lu+gPGjnJRvIWtg3toOPj9eZEfnD9FuJOB1JrrNcJtFZIV0tURYnAIFpFWSAMQty4dRNaKyTJGmVdIowiDIYjyg8AUefKguReZVVBauq/nuPAY/QxCOAKB1VdYbVYYb1aQjgOQs+HhkKWpqhqyndQwsHO3j663T7ml3PUqsa1G9chZY31col0tcL84gIcJ+b/IMjOExoQSlkkSLQix+SUGaRHsdiwhlqd4geTX8Jf/yt/Ab7vwHMo0U/WQJrmOL88h3A3Aw5BEKDX6+Hs7AK+7xsKVWEXLd5vsaD6EwxhF0WBbrdrF8/Ly0swoktVsyN4okHp3nrrLSyXS4OoKMia+mRRFtT2puYGG+5M1yHUT9nreJ6Hvb39jYWqrmvE3RjrdI0sKwA42Nvbx9GjI3ieh1WWYX9/H8/cuonr+/t4/pnb+MbXfwedTozPf+Wr+MIXvwjP8/Dm62/gW3/wBzg/O8d777+HUtVwPQ9FUWK1XCGKO0jTDO++e5eoUmZeZ2SSBSVKuUk30ewtC66H0DbU2KAX0C1HY3PJURt/07E0ahw7HLV12J9msybpVSubEWPgazXX1q0Ru30+c8hHdAyuimJv3Mp/SxyN9t9XGdNXneNprvfRz/G4I7ftaDwJWXia7WmO3W6LdmCkbUBfvb+hopqN7SPaR24c076Hds4lX/dJ29O2v2h9tu3YPgktoi/b999GaBTlgrcCgEopqxLHRXujKMJkMrHUn729HXS7HSTJCqPRCDs7O9jf37dRea6p036OOI7x8OHDDTVTNu6FEDg9PUVd19jZ2bEUImZN8D+eQ7lYc7fbRS1L7O7uGnXSwgjr0HtzXd+yVlgSHBBU36sgVIHLFTDVKM8yqz7JQSoOZOV5bu1Wkv6nQDojLXwMf85tyWtB214Ow9AWN23Tr/iYqqqQmFIEAOzaxm3B9nXPoB7r9XrDxmyjSHzPfCxT3DnXhIv3seMjhMBP/ORXn9hfbX98Wkfj/vv3bIdsL9J8w9xh28Z/u2NzR8jz3D54+3tuOO50Ukrkhgfa7XSshm8URTbXgF9KMzAca5y3nY62Y8H3xt8BAlJRhV4lJcLAh+9TwRUhAOUQjcFOBDbqDaKDCGE8W8BBAyOy108GqXHQhIO6KiCLDBogeV/Dk16tEiTJGqvlyhYdlIbiE4QBUiNTyahOJ+6g1+9BKYVer0u68kKgLAoj+etASoW6VCSpa3jmvu/DDwI4AvB8km7TWsNxHUpu2vK6WZZTaUN9oG5IyblCgCqB0/51VeLi7BSlyRug9xUjzzNrQArh2MEhZQ3HceG5DmrDUSTqiZnItEZdVvBdz8CIFGGmZOQMca+DtEgNv5FyYYha5UNB4LvfexP/t3/0B1jf/ElI1URbXQcYDYfodLsQjoujR0coK3Y0WoWE7CgxP7XJ0zBOkdUOF0RrU6B8DOEIqzzURkVooaS8ArKlRIOgCABKklwxgCDs4OD6DbhGwjPPUkAprFdLyKqC73lwfQ9+ECIKA0Qx5SaUVY6iyFHVEp4foBN3EXUiuD45EgJkawlTZVUpokEVRYF1skaR51TjxfPQ6cSojJNHvHsJCIHheIruYIg0zbBerXDt8BCe62CxmkOXJc6Oj6CNlDQ9NzsaZoGDcSJMG220Raut2TCHBvTF9/HXnjvFpz/1EnzfhesIZGkGV/iAdnB0eoS4Q/k8nU4Hs9kMUknEUYzT03MLOQ+NDCDL2lKSoAu/JbXNcHNelFitVjg7O8UqSeyi6ph2LMoCs9kM62SNNMtABUMrlHkNz/chayoKydXkXde1wQqlzbxk/nZceu9hEEBrSiSHEAh8H57vQQsgz3JoDTz77LPI0hwPHj7CfLVGVdcQWmHQ6+LGwQFkXSHL1pjsX8fBtWvodXt45+238f23vg8Y576QlORNTU5OBDtDCobWtBUhpbfRhvNawRtNqB6PMad1LKEd7eEkmvcMKibIDrfifCrjfLfNKs5v4ms2Z9Ab45Uceb3RnZoru/a5Hlv6tNzcWzT3r9sfPOW27Wg8XoysbbBufSW2drni781489Ubhz3aeIBo/b/9a9s4bYIsfIFmJ0aTWl2g9RxtI7YVPLFnfTIq0Aalth8bxnFtEAe2MR6P0nOQiOcPjc1+RHUT2kY0v6vWO9fNM6D1vBsVrbc2ejbHnkdYERZWhYS1c7YdjabNHj9rc9/isc+1epzaxQ9gERLXsZ8prammkvmchu0mUsX/GGHwfA+Dfh9xJ7J5D4z8djodEmMIQggBjEbjjfphdV0iSciw930f3W7X/r6zs4MkSaxRXtckqb1eryEE1YvgICEjxCzByrmKbPCWJeXnsdhPbgRjRqORLWzXtk8ZzeYiq0IYdMbIujNVVmkqetvvka0VGcq+a6L9jhAbSk+ciO04js27E0JYdU5mgLQDtBxwLYrCFuljBJxtXpadFYIFmTzUJvBVGwENz/OQ5Tk5VYauJQSpiJ6fn8MPfIyGIzvHthE0FuGwTp8G2Vgx5d1x+zN9i9GbKIrw1a/95JXjob09NXWKIRNOCOEX1i7sAcByvrYHVF0Th5rzA/i4dgfiY6KYpBO1gFWW6vQowliVlfVi2xSbNuTZPidDUnzPbS/f/i0rOKCEI5hrsFNSq8p2LClrC0dlWQbhmLyRFmLB2fnL1QJS1vbFeR4V+avyAuvl2hgn6UZSNC9mrks5CXEcoNvpYDAYYJ0myLK1HTzsndrBY6oQxyHBdFCaItaRgyii10ztSxNeXdfg+YfzYkrDxeY2YzSFByknGDHdoK4lAA3P9SCVBJRG5HlYzeeIgwDpeo2zsiTjWRFk2ekQV55lkJMkQRgGcL1GkSFNU5RFCc+neg3rhKpQXlxcbCgD1XWFi4tz8r49F3mWw/N9lEUJAY0ojvHlQ4nffO3vIb35E9DdfQCAVECS5vCCCJ5L0X2Ho7Itp6CxhZoVSMHkdQgTdRe0jNsCumbBUsJQP7CxnBmj2pxPKwCO3UGznr4QKMoclxfnGE+nCMIISgFFkaE/HCNNlvSsmhZnKRVqqcj5cF0kyxRlVaHX7yGpJOaLOSEYxtAVjkP3rDSkkma8CASuB1kUWM7mUNAYTUbQApBljbKWEI6P8c4O4riLNM2wSlaY7O7ACzykqxVQ17g4OzUUF3bGgcY0abWn4bi0F0bbVpr3oabSUIiPfw/7n/ssZpdzpCnVWwjCAN3YwXI5Q2Am0aquSbYwilDLGkVdmZwnH7PZJbIsx2g0xOXlJaqyQrZOIWtSWeLIXJamSLMcWhOaUZYlyqpCVV0CWiOMIqzStYn+aAvn0zM40HChanq3WlFeitCC7FjTHlaJydg7yiAkpQSUkiB6tEZR5VBaIggDFKaYnoLGxfwSab5GmmdQBpEt5wnOF2/bZhZHl/BefZ36fC0hFQUuiOLENDXTyKreNIyNM6Xt++IezGjBZrSUbszMs1vHgB/Z/mgcgw3DVrMDzBfexBik7TdPsspbh7bG8Ybzii20W7QivWrz3HrrvB99E+TVt+6rsRU3jVylt4qy2vvXG3+3b6ltxG86Ca3f2XDcvrMnRLcdp0XnQTsS3x6v/JMM+TYV9jHnaut6/E55/eUnEULAaa3h4PNYw9fBxou0qJTaeBaqm8DrvAKEIqMb28IdhD40xrXe6LKOoVLz9Zs2vzrXgr7k+gdcG0VZhwNoiXBs0aKFaBeZa5wkYkf4DXLu0JjkAKnQAnCFPZ9STTDUMYsP0b9NHR/NMq4OAiMgweyH6XSK69cPsLs3xv7+HgaDITqd2AZ/PdcjmXRT46soSmPDCSyXKzx8+AA3b95EUaSoqtwayBz9Z/SCjenViuSmmQUDNFF0LmaXG2bDcrm0tXbaUXm2Kzkvg9GGs7Mz9Pt9DIdD68BworXneVitVtZoL8sSft+HNFXFtSQbxxE+hoOuRZoZ0dZKIVuvobW2lCfeh9EXzh9p28FMG+e+w3YWqzxxqgAzeDj5ut/vWypV4Ie2bziOg7IghgHZyBqpqUMEpQhp4WCRAoQWUJUCFODA2VCm6vV6SHIj8501jpsQAoEbYLleWjRDKYXACxAFkUU5nmZ7akRjfjmzjVYUBZIksTKz7DSw/FZRFFYdiI3+siyR5zn29vasp7rNWVOK9OqHoxFqSRKoXC6d4UXPpag1d8pmkDUqSUxVYIemjahw9KAdRXDQwJeO66Jmp6ossVgubWl4vkYURTZPgrWQubP5vm8474GFmRja01qjKipoSUW6AiOB6/uenYz4uWgyb1cGRws9aFOQmslSqYYXXlU1gsA3nGqJZkGgQlugLouqLOEHvh1M0ORUSiWJeqUUjo4ewfN99Lo9ot+YZKLlcomyKNDt9YzCFSEQHFFerVbY3983lYz34bjCOmo80C8uLrBeJ4ZiBgyHQ8xmM2RZRm3p+ibRu7QDmx0sgCRY+/2+zd1hzv2g30NZSXhBhG9/54/x//w7fxfHeQB97TNwd1+E091BFMcY9Pu4nM1QlxXnnjbzvR0lrd814HquUZ9S0KD6IGwgMQ1IOE207fFwZXNivb14tgwEQGCys4tOf4AwipBnuakTIJClKZJ1AqE1At+D53rwfA9FlmOZLKEBdDtdXD+8ThFlJW2RwiKnopbdXo8kex1hihYqnB2fUjDA90nLW9aopEIYdzAc78A3MO5qtcJkMkFv0Md6uURVFlheXiJbrzaNHkGLPOfTNO3BTtqWMybau5nIernGM/f+Hr70wy/Bc0glajgcQmvA9z1oDUxGEwjhYL5YIC8LFFWJwlKWgCKnehSy1fcAQNXSKujw2PF9H4vlCkoJk+QsTeQQtNibyLudS7S2yJ+UGkJ4ZNArRnRaz9PqC3ReZQ0vZcaoVnpT8hDUhjUnNENbw6IyVMF2sGejh7WMsPb1P4g+c9XfT9q2qSZXngugxOqPcN5/VdsTjcY/i3MDaOemfNB1tyk6H0Rzab/HD+Lzt4/b3q56V49TaTRsFrxmmlzb6GdaEDsNfG/N2tqOtmOrPfj7bTptO4DI+ynVIFq6BVVxfQUlNyX0+f41ZCtO1DyXECQC0iAX25uz8R7aW5vh1UZStFIQorn/bffOOo2C6NXt92jPga1+0IKueB5lJ0hrZduEbQnHeBi9XhdhGKLb7WJnZwfj8Rij0QhS1rh56wa0CVh2ul1IWWM8nqAocqzXS2vLMbVdSgqkjMdjyk8zORK9Xg9CCMtSuX79OuWXoUn6Zpq8EMIa4sPhEPP53Eb7mUbEykuMYmRZtpHYzcZ7GIY2D3W7//L9cIFTDlyyczIcDm1CNzseApTjwM7QfD63gkOMTmitkaYpBoMBFouFVYMaDAZWtIipTHxvTN+tqgqz2czS/oEml5j/5vvn9uLcPaZTFXmBsqwQxx3rCLBNJISA4wpkWWprZDDNipxMbwMZYueO7e/RaISLiwtrSzPditunTZNipMbzPNs+P/7VL10xfja3p3Y01ivKPE/TFPP5HPP53N4A05PaWrsMJfFD86Bq8+na6kncGZkbzVx9DVJ5qU3yDb+kNv9xNBrZ8zD3L8syy6lmr52PaU/WWlNuBENhHLWvqgpplhoJR6KYCFCRN8/z4LkuPN9Dr9sDS5oymkNRFdi8hrYpRQWqGvjXdb0GEhOOMQaVKdRH1YIz82J5EqLE5wJhFFkYzvM8UihwiRrADlDFsrJOI0+mNcGnpZHkTJKVGSwMZ66glMLFxQXOzs4AwMjNjlAUOYSgwlO9Xg/JKrH1Anw/gGNoGPfv38ODBw8hZY0f/MEfNIWxiGt5cnKCpXHg4jhGFBHVSyllKVccMZhOduB7vuUO8uBkWJaSwCrroLEzQglgHoqyhnA9fO/1N/AP/qv/Gvfu3YcUPoLP/U/gTp9DFMcobYVkvWEU0tokrgigalO93chnagWHF1BjCDpocjZ4hLEjJ9BaUOBsuBowCzfX5oDjYTrdQ9zrww8CFGWJMs8pD6gskKxWqKuCHHBT+LAsStSSHInhcECIm0Ho0iTB6fkZBIBer4/RaEhSpWYMF1lmKGEuqrKCcFx0R2P0+kPAcSi5PM8xmY7R63SRpgnKPMdquUCyXABawrHdfZOyAZBSGC2ZwtAX2s6dts2tpDbJwArVt/8/+MINhZv7E/gu8Morr0AphdPTU9y/fx+r1QrduA/fD1FWJRSAZbLCYrlAVUujnkQUMZ4DHI740EuzTn3D8VUGxeB8CW0iTS4fYqNR7XwKrSkyrgzCSHMUG3Sb3isFbskwUYBNrnYcx9Q/4S7lAaBq9GyQlFUJpnE8yah8ouG/9Xd7/m0bftvn2d6eZKQ/dr0rhtBV5/mTGPmPGWpPsZxtRKivMPae5rinujeDAnzofq3rb1KAHr/+VY7Bh93f9jv9MOdjs31YGQxgJ0OAqcGPC69c1ZZNngLM+Gmisryx8dOO9vPY0FqD6q/qjX2BZgxy0JGNQja06lpalKb5x/fH7f14mzRO1eNtvI1wCLtGEKJCNoazMeYZlRECFnng02yjMpvnl/A81+ZNdrtdi7z2ex3s7OwgCkM888wzuHb9Ogb9PqSSmE7GkIoZAxFc14HnEd8/TVf2Gau6svWAKMEZ1iDXWhsVpq6lPC0WCxvs43Znp4GNZEYZmBXC6k9pmlq6DTMlWHCj2+2iLEtzv6G1A5kG7ziODSayDD8fI4SwkrJAw4Lhv9k+bIsMMbOmrmtUZQnXcWydpdVqtcHGYRXQLMs28pOZCaJ1o+zk+yTgwffEAWq+fx6H7VxZYey1dqG9NhJCSdoFqpKUQdkRYBtaaYU0TWz7MKqSJAkcx4XvNSpS7DiVZWnbhcdo26FiZSn+x4hOZGxOzqmuqgpf/ZkPp059JEdDa+KSPXz40HpDzD1jI5Y9LO5k7QTytvfapv20o4n8cqnQVmFfJJ+fk6AB2MTM6XQKIYQdMDxQWeoSaOR0+RrsHJVlicJIiTmOY71sq6QgjLPkuTbCwM+hTDRSAEbTnQr5aWjUsmxFOYl7X1c1/MBHZShYFNloHCAHAsrkCni+j5mRMGVVHFbhYg5ilmUIjAertMZ8NsNoNMJiubQOiee6hq+ubOcQQmBnOsXx0RGyLIXruYijGKvVEkVZwjed/9GjI9y+fQuvvPIDePjwAVarhFS66gpKK0wnE2vcLxZLZHmG5++8iG9961v4wz/8QwgB3L51G8/duYMkWSEIfJRlYaIbpVWOoEGcIgh8CEMhWa1IilQrMpwJGmVjmpyLIPQhBEyF7D34vocgIBUJR5DjpQGUVU25GMcn+K9/8Rdx9733kNeA/2P/K7jjW5acYCVwjXNgg2A8RMyCokE0O4s2GdqHHUqOaBwNpn9oELRuHQ/qOcJSp+jElCDNd2P2cVyMp7uIuz04ng+lqYK64wi4AIosRbpeUQTDdcz7o5wb4TjWQBUCSNM11uvUOvVhSJXBtSSJW6k0aoPUxN0Y/cEQftBBXUssVrRA7exMEQU+8vUaZZEhWS2xMKplTou4wmpRgFFdMwu9MEa2sC4Xta39u5W/oC7vIvrO38Hh/hQHuyP87Nd+Eq+++j10TLRlOp3inXffxdnJJX7sx34cB9evodPtYpWu8Q9+4RewWCyRmhwTlkZtJ79BEK2oqqhQned6Nj+slpuFJpt5iu6RkYhNlEC0ZFttQ9j3vcGA2Qp4qJY53jZoBFwwx4rRDb6ecDaRig9yCp401T/JWL8ymrvxrJv7POnaatvdbN1H+zz/OhwNPuaDDPwnHffhWxuxfPL5tu95o39iU0mxbeR82Dv9MIfiqs/bDkOD+vP9OIBmNIPQgvaxDY3Z3oX9nim7lMnYDsDQPpT0SsV16f50q1gZABDX3POaeglVVeHs7ByUp9izSjoAsFgsLCWFiuWSw8/sgG3njilXFo0QHAhp2srWEGs9Wdv5YaoU/20deLMOeB4JzMiaaDOdTgeHh4dQSmI2v0CvR3Sfvb09DAckL+66wM7OjmVMPPvssyY5OEOyWmA4HCLPM0tDp4j7EkKYuUuTseq5HoRDa4NU0gZVuYYQIQcSYRBtqBmxcc1RbynlBsWnLf4TBIE1/qfTKe7fvw+AjGp+P9x/2wXsOEitlMLx8TF2dnYsG4TtC34nbM+xjWYLf5rztSn8bByzoiAHZPndAMZeNZ2WjeiiKOwx7WRyAJbO1e4PHDhnA56dEm7HTYcht8Z7Gy0ZDodYLpcWaYjj2MriMgvEEZ61OZRSlppWVRWKMrNIFI9hz/OQJGuEQWSdGnYC2dFqI4iMOrU/YweJHRWmcfH+6/X6z9bR4CJgXEq9XY+CKUXtuhjcsPziOQrRntS3eZ2N4UYVaYUQyPIcRZ5TJLcoMJ5M0Ov3baOyQ8CDmpNt2hE6nqjbESM7kZvIIZ+joSqxqWRoS7XpVCbyXuSF5U56nmcijAJaUUVc3/dse7mugyzLTbsQ1YZfOicBdTodpOu15ef1+33yLMsKVVUiywrUxiDyPKqIzPQyxyFnolEtYMUuivaEQYBVktjBMJtdotPpoN/rIgpDKopnBh07I8PhEK7r4tGjh8iyDFmaIe50MBwOoHWNPMtRS0qCOj8/N05ajF5vgCzLcXJyAsdxLAQZhgEGgz7W6wSLxQLn5xeWVxlFmyjYep2AJ/jAD6AVLIe51+uhLIgvGIRUUZwHaN/0i7IsIBwPAgJplqHT6dgB8vbbb+O3/uXv4Dt//CqSzm3EP/6/MGo5jnU0NpNVW5u2GDwNZLcl26mJniSEY/Yx8UwLc5udYHenZ9TcLw3v1hi/jXNj/4fBaIqo0wUcKlamlYIjgMAofmVphrygsQKtjBNLeRmUnE73xIn8zNNXSgE1OTnwPYSdGN3BEJ5P7yVPM2QFFS8aDAdwQTxVWRVIlnMsFgv7XKw0Rb+bIIJxpDjCx4u1jYCyty6E3U8pDXX+LvTv/2fYHXfwqVc+ji9+4XP45f/ml3B6eorRaIQf+7Efw7179/DZz34WQRAjimKcnp8jjEI4noe/+3f/c8xmc6oPYShJpGRGxos2qFFVV0QhE8JQmbT5vgmEKK1sHYjmjXC3aBnSW8bfBrXFOlet49h5sQ5Xa+f2gU8wWIWmvAtewLej9R91u+qYJyEA7e8+6FravtsP3u9pDfmrDOx2rt4HbX8SZ+bDtic7d9hwNJ5Ec7rqfG1HYxuN2DaSeWuvhR92jx/UDu01mecv6rmERsAISbQdDTquoSxtndFS/pRsn5OOadAN/g4mKMBOLdDUpGlfj75r00S2JTfpXKyK2U4e5wRtYdd8brsgDKBU3bpHsiFcx7U2QzvKzvs5rgPHpUj2wcE1YwhKjMdj7OzsoNvtIQwDCOFgMhmj0+kaqm+ANF3bKD4AzBcLRGGILE/huS78IDBGNqkaFTmh2Bw0FULYBOmHDx/YOjMcPPU8D8fHx6iqCru7e9Caam2FhmLkuC4ePToCNDAYDCztaGWCS4PBwKILbODGcWy/57ZglIBlVWntD22Qmh1JZiGwzdHkfyqb48CGO6MQbCOyodtWYmLKEL9DYjSQ08k1KrhmxXK53BAREoLrmcEKfvB12wFpvl+2E/M8R7/fB9CgJe1nZZoR57m0i/YxpYqVtRgBYvQniiIURWFREEJeiPqcZZm1dfg5qrqwzguj8qxWVVfKighxgLuNxrBd3ma8MAWsrVzFtj4ngjN76Ee/+LknziW2jT+Ko9E21Ou6xr1792yuxu7urk0O4dwIlpRkFII9JEY0nBZdiRuN9Ymlob5orRCFEcIoRK/bhXBd1MZobE8OfF9KkYFVtRq0PQHzPhsoSuvYxskAqT/VJCda1xU4ki4EKUaVVYkwCG1V7SAIIBxyJDjafnlJ6jfrJCFUoyytwtJsPofr0jkXC+JGMhUijmPcuXMH5+fnpsaFQJpmGAwG4IhSmw7G0N3O7q7llNd1ZXh9McqSOhHzF6WUWCcr+J6HvCiozYyTU5YlPAMB5lmO+ZyKyHV7PXiug7gT2kFF7UYTRVFWiOOenUiOjo5w7dp1kGxuBClry1dcrRI4jjB1QGhRieMYt27esnA0oTwmcmeMxDa8SIuLsFGHOI7NIiPgGph4uVig1+vaAbSYz1FJie9891X82m/+FvKX/y24hz/UGAQ2Gt04FXQwGlvPjJgmV4PuTxknhd8jNBcfI+eBk7OEhpF5FbYomLlB2IwGu8hpu7+Gg063j95wRAuxYEqEJrUtn5yrWlaoyhJVUaIsK0IsNGmaa9V2ljgA4MMPIwRxjCCM4HomLyYvkaUZvMDFYDikiaoqkSZLQEnML86Q5+mG8WwaEZzwYqOH7Dyxsb1pqZvmbSQsVbZE9qv/IUKhEMc+Dq/v4/JyhjwrDFLI/V+g0+mSQ17XdB5HoKjM31pDy+bltfOcXNelBGP7ulsIAzSEyzVctlALDYvcmNtvP8xGt/mgzaJhAlZYoDnfNrrRPrJlvAIbDtCfdrvKkfizdDT+VdzjB21/Fo7G059jE9H4KPd4VRu3v7uq3bcdmSfRpZ4GueHgCP1sIWuci2aCB1fd91VoihCMGDfnbbMc2s/SRlU2+97mddr1Gzi63LYLyMmoLe3YtYi4AISw1NvhcGgDL1QcboDhsG/zK6fTqT3vrVu3oE3eY7fbsXkKruchikOLWIzGI8RxbMVi8jzHcrXEaDRCkiQbakOjUR+uK6xYQ2kEVDzXw2qVIDbVqTnKzvmvUBppmiEIfKxWVEdoOBxhPp+hrisMR0NDdeKaDC6kVIijDkpTUPPk5AS+7+PGjRtQSuHBg3vo9/sYDAb2XXKugVJUwG0wGNgkaDbomcLMdp0QwtacaLNS+N6Z1sROHjsSTOFiqhZ/l+e5NezZGeE2YYfDqki18jiTJMFyucTu7u5GnypaORlZlkGYftQOUvPzc5FXlrjtdDqkSKWa3CIOum+PL35OVshqU624rTjPuR0sCsMQqxVR2tlJKIvGgWYnhdusLHOEUWjvn3NeXMdFlhWWvcDPlhvaPLe71tq2Hd8nozgsh8tIDNPyOdf6J376z1DeNlmt6CZbE0JeFMizjIwaA6UpSVVZ2TmIOx2Kopq8g4bGwdFMMsbaEKaWVMvi4uICX//61/Hss8/h2rUDmhCMwlBVVpZ3LiVxo6WsADQRCnqJVO3WbXUylkCjJKccXdNpy7KgSKqSCMMISkus5lSoi4u7kNdHspPzxQKO42CxWCAMIyRJgt2dHVzOLpEXGUojj1mUBeKIjOC2onwDj/lI0wyT6RRBGGCdpsS1NEnXLCUnpURRlohMh5FKoWNK1ld1DYAmhSylJKowCrFcEI1qNB5hPpujNAhLVVWANrkoaYrxaISiJLqXVArz2cx641pp+IGPwA/gBz729nbs5NX27rMshxeECIIId+++hzAMMRmPcH5+Bs9zEUYh8ryA73tYLldmgmA+4QphGJmKzi76/QHCKIRWGlVZoywKSKVwcX5Omt39PjqdGIDGYDDY4HkSF5Sc3m6vi3WSIAwClEWJxXIOqRXCMMbDRyf41d/8l3g4/QrU+EWIoAM2d5v/k7G/aQWyZYpWroawhjRAxjTVhXCM1CchCkyx4kXXysy18XhoaNFa0DU5YloLQDhwgxDj6ZQkWQFw5dLa0AJcxyUFKsdUVtbUpznyLRzR5AA5NJ60cIlmZoqzVXmF0A9I57xDdLR0nSBbr1DkKfJ1QnVngE0nDBrW0QAbKNo4WsbRME0BGNUla1gbR0NJpL/9t6FP36RcKBcgPrgDiMaogIahJcD0RQlhEEelG0fMYUNJOCDBhMZj1IYeofVmdVt+i2BHySAgPAc2mTWPb08y/rYN5A1DquVoAE3+BjuITecQG8c6wji6TzWLb7yop7r/9jXb59HWX93yvq863/bhreNab6IxJNtnvOJWBITNYXl87GwhMC2qWfva7UNYipfG5NZ5WjvS/bD6jx3ozS78HkTzdE92NEyAgcPytEOrTSm677k0LqlyvLb9lNdLjlC2z3/V+2uqraPVHu0Gb9ADduBpTiPHgPqbCxYtoXZortCoGgm772ZfVyDhEr4Wo4Wc+N0egyRaImVtDPzGAWlvDQWHmAK+H1g67o0bNzGZjAEouB5F9a9fv47pdIokSdDv92ldCEP0ej3kRW4dCgp8KHS7XZsDIhXV2+lEMQLPtwU3OdlYSgkFDS/wEEcRooii8qvVCp1uB1VZIs0yaxdlaYY0S+F7HvYPdnF+fgbX86BMdJ8NQ88NEMexXfvYCHUcF7KWSNMcABnMs9kMk8kESimMxyMIIfDqq6+i1+uh2+3aAGCSpMYwjxCGASiIuUanExsBGWkTl8/Pzy3LgdfZxlZzLJ1mPB5bW4CNfzZMAVjHZDab2ag7B6SZceL7PqIosnK0LOvK362N2hPXlmhH3lmulm07oKlfwRQ8gAx+Rr/a9Yp2p1Nore27ZKSLUYi21Cz3az4nX5vbhNENzlfmmhjT6dQ+m+M4VjmLHQbel9taiKbCN9HfgseC5VoTg6auK5OfY+oyOQ7yosCg3ycFRaXIXtYaQRjCEcLS5DkIn+W5BQeggb29PeR5bot193o9SysbjUaW8vZnimicn51Yz1UpheVyidPTU4JmjNRZbHTq+70e7eu6UNAbCzi/jLqqqEDYht5vU9SqrkrbGRaLBY6Pj7G7u4fRaIiqqlGZmhJAS5nJ1C9odyCGPcsshwN6cVmWIQhDxKZTO4K46+RQkLc2Xyzge75Jfm7UkjzDcVzMF1guE4vk8EDodrv2edpFXvhe1usEZVlYNIDpU1prGy3gJKvFYmGTo4XQ8AOC1h49emRRJIo8wEZjiqLAer22yBGjFEqRohdDbjRwSKaOkta15SdWVYX1cmUHaBTF8DzXJobt7e3ZiYMN+263i8vLSwRxCCWB1SrDbDYDCWgpo4gQWL4fR3NY0YsHLk+IL730EjzPw+npGfr9AY4eHVmdZ77ejRuHYPib+1UbCmxT5toLw3xxTrCfcrBYpPijP3oNv/uNb2IhBhA3fhDOtU/C6ZEUrhZNhE7rVmTZ2CSuaWfmINtFmS0x0ZKXtE4DGwP8eZMTogUbRmykMMbRMsAMPas/GKDfH0J4HpSGifK7qKoSUipAkCqL6zhwXNcolJBxL4QgfWytKFm6Jg6m53oIowhRHBGft5YoioxqM6wTJIs56rqEMHxkcgxMPRFocB6K8ZBatkxjgVFOyyZixNQxrTWqh99C/Yf/BWwdDuM4WKolI5JPiMxuG/RPssKv+rRttG07BU+61vaxV52vHa39oPPxPm2O9/a5eWHYpkp90LZ5Hj7mw4/9sMTwJz3PxvUEYNWLrtj3yZtz5UvajnZfZYBuR8mb7xphEg548fGs2sfn3KRjPbmt2tFP/pvbuTHSG+oOOasufD+01AemTTCVFoBF/rnmECHuNdXBMfdMRhEPp226Fc8xDhzHbz2Dts9EeQi8b9vR4Gd/3FGyzraDjXZu2l1AabSchDY1uj1PU4RdCCAIQlR1bs/pulRMLYyaKKysJTrdLiaTCTpxDMd1sbMzxe7OELu7U1y/fh2uS+vjzZs3rTxrFEVYrVbWqGOqL1OEqYBb2SD9a0Icdnd3kee5jYAz3YcDWu06D8zNZzo3R8z589FoZCmmURTh9PQUk8nEUpuIUkW2SpbnqCx/H1bMJjH0Z8/zbC0Dpjjlxkhsr/ttO4TXw8FgYAOI5Jg5Vj5WSon9/X17Lu6LvM5vR/mB5t7a6qJ8/bZqFFPdz87OrKQqt0v7epyjwIgEo1br9Rrr9dqqSbXLJPBYvby8tG3ANTXYpmQnhlEXdoIqU5PKES2arKEq8XkZZeH6X+zstYtMDwYDWzmc0QJ2hAJDe+N+zMnoTP/a2dnBarXayKFlZ4RFjYQQ6MS9DbUqdqqIDj+zMr88L6zXa0Mx9zZoT+3cFkaLeK1hdEgpjcBvbDXe4ji2NHS2XX/q5772xLnRzh1P62hcnJ9uJKLYSJ0m3RzXcW3UhTukVArCc22nb+dRJKsEg17PPkS7tLvnOpBVifl8gdFohPfffx+/8qu/As/18Nkf/izGo7Hl3UVxhKos0ev1sUpWuLg4x8MHD+C6Hnq9Lnw/wPHxMYQpVT+fz225+Mwkgfd7Hds5i6KwnapdCZLhzvF4DAB45513sFgs8elPfxqe56KupZU5Y4iToFcqIMeDVmuSnmODmald/DvfB0cfuHP0+10oXdsJ/7d/+7exv7+PW7duQSllO10b+nMcx8K/PMg4mhMEgc3VAGB5glyQBVLZhDp2ioSg5P/pdGqhNL6GdZpkjaKocHmxwGw2w97+LtbrJaqqxGqVYDgcII47FuqtqtJcvzRRDFKvEkIYr5llPh0zKYdWRYMcTYGiyAEILBYLTKcTxHHH5LK4ltLm+z7u379vkn5LBH5gEtJ9CHg4OTnDH337O3j1zTewSFKIvU8g/ORfgNO/Rqa+aBn7JjovjDHtej5FuEWTKEz7OcbmJqPDKkkBjQ3eDipykJM/Z6NEbDkaWsNYG3A8D4PBEHGnS4nkwiW5ZDhGmpUcZKkkLOpinA0qlujCC3y4fgDP820Okawp/wdKQpUlyjzDcrWAkpLYXiZnppGupZtmJIidKjIsQA5X21jbMtC5toMu18h+/T+AI5uktG0D7jFH4ortaZwEPuf239vGfTto8bTXvOq7x43Xq4/dQHy37rNt2D3J0P6ge/uojsb2fT6tY7N1lg2V16dacjTAEqPmyhuOQWNI83cbd9n6m/EG+sBxmjVs29Fo6h401KGm3Z4uv2Jzo/HoeR4iQ+tgg8P3Q3ie3zLAlZ1D2bDg52znOkJoOOYe2cnnXEEA5PBrGpFsPFEdo+b+22s4yYo//j7a73m73YUwzojg80ls5D4Yg5knNcox8FFVpFQYhgEmRkjE9wNMJxMsVytcv76Hw8PrG3z1nd0dVBUF+C7OzymwF0Uo8hw9E4QrsrVhIyijqpRaBcy25H1Zlri8vMR4PLb7cW0G5sXzmjYcDpFlmZ2DxuMxBSWdRm0oDEPM53Nr3HueR0VAzditqsoa0rymC0F0ntFohDAMcXl5Cc5lDMMQSUKiO2wg8/1zkMX3fWuLsJPBKk5sqEdRZCPm7MhwHgQb8KvVaiOfgIOibGRv5yQsFgubO8FRds5P6HQ6ODs722g3123svvV6bQOm/C7Y+GcUhB0RdjiEaOp2cUCSxX/SNLWCAMxkYIoS50Nw2yyXSzueer0eFZ4198UOmOM48Mz4qmvqo3xdoKEpsXTvYDDAfD6HUsrm1fD754Au08s4OM0OLz87Pzc7l2zrsaPKn3OQlHJTqRYd23IcpGijIoyeWPQFGp1OZItktymG3B85z4aZM1VVmcLHgU1gbyeG81zEAd8vfPnHPnwmfFpH49H9e1bFhhdM1oFX9aYaAxfnG0/GUFCQdQ0Y7xSapBnv3buHIi/x3HPP4ejoCDs7O1adQNUV0lWCNKMOdXp6ipOTE3zve9/DV77yFVPsrbaNwB4WV/+VUmI2m1HV3vUat2/fBpS2gz2OY2s8LBYLjIZ9a3DzQOdOxVEKADg/P7cdlGGk4+NjyxnkCYfl1XiiahdHaU+A7733HrIsw507d5piKGZgt6HCKApxcXGOqi4sf/L4+Bhvvvkm9vb2sL+/b5OGaP/ITpyr1cpOCjxJtL1YxxHWmfB9H8vlknibDvEVeb9OpwPf9zGZTDAYDDaiBdah8T2UtcTx0SnKUiJJ1uh0QqySORxHIAwjO6m1DSeeLGNDA2PVhW63i9FoiKLIMByO7OByHAfz+Ryj0cRc34UQwKNHj3BwcGAjFVVJ6lgky7c0eTIC5+dn6PX6mE4nNiclTVPkeYGT80scH5/i2995Fct1AbXzEvzDH4J3/RUYcoWJIGqUd78OqBrRiz8JL6DEdqmUdRo2BpopgGZRDSGYgWBRgPYh7NwwFsBtZc1EYW7ERA9dzyNI1KFq4RS14RwDmIiW2jApfJPQJRwHtaJq1LKujDNBOT5pkqBIE2jZFKPie7fohGDDtzGC7bSy8Vxb3G1jEAlzf6rOkfyzvwW9fPQY5ehPs32U47eRg49iWF91nW2HYdvRaAdmnnQfV11nO6r/Ycde5Wi0L/mkYz7K8z/xumLzu8023j5H+9irr73pHFxNq2nvs7mxitFVThzNh+3IJp3Heew+n3Rfzb1TvQPHIWli/qpRqqFoPh/XdkR5/Gz3DYruNknMPPeyIgwbKO12adpiszYvf0+o2OYz8LVd14HntlEQGFTGKCg5AnVNOYBc74r4/D4m0zH29/fRHwww6Pext7eHqqowmdCczVKi7FxJKeH5FFyjpGIKxFEuX1MrIo4jzGYz1LXEYNBHXUskq8Tm57EtsFqtbFTbdamCNdOB2EDifX3ft6pIrO54eXlp6Tu87qzXa/R6PSyXSxRFgZ2dHZM/Ccsc4EAer/3dbhfL5RJnZ2e4ceMGzs/PsV6vsWtyKZ2WPcXrLRuEnEwcxzHm8zl2d3c3Eqr5PWZG8KQsSysi0+v1rIPDdTD4HttSrG3qHdsel5eX1qmhwGgPK0OdZ7uEE4J938dwOMTp6al93ouLC+sIsNRrr9dDv9+3fev4+NhK3XKglW0qdvzY8WFjmxEktmOm0ylJm7ckfx89eoRut2vRFEYjYlPRO8syW5mc54jKUIg4FyWOY6suxQ4C24uMvmxH+dnI50A1K1Yx2sQOETtx7Hzw1kaFGNFgJ4VpWErCOvuM6AghNtqKxYL4HTgO5dTyfNaWJd5GolhxldeIsqjsc3Cbt1Vm2bn6/Je+8OFz49M6Gu++8YZRVyKoqR3RlhUp4MwXcwz6AzI8yxJhFKBWFS4uLqC1xs7Ojj2fUhrv3n3fQnmdTgenp6e4efMmPCHw6MEDe51r16/j/Pwcs8tLnJ2d4vDGNezt7aOqSgMfRoZDnlmeZlmWcD0XyYqSdvgazNlrDOQccRwhMJ2HJxrujO1kch78VVUZiMpEYTVMHgJN5mEYmY4kLb9UG5k5qqZNA5tfHE+4SlERHaZvMT+QOlENqWpkWQqtNT720kv43quvYj6fW/k79rrZ2eAJhFEZXozYWy+K3E487cSm2WyGk6MjJKsEh4eHGA6HFm3ifbktOJEfoBojZVXj9PQSWVbijdffwM1bh3Bcba5FxRajKDT9x0cUUWSP+KEBqqq20aBOp4Mw9NEf9JBlqYkshHZSrWsF3wsAQXkJnDy2XC6RmsrNrkuDTiqJIidHLUnWUFrB90nJZLVa4uBgH67r4vJyAQgH63WB45NzfP/tuzg9u0ReS0hBuUOCjWCloLVCcOcr6H76r8DzfDTRU4MctCKNLfuctiYQuWVgARzB1aJBOLT5UpgPNigdrNYC0rl3XAedmBLXHM+FAEDF5IRBN+hQ1/OoeBQEoRhZhrLIoerKUKQ0SCrROBBkNVpnqUlf4URunjzZMHH4UTccKYvgaG3rWZRv/hqq1//JBoWlbZBvb09yCq4ywv8kzsaTjNgnbU9zjavu6aNeb9sAvcrI5p9Xt18b1WiOad8HzxlPQlba93HV/bYN5razLESDDmy/o/Z7o5/tatDt9gG27//Jz6JMV+VAmGNbgPuk3XejCrahHdmO6rQcD/N8MMimFXTYRliYbrnlgDhNkdl2m/J37X9tDjtTqMhY2BQuATjqTb8r1ahPcTCG17G2M0HPQvcdhAH6vUbREdAY9Hu4ffsWAODOc3fg+Z5Zp4aoasrniuMYzz77DDzPx2x2iSgM4fkU9a8rQsj9gIJUq1UCbRB4z6couu/5pKIHhZGhMi0Wc7guiVDIukaSrO3aNJlOGlWeIMRymVjaL7MQiqLA7u6urSTNhhIHCts1IXhd43VnOp0iTVObkDsajTai8BzhVUphNqMczn6/j8lkQgqNptjZ5eWlTf4+OTmx1Gqud8DMB05+dl0XZ2dnNgeB362U0jpNLHW/XSKgTdVhZ61da2G5XCJJEtR1jb29PRtYXZtq0vxMlh5ujG42ljmfgPMP+v2+/Z37GNPG0zS1+3K7HRwc2MAwH8NBTA7cso3VVlXqdDpUGNg4UZyQzrkcbNNxzgc7eBy05vcEwD5n21Hg62vTB9gpaSew83htB1bb1Ct+fr4O20bcJzk5nQPOnETPbV6WJXom3YCRMnaQ2CEASN65Kitry/HzaK2NSBCs/dp2QmrZiC0B2Pi9fT/sVEkpoaSC6/rWXmSkg5WmmL3jui4+9+Off+JczNtTOxr/9Jd+Cb4fIC9yKMOxi+KYqkUbybDVaoXxeIy9vT3K4Tg7gR/Sy3jjzTdw48YNTKdTDIdDrNcZ0qxAURS4efMmXnvtNSyXS3z+859Hvk6xnBGkOBqN8Eu/9Eu4ceMGPvmJT6CsCmR5alSgBNYJTWLdTheO41n1Jtd1sTKyp1Ec4+TkZCPBiCeYuq4RRyG63Q5RhtDIrDLUyMoKPJA5CuB5DmpZgxN62YHRWiOKI5PYZRKDwgCOYP6kRL/fx3g8xmw2w2KxsANzZ2fHerF1XRunQ6MsC3h+wz1miJSTl3jwckcAYFECAFgulxZRKQpq9zRdW3iQr+n7PhwhEAWh5QzzRLa96PE9832kWYazixmWizVcx8ebb76JGzcPMR4PIISmJGMDEYZhZAc/oyocccnzwi6aWmt0OjElsTuO6XNdw511bHTFcVwLn3c6HaQptRs7ekTRMhGMSppJOwJAMn/rdI26quA5LiAcOK6H4WiKLCtwdHyC1XqNpCywMmoTQjRFEbUW8A8+ge6n/iK80aGJgCpDBzLSjbplADESABjagxlkmowWY+IAaDka7LRwAS2xmQBs7Q3tNGiHZooDOR6u65l+DHsdpShHA7UiHrg2+SUwRozW0MYQgeaEdLof8H0KWFlYfpgPMkLtpikpXiuF8u1/Bv3GL8N1iQq3XTvgqug6n3/byWhf//FLfrDD8qfd/iToy5Ouf1V0+qp92u28nVPBx2+/i23u/bZz0m7zD2qfD7r3Nqr1JMemvYvxXcF5DI+jHU+6j03qVJMHgRbaZu7hisx0dh6U3pZrpWs6wgE3K6MhPI6YwrXZTk1U8MnPre1xm05Zs7Eh2ZZr5XZ50ntpB8WeNGZ4PzqfhOcrPP/8Hfz5n/95PPPMM+Ro+ER1Cl0KnuV5jouLc0RRhL29fWJuugInJ8dYr9fY2dk1gblGNh5ao6wqBIbu0+mSMEe328VqRWIgvEaRQUV0j6PjY/hm7WFVJ2WSWTlZmlkBRVEiiKj+xvn5uTW6bt++jX6/b+tNLZdLi5KzcTabzQA0xmY74TfPc+zv7+Phw4eIogj9ft8atSygwpFzVnJkJ4QNcGY6aE01Jh4+fIjxeAzXdXFxcYGiKKyDwchJURRWBYtpRxcXF1YFKooim2d6cHBgjUlGOhjd4DwSloZlg5gdIa6dwW0BYINp0DYutW5qeTGljY3sxWKBsiyxt7dnHQm2mZiG1el0rJPAbc7S9vP5HPv7+5jP59Z+YieIqU5tg5wj94wg8PsAsCFjzwb0aDQydb4W1mELw3BDSUmYZ9etYCyjO6yUxYpXjBLxO+YxxjZBkiQbRYO5bfm+eLzzGOScEX4mdvZY9padkzAM4XsByrKy8wejStyHlsul7XNMjaQ6aeQosVoWBxK4gCIHbgFW8nRQlRV8P7R9oV0lnO1HRjq+9JNffmwe2t68D93DbJfnFxZC6vV6iIIQupaAUkhWKyzmc4oY+D6yXg+yrhH4PsLQw3g0wOXFFL1ODM8ReO/dd6CFiyCMsVgssFwusVgscHZ2ZqISMd77/gXG4zHeeuNN/MhnfxivvfYaHj54iHW6QqcTAhCI4wjj0ZAM7aqEEAr9Xo86rVI4OTnB7u4u4jjGwcEBlsulVWXY39/HarUyXDvyoqfTqR2M7JEyv5A5jwxNARpS1RBCG0O5hnA0YsPzLMsSvf7mQK7rGkVZoNvpW5lXnjRZYePy8hJRFJlCPDSBHR0doSxz7B/sWieKowFtOIwnIx4seZ5bKhLLsnHVx8vLS8RxZGFHKSVWKyr6tk4SqJq86fF4jCiKTDL+rh1MDBNy9AMA8izH5cUlBDz0RyNoDZwcn8JxgDD0CYHwA6OxvTacxcQ6MRSJoPbKMo4aaWRpicyoWEDPIEwSlRDaTqbcvjyAOarBC2peFDZyXlUkcVrX5LmzVKysa/iOQBRH2L82wbX9PYzGY1R1heOzczw8u8Q6TXF6egohBN577z0a0EJAHr+G5OIddD758/j/0/ZnzZJl2Xkg9u19Rp+v3yFuRGRWZg0oEOAgdrPFGSABslstmcxaZnrWg/SgN6l/jUytNpPYD6K6zWikZEaKUpNNIyk1hwaIgQCIBlCoISszIzMi7uCz+xn31sPe3zrLb0RWZZuV3CwzIu51P37OHtb+vrW+tVb2nV8GkgKSqxFfQ9WimCMBdSgDoOhZPkPH6ln0gkBfa6sDARj8xuwKEsrZ9ujRO4OubYfKMLy8SKCitxhB6hKoRpRDeTPcTAxhGM8SvOw5wXsOFCk4eVnK8tyWGDUW3js0f/xP0fz+P0BiLfreCeHU3qjh8u+Cq6dAWcb7Kzzx//98fZ1oxNP3/jRA/3WveQ5agacAePhu886YaWLA/fNVZO199/++3w3foWvtnb8ITAM47uLhFXsqPAHqP2lu34mMYBgTCfqZoVTru/cKWJzL9TieYUzP+zGFP9np+ic/+/t+z27V/A6u85DvED7Ha+RFHmyG9zEHTDfTOx+Td+/xfI6f/rsoC/z1X/nz+Jt/82+gHJXY7VaxLKsDHJCOgpd6Pp/A9S3qpsZm/YjrZ9f49NVnaJsGz57dYDaf48svvwxR5zQDvMd4FHP+dntsdzsAoQBFqIqXoU065HkBYyzW6w0Sm2Bnj5hPgkwWWYKm7mGNRVUHnXrbOLjeYLc9Dk69sRUPK5vcfv7555KrwHP0dDoJQXDOSQSCDeh4llprBaxR6991Hd6+fSvSHuccvvjiC/Eer9drkW/z7CUYZFSBwJuRl9lshtlshvV6jdVqJdhis9lI/oD3Xs4wJhXr6Eff9+JspITaey/yp/l8LgoPXTqWhEhLaCgTJ/4JztTgnOLzUWJDQHxxcRG85ooMMxIBALvdTpKfAchYE0jP53PxlDOfhKSCESdiMUrSwz4J65/kgt/bti1ub29lHJumEdkYE6WZRH/2/G0ric50oDInhfuU+VPr9VruxZihOpU+qziXVJawqIDOU9b5KSQfJBXGGJGD8XsOh6OsJSaZkyDzzORaJfkqyxK9GypgsUoXbQjXJ+dbIp4Y+s9w7XDfUNqnm2f/tNfXJhrPbp6hyHNksdFIW4fQlPGA73tcX16iLDLA93j1xaexwg1wPO5wLI64Wl6hrmr43iMxwWsMQEJ1lOS8evUK3/3OdzBfLrA97NC0DX7t138NRVFgMp1gMh3D+06McVU12G63scGcjxUjEnSdx2r1iGfPbvD4+IByNEJTV+jaoMerqlOoXFXksEnw4NBIARAmOZmM4H1sfFfmSKzFqTrB9Q5FkSLL8piclaGpQ3lY+ND7YLvZIs8z1FEn2vc98iyHgQve9z705ui70JSvdz6WBB7hcNyj7QJrfnZ7g65r0HWNEJNQLcTHztoZVqt1lJA5zKazQPqKHEAbIlFVDWNCz4Tj8YT5bI40tWJksjTFdDLB3d0dtpst+liFaL0OsqLpdIbvf/+HKIoceRka8ywuLkJOTlx4p6pCalIcDidU+QFNXaGujvAudEQflSO46N2pqgqrh9CxvGlqlEWB3vVg92/vgaau0TngdKqBuPmNCUnFXd+Jo1QDnjQJyfd9H9aIsT1c38P5gZRkedjITQc0TYfj8YSm6dC1LeB7pFmKz9884Dd/99+hrms0bYPeObTOoOsHOYL3XtY5rAH6Fsff+X8g+/4/R/kX/zcwy48RcjOi15+g3IeETi9IP3w+OjmDdxcIsiVVrUngvAIiwhTk15RGDP+ONwzSHu+9eHrD5RgpC18ulySZ8KHqWfiYURGToe/FmWs6vt6BWFo/FZPm6z/+p2j+3d+HibbAwylwNwDlnxaJYOTqDFxrN/nZbSiQekbP3nfD+p3qp374u9Xf9eTB+anwmSfA3ZBJGrmmeedaem4BHQ3T/xZAHRaOFHl6P9HA+TwRfGIo+MBIbJAFkRQaSK4R9PgPMpxheZAIG4TqUVbuNctSIUIwQJLYIN/zPu7rsMfbvpf9oqfEGOgiVk/uJbwpALWhE7Qkc1sr15TlEUscW7DEaiK/K0uWIz2gi5HKgbkMc2atQdf34WltIvuVZV9ljcicOKRpgqLIlccww3wxR1M3uL19htvb5yjLAsvlEh999BHW6w3+3b/7I/zjf/xPlC0clgbLVeuIVNgPwQYl1sLDhb0Mhw8/fIn/5D/5n+N/9Gd/HofjAW1do8gyTMejIHHyoXDJ4+MDrE1gE4MsTdC0Nfb7Hco8x2w6Qds2uH/7FuNRiWw+C31rfEgCb+oG3gPXV9foug673R7j8QST8QSnU4Wu7aREfm8sJtMZ6rpC1/UoygKH/QF5HmQn8B6T8RhtF5pu1hGUTWOe2ZdffonFfB4qGkVFQ1mW2Mc8ReZP+Aj4KbF6fHgQICay4FgKVJx2SYJN9BizeRlz+xjRv7q6wnw+F/LCyoyMRPB3zBnRAJGed+5T2kDmOJAs0KN8cXGBw+GIzWaL58+fC8Dsuh6n0x51XeP29hYPD49SKWu1CgnMWZpgPJnAR49+lmVo4tnZRYDaRqnSaDTCarVCGvNrR2XwbI+KEWysGhokuiMB70ze5hY5Rc+5tRZFrBJ1OB4xjhIlfucilnQ1xqgeXQ43NzcimWrbVuXxhPdQqcEKbexrpiuN5Xku/YZ612Nf7VGUBQwM0iQFbIq27SLgtoB34gzt+x7WJKjrBmwoWdcN2qaBseasshSJU9u2OB6OqKsGi4uFmPOyHOGw32Mxv8DxFIsB2ST2ZMuRxGa8p+MpRtZqlEWJJE0APzTZ47phTghVOIwykDzQOdE2HSpXYzoJBZK6NpB87/2gIAlgCtaG0sd1NZBkRo506V/mZX2d19cmGre3L9DGhd53DqTunpwAAQAASURBVHd3d7i7u8fV5RKJBbbbEBmA8TicDqF6UJohMQm6JkzgZBQY0aE+IC9HSJJUyoLVdS1htaZtMFnMUIxKVHWFtmtxebnEdDqJ4dapPHA0sTAmSEOyjAB5hbZtMJmMpZpDWRYIXbYPyLIE8A5JEhKuVlUl5eZYRSmEozbIi0xCYZRTZVmK+lQBzqPIwiKbxmoZ3oWwfRm99JPRWBbC4XBAYoEstej7kCTvXYu2qaJOPkHXNgiNhUL/g6auMR4XqHyHtCyR5Zl4uOCD9GRUjGC8gYXF6XgKncwzYDqa4Hg6AQ7YbUIE59NPPwUAvHz5HAahf8hms0WWBS9A17GKiEHXObx+/VY8K+v1FofTEeWojMlGCR7u70PyvDdoq1iGsXdwXYfl8gJX19d4fHzE42MwdFVVoShLJNZiNB7hxfMPcHm5RDkq8fLlB5jEg+N0OqFzHkUZkqgYIt5ut/j888/xO//u9+ABYdgkF2TbIeLDyh1R0gPAIXhNRV7An0dvg+l6oGrCQcMxRgQ4Zx7WoaEbMBz4fbXF6V/8H5D/mf8lsm//MqgTD58Zemfzu40xAKtYmfPrmUhQGAUIHwxAJkQV+MUKsNKxYmLkgX9X96geAhCt91BmN36INxpAMu8V4TPha0OeinT7FaJkogSL0RYI0GKFqeb7/xzdH/xD8eiGRHoCQP/kNr/a2z9wrQHUDx83YkDB334F4D5/cSDOfjJcU8lzmLPj3x1dRRTeJTzaMy6kT+n3B5IV14AZIhb6GkY9u3BSDF759z7B+547Esim7WIfkpgjYYbogFFHxkAmAGNcIDhPiD8AeBeSokkYu24gw96H5qzGDPkRYThDL4Yh7HZ+z/Y9Qy1P6cPeDG8fygA714NFFiyjh8bA+eBlt5FsWGuDtNADXduFvk6+R5aGyEbooxETu+3Q2boscvSRNCSJxcXFApNp6A2UpRlGoxFm8xkuFheYL6a4ulpiNptitVrh5iZEq1ndJ1RFOommfzQq8fAwwa/92m8gsQlaH4CGjA/tS+xDFTyksZSs80DvkZjQH+Pq5gL/wZ/7s/grf/UvYTqdoK1b9E3wdB+PR2wet+LBXG/Wob+Dc6iipJG5C3VdI6mGfggGBq5zkt/w8Hgfnzno77M8RV5kaNoax9MBWZ5iOgvyo+PpiMXlQio/5kUWKlV1NZ4/DyVXN5sN2j541HOToW5rePQStSjyXMrDB6eRRxv7TrVti2WsALVerc488F3X4QBgsVhI1UWCqLbrgLhG8yjD3sRkcKoEKM9i82GCYMprRqMR7u/vxQMc+kbtJSGd9o85KGx8TOkcIwmMciwWi+gEnUpEiL4e4qDpNMdqtY4EpcVoNMZ0GprGlXkWGiLneWgH0LawxqDIc2y32zAmbYs0SXDY7wHvcXN1LZJj4w22m63YqNvbZ4CJOawmEEzvQmGbMq4NYqo+SrmmUeJtTWh2WNc1HqL0LUjPR0ijR3+1WmE2m8k6I+A9nU5nvSoAyNgy+ZrYrygKjPLQQNE7jzzL4XsPB4fNYSPRnLo+SoJ6YlN0bS95E6EalpV5CT01AmZgQQGWQS7LEdJJbBfQdKhOQeZ06it4b7Db7cVR0HuHxKbwPhYFMBbwBs4BaZLBOY/9evvOuiJ5Y7RMnxuUaYXk9ybmKuVYrTYxdyWBdyGfWOOlyWQSvrsfSgxz7vR3DLb2ZxzR+O6f/AWRnuwOB/zb3/otrFYrVH0L2zl4Y5DEB07TDKyqkSa5JExdX18LMzqcKlzFhTgZB+3mi+fPsZjNkaah6UvfhjyFVTQM3/nOdzCbTREa9LHNe4LRqASrhdR1kNj8wi/8AgAIcWBFI770YLGcHn9Oj3vTNDhVB8zsDM4hJjIHfd52u0d1DCHGxWKO0DW8R5JkcK6LgLqGLs9KiVRVhdBVSGoK2sfNZgN4YDyewLVB6pTAYpSFnJDNwwaTcYmua5HFush1FTSeVV2jbxpsTke4PngpkjTBw9u3uL9/hLVhPOumRlM3+OyzT3F3d4fxeITrm2vMZ3Nh1/DA4XhAlqZou1Z0gGkSczjyHFlW4PmzF/jTf/pPwzmHx9UKbdNgtdrgt3/7d0KVq7LEn/mzfxYvP/gAXdvig4++iY+/+U188PID2CSU8xuPJ6ibGuNyhO12h9VqBWstHh4esF6vcTyecP/4iMf1Cnd3d1hvNujaDpvNGqfTCYfqFD0UDk6FTwnQ9GHCTeEjgPJmSKYU0K+AzJlmOhoEraV+xzOtNpxUcviDf4jk5ruws9tIViJgghSBhZCDCBh9BKRPPbb8HIwfPiuuZf0eDF7tCLBJMNi8bMDlJD1PwLDCxF4uqp6R5CWC8eAJV9fn+Gji4UMZbOc9vOtR//E/Q/P7f18akg2e969nuJ4MDLTM5qcZv6cym6++6HCdIck9PE9iv468aCAS7yuPekYQntwPJUXhn18d3fnq7wZIPodxff/nhCTyUy4QCmtYWjgAVMPoxNn92uE5zEBGJcIBAyQxYmCHak6SbA7A2KFaEp8x/C6uVmleyed/Nw9lIA+K1HrVeyWOX5owEhje0juHFAkAjzQ2fmMxgiSxKLMczvUok1yq7oVqeBdy2H/00Ue4urrC7fNb9F3IX2zbFklqkRcJylhtj57KIJsIVZOstVgul6jrGm/evMHLly9lfDabNSaTMdbrFR4fHbbbHV6//gJJapAXqXjb+fyhqWWHJAnrpigKFGWJ6WSCUVbim9/8GH/iT3wXH3/zQ5Rlhs12hfXmUeQdzA94/fq15B/Qe08pzNXVFZIkkQqMBIBPi6dQdkxvMq9POQrzD3UfAhYpYc8Day12ux3+8A//UBKYKVHhuUvHE/McmOhLDT6VEtTNM6rBiAHXFMugJkmCy8tLyZEUjz97PMSfVVWF9Xot1Z2Yg0DPNgCJXhAMMr+BBVjojTYmlBjd7/e4vLwEAMml1JIm9ucY+mSFnEnOHyP2rGh0cXEh+Zssnz8ajZAlBk0T9gMT1AlMmYDMHI80TeNaCDmRzPfg/EhPj6aSBPckSbBYLGCtldzQpmmwXC6lX4SORGiJ0eNjKLnvMFRiYlSBOTTaY8/7pQOT4zSdTqUMMHNX6mN9NuckKZRuUybG9zO3hpXKmJvCsYbxUT3TSbsExPtOk6FgEm3Q8XgU280qWLyWLkbANSw5JMbEvObDOzkdxNO6p4vON+JaCHL001luMm2w5ObG8dTnjJZH6SaEwJCn+3VeXzsZ/Hg4RLZsJXz4vT/+Yxz3e9iui9GOSshIUYSNVZ1q/PCHP4RzDt/85jcxm80CY8wyVG2L3gUPyX63x+PjI7797W9jOp3giy+/wOlwBLzHP/p//9domgY/953v4Bd/8ReQ55kMKntidF0LaxMpDzefz/Hw8KCYqJFB03o2atSYy0DjvdvtYqiywnK5xHg8DrkpZRmMVpph9fiI4BB2KMtR7OcQSuS2bYvD4SD6tiQJnTzTLEPbBoLUda3oOSeTCfa7Pay3krQ+jc3rttstXN8hy1MUeYH5Yg5EWcDhcEDTNVhv1jjsD+FwN0O97a4FmqZFdarQtA2yLMd0OsH9/T1m8zn2+5Aj4QGMWN7MBqkM9alJGpq9jUYl8qLEX/4rv4xf/pVfxebhEQ8P9xiNx7hYLvHDH/wQ3//Rj+A9cHNzE5l3CKXe3T3g7v4Rbdvg4T4QCecddrsdTsfQVZy6Qs6t8x7O93BwAtSo6+/7Psgg4s+GrrROQgHO9QLqGQwIHvZB/6/Bj/bEfpUGnJv26cspwEkvVZIkMPkYo1/638HMXgwbGASuRjzARsiKAvS8HwQpwhDFGDoTC2nQ9wFGTtRvectPSIk8iYQFzr97IBXh7/Tm+kicbFxvjP4Y8YQPJATq/a4+oPq3fwft578tQFAnfkOV7+TnOAfve+mo5k8yZD/JIL7vdyIlG970JJo13J9U1vLvGeT3fod58rP33bleGyEZmb1LrCYtMk3vjpP+2dNnFAmcfIZzb+AdZG/wOsN73iVGw7WHKIzOIQhdoiFR0adSKHjznnv0cN4BNjSd/DrkkBGf1FrxNJ7NiDHw6JDGQ9UgNIQbjyeYTSe4vg4V/z54+RLlaIRnz57BGoPb57eypD/66CMcjwd0XS+JtgQRuvpNVVX47LMf4+p6GUpNliWc95JMevvsOZwbxu94PEovAgJdgkV6TNu2xff++BO8fn2H9XoVZLuxjOvNsxtkmUFZFDDW4HJ5KT0r8qzAfDoD4HE8HlDVR5Rljv1+F6vzLKQMLJ1xt7e3kudQFIU0nFsul+j7Hg8PD1gsFmeEgpKW9XotIGe5XIrWniCU4JmJwwRi6/VayAKLmtAra4yR8qg6KZUgjQDYGCPkYrVaIcsy6aXEhO7VaiXjzh4MBGiMchNkEgyz74TzHqeqwmKxkMgNn533W9e1JAWzwhRzH6bT6Vl/C+Y6cMyYA0tnJ6M1BNd1XUuew2w2j5JoI5ES/kmM41woV+u9lxL1bX0SMMvzj4CeScX04ksVIudhYCXJmuuR1cmSNFyH+n8qOOjoZWUukhfOOXMQSFIkHyLOB/EZ5We6z0ynSB+976wqyipWTHR2vYPFUG0JgGBDgmvdMJCJ5957iT4xd4TqlrwIWC5ITRshmaGgToKqqmV9AxDZE6WS+mfEPsxVJXkCWG2ul3LA3nup7EXCxfXCMeBLpPGq0hbnXZMc2ht+NwAhXHw23QtPnwt/9Vd+6b32+Mw2f22icToNel0Mxr46nnDa7XH/9g1ef/kFXNfCGovJeAQD4HG1wm/91m/h+fPn+DN/5s+I1nB/OGB+scBqtcLy8jJUrdpuMV8sApGpK5R5ga5t8Y//63+E3XaLq6sr/Kk/9YtYLGaSYMQNcjwesd3uhYUlSYK3b99KPWdm2b948QKPj4/C5Pb7vWwaXV+ZC4DkhHpAJmlXVYXqcJSNUlUV7u/vsVxeYDQeI01Cd0UaLmo/8zx0aO0Jgr1DXTcxqdjC9yGcSPbcO4e7t29RFrnqYxI8qsaEsH/vHY7VCeyyGhZYgjRNMCqnqOtWFltRFEHOdHWN1jnkRYE0SXBzfSPdSUNJ1HBocVPt9/tQnelU4ft//COcThU225DAX50qTGdTrNcb1G2Dw+EoLD+QABfK1uK8ugqTlb2LznRrYbXH1hjAOPjYuVYaUxHMeA9HBhFxEwlK3AmKIAzL3HLsnoQAnxIM/TuoNf/0Pf7JnnhKUtJyiuKX/vdI5i/i790TL37oaK+uKOB9iHuc/RZMKB+iEOGngWgY9Sk1ll7HNTCQCX1hH6KT7/39+Q0EUhBDKMZEicbwS1DWQZlRt/oU1W/8beDwVvbEU6MFP6xhHS3QHv33zYkmGk/B/zsg+8k1v/r1/s9xTLUXXobGh3vhS3vQdMKdln4OkZHz7x4IaPTUS+Tg7DbOSPD7HydGSRIL15/Xbj8fY5LfoYHc0/H5qvHU/xHgvI94vZN06ByMJzEeoiHWBqIc+iukci1+HtGBQHvhPZCm4dCdTUfwUQYwnc1wfX0dcsoWC5SjHC9evgieTxuq2GVZhpvrK7TtCc6HgiJvY2GSsiwxnYYkUlYHnM/DGRX68UwliZiH/2KxQNt2qOsTNpu1eEUpTTDGYFROsNsdBIQRrO73e7x8+fLMS//mzRtcXV1hv9/jcKxxext6Bc3nc3z22Wchf3EywWG/xsXFXLyrm+0WH374IZq6ho1RKcCjqk7I80y8mk3TI88LAXU8WymZYBGRq6sriRYQ2PC+Z7MZVquVnI88e5fLpVRC4hlEjyqrBl1eXqKqKkkcBoDlcikOwizL8PDwMJxNdig3GvopXQh422630hOKHmYNbLUdoUyNSbFs1kZwSCehMUaI2MVyiX3sb6XBJR2U/KyWWfM7PvvsMzx79gzH4xH39/eYz+cyryy0w0hSSMgPJXjn0SFIIM9mwnlenlWuAiA9Nvh+JkXrHg6zyeisiAslOASltEcc581mg9OpQl01uLm5EcBJJ2mI/HoZZ1YE09EGkg/aFY4rz2BekzgJdqh0SZtCLEbSxupldOpR1qdlVYwUGGNQpMUZuKZDMDREnknTPxI63hexDNecRCNssDmMpnCPt22LIi/RNEOjao4v9w3HhQCf/+aYsSE1I2BMTq+qSpQfJNQkCiQpfD7eCyNP3Hu0pfw7SxhrDMT553wx6sF1SmKUpunPtmHfZrc9y04nEE+sRRIP1h//8Ad49emnaOsKRZ7hsNvjBz/6oZSw5QRdXFzg/uEep1g5aX84YL1a4aOPPsLbu7e4vnmG0WSMxWyOw36P3/7N38L3v/99pEmC73732zDGRwM/VCrpusC6j8fAipkIxEOA5IPskxPKOtLiRXdOFu5ut5P6xjb2aQiL3uB4OCKL+sf5fC5kp6pOEfsZVNVJwm5DBSQjiziUzbXRG0IZQvBWW2uRpAlGZRizujphHpOlirzAxcUCaZYhsRaX1zcYRQZfliUW83kMk45jjkLobO6dQzkqZe62pxMeHh/R1DW2mw2OxxPqusLd3T32ux22ux0Oh30sMVfL5zyUQQKThKNkiKAlwgsBVrGyU3DYD4CeUhuOmTHU1MfPGpZNHaognG2IJ+v03JPKSi1PpBZnBMQ9+dUT4Kt+9lWvn0Q0fDQiSTlF8cv/KezsNniH6K2OhMH4IfpgLOVOyofuvRAA7z1gbcy/IADlswz5AkNC8NDDY+ABmoA8+VyUqyj4LPfihdgQlA7jxctDnoTJ7z26V7+D6jf+rzCxn4zH4M15MprScVgbu6dE4+xlCMTt2bxqYDG8dVg/T/MdBhBL7zi7SPvha2Q63g/Ewz1oReogXxKvug95VUaBbrxvjRG4x1wJ7hOSKH394e/64+fPfb53eB1NsMMz87nfT+7eHU/1je+MiTEDyX9KbIBADxMSKLCTfFyLxgHWo8gLjMdBcpNmGbI0RZJlmM1mUsa0KApcX11hNp9hOipRnY4YjceYTieYz0LlndVqhaqtRZICIB6yAQDUTfA4r9eBHDw8PGA2mwnhoNyF98dqfswRo+ed/QQeHu4BhE7Crnfoo4w2zwu0TQfnhr4M9KizMMrdXejLdH19LZH5rutwiPKHy8tL9H2P9XqNy8vL8EyxJ9RoNMLd3R2urq6wWq0kuj+fzwX00gMfZD2FAEPKa6jV5/4jefnggw8k8q+TfwkI2TeC4JmYgQVbKAki2ea/tcyV8gxWI5pOp1KNkdiDv+f9UtrCPhSaMGjpSNd1uLy8lN4SSZLg8fERi8VCSn/SqUjgSBmKcw6z+Rx104gEKESNQhSH1Zpoe+jcnEwmZ+vGe4+rqys4FyL6lI0dDgdphkupk7VWiAYlRiQbXeek/DylYcQ12o7RmRoAawMLL55xesDp8SawZmSEUaMsywFvzmRMxDZZnqGqjiLhISkgWGaED4AAZypP2PVaE5HJZIJd7JXBkv/MfdAldnVCNB3EBOTc2ySji8UCiQkJz0mSyF4lYOY+JGBnLw0pumDOu28HwN3Dwwn2o4wszEGKPCvOIje6NwaxJonBcrk8Gxc60J8SM74ooWKJXO2s4JqhNJFSN46HrpBFgqZJiO6rxu/hOmGeELFwWZb45b/x1/DTXl+baKw3IbSXJElIfvQ+eKm9Q56VYAHDzeMDXv34x/jy1SvsdzvcPH+GH//4E7x4/gJvXr8GojF6eHzA/cMduq7D7//+7+N4POJP/ak/hXGU4ZSTKYosx3q1gncO/+Dv/wN89I1v4PmLG0wmpRwUTPbpug59FxJPOejs5MkDlpOVxQpTQ4frHkWR43A4SiO+MNBGqm9UpwpJOkxq27ZIYIS0sAsjDQTvj4eH9x5JmsKaUHJuuVzK4cKOpdPZDDe3zzGeTDAajTAalcjSFF3bAR5ouw77wwFd1GIaE8LK28MJ++MJu+0O6/UKD/cPQXPatZK0V51OoXJS3Fhd16P1AUIOYMqLF6TvfOivoOCutaHzNaw5e7+LwMnGag3aoGpg42GkudUgYwKAnyyXCRDER4B+Lg15Els4d/DHn73z8u/KXfR3P5VHfVWkQz6j3ve+7+L6S0dTZH/iP0b67V+GscmZ8x+RTlmlR4d6fk0MfPyhifMHY4ek7/jLp1EVHd0QaGpA+kAf/fl4mHe/W/7pvYBtRkHOBz/Oeb3D6Tf+NtzdHwVwTY+3IoDnYDUQnTOv9xMP2/nw8t7Om7vxuj8takEp2PlYkWikkSg9XSMO3g9a1vPXQDS0bIzPqj36/PfT79b/Du/9qsjK+RicE5B3iYZ+PyMqTyMM4e8/6XuGvRN+79X73y0PK9fwQySS1/AeSNCjyNMQPc0zvHjxEvPZDB4ef+IXfw42sbi+vo4e3AzGBCDYuh7T6QRpmuGzzz4TewrvkSWhAlPfdTgcDyiLQBL2hyMeHh/w8oMPsdvtRB9eVSeURQmbpmibBjAGWZpFm50gsRa7CJx32y2qqsY3vvFhKHNZliEvLkuxXq2R5YEIpVmoQshk4slkiuuba/zwBz/ExcUFjDECkOlZp96aQIHa+rIsxYt5fXOF9WaNqqrw0UcfSQds7z1Ouz3KohRQgAhQurbFzbMbIRcBbIRIY1PXaLsA6LWXWzcNo0xpNpsJaCJ4PB6PuLm5wcPDAw6HA168CFFbymp47tJry88zQZo9NHQehC6/CUAAFCMtJDlch4wATKdTPDw8oG1b3NzcoOs6vHnzBpvNBpeXlyEPEpAIilQj8oMURTsiqXUnwXEuRKLr+HtGCbifKDfabDYYj8eCL+i81CVfNWbYbDax1HsgDbPZTOaBYJISq+PxqHptBJun5XoE2tvtVtYQCVSSJBiVJfIsRdPUcs8kLgAEkJJE8O91VSNNc7kPRjOC8zRIp9gU+dyGDs/N9QQMJbSBQY6svetN26KK0T7mJ5AMaTk8P08Ar3Nq+HxN02AynqBtWsC/Gz2hakNLnukUIdkjEOefzjk0bS1RVK5VSsb6bpB7l2UpEnXusaeOUH4PMPQ04/u5Lgj4ifsAiDSMxJD4bqhOasUe8Hl5PRIYEkwth+Nzck/y3jg+29ijLsuyr0U0vnYyuHd9BAddqNCRWCQW8N7CuT6UPwNweXOLxfIKH3/nu/ij7/0RfvSDP0TXt/ijP/h9GEotfI0vv/wSm80OXdcjTzOY0RhNXcN1PeqmBqyFi3q7LEnRuRbr7QplmcG7OYw16NoO2+0B89kMQIK2rtB3cbHYFIvZAnXTCEgP3VJ7nNAgTXJ8/vmXaJsWvjdwfZjwpnkTF2G4jkdgtR6sjmKkyZoxQFHkwqpHoxFevHiB5y9f4hsffwTnPWazmXQonUwmGBUjpDZ4SjbbLbabLR4e7oPn4XjC27sVDp+8wqtXr8SbsF6t8LBaYR+b0zHZrI8LxxuLtg89IYjzqFG2Ua9srEXf9eKbDl7xIRFaPMfOoe2dAFZjAMeqSQTgsYpQ8D5GL2asNBHkDi0GmDWAVu/6AJp8SHYlyXDUToGYewC2ibFArKoBP3iqB2M2fJOjx5U9JjzARNIzj7EdQPzwpUGK4YHYGEp1RTYevg9kSMASCRQI2gdQqQ0tX8YY+OaE9vf/ProvfhfFn/5fILn8ZhizGGFgacrwvS4+h5EefDEcFP7hwnMY/bN4M8YAxg+9BMIvwrzFWQ23672045B/G3qtrXzEiJSLhIJNA8O1pZ8G3xu/sXv8EY7/4j+D6SohTmEZDfK2d4H68D6A5NSqriHmbKy5yKwZ8nU0GA7vdWBi/LCuwwH5tL2DpooBG78vapHAITn7jIkkOjEJ4M8JW7iOl3cmyTm5YDThPDLBaIZBjB0NayP+PiTSu3hwIco4jRDA4MHsIEnSZiCdzHuwUa7oVNlW7t9QZlrH1UIES0dnwjoJEbokteI5pWd4Mhkjzwup8Z9lKW5ubgRovHxxi+l4FKrMpEMuR991GE9LmCT0XmiitLXtKiSpQd/1aKoEPuvwrY+/gdVqjcN+H0D+qERW5ID3SJIUMKH07Hw+Q987WBhkSYoXt8+DBzzJQnWpLoCP/X6Pjz76CKPRCD/4wQ+wXC7x/PYF3rx5g7Ic4/LyGofDCXXdYj6/iBGQAmmaIUtjmdTeI8ty9L1D0zbY7/ciaajrGsfDQfIvbq6vsV6vg8QhgqXV42Ms+FEhsRYfvHwZ5L1VjeXiApOXwYHW5i32233I54OVyHNRlJhMRphOZnh4fIAx4Xehy3WLpmllpZEIMK+AIAVg/mEpsgnmHr59+1ZA036/F8kMPb9VVUkhEZ4tX375JXa7Hb7xjW9Iki6df6vVChexKpRufMcIyVOVgvbwEhg+PDxIVOGzzz4Th0aaZdgfDoAlsQp5OpvtDvv9AZNJKAaz2W7xIjbBq+oWI5vgeKpwqgLJuru7w2w2w6k6ibTr7du3Avp4r7Q9jJgwL4M5CIvFIhY7OQrBIwkjkKNn/OLiAm07NBLcbneYTGYoy5E0b6MEjmNT1zWaqkY/apFnObIkxWhUhjLudYO6qrCYz7HebGBgMB5Ngo21wS52bY/xaIJ1vUHvKoxHY2RZDubAajlQcKSGnxdFiTwvcToeYWwg684DVd0IIQvVoKY4VSdZK70PUnDnHNquR93EErYl1Re0PRZVFUrRWzsULzgeK1Uy24Q9bhOkaY6m2aIoShyOR1SHkxQjYONEJlgvLi4AE0grFRVt28p5z0R7KlMCqckkIkoPv/eIORpBLs7oG0E5gT0A+TdJACWIJBUcL2DItdAJ67rcrE4A1/k/dF7oSqp0fFNqxvWqn42RPBJLTerYe+3rlrYF/gdENN6++TKCWC8PlqQpLCyaukXftcH7k4YchKIsAHi8ef0F/uh3fw+//i//JeaTEbzxODUV9scjDrvQ9ZH1x8mm0iyFTUKn5+oUQMrDwwOSJMHV5SVc38ZDKzxoiCIY+D4wvb7rIzkA+q4DDOBcIBvAUFWk7130gvEQt0jiIemBWMEASJMUs/kMeZ5jMp5gOp3i2e0z3NzeYL5YoCxC47vFxQXGkzFskuJ+s8JqtcJut8fj6hGn0wmvXr3C2y/f4rg7SUfwpm4kXIYIlnrXC+Lp+hDNcAbo/OBp5yIKJRYHYEZA0ruBnesQqQbqnM+zBRGBj1X5FBo86wTqoJFW0Qt4ITj8mfZCvy+R+quW3+DFDonoT6MKgfCdV5ri5zSY4veeSaTsOXDUnnV978y/Gd5znsehwaQeV15P7leNn3iQYZD83K8i/7m/AZ8WofJO+IZIBCipQqzzP8yvCk6c/917eGvYUw+gXI2/VmCWEQ1PTzPJSHijfLc40z0rVvnI4Yb3yndHANof7lH//j9A98XvwveDoTwbE/XSYP4n/Z7SKL6X3rH3ff6cHPTxGS0Q/zMIpVO9cfIQem8ZY2AVmdDJ0wDgVJRB8jCsDWOmohd6vbBjPPs0UEI3XFgRFIR5Dw3hotTJ2LNxD+solBfWcolBokR+7UUOxe9LrImHxlgOM9oK51osl0tJPuz7HrP5HNYAz66vMJvNYUywnx9++AHggfliBmNd0JwfDhiPgmyJXuTF4iLKZ+ZYrVbi+STYoD189uyZ5Ap0rkNe5NJ9OUR5R3j79i3G5TgCoHBYX15eYrVaYb1e48MPP8Dnn78S7yzr+l9cXAAI+XTz+VwOX3rLTTL0KmCfg91uJx2lAZwls1J+w2avTBh+KksheKe3+3Q6IUtDR2KOga4eRbDAA54dtI0xkqDJev2U3zDpmPIIlmddr9cyv/wsv4OSMBIIay3u7u6wXC6Rpim2263knuz3e/z8z/+8yIB5r9fX16GwyGwmz6bJymg0wnq9xne/+135/WQykTwPDZAJ/Ohh3+12Ujlpu91K89jVaoXtdosXL0KBDZajZUI+k9LDGjqXPmlvdZ6X4uWlnPl4PEqTu4eHB4nekGiFTtY3Um6X0pzr62tJLJ9Op5KXcjwecXl5KecJv//Nmzfo+x7Pnj2TJPjpdCrSL+ZT7nZ79L0761lAIKhzC+jVJsh8/cWXyLNMIjusxkSCpueQpXqf5gkQYxD0nk4nKbHKPAmWWuW12XWbUaNTXcEmQzdxRi0CMRmaIQKQZHYqUZi/wIgImwUyCqCTuLUUkHkZnO88z9HUtVQx5VgQ0FdVhR5DQRgdtbDGIolkjr9jfhHvRUeI9ZnFqAsrRwFD5SZG6ZijxbGhk4Y2QLqCx6ILJP4caz67LlwAQIoB6XvxfigqQScAn6coChlz5hzps4R/p6QLgMjZ/ub/9D/ET3t9baLxxY8/QWimlsiXJjG5cLPdIsuSGMq2qNsKfddiNJrCmBK+7fFv/tW/xB/+wX+PJDGo2waPj2v0TQhttV2Hw/6AtmuHcG0VDHpe5IAHrq7CQXI87VE31cDmrInN8woYWGnGkyShe7f3wSOfJGnwOGUZFosFRuMx8izHfDGDzQamN5lOMZ1OMR6NcLm8wmg0A7zBxXKJJE1QVxWaOnSqvl+vsF6t8fbuDvf399hsNqHL52aNdUyg6vseXd8FjxkPn26oid9Fb0WIMFj0PujkrBkaXAVQ4tD1wzUABarskAjrYiM0biaWAubBRXCmZSn0dBozNErDezrQauKhF6AmEjDnQPypjErfu/7Z000qGvHoyXhXvuLFuS1AT12j73oQwL1Dbp440fldeoPTW6OJA4kZtYwkenp8nt6jV2Fh/u7sGdIC6bd/Gfl3fxUmG4OebB0pGYIVPvZsGHzMKg4k4HN4N++ZUQkr8qqBnzC6EYlYdPqTZDDQwSiGFqsRxA634NF+8q9R/f7/E7Y9SvRCrwM9Tnq+z//+NIIwJM3r8aOUbvg4I0k4u4bkU8Ai9FcI/RAAwFhGcc5zCYwxMF5HHs6vCSUTekey9OTnJOdna2QYubNnkIhMJBVh7YR+P0lihTgGD2AP8p8k5XN5lEWBoixQFCGROcsyLJeXsWpPTJIej/DRxx/jKoKgtuswKsvQjNT1uLq8xG6/i7X6w+HlnYPvB3vVRHC63+1QlIUAVyA4aTabjRAgLaUh6Fqv19Jtlo3BNEgYTUY4HA/iJZ7P5/Deh7Ki4ykSmwgAYMK1LvHJ6C9lKZTpMG+PiZ0EDg4QmdCLFy8kubmua5GSEAjRm391dSXVh/Sfz549E4828/1ubm7w5s2b0FAuAkICAIIEAgYmqxJIh0hEI0CN3nBKcNhbgVWj8jwXAkJpMasnUbKlIwgEEff397i+vhYgaMxQWjNEyNozXTiJ1Xa7lX2pATXHmWM4m80kKsLr8Hn5PHSQSaWnCADZY6Pve/FEs/cHk3FJBghaS8rKTiepUFQUBS4vr7DZbDGZTOC9x2azEfBHIEwvNPMiQmncsB/u7+/x5s0bfPe735Uk9slkIuVc6XEmgWuaBhcXF2fJ8PRgM0JwOp1knZB8pGmGpgn3xDwS7XkmaCUJIHDv6kZspT73AQhx4PjrCAXBPWVdTGjf7/eh7KxzkldBQsI1RdBL4p5lGbwJygvaORYb4Oe4jphXQ6cy1wlBMNcEAKnSyZwIkn4t9aHd5We990gwOFt5r8vlMpAUa85KHzNfI00SFFmwWyQFulQxc0ZIKLSDQO+Xp/+mjeI8aEzBOaMkkvOlHSN0CukcJOIWLfsDILaFc8P1QHvIXCSSTh114doAIMSK98Nr/UyJxpc//LEYgTRLg+TIe9jEYrvfYjIZIc8smuaELLPouhrWpphMrlEWIzjX4wd//D384Ac/gAdwOhzx+tWXOBwOeHwMHv82br76FLpY+zip19fX+Oijj/BH3/te8PhHkMmJAkLn8qurKzy7uoZNU5TRm9JHXaWxoZ75eDJBmmVw3mG9WuFwPGJ/2GK726KqKhwOBwnBut6haTzu7+5D+L3rcIoaybbvcYphvV6SpMOh3/fnwJKAAZ5yjAEY07MQ0H4APcyboGc7HPKdyH+4wASo2+TMc00Ek6QBjFAGRtA86BETsCY97yfct4nJyeeEhP+mp4CbmYCqd72QonOP8vs9ze8jGk9BOceMvzvzjJvhYXVEgc+goy16aJ5mdujPkeXrewpzdJ4vQI8KDdfZfD8lHE8iOfpZ5XmyMYr/4H+F5NmfiD9THasVQUMkDAS+8i4N1nE+xoGseACiwVJRCYOhw99whbOXj6Iy/yQpnOvaGKA9of7eP0X3x/8Ejt4dIbLnROLp2nj6b+3hH/pJMFfByLMPVZIGckXSrKfYeUqF7DC2nprgYV/oe+E1GE2j/IjrLomH2dP1a0yUOz3dvxi+z7lepF6smmRiD4eyLDEaj5Bnueyxy6sFyjIXCVKeZ5gvFkiTFJPpJNofyjgTXFxcoCyLKBOwsicDoCtRVScAUW9e1ZhOJ7G8dADp80U45CfjMT758Y9xe3sbDkAAm9UjsixFUZRxbsL67boeWVaInEEnr+52OwAQrzEAkcVYa0OuQyQYBLXH4xEuyiqttTgcDnj58iU+++wzJEmCi/kFxqOx6Pw5B9T+s648PXwABCBReqrLbTZNgyRWKqrrGldXV5I7kWUZ3r59KzKYx8dHAet1XePm5gb7/R7Pnz/H8XgUcMSGbPTQbzYbAXFpkiBT8iGWQmdVpdD5+SCggomz9HTzmtPpFPf392c6+8vLSxwOB3z++edYLBZgwzRGcVi9Rucn9H0vwP7y8jJWUFzieDxKVIKeZXqnGR1htSbaQ920jtWogCHJO89zPEZpmO4roasAUdfOkqyHwwHGGOkFwKgJzzKSBN6PNDeL90SyQ/D1/PkLbLc7AbdNTPDWzgESMH4mAP8EVZT9OBf6fxDsAkEuxYR7ep9pI+gF1/kGWj5GsMo5Cb2/jmiakHNiTCgBzPOJZI6Jxlzr3nv0TSAxnCMAclZR2kYywXxWStxIYpjrQJLIMq/8t04uZhI5S/ly/5vEoolkkg4Gli/WsiBeR/+M36HBPJ+P64ZnLxPJ35fo7L1HnmUYqeZ02rGYpCkcBrLvvZIsmSDf5tzsdrszYM6oL8eJUQ8Cfq2moBOBUVa+R1eN6rpOSI4ufsBnJ7nUxQV0Lg2jSyQWQx7NgJdZgIH7n89CbHg8HjGbzYSwkWyS1PDnnLO/8R//Tfy019ePaPzwx6Kzs8aiaUOIuSgLjGdTwHiMyxx9e8J2s0LbnGLIpwy9IyKDomfR9Q7VsUKeZ+idw+l4jKG4DqeqhjUZyskkaJ4Q9PfWWIzHM7Rd9CZ3HQ6HY2hE17TYbjaojkd0fY/14yMeHx9xf3+P3W6Hze6Aw/GIvu+kUkbYhBbOWHR9Hzp6W/Nk8ENCdByuAfUai84PiZB8CVD2gzeZuQvw7Io8NDST5ChrAQv0Lizwc/DtANfDGpwtGlnM3oCdcJ0brh8ATJCGcGGTNYeNnMfN0KPvz+U+Bn6Ae0+80Bo8cqNLcpc5TzR9X8LvU/Cpv/dp5ENc7PGlpVswEB350wQrhi04Rmffj6Hvhr6f90VWhsjL+6tTvf+e9Tiek6d3fq/nGQCKGbJv/I9hZ7dIP/xzgVSQSDo/5GXEa8MyBBF+YvRgDW5y9bOhozXM+6ILw/2F548j5gYNP8ej/fL34HZv0H3yr4H2FP7Tz2bPcxHe9/enkbEAXN+NUIWnGxK+n/5ORxU0CY+/jRIkzmmPJLHoex8P63MiLVHbsGWDcU2SCHqTIGc0Q+QrGN8k6JiNQRIPb+ccnj9/IZKKFy9vkSQGV5dXAEIPh+e3z2MluBbH4x4vXrzAfD6X5wjSjRQeoarR5eUl9vu9yIuOxxOOhyDPAL1qJlRnur+7w3g8kUisPqTKcZCmMJF2PBqjbsJBSVAXyrS2ksiYZRmyOFbSwTkS86qqkSS5eEjbtpWCGzrxkocxva9FUeDNmzdS9pXgqK5r1G0NY40k+hpjcH9/j4uLC8wnc3z55ZdyeOtymQQC1BO/evVKynJeXl7ik08+kSZ5BDMAsI6lUQFIhIWRYb4uLi7w+vVr8ZRS9uW9l0pHbEzGpElKEW5ubmTMmrqGjUCFgISAkWUt1+u1yMKMMeItv7y8lKIjTGLWPQ+o7+d1WTmRRI/6bQJCepHpaSZwZnUmRoYoESPh0WOvq09x7RKcsSIPAJHp8LM8J3i/lBtpW67/I6glUBRHHc7LdRIEHWIkg/PKSFdYsw3msUIjz3uCXe+9ELrtdovZbCbSpjQ9T9wlAd3v93h4eIBzDsvlEnd3ofwxJXskAwSbunKQ9kQT6IYu14EEag8+x4XVjvRaFADtvOwBEjcCXEZ1Li5C3xhG6DjmJFm0BTpCwN8fj0dZA6w0xcgG7UPIuejgDaRXyZDXkYp907kE2vPP8dX7A8CZjIlzTftNgqA9/G0bOp+PilLKHidJItFM530gRDH6yfEhQYHzEkHk3OgEduYm8b50IjaxFtc3Izp1XQtZoEOGe5eSKxIhEmeOBcmCzu0gOWTUheuBZyM/p7EhSZXeS7xHRoN4zjIyyTlipLGu659tRGN1t8IhGiVOprEhqebYNDgeD3h2fRWyy/seX776HHV1xOGwwcX1NWbLJTxCcmJTNahPNVbrDQ6HA/aHQyAJVYXFfIHOGewOtUwSvR/H0xFwCY7HQTq12+7wR9/7o2Do6gpd28g965BS7wmADJiIHAbfASYkUdIxyuhE8GIPIUcaOvGeK6mN9mqHyQvSHe/du2Cbkg9AKjYBgDcGDm6QwGilhnfwfpBB8VoB+IRqW8FQAFCeVJge3g+LTHvRAStyEVkGEVgGlca7wJuHLg0DjZkcDDjPI3kaoXhKWobxejfiEa47NKfjz4b7geQvvBNRiNXHNJCVa+Dde3p6L/ozQxTlnGxoovKV2+grfve+CMfTlzMJPAzyF38S6Ud/AXb5LZhyEjMtlETKM2oRBiUQXPalGBivN+bdjuMilYrvU6Ie7heJXDQn+O6E+gf/X7Rf/B78/m4IkCiypok0x0bnu+hn1gQv/JeAGdoGwHlHbb0WBy3r+VwZ6KR6XjMY0Dg26CJBBRLDSjs0vilCXlBoaJ2kCWazGeB96MlwdQUYg8vrK/R9j29/59tYr9aYzqb47ne/CziP8WiEtmnRdi2eP38uh2GeZzidgoyFMoo/+MM/xPJiiXJUwtoQYQi16Q1c32M8mcAYj8ViLp5v770085pMZpIA23WdVJvRSX7ee/GETqfTQDyaGqdYMptVfujpK8sxrLF48+Y1+r7HYrHAxXKJpq5x2G2lQlJZBg15IDCh8R3zAljViXMwm83OIhvWWjx//hybzebMEcB52+/3MInBxfJCwM3DwwNubm4CSEEiXkB6bQnueVAToDEacDqdcHt7i+9///v46KOPxHvO7shV04hG//nz53jz5o2Ajp/7uZ/DJ598Ij0JxuOxOM5+8IMf4ObmBgCk1C7167p6D8+Jtm2RpSmcAlCU3QBD1RljgpTh5cuXsNYKaWFUhl5/Y4xEcEhAGHGYzWYi+WKzWWutRILooWZTO44pgZ4GsezX0HWdyOLathU5GH9Pjzz/TTvcNI2UWtX1+HWJYIIiYDi/6SXXZw3L0hM0chwWi8XZGX0ZywNzzEikptMp3r69l74fLOWa57nsCXqpHx8fMZ/PcX19jVevPodzvQDkqqpwc3Mja50kCYDklszn8zMvN0mYc6Gi0uPjI6bT6dnc8372+6HMLeVD1lqJ7OgIGtcjvEeZB2LFZom0D7xv5pHQBrOiF4Eyf84oCeVGOu+AVY6elsRlVOR0OiFJU/Tx3GRSP0tF8320PwTs/H6Cazp+dQlkgl2SXMrisiyT/hr8LpKD1FhZjwBkDGxikcZSxFpeGSqZdhiXI6l2xuibjoQKqYpkW0ecuJ9oXzmHtLValaPxJX9PKRfJsZbhaiyke7lIFEfJSSllpQ3gnDLCxLVAokInEOeVESjeI+fAOYf/8H/2H+Gnvb420TjsKvTcYMag68Lh4ODReoe+c0Dv0VUNmtMJn33yKf7R/+sf4uHuDUbzGfLJFMe6wX53wGGzx+F4wrFusdvv0bVd1PUV+Pa3v40XH3wTpzYsrtNxCP0FL8QBfVtLct7hcMAXX3yBx4cH9K6FU4lfgQwEUkH/svMeaTIwdOd6wHewBlJy89wzrmU3SibhPeCHWsjnZCJKoPzgVVADDqO05eE9MXETFs4/8fgLeejh/BDt0CCrdxbWDp4BTmmSJEjSUCksHLy6jKwBEOpKk9kOzx6lWhiei8+hQTV/N2wUJ1hQkw0NBt9HNPis+iCR3z0pC6TvEzHZQJMF8YI5RADznpKoxr9zP++LSjy9v59ENN73Z/zH2ft/UnTj6bX1PfbOAUkBO3+OZLxA9u1YUi4tkVx8eB49OI9raOqAM/Yq5GJ4nwTtvEO//hS+awDnUH//n8E9fgK0JyHGwHlEQt87iQb//TSPgQcnPZBnRMMnZ2t4mFsCZ15zIPlhzwc5F+VRw3tMTEwtAOMxmYwA4zGdTjAbL5DYBNfX1+j7Ht/61rewWCwAeMynY9RNg+fPn4u3bjFfYLNdo3NdBFdj8U6FdeeRxsOTXsjh4Myw3a7DYZGEvTqdTLE/7LHd7PDRRx+jbRsARgAE4JGmGYqixGIxj5WPRmjbBnleIElSjEZjfO9738NyeSEH3+lUiXyHxIQNrA6HPZI8FPMo8hyvXr3CfD7H4+oR49EYk8lCEkw1MEoTi7LIUNcVvId4+Ky1eP36tVRySZIEm81GACKjIcfj8azWO7Xw7LnAA5AAZjQZiYyUemAe4Mf9EUVeSO4F/6SGn5KW0WgkZIYAh57nDz74QAiJ9x5JzN9j8jkBKBOvq6p6B6zS4z+fz+Wwp3wMgBzanE8CpD4Cee+9gN2maaRhm85NIFAicSKY45+sWMU+EbwXAhMtn+A+IyGgTr5tW7x48ULmnIBnMplIRK7vQ0dwRoOCtOcgUQY6IZk3wC7o1HwTwBGc0rtOgMyIDpNf9XhT7sW9xHWtiVff97i5uZHGiqPRCG28ZyYps8dCkBCFiAAw5C3obt0aBzDhvO87NE0gyow8MSeB+RMsSWxjHg4JFJN4uZZoI+g91/IfEsLjsRI7SRCs83D4LKI2saFaZ5YEPDAej7Hb7WQdct9pCZX2smtCDAwAVsvbSEJJQvhcWlINBNCaFTmSSJ5IBHQkgPPM5yDwpuNgsVjIcxEwc40RfOucId4TSRWxYNd1sH5wGmqgbqxF07USYdG5XoyEHI/HkFsVI2LMeaL9AIaqTXmeY7vdyhlG0s8ohLUWy+VS1qm+F+ecFEoYj8cS6SWRJpFgNIxkSzufaK+5hilBJHHUznGesRr/kGzo72Gkj4SWa2IymeAv/tJfwk97fW2i8c//m3+F/alC2zqc6gaH3RG77Rb73QGnNuQuNE2N4/6A1cMDNusNjoc9Eng0fQ+bpjAm9GGwCOUGWUVp8AA4ZFmK62cv8fKjb8EYG70KFbI8R5okaJsjmipk3xsVOn54eMBuswodlp0HG0GHQbei9+XEcnH0fQdrHAy8yI6CbtvGrrUxCmCG5FpGKvq2EalVALUBBIUmgvadCj1DQpaCfcZI9RGoJFXnnHwnADjfIyhorNxjWCwexqRIs1yMDA8omySQTssRYzrnYj+DQasOnHvlw99bONcFSZlXz+ED4CawC970wcNOw8yxtsae9SrwGPT9emwEDsvPlM8+jpF8HwbSx2sNhIKsMo4NAtkUT3vMnnXORRI3fE+QycWyxl7Nkw8SuadE4+lLEwNNLvl0ckUfnpC5G18V6Tn7fFyzT6MvMBamnL3z+fTm55FcfUvGahjmIXIltIP/M4B/+CG6+x+EdVJv44RhyDcwgHdRegYgS1JIKWivck5gYO3g0SbhJJFNrIVNQjfxADJCM0ubJDLXTz+bpibmMqRSVpplMvM8GMCry0skaSKg4eOPP8Z4PMLV1TWKIoAhjx7jeGjXp+A5ovd1vdkA3uP29hZNE7zgb9++xUXs0zCJBrtp6zOPXgAQHRbzOe7u74LRNyGf7XQ84WJ5EQ/3VOrcd22H8WSCLE2xPxywWFyI1386CVKh3X4HeCDLcmT5oJmmzKLIC/TR2z+bzVDHCkW6oRLLNFpjMI4Vf8qygImHEgFGH/W9b96E503skNBb1zW6vkNTVwIwCZqDxGMvhzFBndZP931obrbdbuUQ3e12WC6XeP36tVyP+QVA8GgejgfMZjNp/CVlJmPX3f1+L3kF6/X6rOIPSdJ6vQYA0aRr3b12SkEBcHoAjTFn5Gi1WmHK/I8IBoUUW4skApEkjhsr7kiCpfc4HI/Iogzi5uZGemnQM+u9x/X1tYAaEhkgAD96JgmwKPe4vr7Gfr+XRGa+SGCeJpwSLDPiQhtC+Rb3MntB8Lp8HgDibSX442cIaJhfMXjzU/TRSckIQpqlKIvyzLtNMNP1PU7HI9quwzTuUZIqAiFKd6oqVDjqoxxmPBrBWyO6/CH5v0fXteKpHvIsUnjvcDpVsGkigL/vQ2PEJEnw/PlzNE0dnqPv0TRBjjafL5AkoYRw6BYdoqMEjSEylMR1DhyPJ5RlAXZk996hLEfwfuh1xRyiJEnPcnC017mqQlVOesCvr6/lnKOaQtvS4LhIYw+UEyYTOgtiuW83SKtns5nMcTwGcDjsJdJAQh4IfImmqWUNEfSmaaggqokBy6bS1lFGCQw9UQjkAUjCP6txMUKn1yBJCwFyGUvjktC2bRvKgXsfCmn4IWoQnLVOHCO8R+6dpg4YNEjgwhham2A0KmFh8ObNG3EsMMeBDlHKPkmm2rbFdDo9q9YFDE5bOmVIBjmezO3hWqbcimSRhJFRkO12K+PPfI/tdntmB7iXKZNi9VMtPWWuB3vDjMdjsTdAwNc/04Z9/9v/9X+KTz77Aj1SOJ/AmhTGhUmDSXCqQ71vF+U9TVOh7zpY40PN8zb0s+Dh1nYtOtcKMyqLcGBaa1GUEyTZUHqOh0GapmjqI7o2bC5OFsFaYgwszNkEBe+nhUMn5VAHwB/YZp5aGTQuFjJk37VgvoVhJRjHbtWhtKSLB4hTQymtGkzQprBkbe/6UM0nRhWIG8M0GCQ2Vf8ePPhJmqhyl0Pt8PD5AKq5WAnMrLWBdEWjRM+YEBElweLCCvNh4HwD584lV+/z/AcwAUjM6Cu89vydfo9+zvD3cJ2nGvunAD58fvhORDkc+3pYa2EQ5HD6paNVepz4u951cK4FNftPSZgG+e8QCXOeUPxVY6BfwQOupWBPSIR6vS/X5OnY0KNObz6Jr0TioMaMkYt4DSmha9Qv8P7v4u+sMbEAbOi5cJZ0BoskyUGWmySpeGQSCxgMUo5ROUJe5CiLElme4vb2GYqiEJlM0zR4+fIlsizBbB5ABbsc03PDsDVLZ1ZVJcafHkPqjRn+Zwdl7o+rq6vQ3FIBKmqJ9/s9DocDrq+vBbDQ8NPTyBLc0+lUgCoPrGfPnolXjkmnbdtKKU16J1lSlAeOc6F86WQSymrvdjspW8jGXkxGJPCg15jeLd0wS5eS1B4255wksh4OB9ze3mK73UoYnwekliORzHAeSCJYlpRAsm1b3N/f41vf+pb0S3h8fJRythcXF3jz5o144PTeISnhnDBiwvs2xojX/M2bN3j58qUQFb738fFR1iajHjc3N+KBZM7LxcWFABMCO0qW6L1jaUiCIGOMyCpYRYgRndvbW2w2GyGyOqpB+QQTqb0fEoO5ZnWC7MPDA66urmScx+OxALTtdouyLDGfz6WcMJ/fWiveUMnPKUvZBwTrBHd8Jo4vPcgEzIzYUI5D3bh+Jg3yuC8BVq0BrBnkHdyzbDxIrzLXKsdZE0AtlyL41jmI9PLO5nPUbSNzQ3BUlqERbpYM+n8dxYAJlTF5LYI0Vu2iPSHgJsjjXJBkkaRwnABIpJBlhbUkhh3AeQ3229D2SVex0vkePHs0qSUBoX3R0QzaQjoR6DTJbCJRF+2hhwnqFc4zMOTE6KgCf29MKMvMSBZxB8eOEQdxmMSSuX3fS78RFgvgvXDNsbIbIxU8R3RFJdoQXWGL9pxnGckKyQuJjL5nViujN58APUkSeOexXa/hvRebzwgZI0Z8afUHZUm01Xp/JEkiRIfjx3nj6wzzqn1BbKMjiFrhwufgeGtyw/EhNube517ThTy0o94597PN0fhn/+TX8V/9nf877lZ71A1Q1x36toE1Bq0cVn3wmBqgrk4oihxNbKJHj1jXdhHU+NgkCkiTBGUMaVpj0Dug74ZkHi6KkGjUoa5PQFzIzoVmb9Za5GkGx4Z9iUXvOllsXdeg7zuppKAnPzED46ch5Xem7PfmAut1ro8eXUYcovQDJpSfdQRt59GTvo/9LmJCL72FQf9O73QE0Coaw8WZ5rERVqxWY2IUgZGD9wFzIHQM0KEyEpengBWAIiEAjEPfd2B5XHr0SYgGTzyG+8dTOZF/7+800TDiUh8S658SDd73EP4fvtMo0kbZjLWhadpToMz7IqHi4TAQKIfetcMEqM88JQ5Pt8050QAgHqV33zdcBCG68R4icxaFiEPk5Vr+TKLGz4a/s4zruawrrDXdM+LJc+heHZGUDHKsENGDYQJ0SNpOkwSpMbFRUy5g6Zvf/GbwQM5nGJUBhM8XczmAZpMJppMxPvrooxCOztIh7O09ZvMpvPM4HAO4OR6ijChGopbLpYAblrLUYXfuN1aaYYjZWisHLA81nRzJg4KVhbIsw2w2Q9d1ErZnFSWWWt1ut9KXgaCDY68r5NC7RQ875T6Xl5dS9aUoCklAPhwOIkXSOmAmCWv9Mqv8AMBqtZK1wGZglNSw2s/Lly9BryPBMYGT1kvzuSmBIagmEKfsQ1dqoUSLYIjdiXe7XdS4vxINPEkLPd/U67OXAskA7TyBAvM/VqsV+r7H8+fPpUILSY4+qBnhYPI3ozz03LE86tXVFebzOd6+fSsyEUp0CbpIprhe6QXk3yXBNIJbVtdiBIf5KewPwTkAgOVyCe+9NHNbLpeyRzkPHDuCGIIEnah5e3srlag4rwTJBFpMvKY9pB0g8CP5ACAk9OLiQmwmoyy6MpaWbNBec80QyHgPjMqxABfOkSa8QIiIcF/zmrwGn1+TLwIy3m+ShPKp3hopocy5kkgBhn1KzzABW1qE8dXklzaH65VYgWeIliDrPANNwnhOcP2FSG2YExJDzvfTEqh8BgLi0WiEh4eHMy8z9fY6p4NOF3rwCfh5P7Q9AFBm+dl9CjCHR63KnurnoRMsTVOpVqRzQygF5LMxUkSyqKs4sZu63nOMfpGIkhxwTVCqpCthaY88ADmfOKccW8oDeR+auDFazfnnzynBrKsKTVXLPJOo8xzRAJ12gQ5svp8RY5ZXpvNA5xnxpR3IxJW8b5IXvfc43oMD2QoB4prkz59iLZ4BtAl0+vPetB35mUY0vni1xt/+r/4efv03/3v0KNH1oRJSkhjkZQHvHZomhABtYvHwcA/X92AT3K5rwcpGiEvXuV4a0nFRAh5t3SNPhwnmABhjkKQWfd+Gz3ah2zdBw7gcI01Cp8q2beB8jzRN0HUt2qZGU1cyGfwvyzKkSQBWu91OQAoXSJoMGtkzMOgD2AsH1whd18o1w2Q5JNaGPh9u6PZM40LD3HWq/KwN/87yqP3revE2JzYD5UHODZ3LQ1Ksjx7q4T4FyPshWsEDks9Bg8j7IfsNY+3QuyelW2XVDN2HvfOSJ3HmJgcwdH+WKRep1IBvtZaf+QXvAn0myBv1fvjQV8J7H0qqxgpMHsFr9hRs85n1+OhNFjZiC/+k3Kv3XK/vSqe8RLueyqUimXZP8z782V+Nuj7/1ONDMqWvB3MeOdERPPggFQy/H+Rk4TrD+54araf/8TDLshST6QhlOcJ0OsHFxRJpmuDFixf44OUHIecoghuux29+82OcqhM63yHPokY/z5DYJHpcPSyGbvSUDIQDqxMCEJKOuwhKHbrOBQlRBKUEUDy46D0l0OAhzgOHyY70ktNzyIZjrOoyn8/R972APWMMXr16dQaKvQ/6doJ0zj3D2gTMvNb9/b0kjd7f32M6nZ7pfukFp8eZwLcsSzw+PsreBkISI9/H5GvWnT+dTqJZZ1SB+7/rOrx8+RJ3d3dSrpQRCR7k/DkbqxG8Mr+CXlKON5NLu66T5m2j0UiSvzk2OumXRIR7j0SE4IqkgUCTZWZppwgMdTTr+vpaPPVMwqUXkgCTQJR/155Y/vzpeiFQ4RwxGjU4sDqJDpCc0KNPrzPBPr2mWmPOikaPj48CMujtpi1nWVGCC65bgr26rrFarXB7eytzybK29/f3ACDjQG8m9w+fm4CUOQUcF3ouCWiYFD44/gYJC++V9k53J+aepAOIxIlJxXr8uI91GV/OJfe7tt2034xw8Iz1AJpuiIzQe0/JzsVsLmce17D3HnXTIM0zcQxwzx+Px7Nk377vZY+T/BKgkchp8MlrMTrEa+ronM5h4P7ShIPRVOIlnaNG7zslf1yXLDzBtaIJmY6ctm2LBEacDATVXdfBw6OSYhHl2TU0LtKVoHjvrNjEMTudTmdVsAiSCV5J3jgedBDoykfEMnrs+r6XqAPPR0a6KOXiutSwl4Cb+57PQpvOKngkOrL/0xTGD2W7Oea8l6eEh+cto1Ik+nSm0CFGG8bzioSRNokEgESLNpZrR+fVaRumpWX8GedCR0B4nbquJUGez8c1S+JojMFf+uW/jJ/2Sn/qO+JrVCb4xV/4Ln7zd/4IXQcgSWCSkDtwOJ4AE0JKXdvB9R2yyOTLPGg0WcOYm6OuK4xGBdhWvu8d8jyDdx6jEZD4IVEUwGDMEHp36EiB9x6JsWg6j6qp0XctQpnVFm1XBw9428BFI60PuK7rkJjgrecEUnPqvUfXOqmZD0A2lTdBxtR2PVxsW9/3DuxxYIyNOQAWSRIbHKaJeLCTJFS3CXX1Q/UoGBufLW6yfAhlkZiFyWXiWA8f6+H33eARomF3ziFPMxk/jhcXDTeTDmmS7PU94F0A7Br46+iItRbOuLOfncnSkvNmfTEN4IxAEtjqCMfTKlNDHgGbqjGaYsPB5QEg/j2+lffHazx9aRLC52a0BniauHzuMdMvfd+atIR1YpGm51GVM/Ljhz4K+lrvRDeU8bDWoO872OR83IYciQTehWpJ3nmkMV8hTTNYiyC/MxZ5kUsyY1mWuLq8wsXFAmma4fnzWxR5gW9/59sR8BUYjUpkWdBTd20b+zFUKLIMSZri8fEx5GxkGd7evUWaWoxnY1R1qJpy2gYNflmWKIsCq4dQevrFixdI0wS73THKkEocjweMRmOkaYLDYR8PjBpFMRYgRy0+gTCjF5okbWIlO+ZfECyuVisBtZQsEEzrBFZGOTabDa6urgT86AiiBn3X19ewNuSNEZiTzF9eXgr4JpjUBOWLL77AxcVFqH6k7uHu7i5IS8tSPLHs1EwPJQ9Cjgs9onVdS1I25S9932O5XArY2Ww2AkKn06l8B4EtQQN/zkOP30WvIw9BRgC6rpPEZoIiY4LMiWOvf35xcSH5BXme4+7uTqpb6YoyBJqUB1BeR8BGLb2u9MJDl8CJ9m6z2eD6+voMKNCG8Wx4fHzE9fW15ALqe+K8axkK1zhlHEw+n06nktjKeyUoZcSKBzwjOoyIEIDz+a6vr99Jvr2+vhaySYBBUEiCR4kd9wswRDZ0FSBGKdgHg5EUgvFtLAPMseIzkzTovhKa5IZ5DPkNBNqz2UwifPyTnl0mlWsySGDGfU6CxLXFv9d1DWMteu/EcUEngzEGRSR67LfBCIQk1F8E2SXXPPcagDOZCsEhn5M2hmCRBJPXYYSEtuop+aVN0ECa65mNAQmg2fBSV8zSlZPodGmaRuwU75G9GvidVVUBEUedTicsl8snCdxDjhNtrZYhkZDwOThfBPgEzVxjTdPg6upKCDvtAPcM9yyvzTHlmOkStNpxyj2vCQPJgfbihzMxXI8V1KbT6Znqg1iV5ZhpR4kddY8NOl/oSGFEg7aAY09yT2cZz27KUrnv+V7OH0mWjlrw+YjtNAmi3eZa1WuPdoA2isSBzm/uL64rTZT0/DDC9nVeXzuisX1c4dNXj/jP/y9/F6/vD2ich3M16vqENCniQixwPB6QJBZd16JuaozjwBpr0LUdkjQMRts0MPDI8wz7/QF5nkXjC8B79G0viW51XctC9Wbw7DVtCxcNcJKmgA8JpWlq4VwHj5BAXdcnoG2QGHvGLGm0jvutLAZO0BC68mI0uEkHQHkOpMnMw2to6KYZZRM9ClpzT4NlkxT1kyRFWdyuQ1lkZwDJ9SHqAAylXGnwdERDh6Zl4iWK8K6HOzxPkNl4f55zQAatr6E3un49fa+OTvFzfA2J1l+dF6D/LtENjvZ75WD+7Pdf9TojEebJ98XnP5cuqWd/KnHi58z5PXrvhwaCzGcBhiRr4GyOOBd6ToPxyeF9kChyrrQhThKLly9fIE1SFGXIc/jwww9jkm4wVtPZDMuLC6zXaxhrMJ1MMY/lKU+nKnrkR2jqBofjEdvtRkphEuTRiD2VELCLs4fHZDYRrx+92EVRYFSMAA/c3d1ht90iTTPMFwHIDETjvKJNAK5TtG0wdATglMroDs48AN+8eYOiKHB9fS3gR8sa5vM5ptMpPvvsMyEJDw8P8T5GAkwJ7pmPQbkNDxP2NSiKQvIhCM5JBChdybJMDn3q6jW45TgSsHz++ecijaDdWy6X2O/34sGkNIS6WnqftQaaOQKS+K3A8nq9lvdQt39xcSEHCcE6PZm6DCaBKgnEw8ODJC5Pp1NZwwAkQXw6nWK1Wsk1Ka1gQjgPRYJwfTCu12tcXV0JeKU9p3dd55Pc3d2J84jSEXrnKKPjeqBdB85lFjzwdW6GBpbayaJlC9wnnAeCuR//+Mf4+Z//eYmOEOAwGVwDyel0KmCSa41gYTqd4s2bNwLGWfWIyfQ6UsnIAG0wn5ekTjTn0ZYw5wSAfCeJA8EubRTlX0AAlfx+3Vma52yWZcizAl03RCS41xh10iSJXna+h/uaY8Aol65GxchZ0zQhsp0mkkirPcovX7zELia48rzkuHV9j9lifpZkS1tAIMafafDHMeV5wmglAT8JD6OOT6PIzAngGuT4cV9znkj26UTg97F6G+0CcYduEsjPE/DrSkVt00i1KkYOGW2azefo/ZDboUsm68iediDw2UmYuV9IqOk00BXWSMC5xrjP9EvLM/kiGNbyIM6PjqqRDJBkEtdwPLhPSXC1yoPvT5JQRa7I8uCWVGe0drQw6vtUtsTvoT3XmILjwM/QpjAipZ0mHG/+ne/TOWS8F+4djdNoBxipJE7kucGzXUtXuW81SfqlX/1l/LTX1yca969xrBP8w3/0a/hn/+K30HQOq8090tSgyGYAfNxkPbIsbMambVBkcaP1Q9Wnw+GArm3huhYeQJamseqPQ55lIVLQNkjTLMqxgmQkzzN4Y5AXIRKSZqksrq7rkdgc1qYw1iFJgONxh6Y9YbV6hG8aGDe0WQcA1/cB8rlBh8kESx4UWRGrbDQtjI2hMVbo8RZZRuPXwzuHNEtj1CJ6cmJeCHyY8Op0Ckw4OW8h75yDTTN0LlRDstHweABt08D1DdIE6BiRAJN4gyfff0WeRGKT8JzRWx+M2nkitP4MDxR65L13Q6UkdX1uWGOMVC/iZtbX1BELWWoGYT0IIRoS6UPEY+hg7VVlKw3oz0nR+XOHvw/kQpOceNWzta2JhvdamaXzG97Ny9A/089KI/E0cuO9l4hO6MFyHr0hwaPHr+s6STK7vLzEZrPGcnmJb33rG7h9/gwXFws8Pq7w4YcfoizLKJU5YDwZydwwwbDIc+RFjrdv3mA6m6GuKwFP89kMp8MRZVEgjQAYgDTEnE7nsDaA3/VqBeddDPFmKMpCejTwgGqaBouLBTbbrXhb5os5yqLEZrtFkebY7waPv/aMFkWKqq5EJ87n3+12uLy8lBwE/o4Ve5bLJdI0xXa7lQZnPIh5iCwWC3z++efigeccsQrUYrEQqVKSJCJ9oBFmvwWGr+klJdiezWb40Y9+JPfCZwAgciSCJx4o9KzRU07QzXVHcsBSqtx7WtLEbto8mBaLhRxABEFa4qABMYkRozOMANETz1KmBBCMfvDzJHCMbtCzx4OP739KJIBBsqBzKSj3YgLubDY7kwzsdrszJwkBdt/3uLq6OiNBjBRwzgCI7ILgi95Hev7o+Sd5zrJQl//h4UHWkiZwBA+8NueTczHkvZlY7asUiR6b0+m9zogwySzBOMkCcyc4bgQ/lGVROhO6w5eSvMw8CZImStQIKDjmtJnckzrSQWBEQN33oZIYAbIuskBAyXEk2JvN5qiroa4/AFlr2l7TKw9gqBqkogUkMJwL5gzpxOE0TXGoTnKPOt8iS1O4rpeeKCQBzgUFQ9O1cj+6aZ3OYyLh03uA+RH0+rI6ljFGbMKbN2/OSA/PDHrU1+u12BxGW2ivWLqY4I9eaH32aYk0QfvxeBQSph2DzC3icy2mM7lvAtfj8QhjLRyGyIU+57l+Ge2lPeFazrJMnEYcA5mH6NknLmPyPW0cbQ/tJskJSZgxBldXV2fv0U4DvT/0GU15K8eahE6q9GHI5wRwRsoF4EfMx/snieCe4frUla+0Q5pno3b00uHEvcPzlGcIJZe8Lzq4uD5oM0goNRnTpIkRc+4Jbce4V/knxyLPi5CGEIk27/kv/7W/8g4uevr62kTjzZefwNgp/uh7X+D//F/8HWy2JzRdi951aOsWfT944kPehUddn9C1VQCr1Od7HzwaPjSFYxJWloYO4dYYNE3UJio9L3wsCeoTLC4uMV0sMJrNgCxBNi7Re4/EWaQmQVWdsNmsY+Mrh77r4Os9No/3qE8VEmtgvUffhvvu4WKkhSF3h74PeRZ5lqIsCrRdd1YGNSwKJ6Sj70OSuE1iaLGqYWDkOZIklN1r21aUOfSGJ2kM54VefTAwsIkFq1SlSYrWtehicruxA8gOqb8IDf0wEJA4vfA+6OaNCYnj8CQTHon1kvQrnvT4f9eHXIi+D1W10jxH2/cAHFIzGDGChSwNBqN3wXMfDGnoWxIMIdD37VmINCxij74PBQLOMhkI0G0CixQeHq53QjqstbD+J0UqTBgbbuBY9WtI1D9n92fSIx9yULhRJTzrPWwkiFo+Fta3k1LH1pjQqIihaedClZMoDZzNZhhPxri6vIBNgPFojKIs4J3Hx9/8OPRrWCwwmUxQFiWKMnRxZYWk2XyGqq5UlY4KiDkPieobwf3onYeHxy42TLpYXmC33Uky4Wg0wmQ8xn6/l0OqritMpzN0bYe6qoJHK65jAChiJRJ6tWlIAYget6oq1E2Dsigwjt5yygCqYxVIeJT2pbEUpPcO+/1eOvHSS6e9RjpM/Pbt26BZjgdz13XI4+GSxQNhFD2RNOIEnqvV6uywJiAhSGFSNoCzRF8tcWECL0mA7j+xWCyQpqnUg+cYaQkB54mHNZ+N19MAUq85nTjNw7lpGvk3D3OdJK07MvO5wgFyXo+fh7nOY9PJwSR6BBM8zI0JnbsJ3Pin9uyzwg3L4TISQbDEEoy8T8qOnnpCGTkDILIbHp6MdOnKWnqfAwEsPz4+ikdWR7r5fg0+CDTkvIoHOwEvCSlBSNu2mEymaOo25tGsYIxFUeRxXe2R5UMeCAlQ+GwXSHweSGLd1DwYApGLxCDPC1gbAFqSpphFoNv3lM/2mEymMAbYbLZCgE+nI5qmRRadgOPJJDqKQp4l1+UpAtCubVGWI5iYgpfnAXxSZlSWJTKCzbhnZrN5tNk9eudw2O8xnc1gjT3rm6ArvGk9OQEhQRXfoyUq4qSLFr/vQ7noNElwPJ3gncd8FqKg3jnYSIwvLkJTv+OpQpIOpVfL2C/BGCC1CXrXI0vD2kB02rx+/Rq9dxKx5J7Vsjld+pOSptPpJP1S2rY9y+mgNI4EmRXQWFlJRzL4Pp5r2pESxqA/Gy8NFCnhvL+/FyJEZ4gQbGKV2HMrzTIYAEfVgPL6+lokitqpxqgTI7MkMlptoM9Ojhcjqoze8fwg8dMRfxZ1YOSW983n15FQ2nWe49rBQmBN0k97ybXH7+X8cqyZ01AUBfquRxI/w+vz71yjXOe0Q3xm2gySA9p43YOFz8OIIqPRdDTwvNW2S5zWkWyEaOIgZ+c+KYoSdV3B2qGHFc9ISsVDe4k6yvyZA1Mi5Fv3YAnnv/LXfzrR+No5Gr0HfFejKBKk1qGpj2i6Hs471NVQ0kuHoE7HA7rmeGa8udCsteiaDl0bS+zFetRhcgyaJoC9ujrKIWaMRZ6V2G1DbkAyKkIZ3K6HSRMkaejVYdIUk/kCk/kiapP3qPsWsCnqrkfiPaz38C4Qns479N4D6FDVdcwJCICt61ocTicMFYS8sMCQY5EM4N4Y+DrmKbh4IFd1XMDhv7wsY7pzaBzIhR/G2MP7kCPBsRhlOYwBkqaCpcc81tpmhCgBYMyg73cxSsD/Wxsqe8EwWhH+Hb733XBdqGbVh4paaRrGxgBZFrrZGh+KFHkDJDaBgQtljlOD1Id5YoWtIlYUCgnAgUA552FNNGLWwvsebddIBrRuLJjaLJyxHjBJqLiVkKUztwUhjwIYkqNpTICwgVIzNGkMXduH/AVGg7jGwoQOEiZjQkW1LJZotUki32etQZaluL6+wuXlEnleoChyXN/cYL/b4aOPvoH5dKq6ofYYjYLUZHl5gbat0ffB4FA3q6ujBH2vw+vXhwhuDNbrR+RF8C6EXITVYOQjwM6z6IU/HkTf38ca6evVJhq4E77xjY+CwXYeMBZFOZI8gXA47eC8F08hjeQpygqYFMYKR/RSMkJAEFxVFaZR4kPyUNhc7EHf93j27Aar1Uo809SKc2z4XdZaiU6w5CMATKZTfPLJJ+i6Dt/5znewWq1wfX2NKgJaygdWqxU++ugjsVMkSvRIMfeDkiTqiZmDQO8d1xOfZ7lcisfv8vJSklOXy6V464GhfDaAM0I4n8+ligwPHHY65oED4EySwQZzlGNcXFzIWDEvg8TNOYe3b9+e5bMQSAN4p3IVPdP0blEO8RQ0rFYriVyQLJAEUfpEckIAQXmWjoJRQqMPYo5NURR4eHiQz2mZBD9Lzy+BlpYRsMEePYlpmmKxWAyykRiN0bkSmjRwnbBjNH9+cXEhXmP+nON62Idco+DJZQTNom0DGQ59ewZpA89I5zyqUwXvhoZ03H/jaDuccxIhurl5hoeHBxwOR6kGtV6vI+gKY05CrKvbhO/NYI0Vj/ByeSm9O0blKD73QP77vsNmE6Q5ZTkaSJwHyqKMYzE09AIM2qZFluU47A9CnqkcYCSJNvtpFJxOARJ/rjsSz8PhAJsFUF2UhZDZIWJp0cc56bvQ56ZrIxD2DnkylOzlunR9jzzNRLLISNTq8TF0Uo+lb3nfg8zaSK4TwSOjl4xQ8f7ZBJJ7apBcD4VxGFGlTdIOCHrQn2IrPXZcV9xf3JPcw9wHrIiGiDwO0SvOdUJizfFndIA2yhgjBIB7VhN7Ekid30RHB/N9uJcYCeUe0vKitm2l2ABtEEt+G2PO7LVg0BjJ1BFWnlN0/ND+0WlA0M3v4f1xn/McykcZ4LwoZDSh0XJFVtjjtRlJoP1ktOxpfgYJKACJgmh5mi6gQMJFWz0oZQYsOTiVUolQ6CgLpaSaFIV1RrmdP/tcIPtfj0J8baLx5RdfwLkMh32Hb3zjOb7/wx/BIwBFmyRoIoPljYeDsX2nKRk3RPhdKBnrfeimCwCj8RiOFWbSLPSdiL0g+r5D053QHxtU/RE1Wjz/8GOMRiVgQwUAOTxZmi8u7CN61FUFbxIct9sQ5fAOgH1H5jK8LHoEr3+al9LzwCZDPwM2EnTxGXgF3wfveKz5EyfehyqiPiQ4k2DwWg6BbDz1ADBiYP2QD9Ka0N+j7VoYOKRp+C5GT7wLUjUfizTZJEGWDmDbWIuuTeARG6f5UJXIRelQkoXojPMe6PsQtXGhkhYiQTbwgDOwJgG8jd8Zqxv5GM1pOzlwEpsjNNEDyryAMYgRDwtranRtjNgkXvIhEpvAmPMyuTaSGCaiJ0kSe7iEvhTOhoT5NEklyjDki0TSZ0IidpplcH2P0XgcQVeBySSAjcvLKyyXF0hsKM86jV2gb589G8KoWYYksVguF+h7J5WSsizDar1GkWWYTsLBu92GfghFnmO332OzeTzzjmoPiE6upKGmNxfGoI1g0dpQ35+Va/ouNLZK0xSr1QrA0DeGxoaHNr2HNECU0RDAtW1o9LZYLOSQoueFnmmGdXnf/D293/QyUw+sjSqNOT1Yzjnx5BGsLhYLMczjOEdd14nGfzQahaZjkaRdXl4KMBuNRmijlx8IB/jt7a1UnuG9ahBALzi9O6FBVyN2i83SCMystbi5uTkLUfNApYSJ3/3U0UIAAQxVgdgLQWvjOV+UFhDwao/+6XTCfr+XynkkCG3bSplUAnGC2tFohN1uh+12K2VoOSeUEOgIJCs5BZA5eN0IsgFI5IW5dVdXV9jtdiIJYwRjtVrJfBpjhNwxasSDU+fEkeTRC+t9qHz0+vVrAd9ca3wP19yLFy9wOp3w+PiIy8tLGQsNcF69eiUVcrRHcLVaCeniGud38zsYLbDWSv8RwABRUsT8JpLSLBtKmxJ0cLzXqxWur2+EtOj3MXmTZyyjaBxzrt3ZbCbjxvU9nU7PolKMSGhwstlspFFb6EIfyC4LKBAYcT1zf9OWEIRquQ8BEMkEwSnHkfiA+4p7UnulKesiwOZnxuMxTJKgi9XqCJi1PK6NRJR2ZDqd4ng6IUkTAbpnlcKUFp2knf/uuuAgoH14uid51pBoMPqo75kESz+/c07sPL3wBJQEwgTyJOQ6zyBVZ7vOu6DtYzllXk+TZl38wXsvcklGPilj044CXYEuTVN88cUXQoTo1KC9Y4I/152Opj7FQDrpnoCe+4MEiWugLEuxxxxn2gXaGi0N4vlHgM61RZvB7+XfrbWS98ex8d7LmsjSFE3bnK1TXps/457m70kKtGOXY8WIKZ0YOjrFtUn7rPOEuK4YDeO6Y35R1w3X536n/eD1aWP4O9pQ2hCdg8N9yHX9dV5fm2gsZgs0rcdyOcOv/PW/gv/2X/wr7A47tJ1D23QySbwJMtckD7InsqRBdxoAE8PWdd0MXuLEoyjDJHZdG5lUCJEa16GpT7B9g2IyRlfXKJY5kORRatTBKy9V7xw675CNxri8eY6rG4/N4yPu37yGNUCWJBIN6PuQbEtDZ61F57rgdY/gPLHBq57qSbahFG0SCYc1JjJJRkV6JIkVb4nv+wji4+DG/I227+EltMYE2xQeBt4ALuYdeHi4NENRlEDbhAT5uChtlqM3sdeBR2Sc4T68Cf1FfB8M/mQ8Q5oFIzoalcjSLMrTfPhsmsJYIE0TrNcrONejOR2xv7/DMWrCZbP40JgxPk4cOy/GI8tymDSD79kUKeS1sDpXlhTIkkHbSC+uiWMdNnk4vPmdaRKjMQgEKDEW1sTqFNZjOp1EwnCJyWQilX9GoxJpluLb3/pWlIY5pEmKvMiQ56loZZ3ro7ELEYzdfov9boer62tYE3o4uBhBWG8eouY9R5oZ7A8bGOOwWt2hqcfY7bbRSPbouhxJYiR0Sm80x4pN3BhWpZdMxiQZaokvl0sBAc+ePUMdq4fQu8x8BTYlszZ0fD0cDlJxSINbGnSWVJ1Np9jGcD9lOWyKRw8SQQzvhYSIicbOOel1oEE0Dxc+5+XlJT777DPoEppaWsDnJ8m7vr5GkiT48ssvkUagw2o1BCGB7A7G/nQ6SWM65jdUVYUPPvhAZEAE0JRB8d8XFxdykPEetWSBz5znuei1KfFgBIJ7xvugG07TUHueMi0dXeTzlmV51tWaIJHeNh4oTFonMOK9ElDy4GC5WD4HZWD08NN+03tIgMrIBRsR8nAiUKFHjkCGxHS9Xsv4k2BeXV3h7du3uLq6EhkG71vLxLhenkVyz3HTxI1SK+YZ7KNEMMuyszKv19fXACDggWPMRGydA2OtlbyXy8tLAXC0PZxv7VXU1ZBCNKuU/TQajeRZQqKyQ5YNnmwSDe+9EGVG2LhH+G+th2cuC0mGlnYRMFDrTjJISQ6jCgRfBIWHw0EkhgSgem1wbRHo0IOvQRblK7qSDwkMHRUkk4ye6VwM/cycF2Do30C7wAi/c0762xAMHY9H5Ekq9o5rMEhuOlRNLYSYz8ly1H3TynqipIVymUpF0MbjsdgSEleRk0XMQ8cDSSrtJsed96UdTmma4uLiAofDQfYR95X2umspEK9J0kd7xDEnAeF7tFSUe5RrkftJS3sIlHU0kTkqvBbXF4kdQSr3AaNQtNH04DOhnN58OevMUJGOtlGDXyZfE/DyGk+dd/q5+T5GKLR8kyRAVzLj/uX+16Cc0XWdI6LzJnQUhePI3BItBdS2hXk+mpRzbjRB4TMQe/NPvic8d8C3OreEpEnnk/CedJ4NnYNcw5xzjhGdO1/n9bVzNP7gd38HsAk8UlR1j7/zd/8+/vF/8/9B2xsYEyQ4BIhD6Aswvj1jbRqYdtJfYmD1AGBNKPnK99LAOecAE0rW2iRDMZ5hNLnAd3/xT2KxuILNUngDpf8fDhU4h7ZuUJ+OOB322G82qI5H5GkK70IvDxo55mgkiYVDjAwotktSYZNEwt/0lhtDBZARwN33veRduL4PSfBxrHjAMTSaZIksUHa6TtMsKHmSUFWI35XE8rHGBqCTFzmKvEAaD7DT8QTvUozKseiinfdBXw+gnBSxaWKIGMj39h5ta5AmGYz1MHB4uL8D0MO3Ne5//H109PICg27UBFFYAFchbA3EnJYYOUlsOChDt+qQ3xDGJhGDybkO6yH0avGAJHamaYrJeIw8SzAaFbi9fY4PPngJ74HxeIRvfvOb2O230TudymeyNMPxdJRD35iw1hYXC6nUs14/ilFm8iuTKYtRgbdv3+DZs2fYbrcAQuj39vYWu90eSWIFYNKDsd/tMC5LNE0dy0iW2O93UZu6RdMELzLBDBsPcc9QRsJ9kGUZdvu95IroEHZd17i5uhKvIsukbjabUFEogs0f//jHuL6+jtrxtfQgWK/X2O12ePbsmXhUxuMxHmOfCR4sr169wrNnz2TvjkYjfPrpp1gulwI6CH7ZLIreaib06nyJLMsEJHA/8PBm5IEH05BDUst6ybIMXd+jaYfu1QCk+ZPreyzmc/H+UeJCzzznXkuO6JHVnti+76WHBcE7Dymdo8FDl8BLe58ZHaA8jQaeQJ22kIcyvXT8j+CS40DNN6NCBDrU8fL6LK1K2QDX03Q6lQZ1PNiYq0NAQBDG+9XRhSRJhLhxvukd1vdL0MJ7eEogSfA0UeI8cw/wYKZ91zkU/O7lconNZoPj8Yj5fA4ms5LMk6Ds93tJjOXcaAkFIyK07QQDk8kEr1+/xjTKIWn76DTguvHeI88KNE0r+5CEIICMBG03dLLnfgdCQ7u27SRaoAEpgRjPNX4vnQWa5JEkpmkqVcoY6aAscTKZyOfoLWVxBD439wQweJ4JdAiACHL5O44rALknAOLNJngBIPkLdEo89UaTXPAavIe+D9Umd/sdiggY+ZndbhfuPc2EmBMst22LoizRO4e8GEAeCUDfdfD9eblaPquxBk10dmjbwDmhZ502nGOg15DOXdKSMXrQGf0jJqL9ZzTmdDpJzhi/lwCQxEwnE3OMNUgnIdSkgj8n6eU5TNLLdc1n4v6nRJHXJ+gnKWEkjgSee5pnF0krbQDvXQNbRnO4lnQzSTrluF9YdINjTdvBeSF5pIODOR+cU01QNAkmJuDPy6IQ6RTPAcqoSMBYBUxHPOgooB3U+4dzrhPUtT3k/ekxp73iOmEi/YBLhzkBIBXsuL41QdFrnXPIF89DbdettfgLf/XP46e9vjbR+Le//m8wX8wCOUgK/Otf+238H/+zv4X9oUGSjs5IBA88azz6rpYwMd+TJAnarkPvIxg3VjVy88hSli4zyPMgz3K9w+l0xGhUxkpOOZKsgDMWF5fXePHBByimU5g0JDIR9LKcXGIzdE0L13VoTkesV4+oDgdYIORsWNXfIEYAnPPwsRke9Wh910lFpHAIMHfBSZJykoS8Bi7KxCbC/rq+C1KhGOGYz+YhSdiHZOOmrmJ4mgs6Msu2hUMA88bGrszRK9fGxOCqOiGNjPl0PALGYL/do8jys2oFk8kEXd+hqvY4nYZKMMYY9I4Rqiz2RbCojntUpx2sAVzXIIlJ6aye1bseRV7E5oRd3FSD9jTLcoQ+K7F8ZJZHidIUdVMjTTLsdgfYJGyIUTmKjHmEyWSEq+tLXFxc4ObmBjfXNzDW4LA/IEtDe7+u61COKN9g0lIusoZB/tECMMji92+3OzRNHQ12CSZBsVMowRVJYZInsrEJsINsK4FzENBlbYKmqaMmPEd1PMSqLC3SNBFgVVU1xuPJmTyCHam56QlACeqNMZjE2vM8oPi9i8UCiTH48ssvhVwRUOZ5jioe1mVZ4uHhAS9evJAEvOvra+x2OynjOo7J4VdXVzjGhmH0wGsyyIOEwJ9A8+LiAtvtVgxj27ZSAYsHDu0FE4BZt5sh/+l0etbUKEkSLJfLMwkWx6pzTg4+54ayk9Za1FWFN69f4+XLl2KDtJeO3jzv/Vl+BEPRHGcAcqBohwrlSAQO2uPa971UTKI9IOhlWD0kz86EZNHLyIOYhj/LMqlexYOVnuHVaiUVmoBzsEfwTmmatVaiYPTIsocBZVok0gQGlMxwLPQBNJlMBAgRdPN+gOBNZfM+PiM9hdyjjPpwH9Amca6fEsQsy86SbrnGSAT5M/6dYEIDV00qmUdEzx+bNRIY00NLsK7HlN7Np8B7NBrDmkT2lE6Kt9ag7QbZxWPU/4doXY7qVAmA4ZqgLePeIdnU64Zkhx5ZOkp4XpFQcv5IZvldXOece75IWLWkTwMfVu+i1Ibfx3ukLSJBBCBrnvPM60kkshsa63IvE7wRmHVdh957jMajs0iJ96HwTJENFcH4PE3TwCYJ+pjrSPkl922WpvD9uwnM4ZwZwWHY25qAMRLBKCYBGZ+NfT4Y7eDz6gpPmjBwD+toLKMYBO4cC00MNAbT0VSSC51vQNtNWY127HCv6/njHNL2kWzpPCNGhXhPdFrwuUnYtXSHNo17n84J/m6xWMj38LtpW7SMVdshIZVx/TOiyDF5WgpY72GOvR4rXZggz3NkSRok2/FM4XvpIOR1WTmQpJBnMO2BMeasLwntB4kHnXGU8HI9cPxpczkeer1T0aLXJveYlqlxnfNMBwapNQBxwpDAcL7TNP1aRONrS6fSJHhFYA1M2uPDl89xubzAbvdlSBA2T3MwOgAeaWLRtOHgrJsGSZIiSxJcXVzCqEQSfjZspNCYzbuQjMwHDzIZg8SmQAQXvQdc2+Ptl18im06RT8bi3QNCbkLvohbQOBjrkWQFZvMLZGkO13Ww3qGNG7AoyjjYKWCA1scNk1r03qOIoTp4IC89RmUJm1iURSmNBJMkRdO0IeE7zc4qFXR9h9FkJKxyu93iFA1y39SwCIm2dVOj73rZJMYBbd2Ayc/BwAcPat80gBuS01zs6N22LQwapOmwIK2xeIAPXctjpaI0SWCzUOUkz3Mks1DFxxrg+e0N2vqIIk+wmMfGZ8UYMKHpUVmWwTteFJjPZ/Ax+jOdBu9QqPRkkaUJTDKU9iRID7XkU2RpjrZl1QZKzzyatgZLHF9dXqDrT7DeYrO5w2I+RZpY1E0FmJCbUFUVilFg+9ZYTEbBG3o4HiWHxhqPpjrBwCFLklCIwLmYb5Oha3tYk8Aai/EoAGwDj8SGfIzD/oTb22c4nk5wvY95QAW6zqEoxtLcrK5r7PdHbNdrLBYLLJdX+OyzzzCbzVCWI2RZIQcxPSebzQYffvihgMxj9G7psHwVDxwmKR+PR+kl0TUNPv74Y7x9+1ZkOTygjTG4vr4+CyEvFgvxhtJTzAgOKyVxf7LPAj+/3W5BPTiTdfk8BHU0cDxE2e+C5WAp+aLNuL29lb2eJIl4AZ+GwGmseVA2KnTNg53GvG0aadBFGQI9RSQ0BFC8Lr1gOopBTxFJiPdeiCi9SkzoJwCg7I3jwvfRaNOjSOPdNI1IBQiueDAmSWg2OJ/P49ray2FKkMpDh4AdgMzParUS0sM1RRmNlrbqXB3aHx7wBBaspMNxItCnzJXrjr1j+Pz0mNKGAZCDm7aBhxjfq0kpv4/Em4CBHviqquFcL5V7mNuT5wX6vhP7rMESZYvsDr/f74MEp+1ConQs1sB74mf4ea5Belq7tgvVB9sO6/WDRJfohWzbFpPp+MxryN4jdGQkSSJN8mjXy7KUiJO2n00zNGSbzWaS0K6JLqOEJCLAACw0+aqqCrPZDJvYY4IOBs4T81VI8vQ+4XeSyFZVJXI1PhdBHPchARHPBEbodNUirh9GiwhWucazNJEoLt/ftm2QbMdS4Vojzz3jYDCbzWR/seu763vMJlNxrBRFocoqB/DHPBktM+Ezkiww6kAbxvcTIxH0kZg9zXugBInPqaWH3Bfcm9Tmk6BzXrm+0jQ9a6SoQS0jLIxw6vKy2smhiYsmWow26bklUaItZlELfrcGs8xN4zrk+JBEUDKpIwp0IvR9L/lPXNd06vIso+OGEjo6LJ5G3nS0gsROjxMLEwi+jMnRHBvuW+4H2jKuD73WiZf5LNyzmrwPsqghf5hrWDt+9P1rJ1gY3w7eG3GK8OyireVLn0lcUySJOvdFr3k6Pr7O62tHNP7Nr/93UaLgYG2G46HFf/l/+3v4zd/6PXQu5Bs45+GNhU3SCOwNbGZEhsSDKI0l5azxscKRQ9+FKkdd16EsRkiTCFQ6hzTNY+lXg7quMJqUoRN2MiTwjCYT1HDIxmO8fPkSWZbiyHJ5HmhOHcp8hIeHOzR1hTzPkGUptrstnA3yqMl0EiMmEQBkGVJYSQ6rY6JY3dSh8lIfFsBuu0VehGpD69Uax8MBCZO+Y5j8eDrAuQ6u94CLiTi9Q1VXMgZwHfJICpI0AN2Qb2BQpBaJDZU9eFiUoxKT8Rje9SjK0OmZTHU2Dc3CitJiMZ9iFI3JYrFAYi1G4zHybKhg4b3H1dWVbDQPH3uaGBz2e7AC13Q2w3a3R1mGRNLEWpjo0QqLMPT9sErPOXhFYsWVuHjDxvZo2wDw2DmZBobGtG1DjsdoNIoe/xTeh010Oh3j/SNGe0zs5FvBxi7YaZbFkowhpHo8HFBI4mS4p77rQv30qDcP4G2K3W6LtmkxmQ7GrG4aXF1eom6aWI453F9dNyjLoX56AGNHOeRoRAn68jwX/a6uxFOWJba7HfbRO8hDuI0G0sc5oqcPgBzcBM/0qDNMnWUZynzofdJEbwo9bOVohLdv38oa4YE3Ho+xjeUHtdeJRpF/50G7Wq0kHyYrCpFRlTF3IsvzoC30Q8UNRhT2+z2AwXtCUMZoAMEUDx16RL33Zwe9BqSHwyES3VSSn+mh4qFLqQgPcB4Q1JeTMNGIPy2fqCMVfJ+OPGgNNQ25lmppaQyfnX/XYe5wcPTy7DT6OhmX7yFRY0UmXY+exKfrOvGSaikIiSsPZIJNEo/Hx0cBEjyMTqcKiU2QxEaRbRNASdeH8sLH4ynOi4MxLKftURQ5dvudkCdNZHSEgN5RIJDQpo5Jn2UpPZrKokTfd5hOZ4GEpQnaZiCGZVmg74Nc5rA/CDDKshRd15/pu7uuFdtojFWSAoO6btC2Axk4HI4Yj0eo6waIziV6dAku6L2kTfQ+RMqNMSLbZT6fznvR4JwySEYqGOkkMGNuCDD0D9DJm7TRWgtPIMg1X5alSFD4/LwH7gPt+CPw3Ww2QtirqhJyQ3DJNUjyT8KgPeRcbwT/mijpBFuuRUYFnfM4nQKoZ3S968P5mqYhukywTLBEwuERcguNMej6Ppz1xoh9oo1g0nQ5CqX0mX/CZ9K5OhxvrYmn3eD4EeiRGGi5FeU3OqKiz2mqEgj8KckjGQdCfhnHmDbSWivnDdcz8RPPZAJZrg8dXaad5b6kLdKOC66t4Gyc4uHhQWweI5+MjtEOM6JLkM0oE69Hm6aJppacAYOHnWSD5IrnIwks75P2lMUPtIOcNpjnK79LE4TgxAUSY8Ux9/DwIDLh6XSGPC/QNDWqamigR7Jq7RC51VLdPC9VXqCPTpEuKmeSszwmVkIM+3coTx6aX5/fM//ONci515iE9pdrjj8f7OC5LeB6+au/8jPso/H5558qtmQBn+NHP/gc/6f//L/A5tChd4hRhh6j8Qg2SUOVJudwPEX2DxNAOgJo9a6X5GOyzqau0cPBZAmsSZDnBZIkhXNAXTVI8wR5kQUvk7EoyhLV6YTLyyvMltfIyzGmk2nQUsYIinM9bJLBw8RJ61GWBao6ls3Lgl6uaZtADizQdS26tkFzCElubdOi7Vqp9uC6Dt3pIA1b9Kb1fQ/0oU55kEkZJEkw9Flq4boWF4sFPvjgA/HmBZ3+AkCP8TgQnuXFEot44Pdtg+vlJZq2EXnHxeICbayCUZQ52qYV7XFIYCrx+HiPpg3Jbl988QVubm4EUHHRsjPt8+fPZaNTevA0ubRtw3c8e/ZMKnzQcNGDS0/imzdvcHt7K+FjGl8aaBpZGjYaocfHR9ze3qLvQ6Imv0trJ7kRKEOhPIGSIbJtegEpQdHeW85ZlmWYz+cCDHk/rN9PwMa8Bd475RQ8YGhAAUhjJUqFeHgzoZqHrDEGb968ES8yDXLQDxcSVqXciSCR88Br8BAmACzL0HhOh7HHMQ/j+fPn+PTTTyUvYzQe49vf+Y5o95m7sd1u8eLFC3Qx6iAEVyU6PpWdUHvbO4cufi+B/+l0wm63Q9s08MpDS9KVpinu7u5wc3MjnkH+nN+lk6IZkiaI4jhcXl6ibVupMMREWCb+OeckL4O2R88XyQO/n6F+dnJmxINrnoczjT5/T2+a1l1T7kTvK4kfiQmlYvow5oFKLb+WUjAnhWCEBwHzXggueLByPqiDJ/Gip43PQltP8kqiwrlgyUeJgB1PaJpODu26roUIcr8StPGZg13x8HCSFElvHasBaS8390x4n49lU7MzwE1ASA++9pxS9sdn5fNSnsMIId+rpR2Pj48C/hlJ0zk0wADWtPeZXl3aFR7QjGLo/UvbxigMPdtcK3Vdi+eee51knJ5ffp6yGu+95H3R6UP7TuDDsddrhR5a7jNGfaip517ns2ggDQyV8ygZYe4SHSKMcPHM1PpvPgdB0uDZDS9K7YYKPQOx1tcNRDDct24IyPXI7+J6J1inBEvLokRrn6aw6SAb4xzTI89rc43p79PSHu5XrhnvvTS1I9ClI4OkgZIXJq+z6eNqtZK1zbOfn2duho4+8n54ftELz7WjHYS0+VxP+pm1Pfbei03V309yS9tJskeb9tR+c945t1yfjHJRRkQnlZZM0e5o4gZAznXaVEYPGGXgfvc+5FjQplJVwHHX+RZ93yOxFnnsHwYMlRTDWp9hNBoLdtDRpVCW/ryhK9ccYCV/Q8vkgrRxiEpwXQ4O2aGJJa9HZ4GeW9quYe8MFbc0KQWG5pQcZ0bZ+P3EdH/tb/4MO4M/Pj6g75ngl8C7FF9+8YC/9bf+S/zhD9+gi83qTBIa9pXjAq7rkXqDugq9AnhjSZKgdw6nGH7lIqEHpzc9kjIDEOt/uyGhpRyXGI/LaBRjeURWfTIF9rsTRqORbArqwjsDdK5H2zaoqhOOxz2Ox30Ix/UJXNfjVB3hXI++bwF49F2H1ACuH8JIVVXBJgmM75HZBmmW4vLyEs9ubmBM6FJZ5DnSxGA2neLDb3wQK1YBL18+x+mwh+tDSFl7ABYXi6DvTwOQWa1XcHFT53mOcTFB14RqVadjAGyz+TyUWGtahK6Ng2QgeKp6GBOaEXJBzmYz3N/fC4DQHgoAZ2X+CGiyLMPj46OADB762pDqMLD3oQyorlRCY8XNoMuj0vt1OBxwdXUlB9R4PMbnn38ulYRoGGiQKRfRWszdbidgd7FYCNi6u7vD5eUlxuMxXr16FT2RwVOzWCxwf38P5gAcDgeRkPCgo9FjmJtRA+3tJYijzEiDzCRJRANP74DWw9MQhg7gG+RRInF9fS3acALQy8tLAd4MrxPEUiJFuQM9913boonhdYIKkp+yLDGPFU6Y4EVPp/ce2/VaQAXJAeuQ87m4BmiA7u7vgWjUeTiFZlkXqE4nzCKJ43hoz6f2LpEAkyxQikAjyWfV647zVhQFttutEEaCYnpOnQsSn4eHB9kbNLRcO3VdS08MJhezwRQA8dw556RHgQYcutKWeLLjS3K4lCSCJFlLFQiKKbPSuQVcS845AXGXl5e4u7sTcEISzUOZa5rjyEOEYJj/aVKjQ+n8DP8LAM2jbQavIu0Ix51kjoc6iaRzPbJ8kEJxPHgYct1TKkQCVFdNjI6nZzkKBKVpmsre5LhrnbO2XTx/OCb8HgACurm2iqIQIFKWJd6+fYu2bXF5eSnPRSBCB4uWgxEgcf651ygP5NwSoBGIAJC9Qg+qljHwHrke6GUnsAVwlvDK8aBNoc3lPubnOL5a5kWgyFK9mlzwmhxfkgZNtjSp0HPKtamJFNettgsEhcP3mTPby3sJYzYkFPM7Ge0hOQIG6bYmu9zDZ3Ika+HNkBvA+ebaoUedxI7fx0IKWgbJ9dh1nciaOG+U7RDs8drsrcHIB8dLkxgtFePZQyLL7+RZxgR4khE65XQpcdpTng8k/pSG6fnjumUkgECekRSuKdoSrhGdK8L1zIIFOjLBSlyMOHOcGBlhVTySGEZmd7sdZrPZ2X7hOPH5NUElPuGLe5i2yHuPxIRIOfeoljE5F/pNPI2gBXvYyj4n4afjYrPZYjweqhnqdVYU4bzQRSKGfXlecUrvez4z1zB/p+0en5FrRdtBHTHlnuAaSJIEv/o/+RX8tNfXztHougDSneuRphZJagDTA7bHqa6x3mwxmoxCSdq+AywQOmuHhkBZnmF0McN4PEGaJqjqGi8WCwChwU/IdUhiB+UcruMBXMH7sBjrpgbgcDweUJ1auD5sot1uFyoKbXbwXej6fDyd0LUd0jT0rzgcdmjbBl3fwhqDrg/ldBNrMCoyTMYjvLycwvsEi8U1rq6WaJoaozyUSFxeLLG8XKIsCpSjEZLEILVDSNpag7IoQ0lYAPAujpdDlodu5VnaoU8dFpc3yGIjO+MduqbG5vExVF6yCU7HE/q2x/FwxMXFAm3X4VQdkRiLwy488+JiBmuBLLfwPo3yogxlOUPowI2Q82AcmtgUkYabBpBNmGazmXi9drudHNxFUUjjJy5UAvjHx0c5bOn954HDg5dhThqovg8acHrHWb+fhpLgksbv/v5eNiCTM7MsE5K2Wq3Ec81oDGuAW2vx8PAg90fyudvtpK9AVVV49uyZRAYWi4VIDxg25D3pA5PhfeY1kMwycRvA2VhzbHjAkCRwo+pDlMaWeRjr9VqabW23WzGcNL6auBA4e+9xe3uLpmkkic45hy567LuuO6tY0rataNwPh4OAHpKkafSyc6/xPTRUnF8aJYkGqfB6mqa4vb0NQG0yiSWgB5lO27biPZrP55IUf3V1JZEWgte+78VDOZ1OpV8IANzc3IgeervdijdLSz84L/T6a2kSgQzJIyU9jPC9fftWKvlQw02vtgZH9ALxcKVHjPe+WCzkMKHMjmOlwQO9eLqELeea/zG6wBedArqqEr2XAM7AAj2QAuCjB4tjxp/zepvNRg44jsnhcIA1FqNRiPpoQMgDTR+YlOtVVYW8yASU0SnAw1HLpei95YGdpufSPeBc+01vH2V3mlzw2SgLYLSJ464rZGmpEKtvcdxI+pnnAkCim5R/cA0QyJNQEfB57wU4MJJK+0ECwOgCSYZ2AtAW0NmiQRMlKXxm4LwpmY4Oa0CtwQr3gY486AiL1nxr8EJQZa2VnBJ+nmRPA3TeA+2jtqMEcPozXINhDAYvrLax4Z6cyLr09fh5jt9yuZQ1QiLEvcA1Z21o5tqqCD6JdtMM/Xr4XpIyeuNJMjhWzEPRnaEJqHkdTcC4bhnJorNtOp1K1EMDVz4jnVB0WG23W8nlIS6Q3hBZJvIf7lsto2OEikSGEQJKqDgnzOFJ06GnEtc9AbYmwtxrjLCSFGtnLG0rSQ4dGbw2yQCveXNzI/vp4uJC1jX3qfch14ZRc0ZRuSc3m42cvXSWcg0XRQHjz3sTcW+HNRGUOCQEzF0KzzlUENRAnucS8QdtNwlo6CfGHnWdIqAt0jQTBwadntqO6IiyjpZr5xL3Ge0/r6X3Gu04i0zo9fqTXl87ovH97/8AgIvgNkfXOmw3R/zdv/cP8Tt/8Bm6zmN2scB4PEHbdWj7DllRICky2MRK/sB+vwd8qBKBBNjv9gJgehdIgq88tm83cD6Qiv1+Fw+LcHCs1qshfEX5grUwXY3UhsU8Hg9J4UWe49nFBRbTCYqywGhUYjIZI0ksXrx8julFCYce43GQYaV5qJpkjcEoHkCJTeKGZ/8Hg65z4pG4uLhASAJvUJ1OyNIUVXXCdDpB17foOmq6M9TVoJ/zPnSBdc7BJglOTUgGhffYbLdwfY/xZILEevT90DCJrDMAhh5ZmiPNUqRJgqYN5S7rqsZ2t5FwPw8zLmTt6fA+dCulDp4b5+7uDnVd44MPPpANrA81ei2SJJFoyVgBU20w7u7uxIDROw0MSVY0TFzw2+1WPMSUr7C/AuVjHAdKChjRIDANXoKNgBIaVgIBGlIe0FoCxq6j7GvBQ0EfZjw8qPXU0YDlcnl2ANAw8u/8PDewPvi2ux2uo4RI53GwDC4NBaUlNFIEnfQEFjFP4ng8oiyK0G9EHcSStFzXSJTkgwdy3/fII2jWz3A8HoUQnk4nrNdrIXrT6TRUlVOecgKbNE0lRwOAkISnhwsNv/a+8mDjnD08PAiR45qkOWO0jASRAJfX1sQCwJmR1ZpZXrPrOiyXSzlseOjx0CLYpGxLDKySqjCC5pzD1dWVHMwPDw9CKilFIDnQ5IMeSmqdeUhy7rVXDhgkjQRCPKw1YdHh8yQZqpwxssKf85lJnHg/LIuZZ6Faki5XOZvNRDqonRUcl3A/aciviOvQOSdjT7BLZwUjAF3XYTyaoKpq8Rjr6CslnTpyyEgUbQPnn/fFlwaxjA5ybGnT6A0lSDjFpnxabsXIIeddy5wYGdNSE46rtgeaAJCwaAkGv4/zwj1NcMezibaLdov2n+PJ9cq1zufUuUesxKeLAxD0kkgQjHEv0X5yzvnSwJXjwntiJJjPSNusPbTasxrGBmfgiKA1PGMi65nnEdcKwR1lk1wXnG+ejYyYlmWoeLmPDhG9VmiTQgnz4M3nekuSRIA8x1jnb2hHG5+bJKLrOnEI0i7TAcG/aw80x5dnBKMJXG8k0ZxfPZ/au897o+3lHNAG6VK06/VaZIBawsR54B7SxJ0RYABSDlyT9CRJzu6NNptrQDcl5J98UYLKvaUrB2rJI99LO3l9fS0gnraK88txOYt8dR2aasg74vcFB8H4bN0Rb9B5bgxk3dOOBNlfKPvP/cU1GHDP0AGcZxpxBGDlDOUz6jNBy6x0dEXbAs4b1xJJipY00umlo6d/8Zf+An7a63+AdCo0bEtSIM8zeGfQth7f//6n+G//9W9juzvicKrR1D3aHsiyAq+++ALHeqjqcjgcsN/v48HpAdOiaztUdQ3X96i4CXqgtBlCgzaH+Tx472FCA7FZrIxQFDk++uhjPHv2LBwmqUdig9G5ubnB7e1tAIeHAyY5ax6f4Hzo8+C9A4xH73t0fYvJeIS6qZDlGdq2QVmU8P3QIbQsC7RthyBJSlC3w+JLktCsr4ubZDjYUwAu5lJ4FMUIx0Mt4KuNnbP7rkMeDZSN/TFc7zAax2ZAaYq6DoDSA5hOJmjaFmVRoKor0W7SENB7X1UVXrx4IaCFhzABP7sKLxYL+TlBOwEXPRx5PtTW114e5q3w39ycGrgnSYLpdIrf+73fw9XVlQA39kugbIVSIn7WWovHx0eR7NA4Oufw+PgoIUgaFB7QFxcXAgC0DIzzRQNMTT6NP4kDr0dSoz2kuu8CDxnKKBh10d5EGgMCe93MiBuZXhVueGMtJtFzrnWk9E5wnji+GhRwDMuylGhV27aYx8gKNdc0bsYY1E0jSf1cu/QmGRXVYXha1zGngaJxbtsWHpCKWTxoCFzbpsFI5TloqQ3HLk1TaQpI4HJ5eSkyE/6eBwwjVQT22tulDzd6DaXOfjHUjafXWR8ufR+KFKxWK5FP6UO673tJJCcJpuOEMi2ugZubmzMPMUEwG8w550Qawf2qjXyehx4klDWs1+szkMH/uLf183Kda2kCE3R1zpKWc3FuWI+eXkquKXpEw3glSJMhb4cHHL9De2UZzQhA1+BUHQWIMcdDA1auSXrf0iRFlhWy7rjnebCyXDI9yaHKW8gFYu4Gx5ugV8tQSBr4HtoL/sm1zhwXDeJ5j3LAKpBFcKl/x/+0fJWf5/NwPjiHXB+8BjD0i+J9cv64hrkmCI4JFPl7wgD+nv9paaOWC9L+M2LINdT3vVQYorOAn+E+IJlmJJAOE+YTUKZDsMT75lxx31FqRr8FxwaA2B2e85oYEBgSVFJqS088owDcq7Spo9EIznu0/ZAMTScYIzwXFxcyd9xTnFOey9xzHHt+lmuOIFgTGI4X55g9h/g72jIdFeO5QWcDzzTOESM9TyU8nAMSI21X+Gzc0xxn5nJqQsjoh3ZSMfotESJA7PhT7z/Hi+cM75FrizabUWk6qfgcXHMEz8zfoQOO0TbeD500rLrFcu9sbKlljVVVoW87ZOmQl8j1GcY/FJGgLaG9DeMb+n1pOSs/23VDVEbLvALGGIrocL0Oe3dw4Ojol3YO67WlHQ36nBxw6ZDjop0KnCd+pmman20y+JvXbwHjUddHdH0HA4u+A8rRFD/68Wf45JPP8fmrN7i/3+D+foO7+xX2ux18Fw6dLIK3w+GALM+RZxZFEYDui+fPMZvNcHd/j5cvXuDq6gKTcY5yVOJ43OGb3/wY3ofKSvPpFHVVw7shU54AVJrPIbS6IODJswxdFwaxboJ3MM8SbHfbcGilJdIkw36/Q5omsBbBQAGwPosN+oI8yRiLNIvhxHTwvLMZlDEGbRfI02Ixj1WlPJLU4nQ8ohyVcK5HqHIylBKrqgrPnz1D37cwMOI9qas65IQgRdv6M2MxbIwMdVMLSAOC0aWkhyVQabjYZ4HgVnuKaGgJ3unF0jIpblAd+mZIn0aIm9qYkLfy+vXrMz0oQY0uWUeJCeUljFoQRBwOB7h4qlCORENNJk8itFgsJJeD3t/r6+sz6ZDuDUEDYm2Y9yaOMTcjx5QbleFnkgV+H/X8jG4wt4Cgks9LQwEM4JwGNE3T0Omd4U7vkWaZzAU1vMAg9aHhplFgyUDOYRYPsTyCHnooCSQOqtdD13VnZfzyCBhohHjvlEuRvC6XS2km5b1HqsBxWRS4f3iAjevBu6GjOInFeDwWLyBJF4GjtRY3NzdYr9fiiWQ54CZGAQnIGZGix5SHIceZpIYgoyxH2KzXsq9JwL/44gtcX1/LgcA90vd97AUT9qhICvLwPU0bKtK8fv0axhhMxhOkWXgeShR5H3le4Hg8xIhNiq5rJUpRnSokaYKLiyW6rpXSraHjtBPpBb2doQvs0HAuTUN/nyRNBDQEgBTKdzPCErrRMA/Joq6HDrgsC8uXrpI1ENWo/TVDpTlq0pm8qecmSULvHe88ijLITjmn8ViS+QpgrIvrsocxYQ5228MZCOX+5SHIyAxJvJZY0PYwwqA9wbSRGmwDwYPKLs0s2Uqv7Hw+l33IfUXSqQ962iKdx6GTXjX5fBpx0dEhHZXWUSwCC54NWt4CkJTwe4akao4Zgf3gJT1vjkeSyvHhHtKARI8zE0cJcHSkgffKRoaMWOoEet47JYdcDyTz/NO5IJ/ifk/TVOU0DFWuOMf8U9tOAv8BoBq0bRMK3HQding29M6h7YcmfLr6F6Pa7LVCyRvzHniOaQDOOdcVufgalSOpTFYUBbzzYZ+2wfvfdq3YQe+8RAaLokDXduj6QT5FW2pMyGfl+inKQu5hcBoMdtJGIgUAqXJC6ByBsH4s2COK+ynggAI+9ivRkTsWbXl4CFUkSeY4V9r51/cO3g9yPGOsRAQocWLuHq/PvaGT9RObyLkAIPQ0s6HyGOeS+9I7j67vBkdcJIfaeZSnodcY7SnxCO9Rl6UdniWkHgRs0KAohv5m4Z7D5zQh4lw512M0KmVsNCns+6FZH52r3B90suoIvyZu+kU7RDuinR/cI/wccdOf+4v//jvXeee6X5do/Nvf+E0cjkeEbPkMdV2haztcLJfwPizC6XSGumpwF5ON+67H6vFRwonGGDw8PMB5h8vlEklkxM47ATeTySRW3Kjiwgub3cbJphaQHgZuAnq35vP5mUeMRrtphuZboe9FEXtVcOBCJaw0CZ1G6eFv6laYdTCwDnUddXkZQ+U9rA2TfzwcMBqN4byPG2iQ2lADOJlOAoGwBqeqgo0bR1ce4kSmSSgT3PcOaZLCxINrvQ5ldJuWlQUS8VJrfbiuYMDSpzoEzoV0f38vZInEgp47gitKh66urs6S+zj+NDoca25+LnQeuDwceVCR9FCGQABxPB7h4uHECkxaGjSbTlHH9UCPp046pnaY33d5eSlGiAClqkLnanpAV9HLQ7AintW2RRIPRo6JjnBwc/JgYUM0glnKtHQlF8oNtHxHy6k4RuzmzgptTfS6d30furybUI5Rg5kA5oKk8HQ6oW4a9FHOwHvkfNGrxVyVrgsldFmWlmSF4WgeCjTiJFZlWWIymYiMqixLFGWJzXo9HMgRxO8jOeEzEqwdj0fs9/t3+mn0fahAxsOQckDOQ5qm0myK0VMAZ/kU1Idz/tq2RVmMkGU5bGKxWQeZ4Xgyxul4wv6wx2Q8EfDJg8Rai+12g67rkRe5is6kZ3psHdljXwUYYDwax3tNIwAvkKahNGxVVxiPxhIl7Ptemh+yxGTXtdjt9miaGmU5wnQ2hTXU2nZI0+gJTixMbD46hONjKWirEwJ7ZNnQ/8T50KG+jN5izpExJnrlWliboG3ZE8TImOo8BI6bsQbGJsiyNJBna+GcD44ea0OVQDM0ndJlFpMkiY4tRBvdIY0NUmnTtLyDQEPrxXlPnBeCHi1nAs4TfzXQ5nM8PDzIwa6bvPG6zHt6qtXn2BE8aHBOTz6/X681/ozXot3iHuD1dRROgznKLgPICUS2aepYPCSPUqUxTqej2FCCPZINEh7tLabeXztpGDV5Gs3hfWkZiY7gaOJFRwwB+Hw+F3kgCSFBOvdvICJD5aP1eiV9FbIsh/c4izRaa7HbbVUkOBeCSXt/qk5wGKK1WZbBxUjdeDwGjD87wxhlDBikhffhuuG5KxhjUZahcS2LtLjY98r7kFRcxH3XtZ14540xyIs8lL93Tkr3VnUoJU1iWNc1eheAYJqk8AikfTqZyhnnnDuTDXI+sixD0zbIpEFwWG9NG3JZkyhJa5sGxoYc0qqukCZRTpsGqXYf1yYr4XFNhCjPAlmW4fFxJftxOp3KOci51+uCTiTOK3EMz6u+71DXQ+RUip503dk5q0vz9g2b2MVIaZGLHXHeSaPgvu/Rdm0oe2wNRuVICFCaBhvtY5sG2lUSR+5ZLdfiOtf3GohAiHyQFIgawA/rSzs+AGAyGaNphuhkWLvBpjOfj44gOhp0ZENHKLWdI3nQBENHR3hu8t60euXf/wv/Hn7a62sTjd/9rd/GZrORha3DTzSYT401L304HETfbK0VzTwA8QIx6ZWeFYJSJqTS2NBjwL8ziZWaWcphKGdhZQR6SShPYMIrDyWGQI0JyYEXFxfCTtnbgYcLm77wYCawoayCunMSIb6P36nLepLAsDIMJ5fGlp5BY4yUsiOhIPCnBODFixdi7I0JzYjooeEBSw8yARw3Lw8O6jkJRvkdBPC6IRTnkFUdCPJYJcp7j/v7e1ncq9VKqkoRPB6PR8znc8nrIMCWcngRYOvqHszXcH2POs5ZExOdGWWgUdXed35+CG+GDbZYLGR9saM7Nya1ra7vkaqIBjcrDxp6o55u2KqqpFwrSybS40vSwjngvemkch7gukcKgQn3IeUoJJA8sL33EhrmnJBE8gDnd9AA7/d7IWjOOenroXXzfd9L6VxWdiJwSpJEqvNcXV3h888/F+NKgJbnOe7u7rBcLqWDNNczPSf64GE5ZO+9yOV4UNHbyXnm2h2NRmdlc2mT6AHkmum7oZQfq5UAOKu6oj1+h8NBEs67bkjIIxl/qr0mOWaVIB6ytGFco7oHAYGZBrVaEkMy3zSNXIs9BXQIn0CCB9XT59EHhpbBPA3Lcy1zHHltrfUlqeZ65FlQliW8CcCFEiIeyl3XwSL0BqI90M6IruvOQvhc7wAkiknyp73sOt/jqPT0vAa97LwfEhutA+e6Xi6XaNsWy+USDw8PYiMJAHT0geeIdmQAEOcY14uOWhD40a4w2qZldLwWzwS+X0vAaHd4znC/8AwA7DDmdPBJRHyIAhKE8jkIZjk+XCuMFvP3XMu6BPPgbT3vik7po55zrkXek3YQEBTr6AMlpxxLHYWhUzPcf3Emm6Ht5L3raBht/el0Qo+hFCyJS/hMKFl/PB6lotPpdIq5HgukacgRYiSPZdWJa4hLtI3I0wyF8pzTZnBdcT9qaRX3OW24zqfiMzHHQ1fC4nW2262c8TxzwucGaS7XY8AfNhI3/w4ANtaiasJ5xZwpnnMcIy3rEsIW75uElSoFjhMdeJxjjgOdCNz/uvgGx4R7np/Lsxx9JNAkyrQ13DvEWTwDaGO4brS0lI5UOj71mFA9oqVewFAJTeeUcV1xL2unBO2fti20XXVdC0kj3tCJ2ZwnTRb0WT9ErPMzgqQjiRw7rVwhxqGNSpLkZ0s0fvvf/MZZOJRAhRNOA0Ivj072bduQuLlcLkUffXFxIeCfXmwd/uUCpXHpuk5CZBxEglluRq3X5+TqMKoO3wEQmQ3vs2kazGYzSTKm7vvx8VGkSIwSaHkGk5lJMig5IangZDMXggZZe3IoVSEZ4XNzM3KREaC2bagapYkFD1dWW9C1/xnO1RWSGM6l/EtrEGlkqUE2JuhmF4uF5BjoMBwBDOVO/AyNIr3lrAp1dXUlwIGeRYKE1WqF6+vrUMauD71WAODNmzdYLBZ4/vx5kJvFNdj3/VkDI3q6OQcE2RwjPhv15wSzTdviFP9N3T0QjO3xcEAar83DkOuP0hrOJUE/jZgm1QRtfd8LkOABR2LN9aoBos7B4HcSvNCb9tTD6FxISL+/vxcJ0ze+8Q0Ji9/f30seCeeL60ETB1Yx4nsPhwNOp5M4EC4vL7Hb7fD27Vsxvrw37l06E1ial9IzOiwIlulkYA4FIzAPDw949uwZttutJOpTO0vwTeNNvf/bt2+lupMuNsC1Wtc1RuVEwCcPCxIUDbD54kFAIktyzMOJoIhabAJCYDDkJEda2kIwcDwe5Z41aNVJ6IyaaM0sbQP3MNcj71NrjElq6YDgGtSyFNorrhvaZf3clCDy0Nbr+yxsn6YiN+E4iR12IULHMdLRCIJQjif/rXXKBGe0MxrEUOdPosv8Ig0yOC506FBHXZalEC8CbtpZ7hcCbK45Elge7E8lJlxHHDsdwXzq/ef7eMhz7Jg/x3NXrz86MDSB5Hpt217AHoEcwdN4XMpa47rStptRS0YSSUI1sAVwBu60VOPx8VH2DJ+ZY8gzgNfl3tZzS6Cqe0Ew+sVoqI58EFTVdSO9DLgnuIfoTOK805YIRsDwTATrYT4squokeAdQcsrY84tRcuYnaVLLNcP8M+ccLIDEDvfI9/GlSTX3JedXn2W8X64FLdnd7/dnIJq/Y45DlmVxfoZ1wPOMkso0HYoHcO0lSYJTVSHJ0jM7TLLCs512nvtR4wO9Lvm9+lwGhoIbPI95PZ513De0HcRnjI4459A3Q+NAkn+uZZ6XfCY6Tuh04LqgYkY7L2gDdB4g9yWxrY4scO9QhsWznvuXa5TOPeIQ3hvXJPe2yK2fYF/tSCG55T3TPtHuECvxXri3aAe5BjXO5Dr99/78n8VPe31tovE7v/lb73hwyNx5Q5S0EKhqVsXFTJbLpDydbEjDR48rDRnr6OtkOC44bmpt1DkplGvokCsJB4Ep75OLhAucE8TvYnnKtm2lJjNDVQQnJDvaG3w8HrHb7aRxGCUg19fX+PTTT/Hhhx/KM3ET8/BjZIbfT8BEDy831xAGzuRPLqanG7mqQkO9u7s7GafLy0us12s5vF+/fo2+7/Hy5UuRBnHhap0fjYn2emkSyI3AbtHaa8yDkmvAey+kjmXlKP95XK2kCSBlSAAwiprKLAuVLwi8OGf8HkZsqHEm+Xt4eJAEvqIo0LQtkrgeSLx42HnvMVUeRsr8nHPS70KTDkYf6IHouk46n9OQ0LtDw+i9F1DHzxdFIaRQewXZnZmfpxFnFIWGmYc7950mEACkehSAs9LHNDQ0bpxPGjTua4IKejjpCWajRspICPQ4HgRDy+VSIpw07rPZDOv1WhoxMnK5Xq9xc3MjYIOkhAaVQJKHDRNRaSNWq9VZJZPJZIK+GyJknK8kCcncDN+TPPFz2nuuQ+I8xDXI0pFPHdbWB6UmSdrZQuOviQ4PBnrN6JXS1dCYB8TDTednMCJGpwAPDR2JIKjheuM64rrWnjd9+PBg1HPifciZ69zgEaftSNM0SFKqWiKpPCT5Pl6TByidNDoqyfWogbeOLuooAG0YD1lGKJ56+PjsmgwQnNG+8n10PD1dC4wuEsTwPU+9qfwcX9rDz+fR0Q9G5TjOTMTVY8Ln5nopy7EAVD67MSbuEY/5fHbm7ec+BSBOMdoYbetZzENHwHS5bp6pSZKITMw5d1ZdjdUFNW7gWtcASTtC+FkSU517xTELhM1gNBrLvuK4Ul5De0ZwnGUZetejc0PpWlYmCvflcXGxgPceDw8PonQAQjn5vg/jzwgl75H7m2uGOMlaC9/3sMaenRVcX5xjkmGe5XrNcN65VgngOdfEPLQRHGt+lnOe5xkQZVe0UZzP8B0BVNPhynUKa+CU84vX1nmhZ46HZMgN0HNKzLbZbMS+c7/pyCXPIj4rn4H4gGcd92GWZaGxct2IDeL+44t2h3/yHOb9UUHDdcIzVX9G20/aJD6Dxkl0JnMdkpxwTZIY8D3aaUFMw7nhd/JnT9URJNPEiiQMvK5eb9re8Jr8Xh01pk0jpvyZRjR+47/7NfHc04DQuHAyk2So+09wRu01b1yXxuJ1iqKQvgycDB7SrLNPg7rb7cSDfXV1hR/+8Id48eKFGBt6WqfT6VllAQ4Sf0dCkaapHBTa+8DJ4KLQiYw8VDVp2e1CXofue8DDRV8rTVMBt/w3N03fBz02q6MwdMVkWQK71Wol4I/RDRp8DVhowAHIRiGA0Acc5y/LQglaLiaCKwJoGlRuCt4bgTeNANk6ZW3b7VbKAxL00HthrZUqVFz4vHYbgX8SFzbBi4TN1UFIsEiPnyZcNGKUq9R1jRcvXsj8sA75eDzGLj6PJsqMPLhuqDaiI1WPj4+YzWZnHgkCdkbHvA9N4JgA/XTv0IuZpqlULOJ8c445j9roEIhxrpIkkQZxchAAAkxowAGIVI8eGkbn6roWySLHgj0EOJY06gQ5OoKh+xIQVJCMaILCNc/3k9hzr5FcE7Qzosa5oSebe4iHy/siBvwMv9P7EJE6Hqqzw6xpQglhPjs9X/weGnZ6FjmWJAU6GqX/0zILer/pWaXHT3u1SS60AwEYgLf2rvP5ue+4RughJmBL01TIGKO0+hAniOF1tX3mWtcHEeeG88Sx4tlAm2+sBewwB/xs3/fwvYPr+7Nra9DNQ5MHNuVHcoDFcaf8QO93gjSSLNoXHrzMw9PrHxgkWnwWkid9Xdoo2tunch7tLaXN4BnJvcux0PkkdGzwutyHrL6mvfksNKGTWAmi6E2mXTBmKEnOeyXZbJoh306DF54V/J22JVmWiZ3i2Ukiy7GmvaaklWcuz1BKiHnfXC/8Xu5Lzrt25O12O4lAEazRYalVAk3ToiyHyALXjCbLlB1SxmutReeHPkp0gPR9j+l0AhYveFo9qihKpOmwDrSDhqCWRIOOT2stXNtJdSWNgTiPtD3cg3TYcA7pGOC4agDLPazBpI52EaAGx8tYkpM1VgtzmaP9/9H278+SJdt9H7ZyP6rO+3TPzL24BAkjwCB/sOkQaRF8QLJAOSz7j3bYtCSQEqEQJQGySEc4GJTjBoIDzPTjvKtqv/xD1ifzs3cPMH0j4IqY6e5zqnZlrlyP7/qulZlDtQG3Fw/TWPYPMmdXTUkgwDtOuhiTYxXyA98wPicWyB6dsb+jndQns03TFMPhWMhNkmpXiB2T8CPInbGDp/hO1tYkAzaHHHkvOoCdOVHE50PqmpDjGQB+/BKJBckzvgUMZHtibTxW1h69ZC2Iw25Xs/8ymb/b7eLv//5/FD/3+upE47/6f/zzuLu7K+1ElP8IVLCwGCDBnWAK6+HSEgJrmqa06ACaaT3AuYzjWEBtRJQN2s/Pz6V1Y7/PF9N8/PixCAJgYsBHqZQKgxWd1i4uwsFR4Dg56x5jgD30BmsWFQfVtu3qbglfMIcSEQCo5GzLevx9nucyPisZ4NCsPmuCUvqkKDb2sl5N05T1naap9ABy1BsMu5kG71fAGXAxDoB3mqb45ptvYrffl6N/I+rdGQQmABQ9ucyh6/t80lTURJU5/vgXf1EYf4Id62kHxwVp9INSXYFZZA2Ox2NMZ+PeVgtSSjEO+Tjhv/iLv4hlWeK7774riShGiN7C+FxfXxdW3P2PvnUcu8BmWAMukXJJk302V1dX8R/+w39YsY/v3r0rrWtcrEfS23V5MyvBk6Na+X4SYFphXMVyPzd/t97d3d0V2br1hKR+mqbSpsgcKfUD2Dlzf7/frxJabmAnUOEkYU3R+XEc48/+7M/K3g3e52QA2bPP6/LyMl5fDqvqJi0iOHvvldgSEiSgEbU32ewcQY2gS6C0o46IApi2jDTyIShs2SxAoE+rIdl1Zc+Jyha0IBeSE/wz321/xvid9DNXXzpndhgbvri6XH2+VKDPiYafhY4YKPmzZnRZU8aHvvg9rJv3xHhubvlC7xgHTB72DHECMGSd8U1935fq/JahZv3QFf7cVl6cdFoWJj/MovIZ1hr/jR/L/mOI/XkvDLErIs6tiYeiPwAe9AEyw/50C1CsD3yGRAG5cfElrbyXl5elyoj8WEcIiZubm3h4eFidIIZsSDZZN+Roggxw7FjF5wCXl5eXpSWU/WypSXE84xB8Dq++76JpUkmsseHMQl/Gzc1taVNClq7AOI6XZGHKh3bwb2RowM+z8PfIw4kh8QqdtJ1bt2hHZb3APvm/9Y3prG/TtDGO0xeHF5xOp2jaNk7jUJJzKgocuU9ljxjmjejotpNkZIRdkBi7EgwpQmsT9uVN2OCAsq/geCp6xri2iTW6BEFjX4aMfBgKiSp6ALEEpgEDg4+wCVd2Dd6xK5NOzAWiAL+I78JPEF+RoZ/Fz50sgP0sA34OiUhiAu5ijbDDeZ7jD//P/1n83Os3SjS+++67+PDhQ7x7964E+M+fPxcDuL+/X/Uoj+MYP/74Y9kYhXOjRYrgSvuVwTKK6PYSWCuSDhwmwAvHlFIqZU2E6vOrAYC00qBMEbUXcAuItyxq3/dxfX1djt58Oxzi+uoqX1Q2rnuXmc/j42P88pe/jKen58L4T1Mt9+Vj+uoJJjkwttE0NVPm7Pz7+/sVOwiTQdsHZW5+xyZynD5tJZQ6KcvirB1gOE4zn3qVAzd7UQDoOBXki/NgbwayIvDBNHqzFckWVaiU8v0OF5eXcXN9nVsmztWT/X4fz+d9FBj9/f19nE75hlZ0i797HQwW6e3d7XYxzXOM0xRNSvnyRB35mlKKmOvRvE2z3psEcAccExzdpuC2I6pmnIbkIIoDJ5kchqEA+bbNrYTDMKz69mGz53le7b0hmNIyAwhyqwqBAxCCUwHQ4zQ5u515IHfA00/Nlb9zVjpMaESsgBgbnmkvmuc5TsdTPh46rc/Vh7nKepnbGXCU8zwX22a/FX3YJDFNU/tln59yMub2BtrUmCM6gBOmdYe9AMi4afLdFpAK6AhAkyAGYYKtoetuSXR7Dj8z4IFxMtvM89ExPkP1bZvEOIixVlSgCOJmYjM4T8HJVstS75iwfAjQZXNl20TTtHE8HcsRnSmlmKc5Tsdj7ErVoR7Fmn3Q+jx8frcFubzfVW3mBaBH/vj6LZPnIM3Yt4ALUIBdW4ZbksmJDHJlHk5q8AXYS2XJ8xG0jH8Yxoio1V5slXVhP4DBJnEvzyXvL+CYd+S1LBzCMJb2o7V+5BOTliXOe+/WyTI2gny3CRGAnKomFd+tH+H70HEnLNuWTrdEZ/xwc6441cT78fHpDHD71XpQqaSKnZp8MS+6fjgc4u3wFrtzq2BElH0CeTynAvC6LuvAy8tr5BPY+pimNcucUr7sd5qnSBHRtG0cD8foujaWsxzaqKAY/MQaQcYBmG9vb0sLLsAR/4geQFwUpj+WaFL20Zz6ZgCemiZ2Z3+zxNkupnpXRaQUXZuPmY0UkSLFNM/Rd12M0xiHwzH6fT12GV0g1mIrkMj4b2IDYBY/ZIIVn89BRCZV+BxVH+IxP8fPlgT/eIpOyXPTNDFOU/E/bdfF/uzrH5+eomlSpPNR23RLXF7lo4TxJWBBsBe6gW2gAyY/wEzoMvOGdLevQIYmt0nG8Vn2z/ZhJqZIFoi128qEyUx0l6SGWMNcTPYuyxL/6D/5/fi511cnGv/tH/2LUv7kJlsHYQToTBDmB0OF2TMjt10kggSLRbKB8wS4knTYkbs324CDgO8XjDXfC/D3xh6EiRKzQfXP//zP45tvvolo6q2cbjHY73bxeE54Hh8f4+7urizuPC/RdH28vb1G07TlmS8vL3F9eRV918UwDjpuLp1lkM/F5p4JkiWXosnQD4fDqm2KZxB86BdHgVF85tJ1XTw+PBeHh9P79OlTRIpo21pC51QNACQZP21SbFiHGWf9aU9wkH1+fi6nk3ErNJsA/+bf+lvx8cOHiMgBiURit9vFw8NDYQfRHZweYMvH5sIMIB9kA2DD4LyZlJNHABS89+rqqugGzj6iblhz3z8AhgoL687JMIyRDcFbdoVEnLYbQB56DDPPuJk/Jm7WyKd80buL82Nedlp+FnMEJOBILV8cPWMikGzb5gD1nDgXkaJJbZyGU0xjPTLz6uqqsNVZR9vY7+vpQlTcWO+np6eIlM+ihxCZ5znu7++LTSIXABbzGoZh1a7G3M3i4GtIErZ7Fwiw6BJ+pj0nsHb0+CI2iuOv0GGYy4gaULB51hSdN5Pqkr1ZLFcVWC8HHYIUYAE9yIHsy9uDx5FWzPURtZUdz4kJeuJqDL4dm8SnZcDaRj46vAZffDXjs1xMkJi5xGdg426jc2xB5vzcuu4WGeTE9+F7kbHbjLxnDxLG64gc0Lkc2PO9TeM4FvKuVrZr2x/jhp09HvPJgBBAxEh8AVVjbKoSPvV9xCP7RIM/GNt8RGvdhMs9QrD8JKvEGPwKtkx7h/cy8Rx0nnWjQurkDzIlJxO7VRIJ08waUZVmfU6nU8zLHMv5PZeXl+UgC+wWvSDOVD+4BPswIuqhBtOZoGpTU8Bh0+R7N5ZliUbJJjaKryE+Q/jUpD5WG4ZJNLZJpqv4wzDEbr8vFYaLi4tyGfDpeMx3gzV1bxfAE//KeJAfrbFOHvH96Jl7+LcJOTqGr/D+L/6Nz0EXtiQNGIfkFPsCd+H3WQ/03NUD3juNUzRtvagSDAB4dpxDD0yYtefkJCLfz9ZE3XhvssvjRHauqLJ2TtI916urq7IX2D6H/1wViahkMzpFcsdaYv+ufkC2Oq451ru6ijzbtl3tHe66Lv6Tf/YH8XOvr040/pc/+dN4fn6Oz58/x7ffflsmwYBQJicGTJhAC2MDe07PNSCfDBrGAfYjovbEvby8FJCN08TRsxcAB8SzMIxlqWVvl/qXZSl9mig82fdPlfSOx2Pc3N6WvQOw+d6fMqqvEwd2d3cXr2+HGMZptek04rzZu2kiLVH2e7CwERE//PDn58u73hXQ63YJmFECBGvAiRy0QdHOhRHSu81FaPv9PqZxiuOxXl7lI3ofHx/j8iq3K3348KEYk1tm6BMkmUEpT6dTkTN94uiGW7JwHgZUDvoEVgzw9fV1xZj3fV/awJgryaLbaNC3aZril7/8Zby9vZUWONqHnMydTqdy7DHPY88Fa01rE/M1m0eQm6apXD4Hg0j7HQk8wJ3g4wAAGwlg5ffYIcm6e33RNcARv2PPlRN2givPhWUDuNFKVwFhLekDcOgtJ2FnY/U4jvHtt9+WhOPjx48laF1cXMTjw1O8e/e+2CVtQACIvu8Le0sgIjCR2HCEsw9rmOe5VPpw/IAk73lg/CTFtGKwDlQ3AXbMg8DvUjbPwnfZoROAm6ZZ9TvjVwmWTgxcpTDABnjiY3kmuhSxBm4kGAAkxoqtGISbJcvjqHNDN7Ku5MrStqqRdS1f6mdbBLACILAffpbHnO/9YL5bcMb7kAOycz83Y0FetDchY3yee+K3rQ2Vwe5WIJZ9S7wAWq7QuUppQAVhsfL/RRb5BCN8NXaV5VCTGHTfSSTjxlYh22gzpmJY9z7kthj0Db/l9hO+axzHciJUHmeeh4/cNOuK30f/IEW8v42xArTYt8HhMYfDobRbUa3zXsMs3ybatluBz211Bb/J+vZ9H3OqesPmbfYV4u9Netr2+Du+Yzx3Muy6fsXWO4FHT5kHduZ9TYwd+Zu1NoDGXkmMkO/nz58jUoq2a+PynAiQcJgpt+wBwSYntqQEdulYgB6YsGV8xCBsCjwHViJm+JANrxGVKWMPJzL4MmSIjlnn7IMggWzLjNtkA7IgJvMcJ4f4+13XRyPdxZ8QW8FlxmroAD9HlszBlXX7XubrPVBOrrqu3hUF7kaHXeGIiFXsJB5B/rpzgbFCpEEOb+X7n/9f/ln83OurE40//pf/TWkV+PjxY2EJcEY4NZ944gzNWR2DJPGg5w7gQ7LCIlxfX5cTY2DQccyw6LTmvHv3rrS84PS3yQZCdikPEP7w8FBAFIuKkbDZmuB9eW6roqUJVuru7i4O54vHfvnLX5ak6u7uLoZxjH53sQpaOJa+6yLOZTkSg5TSuW98iv3FvlxGx+VRJF8oJsDOThUwRDLCyVP87Pvvv4+IKCz66XSKl+e3Iks2+y7Lki+rWaZydCibQUm4ALv//t//+9XGXQLW4XCI7777rrRuOVNmzBgWcksprdo/2PNAexEnfnFK0TAM+fbppW5iAhhhXAR1l3ZpIcPhwirgjDiemCoDQMttgRzbPI5jadtBPlSAzBKUtqyoTJPbyHC+nILlz6SUyj0BpR++qxdUwnqaEeEUFf6NQyIgEXBwPtgrYALnSDKBY+26Lt69e1f2OJAEIV+XkC1LnFllyafo2noQAu7Jfc44YsZiR8z3WBZ2yvZXsN0eG74BlpXA5V7tn9qPgSz5LtaNYIb9IHezlug+yRrfhc5uAx0gCqfvRCOiBh4H5AKu5vUJU+7ndbLpxJ5/55u5a3uL2b7ct17bkvjODJLbWJa/vPXJDCoAjuQlpVit4XZOrl66GsH6owvEE2TqfRs1samsrCuJtjfLBkBkYDHPtXURHXXCyDzxdZYzyfVut4/j8VQSElcv5nlcJUu2HwCs4yt+08kT80Wur69vkW9bTqsxQzRBIPokopQixnFYkXbsr5umqSRhrloBGpGxK0sRsbqjKiLKaXgGnls7/v777+P6+rboEZvmwQAmR/CXyHOYKzDFZ1lvfN8H8mANDQ4LlnnLF5xaN72u6CoA1r/DFkgIkQcAnnEhL/xurRoORZ+6ros5Vf8OBqO10JVQZAGItK822WT23LYSEasT77bkheVEi7VjsFuGeB5zxqcBgL0GTiDwlXRSeH7Ii3E4puArjVn9PhM3TrgLURUp2qZW8O1niaNgA8cgcPA2AXQ8tk/GvvkcZBlzJpZga+BJrkvA3vhuk0nZ/l+LPNATiH/kzEFHxCO////0f/3P4+dev9HN4DgAyuIAWjIpswDueSXoosxMgBYPZ3XbMifZ7/fffx+/+tWvCjtDjxrG4U3PjAfWihYvlDpinR1+99138f333xflYg9C3/elPIgBPzw8FNblOAzx+fPn+O3f/u0SeCgNtqmWQ0mksoHOsai8ejwe44cffogff/wxfvtv/I04HY7FSQOEMkO2j2EcVkHSDgSATRJkVhtjNHDv+3zCFK0tt7e3cTqd4he/+EX88MMPsevzmeCAJeR1e3sbh+NrAb6ATYA+m+npLeUiQtbyu+++i4i6cW0cx3KLNwbi/SQY4O3tbWHkImJ1ehkMP7qXN+ZdlDEzR7flYZw4MPQGnSZok5x4M5TZc7PsZTNhqqdA0A4DaHl7e4vjMd8jgmPivVtnQEWEhI4AXjd4nlZBGpDFMzBtQAKVNd+FA3jg6D4cIIClsDfnahCOF1sDFCNn+wACJwHI5VwDcioe+XNNDKe6KdhAZfvcZVlWTCy24sQPhw/42LYY2Y7wTWVvQaptSFRWGAcJG5U1gjw64lYp5oxtWtcNBtxz7T0aBqusrXu5HaSRCTrlRAX5bJkyXu6bj4hVcM1+5yLadi0/5pz3a8RKf2Esp2mOpqk9v+gViTrfZTCfv7u2aLn11QmZ25EIxGYkAUTIgTXGXwAcAMs8jzlgt+gIpyQBNhiHmV7m5u8jZjoBYZ7EUMBxvvuhridxMcs92zX+kXUwY4pemwFmXQHNfNfb2yHatlb4eL9tHf1Gh/KYxnLMKwkN7Z/IBluADPSRvOgQFZ2u64o/Rc9tHwZa6DsHyHzzzbeR9zfW45VJtg+HQ1lDiJqmaSJSiqarSZUPEjERRYsXtuAODdtt13XRpiaAYIyV9cMf+TANdJn3G9Daj/9Ukm0cQJcAp1FN0xRLStGcLxYEezw/P5cWua1f8Dqi767Y/NSYAKFU7SGX2E9BnGK/KXrsk/Aco5zMkExZn93aZP/lBJn4QxzHRvBjzMfYgbnzbNYAfGLCAtl3XReXFxcxj/WYX8+FOWzXl9/hY/h7rf7Wrg7LwhgBAswYmt/Z3/Ezt9CDj8CkHz58qPqrggH+w/cLOfkymfcHf/hP4+deX51o/Os//u9WzKETBoDg6XQqgJcjIp3Nw2gASABmLoETRAGiOGnew4J1XVeywYeHh1Lu4X3u03WAJqAQCAkyBGeqCQBaHDMlzl//+tfxe7/3e7mtq6nldZx3uejpPAYCAI7rNAyxRBPv3r2Lf/fv/l3c39+XUyCalGI4nlZACmVt2yaOp0MZFwwPVSG3raEMJAJ2/CQIFxcX8eHDhxUoAtxeXl7G4e1UHAWnctDqlJql9LVzwyjO7Pr6Oj5+/Bjv3r0roJXMGqf0q1/9qlzYBvvH6WH06r5//35lSHwXusCJIN7EbtYX4yK5dOXBYALHzHMp1/OCdbBhkzhxkhUgcp7ncv8Cp5q5omOQzgtg63FhwC7L2/k4aNqB83kcjoOaq4vosp3oNE2F0YvILBX7NADYZpDNsrjUzrjRUT7rqhGEhUF4tdMU0ziv5orNA1zca4oMPQZkZpbISRnVIuTkgGY2ycmQWTIHG282xhcAWPE1h8OhXE6ITtIyx2fRk20gcXsE/+ETtizYFpAwXvyQq2EkJE6kqLoA7LdVkKwnFQRic/mgjUO0bfOFfWV9X4LWKT8TXXOwh5nPttNG19XjiZFvTXwyswcLjoypFG8BFYmJ5xkRhSjgvYwDYoA1p4IPWGKvgSvg6J/X6tOnT3FxcRF3d3clNjFng70a67pzFWhZ2XKef967YkABoLX/59/oAGvInTSw/HmNutKzjd/k/hraOa3jef2beP/+XbEnjk12xYzkyqCV9/t0N1fC8cX4Jfy52XHLLZNKV0WuPvnSto0veXp6yu1fTRNt35XYYaYf+fG9/Mn6+HnMZ1mWvNF4qS096CFElZM/9l6gB4BiTvViDCZo6brYfn9EPSEPuUdb9wJYF5x0m4gwlmOd0GX7QscP/tzeUE0yiL8lkYYMqy1vqVTsXB1lzPh8fBqy5HudJBnroRuuSP8UjjSx4TiD3dlPuPrKZ/uui76tdsyfyMiEhb/PstnCb1fhHHexI2IZn/V3In9syGu2TaCRHR1EEP74E+OPbaXUSfTV1VX8x//k/xA/9+p+9h3nFw4XYAbDBlhhMWgPoccSZfIkEQgXv+DgfOQfrNOWqWHx7XRwwmyiNaONwwJEweTQekVgpxXCZ3ub2SZQUVI/Ho9xOC84c6d1bByGcmQjSgujczydoj0Hit/+7d8ubE/TNBFzZciapokff/xx1S7T9XW8LguSmMByU+WgrOYgzeZvLkkjG8Y4uN8DmeIcYMGbpomLy11xMCQBfF9ExN/8m3+zACyYJU5/6vt6FDAOF1mz38FgivXE2bIOw5DvL+GYXk7Bwog4UQw9tdO7uLgoF/yRKPh2ePQQhwaDTTLnDWtO0Ha7XbmVnWBhYGddgWHn2EcCPM7Fm73Z80HwdFuPHWnTNOU4WRw3DoT1x4mQlDM2Agxg3n3Q2IAZXWRqRpX34BQjcu8z8+37fDy02wHMYuX1bWOeKtOLbgNgXGZH/nwfQYP3uORvsGWW1MCy7/uip5YJ72NNmDMB0lUNV4AALXd3d6XvPGJ9+MBPJRS02vFe/2kQjM7Yp5K4+rQx/DJj3DLhJAveF7WtCFV/m1YtDOxfGcchUqqgApvKVYO858BsoeXvVll+lqt4tYrEuJgPcibgMVYnStgmcnE1h7iBvIhvTmbbti0tpiSJ+GbaiA2eIyq76mTUx2+7xQr9cQKadakeEmBm0nZsn+a9ZxyNPY5jqbriOyKikEvINI+zthmSMH369Kn4a/yfQVfX5UtD0Rt07u7urujPsiyr48qxCdbY/pz3931fTnpkfNYVJ6p1jxptfbWlya2NVPrRNXzC0qSiM/hCfBKADRvr+760qfICoHt/Q8y15YW+dk4PREb2wyYM8FHbPQ+QdXw3fp01jKj3b/Ae/CZ6iG9BpiRYBtPMmyQJHWfd7POJ9ZA8rBNVJcCxx+bqrKsLYEASdvwNDLtJKlqPGTfjMtAGqBMfnYzT5gW+wRdhV5aXYwVzxNbbto2+62PeVDPsJ4yrbK8m6p1MOG47scFvsDaPj4+FiAVTW9b2r/gYqnaM1XqLDm1JZ9aI5+FXPJavfX11ReN//h//p3h8fIz7+/uVc88L0Z2Dax8pUry8vpxLMxcxDKe4vLwqQnt95S6M3NM7z8vZmJfouj6GMyvUdrU0WZV3jt2uL205u34XN7c3Z6A35FMfuu4c9FJc7C+i3/UxT3MsscQ4jDEvS6SIaLsMaIZxjOenp7i5vY3D21vMy5JPjXp6jP3u3O40czlKFvbF/iLarou/+OGHrExdG+OQN8oN4xCxRLy9vsTV1XWcTrUU3KQmjqdTpKYtLUbDMMbf+lt/M55fXuLu9jYOr3XzL0AkO6hD3N3dxrzMWd7HY1xcXkTfc54zgTazTQZwvP9wPMbl5UW8vLzGstCekGK36+tRgE0Tj09PcXjLx4dyrNvV1VV8+PAh+r6L/cWujIuyrdmr6/NRtLBn2fBy1eX2lqMCm3h7e42b63wG9TAOMc/ZqG9uruP7//B97Ha7ePc+H6X87t27eHh4WF1K6PYFAhPAGEOgdOyE1Ywx1RGXMjHYYRhWjhPAi2ET1HBUb2+Z5czJRcR4vuDo4vKiyHoc8xpFENyamKcphjMwd4UEh5BSlhc2UtjBZYm3w1ukSNH1XeRNkW2MY02SjsfaWpQdWWUEcYoO+BFR2FTseV7miEgxn3uah9MQ/a5XYJ+jyYMMjpp9fHyKvuui67s4HI5xsd/HfGbRnRylVBnA02mIXb+LvHm4MlsEXDtEfkfgBCgawDjxwHHyLCqQdsCALXRrLnZf93oAdHHeEZWFMvuELTBffJmrQq44AAJcDeK9fDfBl+ciQ/SPgGTgzVHGJh3wxRAAgDIAeUSUFgr7kQh6e2syl9diOgPwVCo1Bgr5OOEaqJGN9zigB6cTt99yN89wJo4uzzZcT85jHtZhxgSYgvDKfrC2bxH8ObyCZ7q6wrMNyKeJjeZNXF9fxevrW7A3Bd3w6XckJoBLCBYAFxUD2jvz75Zy5DlzQz+G4VT8+zRl+ex2+7PudNG2XRwOb6VCxXuenp7j5ua6tBxl39LHbtfHPNeN7PhJCBeYTUAzetm29bCXTAQd4vr65jyvLsZximE4rdrzWOtlyZWZbAPzOdHIJ5PlU/z6c3K6C04yqyw1J1fmk7myn9sXMgRZmxyhmoB9FYJxGqM/20Pb5uNm53mOJjURKUpr5LbyVBjtvm58bpom2qaNBIgbOV1simVeVtXkSOs9SfM05SOfz348lojUpIKNXs82ij9DF6ZpirbLcSXb1hKxRBxPp2i6dgUUnaQBwiNqC8+6ara+kBM/ySEcJoCcjNUYU/doYVd0H/BciELmg+6xL4OYi0043jJ2vgNisZ7sWS+fQ86Qs8jAFUXWxZUN3mdg7sRjmqZY5jnSGcfGUv3aaRjKKWOMwXGpaduYxjFSkwLIkSIiNbn1rmmaOA1DpLMPj5RPMmWep9OpECDMCcLIGAYfCVarREbtMtp+xtU9yxC5OsYQd/5aj7f9X/7kT4vhscj5vzbGYSoLSeaKE0JZmQAKDVOSz++udxzw+U+fPkbX9eXUGI70JMmA+SZ4uxTlbJbs0OU4G5JPMKLUjoKQ/WZFyfsrYDVgGLzQvs1xGPJJC7QqwRZSvo7Ixv/4+PgFiPJRa+XW5NMxrq+uzwG5OhqcFe1Tf1kWyzhh7nlxnjgJgst9Zln7Pp8QdHd3F4fja0k4YTTdekS2zPjms0G+vNQTeyKyk7u5uSk3nfd9v/rdMAxxc3sd+ZjLeXWmOGBgv9+XY5eRH9/Jf8MwlGTC/ec4Yhsf8gPws06UXtFbnlHKyGMNbmZIqTKgm+ghhmyHzHt8IgQ6llKUhB27Qr8B2mZqI+oRvADIJfK/2adDJSXPtc0JRN/Lttf3Y2yDQekJnqdIkVaMPmv0zTffFHYHGwBwuirqUji/B4i6fL7tbUVmtE2QQDZNPascR29WDRt1MmK2s4APVUxcseE5OHInJwYRPMf2Crh1MpPP3+9L8ssYANc5Qa0BjzU14KbiFVHbSNxChq4AFLAVs3bYsdtH7ItoTTGr6JYoB2r0JaUmdrt6cz26kP3HLvq+Ftaxi7z2XWGA8a211aPqqBPnlJrSfmT/H8Em+arT6JarpfgC2988Z1D+9va2SkqQjys+yGUcITbWxwmjYw7oToLz+tZNmSSLrnwhP7c0UAkjFni/CTqK/HgGR3Pj4y8uLuKHH34oPt0HDPDZaZpKmzJrzncChvu+L+1izA3Zsu4ZK3QRZ79hQIZvBhM4KTc7bvAImLq8vCz957DuJPskUdZR/o1f3u12cTydYo514m22F31D7q6iwkh7LiT5l5eX0TZtzMu8utAR+RJjWJOmyadQzhuWGpnPqVYcsUnLx74IO/F6RkQhGtwFgp4ZfDuph7jjuawXa2X8QWs3PtqV6q7rVndVcWwqZJ0JAWO2iCjdEiYA8X9Ua6otVtLAuJT14j9+7oSVeOV4ATlkUmhLeJwOx5hFOtk/9Pt8ZxfjZyzWScsdPzUPFb9ARtpn8j2uTONXHMucYGE3tgH8A7qDX7fd4F/atv3rTTT+P//2/10W3Wzo4XCIi/3VCizhJFA+s2J2xhiHQQgJgp0AAZXd8QgNBglFQrkA6xg3rQwoPKCasTLO7YY3lwBhNqZpKqc8MT4Mf7fblRMj3DrBiw1bfd/Hu3fvCnjGsC8uLsrJGyg7ZWtvpD8ej2XzroEmc7y5uSmtYrD7MG2ARxz+u3fvSo8zLSPumQRE4SROp1O8HV5imnJLj1tCGBNjHYZBN2BHnI5DOcmJFjSU1S0cFxcX8fHjxzOTdhmH49uq3cNBAUfujNvsIJfUsHmy67pyDDKAj+caBNECwtqa2fBpJDkhfYvhVE+neHh4WCWTOAB+T4Dcnh5j48fJ4nB8AgkAmnV3b3REPXXIyX9ExGk4FD1D7wvLnOoRxDzXjB42ybxoiaAlB73kvdgMQQxHTfDZVoQsByeGjAk92bJTrAPBiO+w43YPu9cS2WLvyBSZ8JmIWAUVEk1XyfBX/N2JjX+O3+FVWwPyHSJOYBhbxPqUJtYYGTnIYX9OhlkTZAOA3SY1Tr7RRycqPM++FgBp39n3fTkEIfuNLub5p+XL3g50wOX9zNTWVjzLNSKz2maaa0K4rgDZt6e0lLtPtkcdL8uiSsC0Os6x7/dFv/gMhzVw0hzry+/yqUy1ZSylVHzKdh2Qcb7j5T7yvpYsf3w5tnM4HErbcUSUKhL72LAfSKxlWco+CMbBOtlmSFaZM3Jh3b2fCD/s5NqsucG238d/4AOq5QbsrBtrymsbn40dGLPbWwFo+B5YXScQZpqLjjSp7L+kZYqWWyc8tnkDM8bvvRAmHbAlkj63QJKsMY+kViy+FzwwzOtNzVvyAP9ZK0nr/XQQZSU+nPexmczA57CeyNMVROyL2MKJRT58hjXDfpEdJBRVM+SG3+GAFuI330syzfv7vl+d4OTEivnyb+YGKWcCkrlb/x3bsAH01zKkpXm/38d4GmKZ6+Zs+7xpmSM19SANMBk6xc/RiRLjxkoiUWHaxgWqHmA4JwhONtBtXuinCSPiAnIyCeSE+2s2g3/1Hg1edigAeAwHJpUMjSDPv82UIRgWC8UE0LoqMs9zfP78uQRRFv/h4aE4GQAqp9+gFAZJBDmAKGNgfM4gnR0yZgwLh+NxPz8/l0DDuOhXxcFFRHzzzTflOFycCeCXRSSY8H6Mkct6YLmY90/9Cbu1zeBdesSAYM9KNn6e808F367rSgWB/SRcOIc+IEeD2XEY4+3tWOQK6Cdg+EI2dGIcxziejkVGZuXQOfQBvey6ep8IRvLtt9/Gw8NDcQokXKw/xhxRb5YmccMgAbdOTJAf3828AZN2aHwPbD8vGCBvDmac6CZrYLbebD8BAAfEPg2SrXKM8lx727fOaV7msl5bxtrJ9OfPn4t8SHoYO+PGIVFlM2vHehlUREQ5gAFWzXaO82f9cYQEHmzFrCD6zVrBrFmGBHn+DZC1czZQcBKAXzJgYc4AyFyZ/VSO8Y2IFRGBX8jzaeLysl6AxcVpeYzVTXvu9NEzBsbFYRvIit5wxmm/zLy8Lmb2+Qy+DlszeAbIuOcXgie/vqyAoC/5Z5W9M3jr+30BDvgj5jnP64MMAB+51/v6J+07/6xeGOkEiksc8WPMOY8v4vn5pYwDYEWLKL7s06dPZW0j4rzPqc7Vso2Isv7ofErpfOJgE/M8lHkRz5AdCTx6ADM+z3M5in1Z8gEtrA9JKf7G4Ak5OTayj80JOXbtZMHVYPSTf2Ov1hPkgG1xJLnljS3jz2yTfJb3AMqQDYQEvsEx1mtDtYvvxL+O4xhNaqNp2xUeWZZ6ZLdBGS/Hpi2Y3SYZjo+ughhz4EuayJuOHUcsL29Oh9zBJ1Jx9l1NfBdjQi7ID92g5Y/KEe8z8EUGPN8v5AYOoUVwm5QSsyG3rKPTtL5wkpNG8Tc+KY6xWEcdJ7cEhwlaKuHs/Vz7oHWXC3PHBlgTZF6SozOZ4P0e5ejdsSbIxAvW3sSHW5tSytsCiMWZ4HxdVWZMPPN3E922YeK5O0EcB7dJG+vFfire62Tlr3p9daJhFtXl6GyYsRIIyoIwaTMyG4eywxC2bVvuLMBRYHSAbxQShbi8vCynD+12u7LRGUfHyT8WiEt8CB/DcB8ii0IQYEzMgzYv5oxsCLJ8nrI3zA1HitIKRjWBTcQ4do6B5ZmMtWmasmEV52hFIYi6opJS3cgeUdtzItZHsNEWQ2Bi07uZr5RSXF1XmfB+DIQgfHNzs2IRLi+v4vJyWlVJXNanEsM4bMDDMBfH6ITPp+bgVJhfSqlcAufeaLMrfA8OG4dlJ2tjs+EfDodS/m7bJppzUIJleHt7K/tbeDbOyAmMmR3GBYvjEibrzAvWHnnWFr9Uqn+AWeZMkgoQZpx910fX1SACq4EuEuQItC8vLxERpUQNg8nfzayzFgbvyLM9B/NlWcqBAsyjOKiuWzlI1h32zeVf9J/EHHkCvgGR21Iw/yZRZmz4Hb5vm+Bhk7SN4Ltc/s77muqlhQRziAKqAVdXF2Xt8UNt2xb9Suf7JK6urgpjuL01lnV1OR4gSrXz6uoqHh4eVuwVQJU2QhIq5GCQAzggyUJuXuftGOZ5KUF3276VUpRT/wCFfDf7Mdzuk33JZYxjvUzSupNJhBqsDaJZL0Ca7Q+wCShF/2nXJC7c3NyU05j6vi93BXVdF3d3d6VKQkWwab48Yhw5kgSir8yRxI9xMWaOEUUH8YMALH6Gb3ACan13Dzb+bVmWkhyawcaP4UdJ2DktCP/i73BS6DYUCAPkik9ysrCtFriiBgAl1qGnTlJsxwbvxHR857IsRe/wCSRPx1PtfECu6BBjsT/mufNc923hp0wqWQb4aZJu78Fgf86yLDEcKkGwioFNE+NpfbEi34kfh+hEpuAFbBGQTtUBf89/jqcmCgy6l2UpJCnVfMZk/4ntutqMP0PvnQDgG6dpKvvMaLEC0wHUIfewnQ8fPpRLjVkLZIK93d7eRt/3pe0b3XHCytyNH431fPkgwJ94Nk9zTEuUrgt8YpbLGK867AB7xvfii53A58/W4/BZG56JzBjbPNduHmIg87HPM+Hl6rcvSvRnHLv9nT/3+o02g2OwDJzseL+7LE7m4eEhvvnmm1Vmb1DvLLJt802cgE0MD2GSIWKITNgL4oCKQmAkGBjO0uAEgOYj43xBXtd1K0YAh4CBENRgvs2ywAhxSR8MIsaHs4GZYiPTsizlLPGt/Fx+Rl5bReT7SDIwamfpOG5OlJjnuQRNs3kETJJFAl3TNLHb19OOCEZmPRlPRD2+NaUmpnFeGbDPqEf2fJ4NaG3XxLLUVinGTEChBcslXlc4fMwb+rMtaeME/extUoJ+sv4RdZ9H27QxTes+d5dAmaeBvisi3oPAGGGJzDwRIJAZDomA6NKoy7roUaS5yBU5Fycb7SrBY00j1ueCA5RNCDAmB5EtsCOQOihjr4wXOwe4mPl0BcS/47OsEeNwEss6eCMjzzQgpjWTcTIXAzu+0/8hB3TDjCWkigE0c4K1zVWJvEkWeaKP2ce8RsRSAq0ZY+xyWz1zhQ7dmaZ6ySLJOfplRg2bwuc6CefFelj+TnqRKYAgpVoJMLs4z1Ps95XFZl2zbdTN4i8vuV2z3kif9YXnQQhl/d4X8Lhm7FJcXOxLsm9whWwAeCSOvE6nuqmZ3+FrXAFGNjl53sfpdFz5GmyFWMSpbNaTlPIlem7Tsszsl6l++94hAwT7B2wZv+l1xJ4Zl9l15EAChXyQq32hfZYTdoN1/r7VJX5vEEXV3FUC7MuxxkkMOsNR+zDAjMdk1ZYgjYho2ibGuZ4i5vY2s7kmYvAZ7M+DJTfpAKFhrGBQB15xMtVEiuOZRU4pFSyyLEscTseIM6Fmv8V8XH0j3o5jbhsHsN/d3ZXLf0l+TNZiU/M8fwHeSQgByU9PT6sKG0AUOWE3+ApX6dFzxwcIWnCR798wbqRFm2TYGJR1+jf/5t9E27bxq1/9qtgAdoRf3V7QadzKEf0cRgPZxHo43g3DELEs0TX1WFn85DzPMcdSEg3jAWyQ51vXpmmKvu1iOPs1ZGifjNz82YiK+Xg+MkQftvecEAc8L+Me/Dz68jV7NL66ouGAg0HyJ8pEZgkbQnCycUXU/QsIwApo8Ezp10kFi+kJIwCCDXsAHJABFBH10hxK0oDybaXm3bt3BQwCWLn3Ywt8udET4QOuGIPfD9BDUQCQy5JLjAa7jM99hAbLyIV+eQATc+VzKDDJFd+HYyAw22ny/WYkMFx6ed37uQW8KwOMyvLwWYIh+yVgjXFKKaXY9V08vzwXwM53ATZpRTHAdakXwzMgYnzoEvJ3wsE4/F7swMYcEXEaTnE8DCvw5vYkSsA4VhJRJyS8nzX1HTQk3bS34YRZQx+2gJPwmiGr1NReS5ewc7JUezIJ1Hb6PIs19zwYF3pPgu7gb9aToGL2yvsdXEliTQ3OCaJOrHDmduh2jrzPVbFtckrg8Xf8VDUMG4ZoIQE3K0Q1ArBnAAjLBGmSmbVDcNoWa8Bei17n/QMGnTgBKJADLDz7o7ynxADESQjjAWgSBK3rBgPIGBvo+7603RhwZh2rnwcUryse675qWgz3+7z/5/n5uYAG9rTl57XlZDsfmT1N643ETi4jopx2w9pEVKDcNLliTjUygj7yetobyQsAARuE6cfvTtMYr68vcXV1VcaGjrJujmWckHV5eb1iqlkX4gfA22w+vtOA2TGVF3J3bMT2nORhT9sqr49bx5bxY/hQqkw8i4QI34EcIPPYP4L9MFcTgtgfoNJz4OcmbUjYIWx88qBt3+QIetI0bfTnOIANsFfSdm/5YkMXFxdFRiSO8zyXCjhVXBNhro6SGDGmNqXVnIxj7i72cRrqJZuOqdYDfAp+ab/fr05jxG6Zz9ZnA4ItO7BgiR9tbpOCeGVdqZbg0/kd1VPkHlGPxqadjqot5IgrQWA98AMHNVChNfZomib+zt/5O+V5AGySBeZLF4ZtHPugXQ1/6ZMtia8mvPqui2WqJ9zh57BRKoLEcJNEfAYS6eLiIsZhiHTet0W103pobIKcXJWlGopf2VY9HZeQB7Kz70D+9j9f8/rqRONwOEaDcRzyZuTTcopWjKEByfF4LHdEwJK5n57+RwdDKw8C4TbobbLCe0gsbm5u4uPHj6uf+xQWQJId2YcPH2K328Xt7e2qPF9A7jkhIkADnmBanp6eSlsYToaxmGUBRDqjnKapXGLjnkmcA99DBs383YOHwROcfY8E30tAQynGcVxdlkR2z4vPuppSHfC5TH9mXtumicMBh9PEbtfGMufjjqdpiq7t4ng83xR/sYu317cSEAnSbMZC3hgP43h+Psa8nI8mnudYImKa8pn9wzDGMucyctf1scxzzMsSy3KuqCwRyxLBGesR6XzqxxLTOEbEuV96yafKxLJEd76AZ5rzSUBN0wZHLU4jSXCK19e3s9N6CzasMnZAH+xce5bDskTkI3ybGMcpTqchIkW8vL5G3vwZxbiXAg5SjCMnaXSR0hx9n495TCkfucn7AKr5GNxa/SrAcpkiRcTb4a0AsbY9tzHOlY3GXhzE0YGrq6tVEgbQwTZgzEj4XIF0NZEkwi0N3qxpkNW27aoShoxoe6DiZgbR5AL2gQ3YNu10AeluP0QmkBcOmttKE0DKbZoEBleW0A23JOaxwHx20TQprq+vYprmaNu6r8J+ymvDOMxAw47ygtmNqG1YBFFujWcdnAySbDEnAmvTNKtDCpCnL79jXiQKJAL5uSclhr5FPn/m06dPJcHyZkT8FG08JIQAu92u7qED1NQT9Srjvpzt/ocffjivRxfffPNNNE0bT0/PcTwegiOj0Q8SGnTFFQ0uDCwbQsfxvMfuGKfTcO57rpUuAPw4TmcS6zJOp3xU7DRVEiciCmnFmjvBYG1TSuW+I+KR9+Zgs67oucqPXri64CqKkxmDUYAotu52Gdsg+r8staLOz9yKxDMAbTDaZrn5bETEaRii7dro5j6atgmO27+4vIzpPBYTaGARA3J+l/89xCKiEFAIMHNijE6bDB3HscTtl5eXklzTHQGxYmYam/GaN00+MneZq76aZV+iJlDEmu1pYeiH24G47XlbqcGGt+SDY4nbvVh35Ives24PDw8REaVlMyLvUcMmId/o5sBOIW63bT8kRd4rQ/sbbVCOScZzVCtINt3K6dYl7NJrY5KNseJfjUmtX8PplI8pjnxsbaQUkSLGaYymrYcpeKyMz3PGJol9TiSIIYyF5M/4qmnynVjcu4FdkYS7gg6BSFxm/tvvQha/yeurW6f+5L//nwqrQbkH8An4wPmaKcUpk3yYSWXA/BtBYkwoOuVlmB2GTGZLjyDJBU7LlReACMrNd1HiRNgOiHa+bFaFoQYc2ajbtp6AhIxwKhgv8/Ri8llYCYzfCofc+TvO2EGC9TCIMkPI9yBXn9XOd93e3sZut4uPHz+W9WJtbaRmf3EsjMdsCGvgJALDtTEhB9rGkK9LtRGVnTGL4+A3jmNplUOOrD+AgWduqxgAVuaK06aS5VYYACpBCxkD+viezOau+6H5znGeYn9xUe4iubi4iB9//DEHt34XcAXom+2GF99TGefK0LvsCktptsLrh6M3gDbzzzhcLYmo7YZmYbym1k0CqTdLwziyyQxmxa17Tk6Qo9lJM+h2Z+M4Ft9hu+K92ImBg8EQ8nXAIRDxM0gWV5yQG/MnAFjvzTIyHp6DrQMUeZbZJdsYm3IdgEl6lmVZnewCKLD9L0vdrMnL7DZry58+eAI23xtq7f/8DBMq+J2IfA8L/gm/CGjHrszEsYGcPRzby+Tatl/th6NFBFBmoO/2DMbOvjq/ZxiGAjKsj6fTKe7v71f75oh7Bg8RUdhZP+v19bWAQOTa930hg+g95zlutYCgwybtGwAsHPd6Op1WbR/Mw0fnAiis6yT/JKwch8peIQg4QDXVCWRK/Efn7u7uig6acLCfwRaQE2vGfUlgj+Lz5ynarh5nvGJnh3G1qdvVTmxinmt3A597ObytOi3QD+SKfySZ+qkuA+wBLOFN+I5vyJ65m/1uIn0RB/Bt7a7uK3H84ZlOQljTeZ7j4eGhYKEff/wx7u/vC06AUKBSjexdjWIsdEv4oAH0pm3bosP8jvhlHeTvYDn8+bIsqzZf5Mz8nCgyHvyecSVzcXx7eXkpOIkxeI+QMYJxF/828Yt8sHfmxfezPvhUE+Z8ntYtbA2sShIHbuFgAPY3ISsn+hH15CxIcNuf5RNRTz0kQbHvt21u9RPfM45j/LP/4g/j515fnWj86b/+kzJBslrAgBcVBUQ4BAs2SFPVKANItZWCzzdN7QskkGDgVgYEgOLBPBCs7bwiYlVVccm4k5MyCCcg8TsSBUqhZtOYCy/vj7DisNgRNRi4TQUnBPjk53yPgZBZZQK5y5x2Ls6Et8puMOCghuOC4cWB4izbti3Hm7LuBBHmzvNdwt4mW8yPtWdcOA+zxU40eL43XPF7nsG/fYDA1rmzPi7T20H6kAHWDjnhzAk06FZNvPJldzZU5t/1fUSzPgmC9e+aNrMhqZbT2RTnwOwkIo8xs8PYqC9eAzhExMqZImscolkwJ15m6plfRBRn6o2uyNdgGrYMW+D0NjNXJgeQMy87Qr4DRw/4cpKVUipOnM/Q1gUpAfA3qNrahYG7KxMmE8qeIiWu6K7tAR3mfW4HNKh3Egzrh8/wkapma7EHkhSqC95Y7LXxJm7YQldfmAOMoKsbrgJB7tAu0jRNAbXoJhVrM6SZUR9imuZyQhmsJkHUQHq328Xj42P8jb/xN+J4PMRulwE57VP5hJtcxWyaXOkGmOz3+9U+MCelVNaRO2uNj9lWtkl4sAN03j4I/+Ck3Em/fSZtWuirE1/HFL7Hvo/nsqeGvxMHGC9zYg1JLh4fH4vdcz8GsodV5jh3dBSmH30GVMJ6mswy2UDSiw9A94j3vM/7thi745j3RELYhAA4c0wpxb6r6wgeGcexHC8P0215d10Xn58ei09h7Ngico2o+2XMjBNTkKPfb1/oJIY1cPI1TVPEnC8QZl0BheM4RtN39X3nl30M8kHuEfVeLnSE8eLbSK6en58L7np6eio+k5i42+3i6emp7As9Ho/namCdP3pOxcGkxDRNpXrBWPk3bcNeF+LZbrcrJ3x6wz+2mFIqJ8gxBuwJ3STevr29lVPaeOHPGIvXCt0iDuJ7fwqDzfNcqjvYzvF4XNkmCZyBPDpl/WjbjAW6to2urTHCSa2xjDGe9Ya9QIwL/MX4IFRdVXGSiF1ih6zHP/k//uP4uddXt059/PixOAhAPf1jLDQvZ5/83SUYbwYH0Bl82ji3LAQLj2N31phSKgmKs2szajc3N4UxwhHsdrvC7Jgt8TGZ7969K0I3mDeTRG8fTsMsGUbm6geKYLCME7GB4vC3ZxkTuHjuNnkg8GFgbi8wC2bnxlrwQvYRUeQE+MA52VgwfjsQDDQDi5qhuxyLAzFL4QDJ2Gy4ri7wfQRQjAXDh9nDYCz7iCjOjJd7ZXFOrozwp/vk7Wjqn1Nxcgb3u90upmVeAQaSub7v4zgM0aT1iVqWNzrkpH2328Xr63rjJWCftWYM6Jz32FDBgnHestOsZUQ9Nccg30AMe97+HdAOO2sA5yDFuttWcL7YCc/EblkD27sroIB3wDTvw469d8q2xHjxC+is/ZerlU7QXDF03zbAEqeN7zC7xnrT1rQsS2HqkRmnvJDoARZub2/L+/hOAjhrZf/J/TYkPjDT7AWxHbo6hg6SADFeA23bEQw+ceNwOJZjZYchb+TEVxL03F767t27M7GT7Zfjv2nBzeM9rapiMNr4cx9/jn1tK61O+l2ZBTxhA2aUAX0m35yQ2/6wqy3BsWUdXV10nHx9fY15zpe/uhJrXwao84ElkGLY/7t374rf8bGpfCf7Swxm7YvxHV5jYrxBkFloYriZYFoODWYdVwDF2IGrHFOsT34k+ev7PqZTJSKQx83NTXmmkyJanJu2nlLnagR2b6KHsXp9GQuxm/Gy5pYlumlQ6wSsa2trE7JFNvO5mrBtc7Fueg6uLplgoHpiAAn+QZfwRd7bwUlQ3jsYEcUW+Tf4Bd3CnzkBTSmVvViMn+/l5XiPjwBIY2vgC5JIyGfbnBMx7J65sj7YPPImTrF/y3sT7RtckcdGvIcPm8JnoDeAfshL4ivrkBu20wovmLByhcexEb1wXEQ+2BRtZB4j68nvnbjyLLf5/dzrqysa//K//BcrRbVwmcB+vy83grrEziITdBywWUgEzCVDJBjeQ+AEBmV0wOM7ItaX1NjhY7RObMyWIHyexXcCTF3+IpAidPc8Mk+zWHyfHfB2DA5KZviRNeNg/gbm/B0DdqkVx4OzdRuBGUw+Y6fmli2DCzO79HvbwPisK1awS9sEbZ5rSTNifR773d1dzPNcGMqI9d0XZpktHxtbxLrCA2BC/vwM52FHayfs5IRnALwIaIC1DCzzzcLWSZ5/OB6iPbdfEeQLiG2aeHl6Lo7Z4BcQZIah6lA+MhTQvA1gTk7dCuL+fWzPsiSAE0jHcVyd9oUtmEnhWfyM8W6Z9G2SQfAH1LlKYH/BejAWqqaAVmTkqkRErPYjbKtovPi9gQMOdlvRAUQ4qPNcZEHbJT30BD3LzO2QLp2TyGG/3LHxzTfflKSJFlI2diJfgI5BBcAJ2bky9fj4GN9++20JdABpg23mxdrwc5IbWlxYM4IfdrEsS9zf38fDw0OM4xTjWPf+vL6+lkshaWsi2XEQzfdT1I2k1o95XmKa1sdxcga/ARn6iJ5h4+igE2wIFM+bz/ikNAdpfAjA8qdaTrELdMFJvltZIqIQe4AKqu4GTawZCRZ+hTVDd0+nU6kcHY/HUpFDHoAsEyQkyvgMyLlpmkpFCH0y6MaPvry8RNd1hWR0ZQv/w94BZMCpjLZ7x7zdbhfHsZ7kaGzRNvlmbUCxWVh0Brkz30JqpMrKGxe4amgfi1zYj2DW2rjBhIzX28m/fc0yzdGkdVfDNE0xTlN0u/Vlr04YTGjQIkmlk98b6OKHsBGwDz+n7c+YzPGM8SI/noONWB5OTJxYENfQGxOv6JkJQlcXsDFXAdAFY8QtGeT4iSzQL1fVkQnkBVjWY+M4WeaJD+QYXF5t25Z14DtpqfRpk+gcaxDzUi4BBIPZt7olmd85+djqiclek3n4Kr/s71gb7P2v9cI+giNMHqf9lIxLIJcWD7PhKALvMwjHiReBxpenY+CMCCws3HazE9/ngM3LzmqbAGBkbDTzBWoRa5DvcpmrGwZIZLFmU60AbmcAqPJZnDCOCECAQdgAGAOym+e5bGQlE3cy437uiPVxaMgO+ZuBZ134O4A9IlaVAgwYUEqlyQHY4ybZQU5OXnjG6+trGYeDuGVuRgU5kaw4UXLwcLDHIdkxmokxa4me+Xk4V3TqdDoVRqVt1/PE2S5Rq3P8vMx/005EEHJCQBuYe+ObJkXT1GOCnRy5IsPmbT/TwBB9w459KRhVQ2SG3m3BP7bB2m0ZN1g2QCTOE3C9XU8n5DD3jAc5OGmmXcZ9qF5zJxmsm/VsWeqxisiTsQHc3dtq/8ar67rSWgDThy9Ar969excPDw/ld/xHyx5JyOPjYyxLvoASf9n39c4N2DTrq9ffG4qpUgBYT6dTuRCUZ+NHADesD2sD4KD9AGBMggfTSDuGfS9rnlIqlw4yVpLgLXuKTjKGaaokybLk/Qh50/5lLIvA2vl36LYJnq1O2KeQjME4+7Qg9LuA2vbLPWf8h70PwxCfPn0qegBQMwhhnE4OGacrSsQqs9MwwMQe+zxABWsHiDSoRMcdy52cID/mxc/ocuj7flVZ834OZEv8tJ3ByJrc4rmPj48l2bSvWpal2Pus+ESyTuxYxtoORIvM9rjxpmlKO0lExBL1iFziAfv+vE4m5czmI3MDSeSGz0GPkYkTEnzR29tb7PtdOVnK/upiv485lhJDDM6ZJ1UvTnJalqW0RIGXAKjEYnAPZDEJmlsq7ceJ5Sbi7N+xP5PJlgOdMbQqWZ/xTyTb7P8lFtne3PHhGIOtmhDBllxdQuaOa8Zl/jnywL/wp+0tpdz+7p+TxG+THXSdcTBG7KwkwNMcnYhQV3eoEDMW4xjGQ3xArtZfYx/vKXHiy2tLvH7N6zc63ta3AhoUNU3tAzO4x4nCTG1BHovmFh4yvS24w/BhTPhuFHQLviPWTpHfMReClReTwO3nEFAjalJjUMvPWSSDIRsgSmQwx9/djoJCIs9tMuYs3kwKjsJAgu8w4+7P8N1m+a34JCpmW1xhYizoA4HR38Wau/d5yww7qXSC43X1eA3A7cztBLesh520HYaTT9bAIMFrxHpYhu/evVsBKBsz3308DqtTNPj7PM2xU78kYKVpmkhdF9eXVyXJ4PeMF6AAgOVoQespc+66rvSnI0uctasDtk0ngQQknhlR90ugk3ZsrAkOmvEAKvmubaLGswn+BnUEUGQEm2KwzffZEaI37g03GwnrZBbXYIBjFm0zy7KUnxuAM3ZsAjkS3GHtSMrpj7cd+YjOlFK5LffTp08lACCTZamXkqK3gAjGx1GjDw8P5ZZdkgLsAyDro7WRM377+vq67AFwuwinvtjf2odH5JNmAIveYLvb7eLqKp9YR6BjfFTLAAX2c9mfLRHRFsaQRNMABRDtxA/ggg6S1BFv+LltiBe+hfXjJDK3zTmWWBfwY998803Rd0Ax+18A7+g2n8f2Hx8f4/7+fpV8Ab625AlzcgcBOmq2mfWy/8Q2sSXiCnqC34WpRR9JDNFnwBxkGvq4LLU1DyLINmM/1zRNaXVyVY25pZQimnwC0zb2juMYzVLbf3ku/gR5o8/I7vXtLaZlLqdEsVb4QycojnP+jmmaSrcDsQCgzb+3QBgf6lbp4XiMrq0trMw9ImKc6lHk6Cp3WVA5wifRPucrCkzeojv4ANZs2CQ5tDOSHPtYaZM6YAjWlKoR3+fKHbrJuMER2AAHu7j6YKLHQDminiiFHaPH6IZJaHAJ4+n7vnRW8N2Xl5flpCyDc6rUx+OxnDS6xbVO7pmndQ1/YxJhW53Bb/F5no/cTb6aBEGfIL65kHSb0PM8k3uMxRh2OxYnej/3+urWqT/+F/9qFTz9d5ywB8eCz/O8ShYsaJSTkrCDgJWBeywiKsDhu8wCEFQ4h/n9+/cFdG9Z2S2g+qnA4/+c1eKk3ZoSsd7ghWN1sDNDa6dvsOykCKVjUXHKgACAFt9ncMsch2mOmMa46vqYYo7TMsY8R+y7XaR5jmGeY+JY1UwNxRTLeePRuoXm/v4+IqKcCQ4jYR0om5kFJDMY686Ot43j8bRydnXvyRKnU22Jyhf1RfQ9cqhBojqW2sqAfqCb6Bfra0NhDbatDKw3LB/jRGcBhqwdASDrRj31bFnm8+/GOJ0q02uHvL+4iNNwir7fRSxLLFFLl01qIvR9bgMiEWUuGbBdnedU2+S2rVV2RGZIDRQNsiqjUUFKtfW8yR1biagHQeRxpBUjDDDY6ioOjqDMnAAjEBzYHM9wYDIzSGXA7ZvM0Wefs+6Pj3WjYw6mWa+ur29iGE7FGfNcH2+421EhiEiJk+Lmlf8jKUF/cmtT3dNhUHJ9fX0Ocimenp6Lb8SmYLuPx0MsS5wrGbUCQMLFrdTX1/kSNy5zO52OZ3vqSyAkOR7HMR4fH3PAnOd8LuOy5DnO+ajo/X4fbdfmoxujsnBdd96r09fNxtgNtvX29lbWpG3zcdRZRruSLOKnx3EsR44TTwAJNZGcYp4BWrvzhu7Lcoy0AQ8+0z7A9zwY6DmJMzFFBQ37MPkCkQboI+bxWWRgooN15/34pIgoSaLJFD7r4G+g7/9MEvn7SFzNxpvRNMPrmIM+e58Ha0bcRFauPmCjbid19YI4t42xxE0Td6wb4zHwmpbad9429bSnZVmiEYjiPb4AkHnj76bp3JbUn+U8zVnnh7FUjN4ObytCkjG5FYxYTZyircaEKTrBWrqFqySopyHGc7LG/VhFZl29X4m1BQ9wmAyVTleCHR/APCbyDGQhKtBl/LmBrCsy+Ch8M+CcNXeFdHt4geMI6+F9FsRhwLKxALiNuIFdI2fm643pxCST1KwfeNHECoCdzoWLi4sYzslE13VxeDtEpIiLi/PJplE3+bNGEbGKh1tizpjUMXdZltj1fbRNU6pY86QuApGIrKUJd9bVSQ8JmRMN/CWvbbWDOMs6tW0bv/8H/zB+7vXVFQ2zuBi4Aa97zgBp9NQzEQMDs8oo3NaxMRF6OqkcODNlYVAmNlf91m/9VsxzLnHByhEwzEQY/LtHmsUCuLKICN3MloPINglDwVk0wJjH7LI0QQq5elG37ImzW8ZmpjpSirGZYzfPcRNTtDFH7PtYlhQxRZymiMd5imOzRFpStKmLiCaWM1jtzkqGctKTm1IqN/Q6ICAPALUdQdvmpGEcM0DlNKa27WKelxjH6QyUepV/mzPwWyIlAkMTKdWeVzOJyAnZsI44U+bCmMdxLDeKwiyiCyQoJHPeoEWLRkqpBNDDoZ62dTgcy02iHJwAeCBYnU6nmMYx0hIxArKXfJsoYIw1Zw68HAyYT23Vm6PravJDQDeDhHx96RJ26wpPDegZGPL7DKrjHLRqor0+vror/3YiZztHfwFLMEDoPtUPWGNYU/YDAZhcMmefAMmU+5KxT+axLEvc3t6d1zAiIsU8R+x2FzGOtdVznufSnnQ6neJ0GqJp2jidxtW8chDNybRBLkEms9x5z848L3E8HopOLEvEp0+f48cff4zf+Z3fifv7d2fW7KacslJ186oAm7atekBLJODs5eX1/DNaRfqzPrZxOg3BvSvDkJOD+/t32Y6aNro+r1+325UgkVKKYZwitWfwf9YdAhMkweVlfw6mTTRNW+Sc5V8JGnSBRIh1dp+zYwxrlv+LSKkN7qjJTHmtsGHzJALoEQHcSa0TCkCoCTPGQDzZ7j/xfjP0F/vZJv18BgDuk2vMFALUAWfYPcANIIUe2EdAPvA9jtvsY9oSK2bGHSuxGTOwHpOZ5ohKvpCQkIzwHW4dYV1N3Jmd55mMw60t7iC4vLyM4XQmM/sUbZNJmoszUMYOXTnBxxk4AmCHl5c4vOZK0c3NTTw9PeW5j2O8LktEU6vXgFSPm5+BJdA7iAPeZ7A+DEM5HtjV/HmoXQisOToZS223NVaAnIXoYW2JkegxuuTKixMQ4vnWN5sw4kQqEhsn9XzPNhlhnH6PK1rIkI3m4B70n/csyxIvLy9l4z52YPzB2Elw0D2DeOsZeuCDC0ykEmuW5XwX17xEWiJO53vmpmmKZZpit+tjOM/XxJ0TUu9fXZYvDxHh+8v68J2h7pgUsaRYterbb0VEaT3bEufopyvyW/lga+i3/bCJiZ97fXWigTPBKAn23jCHQjB4FA5A4Q1/PNOsF4trBmcY6mkmZsgBjQZilN2XZYnvv/++ABoCFyz8NlOtAPGwcrx8nxMjZ4dbB0kws/BZ9C1z5sCA4jZNUxwjSr8s9Vg2FB2Ge8vIR1RgxJj2xzGWD5/jF2kfd+0umm6J9vIqjk+v8e+GY9x8exfjdIz9/iLapYnjNMVu38VF18Uy1T5LvhtZUoUi+QP4er0djPN6frlR2BUcDM+OiTk5qaoVshqE+A7rAlUlAjbf68MFTqdTaTmyA/NYSDaapimbJh38OA7v7e2tHLWJTGhLICHYOjh+RquImcyfMnjbBzKjlz+PuR7ryvsB5HZq6CX6hkNmXAYtKa3vANlWF5ANMu267tx7+7oCTNZV5oMfgJi4ubkpcyFoEcyc7NLre3l5WY42xSZvbm4KG+eyvpMNA71pmkoVlPVmrwtsnE/J2+8vgosSeRYyjujjdDoWdhJ/mOfereyUNqKXl5dSev/mm2+KnCl1E+ztZ1invq8noJlsyb637p8C4HDqHkA0pRQfP36Mu7u76geH02pfhRkykj98PJWK4TRE29TTYJ6fn0vy4/YlM+gEO/zdOmmp92qQ8NP6QVsHnzOwjqg3dgMsiSvYOSCKoGkQh89grMzVwRV/zH8G8dvAS5LKXPiZQYdjCzHW6wOR9/nz5/IcA0N8n6vfMMh+Bj7U9up1wQ4NNnw6DrI2WEJHsH10nhdz2n7XPNeWSleS0CuTHcjee4wAvMiA9SU24m/weeiZbYdn4me4CwV7A/DzXSQLp7HqFeMloWOsruoAyNAF/JEJIsaDrZTvmua42K3v53EMYS2cLLEW6Ak+nkMaTIaiz9vKv30Kf0e/WZ9hGFZVZ+zEeI41R+ZOpNEBV8r4k3Hgq4wN3Wrv1lNICuaNPPHp7CFD59B1+1T7ZvsC6ym4puu6iCY/w6dxTtMU/X4XsxIFZO7v5Lv4z1jF5IDbzfiM7Y64gNz501Ui+13+7YNI7Je87jwHPLqTLiLjr3l9devUf/cv//iLJALj9WBdFkTAvodgzXLXuyEwIByVBWsnbOeCk5jneWWwZK4GVhi6ewINdsy4+N9eaFdsHDxRkG35jzGi6BHrTeoppRI43TeLbDmJgLOvUUKX/pyNW5GWJZ9Q0L09x7/75/8iPvyrP4lv5xT7fhfX7+7j/pe/FfPf/9/Gxd/938RzjHFxcRXLtMTr6Rj7u9u42vXxfN58SuBifVFKJxcoPjJHrjiyPOaaTbs8x/pacdED1o+1caIRUTeGMjbWFEfBuHCEZrKsdwQqWCwcKeNhjd0nWwNsF31fnSVztN4amBNICBgk3tfX18Xx4jwNmBmPk2MfjwjwdCAxg+c2DAITCSsOEh1G5nkN1okSumBbw4GvqxjTKjhtN3ljE8gBZgsd89ibJu918O94DjaEvhl08XPWHn2o54Wn0h5AWb0GzFo5pCpVWwSuy79tc7mVKcsn3xx/WCU4+/1lPD8/lz0P9APzDABN1qt2BbK7Lt+2e39/H9M0xe3tbaS0lAu4IHHatj3rS/XV6O48z3F/f19sAJ0g8Pd9H+NSwRg2yPebifUG4HmaYhrqHQZuq2H8Buf2iQAxfJtBMCDDvgJZmnF0FRiwjr3wDIAGftQb+wm8ADPABIwkier2CFjsh7YwJ2WsB4mP2z9MNBkUmjl2guPYxvPt792GYf2xnfE5gwf8CsDN8ZH3uCIM2HO8x6eZSOM7mbt1Cf3I7W55b9nT01P0fV98IHpCG9Q4jqUn3gAJkEVFmljFsbz8vLQiqUr29PRUbJO2YO9RMNFTWPglVzRcIUeHkZ9ZYvy/5WYwvgWyTrDmeY4mUuz6egKjE4El5dumIapYM/yVySond8ZfxKWUUjkVjPG7ggSJy1o4MSLJQsb2h2AnZOQ7HMA/6Cn+x6DWFQaSHWz69fV1FS9MUI9jPfUJ2ZHYkljxfMdFJ+5gn4gobVMG2fvdLtJSL2pmzsMwRLfr43jWU2IjeuX1JX4Q49Eb8Id1j+ezxmUsbRvzNEWK9YlSxiH2L944v9VD9A852dad2NjW//F/+o/i516/UesUCuAjyBBKCVLjelO2s0oEzPNQZpcgtxMmKGFkAIndbhcvLy/lWSiRF8QVABuhnbSP4CVgbB0DwcGZM0ENR0tvvkEgDDjBylmk5UTQY+GQMYttgyfLRlEdPCkDM7e3wyFeul18uL6J4W//bvzF4RDpYhd/+3//v4vrv/N3YkxNHMchpnaJ4+kUzZKiSU0cD4cYD2+RNsyze9lh0lkPy9XVAADQPFfnYt0w47Hb7eJv/+2/HX/2Z38WHz9+XGXt1huMNZ+u1JaTK9AjQDMOkGDpU7yKIz8DZ29S3h4KgNPxZwEZ2fDrs/g8Tgw9Z+x2vjyPlhEz9VdXV/H+/fu4urqKjx8/lvsSXI1hbQy4LGMCGvNHjm7Bc3mdsZIIwdAsS91U6gBLBZCx0zPuRHCb/AFYzWQhF99UzR0QZgFJqtB/fk7yUtvYDqs2GfsVfBQ+DN9hQAX4OBxei73R+kYv/uGwZh5Z12HINzBzPwG20Pd9vLy8xvE4rI4iZP4QMrCqtg2OdyZgdV3exJ4B+lBOBDRZs2WAzTr7yFV+hs+NlGJJ635h/DQvbAqdOx6PEfO5h3iTLAAmTQydTqdSvYoI7dGqvtsEEckXNmOZRcSqF95AAx/NM9zWQ4A3meBkweQALWkppdVRlU7QXRXh88gCnSOpdFWQ91EpNTD1/Pm7GUnkiQzsn1gz7+UCOGHv+Eds2LFonucVoeDkxBUHE4WsyXYdAIYXFxeri/3Q4d1uV+6DIHlFvrRLoqcGtPOcj2PmOGROuDoej/Hw8FB8DjHJrdG0sCIb9G9bzeJnxNp+10cjAgsf47ZT9AwfZ7lu8ZGJCttCsS/pKLpJvBvPG9ZfXl4KfuB2evZtGT/Zp9gOiDdONvl+qmnet+rPOd7jRwDOy7KsTs7D5xnjeS1MWKN7JgxNYJrE4Hu9BtZnH7bgNa7kXG33dkLG+4xPLcd5yqdDOuEHO4zT9IXNGAeYyADPMj9X+iBf/zJyPM9hiWVeIjU1wdsmTNgqfgMfYVyDfBj31qfYJ3ktvub11RWN/+r//l+uHJ2ZMhSGhQEI8HMcCw4XNgNHgmLz+f1+X1g6Z+R2CBGVRXCQMaj35xgr1QOXj92+xVgAL8wP4zJ4g40h03UQMJPNd2AcVjSMiHkxVpSTnlqXAA18GbMVhramcZxiSn10xymupymG8Rhv3RJxsY+0pOhOp1h2bRzbiGVcYno9xv7iMvqbq5hOp1jmGjBYb1ck2KfhIOMqB3pQWfp1Zce6A9D63d/93ei6Nv7X//X/W4CaAYJ1YLergZ2AS1A288MabAO1nQDr5yTJyS6B232JrEcODhXEO9GEzaXlx9VA5kQgMSOE7IZhWDG6OCS+h0QdmfT9+iQIkkHkaNvYOi7342KX+dbiNVghMMDowxibIcsl7Gmlv4DOq6ureHl5KUm4mUknSQAMgifyANxRESDpKayjEsjdLl/QBbjGPuZ5jru7uzidxtVnHYyX5cv7OvjdNNUjUwlMWU+byLdW55tzWaMMWC/idBqKHB4fHyMiyn4eNowyXvwVtkEi5eCaUsQ4DkVmtA7k761s8jaxAHSZKHh6eorbu7uYlrl8P8fKOql1SyE6HEvExW630kvGg68GeHuPDKyZK934Re99wE5tX7wIYTyXdkVXzlypMuvP7yJqCx/sJIkxemiCx6DLCRCtk+gF8qa1Yn3wQB0Le4/sY5Ej+0JICG5vb1dkmGOcZWI2k78bQPFCxvhIV1QMVjwfvtfrbVbdQJQ/AWyfP3+Om5ubIlsDPuwT2bOmVDN9gAF3bLiqAUDaVqW8vvhb/gObYAuwy964XJ6TItq+bqJ1zOO9EAL4Rl78HmKGww/wkegMz2vbNppIEUvdh/rw8FA7BJraPlQJvdpaZHIBf+64iFywLbfBm4hBRvgoAL6Tcjaz+54O1oLPW6+3+os8sdNxzIdYYDtgMtsgSTTyRB9fXl5WBA96bJLSMZ6kGh01yO66rhAQyKscJ980+Z6T5ssW9kgpTuOXVUDjSuujCSAnbE4U0EFkCyk5z3PEvERssATr5MTOdmBsin+zr9hibo/HuPhrbgb/jS7s44VAUQyUkknYkVqZnaTgXMy8EVzsIFkEGGIm52oHQMoAD2VB0VDou7u71b8ZF8zVPM8lKFig/IfAcRgosB0rY7Tjd4LEInqTqJMtjIb5wXRzmoxfZixgCyOisl1pF2kYYx7eYu6WiIsumuiiHyPmZYpx18bYNdFNEfupibbt4m0cYh6HuLiobIJb1rabfK28BsFr5jHFskRZXwcyPo+BMBfk7f0GZp9TyidTGTDDZMCqIHd0gjX1RVYYP8EOR+f5uXXKesFG3ryhvZaQcXToP6AXB0BQdXUQPUZmyAndTCnF6+traQUg2XPb0zSNcXl5UU4gccWC523ngg46MDHnrH+18mDAaRLAlQbWBqIO4AdbeTqdyrx9URi2QbuY7QcbJTg8PT2V303TVG6HBsx5Az/jAzzA+GWWO5+owtGc0zSV5Oz19Xk1R2x2HPMpaimlkkDW5LqNaRrL2pJY7vf72O8v4u2tnthGmxPAwQAdIEJwRK8hV0gsDoe3mKaqq+hlTgTfYrfbl8qPgTEVhtfX11IxKTrQrqvVTjCQA3LFNve7XQzHdduPwRP658oEL4AHuucqhmWP3+ZZrliiB/Yj9Ntbb/En+FX3g6PjxAHAj20mogZm+0Xv/+B52wqBAR+gjJfjh5ldfB6fd1LjBAy9d9swsQAAge3w79PptDoeHnl7rQ0m8Y+MD4JhC5hcJXIi51hJFQ77QXdtbySqsPUkIYB59MH2w++R05bJRkbERxhkxvj09BTv3r0r1UUTXCmdW5W6eps8a0RHA0mDgZgrXU6ubSNbVp0Efzieoj1/F5XBiHMcbXxgRyq+lfkbdFJ5ZbwQk6zHluTC7k1q8Heeh28ivhwOh9J2bHBvPcUGeBYJv5MAy9sdCYydPyF7TewuS90vwmeJB7Zh/A6yZ0wcCWzssq0IlXWbl5jPPoXqUbH/iIimVqzs40xqIXNkYTtn/MaCyIo4yfPblGIc6oEAPMdVfXwLz3JrHd+5bZGPiBXm8ffjT//aL+zDeFyiIojauaD0DMqO0aAYI359ff1iEbeZE07TgQeBwPLy/ThAgkU2lBSn0xBvb4dzC8ThDIYQ2FsxBJ/c0nWVZfsppccBW4EwVrfhVCZ0Xblxqw+g3smWs30yeH7uIMs68NlxHKPr+xjTEkNMEX0XqWviNA3Rno+4vdhfRLQppnGK4TRGE1lOMc/R73bB0azIlDnntYk4HOolSxxBmxVzfW75slSmzA7Ijohnu0xcgV3d4AfozrKfgtOoOMHqcDiek5V6kpiZ0CyzOXa7fVnjcZwKe3Y6wVS10TTVQWb9qadzrFnVWkbkOThuEgTW+OrqqrQFAVQvLi7i6uqqyDgncwe1yrRxPGYWPl/4dV0qGQSoyhbVhAWwgJOjqgaoZIw5MMzRdYAy2uPGFVByixJBgRM/kAVtfDmJeD2DsDyXy0vmPkbX5ROa+r5e8EUAxq5xgFkG3VkXUxyPp5LY5SS8nncP+0sbxfPzc3z8+DHevXtXAH4F/vt4fn4tbV+wgzmB7KNpbsq8aZ0iQdjv634uAhQyh9X7/Pkhbm9vI5/G1Menz58jpSb3eS9L3N3fx/F0jKur63h9eSnMGYwuyQWJZUSUvmTGukREt9vFrt9F27WRznq6xBJt38fVueed+c3zHKltYpnnGOe8aXGa5zgN59bTtN48TNJjoGSATfJY2LimzW0DsUQTKab53HLandtdYomma/O9B5GPH2XM2xYqbBeftmX7CI7YlwH+lpTgM1mv1/bhJM2EFfoE2+jvdEwqwb6t+08MmOwzeBY2acKKGBFRT27kedyY7jnQVuLkDf1xLzi6y8vv534VVwEci9ZkUW07oRIB6N+2R1cSZln5enwgQJC4BkmA/dGmSDUbUO/L2rABJ4T4H+R+PB3jeE7q2ibrUtO20bRt9ClFO8/R73cxnn3d7d1dNF0bqWni8jrb9K7rix6nlGIep0htRBMpUpOibdqIeYm2qxvPXZ3F93KCFfikrMm8xOlwzKcQphRN18TL83OMw5gT+KHe2eGEcZrq8anETyoP6I/XhM+ZoMVm0GX2wbA+JvlIJtAh7MQHD+CTjQ/RH8gmbBE58Wx3t2yTTuIY8XGe5+IvjTeRAYQhNu7Ld1kX5oWu4lvAsyUeT1M0qYl5OWPZM0kRyxLpnNzZ5tv2fBrUEjHOS6Q2RYqItmliGqeYlurHGPOWlGattzGR9+N38NPzXNssXZFB1vgWYyt0wt+J7Zoksz800e/k6edev/EeDTM/EVHK+QQj3sugcAJMGOCFQFgkPrdtW4GV9QY3Bw8yamd+DiQ8O/89H6N6Og0r59Q0OIMMuPKxjCmWZb15ikDt6gfzwiBQCDP9ZnzMwpjNBnCTpPB53o+c/T28jwu4CA5WsrZpIkUT8xwxvo7Rp/M53jHG69sZvDdNzNFkANKkaJYm5mmO4/FUjHRZogS1DBS72O0q0/H6+lZkgZyXJaJtI8ZxitfX1wLAkAn6YiNAd5gLOofBOSkhuYiobQgcvUrQyTJro2lgcDjlqivvz+1GKfLRuTVRzo5wd16//B/6ir5n57LeW8QNsrQX4fjsNLyxeRiGchkXz2nbfFRtTrIOxYnc3t7Efn9Z9GQYhri5uYmHh4fY7Xbl5mFaiu7u7lZMoqs+Zi6XpepdBmg4kNqHTY85Ool8SYbNcubnZzlP0xRvb4c4HI4FPIwjJ1zlo15TqqeSOTAT9LL9o/sprq9vtJl5id2uK73K7HGgtYsTlVxJxYG+f//+rL+vK9vKtljPPL++vi5J5OXlVVxc1NOuCKj4qKen5zPgmKJp2nj//i4zt30fTdvGxdVlCRBX/XXMyxLXNzeRoure8/Nz0XsScMYICGvbNpZIsb/IfdBlf0fKunx7Xvv95UUsKc7HcmaQ3/ZdLBExzXO8HeVb2gq23f5kGzWYdLV5nKaYI/cKn1TdOByP0Zz1IVKKYdSm4zNw47uYM76BSiDAwmADIofPmkW2H3UlwskFeuu9DmbfGQuJFckG+ritLhDg/XlshYSVefUbgGI54GPzAAEAAElEQVQwz/ghBCKiHB9KzOMER8cNV4Hc60/M5btoc3L15Hg8Fj/CngcDlG2FFtsfxzGenp5Kcm/fwn4MdIQ4jjxgtamoVbKkrqOBKc9y5QkZY8PYbkRE13cRKcVuv495WeJ4qJfWvXz+VMbUNE0M0xhN10a/362ONk8pnXW6iX63ixQR81graDFFRLtE33WRmiZaJbXoF8QsCZ91LqUUaYlY5jmWeY626+LqIt+F06bKpkfUQw+wu66r9zzht4mbJJqsv5ltxg6Wc0XEh1fUeF7XC50HyLutl2TRe5F4hg+0IcZ5zwrJhYkl8B+2DumC/eIb2Q/CuHjZ/vlOfDx6CNFL7ALbFduY5xjnmtBN0xQxLzEONaGi48TkOonJ/uy7lvkca9uIUfgYffUBQ/a/TkKwQWSOTFJKEUvVE9apkux1Aze6Y1xq3OV1r3F33XFiotsJ0l/1+upEA6UA0HvhMCL/PmJdGuJPl99QIFcCrPhmXXnmtg3AfyIYEgIzrThygsUWzEdEuczIlYhhOK5YPOZLWxbf64CG4nh/AaVplIP5mq3BiThImZ0z400Qwtk7kPi5udqQZQ1bAfhOqbbBeS5OzpA7a2vGgve5JIvC0m/um5dZpy2bQOLF75ENjIeZP/dbMy5elOPNCMAgYlzM18ZNAsR3WfYuq97d3UbbtvH58+fSX5tPr+gjpXbVPoT+UlLF6JkLsrm9vY27u7v4+PFjcOdLDtZN3N/fxePj4xcn2ozjEL/85W/Fp0+fiv7icDnl6f3799H3fTm73bqIQx2G4YsLkbbJnzfq4bzYtG32lAoe9tc068ubAKxUIDnhhJ9jd1RvHMhw4G3blIpkRA1sebxZ525ubkqSQc87ukr1hc+cTqe4u7v6gsyoDroe+0eQywzwVfFdBEjmm1IqfeMkOIDktu+i6+ttyfzucDhEajLgBoAiG3TJ7ChjGoYhbm9vY4klPn36lP++LCtWEn9Tma/1/gL0wACbz+FjIBuQHb9D/owJ3VuWekO5fR2VI8ACvnKZ5jJ2Pl8T7my/t7e3xQc5CaI3HHn4xmniDrZMXGjb9osL+xw88amORdjF8/Nz0Vczpt5vZFKB9+A7ndzjs7bJr+MWcmTt+r4vPpXPUA3Cvpg7eoZM2URsUIbc+ByJgpMRfN319XWpgIAHzIQzX/5knSxXvrvrav+8kyzkTDLFXIlvZuEBifgdA8+u62KZlxjm9f4cfodP87zdheAkOldlz0fj7/elL9973vKrtg3b36JrEbVNEF05f6zM8+3tbZUQwrYjUy57bZpMChYbEkHTdV3Z58V6IjPm7bvFmIdbFbFbNuhD3EXUexmQP3blPVXoMrbh+M4JY8h72z6Mf3ACD34yWcY6ueXPJDAVV+syeuYKnZOITIq9VVwZ58pVqq1ZtLWxjsQukkoSSfyP/fVut4t5HGKa6x4nHxqA/mM3JvjBPIzffqtr1r7DcdwExpbM5WeMkX+z/sQ2661jy/9fKhoMwOC2bdvCJLBgVnyUiUlvmQvAn4WKoKwYfMbMCk4novaR4SBSqu0qVZjNTwa+lPLRbmXRurpfomm+PF2EoLxl0RgfDh+gheP3WdUYFo4W47SzxDgiogBGgOGWCeNPxsfzGIPBeZ5nlEqOwYODBbKHeWHNCFCA8Ofn59VavZzbQPb7fTkVw0yVQScGsK1c8L3bMqhZipLNR21fQN7Iwvrmqhfyh4lANu5ZxnllhzDHw8NDec76pJ/M1vpUJDPRz8/PK3AHQ26gTOXh3bt35z0KhwIO0I8KHDJb+Pr6Wtiy29vb+PM///PY7fIGbub5/ffflzVjvfhMYdRSipeX1xKkcNYOPMiRtePlZM3AjJ512zEOCluLiLLxkn0bVHJ4P+0X+VSaemeIk9K8rrGyJ1dYrWOMP4813/jtU7+8Tk2Tjzo2CH3//n3km7Cn0p7ldgLYMOTBDdeMhb0zXdetLn6bx6kcY0nwfnx8LPq+JUYITK9vr3F5eRnv3r0r8re9YWdmuAwoAQv4eDP9zAPwZXbTvoLfA1CxnYuLixIb0AWvCcnbrquXQW3jA8AI1nLb0kPLFgkxGzUZH5+hnQQCIGJdhcT+TUrg4/gdzzSQIQb4wjL8N4m+N+eis7xvWZYV8PK80XGz4MRZz411vr6+Lp81O8yaA+Acl+3bDbj8vv1+v6qMoocQFCSWXgsTRfYzTs6o8vBegxcSIoNaxogOeO8Kf+JvAIP9eY3f3t7i/v5+lViYEGUdmKd9iRP90+kUbVqz4gUzzHMsUSsL7m3ne/lu9CzLs16C6EqKWWgDyxKDN6fD8Xn0gTFYV4mz2/tw0D0no/j+SgKt7/1yorUsS2nxpHLh5MVkMDqB/fK8d+/eFZtjDMyXmEzsNSG53UyPfpocxq/xPmTLvJERn4s47ztt2khL3ePDmjkhJQlCJvgE/ICBe37vGKmpZD3JjkklxsYc3S1UuxBqBaPt6oFI1gkO1PFeFpMf6D/f46SEF+8z8eXq7Ne8vnoz+P/z//bPV47PTtYshQdk5gaDdIkZMMzvt4HO2RIKYWNjkVFElBqjhiHIzjCtgggLYXDkcfJq2yZ2uzVIZ45WUAOULWNhNsNsHL36HhMLa6bUz3eVw4GJ5zhD/6nPPT09KUOuBgDoxqEjSz+D/66vr8tGOZgM1nrLGFmWBig4RhwDxoQC21gYnxMVAgrPc/KJY2GMzBEnwPcgFz6HU4AVR18pVY7jqQBBl2mzU80g6vb2tpyS4bKyy6xuw8AhswkN8HlxsY+Ipejysiyl9N73u3h9fVtdMNU0zXljZRttu76Q7v7+vqwLuuP2uuyQ1qd2MW+e7woRAQkbtf6a2QJsmin58OFDaVnw+sEi5b0RqQAc+4WIZuWAHSDneYphqBU+gD6bTU+nfJoTwTXLNIJb5nkeeprtox4djS3gU1Jab7RjbbmTw3PGNoZxLBsEsUXWxJs+uUuAuTuwutweEXFxdRl73WxP0gM5AlsI808ij68yews7x7NoVTLAo6ULgOmKgCsn6DUJJJ83eKD/vWvX+xrQQftRV9JZYwdaEzSXl5eltcyJJwk2MQGwS2LOXkEqYTw7Is4nlOW54O8Yq+Mg1V0TV8zN7VboFTHMAAOCBZ/hAxNeX19LRYF1oEIKGHSlg/jjChm6YIbUwBog+vz8HBcXF6tqlivJ9gcG7SaosCd0wwCJJMLAGN32WByHKmlYCU2DWMeLlFJEk0+l2J6K5/jvmMLf+ZN1KElwpFimaTUP9HmJJU7Sf/tGnml9wA/3be73Z3xONIwJWEfWoN/vAvDm5NwJLbGQ7/Tz8Xv4SuzDcYt1Q69MmrJuJtCMC9ERvhebZly839WjrX/aYihs2T93lwLfx3/YHN9tnMf3mrhwMpZSiq7tYhrqiVjoFzphAgZZ8jL57STk9bzfkjl7vezjeSZjZZ2REToWEdHG+hQx1s76yc9I5qw3fM92LbEDn3DlZKRpmvgH/+jvx8+9vjrR+G//6/+mGAbBkQlwkss2I2LQLKQNGKNxSTtiXVq04BAOQQYntK1oIEy3cQBStg7Li4tS2wlmBm4owG3rgBiTN3x7/pYBfePMEQYQtofxY+x2Tjhs2FJuQI2oWTbtNWZLSP7Iap2157HUUxcYF2szDENhPbwGJAJuM9oyQE44LQucj5NOFBxgjDwjaoXMgZ31NEscsW7forUBXfC6u48SHX59fS1gyHtyWJPsYFK8vDyvWH8CcF73rugDDKpBGcAZgMD7cDKwvSRrl5cXMQy1pGpnllITr6/1uEvGnG997mJZ5rJHg3mgK8z7eDzGy8tLYaBSqsdPojc+AhU7Rp9IgNzKyHqw1i5Xs3aApt0uH/l7c3NTviMnFrk6gX4h7+wgc8sfP/NmwGmqzKzbLdhsj+4iB/ah5IMB8li4/wI5XFzsVowbNvHx46fo+7p5EHBLUCGxMwO0LEscjsfo9+ubltHFfd/H89NzYZ9w7vy53bMBMTAtcwxj7k/n1u+tXSJHs4DIEB+zZfzcvmNfie74CNktqKCVx7bvwGjgu8z5aEYDURNB2OUWXPJ31hg/tu2H53k8y6QM9k4rYE0wqzzQTVeaDGhtf/wMVpi14pkwr24HtC/iOQCYrsvtd7TiGQwPwxDX19erNhP0kLW1z2YtYHldFfv8+fMqRkfUKrZtmzVFF7BvgyA+z7q5EgEJYdZ7S84RH/CVPB87cJVhSxhCFGXCIn/326nGQggSvge9YK0c69Bx1pwW0SY1sai6ztyHYYhhHGNJUdZ5m0SyxvydWH2x20XX1nuZALTohdeauaaUYk5Vf0hMXD1zxR+5sU62XWKsSSInOugk67RNBohlkGdOmnkPOol/IGbbJ5iIhcx0PC7gv/vy2FZXMbeEpJl7twvZZp34IPN5nqPvulimeoGjE1MnL8YYrIn9lcc4LUuM55MJTaAyJ/yT9R9fg9/Afss6jHUjOJUk9MzrTPxjbOiF44CTkJ+KJVs9+of/9D+On3t9deuUy7AYMl+GEyXo0z7EonpDF+xoRGWLtgtFMODZCIxbO50BmiHjGQgHoWansr4jASX0QjjnqptgqoLTl0r/Ha0sXhjGhBNi8Xhm13VlPwtg2AkRcmQePJtWHXqEI6I4bBuAs1kMwkpr1iuiWSmREy9eOIBt4HLZkYDq0jvr539TaneS6IyfqoKDsMeHMWwZAsbB7wz6fGEVzhD54OgIJOiZgwdBeRhy8OMGWRweLPCyZP34+PFjYQPd5gZrzxxIjFzuRpY5oUxxOmVZfP78OSLyhtDD4RDX1zelAsJc+I7Hx8domgoWSU5Zh4goYJ+TiDIIqyDHl1g6oNgxAjoiosyTZxcQuWEbI6KAcCdk6El+xhLcrA1zBuvDIQToNWub9WiO3a4vTDZrd3d3V56N08eGsk3lz3NMcG1reo3j8W1ly22bW31yIt8V5nsc88b1x8fHwjh7/gCKy8vL6Hbrlhh04Xg4xLffflt6p/FdJAlO6Njf0/d9jFP2odfX16uKLmSEN+3O81zGRgA2UCNJp62KJI12L+aLnwS4w6gbQG0DLr7M352B0RB9162CF6d8YeNO/F3ttZ/HZ+DfkJPZXGLE5eVl7Pf70jZHvOGZjJMYsB23WeKIWt1m/5JJDOSK3zOzbObXjD6AOKV60qBbYfAbtCqh38RF7NNtnPge1gIw7ZjoypRPkkLGJHH4DM8JX8zYeYZPJXMFw98VESUxdCKAD6bFFF9v4mRLUrJGjNWVEex3t9sVv0wlFbkR4zkFkDHe3t5m+UaKcZrKoRY8l8+nttoScnLyg0wAbZeXl9GmnHCjL+iA4wwxn/dM0xSpbWOJL32sYzOYC3uwT0aHTSIZn9keSBxMxlINcGWb9cEODcyR77IshUwhphBHWEOPwV0f6O/WfxHf0CfjQuMz5uRqnn2EEyE+k37iexkbY4eMc+eC7RHZHY/HSG1NbhxjtySM94HxQvZu0crjrIkSn/ccKg5e34njNbXP4r3G4MZsvBf/9HOvr040jschUkI459sIFzbt1RYc74jPytxFSvmEhPy5fLITARoldrnKiovTcACwg7ZhAi7MYNTA18SysJhztG0X47jEMJzCexWKw5BgcZI4VxhQsxUG1YyHoE3PoXtVI/KZ3YBiA1wU0uwSyoDj3rYZvb6+looG8iERAtQCLC0vTpY6q3F0HdWN/O++Xx8Bmde2tv7YiG1cOFFkiJEyF++fAWwhd3QJ5sTVCpc5cWp9n0/pQZ9YF5e9SeZoTZnnOZ6enoqTASjm40hP8fnz5/juu+9Wp0lM0xi3t3dxeXkZj49P8fr6EqfTkG0h5TssUtvGaRzi5u42rm9vYzidIsUaANkREKRJxOj5n5fcFtO0bdze38XT01M8vbzE58+fYllS3N/fF+f7+fPnoq9d10ffc04/+3N2FZiO41nfl9jvL+P6uj0DoYvilH+KhcEGzVoSfMy22lkaODnAmT2+vr4uAQr7ubjgpt189PA4HmK360sVgaNk+74vl+JlZnmI3Y79BvU0q+xPDrHfX0TTpPP9Ers4HE5fgCjrKmAp+6AhpukQTVPPkQf4Xl5exsPDQ1xfX39x+ghHZV9dXcXr22scTsfioNmng93iU0iOsH2zz1QraQObl3oLNUH/6elpdb8KIMdB1u0GBgTzPOeLn46nfBrONMWu6+Pt9TWWaY6u38Xlda5CTcMYJ7HNr6+vEd0SU0QMUU/uSilFWpYYTqfouy76Nu9pent5jcfHx1hk45zFj26jK66IRMQKiFDx4iAFbIp1QneJS9sqBO8nYX55eSntk+ivW0EJwm5zYg3xS9tKA+AYuyGe+B4J/CbfYSLANsd3ULldpAPYJ8/DzwPI3C6yHRPxzUCEP0ky3QaHbLZJH61pjlv44W37KgkPdmMg4w4GJ44G4fOcT02L5byxPpZooi1xG71BpgCjra8CAPMz7+lxp8DF/iK6plkRICUu9n0sKYPAx8fHFQmJnyRGGZ/M0xzDOETbtdFEPhUuUop5WWKac3IDeHfCEbFuReKZYA9jinmeV3qAXiJPJ3JOZkgabYv4aScQJn+Zn3UL3WSdkaufR6wx+Wjg64qDQT7+wR0SHperC1QOmK8rqdsEK49jjk5EjH/HOLEn/MvxeIx8hGATMc/Rdm0sKc5He3exxBKdKv2sleOG2489J76Xf4Nx5mWKaYHEmPNRunPFk+6YQI5OMqyn2Abzsk9CliaBvub1G9wM/l+XiRrIZyefQdayLMXJAByHYd1vxoSyg65nkvMeHCvBAGe73dTEouO0tmVqhGPHxOfpUeU5l5fXJcEx4Mjsxmnl3HHcjOPu7k7Vj6a8D+PBeZOAcasrCZSDiRWYthbG7mcxP2/WNSNO1g0osxOIyI7w+fm5nCZCKwuKxloRxMzg5XHmFhbWkTYEABRgld8bINhYeaFHLhm7ysH4HQxdqTBoIPnwOdAwjbDd20QUtvnTp0+F6efZ0zSVNWJ8lsnpdIpxmiK1tULGnJumyednp+a8mfm4SpQJngSgiNqGcxpO5bzth4eH+Pz5c/zyl7/Mx6x2u5jOR4LiGGivgWXkO5ir9664LQaW0XbCe7BHGGb3kxoYuX8c+XhzOEyW38/fzWBiR9vk3Uk8MscRclIc9ovOceoKa2hG3q09ABKSgR9//DG+++67AiyYr50ycseW6dt3y5NZIea8RMRxqK2RtYVrKje7et6QBW9vb2UfgVtE+76PputimrMufP/99/H+/fuV/iFfNknjE/FzvrtjHPN9F1fnlkB8jIOQ/ZyrWjyXlj23jtl/RER8/vy5yJU7ZD58+FAqnp4jDLAZUAgcJwnsBzGJwXwBF7Zd5OwE3HYIWOK7SQTxyXwXvg9QExFlTbEXnu0qMzpicMW4fA/C1dVVOfnHBzSYoWTPBv6E72BdYO/5DmIAQNxJnIErOrK1x4j1qTh8Fn2l+g6xxs9N5mFTrA9kU2F905eXAfNekmPmOcz10j2ei5+3nuM3qA5SveDFc7cnFBFXm6aJZV6iVZWAOc3zHG3fRaMqAT7L78WPGBQ7BvIZktAmUrRn+zHQjIiYljmmuV6ci6928mCfuG1xAvwjW48ZEtOsNok7/pox4V+RH/GCz/F+E22suWXo5MPjsv/g3zzDeIh1cqKCLlt3nYQ40WAdmWtErE6dYr2QdWmFmmqrMWNpuy6Ow5dkhvXb8zQmQYcZl9cCHYDcYx4eM3ZcKirLep8H+sfzTRq4/c74k+/F9m33//Q/+yfxc6+vrmiwWAyYBc6KVMEAxwvi+JumW51TXB1dH8syF3BihTaoJ6BZ0ARcJk+VAadu42ZxrfQIEcbf7AZzYhFg2ugDNvAgsDpg8FkW3OwSAZ95MQ9v5ObZVi6Ch4Mmc0NRKI3zXgIbbQ8uKfIe98ui7KxPRJTEa7fbrTYgdt0udrv9yvHZ8RBUvO8BGSCXlFIxONbo+fm5OEQCvdtw+JPvqi01dVMuJzwR7AzkufDKjAbyg5E2a8xJDVsmACddwMl5DDhu1vXq6iqalOJiV081st7i6ADNANJhGOLy6jKmuR4jd3NzU05AsoOiBeh0OpVEys4bvbHTwFm43JtSKvdCmNliHdEdJ4I4R9bIrXN8r4MeQci24KM68Ss4T3SGTf2sBT6CI2wZ4ziOcX9/H03TlHYLxseJPGZFDU7RJQA9a/Ly8lKAJuSH7YV9G/hIVw4AsG9vb/H4+BjjPMXT83N88803JYmvoDyVRMNBjOoFfdrIhGA+LUtEyknAd999FxFR+rmtj6w/dsKfbkMBTHGWPjq9TW5YX9pQIqIQI6ydWUS+D9umvajr8uby6+vr+OUvf1mSWX8Px5fig9FLdJ/ATUKFLrnVk/EyFpIXdJrvhdTI8aky+29vb0UWJsx4JnM20IO8gYnmtZUR/gsiAr/NfFxZcPxCxxmf2WcnWhHro8KZn4E/8ZoXccMHIQB83GblPSsGkd7XtG3XYA2QmxMfAJKJPcdQnusK0Ol0iqbvSpKCnZKUuULLc9nzwnowHvyVCSV8P8nhOAyRlij+hvjStm1Mh0NcXF2u5Mi8t10a6AB/OsmI0CWQTT75iN85OZiXiE7rw7oa/xADeaaZcyc7xijgIfydwew2cfdBBcREcIMTP2Tg+OUklhjtBAMf5wqh4xvYjDnzXMdqfAO/Ayt5jYmFyMEyPh1P0aa6VQBfhl6Z9DAZNYy1zZO9PmA9zxMdcQLt70AfvJ5O0LcHHLmKZVn67/gSsLWxme3amHabiOE7v/b11RWNP/rn/2LFXKAoWQhrkGQWc1nqBN02k59VW1yYqFnsrutKiZJTPHA2BEgWys+A7cbpo/zbE43qorWrRSMQ5jnGChwWwWnxUGYM3CCMVic7UsChAwmLalnZmHGw45j7tdn0h2I4cDm5QSkBXqybqwSsAUEL9hNl96bscZyi7+sRg3wHjhfAxtrYgaLkZh3Qp4iapDJ+GCccilkyM4u0oSAPnIeZIVpJeI97htE7HBPBGoccEfHrX/961UrF+5umiXGaou3Xe3LQlV2/i6SARUDe9n2bTVqWJbpdF6fzZnAAMSD2dDjF4e1Q2Gt0zWykHTkBF/0zw4le8TmcLoELG8FeDB6Q29YBGoAgD0AplQbGhM4Y2Jod3bLoBMptG6JbCpkfn0GHSCIPh0P86le/ipeXl/j1r38d79+/Lz3xzJMgwoZ137GDb0Ke+Cz3zbKO6PA85xuIh7Hu8WJMLy8vEfMcXVtZagdLxk2lGH/w8vIS17e3cXWdK3Bu12AtaMljbhHrk/Xw007oY1qX1fkM/hPwfDweSxLkfnZ8sPWOFydqmeEEACF7g3PGYFKGBI05LctSKreMhQBKSykxAkCB/yQ5xPbN1vJzEnhalbAT+1MqOSYNDJ7QFbemoPPLspTnuo0CX2SCBpls7dKMKHbL+jJ2J1voE3bkiiJJFv7RwNJAme/1xneDNl6WM1UFKkXYqZlffAs6EhGlSu0kpCSdTYqmzfsbd7tdqZgxLhJvg2XW0BtqkZNJSY9pWfJN9m1aH9JSWmHPYzEpypqYKHOyZCKIMTPn0+kUu7Yr67HFX0uTfQRzQ+/QS+OIiFglBCaLtvECjGKCD9xhQO7kcVmWMnb8I3MDE2yTWcdAMMbW9hkX32u8aKxjWXpezB0bQu6sGevDdxi0931/vpxvWMVJknaei54yhmVZounamGTvfJerSfgEbJI1Qj6Mn3W0bNFVEjBjCmy2yHBe7+Fx3GSu20sqra/YGuvnmNC2bfzBH/7T+LnXVyca/+qP/vgL5qMG/1SYJ8A2Ry3Ocz2pxJuosxM+FRbGgdVK72wax4sgATVmyqgYEDzNzpnxwNBy8KkKOk1TYSjza60IsCjIAmeJ0946Yo+VzwOcyYbZBIUBAyYIBmaVUIAtk4aCsolyGIa4u7srBgUAw3i3Y3SSYsfrpIl1OhxOBTiyZpTMnal7jwoGj9KyTowbh+9qELKDRcbBuL2NF2DOAPh0OpUqhdfCTL6ZMwNiZ/1mUDFmly7bto05fXkiz3kg0bddYdEMzB3AkD2Benexi3mpN8gDKI7HYwzHIeapbgxGrqwzZVxs1GDNwARQx1oBHCNqBc+sFPM1i+Jnor+2FdbYN287+YGVvr6+LqAQPdhueEOvkDksJ2yumXcHScbHOLYMJ2wl9k+VwQAYksMypoJi0gNbIaHl58MwxLws0e3qsaVOJJZ5jrREAZrjmO+nYc8QdmKW//Pnz5HaJr759tto2zZ+/PHHsk4k1oAQZIauk5wb4OBP2qgEhcEeQB09NtAwEcO8WAe3oqBPZnS9qX8bAxz0SRzQd/woARRgaYCP3W/Hji/lWbav7Vz4PUkM64NvQk8BQ/Z3TrTwKfie6+vrssfIIIZEimc6cXdSz90VzAdQg3+3n0RW7KVhXoDDvwzo8yd6wprzbOTqeToh8fN4hgEWdmmAw3q7BQ1b5LP+nmjy0dGMn89hJ7DiBvzEM/SF78Z28QesW9GB06lcjob+cgxw07Vx3HQUuEplHbBdAeBdwaGq1DftisX3c8Z5Kkf3+uJHkkd0mvfbnlgH1gCdw4e6ImoAS2zAh/F+k5omhfguxwPLjjFDaNrusW3mbpvegl6eiS65YmEZ2LdYH9BX/y4iom3aaKLuPUYmxk7YBL9fliWWlK97dQUYGzae9PfbT/E75OSWNeMz4yT7KxP3Ma3bG7dkM2Py84xXt7aDLUbkfVF///f/o/i511e3TjFBQLUXrOvqQjqDy8EhD/jm5mYFArmkxgtltpeggeMlM4ax47KycRzLhUfu5weo3N7eFmDEJjYcdTbKMfq+WX2ng+GyTKtbbq0sBnMsCAGQhTQ45T/YQEClwZOZvaurq/I8nAcGTgJlh0CZblmW+Oabb1ZVER9JSnCEWXIrA/s3PC8MKDuPdZ83N/a6LQlDt4HzHIyIpGfLwvi9gDvff2Bm3ckCCav3y9zc3KwAPGvKs2HtCLZm1A1OSQ6fn59XLTQG7M25okF7C2BnmqaItl7m5wTRwMUySSnF5cVlzFETKVorLi8v43Q4xTzlgMrxsIyZda7rVYNdRGVMXIVjAy7y9glNdkY4K4LLPOf9Tu/evVudCOf9GA46PIs1ozqJXhq4eB6n06kE4i3D68TFCbkdLnqD/Bxw8AuQB05gm6Yp/oZAA/Djd67uOEnaJkQ3Nzf5Nti2/gw2chzHiDnfQuuE7ptvvil+yfMYx3rcZrfPdvzjjz8W8Mf64B9pgzFb1vd9ITOcsLdNE2mJMmeYf0AAdgPJw3cybmyfdbU/c4B7fX1dHdmJPrjqvN/vy9jxWRG5KoINs36AO3Sb9yJj6wPJRNd1X1TKeT66DHnGevJZAzdiGL506zcZR9PU6uqy5AvieGEzxFpsdVnyfj2SBRMVjJlnIyd0EX/I5+Z5LgQC9oi80XeTV/gHknj8LHbMXStmrT1+ZOT9f3w3JAkHOwB0tz7Em8S3vnyapliigjWz1vhtiDv7Q+Tt+LQdL3GEVz0Cd4nTeFqRGOCPJeqmZsZDgucKO/92PNoCuVKxbZpVMmsQnP+olQ7WphK5Y1lnM+7Mz76L+EcboZNv+0TsDX2xDEssbJpVsrP9vWVEzPTeoi2QdgLoZ0esN5HzfDCkSZtSdTq/0FUwG3uLmU/5TEoRs/boKCY6afJ4IqK0tLKufBf2RqxALzxP+9iU6vHddd1rcsWfbh/fjg8ia9s59JdVwfiM32v8ih4QY77m9dWJho8BtJGM4xBNsz4LGGGTaMBaMrH8+QguJOPlxMNsJ6CFiogzW5wcCszC7vf7FcsJuwGgAExlJ54DAbfrep9DRD0vnAX2TZQYLgDDiRELhNHjaL2BKaI6OvZBOHhHRHz48KEESgcFgsjLy8uKYR+GYdW6APClKkQP5dXV1eqoXT5n47cj4XMXFzlQkggxd6pBjAO5Ac6bpomHh4cSRMzqONEEgAPQ3GoV8SVT7hNAAEi0p7l1K6Le/At4Irnw5mAcFXJGp25ubkqljDVfliXmZY55/PLECjNhbLp1lYTvTCkVubEhdpzHiFRbVtC3w+EQ8zhHLBWImPUFJNFXTlULmZkZYn8RTDEyMmhHdryvbWtrITJ4eHgo+o3slmVZ2YmDKPo4DHmj88PDQ9zc3JSqhhkTkg+DPTtp/Aa2gWyRNeMhCKOnAPW2bQtQAEz4xclk2A9kBzoMUIqoPdDbo0YB3MM4xLTU1lBXx6ZhiLapiStJ7cPDQ1xeXsbFxUVcX1/Hx48fV993c3cXx9OxrDs64PFQ4QKEsD6AF+y0gIuot8e6vQmbNLtulgz7wb/6fgLiBjoF8YQtwtAjE5M7rDU2hC7ZrvHZ+BrWyvpouW1vbufZP0VibNla5svPeK0r4bV6aiCB/jLvm5ubQu78FGOPHC1rA3nGxO/5DgCNW8wMVvMx2E2JnzzTgC6inqLjJJxxObExEWBAzzz5XmzNdroFNfybcZugwe/Y701RW8lYa37vVh++l/iKD2IdSX6cEGBTxA4qj/j0YRjit37rt3LMb5u43lXb27bt4JNYC/bWWV8MBrMerC/VRdfnec43g8/rCq67PgwOIZsYM3IGA4Ft8ImO6fybWIlNeY3RGwN7bMR4kMQVGTMG7B49RhcYF7pov4RuuCUM2ZvQcsLDXLZr4u9Fdl3XxTROMalbgvc6nhqjFvCfIkbFGZNOvN+67ySI56KvJM7osgk2nmUCne8olaK2KxVUSDxiPGsJ3rbeW07bcW5938+9vjrR2PY4okgs+sPDQ/R9t1Lucay9fGZQsoIco2nayMfOAjy4lfoUEbV8ByCk7MvPYLwI/M7ECKC1tSS3SM3zEm2b7w04nYbY73fRdZRcYTzb6Lom+r6W4Bk3DByJDs6KhXcmzvv4vAH0FgCjYMjUjA7KZmdiMIsjMXOFw8lz3Mf19dVZHmNcXFzGsszRNG28e/c+bm5uz3OIwqC9vLzGfn9xBhbzeW3zcaOsuYM7DFiWdbc6BtGsuMdrA3LVB1kQ0FyeNSsDoEG2GA9gED1w4srauNUPEAIwhkVAxu5ddiLhtWubfJb1Mk0xj1Pun13yiRXjOK7uR/B6O0DC5B2Px9hf1AvPpmmKvusjLSnSkmKZa486gQJHR+UFR8lJVKwL+uu+fOTkfRMR60CF4+Hcees8DprxRERJWgEIZm5sp4wD4Ild853bVjC3KRlYGfziF/hedNV93ugFztuthRHrIxOp2uHLAE6u/ECKoGPYxTAM8fz8nDfZnxnm/W4XkZZoIsUSKbqmiblp4jSdxzDPcXF1GUtKsbvYx/VlPnno8fGx2AFMP5c60vOOT0kpRT7zLMVuv4+27aKNFH17XvOzbuXja7tIqYnxlMHiMK5bgGhrQB7cJbJNYGGd3aaEfUbk4IQ/Rk6sF/cUwMKjV2wWb5q6Vw3/xhG0fhaxytVN2y9+iJYaSChXorBJ/IT9Bkw+yQo65ooDc2QOlhtghf0eHGlMG5SJBbPq2Bq6b11knNg4OoAdoc98hjjkVmM+Z8YSm3JVifkyJuyUMW3BvsEgZA0g04wrY/b8DTj5DsZjMDmq0j1M9VbrKVJMS+3CMMBGHw0OeZ5tiDmVdpSmiZTOax5LvssinQ+NG8dy6hSfNXOPj9/ajKuFq5jS5j7/YRijjyViyjFmnKZI57uSSBIB9azbNnlj/4rxE/KnCu+KPj7OMcLVCuKSK00mm00a+xZx48GfIg/BU9il92ZYV8BHThhMFBkb8Z6f+tP26wSZeQ7s2ZmnSMsckVJcX9W7iOaIWJoUp3GMlCLG8XyX2Wa8Jvise273ZNwkv8jDFSRjTBJWk9rGKPOcj7kFb/EMvxefa7/CGlrmjAc/8pu+vnqPxr/+V//DChwCOnDSPvmCbN6OAiUF4Jn5MouQ2dWXSD/B5iJQHDSsysvLy4qt4zhIAHou8V5Gc2YMj8dj6d3PRpFKEDCDxHeSPW83mRN0YCDdnoCD8kVbnGBDAOG9PMdKhAypLKBstEwxN4/NTo2bglOqygNbAusPUCJwp5Ti6elpBdSZC46WwM++CZy0gYedhpkwAxFeBCa+hwSRz7vkvA08gCEbBKDAiZCdImwv322nZ/k1TT6u1b26GCyJI84VvWNNfTa+k2zmZweIY2X8gN3Ly8tyM6rZdoAm32VAgjMfhiH+4i/+YpXocUkZJ3sBHEmuCCwOvBHro+yQveeCHfhn9I0zRt6DT+DfZl62JzmxDoBo9IbP8wycMqCWiqD9TUTdu8Q8PWYzUuyPMqOOHJi7kzP/m+qIGWQqayS6JFe+G2YcxxjnKcbzOtGeU45VbttY5qrzEVHuWxnmuocK/8l6Xe4vYtCmTuSKbbDeHi/fgd6aQEGvneyhc8jZQI4EH1+9bRcwwHVLJb7EssWPk4TQssM6shZum0IfAVCcIoeP82VT+CGqoLSvuCWIBMXgiJdbd1lnt+m5V5v3XFxclEu5toAK+bKevPBtjNk/92ddifFzsUvitJ9teY3jWI6BR85bMGS/ZvYY9ht7RSfcfurnbf0x83GyYx9iX8c62Cf6sAGqHX4uurKdt4nD7YvYYjkiP4g17mHheY4TfB9EHuM2iHQschXfCeIWaJoYYvzonG0HWUF4Oe5G1AQVP4efZc74SGzbFWKvO3LZEq7I1EkqeMG+3e2A/IcOUEl3rPJ6sLbMi/e5ewQ9sQ9kHIwVW3aVzv7TFUnv+3ISjl5QQcIHoIespXGNW6rczm5M5RiwJXqQgWNVSim6tD6O2CSM/T1427rG/InB9gHgpd//g3/4hb1sX19d0XApBVCLsyIDxVG4ZQFwaeXAQJgA1RKyt7btYr/PWR7HX5qN9WknPiWCwM6pTFRBcp/1LpqmLT9z+9Dx+FYcG1m32VyCH8wmiwAYRw5m/mxIOGQnJLAIACPkwtgIpk3TFObOTBaJHd9FHyo/I/CP4xBXV9cle0ZBHCRoLVmWJe7v71ff5YycuR6Px7i7u1sxGj6py0yQA7X7pq0nKLmDhQMmrI3fY6AJwAS8YbQGVhiY96Z4LwMOjGTZRs7n3XKBc2MO6LcPH6BNAON1n6cDgsEJTunx8bHogYOjHbeZXOTz9PRUABlHqCIPHARjcjBzAOB5TpJxPtYf/s0Le+GZOGMHRrOX6JMvxyJJcQsMOgA4RF7MHdD58PBQmaa5HouNfgIEHCyY+7Is8enTp7i4uIi7u7tSKWU+fN/r62vc3d2tEhU7edgpwC9jIFCTqGJHNdntIlK9lRmd6/s+5nP5HllcXV0VwFYceVfvYyCZSUvk4zhFXmz9g1sQrJvug+Z3Zs6YL5VTQDk+Ht2a53pfAaAaoMnzqD65muH9ISRe/MeYI2KVNGO7BHAfWtA0TTkm2c9BF9AjbBdfjL7ZJ5kBxz4I3MuylFZOZOf3smacYOak3HrDOgFkeIZJD148A73CBngPcdhEDbJBlq6mbJNqAzZ8r5lvfL1BmdtFbPP4T35OzLWfQX+3/oIY4rGSFEEMAKhKMneu5LvV1QkvOrz1kdg2a+V9Z45zrtqhr9iXdRRd2CZt2/2BW5+ITlp+6LpbA4kHfCdr5/ngB/D/xNXHx8eCvYzR0B3mwOfBgNZD1g18so119vn4KpJudAlfTAy0f+I97uww0bXFBXyez20JP7/Q4W0lDZ+H3eKHjLv4Xr5j61vwfV4X9B5Z8Xn7DxMA26TK2MFkrONxqURFimbzjG1i7iQKOwa3uaUS3bEdfO3rqxMNFoIvhWklMGIoMBkoJY6fzaJuVYBlNTOYA8xF3N7elJNq+ByBd5qm1WkdFjCOEgdUz1FeYlmys765uYmXl5fyfeM4Ba1aXkwWjOcTNAwSMFoyPm6ndaWAoE65GtDPnM3UWn4GkMgI8P7u3bviPDnDHgdMAMnj6AK76rqu9BHj3Lcl+2ma4v379/Hhw4dVOxPPR7FhKkm4MDS3QRFUWHPWhMTGDg0nimERYKkAma1DFsjDjhSQ4jYIM4+uHDEenLYD6LaSYvbUJWTmgJNxgKdawPqRVA/DsLoU0DJDjyKqA8ShMhYHSV7I6OrqqgBmnuHSP60L2JN1nXngWDmthWCD3RLQnORaN72HAVnYOQMumqZZ3c6OjqIjBB8nD7TPnE6nuL+/X43HTKCP0AVIeG9JcYBKujnm1odHPD4+lkQGQIPs2ERP8EJn0SmfmkO7jatnwzCUM90vri4LO0klo9x0PU4xn+3DNr6tQpFwM8cU8YXvQScgZFwJ4aRAmH/W3AkbwIq+buSNDlg3t8ywEx4HfieiJrJ++OGHEh/atl21wxHE8bH4JmRixttBEZ/HcbTM3SALO0dH+Q+9w9+78kAy4n0s6LX9uuVtYML3AaxcUcbODQLxecSmZal7yJyMGPxhR37eNiHBZvFFyJ745yo8n3FlxcAR+zVj62qTATh6Y6LOvoKEkqQBXUFeTt4jovSje14GeAa2yIlxm9whbhE7eNayLEWH7KuxNSdzyItEBD3ABoivHBKA3V9dXa32bfqOMpIL4hY64/YcyBLmgy6x5qyB9z6ZDLHO4StdmXGrFb/HFxmsowP8znHGds+/t4kszzDbjn92QszYTPQyDmQDVrVNIxPsj/mxbqw1MZb1sw05GXJc5ues4TYBdHXSOuHEApILubntDR/AOO0vGOO+q8cB8132iyYjbRdOzF2pMdlj2/+rXl+daKC0AE0Uy4aEMwUkWMlIOjjrnQSETah2cKfTqZzIYfZqnuf44YcfClhGUFY4jAYHWUvs7QqsEDwjIq6u1rc2A06Z5/F4LDv/UVgUzCzPNNVzkklyzCbBduKAAAYGZHw3/0amKJZL1GZdvSkKpic7/T4iqrJgsLRoeP0wGLeRuVxIi8Q0TeUkFH8XQchJgBmg7ekZzAcmcpqm1V4gAId1CoMz+8R62JluWznMxNpRMC7WD51zwMQhuQLD/NA3goNPjmLuWwAB+8T8zRL8VEK1dRwkOdM0FfA1TVPc3NxE27bxO7/zO2VMnz9/jvv7+2ILfd/H8/NzCYQuv27bBlgjJ9lOHNA1AhkgwYDF82INIRCQM7ZmJ4wOmknDNpAzwMVgzgGfuaE/kBtmdHDArLFv0PZR2RG13QSAwXfaMQN0GOOWYXMbA/5gt9tFapvoznZOVQxZpLS+8A69XpYl2ibFbn9R5m1muOv6mMa6twSdJbA+Pz+XqhXjt3zwK04+27buCcIHu6UPGWKHbr3AN3rdAVoRtQrJRmXslrY3fuakh4qm213Ru6ZpyuEC6KqrL4BWwBmVgS1Tji/xUbIGp+ibQQWy8X4TbMxEhdtvGCNJKb7KSRJydqsV6/v4+Fh02oyyARwv66z9Kr/jZ1u2GD9pv24QZH9LrGHs3qvBnKxrZvZ5IT8Oy2D9GZMr3bwPeS7LEtE20XZ1z6PbYUwCIUe3ZrFO1n/GOk1T3N3dFTCMPeM/Aa5OzNj8TfLsSqET46urq2jbdnVBp4H73d1d0Q2SXmTMs9AfA2dXW3k/cZexW8fwjdub0j12x1YnK+iF15fP4wfQpaZpClm6JTienp5K3HIFl5fjum3EGIm1MRllvccv8wzvX2R90Tn+3IJ65mrMgG7yHidYBveOkegoOmMbR8b4P8cw67LJtxQRaf6y/dJ+A7y11XueRXLs72I+X/v66kQDwO4Fcm8ajtqgjwGfTvkYVJSJCWHYVoLsqJpVIHIp//d+7/fi8+fPq+qKF51A4YXK40irjJjPZhZhfUOzWU0c5/X1dfkZ/8EG9H0fHz9+LA4OIBVRjzSzUiE3O2oMHVZuC3Kd1bOhC5D7Uy0UVf4p5rmWnAFOAFxaMHwvBkABx4czIMFD+a6vr1fgBVDswLtliJwZ+9kwuA5Cdi7onQE/YzKrgm4ZkNiwbDA8iwQaR2JWk3EQAA2S/AwnqAYXdtzbTV1O1L3PAuNHpx1o0DGABPKmt5yAyme/++67wuQgC3SM9zmxYm0JrAaHnntErR567xZB1z3gblHZJqROrLAVwLuTz4got3a7tePz588F0PNMbIPADsil0kI1Dbva7XalOoesWW8He9sB4BNfsd070LZ5v4YZeQcTXmaLI9VWIoDVNE0xjVPsd+tLDZflfJLero+3s3xcAUOeKdZ35CADWufwv6w7Y3IrBwAEUI48aFdBL/HfzNHsr4Gufbv9R0SOMxxJbhBrBtaneqEHrqovS93H9/LysjpRDh9ARcdkCXNv27bsgbHstgAKwE2lCb0144edYr8Gs8gIW2S9+RNA5Pdv/Q8/N5tvPTcIw7+YCXV8IS4YVPmodjPFtl3G57i2TahMnKEj/q6UUmkzaZra9sYaM5dt/AA8+zmMN6UUp3My17ZtIeYi4osN/dgnskIuzBkfYdDFM/Gp1h/GbJIQcM4c8Yv4SeSCDzeR5b2v6Jmr8VdXV2V8yAV/bn/Lz5gvesD3s14+uc7jxN7QGY95SzBvZWpS0/jRusn4IQV8MAikGmu8TV6dHOErmb/JQsawrcTxefwYawoO2uIM6yc/h7DeYlqTaJYFL+sudoK/4Pfb5ITn+rPbFsH8kPOx5ZtkxAmMk2Tsy75h6wPQhb/2igaTxongKNg04wvYUCC3SUXUbHwYhpKUYOgoUWbVbiOluuGI7DainihCcLDC83kL++bmJp6fn+N0qv36GCGLPY61ZGVAjODdz8r3MTYr7vX1dVxeXq5OF+HGWrNcTVOPlMTJwKTSOsN47LBZAyvFFkjbueff1SNjSYxg3egBHccx7u7uyjo7iDv7Z00BGcgcFr8mdZW9QC8Arigq+oCs+r4v92XYoNu2XvbIs/jeq6urEuQd3Hmu2SD0lX9v2yxsZGbsIqKAVQI4TsMADWfLmA1KAHWsFdU8vsdAHAdnMMqcsQGeRSLAZxgXjgTdnKYpfvzxx9Ku5T1GVN54PhUnElOXdg1s3CICc0SA7Pt+dWTifr//gilnXN7bQ4C2fiEfb/S+vr4ugdAVPtaI9fdeFX5e7aJeOIj97ff7shkcX0BQxh9gP2aNCPbYlX0Wa+c9EK5wIZOsw228vL4U0IzepGUNJtGv4/EY01JbkOwL+76PJqUYl9o/T9Lm1k4ny6zJ29tbsXX0fJqmcrIda7ytxvoGZgc19NTVOewFfw0QA1TBZLZtW1q8eK4PsfCeNnRhHMdi/9fX1yvdBXzga7FDnukqGWDB7WEAPX7GXSQGO+gFAIf2OL6f+eMrAI1OED1W+9mIWOk4tg5ZhZ1gb2ZT8VX2g6y9kz30y6SHfaYrIZyo5u9izE52uq6L9+/frwgT7NXxkfUwaWU99CEmPlwBvaBFG7bfvvT+/n4Flkx6Wva0uOIvTPSQhBt4M3eeyxqzTui+CSb0A2x0c3NTiJG2bUtrN8kXeANdQE9TqsSgbdlrZNAJSOTAC/sA+1vvJ9mCdOKNCSr+jZx2IkaQrf0otoNcIFkNcEmCtu2cTkz5GfK0nNFpdN9J3jb5d5LMWoIveQay8nN44Yfc8suzGTPfic7gb+0PTHLaV/JeJ288M6V8OyAyNUGbIp982bRtxLKuhhoXMWZjSb4bPUP//Kdxyl/1+upTp/7on/9R9H115PnLm2gavigFZz5n0DSff5diWWAPyeJyOZzAzWJyGlTTtDFN1YgJjBgUAMXADDaLsWGQbdueTw+6iGGoJW8LCKDgdhye//b2UhwHPZZbJhqD8AID6nCg3rxqZ2enwMKiDAR1AgFAw1WcDFLb6Dp6/A/RdX20LcZQGUFABnIxy2ugAog1i4Ij9zzsiHG6JDsGosUYIlYBrWlyyfT+/r4APZIGswB25PzbLDPBocqjslGMHWdhB2C2g7GTxMGcmiHbsv7oAfK1obKerBUOyOws44+oDIcTMZ5tuaLvDiBOQtEfggDOmM3lgKtvv/22VLEAMBywAIBzpQr9Y80ACcjJrKvngS4x5tfX15jnvKH54eEhbm9vV3sLCExb587tu6yp7+jg5eC9bdHg3+ggf2d8Tja3zCyfgb22n7B+kkC4+uVgjw9zCwayipR96HA6xW6/j2kcIzX5nqJ5ye51t9vlYNHUFtO0LHE6DdG1baSGFox8f8qLThizDToxdUAm6WRflH09c3GrHfrmhNN2YMLE309Qs70hG1cfnFDjY1kH7M8+nP9IGM0MGyDYVhgvQNaklisyW6KHOdhWDFIYP3tqttVAvhtf4IqmN/yagbS87cOweeaKvVmXOTHMPpRk2mDDG4rNulpX0QHihv2r/dhPrbHjG383A+2WMBIZqoocosL3l+S17yI1DTfYnePgObGPZRVfl2VZXUqHX3McM3NvsgoChhjjfTrex2WgyDN4jqvaEVHmvE1C/LIOoFfInPZHyB7itOWDXrqKAJmCD89+c4omNSs7qYx2inmZv7AH2wix2NVREyboV4lxS8TxeDp/9xBdxymKp3PiXA+SyQdk5OP6nSQ3bd7wnC8ubGOcxnwUPGvRpJinmkSZQMz6F2cc28Q8T6hQpOZc3Z60gbpJ0aRzQtp3MQ7ngyra2s0wjuP5PXVPcMQSKTWRUpSfDeMQfUd3Rf5fHucc6XxKVGrS+XjatqxJ17WxLJExtdahbdpIKSLvyT1XUWZa5KZIUWPdOE3nxGSOvq0nf/FCV7Bh75vKuru+6PIP/vCfxM+9vrqisdvVDby1HzZHwK1h5dcSeQN23Vn/+vpSnCughYnhiMyu3N/fl0oHQQPjcIbIM6ryrJmc7KjSFwLie7fMdwWP9WZSgDkgyGV6giBjOxwOpSUJBgxjNxAhieI7HfDtpLZsPfMkQPV9PWO+AuV6+zMygaU2O0JgYZMrcmGdaLOAIfe4tqDD7LKZMgA5QdCOExnhoJgTAMdzrUnstFovxoZztWNnjbKB1ITCbJl7+AGcMLbe84O+sW7oF0CI7ydo8H3M1eDHLCXPx3YsR1dJeI/BK/IBADiZjMgsHskc4x/HsRyI8P3338eyLPG7v/u758pfvm2cNgPsncAK84QOsEboCMEQ2bBxGBuy7Hwik9uZfFcHrOi2f54EmX0pzMtgDjtDdpYle2qQsdshsG+zfK4W8H32d05ssXOSckCM9YK1KExo1DXkSNpYlmhSE13fxWmoF3mG/U3bRX9e96urq5inOXZ9H6/nE5acsDF27A6/7XHd3t6W9y7LUphEvo+1oXLrVjGDKjOT2D/+wATSFojx3WxcR6ZUgAFIt7e3KxsGdKMXXh+TAfhf5o9dkhBM07S6VM6VSGydI0Lxya7kMW/vwXLyYTbT9kjLLX6HFzoXUXvHnSQRR/HvJnycSLk/H7vbVrlZR1do3KoESGcPATKFQJimqSQFEfEFSGGNePEz/B1rAqGI/v1UyzNrnJOJiGWubXHLsmRQ2NYqseXMv31i2tafEsv5twkq1h65U3Uwy8+YDdBIpnyRrWMEPssx3qSLiQ10163SJLbFT5xfbs9zEuBkIiIiRQbT+FC+syT1aX06kpMzxzvG5/jgjdasYSZISX7rfhhIU/wVsj6d6n441up4qCfLpdREk+o+hpRSxFRvJUd2/NtElfWyJNjLhuybloizWKexVnL83jnRBVExRH5fE/OspDXV7pu85pWwh9ByHGPMJCrLkmI+JwwppWj7enWDk/yUUsxLPYBiFHnRpJq8suYm6VlH66hjiX3Zz71+g3s0/vu8sOqdjYjVpm4YfysbTpgA4DJ2xPom2ZeXl9JbjeNm47YDCYsVUUFWUYalnv9usDkM1VE4C4+IkhQAhuxwxnE4Z7rrIzsBCyRdPl3KQMQJAc6KOz52u128vLzE29tbvH//vhitlTsiyj0hTqL4M4PLegLYOI7lhmWcN3I26NiyxjCy/Jw5AOrMjJjdYV48h8TEY3XbQ0TdTIZj/ClWjQCFzB0o0QMCjo3ALR0+3tWgyokD8vacABLbzXxb4OKgT0XFAR6dYV2dVPhEGwdZ/vNGbTNyBlC2MwNeb0LGXrdBD/A4jmP86Z/+aTRNE/f393E8HuP+/j66rotf/vKXBehbTwgeyI25k4RExKotL6L2+jIfghTAx5/13Hz5YNu2q/sttq7LwZG1dMuOg7OBj20bNt8geRiGeHh4KKDHActBFnvh36ybL0YzwPWa2Cb5HaTBOM/R7/qV8y9Vpq6y5rQJ+SQa/IDnjD3Bcm/1jX0NTkwsX/wDSQcVReYK0GqapgBT1nW7TjyfRBObIHkwQYOOIVsTNNwPgx+LiNUpW+iKSQZ8gdcf++B4XbPBEeujt+2nqQ6ztujD1kcCePz9fLf9TQVdXTmq3ZWfaZrKKUXWeQMmqjSMiZ/5OejKNp76hd6ZCPGRuvgj/s7nfUoScd4HgtDW6I4A4wHW1gQS64p/XpYlUpfXhmQbksQ+hldJ7M82anxhMpFYQ8WWOeKrkcnr62vxmej4NplH70yEWE7I2PHahJKTchJj4wMnco7R6D7yYmM0vnaLlTK5Ue/0MsE5jmPMS11/9BidIYFhHx2f+SmQCl47HdcH3QB6IRqQ3bZqD4njBAIw7s4BJ81OTlgbZGdcYF9u29+u29ZO/jIQjk9j7MZAlgvvNb4zrnLS5tiDTrNW/MydEtM0lgsejf+a1MQs3w4h4XlCZmxby0l42rb9661oAIz4UoTMBt6IevybB87kUAw7W/flIUhugR3HsWxusgLgJFESZ+4oOIwISpwDT4rdru6rMHD3RsItKMvv++ljzPhOBM7PmYsTEgyRPRsE5S27hmMDIMLqboPr6XQqzNLhcFqBL9ZkOw47FFcZ7LQiamCe57kctQmgwJGi6Mjtp0A7MmL86APzd5LoJI11AHg5WQN0WPHRPb/Hp2l4fwxrxp8GYTyHMQIQcezojAPXlmlizHyfnQeO1G1+7D8wsECOBrQActbebRXIhO/juE82MLJpPyJXHmhDQl/+3t/7e8VOliUf5ffw8BAvLy/nSx/TuXRd2U2CinUcW7BTxA65W4CDDNATgFTb1jtmkAEEBaDPxAUywof4/cjr5eWl7AVzHzlJqgEsOgo4BIQ7uJsscCXOCSjJgYG0GVrAHd/HWPCtyJdgPwxDzLFEH/0XATGinoQEqPYauc+a/7A3P4OAGhFlTMg3op58h83hK5g39uNWGeZgv8m6cQyr/S/jASRaJvgr26VjCskV78N/+n4mAwN0j38TD7Ah4hvzLgxnxEoXkWXTNKvDUhh/Suv7BpA7DK1jWUSswBV+2HMwkHRFDL2DIHEVhDlQ7cTHoMO8B2LAANIyMjDlREhsnt9tY46PHWa8jkNUVhgH3+mecesxzyCpRVbt0sTpvGZccuo9H8wZgieleiQ35KiJjoj1MejYoXXVNsQz+C50BkAMq+2DKNBDkwbMB99jwOujnbEliDZ0yN0H2FrxIXOtRBAz8NuQBuM4RYq8nhx+U4F4ir7bl6QHXWQ/HkmtuzCQD3ruhKht27i8bCOlutfImGG7l4nYaXKAGOdqufVwGx/th1lPJ6OMi7Xhe7EH25X9o8fmBMA+i3horMXc0AkfvoOsIGGYtxMp6xGxEPIb/RnHIZr2y9bqPOextBvaVn7KZoh72W/VE83sv/6q11cnGjCLlFZgb2BhttkXhuh+UWePEZUdIlAgUC/ulhUwYGLBWASzqwaA+T3rfmkW1MZWMnexAX2fy1VbZnKrKLBLzJmSNBUBwADGCXPIonPCSUopPn/+vGJQADwEFhwRc7+42Me5yXvF7OOYuA/BCZJvdXewYJ6FdTidVgyIe31JdJyE2uG6BMvaO7E0OLWher78Hr1An/gsc+FzXMrFaWCACICImaFt8mp9IkDDuAEq0TWvD3OMiFUC5O9AD13B2Z52xdoBzLbO10wT8+DFBU8YPs7UY3HC6xNq+Mxul+/AuLu7KwDn06dP5c4WABTyMsj3utpWkdPhcCgbxt2m1nVdWT/kAJgkqCEHByT0kUTFMnPwePfuXQFg2I+fgzxIXg0U0Sl028SGEwsD7/1+v+rZZxzo5JYdQ99IGPBhBMGu62I673HjMkFkGZHPSHeFD9Bk+6Olw5uf+T1z3Po+PhcRJaEkoDvw8G+DUpJzwMwWmBBQDaTQycPhUC6zY01MdJhIcTsGYJ95cLAB34nfAkzgJ7AN/kSH0HfkZGC/PUrXrCQEAj9DR0lSGZOTHN4DoLSNOxG2PbhdzOsGEDGj7jmwtsjOe5pSSoUBxobtP/jTSZUJCp7Petkf4F8dDxi7ZWu5+E4ht6V5PsuyxHLOzfhOxl/BVr3ID3+FbXL6FJ9zZQW7ta+07VgvDDA5NIEYS2XMjL3Zdts68S6i7lNyssfa2bbAHPhFJ03Iwphqu4eMcXVtV1p+OAKd9xkg46P5mQ+9QFeRCz7GQBX5LXPeV+FK59Znep0YhzGbq5PYhffaYUs+oMH6ieyMCU0cYwfGto7n6IFt1aQGOshzTNjaxzoeOKn2z5yMWIe3vpvvmqYp5mWJWf7I35dSiv1FJXmsd9vvMLGZZbGsdP7nXr/R8bZma5kMp7+Q/bJgtCIBqFiU0kOZKrvuBWWidiR81uDUIBbmBwDnDDOCEnJtV+E7zDwb3GJgefy1BIhTurm5KUwpR746WPBMDB9H3jRNSS5sGDwfMMPRloCylOqFh5zrjvPMCc1lHA7HYkBWSpIMsl0bPMHWfXnOYA3gDDqcSOIsaXuzfnDZEGAWQGlQhPFH1D0zMLvPz89ZSc8B0RvxmP/t7e3q1BqSQU4cQh/YaIreOJg6+GFslP2d2VvvnCRRbmd/Dv/mvU4ukL03NlOp8EVJrB/PsF5hTySxsK+AKQAh/exvb28luBjQogPDMMTt7W2xjYh6ROaf/dmfxS9+8YsSTFhLABXzMaDEqW/tm7Xk3+gUe1f4N/ui+Bl6xPfQesj6PD8/r6pAJC8RtWVrWZbV/TucasTvcfQkq4DWT58+rY7PdUsPQQs9Yh2ctLJ+JkaclDIng1oqUJwe9HY8lHF//PhxlWCm+dyrfPZH8zyXqhBrvQVy2J6BE/9GjowH/8W/0U/Gx79pA726uirgx7Yasd5Xhg0iA2TvTf7bikwBRF094QY7RB9475bRdhULcIS/x8eaDGF98J204iAr9BifwHehE25hMIByjNhWf6dpKgcybAEGa2AywWCs7NHRHJCNj6jG35DMcx/SOI6Fcee5vLZMM88iQXY1nWQJHURvvMfKCZ0rBAaAtgviI+OzzfEnfyeGumK//TuX+aWUyjHI6Al2f3V1tarEs9boBM9j7V1VRS5UGX3vDETNdg7Iy5ULno//8P4+1gU/SVeGE0r0GHtx1QTsQZxJKcU4rfv1c9Xhsu5hifXFyfgDk4vYsXWT9TSeyZ9dtzw59mEn6BpYhHUwGMfHmDhGv7BxYgzrjo+wLI1F/PzteDwvdJoxOKlCPqwHsdrxwTjV/sK6Ac6zbCo+rXjPyQ1zaFMbp+G4embB5nE+kUrEnXE3a7OtruXx1v07X/P66kTj/fv3RXkYgEHElv3xe1EQAraDtZUL4MPC59/lEo/B+bJEzPMSXERnJanl4T52u/58Jvtp5WwRHt+LsQDMnIG2LXs88o5/PoPC5w3v6/7Wea4gY6tAWwPFaIdhKP3UjIE5O9HhewB8ZNSwP7QN3N/fl7YTs5Y4yJRSAfQ8E4djRwrosGGZNY2I1a2Z7tF0UHSy6bYRM4jzXFu1CITbTepeRxIwO1/0APliJLTO2IEQDHCCBhYwSVSmkAUbR6lAwXyaDRzHsdxcH1EdPQkHz+bfTtL5N/3LOC6zo9gB4+M5yJ4gidPnZ2aGbLPeA7VlWyMiPn78GH3fx7t374rubBMlJ7folgMQPzMoYg58L7I+nU6rhOjh4aGUvn1KCmPF8WPbbudkrr5DJiJKC6OTR+5OgAGnlfN0Oq1amfBP6BpBm7m6dQJ/hJ0yX9Z62/oQsb65G1mkZn10dwm4TROLwCXv51lul7FPMSif5zlubm6KvJ3I2j9BAkAYsRbI/+7ubsVCuopqwG3g6vGYQImodyQgPwdtr7cZR+Ru1tABc1uR5r8tUcSYvE5bBhefxJqxF4Ug7fmZWebzvId7U5CnQZMJHgMYA0p89evra/lOk23EBQMXQK0TSeIMcd1rhr+yvFgnYg7ywzZp0WS98Cm8j3FDLNA1sSxLzEoOl2WJ17e3aJumEGeAR9vjFszjp/idExL0MyJWe/nM8uMf8RVb0me7n+bm5qbMFfnZ1nm2KxCnYSh35JDo8DnWGJmT8LLu+EOeyVrjZ5CFKx0c0JOIp6c18dS269Zd/HWkiLatxK2xm/2fqzbEdnSONqdCAkRl97PMfPrTuruAvzu5wDfwfR6PY6+TQnAFeoc9sUbGrfYRjjWsqT9nkO8KkLHcIjvgu0wEOUmxb8r/zhIr80wR/a6PWCKG4RTzNEd/1udJ34Ffw86x7ZLYL7FaA168lzUD39QktCYzX/P66kTDiuU+QBQBZ4qg6PGj9QR2kgnk9zUxTUs0Te2R3+8vFXy/vLDJm3iyw2xjnqfouj4imtjtLqJtqZzM8fLyGik1welYJBOAAcYHALMS5XEuMU30AKdYFtqwOLEhJzXZ+S/Rtn00TRtt20dKbXDkb1b0JZYlJ0/5+IKmMO/DUI/PjGhiGLgdmw30lTXBQACZNzddAQgEfpwVn4mowJH52ZlF1Et+DMhwbMjfYJneXtbEJ3TBbFl/CMp3d3er6pGd77LU1oiu67647dYJkpkX5ns4HOL29jYiqjEb7BoQIkOCH8Gf5/AzXj/++GN8++238enTp7i7uysn7+DsfZHi3d1dXF9fx8PDQ6l04MRweAAGWk/MYpFgIksugUTvSSoiolTAGEtE1hXkjKyQqRMdkiTkhJ3y73/wD/5BLMsS//bf/ts4HA5xd3dXCAOYS+5dYG2sOwZUbsvYOlLvXTKwRC8ByowNYMMpSRw0YSZtHMfSP5xSKsfyWhdZD6pHDppbZsn+Aj+G7AASAFJ8isfipBodNGFje4VIGIYh9v0uxmmMZskVjDQvsSxTpKaJi6vrGIehkBBmsxyYnajaJ3Rd3tPgvQSsldlwWFN01eyk2Tz8EAmD542OmBxy7zI2TnBmzBAr6LDtl7UEuOFLzLi7ouM1IA6hN8S4bVJk/4E+m63Exnw0txNZr3VElEoyz3BlDZu33jBPgJzjsFtuWHeICmIyc4IZNpnAevI8/m5iiZZmfod+e12td64WMzbmRczC10PAvL29xThP0Z3H27c5gU5dG13TxLhkf7Xf7eLqNncUzCkidfkEudPpVO7pMBlDnDNAJSEbTkOM47Rai+E0Rtu1K9t2zGBtHDMcI7ZxCX+FfhxPp2jOOjFSYYtY+X8DziadD9w4nCKWFLGkOB1rl8C2FbiuW+QT6HZ9tF0Xy5w3X6OviaNWo4m2bWJOlVnHBomNOTFJMU9LDMMYsZx9XtdGOmO04TRG13fRd30cj6dY5lyxmKfcHhUpxTJHnsdZT6JZYl7maNpMJrfdLuYlt/vEku8A2+37QvL0XR/zvERa0hc2uQX9+Hd01cmIMYExKb83BrIv4gXJYyLT2Kpt2xjGMZZYYpmnmMdz+/y8RKQ4b8xe8rzHKZo268K8zBGJ83UjpnmKtmnzscKRE5WmTREpz/Xw9hbjNMUy5yRjnqesW8uZSF/m/Lu2yydUTXNEpDgNhzJnCD/wg+XI393qGlGr+lk2X7dH46tPnfp//Y//8yr42/HARrLZ0728zjwZXEScgUFWbsqVvAhiziBdhfgpJTOIxAhxbrxgW+jRJlDgnHk2QsdRm0m0sm0V2FkxSZEDwDTVy7AANHwWB03GnVK++wBF3u3q3RgodWVTxzienQ/MBQ4Ott6fYT5mJgiSsNO8aIsCZDBWQCTMPorr1h2DWWfSsFcuaxfmJOpFfvwOuWIUgFzrI+vrZNSVEDMTT09P5dno7TRN5cQh6wLyd6sFujWOuSWOi8rQU+uny6z+N/NE9gA+AIJ7StFFqinMyQ41ojLh79+/XzFL1hmC7bLk/TZ3d3ern5lxZl1Pp1N8+PChzJVbyCMqG+INvKwR+ti2eQOpARd6yjMYryuebjdC5tgNlQYn1N6rwzgcWLquK611+AtX7ZwYeE+KQW/E+pLMiArQSIDQta1M3Wdu4OgEZztu3ke1x60mW4aWP61nJAGAWWRstht9c4ncAQY/gIzcwkAgZqy0eDihJUmhUlSC8cZPYROAawc7iAt0apuU21cADpHNtpXDNgPDamBtJplnu60IWTuxtW9DR5AxL8aDvQPCSZL7vi/kHONgz4/9AvEWn2CCjDXh31ShrH/8nHiIvUJmoAPEU8sLPXVbj+fWtu2KbODzTg79LN6zLEsM0xghQsnPx3fbBzvRcXJp1piky+tUNlunWn3je/B5/a4r4zDj68qgAZnJBL4b8qxU1s4xg/2Dz8/P0XVd7Pr16YsRtW1wONXEEzxVyJJuXWHAX47jGONQT8zCP3stjVXQVyfO9lFUjoj14BPvh8UP0kLpCoCrI6xZ/s4xItXxE/f5Psdft73n5KgtMQLc4DjGuIzxjBWdINtOt4w/P0f3ICnsm/Hj9oPjNJV7jfz8/P6Irl2fLujDkoyZI2pl2fJcYYqmiX3/l8cq2xC24goTvzPBwneYdLP+oJ9t28Y/+y/+MH7u9dUVDYIbi8FC8jPAJf2PnBjlE3VY4BwE6ue9echKycT5bsAXIMcgnUUi0Dm7hZWJqKcFwAAg9C1DiUGZFefnVgw+gwy2QYrvZNzu/ffFUNfX1/H8/FzOI+f3lamrF9ewHhG0JNVLXfyfAyWfQf4Gy267Qq5d1636hY/HY7y8vMS33367mi9VDZfDcWpO7JC7+2z5GXpA4DWjYnZh2z8ZUZNcDJC2GgwJkG4d4/ne1AhbzRpSHTAowvEBeEigcAQOSP6dnTgOgnU1WOO+iXEcV/tjOLHJifNPBWEc7sePH1dH6UZEAalUmfq+L0klY31+fl4dW+mA/s0335SEap7n+PWvfx3zPMcvfvGLLwADfwLc0TF0w/3/lgdtk8iblhIqDvwO4OfPRtSNdwAv9N7J6rYMz7qYUQaQEUD4DnySddYBhwoLwYJkmM/w3RF1T5uT4G21xJWPra4S6PludA3ZEiiZq8ve+DKvD892i5/ZckgS7yNz1YLASADCP6Hb+A9stmmasukbGVrmyJOfPT4+Fp1mDA7A3ixt/2+fYRIgolYzARc8Hx8F885a4BudVCB7dMnxymSGf+59HAYGXGLrgyvccmVyC/nYFgwU0UESEYAwCQZjZa0N2GkfZE2RneWHH2It3a5me+G52BFkCbHaIKZLXUzyY3yPEzvHbz7vyg7fAw6IiGJX2C+tpawR8mcdLy4uouurzyBxYQ2dZNOOh62ZUPXa4gfQb543DEPEUtvI3U7ctm3EklZ+h59ntr2CY+aebacpMQ5dsG0jbxPByBf9SSkVG6AqzJhZAxJj5u1kBN139dR4rOu6OBwPsdvVwz5YN+Rr4orku2mamKc5jsd15d0VPGMEyw4/ZZLF64NOM04T5iY8vHcH+3BSUp47r59dfEVaH6VLIohP2iYaxpW8kGHRl+REpibOJrZtj5YNcuQ7XCHz79E9+2Vs4+deX51ouK/UjIFZIATuzblmiAy6+I/BMzkL1Nm2s0g7XQS+rYpgVO7BdyIBqxTx5YUufK+DkzctMnazituA7UXwe3H2PMvMP73VfB6nn/vrlzjrTvkcAS+iBj2CIyVy76chwBFEuq5bXbTE/AmurAlAh9NneA+g3iCHQO+MOKIyBa6oIFcYYdaPzdzbz7NOBGDWOCK3I9DOtG2jAZBtnaqDTdu28fHjx1UWzzNghryRzZv9cNpO7FJKq9vObSsEKQdl6wYOwqyDARyMvnVuGPKG7u1eAXr9kStzf3p6WrEntHMYZD8/P8fNzc2KpaWH+O7uLv7oj/4o/u7f/bvxq1/9qhyDiy4g720Axd6GYSgVJFee7OzNWuITzOyxbnwPa+vAZT9kxpnPMmfk602DgCEn5oyDNTZLZmdt4A7oYVz4QAdVEhOO+jWItu4bGDZNs7rMED1C5rYb+yx0xqSFQSQMOjbic/sB+tgn4wOguXJG9YGExqQNz8L+/POIKDY2TflQCtohncyYfXSChk9yDGG9GZvXkrVlPG5F5Du3SZ6BPJ/l4At8QkQ9OpbPOcHg1D7v7YLcImnGP7KWbs+DXGD8ED7opteU7zidTqv9Hvbl29Y/ZG/fgTyoSOITkbmJBnclkGQ4FgBiCoZY5khK2Mwi8znGih6wD9EA3vueWAOeafKoa+v4WIfdbleOA0UfqIB4XyTf403Ynjc+ntg0DENufTnbiisY3PDMeiJ7t0iDgQCgl5eXsUS9xwd9zPYzx7ys98ah9/yJ3DnlzUCamERFxu3Ftl3m6DU3yOWZ6BlyKzE9rSsstjNe+FK3EMZSKx3YL37IyeuWCOLzxnv+XuZCC5HJBeaO3qObHut2X8cSdf58R/37+tQ99MaHrdhvWx+dfJd4GevuCdbL83T13nsWwS+st3H0lrDmWfirv/ZEwyCfL8PQ7VQBfhGx+h2Dt9NYlpohO7BuFZvvxwEjUJiKbf8uysAi0CqBgZmFQ1AYt+fKIphlsJFR4kNRUBAciZ2sAbZBpsveOJDCdERV3rwHpR5nSGUkP7ueekCygfwiqoNxjzXKiBP1Lc28f2u4GCLvwxl+ofTtegM462KGOqIGOW7iBdwStJCNN0Vvq1kYjpk/BzkDIQKUwcgWaBOoqXigm7AbrDtrgwMlwQEYkNABMGtSuD6PG12wTKiaoCMEJcblfRXby+54Bs8x4GAuOG3Ig8fHx7i6uiqbWZmnq4B+/vF4jNfX1/jFL35RZM2Rq5eXl6U9iYQQEOi7MPAT9ilOKNxWwnyQh2XH3MxkoXt8r9tqaBFkTSEdtokxeg3wSimV1j16wvk+J2yso4GEAVlElJNuSDrM3JFIkuCY4TYzx3paZmY9kYl9EPbD+w0qADC8Dz3HZ1h3t+y12Vr8OH8nWTaJZCKCz/Fsk1AGz/7MPM9lfRizddRJgf2CWX/7HwdLAq2rQ7ZL/IuTWesnumufbp/Cd/izyJmNzpyCxFgBBYB9J4hu1/EldyZFSB5NIBkUWa7oA+vId9CdQJx1hXjds71O8JzY+o6ibYtu13UR8xSTCCHsz6QiyTU2iX74sBEIMa+d12uacu97SusjfEt78Jji4nJfTotCj1g/bJ+Y6dZJZIs+FB0VoN1ikLapbUXobkkOu35V/WbdpmkqvfoGs0W3I0XX1wqP1wLb3XYU2Jc5oeaz6KTX3sm3bWpbMfipxH6cxujn2roXsT7VDFs0GbHf7yNFTT4M/E3o2OY9BvSU3/E54gC/35Iv6CP6wPyM/ZwgN20b01yJFOadP9+UKpblaqLaGMbkDdjB3QApJXaLl9iOnoJJTZ4yB/7EX9hf8mziheWIfeIrvub11Xs0/oc//tdlQdu2LQCHQaFkDkSA39PpVFhmDDAHj7GcLERZ3QaDwiA0lwPNZNpBWoGcMMDMMkYyOBYA8OnqigXNgnnjLsZhprwINtXqzrZK48+h4BG1/YxWE1cBhuEUw1BvvMVxZwPIm91ReDNoGJhZsYiawMCiGdySxGDIW5bB8yMQ4hRgvSOitOqwlrQcATpwHgBlQAOVCgdkZOj9AYzfgBS9AOSb3XKFa8ui24jNhLD+BoLMlYSurlFl552Ms3GbCodPS+E9bj8xG7MsSzmTHcYD+TtA8Ht+52dY19yHTUJAgLy+vi7rg80ZqBJEOMK37/t4eHgoOnc4HOJ3f/d3VwwrjCh2tmWTCNI4LjORLh+z98vkA0ECsOPWCfsR9ASbwE/YdvE/lhvB3YnslpWjKmP9MTMJ+LNu4xedfGJvHHPp73GydHFxEZ8/f16dLIb8sQuCr8E3fg15kXQyT9+pgz9kTug8sjXr5cqhkwS369ifosO2WTPhljHvb9t6d4WrAayvWxlsizzXQJU1dgC3j3PlwWw732XSAR/GPS0krl5rfk6yBtiBnbYeIk/+baDvfRr27SbyHG9ZU4MMJ0QGqCbb8LkkOxAc2BfPurq6Wl0M62TR7UvYEM83wMa3oYdLyuCY+QHU3Z7jJJqf2T+xnsRPnoPcrW9tU99n+V1eXkTTrltjkCkEAImSQS7rvk3YIyLG6ctOjQJixeqbzBzHMVLUxIrP8Tp3y5Tnrt+TIpZ6iAC67DYZ+0lkjn9wlY9nbkFlAdVNrdK6rcbEA8Tv+r1t7Pbr267NxJvUNhZZ5loBIQ577adpffS2saIxo+8LQ46MDT1xcmICFlswXrBvzZu+17d/l/ge+QQvbJPxMV/mgO9mfsQLtzKVFumlxortfJxckVTgg/u+LxiNNUC3TRagY9iBdeEf/6f/KH7u9dUVjXxSQ4qmqa1HGeQ10XXVudtp5569Y5zOR6ixiE2Tj4vlZz7znsBpkBER5b6O6mwiUqrAkEUwy2YmH6fnigABZfsZhO5Ln3B4JFl8L/NGcR8fH2O32xVA6+9EobxoGIKTI8AIhoICoVwOHNM0R9NkozVjZ8VFqUhMHHQxNisuY0LeEdVh+bQZ5r0FHr79GCPhfTh2O0ccrkvQPJPfOelAJji2iApK7ewBR2YlrKMO5mY5cchmQthrBOvBz2HtXSlgDqz5Vra+nNGBzoyIN9Hzn5kh1pfvQ39sD/wbXQKgkdjQewuIWZalAAwcoJkcGBYS0d1uF999913R7/v7+9jv9/Hhw4d49+5dTNNUSvNeAycYrhQxB/QCwiKinqzF5k5s3a1EkAcGHsgiIopDZW4Ehd1ut2pVM2hyUsL7XanBD/JzgBPVMP4za4d+MU/0hBal7YZrj4X3bRljghY6DkDAjnyiCDaC/A0WzHBSbWzb3FbiY4zROydXticSH/t0KkKsHUkaNmoghh+0P0Z/eQEyDOpYK4MM/jTx4OolYMjHPGMfVHsZs/cMYb9OZoh73qNlIoE4ga0Nwxh9Dzu5RNvW/SAGzzmxTSv51+So+gMnEHznliyynZk0M5sKo+wx9Dsu7BzjcCZZarU1H1aCLvQ9oGs6x6eugO2maaJpm3yS0VIPyUhtG6k574ua5nL6kw9iyRWAfKrPcDpF09ZkMldMUkQczs/sIqLeIG8g2DT1YAAqE9V3LJGaykRvSaDu7BPwO1mH60mB0zRF07bBJbpvZ9sziUGL3DzPMZ/B55IXNRoB+KZZH4Zj/V7miHFkb8KuxKmsl6dV1RbbmOd8lPUwjnGQPxzGs09c5pjmNbvP+mCb+AjHULCB/QKys60ZtLZtUyrfJgWwbcdZCLn8vVl3nLzvdn1ErI8f51ld38U8nWN6LLHvM5kzL3O0S1vITus6scAVT04djaiAOyKfIoUs+LPt8mlitMNDLJBkmHD2HgzfqWUMyPt4OWnMcqpzNlHkS0x5xhaDOsHA95oM7Lp6tDxrSGLl8f1Vr69ONJYlFcXPjn2Jw4Ge0PVNx7ShZOPeR0qUWE/Rtl2kFNH3tfcZIFOP0atZ7TCciqOnHxVnllKcv7uCS+/J8OlTMK4kDyxWdj5jdi7JC9hH1+Wjas1owaqO4/jFKTc+59+MZUqpgAOckZk/5rMtL9rQ8oI2cTwOEYERVcbV4AuFNAgoDImYMJItDOny8nIVuHkuFZRJgSIiVmOnb9v9nr5FPCJWY3OygyNH0SPWJX0zEmbQeB7j6rqunNTF+mLMyJvvhIHCwbilxEHFTs6su6sHZvYAoQb4fC/f7T0ZrjTh9HkPjo89KzgQ9/YjW8bE+31ZG4kDgefm5qa0BaAzBrWuVCI/NtYzdmzy5eUlfvWrX5Xb7D99+hSXl5dlYznOegtosVX+DlDn9+groA4dIdnAprYXgQFECXpup8G/DMPwhZ6klEpFZ8uIASip4jgZxVZY2/VZ4+uTn/jTVRv0DPmQZLjP2/rOnioHAustc4G1sr5b/22XAC234RnsOwEAUCMbdMQVIGzRLa1O2HhhW2aem6aJX/ziF/H4+Fh+Z6aP93l9eJZbWGx3VPGcpNm3RMTq1DiD7Vx5r0f74kMd6CEGWA9YQuzYz+HZeUxsrFximiq5MU1zSfJMwuz3u8hwtN7LkO0FkiyKb2C+TirRZbfOkFDwPcylbdt4fnmJ1OTTqPb7fZyGxwxQD4fYn3axnA90mWOOJU0xTNO56p7iNE4r3dwtEW3bRds2kdomWiV4y1xv916mJeYpA6fhNMbc1taZ2koTscxLjOMU7RIxxRxDGqNtalv1PM/n94wxT0vsdvt8XG7ky8baplayOeSACuQ45lObIqaY5jNoXiJ2u31EpBjHvI6HI8d+png7HzqSZdzEOFbyp2nWbUh9vztrbSr4oox7yicWRSyRmjbG85jSNMccS0RTq3pd00akJqZ5iTj7yoszPlvmSuZUvHS2h7fXfNxsijiNwznpy5o1DPWS2K6rxOhwyomubR5bM7g1iURCjx46Wcl6W+9XM87ZEoZun63JVMQwno+fbfN+CBLdZYno+rYkstN0rko0baQlV4K6vo3DYQwO2Wm7WqVIKV9kl98c9chZXmmJeZliYE9U20W3y/67a/HBWc/2uz76LssgxZf7M8F9TgaZrzEC78cXbDtoXG0hppusx+63BNc2iSY+sl6s3dZvEqe34/jLXl+daHjiCCRn5TWjjVjfdpsZmgqIDALckmKATIXj6uoyuLiFlp6IejJCHZd7Cuu+DwTMmABifAeLkp1X7VtlMaoDn8VajKUs+/LyUv7Ni6BKQARU3NzcFEVwsLUCIWOSH9hZJyH7/b7sBUBxdrt8pPDLy0u8e/cuXl9f4/n5ubCHGCgAFYDMMwCgKPDnz5/LyVIARQdN5sn87GBgaczCmyVgE6JPguJzNgSey0ZUAp+TUsZB32/b1puweRHo7KxYH56JnrgaxNyYg/vEU6p7TQC9LuNHRNzf38fDw0P5txlP64mTC/cdw4iSxNBfjXwYq5NGgIP3NzF2s+MVtNRWGYICSSb7ZEg2va8Ixn4Y8gWT6IeB26dPn0oSfnV1Fe/fvy8kBONxFQx9MmiNqPdumJXelpqdEJLsu3UC4ETLHYm595/wvfghEil+j8zQMfwPFQF0FzCME7Y/cXXNQR+78oZpP9MA0EGCSkrTNOWyPb6XthZ8CLf7IkeTBRA4zAeihiDId/J++2v02tU/5k8Q4+fojHXAR0YzJuwdGbHvD8JoW2mLqBuVTUQhZ4Iz8wMcOTk0kHELJj7ZtopOkBSTvDA2EyPEl4j1RXD58zUp8p/IGCKAym3WnynypbF147/3Cs1zlBZKnln3+NVe620VifUZx7EwsPnnkduZ5PuQDUCKuWKz+31lUPu+X+0bSSnF8XSKi4t9kZOrXtM0R9/1K7+MTK33rBOAdp7ncpIPsYz3I0MneySDNRFY3xHSdV2JeZBo6dzJMU5jvG0OCTCw9uEMW0LKuo6sk+S7XpN8/Gth1FNE3/Xr2NG2sWvqXoGUqv9jTSBYXLkbp3U7rQkTLhu23aaUomu7cAcJPtf6DRB1RRmyw8SEMQkVLObEmhjMen+bZUilnOdWEmuO8xRL26K/s1ai10Q3z7L+8Fzkhc/3PLDpNQFVKz/4CuQEbjSwxydR1WCu1d5qvAcLMMZpHONyf1GOFY5YH9REXMK/812Mx5URY1qTgiaC8P8+/OLnXl+daCAYWPt1T2JdFCvCbtcXxUcAOEYMDQaci+sAFvRlUoI2k4Zg/PusnPXyPITjuxlsFChBBgEXMY7DFyAuogYsPmugwzj43DAMq550l+YNLgCzfIafG9CSGDjJgFGGuXV7BkmcHRsydPB3pkrwJ6ieTvkOBhg81ghAQ9DYtkphRLRGOdCaaTSYSikVWe12u3h+fl4loAQh6wTtD7DZ6ADGbfCBfFknkhsz0F4L5gdYJeFFVyJqD6yTVf+cgPn58+di5D7FyEyx263MbPAz9reY5eE7HQCQNY7A3wODylo4mTGLhn7C2l5dXcX19fWK3YyIkpzwHwk0m1gBFIz7+vo6Hh8f4+npKW5ublYsKrpsOTrRYz5+LvrKGjkAmBUy2EOPkK8rSDzfcvU4uq4rl3tZD1wlMeuDH/PpPw5atht/D77RCTAkAhWSyubWCxDdfsF34vPwHw5mDhaMiaTKYNwJAvZkALHVQwdj1hj9Yg2c2ONDtsQA73MfMLYNqOH7nOCz3vgy72+z32UuVGphs1mLiP9fe++2G0mypektP8SJZJDMrOyq3XPA9NXczggSBA0kCNCzS9DoMHqCARo9mIuu3l2ZSTIiSEaEH3Th8Zl9bpmzKwvYl+FAIjPJCHezZevwr38tM4+UlGV2Om/I9howBq+RwYCrsAYa6Oq05hnc4EuZM34dn5v9XBNddw5alqsqVwCntVynNjk/sxyfSRiSOXyG94PUF13n59gnNuBEybbEiVokBWkD9Xpe+XZS1yiBx17wqcMwpH1UJrJI/l0JN6hEfxynsTMTT7T54h+s6zk5XMS5mx86YBDL/9EP1h59bNt2dpAIuhARM3zB2LExbNZJpYEkz8K+q6qKXkw1+pQIAQFQ1nD6//QWP1dTkVHX9dMb/iLHVgNe9B3QXMpnjqsu8h2HiD63V7kV2/P32+V5npN6bIf7ej1s/8YL+Apky9jto0yIsSZumaIChn/i+bZXdBS/xPMglPEtyIDnRkTSS4/BviqRKFVufUKv+Ax4wLjN/olEnESXuAF24Dlclpfj2+9dP5xomK0rF72u81GD7l08Ho/x/n6Mn376KbquS5vmcIQGpgTJt7e3WK+n0hjsKU7ePWE4ZAuvVnYckTezmk0dxzH1mPOZiDHO57zx1Q6/aeYnH2C0sLs4XdqyUISmaVI7h/clAAq88CQojHu32yVmEVag6/KpPbDIvImaMcDmkHSYpbGCME++R5JDQMJ4FovppUKw9+gB9y1BHU4NhbSzR384cYfs2W1mZT8pTDoXTsDACSdiJsuOZRzHxLzz+5ubm6SDrqCwv4b70kqGQ9jtdtF1Xdzd3aXxmDlEBiTj3hyKEaNLp9MptXQsl8vUC393d5fKpzyDygKMHnL2nCj/M387UtYa23DyRw8n8kT37UQI1JUcGnZyd3eXxsR4/+W//Jfx+vqadJ+3u/s4YLOWTuSc/DnAEET5jI/GJYFFXzIBMs5OweO7Tna8l8og0kk2em+W2rqHXAH+EfMT9/gcczHrznNvbm4SsMR+fHqcmSSSENYDX8ScDVbMquFvGYvb2QB1tlvGbrCAH+G+jIPvsn4mFNApgCxzwZcZBLsFNCK38WEzBE78qIkm9AW7NtBEz1gT+zH+BiRR8fP7OmCqDWBMDmDHEZH8p9lr7HkOuHI7n+9NRZP3jBi0ns/nuL3dXqpBXWpfbpr8QldIAhM3xCBijpNDH6PK56tqesEctur9OfbJZsqRF3GJubrLAdnTCkqS1Pd9tE0b57P3SuR1yf35+YV+ZV+99dE65YqzmWT01ffmXk9PT7HZbFISjg+sqyoWarsl0TQrbz9lvQPw+QQ17uvkHnnYl7lbImJ+hC8yMOEWwzjTcXz+8TJX+zJi85RIZBCKHkyxZRlDP2/NzpWU+Rq7tcdyMCgdhmHq1aoyYeEkwYQrcwc7oNs8m9hqf2q79s/y6wLmrdesE88zCWx/YdIBm+D+JndKkgldBRfg16iI8n/WyuQZcZyqPDqCrwTDuOXJCYXjnhNCnoPvfH5+TvZB4mdSnpiBL8Sef+T64UTD7Uc24sm5dEnxCURuSdjv98lYlstleqlVRKTWH5R9mujUK4ggALo+WcWsPMp2PnexWuXWDsAKiklbQdd1ifWbFKeOccx9hyQidd2kNqTD4ZDuZUVD8XDQbKZNR+Up+zwej/Hhw4cEwkrmhUTMxwhaWXHqyBmlBAzwO5TWgNAAAhAT8S0rS/CPiEvSt04BxH3IZOgYLGPBSM0GmEngMzyDVokPHz7MwLyTCs+RpIsx4OBwsgQNMx9czI8XY0VE7Pf72G63qV3j+fk5sXFuc2NdcFJl+wGVi4lVXM3GxeUNXnzH62SH5CogcvNlZuR0OsX9/f0sOcP5mLnCFrEB21SZgKKLEAMGSDhUA0/s3fN6eXmJT58+zZIZb7BzhdJr7fWi8sHn/NZYgmTJNpndNrBCR0swi84C5jLJ0CQADpAi0KEDEZHGRXByUmBd9PMARbZnmFOea0dOsoLjJ6kw00WFAJkQXJiLD4Vomia157jSYlDDzxiHq2vYMYHJCQa6BHAnwTHxYWYZsOe14p72S32f3+vgBII1cGLsKlxEJLIJksMxzDJ2UmvZMVd8P3PD5/MyS+5BywaV4Yi8ETO3XuX9BMiRcSFPEwPWkwl8n2McLwnXYhnv711U1fwoep5NQu19c8jTzKvXqIr5iVb4NnctMC9iCj9nHgDC1J4Rcx3gmirXy4gxYw10HB01gx8RMzwABmA8gCTrqlteGKf3MfB5yAtXvkgej6dTjBcswTq7ouRE2PqDf3IrIAQAY+ezHiPEXxlP8NNgHXz6MAxxPp3ifMrvfjLZ1dR1LFfLWSKQkud+as1DHoDcRBpErtBbnvhdryc+uSQFsctJF6YqFvey/zfIx97RL3CAiRfrlJMk/Gyu+E0x3MePm+zAxpC7Y54TbeZrcgz/4M4Kf94dKmUVh7Zy4gxxh1jlZNlxN/mwMcsd+fH7shqPXJz4EZtd0SPulZULbNqEw+9dP5xo0BLhBWRRFosJ2Oz3+1k1Y8qYMyNLFlZVU1uPKwsIdFrUuUKadcYZ+8g7jHU6EWS6H5krCkqgsWHwdtthmL8AkM29KBJJFAoHMCtbRsg639/fU48+QWK/3ycnTZWADJI5oLAGHyg/IJZxceQpyoUilAbDWDEeZ/Jl4HcC4eCGPHBaBr4EStbO64RcaEfg5wZpOIt//Md/TC99u7m5Sb3GBGWeRx+ijYe1dmBFFswJJ2x21kCSz93f38+S1Ofn55SMmK1GrsyjBAtUu9B7bMjJemkrZlNIZJEPrXME13HMm+1hCM3WGRxgf+iNHSRrAOPK/L4XbH2IgpME5IsOMHeS899++y3+9Kc/JZ1AbjhDWuMM0pBjeUSn9Yw1NrNkn8EFUDmfz7PTpQBeyID5YWvZv83bMVlr1gjw52c6AXBQIBA6mJjR8wk42R9mwOnAN45jShZczYrIR2W70rff7xPgjMiVKubmoInOOgHl86wFBwQ40CI75Ijt44OZR0RulSqJDtolzSbyvASKLrbsPWfYgltK+Q5r7zXhb2yOOMPaIhuvIQwk9oh/M7vc9/1s/5LvbbBVVh34PQGexAXdfHl5idPxPG1sHsfo+y7axWLaqDtWce5y9Q6ZmaRhDE48/XIyQC7rdDq9xdsFOAEEsV2z7swZvQMr4Duwq6qqou/6dFIU42Ksx/f3qKp5W591A7vGfxl8oc/2EVzMtUxcIBwtM2yD4/AB/QlvxBjDmOMP4yCxxuYYK+N2smVy0cRSycq7EoK8ISp9cAOAFPlP98jP4R48c4j5vsRhyIdQbNar5DvQ+0kXzlFFNfPD7FVEp3meSUIux9vM5ufTPU2iRMTM13Ehu+12Oxu3KxGst22g7/t0xLyrHMjFF/7NiQT3RPeI6WVl2mQc+mhcRZWcuGIZW89JSBlv13WJrCvxVtu2MQ5jNPW8Soc/5r7oIP7IRA9rxzqYROGP467bBU3k/qXrD5w6NcTh8H5h8atYrdYxHR13jPM5EhPoYBpRpQzvfD4n4/369WsyDmd+gA42QaEksMcoyPTOiMweOoMkazULb0YRhTHAi4hLls4Y2oi4nPN8cZLO6mh1ishMihlML4RLyyz0OI5xPL6ne76/v0VVTS/lM+BkgSMiBS1+7mTo/v4+xjGfDEAwIWnCqJyB2vFRmnayY1CA8/D7Psw6YWAYk08JQyYGLmXiwbsluN/hcJgpPOvK/wny4ziVU90+YQdk8IlD5zuw9MzZIM+AnQDrTU/WS+bPGO2gkiMQC2emC51E/3wvM67sX8IhOGm0TLARg02ezRqjW64G9P38GFqvo51MDmLZdgCylj2byT99+hR1Xcfj42N8/vw52SLOjWCPTAAXyBV5uVWitF8+42DHepftS6yngRNzwzewrmah+D62SMIIAGHdYbBx6k54nJyxzga+BBJsFLBtXWHtID4IJPwcmfIMJ/w8n2cCsPwZV7Hwx7SYARz9O2wbfwDx4vK7fQ5+BPLg9fX1Mu+I6YjXMbrunGIJtoQvMoPu1hH7NFdqImKWiE2n/YwXAuEl/bw8ojidTV830TT1xTcuY9qIPT82lsskTgZJddQ1LXZTi/HkG6Z4yruP3DblpNs+En9XVdV0FGmd32LMRuhhGKJdLKJV5WN9IdOO7++Xc/3zy3Ih7Op6Ohp2jIjNej2ddlVPG3VZS/TJ42At8XP8XZ5whrzGcYyqrmJQwsWaNk0TQz/MbPJ7J6U5zqO/VBRhvL13AP+Ej6Jdkjhqn2sfBBFwPB6jH3JFvooqluvcnsXn3cZa13U0dT11BgFC+znwt11ynO2ibWNzIUexxaapZ3uA3l5fo73E4rZpog8fWTrpHDaDn3RsatvpiFcn+1O1Ii4bznOFyIkep061l2Nbq8u/8aXDeImBwxDD8G1lrmmmw4E4kbRupj28pa92os16oFP839VUCAET1QB2xs+93FKKPqG/jrsmjjiQxrHA6+5kg/Hgu41J+AwvkwTnufPABxV8r7JZV9OL/rhXdVmHuqmjrfPx7qw/a2eC1bjBlSkuYxgSaLdYoTfWrR+5/lCisVy20bYoLkeK5pNS7Gxvb2/jdKK8m5kq789ggv57AjjLmF5Ql9kQJv3+foyqqi+Kd4y6HqOqOKM8n9JkwVHuM/CC5ZgUahmLRXYcU/lwjK7LPbYoM4GIZ6C4rvTgkFF6gPcUHOuo66n9Y7vdXpKQuAS3zAxFRGIuWHzu75YYGGqzCCQQZl3M7jNus1vO2DmlxyANQy3P8MeQmffd3d0M2NBC5soK70JAjga/ETFrj3HfML+LyG8tB0ST1CB72lyQD+ff13U9axlxidCA1QEEOeCUDofDLEkFoLiEi8ydkAFMXRXDXpxoczTs7e1tLBaLlNTChJf7Mdz/TvWLoHx7ezvrmTUocNBjjxAA2OuL7sAQR2TWCB3yPblc6fjpp5/i6elpZuc820koYBR5OGkDjBtY4/jMPBmgcd/SSUbkzXSwMszF5IH/zdhNItgWXIJ3UoAdJtAx5PI/v3NSzhrCMhJoGQ+2hYwYG2P3fN06YwLE4/bGWPTYgNnVFapiJXmAnrJ2yMrkDMmr12a93sTpdIzTic2xgIbp6HLIEgM51sosZm6/a4IjQ7nf1Bbbyz/4SOQ+phOgxqjr6fuTHoyX300tTiRcAJ9xjDgeTzPfSrLJGpZ7OvALXK4KlgSCfbWZxcWySsSK2cS2beP1/WLTTRMxRqxvLuRDVcfmdjqMYblQhXUYomra9FbhGMfox4j30wX41U209by9xmvnsRM3iDtt2yZCiDnhV9HVU5d9Y4zTUa+2IUg6SBT0CgIEPY/I78hhDYwBDGB9iI2JMrcrn8/nGGKIt+NUVR87AfO2if5CNDR1NenNxV7R92kthwkIVlUs2ibO4xBVjBHjdDpUFez5zBWriIhxmPaB3GzWl3gxRNRVnE/dpYV8Sj4Wi8ubspeLGIZ5K0/TNtE2+eWm4JdhGGK1no75jRjTeOqqmfZgqDLlteq6bkoQL0ly3/WxuZnIwq4/z4iZuqqjbqqoxyr6fnr7NzGoqqpYrSfdjTHv/3I12xUAfBvxD1/lWEr8QydNvLhKb//v/Whm/l1dQ0/u7+9n+Aas5CQVfQLcu6pD5Wm/388qrB4nPgSMa2zpmDNc9K4ep+00VVVFd5HfQTiJsTrGsY4QTI7tEOH23967gg/iXsRPx8Xfu3440fjw4cMMVGDM2aHnIJJOmFitYhi+fYMjgcoBDmfC5OnNxpmiEDc3tyl5ARwBkFFYs6I2GAAVDJZbqXzyyjjmzVbMmaDuIO3gwTNxNrTa+DOTgp9jGPr49OlTWuD7+3tVF/J5ya6aMDfL2Qy3AUJd51Ya1spg12DASo1xwuSYIR6GIb00kWDiYHB7ezs7499MlFkoOxQfq8nfJDgu3xGAXRpvmiaVAbnKgHZzczM7tSwiH5mamJghv8jJSQ+Bs6wiIFMHTAwckAtzjyzK05/QQ05jYSywGzc3N7Oyp4F3RGawsBtAjQ8nsLwZH6dJWC8BprY1gwlsj++TaAGSvVeFBMUVRH73/Pwc//W//teo6zoeHh4iIveRDsOQ3vTsZMUMFM7YAA4f47Ug6fT+IOuFQTjPz6X87Cu8ziQC6B5r7rWxjnNvkxIERCqafBZfhx7zfVct0E9sB/k4ueT+1jP2oeGbGL8rLswb/UVvsYfj8Th7TwzVQFqhDAjwtwTy3W4Xt7e30TRNPDw8pDH6VCzabSFiSKYjcpWvbdu0/wQbc/+wGcjjMSdnGfT1M/YO/XH7JjKbZJWPmoQQwx8RL77nA80G8rdBsn2VfRb38mEGrAv259MemTsnufFsxuGWHSdBrCH/5v58F900UeXkwuDI1Ryf7IitkQzwc5M33N8HCaDjjIe9XHy/9CnERnQYObDexHbjC8YBQHKizhrV9fSyNa+DEz38I3JkvPhk5u/1xU8Bjt3yhb2g1+iJ7SpiauXi/z75iHGYgIBUwA6Mq86nc5y7jN2wVTof2HCMnF5fX9PcvObeZ4K+jeMY3ZArJYvFItq+Tc92Et33fVRdlXwrsQsd8H4Gx0nmy7PdxoQ8LEd3zWD/rLXBNH87meAPviAin26Vqgx1PsjBFWrjUZOatgfHCeut8bUJ/EXbXipGWa9NdHAv/Lhxy3K5nJ3aZoLGmIHxO4lwQsjnvMf3R64/9B4NnByKVAZlHs7+geUyM9acRMG+iaZpEjtN+wHOf7lcpCQCBfe54j65hCSnTAwMLlBQH7Pnk6gMtll0nDnKbxaU3+PMzHKizOUGLu4zAaN56wQOaLnMTA3tAcgYZQGk8TM7mFyRyfN1GwqBCJnbeSJPlzAxMBKAcp4Yc9d1sd/v07hgHXBw3qcAcKQ/mIrP09NTWmcMhoqWK0I2PjsCB6zFYhE3Nzfx/Pw8K53S68h8+duJD+1DBtu0rJHk8Uzv+0E3YPIwZp9EE5GZ3ePxmPSe0uz33ghthsfA22yeWRVsKyI7C2TDZ9EFxmFH7J5hfgaYtiPju8gR1hl9ZL3wDff39/Hv/t2/i2EY4suXL8nZ3t7eprGjw+v1enasrBPF19fXVJ1CLtgq46V10gwWfsjkAsHMz7BuuzKCXjjRZ7+QqxX2S7YRA3/8J8Ean+TA5SSZ3+Pb2MOEPwFcWle80ZygX1X5IARsGvmwZ8bJPADAbZT4F/TAcqVaid+9u7tL62A95KSeKVAOUdeLmQzd1oX/hrF2gkwVBXIEefN2bbd9+hQ3dJ+/0SX0zWQF4ylbM9At5Mz68Qx8BPIwuOD/jMEkkhlI/Idt0D3WTnLHcYyu79PbiK0vZk4hMtATg3DLgHha7q2kQg1BwzqW7SCMCV1xNdGxGX8HfgCEm8wDkPF9fLJ9IDLHxpwokWgiK+TvhMEJY1TfVjutM5X+b79hJtnxxWvP2i0Wi9QODUnEhT9k/m4NNklh3+8WttPpHDHO3ytjWfB8qqbGOdNJoe9Jt/Adfjb/59/gDBJhfD+xz8+wrnjfoBMX1pvvu/2dOGjs4qTSABkgbtKT9s5ynMjZZDqkVYlfXIXgb1rtSDjQQbBcuXauxuB/Hce5ZmTrOI/hxmj2FybluFy1yDg0kw3oMz8rMbAJQOzXieHvXT+caNCu8fT0lDbDMQgAApv/AGavr4eIyNnTZrOZsUOU8ilbkon7DZT+bkTE6XROgQPlwwka+AAM+L97OB3UNptNepOxgzqGCTOAsjFn7utACsj0EZV22pPDmd6IWVVV3N/fX15OeHNRMP4MKcmgVQlF4MJB00qDPD0HxoqMzLhxmbWJmDMJGLMVq2xVoW2I8dghcgQp48foy0DLetV1Hc/Pz8kJcU9venfSgGNlngaggAPKtjClzA8HgkPB0TA3DBBnAOPCHMo9FRGZgaQ6QXDxqRdeDwcQPkfAZD3QI/QWeyjX1vuVyooK9zAjifyQMZ+zHNAB7AtdBSRwX/4myeZ3JH3DMCR7fH19jZ9++ine39/jy5cvcX9/HxFzhgSAzP8Zl30FAMrgrJQ3cuF7JHm01jHmm5ubGdhE/5Apcnflwr4JcFTKnHlQ1fApdHyvqqqUaDZN3ifB/fnbxA724MomYyOBsTwB0w6MBnz4C47FdqWiqqp00IJZVgI+zzPb6O8dj8dUjSBJx/aGYYiffvqUdOBwOKT2JPYODENuWTV4xYfD0rFu09rlNhiPBzvj+9g6Og/wQNZmYhMLW5AQPjiDz9oneF3sV12pMghlnDyDMbEurINZ6sRuxhzIm6jj51TPnIBGsEexTyCEmFTGAQg//EDeH5APDUBnsSMDvu/FFb6LvbI2Tmjsj0piwQCaeyMf9MlEC/9nnf1uC+QxxLebflOsidw25nZs+2X8juXoe5ioNAHoWI8enM/n5KNM9LiqQtWROcaYT9w02UGSgW9Dj/FRyNuVbwgI70GzfjspYmwcyFAmCQavBvGWEWMFs3yvEmEfiU+ynZFAGzgzR/wY+gmeZMy2Q8aALpYyNdBnzKyxiSfGgc3yN3bXNM3sRD3mbTxXVXkvJPK0P3YMwl5clfC7sfB9/M42aX+K7GyTZaL+I9cfqmicTqdUCnd2huGwUFVV6QVdeYc7IMiCp0Ixz0YzO0tQQOjTs7LDJyHw82G0LTSOlAX8mqGtqioeHh7S3gGeSfDk/wY0jM0ZJ/PiPsfj8Zvkig1QdswA53GM4I2xODEU0W0tLLhL2+OYy7c4C5IvywklMaiFSUdOtInc3t7ONsU5WWHteFYJAN1S48DJupIU+oWO842bi3RSRF3X8fLykqoqVIKcjDEOHHzX5fPkWT+cBRtA0T3vCTGzZf0xq+hgZiN3m1+ZwPE5klGvfdM0s6QsAYcxn6wCWIQdKts+sEkzfcjZgdrJKt8hUMCIAJxIhFhX7MG2GTF3jAQF5ATINOjGRu/u7mZsNLbG/c2AARiGYYiPHz+mlpumyeeQU7EkWNd1ndo0qXrWdZ3e/UHgQI8cMB1ICDQw/OgHcj4cDgmMu33S4NYgDGCE/Tgo8XvmwvqSFNtWnaj7/07GXR10csSz0FUCOXLA1tE/dIWg58oo33FVgbECbFlD1hd9jpg2iL69vcXpdIqXl5ekB+OYN+lCRGHbTuTZqJ4Z4yx7gwCzdsybnzsBROe9XiZonCyU8zH4NOBEZ1gf+weejf8BQABSLWfWj7lD+E37CmK2lrYf6wb+z0kn4y1jH7rohNwV27xW+cREJ9Q+7Ypxo0PWfZNg34t1fLckT4wL7L+5D3prQAh4Yq7eRxhxYem73J5UVvqqmL+h2nJkXuir/QgxivZD7Nu6hy0B7PFf1lmIItbCVaOU/FUZ1JoIGccxhrFPPtN7pkgk3YqHvvN91sbkBHbhZMHvFnFs5XMmh/kbotDvT3Lrk/2RfXXfT5XDu7u7mT4aeyB7bJPf4ytZH36HfjkWY/fYO3gTu/IeOBMLZWXQSTJ+E/LLeLpMYMdhfgohekziMJH7+VURkFvogd9vY3sp14hne18gMsQ3IBvW4/euP/TCPm6OgzMQYyEAuwSYYYjEJgI+nYkzEQL+JITcr8a9MCoYf7M0zlIROEGHQMtZ506S+r5P7KABJwqDo2DuGK17Qc2mEIiRRVVVsdvtitaGIdbrqeLx+vqa3uEwGWxuN0FxcQZt26Y9EFzMD+drlsKsD+y5y70GkGWLBoEI43BwxNGgE/zcTBlVIINrnD7rCTNjZuF4PM4MAxAJcPU+FPqJz+fzN+DPPe2sCWz6+/t7fPr0KR0NW1VVqgjZsCMi6Q0ysc6hQ4BdnsGzAbU4NjOy6AxriG4xfvfgRuQjfc04AJQZE3rN9zj5CT23jfreZirQHVeovCbIy8lAxPxEJiqH6NL7+3vc39/Pxk8iez6f4+///u/j559/Tienea+GQS/PJGkiucp2Nc4cKDa1Xq/T0dLYghNCV9z4P84YNo6AwVwte35GklsCHCcTvgzODa4gAAwoeT46xu8dBJARAAY/HJFbCwzOzQga/KGHZjO95vg399TjF2lLqOv8UitaIrxOrkj+9ttvUVX1rDKQ21fPKTG3P8L+GSPjxxfhQw0cHHeIXXzH1erNZpPiAD7zcDgkAGQQY4YSsIe8IVLcTmhgzdi9D8GJqRlV/IUZfvQQvWiaJmqBCMvDuuqeb9uaN8i62ovM3F4HOHTsdSWDezKPknTCDpm7k3Y+ZxIGcF0mj/ZprsAZhPEZJx+slcdi33w8HqNZZLtDd7qui816HauLfpREDWsPoenxkDjgE5Ef8QSdOZ/PKRHBnvFdJnisewbxxNXTMSe12CGyjSpXiyBP8N/eJ4SssMH9fp9ajQDYbr3FZ/I7k06sMevul2tajrYrxkQCgr55/8l2u014lL/Bi+g6+kG1GDmhT/YR6DxydVuVfSfj/x75hg05dhgvolMmZ/Cj+F+eh74sFouohvk+ONsuscJrCVkBaeX5sa7YN/7P+N5x3ckyn8OX/cj1w4mGmQScAoKZKgxxcdjTyVBTsjCdsPDy8hL39/czozDzYvCBMhIMDGqmSY0R0c4Us2SkWDwDLLJPFBADRIg2Gis6gkepUBiXlTBKMw8sMIt2Op1SK8E07jo+fvwphqGPYRjjt98+R11Pfc0YLIGCLBUD8AZT5kdgwbmYWeQzBsjO+CNymQ1H6fctOPkhoLD+Lr0jHwcNmEzuFzEBM9Y7Iu/pGccxvduEuVhn0A0MZL1eJ5bT4NWsMCDHffDoo8Gb2THWsKqq9BZws2LoJPJAhxxs0R/3Hbvk7ZKkddnBle+XbKsDKw6HSgby9eewEZ84Yb0322dQTa8u9oKes1a2v2HI/eMGOJSDkUFV5QMZhmGqTjw8PKTvrVar+Pr1a9ze3sbXr19TyxW/p8rHHPEdlhkMrDcyW9Zuo3Clr0yq+TnP8rsvCPboJG92txxJYj58+JAScbOcrjiwDlzoiN+lUoInBwQCLGsCuYNeY9usJ3YRkY9+xseZ5XZwNXBGn50cO4HgAqQY+CKnXGFcxDguLrLnBYJDjGM+jcYvyixJH9tV9ndUn+uoayrpQ2w22+RTACcAB2zG8jgej+n4bU4jPJ2O0XX9xXfn9xPYxgEKbq2ZTgoaUkWA73gTKTZCMmW9HcfphKNxrOJ4PEVV13E+T6dKjVFFVPN2Ep6BjnfdtH8lA+uIqppeVotfsw/LZGEeM+yp24ENQgBwVModK5mDfUSZBDphKMkVxy9+5sr8YtHGGHE5+Wg6UpYTxiLissl7Oh4/xdMhjzsn8EPUVRvjJbaje8Rv/Fld17MXeBIvTRL4wBPGyfixfQNAqq0+MAFfiSyts8YgtCYOwxBjjFE3dZzOnIzWxWKxiaquYrOZ4u1+v58RBjzD+zdJLHa7XUTkVnEnOyYU+S56A+mB38Cv2m8gKxOX6AWdMcY/6+8kevgeSAe3QiJv1sjVW/Se59kHm/DxBbYosUBEfCNTJ948D5tEL8GOJsB4LjbRdV1U4xiLNm8cN4blWeigq7cRkfY8OznlOyWJaGzu2Gjf5Fj3I9cPJxq+GDxOpa7JAseI6ON0IiNrZ2UjAKRZOgIYAmeylMPNuk+Tnr8V1mwchglAM2OJkByEPZ6I/EZZvsNL9WAZDEhhGVg499c5y0QZcWRmEodhklnbLmK1Wsd2u50ZH++TQElh981gG+gZnDMfGwHsHHKYBTAFGpf5rNAYEBt1I+Kb9eHi/lSKbm5uYr/fp2TClQe+b5DO+kRMxovsqerc3t4mHaDq4HGa8SSjN0tYBgd0AmaaewNomA/3854NNpFTVWG9mYNPnimBotko1oE1oVrDhWP3efF8n2QKe2L/jx0KYIp1MBuDjhhcMnf0KCIS+GjbNlUhYLh9T+SI/rC+rjrRRrBareLl5SWen5/j69ev8fj4mBI0ExMQEIB6J7bovcu9Bj+sM4mOSQS/P8LBs2TLqypXv7bb7SzZchUNnUaWh8Nh1kLC53i+j5ImgBqQmBCw0/fGP/Qf5h+Z8HMCHsHXp3XxWQ5ocGKDf8TvOdlhHW2DrrDBgLv1xP6hZNGmeVZxOh3T/fHRjg0Go4zHpxxldpZT5RYxHZWbN0PC5pqUyhX1XBkhTjVNHV3nk8vyBv22zf4BG5z0K6LrYHI5dGR6h9I45ljh+OUkr2Tcq6qKczfG/rCLzWYdYx8xjrWqGbkiBFAFFHZdZpyxz/f3c/R9F+PIEcD5/R3YP22xtK7OY3HerA/oZvy0abiCA6BCp1lX7MTx0Qkp686/zQKzzmPkVuxh7GO4tFdvbtazxLFRVTqqOtqqmc27buqom0Xys+tLJRvdbZv5kdrEdZIqwC4yQE6WGWtCjDBR6fbeiPlbztk7wbPZM4edY38T0F7E+/tkk+/HKRYeT++XhCkfl+5qk9fUYNSH/Hi9I+Z7NFh7PgOr3zTT/oPdbjdLIk1cs674P+yCMWArTnbLDhla+0pyyBjRdkZ8cSUBcgc/jR3yeSfL+AbGzzjLuM3P8XtlTGGsZQw2MXZzcxMxDOmdOXyvTG7RSVeAnBBZt/g8ds44TQo6RvB5Yief+ZHrDyUaDuBZCH3w4iGCFH9ub2/T5nCzqxG5nYfJuQe5aerYbO5mTCWK9/b2Hjc3t9+cUIGyuWfOY0EoPlLXQY7kAVDStm08Pz+nF8wwBzZ7w6CbqUB5SBYwMAcUGyOGiONHGVFoV0Zw1pQmDUZQDpTSJ52U1RGcJqAZwIGj9CZYZFZVVeq39hqaXUbuOEzWk7/NFrviYUPAiTgoIRP2W8COmgnCwfhIZJKR0+kU+/0+nW7kxBbA7qMPXSWAGQEgMm/0lnG4+sO9uV/JCDsZcKA1aDMoBGRwH4J5RE5yvUEbeaEjjIX1RzdoBYOxQ64AFMbjgGMWw0wKjhE9gInC6TInM1NVVcUvv/wSnz9/joiI7XYb6/U6/uEf/iH16X/8+DEipqO1sQ90hfFHTGyNk1+CConV4XBIRAD+xK18bonxWhFwAPT4KT7H9/u+T29BN4sGQCoZ2XGcqmpur+DysZ0ECgc5s4/ev0PA8z6tiDkD6VI5v3eQd4DjO8zDLRa73U4HWAzpjeOsC9UtbMVABF9EEtz3fez3++SXmK8JCYIhfgUSgbm4IlSSRzzXB3SYiLEdWweQw6RXUxUdMIpNTL4yA3JXkSdbyu2ZTpin8dVxPPaJ2EEvGCf/93gjIoaRl8nNT4Bs2yb6fkjtgvgV4ocBDfefgNo5qmpM6zaNbXpPyGZzE7xkEJ/sOUC6YM9m6C1H1hQfZSYUG7FPBF84UeF5ZniJ1V03vefB30F2/Bu7QI8YEzELO/JcfB+3b/IdAKU36UNKPj8/J1mRIMD4ez9jRKT9XezTAwdh38SFqqrSex2Ik4wbGfkFvRG5TQs96bouvnz5Mou92AU+HH02EHbLDYSLkwY/A8LCe3bxicRSYwXmzNpwD7AL/wbHlZv3DbxdKbC+c39jI2TMupuUBp+aXOIZ6BVysk/mFDzHXpPXfJbfQQASK/k+zzDpGWNEP+TOInTfdsT/WVP7fdYP++f52FKZvETELJ6U/vmPXD+caJitQXARcWGfMpPMwpL9+m3WvEANwThw4pBoh3l/f51VPXBosJEEULeMMEb3fBqMAexxEGX1gQDJzzE8xurTOHyxAO6Lxhk4ay5ZGhKWcRzTRqby3RD0XBv4OyFxGbNslfH9nQQ5K+Vv5O+5o+gYC7Ji/VkT5osh+YQMnLQBgRkTM7dt26bK0cePH9OL8dxq4ATLaxOR2VTkCzvEi2isZyRB6CYJB4kaTgTdMKhhTrB9BGCSHL+kCpnQEmanzLz9fByOW1cAZ4vFIumTW9bYS+BTt+wwXF3ZbDax3W6TvN06ZkBiHTyfz/Hhw4f0HDtfgLr9gxMzO/AyEcMOXeb9u7/7u7R/5u///u/Txm/GSLAHADA3xouue38FP7e+OKlLbOVlbgABM18ReVNyRO4bdhLo3lon/5AT1ontdpvswQwtAREgbdBlNi0inzSD80eWBv+8iRaZwQY64Pd9nzZjt207S5yxIwNEfo/uf/z4Mfq+TzJ5e3tLfeEGnARuV2kgAJA3gZD4wnxIFmBL8UeWif0vPod1mWy7n93bfh2/iB4Si7bb7SXGVLMxGrBGxEyu+AODOAPaaS7r5L9NcpjV53n4y6ZpYowh2kV+aSY2fDx2ETHE169fYxyndlti3nSa2Pxtzfj6yT/10bb0fI8xjhFd10fbTscPmzXGZ5aXwbxjpxMb/m97M4FjZpb54T9NSuLLEoiKfNgA8QMiwYCxZKnxS65QoJMQbq7GlcCSse12u0Q0GITzeY5uB9ABcvnM6+tr2tsGsXF3d5e+Y6Dn+G0yzp9B1iSw4DLHBWKIqwbYqFuXXZ00Uw5oh8zhj5+P/bNujNExkL252DljQr7ohJM01pDfGdhj345TyAIb8no7ScMewQ0c2W47Nt4xJiNe+9/oKHIwEch9GLeBP5dx883NTfTnfLKkYypjdNIFVkLnHHvtn+p6qvKSDPt3VHeM0Z2U275/7/rhRIOAyCKTdU3APwdvM+tmCBmsT3dgAcjgUZC6zsqKQlpJmqadBX1nvDg5HIj/9oKizCQDZWZMYIdhxOCc6ZmhtAEzbxYEA3R2i2MGIOI4AA88CxnxGe5pB9N1XWJ/DVifnp6iaaY+Yd7Yzby9f+FwOCTACAMMwCqZMLecRWTQQdDabrfJiZHowNT4tCjuVfass0bv7+/x8vKSqkyWG/pgkJgZxgwiSrmXzKIDGbImeXXQYD7cC7l7ne1AqQ7gdPi5qzbWVbOaMOkAD6poVFdwxmYrCKAkJPwOvWdt0HczjU6G0GGC7Xq9jq9fv0bf9ynhZe5mvMxOm/03g8Lv0WtOgSMxdWWI+f/bf/tvkwwYP20/dT3t/eLFmPgBWCq3tjl4QjYsFovZSXTYH4mdbdt6ZnCCDRPEfHgEumLQ7iO3sR/2WJhd4lkO3Aa2BAROfCmTfXTI7WuewzAMsxZKgBntbMzbJ1zh+1nLrutmrRBt28bLy0uSkRPvcmMx/0eX/R6B0kb5mdspXCUgkOM/mBe2zYXOQ44AnNANnuXkgaNzJ1CYfQC/n2LC/D069NTzLG/q5PhgdMQ6BpuJ7nn81r2qXmifX66Sr9eQMVWq0Pg5x2OfEi7i3+R7VtH3XfT9cPkDabOIvh9isZhXHxxn0bny98Qc1sdEgv2/wY99KDbv2Ml80T0n4YwDP2dfzz3RbVdlDKKQNWsEyHTfPCBvt9ultk8Sa8CayUTILJIIkj/jHjZYUy0sATn6t91uk8wcu7gPiTH2Zh3wcdL437u7uzRHZE/ygEzBPP63CUjrJveIiNSqzDoiJ2KmScuIXCmnewQbKl9HMI5jPD8/J93Cdnk2tgB2MZlqufnfYKCyIsw9IVTLPaYekwkb7huR41GZMLGOThz5GYlBWZl9f3uLuspJOvfEjxm34lOxHeK7SVYn/MwTnXVbFyQeckFWrqr8yPXDiYZLTgYabbuIl5fdjNE048gfs+0AOTsJs8DH4ymGyxsmcYiwyE2ziGHIWRXGzekMBvsYn5XZpwFERAIkNjAW3X1tfH6/3882CJfO8HA4zEqDdV2nt3rieCMmRwaIjpifhoMxAChoEzkcDrNyP04iIlJSYSMzGzjvHc5/A2T5LMrkDNuMBaVZj5vqCWvNmhI0XSFAL5ANx+nVdZ1anBgzjpKNay7tkhi8vLykIELixv08TsbligRGZBaCeyEbkhwn2HZYfmMxBuqEyC0orC9rzLjMmBBECcYGeIybsSJbHLrZLrdV2AHS0sJb3nFWfBaHeTgcUguT91hFZKAJMMc+nHSXiXtEzE6qIxH1c8dxTMGy67r48OFDNE0+fpkEhLE8PDwk/2CWlHHxHK6qypt+SWjQc3TG759APswXJ8upMCQaJGZmM9EHryl6xv1KdhhnbgYMOZaJLCfoYVsAbds2p5V5XZg7/sHHjcMuMv6yvQKbcZAC0PDisTKIGRw6fpipRwZm95grcoRhdPLF7+iFZz3NmDrhmZ777QvMCKjYutedTeTjOH/rM2Bq0ttISSU6OIGKTGDh//h9RBVNk9fMbUD4dvvStI59RFS5xYi5TL6si7ZtUgLF2k5/N9/4tNxmQqtxH9OejTGauomoxqiqzKS7f95gnZjK2sCEMm98puMR8d8YAZ/Jc6wXbsm1D+q6LtpFrrb50AH7X5NZHie+lfGafOLn/A6/zFxJ4tEl2nyoyOKv8eXb7Tbpa0R+zxDdDLyfDLszC2+Qik5UVZVabbAR+3VslySI+aNjTiK+t4bf29dgX2u/6Jhj0sbfM6AG0NpWTVKzhmU1wDZqkMv64FdcTbH/sQ/mvuAAJwGWMSQt+mQfyBzQYfsRDk0xMcu6OBnl+6W/RSb4qUXTRFPnPWne4+P4x1zQIcg3J4hOvpAPuN6x2/aCvFxV+tFEoxqR6u9c/9f//h8TI8cJIxlQ5b0OBFzAAgaOog3DEHd3d8kAWXwUZFqYczRNLgWhSFOgyCDYCobC8nMMn+CDgyVbdJkXpTWDxAIZ2GI0Zi6szE9PT6kiwUuocBwOsF5ALuQBaMcZuLJgNgnDQd4AAwzcp1659abr8uZTgEzZUwiAdaWHcQNs0AOU/ntlwsPhkJTS572bldpsNvHy8pJkQxLHvAlSBq1OlvgcCYLHZzCB4+d71j1YIOaMQ+NyO56BOzLEaRAIeQbJIeMsmQEnMF5X7oN9oSdmWrApV84YOwHCv8f5lAmJN4ZBHrgnlfPJCVBmRCLmrS2WtdnEiDmDA+mA/Tg5dnuNE0vmCEgx+GZMrKVL/tgWMjdYZFwRubrq/T8EIfaZIavb29s0JmThwOhyNXJgbE7k+Rs7Rx+xN28wL4M4sij3blA9dJuOGThXrpiHGXr0yufas24GlfhUfo9euzoQEemAC6ofTmTMmpkc8DNZM9aYtjhsDP1Zr9dpPxzyR+9ToF4soqrq2b4C+3H7ckAHbF9VRTq4gKpJTlJyAl4CtcUi2wdz6fupdQrf4vYYnsnxzOhC8hXVdHKVbWqSTx9T29MwA0XoA3tMHIeR9dDnaoR9Q1RDrNc5MeZ7yJLPsjasIbpk+yBesHY8y7bI/XieAWopW1j65XJ5SYhyTHU7K2uKnBk71Qbk7hjHs1gzTo4iyfEmZ/xtyYbTxoVuknxY11lD+1SDdJ5ncozPnU6n1G3BXLFxv1TRLDxxjLiAfJzUQ4CUNoROuGefe/B8SFGIB68z62ufDpYirthf21f7Wb6PkzGIKHwISSC+Cfk5oXNLOvMzUcU6LZfLdLgB43Ds5hmQ1SWuZF09H7CXCXo+w8EyPIuK2dD1MQ55LwfPhux0mxvrTwx38mEZYhO2e3QZH+92QeyMuNv3ffwv/9v/HL93/YHN4FW8vx9nR8CeTpMDrus2TR6DNlvAAA1ezMYzObKpSSH8FtY6quoc4xhRVRHDkAWCYiIUgo0dHAGLz8KMwsC5nQhg7MBv0Pf+/p5ajRgzrRj09NrpGXhF5BK+gaGV10laRG6tiMhvhkURADsos5mciEhtWWaHXGYbxzEZEPPDSXNPZ/Bm3/m5W6/e399TUnN/f58YPvdxIn/GQ5XGTBWA044AB+CWL4C7lR+9APSR2Jo1cOAiAJhhZq7IFuBRtljwN2uKvJgD1QPmBVAtgzry5lQxgJA3nftzjMfthhGR+uzRWRI89+GaHbL+uirBWkXM3+NQltL9HVoOdrvdN6ANuZCguyLjZ2GfBmUGLCQBfM7gzOApIvdPo/N2op4TtohO4vx3u92M/b25ufkm8YEUwB5g1mEobTtOJgk0HDDhRMKEBH6prusYLvN7P75H2zTTKTttG12fT4OKiKjqJupmjP54vJTa67i9vblUhWCIaXmbWoImOU4He5zPeuYwxMS8w/JPfzLBlH16RBUc1T3FhOnFqn3/FNPG5T76/pTuc3NzG5vN9I6TfO+s4+ivE0vW0rrpAJ5ZTJ+PHxeWfkhjO5/z5kfWxZv8DX6rKp9SZiZ6SC/PaqJtM8gAAE+ns00vJMSGTycqbRdZny7J+zjGom1iGC4kSt1E0y6j68bouiHqOqLrLoeX1BEcz3o+naJumqiqOhaLNsbxHF2XW4zwWZOtRkRMx5y2LW1ox0lW4xjjMFxkdak8jEM0dW6xMkgygeBKoDsKqmp6X8Mw9Angtos2NjebOOwP0baXAwcu9jwOY3R9F8vFIrquj6quYtkspzEPQyzaRSyXi3i7HEjStk3U9WUO1bcxxoAK34seEWuxd/wHNr3dbmO32yU/hc27KoeOlv4GMI7v3mw2qRqPL+Me+CPiGPfAL69Wq1TNx0dhE07AAKsQd8QQfsazXHU0QYGOGGAiS+IqftA2Y6Bd13U6iY+Ww5eXl/Qi5FmyPOb2IvtNJ2/YkwG8dYv74BcgAZAvccZ6y3qSSPB/y4j4g58x6eRE1LiyjGH2467IQgqDSyJiNi5k4ISKJGK1WsW4GOJ8OiXfT0IZVd43zbO8J9CtUGCYFC+qOWELwY1NWCZOnpAB9/m964cTDYLUOLJp+j0BWVh8M3YYHyVSAimTcw97xLzFY8oQVxcjOEXb1tF1+eVFtPoYXGKIJCoGinyOjeZmvl3F4JQTFPR4PKaFjohk/Bh6yZq67G7QaUYHBeK73iTs8hmyIClCLgB1G5yBE9kwSZOZe5cyrWQuS7v9raqml9y5JQjHyBgwNIATJ2hETM6f78NU0xqDg4c5LQ247/vUz8pGO57L2DFuMySwCzYY+mMj8oZxDI6qjRNks3PM0S1LZixYF+sATsRVK2RtWby+vs7YJAwewGJnb9aTtfBYfJKJHRyOC3bN+ols0FPk4rEjZ4AZa8e9eMkUMmJuzBl9x8btrH3qh2XIc8wgYRfop8dmtoX/O9k3o8TvkYsDhs+Pf3h4mLFDJA34HpeWuQ9AgPYrHDpryHzGcYyHh4fYbDbx5z//Ofkp/JiT54iIbuhj0PiPlzHV1RhjVLFc5TfbP7+8TDo4RtR1FUPfx+trfh9DJh1ofZlsjzYrAHTE1MI66UJ9+czrTFfwHRERq1UmPKZYMenH+3sXnMzEHPEZVPvymk2gffp3HW3bxGazzkBVrG+po66QDcMYdd3M7LHvx1iv2UvTzmSMb2a9sFXsMIPW6T0afT+tCyRFRN576IrTFANhKyeSDP3tzhHDUEVVtdF356iriLa9MId1FW11AXwNFbCI1WoZx+Mpmpo2zTbGYUqm6qaOfsytgm7ZmnQxVwUXi01ETElX00zJEjY3rU8T7VjHdDRvM5MJvsW+yMRB3/exWC7i/fg2Y8CjGoNE5+Z2kwiJurncr61TctIumgvbfanAX3TgdD5F204tXav1Kvmcvp9OLoNkRMdMSpm44V0HsNzTOuWkA9v2fh98I/HYVWy/s8btLAbMVTW9vBdA3Pd92r/oKjaxt+u61Hrj5Jp1mIiCt1k3AfNFx4ghnoMxSwmwiZeMwwCTzgh3JpCAUCF4e3tLNk2sxlYNxJ24uqrhKoXjB62qJirdgYFO7na7hDGMN3OLYG5F5g9zcxWae4NLeA7j9lyMV/DjrDcdEtgGz2NN7J/YBwKOQq+Q1ziO0fV9vF/8TD8OcbocnV0rdiIbsB/kOGQJusP4XL12THUF3cSacZZ16feuP3TqlBeHsi4LYnDEZyLyJu66rhPYcTZLcD+dTokJnBKZie3zRiYEBXCk0kASgeNBWQEnVszz+ZzAEQvIGFBwfu49BQYiHz58iLad3vXhkj/KiIGamTVQpfTa9/0sWGHgp9MptRwgQ4yaU2SsNIwR1s0bVN0C4g1n3pR/Pp/Tedyn0ykp+svLS5Jf27bx+PiY3nQeEYmBx9GRDNBqw7rgUDgeF0XG8ZFYHY/H9BZpJzzoF+CAUjbjd0bOvXHQ4zimt2TbiaMjOAX0hXkwLxyHgY7Z+XIdAEXeFA0rgw6bhe/7Pu7u7pLuISdsi3vxO5wB43LLkJNlknwng04AcLhmpJBfyV4wR8aErqGftOD4pWquvmQAOH8Tqqtrq9VqVi3lOyS03KusSnhDIYGyZOd4BmVibBkdYK5cTlhgLQFUw5CP7PW+LpMpTjB4hwafQX4vLy+z5NYnngFQciVk/nZ3rsmX5jGZpV8sFlGNYzQXHWfM9nvfY7hmjHTkfUPlevnn+Cxs0KCNz6IrrIErPdwbG2eudZ1fxGmiw8HdzCzr1PeT714tL+99WFyY276fKgRVFVVcxl9FVFFFPwwx9H2cxvNUgxjHaBftVOk598k3HPavsbjY4/l0ilOV3+8xDhF11cTQD8HL8aaqRiQ/g4yXi+nlcdN6TO+HOp9P0TR1jOPEUsblpWt930fTNnE8HaPru2irNqpqjKatLwxnpBfPTWB+friDGXB8ybR2WZfKl79Nfq5JMcoJOj60rusE6rxXDb3ISd4EJg+HQ2pbMvnFhmknlAao6IUrsdgj68/+Hb5j24UkwLfSuu046kMZnHRSbQc0IiODbfQP22JePnUNEvR0OqXqqDczs1bEELfDQADiU9B9xuCqNr4buZWVfhMzjNWEi+MZyZVxiFuZuSeyLA8ycHJm3Wf9SQjBjciBzzL+kmRjbe0r8KHeRI6um/hxUkwM5c/t7W2q+thXl7jWPti42EQFuNU4x2uMHREDwGbMn+4g7umKGjrlihpzIenl5D+6HO7u7mZ41XL3u7HQ3VJPkIW7EKy/v3f9cKJh8AIIxGBQBPcU4wScLWLELALBESYeIAro5PP0IloBeQYMsVuxHNwweIISTL8rMGYMxjG3vDh7c2AslRlnyrwYgx2De/8YH46kZCtQIu8RwVFzQo5BJsDp+fl5BsKoRFAudf849+d0IRwl7Sk8g/WkfBsRib0wK4ThfC/hJMiVPZ/8nDU3aET+yMVv/jZLgI5EZBDl5C8iZntNnJD6MwQCt9KhbwQk1sygFbCLvFlzz8N6CbDF6TAGJ1YEb5e0zYRwb+Zv8O238RIMAAboEXNwJceVQIINNmzg4uAUETO7c1JCb7iZP/646kOSAQhCBxg/eoUc5lXPnBjZ3vk/8ieZR97v7+/pQAqzmNgp8zSbbRDm6qMZr7IiQQBingRkO3cfs+0Elu9NALaPJpqZvvH5qqqiiny6D3OpqurShtLNdA3ZmWTx3PCBfJ51JZED9LDGicVeLGayMguGfQGy0C10HHmSsKD3EfnwCe5jUud0OsXhcEh6AyA8n/voO+1BGOZtFu+nfCIPOmmWcmLg6+i7QUCLvRjVdJ5936fqyyTjqZKT2OOmndqD+pwcIuOp4jT1W097K6ZEY7GYXvK2XM+T6ynZ6C7ybGIch6jqKiKmv+uqurROjUnGflmcyRzGYH9M+wprilxNchhM2T7NgidyrcqMOToPOWQ9J3bgA4jF+CF0Hd9YtlzjR7ifbeZwOMTt7W2K/RF5bwU6xx+3dPJcqhLEk91ulzZzEyNYa/sC9rctFotUkWcdkT+Eigkj7oF94hPRU8a4Xq/Tse9OOFhfWsQiprhHJZ/YA07BnjhhEv/h/U/2vU4m8OlUM7DjiEgdGvwcObLuzBXfbJLLeMrVAOswRzaP45hsH7mbDCTBJBEyGw/mRK+7rksH9lAVYxz4FZNIVK7xkczBB3MQR/h9ScqQJNCBQts5MvXhSMRuklNInYjcVt1UVdRVnU6HBB82TRP39/cpTln/OXjH7dP2U1weO0k/PrMk6f5b1w8nGjgVgBoAhEFx1j3CYFHYFIRzQ/GpMlDGPB6Ps03JKBCGjuLD/BEM/YIrA1qAJOUvyqD0ci4Wi/QiLzMoGAMOgeDswOu2FcA8SYYzbJfSMWwDNAKowYsTIZwTf0hwqGoAhgguVIwIGii0kxucG0cpMm8YzzKz5ec4TZwM59+TReOsuMz0IhsybKokdsAR+QWAJXMOsPJeBYOjzWaTkqTvZeXMGf3B6WRAE7MyNbrLWpUAkXW0ztV1ncrgnICGfBgL4Ji1MUNoPfPL5QzSS3v036wdjhyngdPFJlyeR+boIPM3c2LWzqVSJxuAOLfROQibjWKc/nnJqJm99jF93JvPoB9cJg8IDoB/dIc3yvtYXL4DKeHqiAEBdo98PSePg59zf3QMfSNwsi48g7UkCBBkFvUyxshtZZ53denX93yRQ9+2U69rzI8ALxk5M474SXTF8zMxgk/iuWXCZF8SEQkkOsh7Ld1y4uS4JLBYT+zTbYjn83ny6eu7eHs/pntObUIcn4kfHmb+cLlsLzpZBS+sm75bRVU14Xg6jhHT6YdDNE0bdQ2pNu0jHIbpT9d10fV9VJc9K5A4fd9PyWPTRtMAAKZk5u7uJqKu43Q+xXo97QXxetU1Vclpj8I4Dpck5xQRuf2GOIeNo3veBOvWDezcp5Bhn/hLx2KTaK5ipIQk8rq6EmH7NNGDf6GNAx1gnam6u6XSbZ/YERugqSKjo/h3/D6A03s7qN74vU2MA12CUEKW+IyTklfjHZIDfIl9H2DYPgLypKqqeHl5SXGe77++vqbvs86n0ykdnRuRN747kYFUwP8Qf5hj2SXBHksft0+ssh8hnjvGMR/iCmvDnPFhyIv5McblcpmOPHdlfBiGRBrZJ+CzwYaAYXTOMmV8+A7WzzG+JDzRr8n+6hRPIuZdBsR9P4M468q8W7KQ8TAM6QhjKnskbfh7t7JB2DPvGCOGMZOBrkaZ0OX/ToRMdEOUmeRlnl6niPlLgX/v+uFEg4VB2VBOFMF7FKzsAEoU3yWiup56oQHRPtrNx7+isJSTXl5eZu0tgGGX5Jxw8Fyeyekp3JuMEuEBBAyYGBdA0UAUYzFTaABoAIRymRWhNO17Mq+madImNmeTGOpisUitRa5YROS3aaOYEZHugXOMiJnxo5wOLnzP4LC8ygwfneG7KL6DGAmqkwacCHPk+eiKwacBBwbsagXBjONRWUe/BNGlXt/LLJnZILP0blWJyECQvTzI0mwpTDbrSOnbCYmZQ2RqxsEG7z04PB/ZoY8kQH4xGXrqTfc843sJPs/zWrEGzNlJg/XIIJ57kRQbXJdODQLCQItnE7AZlwM8PzMDg0/yPc1sOoi63cBsMPdwEGXsHh/zxRaQlX+Of2LsyISW0BlT2jRR1ZnhRm7jOKaWGWyccTVNE+OQ21ZIBA0gsSvr2PcSWqrPEfmYc9aTOWCT+GB8rIMyOsWa8GzsCGAIkXU85hesEuzN9JV+lu+euy7GMeJ0Oscw5KrfZnMz09uUrF30dbO5iWnzso8sx67qWC6pgkydTYvFMoZhzoBHTC1PJBxV5P50yIf1eh2LdnmRDZuQp03dwzDEarOO+lhF3w+x2axjHIdLK8QypqN2I9hjcXt7cxlPFcOQfRz2jX5hT6wP7zzBPg3mlstl3N7epp53fLJJB4BcuU/APso+Ev+MD3XC2fd9eofC9yqh5/M5bm9vZ0fmokPYSAmesH+Dy4hItgWhRbzEBzi5xqfi87g/bcgQo36+9RlZ4k8sD+aLrpuJxo6QE/EMXOQkDz1GNmAAH6RiwFtWt0yAmqhz+yvjIYY7UWH9sCVad7+HCcEUJpzK2EHcxh+wqR2CyGN2pwvj9fHkJj/RmbJqY1LDsmCeTkKZgw+NcUfL4+PjLJ7jX5kPlZ/VahW73S6tO3srSPStwx7XbreL9XqdTuZs2/yC4+hzjGJMELrGntixdcLPQ9dN5JXVfONU29Zfuv7QHg0zgwQlFNYA4/Pnzwmo09bk/mmCFs4GwEMAs6J+/vw5bZxE4T98+DADJtwX5TVT5QwOB/P29havr6/pDcmw4S4hWvG9D8QGyfNwhiguIIv9EgRJnBkZK8kElSIDdVo7HOg509s9jQYPOGrKcE3TxNPTU1RV9c2JEBETGOOleCgRZee7u7vkrIZhSGyJQSQK6LIlY0KJUXZYAwAGn4eBskMqkxUnQE4O0DkzLn3fz1rBkD36wB/ra0QGKQB+xuPecwcN5sVFiZwAT5Dmjx2HAyEOq0zSDfzNLtgxwqw7qNzc3KSEgk1gZh5YB2zXe634m887oUE3GIOdrYMwOszYCAK+vAYZ0M1PsvHv0Bd8BjqCPJG5QT4XznK1WsXd3d3sSEj8GrpmxpP5e05Uw/gdto9eEvj9PgkCsoMrawrIMTFiH8NzFqtlVGKDeX/I6XSK0zEHKcaWEqeLLSA3XhzG52DIkDdtStgTMqJtsQwu/O21IJkzqeBqYN/3swMw7IscVwjKJDFm5NBH+yDWrq6biJF2S0DHVD2YfAEvxpyqApkgmTZ6n8/5MIZpvZvouinRqCrA+xBNwzHWsLvTBvqsT31U1RD15Zh2V8iGYYjXt3zs9Xq9jrqpYjrWnfdXRFTVGH3PJuM2+r6L0ynrVj7pixa8dgZM8Av4OeJRRH6ZGP6Nz5HgMl5ft7e3cX9/P6sKsFZsck4yiZxAN02TmO+qylUHJ0H8IdEmxvKM19fXdEKh/RLPZ774etbBrLn9pW2ANSHOR0Q6NMb2hL47lmP/Jh8YH/7Ue4uoELBm7+/vKSGna6CWrWN7m80mdTK46kSyxXcA2uiIK/DWCeSBXSMTy4vYXyYXsOjI00SlYzn2bP+OLvrZfJbLiRn7/rjw9YwNfGTCjKqdiSz8hkkRZOdKlKta3M+kFVUcbAw/kUihS+IEoc76WRbGLcjLcnaVm8p23/dxf3+fknpsLbWjR5dwlslhkyklIYSN87fjEZ+37C1D69SPXD/8Ho3/9B//v5SpsQAAChQJx/D29haPj49pQ5MDEkbiz5t1NLPs0hEKgZJZEA58GFpEJGa8BK0IFmXmb+bllwmZ6SEDdXb4+vqaFg3HZMBCgoSi9X2f+meRJZUJKg3OZKtqYgdfXl5mSuDeVeRKtv3y8hLn8zk+fPiQNgUZvDtzRrkZ18PDQ/p527Zp41zJPjgQPD8/J6PAidnhmhnAOZRMAUkIQNClXVemuFyJYPwlA9A0TTJUNoTbifPMiEhrhW4C5Bg74NMBxg7D7UYAb37GZQcK0+FTzMwWONlGV/g+9+TAhNVqlfowSUiRqR25HT3r4LYp1oV/O7g6kLrqQlscv0fvKf2WrDPrwhoiM+7JPHGGHiM2Z8aOcRhwYmvoOr6HNXcVge8zR+u57d9VAAdP6wHA2L3tfgb6YLa5TLLQG67j8RjNZS5d38X2bpsqsPDnTdNewPB0utHUxz9GjGymnfYPLJfTeyQyo3xOpIeTTTaYM8YykWL+TdMkAgNdYE15ezJrbd1Fx8q/ravZB7GfJ8eQzWadCJO2XQTH9U5sbh+LxTrGMaLv8ollU7Ug7/mp6+nI4BjHGONySlOX3xMzjGPUVT7ZjiB8Pp8vx63mKh/6aTb4svLRLnJSav30utOuhfzrpo7zuYthHKJtmoio4uHhIQ6HQ+z3+7QWUxyY2rxcASRJc+JQN/M3pUNeTXY7/W51SUqHYdoYH9VEItHS8fb6FnVTZ5B8iS3MDcLs3HVR11WKU8zfwBRdQtfxw06ynXDgz0wY+mQd65LXhc6K/D6RvFfDvoLPAtC9Vu4SMLmKTwAT4INcLXBLLz7F1XIneMzRcZNYROxHlmUc9RgMMPG3Jqgc9+nqcMUfG4fodGcK92PML5xyd9EJ1hg9clz0OpscZU3BefYzZt0ho10FxyfwGWzIBJOrw6wJMrZdliRZCdSxf76PbhBvHUeapkkncCFf40pis6twjoERMcMffd/H0PexWuZOia7vom0u+io5mFB1xcWJMHplkg7fx1xMtNnG+MN6/Hf/47+P37v+0GZwAxgmBXhjYBgRGaPZRZchzdJaAIBmSj7v7++x3W5nvYkIgkU2k1HX9eyYVcAaTov2Gsr+br+wErhsiMGQxKBwlK4AxQaaGC4O3a1QmZHKwMkJGf8HEJiRsUJ+TwkweIK82UU2h8HOW9EZC4aIoron147X4MkJRkQGki7hAcYYe+ksF4tFequpgZbfA4LjAWA7uOBEAJMELJJVy9YsFDIDKBlIoUNmPcoEyYmLf2dnSDBkvmwUtC5HZOBtZ0wA5Lt2AF03vR379vb2m2TMAMiyc5XAY0LmyMX6bGAQMW8fMpAgSTaYxnmhR8yZv0t/Mo5j2khIAoafwL/wc/QGXUKOsE7MhXH798jFlVSDYVc8kJWZMtaWcdufkWChoyTL/KwEJJYV62uHbzB1Oh6j77qIcUzBZRz6CyC9APo+ZjqYGcbhkszn4x+xGfxjHnNuK8DnGWCxhpxM57ac19fX1B7KZ5Endonv4T6ugHh9T6fzrHrW930cDq/R97mlA3uZ3gtSR9NMOvp+nA6sGGOIvr/40GGS5ThcKmaJ/DjGMA7s9b6sSR9jXJKBpophPEe7qGJZQwrBDlfR92PU9Rj90MVqTZto3pOF/CB4JnCfyYthyD6i6i4nr9U5SXk97KOKiNubzcxWHPe6btIDEoCu6+LExuNZcrJIbXpd18XpPJGD+8N+Vm3AnheLC9DvTjGe2Qxexbk7xzDqFKhFG13fRdedEztPZZ5YjS9gf6TJM/wb/sqADgIFgg2/Qwyk2j+OY3z+/DnZghMwk3QwwiTHrpSYcLEdo6eOMZykxXfASK4Oum+fZxNnnMxjA8QI2myJf7bD1WqV2o4hdzebTdzf38disUinJ/F5+xriKn7esSIi0v5L7A0sVsbaxWKRTjNCTti4ATq23Pd9OqEQ/QIr4nvRdyfnENFOurxHAqwDmMfHOO5hL/zbBKuBPlVfdyg4ZrAGjI84gP5YX1yZsK5CHhsvIiPGzhgTudH3U3tU3UzNmcMQ1TjRL4vi2VzG6E5AkT+/N1FifGaCleTLuKAkUv/S9cOJhheIdyH4QogYYak0fB5FyD2t+Qxr9yyTDBAADW74PskHSsg9vTOf51Gy5KKkGDF/w6oVbLVaxXK5jP1+nxhagiMZPo4D9tXMJEmGM24nNC7vsqFrs9kkZcdx8lIrl5idxFA5IuDyfBu+lZ2kwDItGQQAPrIhAURRcahsxLZsMQ73oVrBLXcnRwBeHwrgU3FwmE2TT7Zi7dFR/h2RX3iD4RK4XLbFkDAwJ40GR8jMFTd03oydg6N7biPmFTYzDdgAf6PDyNxVDdY5BXe1ALjs7gTOQBabQq8BhQA/gLfBjNfJc+c5fN76bYbKMgOUskETvTZLix0hB4NQHBvPBPyT+Dtg23nbR6H7BDsz9KyB2R5+zokyrCXPcUuZgQPfIyibVXLiAdBnfOgy37PtOpBYf82ClcHLZAn3Zu3Qp+PxePGJ80MO/HkHXjN+dV3P/CtAFvDAHNEbPkfC4WTSBE+pd+iKfef7+3uqKmMHfB7ZuQWRSpPXq21zfMpVuypOp5zY+3us3Xo9bcLshzHapo52sYhmZDP+MSV0VZUr7czLVVX7K8aA/ZtggsSzXTIPxx5siPaNpmmikj0OwxCfP39O63E6503T1v27u7sUJznUhbVnvZ2ospa8k4X4xUblvs9HnPvAEwNNQGPTNKkq5g3ejtXo5e3tbUoYvK+M//vIbyfMAHl3OJS2SazzQSQmDCG+HFNXq1XaH3l3d5cwhdl9EkHGQUyLyCe0YQfoesl8uxJxe3sby+Uynp6eZvEcAE7lmXYt9Iy19Usx0VXa2Fxhtq6WVUriDXrsrgdiHs9A702ImHwyAYNO8hm6R1g7kjriq99DAY7ipCoAvu2KZzAe1odYye/x38Z69lPYJb4OjGQy25fnhy4gRx+8kwjhYb5fEj3Er/s+ThxN0Nuvgw0sW19OLk3GoTus649cP5xofG/TKYZslhTFQxm8iRYjN1jBUBAcgieJwLESuLzXwwaHUu/3++RAeCtn3/eznf5UOGBJGM/pdIoPHz4kxSZBcQbqzVz39/czgG6A4UAAkP4eOLPyoZjOaAmqZLcYl9lvnsmxs8zPBoAikRjwPBynA7plRaDCebuFxuPj/zh/vm+HhJE4AWJ9DZCQTdkuRSCt63p2NBv3B0ygY7Bi3NMvZPP+DW/qYw1JVg3unOnbSQA0S4DuRJKflUmXKxV8xnaFXJwYunLUdV28vLwk+aOLZsz4rIEwhyE8PDykpIh5mak3+MUGncQ6CBpIokvYjZM2g147bwAGYBFn7iqbAWJEpBYabIPkxGMALCBnfJEdu23XGzA9f+bnE0QiYra/ygkeAAIn7WMRTWg48fXPmDvlf0CNWTZXXJg748e3+f5UHvDFzAGfyfz8fM+9tMeykmTCIAVIxQ3WyuMlBngdGQP+DX0oddrkCWCUz3EP9Ix7eU4kmgZ+DvB83kEYnen7fjrtZbgcCT3k9ynEyCl5wzf6M+nffB7ojBP1MsmnrYV2F0BVroB3s8oSMbCq6zhfYqeBIWv4PeKJtVuv16lPHj9BTLf/LkGNW0rQEwNT+232lHmDNvIykeCkoK7r9O4niDj64V3BhLDk34BQtzRxtW2bACky9pqUCT/xh3jB3Kz/xEiTIFzEKmx2v98nm2AdhiHvj+SwBICoiR1kzB5N69M4jnF/f5/ment7mwhKZEmXQ7nZ3DjCiRJ6aJKY3wHu2TCPT4M0w9eTVEKS+aQ05IQvM/nMu7YOh8OM4BrHaW/kfr9P78SwjVHZQvdc5WduttX1ep2SMNu/mXz0Cj03OYXvYU2IP9izCVr8H36MWGGMgS+xbzDBVFbe8DckxYwRO76/v09xryR1HI+QBzHB1Zy/eqLBQNw2hBOIyNmUM0kUzf32GAMJAMZIhkRwRAB2TA7ATTOdxsQRcM/Pz+lUCyoRBBHK+MMwJGdEnyaLYHbO+xd8EhaKAmjAEFzZIBjgqAGrJSNI0LWiuaJAcuTWEAMilI/7cU/GV5bQmM9ut5ux7K4C4NDMstoYHLg5LcFsKuPjZyitKwYGdMzD5Wi3QkRk5thMFQEIObPuGGhZli6NGcfIfQkCBGC3/jFeM0mslR0Oem5ggjMhkPAdgjUOgWSHINL3fTpZzUkpgNNOzAld2fLEM9Ens4J83gCez/lC1k7MWOfyYAIcEzIFrOPkzXD5LHme6yQF/cGnMEcSdTZ3Axj4DGtqZtttGKwvtkeS+fj4mFrnDofD7Hjin376Kf2cvVI8Ez1j7LYp64xBgtcK+di3sR5muZAPAITLyZP1nfu7MsNYaJ/Ep2ET2U/lJINA57mU7Wau3jIe1he9sL9h3dFvWGA+a//Bz/HlBrTWOQgP2x6fBQSW+6EcYLF390UbKFvvSNSn+VXRtstLonZ5k3s3HTkb47eb3PFD2D0y8KmIJdsKsAPk2o9ik6yX15z9bm+vr/H2/h6VkizusV6vYxi9P2eyVaoSxEP+/fr6mkArPtTn/qPbJnA4dMUJivUVkMTakaTzO5+Q6ENJ0En8U0QkfwBYd+sH8dJk0Gq1mnVGAApNPjkBWy6XqVW1qqa9SPgX5OrqpAlSYxiqcE5S3F6Hr++6bvZZ4qV9Bp/HJkp7Rw/QObPYfd/PjsUFL5Ub5lkX+3fsoMQJfN5dDxC51jP02xUKxgiwJbkg7nsPJ4QPcYHYUXaemOT2pnd8m5/LOrIujNV+nZ8RG3m+kwzvmUl2dvk+BBSJLzJhzMZ3JvXbJuNh4zsSZOK947Fl7iSYiqGfaX/qJJZ/O16b/PiR6w+1TgHgYVxRKDPKZKcRMXNQNnqO1vPk+D+ODQXHoGAGzudz2lSDkEk61ut16o9GuXAYABxO24AN8QYjSrSw5U4McEoAH5dEDSL4mwzehkygcpbctm0q/ZnFNUNbBmr+Zp4oPskO8ttsNvH8/DxjQb4HijAW97SyjoAGz8/Zctl6ZGDIs8zacjm7Z939dlq/VKjMuvm3GVcDE78B3QEZx+KKAM92GweBvTRCg19+znpETEHQm/zQD56J0TuRYmzez7LZbOLLly8xjuMssKLD6P33xoD8ANM+jcMMCHNhvnwe3SyrFDyjaZp0wMAwDEnWMO04KezOMmXd7ci8PmaNnNQwT8bPdwAjBpWsD4ER2dsuXYnjGZxl7vnyvD//+c9p/gRXM24R83dknE6n9AZiWEvfG7vns7YT5ufKHMEcBg+fZZLGwc4tXa4gm611hRq9y75hXsHARsrE23bu9hGDZFf8vCYmAJChe935jKukbntxAmQ9wVc5mSb5tM3xWebNejphYm+Bk0nunedYRd9xQtAxpk3Q9Te6XVapFotNTCdJ5eoLY3NlxUk2ug4ots7n6lR+l5Vf6jZGxIfLAS28+HUCdBHH0zSm7Xab9AG51XWd9G6xWMSnT5/SHgDrgUmYqpo2r7+9vcXLy8ssueFz2BMJmxl/wDr38+ZwvzGZ5Obu7i6t393d3QwfML6y5ZD1dIsK8+YP9sL48H3Eduy13GeJb+G5PvkJ3zEMQzw/P6fTHRkr8vKR9o71zMcdEtgG1QfWHADvPn/iAbGShN8xwnrrLhN0krlERHrNAAkhscTkMfeEmOIkPLCYKxv4E54BFrIOMVZ0nMQHW/Lz8SsmGVlr/AN7WVg7s/fEOetlRE6m8A3cl5YrLvCh45hjuUlO+2LihX3iarmaxRL7B3SYdTHu8P1MbrmKY2KpxGX2Se4EII7+yPXDiQYglp44DMyAwVUDgkPTNAmA4fD7vk/9zhw5idIhJBiJ9XqdSooRkYA0QANF/fjxY5xO0zs2TqdTPD4+pntZWUuQ7wDtxYOl8bnMDmhfv35NLCdOk4UCwJAAcU9OvkDRcH44DZTce1X422V/EpZhGNLGdwwVh8fYAPBd1yWDZm1QOK8xwcUOE9lhGB4D64qhGASh1FxmvJ1ImeF11Yi1Mev+PWeOAbtS4cBsMGE546iYI+NDt92mwvidnBhUIReew/i4F4A8IoMhV6s8hnEcUzWLdUG/vLGQeSI3M88GbIzbbSXYBve1vSI31pIStBO2iEh2HDEFDRLWpmni119/jd1uFz///HMCC14fO0LuRVC3bqJr/N52A1h2C4TXh2Bq0AE7ikywIyp0sGF8liDEMxwIImLGSMFawaKx4dVVKSfIBF9YSeaM/Zi1hGBxQuYABxDCX5nZpv2Ty+QA8rZdAFa9PiQTJXHAv4kBtGzha3lGBtiLmd47oYuINE/0nmQA2wAoYVeusOHjeB6gANslMfOeJwAdMcssI+NzMshzMuiro67yiWN13UZV1TG952KMMfrgrd62Za8DdlTXdTpjH72wvRn0YscQP9NYpvd7oE/IuWmauLkkB64e45+JN2Z9racGw9jyfr+fneiD7/Abyeu6Tm/Ttr3yB1t2sowe4x+bpolPnz6l77qq5Gqd2xfbNr8Z3MQELLjBqjdMV1WV2rBKX0KyzDsM8GfoAhVqx7C+71MFdBiG2O12yWegp9gLHSDEVPtmLnSCkxSJTz7dj+SJ5AGdj4jZxm0SNvyQiUb0kXgDWGbdeHs2ILPs5TdugZwlYcX+wValH0BvSoafZMKYwYS39Ye1dfKIvrPWrFdEJPnxbCeiPBP/RJeLyTk+Swwl9jrGOp7iA/w7/Bv3Y62dcPfDvErrpIixsbZU0exbje2Ipay719Cy8LowR8bpef7e9cOJBpsFzSJjuG7xQDFYpIjMnjIpBkcVAmGi2HZeTBwF4rXzBMG7u7u4vb1NGXXTNPHx48cUSOjnY1ENmsdxTGdz83z+7546Kw1JCiAIhUbwKCD3ctaH4+TEISs7C8tGcGQyjuNsQ7SNj3sQKPgczyRwGYQSmGDQSFCcVTMXZFVWQigxc1+DI/fXEgwMvq0fDkj8njnTR1o6XO7FXHgW/+a8drNsnr+ZOpe7MSASgqenpzRX9IOAWIJZHIEZWHTMLJABPM7GzC5jZVwEQSdyDtZOQAAMrCl9zdgewYd1ZJzoMUEGR8zYkRWAwAwKcnCVBBu4vb1Nz7MdoSsEdMgLO1lkjC4zH2RD0P/111/jdDrFdrudtSV4jPgmgg1g2Ukd4AhSwOSE16Y8QhKdNVg1AxsxERIOZHb6bnkpHTl/l4w2//fFWtqevGbWzckHtRfbPIs9BtRGWgdszMc+E0xL9gs95PkmVJBPXfPehzEiACb1ZfPsTTw9Pcd6vUrrRSJo9o115VlOqNh/xvpSPUYnsCt0MCKDJPTjcNinZOd0Okbf530/E4ChvY9W4Yi26aPvh1gs2hiGvKl8GPuoqtxKulwuUrUL38+b2M26om+ukpmBxqc6EZz0cnrWbreLup5e7nc4TMfhPr28TECH2FU1cXg9xKJto+3np+zhayGu8OkksraN75E/Tni9Adg2znr4mcQ86w7j8HMA+SUJxH3QOY76vbu7myXttiF8OGCLuGjiE9b+8fEx9vt9fP36Nc33e2RNXdex2+1mvpa1AxtERDpl0fs/2deK7RHTeWUAdoddsif1/v4+7c8kZnm/KX4Ge3f8c+LvBNeEIHpovXNVl6QF8O1kA9vFhkiQTJg4wcGXc7HuJrSJZ+5ocdINEUHMICYRw9BfxsYYGHPE/K3frniAZZGR74culMDdRKrbVBn/OI7pnRwkd8RlkugYsq9lrq4Qe0wk5GUi75hu4gRdXSymk0m9Ln6m5/dHrj+0R8P9qQjh119/TS/Uw1lFxOxtzCg1YKFt23h8fIzb29vUc8eL5XwaVF3Xsd/vo6qqeH5+TkaGUby/v8fDw0Mq5ZLN4TxwUOXeBQACSkaPKK0OGI/BG3PwBiorEEH+5uYmsX8GEMwNQ0SBypIlyo2snEF6s9x2u531/aFMXdfNKiesHWMhYYP9Yy4kHHx2uVymIwoBzSg13zEQYk5836AbJ8Pa4Rh8kokDAMZAmdUMKg7MTr5k4yJyAmUWjO+ix957YEdAkgmD7Pl6z40rBq6WsJbWLxhrnJ+BPs9FZ5EBa4szisg97g6aML+cFPb8/JzkwfetizDLBKCSyaJiaQDEuO3M1ut1vL6+zlodnWzikNCTYRjiy5cvMQxDqmLSX/z4+Bi73S6NyfoEgHfwraoqfvnll2Q/5/M59TLbwUOOuApFAkzA94krZoCQAQSDyYrT6TRL3PzyT/wPoNKVUCeN6Cs+0893Kx36zn1cefJacP/v2Sk6l/upq2QTU8BbpPF7vIwJeboSws/QQ+sJOhwRsdu9zBIXdN563HXn6Psuug7bOUddN4k9RRfcSng8HuPu7u6bSiJrxDsnFotFIpBsQ6xRJsHYI9bG6XScgZ3T6ThLdjJ7Pr3QbzoWt4phvJAO0cd0UO60WTxijLe3OchhfSIiJbGMDbDgpMubX/Gp2DqV5YiI7XabfArrtVxN/jfGIeq6jWEc4u3tNRaXF/D58yZUWCMTEq4isT7YpPdL2DfyfXwj+sNnnBzD/OLL7+/v4/X1NVV6DNiI51QikQ0Jf1VNb0FHD0wEwKzzPeZrJhwffTqd4unpKfltQPkwDOnkPmIWlRQSXeI2e1uoJrCWbhPGN5ssOZ/zO7GwZfw4R8vjg1mH4/E4awE3ucPznp+f46effkrjc/ue2065/83NTSJ1vQ8GG4IYNBGNzvhgCvAE80XPsY0yoXF1jvt7DCbGGBNJMokxY+L5xrA8b7PZpLZgEmXbqUnl+/v7pJ9c3Mc4i+/zWeSA/qBzVMXK+IUdvr29RR1VNCLrjWdJJMqWLmIW9zMJhO+NiFknCnPJVdrs553w8b0fuX440WBRuDEA4eeff07/d+/vdrtNyQYKhJAjpn52+qIBdm578aJ6sXCqKCbGjaMxIIvI7BcK5oBvQcFokPgwHycajAGDx8hLFhvHZ8AUkZMXPgc4QulOp1MqUyMLOzsUmEBN9u9qUTl3K6WNu2SAImLmaJAB6+fEgefZyL1xkkQJZ85YIuZv+vZ9ARGbzSa9cBAwyn1Rchwx3+WiUoARtW07e2s5Y3PiZVDFZ1arVTppxTI14++EICK/cBCHyGVgguGbgcAZkuQRlGlD4nsEQDsD7ovN0RpBUAOMogfoKIGD/mjGi+Mj4eZZMLqWXV3X8fXr15Q0QiRQ8WOs2BPjMIBx8uqXG/F5QA1rjg+izSkiZnulANHYiRNXZID/oErn3+OkkTs92i7ZO0iiMwQ290PX9dQ2AmvJfAAStM+xzuiEK1Fml7nwHwbr4zhVZZw4eC7cL4+9iqrKzDJ6Arg1Y4ff8glaDk5cBuXoGs8ex5jpsdm40kc62QYokaQjN2yB9tiSlcSm+RwMN/HrdDql6gcJ2rT+ExhgrtzHibMrhJP88oEJACpIitfXQ6xW62Q/+Dmqrtij/Rk6bLniq9ARKgr7/T4BBCewVVXN9lX0Qz9LAFkXdw9AgrF2fd+nTc/40NIeuy5vlMbmGDMA0QmG/YD1gzHQWoTeoa8vLy/pzeOuZHMvgDXydPsgn7HNYovEMN+LzeDoN63RkDAmPrAV5BAR6RQ/4lBd1/Hw8BA3NzfJtiFsWAMSINYRrITtQW66uufT9lhbEzLWUXCZk7i+7+NPf/pT8tnEcWI3hCU6i32/v7/Hfr+f4RLW3CQQeuSKOLZuwgb9IAYTz1gXYoRJWBIK4oDBsJOkkmzhNQWO+X6u91Sia+M4zvZcoF8mNZkfccRJogkbk3rYMN/Fdkoy1dikrZtYXJIkdBdfhnzd3ULVq3yVA3Hhe3ZZytvEgskxr/mPXD+caDiLdp+4y6Rk9jghZ2QGqgS1iEjMP1kbk0I4sDNmXZ2Y8FmAP9k1TocWHxZhGIYEanAeEbl/jYqEx+3z8+u6Tq0E3APZRERqe4qIxFzgRCLy6S6ABFdEzGLigN1eFZGP5iX4eUMjp8kwHxwgAASWyMHL1QwUF1k4sCE/swBmip0hI4+SuXFw8rPNHLMxPmJe2XCQMUtDZcLJU8R80xj7HVwSRPYGEWUC5c1pZsMjIskRZ8TaInvuh42wdvTs+sQdnm/9GMdx1nrEPQGQ6KJZwYhIsoCxKdmeiEinqnAPvgsDg+O3bZmBHscxXl5e4ng8xna7TWe34xh9/Ct/WE+cILLGaTIn2zh+AucPCMM5M3cDfbPuZgYBccgcG3CSbkDntXNiiszwiQ6gTZN71F0BwI4M5JAnDDD6xX29DugCYLlMEJADMqP6grwMXPn81L4Uad0jYraB2P3vni/3ACR4/mWSTdLe912cz/NjOMtWgzIhmoiHqRcdkIYOoxNlso/MHGfcYoNOArycfI3jfOMxdvLw8JBYZzOQtOROBFUG+cgBkM38XMlBD93u9z22H/KrlD9jcwLN/fGxq9Vq9v4l7NygMSJSFRBCgM+U77gh5uGnTPDYxt165DjsBNVsL/4An4Uc27ZNY7u5uUkHyJzP59kGbnSIFm7mbV/GmrjiFZHfF4FdHY/HeH5+TkQPMn95eUn/J7Hi59gl42Bdmft2u017MBgPMctrSBuZExnbF8kUugMJR6UFe2BPGMmGyVowmGMfb313gumE2UQo64aOQOpgB76v1wXbHoZ8IhRJCnEEnAbuYm2dJAF6iW2QBOAzJ+PoCvaEbi+Xy0ROGZRXVZXeY0YnhVt6uUzqWf8d20xMOQniXiR8VLycwBPXsBP7+jrmhxjg20ziYLOsDdUS27+xuHWDOEwcYG4kZ/6+q8g/cv2hioZBgllOJsgAWSiUDjYkIpftHLgxINhQhO6sqwSdsMckHbAP5/M5ttttKpVbMCi8AZE3EhEoWRgzpBG57IYRo7w4eEAySgpIN0uK/AD/7NegLcuOAWP3wmLY/NxGVNd1YqO7rkuncBnIoHzeyE8CghHZEXCfkjUEwJrVNFvFd/k58sMokbcNwIDZYLfc0ItMHbzLkx14noO2A74NDQflRCIib77jDwEOmZmxcDBHfgDfqqpmrBHGb6fIOBg/RozjwnaYO07fa+/A4kTRp6WhB+XeCO6JfmBbVAth6pkPDCPrSQWvruvZxmbLijHYTnz0IlXSiJjZotfQ+kPJn/WzvxjHvFnUiYorbK4yOWljLMjJ5WzkDgnQtlObodkyQIJPrSmTICd+/I5xmZnGNpmDy/EGtoBk2Dz0wcw8fmS6xxy48nmeyTgMTlgr/KDJB68L+or/XCwW6UQjmDbHFFdrAU/Tc6dqCEnk3d1d0h0ACHsc2ETLZn/7aGIQLD2yww7Rl4gMbPgswIfe+bZt08lA3ttDFduM4OvrIckdX88BAfhp1p7DRZjn29tbAqNOwkz82O/QnonMl8tlaqXshyHapo0xxtn6+sW7Jv+cBJb3NOnj9hmfcGWQ5lOBAI7oG8/zHgX0eBzH9PJaEj2PB31x6xNJArEDO0XOfMdMMXGHcfDd19fXWcu19/7gb/jbMdr6ZrKBBILN8VQSXIEhUcDeIF5JVMBAJm5NBqLzZv5pqXUFiZhOTOGersygV/hMYgFJ6fPzc6p4IAtXNxzX6NygOuPWOIgEMOHz83OKTfgS1ge7ZOysp5l1ZM94SHRd0TscDglrEh/xR/g57MTJP/qCnnt+kKqumLjiY/IJH+pDYbA/9p6wHq5ojxGzeHg8HmO/388OMImYn+5G0oj9+XceF/gHX0zcQJ+Mzfi+5fJ71w8nGiwEC+6HGAQfDod4eHiYGSxvmLy5uYnHx8dZtsdkuBeKQTBz8MSp42AAHtvtNu0ngCXAoflUHISLE2ZjedM06SQHnGJZGoyYlGy73UbXdSkpcBLEPbxpvgTRZOYoLIpl4GGHZZkDOPgcYyPps9G5Vc1JAs8tQaZPvkIG/M5rze9RTAyL9TLgZ05O8CLyKVvIBcfkyo9/D+C343ayglPiud/TKWf1du4AYvcVuwLgpBOwzb1x8hiznQvPQtexGfTQiY5ZS8ZUJpBOqjw31t8sP98xWMVhlMwpz2BufJfr7u4u/W6/38fDw8MsScFR47wBCqwHcgKUAd7RGcAqgZTPAt6wI/ewYhuM8/7+Po7HY3pbscv4gEXLgb/LpMzlfqoC6AVO2Iw9n/d7KbAtnoNf4BnIhcSTAOMWDtuaE/KIXCVFJtZh7MLsGO1BbsliHdApxobeO0m2/dsve33xF5YvRNDUJtTHly+vqRrOfBhnCUxy1TSDwWGYTu1BP2nn8XoDygFrAFieRfB0iyHznGSaZcNePydU4zh+p70nt8GVvhOgh8xNWrEXCt9icsYnH7kV1ODBP2d9nMjCmOLb6kWOIyXhg3+13318fExg0HpBMoXd4wtsH24jub+/n+03gZ1mjbENknLrMnIxqUasRr8dY0num2Zq/4RgQa4mJ5A3wNXVOtuUcYO7L8ywoyPlH2wPuRCrXC1YrVbJf5AkI8O+71ObXd/38eHDh/S5t7e3WfWCKoeJjRIss+acnEUlBIz1/Pyc9pqBzUwyEstLUs/JNHaGHPE7rhAxL2TnJBWdNe5iHfCbu90uVZF8UqmrrKy9bQSZYkdO1tE9YpD9juOnSRbP350gJVHkShHjNhlHIodOMgaIWj7Xj0OcT9nneZ8h48FP4dewOcbl2E0MYT4kofbv/I574GddKPiR64cTDbMqLkc7o+37qTe8fG+ET1FwoMNBETDu7u7SInBvnF3E1LP7/PycKiaMJyIfGWrWGqHn8ngu51GSRdDn8zm9AMxBlbFtNpv0ng0CFL8DZJTKyDzdukAQpwLi4G8lZdGdkSJjHJcBA7KixEyS5kwUg7LcGBP3JKs2Q4GzdusR64syY0QGyQZCJevhcXFPsxDIA/0qWSj3oNvZU/WaMQGqCDl5QWdw5gagJShFTgA9nAD3Yo4wshExM2bmgsGiMzgzj9ffdVLJvw+HQwpYdmTImsDJfUlsXSpl7IyLZ7q9wEkSwXsY8ksv+YyDF4wiAZkKHp/NbO9rSvIp/3NAAPs9cJbc2+Pm+QRvt4IBtgyUGVdZEWB+JeOHntqBE2S9rwv7R1+RmZNn5mMw5mCKr8G+kV1EbpFB1/FrBq78zr4hs/T5LbfYxyTXbPskBrYz3we23uSIgQNB3eDteDymU/cAnF47fI0JmWEY0r4fbL1pvn0ZGjGCKgPjdLWKtWmaJu2p4yQiAq0/P/W6L76RtX0muoOsVqtVPD09p3EYqEx21M32QQDonLw6+XTSQAWk66YXthEHImJ2eo5jBsCLmOu2ubGukp9E39BtQOpms0lHOp/P5/S+DZMsHBv79vaWkgiDPGwIwG8Qz9/YrKt/Xdel1qFSp/EBJCbogWOtK134dGyf9S7tyxV3+xEnL+g1gBb/yLu4HNMcuy1r1o/fYfPcH/3iuVSKWUPmwsZy+vLRYWyY6gXVLcbFnACg6P12u01+kWP/u25+StfNzU16LkDaZA+kJrLmuY73+Hzmhg4jM2yB/1OZ5PvIjdZTH8LBn4eHhzQ++18nfjzHxBI6xfowr4hcPTOR5/VzV4HbsJAx64o+Ys/ch3s7yRiGfPKXT6erqiq6U67UmFg16YbcmTv6zpUJkpwo4D9NivBZd8MQI92R5I6Wv3T9ofdosFAIBtY8IlKGCqsEwIAZ4vdMxCUrgiK94zgRlCgi9/ohWPryYCy9Qevnn39OZfVhGNKmORYCJwPjQDAvA4ATDhwewjZTwr/zgo4xHY2YgQgAdLVaRqjXztUgnoMDw+GeTqfE/ACoy7YvADQMCuvlfnicGgDVm5ApiQJiXGJGEf0iJAKPgzhOD5lETMCPN69mpjLP32yTv+MSqw3frDxGbOaSIO0gimxxzKxvMoI2HxnIGjvoozMRMZM5zzfTa3mj2wSdshLAOFyiNIOGLgLG+JvWCjP1DnjMyayLkz4Ck09NcRXDTjoiZrrI52A53LLiJG6xWMTLy8uMNeVoyP1+H4+PjzM2+fHxMbbbbXz9+jWxvZwot1gsUmsSe7bMUEVESlq8NlRR8Ukk3vgCZGL7JcC78uCATWLEWqDT6A5sOGvt1pSyeoEcnTSQjBKUnLg7KeJMerdAArScWDKPh4eHxBxP8ouo6ypOpy6aZjpmdhyHaNtcjaOiAB+AHqxWywswY/PktE+Bo2m7DuZ+jJubCRC9vx9jOqGpj+ORvQN19P2QCKaqiqiq+pL4c6JRfus5cSWTJXVEtDGO7K2a9Pnp6SkeHh7SGjnBwzawQ9bDxALkFn9PQG2RNsGez+wBGSIC8qKLplnFarWMt7f3YM8H9oHtobcEaXzL4+Nj0pdhGGZHxqPbkCP2WegCLH9JHBDjutM52nrq814sFjE0Q+z3u6giZtU7bGSz2SQZIkf2NqJDfmFmVVWzTe7oNmu1Xq/TXhuIO3x/VU3tM66IQmoRa7BR1omN2YBEwK5l7IScWIC8TcTgc/E1HjvJuolD4ix2Z1tG19w65hba75FY/H6xWMTt7W2qzOIPGCPzv7m5if1+n1rEXd0yCASPoEfgB1fTieskco59xHFXMhwTfAKYcQKdIk588aXEF7CHfRbkE8/ws53guzJBwoo/dyLhZJoYhJ7yGROArDPkhCsMYAeT7I43TgDQPeTnfT0REU3dxFgPUY0RYz+9ZLOOya92p3NUY8SiaeNucxPt5T7DOb+EFr3gb3Qf2TA+E2z4P+IHc+Vzbpc0VsSnmMiFWCr3D/+lqxptKX/h+n//z/+UjJayD+/AwLEBOpkYggAUl4xqVVVJKTFMFgvlRPkwFJ6FAZpNdtWFE5NgkmzkVVWlzVQwmB6XS2kYEBt3+Jmdhds6MuuVmXlnysMwnVTC3gkUBqM1s4oC0duJU8lsX1YozwPnBTDHsaPogOeIDJ4eHh5S5o2C4cj3+31i1MuEzH2bLivaWaKoq9X0MirkiaPG2Tnpc5+1gRxyxvBZMzt0s4L8np9jXAYYBo9mnNEBvm8WzokJDo3xYYCciuEqIIEcZsYnBXn9zBKh69ZR1hd9RO7MnXFhS25ngi3ifjAnjA2g/y/+xb9Ijq1k3/xc1gkdwbnCap9Op3QaC2uHDVmXAds8i0T24eEhnaJjJp2WoGEY0kEQj4+PswqCAzpn2+NH8GGAJdbCVRH+5ohMB2v/jX37pB3uzZqxvrCR2KcT7zIIsE7oAn84ghi5OQE0sw7wYI0IoCYn0BMnlLYZApEBmvcyIGeA2/l8nh1D+/r6lvb6cD8SbPycyR8Y1il5WKYxA7Sn9tVzeg52x/gOh3woifWxZJvZ/8S6vr29ziqnrj7UdSaS7FeWy9xySEUANhLW1mSICQ4z7oB25mJgxXdMEJGAIBfIGbfrGHiZaQYERUQM4xjnftoUjN1TTbHvdsXULWtmcc2o53enZAbclYWIKcHxaXM+4tethMiD+Zik8TiIH8iK9cVGWbP1ep0OsHCMZ37cr4yF6AUkGD8nMTQjzO9cXWVcrrjbP9ze3qYY6Xi23+/TcarErPf390TeYousk48OZw3YG8T64K+JJQBt1gJ/4HdeYMO2ddYaGyB2e1+gZQI2ZG8tNu5kiHUlLiB74hjPBsg7XuN7bTf41pLApv0MeZb+3TjVpI3xHNVeV4LxYU6GnKAu2zZOx3wCGWPj2cYuYGjHddo/8YUm+jxW4ogxkH2QYwwJI/c38Y3O9X1+MacTnP/hP/z38XvXD1c0yPIAASysey4BAQCOup6OwHQu41YrZ9IG0CWYNWBgkXkbtoOlBcp9InIfnctCJCB2hHYMCBZHHhGz7BpFoE+V7+fscn7sWkQVyyUvUOlTcuENeRidy7cYLADcb1knMLMOZhbMTDFWlB1jJ+hGRDw/P88yVP7u+3xUKs9EhsgYoMznMXwHJGffrCNjAfg9Pz+ne/oZVMXcuoDTApDY0bA+ZfUH+ThwlEDNTFCZTETkE1ZcGm6aJgXN8/mcTiOhx9UVE2SIzjJP2uMAAHb2TkJL9pzve9MlazWO054iV5Ss/2btKO9HRLy8vMTDw0P6nJNuP9eJLvLZ7/czHfjw4UN8/fo1vSPjT3/6U2pRdMLFuhG8aPswe0NrXkR+iRb6QaD87bffEjhxosUGXvZy3N3dpaSVVg8cKqVry9u+DX+HnhAcsbuImAED1hUQGJFL7VRmCUxlqZo1KME/7BZzwt7ReZJb+1uzUjzfCQa+zz40IhL4dNUW8O7TV/BlrvIATI/HY2q9gxm1HwBkUMnZbrepH53WOfwVukByQZLuCidrgT8FBAP0+Dw2wDjxNSRQzPd4zD7ZQM2sPPZjkggboeJORYJ7AySxM9pzka3JMJJu1tLVWvsQfEvbtvH169e4v79PQNgABF1dLvNBKsjWeueebvt2QKb3grBXi/hq8qau6/QiVsCv2XUnTCYiaKl05YF1ZczYO0kS/oo1wVdY35C5q7+n0ymRek6UmIM3ERtAm3zkfiaXHGPQcSc32BPxwYSM58PaYsOsX0Tej4o/J1GlGoauIgf01PtA8GuMjfFZ16nAm9gxKcj3AeDIwuCfOIQPMLhHlmBN1te+z7qMb55IjddEnpGwuvvEXQD4ZpN3JsrxDQbx6APEgKsb1imSLXydwfqxHyKkd8Z9boc1CcTnkGdd16kqyNjAirTAuXsEn804sG/8mxMhk6PYP/I1PnS8+L3rhxMNTvcgcJebuKycCNoKihNncige3/VmZLJLgiEgy9kaQdqBD6eEsMvSGcGAKguKZCfkwOOWCgdxlAIFQDlZwAl01xeWlTOYq0sPcB1d95aUg+fa+TkAu0XGAdyMNMCK+RlMcB/WgOe5PEqlxEAIpTc4wYn6OX62gxy/p40GRgqlt2M2aEd3SFZZe77jihpyKo2TdSPIMRYzxyTO6CU/9+/QTcbtZAOjRLZ2wBwK4D8OvE5YcfzclzHaoVi3XEUq9YU/ZkO8Ecx2AtvH+r68vMTNzU0Kgtg3IMOb2A2EsQuAhwEYtnB/f5/Gs1gsZpt6CbBOjgCIfA97jchHaANUGIfZKtjNpmni6ekpVa/cmukSe0TE4+NjqkD5Pk0zvSjt06dPaY0MYJE1dun355As9f208ZONlvv9PlVgsElXDGDbzOwiu6qqZgwy/stVJlow3I5AkCVZt07hx0qihkQFsGvb+Id/+If4L//lv0Rd1/Gv/tW/isfHx2iaJu2x4J04k5yr2f429Iln8fzX19fUQgM5AEB2FdPjLVlJbJ+9Hfv9fsa+2k8Q4GHCpxayaiYfvhvx7ZuC7QfMupsFdzAnYBvIj+OYXvBmXWLeVEgXi+mlg4DJm5ub1Kpcjo05+oAF/vilsX3fx2K5jOMlCQIYUbn1OJ3QITd8M0AS/+QuBHSTtUQeBj2QKtiXiQfW1eAQQIWciDu73S5VYtDh7Xab1uR8Ps82rxtMA6y+fv2aqpc+0pcXbzrZrapqVm0gFmL7EBYmZvCp4A8TDcjW70mIyADYVRzGgNxdmTXAxk8wHq8Zn3EswA8Ri8Bsfd+n9jx0nZhmth2/QZcD1TpXjVhj2wp+y0kyczdx6opLRKQ5Od547sRX7NSVBp5hbGHS23GU75HE+UQ4k3CMBT/3vZcnjxGxXCy+8Q98hnvYF7mSg19gjG4BNiawT0HG3J9kyp0EJl0ZA3jfBAn3dOL4e9cPt0793//H/5MABsploMHpCeM4phKys39eMINBoBj8nuDtjNsbdhGQM107M8DsbrdL/0dBqBD4TGic8e3tbWrvANw5ILIgsCiMwQCWoARDNi1olUAhCzQBpmU6A5k/rshgjCga9zcTHhHpu+xDYYwYm50MP/fb01F6HLmTQn4GoDfYKUuKBG9ABfJBqUkYInLp3AwiOvA9kOyKVZmFIzecNnNkHR3kMFZvlENOMC/oidmPiHz0KKDGjg6dK8drsE2iSqnbG9l8EYC8Rwlngi6TdPIMVxrQWxxoyf44+S8T0IipEkEFhPsYlETkUjHrhT3guEmAnOQdDoe4u7tLb11lTGZHXRrmT8S3pV3bHOMhAKAPpdOPmCo0rrK69QRdNRtG8HdygS4Pw3wzvJkuNs8CRkiOXDllrmbW6V13OyEOH18JW02ibWDJnJCBK3J+/wM6we/c9lW2MGHHzN9tG97/xjioVux2u/j8+XP8+uuv8Xd/93fpZWXjOK+OlUduMqbsPzPIQOcAypMNZfIBAIFOTC8knJMh2ITthWcSYPu+m/k6J0FVRXvVW1qniIjVajkjY8qWFT7nNkeDc3QXuWOPyJl7wzKy/j6Ck4TdDLZlhg6yX8kgpKqq6Mb8wlhXlwCDJtTQFeJCXdfphXpUcrlcJcDPWseXy2Xa92Km2ywxc2duJBrI2CTDbrdLBInJSUA08vWJPxBTzPl0Os0SDOICa+G5OblwZwdrdnd3N6uMQIIyN4iAuq7Te1l8rDZJG34AW7HP8rowFxIRbJ3POBk0mC3BJT7DR+1yAAT+Dn1j/xxrDaDH/7mFHbtGN006msgjPtle7JPcZu/EAb/parbXlvWGXERWrrgRA5CTMUTTNCnxQgbIF53Bp6CrzJf1G8cxqnGMccgnT4EJvKYmOB1nPWbG4rY1sIkrIayNcaqTDr5nf2+iErk56UPHhmGI//C//k/xe9cPVzRwbjB0gDZYLwzEbCYnM7jMFxGJhUIo3uBHqRxghFICqmEjYXoIUoBlM+4GIcyBbJuFBVQg8PKFcRiTFbpUYByUje1weIvz6Rxd30WMEcM4RBVV9EMX2+3dN4rlBArFd9KDArjVyArB/Mxwk1TxeUAg8gEcOinEiM3E4Ch4HgZuQ+BCGecBPB9hizESOMmamSdyWa/XyehZf4zfiY7bqmDj/DMuWDXvAzCgpgXOoAGg5rIrY2YMBDB0xcGLMbq8nwyvzUciAm45q9wMGWsQkY8F5nswG8zDcuS52KI3sfFs3wtWFeZxv99H13Vxf38fXZeP3GzbNgFOnuuqAgyI2zIMmsyaINfdbher1Sq9a4HvWr9JftE9dNtBhu+QkMGKMx7WkJ/xfB+NTTsArSTcA5+Ag+VZ/DxiCpicfuJxlVVR7oP983nskLWmemCdMvg0SPXb3GG9rHPlc510Mg8nqwQrqkmMn30RjPO3336bfb+qqvjbv/3buLm5iU+fPl3WMJftAXqOJ05e8XXjOLUUMUbGS9yY7GtMoAa/P44Rw9AnX4O/NMix/LIfqqOq5hstI+JCyuRjanmWbRufb3awvI+fadDDOPHtgH2qi6w/wBFwAoDzG7OdbDI+J/aw8maiV6tVvB4yAYePoMpDPKACx+9JAPCbYAKILEiJzWYT+/1+5lv7Ph9Zbp1jvMRBknp0EOKCVjN0jkokvtzfj4j0UjrkjI+jNY8L26ZSRHyjbcs2zXpgI8jY82DPKhgoIhJg7/t8EhHjtp/DlsziU8F1O6aTU8cf2439KfPwi/PwuRDC/A7bxA+byUbPiZ3oOzbOM0lI8yEU3764kwTHJFqZeGNbzAG850QRPGYymJ+hR042iWHWZ+I7z3Ecv7m5Sce0I2vske87ocJnodMpQarqqAuiy/66JBKRpckB8DJz8L3Qf15MyJhcqXd1l/GjD+iCiRLjU8dCJ99/6frhRANGy0pflplcviLjKpULATBQLz7G23V5U6DLXfQDkjUTuDEKlN7tIigkTJjbsSLmfWoALoQakfeCYDzPz8/peRwPx9i7rounp6f4+vUpxrGKuLxsqu+7aNtF3N3dxf32PsbI5S63nLHwBBwCkkEdyo8TsnGWIMHg3QkJ3/faeA0ddAhKKBeOzk7HSo8cS7bJ1R6vs1uO0AlABmMDJHpdzBAD1AysmAfj4UKmGBr6hKPweqBDZn5cWkbOnr+Pdi4TGh+KYNDhUueHDx+SLuBcXalijfhO2QddOlv+bSYK+6QNicSfz72+vqZTnmh9ipgIgru7u3RPznP/8OFDeh56yWfK9gvWyDZ/f38/c3rolQOREwPLAH0AZJnZfX19nQFqgIDZp2EYUrWVpArW2s+g/QCdBqR4nwTtQdybdSSJcLJMklxV1Tc90rSG4B+wcRKNiLwfwqdboQPYDsljqYfIj830bCpFf7ENH1Tgyg02Q5D/m7/5m1gul2lvT9d18fPPP6fEeLVaJ9bTCQVraRLKJ5rgT9Aft8dN4817plwtOx7nQdQtiwAaQDPPmxK03E5ngHA+n5L8y1hofTXTagDE/4mVMKcAceySP668GLAaFKCDHFJC7KUyxmEBu90uzudz3N7eJkIPgmK1WsXpfEp2yL1Zd3TPxBU+mSTFbTFudwH40w5nP2vChZhm0g1WGt0weWg9BhDxh70VjAH8QLwhbvMM7N9MvZNw/LoPnGH+b29vcTgcEibhHvyeueELqHqQyHBkLLJ1IoYuM2evlwkj/CvJM+PnniSI6BN+Azk/PT0lm4qIWRKKzZkwciteWQFzYgBYZR2J38gGeZZxCj+FvySJRJb4ap716dOn1NLPmmGXy+Uyzl0X4zAnag3GvV60QxErsk/IySP+3AmA/b59Gj4GPwY2nWLVe9ze3CZ9whehb+gM4zY5ip8eNC/7Hnfy8PuIfGCQcRGx2cmLEzAIavtM7IjP4BN/7/pDx9vC/uG4qqpKG01h2ghUtCphGATL8hhMZ5UIimCGcrml5P39PYEdHDOGSFJilrlt21S14PlmVe/u7mZMGv9nQ5oF3DTTy4L6fupXxPh2u10C64+Pj5c2gunIw8lImgvLNrFtTbNMgALWnHFz4UAAZYAB5ozxuUTvAEdgtBGjnMwfBbQiwkYBRjA+398MDEfiOlFwUHQCYCOFDYiI1KJTBmhXbwgwGBIGRrsKgArn7P55Jxw8A1k4USDRcPWlZILZi4D80T/sgqqKwSEyKQMROoM8zNCYPSUhcIA2eER3DP7QFa9vBk7n1OsNADYAOJ1O6YVXBOaqquLDhw8zgF7Xub0C22Vs5ZoZMHNh35SnCcSMs67r1HqATjE+gg3+ZbFYpJZNvksgLisS2J0dNT7ArW2sJ2tGy57ZTJID67vZ8+VyOmIXu2NM+CXuhw9jPARDJ2/4YdhpjiWl+kJF6PHxcXZCC5fXs/QdBnOAQldu+I6Jiaqq4m/+5m8SWLeMnHxP85iO053mvxIA403RTaxWk6+DST+fu1guqUAPcTxStV5FRBWLRRsvL7ukS03TznxEXdcpieMQDVc23S7gxH46GZAXSZ5SyyMnAnF/Pt+2uQLOn2luOVkyAPweuCZxx4/hg7B/JwFOYFg77J3KI4Dy8fExsbBdN+29AnxXVRWL5SIG+QfWG5sxqUWlhf/vdrto2zbtjcCvfvnyJTGfXdcl/+X45viBztuvYdvIB90i4YfItF9HJgb42KJ9IOQgY8TGWQfWiOdjx3d3d7NTET0+9J/nMzZsyQkbFQXeR8LcifPgDtt7WU0nOcm6n0/a5Pk+Qta2ib/DR+OXHSvQGSpEkBCHwyE9xwQy+3KIfSQwxGLk4+/gy2lfJwFjzbxnAoKTt4gjU9rT0K9aNhERMfR9vB+PsdGhLG4/w4ZJ+D3GkvByNdKx7fb2NrXnElvw0SYcU6xfrZNfKOO0YxFrCTHKPfDRrh4xHl73QJKGXYBzwAskciYCnYSBdbAJ9NdkirH7711/KNEohUywioh0TjYD4Gc4KMApgjXThsM1+2SmEePF4ChXHQ6HpGwohQECzoI/CJZ7kSgQ4HEcbtGg5Mc8GSuA30yuDXQKJIuZc53Y6U2aK/fFKDF22gpwPoAKKwFyQiEAa+7tBmjzh8/jlNzHaWYCZaa8ixzNjCMH1tPsBIrO+e4RuapgxtcKzMZsxu8NljhZf5cAiM65RMjas8YkqyQZpT6N45iYEsuJJMvBx/sQeD5zcCnT1Qra/GALDMgdCNExHIjLtsjTbIITcgIaAMosG9+LiGSDBB2vl1sjkIuTf/SfdQAw2Y5ZG9aLMUXMT0xiDsgTZpSLsRvoYGcfPnxIvsEJBKSH1wy7RrasL0ABeWN/zHUcx3RSFTqOLqEnBjr4qaqqvkl2nJRE5OMxS+BJMCWQOlFG7/FltkFO8TIxgN4gA5gyjx9boP3FCQWX9QzZwlaSxAEuPn36lCoXHFvqZyEvs5cACa+RNwnf3t4mVvPm5iZ2u91Fp7p4f4/0/YjptCReWArQxqc5uLrdkP9nEmF+AAZAi6SOsb++vqYTlBaLKdHc7/cpFmE7tMMxnufn5xnBwBixW/ydj6CmbQkdgFEHaDq52263ybe9vk5vY398fIyIXLEzYTH5rLxR3VU3n5TFmgCA1ut1bDabdPQ64AcbYp199KcPb0H2gCz0j43Jth/itm3a7LUxhtcUopO2GbcL4VfQYypB+FOeY8IE4G78AgbAV5ukY86WNbEVfePf2OL9/X2SAevMszlxDN0oT6w06Ht6eprFJ/SHz3Ofw+GQDvdBlhxEEDEdkkGcdgXQ/zbhYtICYhjG/3uVF/QeG8cPNM28HRSZlp0KJN+sF63T/H68yKbr5/s/yiqCbQj/72QVgJ1tJu/9YW5gK7d6cj8IrIjLBvaLnJGfW8icxOD3iEvo2WKxSMQJ5DC+2FVR+1tiuTGhsSR2X64p64adWof/6olG2WdH36U3ZxmIshAEAvpt3erz5z//ORnM6XRK5V4vCIBzuZzOU2fjGQpmUG0hsYeEyonBNg7q7e0tOQYDbhsvQYpFwkBRzojJudDbaEMzUMB4DJSdWY/jOGPK7ewwLjtHO1UzTx8/fozlchnPz8/J0UbkDUoG0e6lZ658hjH6uzzX5dSI+THCThQNiOu6Ti9hMpvgCpe/R7sAzE3f9wmUYkCseUTMDNVtMv49Dt1GhgzMMn+PDWMtCbgu/+JYnEAiN9bVbKdZVwAclStAJnbEyUtuX/OGTpIKKn44mcViOt3JZEDXTW2LBG32wCB3klyOf/WJYU4OkLMDLM7UpVfkBEAhkOPksWcfAUxSxLjxIchzGIbZSUJ8xpUHt4K499m2wjNgy9Dh19fXb/wLzCs+ip+5IsD4zGC6SsW4zCaaGcInmSWyvbL2TpIhRaiMAKAjIsmZtcdvuprDPdF79NftpZANTn7MVjMX2g/cX26ZAEo8dvs+ZIGNe9PwOI6pggyA7rqcGGIvLy8vad0ico+0bdfBeLfbzd5276BJvImYH2DidcCusQf8FK0ffA5g41YGkkoqJMMwpKoAyRVyZd8WiY9bm9ApnkdHATZDnEJvAX3o6Wq9iuryPS4qSk3TxH6/T0lSSSqRFKGfjBs/hN7zN5f1FV/rRIoE1CcKoXsmeRgjuoP/apom7eckSeGzJBQmgAy48PXonvWdPTPo/Ha7nW0s5zveT+Q9UugOuoD+Ig/2FvJ8wDb+ylUYt+8xxvP5nKoOpQz4AzAdhiHu7+/j06dPqaoCdmGuyAUSCLzCcfcRuUoK4WfbcAUlIhMf6A06T/wlXpCwQuawpui5kwpX9Zqmif5iy8gdEvZ0OkWlOG4wDSEekXECcyVGl1jDfgf/RCsV9oCvNQ5kHp1a97APEvvSZkweO1bxf36PTJE7Ns8f7AufRgx3/OGeZfsuvtOkq/3h710/nGi41WcYphKNBYfw9/t9+jdHS242m9nmRoOx3W6XXsaFwqAkJBoIiX+jrDhos4ZmyQnEMDAwPAQ/96wxBzsxBM93WFTG5oVlEWEmUSIWh8tKggK8vLyksjaJkB0JxuWXYOHweJ7ZEjO7zIlgDjjgskIlIxAQQ74Eecua+/JcK65BKvMlyDEH7o+8vFHOpTkcDwwCsuV5ZhhYJ/6NQ2HOBEwcC4kROoVjNwOOQwIcGGiy5ozRTBdBAcfFHNgjQHJO+xVr4AQE4GtARqsNeyaYAyVkt64YsLHWvBAK8Ig8CYxt28af//zn+OWXX2bBiWfb8eHEDbK9fi7LIzMnTZyEMwxDereFk13sHn1Erjg5/kamMMsAGfTZLU/oJHKhmob9OTkzwG6aJu3LMhmBnjpRRN9cYUEHzN7CzDpw8R0IHNsQ9mdGFFDCGAny6FNEJKabMZokcSJYJjlOjEyAmIBBlj52mfsCpLATtz6yfiWra2bU5AprNwHerGMOwvgd9MStCxBEyGUY8gsMzUBiD/gD5kcVzYnk+XxObGxEJF1GTl3XzRIg98EzFpMErAvzioi0qZNkCaICP7BYLBJYsl7e39/H6+trvLy8JJ35+vVrqjKTYLbLfBwozyUGPz4+zmIW3wPY4MNYR6+7KxyAHyqJxCZXvgy22DvGGvtdLrZdk21+qSe2QsxiLdDpiEgtcdibwTw6R4xkrZmLwTNVA3wg+sdcIPu4H61HjG2xWMTj4+PMvyHniJjZTESko8iZi9ubeKkecaCcG0k4Y+cPn7ctmgXfbDZprewDAPsma00MMXcfXALuYo4klSbkIMwgnhgXb6unnd5VFcYAjrF9+f68PJafGyw7mUFv3FHh+WErfMaJlP2M5XE+n+PUH2PRtrNECT1wzOI7yIfYap9n/2Y7Qvb+P/fyWFhr5mpSDj/Cz8p1Rud+5PpDm8ENmgH5OF0Wi0FR9ibTxugw/oj8htyIiIeHh1mgY7FZCIAV7A6K47YPgiWCY7EpC9ohAE7ooyvbWzgmr2RNcWoR85e3cbKEqxbOZEkkbESABTbqMX4ABif/OKnxKQfuFWZ83McyINgja+aA8vFZQDQO3YCBnxnImN3GSAEPGLJZXIwIo3TQYX2sY+gO9yb4mfEx24DDdcJopwC4JjiQbOIMCR44fLO+GLOZKAInsrMhOwksW+N4rgMlz3LvOA6WZ/AZA+evX7+mMf/222/xyy+/RETei+A2LdbObAl7m5DN+/t76rtHj2HQ0DP3LkfkgOi5u9/WQR72zuQBjKPbsMyWuhUOdgsHiW5RHQMMe37oLUfs+u242Bzldldd3DLGuBwUWENk4E2c3m8BQLQtwdaRZLLuAF6YNp5BsmUfQCLJXB0wHUDcymASwSVxKtMmFkjgLVvrFTLxS+bcEoZekOQQCNFP/kYmtiN8pquntk+SQuuJyRtAFf7DLQpew4iYnSSDLhKv9vt9utfHjx+DzfOMg3nAIJvVBcChZ26rcdsP4ybu+SAMdJJ1sH8lcTObjn8BsHKaGvoC2Ou6LlVQ3E5p/+pEj71wJt6cBDumMw4n7OiQN/QbP5g8ZL1MZN7f3yfm3aAPu2nbNvWb829IRjO5zI8xUh1lnXyKkiszkBTI3sQLa8JLSauqSraNTaHLdGiYfDSBCOE0DEP88z//c2oTpR0cTPC3f/u38eXLl0RcEdOIEdYpEwT2l/yOMbnihg1je9/rvsAP+GRG9IU5Mh+ejW4Z5PIsxovciResr/ddooeu3KYkqJ53iOBnkIFfw8D3TOpYZyC3jdmwQ9u+K3JOcJ1UIe/j6Rx1ld/nYwBfYhDsHPxtYsv4xGsGDsUvIHfrHM/ycb1O2u0HnNTw++9VSf7S9cOJBsyqJ49yNU2TwLJbo4ZhSLv5CaCAfb4H4KvrOp2DzWddbo+YHMh2u03Gy6I4AySwkDiYPUVBnG3SB0j270AcEbNWDgN6lIRNTAANM1cucxmMOdiaDXeLkBl0FM/KyH3f399TyxkBBjnwGXoxYa0xWgIPDtSnSqBgGDlGU7LIzNnB3smUN7x+jx1FDty7rHgQaPhj4Elw4iLQuB0Lh+TyM7/7b2XyDtqsg0uapdEhs7KFij84SFeA+F7JZDN3O1LLHHnBTP30009xOBzi/f09fv7559lbtz1H2BKeC7ilfdBBGn0yQ+3AxXqZmY6I1B5phseyqqoqVQQISl03vRGexIZEwjZHLysbXQEX6IuDOQQBoAY7JXi5GoF9wuSx5sjLRAJr7GQcUGQboCff/gn/6cQJcsIJKICXwIWeGBDjd3m+Ayj3wsZMBrDGDlIEVUAQcuAyaDdbhx2ULByJAuw4/hRfjM4gFzO7bsPER2M3gGJXb8Yxkn3gM5hD3+e9ZZYVVXk+CxBizOig22nwzc/Pz9+0TGS7zNUcbMH6bRaQ+fvABVou3ApFZdrED34M9pnYg78j+TUbPI5j2sSMbpBcn8/nuLm9jXh/m8kegGY/aNKE+0AmGIBjj7TTuNWLGLLZbFKFAhkbFPNzt8CSbPOyz4jM9JNwUd3Bxp14oY/EEGIbpA3rwT3v7+9T4lBW3co9Lqwv1aNhGNLBDJwuRkszNkdyA+kEQ8/7NCwT/MTNzU1st9tk14+Pj7OXIFtfI3KC6ljAwSXEtfP5nPwVPpr5MF/IONYG/XIcLhNF/u9XErCu6CXJEb6B8bHu+A6ITZNL5Wb8hDnHMcZu/qJl/KTjUkR+Fwq6Y9+E/vm7Jr6Jg+gX8nNVrCRiWZfNZhNDn9uZsXnbOj6NWICumfzi/mAFP4MxYztONMB0rG1d1zMcyvqZIOQejveOpb93/XCiYVYd1h2HiHPCAZsdYKCUq2DWvSAwL1U1bZbjZIunp6eUsaNUMEwG3jjAspRn5+wgEJHBaNl75oTAc3F1ALDx/Pw8Y3ZgMux0CYbuXzfYBojhLCn/oizMabFYxMvLy6yXLiJmfaOcinI6nVLPpFlBzxsDxPAYM8rj8psVmjmh6MwPQ8BBd78g7wAAF2pJREFUuT3DRoAx87OImFWVWC8nEIzVmzjNwlP5wKB/+umnxOTxLNh6l9Vhq9ANB1acDAAkIlcF7ETsZHkOv+cdJRGRGGPmDyj2JjPK7AQBA1+ezRx5LowLzLbXyon1+XyOl5eXNF+3IRKc7dh3u13SLxJnABk6xDOwZSdyDpQGKOiB20Q4EtVOjYDF+gOO0DMz8gBGyx85WxepSFrfYc289uik2zbLZBRdB8Tij0xuAGZN0Lg1xolmRG4lQu/MQDsIkvgQIEv7IoA6eXXbImNkzQChTupoB6JHGt9uJrQM3KwFfsatMyRRZjHxIdiiWVXP0QwtNnA+z983NAHeYSYvqm/4dyciBFnsG79NjCF+GHy7ysVz9vtd+r31v6qmE5+wBScSpX8nBnF58+wkhzrGcf7iQaosJI3+N2ti2eIz0RnAcIz5wAX7ItaLdd1sNhHjvAUGksJx2T6uruuU+MPEV1VuZ0aPDGDwMcydz9INAHsekd8bYRCE/aKfxFXrl6tOX758SRU3NtibdARokkiez9Ppbn3fz1qen5+fY71epzeRc9IWJ3KZeHAF3aQbz0VveT5JPPqI/LEtx2NwGTLBdvC5rsw41rrSUcaP7/lT/m8fhf37ft7LaOLPxCo2UlYFGE/f94mwJs67qo5s6rqOEPmFTZzP5xiHIRaqlBgfOvlGL0wuYZtuRTPpCIGCnIk34zimKiCfOZ/PsWzz+pdg3jgEAgY7iMi4lBjCGiM7V5qRY6k/Jjr5HImefQdrzTyRK/d1QvR71x86dcpswH6/T87T7DjMOI4EozbTwuepbjBpStKAW5wwixaRWxswLozXi2sD4YQXBwDujWMl8NCP6xYIQDqVF4wIx0AAe3t7S0ffmhngHl3XpXPmYUDv7u7SYuFgvYiAABw5wRDZoaBuN3h4eJgxYxgon+GeZistF4wD1oDxoKA4HVebnBSwFjg2QCFMBr/DYRpQwYCYeeSZBHgnTawzp7+QGMIS4Mj4LOxJ2Y5BMC5PLWrbfFyzGZGIDBLMELvVhPuXbwJHXt87sciJGfdCDqy1GWQH6bZt49dff43tdpsCGeuJDnJ0M0kQAQ2954QQdC0iEtuKrA2QnTiM45hABfpusE1gcakWGa/X6/jy5UuSZ9d1s5OyAElOVB1EDfyoKACmys+Z2cG3eCM58wNwwLDh83DIVCbwO9gHLyjDP/Bz/Ar2CgDGTl0J4PlOxtERO30fy2n2HtvCd2B/6BG6ZLKBXnXuTYAxMWTwZZ9s8EkiAIhBP0ywsBaAUuRr4gVdY/0d+GBSu2468WkCE01E1BExRsT8eGJkQ2usdZJqC/4OcoJnYQNO9Jj7tP6LGMchbm/vLn5lOna37/3+qDGapo9hGKPr8n6Mvh/ifM4grmmmM/Y3m5uYjgIeo2naGZDAt7stFYBnP+n4iT80eYa9sz4GujD7x/dj9OdzNFUV0Q+Jnf/y9ltEXUUrxtetw6w7+1VoGfJBG/hIxo1M+75P70Zwws3xoejR+XyOu7u7pJen0ymx/cYXERH/9E//lJJd4gD3p/JF7z8JMsk38Ydq4HK5jH/6p3+Km5ubVD3Gt7Ee2+02/vSnPyXGHr3uuvyCRbeTm31frVbpZYEkc3zGusm48ENOHrhMouFr0Q8nxY5tJl1d3YSwdAxwWzO6aezTtm2slqvouj76boi6bqKK6aWadVVHVdXRtHX0wxj9MEa7WEbfdzFGFefu8o6wfogxqqjrJoYx4nTuYnGxwaZp4nQ+R3VJMJA/+mUCuKrziU34Qny3wbIrF8gaYplrtVrNXuhqAoXnjf0Q3fEUTVz8W3tJLPshTn2u2juB88tI8eXfaxUGLzEX4oUTNeNcYh0/Zz0hU7lMLKPr4HX0xAm8Y+nvXT+caDh7bpp87FpEBktOJhAe548zQZw8bQCAQRwVnyWZMIPMM5sm98M6uzeTCpjC4fh3ZkIQpNsGcoAY4uXlJTlTJ1YoBQ6EKk9VTeVSnts0TeoJx4Gz+BHxDcvO/c28GYChaMwJZ8OikwU/Pz/HMAzpaMOyKuN1Q/H4GUdEmoFhrmZPqqpKFRgHN5frGDtG6OoSzhJmn/XxXorFYpFePAbLjtM1wHIJEgDHKVc+htPzxhhh6ZF3RCTngp7gaFwBMJC1LnD5RBscuSsMODWDquSoxtwHy7/LjevYGt8lcY+IFKzRU07tgeWpqirJE4BLlY6AaMfsTbasqRNXbBYn7bYe+wkSAIIetkKCgIx5MWbTTC8xxJ8wZ0DCYpHfn0E7Bv6F3mXYSrdSuWxslt0sI34ARpNnb7fbBJ6wD9bXgQFdxYYfHh7SsajcC1ki54kl36d2CzNT+D3GB4Fg9ho5uQpoFg/ZYF+sMevJc1g/kwL2yU5wSpbUvoy44P5iZI+v4j5OIA1Y+J1t69ukZHoXxxSb3mdVdVdt8T/YuZNxV7/Za4A/5vt1PT+Fx2uMLq3XmwSwxzFXKksmFXs32bBardMzzRKb1LLOIou6rr9pL8O3uXXIiQfjHs6ndH/8/jT3JlYXG90f97PKT7tYRLPIwJLkHttiDMQ/V7u9bwZ9wEeDCxxnjRPwFYyXSkpVTR0QkH5t28a/+Tf/Jtkef/Oeq/P5HLvdLh3NS0Ltd/GY5aW9arlcpniOnkKyoL/4BTPd+GHe+2B/h5wiYra53n7BSbN/jy9A7iWxwloSQ7BlfGdEzAgJdIq1cZWCeGVsYEL1e3/33ZRgmwjpuz6qS1LTqvVvksG8HZfxk0xO/qJPCRjrw8VzsS3ue1JF0ZiSZ2Fv9i8mP+wHIyL5f/TWCUDXdTFckkY+Q7vY6gLeIZpIdlg75mAZ2HawNezLLYL4FRPDtkX7mtLfE1v5nZNjE8l8B32yT/5L1w8nGigwTMpisUhZFJkdx4rRl4egx3GcHRUIGDfIdgsAjoc3+wLuMAyqKZyeQRDEgX39+nVWujOws/GZzcQpk8GagQCIspAGwYzdm/vMQMBg8p3vtVw4ULnsyX2QIff2JvqIzOy7191A0eVFs/DuNUXu3A9l5Tk5cObNoN4IzXfaNm+KpZ0AIMYJSbRmYEjDkN/8bLbEpe6y5G2Gz+wVBu2+cECOGSSSJxgtjJ/NoGZofDKSWRzGBNjjYv3cTugkhCCGbEpmgLEQSFwutsNBh3geSSXsHs4Mpgz58XkCCVUT5ouuAgQZC0GQ+TMnmG+CLfLkPsyfNjInDNgyAAZ5U3my7NxiYufnhMFVBDPjJQtMokLwwdlbRpyCxhrgbwBsTjYZbwloGScnh7EnzCVq6wj2BTsLCHCS5zUBIDnBt5/AphkHbK5PObOP8NpBSpj4MVjmWcgOAIMN88d6wP2xe+aAreCzXRlm3Qji3M+VFI+RcTI27o3Ns0eAmOAjWb2/jrXmOFAYZe49DENiqPk/z8LP2ZZZX/QFUsWVcpJJ5OlkdzrIIIMM9O90OqU9eNjWYrFIL9Tj4kQ9xsO6R2SARlUHO1u1OYlkfSYZNzGMY9ok7lgHMGbc3Pvjx49RVVU60hq9/ud//udZnGDNV6tV2qeyXE7vxfjtt99mjDnJwefPn2O1WsXDw0Pc3t6m44AhHLzvhjWiAssYSTLQJZIDZEqCUlVVIhuIK+iNbQ68wjh9OAE2zOecrPit8YwbXed74zjO3lNmkpZ1xC7wudwfLMb4mSMVLie5rCH3QI/5P3+jv2AofM44jFMlo6pmPsbrzP2MV1ydII5lvFLN/BnxoST9TMKNl/sSF8B+tiWSK3cMoMu2X2IRxAT64cS4O5+jGjNOMLnKvI0h8R/eWA+uMAZydcoJhAlKcIFl6HiJ37dt2vfnpC+S/+Qe+D58o3HLX7r+UEWj3CxsRTUo8IkM+/0+tWRg6JwYQvB0GRDQAEAkgHrTHu0efM5lV7P7JDvsY6BKQBmWlhuCD/NC2Zkri0p2ykuj+L0TJbPTJGJ9nzc52bEBxBkDhor8DJDMSBJ0I3K2i0G6HMc9MRSX2A10GS+KynNJJgAlgFa/yMngnDUGPNOSgd7Q8/76+po+i1NnjrCwyNRJnHu+/YZQ5kDgN9BgndAlStafPn2aGV0JtgELdiwkGu5JJZCjo3ynDMwGIQYePMeXHQX/x84AF042vG7YD5/DITgB9tp5/T029B/dYi4EA7MswzD1e7NGyA/dcCul3wsyjtNG1YeHh+RjzPSQNDMnesKxIQIj60AQ5ohH6/Qw5BNMSIqs/6yZk1+eiS/DL5i1L4Ovk3XrK77SuoOPs78yc48PMMlCtdM+BJDiKgT246Bh1oqxcp/vBS30AiIJJstBiPsxXwMU5my7cpUQnXJSaQLD5X3G4pK9Yw8V5ZKlM+liv4l+u5pgBrHvpyo7B15wMpPBHWuEXJ2Awf4zT4NFZIP/so/ADvC/fJe4uVwukn+w3eJbTJ6RACCz3W43Y8IB+/iuiEhzPZ/PcbPZxLhczeIaY10spjeKQ24YDDHHup6Obscv4WOJb8ix7/t4enpKlW3uAxn54cOHiJjiG8kKwBh//K//9b9OzyVBhkBgLPZfgDhvNGbtnTCzJsRVbJjxG2wTC7APs83lkan4Ndse9sMeEKoz7FG1fEvCh2QXe2B98VVURPx5V9WMtUwEgRUgcbzWBpmOWTO/oA4ItwOfTqcYq3w4gn0N8SMlCWM+4GLyB21EjAlfcIqUwTcVfa62bWMQ8YSfcsWTdSSmuR0JX4JvQFetO2DI9/f3aKr5JnnubRwCWY8e2YeUZB1zsB4SJ40lmD+y9Jpan50wGPORCHNPWm2NXV01Ze6/d/1wooHiEMhxqAY1OEgGjCDcKoBBUrJkUmYfYUcAHbALgAUzA1QOYBUiIikPRvb58+cZMwarSMIB+DU7jFExJzb2ogwoHIxuKgv2eSMvCgHTgbGgeABMDB7FY27IvQTv3MfVD56FsgG2nNU66eDFPs76MRQfq8n6uozM8834IEc+h0Ok4sXV933aK+CeXdhqkk8ACGsAuxwR6cxx1rPM5Fkfv58FObOeHCHJXgD24BjcjOOYwB9rRLILiMAWXNrGUeHsmbcrZcgWPcOZk5Qy75JZQq9xgC6FmjkzwAEkYaNcdhpd18Uvv/wSu91ulmRUVZWSEm/WBRCiKwaUlLUPh0N69wDsIXobkfdbDcOQwBG2D3B0xcHOEvmh5/gPkg/WANnAAJqIIHCYBXeFAcaGZzNO2CgYULdQASyQBXpgAoNEizUjIPA7gAC6iK+wvTMes/PoBz7YbJx7v8uxWr/NTqIz+L+ynxf5OqC5xcWMKj7BYAWfhfw8d4NuTlcy03g+n9PeIlrwbAduF0O/DZogF3ywAT4Ff2OSB33HR7A2AEh0z9UWqqwGfciU2IbfNbnBPSBn5snKKZqmnpE9q9UqPn36lNh/nhPxbQKFPpLYtm0bzThGu2jT/9nnVld1bC5Mvb/LeDvZCn7b7Y/4S3SKCgtJX9u2sd/vY7lcfpP439/fp7WMiNRKyfyczOInAEP4CO5NDPSJY4zh/v4+kWnDMKR1cqufE3tsmxhDjIUU47PIwCSqK6D4FezIVQTvK4Ipd/cDeogPI2Hk8nHdJrOwTye16BlkH/J14shamcTAv7kFlLkwD2x86PPhGY7TXd/HMGbCGX3lXtiYMeVkz/OKCLjBlRTvMyXJWF4OQ8BOTExzeRwQW47ZTojsZ7GZFF+r/L4z1g8/BEYgmUafmBPxj3VyMmYZlkmqcQ64CHnwDC7W2nPCll3FYv1NMrjaSyz/vesPbQY38MEB8CCyfCcABjX+jjc1MUl6aunDi8inUBC4mqZJVQUMm+f4yD9KiDgJsyy//fZbuieZKeMyk8bzvdAotJ1DWc70BhoughhsOp+LyEkW4JH/Y2QusXtcZrCckTrQADwIYgQYTsagtY1ErWTQInIQhMll/8b9/X26N2Pk31++fElKiRMn6GIUblEoNxtjtGb7WGMYxd9++y3t/0FPaEOgB5a+fAwafQRwkvCigwYOOEo7BfSIJAU9xskRyEiwAC08HyPFKaBDbs2j+gf7SrAx403ybTbezAb6YdDM2gKekTXJGC2P3teCTiFXrzWMHwGZdkkc1c3NTdJZb5gDGGALdsbMg7YH5Mr90Uls28k1AI77o2tO5lh/7Iq5WS6ujgE8bD+Wn3XETp8xeazYitlWfg+IdXBgDH0/tToAttEL5gzxwnMYH/N1gpMC/zBvfwIMkbAhQ/wO93CC46oCv+OZDtZOKByg8AHYBKw2lSyCLc84HA6p9Ye5QA45oZjspZ+BRfQRO8Jvk3jg37qum71QloTfoJ0WpTJJG8cx7SVD7rvdLhFMJATEAcZALHHCgoyoQAB+Jz3tou9z3GBcHufNzU3y/1RGIOnO5/OMHKiqKpar/JLZiEwARJ2PdycxO52mE+m+fP0azaL9ppJZVVU6NMEviYTM+/Dhwyz20Zlwf3+fWqoAcOg+yR16jozv7u6Sb8Pne/O1GfmmadL93QqDvPHZxB4fbIEOW49J3iHt0C1ijhlj9NxthcY4TgSwTyorrsjMwfb8HWOu1pn4NYttEsxAmfmj7/gkSEPbYUm8oGPWR74/2WkXfZcBP/GMOXV9bldnXWxDPA/9NsmEbtG10rZtajs0drgMapYo4oNoaQW3WjauRCAj7o3tu5WT8RjgO3koKwFOXkxO+jvGY/aflrvJbicV9tvEBdYRXTPJBHHFGlnHTAAjk5K4/EvXDycaMCucDoOjZgFQZjJwhIfDI2gxyJIZZ/IR+RQTBIEw+Jv7WplgJHAQZtlxIl3XpaPmyHj3+/3saFAWGUVB0GWvOq0aZthQFBydwSGABoMzsOC+OClag0pFxvgJWAAx7mUmDLmTRBBgzaTxGbdcwZiUJToUHBAISFsul2m/BT2KHz9+jIh87j8tB+fzOe27ub29nZ0sNQxTfyJ9sAQIEgwMEnlzGhRGQvD2pi6fHESSEhGpFI0TA8Q5aWCNeS66/vb2NtsMbFCFsZqRRnbIzEkhgYTPAPKRF59F90lIcJgAY9grKgnM/+bmJr5+/ZrmA+hAp+q6jn/8x39MTNzxeIxPnz7N2C0ScWyPcrP3AFEldPWMsWF71lOcHoFssVik56Bz2C9Oz60O6CTJEPchMWBM6LyTEQgKxsP3WXfmyRzxScwJuzcbje1jgyRNXifmYPICP4ifYI1IOGHW0QGTHFQe6btG7maM0TtAC8ku44iImR8iECFrwJSvcRxTOwe2hi8yCMCu+b8BRMS3bK/JIAcwqotUDJzEubXEbb3f053St6PjyJPPmjl0Mu8KsMfI+pEEcj98tFvV8GfM3wy222UMarETVxmtu7y8lpPOsG0f7TkMQzooAV+fiJ26jmHoo71UvP7zf/7Psd1uU3vh33z8KcV45ju1vm6iH/NJh4fDIbXQst4QbtjThw8fkn2QFKFzLy8vs/jlkxFdyUCvbGMkAz5G2r9nbQy+nczg34lR2A5kIWDbnzXhiu7jV7BD1tOVAnyEsQHxjPiIvaJr+H4nougPvycOG4s5ETYINgD2z/E/BpOM1aSF781Y+J1JW/xwFRnjzEiIIR/IwfNK23PyhI2+v7+luOmkxX7aBBDPZI1Ksq/sGEDu+GHmhGy8xvg/d+fUdT2dOjVkcgo9Yl25jBuM29Bj5mGSkTl5XZ0slAmaKyPMD5suKzGOLybynOygLybMfu+qxh9NSa7X9bpe1+t6Xa/rdb2u1/W6XtfrB68f28lxva7X9bpe1+t6Xa/rdb2u1/W6Xn/guiYa1+t6Xa/rdb2u1/W6Xtfrel2vv/p1TTSu1/W6Xtfrel2v63W9rtf1ul5/9euaaFyv63W9rtf1ul7X63pdr+t1vf7q1zXRuF7X63pdr+t1va7X9bpe1+t6/dWva6Jxva7X9bpe1+t6Xa/rdb2u1/X6q1/XRON6Xa/rdb2u1/W6Xtfrel2v6/VXv66JxvW6Xtfrel2v63W9rtf1ul7X669+XRON63W9rtf1ul7X63pdr+t1va7XX/36/wFNSVUklE66SgAAAABJRU5ErkJggg==\n",
+ "text/plain": [
+ ""
+ ]
+ },
+ "metadata": {},
+ "output_type": "display_data"
+ }
+ ],
+ "source": [
+ "plt.figure(figsize=(10,10))\n",
+ "plt.imshow(image)\n",
+ "show_mask(masks, plt.gca())\n",
+ "show_points(input_point, input_label, plt.gca())\n",
+ "plt.axis('off')\n",
+ "plt.show() "
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "c93e2087",
+ "metadata": {},
+ "source": [
+ "To exclude the car and specify just the window, a background point (with label 0, here shown in red) can be supplied."
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 17,
+ "id": "9a196f68",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "input_point = np.array([[500, 375], [1125, 625]])\n",
+ "input_label = np.array([1, 0])\n",
+ "\n",
+ "mask_input = logits[np.argmax(scores), :, :] # Choose the model's best mask"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 18,
+ "id": "81a52282",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "masks, _, _ = predictor.predict(\n",
+ " point_coords=input_point,\n",
+ " point_labels=input_label,\n",
+ " mask_input=mask_input[None, :, :],\n",
+ " multimask_output=False,\n",
+ ")"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 19,
+ "id": "bfca709f",
+ "metadata": {},
+ "outputs": [
+ {
+ "data": {
+ "image/png": "iVBORw0KGgoAAAANSUhEUgAAAxoAAAIYCAYAAADq/5rtAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjcuMSwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/bCgiHAAAACXBIWXMAAA9hAAAPYQGoP6dpAAEAAElEQVR4nOz9Wa8lS3agiX3LzH3vM0TEjTtn5s2RZCaZySRZTM5ksYpFVrO7utEPhW61BAgQ9Av0LkAQBEiAfoMeBDQg6UmAHlutQqO7WqqBYzLngTnnzTsPMZxpb3c3W3pYZubmtn2fiGxRECCEXcQ95+ztbsOyZWtey0RVlWftWXvWnrVn7Vl71p61Z+1Ze9aetX/A5v5/PYFn7Vl71p61Z+1Ze9aetWftWXvW/v+vPVM0nrVn7Vl71p61Z+1Ze9aetWftWfsHb88UjWftWXvWnrVn7Vl71p61Z+1Ze9b+wdszReNZe9aetWftWXvWnrVn7Vl71p61f/D2TNF41p61Z+1Ze9aetWftWXvWnrVn7R+8PVM0nrVn7Vl71p61Z+1Ze9aetWftWfsHb88UjWftWXvWnrVn7Vl71p61Z+1Ze9b+wdszReNZe9aetWftWXvWnrVn7Vl71p61f/DWPe2Df/zrv8U//k//Q57/5GtohB4PCMGBE8E701lijIQQUFU636EKqkqMkRgjAM45RIRxHAHYbreEEAB7Nn+f/xaR0kf+3TmH9x6AcRzL33n8GGPpR0QYw8QUAiEE+r4H4ObmBhFhs9kwDAMAfd/jvWeaJhs/Wp/DMDCOIyLCNE3cuXOHzWbDOI5M08SjR484Pz+n6zpCnBCJeO8ZhoHr62tEBO893jmmYSww8t6jqmw2G/bTnhe2p/zp7/0+2+dOie++z+N/+1VOxoD2sOn7AodpmnDOFbi2MOq6jhhjgV+GZb6fse97XNqzPBfn3OJnvRfOOXtehKix9O2cK/COMeKQAtvT09MFDuXx6nnUc8t7Vq/DpX91y2vqVbjZCBsVXnnto3z1v/pv2Sic3D2j7zt7BhCBPRNDp9z/+Kv82h/+Ju8/+ADf9Ui3xZ+eEjc9QQSiw0/wzje/z/tf+3vujkJA2XvFCYgqKsq0Ee79wmt88Y9+mwdXjxBRxHVEBKRDup6I49pv+MQ/+m1OT+4SgjKpsh93fPDoQ7ZOeO7Oc8j5KRIDlz/6Ke///bc4lQkEJhdRHxGNaPBcxA2v/PIX+fgvfIYoavPF4YPSB8ePvvVdpofv8Zf/x/8zdx9c8VhvCDFyGhyh8+n86cF5xAlB7fycbDdsNz2qIK7DO0cMA75zjPdO+Cf/8/+MHz14mzMVTtUTthv8dgPiiFOEMfLWT37GxcUFExHN5x0BAe8cfiP8wuc+g4gQI+A6EMMtVdApgio7p5zdu8uP/vVfcf2X3+E0RG5cYBLYug6GCbzj2iu/8Z//OeHOhq7rcJ0nAiEGphAYh4GwG7h68z1++O++zP3JQ4hMoriuQ3DsdjumKRCCEkJgmibGIZTfY7TzfP/+fU5OtogTMlpmGpNxs235u6hKrM5j/fyEsJsmXn/9dbbbLZvNppy5TdfjgN4Ld+/ewSOggRgDXmDsPS/88qd57hc/gbt7Ttdv8M7juo6N75EYCSGye/8hf/df/bfc34ETZecVnLANSiAyvXTOH/zn/wk3CFrR4kLXNSLDxLt/+Q3e/cb3UYHJCz6CD5GI4dfo4N4nP8of/sv/mHfiNRFhqx5X0agQArubG77+f//XnL53TR+UoIGhs/N6t98wjIHr/Vj4RNd1MyxZ0qeaBoYQFvOueQXOs/MTn/v938C/cE5/5w6bzRm+2yC9IFOk73vUOWSY+Jv/+r9j9+b7uADee8ZOkLunqBPCwyvisOPzf/glvvTHf8B7+0uuo/EIr4LHpxMQiVPg+uqa//q/+lc8enDFT99+h5tpZL8bmMaJj33kJU5PO37/93+LP/uzf8bV1SUhBLz3FZ1XxikSI/z0xz/hX/0//hvCOEGEje+5Nygvb895+ewu027PTiLx3il/8B/9KV/8g99DOm/4p9CrsHt4wY+++R2+/Zdf5mevv852s2UYB0h7pKo4ZMGP81xq3M3fZ7qe97im+cda7mON7+c5qCocOWP2uxQ+mt9ZO5c1P8zzzd/VfDJqXJzT9kznd+v+7TkBdYvPFvi6st6Mt/U8WtjU/dRrqXn+wTO4RR817637XMhZGK81OhVtzhVM1t7N74dKHqjnuTZubu28630JVPvRPFfvVZY9VA2+IKtwq3Eiv5/7zXJjPY81WOf9Kv07QSr608Km5rM1jukK35hx0+NkKX/ZeEqUiETFBQcIsYv80q9+js9+4bOM4rja3/Dhwwc8fO8D3vr+jxk/eMzzJ+dc7fY82l1zHUfGGNg6z3ObU877LZ757C7gZaBcxZn2vPwfvv/XB3vbtqdWNMAE+qgRjRAVFCHiEFFCQ2BUlf2wp/P9AqAt8tSbvHbI6k3Lm51/AoUYt60mBOM4Mkwju/2+COF937PZbNjtdqgq42gMTVW5f/8+AM55gsI0TUUpyExyHMcyblYisjLiO4f3JOFlous69vt9UnBs/K7rinKVBX1VY6YYXU1zcCgTzvkFIfLel/XVykaGS1aKZkSdYVkz7JZY1kpGfcjKnogUBMyfZYFIVZmGcYGEbf9P024jTgslJR2SGCLTfm8w3Q8zEczPhwAScU744O13ePToETc3N5ydebou7a9zRO9ABUEZdSIITBrBGQGWGBEURYkh8t6bb3F9cUnUgPcOjZEpanre2ZMu0jlhd3ON4hlC4GZ/xc31FT98/XW+8IUvcv/eGV4cJ2dbU2I04oAQIkqwcdWhIXB+dorDcEWEQmDHcWScTEHZ9BuiXhiEJAtcRqzqNu8rKAGi4iZH7zsQ0BhMgfIeojJe7/jpd76PvHDG4NK5jAE/TeA8MVgf/ekJ2zDhxpGYcFvEhteoTGPg4cOHPHfvPlNUJNr7iBCiwhQRhZGJ8/NzbvZ7xDs0RJJcYeceCCiTRB48fszp9nkUwSlJIYYYIE6KIkjfE50nIvafGONwsmRmrZDTKut2APLPn7/VTDLvX1wRfAr+KyCaBBnAYUKBc6A27w8++IDuoy9yen5CmAac80gMRB/x4ogxEDoh9I4YBR2nsv5JI+qFi5trHl1cEPoeSXhTn90hTHiFx+OOwZnSTVQkgERFHKZqiPD+B+/z6NFD9KxLSp8SKxiGZPTxJ1smf02nAlFAIyrGX0KiazUNKk1ZKBP1HpVHGvplgFbw8JOf/IQX/cc5ccImCq6b6ILHI6gIURQJkeiFYIiGqBKi4mLEdT04IQr8+Cc/5hd+4ws82l8Re1cUDSeZL0U0Rm5ubsygJba2EIJhUoxkAenrX/86n//8r7DdbtPaQHWa6bEKMSqPH1+QsBrnHeKESSJTB/sOONvwy1/8PL/zZ/+E05efBwQJ4MURhpGf/vDHfP0v/5Yffffv0esBorK7uZn5qzhU40KgbIXrmicfU7Bbvr72TP6+3een4Rs1D2z7q/FgoUhUQnH97FKgPaSV9XyyYnPb2mq5RoUilIYQDhSdVqZp198KeLcpcO2Mnpr/ylLuYkXAPBhrRajPRplW+WxlwDUlYJ7K4dqfpq3tdf3dGizqfW/HWsP3uckCB1rFr4VPMeSKzAJes8Zj+J8VXyem3MSoeN/hEDREMzhd3rB7dEncj/hotHgaRqZxYtzvmeJE0Mgkkeg2uI0DZWGYKTi5Atd2Xk/C/7r9XIrGzc2NCcFO0ABZh6wJRCZUZgVUAvMiskCe38nImCddP1czj7xxXdctiF29wXkT20OYNd4s8APldxHh3r17BdBd1zFNU2GC261pl13X4b0nhMAwDOX3rIBki9k0TUUZyR6FVlA3HJuRN8+l73t2496eT0Jc522+gqDRLOm5v/qw1gTzNqtI3p98GGpLVK2t19p7vae53fZ7JqTtAfx5Wmt5qltZd/qfJvhMo3mJukxg1IRVj1nluiQ4TePEsNsBhhthv7f1e88YJojO3js9YZDI5ASnikZwMSkZTstBHG5uCF5tFPGYPB9QcUSUoHuuLx7z/Iuv8uGDCx5eXrEfbxCE559/kUkVQekFrvY3qAYCSpgiAbMqERWfFCad9kgSMERnguA6j+886hynp6dM+ZxqJJPtliTkfQ0aESIiZgfrNFvhAhoVfGdwDpF4saO7d8q1jMSTE1wIiIDzWuD+3CsvsR9HwjCiCk5mq4+GYIJkgJubvTFf50jaAYqg0wSJdlw+fkyMBgmvcWFlUQcjkdEL4j0xKTFOFefMmjyOIzFGduOI225wp1uGYc8mE3YnOJetxgGY8a7+V8ZMZ/gYft7WRMzz21qrVJVQbc6hcF0p/hpNsDf7KM47phjY9D2u6wx3wkRXlHHDfRVwZye89OmP8+jvf8qZlyTFmqIxAHdfepn9YMYYZDYeFLrsHPtp5NVf/DQfvvEO7magi7Z1AoaPAkGU07t3GMeJ8XoC74m+X1j3spfo5U98jLfee4RMEx1qHkOV4rE4xsjELfekVc7WlMV6LSFG9tOIIxLCSOeEKUQ26lAgONBx4mOf/QzffPtdNmrKvaoxegUCkRFTrC+uLhnCANGjzhQNEUdU84Siiu86Nicn3NxMCRc80gn73R6S8qWqXF1dVd4Mv4BBiAbke8/do/OecYqJrwk7GbmUyC/9wif5/T/6I177hU8xdYJuOvoJ4hR486ev880vf4U3f/hjHr7zPjLOkQRZuBTncCIE++KogHibQejY2VhTBp/UROSAdi37OBRa6/6PCbql7/adI6PVuLW2lrYtPD1QPBotXWnHOAa3NeWk/TstoKzhSXOs15INc+S56fLdtb1bPF/NY8040K5tMXb9bLJlxgbOT8QVbQyRR2TL+vta6WwVjnrdNQ4VPHJihhWdIzvatbWwk0rJWFt/S8fy906SESatEQdhmgjDyHR9Qxgjj958h93lJeP1NW4M9DjCODINA14cG9fhNdI78y7HaEaotf1aUzTWzsrT8r+nVjREkiXcSTai4Z0nCJXVdHYrFSVCZ8G//l51DhvKz9cCcB5zjdnnvtYQuRaO898xmivUJ4Ug/8sKRh1udHJygoikcK4JjW5hYXDOsdlsUDUhJoc4bLfbMs9xGthsPOM4FoUmP5cZysnJycLrkEO3zMolwCy0mzCo+Gqd+WdLQPM7dShard3XikXN8GttPCtObRhTgXecXalt6MIUpsIkWyJYa+1rylDdV/nbHijrq8dMpxxQ+s0G1WhCgEamKQnNiUmZO1zYnp6Y5e5kYwJjxssYcL5DxSyad15+AblzwnQx0o0RMu46UCeMOvHSyx8lxAjevCriTEBTo3goilP44I2fcX56Ttc5zu+c8cr5y4Qw8cGHH9D1HZ0D2Q9cvP8ecRwZnZpSIxCTO96Lo3OOh++9y0sf/RhIh0Uvmo/FeY/fbhgvjMnEGM3ync8NS8K1IKRYKI14x+AdO+/ozKWCYB7MyTsmiXYuhgBbxz4EtuKQZCUOCr7rGSKc373LdH1D3/cmQMUcWANhCoh4QoiICp5M2AR14FzyUoWJd999l904mDJWECZZxYGpg/sffYXTO+fEdJaceEOLimG6riNu4ROf+yXe+ep3CbsJjSYEZgXecD2dqcpa1Qqpyu3K9pqwU2C+wlA0CbFrfVl/SZBPCKsy4/0+BPo7Z5w/d5eTO2dMTuicp+861HVIEoyjbTKf+9Kv8zM63vvuD/CTKeGDQDjpePVTH0eFIrjWtEBEEI3IyZbu1Rf41T/6Hb7z7/4GvdjZs6oWzueFHYFPfeoT7McB128WdGxhIPGeFz/+Mboh8ubffQvZV0qCQEi0sg6pbI0qa/jcfgcz7RtDQE48zz1/n/O7d5CuM2+ZE/NEppCTiDJK5P5HX+ELv/ObfPfffplOTAES74gOggjRC698/GNcXF8hW8NQTWc3xJAsjybAu87zhV/9Vf79v/trEHDeEYLRut1ux+nZHV588SWc8wzDiPcR54yOz7TYBLDnnnuOX/+N3+CrX/5KodEvvfIy/+Jf/Mf81pd+i03XmQfJgQTYPbrgG1/+Cn/7F3/FzcPHuDHQTRGnFv6sCYa1USkrxa2QW8/nmDJ4TABZOxstvrfnAw4Fn7aPVhhseePavNoxythRiyLbjlPLH62iZR7CFet8otFr7z/JWLGm1NQKdK285+ecc4R42MdijStw1ywHkOmRzvRmZQ41TWthv+blasdu92KBY7IMTT3W8noNBochVscE9xqva8NOqzAdg3/mKzGNWSsZa+dl0SeH56CMoevf5fddMhqZlVUZd3u++tdfJu4Dl1eXlh4wBVxUNl0PRM7OPCdi3n8VMww5mwQhhoVCXObPfOaOKbdPwt26/VwejYLEISYLfiDokvHWCoQqjMPAZrMpzKo+YG0cZxb884Kylpj7zM/XFm9VLWFIIrKI563zNU5OTorwXBOi7Jnw3nNycrJQPlrkzN6HaZoOciTA8h6sT2Ecp7JuFvChjJvnsd+bJ0N9ekBMMN50phBpGC1WviIqtWJQ91/Ptz00ay7C+qDmvaiJRP1OEfxdDj1pLCoAOj+7No9aqThG6FsCXudoHDAFNeukKcGOOAVUwYtZc4MqOGGIgeg7PvGpT3B6fgZdshY6D96B87jOg3r2IXDy3B0+/6Xf4Lv/+i+LshPCBOKYnNDfPee1X/gUru8sdtI7swKLQ1wH3uMwy+flB+/zzYtLPvKZz6L9lt1+x7br6V3HyfYEr8rNgw+5+fADTpxnchbOgzhc7yw8ZYKNd7z3xuv47Smf/OyvIC6J6En5D8FyEuqW8U1wizjbJdzBIwTXEe/e4e5HP8rFB+9zshf6aUJUuCbysS98jv7eHVzvONt6tPd00eG6Dro+ES9wAbb3nuPm8oIwTkQNBFWGOBFC5LVPfIztdmvn0XeIeFQMftGZN0KYCL1jFOVzX/g83/vxe0z7sQhxMSq+75Btx2c+/zm2p6fEfL6TpQkBcZ7oJkQDYz9y5xOvIY92vPOt79NhjCLnMGgS3m9jLrMF7DiRbYXbct44NJDMjHV+95CAz2piVLNCadY+th0vf+o1/Ev32Zye0G96vO/Mi+E8HQ7vHHsNTCgqkU/+6i/zxve+zynmhRhd5PO//Y/oXnqObrNhu92aR6ii1WDnbCKiZ557n/gIn/7lz/LDv/oqLhoOTSjXYeLTv/F5nv/4R5BtT7/dIs6TQ7HyerMCGk+Vj33+F7l84x0uf/qWjaMWPpiZeP1egdcThKd2/1QNb7TvePGjr3L/lZc5ef4+nGzB9Xjf4zpHH1Ju4cYTUNhPfOaXP8eHP3qT9372Fq7vEuwdQwx89FMf5/yF59icnCC9x236otShhociat6jCJ/69Kd49OiK1996m5D3O9HC7XbLF77wBTNKiS/fZR7ikifFOcc0THzxV7/I2faUL//Nl/mjP/oj/uRP/5S7d+8i5p+0vX18zU9+8EO++9Wv88Nvf5ewH9ioSwYYwXlJhhETlI3WJnjKrIC056AV4o4p3mv7sPb7be+s7e3y2Sd9f3hOW6PXgfDUvFMb3dp+yjmvxqrDUepn1+DUwm+NL9fP14bbWk7K77ZrPqZ01Z+JJFytvmvb2mcZJ9vv2pyHY/uzJhvArNy0OFbPud2zvAftfNdgW8+tlVfq947tzRo8juF5DSs4zHdZ7HH13LJZblVCMqYQ6Jygw8R4eU3YB3xQJEKHM8KuCt7RpYBvn1hGJCZDKPZzBTdqQB7jc+1ZuK09taKhySsQQiCqMowD3nd2HnVp2c5hUarBkjMr5cHWZkCurVyq5iHo+35xgNbcs1k5qIFQC975+6ykbDYbfNcV4pHHrEOpvPcljyLPxca2d/LntZIAsN/vOTk5Kc+M48hmu0V1ouu25fn8k6R8hRDYbCx5dRgGpjARJ4XtKS4R/Lx+Jw7nPSFMZZ21Bp3h1XqIMuz2VW4KLBG5VfxaJTA/X8O5VghrIlArXTWcb2MoLRHJ49WEpyUy87Omd5f99J3F94sxWVAikWEKhK3n5U98jOc//hFib96Hvt8y4SzhTUx5wjm63jOOE3dfeoGTe3fQB5c2pncEp+yJ/OpvfJHu/JSpSwlcLiUyg4W+OUfE4aJy4oWH11dMYWAIkf0wcPL8izhxnJ+dEW5ueP+nP6WbJvNaicdQTwi+RyV5OOLESed446c/4SOf/AybzR3LFxpGXH9qSk+M5PDGBSEQEBwQF3AGo0m9dDzynrNPvsYf/s/+p/z1v/pXPPzGt/AXN8gkPP+pj/OLf/TbPHj0gA2wVSFGh8djbh4LQSohfgTzsMTASy9/lAcffMD9l17k+vqa5154gWHcJ7j5haIhKQTLRc/WeaJObE9POLl7znRxkwijKZ9TDJw99zybu+cEBZdyL8BCxmJUxnFCp8AkkX2MoIHRMlKQkHJuRC08KyrgKi/njKM13poH97jV6ZilJ9OnNUayppwXemkrKkUYonWGiHD6/HO8/KmP89gFS1CeJnxI1lVvYUjqHCqKelO4Lx5/yBADJ9Gg1Z+e8MqnPsG1DwyjxfQ6vxJ7HAKKckNgHyYe7q9RL0SXCkQI+DunfPYffZHhpCOIKcFR5yIRrQFnEEU7YUyeQokRjZYYnsOnao9GEXQr5WtNYFzbE1U4f+l5PvG5X+TSWd5eH3scSpgGNDhO/AYX1IxozqA/qK03Cz+W+CpED5//9V/D3z+1ELzEY7SbrY5m4I4lzykivPqRV2camyyLCPzhH/4hr732sZTXOHuSYI4QyDDpfU/cRH7ti7/GP/3jf8prH/+4zSma5z7uR95//U1+8JVv8L1vfIvHl49xIdBH89k4J0wOohMkSZgOEt0sSEkdt9/m+/1/s7W4t/ZdNdGFXrAqON0yTpuUbZ7pdUWnnc9SrmHxzPIMHwrFa4rLmvB6oGSz5JFtAvb83Myz2/W2Y2Zc1PyfEdkSolzPRVUXuImu07waBmuyQLvOek0xhSk/SQFtv2u/vW28YwpM244px9aR/ahx6JhiN3ey/HOxH8f1ZVMSMlycQ4j03tORPMYh4pIMErGUNzC+iAoOTYqGI2KGnGNK09O02/azbU8fOuUc+93OBIkY6buNJVvGiG+IfBbUTdhdImDrBciCawihJE9P08R2uy3VoVrBt3Yd1hWT6mTtHB6VBXBjTgmhxVz9ZsWBk+2W3X6P956u60xwc44wTajGFPYkluw4RfrelIP93vI1drtdEfK7rgNRpiTw7nY7huTV6bqOmCyntbBehEMxOKsTuq5HRbiZBjqUOEacd4uDsbbxXectnKciYlnByHCqCVzt4akPSX62VvTKHshMMDO8bV+PC1Kt0tDiQz1+3YcTKQnF9Xxy0KsDvDfFbIyBDtAQic5c/4LgXcdA4PTeHWLn2A3X9F2P8z0hKuo7YgSJIESCWnjCKMKgkV6EGCZCZ14SFPrzc6IzLxc+Wy/FsiqcImJVImK0/rx3PHfnLoN4fNfjRHn++fs4VcabG4brK3QaLemr26T4VDUPRQqXUGAcdrhtn/J3DKabk60loo97eidMcUomZkW8hYIVJpKI+AENjBDFs9909K+8yD/+L/4z/u3NDTff/gEuBEYP3Dnl8oN3uKMOn6hYkDQLxZSEROVULWHVdZ5uu+HO8/dRjbx4/hJTqgCHOFTMA6Fo9ueiYUKi5bmgykjgcnfDRnTOzQkRFccYA/swIrqhw0MqVkGSFbxzaT+wqjtdZHQmPPbFM2BCaIgRX4VM5DC6bLErNK6B3Zoi3TKdtWfr5hDy0K0A4hPtISoaLazIpSyNhxePeefD9+HuGacieOxfJ5Yz5FNhgs5h+mCn3H/xRU7unBPev6Rzjuuba9754B30fEvfd3RZsHAuMTSScucsAb+zfeu2G0aNpBg9osA+BnYauNoPiPdsZYNTMZe9OBNoJXmqUYJA1EB3dkJQZSMOR0QMIrPhKgnxlvOQM1QWm1AU/YyP1VcGU4Gr/TWPLi8YtnB6xwxBEs2L4Tqj4SEGUG8M2jnw4E43BveoxCnSnZ4gXQedYwwTOik+RoIq0nnUQYh5v5XOOzSCqOPBgweM48Q0LcNeXn75JUC5ubnGN0VUVJWu7yykD+i7Da+++iovPv8ine8tIdSZD/Xygwe89aOf8oOvf4uffef7hOsdSDDjFelMJGWN9Jkdq6yoz3hYC9Fq/yuJqVK+SF6FVcw+bE8S6tYEVtI5hUMB53+ozlPzvTp5GQ7XsqZotErXTCOM3lO8o7PC1ioH7XprgfxY/7nVil+dnG7vL3lsy9tbGNgfeZ/Ln9TErg7/Wsh7a32twHqt1eufw1cjVMbN+tm1vhbKgj2weH6ttfmoWY5sFaZj8oqIFEW8/r42kq/tWxmD9fNitOu418T4jyZzmhV3QC331OVw3xkEhXeJgmRcT3xt4cJam8gtfM5gLcffb9pTKxpeHMP1zkorimFknAKu76ziToUENZAkMZX8WVt6tp549hrAeqJZvWEZUXLuQw6Vyr9n4bpYChX6rrNqH5OVvPTe0/U9iHK6PTErzzBalaIYrfqOd4zjnk46us62d5omxNmm5VCtrGTEGBFHCbGKMZa5ZOHBe1/K4k7TNCNmsnuMIhA9/uSU4e4J4eEVJ7gSg14LMSKSqly5BFPoXMr5kFx16JjFg4XSk+GV4Z8VidbaijTuvkJgdPF+7j8nytdEsV5He7iLZUnmeM/681nhEfpISZjeiyU0+xitUoxAH62STKdwdXHB3fi8ebicR6LQ+Q24HvEnSNfTqZqy4S2Z3J1uiQ+u8SoMEnlucMi24+LxJc+fPM8JnuidWfdT5SR8D111tKbAtN9x8+BD3Mkp1+PIlUZ8v+Xk9JRTmdA4Mm2gkw7NnjQRegE6IThLBOtcb1Xfxj0SN+ynkTBNnDnHcPWQ0+srpjgwaWBLb2EoTkv8rVnsl7ggqkwS6KJyEhynmxPkzhm/+Z/8R/x3P/sv2e6veHx5QRhHTp3jXDqmHsaNw2Eha3XpTEHpVAhXI3sZeO4LL/CT17/KZ3/xF/jwrXd54aUXCH1Ht+lNmXAOEfvn48TQwdR7+sncvfHEc/7yc1w/vkSngM/ilsL52SmqkW7jiS6m9ZnAFDXSeSHi2aR4WrfpOX3+HiMRVRNpFQudi5NZ01WtvOKkprBGZxXANuIrfGW1tQLCkpFLKfGan83NIbhoeKwdZt3P3kyUTlJ1PrNHFwZydnLGxjlCVDrFXOWpRGLEFMHoSTleAuLw2w1dvyX4awLK6cmGl+7f5f3pyjw9vrMqYICIT9ZutfyFENmoECKc372Hdh1xsLKLvu/onBDCyKQjfW80tZOOVCprpkRiOR8nYpXd7r38Mu9976d0o+DU4bVniBaaG1IYUBYiQobvKpfL3o68BybwmVFM2YhyfXnB9ux5nOtMefJWOhjvLa8h0RyP7YN2cP8jL/L+T99EJ6HXDZ3f0p+dczNNxN2ezeaEzjl65xDfIeKIPYj3xk/U9jiGwMuvPG9eT515lveOd955A9X73Dm/vyhC4nLoVOfpouf8zl1efPUV+pNt1mZMWNrt+dn3fsDX/v1f895PfsZwvWMME1Esv0/U1hOSfNDlnIIkLKmBb7Ysh2jejiTAmedDSljq7FlKwnMSvqJqKuu7sjsVT3mSYLoWmrEusK4L6sda/f0xD8XaGYX1cJH5+VjldmSjhNGKumzp2npqIbcWeoFFpELLN+v8glb5yn+2hot6rXXFzkVCdDKoIZQiD9lQW+/N7LE53m7b49rguphH82wdFXNMWdK08DXDz7G11wpH29a8Tcu16ALG9VyOrb2MJWK0flWpWOJz8ehaTTxTMFQhBi4vLlAcKt4KRSCgMYVQpX7F1BplmUvi85lfg0/z90IWFOHIlh5tT61oxBDsX4wWvztFuq5PRCtv9MwAJDF7tIpvTJubM95jc5jygmpPxtqhr0vi1iFNZtHvDiwG+b1clrYW/rM3JZegrS39UdUEm2TtMCXJKk+hdv/Hzc0NQIprnq3zIcx5HFnIVjWBL89nGIZFrgcoQwqrMkFBeP4jrzA8/hEn3i36X1g+ooUtZK9OXr+IoHGZ1FkTprzW+pDURKz1aJR/GScSHItSwnIv6z5bC059wNaIbW45L2SN8Ec1XEQjN9fXhBhSVRasjGWabxCzZt5/8QWGaeSs7+lcCSTCJwHIBJmEv6lk57brGUKkC8p2Aq9C6D0vfuI19teXnInAFHHe7oKw9Sam7AQRh0qkx9EpbH1PhzAOe4bdjv04sL95xHh1yUYDnXPJUuITkzJrcECYggKeYZx492dvsnn+eTZ37nD58AEn5+fobmS8umEaRvNaxJi8LJoqVK3nHwjQBaUbA+fdBlGP67e88MlP89IvfZaLi29x585dHB6ZFOkMvhItQdusMPYv9+oAN0auP/yQ7/6//orH77/P3/zoZ7z2yU/gX3qBDqFP4msOtxLU7h9w5tr1k1XbcuLY+I6bmJmnkdsxBDabE0uYj7NXoISCaMqLUIUQkSnixoiMkS6CTJYXFUJM/0J1RpYWVKmZoWrNCxZtDU9rZtwylXIeUsiQpu5jVPBSlKYDASg9F6IlSIzTxBAmxDkCEU+KyU046TB81qTMkKvxoajrCcHCzLx44jQh3op9oFr2NordmzGkULNus7H+MfxmjJx359zdnHB5fUN0I1F6ojdBuuZeAnN4oyr9yZZRI0NIHobQE2JkTHlH4j2+EoprmnBMmCh7Uu3NabdBJoV9gCnVgEzaj9cU/qiWYpH77VC2YvfV+KBWex5h0/ds+p7dNCKdFX4QFVyqOOWxUKYwxVQ1Jil7IeITrnbpDMgUeeH8HjJMxM2E9LNxSpLwfnp6ykdffY2z83OimjKvQZH9xMP3PuAbX/kq3/67r7L78DFd0KQMYLx4JZy6WDcbONYGsRafayv3k4T5Jz1zdL9WBDVDlXUBruYZcw6VW322nV9+5+BZebq5tzxs0Y/YzDXJf/Vc61CtHGq+ECqPCNX1WLfhf/3K0/TR/l6e43Yl4ra2Nq81b8GqcpeZcTX//FwbhVGM12J8oVasjtGGtXGfNN+2ZXreGsdb78iasmFewLnvOY3ALejVAczsCys9DxYhQ1YjNPEKFr7JTD8WsiNZAXm69S4UInvwKFzW2tMrGsl9bRstdN4bE0+hU75ixHbXhjFqi8FOVu60EM2IwrKUYz5oWVkADhKdVLVYetYs4S0C5X91InhG1ixY5JK1raJyc3ODz3Hvaa6zMGJjtApGjJEpjMB80dc+lVAVSXBLz+12u7LmcRzpO1eUGAUrkdr1hO2GKZjQlddZh0D5zpKCa201P5eVO1WdLyGsDmz+u35njUi3cIZDd62IfZaVv+yt0WoOa9aQDL82l6du9Tj1u9M04fuezXZrQla0C7DEjPdEhAkYQkhlXK0snO8thj1IJMiEXZkmBOyCvhADDCa4TZhA7cbI2PeMd0+RF++xv75gGy32XZOEEjHlRVI8gTorE6nJMt6fbJHY4XuPD4E47C1eMg6oRvAOJxYWpDN3wnmHkw7HhA6R7fYEh+Pm4prHHzxELq4Zd3vGy0vGmx0unauAyVI5qqk9G5noWK6u3fmBwMP9nseXF3zsS/+Ir3zne3SdR1MY2IjdieBwJaa7EEfM+jWpMk4Tj99+n+eCo7u45sFwxfSRVxmnkSkGy/FyFcGTJNw7U5CzgDsFs2wTleS0MOXBOW72e85DoKtwqnhL078olpMRo8IUStUrXLbICuNk+QmnXZeIsi7ucXBOjKY1Z6A9PzWuts+hWko21u/Z89j+axamLWxQoxruZIMNc9lHyy1RxjGwGwfG/QgIrrfKU9nCHApOJlhOE523ogcxyf/Xuz03+z1bPOHEFPauU7zMnmEV2/tRIzFMphylUsT5bqVeYdwNdimpOJyMdqlfD122zidjRUzrI9HIiJ2RDpeUjIkhjExTwHWe3kTymYkuQLsuDtV7oaiF200TDAP9FCAEyEaumAw0+R4czTl/EcaEN1jFKbwjpoTwm93ePEDe03WCF8WJwUQdxTtU8oZCsPs5JFh4ZZrffj8gCMN+pKfHu8547abjI69+hHv37uG6DYh5aGU/cf3+A775N1/me9/4Nh++9z6dCm4M5n1KVec0xmScXtLV2ww8cBhesgbXJyl5P287dnaeVmFZW8ex7+oQ7Py9CbnH19TOqYVBzZ8WMkhUkMPE4jVht+XH9Xe1nFQrK6vC7MrvbauNgHV/q2svMRf/cK1Wro4pVm1b0s2lQB9TCdinGTfLeT8PbtVz0Orz1jhaG6zX5LJ2n4tSn5WASv6tFSdTMlLfInjviNGbzJgMN3WrFfSf76zqARxbevHztKcPnVoI9snl5ZM7MHknXIq39jlePwTAWflATWJTTDG2bo59zouo4yQz4IdhOFA8clnYXKJWZPaC1Bu8hkBtHke+KTwL4XWfp2dn7IZ9mUsOk7L8D0HoChLkn3l+XSdljvW8Nv3GynrKXMEmfx+CJfI5EbOCdT1xs2HXdfj9jhOZkTQjsIhZypxfJmzn5txhjeTaYrXGRNqk1FZjF5jjdEUOSrvlELLs7ag1/DyXDJcMtzXNv8yhWVMhuAiu90w5hjvhoKJWeUEpgqQanScOI6N6cxh4mESZdKKTACqMZGEuMo0DO50YnOKcWTJvXMR/5AX2246baWKrCr5DxKTiACDJu6fmVdhMym430Y2K3012yZ0qvu8JZzCFHt95wjDiNRI1oOKJMltwFVAvTFGYRLm8vuT5O3fYKLz2yiv4aeLDGHj8/geM1zv6aTLhtdoz6+yQCU0aCc5udL64fMQ43NDducfDYc8nPv9ZutdeZnRWcWsIgV1nyd+dwKiWcI84QmKkcYpEEaKDxxePueq3jMMenHIzDlyHkRADGjyiMSkcSekVYY/F7gdMYdmFwCDKFCI+2ngaFec7Lq+uuD+MXN/s6E9O6HorURyzoocpf+rMQ7jbDzy6vmYnajutwuXlJRfX12iMbE+FKWpx3c+Mz9hs9nY4P5+1NYtoLRQUPNc5vr1lqKpY/oUqLo0XQrDKYuJtHQJjtKTv7HGVEHj84BFT59DdBOrROEHviL2iaiWEQ7pXZj8O6M2Obd9xrdE8nkG5enjF5dUF8S70/Q5xjq7v2TpBvC93smhU4jASdwMyTOYlCZHgOkLnmMLE5c0NVzc7q3biLOS0g6SczgpTUGXaDQyPrri5uCwwCqroNHEzDlzubtAY2Ww3M3MvZazXhZKaztR8IKoSHIwxsr+5IV5d06N0GtkC9Km0gYidQYxWTtPIzTgwOSVopN92SC+oduxi4Gq/JzhH9B4fha3LoWsR573lp2BGn/1ux8OLC6Y4sY8DijIR2cXA5X7PEIVzv8cHU4w/9YlP8NGPfITtZpuskA4dI8PVDd//6jf49t9+hUfvfsB4fcMmWhikTxcFqojFZTMrGS1e5s/WrMuzku1WFY36Z/vZmuh2m+W4FhhbXpBlh+Pi4JNDWFreWM/1gLfYLwfftfjWGjNruB6ucXnDdDuvek65tXy75cP1/A+NcMcVj9rA186/buXsJHqkstzzlr7VfT9pr+t2jPfXY9ymONV7mQ3AT1IgjuFvC8vbhOpszKplmHa/WiWj/m4Nb5RsdDrEy6IEi4VgOudKlUnry3iT5WLM+XWxGmcNJvVe1WkOzTUqM345WRjMnqY9fdUpQGOuJjXH8IdxRLwvl8tBEmRVLQ4eeyZGS2abSxZKuixrFpBrwlYf6lqxqK0s9T0U9WbN4UtzEnEGYi3w5mfzwa1dxcNgTEBEFjeD57/tKGsJjarfzWPl+eXwKPt9RGNcJRYCOKdM48g4Bc7OT9jce457H/0o8WdvIMO48CJkBpBD+jOS5KT2OjRqjSnXsG4/XyMYRbvmMEGqVjhqS0FeZ10lzLn5LpKs9LUhYfXYdVsc5BwSpElBc46olvvinQeXypACPkT0aseDDy7wXc+Lr76KP1PYbvFdT7wa6Hvw3YYpBIb9QLzeE272BhPTdhid8Cu/+gU2QeDxDVMSSjY+mmXUOcJ+YnPumcaRXRi5HPZcayTc2XLpI9HC3nHARjuL1d5PMExMo+A3Hu2CJTG7lAwPTNFyh7owcfHO2+wfXzAME3e2J9w72XLz7rs8ePNtwn7AZ2U2+0USnFSWe5qFu1EUlcjDt9/i5u23OD3tuOeEToQv/P7v8N2v/B37Dy+YrvbcDCPb0w0hKLrZEhG66FPVmogOE3EfOducMA0jl1dXjOPAtYwWN351wxQDLti9G/SKOFM4AoL2IEGRUYnjxDANeGfFESZN+QaSwkZ2I9Plju3JGegIQXAbsXLDzpIiXYiE3cTu8RUP3n6XRw8eMSnsVemwiwMvLq7YbFJxABwxWuhjth4Z9U80Ss0o0DKWNTytz16LzevKM1CJVZnO5DlM6ax47y0HZe/54PW3GVG2bOjPTvHbLd2m585zdzl/7i79iZUgvri4YPfhA/aPLrm5vCrrYVTef+MdHjx+yHT3hngVcJ153Tanpzz34gucnp3S+46bixs+fP89hocXyAeX+JDyyoiMClvxPHz/AY8ef8jJvTuEsxHvN3R9T9/33LlzB7/Z0PmOh48es3v4mJv3H/DgzXdgCihCTHTyanfD46tLHML5+Z1kaT7MzKjpTM304bDK1e5m4CYEwmPBScd4vac7O0HOJ7anwun5OZJuxQ4hsL++5vrigsePHqWQVk/n0x0wIXD94UMuHzwgng+wV3y3I55ObE9O6Da95YE5IU4Tu8srLh9fMDy+wU+RLvUXojLs9jy+uESYCNHxi7/0Gr/82c9x5/TM7n/CoSHCfuSdn/6Mv/rv/w3vvf4G1w8v7FZ2hT7DoCpo4EToxS+smsdo7EJR0Nvxu21LPnIoSNZjLJTvaq9aRafppOz7oTIx50zVwn9rzGrX2LZaIdVwvGz8sXW3QmottOX+14TstbYqhKbPWpxuP7d35oqZ7ThPowy0SpSuaHprwvhtvBuWRTLa9dZejdCsb02Qb9evTzH+2vyf9rlDJZMiIz4JT5bvHSpq8zvrcMwyq6qWpO58JrquT387LLuQ+d0VRbWso5ljjXP1u+VcFLnVDHjiXKErT2pPf4+GZqucuZJ9dCb09D09gobKBRcs38D7lOyG0KWYU9Rc6BZSUmuiS69AnaBch93klr/P/1ogZkWjPjD1Yahdj1lRqIGZFYghjCUUqHaJIZTE0TZZ2caeL8LLJXutQlFnybftPRyqTPn3BKjt6Rnd2SnDyZbN+Tk+XCwQrgj4cSpW/9rTMRPhQ4KQn6uJ06JkHYeHNe+/iJQExZYg5b4zLOvP6+8zbHIYXEsoW+ZQ91PmqCnHwrtFmJZ5nhJ+SCSKQ93Eg5+9zaOrx+we7fnB9B1e+dTH+eRnf4nohJvdnjtn55yenXF98Zibmx3D5RXjuw9x1wNOU4JahDuh4/J7b/Dw6z9g1zneD1d0AV58+WXuvfAC/dkpXJnn4oMP3+NxGLgJcPHxdzk5u5vKBipOHahnePCI3RsPCDdXbLoNp2f32Ny9y+ZkYwpkgvs0DEzjgB8Cvfa8tDknBkEfXjLs3uXx3/+Ax++8W25q1hT/LopVYvLLsqwzY8XMF7sRefCIr/3X/w2f+u1/hLiOdy5/wFYc8YNL3v/693nv3be4c/8O3sGd+/c4eeUFzu7cIVzu6b1nuLrh+r0PuH50xfs/fhO3Gxm6HSLw4r27vOC3XL3+Lvthz3Tn3JJot1v6zRa/PeH0/AwXLL9i/85D3n33bYYOdu8+gAjBS6q65AjjhF7v+fCNd+g/eGx5VtPE6Z0zzp+7x/0XX2C73fLonQf89Ac/5NGjRzz68AHj4ytOgoAK++SN7foe3/cMk13kN6XcrSLcVHhIOldrbY0pzTTjMLTzWMtMUzHBx6WQthCDefCiGW3Gx4Ep5Wb8+ME3wXm760EE74XTsxO2d85BhJurK4abHTpN6G7HSfQQIsPFFa9/+weEqFxO79L3PyZiiq3bbui2PduzU154/gWuHl/wwaOH6DByOsEm2HNTiHjXsfvgEd/9i79jkoDrekJM3sR05k9PTnjhhRfx3vPmm2+g42iVnPYjMgWGkGlhACfce/4+nfNst9sZxg18W6bewnUcxyKIjO98YIK4CDdvfYjb9mhnXncvHXfv3uX+/fuoKhcXF1xfX9N5x83jB5wEY+zX73yAO98Cgfcvf8jl5WMuuo67z90nquC7js6bonfnuXuM48CDDz7kg/feZxwstPMjcsIjVbzv2Z94oo5cvf2AV197mT/4vT/gY5/4JF4cvTicwrQfub645Lt/+xX+/qvf4MO330PHCYkWbqlOmFSLNT63nC0X3e1W42O4e8yy+7RCWv1uy4fhuPe8HWNNQL9NSK9/r/nQWrjw2nrWzuiTzuyxuc79H/cetO3YPNu51d8vCsXc0vcaz86f18J+68WKzfxLPxyjhk8W+J8Gj+qx6jCrY+022nDbO2s4+IS3eBIfODav4/M4/k42RAkme8YQCDGWy6Kzx8mUjup9WZ6DZqKLsYrcJWsmnfQMZmx2OcT8KdrP5dG4udmTYkOSpVQgxYGLWvyvSLbAzQnf5bK9tOgpTITJdK98ALPg2/fdzFzFxh2yFyCkcrnOzfApDDjVvVe1mFrN1ZRmG6FUgrRL3pTOd+xCMCtVjEzJCyGpLK+FrlvpwGEYUqJqut04Je7mA74fhhTLrnhnt+vaxtqcpikAQudcsRBogq3dXC441xODIuoM6ZxDO4ff9OCFEKIdeEyzVWYCmpWr2rMRYySGfDhJlllL5ixWU0mx6hrJt5u2yduQEufTTZIZXbNSVhPzcRwtn8fZxTKxVvgwYUnJIQpW2jdXCgsxWiheTLeAZSWlBEElbTptqu2VJwa7Ndeq80yMw5TmHRBxTIy88+M3ECdsw4YueC5+9A5ff/098I4wGTxEUvI+FirlQ6QLEJwnOiHs9/z3/6f/K6rK+eUeJbDbQqdw8fq7lhDfdYj3RAHdj2yi3anxV3/xA/C9WdtRdiIMvaOPA3p9QacWvoXvcBsTgBApZY2HaWQcRgQ42ZzSdxsrSztOxGHP/uba8lNCNGu+JAsSENRitdvQqdxcsPAO2U9897/7f/Ltf/+X4DvGIYDv8PuBh2pn990OYpjwm554Z8vLr7zCwwcPrIrNfmS4ukbHiBPPS+f30BDMM3O148d/9y1GQjqvQohmGRHf0ffJ8n33nGkYGN57yM04MDjlzgB9TNXEnBBjwKuwu7ji4u9/BFEsxcNZMrR4z9ndO5yfn3Px3gPGcWScRnqFTfD4YDfHBxG22xPzpoRg5yvdFeR9VxK0Yb7ZPJ+ZJzGmjOPphVnRqJ4pZ49AJKTE/RwKkuhP+jufQ58LMKjYjfHePMdOHFOIdoO3c/ghorsrrj64SKFGkT6ms9T1TJPhkqjDpQpfnXq6G6ueMykwjujNRLwY+ODdxyCwFVNcfUiWyM4jkyXYb1zHdD3SOUUZLWcgJYyLc+j1DZeP3iRG5ZTMDwzvxXWoREK0+vB3tpaPIGpVt4pjJ8HE4LMUjp2YRyTzA5+q/YxxQgE/aIIX6BDR3d4U186KL1x8eMnjH79lpbHT3g5xwntlIx0xKNPVDXHYIzFyFScEZVJ49OE1MSalSpW3RfB9RxgnywWJRre8CJ+58wLjuRK9J3aeuy8+xz/5k3/Kr/7mryFnW6tcFSJhnLi5uOZHf/89vvP1b/LW3/8AGaxmvgerlibpfo2sFJByWTQLJwKiq9Usi8CuVLS1prHrYStrlvbyXCN/rQm1Bfer746FFEnmA9Ueu8R7235rgbHOBXyS0rCYm8wFTbKXvlbG2vfWBHZYRkhAe9O6K7xbWAqGrZfnGEzqkM2Ddd6ifLdGwSftS+bbNe84pjgeSMoc4swxRamdZ93qsLM1IV4Snait+f9DFcUWzu0a6z1cCPRH3m2bwRyoQv5SL4XfZKWCvJf5jIhDU1iniDCME5uNyWVm+Da5SUs+jZKFzSyLLhdrY1SQowhX5PNTHjQ5T8RCnGPk8e76ifCEn0PRCCrcPbtr1Xg2nVU2USub51L5UrBKJTER+ZzPOVVaT/4eNBX7yBsEuZB8QBHv5hh17DKkWdsGnwR6VYsxN8abw0RM6M018adxSETMEsld5xlHE2gnHTk9PUFV2e32hGC3f4fJwqw6Z2UGp3GEaHdqEGNSDpK65RzDsC/EL4RA7ztzaQPjOEEQereh7zqiBGKw+vFWNUat9nqMiPj0bGeJq+NA5x1u45kEJiJ974njlEJDNOWwzESn9vIIChpAtbo/JBozEVuDT4w33ZmGE0oyZGvR8s4nQXm2gOTvnXMECUX5y/GS4pPnJnuwEuycn290n2KwC2VE0rqSwmoFoIsmHazYJaqki2hAo+fk5C5Cj0jAtOFcMjXBiA4fO5zaJVoi0EVFhwBM9BnPY0yHwmLSM7MdiUUBO7m8MYaQntsMJlwQrYpLHCdEAl2BjzPhb9zDZCF5KJxg1WxElDCBc5ZnEsdIvLkpMZIxhRluEbaJJ+nuhqDXZtlIypnTSKcWCz9U3kIFJicosdAZIVvKU6lUHJNasnU3KDINKENKsjZhxfILwCUrNTHS73c8/OCnpmyChVem8+E6hWi4p8GkD40RCZFN8rRNwepiITbeoMrw9odJyRdOVNmmczSpmkJh16YzZo9h0DmeVEwAkxCJDy55/OEFHsdGYxKMMQbR2b56DSBWDjCmM5/d4S56Rp0M45wHnZLAs2RkbaxzvntDJN1Qns6I80YffNoXagOBBtRbDkE0gktHYONcYhpzFbiagYWQLVhW9lUkJf/GyCQzW3GFAZlgE6dQbqYGhWCHIohaAnPhgGpVlEIsSlyhJQLRap3iO1dyTAQPcZY1i/ibvLhaeYpQTTfX2oNRpeQzdGEWLK3DRLNshPzWjJ8xomJhFyFb8KMiEQtR6h2oI4gUG4ZzSSCPgBiCiFhYY74zSlCc9NAJ6iJ9KpygouYtjVZS3Hi0Cfl5rhIiW1y6SEuJokQn+JhK6p5v+dXf/S1+90/+MWfP3cN3zs5qCMSbgct3P+Abf/Vl/v4rX2e4vLYCl0n4yPvuNOdhZOEm4wTlzJLpZYJWoQNSIYnmO0psDcmfvFAqbmvzMzPtqT8/Zum/LUevPMc8zdJfPFZENy8nmQiOxM/nz9qLgzMu3eZRWVtH2+/ynVj2J+9VKVOd5Jz8bh32nHlsq4DU47aRA+2c1z6vFY01haxWZNqV13sGWVadeXumbYu/V9oarGaZY5lv4RZKWmNcqDw5x7D0SR6Gts8Wd2uPSpnzkT6e7M2oc3lo1q6zUl3Dl6ScKliVBw+OFEqcvE1E1IESmZgvLs5hgLNSUc9Ey+V9IFacJT/RVqor8/FMqtx44YePHxysda09taIxxcjJySkalXFvCdp2gZNjSrdoi1g8eZxCSk52xWq9SBRPITtWAtcVYEtiphpDk8QsqeLLrHlJNLLpUvK25gvAoml9IZpQ0KUk4e3Wbu+2iwQdPsWaSRKqx2kohFYQ+q5PN3E7yzFJysM0WpiSSwQ6x0pv0jyG3Y4wTfTOxsg5GbYmE+g9pn2TEncA0IgXh3PmWdkPA1wrvfNMITLsBjQENn0P0UodojANQwoNOLyTwqz9zFW+Ko22HOgVy4JL1s98INqkwAX5rMKd2hCyNhG+tjQtiEN1yOu+VJVpGgzeddiadVbYplUJmvND8v4sD3xiqImImUGhJcAsCFVtycmGgWJlWBzYJITXcM3EIyoqsQiwuXJRJorZOoFaGcwaTtmKYcKhKzdD1zCuiV++EM2qWC1r1Wu17xQsyPtnSm/uV1XRlM+kOiuMihkPRGZPlJBunI9VScHKQpfbglnmZ5Lw01rmMtyzhTZf2FjgHQKkc3uwX2l93vsZ1o7F+1qejanCWCwXIiKkykgQg+2X3QQd8akqVgvLBf5y2OZz6RYCRc2wvfN0qR+7ODAnRudqfanalM4GlLLu9P0sgBmTrqEaajxJFndNCF/X91dVojadqybjhC7i/03XNLxx4pbv1esv8GLOeSmwmem6mi6azvZs7cvCspGvlFcWD1DMno0pETKFv6UFmOKbLg7MpMAq1GQl0cbMnQatzqzOl4jl3wuuJcZfw6/gYLRqb1lInkSJvWMSoN/wsc98ij/+83/OKx//KNGnMxUUPwoXH3zI9771Hb7xN3/H9YcPkSHYPSuyTAaeYdzgREXb1sJNWpqbP3vaXLm2LZ7J+1iN09Kj+r02zyH/vE1AfZr5tOs41k/NN+swx9xHG8Z0rL81mC6+L+NCjh7QCla5tXvQCrB1/3U4TKtAwJPLvD4tjFslr13z2t/tHtyWZ3HssxoP1nCnHue2vm57v32+NR7V7y1ya29Rc5+Eo8fGbs/oYl1l3Hl/FYsIGKNFdGSSJOkFM9HMfcZKFrCHk1G3zfxuWm2QcKSqjUq6p+3J7akVjX5r8eJehI2zG66jQiCmG0clhZ+Yi9A7Xzalk1ngDONkiogIpPxZSZc5ZUtvlyx4nesMlGLhNp5ZOPVJ+QjTWBSEEEbiZHdiuCQ1SAqnKVa0YEmn4zRYEg1mgQ7DZBddbXr6rmMcJ0Q8w7Cn63qcI4U+2S2y4gTne1RhmiK9c4T9nk1KCBaw0ARVNp1niCElsAbEQe98us11vrzuZLMpl6Fc39zw8OIB515gigw3N2wgrUOYxpHeW7iRCAyDldA9SBYXKYG6teXGOccQpkU+Sjm4MYdqrIdGsUJMMjLWCgTM79f5KHWYV55z62auhTON4cCdXIhQsehrEeJMM1+Wy7vNOtUK37C0sKSPyJbstqkml2fDFExQsXqsrTAdi1dsyTScc0VIrglZXkcL78VYlRDUEvQMl0yu6jGzMg9zqEANtxJK1xK+pNzkfaznkrTDxbzKnHXJII9ZgGqYZUWnZsoheeZMaTlkNPkMZBgXkTbPSSNTjEwpn6pWRaySnkAqdTqOk1m5JQsKS0EODsvP1s3OxmyDX2PknbOL7RQhqFmrJpRecgJeFpDrfpNVjCUei5Piec3j10JfEa7ThZ5CFpylhJumNy3sLXm2TNhP69BEu6HQi7WW52ZGgEMckgqmqqYszGc2Pa9alKmoFMNTHiD3E1P4gKIQYerMwych0odI9C4pO1rWYOO6ufy6ainbnJl3CNlbXmkqJKVzhb4IgqSS5NE5grdCEnuv3Hv5RX7/z/+Mz/3qr5g32hn8JSr7qxve/PYP+Lt/9xe899Y7SIg4JXlE5pvR6zNfw3I+s7NysabIt4J1SyfLO04W76z1k8eeMUYXtGJNWK9/X1vLk1pLt/KPY33cZmU+oJXoQnFr6dSTFI78TFvwpfo2kSujyWv914a7mu63sGqVofb72+bYttuUu3zAa8NjLUvkd1uvyxoPXlPwWhipUsLX29zNFqZL+KzfQXLs3Rre9ZyPGUdrgxnCwXuH8zlUrDKdu20fbmuSDOTZaNP3G3ZTTAaxWdMoZxkWFcNqPjHj+mxAWx9z/r8nAiPXE4Sn0zOeXtE4vXPHJhYiGiw5UaPV05e0ALPwu2SRotxGnDWwXPa2S3datJVC6svsOlJVFe+ZUnUOL0IU66dzHVGDhWeJMo0THkqZW8XhBfquNwakpiCcbLYpOftkQZQ3Pt0R4h0xRLb9xtZ3csIwjkyjcHK6sdt6U4zdbrdnGAemdNGfV+g780h478m2/2mccL2VMN3tdjjXMUVzT9tt5aZ42QVZFgd/fXPD1c1j/HaD7PZ2y2OIqVypYVLQiRjs3o6MQNM0lcsIVa0EqHdzsnWdWO/Vlb3p0h0pc3lftzhkUB3WLHtXikV9uNYqXmUBuo59rYnIGiOTjEcsiW8hJDEmwQIuLi8sFwWzFsWQQ2yWBKkWissYFeOOysF8siJhScgs+sxN63NQ9W1wD4u+asYfm7/LHCtQ3EZkb1tfTehs3KWiMs8xW3d1QUiNabhZCKSWJm3vAoeXY6qqlUOt8GahALEUZtbeL/ApFsYsZJtgl59wmLAsFU7m94pVilRaNsxmcNVo51rjos9a8TM5RgiTrTukZzNe5fMUYyznJ5cbrOeSfxexW8tzcvICnzXlq6Q8C+dT9aWouKg4Z9X+NFI8PfmejIxHxVuQJPe2YEPeg6w05P9iSOE1CbsXnglJY5qrbIaLzmFjee9ijbM1TlMJF2RGWDYC0czoKMxSFdtTyfRG0pxtguZRnmlT9jCXUo4qiPfcOGWvka0KXRAioVReM6VFy3ytDK035SsLKingMwYL0TVYZlzO89KDWP6o0XKWRBidciMRf++c3/3D3+O3/+gP8Ocn6f4dUyKmm4EH73/AX/3bf8fb3/4B8XLHJvUXxslKQHsLWWhpZW3IqZWN1jBTP7921pa4mteft2ldGF5vh5fBPk1be7Zey5rAZlrm7NlsvT01Laznn2lSPoN1cZma3q6N3fa55pHJ3x8oDUlxTU8AicdW9De/W1errNvaXra/5zN3W9hYC5fFvle8wA5jFc7cwLmF1xoc2nbAX5tnRNbfW8O5Mm9IZ3OFPzf4eqtSBQfrqPnKQnm5pb8WxmtyxdqaaiPBvKfGv82LkN5NY15dX7MPoxlFrONZaRBZ0OWD+YjdwVb+vkXZmNelBBfZR2WSJz8PP4ei8b/63/yvOTs/N2LsXbHedn1XLIrZI5EnnQVXyVndYqxCSZWnaqsUM+MyTdZu7L25vjFvRlZORNhst1xfX6Nq1vBpmuj7vliC+74rlq0s2Drnae+UGIY9Nzd7nBNubnbEdImYT4K3otzc3BCjcrLd2qVwMgtn4hzTOKULCucqSuK8VYcJId3+PSLJ8hvixPXNjjfffLMQAlOkDIZbb8nwY5jsboioTFc7NiFZb9XyXHIcNpXwlpG9VFlRRV1YHJK8N7kErvH8mRAWARNZMCSoDoTMloz8XiihNnb3ST4oa4S3WO116YHJY7QMsvWI5Hm6guPC6ckp/aZnuryyPAWNSDw86PXP8vZCCdD150SQQxpXvsv3d2RhvzAMADli2RJZrCl/X4hmdehrOK3Nr4ZtXca53JrqrMKVSVn1eGntzLiRL5q0PmYrUWZelgxm72ZL+G2CRz3fglscWuDWhIKipEQtl8stGKEk3UGy4rlyT0tSEEKcPXoxiZCKxbdaMt0y5lvUwqamGFCNdMm7mhOr27VlJV8bxaqChDGLap9rXDAPgRRvcUTsPpEk3KLQda6EK4lIUrQSDHNoTQpTncK0oAtLpT57FW3oXCwiJngZrc130cyV8CzUzX4XoVR7E2cJ2HXLq1O1EKslrUn3LEn2qliLjVI4w0hmJQXKTddFaU3wiRoJCJ0qQYXXH7zPj99/my985JOcdHcYNSyYsDReM+/mOSpquXoxh7Wa4j0rG1lfqjzIVYjn2Dl2Eonbnl/+zX/E7/7JH/P8qy/Z+Ul5awwTj95/wNf/+st862tfZ3+zw+9GtqTCJdEURuOt5m2KFd7VdPuYoFfjW21IqAXr+rkZW3VVaGufXRNm14SsY+2YwJVh2npkarpQC3tP09q+6v7qOdZruk3Qz/PM/dZ0p8aJWgGwPpo5yTotbMddo5N5bxfK3RFBvX6vXnNNw9vPVLXkXR7jPbXisYhYWBl7KUCvr09l+fkafh8Ycpi9ocdwqt3n284MrONL/W6maS1MaD4/xuNaWLdrXh2XmbYaXCIhTsVomXmMyx6hdl5J1g6q1OVwsxx5bK25BRft7i1Rep7OpfHUisYPf/yjIujny7WmdEDWwkIyMq0dPCPodnNt7q9cCIgxcu8cvus4Pzvj+vq6XLDX9T2np6fEEHj0+LGFTCWB2ydL/nW6fKsGb5imyrWUiLfOikot9PZ9X6zy4zgSQmCz2bDdbOg3m+KdyUh7fn7OfhgI04Tzns1mY5VYEOI0crrZcufOnVIa+NHFBSebbaoCVLkiscRFiTCEiWkCN450XZ+SaZnDRDKzSIiRrR/AwaHPwkBbRhY/r6G+LNH2rWMOK5j3zSaxjGktCmUl0GTPUhZ26z7WhNL28NdhRDn0qGY8MUb6rmOarNLZ9c0N4ziRrY0uWSXbMdYYR80EjjFIs4of6ScL4awQlPr/KwSwZlI1wZZUgjM/Xyty9fv1GlYZBBRcrshYnnaZG1DuuFkynVDAqMmoLSJ2aZzMfbUwVp3DZA7wR5fzbeG9FlesWHUiTbAplwZFq9fUsbQqLoi8JG1Es9W88mqZQTopH5T3LXSK4sGI0dY+hWCCOEumvAgnaEJWirIsjqDLO3TKjmhO1nXFUxtUixc4hyjV1QTFQYzTAc7WfWo1zxnP8t7X86ecHXHOilUcZAOS7tBZvitiShlyuJ/1/uWWrf8xRtBZgVetwrpssOrNlVAUmY+4Jmtf0GgV4qIyorxz+Zg3rx7xiTgxhIC6uSjF4RkSgluzYlu1P1WHSO3VICni85xqa+SOwGuf+0X++D/4U179hU+ZByOtwYsj7nZ8/6vf5Ot/8Td8+ObbSFC6pHxNknPNUr5Zho8NehCKlMdeo2//w5uw3LnmW5kNQceE2tvofCs4P4mm1Z/XwmE99AHerQjVx9pME5brPtYnzBcA3wb3BT3OoXdNy+8fu+Ct7WcNLguFZoXPtGOtCcJrxkH7uZx2Tc9b+GRZpCi1Dbxa2n9kseVwS4Xva/tYz7/2ONTrb9uaUlz3V4/TKl/1FFuF6FhrlZljyz+meEBl6NR0zQBKjELfd2x6n7zaUuRc51yKLNLZQJNkeIOVEpkVdSfHywYvFA2wIhjA2ebu0TXX7akVDbsd1uJbw2TEMMSwqKNrzHUOFck3epuQZJO1sJ5ZSO77flY+vF/0pQoXFxezppUsb48ePaqemS99qwEyjzsflBCm8nyx6DfIFEPkZrpJ851j/40IRMLlJScnJ5aMjc3ngw8/LGEmYAqPYEml3jturm+4ePy4VJ1xztN7T8CY7jQMSTA3AarrOnRyeFHC5TVdCJbPkUpZFoEBQ3QrWpEsopkjqSYNf/bq1EpBnaOR4VUzSVP4jCiKVAJz6l+pDng0pjuFOQHfOQtBQ+eyfhle9eV9RRDNY2Jwz+V3M82vvSf5vZCIkcaIs7JBtgbvbX6NpwCRFFp1hLHFiFbx5wkTk9CZQkMS4TTBkbIPIQl8koClKYE6UieW5h4TsTdJNoWOaAllmTd2yQhIFkaoPAg1IddU2hmh9qLkz4zRLVgo2Vk6kZLGCtVxSCFuVpkCTQmrIunm4wyrtElawdZ7fBKdDT4zA/CSbyyN9WTSOnPojuHwzDgqeMScwGZzEWASU4gkEcAp5WSpISAxGhwyXhj+2C3RJSQsrTmHCwUNKbTK9t9hXosQIuJn3Mnhht77UkI038oqUPJbDFcPBa2MFFHNWxzUSmF7BR+VvRPMhmI4I+kSSolm5fdCujzJ1huz4cX7BMOwFBTUkv8NX0nCfiwwDeNU5lwXVTCaOs3ejozHkpiZqzArzuvK75YPNIWfqSTr26xMwBxOmJWJ0meY5t8rxp2tcMm+WMLhxqjgHCEq17s919sTOp9ujS8yZSVwKOCXQkHGScG8Hzl/xVi0pFzDVOCgMwUhotx/9SX+g//4z/ncl36NIEBnNFemwMWHD/nW336Ft3/yOg/efo/p8gY/WWEQh6Rytdmr7NOqxCoCVpuYabLRgqWA1ApKNa+slYM2Fn0Bk3rPKmNJ2YMV4eugLYnpwbu3KQCtUero2Lo2wmFf7bt1q0OArfLWejKwyLKv2nvc9l0b4ubP5pymjNzFe1YZ5OpWw6pWJjIfbeFi/2T29Ob307ha7WWrWBTVOuNCziurWMOaoF/WX8+j6uuYAnRsnaysae3ZxZpjxPsq1Ld6b82AuIa/tz132zNrrcW5tefWFNTaaDXjTxbuIEckZN7cec/98ztz/1rRN3uE8kHiAxlGtSlpOYtZIZ6ps874k2XO7dMZNZ5a0fApBjmK4LtEgK0+YuWST8/6biEY+pT/kAGXK4NENUYgSfANcZnUa+/7qizrUnC2A5CIUb4zQmfNNrvy8wbEDGfvEe9RLKZak2Cu1bOZgcVUWjVirqjdzUC/3ZZSkjHGUsKyjD1Z6NJwNRCjlcQ9PT2lS+B2rg5hgM3GbnYU1+HF4/HghCGMhGFkurJEcEnzK+FD6XfvhE3XmSUhhTs4cawRca3mDSwQuiBF8gyJsEgSlySIlYovcRYGRVIYB8I0WKJ69vqAoGLwrW9LnUN6zP1nSo0JMZLujlhUaaoUkzzHKYyEMHF9+YjtxrP3ki4Pm+9aSdtrybFJGTQ4ZKUqW98hHR+U5Imhwg3Jwq4JqSW+G2aFT7I1NuU3pDDDSFwKX9HKO7uUXaxJoXFJCNN63oVuSPl/Ph/ZC5HnEdUUPOelCJ4aTbA0Y1oWLisPBsJIUs5o4r8VhKncRqr2YjkPYaZHBjs341kYQ1Jc3SJfRlFEo5X6TKVrszcoqqBqyc8xKbBF2U9zLIvFwjKdcxZ7r+kOCbW5FdqQjBZTlNkwknIiQmVhNCUzw0sITojRldwMjTHdHG5wVGYlwmWPrLM8r4xJInPssHe+eJfymcv4HJP/oDvpCVeXOI2EYEnhiidO6ZZ7IQmgAhEc6SLJkDEjbYaI3Z2S4DTDLCtzEZW4mGeGi+LJ5CAzs7LD4lOiuhbeJ7kaV8W1YtZ3i7JaspvQ7BojyxOJPid6YGRlFnCysj+TMqMTmvhBVtxzXyFV3RpEOfEnnATP1dUNl5t79JMNp5o8Bt6BmueoE4E4e3411cHOFbwkeRlUI3Z7lBUa8dE89MMQOHn+Dr/zJ3/Eb/7x73HnhedQSZ6/qAyXV/z029/j7/7Nv+fi3Q9gDAVYRTATwYsp42CVkWsheCGYaDYTzIaINk8DOPiZf88GuhIt0K2IA1pRHW2EQXfYb94y3yh/BS+KmFs9vyKk589rHtZ6tMo/ZDmvqtVe/Px9/Xfd3/yu4YHgUmSE4ewcXhiKYtcKvO34reepCI0VtKLOUFnbq7q1isvas9mTXBu9IBkjaoG1mnN+1j60fSId03xn2jFhmbyi3K9U4Wwi5XwuntdWgavCZHXGmqNGwRXly2it0Zs21Kpe51qftdKwNlY9Rv7eCYsbzJ/UZrlnPhNrCk1tcF/iTzK8OkrEjohyerJlgxnwXdpv4wQG+xBDpWfMSogK4GYjxbI5JMmrKlm2sOiB/FmrEN7Wnt6jwVyuNjNU70y4jRJT4qEmJuhKbobGOU5RxG7h3u13KZ7ZmHPJv6gIagZunRC1sDpUrrkWCVoky+9nTbFsqmPRT4xxvg8kCQ6eeY4iYmFbMbLb7cq8c0x+jocHGMehjH1zc8M4jpyenrLdbk0IqypAzQcgouKJajkb0zQSpoGemJ6fY/ChqiIV7XbsmlGsuVFrt6U4wUVXktBq929mPPndDMtSJcp1RSMuSlwF891uV25T3263s1LD8rDnPQ1ql6TlOWflJu9fXm/XzfdudEmxEjFl8frqinEYjLA58yJkpStWc4R04YwqzuXDKKQrrxYMpByqzM4rPpSFNXS2+kgl5xlcgl0Mpw7H7I0oVmAnTD7f/K04L6mSkithL61lBkjKkmNMd1OUePtoykTM9wglYmBx71ath/zPsIRiIMiCo2qlLMzryYsr1cGi3U3QWoNmwi6mmMWkfMR57IlIlFgpU1qtdfYoxUgxSmT1r5I1y3wtOdg+zMqwU7MGl5AzlBApAnTuX/O8Mq5X300KIUKIYvc7aLr4MCXQ5fNfnzFL+F5aJOuz0wp7ZSfE453jZHMC4pkiSLKub8Uh6ojBAOgcdq+HCGMJV0pKSF1usCiqM9wyLOYk64QnNcNQo0XSlA82+l7/pXO0lC5DJNJHlE2vvhJneSjZY1oXAZHUjyajgGiqSBiXMB2nYAphDKX4hnl7NXnehX0MnGzv8InXPsNGHbtRrbRsXjSz+uMUegedd8QppHPtGIfRPFUh4CTvX0ywFlQio3P4jfBLX/wif/af/ke88rFXkU2HRMvrGYeBB+99wHe+8jW++dd/h9tPSDwUdmcASYmvfppW09Ico74Wnrf2fFucoxZy6ufzzwUP4enmt+zs0JhxTJi8bf4LmrgiGGYY1JEOtQxwbKzCk+L8dz5bRfl0y+fr/o+taRZwK4+DLPto3137rqaxreA8C9uQlc66z58ntE6gFDhZe7q2ts9j/n/WFutuPl9T4Fr5JhsbWuUlP1OMc418+KT2JOWvfa5dy9pzFoo5hxQ/zVzyGrxzOE9iXsmwlWSSYkxk9n7msvcH/THLOIWhUq/BVEyUcidejV+1l+tJ7enL2/YbnEvKhMzabd9vbJqyTA7On9mEZ8LQdT2nYgKu9zMDruPU6woeGZnt1vB+0X8d6lMLxLm60X6/L7/XAsGalSRbd7KAXCs+eYw812maSsKsiBRhehiGonSIGPEeBlM49vs9+/2ek5MT+r4vfZyfn1tOR7JOT+PEzeU1U5hwOnLS+XITqsZpEQ42K1CTWcYrWOc11h6EaZqKwmQJp1qE0RaurTI3E+yccDUTsXLze/q973uur6/ZbDZF+ZLkHl54pKp+2/yRmhhkxaMOsatL4276nvvn93jD/YQYAlNQam4QQsXQxeKwTUhS82ZoraCGWVlgtrZHIIRlbGtIwrlLakoJYSNZ7iJ4NS9FZrBoTtJyBFX2GopVFk1lnNO67H49XRBPsAstcS7dTi/lTEY1id5CQ5IEnYTGGBWVWUGUBAstcJ6VKruTbcaj4uMR8g1x5jEqZqcMWygsR0i5FOBy/D9ZgQPSfs/uf1NOaoIY1QRq2xuF+hY4ZniS4K6Ay14y1G4yQpPwbcpCiFIE7xghVPGrxcqEBcZMKuVCJFVBgn2WNacsqNX0LYQKfzL8Ktp4jAEJVh5825+gkzGAXGEuBsOJwoxCoOsSHmbvVwq1yfto21vTRRtFM8jqeUgjNKoZlsrD1XO16hE1w3fG+bqPvN95LuWrKQl6wSBtF/0lw4Bo+XuBD0seyGSEi4AyhgBxwif0kAAupgpyAmebc2QMDGNglLnYiOlbMTFvZVJHJy6VMYcQBvsuRrxkj62iIeC8Xc5JJ7z2C5/kn/+n/4LPfPGX8RvD105tfR++/S7f+9a3+e7Xv8nl+x+yCYKbIurmCxYPBBmNZbFPI4RnPmUGh2n1mTW8a418t41RvE3ZM+DkoM+nEpYa0aQ1otzWVytAlnN35Jk855of1rytHnu2NmfP81JoLHKCBlr1u36uFfxz3/Vn5V4izRDRYvBr130YerX8vVU28ufOyaIoybxvrih6q7RIdVbcmuPfrrWWqW4TOJ9KsWnn8wRFtN6v+jOpPlt7vq06+TRzbRWBspe3LOuY8pjXWZ+32vD6pLnV9NxK6mdcrQ1xmjzhaS9r0l6MP7kISnNZZk1vE32PWcme0cLecy53+MT21IqGKRl5Fo6um4XFeRG26Fkwag+yWYOc63BExGlFJJe1itcOVO3eravptBp9/nd2drbQZOuNrQ9wEVg3m0WoUD23mjjld7KQlOdi8du5TJ6UPrJ7Oj/T9xYqtdvtCCFw9+5dRIRhGhn3Y1I0RjqJnDqXLnyLxZvUWmq8W16MN+/ZYe3y/FwI6QZvZpjUORAwV5TJfZhHYVYoaqWgVvgynIZhQETSeqHG+LrfGEMp2dYmma1ZJfJcs8LWdR3b7bbA36tjChNTjFk0KHCKGlNcPkAoxCmhblmPzBOd58lsGVh434J5IuZzMFd82EfILgJVYyhekxVRzQsRVdMFkjbeECa6OOdgIHOYg4igrrOSq4BotvqTQj0styUn9ipUhRFSUnPMyp25W6cQiC4WpWEmV1lBMotuRaNKHk7NsBekVcB13twCeRlpfYLggxSFNYdIlRcLQa3DJcySP8O4sQhrsuEIwGxpc05QnRbKQAym9IQYGUTLnhrdsrk4MU/hNE2MYcKp4jRZ25MVKc8t/xzHsQCoNQa0Z7E2AsRoJaqnYGGXTrVUlJs0EDXgXZfij01Q6TB89ip4cUWZdCkv44D1J6G9CPFVPsUy6VoQlcUlfgvljzkvJq9DRIrgmfetMLNM/4uymvc3wSLBNBtMCnwAopR1CLLET2f8xTugSwYhrCx3nEYLgVJl46y+mFNloxAISV+1/uKY+u88qoEpzt7UTedx3uNIgrY3Y5B0HTi48/x9/uTP/4wv/eHv0p1vib0gXtBhYtpPfO/LX+Prf/t3fPjOuzAGNlGsIl6MdhG7P7RO19bhp1Ey6u9rT3BLS9dajYu3JdvW85tfZtVKujbGgpfnfay+O6aA14pAK6i1BrX8XW3wqr2Ia0rK2hwN/im0u4muyN/n+ee+WjmkhlmrSC2rziWIJJpYr6mFQ8sX63/1/PKzMepBbiZQyjjXgnrZ29poRJJRtTrD1Xrb/eEJOFrDJL/beliW657XU8NkzUt1TOFdk/NyH+1cWqF/bb2Hc1yG860pme3v9bNr82ufreemFbxEmC+0jcucDgurzeVwk4KgczjazF8VzdUybVZl/wULM3Z20Z3RaJKxWNXGXlnXsfbUisZMVWrAy8yYXSZ2sTqgGXPzJVAzkEQ84qyf2nNwjPjUn7UHrHWHttp23UeNsCLCMFgeRd/3C+t6/VyNoHV4T30nhaoWb4jI8nCP41gExVxvP0arvT+OIx9++GG5O0FDtMpTYkIPImjMN9wuD14hFhpL6EPtGagJXVYMauJZt7XDmity1fdf5PWtEfF67zJByMrKZrsp88vzyDBF1Zh8VTkL4ORkvutkv9+XkK5WERLnePjwASFMjNNEGILF+qfQD+ecCQmpxGauo98qZiJCVJuDQvL6zMHqgTmsIL8fktDaWjcy84gCsfa6xVQsQCiKUcZX71OlMlUmlwoX5P0mK5KSiIMJbBnXwhQSg6RcdJTHizkcy1neUlGkZLBkVifsw2gnVeZzPjMjSyYWmWEyJctpETklu2hnk4jEGa/yzekiFtZEoMrhqaoNSVacjLYYjlhRhRCyMmBC5rwXeR7JUp0EYefsHgNNxes1PVxyt6IJ3AenQSPTGNPdNQEXA5Z0rfQC3rFQ7hfljCvlKAt+i1yMOnSTfJ4jU5wQB6fbjvvnZzze3eDUWeims9A+l4R4SbCV5LWRdKu4CJaxscLzrbAFhUEpsKgSVXY908n5wyUjnJ/JZyOpeKjLOWuV4SFdPOmLZyomfJTFpZrWX6OsqjAfrFrgEPCxXEIl0pU8PlOuHV0QJEYmgcmbXrKJllOUlYacx5Y90OKyIhrKvUvmmfNMKrjeEQTcScev/Pqv8if//E+5/8LzsOnwznIr4s3A2z/+KV/+i7/g7Z+8QbjaWfhktEIU0UHsXVGuMnwXAkuzd2t0qv459yGM4xwNsCZkr/Xj3FygoxVo2/1fbE/T11Kg/vnCU9o5Hft8TbhuDVhZiT8mA7T95PmWZ45qUCbLWLXIWZ5oIx4WvLkOL6q+S3aExOcP8wfqObb7fEwYXfJhFry+hWs2ctRh43Kw8qXm0cpepc+fY49vw4ljilb9dwvfNVmmfQeWURpr72b41XJbjRNrCku77mPwaeff/r7kBcv1t563Fg4ANzfXxXBmhXGcFQ1hptlUc8vnIsRUckLElAjVig9oiYxQzd7q9H+NhzzzCe3nUDRmy2LWyo3454VnRJf0bJM4s1AckoLSxBDWxLZVNGqLOSwJRh1rWm/A2iHP79ab+ejRI1588cWj7qw1LbzNC8nPZM+F9/PGZiWmCJOJKOXE0Ln8rAPn8OKJ0eJ4DcoUJMhj156XnIXZEs46hyV/duxgrr1fhMRmn3IIVHtwW5iDKVnjONL1XblALK+7lPITu9Rws9nMYyRmkV37eX9r2Jef4vBeOD09Y7q4wdKFKmE8JQbHlFScYmFALWSkZhg1blFVfPG+s3CNuolZAHIlptxCxWRFHLFKzM9KqqrSdx2xW+5xIQ7OwrFcRRzy7/Z3xmvAW+IyKM515CT3ltGY18UXgcy5uUzzWdwUpU3q9aX9ydbwci5SnL0e8UIiZnwo3pFqHpbHMJeVrv9FLEHXyhbX5x0E86rmz7KBIltxlsp3rgwm+FylybQrtFy8lhXChLupypwpeCmXJ4V/dU7oMYu0U1O8YpRyfosFNZ2BaZoYxxEROTjnNTzK+iyLj23f8ZmPf5SL6xurniTKRlyqTMYBjYrB8gWcc7OYICw8ADVO5/2ILGlBsWklb0aBfUsuUjnXmT66fAzInitFF30UxUJmI9jMF+Y677aWSqhqFY+CWoLz6woVwIhaiFKEkUjwll/jwxwGIFm5SPhoXj8rIpHh57sOVInOM7qeySkf+8VP8Xv/7I959ZOvEVyETWfK0KQ8+MkbfP8b3+Irf/PXXF9fsfEbXDDjkXPe9CbvGEVgCiXU8kAQkeXSbhPMaoNSCHHx95qAstZHK/ys8cwyt/x78/fBHj2l8FnP82nfaQWxuux4/r5WdG4T5OvnS9+J1q2tQ5Lu2+bAHBMED5SEWD9bnUk9FEhbpWq1vxV5yD6bZbDFvBYy29JoGWMsRQjaVuNUPZbB6+fb6wM+u7JemQn2qiD+JLzO/ddj1DJiLU/W0QJrONhGtpR1Z95fPVfDql5bO68lP1zKpccUq9qTZI8kPpgqwk77PaiaEVANAwQW9+4AUOhslokOcd1kTTOIROb8u2Li+/nsB0+vaMwItp4wltvaZq3FzIEgYmVgQ8ylAn1iRorI4ebU/a9pg7BUSNpyuYdzgO12y6uvvFLWZYER6WKkaKEttVJRr2cJFxbj1xYi53yBXX7UuzmvYbvJCdNpDeKI6qx85X7AYTHxpOfrOxWycOrcfGjauUmywmgpjZn1VVkefGwKJuympHDnk/Ux1fhOumRWlnLOxbGL98phDjHdzaElOSlil2FN48R887F5Cby35NcYR5xzpRTxAtYKEavO9dy95/j4Rz/KB2PEBTWLEfOehxisGpOby7YWQR0tXg+lSUaXWYC33GuTlmKGZS2MY4JUHQdqAn5DnN2JeS6SJ8Tml/pzKQxGWVh8c4ldTdaEHGpll9C5IsRpTNV4qtLMhlMCEvGdn63wSbFAsVK0kkP+mtj+JHjlOOJpmoqlOocZ1J6mDI9iLBDDaVcpfFMMwIYcE23wSrkwFTMpylcB8tLDONOWfK5cYdzO2157l5QNkUoYS3CJlQBcC+ZOiI5ynZGg9EnZcwhxqmJb1YRkl4plDPv9bAhIz9idQZWFNeNdArBzgsPCI0/6npPOM4wDAWWDQzR5ExIDzqEWsfflPMKsDFr52IqGVoxR82Jzsndad3auZ4WlXF4p9smck5F0z3SfiX2X7pXwmY6nkMV0Dm3NCuXMpPVoFeblmDfAZjDTG6Tsq6J0OpfelbJD1tPWeUvcDopXYUp75kSZ7DCkaEZ7N5fNdZhyIs48c50zfjA6x/2Pvsjv/OM/5FOf/yyy6VAviHj219c8fPs9vvvlr/H4jbd58Na76H7Pibmn8WIVBCOa+k1Ks5NScS6fMTSz8YyMmaYshU3bzkMhzYxV/oD25udbobRupcjDyphPYw2uP6tlgAOe1Ozw2lraNRaFyrlEH2c+Y56hw0sHa6HvmALT8u3y+coc8zet4WQNDmtrsa01pbbgfma4CadFDqM2asG65a+3NklnNZ+LWE4ZypJ21rgzVwypqG4jDNfrnflfxQBrGNRTWpnzoSLX9FeNU/Y8xqOwbodYe+8YPOt+67VZuCxl75PwYGeYJVyOKRlLRTHTv/wvv7+OW/N7c7+zsbBDcQwxsJ+mpDNoOWgikq4XyAr3nLNqMlfmUbPyIWC5f2ktIcsRktmWWC2RZq9va09f3raqsFQTpVpLbQ9dLZjXWmF9qGOMpZpHWaiLiMz3c9QW7LyRa8RtTdCt55N/1u5CTYRqfqcao/LK1AhUJz/nflpBO1s4SRarvt/MISuaYvNTrX/nzHqWhT8FxHm8V9gPxfOzuOiKGqmXjKl2G5MIWgipDGQhcHmNQIrnzMJkhkPn+5lJpAo9zs2ehfpffi5bmGslr3hxUj7FNI72bEjhZD55OKY6JC95GWS2PBaGk4QmgiU+jxpxnUfHgTvbTYpzr2JsJQngflYEazwoOAaMUa3CT9ors7gCKUk8M4iua8XfhOsoUWalMQpmrWYOvcsbM9/RAkGMkboOFAdBi/KIagr3AhGf+rSQs4RiZa9zkJ3IvJ9lH5yAmEJDKWGcFItCMOfzomrCZoyWY6Q5sT8piy6V7hXA+RURIo+tIEQIifCpeWpExMoe55CVaApWVvalwD4LvA5kLjXrcGiiHVZhTE19UxPqfGLkImoCnyjohMtCMZmwZlGVuQwvER8UT+VpzbHBZoqYBTBxJUQthmXoEOXMzUxQKvpTaI1mr4UiTHiNdBoSnGZlys5sQhoUn+efQZ9/DYdMQFUX97hqgm1L38h4F0OCUCpTvqCHJAVgDp/CWdqXJBzTqFYefBFGY0wwFzEozDbjYs2kyedjfrYozqTb5QuTLiwylfw1b5Ag+NSlJqVa05oKyMQlRcSnVB+PdsJehO2dO/zW7/82n/2932Rzfop0dleKV7h68Ijvfe3rvPvTn/H2z94g3OwJ4x6v0Gna/3wPAQl9Ufok9Imb77gplWG0QLO0mte1gvjMDx3eH3qt1wTEFieOCctrCkP5OzOWlXfafheKxDERvlE22t9john5szpHLuec1bQ897kmm6zJDEv4HAqxJQyLW6r4VH218omTLnleWmt8UsSExfN5He286+IuLdwOzjEw5+rVaz6igKb1zUpQOucNjtTwKML7IThWWw2XY0pGUYhq3vwUOG3rXMK9fudJSlotz5Q+oVRygoo/NPhdK4TteO26Cy1jhmVdXOdwfrMhrswpnfkowsOLS8IYkVSxsRgxUURhilp4HYD4lOcMZnRBsg27KB5U58o+T+GxUML+fg494+dJBhe6zuMqi9QsYNbCZr2ZifA7c+LMBGDuN2v4+Z08+TVBthUOc9+166t1aeb36+/zRjo335zYKhRlHF32Vbc14tX+vjYXqhyFtiKWWZ4F1ZCspiwuNsvKRm35sFK4y/yGpRKy/KzMTw4PSVEYUJzzZZxSrapiZBn24zgWITorGLVHJ1fVUlX2+33JZRnHkb7vDyr3LCxnHO5B/s57zxSzcma5D5vNhn1IuRtaEQ1v6kDLCOo9jTGVq2XOHyh7YhtU8h0y1hYhKd+dUO1hhnGXKkM4J1kLSNb99L6IXQCXFSixRGpRGNtbVqv8ApGc7DwTIOcpShqYpyJN3mxbSQg/TF6s4TArtK13Ju9x3rN807WIVEnn817VsF07w4fGgST65zNKJUOny5hYCV+kwskWV5KBGhGh8x5NBpN5Dku8MmgIzq8bNdq1tefK+fVQzpqWtbka+ZmD8EatLJEVzHKr88TKXFZCJOuzVcZLfa/NYwnfGSpt6NYMgyXMs9DiRJDkjZyF1YRtFb0t4zdGqLrV47WhercJEfmTdLQQpSgfqAmOVo1HoHMMXognHZ/79S/y2//kj7j7wn2CM/xzwO7imm9/+St868tfgWHi+uIilzCzM4GCMw+eT2e+xtU1AeqYgNIKwsd4iwmsyz3OBr6a/7V4Xj/3pLY8W7mk5lJgmuWAef4H7YhUWq+9hUGNJ0t6IWXd+bP8ThvGW/O6ti3gnOj12phPaq0c0QrP7RzL/Kop1WMe27NaTllTLm+jVSZYxgUtEBGOYlaDg7WssKbcLMas6Ndav207pgSsPdOusb5D7VZFZmXcGsfq50w3PD6ntbU/Da6s0dC2vxq2x9aT84v77Yau7yjKIYklijCQy1Ibb2/PRIyW/5cvT3XOWQhdsCJERj8yLbHLfQMmqx/f3WV7akWj63waNG/IoQYotRa8+JkJ6goTkNxPZelVSlhKfaBuZe6VpTq3/F1tYW+/V/ul/J2Jcn6+JtrHxs3IXSsMB4c7C06SbYCU6lMLBipJG51MNxexC9hCDLQhay1CiswhW4Xh3HKohDnErGZKMdp9HjUcsnBUC0gt7FsBaDFW9X0uA5wriI3Jw9Guxf5eCjFlDYmxOucQtdjq66sr4s3N4vbvlrkviEgrXAGC3bSMpL2I+WI8BRW8LC+AcrIkXu3eW3gHRakrLKc6P5mYibM7RYiKiSuHDMk5xxTDARMtsCqWCz0kBDLf/VDvYS1s1mcmwybnGKzl7fh0x0WOr88eOVQXoVui0OWE4EaIWKxR53jQ9gy1sFgIALaIeV8SA67xd5H42Agpt53d1luJLuFV40N+tzVs1M/Ufa2N1wqltzHGuZz2oTBStxbvW6GhjJf2LrdaGF47R23/7fzqPtaEn1aYamnIsfXbTe1LZlx7lldhgOGhy4qGMbGSizM5IfSOV3/p0/z2P/tjPvLpTzA5GLxLhQEiH7z1Ll/9i7/m7R/9hPHRJUyBOOytwAOCOE90pmhQnd8aL9f25jbh5OkEmfnujcV+Nud6DUe6ShE8ELRUD4xbZR2NcAxz2OihIeNJ8z/kZ/VnvqEbZdWZvnLIm+t+2nCbzOfyGMs1p+IZsjSsle+za/uWlucxGywP5Z8Z9+dQmOXncvBZ/W4bVXHs/C/pDQsFH5b8u+5hDrNcP/s13qydf5gVrGPrWJsrMhsq6vWthe7VsKIyetdzrvcit/bMFYG7irwpz1Xj3HaOjskcbWvnVY+V53Ebv6vn4Jzj/gvP87v/9B+zPT1hs9kY7BIcnfd02xNcirDJ97uBEFN1lXqMkJULVeI0sR/2qYCNN4OJd/h+g/guHYF/YEUjxrk+t2rekLkGvi283oDKZIRDJMeiHbE6LRJSHFEPQ6dsrEPLSY0cdd+tZrsm/Kuamz/HT2dCma302VXW5mm0yFGX282Ce/YCLA5rNX5ej6qWalS5Dr+qphj6+V6QmkXVd42sza8cTubbkDPsMqzyBXo18mahOu9phnEt0NQhHy08Wwt4S9DqPutn1nJLbC5zPsqiP63g4GC335e/Jd2aXLuZ1whFLaDMglZMIQ6ClWJWSBd0uXxFJilHIvGOWlDPY5UxijNTyk3DRgiYDw65H/NJ2rznZL7s0VhUNWnGofQZF90uCEHCqzrHJysHU5yrt+XPa6WkZf5FiE5dLxiqUkLwcunURShdJaTUOFPGWCHYNnbNfurCCyWA6ICRZVjmM90qBLmwxXoe2RqM5+drD03BYWXhIc2tfr7uu8XBdty1PLPW0l8/X+/FmqX6mGCw6L+B/8IL0ozVrqX9vqUTx/Cpfrb+u6Zzi+dCJFawP9iHarzl35LCzUBFiJ1j8sIkyr1XXuL3/vmf8qnP/xJse9h4RJVOHMOjS77ztW/wva99kwc/e5stjn6ysz2EiIhZFi2l3LyGdpGkO1hbW3mvxqljikj++TR78LThUy1/PIYXrYB2bPy1MVr6Lqn0Zv39bby9rGlF0M6wXJtre26fBnbz81IMQWsREibIrC5/Med2rBoHln3Pnuk1L0zdWhypeWtNT2peX8+njkCp4VjWXwvqHCoKB7BgScfqddZ91HvbwugAbqoguVT5EnZr+FXTunAkib+mYS1NaNewdgbyM2v0tIVPS/Pqz9aUnTXFou6z3tOWT3Vdxysf+wj/4n/yL4kpLy8rGZLWnYuWWn9qURJihWB8kjNiqlJV5BNRM5jYTFCt5GzF7kDSHJL15PZzJIMvE7qIcxhG8+DybxE0hnQhUxYW1ty32UV/yIiPHdqWqSyncWjVaFsR0lPVkVq4mqbpwNtRI1V+ds3K2x6oVlBuGUEer+u6Um7UOZfSAgTxrgiXtcei9CGW75AROSPkmkUwvw9YKEBFmMv6Ugxx64KvrbRrwke7zvaA1MQzj1ULEi0jiXG+rbvFgxgjEix0JyzGj4QAnuXN5u2et3gwz1GXh1WMVFpu3Zw0b0qJppj8+RwcrtsUWfF28WK1ZYbpGXdQu+m4fJa08tQW8fwi6Rbk2CicNnc5ut5DIm17UN87cVhFbA1eho+zUiDMeKOqJYyqhNNpJciWIJblPCxW+RAPjhHhhSKZxqv7yng6x3LHIpzYOTBPan3zfCv4AKV6VPlOZ4ac51H2O0Rwh8ymFSrr3+uz0yoCawLTsfDQtv9j7ZgQs/bcMYVg7f1j56wVnlo6etuZrL9bCI0N/bmNR7RzVBEro+wduw7k3gm/+Y//gF//0pfY3rtL9Fj/U2QzRV7//vf58r//S9574y3C1Y5eBURxviOEie12W11MKlZYIcXBZ49ibXhq51sLYbVBZw3Gt7X6/KpqCaethfHbhOy1/lp+VebNbIzKn9f91J6Nxd4jB8+3e31sPjWfzX3XeZC3vdPCu11nbmYsUERmz1gbypvLKrfvtmd3sRadY94PBNFG7oHZSFYLqLWA3PLU+vkiv6wIqnCLVV4p/HZNk2r3p75NvqWZRQ5p5IH8zNo5KPMRytmp19Tyu/bdFmsWNJulotDSnqPnzJj9z3Vu1lpN29f6qOWrFs71+avzg4FyR9vklEk0mTlypI4VO9GgizvYxHludjt8dGxTtIJUil2GvV3orIWvOhGiaDHUICCHdpHV9vTlbesqUDprnM419ZobjS0LiU6XglgNSADXhErl+uktQYKlJSYDT5dy2eJw1Qi2WEIWYHU579qDMsXQHHKlLh/axlqvxV7XRMEnIlALQrXgThbgBOqqKhrV4varg3Gb8NIenBlOS829JlYLT4Usk7lruNR9t6Ebea15TfmuiEyQgMIA19yUrRWmzuFp1yNOIBhj6Pu+hFPBoVJXE+wWPrMA6lDN1nXKP6zHKixpScSaAmlLvBYxwTRbWtIeNy+gGhHv8Q5Ercyx6pJ5Ffiw9ECR9ZJ5gDLWYp0rMJy/yef58G6LNdjnAbSyTvrkDRMopYyBKp8knato6JXfXDDQFTiWs8x8Ttv4YO8NDrWXIf9TXd4+vxTWmzsMFsJp2pdqnKxo1BOt98dKHa+fz2PMrD6PrbXy52FmT9tauEIV3sTtVqoavre1Y0LjGm28TZhuaVPBo6RU5z4X57GlfczbJc6UjKBK6OAXv/Rr/Naf/wl3X3kRXCo9C3RBefTWu3z3L/+OH3/n77m+ukb3I73CpuvAO4Y44XuPi7MXKFOJWOXMtQJOK3Tk+T4Jpk9qa4pgCXFslI0Mx1Ji/EhrhbXqmxUyVtGCysi14Iluyf/bvVrDTRuNQjdrup55/zF4HBP81/gYZPpnYW813yhzERY86ZgAehDKpEpddKZukcq4xTrMc59t/1mhVNUSimz0cC6jX/eR17YWAWJihxRjT1rhwfpamNRW9va7WsloeXLb52LNyYZVzzO/u+bREZHFdQn19y0cb6M3h+/PJWzXz8E8/3ZOa8+swac+I3U/9TlZC+3NvHocBhgnfJciJ7IymXhm9FIU/DG5NzYnW5NNcq0ftRLckIz+qvgKd7x3Fs4fI9551JEKoDwdHJ9a0di4fq4tr+kyDzGVpu/SYTeFOR38rGTMjCzGueqSE49zPmlNoDnhWRwuVS9JjxLCbMWPiVi5LPSJA7okaIQ03mxNUrUqMOTbbsmMZ7a+5jm2BMKI8Sbli1iJRBNaqtARmWvpZ6Spw4fqZ1SV6FwJ4YgxcnZ2VsHHbsgW5/CuQ0KEONilYULJa2hvgJWkddcHodZ8o8WykMuLalp/mILVis+CaTnAWohUrWSIzDkgNZFaCAFicYFFqINU2vPQUpxbbWlumXCGyxqDCAIuQDcZwqsKfYggMYW85ToJmvIeZitJtuJnGOWbruNK2Eteb1Ts8kSRRATtPgXvvFXXyQpDUhRLPwm/S6yjmY6MhKdkUQ2kcg5z3kcWvQ2OVdnWYvEhzSUW75sRmtkjU2RGnStjpR0uPKSrzqHhtZSQIkTIKd6qmipXZQX4UNCr1cKpsuDlnchTKBW3NMXbi1RezRnmmr5TjAA60hlVy6XJOEcWnpL3z/tcchdgzjHJqqJPgnWu9BZjIAYQ/MIqXM+jVE+qGHUp1FApJ6XkIWlP83nhcG21gFG3/F1+R6p/i9bMs513/TP/vipklIGzwKsz7PP+ViasDPNZMDi0DtY0qqypmc/s5U6DFwShKBIZDpI+jyGmcr9WDhmZvb5g50bUqk25/IFzBFW879gReP4zH+d3/oN/xid+5bMEl9bnTWkYH13x7k9+xl//63/Dh2++g4tK2O3mC/68szGyclaF32nM5b67RZ5hu7droXI13Oq/2z7W8SUL8wmulYdkUYWwarNyPwt3CKnweRKoC+JJ/aT9Xk3jYI7J4JHPx0JpqASlej1rwnX5KUWwOBA612h1/fsa32lhvQzrTX9XvNKetTW5dN6TCbA5c43hNeO3VAJ8hTPWxQzXmvfVc2sF+0J/KkWyhkt+v1UC5jWu04sgdiYtSngh0B3F19b4UOhqQ0dv25P2uRhnXl0/d5shxn5fCvOtLHFbP+1YZb7pfy7js42ywI28hvpnC6d6Pq0CVfPQY4pK5pHkcdMdGPubHTEKPnqmYaDznmEc2Ww2JlOJMCWZc5OSwsXNyoX3nckMITKFia7r0SRPFT7kOnQKXD68NIPopufO3bu3mKSW7emTwUWIOPCOqHbD8OLwK0UjygRPVcFZcsnMiJNQkFWFzIxcRo50syEUS2jnct6A0vWpBKHaJWrgQRPzrJedBDZ1njBGlIB4m2MWgDWHc5XNN8t7TO5Yl0I+THikuBXtApNglmcOCViLcHVIlZNZQakt+iJCNpQoWGnZcSROAReCMcxkgWoJbN93hOQ5yOMUpM7zSHJlFsRiFFRNeHb13tjEF+EmBaS6DM0qa8qfVQnew34/w6IhnFmpWOBXt0TF4iVp3OL1YQyi9Dg6FfZjAOc4dR2j7hnjhLC0qsFMROe+ZuZS15JebxaBXRinmCcOsoJgS52nW8U9pnHzd5mIJzWoEqpTCc4QF8wsKzD5GREpN4HWMM5lb0sFKE3rdEsGd2A5yYK6y1ZjiCwJtpNqTZps3y6FHTpX1pLX41OyoOUd6UIxqXHYAebiCAVPC8TTWkyhyFWoksKhihMtd4povQbSeFnwEqk3hqw4CLMi452Nke0/IrM7PgvdWbBXSYoSGV1mQQMS7WIe+0AYqvZ8sQ9Vy3SqZkj58xnD5nfr0uO18FT3XQv/ayFNqrkEbmJ+lWUXsaTc+gwWQaH873hrGbAmHHLl41Zwm+eQF6uF0VeFNYQU2ligYV5qTeex6xiIROfZ3jnnd/7J7/PLf/jb+LunTCJsxeMRhus9b3zvR/zgK9/gre/9iP3lNSow5AseUaTrmPIcytmYaWEIgT6H36aQu9rD2woUazhQ09x2z2ve0gpZ2UhSP9uGvx54VhJcszJR8N3+LJePaoPfLLltu9HFqJN/b8/e07QDBaHCvRr/1hTmGr55/fnzxfqrPuZ/bmk7yBZiyXDOBqRcLETKM2UuauEo5e4cIKf4KRTjjTBXS8qt5bnHFKQ6PK3+7hhsMj2rC7Us4C2YpTqHfmZjUCW85/fafajnulA6qrHXPLyra2Metx2vnXe7v+1n7VgtXrTft+cMqoIvFU2fxYT5uXzGDpUfFn/fppDUnqp6b2Os5OLCF0xOePjhA/5v/+X/hWEaOT8/59VXXy05xvfu3WOKwQzhiVdfXV1xc3PDNAUcc4RN3/eMw2BKa+ehs3DvzjnOtqeQZI8xTOzHgbv37jEOA//y136FJ7WnVjQmmQqz9yh9561UZDqAxVoogvQe1OLnVQQk3bBaAdmLIBrM0pwNJ0nIiWEqVkcRe++k6+YLo1LyZ754BMBtujKXvDFZaFQNTNNAiBNIVwmX4HyHxHQJV1JCphBNSAojfZKHxxDYbLaM6cbiqBCT0N8Sg4wcORa8FtBbRaFFPEtoSiFWMcWhJ/JUWy/qAzFNobgNa4bSxjPWwkUWWOtjUCs/XbrXI1sm6jwNmG/3zvHrAMM4st/tyhxzVa261QeqJYY1M84tVkx8lSilA+98KreYmZrOz9WEL4RADPO4fd8Xb0a7j21rhbS55O/SLX4gCKoeMHl71iw3benJYkXIeEGyoCThSZhlAw5wqJK3WBK2Gm4LGDYMuQ2Fc+JKXHLbX31b+IJoMyumLeOr8b1lVvPq5lYT8PxcG8den6V6/rWAUX+eYZ77q/E1f1bj6CrTXhEU6/a0uLTWjsEp/51bNvhknMzfH4vLr62PtaLRCjcZxmvz+nlbPfe6mQAbqW/3WGP0q7ASQUXK7bd1+GKnphRFgdALNxKJ2w2f+/Uv8nt/9iecv/wCgzfv8lY8ejPy5utv8MPv/j3f/9q3uH7/Adt8D0/y4NVnd3kZqwDLMNNQ8YUaBvXa2v18GhyqBY81nDSvhhwIn5lW18LL0wr7P89+L/fn6fu47QwUXDwS+tW+v8Zvjs1h7VlNMkY7/zVeXdPM+pl2n4GiqD1pze28boNNKwfcttY1gfdQSZNZkG3och110N4jVo+Zn1kLhYVD/vE0raUfa+8XgVyXnrbb3mnbOkyevi1yeXSpyN5WQa8e/9jnNU/Nf2fZzCk8/tnbhGnicYi8/rVv27Mx0vU97nQLWOXYru/ZbDacn51zstny4dvvJNnb8fo77/DwwYOiCE/J8I6me6hUOdlumaYJv+k5Oz3Fdx3/8n/5v3gibJ4+GVwsNosYIEa6rmfrLawlOo90HaAM494s/aIQI9MU6fquJK/OgAs4h13WlUQpu3zLcX1xwUnXcXp6it2YiykKYWLTb+hweO/YTxPjMBFVOT09JeIYx8AwDOzT7bwzUQ9MYSSEwJ07dxjH0RK/R8em2yDe0/cGjpOTHhEL9tCwZz8MdB72+2tudgNusy2Hqa3+BEuEq4l6q/Hnf/OhTrefMpe7y+54ScLzGjKuMbRWyGs1ZVVF5bCyEHAghNUx9FnZ2O12jKPBs+97O+jVoaoFmSKQV8JQVmTqcWthKbeFK5uK6NsLZb5d3zOFkDxjEIMiLJPlsnKw9Ab1xRVdw/M2hlULPoXhiVudf1YJavgt92wpcJRYTeeWaVFUrvOQk+TXQmVmQb1lWC0hrd+/zXMVZd6bhTVMcxGHdSZXr7nFp5Z5z8T00IKXyyi2Vqt2j+p+a69hu4etoLK2N62A165xjWkcU0bWmPFt79Xvr817QWsSHcpwqsds96JWKtZyBp6GobdwmR8+eHT13Xoc1+L4UwqMmXY5LJzBGQc25SN9FhBGD/tOeOHTn+R3//xP+MQv/gKhE4Z0gWOvQnx4yQ+/8R2+9ld/y4fvvw9joA+QAxdDCpXsZJm7VBsO2tr0xcjlZgvkWrjawujTeJ/WYNHykUP4Qj777ft1pavFHpMs2Q0dXhOYju3JwRwrS+9xYf7JbeGZb95Z9lvMLkdbDdP2Z/2MiCRz9eGca/pV/575WOZzmffVNKu+9C2/l8d8Gg/Gbcpo/dwxGtS2dSUNSnz/kdYq0DUO15c657EzN1qTgY4J9LJibGrXmFu9NzHmoL91HF6DxW24fYxezw8dKpDH5nxbP23+Rc2fFu9UuFEblcZh4OrhIz54771qTWmCIsa/8z4xG92sML2Vpt9uNwzDWAzHvrOKe6itcIx2hcDNfgciDDvh5tGjpz7LT61oPHj4gLt37nL/uefY9ht6Z26Vm+sd+2Gi73v2+xuub65xDq6uLtkPe/b7kdOTU+7evWvCXro9Vwl4D5dX1+zHgdOTc3Ad5+d3uXN2xumm5+TkJN3fYSW5LKQkcPH4AlB2u10ad8fjxx+CdAQ1q9I4DFxeXVZej0CIge1mw9XlBZvNhqurK05Pz9huzzg/u8PJSWLW+OTyVNQ7/GbDww8f8ODRBX2/5c5mW9z2a0iyCAupDl4RcpmrcsDsHYhq3gulK7F4QBE6s2P7wCoJBYFyCFJ9SGqhPr/vnF/cUFwTPucsvn2fSsZmIgJWgWcYBpxzxROQL+CLsrxzoFUgpiYxrW61EDsrh1Vsf2qLRHJVVMD3Hadnp1AEGI/EgKiUueZ5uhTi4/x68n+2FNR7WvahIvoHZUdXmEiMsRCjdQI371vLzIrKUP1Ned4O/1r8bT2no4S8EfLrtdU4MhO8Q2vs3NfcZytQ5TNQK5w1XGvBt+6jHaOGSxaW6osua5ivvZP7bgWXFk+zu3mNKbaf1f/qsVuB8tge5L7WFKF6zmvnZAHbal71uO3abptTu/f1sy1cW0VmsU9H1lvD6cBzWMkUt8Gqbs45KwCnglOhc8IUo122FyyEMnaOk5fu8/t/8kd89ku/gW4c6j2d2B0aw6Mr3v/Z23zv777OWz/8CbvLKzqNxClVHUqGk4zg2cvbWnZByRWKMu0osKn2pfYyt3vTCn1reLomeLR0Q5KAn+l37jP3n8dvQ7mysFQLxsc8yPXvazStzKv67EnvtuegbSJSBJ72HKYnFrrB0wiWLZwP6ODK80/DC9pnjwmsa+doAb+VMeGQ5re8ql1zO34OExWRZQXKhk7URuEWD+sxatxdC8U8Jmgfg2uZT5KEWnis0cjcTB5a4km7r7eFN7Vzb3lBHqP0pUujYkt76/5rGfDYmlo4HITCV+/V/DZqZDfuGHU6MCQQwaniZc5R1hjRMDGqEpKhc389lHf7rmfSYNAXk1+is39GYrTINS0MjrWnVjSEjt1u5CeP3sB7z6bf4DuPRkuYnqYrlEDfe3bDjgcXj3n48AEvPvc8u5srNE6cnJyw3++5uLjg5GSDeMtn6XzPbjciDvpu4kJ3XF5fMw7vMU0T4zShKcSEKTLu9lgCbGQcB7yHV155hX6j3Dk7t4TprafvYL8fODs7I4TIsB9M0YmKwxHGyF4GLq4G3vvgEWCCrLm/zVNyM16jwKbrOTs7o+tPiNOINhaujBhrLrL64Hrn0Mrikb0H5h0Zofd0Xcc4DuTYX0Mm24WaEBRPQwx4v7w9OjMmWLduiaTQA+eK8J7XnglYfQ/IOI4lDGyz2SwOQs08qZhibqpKSOWC28N4TJCaBRFZCNyLn5KZZ2SYRsZpSsXdMKUmuRbb29dz4mjLZOrx6zlmuK01+97+1Uyndh3nPTkQYmERn9taNWUxhnUmKCEosZrOkpEdembWwmJaRtISsHaNGV+zl9DmumQoC0HFLyu31GO2xH/xU2fJs2XsrVcr/12HsizgVb17jMnV/bXfHfuZ32nLW7fj1s8em89abPGTxs7viUhRruvPjsE399Pi/rF5r53PVlCr1yCN4HabgDnPOccbL9dxKywFLP7dDBExKuqFGwLxtIOTE371936H3/iD3+X8+XsWD+/Meud3I4/ffo8v/5t/zzs/ep14vWMaRlDwndit8RpLNZJcSn6h9C/WMt9XMI7jUmgWQZNiXHuN1+hODde2xO0xYbSGp312WNVo7Vxn3FVdCgq1cSGfr7pq0YE3pJn/jA+6qIzXPru6p096rqGHx5Sdlsas4W+73trQBrOSsTantfFa5bk+2zNeG11bE1xbYb7tP/eRaflRfnGEzixpVOZJy3LpM34kIbLBzzznmsav8fJagb0NlmtnoG23KSnrPNoBh5dL1v3U0RbHaMxtbY1v1OPUsFjbj6dpNd2u5bk1Oi5iCqP0qSBNSvImPeuYDZr5rNdzTL4n2ztvxtuQ7g3LK41YGGpUu6PMOYekGijqnm5NT61o/O/+t/97PvOZz3B29w6nZ6ecnp/Tbzecnpyx6c4IYaLrhBAGzu+c8Nxzd+k2G7x33Lt715JK+h7VyP3n7rHZ9uyGPYhnmgxBH19c893v/oAxTgzjzkKghoEwWTLLxcVjxus9u6trbq6vQBTn4Jc++wv8j/+L/xGnyQMyTVNSQBz37p7T9xticPT+xKyW3nN1dcW4D3z9a19l6np8tylKCCjb7ZZhHBl9Sr7VwCsvvsBvfOElvHM4IipucfiOCWtrxC0T8tmdbRqiVUOyakYiTVy/LK1atYuy7rdF9nZu9SHNSkLNRHK/Wajc7XZ470u9+LyOOqQqz+MYsVNMEGkVifqwtn0Z4ToUPsr8sTKVURXnPeId4zhBZ9ZHRQ88PPb7MpSnJVytspFeWqxrSUwOGUh5BrI8fhiyglluWBP2YgSkJCCbdyTta1XbuvxL8MihTPV4WSCeYXooENZK6gJeQsn/aZmpCV9LprkmeK9eXFkxwKUCYX22eFArTIVIVvdo1OOtMch2v+t+jgl99Vlq+11T3o6Nv9Za5aB+P3+/xmDa79bamiDW7vmxdT1pHbcx1Za+tGtdhwNFsGnP4wEdze+0c3LC5EC3Pa997pf47X/+z3n1Ex9n1EDwziqURXjw7nu8+8Mf88Nvfoc3f/hjOqtETHAWk+wUrJSZR5NHwydFKIcXHXgD1Iqd5DLeqjPNqfH6GGxqmNatFTBruBzCMCndahRlzcue+4Ql39BoXuE6pLWec91q5afur+Zl9rvQLmltjS0u5d/X2m3KU0svjsGrPgs17Vhb69OEAubW0qVjykD9TH3+68/bVsM8K4htqG+9tnY9bb8hBkSWVvWixGgsxLeFXd7jYwpcPcfa0Fl4YPXMMdqz6FPK/47Cpl1v4alH5lhg8ISSzre1JX+n5C4+CYdro8zPq3DMdPYQFsaHhZPOcyWg5MJIc4uSvJY6G2qyH9MnGUPTgmba4PDpcyfKFFMlT1WYYskVfdr29DeDj8qPf/hTXvnoR3jpI68S3cCp6wgy0IeUPKweL3ZZ0cdfeZVpfw/v5zJ7d5+7y/Z0C2qxxbt336f3HX0nnJycs9+PvPHWm4Aw7gd2ux3X19fcXN9wc3PDbrcDr5ycn/DcR17h3r173Lt7zsdefZnNySniPTe7PTc3O7abDc47XnjpJTabLQ8fXxL3A9f7azyBbtsxoOydA9+xSzkbCnRdz6AQnGMKASd2O+y4n+i7DZIE2Dge5mfUpQTz54sD2ggWWRCc8yJyaIgjToBzpVqFsLSgFGakZqHI5W/rQ5/Hz2PNhM3+F1PsnWiKsUwXy12mygTb7ZaTk5Ol9TYaPDKSQ5qf8+QyiySB16cL0RTFd10pK6pJcEa1WKsk/R4TLLquSyWFsQuwYhov0VjRSBgnJjUFbSOejfNMPhFQ5+ichTdoYsLiUqWa3NeCSR0SjHyw7TAurU7l2bQ5c9WqRBBSib5cQSNXJ8kCQek/70kwN6h3HhVfRR5r8dQgFEuuwUDKWnwaw1TlpJhKriTlmoRyMcUv70GDx4WYpedRq/gkzlfKgLlkNWkcIuAdaLS/s5KYK7BQEsrDvB8Jbhm3NJW4dRXsixqVAJKZWSsUtUJ1K0isMeD679bqHMNc4QiRhLMJTprOctpTSYwxe6jymb+NQbZzqAXLlqEcMp1DBakdT+qfagKza/D7mODaCkK51Yyy/U4ii7rkSqWAIKXaW129y6xp6+53l2hJgBIqJSlcygeHOGEUGDee89de5o///J/x8c/9IrLpGYg4BR8CNx8+4qff/yHf++a3ePDGW0y7PS4LhNYtUa30rVUscxVDXho5ui6HxNpixjGU6lKd94QYiSEV56hCauqQK4NfTXsSnpJpjS94JOTKgBkHZg7fKrgt62/Pc2tMqvlUDgur2zHloOUvh89KoaVtn+17xz5rleVsSGnXnHGo/qw2ZNQ8r1VA7Odcyhl1ZW/qsdq+898Hwj1m+MpCnIjhVilHWD3bCp5ZRmrPdat8r82n3adjNEfEwmey5xEOQ+Tyc+1Ya7Sm5ZVrc4blvtVhfGsKRIZjORMNza77aPfHBGwpckWWl+Y+lzBa83q047UK1HKe63xziV9LmK3BZ+37deXX1lZ/r6pJeTzBHBlGvxavLdad+mE+O7Y/OT9JURXUCSHLNdHOhBcrjRtjMIO8rBcMWWtPf49Gt2WcJn72+hsMU+DVj3/Mkon3I/1Jz/b0FB8jLkSYRkvIG+2ehgic3bnLyekZp2d3cM6x3Z4gbsP15QVhGrm8eMQ07nn3vXe4vLhhd7Xj+voGEeH09ITn7t3n059+ge29LbJxKI6u7/GquL5nDIHnn3+BYT9wefUW4jtOz8544823+chHP4LreuKw59WPvoJzwjvvvs/p3Tv47QlDVPCOgG2aE7OG4xweE4CnYV9qEXvJ++4QyfdqZDwwqSyX0a2tX3X8a23NLUqAmhU7xMgUMnFVQoyEqHR+eTjnMK3Dg1/HCufxWqLr3KyUFAUmMcoQAtvtdpEsnt/r/Zw3YzknUpA36vJgLSxlkksHG7IfxmtLEYqsX+Z645qF9VT+NQtOzpkALNi9I1MgilVf8Sm8IrHwFGaWppqE8DLXNAZJGFjEWku6Z6Fa14L4JqFz7sjmXW7HzjX+NQ8yK42acCcTEKu0lvCoEii09J2ZlpLjJAvRExB8ecSEIS3KbRbYa0J3EKrWNE1E2/6R3q8ekGpaxesSLSZScrEDDoTJJdHNlmEtSky+6X5BdGV+9yA0r7kZtx6jHa+2IrZrPVBuKhhk4bNmODFU1cdSGWxZYYTHYFtbAOt51ox7jYmXNTZrawW2XE57ZsTz2aGiGTUdaBWJts/bhIzcv02I+afM3xkarQsZ9RqDS6E9Kng8GiMbl/IknGPqPf7+HX7zj36XL/zel3CnW9zGvncxMjy+5O0fvc4Pvvltfvq9H6LDSBciLvUfmXMpvHN4N4eM1jltmb5nxmwWZaORwzCU8soZ3uKWl7CWW8MrWAuz8CNllAovSHQrK7b594av13uTnRo13c3nIZ+Pel7pgcW5WsPFY+O1+wUpzBcz8rR4Uj9b09Da09sKfLWw2vaRv88elFrBaMds8Xym60bPnHSZMSQlYV14Pybsl78zMUyGHiQbfo4L47dFQxxr9XOugnXdZw2jMm9Zwin/nj1ixxSHNeXnWGtz1gqe34JXyzYbBvPaao/ZmlK6Nqf83gKXVvavfr5ee42/a0p4Zumt4vCkc7PgM40cdBts1hQtEUvm1pjLW5Muza37WfKSTIOdE6LKLFuIGSTzpbsqYsUwynt5TId0KYrmKf0aP1fVqa53xCny8MGHTHHihZdf4s69uwQ5J6ij7zcm+EchqOPk/A5d73n33Xe5d+8e5+d32G63XF9fI+J54YWXeOH+fa4uH3N1fcPlzchbb75NwHH//vN89FOf5P795xaXxgVGcMoUFO86Tjc9u5tdIaR37tzhtddeA+Ds7IxxHHnn7XeIruP0dJOSg4XNZpOQJyU6J2KXKynlZD/TFg3AOTm66zoTmBuq3yJojehFcE3r6Pv+IJFrJpxZcUlMyzt0nC8tLISBZJmStZvPtXg41uaY1yEii+pcMUaGYUBESpJ3+16OiR9SzeVSdWqlicxVg0KMhwy3WncW2HIlqHotNVMqnyVBwS4ztHmfOYfZQNcPtuHyMlGzJtpx5TNIgm91AddhbP2SCIskN3fVX6tcZsbUwgPMakAVOtcy+JYJ2O+A5nyeNYawZCSLUCc9Lni3nx1jtjXOl71x7gBeyJIM1oQ6hwu2iXD17/Xc1yymLYyWwthSCTjAjScQ+7a1/azhztMw6Lym/PuxZ5+W2cMMr1poLriox1nEsXm0glC7H2vPrM29Fm5qgbjF8SExwk2APgqd2zLEgGy3jCeeT/zar/ClP/unnL18H+m8XdA3KXK959033+LbX/sGb/7oJ1w/eEwXFJ1Cqmx4SJ9rmlivLc+zDjFVtUIkIubFWNLuZXJsXkt7b9BtgnMrjC/gwuxZPQbf+vd6znXFvTUBvp3P07YDerBCS27rv8XpGp6LvlfGa99fw9m1MebPaiOXoFWO2Np818I9yzOCJdyu7OExulKfnTV6tqaAPA2NqgXzY+1wH8woRCNkr53nGt9vo3lJeDo437c324OsgB7w4pV12Xqz0Wo5h7JHi7U+eV9aHlvPIwvemX/X/d12fuu+W3it8du6aVwaBZ1LebXnZ3R9Xz5rjXDH9k6qPON6HvkZ13mcd0U+bGF6wNdvaU+taNx//j5XV9dMMXBzc81+2Bk6hEi3C2zPzthsJrwoo4PLmx0fe+VFwjTy8kuvcPH4is98+hznPX0X2GxO2DHQ+y1np6fc3Q/cDMrnP/8FtnfvIm5WLmYXt9D5DTEG+s4UGxD+36z9V69tSZImiH3mvvbeR1x9Q6bOSFlZlZVaVFZVqhKNZoM94PQLwQbBR3L4MuAQ4BP5Y4bs6QcCJAE2wGliZsBBT3dXixJZlZmVKrS8EVeee8QWa7kbH9zNl7ktX/ucqGoP3Djn7L2WC3Nzs8/Mzc232y04AkOfDo1rcHP79m1473G22QJINyRerC9w685dLJcrJLmYmEFStS6Xy6JcZIto3PLOk+AdONSgTU+ELlqASDua2aQt7zyQb3mOMQLKqy59lHHJYvPeI+a0vRZM2IPpWkiGEKobygXcb7fblPo3M65mJivQW4tLvrdjFcNAFLmkF24tAhmbTR1swRwg26NpJ2qxWABYjzssPL5TnWGJXAEO3bZuowKzDXBdhAihuh24FkgjD0zpg3GuUT+nfRItRWrnOin43P8ZPtTty3sSMhF45CmZ8zkwo9u0ZwxK3xRttXFox2JpkpRLLcTkpycHUoft9ZxOPLVoA3bdR8uzVkFoBWnB5BzAlosRdT1zykMrIivIdb/0uQALODQdbXvakVHVTTTecm7G1pxL1ZdWX1uK045zbnytZ9IHgGeCD4QupsQCW8dYH3R45lMfxff/6Ad44TOfQDhcoPeAj8Bix3j0xjt48Na7+Olf/gQXp2foL9ZYhHTWgiPAXZINOpxV36osY+66riS/sOtd5kK8wJJMQ2jekit6/DHGFF4IatJOrz/LX7pOW5jb8yZt6PVReA9TAGbnpSXb5+bP+5QWM6hEJpZnrd6w/Ck8X/WhGqfm/2Z39vZXv5/WMsolven8ggQ/jc+3dJ+mVZqviKjqbzn/Wn2Y22HVpcUj+8aov6/eZTa7dfqdHJVsvtNYQtfX0kGWT/fJl1Ypn+dwM60DLA/ZOSAC5gxFkeegtvzR9eodNo19rIEjulaKjVixxdLN8uFltLHfSz/XF2vw9euVPtlH37LDXeaj1tPp/UbWqwb+2MezulzZ0Pi9730XZ2dn+LM/+zMM5z367Rb33nkbTx49wvMf+yTW5xdYrFYAIg58YpLj42NwJsZyuUTXLTEMA3a7Ht4vsVisQHGAdx0OVh7Xr13H0dExAhz8okvnBdSkDX0PUL4QBg4cgYAIH4GuW6LrugrIPvvsswCAzXaLAyZ0ncOzd5/Do0cPAXK4e/duAomZAWWXQUB4IiwQhoCld/Be4lg9iNJWu534yhhRE1QmpqFY5HuxyCUGTs5NhJhiw9PZjfEgV9/3AFL/vKOy5S9KsMS9G2aw2aJijGXczIzFclm2BPU4gDFrg/wufdF00OMqz7h0rkAbEBZECQ2BaezoxMtKacswpmizcnGc9qZLfRaYSWiR7bcoXg2Si5ImQkBdjxWodmt3DmSW9jAudv0uUT6DsUco6r6VtsSbMwfqCNWWqsy77lOhQ2MMliZaIOv3iMa+C8/quYYBGhaI6jmrQJJ6xh5wt/Ng0yzPrTk7l8KLLcA4AcNmLoDRaTGnTOw7cyBmzjibtMe150+PraVw5Dtr5F8GImy7tu/CSxrQ2jnV87APwFJCDFhGAgeHQIR4tATduYFv//D38blvfAWrRVfud1kMwO7kDK++/AZ+/u/+HB+8+U462B3SOQ3JHJWAC0BuCv41LeU7mxIcqMGjcw4he/ssOLbFtkduDEVoKW0bVlraYACon7e8N0tT05cWn+rSkm9W7ln6zX0u/8Q7alOZ23613tfJRKbf7wdo+8Yn+iTtaDBA7edsf+33UQ7ToF6XUlr00XS1Wez0O5ftTthi16blrdYdVuR8Dr+bn0ddh8U2V+1X63dLV0072+4+PWtlTlmTSidJ/bof1hiarC0jvyeYAjVGaa3DluxsyVvt4NQ8QuSqOdP1CxYU3Wfrbc1BmsNa740OvIgcNVWFr+n5svy9r1zZ0PjWt7+FzXqNmzdv4F/8i38BT4QQBoTtFo8/eB83b9/BsNtit9vgadyBEHCwSsaEDH636/MCZAxDulPDgxGJAXJYrQ5xcHiE4FwyIFw+KA2dQjVPBnkwEtjuOoeuW+D4+Bq6zuPo6KgwRiJIgO88Pv7xj8Ej4rXXXsX5xQa0OEjhP8uDcplctbDzIdrFwsETm+w7ESBfMZxmXu9rgVMJakwXe/Kax2TIY2QU7zy2w5jpSUqVUjYDTK3sNUNp5tC3lRONjNX3PbbbLVymOWxsYy4xxnIQWVu82jCQdioBzwDT2G/NvJpG8r54Ca0ybCl8AmG1WjbA0tjnInQ5GSc6/KBeuFNhTkSwy7UOkUiDa4I7xmjMzpQ2mJNY4XnFNhG03Ox+eiYyIut4yzZYsd8DtbGg37FCRmdESWcy6kupCs1kh9KAWauEtJEhvwfl6bWeIw1i5HOdHKG1S6NBsOY3oumOUpOutj7UvDL3rubl1ny2PpO/54yL1nOt9SXPzSkhOw/aCTCniFuGxFVoVstpA8yIEFYe4dohPvWN38XXfvD7OLh1Ay5frNqFCDrf4IPX3sK9V9/AL/7qb9BfrIHdkC/LS97NwDEdgs/r0Lv6dmMtm/UOrPU0a+dNUcp7wJbmK0sTDY4/DFCbK4lf//71SNEGN9A2eDX/TftSe0lFfujdozmg0jRm3Nyh7r/7GCugWz5L8e76PK2dH91nCbOWSloAda7tFk3t2rBOlxa9WnPQqs++Y4Gz7OpYuTK3prWjR8trXXTWRAvuJ4aOfneP3NQyZ67o9ij3Yc6AsqVl5Ov2dR/1dzVQnxoS+/pr+z6ZP0bKNql5Vs3L0eEhPsi82HIItPgxScda/xa+kGZV3/XOrXx+Vdl1ZUPj7PwUF2fneOGF5/GZlz6Nl3/zMg5WRxj6HmFzgfvvrbELASmsieEowju5ATpmAohXI8D7Ab5bwDsPR+ns6Gp1gIPVAc53Wyy6DgBh2I33NzgQOteBKR+aDiF7yR2GfsBms8Ht27cAjIItncnwuH3jRiIKAev1GiFEnDx9iKHv0QdgN/RYLpdIMeKZKSPgfPYUIeUSToLSpX88FSyALMBx90EEqt2S0wtGDA1yDt45hCEAPG7LM4Z82JSKwGZOlqzDuIi0p1f6NQXgo4Eizw3DgNVqVb4TAQFMs2ZpAWhBzJwntgUs5dlKWKsy129ZDJ7SNj1zoutut0OIMcUVxtHQqIR3TudYz1VbgOt5LYe95ZBf9QzAPArvagGqzzR9Ur/qdmpPTfqnhYDdwtRzLO8HAza0wCrZdFS5LJaXaDxj01IqViALDSJzORStgeQwDPD5osd6q1avo7any7Zrx24VnTVEWkJRxtdqR2do2qewbdFGrB6fFfz2vgRbbwuISLGGfGte9BqzbcwBHXl2Tn7od21o5qxCBioD2NYP6PWVno0g9AuP57/wGXz9T36IW5/8CMh3WFAHP0T0YYeLJ0/x+l/+DL/6938FbHZYREYc0sWhSeZk2hDKPRqEUX4JfTRgsl5UO2bArGEFLKwMs7K+lmP1+m+twRbfo7G+576zpTVPc0XLd22ItWhi150OKLHOIrsGLJ9YoK1/1zS2fdo3Xt2e/q7i/WL05dj7mX5Y2ulzjjFEMNX8bR0Crf5dFbBZXWvH1qKlrTuNbbrDAci81fNjZcmcPNB9qLBQZnQrR5t8o+nspmvBjsfqgtTUuDa13h2TtUx1x5RG9V1kczpAcE0Z64ys1d/PzZ1tWz4veArCm1O+9N6DHE2cJ+Wn4ue6/RFf6PVU5JM6Z6nH0JKTl5UrGxr//J//N3j/vfexXl8gDAN22x2u37ie05du0fcRIUZcu34Nzz53B91iAeocUhhQQIp8SKnkjo4O0XUeoHQTtiOfUklSBGiAX3jAd9hut0mw+JRxxPuUUUeATOcchu0OwAKHh0e4du06lstlxSgHBwd45u4dMAH9bg1aLnHnmWdxcnKGDx6eIOx2iOB8i/mugCBH6aCfYwAxCRDPHgSC8z4JpsiAyi6UZycdEHT1YdWi2EIomWKEiSVsyYkyJErj7Dw4BJBb5SwBmbkjpzAyTulFwemgNTAKdgmjskV7mIjSZXf6cr4iLBhjP5EOuSUPXi30hfGstT4BbY4Qwxi6BJKD18nroQWyvSxQ00/qDiHAxZT1IBDQbQNWvsPg0jx05EuWKOd8qT9lYqo9s9rjGGIo+toaDY5QUsgh7yLlSzJBXqY/JRiQyCftFZ8oIAIYozCxW5RJ7IuglhixtBNlhay04cs0pMY5jbY6t2F/FsMA6l2jPMpIpD0jYFreRjTmruu6Mrcy76IE9K212jiROUrhU4kwkZM3WYzsZBSU3sORg5yK53ziReoPmb+RFRMV73cx7yZKs1Kear5aXm8PSme4tEIT+afkvBbY1gvWml9b5tacVhxSNODjPNclhTAAa2a7VFGam/yc5FWnVGH6qfsnPCS0y32JYESK8CAgZ4OLyGmmwVjAwXOiew9g3QHXPvIc/uCPf4xPfvELCIt0q7cnB+oD+vM1XvvJ3+De62/g/TffRthsEfoBIYayw6DnqMuKWNIVa/3Aip91nxko2aRI7T7L56Rop2neAsctAyLJC33BZaJF5r6UhhQoN7+L64GLAwL5Yq70RhYTSOqgBhW2bxbsy0Vec/xmweHc93bccwDagrsW2JsYu5ieZRufT/Ro1avXMSveSPIph2NyvRbJze8N6d1VXbekxhfnHUceZzOBA8CMSctKDdz0M63Q1JbBUc/xuKME4mqnixwQuI58kHYcEUIDyLb6NccLFrimyJD2+QPLG9UN6xiNPyr1JvwYaepASX1q71gX/kUlfptOKD221vqp6hcSN/Sq5UFpw/Kird8aN1WkSHq46rfULWH9E8chcwkdjYK9kJwv6fK9Qo3EGznRDxHBC9VUJISjlGp/bB9XKlc2NIY+XYJXsiURcHp6iuPjY3jnETl5xA8PDrHoFjg/v8CTk6fwSDH96YxGl0HigBB3AAI8eXRuiRAJZ2dn2O522EYG0wAQYbvbjSAROWsmCKBkHCAOCIGwyPVvNhsAKBmXvPdYrlbohy1CCNhsNrh16w6uXb+Dn/3tr7FcLHF+sUM5A5EFr8s5g/vdAHBSYAtaQRaxqJjCRDFtuY6Ke8zaJIIhxpz+M8aSqUnnM+cQMnAWpZa8wl23QreIAAaEPojpnhV9HWsvfWJOlw7Kjd7aczdavlxSL1bZqbj8D0ASmkNIh7d1TLIGhLpdMZ4q0ASaLEhJL1vgoFng2uuojYHSfmT0iIAnbM4usPA5bnsIcPm+B7HaZZeKmRExjfMtykd5Uqziy+RIACDW8z+Yy+PGOlIGKStwYoxlfm1oRfmp+iBAI51Pkr9M3yCGCcZdG6Lqaf3sHBigJNkLP0O9LyBSlIDcANyqQ9Zga2dhAiyASrlbepWfPNJv7GwyLAJCtvESQGYx3FR2uGLgFDBMRQNpemtF1goL3LcNTgntjXKLUvYkMZS08TRnSGj6aAXV4hXLdy3vc6OBEfjYPuTvZPfSab40wNyOu7kGsuGNyCBO/JivxQAoncFgR+g5ort9Dd/6/u/hC9/5OpZHx2Cku3A4RAzrNe699Q7++j/8OU7feBvY7bDL+kE7dLQ30rkUOotYG7CaNszprJSk3pbnWjHz4OTUkbNqznsMM0B8HwDXf2v6AUj36WD6OZCdW6Xf5YFZPtL90CDHglT5uQ9Eaj60INgWkduttq4CVG2bUO/pMe1rX9NXn7cp8xBTiHN9kWycINIWv7Ta8yLnOI9DvkMt23RdrTascWSf2Wf4ybzEnKjGkSs7rIWXqQ5zLTosO1RjjDXoV++2+MaWis55/HNj0u/osMVmiBiQXUbT98c13959u6y0eNIC+in9MdnB0t/b8dl29BppvWdlhegxy9uRI4ahL7rB0i6dTHCQiCiGyF5pc4w4GfvQ3rUoWOKKBoaUKxsab7/1FmJMWZxu37kD7z3u3bsHIkIfAkCEvg949OgxvAcePXiEG1/7WomHFQKVfy5juggQOsBRupdjuYQfAmIO8+i6rmRHYlYXHhFhsUC6WCQyHj55jFs3r+H2rRsAxtApAPAsl4URnF/AdQEXF1vcu/c+3n77bfQD4JZLHF4/hss7CzGm2w9Z3SLtHKVzG86lLXiqx1TiodWEaabgbCDoeDfNbJIaDzECpG5OlvrJJWONU6hTHIYCYrUClUxCFrhbC5oop0fzvlaqhom0EGwJIPuMbm9O4YiRVQQj1yFXtu92ccnvzjv0MeDgYJV2wGIs4VTiARnFfN4ZKMZ+aqPMhfFkyaKdi3OfK3phpl+nihZAdd5A01CPV/ezvLtfx6qSPX0jNpn0syXkLKhtAcryngmT0G2LJ0TXaX/Xn82BBwvIW3TRdcnvc2DoKnPYUqhW6es+62dE9lg+Tlh7WoetuwVEWyDe/q2fnTPuWmVufvcpzFb7rb7J8+lQNqULJpPgBJFDdMDWMehoic9+7cv4+g//AMd3byI6AiKhYyBut7g4OcUv/vKv8cpP/xZnDx9jyYxF50vSDqG5PbsjAFMnsdD01EaK5jObmadlJFQ3bDd4YY4m++hbnuN6LuaKrefDznPM4BKYhni1+tXiw8uKDR1tgbKW/LF91zxVn5OYAkI9X/rZETzVur0eaHsO5wymObpdlU5zHmw9dqlPj0nPhY4GSPys7mNC7TDhxudFZpDaPTZttwB8SyZpY6EKidxTrs5bKZJgX4hjC/O02rN/zzmPWn0TnGTDmW39l/G3xhaWd1p16DbEIOTIODw8mtRPJEllzM6N1rlmrHqH/T9lufoZjbMzHBwc4Ctf/Squ37iOi/UaZ5sLLLoFzp6eYbjYIA7Jy3729BwP7z9EGALcYrrIE2MnQ4O8A+DhugVefu11PD2/QCBCGCKWy2V1GC295xBDwK7fgbzDwns4T3jn3vv4xte+AuI67MZ7j81mg912l7xPQ4B3Hc7OHuGXv/wVHj8+wdOzc9x+5hlcz0YKczqz4bIw6jzBZcUSc6hRGkrbq6gXvWZCWXhawcnn3vscopRCCpIxlqxQ53M6RSRvfORYQqec8whhvPtD75LoxWMFcDrTkJS0vhW2MCnqRSXjaS0MHZbRijuX5228rhgtjDboEn7R507KAsgLRkLZnEqHPPqQRs8DkMK0Sr+UMKz6H0MlBOZKJei4zuIzFRjt1MeCJ1rAW363gjPG8ZIcq1CZefQ4KCrIL1aEzyl8LeBaArBVh1W0ROP8aj6/DGzNef60Mtf9tABffpd51fOk+aolSO08aH7TCsWCTt1X2V20a4Co3gXVc9sOA+DJ/BbloYBBa250fa0+7pt3TU+r2Gyfrgo6CQCYEt9SuumanUN0hLDwePbTH8N3/+Ef4fanPorBEzYAOhCWIPRnF3jj1y/jJ3/2H3H+4BH4fIuDyGDH2Ib6cKLupzbe5V8IITuJxudsLLamh+V9K+/s55ZOdv1anmnNoXw+ZzAkUcZV31v91XOzD7TLeOTzfUaNfsburLWMA90PS1srKy8DhHYeLouHl+8sH4/tAckZZZKWpDcn7++jRWvtTOb+it6hFr9ZMK3Hp/uhP5dEL/vklOY/IkLnHYbYTjIhz052+Br9quQjj97yD1t03wsd4/xas+vhMppZ+Wzn24L6iUymxClWHug6W3q11e+WY7iqyzgr5VnBe+v1Gs65yoE91pN26mIO50sx2zlk0qRj17Sbm2fBFVeR/VKubGg4Ity8eRMf++hHce3WTfzmlZfhlwssDg5wa7ECuac4eXQCB8JmvcG/+Vf/Bj/64Q9w++7tknaWmccYbQDglE+cvMPZ2QV++rc/x4AUb7boXPFWCTGTFz+AyIGcAxOhjwxyhF+98gruP7iPF565i91uVw42x5gyKqXbtsdMOD/5yV9jGEKJeV2ulsnD3PdwPsVZx5i2sMMQsBIgmb0BjtKBYyG2hCcVIJ7BhmYgCZ2SEuP0oFgK+SFESErbFCJE1UTnmNBcX7dYFEGmjYHdbjcBRXYhWaYsTGyUjxgxdjtRexCJxnsZxNreZyGXfjgNj6egVegn3poEKAmQg18MeJ+zZbHcsp6/QAK9tSct/bQpPi040HMk32salc+yIpHPa/Az7pLId614fE0jDVTnFrMWepqW+nvZuNZKTrerPbJzdWnDstQr31P6nxXYQnnnqKrH9ru1QyQ00/RqFUs7S6vLQLDwrv1M98PSWH8+p8gsYK14phEe2OIDGbf8beOpa1q1x7Zv3LpYR8Skz2buNd00H7c8jLI2IkeQ84hMIO8xgDB4wtGdW/jOH34Pn//mV8ByH4Zz8AGIFxvcv3cfv/npz/DqL36F/uk5aBeAIV1kGdVdOLqvdixWhrTmjZnLoe4WL9uxtuq/jO66D63+VGPgtoeWiCr90Zq3uR1mPYd2LRYaNPpi6acNo8vAo5UzVnfo9lv8remmf2+trdb3QHuHID0XwVzrszLHqdKqz9oZpWWDXgtE9d1V+jlELuu/NT691qyXfB8A1vVpw4IwXReCXxBrwFzGZsap9Z6VW3rcLWxQ+oPcZJyGK+siPGq/s2u2zCeN3+uxt2grz+1bn5pGrR30Vr/IUeET+4yVS1KflZPyng5ls/UVXRCm2CuEgEXnsd3mC0RVNAuAfN4rOXe8dwgxIuTQTAaDUGMbfba3tT7LWC6RdbZc2dBI6Wl3+J/+9f+Enhmn63McHB/CLzr4rsMz3QEcLXD6+AkQAz54/wP8+z/7d/jH/4t/XG6EFmaMMaWuJSZQPgvx81/8Ag8eP8GQhenQ77DbbtF16VC4TMDBYoUYGT0HLA+X6IcecbEEx4i/+slP8Kc/+mEl3ApoQ/KoxQis1xf41a9+jbPTc3DMd1UMAf1uB8pnFUTgO9+h65ZwWUi4fHtmCBHMU5AmC8beMF0mXzGY3XKNzGAX4fwinddQt5KTc0BO09iHAU4OnzHnNLxTxhZGsQI+xpgNPodhSCmC5RC9Zir5XS/mfQJDj8nuXmjQZGPcJe64pXSsgC/gkMY2+6EHkGJkUSlv+ZliN8dxzCwSGjMsWUEgv7e+S3Mz7xVwKtxMgwYRVFaIa3rOdLQJAIUsySjFqNgohVCphByTce0rWolU/SRUBqkt9hPhPQuk95WWorAAbe69liHfAoaXKSH7nn639V3Ly67fa4HD1ty3ANVVaKbft+tQA6cWeG4B1bm6rTKee945jyHmbFDeAYdL/PZ3vomv/P7v4fDmNYRsYBxEgLYB2yenePPXr+A3P/sZ3n/zTaAPcPleoeiAwTV2woyinwMKludHXm4fvLXjvQpYaYGJfe82gbTY8mrOmZMDSw7XWpCr/00dWPvPU8wBWalfA2vtgdV1jINA0Uk65NmOtdWP/xTlsvVeADlG95ZeLyHGKh4eGOlnw+Wu0o/UVu1A0WUfb7RAvh2j7n/5jlOIkTZi0nNq0JYmBMCsAXnGjtdGYwCj426yk2JBamPMmp/138zjBYNFTu5hkzmZRERjYoXG3F1mBFk6lmcbY7M002O24az6WUsDLTeIWidT5Dlgt6uPF4xGC6XjC0QpoZH3qc8xICj+0AZuq209HqGldoBdVq5saCwXSxweHmK93YI6j9t37uTYTkIMKcvK7du3gSHg9OQxQmD8y3/5/8Uf/PAPcfv2bTjny+HoGCOGfkDYDQA57ALjX/+bf5sOgjNjEWLyXAHq4jztlcnE7dMBmCFEcAj4+d/+Al//8pdx+/YtiLHBhSAp5MpRh//wH/8cJydPESPnW8VjBqwDEAOWyxUWzkPOaqy3ayw7j+ODZe6Ly4dua8/GkE/se++BHEIhE1ZyEDOX7TZ5R0K9fA4NA9LWZwgRMRLCbovt0GPRjYwdQ8h1pUxWeiFYwSQCVD6XG9Cl37JbpLOptJRXa7HZoheKFka6fa2QOQvEUd/XoEovRr0QxsXH6DoPBmMIAY4TIMmyNtcni52yPTCndFnshQp46cVn6Rlj1OfHZ0GnXZBEKexLFqwFAvtBzfQyqPJNTFmCJJNS4DgqUzU+3Q8rJG0/mHly7ifV1wbg5TPRajTSQvhNnm3Hgo4GoqaF5uerGAYyT63vJn29pC47xnTmfp5mVwmvkbrmwn+0bJHdPL0OWuBD12HDveQZC7btrtU+OlgZU+hRHpK1nGgEQkq5vOgQHOETX/wsvv3HP8LdT3wEu4XDxjE8OXTbiPjkDA/feBc//Y9/iXtvv42w24D6Hj6ndQzEYE8IDqAhZ9y7QmkZnJpGdmx2DlrA2oJyzW963i6j5+zvPJUZzMlpYflK8xtRfYfRnPFQ2iGUQ/CtsVlwPt7BNNUNpdDUGN0XzteiwWXPXuX9fe/moVfPlnM+DTlT31s13785A6B6Tiu8mTJnYMh3++Rf+k7OJ6L85CSwK9Bq9XxxXoqMm+mDHZ8GqhXfGHrtm9OWMaPfKw6viQerZXvU6ylyrTNaRkMF6hvruzW38kxr56wld6282Fe3/CuJdTBvY0lEjWBQ5xwW3SLRISJfEKp0So7+YIwRQ7rNJMIv17f/yQ2Nm8+9iNXBAVarVRJ24k3hdOHewAHUOdx67hkEYpyePMF7D57g//n/+n/jn/yTfwJmxo0bN7Ln3KEfBmx3OwTq8P/713+Ge49PUtqyMGC97dH5RQY3AczJ0CZKMYQMoOtSStxh1yO6lNnl/pNz/A//6t/iH/+jf4jdbg3nCCECkQjEARx6PDo7xV/9zU+xC4zV4QEu1hfgOCDsNoi7DdB1iM5hQACHCIZH5zw6eIR+yEK5w3jYuGHNQpR3zGnHQhZi2SI3i6mkt1106fJCDilVY+Ys5z1o6EFxZLqI5E0OMSYDCpS2RJF4S7ZHY0wX7MUhlJ0bZkYYhnTzIwOd88loWyyScRUivDq30QIUeuEIUB4PotVxixqg6kObYz3IXvd6y1bqaQGb9C+C4wC38FguOzgHOBLP2ZimrQbIDFCAHEgdDzEQ0qV7KaOaHbMFErXiVBOvChFVdVnPtQBV6aMd31zRoMjOCbr6sD6HmM/6UM5W1fZU2NICXROFh1rmayGdUtcmgw+MnCY6A1uiaidE09JVxl5KwMAs4IsrPmnNUUUL1e85QT4LlhrvlvXkHDgohSf9xchOcwpVUl2ShLQxikKX8Du9g7RPwelx2tICzvY7eb+1tuZAdXax5PSIrpJnlDfiPfKa9Q7RE/qVw+FHXsD3fvh9fOqLn0O36NIuBjO6yBjOz/DorXt486e/xJu/ehlPn5xATiIxGAM4pQd26XwFh8Rf9p4i3d9ZQ06DCcDc3zE/dkvrOeWrd+5t4gwbimINydJ3pLEWMCoAcIaPdf+0DNVyZZZnLjGY7dopazUJ27R+8/m3shxUnXPGjvTR9k+Hblg6SWnt5GjQptuy4HGkOcHRuHs9CaPMISfiDCwp7IGyW9MCxro9bZw6KAIpIxxAyY6nxya/N2XIzHireSVGSnwi8pRBOWc9ufGQdtUGc+mnZOImOHBIdWl+bRkEUvRzhNGI08/u42M9H3ruR/piJF7uNyBps1mla1b0yf8XsJ50M43rTc1ZS1/YtSt1suq77uuc/NR8MSdn5NnJ7n9Muly3J78vFwscrA7Q0y7tMjkCcZIb5Gvnn8sym0AYYuKRdE1FBoQxJdnRParWFSdn7lUdPcCHMDQOr1+Hdx7s0tkIJ7FdYMTYIyIPwBFu3b6NECPWF2f4i7/4K/zn//k/yYCb010V+fI+UMqx/tY77wDkUxhUSKlJpTjn8/XqCSz1ctglEHa7XZqQkCfOE95+911sdzskH3dEiACTR8cBjjxOnp5hs9mBGVgtV1gtlzi/6DPDpcxOfT8ArgOYMPC467KKPuXuJwLIIfJUcBaQQCjGRfpetmvTpGpLVc5SLLr6QLFeT0M/AK72sAF54RpQInVbD4Oue7vZIl1pn5WxWQBS/+SGb9RGhv4nC0Lf/q3p01qI6e/6Mw0cNODSbQMFoyV6IGJ5sMLu6UVJ56Yv75F3i1KlTAsBfQ2QOae8JkLStFGXemxVO0rZyHdCbyu8awNl6smeA5xFYEcuOyj6vZYim2t30g8jLFvnWSRMT+9qsYBVxSN1eN9Yf3UXDE3nyhqCmhebNG/8PffMHIi5rOwzEgvgESMz/wtZZthduzmAuM84bPV3TrHb9Wjn1L5fFLP8y4tQfx8dEDqHwRNwvMJX/+C7+NL3vouD4yPAZeAfImgY8PC9e3jn5Vfxy7/4awwn54ibbRoHjW2NsYCpX50FhbrthtGhS53Gmye0tqDUAtHaQbLfKLMyqwWaowF8zEYoZCNjbr7tpYm2H1fhWT12+3wr9j49F8HR0mCUqZYWrb7N7aBdaf0YQH/Zu5b2Wj7JOOVzK+PK85kf960PuwZbjrLyDqQPXG59bgHxlszVY9eAdHwupa9P72MCGluygUqPMMlUSOTQuTFVri5zskPTpDXXVs9Xut3wr9Wbtm8iUaM4b1DPRTnXiQZfqjWu8UtrfVc0zEd+5/pseUIXO7/WSNXzWeYcbTzEnKNxMuakTCPkd0Kc3qcmM+2dr/gOaIf+6r7Z/l+lXP2MRgYLZYHm2RTr0bl0U7ZzKUf97du34T2w3W4QY8T169fhXDrgvd1u0XmfPAV+kXY2xLOB5MFnllu9p9mTQghVWsMRWEQMQ9odOD4+BABcbLYIzEg7SgSCRxgiQh+wOV9je7FJd2bkS6TCkOLaXJeYOXrGQLHkfQ8xYAgRnZsqJL19rc8QyE/v/WgUqYmrremUirelHvRC1pmYmKgcZpRiz1NohTHG1jG6blGelXhLfQdGS/BJvTqNp10A8rtehC1BMgcUW4aF/jvt1GRjzjF2OQTOOQKieMZagI0yZsm0ZKUYwdlNMfVQSD1zHpl9ZU6BzD1X8VGj0ChLm3VUz0odAtR46oGZUxx2rib9ICqXmgGojQJMDVL5THP3ZW1VfIB2qmTdnj3TM8d3pS8zYMj2Wz6LSk7pz0vd2TvQApytsUqfO0WX1pmNv0uZG5v+bt/3ljfEAMjBnXBcZ68BEaIj7DywWxA+9bu/he/+yY9x9MxdoOtABHgmYBdw/vAx3nv9LfztT36Cp/cfAJse2PZwcBg4h/8RlV2T1ly1xicGrS42LlrLxDma2NICfi26jXdFhckzen3L73ZsKclHEUFXKvvW59+32DS/Y9+5eErngNgceAQSneyh0xZAL++iMr8m49N0tP3VbUu/YmSAx3DElkyZMxCs/GoByjlDoV3q0dm1N8d7+/hVh8NU8je9DMA1xzbfwzpt/1yx/eLshW+F+u4DrhZH6Hf+UxRrHJH5TH8312cxOjUukGcukyUtbGHrt/1t3esj+tS5dDHpth/vORNsY7FUxV+ECkzIGdp0brZNs79LubKh0XVdid/TE1AAbe5ViFwO1F47voaFT1mfdrtd+bzvexwdHiLGgB6j8eHEo8/pHIQOxfHZMBGCacJkKmC1GK2z7XaHdMdEyojQxx1iHBCGdKkXDyHdfBgCDq8do/NdCjfylH8HyBPS2ZmUUnbXbxFjyDGcVFLR2u3fGFPaMAHt8rmkxyWMoUUiUNPPFGtHzmEIQxVG4rzL90OMjF3AVBwXigYveueDKN0XIcyW6ObAPGb2Qq5DlKVlflu/1NMyFqxQ0eOdgu564ejFYAWrVVppN4MxDPmQpEuH5vV7lTJJHybMzeKdpdINymmLrdCx45v03y5g9X1roes69dg1v88rgnmgZesstHdUDK/W2HQfrloYXKUb1E4ByweV8AYA1waPc/QjoolQ1KXl1ZT5srssc8BIt9WiQ1lzKixxMqc8Py/W016PbwSXOnNbq7/WiGkZRBa8za2fVv3ybAsoMpB2frOSYgLYAdETonOIC4/bH38R3/qjH+Cjn38JceHSLjgA9AHbswu88/Lr+PVPfop7b76d7kza7tDlm9yZkqxjMfh57KP0w8oPCwjmwKaeJ8uXLWOmtas6kSeGb23GON1H59LFtdvtdtIfeSbpUjmrN87HXJkzvC0NdFuaZ/Rzc+tCy/qxPkzesUaVbkv3dxJC2uDLVt/tnAq9WPHIVdb2SDeUQ9/6Tqe5eWHmFIbqp+fu7FrTf7d22Oq+0mRsLdpJP+yup01gottpzvGHkPHl/Zw1S4eF2jmyPFZ+Gpross9xZMtcKFmRy+Zzy1dWVhb8pJ7Xz7R2Yco7zDn6eppl0OIETZ8WjaysaBVd74QGyiYomEZEJ08dI6Vvqj493lJHg78tLa5armxoaGtWJlwfIvbO5zjGceF3iw5HB4vKU87M+VbsBHz96hDLxSLdbJhjPSOnW7a1d3ez2Uzux5BFXLYP40jIdCP2Dr5bAZKhidKOC8cB3kU4DFi4AB62cOEAsd+hy894ADwMcBRGj3fnC1BNOw9t5R5CCtMSQ0nidUMISUjlG5flgLhMdpRzH5XgRAlrInAxuOqYXi4oxQo5qxRHxsopIpmrPrQUkl58luH053onRL7TzwGjolksFtUYJWyk9b5dxABy1jIG9xGBI7pFJy6GTNv6ng9pOwlaG9IVIWmFrdEzp/iqYjwHtcCSez0ayjNv884JIUuHkR5VN81Y2saYp/HSzJYR2BIimu7687lSKWQaY+h1e6Vvqm3tpbH1zwEkKa344H39s3XOtWmVaUUDjMrTvp+E+9Tgvgzg68OKNoTR0s+uR11fa+3NrW37XGv8lWLO3zmJde48IiLCwmHoCMd37+DL3/02vvTNr2F5tEIUUDJE8KbH+2++jV/8xU9w/413sD55ilW3BHYDFvm2cCYCeYeQaZivRS00EXq2+NUaCfJ3teOint1XrNdQFytTrIyUd/X5DGkzOcC2k7qkP2VcPF1vLYBkx2KBkv29BbauUqxcST+pRCHY8Kp9gMQ+P6cv7Pd2fm29Wo+1+qDbTr+HFPoyQwa9Fg01mm1oPVuHwU131OxYRYfr71rv2DnUu3dzYWhWHxARQHWWoX0yc+zn6OyRdWWfs3hDj99ikhYN5vSdpYH9Tj3UDBMax1fLVztGS9+5dsqaB1frvaVXWjLX0rwlyyxNOIMke0YUQHFgMEdgvUnvCWPTWKfFgURUzk1aXSXj07w2x2NXKVc2NEIRUIBE/wVOnn6KSIoXBOc8YpDtGyDGMLlafrPZIIR0IR+ruxYS4HMY+qHEoQuolsUnwlrf0ZAAKrDd6d2DAd536BYdhshIWxTA4dESBysPioRbNw6xpJtg1+H4xjXQcgl0Ht53wJBS3PkuZ/EA4WB1gJiNB+fHy/daExhjrHYzyuchlvfq3QzxanLzNs0YIxxNGTXGWHY6pOjv7cKUn96nHRTmaRyuDo2yC8X+vg+Q6ee0UKzipJHtNaNQWmPQCy+ECBdCOnNAwNnZeRGCepHod0pdsb70jkjASy30tXeLaGpIzZU5Aa5BChFNhKLt62WlpXDl84kSNEBLt2Oft+FHVxUwUq/1AAstdZn6n+ox6TL2Z/rsnJLcpyjs2K/SB8AAvD3ty3M2paelu+YnmgEZrWJpqdu1fW8piNa60N/ZeGFdEsQkUM7+FBYe8WiF3/rm1/D1H34fh8fHxVjwDGAXsX7wCG/86mW88vNf4sHb72FYb7DwHULYocvgJSJ5CGMOm+oaYLQly+aA0hxAB6ahaXYe9RwIIGvRcI5PWgAJqOdiH9Cw/W/9va8Pdof9MrnSMlbs59N30HR2tMYzB6T2FQ189tW5Twbo5+xP5xzA0yyGUqxz6rK51jqrtX6bMrl8Nt9/W4fsXrRCRC8rBWsYOszpdI25UvuojJRW/fLTgmVN3w+j41r1X1Zaa97qDw2gZUz6fWAMT58rjtLOq6ZHy7Gh67zqXOl+7tMx2hFfUvhfsh6KHEyfVDp6DPmcvqvn78MaHVc3NHLmJIBSxqKcNpOcS+FAOU1BiAExBnBk9P0OxITFYoEQUtrY9XqtRkElXV7f9/BI6bhGQ8MV4yNGRoyDSiHrMAz1reEBcYzpBaXQrL6H6xbw3mG72+LunVv4r/6r/xKnT56gvzjF0jscHt3ALkTce3AfN+/exXKxxLJbIg4DwAHM+bI/53B6epqMLHBOo9pWWMJ8MnnCgGlnApNn0veycxTLYUtxuhAIIQyVAVMEQq4vNT0ymQ6/kTAvDfqErvpZK2jmlHpLkWkwLp/bRTK3/dlSzuU5ZkC17/LhL3IETx5DHNIZDc5b25ExRM67FA4xBohp75xDkEPieVGKZwJAvjxQ9YNHUCxCXo9ZKL5PQbf4Yq7sU5yl7chIuRQaQFAJAS1AYkyXU+o5bnlhdFtznt0y9uRkmfRP/92m1zzQtfVohceg5nNT4MyZZaxiG5+XjFhEUzBzqSLgNPA52gltLwMBLdnBSDuYrJ8xr+t+6gxeTitTGusUTGjXqW5XXiQZX+6LnmtKQVOAIwTvMCwdXvjcp/HNP/khnv30J7B1hOA8OiK4PmJ3coZ7r72Jx+/ew29+/gs8vPcBeNtj2S0ARKDzCMzwjhCY0421VHuSRWlbA9YCGK34Qkjhsc5Pgf0ceK1ws+KdlofWzkFrHoW+Wt7ZmHm7VltzrGWx7fPcTmRLlu7b0bE2w6XyJ8vjqo5G/+bG03q2JQ/0+mFArVmtkwABS61iaTT2Y3rPk3UC6HFJiWqttMZn+bY1Fv23NaKltEB5U17sqWO+qOyJXKeLtUbBSP8kUyUFfrNWgx1k3kh9b8e4r89X5W1dHLkUEaP60CrVfKt6LV3n9JRgAlK7DBpbtfo9pwv2jUnzi0QV6TUtMmS92eD46HB8j5CcV5znkBQ9tKDLY4Byrhb9qLDQhwlxa5Wrh07FdMleGEK6NCj3kwQ4x4ghBGw2W+y2W6w3a4Rhh2fv3gTIpUsNB0Zkh65b4eTpBcARB8dHuHPzBhAGBDD6kC9/IYnpTyE2VLzVAb4okLSohyEka857HB4f5+cjEAPAaYeF0cE7RgyM06cPcf34AFs6wPriAi994qM4ODzE6Z8/xZMHHySgkDNfDTEmzzOnHZzFYoGjo6M8R2lSvPcFtImAiXH0ggtzpD5zAfcTpmTkbCvAamAMDtisCAsOOASB8/Mh72IIIIAyyhIjiJDIKfoyc7jUqFpYqbEwDGmXgRngmA7jO6oMIes90Vt4Nt5ZijCljn9tKmwG5DY5ci6l2Mv0EKHuKG3VM6d0yt45REmCGQmLxQFi12FwEcsYQOxBlA41pf6iGCuOPQh+bJuyR1kbbsXASPQjjCBoMsYYpwYKlCdW/14JC6oU576QjbpueSb3z4lAFLHe8lTXcyLzoneaKuCl+jsbWgeugPpcaSkunSyhZcTa92XckklM+H18nhHCUMI00+coPwWQtMA/cw3C54Rp+U4JcCnFo5U98q210RLUhc6RIbG2KYsKwBjrqtZEHpQ8S3mdyL1G46CUl658M7bj5JyZGosDwXGSrMEBcLnlELHwHZgdNguH7sW7+Paf/hCf/d3fhu86DIhwnuCGAdRHnN57gPdffRPvvvI63nn9DfS7FJYaly4pPU+AS/zDBOgbakWpSnY+ymfQUlipUrQyb04uZBU65zFHhh9HnfUUF4Ygob8JbWRO7xERqOvK3HCmM7nUW8p0mgvfa4HFFtiwskHAS8VzprQcCtoos+vN7uLUHVYSgyEJ+XI427TdJNOyw4enDok54+gykGKft2s0rV8NtqfvWVpWw9TgETXdm2CyBWSVMWz7LrKy8LA5TzFHm5iZc84B1QKi9rK0Vl8tDYocJQAly9VovBG5Mqfy/CjzUPCM8J7lzdaOXWvGW+ejJn1HzqRFBMop92UVp8D2JqEAcDlDp8cs+raA66zkNWgfeSxlY2BJz04jX8UYEXm81wKcsAgnN1529jDI+3yp8zQyojVPrXVuDWEd6aIxg3ME36UrJ9ghpf9Wco9ZZJwoQiXrM4aG8xgEqwqN5L0iD4wO+hDl6oZGH7AbUtgPGOmmwXyvw2a9Rt/32Gw2qc/OYblcYXl8hDu3b2O93uDiYoM7d57BcrlCCIwQIi7OT3FwdAxiwpNHT3B84yaYGIvlAiX/cz6ILYDGOz8KmAyGPUlaL8a142MwAN8tsQtbWVMY+gDnUuYTAuHx4ycA0n0Vr77xOj7+8U/g7rPP4nz9Zhov8hZY5xEHLnddSLaM5SLt7sjCsrHYwHiCX37XHq1C1+oATga7ADpKCpldWmiE0cui6wRz3v2RGqdKLSqwCLWwwKNhJAtCDozDjYq75XXTRoj9ThctaFtWsRU29nsNcidgl5KXK/FjXjKUQpII48VWBJXqljGZt6K0matx5+qK0SFGiw6JkX5Y5WHp0TbCRlBUf17XofvqXLp40nuH2nDj2TrST9kta05T9Z5+twWWigLCNORE/z67c0N1H+eMDGvY1GUKIpi5MmpjHM9w2X4me7umh93+nhtbbrBqW0qMDEYdGnlZmQNEcyF4ek6c7Zcp1PqDgC4rwqTA1XwQYeeSknGcwLwnB1p4REeIR0f4re9+HV/54fewvH0d8CnReccevB1w8fgE7776Ot769St479U3gX7AbpOyDPrOw0m4ShHiKEaTpkVLnshOj6zXQhszv3rtlHnMbWrjX76fA7jpvZrm6QuMlgvX/Snzoni/hEqGRprJmfnbB8o1aNFGhAbOH+bs0lzbLeBT9UF9Z+W0bjfGWBIc6M9aBlHLUBjXKZl60++tsBcp9QF21Z6xF1qGkf5O180zz2gAPedUs7otjarO6NQGyXXZp0OFJpqm9csjaCRSdTOX3QC7A5aTOVbjsP1sJevBHj62fa/GmeeHxTEiuh6AOFSn81UbSNOxZ0NF8LYqlh9b+lvaEQyod72IJgzV7EvN0yMWu1QOMJc7NCbzmtsIMV1MLREDyOsmMiejgWoeBusYASUz1Zh1P6p3P2S5sqEx5PsvEBkcAra7HhcX59hud3Cdx2q1wrVrx1gslogxIEaGd8D1G9cROeL6tRvl/gwigJzDervBxfkFbl6/gccPHsGhw2J5CJ/zE+tBMjK49WKVJk+uGDwEwBHjYLFADBHBdYhwWPolIkdstlscHx/DOYLzHRbLFYAA7AhPTk5wevYLxBhyGEKqX9oEUGXASv2pAzkqUGEEmA5RCZkBrGIYwXMKB6I4bldaASuldSCrgOZcvPMIYaiYehQUdeYrKQmsJV+gFcDyzwqiiWI3xfarFSctf9u6NdAuxlOMCBwQshCSS5QYAtLyNjd06Ej+p8hm+yFKZCIYUHsR7FzYOdc0as21XtRa2GoazG1X6svu5Oc4RzXNq/dQlzkgvRdgq88dXDmsq9+Td8TQnvYjCWVrYLQUawWaLgFfEq4k7+n5s2EMEtJoFZ2eq1mwxzy5j8Qa4/b9uXWxD0iMIZU0mZ+9/btSaRuCkQi9Y3QxGRkApTsxFg4f/9IX8fU//hFuf/T5tDPhCB0csBuwfvAY9998Cy//6td48O77OD95Ch8ZPITk+Vfr7O/ab2sIyO9W8dpdJPuOfdfOt8znHN3tnLUA6iyAUuUqh3Ftva11KmtEAxZrbNnv50oNEuvPq7EQVYJ0325sC2C1dMowDJN7hMq7XMs9O0ct4D9nPKR3uAJM9n27dsszDTkla9W2r/tlx1vrlrptPVeVQa2KvtjQ9rf1d+lX6kSzTmaxoKdrLdXHE16ygPnD8PKcISbYSuuRUX7sca7w1EEnc7NvHc71B8hLwLyrMdMcn6Tdh/06wK7ly8Kqbdu6j855LBaLhrxL0RxknHtgLkac1EvIBnhzH+rvV65saByvFji/uMCw26FzHh6Mw2WHm9eO4BZdzqbB2FycZu8FI3LA4eERwhBySINDCH2yTAm4fecOnHd49tlncO3wAGGzQdzswKsFdsMmUwDZkxwzUORyaZ4IJdlpODpc4trhAcAEJo9rN27DO4/zszM4vwDnTFHkPQgd4hBB3sNzPiPifTrkrQVB4y6GxAy10qyApGIw8eaUwjWoqZSiHKoXY4qRvbJUGEIYslLaPIJfexC3NKveK0xNrqpLAJgcMJedEBmbjVu1wlwX208rYG04jo2Ftopf11nonY2MEBm77a4C7wAjxHwPSwkccRKN2BY8qr0JSKExxGLiITdbozXYnQKeUn9pdn5bVY9fioSRWcE0zlO9ywagZHFjTAWcBSVlzOqZlhIR4SQ00X3QdemdPWD0UrUV3TwAzJVOlPc++tm1oo239J2fAL59YEz3WSsy2Unx3o9ngMyY5taJ/XtOYVvP9aySq5RZawyAeAU1nZNMICxDupwLDhg6h4OPPovf/5//KT72uZfQLZfoc6xNFxlxvcbjt9/He795FfdefR3vvv02HAhdTKEE5NIlp2KQXhUQFd5q8Kp+z3rSp+uvTfMWYLd/T8Bu43lydWikBTlalrTaaYKPBh5q8YNtr1Xs2vhwYGt03Oi6Eo/WO5otua3nahJSY2SsfKf1QEUbagM1yxMtg9+e7Rl/n+pw3Rf9ewF4qHcL7O3vluYtWkz6QbUOsfS0/dF9mgLLeh51u0RU3XBun89kbsrwtAuC6jMtS1uGh9THGOWalNYOYKmLHBijEVWfdQ1wVQIhY0AqntTnX1s0apWp/Kx5zspgacPyf8yYoaWrbNkb1qj7hhpb6v46R3mnZYBHxrmc5PTYN2f4KYc+y3wbXrI8rHui279KubKhce+dFGe76BbovM95ehn9Gjm96ALeOThmxO0uhTT5Djdv3sDdu3cRYwqXGk+2O6y3O4SB8fxzz+BwQYhhAw4BQ0wCLuQ7K4RJd9stQj54TuSwCUPeTmN432FYL3D31i2AHMgtAFrkXW6C9x2c60pccGSAyYntDOd9ynySlajY9rINpZWPjr2UfxbQyCSJl7XKMKMmqVJQNC5KPaldtyhtAKNy1V5v26ex/pohtJDUh8Nbnn39t/YqzAk4oQ2ACS1ayt32Scamt2CtstZtDmFA4LRzcX5xXgkVonwuQwAOdFq4toLRVLf9TvdzTL/XgsV6emKUGPt2/4W/WjSxwGVOEM0BEPluHNu8QGgpQWs42L5pACA8ZL0x+0DfBFyZz1uhFS3Q2aKT5T39Tg3OreCt57XVxyKQTV+K4gNP5mTf3FlFZGljv5vrV7uu9pwTpbHbtetzOJVzHgMIq7s38OXvfQtf+v53EK8fYPAEHwkdOfTrDU4ePsHu8Sl++Zd/jSfvvY/1yVP4CLBkUyMqfKfnyTog9Pea9sxakbYzBFkguQ982c9mD4ab+bI8ZOk8N48tGWjrFVrMGQp67LaPesf0qrs4+nM7ztZ6ae3USr+1gVXJGlsHpvyt5YvWG/J91bcMIC29WwBtbu5a/GbHPLeLNUcPO25d9Ny05k5+ElE6l4n23LXm8io7B1cBrpN5iyl0yqZmFixkdd5la21faa2pqg5DZ6C+VqFVn+2Tpv3cPNl3J31TfSDan+zmMhq01rLul57XlryoiGLa2263WCw6OOcBZnOeogS91U5S5iKf0z0p44BbsvbvU65saPwf/sv/fTY0OqwWS3S+w/HRIY6OjrHoOpydnWG5XGK5XJb7Ia7fuo2TzbYoXwmpSoMgbLcD3Mrh7p2b+L/8n/9PeObWDRAGgBw4H07xPhHu9PQUT56cYNcPWC5WGELAdrNBn28VH4YBYRjwkReeT3c0UAqdIhCc67BYeXAGhHAeqQsJQDIhXxA1LniiNjiriT5a8yKkBJAzjyFTklmrvG+EndyNMWFgl+IBZaeFYu2RHZmxrVDTM+MFSVYZxBgqY6Vifq5jAoH6kiS7MPW7AlpaxSozqRdIgl6nQrbj0b/HGNMZFhoNN+9c2aXhEkSNxE9R6C0+lsvLBLSqrcaWsLfAhTn3gsYzHZZ/5t5v9aXUaWg/BfQzh/MxAj/LC1ZQW+HS2qaPeZdR1oD17GhPf6sfrXY0r82FDdixt/hFnrM7PvV40+d2Te0DEMyJB3TdlQEeL++TrmtOOc0B1hatdF2Xbb2PdQKyPkRWAQB1HtvVAp/92pfxzX/wIxw/exvBAQsQXCC47YDtZounHzzAf/hX/xr90wusItCfbzBwxMApe57LoadO2lLgxK4T+5nuI5l11gIDmk/a68EAuwadtAGkn7EgxRrgRDQeADUgx9Zvi57/ii9mAMVVFH5rXe97/6r8qPsBZDqYUC0tEy1osuvBnoNqrdOxYVSeWdv/Of6w/FC/S5WMkWfmUpraevbNRUt3aX6xZ0qsM9O+O/f5nJzRdL9K/6Qf6czrqF+rULusy+bwgPzdrF/10zoVLY+WV9QWig0hbsmEMpeNndOrrhv5WT1PVNXZOntl5caIM+q6LX3suC/jq7kiuDPpWgDZsTle8CzOJcZ4vgWIIOR8I+l/jXWk+zt+ljDUh+nrlQ2NT3z0ORysVgnYDwMWXQcOEbvtUwxrxrDZ4vrBbZyd3MfFxQUWiwV22zUOn3kR3nfodxvEyNj1PWJgLFYrkPPwXQeAEcIW9++/haOlg+8W2IVkZUnGga7rcPPaEjF2ODw4wsHBQQY3Hs55LJdLuMUBdiHd5eE6Xy4UYhC6RVdAgs8X+FEOp0lSjMruh1h2ib7WEyMLAxlwjBOTGNHD+QiE2nOjmUtiDLXwAVKcHTyB4NIBx8jwcNj1O3SGCfYphRoE1xapDn+Ksb7QyoZWAYDvOoR8WzlBLQZOoVUEqsJGfK4nhlClGpaxz/W57/tqR0KHbOlSCVbHCENEiBGbfgf0u5SSGCkzl/cphA95vrzvADjEOECD/KpPDbAdYwSHkNJvmndG8F97V1tzYhWMtoU+TNELf6pMqeLJ8SWMQkbebdSpx9QqeoyinHQIoy6tXbb0Igr5LXDUvNjqFww/cIwIBkwJ6GkZJLquFmgd66nkriZUkR1pbGmHLMZYaJHapywryouwkz0qHhtWkohkQY01fMe1YMF6aldmODlSaMwmxOl/0hvXdehjBHuH5z79SXz5T3+Ej37xsxhWDmswDuCx2kb0T57inXfexhuvvY712Tk2D09w/vgEPjCcd9iFvvSDY5JzzvlsoLfD88rvwlO5T0nWYDIJVva1gLJ8J6BR88McsLFFg9AxbGPkZ6109wE7zXtzO36T2GymiVzYp9T36QP9uYzlwxRL5wIu81okpDTyBXCZ/sj4tVwXx5voDNv36brk5HFtAH0rbyegtAHGa/CFQmvR6y0AOCVMeo/SA5Pd8En/eWoAjMB5dJYRJWfFrGFVfiYBpZ2Bc8btPl6XcEnkHftRxI59L+JaQI8p1rhrkKnSqS3ZO5G3NCoJjZO0I7IJzHUlPBpHUtvcOprQWfqndqhbxrHtR92ncWyid9k4RaStFs/tMzzke5fn7datW7h79w7OT8+UPpE+jM5HwR0xRnBEivIR+s7wsW5TjBSRe1c1Nq5saDx9/128d3aGk5MneOWV32AYdmCOuFhfYOgHHB0d4+joCE+fPsXQD7h27Rr84Q38Z//0f4fVYQfq0hkJ363QDxu4yDjMh7Op63Dz1i0MF4+wwA5HK4c+AOuLC1w/uo7dboeLi1NcnJ1huz3DZtUhBMbT03M8enyKGAnkPJY3X8QP//gfpY2iIZ25IOeQgoS64v12visBNSFGOPYAXL4bhBA4nV8YwpAWPCIiU/6Xlp7Edo+hOAIsGICD3AidwG0Ac7oDA1yffdB3XQRwPoDJ2LoUpdj1AQxgcKiUtUy89x5xaOf8FoGqmUR+H4VeLQTkgOyqSzdtxz4d0OMQ1LNZMTIXpk4CLwA5pSQzg4cA+HxwLYYCCLXi1322YVctxahBaASwjIRdYBzcvpHA3bsfIBIB8ACn2+pBIshCUS4V7lVKSxbkZQfIbJiUDWeTegUIWvBbvldLuxWaJkVS0apJa845US00tRDrspoKyghk1QMN8nUdc6EudntbH1C0oS5VH5ESOUjdUq9WRFLHJLREeFcZTESkLhRt85PsGtqdF0B4ggovy3qulKqih6MRXHH+L4e6Zh6T/jK6zikDLDkqrNGZqs87AcX4CAWEJmeBjEkbIqmP49qWRBbJJl4w0HPA4BzYJ+9VFwmOGeCQwIrvsHWE/sZ1fONPf4Tf+va3cHC4wtAR3NLDDQF0MeC9X7yKt3/xa9x//108fPQQMSRnAjiHYMaILjtrOnJgl3exOZYzOnrtl/UDjAYQESJiATzzCrxtdOmkG8453L17FycnJ9jtdoUf9inufYBJey/NiyBOcrvodeEeQgmpLECcpiFPGsikdsbq9TMWmMjv9jNt3Oh2tVGzj66l7nE4E/Ce1REIXG6KH5/NFzCacVlaSr1z8zExPoxcbIU6zdXTMj5i7NOuWwZriUcBIg/moWq7akdkVpQd6zT+yAzKWTHTmdJ0f5NzqU5Jec+KJ5JuHY1sYnEAUHFoKAk9rhcaDa/W+C141TIVcTyn0eU0/iw3RGe/KxFATjtHMmBFGltyUhb4jsvSnFuQDgCRQ+VZKI4bkrVW83MZq5IXduyd8xBDmLOTcTQZ9hvsQp+5HS3903433QGKY/gSUqKiLNRyHVP93dSxM/2wz/f57DQkFXh6AGl3I8lnMU5Bacc5yiFXRrkXTy5KHWIEfJtWUo9OI3xZubKh8cH9d8HMODhc4Hd+97dxenqKYRiwWh3g6PAo7R6AMIR0J4MjwsVAuH79eom512CMOd8MHlOKWZDH6dkF7lxbJiYBY9tv4Tce2+0O680a799/HzFscbhaYrPdAUgXsq03awwD45MfuQ6U7byArvMyI+MCz3nu5QZzQIQIQJx2PySXtAAamVsNzmMGsC1QB8WUNvyDMsrVwLO2ZPMi9ynLscurnsFVtoXKqneEjroJKEtMMBWwBXCpLD1SZKFpANhSFPK5DhnTAsEuzCGEZMC5+oCWBQxSP1CHUrXKMAxYcAqXgpND0BL2VpabmbupN7S0613hF/3s6N2o3y9jMN7Sqk3Fe2IYFsOm9TxqoKC/K9+nD6p3xjIC5kkMdyVAR17OUqk5Zk0f/bcofudH4ar5QRdL70mP1fvyt+1HK1RNgzhLL6lDQoKsomsBHcsPI1VQgRwNFOy8yoVe1vut15A1qIB8uLahaKZhRvXvduyinGWHBUToooD5tCbYEYIHYucRFh0+8eUv4zt/+ke48dyzYO+wAOBDBF/0ePTeB3jtp3+Lt37xMrZPTxF2G8Q4ZuuKeX12XVcAl50DPX79WQE/NJ/+tVXq8U4v55L2Pvjgg73v2mJlxJxsmgPHwtjl3WxQ2zrm3tdyAWos+r4b4T29WzM1WttruLVGbPvW4GrRpzyPmperOUH9t14PrX7qNq2jI3euMvZHHDEFZbb/rTVejyklhQC3jUxdh/R1uoa1HEvrORkusTgwK89MLkV+Tb5RQ2/osdoAmZa5HWHLL26Sqr1uS8sb3d5IxyxTFKbRhWNMBhjVzxBRjjipns5tjjtA9sxjmvMZOul51/MiFFNtza3B1udz68HiFfud1d+2jhZNWk69Vh/td0+enODo4KAeez6/PDYoFZj6GtEdzrkJL7TGeNVy9fS26BFixHbTp5S2rsPJ0zXIbQGcAEipVLuuw9HREQ4OD3Dj5h0sFgv0w7YSksycb+xOnoS+j2DyeOud9/H0sINzEXBIF57gAWSrp1utQHEJIuDg6BBHR9fhn55jFx4jbnu88OILE4FHRInZKTN89lx47xFDnzL4EFVKW7Z3hcAWnBaGcG0vUpkoM0kiUCyjSJtVLKB3CEOyPnd9j8XMvDBz9rDG4jXUaT4duRKWIH0qApqmzCNGgCg3HbMq455s9avvLEMW8ECoQJ8uuv6WQaNpK+2nuzLkxuhEh4uLC0iIEKimp55HO1d6W38uPhpU97tWyBGk8jFrZaQ9F5ctTOuha/EcAPCeeiQ7GzB/u216EPVuBmrgposFCKOhUa8P4cEWsNo39laberyaFvpvDfiJqMSMW1ClwZpdy7q+CbBsgAgtiC1fJTpi9JKiXuuHh4eJRzE9gzLxiBlaW5mhgVbTaPIOPTE6dliEfGbCeew80HtC7wnPvvQJfONP/xgvfv4lUNchkoOPBPQDto9O8PYvfoM3f/0KTk9OcHF6CmLGbrcr4FnWq/yzfZeQI2tg6fG3eGQWyJv51zSytLGGzVVKCzzq+i4rLR7f18/ZtotRWM+z5ttWvfrzFrCRotfMhwmlmgMbTQCm2rdpp/Vzdg3OjVG/29p1bZUW0JvI0tKv0QOdnhl33eyzczzLQMER6dn5/rXWxGVj0J8VLDHTRsugmjOihA/EwavfUX+U1tp0n9FvVO88V/NvHp3TAxXdLUg28wrM70poo8m20dIFl5U5mrbendtNtfL9srabbRY9nHV1DmHMcX2XjsPWDyBFh1zyrNXR+8qVDY2f/PTnAKeD1bvdgDfffAeb9RZDH/D888/j9p07iPkGbebkZf/97/8YLa8yESkAnLxuy+UR3nrnA7xy9gSgAbthmxdTAjTireYhptAcEHy3ABPhwcNH6BZL/IP/7JnKs14s5xDRibPapTMQi8UC/W6bbqKOQMjp1ORQdsmy5I2FLpNMbaHZEkZA7aXXz1cgIpPK5ZuBC+gRmjmfgaRtA1V4glyOlIyQOjRGAyrK4WJWuGtGnwrkqedCntehM3YOpBc63tmC6tbv8oxOkSrKOHKKM2QCzs/PUzhO1nFO3TDUqrupyDCeO9FjTnMwPTwo42HmyuuoBSbL3krDgIhRLqNsAxBNc00PNs/UoHb6bglTy2uNaPReOe9K+ugYp3Xa/mgecc4hKP6w/LUP1IPaQncOKE2Uum0HSCFBubR2EGxbdlwt2kONq9muAbiybi2/MXO50HRufDq0ptU/C85bdZXvCGCXQj1TWKhD9A7bjrC6cxPf/cHv4wvf/jri9RW2xOgcgTc9dk8v8O5vXsH9V99EfHIOOrvA+v4jwBMGGndRhIaSu10+s04Jq8T1PIseINRG/L65mswPGrwFVPS6rNg51PVah9NVgble//J30yBUfS80a+hMW8dcvLgtGlhbnrQXj05AfwN02vaaoA2obphujbM1Nhs6q9sQB8qcXLH01Y5Nq2v17lCiDSdE4RxQHEa1vrN8bOchOanEyZDDVTRpaNQhUvSOlNSh25zSwBhrjiZ0lr5N5JIag82cJJ87YHLebaQEitEwlZdj6JTVj7poWQggh1ur3RXFw1pH6rGk3SFf9c+OW79T46upzNaySMtZ2+/W71fR2/adfaUlX8o6RwrZBU3BfVrLKeSyWstEJQmOc9PdSo1ptHwQva5Tktu5ueqYpFw9ve0HZwDnEJgQ4ReH6GKHi+0p3rv/CB88epqvi09K8ujoEM8+/xH0Q58PfwGOfF6AKaY5xpTmlpnAvkPEAn/9s18jxh0i6RjlcXudhwCXT9WHGNGHgNXhAT79mc9gsVyVS3+qiXBGQDCwWCyKQNBCRDz4RVGpRV4xmRMjYOqR2cd8wHSrbfyO4SjtIvQcSkrVsougbsTU9XXej6GOillijJVnCdBAINWtFZEUG8LSWlBzwkq3pQU+Zp7VdQs4bO0GTf4W5eGAMPR45tYtnD+9ADsH5nwrdEP5tMBHEVg8AoMWmJM5t8Auw8umwNc01n1JfeAqBELeadGm9bsF06k/rs1rag608KUMKNJ2/1S5WuGihaE0Y8Mi9LMT4dYAhbpPVd9mBLluo9BZtVH3cTqflk9b7SRBXPfTOgnmlDlMW3ZcmhZ6rvfFru8DEy2jJMUnA+w8tp1H8A5D5/Hbv/dtfP0Pv4drd28jeADOYQWANj3O33uAd371Ct597TW8/8ZbOGCHYb3FwBGRHQIYXu2KzhkE+vPWmQDpt/Z0C6i3dNX00+/PfaaBZYvf9GdzbbVoqj8T/mrxjW53vPx1OoetdV5ohSS/LM+2eK6a80bf9fvW2cU8pl0XR8llNNEGjvX4l3YJRe7tAyX2u7n5SmHKBGC6bu347T/pnx2bpS0zikxOj8SKl3SZC/GTepjH31ttaXDXkgktWsi7FX0a9LS/T+QkpsaLftYWrW/lOq9WCJz0xuqjplyVuUJ7Pdj1NeEjGnGXxQ8tHWlp1dTTs2UMubJh3HNzpH9vPWPLvjmo5EkS6bP1JUw7YlawOIZmjCKq56mF4cpFyKZ/LVm/r1zZ0NjulqljMQJIoU3sgIEB75Y43+xw8+YNdF2Hvu9x7eZdPPv8iwjDeH8EsxL2DKQDj8B2NwAHB3jxxU9gvflXcN5jN6Tbx51z6LLhMIQBK/LwRCBP2A479ENEdD2efe4FxAhEGuNXS+iIhNgQUogLJU9c2h5NB76t0C9CLqeH1f8SCKkJbL2nZL6rAN+coIQB5FAeAgWStYCy/dUKu/Qp8uQZlBja0ctjAZpVylJkPlugXQuhFqCXOvXhUNuWfQeow66ENvL3YrHA6uAAfHyEpyEAkHCq/Z7fpiKksV79XowRMdT9rEKTfDte1+4PWwNNYtz1P92upQnz6JnRn42KdWy0epfT/+Q93/m8VS5AvQ1srcKqBBHPGGyKZi1Qvz+6+GqlBSCKuT4DbFqlKYBzsd5QfealGo/mo8Z8WSCov7PKaC4sca6efYJ+SR0GR1gvgBe+8BK+/aMf4KMvfRrwDmGxQAwBbh2wfXKC9195A4/fehfvvPI6np48RrfosA0DBpedLj6d8Wl5zvVOi5UXrT5XIZHITg+MhkdLpjUBhylarlgaX6XY5+Z2j67KX0QErzzr+xwo+h3K56ws7VpAWXvFL+uLvCMXyNo1bh0GMHO4r+59NLHj1jTUgLAFsmRO89GjJi3sWpxrV+ssOx5XnHoy7Hq97xuP6jEE0lY0IyA5VNvzbmX/nLzYV5p6wnxveccWC2LtOoo0Z4ykt62cci7JjKjarfEBV+/p9+dCjQCJ+LhcHuixEjAbCmT5sRq7wYZXLbP1XeG91lzOzR8zp/tPaNSF5XuWZ9thhoQaj1WYxz77IfnRlisbGq++9g4iR3Sdw3LZYblcwHuHbnmIyA6rg0M8OTnF9evX4ZzH0dE1LJYrxMjgCHjvIJlmUqdT2IvvPDqfiPXSS5/BwfF1bNbn8IsVfARiiDg9X6fYYHI4jxFHqwMcXTtCCIwQGD4CH//4J9H3PZjGXQGhVrLy5FaN0ZvmvcMwFPcLgAweZR4J5RIbOXiqGTAlSJl61iLXlxnpRRNjLHnXLfBFjnOUDABSh/ceIMmskw5wxRwixswlNl12c6RN733yjkGHk+WsDFEA7jjHwzCMuydiHFEeqgKVxISu8yXsahQUbd4pRhRnD36IJaVfAqz1hW9zCieFxckWOsAhGY9DCNicX6DfDQgAPJLrRRtOen4SKFUhUqYt3YcRxE5vbBaB6LsO8vFoxKDMKfNUWCWQRdUuiVU2Ff149BhF5uZz6e92W4n+WbjnW33BsaSNzJsypq6pAah3CwmJV3UYgu2X5o/i2ebcvjRKIz2sCdIScFYx2bE6atPUlhZYseO3a7ulCLSHmGMsByxbdc0pclmzfd/j8PCwnvOsEGImF+vJkmcoxdRSTowQmdF3HsfPP4Pv/PEP8Zmv/jYWhwcYYoTvPPrtDhePT3D+wQO89YvfoH9yivtvvoPdeg3v0jgGjuBuDFPocmotTh9oMQk5p+RUv71zgKS85pRNKgIlxBYu1ZcOlwuAE49yoVJZ73LQveYJC1yhfmr6lt8mc6OLne8W0J/ju2ll9Z9ziloDq9RuffGpXl+Wj/aBrZYcaLUN5LucQijzlNZpIvy+uyUksUg1Zq5pNX+2rd6J0uOZkpL2ymm7LkX/idwRvWYNUSkSaUvU4rFp31ufEWGUa0l5KxYYZZvMn3aW6Pr2GRpWZhTTJutRYOT6WYNiTtfIQpsZ/xwfJV03Gr0uh0QxoxiIUoS/kEOKGe2zj1bW6rbHZBQ1ftH91n0svJXD4CkPVa9Py5d2nHq+9pWrgPHSvvob+TNqJAUp628GEyRaJvzkO48wDHAkUUPpwH27XxoHjkayfAeq1+lVx9cqVzY0Do8PS2YRIMchAui6RQIcIcD7BbbbLY6Pj/DMs89guViiH1LUoycPTw7OMQIB2z5DQiYsnYMj4O4zz+Da9Zs4vzgDhgEERt/vEIYe280aALDwHnfv3kKIA4bQA2DcuH4DH3vxo1j6JSJ5cOCkkANjsVyAhy28S6lXCOmCJUcOy+UK2+02xaPlmDSmdB5EjIsBnOIWkYVhZHBIRktEfVCvAhyYAt3qeyNcE019Pl8hACxNPhElSegIIIfOeWyzgPLOJeCuFIII92EYUj8DwDn1pHi8ORIi1f05PDxMFx+GIaW2k++BilkZSYAQEZxPRmPaRZFt/2mIF1Ha+qPI8EQlNRoDYHI5zKAB8NUZEuu965gRPTDECOrTQhy8g+9Tml1S6dmqBeIoXd6Y57sUJbWswCoxuEogpV0xMSZGgZjCS1RcMNVhIoUvaGxzX0iXNW7IuZKPWz8rBjxQe8QLvzEXKSex4JJO0YoPK1haikmMz5YQsllxmoaAWLFIqZ05K3uhQg0gZ3ag6k7X52HkOaM0KxBPCZRLQgWr3Cw/ljkwGk73j4CSgCGNTvWvjB2FDtIHMvwn7zhOACYQSl9TWGWEQ0ozTTHJj9h5bMDorh/jC9//Hr76B9/D6toRyCUZgAHYPD5B//gx3nnlVZw8eIQH797D5uQUcdsnkMsAeobHyM9ElFPWRjiqlgrAMT2bwUMyHBOg6ByBYwAJHbOjJXIERRaBhHTvyKBoy/A+rSNtRIwARKgo4FADf8uPBEHAaY6m/LzPINV1ad5ogc40lvbB+H0Ggb1PokrooXabte7QgLW1XuUd27blM7mw1nmpJ+svJKRoZbnIEnYpNl9CNZJepULxqg0DoKVOkXk2jE7TNMmSkRatsm/3XOsP+U7OciaeADinuYZLhm0IDWfNzNyVfhIBylAbcWCSc/pMjMy5BfSVHGnwo/7MkQbOXDzUAhJbcszWMQl7U59Pd7e4kqU1bVLYmRj+VVuU1jfRuKNP+RLd0etez1mLp23oX+JQVsxGVX12zkRMEI+yN4acJMjXdVe4jfdHXeg+WpnSorneWpHVMq66dv1arol80TwvGBaIAI0OWRR/wdyOVki4jQhEoq+lH6PDrDW+aV3z5cqGhgaxaYGMTJ7kUSJs36czGc8884x0sfqXmG3IixsgB3iXL4Vj4Pj4CNvtFn2/xna7Le1fu3YNfd/j1s0bcN7jYr1Od2A4h9Vqhes3rmN5sESI4wJzOr4sRjifBKF8v1wuAdQhXUI8ASpR3fQtAn48PDOmZdSH0MU7pCdET5h+TkpqEwUcUSZQjHG8+M4lj6HzDouuK32TPswpvuVyCWauDja2wjN2u12O1fVwbtpXDcS0Ahtjq6NwRFEQ9fjqzFSFzoRq4dTAenpI1Frz3ntcnJ5iwUlJyGGmlvKt6DNWjFbR/XXkysFtLQRT/1Mi4nEnaPQCiyKX36v4XiVXWkpsTjlYI0M/z5w8xEAdzjdXtxh7ehvVAnoLEsY6xv7rOltAqzUmCwD0WFvPXaZ4bTtST8he14mxABTjcQ5E6Nj1VpuWx6zingOw+pOyJiiFdNot7EApXaj0Ocnc5MUKMafZ9g6x8xiWHT75u1/Cd378Q1x/4TmQ9yBHcEzozy+weXKKe6+/iftvv4WThw+xPjvHbr3BZrtB53w+I2AMQk0zMxSq7Ln5cwR6TiwN50JU5gxK24Z8VntUp+E5+/oi63oEoNOiAb4Fxq0+XQY+WvUzcxZMUzAo31uem8hT9azWXdLn6mxXqyPSR67HoftCSn/YddUal362FSY1V8rcNerUbYpum5zPNPJMz8Ecn7bGNDfHmoe08WedFrbIs63D3voge2ss4pS6Ks330brimQ/xnl5nlg51AyjGieY7oqnBq3/uOw8n76d+TEYEbezoudbh9NIPkXdy8FnPddGNvH8ur1Im/Ud77OEKPNme74jtViVQSo3MLPBa70tbdb1XW59XLVc2NAAUC7xStAAWXQdyhO12gPdd3tU4RvFsZQMjRgHGgM9uMeZYDAaOETdv3sD5+RkWC5fqwKiIb9y4gdVyiYuLM4SYbgTebrcIHNEtl/m5dEle13W5vylunZyH97XAsecJWsaEWIplEqhWALLw5UIwIE3ePqYotDNCL93UKM1Q2UXxoPEwPDNiGFO6hhDg3RguZesNM0LdglC9ENOuynj+wCpWYLzJu6ZFfW+AfkZ7b/RP5xxiqIVq3d9RcEy8eIGTFzeDNPlcYslB9SLaB4DnShF8PBobE4AxQ9Mynua4MG55t75r/G373hLCzhFC4CbvkeFdoYn2VM0pv5ZSiI36Z2kwo+QnCiiHGOi2K2B0yZrS7Wka6fWoFauj6Za4VvganOlxzikyy6Py3T6DSICUU/0M6uxOFI8zpzAqx5RlhcfgCcEBw8Lj7ic+hm/9yY/x4hc+A1p0IHLwRAi7Hif3H2H75Cnuv/kO3nzlNbgYsD0/x3a9xvriAiBCzxGdc+XCTUu/3OMJPVtz3/Lg27V/2Xzq+bIguvVca+4t/eeAlJYvrTakPutwsSB0sk7M+twHaMc+K284poZ4a+wtmurx7DXiGrxp67OhTTHGFILZ4AXdh1Y/tY7YN0cir0MIKdB1pp9ats/xhpZtQtN5nqkdCbrd1o6KDntrvdMq+3jZOuPs9/psoF0j6SEAHJtQca+eYS5OP13/XP/n5lvr2SEEkJtmlNq3ZvfxUasf5pOJXBIekr5N1qmppzaIpsb7f4pixzvSZkxPb8e3bz6YgYv1RZY5EHAhb851YiJfx/r/7kZVq1zZ0Oi6bhZ4DMMAkMRCptsw5dI+AGAOiHmnYRh6DEMPv0zGydAPKZOUI3S+wwsvPocbN66DOe0SyLmD4+NjLJdLnJ+fYdf3GGLAZrtJhgAzVgcrADGd2fCuGBjMksc9xQFLfbXga6dwZWZlMmeGiHEiIGtGaXsiihcCKAcEpY5ReCUvYj8ERDcylqQu00J+XAC1EOz7fgQoMcIxiiFnFYc1TioF4OpFZrdS6z4IhQgh1vTQcbF28cv3XOKwqeIzq8Q0IHQub/kjhRLJbddpLDHtKijDR3ZgktAZgCsog1qBp23afYpb07cczHJ1NiFNc80fVlHpemseGd/Rv7dCKVoAQJ6vgCDlNInmuJwGjLY/QBbQxrsG1IrX7gjMAbiyjqj+zI6vRfPWOCvhqdasBWE6Pa+l7Vydum3L11Pj+3KBTZS2BebCYToGHFMKj4oEsEMPIJLDpgOOn7uDb3zvu/id734b7nCJoXMYCKBdwObpGbZPTvHea2/i4Vvv4uzhY2zOznF+cZbuEOK8c+Hl/IWVSZrW4zkJvSbl+dZ8aPrZQ+P7AEULENbrsS4toNr6nRR/6e9b/bHv6yJyTRdrZJMx2Gy9c7yUwkrrrDtaTrcMiBYtreyYkyUMNPtpx6jnQjuW5uakZXxpntFjtzLMfg8Viqo90zKeOZ7QdJuG3kyNWQCTG4/1OFrzt28ubH/0c9Z4k7HYOvV8WppagFwiG1yLhtM+aBqwGavdlRHZ3HL6aHlgZbeUlpHWkrvyvuwwtpyiLRmin7Gpm7XsEVqVOSfKoZvT9OL2bpE5mtoxt/RD6fcMiLd0997vdbAVHcEpY6Qjl87xImEje/p9bo1quo10RTVqiwPmsMVcubKhYYXMGCaSYtcRR0ODKF1Otd1tEULNcCmlrBxsSTdosqd06Dp70UMYIAfilstlORx5fn6O9WaNGAN2/Q59GOCdQ7foEMqB7YAQBzB3hUBdl84UyI6KZN2Qhal3MPTOhj6UVw5KzxC3YnpKsX+tRSK/t4BljBFD3rp35MvFbIwU29ip91wemzfeWAHqY+GyG6JLSznYrU15Ti9SEd56e7cwnaGH0DrGWFKvaV4QegvNrGJI9Y4xk1Uf8kpgZgQeEMgBbpzzxF5ToaPHb4WFLG67gMo8oVZIVhnpurQiXB6sKjqPz0XoA662Pf13xUszAiPRvL2boWk6GVeMYDd+VnnTlTKc9I9QDDaZl77vy30q2rgDauA956UVY1zatAL7MmVejUveTX9MxrGvWIV+VaF62TqbU4wgqs6XaGXqY4RngJgQQNgREFZLxIMlvvB7X8Y3f/SHuH7nNpgIAYALQNjucHb/IU7vP8Abv3oZ77/5NuJ6h+16DTBASrF674sDjIDi1dTgbBz/1AO9z3CwgMM+Z9cQ0DYuNK3sWmvRswXUWiB2DiS32myNW/orAKUCsZERMa3f8tSk/QbII6rD+DQgadUp77acDhUdqPxvLw01LaVeGH2g37U7gC26WmC2rw/6cz0uW1pgUeuVuVLP7zSUb05utPhqjp9avNMa59z6uKx+ouyowzQUaI7XKoDcqLvwExG4QQIN5Fvv2v7Zv+dkqpYpLbmi6xhpCQDt5y/TFzHUBmmVHXJy5qt2ZAFTp5LFRkWWe48QRiPHGswBPKlD9GgIQ0o2ouQMc3INSUh9xx2G3Q5yLsiOvZojwiR0asQ61ExUcxUd2CpXNjRsWk75F2M+IM0xe0RZdHq+YCRdtOa7ZIQsuyVAiXGHEFKoEDnEENB5B0nFRURYLpdpZ8Q5bDYbbDYbxMgYQkC3WKTwqRCKx37Xb+F9l0OlGCAGOU75n8PUkzDG406FhACUmCcyyjmMSwRWrqUCxnVYVV1qxZA9LhxBERj6bNyEkM+zjIeAhxDgiOA7Dwq1l7zy/BNVnrW5Ugl9tIW+zPeccCWSC8LGfogAannkq+1UFR6lQ/TSIetGfyIXweiIsFwssaCUdYFiyOFlVPohIQ993yNgqqxaCnCy8+BoMu45Wm42G3jvscjnY2wbuUYQ1cBJA4irLGqrrLUntKXI9RqWOQlRsk+NdersZbNAmYHIoeq/VmgWGOo27RhKvTwadPvASKtfdn3LGt6n1K9a5oDth61vDlCBuVj3Qifn8kFv5xA4IBIQlgvsVkvc+eyn8e1/8Md47jMvAo4xeA8EBnYB64cnePrBIzx860289fIrOH30BP16A46MgAi/WOTsUKnvPp8YFGMjDerD0WMuDKY1j3XYXtvpoT9rhcXMGQgfpkzX49WKtKtvm299z8zFaLN9nuUDoBlaremoaSmyXgOP1jst0JZewCRpxj7aij4jjknbN/rUApVz62ZOj9gyJwesETEH+q8it8eXUC7Cu4w3WnOr+1v+Rjpsb89X2L5andMCt/v6omX2ZXN5WZm0N2NIWKOg4gkzx1cB/lKnjaLQbbVALxFAzkOnc23pPflb5EpyWo7PD8NQpYAm13aOWL3dakPPCZB1Uw05K7oAtR7TdTgixEY76dhBiiQq+lX6BZ3kYV5u2jkkUCWD5uh41fKhdjRSZ0SBj95YAOAYseu3+eAl4eHDhyAiLLxPhgYlz/JytUQcegRmHK7SBXuOgEiSDYpBxFguV+i6DiEEXFxc4OLiokyY9x0IwGKxBNGAx48eY7PegNnh6NCnQ40AEAMQMziPKduJdylbCwOIYYAwpTacCtDLYPbi4qIAfMaUkYTwJRwl78yIJ10OiwMpNS0kRWs+pyKACEhMHoYAsEOIIX3vPRbLBVy/Q4jihBJvEpdUt4t8TiXboykBAaXQEeFtzv/2AQlSwYNtfgABAABJREFUqk4zZcvL1hIa2hCR9IfaUJW/5dko+RYaglK6WpSlKNTIxbr3jtBdO8K1u8/gyclTxA/uw/EYkpWZFs57BDnTkzOoSf9HoRNHD7jW+A3BoCkm3gMgnV85OzvD0dFRut/DKMay6FGDSz1mK9haoSzVnJm5sErGKuqqTzkMIobEby7TWYSb8HxLker1IEw2DEM51Gy9OhYUWMWjvUdzinKfkJvQBTPArUG7y8plwvqyQsn3UbJr5caTMZHpTJkXvfMpAx6SIUjLBbYEXHvhOXz7R9/HS1/7XeBohUgDiBmxHxDON3j81j3ce/kNnLx/H4/u3cOw3WJYb4rnimi8wdg7j2zZpQw2XHvgiVohkjUNNBho8hanNSgfpXpaM5KK3c3QP+V37UGf0HiPQZJ+n9Y3Z+Tsq6f8JJSL+YLSkVkgjMlHSl25XpH/QEUzohR+Kmtefyc7hXaNA7VzqdVXO48Vvzd4vwUsKsOAx93mOeNCz4mla0teJepQ+b82vWisuPyU1PNzxoSlqx1Ha37L54olrjq2y+SCxhj2/YoGNOUL+6wtOiwsxghWoVN67oVHc4v1MqTp2IpeBGNoGLPT9WUMJ5bdgnp3DSpcuiV77U56jQlIreO83gpbTI2dFkbRWEYwiN49kN+99ylLpUS8MBf8ZY05O29SB9E0eUTr9xhjSRyjaTj2t866WbcN9LsdvKfqPQDlHrW50up/SivK+RqC5JRqYcar6E3gQxgafd+nF7p0HwY5AMToh7543Yc+be0sFwu88vLL+NEffh++c/AEdLmTPPQ4WObdCAY6SjdO0tKDwLh/7x1cPzrEdojFAy3Zp+SgsoDs5aLDcrHCdtvjF7/4Fb79rW+BhwAeBlDnwSGAspETOXtpFx0iB8Q4YLs9A2EAMI0hlwkVZgkxhZREJehbAkGUiJ6UsshDKIYacp+opK0F2FEKiQoOkXO9jjC4ZIghZM8VZ08BkHIl53sJIicrJKbcs4hqd0giDZnFcz16e7WyyrNUxqKFuB6LvdG6/FRZv/TuBPM03r/QJwP1pqUN2RkbUxImtU5gWmCR5+mUA77wra9i+ewz+Nn//f+BQ0qKqFz0l8fkFx3Y5H4v/WW1lyNgwcyjHqsUeUvvRKxWKywWi+p5LXBaws8+2/o9f1D1ySpUy5+ASdfXEFQAo1Mxn4XHMu3ZtFfeN6Ff3vlED54CC13s2inP5LVjQYMdT0vBa0/5hG9rIlc/W2EVLXBhzw3oNkQRWi+Urj/dapPCm9hRykIcGMRApLxCmeBjXtuLBQYOCN0CODrAV/7g2/jtP/wOljevgR3BI4B2AcP5BZ7ef4T3X38Lj995H4/f+wAXT0/B2XERKWfgA6FDOlAOUEptTOMWOUCgGCF3CQgwT8MYDXI7Z3PzLDRI4XwjyWXndpyVNqDSn2ngYb/Xn1n+1EX3TWST/V47mrR803wgJfFDnse0753klKZbZEDAMAMSNizp4a3usIaBpUdrDdixtww+O845gNeSJbYdG0Z9lXWqaWff0QCSE1F0bXnnWjs0sqEGwJPLKelDBYxt+5rGOvxsjlatudf12LG12tL6LoWa7Zfvc/Nlgb1ur6kzqU6XXckh5nJ+I5GRi/4F0aROLjqR8n047fGLbrPFQb3D6SxgWsvpTKCdA/33LB9FgJwvu05gmqyX1rpt1W3XcyvUnUQdKpkpPkKbEEXan4awzxtV1fiotv2kL4Ir52gCEHb9DkfdAYAx2oMx4pMprygLDajkHpjQUT6rUfpMJeR2H7+2yofKOhVjwNnZBfp+B0aE98niS2A+MZpfLDD0PX7+s5/h3ffexa07twrocs7h/r37uHPnDkKM8D6FlTx68gTeEd59+y388pe/BAAcHBzg/Pwcm82mWpCRkydbe8qdc/jn//yf4/joCJ/73OdB+YK75WqFzXYHZsZ6s8FyuUDkiN1ui2HYYbPZwpppIqzSAkuhKFws73yOYggYhoCuS4xTpSwFUoiTulHcAj67za1DuSIDiJzuFYgppz0jhUotsqBg5jG3fWR0XR1Lr3cQ2CjoKsQqGxsWODHS4tqn0K2CLGPKhoYOdyieAUPnlnAXGtmwpil4TnMT+h3IoxyiX6/XiebJiqpoLPXqA+eTGHTRatqLdoWi+ye7JeknJuOoFm5DWbTGWwla03YNMK7uZbB9t4cli2DOAqlVr/YuF2NDYv4vabO1Pogo7eSp/lih1lISc9/ZsVi+s5+1+LtVbPjP3Bh1/QNzuViPGaCY1pljYAAjegLBYReBzqcMZ9E5PP+lz+G7/+hPcfe5uwirDtQ5EAPDeovto8d49N77eO03r+DtV14H9QFxuwMPARKGZs/KMPOEt2vQU8crzylIC0hawDf9BDTXarpIFXPz2wJSQn8rj7RsbZ0tahVrfIw0mOe3ircycCthiOIMcQ6eXNXHfWu4Mmx46qxp9VnaEXkvPGvHbuk4kS/ZuN9HH2vAMccJyNIe3BbQ0/2zcwdkILdnvlpGixQtg2xf55xiWh/WMsBNDoRfVjSd9p3LtOOw/ZHvdATAPnln+y6GAe15PoW82sscpsZOmcuZsdo+tWS5nAOQ51588UV88MEH2Gw2WCx83Q9M17W0oeV3NLqo9XvLgJHvNc4YMU/bOaH5dtSxI7/aosPlqzW9p0zlQhtvEdUt6v5454rTj1lk7uWlxWOCI67S36uWKxsa5+fnWbABq9USi2VXFvAQY7qsJo5C5NGjR/hn/+yf4X/7X/wX8F3EEHZYLhe4feduAoCRsd6twcw4PDjE2dkp/m//13+G7baH7zo8PTtLIUtZmMpZDRFu0rYs6gcPHuD/89/+S/wfv/Tb2O6ScUHOp2xUzNm7TPCuw9Bf4GK9nh1rAV4k2at8Mi76AVEJIO1F0Z4wQu3dbgk//TPIGQwat4y9IwwhGXfJmBngFQDQVi4wCk2bxk0YZgrUx4UiC0KDJgaXC4F0/boefSB8jPcf+6Y9BC36Son5ULQ2hmQnBBNwrhdFfj9GHBweoHMe3A9YUPYbG4Vn+28BphZiGrxfWrJk14u2gAMGyI07QLVRJ2ElbUFox7u3C6pOTeMPIxRk7eo4Yo4BEZTucHHTuGXtHQTGNcENU2MiqKk+J5M/nN35agEm248WmGgZGGNzbQC2TzloRXJZ0YAhUvqXW4Mnn41kxoKzAeI8QufRLzxuPvccvvWDP8DHv/IluOMVYs5EvD1fg3YBD9+7h3d//iu898ZbeHpyki7n7IeUWc+5fDHV9BxEy6jSdJwAUTNmuTdHK/LJOqp2zdo0t7KxBcxaoGyufzoc8zJjpcVHVsZYJVw5adT5Jsm+ZOtgyOVX8xfN2XGlMbiSsnyOb3UfNXBqndVo/a3HJTuQrT7Z+kZacDFitbxvzaMen9Sh1+tlcrYl++045vgFwCTcTI8txjE5zHgX1mxX9vbPyjbzVAaA+2WRpaXowqvI81Incwn3sf3KPakAvabdbIiuadauCf133cd6HfV9j81mk6NEYqG1fka/3zQQ4Sd0uQrP6b7qaBUYQD9HV/3M3PzJGtSyqMWbV1Adpc5x3NPvgBwuR+ksRsIdV6tc0MLfxXD4sO9c2dA4OjpCyRgFBiPktLb58DIn2OrcGAP869+8jL/6yV/jG9/4BpbLJZbLFYgcdv0ODMJyeYCLi3P0w4Bf/+o3ODs7x3K5wNOnp1ivN1WcnF4QevJEOIcQ8Ld/+7f4xS9+iS9+8bcwhIh+COgCo+s8Dg+Psd1usNttcXBwkA+WD2BO2lsrMD25KVyKc/YsQkqZSthsdunQOaVLtqpL+9xUgI4xhih/a2ESQ0C+5BfO0SRbif5d2unyYVFWsM6Ow9JLM3wM4w6Jbqdlqdv6AJRD7uM4CUTTg3kCAorxABOuwrWAqQSr6UcZD1I4lPfpEsPQD+icT+EpiUUrL4Wu2xocMgfk2ovHChXdV2YunZS6Kg8/TT1Ouk+s5kzeswrbth9jrIRjaStTTHbTJv00z2re2Gfc2FvbdWkBU+nfbDhcQ2CXPplnNHiy49UywXqO9BgrA5rr0AndB00DqxwskG71R9PU9pOIyg3MlEOogCQnezAO/ALMwIYI7uYxfud738ZX/vB76K4fgT2l3RAGNk/PcPbBI9x77U1cPD7B/Vdex/rpKSiWPDOpPVffh9Eak52L9HtbMQp9NP30HGqngq2/FZo29inFb1vgo+vdV4edFyunpnPVBhL6PctLLaNGr3VuPAMge+indEgyo5aNJbzOe2gnr04qommq+235Tb8j+lGvgcooN/xqxyt0sSFzti9XAcBaBuv6yzOcA3lm6tK8Yc/5ybis0WLbsPpddp8nu+mYOtGkvhYGsbpxQhPCRGbP0UrT2q4HSw/7e+EtjHrU3ruhx2FLKxQu1YsKY+ifUrSDqOh5ZuVpZ3zwwQfj2mkYL7Zty3vpw1pez2Edrde0nqjHJWGO9Zpp6U1Lu5YO0TJEj6Gm7bz8lXMYtk2g+DOr+qT/zJyOLnB6irJTKgyh0F/mSOpl5kkonB2/FZeWNpfxs5QrGxrOKUCuEvRyZHTe51hUAVfCZBF//Td/gy9+6bewXK2wGwaAgSEMGIaAMOwQI8P7Dn/2Z/8OwxDhXDoo3Q89uq7DYrGomIaZS7YpZsYu716kz4H3P3iAz30uwnfp1u9+CNhst/Cuywe6CYtFlz1N6QAsUzrA+u677+K5556rCCkeqRiTsTEMASGnru37oey0VEwX6y3i9P6YGUQzf+XxZC7xgKAxW9JysYRzPi32fE6DkA+UcmYatIWRVaKVIATKXFkhob1cLUUmn7eAiwVumgb24Kjupw4RGIVZBGG68McFl86mnD99itj3yRMY890Abupl0QtJC3AWSWoWjlVSUkcFZIkQeDo+Ma5sHWVOHFXtzSkpCyz083bh6+lvPd8am22vajM9WADJ7HNWCaYvZ5TWSA/NSzHG5lY6ML3wSbc9e/ZHyQ0bjtcC0XO0sM9Jv63ibr1frzfKuwzp+8AR1HkE77B2gOuW+OTvfBFf+dH3cevjL2LXEXbeYREZfjfg5MEj7E7O8OrPfok3fvMK4noLyqGhiQ7JEeIkyQSmvGznSwPJ1jh19rEW7wn9Z8dsgOh0nsYD5VpGyju6Hd3/qyi4dp/qz/QY9E+bZVGv+YksUHKmAjmIJQR1Mi4DNvTZreSomtLysiIGi6WN3XW09Ckx+qj11L55dW4apjk/x9PSkqtQHGsNBNuPGnhOQ0yuAoIK2DIOhsvkph4rgEv1IYCin+UzHe42azCoYuVkS1+WtUxUpUmtdC1NwbPud1Neq9+sDN5Ho7H+8e+qDaprn6tnwoNc06klF+xa1HVP+47ZbKK6v3ptybhqrDg9nzdDlMk8a4fa9PFi4gGYruFsw5asZmWrgvPunFoPNpQYM/Tm+oNZ2ly1fMisU+PfYniEHNrTapJAuHHjFpzrsN322UuQDnjHISIMEc4Rhhjwta99Ha/85jdlsvR2prQ/DAP6YSh3WojC995jsVjg7jPP4/Nf+CI2ux7Lg0P0Q8C2H5IAHgIOD1bw3qHvh0J0sSJXqxWeffZZOOcwDAMuLi7QLZYg8uj7LUJIBtCwCwATum4B5xboOj9RwnoiLCjV3wE188cYU8iDSzmTY/ZSJmOrEBW+60B5gZWsQHFGYDiAwwj8ZWE65wrgEcFXGwbTGd23iNK77fekWAEuRRuxTWPI1FH6gmQQcYx49u4zKXSvH9Jh8Qbo1uNvKUhHrhwan+t3U+lhXK92vqV/GvQWQzOiXIyox9Yar+6HfsrSS4egzSnMufMvM6oC0fRTlw8jbFp9tkpCx/O2nrWltdsxGYFRprquyzzGH6oocGjnBUiOOALgxaDtOgyeMHjg5ic/hm/9+Af4xBc+D3QegQieHfwmYDg5xdmDh7j35tt477U3cfbwMfymR1jv4EqWjanHS/O6Bo2XGX92DC1jSj8DTM/qWCNMr4/6/Wk/tJzRddizcK3+7x8bIAfdpbSMGf35vvrG32nCW0RUxflP+1eDhmrOTHvzddRzYHfuSkr1/L1NWe3yjrjE6Nv27FhNr6Bldos3WqVF53EO2s+3ZKAFTJrX5+SFjL0A8pmw3uTIS7rM8sFl/CD9Gfsnz2AC8j9M2ScDdbvpj4S9NI00EI7c3v39+5R99bXOrCR5xLOONlvm+ljpjgrTTddK6wxXbhiR55PV6L7V9dXp/OfGYWWKNqjtM44ITLVjp+gvY2do3tT1Ualv3HFt7eTMRRxctWg+v6xc2dAouxiUNFphYiSBKuQTQemdx/G16/jaN7+BPjJcCNhenGO5XGLXD9hcbODJY7PbYtF1+OwXvohnnn8BJ48eYbla4YjSuZDtdpvuPtBKhhLQ7zpfhOdytcL/7B/9I3TLJXbDgCcnJ1itVliuVgAR/GKJCIfQB4TQwzmPGEPyRgVCv+uxXC7Hm7Wzx0EyODGAPgzohx4pWwJK+60tt/HnmJpsjNedhmyI0QBWwBSUcucDoMigEFJ4GlFJs5a2xaaeYfldDiRar41uV/+rgB2mwkPXr3+WxVT+p61wTKxi3R4AeCKMl9dlzsoCUyL+0/N5xwCuGFs7Zgynp3Chx4N3304p9TiCeZqBpBLYeYHK9mGcWXwa4KednhSXnd39YKYxCwYwphOm0ZjQ9GqVlhHG6jv9GTMKeBzdF6Ox0zIuLPisnlPgp2yzjvgVslWdJ2SM7UTN63U/WU39vLK2/fPkUHKfMcAcyz0fumhw1QKl9rn59Tk9E1J4sxCVIPsDFThJxAGrXRjPgIdDJEJwjMCcUxYCXQQWnBwJg3foO4K7cwPf/sH38JlvfRX+2gF6EDwTlhHYPjnF6f2H+OC1N/HGyy/j/XfeA4UID0q3hAtwSUIBlJULkPmONNBJmY6IaoAvz4wGQw2cLUgZNR2rvznPlXVSSF31XOvf5Z1WiEpqd5xT58SDGxUoHT0wLeNO+lHWhvqUslyX238JecFCCKcM+30AkROvc5bdkNAFUElXOY5X9KgbqdQA07K2LG/Oj1HP4eiE0zLd0ljaygg40ZgyeLoCCNkHvse629+3jMkrhpZXdY98Pd0h37cLKp/Jv5ouErWReZcAQtYXhZfzroJLzlMI0CdxVUU1JAJo6gFnRo5UmOoFLa9aIN4atRVtYpIJThxxWSyIPEvqtUjvvP6nWbHsbnJkZCceyp1L+/iRs1BgtOVu5DhJVjNXqvHaNjDuNkiYoA6Rtoao7vco17jQJkODFN7KKCmU9RoS3UtU98/uyrbnbDyMX97jMTW2yOci2Shnmy2xZgqLqL9CzLoyf+Y0/xr9mGQVJ73Rpnj6f/4+Klr/XcrVQ6ck/SJGIJh+dwg5JCrPC7zv4LsO/8t/+r/CZz/3hXL4BwIQnYfzHWIEDo6OU/iRB/7p//p/g//mv/6v8ejR/QIg1us1iKiEKAnlRiGVFsKPfvgj/N7vfQ/d4qDa5QAT1usN+iHi6PAAPh+Sct7DRYcw9ImZVBxjiBGu8wj5ZtcIKiA0IoIREGKPJembqBMTloNnToSRUxhbJqod3+fy4vfOpW13l7Ij9dxjQQ6Lrks0LNiC0sV0sc7/rBcd89QIKgKYx/hdC8JGVZd7vofJJgqnAHfVNziA/ETxee+zcZVD8ICKNsJjWe2nRZwxrEdEzxHBL3CwWGAVA04+uAfvAI5U1VVlZVGG2ZxxUeggdKHM+FkKVRlXZCETCr1H70o6CzPn8dGKsIpTV9yi+5KwbboRfnxfhHTbQ6x/aroWIUsEdkmYRRLVKBIU6udohCgRUPGOBg36zIsWxC1DwK4D4U9CAj6dcwg83W+y87ZPYWka6DWr6VIBklCHSZEIOHk+B8C0vFpE6vwKON8R5ADn0XuH4fAAL33zK/jqH/0Aq2duIlCAiwEdA7TZ4ezxUzx85x7eeuVV3H/zHZw+epLSdjuXzmtkGefzXCQgYL1WKHwhBrFM2nTOKNOFJoBI03bUoXrNE4ikDm0s6GxJIx+25kdopW+/jhGlPg0cpQ8i/9Oc7/NGqt9V00GSa4hecwSSEKbICGpitVEwts1ZDrsyQjljUJwOSGfJRhkzdqAFSBKfTQ0y+V5/3jTwLQ8r2uk2qvdYQrbcOFYe04oLANXADaYvmibA9OxWawy6jM9NZYPVT7q9OUBud3daNLF6saaPrJm6W+lvAecAKMJ5MSBFximnqFpLCcvndOs55XMsdxzUdGrxsg3RapXyXhx31Thf7suyy0GoohnK8Dgb3YZf5KdT30u4HWNqbFR9N/SW31NoYnsco+6sdcP4bC3jrT6ztJtgGx4z1MmzvjgOM7bCGJIUQU2axHzPmT1fJsXqurpfMiapM/NQxnaUPywyzkY+sJgT2clD2XihUXrou461fqt0ZBEBdkeQAHIgptFQdLUxqmlxWfkQOxo1YClMb4SlxJq++OKL+PLv/A5WiwWOj46KYuz7dO9GOA7wfoGQPZb9boNPfvIT+MY3voH/8X/8H8DEOMiXnWlGCsYz773HcrnE177+dXTdAsvlMu1kLJflfIf3Hqen5wCla9rJLQAesNumXYZhCIXmwzCUy1sks4YsDGQBNISAwcTD6gl03mEIQ+m3fUbT0QpBJ4qKHYjSYe3FosvfAwAVmo8gqQZN+rAdlILQ1ngIARR50qcR0I7Czy5cveCsMrEMXW+bjp/rXRcr9Pcxb2mP04r05OAisD09x+mDR9g+PcN1Hrcg9TsFqO8pLSEl9GgJ1bn+yjN6J66lINg8X36q76ZgeuxHy0u5b0z2UCcnpJYNmP0Zn/ScJt5CMa4nisnVAtYKXAsEtKCudsgEfBHVkrPRvxbwsv23h4t121aQl/Xc8ALPCdtAQO8ICxAWgbDiZIBGAvrOYbvq8MLnX8LX/+hHuPuJjyE4AjGwiMCSPC5OTvHgnfdw77U3ce/Nt/Hw3geI2x4+96PruiJ3vPdwEC9ce60C0wOAmgfsuSIdOy7KeAy7EmN2qlTnDMkWjezn+uI3ey5Al0l8sZmPORroZ+fuAZC/rxIKMBeLPeHBxjO6WIBc64t5T7F+X68lu2b0eZM52boPGNlytTjy9vqYm5s5oN8CjLof5Xk3XfMtI2JfXVYn1Z+FMh9j3YCAXavjZ4v6WuS3vGfX5xw4nWCvS2hs+UEatzsopZ6MXXQ7RR5nB58YKYykgvkS54/QTvqgjQGuyTLBRJpG1U7CzLLQfGN50BaLT1oYba7MrRP7uWDh1pq7DOdcpdTvJ4PDe9FvORzMOMek/Q9bij7AlEevUj7UPRpWMcnvq2W6J0MAPpCyVN3/4D7uPuOwWq3gvMdi0aHzHZaHB1hjm3YMYkQIA4YwAMOQ7rpQyk0UX/GmKH+PHuzF+XmVXQFAUcwhBBwcHKLr0maic0AIhL5P7cYYsV5vAOQDmjoHckxGVgihgHY5I6KVq/7bLnrN9NYrYQ0NbWQIk/iuQxQQFsYDhpxjSYmoePvHbb1MBxqZxGbp0P2fMB/NL1Q9Vp0xRdpu0SG1O/Vmt4SJ7d8cqIsxZ5oaIlZugSfvJVDmAoM5pksO1RzkP2rp1ih2boqBQjXNxrAdN9l9kMOkli+qdrKobQlGMTQm/WAxuts0Er6142Ee88nr9xKP0NjmJcJZ00dAogCZOt9/e7t6bk51v+dAZOpq+24NSwsNNHR4lQbZ+pmW4N/HJnPCVoKsfCR0MYVg7jyw6YDjjzyPr/74B/jUV76E/sBjQymUyvcRfHqORw8e4t0338Jrv3kFj9+/j2G9TaFSjqrLH22IkfTCGkQaPMnvNgONHrs2GiWLXtWO4X87V9K/OXrtMwD0Z+NzFoq0M7LNGRlCq6sq2HFtzRsbLXCp+UzzVgSXcxpWFto+Cf2TgTKCqRYQb4WE2MPszDxJ62oNEDuu5vqb7G2PTiN9KVwL6F8FjMi6Fzm67z1LvxACHFIoog5FaQHVlgNF973lNGzJUQtmLb3mBwrItgGzfb52oMyBZNu+LfpznVygfhcFM+hS1kkDqNc/Ux0h74wgy599a8vOadlN2OM0snytx6D7NPeupYctc+FNzTBaJHpO70uj4pyTOuf4d4735nCjpUMLk8g7LreZkhyNhh/HCM6ypKV7NT6xMobZ6ESRO2TkwyUyVcqVDY3VaoXVaoWDgwN477FarVIFXYeF70qaOCHI0dFRTmmbDI/ddgsCsPAdhmHA0PfY9gN2Qw9GSs0FSqFSp6enOLp2XA6EFw88JSNDh42IMXFwcIDNeg3nF1Wmn91ul7cLfTpEjQgOsUxMP2wAEF5//XU8PX2Kz33+81islkLGZAyFfDt4YPT5cLkW2NrwSoq/FmzyU8YhuztNEMajcE+CNxliKWOWMB+gVUWIYbwB23r9HCBR7zpuMSmi6fakvCtFC+lq6xz1YpGzMjYueKx/3K6VYpm8pVD17xNBT4Q+BBATdhdrnD05gc/tDIHBmUi6P1KsMmwJpao9cIlTnCrrJIC1lxyo71lpgRM71lnwOgFzdR9tn+eKFTDVdwrUzQlzK5Bkt0/GWIdnJKNAAKs1QKX+lnFgFe04N1T1Q+hr39NzaRWtHXfLCCnC2tRn+dPSlojQMcEHl+Kjlx5nFBBvHuG3//A7+PL3vofF4SGGpQMvCBgC4nqD9ZMzvPJXP8Xbr7yKk4ePsF1vEh/HdMbK5bUtfa1AowqN1MBSyya909niNcvTmrZ12Mo0JtnOVWvHaA44pX7XAFHTU+Kg7ef6dzvvVglOvP1AvlB16jluARRmRglnMLTXvNei62UKubUemBkxDBDQ3SoWtLUAcgtsz/VBg6xq7MbQq+mNAhSt4at5rjUHtpR249QJptvV67yiG+o50XJBntOx83reWkXTzdJE03qi9xs8UeoUoxMEogiXw6JjFJfSSL/Wbqset11v+kxOS5ZpPS2v2jElQM0grudSlwSslUOKAfL7d+3sp1au67HL93os9h37rOY3vVsidJS+tUJ2pR1xHuv0+2ObaczyvnYwpkfaRtmEdupdO9YWP07mpqGLeZxMxBiw2/W1THF1OL29+NPKiHrHUtEhDyXGdDCwhW0vK1c2ND772c9WikgzOId6YQDJAHnhhRcQA2G5XIJWB+j7Hp1PZy1673Gx2cJ5j2HosVwtEbZbfOxjH0tnOjqHxWKBg4ODIjh2u125dl4rxtVqheeffx7H165jdXiUQgryd13X4ejoCEQdiBjM6QD4bhfKYokx4KMf/Sjubp/BarVKseAsqWzH2OeUrnSMwYwcq0vt9ATKz9ZE2Lhw/Z54REHJoEo3Q/TohwFLTl5jlthxIkAJE91eMbbm+sK5/2h5kUYml8WnzzjYRWS3fq/i7XTOlTs4pNhFbmlnDZPo8vkHOKwWC3S+AwEYQph3R9MIlmzfWnNV969dpQjeVrz/nACea2NfaQFd3W6rTju3LQUazdhb/W7NJXPNI5UiZyrphcUJYeuz3umW8q/6QrVaskDC0sUqHP2eBTJ2V48Mn7TmsdVfAuBch40Hdkcdnv/iF/CtP/kBbn/0BTB5wC3QMYMuemzOL/Duy6/g8Tv38MFrb+HJ/YfpTBMonRdwSPza+VlQw4n5KiBm6WbX1T7QaddBPT+jwaFBp27Php/oujQgqudo/N4q3RbAk781TVoeShvbP85QPadza7TvezCr9O2Y3rVi26zphupMyNxa1PRLn0/HXdZqI3zMygALXjQdWjwxK3+ynTHHK2J82f7bsi8kq+qHtKm7MCOTK/oo2rTlVO0Q0XwqdbR0jbyvIwXm6HhZ+Ko8K71L9Wter3Wjbrt63/BPc4fa0K3CBS4dXreOu1zjnnlM8lBM0CZ2adE+1docgxiI+ruW/LHjESq2+tnCE5ORGN5vtadqFAhVdN1Yx9yezLTf9u6YObmmQ1dlfufWpx3fMPTJeYyydAtbzenZlpEj444xn2V2DhFIDi+q67sKvgE+hKFxfHyMEAIWi7RjIDsF6exCWrxdl0KjQOmsQwgB3i0rL/4wDDg8PMQQAvq+x/LgAIvFAv1ui8VigY985KM4Pj7Grt+Vcxb1XQQoqchEaCwWi3ygfPSqh3wAKmRA65wszAHDboOTJ4/Q91u4bKEdHh7i8OgIb779Fn7161/hG9/8JspB6sh5F2aAY4wGT2SwazOMFM0oGpCJ8GqFC1Fe1C7FeJWD7S4M6d4PyzBmcWmhy7FeSEWIEcOhm/Hy1OBAPtcAR7cnceMyfruIdNHv6xhieymjzKP2zmnmJiL0iGBKl/YBadkHTrdk0ng2r1nmFJCdwwoMzFcGSSvbAlhzC5KIRu/QDL3m+jOn4FsAzc5Zqx85ycqVhIduI8aahq1i4+51G3uBzrSnFQjTRWRESzFrBbFPaFfzL5K6AeLHeUNxCsjnwXucu4hrn/wIfu8f/hgf/cJL8MsFiIGOOoQ+ANseJ++8h9d/8Uu8//ZbCLsddutt6udikZJREJWdW8L8jlda4+1Un7NUbPCENjxt2N/47H7jU38mfdChry3vcDpfFqvdmPH9cRG3xq1/b4XGtD6z3wOo5LH1AAqPk1mDc7KiAgZXVMLCt9Zwa43bvrePn+347Tq8rH5pw84ZMMpCK5NbYHPf39XnvN+zq/usdQXyGpTPW2mQtVzWc3SZXNTzYef6KkB7fAGlrxKtkL4WPmq3qdtu8d0c2Nb9sXXK363dvqvyrHOunHeyOr+SQQ1+K33eI/a1/NDvJXk3D5BbYNp+J9/rdubomlRBvYaKLHb715Jur+VEsWNt6far8Kn9nlyKYaE8AI117G6ENnDm6mQe9zYZ06MCVylXNjRu3LwDifVKC7lLE8BAP+zgQDhcHcA7h8ePHuUD1cB2t8bFxQVijLhz5w4iGN1ygfVmnU/Kh7wDkcC07xb4xCc/jT7ssFmvcX5+DuJ06PfZ557H8uAAb731VmJyTtt9u36LPvS4uewQhh7EEefn59jtety+fQtnZ2cAORwcHKDrOmzWO5ydr7FYJOIOMaR/IYCJsDo8Qh8ZHIFhu8Nuu8N2F9CHROrzdY8Y8yl/4RnKDEljqjIposDkvIjkN7cCkSNAXbLXPVFKa0sEeA+/XIK3WxApjxdROrtRCV3jOUwPT4RXjBEx9GlHJnOQ9N/e+9ASTFYA6HpbCzdN15i/XQs8aUdv7dntfyvAiAgIAKXYsGRIhgDilCWCcgpM0UNFpnMtwCfGgcsgEpyzSOW2ZJXxCDLHkr0bzHsFSpnnMh81SNX9sYdW6z7XoLkSoPKMrj7PLYFGoSmfkYQ5UTkTUo1srzBJ49ahc+UbRyl2es/unbx7FaOjUk5a6gFprK5Wqvqn5R9NM5fDHMXISlnckmxJZ6RkTIwATmvNJdp1cKCBQXDoidIh8Lu38I0f/SG+8M2vwh2vEAnw7OH7iLheY/30KV7/1a9x/uAx3nv9DZw+eYJF18F7h2WX5tU7X/U5hgDJBpX6LiEQBEmzWbyDjkYeV+O3ns+QeaSsqZh2FgrfU6IpE0Z6uEQxqGwxDAEUI9+VA7rAGIZGKVNbOUgK6Z+aUi+5XpCM9/wFUepHCcETPuYpX6G0FXOoZrqniSjtElmaWGDSCtcE0oaGrNn0jDKuiUv2uhC10dfg35m/tbGT6NdeB5eFLVgw1QLeU3qNv2R1kX5S/bzu86XAWvVBAx37ef33qFtqQ2LaRk2HWOYGxCgmMdfvWf3R6pP9nVlS0CLzW6q4ZWjaUvVfZFYRWknOJPnXDqfZN78tOui+l0h9opxNjMGBK8eWrlPCqh1quVmeJT3+vJu1x6Mv/WBmRA4lg5lEYYBlB2tmJ6QBvMvvKgOqXLdALsnyEPMdKMTlduxkFCR8JTSzDikp0zBnLlOm5UP6AON6Qb3exQFnsdAcz819ZkOt5kpkRuedShxEJRXxPh2uHUAFe2T5xggAkn5TyqfUuQ/j2HJlQ8P7Vcm8RM5hdZBeZTBo6IAhIg4R2+0GDz54iNXRIR4+fIwnZ09L9qjl+gL90x4fOzwAdR4L78vac+QRA0B+gRs372C32+D6tZvo/AOcnpxg2S1wenKCT929i5c+9Wn88je/wq7vMYQB5AmbzRoxDLj//kPEGHF0dITT01MsFx2ePHmMyBF37jwD3y0QQsTh8XUw99huLxBiwC4MCDHizrPPgLoFtrsBznmEvJPRB0YfkpLcbPucr7hOKVmAOidQJ8BZ774AKZREA+zCkH70YDoAu2GAixF9GLDsFghMoEhYkAeIMXBAAJeYY2Gc0p+syGGE6vg7ox92KU1mTjNbxlHkVDvuWSsE643TwEbGL59LaW1d275bg0B+l58eKQtCiAHOMZbOpRR8IqCydB/bHQVH03ABEpBU90ZEjqN+KIc+pK5RKWuh2FKSU5CtAaP9vE3Hsc6itaYLPoqRkSWg2tFy3kFnUivv5Tz0rR2guXFoA0WHRlWKFVNBqseQPpoK3lYYTFpTKD+zKSmdKqhI85JWmK2xiMJL/9LwBQiDkqHvclYozlqFHQBi+JD75DtsCegPlvjCN76Gr/3JD3D03N10l0uMWJFHON3g9NEJ7r3+Ot569WWcnZzi9MkTUIjoQPABIKSU2jI+R+NOhc9zI9nxUtfHM1t6boqckfEDE/omw4SEcYvTRk8/A0WuCOAsNwNwal/TthiMlNODu5wgQQwfncYzs2aQtZUUQFlWYrgI+ITweAjFSPHcBkRE+VZkGuuT3/Vt323DdwRdukQWXqVisEi8e6J3PhgNGmW48JyJn9fF9tue22sV/Z3ekWkZ1zp7mD3YX81zbRFlIDeKAwv6CmAyfbOAUIBLaOzCt+QKg+HITeZGxtg2TrgKpWEedZcYxCIPpD0LJm1I7timApGghGYRwdwjxnoHZ05GlrGRwHMuRjYjKlpPz0bY+bT1T3YkqKym0ZjPPyPzmGYZNKm7GN9mHVj5rWVx5bhSpdbXcZQrnJwHpT01VS3azQLkJNSKc0UuIHRecvClURNlavMom8Sgb2GL1lyK8W3HVun58uX4nDhEWmHNpeYZzGBpbd/Rn5fv88/lagVwvkg76xCRLS35Y89WF0ODCClludm9YM73s0wx3b5yZUND4ul1uJJzDiEGkCccXltiWG/x8P4DbHc7nK0v8MH9+4BzWF9sMoE8NusNnnv2BTBSuFLf7xBy3eebC8TIWB4cIMaAEAbcuHEL64sLxBgwcMSDhw/xu1/9Cp594Tn8d//9fw/nO4A8zi42eOvd97A+3+Lo6AhMDoGBp+fnCBE432xxsN3hgH3auQDh/sOHOD4+HNPbRmC73cJ3C2y3O8TQY9ilywL7XY9hCCA4bDYBYQiThb5YLBBCwGazKedEYozl4LwtIgBFGHvnEmP4LhkyPFr+lHcnRgDCxRvA4BweNioz7aUvQqRhELSYXAtibSRob5+EO0mxAgmYZlQQhdDadrPhCnohlUQAVjCyGGsBm/UGuHZzHMMe/td9tQe0dGkd3GrVVfoKwAoLS5OqPqAC91c5AKe/03M3zjWKkcFQ94QgYXF2OZxOeebEdNlX2lul6d4FTYvyTAaKrUOJljb1vGIyphY9bF/s9rbUYUGj7T9RrTyknUjAzgGO0yV8AgQIDAqEQ/ZYO2B9vMSdz3wS3/7jH+LZT3wMfrEAwoCOHGI/YHPyBI/fex/vvPI63nv7bZydnaDfbMH54j1XlPXUGSA/7TrVxYbqFcVJCQa0Yri1XJEi82Prq8OnAH1fhf4pcmMSBqppeomCl2da89j6W+rZp8xr0FOHEEx4yIxHCqVOTvoxAuga5Ou67Pj2tSUyVu/kzL1ny9xYgGk63jl5pH/fx3fCC9HU0wKuLcBo6y+0iDHJJ0N/DYLmaKDbaY1F00E7yOb6l2s1dXJZA1pOtWggfZoLeax20yajmRoP076N9djvGPXatuu1xVfFkDNOqEJzc1mQ6Drd0j5a2Plm0UszYNoW+WwuZEfXb/uTcNj4u7TfOktqaUTFQLy81GtkurZn+d7IpX3zpOmh1404lGJxprgRC1Abn1m6Vcb8nrb/LuXKhsZ6vcZqtSrnMpjTPRdHR0eIiNieX+D8/ByPHz/GZr1GAOPhw0d49sWPIHCP5WqFi/UWznk8PTvHZrvFwEAYAnabLRwBDx88giPCtes3AAAhDHjyaI3F8gB9P8B74MnJCU5OTvDpl17C7Tt38ODhI0QmPHnyFM4dYHV4hPuPHmN5eIS7zz6Hx48fI4AwhIghMB6fnuH99z/A6ekT3Lp1DYscPx2GiH6XDl3vdgOGIWUiCH1f0tkK6O13O2w2G+x2ByVvsUwaACyXS2w2m3LGRHuepAijayAdOSJyvpwuH9hKtyKnbVbvHCIPBfI4l+7rcM4nNIRaiDNzybClt+alEBycS8w9DEMlzK1Q1wtA5l94wSp6Gz40LpzaYCn9ICq7KhMlr4SHNYjkM+ccnE+GK3heMMwt+ppuI32qcAaipvAu9ZnPbVtN42OPkuP0x4zQoUa/5wSDEiRFwIuXhgqIQkNhXNaGKF1NI0sDu/tlgaGuV/ONBaX6ZwskgkeVp2m+T1gX80RNbDWvnL3UDHTkAUYKZ3QOF45w/LEX8LUffw+f+sqX4JYdQA4UGLQdUha0h0/w0z//Czx+7z4uTp6iH3qgS2Gg0QGI6VbjOSvPhkVo2sjftt/VWtlDs2TaTEHZXEk0TXKp1Rd93sqCbv28BWJEbVA5Po9mHVmTX4H/a6+15qvWTmuTDpQu4JMMakXmFMdQG8C3gJb9XvdFdh3Sgd3982H72TIGgDE0Qq+/ag5MX7Rh3gKH4xim7gm73lpy3uqGSmYo+TAXPiXft2jZMjg1sNROD70erJ4a+5vGOc6F/re/zAHLmvdl7LUMsPrtMj6Q58rvZq9B2moZahoTyA6BrQ/5W6FFrmRiZFzW1zYPtccxV8/cGrN3VrTmcy7sUPP+NBSt3tG4apHIgZZu2yerqvloyDcrUznPQwqPI2y3WxlV4anWurM0adF7r1yly+WTLlc2NM7Pz0FEOD8/x507d9IB7r7HwdFh9vYPePjwIbbbLTbbLa7fvIHtdof37t1H1y3gu01JIfboySn6oU9bXTEBeoSI87MzcIx47vkXEGLAdrPBnWeeRT+EdKYjBoQY8cabb+LTn/kMvv/DH+K//Zf/HWIE3n7nHj54cArXLeCdx8PHT4vwds6hW3Z48Ogpzs/X6PsBu90aZ+szHF//TLphuh+w3fbYDamNYQi4uLjA+ZMncH6JgR2GIaDnAIQe680am80KR0dHhUaixPq+x/n5eWVktASMLJAKOOT3mbIlPvSlbpKQBLnTI1+Wo4WoTH45p2GE6ChkAeIxA4XsvtjUvdIvYTphWJ1OV96x3uN6kbliWbdS+zKPuzIWJBJRtWNjAayIVtl1IxIPdC1M5rbfNUjSW8e6b+n36cVtgMDVqSCwQkLPMxGVPNwjjdSY0fYQjm20lSMjhUiBs5HpBJhls4IURGCkXY4chOSdhzUCpGg+LuPKlemD1uP8TYGnLVYBJ/7iSrBboGaFZWkzEWwyd7rvkzqBKra24kkGlpx2NIgTzw6UwrXctSN84fvfwZd+/9tY3rmOHgEuAqtACCfnePLwIX7z81/gvdffxMmDR1iSB/oeHcmt1jEd1svGgISuWTBg51fW6KUH9xqAU9NLcLqlkQbQspYkzDNTCJL0YE7xaaeKPjhp19M4nykcRa9rKSFMs7jJe3L+7DJlZ0Gb9WhaulnQSZR2kO09DVZx60srtTGj/57bOdV9LfHRBnhKuYrxoudhXFd1KGFr3HN12v5bQK9pNQew9XP6vWoHi9qGn6bxHN1adBojK6ft7lsjLXmVPkuGNpGA7qlDxrZR8VMDJCadTxPTpaVH7PcthwMgw24bgnOAEpDd7xEnSJKXsZ+ogC2F0diwckD3sQWUy9zT1EAFppksW/1t0cjiB3m2nO3iaZp++/s+gG35uYUpWvRtrY25umUce+e4okHeF8/JM3S4YowRjmsDqzVWeacVeWCxq1paVy4fakfDe19ius7Pz9F1HfrdDovFAvdPT/H06dPU2RDw0ksv4fHjxzjvH4M5Za3qug7Xjo9BtMFu2KFbdthtdzg7PcVmvcZuk+7a+OQnPoaPf+ITePXVV9F1HW7dvoMYAz54/x4WywUePXmE0/NzfOGLX8LJ0zX+5qc/x8nTc1y7sUS46NF1HZ6ePkUMAcfXruHatWtYcrIyh4TEEMnj/GKLR0+e4va1Q4SQjY2+R4iMIUTce+99vP3aa3jps59DtzxMOxuhx7JzOZY0TeDFxQUODw/BzOVil4uLC9y6davKmGUnV77Tyk/+i4zkKcvvDGHAMjMehZB2PxCrm1E1MxXFp5hkGkbClUBpKTS7iGz4QstokFJZ8ahTBlrBo5VJS3DP7gqFiAjG4FBC8CIzugY4uUyBxYZyGt/ZJxgA56dCzyou24eW8ii/pw8mbab3ACgBTzTmjgehbJ1ztmM0sAZEqbEaUjJw9fzouuf6aJWE/ukyKG/RQT/b8jJpYWvp1Prd/tSg3SrAiYDn0S9XgQ9muBhBziN2Dmti4OgQn/jSb+FrP/4Bjj/yDIJjMBOWAfCbHrvTNR6/+x5+/td/jXtvvYOw2WIJhxh28J3DECIopnAz56ic4+i6LsfQTvuhx2rH3lJE5ZnGelS1VTxU1z8azZa2wuvANIShDczal0cCOt0jAEzB+1jHHrDRkKtjB+pnxfCx61DTb9brqDCbNURkDFpWttbMnPJu0UbTufVeSz7a91s7gnOFQNVZw7l+jX1LfGLHa0HY3Fitrqr1TDvs9DIg1+ongJKlsdUf/bzm5wnPxuySIAciD8YY5jsHpC099ve53klvPSe/W53clGkzoVNXLW1dnO/BorzsGrtVf9+yTx/qndMWP+7TBfK9XEuwby226omYGgr6vZbzR3SxdTq0DLLW9/by6VbR2KYS51mWOVV/9az6XYq0p3f95su8DJorVzY0nn32WXSdx8HBYbqw72BV0twe+HSR30c+8iI269u4du0aPvGpTwJ+gWtuBUCEODDkBb1YLgFi+M7j2rVrODw8SGcPImOxXMH7Di++8CJOT5/iYLXCndu3cPPmTWy25wixx+Mnj/HCdouvf+MbuHHrLg4OjuEXK/iug/cdrl2/DgLQLfJN451DHyKWfpmI3DkAAx49eYy4uUDnPYYhguDAMYURPf/88zherXBweATyCxwdXwM4oHOMbjGmdD08PCxgDwAODg7w8Y9/HM65Kn+yVmpaaIzfJS+xI4cgYTtIWS9CSPd/MAi+67BwhN2wQyQGD7FSugKygDozlmaydB9HBtgqdlXncLaHvfXCai0YwKR/08xIdUDTdIsSE0NILwgLSK1V7vLFZqNRE6p6dJt2YZd2MLXUx2cZ4LYnmTBVCHZh6/aL0BKDwAhLSD9mgFy6z6DeYXDOpdoE4IOTl98IyDnDSV+mqI3jfYaGBWfSzxhrA1ietcKs0M8ILU2vuR0WABV4jI3v7TyXtojK+Z6cTmg690QYHMAdISw87nz6U/jaH/0QL3zus0CXstB0zMB2QFhv8OC99/Drn/0tzh4+xNN79+ECQJFAHOG9Q3AER75keiLQeMg6RsRsgGh6WO+7VRR6/lv02Vd0XfXcjcDZApu0mzHfloAvCzatEi48QgQ2h7qn81d7R6s0xsxNQ9WuG3vuQ/fdnkezQC5XWNGo5qWc8W4GhFiFPld0ncxtwKSftZ/J37JmWsC52Q9K/+QGc1vm+5+N5dg+g7DvYPvsDk9eF9LXufdbpfUsM1fnSDTPt4DUFPDlfwSk27yz15imstyC/8v6PQHV+nc1dsurdf/Q5le2pkYbTNtCQNqpaALozI8Sglj6095t0e1Y2ly1TGXTVNcA7XNqVvemz67c9N7xaAdY29BrG0Bt2dJua24c9vsiE2OEnJesNDzVOqWF54A018MwjE4vl84PtvpMJP+7ermyofHjH/1hakTiPdWg05VpAJgR8yHplEHFIYCKp1gGN4Sh9FOy+sS8Td51HZCzCDz3zC04RwjDAOfSCflh6BHikA5mOw/A4Vvf+N3ERNnjQJTAuTBmENBJCcTHyAAxhqEHEcMjA3XOOwnOYbPdAreuwX/kueTxl/CJoUcIA64dH8H7FGKwWq3KRIgXQC4atMyWQp9ivjZ+XKhOYlpAOVVnCiPxqVJg6EExgLlHJAfvOhAz4jDApyOqYI4gHg8/xSh3nKC0r3PkwwBiGyPfUvxNkJ+VW0vo6tKK4weSCCOXNDaJxyQbXQIEbR9iTHzjM50657DsFnmaHQjtrFYC7LU3n0pK0Kk3qy4j8ClbxpmvNG0sgIvlWZ6AWSv9KuHVNBCEdhKSlBQgURpD5Ho7uwUCWsB+3yE0LagExAAYw1cklXDeLSGX6UgjfBfFnepKw7bCr+WdbymxJvjK7Y9EQjEgHCf+SsYdSjYnMINzOkzPBJfz+AcwBiKcO49rzz+Lb/34B/j07/423GqJgSIcGBQDXB+xvv8I7732Bl7+5S9x7733Uoao3QAHQteldegXfkzgABR55DufjQs0i95hmgMxLeN5/H0Mychckng9Jv7R74xtRRD5IkPSGTSRIQzm+r2WId1Srnp+dR+ToSFzKeGOY9ij5l8dLhlDHI1q8RzKOqD6vRa/W4Bg5Zq8V5SyAcBjvfM7pq3npf9TEKT+YbojZz2NbaOsDTz3yWWO3LzdOa2VJEkkXbs4VEZ5Vtdrf1rZJT91PH01pmx8M+fziLJmeJQd1gBr0UK373ztkLG76i0APr6fQn7FgaPXkpVR9buJryVUR8LlRxhIRR60boDX+tjKOq1zLR1af0uxO1wtR1/BBcCUNrnnzmUnqMyfwha6n3Nrq1oP+XvBQuMr4w6bxiFzRkol/1i3K4YrQ9xvLf3R0q/MKuuWkidWvk3GVOpp82dLn7cwkZab++oQGaRlr+y0FbqhLZukXuENMTJKG6q9Odk2V68tVzY0bt++URaqFZR68JYwujMpuxMDWKgFsyh1SYwYM8E5rya2Q98nAwMELBZLdB2Xi/pagk5ijZOCGy/yA0brDVipBTumPVssFgjxCLvtNt3hoVKDxZj6sugcKO8A7HY7MHM5AK4Vohyy1rQpsdaUQPLIk6PnUPLYE2WhFBPAEa9KyLnhPRxcziQUYmbW5N4tMa9WeLSEjJ3LOSZvKW0ZUytMrLSLKWNWwjONDGJ8FbFM46Vw8k5pOx+m9eQAvvyCLt2OPCag14K1llLWiLDen2mDek4IavwbKGcmRAG12msp55ruI33GStLZBlJ902tC6rCAQ37OretCNwOK5HeXjeI0VtkZGVOmWtpouaS9r+OYp3SdA1d6PBNxR1nAChgSo5UgYchpDJHzu+nukugdegL8tWN87Xvfxpe/912srh0g+MQoB0zYna9xcvoYT95+Dw9eeQtv/eplbM4vUopWoSEBgQB4SndWQBmBWXH1fQ8iyucg0q5GS3i3lJulgwV2lIFReVx9Frg2YLR3Nj1PCCGqHYy2opEdKlFu1ps+p5A1eJbJkn7GyHBuCt41DbRREUUhSv8a77RAaYueFsxbAClt63mRZqfKf/y81f/WLs/Yh+Q00DS0IRj6c91/O047ZguYiKjIzklhZHg21sPqfAKbPs3p/jkANZWvqVE1lRgNjBEw6TnS9GgBuJb32c5lS8aOdJJnFA14P/gSs55BWTy7nOVZ6x0BhorYmPLZHGC3Y7f9Fz3T1GNAk5f0fDVlLajgDn3287L3WyC5tM/JyUyk52c6F0Adtt3irfS8/jfyiGSdsrSsaGZkVmnbjXOyD7BXdFW6rmXk7ZtX26eqXjMG59J5TLl7Z7FcYOEdzs9Ps8tmugPUwhYaRzNnx0pjqII+9uGsVrmyoSHC0Xqt9GTJwg751m/mlJlKBsk8ghnZ8pEByiT2fT+Jx2sBL2YuWz3yN9E0X7BMRuuQpdTf97uiNMsBqBw7jUx0eb/rupSuloAhG0a73W5Sv4xPLwhmLnNnFaCMTaAwkYPLlqojQh8jmFO/ogC7zMAc2wunBTQrZYQ2U7c+s3227dmwsH2C2Ap8xFi8ZC3BMdcXT4RhCGBKt7U/fXqSgQ5no6xRmIunrlXmxp6/rNq3dNF8W94tc1q/N6fk9HN7+2L6W/7GKB/mlPyUxtMQgBZYkjrswfAWOCYZe0OhaR4Uuo1rdD60oUWLOWBe/Z0vakPMa1n7FtmBvMPgCP3KY90RPv5bn8d3fvgD3HruWbADIjE6Bng3YPv0DKePn+Ddd9/CX/3bf49uFxAutmOoWFbCc0B7bi60TBIa2/lvgjP1rpXLWrnq8EidgKI1J7odHUqpn2cePX5yAakFAPscFfpni0dt2Jwdq5Yz9m/97L4dSiubNe3quqe7ffZZPf65tnSbrXHZtafHNgdyJnd+mBA72wfm8fxeeYamjpNWv1tF97El++14rQ5p0aB1lsY6ZWx2LD0+3YbeaW+tE91ua+yWN22be0vFM/WYmyF/mPKBlQ/y7j5PN5ddoLqvrbrq7jJAbUekHhKRmFKAVaR27dvSkgWaZ8vaN4aX/N7i67n65z5vvW/1mqwRCWFv6UWLt+pnRiPS8rLlx6uWyzAXAJycnMAT4H03YqA4vg+gcoDrsVdzRvM77ckImflyplzZ0NAEaS1eUV46TaoYG1p56thNq4xSaFK9AyCTLulPdRt6C7alCDXzjPSrt6916lqtOLuuS4ZGHAGAPqAjl8RoD54YKQDK2CVbUtlFSebghKbMyQyPIWJgBntfLo6Ti7NiTOluHQhe7c6QEQxWIGnaVFuujYViaWfrnYKZOkRptpjvqn5hXjHCxIDquQ45fIpz9YeHRzk0bWha42Ucajx2nLOCbM/Y7DsVSJkZX4vugDKuZ+g1t+Vdfk+VNpVVRYMZBdqK37yKgp20YwCnNrpbYG2uLeHZFsi2wrsFOED5RmoAHadcZJJRttz27Bw2nrB47jZ+/0d/gJe+8jtgTwic6d0P2F5ssHl0godvv4c3XnkFb7z2KmiIGPoBnfOIhBLfbMcnfdIxzTaO3hpv+v2W7N03HwIma7Ozpqn+3cpzvbsldLdzRZScQjKvmm/0O1ZB23myxRka2rme8+xXa07x2T6ZNAd4dT/F+A2hdrRZuWfpOlf0Orbtyffg8bZoC05a/GH7sa9d+y4RTTyUhWYkYY7z7en5bfVxjl+b4KYxjvrnfmNHjxUY9eacvGzxpP5c02yOn1v1jkZF3UcJQav62JAVwneWn+2YZ9cSA9W2LabzK0DaOkhLX5VMkDo5Oz5TGv4UdUGOipGq18WcrtNtteatjEkNpyUL9O92bvbN+dz60LpG10s0hgw2d/1MHQXfonZot9Zuy1Bo1al/t1hBsHGR20Q4OjzEk+22hJ9J1imtR217Vu9zlNDnmn5gBtP0/cvKh7gZ3E+2IeV3KfK5xHppA0ODdPlcwo705Mr7AKrdCnlGE1ZPnmUUeU8rdCGmGBJi+CwWXTm7oFO1WmDAnMIdFvmAOWj0+C2Xy9KuGBXynY1J3bcz1HUOYRfAGA88yjPO+bzLkheloYGuX/4W2o/gQ6WyhEOk/ecxdN+sUtHzavnCbuPLYrWKxefb4SU21wrgFCfuq/7rfjjvyiU1wi+SMtMaKenL2ntnF7nm8aqvzHXYkylCD61gnXOTvROrdK0SaYEoy+fST/tZwpUuHwyb3sFgaafHrOu1wnoOKNjvNIAKmXaX5TfXijeNqb2DOadsLgNfQhfivNPAABOhR0TwQICDO1ri81/7Cr7y/e9hefsGdp5A3oGGgP7iAuunp3j07vt44xe/xv0338XTx4/hnQMxp2x1MYI6n9LgqjWo+5XWPCHG6UWfdiya1i1A04pbnspCmdvp3LVAsvyuPcU2A5ydF6voxnFOPa7Sjg090p+1dp3l3Rbo02Owv1/2zD4gJO3pfrbqJRLPXtsJZ+sUXbAPXKfvU5VzckGe13Le1mN3Nlr0sGC2Bab2AR07Nr0GLT+29EurzjqMT7dd+3qsA83WTURJd+51Yk1/b8m81hq0dcm/NLdiqAH4//P2p8+yHFl+IPY77hGRmXd9+wrgLVgLhdq6uhrVG6ubPewRRybRbChqbGQy6S/Rp9GfMfogk2ZMxg+SzGhGTtNIVrMXNrtrBapQ2Nf3gAe89a6ZGYv70Yfjx8PDM/K+iyYphz3cezMjfPfjv7OHYAcnwbIx+p6vl66pYpR8LXO67lnCnKdrn65xnimeSAQyesflNMoYg5hJUl4avpthiHVrn9N7fWYlc3XgK/O1GdtLOUheh03H7rS8zjEs9LS9kNPt8Cnyj9I+rNvn60p+lgefeR98kVIhEaAmkb6TgED5HogYKqHXcX4MDfZsbFsqirjmaWdDy9fSaOQqrvQ71Qz4BGAo8HMJEMwvJefcQI2jndf47cYYlGU5qGcM0K0jqPnCqoYhDU3H3LerG17H6zsxA2uaZvCuMQat6waLoO1pv3Jini5M+ncEaCTh+Iw1khiM5H+RMJhQnxOJQm6ikdebS4yUIESzDPYrBGWspO+cpPJNx6Pzl85nuieHkgM/WIO0LjVf072Vcu+F6ZNo1bXDcrkAkUbaGsZcj0QIBGsIXZbZXPf1GMHsiff6y0rrSNc91peZwax7f4VQjvRB527QrwFwGa7D0zRO+lluqpOPKZ+nsf6m7xqikEToZCmS/kzzsjCv9n+s72PSp7H+S2JKA3YcwkIDjQXagnDxxefxO3/0I1x85rowC8Zg4gm+7nD85BEe3vsS9+9+gc/e/wjHT/bh6iZk9AYcGE5cd1EFmmAC+MwZjZQOaZ/T308zT+l667lK8zes249xHkbotp7ttE8nhVbMAUQuJMq1zyk9TMHFWMlpZdrOWF/G6M/YWJ82r/n4xn/v3xmAE+6ll/k7+R2QXvI5nUvnSZ2f1xU1fciFamN9H2tjbJ9ovdkMrTy/bp7Xmbml/TlpvrWOnIkee2dlDUbGu64fp30mbT8f/9g5SvulUQHzKp9K79fcp1rG1nuMkQDQCyqxeien5zZljIlOWLPsc0OrmsunlXS8ef6wlX2ajS0VYJyEO1Jz0XV3YL7WJ9G5k545aZysEQCy+tK5eqp1Ag0ZyLFnda5E40po2w5t20Lph3c+Ci3Sc57T2ZFRIB1AnGeQ+B59zfK1TafSSy52aeSSGYD15DIbI74p4KuqSkyEkohNY2B97DLR3xV8jqm60k2eai+IKDI8+tN7Cber9WkbqtUAsKJdyedslRhy5C7XHR5rjDhs6oYk0zMiwVyI4lwC68Qlue20Fl1DQ/ZEIJfOWf73GGOhvytYGWzuNXHCvfdwIfFgSgAHa+9GJCMYEsmua9E2baSH8nPkUgg/y7IcvYBy4qJ9IiLArzuUw75rXfL5MAPt2J4cazOvOz9vOVjRSXHoiVhex1hb+ll+aY29m/dlbM8MJI0jTFtaRy517Zmzvh8rkpY1oIeAaCqhJnXqkB5D2RLBG4PWArOL5/D6j34PN777Gux0ii5ELkPjUO8d4ejREzy49zk+fO89LI+Ocbx3AN9KNCkmwEuDMGXPvBfWwhg7MKtMmQstuY380y6+MeA/xkSM1TPWhs59fm6Ze61het7ys66fKe0aA0xj4Gdd6YHOOCjQ/Z4zvOnvaXtje39s/3wd8JD3tQfFAJKQv2P30RggziXyqwKBVYYlBQZpdJh8HtL7eCBYesqYVkE1VjQCqfZp3dqOzfc6M5GTGM8xcDaco/XgPa1f2x8TIsk41/sTjdFNrTenX1qkzxIqX5fxpBNwkhnVWN0q7EyfTc8AMwOGVvZNfr+mJc5zpuXqv+935EljGWMC0vbzfZCPOb5PI2MamY903mSN198RQC/cPqnkZw1r6vs69CM/D3qGx8/+6tjyfaafG6MRYOVfUfTY2xDF86vv5PdBug7p5wwMZB1xrQgas+FrlVMzGmljSsRSyaqaIg2BgfSmZzxEJxwn1stkWGOitNh3HZBcPPlCAFhRHY4R7VzaqaBb39dCJFzgEAxaKEiVSIsUbRF9OMQggjUFNEKKtf0GtqZnxLquFc//2J6Y0ygQT0EjGaBrGew11yNgrIWzHEIIGzH9YFFc6bgtmWiapONLx59KD5S5AQAmgmfAB1t0teljIJhljRO/vK6c+Olcp4Tah/1AJNJuTwnPTBQd01cOAQAX5zzsEwLYmDi31kOSLBLDEaNkAGRCwrqUwQ0Ek028BHRd4tgpqL6pXy8iiTCWOph3na5fIHAQUzoK4RTBHKKkQNyP49jCnDBHwSWH+R2QGOqditO9qt+xoUCMQzAlJRgGsDDxrFkrwF2jQ2lJz1BOmFcviAQMhDXRtVOCZjSKSnCC0zECChL18gKg8zICbvJ+5GA4/U77ZMigCAEAau/gTQBIRkLW2s7AW4NmVqKZFXjt9e/jtd/5bWye3UULD3Ye1gPd3gEWj/Zw9OAJPn7vfTx69ACHhwciGHAOtrADkKe+HybQPgQal16oqYYX4dznF3kchzW9vTx7Yc6JUJRVoD0enjuEIGsyj6BIUxgEIgsQC5OH/mIaM4nTPqjgIUookTmHp/vB9yGiOaX13OcsIAiTqfsk0qJ0e6M/33FPej9oK90XaooX74ZkHMBwL6XjUtqU7hv9Pdfi5e/3/QC4n3SRVlJ/18ZLX297ebH/Pfk89pgIgJG1YkkMKQIo0YCqMEr7mWuDcjCUnpGchuoa9vRD/ueVxiMdKw3oO2PYjzHQos+m/UrbXzfHaf/S/uc0L20/389jwDNngNO61oHDpwmA0s9yoWlavzwDAD7Q4FTbSOE71Ybpi33d62hcOhfp+FOGY4CBaBz0r1sP+WBcoBP7SCTJC7UP6OlQehbGtCZja5XP3YAhXtPfMVwY62XJaRPAkHrKhAbkPh4zbUyF4XkfJbrWcCriXW3CnORnLfarn9N4H5HczZHOJ2NcJ0gZ+1s/038eHkXItyZ3MgJWTPqcnU0de3qmB21p9FMIVgx6migUzvfnSeXUjIZK+VWSDwy1Eym41AEoke4BWf+5D7kk2PswiCH3mNv5Uva5/hu7OLRP6WWvmhbmoYZCwXLKQOmmq6oJvHfi+GQtTDAHU6dva9LpCxc+i8O2TTZ/LgUa29RyKZMknYNcOEwM7zqYYJbBbuiADqKVS0nnKTI9CYBIkwdyAIFkLAhyuRm1J/WrZkfpodC+j6k/07VJC0MYqdKWESzo2oxd8LqmYWpBZAAX1iJ+TqLtkLi+IQkkgZ0kjPPM8EilwarSFNt6SgBAjOPNQwAR2WWWSA4pgZM+SgfHLqq4sFACGt4NQ/Re1jge8MFuWl8GDEr2t0o3pK1+D8jlthr+MifeOYCI85yAyCFB0nlVMJP7H8hbRP3z+nuurejrG/bxaYXBaC1FJ290HoW1PQifVHBVgUvfeB6/9Q//EOeuXoJnD8eM0hPaeY39J3vY//IB7n30KR58fg/zw0Msm2UUkqRa3HiJjmkawghSkDu4eLAG8OjCsYBY773k3whz6pxqeRH+drDW9CA2uVSUFmEErKRgUseVnrvU3C3VSka6Gs78ihQu9H3AWOVAJulDPFdImITkd30OegbTyzx8ngMmLWNgAnkd+R464cJkxsCRV/vfn3m/uqZP3bsKzuT8CK2RcWlOqcHTGRgY63t+ntLnc5tq7md/8OxgHsNeHNs/K/WP0PD8jOt3KUge7esIQE5/z8FSfmek8yFCw9X5S0HaGGhKmZ58b6yzAhgH9mH8nqBCJmUy9HWvYbdpVaOXj0ufybFLChpTgJ2OaxUIrzGnG2zjkftY/ujrYx7eXcl85vOua58Lh1etASjOydh6n9xvTjRxyWeMlTkcA8v532MnWfFEOt4V88GMpBAoCmDyc5Van+g8jZ2HtL04v7F9h43NM9ja2sLx0YG2GK6Icb/AdMwDGpatKSgIe4wk6uRVEnVi+VqmUzmHOvZ3bgaUEn3vxUm6LEuR3jn5W2zKZPBVVQ0IeboB00tfL0JtQ8F7KmHPHZVTE62UufDeR58Q7YdK6ImG7aZ1jRHcfM4iKEGfayJllmJ/lLABQRJr4KHSUQfvhxthANQ1u/EpDnX6Mx2vPmeMZNhm32uA0mfyMaVEPSXO+feqDcovi7FDnqu7I3Oa/ATkHBu9uDrGfD5H1zlMQn8V8OXrk7c5jJyDledkbBwvLe1jHJsRc5oxqEJEIKbBmvSHGX1ksZELbV05aSwrbVPaNkVia619qi1++G0A6vJn1/U7v8DT3/XxdC8NwUkCPk8zLwR0hYStNY4wgQU7hqkKNJYwuXYOP/yjH+HZV14ATUqwZ5TWwi0bzB8f4PGDh/jso49x787nePLgIYyaUSV91N9zhiP9mQONsb1ONNwDcT4TUKN7q23b6Oc2ZmY2dgHpPnbOjfpwpedTP1e6FullRj/S9rTuXGqZ1r8iZBgBg2Ofp/3PadPYHs3bSC/p/PdT76WRQiRa6jEBylg/0n6nn+nnTyspuz1W30nMRrrXUvqlOZn0mRx0pv1LmZEUnJ1UclqT9iUFw/q7CvuGdGEIstK7a2z8+dnM+/K0tcr7n/+dt5/Pz0k29rmpn7w37kuVltPM9br3BnsAq5rp9Nn/lPrzImB3+HcK5MfWS5/L74A479w71efn9qR1XX/Oe+Hz0+Y/H1tOQ2KfMsFRaqqW78cUt5DpmYP0GSIaWN6cVNI5lXMl2qbDgwO4pgEQtDFrfIVOoiWDNiLfwRFvEcaxzknl1IxGKsnPD7J2NjULSC/WVHKRmgyBh+rYCCohJkM6wDGQk0bB0n6oyVB6IeglquFmUyf1nLBppKjeDIjj2NOITesujnhxB7u5XFqofcwlT5GhMgB3LCDJ2iB/55DVWBx70rntL/lVIqDjIeoZs1STYoyJDF7al0hcmVfCda4DEKnGJp+X2C8SM4/crCu/nPTzdZKdMamdxrpWxjAyJbQKBscuDCWKzjmMmUToOFvnZB0QzFxCFA4yBhy9IzAqyRib55Q454xaPu4hgRsSqpOYAADJhd6PNwe7uYQnggLTS4XG9no6R+nlmp6T/AwI0zy0c877fRpg0/eDYL2JTtogRlcamLNbeO0PXseL3/8eytkUjggWDO4c5nsH2L//EHt3vsTdTz/DnTt3gpY19JGHgok0PO+6vo6ZFKbgKsxcfK/ruv6izfIhpGeLwvODrK3caxzSfoztify8aR/XrTmSSzPtT3rZ5tLotM+aGyn/7iQQddK+T9uJ4xutZRVEj+3ZvI2nl+FcDvsjJopj9aVAarUPq2dbnyUaCnbyOvOxpG2NfcbgeHfoZ7lQLp37aJ1gTNSKjrU59tlJDF36+ZgpXz62wXdZPWPMqP6+VruM4f7IaVRaxuhxXs+6+XgakNU570E2RZPBPCpZvyeGdDY3Bxzci2HNteTjXEd35TZjiLZluHfH1jTWieGVl/YvFZCk85pbdKzQC/RrftIaPO2ztI0xDXpOW54Gwp9GvwYMxQj9LIpC7u5E46T3cfrOuvHmdCHu0aAia7tuyKwIIFrpf44h182bMhXD4EPDPp2mnJrRUJOpfMPpJu6zevfmM8wi/VJgrxswXnBuKGn3XpLfVZMJbJIOPR38GPhS6WxKRHvguWozmEbBSjef9k8TDqbANR1v39/hYo+ZEuUbSNvS9gfqTzCsZgkOG9GQgXPNYGOlGh1tW21wc7Cj7aV9T80m0ss49h1JCNyMmUsPlL4/9mw6fmaRUDi/epBywp8fdK03dcaPhCLY/VsSTdhsYwaE35u2iWYg60pKcCJBNL3JyeBZAOzTcJ+9X4dBb5+erj0zizYjYQQHlyAhJnpL5yJn2LR/JAgE4GG29BxArQKX4bkZYwjztYifeQ/QeH6IkwBh+v0q8R6u7yqxWgVT+VjS/WiD2R/BwJUGbWXwzLdewbd+9LvYunIB7MLF5TyW+0dY7B/i8Zf3cffDj3Hvw09RL5fwzCisBSg4cIZ/+VlI6V2q3Ugj4uVzoM+njno5UFJhQTo23UM2OxfpOg40a9na5WBkLWjP1ikdRwoGx0Biute136l2OO/XGGjIAXB+Vsb2Wb7HU41LenHnazE2T2NncwhihyBFBTi6bsaM+xakf+eAK293CPw4CDFWhTnj5wWj+2ow7oxW5Pdu2t9+ff3KGPLxpHWNAbV8H6zbi+uAbA+kxLQ1FSKm9CAVMA6k4yNzlM//WDkJ8D2tjNGptL28Tj/Sp6fNR86ADO5FDtB/hL7mZmuDtfc+mhzl/VlXUmZjrB85mE/XKsVHcS5OOCdpnWPnex3NCV+Gu3N8HOtoRoqz9Lm0SpjxM5X2I8eBapKYzsfYeRybuzF8BMg9zexhvIa0dfCcWKgktFFLruEZ229AmDKdv/CJ0sTTno+vlRk8lUanhDfNBJ52UpxQzQAQqxTPhEVPJYXpxZ2D1VSCtnJQMzVdCgrSyFJjEsc83K7W07ZteG/oVJ2qftf1J+1TTgy0Hv17YK7EHmwYsMEnxgakw8KAUNsNQWdox/CQuOUX59hBSPuVEu5+rTKJEg0lqmkZG5/2Mc7DUxRueVtjfc8JLRMDnY/SAdeJuchYVImTDsRgfpKxpcRHIglRsPsPXD313L4oC4LmSQ9oWDsJt/v0S2sdAzAgBN4DVpHw08fWvwvk87+OsOh78UyZodp5HVA8qS/DttbvBe1nus4nSV2AEGXOWrjCYPuZS/i9P/kHuHjzWZhpKZqJ1oPrGsf7h5jvH+LeZ3fw+Wd38OTBI7hG6FZZFFE1zBCaag0N9sAYuNU+6tlIL9H0UlVapKBUx9Iz97Ti/5JfUOkcDLUkwznO1yOVnqZzlzMPaX/S9c7bGgDA5PN19GYIgIb9zfs6BqhHwcvImMfobd7nsX6ld0bKMA3mK+l3zgwRncQ092XY/vgZEg1WoCMjoCufH90jqfBIzZK0f9bY6OeS9i+tK73PI6NIw3Oaz48+P7a/0pJrB9bNUTqmwXysoYVj+0r7lwrv1pV19OQ0ZexZ7X8OopkZ4KGP3OC9INEYY4LGgOUY2F45W/LhSn/HcFJ8P9x/Y3horI7wYdri4Pv839h85TRV//kkaWXadj4f+VyNfd7Px/hcrXvnNGXsvTG6s67Nde2N7c2xtRgrZVmi8R2IAx13PEpL8nUZO0dkjATi4bS9vi+5MmBdOTWjUdd1VMl471ciC6WdTC/g/MKVy9TE/Zk+o0BeiKJH1/GKViKfkFRyn16IvVall7blPhp5SYGNtqv1N00TpZjOObAfqry0DR2jGbmAx8xKuq7rk9apEjLMRUcsoW2tjdL7lMDonIKHhCg38xo7zFpin9NnYv2rqu7cfCpnAHKVuAIs5yTjQL7mY0AhBzm5pCoeNlCIEgWAAOc6eC/hTRO9qxDPldUOJTu8HqsXnUxA0BpBqw4SIyBqnygwHhz6o9vU+zByUgZOaV78ZbBPKDqKxqH184r+fU5A+QnDS//qez9G+LLvCBT9T7zOaQQfYccO5i9riSjpK0cJG620n0qa+j7m+6mfG3mGTIj0BAad2cJrv/s7uP3914BZhdYYFHUH23Ro9ubYe/AIe48e4c7Hn+Lx/QdCv0IySE8Ex9w7kCf9shpRKs5n71xHYT2BIVAjonBmfRy3tRZd5yMo1WKM5tAhmR8jZpfOawhq0pUAEeAcJ+3GqYrzFUELOF40DPR9CQuV0u1UG6PPp8yenr0cBOZZwSOd1X2c0NsUBOSXZk6jZF5MH2kKiCZ8/fYjiSpLcr4YHOeCINpmXafktEW6PAYM0rbTv4lWz0Y6dqC/C/rdi8HvsWdEsV/MQyFZrD89KyMAIxdipUKd9MxoSYV2OUM1JkCIea0IYOppkc6dnl/KhHkgxDVZYaTwdAloerek/U2/y+8L/T0HmfFuPj3vcOqyjqkaA25KA8MHo+/pvdH/LZeEH3k+XfeTQHF6v57ErOizQLKuoUM5g5jf/frOaUq+H1MBSroX41mEXjdD7Jfvh3x+8rnpxyk1RgCdzQFiqyePbLC+hBjCXbFOjq/yd5IPh22EP09a23Vr0PdY6ov4kNSUedXNId8PY/2Mc+SCGXqkgVLnGIZeV07NaJjgbV7XDbx3SUbYVQItYwohZa2EZLXh4i2MhQ3hGDvumYHU/AkkCUgmkyq2IUUnZ9UkQCdrTPUujpEi2UEE6hQvXwHW4R2SkIMSslMOXLjmwZ7RBa0CGBK2NiA+InFG1cswXYT0wKZgnUjMfPpDJ1GrjBE4ZQgwKFFYC2sKeG5XmAfZ3AwOTIGY/gRfiMKK3bmRALvMEj6SWICIQX9o04PCzIBGtPEcpPkAs4TDBQBLBl6MhsKYCcRh/KaISNg7BxgLAxPDYQ73VcieTQHQgoMkWaTMRASLAp06xENABxgwjsHGAJZg4FGaQsJehqyWQUYczJPWEI6IXALhYAGuaquKAPoZkqAtFY1YMtHnp3MdOucCkxnWU0PmFhQJJxs9rHIpR2hLgOFkzwQhQiSs2l9mCWcbGYwQLo8VfAcgoeArLaR9554RYlGDkiMUFByPZVUD0AA8iXZN9l0Sm50Z5BX0KqXs57ULIW8NUQ86jZEs3VyAQDA0ZLaYnEQKY515Eah4BmAKeAcURDCW4EqDujJ49hsv4Lf+8PewffYMOteJ5q9p4ZY1Ht1/iEef7+He3Xt4/PARurqWKGU+0AxiWNh4fhG1Uh6eHSwVgEFiasCh3wkoBMNQoGHMcHpIjJwza+Uc2lLpjPyTbSJ9EELeX1TCJARtL7OwVwwUNtGYGMDBwYOjpk3HJEjBxHX3hsBIBAchOKVIvMQnC15oPChEQAnzwTDwrgdA6hCo3I7sQsmK7vVsGhPDKwp96IVLso993DIm7HMVuAhTG+hBCJYA7nezZx+CQIQdYgjsVRAgZjbCbCkzDKhO1UR+RBJ3IoyJWUJEpqYjREILhGmR6H5G4kcPARhYQoWHu8sHembAsMRCU8K+h7EypwQ5ZaGN6KydMBrMDIohj8M0jJgNpYAppeVjYDz9p/Wk9TFz4s9ohK4RgQsLoEPBHgU7WG9ANEXHDs7IXjTwsF4CsXOIepZGMVOGN72jB/1L9icS4UOKf3IGcR2Ylv3bg8sU/KXAKhWIpc+sA/E5gB8HvBQwSiCgemfkQgF9nxVEcjgj/bkC52B4+H46loEAg05mslJwPzCFhJAPvRa1SpY4+P0+imvVM8Xar3Re075qu0pLcyy00v+RceVrnIPy3Awx7YexwSDA9PdXvP+Gk4ueTq9ih9gfUpiTMWwjzIIy5ENmWjCKD2DAkpX8acm4dTyKjVNhQjonFEyHmT06J2bq8QBlDH6+n9btL/ku8e1Cz4waMwyG9LRyakZDAZX3HnXdD1q/GxK2oKpBIIyeUbtalqwAjEEkrGMcGjPD2F5aMplMepMrMwzplquJU8KR9q3jNoDUxFGJAiAHBgsKDJkLuQxNBJ/s1ea6SADIEKyn/9ZF90kPn/cSGcR7H9uM/aAgZcyIXFEUcV6AHq8RUUy8o/XrBRrnyPcamDSkb2+mhqROPWwMzanQHzCKfgbOe8n1EYilctNEonnQtlNTOA6XalHYqDnSaDuDwAFYPcg2ZFBng6gehDJJfkgAseZQRJLCwWEy3YfaVpzXvh6dY1sU2NjcBFlxrq8XS3RtK2vFSq76Wi0ldYeLSMAhBuvILMwFpfsmHHbwkAAOclR4JFqZ4VgNUlCixDBcLNaAA9ETJieMk4EpT5LQx6H/IcO2hhPQnivgNSAUqsHTvgGwDHQEtNYPzlS6HiYweyCK9ZGyWhboDNAZj7PPXMYf/sEPcenaVTgw2uNjwHm0dYvl0TG+/PwevvryK9y7fx/LZS1hzwuArMwFDMGxC4AIYGMCeCUQG1TcJ2osTClrZMJYYt4V6ZZjB8OEgiRanAIngIAOsLZE4zp40wOpVG9VsEFBFibkeGHygRkg2d/hDDN7GLKRoSzYBW2nH+4lEuCsNMyGratMtGMvY/YsWkEicHhe6SSxCHzIWJGOORf6IOtk9VIPG1sSb4a9ZcM9rvuZknET4CNH6gEDEPnQF4Yn+bb0XvZm3AtSPBO4NXH/6+6Ws+ARm4pIleIPyUkU1kw2soANAjxMEMRQ4Jl7MFUiaM4IETzq2aTAOIBk3vR3C0YRRPyuY3SeQV7YQoQ8OGT0jhEmhQz1UoW06FCzM70OeKeRwchQAI/j4Cwves97AN4SLt16Dpeev4lfvfMWtjamuLS1hcMvH+OrO4+EbjOBXMhTBCsgm/oogwOQn2lTdAwUaVs/rjHteVzj5C4bMH251iRjCnIAnM5HPpfrymlt0ymcX+EfVwOprJRI1znsr96Mc/XR9cyT3Hurz4/9nmqK4ueEaAGioZbXAdV4KkPX07ldx+ye1P+0jZPWY90apNq+/P3ceqP/Lq8l61vCAHO6pzNsMsbUA4mGIbP0GRsb0dA3LWU28jlL2zXxfJseM7KP+GZs3vM9OIpPg4+pD8+LNQ9gzHqTsLHytcLbdsGjvXeUpgGnlS6w/nPcJxJB4JhRBIlaBsiB3kTDe8RQuCmTkW/OdUBUf0bOmRnsHMqyHABsHUOutu3BrB1soFxjkpsN6PvK8eUce9rHdL4UlDvnJT6/MaCiNz3QqCHx71T9l6k4c6I7OBxIHPmC5FWzZOvnuco0ndN8T6RjSk3E8jlLx9zP0dAcw4X10TrS8J66FmnbnkNbwWSh7TrRZjgeAPSTLoW0/byk41fMqP1O+79cLkWqqvNA6QVxgtkWELNMK0Ds2xYtYtr/fH+n/Y+fZ+sRv4NIc8EEzxFORqYRFExNmAOwCwSKDQhleCaMh4M+zAOTjDNTYAPL8DYAT0I0A+BCgCMxAyYFhVKsJxjfJwpTbZQJTncdeZjtGb73+m/j1je/AcsMNz9G6xy6xqNZtth7vIf9xwf44s4XmB/P4doFJkHAV9hC/K7CPndBKm7IwBZ6EQCGLCymYA6aQARNjDEgS2g5RBnTPcZismfIwlJyHpjRtC2MrVBWBp0R+2M1hcx2HMiqICUwPQx0FlFNr0ACEHMv62RdcyDB5ECmkUVxDMsMCyMaPzAa0wpjIDdU0OZxAL+F7A2PIJixwsySaFn6M93n1XDewZOMyVoDtqn5EQ1MSSVvQLiMWebOkAgbus5FBlM2bK+RFCFMYIpMz2iwIlQW4ZHJN9WgcH/MEmBFJFJ4Ew4uIfhlgWBJpPW695UTiIxk4A2YAeLePNiEM0xk4F0Ha/RMqyZm1YRJthT1fcPw3HOiAczBT0rjlT7p757d4PvBjGT7MFoCeI+iKnDsWrzwO9/DrR/9AEeHe7D1Eg8+/AyfPvwLbDBQNgzjAE8GzoqmjDItvpb03tPxRqYjYYbGQFB+r6tVRT5H+djGmIt8/p42J6dhLFbf0/q1/6vnNDdzy4s0Ow7yx9qOJq6nfGcMXComyvdTvjbRPD1JHpvWsw5Q52A/N1XMn193Pz9tLv4+342VfCxxX5/w/NgdneORMUZoDC2sZ0pCffJUaCfBm+HuetrYxtrpv5cWIgwiuXdOwk1j5WuYTvWEUJmMNMlI5KwSm3pmRls3aFjUsZubmwGI9DmWU2LUmwQYGEp8HrJLSrmpdHJSE6yco2TugWfKZa7TRoxugGyjaQJAVTOncyP/huZd6TxqHenfxojTTVmIysdxn91TwSAZM7AJjO+Fiyklvul6pI7rAybCrJpypXM3yuGO9D13uE/3Su5roe3VdY2qqmSOEkl4eihVsmaMGUSy0X1hyYBNMLmwBkUlgNhz+I7Xc93p3ohMZpjH0fGTCCFBw4Mu+8PB+4SRopDVO5KNVcmefKpsSFi/pHrPIm0eY5byegaMD4YSlTifACikY9e5AbNIz1mAAhFCtnjuQ+iCwaZF7Fx4DwBgARdMJBSc9aYnPpgOqbSXJPuxNTAemHH/fJgBqT+o/D0YbGTPC4i1KArCyy/dxgu//R3QrMJicQyuW3DTYdF53H+0h73He3j8YA/LeYt62aIwBWblLqrCRNpiA5AHGC25eLaMmlAy4I3B3BTgKMmmwcXKQQNnjOlzuTCjIWVIKJoskjFojYEjAts+0hwizyBmNsYgaEmN+GYZCS8MY6LJne7ZmLHWhX45SRSqzEjbNujqQ8B1EjChdXCdAzoHy4SinYPbNjBwUq/zTmiMETrrScC1aD8IhqwIQsBg6vMBOWYYU8D4DsweJUQzI8yqaEHVJwFAb6IEiRjGzgGOUVoDS4Dmq6vLAt7mOVZSCWxPC1PhhoGNYJz0WQDEQNWRMLmMqIk1CFoI7rUA1tqwN0UAJPySmNVG2kqS6ZdMr20xhQ0mj7LPTKCz3hv4thNNfn+QV+iCMSbYHq+TFg6l1WN3Vf6d0FA5z+vooT6fCqgqa9B1HocPHuEXP/kpnv/t72K6u4ujPY/dW9fwo3/yX+EX/+6vwY+XICemG54NjAVMYhad07AUzKbrqneA9lmfTe/Q9PcV/62MRuq6D7BFhhtyELhuTtLnB74Ea94loiRyWP/ZunVL50V/VxPC05ZYJz9NvJX0MRlX2oc0uAWQ5NjBiHM/AV1yx61jFtN2x+61wfqA4/yl/RzbS2OMbN52vk/yZ/L617WX9l/21+pz+RysY7jycaX7dV3f8/4CIsSz0H0+Eo6aebCPxs7LGFZSLKNJqIkIZOnUQty0nJrRSBkLNUdKgaWC3Eg0iDA/PkazbLB/sI/NzU20bYvtnR20rsPW1lbMdK0lmkDRqrQjJxLpxZIejK7r4L1HVVW9UxsCkKBeFZVeUClxze1HtR9pKNwUBGvMeJ2bsixDm6sOTukGzQ+btTao0+XiZfYga2DBQNNH6uoyEJkS5hTk58yGjmcYvQuAXyV6o6B45KCkplDpM0VRxKhd6VynDJr2Wf0bfCKdyttbZTZlHVovmZJd18IQpB4FPhheSGMXwwpxScaXj1EuaURBke53IpFseHC0Sw+oJIBvxhjN1z0C9Awfh/f0uzFGb4xI5uZ6a4sNpjg54WOgUBAYQZgBGYOOPWrbaQcEWClB8oBxIkEzCRA2lkCdRYEJQCS+LUSwNjDRxEHy3EuFvPfiQA2LLrTFBDHJ8Yzds2fwyjdfwfb5Xey1NQ7nTyTvTdPi8NET3D88wnHd4mD/CN4RphsbKHfPoKgmaKsSvihQViWKsgSsDUwNUJaEoixQVRWqsoS1Yg5pCwsqbMhh05trWmtgygLFrAqMgIk0gCgwBba3ny2LAtYE4YOxsFREKbea5xAB3jC8CQ63QZuheyj6RITtJyZwIfcLi1EZKxMEwDuHpq7RLY/QLZeoD49QH81x9HgP+w8fY7F/AHt4BL9cwrcdXNsBnYMxZdgXDIaDsQbgEPhDHS5AsIWFMVbGYQxABhYA2IhfCwr4tg8vTsYGhjMEtyiSRKJgOJZz23mCqLuFKalgwE5ph4B3Zg/vGWQ6eHYgaJjxwNh4BryFYjRNsik0Q4RUULqoUQ6JQMSw3ATGUP4WLYwVzSlsz2ibAvDBMC3sAUOQ+oLgh6xBWVThvACdn8NQC6uMk1+9++LZzYDIwIY+7BlgHOTm4DvSjUx7nJacbkR67j2mxoI74IO/+hkefP4A//Cf/GNcOHsRB/sPUVxxeP0f/Qg/+7O/RPNkAUuioer9+lbBp6LutO/9XdUzhtqv1Cxaf64bo9ar95x+PpbPKmfK0jq05CA8fzYF3Nm3yZzrOg7D8urPtF+5KRjz0CF8XX/yu42Ze+HPmvt8HTPQdV3EdulzY2bp+r5nDmdmHPTn85kD3FEQTeuZkLTefA3X3e/53Ol7Yxqlk5iOtL8qRBl7Ny3rsEdu0UF6fmjIoKzb54O1ESc6GGNRliXqegn2AVMlmCWv66QzQBRMqb0ImhSn6L7Knz+pnJrRUF8IPfipXb8eDA1/23Ud6roGgfDvf/xjfP7F57hx6xZ+8IMf4Oj4CNu7O2jaFpUdZr3VyfPewZAdbIp0k6cHKn0m9YVYLBaRKKn0O40klRYlGJrXQutN64xSyFDSPiiwB3ptj6LL/IDoM+lGj+Cfe87TkIEHRQ2GMUZMgpLLRxkpk40pbU8JR9qXSBwTh2H9Ln02PZxjxC1/RucxzamSMoD6nLU2mrAZYyQLevJ+biKn65Da9Wqx1qLxHZx3aLsueA4TePW8j/Z7MF8QiX6+Xs654My8ehHF/RcYA8nGSZG50GbGiJYwKcGZNJgYkfoIBJOMsQshryP9lw575ZI3BTiRdrEyRURofJC8chhLkIAaBnadJsILoFelXBZoSpk5Y000GSECOhAaW4IKC08ADKG1orVrDcEV4t+i566qKpRlCVMUKKoKtiyEMSosds+dxfmLF9Cyx2N2AAibqlH0Dpuuw9VygnIygy0rlNUEVVmJ+WJhgUr6YayRddTMrAQB1KqZCI7MIJFyF57jAlIAmRw2SvQ50DXiXnLOgz2aXCxgUKTrHM2QmIXx4uHWTmqg/rIA0CVnzlBYG3027O9NAMwXBGgxwTLgmw5t3eDR/fvY//wevvjkUxw8fAyaL+HmS7i6BZoOpqlhqYPznSTDZB+cS2Vvgoz4bdgQstcGsD0pgM7JXHsfEr6xaICshbEWrdK9cMl5+JiPxieXvvcexhuYsC8jWETwrwGDgvSOnUjsGQKOiSlebCohtJCz1ULiy4MIjoJWTc+qn/U0yGoADZb8OWHdlBaZgmBNELgFZsUEzaoJe6woJ5hONmALA2/30La1nDHXiabJdRijsfJjjQ37Grp2UuG+0nhHj9G/lfcI6MjDtoSd1mDx/hc4+Ogetp+/iunmFo7qYxTndvDS7/8W/ubP/gJVy6jYBrDUa14GtCv0ZYyepZL49A5I7/Vcwp6Dt3UgPP1e788xhmXs3Zze5mPK32EOjt0Yrmfaj5MA2hB8rn431r90H50W/PX97etM0w3kc5NaJYzVwSP1rRtffpcPmCs1/xoZxwCUh+9z7Vf+XNp/fT5nmE7o7Ip2KM6LocEeWrcPcy1j2s98DBnEWMEiY8yXIVJvvOi7Z4IGPZ2XsTbzczjAEsxDRp+EYU7rO9Uc4muaTo11koOKPQXxZVmibVu0bYuPPvwQN27exONHj2CMwdbmVhyUAvQxDpVZbN8nk8mKVDxFcWk2cp2gsiyjhM8lC5gTGh1PmjhPP0sPQu6/kc5J2i/vOZpMAT2zkhLIVDWfMkIABMD5EFXIKJOhi4yknYQbD0Cgj+gkNuDqf6EmR2P+GhSdGmmljwE5xXnOLzjGKoGOWijnJAKTMk2BmXJhzzjPIOdgbRF8tg2i2YIhGJgoETNkYMhKXG1QjB4mETokOhJZA9e02jGJgBMijAWxsUgfuJcM+xiiLT/Z/Vn3wZREQIwHQSJ6pc9FAhvs6cUhPjwQfvRaAFXf9xJyNSDywUxKAT6SkLgIe55jF3spO6j3fxDi3JslKnMAiPS2JQMEYMRAtIbyTOhsISCcKBqMgAidtTiyBUwIfFBE5qBEsTGF26hQTSaYTqcoigKTyQRlWaKcTmAnFSbTKeykBBUFTGlRVBXKskJZlDA2aAIAFGUpjqXQYRiwpeBDwYC1aMGwIJRsYENW9tYQWuIQyUrWyqO/bIgYlRdnOXGQRowSRCTmDXKnBXGq7mvy8FYDH3A0ddK/mRKirGvD0g87IN7D0NFMPtyfBE+qKQrRxzi5sMP8EyAaoGyP6g/LIWIUDyVNnhmtFTMezwTHgJmWKCYlLm3fxIUXbuL277+O7niB5ZMD7H35APc/+xwPPrsDPHyErl5iuVyAnQX7Dso7F1RCzTxNoC3WWDhj4IsSAIOKMpoNOe/A1sAbMUUygSk1gQZ6Kz5KKiwhMiGGPoHLMjDHPf0qikL2IE9Ea2H6xKkAB3q4hAlWcOo/wgH4bToHF4QeMZAGM8AGaCu4zg3MF5gZ5FoU3SJGGlOwrgymMtjGCJOhmrNJNcN0sglrCahmqOs5vG+xXC6AZgF0AYoGLXzYfhKJinnIYOr6sp7cpIQ+rId3LE79tJrRfQz4xLFbwhIOEypQdQz2HX7+l3+D1y/915iUU2xub+N4/xCLAuCtEu1+jQkTyAMMM9qOthHHlHyveDwFOrnwK2cw9D5cxwSkd37+Tvp93ubY7/l8pe2lz5jAYAtDpd+vgsSxkt/RnD2ftxvNF8O89EJLrIDW0zAA+RyOmbCtCPx0b4bf02bTFvO683nL1+0kRnBMkzH2M38nxSQpFhvLvTVWf/o3OwZoPNBPDsIHa7pmvGP1pCXHnnEtFBNTL/Dn8Dl7DSmDwd4fY0jTPngOEUNT/EIIiu3+uafNm5bTJ+xzEtGnMDbmlJDGPcgK+CkLE1KVA4YY00mJF194Efe+uIcXX3oRW9MNTG0pgFFul9BpAU4KwooyXC7OwXfi7WiDUzA7Cb4ZmQIARepr4T1810XuWic7bHH0DIBukNT0JN0QOqF95td0sWRhhhxjUQSTCHi4IK1KCZVGqfIefZ2hXWMI3olZgGMGeUZlCIY7mIkV51NbwDsntrCOUZBFywzAwbMAbTImbBCxfxZb/34jRRjDDHYEYhPAe79x2UlYRo2QpJc/gGC7H5IdUmLqBAXG4uhqwqXv2KOoqhD6sYSHk6gxsLDVRPgh18BwC0WZPtjN64oZWBB6kwtGMHUwjLprYCsxvwIZTKjA1HkJxwqRptYEeGNROmDqJOKR7qEI0MMBsoHp8tGpM1ELk43SfO98n8gOEOloxqwJWGCxWAKDUQRHD9l4NvwHgyDRDlJ2I3b+5CFSfRNCZ1oKZiUWMAa+KMCFETBuCGwJ3giol71WoCwLFEUJUxaYbm3ATCoU0wlsVcKWBYqJaA/IGlSTCpPJBFVVoQimRqYoRBod6kz9QcSen+I5i5dNHGKwNY8AXu8/k5h/IJ5jYZoSohPALcL5CYFB4eDAtreRtdAgPhIW10IvOGnQEWKY1IS0y6WoYRSBaBPcNxyYkEHHODgwKwhkfSL+TPVKevn21fZhJ4d3FyGdPFZaFb4zg2cHo4j+NGmbTEYYHu6f5/h8aK40qM5sYrK7gTM3ruDGb38TzdExHr7/Gd558y0s7n0l4YCJxd/GEorZNjY2pphOS0w3Zqg2N1DNNkBlgWo6gbUWk4kwk0Uh+48K2a8IZ0uELMHsiAC1F4hDUA7YUIx+1n8eLkIX8U2YR728dd/1L8k0yLqZ/oX4nq4De0Qnfeck0673HnAeXDfo2hZN24BZfA7rZY267dC0Huw8fN3C1Q24czCOUdpNzDbPobQEPniM5XwfrpmDjvbRzI/glgvwcomi7WDqJSj40DjuxE/FS/x6WV8OoKGXlKe7znsGa2gxz0HaGjTnjJjbJAU8cYZG/uYAkq21YEPorIc3wP6De/jijbdw/tlzmDd7KIoKO5MJ/vAPfh9v/+RN7H/xEFMqgUTAloLCVPuf3o9qSpaDsJSmpkxF3Ou6TwC5543QFg3PnR6ykxidMSYgB4bpcznYTp8V4QJUXBOYDDvqc5DXuwI+kz6n8zhqdpOelZRBXVPifT/yfj4fKTAfmzuD4ZppCR5do/VqPfovFbwqs6/PD5h7YGVPAKv7eDCPGO79lBEY81FNOjzklrKS9yvuYUKM/ihBJcJ8sGp0DXxacYILNOmw1puOLx1TxJZAn94AkvPOBByadz1f615uKiDIB+yrwYdSjMOBLhNJZMQ0gffTyqkZjcJaFLZAF+xp1b4+lerLfMkht9bCdQ5//F/9iRy0cJG6YDfmvAM5BrOC/D4fQNcOTW7SienU3Cb7l3LbURJChLKqBhy/PNP1YCk7ODqWnGPWMtxQskQy18pkYGUTa1smAH+jtvJAlN4CiLbBCOE9PTuZu8KimFVoDg4DgySaJGskAo73knSMmcWx0QSmjAwqFkmUC7b0Yg4g7pidlfl0LuSgUG7XyBbtyEVth5qKEBD9H6JUFzRIKOhDmEs9VC4wbBadRMMhg2lhUVmPzjvAeRCV0gaFCxISxYctCVBkBtgFhkLGUXmLKSbwbIFJgersOdQXzmBZt5geLVExYQ6PyfXL4K0ZWib4pcPy4ACL+XFcF10vYqBMtB5y0IQJ8wQ0hYQM7fdBANlByh4vsl7GLdqZYGJB1grDrKY7ZYF2UokmoZAoYwL+J7DTKWxVoZxUsJMK1WyKajpBMZ3ATCuYiZgYmaoQ5mFSoawqVFygJIkUZNSMI/S1hJg1+AC8HRCADGKknvwcnCT1WHc2wpPKekZCHfAtImLEAB/3D+V/cvYxhcsrYHNKgOZYNRGMZ2WFCK88sVpSKfNYYfRMTV5rZNLjN8Pn1mGCkZk+6ctY62g3B90Pax72AIxBeWYbz3z/W7j48vPYe/AY7BkbW5uyZ20BW01RlQa2YAG/xsIFE7DKUET/zIy2abB/cAAPxtb2NqqqGvoixD6sSvaA8T12mu9W5uOUder3K6CBAUs2wvq0eCMmWBbBidt5WBDQOriOYEwJ3zk08wX29x5hfvAEe08e4ejgEAdP9tDMF1jsH6A9PBZfvLYDLY6ApgG3reR8YQYxw7IBTBcBrJibikYX1kQtPgUhUy6VTudiDICOgUi9i5SvrkD4zd/9DOWbBk1zAIaBNQW2JjuoD+aovIVzYsKqkuLcvCSVqmq7Y1s/BaBAb66tWtWIORIz4lFGZGSM67QRY5+PMQUDMJ0A1VXglYrM+ndSS44xyXb6+7rxrBsbQksD6jLSjuK4vKT9SiXna+8GZdgTq4nYDmFA5PM9kGujYkj7kTnIhb0nMVEnlXUMSeoK8HXqHtsjvRCj97NRKxDFToz1DF4uEFiZ17xNUqG6njePpu5WMnfnZzz+RL/f1UXCkppD97uJTrr8TiinZjRUzZyD8Pxg6kGrqgrWFphjESMhVWp7LS8CEO7JGPHL0DpScyjd6HVdx1CnLjPLSW1O036kz6ScYR5RISUquvC5BCEdq77TbwTR0ycCiPh8KgGROgF19kzbFEZINACeWJJxOWFCOiLYqoqJ1Kw1oo6P+RMs1J4YrJcMABB84dHBwasJEPeMDMAg9igKwBZi8kTEgAkMCxiqaYoct7DqunyBiVSJGQkTF/KBGNubF1giwEjEIzIGpUGIMc8iwUch8V0MBX+IAGTQiaNpMIVyKGLceWumAAgdezjjYc5dwPZ3v4kFdzj82TvYaIFFaXHum6+iOb+DtihQHy5wYXMLO9vbWCwW4vSr6MszuraVfAFB+knGoGtb1PUSO0ZswY0J/gUg0RiUokUgEDrXYblcwhqDyWSKqpqiqjYwmU4wmU5QTaewZYGyLCXrdFGgqEoUlWgdQAQOUYcIwW8iAEEPiEOtD+YyEbn3Gc11KGL+FLQJIh6CCWF/BQwj5pJixYcjZ0J/Hzvv8vdQqrdaetjbn42/H7F6Wvn7XTtpya/nk54cHwOHM5pWGS/N+L+0vfTLp/Xt1A//vQsT0JQEc2YD57amePJ4HwfOB98KwhQem9ZiWhUwRvaYIzF3hA85IpgxX8zx+PFjnD17FtPpLAhXev+0npaKBBg4GTitXuQnS0nXldMyKEPJH4Gpj+g2eE6ybsKhk7NZkJjrlsJUOjCILcrdTVy8soHCPCd0hhlt26FdNjjeO8LRk308/uohHtz7Cot7d7F89ADt4RGocfB1A1+3gPMoDQHoJCkkecCqTxUCPR4ClRysjjm/Pm0edE19J4n60DLMkrHBQWMOjwaHMA6oqEJLab6YVZv49O5MNQM5bck/T/8eMkOrZln/KSUH1GPf53jhP6Xtk5ghTcaZ92cdgxT7mPU3fS9lhsbMe9Ixr/PJOM04tCOM9Wc3X9P4nRn6CozN89P6NQbax87E08a1rhBR7yC9UnqzubQPOQORv5sHEBqb/7yvg7VFEtAlZwiTZ6PWCKt0Iq4JCy4Qn5mTBWxPK6c3nUoGnDozO+dgk4hMGm2IiCQPQmlhbPCDsEZU8CzZn+HFzAos0UeU6QBzlFBolCLv/SDqlUpKjOlDn6Z2irkUJSVyuUN5Ps4xlVq+yfufKQFQFSNH229wr3YEK9FgMDt4F5gpa4KmwsO5NjoWO9cCVIBNAQMD6wjkCSVCxC/u4B3DkIclB4n2b0Im5eCYDUIHgikka7HXUJUgVE60GdZaWG/FpCnYvkcAqUwJI6imLVBI+EhlJBjCGIotn6wFmd7HgkI0LadzbQ1cWQC2BFsO82BiJmwOm5oBkBOAo/NtmdE5B+c8npQWbUWA82i8w5fzBWbXr8NWBJp7LB88gZlM0e2ewXIygS8rlNUWlr5G08zBhuG7FkVRYlJVKIoSMDPYII2bVBPMZjNUIUN9NZ1ic2tLnNmDNs9aK5nb0UsRe4OXMA4WYB8+jOpkPeiAfN/pmAkonUfpBEv0Fw5iJZpFnIiyXBROdGWBwePA/RIROgohk0M/kF5USQ05IV5/oVH25hgYXr2EmYfPngQo02fWEtwTCGA/vtX3V6Q62c/0uQH48BJOVumI0iLvvUiqaCip6yV/QSiRAClGD/4oaa8PKjGco1wCln6/CnhWVe7D71eLnGfZobYkwAI//vFf4eC4wc6Zc7h44Sxeev4GLp8/g0llYA2F3CvhgpPJxuHREXZ2dzHb2IBG0BqTNudSuqfthacBv6eVPPLPaeoHhbFRL0iKu5s9CtdLBUEGbDic+ZDzgyE+RDBovAQz4JKBilBMJzh3ZoZLN6/gtnsFrvXojg7w5P6X+OrO57j30ad4ePcLHD3aAzctivkxTNcA3MHCxzCy0oi0nedAyOfoJOAyYODC3z7Q/8IYuM5hagtpj0vRkAJwniUppZdoiYBDLq3OhZJ539L1UYHmOm1IWi+HuseChaTjGxv7mPAw/fyk85b2/aRnYieTcpLmZbgG48+c2FagUevo3RhjNDYvK3RvzVll7k2dUkZGhIynP8ODvz0jjXKRr8cYgE8x3lif141NyygTzol5bUZnFBfl8xFakSeyz/O7dOzOSfdxmngzn6+8HgmKMWwnxbK5CaMmgVWMrc9HBmUwaTIir5q5NczaunJqRmM6ncIYg+VyOQDqOuiU+dBDL/bhYiZljYTZspqASyfHd/E7GQLDFha2KFfU7AK+3WACVcuhf69L4KN91H4PTKzCeDQ0rmalHqsj5ThN1Ep5FEVwYIYHh7CLYHF+FBNngu862bSkGhtxOLYoQwQVjyIwW03Xh250zLDlBMaWMBAg39TinFyYAh5NiKiThvIDAEbVFZi4MjiaIlxIAIiw5EYcN0NIXvK9UzlZyfAqOSlCYi4nOQRqS9FJmsjEd3xgssSUqvfpYAAdDGqINkMdSYXpMSBiELE4HBcWtiyDc3ABVxRAUWIymURHYxsi2GBiYQqLiklyM+xsw+5sgGYV8J0foESB0lhUO9toSguGQcGAmzlQqWuqIUUR4uyHNQsAAapSJIOOQmJDHkodjAcoS/oob4rGyATwH6qLwJhp8PCAJhMBrhh8Hd9zKBEMNCLIO+EKijWsGCgwR1qeaiZOIh7pxSr7ac1FSAARD+ZwUE8fu2BYRzaSnhCHESiBVaIf2DUfsmMzJ1IalcQE22jnnKixkQSzAAYqf5X0REKvDsPh8lbaUWSanAiATK9dSoUxFBg/aZtDmFNhOhjirF9OKhS2CGeii0nuRBhho9Aitpu0rc7U+k9sa8eB9zjT2P9tnZO8HmRwdmcHzaLBw6+e4OjIYXE0x85kiu2iQLk9w6QsxYTHEFxQdRoiOb+l5LXpumG+hGEZl9iN9fUkoJw+m5eUfg/37xr79rxeAEx9mMj0eQug8hQ1iAiJDQFE8wgFHbIPQ19cB9LkNZAkmjAEMzEoplu4eP55XP3Gi/jWosZ87wBffHoH7731Gxx+8CmO7z9Ep/4d3qMMAhNnVtc1/z1nKMYA5eAdiAkrSBxEDUg038agM0ZMZr2HJ8BxB7YklqG+rys9W2l7OYYADyW66wBaWheAxNdzVSKcrm9qPg0MtbfpHOSANd9DeXka09rTK7Py+dg4k8kfrS9vO19DhvgAMI2Z9HBmRr7K8Kz7ey0zH7Z1FLZk4DpnJNO/87rj38ma5szjOsZ1HdM4Vv/K3ss+y8c6xuj4INBLLWb6fqiFy3pmUt/Jv1tXxpgN/VzM8oXeLJdLTIreFF4F9PkYKNxro/WqzIhIo8pEoejg/j2Bdqfla0WdMsZgMpmAiFDXdWiEB9qF1GmosCWIfWyGgxpQB1ZOQ4SashyEzW1ah6bzmEwm/eWfEANtT/uSE6ZU+5IStDFpR0qg9G8dW7y0s8XoCaYfbLpI5IBo1oSkfec8DDnAtaCQnI8KwqQyoOBY3XmHeVOjdR4ImYgNDGZnL+Dw0b6YKHlG13bwrpM5MjORzjsHiRufAKjOwpCFoT7ePyDYbgEHO5mAiwLeuz4ySWFgbB8v31qD6WQqYMca+KqACWC/UuBvDKwtUFhxMiZjRNJvxYkY1sJR8BcwgLEFGEAxrVAWFgURYAUg2aIQsyJr4K1I4hX8DSRcATRqxB6Ev9kALRkUZGE7B28AMgL6Kw+wKeFdQPZEAewJt74sKB4+2Rti8mOYUfhOeTQQu3gYHTGW1RqfHjBMcgFEjQYBhScUrnfptMke64jRJaqKlJmwDihHDjgT0BnutSdZKTwGzEY8DdwTkdjeCIFckb5w2qtMeMXiz5Jf4vpcmrB0jFjpuU/PvtqO5vQgPX/9WXMR0CNz8NU1TS+fVIigNEz/ds4FsNwHnDDcm5M652KADNd5LJeNJMcDo64btG0rghowuq6G68SUdGtrC5cvX4ZzDvO2RhPsa69du4bd3d2BVoPcuPlJukeVxslZNLBFnzhQ/52qMIJZnYcpCly+eg1vf/AlFm6Bjjp8/uABrlw5j9msknYRIluRXkwGH374Ia5cuYIrV65EOpjvKynjktd1e+IkwJc+pyVvb51N+tPqRBL4Iq3TAeh03hNgTRRCHlDP4nN0UmcJwuHCudNjZBiAk2ADthB6PKuwNb2AV65dwgvf/zYO7z/B2z97A3ffex/3P/wY3eERTNOCyIJ8DeZeC5A7ua7zOzypWLF3hYNEQxTbDMBB8hURS0S3ggDHDh6aDLMvq345/TwO/Ed875uZl3V7gpQBSu6FdYz0aevMPzsNCBwrAyD296tipZy0twfPoadrOfDXd1Nck9OGpzHtAwYkzaG0xjQvp9cngXp9PpWuj+G5nJFN6xob89j41423/57iPT/2DGNVO5XPRa5NUEsIYGgdpHXmdeQWNvpcOteGxAeUvAsYRepJ0xusMO4yqkF7aSjp/ish8mKy3s/FfxFGY1IWmE0kCd5yaTGtSkkM1bbiFByeq6oKddNgtrkpoLhrMZvNYseZRTrnvcd0YwbXdeg6cfKdTqZgZhwvFjg8XqCwBrPZDM45HB4ehuyE4i5QlQWm0wkKWySDDZstnUKWKEiULHrcoDqJ6P04jDFo2zaCDPGHkHg3Asb7fA6TaSXMghLycKF2jWTIZR0viZRve3MThWFMCu6lleH/kvHcALDo2hZHTQuQRGdp6gZL16A7s4XSFphOp5iFHCTMDFNVQIgwor4wAMTxeHsKbwmz2UzMzGyBaiIhSamcoKwmmEyqAMpsTFYGE5K0kEi7NVMuwcDHA56BS0AYJh2bHxJZcT8OAhBrJONw2BfEPQPEkMubmVGyw0TD9TJL/PmIc0246BkIEaksxPzLmaBpsQRvHJz1ADtpx5cIcbGkeyFqCZgxaXsH935Q4UIjF86cEkv9mjFxGaEMwyYmFN7Gz3R8wnBYeEqC4RIBwRndepbQpenchnPuDINN7wnACU2oXMArKkWNc0VwwScmthcrYHSc/pldwNzbm6qaXAfkvYI0+SD9TqP2MPcEKj1zWPk9zBGLps87j7ZtsVwuUddLtE0Ltefn0E+dN8kBwgMirrW7tpfguRCRzgfzJx1r27boug5t16FrW3TBT8c7h7pp4L1HFQQirnMS2S4wGd57LJdLOOfQNh1c43E8n+Po8AhN22CxWIjwwncg9MxMVVV48cUX8cwzz8BbwtaZHTAzvrz3FWazGa5fv4arV6/CWmG6hbj7AVOoQRh0+1AIRSi5JwBrDYrCBmGAjUIBYFy6BwijjpBU0TFw7blnUPNP0XYtbAvc39/Dk/kxtrdngIEkzPYGLmwq8oTGdXj3/fdx8fJlEHOvKc0uJxVWDaWiHD8f3LusACpI0vuN16+3Ao24bwc6hbhXIxiJzEDYvay7S32K9K4In+l+I/mrJaCGBIezxgAh54ghiv5owkxocIzQkjMgNmB4gBhUiAkqiFGRBdoOIIrWdg4OXBEmz17Gt6/8CS6/8gI+e+PXuPebd3HwxZfAfAGqDUzXAc5JAi8wHIJ5BAiOeeCcK9HTtEeIplIDMAuADQXfQaEjkakHw3iGZQCeUVqJ1ifWYat+k0jqHwP5RL0DeQqCUrPH/r5ME+z64Nc3DkT7fTYsef9WBCnZnvq6ZQCqdTLXPDcmVRYweLp2c0ZSzZDz73KAnwpngVWGIy3rNAh6V46BTzXTXjd/6wF+/52eOaV1HkOtVVrXOuYi71sqeM73zBijytKF3lk9MCFkYg/T1objwbhWZsUEMGt3HcOUz7/eQyas+WQyEfP5E0wJI4OSzeOYNg9pH/jpDNZYOTWjsVOKBsH7Ak0lavzOdaibFl3g2Jq6waQqMTMGVVVic3MT86NDWAI2NiQZ0mKxgCXGcb1EWxgsFksQSUbt6VQiRHVtA54UKAuLzVkF7zymRgb2ZH8f1XSGyXSC0hDYi1oo+gLIvEiuBfZwEFBLVAIgOARJp7Ho5471lo7AvWkaAAxDDIKP0ksCMKlC9mCSiKNlKcxG27ZomgaGRdpTVAUa38GzR2XF3XmjMKiEMsd2PRw6SBQuSxUqiMNvG8ZSmArXX3sZly6cw87uLjY2NoL0TMdMyV6nSNQIFEOmRkYPyhSuGNIkhVd+U2AnGJbi5dQ7COjcJ3GVV/Z4Tzg4HAyj86/RnJIGA9SAg+nr0hsx9CP+8GG8oYWChSlQ/sR2faQvBClif0YSe0SDcDX3IBaxj/3+GtDH4HGtxEdMpsKrRHB6eLP/GyIUiQQm5kIhCWebRkoaSERCB1JVpgJ63xFkCWQCNYcAM8OFaGBghNwrweyBGR0hhuHzPjEDC7blQmzULweRCVcKHKdDz2CYqJQYKQOn2SyMsSBNzBnC2jgmdM7j8OAQe0+eoJ4vBLgBkLClPm7KmB+Bgk2yV98GiCaha+E6h8WyhZixe8zni0hE67pG23jUdYO6rlHXS3SdCBOOj4+xWNRo2w6u69A0DZZ1jbZtAEhW+rpp0DatSHvC+jkWcKemXP1+kTWjZB8REX7y1gcoyxKVsbh66SK+9e1v4hvfeBmVKfHBu+/h/XfewXM3buHa9WewsTUTkBc4TrlcKCSwCxQlRNQjFnMc5xhtxzDGhXCzYlJlTRJiGyno8pI4HUY4DjY4s7UJ6xvAAdwymsUSR0cLtBcIpQcKvXADg8sE3HjmBv7lv/yX+L0f/l5Q6/cXlfcJtA1cMjMwnx8Lw+daEa4sDgEv2qSu62K0Quc8mqVD54IQiRBMOYdSbfbig6bSXec8HKz8TMxE9XwzO9HU0lALZEAx7DUohKb0PmSF1yzpIhTTxJNVWWI6FSFOVZVRWCUmbRTNHDw7WAtw24pfG0STSbaMDKExFCL8SeS+siTcfOkmnn3uOh7/4Lfw4Xsf4uN3P8DxR3fhH++jODpG4ZZwvERjHDq0KBsRdi3Zw5EwRYUnkGfURoC9S5hPjZSjIFJNBTkw50XwL/Lsgsms0m8SzjOxXOizs/dASr6TdYomNxAaBdP7GChfFKNJh3qkGb3bhvkW1oGfVIMZ1z0D3qtMMNb+nUvFx9qLdTKt1H+aQuiZjVRCvk5DEfc+hqB4HQN2klYhH3f+fj7n49qRoWZNzqEbAG0gtRLRfQe9poWxRwD63FuajM13rv1YkeJnID2d1/S5wfwHblzuvYChjNw/8EmQnYSum3AGRNBsokN1iiny9nNmd6xP+R6ODAOH7ADB0qfrWngEn+fkPaN3NQPkh+u9OqfJ916EFRFTPWXv5+XUjIYloCosimICnnGQ4BXY2tyEY5FELJYLAEDXdigKi+l0is3pBPfv38fhwQGYBQhszGYoqwrzZY3jo0OJ3V+KhmR//wBNXWN3exudc6iKAqYkWENomwZntrcx3dgIvQrmPSQEn0hMusRcR4mbXDYeRkyXXO+fEUEK+fh7HyFDJr4oymBSJBuqCk7DRAjSdcktAgI6aTAwTgUcexgw2rYRkFeUsGaCCKr1nyewE3DiDaNuWzRNh8nWNp5/4QVcvnwRtiBYa7B19szAhGhMHZ5uH0olGytQ9+kl3UrjG4tO/HPsyyjh4ZNfoeyXsR6P9omGv/fX5ckHQ80Y4gEnymnC2vaZ+/qJDJQNYB7SFb1smRlOzUY4aAwQgL/nkLRLnbgEmPWmRPJPwZI+I58RumA2pEBfHL98vLQ4dCzuAxZM6VwaBrN3ojAc1LxhD5ZlyOTtLSpTAMEXg4zp6w3AIJfO6EwTyVxozgP2jM55HBwd47M7d/H40WMU1mJaTUAMTKoKbV2jXi6xrJdoWwH/enG1IcdBXddYLBZomgaHh4do6gatA46PjqNmoW7qAF4dXMfoOheBKQ3OlZhHxo2XnCMHTlTJ/e7SyHD5ha7FIJGieY/WNZgva5TGYm//EB988hn+/K/+Gj/4wW/h+7/9XezubOP9Dz/GBx99jJu3buGZ565jOpvGSGGg/lwDfV9EyiVMCQXJlvcczcnECnIYIjzuZ10nBsCEne1tlKVBxyIp77oO+wcHWNYNJoUAcXnUxPd2d3fgXIcnT55gZ2dnMA89zWLAWzx88Bhvv/2OaEyChO3atauYlJtY1Eu0TQNbTFAWUxjnAN+iLBjgLko3hckWgVDbtmGPi7rFCDpA6zo4ENrWgZmEyQ396VoH5xnGaP6cXvMU89gEYNw0LYhEe1/ZAoUDDg8P5KxYg8V8kSRKddjY2AhMnviabW9vY7IxxdbOJra3NjGdlagmIqwyluCYJMM6OWFKAqg2FiBqBciTQTUtcfXGM7jy7HW89lvfwZ33PsRHv/oNHn7wCdqHj0DHxzD1EqY1aIyLe4a9gzMuaq5S2rUS5YbQ02kVMGXgUhJg5jvw6SUHhmNl2BeCSldT88YUoI2Z7owBtnQMY+2fxIys05SMMSLxd0NQs/ExP4a8jp75Qn//rZFwa1tqhiP3gou0LO93CvZPKuv6t2K+iXHtlHR9dczr6h0LvhO+7DVYAmjis2MJKLXkQq4xzcVJzKmOLfwV8cEQEw3eQN98f8+n40CkIz0jmI5h3VjGGOIB46cWFQzM53NhikLI6wEjk3Y3G/PKORhhZsNsfW2m+dSMhoSrtXGTTadTLBaL0CwD7FEFx+yN6TS+d3x8jDI4G4vUsMb29nZUM1sSk6KtrS0QEWaTCluzKTY2NsDMmM/n2NzcRFUWAHsUZYmqmgw2rjGS68BaG/ugm9sBqIoSHQNNK+pkazXudoga07ngM1HCGApmFMIUNXUrDpoImaZZEusRRFVsjIHrJNKWa1sx7/Ae02qKSVWh6RqgBYgdCltBRfYquScPEAxKlGjg0XqAbIHbL76AZ2/ehi0turaBazzOZkwGcLpwhWObWMvX4Ur/cxWV/AM48aBLUeln2PcJsBt6U//n6xclhH0ghdNbN3RJmIMYhyFKW7XfygD0zAVCkIE+a71XYs0cM3p65mGSxcE/oOPETyFU7ANwBdlYpzaqq24CAwTOwakwRwr+1Y8BkLPtXYembbFczuFci65rURQWO1vbOLdzBts7O7Ahyab4eyBKgFLJVQ4q5Hcf5/mLz+/hzV+/DQZhWlbw5LD/5AB3Pv0MX9z7Ak8e7WE+X2B+PEfXdehcF02XPIf8LQkBlznSPC6qVeIgbQo25zxUHRP3zpIUsnhTJNQ9se2YAUv9nOr7Qfo9HKPunx7DK7GW7wAHibrWNA7z+49x/1//O/zNT3+OP/iD38dv/9Z3YYjx9jvv4sOPPsbt52/i2vVrmG7M4rr1Jb/0+72jwKwoLLwj+GBWpUBTo0OF14DAMJVlielkgv35QuYZQpfrpkY3K0Mo5v5VQKTYt2/fxttvv43XX399kEE2ne+26/DvfvyXODo8xPHxHE0jZqtbW+/jyqWrABOOjo5wcHgYzNhEyzQ/nqNzDl3QWrVdi66VHDtN04pJrnPw3kUxQ+ccWt8C4XLX8NUUvmuaLkr8VENuSLTCVBYDvx1rLYqiQEUWMyt+htPZDJOqAjNjtrGBrc1tzGYb6HwB75foui7emQghzKuqxNbWBs6c3cWFi+dw/txZnNndxubGDGVRwMFJ4ACjIald9LtxZGCN5Lc6c2EXm+e/hxvfeQVffnoHH73xFj7/1Tvo7j2C3z+E5yXQtihaRgmGJ4/WOEmo6ss4R2nJJa1jkWvGwFpvgrZaxgBpDqK0bX1+jHFI7z/9bKBBOKG9QV/XMDr5fTQmRT7NO3lbJ70/9m46l9rXPBhPXqcxkgwun5v03XWO2+vKGDg/6dlIc4Bgxtn7Ioy1fdo5ESEl9UKfZEzAeDjYHJSnkvvUDyTvf1r/2BiV6dH2YxJr7jGL1jHYb+iFcOvvxb6dVOuj9GfciV+mRfLbEdp6ubIH8jF8HWahf0/uudPsBS1f2xk83bA6waU1MNagLIIjcpj0/f19kBGfAWYB7gcHB5FTt5bA7NA0S7iuwsbmJupaJvHgYA/GiBOydx3YOxSFOE1LO33aeAZCSFKZ1OVyKZ2OE8HoHCfSLr1Aq+DcKSptVdN751CG7LVFJQ7nRXBebtsm2AdLmNXOdWHjA03dRJOUrqthyGFrMsHZzXOo66VI/nxIuEQEgulBJROcJ2BS4ZXXXsJkawfLtkPXtOjaBhuzSYywlZavs1H+vhtrtQwlJZEQDtpafeskoqZgZ/WAAplvYX+QuVfRn5bZSn/XyzN9P3VA1mfiu4k9fHrx6mdprhk9AzIcNdti8QtAcGz2vjc14mDmwf1kUgJG+/6LBLHzXqK1BemImo1ZTyiQmhIEbQkLA6EaEHmpZ/6V8e39kwR0Nk0r2csJoODjUZYWy+NjfPDZF2i6DucvXMCt27dx7vw5FGUJGyLNjUlEtMilIyTXe+DLe1/h7/7up7hw8QqOjxbY3zvE22+/jV/96ld4/ORJmGuxa4/zn2hpfBKlJEpavZgXauQzsNj3i2+QQRD7ACwqZuekvpDKHQyXMEthPlljigfTEdmB/RghUci0jylTrWGN+2f7fsEYMEgcb9mjWXaYf/kQ/59/8a/wk5/+DP/oT/4YL73wPOqmxhu//DU+/uhTvPDiC7h+7Qomk4nUZwi9g76Y2uTgJoJDS2AWJqMo9J2w3xIGXpyLGUVp0bkWnRdt2bKusWwaYZYNklzvUpxzeOmll/Bv/+2/w+uvvz7YB+mZOjqa4+HDx5hOp/j008/x3vsfoGslwWhZWXRdi851Kz41TVtLXV7Bl+SviOcxBWdgqMkemwTAhbmXo0AA26BV7EFsBMLp+hrxvVA/OwUv4gNnoxmXNQWKosLu7hnxlQn+cdPpDNPJDBcuXMLuzg72D+7j7udfgln8gDY3Sly+eAEXL17A9evXcPbsLja3NmGDrwQVBi13YDCKooAvRHptiwobO1t47luv4NLzN/Hkd76Pj3/2Fj5+4y0cff4Z/MEhDBNs28B1LbgwIGuCaWR/P4w5p6b3frq3c8Ae555Wn0nXP60//T419xnTKqxjCtKgLXmf8zbzvqRjWKepOImJSIFsar6Xzp/My7APqZ9JPh8RSKbzOtJ2fnelbaZ15oA5navcKiKd67G5yQFuPg+xv6H/OSjW/qaS/BxQ50EBFFwDivf6seT91zlNQ8Pm/UstQsYYsnTOc6F2XIts76dMst65+Rqk7eTzuG6P6rNptLCVfZq83zmHnY0tLOfHcc89jckYMx/L50v3o8f687SunN50KtFmaCfKsgwSI5HQq3qw8x26usGkrABjUE0maJoG+/v7MTtsVYkj9flz58SxejIBe48i5CvwncN8PkdpTJRAlWUJxzKpMmZCXYsTZmctyrKCtaJhcK4LnJ0N17kXoEQc1IoWnWtQFCU2qlk4EAywODPr5pWQt0AbMqJLBJoOAMMGPwsTTEa8dyhsAVsWmEwqTMsKVVBfFRBg1HXBod0W4W3JddG6DrvnL+DCtevwtkTjgr1318EQMJtNRx11TiON0HIS0M+fy8vgvdSjGZnwKh6mXvqroNaQJhJM4BYTNDpzaCmxeQymRikdicQXYoPt5fD5EI5YGDdhUBgJqGGV6ipAxarkPyUsYWDK7BhjwF2fL8T5PvxxejmvSkgUvAXpCIlGzJL4OKh/k0rCFSyBCV3wodB59N7DdR1a58AgdG2LtmsDgxvG2AhzaoxBWUo43q7r4r7Vv9u2Fc1d28I5h+WyxvHREZYh4tr+/h5Y+TnXE+SyKnD+/Bl8+zvfxuULl+CNwVcPHuAv/uIv8dyN53Dr9m2cP38epuilVuklkSykrjaausFvfvMOnnnmOXx57wEeP9rHm2++iXfeeRd1U4tHR1CyiGaAgnNPlmU7EcYLf2fDNrWZxD1RIQcQ6YMZVKoqj1s3rVMeQm+Ohzj32kT/DfX7nZUHSC7cwZ720GDDRAZFEILUtcMnn97F/+P/+T/jm69+A//wj36El158BY8fPcQvf/4GPr97FzduPIerV69GzbEAYDHw0v3ZD1f3uwFpzh0HaV+j3BHF/JwMic1O5OG9i87A4p9Xh3mnMNYh3Th79hwWiwWOjo6wEc1dM0afPSazCS5euozZJ3fw+Rf30LWy2J4aeG5GzTyisEEvd6JgMiJ5iZDM+4BCJQERhqtASJ3KlIklIhAziiyMcwRFJP+IKDIYoYOyjkWJ/ePHMeJZjApGFSyV2NzaxGy2gd3dHZw9dxa7Oztw3Qbmx5/j40/uwP78DWzvbOHGjWdx7epVXLp4Dju7WyBj4KFmwWK+S00DKgtQZVFtznDlpVu4cvNZvPK738On//Fn+ODnb+Dwiy/RHR6Cl0tYYolSI/HXVwBTDqbHmIoUrCpAjIxdBljHwBRzHxo//+40UbKG4C7VRq4yG3m76+7RMRCWzseYE7HeAWPAHFCG+OnjyQGuhnnNnbVzBicdg9wfw3N20jjHQLCW1EQpZxb6d1cjIg0ZjtXPtY5UC5Ayi3l/0u88GLn/yZhlx1jKBW0/186N7Zex3/M2xpgu/X2MUQYQEuH148uZ0nwe8zrTvhgTRDxhfxlrMJtOsbOzg71HD1f6cpo9kZexc+/5v5DplPg+2IFtpAA4kTh738GwFbuw1qHtasw2NgEjtqcbGxto2zaGpCWCRJXa2QJAKKwBCNjaFEdnZ1rMj0MCO+9RVRO5AK0RW1oygGXM1UmwFc1CYSbwrsO0CqFxg7q99gATie9G0UeoaNsG3CLWba2FNRadEzOrqjCR867rGqgKIGSnZicOlioFK8oC3nl0roMxJKZV4DA3vr/kwiXpAbQAfGFx6Zmb2D17Dq0Dlk0HJkmw59hjY2MaQaOG9h2TFP2XLP0mA8CrTnX9M8O/1eGUCMFJdhiaVJ0Amfts8GC56F1w9kw3dATUoS0xVeIVIpL3SwF/SuxTadI65ipeLmTAGhAgMAvq+xDbDWvfdV0MKychjS285+hLIAxrBxecXLtOHI5BFH53gJFwdS5EdiOItsF5j6ZucXwk0grPjLZpsFwucXh4iLqVCEnL5RLL5TJo7BjOO9R1jaZp4hjquhHwKAMcSEU0ellVVpJsjAhFWcBYwp2H9/Cz3/wK3nncunETv/v7v49r167jow8/xt3Pv8Brr30Lz954BhsziX6W5qTReRVgKj8PDw9x7dp1HB4e4u5nd/HJR3fwyUefom07eMi5lJAMFPtJkMvbB+ZNtQjKlA0cfU0SoEAWu+9L0Ebmn8uf1KvpU3xKQCr1t9TXMWQ0hg52Iu7gwd/MCrAcSEJXxLat0TwFDnXd4Re/eBMffPAhfv93f4gf/eEf4vaNW/jq4Vf45S/fxJ07n+N2YPJ6DUeIRRqKngvvHOA1waaH+MlIPhuGRJtSWhXccXH5ymXc/eo+QIDzHp33WCyXEp2rKgLIWpWYXrlyBXfu3MHLL7+8oj1kZkxnU1TTElvbG3juxrMoK/H5IbLwsGCqBnPZ7yO5YEWLgyhBV+1UytAN1tUk/OZgrXmFNuirBETtRVw4KFNKwfeBwz0QTAGZgw8OwzdiwtVHUwIMLwDvsX8o+YqIJArZZDLBztYOLl24iCtXr+D8+XPoDo7w6Je/whu/egvnd3Zw/doVXH/2GVy5ehkb2zMQAx06eGIY74DOgA2hmJTggnDxxlVcufrf4MXXv4/f/PwX+PjNt7D3yRfA/hy2qeH5SEazhrFI50PnKl3jlX/9FI2WHMRrct5cG5A+G++KNeBmjME4SUqcj+k/d1kBvjSkC6PMf/J3ZDY6H5PvrgP6Y0U/zpmjMcCZMhtjADSPTJQ/pz5Q6d2r0u/Vfq36Fyi+WhfaONdK5HM7YGqy+cyZsLS+tD9jv4+9l9c9xiSMrcvgWTM8V/ne1d9zE7mx8xjnpXNRqHt0fIyyLOI9ua4fad1jezB9Z9h/A8OrCVhPKqdmNMbi16dcoWcGu07Mfwxhc3MLtijguJd4lFUZtAxGNA7BzlUve2axW7VGwpYSiX0uID4hAZ+gbRuUpcRwn04nokoL5g6eHTZmsxgKt7AWTVvDUiGJ74yYeREomDkZwHdBaidMARFja3OGqiqjFBUAum6Kvb29wIwUcJ1EvdnYFGmddx6L5QKVKTGpCrHv7bo+vKOVhRctCcObAtXWDq48dwNlNcN82WK5qEFFAViG61pYazDbmEn9ETz1ZmJ50f3RE5r024wxCEzPCjngXjIkf/b+BswiAWVeJdRxbyTSYNaxo5cq6D6Kjs1By6AmC2pi5NmrGDiMJ5d2+Jg8D5HJSdT34N5BOYxTJSHOaT80YEBwDg5hISMD4LxEcOgcXNtFbQnCWJqmkZwm6nfhXNA0dCiLAt4zuk6e0/ws3kv0oyaY07Vdi8VigcPDw8iILOoadfhdmBTRQqgsnbtUUmQwmVQgY9CQhy1LVJNJHxCBgOnmFja2t7EZ1kEDJjCHkNSdRFOad8CyPNdvl7DlPAMNATu8hwtntrG9tYF2WeOjd97F//g//t/wD370I3z3e9/Dnbt38bOf/wLLpsaLL9zCZFIle0Cl0AaI5hpA23Y4e/Ys/sNf/0fcu3cPB4f7AmBBYEjEIg6XmfLpHPZD2Ijyq+do1jjYmxkRTXdt+tgQmMgckT6UnBPKXhRwFZgNBtITlQMvq+cSOhbd+x2Q5GYhQpCKk4TuZPFDOTw8xr/5Nz/GG798A3/yx3+M3379+2jaBl988TkePnyIq1ev4saNG7h48UJggGQRCWJe6pM5lIhMnYy16GdG+QUKC2SMwfbWZqjHh3PHWCyXaLvgRA3ux5bcEa+88greeustvPTSy1E4QMoUgMVHYXsDi+USV65fx9kLF3FwcBSiy8yGzAsw0PiRmnBS4n+kk5sBu7HFH4ADKKMxFEpw6HAaLtR7TUwo/h0UHOxjdKUY1lmipKlkVRPCeu9B3KCp51i2i0D3CMdzCUn+6NFj3Ln7Oaq3S+xsb+PipQu4cuUybt+6hbbzeOfdD/DeBx/i7LmzuPrMNTx34zmcv3gefmJh4GA7h4KArq3lmFUF2qrC5q0r+J1n/2u88vpv48O/exMf/d0b2Lt7D/6IwW0Nwy6ur6Owj71u62GIS51jXW89Az6oHlMwta6sA4f532PS3xwcj0nCT9O+lpMAUwp0h++lflcGBL8efHGi+cyZDiEaK4BSb0PVDqVF71INZR/NipK1iJSIVctPGLntB8xImlU+n9fI/CTzETEg9W1r//SMj7P2iG3mEvP8c/0uAm8I2BUhWggBz8nZT8ak9HhsP+VaGmWO9MxTEDB5HvqWxGeJokBhEAglrsPKTIfPTWQelQHMfdjGmIuxAEB6twp9l3qbRkKqE1E/P4lALb2P1p2bKLBDYqKc4DPO5/kp5dSMBiCTUSQZB6OESqYBLth2ExHKqhCwbwQQMkSKu3BdzDJeFbM4qLiAnmAKi7KcYHt7B845TKdT1HUN5xt0zmPZNNjclI1oizJOVBGAgahw+zwTk2oKIonGUxaSbA4QwE+W0AbuzBoDS8B0WmFjVsnConcYt7Co5zWKssTuzgw25P0oyzKOYzqdwHUtiiDd6lgcsxwAuHCYrcXSAZu7u3jm1gsgU2FxXOPw8BhkCJUxgHOw8CH3RpGMhyJISKVIaZHFX5Xgy68qSWZ0vpP46F5s9n2/e+A7l1YYQ4kCJGbqAfhFZkEfNTLPSA6EFzQffRz0AGshUCS0ynR4p4RTDcx6Yte5LkQpkpwHLlziTUiO5lwH5xpwyMUAiMlU3dSiYTAVQCZEHvKiWQimDZ3voqmRmhstl0tJyAYf8yjUdR2Zb3HyrHF8fBw1E3Utf8ulW4Q1EwazrEqURQmGkzCj1sbDXxQFppMJitkGtrZEozGdzVBYg6NFA8dAUVYoigpgj6Zt0dkZmjO3wd6jZJlRR4Aj2b/L89/EAWmCICNOsok/iC0kdwuHaFcSKw2gQGR9Qny+dB2+3N6Ce/Qhzrf3cOP5F3Fmfw//4l/9GQ4XDX7v934Xn3z8Gd58821YW+LW7ZsShpo9mDuoiRCZAkQhJ05V4v5Xj/Hpp19g//AQ5UaBclrCLWvJgM4ADKOgkHsgXJwAYELUHLYmzanWMyBBuDAAmMkfeon0l3NSRQAAAwZDHo5txH2vZxGDpoLWYni9DyXCgIUFhzw4qTBHQyQqhZXhEOq2wxdfPcQ//3//f/G3P/0J/uRP/gTf/OareLL3GJ9++hkePHiAmzdv4NmbN7C9swHvO5Q2SAPZyvk3DBcYm853oKC9MWSilkiGKbqki+fPoDCEAg4GYma1qDs0LeA6gi3GwdDly5fx53/+71EvW0ymVTiLYnoqS+TwzLWreOPN93Hp6g08c+sl/PrdXwPowGxBUI2xgHv2YmQIH7TQIRogEjCk5l/qV5OCXsdDm2xdJAbAqYlfsp5yWfdhKg33DJjmy7DBxNc7B3YOpPEmTajLeRTWizaJGZYmmFWzSGs8e3RtF8P7tk2N5RI4PtzDw4f38OEH7+DNN36OS5cv4dat27h16zb2Dhf44qe/xpu/fA/PPfccbt5+Bs88cxVbWxvoyIF9B2MBCwaxA5FBaStcuHYZ5/7xn+Dl138Lv/y7n+Pjv/sFDu/eg9k/gF0uwNzAUwtPQEEWCGZz4aDBcBlORxeZC5kSZfxWQRLQ+3mqQEZBE2VrlwOfFNimWKE/Q+NSWf3+JMn/WB0p0E7LUAKsuAUgksACTA6qmc/fkWRqiH5gDI6+PmCAiQd0NvYNQ9+FIe3o5yKX0lvIvas5lVK65LJ2VJOQMxgrY0iez7Ua6d+DOnh8btO+jzGHaV16XuPzqbRE50LHaIZzFWm4MngJsB4kmgYFVjEVUMn/0neGaxOMLQOTkX6udJ8SWZgKMoiGPlFSRe+kn89tPv7YTsKQKqRSul2WJZrFPBG69Pceh36rJnZs7plIXWAFx0MsC2T+VxmUp5WvzWgoF6gLVRTFYKPqhKRqFl2ajc1NeOfQdh2mVYW2bWOSOJ1MVcMRSeKRxWKByWSCyWSC5XIJpg4lGMfzuYDOrguhAwuUtojSI2sloV/bdtje2Y6RSdThtrAW5XQq4I48PAvoKaxBVdiEow5LZGRjlyH6li2EqRHTqWTiIcAR3qFjYTBa71FOpiKNcw7L1uPcpSu4fvM2HCwODo+w//hAbKxBuPPZZ3j22WdhjQ2anKGKLnf6GmM2tEheCxac7xns1eZTpOTq0yCfqb+D7zn7AJJ6DQTHiEjRSUo3MAFkjThvOj8ggt654AzPaFox3/HOxzVpOwfnOokYE0C+XkZ6GVtrogmSSgfacDmrmVCfpVmSuykDsqyXwTehw3xR4/h4AYDgOodlXaNeip+D8y2aqElIpA5h/GVVoiyr6JhfFgUmkylsUaGsJqgmU2zMRMPVdi3q1sFNd+XvVnK+bGxshH4tAQPUu8/Dzc4L0wJgGdeut0X1nuGvPAMUs5AbJJMGBukFy2L1Z5AMcFxHyY68kILoHknrblerINKM4QmRZWY8fHIAmIt4PDmP+6bG7cnP8corr+DHP/4xdnd38dJLL+Hu3bv4zdvv4Nz5czh3dlf2gldtlwdBxlWWBufOncNPf/IGHtx/CFMA1565gsPDJRa1g2NNeOaFyVDwiOSiAkRVkF1o6ZlJS3rxUfSLWDVN8G7VZCGtX4FmXAPEqVx5Nm87r5dITGiM6bXFsvYIoDckJiOCsRbsPRbLBh98+Ak+++z/jldffQV/+qf/CC+88CLu3PkMv/nNO7h3/wFe/eYruHz5nORFAIHR+/vo3k73uvc+OKbrmGQPzTY2RBscQaHs52VdgzdnkHCxwzn23mMymWBzcxN7e3u4dPniYIYoLNmt27fwr//NX4HtDM+/8ALuPfwKra/hWw9EejWMs58GJ1mRSvrV+VZmLwUcKbCVcRdrzXNM8D3ITVcNqSQ/BBLxHhSkk0VZwNoQxbBu4CB5T0j3HRkYU4CU4a8cSu9BXqJpNU2NrmvRLmvMl0vsHx7iywdf4YOPPsT25haefeY53HzuFq5cvop3330H73/wHq5evYznn7+F525cx9mzkgCyazuYxsu9VHhw4VGUFbYvncUf/Df/EN/5wffw1t/+FO/97U9xfPcLmOM5irqG9Q6dcYFhMoHZEFAML4BP52Nw1tYwGjk+WAFuI8/rWudn6KQ7Ly8pI5O3p999HX+QQR8BYRs4yo0Dvey/Rbj3dAjqy6JlIOzQvo70H1jNdZDTuAFWCOBw5a4Iz6mGbQzI5lqcdeMXkL8q4Y7nw4jgIkrTR0D7GKM49lk6hrRvaV/XRYgikkAKOu+5Pw2oD/k7uAdG6kr7szL/8kfSbwpMRsJQZLWOrd065ngdE5yKt9gzmroWYYgl5XpW6sq1PcP2epwnvnzKZPRYUennacqpGQ2y4uRNrldZOfYg9qJeDZ1Uj3vPHJPspAdHVV7zhaiMt7Y2JfZ8iMZTUAHXJQfPShzzruvEybqwqGg64Pza4NBaL2twkDQbY8RZkRnTqfg4kDEgFlvAopQkSmQIbE1Ua04rCaOrYA0QoqGLsbu7G8fpfYhZHSbchb6UZYnWizN3HZgpBqFuZPE3t8/gyrVn4Dwwr2scH80xmUwxmVT483//57h58zl477G1tT04TOucwXNJR/+MgLqesRBbbO+CaVInmgN1Ek7N48C9OVM0dQp+Ez5E8GqaBk0j4U7VubhlHxOcKbOgOR1cyL6shF0jgMEYLJsG9XKJpm2j3e5yuRRJOzPqpsF8Pod3Dp4Z+/v76JQh4D6zc0+oRbMi0V9slHSUZYkiMAsimSFMt7axfbaC6xxMIQ7PAGG+kGRxtpDQxoddCV9tRzWp9yyM1ewMji5+O57lh160Hs57OCqB6W6vYkVPoBjoo0CBwRZRUg8ogA6mQAD8kkF8LEAwWW+50xhRoqjvcwDovY1Dv0dIWyBINKnkglNpCzgkDZSzzN6DbBpaj7DfTfDemT/G8+2/xoULF/DjH/87XLlyGds7W9g/2MPb77yL13/nt2VcnEihkgzZhalw//59NE2NrekGzp+/gC/vPcL0cIH5so1zoRcCELRkJrsQsnOhdCAvYxdqfq6AsQRGfd0peBkLkZjXPwZ28ufTC0fnRiOXaWIyr5mnQ5AJ7z2WdYtfvvFrvP/hR/jDP/w9/PEf/xGOjo7x1cP7+Nu//Sm++53X8Nxz12ENAcRBzd4Lh5SpARCjKXFgMimcxTO7Z0SbbfpxtG0XzQFz84507l9++WV89NFHuHzlUnhGZX4i5dvd3cazzz6LL758iMnGjpiK1ixal7YP6TgAW4YATViqjAKL+ZOVmx2a0FQZI2YvEcVE9AdLwjxoyF4FCWkiQ4SeegMwCMaWg+h/pOvFFkUh5rrKcAS3Q5RVhaoswU5oowpQ2DMMawhsB3LCpJDvUBqLopoA4KjhqJul5Fja38PR0REePX6Md995B7s7u7jx3E08d+M2Fh9/hnff+wDXrl/Bq994Gc/deBYXL56DYTH/bDpGVziQbURIWJbYvHYeP/wnf4qXfvBt/OY//BQf/Mefo773CFjMAX8EsIsaZiKSO5/Qa/EScDYGWnJwlgPMtORAdeyc6GfrwHdaTrIj13Om917a7oBBTc7tCoPDvUQ5kXGjZzLC5yRUeBA9iTn68p1GOjwG/E8CpPm78bMAfNN5S4UNT2PgUjAsWGG4livMEIbPrBP8jJV8D6TrMDZfigHy/qqAIWdSVFiwTiD09y16l47tJQk80gt5coYlZzjyevW9dX2MmjIk7MfYfBENfc8G7fW4VzG9atdkDr/eHJ1eoxES2EGCMkm0DefgyURViqEgVSWK2QWYfdBqEAorDs0b1gpH5OUi88wSqxwED4jtOBBDgNYBbNrwrLGhE8F2rLKSV0NNsvSMu86BwTg6OsKWNSjKAs4HzUZYqOlsCmMNiqIQZ13nxHAkMd9xXqI4OO9giwI+1OGZA6huUZSi4WjbFhM/Qb1YAgS8/fbbmE6n2NneQVEUWNYNfvD6N2DsBK2XDMZEBq51uHv/Lo6OjjCZSCjbqupNsrSkBHGMqKcbUBO9OaeO1YDzHZpaNADLoyUODw4jo7Csa4AZxli0bYO6aeACY9AG4O+cA8Gi6zrU9RLLZS0O+l2H4/kc8+USPqxb14rvQdd1sMagXi5xeHQEFy7itmuxXCwlIVaQiijotrYIhw5R6yVjNWF+KlgrZnOTiTANoiErUFYlGBLRyTkffRW6TiTEtjBBOslYLmsc1h2oFq3W8c4tgEt4GPgb3wFMGR2+QYUkJUukNyqN4nmQ1nsGkwW4lwCgPYzqci1E1N9QAUD3zCHQc+nyTATacsNDSQhHyZlI+71gyeTdRCqjBC/+L+TOYIqajCiXCQxG0EeL1FXvj5DoTDQThMWywRcb38DNK0d4441f4t1338Z3vvtdLJsN3L37Ob75zVexuTFBmgRQsnj3RHi5XKKua+za7biewksQWueg8XfjeA0FYBmmMCFVei7WqfhPuhTzsk7KNnYm8+f09wFTuAZM5GBG+6bviHmNAzHBQXwihNbJvuq8w8HhMf7Vn/0bvPfBR/hn/+x/h8tXruPRo4f4u5/8ArPZJi5dPCe8GQ3nY+Cw7jlGIAL1jO9sNo1mszbRgiyXS7iugy+KoLbvnRv1Er1+/Rn86s0/ww9/9/XAgOj8yJmxlvCNb7yM37z7Zzhjp9je2kXTtXBduzKvUaKnjHBgo4uiSExy4mjggm26BhFhIN6+HonmK9YXmJKUzhqSvCmBKRfTL6moIIpJGMmaYBJchKAOLeA1AaCYBBtjMDUWMAZdJ/PjgmBChDAe1LXommWIbuhhAMw2K1TTGbpuKXmVug5Hx8eYH89xdHyEh48e4jdvv4crV67i1q2bqOsGn312F9euXcWLL97GS7eexZUrF2HJomsZ3rVoXYvCNZgWM3TWYufZq/jhf/u/xsvf/x5+/Zc/wSdvvAm6/zm65RKmKWDhUbCH962Qt8TGPRX8KQhZB9wU4J8EHk8D+lLh20llTCquv+fWAWndad/WMTsImtU0A3PcZDoujJsjpePL5zF/Jn0uZbBykDr2Mx0HSMi4H5nzlJEa+5f3Sz/3WR+0rejLlPs2jMx3/l0+P2NjXldXrpWUe7rv03hkyDV9UrujpOS0emxvjK3FgDGkYRLDdfOTnpW0DhVEDfoS6JkpJJBLvZiLO0MWpOOk+3Bl9CRYQ7BZqmEcMvtPK6dmNN559x10XYeLFy+iKAoURYGmaYJZ0yzYyhrUdY3OOUwn4qTNYBRlib0nT/DJp59ie2sLZ86cwebmJlzbYT6f4/HjxyI1O3MmTkY1qTCbzkTikKgaq9k0gKd+86hUID2k3kUvNhhj8NX9+9L3qgR7xvHxMQ4ODlA3DaqNaTB3khC4ot4WrU3Tejx6+Ag3b94UyZZzKMtyYG/q2cu4Ayi//+ABClugaVvc++o+zp45g0dP9nDx4kXcfv4lTDd30bJH3Tk4Dzx69AR3P/kMf/Mf/wb/7L/7p7h+/Xq41M3aTTDG6eafieZJ8nN4R5jPl3j86DEePXqM/f0DLBdLLOZzzOcLHB4dYrFYYO/JEzSNmBF1zmF+fIzFciEbzUnIYRW6N3Ut4L4oYshX58VBTf1WmFmiqQSnNTYWs23JlGtIggJUkwmMteJD0TmYcGGLz0UDJoMFpugC8Dj2DHZqQkXguoVzy5CpuQYRoXV+MC8RhHgJB4lzN0FnbgHnzwPbV+OlIcLOYDrSegCuB7TciGQqSK8S3n9AyOET6bteNMCA2Yg58Xy6ZspEIFQiG3jAfyAD1umak+ouQuXqm9B3NKOZ4fmYB0H7p9qRoeNbvHR1Xn3onweOZ8/i4PHPMZ1O8OFHH+Abr30TRVXh6PgYBweH2NiYgYPpTs8mIaxzG6JhIYa+FqlxYHQSQEhkZcb10htIDvvSS2JWTSbyS2rssh675NP303dzG/L8uVQT+XWkQPFiIQKMhe/EHNDAgNnFHB5EISEWi/nOe+9/iP/pf/5/4b/77/97bGzu4ujwEL/+9bv4oz/6fRjLAFzYdyOSPwjwNQhhpiFmISL4qGCNjT5uzjvUyyXarsXEW4wNjUgyiwPAYj5HFYIDxE1JEmzhhRdugYgwny+ws3MGX93/qu8T82AdZb7FJFcZAk2UKfuZAgOqIW/9ikmDbKv+0geCsAMMMMcLmpTZ0k3LiBpGCky4lhi6NghGOkPo1Ew0MC8GALOD8eIbpaa+Oi7nHLhpsSQDzwuAGOw6YTJtidIYlMVU+hjMq+qmRtM6LJYOx8slPr/3Bc6cPYObN29ivqzx6Wd38M6Vy/jmN7+BGzefwaUrF1CUoh1znUcLAJMSvixAhcW5F57DP3j2Kl794Xfx7l/+NT789TuYP9yDO57Dtg2sFYFVz/znTMHqvlq373Xc+kxqyrbuvRSwrTtz+Xv5OR+rM+/z2Pcr4JLQ76NBBcrIMJgdYHqznpwepAA+/5f3P/09D/Gag2jt04rzNtbTunXzsI7ZUMFgWtegnyN1jJWc6csZnLE6xujreuDLESinjIiYTA5kL7Edk/n25XOV79nUoVvrGP9bac5wrHm9WnKfpOHco6dFQrqiyf3BE9U49e8PmNMTriLOhJnDPooC4TTmhlpOzWgwPN59/x2AGDdu3sDm5iaWyyU2NjZhqJe8F1WJpmnighYBNJiyQN02uLq7g7v3vsBsMsWVy5fh2GO2uYGjoyO0ThiPyWQCU1gUQaK/WC6htmRV16KaTqP6Wn00GEDruphyXaTxIj1rXQdblfjs87tomwZNMPO5cOECzp4/h43tLXTOoSoLkfh5j/39J9h78gRnz13E5tYWjpcLNE0jPhOFBTmRKrZNC5D04+DgAEdHRyiKAhsbm/jiy3vY2t1B7TqUZYnds2dw+8UX0TgWK3VPuPflfRgA585dwIsvvIhLly6jaRpsbW2tqPD7TbCei1yV2Bg0S4cHDx7i448+xuHhMZb1El99dR/vvPM2Pv3sUyyXSwF3ZQlrjDgfh7m31uLcpcuw1qKua1ybzWBt2ftaeI6RL+qmDtGCIJoQAE3bRhMPte/boxkaVwXNhwMvPdg3aM+/Cr97sSe0m+FAFBUwOxsi5qgvSUr0QsSqeAjVBlqeZ9nAvUYhzOnm5haYGV2rBEKlT3rYlYAF86KQUZpTdUHy06dnVwlJ+C90If5fQD/pL6GdwEQwg2CVzwhWItQ/EOqX56SK+C4RkPgd9OBoSFd0TihpWxkVZolOJKBeK9Ykd9rv8HdwcKubBgezZzCdfYAnTx7h6PAQ080dlGWFg6MjXMYlCWAVGtZxGmPQNMtgyysRM4A07DAi08PJIOIFxr2KOi1jUqKxctLldBKz8f/Poqr2opqAWHyZWMNeBvtZCgytCT5xH39yBz/+8V/gT//0T1GWU+ztH2M+r7G1XcIY3dvDyy3ORZRWAQgXqTB/JWxZiK9GoE1N00RJPPOq6Z73Et75ypUruPfll7h162Y4vwocJDT65tYOXnzhebz7wR1sbGxiMp2hns9X+hedJqMcycfNrXPA6ucCDEEsUdxn3ocgE0SRoYhRo7yH7zp07OI7aiakZwEEkLHB31uYMhWGibDfwppJtJH2XRd93wA5zxIIQsZnDAUBC9B5j2Iyxawo5e+uRdMsRdDiLJgYRCFm/qzCdDJD2zRouw6HR/uYLyyO5kd49OgRdnd3cf36dRweLPHpnS9x88Z1vPKNF3D71jO4cvUimBgNNTC+g21FG9zaBmVR4vIrt3Dp5rO48e5HeOMv/hZfvv0euscPwccM6w2oa9Yw5qppHGfa0zUd2385yJR9Ms5w5O/r5/nvWt9pQOkYyF/Xh9WSPiP3hbVl0BKuMk+plP3rSIj13dRXSc/bmBBSn9dzkJvsrKv/JOag9wNc/Y6Ze//cU44pX5uceckZqNOUuHZBXZ9GeYpjT+76tD2lgakPzeg4w+eqQX8aABeT9L5/uZD864wrtp+8ymDJWxSEJJTMazq+FHvkYxd6Oh5uWNsfMNxPKadmNM6cu4A//of/CLu7O2BGCGtI8EyoqiqqyawFpkXZ57wIE3Hh4iX87plzaNsGDx8+hgcw3ZiBrMEWEZiA46NjnDl3FhcDsFWpuEbJWS4XmNc1YAt4EMqygC2ruHko2O16ZnSeYYoCVTXBbHML3nucPXdeJhIChI2RpGaexAikrKYgMLzrcOHSFUw3trE520TdNJhtbgU78hbGhHwizokZj5W8Gx4EMhZ7e3tYLh/jq/v38eTJHmbTKW7cuIlr157FV189wLmLz+Do6BDH8wUuX7oESxb/+uf/C27fvoWiCBnJC/ErGGzuuKa5+ssPDoaABXmvbhw++uQzfPTRx2jqBk+eSDK0X/3q1/Dk8eLLL+HK5cuoqgpNXUuoVu/gwMEHo0HddiJlWy5xcHSMrnNoGtFmtM5Jzo/OYTk9j256AcwM11nJgXD998HFtO+jZ7Atg3lRf9AFMIaDYAiURIxhZmBZS5jgIHfXwyPgXpgAjQBBSpRkquRzUqmF7DXvHKpygul0iv2DA8mUy0F6nFxMAm4ogi6df/WHoCCdIE60B8m5j5aS8VmT/J6ISfX/aduxsgD2SduW9wwF/YNXHigZd6iXw/xIRhdWjkKe0OHoZcGifdzc2oymhfVC7MKR6iE4MBvG9Nob71Ff+DbKj/4CXdfhyy+/ws3buzDGSBAH5rjeAcsGSZtE49rYmIE9o2061MsFbAEwu8CmhehLNLw09SxL19dfrl+HgD/t2bGLbszcIQUn+WcnSRDH2iIoYQfAhLKo4MhE5t2zlz1vgimclwhDv3nrN3j11Vdx+eIlLF2Hg8M5NrfOQvJmrGmbWWcbAR3JZQjAdw2qqdA73Y5102DZtNjoHMhQNJ8aXGrwuHnrBt5//z3cvHlj0JxzTtA2e3z7W9/AL375FnaqC9icbaJZLBBZdZ07jTYWhA7WJMkzFWxZPfsEDsE/KJh36n3USxQBNiGqCpP0pbSYVJtwnZMwkc4H5gogVp8c0/P8CMxGBHJy6q21KIopiEkEXE0j/QHDMKNrmpB0tA/zLT6M0rGiFJ+YyXSCDT9D27aojxfomg4cIoaxd7C2gp2WmJDQ5bpusayXqJsax4s5Hj95gu2tM7hy+QoW9QKffPIJbt14Dq+++hKef/F5bF86A+M8CtfA1zXKygKFgZtN0VQFrn37JTzz4k189Iu38au/+mvc++A9NHv7KOYGaFoYeNGmwcncs6ae1NUL6wWh16lEPRcGKOhONT3rGAjdXyloPsmUakx7sI4+5EB3TGsSxB1hL+UZcgBjKQafMUgDLAzzWuSAfox2jI0l7Q+r5AiqcR/SGH1G7q0+b8O6NvK5GtMsxJ+EPmJlWgcgmhxPcCPvjo1Hn0nBek5bT2JG036mfdTPnXNRMBPv1ay9AcMDXvlsbJ7yfZUKv/obPtQfMEhfOEb7S260XnASxuKYI19gdN5d0K6it5ZwnYsMDPs+amSKsWLL6bUe+s3xbx+/ZIilj+ANoemSfgCnKqdmNC5eeRZN04KNZPQuAVQz8VGYNy4mugMzPDyYrGTBNlZhDUxhUJkS3/rO93BwsIe9oyOJBNQ0aL3H7ZdfxM72DmAsjK3AwVGugiz0bGc3hnVt2xamCGYUoY86Z957bO5ME9MmDodeDpglQhFC3vYJv4RpMsYCxqL1jGKyBccGZbUB6z2uXRMn7bppUE0qOTxBMlYUFWzncfbiFqrpBhbHkoTs1s3nUVYTXLxwCW+99S5e+ea3sL+/DzIGm7MZ5vM5FosFlu0SF69cgvcOW1vbIgkDQyPNSMA6tfvvM1frJogx31lkbOKoDnx29x4+uXMXddfh7r0v8Oabb+LTTz/FzvldvPTqq3DO4eMvH+LRkwM0yxptMAHrnIaJdUECyKBr3wWmZ2SzEsAlw16+AZqd7ddAGQglHAAktq+EfyRDgOcIduQdEw+mAhjB7XrolHgObUvBDKsMwAA0Dzl8Qv8Zh6zgZKysfSkOkU745JC9XBkfRJUqqRZVBTg9zzH+U0vKJPTD6RmS8L2OhyPJSChAwjxE+ggfmCIkHeuf16Y5bzAhsKztkc4R0LkWTV3DhEhwZEmySqaqhNCG+IIYgB1ABswGxlTwrsHx4RyWGSURfNOGyDr9WfUOEAGw5hooATZwnUh/z57ZAJGDoQqeDcQzYXj5rAPpYxfPume+zrs5KBpjGNJL+bQ25On7+Zg4gGlEtZSsoS1KFAGoSe4VyddjDaEwFq7rUM9rfPzhe7h6+SysMTjcn+Pq1Qvw3InDdNZO/OclAhMjmCB5j1lZYHtawTOhNEZ8qsmjcR3qzsPDDvb0QBACxuXLF/G3f/s3gQkKTAz0UnOAq/HSredwZnOCerHAtJwCnkAsIUTBPYCPAgDqzY1SoMpBeskIyRQNIeZLhYmMLohANjANYBhiOOpgJjPAFpjaCaqNbRwdHGHZLjAxBSjQe2MBhocLUr+U2QCLJr20pfSZGUVF8G2HZVtL4tdAR3JgZJjDjAVNVutBtkBZlphMK5yZbaKpFzHk9mKxCDRE6phMNlCWvg/OEf4tF3McHDzGl1/u4MrFKzg8qPHhh/fw/O1P8fI3b+HlV17E7s4WUBC6ukHprTimlwZtWaGcTfDi730HN157Ab/+yRt448//GstPPoc5OEKxWIKoBaGDt2KeSjFATA/KKbm0dL1yx1Zl2tUceihQ681g03OTA/V1zMRwj6wHjBGknYJuKBjzLFm8NYGkV5Bm5K52bJGGek19QPTnOrqSn6ek17LryCR1hLmmEFSfQ/hnjbVMiOA1b7OPtLlaUiZO12DI7PiVeY5jIRowVvp5vrYprUz9OtKopuuiYaXMh74/NltCRlkvR7lzCYN3B3VD6AcR9UEceOhXoe2lTKT3QfgzaFv+FovjhHkO5ltgNfEM/QzCe8UGGq9K72v2YowMZjCbeNJsUYiAJMxZDO8dcEQ0ERUgFAO8eO8TBkiZkmSNSOeGADYRa5+mnD7qlLGwhXI8FDdQOZmgbVscHR9jc3MzbAoBlabQcIEQCbQHOt9if38fX93/EkQSYvWFF16Ijtxt16Gy5RqnZ5EqARhE/gB6biwFCAMCFhzI9TOVmPgQHaUsNR8HonMTs2TmlrCzkhClXS5FcmgsyLtBDGUKfirbO7uYViXOnj0HIovFooYpCnTOY3NrC7YsY4K2ruvwxhtvYGt7GxubG31fsvln7hd9lfhqdm0BCSK1ABbzBe7evYuNjQ28/fbbePfdd/HgwQPs7u7i2nM38JujHTzwZ7Hc2AR2plC0LfhVb2OBvgUgB445jBkDVj3y7oELT7/j/oGeH0BCdAAYzyEgQHguXkqhIhIGxQSgJd8E4BxBGBKwnWL+AJiAIB2XPdl6l+xlBEfYMMcRm4eWlICmPAwNx5N8nIyb+s8Cxk95iDjNA1lG7LWYbIyAag8CRYFDf5lrB+P8IBAbUByLTG1vZx4JNcu4jxcLENRPgxFBYew29QwYISTTk7g9ZVlifsw4PDwEWC6JpmnDeRMAAa8mWkLcrLWYTicwxqALkYwmVTUcWjKW0zAS+WX09y2nZVTyS2oM4Jwk0Rtra0zimrdjjARH8M5IYkkvwSxEeudx74svcHR4iI3ZLo6ONK+LAfl0E64MLs5zalcu0dts0JyI1Jm9+KcJvTbRDjof43Q6xWQywcHBAXZ3d5MxCb3pug5bWzu4ffsG3njrA2xtbqAsSviuDaCAI0gQEO5ixBSNGuNCRDoA8cIc9kXpk/zqvURONBCmunMObCysEcft1knwj+3zZ1E2U8wPDuCZUXgP8iYyBr0mQ8KjEwiFNZhWE+zt7ePw8DCYBCJq6l3n4r2Rgueu6ySvjun3TNM0cl6rCtZSnMuuk5xUTdNguVzAOZkdIjmHZVlKgJO2Rdss0bRLdF2D+dERHtz/ChcuXMTR8T4+ufMhPnj/Q7z66su4/fxNnDmzhaZmGONguhZwDJQMKiYoZhO8/ke/h1e++Qp+9pf/AW//5Oc4/uIr2MNjlHWDjaaBL4AlNSAjgVTYRF01DBvYIAhLIwSlQDc1dxuTYufRetZllNb1/7pmSWPndIwJ6P8OdNVn2rfkVpA9dzp6dNp+IgJBvQh48Lm0mfq10aBPaVt5igLp7pBhGNMyEFHccyn47qX5q20CQ2ZvHdOX7w19T1MsnMRsDAQnY2MaWdt8bGEAQndG+pi/lzO8WleufSEezojO20o/svd7RnJ1H3FcbwoYMND5kTXRIia5Hux6LUyvkTnZryo9i6cpX4PREOKrnVCg6NijmkwwXy7w+b0vMJlMsLO9gzKJmMTMePz4MebHc7Rtg6IscfHiRRwc7uP8uWuYTGYx+lRRVCDqL6xcZaVEIyUuegj085Tr1InOYySn0hF9dzKZxHY0P8hisYQtyij5LasJ3HKJZV3HaEZaZ1mWwSZZGDDXeRhT4MneA/z857/AP/2n/xRlWeLw+BjHx8doQ1Smzz//HD/84Q9hre2ju6zJrJpLaWJoVKj6VIpzDl988QUuXbqEv/yr/4DPPvsMBwcH8N7j/KUr+HDn93G/LqOPiSUDFIkJmrLOgaGMSB3JZ1AuF/H5wXkMSFE4cop/gzlKJzly8SmCV4CtDIu2RYGDR3/gEj5DmfTYtuLupE+qMyAjknPdM03ThXHEQJehf6FrOgehTU7rzpgoDwgx0TFRv3YDIKqMkjLJULaO4hVCOm7mpK2e4eFBb3UedAz95ePhZT71EorzH9YIAMXoFmEcXtcusC0JXmNlwrjvozMTLKtz8P4BlsFJWMIg19FMiojE6USzzHuJMLa1tY2yLNE5MdHbPbOdnYEhc6FzmANzLWPEdd2zWsYujq8DUNJykoRyrIxddmPv5QyM/rTBnKltxDSAgxnV8fEcx/M5NjfOYB5yD4mkzA6549gweqFF0r4xBufPn8f9vSOURRlzH7HrxOSy68BVOZDs5eN/5plncPfuXezs7MTGiAm+Y1gieNfge999DT974y1sbGxhOqngmhpMvreTDrtdct54WGPRtM1QMk4UtKYUtb/xLoiQF9Fp3LUOXDC8kaSsEqTCg2yJLphq2Y0ptsoCi4MD1IsljDcoYETTaQLDDmF6qqJAURi0XYt79+5hY2MDk8kEgEQlTEGT/kxBnPMunFUIgxGYjaIoQEWfiNYYg83NTcxms5Bz6hh1U0tSwEAfjLHBkd+irpdY1HPUzRKL5TEOjvbx6PEuLl2+jPl8gU8+vYMXX7yN1771Km7ceA6bGxXgnGi3G4/WtpjOpvDeYePyWfzBf/u/wYu/81v4yY//PT7+2RtwX+2hPFig4BYFyb1kDNBxB28YXjKARmCj+zcP2pBG2Un3T3r2o6DQr8/GnYPOkwQPJ4HSdUzGyjPZ80MaROPnbaScBHxXmaDk5qD0nVhb6AehDxs4bCudy6f1IQfTObOg9UVMZvp5yddhKETusVouJF4XbCOvM99L6TNjAqOxfqwruQZq3Xs5Y6CfrQDyNe/l5aS9N6wA6OHEKqOcaqv6M+FXIobFvmTvj92DOfN5Ujk1o+GR5lNQpNdLeauqwvXr1+Gcw8HBAWhBMTpT0zSYTKc4d+4cAODJ3hPs7+3h7LnzOHP2bBiARkRwAdQPibH+nko9Uq5qbMPqu6ryipdjwmDoBmjbdiB10sPpvRhsaLxtkMFkOg0mCzWAXk1XlhK+F8xoG7G3rSZTnDt/Ht/93vdw4cIlHB4d4+h4Ge3W1Sn92rVrKMsS0+ksMFF60IYHJt28+rsP4FAxofcSdrLrOhwvl/j4449xeHgIZsbZs2dxuPEs9v0Mrl2IZihscjVL6vmIHtAigN2ASJGg5/hceCMyZYJaSHmLXuuBlCEJDtZhDKzPKHOhQHjwfqg6gmf9VNmIZNqETR8cMgpr5LwXQGIMiHpGLTIXYdzxA+q1AdKBJGwcGBwZI47PyaE1cVyc1sXAjQtT/A//x+/g//I/vYHPHi4j0IuzGftOiFFeknHrIDVhWs+spJOgAE0vJYrtjEkNZQ8PGci06NYAI/rNcHCQhekz/+q5U4m3CSGyWYTfEHM/H7WTRVmgrpeo6waz2TRGsoML8ZXCnI0R5XWXyNcpY4QUGNpT5/XnhDYXiOQl1aimz5/mQll7yQLhkpHoUPCq4vdomhqHh4c4f9bFXDPi/9IzxoM+yA0zuCz199lsCuwdhWhJQdNhLeq6Qdc5MBexnlXpmcf169fxxhtv4LXXXkucMQ2IZW8QeTz/wk1sb86wrJfY2tjE/OBQhCC6lwPzUBgNcc4orWjOCQggW+h/WZZB+9E7YUtWeopa2SiwCSaihWf4tgMVBRw82BiYsgSTMMTbZYn66Aj14VFIgmhQ2gKFMTDEoBBy3cDAu25IpxPGQplulezrvEUBhO4f54WfZ81zZCIjqHef95IYsapKdF2HxWIZfeiUVJEtMNvYRNmGnBztEp1rUdcLHB4d46uv7uPKlSs4ODjEp5/exfMvPI9vf+sbuHHtEiZTC1gGTIsj51BMLCbsUdEMF5+9jv/V/+F/j8++9x388t/+Fb56+33w3j7MnEHegbyD8UIbWu4iLUz7Phh7AhjTz/W59P4HhgxHOif5WUppXOr7oRLy/Fylv+cMx8qZiZ8JnRrN36P3JIbAeazddT5f2t++bv1uCDDjh6DodCzj6KXWaZs5dtLP1vkl5MCdIeuQhrXuH+6dqfP3cqCu36egPgftY31K+5zPYVpXztCOzfHq3+P7Mm0772PKJI0xHSkeSesZqzedm3XPp+MHxFRKmb18jvP5N4YGWDhdU2TrkfYrZ0yfVk7PaISbiVmSG6kJCxkj6mcrtl4Exu6ZMxJBIwCzDd7oVdqecf78eZRVJRduWcUQpkxhIUcuqTSyghLdnMvV75Vw67uaGC4FB1pfKgnLAQAR0DmP4+MFtre3gx+v2MOBJN+E+kakGSfF1o1gywI7u2fwi1++iR/84HdweHyEuu7QhAzRevHfuHEDW1tbKEMSwbSsA0zDqBE9NJXkT4zFYoHz58/hL//F/4L5fB7HtrW1hbtnvoHmWJzaCaS8gMwfEOihmsv0zA7HvvRgX5mG3q9AvlDmsRe394SWs7+Ve9bPc5jcG1T1Rd+Wn/r/p4O1+E04LAyxgddxqqo3rSIyDWmbZOK4tW0OTAYl446gPNbT10sA/s9/8jz+6LXL+D/98W38X//5b6Br2TNOfR3ECdFLZoEjQ8ghpw1W5nJ1HpIaSBmafsBx3428nl9oRAC3krNE928XouwQSWSitm0xm4m5h2hBen+Tqiqxvb0ljvn7e5jP5yHksYkgkXoLxQHxO4006mll7IyN1ZkTbP3sNJdG+uy69tJLcKyedX0STZ/MaVEUYEfw1qPrRBJ+cHAAF+jSfD7HdDYNURRG6ld6MgIuzpw5i7v3n0RtpDEG8A5N24g/ly/Xjs97j7Nnz+Io+OXFi5vEdpyZwb7D1sYUzz//HH76i3dQBa1yvNCyOaJkPxhjxOHWcJTSaThrpHRLc2lo+OjAWLFwJOgWS3DHMFUFmhB8UQA27Gsj993uxQsoLpzH4y+/QrOsUTQAwcOWBWAJrmNokjvdq6lwC5Dw6y5kZs7Blus8bBH2eWA2xDxMnx1q4/X+KooSxlhYW6LrZqhr8eOomyZq2ovSoCwrdK0wGYumRt0xFvUS+0cHOLO7i6uH17B3eIjPPruD115+Ga9+4yVcu34FZD0cd3Bw8I2HsR4oC9hJhee/8yqee+EW3v75m3jjz/8KT977GP7oCEVTw7QAvEPBDG8S2pjct3lo0LSk9/wYqEzPV36GcrCazvfT6krX5CQasR70Zc+NvK/gNe/Luns/BdqShwggg+CvpOF0GbYQYaAfjDUxTc4wUz72MeHtOgYhH3vyweC7de+O0cv8mZQ51D4+re40EeNJwiKtL21jyEiNM6zpcznNTveaRpUaG/PYHhorY/syXZfURM079dcd9wVKz8Tae5R786l8jEpb1yXEHSunT9gHASURmITf1Qa0rKqYJVtNMLwOTDseOmiLCTY2NiQErffonEcRIJtIPIdqQCKKOSpU+rlOXZqaUOkkqtpaJ1I1Dyp5BUQjoxdWvyjAzs4u5vM59vb3JT9EUQQkRyHJXxc3dN8fcSqfTWdYLmvs7OygqiocHc3hvWw81aBobhJmxmw6jSYQvAYgpnPSr4vAX2YJsarjmi+W+Pijj9A0TfRBac0ES7MB5rlEX0CfLA+DOkM7jN5sSL8PTKeqDvp3JQpBtNAB95J3AtJ4zgNWIryvUD8+o3Ul0Hv4/vC7ntkJfVkzhwJSxISEvY8O6ox0jP34+vppyDuF5/Xy15j6HMYtfNgQ6g/3LOMf/9ZVAMA//v5V/A///K3BuEnnPKW5CRPR9yT8Li8hMVDPRz5oGwhgjShjSPL1Hr46IKzxOYIm0KQAijrXoSgo2JAvsbExzeYhhHasbPDTmIKDH0dVagbmPosy0+o+GCvrGI8xYn3aMnYZjtGgFBCNSXyUxjyNQToNk5F+x+DILFpr4IwBGY/OOSzmc7RNA9okHB4e4uz56VoG0ofzMHaRnjt3Dq57X7QZYQwUEmW2bQv2U1AxDtQ0ktDm5ib29vawu7sbtVvEBIKDdw4Mi+98+zX89d/8AhuzbWzMZjhoWxEGKIAjAvk+fn/P/FPQvHei8QDEdEPnKNBHSWohyWFFCyeAzRgA3sG7Br5jEBvwFDC2ANjAVhZ2YmHLEtsbG7hy5SoO7t/HvY8/RtvW8JMShiSSoqYqUcFXURTJBS/RYvTeWAG+YIhiRsZmrQ25iaowjmGUJQqMknOaK0CYiaoS/8n5YoH5chG0SA6AR1EaWFPAVR2apsF8cYRlbdE0NQ4OD/Hg4UM8vnQFjx4e4KOPPsO3v/kKXnn1Bexe2IYnRkOtMEDOoHQlylL8N779D17HjVdewK//+qf49V/9R9T3voI72Ad1NUAmrlsOplPtRrpvRMjSn5mTytMYev08BetjgDrfv+v+zscQIxGOgemsn6l52DrBwtj4eoakNwL0nkUDJirmpC/aT8UHyTgSZi+d+6fRzpzp0JLSwjFG6SRG8Wklf++keVq3nk+j/Xn96bvprswZnrydsfGmNPRpa/x1yoBuZMzQcrFYYaRyZkFI4XAc/f4Yzldukqb75j87o8HAIDSggk/vGdVkGpkIADDhAuiCc15ZFHDeo6kbwU0+mFPo5EPV1x7eamg8E7k0AedFiCfeoiwlQ23KdOQbMJ0g+RvQvADMFP9WYo4YQrNPPMXM6LzHbDaDZ4+Dg30QCBubmyishLe11qAoTLw0TEzM4zGbbeAv/uIv8fzzz4es1SQZt5d1yA0C1PUCk0mBalJgMq1gNJyrUNgEiw83aEoYgkIUEvlB4q4XZYl3fvkrzJd18B0RieQXc4O6RbTT5rTuuOf6zabQTtY7tBnAdnycAtev3Y6vBwIHoX8eSgc50Y4gw78cAXr/Vd/acB56diU+Fzmk5ABw5HuStinG05c9LeZZSAixgmH9TDUWsT2iZMpCHwMQ4mTcqldIZhMA8J2bZ3D9/AYA4Jnzm/j2zV28+clBYGY4Yb6CrdGAnKwyBhw7vsIj5X8Mf0/fjcOROnXtB7tP90UYmyYd9MzopmcAAHXboHUtyJZwntHUHQAjWkD4sLwUhQIMj+3tjRDeU/pqje4fNREK42REbWle1l1G6wj8OsnSGEjJL5cxE4gxydjTJHZEYmaqwpTwadIvTn5frUOBphzmEFmGLFzXwtAEi4XkDjLWYD5fAlwivT4Hl084s/0G6rXM29tb6Lq2z9vBDGMNuqZF3XXovIfxHLB7vw+JxJykKApcv34dd+7cwdmz52OoSYaHpB90sOTx4gu3cW53G8dHDTamUxwfHob7xAsNCptPaQnFKeIQeUv6m4K+Ydx8QCeMAQkDE4669MfBuWBO4DtYAFxVIJJw6tVsis2dDZzZmOK5K2fwjReexU/+9m/x+OFDNPUCWxvbmJZT2KLAJOSP6loK4coR1kf8F5xzvZyAgaoswQxMqgq2sCht0S8HOCQoXAVSAMNak5hC9OaomxsbsEWJpq3RNA2ck6ABZOX9aVGinEywWCxwvDhG0zVYNnM8fvIQF85eweHBHr788h4+/PhjfOu738Jzt5/D1s4MddGAGkbbNqjKBkVVwZYlNi+ewe/+b/8UL33nm/jJv/kxPvrFm2if7IMXS9i2hmmbuF6eOWQZN4E+soQf1yVhQQIp2MsFgqnUeh2QHGOc83OY15d+nr7X37hKzeU3k9AOZWKSXgM8NK9JGcW0rPt7CKBtMDfMmR3VFAcGJHlPGG0OZqur9C41RxubvzFaJ+/KZKzQNZ2j5J0BbjmB0cjp8Jj5Tv670t60b2pC9LSiNFt/RtyoA8nmIGVMvk5R5pkxXJcx5uip9SRz0+9DqXtR1/BE8AnzC4gQAgEzeh8Es4ppSBjUiFjIxGSlKRpjBEyg5qunKKdjR0ITlhQwQS6ZAEYMCsATuqaVKE6AxPc2hOlkgrIoQAy0dY354REO9/bBrcO0rOBC6Et2kjUVLkRN8oDzDOcYhiyIDAzZeDDTiBXp5KcLMIxOIJdx27pgT4xQZzCbCQGFvVfOXxiiwjCs8djamODcmR0UlnF08ATEHmVRwZoShgqUpSS0ck6ivVTVJDBFJXZ2drBcLnB8fIR6OQe7FoY87t75/9H238GWJfd9J/jJPObaZ6te+aquNtXVHm0A0IAcAhRBkRA5MiR3R6KoCGlntDu7WsWaiZA0O7uSVhET0j87EQyFIiY0RrMjL9HI0ICwhEd3A2igva3u6vLm2WuOy8z9IzPPyXPefVUFrnQiuuvde8856X+/78+/j6pyxktDev0YI4KNa3yfXFo60x5n94AZozAojFAUqgAZ8errb2Kr+qY24F5E7K086gLAbXpXbYwlgCI8VFbEC9ALjWOSb7P+qQHxXgCt59tVxIX6eyPASEn4ZlvHxAFKi1LqTWewrnraOAsZ7T7Vc4KFTkZaJlVjDyHq93mLhe8TGJSuXP0Vl3bO9z8gJJ6x+EGH7fqMUMIHvbmKxc256TqC6XrSfv65EwD8gxf+AQCfee4k7UsE/7q2jUE64OEdvrzQU69b9/GWgNNxpxLNiLyWI5TXdCN1u/8I2sQhATt+rTXVxuO2ZoFWzIoZlTFoIrKicpXEJc3q2PMWxxG9XsJw1He1NOxvw9EAhLLTikBogzTCqSDaYlOXUHeBRFeLdhBBD+/r3h/+eyeQcCcho8sM/TuSJMWmqozwKSt9Ub1a9j1AaLGMws9tBCYmilJnMRAUhS2EKCXMpjmYXg169s2JW1dboNKePps6VTEYDqjKytJ8I4iEtK6zGEqtKY2kMgLlgaFpXHy8sHHy5Clu39pCKzDa0VtsSnSFplQ5y+MB5+4/gypyenFKImO77gaksVY4uw9AWBNu/V8kBL20t29tPHjwcXpC2P7HQlrhqLJF6ExQF8YUBXoypdzZQmV7VPkclBWM+2nE+krK0nLMxvFVPv3zn+KJjzxCUWZsb+8yn1WYyrC6skSEQVUFuiqoqgxV5UTCsDQasLo8RqCIpaCfxpw6cZyV0YAjqyusDgb0pKCfRCQSIkytyApBht9r1rpu6yD5tNH2Nk0/jRkN+oxGNnA8ihO0jBBxD6IBUTJkPF5hMBgBmjybMtnb4uq1i7z21mu8e/EDvvuDV/nt3/4sX/6Db3HhzctkkxJVCatIqEqyfE42n6DyGYaCjfuP8bN/4Vf42b/4q5z4yEdIDh2H3hJEfeK4jzQR0vE2pZUjYRqktV56Wu9rpiw6mwcB4O7e9vf5uTvonIZa2kU0BRG4FzsWHX7uasObPhwMyLpg9SBaFr7vThp0vy+8i3go8IiAI3Xnxf93p3Z9W/5ce6E2BN71vcH8hm11FSbddvz33QBmvz4L2wre390PB81fd7zh+/1/Uoh993StkN227rYvu1c41u6YFu2LRW15dAQOa7kSDQpBZWyWSi0iKm0oDVRGoI3EZiKzGLPhPfZfpQzKYThtrOudLeYrMEKiha3tcS/XPVs0rl69yuHDh1uTsL29zWg4Qke2UJDSiiS15tc4jpy2yEa2TyYTjDGsra65Iks2Z6/XNHlpsjmUwhajcsFakUv5F0cJSlW2/obL4LFo4f33TfCUt7jYytI2cKuxaGijELrJwOD7ZbUGon52aWmJ69evc/PWDQ4dOoJHAT5Djg0a16yurDKdTjlz5gwzV+E2jmO0Uty4cZNLVy6zN5nwyCOP0Ov1SOIEuTDTlD8gi4NO/R1eWNJGU1WKm7e2uHr1GlWliCLNaDRkc5KRbRylnJaBRr4tq5p95gr7tzE4KVe0fxM4zbbVLApHiB3+cdKwB8Ci0Y4HY62dH1zbvuaCcCBYNFtiX7u+q75d415tvzft+fFA2zMLY/0ZRWLqDodFatxEh8vQ+c21HfCRejaFf9b7T9Y9refnM88dZyfb4a9//q/z55/88/z8s8f5u//6tXrOWto2vDWx3XbYJQH1HNY3tSYujO1wb63n3O8h015e42WYgxilH7GoK7+DtW4URUG8HKGA2cwWX/N7yVsptNPQxlFE6gt0Voo9p8WOpERJbD91A7pbPQgYwyJ3pUWMOXyupe3u/Oafv9N7um2F9/t3Lbo8jZJS2toKnbZaGsM7tIcQdVFK3L8Cm3WqLCvyLKtj2ubzOVVZkfTulPKzYXZhDFsSx8yzDGg0fp5B5kVh69JIX0tif+wBwGg0YjqduXe6VNN+Vxpq17mPfexZvvGN7xI7N9vt7e0mIYebkxAwdYFiUdjU5fXecF3xLlhaNxlXvHDlq88bR3esYdqgi5Jib0pVCYSIGfUTtOojIyscJ0JQJZKPfvxZ7r/vLN/62gvcvnGDLB8wHo84fvR4DVpEJElc7IkQsHl7kzzLOHb0GNPZ1LrmGkPiXAe9Ui0cZxeoQRAbuADg+GeiKKIX2WQmxhiyPGc6m6FKBQiXvKRHmsaUxZw8z6nUlKLMmU72uHnzOqeOn2Jr6xbvvv8mzzz3JI88co6NI4ds1XNRkSQRqpzQT1OIIvr9AY9/7CM89NCDvPz1F3nlG9/m1geXKCcTjBFEukKqkkRLV4DUAS5JTU+0T4wiDjofi0Fld190FQ93Aoldl5AaJHMwDbjTeTfa1XdhvwWmG6Qcviu8P3x3yAq69wthvT3KsgoEAlOvcZvCt7NjLaYHbYDu/6sDwB3P2CcgHTQXC9buTnPXpe1dQfCgPi9q86B7DxQIPDS5Cy0PrztZ1n6Y627vaO1l2vMihC2k7RXy2jQIBNycyk6gt2xn7vP0EEC18Of+PXq3654FjV4v4dq1qxw6tM58rhzQz5HRmDzP8CCuKHJmswnXr1/ng4sXmWcFzz3zDIPegJWVZbRRGKVqQcP3W1W2+qoNLq+slOzAlqoqIm1NYEVlUJVCY8jLwlkkXC5zaatCa2VstosochPkfNiEIYp96jVlrSjSF7dzRZ8qC7b8IuhSURYFSitsHQCrublx4waz2ZTxeIk4jun1BrXJMU17Ln5D1bEfRVFw9epVrly+zGwyZW86YTgacezYMdI0RUa+kNTdCdl+MOOJorbzGMW88foblGXVjE8pbhz6GLmOwBR16lWBacC/qCE/RsiaOVsC5YmbwZW8azauaLTknsAYYytX1yjJH9S6HeNkC3d/h3A2WabYV73StiGccrxB+XVGSLCFr0QDTKVjXL74oBdDrE+6qwlgnKWrnnAnJlgE72B72Mtmb9VuPVDPTkvMcQAGd+AfPb3C2SNj/vEP/jF7xR7/7q1/x68+9as8cmqZNy7tNuN1bbf75EfZnrRAjKnXrZGG2v3wNgEvNxoHxlriq+uvncP96+TlD2OauTRQxy5510kQzJ2w7XtqjAV2ylkw016P0XiMlLYexHw+ZzQagtiuAWhLygiHSZuRhAw7BA/hvf437zvfFSIWffbP3MvlGeNBjNO/MwyGDWtQtPsUsog7tOn7Key6ejO4D9yzaYZjW6cksW6k3f55wLBIUzgej23NDq2QsleDZ4A8y6jKEt1LnOATnHdCYVCyvLzM9vYWhw5toJQP9LaaNZtaVvHQuQdYXh4zmczp9Sw9bbmWmXY2G39pbTBVhdGWn4SB5BiDEUG6W9OcJLCuwcbdqrVGxDahCZVBmgqtpkzKithUrA1T5tOMpV6KEMbGF6mSYycO8/O/+Gle/cHrfP97L1NtF4xHSwwGAzACoexpVtoWoByPx4xGI4Sw8TNxHNfZ1rwFxidTqFzweLiPFgnBHlx2NaVJklAZW4lcCMHh5SXirW2yLCfPMhsbaayQKvuSJOkzcylzy7KkUgWz2YRD64fI8jnXrt/k3Xcu8syzT/HAA2dYWh5S5IpYGrJijkhjlDFUPU262ue5n/9JHnr6CZ7/wjd4/TvfYXL1GmI+I8oFsRFIo10abk+TvEXNnYFgnQ+M6VgA1D2Y9/PglQsHBWF3z20odBhDq8ZJt/07KSO63yul6vMfKkYXacL9PW3lU/t8+X9rpa3WCNEkqQFJLIWNdTPt5w6iVYvoXhiTKqWs2UvoftT0sWNBd+/qZoW62xUKOaFgtGhe7iQwhYJSOL6DG/ac/96AdThP3X4Gr/wPcrUForYFX3Q+LxLsjDGtGA2jVBNfbYxLBd4VS3G0lNZ773bds6Bx4cIFLl686GINIuI4YjAY0u/3EUTISDCZ7LGzs402CqUqhsMRBquti6OI7e1tKzR483Uc1ZrNoijqqsxRZF2RpLQuGAI7ab5tYwzSFYsK06qFmStstVy70EVRYGgCxI22Akc2z8gL67fqCwZ6jZrVctr0mwjqTCvaaFSl2Nvb5cKFd62QkfZZXz9sc7/3+zzz9LNkWYYQgjzPuXnzJlevXmV7e5v5dIaqKobjEU888QRCSluzQx5cdKhZ3/3my+bgCYSIyLIpRWl49933gCbN2YfpWfLxGYotqxm0wZz+zZ6Q6yZ2whf3MV6gME6gi1oEPyCHwSfjanE45uAkZDyYFYBPh+reEhalEwTE0IGmFnisd7nrdwtwOtc7JxR5IN28B9cnC96VagROUF5kqd/rxy6cNr5NM9ujD6E+3k/fiydOYPCP/PxzNgj8N17/jfrfX33qV/nMc8etoFG/3iBcVh4hm3B3s6jtkCHXi9ueHyEC0GraRMQEA6znvLZYdEcctk0zt1g/UK012XxuNSqOBvjqsVL6qqJ2fbTz349jWwzOA+PBYND0W0qMsv75PgxStADA4rNxkLBwEFPvXqHV4yBCfi9asm4bXQYv3P70Ftw2ANIta+ed0neCFcpsHIXd33leOHpmaaEVOPpW+O4wIHtM20Ja+7O3RNgrclWrvVVIKY309YWC8TYgDI4dO8aVK1c4fPiIAypuDo11lzWiYDxe4pFHz/PNb3yntmiXZVm/T7v6O6EG2hjjYs98Fh5Xo8cJGV7Ib/aypUm1Zd0L1k4AE8pgXGFAoY37rNm9XnKxKugLWOkNIIFhLyXq9UiSCCMMz3z8Kc4+cJbnv/Ei165eo1QFo8ESg7SPrqziR8bWwuK1jr6vPvbQ7wv/2ScRCSsU323f+eeUctnBHIiQUpKmKUvLS/QHQ7RR7GxtUxQZuqqQIkZGEYOxRFcVRZ6R5RlFWZAXGbt7E9ZXjzCdTrl48SKPPnaeZ555ktOnTyJ6EUIoVF5RIiiNJk4S0jhhdOIIn/qVX+SBp87z4he/zKVXXkdt7yBmGRhlg8V1ZQVVYTDSZU4yCwDbAhDcBZzhPg4tPi13ogXzFQoNLSUGBuE8IQ7y/1+kaW8UBm1LRpeG3Em5se8eY/lJCMBbwcrB+bV97cZ17aeZi8YRfl4UY9HwuP0xL4usjotA8CLwf5BAsOg9vm+LCg+G/VlkPerecxBPCPvSzVa6b04W0Ob2urX35qJ2DroW7VfRWcc8z1t4eNHZ0Z7/C5p1qgUXajx+0J75Ya57FjSybMaRI4fZ3Nzk0KFDdZ+kFFjrmfUHnUz26PVThsMBo9GQKE5577133GTA3t4eb7/5FqWqeOSJxxjW1cQhkpENgEtshg3LFItGYjUQxwk2q4bNHOUzeoBzTQo1WCLMVmWFFr9Bsiwjz3LixD7Ty3pWkxRZUOQLJCVJzGDQt2kTlWViRhqUUUhpMEahdMlksgdIVlfW6PUGbG7e5sKFC1y6dIlbt24xn8/JsozlpSWOHTtKkqacOnXKVnmtLRrtDeg3RPfav4ktSClLTZYV7OxOuXnzlhUSpGSqDPNDT1JmJUIKeonN/mOVxLYYljEgXdwG0Gi4PVBH1JmU2tDTkl5H82pgL/BWpFAKcO8y4Os+1G8XMgC99kYTHkyvWfDqk2CNw7aFkF46wP9Rgw3fL08cjLHVgN1812NzMSv+DQ3YDiQN0x5bWO3TttH8HQIbT3o/89wJpsWUz77zWQB+/53fZ1pM+cxzJ/j//Nu3mrmo+xIuhsHme8UKTMa0LUKLCJVxM1Gv5yKC1hZe/DikaY+7LkQIteba7gGF7q8gohilNLk7u5KI+XyOUpo4EQhjA9I84SqripWVFZaXlomdBjfLMkajcZ1YYcFwXGDs/vEcBMAXfdcNHuwy+jsJCwcJKmLBGT7o/SFjMqbJMJTneQ0eQgn3ICYZysDhufNMp9HiCuv+ZHqE630vVxxLlpeWUCqwLAjb56qqHK3VGCMdHWk0euFcnDh5nG9+49s18PN0TxDVKcRB8dxzT/PVr3wbpRS9Xq+myT5Fci2g0HYvMUrb2ivh+pgmC1Q9j1j6h+djhJrtxmJiY44gShJkZS3ye9dv8+YsQ01zzpw9Qb/Xpy8jhIjoDfoURcnS+pif/vlP8d47F3j5pZeZzHcxaNKoZy2rla4tQsqNyYOlyinkwsBcD5C923BYt2ARcPRrXmuaHVCufc6BwXBAojVJHDPo99ne2mY2nVKVpT1fBuIkIY5T8iyjLDLmWUZVGeazjO2dW+zsHGZra4tLH17m2Wef4fEnHuHw4WW7K5Ugn1dUpaaKK3QqSJOE+548x8n7T/H6C9/jxS9+hesffAh7e0R5buMedWXrqwhAGnRTCqUeo1cydoWHg7TkXRC4CBR237/IHU2b/TQlXKOFn4NHrECuWvETB4HLRX3zfQm9u8L7amtN0OzdwOuie0JQfjeAuUhouBPoXvSug2hjl8aGGbu6z3dTPncFyjspl0JaUp+Rjjv7IoFn0eeDhOKD7u+O+27KpPBeaFNyP+7uXDf8pHnWYyyDqZNr+P97wbTBNVj+b0xzGO/xumdBYzweU5QFy8tLNpgskOaFiFCqQghDf2BTyS4tjYnjBIQkEjGj4chV25akaYLUEb1+j/VDh2w8h5NI4yh2KXBj0jRBiCUMTdYQgQsKjyRlUZKkSWMNEDYgTgobA+K1NgZQuiSVKUpVIGJkJOn1UiLnE6u0rjVzw3jIYDioc5d7E7aQjcm1P+gz6B22AeOxteoMBgMeeugcu7s7fP3rX+fWrVtMJhOKomB5eZmzZ88y6PcRBvrDAevr66SJFZykjFwQH63NcafPzUazcDjLMuI44d1336NSzkQuNXuHnkYRoXVOHMU1/DYeCGDrghi30YwD+SIANzWwdgDe4nRTM3F7qwPF7chy3+MWsa3BWKjxcLchRP13aNnoEutGS9SAXVF/9Nond2+o2RdWCJIB4fGCcD2b3bYJ/m0JGcaN2/bvz//UWU6uN5r4NgS0Vz+NePjEMv/q1X/FvJoDMK/m/N47v8cvP/bL/L/+t4+TFWrhs/66cnvOP/7K+7aFA5lI53k3N6EgdOBzfg+YZl5rJuLfRfNbLWilI4gH6GLXplR1c5tlmYuNsgKSFKEWTjEY9ElcjIYQ1nrZH4yQMsJbmsITYPvQiH73qhVaxCgWgfe2AHCwsLJIgOj24yAG3RUyfHpM71LhlSzdnB1N3NmdL+HckIoir620cZySzecgVu/6/P7+CiInRIYMK4oiMqec0XpgGaXbJPUpCeZgOBjZyvFlSeRcRjHezVEjI0FZ5Zw7d78tMLq3x2AwaGkRwcZX2XF23F2C9Wwxf3Cpez1N8AoOV7zT1cmIHC+S7t1GG5vMqyqbPVMq5qXhjR+8ya3bt3n8iYc5ceowvUGCkIK034O4osgLzpw7zbETR3jrtbd59633GA+gF8eYygrLHhihNaayPu9lWVp3rAB0+LbD+JiD0m2Gf9f/uTkwWhM5RZ3ShkrZGBDruhiTJj1m05mL0VAYbYvo9vpDm+QkyyiKOVrlFOWM2XzK9vY20+mcW7e2eevCezzz3JOce+hBxsMBsQRdaSqpycpdqp5zNV7q8dRPf4L7HjvPt778Nd7+5vPMr17D5DmULgicMG6zHhT4NbqHc9Ds3/Y5vFta14U8OKBbd9J632t/FikzQqDYpT/NHuhSxOb3e820dC99W0QH9wN125dFezX08w+/X/S5GysS7us7gfhun7zbejf27k6FGQ/qU3fr3evVFbz+KFd37cM5Ocja02X5WulGYRIowDw9MLT3YY35aGJew98NNImgfojrngWNKI7pCWHdjfLcFuWrpSZBWQlSo1k/dJjt7U3SXp/hcARCcuP6DdJen6XlZeI45oFzD7Gzt8fS8modmAaO+GpD2ndpMHWz2aXPi+4YspSyNgF7ZucFFCklBD6Y4FLkaUUkEycsRMjUum5pbRCRBYtJmlr/NGd2j2RTdTaKYhASrTT9wRCBQogISUwapayuHGZptMRv/OZvcfHDDyiKgvF4zEPnznD0yAZlVaCVpigqTp06VWsvpavjILuBChwsQbcPiQV586xARgnvvPs+8/kcGac27eTKfShl65WIgLj64lV2BZuYAr+ZWi0I6jtcb1pgu9b6m3qRWkHSINp4SRsHdjsenH4K6lcL951pgdsQ9NeFg42p5Rnh58u0p7QZm23fBBorK9WLuo5AYyZYPO6QiAhg3I/423/2SdL43pjfP3n5n+z7/MuP/TL/+acfvOuzRaX5N89fZi8ra6BtFs152G1j6sm9M5nwc2udlKSHKH7cOvCFFqZZS7eZ6rigorAZztKIWZZTVBVJmrjXeMBnY2bSJCXtpSSps4ZkFf1hhBA27Wnt9BIINaG25SAm6NeopfE+QLu0iOGHnxe1cy+CyyKGuVhTab+rHKC1qa7vrJ2t26YROI2wmdxCED2ZTcnLkqTfZ2+aYY2zos4C3Yz14J0hgJPHj3Jrc4s4WrZnz4CUEUprykq5jG5We94kZBbBewWRjFhaWWF7d4dDh9Ysndd+frDxe1XF6toa5x4+wwsvfAcpB6S91IIHdO0q0F0L45hg6PJXb3s8PQgZtm1UaEFV0x4bS+LjgoS0rphKG3AuW9YCUmKE4OKFS+zt7HDu/FkePHeW5dUlu5cjgeiBoEDS4yPPPcWZs6d58dsvsjvdYzQY2bTfuaaqyhr4A5RlYVMJ1xlvfJsgopg4BVHZ2iM2dsMFydPMo1fOtNw3HX2MfT0obdO3V5WNqer1e7ZwbhIRz1MnEBaoyu5FbSAZDEkHParCegVU8ylFVTLL5mztbrG1t8mNW7f48IOrPPPkk5w6cYwoMhAbShSVyal0QZSk9JI+S8cP8+lf+dM8/uSjfOsPvsDlN9+h2tpBZhmimBMrSwE0PqOgcyfEZiLDZfwLU8beSXMeArXwPHbPe6j9rkGfMSCb87zIhSZ8X63IEiHwbKfdX0Qb7iQAtc5kMA4PrsHxSOdabNwOsJ7M++u2HPTeJvGC8F/SsALfV7fnHN/0YLR+T6ispB0LsihAP7z8WrbOdif5T3e+D1IW+XF0lRXheMM2gzfTpYmL2ti3TxaMp9PhYI6a98ooqgVpTKMore+rBYLmmZruu7hmiQCNVQgZkMYWlva4RqHcPpZOoPC82I8XDBotTP0pVEwaLL1sI8Q7X/csaEhhK6MuL68yn8/BCPcdVLoiTqyVYF0cYm8ycaA3ZTAYMhovkfYHyCQllhFn7n+ASmmStLGMCOHdopqNp4WNkRAO7IWm0XAx22lsmw0VHkC7UK6tYJGkEGg38ULGiChygcQu85QySBFjtEAZgRAxUvp7rbYrFjGRTLn/vge5dPEKL3z7RWQMTz/zNEeObCAk5MUcpUqEsK5hhw4fJkkSOyZjAe+idJl+jHfSBCAMRVlSKcNsMuPKlRvkZUmMYVcNUMkyVZ4HGykAFSbc16HIIbDaJBqhwW1OjHb5lZsYBPw6GepnG0HEffbJ0Wu23xkTAXhsopbxoBTh+ubBlxC2IFewpiZ4e62N8H0njGywPyjn9x/JJvjdulOIpvsGZ+Exzf6pGbkDLVqzO9f8xV//Jv/d/+5ZjqwMeHfzXf7q7/9Vbk5v7lvTaTnltZuvtb777Td+m8f/weOMktG++zdGG/z6z/06D64/yI2dOf/X//El9uYljSXKC2OiFvS8q5kI5nwRkGzkDzfnsrEo+fe1iGYA0vx6+SZsEG0foQ1GVURSIkVMqXOKqmRIZFORErntZOeu17f+7f1+wvb2Htm84vhgZEGlUAhiJ87WA6rbDM/Hor8XaeO6goD/t6W96QCA/fMWgof2O0KN5J2upg3QWnX6d8dH25cfMy6Gxa2d1tbNczqfUqoKIWOm8xKtRJ3wIRQ2wjb39d0YVpbGXL12zbnVRGhlkLFNP1afVwkAAQAASURBVG5pkCbx62rcuXc1ivyljGHjyBGu37jO6tqK7bVs9pIxxhVorHj62Uf5+je+yixLSJKEXFqXEa0WM3Q7d01robIKQNRWXOq9Y5xQJC05bPiF9FYWg6jdwZwLktEIJEZVoAW7W7u89J1X2Ly1xcOPnOPYiSP0ejZ+hchQRpbPLK2O+fRnfoa33nyX1155g1HaI0oiqrIEBHlRWku0k9p9TIx0fdFCIoQTpkRERYnUhqpSYFTNKx258/+rhQQPDrxiTkayVspUqiJJEpI0sTEwkSDuRRRFwnw+tzEyzmPTKEHaGyGjlCybkxUZylTMywmT6Q7TyZTZ7pzLH1zlo889zcMPn2VlZUiEt6xUoDSlUhAbkrjPqSce4U/efx+vfPM7fO+LX2P3g0sw2UUwI9J2fEZolOmcPaJ67Zs90Aa2izIVhT7siywjXcWBn80QP4S0IbSQ7KNBGIwpbdp+ZePYPI9y5Hoh8G8HorcVGNbLglY74AR1E+F1Q2F18HoQdxlrOGf2huZP/3gjfDUCuld41XQoAMVd2tx1SwvbDgWtgywYYR/CedtfQLlp/6AMW12Bp8Ub3N/hs914mEUWhkWKKuH5c9CnfeMyAc5YcDlZr3VpLF0QTqLUBmSaQpwBEQIbZmCEn3dtM0mL2LWp24HhQCsjT/C9cRgvdEW92/VDVQb3Gvhuyllh2hrDOI5ZWlrCGNjZ2WE+n3Po0KHaJ1FrW5k0SXutMvHdkubdhQqZt3+X/+x9d8MFvZvELjobqCv5ApiqYf6LfAOltFVjx+Mlxktjvvi5LzKfZ2wcW+f06VPObKVRymb9yPOCo0eP0O/3nTXjzhVPu5t3EXgx2CDPNEn4/g9eYzab1e5k+aHHQQiUslkovPTq3u7cgxqwY+pyuZakSmct0O4GYRwTc8GmNRjFSbqhSr0WDvyfjbaj9fe+Qbv/ifqtAdC3vwnXeCMLtEGoFzLqd/v2HLLyaWwNymbR8WkVW0PyL2m33fSradtLKV957RY/+7f+kP/uLz3Dp558kH/4C/8Df/63fpUvvf+l7igXXl3hA+Cn7/9p/uEv/A+cWD7Ol1++zv/tf/out/e8JcO3HQqeDRD38fiIxQQ7nG5wPqleUPHr7e5qVrkZt6i1Hu47Y6iOPYO+9UGdltNgXLrbEiEG1DgYuw+U1qSpzdrmLZJVVZGmPduKFBhFIMh2+r/gjCxinF3G0v2um9En9NEOn+neG469qy3sar/uRJhD7eS9EvDuGP2zGuoMIkopZtMpRVGAEC4Y3AsAi/sR/usvbQxra+sug1gD5GJHi/OiqLNIeQDiWBNhALnWmhMnTvDiiy9y/vx52kKw3RnG2EJwjzz6MKPRkGyeMRqlDljZfSqR++b7TuMJweaie32SPB8vJgR1UapKe/c2F5ysjU2fa4yzHtkCie+9e4Fbt2/xyKPnue++U6wfWkEQ0e/FFEWBEHZvn3/sEc6cPst3vvVtbl29STHP0QZm8ylVWbC0NKJyVooIZ6UXzmXGnVUjBDERZZljFTscTFODK6qz7BmXtbFxK/G8fTAYEMc2Q5n/PJ/Pmc1mtgq8sQoDGcX0+kOKMicvM1uos1TMs5zt7W1uXL/GtauXeOLxR3j6mSc5feYUg2EP44rzqqqkiqeUUUmc9ukPR/zIpz7Jw+ce47tf/hovf+tbTDdvw2yXqCyIlSbVGo1ASYPyc+FiOJpsRjiX5wZgLjqLBwHEFnAP4kDs7mxjkZAmdK0g3XcjfGxFAxfv9cy3sU2zyGEGJ+Mll2CMi4SXLuj29x/kEtZYxpr5a81ZsOO0S8jQBdzdcS6iq92z2r3vIBAffm7FfnXeeTelUaikrtsUC8bb6fOi9sL57/bxoOteFFP73uPobOQt2BhyofnIRz9KXpXc3N5id2eHIs+YT6foMsdUFVoZdOmd6E3tYtVcUU1Qwn1hazzFoCviBcUdF133LGjMZrOa8LS0A6bRDsznc6bTafPyOCLLDMPhsJYChRD0+zZYzmsUGqvGfs2DDJil/xweYp9RIwQTYfaBUEDw7/Xf+Q2ZxHHthuXv8e+RwSZqEQ6gKhWRtCaqkydOsb29y/PPv0BVlZx/+GFkJJBGYpX/McZAmvY5dep0HefSNR+G1yLCeNB98/mcJBny8ssvk2UZ0lUrN8MNGzjomJZ0AFK7LDT1YGwjjWZ6nzDibqwBg3FAM+y7Jzp+/QSePIWuDGGT9QhrQtxoeMI7WoY60RZcrEQevE03wDuE4B7Y6qCfaFCVIoq97224xmLfW8J+1W17RG8PA7d2M/7Cr3+T//xnHuRv/NJjfP7XPs/f/frf5W9++W9S6SYn/t2uWMb87U/+bf76J/46lTb8v//FK/yPn3+vJvrdOaoZjAjIfrBdWvNqgh+7TFF46aQWB/BTLJygWo/bC3hu72gvpLjsbGVZgkhr4CiFtAW5jHAuinZPp2lKkiSMR2M2b29RliVlWbh+yfZA6iE0oPQgBtRlUiHBXES0w/PVZS4Hade6z8Hd00Uu6mv3u/D+Rd936UP4Lg84pNvT09nMChpAUdhUqYlz8ZMIRNQ6JQcyxtFowO7urssu1dZ+2kwnlfOdp95jQuyf16WlJbIsc0HPIagIQVvFoUNrPPjQWb7/0huWrklvHXG0pUMTFwGZRWt6kMVJOCFGu0Bo49wHEZJIRnWAtMFglLP4RoLKVV5HC3a2dvned1/i9q3bnDv3AIcPH2Y4GhJbfyeEm6u4F/GJn/hJ/un/8k8oswopBWk/pT/sM5nNkE7wNqpCukxH9amU1stAqQokiDhCV3offfX3h8cncklTvAdByPvCOfIWdyFsUpXhcOiUZTnZdIquKgQQCckgiUmqhDyfkxc2w1xZ2lT329ub7OzscOnyVZ579hkee+xRDm+sQqwxymBUgY4rCl1SqQqTDlg6vc4n/7Nf4L6PPMzXv/hlrr76KmJrFzHNiKvSFgsTNu4j1o2LoS8c7zPmhFs4PDNdMNitQRBeB8VLdO9fRIe64FoKgRaehrod1znHBykn2mfSpZYWZl/fjKGui9rd++FY9wlBwd93opHh702D1OyiGXv7mTuB8fC9B51f/1s3BuVelLGw321r0bVIaDBivzDTFSAOajO8b9FcHkTXFym0FtEz9xakp0lY4VujeeiJR3nqRz5GsrZENptSZjnTvT2uXL7EzUsfcuPqDXa3Jmze3nQ03fLrPM8wRgLe2gHCWEEGY4v4RUmPaEH/D7ruWdB45513GI1GaK2ZzWacOXOGfr/PYDhgls0wxpBlmX1pHHPz5k2EkERRTK/XY29vj9FoRK/Xa/wI3YSFUf7hpHprRyhsCCGazCNuoF7zGAoPqhOjEW6G1ibykxVk8AjvsWkURf1+n9lKCEkcp+hKs7K0wvLyCt/++re5des264fXOH3mJD6dpy08aM39KysrtbYoTGN5tw24aEP6PiqXX317a4ubN29ZbXCUgozRyyfReYmqqhqLG221+MYV9XKSQZ3dyM4J1u3APVNzqvCA+2+NqUEntbo6YHmGWusfQKtQfxlkTXLMwTfcfKAr79Rth73RWNcfd/BqTYxo4AnYYFWfs0gZTey0AWExCRG0bYF0x+UmGLeo+2UPozGGf/gH7/LtN2/x9//yR/mvf/K/5lNnP8Wf+80/x/vb73O36+zqWf7ZL/0zfvTUj/LetT3+yn//HV65uFPvWYz3uz14zv20dMGHn8xQ8BBuD2hP6NyXjTtZo9FrvTwwTwhhLSBSRpTG1Fne4iRGG2Xpg8Clqm2eD89oHEdUlVUcxHFMmqaUZWaBhBNmWgJEd1xBXxcx0kXgvjUtAeO41xzvd2pnH5A9gDCHNDBMpdulDaHCpgucWkzUGOvmKGxsWpZlLljbuj3aNpq2ESKIg9PYrzqVlBGsrKy61OGq/t0KigmqsDFott9N1Ne+IphuXqyWPGM8HoVkBS9cKl3Ri1Ief/xRXnvlLXCWESkijGwUD12AYbSuUx+Haxi6aoTra8dH7RIlpSTyoF7bGCITuKj4JBIWz9m6TcYBviiK0EYzn+a89/YH7G7u8MBDD3Lm/jOMl0aISBL3EpQQFPOcl199g8k0Q2qBjKEoCzbWDjO7PrPtG2sx8QjaoK3wYVxMj7CucdrY2lJS2tofBqeJd+fLF1P1NFAIYYV+0Qhs4RyGe2kwGFAURc234zimn6TMpzPyPLNta0UUp/SETRhQliWVs5zlecZ8PmM2m7G3M+HSh1d5+pmnePDBM/SHNsOUMTaN8FxPUDqnn6QM+33OfuQcx86d4Qdf+gY/+PI32L5wETOZgKpQVE6SEjVt9u5t1tPCYEwTZ9Ad20Hn6yAh+yDQvQgYH3Sv1oEwgD9f+wFq992LgL/9raF1Hv9I2fjth+85CLh3MdEiumctiAdZXQLc5tsiYC7+rgWfw/eFwf2LAHxXaLsbjbdFC8uONn7/O7rPtYQGx98X0fGusqI7nm4fu+Ne1OeDhNauMNzeX6YWrDUGhXUD/Y3f/i3+8LvP81O/+HOcOn2K27evs7e5CShOPHgfH/nRj7OycQStFLPZjN3dPUpVceG997hxY5NKRVy/epXJ3oQyy5ns7WGUi1d2yTnCYqJ3uu5Z0FhaWmI4HLK3t0eSJLaadZJQlZXTaTYbdjSyPub9fp8sK7h9+zbXrl1jPB5z9OhR1tfXXeG8ZlJDt6Q2A7D3eJ9Sz4T99yFT7m6gEHB0hZv6Mqalxe4KGmgLmLwUXVW2CJ6MJBpJFElOnz5DWVR87avfQCvDE088SZw0gfJa23dXVcmRI0drt7M7+YU23buzpOw1ib1ej++/9GpdURlAyaQWuiAoCqRqFk07DqKBkUKIWivi/KZq8NkVNmxQEfX3NfgFbOmuxk+1Cw1F8P/2RDT2BPaZOVwMheuPFz4AG7OBFypEp20677PP+7TFUkrrXubbriUuU7cT9lT4cddfhO5gts1XLu7ymb/zZf7On/sIv/KJH+Ol//1LfPp//TQvXHlh/5jd9bETH+Nzv/Z5VvrL/MuvXeRv/vOXmWaqbtyP27MD4ebc968W4UQYb9P1+Q8+COG2QjDnnXHXwpf/LbjqQomO0fuUob4mTeqYq02rWj9V90ApWysnSRIGwyFg0w4nSVoX1LMATjV7rxbyfHfbDCf8t0vE7+W6F4HkTleXURz0XFe50rWEdAHG3YQf/w4pbGChFNY1LZvb7GZa2UrceZ4zHvVdI1bo9MCl+77w6vcHrg++X9pZkGMKNaesXP0idza659uPwRjDsWPHuH79OsPhAzWN9iDZGIOpSioV89RHnuA3f+PfoSoFxitnFtBy2yG7ZxfMfff+kD9IF3umtXag3GnyDWihLMhyIxIChHSZEpW2MX6AiSKK3KYQ19j+37y2xd7eK9ze3OLBhx9g9fAqcRrR6yW88O3neeU7rwHSJekoySubbCVOEtJealNEG0FZVfR6PZZXltHGMJ/PnBBis8pYQ6EkSRPi2NL9Is8pXWKBFg30/FM4IfAuINy7THtQYZOjCMYyJu31mM4mlEWOEAYZxaQyIUkMZZFR5FOULjF7ink2Z7I3YWdnm2tXr/HUU0/w9DNPcPTYGmiNygWz+Rwp5vT6MfN+j2F/RJym/Mgf/xnOPf4EX/13v8crX/s6TCdQahtPWR8Jz1sEuNScBxXX89e9pBENg6LFAprTvboguQs2Ld+2MWo+5bQQ7LsvbMPThabAn7cyL6pt4dver3Q5qL+hEL7I4mEMrVSv7fd1OWPz1aJ5P0g4CL1Qui6rd7oOUub4LKKLgscP6of/vuEffjCLr+66hrjU/75IsFj0DOx3yf1heZYUglgKRsMRo6VlLn9wka99+cscPXaUnZ0tZnu7GK2IpeTw0aOsHjvOww8/zAsvvshwOCRNUx599iN8YuMocW/EZHePye4eVV5w/cpVbt24gYxjlLFeQ3me31Pf7lnQOHv2LFEUsba2xs2bN6kc4UuSBFPZCez1eq4wl62UGkURw6HNgb67u0ue57z//vvs7u5y/PgJ0p5ldH4BvPYszAwQBlh1XaDCLBP+uzD1n/8uPPA12HbvtExxMWPCmNrPuSzDDCCi1vaPR2PW19e58M77vP/B+wyHI06fOo3A+7xFtj4FijTts7KyQhzH9WG6UwB42P9Fv/n5sH60CW+9/TZKVSRJShRFTAanUUpTlKUDgSo4M6KhD8azIC8cuL8DQoVuQHzTkeZ5C2rt07Vfv2jcq9wv9XPNkN09+w6zqH8Bag2NAFuZ3PcraNu4tgneJrzQE8g4tajjntXapk+VQlLRCKT1ugRttwiqb9u4/jkGbGiPe5Zp/qv/+SWyQvFrn7qfxzYeu6Og8djGY6z0l/lfvniB/+c/fblu1dypbeNjWTwYCoS0cK3COa/NFQvm3AlZ9bQJ0XkHnTm3P1feChlZAbMoCtKeBTvZPLOaRtWstTFY4T2y1kKb0tMK5Vk2J4mt+4bxihNh3SRMpzNt5tD+96Drbr//Ua9Fmq17vboKE9hv5r/Tu2thxfvOuikqytJq94xGCklZVXjQ7M1xHlAskvv9laYxw+HQWkT9/TTur6ryKSUbhUIowHgarbVmY2ODV195jQcfOGfHjaxd6ez5rKiqkpMnjnP8+HEuvHeJOO4TxzFFVdTvazNrH0919/nvaq+7SirbJ1esVUhbb8jREuu2Iqh0k0JTWv2HVVxJAa5w6Gya8fZb73Br6xbnHj3HxrENDh1a5djxY3yvehkb7xbRH6Q889wTnDt3jj/4/c8hIslwOLQub1pTVRV704lV0tkVI46TOhW7lBFxFNfKJRlJyLwbmLW8IJsxC0SdutePf5EW2a+vLdRrU4cWeYEWNpONkIIsi8gLVyRMWyVI2oMoNsxnE7J8jtaaGzdLJju7bN7cYrI7IU0Srl9f5sknz/P+hSt85UvfIC/2ELIiSSKStEe/N+TQsQ1OHD/Guf/kx4jHfV747B8gdyp6paW2MoqdEo2aXhtouT4v2AEExG+fUO8vr+yweGOfnmXf84v+DefTB4I3VyCSH0A79mdoctaRIJtVG6QuFoq6wmS3vUWf65kKnm0pd/0QDrgWzcNB94V47V6uUJDyc+DnwRdN7vZhUT+6Y/b4bJFi7U7XIqV3V4jtCn7///AL+1IbeG9JuXWjyiZThktjltI+k5u3KScTVlaW0UXJ8ZPHWV1ZIS8LEiF47623KaYzrl++zHA45OJ77xEPhhw6fpJsNmd1aZmjhzYoizlxBCsrY06ePsXeZIIOEirc6bpnQSPt99FKMV5eJklTKlURJwnzPCOKoya9bOSrmEbIKEZUmuFoxGg8pigK9vb22NnZ4cL773P27P22srhoa+q6+Y6hYVAGqJw529fKQEqnqfNMwQIggxUUBML6l9WXqA+qlJFNnef8ir2mwbjMSsoxNHvQLYHQ2h5iRcXxY8cwyvD8t15gOpnw2McfZTjuUZRzt4EUUtiqtsePnyBJktr9yhca/KNc4cGCmJ2dGZcvXQOsZkABxZFnUNpWaR8M+iwvLbO1tU1ZlM5Fxs1Fra1zh8KDSgLBK3ApwoNRL2QEYBMMpvapbwh+IPe7g+sFghAQdzQL9W8eROMAtbvdImBsGtZA2BBNd41/j9P+WIFFu98EzLdRSWyfCQWpAJR7waX5fyAaubY9BzJNi/XT9oPm/MlllFb8ztu/c+C6Avzu27+L0opHTi25MZn6vfVcCtcD928jiC0iivc2521BKlg1z2BavNHUAfr1Yw612tSgkjwrMaZy1j1JnmmMthXYfeStcRkwlCoYL/Xp920hOe3qP4xGA25v7liiLyXauNiiAEzY7uw3Nf/HECS6bRykLTyIuXZBTHh/CAAOMsvfTYvaeg/GZYmrQCkKF0MRpz2yQqGERJuKKFjaWjBf2IhBCkOa9igr6GGQQiGEJhKJU2pUFgAZ/y7P2NtzKIRgaWmJ3b1djDF1Io96vIAxEaqC0XDA+fMPc+G9D/FBz921OOi6014I50ppay0z2rgCprrueySshUK63a7rPS+QkSTRsbPkYZUs2rqOaWkojbHxL9qweXOHH0xf5ez998FDZzh59AQPPvgAr33/DUh7jNIeO7u7FEZx5tz9zPYmZNMZ4/GQaZ5x6vRpjp48hpSCsijZ3d3l5o0bMAEhJdIIN/fS1rCKSnoC8iyzwo9b2XrfYp9TwmfxM2ibv4bgiLVArBDWdVlK6WKwJCISttBu0WOezSlzRSwjrOFLs7QcM59NmGdTVFxSVTnzfI/N7Wtk+R4/+uM/xnRe8v67H7CytszP/ux/SlHO0KZEG1sIcmt3wvZkl82dPUoZM77vfvJLlyi2toiMAW1IhLTFdAXkpkJJ44qDNkU/pXDZxYwNmq0qbTPjOZxgPTNsLRdj3Bny9Ffup64todS76/nz662TgcLKynxNPAkIV69lMW1YlCXJxynZdkXNg40WYOw4Qkzl41i77/FX6HJusFZpGzdl9324D0JrR/0e0cQ9Wh5rvwuB9oECTOd8dmllVzAK+xzeF75vkYvRQcqnu4F8KWUr+5xSNrtmQ2Ob93TXKBSaDkpEsUjJ0RVMF81feBnH0bXDREIb1Cxnd3sHM+ohKs1yb8jG4SNoo7hx/TpZNkNKwfXrN9AGSqXI8pLpNGc6z/jIs88QYc/45z/3RZaXljDKoCtFHMVsHD5kYzqqik/94i8cOH/+umekK6TAaBuzkJfW13d1bY0oiZ3rTh+t9b4NHcUx0ljXBw+y0zTl+vUbXL16lbNnz7bbEY3ZrHvI7EEQVC4TFLWmCVft2Zqgvf9x7XOM00AZv6CN6V0I6fzK7f0No5UgNHGS1AfZphAU2PRhgrSXcOjQYfa2J3z3xRcZjvo88vg5RGyIdOy0fprcWUMOHz7cVEG/x2j98Ao3rt+8RVESyZT33n2L6WSOEJZoTOJVVLKELkuGwz5rq2sMR0MArl+7aRlJXb7aE1Nq7BmCeiM8qvdzuSiQSgTgogH4bSHD3teG4u3fA89u/BEKLSEtEG+Mcw+JrFsFAcHuQG67h9zghGX8CEHx5heITj8Faz9OLWe0tFZi3/+pZytspQPQhWjiRIDDy30++tA6X/7gS9ya3WqN99yhc7x1+636u5uzm3zlg6/wUw99ksPLKTd383bbxti9X0MHL2R1ZruRShaMZdFlmvvCdRTttq0WSzgBpHlhDW9XzqJswlCbjaaY0e+tUpWWMdrUnG0Gpk3FaNxjdXUZm5mnZJ5NSXupBXtRRKUVypjOmPYzi3vVEN1JQLiXK7Swhu12BZA/Sn+6c969L2Sc3UBWT8OMNAhXLE1VJWWeoVWFkAOyvLLVrj0OczTxTppJjHUhPXRog3lWMlwxGKnAaKSw2vSqrFBK23oQorGadQUNH+8WRzHT6bQuTtdixCKiLDVlqXjqqaf4vd/7A7SuiKKYOLGsq1uUyw/gTuu4ELwYe4o8DfBZsoxphCbLzJ2vuvDHS7q6HaZOKyyMc6kyAqRGGAt+ZAnZXs57b1xgZ3OTcw/fb/3p0USJQEgYjcYUVUmhSz7yzFNQKl548UXSfsLGiSNs72xx4cJ79Ho9RqMRp8+eRinFhx9+SJFnCGOFfJt2OCZC0Rc9qkhT5GXLlcQY43hASEeEl0YsKBZNrGM4p97CEcURSiVWUIwiZBxTxCVlUaKqGCF6GFUyGI5J4oQsm1OWBX2TUOzO+MErL7E7m/PRH/kEVy9/wJGNFY6eOIwRhn4/IY4FCEOZa27c3uW1Ny/w+gfX2FYRcjhG5TnLy0PK6QwzK4iKAmkg9bV9lBuLz5KITf/qqwPJGjS6wpFuLtz2tfzIeIXO/n3UAtM0yi2LVTq70uEXnOBt3Pt9RsCDhOHuvm32buMiZa9mjOFBPiila7j/66xjGOsWbkwtEHnwLoIxh7RPEwjfnXd3PTbuVMOi28eutaIriN2Jft+LEqKbdav7ntqKFNZz8+/XLp4xtBAu4EN34yd3UySFwqK/f7+gYp+xHvqGyFivdxlJtuYz+v2UXpaTKUVlDCKOyIqsxkRFqVAI0v6QW5s73Nze5aWXX6uLqe5N5yS9AUePHrftFBXbO1OMMezu7t5xfP66Z0HDbxq/UZIkQWtdu0/VgoUzoXtBQbpAbT+B/X7fbVK4efMWly5d4vDhw5bpOE1Jl1m33Zy8j2Iz8f79YWq5g7IK+MUJf5cuVeKiypG6LGrCEEURGGuiVlpz9r6zSAQv/+D77O3t8sCD97OxcRikJpYRVdUc1uXlZcbjEVEkayJ9L3O+SBIPN3SeZ0TRkFdffZWysnnQlVaUvfUaZ47GS8hIkOeZJZhSIJUHkU5no6FOk+qDtmsk2Pxj9/ICsGcll0DXb8luCIG9mmwRwcYTXQ8UGl05Iclu3Knc4dJWA+e1+t51iqAPvm3tum01PoBRmO2L5JToR36sIaZeSRQMsa2/aF9Nr/ePGwc+fu7Z40gp+I3Xf6N+bmO4wT/6U/+Iz5z7DL/z1u/wF//NX+TmzNbc+I3Xf4NP3f8p/vgzx/nHf/h+0yFP0NycG+H1GfvnvpmGBcSutYadwXa/CdvuCCu2H8ZybIwNnh0ug7DakKIo6irgeVFQVRVx0gbh/r/RaGxpgAtSlVKyvr7O229ftEqAu8QntK18P/zl6cJBqWv9Pd327kWIuNu1SEA56L6wH4tAcwieEVbDWpYlWZbViiDv5iID46MQ7jxFi9v34z16dIP3Ll5HqSVi09BRW828rEFX99nu3/ZdR7l58yanTp3aNxYBlGWF0opzDz/I4cPr3L61QxynByg77nx15y5UanW1iK35DL6z9rjFgDA8STUADG71beW54drVa0ymu+zuWCErSRI2NjZ4/PHHMLGg3+tx4YP3ue/0GX76j3+ab3zzm3xw8SKPPfYIWTZnMpkAcOnSJXq9Hg88cD/z2R4XP7zkeHVkaZ2IIZJI4VKbF4XtknN5MjhhwwiEK/glRFuJcBBo85jAu1R5n/hqWKFKba0Y8wlVYYiwAfZpmjKfzVBlQSQk8/mM25u3+epX/xBTKd5+s+KB+z/LYDDg8OFDJEnskhnMuXbzNm+88wFXLl9Fz6b08zlxqfnZX/rTpLHk21/8QyaXrhLvzhnMSuJCUcQlSmiUcQX/EGgPDvXibFtSeGWldz/y7k4uOUwneLsRkO0OcdNnSawTYiwcbwvdQtiA/Cbabv91J+XDHWlPsKcXAdjwPfV5cIWDu3TNf/YJdrrWVm9vD/t5UJv3Siu7dLDLL7ptHTS2MH7lXl1Qu/ceJOyF7t7dMxJi0Tu15a8QWy+iSd1siWFbUoi6qCi4qkXSJmUwlcWv2hiy3BZ09vWEq0ohpCBOe1YZEttyC5EUrb4sLy8xnU6JoojxaEw+yzCloijLIDvpna8fStDwUfyhtBf+7dPK1rUxRNuM5TWTSZK4WIWEyWTC5cuXOXbsWP3sHTeOqhBif/707ubYH1QjW5rwsKiLsaqL+rdW5oMoxrp2KHfA7I29tMeRw0fIphnf+sa3wcCjjz1KVmREiSBx1hFrVamsAAKtIPCDQMVBWof2eJpKoDs7m1y5cqUeV5Km5GvnrJapnn/rHlCVpf1OKTwIFm78Hh6EMDlQl7QYqUfvgkY+ad9jArAqaAr4OQIlvLgg9ledrJ9uA2BTv6s54qHVwEPgNhR2wF9YbaXRjeuFHb/VPmKw8+K5RDPIAL4Lj6zrttuIqmmztWZC8PPPngDgt17/LQB+5oGf4X/9U/+YY0tHubI55088/Cf4/v/hB/yF3/41Pv/e5/mtN36Lv/+Zv8/PP3fCChpCBJMvFrTdzFDD4EwgLJp6/mtUua/fzZj9vmhPhR+3aBY6FB69H7uxvuNlVbrkCREYQ1WWdq5TWTfj97HWmiSJ6fcHdRa56XSKlAlgTdaGu2v+uoC9y2h/GK3hQQKLv9+DkdYKdN5/J0bYvbrWiXu5POOHdh5/98bmNBlb1NPTV5sAwf7WZHvp7otF/YtYWlpie/tNNk6s4zP+2BibhKpqtOailmLazDFkokeOHuHdd97jzJkzLUu2vd+OpSwylleWOX3mJNev30JWKTrQzLe0oP7/hn1r0xUmuprT7ljrvdCCFPUNtaBuBX8717XG00Dl3G8XpWBXRrG9tYfWcOz4Sc7edxpMxYUL75GVGUbCaGmJWT5ncm3KT3zyJ3jllVd4/bXXePjhh7l48SKTyYSqqsjznPl8xpkzx3jyycd58/V3KDIbwC5EVK9FmqZoo+tMPK0CXca6fCltXZX8OvRHg1qReLdAVc/bVaygB8N+Spb12d3ZYT6fEskeoBmNJNneHtopIooiQ2YJ+Txnsjvh3/7b32NtbZ2Nw0dJkpQsy5nsbbM7m3BrZ4+8KIjRLCURozjlO6++zv/p//Jfct8Tj/HNP/giHzz/fdTl24jJDKLKeiw4DbQRAuXqKKUtC0B49iXSJUjwMUNWL2gVKSJqA+n6X/uhtd8XEOnW/Fmh7mDBPuzbQd8tUkb6lKzhd2EGz4PWMFTY+tiUsK/huagFDq/BW9D/uyliwvYW0Yju5xAzdft00PsPmruQboa/h0Jcd259m2FGt0XthQJHl7503xW2HWZPBfbVcoK2Jd0+53GJe7+2jp5FkROnCUSSvdmMd967gDGa5ZUlRqO+DRlQYJRibzpjMpuTZyVp2kPQnOdSKISQ3Lx5g5WVFdJej5WTJ6mqiklQzuJO171XBg/THIpGcxj+HU5kGHTdvcdv0vF4zGAw4NatW9y6dYszZ84sBN7hM91sBHfU6MG+/iZJ0uqnHVz7+TA1rpQ2JqOO3XBB4EePHiUWMW+99xYXLrzPsePHOXJ0g6zMiIxAE9WWmyROWF1dc/3f37fw86KrRUACCddH/L/77rvMZrO6IJ82BiMTtFJ1UUCwgZp5nrv7qEGIB6TCv980QkIbz3rg0uociP3uUPufFg3YFeHBCMYWvL8WHWoatkBDYgjO2MFtC9G0bVOrep/kCLF2BrFxDm2sr24NKsQB4xbhWJqWum03TwjWRgk/dv4QX7/4dW7NbvF3f+bv8tc+8dfIS8Xf+mcv8z9/8V3+0h97iL/xy4/yuV/7HH/v63+P/+aL/w3f+PAb/Nj5H2V1lLA9LVvCsBCimaP6Xy/E+c93mvMGjLa5hGj/JRrBohY8pZcv2o5uIaiMXIKFoiiYZ3N6yzZbjnHCXb0uNIS93+/TS1P6/T5aF2RZzsbGqhXOFWjV1hB1Geki7d2ie8KrS+j9tUjIOChDzb2e4a6Ga9FzXeZ20PvCy9OrMIGG3fJtmjybzSiLEoAsz5zGu13ISgR7rAtM/D2HDh1iPp/XAr4PNrba6qlzGzLEvvjjgrnwY1tZWWF7e7tF1+r7sEyzrHK0Lnnyycd46buvIIQgClKct+bNAZ9FgmWXF8DiNQ0vC4SMc7dxE+SOlj9TXnGCmxFv+TZGUNZ1RWSrIK0x9lwJJDvbu1yOr9BLJUU+JS8zhuMRD/zkJ4jSlHk+590PLvDwo4+wdfM23/ve93j88ceZTqfcuHEDpRRpL+XGjRucOnWGJx5/gu9/71WKvCTPciIBaX9AWZYkok+lNQqDcFm2lCrB2NiU5eVlTp96iDiOeeml71NVZc0zF82pH5vffz5zmMYmhOj3h/TSHtPJhL2dHcoyJ5IwHI2Y7Oy6fTkl6Q0oq5K8zLl0+RKbm1t88MFl4jjFGCjLjEKV5FphhN1bRW7QoyEfvPM+t67d5sjpU/zCn//PePvRR3nh97/IjbffpdpViEoQGaBUSAwRYFxMiz8iXeWEdLGmNquap5GNy+dChYW0sWgNHQTr3tSW30XNQ6yFxCVW34dnDtqPft5DWtHdx2FSnHCvdzN6dkH6QRgq/Dd8V03TRLMfugC6Sz8W/XbQOEMBt/t8SEe65QzC93cFpK4QEd4b0qFFvKbdzmLlxJ14TFeACjHtQfyhK2CF7bm/3P2NAttasSuGq6uUUpIrRex+u3F7i1W14uoFWR6tXCKb0XiENpAkca1gEK6YcZblNglUv08v7dMDNo4cXbh+3euHikYO06SWZVkPNoz0DxnUosXz30eRRCnratXv99nd3bWE0A8umFQfKGgHLVpag1D6Dje5b9cGqEdEoslR7/vjrQtGtrU14Ybt+jfazRFx+tRpqlLxwvMvUpUVDz74IFvbm/SXe0gRo7Ugn1vf+iNHjjrhK7I+ufcAThYdgvA3Y0xdPPGVV15mNpuBAw3TSqJ661CWxElMHDXjqSrVQEvR+GWL0AIhBHUwJC3IHvbQfhbNLy3IailnbQvwn2uLgBC1BcWmtAJcIL+j0A0B88+6lrRpB9nVt5jmgxcuTGBdMNoOVgQgIX34pzG9MVob4ihCYOr3NK8TdbeETwF7EDPojNsY+NlnjhNHku9d+x5f+0tf4+MnP8671/b4P//3L/LKxR0Qkv/p8+/x/Fu3+PW//Bx/7RN/jU/e90levPoiP376x/njTx/nX3z9w7ondWgNYR8bgSAE/HXH8fusETCMk6jEPuHD3eFe7IUIIUQddG7TkNY/Uktn3q93sEKVbTKfzWthV1UWiAgZ13Vr/NpUVUW/PyDtuXtNk42qPh9+oIumvUPkF4Ei//3dmNsP+9tBvy8CAgc912Xwd9ICLrr23+/opVN2aK3Js4yitMktqrKqwc2Bk0rD5PB3GVsLqKrKQE1hn0+SmL1KkRc5o0GvJWQcxCR7aQ+AsixbdYXsTY4Gm4qyynjqI4/TH/SYTUqSKD7Azc0qh8I271VgO5AmiyYuTQWAwDrDtKvJe79tKSSJjECK2oIQpkhHCJI0xWfaunXrNqdOHiFJEo4f36A37Nsg615EGg8wkeDqtcusLa3xsY99jC996UscOXKEhx56iCzL2N3bpSolt27e5pHzJ7l5c5PNm9uUZclw0Gf18ArLy8sgBUr3KKvKVR43iFixsrLCI488wng8BgGTvQnrR9bY2dxraVdDodbz5crVcaqzQCKawoZagzZEUcJotEyezynLmVXsRBFlVTGbTUgHQzSKyuRM8x0KlTl+GYMBpW29Iy3t/Jo4IopiKlMxm8946423WDu6gUwjHv2x5zh17izPf/mrvPzlrzO7cRs1mZGYEqmUdSPrbPv2eod00mvutfs7wphqHzC0/9qEMcZ4PuNUYMLTWPsOY4LzaghqSFHv14X94t7pww9zX/1f5ze/Zz1uAloCpf/saUj4/KKzF+K1Lvivz1QgQBlj9tOEoG/h/C/KMnrQWH3/wn5109GG9y8SyA6ay64ivPv7ojbCexcJdQe135q/cG6MjbMpqopYQH84qr+TMsJkGfOscmmx7V43SGRksXc/sbXvkI011MbUCba3tzm0vuHOgeHwxsYd58Rf9x4MHoD0OLYBfEVR1IKBvxYx1O6msO+TCNHEewwGg3ry/OaqOxnH9W/WfbvRsoUCzSJm4jdvFNnJCrVg3reUqPm+JUnaBlxmnEZLcfToUSIZcevabV55+VXW19cZDAdcv3kDtjTjpSHro1X6vQFlWXH06FE8Lo6idhzKnWI1DhI2hNOolGXJ1tY2V65cdaAsIo4iJtEhlLYSbhzFRJEPTLfVmWvpwuNQ/z/h/YpD+Eqj5TfU7Tff+gNjQXj9aL0UIUgMVDvhn67tZsymTktIKGz4tj04cqDeQXrXtkB0266lDz+xDcCSw0MoXaG1gjh2bnS6Ne76LSJ4V1fo8sKQsCRXej2VMHzmWRtE9Vc+/lcA+Bdf/YC/9c9fYZZV9VwZY3j54ja/8Hf+kL/9Z5/kf/MTP8KPnPoRAH7uuRP8y69/2LTtLQxOuqrH7dM0e87VlUTCbhurnQuBYuCQVg+rWSfR7AvXX+HGbZvzkSL2LWr1Prh8E4MViPtphUTWBd1CQuvPQ5omLC0tMRqNuHl7x1Y9xrtfKtrk9O5XyNjC615AZ/fqauZ+WEHgP9bV1Xq1fpOSKGDAeZ67ukdQqQoLhiQGO893asPuKxtzNx7bfOshyFdKETmAX5UeeNokG913t7WKmpWVFW7dusWRI0cWzKt1V6mqgmPHjnDixDHeeuNDiBra3xI2gr36R43V8X2s/3WuIVrbYnkytgDZF3P1tSiE8IkOPDCFOIqIpETpdqIUO2cGgQ0WFwKybM543Gfj8GF2JruUVYU0miiJ6Mu+pe2TPXpJymc+8/N87nOf5wtf+ALHjx/nyJEjrCyvUZWaf/2vfpPrl29bCyCSmS4g2mE8HrO6usrm5ibD4YAjR44yXh4R9zVJmrK6ukIUSYaDITuTLVYPr3D75jaJ1nUMhnV1Kpx7nM0A17gVm1rQwNgiYhhQrtZWHKfEcUSRS0oBRZpSKZsVsSgy4kQiZIU2OZVWliW4wp5VZQOUkXZPCWVT38bxCAYx17ZuUJQ5UgnoJYwOrfLTf/oXePDco3zxN/89t99+F7G7S1xkGF1gtMbaN5p94yPQwuQn1uPdVmG3u7FxM/QKU+0VWAia4lON5UPUgegNAZZSOsbrlTPNvu/Sx3DP3CvdWaTJX3T5dfNWSRHgt66iZJGgUHutdFPfd/rhz2k3sUDXMtMd66JA9rAP/vvQwhK2fS+XVR7vD7ZeBOzvdC1Srof9WUSPQo+fqqrqOOXuswetX/190LUoihprcFkRS7uzhcsEm/b6CARaV4hYkPZ6VGVpM7IBcdxYw4QQGFdHzscXG20olXXBNNxbrNw9CxpVVaGUqv324jhmNpsxHo8RMsJnO7KBKVG9+DY4Vzui1MR0GOML14q6EGCWZfR6PXeAG0nWg3FjDGiby9qDI++KIYV0B1rW0rlPS2aMqRlumOoNbFGXJEmYKVeJFb/w1EDXed+6xVEcP3ISlOB73/0u2zubPPvssyhT1pLfdHdOuVcSxSnrq4dIkiFx0gchkFFz6MJx3VVjip1Hg/ULr1SJQfDW2++xN5vbGhdSsCVWyM5+mrIoEdjK7HEck2WKsrCAwtYhsNXN24IAYLQDHxD8D6+zaDSgoiathP2Xwr0nAPbuHpx1ocbrfmzCS9U6eG8gYAgIzRW1ACBE3Y4F9TJsqsbGxo/JaET4veuHcMF/Ns2hoFKNEBQcdbxGqgHigbRUE8cApCBY6sf8xGNW6t+dF/yN/+8P+PcvXAnmPJCiEMxyzX/1j17iK6/e5L/9C0+xPEj5yccOszSI2JsrC+eFHZPZ13ZAbbxg5ue8u70C4bLtgx4SUzc+fw6Eiw3RxtWeaQQ2Y0RtrfMJE0QUUeYF/SS1ldcNKKPtXrW41Z4FpTDK5qlKEkGaSiIRU8xLRoMUTEEsIquVsQfb1ahperyIuHs6sojoh9913Q5CRujpnY9N87/f7cwe9Hu4Rl2G1o1nO0gzdhDz8jTX/20BkESYCKMkqtQYpRDGxrxUlcKkITYPzlgHDDSaS00vjujHEBtBrGN8FEOcxAhpq1sb5xbkz0qd0rPDyKWIOHr0KNevX+fYsWO1MssLIcYAMkYpw6Aveejcg7z95lWUARE19VWE25v79bL71/2gdQufrPeXNhiXpd4IW4vIKFNXw3YEBExVJ6IQyvJDVAVSkyYJ9z/wMBc//JCdnV1UZas3a1PV1jtjDNs7mqrq872Xdzj7wFluXr/JujrEeDwmTVLoJVQioigLdva2+LnPfJrP/cEXeev1d7h9bRuD4oMPPsQoMBVoI5BRTGUgz6yV4vz5hymrnGeee5r7zp4m7SXMsz20Vhw7ftzxTsOJU8d47+33ufr+dQfiFFVVUlUFVaXsmXWppo1zE8N4NwunczFWYVTqknw+ZzQccuLECfb2JuztxCilmc4yhDGU2Yx+bxljsLn5/RnwShwdWUO4E16NVpDE9Acp4+UhQmCzbkmBUhW9fo80TTj3kYdZXfuzfO+r3+a1b75AfuU6yWxKVJUUuqIQhgJFnCSIShMpbEahxCtW7MaQ9Z6RNMHdNvskAoQDd549+krNDYsQCBHX59piEGv5kcF+DOmR+6JWBpmAH4cCErisT6L5vqsUWfQ5TNxTg/uWa7dvqHHV7QpBNdj3s9NxX6qzWXXcMA8C493Pi+h0eE8ofITvDWnoIg8V/7fW7TIDYdxG18qy3zWr4T2LUuqGNDx0udpvDWq37cfXpfOLlEn1HLi1EsJmn6q0tucyK4gRlBiiJCJOE4SSqLKytDuyGeqEiC0WcJnjpIxIEpvxca4zpLT7pSxz4iRCRpJyXjYupXe5fqgYjXCwg8GA6XRqJxAP4gR1dgan7fAaSfus/ezPbyi5pWnK5uYmg8GA1dXV2t0iXGBbQRjiOEJr0Qpok8EiCGFN2FLIWtIO3+WDOH3GjHoBHXMOfY+10xgLIzDasLayzni4zNbmJi++8AL9fo8TJ48xnU9J4hiEjfZXVUWE5NTps0RRShTZWg1aa0R8cFasRUTB/oDTfGi0sdovg+S119+26YaNIS8U2UOfxCCoysoCCbPGbJ6hqop5luMtBv6VNYgkCL/27QNGSMfAffAoAUB1l88A46t1Yxq3G+GBTCMk1GMNhYZgDgQOmDhNkO1ZEMxPE7ZeU0OnFWzGE4xSWHcrT1AqVdGssr20Azg2VaVtuxG0/Fo1QoF1YQrnw95bE0A7RZxYH5DGEd95d5O/+g+/y4e3ZvU8GEQ9vnpeXP//3QtX+N6FLX79v3iO5x5c59jakN15k0qu1TZANyLf9bE759C+z//iBcZGIrF2GS8y1QIi1DFN/mlfoNGYhhkBKOdSYZSmyHPStGc/+0fdf1YrqInjiNGwz3g8cEo+O0tJElEWEAnhi8LXRL57LWSCHW3ZIu3ZQVeY/CJkkn8Uq0j3WpTxJry6DPcgxhze33pGWE1sJGOEkahSUWS5pdVGoKoKYyK8NdE9ta/9ul1plRRpGnN4bRkqhVFYJY7wwlLjKmSRjwNinXn37zfGcOTIEd555519QY9CGoySGA1VqQDNU08+wR/8/jdtHafIbgQhnGJCBkLMgnm74yW6Hx0wMS5jkYtnQLmKDFJYQQcwUtDrJYzGA06cOMHu3ozLl64jpWBtZYSMIoSE4XAACHb39iiLksilJ1XCBh330j5n7nuA67du8O77l9Fas762xv3338/m1hZZNueppx5jMByg0Gzt7vLJn/5pvhU/zxuvvG15QmWrYFgwrpFSMRqNMS4RyOHD61Qq48rVDzlz9riLRRBsbm5z5OgxEFZJMBhGPPTww7zyvbe4evUakbQWhShJQSpnBXa1pYyhKhVG+YKlkiSKefDBB7h69RJ7ky2Kck62ucfuZAspI2v9iiQislluqrKkKkqkBpRxgrKyW0gbcMVmhQAigXDW+5WVJY5tbCAwZJmt6aWNRmPXrIwUK6c2+MSf+jkeffYjfPXf/C7XXnsdtbNHPM9QVUHiFJ9GALHDAVQ1aTWAcrwtErLGAiKye9Pg6bG153pBKzxDVtDYT5tUzWP2g21jXGxQ610e44SKgWC/s58+HUTz7pRdz5+Bps/t+7pBzneiVV06fBAdCAF7+H3YxiI64t/paXQ4z9493ic46La1qP/h55D276Ov7B9H+G+XX/jvFwkUYb8XxdSE4wz/Fm6zWbxh94NxwgbGoMsKYazCrNIaXZXWmqcqWxJAWfyb5zllWZKmttjzeDxmeWXVhUlUdb92d3c5dfI+ENb1M3fZ7+52/VAxGuGEaK3rVLX+czgBXckunLTwd+++tLq6Sq/XoygKptMpQoj6/V2Xp3CTLJKwu/1YdNDq+Axj6mrm/rfwPtDWV1RIKq05efIkxhjeu3CBDy9d4v4H7idOEmQR2crb2KMvpSRJEk6dOmXnQEpk5DUTZl//7n5ZE6zEV1+GG9dvcOnSJfIsR8qYcukUanAYlWdIaYFEXuQMBgOu375t8bgxTjgTTjscuEWZjiAgRFPlO/zFC4z+T69JFB7aegnD1PcFD/rFqYVSf2QFgWZZhCJIGyo3GnjTUMBwDgPNj//L+9naYqoe6Jv6tlpgldIVOfNPdtfGCxLCaTubcbc7YA/8m1cn/OT/4/Ncujmj0sa27YO2gvHUPQ7G/eHtOb/y977OyUMDLt6c1eP2Y2/maX/bzV/B3y1Boj2eZg7d8w5A1D0U3oLRbsYDfmGccGgabbD35VVO6WDwwL3J5oKxWhR/JvqDPv1e3zZhDEmakCYJmbA1aYR0fvB+/Q64FjHWexEUupaEkMncC2BdpCTYT1M48PNBfQoZ5CJGHbZf00cC9yJjg/4m04nTrsV1vSFPFwwaY+SCPVK3ZOMPtODo0SPsTOf0R6O6D1JKemnPpjhVygW6Nq4kB12DwQCv5W2PxQMqG1tWVhUPPHiW1dUlbt7aBFyWJylbmtg7ze/dMid1Lwt4NcrHHklpXQiSmF6/T6kUSkB/1Oe+h+7j9NkzFJUmXVvhygcXycqKE4ePcO36TTY3t7Caf0kUJRgDynhnG81kmvPBB5dRGPbcOu3uzLh5c9umiY4kWZHzk5/6CSJh6KeCsjI8+sQT/OCl19ElSGIqVSIjSHsxp0+eYH1tnWvXrlGVOceOHKHXi/jc5z/LiRPHOHrsKLmuOHXfWSpsmneMVYLs7U3J84rpxFb17vV6LC2NGY+X6I36qAiMtoUgYyHsOZ3N2N7cZro3Ie5F/Mk/84ssj5d4+603KcuC8fKQvb0ddrZ3mOzs8dnf/ywISV6U9MqixhJ1AVhPV3TjIiuJMMYqJlbXVlg7fNgVEVZUWlFpTaSsgJj2IoqoQvYizNqIP/Ff/Covfe2bfPeLf4i+dJtonkGRY7RCGShjUEYRaeV2rUAjXEZCK5RJFewhT3/FnYXaRTy/xkZOUF6ssfZWkf37dBFdOQjMh/3o3nvQOzsPWtVTx61H1Dy/3cYiWrsIE3b7dk99ucMVWgyAfVabrguYz+rkn+1iskUY8ofpV3dPHPTuexkXHFCHpIWxmvu1VlR5TpZlpEtjiiJn88YWRVFQZjl5lpO6LI9FUbg4DCsSHDpkLak+Hjs0MkynE6KooNezVsN7ue5Z0PASbJ26FmsO0sYQC9EC/l0JbpFU6p/3v/lYjyRJmM1mTKfTmmH6QVaVTb3nhYQkSTrmp7YbRDdLVXfBlbLp9Rb1z4/RuoPZNobDASsrK2TZnG9961sIITj/yHn2phOc+h+whVKkEGwc3qDXS11tAGdBkU38Sdd0dqfLu53ZVLtWW/jCCy8ync6sECY15fHnnKRauXSgcO3KVRAi8P2z5m0PkMMN2lqvjqak7kcAX72PfkNpwQjvXuRXxLMHE3zCtR3oYYxw09fqkR98JwOgg5nGuFsagaUtGNj3+qA87YWHFmi0n5UHRn4fu7G1wLUnqkbXNSz8uLv5Zut6HsJw8eYcX5m3dkvzs9J8CMQp174GJeCDm9P63S0nJ9FpO5T8avJvpYH9QkbY3/DvRqjYvxp+vYUvr+uEEeGG6rR57hxaTa2r25Bn9Hq+KBvBs6CVrs/haDRiNB4BguXlZQb9AUmaos20WXnT9hO+J421H+kCAeSgz9D2oe2+405nd5Fg0qWJPlHF4qDm/aChqylc1J/WPbIBMDgt1nw2t64pSezM3n6vN3ZCOu+u23JrZwz0+0Pev3SV9cOHa5BvjC3Qms3njrZTv9vGEi3ufxRF9Ho9JpMJS0tLvmWMUdizbTP+5XnOysoyp04d4cbNG0Bqg91dYVRfWGvR3PxRLu9aoRzojOKYKEkwwhUKjSJQylasF5r1I4eopMakcPb8ffQHCZfevUBWVURpSlkp0G7fahvgDAYjrSVoNp2TZbkrX215iFaavWqKkJI4tsVWb16/xeEjtvirMpo/+Oxnmc+mJDpFCNtPQ8XpMyc5emiNOIoZDlImk5zxICGO1inzggtvv8Mj5x+hiiKuXbvGmdOnbUVoIbh88SL//J/+S25cvmWrIWPdjHe2txgMBqwcXufo2VMcXj8CwqCKnMnuNr3hEsdPH6XICvZ29/jS177C8njEr/zSL3HfmbMgcnYnm+ztTJhN57z86stcvXQVJChVORrj193tKx3QSUA743q/32NjY4PxaEyUJIBAaW39zV3mM3RCkgpEIqnQbBUzfvwXf45TD5/j+d/9Ahe+/wrVrS3ioiACKmWtfREaoa37meWXGnwtEo8tvOAP4BLKhKEKXfrQBZl1fAKC5ogF50P44PP9tCd8f1fhGv62SPHh+99930Hv92NcRHMtS214QLdf3bGG3++zYAbjOIh+dvsZCmz+ey88hP/594aZ+fx3YUmG0HLtr64yPRy7dycP52TROw6aAz8P3TGF33evWpEUtruAFxljKKuKoiigyJlMJ9y6fRtVlpjK0ue8rEjTlCRJamuGMTZD4fb2NsPhsG7D9++tt9+iKg1r62ukabqwj93rhwoG925HYcPeFzEcHLQnu5uVKpRm/eR7Scq7MtXa0AUbIMx24Yvf2axTBmOqWgBZNAa/Ef3C++/j2PpPlq6Kt79PoemlPSJijh89jjFw9eo13nzrTVYPrZH0emRVgXCuRMaqERFGc/8D99fZdCygaB/CRT6Hd7uMEWRZwWw6580338Zoy/T3coUZHbEaZedSZomVdFYhT7A8ghQ1uPWuO766p3Bg1Zhun7puOKIGuV7WsH30f4vgS/unDICNPxw1IQ9eiwPypm4mvH9B2zTN1IPw+Nu0frE4WQqsi7UE0+zPOqDaPxEAd1tF1mZLawlcPubAMQxjahZprR4iSI0JgaeKgMAlLXxnc38gEHXGJ+tnwukMZqOWN0znC+qJEfW5an6rx20MInBZ8wJasKqN0CT87mgYjjGGonBuNFrZirO60QzLKLLrHoD5NE3p9XpIKdjd3WU6nTIej9m8naFUk/nOEviDU5N2mU/3+3s5b12gfy9WjYOEn0XtHcTsFwGUO72n+2yLiRl7qn0MW5ZnlFVFX/ad65R2aybq/RO+o9WeaIS84yeO8/1XX3OucA3jS5OEyd4eqqqaTSkOnjuDpVdHjhzh9u3bLC0tNcJosLcNwma6koYnP/IoL33/1Ua7J4TrdyOMHbT+d3NX6/5W3yMlcZpan2Y3p1aDbgscGq1sQHMlSfp9pIFTJ4+x0h+ws7WDdGlMvTVV64rInx7t6KEPnHcuSULa/5DWJVmYCCkjLr1zgcOry8Rpwje/+lVuXrpIjxh0AZEgjiNELJnPdpmkgocffJAym7G3c5tYRsRSMur16UUpt67dYO3EUa5fu8rG+jrJaEw+z/jX/+yfc+nC+0QmwesXijIHAVU2Jcv22N29zfz0Kc4/ep7Byoj1tSVub91iZ3eHQ2vrrG+s2rVTms99+UtEUnL2zHGeevI8w8GAWMY88cTjXLzwgeW9RW4povZ1K6gTsViy0cSBRZFgNO6zurpMfzhkPF7GCEEUJfW6UFbEFUgFQmnWlpd4/bXXWRmvcubR8xy67yQ/+Nq3+cEXvsre+5fRuzNirTG6QGiBFMbG7JXKKgj9HvIZLrEWPuVqBwk6gvmCc7mYloR0OcAI7v/eC6ILxMP7DxIQ7vT7ouugvjecpo1hhGWmaNE+M6HC1mOpbj+6aV0PEiS6V3jG/RVaWkKM6bFj+M7QKhAqkhZZa8I299EwY1q8Lmw/nLuQJyx6d9j+3daxlXShVoriXPCCvggroBeFdYmKtWZ1ZYVSVRbjGos04iSl1+8TxzGDwaBeJx+Y3rX4JElCnpfMswlyh5an0Z2uH8qi4cG/1jbi3JpzI9K0XwsKYZBzVxvoN15oLfATE0qaYQYqP6GhgNNNgaa1JssyhLBguizLenODNc13+xIGYnvXrPC9foOkUWolPWJWVlfRWvGd73yH6WTKU08/xXQ2papKoiS22F1KZCQZpD3WXO2M5hIhPbkjUdonVQvpNJCSqtJcunSZyd4EGdkq5clohULEVEVB5fO1C6uZjiIbOyKFsNYQD8ChsQxQw94GCAc4VzhmXverRraSRhdqDdse49M8HkjcpvW5mQN7YGrbhNeOhM+HwNm17fUK9vnAjGv8M+EcN/c1sN7tS7fuURhQXrcvagaIqeqUofv7Z3BKyrq7VvNlNYJxnNQxCwbjss14C4eu+9yshgnG0oxbA7h3emFuEe9oiJzGiwe1KOECHZr1hFAdZzGnXDDnjTTpxSKfvcq/xhbpkyRxgjEaVdmMRHYOPXNpddTOgNaMR2OWlpaJooi8yCmKgjRJHK24O8i3Xbuze0D3fn/dibkd9MwPcy3SOML+glHd/hwkSHU/L+qbrelg6PV69Ho9+y4HdmsXA4/VaeYsbLJhlNi9LWHj8HoTg+NullISu5oLPnmIdG6ItQNmt980gsbrr7/OAw880ATe14fZ7ruyLFC65NFHHyZNY4rcWoR0sG5dBVao+TtoLg+6PK8zBqI4QkQ25i8SEcoYKm0DwoWGWESsjoZsbW6ys7fLcDSmn9r4rDKfMt/bJjaVk6ygJ7SNAzDWcmOcWyUabC0GgXGChhECLQSVlMgi4tq773Fx1Kcsc17+1rfQ89IG/AuQMuUX/+SfYW824Stf/hKTzZtsXbsKImI62WNna5Ot7W3msxlVUfD9732Pnzr6xzBVwWTrNktJzFe/+Hnefe1VF/QeuXVyewBDJSTFJKLYuU25fZsr773NMx//GA89ep6VtVWKKuf6jatUsmJtZR1hBGVR8vabb/PFz/8BFDnHjh7j0UfOM0x7CDTSeIuAA9a1cKqdpOkBt6OPwrC6usLKyjLD0YgoTtibTBktLWGEjaEoK81calRZkaBItOT0yVO8/tobPP3ss6SjPj/6sz/FQw8/zHe/9HXeeOH7zG7v2kDxfBejFUJrZKxRVYUw2qaKD4RxhYsFjSRaKWydjYPPcVfoFUI0bmJ0FCSddyxym/HvCe9bpJH3ZyJ0Kwp/62qtw/74tr3yMkywYUxA+02jvPX3+DN5J+Gr+13Yrv/b40bf39Al6qBkHv5+jx/D2IdFQkTXrcrf2xUi6s/Ojbd7XziOsI1F41z07jsJI4uEsQYvBPPqvi1LK1j0DSRpyokTJ6y7qXYJTmRce7sMBrbWjnL11/w8er7h+7C6ukK/P0AI69J6L9c9Cxp1RVmt6xR3Pr1tFCX1gsL+yP5wYroT2pXkws0Ufh+mgQ03eVgXI45tJgsvbPjN6QOBfIC5n8Cwne4BBMtcJIayKFleW7Gm49s7vPDCCwyHQ44ePcr2zlYN/EAjsRv81NnTGGMrJPug8yjan/53kfZtETP0QFhpy8DffPMtGpApKI58xPlhl3WlzkhGRKIZX+3GLLzrEy1qZhyq7W7c9g0OeYr9ERS1VscfBi/x1yDVv7cBt7WvvXCVu41p7gkVPbX2oGm77lbQvyYTU6uloO2gS/VoRK05E1HUubO52WtPTdCAaSaueSLoc1ONxFni/H0+nXCtiW2D/HBMXhDzbVvFZ2fOu/PhnqtBWHceRLgsop6UBtuJYFz757xpLHC5CddVtK2EImkUBYuwuv+t3+8xHo9I0x5GG1uTYTQiiRNbWKz1UGe+jF/N/euy8PJMUoTzE0rZYUfb7zrozaL7ITxfwUz57gnRpovhY23Bp9ti08+Qnolg/3upfTgasTIaIaXdg/7JJvMNLq+SxmiNFlYAbtp2LTphzxjDaDRGG+PcXRpGaPlBVCtuDrq6gGt5eZn5fF5/3kcD3ceiyDlx8hgbG4e5cukGcRSjRUl9koWoYz26TNnymvA7mj3SIYbCfbbPOF4Q2TNgUzwqK3RIQQQkQrB14yZSaE6srXH92nUmlabSMJ/NKOZTEqGZTPbcwmu0KW32KqPRunJjtidcClm77OJoeBzFFETku9t8b7LFrVs3mO1NiEVMWWpMT/Kpn/40zz73BL3RkPvPnuS3/um/5NpV6z6bpCk3b1zn8pUrbG9ucrXXozfss3njOic2DrO3tUlfCL73/Lep5nOb5QlXmdhZroQTepTWVEYz27xNb3mJr+7tcePmTX70J3+SQ4cOs3Z4hevXrrG1s8XJE6foV4bHn3yCW5eu8tp3v8+lC1f47vPfYTwcQFURJYn1UIhjhDFEwtVLMsYpSrz91ivPJOvr65Y2JClCSL730vd55plnSfs9EFYBNtUVhdIkAvpE9Pp9Km24ce06x4+sQhyzcf8pPnXiz3D8icf46u9/icvvXKCk4PjRI5w8epg3X/4BpsyJjEIaQaQipPGWaFcXRVoXK4kHuk4+0q44bq30afN3IbDaZeEoV0B3BaAwRDKq073XWTVrgG2C+0Ut1C8CpOCzZx1g0fV9qPvmFEAeiHfAf0tIYYE7T6AAu5OypHlnO+FL2H/PA0Oa0jy/YCgLBAfvIrVvfB3F9yIl0CJc1sVu3esgpUb3mW4/us8fJIC02u0ohgQWD4vCupwuY92XK2OoyhJdWM+fSmm2trbo9Xo88MADrTnw6+ktG56Xx1Gj+JbyP4JFwy+a11T1erbYkgWITRVwpULhodmcoaQYLlKX0XYnNXSdMoY6nqMsK3zsQhxH+I3oNareuuK/U0rVEhvA0tKSXQxjQbnn/EZbX+NExihtc4CvrayjleCVV17j9q1bPP74oyhKiDy4cGPVCiMkZ07fDwiiSCAjENIFc0ubZcNi1pAgtGMb9mllBQgpmU8rppOS9y5cRiNRqkQmKWrtIYxxWncAl27UH9Amt7sDUMZqjeoaGqaxSrRwY4twNECuDcgamcDU6VINtWkkJHq1ANGAWw/kfdfbsR/Wfcc4QOxbE82ddS9MmD3HtAUm4YGyI8S2TxKhld3A2th1j0QwfGcjEWFbpt4n/rv2DHigaOoDX8+W6UBNN+4Wnq9f0AAg0xl3LRyBr30YnB/XSxH0nwU+rx3tSJtUmvr9tTBZCyFtq5HNbNSsq++nUZpECqQx1qUksikoK2N92q27iKjnUQGVMcRpzGhpQBQLjFHoyrA8Xna5+e04vRODMdoyfExd4dczS0urAhrTkYVqD3AfU+TBfIs5xPVoTT0bjkbQaM1Cn2Ah3L6vMYPfhbYiscez3rLQlJAJUsHSMAsPWppla2KThDvXHhRLabC1bFxSCiUZDIacOX2SvZ0d6/qCYXk8QhowlcEoFwtg7PPKaCIT2TNnPB2ingM/vtFoxDDtocoSoRRSK6SJSKKYWMYUeYnSCuXyz4YAprUPtU0V6xVJeZ6TJImbHyf0S+3OZ4SqBMtLIx595DyXL94A7apSywybyjexSfBsdgJX8RZ3zlzNirpp0zoHRlSODnl6VyKwvK6fJhhhLQ+6tO5+2hgkBlVUKDFg78Y1rl+/yiMPn2N26wZlUaLBZpgqC0S1R5lvumxQztLoAKsMzq5NPg64zEqWlEowFYiYqsy5cXkLpSrSxFoyKglnH3+I537qx1BCUZQZjz/5GPf/jf87v/2vf5MXvvltolRw8dIFrl65SlnO2Nm5xUiN+cJnP09VlPSThCSSXPnwEujS8QxFFEc2u5IJ6iYIgcamoZ3u7VFWindffo1ib85/8umf5tCxw9x/4kHyQzkffnCRo0eOkfYi1paWEUqhq5JSlcynexijrLuXlFTaEEmIhXA1PW0K2Vo956YpilJWVg/R648QQtLrDXj1B6/TT8Y8/sRjJKmtHeVT7WstySsgNZy+735ef+M1Dh96DqNzIgxJL+aZH3+SBx89y8vf/T7f+OLX+fCDD4k5yiN/7I8jjCJNBSrLyPdmLnanYjqdMBgMGI2HXH3nAsWtbUsrDQhtEM4tzrjEIX73WQWp07BriHDA2NE1T6cS6U6eadyMPA2IPHU3AuVi4SIHSCoRFOa1Eg+xjDAysspYZfGEcfvNCI8B7HkRXvkqrXuYMDZOSnt1iZTU1aYERMInVPGCYU3ICLmgdkKi9ZwwDr8ZJ1iLeq6EsIKsPQZWgWzPqXVBp6aNosY1fr+GdNLTaH/GF6U77yrIDwpS328FsTXWhLR4pxbiaLOR7vMhL+5aYw4SyBYpTsJL+thfh3uEtEJvLCOYFZDbZAevvf0WO1s7RAbWllbpJTF70wnLKysURzOb5lnYREKlqsiBtN93OMSuZ4REV9rVCLo3EeKHyjpVliVxHNcCRh0roay/qWcWQuA0RxKfXcZrmVqmpwBIh7mMw8kMN0kj+dnN7KUtL4AQSPI+WNy/p9frtYSlLMv2L64DMggr+VtNjmEwGJImPbJZzre/+W3iKOKBB+5nd2+3DrC2bVkmv7K0wvLSKkp5LZXLaWwCFwSv6w6ARKPN36/V085tqiwVl69cZ29vRlXZA12ky5hkRDHP7DzJ2G44Y1yWJfDFgTxIseDMOELQXDUQ8gjWL2jQN3vf/hiYBtgHwsY+HyhqENAIGw1Ab6Hn4ME28G3D4oaiegGq/Wwzt+5m3QA4f68AjNJWcAwKbi1s24PSZtB2HgPBrDs/Xiwxbtx2SkME6cbN4jlvhItOu7id5CIk/RoIL0jiz00oILn+NhuPWqDzzNDUJLNmGPU4hHQRmXb+aic0YQsVaq0xy8cR1+z9VVlQpVWD5/Eg2dEIn6XKGNLUFYTrp8znM2azGetrhwFNFEuUskKKxYi6ZbERBEzNjdkY47SNHkz62CV3zkSM94GuC2jVi+ajlrzblqnXSCvhsnREpGniFBj2nFuAvG+Xuse9O5xzlamXsyvqNcoaowVCRM07OuP1zFZiNe0QIQVEwvD0k48hpWS6t4NWivXVdZbHy+zsbNvYMxljq6LpeltZOhXSI/uvwdUjMrYK+PLymGw6Q68tE0lrkZRCkMYpSnlXi2b32mG3GaSde0vv1tbW2NraYmNjw43JnxOX4tNIiqJCac1jj57ny1/4BkYbYmlj6SwajhDGBxXTjMsYGyfhhAttnJZee7cQhcIJGrqx3FdViYgklZ7VvEYr7QQ924QUUBWGcj5jd3OTl1/6HiePn0DGDhxK2NndJptNSWJsHEFp6yAZ7V2Bmr0nnAAitMKgXeE7uwcraUAbqsplgkFiIonsxzz61JNUZUU+m2MSxQvff5mtzU0ObRxiNB5itOHyhxe5ffs2uip59umnOHL0GK+88TZbt26jen2ObByy4MnR0kqpOpbE+HkzDR2TwhWtqxQ7m9vE8hKf+53P8thHnmA4GDCdTLl+7Rp/ePmL7O7ucvvKFaqyQFWl5Y8od441QsSO5LnEHZ7mSEdvAjqfJCmrq2s1oKuqivks5/lvv8CpkyfZ2FgnkdLqM5QVOI0Eo20F+rTX48LFDzlx4jiJKDG6wuiI4TjlE5/8cZ55+mkuX7rGW2+8y872Dv1Rn0uX3qcqCwb9HqPRMj/+8Y9y4sQJ8iJjb3eHzes32Lp2gyov0WWJLhWmKKnKkqIoXR0S5WJPrUvLbDYnqjQ9aYG8v8crbmOjEdruB6M0lbLV3DHt2gpGRVZ41catX9xQFK3dnrV1zaRx4oIH2J6CG4PQjn8ZQeyqshuX4lnhqokZR089+xAaI10/XdC8ENIp/pzSwtM4YaxLoOPTtTIaQ+VpubSCUYMPnQLHCTW2EKhzL+zgku4VYsjw767i7aC/7dFsaFf4txTOvVGImj3QUkm1XbK6/WpbptqCzKK2u65fbauwqPcEsnF5TpKEsiyY7O4SLY8wxlo6ZGXIswwpeiRJTFWVZEXOqJegjWJvd5ebl6/blNFJTJwk9AZ9dzYNw+GQw4cOkcT/gbNOCSFqv62wDkVongozRNnPUaAV2z+JYTBQOPFds1Lo7mTntr3w4QbyAsbdFk1KadN+uQq3WqnWb7WkiWB1dQ0pJJcuvs97773L8ePH6PVTUhVTqpIkSRj2e2BgMply9r4HqCorlHkBSoh2Rcy7XYs2e1XZVKHvvvsuVWXdSJIkZr76kGXsrUJHdp72uyA4pmFfWkvfXjfvtf2Nl58Hl41WwgtM9nw1blgecDZn32lbjdfkBxYVUcNYGh9/33bgcxrOAd507tumJnheM+jnqpErPLj2nWoIZK12MbbvSisSxzy7BkGBJb51j2oNUCMKmdaM+QZEMLeiBVCECJ5raX72t+39jv0cNVrtpgUPPQPpp24bRFO91dT/c0IR9ZyH6+5m2z7vv3SxFpaYOQKujbX/u/mRUmDW7q/HWJusjU/24KewbdFUSpH2EkbjIf1en+2tbaqqZGV1mTgWZE7BoJ07Qq1/s7LEvvnzmWFcSY5wQhtaIDwTNAv4lWPqXtAQjUCWRLH9WyuEVkhv0bV6pFpzHky1A7/avabTXngj7fMviILKxN5K49fKumv6dMTSCR5JGvOjH3+aRx85z/PPv2iBXVXxyPlHXE2TiNW1ZQId5b62QxcIN1kYI3xSJA4fPsylK1c5qlwcg4xqS/d0OnUuq2mdLGHR5RU7Sik2Nja4fv06R48eDazYbXcCb5V+6Nz9jMd99nYz+v2IsjI2ItKUoDOMruoshVYAdGuoS3xMRHiGEKLW0HowjVJERhPLhF5sQardq40rCcIWuBLCunUlsUQirLtUWZAGCi7/n3df8zS4vdY4umLnzCgHkN1nEbEPZFZKMV4ec+X9D0iMYG1tja995SvcvnmLT33qU0z3JsynM4aDAZubm+RZxtJ4zK/9+V/jzbfe5nc/+wVGoyEnThxnbXm5rlfleWK3ornwtEq6bIZRjC3Ya9jbnZL0d/j8732WPMuoCsunVOlceuvkLt5i0axrHC2GI433A7agWCSJkxikIHMpceNYk+cZV69e491332N5eUSvn9Z02is7/b+nTp3itZdf4vDGBsYY4iRCa0Ovn2KMYbQ04vxj53j4kYcpy5KyLJlnM8oip3Btrq2tICMBJfSWeiydPMyZ+ClL54yF2KJGnVZIU0qhVRjrWhBXhkhBWTqX9LKkLEqqskCUClUU5Flm+1FV5HlOkeeUpf03m84osgyhDVVekM9zpBboytZOMdpb4GzKU4yqq7ejDdLjLmMd1LTSCG3d14RuOHcRuIER7FktDA1FNrXHBsbWCTG4RCruDmvwlVa49xZpIRGR5YUaoDJ1yKBPa4631IpoX/D3Itcmj0Oh7RZ1EDYM+dFBbk8eH3Y9cUKBofveu12LlOmLxrJIWAI7r9oYIlzSH9FYl6QQpIMeylSYMmfQi5lPrMvrvCqoKOkPBwxXxkzzGTKNmGcZs70JiYyJB2PrVislxTxHCEl/PCTqp9ze22Ftbe2u44MfsjK4jzWowbnToobxE+HkQZOebZElw1/dBQqFBr9ZmoVs3ukrlft3+Mnv+pn5e7uSY53BJhB4wgWXkUQrydJ4BaMNLz7/AkZrzj/6MHvTPReZH7G8PGLQH1AUiiJXnDpxhqIo69RfUtry7d0sU915aLTltObK35fnOXmW8cEHH1CV1lrSGy2Rb1hNllLKSZyNi0CtyfXa02BzegzhGa3FWvXptkCmFhQgRAs10WjUTJZp4v1APUA19fua+9w73W2mBoltgN7WVZj6UVpt+6Zl854AKDX99fZW/3MjKHnw6NN0yiiyFoL68QZ6C6t+pRarQoEpHKdvWzTWNjfRtP4vcALMonEL2lEe2NomBMBZhLPgBLka2NL63JpA19dgN9j2/H6ogW8A34V18PEmfluhW9XrKYWrMSAlQlT0XAapqlII0Sgn6tcF+99rkIU0LC+PWF9f5+LFi8znGWtrq4zHQyabWyB8JiWBt0C4QuWty59nKQSq1tnZQXhXKlPLbSKo5BswD2I3BY6w4yypCKSJka5Cua4EQsdIgve4nSXdGhtjbHYt/M4xRMIWF8O4AmumW0fCZ7YpiSLnlqpdhVncXApNHFtAnvYSDq2v8eBDD/LsM8/ST2Oe//bz7GzdZG93i6eeepqPPvs0ly5f4ulnniLtxQgvPAVb0Ft4hBH75tMY4TKzKe6//zQffHgRVRmEiGoBLk1Tdnd3m/TlIQ26w7WxscGbb75Z7wcZLWbSVVWycfQQR48fZnfnfZK4z6TIKbI5Va7Ragamid0TNV2CSChb2E82gpRx9C0S1hIl3VkVWqOMrdAnlM3CYrShUi6VrgAhDXlWYuLYWiyimEfOP8x4POSl7/+A3KVtDgNxq6qy59i5XNTz7c+2pi5Aa6xsaumbxhUlDPiCECRxwpGNDaQyXHn/Il/9wpeY7O5yeP0Q77/5Dlk2t+mNq4rJ7i5ZltHv9/kHf//v8867F6g0mEqzs7XN9s2btcJKClFrnRfxbBnHxFEKMgIinJjL9u0t5vOp4zk2wUakcdYjr3jw8UTCCSkaEQdkM+DdURTVPEpISRRHDMcjlNY2DX6lqCrD6dOnuXjxEm+88TrnH3mIJHXWSpp3NlWZBf3BmPffv8jp06eQVWU1u8oC5VQm1p1aABH0kpTeyAoudu/4AsSalD4GQ2wMymenUo7+2BE6EmlaPMV7ZkghnQtho6St8VLl3AZNMxK/n7SurKt2pdFFCZVC5SV5lqM1VEVJkRf2vyyzAkqWMZ/uMtndoypKJ5jMyV1RX1WVmKrCVMqe/0qB3+/KJyCxAjDGuohFJEij0FiBPnKxFgbrKquFpXXW69KAdjxESCrPP4SN+1Ha1fkSTaIXIYVTRnr+FrUwYovPdwV3d4/3vgmD1P1c+jnvgv16pTr7v2v92OcZA67PskVjwneFuO4g60aXH3X5Z3gJRI1jEcJCFG1QVUk23SMVimEsWUl7FHFEnle2AngkOXZkgyNHjxIJaS2+ha0mng4HJL20drHzwe/nH3uUtY1DfPXrX+fCxQ8W9qd73bOgEWpjvMbfB4iEv3clvTDLVJiay0+8n7iwWFPjgtVmUN59yBhV+0b7K/R1C/sQtu2Doq0GJGY8HrusNilCqdoSUqfYNbC8soyQMbev3eKV7/+ApaURhw6tcmt7k0hKVsYj1pbHNqe6Lji6cYzxcJlsPqnb8ZuqHn8wp+1N7YCd+y6UXLW2GpsPP7xkTd9a2+D0pXMokVCUU1fIzL7G5xkCnHtL94A4SBsIHx6TWvcOB+S9mZQG5HokbBUb+4Ul48Cz19Q3v4Wj7LQdfN+03QghDVyxz3jxoPXumo6LmniFmheP/2sXpnbDVtuDCAJGfY8a2F87iCLYt3T+O0M7IN530OCAXTgb1FU9wzlv5C7p6W0w7s5k1p8bgS8UdkSwrs2ci4Vz7pPmttoOxultHN4S4hmgzxaztLJCkefo2R6rq6vEsWE2m7K6tkIURywvL9vYiWD6vSW0UhVaVYyXhjx07gFeeeVVbt/eQkh49tmP8Ptf+CLSaHy4vi12Jm3FcGd16DIaD5hq4UvakE0PgkBRxzNJGfgCSwQ9Jwi4d9cz4KbIWHCqS/tMIhOUKpDSamztuJQ7xxDFdo5lvXG8O6mN5fLZP7wyp9frkSQJo1HK0rK18vT6fVZXVhiORsRx7GoJHLLFy1bXiBPB9tY2V69d47s/eJc33niD7a1NPvKRJ/ilP/MnefChM5x/5CzpoMdkOgGcC6XbcMaAEV5r1qapdtZlLSgdPbaBxUjG1Vqw96RpWvMKpbXN2CRkC0CFTN0D7eFwSFVZlxKbLavt5uBpeVVVDIaGh86f5a033sUoRTGfUeYz0IJIKBvX4cW6wCpirRm6ppWiPrC2ZoK/rNZWY4zdHza5iKrdNiJvyVfK/q0VRitWlsccPXKY69euMZ9O6Q1HdVygt+zZ+hc1oq6BtDE2NtDEus56bcdv+Zavei0xCK9giyNOnb2PMw+cRYqI1199jV4UIwYj8tmc61eu0O/3qYqSOIrIXZ93d3d5/tvfBhHRGy0zn82IgetXryC0TWJijHXD8Lw1LNwVxYn9T8YIGdu5EzEGQZmXtb+6nVjt0poLjLSuN0mSWLc0IfG1doyjBT5lfTeRjIws8I/ThCRNKcqSSimKssQYQa/XJ0kSLl26xO7uLuPxABElrT3XKBkNx46f5NVXX+HQ4SMIYQGtlM4dTET2O+Eyjjltsa2ZYtzaWDwsHL2URiAJktZgbLE/4bX4bj3dOfE2ZBUBUjpB1wqvNa0fRAH9FfV7vTVOChdMro2rqq4wCCph09UbnzpZG4xSzl3QWjp0pRDGWIGjKNFGU2RzinlGVRRkkxmzyYTJ7h7lLGO6O2VvZwdVVBRZhlEaXVXoQkNpXba0ssKOdHF4hhJBZZPkVMrRTOsKJ6QhFtrGURnbd2lcgWZhHB2qrJBhAvoOtUInFB4sjWgngvB0Y5EyPOQTiwB8VzHuMVw31tg/H2JY00rf2RaAupg5xMXh7wf93RWSjBfgPK8THoPZ/+bbO+g8p6cF4yRl6dARqmVFXpbkpiItFNnNTXpJShLHxPOcfD6DXo+V1SVKVZHlOUVWsnH0CI/cfz+lhp/6xE/yuS99Yd+8LbruWdDwBCC0LvgUqqG1ILxq/BqA5e6EdRfRtxWmM/Of5/M5vV4fIaLWs90UbaFwE/a/K+TEcUxZluR5Ti9N67S4vnAJQrC6fgit4aXvvsRkd5ennn6CWTZHSFgajq0vaCrRymCU4b6zZ5nuzen141bMim/Xanzv3YUqZK55nvPaa03++EKmzA4/gdEqYOJW+yXwQY1Qw+9ws3eEAC8JW4bnfwqdUQINZw1c/btDhx3TCBkmALn1W7AMXITfGJzu1/bXg2bh39jA4aA7HQDsu9a07Sd/YdvC+6F74o/TvLv9GYLTbhumOwft+/zfBv+uQLiqBZBmXG3hobMmXmiiaa87p824O31rPWca16lg+gSOKPoc/gvmuGW3qgGf17I1Wvql0ZjhoE+WzVneeZ3Tp09x48YVytJa944cOeJSTVc2T31ghRRCoCpFls84evQwJ06c5MSJk7x34U0+vHiRT37qP+Hd9y7w1tvv2PNubEFA79etKFt9D+lK1D1rgaQmhHaMzO6Z2BZLQQjQqrAimPSgz06wAEysnX+6pUX9ft+5lhriRDAYDknTlDSxme5G4yFLoyFpnDAYDEiShPF4zHg8RgjBYJAwGg6JZIIB+v0B/X7fZfeb0esllKWiqnwijpSyrCiKCrDVWt947U22tm5z8eJFLl68yObtPdI05Sd+4if42Z/9GR559CGOHVulUiVbu3s2kYSUtezst5vRBoWyQoS2u0RKK2S4SGtAs76+xvLSknXpKCoYWTqb9hJkFJHnuXMna9Yk5AMQJK9wv49GI+bzOaPRyO3X/czauh5VPPbYw3z233+BPJsx6KcU8x0i6/yBDmIzOnIn3gXMYNx5khZQi6j2WzdG26JWwmpejYFKOctH1GRhMca6FfiaJEkcc/jQOm+89iplWUBu4zp8gHuTDti4Inwx/X6fwWBQuyZPp/P6LOZ5Xlvys2xONp3YpALGju3YxmHuu+8+EJJrV69y9coVoigicZp1rRS7O7suzsO6xXghWStN2ksxSlEVJZnM2N3ZZdDrg9NO6w648nw6coGgHnxHIsEQ2aBead0HnfRW+4xrbLBymiZUVUFR5E29J6zXQRJbIWM0GjGbzRo+6QTSpJeytr7Ow+fPs37oECKyAG8+20Wpil6vx+7uHlubm2xsHCJ1gkazFwJwGcWkvQE3bt5mdXXFWmedyiWSMTjaEMUSQYSUCUJEGFRND2yBQ6t+kUYQmYB0WsnCCRqmjuETtPm/zWYsal7l50QARspA0eV4iWdcPqmM2w+RjOp9VaDBC05Iax2MhbtPkAif/t444coqmITWLrucFQiMc/NCW76ulaLKC8qsoMhypjs7zCYz5tOM7c0t9rZ3me7uUWYZZV6Q5xl5kaMr6wImlMFU9n2VLjDYc4bSUCmkNrU7l51XW4zYmApjfOr8Nt8Iryjaj/OgwZQhVu0qpxsa0Qb/oeK6+1x4NRgvctbK9m9dAagrRHQxdPhd14oSKmCszClrqCCEcDVlIob9PnHsil3f3qI0wu0TG28ToZnuzpkaQxzFJC4pkhFg0ogbN28TxZGNDZKCG7c3+dYkZ+XIcT7+yZ/giUce5V6uHyoYvJtarLYWRI3PXGjSsovbSJWLJDL/uau58osdLm6v13PajrgV33GQOSlcnDBtbthWmqbMp7M6tWIURdYfcz4n7fWJophiVvDd73yHOIo5e/Yse8UuaS9hdXWF8WiEoaQUijRJOXrkGLNZTmriug/GUGtKhQNuoTWo1ecQJNNsqqqqKIqSd955zzJnCbtHPoYSPcqysH6VdnA1wRLa+04GpttmBdtA2WldECzol2mQaevPxoFp0d8NwHbv8IKL84tvAHzjBuVBdN1X0TRYg3c/Ty203xUH/CipEVTdtqDOouSlG+H2iMEJ0eDTKYGwh7IV1x4IBX5djTaoStWiU01q6kw3nTlHNIm5/N0mHN+C6TeBK0o9c6Z+hxswjQuZaIiPaQsndS8OEHpbgooIiKNjAv5KkpjV1VXW19e5cuUyVVmw0VckiRXeK11y7OhRzpw53fRJ+NguP1v2/dPpjENrhzl0aI2PfvSj3L59la989avcf/+D/B//y7/M7/z73+WVl1+lyBXTSUZeVBgkWgqX8awZk8/9HgWsGqzbRBwnxJFESgtuRqMR/X4f6cDf0tISvV6PNE1Iewnr66v0+z1bRTWNGa8MGA6HtevmcGiBotECrS3jjpMEbayCpChyBBqMIM8LF/RZ1cB5e2ubG1dvkKYpeZ4zmexZVxNj2NrcpSwrqkrZoNf5nNlshpSSsjTs7U3Q2gaYKlURRZLReMRzz/4Izz73DI8+eo5jx9c5dvwIxpRMpjs2DTb2/ZGM8X6MTt6ylgjdZPprxFK/IwxJmnD8xHFu3dqlKIqaJvsAeZ/i1q7x/lS3tSDtLq01Gxsb3Lp1ywpgBGU8RbOPhYCqzDh79gzLy2O2b95kNBwx2blpA6md0Gwcwwx2NMbIeigieLfXAoIhTXu2EJtzZ5FRhKgLwhpkFNvaFhjnJmhfM5/ObCG8pMd0MiWK4rrwlaVVTsAxzj2kdpUTnD//CPfff5YvfulLyDhiZXWNJEmYTqc1v7p8+RJRHBGZRtAYDAbcuHGDCs2Vy1fJXXGuQtv6M9K5ryWpTQHrFSlJktZroLT1gd/cvI02ispAEklb90c4muXinaS2QCpJe8RR3wppRAgZgYicECZskVIHiL1bhxXMLVmdTiekcWznWFqXQOOyxPX7A44dO8b169cRQpKmKcPRkKXlJTaOHeXY8eOcOHGCpeUlpBDk0zmbm5s2C6U2ZFnGzZs3eeDBs/TEcKGS0dPi02fO8Oabb/Lsc8+gfQI6BEY5TCK1zTKGQArthHIH9KRxrliOhgknhzff1PzUCwN+vYMdiaxwsVV+j+paIJF1akjqtavPi/F1cIRrxyXzEAItHT4yzpujZt4CKWPr8umVbl65gs2zZ+rx+fdJRCJt2msS4mFKamCAYJ2T6Ai0NC6YHExZURUFqlKUmSafV6iioJznzCZTJju7TPcm7O1tMp3uUWUFs60dyllmn81KTF6gK0VZ5kAFKJSy8VVamTrVrpSyzuiFVxgFCg1Pf7TRiMi63Qu84GH3p1VcdXCDAyK15WiBC753w/MK5dgXcqzXeL9bVdfi3lW6dwWK/V4vzW/NczR7xD+nrFU9FW7tZeyKdcYIEVsrtDFUThng8WJkHEY2BpFXCKkxpsAIRyeiiCuvvcFskmN+9OP0k//AlcGrqmplcQrNPpGwvqtKa+sqBDYdn25rpPwVBpP7yQqFhvBzONnWJE/Lfaslbfqidk5i87pWewDtwZLSmnAVNvhXCkGSWuFiNBy7QoQ2gG11ZZWegZfffJOLly9x9r4zyDQiVpLDqyscX18lSgRZUSGNZGl5hVJpp8SxVVxBWJ/byCe33C9ktS93aJy22GADLcuqZGdnxtbWnDhNMQno9bOAcG4L0lVets9qY5q6GRa5h03YeTELfPJr6gi+SFLtDhX+hCPITlvjXWpCKFITV6jdt4Q7uI1oUXcQb0oRmBaoN7Ld/7a4tB8A2e9lrbmz2jBRt+0ldiElQnntvPX9lwLiOGJpeczGoUNEsU0vKQV16jetFRfe/8D6fUpJklhf96qyZmA/l0ZbbbgRwqY5dOPWmLpojsft1KNw/ze0grf9fRIsoPZtYJrQeeHnyc2u41EitCT6e2rhzTIZ6dIS+wxNMrK526UDUlEck0QWUAgEcRJbQJlE9Hs9ZlnG5Q8vks9nlFdf4+GHYq5c/pD5NOPc+fM8+fhDHDo0cghJ4tNSR1LUAh5osrmiXFI8eO4k09kOWzsf5etf+yb/5J/8M/7ML/+n/Npf+CVE8afY3dzmrbfe5o0L77KbzdEkJEmf0WhEmib0e/3axWVlqc9g0CdOYtIkJU0TRqMxURTRSyRp0iRtUM70brShKBVZntXriLFxUvN5RlGWzHZt5rr5fEaWOe29lmQzxe5kj6K0FoOiLJhMp2TTOZGxc5p5n+kiJ45jiqKiyIuamYGPU4hInPulMZooikmS2AaHK1geDdjYWCPt9VhaWmI0GrKxsWH/O7zC2voqx08eY2lpzGyWMZ1OyfISVbv+aKiqet9JIVDSplWttERUECURUnuvQXuvkJLISE6cOMG1q7dtFiTlsj2hSHoJ83lGZVx60sWyrKMpjaViY2ODN954w+Z0N6pzs32JNgZVSI6sb3Dm9HE2r19HyB7IHkIokliQl3ldrLD1Ch0cNidg+AxUylksitzxJ6FJYkkcS5LYKuerSlEWE6sBFgIjYoRJgAhVCgb9ZWZTxXSvosxBRbawH0QoI10BvIgIm+lIKIOuNOceOs/u3oTZvCJNUqa7e82ZBebzOVVeEonUdVvS76VoE7OzNeHcuXPkM810N0cIZ5nztZ2EJI57VhjA0pWe46V5aeOiSlUyzzOSJCVGErs4IM+zpIxR2FicJE5I4z49MSTyRQwjW1xQCuEyn2n7OYnRUlBpGwA/L2ZgKkSugZyKiFIqikhRlsJmfhoMOXXyhItDjJBxStqLSHsDjIYyKzEKelEPIQRb2Ta3bm2Szyvyec58OmMynaDQjscvzupjjGI4GKC1YjaZ0h/0rVJICEBZMqk8CDcY4dLpS0s3RUd2Fs4tzNPZ2oLhybhp8y6/EZVRCDyGCRREwgkgvr86BJc+eYF7qSX0jQJW2nWz21wHbwHhk1x4hW/zA8rzH9F4BjR6BmeN8X0InvMClU9RiwSRRsg0YbQysHit87wXRI3SFC7AfT6bs7uzw+TWNnubO8z2Jsy295hs71DMM1ReUM2nlHmOLitMqZBKoyvlclvNLWbUyronGmsRqgTMI2XTsRtpFbNC2sonxiCpnDpKWCxlvBVOoEUz74tc9BfVnuiu8yLrB+zPLtpgMf+3X98mfkMvuBcRKFWMTbvt8YSUKRptz6gLwgeIJAjvKix8n1S9jsa4xE9S2rgapI09MhVKTdGxJh72uJfrh4rRkFJSFEUtuXmmGEndoed+AzcSXViJO1wg744VWkS6Gojws7eQhFaR2rQrIxdUaZzfZ/Csm3jjGLbPOmKAJI6t20Y2J4qsFmltbZ2l8RJCG7721a8SRZIHHnyALM8YjYasrSzT6zmf0SiiKGF9fYPpbEYUJU5ja10DokjQpjZ34LrG+JlrjTtJE27cvEmWlYzSHoPhiBKb0k47sFwr0DVN0HCzEu3N7zXcLYEn7JcT0pod4PXkTsPtfvHahFoCccJCLWl03xgKGV4oEI3WvAbapgnYpf6xeUMow1oJBq+ybywzzf2yM35LRnXQpqlTpfoq1qdOnXQpVa0fdhKnbj00u3u7/z/W/uvZkyTL78Q+7h7iJ65MnZVVlVmqS7SYltM9UIMBBliCBiwBghwILs3WbP8W8oGPfKLZGp/IXTOurQEkaGtLAgssZgYz3dMzLae7q0t0VVZmiZQ3r/yJiHB3Phx3D4+4vywBIrqz7r2/XwgPF8fP94jvYbVcglJMZxOs7Tg7W7NedbgErmJf+L6+iE9ZDumVVKLzVWKRhZBw69JGJbkCKnXz2LqlCxMsFyLKC6MxphAh4SW+uTA9KYExJoEJlAqbZAAnIcBTQKtMKGtdim0nsKWsVy1HbSNhfaeHdPd/Tfv2v+PLN6+yOHuZe/fusbOzzT/7p/+Unb0dCqNo2qCohhdxCkCLIhpA3NHhMZcvXeTGjWsY813Koub73/8B/7f/6/+d3/zsLf7ZP/rHfP21b/D6C2/wd7uGFQ6vVqybZZIrbRuTIj3rtWa5aoKyZjk9Oub+x49ZLpes1otAN2lTQvpyuZRrO3G1r9dr2mCx76xYXq0dhmim3C9jRGl1QsxgigIdwkEUmlKZlLc1mdTJS2IKmM0mVJXQDdaTCbPpTKxSwaJbliVFUTKdTpjNZlR1hS408+15CL+ZUBSGoijDfTTOKRbLFR998pDFYinVrL0XS7WHRBHsJeTCBJAxqUtUVWG0CiIpKFBalFytNEobnnnmOj/60c9Zr1dZbQBPPak5O1tI5diBsnU+FCFfmHt7e5ydnWVrPtuE03XytzGKN974Ej//yY9FLm9t0zULtPVMvEY5UsJ+PIyK8hVw4TclhpTWDBVBh8W7FpwBbyi0kgTKoMTFjbmoxXpb1zU3ntunaZ+g9IKiWlOWGlJNkg4QFizjC5QrBYRZw/f/+M84PjmlUhN0Z9CBYlgpMay5ZcdU74UwGCEp2JpuYWxFoTR2UVIsDNcml5P80kjIm9YaXdYpLMwYQ13XTCYTvFMUfoqyiu5Cg/GKQmnqsqQqDBjQylCYEh1Cpep6QlFX6EkVmBU1VVVSVIV4CREZWVQlqihY25Ynx0esmjULt8aUivZ0wcnjA1brFaftkvuHB3x0/zadW7F3acZsu2Zrb5v1GpzTtHQcLc9Y2pZV19IqD6Vhd0cqg8+35vzsx99nuTjD2pbTsxMpsOgcmA0FIOlrKtx8/nnu3LnDa6+9tuG8KKRloooSOwyDSWf6YbJxmqsbLNL50dt9+ry3uJ+nvEjSR72czu6brgmbbmIozJ4R3mYA+sfvkGMnn/ZbNrxv/vvwWZEevlfAdVozEPcuAR4pl8eAnk+YzyfsXr8s4FgXKIeEWzWO9WLF2fEJZydPePjJPU6eHHJ88ISzJ0ecHh6zWizwzRrXdbTrRpLj2w5vLco75jbsDwihA0YJ+PYWq0jACoXU8DAhn899elG6TV6HKFfzcMOneTXGoVCk++Vz73zPD8K9YCBjIep2PVmTc15q36T79EUYk1coHNb3+rEfpUZ4b9nb36Woyw3AefPxuYHGdDoFSIxT+QtFFXKccCMhQn3593GoVO6tGDNM5aFTSvVsEZEmFoagBHpgE//OaflUKpKnUuJOdGE7RwrzUEpz8eIlqrKmrid89OHHvPPOO+zsbHPh4i5guXhxj+3tbXSk7VQFKKnAu1pbiiweNy4yUTKDt4MhOv60I55TVVVwD7fMZjNahHKvrALLeeCPM5HJwbpsjg7hQkSvvUWi39TkHCAw3vhMQimGcMNHBT8o/j7N9uxmMlHS39FSkgSqip6QDJV4T6TrTC1K3pWszzIJ3D/C922I9wrvqKIwUT3aD90RTpVFbrRhsVxw584dUCEcyjmUMsLM4WwIqdAoDc16TVlVQYD7oSCPXRJChbQOlgGtk9A3xqCMFrYOpTCmSAWsFPJ9UZTSzpCsmKyHab5HJiZ530ih6BXBWitKYKTWdIHyMxYnixVs08/QFxBCGbsGMvBvH76LO7yL61rs3R+DXTOtSt549UtcunSJn//8p+zt7fIHf/AHPPfcs1jnWDXrDDAyWP9xbmhV0LWWJ0+Oee21V1EUfOc7BVevXOWnP/w5b/3iff7PH/zX3LrxHKv1msPFCauuoevOaNs1zjqcsz2tKdBS0NqQuGt6q65CQTGU4mVZhjXnKVAYrZlOJ0zqOQSrY1EUTKZTmTtawMVkMgmhVAqjLfVUvCuqCIpHIcqaeFSiglaE66aUlcIUKtQpqpjUk9BOCWHRIVa7CADRWStz00NnXQpTWjZrmrMT4e1vwXae1nY4LzURPBIWFTMnBmOtRF6XhWE2rbFTh3PixdOVsGwNamLi2d/bZTabsG7WNE0TbqOk1lJQkv1o/fdiYbiLSkiPPG+5XDKZ1gM5koxLgPUtqnB89euv8y//hbDEbW3tcnRg0WuH073iVWQiQ6vceEKai44Q3519Za1FqwZlDJURD5lTEtOeFC+lMWWFrhRd07I+K2m3auriEpOJASMFbIuiZLlY0tXi8ZzVUypT40Li9ayaM9/fp6pqCmMpCqRmSfbuEm4rYUt1XbG9tc18a0sslUqhvvk6RVEwn86Y1jPKoqQMCduFljDgaGSYTASUllUBpaMwAswKYzBKU5mCopLEdLlGKGy9g7KqpD6Flv7SYX/VRofivT4ZKhyedbfm4PCYznZo5ZkYjeo8dtXiHCyaNXfv3+P/+H/6P/Do8BEfvPcBH394j6KsqestprMtdG1Ay1zurOV0seDJ4RN++7d/m63ZFvfv3+fBg3uyPgrFxYv7UmU8G6unhYhevnyZd999d8Bi+R97jPNQcyXyaUdcM3EZ5lgnt6cN9KYYFp2Ri4wV2NFTwrPOK8Tnz+qf1/+ee9/7nDYg5bDF99V6qIcp5YhR93n7cpKOfh5p3HIpIT1a5I3tHEYX1NOa6d5VtourPPftL0s0gnV0yzWnR8ccPHjM4YMnPLr3gMPHTzh69JjV6YKz4xPccsl0UeNsJ0VjfRtYsiTL0OtQlDKAJqeUVCH0DDxX0ag9DMM7fwiQGuq7uQ78tEP0skxX+ozzNx2DnGWiDqICK5XsWRHgRSKGp7VlHPoF0kdVWX6htn2hyuDxgXGzzivijhuYg4Gxcp+DC+g7tFfON9OWxcGKiyoHJ31HDidAZPmISnOeYJ6/l1KasqzxDtZNw6WLV1BK8/3v/4DVasFXv/o61jbsX9gVkBHiFzsvwStFMaFzQBC+Q0re/shdmOPwqfH75t4g5zzL5RLnHFVVcu/+Pdyl2O8+KK0KGzngk4TywWItSmsCX1HRyCzkveHG99bEAV4IIAU3omRlIKHGHotoefH5ueGh0kxHHwCUAYVMsYhuaKEAlL5PPRtwidxehf+HeHNF2vySuzd715jhIO8tfVdPKppmzYOHD4JlMAhCJMkLrajKIhSr8RRViXewvbXN9vYusaSHNloq+yrhXPEuMqcooTN0XaI3jfkE8XcB52IZbJqW9XoRYk29UFW6WIQp9GDX4hePhf3Gx7j63rISf49zyjVL7Pt/grdtuN4loN5bVuQebnmIXjwazE0TBFVhKvZ3ttnZucT29haHh4ccHDzm1q1b/P7v/22++93vUtcTzhZntG03CO/L7xfXgFaSF7hcroBjXvnSK1y4sM9sNuP5Z2/y4JMH3H3/Ax7ef8ByteLo7ESKJtkKo+cUpXgMImtTUWi8XqUE7elkkvq5mkyYbc8pEriAuq6EvaYwFEqUz7quKYwAg7Is0UYzm02ZTidJ6SwKCdcqiwIJzJTxxwibkYsWrlBrQoxnIWQvya3eO2KdgIdu3dDZNZ312C4AhrZLnPyd9WF+EepGWPGGOZ8qK3sV849IHOsuG1+frXmlwBhouo6mbWkmtcw1VzNVWhRSpUM4gZU8jetXuPvhx6wC139kDdKql/n9KurHPC3fTHZYa9nZ2eHk5ITpbBK+H8pRhcSnt13DK6+8yD/73/0BhdJcuXSZd379Dm/+4hccHx71bDMqJsqKIInzV4EkngYwp4yEuxoTkp2Lgq7tRGEtC8qqFOU/gs26pqwmzObbaez3dveYVBVf+/JXKOpKquqiqMpaQL2TBN26NlSlPLesSsmnCG00SlFqg9EmVBHXYtTqOqxXqdp127aSs1EYcNBph+0cUrtXkts1RfAq6XSN0H1aiLLBWnwn/bxqBJArbym00J92bZsU4PVqJQB37bGruJ/I3IwaWdfZMEc9retou46zhXgOOzrJ3+i8xOJ7g1Wa47Mznpu+Bsd3OWsXnB0es+SUI/+YyaRk+8IlqonkW3RqybooWBwcsjg4Zra9zVtvvslqtWBrPmN3d4+vf/3rktNJuRFoRD0m7ofXr1/n7t273Lp167ynYgCSz1uvz4Pn4f792WBj5OHLjmTWS3pT2Nf80OOvVK4YngfwSSHwHus2K8keidvfqOCqvh3jz5T1Yb/16dEp9mH03pEtChWs5qF9CiXkHrEYpvJSewVYLJZYD0VZUTc1RWUoQr2aUhnKSjO5ss/N61d4UYlb0jYNZ4cnPHn0mIef3OPRJ/d5/N5djg4OWBwfoRZnGNthVysKHJ0H7X2o5A5oMRCghop7rtfFvzfNhVg7aGxMy+dDPAbRPnw6KB4/J93f5B4HP/hOwttJxm5vA5BiOF/jz/z3sSFQ3k3IKZxzvff5M44vVLAvf3C07K3XjbBFlOUAJISLIDs/R4N5p3jvU9XVQQf5YfG8vC15uFW6Jvwewc+g8yBZb8edqcgSs5XEIs/nWyyXa378k59SVgU3nr2GNp7ZrKYoJL3UehHgzikm023aVpJllFFpnQ8nZwRH/twAj98vBxkyEWXTjkWolstl2sSFMUt4ooVqM+gN3gXGFB9K0itRfEK58IFXQxqbBJso3SMQlL1TkiMEW3oEB/G/EazgR9creTZD0BXI44OBxuV3ksSkQAEp69pmsbAqvUs6P/23T/QyhShIuYXIaI2vKnyIyzdGszWfs7OzK6EokwmFMRIG4z14oTxs2xbr2mAd7oLHI7ofZaONtKbOOfzZIzh7SLRE2WBFcFEJCwMmNRks3jZw58/wtsV5K5YWH3J2IrmC98QkHOc93jb4s8OsyJFPG0FP8awSeFNK8oiUAu88ZYBtWvXJrbF/hYGiJrq7UX0OUlFMQuih4+xswbVrV/nKV97gq1/7Kl9+4ytcuXKZw+NjYSDyjpBmf25D7r2SpA3t5OSUpmnZ39/jGxcvcHh8yMUbe9x87RmxHjcNnbVBqAsLjlJSV0CbWLHVUxVQmEhQoUKeQyWgoTAUZUmVlEgBh2VgkBp4jaRhidghAoI4jku7YNGA7SzWChi03orHwUpxKuejfPJ9booHMOALYshB/q9z0QcoR7+5qbCKdO+ZyNaN810Clz6MvfPRRd4neg+NMw6jPU0qdhc8v2Fuzya1LDl8smC/+OIt3nv/dqJxdd4n63mkRNVlkZ4Vj6gAKT2cD9euXePx48dcvX5V5AK9HIpyxnlL5xzb8zkvvfwSTx4fsr9/ld//O6/wj/43/1uaZsVisQAI80Hmeoq39kILipM6BUZpCmVSPH+fyC4huTF2Pcrz2C/rtqVzsYIEIUfBM59usWpWoSCZYnG2CIYDaNYNeI1yWpKgrcUoWZ9t07I6g65VrFcrVqtVkldN07BqW7QWmbReh2J1xtC1HUUjFKvOerECK0n+7ForjFoB+Cnd75+FKiitsGjFxNr4HvG7WL4glpUoy4JyWmCmEjZaVxWTaY0pQhy+knwNFdagLSyNaWjbjjPfctwsaLuWwliUKrDeM9u9wpVv3eDw7JBfffBrfvXeX3K6fkTbrelWZxw99JhiEuRFX2/ijnoPV4m3t9Kwszvnv/qv/kteeulFWgfeDpXu8RqKSt6tW7f4wQ9+wEsvvTSQTyI3cy+67HjxnKHVfzhH8s/G98yP3puRhcz03w4MR/nfwzAnf+6a7NteISXkS2VrsVdIw1CrYR+N3y+/LxAK/Q11ur4v3OA6rfvzbKoTpHpZoGTPLoFCB0rhyrJYrtBdhzJFKD6nQ40kRaskF0/rNc5ED5ymvDTh+pXnuPH684BitXYcHxzw8M6HfPjWOzz84C6Hn9zn+OAxtArdSuHVAqQKu7I4TQJfw/E6DyDy99fJ2DrU58Z9OdaF434zLgnxaePhIXDmnAeQQ5DX7/+bnp3/Pgbn6V2DMarrhO67s0/3iOTHF2adyr0QIELH2d6lpLVOoAO/waKfAZFNaCreZ3zuEFyoc9eBoP9sRaaOEquW7xMBx88Ohb/EW6eZzbaoqpo/+Q9/yqNHj/jSl16kqksuXd5jPp9gTKTfbfG+YN14ZtsTHBIb3y+c3hoXBaS8w6ej1XH7i6LAeUmUBDg8PGI6mfDJcklVT5lvbfHk4ECSGbMM8PhaEqurA381Ia+j6y3d4T9Z2pl8Fhg2vEfyDaRVPciICmkQUgMRmRZXr/xHb0TEGxGMpL8JydPk94oTHlECS1FwJb5TBEysVq21Dpz9QsMXLc0uxsubAm8tbSfVUnVIFrVdk555enrKydEhKhX88onuzzuPO/oInrwvXquuQT/4OcpJtVdnLdZ1SYlMXsB2DQF4kAmDmG+Ubwz9fMnfPeRrhL/xSqyV2TrSWqEm8xGbmU/zP1rDdFY4MgkP79E2FIHLvk9ATvfJ4SZa9bWmKCqqesL+/i6XLl3gxrPXeO65G1y9dpmbzz/P1avXODtbcnpyKqxECEiLynFsQ/5Tq6EF7+zshOVyIeFLswkv3HxWSCHwdF2b5qHznShCSqoGq3RPDa5A0Sf9Rs+QWP1tKCTmaTuLtU0CAo2zOGtpg8KdEi0R0BqNG2LJC+vDCfmDjV4n5FnWWVz43AWrnSSZB8UMoeyVeeFTXoH3YhV2qrd2jZWKuKOd3/QCSAjeNJu1N1UaT/0fvB5OkniLrs9bie+mlArsNYVUPQ5sQVeuXsYUOng0GipbBzBX0jSNECTE6zP5ntqfHc45rl69yp07d5ICNt5zQELs2k4KfN184QV+/KP/F9//Dz9medqyu73L9taW9F0jFnwXgGIX+kQHcCEMOW2gdVQJfDvnWCyXEoLoHJ1VyVAlYYnBYt+CpQozWsZCeZlX1rc4bBg3TdfFpFyNZ4LytShi3lLoEDsfEriHamTvtVdlKbk0gUIz7lkKmFgwiIImclHW06TWFLoS+eeFFUwHz5opNUwsRSm1W8qipKorqrqmUAV1MWEyqSSUU8FkUjKZTaj3KvQOzLamVFVJXZfBkNFL/IHibWVNeevoVh3O9UaWaOgp9ASnDT9/+y3+m//nv+Ct37zJowd3aZbHtJ2ncW2yXxVFganEYLC9t8+1q5d540sv8vf//v+S115/jVXTQedSYcZ8/gwMG+FnVVVMp1NOTk7Y3d09B4hzmZqopUbHeRC9+bvzF0ribbTcDc/0gw96IyxiEVXDzzdcIh/lXgxFuodK1weyA5EQQd/q4/ZV9t/0q49KtR8oktEIM1amZV0NXls0ZEsAGCaqATgdyCeMYmdnh+2dHdqmpe1CYcDg7Q+0A1gVwoGSGJW5aGK9GWPwpWLnxkUuP3uFr373mzSnCx59fI8/+ff/nnd++jPawyPKdYtrOrChbfSyfRPAyJXy/DubvWhODZ33UX59/CyqWfFem3TufC7Ewcv3i/x7rYfhrip/Npu4ABm8z1jHjn1xciLhuXrUpqcdnxtoxPjF3HMRlaQ4raMVKCo2WvdczdAnX23iMs4nZj4I8fOha6e/ZmCZ8CTFSgqInVdk4u/iyYgdHu34srFtb+3QNZY//uM/BuC1115lOq3Z39+lrmucRaj0QCa+NynW1llht4qhCrkXp/fOnBMlw7+ztsa+LkzBjWdusLu7w5MnT7j2zEVOf/T/YPrX/kvqqmZnZ5snh4dB6eoXhw+C0Xthlo8LNI6dCivbB4WT9HmMVhQB0YdDhd8jyEhAQedMtGFs+1yCtPC1GcTNSlKyJpjqMUUhOS6xaqo2aAVtCBsRw2wIyXCykToPtmtwZ0+CB8Bm4UIxqdknxO+aJf7ODwRMOIc/vY+rdwNbWIk6vEO3CsXMbA8Q8E6KHnmC2zqCrmgFFAuOsFep5GKMuDIK69gfRVkAOgvr6D1/IB4XpaNlnhBbGZVcFazzRkKytA4W5mi5NwnQRmtRWcnGFGOqI1W0UZpSl2IBLUvZxANg0UbAm9aa6XTK1tacnZ0d5ltb7Ozusbe/z87uDtvbEybTku2dOVtbc7yHJ4dHHBw8Yd2sU9iObG4aFQNfgyUmTi6dNvGwoeLpuob10Rr95FBCXoy00wQFS+ajsLBEwZyAAYEcMciSCNh8tFY7lZ4jgCHMGe+xqnePD6i9EUpPAei9nFMRPEdF07kUMhXno7OBJjAo0ZGlSSub1oWPQDWsU6f7vsDnfUS/3kM/5O304V3EF0YCHXKPvu7OoL89KBdyfLo20FS2Yb05sB3eT5mqGqUdWkko5zPXr3F6coa1oV+tMBCul4sBENq44Ybhjxa96WwSKLulanCS/fQLSSmRuV3nuHjxEr/3e3+L7/+HP+fhvUMe3znm+JOG1XrFerWms5LMaZ3Dh6Wmvfwrwmg656DQgR2QZBxKhi0lidCyJmVNl4WmKC2qjIYcyenBQ2kMRaUpK/GOmeBRiHk2ToPSBmOEea0uDXVZUhaGshSZWJUlRVlSFqJQF2UhbgXd08dHj3dRFui5wlSaqjQhIdxTGEVpCrQSgpK0nxRmkNRcVEUvn6PsUkqSdE3cJySvS5tQDA6p2+CDyiLjJJ5wTyS+CHuy1xSAocbZEO+v5Dpnm6BkeTrnOH7vCc995Xnmz13k5OiQxckRnV1jbYdC8niqSnKdtufbXNrd59WXXuT3fvd30Ao6Gz15rvfkQ28c8IGJcrTxvv76a/z6rV/zve9+b/DdQIlXvb4j320CzaMbb1D8h1/3BkKlhsAoXjfQX8IN3adYk8fAJlIzK0VgYzqvE0WPhidXpPs3Gudz9O2lL0AZPrPW9fIsvk8ENpnOmrdSoooV2nusdpRKi/fCB/KJQkvahFN9SKaXdsV8D+WCvNAarxVu3QQCB8vUeNbLBZ0pJa9qq2bvlZt8e/b7fP2v/jZv/einvP0XP+Xs/gNUI5E6WJnDkaI712/iGOWKefwMF5m/+vMisusNVr3cG493HpoV9dWnhmlFg+Bo7JNxPgIYH1nM5NzceyX6EQNjcS6nTdRjIRV5XK/W59bQ044vFDqVF+yLFLNt26JMIVH2haE0lYTShFj2uEiH1ledTeRhGFH+exT0UWmIna+D6zd+XpalKFzWohGKSpOYJkT4dW2Im1ZBIQsWVecdnbcYJXzyhoKd2TYf/OYOd9+9w5Vru1y+tM/e7jalqfEWFA5joMPgOmFYsd5RagmbsZ2hLT2lVsLvHywPWke+IWEiiSwgWScTYx2HwASKouTSpYt8/etf49//z3+CXWleMCd88sP/FvO9/z3bO7vcuPEMT54chpjGDoIF0hMT86TKLSrzNEVgEa3qYWOXBK+IamXTSUl/0FtiM4uKNqGAU1DEFdGaLgm6SkVhH5SvsAi8d4G9Crq2k7hobSS51Fnc+hh/dFf6JVqjvcOfPIRPfibKjXeomKOQzhH2sQhaQBawzRZVnANiUdM9PR9xEUbFyEu/Fb3yH62CQofXU9akavDB4mi0KPRaqeRFUcG9q/TQg5ArN70QCxSzJjDeOEWhRRkpiiIpu0VgiqnKMtSAqJJCa4xiMhdr5c7uNvP5nLKoJCdhMmEym1JWFbOpsBlNJhIfX9cVZV2kdlalKCTexbAbAXrCtNSxXracHN1nuW5Ytm0ogqhGQtcLt56PbFr5JjU0AKTNJMxS3zl8a1HrNgliAIsmhNQmi5J3Lhg6COEiPlnoUxgl+tw4R0ue9TZZ9GK+TLouG7M87jiObWToGioIoIwApT7pPm7yStS2CJDDWlFIPoIAkAB4QqJzArzx/ilkVN7H2bRlDH4qPDiVFDABI2EzUl4shng6Gz09C9aNp209WIfzCusVE18z0R5lPDdvPc8P/vTPmU63MUXFBEla7k5OhPZW+UBlbDOgFBTTEJiUG8ems4r1esV8tkWsxp2/isaiUTSrFbNJzSuvv8Dla/u89et3WD7y7G1f5PDJEbdvf0DTNslMIkA6UNaWhqoS4gWURxkXlPsihAUW1FVFUZW4kKgfQ4yi0a0oC8qqCDk8pgfoCQgE74OKIbP5PpBv7GFf1IOA0qCbDJW+jYcCG8NSAv11v356bxjZ50mRCBpHnIeomLnmw3oIvzkn93YqeZV7Y1VwRWNCleK+aS6zpnesxPOb1iCBCVKU4IOjM95+9y7KTZhPK4piwnx3F+87CEbMwpRM6wllUbE1m1K7lls3n6OzwoYXvcpF0r+iQmb79/Y+MPuRlKwrl/f5xV8usN2Ksp6G/UlnhW/jGMS9k2T0HFSfT24JkSdyzVAODJHH0MOSj00XVH9G18g98plyHlyM9Sr5W+Rafk7/ncKbsaezv24IsPrfXZoDckRDpHNuYEGX71w6J3qGfOijmHOonaLwHdobVKHofJv0Oesdzhq81dhO5LRCY+OcDvJUanDKM6KsXWmfvJvWtaAkx0kXimJnzmu/+9f50u/8Nf7D//ivef9HP8QcPqJWDhc8zV0ACrK+iUL6XN6GCgaHFJkz7BnxpIb+yxPiVejXOF5Rhow9cuMxjjl//ROyMYryQ52/TtHXTfHJABqBryz6dJlzokt6j3GwVc4odDEU2p9yfCGgkWfb566VHG3lzFNjZDXuqNy6ld83T47JnxEts13X9WgtDGjXdfGmqW3RC9MPeNSKSQpERPY20NDOZ3Mm9YQ/+sM/xNmO1157FfBsb+8ExazE4zg9O0VhaJsVu3szPH2itfM9mj/fjz1ytdYNQNfY7pH3d1Vp5ts13/r2b/HLX77Jgwf3efmlV3Dv/JIHf/n/ha/8XXZ293jh1k1Wq5XEt3etUHSGjSa62L3vFe9eqYsTM1g1CxHG3rmeKrfXjDJlMwgo7+hcQxCzkviKgD5nxcvglQq5BV1SiuJiEKOYo/3wR/hmgb7/S5rTQ7GYdA10bSaAk+YZ3kmFcZc3inMLhIVLl6ZfMKr3GPQhbf280148Bn2scdyUJHZfZ9VXi5g/E4RavEcOGIwylCF3IIZ1GVNITkBh8IH5wpiCKljqJtNpoDYVy30ZrPfT2ZSd7S1m05p6UlOVJZPJlOlMKk1XZUlZGqbTCWVVBPgYLLDaSEqHipufKJFiebesA5tW13W0bceqkxCi09UCjOoVDfoQwARCQ79GMgZZuyrUThFtOAJ7mWsOnE33HLDVeYhW0aRME5Ql3xsYolXPxuT3UCHcxU0xghgUkabXpfnt06MisBlb2p0PxeLSevUJHMf1E6+x2CTfcjf5+fWfbQL9R+FvYZDKz+2nbFT8hkqD9z7QAzM8N1McxjtMhBpJF4p9kG0y+BZU3/eds5wtF4kyeK/p2LWWXe9AOSZUXL18mcVCCqdZ59i/qDGmDF4HAfvo6I0+vw9Av8lK+NRlHj9+zHy2nXLbcuVGK4NWYsA4PT1le3ub3b0dfuevfpfCSW6CtQ5rv0fcfsVSG6KnlYQSKiPeW5kjPSCOSjmIPmEjkCTKz8Eojvp8+J28XghvUCEqI/V3FH0OrAUrcix/xnBMh0f+kVdP+z6Tsak9bLzn+L3ysRpb75+mY4zvG/dikfV93pD1Ic0sFnAtCt56+zbrtQdVUFeGsi6xSL0MQwB4pqAwkpehvMMoy/7+PqvVmriza93rC6nFqg/F69vn43IAFDdvPs/tD97nS69+ORmMMkZQAU15ihSMxj2bAU8BD/l3T+u7Qfvy8cim13kGqc1AIM4f50LI5gbPRPaCWT2GdLcImc41Q/4Yvn+c51rFVRdkV5Q7PhTQU1F3kO9dqENi8Xjb4a3DFQzy7ZyLoYtDa3/eZ7mSHj3nSkk9DKVAd0o8iUbTtS0XLlzk8eNH/PCHP2H/whW+93f/Ls9cucKf/Y//A6vDA2pvpZidCn2gBFxppVJ0zhgMjMc3nx3JAJCdPz7G47fpnqnfPsXT8bT759crlcucp7TN9zmezjma1Yr6cxbrgy8ANKJnISZtx4mboy9gACgGG7dziTpunCiVu542gYvcwu/DC8cQrRxF5m3x3qcwLwEAQ+aA3nIclVVxJc9mMx49fsRPf/oT5rMZL738MrPZjLKsJMnXOy5c2OPk5FQYX5DY3qKsiMxBsV2bESifOcn6c+W9pTCc58rVfR49fMLf+3t/h//+v/+XfHD7Dt/51vd4861f8P77P2Z16RZnJyfCRGIKXMgdIACpjqhIxPu7ILB6ZU5YmjQ6VAVu1muxDnuPbxa49RlJl4tWWdvQvfcfsM0SsKiionjhr2Hv/gVueYRqTiW34cJNfDHBP34XbNsr5ATrqgohDWH8aq1D/o9BxRjgpBTGXurZx/LvpbiZSYpwzB2KuSo6AotwrSkMhSnwId8oAoY4h+Kmo7VUqi3LQhhjyhJTKExNCi2azaRoXFXVVGVFERJjZ7MZ8/mcuha3vwpeiOl0GrxyOllLtZbQEEVgryqEfs95C6pD4RJ1qLV9TZvOdRytj7CLPqzQewJDkSFVJg70thEg22wb6YFoUIxjTZgwX9KaUQoVQn5y0CYKfYA5wasZE+DT3I7GVOewedxuBoJiGyLgEHzSb5jihQvti/SLRDd3XnVc9W1XEZSq4P08H0sbFifgGYPR5HXVw7yafL1+2vFpG8tgIx8oSUMQNzxn8/P6xzxFocmbMbiPjB1J4ZTvHI5V17I4sjw5W7JzeMTlS7tcubTL7vac2XTKfD7jycFBmNcVk9kcpRRNG2PrddjQ3OB58bXyvrl8+TLvvXeHF269NPBo5+8egW7XWRaLBVUlG5/1a9pgbfTGJ208KvRKqcAx7/FtPs+q5J0aAzYfxyiX3+k/uVxP8K3/PYrcAFZSHt1Y8QxzQG6z6ffziobL8w7V8LtotUSpRBwx7mfG9+23h/6DdM94vvz91FzD0T2iN87jQ78HKm6UFADVHpTGWs27t+/gCDH1SoMyFGZCUVRopOitMPiFsfSeq89cDUVTZaYOQwufTiE/BrhKKV566SX+7b/7d7z+xtdSH+aRHDno/6LH04DApnb1MgXiJDs//nmY5HlwN75fmreac+flxk7lGXwmEQ2b2zn+fSwTxxf6sAZEpvUeNwAsaZ05PLa1NDovc0AAeZsZn8ZgY2z08QHwawfWKbQVL+VqvWa6tcXNF25y+4NP6BrHy7/1TRat50f/5v9DcfQA31lManMI0836OLYxnyefKuuzdubn5ffJAeI41zl/xqZ+GI/PpuOzvt/UbpAVuFws07r+PMcX8miIAqQHneS9hAuNqW5zABCv/zSrXw4Q8t/zwZN8DT0QHmOwkg9KbEtZltjODYTyIOZaCauTBybTCX/6R3/C0dETvv3tb1MWJVtb23z/+3/GZFLzxhuvSUKTMiwXC6p6Ttc5ysrQOankbcxwUkQrWS48Nk1ERT8J8z5q2xaUY3t7xqVLu/hXb/EP/+E/4F/9q/83P/nJT/nWb73G/+LZgh/+5F/z65/e50xvwzNfD0pf7xmRDUsaoJTqC3UphXv0DvbRe4HHv0aVhrZphS0oKImqOUO1KwpVpDEWizBMgis9buDqyfvJ7ayVwk13cKtDGZvpTlISvBf3qn7KfDCBLUYp3VuYIIUx1HVNZBKqqpKyrFI/b23NA0AUK1pVSTiR9lCagnpSM6knoRZCQVEaZrOKre0589kcE0MnSgmTmNRSG6Ge1AJ+lBRTqyYVXvvQTjWYs1HB6i3sckhyriSzOmtpXItre6aqyHSVxHXo56gs9YJWDZSSaOGO8f3RlivxlTqFMSRriJfwssgSgw/VsVGITV8LzV9SlgQMqBCiozUhmc+FdRneGSFfUGFTGRpHVNpbpD1dUtRcsPzmMcVpzeRxQnLXAHKUFOdSUvXUupFi5sE7AbLK9yQFvfIXlOvwktHLgToviFUEKnrzpjJmwhuv8U2Wr40AZaAonFci0jXDLkn3jtbbgMRGltD83v01yQCjeusvVlzmomAp0AWrZs16teDoyWMOD3a5fvUiz1y/ztbWNnfvfERVT6inM5QWOdGsW7wT79ogM3GglPeHMYbd3V2Ojo7ECBD2lrGCLPNKvLSr1ZqmaSXRuQjjocYgsFeOI5AdgAnf9OMWnpBAgVNp7veGmiCrg4yLSqjM5fMeY5n5ajB2eZhgfv80N8ne4TMUXK/iOA8VQKWQ2PXR+bGWzGDuqVHoVvZMrWK94Sg7ssvyq6IRILyIsBxGYCEyxgTab1SoF6QL3r1zl8cHp5TVTKK5tArhGR7vCjwS4uYz2WY7y61btzCmwNo25EuF9b2hu87tuaN1WFUVu7t73L9/nytXrmw8L/856P/RZ72h54sBk/F1+eXRcJP/+yxPyVDX2QwQBsa7KMsyo4x8FAlJGD0zvywahjIDAv28dpk7SEKcs3WUlT/AhZC1LhIjnE9M3iRf47tuJBTSYuiIjHNaaxwtyoqh8cYzz+BUwfvv3eWn777Hra98k1tPjvjgT/4NanFG5aT6uJWqOzjFIAxqkxzPQWPe/rywY36Mx3QMEp+2D4x1p/z542T0TffPzx+vibztcTzbpg2sfZ9vbn9uoNF1XbLuxobmPNR5gzZ13tMW6hgFRkDhvXgk8s+jR2PTMyLA2LToNm3muUVMkos908kUow3f//6fMpvPeOPLb6CU5t4n93n77Xf45je/zmQypW06vFOcni55/uIzLBctYvXtKEoJrcmTCZVSow1eDdqc2pO9z3iwV6uWoiy49cJNrP2Ar37tVaazin/7b/8df/mLX/Dx3Tt8+atf5atvvMpiuebxwT1OTk9ZrdcsV0uapqFZNyk8puu6YNX26W8ZaPDtMc57amOo0/hpfGkoZ/vCXJUq7vZjoTyBzUYl17XkCQhgqCrhivfeUZQldSVMKCgv1ZDrySDnYDqbUk9KnJN8E/EE1BQhGXgymbC1tYXWAoLn83nIPSipKimqVpby/LquQuK4Z1JVTOqQR6FMyi3RSuHUCgjx9ZnAdy7Ow76GhXOOzi1ZLxZYG/jJg+UugTtUohiOylHcBL0P/DLhXrGSqO75B/u5HBVnD54C51Ro01A4xUJsqCJZMyVfwOF8h8MNFJoISDSgEnMFmRLmcMGSmB/KE+o1DFZhb0BAeMlzBqV+XSpsiMeNzE+RQKHzLtSCIesvOUwiEe2XUfpbI/SaocbAMFEyJGsHUNZfS2YF9ulxohL18b7nZBbDsMaxAB9vBqm50ZI3UhRikt1Y4ev7umcrG28sm9zwPQjNzh0olNIPWimh/4ybsXchtl9ypzQq0EqLAcE6j1IdPrB7KTyPHj7m6OCAoyfHWGtpmobFYsF8ucQUwpC0XCyD1y3ENsf+TmBh2H/OOepaCuQ1TZMVUcw266i00q8d5zpJtO8M6BGVuo9rSK4W2RfHCMCB6jgP20J/STZ9mpc+yXOfKedquEzSHD4/pgzG7GmWxRykcO68XrGLP3z/jNCmuBbHgFS2pADGxlbnwXk9cHb9h5zrp8F+HEFeaFeWy4epsR3ce/CIT+7d5+RsGVJsNY8Oj9HlFHTMCcuNT0Ipr4Lg1Bqcs0ynNbu7exuVtrGd4NPAQozYsNby6pe+xM9/8SbXrl0bEM5sWmfj+2xS9McyYXyM1/Xw3JBjpuK6ztkKHZuMHZue3/8Tr3gfWjQEGkWMCpBH0wOLiBUzr26GMHK5P3hT73vZlr2fJ3qnw7s7R5fl0XVIJKH3NjMQn1eIP0325kbv8IvMKSf1kZy3gQBGYiqmdc2NK5dYnC745P4x73x0j5e+9T2WTx7wyZu/RJ8eM9F9IVzR64Y65lBXHe4d+ffj+Tr+fRNA2XTu064dPzP+nZ+/CRh91pHG2Fq6tqWuPl/41OcGGrFBeTa8hCX1MdZDas2n3ycfjHi/vIp3XACx2N7wmj6eezwgY/Ay9pDkG2/fHodtJaF1b2+f4+NjHj9+xHPP3eDa1cuowvCHf/hHXLp4iRdffJmrV68BnuOTM5QSzhJjQjy8UgOAkQbS+4xxZ6QYZshb5PfQHdofhrPTNbOZ4eVXXuD27bu8rG7yzI1/xo9/+CP+8mc/4/t/9hecLZdoLYmYZVWjjaZzCmVKTKWxzTpUFIWiECVXlwV1lSl0pkiF5UxMeNZS7VchFs/IQhRD6SaTCVvbW6jg6pzP5kxn8n3bthRaM5/W1FUt3oHphEk9kaJKhaaqK6msHGoaSHhSidImsYzEcSurAqOjwi4ArTAarcug0Ii1XeZoEGrOhgrZAgSaLtYHaPo4f+/xKtDfep/CKKIyPjbAJkXGgcJk8zA+1wsApS+GJ9/HOSAGgUi16pxUGzcxnGCspITrrOuwrm9PbH8KQlO9p8lDAhpeicctf5dkQfWuf70QKxvPM2popZdaDA68TjSpsT+kpoo014V3trZLyrTcQ9PZ6FWL3gv5aX3IKUqb3BBs5XaVaN2Tvu6gEc0mJuD2YU8K5WPoZGb40OM1RgJfIAwd4xjccEo/JzivKOTH8G8BqlF+jr3DuSue7Pcx0Igyz4V46pg7Mrb4xWtyWaRUIHNwIdHVijfLW9cXPHWWJtTEUN6jXGyfZbFahPDBEtd1rFcr7t79kA8+uE1dF/zW179B27U0bUvddpR1RdNKBej4ntmLZVNcDdqvFOzv73N0dJRovTdvirH+i9wvgXw7HJ9ht4pV3cfyOL4nDNis9OdgLowjsemqt97TM8rF9xuqjEOQnN//6YAj76Pzx2AvUww8ED61briOVAYEUtdseLTID/WUZo0/HIEVTwI7sZK91oa7Hz3gl79+j0ePH0v7tMGjUaZAmwKTQkhVwE15v/j+n/IoZbnx7LNUVYEPzGI+GWjOK2nj9bqpH7337O3tsVqtODs7kz3vU4DCpnvmvz9NHxp6GYaK33jfj3uF971hKZ6fg+k+xChfR2r4uQp5i7qXkf25YFQveyNIiN/1MvnpgCrOmvi1TtEcEMck/u4LsndzWGvSXtB0wijXdSox3tkYMRN4+/N32xQ+FPvBWqG3996jfAjfjHMTMYgVCtrVip2pgI263uaDT454cLrkq3/z73F8eEpz5z38+gyjXGLx+yxlfazn5n21yQOx6fqn7SlPuy4/P2d43XS/p4HkTc6C/g/xaBwdHlF9zjyNzw00BtULs0aYoo/7HndmbPAYAMQj5k/0Rek2cw6P7xUXWAQjPZA4L1jSogz/7TfcTOFD6i3MZnMe3PuE737vu1y7fJXd/V3ee/993njjdV5++SW6tuWtt97m/r173Lv/gN/61vdYNy3aCK9/5CmPllPvIt+zCOwo2MdCqW93LvmHhyh9jpOTU2azKc8/f4MLF3Z5+OAxv/e3/ybf/OY3+fCjj/no4484ODjk8Og4FDOTQk/RvS+sCw6tDJUxbG9tMZlMw9iJ8jOfb1FPJngvLDExRGkymTCZTITBqK6Zz+cUhVRMns3nTCYVGEtVS35CdL2WgQ0J2wkFZJark1tZcqEZgazHyL9s81ivV5J/4nprSW5hjsA1Dxkjm3tROQNC1dy4+Sqs16RwfoEH4XI9UA7lfJ02taH1uw8NwpPyEwaCyUtgkvU9gHDeoT2JQzxgi/C97QWyt4lOMAHX4HHRysQXjKumD6NSfbuG69THF5a/bLBg+SjQNrGUOBRaPCQMlSgb47Hpn2tdP7djhL73PSNNvxY5V4emB0X9OgbS2kqjleaOtDkWf8J5JLRrtKHj8BmgGz9TE5NHozLZ99cYGEQ2KwhECFEhHa3n2M0eULYPVzinmETDA6EKe+ijmDkT83fCTAxWJqnv0LStVGZ2UjjSdh1t20oy93rN2ekpy+NTXFgj1lrOzs5YrVayKXsrtLBtG7yUKlCoGppmicdTT6ZIXL1jtV7Ttg3TacHeB3s89/xNYYzD07QtGsVytWY6m1DqqAwPVfDxYa3j+nUp3Hft2rVs3+jn9bBrdZC5HTG8Ji2eMD49C5iEcSWQESiOSSE+JJmB94H2M8yf+HF4B4+sEx3AvQvP3BR6Nwg1yh4jAGUUbpt//2m2u4E1M/ZLvp43ABgVwuCCfBsAoBzXJP1+MwASVqEeVPW3D9ZmWcw4B9ZrfvSTn/Hu+5/QuhJ0JXM8FP40RQFKY7TQ/Xpc/2oD8eRF7LoOjefW89cDIB7m/aRW+k0KfZwa/XuJ1Vyndf3888/z0Ucf8sILL6b+lO/oAXl6jB/MxWhUih7HOA999jPPd8sNB9K+fKKQbI9pDcS5EfZA2WYFRIjyHfo/Mp9pk4ENQr2h6BHoQYjChZomsU0kr1jsyx5sDPWsHtz0S2d49GAo9l3MqZT31Ym4x3tPUfoQOVBiYy2jrqOzFmd7z4fzThLIA0GIVn3x0tgWkIgMYceyKZRdayWFTDU0tqUynpVdcuXiPrpsWDTwyf0jDouKb//e7/P9f/Hf4roVBbKWW+sGY50DvPyzvH/ysR3nKmcd2vdZvi/EpZYA21CGxlMSbXWYKptA76eBm6d93+vSkkzvXMek/k8MNPLFoFSfSNu0LWpU/Cm+0NOAR36/nPY2XpPnZ0REloOUPn57c7JMX802By1eEkYDBaDNQys8TKspk6qkLiv+/t//X9E2Lffv3+PZ52/wt/7m7/H+++/zq1/+ivffe5/CFFy5dJ2d/Qucni2Z1jq4Iws0GuUKDJrSlEHx0xI+Q1Dy6du2KX7OZxuerOvwXTh3sVhhjGE6nfHCi9u4TqrEvvbll1itViFMqmWxXNI1DV2ozluWJbPZDFOYMAZaqE3rWjxHCF9yVdcYEzcihF0phDQpbQYCM/60zmG7LghRP2CV6pqWdr0O8c49UIx9LxbZIcCIC8wHgZcry/FwROAZW0q6R+zHaAXP9gRsvpnmG4HMjP6b9H7DjWQzU1i/oQ8BhUOIL3rlOIYJOSJrkEhEKSomfeSc7hOfszakGihRkKheWDtgHUouwdBqAmC87hVm1Y+D96B9n2A9ZBHx2NyrkL8bDiFlzeJ5Aa8i8OlDJnK6P636EKi4GSeg5CO485kyEDcmARAxNyXJFhXfKViw0obsUV2Hcj5VPO+TzEFpTavDZhGGSCkS936BzPXO9jSFcW5HK/bYYACRplHOt+FcKbDm8aGAW5R9bUjob5ZLuvWarutYr9es12uatmW5WKBth7NdCk3quk4qRnsPIfSz7QRExBDJtm2xjYQCNc1aKrnanPHHpncYJs+K8hHrsJSF1HLoWo/RM/Z2L4jyUhiKqgxUmZ4L+7s0zQLrGppuTec6WifkIauuY+FadpSl1BrtRINxGIaLk0E7Ll26yDvvvIvnNRnLTHFw/nwIgsiBIngzgvcozAvroyW0p4KMygiFxGyLYhUBpLTRx0mBonNO8lfwQfvzwVvQK09KBda56DUZ6BBjxaCPd88NKXLEMelDvDb10eC7qBgmTTQ9iSHYyMBsOHHTMzZ91gMgFZKzowzK7uHlM6Pl2Z3T/PlPfs47HzxA6RpdhroIOre292sDdKqQHBeSIXqRggfLw958wqWtOd53yXuahit71yTJ/PBzvMnkTH6h58aNZ/jhD3/IrVsv4JLnyyMhlUEmZ5A5L1ir8BkF9dDivckKnt9/fDjXh5XmyqsYM+MckLxQbTTGREu/CTqaGYSgyXf9c5SK80slOvZcQR63NZsdQ3CVD366d5wXPQjsdcQwBsS8E5kDMfS1oO8T50W36LoOazNvR/SUe9njnXVCBxz2gx5jSsidVkEbsF68+17qUTln8RpaZdCqwLawtb1FXTxiVsLJ2Ypib4dbf+U7vPc//U9UKw2tTQU24xrO99txOkDucR6DkLy/lLep4bGLFCqB+qzbMEFWiQwqUverbMxSPbl85DYAj7xdm37P29jZjs467t3/mOn1axvmxvnjCwGNHBQMk74ZdHB+fr4ZDGJmGSps+YadT+5NgxEXcA5axop7HsI0ziPJr5H6G7C7u4Nzjl/96lccHR7hLGxvzflbf/uvy2asDd/69nfoWkfbdly7cQOtDW3bsr1dhCqJvecnJgdKnwWKTXxAgi5tmsOFrNJnPZqNMDW8s9Zo5YWCdLUOXgqhbxXWo62kxHhPqC3SJykao/HEcBOZgF1W+dhay3K9lOclJTwunBBLTl6nQG4i1gcLKngfYtvHirqKr9aH0gRtIIAOFzb8XoAP5gW5CpyzwYznSwxTiVaWvgEu2/3HlmmydyYbo6hU+OxnrizkKzkVUIvvanOrWlRWwRIoVOnbLhYzL4plZwdVlWP7vO8tpjlFYLDRZ/SEY2CWbbsJFKgU1if96NJmk8aLnJLUpe3Vo3ogmL6PfRMEXtYOH8GBd6lzYk2UHADkfR7Xjacv2ujTNT1I9/Hd4nwJgE4h4CWNmY/jKnM0UqcO45V9UBhchGUhj6QPGY0gNpdt8XPrLM26oWmblP+0Wq5olwva1ZLFckHbtCyXS87OznDOcnZ6Stus01rsOvFGAHS+S30a31mK0MX4bWGFycdaK432Kq3btlnjnACN/f199i9dZDKdMplM2N7eJrKdTSYTZtO5hEfVNbMQHgmSBzWpZ1IlOkwJoZc94fbtd1mvG4ogC7SJHPmycs4WC5zfCyBN5lQypaQ1LlfE95hOZ6kI7Hj+B9bpc/uO7E1xL+nXBT5Yb8PaXK2W4s2M6y7E51dlSWFC8TpjcJ2l6TqIxBNKhcJxfUikUkJS0su7MHdGoVhjhS1XRM5/7gbnbDqeZsQbnhRW6hewZn7akV863tP7Z6i0fXk8H9y9y90PP8YUFWVZA5vZ3MYKbt7mNFeQvC6855nrVzFaCftj0sA852hfU9tz/UPBObAav3PUdUVRFJyenlJXE3LWSgGjwZcb9ZcoUxKTUmxOb5CL16c9x/d9+jSgEYt+5vpRAgwqesJ0ABqKoogEKuacXMuam41n3z5rkTDJZOwa0AGGG2Tv1t9ksJdH4x5xb6Q3Olnbe0W07pPL+5+kmysl72pUQWGkcr1zjtopus7Stm2QrxZrO7pO07kuGS6djfNSwgOsGyrPsX+0VmBUrG4m1Nl0PP/cs3x098fMdnY4XJ1y4/Wvc3j7Y45++SuqwoO1ZJBgI5g4N4/HYMQ5UDrNP8VmABBrQsU+1iHkIfeD9maDfHhU/7eP81dkrneeXvaen3tPkxNGKcnRaFpszO39jOML52iMO046wJwLYcrBSLx24EVgc4eOY+3y63WwikZvykDRGLWvyzog94aMLZDiDZENVmvFlStXWC6WtI3lS6++ytnZAqMNZVlR1TXXbtzAWsfWzi6rrkuMKPGeMbF1DJj6v/vQivNgQ4RffK+obMXvZAG1SenA9yEb/RpVyRrkQZR/n3kK5BTpoxA3H+MfvXe9ghaVrnBBDHEDpABhbHNQWGM+xIBOMLxgfEb8TDGkhotAIyoJOW1iVDMHp0cgFjb3IdDoCyjlFdBzJOCz5ZlbpfN5kTdgMP8iJXDfcIZCMggBn1k1stvF+iLkinevQ4W/AzrSuv8qe7+EAcIvce15fCpGGJo1WmOjHSLvFm8H5+XWoCGNZR8CKHwg+bzqhWxUBsaWOAEyjpjv7rI5Fz12ad6kjVjCXmyYb0Cfd+JJ8z9uvvnrta2wY3Rtx3K5pGtbCPLAdh3daoUNyn3bdrRtQxvCjmy7Du76jqZpZTNrJTQp5vHEdsraj5ueFWubdSnB1NoOrMN4N7jGGJFjRSiECAh7mtE4pajqCmcmFJMSo6UCdF3XeCdkGWU9parrxAgYZaMxUjhzuVxydPiE27/5DUdPDvDWcf3Gdb72ne8y39mWPCsjhZdMUkxiwchALR03Rw+lLsWqrxVlaairiulsyrvvvM1yuWaipH5FpK6MRA1nZwtsZ1FlRb5uGGyVw/npvWdra87x8TF7e3vkx9Pla1g/yUKhwrzSnB6fcPDwEWenp6xWK5bLRWCrWrNarrBtmwprzuZz9vb2pJifNjQO9vZ2efbZG0xmkzAnFRKiZ5PVuFc2VACj2crZoOxvAhK58vtZoOA/BkB8LoDymTcBx/A+/X09aPHgN53jrXffo6wnaF3iApHIOBF5089BG+N9kdAprRRXr12l7Rr6sOQ4H4Z7/NPeG28Hfd2/msN3HTdu3OD27du88vKrYZwDkAkyLRp1xOBCYDPqFXefkrb9YH7mYDi+lh/tY/FwriceH3uoFSopymVZoI2EtMQ1PKb2HfdP/CyBu0gHHsBC+plGwGd7VD8q49GK3ycjnLzJ4B3EAByZC8+DTrJ3Hl+nQ8HaMuTvWiee3rZtaTpFZx0dli4jFfFZf+cAWcZC9C7tFcZbtG+ptNTJeuP1V/jLN2+zfeUyx7bj1b/yt/nzTx7gn9zDODfQJfIjX7vjcSN0nwr76FA36Q1uY4DytGd81vrNv00ahQ/9QOyD83XugI3rA+fRRvHo/gOeu3b1U58djy8MNOLL5YpnVP6VGoY65YsmD2/KFWmhrO0LnY0TmuIx9l7kgGQTeIigJ95/oAQNFB9PXdccHh1RVxNu3rzJpYuXMVoQtLdSZn0+38I6z7VnbnC2WLJcrbDWUdd1UvQk3EioVvM25wBKB+XRoxLrU94uH2k2kfoIEJl7PF2wlubXxDoZcbp7T1qoccOLnorUP8HSO6BCzWlPFaQQmwgUvMe4mFAmeQ0i3LPQHidCOoPJcfD638ORJ9n6ADQGwje+T7CPxOkQKY7F3TpkUPKQ3MJDoR3mbkDybqRUD56X/RnpH10QVC7kSeTXRUGhA3WeKLFRQMfnZfeP/eZ8SsqPlogEvsIccF48WD1AV6nib1T8ohIOISwoX3fZuWJFG66ZqAjKxf2YyuyM6wM6F6lrQ75JuG9U/uP8iTG3EjcrIQZxrfbrDRS9ezj19chY4L1P1uyorDeLFV3TpBCigUzpLIvTU1arNdZaFssFq+WS4+Nj1qs1zXpNs27SnIrPESt/7yHxGUCELlgMwxxVJAtUNKLmCpMxhrIqKUOdFQqDMcKkZopQabouqSMJgjFMJjVlWVHWpfwLBRrLogSgrEpQYAKQiGMQq2WrwNATZYwL+THOihq4Wi45OznGK8/Pf3IkHlU8u5cvU1QTyqqUsRHNQOSS72UXYTM3gX1KVzVGCflCUUhYxvb2Dh6Ns4qudfIvkC0YrVFas143rNcNrq4oQkVmT+7R7udlPkevXbvO48eP2dvbG4IJP5Sr+bxxISzMWUlk1yg+vPsRP/mLH/PJh3d469e/5ujoiOVymayiShZgmqdJqdEarxTlZM6XXv0S3/rOt/ju936b3f09VPBq9eNhQuiHKIjamExRe/rxNICw6fOhMjY8Z9Nnn+e+m+7xORqdifehwiPeJofXhg8/ecBy3WF1AV7CcMfei7FCNaanj23UWhPI6tiaz9namoO3WOsSTWrennhdL7IzpSnJzw19pWRe7e7u8dZbb/PSiy9jbVadnhjmCjbseclbOpqf8nkwLNB/Bz3phOQIDUFJlLE6mKIH3sos9yLmtwrjXvRwwxiwD0G5O/d5MsaqDPCkvTX0YQY8eq++fJ4btQbfxetCX+TrygBG96FcaV4EK9TT6rRorULeWBHubajLAusc67ahaVuadUtnLV1r6brAEslQDwWSfuiVwYQwxQJF1zQURcHly3tcuD/nZLlkurWL3zM8+/Wvc/sP/zW11oHa/fw8/tQ16KOnRgXmPOKEkPD+7B753jI21A/12LHBdQh00mexbd4LC1fQ2ceyY3xt/kytNL5rOXx8wNajx09/z+z4QsngY4GUGuhlwMqypCiKQYeMBWM8xig2v+9TkaB8Sr7wciCRM1flAqvrulSDYTwZovXvj//oj/nrf+2v843f+jpVWfPRh59w//496kLz7tvv4lB0Dhrb0TmHRUI5ylCoL1p64yKA8/F6EVhJcvAmi1x8P9K5kb3IeqTmQspTcUl5VD4XK31MakSssV5GqoxMEDaxD2PYShR2YUxTrkUSRjGZuncYpgmKgCTFMIQgvksSoOGQjTl+LhaF3suRCePcshH6VQflvben9Iusp6HNcU6wNsb+Vj6VTRgf/dwD5VTI91YpmT7HUGm4vKfpuqCcxz4J/aLOK0/pX7g+Knn9u8cxko9jLRSVWZF8BJyqzzuIoSB53w+EjHfiHtaSMCcF/pzwi2fMW3HdaK0DkO3HtOsske2p67oU6w/QWEvbNjjn6Zo1bbNivV7J2nROaE6dDfkaluhBiwUmxbovOQWnp2ccHR1xenoqlqqmoT1b0K6a5CFI3qvggpbwF/FkxdCE1NcuZ/6SUBm0whcKbUwowFhgTJF+r+qSIoTMFEVBPZmE6us15XSWaJaLoqAsCqnRUhTowgwoWZMnzGiUMZKnFeROmlA6rqLeUADBy4CSPB8l1mDjexINP/IgKoJsQLKNdD3BKc3Nl17h7bffpVks6Kxia3sf67OquwMJIv+N8sMUpcx/rSUDKLj6JZ9Go01BUVR0ncd00Ky7wO4W5byhWTUsl2vsfCbh62q4/MbKUPxsf3+fX/3qV7z00kvDtTMAhP35Qj0ZgG2I9T85OuVf/w//hl//6k0+/OA9zs5OU3haXEN6YAxRg7UmG/QRh48f8clHd2maJV//1je4cHFf3kPZMH9lO7WdRSlD17VDRSI7vogXYZMCs+n6TTmRX/R54+s/9bqRUhL38qjMOOX58JP7eFORe8k2eS7Glutz30NQVGWsrl8X9kchPNBkXBPke+smg6Tc++mAS/JFnHgJtOb45IT5bIu2lfGMOaIOAlFAr5jnpCAxdHc8R6XdMbQTSMQEOTCROW6UyP0IKGL/GGPEwxkMELlyGhPEx2MzNkDlfRTp6n06twckUa4MemvDet2klEYDYjov7HdKgVFQGiOhmGoY7q60UPluMjzrsDbjElVKwp2M0RSloW5L2rKlbS3rVUujW5q2o+0k/DUaXXsdUWGVDntTHxqM7/DK88YbL/Ef/vTHTOqKg8UJ1157lftv/5rm7h0063PzbFN/DPopOz+2oQfEw+iIfL1HHTwHh/1zeuA+9k4MGAnpAUcckKcZKDbr37JVFV7hO8vWfOvc95uOzw00YkNy5bxpGkByBMYvNA5xyhWY/KWe9jKfJlDztsTnxM/y87uu68MIRsIrtikO3u/+7t/g+OiEpmnYms95+PAhZVFy5fJFZvMZZ6s1nYduscC1DU75pDCI8iWWz6IoktI4HvQYw03GDd3XK4Ch0tx7IbxHnu37UKlepqoR0ECsEiF/wma5ELny7ZxPjEF9rGAfvhSZWHqQBFHU+FgNOsSGR4QsdvDRxprASw6B5LDRsxDoJSNIGF6eKeQqtiFsWF73ZCcRTCSFvFe2BZjGe4eSO973lUkHfRfmpJivU2547JfY0zlriCfQM/uoKkbhJ/0zZifKBcVYaIwBQhcS7JXqw9Ny0JYsUYN7k86R9SUbkfExJ2S4AbVNg22bxNyhkBwAayXXYL1cpSTkpmlSsrK3lna9Sl6HWEOhaRpWywXOtnQxxIheAc7gZBqnNAfpQyTzitDpXcKm2sfXyvouJ3UqrChV1nvDgljeRUFYrVd8ePdDTk5OcN5x9fI1vvXtb3Fhf5+dnR1MAA2mKNja3mFra4vFYsHJyUlSZLUp6CIlaniPaFxweLzJhLwPeVXhZxjIsJkOSQUEM4jCmxdT08r0VLxao5E1qI3BZZtGPB8VamRoKE1F1Vh2vOHZ517g9m/exRS1zKMQ3x3QTS+LfZTJIkdsJ3Op9S2t7Si0ptCKuijoVMvWdMaF/Yt8+MHHOOeT98J2wgBVGIPRBWenZ3R7O+jQPy7JhM2Jp1rD9va2hLx13eAc7yD3gCZZhafrWgl1azpOnpzy5z/4C27/5jb3PrrH2XJJF+SnKiS3jajU6d6QkOf7KKAqRL4/OXjIb959i5svPMvO7oxLly/R2o6jo5OQN9cwm82oq2kCuJ/n0E8BJHHdxGOsFIwViv+Y49OUxaedJw88D2pUMMYoFIenxxwen4IKYYExbJBe9oz37HzPyZ4M9EZFh2X/wp4QHLgGawtSGGp2X9jcJ/29NwMNIR6QtX716lU++fhjnn32+d6AhQpAPsizbA/E9YAhvUdU3BMgkR5IymYONDKdQQFOSaREHhIZf8+NtdaGGjiRpECZQT/0v6toyxoCDR081BGA0Id3xbb0aIahZTx96XpZIhf2lPKhHV3XJTlTaoUvLNYWSeGOIYixnuMAfCRdMXqleoAFWV5sVYa6XY6qrGjbjuW6YdV0yRMe5YkYJhTKmoBgHNoKCPJe44oGXWi+8eotfvjTn/GVb3+bO++8y+vf+xv8+MG/xNjm/Lr4jEPRGzWkyPG5qZjGLDeYx/k/JlDKjzH7qvc+0w97yn4xJDu8HqYepDbm+8G4/d5hUGzPt9jZ+k8MNLq2C0mBECdrZNvIQ5TyRqYX/RThlS+W/mXHaGy4IccQgbhQrbWDqtH586KXI8bNR2U3emKMKbjxzA2Uhzvvf8Cbb/4Ko0t+/rOf8/LLL3Pxwh7WeXZ2d9FFyXbX8fY77zCdb7FertO7OucwoVp1HNSxpQcCO1NeBCjzGESgkd4vi0F3IVyjtw5ENY1Rsd3eGhHPyhVP6ZMQ7hTme0wYjYJU6AKDUA0ApB+jkFSsQcdcAp8pO1myWD6esU/i7x7SRtULcILlOZ3axwHnkz68mwphPPmYjxOyUsx+XEweMJxj8ojnd17mW7wuYptUOyK8gR9JhoESlAsIRaKije2DEBblEd87w3UQn6HoY75j/Q8fcgucc7RdGxLGbX/vsIG4LE+gs5bVcoFfr2nXaxZLCf1r2oa2aSSsqBGWI+cdOI9tLa6TmiLWtbRd5oVzsf1eEuIGoYw+ACPpr0iZrALLjFIqrBPxBBRlSVWWaKMpCgEJVV1ThMrtVVUxnU4pyxIKHXj2CynAGPIHilK8CDqsPQkv7JmuPB6vNW3b8fjggHJnmx//xZ+jvGayNefWSy+xt78XaCCVFHosSrSpKMoS3TmcXopBw9mQVCiKZwKl4d210mBMkI8qyUfvIwxXYDLFMsqPzPggxg+Zhx6XQpk8Ej6plLj6rc/owv1wnXSdxWuDOLkKMCVf+ca3uPrMc1y/do3lqsEUJjG5QAz90Xjfb+pRrrdNiy6M1MRVYmmdFIa97TmmULz44k1uv/cey1XDcrFmtRIronWWslSYQnN6dip04JMqzJOMHjVXxMK6syEEUSnFcrmUUNaoHNkAqD0cPjnk5OQE27WYQoORvpuUNVtbNc89f52rly7ywfu3+fHPfsTjx49oMya+oiioyooqeLLEm1UznU6pqoqqMFy/cpEr165y9fp1/spf/6tU05qHjx+zt7uPc5qq3GK9WvPo4W3ef+8OX/nKV6I433DETbz/RPYplZ3fy848hMTZkI+UQnDzuzKU1aO49P7w2X+H3yWlMp7p+3OjkpeeNrp/vFaAt+HjT+7TWYuP0RA+uOV8T9yC96GmgRr2le+NNvEDFyIBtuYVk7qmadYoJ+GQkURDZORmXSLdLe63GbbrLcrhWVbyL7e2dvjVnTe5cvU6IKGFNtwyGXhiP3mhh437RWpX3Hey50hdJ5/2ut5ARJobWutARRuVRxgzSEX5RvAO95KoZ2RKz02b7DBUK+pYDmFtcr3SEO7lg+709ENl7ybhkmEHUxoTPOhKKYqQ0yqGLE+DR9ueyTSBCutTH/QgJPwjGLt1LMSaKdhanhnJcIrCUdmKoiop1h3rdSFMqWsCVa4Tee4tGFFurHe0eLxW6LWjBC5f2ObaxR3e/fUvuHTxGmW5zYWbL3Dy9gnaCpW6DXVztFfnQHhkf5J+smm+W2cDJW8Abdqf6+dcJqZ1HY00Ks6fID/CB0nfUoDOPYnhOeGn94FmODOIjvFL7v8ACW1zzjGd1Fy+cOFTZkV/fAGPhrjAnbPosEIVPUVd9A7kiLW3qPbK8xiE5F6F8ev1AjmztA8ASb+Z5wpj/uw4OcXSELrNeUIWF9N6yqQowcOX33idw8NDLl7Z5+vf+AoApjacrZc8fHIgsaAOVGexqxUmi5+PCyV6NKx3aO+GCNK5ADRCXK+NnEPRiqBTjL21MUdDDue7PslcLuonZ5pwww1E/hj2tU+/i7Iew6PEEhqVdY/xcdPQoZ5A8HIocEh/WnrBR3qT2IIweV3cYHqlgQDy+jY6Iod5VHoGR5LTPXtQLryTQFU9CNCB3lJr0/Oeh/Z2rusXPb2A9woa7xPQUF7uo4O1xtKH5fgYcpTNtWGbfd+3WV5N9FJ1XYdtWlwjYGHdrENCW0fbNLiuwzVCaLBaBa9BZ2naBts1WCs0qN4HBhTrSEUJI0DobMYoZlFti3MdrbdYghVM4rJwRuMDKCpUgXZQeHnztspc91pRVkUKJzJGU1U1k0kdwo5KyT+oSnwhNKix+KLRksNQGBNc5kLCkL43kni7atpMJvjAPtSyXrdhfgi48MEyBWAqk/jRcyAfrVzelHQYzmzBjZuad375Nna1ADST2Raogno6pa7qFB6xWLa0JwvJd1AlaEm4dF2HUuIx7OVbAAm6APRAYVTEpLuwZpSiixuRF0+H8wpthDPeWYXWRSjiKBW7tRJeeaWicSLkWXmhsI2KqnM29InC2ULCPduG1jraYsLOszdZF4aD4zO898lA452T37VGaQnpMqa3jmljcE5jfIE2UGhLoT3PXL/Et7/5NYzyvPbKLf67/+5fcXjasFi0rFtHYzu2Ko1Ze5btmtNmhZmUROu2URmxBAz2CO9kLu7s7nLw5AmXL1/ujUvOg1Pc/s0H/PwnP+crX36DW88/y+7OnGpmMKVJRB0PH33M3/0n/zm27Th8fMTh4ye0neRmRG+4FGaL4khkY13X0ibb4X3Lat1ycrLg5z/5BSdnKx48esSDB09QekpnW8nhUo7WtuzsXuLZZ5/B+y7JvH4/JMX4Z+JClAEUnl5eyNzKTxQlkQ2W+uhVPyc/4wOGHyTlduhNGSr3kQY7B8zSrkgTHNsWQKNSBOJNHh08QRuF9Z2EKepQUNRFq65c34PNXnHKmxIfI8/suLS/jwtsbhpwrk0Gs9ySDgqhMPWQyfn4KKc4t5eEnsGgWTWWopqzWFtOF2tMUeCALoSOJgNfCHFW3qKVFTDiwHmFhQHg63WYPqwqKpDSdJWU57LUlIZBAdLYQc45OrL8OxcNhcGDkArlidHJhzngnOxpEdz0h8PiabA9lAzUbs57oQgPG3FuNY9eDZ2mmMcbA05YnozRwSgplObaaHRZ4L1JOk4XogO6ULFchahuAa7i6TUh0R08hbIY4/CZcVkTGD8jFbnqvdnGeMlhqSqKusCsVuhCsVqtaFsHreyDCgGfTolh3Rcao0DrjpUuefm11/ijP/pTuq2Gtfc8962v8dO7bzM5PsN4R2scVmsmVoPtw9eywRfPOjp4tx3eiYcurrXo4U1zAVJom2jcDOQGQW7oYLjBKyKkiUZSHzrUR41HRa+iD3lpBu17hsVcJ4pYJc0JpbBG0Xlol0tU0/B5js8NNMbxn0nBZhgOMj7iIsiToePRu/16b8imQyx03aAN+fPy2LW4uYzdsTEcIG+Hc46qLFmv12gl9I5XrlwRtDadCjo3BfP5VJC5KTg6PA70ozaBGBEeIkSsdaGtBOtSrB8gi1zo6kQhcKngC4Bw20fhkydvey/XWT+01uc/Yz+d78chI0cO/tK1I+An6DZs+FoFC0ycoH0SG5DqH+R9nSveMcFWqficsCBGbc8Vjfyw3qcY2Fwox326F9o9dJDFoZJSFuk/kyVAZQuRHsSAbJHhJcF7rPO0YVNr2nUqfBaTSOPv0SUb/8XiaLZtIXggYjhQPL9rGrp1cOUm64rFdjYVU9Mq5DPQK0AdVkL3QsXTNPbhLQT09jUzovWnnJRoXVKFvrBdx+LoBNu0dNqzf/Ei1599jvl8i2k9YWe+zXQ6Q9WaIoQkCXiXRLzenS0W1mghiTjSqlGNBq2wnVCIzmYz5rN5nzsV7llWFU1nQ+0HUZrLeiI5UssWj9R2EDAApqxw1qECI1NhCrSRitextktnhR2kc56qrtnbv8CVa9f56IPbWGVYtQ6rWpatBU5jJ4IuU5K714Y2smN5UKpIOp0kqeYECUPKv54Kd0QMkNYKeBe8GPRw3QbWKq2cJO25YdKe99A6QAsI0EqSZfHivWltQ1XVdE6jzIQy5C6URcGsMJJjYopgLOiTu5US8KJCwilBoTG6EC8SjsrAbFIwq2sMsDWd8zu/812ms23+L//1f8NquWS9WiVjymQyZbVaslgumU+nAmICSI5GmF7Zgl4R7rh48RL37t3j8uUrSZZ1XYtWBX/4x3/Mj3/4I37wp3/KfFpR1yU7exe4cOkSu7u7lEXBe++/z0d3DsBDQSGAvVnTNLJ2AZbLBV0nzGKytm2qaWK0rKSm6Vi3HSgBY+um4dHDx1STSmoYlAX1tKaelDx74xrXr10R3VlBTwvq0/rId0uVGYqG32aAxIP3vSIS132SlW7M6jj4i+HRAw21IQSqb4dLl1rrsrY4chrZpBgq2W9OTk9YLpdEYyFJge6tq5sMNNFKO9jXQksUkhy9u7PDcrXEu1YULCd78CAfI71TZr2P9/WAVimseKDkh+dpVArbrOuaJ4eH7Ozs0DqXCBIgDGsM+3R9n3oCA2DAft6f15M2GU2jcdQYqTHjUQL8lUp5ieJxiKxnw/1P9C0JB4ogKpLORG+P8noD0JDogQbLaGMU4OVJkRfJeBv7QEYm7aidy+eXRBU45bMoCEuslxENyPFh8nssGtj3ibVd7/XXHmeFtSp5OZQPfzMwMKfwSqUoS43WNWVhqMqCsjCsVitWrHFdIAbB41E4pWSthj2roWEymfHaa6/y1tvvcuXKdeaXL3DpSy/x+Ke/YNZoaqdofVgjqShgprNmfe29y9b7px/Rm62yOToeuzy8eBhqSTbW55+nIIV3Dj2bpHsNjAxe5pBWiqOjI9r/1EBjnNMQw6WiK2esYOYNH3dKfIE4IcYLLgnAbOEN0N0GsBKfnXf2IJzGi5Uwv15rscaqLMQiUqVJLLbh4MkTlD4S4eFgtWpQRlyBMZEyDgogMemIEBCGDJUG2YV4Ref7uhPR0uB9SC7zPTiLllKpBu2TEpksb+f6vBeu4yPv47xfso6MJ4pQi9LR99f3rBTZRE6WKfkrsh8o1QOmrBED0DPYTGOhnTiZs29EWe5j1vE+sBpJ3kESWN4nPnzvfAqPaBuhI23bVpJAG6lk3DZtsviLB6BDeQECbYgxt9bRta2EGDUrAR2R/tTaJCS78Mw858ZHi0Fyb/chW4ow98N81Makyu1aa4pSo3SVvGR1XYfkRIMzUE7rkI9QpfCPIiQiF1lisyiPoTKsMYEpymHbjrMnR/zm12/x9q/eBA8XLl3mW9/9bYpJjTYlJnCxJwP9wAKbdiEcvnf/xvmnwBCAqJak5rIsWa3WVNMpppqgigoXFGgcuPWK7mTJcr1muVxKuBSKk7NVmH9yb9dZfCs1IWL4lG0dTdfifdPTM+fzUgmhgtEFlDU3X/oSTw5P2L98nbVTNKsueGdj+JDD0xIVpSjz5HcFlmze2d6u6zt8VvQRlYWIIAp9CkdEBUXbS431rqEoTNpAZZ0Gq6zOqk87J2EDBE9TUUGQzVErM0UB2qG0KJJG6fBPURUFZeHTmBgjyevTac10UmOQTV3C1yYpHNTj8QYKbZjPJuxubzGtKvDQNg6P40uvvcqzz93gzkefsFyc4ToJ6ajrCcaULBZL2u0OpcowPr0V77zBArrOsrOzy9tvvxOUtSBHA9i4ffs29x88wCjFpNTs7m7z5tvvobVhOp0CitPTE/7sB38hClxUspxPeUhxHCKFafQSRnkjNUmMzCHnBDxohfWWtmkojMIURljDqpLdvV0ePrgn4YthDvSvppLRZbArRpnnY67OYAr1p7nzsv0/5thkyd90VnRSDPbUsDWMG5oUIeV4dPBYQqJScc4YDBrfaWi1HTxzdI78Lv1TVxVKKZqmxVnx7GpVBgdZD1YjQUsM6437RhRkHj+oHzR4LgSrupBY7Gzv8vjRAVU1QWklst73se/OBmpub/BOS3FI5fBYrApecOcT0d4YbMQjzzkriiJ4AAziSxCLdJdFOWhtMu9tvw/aGH4cgUYCXb6PMPBDDw8QvDz5vIy/Ba8q4pmwnXghbCiYh1Nimc+MBZKgrtBGDFNxj+pzZi3gwn4YjdYqthqtHSmvMuiBMVTKBcOZ6mJOR8xdkVoikUBDQqz68GkTDW6FGYANozSrVZf0Pu/lvsIXYrFKo7XDdR3P3niGDz/8kOPjJywqeOa3vsKD37yPPzqjsh1KQWckP864XicdH5Ij54hMjU87eu/u+Wig4f2Gnpz8kGCz846A/NyxHj42Sg+e6z0+5ASNjRtPO76QRyNPOs0bFpOhcqU3BwN5J+QvEb8bozD5qgcNbdsmkDPunDwxJh/UHEnq6LIdgRZR6IQWjUxR9RAsArDuGlAabz1tZ7FW+OtTjOxAeQ/KeAcocR/n7xaLdznvBgMUrS+ywcm751YfFza3qIjH+dL3ZwYERv286ZDNwp/jzZaNNYQGbbiPeBRUQuI+gBLSTxBc0XtpotdGQpH65DggVZOW+MI+B8FZaUPXdfhWQoxs17FeN7SdVEs+OT2lW63pmja4QNuUrOyspUnFfLpBCJH3Dh8SlL3r3dceAUVtiPlFBUt1YDGSPUolRU6nuQixtoUxYiXWqt8sdCn/IlgoQh5PWVXUdRWoUMsUclQUEn6kY95BsCjrwDIS47XFeh1BjYvDGCMC5RUSA5qEmnReAhxKxIoxnW5hO7h9+y5du6asKqrpFF8UUBR4XWBRFGbIGCMhJ0XYIGKwWqjfQpa3ECwfsvlZvAVd1Kxax6JZcHiyFIUtUh07iZdFabQuWXdC9OBsoDoMwJskH8RFDeL1yo0OaVNFgTdYZ2ldJ7UumpaL127wu3/nKmZWc3iyyqZxz0QSFfuwaAI4TKpSuiauj7IsEMNmn7gZx4pg2SyNQRUq0b66wB5VGA9xw9UKo3MCi0ATmxlmQDbO2hiUlxCoqhJgWtc1VVViSoROtyypy4qt6ZyqLJnUBlfImi+KqACEie08OuU/ZOGqiPLd+SZ8p1idLTg7PgWvBMjblulsiytXL/Hm22+zOFuEXB+PKsUjvF6taVsJWdLEgJteTvVKU9+vxhSh3kWb5JwLMifO93WzZjbd4rXXX+OnP/8Zjx495PhE3mmxXFKVFc5ZDCYx7MTwrLgJS3dnBh3pEZRX4IJXFAECXqukaJWmgEahVhplNCdnJ/yt3/9bOEJOTZg/MdwyHtEhIKJdp1oyKJU8gRF8bD48+Tcq+2/6Ni6BQT5FwnjJWpquGYEPn90x/13u0+e4pXt4WZKHJ8fiWURhMHglSn/qi5HRS/7waexVCiPJ2uw8s+k01LuxKC8lT33XDHSK/D08KnmyI5iLEiuq45sSxnX2UV1PuHv3Q/b29jFlgdUQqZCxIYTRWrmrL+hcBzisb3HKpfwrRU+MkwO33JBRVVXaI7TRIv9VkN+u7WWrUvjGphyQ3EAXmSpz1sj4nc9C2H3QV3ovEnhlkky2nWW9Xgm5w2LB6uyMxXLBerVm3azTOV3b4e3Q2NzrWCqF10ewUZYlk8mE6bRmNpuwtbXFdDplNpsF44AYEZSSfU+8yhob1k6nBQjo4HHVRqOdwziNtgLOCudD/+kkx4tsDyuNxtQ1JhjBjFmjtWe1coDDe4mMaTuZLxqDNR1VUfDG66/yp9//AdP9bar9fS6+8jLHP/kFpukwWtOVwWDYna/oHn+PeRGD6b8BlOQG86hvblo75zyDme4WK76ndcFmYJGnAYzJKQYRSUFOzabTQAj12ccXDp2Kgj7GbDvfC+pxgzYhpHGnPE0Zzj9PidN+OJnzBNrcSxFDVKDnHy6MHijiuYUSJYuzC9YBGRxRBLpEwxn7QQpQyQbUb4hReCfLemtxLiqrct+uk+RIF9xrccOLynjMI4ltEiUt9Ici41jOvQY9lWfaePJ+jpvnhn5OLvP0jOCdcn28HkrcyOlefhhTGvNUYqiPstKPsbhZF0OF1iva9ULAQgg3ikKss20SgF3XslgsWS4XLJcrVGfxnU15BzEsyXYdvnPpuTnIjWOA6utuFMZIxWKthF0m9kFQnBVIITbX4pDk/8l0Sj2pmYTqyFWofxBzEqLQLIpSLJohmVkqJ4eENK1xZYh5D3OKuBZUVFbjnJb5aIxGmUJc+yEpuOs6XBBWpdJ4ZXAuJG9jkgYQAWnuDXTeUxUGgxYu8TB2q+6MnYuXmO7scnZyiCpLqskUZzTKiDdBIYmd+boRDaVPxItzwfpotYuKvktAA6UIrMhhc5S5LaEH4qWQsYtjE71FPSDP+yrfrJ3rq/Q655IXRbxZHVpVITytkVwn6/FOoVQByy5R0UoctCHWqIjVpLWWXJPIIqaAMngzrbVUwcqqtQoD0FsmvRfWJW0kDrYykf9eB49TQVWV1BOFQkIKylJCyFLNAZDieHVFUcTQUMN0MmFaBD76Qu6ZLMjKgxeFp+uEFEBrDbbF25YuhHq1a58U0iTnLIOEWh9M2A6PV5KnJrYZLcbRGBKKpfOKS5cvslqfsV4KHXHXWPwEiqKiXS1ZLlfiJVCEDLDhJjneKwpjqMqa05OFVAf2DqtkflwMrE94x8GTJ9z58A5Ne0bTnmbWOCm6qJTGa0cHWNeludo/z51rR/RGxbnrFZiixJSl/F5K3L5SEmNeUPD8iy/x5a9/k6aTeRllsvMuKLA+7ZtJ/GbiORINhCdmFumw7Dgvy8dHMqBkcrG/v0pjPvaGj7cJf14HD/cAyd/I9plw7bJppBisIhj4IvFByDEYVe6Oh+zHY693uNRZtIJJXdG062DkEAOQdqqXqXJ2JieCfFIkD1XSVfx541z/vByYqVCwU8CDD3krOngIu04ou9tujfMNUofD0jlLF/JtBGhsZvfJcx5yBS9e11kvoM7Jnh9DmJyV8YqAor+mJ5jJw3l9mIMWl4bLh/286zrWTctyseb09DTRiscaRr7rIKOFzRVTvARO5YnbfTscyokBMzIQxuvbVmpVOOeSoWQymbCzs8P+/g4XLuwz39qiqqRIqCeGqws7YpSPMbdM5KzCGIs1RkhHYmiV1qhgXIgGzkIrdFmGehYKUyi0gdVSKNqt9eAVTjm8CWG4as2lixd45pmr3Ll/H681z3/tq/z47XeZdI4iJPmPnRQDsqSkT+WezqHMe5penM+bTQblTes9n9/j7/PP49x7mg6fzrdQmSKEDH62LIIvWLAvbuxxQvXIeHhevljGyChZ6EfnjY+cziy+bE/3Os4B8Kld8Rn5/aNCEK2E8fvoIYkF8VxYiN55qqoCpUICuKWPjdXCu5iUezmslWrHsUKoR9F2kf5WKg53XYjjVoGSN3OrqrDpphocxHjF3HJKNjnVgDYuvqdWKiQpRzTLoE/y843u6eGstbTBYui9x+Bp1uuUn2C7jtOzU54cPOHk6Jjlasnuzi6XLl1i3YhwWi1XNO2a1WrJcrlMBbHW64auXePadaJJjfHn0YIX25jnpuRAEHqKPwBdaIoqCBJjBmEgxhh01ecURHYjrZRY7esyWHBEyK6bhrPTU/7y539JdyZF2l7/yld55tlnmW3Pmc5mmLJEReriDCTk4SzOu6QUhCbjHBSq98TlIUZRmVNxagVri9GFJE4r2Q4E2PdLVRLJdGCTEMtNtsDCnOktStqHEBsvYMCqwLRRFFRbcy5eu87J6THVZEL0rDvfgRPrWUdmeQvz0gUqXGd7qmClI2mAwyuVcnmUUoN8EufA+t5bF8delOqepz6FFkFYq5lylgllpSR+WeZLAVrOMkWJ1hXGTIO1sRXgpjXoCqUKSqUD0JCwqeieN0aHcRtZjrQ4oo3uc7TydpQGSt1vnNPpBGMKyUmpC+YTSYA3RoCCvJfM52SNzNaoyDfR7Hujgoyx957Ot8Jq1np8kykZzmFCH9vgkbOhL4UxLIZuCShUyaghStLYexItpmgVktRJVlAX7m2txa/XXL9+Be8dZ6dnLM+WtI0o9WVZslqcsVysKItS1q5yfbXaNIXPG0ZmszlPnjzh4sWLAiDpWC5XvP76G/zgT37A2ckJCs+v33oLvKUIFL6ST9QTcqybLuxbDHJnBNAPtP2MmtNiQl6XR0JjSgVaF2ztXWD/wj57+/tce+YGzz3/As/fvEVRz8QwEkMpwx4T5bLzvUW9f2QAtookR8a5kT4wL32uw5M8jONLfAA6Q1Cz4db+KXt0YpXLLdiiUJ4tF/JuWmdAUolnSAnhSf7O/R8urDfCvfqvjBaKaA0hrybuZ6LIxnfN3w8fQ+18dk8friXtven87HrDsI3GGNbrtZBQRDCkHGhNoTXz+ZzlesFqvcT55J9PYbyR2GWsv0SDRNzbcv3EeanPZG3XG3UgAAcfwpV6Bisg1YmwGWlJ/GmjMc81qRjqOrAQrkI+letEl4n9JSQtDq0LlNJUifWvZjqdUJYVs2mNVmReeZM8CdoolJb3t12H8wIQzs7OWCxWnJ6ecnZ2xtnZGV3XcXh4yMHBAR98IPv2dDple3uby5cvc+nSJWazGUUt9226Rgy/Tjy+XeEpnEI7Q+FBhSKLRQirUkbmEVF/DTKurErmGqoqhBqrBauVRERIPq60XXQJTdeuee3VV/jk4SNWizWXL+2zd+s5Fr94i5lTGFSaX+fmOIRomN4ILB793luey9wcdCQYvQFI5MfTwMb42vEemntccn3xHDhGjM9tKAXxeY7PT29ru6QkJcXeDL0HcXPKF8wmUDEWnmM2qrwTckG26bz08kHQxUVSmCItuDFgiffVQanogtLkQyE3p8EXAia0kNYHzwOycIiKUL/wRfAEo00AALazSfjFfAHpACWJY3ETCOBAI3UhtOmpCxN4CkLCdl0SGE3T0FnLetWkMKGu61itRNkXxNliu2iZ6DIh5nCdJCU3a3GDrlbrdA86y3q1xnknlv62ZbmWegqu7c6h7xQfO/AW9OMiORY2xYOboqAoJhJjrzVlUVHVNWXwEkQmIkqDqcRrMKlrtNHUleQn6CKEE8X4zGBxLopS3IVBKRpYCFSMQ/WBqUk8JKdnp3z4+DGLd3+DMgUXLl9m//KlADAMyhQCNMi2IwVeiYLolViJDAxc1VorCvo6L8JCFi6PBQvzOR82SG/7eeo9GGV6K5WXeSiF0zzJCxAmYZqXeLrOobSi6WxP3efEC9S0Lc1qzSuvv85zzz7L3v4+BwfHFGUlbQzKpMWnUMEcFCpZvANgLy5vBVrT2C7JhLyIlPMKr/oqyiITDEoZtIrhYQLkus4ymUzQWihgSTImWIeiF0ibkLgc7xfkEGCUwmh5IaW8JFfqAu8VE9XX2SkDGNVG4vinU/EgxPlblUJ3WxiN0S5dE0PetNbUJZTGJw+XCvLDe4/2Hcq1yRrbrte0Qb5JWFvv7UpWVycGDKKV10UPhChyrdID+uTemqbABoXEi3W5Z6kBY0UFdNk94+Zn8aA8ykaq6fhMMWRE8guC8h1Dfrqmo+sck3qOVorF4pTTxWnwJNnQz4bluqVadxQmhBzqXtnNmQUV0bqv2N3d4+DxATu7e7Rdhyo0i+Wa/YsX+cf/5J/wx3/0h5yeHLFcnuGaJllpAZRxLBYL8B7bCniYTiegFV3Xhp6LORqxI0EpEzxIClwIU8FgdIXXNV/9xrf4h//rf8RkS+SYtY62tcx2dlg2bZCJvTU5H9MkIHtRElRTByoWas33Sp8p008BBir/u08GVpAY2dJlUX4PLwriJzNe0Ydwqf7DcG5ywYdnaGzXsVo3Se4rpQKolevy9ufyJLY4gt4h4JE/qrqSva8J3qm4l8caRhmIiNeJQyqXpb0SlqpC+1GRMy9hpvEQA1XN0dEJ2ztbSUEsC83zz9/k2pXLXLt6kaPjYxarM1ZNy2rV8Zvbd3j4+Anex1ysfkxS6BWSR5Are3mbOhfWLb0HJskB3xsb45yKHggXgIVHvI1dyCnsuo5VI6FPLhKQxPoMqgikHGH2eMt0UlMYw6SqxPIvPSwhU7ZFoTk9WdC0C3wAEXUtea8CcmRk4zPqSsKFJ3XNxYv7PPfcs8znc4qiBDzL5ZInTw755JNPePToIacnJ9y7d8r9+/fQWrO1tcXFKxd49rln2d7eFtnZiSGusA5baAoTjLe69+gXXtisJEyql/lS5yiSmxSAAW9QSiIqvHXJY6ucpW0F9M0mU55/5gbv3v2Qw8UZr3ztt/jZOx9guyVWEvgwaaNXyajrfQgjRhLjVdpvXD9vwxKJ9sd8YafP4liMwMI5kBJXbq/+9OtZDVd/MvCqwFCV6SNDoC65GfOqYjKt+TzH5/doSAtS7Kj1brBwxyAhxl3HTsgF7djtM/ZAjABUOnfcmfl38ntkQggdFawpJjAciADrXX5FWQYvRsjLCP9DIUqNBy2xAaHMGxhvMd6GPVZiT72SCsudc5SmwjYtylo0pASj6L5cr9cpT2O1DixGoVq49z7R9i2Xy3Ru0zS0yxW2bVmt1ljbhVCiAC7aTlx9QZjYziZgoVwX+iTOXh82Pyuxo1GJgGTBA6CVuFBdGkxZoItCxt8YqlqnfIQ876AoS6rZPFln6rpmMplIiFEduKxDgnJZlqmqsiijfXiOeHvCWAfAkM+BfqLFcZZjHA+Ztm8fcgWCVVFcpxqlHFjLtJzhfMHNWy9x//3bGAPz+YyiLFFFiS5LUDqFEBHmSp7e6IKSppDK5f0cVVGFk80i9LMOYXlStDCuDUme877D2z6xPt8c4yaFz+hzo3AJIT+OnqXMeS80jt6jrMJb4TAX13BIhG8dVHNOVpaia1GqBwhohQv5ETH5OnmVEGClVQgJ05JwXpYFDkVRhKKdKZk40M1qExTImDsl/4wpMCorzOQ9Js6PAF4iyEjUwgHAVNpjAvefnCpKYlkUbNUwn9YpST4CBuU9tUHAbVVSFkXfVu9RRiziXdvSdl1KRI1zLT9knIRW1jtP11hs0wyUAB2Fm2cgD0EoFXMLt8/OiXbhaIX2YfMG8U45svtlsjOX0XHtOByR/W7Q9uhZVIrePAI+3wDjp76fr1GB9dYL+0/n2N+eszXdYrFasFidsu6WdN2SopigdEFrYdVYTCHJ6oUxYT31YSDOCSgvFHjXsbO1xwe3P6TpHJ3z+LVjuepoPdz60ss8+/KLrNtGlM71WtJnw161XC749//+3/OTH/8Y4z3GeP7xP/7HfPDBB7zz7rssFwvarkE8XuO9yKN1KXmCYioBU3Dtuef4h3/wBxR1ReP6EM6iLIQ6ul1l82Jo4PI+JBJvAAneCx9/yvm25/fP8bzr/+i9AMmw58NYKje+9KlHNHhEZST+HT2aueFvfEhce4cOxhUCIJXrBnYo+hNCF/h+fkFvqPJe5KpDwlvl6EMqnxZanbcxT1TOr0tyleHa6YGYp1CGybTm+PCI+XyGV6IkVqZgf2fGJx/+hvXZQyaTGo3i3p07mHrCtasXefT4ES4kcxPeJS5fpXVKmB/UkMjabTMQZEOsVCREGAMM733yVGgvyqDFs+5a1m0r1OjWJRYqrSQpui4rbCt5dzgZo6o0eDoUFqUsdWGYTabMZnPqumZray7000XBbD7h8OiApmmYz2dSLVqJF7vrYL22HDyW72fzGSfHJxweHPL40RMWy6UAlOS92GJvb5+vfvV15vNvobXm4cOH3Llzh48++oijo0OenBxy+85dtra2uHHjBlevXmU2m9F1lkKFMNJCwk/RDuvBOiOhjtpRFOLxkER1jXJaQBaKujSomUSWaAWr5VrAXPDIq6AHOO155aUX+ej+PdqmY//SVWa7F+maezjXYLR47tMcj0g7GpkDoJfpFz1IJANjAhieQZRLXD5ihFEDo+YmQ316dLiDz67PjYaDa5Le1F8f9RyJXJAyF2iP83E9fvrxhVinYsxxziSUx3XlwjDPmRhbv4cvNXxGUrgy6+Q5103WobmXw1k3EMpq1JH5keoCeE+hDV3booDSSP6F9uIaOj05pWtbTk9PeXJwxPHxCZPJlOlkysHjxyyXK1arNa11oDSL5YrVYpkAwypUtZV2asmWbkPORrA4dCHsRpSULBHaSdJ4LMTjs/6JbDWifFgifWJMpixLiWVGy6Jrmia455AcAqMwumZSVWGs+pyV05NTTp4cAp75bMbLr36J2dYW9XTCZDZjOpGkrclkkuLbVfTKmD6cJFqC4+8qUtox3HhdCHIez4+Ixj2idMvGo7NNZBjdbbQZxNz2oSGB5cdAkQlxSZaWa8rC8Mz1Z6gmMzxQ1FOKcoI3GpQJ7TjPdhZd771QyRLMfa8U5pt3qnKMAx3mfbYhivAQRXygYPhghQsMXDFcSywOse8iJ7dKdTFUsFCUXoSpUgXGeCQHoaAoa3whYLIwPeDTIWcBVYoFkQgU+vFVGc1t/tM5zyQU6YvJ8b1sMAlQRKFmQs5D4RqKUGyqLIs+qT6EPQpIlLGOXq/pbMpsCpPKpGTKOA8LU2CcxBDH5HnRXBR4h3KRGEDqdCTlBoihNEqJRW6VKTTDowe0hLnaK0uZDBopm/nhleqVSzLLpQcdU6bHSiv0HjUfQUH/nRsAjR6sy3zrn51vVkDGpH++rWOlN8l/67GNBWfprOXihQsc3zlmebagWa9YNw1lKYUXu2AkcYg8itSV+ftJfymcNnSuYz6dcnRyHK6T76yTgns27AGTyUQ25noS5oq0bXv/Iv/oD/4pXhf8/Iffx1vLo4MD/vl/8V/Qtg137tzlwcMHrFZnyTDUtS2L5QKtNavVmt/85jccPDmkMCWXrl7nn/7zf05VVykHI877siwHSu14zNJnrp8Pg/MAr3zKFhnvYU8zsgF4p86NSz+j7Lk592nHufZm++mnHTGnBT773HOHGmfrhI/Df6Ji/TTA9bS+zr/PjzxufpPhAIJxICjUi8Ui5DYpJA/D8Yuf/Zyjxw949OAek2nFpauXOFs27F26wv6laxitaFZrnCri3QbPyMcprq1UAT3Lr4gyKAcYm4CGcwIkCHtDay2rZi1hk152MFMEWRqs1soHb5HtMFWg9K0Muzv77O5sszWfM59sMSmnyUPUtQ2d7VgsVpydHrFeW7rOc/joCdY+SkBDqNld0h/XqzXT6ZRnrj1DWVVixFSatutYLhccHx/zm3ff41ftirIq2d/f48KFi7z2xpf55re/w9liwZ07d3n7nXc4OjrkrZMTfvPuu1y9epXnnn2OvZ0ttDWYUKjWhBwQFwxWVsd+tYGlShLu9diznUL3Nc267b1EtvcMTSc1L926xZvvvcPhZMqLX/8Kb/7PD6gaIWqxgZ0UxBhXVSXT6ZTV8RnduukpkZVjWFRvOAfj3GDDvE/G98wQOwbb4/M3zfMvcsR56wJA/DzH5wYa49Cl+C+6p2OOxNiCFhfApnyMvDPyztGhYFR+n7EXJP8830x1UDZzlqxNQKVtWw4ODtje3sa1HcuTM+7evcuHH33I/Xv3OTg4oFmvWbcNVVkB0HWOoqzY3dljWtdMgnL04Ucfc3h8LPG/HkkcazoiK0/M0wCEpcL17+pVoLr1HrRYPqKVUAdlDyScKoKGIiiEVVVRViVVJZWS6+A9sF0nlh/vsUpjCimQVZQFShGK2EiBsLKUpFMdch2stTx68IAf/dmf4pxj5+Ieb3ztK8y2tqimNbooUUo8EXFjDJ2Mxyd3YNbZobYJxHhfFcc9jo0H79WgHkraIEIfpTFM/NtITmFO3QJiLdeZ18t7lM9C+eIiyRS5KETKquYr3/htvIdissXZukMXhQhKL67q/L1inoJW2f2CwineExeZBMUK5fvkaFmoLlix42ZIyhGSNWCSAihtjlXug8cneH4iLW68h6YHfD5YziRJOKO6VVHBN+LeLsRtTrbWtJKcCeUj5etoAYvTMM0DRZ8/pENbTAZc4rgW2lBg8IE1JgLgqjJs1VMubk+YBctYVVcSz29M8uSQntWPvfeLoExZvO9QVoGFZu1Qts/NknoUrp8yqq8HFNsZ+zEqBj4AOZXx0Z/viF4GxVApsnvK3IuAwaV7xsMyUpCSRam3LOXKaH+eGn6e3cOmz3NwlbFxxXsM7u1Hubpj1W+4PqPXwAVjiOss6/Wa3Z1dCclsO05PTtna3mU+2wlU4m1IDJWK4d77wGIW8lHSM2UjjvHyzjsptOd71n6vItsZySuNKSEQH8Q+KqqCf/SP/4Dnrl3lB3/6J/zJD/6MP//xT1JRPlHSukQ77ryTMAmkYFpZCSXyy6+8ym9/73fY3bsgSei6D4uM49w0zWBsB/LMR8OEG4yViEEZJyfmynPz5zOVAq+H9yebzznl8mcc4z38aX+PE5f75/5HgAy5yTkra/Jkh8/yHL5xmzf9zHWAMZjI++hpQMN58Er0CSmQ6kI+mISEzSZzlqZiq97i+PgJd1cLLl25jm0aCTVyoYig8ziGod+9vtMb52LB47yNXxRoeO9DVEMXZAIUShjRUNEIh8zzLuYfaPZ2trl69QL7e/vMZ3Px5K5bjg6PePTxIevFmpPTU5qmYbVasV6vWa8kx6NrJQS5sx1t0/ZGMLog4yVMUmtDVZVUZUU9nYQEcCFd2d7aYn//Ai/evImeVJwtFzx+fMCv336HN3/9Nju7O1y8eJHr15/hjddf5+joiF/88pfcvXOXjz78iI8/+pjLFy5w89Ytdvf3JY+zKDBdSVl0+BBibZ2mtUIKYwqpJVQWZjAekb3Pe1CsWK1WyWAcx6goDC/dusntex9y1Jzxwmsv8uYPv0/RNCjf0QVjpxjGxGNflRXL7hjtoqeR4NWSECqPT/k2uRHfOYcRJJLmxljPGoT/jeby04DHpuOzwYfsE1XIg/08xxcCGlG45Is4f7n89/ylckt1fr/8OxUU0vBtitXNr1WjzowKfK5kjRdxLnjitbHdP/vZz3j48CHaw6OHD/nwzl3ee/ddFDCbztjd2eHatetsbW9RVRVta3FWKhUrwLiO09MTLlzYo6iEI14XJYeHxyyVhD2VlRT9qgIImEyn6EJjQphGFVmNyoJqMqWqp6FaslBUTiZTsdJWJaYM1KcpgVWHfI4CYY2WTliuVpycnLBaLoXtqW0S40PXNVjXZYwRUJYVRofrrWXvyjWq2RZnizO8LimmM1RVocoaVZQoXQmDb1hEaUzx+CyO3rsY1gFCl1IkQEJUSlXvlrNhs9Umuhe9IPVsffmBIVAFRT5uCi7q7Cl0z+aJci6GjLlBcpy1lvVqRdO2XH32BbyHx0dLtFkTS3FqExKw5S3FezLyJkRPgxfpBKmtChVyD1R0naoYitRzgcc5rmOyGL3ib3KgbnQII8o8AhFA+Bq8HiT6x/ClVovlY8xy4r1HD5TP3KrsMUTgbskrt2sc2q6T1yHS9JZlSaF1KmaV1qwKYU1e4RpZt1vb28y3pmxvzZlMKwotYLVftx10HbZDmGB8HHkCIA9zZ8DnHRTPoPhHJctlkyfJIxPGiR7A9GPXA8AeSBBc0JuFsc/CV2IfJ5AgrSCBa/r3cWOgEQFG9h795723zOOJMThjZdTFVmZKbHyDZMjJZGb0gOSvdu4907tIm3TgAY3eIteJJ+Da1WscPD6ga1vWyxXNei0GoLBWRG4XdJ1N7xJr0qT+UWCxGBSrpsEUJSenp0zms0SR60KCqTJ53RFD4ueLIMQrTDXhb/ze7/Pb3/0dPrn3CQcHBxwdHScLslICeLa25kwmE5TWzKZT9vb2qSY1VT1BGyn4Z71HB+937PJcYR0r6Bt/z4RaDiDHYHK8pw3nSD5Y5+dkNChEH8lnKRrjffppCvimPT0pM59RG+Cpz/6UqzxD0PC0Nj8NcOTKFgzfK5HabARzPcXz2dmZXO8szokV/uIzz3Dzxg3WiwVni2OKqQFlaL2iDbW0IDL09W8XwUURDDw5SAAG7cxBRR45Mv4s/z31p1LUZSnAPOTQdbaT/Etnubh/gRdfeJFLFy/grOPk+JiDh0d8cPwxJ4dHnJ6ccXx0zMnxESenR5yeniSQ0TahLpVtgN77ku/DfX+qtNcLQYNJe1bcOxLF7WxKNZ9z+fpVrl69yisvvQR4Hh8c8OGdD/jwgw/Y2dnm+vVn+M63vs33fvu7vPP22/zqV7/i0aPHPD54ws7eLi++9CI7u7uYtqMrC6yRcgaF1cHYqjHeUliHsyp5NGLotzFSiyeWRlitVoN+bpuG6WzCK7du8f6d2+jdORduPceTJ0cUTva/uP5woAysTqWIpVRu14F6tg+fFnk11FnjfNi0dntjW4wk6BmjPu34bDAx1NHjNXEf164PTf08x+cGGjAMg4q0rePGRMTXtm2ifRzfIxfIOQDIAUwEDU/zZOTWjSREgnVpTNMVPRzRKhAVrG984xvp2r0L+9y4cQPvPSeHR9im5ZOPPsbfv8fVa9foOstHH33C1nyLF154kaZpeHD/Yx48eMgrr77KN77zberJjNl8LiE9ukIpHcI/ilRQRhUFzqikBETroSRuSbhMVAiighm2316Bh0HFZe8KPD3vflXOubh9iaZZszw9oQ0F6qTq7ToUqurouiYVG2oC8PBaoasp23uXWDaWop6hyyneVFhVyJRxvVV9IOQRC6dQqIYcg7h9hHCSqKQEw3dov0/WV3y2oUSrLsONpJ8zQq/pQghaSnz1sUqoGgjhqHBZJ/knzvVJc5IYruk6mT9lIYWSdBA8RWHwKZeg99zFuRTnnTZmYJmTqC2TNuBIqGC0kbeK3oaghONFgU7AQyZ8qochD8qs7oqkvCmt0b4EG9ZnK7zeJhXNcjgkLyUJM6XEwxQK8KR1432IU/UoAlsTillVJgG8tzNnf7tkvjWnLAqKokyhchr6mOvwItELIRa+rFCTCtZ+u0Z51c8FRgIx1+oG3ylCtkj6fFC9XtleOfb9HApadgavssNLfw0t//01MdRNXsWn95Y6H0NLrw+D5bxL63r8bk9TSiE6cpI2m6y7Ptnx8+7p/7bDNxo8U2ToZmU1pyz8tA1Ja00Xw1UVtNbiuo7jkxP29nd58vgxjx485Mq1K6zWq1BlW7zDTSPMQbKWSOt4YF1WkrviUayaNUrLz3I6EdlPRpyhovxBTC4+3SIsRfmg855iMuP5F17i5osvD8B2rGuSvJKpb5R4mz201on0GhgTz4cED69n8Fkaq6yRzj+9zwdzYaT4D4+YDXb+Ws95kLLxDhuV7U954gj8xHbk4OvzWFE/9VylzoGoTeBi0++5jB6HXeVGznE7ctkilvi+GnZhTCBSgPfu3qEsDJOqBG/xq47FqmHdeYHIxYSuXcudRgkqPXHOUFcZGhP6/W4sIzaBjvx9y7IEL8U6ARZnZxwfHbF/YZcvvfEa169fp2saDp8c8dav3uTwySFPDo54/OgRh0+ecHR4yOnpKcuzBev1GZ1dpbChPsTXg+rQRvberrO9jAegAG9iVw72SqNkf02G41h4ryigKqjenDCZTNje3mZvb48XXniBF269QFlNePToEW+9+SYf3b3LpUuXePbGDV579VXe/c17/OznP+fg4JCj459z6dIlnr91k+3tOdZoTNtKjkZhKApNURoK7fAFKdfUez9gAauqKvVvk+XdeeVp2zUvXH+GR/fv8+j4kGdef4VPfvVrpsZLInk21l5rqumMxXqFN6E+lpeIC0SDC8x0Q0Cae/XGa2DTXhLncP77IB8pm0fj8/L5FUFXPq/kO2mM9z5F3HzW8YWARt7gcYPyl48Jvp8mtKJQSVaQAYIf2jbGCl2+wHLvBvTFv+J1wMDdmt8rVv/2ShSEejblo08+pkDju4579+9TTmquXbvG8dERi9NT/t5/9ve4fOUqx8dH3P7wDrdefZW/9nt/i5df+ZIkDQNtB17XwZVoo4EUE8JlvO83RlF8HYVW4EJybLBku+xdCPfg3AQRdBwt4EqBLwqpxlsUTOoZ63XLar2kadZUXZMBjSXOdnQh3MGHcIGus1y+eoPFqmP3whXWLVjtpUiV83jXYozrqVqzzdN6UohIbtkAUI5+E8+UGYco/vl4xXf0vr9/VLi998F9GUPsXFIgle4pgr2XOWFMYNJQosBbXaaYxghuBAhoqTLrJdnPGIXRvaLiA8Xf2Fow9EjEsYkoKn4Xnhf6S7wtYZ6nqd5XkQ6GcOKmna8ib4MnRS6R8ChlpHaLPwUndUGM0uAkN6ZEM9eIcC1CflJibNJUVZE2vvP/ZH3GJP6yjGxMHuUjk5nFtpZYwk8250xByICGxFVZHAJYXeQrD6GGosjLC+aK1RjUusy7Au3G8yCA3vH1+bxKn8U7bzpyz2q0vvf3Girw5xU6AT/nFc/BE3oDdwI1HiBjltKBbSeuIwa1H8bvff79IhDvGb981g3h96cCDflehYkn3gyVQvRiEb3T01Omkym2s3zy8cc8/+JNmrUw41XTaZK91nYIQFQjZVCeFcGiR7Fer9ne2eZssWAyn6ekKK3CszNfjfY9wxkZ6IBA2qDFIELYC2xgqMHJs8Sx0iffo0I+WLDm+ZCZIXK9Z1Uc70mbgEYyzqk+MXPTeU87Pu27gfFmdF4K1RyFVH2R+2985sjQGP5A8/mtnemy0T2HDRs+M5fBec7o09oXf4/vNw77Gp8XD60QJsgwZl3bUte1zGF8yK1SrNoWukZYBylwGlqr6FCYqsDaBsUwt7U33CryfKoxWB2HS8XvNwGnBF7CPmi7joODA5ZnC1584Ra/853fpqgLHj16yC9+9pccPHrE40ePefjwIYcHj3ny5ICzs1PWyzOaZoXt1hDIYzonJCJjr508VyVD7mB/9G3vXUTWXbqGPj05GvBUiNawK4U6EU/5w0+grmve/fWv2N7e4dLVZ3j1tdd57rnnALh37x737t3j0qVL3LjxHP/gH/zn/OJXv+Ttt9/m448/5uDJE27dusnVq5fCHlZQlAWm01TWUBiL79ygenkqmqjl32QySa8UC0i3rqOgYIri2QuX+fXtd3jlxZtUVy/gTxYYr2jbJhllG60pJga1MwPbSeHgzqIcFF4olbssxzPq2lHZfxrYHgOJTcen6uKc3/U2GfeHN0RC59brpz4zPz430IjKeg4QxkJ1DB60ieElPV+3DcpEURRBuRTLdCxO54PlVxQD2UAia1SMrU60hQQ3rfcoFVlLXFDuIge/3Csq+Dom6CiE9SEsg2a95qMP7tCs1zTOszw9A8B4T6kLDh494pvf/CZf/dpXqSYTmrbh5isvcPWZG5iq5uR0QakLClWIdR2FVZpSF+iiFAYYJVZe43trlsOjlQuUmwjXeBxsU/V9m41FtEb2qqj8N9VwUApViIZcKENZTyjXJavVitV6iQlAw9iKdbNG6RblTbDStrgWLj1ziwvXnmO+NefJ8YKyLjHlKmh4sbBckawX0V1uoyAKilUcI9WbFpOVPioBIhQDC1EYl3iOid9lgDItrECJGgVd2qpUpEsN91Mx2d0kjxAJMPSCTsBGrOYsFm2FR2lRLH2kqc1rRiRFunexa6Ujigw6WyggGCwWqEArqhxSlSECJReKQPrEGZ8oGGUi4L2nVC1aecqyCMnPJZNJzXQ6ZTpTTGpDXdZsb80pi5K6qqjLilI58ZkNNrkgqBjG/Mp6syG3hESDKKFmDmsboU0k8y6OlLqY1xH5uYgGBeWISfMEtrWISSNgjkBgYOmSXoIGAAEAAElEQVQlY2Y6J3QteJesn/nXXhlRHMkErg++tvy8qFj6vv1xpQ6ByfnQKWd7goGB6p8rDkSgHdo/kN2yHuImM9gUlArJnOc3gKjwbjqiB0XuHq/rFfnhffp3PH+/XAkjyFdP14bQPyc1IWxg41u3Hfv7e8y35hw9PmBxfMp6uaZrW/xEOONNEYxGvidA6I1NoaeiTAfWbUtR1Tx++ID9ixcpwp7gwnjFPI0I50ea6bk3Shz3yB4gRCI6eKRiCJCAEecCFQ8ReBAna+jXPhTxfLJybpSLf8u1PZ4TY0NsvxqNSz5O43CFp513/n3D6voUZSS+g1yQv9+mE6E37qjRV8lK0oMw+aO/dnibwXru52c80ad1nb9PXFV9n8Q5NAT6uYEgV3QjmM/nSh+KkrU/zK35fMZisZR6Q6FZnRUuMu89yiuMJ5C89MYBpbwUic329mgx915ychR9JIfUsYnANYRDRVrrtI6j/iV7nXcuMeaZwtA0DfcfPcZ1HS+/9DIvv/gS7WrN++/d5t4nH/PwwX0ePrjHo0f3OTw64Oz0hNVqQdc2tE2Dcx14yXmLnl2brY2woWeRBb3l3VmXzZ1szBSQAJXoej63loc01qITnUkooyUM2HZrVivN8fETPvnkE97+9Ztsb2/z4gsv8caX3+DC/gWePHrEgwePuHj5Ei/ceoEXXnyRX/ziF9y+8wHvvPMuT5484eat56XYbtdSlgXWFhSFpVEttRVykcIUlN5TOIfRjrKQWjyTugLvWKpQ0sErWufpnOeZZ57hvTvvo3TBV//KX+Hhe7dpTk+FhKRtQu0XcEYx3btCXc9QzmOXaxaPD+hOjiiUQndNqDIfp330PJNkc1wvfSHMjNEw7qLZ3q6UQhk9LMIa9h9Nvy8m2UN/CEPmaD0Hc3izXLI4PuHzHF+YdSq5mbMNL1qizsV0OZcoFo3pwztAJlmscOfSogmvqvpNXzaa/ndFZAGSd7c2FL8LSpxwTYty1oU2KZ1tGmHxai3Vfruu4/qVq1y6cIEn9x/y0d0P2d7eZnW6wFrLfDZnuVjgvOc73/0Ot155kaKaiMvedSyajpPVGl0WGFNiKFDeSpVYpVFFhfNa2GFi4mxmMTRKobVPcnWcUA8jfST0b7Ts5+dqE4RxNg7ae8oStK6oSs1sWkkYQ9OwdkA5QbctqpQ8DtYNTlX4ahvlHV45fKHovKdrOwFraoJSJhTaCjkEhKJ5hRkI8RRqpFSwYEeQkhexyxKQM2uIfNdb3uNGkTxgpg+XiX2XrtU9E1acvyoIvzJkKuchEmmeZxtMbpk2WiVWF68zJS/sHw4HsXJ7FAxW3KtRwfZRcBCsFXiER1hiNJUTBbxQiolRzOuS7e195vM5s9mM2WzKZFKxXSvqUqV8nehREUAn1aBTp6S9OqSdO49SLgHz9H79iybAWgbx0FvTpJaHi8wbztM6Q9t1yaUe3eq2c2ivQ82SGEZHEJrRIhzmSFAspM977884dtprhVO54jBUKHISiIHC5W12XvxP30WDw5PmRf/s8MVTjr7wm6gCzmTtcsOybE+zXOfy9NPi4seK4v8/1u+NoIYxN06mlKvoOfX9JogPCpWCTtF5h9cSInrp8hU+eOctTg+PWS/W2LYVC7H2eCuyweMDlXhfITx5a4JYjPkr5aRmuQrGjmhYiMm2GW5z+KcXhcvO82Eu9+8Zvc9pV00hcsr3pAEJ+NMbMeL9NsctZzI6GDKkWFh/Rkyml2cMiwfmc1FFoBLHI3+10TgOQWn09H72MQDcG+Zc/qyxwSJ8mWR6+o7US+f3M7I+p59v4yMHNEMAoZLMzddIb/zM29wDC6UiuB8nzse9S4m+4QHnKMqSddeKjJQTReZkb2ZDt/mQB6gQJUvoq/t9Oe9Tl2o9DZPpY96TT0MRdKfwT4Uib0ZLnQ/xdHvufXyPo5MjvvGNb3Dz+ZscPHrMz3/6Ez768EMe3n/A0eMnPHxwj5PTQ5arI5p2iXMttuvQFBJKG/Y/hZA0CHYMwZi+B8RE1rvAjNcPEIPxl3EejXxaRHJ9VKCdFZOe1hbtNF3QC7QNeS2qY9muWZ0c8uThff7yJz/i2rXrfO23vs71m7d48vgxBwePuXL1Kl/96pd5+Usv8/777/PBnQ95973bPPvsM+ztbePpaLpOwtu1ovWWsmupyooJHucMpSlDeFOB1orppEBR0rQeqxSogkYr6rrm2uUrLM+W7Fy5yp//4C/wZ2fQSY5hYYTps55PmV25zqUvvcHuzkUqbzh78IBP3v4lp/c+Qj05wNgGsKJzKCXmTiUFK1Xoo6TmeU8grwxznMG2H/VEg+q9zjIJgy4qunKR7bNk+riClC8bhkpyhJWmbVqaxYrPc3yhZPBckXPOJRdS/ln+Uxsz+CyCFfnbovK6BGPBwVBQjj0o0XqUrAKjeMVx+NRYKU+W2xCfv7e3z82bN5lvbzObzemaDq8Ux2enXOhaLly6RDWZYkyZkrWPj49QqkCrDlMo0AXWi5vdKfCFAqWRUPRo+dfkZtRN3qH83Z/2d35+dOuOvU3e94pvaQylMfhQLMc6x6LtWDWCtpumpWtbmroRwedj8m94NyV0cN45SlOLd0D1rtqYwGxUn9Sf052iMvU3tjVemwneHLTKP50Svs8lOI2qzKa4eQVeRZrXkHuS8jfAqyLsHb3lMs2NgNV6aBs3EZ/9Jj9ddo2LO508IKx4oRn0oYCP8i79MzgKbSirgunWhOmkZmdrzu7uDns722xvVdS1p4gVwVWvHBrfx6HL8z1ifYrrp58jA6V6YF0dgdmR0j4Yp9Hm7SPNtYfKaSKjVqwu39lOmNc6KWDWdB2dDTU9HH39j1goLoX+ySqJAtR5qfhq47maVBNk03oZWirzxbJZQcnfdXD66LNNfz/tHIcHqwcW0afd69Osz5tkwafH52++z9O/3PweYth5+v3G7Upzw/deregZuHDhAu80LUdHx6zX61R9eBB3rDSxYNlYjo8VMqVUCPHsvbeb3jPstRu/U9l/P+0YG3pUJnvGhrbB/T8FCA7eheHSjHI6/tF7oELehYpzXA0u/DQPxXgf/bzHFzl/03rzbJ7nUbEff54/82n99altyDWrL3jE/en8WlFpb9ISm8p8Puf07EwEbJD7ufI8vsXYaPhpCbqbcjDGfZEbeaNsL0IdDJzn6OiYu3fu8tJLL/G7v/u7HB4e8qM//3Nuv/cbHj64x8HjhxweHHB6fMx6lbH0EfPl+rE0me4W97in2VrGelmuf2wyCo37P/Zdenfn8L7Lclh6OVMEFkhjgielAdtZbt++zZ27d9m9eJGvfeMbvPTyS9y/9zEPH95nb3+f69eucvnqVT4KoVRFaZjOJqm9/z/i/uxZliQ98MN+7h6RmWc/d6+6t9au7uoV6wBNYCCOTDOkaTQUZZQIG7Mx0LRQbzQZn/l38IEvGr5IpIYmcmxmBBoGEIl9FkwDaPRW3dXdtd5bdddzz55LLO6uh889wiMyMk/e6sLIu2+dzAwP3/3bl0wHOiPzuNqD9bh8hBqr1hRTabJMM9kao42icuCUBJ5Q2vD6G2/wwx/8gNdeuUeF52I2w5VlYDQ0WztbODdie/sQdu9gd6+zfXidl7/4dV7+0pf59N13ePSvv0f5/Aj8Gfi5ONp7TYYE0lEs4y8fx8ewMGpovdO9WreHg/vtxPKiWhR8ev/Byr7S8kI+GnVdd8JVNpsUYhWXZdl8BkLGZtOZQLTPdUGy2mcM0sVIQ+O2HNYwkB9iKOL4oslHurDpPE5PTvjk/gNGozH/3r//7/PJg0+4/Su3+fNvfYuqKHj5lVe4dfsOzjp+/JOf4LySCFNKM9na5vrtO2R5Di4k08GFiCki2WjMceLY1qxxXxqzqnSATo8h6zNjkQBuHMmzjAzIRmN2trZw3mPrmrrJKuolwU2QJyod7O2RqDGGmNAmStFbJ9+YWCwNVasCI5SGzexKo1rzlJRgDCtCYy/d328FHclfahraUHoNTsCHEEM+Soh0KyGKTEOMb798ySITEVpX4ijdRuoJc/U+qSvSLo1jMs7Z29lmb3vC/s6Y3Z1tdnZ22ZpsMRrljEe5SPi9J9PgfBmYpZA4UqXIUOFcckZ8uyZ9WnSI0F0noRz6rc9oxKKITKZoIvKQIM97Ca9YVZayLCnKinlRUlaBma2tMB7hvigjyli0GLLosIYy1iQDsElMyJZGGwDgINHQnVOfiOw+D6xk7CP87QBw31uHYL7pPZIDwa5mCNYS/5+h3mcpsry2g9xbae6yRmPVuLqMRrhDIYRnVVW89NIdqqri4uKc2WxGsSgaG+4owU3bveoMGmMaE4SVSHAtdF1uc9WzDqyBjvN/+u6m+9Rn5BV0NNtp0cE0LbyJuJ8HXZLSOD2MA4fm86LjTIniBn+smU/fybSRgrKMj+J8+hTrJvBoSPA2tI8vem8GBSyoRuIrCV4lcMdoNKI4Pl7CUavWaQlGrNBo9McSGe709/RfJCzH2RitxJfz/Z++R57l/G/+7t+lLEv+4t98iw8//IAnTx7y/OgxF2cnXF6eUSxmOBuCeyS5jKx1weS3e/4bBodlIU6f4V7FZK/anyEmtV1Lh/etMDm+WxQFRmnyLAMUWtVk2Ygsg7q2PHvyhD/+g9/n23/xLX7pl3+Zt97+Es+fPeH87BQ9HmMUjPOc89MzMm3Y2dkKptCiuXK1wxsnmc+pqY1BKY+SqBTir5Nlkki09tQ2mOU6OLh2ne3dXZzSvPnVL/OhVhTTOVtZxijPGE1GzIoF57M5F7MCPyoZW8fO1haHb7zG4e1rvHXwJT7+9nd49uQHXJ7fR5cl3krIem9MQ/8ORWDrCAOvoB/7pc/EDgl5orJAI/6fvnacH59s1P7GjIYJORayLGucr5o07q4NbZbWkTO8fPiEW+46FaWTiZ/7zIdSqlHpxv764+gzHJEL7m9Mw3g4R1GWHD07RinD3t4h59OfUD95is5HvHzrFpPtbUw24uxiysn5VLJrOofJcrYn29y9/TIjxOHHKkflYF6JGtIFB+o4E43qmecsE3P9z6uAZ+cC977H93TCiESdq7QfpYmBMMvaTK4eRe2iSVKUqMnLCvFb0cm4+hKloXCBS0AoUV9b7xpA1j8PwdN5aQ2acftkLRSNE7H3mTgZQxMaNjIn3ldBmtMSlToyEHgxd6IFnoJ0Yxzwvq1/9EMIkk88WaYk4+ooZ29nh93tLfZ3t9kZ5+TaMzJKlluJGaDCo30ZGA0HtadtMaypSiREPYAS5x+Jt5SA7Ky5HyaWmrUZ+JyuwzLgau2zVZDuKSOrkBnNKM+YTHIWRclkMmJRViyKkqKomC+EAXHOU1WSIV1pA95KgjoVzeqSebr0vPsVhJrr1JHzvjnx0anZITZ956EQ67IXyrXEUzwLq5Ds0DpfJYVahdD7n/v9rWpLzPbaTMSd9+mevCHCoC84gmBColRjHlIUBdvb22itubi4ZDqdUlZl6KNN6hjbWeekHIVTbfjzVqjcLyksSgmzoXVI59Tv+6p17TMk/bVZRSj3Cchmjgm8VNA5a0tmSD04uW7M6wjvq5iVlPBY987gXAfOttTzAfd0/TlX4cEhxi8+bzUGrbnRqn16kXUhxUW+XYft7e2lPvq0Sx9WpjhSpQLTNXPra1jS9uq6Zjwei5myVpyeHPP+e+/zja99nTffeIMfv/su77//Pg8/ecDR0VNOjp9xfn5MVc7B1XhsyOasQn6p6Btpmnu/6uy2AoLlSKHpbytXdQVeGVrLtH6fiVMKqqpEQsZL1EhrJbO5zjJc7Tl5fsQf/v7/xA++/11+5Zu/yhfe+iKz2Yz9g0PKosR5z/z8EuMl0afDYcsarRS1rqh0idGGxXxBPs7JMnEINwbyEDgFlWFCpCyUJh9NuPvqazx+9Ih7b7zJ7/zO71LOF/iqYmdrwltf+iI7+7sc7G5hZ6e4SYYttyhLzeHBFoeH15nkd8gzzfmfPcXnC2anz9DzClvFVAHLOL9PB6fPhxjgPv646l70YX70wdJKsbu7u3K/0/JCplNRSt1XAcbf8jxvmJDoNKqzZfMo8exXHUSTPltFgEsbrXQpVcH3ubj4XrQbTxFqZIh04GKNyqiqmu989zvcfeUe3/y1X0MbzZe+8hU0nlE+QuuMspLENkJfaFxdszPKOXv0iL/4s3/DfDpje3ubt7/2NV5+8wsUeCrjsQpQwaOhQ6wMc47xWfrbKiQWCc9V73VUux15n/hGmEBZNKFoQ3Wj23rysoLGKyNEWlEJkRKg1BDD07bScFhNfY0KrmZdZiUtq5CCVr6lNnw7Dpl1YuecaB2UAqNrop+AD+MwWYjrrST6xCjPGY3H5FmGyTLJItqEMG1j/7cMR7SX9YxyTZ5rRlnGeJSTKSG6jdZoLKohSgODFbRAGvBOnJqtV6SZyBvH6sAcee/D38h3+LiKHUYoXbt4bdch76vWvLO3BLOC+I4K5oHB/Mkpj8k0Wo9xkzGTaKpX1izmC6bzgtmiZF7W+Mo20dAaC3gViZamQ9JDsgqn+cg0NveiG7lq3bxXIsqB5YjGdfTuY3qvV0XNWh7z8rMXQdr9d1a1J4TscrtNXxsQpvFzPwpgujdlWbK/v4/3XrQZRcFivmA2m7G1u9M42qcCo7Ttob6UUiGJlg/+fcM4wvU2q9NWuD8pzlnF6DUEISzBpvh+ioP64Xn7cLsjROsh9cioEe5Qe+Zlnj6EUPZKd6KXDZv9LJdVQoX+s6tKnGPfL3Ndf+lv8m+5zavi/q8a/9BZHnr3qjVKCXwx54ztg/Y0Jn/z+ZworItj6cOUfrtKKUgCmnjvOzRJv6Rnss+UbG1tCWHrPR99+AHnZ2f8+q/9OnVZ8id//Mfc//g+jx99yunJY05OnjOfTakriXhllEKUFjEfVFy74DOnEM1yMva0pKZgfZP1dOwvUoZgscx3WXsSi9E+5CeJZpiSgVzXNbqSqIraSHj6p48f8nv//He4d+8e16/fxjlPluXUlWU6nWOt49adW1y/fQOFktDFSgTQW5MJygj+d158PK2rqauSfJRzeHANozPm8zlb2xN2drbZ2dnBZJo3v/gl/t3/1d/m4viUcjbl6OgZ7/70PbxRXL/xiN/4W38Hqm20XbCV7XHnxh7XdsdwYLjtXuEb+a/znT+aoc5nGHUJvpCocSsix6WM3hATu+7+pyFsV+1f6v9oQx4wpxUHN65ttM8vFHXKOcd4PF7iiJQSVbm1lvF4TFmWzaBSKWQK3PsTjpeuH6quDyQiQku56zi2WD/9fd1laHMrwKNHj/mFX/glDq4dyrXTCu8dedDkFPMSo7OGKPTeM8rAVJ7/+Z/9j3zwzg85Pz7BO8ef/8Ef8dYv/jL/3n/4H5Fdu0GtwCuHQ3X8EV4EwPfXJM6jYTR6z9riG6SVro1IhG0CzGgBj/cStlTeSprqEaOBSG6YOFrE3ZdWQMtk+baBlcxFU8Uno2jaa+0SBQ9LHRN8QbQWlaoxqZ9IhjZafB6slcgJwYnaGEmgmBlDbtq+uswuWBeyrXf8IRRKKzKdSehYoxnlkuU6N4Y8i06ulhiPyDWzEH8evJdnMUIb4EKG6zh350N+FS+fIzHtfVeyF8OXLgEMRTBxCppE1UXR687i0H1PtzCt12GIgymTjg78I5EM+bGjGuXsbE2Yzksu5gUX0znTeUHt2ySPzR4HUwZxZl3NJPQn3K6R2CG3e7nZvXsRYr7/OSUE++uzrs1Nx/WisKODxOOafsbSgSMJDEoPg7WW0WiE1or5fMb08pKiKCirkrHb6t5ZurHa+0gxJWryLBPzia1s5Ro0YbeHxt5rd92cmvGwzGf28Vg67iEmZjAsfGfMDQQPOCKOK85HBm+hSQQW2+v6tazlFX+mMjTP9G8Kq4d2RjX3dz2zv0lpmZz1J7nDQPQWJvXxXEkgB+GOQggyCe6wrLWI/1Jao3OW4x4OzHlo/mm+ibjueZ6jlISQ/atvf5tb1w755q/+Kvc/+pj7H3/M40ePePjpQ87PTri8fMRiPgVH0JQjketEqtZo8mOoZoiWC928CA190I8stmL+Q+u/qlzNlAz7r0r0UY9CB4YkmMZjyUyIgKUVyhiU1lRVyQfvv8eDDx+AFzMxozO8F03Op/c/YbQ/YW93l8l4zGQyYWs05trhNQ6u3+Bw7xr7+/tsbU/IQtI/pWA8GrE1niCUj6OsS1RIRqi0YWd3n0/vf8pYG9544wu8fO8e3/3+9/jo4wdk3/pz/vbf/XtyXpy0hVdU246tV3eZPL+O2bkG6jmaBTDHKgkosO68XFWG1jxNJ7Cqbgq7lFZUTujZURL2d115AY2GEGTOSZKl2LkxmtpZsnyEV+JAPZpMxJbWxXjtXWc/HaIvKU+wbwZca2+utMbbcLtdjytLJbq9Ay5ORHHAQbIaiJQO4PfBFMxZtNJUtmK8NebWnVugQhg3FZKreUdmMkbZuCGYINDIyvPkRz/l5MED1GzKbi5ZY+uLKT/+13/Os4dP+Hv/4B9w8803WDiP1xrntUT3JIkUEP63TpqwlhDsHZ6lukOv+kSyFN9PGb8Osu8dUJWaLvVyZTTSet9I6MIk439QKol+4MXYIh2ySqornERM6BGYKmgPMqPIshxjsib2dZYZlLHowGhEolqAo0bVdDVLxPl5VBMNCnyQIMS514GYJzBqRotZntGarZFilGchEZCYDgmRLMVFx2eVSpJ86Nu1NuDxnELL1OLxtm7W2eE7GdElNZtv7kbU7iwBlZAF24W5puutk7HGO9MwXKp7z1Iko1X7WwvsEubQeYky5MXfIssMOoM8yxltGSZbOZN5xvYk4+LScDKdMy0qnLXCbFkXxqdwIR/JVYx693ff2exVwHPo+SppcR/x9essEV49Rm3VeFcRX1d93pTxaPeMxkRCRSZhFWGeyhma6DwE4jkNeS7CGQmEoLG+Jh+N0MZQlguKxTRkFC7ZDtFxtPeMxhPKqqK0ZasNa/bYN0y5hLi0jPMRrqrRWwzCtcYks0PM9qXoy8RuyrDHOTbCLFJpYcy+KxqGeOaXpYut5DeaCss7MRGnjEngVZrDRrTw1taJObJrxl95F8KMIoSW82gdIwNVOG8xJlgLqLAiDawP76kg4Umi5AlMG9r/sLeJYEe+uwampnC9gV0r7odPYE88Oy0uWZY89VFU3L6url7mtCpAQPw9ZcRaYaNdqh8FOERJWHhPa9XSK2qYaFt19/tndTla17CJmrQlDLbWMLu84C//4i/42le/yrW9a3z/uz/g008e8OjTBxKq9uSY+fQC66YBt3Z9oVRorzEFbaL4yXmxLonCFpgPpUNeFLU8tj5zvSpi3tC8+mW5bnt/02c2zEspwcdK6UAhiO8fXqJgelcHnJOhlaIqS/CgdUZVFXiv0CqjqksW9Yz55QWTyYTJaIwxhmdPnrC1u8/W3gEHBwdcv36dg4N99vf32dvbJTc5RVFKTimtGOdbslZGczkr+OrP/TwXsxk/+dGPuPfGq+Bqvlp+hW/91Xf46Qc/4cZ3X+Lg2gHe3+ajDz/l1Tu3GO2OqE1GducWe2+8yqP3f0rurSSdVUZcNgfWtGFI0/V0rgl73NIUy2se76ELdeTohzuzYn+MAluVjLMuY7qqbMxoaG0a06kU2QshJIurvQ/JjuSvR9SO1qYqVgHWPhB08YioMLmGOEE18Zi9F78OhcISMz/b5nB3EC6JyUIC+LTSTSI5kea7Ro3uvWPvcJd8LCq1zMQQmzIv731jt9/QzQpMNuLpo8cwL8i8F87BGLQHby0n9+/z//6H/3f+13//N3nr53+ehROVrPIhTwS+kdJ6CARRn8FY3osO4EilJm2NthXV/KdZo9juSqCYtC3PB1TkAdF0T7ZvCBhN92D7pG4E+PGJbpCXb/cwPNXKM85UOH+SN8IEpGyUxeg2Jnk6xlr5QJAH5EJcZUcjxEnWRCQiChPjFgLeW2pfC0GFwhIyeCpJXjfKM8ajEVmmGWcwypPgB0rYFetlFdoQzi3B1iK7Id8i0YREgqVFfOB83TGf6AL3VvPRQeoAtvUv6ewz4nfTEgyBIYscoOojwfZcGp2cHbusNYi/y28S8hYDOleMyMhHuYTs3dlid2vEZHvCyeWc6XTKfF5jvYTIDsaStIkR1ZIUJ5XyNn1HBmpDxn3V70MMyosxPOuRLGwulRoaz7oyJHhQ6X73nl3dp8CshoZSbR4LkdwqvNNs7+yytbPN2dkx89kFZVmIX473eOsYZ4bbN29w/5NPJZlpNB+Kw1C6MY8Uzalhko+oFgVqXxikoQStWqvm/Lf71O5V+l3qt9Hx0rsYGYC07bj3UVueBjuJ9eJ3a1sT3xTu1rXkJpB8NDVVVTb9RryF6sGFoIVshDzWIeSfRnlFpkTgp3VwbDUG56F2VtLLBD/fhhFLYDGRiRrYc51ucjvLDvxOSwrHu79HEqYrmOgLEZdLNPfr/ZqOJxlLe/+XJeHdMS+Psfm+hKeC5lgpilLCwOtk31PYvTS28D3mtOkQhV0k3ZTUukMp2J5MMMZwfHTEv/5X/4p/59/5Jq6yfPsv/pLHDx9ydPSU588fMb04ZbG4wLlofpqY/UXmCA/eNmcshaNRqNVZk7BOzrpO3RT29RmP/v73785mJaWFeu8EfxIP4ewmUUaV3BUXmHrvaqyz5LnH6BEoqAMDggJHLXCkdLi6QjmHD2ZthTGcX17Cs6doLclqR6MROzs77O7ucnh4yLXDQ/YP9rl27Tr7+/tsb29LQBSjIM/5xW/+Ci+9epeXb1zn7ddf5//xX//XvPHqy/z4w484PX7KfHrB+ek5C2XwleFwZ5fn5ZzdO7fZe+0uem+L6tJjcbjK4WwrwEjX1ycaU9ezCoq5Sujvdf+8hjrNcUlgQnoHFSEpqnWcPjvaaDdfyBk8BdyNlDeENCzLcolg0lpTVVXnUDbAHB+SW8nR1qlqTmZJFMp4kgvP8kWO4xKTC4cKEpza2Yax0ErL4QtEn3M2AGwLTiJKOOeEsXBxORv+rtNX89k5Ls/P2JlMWHixS9bK4LzE+8+dwj4/4Xf+n/+Iv/1/mPPVX/smpffCmcY2gu+GJuCRNHLSiqgkgZpP6vfq+X7lzcomUtF+vasIsLbuOnW5D9xTOMxKfHVGec44V0xGckyj1C8WrUyzQ8KNtyFnrbCkwxOIadmTOYhEDYo6PpDxOHwjjVRKtHl5Lo7e41yS4RmjGJn0EkdmMM45MgyOGHe/JYRc8ywljqIUPj4DOQ/xvqR3rctoREA/gPBVDKbQApRYDCkiVoGmUZGK7Cxfy9RFhnKZwBdmJDArtGZqWntULVpN2U9hICcT+Tve3mZnZ8HZ+Yiz85zL+YLZoqC2tsm3MaQBSMum5/iqsirizjIB89n6G/J1+7zKOo1LPJMv2lZ6v1NYHtuUM9maomxtbzHZ3uLsXDGdzigWC8qyoCzLxiR1Op12bIv7WhoVGBgf8kzko1FgLkyIE7HMcKYEbCo170dMjM/7daOgqqqqJQfYtP12zl24pgID1BeCDcHKdP1iv42Gu0NMS7vGe7S1ZMawvTVhb2eX/f09CWpiHWVVU1YVRVmxKEtm8zl1NJm5Yss/r3uzCeP7s/Q1hP9fdAxrxxQJ8vC7WHJE7YDr5GYaYkT7BLVSSkx1aH2S+oQitOc/3iutNeM8I9OGo6fP+OM//BN+4zd+g7PjC95/732eP3vE8+fi8H1xfkxdF0At7ks90LVqPfpRw1bVjec3JXKHGI++KVpfgLZpWS3wgSGOtO+3EM3p8zwHoCwLMkMIjwsETVX8G8Ozx7sb6UHnCskLpDWLhbzy7JmsQZaNUIhv8jiYXO3t7XHt2jWu3bzBwbV99vZ22NqaUBYFZ+fn3Lxxk0cPH7FlMnxRUMwXFJXj0yfHTOeaywOLG2VcPDplZ/c6119+lcePH0pgISsR9zrJHgP8qWtLnudLDF6f9u771aU4rs+EDJ3lfjn/vBP2xZJ23IROVe2la7MH22Zi/cE2uTVoD6KJWZchaDNsw9OagahR/ZIuWnSYESDRJnyTCSA29UraVMbgnRwsAfTtpe/PO+0L79HO4sqSej4n854tk5GZnKp22NxgrMJWnupiyh/8D/+E0lb8wv/ib1I4CX8buQqNEkmvC4nfltY89pv+mI4zPVzxWfze5UpfpHwWwiclRoaiRfRbjERpazoQkvJkGXmeoZVDNwnyHLZxxBamscuuCLPgIaYWSn4PAI9AQDdiKxLzKIVtfIo83tnAHECmNXmmGY1ytiYjRnku4VyNaehwkXQG13YVmQSPR7Rpol1px+8JTIkLGbCjRMmD9SErd5IsxzkXst3HcLxtJlmIV1FMs1rmKV2HdpzQNY9TdCVsLeFHQ+SIAyvJMx/CHMuLbRLG2E7VQZ5KRZ8N4V2E2Qh5FxEt0ZZWZAomuRBSx+eXqLNLprMFtqo6RGmfcOwTkMS9viLq1JD0rVmJFUTRpoRMn9hMy7q8GJ+FEOsLgT5PguwqeKgAg8IGgtYYgwYOr1/n04efMJ1Omc1m1JUE58iNwN/ZdLbEtA0RJyoQ3luTCU+ePOHuK6+AokGu/f0Hloig9B6t2pc+kVTXdTOmPlxLia+h8YcWG8lxJDRlbKbJ1Nt3qtZJKNRIDCmtyEzGltEc7O5w88Y1bt28wfXr+yg88/mck/OCp0fH4DwLW+Bri/EKbTIq1Z61JSI4CcDS39eh+3BVueqdIadV2hkvlReRhPcZ1avqrfxdtd9jviWtNJPJpENsp4T1EMO5KjBA97duroh4PieTCRlw9PQpf/onf8o3f+VXefrwCR9/9DHPnj3j7OwhJ6fPmF2e41yJVg68DQJKw+oV7c53HYPRn4/gONt5N4Xx/bqxrIt+FMtVe5bUJJ1bv7+UiY/MgzGGsiywtmY83oIQgkbwmeAhpUwwWZQcXHmeCx/iarRXWO8bHGgt1GVBlo2pigXz6QVKKY6eGu5nGZOtbUyesb095uBwjxuHB3x6+zZb21tgLfdu3uLxgwc8+PAjnJ8wrwxzN2FRK/YO9nDKYcg5eOkuD0zGCIMk410B1z0dK5/+HeszYClM6+9Jep4H6TgXwgI535dBriwvlBk8XrDI9TWSG909aN6LRLquZWEiBxYT/MXnVd0uXEzipbTGmEykr0F64ILpTlmWbE+2muzDKecfVc5Ka2xdQ8gGXllBFFmWSW6L0JbHh7xqjrIoGI8n7VhceuBbLj721Vy4sqSYzfBVyUQbRlqTmZzS1zitME5Re0tlFdV0yp/8099Ge88v/MavUwGlcyGTaLBL1kEjswQsl7UCkcEYgr+RGIyagqtA9DqCpH9509+GgP8Q0vWBGW3mEP62TIUhM1qyrQekKsSrw7uaytad9mMX3bVJCYlYoV0PeRYuj84ahiSuTxxn5YWo8d6DEzO6XAUzqbFhPBoxyjJyYzBKREce8evpEymReXHKU1sbBhTquah16DHJLmo4wPkkkROISjgyF7jwrKsZicAzZqRWcSzhlCWL1T0D+MBQROJcNUuYmpakf5US07YmQaNNCb5o0yxNKS9x2r2tybTGKIXWHq0dzoW6SsYxyhRaj8mynCwfkedjjk9PubiYUlV1ZwztOVg+e43UsEcoDp3ZPpE6RLSmEqT0t3VEUIQdm9yVVX2vGq/37dpfZRudtq2VojHevGL8fViUrnu8v9ZacB4T8uoUVQXeYYzi4Po1UDSO4FUtARW0EphXlMVSX21wCVqCT0OmNNvb2+IMbjTWdzUCQ2s5tBar4Fd6DlJku06ztWrNIo6R9ZLfJUSvaPFsYooSo76YkHdKGHGFDhFwjBGzjcwYMgUjo6lry6PHjzk6eorGc35xxullxXReUtW1wKQ4fq/wuoXBnfXxrblMf92GNEMvUlbdyyFmUCqyBJfS91JGcV1/q+5lem/TdoaCAtgkEzw4NDrsj5BMrRn58jzTM5T6rfWJ4ZYI7M7RWitMhjGcPH3Gn/zhH/ONb3ydh5884JP79zl+fsLZ6TFnF4+Yzs4Rhz0xx4sY0dMV6q1j/jZl5IbWM41CFr/3GY6NnO6T+kPnJqlFn4Hqt9tncCLtZjKxH6zrgiwbESOByjsxCqVgzbquaEyyRAYs+cbiGVIiWqnLMtArMaqYIPW5nZJlhmoxYz695OjxI06fPuXv/p2/w6uvvMonn34CWca773yfT56e8PLrX6PS25Dl1Dpjd3uCdYq9O3cYHx5SXZ42uDzCiq4AhM7vfVNyoGNmOnSHUoFHar63jMM8mRZB0vnp+cr9TMsLMRqRuUj/CXerOwsAgljiwGOiv8ggNADci/mU92DrGqUgQ1OUBcbkUUSLRlPVNSenJ4xvjzrjShfbWoe3EiZTocjyPKjKfAgNJocg9umCM7jJskbF1gLWSFDEtrs+IUopvLPYsgBrGSlF4GQwHqEStcKOM6gc2w6K6Zw//Se/jUHxc7/2q3ijKW2NVQalHKoxr0mBVzNTVAc/rJbCRilJBDUqaotWAN6hMsRUrAKs68aRfvbeIQ6UCmMyYh4Po4Vg1UGb421wbxaKOW2xg4ciAR1LOi7XMztLz4lrpBk9xgAvSf+8pPbLtGJsNJNRxtZkRD4ShJ9nwmSohvAUB7SUYfHhrLkg5Y31YjZsAoPpvRKNRqLKdM5hvWTe9q5NCtg89+E8h/MSmfSoAYlL4om25DKn4EAV1qMN1yt1XWAwImOROLNHRiBqnMK7Skt45MZHRuskWzwYoxrmRWvTRAUj5CJRSmyQTaaacxElh9poxlpCDo8yzdhAbjKOjk87yG3onPXPZ5o/pIv8u+dm1dmFbubeIYS5igjrI/FNiLU+UZcihZRhauFv99mqOTRtqtQLanlMfSJkVUlhorfBg8lL25Wz2Lri4PAA5z3FYkGxKCQ6YWCYNSEgiOoStHHOKkWW3mOdbcKfW2s7ut912qGhsgr2rYN3sfRNDLKsRaMdya5uQ0rH9yLC1jojDf6RZVkzt0zLmlZl1QjQyqJgbp04sTqL0RLZQSdwqPJeEmHiiVGOQp6xzvg68/MhTHmzzF1COP62jqlfVzoM/8B7nXVOTuUqxnwTpjiV5g49j6VjhpvsafTlDJQdRpuGQQdJbkuwgOi3F2mgVBhAnF2C1/uMig8Co6qqmEwm5HnO+dk5f/T7f8SX3voSjz99yJNHDzk9fc752Qmnp8+ZLc4lciSR/I7rFwxaX2CvXoSJ7NftW7CkBGu6/30zw6G2rh6zMAKbjDeu/5CQHCoxfdKtP297BxzO1dS1BDPKshyUJJO1zdziGCLu9yHZr8apGqMcuAxrwdqK8Sjj5PSEj+/f54tvv80HH33IK/de4mxW8Ojhx6jJPuO9a5wtxpjLnFGWcfvGNa69vMOP/9Uhp592z39d180ZM8EqJ67xOoZtHZyM7fWZjPQZCJNlnQQB2vu882iknTrnmqR8JsuoXRteVosOqrFvjYn+ojYjXjDnPZWtyVQWDoPFmCyYFKlGi2Gdo/aC0A6vXaMsKzkTAWDHcUVmQhmNCnbCta1DKNAe8WHbRfeKoHlp51YWFd7HcHLLyEZFgGOtZHG1joOdXYqiwFuPrxU5UODBKDJlyIuakVPMpgv+6J/9jyjg67/xa5TOSWx0JdF5YghUz3JYPu9XS4m6RfwJ2ndd836Kdvp3uSfoQqnYj0/qe2IukT6hj++PC+KF1CrtwId2xPROQrxFG9jQV2QqPB2iqENINR4Lvdl7AUYRcvSRq2QwHmCEcLhg45pl4oMxGRsmecYkz1BBwqjCecVHJgOc042GpMNMEzLE06qcIzMhoW11wzzUdd1oImrnqF3LyERNRzSfcsR1i0yHW9KSdJkewLXr1TU6AwmF1moj5G9gHHyLMBpzyMBUmOBrkeW5MBSReTQKk6V+GLqVwmiPwzSmU85H7QagDNpk6OD7mhnYGWfkBzuYfIzOco6Onrc2uFlGlotQwsXzmMy/L61cPiddAqWzJL073wfgQ4xOv/SlmKvKpkKAtI0+Q7KqzrpxXfV+//f+fOKa5VnOSGegM8Yaisowuzxlb38frTVFWVKUwmi4Rn1Pw/REeN+5q84SQ2orD8r5Tnbw1EdkHTG7bj2GJLspI9ff79aRNzUJVB1JYrQNr6qSLI+R0lqJYl3XxESf1lqstSwWi4Yo0r4NqhFtx7XSkphMyw023qMxhCRNAj9NjTceFQhN38A5IsiVNSCaAokgQA8ckauESpuWdUz5VYxxv2xKXKZtrXon3cO+fb+AEB8bBFSALw5nXUPkDflY7e7uopRiNpt1n6s2cmJ6j0Qw2+aUGY/HjEYjFosFf/AHf8DNm7d49uQZjx7d5/LimIvzY85Oj1gspoIblcYHgWkn+uQKoeSm6/hZSt/ef+jeXdV3yoyshkOr3x86Ty3hXBN9ApUKgmYdGMIgfAwEB56QL8JLlKr2vmdEZkdopIhjI4Ee6BdnwQdts7U4q6mrmsdPnvC1r3wVk2UUZcHXv/5lzr79A7LMUZRT/GLEOMuZTjPOJp5qfsG1l25y8a6hmndzDrXn12J6WvNVMCxlAldpNfp4IdJ9jVYjwBIThYcblI0ZjboWm/EsaCzqSoh/dCCNlcYrTWUteLBeTFgMitqDMpn4XXSIZoMLFiVKGbyDqhRJldjlJ1qS+J4S4kx7LdIbLxJQSSFfiXO6FyJJJL1Q1RajM4w2DVHnncOYDOuESxV85qnrkovzM7TSbG1tUVQFCh0SRcH2zg5Rel1UFWW5IPOevVGOqUpq57EG8I4RCuMcmReV+MJaxijcxYw//Ge/jTWKr/zaNymVw2NFouuVIFWiKCpIhQmOt+EudBydvW8c1OSQSP8xskyUnCmVAFBA0SXTUzag6T5I+L33bYUQ9rcV+vikgRTYqeSChlE0QlWJ/hS1WhGQxyyvQoNESU9rPtQpSubQ9JqcLfnNN19SIgLVNTnqcOtacl+MRyMmkxGjPCPPNcoQollA7VWI5BCYDO+b9uRsJdoHwIXQizEKjbVB+xYAWSSa4zvWWpEIh8g03kn2UxcYeu9SJsKFuyn3s7Y0a5Y6koPH+9Y/ZGkpm33pSiCNEjMnE6LOERmHLBfmQQkgN0WJNlqSHhqN0SqE/xXALoyGw2hDbTxGVSF6WEiS1Gg0LMbHeOFgjEZ5iTN+w2SMMoWvZjw/vcAjQgVdK3SOxE1vhAABKHsfiC4aya33IsVVphX3OmdptTxtlJh2fXpSNO+DhiicvvgxNNknpq5CsCnh3yfo0zpt90N7uOynMFiv9/uqttI2V9WNRHZuQhJWoLY1tatxXnGwf4NM5VDVlLMF5aIQQk2FQCBOtJz9NdJagnc0c3ICJ0yIBKVUq2GL40rHnJYu8ZKccdXCGRRNyOhUKtjVQiz7HHaEXV4k0nVdUxTCVHlcCEGrG8ZB3pOdiDDK+fYMqQ6MlvNonXDeMSmm85JrRykxtfIqHEfVCvJiCHGjDEqF9QkymGZdAxEtsFQFAZ5rYJJL9rtDxPue3Gip+Lavoac+mnIKXG+1Ku1FSt/Tvb47+9vBObEDaduEOS8JxJr5qqZuFE35SNMQGNzQcAxIoD0YHyOt+bb/AFvm83nHfCgdnAk5XhSqCZfvPFjnMTpjazTGVTV/9qd/ii8KFnrGJw8+Znr5nOn0hIuLE+aLC1k3384z4SPDFJfXqb/+zag+I+PRZ8pT3NJ3eL+qr/Q+XT1Gh+/l9JLHilR7HQVngveib0XQbozCeJ046psQySrhxoWOFYhGnmeI5Y4N7UaNVRxb3AEZl8WCKzHOYJAAQ7X1nJ5dojLN/o09Li8v2N3d4X/7H/wHvPfgORqPqy3zomI+9jw/mfP04ila5yyqEu1twGe+xWGBualjbi/fMnkqwBjT0FG+cRfwnmCq3zLUjeDYyQl1PvoPK0yWC3xUCm+caFU9FNPZ4H72ywvk0ZCsyXHASiGX1AmAU0FV671EX8rynKIscYXY4OZ5DloHvwwh1HKTBeKrPaARAaThO23QoCilqC1BKtRKvK2zOFehtAdawir+9V4So2lthLGwwdFWJiMhU7MM7x3FYsFiPsVoTWbg4kK86vf2DvAednZ2cdaitBKNSV2TKYWqa0zIsQAe6x3Ga4z15GFOjDJsVbGtDdPFgj/4Z/8fdq8d8MpXvowzolkxXqJcREYjHt1otxvORJOVGyKgbREpzcwj0mrNK9Lr6WlDlnUuNTS5+SIY67brSB1sOzAgaae1T47AJ9EsxbE7h/ISirEFVD65vMvjW0Usd8sy4IrfU6DYB5aZyhhlOaN8RJblaKPAiMbJO4+3Hmu7xIukBWid+BpthnPCLHjx0YjMhXNypqPPha2tOLkHrYV1VpzBU4QfGJDaWtGaRe2Gk+g4BILfeZU4ljcymmZJGjzdXz6frnkSHs9XGCQWt8kkohpBnWyMJteKPM9aZlJHjYb43WTB7lzqS44TEzQZmTFk2pAZRxakI1EopFRrax33ZqQVB1sj1N07WDwnJ5eyzniU8ZhMGIYsy0Lced1IH+PZ60vyo0SzjkRg6LuJNN2T/mgtd1MnN6khWKDVqvTO2zotwdA57fse9BmPVUT1Kili5/2IIAfeGXp3FfJPz3nMqVE5S+2s5BOylhs3bjMZbWHLuURYmS+oq7pFenTvclcqKuavo9EI7aEuK7Ymk0aAked5h0FPmYO0NFoEkPOXmSbnTmQO0lDqfQlgKgCId26opHCp/35MltkKOwYo8PA9aiPit/aZF0sNSAgq29zWhpFAzqQJTKA45q9mFjsEYhLMJWr803rpedDR9EsN4I84dg/amOU2iOcya5i4dcxvNAvyyTpJD63vWfd+xLc6A2oG2LAx3jdJ5pu6BGfXsEUq2VOjtAQA0aLZVroVdcUQzX0tWTPvMDAV6B8I+bwqF4SZI7RSvPPOD/jovfd56c5tHtz/iPOLE4rFOeeXp8xnF/hg4dHOMzAW/Xn2xrCqrMOlV2m0huY61O4QIzH0zpCAZbj//veuabm0JfVamjVYugSc0ISv9jS5NvrwSN53QeCtkt/6faXWGIASJkUEx4qqqtFKczGdczm94Patmzx9+oTHT57y9775tzg6+TYuy1gEIdlsUZLpEfff/5hXM0PpHLn3IpoI5J5XvhGIOYQJgBiBk0a466zvzEsFYUXKqDbWJMkFEzwYgsBYh85HWDx1sIxQwNHjp0t7NVQ2N50KwLG5SEFaaLIsSFQdJgu5LuqwMToLWRyhLCuqqgoqZqiqOth+G6qqboC+DUS8Mm3eDqlvmwVyznaygTd2gT4lnoW7tU4IOfHYL7BWCJEITMtiwf7ORN4Pi71YLBjluaj8iwJjQjZaI+YhTS6k2skGID4mOnDQGtFoizWKwnoYBcGJNYqZK5i4DKZzfv8f/Q/87//T/zOHr73acpu0Epfowxf/DYmHmhj2/d8T04KrSopcu4hsuC5cTfBvAkTiuqcuFWm9PuHUd1BcV4YQf5/JiL8ppcizjHyUMR6PyHNJAqjwuNrjlWTw7DJEgI/Sw66PRSQwrHOinbCSTMg5YRJsLc8EsQdtRCSKvaP2teTwsK55HiNXaTT4uA5KkmX64EeBx/QY9xi5yvi8YTb6gNqmktZw1xVBakqJRyQyMne5/kpDjaOqTMc8ygQTsyphNExWY3RkNBSZEXMbm2Uhd40R5kB5bC2Ee55lTWZxbUSKZJRmezLh9VdeYT7/kPmionI1I6twpePatcOOjXQViNrUqQ0ISdG6pmwp09kQgwNnSumuj0Naevxx516tQ/j9M90/n1ch6H47zVij5HoFAl/3PrRZY1f120owgYTF8ggiPzjYZzweczG7pCgWjcTfOYcywWzKuSVCU9oWoZW1lpHJ5UxVogkrilK0hQPwrQ8z0nV03kLVHX/UEsq56c5rCE70Ycqqde0Q8D2zkiWCeYCBW1dWwcd0DTqSZpb9jIb6S5lH7z3KrJBK+2UisxlT4gA/NMb+WRza+6Xz7XzDnHTrCoE5xIS3nS5NoTOewXd67yvaNXXOBWmyaOUaf46EUe3PaejeRDhV1+KXYbTi6ZPH/Mmf/Al3X3qJh59+wsX5BYvFlOn0gvnskoYodD4SCd2ynqdYOf+hso5xWCc8Sc/YujuyqSblqruwjjnp39fUaT36mIlArxbT/d64Qe5NXQ9HfBqEzfKgGYN3Dh+EHWVRcPTkOa++8gbvfP9djFNcnp5SLy740tff4v2jObnJKGcXHF8sOHr6mDu3tvE6wyLMbbzPkm8ujFV1gIkwFlqLBiLgfB/ubLR+wbf4XEzA0nkFT58o8NJQVgUqF5zsnLR7dnyydm9i2ZjRKMsKk4lD92g0ogrIIkccv7Mso67qJDmfIAXrfaMar6q62bTM5EHK6Bt/j5g52ANlVYmqUseNFDt/sUe3zYWH1vY1tq1UCB/o24ghMVpN3Px+dIQo/nVO7GW1Uk2c9/F4wvb2DgQCTuwqnSR3CVIf66OJlzjgEUxe8KCVQ1lH5hVj7ai1pSxLds2E+fNjfvcf/Xf87/4v/0cmN27gtArOkmKmZhTogKP8qoupVKQem4OfIpqh0r9Mvact8Bx4bwhZtENZBk6RU46SoSUk7ukwGkMRKuLneOH7vw/13yfe+lLGSHhGCfxoPGY8yskDkxnHJT7UTkJ3hu5sbMNFRsM2JnmRkHJONFu1q6mtaxhwZ+V92zAZQuhEYth5j6PG+nqJkNJGY7yYL0HWIMAWCVs8XaI5jkWHONx9tbpIO8STBKVC9K+4oAiUIWhKIvDCC9DDUtcepSzWGrSWHAfi8G+wxqGNRZU1xkjY4sxIqOC69hhdY5QwJHmeByYk2Lr76FROyA4vmrQsy9kaad54/RV++sFH1NY3+3F+fhEiw7Sqba1VRzDROXsrzq3SqnPfhk0h1pd10r6hkt7JdVqGTf0R1iL5FX2v02AM9dHWE810CoeUUozHY/YP9jk7fkZRFMznc2pbI5mlswZ0xX47jqThmNZ1ja9FoKO1mLRWVYVK/H5SDdAyw9LCgaF5R6ayn1m6Q6j34OUqRiT9rd9GOrd141xe29WwfWiv0t+j8MKoNhnhOtgdxyfMUBA4DOAR7/zgWZMvsIq6/+w4qdvGJkwzq4exsh05CzRa31aG3Q0H7pEkdsRcYF5wplOyx1mWNb5Eq/rO85zZbEaeG0ajnHKx4A//4A/Y3d7m9Pg5lxfnzOeXLIop82lw/I7CJmXwA0u1CVH+ImXT9q46u5+1/c9aF7pCRYhR39poTU3STZ3hnFjaDDGpnpYxMYl2Lu1naZw+ag1aH8raecqq5MmTp/ziL/w83sHl2aWE6nElL9/e5/2jKbZa8PCDD/jw3e/hF8/5+u1fYby7x/xyKjDRt6fSezBaTEtThhilxPICF7SZkZHwEpuXxBwx6gsTskDhxVyVkIQbhc8N127d4PDgkPd/8lOs0+R8zpnBnQdbxpjiiroWwrquJOpUVaXRT4TYquq6JcCJmVLFocY5H3wxIvA0TdQN2fy80XRorRvn8mgjF+3QUtV2s0SeRoprLc17kaONwC4mfpLfRUpQ1zXXr19nb3eX2lpeffXVxnwqHk6JpRych1Rw9jUa6zzae2xVt9G0bE3tvGRoNQqlPZl22LrC1Y6x3uL84QN+97/7f/Ef/6f/V/x4LGYYucFrHaQW7fb3SyQy27VfRoCblD4RHtUn66QSLwZklhFtt15X09AHEmndFwFqKfJNzZ36CFuivohUPjKUto4cnqhPyyBVw3c1F2Iuo8SEz7a/CzMh9upytoJWxLW2olHrJm36htFQWvwisuDzoBPb3kypJtKMVm0CTOc8zlbEkM0xWoZ3DjlSntzIPctHIcpa8OOYTEaNCVRV1dR1hbWOqqyYz4NpFypE7DKB0RGmOpCFgPifKFRwZK+xzqNq1YTprK3HaE+dm8BkyDxzY6jqoNnIM4wB6yVDq9GGLFcY7TAGtBUt2OHeHi/fucUnDx+hlMF7RVnWGBPPEIHR6J7X/lkZ/N3TmENFhjR93n+/bUMc5DcpV46hV/oE5iaMwSBh0Wt+HZxYRxQuj7vV6ESEZ0zGwcEBnyhNVVYURUEdBE4oQsx/NbjGUVrd9OBb2+/5fMZke6uBB6s0t6kU0/cn3pljQLQrCPchJqJfd4jQT591f18+P31GeFXZdL/Ss2yd7azFOia4mSt0UE6fmVhNsq5a6WEmeSPiV9Es2dL8/cD4wu+e1eNcxXT55CXv5T+iK273USuNV2L+F4WSqNbBO+7pUMSl+KwsS5RSjPIc5R3vfP/7PH74kIO9XY6fH1Eu5tTVgsXsEmsrFA68kyAAq0mCtfDj82BE+vdhqP8+bNoEvm1a+jTJKljc/+t79zsVAGjtG2uX/t2I70X6pQ+nUtqpmbcTyxznxWQr5g4qy5LTizNGWyNMnvPBhx8xvbzE1iXbkxHagK1KHnz4Y46f3Gcrrzk+OcYqQ+1VkGJ34Ym1DhNzssX5B+Tnfcx1oYIgPYw5Lki7qs35FdhNk21cZTnkGYzHfPWbv8r+7h4PHj3hsnqOdxvcXV4kYZ/SLBZzxuMRRVmJelQbimIR7M9bRkOAmRBT1otDa0QStbKN2cLWeCtEdgpESu0oqxKUwmSGi4vLJgqDZBgHpUwHWHYRjGqdQEkdknST2MkmY5X3g21xXaNCeNAoNffOYULYW2nLNBJwvMJr8Mawe/2AGwcHnB8ds1hcNu/W3gmDoTwEe73MwpY2qBymdUVtRVX26N3v82e/+zv8L/+j32RqK3xusF60PCoelHXbcwVBsEn9pm4Hu69+LyV4ruovlRYsMwu+AwT6yHwVQTY49hWfhwiDCBRiZs9IPFsrNuZitiYX1nlPEf6mGhGQ32prG1OoeM7qum58L+J9wCucaxnhmGxPgIM4Iwvx7SRZYUKENOe3LnG1mKBorSTfRJZx4/CQTGuuXTtkNBqzs7PNZDJpbDZVEivcZBFZieZsnIfcOKgQbzwiXBEslHXNxfkFR8cnHJ+ccnJ6xqIsJfpVaEMrg3MqEP0u2OCHu+2FqHS1xelWujTKc9H2WEdmHUYZqsqG3AExt4Ajsx5yi3YwNh6jDFp7Xrp5nfPTEy4uSyQCi2gXPb4x4Wr9tobP6CDz2jvnnXO3jpjv0zobnN2hsupO9ZFsitz6dWMZQpAxxsqqsa4ay8rSfzVwHFVZcv3adbx3zBdz6rqirMoG4cXX+j4p8W6pIDgiMNIK8feLkvo+/FkaVo8xTEngPgxSrDd3GX5vuKx6N2VIu0eqncem5q790te6NX15iIErYr1VjEbfcb77IZ0Hjfng8nos28vHMsSoxzGsXFe/vs10DuvO8LqocoN9Djxu71riaxNfcY7RaNzcy9SHaIj5LMuyyY9yfnrKv/wXf8pkMuLZsyfYsqCqShbzGcVihjGIBsUHwOwV9AQa64Rwn0d5EWZhCMYOtbNpv5vMa4jZT4Uz6b1IYacEaGhDdXd9vFrNxBC8XdWvhyaCpA5OQF4LnXByeUzhC37xb/wSP373ff74X/wLJrvblLYK4XYrqsUlxhVshwhkTmVUzjf7L3NLmB1CyGsf/WkD/FQ6CHOkRMuf9v3OAiY0ICidBcY54+4bb/Lm176Cun4NtbXDL/7Nv8mf/P7vM5tNN9rDjRmNy+mUsiwpwuVIF1iQmGkmIr87xqOxEOpeHO5G4zE7OzvC8XvAS46NqqokP0FMoa4U+XjUZGVNo350nDKTA+S9qDLz0UgYh6C2zHOx7R2NR435hNZiqkHgPLWr2d7aBu8pFgXKeyaTLfJ8BFqxtbWN1obRaCIx071Ir71SbO/v8uu//Msc37/PfD6jmBVU5UJMYTT4XIt5jBc1FA50JfadPtcsXIGxNVld8Zd//Ie8+bVf5OUvv8XCO5zXWGJyKxrNxrB9eATgq3ZwjQiEZUCgVIym1JNIRADs0z4HJEy9bmT8qnNhY7upQUNf+rcOYPV/X0V09JmNNCRlFnKotNKB2LdDWQiOMzigUtGvIs0FExyybd1oM+L8nGudvIXB8MToFxFHmSwPY9GNuZpCoV2JAWxtmS/mwc9Isbe3x40bhxzs7bC7t8vW1hZGG6q6olgU1GVFuSgop1MuT44l8k1wHK9qj7MS9jmugQ57nXmLUaLZGY1GZFnGzs4Ou7s7jLY1O7u7HLx8i9dfuYvzitl8zsnFJQ9Pjnl+fMLZ6QWLRU0M6dcA9Wi8HL55HxIf2TpoYEQrY7WlDg7huRMGIwaBiJ+9DuZazjPRGUobMqV4/d49fvzefaxrpU8iVQKno2Smdx57iGeJUIkv9JBU/M2suEdKddmadUh1KDzmUOkjsvRurGbel23f08+6N/6lPuQT0e48fIPeXU1aaD6p5Kvzjhs3bgBQVRVlVVGVVSstS5jRWD911G268J6ocRDTqbozx02Zjdjn0ByGCIZ17TXzfUHCaai9lMDpMwHpfq/LAZMSVp1xKok8tQlj1n/WsoNDZiUrfl+j0UjnG/sbXOcr6Mp0bvJDuqm90TdXerWpWafNK8aQ1u/j4q2tLWazWWOW08k9ljQZA3gYI0ah//Jf/gtmsymlVlRFgbcVdVWymE8B2xKGITJaXPuh+Szh7F4ZYgyl/ouc7XWMn+rcM9/c4zhmkmdpX+vol9VlaMxDcFEpln6PTKO13fvTzFs1/+kwGqkJ1RBzI7SBQLb4TjwPl7NzTi+POZ2e8f0fvcMXq5rX3nyD+aKQfp0lz0Ary9Y4QxtNvrVFUTtITMc751BrVHBbSKNJGU0b0U6Bj74mLN87mV8M9GTwTvHSvXu8/bWvcePeXczeDpd1iXGei6JgVlVYt9mGbcxo/PxXvt5IX+MBjyYbrS2zOIdLApHWsdto09i5xYRfNiTVa1SSNIKL4Q0Mj2QhukxGCkD6yDf+9UpCZWpoCHcZZwY2Z5xtAbC9bfFOk4+30VZCL04mwjShNHk+llH7nEpnlM7yr3/wXV65eYNqb5uirnEHu8yrinw0YhSYp+085/L8nMXFBfPLSzKtyWvNxELpKsgULKb8q9/5J/zHb//fsD4nd0Y2yHhcIsDwgVON39LSv/uCyNtqXSTbrSvtyicVbAyb+MxxLRN+w3vosAl+CcY3Y/J0L30qVZN7kA4wSPY8/ektEwb47mvhN09LdPZLZF6zLCfPx2id450GpbFKxuKdZBFtkukBta+CdsI3ZlLWSoSoyse4sjIGW0siJR+9pgNAkwBkKkRcA61ztAIJlyfaitlsSr1YMDIZhwcHvP7qvaCdGFOWBbPZnPl8zunZE6qqpKok0IKtLXYxpyyKJsSmretgEw9lUVFWdXOPU6Yr10ac4LOc8WTCeDQiH+Vy7jXko5ytrW22trbY29tnb2+P3f09vvLaLtlbX2A6nfH02RGnZxc8O3rGoqyxZGQ6By0mVXIsRNupMWhMkyen1h5twHhHjSfzGZl36BBFyjiLIYSfNTUuA6MdWZ4x3p5weLDH85OzcH4VqBAe1cdjsYxEUrixJAWGYDqVMkxy0BTR5DPcmvRMsiRoXF3Ss9knDnpt9t+LEdtV8lu/ng7jbcYVPjs5eC2N5kny3ARHU6U6zxFbsoRlVD0bcYHRpoEhEg2vdI7969clSGRVUC9mVPMprirBjoNmXDWTybRE/3MuiQAW5xP815RRTC8ukSSTGk+rDUkTlSZDa9pfzxNs5iOwnN9oxXtJf+L07rvETmeAPQHSEu2uWD4JsR2Bz2kCTujPtY161C8+heGq/RzIwuH3E0J/iXHrL/8AM7HE0ASiLP11IxLG96Y0zPsO9rsKN6iI3GL9IJBJichGAEqLT7TSQs3YusFNRilefvllnjx6gnWAUdTe4rSYsSrlOHp6xPe+81d4W1PaGqUsVb1gUVxgbYFSPuStTYIIpNz80BwHjqNvnvcFHPJUUFWXye02FE0ZxY8vhk9vw6xKO5EBSzV0HiGGvYshkxuqIB1ZZzzx96vu5FXP232OPr1R8NT6/+J9iIhq0Tpq0g3OgVZZC+uiZlA2Pggm4xlv10xrLY7USuCgUUaydDlPMauZns+589ItZsUFRT2jqks+ffCQ3dF1ar3AKo3XhqKoKasKaxRTZ8VsOlktiY4o1kW1dUgwGM1ka4t79+4xny04Pz6VqFfBBSEPwv95scAGTY5oUuJaSFTTL779VXZ2d5kuKvbmFVSXVGXBp6f3eedb38LOCrzdTPu6eXhbaOI+R62DQpxaTdAOCK7SwWFFgJ8KO+Stk6NlPV5LhCiCHbsyRvxN6cCvxn48XnZA2gvrIdm+XXOwJTRuPBBdQOJ0DF9Im5olqqIsRPJAKYPSGbN5IarPyqFVJgcu4LAI2GulYGeL/HAXffMGr775OtPpAufh1ksvsbW9zbVrh0wvLtnZ3uHx48dob/nRX/wlx5885PTRU1BQLqb4TIOv+eT9d/n4/Z9w56s/J+NS4HQk8lNU5Nv/+uSyDeO7FSApQXVLlVqE09Eu+C7BQWdEy86WnREkTGHfVjfabKdFr+C608+dPXYxt4fCJ0kFY90uYamDf04w8wtMU1fjEvwenEPAhRDpaZhL8dFwOB2c/50PiMo1SChObDTKJS611mRK44wD5ajKgunskrKYsbu9xat3b3H94DpGZcwXM6aXFzx79ojFYk5ZlpSLgmJecHl5ycX5OdPpjMvLSy4vL1lMzynm88Y8MTqmAx2zwYbRi4hDZ4xGOXkumr88hBWdTCZMxsJc7B/sc3BwwOHhITvbO+zsbjPeytnZ3ebg8JCDffGZeOPVl3n6/JjHz06ZzeZ4HxCTF98T5X1Ya2HknfI4FTKeW9EmiRO9QVtN5oIplZNwhD4Xf4wsA6dqlFNcv3bI2cWFBH3QpkHGnmhTvaxCj2d7SLPRnKeBmyOgq+tP1GpwNi/p2VUN/IxMdvtMJ/Av1u1LLxuGov9e8qz5XeuOY2tbTRatDcAxzIytKjGfgEKBCb5r3nP95g3yLKe2NWWxoCzmuJCcsgN4fDAzCHdEx7ak0WYcWZZR11UQQPUZxVA5lPYuhzGutSleb57TqbmCSe3Aqx4xaMyyycW69jt1evPqlIS27+7RchtXTi/hXiM+X1VtJeOmekwTw+u1xHzQvrcalwwPZmgcQ6s7qI1oliclHuKdbM8YdO3w45bEu5qHEKlaS/I8Ywzj8ZiiWLT+iUrhbDRlFLj0x3/4R5TzOVmmcbZCYSnLOYvFjK4gY/0GLjGwQ3V9V77RaBWbNVzt46B8Cuc0mWlNelPyN2Wm5X3pWCuND/Af6EjeW1wev7cWD+vKJoKBtk6rWVleg+Bz6C1VXYLKMVnMqxRNOH0jME21FHGhUxgU81iJxkr6rOsqRDyF589OePvLb2OMmO8XRcHJ8Snbt28JrZnnkpPNOi4vp2QhzH4UfgKtk3doX5twVjXMFjNOzk443D+knIyx1jKZjCSRrslwzmJq3YTR12iU0UGjLLTm42dPsI8f4pxj+8fvBsbLUcwuceWcyd72RusPL8BoVG7ZLsz74CReOyEglCLG4G/UMN5hEN8JHZIBaXQjMfdKE0FMk2SoIQplOeP5UyoyGb5hQmJfcXMbnOXbw9rUCcm/QoxSbAiXacuqUXF67xmPx5yfn2OMoVxIHpAmIlBiw1qbnIO793jrzVfJAtKblJZnz4548P673Lhxg19//S7OOOz2NjujO+xtbbFwFW9+8Yv8f//xP8H4HL/wKG8xGoqq4Ht/8Zf8h1/7BQrvsCETkzZ9KUSXSNm0DKlar6r3Iu2vK6k0aJ29bL/vVePsE4bdel2gnPYNQbul0+zyrj1bPvXziX4UHmvLTvSihilBIjSIr14AAqG/TBsIvgLi3K1DPg7HbHrKfH7JKM957d499nZ38c5xcX7Og48/ZnY5oywXnJ+fcXZ+yvOjI07PTrg8PWMxmzGbzYLpYUldW2xdY23ZrEMEDG00q1ZKnHLkgmR0E/Y5qoZVcMQ22pDnouHIM/FnGY1H7O8fcO3ade7cucPh9escXjtkd1+YkVt3bnPnzl1Ozy54+OgRs3kRQl3LZVZJgq7MmCiTbjShcdxxTDpIw4wO/h8++lsFMzids7Ozw+XlZUhcFkMmN8BjzclMCPwN7OMjcu6fqaFzuO7urHOMHYpuktYdSoY1VG9Vv3pgXI22UYlfTspEXdWnxzcxKxppbyC2Dg4OGE8mTOdzMZ8qK6qYXbnHRMX3o2Q5FXbEse/s7OCetnAkjmtVmNRV5kb9us6uhodD7w9pzrt9dbVM/fovRiR99rLufH7W/j7LXIZK5/3Nlv+F+vss4xLwuGwt0cVfyeFsO0MpxdaWBCkYjUY45zg/P2/4NxcCf+RZTm40n378gJ+8+yOMVri6wjuLczVFsZDs0viN4clnLekdcd537m8qnFF+GRdHf9x0MWLYXinLifua56rPZCQ41bXMQLf9FzgkSRmCC32hUkoPxNw7mclXtheZjrTNIWZaKdWhL6uy5HI6Y7K1xWg8BgVlUfL8+QnsFXilyUdjTJ4xGo8oygU7B/ts7W2TRVPukFbBBJ9h6ysIjKsk1DVgHGfTU9TIszvaxhjDlp40Y9o3B/gg2Inm0iYIIC0eQrJd7z2TyYRbt2+xs73N9u422ztb7O7usre3u9H6b8xoLMoyLGDLwStahiIm64oEfnu4VFPfBxt2HeK1qhAH2tU10QjGNuHbVOfCR2m6R7hPZ207juR5/wBBkEAqh3YqaES8ROJBpAp1WTY5PuKBK8uS0WhEWZaMx+OOg3lU846zMbduvUw23ibLNfNFgR9nZNtb6Dzj00cPOb28QBtN6WpKHDNvyW8csnN4Db2zhXMWbcScQeLKOz760Q+pzi/w422sNjR5CLVPpOQvXoYQzJJkNO5aclG6l0k3F2wIyaSE1yokdJVka0iaumr8q/r1g1KLrto71dR4LyYjHpswk210KcmWWw2OId4DrRQYg/JecqqgQqK7TMJLWktdFJydnOKc4/btm3z9y29TLAqOnh1x9PA5s8sp52fnnJ0d8/jxJ5yeHHN+fsbl9ILFQhiLupijvKeuqqX9sd422UJVHecXpSzNYjWSmJZgVhQhCor38m6zR141IYAlv0WO0opRNiEzE/I8Z7K9xeG1a9y+c4c7d1/ilXuvcHj9Gjdu3uSLb7yOV56PPnrA85OzNruzFvMmghQFFaTprmXoI/GmBPCEOyrMR5YZvJdIYdpkTCaTECEuaidld3yiqUqR6qrzl56Zoc/ryuD5uKKf/rMXud8pvEslbUPPYDOfhjS5YXz3qjEJ+B2e+2SyJUzgbMZisaCqSmwMuNEwg239ztx6v3sv4dCnl5cNI5MSRP021q350FjTuV4FnzZtc9W7q9b0Rdq/qq1VdYfg/tC8N9n7oTJEgG1yzzYpm+7vOoYQlvmE5M0GLsb34zqk4ZSj8C/Wq+uKqjINgxG1ytbaRmUQg2BopaB2/Jt/+a+oioLRSMx0HF4014tFoHc+G2G9rizdsfTu0BUUNDBTLfsPtf6yhqgRkHXTpHkZVJLcN8Jzabu1YuifycyM8AhB3Wp3xRYlbW9duQrets+XfTri/mmV0ZevrGo39TvtBN7oOZDb2nF+do6znoP9Q4zOKMqKp0+fYq6dk2VjlAprqhUq0/z9f/D3KS8vg+m/aDaUi4Iaj9KCQ7MsY7IlOBmlGjq3EVypVnMuwj6xRsqDr6rsjwmBjsRwUgehYJaLRYZ1dXOWa1svrcNQ2ZjRKMqqkTylBIDWWqIhWLC2JM8zvCdkUfRBkxE0FikShEYtaWOoQ9VmBE+BQF/LoYIWRKkYrqs9HHIxdCO1s0769xooA7DQukm0p5TCVa1GI5Wm1nVNWZVsb283Y2kOqIcxBirLOB9x7cYhoDg/O0cVNeZgzvvPTzh98ow7L78keTSUxnqPn0zIVcb2wQEXs5lkFA35DzIF86PnHH/6iMMvvIXVCgOtORrxvGwupbqqpPsJdPZpqW6qp3+B0mca+sAufTYkmey/s2q+LQBZBh6ptDgiCx+kJY2TnXI4V3cATv/9IeTbZMn1nsxkmACcs1xyOswupxw/f47Rmi++9RZ7u3s8efSEH3//PU5PTzg/PePo2REnz59z9OyIs/NnzOan4oNRllhX430IZhD03ylD1kWqMq/INLdDDdL95p3u7ypoGOLfMB3EXF7OKEBVidChyitGpuTSOvR5xvPjZzz45CMmP9zi5s1bvHT7Dq++9hov3b3LzVu3efmll3j13j3uP/iUo+NjJpMJWZ5J4jUfbV01XnWT6MW7WaGRGOKW6PMViU2ySvLOhASiPiB2pVTIx9NiiyGCdOiMDX3vn+EhhnwTbUN8J76vB8Y31Gfa79Ad6Po+LZ+P+D1KWPvt4kFoiu5Zv4oYjMgrra+1DkSWY39/n8fPnlIUBUVRUJZlc5bTaXSDRCxLBiOxp0PY8/TZi8CMZWEHbArYBoVZCQG1ybub1Lt6zJ8d5m8yhk3bWVfWCbeWGGG//m6ua3PVeIYYnDh3EWYOrKXqvtu/O0L3BAJdt5ErnfMURdExq236V0GI6kXLbZTi6aNHfPjeexgF3lq8F620MBkOo8SklyvWeNX417FSQ0UYivadKHiNgrvU7yI9P/Jb3/9NJwxBy0B09ncA9jX3HyGmmwzsSgIHyZSGTVo3neOqEucT9y7Sg0plzRZ03vddvJKWjoldeCe2W9eWoqiYzeZkmeSTqyvL6ek51xYlO7sT0OIDJ6Su4wtffLPJ2xbPrUboQgHbNRDC3XvXwLNGAEqy/koF+gGiUM5aSz4aNX40XgC69Gd0MGR0Qr/aGu0cuVKoXkLXVWVzRqO2wgy4SJQo6qKUSXhxAsd7tJPNKEOs9IYjjuqyaHsX/hEOrFeKKiQU6yPqlnOWt6IZFr5LkGRZhgsSBANgJPlfUVakeUVM9OwJTEieEPExSZ/3AjQUrZlPBCJAIF5gXs7Ruebwuvhi5EazleXU4wm+tpw8P+buK69Q2ZrMZJTWkuUjtNdcv3mDyydPhMDyElXHoGC+4On9+1x/64tUCWHv/WdDEFddrs8isbqqrz5hHv8OSdKGxpTW33R8KTGSWkEMESvCoIoTjPCx4hvgfdWYGrX9w1VAOz7Ns1wQidYYpbmcXnD8/DmZyfi5r32dsix49vgJ33/8XZ4/O+L502ecHD/n5Pg5l5eS/bVYLKjrAudqrK0B8W3QGpS3RLfJsEoN0ajCb1FrR5hXu0DpSFX35zWAO/IdsR+P3LvSlzgl+TbQCuYKZTSTyYTzs2MePbjPj374A156+S6vv/4mr73xBjdv3ebuK6/y0st3+ODDjzg9Oebg8JDM6JB3xGFCuN7UTBFC7hEncCVzBmfEDC0fBbMdrRmNRtT1IjkTy3cmNbf5vMomZ3SoThxXlDitIpZXEZd9QvTzvMtD41jVd3Mwes+dc2At164dAiHyVFlSVqWYJuSjpavV7NcAkxAZyywIC2A5XOsQYdkf1zomcwjGrhS8JMTWJnA5hYF/nXu1aemv2zIB2T7r/9Z/tqq9v86ybm9X7aEIMlVLgwyUlMlN260qsbPXjR+YkoAGrg0dHpno7lhaf9bMZORK81d/8W3K+YIsC8yKc9RlQVUWEuzBX23G2Z97mGn8/+A6DfnPqDiPpK1417wPyQmT0oT5B5QyqEhgRcaowTWeJlpmX4iDXtqARnjg2veVak20nIv47/O7RylRHhnJCLvEjMpiTLZ0x314eZ2QI6Ujmna9mErNprOQCFpozHpRMF+UTLZhPNkSx3wl+aSOjp4yrjzaB+sXD95JvqzZbAZakWuFUZraid/nKB8BNIl/6xg0xrnANMK9e/eYTCb80R/9EQDbOzvYusYoyeFlreQCq6q6WZODvR1eunWDi4sLPvzwI/5Pv/QLV67xxoxG7S34mGhMYkR7DSbPcVVNWYptuAomFjZydFpj67oTKjXurg4MCLQmSQ5ZSN9RQ5nAUNREDqwsy44Evk/ApsSiaCmCGtJ7THDGFSbCU9YVVXDUMcYwnU1RSlOUJdrDyclJI8mPQMRojdKWgoqCGrOdU19KzgxvPPOyQI9yjs5OcEZRWVmzal6R6YxqUXDr1m0+UT9qOH/vvdjxe3j48X2+pqB2lsyrjt1jlDymkpdNJUDrAPHqBjZ5vix564+hv0ep49+qsa7tticZ60SD8WoJiMW5R+YUovlU8AfyHsmq7RpitAUW/e/tnBWgAwLJjEEDtrJ8+uknKAVf/MJblEXJOz/4AY8fPeTpkyc8f3bE9PKMi7PnnF+cUVcLysUMfI1SXnwPyAGHMWFeIY+AV6qV6fhWKidCB9UBxCphNFKmo8s8+TD3gXMUEEZcH5RqGA+8D5oWDy7YdVqo6wKjM6p8zmI+ZnpxwYP797n143f50ttv84Xnx9x6+S6vv/Ya1ll+/JOfoIxma2cHHXJspIgsajRjFnaIUUNC9C/v8JkPiQ27mk6lBCA71WqyXoiB9T5KRDo/r0LimzDQ6TvpmRxqb127iq7T+OdbBu4wqdPncr10beN3rTU6y7h9+w4KKIqFMBql+Dv5FJAxNPcuPIh3vApa6D6TcdVUltYxfI1Cr1XjGCZah+felXoODOdzJsBXEfqfpaTz6EfXCr1t3E4Y3Au81a3Z36p1U2vEJ0o16EipCBvjJqcNRJ+iFoa3eGiYeYmMRkeThlhIEIhgl/iNpu8LCHMYI+FKT54f86MfvkNmMmL4Wucs8/k8jClqQtTgTVxbIpMep51Gz2tAfoIzoANr0zvVzavS4lhIfTGC0/wLwqI0Ieryu6p3xyRflLUKlBUte0PE995cgfevHI9qtY2tiXyN1jlBjh5bJC7cEFzoM+wpXIgajcWiYD5fsLOzw2xWBjSjmc2m7B9elwBJiF9xVVv+9I//iKff+zF7+YRiUWDrCm+9mGPXteRoyzKKslg67tZZSUSslEQcJApsNHdu3+Sb3/wmJ+/f55NPPmnwrvYabXXr9B6YZK01W9tjPtoS1uHp06dXriu8SGZwW0vUAGdx1lIJ5cG0KNGI+dTWZEKxKLl27RrjkeSg0EZzdn7GdDpNiLfgPe8dytmuPaDWwYwlJtuSBGdlUaO0RqtgNx85bi2Hva4tDisy3XDJqqIIuTVyuQreU5U1TmvMZCJaFufw2rCoa4ytccozXcxxIdPw9ihjMZsxGkt+jrPpBRcXF2jvuX6wwygzqNqhSk+uR1jvqbyjAvavXWc03pKQjfWCiR5xUVygd0dc2ordOzcZ7e7AUUZtK6xV5IhW4+mnD/DFlGw8ximDVTTqRBFXXC1h6/8WS2RUIpBoiFUfga0iFaZ03vZJH/E/8cJLZ0nV4DAVL230HfDt82Z8YbjrnHH7jEq/dM2cus60AjRAeY+t69Bz6/Dtm8vpO4CiyUDvPT4kT2wIfi9hRrUBnWmJOuIUx0dHHB8d89YbX8B7xzvffYdPP30QNBfPOD05Yja9ZD6/oCzmlGXRAtV4N7QCJMiChza6ZSpxjP9R3XWMNvZiQrXinJAwKNAgyBUrTwpY4/5Zb4NCtWvqaK3D2Qq8Z14tMDojn+fM5uc8e/aQ9378E77x9V/i8u0vcvPObX7h61/l8dFTPn30kP39a+Q6p3ZW2jUGh8IrhVGgA9wQ8ygBfDWSkyPL82Yksmq2Wbi4v0O5JYaRUIvgUnZ4iedIkMhQK93oTqrztzlf8mO32aXhDBFL3fb7bXwepKwn2gHHb3EV/JIWQ+HFqdX5RqBptAKTcevlu3g8VTHHlnOqco6Ep03DAXtwkmFZbJHbc9dOU7TQtq4klC7ib9esoYpBAJI16NBUXSagA63CfV5imFAhBK/vgF9BgS7gM4fuNQ/L+9iOYYiATN7rMQ994uWvowxp/mQGETYMn6gOXxXyoIhEPp6W4Ce1NOMWbinf3rd+nYZu7ghKWiFJx2Q/hY10I0aRWGNIe8nuq/QwBLwVBBxKSd4sheBpsaYIbYXAMtq1ZyMdX7NvWIyCPDeA5d133+Hy8pyJkSRrOPG5q+pCUDJa/kkIw+7S+OVzFbUrbUk0tkm0qMgUBHQfdQYh54OSQD2RyA/0QN8EaBleOtJNUCqepfCs2ZruqH3P6qY9ATox35QRtnA7+ohKFFAXtOAtHB++H3043xe2pvNLf7fOol2B923QoqRS+16cW0KjRA2RDoLBwG3igdp5ZvN58IsQUzlchS4ucEpBNiZTFnTOwmb4ecnF08csolCUlq5y4QzGCJjetUJDrU0bXZ/WXFopja3h0/tTfvvRp+ILU1V4rUWQ6UC5ltHQWmProLGrLjk5b4MjbVI2ZjTy0XawtxXUUAWNQaYzPBqdK4paSI6jkzPwXohzLWoiDxiTU0cnbCOZia13oCRxmmgfauZFCeiQDj4APJ1TVhUQknhlEg3AAjqTeP2VLRNJpqIISc6UA+eEUbJoauuhrMlyFRL3WcqqYjIZY23N+fk5TmVMtrapNcIlauEGy7LEhjwEzkmSM1vWErbXOqaXUy4uLyltjVOiLrWJI7lWYlJjcexdP2Syvc1oPOFyIeovhSHLDGenx8wvzlHZNVSWBYf7eCniQQ9/X4CiaC5Tejf6l9N3f+sDiPRwLWkpEqlA+sw5lyCTPiPkAjJZfjf2l0rY0r77Gpr4r0mAR8tkJNPrjC1FPKsATgQWAb9IH0qFs6hAi7T2o/c+5Obhdb7ypS/xwXvv8+GHH/D8+VNOT485PXnO9PKMYjGjqhaUxYIYQam7xmEdIiImeZ7inJX73r63WpKzjPbXl5R6S9YbGo1jWjX6XjnnqKio6pKiWIij47zk+Nkx773/Lt/4+Z/ntTff4M69u3zlS1/hgw8+JMtHTHZ2KGvRbCpjAIX2AbHHbrwPGaJNkzOijQ4XtSKi4YlnMDKOMczv1ZKuhNht/kPyfRlhdd4eIAyXEG6vrV43TZ2l31eNfcU926gsdewDAZ8226fkl/vsSEGzjJu3b2NMRl2XVJVkPW79MbpNqGTc7TPfqTMZjxsCtclxECosmYaknzp8hu886/fVcegMfkKhZuiHZm3ajlLYMXRFWyLvs5R1+7lkmtKDi/1n6zRnLdHWoeLZCNl43waASQiutvO2rwbmDkYMk8pat0Rv8nq3bvJSPA99uB9xnlp6aWBqEdCrFI52pf1ROBfk+RilcD0GJhZnrQTMQawivvOdv8IYMdeNcysK0Wb4ICDyXuFTIj5pdhW8aTVJ6e8tgRwZAKVUE2EobbPxW4n4OL0hA+dlCF/7KGVgmcBfXYLuqQNH2vbS+fokOInA+3oJlqRjGyrrhJZdTYSYDtW2wuiMaAURx5xMuDubhJZpcGP4bp2jqioWRcFoJOHka1WD99hqjskMXim8syyKktyImwLOYl1rrdNqoVo/Go/HetvCMCxaSY4Xn8BG72oUkCmDK12TxVz5KDZUKC9h/ZWSsMuRkS4rT+XEZ3tYvLZcNmY0js+moFRA7PHCwcLJAhmTCQHuQ5pz72BeoIxKDoFq1d0BeCwWCyYT8ZKvqoqiLCgWFcZIpnAFzOdzdnd3sdYyXywY5TkmCzkQEntr660wJl4SpsXMz9P5FBPMWuJYKldTTxd4axlrz43DA2xdkxvDV7/8ZWalOOuMNDx5+Ak7WxMKW7O/u0NdShKdeFEXi9YcQMJrekxm2Nre5vDwMEj3FLUVP5coId/Z3iIb5UwmE9QZeC/E7N7uDsfFgtnlBQc3booDjmszjMrZ7l/I4Q3vI5SrkM/Q733ifqissnmP/Q2F60wRuks+9/tLHav6kr4+UfMipfX9CUENej4ByyVo4YAsM+QmC+HlFI+fPubxw0d86a23mJ5f8C//xR/z7Mkzjp8/5fj0KaenJyzmU8piDl5CGHrXBi5Yt+ZD3z8P04v+Wqa/DZ2zVf0OrVkq/YoMQfxnK0tRzJkVFzx++pg3vvBFvv5zv8Crr7/BW29+gU8ePuT89JT9w2vUkcgLmlCtl89oXddkSmFVzKDbRhXrS4Nj1Jc47s/bV2OTsilT8qJ7/NdxRl6kj5RRj/+01hgPhwcH5KMcWxVUVUgmGeBhv60hIjj9rrUmz/POXn7epQ8zV2mIN3EAHyo+0bIN9blxOwkh99ex35+1bKJ9WcXs9IsIdaJEWUpjMjjAzK3r97NohVIhlwg/l3GR1hLEIprdxnlFvOK8Z5TlKKV48ugRjx8+YqyN5BKrK2ortE803RXhiI66laXx9wn4Zcn8MFPQPyt9zctnLatoiRcpq+bWryMMiXyPDEc7hs37TIUX/e76YxdYkw1SWS09vAzPV9FO1jkWiwVbW5OWxkFjQyCT1izNU1Yi3FZKfHnivLsMUSLYCWdOHtL8nv5tJh7pLtVLORAWRazbhOEwRnCwpF8U1mHTE7O5jwZZWITgL1G3gxLpYN1+DuIvOdhyOT0xNrIH6pYTUoZZWWNseI7BjGSRq6CdyCZbLGqRCIy3t6mqmqqyGCOEmquDhsFKyEulNNZ5aiuqJNSIRVHhwxjFPKsKC+Wx5YKiLMmzAzSWPN9mFwU3b+DrihvXDvHOMZ1O2d/fYzwe4Z0l10JAV1VFURRkIUSYrWscUNkar8TPwiskFFiQwmVZxiQfkY1GZHmGtw6vNY4QDcvVnB4dcfDqGzGom4RbS8JTxoupUUvpiGOdVZJbH0U7A1KSofJZnqVAIwUeSxdTBeW6b+0Y+xqH/ue0XnrRVhFCnXfDtIeIpL6tfOd9TZPLITeGPMuoq4qfvPsTtNF84fXXef+nP+HRgwecHj/n+bNnHJ884+ziOcVijq2rIAl1iMmF6TBSn4Vg6a/30G+rmIZ0ffrPNxnL0Nr22xhiCmb2krKaM6kLirrgcjrl8aPHfPmrX+fLX/kyr77+Ktf1IR/ev8+N23faPpD7nvYZgap1Fld17aMjYxHHmkqYJpMJi8Xic0Ow/XCQ/TVat35Xtb3p+D7vM7RKsLFpadfcMR6POTg44PjZU8qykDC3IZlk9EEaEop0JZntvkaYG4mMobC9L7q3fbia9ru5yd16eNhObvP30nGse76uvc92xrsIYhWsSMfXrGEiQe/XSb/393XVHGwMgX3FfDpj6OGSqxibVXNadZ87wpRE2xLhUvquRB8E7Tzf/6vvokMwmYiHy3KBtRJZsO1gOYntJmdAxr38m4xr2aS4eX9AezF0//rrsApXD/WxDsesCzue7mlmsiVmrsEDtlo6A5v2n/6e0gORjvLOSTJYlpUYfTyXrll6N8RUVmFrG+BXGLevm35cSFDrPRgjoW+10tS1ZAZP1yP2OZSXLF3HiPfSZ1qJoVxMMkmwHFBKNG/GRyGoUKBZJs+td+jgY7dp2ZjROD09l4UPappUlx9Vi+mhlEGIzW5MziSLEycufyPx3CGcm++tvXn8HSRySTSDiNFpJFSiZHv2SXiyspAQo7W11EHlFLUuKhC4zosaKMsM2omjqTYhG7gZMckylFbcuHatiWiVjXKMahOdAOR50MKEA1qHCFbzxaJxkJdwwK1WZ7w9obaWzBgqhzBIZcXO9pijxw953VkqK7kLuuaBvQszcGeuAkoK2c/0QsVn6wj2obaG+h4Cyg3iSA+pUs3c+kxD/7L0++j/3p4jILHt7I9F9/qJdZooG8mljLaPynkmo5xRLonrphcX/OB73+eVe/eo6pq/+Na3OHn+jJOjZ5wcPeX87JTZ/JJFOcV5GzJiNyhY7gDtGK4qmxALVxFAQwxnn4jqI/+r+r2KsO7vvfNiTliUC5yXRGnPntRcnp9xfnrE6fGXef3NN3n7rS/w/kcfc/3WLTxKEoOaZXthYyTeeCRAo0p91RihaxbzsxL8q+7KqrLJGvXbX9Vm//efhWnqv79unJu+q5UK5nWa3Z1dnj15hLWOKuQuctY1EQHTPb2qv3hH+xopWb/NGbNV3/vE7xAMGYJJq8a8rt5Vd3/V/q8jnF9kXFfB+v6+rGMI5DNEzf0qxjW+c1UQBCUEA33NRfw8tHJ9+LAKhwzhk6FxAsS8CmlbXbgp9IpSGtPDo7GuyQyzyykf/uSnZCiJIKTEPGqxmIdgN8JcSESmjiv74Bqtgz39fYs0VVy9lOZq5s7w2g2Vded2iOkY2v9N2+u+t2xBEdtuzamW/QdWt798Tvv33vuYqmF4XOuYlj6cEqG7mE9tb++jlAo0YEZV1whRnzUhlKP/pNyFtu02qM1yn+k8hv5mWUamNCOEmTDaNFZK2kjEKd2hxRUmE41OXdcsylKisH7e4W3n08vms3Vi92UyyRrsotNqmHSe52gl4bRssJU2Wi6ODwvkXVBDhhTs4rsgBENmDIsiSBsh5NkIDqHGkBuFRfwubGWDVMyESFIhS3kIRzYa5YDCGk1Rdg+DSMM8GeLonec5xoHy0oYLWhgTtLYKiXw1nV6A94zyrPEtcU6kdlprxuMxdV2T5znz+ZyLiwtu3LhBXdfivF7LeL1WjCaTxiHUGLHNK4sCMjh68jg4/CghxlkBVK7Aq+kBW1c2IXY/j9JH4quef1YgF99tOPeBcMkpIBoyn1kCwAomoxGjTPb8+dEz3v3Ru7zx2us8efSY+x9/xOnz5xw/f8rp8REX5ydUi7mElgvSisbhPjrfx+mpzQmDn6X0EUhfI5QCzSGib10ZAtR9gNcWjXMEh+5CznhdYusF7/6w5Pnz5xwdHfHlr32VL33pbe5/8ik7u7tNltKIUOqQ9C1KiWICraqq1hJg3nsJCfg5lb6Q5bOUF3l/FbL+vM7L537uAJNlHIYQt9aKNK8qy7WwaxWxAoi5qeoKoLo9/mwlNT9Yt959wjWO+UomTUTfK9v5t1le9I5fyUivaHvo/SFYMdRi13CKBhUqFEPxLl6EsUt9t1aNQWvJFD0ejzuwsztK8ScZ0rRrI0LRjz75hLPjE8nlFTSxVV2HgCDp5KLvRiuMuorJ78Jv3fk9ZSpSZmOp3Q2P3hCTMAQHm/n3NL6r9vuqOzQ0jrQtHYID9fHazwLThMmwWG3JsjZaZVo2Zfjb8YpQbHd3R0LYexFQ2yCUjyZ6xhhx7vZJEmuWaZgUVkZ4GIWmXrU57+LzLMvItGEctBaxr2iKphVN/pKWiZNneW4YjQ31VkZVVhut4caMxuuv3JW8EoEQjtJ5sU20yeGRzIJ1VWEzLU5SxjDKc7QxzUJFiaMNmgYT7G5lIhllNQbfPo/htbZC2nbvHItFEUyWgkjMqZBVXEtCJ6UYT8ZUVY3DUdVRNSSShyzLQuZEiQhhwmJiW+2LUjSOasJZiqMxCGc3mUyaJFT7+/tkeR4Al2FnR4ijoigw2lBaiW3sqhploLaW/f19jBGGra4ddS0MjK1qjo+OsFWNyiZY58gytYQAr0RoSelIj1JCt1eulqom6qx+vQgdG75odd0GGK3oc6h+HzGtLl1tRVo/Sjz6bcf1cc6GRD3txRyPxoxycap68OABDz/5lFdevscP3/khjx895PLslPOzE54/e8J8ekFVzMCLI5/SCq1MxyHer16WK8umTMkqYJgCpAis0rVd1+Y6CWhaUsQyLHUJGh3vqetSnM2oqa2jqiyXl1POLy+YLwq+/vM/z/0HD9jZPcDoTGCHaQGntZbMtKGHO4iMbuSZ9Pysmp+8F1/oPuu+0yLtLuL8rITi0B4mZ2Vl6Z2p3vufZQx9JjvpZs0wknVOqnsku+ydOy+hlexTWZbM53PRaOQrRtIjSNL1z/O8CXEekXBvCs0ofG9cm5SohZFp+WZuQxJm30gcITXti8/jM/mdzu+xr864emesu68vcrb6QGbFu/2DE+VXyXyghz/Sg9knXL3vdLV0hpO1aeBurLDisKtIZDXVWhWH3PG23ircENtwdO9yFBam9bxr99uFumVZSsZl6PUhn533EhQmnUc4OzFS1Y9++EO8FVommnYXxTycocScKuDndQxozNjcjLt3uoeEbXFeadU2lOuyxmElA+j9SuCiVMJHe5owtimeScfYn1+zN2v68AltoZQOjvWemCogajaGcH2/7035+hi4RTWRwFTzdxVOTHFNahomvztGozGZyagred+66KMheK6uKtLzhYvZ0pO1DMukg7+nMSbk3TI4Z6msJLONNDHBrsI7R+Ucysn3TBwXguWPQydz0pHJyHLyTJNpRT4esT2ZbLR2GzMa+yNLpRHiaTJqQVc4DJHpiFl8jRmHc9I6kLcJUDT5JGKXPKgkI6Ohca5CjwxKgcnGssghY7fc/ILR1pgqy6jGwRehtmxtbXUOsiCiinw7xzuL0RlZcDCvrW3sKbE1O7lH+0oOjzZ4Gw9xF7gaYxiNRjIXBePxmHKxoFyUVFXNaLJFbR1ja9BmjFKX2NozzsdURcnWaExhK8aTMfXlJXvbO2RodkfbZL6k8GKnaSvH4uwUihlqNAaV4b3pHOh4cTPdHqAWKcolcL4lswT++wCgWmB6FdG+BISbCx6AfAoMQ2jLBvdEeNvIZtrQaxHapdGoOrjQ08dQDXfvvZcoXb0L3UqmfJBELEfI0qjgXJy8G5gA7204AuKIp1Dk44zxJMe4mp/+5Cdcns852L3OX3zrr7i4OOXs5CnTsyccHz9nMZ9RV5XMN0DbuEYpY9UA0M8uaBks64B4/N4H+H1HtqsQwVX9xrqrmBbv5Qw4Dz7CC62hqtFujvWe2lfYn1TUdUldl3zj536Ohw+fcLB/DWMkKRFag5ZETlVZkWcZu9s7EgBiOqUoiuSsdccVz4i1NUplS+Nsib/uu625RDq3FB++CCHY3/xuu80IlnB8n3HblBNY13c7hpa4GGBo0zOQnpMEzoRBSohTJeYhGMON27eorEV5RV1U2EWNqyxM2jO4TKAvnysAjaGYFYIkFQFO+Hb8MRR1f68Scqw/uz6hFtdZty3LGQi1O0xMQ5y35in9vltpMh0iSvkooAlnU7cHqr1DL8a8SpjupudwRlNYrZp6A9ucLEL7UUeAHom8NKRpqCwws3tmhYhNTlwUBsRIN9CIAxqcTAT/YV2Uiey01IvhhkN73bm3XF1nR8O4Y+Q6Hwa+BNc670kqOmcddVGKWZRyQtiSmBvHFlv+B4kA5Mi0ItNQFjM++uh9dKbwWmzxra+YF1PQQTLd6G6Gz3+36M44W8YLVNCaR+ZBdfJmKMko3fQUOcFlwr4zv3S9VdAyNRHF4r3raVB0u4c6M2Hv5T0CkezCOWgc58PZaNrpbWHLZLQaGq1NEgpYfssyHfJtxLxYXQag2+oqpqmtH31AsiwP77R6tk0Efa3QTe6OtTWjUS7MJQ6PDVESQz45pyjLWuaiHTqcXQUSqlnJCTBakSGMRhYE+joklSzrCpUp7t69y9MnT7BVJZq3MO5CRbjnIWonvODmSCNFSyWjDcYYJlqzOxo3QZw2KRszGuMRTEY5SqvGAU84YfFpiA4s2oxRiJ2Xsx6Fpqor6qrGeYdW44bjSqWoNjASWabRekRmWiJINnVEbSVSj60tWtWMJga9M2qkIlmWBQ7W4ZyXvAZK4b0lH0k22UaKa0yjmVDekGcSCz2iERekMsKNdzntSWPu5KkWkiDl2sEBeM9olFMuFkzLBYv5jIvLM3a2t6iVQ+UaO1IsUIzGiunxXEKk1p49nYO2OCMJBPGaYjbD1RLSN17kIamAALiIBLqIyfcIAK3aJIdwFSAbLnHPhtoQzj3ROqSIFQbGjpDzCUOSgpYULXZpHNWZV7/tdVqZIcKz+Ydv8n14JyGa8zwHDz96510uL6ZoMv78W9/i8uKMi/Njzk6eMDs/YjabtURsHzq2gxxY0c324SqGcBWxP7jmA211JF++PW+bRGZ6ESZk1RglWbujRpJ/Ou+w74lpgXeOv/E3fpX33vuQ6zdvSqjqSHSGsNAuBGyIZjWARPYyqxxOW2Lxs9yDVfPZfP5X9dsi03Xlsw19kzn3NVwt/IDuXPuouiFIAuHsnOPGjZsh6ZbFO09ZlI0QapCx6MEu1TRMyOnUEr0qPGz8BYnx5Zfn3b2Owxc1hW/N+U8I0EAjNQKVBuqGUN2DpTeZlCCNWGYYrnX/AuztbPFrv/RV/uyvfsTFdL7cVY9m7MPGluHpjmXleBsGIyFYO/A4FWileKjtf7jZLrPSgVUNE5cwb6FeozEd0JYmnXYI/153A9W7/ar2AVpryrJke3tLfkpMxTvzTvsKmpooSX765Aknx8eMjBbCMhCbafjTzl/6Y++vabdG6oBvtOkIktI6fWFlv05fi5IyGzHJcopXotCmb2nRMAkDcMYH+qqvQVaRgUm0TH0tddQwad0/0+LPkPpZNnmw1p2TK0rDZCiLdZZMZQlBMsyY9QVtvQYbmtcYw3g0oljMgy+oCDqNFibGOaFDxltbeBOE70rh67qxCtIhHK5Vikp79NhgxiOcVtSlx5eWjx8+Et/lWs5kZDQ1PTPqMD7nAvwMJUZVw3sypbjMcra3t9jd3dtoDTdmNCaTLqEu/zQeIeS1HoWFizbUCqtFPZRlGW6sqcqKLBeHEmsd2ojSUzZHHGGyYG6lCfGzY10tzijWVozzTC6/0g0jIsGuLNrECD7daCEKyRqsVbDp9K7hrrWO6EfMoqx1QZq3/hB5PHt7e3z68QN2traw3mKUJ8NhixnzizNsMefw1g3K2RRXlVTaUVULsDVHnzxEH5/BosBYh3a9rJxVzezikt3rd7ApQFkiGlv0uYl2YojwXFe6xPuwU3b6t1UN/mxRYFaNo2mLhBFRXcZ1SJUZCemY+Gmojg+XTgHj0UhM/pTine9+n8uTcxbzgo8++IDZ7ILLixPOzp9zfnKErYoloDfUR38em5TP2sYQo9FHIv321tV/kbEP1Wulv0GG0jsv1lq8CmtXe4qF59wr3n/vp6L1RPH2l7/Gp48eceelu4CnDgneYhJQF8IGNrlXjAnCkC4h254V95nuxOC8+Ozr1S/rzs+/zdIRIsAA4b5cb6g45zg4OGj814BOLo2hMLEiie22E00zszTaFFGSySDxkgorVpVVMC1+HpRYAj6cZTXw3mA/a57FM+gSZmiVgOArX3yNey/d5CtffI2/+N5Plvpetx+f6Uz6Hm+RoEeVPF87wQ3GMsRwtoTmMCE3tEZLzMrPWJRSTKdTdvd2O7+tu/vRWXc0EmHo+++/LzAuMik+mFttuGjLazXsWxh91joE/xr4nz4fIshVoJvwXVv/fp00zGyKi+PnaM0S6/tAqK/CPf33WxOvdvyRxsuyjPF4xKJYNOveFYgHa4XPUK5an1XvpKWzJrTMi9Zi3u9Op0Fw4iTYUDANVlq091k+Qmc52gUhi9JoI2GTrXM4BU5BiefLX32bN7/6FSqjOHr8lJ/86bdYzGfYOlgFOckzhfNkKvHdaMZGcEOQZLw+JA22XjR0GselrchswaQuNlqPzRP2GVDaiUwhEudepM/OKZQS+0IVpereYnTcGCVZXHOF0rLpxngklUZ72HMDSrmQFVaIAHHG1g1TrDMDhHCW3tImb4lctSCdltsNnG7lGpWuVkqSovjIFEXmyQWmSVCH912uri8J0FpCrR09fcIPvv2X3LhxncvLC2aXU+zTU7i85Nb+Lurpc46fPcdZyygzzC+nFGXBT7/3A+zjY+xsLj4biArRGIP1jqqsOH72nL1Xv4DSrWgmPcQpUBka5yaS7EGCe4BRCE8h2bNVDMVQ3/HZEsCUyp02+2Ppjw8IccvbEKarQlD2ga0wS22dlnGU8+i9ZJwfZyMMmh9+7x2ePnxKNSv54IP3KRaXXF4eM7084fLylKpYoFWbC+QqRL6KwF8p2R2Y+yZtripDa9pH3P1Qg6va3gjZ997vECyhNMgg3P8Yaq9kjvOOjz/8AKyYwv3cz/8CDx4+5Padl4P5QYATxnQQUuPPtOJMSZ3V4+4Q2Z3PS9N6obLufvTLWoZtTXubMPV9SeGVZ+4Kom2IYPDeSx4g7xkFdXtVSQjKoigoy7ITPaUzhl53ApVFUBQTXUVJqlLx3WDrjmphygvCw1hv07MfGed+nX7LXSKJjQnMofLG3dsAvH73dsNoDI0tJZCGz3NqetaDI6jWp4y4/quKaugBkfZ3ccTgG73xDJ3DIcIzlo4PTTLv9ryGtgbxR3f1O30r1TURDM/LsmQ0Gq+Fbf25RsK8ri0ffvghWSbOvSjRukWN3lBZBdP79yz9HMcQJftD8xsKdNBfw9heFHzGgDVpX/Edrds2h9ZmqG2BvWZjWJq+p3TXsTwyFdev36CqS05OThp/4qiJyvOMuvaNaX93jMN7Gf+mdSOskpQN0I9EsA7udve5xbfRHLyqK1xdoZVv/I6t8xSVpbIeagdW8sU5aynKsjnbNQ6XGfxkxJ27r3Bw6xYL5RlPdpi9/5jv/9V3wrkQQY2zFuEnrDiex4BNPkwpU1il0ZlBj3NUnjGajLHeM5kYblyTaFlvvPHGRvu3MaNhFCGOsIYYptWLRsAokSplOtqseXyMX58SMEAW/ANEfd76SShozJS00o3Nr1LC5enmYAdOsHlP7M18CIMbQX7j9BI2Pc0UHZOeKCW24dEW13mLIb2cNMzOEsDDYxG7tXpe8Gd/9CfcPjhgazzivXd+BBcFWGHMFB7lJaRjVkNeeVymqOuSkfVoZym0x2YKFxzRHQ5vLSdHz3kLhfN9YpkwF3E8j2UI0bV0wjJhsY7xiIB8FRffRwwdFe3AWFNg0Umy4yG97OtCti2NNzKgPT+DNuFNt+/4UspodPoBlNaMRiO0Unzw0/d478c/Bqf4+IP7zGbnlMUFs9kps+kZtiy7w1lDnFzF5K0yUVqFkIe+r+on/r4JcRvrpmveP/+r2lvF6K3qu7svkTCweKdwyoIFX3qml55PPnlAno/Y3d3l5u07nJ+fsrt/gPIea1vpVtq21lpi8CfjT/vsq4c74+h9TomzVaLbdeu7imAaKquY6/TzamHA+vFc1ffqouL/r+w3zQ0TEWmWGQ4PDylD/pKU0YDe+fctYxG79u2lZTwec3Z21sDmFnGLpju+J75SqxF/XxjRZ7hjvVWOrAK/fMJspH1dsccrn6hmyEPn4Oa1fXZ2xIRnd2eLG9f2OTo+G5zf0lh782rWeAiO0GZdp8HHUQiRmC31llcrjVPDprl9WNIf65DAJR3WVXenczeCZQQDc+8Pu8tgLfcTGY3t7e1O/VXMfTwzJpi7TC8vefToEUqJxYZHIm+6oNl40SJwsvu9A6NZPa6hufXXAFomaR3ckv1qCfAUr0f42//cMojJXAb6T/tsz51I1vt5NLIsYzafcXCwz97eHs+ePeP09LR5L9IcQ1GahsBDHEvKmESmpq5rmedQuLNk3Otgb1yzuDYyHy+5tpwEN4mm/ZV1XM7nzMsSu5CIitZabF2LNsM5vNJYDa6s+OH3fsjCekoFP/7hj3j+7gcUVY31FlCglTArWuFHBqU847FEuSqKktu3b/HaW29x497L3Hv1VW7cucVkewtlNA7Y3hqRm9U4fahszGg0m6oUPnq2u5ievOWQ4kFqVdotxx554j7xETcwdeRt+koYBx82CK+bLIUNMeydMB2JhLILXKUNpQjMRJB8OheciKCuq8YeH6JZVQCqSxcMLJAp2Mpyjk7O+fijB+i6ZnZ8Sl4iDJkSNZjCkynIvCb3GWXl2DIa6hrrrBwS74I9ukUbcfJ+8ugR2otjE6oLLOJn7zeXjaXvbhLDfAgxDEmCNu07Xqr0u1AR699dfgdB7ro1iRqaRzq+pXjWPUIjMpyjPCcf5Rw9esqf/vEfc/3gkA/ee5/FbE5VziiKC6aXp5TFQkz8vGG9R+Xq9UjLkISuX3d5zOuR7iok8qLE6YvU6xMKQ0TcquKdw/mYf1Kc4gDqSjGbXvLxxx8yHo/51V//NfLxFsViwXhrgtBCvlHPN6H9vEcp3TwbGvcqpPBZy1Vr+6J3ZlPmZZP6/7ZKl3gQnDAajbh37x4fvPcei8WCxaJotBuwIipN/BuEER4aae1sNhOQ2Jt7yq6rHhXsWL4HfSFFOv74ORVcdIQDajXs6vedVnMqmVxaxwcOa43u4LV7os3gv/qv4D/7z3j93u0lRmOIKeqPXb53u+ozIYL95DcJMy+Coc5y+favahqlc+eXmXU6dfpj+1nPcefdDa5bf33SvYsEdJogcqmP2FVvfYXR0Dx9+pTZbMYkJJsDkS7HqEibzLQPU6H/vT3PGt3R9KdlKBJTygzEtqKGGGhou+Ez1Wo1+jA+zWfUZ3zF6qQb+XCI0e//jXg8pSfqupYkoFXJzZs3uXv3LsYYjo+PE0sH3TAbq2Dw0LrENVRKdSKUSUACtfLdVaURToS5CDMjuK+uCuqqJAuWOCbLhClBc1wVIalj0OQoJwy9EZjoAVuWfPu73+N7P/4xlQsYtC4ZbedoM2Z7Z4dX33iNN77wBW7evsX+9Wtordnf30drzdnpKa+9/jrj7R3MZNKQZkoprHOUZcHlxTmLRdXJIXdV2ZjRkNj/kiJdGyPe/C5IuJTGhRTpNOBJnKu1ykAFT3tEYk/IdW20bJoPbfm4eYjWoXEED0SgOOoaRkYWv6oq8jwmFGlVfHEz451oPqsQhSl8bzQyob32UrSQM/p6LEmDEGCkgIODA05HY9R4m1deu8U7p98BwmV2os3wzganHZhSgRLGJgt+GdpbycaoDWioQ4K4xXQW4idHJ8HYM6C6Ks3ufoW6nYc+mVvL0LXAo/s9+ip0AVVrdtRZjwEiMg1b2DyJ312wTfXpeNo6fWYm2mYDIVyswrqI9Hp2nkFmpIVTbIBRnmWy/66VOLUSD4ezDjPKGI9GzC9n/O4//+doFB+89z6zy0ucLVksLpjPL3C2DjEnhpmDFyEmY4nSk1WlAfZp++0hB7qanQ5DSrrj68iY5dJKFaOjbft+H3ksjV+pRNobefjVa+OC75QPZ15RB0GEpVjMUWg+/OB9snHO3/x3/xYnJ0e8NLnXjMWD5MHpEaueVlgh0kDfrGeD6AcITjqz3aysJuqWtURXtdGJctXbvPb1LtOp4vsqjp/Oi2H6rSmMarckJRRj5Y7pEYBPzN8G9lIl+41SAmeBLMu5desWP3n3XabTKbauqMoCW9cwGrchasMdlvG16x+FRVplZMZgbR0Ihzafikt87zqL1SktnIvzFSdy3XkjBYu+cZZszbLi++19HF6LuEzN9NK201GFNlS6IQNr/Prd2/izM9R/8V/g/5P/hNfv3uavvv/T7nlTcY98BBygaCT8eB+YLo/CdIgfubJhfh5iRKjMRDygwnurz1acu28yenfxjg9janxcVHKm0hYjvOv93phcx9ElfUbtV0ICsrQ3fQZruUYzl8bPU0mC3uV6avBeK6WafBn3P/5Y1tzacJ883lm8jVGIWFO6xP0QkxHXwYdoRB4/yED3xx3H3IEdqZlUMD0VuL/MADgrRP9oPGIymbC7u8v29jbj8biJIqqUoqoqiqLAWsfFxQVnZ2csFgW1rVtf27DeLoR4TQVqKROSOnjH38pSAohYo3jy5An37t3j7st3cdZxenYacL1ENo3J8uTddEVW3990nVJfkXV4vk8zJg/kLmoJl2+DhY33jqq2WFuhcNQebh1e49nzE5zWcLjDy3fuMB6PuXv3bsgWXlOWJUdHzymLEm0yJpMtxpNtbty4wXh7wv7NffauHXDt2jUm29uYPMP6NpKUjMVgtGZ8Y5/LumI2v2DsKknkF4Zd1xKMaW+yLVYEtWV2sVk+qo0ZDZRkLwSazNbeeZRWZFrhfY0kMonSZ/lc22rpQLdSAfGLABiNsmDj7oU4RONTx2gviKAFR9G+2jVMhlRtY5rHPhqmooFHCmOEAZIDK4ehrh0ynFTq3XUgSi+lsYrMOg5u3WRiMvb2D9i+dQ09zqjnZThAHkWG1pnMSSnQDu2RsGZGI7ogzYQgedUa5SpAU5yf4bGobBSYFtAqIAVPyE3STWfUvZQtAMS376EkekG7bnF+hD2MTmoKXC/LcroeLsoIfRPBIF7GaL4WxwSI9shHgCzZ0VOiP90870WiLUAuGacnEAZRS6UbgBdtg03UcGhNXVVoxJ+mtharLFrRAB9wOGfJM8PWaISxnj/43f+ZelZxcXJMMbuEek5dX1KWlzhXBXVl0IIswZFl4NMnyJee9zdgoDTrugKBeGiIuqSz4bYGf+2OtYvUxF9JKxpCS0riTJ1E5+nPN7UJTgnUPpL2KFASZEIjZ9Q6i689ZJr5Yoo/9Xz84Yfs7Ozwi7/0S5w8e8rh7ZdFkODaBJ6ND1g8T1o3Gk+nWlqj0XQk/7rEScq4BIZu5eptxpSs06L0f9dhLClx1a0bxqpo7mLDjKwYWgof253yyfzjT92TIuOW35xv+0moSxS+0Rxo5dE40BLB8/aNW9iqxtkKa+e4eoGyNcrWbZz3CJMiMxT6iP5+oNBKnBKVt2F9ZIKGmFugb1IV1zJdjpSYB+/qZjpaaVpppW//51O/nrjuCWPTE5IknXU+6n7f8bsPu5DC5KTutYM99vd24L/5b+DiAvXbv83+b/0Wtw62OTm9aN9x/TuYEo8BRsYpUHfHGi+GD4R8DBu6xAWk59AnSt2QL8g5wbkBJjX7AQQ3yGSMstntseyuY+e+dWAPy+HRI2NFQLINuPLtNLzHpHi+dw8aSiGM0VoXImsq6l5Y+A59E1alrmuU82gP2sOTTz5lpFSASeJjal2NrctmvZcFFME0XJvm7EemIl52ea47nxVdS4S+pmidAAQffGLjCkd8okBnwXTJWfCSNPOlmy9x+/Ztdra3gwmTARW0Kg1zIu1HZ+Tbd2+iUFSV4/zsgsePHnN8ctyup9Fo78mMpiwrvI94Jdx9xAnaBFgRaZu6LDF5jnfw6OFjbt68ycsv36UoSuaLeYf+tDZquFdrN2JJBa0drY2KTHlrTdHPSZUyTM27Cey3zmKrCvFpznBmggGq2rLId3n1S1/ik0/e594X3+Rv/d2/xeH1Q5xzgWmzbG9vo5TQy7HfLAhUFaKFsM4Kk0ACt2WrsZ5AF9U4j+Sccw6joZxe4qylLEuyLAtBDTQH2/vkeU7mYXLtc4461ap4Em7WS7KPOtjJRgmTXE7XeTdVx6WbJiG9ZDFEOtW9FCmRkuc5dVlB4GqjE7eMh05Ug8j5xrHGv/ECVVWV2BNGRkPSv6ecbnpY0rYCVYcxGdt7u2iT4esyaFlyai0AWvmgrg/1BfESYiIjmdEBQ4jsoIT4NdrgMVycnmHrCq22aFeU7lhYBhzyvEW2bf0uhy5RtiQkcKrJ6Ga/HODI45MVfgUrpSkREq+Yy6A0WPVeSZBgWrdRQycX3vXCZ+LjWbWJo57UGY/GZErzve9+jx+98w6Z0iwuL9HKUtUl8/mUsiy6DnwdAuLFzGJSJmAT8jQCqyEiNe11iKnZjPy9uu/+b1H13Udqq6R8/dJfL6VaJiYyVvGe1nWFCslBT46f8/5777G7u8drr7+GrUpMPsJbwUfOJ4yuAKQOzzWUt6GvBVk1zriig3NS7V6skyayQZ2+NmqoDK6fPFgaWKoT7VyvHtG4/K3TYULWJ/UTuNuVJidRcLzj2vXroGQv67oUHw0bpN7eE7Ul61dOwoiLtLQ7kv6sl9ZnTavD2qzusw7M9eGvWgOr2oGsHEdgr5MH7Y531xJeu3dHPvzjf9z+/a3f4pW7dzhNGI2lueE7DOrgQJbAvDCMfelyOvJYUrzdbSoSmuH3cBcjsbPKL61/5rv76Jd+60ue27ENE9lR0LU0ZhWOYY84r+uK8XjU6WsJV4W5pfPXSlMWJY8fPWr4HtB4XzUJ5bqCvqvwh9wOpRQ6hudPDl0f1l7VXrqvTebpIOzq7HlgGqy1XL9+nXv37nHjxg1GoxHGZBhjyLKMqhIhXF1VFLZGKaExJCrURHwfA85dzEvybMS1a9eoqopnz57x4MEDFosF4yxrfCH6Z6u/9ulncdgfURQFFxcXaK159dVXuX//PotivmQ2JR/Xw+D0zERBn7UWo/Pm3WX4wODv8fxLmwprHZW1aJ2hTMZkaxfvPcViASi2tycYA/l4jAU+un8flOLmzZts70oEtDowHscnJ9Qh7O1isZA8Ut5z8+ZNbty4QVVVjdZJMo9rnBeafLFYMJ/PmUwmzXwb/zmlKKuK7Z0dAM7OzxvGI6Xn15UX8tGI/6Ljj0itdYj64pq4wOnGR2lhtG1LiYeUcIoqrZjRMdaDllGJUUZS9VW0ERsiavqAKD0EfS41zkXGGN/vHpwl4k6JidNoZ4tsMqKazXj55Zd5L8tY6GgKJlnKlY+A3kvSFS8SW5EuBXMRwlp6h9EKHULylouC8c6aywZd6RwB5qEa2DcoAffLTlUg0pi+r0targrx1mVYBsY7sEdD4S2vKlHalM6nP95UAxCZTwlCECNlSEz/8VhC2Z6fnvJ7v/O7eOtYVAXeWyq7YL6YsigWDSD9/1dZOoMDc/632XcaHnaIEUmJlFXtpHvfR5IRJojUyqG0wtYVs+mU46Mj3v/pT7l2eMj5dM5bX3wbnWmKspKQfMasJPyGhAfrGKJ1TEhnzINv/4zFR9OeYWQ2fG+WycqOu3J6d3zC874Qn7y8VkNS1EiQO2fZ2dkhzyRJa13XL3Sf+ki/LMslOPKiRNaq+QxJfVP8153c6nY27W/T8uq9O/jpFPV7vyc//O7v4qdTXnvlJX7ww/d+5vY3LS8Cq1Paoc/Yr1rzVfhq6Nm6saxac6/W+4v1+yiKgizLApG5LLWGvjBMcD3A+fk5l5fTxkQ3EpmRIVJKg1qWrAt9r5cEpnFeaXbopbFsIsBI+jMhdQEr/Dattezu7PLmm29y+85t8jwnz3PKsmR6OaWuhf6THEbRDFijlKeqSorigvlsTlmJdHxvb5+b129w48YNAC4uhEm+efMmz5494+GDB8GEygWNTrLGSqN1V7AYSwydPRqNuLi4YDQasbe3x40b1zl6fkRVVYNhdjc5Qym95JzrCAjW4ZL0b3vm5XxUtViu5OMttBmhjCQ1rIo5k5EhC9rSg8NDvvT2lymqooGZ0RexqirGE8/+wUEnopiYrpmGDo9jL8sSay1ZpkLyQdn/PM+JGh9jDFtbW42JWerkr7Vufk99cNaVF9ZoRKKg/SxRE1KpcgcQK9qNSYB1H2CnkUeUarOJ9w9B62TeOitFJkQpcdoTQlm3DERiYxn76kYlaiV9VSWZH6NUI2VqOoBRASER1WRnGzMeMS0Kjp4+AxtGGM5TfLcrdRanV6/CP0Sy5YNTuHIiKauripPnx9y9eYs6cZjq+030RGKdT6uAzpDGJx6q9jLE8a6WTq+6pH3Esqp8doQol7XfxxBR23EEth6DknjSlSXTipHJ0MDv/97/RDGdS+ZNHFVdUFVzZvPLTtz/n6U0Z4kuibKO0Fm3Rquk8mlf/Tav2sP2nYjwhpCZPF/nxA5ddXMfAKd3d2g8EdaMRiNsJUwhWlNVBfPZJU8eP+LH7/6Ir//8z/PsyUNu3LyF0eK46pVChYhs/bEPCSG6sCYIBXpnyYcF6eTk7TPifrNkmJue+0Gp2Jp2xLdKtWAhED1+QDKYPB5koFat06bFe/GVsuG9yWTCZDJhUYnqv64qMTMZIDyHxhDbLEvRhjTzTfDJqvPWb2N5HVYzCEOO6i2hONzmqn0aOoNvfeFVdrYn8vvgKATfHRzswX//38M8JOmbz1H//J9z8Ju/yS/9wlewdj18ms3m/PT9+ythwdBaXzX2oedXndUhx+F+vSFBRfxtCMZvAt+W2lkhzW5wdtj7i4sLdnZ2ls5BGtbVh++Ed7LgM/To0SMh7HQq4Iih81uGY9V6p4FQhuaXCm7XnflVa5VqyRuKyLcCQIAvvPkF7r36Knt7exhjmE6nPD86pqrqhvGqa8vJyWmIBCfndTweMRrljMcTdm/t4z3M5zPOTs/59MGn5HnOnTt3ePnll7l27RonJyfkec7Ld25z/+OPw9qla67w2AbvpPdeqWA2FHwwsizj5OQEay37B/vsV/s8e/YM6FrWpDh91XnvP7dWzMeiT/E6uJjSa3LmxPzSe5gvCvLJFkqPcS5jsr2LMZrz02N2xjnYmr2dHbTJKOua+WIRAhaJlnBRSB4LZ12jVVJKNYxx3MMo1MnzvEk4jRKzvPSsVFXV0N/zAGMicxLp6jzPybKMLMs+/8zgcQD9BfeIPXy6WVErgWoBSlSDxQWPByEuRGwz9hMvS6telIOWm4yYeToWpdo4zrHd+H4TEi20kQKG+K5IDdoDm2UZdW3ph7VN5w0K6x1WgR6PMKOcfDTiww8+oC5L0EqyNQZfBaXEdrFBTpo2G7aYWIpplNchJElwNrKOi/Nz6qqW5CVJSQm+OKbWXKpdm1VlPQOyzGhsQuz221+HxIbGcJVkoUPoe7UEMFMuu4/IInOpQr+SBA4mozF5lvPB++/zzne/T6YNznvJRO9rZvNznK9/JiZjEBAp1ZGIrEOUaem3c1XErRRprkNAw2vfmhikz+XzeuIjMvtDY0sB+SqgHuvFdTdaOBtna5R3TC8vUSg+eXCfO3duo0zGrZs3yIzBeyuJPtVwrPahdRhC1H0mbh1xsqpchfQ3aGCNGcnyGBtfpcglxucpD5W+H3IPkc5xxdgGo7+xfNfTOp52n7VqfXmqqqJKMtz22+jDjrTPxWLBaDRaykMwNO703g5p3Ya+r7pjsc46WLbqbKUlfT/PMn75F77ahLO8svy3/+3y99/8Tb7y9ptXvmqt48OPH1JV1eDYlu94t1wFz9eVFE5EHLzKdGqTsoqBvIphbN713WerzrNSisViwe7urtAEyT51YEUwM4mtRGffx48fYesak7dSYRHIitmUc60fxNIc18wpFaYOjbvTTnKu+0xECtvSULBRwPOVr3yF23fukI1FS3B6ekpZllxcXHB5ecl8XoQgP0GAHCKAOmfJMtNEidve3ubw8JCbN29y/fpNdna2efzoEe+88w7vvfcer732Gl/60peE4Tg64vXXX+fatev8+Mc/oSjKEABCEj331yGa+MSAEtHipiiKBlZcu3aN6XTKfD5fEm6tw0Hp8/4aDt3rdXuglORtc7XQE8+ePWd7dw+lJ5S14vqNm4Di/OQ5mXK8+873sHXFZGub2aJgXlRczhaUZdkIbST/RdWx7lFKNXc80t2R5vHeh/D9woBERjVGkYp0UoSvVRAGnZ6ecnZ2xu3bt5u6m8KAF4g61XfkXl7EgZcalVc6gdhOKjHo5FWgJRr7pi/9MaV/I6PRV/P0NSd9CWyToM+1gEgAge/03QHCCqITOsazf/2Q2UcPqKtanKmC5sV7h1dZg8QdUCFOYhGIOC+/1ShCIKWGe1BKcfL8uBlvHwDK55bhWBdp4qpD0SWwur+nfW9yuPqEwarLl47rKmkMdBG+C4vVfz9tIxKqfVM5vMc7R57njEYjnLX8T7/3e2gvzJ2tLR7HdHpBbUuqurxybH+dZRUBsIowXvUuXE34pgx6f7+77/oGoA/1FVW7V61Z2kd/LvF7WRSMszzAExv2taIsC06eP+f9n77Lq6+/zscffsgbb30R5wUpSRCIn33P0rMlZherJtOdz+dyXnzXVXXdGIEmgkt03FeB2WhCu/oIZGjGqCIz46G+As5edcaGkK8LjsExMZT3ktHW2lp89Hpmt0MlPRd1XS8huiH4lJ7lobFuUvpjSvGHBINYvpubwkmAqq7503/1l/zar/wck60JvP8+/Of/OQTpa6dMp/DDH3Z/+6f/FL7+dQg21J1y6xb8l/8lvPUWi/mCf/3n3280SFeVqwjWz3K2U5ywCT560b1aV5b3ZDXTlOIrYwwXFxfcvHmzI7To33EVmAyfRDNUSnF6epZKAxtfhwZubixv6OH9gfci8zEET/tzS4UKTdthvs459vf3+cY3vsHh4SGVdTx+/JSTkxNOTk6YTqcNITsebzEejdDaNPRWbNO5urn/i3nBp5cP+fSTR+zsbHN4uEeWZcznc05PT7m4uODZs2e8/fbbvHL3Zc5CHoxf+qVf4t13f8zZ6bnQkEveqsnaJEIMSdSXB0YjZzTOuXnzJk+ePGnG2Gd+rzrTHTyQrF367hCz0TIZklphNMoBz/HJCa994W2OT2ZkFezuH2CdZXp5wY4puSxLdra2uXH9Onk+wuRCsvddBzRtqOR4DmIpy7IxGcvzvPExqa3FuXa/lVJNG6nvap7nKKW4ffs2d+7cadpO85JcVTZnNJxvM2i77uHtLHhAILK4IraX0IBQ15J1W8LhOmJYwnQzYkkJmHTRrLNtiD5okgZ52s2MDkHp2CLzETnZFIiJak7GW5QFW1vbDdEeD6BkVGwlhI2K0QT7tp1txof7HIyu8fBiip/PRDFhNHVI+gchpbsKUTlQODx1QO4VMaKFw2mJulXWNdevX8MoqaMIIR5TdWeIfBTD4HaJCFgFUFOH/XT9W9alD+RlzKuBfx9Yd/tOGaLG5lKlz3yvrkiPffgqn30cBlopXNAMyfaEyBy6XYP2bCZJxAjaCmA8GqEUfOfb3+bTTz5hQhYuW82iuKQo5wFYdqVVS5SmSiTH8WzGR02V5Qgg6edVBPvQ9+XSMp1DRG7/t2EGJSIyWmJEKfIs7yBOgto/EnyrwvJGZDoej1fOQdaEzrjTZ3HPqrrGKI1GNXdRO09ZLijKjKdPn3Lt+g2+852/4pXXXkdnI7SH2loJ4deuxNK6rV3VBGE04/M9sj8snQgOBvpJ72PnPd9etsAUdItv7+GK/V9ad+9DBLaofaG9M8lAlqR5qkVeNOeIRq/pwxd5T7G0jj7etf74AvGiDRjIRzlbO9ucX17gracqqxC5TmDwUj6aMG4VGbiwbDokd41agD7REPuO0aKSEdHAmv5yq3Re/bPYhhmWe+qbc6sUS/dqFYG3SvDy5Okxv/v7/5pv/so3uPvWW/h/+A9Rv/Vb8Id/yEalz3wA/O2/Le28/DIPHz3jz/78exRFuTSudbClj5PT+uuEG/H3oTVY9+5VbYZaoYPmpfRL966oiBvS8agGVwzNMx1/LEVRsLW1Fe5Ucr58MoQUNyrQRqIqHh8fkWeG9GwtmZg381lqtDvzFB45j1Nu8LytwjVKqSABT4I69M5ibS2Hh4d84xvf4ODgkOnllIePH/P8+JiTk1O0kuhSW3s7GDPCZBOMyckyTVWVfPLgPrUtOdjf5/adlySZXFVhbU1VFiwWM2azKRfnJ+JjUFZNlLTpdMp3vvMdTo6f85Uvf5nReMzjx0/5yle/ygcffMCzp0eQWm00cDPQUz1Gv7Y1qlIUwZfk2vVrHBwcNEJpqd5aK1wlIGjWMdIiyZ6277Y0R7sfMdeIIs8y8tEYpTQvvfQyX3jrSxx/+4cc3LzOeDyhml9SzC8xpuSVOzfZmozY29+mJgRMsjZod2ww4ZKgQ9FscjQasVgsuLi4oAh+bJOAg621TXZwgfnyW2QatdbBz0Zwb57njVBna2urYy0ylI9lVdk8vG1AYJFg10qFUKtaorxYB7ol6J2X6EqZzqhsFfydPbZ2jEamAdKpw3c/KVJ6eRpHcedwgaCOnFdEkjaogaKjyng87phrpX11VeGW6ABubYVzdUDUisoG/jkQXT5cUB98KErnGFmNvr7P4de+wJ29fS7LBaOnEx4/esR8XlDWYs8nIErCBFsPVkHpPbVW1N5jlCfDk5sRTmUUWmMnY+69fhetxK/AKOFeNS3TobRJLkAXRaqEwOg/i65McU6ES+Kb+SY1VdwX12ulJU5jW+l3AcYR+cbfVNMeEMzWfGK+1rYRiS8XTcl8u38uaIziMDrInkgYpcOU3yvnqV3NeDQiyxTF/JI//aPfJ9ce78BRY5kzL07xFFgXzTMSUye6Jf1dtYvRLEJzrulmBN1EKrjEOChPE9Y5xsBHGPhlQm+YyYRlR/m0ngAU0fIVRdEw3lHqHOcQfbX6WhBonfX6qv0+hSdnZPn3/vgrZ8mzPOTCEULB24r/H21/EmNJkub5gT8RXd5qz3Y3390jPCJyjdwqt8qu7q7eCJC8zIkzIEACvM7wxDk0QRAgeGueh5cBBjM8ECBnME3OoZuYAXum2dWVVZmVVblnRmZs7uG7227P3qqqIjIHWVRU7Zm5RxVbAh723lNVUVk/+db/t1jMODtLefHiFYui4uOPPuHdL37ZWg3dvZ4xvcjYyMZctA/ddhvqz5FQiFsZokZM8ky+FKKO2YAGFKeJ4seMu3fFANSMvnu/juoQQTAguASCAe0sL5EAIT3KjmPA/WoOkNMu8NAnS4yR6AKjH/Ii1O0LL/eyqqMjIcmq1ggMSitEkjBYGyFeHSCx0NOVKmy90r8zrj9+jeUY7VoEgUZ4OHNqZcLVpUUXIloTz2mEhe5Ho3kNS8O01rRdOFeVtjZ6lbZ+uSz4kz/9K9579z7f+Oq78C/+BeKf/BP4L/4LqKpV1a4uaQr/5X+J+U//U4wx/OwXH/DhR5+F919lfWoLTP5zvDeuYmLbe+Wq+K2GJeAqRtkx4AIP40qYG+OZJr/zGu2q7wvMaPjeABi+IOC0++/diBBxrKWp16VrgQTLnyQCEiirBdPzM8uWGgXC0y6Nh85vKBgafeGCsNEQ1Jzw1HZRvXJ+Aalcu4XAJDX982fqYLTGl99/n9H6JscnZzx+/IT9w1eUVUWedNkcriETgxEpnf41RLZG0s3pdTMSUXF8NuH48AVn4zNuvvVFhqNrVEWBUQsOXj3l5OUz+r2EXj5AKxAmJXGJn3d3rmEwfPbkKePJlK997WvcvHObJ0+ecP/BWxgJL1++tMJOklBVysLcOg2E8DGukiC8KF2xWMwx2tDt9uj3BkwnM8rC5vBApmh9UQBfNX6+JGmCjbXw68TDD9e0JF7yWitAIqVBpAPWN3a5fmOPv/23/zYH5wsGO9fore3RkRlHzx4iRcFg0CVNU27dvkalJyyWCq3ruEYf1O0tG1mW0ZEdjo5PnStZQprmzGYzQLJcLhkMBpTVnDzP6XQ6CGFCEL8HZDLGsFgsGiEG3iISJzz0fPateyuHqFHeXNCIBv4y6d9rH2PzXeyKBBHCjDEhUUl8bxAeVrzrMmLgEUwkIiQwAUKgSixYNIPAfbsNUqaBabU+hhddxJobGCptBRtdGIZrI55/+pBRb4DJM2ZFiRIJJCnaKFTlGCMpKZOMCsO0KFhqTSUkFZBKSSogTxLyvMtwc4u/9Ud/ixdHx7y3d5PEXIQ3Xak1umTurjwMIw1H0BBFLieN4NLmg+GNV+qgWm1sB2xe/pw9MBq8xyWbvw1dt+pgrJloyJIEAfzlT/6So6ND8jSlqqygOZ9PqarCEQjLkF7WwbYFo11ihvvNNHaXMbeuTxKEqPOn1IJGEjHUqw+deo9aS4LXwPiySsD3r4/jpXyJhYxVTItSKsRnxUxrWDMtJuUyDWetoVINkAf/juViyeHhAVmnx1/8xY948N4XSKSkVJVVgrzGcnFZieetnmdzaW0Rn+0rsPtGBPYh1NsYx0vo6soxWfHOlW2JnvVWi0sfFDXDI1oXL2MWL7Q3EuqlbFqQLRNgg+i3trZ4yCeURWnjNMqSGr3sYo9quf2iEmrVmeAkrivHZnUx0cvaD0fXiOhSS3C47MxaVS6zLHz40SMODo75wXe/xtp/9p9h/t7fQ/z7/z48evT6Lty/j/nv/jvE97/PZDzhz/7ilxyfnK1kPq+yvLQ/v25vtvvhacIq68dlNPCqa+37rvoe7bIL7a3vbWqc2/XE55OPG/VCvg8Afg0JR0gRYEO90G7QjXMqbo9vc3tc2woQrbUN+pUX72v3178j1OGGJcgz/j5hATQ63Q5f/er7rK9vcHBwxKNHn3F0dAyJob82YNgZsVzMefXiMZU2bF8r+Oq3/jayMwCjUOWCL7z/TQ5e7aGrkry3RqEUSZqR5Rm7129xePSSyeyURHZZG6xb5au2TOt4PObmzZtsbG7w+PFj/uqv/opvfOMb3Lx5kxcvXvDWW29RVRWHh4dUOH4ujsESEuUUBp4pVkpZqFdtEcCGwyHD4ZCiKFgulw1+9ar12i7a1K79caoFP0dxMcauqY2NDW7fe4dvffvbvPPu22xfu8azX37Azu4OJukhFyXPn35GIgx3bt/i7OiYb37zWyhVUVWaJMlC+/I8D/yM/zuZTADodDrhvN7Y2Ah9WSwW9Pt9kiRhPp8HC0Zc2mkCvEeCd8GKY0GqN1SAfC54W7iIFuGHth2YFBPfC/CircmM6/bfG0Fb1Ad+u+54UKqyduNov+fixq77JVsbdjad0e8PAipEXMLCE4IskWilMFVJ3ulyOp7w67Mx/f4Asb5GP88Rszn9NEMKSZ536Qz6pP0u3bU1kk4Hk2fIboes32O4NqLX69FNO3SzLoPRCJ2mHJ1PkEnqzrrVQZeryusJcnMc4nqNfWBFnS0NTOPi1cLGqja0D5arDmZ/3yrmos10xBar9ju10nRyC/02n8348Y9+ZLUjZYVAUlUFs9nEakWMIZGJTeYYGKGr2xlbLNrM0WXB0a8rjcNGeMbVM/cCiLOM1ox/WZbBEmHbZtz1NFw3BtI0wTiYaiFq9A6fpbVtBYzny+/9VXOptQ6CRv0sxCulSQcuFzytYKQuCKlWmCmYTSbkSjM+n/DZw4e89eBdEiGpTAV6df6RNymrGH1/yK8qEb9t3UyxeyYWRy8Ijyva9SaM4FVtXcUcvknxz7Xpc7str9sD7SLdehiNRqFdXhBdRavb7/Z/7ZxXF/aXL55qX0VTXkeHmvddzZT65y8bj887B0IITk7H/L//xZ/xB9/8Mm//4R9ifv4LxD/6h/CTn1z+4He+g/mf/wVifcSnD5/yVz/7bUiy26DtV5wLl621Vf1r8wTx7+21exnD1qbbq8Yq/PI6QfcN+nbZOFw1R0VR0Ol0HMjCxXUd1ln7XDQwm89QcS4nc/F8iPfbqvFut9vGGFqFR2zVaI/JZf0zuDMEt1ec0inNEr785a+wtbXF0dExH3/8CScnp/R6ffJel6w/pNcdYeQ5S/MUIzWn5ydUVA4FcEa5nGOqkt5ox2aPRqKqAqOMy4RecuPuW5yd7LPW65MnGUmWUZZLlss5h4fHCCG5e/8Ob7/9No8ePeIXv/gF3/rWt7h9+zaPHz/mvffeoyxLJpPJxfnm4nq0VkdQsrYCDIfDoKWPwYY+D+BLPNur6EFbcO31ekgpmU4nvHj5gpt3b5HNZnR6XfoSilJxenrA0f4z7t3eYmN9jZ31da7t7fHy1T7j8ZzRaINer8fQ5dCIz0AhRHB18uvJe/QkSUK327VQuG4t+1wYJycnnJ6eMhwOAw8fx2x4xf3W1haz2Szk27gqHrhd3ljQ8B2JtbIBpSnPguTfyKOh6wBEz5D4uozRKF0F7N5VwoV/h18E3nTj7/FQtv57mqYkEdMTPxsTP78x4wXpXaUAjk+OOT4+5ebNW6EdFwiWlPjokIeffsrezi5f+trXGPR65EmC+e4fUBYlWZYzGAxJEpsdXCaJzZWBoAKbBTzL0InNGi6SlFymCA1KG7SG0cYGBptVNG7D68plh/aqPl31W6POVfe0iNtlB8qb1H/Zve1DyBJtTyptWSVc1vPrAlArhcAivWRpyk/+/GecHB2TpwlCgqoqinIOora4mZbmclWJD49V/VmldbpqTGIBvW0pbL7XIGVCmmQIIYOfphVCrKnWQsJ6dtfidGvtUJyQ4FyLtF7VnloQX2WFWnWwtRkNT7hqkAafkf3q0l5Lvn4Ps+ffobWmKgvKYmm1TCLhV7/6OW+9/bZ1R9K1FnDVO9r9qL9fwjhyeTC4EFZrb3B8kWeEhX9PXH9LE7/i92Z7Ln6+7Nk247Kqne3vr2vLqj2w6p2Xtd8IAcawNrRJqVSI3asuvPsyOuKLzzLs90mjzZ9flnzN+wzGXBQ2fGkHkV6219vCUlxWrnOl+PFf/gqlFO++cw++/OWrBY0vfxmxPuLDjz/jpz//4MJ+vExZEL+/3bZ2XEZ7XbXXWnzmtpnpdlm1vla3Dd50UuNxvkwwuoyGXzYGHnFKKeVAXi5pP/Xa89cm5xOWRUGaODQmYelffG5dJfS2+xN4L6ORNOeyrSBYVb+MwXy8pVIIEIY7d+9y8+YtTk/O+OjDjzk5OaPX69vcN90RneEew+E212/3GG7tcXj4nMFgg7PzOTM1YzQcsLW5R6/TIUskqZQYbPZtXRlUVVGVC87ODhmu9VlOJkhgvd+jKgsm4zGz2ZST41MMmnffe5cHDx7w8ccf84tf/IJvf/vb3Lhxg8ePH/Puu+/yy1/+ElVVFmRC1Eqqtqs8brS9UqMsS4bDIaPRiMViwWw+c8NxEXK5Te/iM0ddIpRcJpQXRcF0OkWLYx5++pD+2pBvffe7DPoDimpGMZvz+9/+DEHBl77wgEEn58a1W2xsbFLqGaNR5hBRrQePFxj82eZ5b89T+38+n4anl36PdjodjDFsbGyQZRlHR0cBfSrPcyaTSVAU7u7ukmUZW1tbIb7odTQ6Lp8LdSo+qGN3p9gtKr5fCIGOXC2Cb73WVFVJmiWN++NFEm+uVRoTX2cMZSvcwW6MCYdXjHQVHwA1ccRpbT1PIOj3B0zOJ9ZkmjQTAgbCqzVpJ8Moq/HY3b3GzZu3mC8WaDSVLlHKHqRGCLRIUAZqn3Ccl7SNsUiFRAsbw6GdBk2mNoFOYixSQXBtuISAXvb9svm8jDC1iwCapoqLmpur3r3qEG5rDtqHc/sAWyUwWp7iDTQ4pkZHUlqRJQlZkqIrxU9+/GPSJLEZ3JWmUjZYzWARceq6nH96dKD6ettM0usk/Te5FtfRFjDsmgZwTLwCE6xyNujQGDDKwgzabWEJsXVpMbUSIAzTar9xK9DXLkrxfoz/rYr38JoUf70Jv0f0Od6XF5myVQdn+73GGJQqbcIjAZ989BEnJ8esjdatJp3LmO+rmI+rhPSGfN0UJqPHRTRvll+6XFBb9f11v19Wrtrbqw7TxnUu7PDPXdrMkoAAFNJzpnuMaVg0rqJFbYaraq3F8D68pvZyWrCqnXFb4/vq62++n1cJbJcJI/6+VevP37OxsYZRCvHP//mlbQDgf/qfMEqxsb52aTtXtfVNhNh2PZedx6vKqjP4qnLhvpqzv9Cmq8btMoGifV9cYtQkf890OqXf768UIP13Y4xbeE2avVgu3LnhEhbjz4z62fb7rhwLIj6rxee+icBrjAnCkgFEIqmUoj8ccP+tt5hO5nzyyUOOj60lY224xnA4Ih9s0l2/yWj9OqVWbN/MyAYblIuSYX+dG1sjhoMuqYRyOWcxO2NRFCwLq7RLZcfm0hj0GK3doSh3mIzPODk8Zj6bkGU5QiacnZ6xPlrj6PAIIQVf/vKXeeutt/j444/55S9/yTe/+U2uXbvGq1evePfdd/ngt7+1nJHrozIaSZ0M2p8RXgjxaFR+TrvdLvP5rE7J0Bq7VWuo3q8X6XjjHFgxF0VRUJ2cUi6tNYUk5b13v4ReLPj0g18zPnrJl967z707Nyhmc9595wGbm5vIbAMhEvb3Dzg6OmI0GoUg7bhdq9yz2wJGkiQha7jfm51Oh9u3b9fZwIHRyHrY5HkeBCUhRCNw/H/1zOA2cES4A12F5CBJkrAsiwtwtX7AYwjCmAGxCT9q60T8bNuycdVG9PXVzIsIgoZ3/4gFmLjOtvZFymYwupQyEIZVuMvKIdqsj9Z5+vQZ9+6/BVmGcsHkSE1VKYRMkNJKmcgELe3BmxmBUSA0tXbCLxKnAbUQlSYSQC7XKl72PS6v0x75krQY+HDHawwSr6v3daW9VlZt5PAuBFI0N/tlh7afb601/U6fLE357a9/w9HhEdIYNHadLIuFzZmhSmywnmgcHm20kHitxv9WjcdlfW3f37ZaePNnrV20vbdwglhBw/hDqSns178J90ys7RFhz3gi6/dMXIcfN3/oxQS8LRS0+xMrDuLA8VXj4J+9jCGJf/N7MjAxWlEVJUmaY4Dp5Jzf/uZX/J2/+/dQhc1KbbOhXk3ymkGVV97aaFctZNR+0ACyaRx6rWvh37R8Hi3T/9rlMrokWgM5GAzCei7LGnrxKgGsXUzkO3zlfX8NGvR5SrudqxQob8JkX8a4dzs5O9ubiH/5L+HwMK4Y3n0XPvyw/u3gAPEnf8LuH/8xnTxjWZQNRrZ9dlzFEL2uz59HcIgZn6ueabfrbzp3lwlW7XZd9pznAabTKbdu3bL3CxoahlX9sTTS0snZbOZonqXRWpvXJlX8PP1b9f11c+LfLoSNyxBS8N4XvkCa5Xz2+DGvXu3T7fZYX1/HaDg6OuL6YJ3NnRGlhvP5nNOzQ7JEc+vuXQbdHlovOX71guPDl0zPj1HFHIHNFYKQaC1Jsx553mFtNODatR02NjfZ2tnh5OCQ/RcvyPMOUiRMxhPWNoccHR3x8OFD3nnnHW7fvs3Dhw/55JNP+MIXvsBsNiNNU65du8bB/j6O70fQXO+1V0CtmCrLkvncBkTbIOg88HmvG7vm2pcXAvHbay4+7/w53pEZiUyYnJ3z8QcfsTnc4slnT3j84e+5fWOXb3z9K0ihGQ76PHjwNkmaYWRFWZT0+3329/c5PT1lMBg03ulpTyzYe4uEb4PnYXzxHkHePWowGATrx3K5bOS/E6KOgfZeBb1e78rx8uVzx2jEPmDta3BRK+ShRmPpyTOuwc1DCBvF7xLnKWXdWxKXOM0Y3O+aPM/qSPsAbShxLwFhtYipw/5VTuO5ylGjNiXXxNfChQlGozXKsiDrdO0CNITEVk4+JnFaiq3NLX705z/i9p07dPIMlpqT/QM2t3dIkgwjbF4NtAnCgoXqlEgJQhmEkQhhNR4IUF4aNdbH26IueX/vpja1aVJo6d4i9BQT/m/1frWFxF2LpQnhcDq85qWG6+AyqcNgUTdMXFn7sPDCZngpzhXF1NUbE/5aTVHcI88wey2p65Ex4LPUe4Ihona7dydCkGcZAsFf/PhHdp0lElUpG3BVFkGINHiIUOsAqMqLWvYmetnVAc2XCUE1w2/Xsr3f5/9IgrBumTMVBA3r/1+7Ntnn6/qsFcMHa9fB316r4e83RiBDEiqvE7aHo2+XzSAq3RaTQWOcyMTNXwxH7YV5E7WlVhi0LZSxpcG7qFzFZMSaGl+fNoZKK3KtEYnEKMVvfvlLfvCHP7BE0tTCVJNGxQJX/d0vTin8jgs/NcYFd9Wb70X8YyygR+3+NyUItBn1VYxbfRBeXDOulqgDAtPa43WkiV179TRFZ0AIaPX3ugWAHbg0z6zQZRxSoFIOAr35btvm5tvjRnd7PVdtE6HIiMvXjh+PNrMc/22PWbPnzeJeH90b3R/VIWX9OdQpaP6N+ubH4NatPVvPP/2n9fXdXfhv/hv4d/4d+Of/HP6j/6jOufFP/yni7/09bt+6ziefPiUeyzYj+lrhBzBtxQVOqeFOVGE8nXV7vj5VcJTdkmUjwMh6XzTWYv2+UGd4z8XxN345hRPNhInw50YYypbWObyveeDVe0DgkBpr+q61Zjgc1oJGbPMT0VdT04ZEShIpKJZFY35XCVv1R9PYfb7N7RJc1mVTm/06wUxK6SDway4AYGd7l2u7e5ydnvH06VOSJGUwXKOsNE8eP8EY2D85Y3jtJsr0OT2d0B/2uHV9m9Rojvef8vLZY2bTMaCQpiSR2n52y89IELqkXJTsn59y+Oo5g7URd+/e49q1a6z1erx49ozlYs5sOmUw7LEsFrx8+ZLNjU32ru0xnU755JNP2N3dZXd3l0ePHnHnzh2Oj49RpX2X57PC+gr7sFYW++D+8/Nzh9aUUpTLcC6+KWyrvz/O22bXmHWeFcJCHCcyQUgZXJJu7N3i1q27rG9tM1zf4NNPPuWDX/+Gezdu8pWvvcvO9jqT8SHf+M53kamgUhUYK7Qtl0uuXdtlsVgynU4aysc8z1kulyil6Pf75HnuMrcrksSHFFgewgoTdR99OojFYmGFoU6HXq+H1prxeBx+S9OUbrd7Qbn4uvK5BI2YOGxsbDCfz1dGnQeCJh0Uo+OMtWOikQJhpKMNwh0U9q82BiESm/ROCESAhkzI0hSB3cAN5k25QwIToCRl6rJAOzNhWdlEenAx/bwxvm/erUGjNDx/+ZRlqdjZ2mXQGSKRlKrAqJK0k9oMxULS63eZnJ/xf/6v/0/c3LvOs8dPOD445G/9g3/IH/6Df8S0rEiMw7FSGrTASKiM1bCK1G59GTGCQSMqfTZrQ4LxVJCLp5MrTZmjPrNoE24vgLi58gQwPBvd15jb+GCNXmuM1VyaumUe3rKRg8TV2XgWY3OOuDaZwKTZ3z2P0njCn9WubhNr3L3QGbpg+1VWJb1ujzSRHL56xZPPHpFIgTYKbRSLYknlECqqyq4DhEYIx3yappakHpPmXLSFjcs3Y7O+eE0nMkUbjVYGJcCDjvo2+PH3QkRgjFttq9/tmZ2L1yxBjjQzXuclos/g9padDGNs1m0pbeKhqioRQgWBBtrBjTVB1Lp90DaZOr9c3qQEC6iUGKNZlgX9NAWjOT084PGnH3P73fdCPFfsamXb154fxyAZg9AGkazILO55Ziz7I4w9vBP3u4kUBoEJ8lWvKKs0uLEl6LL189fX+LbXQSxseOHAN1s0nlPGr2/vktdizN19Xqit3yfRQqMTQWfQo9PvUhUF6ApUBU6ZIxxwtwbQnoY1ODWEAK2tRc/gsqAHwSTWFl82v/Y3K6jGrrqiQdviMVktZtge14KvurD3mkJIPbKmIa0aiBh6Gytl9/HtW9ftj//j/2j//sN/iPlv/1vE3h6z2YL+v/vvYn75S8R/8B/Av/gX9r7/+r/mzu3rfPzJc0BYCHoiQc54AbIpcJgWndYIdEPQcCDj7twICgcduVK7hSOlDEvHK80Qxomurh5tWnuiOcqehNsmtQXeiE4EetsWfh0MvBtqyx94OlkLHF5otoo++126XF/G1N4Rljmz8aUNpZK0LdKuLVIZMiFIAeMs49q0YwZj2tg6l/2P9s7wrvidqyxUfi6vVGgI4VxJBZZHFdy5cx9dCZ48fs5ysWQ42qTbX0cjINkHVSFEynKy5Hw+Y2N9m+vXd9HFOY8ff8DhiyfglM9aaUqtGu2SUpGmGUkCaZLQ6dqM07PTUz44OeHmrVu8df8+d+/dQ0jJyekJSSpIZhPOT0/57OEjRsM1bt68yfH4lN/9/vf84A9/wNbWNkdHR9y4eYvHnz1GegQq4WmycGvORc05WhCfA1ZYSANCqRA2lqYqq+AiFI9nfHYkiQzu/0IIjLZCho2ZhG4no9frk+Yd0ixHacMPfvC3+MHf+WOOTk558fQZf/UXf8nzx4/ZGK3z/pfeY2uzz2w6Zn1jm+H6JkdnxwhhEaayLGM0GrJcLkPcxWw2YzqdAYIsy1lfXw8AL/P5wnkPZUHJX3s3WCW3R/vz5433aPCZx4UQbG5uAgQhxgtr/0YS9vkKq6piY2Mj+Cyen5+HgY/dK7TWAZfXT9aqYO+4BO1w6/z0z8ZmnyZcpiOMpukSFT+bRO/UDe2Z35wESRcIyASf/Oo3/P63H5KJnHt373P77i3AUJYVSBvwJJTmnXfe4b/91z/kNz//pWN+Jf/6hz/ii9/6HqLTpcIgjQGjMUKQpglJmiKND9qVSAGJqJG0GgHGwm4ajw29SpP+utI6r+1vfkwu0TK1n3vtO6LPsZUirsTLnvFTIhY+mlJIo6wiqjEhiBnJ+He/QdI0QQrBb3/za7thE4F2CDbL5dJtstLHyeFzU1hmvOmPeNWYv86KUR8UTbQmIWwwl82PIZyLkG4II21hou1qdVl5E8a0DZLQsEJGjKPXFNk96Sycwo+XaQgTq+jDm5Wr7wv7vhGnoaw7AJZW/epXv+b+l75MVdaulO0DerV2UdQJSi+02VzBeNK437QW+1VC6WXj8nksIE3h7qIAY38Pny75/bVvIYgUr9kDDe2yWy+dTocsS1ksF5RlFQ4wrzFvv6Ndn3U/URdgGfFP1P+L6mq3n0jIiO9pClai0YyLfRXgNOxWWNAtGup4uYit9yqcWFkgGwe2QIIQ5FnKtZ0N+OEPrdvUP/kn8I//MVopfv6z3/P7j5/wxXfv8I3330H8z/8z/Ff/Ffzn/zn82Z9x7fvfJ+/mFEUZmPV4kBpfTc24RwPiLBq6TYJDJRoPxAI6KCec0BXnmTFebBVhfCBSQPl+C9Fqlwl/L+xBf6/7SbgElTrK/YLLzRPkJ+ocNIEpjetzFSaOAfOMlGfqlFIkqWTVOgCfM8dDVdvfPLNKqy/tcuk2atEOb2Gxe8VOZC00rxY+rirDtTW2t7c5Oxvz4tU+ne6AfLBOd7TFxvYuOzfuMxmfMhiusagM6+vrXL9xjWJxzse/+wVnR08QukKVVktu93YvnBsetcjHBHiNeKfToSNtbocXz58zn814++23uXv3LlIKjk6P6XR6VL2S+WzCixcvuH3vjg0Gf/iYp0+fcvPmTcbjMXt7e7x8+dIqvZ0iBFHTposAKnasPDPd6XRYLOekacrm5iZ//+//ff77//6/D547TcVU89z1yE02XiGN+FxDqRTz0zOUtoqF69dvcvvePWbzGR/85tf87K/+imq54O0Ht/nCu++yvbmGpsAYuHHjJqenZw2+OcsyNjc3GQ6HrK3ZoPDBYIhSL5lMZkipgkXCuxXH68XzQQCz2YzFYoEQJoRF2HCGNPTx7OyMfr9PWZYhO3hVVYFPinnw15XPZdHQWpPnefANS9O04aPW7lTsG+briJmWNvHwQoLXJviBihmf+K/3+a6frajN9rZ44UHKpCFgxAvHo03FAoqNQcnY27vBRycf8ezpY/7iR3/J1s4W/+jf/gds7G4is5Q8zciF5M69u+zt7fH0s8eUpYI05Tvf+0P6gxGL0sGnYV2ntDEsS4VUBqUhSzPyPLHSt7hcGGtrva8qn1fb2Q7Cv6y+1y2sVYzkmxC+eG1cqDM6GVdp61cxnO17w8aQNnvpL37xM7I0sZB7GMqyQAiiOAJDkmR2PjzRMhdRKeJ2tPtzVV/9oQGi0f66/iYwQixgfB7Bos3oXdbuWBBoCxp+X7QZdXuIm8Yztm2rA/3jd17VrjftW7xfm0ATFWliXSwffvop5+cTOv1+Q+nxed77OkG+KYK8ft9dJtC/yXNv3KYr6ITXW7zuHZ+nzjcpQggkkizLyLKcBSK4A2ilXjtytYa0Tj7V0MbDlUKBa0TE29ZafOvuIBrPN9oTCS+xVtk4eh4Ea/cbQjSesZ+s1OIFDb/fkiQhtmj4tt+6uWv3089+hvnTP0V897uMxxN++Be/4eT0HIPhg48e8/LghD/63lcZ/eN/jPnjP0b85V8if/ADbt/c5ZNHzxsKAkILakHHM+HxGPuWXzYn1oFYhzEgSpzaupHaCm/H2Wj/nna8lqcNdvhqOtRsv33EjaW7XicrjYUHQNcuI0IIG4+nraUYY3mUqqyCVaOqSsqqBCyTeX5+DtQKGEv22oqXuv1W3qwTm5ZlFfcM72L6pjS8UXtEt6SUQXpt8jJXAwu0y82bNwF4+vQp2kA+WCcfbtDb2KU72mFzr8+eVrx8+YqkMty6fZP5dMzHH/yK08NnUM0dw53YZHj9WsiwZ64M8bxVZd14vCdMt9cLkKunp6d8+OGHvPfee9y4cZPZYsF8NqXb6VIuFrx8+Yrd63tsb+2w//wVDx8+tPk2NjY4ODjg5s2bfPbZZ42kp+2xiHmThhAirCa/LEuOj4/58MMPA0Me73X/OU1TRqMRo9EIIQSTycTB5lbRehWkaUavP2BtNGJttEF/uMbvP/yQH//4xxwevGJj1OOLX/o63Tzhzs3rXL++x7PnL7h798uMRiMnuEQ5QqQErPuyUoYss65Re3s3yLITzk7PmJzPWCwXSCFZWxuG8fUKTJkkdPKcQV+ytrZGmsrI2iGcu1VJVVXM53POz89RStHpdOj3+wGi1xgT5vNNyhsLGp7pXy6XPHv2jOFwaAPBiyIs9ljg8IJAWwPrBZB4soEWA1Nv5LiuONmeN914actrw2LBI35nIpvayVi6S5IaDswzI1ao6rC1uUWn06Pb6VEUJZ988invPnqHvWrJ2saItcEQREKW53z9m99g/9UrNre3+d7f/mP+6I//DgbodjruzLEaF029AbQ2FGWJkBKZWsz/VQxFm3S0BbjLmPmL2kyvVyMcbq9jLtqbdVX9r2NC2tpt/9kY48bjogbLXvMH9MW62u4lbUEs/uyFZCkEz5495fDowB6WxvqHF8USfxBkWUot2TieIWrfKmS0dt8vG4dVblexABFb5KRIG2vY3/N5GOX2u9rX2useaBDZNhKH73vtl+rbRNAmGtPMOh4L+PHvl7U37l97L8Tf29Yr2wcraOSZhe6bzmZ89tkjvviVr16o+03H7/L7xMVPhkaOjcue/bzCzuva2K73MkGunvPVz19V2kqa1z0f9mW8FYQFFhkOB5weHqCUcgdbQDS4IAW1++TX5WVugk1ABIgZWPu/WuPstd72etyn8Fh4Z9sib1xbtcG6QsXMuq59xKOeOC28dSAy2OeUMY1YIP/aO7ev2Q//8X+MAD5++Iyf/uIjmxtDiMDAnU8X/H//9Bd84ytv89b3vgff+x4At29d45PPXqzc57Ztrm+yXhNW4LJBwjKRjXXSGAulSdKaQQlynoOutr9pZ8HAotwZH2cWK1Fsj60iR7ghcAKJMRizyj3IwpBXDhXQw316oI7FYsFyubQWjNJaqufzebBKTKdT0iRBUiccy3Mr/OZ5jkwEWWaTsD179owbN24EXsSOVU0f47H18XJW3rTtXy6X0X3Wgm1BcCIat8J6V89R020qpqWJsDS4LbT4OVnl1uL5JIMhSVKu7e6yXC45Pj4OfvmDwYDBcI3eYI00zzk5OmY6L3jn7bcRuuKzT37L6eETTDVn0OugtWE2W1AUS6pqSa/XC+tpuSxcfJ/P2WTHsSgKlLY5dXxOBh+D8cUvfpHbd27z6NNPOZ9OGY/P6Q16HBwccuf+XXZ2d3n29CkvX75kd3eXw8NDtre3efLkiQ1JvYznWfE3SRKyLEOpivF4jNaan/70p2Ettc92z2CfnJxwfHzizkfrdr+5uU6WZwgBed6hk/XIOh2khMnkjPlixu90xfbWOl949x7Xru0yHA4Y9josixkHR6+4d+8eu7t7YU1VlQlWCnvWFYzH544nsWMspWCxKEgSyy8M+gO3LxTn55NwRs7nC8uz5zlpmtLp5mhtSNNmrImnK/1+H2MMs9mMw8NDXr16FQStPM/p9XqUZclbF1bZxfLGgkZZlrXFQUoODw+tOUXazdPUxl5k9MIiX8EUxqUtYKxC+PFt8JHvKw8AV/I8D0lZ2m3zz3pmKtZ4CiGYzmYkaZfBYA3YdxukpFhWSKzLlC4rSqlRpuK7f+sPuX3/Ltdv3GBzdw/IEKKDivyZDSq4Kfn+GWMwukIp4aTiiwtcSHGpGvJNNJsXL/gBb4593P9VZdUmbs9TfO8qhqq9Tryw0b5uHFPwGg+aUH9bo+P/xuAFSZryu9/9lrIsbBC4qqwlzGiULlttvVrHuorJaX+O74sZ9bqPF115/L1+HtrZ7Fet81Xz1W5fPFerhI6rBNbL31MLGkY110IsRMV7dZWAFr/7srX3JmvMM6HWrzqjKks+/PBDvvTV94NJ+U2FjNX9XXUTYJrKgNc9d5UA5a+3Beer2vcm7fRzY+O+VrfnqvG/qg9vcLdtp2PG8twyKKVDMfHni5cLrIb5coEo9p9etSZjAreqmbFQYb8311ccz2QP9aZbsH+n0joIGV7RFQtWtUbyIv0WEWmLAzMNVtlxY3cTsIgwP/rp73j09KWDcLf3+XXu7/mTP/8FT58f8P0/+CJZnnPj2iZSCoqywmMc+CSfnuZKxxATCR4I4RhqEd7lNf6+L0Ik1FHZwgpWUpBIEZRqxtQgLMYoqrJEUCFlwmK5tGhjWqGVDu41vl/n5+dUqrJOtUYzm80BjwypHT2xmP9eCerdYKy2X9AfDOhkHRKZBIYSbHJSIQSJsGh0GBu0W9NAG2+TptYVaH9//1LlUnzmGISNMzK15cJmBY/OI+PXY81rWC+MeF3EX5q/X0Yjr1LQtO9DWCCR0WhEv9/nybNnVKpibW3AIE8YdlLWejmDbs58WTAZn7Kztcmgk/H04e84fvUYoef0+jnd3oCT4xPmizkAVVUERCeZSCfIWzhVn2DPa8fLquL8/JzNzc2gLD47O+Px48e8/c4DdrZ3mZyOWSwLuv0+BweHXLt5k83NTV48f86TJ0+4ceMGa2trjMdj1tfXOT0+uaAEaSvoYv7CJ2PM85zhcMjp6ekFfrE9J/X5Zq1K2lhmPc1SNjZGpKmgl3fpd/tknQ55p0t/MGRre5fr16/T6yYYVbKxMUTKhLMzK+DcuHGbTqfH2em5G8sq0Br/zm63i9E25lgb6yIsZYIUaYiPtAhbdsN7KPzZbM5yuWQ4HGAMzOdLzsZngKLX69Lv94PxoL2Ger0et27dCmMXexJ5tKrXlc8do+EnzDM/iUgsYWoxeTFT1d4E/m97s4SJNSZssPi9MZMS+6zX9Qh8JuOY4UiSxE1KrRWIhQsp04Zg4we7KisSNP1enyzvIETi4L1K0IZ+3qWfd5jNZggpUBi+/t1v241swJgEXSkykbm0NQaMIHWKO6vJcJobbbXrjx9/5vwUW6bVmub/GyntTXjx2mpGeqXgcYmrU1z/mzO0KwQsU196XQnBwlgfR60Uv/vd7xpmeWM0MhHo5SWBTa2+rBKeVre9+Vt8SNTaftOwINTX3EHeqm8lYyWiRrJ6vC9jZOP5iNvaZv4vK/Yer/m07n/+99ii0R6D+Ptfp8Rtjy0bWrvcIcZpT4HHj58wm82CL21cx7+J0rbaxDNz1TvbM3jpqIvmvTH61uvqDFWsOIwvm+fX1XGZYO0/WybdbWNhXY22t7f4UGsqh2u/LJa1osdbOHXbllmXVbDpob1eWmE1PWv2anW7QbT6cck4iUioEc1Yt2bbmgJPxMNfbJkxrHU7yCRh//CUf/XjXzKZWUZOxtYYW6td+9ogk4RHT1+yf3zK3/7e17i2s0Gvl7MsbX4ZY2ywtjC1g18AaPE6HRdn4l2NfT+00hRl6XIL2bN1sbDuIkppiuWS88nErUHjfMCXwefb+uhb1EjLO9iz3CPxJImFu+/3+3Q6HUajEWmauSBsGblpJ07wayKoSSkatEAp67aDaio9vMIDDBKFBxOQ0gpX3rKkXYD7zs4OL168uEC3Vq8bJ4o5pEcDzOfzILwAzs1Oh/X0b6KsUvAFXol67NbXNwA4PDhEIOj3OqjFmN/+4hlrT57x9W//AI1EFQuu3bxJMR3z8umnUM0YDnLSzCpRC2XBVISAoqwoyiUyWaOX9+l2+iRJFph574qT5zndXo/JZML5+Tlra2vkeY7Wmv39fTa2ttje3ub06JjD/X0wgvlswdnpGdd2tlhfX+f4+JjpdMrGxgZnZ2OuXbvG8eHRChSo5l72zLIQgsViQbdnY73aCrKrhDUhnCuxMBTFAqU0ZbHk/fe/wmg0oJ/ljAZDBsM1ur0eQqYYIeh2exhdUJSGs5MjjJGM1re4f+9t8k6XxbwMQoIFl5CR9ZZgmbPIT4R7aiuiCb/HfIVF18oZDPqh7jTtkqRW2I6NCFLKxhjGPFSM3Ag1WtXrypu7TqUJRtuES8r53hmnkZKBcDgZQXiG3jJybXePICQ4bYVPahWCs0zTLSLWJqRpapl65RBwDMEkKqQ3Q1om3rbF+sFXlTv8nduScuZbmaRo1RQ8EuevBxJdLBkMevQHXZLMqqDKssQo6GQdVKVZFqUlzknJ2fmE69f2EAgWixLyhEppQoocY0D5DKHer9fqN7QyXL9+vcEwNJiyK+YnaEto6/NofbKnSi08eDN+fSDiNHj1idY+rFfXGu53WpqGRsBd94ZbrU3QfCEcgff3C68Vs8gnXhfq6w31mSbxsFDAkRbYW8CMsZnAZcLp0TH7L1/aXmsFRqMcMohP0NcsIhq16ESORyMSRNqMTXwY1kRfRsFVDuJTQ5pYGGS7TmUYz1jTatwaEgJrTSQSEsH2KXq3MRYJRBuNz/xt3+G1sH6u3LrxqFZCtLvZ6Gv0C0I44cklYTMSLEqMQFWKSll3CpssUNs9L5rCbfPQXb3W7C0Xtfz+4LC0wjIdWldUqgQE58eHnLx6yc07t12+FKxm18r9V+8rLrluagHYg+f41aGdlku2mFXHXdg5FI2VjBG6uWftxNbvd4xp3R77tDLu/dH1+nUiqqOeUx+gHHrWYtgDzbkwFr7Pbu2Y2AKB23uO9oaAVSd7CoFBgjBopdja2sVgzfvz2YLZbE6lFLmxcWxOKguWYLD72dOR7qCPMlYrH86CeJxDm73GuEkrVjKNotl3gQyHfouVdGedPbt0VH/DYiftfq6fbQpBth7txrJ+r0QwPpvyP/zzf81ktsAY+xtuXEV0LlbKWyvsk8YYptOS/8//76cMBl1Oz6buPK1C4L12gAnL5ZLFYkFl7Jk+m80oS5sDqqoUi8WMNJUW7VFKqrIkSVO63Q6pzDBa0Mk75J0OSZKwPtqg1+9boJMoz5YXDhKZkKbSZrWW3kWr6UZtNMRQ3PU5ZNwKFEEgEn7HBcWIR3OCLLXuORJDkiaB9qSZp+cWjQvqBH01pfew1lYBKJ2w7NcgAVDL0U9viXNKK1UpMClGayaziVvDGoPCOJjSNI1R/q4oEQG6wPjGAucKpnilsOHdc41he2ebZVEwmUzI0pRUCA5ePud0POPg8ITR+iY3bt1lc22NYS/n08cfMpmckecdhsM1Zoslk8k0jJ/nq9I0w5CATNjY2eXa3g22trfBGCbTKZ89esTp6SmZTFhbszEOaZowGAzoZBmTZcnzZ8/40pe/xM7eNSazGaoqmczOOT44Ynd7h43NHQ6Pzni1f8Rbb71FkuYMhiOSNG0G+VPznO0YPZ8lfD6b0+l2EcJC0SqpSJMEo1RATb1IL9y5ql2MFRV5mrGzscHt2zeRRtPNcrI8o9Pt0+v3mM0XnJwcsVguEFKQd3rcvH6T6zduUyyVhUJGBHQzzyfnuRXSYoTXolAuNiYnSSRlWXtt2L0g7V5zfLTNOSQiYT2zazBRLBaq0T+tdYjTiBX9saLlMiXPZeXNLRqeyXMMjj8ME+fHaYL2VaIdbfBENY6v8NYEKSWJMz15f1YvpHgtTSxhBe2KiCBz8YtbUylFElCB7KmrjSUMmUwcI990vSrKKizC0lk+sjy3DKsL1EVphoMu/UEXIxzcKVhoz6xDIgWdSjGbzVguSl49f8W1zWtkMqOXJRRVhRKeGGnPx4dJjTUl3vzrJzvWUjZhG1cUJ2jEddu/jkQbAjG2t/vPjoC3TkNvAbJ3xIIIDQLXYrmjv01zcPy7XTsm8DqiJtP1WAiBETbhmXYMpEcp8fV6vHND7JpmB1gaUG4clFZ00oxMJjz68GN0UZKlifVDjjZWPR6u3jZdDwJDe4OZsHbb9zddpfzfKrJaSHwyRyFsrgrvhhP6GWvTEAhpmfvaB7oWrGwOES/IO/9ooS0SmjCO4Xe/Gx00i2EmfR9xrhNCYFxmet+WmthoQlLDsBqc0BiNkfX6EwgSpJAoU4bnY+tJcw2tKrWAEdMFT1ds+xQg0abCGKuZkeWSJx9/yP17dzAGK/gY60Kko3110cLiWPfooPbvt4Gssdumuy4kCEvrKmIW1TE3gVlv91ZY+uLfqmtlgAcNWDUyxgiMU9pYCM36mkREeYiabQkSAi3EOc+++e+tNe2hwHFrxvbZaesjBYGpuTFL97T1t1dGYCrN9s4eMklRSrOYW4alrDSlMvhjoV73IghaYOn32voG47MzKq+waAsXpumm6zItXXS/8y5LAqe3qPeC9Ohp0gsdxlpZhEMtcjlfrHbUzz9OiWX3gtbWPUmIOq6k5YTk9rBjvJVCVxYQ5exkZsENlHIunoayKplMJuDunc3nlnYhqCrDZDJFSunchGyMQJ7n5GkW3I4sMlBGkqYkSU6a56RZxvZubT1IZEKaSdJUh/3rGXyMsQKBqT0WYkbuwhrFK4DsNwkYVVn6LnBKCQ1ISERQRNgx9PB/Xpi8eK54CwHUsLXGQJ5bF6EkASF0o31hCbvZNlpbfsHvOQcHPJ+dUxZzVGnduoQEo1UQeIWohWohwKgSVVbkaZ/ZYs54fGrpk1EY4910leORagGpXWpraL1a/G8hpm9ldrDW2LcZZCEQiSQVksFgwHw2Y7lY0u8PSNIcmXYxzEmThEGvw2I2Ze/mHRaLKYdHL6iUYm1tnTTroyYLVFnQ63To9xzfgiDNMrq9AV/6yld48N4XQdaZqLsbW9x+8C6np6d88LOfMxufUhRLFvMZ3TwjlTl5kjM+PeVsPGa0tU3n4IjlfEpeLpmOx5SVYW19myR9ysHRGfffTun2RyzmM/r9PlPnotW2zF88a+wemi8WpHknKFL82YnRloZG49dQKAiF0ZBKSZrkDDpdBnmXHMtvFpVitljC2aRO9CsEvcGI+w/e4ebNWxhjOD09ZTabMxqtMZ8tkNK67HnUw7IsrIsfFtQoSWqrnrUo+kR8Otxn82b4HFw295YF3piTZRmvXu2zu7vDaH3A5uZmOEMXi0U4X/1a8+MU86kxcMyblDcWNIJbwoXDpz58Yykn3kCecY6ZM8vs2xs8HGW8EGLp00+SlNJaE9xB4s07cbbmmBnwhP3s7IzZdMbO9nZov5SSxWIRAsr9u73vrw0u0/TyPlWl2NhYd/5thsViCcJOen/QZ7EsGQySYII6OTvj5rUbDiZVQoUlzhGzGI9DPZRec3ORaf08JV4IImkuhFh4iwUaP2ZxHb5c1DjTuNYur7tXeAkj/N5cP6Ee9z8pau1P456VggCOybWHdelM/UmSoJXmw48+tNoKx2AqZxasqst8vj//PLTN1f5zHK/QDvgWQjTg4uJ2xPvBF2/OjDe71hqMsUxlSxiy8kMN2dqOqWqozqgPXGMERte/J4nVAtaHflNQjseuHfPkP9vvcdtiLcmbxwjEgeC+bj8uDTQMY/js0SP+jm+jdgxj0g7WfdNycb9cvEU0EFB80Zc+Y1rruekSevlr/Fz4700hxl83Joj4F998RT/ia7Wy4mL/2/u3bc0MrXLKga3tLfK8g6pKirJgPB6zmC/oD9ei4OQmzYzneWNji2fPXlJW9hywzOJFf/f4tbHm9UKckhFo5d0ArbJCKwNCIrV0ViMZGG6tfBJLu4K0tvQGJ3gURYVAWbeioqSqLLZ9VZUBEl5ry0RMp9NwnlWVzXCfJRlZnllm2BjyTk632yNJrXDc6/XJuh22h2tkWe5ci4SLP7DtTFN7vEshQtxIYMD8nAiBae2jOmAbpFD1JHpGXIBMBSa4ZkCSgjHywjlvr3vbg+fuveuQF+RD48KL7Kc6iagxVVi/vvow3/HLHA2yzL8VcDX1vMeSeBuCV3ulS4N3OKTXTcHYGKJEeJcWR7csoXXnu2C5WFAUJQJ4/vwZZycnwa1NRQoRPy5+bb4JFYqZ5zAnb1Ca1jzL7MZ5GIzRFto07/Clb3yHoqzoD0bs7d3g2fOXjIY9DvZfcD4ek2Up/X4PpSqmkykCSGRKmln3KJnldLo9vvLV97l7/y2UgbJSpNIlWsawmC0Z9AZ8/w//kJ/95Y9RuuDk+Ij5fM7aMCdJU9R8zqtXr/jil3atm1Rp3fCKRUGxXDIcrdPpdjk9PaUsK3q9HufjM0ZrI6aTycozZNVvxhhUpQJkqzEuhwo+p4Snnf5+whchDIm0+SikFHTynOl0xunpmaX/SUpZVmit6HZ73Lx5h3v37nHj9h3SPA9n9/b2duDJbCb2Y168eOGsEFYJYVExJb1eH6WqBk/teQsf5+LPbfvXBqsniXTuVHb9Xb++x2h9jTxPQo6p8XhsFebLZUDV8kiTxpgQS1cUhUWwkpL5fM69B++8dg1+rhiNOAikXvROE0F92NTa+NrkGE+0v678NWNVbsppCtIspyqrmvE2TqdeWfco749ZFEUYcB/k6GHuambKQoFNphOGa0PbfgPz5cL5cBuWpR04jLCaNztFaAyLogAj2Nze5tqN6/z+449ZFkWgV51OlyRJQ//yPGEymbLYKKzZ3GlVDQbUCmY6lpQNKEf8ViVDaTPBlzEIF7QYK97n5yGet7bU3pzniwzgZULGlQzYJSVmItrv90zCZUxOk9GKtaEEa1qWZVSq4sXzF9FBKlkuF013h7+BgFe34WIdnpCs8v2MBb+4b+2xDMyAsehK/lrMQMkVz/i6fPLHuI2rxzN61njfcntfcEGM+thm3mLBIRawfJ2eCbJa2lXxG/VauGw847ri93laEM+p1pqDw0Om0yn5oO/cNiyD8Ned78v2hGfq4/a1n7uiVvecracWNvwzF+nHyozT0buaQtzlfYFaUE3Eav9kz6ddulYu/W7wSeLs3oTBYMC1a7u8ePaMqqo4G4+ZTCeMNjfJ05qexvMaryeZZNy9e58PPviQL3zhC6RpEnS/3qWrnge/PmtBVogktM0ymdbtA0QIBrWHu7VKTKfzcO/CMZP+HFou506wrREVsyxz8QhpQHTpdrsOGnM9WBV8P72rkZ9vn1vJ87H+vtoC5xgJbWzQLQCVTZLr3Y4dI248UfRj6hKqCek0/j7BpKtWSlBGWQtcpIfwQpbdohohlLVyYOv0+SMMsdtt/Twmtrjbf1pX/qKdJx1R84Yg6O+r11dTgHG/60iYN25FKJc00JioToPRUSCrO2dMvchRyvD82Wfs7OyyWJy7GA8DuMSMQqAdApjRGq1hPD5Ha1jO5/zVT35CsVyQphllqakq1VCaXqUNNr7t7WH0NMXwGmssjWshVYCwTtw+AZzVYLvvnS5r126ws72LFJLp+Zg8T8kSwXR8ynI5Z9jvIYzm7OwUVZb2uTQlzVz+jCzn/r23uX/vbRAuJkZINNrF84KRJrjvfeOb3+THP/ozzs5OWBYFfa1Js5SkTDg9tdaO9fV1Dg9ekSYpS2Pdr9Y3txgMBuzv7zOZTOh0OtbSORrx4sXzS8fVj0fjvHCB+5ZPyCnNkjTLGA6HDtHMULmzytMQb+gWGBIp2NnZ4v2vf43N7S36/T5p1mXQX2M4HDJaH1kkKAHdTpfpdIZy8UxKKY6OjjDGBslvb28zGg25tvc1ptMph4cHFEVBr98nS3M6nQ4nJ6cYY5jPZyil6PV6LnzA7pE879h8YVI4UBSJTBKSVLA2XKPvzkDb/yrQp93dXYyxkM6TyYTJZMJwOARqMCifHTzLspAT5U3KGwsavvgDxDNwduB1CLJqukk1NasxIyCTBBX5k0vH4EspqbSC1MZdFMsibBSlFKmQVIXd6EqpIHFZ0w4Yrcg7OUrZjZ1llqnZ2tmhMhppFTJURpMYR3QTK3BoVTmiYbViyv2WJCmJFNy5e5f7b73F+tYma+vraGWhcbe3dqyW2miy1CYpPJ/NWF8focqKNEkcQbLCVAx40tbUxwhDTaSE+pnLmPlVTE2McBXf09R2X87ItZmUzytIrGJIL2OKLuuDZ24uMLGOsYjFMS+Y+PgfqDXt4/E4aBMBl9xNNdq0mnn8/CXWtvu1CoRNrZ2LkxS1kBHvk/YhZIyz7BmNvaQba8a/E30JU+nHzTFL8bprCw5xu20ciHDwlLVrT23OjyEum++OXR79GHiBx/pSpw1EsItNbq+12kWtrZH24x0rHrxiJBUpk8mEo6Mjbg4Htl3Kjd9fY67bTzTXyyrXus9fq+9n/X31vDbdQeo9fkFj36rnKqG27cvcLBfX5WV1x30TQgQhWBlDKgQ3btzk2ePHLrDYBnru3bhBYKJX0Iqw5tOU9a0ttBD87qMP2d3dsXCM2oCLt1oui+DrrJVm4ZQKnsYWyyIadgEuANq7HFiB2CqvPJyj3ys2DsHi3AtBcFWA2J+ZMLb1fDUtLoEnjjTz3lU1uJRGeyhp77HM53YIb0AKywyTun1qE1c4/sgFPgsRrD/2cWNdmaQVrBIX/xVYeYPLr+yeEQajo2R09vC2geZe8UFTUaWVcu2x7fXun0L4dZM4VC3rDo2onWo9yEs8nl4p4d3O7Fmng6ButIuTitamDsAEtv1xELmnUUpZQXU+n/Po0adcv77Lwf5LtNEWFVLbnC8eUrcqbYxmUZQslyVJkrL/6oBf/OLnrh0KI0xQrFzYe63dEsYM4+Kbmr/7z22BZdVe9AJGvf40RtRBvIvFwq1lSZblJFkHkaQIDFVV0u3mSKGYTsYIrTBacXpyzPT8HKM1aWLXR5ZaDfdotMY7774bGp2miXXpEQIj3dkjBGiBSBKyRHD/rfs8f/HEWivKkjyzCeR8DNFgMCRNEqaLBVpbeGIhBL1eL+Tl8LndrLVFBe+AmCbFtKShtHACUZJY+HuD4ebNm/wf/5P/hJPjY/b393n27BmHh4ccHBxYRLSqcomZFVvbW/zv/+P/A++//xU+ffgpaZqys7VHkuZhjrI0pXJ0blYsQBCY9Y2NjcY8LYsl2mjSNOHmzZssPUJbZdHZ+v0uWht6vQ4eytsLAlYYLul0cge0kJFmTXS22uLvBXwT1oIxFqBha2sr3Kd1nbQyTsSolArKkteVNxY0mihNdYZuO4HN1Oy+SCkiIaB5oPkFHxgDaX0/K1WBkSQyc896n1jri6+VJcje/SRJEoqiIM9zlssKjLCaFgAjKJYWutTCpYuAuQ1gUms201qTdzqWWDnm0yYWMkiTok3FvFxybW+PO3fu8M677zBcG1qzmoZut4cQos6AiWE8PafT65CnGaqqSKVEGYORspXOrFnajDlcrhldJSxcxbSt+huXq55dJTCsqucq7emqa5fVU19v9i0WwohiQP2h5rZO/d0Y8ixFJpInT56gVIUUTahku3EuIoG0Gb03KfEzsQDg17xfe1JKEpniNatXCXMha7I/0KmFrng+LeNcj8nFNtXE1b9z1bpZLajUTIcQ/j3iyjUaz1VN6LVzjdFhD8cHoa2iKXTF2mzv2rLKotBeJ8E9DBu78uLFC26/dS+45RtjGjETbyK8+7GIr61yKb3s8+Xl4v72v5tayRpd959W76f25/i3y4Rpqyn9vALSxTZfoFV+XToNrZQSVZbcuXOHv/rJXwTXhbPxGbPZnLzbj7T0zbr9HlemQhnN1s4G65sjzs/HHJ8eo1RFYgSZRyxygcn5IGc72wlrLT7YfTyaljiNb02TLJMKHo3JuPUao7LgNPi2i/VeCwd53QuSNIZtN/VaiuY/EdFkG0MYCuGVJ7XVTOhIeUN5gYYZ1w+jrL+5zV6tQwZrMNZ64ZU4SgThzCpzIjpkvGLMKR2claG5pryNwf7VDvbWaJt/IBHSISwad6YbKxgJ63nglZPaZVOu97K6sLa1qS24caxW/K8qy5AA2KNQlg49S5dFyMVhTO0aYoDpbMHJyQmdLOOTjz5urEFtFFVpadeyWHJycsJysXRJ22y838nJGUVp8/ngBBwvmHjlzpv4t7e3adgHrTNg1b6/7PwSQgQGsXLKGCkTMJpUVOSJQRiNqpb0uzlalRTLOUIYBBayd7lYgFEsZobe2hoGRaeTsr2zSb/fcXD8iVtbOAADr2FP0KmgKgvSLOPm7Vt0ez3m8wXLYkmaWlfAQlUudmGdNM3YP9xnNOgzm05triTnfjSZTNjd3XXCRfrGcQNB2EhqRdu9+/d4/vwZxXLJ5uYmd27fRAoLKCCEoFgWjM/HNqHddIowhsFwwNsPHtBfG/L1b3yDDz/8kI8ffsKNvZusb6zbBKVpRg5kWcpiuUBpFfJRLBYLyrJ0fHVFUSzCPA0GAwcH3EM4gSg+b+J11Eav9PsGDEqVKFWGZ7yw4N2tyrLk7OyMbrcbhLYYEtorR73g4S2w/6vHaHiY2KBZcabgXq/H6emYsihDoirvG2oHpCZEcVyA1hqRWn1DpSpMFWkjlSBJamtHmqQsC6c9EZbwFkURfMvASXTKEjafkdwzj0maYqQNpFNKWYuFFKiydANnD4PKZXY0xlhUICTaOGQibUi04u5b99m5tkulNRIdgshns1mAsiuqktJU7B8ccGPvugtIS6y2Wf51tJ2sJCif59m/SXmdEPPXrbNmJv9aiuXmeITDFhBNa4xnCh49ehQ0+0DICusTzf1NhqlmhC9qnPzm9uu7bv9qrb3rTqMPl/o+CxF4mpjRuUqAW6UZjM30MQNtiYpvq8f793rGGpq37r9/R7Od4AUugUVfqZkTryWx/1zNkVBZtxOMuZhVt808++dqtywbtPL06VO+4ywOXrsbKQw/xz5ZLVTYQN8ma3lZ8f1s1hqh0Pg2Gq+JJvz1c+562awjEsBWKSLq91+2Pq7aB56RvOTqJe++UIw9uK5f37MuD+7Qm01nzOczhtU6mazdila/yyCkoVL2HFgbDRitD62VUwlkcI2q2+brsvlzauE1c/DnCAVULobLr0Gr3ZYitYHLid8kVjsvZOwy6Mco6mhjjq17ENgA8/qSCe4+Aiwjruvg5YZiQMdSpwgCjsAENyS/RoSIrhtvMakjH7xOQhoV2iKkQBqN0BZxS3urhXt/fSobjKoFjbb22Je2C6MOuQc0ZqksaIOzPniobysgVDZHiXNtMcbCzS+LZbCCqkrZLN4Gp6C041iVVYDdNUqFYG3lBBzf1oDkZayVZ7m0gsbB4SHPX77irbfeYmtri9l0FjS6HuzGaMn0fMrjJ0949uyZs9Za4SmRNtN7gk0sqIVwKUeaGvXaknwVvWgqlKJfXQ6zpnDfVuhe4BtE/W5jrJXJOGWeFAaKGWp5TpZmCFWSdnK0VhTFkkRa4bxYLjBGoVXFfFaiMNZDJBVsb29iTEW/10MZQ1kqtBBIbS0Uy8Wc86Lg7OyUTt6zCE3SwggfH5/YOY/aOZ1OsCiNKRjcvKrGubFcLgNv6pnfqxSe7fHSSiOctWV/f5+qrBgN11kuFnTyhDRRqMqQZhlZJtnZXre857KkLEr6gz7z+QyRJuTdLu9+8Qvcu1/w4vlz5osJWT6iVE5BkQk6Infwy9bdaX19PRIYrCXDWlTr2Eu7t+UFq4SPM45/89aLWhnvE/JZABNP17IsdTyyHYudnZ0wdrFg4aHEY17KGMPcAVHcvHvvivVry5sLGkagKqvhEBi2NrcYra2hygrV05wsT0CBEQKtnfXBWDg34xBeqsqaHItlgUaQqLS2dkQnflUpoCRxG7EoKwQW6aMyGoFmWZZk3ofUeCHCakWUUqRJasmIEFAVIDVCRvEhhRVQrOABxVLh1VfWDKpJZIIRFh2rLBWlUuxe2yHLE5bLBWRdlmXJfFEGiLuyLCxhVIZ5Nedg/4D1tTVkZoP1hHIm6KD4ijQRXlMULtUMndeuxY/UB5C9CwhQwZ6gipZPb5wYSjaCLuu5vorxNyaaqOi7Z0LbzHOQA2gykkKI+hiO3tU4lk3tULCKafIuBpga+Sccwo4pTYBOIknQvHj+BIFdj0LYNWOwm1iI+B2rO+/N8n7c4kXb1uz7MVBK46FQhRAkMnNaXYtaUzPDUOOvW62ld+8RUtpDTESMsVtvoh0vgX1dmP/A+Dsmx6zQONMWgBzjbAQBAigeGf/dGIfu5IiQi5GqrR/1+oqtGhYNzrlK2J3t1o/VvsRW0LYAF6+F1x3S4bAxGrTg6NUrcD7DPh+bnfdmnIjrWnOMGoJF8yBvui7EjF5Yim5tyrq1F5ouwlpvXrZ1+u9+/KNdXFfkX4i1/AhxMcYr9BNq4dJEwpHwjaVRp8EuT7liHqIH67rd/ibaw0IIyyhLwAiGG5sW9vH8nMnZKbPpmPls6vZjhhBJcNlrj4UUfswAF6TrLTJC+vkVgcAEhszRC4kBT/+0VV4lwtWubZZy735pDAhTWrrt94+ph0o4F2AhRWMqbItrxtJi2Xih3h72/rwRXtnhrXlOMLCfa5pug7Mj9MQgsQiE9LEpEe2NptUrCbxCpn6PUyyE/VILBggdaGm9HyUYjVZ1El+oEwh6ZZ7WGuXw/Ovs3RqlNMvlgmWxACwUtdYGVVUY5cE5qtCG0uUBqSKlhqcp1mVbBCtTrLTQWqMrFdzgfPyKwFp1UpdJ2VomNLPZlI8//oSzszE72zvkWcbRwSFpljIajZBCIBOb4bosS5bFEikEibfyaEvrfV6DoiqR0p3Jwq8BwtiHc+IiMYiuR9+JzplAY9v0sEmbwu4Mv7mcR8a6yNVnvWF8csxvfvVzut0e3/ne90myLh7CWUibKT1JEpTRKFeXMppSKdKy4nx8bveWsHNaFBbkoSwLzs7GAS2pLCtUVdIfrZMKgcg79Lp9yz86JEPf9qpSpGlGt9tnc2MLVS1tvI2wygohraI6SRPSLLNIXFJiHBJc6D9NRVRTMaVRVYlJEhbLgrIquXv3Drfv3qQsFlTlwsZlVRXD4RCZ2HelaUbe07Y/ZYlcLEjS1GXV7nH79m0mkwm9Xi+sQb8uhZQkbs36tth9ZBPsWUWIXbs2070NBh8MBo0cQt6d045ZGtzGALIswRjJ+fkZy8WC9Y0Ny1M7oQQDadoBbOyIXW8u8DwRwbpbFoWLMyqce+Ai0MHZbMablDfPoyFt56qy5Nb1G/Q7PTKRkCSCjcGQtf6AUinOZzPGkxmVVo4NVBaFQYgQLW+MAZGwrGq/Mh+gaQmLzZ6gE98863PrF5byGMNGoErrIwlQVprKCRp5CqljArSyUGRp6ifVLj3c+6rKukp5FyzLMBtKU4FD6ZEIqmWFPlGsj0aUVYFBMFsWdPM+Wlcobc8EoyFNc8piyfOnzxC3bjLodel0cvzZHg4RWgSImmjEWgjPXNhzoOlGYtORrnY1EJFPdVuAMBGX39TG+U0YnVQriwjjGQSKFYys/90ErXktZATWPhKQ/Jg02JgVWlKDwUQWMy9+uKZhtCIVggSDWi44Pd5HG4sIol3+DCGslsTj2dMYL9N8W0N48t/9fDVxpv1nq0Sza9vndLH/SeKxF8KLTT5brfc3tnCQQhCsYY2pCn12gqQ7gGXqwAQCh2qRZy4QWSzKRpqkbm15hqKOFzK+HvcqIeqvATkGA8JpHzUO0rMZ1BssOy6jsF9/RnvNp3A5cupkQ56h8PXU/W0slwuCXnCb8nOmKk4OD1mcT+ivjawbIwa7Oi6ucTsnyYXfoT7gV1mptBdgZM34hvaZptB2iTzbaINdyGGlXLinsUYd81H3pyUkesID1p3J10HNbAIu07W/Zh8MTYkUFSKu0D7YfJfxDBFu7dv4IhucLegMBgyGAyYnBxzsn9LpZDx4523KYk6nY+FXjRBBSWH9+41bgwaJY5RcS4WnPUJhYciFlUis36zL1eOECFdVWFHart9oKO07vfCoolXiBA2NQRqDMDXcqX9WRJ8NBhzykGU02v7RXrtez4fxQrrW4LSLWikUFQKfLVg5QYOwKa11yCLthbVh7NgoB31pLRXW8q+Vctd02HfxP60VVaWcj7gVFgxYxZqqnEbcul5UygaEL5ZL+3xVBUHE4NAhjXXV8hYlb51I0xRTKWpB2Y5c6hg37aS6PM8RQgT/dmPyYG2I3Ui8xtsG43stbYrWteBRVSVJIlkslsxmCza3tzgdnzM+P2d7Z4ssS+n1ukFb3ut16Q8GjM/Pmc9BjSsGa33W1occHBzamB0SEAlK21gkE+JCPc0z9RqJds9lp6xw82fc4R2UNqwWNNoKmQtWJgNGC8pSuZwldeLa/f2XTM9OGJ+c8POf/pQ/+O73XfZ2Q5LasUuShMFgyLk+t3PrYMQxgjTNqQo7n4lMmE4mVGXBfDIlFYLhYMBwOCB1cay9TtcmNHaQtgLhzg3C3jABsjthY2Ob5XxCaQyVUlS68oTa7i0ByAQLTqzduWkCqNkqS5u15AhSKazVz9iT+aMPf8+Ll0+5cX0PrTOS1Cm/kGgjOD07p9PpMBgOGW32GzEhWlkLYbfbo9frB8VZHbtVx+DUZ6uHxLYWs/pegZQpVTUnSQgWiyzLwmfAWo60R1+1boBpmpEmCetr6xyXioNXB2xsbNDtdjk6PKLfH5CmOmRVXyysy1avZ920jg4PmM1mVFVFlmUBohi/l7UOz7yuvDm8bVmQpRn3791jd2eH48MjVGklzyyRCK2RMiPf2OD8fML52Qmdfg+DoCgd4xBxumkmMUIC1tIhZJ3O3JNoDzfnrRAae4Yo45NyWYzx5cI+J5PEZd7E/pZl4HIFSAmlKkGIoC3VSlnNMgJVFRavvFwgEwejawxa2MCpNEkolwWFKCjLirffepvTs3MW8xmS1Pk6AkLaw9UI5vMFv/jVr2ywj1s4SZqwipmNicUqAmGcpOHvi5GGkLG14yrBoFk8k+Q3XTuAOWbUrqrj87zTl9hPsF1f6w3UAo1YeW/bbOyL9yUUwiYFWiwWdcB0K0ljXRduzV3UgMRjf1k7/L86PsMS9hhZqn2/y8/rNBlWYxkzfvF7LIGqc2XYtoiGQOETFK6NRgyHQ9bW1lzm1awWgJRmvpgzmUyYzWaMzyYWDcMho8lEoHQVDu64DbUAHGmvo7Hxa1JyuRuNDZwVYQ0ENzOaQeTtMfblorWjeYj4Oo1xftxY+nJ0dMxgtG6ZFye0hcR6ojXqV7xfIBr7JcxP9FybAXDy6ecuUhAOS/fyuq9+4cTFeI1vSxCob7DCXtSX+gresBZeJSCAAtQwRBeqbDbSL0m/FnyCQoeEpN0a397e4tWTz+j3uozHp8xnE8rFDNXtkCWWVgoU0uWMQXtAApuXKFa8EP7VyqQgrAnwuTBWDKObtzohVqxEwOhm3zRB+NHGICJa3NQu1xZkveIef12IZpC4DzC38okTnF3sYIJxAcmmBrNwVp/SMfY+MLRyzL4PWPYCQVmU4VzVRrn4gbKxb+Jx8HVpVceHlGXhGDmvwXf0ywkORVniBQWf+VubCu2Eik7HJiDr97sBvSaVFvBFOkECQYDRNAjSLCXPO36xhfZJmUbjbtsSu4BkWRbOc4sQaWGFk0TS7/fodksGA8tHbGxscP36DTY3NwGCW463nsxmNlfDy5cvWSwWUd6BOF6iea5fjENr0hXtM36uKMYRjcu08ZeVtsARf5dSBhh/H+eglKLfH3BgDEZIhmtrpFlKUSyQiaDTyYPw6YOwl8slWZbR7XQZDIb0B30ODg64e+8eAtje3LJ171R0u11nTbJxIUIIF79qhdjxeBwUUbY9dg2maeL2j1UUL4xxsY1eALF9sHknUmuNfIMS70WlFYn2Aqodr0pV5FnOxsaGd5gA6jiI4XBo12bi21enX7D9AKj5AP/XXhPBZT9JZGsuJTLoDux4DAYDer1esPItFjVSZunc/61Lmd3/Nl55yXj8il6vR7/bY7ksePHiJdPpjI2NDZTSHB0dMZstQn2LxSJYKBaLBZ1Oxnw+D8qA+XzOaDSiKAoODg44Pj4mTVP+N//ev/fa8X5jQePtu3etH5pWnB4fIbBm0TzvoEqrQdFaI7OM/qDP8ekJi2WBFilCpCjPyDqiqCvrX+s1cFpbfF6f3EibGgHDEwyBtTzUCBFWiPCxGIYS78MttD1MhdPYFkVpzWPGRvX7SbKLxwQkAz+oIbgMTb/fY224RpokpDLho999yPVr1+n3erwaH6KUJMtze3i7QyPBcHI2BiE5PTsj79ikSEZIbALlWCtbayzi3+LSNovGv5kV91/G/K98b6veVffF77uqjZfVEf8Wa/4ve0f9rppZuqxPbaIa/02kDT48ODhoMK86HABNBrUWNC4etj7BXOw77f126+fr9tvDpQ7aamuc6jHzUoK3Ymhnjr+sr84Ub38I17q9HhsbG9y+fZvd3V0Gg4GDHszodjskqWW8bFyUoqpKi9tfVZSFZjabc3x0xLPnz3n18iXLogjMeFwurL+WYCxlrUmP5/my9eKF3CSx8IeZrJnzhrWgJeDFB+hKi5cXYlIrjBljeLX/ivsPHtj5jHy2w9xEHHb42Jo3ixZWw083A4O99jLqr9NYNSq9UK7QbRofTRJqDyWWJSyDo2u3oYszVz8nV++r8GhLw269dVprIR5vYWi6atk1bRxsjnTuNkJoKl2Suuzta2sDsk5mD8ThkPnsnOV8ghn2ECZzSViVzXngNXYidNaiHPk59JpeqUMf6m1kXJ6LpNVG3w+DMWU9Rq5+4/9GDEy93u192sUJ+KBnE93n6/DafG+ZMAbnRmSZB5trwwGV+LjA4G6kQqZejAlCg/8dauEaanhXG99Q96FSKrQnZrJI7BzXKFreWm7dh0XkmlRV1iKcy4xB3zFbQtDr9+tRdeeolNJ5CNSuVVLYhG5ewZW5z3ZNNq0Rni4IYV00ut0ePguyhQ62biZSpPiEwTHwht3jhkRmiMy2XVWKxWJJWRXgvC2Wy4KiqJhO5sznS65d2+Ply32MNpydnYVA3CR5QVEWlEpxcnLiFKPeKtOkVbECrbG/rhAAVpXY2hjTIa+5jnNMNZ6L6FobVRBqhCEvNBRFwfb2Nt/+3h/S6w24e+8eGsH55AQhYLQ2DEKfFxq8Iq/b6ZImkkQIlw9jSreb0x9atCjj58LNTcdZpbwsf3Z2xuHhYWP+cHPvE08Gxa+2yJ7W7VYikPR7AwQ2T5YUlxLYC3PhlX/BMu0C+b2r3+HRIddv7CGRdU4aN9bdbtc+1zrX6/r8vxpu2s+ht95bQBTvJubOZiHDvu50OgGgYD6fR9aLMggFRVFYwb5YcnY2drk3rIBcFAWz6ZRO3qEsSw4PDzHGsL29xfm5Tfp57949er0e/+pf/SsXqJ+G+tI0CfQlTS1M9/HxMYPBIGQq7/V6V463L28eo1EojLJJjIy02U+LSqMp0UpTVZokSykrTd7tI9Kc6WyOzBMsEU/we68sDdV8bjeDm3yDDeKyzJM9ELTxcF0KKSrrXuMWQZ7nFMulQzOwkqGFNVRkWYpWimk5o3ADXrkJE4B0plSPQFGW1qw16A8amhGcOWs+W7KcFeRpihSC8/yc3/z6t7z9zgOWyyVHx2OGaxvILHHBYJJMKF7uH9AfDDkbn9Pv923W7wuIJXXRWl2a0Mv71MWMlQ+KWvVEzPhdJoS8Tjip4wcuMiSr6ris3lX1x0hk/tpVbX1diTe7r0spBZklavv7+/ZQcq533gXEH+7x4dtqtatzdV+li5/wuPdeG+8ZASGSIDTEh2CT+HsV8mph0hP00LfEmdBd4sHNzU3eefAOu7u7dHs9Rmtr9Pq9AAtYqQpVKZQu8PFS/bTG95cyQWuYTqfMbt3gwbsPOD8/5+WLl3zyySccHR6FTNWxcJAIEXi1tqXmMuEw7lfb+mPrb9ZXm/ZXlzdZ4yF2yBgO9vfD/UKIZtyBjoR9JxestqrUwlG7HYhIEBAEn/BaKdBmNC6Olwnrwb/X0MDEbh2W9STY+JeolY1nWiNUrRoaVQABAABJREFU19GuujWWVjnng4ojAbxVfzsw3TIMrn/a9RdDngqMUWAq0lQwGA5IEslg0ANdMZucUq71MHlKknWQwqBQaKGojEcUrLeMd//DWF9/O6eW8UfZOAMpwVQGSFdaK7VWIKrAwPn4KD8fWqvA7NizQwXGtaqqGmdfaWchsNd9PUoplsUyMBGqcsKGc38SUthnyhJ05YQyy4zFcRAYAnNiYpcMaRklKWUIiI33t0ySAN2ZZzXUZVGWJB0Lf+mhPqW7Zuv2mmO7IaqqotPJLV3zrs3GMiLLYolWPiDVIvV41y47brohzPiVasfV9m8wGABWWVeUhQvgtvl7Fgs7/vP5zAbwCmFzWml7v81vsqSqFMulzXViGTEb8+H9y4vC+uHbWCBJmmYYHVkiDEisVl1rxdGRqPepsPm/tPbCjHfx9AY1c+FsW6UctH3UF+4L++YNSuw6FStm2nVeUMQJy4hai1I/CIaVUuxu7bC3t0dvMAgCma4K1tfXyHNr1fAW8sePH7NcLsFYN7qqKpCF4OMPf8+3/uAPEC51gAGy1OaxsnF8nr8CVSk+/fRTJi6vhHdr86kPhsMhPlWBXX+KfpaHNSFlQp53WCyWKG3Q1EnpGrKVqelVW8DzueA8v5nJjLfeeot3HrxDv99jMVsym1lAAI/IJIQgSetku57f8OOfprZ/nrfwYEo2waBl3rPMu0D5tbl08UuOZ3WgRv1+n+PjY8qyJElslvXJZMJ0Oo1cHK2FIpEJ4/NzJpNzZtMZCBj0Bk4wmVIUJVmWsre3x7vvvstnn30WcmZ4CG/rHten2+0wGo0wxgRFhzGGo6MjyrIkyzKOj4/faK2+saAhRIIQGeeTOSJZkqQJldaU0wV2Wwr0UjGZzfjsyRNKh52cGGvtUMoiRFjp1mCxvWstTBAoXOCUdstC69LCzEppTXmLBUZVFM5nNHF5NJIkCXXOpnOqsrRoIi7YWyBIROLMzZZIZWlOIjI6mSNsy4rlchnMvdpojLDxIpXWLGcLMIZUJvz2179htD7CGMmL5y/o9M/Jez2ybk6aSnpJysuX+2xvbfLq4JA879DvDxgMrCBiE5bVLiNBa94Y89XajlrD7jTvEcN3WWkzya8jZqsI1GXCy1Vamc8rOKyqyz+yyqJymYbIC2ZJYg/Oo6MjoD4E/AFduMM/MKYRrooQotYfe6NDfK3FhMYakqBhNDog1cTjF9qIDzg1WB/x1otoZmkP70sk6xvrfOUrX+H69et0u122trbodDrM53PG4zEHh4cOclGFBHnWDTBFSBGuWcKYsrOzzfbOFmmaMpvN2Nhc5+69OxztH/Pb3/6WV/uv3JjW5mIPUX3VWr2qxMKEwQaErnLZuuxZvxZjy5R/b1mWThNlkNJm5vVaHRu7VcN6tpT4GN+nFX2LBYcLf4O7ji0XsoNHckw9zbV04CMsmvvLCRusEnhVqNT6/MaxBFe4EcQyAqbeY1xCSlyDjVldp2gvWxFsGq573ppmXdkqrVBqSbeTc+PGDc7Pz8gza7Wejk84TAzSKNYGI8tAuT0iguuUsHEPUtr4gshFyWtKbe7nEq1LB0zigT5qS4F2wcrWolA45rG2YHomv6pKyspZFbCuTDZ3kn2vV/oEN19t8HFfdo/ZepVDNkQ4a6ujBz5PlGX2bVZhKZyrrcEx/4I0s268SZTU0K+xLGkyPj5jeqUUMrNBpQKs1lMIqrJis5OjVO02e35+Ti5Sev2B9TAIlgw7XtPFnDzr0O33SZKspmlSkmqBEgptSsqiACEwjs5orR0jpVjOF4GZUkoxnU0t+p9b+6X7fblcopzwVixLjK59w+MYLC8c+oXq5w9qDbMN0O0H5kxrhcEFLivP3/gYOn/meE1zDbpihcPIouXAGIQjIFcp2y4w/K592tRxVasEEl/iPq2yjLefu0xJ4uuaz+cWejXLgqAxXy4pqoq+47fSNGG5nDMarTEYDBiPx0ynU7a3t9na2uLVq1fWjc74+CvNkyeP2dratDnH1jedBULQyfLQRyFsLM/Dhw/54IMPKF3yP88X+SDwXq/HcrlkNp9xcniAQNPv9QERXH0HgzULjbtYIqjceef3VjxKq5Wi0sW6VmUVzrb10TqbW5sBsWw+n3N+fg4QEtYpN4beLXs8HtPr9djb22M2m2MMTCYTiqII7k+TycQlbtS8fPkyzKm3YPj60zS1Qhw4N6gxp6enVFXFZDJh7hT1PumiIAluW1mWkSY5aVpxcnKCUTihJaEoZlSVYrEo+NWvfsNiMWM0GuGhboOLmxBkmXU7XFtbC9fHYxvUP5lMLARxESW9vKK8saAxmRYkaYIiYTkv0KJkWdp4hSztUlQVZ+fnvNjfZ1lWZHnH6rcWlYMTVDY6P6BMWWEjNpP5QVZGU1TWL7ROnCRRhXu+Kq1pJ0vRVUnlGAqjFINBn8FgwPnZmKoo7O/aYJAkKEpTorRCVxaRwmtWpHNH6eY2CYowAmmEhaYz1qdfK0W5LFgYw3K54J/9s3/G3o1bdLojpstTumVFT/XJUkkF7B/sIyVkTns8HA6sybdlbvOHWsxkXkZIYkLkGdqmeNJ8xjMtbaYcIRqaS8tHNDdi26LR+OyeN5GmVHCRmNYM/GoB53VanFXCReyW0/jdlWBVcO4AiZScnp5i3e5U0DAEqwcRgtdlvi2m+b622TUWxPxYZ86a4p9tuwhY5sP+NS5QNlxzCDH+u9/8UkrybocvfvlLvP3224zWR2xubqIqxfHJMYcHhwwGg5BAUgrJYrlAFPYQrRR0OoJut8tofUin00EIUKrk4PCAR599Rt7JuXv3Lrfu3GYxX7A2GLG3t8fjx4/51a9+FQhue54bViV7oTWX/v56/hrzbwiMvXepaMfwXFY8OtCFdsRrzhiOj48xxrpiKm3djJJVwq0QmLBPqTXo1JrEWNCJnoQV8Q8mcL9eIKnHwWt76zrDCEYDVvehoajTrTGO20GNUFS3oX2f+x79kKwQNXz7pYzqixUjpiWi6BbdCdpWbS8KmE/GdDoZN2/e5PlziwSnVcliPuWwXDA+PmY4XGPQt5lszycTjo+OGI/Pmc8Ly6g6iFOtNaV3g1k6AcFUIBTrG0P29nZIUolIape3GCVPVQqiGI6GIgew6HT1HvRjEo4yfDyBjQnL84Q0zYLbUZamNeAFkKaSTicLQl4iZaBX2kCSpAFb3wvGxhjKahmEm9p/3a7n1LkVz6ZTtNH0kp7Nspy4KDAJy7IkIUMKiRIePSihqmz/0rQDRjKbLpnP5xSlFTaqsmI2nzGfzXj27CXG2IDiZWHnwbt4qKpisbSWDQ8XH4AdtF27Xiir150LUPfStz8XfUwIII1F6SMIxXa9KaVwWf7CWW6FLNmyhoqAeKW1CTFinsb4MfZJVFNpUZasK0lEXzDWmc9ZM4yp9zhChFiNtuXWf67328Xf31T5F9+/SuF1peKPGrHt5OSE69evMxwOGY/HFEXJfLlkvlwyMpo0TRkM+pydnnDn1m329vYYj8eMx2OX28G6yy0XC7QUDq1IksxTfvKTv2CxnPPOg/fY2Nhy54xwyr2CxWLBJ58+5Kc//SlHR0dWEHGMttecD9eGDAYDTk7OONjf5/z0lM3RmstWLZjP5qRpSq/fdwAEmqpcBAFbxET2svEwxgHD2PtTkWGM4tFnj3j16hUb6yOWyyXdbpf5fM7JyQlVVTEajZjNZijnlt3r9VhfX+f4+NgJHecYYy100+mUjz+2uVi63S4bG1s8efIEYwwnJyfcuXOHyWQS2nN2dhYgajudDuPxmKOjI87PzxFCMJ1Owzh5RfV8tnDrwUJ3W+tE3651ISiWJXnHAh1ppZg6KPE0ta5wvt6yLJ07XUVZ2vZ6oQIIY+HP5729vSvH15c3FjR++fARnbxD5nwui9IhNBmDmk8pioLpfE7hg7WNg8vTtQnSEp0KY5yEJVMElsjbQ0aRpQaZSPIspdvJscHaFsXJqmMyZGIsslOSIEUS/BTtWahZHw0YjUacn50ynUwplyVGSETqoOhcds+yLBASUi1cIiaBz3TszbsJKQiDkhbhSmMzZhoMagGPPntElnXpD9fYFXtksoIkRaQpk8k5xeYGVbnk5Ys5G6MBG6M18iRBC0mWZ2hhzefGMZUXPeLdhgDr7xwxa8YYtDDhsy8N86zTFNuh8TojnJBw1YxHcJu1ijT8MQ4azyAihazXIFxsk+fUhP8rCBtDuwqMqLW5nigJQ43I4pk997XujYnq84yCskxkatfG2XhMDQWqUA5zPmgYI63y5cXeE/tf+r+1lclrx60lRdgHgisCRC5Uyq574yxxNQoIFgHD+3VKh1IlYHfvGt/69rfZ2tpia2uTPMv53e9+x9l4SpbnJMDR7JiD/QPOx2POJ2PKqrDjUxlkkrp9J+nkOYN+l63NdXZu7rF7bZednV2qquLRw89YLH7Pvbt3uHX7BtPJhKybsHNtm1/98td8+umniES6uTYOrpbAS1uMIRU0Rs3Dr4nMBVGcgxbB3aMe14uCcizcta0fDQbXMy8uqdpsPmE6O2dtYwNTaQwSxMUYKSBAjspwT6MHrg26cZgFdrslxPukdSJAGDvrhV3w7roL0jZ1XY11536MhfegmIjfFb5X4RevUbdjZ/vm/b/jsYyZGH9IeWWCwO+5SORy+orYkqCNFygsrYQ6JqpygcplVXB2ekqWJuRrGTduXOfVq5fMZgvLDEmJMGMeP/2M2WzBwcEh+/tHLOZLd14Q5tc4X23AuU1Ulq6nku3tLev+OrcgH1nXalWlTFxuA0srut2uHSd3cMvEujzKJLHZwaUJ/fVMgNaaRKZBsRGUAsYE5ZLSOrhNIERgtL1lXStFJ++QhjwBitOTE7rdLt1u11rzI1emLO2yXFq/7FL7NQhoh8RTViiVMJ8XnJ0cI7DCxcnZabAEeLcMG/MBZaECZGtsMdDKxon4NeeVAdrRbaJ1ExettdMS6yBk+iUjHaiAByMISkdv2cW614G3BjoFjbC/h3wjLh5GOKS7Jm2od4RX8MSJev17TXiv3TnG2GBlbTQVgsRZiPwJ6i1iHoLV/qtfKoFUWhQ7fzaENjl//tiSEeifaba58cnvPde/WPHkr3nljInvj/rv+1sr0xRCCs7Gx9y5c4utrU1OT09ZzKdUiymLyZhjrAa7lye8enWEubHH3t41njx5zHg85uTkmMGg79zUBePJGUo7Wi8l3V6P8XjM40dP+MIXv8T29nbw63/16hVPnjzh5asDZvMFi8WSNM3o5H0wElUJtOyys3ebNM04PTqgXNoYhazXo7e+TqU0s8mEXr9P2u1wdHqGFBmT8SRkgxd42lXTK6/Q8WNSj7+13O1d3+X09BibgXxGsSxYLpaURWld+SrFbDYL+X+2tre5e/ceZVkGsJHj42Pm8znz+YK3334bpRTjsU3y54WETt5hZ2eXt+7do9Pt0Ot2WS4XnJ6e8erFC7emJUdHhyGGRkqbC6PT6Vgeuiww2p6V3a51H0sze452uzmdbpdKleRJai2yRUGWpVSlRdu8fn2PsiqQiSDLc1Jl6yqrwub2ECK42Hm6kKYpk8mEfr9PWZYXlI6XlTcWNJ4cndmGpimJsBqaLMusVJln5J0OShk0kiRNnLtSEhjoGt6wNuvKxAoaiddEGKv9x9iNYLB+cBqonP+pERkyBV1ZzGqJheasmRmFqgrms3OkhJ3tbc6Ox0ynM7vghCHtZAgtEZmFuNOFDZKzhKX2sbc5LVyyEgRpnlOqCmUKl1TJkKcSrUsm42PK5ZQHDx6wtrHFeHzObDpGK+sjOpvPefb0Cdsb63SzGyTCILKEGCHFUhDPiEdMj7AHvApY61aBaDzhFbV/qfAnv7CHpmfGG/83Nbxao8RKVAQxOlbcFttcz5y1GSInZLSDsowImhRcG4xDoDHChGSPnnAarNYoRTbBbOozywaC+t9ira87NGRitVJVZYmG74B/JvT0NQFkdd/sJxk0V3XQl+WTHYsXsNRTN4+6wYj4/uMyrWJskKRwcwZWw6n9QYJ1oXjwzgO+8tWvsjYasbOzzcvnz9l/ue+0uBX7zw84ONynWBYYLWwgeKfHYNBHSuhIidYCRYLWdu2fnU45OTrlw08+ptPrcufOHe7eucP9u/dQSvP06WOePnnIl770Jd566x6vXu2TJAnbOzv87Oc/Z76cO2xuv66sglE4Btoyqqp56AqJX1sXtW92DGvXBC+9xGugqTX0AmttMYmCQYMgYBtVFAvG41MG60MMTo0lCQx3s7j4irBOqIVdNMJYoIH4KSkESaAdF3sWxGO/B90+rumAe4fbW7VeoGb0PPPv+1WPFYH50xiEqUIFDZcM4eLBdA3xCBEyUtDm233kGWMrHNeoRn4OlFbhd4NNoLVYLJhMzimLirIqSdMkclG0gvfe3h7dbo80ycgyqz09ONjn7OzMuk+oBWVZ8PLlPgcHxxgtKZYVStk4D5/PxjKTJVIkZFlK3pV0ezk7OztsbW0xGo2CO2x/OAzuQKs0yLFlPSDFSOsq5RUsHoGrrEp7fvmEWc7VKhWWCS5dXIcXTIyx7nxJmiCSFFMoKlWwLCqmc5uTYbFYspgXnI+t8q4+6CsWiyXF0saDGG2YzWZhXdg4RBcjEsV0eMuulUVMI4bMl7aSquEGiI+jjNe4VYasWuPGOKhety9qodcVJ7z6e2MBuQYx8Os9ToSo3Vnjmf563/j64v3fOD4FxBbDet00Icntme/geisNLMM6b49T/L1m7CWJOxe8tdu/E2kFzWAhi5RpYayvUHT5d3n3OiBkq7ZtMI2/ba1Zw/LqABrG4zPKqmBtNHTIXAXFfMKLpwv+5KMP0Vrz3nvv8eDBAw4P9rlx/RY3blxnPp9xdnZqgQEEpJkV2pNUWprhkdCU5sXLlxweHZPnVgO+WCw4PT21QsxgyPl0QZKk9Jw7VFVqqsow3NhkfWOLxXzOfHbO1uY655MpncGQrNdjfHBMVVRs7+2hpWS2WJBnGZOzsbWmOrj4sCaiMffnQ30eC/fuiufPn6N1gUyGfPj739Pr9phOZkyn0+BqtlwurbUxSRiuDblx40YY59PTM4SQbGxs0ustefbsWUAnm06nnJ+fY7Tm5o2bHB8dBYuaR37yboq1hU0493/t1GU2r0WSJGTOzSzLOxghyDtpCBifzaekWUK/12E8PifLEvK8T1kVVFVBWS7Rus/6xoj5fA7YmCqvFFkuF+RZHmIzut1uoDNCWHAGIYRzSX99efM8GkmPbDCwPo1VRZZ3ydKU3tYIkViXFG0MnXxA4jH8jfXptcoP7zNtg8MxmkxAliYBXrKbd+zgaRtYfnJyhjW0CzpZBkKSZ4JlMSPtpDYoTltf3iyV9Ps5Si2tZaSX2wVyekov7yKM5vTszKabNzY3gUSSJTlJFwt36gPuHIJCIgRKO0RFoVGVtsx+Km09SNAEf9liUfLR7z9GCMF4PEaVJR9/+Huu7WxTFEvyLOHl8xH9rmB7ewdEhUw7+MRlXrNSayE9l2GZCyETx+gYh2sJiWPYIkWoV6liNcu1S5ARxqF+WZ/28Dp/PSZSOroYl8ClW8Hhwh2xu2ysoYnlAMBJRhjjtFvhcKsZKa+NaL+jKYPVDFTbXSZ1WsnZdMZiPg+ygj+IfMKiVlNXFk+gPKMmGlp6p+HDo7WIYGWz76mJXNP6UTOKsTuGECIwBQhBkqV89atf5Z333mX32jWMMPzudx+QJRnT6YwXz15wenSMqjTpoEd3bUSW9UnSLkmW0elkvHzxlFfHr8jyjJt3HpD11qiUQVcV5XKGqU4pizkff/QRH334Ibdu3eIrX/kKb731NkUx49e//oBr1/b4wntfpNsZkOddBmtD/vWf/murIcEF2fvBjBjbttYzZgjaLgZxvFKcS2PVvavqjotnlmvkHdCqoiwWSDR5Yi1FqbOsEmlM7Zx69KK6HX6p+D4kLhY7aBCx1gkfS9BqkRUwcEoCbaJ13tg4Qdjw1oRIwnGCQu3K07g3Hitlg2xt0LBFCcRpZQuXedm6GNUIPcodak0feOszbbV81h9ZCEGv3yN3JnQfv6CVFTSWy5IXz19xcjJGqZJ33n2L9fV1er0ew+GQ0WhEluU27iBNyLQkSSHLr5PlifMFL+l0emxt7ZBnfY6Pz5jPTwJkdb13FINBl+HagM3NDTY2h6yvj0jTxMKmphahyCbTsv7ow2E/MP4xTLExJqDreDcPVWjy3Lp+aGzMn80vAFoptC4wELSai4X1F0/zlOl0ynQ2QytFUdqAz7IoUcpQFCWLhT2vvMbQZ8P2cxozul6BEru0xq5VQtegChcsVN4CFK3jNrN7cbUaaqp8cY+1BZS/SREQEtv54vd/vM/bNCAei8tcltrWU6+ZbTP9MW1uC2O+Tn8tdpmtr9cutTGsqVWQ2qDoeF/9TcbNB/xfVtpWykZfnCJzsVhwfn7OaLQexV/MEcJaABGCR48e86UvfZmTk1O2Nne4f/8+R0dHFEXBZDKh2+3S6XTpdroUZUm3k5HnXfK864Raw3Q6Y7FIOD8/p6pKC04gDbPpHJShOxjQ7fbQ2rAsS9Is49atm3TynP0XTzHG0Ol2mS0KtrZt9uqTkxMMsL27y9wx8T0E08nUeQJcFKbjdR8XS4ttQufKJfF9//33OT8/Z3w2piwsGtPW1hbn5+cMBhY0aOEUKgcHBwyHw8CIz2YzlsslZ2dnQTDxMRVgXQI//fRT6/bV6zXWZhNwwuavyPOc9fX1EHPoBba1tTUXTzkP6y2mZ0dHR3TynKosmU6ndDqdAH3r6b6UMtSzWCwC3LF2igyPHuddzQeDAYPBgNPT07C+32i9vtFdwGi0gQAbMNOxWQ2lEA6PvrIuTNISYlVpsjTF7wPl4P96ncxm1MaQJ/DevTu88847rA2GdF3Ee7fTBSEptOaHP/wznjx9hkxTktQKGp1MgumzubnF2mCN5WyJ0YabN25w48YOeSdB64rpZMqPfvQTHn36hIcPH3N0fMzB8SFvvf22RcsQgjxJHUOagjGUDj4wdnHJOhlKl5QlVLog7+YkOrEBtaVBGpsYUCmNUYqyUiSJZNjv0M23KIslJ0cHlMWSxFQ8e5rT60GaGNY3dugmKT6Xh4gIhGfcfPFsS63ZjJysvGARbR0a32ouXwhDkviDw7CSwXYMvpN3VsobsWn3whWvOGmaO4jNlp5R90godTWOAWu0PlQYciKE/5m6X96aYpP02BwpAlgsZlTFMrTX4k1fRAd5XWn6yDqtmrEWEa2VM236pEPN2A2/+RuHpiNusS+xPzx8P6UUfOc73+HevXvsXNvl5PSUyWzCYrnko8ePePb0OYkWDLtDenlGkSVkg3XSzgiZDen2hmRZwiefvWA8LxGLkl2Rc+vuOyxLzWKxpFpMefXpIdNzGxgmBDx79oqXLw+5f/8e3/zm+3zt/W/w8cef8Kd/+kO+9a1vce/eXbI85e/+3b/Ln/3wh8xncze8xgliVh/aZJRs0c7f2d/vmZ0kkQiT4JN5tRmANsPQPED9Ym0yVEGb69l7bVAueNEYQ5oKMunXpreu+nVUZ6Q2fqu4D0ZXdRu0cXK5de/wUKZ+vbkbw75qCATOaqCdQODbHDM73o3FxyJAHRRr12CtxY6fyYVf704ANNa9RmuNErKxrYNw5zKnxwdznLxtOps4rHXDsuhFc2GclQSkyNDK8PHHD5mcT0kSwY0b17l54zaj0chi3sssJOeykKUFNqErbG9vMRj0OT09Yz5foirBfFY0tMRKWwjoTrfDYNDjzt2brA0HFGXBcDig0+k4q3seDs80ScnzLkJUlKV2VgZJWVghYLFYUJXWAuMFg+lkwmJZsJgXLsawYrFYBHz5ZmAy0TzUfv9xbJY2XmAUhGyG0fL1MTeByRfWO8C4E6LF+lolGAJVaZKI5rT3XDvWy6/dNhMaKzwwTWjVxloJG2JFcYJ3zNj9dRjrOGtyW9Bo09O47stoer/f52tf+xo/+9nPgkY2Ztjj+mNBoy1QNcao1fG2q5KvX8gEI0S0l1ZblV43PvH8tWP+Wk1pCKv+PqvEqvNmPX/+nI2NTa5fv854PGY+n7O+vs7W1jbLZcHt27fZWN+kLBRPnjzhwYMHvPvuuyH4ebFYMBj0WFsbsVwWdFxOjTTNwVgepnAued7dxsbHWIS84XBoUyQYw6JYojBc39tjc3Od5XLO4eE+QluNv0wztnd2Wc7mnByf0On22d7dYzKbURRzTFk5K0scXN8cFh8f1HS1E8FybYBEJpydnbk8IXkQqsbjMcvlEiFsPEOv30Mby5Dv7+8HwWAymYRxn8/ngYH3418slmH9Fi6O2Adb+/XiA+PjNdLpdIIgkaZWieFBDjQC4dFYXfD5fD6nKMoQU+Hbt76+7jKcS4pyGYShWKDI8gyj6vwxFmbYjpUHd/AoXG9S3ljQ6CQuSZ5MgwWi1+lYjY6xmRk7nQ5SCErX2GIxw2hFd9hFSEEiBb29LdbX1xgNeoiqoJicYTJJqZY8/+xTiqLg9p073Lh9h/feuoMq5syXS/K8S6/fZ7Q2AKNYzOb8v/4f/3c+/fhTtDJsb23zb/1bf58/+qPv0elmbK6tkSeSX/z8pzx6+ISDw1cgBZOzU7781ffp9dfQymawRGBTyuc222JZFDb5EQahKxscmUh0mrJQ1nRdliVSQzfv0kkTTJpQFBZZo6xsDMBsNmM+nbCcz8nzlGWvw/HRAU8yjTCGPO/Q6XQRMkH61APOYqG0tu5ExoS/2hN/Q/BLrQUTnCJZNzaX8HEPTnDwjI6nRc1SiyQ+wZYnTE1ta61NbJ58tf5LuHcT+eLGpvaaoLt26zpHhZQyOn8jgcgQEDr8QVi3vP5gjMW2l5kNcj4+PECrysHMNrWCK6WoFSU+4IIHqKjdJnysh2e0PQpSU7hqjrjXcMX9jt8nhOAPvvUHPHjwgO3tbV4d7HM+mTCbTvnlr37D6fmCbm+N0XCdTCiePHrIeVmwd/cBX//ON+mtXSPJukg038k6/Oon/xKlNW996X22dm9hRIKqFMX8nI9//SNOTyaMJ9avVCRdiqLk408+4+Bgn+9+9zu88867vHz5gh/+8Id8//vf586dO5RK8Ud/9Ef8yb/6E0qXOdTj9wu5Wtvhc+nErgWxgOL7H2OXW+2zuOBnXd9vx7ztGmLXXWyRMmAUQpfo0qLbdJJBZOGKEIeweRW8UAr14W4zzNs1oFwkoXIwwuCyLjsrr6psUrSyKMPaDfOuasuW0pXz+0/Cvov7oioVxmgVE+cZ3SSxSqBZVVnlUDRm1iInbdKsaPzD+ksThCH4p/vYgMRBKc8XMw4PDxmPx9y/f5/33nvPCQAeKlohSJnPCoxRzrqtXB3WNbV2UQW0opISIRKn5be5lfK8S7dTURbQ6xk6nTlSjgOwiEAwGq2xs7NNmkmKZcFJVaFVxWJRkCZnYZyrqrL0XGlKJaJ4BM18bl0q20JDLAHU2Yndr8K6MywWywYDERgcE/IKghEIkrAOQ73uFTWDEytbaMHCOlqJTwyXBIuaFYjdM8jG/gl7K6rnMuF9VYmtZXFZxRTHAo4U1g26LcBc9q7AAKNrF9qWgOGfj62csXWg/b3RB1eKomA+nwd4Ub/uPXMVP+eFnFVCyyqBxt6rG2vBW96ki8/Q7lkf31OfQW9WQl0tS05b4JJSNs9GY4j3eP2M5Pj4mPH4nNFojfX1dU5PT1l2Su7cvsfGxgZ3794lyzpsb+/w+PFjnj9/zvXr15nP5/z+97/n/Pyc6XRq4yETm1AxCBlKUSkbt2ibK0nTHKWsMmPQsxZ3gKIsWJYlW9s77N26SZIIHj98bOnYfM6yKNjavUGSZhwcHLCcL7l77y26/SEvnh2QJoKDp899j1sjF4E6uHGJXSftmnVAMZggjJyfn1s0NFW7Wvln1tbWKCvL9M9ms2DFGo/HDWWPlDbY2sdZ+LH3Lk4+/sFf9xDC3oXJM/R+zfr59efcfD63KFvO4updnXwcltaapcuZAnVS7LIsSbMUg61/Z2eHw8PDcCaXLqed3wOxyx5YoafT6QRkrNeVNxY08qS0AkYGibDQkL0sQ2R2TStVkmEPww2Hzbx27TqbowHrGyPW10dsb2+6DKSKs5NjEiH49JNPOD7cJ0tSMifBnRzsc352ynC0xhce3Ofo+Jgs7zCdzkiEIZUZ/8M/+3/yF3/+Y0CgleHo4IjPPvmEw5ev+O73/4AkS/jOd/6ADz/6mEpVZDkuGEnz8OOPuXnrLhubW86XNA3aY4kkyVKMO0zUcolWlhAlBjKgrCqK5QJVlEy04sXzyhGwwk20y9jqguClsC5im6MhG6M1vv+9P+TnP/85Gxvb9PsDQAemzLtQGSdoGGMwStRB3ZGQILz1QHvWHqeFqot31AiEJwgHFw8PY2rGOD5szYU67f9XCxqx5ovw3elpG/eGM8C4k1k4//Bw/FKD2bj31K4tNviufWx5DbZSFb1ulzxNWC7mtl9G2My1HhZTqcZB/boSawLrhGf2X524r231WDXO0UFtVmsghRA8eOcdHjx4wMb6Bi9evmQ6m/Jqf58PfvUBmpThaIfeaJv+2pCjl884ni/AgKpgtL7LeQHnZ8cUi3NUMeHuu1/CINg/HvPqxPrGpknCqJdz5/67zGY2AdX69g2U0kynE2bTCbPpOf/L//Kv+cY3zvjqV79CkqT8+Z//Od/7w+9x//59pBD84fe/zw9/+EPrRiUlqCs0dMJbfVpxEU7YqF1j6oPBQv4lwS89ZgT8Adxg+C4wIgSLWJZIFtNzinKJMYJE1ljnxpiQTblUhXVz0TbINmRcdgS8clltLT55gdGGXr9ntUHRPPv+eIbJx6v4NWLXkAuEFYJKVE57bYW2OqmTzQHkn01kghHGxSIlIbmaf6eN+6kPh8QFNoOgqMqwZn2eAS80CSBNM5T7LYyL0izmS373wYfONVby/le/TpZlTKdTlouKJMkQUpJ3MrIsYT6fIwQslyWnp2cURclwWIZD1I6phTJdFgULBxc5d0Gis+ncwtdWFvXIz2lZlRwdHXJ+PnYkzQSljFe2CGwwo0yshlAgIEmDQAk1/bKButoFGMdrVuDd3Opf7HrziG1+n8db3dIbZ10VNa0zdSXUcBt2HfjVYER0Z9QUgQgxIrX23OfXqBUwKwWIFu91FUMevrdoV1OwAORq1x2rIa7fE1sB4nr8fgiQ48aiQcZ9WPXPPxv/jT+3rS++zOdzfvrTnwbtsZQyJK67oOGOaP3nLe3nreuUnT/v+uL3m18bK+SZK0tb0RALIfZcbvbnsqKUYn//Fe++8wWHKnXOfL4gTadkWc7JiY2n6HS67O7u8uLFC9I05f79+wB8+OGHzGdTlKpYLguWi5JJNqe26ENZ1dnmLR13mbxTa+FbFgsUgq3dbe7eu09/OODpo0e8eP7UHmYCjBHcuHmbUhmePX1KmmbcvHWH2aLg5PSMtSzh6Ohl4Ao8/bRj1MwJ1oidAafA1OFemUhGo1EYzzRNGgosz8inWdaIk/HuUT7o3Wv+vZDnLWjGWS695cLTXQ9P6wEbvKItPse89cMLDH6+YwFDCIva6O+RUjaE66IoghUjyWRwhY3dcX2bsiwLgoYXnPz6XSWEX1beWNC4d3PbHWZW9V4WBWmSMhoOSaRx/rC90KBer0tZFHSyhHs3rzFfzHj66CPG4zOyNEHIhKOjU7SyeMluvtHacHp2wtqwTyI1ZaUZDfssXV3nZ2P29w/5/e8/QiYZ5bKkKisLv6c0P/rzv+Qr73+VtJPw69/8hs2tDUpV0Onk1p1LaGazKc+ePmW5KLl+4wYGe3D5SRVCcHR8xPj0lGo6o1i4JD/lEqVKq7nUNoOrcegAPq5AG5fsCUc93D+jDHmW8r/79/63bO9so7Th4cNP2djcYD0TpDJ1aCoOzQODjrKNegZbG+2EEcuYW2EjRZDUpvfG+RK5JoWFUbv9+GItEG4WDCCslC2TBCHMBYK+itDHjLe7GJ1vTTGD1rtN1C9jareOpjghIuIsQNXa3vh3Y6yffJpIsjTh7OwUjEWIMbIOBjTGW4uuWPj+zUK03uH6pK0G249dmqZ4BBw//SHYPDpRQj3aa+N9LI0tOzs7vP/+++zs7HB0fMRkMuHFyxd88MHv6CQ9uv0NupvXyUdbrG9tcP3WLbJuh/nJKffuvcOjR0+ZlIK8m7M+6rB7a5Nep0OS5lQmYbEsqYqCydkp52fH5L01vvjVb7I2GnF97zrLouDo8JA0P0ZNJbPZOT//2S9YLBZ897vfxhjNT/7iL/jO977P7du3KYuCb3zjG/zspz91mvfLDzfhzW8RkxZfs4RbEEMR24DaGrIy1nLGliVPMBvMiXPj0EqRdhJm03NOjiXz+ZSiLJhORoG4e3/a5WJhUUZULXhbfHbr2iWwAoPXKvn8O6qq6PRySxOkPViSLEMASZqRpnm95kSt4RTYvW2D/LI6YDV2pTN13I7l89y1JAl7RzhtprEP4WX9sqwDl7WLj/PuecY09wTYoHnjaJm1BiiWyxJjEvau3STv5Ny7d4/pZIHSUybnk2A5WSwXvHj+nPPJGCENWgs+/vgTnjx5GgRAvwcs3KJzD4uY/9pFxPbLttu5fSmF0AotfOBtCh55SlvwAd+fLO268U4CGlat1Zc1c66ariwX12xzjRoMscHOj1sQIiHEWgjhaLOpEZVitymLpmSd+6QQdbSOJYzNreTGpNYdvRlD6QPYY3p5mcY+eqoWkNqCixANuN620CKid8T3eCVBzNgEQdY4y5PWjWdXCU6XCROrvse/e5/zWICOaUr7+ViL/aYlZvrrfxIiq0xTyRJp0j7HOy77/YIy64oipeTVq1fcu3ufzc1Ntrd3ODg4YD5f0OnMOT09I8tytrcT+v0+u7u7PH36BKUV9+7dI89zPv30E05PTpDSQkRbt29tZWCR1O5jjgH2bbLafEvjdnd3uX3/Hr3BkCfPnvL4s4c8e/KEwaBHr9tj7+Zt8k6H5y9fMZvNuHPjHpubO3x28IJKKY7OjtBVhZC561ltxVGqadGNLTvg1pe3FgI3btxgY2PDIj0JidGmzi/h9tHx8TFKazKTBWHZM+eLxSKsm06nE+hdyHYvRIiH84y7EIJerxcsGH5deqVW7EbVtEoJF9dlglXF00hfT55mAV7Y77ksyxgOh6xvjEjSJOQC8R4+PuDcOAWwHytvTbbAFYsgDL2uvLGg8Y/+zvetdFoUnJ6e2k1bVsFsXhQFaSLp9YcsnF/arRt7IDS//d2vnbTnk5MUyMTiU9vD1i0NaQlilmbcf/CAPM+ZTmccHh87vN8+O9d2ePHiGZ3cBsmUhWX6y8qakD7+7CNeHb3k9u2bnBwec3x0SJakYZIX8xmYEqPg+OgZWs/Y2L5Gt99HVdY/99Gjz9jf3ydNEjppCtq6XAhsxL/WlWMMak2jtzMIt8B9ACbGYBLLYD56/IT/y//1/8aXvvQOb7/9NkeHBzx/+oQ8lfR6fUu4pTucwAZJK2vO87yZdNYOb2WwTFQZNKUCgwmB3M4kGAkZwTphTAB7DYyJqbVqwmikMUjv3W4iVyrvXtAQJHCHakToHGPtERM8pvxFrb5DDnHtlFFWXCncwnAv8FYc4SQjKeoDu9ZQGkDTyVIwmrOTU8sUGkJgsIeV9SgmNaGPBKULxTIzXsgQArSugCQcnt4MG+5BO+bCMTPRHIS3iHBHcEH85re/zY0bNymKktOTM/b3D/jdBx/SzXuM1tbprW2Rb+2yfuM+6xvbyGrBu+9JTs9OqZDs7W7w9du32d7aoJMatFqyLEvKqsIgkKJDnmUk8gaqKjk7P+P5sxc8ffqCR0+fs7m+zc61e/S7Iz7+zVOqUtHrd/n1b35NkiV8/etfZ1EU/ORHP+bv/vEfc+vWbbTSHB0e8umnD7GIWhfH0TMhhjgOQwa4SkwCpGD84RC7LJmw9uOsrBAlsTJenwVIi4kv8DENimWh+NWvfs3aqI9SlYPZbgfoW1Smqlo6d6wkHJBWA2WzCUshQEqWpeLnv/iAzc0t3n5wj/WtUYgTyPOcLM8x2mZF9sAR/pAIDFTsniMjP3CvSTcE+mmw0N5CSowWod9eCZGkFhJcG+0SIGpMZWG0S5R1+5kvHeOlmM2mjM/PWcwXzF0g43K5CCb9uUNNKZYl8/kiHH7Pn7ziz//0x0Hbb2M0DFq7DN3Cuk1ZtyjNdDpr0AchREAn8/tSutg/gQ7K+kRKjK4CBp4QAu1hUkXbauDWnTvMRerBMtw6MyZYDCximIsTMzoogdur1lLSoKNHRMDant7j9RV+PQuJEgKFxCDxqhO/HhHS5omw0gWJMCA0hgpBDqQYlOsbQUCSbnVLlwm8zUjW9DUSfhDhe00qTX3OCBHQqowTbKS0TIYyXviXYX06qQkTMXDxuPn7Yv7cKlNcIkNlEImPz9PUotVFevGmDPNVxT8ba5dtxvCmIBPfu+pau77XvbOxzhOX1FjX8RGe0TSYyADRHgenKjTeQuJdfmprZSyE1e5Y/v6L/bFX/XUbQ/vo4Sd88Ytf5vr168xmFmXJuunZe+bzCY+ffEZZFly/fp0XL55SFAtu3rxBf9DnxYtXPHv2zCEYQYJzvXRAN0jH5KJQyq5PSUJvMGLnxh5be3skWcLDR4+YjMfg3JLSzoB8uMG1m/eoqoqXz56QdPtcv/8W87JkfHDMet7lwycvkTJFh4S7ft1HLtJuvYW/eGWDBcrQRiCEYTDoWVf35Zz+oE+v2+Pk5LShyJotpkiZ0OluBkuGtyh4YTrW/sfChsQn8bT3eetDURQ2lsfNmxYCZEKn08W7ZIJLPhvloqmUIpE2cWm31wOsdUVIC2qUJylpklKpCpEIdKeinC9IhmuMT85syIMRpCSYyjCdThFSMCtmqMqGCtQxw3bva21pl1Zv5v73xoLG44efYoyxCV76XZu1s1TMZ9OAG9zv97l+/Tq7u7vkec6Lly84ONwPEqPXgCQuU2SMMGOpm6N/QnA6HjMajRisDRmO1uj1elRVxfl0aplEl9UzSSRCWFi6ShUsijlFuQChOTh45aQ068MrBDY7ubFBi6asODu1h+P6xiaD/oDnL14yOztj2OlYv0rtAnZFQtbvIwVMp+dgtAtqahaL/18zEcr5KAqZcD6d8S//1f/Cn//oT9nd3eU//A//Q54+fcpw2OfatT2yLEUmTU1NTfyjQDNdY2j7zWQ3ifvn2Gdrahcu4DQSNBxzrxvEJyZwlhA4hVp0aOEO8KbGOC5tAltrlQ1aERIg+jZYl4UaMtEYg3TJrbywZaK6k4a5XjTHxRjL4IqEVAob9G4Mp6cneC2koY45Mdj7m6V5iMTmVeEIk/8tRi6JTbL1/Pk6/FjpcMETkyBlew2M0Xz1/a9y7/498rzD48dPOT0954MPfk8n77OxscFiNkOJKe+9d4217V3OxjNO9p9TTc+5dfceb7/zNoNuh+V8ysHTj9l/+Yzx2SmL5SKgWnjEi/XROjvXdtm6tsOXv/wub791nydPXvLo0VPOp3M21gacnJwynZ5x/cZ1ut0Bv/j5L0mzLu+++4Dx6Sk/++lP+f73v8/pyQlf+/rXOTg8ZHI+CbJbW4tq5z7OP2Hd2vxQCGFRSYxLZuj3mY5QaPx4N8Y8rDvLrKOls4LU2hiZSD59+JDBsEue5+R5FjK9+nbmeU6n02W41nf5FQiuFj4ortcd2HaKlPPzBePxhJPTCfPFnOs3/ohOp2fdA5IEjEDKlDQyk1taaEUuazVMUJWutVhuLxTLZXDlUs4FoazKOhdCaRFIPNKJz6i8WCyonIXGwzHGeRKq0rBc1lldvdm+bSH049bW/LZpUlN7bRUeuH1NJABaUuMtsW5j4RleAsyzxAqfwmtY3DqSGIwUoP0a8BDSBp+1XDjmrbYYeGWQpq4tZhhNEIBXlshy4Olh0EKLBIF3eyWiZdZ6kmaZU5ZoEg864Omc0x5qZYEkpEwwJrF5qIQAEmc1sbQ5SSSdtEdVOVz9NAmuXtYCDlWlglASu4h52nrB8iAuKn8wbv94ASzszdiqEJ9TjYECmkHr9TsFWZpw794d1tfX+e1vf4tSYJLMAgEYFWhqjDj1uvKmQsgqK8hVloFm29/kvW2rd7RXovFqWjNqCOL6mlfAxXV717zV7WkrXLQyF65FVYUP/kx99eol16/fYH1jh1u3bvHZZ58xnU5JHET8Rx//nlevbAzEeHzGD37wA05OjphMxty8dZd33n2Xnd1djo6OOD4+5vz83LrzaAsEpJUVwI0QJFnGcLjGzuYu61vb5P0e08WcTx9+jC6sC34q5f+fuj8LtiU77zux38o597zPfO6584SaC1UYCjMgEqA4iNRIiZLMcEvq7mC/2OFoP9p+8kNH+EFvDj/4xQp12OF2WxRlUZRIBtkiCYAACkMBVYWquvNw5nP2vHPO5Ye1Vu7c596qupDYTSkrTt0z7Ckz1/B9/+///f/0un1wAi5fvYnrhdy/e4uyKDl38RIra+s8vv8QipzJ8ZBkNsO2yqX93Oy5BrQ0+6+xWFCPMU2iBuiQusFZ4ge+NgVVFPg4jnFdh1arzebmJsPhiCRRKnOylBWNSpaqL8+yF/0b5t6oaopdVSlMdcXsL0magVR+JJYG4IRU+48ynCwQUgNNOulxdHO9YyvxC9dxsIAkTsizHGEroCvPMsqiJI1V1d5zPebzue7rsyvTTSNTboBjU8kxwIZJkKRc9Jp83PHszuDTKULA3t4evu/RaDRpt9v4vk+3260cA9vtNicnJwwGp8ohVC/+hv5gghwTRNfLjOYoipzDw0MePXqEbauSnUEACikrPltZLji1tmVR2jallMRxqjfXnCzNSVPtJK5vrClfSqmaD9NMEoYhvufSbjaYhQFpli41a6nmULTTqo1K7pYn/VmOuNFENoPe8Jpns5QsO+QP/uCPaDR8JAWOZ9Npt5Q5lFhkzjoe1yiT1i9/WvIhpd4QxJm/Lze1mUVPakTLJAFQ35AX/0fti9UkNc+t/7dUDDBcYRQlwrx2KZXijbk2VaOvNO7mNURGONiYCoELaL65ZYGoNVdTc25G89drt0RJr0kmk7EONtWmayg51essLcQfsmmJ5cfVE4uze9ECUVx8nHri9fTXV6+9trbG888/T7vd4cHdh2RZwbvvvgfCpt3tMZxM2X/4CJyArWsvYYVd9vcPCGz4zBuvs7W+wnQ65sff/wH37twimk4UWirLqmokgEII4uGAwd5j7r8vsAOPzXM7PPf8izx38zLb25v8+O13OTzdY2V9lfF4yOB0zMVLF8iygh9+/4e0Ww2uXbvGD37wA+7cucOFCxeI45hXX32VP/vTP3vimpjrdvYa1EvC5vorhR7TMK7vW20MF7WxtAim5NK9MPOnKBZ86GazRRCEWu3Ew3FsNfd9nziOl/jbCqFSgbmiJqpkWUrI87lKhErFed0+d47TkwEgODo8RQhHq6yoqonquVIu7UaxSG1SkZYbhDRRFdVoHlWLfZqohvWyplRTByCMsEFddKBCzyyrcpg347QK3KWlqw/LNJX69/UKz/K1XsyB5TG/CESX/oaFqUrW8gb1GXWufTZ5kbJW5TTvV2sULi1dJa16UP7DEe9nOwwQY770e0obpIsK2iSCQldKchxbOan7rkMYBLSaIYHnkqQps2mkgJdSYlkeUkIYNmm12riey8pqn3a7zepqn5XVFR3gNLl65Qb37j/gd37nd3j48KFyJ9Z7WV4oGq9y7VYeB/W9wMyjBTKr0OUiX8y7aj9G+T5YVj3ANa/B0nUwY2rB72appwUWvQmdXpP/9r/937C6ts7/8f/wf+L+/Ueajm1RkmIoanUBg7/M42eqpOh5ebbHrJqv8MQckRrwq/AsKT/yPevzzwAo5rXqXx+WkJw96ipW77//Pp/69Aq9Xpc03ebx48fMZhHKH0TJ1hZFQavVodvtEYZNjo4Oee+99+j1VllbU/K3586dq3wnkkQxTUoEwlbovOcH+EGIZytJ1Yf3bzEej5WKnLAZnw5IkpzSsrl29SrNlgK7Do9P6XVXuH71BsPTAaPhgFbocuund8BSNgrLCfAZOpzgiTUM/RQDdNi2zfr6GpPJhEYzREqpm6mhEYaKXhvHHKcZWZoxn0fkWgkqS7XBpb76RVkS+D5C+86Z/omz1EEppU4kClxrYUBdliWFLHCEhcwKKDXLRN/esiyWpLEtyyKLkyruzHSPyCSfVDGzqlAooGLvYB9YyEjXBReazSatVotet4fne5W0bq/Xo9PpEIYhjUaDTqfzTOPsmRMNRRERxLEya6kr95iJFIZh1XiilA8WsmrmQtZLfGYxMQ0xYCaMRZKY0n5eNcZYluI5NpvNxYXTErDGhVWWktFwhJQW7VaHOFJO5EphZFLJk5nPnWc5dpzzWMKFixd1qZ/K96FC/zV9yrEdXMclqZ3L0zZYs2CbpGqx2AjAIS8E333z+3S7TSbzCW7gcP3aVRpBoOR39aG4xovvzbVT72HQ2uUFvz5wYFG2U58V6ovQ2Z/PLoJPlFzFoj+hHvDUn7sYM7XgR6qqkyY8UEqt0sSCZ68+vlLckujmXv0YS1hYUl07w3FXKZNVNRbbtoMA0iyjlDm2LZhHc80Vpwq6qs9Vu28flgCcRXiXE+IF0rv8HPM8UasKPfn6S4EVEikEr776Ks1Wi9FozDyKeP/WLabziP7aBn6rx8HJCGm5CGGTxhG7j+7TX+nx+qsvEbhw+6dv8ZMf/ZDxeKRJG8qduSyUOIHhcdqWjWXr8VmW5PMp997/KY/u3+Pajed44ZVX+dTrL/DeT38K8QmeHxIGqqJXFJL5bMQPf/AD1n7+57h27RpvvfUWm5ubbG9vI4Tg7rm7PH70+EPP+cOu8+LQqHdtvahXSIzT7yLZK6pEwyCChi7l+wGe69HpdAkC5aoax5n+F9K0xHUTZXSI1AokJXmegtCKRFpeNtNN4XlekGe6iTlRYAYI4iTi93//oEqQ6l4ZKsBjEeBjXJYVMq+UhmQFJpxFRoUQmiOsLoXqBSt0cFYPbNT104bz+pqcRaLVq5iNrwJC9FF///phOMBQp+ksuPf1e1zNHT1PF8uMrmyh+4nF8vpj3tO2be0greAK26r1blmKm3z2M1i6qbssFxUzSyxe46PG3ccFeIvPps8HVU23yIECRA4ip9n0OLezzfMv3OTSpR2azQZXLl9ie2uTNIl49OgRlnDVl63Ao2bYodtdo9XsVU2mhuITa2WZo+NjBoNjut0Wv/Ebv04YhkxnU9JE0ZkPj455+PARu3u7nJ6eEscxWZqRF0q2Pc+LJZqgZSmfKFlaFfCkRxZVdUiYcwdNutfXTFeidUBkDCDrVcaziWOz2eSf/JN/xGffeB2w+a/+q/+S/+6/+78wGs6whI1tOeQye2L8fFz14T+VwwRpdWEKMHOpwFCn6lVwWE6Rn4gpqjXtwysvT6uinP1cZ8d5/RqbOTSfz/jgg59y48ZN1tZWyLKMg4MDptMZYRiwc24H1/PY3t5mNp0ThiFbW9tMJnOOjk84Pj6m0VBV93a7TavVAlFi2cpwOc0UPSnLS4ajMZPBCUk0J80ThqenrPRWmEQ50TwmySUXL1+jv7rGfD7n3v0H+GGTG8+9SJkX7D9+TDP0uH/3PfI8RlCAZVWO8/VzVf1fC2PV+vWoN4ZblqDdbmNZFmkaUZRKOMYWrupRE2rNmU3mtb6J2ptps2VVBXJ0lU5XaVFKTZ12W1WSBRVdyvQGuq5LmeoYSSwUFlOUspNJKExl2pyHeVxlMKrva57nOK6DZei6SFzfp+l5OLZNo9nAcRzOndshDAPyLMfVqleXLl1ifX2dRqOB6UN2XSUQghA4tuq9SdKUZzmeOdFQBm/Kg0CbfC824bIky9KqWVPFBxbKtfNJdRmTcBhd4LObmjGWqk8CEzyDqCQFrScaQAVgMRpNmM8j0izn1q3bHBwcqZ/TuLop5r2yLENkqmR7fHRAGDbI8xQpc7VhSRtLGFlTWZkKLQcJT8oKmt/Vm8lM1UE/m1KWjCcTfvre+4oTnZWsra7SarUUjcpwzC2r2kBNA2o9KDDBo0k6DMLr2E51jyqURWoCkVgEQsLcLz0c66/9YUc9+CnLhWJPfeIuJThoXR1dynQtS1MFDKqqHqcqX26VHCIklqVVwKSFLApsajxVBGBrBEENekU3yciylNlswng81vdSfYoKxeVpCPty0GaOs4t5nWur/q1tEEswrHnNZQ3v+iZcSsXR3VhfZ21tDd/zuPf4AcPhiMePd2m0O7hhk1ZvlU9unuNkb58gbICArfUer7z6CkUW851vfpsH778LeYYoVGOlchovq/liC+VmnWSZrjCB5/m4no0jLIo44p0f/5CD/T0+/6Uv8dILNwhduH/nIc2wjZCQpzl5njI4HfLOO+/y6quv0Ol0+OEPf8gXv/hFBoMBr776KruPdz80sTg7RhYVvBLlGr7gGheF8i8QnDGqo67IUVTX2QTaQlczptMxvh8ABYNBUc0P9dizCXWpF/QzTbh6bCySmTqyvUBwF4l4lf6r1xGCMn+yp0v931JyoLVxY9yOkaY/y/y8iNdNY/jiXNR51RuSDWLytHtwNkE+u04/keTU/na2Cv2051a/kwYxFLq5sBZkWcrwdHmNVxRUG4Fr24vrafoyLIG0DLVqsamasVDmCx7zQjBAJyTiDABS+76ORJvraQJpqDs9Q56nWJZNf6XF+XMrlGVGp9vA8y2+/JU36PXbeJ5NEDpqfZUDjo5OtfrVCTvnrlBKi+l0ojfzOZIhluWC9EEqypVjl4ShQ5pI1tf6NFutyt3cBIdSolV8XISwKvVDRUEqOT4+YjpVCPNsNuX0dEAURYxGQ378459wsH+iaRlqn8iLAsvRY6oEy65VzvUabmkHbAXMKVqXWmfUeDcAmRACx1HymX/vN/4ef/Nv/RplWeL5Pt/4xtf5wfd/xL/47d8hzwpsLMpisW8CS2PiP/WjLkethCOWVYOo9VQ8web4sIrGU7LjKk7S47ue4Fd/F8sSyWf3LViY/tXfc/9gj1a7ybntHTY21gHB8fEps+mcsuFjWQ6j4Zg8U74YrVZL9XFFkaZa2ezv7/Po0SMAbLtE4aYWcZJTSpu8kAjLJrAtbAse37tLFM0gLyhKBylcLly9wfa5HZI45sGDB0gBl6/foNHpsXv3DnkSMZrPOTnZx7YkAltVB+uX7qkgwpMX1KxRlmVx9do1oigiCFySNNbiEuq1DE3I0ZLdnu9Dfd2yIQMFkjtlVQUoilgB4UXBfDIlK3KSWo9QmqZVbGBjV8IUcRxj6R4O13Gq9c7R3xv5WbNudTodNjY3abdbbGxsEgQBG5sbYC/8MUDRsFxttGqq+UKISqpWCFGpUhlSX+CrYoDC9SVZWVAW4Pp/wdSpqvFZmOoGOI5S/FCDt0BSYpmu9zJXwVeN0/60jcsEGHUJSEXHWUYzquehlFCiKCLP8sXkQU2csNHgW9/6Nt/8pqJuJElOWVBxmut6xLbOymzLIc9SppMJnuviWBZZFRSCChZkhYwZNSYTDD0N7X7a9+rc9PUshQ6OIYpS3v3pbR4/OsB3Hc0d96qEypi3OI6D46rGHjRn1zQdmfPxfb96rHqeRp5sVb6zHUc3UCu6WYW+WFZV+q2jk/Xzqx+m+byibqgTVPfIsqo+DnNIULJu+t47jluhYNIkADUjIdN8K4RyYa8nbovEytafxWTyagwMh0PSOGcyGXN0dEiaJhgTuLwwmv7WIvh5hiqzQRkMaldHD9T9LDXP2kKWZ555JkmpX9OiKLAdhxLJc889R6fTYTyZkCYp9+7dw7Idmu0u7W6fdm+FC5eucPnqde7fv4fteLz+2iuk0Zxv/fs/4nD3IaJIleAB4PuBUr2QJSsrq9iuqwMFidTIyHA4ZDQcwbxQ2thBiGsJBocH/E//7t/xhS9/iRs3b5Jl8OjePt1Wh253hTyLyDOP999/j/Pnd7h8+TLf+973GI/HrK6uMpvO2NnZ4fHjxx+Kjn/YsUjWRdWrYFnKJLQonl4dEmc2GOOpoYLQFNsWDIdJ7fXNzq4QffRmY8rrtXyzdp/rQWg9SV1Gu80AkNX/TbVOixuwqApqaEB/LQ2b6iiX33k5GGZ5nalfBwWNLIMGZ8ehuR71ZOvj7tNZEKUOrpxVApNSVs3dApByWYbYDbRJlV7LzCboeR7r/RXarTa2rmI3Wy1cvbYFrSb91RWCICDPcw4ODnj48CGDwZCfvv0eRwdHeI6rte5VYCCFoBQL5Lk+Ls1crCdfS9dFqhZwVbkocFy4fOUC/81v/SOe/8RFdncf0e01yYuE08EhDx/e48GDe4SBx5UrV3AsQZJEtFtNXNuhEfgUpY1jSSbTEaPhlH5viyIpEMJFAr1enyBoQCnp99o4tktpO1hGpVFfd9PTkOWGUuyaUgSWbbO5uVZNkKLIaYQN0Od87+49fvKTd7h//37ljxLFEe1Wm9u373B6Oqgqh7Zta/U3JX7he37FRgiCgCAI6PV6hI0Qx3ZYWV2h3W5z7tw5XnjhBba3t5nPxgymE4QQZGnBr/7ar/Dm97/HgwcPkQWIctkr4iyw8D/X8Rfx+mYM1T13TEAnEQpxr8UCH6ZoZfYYM3fM45/8jAtWwfJ5KOlr8zpnga2n7UNCqAQ+LzLu379LI2zSbnfZ2tzCdQKOT46YTkdkWUaaZsxmc5rNJpPJlPv3H7B3sI9lWVy/fp0bN25UfH9ZRDRCh7DRJi/g+HiEZbmUpUWaRDy4/4Akiul1uyR5jh00uHD5E3RXNphGCXdv3aLIM65dv8HG5jl2D4+ZzUbYVsK9Ox8ghGLaUKlTlkvXpZ5YLQEctSRPaDDItm0aYUgYhtg2SDxkISkTSZ4VyFKZhio5WJiMpyisZyEwECcJqWbNVOuJUOt/xTTR+7CZT+226kFutVp02l3iKGY0HmFZNt1ul8uXL3H+/IXK3LjValFqdkJRFriOSxAGVcxn/Jo8zwMhGI1HGgiT+H6gJc7h9HSA4zrMozmO49BsNUnTjDiOCMKQIprT76+QJDG2o1oGLMdW3iJlQdgIn3nePHOiAYvSTVEoS3bbXiA8YRhUi7SRFqTGNTubTMBiQpkyUIVOlrJqCqxn/qoEJlU5SAjyPKPIVcO1JSwc16fZaJIkMUkSaSqNRV4sFuP6wLMspYXuuz4ASRJzenKsnC1N8IFSTbB0ohHH86osbzLMjwui6qVkKRWFSDV9Kz6t6keymE5ipjqhEzyZZFm2rTaP+maIlkSsIcMGqTcTDlRg6ThuZfS3CAKspaDG/E41NpnfiqXvXVcZbpmERRj05CmLWIUg6MeaBc8swEIIHNfGde2KG2+ac13XxXYsjahpTWvbxvN9bMvSCj6LZl+F0NhMJhN8L+DRw8fcvn0HKY3utKiSTccJamjl8vG0xb+OItcTjcVzFs+VtfLtAtVeHicm6TQLUqPV5MLFi4Rhg7t37zKajDk4PKTbXyVsNGh3umxsn8PxfHYPD5hnOV/53Oco85TvffvPOHj0APKU6XyM57k0wgaWZRPFMWmWIYVFd3UVPwhwNIfTth3Wtho4fsh0OEQWBbPpjFazhWPZJNM53/zjf88Xf+HnufmJ5xgPYqajKd1Wm/HQw3U8ZvOIDz74gM985jOsr6/z4x//mDfeeAM/8Ll85TKPd3d/tiSj9p1SUTObtaY0lmdEJM5caVgkAKrpWlQJsG0bUGRxv9CVM7PRUtZL6/XXfHrCbZCwBYSwqJYIQFa0JlHNa1PlWlRWTBLzZILzxFEDP9T/BXXN/IpXJZTfkawlUPXPLJahvwVYgBaSOBOc1IPuOp3TAB1qzjq4nken3ebq1asEQYjneXTaDXrtFisrfVzXrZSrGo2QZrdNf6WP6zrVPqG8Nyxee/kVhRjmaoMuygUtBcdWoIklyPTGJ4RFmqa889Z7vPv2u9y5c5e7d+8wGo2Um3ccUwoTZIhqLJj7a9bVqjJSSv04JQbiWEIlRI7gjc+9zm/+5t9nbbXDw4f3ePToAWvzFXZ2trGw+PznvsRsElHkBccHY77w+TdASh49eMB8npLMBI1Gi6OTY7UeCY97tx7Qaq1xbuccQkge3LuD5wfEUcrh4TFXr16n2V+h21/FdR3t0A6NRlOtR5aF67lLyZ5lLeSOHceh1JTjvCg4PjpkY2Odr371iyTJp6sm3puf+ASB73NwcMjDB3uA8hJoNpusrq4qJ+ciU9KjjUZFAzSeFBKpe0eUe7tl25ycHDKdjgj8gNOTU6bTKZPxmJKSz3/+M5wODhmN5zi2Q50OUq9uPGsi/Jd5VJV9W7ERDKotbCXpfxbAM14HT0sEXMcBuai6nd2X6sIk5lCvs0hk6u9V/7ceWyyea8QoMt559x1eevFVfC9UzdECms2Ak5MTxuMJSZIyn0cqOO52OBmcYNa4wWCg90hlyvfp114mLwT7+0fsPzogy2PiOCeJY1zbo9/rE2cJ3bU+W5du4rdWmcwTHj+4D8DVa9fY2NrmeDDg9PSUrm9x+71blEWCECWqT8oGLBAZCzGERaJhWYb9gEGJlpI3IRRTJkkSZvtjbBuyPCWLM9BGsXVwQlH1C6QsKsC61+th1ahEjuNw8eJFWu02ruPQaDYJfB/bU15DnU6HS5cucf78eXzfR0qJH4T4YViBgQhDU1KCCVmeV30WUkriKK5k0ctCgbVpoiiTaVnQCEMazWbVghAnMU6hEpJmq0mW54SNBrZtk2mFqeFohLAswkYD02UbxapvcGFQXMB8XomlfNzxzImGUW/JMrVr2UaetraLCWHpZsqFKVLdZ0CpPZkkY6E7rBA+tVFIWSq5LrGYlKaR3AQCFddZKrUOgVJtsYSg1Wowm0qiWUQSxXheoGgQZybbYtGysB1PuXOXknkcM0tGOK6H73tYEiUDagum0wlRHOt9XTmdf2gQtcTGWQQFQuiNGqoNoPo8EgQKETebvo7P1cto2nFZGm6sOv+0LrMrWXLZlkWdZlUvQy9oU/X1ywQxUpgyeS3YKMsnKCWW9gCoAmc9NBdN4/p19Vd1nrV+EzXJHSXjZhqAdYBkPoNB5xzHwXNd9b3mMtu6oiGRukKlEtrRaMza2rqqEowfV9fEtkE1lddvUp1G8mRjq22pCohtgtyiqJAKy3KwbUePRUEhFxJ75qv+etX3Bjm3bc5fvETYbJOkBWlS8PDRQ2xP0Gz4tAKPjdUevW6TwXTCweEJn3r1NdpByFtv/jmP7r0PMmcWT2l2eqyvbzAeDZmORkwmI2RZkMUR8yim2WphCYvA98l0o3E8nyOLglarpRba+Yx2q42wBNF8ypt/9u/56s//Ip944Qbf+fPvEucle48fkmVz1jY3efTwgOvXplw4f5U333yT116TrKxsMByPCZsN5rNZNf7VOC6rcX8WFTe0M6E73qpeKQlCSmwhyLUhm5JENSoijl5rdFKgdKDVnbUc8tzQ26zFHKwBHlIqYQJRjeAzCUNF01tW1BEaZapGUQlOYVFYkOv+Aym1urxAjQ15BqG0qNYUpaaHnkO6umgZgEYLLAsLS7iUJdhCYjlmQqpPqiStFS/cmPLZjgIpzDjNspIiLyujJ0VNVPelNPfKABhikacILcZgOzaObdFqtXju+ef5yle+xOUrlwiCgE6nQ7fb1WuGVFWVckElMNXKoigYT8bsHxywv79HRyN7ge/T7fUYjEd4rkdRlsRRRJ4Xeh+ykSjvI8/zKctCo6wzyrJkfXOFG5/4lYrPPJ/POTk54e7duzx6/IiDgwMmkwnT6YzxeEyaJGS58hkxqGOn08EPApI4pswzzm9t8LnPv0Gv18T1LF544SbzaEI0PcULHPorfZBwdHDM6somj+/t84U3vgZCURJ294bkacqF8zf50VtvMZ4leAGcniq6yebmNtvbLSgtcgmngxG+16Db62NZUza2HMJmA9cLsWwPKQXtTl+r3aix7ziqaj2fzwk8pZjz6N4DIh0QJIlyMlfnnLK5tUk0mbK3t8d4PMHzPOazGf/v//7/Sbfb5ZWXX+Xerdvs7Jyju7ZG4LrMJxPslqJsnR4pSdP19XVu3LjB4f5+RcdIkpQ33/wea2tr3L1zl26vy2w2YzqZ0ev1q0q9ENBr9/jVX/pr/Mt/9W+YTCM13izIZA6OAhdMsvmf8qHmjo55jPSvSR5QSarrusoo1bGJ45wsT9XqIVRsAGCJEs/zeOONz3Lv3kMePtrVc1Dvono7L8WTYjrVmqKVOc+CW6rguuD2L9gBRh5c7YN5mvPO2z/h2rVrRFFMkqT4gc/W1jbT6aRSlYrjGNfzWF/fqJqQj4+PK2+gotfm+HTKYDDig/dvMRxNyPOSPCtIC0laFISNDleunGNtc5tSuBydnrL3aI8gbHDx6nX6Kyscnx4zOj2iZZfcef9tkkjtKYtkSgKa7l5LMOrJm60xFyml3kuM/Ll+Lhm7e49QPjyWokjlJQ4KjHUch9APaIQN+v0+WZHT7nbodDq4rsvXvvY1xuMxDx48oNPpsLKywsbGBlIqydggCNT9su1K8c+yLCazOTNtCdHpdHEmEwUOSkmj0cCxbZI0Jc9UD2Gz2STPMs3SUCIjma4gGVEm4QvyLKsqSyY5aLfbT/R4GD8M3/exLIvNzU2SJKko95l+nToV0Kg0PqtowzMnGkKoTLd+c+tvUueALauZ1PmwC1RsmT+3eA0zOExGatAyq2oEVI1nUk9rYam/lYVS1WnophbLsgkCD9tyiONoiUNdL8XmeU5W5ISei2d7OH5AmmUUpSROMxwgjiKkLJSDZaGajI304oclGk8BxauTNUGmrJ27CSRMGe/jDkPVMderrIIqS3dYytoCtqAGLK7B2VKsQTjQSdzi5yXqi1iE5+o1641tsmrOp/aY6nv9ZCml0lLXyYQQivuXZ0Wl6CXEgo9v0IQnKgKidj1r71dHtE9PB0t0sLIsFf2sJk1rErqziNFSMCgWlAszfhXlQwVwQivcL507Tx8E1aagE3UJXLx0iSBssLe7R56XDE8GNBshlCW33vspUZKzdf48g9Mjep0WF3bOsf/oLu/85EeURc58PqfT67O9fR7btjg+PmI4GlLkGQJw3Jz5bEYYNihlSZQVJHFMlqYKfZSKZ7u9vU2apkymE7rdLp7tcHJ0wFs//D6f+txXOH/hHA9uf0AUz0miKSvrm6Rpzt279/nUpz5FGDa5f+8hn3juBq2TNhcuXuCn775r7n51/k+tGumxZ5JSMzaMmposVEVTrSPKn0RYCj2kLLCEkuHzfZdGM6Tf67Bz/gL7uwNu376rKXNaKre2BtQ/j0kwDMJtKqGWZSG0SEOVMNcj8OrcCqRVIIWLQEnbCkocUWJJgZTuAm3W/VY2aswr7wKVfFosUHZhFTiu0CX2JqEf4to+Ydig123RarWwHVtRI21HK2q5eL4CZIIwoNVsEYYh/X4f3w84OR5x79597t2/x927d9nb3WUwGJJmKZmWZlXB0cL13nFsHFchbJcuXeazb3yWz73xBufOncP1XKI4qioOZZlXpf2yLHFsW1FqdD+GZVn4gU+n2+HChQtIKYmiiDRNGY/HZFnG3v4+o9EYUIIhKkgzdEmr2kTNPfJ9X1GpioyT0yNc1+X09JQgCLh46TzXrl/BVFOB6rlmgzZSlGVZVg70eZ5TpCkyj7h4YYe8SJnPp/zhH/whX/nqVyhkzng0Z3V1k8uXLnHvzl3K3GZ4OmN9bYfheIxlWXzi5kv4QcAP3vw+u3sn3LgJcVZy8coNms02soRWq02z0UIKh/7qlFarxWw2p9HqA9Bud7D9Brbj6T2vUGSuQoF0WapUZVztHnxydMzp8THDwZDJZEKqTTWzJKUsCtJYySD3Oj1ajRZBoBDr++4DDvYO+MODP+AnP3mHfr/Pzs4ODx8+VD1kvo9tW6ytrbK5ucnx4RFJpExtHz9WgM4Xv/hF+t0eRweHXL50icFgQOgHjAYj8iwjCALGoxHtdpskjllfW+fTr7/Gn37zWwqpt1wkgkKWyDLXQfizafb/ZR1L+2nte8ViUF4NhrpdVWnKUgsCqDlnCXAdl8+98RleeP45Nre2Of7d3yOaRWgkUgN6i32wLv5iaG31YxnIYWnPXI7FFBBjqiJZlvLBB+9z8eJFHNdmOp2pCmWnS6vVZjabaXWp+In3NxWd0XjM7v6hUv5MVHCsAAOXoN1hc2OD1dV1HNdjMk84PjlkPJmyurLKuZ0L+GHI/v4e0WSII1Pu33qPZD6t9bDp6y4WgN4SXersPdLnb8BJBWAK1taVrG8QBLRaLa5cucL29jbDwYBeu0Oz0azAB08zLwokXqDUCsuypN/vEzYbdHrdiu4O4LkeXuDXpOVdwkYToUEIIYSWJ0+ZzWaVF4cQguFgQBAERJreBJLjo6OKEdLv9/EdhwKVnJrmcilllQyYBNDR9KflOFDF2NPpFMtSIkxmDTcqjI72rBqPx9VrhGG4JAn/ccczJxrmxE0WbLruTROe2cTNRmJ+rg96k4yYEzEnbAaHCSatWpZuLpDJrtDctlarycnRCb7nYNlKgUVYFq7rEAQejUZIUZjyt7XE/VwaeALKQtFpPNdjZXVVqerECdF8TpGmeK6jqweCJI119eWjEw2W1hyx9Pv6j896o5QSCNV7GvQSTS1ZXVvl+vXrHB0dcu/efc0jVEFYhZZKE0QJhKj1xMgSE3NX52UoBaYMr/8ma4nawlm4qmkt+VwsKl4mgVpefM21qyeu9d/X6WBnURtD9agvlPUk1jzWTCATiHieh+UobmRdIvXjj6f3Wug//QcdJnELg5BWs0Weq4RhcDogyzK6nTbD4ZDj4xNOh1MuX7vOaDzh9U9/hiyd8JO3vk8SR2RJRhC02Nq8QK/X4/T0mMlkWvVkOLaDZbs4vo8XBIS+j0DQyBoMB0NOBwNKmVfiDJubm+zu7TGfz2m1mji2x507d7hy/XmuXLrI/sO7bGxtsfvogaJH2DYPHjzg5s2brK6ucu/ePZ5/8TmtSrLFu++8WyVyZhwtgvWPuj7muoOUghJbjVPV7INllziOoNnyObe9zoULO+yc22Z1bZWV1T6B7zMeT/h//LPfWRpXhZb3M6iqOc5SM+rqSmcBiidpDBq4ECXSLhC4WNjYosQqY1qeVBRNqZZcx3ZUEF4I0iyj0RMIO6bIpQ6oVXLguj5hq8vf+vW/p8rwzTatdhu1DlqEfoAlRAXGHB0dMZlMcF2XLE9xXZdGo6F4xxqsybKMrXPbfPL1l9XmkqYcHR6yt7/Pu+++y2gyVvREvaGsrqxgOw5hGNBoKC5+v9cjbDT09VNVm0ajUc1Vowrmum4VXJmN1QT1sOAtG9TNIGhJkpAXZdWoaOZ1pWgIlbS6eQ3Tn2YJWW30vV6vev7x8TGDwYD5fM7a2hqtVqviR/u+X72eebwBueazCUk0USo6wGg0oLvygKxwuXDxKucv3qQRhNi2Tac1Q0jJZz79ZdIs5fHjY25+4iYWNo2gw2uvfZbpJOHatRfZ2NhUgI4UuI6nATrJPIpYXd/Cth1Gk4j3379NmqZ85tOfwbMLsjSiLIuqt2g+nzOdTogT1ZDb7/XYWFujzHNWV1bZ3NhkbW2tAm7Mfrq2tqYb0RdqYucvXODFl15iNp3y5ptv0u32ODw8Yn19jatXr2DbDleuXOF73/sOnU6Hq1evcvv2bQaDAc1mkytXrmBZFqPRqJK+nM1m5HnOaDTCcWx2dx/reWVzcnKC67rs7u7SaHhcvbLDvQcPKeMSz7XJckFJibQsFr4g//kf9bVG7eQKKPVcm2tXLnPl8iXCwGdzfY3LF85z69ZtMl3VedoVqCiFPCl//0T8wbLn0/KatgxAFkXB3bt3Wd/YoNfrMxqpPg3Tj7OysqKawZNEm32mZFlOkejPalmM5gme5+N4Ic0gpNPp0Wq1cPwQy3aZJgmjw1Mm0xl+EHL52jVWeivEUcT+7kOKLCaPxzy4f4s8nVexxtOuaZ0e/0Rcpq/12WsihODXf/3v8sILzyOE0D0aKpYt8pzpZMra2hpBEBDHMdPplCzOaLaajMdjGo3GUnO1WaMsyyIIAqbTKQBhGGqAU8U6cRxrF/aIIAgq6paJqc3+pGRxjSfUwpMjyzLG4zFxrJg7QRDQaDSqAoD6vXq++b4sS4bDIUEQIKVaJ6MownXdCmipkkVLVazn83nVP2eUZSsV2Gc8fqYeDdu2SZKEZrO5FPSdbYw1WZStkRXze5NZ1TNOs3nUN/dClri2qC600bZP0oRSwmQ6UQlF6OE6NmWZa9kti7ARKh5bkWHbpqFY9VPY2BUibT6v67rYliqrZVlKkWV0+31ltjKb6gGjOL2ua2M7FlE0+/CJDHU2WXUsHvM0JLeGNiCePkmQSJlj2crtOggCLly8yM2bN7l+4xqb21tqoOrBe+/ePb73vTc5OjhWzUFSoui6i+ter0jYtslu9b2i1ixtchpQSKdOLIwzsuGRKroHFS2GKlBcThyq99e8yXoSUW/IrF/bp6LPGil62rWsB4mL6pqmVumKxlnk58MOU60xfUZLwgVy0bD3tM9hWYtr8NRNUkK70yZOYj744ANkqQIiGxvfCxkVM4RQHOk0iggdm3MbK9y98wG7j+5BWVAWJZub23R7q0iZMzg9xbZtVlbXVdO7ELiux80Xnuf69et0Oh082yFJEh4/fMi3vvlN3n/vp0rhwvPodLtEcazQ4DDAcVzmacaP3/oRX/3a17hwfocsmrC9vcVoNGYymRBFEZPJhHa7zf379ys1nUajoRvvVUXiY4/a3DGJtUk2hLBwXAeE4n67ruTLX/osv/TL36DV9mk0fPK8qIzr8jznj9/8Lo8ePKTuolsJIJzZbOr37Wn382nzsl6BBSiljbRcLGlhixSXOc8/1+c3/u7XaLYkpVQN6b7vV4n1yckJnX6HNM8ZDsaUhUW3s4osbS5duk5v5WV2zr9MNI+xXV+5KttCmZSWKY7tMJnNOTo6REpYWVmpDBmVgaiuJuv56ds2Sl0rpywFeZGwstZnY3ud556/ieOp/qjpdMpoNCLQkttJEuM4i+bS4fCURqOB7/vKKMrzKwOoMFSNgipRPiarJXZmXptKpUHfgiCo9UeUNJtNAh3At1otut1uFQDM53N2d3cV9S+OSZKEyWRCr9dVqnVaQSWO4yp5OHfuHNvb29X8NcG1WR+UURcVKGEOx/NotjcxplZb56/wa3/zgkqK0hTPcbAtSyX0QiV0Ze5Q5AW3bz/k+edfpd/vI8uSW++/y8MH+8xnKZ7XJIoTjo9OiKKYdqujAoVC8Pv/+t8ghOAzn/kMQaPFt//8jwibbfI8Q2ok8+TkhKOjI27cuKETM8XDjqYzHATtdoe5BlqMoe58Pmd9fV0JZqSpTs5c7ty5oxKlToc8z3n06BHXrl1DSsmVK5fxPI/vf//7tNttpMz5+td/ngcP7vOd7/45SMl4MmZtda0SSnn86BGz2QzHcWi328zmc6L5nDwvyLJco7Qxvu+TpspItEwzdnY26PU6vPvTD5hMY8pCqutZiifW/vrxVLDvP6HjLMi2VFFF7SGuY/PJV17h2tUrlEXBcHDKbDbnjU+/zuHeHpPpjEIqGid6Tzpb5a/vk2eBvMX+K5ces/ibYCGssnw9D/b3mc0iNjc3yLKMKJqTpgme5+L6AY12h97KKpatHeVLxf8uLRvhuPh+oNdcuwq0h9OI0eSINE1pNJtcvnKVTqeNlHBydEASzbEoGB7vc7z/CIoEiwLEkxWb+nU9G+NU94Dldd7sAZcuX+azn/1MBayYKqdJEpqtFo1mE89zieIYhKDRbOK6Lp1utwrO8zyvAn+D+EdRVFUyZrOZXo96lKVa8/r9Pt1ut2JYmMDeVFTNGqUqujaj0ahqIDcVXiWIoRK70WjEdDqtABghlKdOs6n6uM4mPbAQRZJSLjmbHx8fV+uG2dsN1dlQbhuNxjON/5+BOqU2hlartTTJTSnGDOIls5raZDIXrN4cbqoUJuCrkhLJ0gktdN4VNaff7/IP/uFvMDgdIIuS73znu/z07XcpypJGI6w8OJQsZkGWpwtZXhbZv+EL97s91UkvJWkaMzw9ZTyZUhY5QppgXBHFVeKTVYZIT0s0npJnLP2Np9JGdPOWXA6mF4uFoNvrsLOzw8svv8z169dZXV3VTYDqDbMsJwg9zl/YZmNzlZdefoH5NOZg/5CHDx5yOjhlNptR5IXi6WYpWaqSvDRLlVwauvmyVJOwKBe6zuoeW0jrjPmcQKtwgdL1f1qFZ6EuVi14Uhkg1s/z7AZSTwzNzybxdGyLolwkKPVreTZwfJoIQJ0GVX/s0yoqUiqufF0xp/4c8/3TAlWFyD9ls9H0lEajQRzFTOdK7WUyneD5AY7j8fyLLzFPEy5dvkpZwsb6BuQ5D+7epcgysiSi3e7S7/dASPZ2dxmNhjSbTaU6FYac2znP5z//eVY2VxVlr1R+My0pWVtf5xMvvMAf/+Hv893vfJeiLEnSlJW1VUZj5eXRaXVwbdh//JDR6Qk753d4cP8ubuDTMgpwec7p6SlXrih6ysHBIeubK7iuq85pPFku5T1xjfT1RMsDywWNyTT3KTWzAtezWem2+Tt/61f59KdfJgwcSlS/iSwKLAm27eI7Hq+9+kn+8A9/QJwsy0EbROfsWHla8lFPKp/28/LhIKSLayW03Cnf+LmX+Gu/8jLtVkJZJpRSqbUJS5l3lmVJp9khLUuOTocIEbO6skYUjcgzODy4y2hs0etvk2cWWRQRNBs02w2EAM/2EFJVLRutFo7j0Ol19Xna1VqXpmlF1TI+NI5WevLDoGoWPB0OGA6HOI5To8ko1aZWq4UQSsFPBUoWDx8+YmdnhyhKEdacBw8esLq6Wl1nx3FUIlVTVjHVa3P9DC3qrMvscDSuqpGmQmGCANu22d7eruao2XSlVKZZ5jbWVXfM+lOXvTX7ldnfzDqcJIlG+1VFcDqNqs86mylXXfWzjyxKoijFdUrObZ/n3/7ev2Glv0KcxLzw/Mv8+K132N7eZjQa8YMf/IBWq0eaZNy+fYf5TImWzGcR3/n2d7l85QqNRsiVy1e4e/cuf/xHf6wqBZevcOfWbcoip9lscLi/T5qmtNttvvPtb2tajmIbbK5vUKQZFy9coMhzHj9+rCpSjQaz2YzNzU12dnYYDAa8/fbbbG1tV9fq7bffripTWZbx4osv8N3vflejm00++clXkVLy1ls/Ym9/j/l8hmVZ2rcjqu758ckRWZaxsrLCcDTQvT6KktNutxiNRnp+eZRlQRj6WJZHUeQgBa++8hIf3LrL3sERwnKQaYm0rYru9p/7YRIAKSXIEtexuHn9GtevXUUIcB2LLEmwKQldm9defYk//eaf6wDeUj1j1pPrUBVH8GRsUgFutcu3vIZpUPZpYIplMZ2Omc0mrK+vEwQ+0+mUosiYxwm2Fy6pklWHJyjzjCRXMWKaFFXlzvEDNja3aDUVWJFnKafHhyRRjGtBHk3Yf3yfeDbGEoWqbLHMjqjv74seveW/GUGE+mHWgl6vx9d//ud1IqQqriYmnc1m9FdWAIizhNF0jEDQW+2riqxlVZUA3/eZTJSa2urqqjZhVYBwPZZV1cQFuGJiULMmmupCt9sl1E3hxq0bJO12u1qnDOiv1lKqxMFQmsxcvHjxIpPJpALgfN+v6KFmHJpqs0k45vM53W6XsiyJ47hKVOrUP3OOz3L8DIZ96sasrKwgpWQ0Gi0lDgapqpe2z5rVmQFgNg9zQ8+qKtSpWfVB22m36fZ77B8c0G636He7CAGXLp0n+uVf4N69R1y8dIV/9+9+n6LMKYqSslDNWaa51Lyeee88z3Fth7//936DKIn5oz/6nxiOx2RpqsziKvqPaWy3qtKzSTT+Ig5VQlUJhUH7bctmdXWV8+fP8+KLN7l4eYdmQ/knKOpFjpQFWIKiXFSKirIkS1NVASpyrl+/xs2bN4iiqEraTOPkeDzm9PS04uQp1C4jmsRMNCfv5ORU86FTptPZ0iJp3lPd6xJJPaBfqNNIFOPFcAhd1yVO4uq5Z5MMM1F83682fMVjTKpzyLIc06RlxuiHVQ7qTccGBTBjsC5JeDbQNK8nagv7R1Fozh5SUgXKT5yfvjIrKysVKlIUBXEU02q18BsNVrc3+dLLr5DnOW9+93u8+sorzCYTHt1/hOp3lvR6bSWRubfL8ORQqf+4Cmm6cPEKX/u5v6IWJKsgz1J9rZQZkaIcCv7qL/0S7U6Ht956C2mpHp1mp83pyQmB38BxHeLplAf37vDSy68QNJtk+j4aOeXBYMCVK1doNBqcnJxw6cp5ms0mO+fP8+477yzxiutB+5mZgKlgmJGj7gFImYNVcv78Nv/Nf/2PuXBuA8oUz7aJkpwiL7HwmI5mKMMkSa+1zoXzF7l15/5Sr5H5+ll0+j+sgrlMg8hxrZTNFcHf/Ztf5nOf3sEWY6SuxlpOADJH5gslvCSKKK2Q2UTg2l3yzEOWNtPJlFYDpvN9vvfdf09/5TyjccrOxUuc83coyJG2wHM8pRyi70EUxRXSJKVUFd5SKQO5OpjPcwUwRFHMbD7j0aNH7Oycp9vrsbGxgWXZlb77AhySJHGC47p4no8lHKx1h253RVO1Mp577rlq3TcV4zc++9lKkciovgVBsESJNRuu2Vw9z2N9YxMpawAUy5x0s4ab62/WL0uvCcp9PamSGpOwGGqB2dMMnQug1WqpqkAUVYCV4YcWRcFsPMX1HHaHp1opzyOeK8OtPM0YnA744IP3abdafHD7Fkma8NWvfo2Tk2MOD4+4ffs2169f4+7d2+zuPiaOE1588WWKvKDdCjg+3CXNMoajEc1GA1nk7O8+Zm1tjX6nrYCgIidsNZlHcwSS9bVVhTLHMf3+CrPJlJ+++y6zyYRup8v169f57ve+x2w+ZzKZaFnSCffv3+d733uTblclpl/+8pd58cUXq4rUZDKmKHNe/9Rr3Lp1i/MXdtjf32UwGHB4dIhtWxRFzmwW02yGRJEKXMIw5LnnPqGNyOIqsJrP53gtH98PKGWhfvZdQCG/jSDA9V3F3w8bnD9/nvdvfcBbP36bEoc0W1Cvz64j/7kdi8TXIgwCXnj+E1y5fBldryBNYqLZDNcWTEanXLpwnvvnH3H3/q4iTJcldsUfWE4qzl6T+n6lvCaspz7O/O6p+6cAhelJDg8PQKiAttVs4YYecZpi2zZRkirqu23heT5hEBCGDUBJ2nuuj227OI4ync2yjGg+Zzo8pchTPMdGlAmP798jng6hSPGFpEBSAKVwsFkAuQYQ/LD9u/69qejCAmz+G3/jb/Arv/IrjMan2LpZv37+09mUUscimV67pvMZGxsbDAeDag80tKNms0kYhgCVr4hZ40y1wPeDqoJqaE3mPKIownEcBT7GMZPJBMsyn0tVb0013Ej5q+qJX8XjjUajWs8sy2J3d3eJ+mSowyZxcBxHVW6aTaSUVc+JictMvG6+hFB0zYZWq3qW45kTDdNfcXp6CixkDc0gNjwzE/Tleb7UNAyL0l1d5cBkSGbRV2hjyGp/lePj4+pvRv7r5OREcY01QpKmKbZlceXqFV586RXyXDVVra+v8/ZP3ubRo8dYFrqiIZYkVE3AaTtwdHTAf/1bv8XXv/EN/tk/++f80R//MXlRqjKdXJxHKRdKUUuD2GxIejJSbwU2SGkt6NbPRC0sopoIruuxtrbGSy+9yI3rN1hbW2N7e5tCJpwOjrRMY1RdLxVQesSJasbL0ow0SynynJPTU9J5zubmNgIYat5snudVpp1lGa7r0uv1Kj51HMcUnQL38mUAMp0cRFGkOIVxhOuo64gQJHqDt22bsBko5LLZJAhDVldX6XTauJ7P+sYG3//+9/nn//yf85nPfIY8z/nzP//zajCb8eF5Hr1el5WVVdWQ7HlIKTk8POTevXv4vs/JyUlF1zL3wCQTT0Og61+uY9NqNhEIXMfFNKh/1CHRFQi5LPsJIC1ZPeqpzzyTYCzQe5Uwrq+vM9GlUlUyVXOqENDsdPACn8npDCmg2W7w4O5D4nlEkRWEQUBZFEynI04HA9I4phH2dNNehy988Qs0my2thlIibEsZAgmBFEoqOk9T5tGcz37uDY5PjhkMhkhZ0O11OT05pShKXEdtNvt7e7z6yVdZWV3lwf37dH2/cgkdDAbV2Do5OcGybGzHpdPpLM77zHVeTgyNQguYPuv6wyUFRZ4SBC6npyeMT4+I51PiaMZwOCJNcybjKcfHp8RxQlkoQYeD0RRDfROWqO7hh93zs5WNs5+zXoyXQulUCQG2Ba6dc+1Si3/wd7/I1YsOljxGlJI8sxGOTS7VZmPG7XQ2pSwkaamMoEbDU0o5IAyapFnE4dEjtndeZDg84gtf/Dk63W0KHEohkaLEkhZFVpJlBZ4XsrKiHGmHozHT6QSgKrPPZjMdaLYqgEdtdAlra5vYtpKtti0X23HI0hzbEvhBUK3XtJXiIKgEoNfTAglaFthUHkyloCxLkjhmbWUVYYmqN8UE/xXtQIMGJtmWpupdFORFge95zLXsbZ7nuJ6i5aZaOU2ig4E0YzoZU5ZFtZ5lWUYYhMw0+u44TlWFA5VcGMTP8zx2d3fxfZ8oilhZWUEgmI6mOI6F57tImRMnM3Z3H9NstZBSqM+RF0SzGUdHe3jeDlE0YzaP+cEPvk+n02EwGNBuK2RwPpvQbYWs9jqMTg9Z6a9y7tJ5Hjx4yOHpMcPxmIO9xzSbTVqtNmk853g8BgFFWXJ6eqLXPHWdFQ0qZD6dK6Q5z5lNpnz2M59hf3ePjc1NJpMJx8fH/O7v/i6vvPIK7777LmEYcv36NZrNFoeHB0gJ29tbFIVSp5rNJwwGp2RZyp//+bdI01RT8oTqg8zzSnXHOEOPx2Olva+DrCzNKvGULFP3q9/vIYQyN+t2O5g9M45TPN9Tprl5wo3rV1hb6/Hd7/+E3d1DLGvRVGtEIZQm9WJiPjlL//KP+r5Ur5R2Oh3e+OzrdFpNomhOWTgEnofjOvR6XYYnpxS2ZDg+oNNu43ouZVZWPlVncZqnVWmXuPRSfuQFWe6LVKCPqTOr/bVUG4GUZFnKyekJjh+xsrZFr9+jyAuSNCGJE9I0QU4tWu02juMCgrLIFLAiJXmaIyW4toXMYqLpmAeHB0TzGZ5MscoMIY3IkEBiUyqJDXMylfJS9dmg2juWxoBlIaRxrlfrUqfT5sbN6wyGp2RZzGg0qlgiruso0Ny2SHSMNJvOdALlcXx8jOssJLkN2D4cDMmyXFVD+j0dyLt4nlv1eAhhcXJyWsXOjqPey4D1lmVVc8m27ap3Upliq/VxPB5XfVG+75MkiaY1qiLAbDZTcrt6vTvr7WLGhAF5DNBT7+9oNBpMp9OFa7neL4xnjlG4epbjZ5C3XfDSz9JUZAlFrtwZ1WNKHNtDYFUceiNdCxZ5buRXC4pCIsSisiGEkgg9OTmpTtY0zqRpWvVsWJal3lNYZHmB7XoUFJwMjml3G3z+i5/m9U+/wmQyZn9/n9PBKVeuXK54ZkBlcCJlxvHRMf/Dv/jv+ZVf/jV+87/4+/z5d7/FfB6TG5QcwUKm1kZ3oOtVTVUjpNCUD0kV0JlKhW3bWFLJ39mOg+u5OLaNbSsutbAEq70uF89vs7mxSbergrOTowOi2ZiszJlGCqmdzqZInf0GYUgzDLEs1RBvrpPt2DSDFi1fkMYR7U6HK5cu6hK2oNvt0mi2KndPoGr0sSwLz7KJI6WylSQJkf5+PB4zmUyZz+e1El+Abdusra8RtALa7bZSvfH8iheZJhlplDE4PmJ7Y53f+PW/Q5pm3Hn/fcJWA1tzwldWV3WDZoDruKpUjOLkh40Az3cIGz7uxCYtMop8UY0wmX99QTdVCxMo2baFb1v0mg1cYeNgk5OjfdIxFmr18Q3aJ0SiKk21LF4ItaqVZbao6pzpG3kaNUclKhbSsonSjFyClIJoniAL5Wzs2y6BsPARlHFMuxGCkIwGx1BklGWO77fJspyTk1Oi2UxL0s4Iw5AXX7jJ6koLrAzKEseykNJC2oKsLClQZXvHsTVVDl795Cf5gz/4A1zXV/QaxyNJ5gSBkhQeT5Sh1+pqnwd3bkPhkKUZtmUzjyKyIscNfPaPDshKQSlsojSnKFWFC+PQLpavsboeAApAWPRlCMpSB/mlwLN87t99zP/t//p/h7LEFjZFrtB627ZpNBo0my263XU2NzdwXY+gG/Jo7zF/8id/SprFWH6gaVgSi0Wlq55AnqW51X+2kAhRkEmfUvrYNngioulFfP71bX71l56n1cwoohmFzJSrq5DIPKcscqRVUlCQZDnjWUSSlKRJznCQMp/nxEmK65aEjRZ4TWTZ48UXXiOalwRhjuM5CGxsy0OUJba3UGEyTXoqSe8tNf8KYdPvryCl6q+SpaJE5HlWjWnLsrAE5JqiY0w0HcdSm7qAEjVmbEdtPrZUwE8QqmqAAMpaFcKzXeJZguvY5CLFsW3KIidNE7Wa2kq5LaqhdZZlMRlPyIuC2UzJ0J4/f548V6IFiUWF2k2n0yqgOj09rb5XfShqPp5K9fjh8JSiKJhOp9WGqzZbm+HpkPX1NXq9Pru7j1XAHs8Jg4But4fnucymU8qyoN/u4e7YHJ+oPpXt9W2yPOfRw4c4nk9eSl5//dOMJxPW19eYzWZkWUKWZfi+jW0J8lIyHA2I5jG3b99ma2ubLMu5/+ABoPbRbrdDnid6fYHJdKob9HvMZjNGo1EFOCELjo8OEMJiPB7RbDb57ve/y+c//wWef+EFHNdlbWOdP/mTP6G/1ucbv/h1Ws0Ws/GE6WTE/v4+u7u7vPzyy+R5zv7+LrNoQqopFZYoaTZ85vMp7XYbx7FohC1Fd0LS6Sha3EqvT5bkzLOI/soK85lCe/MgRwgLz/UZDod02z1KWeI6DmmcsbraBVFWUqDT6YR4NqbdCPi5L3+eW3fv89ZbbzOXJVluKIAlyBgl52qdSTIWiP9/Ckd97Xddl3a7zfPPPUcjCEjjOWkcMx2nZGlKXqjYIslK0qygRPn9NFttMs0mMX1n8CRQ9rRkw7ZthL24JoZxYCruSIGUmX5dQVHUmsalBaWFhaNBN7VTOgJklnOy95Dh4S5hqNffsKEqF2FArClFtu2AThDTLKWIE6LpRCemkf4cBbYEKQQFDgijrGlhC7AkCLFA1osiP7N/VKgwphqurkGJhaXPTWI78KlPv8LNmxcZT8YURU6n02Y+n3L//n263S69Xl8j900s1yL0QxAwHU/Z3Nyk0HuwEBBFMaPhFNf18X2BbXtkWa49Z0qkVKBAUUigIAzDSpBECFElCya439zcrKq/Jp6Zz2Pm8zlbW1t4nk2/v0oYhlVyP5/PmWkp+fX1dfI8ZzAYVAmCAfZNkqDmsFNVVKIoot1WAjTm8wCVKaqpmIzHYwJfV6TThQH2Rx0/c0Xj7FdZqMYfg2QppIHqJtdRZoNwmRK6mQB1CoMp3Ugtv2oudJ1PX1eoUhmhy8HBIf2VHv2VHuPJCIkkbPj0+ufZ2FyvMsE6F00IoZvrYGNtg/k85l/+9m/zysuv8anXPsW3vvVtlf1KkzDYlFKSFaoBECkqrr8JZj3PU1meUP4bzUaDXqerslNh4XoelqeCM8d1qs9fFDmdZoMsjimLnOFwWJkd5blLIUsaWoJwe/tcpcbiOA7NRkAjDJUSRL+PV3PXFUKoclsQLDmBq2utFq/6PTFUA8+yWFnpq6xeT1ZloOfo65/jOi6llETzORKwXafS9DflOdMUisiJk4SV1VWCMOTGjRusb2xw+85tvvK1r9Ludvin//SfMh6Pq8+dazWwNE3pdrvaKFBUi6YqAS/6g4CqQmYy9fqYE0KpYjUbPu1mE99rVP4YFZWmfDpHv964bqp2dYRbgfUmyXhaM//iWCx+yoQsiiK6KyvEccpsolBX21KGiEJCmefMtGt9WZbMZlOoUdSGgyGj4VDNJakWjDxLuXr1CpX5CsYI06IEAs8jzy1lYlYUWEKQxjE729v4rsdsNqPd7uDYFlkSL0qmmlLS1DzuD27d4vDwkO2dc5SJOhdhWcznEVlR4jge3W5PB5OL869qQGcRt6oCVKdQ6XsnHBzHot1q8LnPvq6SJMuhESr1oBdffIFr168rDrHvYzsOs9mMRCY8ePCAH/3oh5wOlEuqYyk+f5bnWJZYWqvqzZN1yl1174RAFhbKPwWEmLPaL/nlr7/OG69tYnFEmiu0VYks2AihaGp5nlNIyHKL6VwyGEp298bMJpLxKMH1AlwvoNXusb5xmc9//otcvPwiSWbrAHKC5cTYrkcQNBCaSgMKaPB8r/rslXKKXp98XyX+lmVjYQQcQNgK0cryXPXVOTaeRrdMhanIFwptjr0Q1TDyjGmS4Lp29TjP8xgMlTRjkWQUqVGXUnQky17MOcdxaTablEXOdJLohuGMvd1dhKVcpwenJyBLGo2GpujAfD5jMBjQ7XaZzyPCMKhoUEpyU0nmSilptzvEcYTnucxnU7I0wbGVwV2SJkwnMSv9HrYFk/GQrc0Nok67UoLZffyQsizpdrukacpoNCKKIo6PT2i220Rz5fOheNpKLjJNc+7du8/BwQHXr1+t9OuPT47Js4Rut12tZUmS8P3vf588LyixdZDiMJmMOXduG4Si7kopaTRCskzRktbX1zSCOaURLhy6Pc9lOByyv7/Pn/3Zn5KXkjwvuHDhPH/7b/8t3v/gPfb2hgxOT0mjhPk8Yjqd4vs+P/7xW3iey2QyptkK1B6pkx6V2Fjq/RpNppNJldwKIZhNVbA1myqGw+7j3Wo9N4o3UpakOkBxXZdmU1Fr9vYe0+v3sCwVQPZ6PU33dZhMp7z83HVsCu7ee8TJyZB5lGDbgqJAqyFKSslH9oL9ZR3m/E1Qubq6ShAEHB4dcXK0p1B6odUzTUUeRRUqEVVPq2UrmWljNfBh+8yHASb1v5/9GaGouJWct9CS+zpoX/TNKcCOCqApsCz13Pl0ynQ8qZIgaQlKXam2bUtXqLXJcmn2JjSopF5L1/qRFThtgF6JobErpUxT0XqWG6AFMYoC2xZ86Ytf5K//9V8lSRSYfTIf0G6HusJ3XYExlsD3A4qi1PyUksAPsK02qpdFkus+4F6vq9g0JZyeHmuT4RZHR8cV06fRaOA4DpPJpIpj4ziu2CWmH05KyXg8ruLfNE0rBb+dnR1Na5xUPW1SKrdwU73t9XrVaZtGbkOD7XQ6FEVR9WGZpNeIb5i43Pf9qqkdqPrj4jim3W5Xwhln++o+7PiZmsHrG+90Oq0+LFBpky9RSkplqmSCW8OPN26YZ5MPcxSFakBWDUKZKrNlmUa3odC0rE6nw9raGoeHh4RBQJHnPDzYJwxD1tfWmM/nHGuKTZooHm2r3VYqTKWs0K9es81oPGY4HHNyMuR3/j//Z7a2tuk1O8ziGYZN7zg2a2vrtJpNJBA2g2rwmEBlOBzS63ZohB5potC7wPNpNEJc26HZadPsden2ugR+QKCrAZawaIYNPMdd0po3nGXHc5FigaYb1M9SpQxsW/VYmB4Zk2DoC12ZssRRRFEWBEGI63jV4DaHWQynU8XltRy7lpTlIBVdyXIcklwpDwhtBmbZRqHLwrYd0lTpQqvmUo9mq00uS65cv8bByTHr21v8nd/4u0Rz5d/Q7XaZTqdLiYPhLZoEziR0vu8zj+JFQx0L3qsZU/WGU1OJc12Pfr/PxsYq8zjXm5qiXpxdmOuJhjL2EUvXqAo+rY9QlfrYeWXR7/exXZc4SvTCrRKlw8ND7ty5wxe/8mXCZqM6rzhenLdJrFzXXeLTe55HGCouaKk3hCLPK5pemitEOU0zyrIgmk10QmCxurLCg/v3SZO0wgRVJUxtNGma0mi1kEgm0ylJlpLqJs04ikFArpXO3JrCl6yZblWb6Rnk7cOvkzAkQ/r9Pr/2N36VCztbrK2u0ggaWK4LUjCP5uR5zmQek+Vq4Z3OJjQbDf7KV7/K//e3/xVlIZG2hYVFXirpwLPUvXrVtj7G1IZsY1mOdoku6LZt/vZf/zwv3OhQyiFSuDq4d8k1l9qILMxmKcNhzHxuMZ/73L8/4uQ4wXZ8XL9NnFl03TXOX3yNGzdeoN29TtBYI0CS5QWu51GUEst2MJKYpf5cnu/pZFlVr/RgVdULKcn1ZuO6LpZUFJw0TfE9DymE1pQQDE5OCMNwqZfBsiy1DhclUXSoOPXNJlKPxySJydOEOE44Pj5mfX2N6XSGbVsEfkjg+kSR6rFK0lj9PlBrj2mANJK4i/L/tELrgyDgzp0TQJIkKVIWleLV48ePNL1ANScaichOp0OWpTpxLMnzjDSLlHiJLMiLlCRVybfnObz11o/Y3NysZLCNSovZszqdDgcHe1Xj+cOH9xlPppxzlb69oqFF2Lag1+tyeHjM+fPnCcOAt99+B8uC/kq/2j8nkxFpmtJqdjQyGTKbRVAKvdYp75T5fE6z1ah6Jw4PD+n3+zp4Uw2tjUaDIgffD6pm/vF4XJlw/svf/m2kVI3Yb3zus9y69T5JEgHK2Mt1XISQ+L6rKyUDev3ukuGXCX4MKDUajap9fz6fk2UZk8mEVqtDmuSVpKbp51T7UUle5Dg6uZUyJ4qUP4OrH7ugdgg6nS5xFLG+0mM+m3Hj6iW2N9aZzWM+uHWHBw8eEqU2WWFAnv/0kgxYxDrtdpt2uw2oa5bnORTK0NJQgc0+VpYleSm1mvdyr6takz7+fU3M9aTy1JP0bwMA1R+zWJNLEPUucv1coaqjQkgNRqnqg6H/qqqz5nzki3XfNmCSUJW7UnuImMRBirKqSug3rK6NqmKUS5//w6750rqN+myNRoNf+7W/ztWrNzg5OSIIfMKwiRDKTNH34fR0oGiTQgBlFbMeHx9XKk5xPMcPPLIsoxFmSAmrq2vMo0ml2geLfpDHjx9XDBIT/Jt1ajgcMhqNKrqT6b0wynzG38p4W/R6vQpEMr1k5j4bL44gCCpwIwiCKqGwLCU/bahZrutWvbNCCLa2tphOp/T7/Uq0od4Q7rgucx2Tne7vf/wg5GdMNAzV6Pj4mOl0qvlZC0oRLDalOp3FTBoTKBnurNkUTBBpLmqWZfiup91g1eYzm81otVoUUJXP260WRZ6zurJCu93m4GCPrc0thRDFCZPxhFKrHbiuz2Q8JXVTDvYPK/3g6WTKbvyY+TQiTTMEFs0wpBGEfOrnX2eezomjiCAMWOmv0Ol2sIRFXuSUQrK+scHOzg6e51WKKg/u3yWaKb6fhVAqIHlOM2xg+x65jebEeaSpMk1yXRfP8bGFg6XpOapcpRvYLaW3bxKGeo9LkaWAUjFotVpVVjwajWh21EYVxzFYgqC5yGRFKZaafoyWfFmWNELltRAnMWmmZBBtx9E8asUpRECr3dL3VfUwGAqHkopr6KQgpJTqeUenJ6RFziya43gu7W6XdqezxAM048b86/s++/v7rK+v43keL7zwAh988AGjyRRbm0OasWcOM26AioMIaqNdX19hbWOF+TzH813ElBpisig71/mqClFfNEWZxeNpi93ZwPmJQLX6m0Lsy6KkSNLqXhu64ePHj4niiN/7vd/j577+8wS6OmQ79lI10EjZJUmCFMpNtNfrgVTXJMlSjo6OKPOchn6NNMuU4IFQ/O4iS1jp9XAsge+5jAYD4nmk6HTmHKWixAD4nodl26xtrpPmWXV+ueZPI6V2oFU0HMuyKIWiA9QrGvXN4Ow1Mr+rX8c8L2g0Qp77xE0C3yaOZwwHJ9iur4J6vXBKKSlkQdAICAIfieDv/O1f5w//8E8YjeeKnmYb6uRifWq1WvR6vQq1NmO5XhVDSGwXLCEJfZteq8G3/+xH3HnHYXWlQWdFIT5B6GsUTymtRJFkOvE4Poo4PZ3pBukGnreC7Vs4nqCUNrNE8q3v/Ijvv3WbVrPDhUvb/Mqv/FV2dnaQQmgakxrbhT5nNY5U4p/re5QkCWi0K82Umdt4PMb3Axy9LpsmwEoRpShIk4ThYMCDBw/Y2tquAiDbtknSpGpqPNjfJS8Kut0uo+EQ17F1MCop8gzPc0jihJPJFEoIAp+T0xNarQbD4bhSPUnTlFarVaFnBjBxXYdGM9QGX4KwoTThz61tKbM6KXW1s6OqaLMZURxVVZX9/T2lppWlOpCGJE0UJaxcuIYnSUyn3dEyvW41fsx5muBnPB6zu7urexqUN4nreeozZjknp8c0wgaNRkir3eT27TsUhUq2VYNmjCUEq6t98jSlLHNOjk+Yz2LOndthfX2DOH7EaDzGcT3abSWpGYYBfuBRlkGV5Bh/lDRN2djYUJTWsWok3dnZ4dGjR6ysrBDHcUU9zrKUNI34yY9/hOcraXgA21J76dHREXESYdsW3W6HsigoipJer8fh4WHVK2dchHO9txpgwwh3gIXr5JUapQmIer0ee3uPSbNYKxcFFVXOyOwahaCGbkxN4hTHcbEpcS1B2GySRhHN1T7nd77A/sER7926x90Hj5hq+VftefkzsaY+DiT6uKD2WV7fspTMsJEuNb8XpaLmmn3UvJ8QUApZ0RfPfg4h7A/93HUWyVm/MrNvPO2c6opVT762SuRU/lB3HS+rCoCUICxFcy3LEkuUWEIuYkQJQqreEilspFRUJlXNkPp7k3A8uQ+YczBV7ifOofbj2YqNofhdvXqVf/t7/5b79+9zenJCp9Ph+edfJM8ntNsd/bkd5jNVMXNcRckOg5CHDx9pSdoeYaiA4tFwqNexhNPTY5SpdFlVCzxPJSOGtm/mwv7+flU5MP3CJycnOI7DpUuXqoR+MpkwHA6rXjshBLu7u3Q6HVZXVxUjotslyzLOnz/PyckJzWazopSaaoeR7DaVijAMiWNFxzJmqUYkZz6fVwmKeZy5/nmeV/Tnbr//1PF39viZEg2gWji2t7c1yl1Umrpn1XhM0JmmKY1GY4GMlQuZ03o3vgng+r0+nWZL9wOM6fT7dNttwrBBu91mPBnT7XQVv9N16bQ77O7tMhlP8ByHJEmZTCZKwSeJSZOER4/2ePT4MY8fPcZ1XVZWVrh2/RqrK6usr6yzsb6p0NFGA8dR/EnXc1UrRi3gNOcmNMdWQqVkYpCGtbUVLAqODg9paXWeTrdDmRdKLlZXLAzaVjneWoJEB3+TyUTdXFQFJ01TEn0dlfOvV3HsHNsiiSMODw85d+6cCqr1IE+TlLDR0E3vulFfZ7lFXlT3zWwildu7pe6fFwTKmyTLyDKFgpd5VvGmoyjCtmyaraZqEBc2aZrgul6FOkRRjKKROIxOVcPy+toa8+lMXWPLwm00WF1d5c6dO0u0OLOxGRWGMAz5rd/6LX73d3+X/cMjJpPpEn/w7Hg1Y9ZUNxTya+F5FhJPEXQsgajoOk+O+aryJssqUK4fqsz9pKb5hx31v0mpyq95LgkbIbPJrEp4PM+rFguDKji2TRiES0nOxsYGjuOwv79P2FScTaWSkeET6MqCixTg6eCiGXaWDBJtUeK6Dp7nkCbKhVaW6ncGMTEJkOM4mtufc+HSJVzXYzQc6uZcxUO3oHKFns+Ufr6lqymIp3vFPG3je4J7jKLrPN7dJZ5P8T2XVrONk1uEjSa2bZHGacV/zZKcLM4ZjSccHBzRbLQYj6aUeaqQNrGgB5i1rd4oZz6DWbfUdZc0GhYvv/QSq70+Qhb4NmTxjOk8ISkcjk+UO3YpMyWTbYEsbWTZw7bX6a84JGmmqYs5WAWZzBEl5LqPKk5nTOcT/IZNp7dCmhf89Cc/odNqsbqiKJKO4xLrTULxeBemSwZhdl238pooigJf+12Yqx1FEc1ms1rHxuNJdf5379ypyvfT6ZTJbFKV2M1GaiqgvudWjcH37yvaTq/XI/BDiqwwACZCNOj1umxsrOmE4ED5JCVxTYPeIcsTDg+VbvxkosCDfr/P8fEBRVFqilTE1tYmZbmgGxjgpNNVIIvtWBUQpLjgkjBUgXK73WQ2m+G6Dud2tgj8gChWCXYcxfiBcddVii3zaMru7iNarZt0ui1G4wmDwQntdofNzQ2KotCbeECn02E0mrKy0td7o5IBlxI2NjexLdja2uLw4JgsyxmNxhUoNDw4pN/vkuc5GxtrRNEc13MqLX5jwuj7Pnt7e5UYh2n4Pj4+rrjYH7z/AQIIgpBcFsynE5JIVZTyPMcLAk5OjwkbQaVKhZD6+XHF5zZJqUrS8irhOEuFLnJJv99nMBhUgZUBE59//gVm8wmu45IXBWEYVH12gR9WccDhwVFVmRJC4KpMmsl0hu06HB3fxXZc0lw16p47d47RaMx4OiPNMtJMqdDx5LL+F348axKytL/Wf49ZD4FKibVcypY+bG38qPeur50mhlkE6k/ub0BFDzaPXaaNLq+XC4qrBGGyO6GSB4GiD8mFUfDSUUotV6sTed3Ub/ZSlZg8nfZlrtUT1K/q+8XjDMinYkv1h3feeZdbt27xzW9+Gyklnu9z/doP6fW6dDpdgkApo7muw+rqKmmq6E15URD4PmUhuHfvEb7n0e0JPK+JbQmiKGE2iwi0W3iW5UuGd0IIZrMZvu/z6NEj2u32Uoyzurpa9W4YTw6jXGXAj+FwSKPRUC7lvl+BNJPJhMFgUAHUitEQMp/PGY1GdLXfh2G5GJDHxOxGUdYILQRBUCXEht5lXMOllDiuC5Yg1n0cH3c8c6JhPoCUsuJlKalRR6GWeVZlzoYqYRSMYKE0taCwqIXbVDTSNKXZbKpAOmwwHY1Z6fe5sLNDmmUcHR1xcnys3DMdF18/ZzqecLh/wMHBAb7v8XA6rcycptOpyibTDGE5vPryq/ziL/wir7zyCv1+nyBQ1BLP88kLRT/KiwyhOZFlmYOUCKH4gHlRKKMwz1XlwWKh3+y6TjXwbdtBYrF94aJS+NGVG+HYtBohUuvXW5ZFqT06zHWUDXWNG83mUnOzGZAmmTFokaFONcKg2nQuXbpU3QdpiSoQn9WUjYQQ5IlSYzGVhDoyJa0FYl6WJa7n4bgus/msMvIqigKEICtyRuMxlrAosqLagGDBFW8329jCouEHFEnKWm+F+XjC6uoqrutRyJL1jY1ak9eimdRUNYxMXBRFfOlLX+J//Be/TRwnVXD1UeiO2QizTNEuXNdSjWa6x0OCUqZ4Cgxm66Z9WUiMMo55XVCL80dtZnU06mnofbPR5GQ0JAwtXMfRTWMF586dY319nU9+6nWa7Rb7BweKPtEIl4I827ZZX19XQgBZWtEUxuMJzVYL3/eVUZksKTXlrl56llIq+cKywHFs9vf2cB2bZjPEthYuoUKWOI5bVR9zTb3JS6UMJIRgPBozn0614rlCppRakLpOZaGC6HpF49kPWQkodNo9+u0ek8mUTnsdx1ZViySKGZxOefjwEXfv3uXu3bvs7R0wHA4ZDAdESYTvexRlgefb5KVqNjdUxCRJmM1m1Zgx880E757nsbbS59LOFp7jMJ1NyLMcKQVZqiSDJRFIRRERSGxH+VAYDfxms43r+OR5ihAFlq18a2zhU2rk1nIc4iTG911+5Vf/Gq4fMo9m3L59m36nTSN4npPZFGVi6HJ0fMTpySnNVhNbV37yPMOybCYTJeBg1m7XdYjnEdOpoqy02i1Ojo+UF0Oa4zgekXbuzrKM/kq/GmudtkLHut02cRQThD69bo+h7yoPEyTzmUr+11ZXKPKC+WyKEDaeBhVOTo5xPTWHZrO5TmIM51goxSEgCBSqr8yopPpc0UyP9YTRaFjJPEop2d7eqhD8pl4/g0CtQ9PpTDefSyxL9YWEoa2D9hDXcXD02pKmCbOZarpuNptVcDAcqWbxNE0r09gbN65RlDCfRzx+/BjPc8kyGylVJW00mvLw4UPKUiU1SjpYGWulieqLuHD+ErbtsL9/wHA4otfv019ZZTweIWWpKL6U9Hrdav02TZuKHpbpvsaFIk1RFJVCpGVbFGkGskAIRxnUWhbj0Yg0Swk0Bdpx7IpKappsQVbKMs1mk8PDQ9bX1zEu3WbtNevvaDTCEjZ5roJZg5h6nsdQgxGGS24CV9PTEkXRUhCswCkbWUoolHhBKSVYECUxlg7ekiInyYpqLbRLiVWUSpntGcsa/7EVi487PpZWKxZ9aer7j3+dZ/3I9WTB/GsqtHV1OCnBtpbpVMvJxqLp2qidqcfp66yif1SfhTb3Av392c/DIslAfwmQuhqgyVb68dTeW40Lk+wsJUmiTrVafH6T3BlfIRPLqt9ZZFnBrQ9uq/VHn4NSnFJBe6Epv7ZjY1t2VUmQUnLx4nkuX77MxuY67XYLYQl8PyRNp5yenlZVWgO4TyaTig5v1D6NOIUSqxgqKrVR8dS9t8bnyIDLtm1Xax0oEObhw4dsbm5WSYFJKk3flhCi8r7wfb+KjzudDt1ul709RQs1AhOmsiGlYkm02221NpQluVz0Gz3L8TMkGjmObSsFCY2qxnFCrJWQjL9Bo9GoeONxnCC0Ws9sNqcRNsjSjNlsThKnVcnU3HzfDxgNx5wcHGFJSKKYeB7x7rvvkiQpzWaD4WBYDZAKtUwzkjTBcVRp3/M81tfXee4Tz9Hr9Th37hyNZpu11XWF8mdK69k0SSZ5AgKSJKeUapH1PA/bsZClwBY2oixxPBfLVucjJRjXZXXBPSoVCNVxaWYVthAEjaZqwNQlJ2PW5jiLCVunmxlUTiVlDkYtSg2eBTpfloUKjvVNbzQaPHr8mJ1z57BsmxKpFWYW8sEV/zpXk838nCQJg8FA+Vsg8XxVNVlZWcG2bApZ0O10abfbbG1tUeQFjuvo4BGSOCGaRRWv7+joiIcPHyqUbjbHKhXHcTae8kd/8Iesrq4oEQHfx2+EjIZD0JNDFiXCsrDsZdqR7/sMBgPe+OwbvPDc83znu9+tZOOqNfhM3F8vI1feALaNZ3k4jlKcyXVCqFvNqueaQNO2FUfd/O7sv0vVrtoO8HF0IFmqhlWz2PuBj2Urap7reXziuU9w7do1ToeDCrnu9XpVBcosmo7j0Ol02N3fxXZUc+m9u3fZ2FjD0pQ3lSSpi2Mcd/OiUJiUvu7Hx8ekWcLm5iaO6zI4HeHYDqCMK73Ap9VqcXJ6CrqZWiVxigN/5+5t1VR+8RKOraqL0XxGWRaqef9jrs3ZY7mEb9IXoYyf8oLxKObdt7/NrQ/u8ODBA46PjhiNR2oRzjLyQpkZqU2sIPA9uv0u125c4bNvvME//+//XxwfK8nsoizJs4zxaKxEIIocz3V47rnn+OrXvsq777zDl7/8FT7/uTcYn57y9jtv8Wd/+u+JszlJluL6gWq4L0vdYE5FBxVCkskUISTTOKcRtDQVLMO1BEI6SKnoPXmhaDWOsNne2sIWgnfe/gkCyeWLF3nrhz/EAlzH5nQwIAwbzKM549GYVqtJbJIlre5i1hJjdFcWZSUMEccRDx8+4Pq1awSeRxgEzKYRrVZT06JUA/DpYIDrOhRSIW1lUTIej/A01TLwPJIkotlssb6+zmg4JElTVldWlDpVoXjYjmMRNkIkbkUZbTYbVUKQxHFl4jmZjGg2GxWiZnjJrmvTbKxUDsS+7xHpviUjPmFAkkbY4OGjh4rWWhQgSuJYVeziJKLT7aheOsfBMsgysLu3pys3WbVGdLsdDcYo/vVgMOTk9JRmq0MURcRxRKfTrqpfrqvMCpNEUZr6K11OT44pZUmepTR0D9XpYECrqRK4XCcIQRgCyu/I81yEBXGsmojXVteUlHSWMxwMiaKI8XiMLC1arTa9bo9up0McJxwdHSp1INciy1PW1lc1Tc6m3e4gLEiyjFarxXikFOWiKFoCfLqdLpPJmFJKwiDk3t172oU8I0nShYhIntPpdhmPp3o9ldpNXoFoqtfDRpZU+19RFjVqohEwcMl1X8hkOlF0otJRPjm2RV4WTKZj8rKgLAqSPKXQ7ILcSHdLEFg/UzHjWSqq//MchvJrUHyTFMDZt39aNf3DjsVj5RP7kjnqZsv6ocvBuyUqZT4Vg6jFdEFtMj2AOkFE6DjINHHXEw6q/bWsqjaGFlbqhy2sAM5WMZarKx+y54onn2fATkD7CQm9lwuKrEQIyWQyrf7u2LYGHUEI5UpvaLtFkTIcTtnbO0IIwbs//QDPVSIla2urXL12hWazwfkL5+j3u1W1uNFoVLRMBUh4WolOsYHa7fbCIFT3V8Fi/zDJugFRTBzTarUYDoeVAqixmTDgcBLH2Pr1TEXCrJF+EDAej6v4r9PpqDVTs3CMiEOv19MCE0rwCUuJFClg6Nnmx7NTp6RNnkpcR6ks9TorJHEOhcVgcMp0qpp+V1dXK93f+XyO4/pVw/FYKNSiyAuNNjVwrZBClqRpwbsP3lc6/J5Lv93iOD/GcWzmE1VOno6nSEsghVXxyZrNJs12h3O9Pr1+l5WVPlubW7Q7bXzPB5Sc7Gg0Ji1z8kxWGsmqtNVEaLTSdRdd/Ja+mHaFlC/M9AotPWdJjYSLugyc8TPWfQNSkpf6N9XE0IuAWCy4ho6lBje6fbREUlBojfpFMzLVDS7KhXkVtkWn3+OnP/0pd+/f4/KlS5zfOa8mZUAVmCpnzowoiQHBwcEBUaScbw2Ny7ZsbGySecJQDhWq6bg4fk072tZOu5bWxXckbscmDJVL5nPPfYKLF89zfHzM0f4BJ3uHFFnC66++wvHBPi984iY7OzsUwPFoiGc5uJZSrlFjRPH8sZT6kpCoPoksxxKCX/zFX+Dtt39CmiTkjkOWF/raKl782WTDsizSLEMIB1mA5Vq4upFTbYaCQuZLC5p5rjrnRTPeklGNUO9ZX/jM4ve0jaBemjaBxqVrV0mLgiTN8BohSZGTy5woTYjTGM9zAUk0m9HpdfEaAXGWUMiC0XjIxvoGrVZTuaraDkk05/133+Hq5fNsbKxDaVM6irtiCQssSSYzEKrJ2EZ5KHzvzR8gsVhZW2c8mpCkGa1mB2E5FGSs9noEYch0OCIQNi3XZYBEUOJ5Nq7nksuUoN1EWB5JnNAMAwS6gV7oUXxmw/i4DV1K1XNBKbn/8CH/2//d/54yL8iSjCzNyMuSrMg1d7+s5p8QkvPnt/jUp15jOBrxG7/x97h69SrtdgvfD9je2iRNMv7l7/wrfvLjdyiKUjmq+x6ttsuLL77IP/4n/4idnR1ybRhWliW97g6Xr10gSSO+9+b3YDJVVcJcNboqSp6L57ua5hNj46lANfRxLJW8Oa5uxksypKXN63QzpW07tJstTo8OaTabCi22BO+8/Q7T8YQXX3oJz/EYakPNMsso0gwHwWq3j+vaVYCYZRndZo/xZEyaRPjNJuPJCNuyaIQ+B/t7VSUsTVJ6/V5l5phlGXmSMJuohkhZSjzHYX1ljQcPHiiwx3OAkiyJmU2UX08czTg+yiqaJ4CFhyVLyiwji2Olsqf79oIgUE2xWUa/32f/8WPyRHv+SAdRWriWj+cEhIHP9WtXyPKc8WSC6ysqTpZmdMIOAkuDSRnXLl/m8e4jhUjaEAauboCUpNFMiWN4LRzLJ88KVvp9Go2Qg4NdwqCHLJVPTbvdYTababnglKOjfebztkIwk7RCT5M4pt/rV03os9mUre0NLEvi+Q55kWHbPiWCZrvHfDbnzt0HxLHqhWu1m8RxpB3YfdJUqSR6rk/gzomEqlaa8SalpEwlUTRlNp7g6wqEbVmEflAB5GmWcnIywLFt/CDAcRTrwPMd9nf3ydIUKVUfi21pU9Q8Y0/sgVReVIWmoWZ5icSqwBmTlIxGcwpKZa6mg9hKw19KykKAtClLqYMlpS51cnKC43lK/l2jtUDFDcdQcKp4UlTNwRg0HVDy+FRS8/+xx19U8vFRCYIBKMtyuWqgH/kRr/pRiksqYVm8Tf37RW9HnT2gBB8KhBR6T9NVBR2rWLao+rXQvbnSnIsUGlyxqvdD916Y6pcJ3hU4CpWsbu1Uq9jozLkv7ccomwRTEVMnYihXT09KLEszGEx8VlP3soQGX2wbYdkqTtNvJ8tSy81bShJdqnfPNM2fUo29JMuZP9rn4WO1VttWzupam/X1dcIw5Gtf+xqbm5uVeIOqLLsVLdV8FsMuMVRPU7UwYKShzZ+enrKzs8N8PleqVp5HT8c3thZo8HRfrRHNME3fJuGpYj1TudHAuxF4MD18hh4pbJsSlNBIWTCfTlWP2ObmR4xDdTxzotHrqm746XTKcDjiRz96q1IDcl2X559/nqtXr1Z8cbVIqgFpaFRGwULRphqqKbHmCv3gwQOOjo7IsxTXEVX5x3VcglApPA2GI1rtjtbLb1ad8yozLyoJVCklaZaxu7vL6ekpn3z9taWmYDMA69lwPbuvJl65UNoyEwaE4lwXunihy22gMlCEoEQrAglVpgYdYAqTLJRVNmt44bZtLwXHJggzlCET4NcR+np507zHxYsXefjwIQjB7u5jjo+OWV9frxD9hQKYUnoxzpGbm5tVw3+9KTtJEmZT5c3geV71fIXixRUCVhQFjrOo8qSpqnKdP3+eG9euI7SUrmMrWkil3S9hbW2NX/jGN7h35y63b93C1tc0T1OlamUWBcuqSoufe+MNrly5TBS9qzYxmVZyvRYslTXMPa5KjUVBs+FgOzZZllJKJR+Ktbywn12wTNJRp7FJlt3CRe0efzTipK7V8ckxN154DlvCbDInCEMm4xFpkjKfzYjnSt+6EYTs7+1x/cYNev0+M62Ic3JySq+rGpiNkkmSBJSy5Jt/9md8/es/r5DWwlpcEykVrU9KDVJJ3nvvFo8ePabZbGNbtg6qVPk202Pv/PkLqvJxeKQkMKdDkAVZnrKyssL5C5e4ffsO6+tb5EXBZDohjZPqWiKlqvZ9SHXo7PWqzwHz9Nk0IprFUErV94GgoKgQMdtR7tCe57J9bou/+o2f45/8l/+YaD7HddX4zYuc8WjA66+/ikDwiZs3ePDwEXGk6KCdTpv1zZ5C3MqCo4MDLK3sNp/NaDZbJGnCyy+/zOrqKt/73nd5+OgRlq6mKXliHUAUGY7tkKYK0fU9n7IoaTRCjZiV+IGHclAucF3VJBkEIZcvXSKaz5TMcJowjyKGwwHPP/88p6cnlHmGLAriaK6a/tKU08GALEtpt1vVJqaohymOlsdM0wTHtqsGTnVLlBeC4eXatqN7JgKkVEpNQtg0NOVVCIHnKmluZImwqGixhp8vfF/3jam5bgAN85mSJMH3/YoeYJzmsyzjpZdeIs1SHj54wP7+HlevXtVrvE1R2MRxqTZWx8GxXFrttnLSLS08xyXSqjBlmXP16mWlQnh8uFCQk1Q9LAfjAy5fusbsaIosVaJ5bvsco/EIEHhewOnpQKmYTaesrq7y2muvK7rTqTKI3NhYJ5nPlbhDlrG6ssL2uW2azQYrqz0cx+X4+ISizMmygjhKCMOQvd19ilLRZ4tSItBUhU6HOIp1spezu7fH6fGgktyNooh+r890ppJc1/UoCyUjbkRDylJRFy3bVqCU3r8UTUoFT0hFSVKqgrJCVfOiWCDEUtOEdXCYpBlJWlQiA2VZLvo1S6UKuSSgYNbSUiCEs7RvTWaKniHjWO2dtR7Os7Sdal02qL8aTRUIV/+N+tVfPCXqP4Rm9bR94KNfRyUKdRCmjuI/wzuyVElYev8nTW3NY8y9N9f+aUImSx9Rv5XaF0GIZTWopTGgPZQqZamPSdg+jCUghBK/WEjwLicW9Z8rBbNahaRe8az3bpbm36KewGmvkbJU1NBaLNftN7lwYZNWq8WlS5eIIiVy4PsBrmPR63Z0j0daxal5nrOysrLUY2lUDh3HqSjpRsXNxBsm5jFx487ODlKqXqherwe6ZzIIgmrNF0JUzAdD/zRiP6aPoyiKijYcael608vhaHl4IRZ9b3EcV/tbVeF4huOZE435fK4cjCcTtre3abVabG9v47puRbOItIlbPSuyLONA6+C6ilvm+Z7ehK2KJiSl5ObNG1y/fo2iyFAsC+0lUOszyDOFWpvAFliaFCYoN59jdXUVgOFgwPr6ukLI9SS0HUWXMD4ZllClQpX1miYlqZV2pHpsUVaD3JKqb8NkfgZdCsIQL/CrRpxOp1PpDkspFbcUFvJkcUwpJb6+cWYCmMzWoKj1CWS+qgRFLDSRu90unU5HXZssp91qV/JpxmbePA/g0qVL1UA32asZgCaANkmflLJKNoyagtFmVs17aTU5jIGY4RBbCISlAh3f8ymkajjOta5z0O3wv/rNf8i/+de/qyZUmpLLklSbBk6nU7rdLhcvXlAc6sDna1/5Cg/u3yfPC5IkpfwQimvF18xUwGqCGt/3VRJjqk56TJnraZI7U1I+q9hxtgG9nrwajr/52aiBmUPq8x+NRhR5QaDpHZ1Om9PjY0UL0IFtu9Wi3+9zeHjIJ55/jq2tTfYeK2GD6WTKYKACkH6/z3Sq3HwnkxHj8ZAomvNzP/dX2D63rZs1y0ohTOox/fa7P+X73/8BQRCSpgVxnCi6Y6Oh5rAGCG7cuEESx5yenvLgwT0ODx6xubWFlCXtTp8gbCGFy+bWebI0071NqgJlGNPWAjB6pmOx0VgYz4syU54PpoBvexbtdgvXc0jThN/8zX/IK6++Qr/fpdNqMDw9YTabVY2pRvGuKNQYHwxGOLbA92A6HeE6JbfeP2B1dYXRSFGxjPb9ZDLh5PiITqejeLSBR56lpLESRrAsKnqjmVe27WGkn817FoVROCrwdPVV/T7Xm0gXy4K8yDg6Pqwa0VfXVijKjOFogC2lUiZqBEhK5tGMRiPA97vM51MsCzY3NyqpadV30Kjm9mAwqMzDzBxXnF61ITWbqsweRXPd22CTF6oSJixBp9vi2rVrbG9vcXp6wt27dzk+Pq7Gue/7zGbTaq0za5QxozLvabj7o9GoAjuC0FNUofUVur02pSxwPZsonpMXuV6rwPaU+EWaZfhBQBFnpHlCXmSUqCQoGs0py4L19Q1u376Ncf+1LBsQas32XGxbMBoNlRyk57C7u8d8PscPGoRhg9lsRrPZJIoSJQ/uBci8wJISRwhcrdAyOD5iMJ5xeHSk+j7yjPPnd5BSMJ5EICXj8YTpLMIPm6Rphud6lKWmBWcFeaQ2/SJTVTqETZzlzKJEuax7AUenAwxtFZTCWz1YSrXgiKhVUU1Phdo7FdJt6YTXcMGFpWSS40yZx5m+DbMW5kUJ2Ho+L5SNYBHqS6nmrPmtlKaaWQNghKqQKcBGVUHMPv4s68LZIPQv+vjZE4S/+OM/9v2ePIcnQR6zZxtw1TzvaQDaEwmPqKV5T0lezGFev/4ez3rU38+yn2QO1M+jelx9nMsS5DI4u0iCls916dx0AmX6IuoArO87vPjSTX7xF/8qtm0zn88Jw5DpdEocpbQaKu6aTqfahHghdmD6kgENyi8qLKb6YNZGQ20y1YWtrS36/f4i3gwCCilpNptaQGlSeWaYhGUwGFQJ5FknchPnwMKHzIhamDjQOIcr405Bliq7iMpC4WOOZ040vvKVrxAEQZXxGj4/qJuQ6iYTc/MXBnuZDkodfN/VtCMVchiAv9CmJ6Z0I1Eoa6510c0CqEy/BNPJtOo3qCcVqsHVroK6slQGS7at0NmZbn6sB/FqEa6XMesowPJE8T23eq6UspJkdRyHXq9XZaCTyYS8VMGzyWTN65pg09xYx7aVVGi18C+UfUzjTt1C/ixt5+zEqAe0RaF0903vzMrKCmWpmgtHoxHz+YE2ANyuqh3GaA9Yek9zb4AqQIiiqJLFbLVaNJuNheymfrwZqJ7vketMfTyZMNKa0rdv32Y6mdBtd3ju5k3W19f4hb/6DSUFh1Du1boXxowBpU4TIcuSz37mU/zrf/3/U41NroNMVZJ6dnE1i5wZfwC2pXiGetl66hgwh2pKXLzuooq2kAusP/8sGqTG05NovYRKwavR7mA7Dp1uF9u2SOKYLE351je/SRzH3LhxA8u2GQ4GXLp4ibt37nK4v4/ne+zt7bG9vV01qSmZ05z5fM4777xDHEfcvPkJLl68RK/XraqM9+7d4623fszR8YALFy4wm0VYwuLw8AjX9Wg221CqJPvchXP0ej0ePbjPbD5T1Ufd5Oy4Hqtr65RSuaJubm0zj+a4jsN0OlssZh+yEX3UZrrUIIp2tRZgOwLbUv1H/V6T/+If/a8pi4J5NONTn3qVCxd2GA6HnBwfMZlMdOUtZzKZMh4rbf/5fKY10SO9eQR4roeUKVubWwS+h7u6Qp7linaHZHWlz2Q84fjoiDxXMt3j0QjfczWbQYEU6v4boyqJbfu6RJ3rJjqp176cNF0IJ4BS8+t02gyHAxCC6WxKGAY0my1832NlRVFzpqMh3W4HKSXtdpsoUhx73/fpdtvVRpplKSsryulWySirhKff7+v1qKjW4V6vq+d2qtXjJOvra5oao5x8y7Kk1Wpx9eoVZrMpjx8/4sKFC9y4cYO3336bt956q/KiiOMEzeahKAqljqYDctNgb+QX2+02R0dHXL16lcl0zO7u40qxqF6RbYQtBBZBGOA3lFJLadZV2yJNY4RtYTkWQtgUaclsOmEymvLcc89z69Yt5nOlST+bKSnHc1vbnJ6eEMexMnrUVZvRaEwpJ3S7SlHr4ekuSZzQareYz2bIIlcysKMR165d5/TkFNd1Gc9jBoMRWZ7RbLa4e++hkku2bF577TWkLHnzze/juh5CKKlm3w/J80SLVkhdoS20qhiAqEzVhFC0lixN0dESZQ0kMvNLVSJUkm/u8SJAUwmBLKUB0bVflXqtUo9dQ0sRwqxvQu/jiuZrnq4+h5nX9QBVV3mr5l+zAKhm9VKa118o4ZxdM/+XCvqftk4/y+POPrb+97OvcbZS/rTH/MUnGIvfn/2c9S+j/gkLGVuTHDztvlT0qqe854edUz0p+Lg94Oxn/bDPUT+3+uev9mzdwF4HaRffi6d+NmFZiNq9UrRJ1Zd4cjzg3/zuH3J8NOKXf/mXSNMYZ8MjCEICr4FtORV1KgzDCuy1LKtimJjPAaaHyao+swFkzH5u1sx79+6xt7fH1tZWVRGOjNqjZqCYeVQZqupkxiQSvu9Xalj1fmcTt5nzNIJExiXc07L2rVaronM9y/HMiYaRzDQBtm3bnDt3rjIE2d/fJ4oiLl68yOHhIdPplPX1NcJGCEJSlHmV9dqOqnbIKjFRfL2iyHTyIcjSjDRJF4gyMBoMabba1WcyF1M1zCk51SSJqywwiqIq8LKEUGZ1uiESIYhNBcYRVQBggkdTETBZsUBQZKokZaPaUk31wXwWk/j0V/pQm5hm8gqhgiJVtlefya4aNXNVWall/HW39bPZuvls9eNpGb6tUWshRKXEYs5tNou4ffs2+/v7lWTlbDartJxBKY2YBGU2m1U0KePYbgLW/f19XbFa+KaYCTIYDBQqGkfs7x9w6dJFLly4QBiGyqAGFQgl84hbtz8gns8ZDk+RpSSXJXGaVGoHQFU9KbKMa1eu8sXPf46Dw0M9MSBOUoqCavGDxYKTanM5g9q5tXuoR9XS9ayeq7fUqjKiEeG6p8nZikZ90ai/3mL8qvfLs4yj4yPWtrZohCFZHCuO+zwinkfcvXOXNE05OTrmjc99jvd++lM+97nPc+3aNQYnJwgEaZxweHjI2tqartR4xHGhXOF9l9PTU9783pv85K2fVJ/x+ORYK9SUbG2fpywVTfHRo8dkWaGdwR2SLMF1HV5//XXKsuS9996j2WzSbndIMxeJkjdutTscHZ/S6rTp9jrcuXeHoiwZDgfq3HXs8WEb4EcdaoPJAIFjO3i+4i42Gz4r/S6ra6vcvv0e3/jG13Eci+2tNe7fu0WeF4R+gG1Bu9XUPRQ2W5sbCCG4e/ceq6srPHr0kPF4RDSfsbOzQ5pG3L9/F8tSVKFU0xwNf9xIEJqF3CgtuY6LcYg3zrVZli6dh6NVqPLcONir5NnVNCQ1VxvYttKYz/Os8m1wHJtWqwlIms0GWTxfJDvjkVYhUpUahDb0k5JSFkynY4QlGI+nyt27LAnDAMtWFUbHUeXzo+NDADzPodEMSJKUIPQRwqLZbLG1tVmt/+1Oh5PjY/b29iqVoy996UtcunSJb33rW4xGI1ZXVyrgx7Is2m3luN1sNhkOh2RZRhAEtFotOp0OW1tbynTOdhCOkcl2ePRwlytXAqQs8T21ltmOiy9RnkQ1JSPL9pBlSTSPmM4mTKdKslcUJY8f77K9fY533nmH0WjMdDple3uTsOEzm09ZXVml3+/z7rs/xXU9HCcgilOGw4lW8rLY2Nhgd3dXU69UhazEInv/Np1Oh5PBgPFsTl6o6uDxyQBZQqvV5gtf+CKj0ZBv//m3mE5nIAW27dBoNDk8PK32wjyvVxJ0xb4sKYrlZP0sRens+gULGQX1B5DVOldivBuemHNoXwdDQdKVSGn+J6uXW7yf1I+vg8L1934KnamUcunPTwNtnvX4sED/Zzn+QwP8Ouj3UUnIX2aVRL31R4M99SToaf/W9zr1aiwBSB92LvX9sJ4s1D/HhyVdS9dMUuvPUUed1XL2PtT35aedrznqSUj1fal65QzIWgcWi0Iwm+Z8+1s/YOfcJT752qvEUYHnKdR/Op0uydAaQKXOQImiiFZLeZHNZrOK/lSWJe12u6JbmZjKsDA8z9OeSD6O4zA9OanoTkVRVIkEQBAElecOqFjeVFRMDNfpdCqDQdPHYRzNTRJSlkrBSgCRVr571uOZEw3jPGyMRcyNMRf90qVLmgN7XMnURXFMFM8r6dpWq1XbZAssbdhSFEXF3U2SBNe2lYa/bVNIiNKEo6Mj7ty5zQsvvcyNGzc5HQy4f/8+nU6nosGsr6+RZQueumVZ7O/vK6TS87BrmZvhBSt+scSxBEjVrPTg8WOSOGZ1ZYVEI0NGXnUyGaPcIwMcx60SCIPsK9fZkslstpSclWW5kAKTkjzNVONsaqTXLFVCtrVzph7YZ7Pep02Ip/Eozb+GFlafKOawbZtLly7h+b4KPDSSkeU50XxeSRfWEyqDhtUbiHzfZ2VlhaLIybK0Sj4cx1HGZUHAaDjCFhY7W9vYWAxPThmiJsHq2gqNxhoHe/t897vfQUilL7/S67O6sU6pk0+TdJkJUKQpQkKn2+G999/nnXffYx7FVfZdP+qoQZZlxFGEEBZho/GhY95cX1NRszjLG346GlX/2xOl2NpRlhJhK0ToYP+Aazdu0u12GZycsLmxya333yeKIlY0ZaqUJRvr6xyennB6esr169c53N/n1ge3qsR6MpnQbrcpy5wg8HE9R8l3ug6yECSJOvdSSubTiLIAS9gEQUg0jzk6OmI+j+h0ujQaTZJYISXPvfQiW1tbPHz0kNFoyMbKKpevXGMwHDIYDLhw6Tye7zMYnXLh4kWKUqk3TafKAdUWanNQTZxqDtQ5th91D8y1tB2ldtLrt/gHv/Hr/PCHb/JXvvplNtbXcGyHQJeV5/Mpo+EJvq9oSUdHh9iWpRSwojkgODk5JghCjo+GzCZzRqMh82hG2AiU/027rRFWi2iu5vJ4NOLg8IBet4cf+GRpQjSfMZvNlb6KBVAopRaBXutUsCY0Woyer67jaGABJAW2I7BscBzlJ3HhwlXChqIGeY7SUJ9Ox9qtVhJFM2xbqd05tUrjZDKueudKqeSKbVslJ2aTNP4Lh4eH1TyOE105LnIs3QCeJDFJmtBqtbRPhk+n0+PixYs0Gg1+8pO3efPN7yllom6XJFFr73g85ubNm/z8z/883/nOd5SzddOqKq1pmir/HduuNs00TTk+PqbVajEYDPSaZzMYKB+N/PCUPM956623K5M+UIooOxcvYNk2K6srrG9s4ro+SGh3WuR5xt7eIx48uM9kPKbTabPS77Oyssqv/ur1ihYXhgFlkfALv/B1ut0+62sb/Nt/+/vcu/eAk5MBo7GiILiOy1e+8gUlS5l/j0ZjRlaW7O3tcTzYoywfs7Ozg+M4fHD7LkmWkuUFw/EUgU0Yzvgf/sd/yXgypCwySmXrrv6VxypOt570CSjLUlcd7CpJqK9DlhYSMU9Rv9eBlZpAH0pXlHWuqXyKIOyHPLEOcy0HrtQ9fJ88Puxvz5gXPGvF4S/q+LD3+7j3/ai//y+VWHzY8bRA3xz1cWV+rrMbgOWAXkq9xn34652NUcxa8FFVl/pRB/CKolhKNMxr1+PR+vMWlbuFAtXyeSwoVvV4SwjV+yOENrasJQjKS0rgujYXL+7Q7/ewLMjyCM9vIITNxsZG9RkNk8YY8Rk/GiFEFdQbSq9JTEwlwlCcjMeQoeGbe3JyclIJbpgY3cjiKmDLqc7bgLTmbyaBqcf15vMakN1USgwVHCkr6v+zUuCeOdEwN6X+r6H2mOY0E5R6nqc490FAKTOUFvgJjmNX5ZYwaOI4bnWxp9NpRW9oBiGdVptWq4njusTzOY8ePqTIciajMROtub22torn+foCKgfFJIkr/q/RfpdSKk5ZoZDGPC9IvESXpjIEGb7n4fsege9z9dIFQFJkCYOTE4VS6oFRZhmT4YAwaNDRJiizOOb+/Yecv3BRcZKjCM/3qgDD89TASZKUNEnJ4oQ8z5iMxxwdHnJ4uM8Lzz/PtZs3KctCIXkVb7Cogl1Qi7gyntHVEUspLD1twkopQTcXmrq41OVvy1LqUI1GyHweUZaFVqQqMKVEIzmprqF636LQ3h21wF8IwTyKdPBIVe6rNydbtkXgByrILQrKXMm3CiBLM2iEdPtd/ubf+pscHRyyt7fH6sYawhIEgerpKcoCy7JJ4pioLBkPRwxPB0RJwisvv8KdO/eYzSO9OCzvW4tFUX2+KI7Js1w1uqqrVft6elWjnljWy5pSKk5+VfFgoRC2jBJRW/Q0y6AsEcLi6PCQ8XDM1uY5Gq0OFhZhEBLNI/rdHv1+nwsXL7Bz6TxJkfGDH/yAr371q7zyyiuMxiMO9g9wfeV/EEcRliU4t7NDv9+l0QgVd1vazKZT5aCblzi2x2g80uMz48GDh5Sl1K6nDcqiJC9KVre2eOW110jSlLd//BOajSZxlJDEKXGU4roBW1vbTKdT0izjueefZzafIYTkcP8As8ibG/LsgjC1oEeoqmcYeHzj61+j223y1a9+ASlT9vcfQqkQl93dhziuoysMGfMoIk+LykByPo8qfqoKnDuKCiRLzp07RxB4tFpK4cnzfN1jYZOm/3/m/qzZliQ7D8Q+95j3fOZz55uZlVlVqBmoAlGYUcXRmsY2vWkw6on6NXxRS68tmainbqFN3aYWJE5iq0EWQIBEgYXKrMo5b975DHveO+Zw18Py5eGxzzk3b5KQWmGWee45e0eEh4cP31rrW9/KcXJyjPl8hiDwqLK27+PW6SkeP3li9OclQlNYCaKVlA4CyjVTStkom5ACvvCNlyqEFALS8wCt0DMF3zjPzbbXeKkoSrggb5YQKJuGCmkqjQcPH6I5v0ASxwgijySRqxJS0ZpNlYm3EEKirmq7WYVBBE+S8liSRFitalvkCTCbrBRYzOeoqwp+4KOuK4zH5AnL0swWG/30009NhDPE8fExPvzwQ6oPMZkgN4arEAKz2RylkSPPsswmLAZBYLx7wN7eIabTc1pLJW22Ukhstxn8wEdZVbj74AF+/OMfY7K/R1Sjmoz3oizgeRKnx6d4+613AAB1XuD4+BizGa3rd+88RFVVODt7CaVKvPvue6gqiaoEvv71b+HiYoGiUHh7fAjP97GYz/GTf/vn+PDDD9FLEmyyAlvnmZRq8OJiSsnXDUX7paH8ai2QFRVRMNFACiO3KaSJEghwDZ2OEWHXEHIcWeU2wbOk9Sobd+/OLKK546yG7QontDE0HKOkE2HY8frCDVq4IQ0HmF47l50rWCtk95s3U2d0xwBiq709rserZs9zb/U6+P665zHbgmvMcdtE5z3wIkf/c5+0XcvEjU25se/4suILvse34NOu+eKrDAK+eltnqZs0vhspIJBvjAk4jiPB7ejmAHyRgeVGHVxM4zpXlR3LrrPVo3IDdlTSC2spUUTv4n23NXYYz7bCP7s4l1XaBv0+hqMRMXXiBHfu3sKbbz7A0dEBgtBDvx+T4EYgIRDYemX8/ExtpTy8xhQmpbWOC666QjzsVAWIXg3AUk0ZhxRFgclkguF4bK9hc0/BGFJZg4H7i7Ebf8bXdpPQOS8FaI2aqqrQSxL4HhXa5iLQX3S8tqHBL1nrVrufG+cujOPx2P5OXjUf+3sxxuN9NHWNfn9EHGvdVhnnUPTp6Sl1gueZxZkoNePDA/zqD75v75XnKZIkNkUCazRN1WkXGxjcURz2UbpEkgyszJdqGvSHA/i6wvTyHOfbLaAaNHWF6eUF9vf28Wd//u+xTVP8we//AQ4ODhBGIcZxjM1miUW6QJT0UFQa+8MhqrxCFA4wHCYIQh9VXUMKiaJsIEVA1DAvRn/UR55uEQYhelGIJ599jPd//pfI0jW+9WvfR1MX8P0AQpMkHKvXVLW2eSpm+pEmOYhTu0vd0ZpkR2nyePbvPHCoLzOsVpQ8FMcxpCR+OC+g/JMmBxXKabTEek2eai5IQxzCGDCFk3gQs6UuhIBqGty5dwdhGFGOjhBGWpik6iJQSM6LQuwdH0GaAl+e8GxUSgiJdbnCcrFEoxSObt3GcrHE7//ob+K9X36I7Gc/R1k00GWO2qk3YhcpCZRVg7JRKKoKwvcoqmB2E7HjimPvRtMoaK/1dABtKFgIqhIvpaRkYDe6obQFGeylZQ6CBml4e5DQRYPL5xfYm5xgvH+MPKtw6/QeHn3yMaqwxPhwAj8JUHkNjk4P8fSzx/jZz/4Sv/b9X8O3v/cd/Ns//zMCnzpEU1WoyhIvn7/AZrPGZH+MKI6gtACkQDwaoSwa9GWIsL+HPC9MVWWJ0WiIXn+Aqq6QFwXiQR/f/e3fQjAc4Kd/+hPURYGDyR6m0wVRs6oab735JgaDMT746CMcHd/G3uEpPv34I/hQeP70KT2/8X8KRxL6uoP3BDO8IQA0muiMHoB+EmM0SLCan6PfTxCFIcIoMXUNZthulrhz5w6gNcIwovnnkRqZ7wfo90kikNeo/iDEaBxbJwkvvATyKTeB85qUavCNb/wKLi4ucHxwiOVySQuyEIhMxBcwwFAIkut0FnL+GYQhYNapqqrgex5qM87YMzUaDkkMoCxQlCXVrAhDytEIQpR5iXSTIY4k0u0GBwdH+LVf+wH8MMKvfPO7ePL4MZ6ffY68NtzawMd6saRk7rKiqGwYAJCoqhqr5RrQAoNhH6pRiOPI1EDwQJK/EZbLBZqyQZ5uqXZNUSCJY/TjGNLzkZ5lyFNKkp5ezqCUwovnL2lsSQ8XF3MopVBWlKdAUWeBRq0hhYSGIInXOMHde/fx4uwS59NLJL0E6XqDRjU2wsZRzbv3H+JXvvEtxHEf0/M5tVl42KzWuLi4wHa7wdHxMdarNZ48eYKq0ljMF5hMJvj80efYmET1sqrw7OVLXFxckJKV5xna1QYaQCVauoaNas7X7aC1mNsA/aYBBOWH1I02zgdK1rZ0Dm0GOYNoodFworTFWFxzgA6lG8uJZ4lXWqdaUPnFzvJu9MFONv7/zgU6kRI43nC7ru5c/nW99dehZeFM/s5XHagu0AmZ3Ay628WE+6lrOOmd7157a2tZtWuWY7WIG6535RruH76of662S7v3vPZ77tGNeO1Stlyjc5dmRI7N7t/ba16lH3UiHVLTPO6M352xZKRzATjCPNf0gKZ2KsVzRxjMYBSk0Bo6ropcY8oF2DW3E40IUNcNQlPGQGllZeOFiUAHQYjxeIwkSXDnzh3s7Y1w6/aRVYo6Pj62gjnsNK3KHL1kjLpUCIIEulFG9bbFCVVV2YKVrATFLJ6yLG0eLTssmOrEORg85waDVklwMBhgf3+fmDnGqcXsHvdgnOImdbNBxc5SANY5z8YORznciBbjn7IsIQ12f53jtQ2NPM8teI+iyHYiv2x3wHHSiSvJGgAQcVtl1+0Ed0K41xVSIBAhJkZbmGW/0jS1CY/WiDD8Ne4wTobzfd9m+4t+H3lOCYBBECAZjUi5phaIekPMFmskcYzFfIWyAR49eY633n4by+UKP/nTP8Xt27fx1a9+laQatcZms8FhlKAoCzTwEXoesjyDyghkEJWqwmaztkmVvu9D9nzA9xGGpMT19//Bf47p5QX+9Z/8BPFghNt37kCpLcbjMaDIgle6NSLcZD5a8GnCuuFMa+kLkm1tGnWln30/xKAfIgx7ODs7w4sXxPHfbqn6bpqmiCKaeEoR37tRCrWiJHt3EAsh0NQ1fE/YwWrpWw4vU2vWmi9QFIUJDQZQqjG5MMBoPMZwNLJGaGUMGvKqSgRRiMn+PnyfANvmYIvnz1/gH/7Df4j/Yva/R1U/goJCY/J1XG+MUiTdWRQFsjwjMCo9ADWu85RZD41jaLshRwCdPnXH7/Vh4e5GqgGrRf/xRx/i/htvIhmOoCAw2t9Hcj7EcrOBF/kILi/x4nEfb9x/A+XxMZ48fYr33nsPX/3a1wAB/MVf/BTz8wUCvwfZ1KibEvPZCov5EtKT8ALf+Hmo+JXWHpSiSvZxkiCKQnhBgG2Ro24aDCZD/MYPfxPHR/v48Jc/x9PHjxB7HjbrJVbLOdIsRxj38fArX0UNYL7e4re+96tIs5ISrqdTZGlKija6tt4mBik3Gxvt37mfiZJI1abv3rkNrUtEvo+mrhHHNDbu3LmNzz//HEIIjEYjy4ktClrkuaqquzZsjBY4Uf8aC/4HgwG4Cr0rQR3HlCxO1bHHVySqW6MWNsGZxoEAJ8GyshkAu0a2hn+BBw8eIDHJz309gILCerNBWVaUjxbFuDif4vT0FvIsw2abYjiscfvOXTx/eYZ0NsPdu3exdzjCX/7lT5GnGUpdQXo+iqIyOQU18qJEGERgSd047qGuK9QliTdEkY+6InrPfL6kqucKmC0uQEWvFHpJD9vtBlWtkBcV6rpCHCeApnwo4gmTEcFzh2tRCLOeNLaoIdEinp9dYjgc4vDwGG+99VVorTENp3j02SNst1tSd+klCIMQf/XzX+Lps5cIg5AMibqCL8nblqWZBWiUV1MB2iQbS0qGFyYPQUOjMvSPxqxFdr4DaMR1wM28RGeed7ywTl6D4/+333ulV1pc+Ufn3rv3onnzGpe79u9fbBgI0XpH7fOb/zrhFXvdL77m1ed3DINXrp2v1WT6mtMpu+vNbmTii66xC9idL7RNuvEy4uoDX3dPu1Zc34bXpY3d9L2bqErOmbjpHdw09lxc4qqP3fQMr2rn7mf2c8YSmkVpWizpOv88s68wzcnNsfX9CEFAuVBxHOPo6BD7+/vY29tDHIcYT8Z4+PChVWuaTCbIshRCkLNos9lY6j8AYgqYaDPnVjA2Y0DPNCgANofXzVcTQlgaFa+BTMHnJGymTzHFlHMDq6rC4eEhUZrM83KUhIV9mALF+YWsONUzlHHeX3ffId+X6VKM6fi9cHHBL4pQ8fHahkYcxzai4IKq3Qx55vnzRsKhl93QmwvS+CW4h+XF7xgiXGGRE1b4niylyuEm3rSstKrxUvqmgAl3bhjHELKHsDfCwfEtQGncffAG5tMpyrJAVRQ4PClx6+59DIcDNEoDWsKTgBcluJwv4AURwjhAmmXwQw1AQngBijwDBBCGPVuhUUgfmzSjqE0QwAsj+BI47fXxd8Z7+Hf//t8hihPcunULzIKlcB9Xqmz7lCcSRKtNLQQltrOsGhTQ1A0Gg75JJvWp8mwcA5oUYZhqVpUKlxdzRHGEF8/PLSBbr1KilSQ9QGjUqrbvy11YiqKAbipbMyVJEvv+OKzHNDmefJ7n2YTV7WZDVacvL+F5HsbjMaI4RhjHJHNbkvJCMuijLAoICGw3W2it8JWvvAUpPWTZ/wb/+B//YzS6QVlXdhy0BliDsqyQpjnSbWYS5D1ofXWBdI0FNp65oI6rxsHj2N2IX2sCCjJslKGjpdsNnj55hDff+Spu37mFJ4+f4vbDB/jwF+9hs90iXAY4e/IciReh3x9g0O/js08+hVIK3/jmN9Hr9fFXf/VLPHn0BEJKRGGESDXQJm9INQ20aiA8BU+Q7r70iC4jAqoHkpY5tBA4uX0L3/v+r+Lw4ACfffg+Pnr353j66BNk2y0ePngLaZohzTN843s/QG+0j5+993MM949w6859vHj+HIDAhx98QN4d4yHrQCvdKq/d5BVx573neQgE8NV33sLeZAQhGghFkoXaqChlWYaHDx/ahZwqpoa2nguPOfaGC0G1HDamHgm/W7tpmWgoO1JYV/z45BhFSgXVuDYQz0neBFsvUW0Xd978bGJv3VivFRdeouqsEuv1xm4WvUEfmck9WixWqKsGi8UCH3zwEY6O9hBFPazWG/zX/9V/hV/9te/j7Xe+hg/e/yUefuUh/vbf/rv4f/2Lf4E8pXwcaHI+VKqAEECWp2Yu0PrEtX+aRtn250UO1TSIohh5Xpg5RUnuSmkUZYG6VojiBKpRuJyS0hK/v7pujJO/sWsGOT9qNI0GV+rVmpIvSVxkho8/foq6VvBNbaR0S8mNSitstyXlkzw7uzJXIds5z5FzdoiYuARF0z0qHEegX0OLdhzWqnEc11ejnO7PLwJ7u3vedaDvVQbE/78cDJRYEfHLAI3rjtcB9/+ph+t0212XXX75q9bs1+WhA8BNySltXY8vbu9Nf/8y48Ldl1513WvuZKIJZHC0p70q+nCNyWhPbM/b7cZXtaltN/3ueS1Ni8cgA3UG7wyyJ5OJ9fbfvn0bs9kM/X4fX//61xHHlE9a11QosixLRFGIosyRZzk830NRbhFGHhbLS/SSHmAoYVJKe05ZlojCEEkcGyU/ZdpJ1KbNZmMpTm69CmbbcFRjvV7bSIZSCkmSWLYI14ljjM15LczcybIMFxcXGAyHVJzP5Ly5BppLB+MxxPsRz2cAdu/jvndzcFlEiCMw/O6+zJj8UtQplzLFlhtnxAOwmy5bX67u8O6gYtC/u8Cy9bVYLDqeLyGEVXgZjUa2eJz7sO7L4N93O4LDThz9EEKigQcFDelH8KRAL4wwGE1okCsC20wdKsvCatIvFlMcnRwhTvqoGyAIYigNSOkDptKya5BJKaGFRgO6picFFaYDUchGEw8//OFvotfrWdoX9Y/xABs+oVu5kZ5BdxYxHsBN0yD0QizWC8NDPrdJw1EUYbPOLV2D6AiJCUV6SPO2UvhqtcZy+b7Ju4kg/Bas8SAkC9yHEu0A5/HBA5r7YTQadcC6gEZV5BSYURqjwRDD4dCCFD/0AQ2UBVEufN8j76qme5LeMxkiv/Ebv46/9/f+Lv7rP/xDK2Cwm8BNPPEGWZZDygACEgIS5HXsGhw8vpRWnbAnP487vtjQcBPfWtDZTkxJRWKgNcm0koOfyEUfv/9L3L17B4O9Qwz3xhCewOm9e3jx5HMEyw18IfFh9j7e+8UvoLTG/YcPIKRAluf47ne/ix/8jR/gzv17+OCXH2B+MYXSAr4XIPCpvoM2lSe02RA9SYW5iqpErRpM9vbw1lffxlfeeQde4OO9d9/Fkw/eh6cVlvMZvvPtbyPNa2zzDKd37uKtt7+O+WaNy8UKv/u7v4OyaTC9nCJdLDA7v4SUnJtgxqgwnl11Pciy3kHnJ40TIIx83L1zC5v1EpPxgNTISoUwjFGrGqvVytYBIOEJqqnR61ENhNVqhSAIcH5O1Vv7/b7dQNgYXiwWGAwG1nmS57l1srAqR1WW6Cc9pGmK7Xbbed9lWYGSBzWE4IJ4lOxLdSh8VFVtlYTWayqASrlRwOHhMYTwoLVAFMWYz+dYb7eIkxiz6QIvXrzE3t4+lss1Tk9vY7ky91cNfvmLX+Avf/oz/Oj3fx+/+6Mf4Sd//G9w684dfP1r38Cf/smf4OzFS2RpSvkckkLmRVFCQ6CuyABvGlPxWbc1gpTxctEjknwiHI88SSk3aJo5zX2tUZVsaBCNoFbazFmqNq0UGRUtJYOoErQHsHw30SRUXti9gRWSGrMu14qoEuRo0YAQqLWy9ZDY2NBNYyi7ys7HxtRE4jGpoYxTR5B3xxR80VpdW5vnuuN1vba7f3udDfuvC3y/7nFdG9mRtduem4yO1/XA33TebjThalTi9frtuu9d5+DYjYC0Y6htz81GYRuR6bb5eiziXt+91utEeq87XvWM7me7ztvuRaSdE0q19aOw04duAvbunrf7XG37W9od/QdAUA0X+qzLyuACy+SAGWJoCjVTwWeq75MkCd5++20MTJ0pLuTMUeY0pVpQabqFlCQck2UZqjxHmq2NmmWJIPAxGlMl7n5/YPAMF1CWdu9nuqwQAlVdIzSOa+4TlsYeDoedOmIcDXABupRUfJijB0mSQBm2COdysJIUR022RmSIz2+aBuvVCr3BoOMo2263Fgsz84cPFvBx+3g2m5m6Uq1hpBQpjfK+x39joR8OKLz5lbdeOS6BL2FobDYb20G7A4p/Z0uTBx8AU5CKC1ERiNt9cPchOCTEoSi+LkcqWM5rd/K71+Fj14vB4MEd7EorNArQwklk0oSDqNaH6SIP8H0B4Yfwowb98R6Obp0S5y+MUFVUNbdRClL40FoalRDawlhdRgjAMxQKz3jZqAgKvfDxaEh7nBMOFAKo6sa6BFg5iYG8hkIQ+FYZiw2yPM9RoYaAhyhKEEcJtAZ8r0bgRzg8pAkShiEWiwUATRKX+RZ5QdrygR8YTwHRwLKshgy8ziRy65gEXhsebL2KrdoDexbd0KbQGjKMEEf0vncTlOjdAZHvQyiNMiMDiXm7HEEpiwq+H+B/8b/8n+PDjz/GT/70T200iw1jKQW22xRFUdjcFAKGZgxdE7km4IErbXLDjfzMu4cUAloaegZ7isz1qRKppAJEDcm3pusVPv7wfbzzze/i5OgU69Uah6enKIoM87MzSFDkKEtJOvPJ48f45je/ienFJf6Hf/Wv8PVvfQvvvPMWTk+PcPb8HM+ePsPF2QXyoqAq0jxnLL+7QtLr4eTgGPfu38eDBw/Q71My9L//sz/Hcj7D0WSCuizw4MFDBFGC82efQ8YJvvW9X4Pvh/jlLz/A/YcPcXzrGC+fPIYHhff+w3+AhDBcVbojREd3qjNHeX7ysbvOKNVgOBjijYd30etFyLMtoiCC9gSytMA6XVtaVJqmNpoZRRGyLEddN5aPys9H0r+RNb55U+N1jGlTWmvM53M7V8uyRBZRNeMPPvgIk8nI0jrdMcFjmde+uq6R55SQnee5AfqFNcYXiyXi+IKKIGkgCAP6blFAQcOTPlarDY6Pb6Gua5ydnWObpvjWd76Fi7NzZFmBr7z1Ni4vLpCv1/h7f+/vY7VZQ0Lg934vxueffYY//L/8IVbrJbIyg/TIuPakj5OTUwyHB/jss8+wSTNT2JLmFwtZUI0Gcriopq0SrY3RoZx/d0CPKc7Kh+sh7iYp08HrhgTsnNFadyhnLjVHwSgymWEG0dqxbjuoVoNDz4E2S6q2tBdBJxlj2GknrgK9Lwv8XjcS8tdxvMrL/B8L/l2Q9GXOed3PO0Pmmr1b75z3Ou143UiR+2y713Xb8sWGTvt51+Hk1ALS10uu8rVfFeG96XmvtPma9rlGx3WGGxsU9nfp3ks7tNfWqWtrn+nWyes6b4TQCALGAhLSk+j3eka108doNMJkMsZgMMBgMEAYhrbI8ng8sZ+PDJW6rhurWEeUazfZmYuSRthsVhgMBhgOB4Y2JBEnJAiSZSniOEKWpSb/oUFZKFufbVkvMeiTo0pAIs8LC/bzPLc5fjC4Jk1To7pXWIOA17gsy6xcra19Yw4G+2EYWpzsRs/dMcQOcnbgc2Vv6+QvClt2gt8D1/vYbDYWI7Hzla/TNI3tb6Lu5jZCw1EMpl+50XveC1+nsCbwJQwN3jA5DONa+vxv3qD5b7uSYQz02SvMhoVbm4FVrJjKwLQe7gimRV036fleu7Qs9998X26vlBJSmdB2Q1VkVVMjCk1NCEgnGmr4fz7TfTzIgCxxSEKovu/Dkx4ZHp4wWvhubgoZG1QxXZuKrQac1Ap5XlggzoClLEvA9GVd11gul5aKVJYlkl6Mw0MaLKvVCkmS4PT0FFmaQdXAYr5AluZolaWUoXRQHsw2pbZ7nkQYeej1xzg+PjCVcn1j3HnW26ecxdStJwETmeCEJgD2XQvRVjsH2kUvz3PoukHocQVPjcLIuNVNTUmjVW0SUwPUKFDkVBm3gYKWGp7nw/dD1E1lC1v9o3/0j3B2cYFPPvmkM/EBYL1aI0szLBcrlLU21KnXmwO2cCRgjT13Q7mySQhhksPZ0BBWN94u9nR16w/7+INf4vTWAwR+H3fv3MWTZ49x6949qLqyCb0PHzzEbDHDZLKHg/0DTCYTPHnyBP/+z/8t9g8P8PbbX8XDt+7jwVsPkGY5losVtuutrfdAuVYhhsMBRuMxktGEFDA2G/z8Z3+Fx599htAPcDI5gG5KzGYLQPj48JPPUIsA3/veD9AbTfDez99FHAb43ve+g816icVsirNHj7BZzsHmG3etBuG8Xe9wdx2BnQ8ciaKNy8NXv/oVRGEAKYBBrwcpPDQ1UPkNmrqxaiScZ8G1Gi4uppbvOp/PMRqNrBeqKKj+CP+NvUb9fh9ak6DF2dkZtNY2CTmOY0hBBvWv/up38aGRIV6v16hrhaamMVmUBRpDj2qT7rSl69DzcVgcEL5EU2tcXszseK3rGkk/wTbdIssKABLPn7/AarlGus2wzjJkRYmH9+/hb/74b+Hh/fv4t3/yE/wf/8v/Ej/8/R/hN3/7t+H7PvL8GZ49fYF33v4aHn3+CKWq4fk+iqLEerXGap3j5dkcnz16RlQps97zO2BBibJRO+/NvFnB9RBcoMYgsUu60M76QbTP7jpN00VAQpkT2YhwQCN2js6003CElHYGm7TtMhaRc45jAHeutvOHL3G8jsf9f+rjJgrRq0D8f4qRdPO5Vw25VwH7/9g23IQdbrqui3e6xsPueRIshcrntWtY9xncNuyyPl4V0XiVodH5LrqYx73uTdEi+tBtvxuhISlu19mmlLIqcVy0N45j7O/vW+rP8fEh+v0eiZJMJjg8PMTJyYn1ynNNHfc5kiTBs2fPOmqmnFAthMB6TZHrw8NDFEVhveue52Fvbw+e5xmJd2WNj36/j6IoMBqNbA5Cr9czERsJzwvgeaERDfFAPg2BqioM9vBNZDyxztU8y+A5jBB+pvF43KmY7ZaG4L2X13/GY5z7zAabm4YQRZEtbsrvi6Mf3J6NKUUAwBopbHRwsb7JZGJVrlwctlwu7dhirM2OYBZIYWdyHMc2AuPivC86hH7NlfDJ54/tRflBGDheyRnAVU8lD4Q8z61h4X7OBgIPuqZpkBseaN8AACEE4ji2uQb8UvjgRYC910A32cVtJ38GCDSKKvSqpkEUBggCKrgiBKAk0Rjs5kkzmNotzN80ecYk2jAiW/0UHTEGmpCoqwJNkUGDNPMViB60XpPs6Hq1tkUHm0ZBK4UwCpEamUqO6vSSHgbDAZRSGAz6pCsvBMqiMJK/lABel4okdU1hxSAIEIQh6fwHJN2mtaZkYSlR71jdLMuptKE+0DA03ngBqgRO36+rEtOLc5RlieFwaN5XgjzPAEGebCFo4lB7akjpwfckaiOVTNQTs5BpU2/E800YkTzMUkhkeYZk0ENapEZmmYw3olYFUBB48uQZ/rf/u/8CT58+R16WxBXXGkns4Z2338Hprdvwgwh//Mf/GsvV2oBi1b477C7CwnIw6Z2T5KZnFNJcnqYbdbO0LM2UMgFWjtGkdUl1JpoG0pdQAEZ7t/DbP/rbiPoJVtsNzl++gGxqPP3sE2TrFUbDAeJegpGRvj0+OUUUhViuZricz7BJUwxGY5yc3sbhyTH6gyFCGVKynOW7KgusZ/Mlnjx+gsV0is1yhUG/j9OTE6w3G8ynl1it19ikGZTw8bVvfRd3Hr6Fly/P8fizz/EHf+tHiJMAn3z8Pqr1Cv/uj/9HqLKEVg15m2EkNIWGIeYATWuYsVFNc0dASEA1LRAXAALfw//6f/U/w7e/+Q6CwIMnBbI0gycCQEu8OH+BpBcDgvK45vM5GtUgiROcn1/akPPYyACyrC0lCXoIHKltDjfnRYn1eo2Li3OsNxu7qUqTL1WUZLhsN1ukWQYqGFqhzGv4QYCmbmgsOeNEsBGlzbpkfpeehAYQhSG0BuqaciXCIIAf+NACyLMcWgNvvPEGsjTH02fPsVhvUdU1hFYYDfq4e3qKpq6QZVvsn9zG6a1bGPQH+OTjj/HRhx8BxjlRNBVqQ4cSICOCjSEFQ2va8ZCa2Kz5g2jXQU1VpCFbGdKO8ho6TLkdvjoVEwTvAUY1BkKQ6p6zB0knh6JjnKBryQhB0Tqtge42KCDg2ee6svXpXdpk237t/uE1DzcqR6fveqpdA2vnI7HzlWt+v2IMXXOwK2NXHLZztmh/tO01b9zet/1SK919td3dddPxgtur3mw8uEGp3ceGMVxdhwRhjKteeg5Ls2Gv0R1HVDfBBdH8rpx3rttngPO8QkjoG3qbnk3a6wgh7RoGtG3ezeO7iV6+0wM7n5sxrK5Su/gBbITEOPFg5qlnMJr0qK3Sia64TlyOMPiBj9FwiKQX27wHjvz2ej3s7+8hDCMIAUwme536YXVdYrNZU320ILCAPwgCHB4eYrPZEPPCsFjG4zG22y2EoCRpBuIcIWYJ1iiKLD1JCFJB6vV6lsGQ57kF11zYzsWnHM3mIqtCmOiM7wMGV242GyjdmGg6Ya3YUPY94+2XQnSUnjh/WEpp8+7YMABaZSfXQcsO46IobJE+joAz5mXZWQb/nkdCHXEcE21VURQky3OijhlHmxCkInp5eYkgDDAZT+wa60bQGnMNa/RpEMZKKO+O+5/xAkdv4jjGj/7Wj6+dD+7x2hENDplwMTR+YW5hDwCW87U7oeqaONScH8DnuQOIz4kTkk7UAlYPuDcgD2NVVtaKdSk2bmTFvSaHpLjNrpVvf28qSICiD+YebJTUqrIDq2lqG47KsgxCmrwRJ2LBEZvVeommqe2LI4s1RpUX2K62BpykNkHVvFtAUJVYaCBJQvR7PYxGI2zTDbJsayfPwHDy7OQxVYiTiMJ0UBq+lPBjiTim10z9SwteXdfg9YfzYkrDxeY+42gKT1K2jJluUNcNAA3f89GoBlAase9jvVggCUOk2y0uypJqfSgKWfZ6xJVnGeTNZkNqR760hmOapiiLEn7go6kbbDdUhXI6nVrPAC1MFaZTShz3fA95lsMPApRFCQGNOEnw69/9Nso8x9nFDBrEJc8KjcdPz9AbTJAklBjtaQVIGKHg6w8N4ptDGGDYNGbD0jZ5FmiN2y6VSl/ZcDTTOIS5r5SUHCsl5otL/NVf/QW+8d1fxXhyiLLWWE4v8PCrv4IXjz7F7OIcSaVQNUCeV0gzKqzWiyI8+/QZVps17j24j2KT46NffkC0oDA0hpipRl+TUEJZlJAQGCQ9FLMZPv7FL1Ghwde/8000WiFfp1htC4iwj29879dwcnoHL87O8Onjz/HtX/9VRMMeXjx+BJVm+Nmf/xlUmdOmZqITNPbMHLQDvXVMuICMQCP1i9CAUIAQDfbHIxwd7mM+WyBNqd5CGIXoJxKr1RyhWUSruibZwjhG3dQo6srkPAWYz2fIshyTyRiz2QxVWSHbpmhqUlliz1yWpkizHFp7mM1mRMurKlTVDNAaURxjnW6N90fbcD60NmaUB1UrAESfFBAQWhCOtX1ilJjMEFAmQlI2VJOF6NEaRZVD6QZhFKIwXjIFjelihjTfIs0zKBORLRcbXC4/tiNOvJjBf/eXAEgQolHkuCCKk2oHutCAqjvvAcaYooDCDqh3/tYB68p9x7thK/dHaxh0gK0xevgr6JDsgEYz6LuZrmJPbe/UAekauxmpjqdXda+td6775Q9hIihtu1qs2AW5XFi1/ZTbrzu/u01yQXzXSHD+zcBxt2U3eLelFN25aHPWzJwU7k+O0LVU2CvG1c79+J26jAdaEwWks4eDr2OBrxOJcsC/dvqNrslgXwNQtIBoMweZCqQ1KMG3pfoI0ZXplYZKzfdv+/z6XAv6kJkUXBtFWYMDxslGfdylRQvhOfdojSQhBDwZGMof7QsCrYNUaAF4bZE6WzRPGAKEpvaSk1MY5yDg+xJhGMA3tGgpJQ4ODnD79imOjvdwcnJsCrYm1vnrez7CKIRnanwVRWkwnMBqtcazZ09x7949FEWKqsotQGZvOEcvGEyv1yQ3zTx/oPXAswoTF6hbrVa21g7jHjZG6rq2eRkcQbq4uMBwOOyoArL33/d9rNdrC9rLskQwDNDURDvSDWEcKQKMR/0OS6eqKsIx2y042s2efhZIkFLa/BEXBzN7hscO4yxWeeJUAWbwSCltXzGVKgwiOzaklCgLUlQkjKyRmjpEUAqewVzkLQeEFlCVAhQgITvKVIPBAJvcyHxnreEmhEDohVhtV5Z2pZRC6IeIw7ijqPVFx2sbGlSRVli602azsVVg2WhgmkxRFFaOlEF/WZbI8xzHx8fWUmWuGB9KKSyXS0gTlmMeGien0MsN4MmWI9ZOMmX5Yjy42KBpQ/+sPNJ6QKSUCEwYijyLHmp+0WWJ5WplS8PzPeI4tnkSnInPgy0IKCISxTQI1+u1bedms0FVVNCNQtSLMZyMzDm+XYxarr9oPftKYX9/7EQPXMWedrHUWhk5SqJGhWFgONUN2g2BCm2BhiyqskQQBnYyQQPbnDTrs5QSkl68eA4/CDAw9RU4mWi1WqEsCvQHA6NwRRGIXq+HZ0+fYr1e4+TkBB999BFOT08gPYGzczLUnj57AiEEptMpttuNoZiBKmPP58iyjPrSC0yid2knNhtYAI2H4XBoc3eYcz8aDlBWDX7wN36Ir3/jm/g//JP/M56/PIfKKQo3m03x0Ucf4Y03HpJnF+2GcNW9SAePM5cqyAsQtOj8rTWCr2qPt5uxvMbLaT5XNT7/5AMMBgPcfeMrODk+ggSwnE9x7613EPdGePrkMbJyQVLBeYZtr4fp5QU+++wzKEEb3u//6EcEWIsCeZqirmpcvCRu/72797A3HEJMPKjAgyorPPv5S5R1hcloBLXJsckyrIoKe8e38LVvfg/9yT7OLqd49OhzfPs738b9e3fw+NNPkS5m+Oi9d7FeLRGAPNMQpIhGb0q0fevMPbdfrusH1TSArnHr9BSX5+fwpcJms8F4PIbWoIrnGtif7GN2McNiuUReFiiqEoWlLIH6qCzR1DU+/fSz1ptYN1ZBh9egIAiwXK2hlDBJzo3xHII2e+N55zmotDYSvsokGPuUw2BkELXzPO6z0nWVBV7KzFGttI0Ws3degNoihcAf/+s/tcCiaggguc6e9mjsmsj33h2L5pcr7+B1KT+7VJZdwMvPvwts3cOFwa8H7a/51qudwTf+fjXq8J9qXHSvf5PM63VgddervPs5/3Tb3DFOXEB8zefXXe+6v7kGQOviZ5qcC/rJccKKQK0R2HroXW87Hcx4aD93I8G8drpOGvpOG9HSTqjKkz40SLlPmP4msQ1qv0bjRCrYWCPQLyi22vZFp0vkte+B+qf9txtJoeKr9PxSyivvno1GKQU86VTGdo1d6O44gDDFQOnZNDQCjwsRK9snoZHTl8bCGAz6iKII/X4fh4eH2Nvbo2r2TY179+9CG4dlr99H09TY29tHUeTYblcWyzG1p2kaLLdL7O3t2dICnudhMBiYd9NQ0bjh0FKGiJ1Q2tICURRZIE55c5k9X2ttgTrn6CqlbEI0Oz2ZWjQajTrJzGyUCCGs6hR7811jh/I3KLLgFpYWAErjQB4Oh1gsFpYmxRR1jjqMRiMsl0urBpUkiS2mx44qzpF1E6ufP3+O8XhsjSoAnaRqxjTcX3wNizHKCnlZIEl6EELYxG2mRkmvjY65QQEyMn1LJdtsNta4c1lF3O98z6qqbO4iG1Xc35yLeFNe6nXHa1OntmvKPE/TFIvFAovFwlo97MF1tXY5lORSI3hA8d9c9SSeWMyNZq6+Bqm81Cb5BoDlrvF5k8nEXod5clmWWU41W+18jrtYa63R1LUNhbHXvqoqpFlqJBypcIwAVXL1fR++58EPfAz6A0OVajP4yasCm9fgemCoQFUb/vU8vw2JCYnGGDTCeCGk5yFLUzIEzCJEic8Foji2YTjiYefwPaIGsAFUsayssZABWhw9KVGamiKbzdoofHE4cw2lFKbTKS4uLgDQJjAeT1AUOYSgwlODwQCbNVVgJlpJCGloGE+ePMbTp8/QNDW++93vmsJYEoPBAGdnZ1gZAy5JEsQxUb2UUpZyxYP7YP8QgR9Y7iAAaxTVdWm5mzzo2RihXAofRVlDeD7e++X7+G/+r/8tnjx52hqlQmL/4ACbzRZZnpuIA9Muuht1a8zpjteCw7oSXsfo5ckspYRqdg0Mvp6EEF1b3xqQggCoF/Xwze/+AKf3H2Iw2sNiscR8OkUcBFgv53j6+WfYrBboxyGSOIKAxmKxQJZnuHvvHt5++2274AIaT588xl/89KfQWuPhg4d45513UJQV0qpCUZRYXE5RlZXx/GwhgxD3v/ZN3H3jK4Af4smzF7i8uMB3vv0N3L97G8+fP8ZyOsWjTz7Ck48/AuoCnvEsKi3ARQlhDB+lakCTEMK10teCikY1Nalw6UbB8xR+6zd/HXeOJgg84Fvf+haUUjg/P8eTJ0+wXq/RT4YIgghlVUIBWG3WWK6WqOrGqCdpKqAp2wqw2nLTW6Oe/6trZaIYnN+jjafJ41OsN8rNp9CaPOPKRBhpjeJndJdauicDKwXY5GopJXkf+ZvCByDgOZ7QsirBNI6bQOVN4H73d3f9dYHf7nV2j5s8u1fuJ26OErrf/48B+dfN0y86dgH5697/y7ZPmyjAF37Pub8LXK+7/6uMoledt5uHcdP3dj/nNdF8wwJ0ms9XhVeu60seXwDABUu7EQ101kv3XfK5qoFzjdYLznPQlaLmyDixDxobpWn/4/Zxf1/tk9aoutrHuxEOisDQb6yy10ZVtHNeq65Ev7d9vLvPtNdv4PuktOh5pPLIgHY46OHw8BBxFOHhw4e4dfs2RsMhGtXgYH8PjWLGQAzPk/B9quuQpmv7jFVd2Zw2SnCmKtTkyNFGhalvKU/L5dI6+7jfF4uFxVm0L1OUgdd3Bqdpmlq6DTMlWHCj3++jLEvT3sjiwFbERVpn4nq9tjQsN0ma1ZGYBcO/Mz50RYaYWVPXNaqyhCelrbO0Xq87bBxWAc2yzI4vHmtMN2WBoyAgAQ9uEzuouf08D93cDGHwmltoz42EcH2lqqxszSg29oIggNIKabqx/cP4hIwKD4HfqkgxrassS9svPEf52ZimxXjWjejEBnNyTnVVVfjR3/li6tSXMjTYqnv27Jm1hthCZBDLlg8PMn4AXkDY2HBpP643kV8uFdoq7Ivk67OFCcAmZh4cHFhr1k1QYalLoLU2+R5sHJVlicJYzlJKy6mzSgrCGEu+Zz0M/BzKeCMFCHhLSYX8NDTqprT5DU3TQEiJuqoRhAEqQ8ESgsCDBT8QUJUpJhYEmM/n0Fpby5JVuJiDmGUZQlPlUWmNxXyOyWSC5WplDRLf8wxfXdnBIYTA4cEBXr54gSxL4fkekjjBer1CUZYIzOB//vwFHjy4j29969t49uwp1usNeW3rCkorHOzvW3C/XK6Q5Rm+8tY7+OlPf4q/+Iu/gBDAg/sP8OZbb2GzWSMMA5RlYSzy0ipH0CROEYYBhKGQrNckRaoVydpyvQuqIk7GRRgFEAKYTi9xdHSMIPARhqQiIQUZXhpAWdUQ0sOLl2f4b/+7/w6fPXqEsqxQVvReGi2ghfHY6TbixROef3c30iiKbK6JEJKoMboN/fNmSJtQO174WvQ9D27Y3AV7QjfkjRM+vCDGr3zn13B05x6iZIiq0Tg/O0PoCYSewPT8OV4+e4Is3SD0AySGKsR9GxnKlABFp549fwbP83D3zl1K3CtKqEIhrypkTYNtVUFJieM7t/HGm1/BaHKCTZrjk0ePoQH82ve+g/3RABcvnmA1P8eTR4/w0fu/hFANjHyC8b61sqNCMmggr7wUrQfeBRAaiuor1MqKDo9GPZweH+D0aIK/+7d+jHfffQ89EwY/ODjAJ59+iouzGX7rt34Hp7dvodfvY51u8d/84R9iuVwhLXLjQGjvYwGDIFpRVVWom5pogCY/rG66hSbbdYqMCI0uUKWfwpFtRevk5ZXCdZ7uODwUuiDSAj94YI4VRzfseJHdSMWrjIKblvqbwPp119qNiNzkUXcP1RKuOufuXud/CkODz3kVwL/pvC8+xCvpVze1uTM+0VVSdEHOF73TLxPN4L+7BkObO8DtkYBuIxeuFDiveXRv2wr7OVN2KZOR79F+h4qbxeRhFnR99sgy6K9rAt1cL6GqKlxcXILyFAdWRAYAlsulU7uA1Ia0Zoxx1bhjyhXjAHqerqFo6zE5T9ZZuwxVin+3Brwk3OD7PqQn0dREm+n1erhz5w6UajBfTDEYEN3n+PgY49EIQkp4HnB4eGgZE2+88YZJDs6wWS9N4nFmaejkcV9BCLN2aQKrvudTsVufaM7sVN1sNojj2EjCNojCuKNmxOB6MplY6rJL8XHFf1h8oyxLHBwc4MmTJwBgC6C67BJ2FvM4Y1rOy5cvcXh4aMU7GF/wO2E8xxjNFv4013Mp/AyOWVHQLazKzxeGoQl+aQuiWaCISwxwMjkAS+dyxwM7zhnAs1HC/dg1GHIL3hn0a00J5KvVykYaOMmbjRXKTfUtw0UpZaM1VVWhKDMbieI57Ps+NpstojC2Rg0bgWxocf9z/3J038XtURRZQ4VpXPz97Xb712tobFZrO2jcaAYPEH6JvIhxx/KLZ+DlLuq7vE7uRAGgNoA4y3MUeY7CePH39vcxGA5tp7rhVh5YzAnkDueF2vUY2YXceA75GrYNZrEToMWjqc2gMp73Ii8sd9L3feNhpOJhZUW6zNxfVEwsN/0ioMzLYkOIFRDS7dby84bDIVmWZYWqKpFlBWoDiHyfKiLXTW2Sn8iYaFULpPHqk7cnCkOsTVEyKSXm8xl6vR6Ggz7iKEJkDBgO83HVY8/z8Pz5M2RZhizNkPR6GI9H0LpGnuWoG0qCury8NEZagsFghCzLcXZ2BimlrXkSRSFGoyG22w2WyyUuL6eWVxnH3SjYdrsBL/BhEEIrWA7zYDBAWRBfMIyoojhP0KEZF2VZQEgfAgJplqHX69kJ8vHHH+OP//VP8LOfv4vNNoMWEkRdNBuobl6LvuFGNaDJPnGL4PCC6nnUDh5fXa9kK/u5Oy7JW6hJyl9IKOHjra99E4endyGCBGmeQ9UlAk9g2O9BaIXzly9xOb3EcrkElELgBwhM9M0TEhANJJwCZqZNTVVDF6Y2+qCHyekp7r75FfRHIwAC5y8ucD6d49bpLbzzlbfgocbli6fI1jM8/vRDfPLRR2YeaQg2LCAASGtoAMqoQhF/1HKg0QI9alNjIxpCa4R+gIODEb7zrV/Bb//mb+D/+X//I5yfn2MymeC3fuu38PjxY3z/+99HGCaI4wTnl5eI4gjS9/FP/sn/CfP5gupDGEoSKZkReNGGGlLVFTxJkUCiMhmFMLSOEKWVrQMBoDNGtHaA9A7469CZRJdK0zFeGIwL58vuiTeMSqEp74L7b9db/2WP6865KQLgfvaqe5GN9MXfe10gfx3A/iIa3pe9x5c5bjbu0DE0rlLbbr6ea2jsRiN2QTIf7l74RW18VT+4e7Kw89Qk0pt5TSN2N3neoVx1PyGZb2ioxr0mndNGN/gzo+QINmqBtiaNez/6jKMXjDFcyU26FhdXdZPHOV9O2D2f+y6MQihVO20kDOFJz2IG18vO35MeSZWHYYjT01sGCDbY29vD4eEh+v0BoiiEEBL7+3vo9fqG6hsiTVulOwBYLJeIowhZnsL3PASmKjRA8txFXsB38lqFEDZB+tmzp7bODDtPfd/Hy5cvUVUVjo6OoTXV2orCkLzxnofnz18AGpaaRA4/wn2s1qQNIGfaEH/OfcFRApZVpb2fcAknbLMjmY0IzgVlAM37KgN3jkIwRmSgy0pMnIztGi6uOiRTuLhmxWq1ukLN88w7ZMEPvq/rkOb2Mk7M8xzD4RBAl67PzyqltFKxbtE+pm2xIcH4j5+Nk8iLorBREIq8UO2lLMss1rEKmHVhjReOyrNaVV0pKyLEDm43GsO43GW8MNWNr8URF06dYNqZ1hp/47d/48a1xPbxlzE0XKBe1zUeP35sczWOjo5scgjnRgRBQIm9JgrBFhJHNKRDV+JOY33ixlBftFaIoxhRHGHQ70N4HmoDGt3FgdulFAGZyulQdwHm73SiKM65rZEBUn+qS4RBgLomzzV5sEkxqqxKRCF5tdfrNVmTkgwJ9rbPZqR+s91sKKpRllZhab5YwPPomsvlynh0aRFLkgRvvfUWLi8vTY0LgTTNMDLgD+jmnXDo7vDoyHLK67pCWVaGa0iDKM9zO+i3mzUC30deFNRnBiiXZQnfhADzLMdiMafw6WAA35NIepGdVNRvpsJxWSFJBnYhefHiBW7dug3Pk0iSGE1DXpD5fI71egMphakDQptKkiS4f+++DUdTlMd47gxIdMOLtLkI63VIksRsMgKeCROvlksMBn07gZaLBaqmwc/+6l38y//hj7Hcpmi0RGUKAQvVkDRmZx/mKdIFXOwBAYCmUnYSuwIEnvQs3WbXGwxISOlf83dAs8EuFKTQaDSgRIhb997Avbe+irKhomR11QCaFrJevwfPE8jSFOvlCqvFApvVGkVKKmdSNHZDBtrij71eH/2DI+wfn2Cwd4CkN0CZ11hczHH28hzxOMFbb7+Ng/09bNdLvHjyKUSR4Zc//0vMLl6yfx0trDIdqCU4CZy40mS0SyFN8bSrnu2rhoaPJAlw5/YJZrM58qwwkUIe/wK9Xp8M8rqmO0uBojK/aw3dtC/UzXPyPI8SjI2L0gVYGhrCoXZ13pGGYXdz27tj5XWxLDlVKMqhRRvtcD29AANP90wHvAIdA+g/9bjOkPjrNDT+f9HGVx1/HYbG61+jG9H4Mm28ro/dz67r911D5ia61OtEbjjiQD+dyJqTY7FrUHQNlKuGDQs98HVdloP7LG5UpTv2uvexrAOvrdnk4gIyMmpLO/ZsRFwAQljq7Xg8NtdUpjjcCOPx0IrOHBwc2Ovev38f2uQ99vs9m2fg+T7iJLIRi8neBEmSWLGYPM+xWq8wmUyw2Ww6akOTyRCeJ6xYQ2kEVHzPx3q9QZKQFDd72Tn/FUojTTOEYZsLOh5PsFjMUdcVxpOxoTpxTQYPTaOQxD2UpqDm2dkZgiDA3bt3oZTC06ePMRwOMRqN7LvkXAOlqIDbaDSySdAM6JnCzLhOCGFrTrisFG4705rYyGNDgilcTNXiz/I8t8CejRHuEzY4rIqUk8e52WywWq1wdHTUGVPsuR8Oh0R1MuPIdVLz83ORV5a47fV6pEjFNGfzvG0R6HbM8nOyQpZLteK+4lxk11kURRHWa6K0s5FQFq0BzUYK91lZ5ojiyLafc0U86SHLCvT7fWsE8bvh6BQ/J/cdt5OjOCyHy5EYpuVzrvUf/O0fvXI9Ab6MobFeUyOdBSEvCuRZhqosUZlQmjIAiI2DxCTbcN4B84ztAqOpjoEbwtQN1bKYTqf4kz/5E7zxxpu4deuUFgSjMFSVFaQBAk1D3OimqQC0Hgp6iVTt1nMGmVvELcty9M2gLcsCVACmQRTFULrBekGFuri4C1l9JDu5WC4hJekQR1GMzWaDo8NDzOYz5EWG0shjFmWBJCYQLKCt5HsbHguQphn2Dw4QRiG2aUpcS5MAxVJyTdOgKEvEZsA0SqFnkpGqugZAi0KWZjSw4girJdGoJnsTLOYLlCbCQgnMJhclTbE3maAoie7VKIXFfG6tca00gjBAGIQIwgDHx4d28XKt+yzL4YcRwjDGZ589QhRF2N+b4PLyAr7vIYoj5HmBIPCxWq3NAsF8wjWiKDYVnT0MhyNEcQStNKqyRlkUaJTC9PISvu9jMByi10sAUHKYy/MkLigZvf1BH9vNBlEYoixKLFcLNFohihI8e36Gf/U//ht89ugZtmlpqD6NiZ6YugB2Q+XNtt3g2VtEahXdTb/dQAWFrU2ETCnd8uq1wFXFEbqLBuX9SKHIa601IAM0kEjG+/jGt7+LXn+AWgOAh7wskRUlPCkQRSH6vT6iIIDQhkJYFJT/w6H0wIdnPCthHKMJIigNLBYrzKcLbOcb7PXHePjwIcanEzRNhWdPP8fZs8dYXLzA5bPHUFVOZB4uuiYADY5oSLe3wMUzyNBoETVj6tbQMF6kxsj+SgnfAyjCIwHRggpoGFoCzFhsIEzEkd6dMVYZKAkJStBu+1sbeoTWuxXdzQMxzcJEQHgNlK+Ie90E/nYBcgdIOYYGnPwN+k7r3YUz/oQwia+6q5hz83HFgv7C9rv3dK9juhduX954vd3TnfOcN9ECSfeK1zRFQNgcFsH91vF0O+DUoZq593ZP4fFIQHjnOs4XqT2s/iPs9YTzmZny9uluNjSEeR3CRdBOn5J33/c8igeqxowH1QHo7Nxwr3/d+2urrbtRNbfD2+gBG/BaC2sY0Hjz4ApmuDoWraqRsN/tjnWFtl6RNm2S9nm6c5BES5qmNgC/NUDco6XgEFMgCEJLx7179x729/cAKHg+rdO3b9/GwcEBNpsNhsMh7QtRhMFggLzIrUFB65JCv9+3OSCNaigJOE4Q+oEtuMkqiU3TQEHDD30kcYw4Jq/8er1Gr99DVZZIs8zioizNkGYpAt/HyekRLi8v4Pk+lPHuMzD0vRBJkti9j0GolB6aukGa5gAIMM/nc+zv70Mphb29CYQQePfddzEYDNDv960DcLNJDTCPEUUhyIm5Ra+XGAGZxiYuX15eWpYD77MtVpOWTrO3t2exAIN/BqYArGEyn8+t150d0sw4CYIAcRxbOVqWdeXPtkbtiWh2kQXsRVFYuVrGdgBR67lmBv9tOBxaZ5tbX+vo4ABaa/suOdLFUQhXapbHNV+T7819wtENzlfmmhgHBwf22aSUVjmLDQb+Lve1EG2Fb6K/hVec5VoTg6auK5OfY+oySYm8KDAaDklBUSnCy1ojjCJIISxNnp3wWZ7b4AA0cHx8jDzPbbHuwWBgaWWTycRS3v5aIxqXF2fWclVKYbVa4fz8nEIzRuosMTr1w8GAvut5pJvvbOD8Muqqgsdce6v32xa1qqvSDoblcomXL1/i6OgYk8kYVVWjMjUlgNYqFlJYXeOWX0phzzLLIUEvLssyhFGExAxqKYA03RqDgqy1xXKJwA9M8rOwg803HMflYonVamMjOTwR+v1+J0OfNaW5LdvtBmVZ2GgA06e01tZbwElWy+XSJkcLoRGEFFp7/vy5jSKR5wHWG1MUBbbbrY0ccZRCKYXZbGZDbjRxSKaOkta15SdWVYXtam0naBwn8H3PJoYdHx/bhYOBfb/fx2w2Q5hEUA2wXmeYz+cgAS0y1IIgtHw/9uawohdPXF4Qv/a1r8H3fZyfX2A4HOHF8xdW55nvd/fuHXD4m8eVGwp0KXPuxrBYXlLYT0kslyne/fkH+MlP/gyLxQqV0KhVbY0MZeUwmT7Q3cyDIEAv6VFOgbPw8n3d/KSOx9yA110deAsWIKEh0Qp8OuDJ8yGkj/tvvoWHb74NP+6hVkBZK4QheUKsCocfIAgDRGEEz4sMoBUQUqKsK5RVRTVa8hJNVSFOetg/2Mfh4REGvQHyLMVqcYFss8bZ08/x+cfvI98uIXUNKajMoFJG5lcQEBKifRe7XkohHOPDOdrIJOvOtx5ZlmS1VEuOSN7gmd0F9Deh8Ov+6oK26yIu191r99zrruf2w6uux99xOd671+a+2qVKveroXofP+eJzvygx/Kbn6dxPwBqa13335kNe+5J2vd3XAdDrooT0WStM4o5JAGCVML5ml451c1+585p/535uQXpL3SFj1UMQRJb6wLQJptICsJF/rjlEEfeaxNwER+gaa6t0n4UpiwJUJyVwnkHbZ6I8hFbUuzU0+NmvGkrW2Jbo9HPb7wJKwzESXGq0u057RqUNCMMIVZ3ba3oe1SaK4tYL29QNev0+9vf30UsSSM/D4eEBjg7HODo6wO3bt+F5tD/eu3fPyrPGcYz1em1BHVN9mSK8Xq+tXGvTNNhuKeJwdHRk11HeF1l+lY0BTuplbj7Tudljzn+fTCZEaQUB4PPzc+zv71tnFVGqCKtkeY7K8vdhxWw2hv7s+76tZcAUp9yARHffd3EI74ej0cg6EMkwk1Y5tGkanJyc2GvxWOR9ftfLD7Rtc9VF+f5Zlpncj9pS3S8uLqykKveLez/OUeCIBEetttstttstQkP1cssk8FydzWa2D7imBmNKNmI46sJGUFVVCHyqm7ZLveLrcpSlzckUFsfw+x+NRrZyOEcL2BAKDe2NxzEnozP96/DwEOv1upNDy8YIixoJIdBLBrafWfyH5+p8Prcyv7wubLdbQzH3O7QnN7eFo0W813B0SCmNMGixGh9JklgaOmPXv/n3/taNa6NdO17X0JhenncSUaynThMcIsnZxnYme9yF79lB7+ZRbNYbjAYD+xBuaXffk2iqEovFEpPJBJ9//jn+6T/7p/A9H9//wfexN9mzvLs4iVGVJQaDIdabNabTSzx7+hSe52Mw6CMIQrx8+RLClKpfLBa2XDzLpw0HPTs4WTYsiiJrJCilbLhzb28PAPDJJ59guVzhe9/7HnzfQ103RrnJtyFOCr1SATmetFqT9BwDZqZ28b+5Hex94MExHPahdG0X/H/zb/4NTk5OcP/+fSil7KBzQ39SShv+5UnG3pwwDG2uBgDLE+SCLGiUTahjo0gISv4/ODiwoTS+hzWamhpFUWE2XWI+n+P45Ajb7QpVVWK93mA8HiFJejbUW1WluX9pvBikXiWEMFYzy3xKsyhHVkWDDE2BosgBCCyXSxwc7CNJeiaXxbOUtiAI8OTJE5P0WyIMQpOQHkDAx9nZBf7yP/wM7334gZE2JRBN22SbANk641t6V7/fh4Rn+8BNEnP/czdq6yV36ADuT+3kb1ydtSZ5XUiESR9vvPU2Tm/fhRYePD9Cr0+Gfp5lSLPM0hObBmhMNXoFWgSjJEZ/OEQ0GJMXLfRRlQWydIv5bIomz9GsF5hfnuOzTz5GUxXwhUZTm1ozQqBNgqRih0yXchtGG1IAAQAASURBVAt6dkGd8+BonQG0KbD2fLc6OH9vF9TddLyOkeD2t/v7Lrh3nRave8/rPrsKXq8/txPx3WmnC+xuAtqvatuXNTR22/m6hs3OVTpD+bW2HA2wxKi5c2cMtUCaP+u00vmd4w30BynbPWzX0HDHHvW/22+vl1/RPShi6fs+YkPrYMARBBF8P3AAuLLrBwMLfk431xGC8raEMGsTR++4nVLaSCGDJ6pj1Lbf3cNJVvzq+3Df826/C2GMEcHXa9DJfTDzmaNHlGMQoKpIqTCKQuwbIZEgCHGwv4/Veo3bt49x587tDl/98OgQVUUOvunlJTn24hhFnmNgnHBFtjVsBGVUlVKrgMlOrLIsUZYlZrMZ9vb27PdYZpV58bynjcdjK+1JEYI9ckrKVm0oiiIsFgsL7n3fpyKgZu5WVWWBNO/pQhCdZzKZIIoizGYzcC5jFEXYbEh0hwEyt5/X0CAILBZhI4NVnBiox3FsPeZsyHAeBAP49XrdySdgpyiD7N2chOVyaXMn2MvO+Qm9Xg8XFxedfmOJ1DAMsd1urcOU3wWDf94f2BBhg0OItm4XOyRZ/CdNUysIwEwGpihxPgT3zWq1svNpMBjYitYsB8wGsm/mV13TGOX7Ai1NiaV7R6MRFouF3fvZucn0utlsZull7Jxmg5ef3d0XXYOFDVX+OztJKTeVatExlmMnhRsVcfFHHMfQ0Oj1Ylsk26UY8njkPBtmZ1RVZepthTaBncc9G0AArMP3N3/vt754JXxdQ+P5k8dEe5KsyCCtDryqu2oMXJxvb38PCgpNXQOiraBcViUeP36MIi/x5ptv4sWLFzg8PLTqBKqukK43SDMaUOfn5zg7O8N7772H3//93zfF3mrbCWxhcfXfpmkwn8+pau92iwcPHgBK28nO5dsBUqeYjIcWcPNE50HFXgoAuLy8tAOUw0gvX760nEFecFhejRcqtziKuwA+evQIWZbhrbfeaouhmInthgrjOMJ0eomqLix/8uXLl/jggw9wfHyMk5MTmzRE34/twrler+2iwIuEa8VKKawxEQQBVqsV8TYl8RX5e71eD0EQYH9/H6PRqOMtsAZN4KOsG7x8cY6ybLDZbNHrRVhvFpBSIIpiu6i5wIkXS9akZtWFfr+PyWSMosgwHk/s5JJSYrFYYDLZN/f3IATw/PlznJ6eWk9FVZI6FsnyrUyejMDl5QUGgyEODsijxFGZPC9wdjnDy5fn+A8/exfrbYaq0ia6IADR2PwRd9pIKRGHib0vT347yczY36XRQLOCkb5iiAAeILqglMBlW1RLSA8aEo0GwjjBZH8fXpBgNN7HcDiwPFbyZilkOVELldbQAhiORrh95zakH2DbUFQv327QlBkCoZFuVnj59DHmzx6T0piTC9D1CDPAYFWtpgPOr4AWtMEINhoYUFEOxS43+3U94NcfX+b83ft+GWB93X2uGyvud13HzE3tuO4+u179Lzr3OkPDveVN53yZ57/xvuLqfGg/372Ge+719+4aB9fTanbHXXuwitF1Rhyth65nk64jr7Tzpna1bddGWY2kifmj1glB3nw+zzVEeU7sjg3y7rZJzLxu7Br0br+0fdGV0ebPad3pPgPf2/MkfM+NgsBEZYyCkhSoa8oB7PV61isehgH2D/ZwcnKC4WiE0XCI4+NjVFWF/X1as1lK1HXO+AE51yipmBxxlMvX1opIkhjz+Rx13WA0GqKuG2zWG5ufx1hgvV5br7bnUQVrpgMxQOLvBkFgVZFY3XE2m1n6Du872+0Wg8EAq9UKRVHg8PDQ5E+2QiDsyOO9v9/vY7Va4eLiAnfv3sXl5SW22y2OTC6ldPAU77cMCKWUFlQvFgscHR11Eqr5PWZG8KQsSysiMxgMrIFDFPHMttGVYnWpd4w9ZrOZNWrIMTrA2lDnGZdwQnAQBBiPxzg/P7fPO51OrSHAUq+DwQDD4dCOrZcvX1qpW3a0MqZiw48NHwbbHEFiHHNwcEDS5o7k7/Pnz9Hv9200haMRianonWWZrUzOa0RlKESci5IkiVWXYgOB9zOOvux6+Rnks6OaFas42sQGERtxbHzw4UaFOKLBRgrTsFQDa+xzREcI0ekrFgvidyAl5dTyeubKEu9GolhxlfeIsqjsc3CfuyqzbFz98Hd/84vXxtc1ND59/32jrkShJtej3VQ1tFJYLBcYDUcEPMsSURyiVhWm0ym01jg8PLTXU0rj088+t6G8Xq+H8/Nz3Lt3D74QeP70qb3Prdu3cXl5iflshouLc9y5ewvHxyeoqtKED0ndId1mlqdZliU838NmTUk7fA/m7LUAOUeSxAjN4OGFhgcjRxw49MihNApRGZlLDZOHQIt5FMVmIDWWX6oNN56qadPE5hfHC65SVESH6Vvs5aVBVKNRNbIshdYaX/3a1/Deu+9isVhY+Tu2utnY4AWEozK8GbG1XhS5XXjcxKb5fI6zFy+wWW9w584djMdjG23i73JfcCI/QDVGyqrG+fkMWVbi/V++j3v370B62tzLgyc9xHFkxk+AOCbPHvFDQ1RVbb1BvV4PURRgOBogy1LjWYjsolrXCoEfAoKSrjl5bLVaITWVmz2PJl2jGhQ5GWqbzRZKKwQBKZms1yucnp7A8zzMZktASGy3BV6eXeKjjz/DxeUceVmiESS9ep3BEPhhh7/JG7Y7qa9ELTQoFwHogAx6Fx6E7AKH9toUa2kUAzMJSM9I9XrwfJoDp6enuHPnjjGUBcqygfQ85EWBRisITyKKY0RRDI0A2WaD6cUZlrNLlNka+XZNkrWiMtWkgUYLc1PS0hdOpEepGhqqE9lkr0sXEGrLi+dx2T6jMsYGOufdBOLd77n9uwuS/2OMjZtA7E3H69zjujZ92fvtAtDrQDb/vL7/3KhGe47bDl4zboqsuO24rr1d6pxDABRtdGD3HbnvjX661aDd/gF223/zs9D63DrCpO0BjnPY73aqYBvaEd9LS8fwYClmUCFHKdBNKGnP0/pqMj2vBbuRMv7M/c/lsDOFisBCV7gEYK83/Vuprpw2SYN7nf5tHRfU7jAKMRy0io6Axmg4wIMH9wEAb735FvzAN/vUGFVdoiiIWfDGGw/h+wHm8xniKIIfkNe/rihCHoTkpFqvN9AmAu8H5EUP/AB1Q2vHxFCZlssFPM/DaDxGU9fYbLZ2b9o/2G9VecIIq9XG0n6ZhVAUBY6OjmwlaQZK7Ch0a0Lwvsb7zsHBAdI0tQm5k8mk44VnD69SCvM55XAOh0Ps7++TQmOWIUkSzGYzm/x9dnZmqdVc74CZD5z87HkeLi4ubA4Cv9umaazRxFL3uyUCXKoOG2turYXVaoXNZoO6rnF8fGwdq1tTTZqfydLDDehmsMz5BJx/MBwO7b95jDFtnAu6UZIy9dvp6al1DPM57MRkxy3vl66qUq/Xo8LAxojihHTO5WBMxzkfbOCx05rfEwD7nK6hwPfXZgywUeImsPN8dR2rLvWKn5/vw9iIxyQnp7PDmZPouc/LssTApBtwpIwNpNZBSfLOVVnZPZOfR2ttRIJg8atrhNRNK7YEoPNvtz1sVDVNA9UoeF5g8SJHOlhpitk7nufhN37nhzeuxXy8tqHxL//ojxAEIfIihzIcuzhJqFq0kQxbr9fY29vD8fEx5XBcnCGI6GW8/8H7uHv3Lg4ODjAej7HdZkgzqgR57949/OIXv8BqtcIPf/hD5NsUqzmFFCeTCf7oj/4Id+/exTe/8Q2UVYEsT40KlMB2Q4tYv9eHlL5Vb/I8D2sjexonCc7OzjoJRrzA1HWNJI7Q7/c6FR75JbTF3zw7kdkL4PsSdVODdcHZgNFaI05ik9hlEoOiEFIwf7LBcDjE3t4e5vM5lsulnZiHh4fWiq3r2hgdGmVZwA9a7jGHSDl5iScvDwQANkoAAKvVykZUuAJnmm5teJDvGQQBpBCIw8hyhnkh2930uM3cjjTLcDGdY7XcwpMBPvjgA9y9dwd7eyMIoVEUpQ0RRlFsJz9HVdjjkueF3TS11uj1Ekpil9KMub7hzkrrXZHSs+HzXq+HNKV+Y0OPKFpco6UxizYVsVuv19imW9RVBV9SJEF6PsaTA2RZgRcvz7DebrEpC6yN2oQQbVFEaEBA2qgQL2C8MLnUIdeDBQhTQbr1bPA401oComucWL6koSlp3Sbltp5XojMRsGqLSAZBiDjpIYzIOyMDHxpAabi0umxQZBmaqoLQDaCJwqibBtqnCg/KUknY2GD+tyAOueZNp/W6ukZZe3QlpVsPKhl+RZHbcQa0RtZNXutdI4PPeZVnf/c6f13Hf0z05ab7X+edvu47LrDezang83cNgl3u/a5x4vb5q/rnVW237RY3GzbuV9qxLO3Yfp17dalS7fnWRrBjQeC6zHQ2HpTelWs1DgAhwd3K0RCap20uRLefWq/gzc+t4c4R15HABwNJV661nfPXvxfXKXbTnOHv0fUa+IHCV77yFv6zv//38fDhQzI0AqI6RR45z/I8x3R6iTiOcXx8QnkinsDZ2Utst1scHh4Zx1wrGw+tUVYVQkP36fVJmKPf79s8Mt6jeO7HcYwXL18iMHtPW32aklk5WZpZAUVRIoyp/sbl5aUFXQ8ePLCVqrMsw2q1slFyBmfz+RxACzbdhN88z3FycoJnz54hjmMMh0MLallAhT3nrOTIRggDcGY6aE01Jp49e4a9vT14nofpdIqiKKyBwZGToiisChbTjqbTqVWBiuPY5pmenp5aMMmRDo5ucB4JS8MyIGZDiGtncF8A6DANXHCpdVvLiyltDLKXyyXKssTx8bE1JBgz8R7Y6/WskcB9ztL2i8UCJycnWCwWFj+xEcRUJxeQs+eeIwj8PgB0ZOwZQHOVcKaBk/My6igpCfPs2nHGcnSHlbJY8YqjRPyOeY4xJthsNp2iwdy33C53T+T+ZTYLGzEcwWAjhZVcAz9EWVZ2/eCoEo+h1WplxxxTI6lOGuEIVstiRwIXUGTHLcBKnhJVWSEIIjsW2CHOKQCc6yGEwO/++PeurEO7h/+F3zDH7HJqQ0iDwQBxGEHXDaAUNus1losFeQyCANlggKauEQYBosjH3mSE2fQAg14CXwo8+vQTaOEhjBIsl0usVissl0tcXFwYr0SCRx9Nsbe3hw/f/wC//v0f4Be/+AWePX2GbbpGrxcBEEiSGHuTMQHtqoQQCsPBgAatUjg7O8PR0RGSJMHp6SlWq5VVZTg5OcF6vTZcO7KiDw4O7GRki5T5hcx55NAUoNGoGpT4SkBLSI3E8DzLssRg2J3IdV2jKAv0e0Mr88qLJitszGYzxHFsCvHQAvbixQuUZY6T0yNrRLE3wA2H8WLEkyXPc0tFYlk2rvo4m82QJLENOzZNg/V6TTkamw1UTdb03t4e4jg2yfhHdjJxmJC9HwCQZzlm0xkEfAwnE2gNnL08h5RAFAUUgQhCo7G9NZzFjTViyBNB/ZVl7DXSyNISmVGxgJ5DmCQqIbRdTLl/eQKzV4M31LwobCXoqiKJ07puDNAnhNPUNQIpECcxTm7t49bJMSZ7e6jqCi8vLvHsYoZtmuL8/BxCCDx69Kj1+qp2krqL9S4lyuVbcy0JFwzw9aTkgnfXgEwhAXhos0hAvGytKFKgAU+Qx7UpK6hKoMol0s0ajWlTo8kTy0nvUisDzDQgKZmz0A2EBwjpG9ygAMFqP8bvq9uohDB/5Ge+0UAwCjMMhlyQVdfKGpyuN8qeew242gXKfNzkif//5vE60Yjd734RoH/da3ZBK7ALgNt7iyt95hoGrbH7aurUqwyhrgHkau11DwamNDdqs3mZmgo7QP1V7/ZKZAROtEc4f7+GjmWjFOhGKrk/qU+79ZjoJ1e6fvWzX/e5pT8K0RnnlO9gjHhzjTAK0dbiaamG1/XJ1TZ23/Hu71Ec4fd+/wf48Y9/hDiJsV7PjSyrAhTgJ+SlHo36UE2FoiywXMxweHyIx8+eoCpLHB8fYTga4cWLFxR19gNAa/QSk/O33mC1XoMdK570EPgBKq9GGEYQQmKxWMKTHtYyxahPNFkEHsqigRQSeUE89apUUI3AepW2Tr2etB5WLnL79OlTm6vA+2iWZdZAUErZCAQXoOO9VEppwRpz/eu6xvn5uaX2KKXw/Plz6z1eLBaWvs17L4NBjiow8ObIy3A4xHA4xGKxwHw+t9hiuVza/AF2wACwScVu9KNpGutsZAq11trSn0ajkWV4uNKxbBC5FBqmiTP+IWcqea35+Zhiw4B4MpmQ19wxhjkSAQDr9domPwOwfc1AejQaWU8555OwUcERJ8ZiTEmneULjn40Lvm9VVTg5ObH9WJalpY1xojQn0Xeev6psojM7UDknhecp508tFgvbFiFadSp3r+J3ycwSFhVw85Td/BTGBGxUCCEsHYzvs92mdixxkjkbyG4NL/6d+7tRrQIWq3TxGsLj092zaf1ssQiPHZ43TO1zi2d/0fHahsbx0TGiMERgCo1UBYWmhAZ00+Bwfx9xFAC6wbPnj0l2EUCarpFGKQ72DlDkBXSj4YmWf86hOqbkPHv2DG+/9RZGe2OstmuUVYk/+/M/QxRF6A/66A960Lq2i3Gel1itVqbAnDaKER7qWmM+n+H4+Aiz2RRxkqAsctQV8fHyPCPlqiiE9MiDw4sUAGtJ9vsJtDaF7+IQnpTI8gyqUYgi8hRTclaAsigN0NMQGlgtVwjDAIXhiTZNgzAIIaDI+95QbY6mpqJ8jdJGEjjBNt2gqslqPj45Ql2XqOvSGiakFqJN9ecA8/nCUMgUhoMhGX1RCKCiSFReQAgJ3ycp3dFwBN+XdpEJfB+Dfh8XFxdYLVdoapo4iwXRigaDIT7++FNEUYgwpsI848mEcnLMwMvyHL7wsd1myMMtyiJHkafQiiqiJ3ECZbw7eZ5jPqWK5WVZII4iNKoBV//WGiiLArUCsqwAzORnT33d1NZR6gIe36Pk+6ahMSJkA9U0ULo1SoKQJnJZA2VZI00zlGWNuqrIkx/4eHo2xV/81bsoigJlVaJRCpUSqJtudW8e5zDAgaNgPOl3DQ03uVlzJEK2+U1EpWJSRzuJGThKKUyNDdnxHLaH+Y6hjAAtMNGgpM2mIYNBKwPltIAQJrIiBGzZCbPgUOqFSTC13mOmDXJExgF+/JMfgV3VNhrTGiFKa2sAUk0V5YC7Fih/USSCI1cdcG3v2QV7utNWgZuXyi7dSLh/1e2/pXsvtwOcs+icHeBuO0jYa4or1xLdpgi3Je3vFlBrkDFoT7/O0ECnTyz4RCv4wJFYogWxMUhRM7FzHo8xOx8BayzQb6aitGlrEPh2bEIAnifhGTWomuctBKqmMcPbaTdHPV4Z7WDlubYStE3mltJe0w4PI3EswRKrnv0sjlmOdItacAFKtlzadyalQN1QsU8pPfMVbWVf7Rix70TB9z1EUeh4DAOMxiOURYmTk2OcnJwijiPs7e3h/v37WCyWePfdD/DP//m/dNbCdmhQ8ndrJLZRE5Lj9aSEBqnCaSjcvXsb/+Af/Gf49nfewTbdoioKREGAQS8hipMm4ZLZbAopPUhPIPA9lFWBzWaNOAwxHPRRVSUuz8/RS2IEoyHVrdGUBF4WJbQGDg8OUdc11usN1e3p9ZFlOeqqthL5jZDoD4Yoihx13SCKI2w3W4Qh0U6gNfq9Hqqaim4WBpQNej0IKfHixQuMRyNSNDKMhjiOsTF5ipw/oQ3gZ4rVbDq1QMzSgj2SArVOO8/D0niMuXgZ5/ZxRP/g4ACj0cgaL6zMyJEI/oxzRlyAyJ53nqe8BnKOAxsL7FGeTCbYblMslyucnp5agFnXDbJsg6IocHJygul0ZpWy5nNKYA58D71+H9p49IMgQGn2ztoA1MpQlZIkwXw+h2/ya5OYPNtJlEAa1dBe0kOvl1jwzsnbPEUy4zmXUiIyKlHbNEXPUJT4nmMj6SqEcGp0KRwdHVnKVFVVTh4PfYeZGqzQxnXNXKWxMAxtvaFGNdjkG0RxRFF/zwekj6piR6EEtLLO0KZpIIWHoijBBSWLokRVlhBSdJSl2HCqqgrpNkWRlxhPxnY5j+ME280G49EEaWbEgKRnarKF8KSPuqmRpZmJrBWIoxie7wG6LbLH44ZzQphJwVEGxh7snKjKGrkqMOiTQFJdkZGvtW4ZJIapICVJHxd5ayRz5MiV/uW8rNc5XtvQODm5hcoM9KZWuLi4wMXFJQ729+BJYLWiyACExjbbknqQH8ATHuqSXmA/IYtoW2wRxgk8z7eyYEVR2LBaWZXoj4eIkhh5kaOqK+zv72Ew6Jtw68A+sFliIQRVYQ4CBshzVFWJfr9n1RziOAJV2d4iCDxAK3geJVzN89zKzbGKEoWjlgijwIbCGEgGgY8iywGlEQU0yAZGLUMr8vrGxkvfT3p2IGy3W3gSCHxJXHQhoFWFqsyhIdDUHuqqBBUWopoeZVGg14uQ6xp+HCMIA+vhggFqSZRAaAEJiSzNqJJ5AAySPtIsAxSwXlIE5/HjxwCA27dPIUD1Q5bLFYKAvAB1zSoiAnWt8PLlufWsLBYrbLMUcRKbZCMP08tLSp7XAlXe1kFQdY29vQkODg8xm80wm9FCl+c5ojiGJyWSXoJbp3ewv7+HOIlx+/Yd9M3GkWUZaqURxZRExSHi1WqFp0+f4mfv/py89sbQYeOCrW3ytLNyhwH3ABQ8A7gNvYD/bowAUTdAXtJGw30M9uK7AG2nEJ/5d900VNrKyU9gsO96+rVuOqAaIPubP7MA0t7PgGTlgkcA4IRsGODueHMdUMSQ115Ra9sr2tC/oClW0mI7DRhKCYGoll+ulIJWrBTFIFR0+qitPeHSexo0xqgRAGA8uo2iCA09SxdJvsrbrxnPOqC+PV3YBbR9nusBd/fQgLjyl/aaDj1HGG+Ua8Bcuf41Bo/rGW/ff9u/rZEFK0LgjhW+hnCevX3PLmXomie47rmNcVlWLO9sciREO56Es2W0xgQghIl27Rj+AKAVJUXz2K9r3T6XpuKsQrT5EdSdVIvBhs122ixf4UijruZ8BeWM2YbiJIJlXemaSpOXXRpjQ0oJYapQ11VNdZ10g8CnyAbV0TCJ3bKtbB1HIRpjNHiexGQyRn9AtYECP0CSJBiOhpiMJxiNBzg42MNwOMB8PsfREUWrWd2HVJEyy+lPkhjTaR9/9mf/Hp70UGkCGrZ/2LA0dajIQ2qkZJUGGg1PEM3x4GiCX/vV7+A3f+s3MBj0URUVmpI83WmaYjlbWQ/mYrmg+g5KITeURs5dKIoCXt7WQxAQULWy+Q3T2aV5ZuLfB6GPMApQVgXSbIsg9DEYEv0ozVKM98dW+TGMSJa7qgucnpLk6nK5RNWQRz0UAYqqgEZjoxZRGFp5eHIaaVSm7lRVVdgzClCL+bzjga/rGlsA4/HYqi4yiKrqGjBjNDQ07KVJBmeWANOzWN2PQTDTa5IkweXlpfUAU92ojU1I54gW56Bw4WOmznEkgaMc4/HYOEEHNiLE/ibGQYNBiPl8YQyUCknSw2BARePiMKCCyGFI5QCqClIIRGGI1WpFfVJV8D0P280G0BpHB4eWciy0wGq5smvUyckxIEy0XpCBqRUJ28RmbDCmagyVa2Ao3lJQscOiKDA11DetNeIkgW88+vP5HMPh0I4zBrxZlnVqVQCwfcvJ14z9oihCElIBRa00wiCEbjQUFJbbpY3mFEVqE9Q96aOuGps3QWpY0r4XyskkzMCCAiyDHMcJ/L4pF1DWyDOiOWVNDq0F1uuNdRQ0WsGTPrQ2ogBCAlpAKcD3AiilsVmsrowrNt44WubuG0zTouT30uQqhZjPlyZ3xYNWlE/s4qV+v0/3blqJYX537j3atfavOaLx9q98zXoe19st/sNPf4r5fI68qSBrBS0EPPPAvh+AVTV8L7QJU4eHh9Yy2mY5DsxA7PeIu3nr9BTj4Qi+T0VfmoryFOZmYXjrrbcwHA5ABfq4zLuHJInBaiFFQRSbr33tawBgDQdWNOLD7SyW0+O/s8e9LEtk+RZDOYRSMInMxM9brTbIUwoxjscjUNXwBp4XQKnaAOoCrjwrU6TynEJXlNRE3MflcglooNfrQ1VEdfIgkQSUE7KcLtHvxajrCoHRRS5y4njmRYGmLLHMUqiGvBSe72F6fo7LyxmkpP4sygJlUeLJk8e4uLhAr5fg8OgQo+HIWtfQwDbdIvB9VHVleYC+Z3I4whBBEOH0+Ba++c1vQimF2XyOqiwxny/xl3/5M1K5imN86zvfwe07d1BXFe7cf4gHDx/izu07kB7J+fV6fRRlgV6cYLVaYz6fQ0qJ6XSKxWKBNM1wOZthtpjj4uICi+USdVVjuVwgyzJs88x4KBSUEz5lgOZuJjwptAFQWrR0HzYQdmkIdhKZBcHlUl/xTDsTzs0vsInyxqhxE//dY5fqcJObnYwiMpd2ox7clM51vuAQuH6x6Boy7eEaTa0c6PWSrS0IbUOySinUTpjZlegT4urzvO5DuDSbL1r8dmk2N1/UjSi5VZZhPfCvphe1hsR18qgdA2GnPUwpol9vju68+j2TBdb26/XnCScXCICJdPmQgqNvBFAFRyc67ZXtc1haHb9v83fPRAwcsQObbA50RA/4GekzE28SsvOZ+y7c55EmMiG4c7VTe8X0n+9xDgF9pVEKPpnW8E3hN66n4XkScRBCqQaxF1rVPVLDm9jN/v79+zg4OMDJ6QmamvIXq6qC50uEkYfYqO2xp5JoE6SaJKXE3t4eiqLA2dkZbt++bftnuVyg3+9hsZhjNlNYrdZ4+fI5PF8gjHzrbefnp6KWNTyPxk0URYjiGIN+H0kQ4+HDB/jqV9/Gg4d3EccBlqs5FsuZpXdwfsDLly9t/gF775kKc3BwAM/zrAIjA8Bd8RSmHbM3ma/PdBTOP3TrELBICdc8kFJivV7j/ffftwnMTFHhfZcdT5znwIm+zMFnpgTz5jmqwQ4eHlMsg+p5Hvb3922OpPX4c40H87c8z7FYLKy6E+cgsGcbgI1eMBjk/AYWYGFvtBAkMbrZbLC/vw8ANpfSpTR5nrdTJ4tyJvn9ccSeFY0mk4nN32T5/CRJEHgCZUnzgRPUeV/iBGTO8fB934wFyonkfA9+P7amR5nbBHfP8zAejyGltLmhZVlib2/P1otwIxEuxWg2I8l9hVaJiaMKnEPjeuy5vezA5H4aDAZWBphzV4q06LxzNlKYus00Mf6+1tr+PU1Tm5vCfQ2hDXumtuUSYNrte61gEq9BaZratZtVsPharhgBj2GbQyKEyWveXsnpYDzt1nRx8414LBAdPevkJvMabHNzTX+6+4xLj+L1jg+Oqr7O8dqGRqlqYy1L9IZ9fO/Xv48PP/oI6WYDWdeGmkIVCD0ZwDcZ63lW4Pz8HJykOxwO8eDBA3hBgLyq0KgGQehhbzLGbDbDYNCDb5QOyrzAwcGBHYDvvvsuvv71ryEMA9upXBOjritQQnBpvQRuKI9fKHMTOVmIOWqcy8CL93q9NqHKHHt7e+j1epSbEseUQDPpYa5mEAJI0wxxnKAocqRpis1mQ8bUdmv5bZ5HlTz9IEBVkYFUm1oELN22WW8gtcRzk7Q+MMXrVqsVVFMjCH1EYYTReAQYWsB2u0VZl1gsF9hutrS5i1Zvu66AsqyQZznKqkQQhBgNxijzCsPRCKvFBvPpChpAwvJmUqBUNaIoRhL34fkepJCkzhXF+OFv/g5+5/f/AMvpDNPpJb72tR4me3v49JNPcfveQ2gNHB0dGcub+vriYor3P/gEP3/3l5hekiGhtMJ6vUaWUlVx5hXyu1VaQ+kGCqoDZpnfD2mUX7SANhW2G60oa1nwD8PX1q0vX6u2DowbYdgFcrvgh++/ezCMaz32XUUYnoquxC1PaNdz3QF79n+45r7a+dnW9hCCKES7BtNNx6sWCfc81+hyqWCA6AA5m6zutNO9h8tjdfu8wyvXXWNj911c+xzm/5Zd9KrvXvPZdX/TjpeYvuN1IzWvBPtfdI8do/Ia44oBPEeKlGqNHSmcvAAbMLmun5xIxI6hI5zQRxv5IsNEK84vaiNy7XeuGkbtPdux7OYQUJVo2KiomwxJQ1h0o3ca8ARFGiCFzWWy95TXb1sc8fGltJ5GOyZMVEujhh8Q2BOggnC9Xh/DQR+Hh6T4d+f2bcRJguPjY0ghcHJKyc/QwP3795GmW9R1YxNtGUQ0TQMvCRBFHjQqPHnyGQ4O9/DpdIokjqG0tsmkJ8enbQTVAYlPnz7F/v6+TdpkmfUoijCZSPz4b/4BXr68wGIxJ9qukXE9Oj5CEAjEUQQhBfb39m3NijCIMBoMAWiSsC5SWhuFBtBY4KyUwtOnTwEQZezy8tLmIAyHQyyXS8vNbxqqHh0Ega1VxJGMxWJhgdxgMLBcewahDJ5ZJdCVLGdjgfuGpVw5MsBgnSlEHGFhAGwTZw0Vmt8NA8Y7d+6YQrK0bnENBgbbriqlK37CvP5GKSvTy9dlw9Ll8s/nc2vcMPZhyVUWMHFzHXjeTKdTK7XL88WlTzE4p/7oWdDIkRL+ydQapUiulvsyCAJURWafjXMmuC9Zjpe9+K0UvoaAtLgJaOtLAG2RXF7PedxyNAOAFdXhd+7mILCRwsn/WrFKZ23pbNxWBrg8FjgBnellnEfjOgbDIIQMWrUlnlOMDdkQdnM7+J3x+GADlvs/jAKrMMaUdjaU2dHMUQGWtmUDgkV6uE/YSOGIDV9DmfHGxhCPC8754LnD/cTPwQePAZcBxGODIx4scMRzjvuI6X3uvfkebBi9bkTjtVWn0ixr+bpoN7Q8zZCtN7g8P8PLF8+h6gpSSPR7CQSA2XyOn/70pzg9PcW3vvUtOxg22y1GkzHm8zn29vdJtWq1wmg8Jh5kkSMOI9RVhX/+T/8Z1qsVDg4O8I1vfB3j8dAmGPEATNMUq9XGWmGe5+H8/NzqOfNCeOvWLcxmM2vJbTYby+1z9ZV5ULBFx3xATtLO8xz5NrUTJc9zXF5eYm9vgqRHxpJSLfjilx2GVKG1UQ04KbYoKGwlhYRuKJzI1nOjFC7OzxFHoVPHhDyqwmzGjVZI8wxcZZUGmAff95DEAxRFZReoKIqIznRwiEophFEE3/NwdHhkq5P2ej1InzYtnlSbzYbUmbIcH3/0GbIsx3JFCfx5lmMwHGCxWKKoSmy3qV28iIevSLYWXXUVDaL5aGXCvlJCuh5bIQChoE3lWluYisGM1lDGiGDcxAYK3aAFui2HH4aDfTUEeNPE2QVxu9/RO3NiF4QGZhHmw1WYcP/j77PHlcHZlfZAtHQd5xmJhtKteLz7uXtc5yHnPrheLWr3UJAOraardKM7QJbHv9amYCBTr3gs8Hm6HcO7bb/O4GsBqGzNL6f910Ucdq9583H9eS6A7/6dI0Bt37keNDfhzl34W6Ore+92LBhPvY0cdJrRMXCvfxwTJfGklVPmtnX7WJn7tAXkdvvnpv50/+PNrR1X7fevJB0qBaGNwY/W8CcxBOonP2jnT2vo0ue8XmgN+D5tusNBAm1oAIPhEIeHh5RTNh4jTkLcun2LPJ+SVOyCIMDR4QGqKoPSJChyboRJ4jjGYEBJpKwOOBrRHkX1eCgxOAgCK+s5Ho9RVTWKIsNyubAgl6kJQggkcR/r9daCbQYYm80Gt2/f7njpz87OcHBwgM1mg21a4OSEagWNRiM8efKE8hf7fWw3C0wmI+tdXa5WuHv3LsqigDRRKUAjzzOEYWC9mmXZIAwj63TjvZUpEywicnBwYMEWR/253cPhEPP53O6PvPfu7e1ZJSTegxgcM4jZ399Hnuc2cRgA9vb2LAgMggDT6bTdm2QrN0r1lCYWvK1WK2toMHhzvcruOsI0NU6KrevayuG6CdRCCFuPY7K3h42pb+WCSxc8M0Bm0Mn3ePLkCY6Pj5GmKS4vLzEajex7ZaEdjiRRQj5J8I5GI1vfiw0eonbFHeUqANYw4+8zcHZrOAz7SUfEhSk47NF29wDupyzLUeQljo6OLOBkJylFfrXtZ1YEc6MNTC/idYX7lfdgvibvE5Ct0iWvKYzFOGGd1cs4isZGp0urYkAshEDkR9ao5+8x44Vk76noHzuguV2MZVyDNwxDCElrDkdTeI5XVYUojFGWbaFq7l+eN9wvDPD5d+4zLkjNETBOTs/z3DI/OFrHhgIbIfx83BaOPPHc47WU/+15rfS1+5+NOpvn5kgjX5fn1l9rwb7letVJbrXSnVLCMxvr559+gmePH6MqckRhgO16g08++9RK2PILmkwmuJxeIjNelM12i8V8jvv37+P84hyHR8dI+j2MhyNsNxv85V/8FB9//DF8z8Pbb78JIbRZ4FulkrqmmhVpSiEvTgTiTYCND7Y++YWyjrT1oitlB+56vbb6xtLUaaBBL5BuUwSG/zgajayxk+eZwcICeZ7ZsFurgCR2LHxpvCHsxSSeu5QSnu8hianPijzDyCRLRWGEyWQMPwjgSYn9wyMkRoc6jmOMRyMTJu2BchSosrlWCnES23e3yjJMZzOURYHVcok0zVAUOS4uLrFZr7Far7HdbkwkqLDnaTgLkuX3G8oQgxYDLyywMspOEF0POeeacJ8JwZx6c65Qlvt+NcfhKiu+60ltq0t3jo4BonY+2gG+uB7s755zk6HBnhlXRYRBpmtg8HnW8DD8+JsNDb6X7XKQIg0bKS0YdsHd7nPeZIxcBzI7z6tpc5Gi7b9OXwqOsLTyvS5dSgMd+T/36bjisLvY7RoanUMwEO8qfu0+m/u8fG33/m60hvqNq0jr9ja2D64H4tQG1+Pe0peY0qM15VUJ971cN8YYuDtjQWt0xkw70/jf7und5+7OHb6Oa2DTM/NzX2/cXe1P545X+kSI1sjfNWwAMg89NqBAiYvWSBQKkBpRGKHXI8qNHwQIfB9eENjoONN3Dg8OMBwNMUhi5FmKpNfDYNDHaEjKO/P5HHlVWO8tALPJEgAoSvKoLhZkHEynUwyHQ2twMN3FjUoygGZww95LOv8SAFUSVo1CY2i0YRihKmso1dZlYMoDC6NcXFBdpsPDQ0ynUwsmtob+sL+/j6ZpsFgssL+/T89kakIlSYKLiwscHBxgPp9jNBpZiVQGveyBJ1pPZIEh02uYq8/zj42XO3fu2MikyxhgQMh1Ixg8M2ZgwRamBPE6yL+7NFemZ7Aa0WAwsGqMjD34c24vU1u4DoVrMLjUkbqusb+/b2tLeJ6H2WyG8Xhso0jsVGTgyBEHpRSGoxGKsrQUIIoaURSH1Zp47WHnZr/f74wbrTUODg6gFEX0mTa23W5tMVymOkkpraHBFCM2NupaWfl5jp4wrnHXMXamEmAtIaFtzSd2EDFdh4G11toaO2QwhYAWHRoTY5sgDJDnqaXwsFHAYJnrPQCwwJkLE3LVa9cQ6ff7WJtaGSz5z7kPrsSumxDNDmIG5Dy32Rgdj8fwTFTajRIxYOZ5yICda2lY0QXRrb5NgLuBhrLYj2lk9A58hEFk3wW31zW+eFwyrcztF3ag7xpmfHDUw/M8i13Z6Ocxw9REprpxf7jMAjdKxpjOravG9+FxwjiGsXAcx/idH/0uvuh4bUNjsaRwqOdRYTBoTV5qrRAGMVjAcDmb4tnnn+PFs2fYrNc4Oj3G558/wq3TWzh7+RIwi9F0NsXl9AJ1XeO9995Dmqb4xje+gV6PaDhxf4AoCLGYz6GVwn//f/vvcf/ePZzeOkK/H9uNgpN96rpGUxPQ4k7nSp68wfLL4rBqW+G6QRSF2G5TW4iPOlpY9Y08y+H57UutqgoehDVauAojLxDcPt48tNbwfB9SkOTc3t6e3Vy4YulgOMTRySl6/T6SJEGSxAh8H3VVAxqo6hqb7Ra1CbMLQaGv1TbDJs2wXq2xWMwxvZwS57SubNJenmU27AsAdd2g0hRVaMGUtl6QpqakZgNr7abTKKIzuN9n5SBp1BrcBdUFNhYgW1YKy3C2WvR8Hi+SAEMQfS0taCe2YIF3O6qvGd47Hm/3XmyYXOfl3z3sOc73rrsXjz8WBOAN3Q3tuh5bNjRc4NxpD+AYGu2zKKUA3dJUuI3sCXev4Xqg2WB0DZQuRarzQGCJTZLTVTf0j7Zjiz/jRVNKSdEoxyh0zxPoVr7e9bB1u5fd+t3ibnzdL4pacGKvew7/lFbWd3eMKGjdclm7R2toWMUp51l3jT7XaLgpUrAryXpTH+xGoW4yCHaN3V1Pr+3Sa+/Tjjf6XDvfvyoPa6+h20gkX0NrwEODKPQpehoGuHXrNkbDITQ0vvr1r0B6EoeHh8aDG0AIQ4lVDQaDPnw/wJMnT+x6Cq0ReKTA1NQ1tukWcURGwmabYjqb4vadu1iv15a6kecZ4iiG9H1UZQkIgcAPzJrtwZMSawOc16sV8rzAvXt3SeYyjikvLvCxmC8QhGQI+QGpEHIycb8/wOHRIT795FNMJhMIISxAZs86860ZKDC3Po5j68U8PDrAYrlAnue4f/++rYCttUa23iCOYgsKYABKXVU4Oj6yxgWBDVKjKosCVU2A3vVyu0XDmI4yHA4taGLwmKYpjo6OMJ1Osd1ucevWLQAtrYb3Xfba8vmcIM10KDcPwpXfBFo6CUda2MjhccgRgMFggOl0iqqqcHR0hLqucXZ2huVyif39fcqDBGwExaWicDTKdUQy150NHKWonlBhPnfpMAy+oyjCcrlEr9ez+IKdl67kq4sZlsulkXono2E4HNr3wGCS6TFpmjq1NmjN8zzPvg8G2qvVyo4hNqA8z0MSxwgDH2VZ2Daz4QLAAlI2IvjfRV7A90PbDo5mkPNUw/OlLYrcXUPb5+bxBLQS2kAb4Xe962VVITfRPs5PYGPIpTzx+Qzg3Zwafr6yLNHv9VGVFaCvRk+YtcH7sqvYxPsxA3H+qZRCWRU2ispj1e7xdUv3juMYm83GjqndPAg34gG0Nc34+zwuGPAz7gNga2CwYcj4rlUnlXY94Ofl67EBwwYmM3tco5XnJLeN+2dlatQFQfBahsZr52ho1RhwUJNChyfhSUBrCaUakj8DsH90gvHeAR689TY++PADfPbJ+6ibCh/88j0IrQxqLPDixQssl2vUdYPQDyCSHsqigKobFGVBSjSGLxl4PmpVYbGaI44DaDWCkAJ1VWO12mI0HALwUBU5mtoMFuljPByjKEsL0qlaaoMMJXwvxNOnL1CVFXQjoBp64WV5ZgYhXUeDrFoNVkcxtQcMoI2i0FrVSZLg1q1bOL19G/ce3IfSGsPh0FYo7ff7SKIEviRPyXK1wmq5wnR6SZ6HNMP5xRzbR8/w7Nkz601YzOeYzufYGG4nJ5s1TEcRElVDNSEYZDNHmSYMeU+buoE2hoPWmiRZseM5VgpVowx6JpCqWCqVQaMWhqZEFAchBIRRmiC6Q4UWZhlAImgMscddSgY0irjYmk0PtFaCEPAEFa4zGOcKpYMubRYc9rjCEKoJkZsB7ABhKXbc0/SsBm6bwlBOVWShoVl2lu/NBgLQJp+iGwnZBXputMxdZPiZePFVSnHhbRvd6jRWG2laadSmlJlX0BBCEUXCGnNuxKYF47t9CPDc5L5vQyUdM4BfhDEOW2Ov7Qt+Dw17xdtOoDMdettVoC7s98wTEaWOXxNEp6/54lJIO5ZdMEzfVZaj345r2iB3yzu45pLW3X5qH8ODgtc5Rxgj2hMeoLt5PnQdbb/peV3jgqMJ3cgERzOESft3Nc7pc9/zoMH8WxgaJ9ExeZMnycaWekXP0uY9SENXVI5sK89fkpluHQ10DWNAmL4lKUiifXm+tJ5T9gz3+z2EYWQ1/oPAx9HRkR3rt2+dYNBLSGXGb43kpq7RG8QQHtVeKA21tapzeL5AUzcocw86qPHGg3uYzxfYbjYE8pMYQRQCWsPzfECQ9OxoNETTKEgIBJ6PWyen5AH3AlKXqmkubjYb3L9/H0mS4JNPPsHe3h5OT27h7OwMcdzD/v4httsMRVFhNJqYCEgE3w8Q+EYmtdEIghBNo1BWJTabjaU0FEWBdLvFZDKB1hpHh4dYLBZEcTBgaT6bGcGPHJ6UuHP7NtF78wJ74wn6t8mBVoUVNqsN5fNB2shzFMXo9xMM+kNMZ1MIQZ9RlesKZVnZkcaGABcbY5AC0FzlvAn2MG+3W5yfn1vQtNlsLGWGPb95nlshEd5bXrx4gfV6jXv37tkkXXb+zedzTIwqlFv4jiMkWndZCq6Hl4HhdDq1UYUnT55Yh4YfBNhst4Bkw6qGHwRYrtbYbLbo90kMZrla4ZYpgpcXFRLpIc1yZDkZWRcXFxgOh8jyzFK7zs/PLejjtvLawxGTwWBgi+xpTapRJHaSWgOP9wTeH9gzPplMUFVtIcHVao1+f4g4TmzxNrd+E0efyrxAk1QIgxCB5yNJYpJxL0oUeY7xaITFcgkBgV7SpzVW0rpYVw16SR+LYolG5eglPQRBCCk9a6DxXkaOVPp7FMUIwxhZmkJIMtaVBvKitAYZqUENkOWZHSuNJiq4UgpV3aAojYRtzOwLXnsk8pyk6KmwKxlcaZo7ktmC5rj04PshynKFKIqxTVPk28yKEXDhRE6wHk8mgCCjlRkVVVXZ/Z5zqJiZQkZNYCOi7OHXmowNKYguztE3BuUM7AHY39kIYAoiGxXcX0CbGO8mrLtys24CuJRtPRJ2XrhKquz4ZqoZj1f32TiSx4ala9Rx7bXXlbYFvkRE4/zshQGx2j6Y5/uQkCiLCk1dkffHpxyEKI4AaJy9fI4P/urn+POf/ASjfgItNLIyxyZNsV1Tcjbrj7M15Qc+pEeVnvOMkl6m0yk8z8PB/j5UU5lNix6UoggCuiFLr6kbYxwATV0DAlCKjA2gVRVpuCqz5k1cwmNPM2AUDADf8zEcDRGGIfq9PgaDAY5PjnF0coTReIw4osJ348kEvX4P0vNxuZxjPp9jvd5gNp8hyzI8e/YM5y/Oka4zWxG8LEobLgMXWVONRTx1Q9EMJYBat95hHkRN05CkIb9QMFWptc7dEKkL1Pl9dgaEAT4SXW+7O9CsJx5tHQn+Xesu7971Qu9GCvg71x2tF5sS0Xe95mTwdZWm+DwXTPF9O7Qe2QWOrmfdbTvn37Tf6UYfXDDp9itfz7bX6b/dtrr5Gm7/8vd44eD7XBf12e2Xm/pXaw+MrDsA2iSFXhv9Af/5qvfpukgGjzM2yF1P/m573HOui9zsfs4RHv6um0R+Xb+0B3l3yQCl/wRIOlWLtgbIbjRHOsaEmzwNAMqJMth3JSXVFXKe2e0jYeowcJ0GitDR1fku9rugqBUlZBuqk5CWRghjBGmQ+pdLl2gpSmw3akuH4vt5UphNo2c3s9bQrbC3t0fylIYqMRyNIAVwfHiA4XAEIWj9vHv3DqCB0XgIIRVxzrdb9BKiLbEXeTyeGPrMCPP53Ho+GWzwenh8fGxzBWpVI4xCW32ZorwJzs/P0Yt7BgAFNjl3Pp9jsVjg7t07ePr0mfXOsq7/ZDIBQPl0o9HIbr7sLRdeW6uAEyHX67WtKA3AevjYC79arWyx1/V6bRNo3TWXwTt7u7MsQ+D7llrKAMAdy+4GzxW0hRA2QZX1+pl+E0WRbVdd11aedbFY2PfL5/I9mBLGBoSUEhcXF9jb24Pv+1itVjb3ZLPZ4J133rE0YG7r4eEhLi8vbbI4c+PZWEmSBIvFAm+//bb9nBOiXY8rRzw4UZoldFk5abVa2eKx8/kcq9UKt27dghDCytFyQj7XWaAx1KU+ud7qMIytl5fpzGma2iJ30+nURm/Y0KJK1kdWbpepOYeHhzaxfDAY2LyUNE2xv79v9xO+/9nZGZqmwfHxsU2CHwwGlvrF+ZTr9QZNozo1CxgIurkF7NVmkPny+QuEQWAjO6zGxAaa+w5Zqnc3T4AxBoNeThxmmVmm5nCEg/t9u93aqFFW5JBeW02coxZkmLTFEAHYZHZmonD+AkdEuFgg75u8z3AuDT8/52Xw+w7DEGVRWBVT7gsG9Hmeo0ErP+9GLaSQ8Iwxx59xfhG3xY0Qu3sWR11YOQpolZs4Ssc5Wtw37t7PFDQef6ykxvOVIzuMm/ldAbBiQG5btNadfGSOXHAkjvucc47cvYT/zZQuAJbO9uO/+zfxRcdrGxrPP38EKqbm2Zt6JrlwuVohCDwTypYoqhxNXSFJBhAihq4a/Ls/+Qne/+Uv4HkCRVViNlugKSm0VdU1tpstqrpqw7U5LehhFAIaODigjSTNNijKvLXmpDDF8yIISFuMx/OoerfW5JH3PJ88TkGA8XiMpNdDGIQYjYeQQWvp9QcDDAYD9JIE+3sHSJIhoAUme3vwfA9FnqMsqFL15WKOxXyB84sLXF5eYrlcUpXP5QILk0DVNA3qpiaPGW8+dauJXxtvBUUYJBpNPDkp2gJXBEoU6qa9BuCAKtkmwhKtRdnJxFLAvHExOHNpKezpFMKp6XBNBVoXXLoD0DUkILpAfJdG5bbd/dt13n/2pnLNAvde7M0Woptwy0dTN2AAd8W42XGiu2DfenmNt8Y1HNgwYy4jG3pu/+y2Uasuteg6D/luO3ZBBx/uItR5nlcYGu7v2gHO7OF27o6bDA19g3FxnaHBz0EgGFcMqV3DaLeNbCTufs5/d/uEqXTt6W6ExqUKGSMQElRfgeohAICQGixj6+YSCCEgtBt56F4TDk3oCmVp5+9sPHbGCNredp/BRmSMUUF9TPV+PE/aaA55ABuw/eP5/FwacRQhiiNEESUyB0GAvb19KlamTZJ0L8H9Bw9wYEBQVddI4piKkaoGB/v7WG/WRqufNi+tFHTTrlelAaeb9RpRHFngCpCTZrlcWgPIpdIw6FosFrbaLBcGc0FC0k+wTbfWSzwajaC1JlnR3gCe9CwA4IRrV+KTo79MS2GaDuftcWInAwcFWJrQrVu3bHIzq9GwPCVXoW6aBgcHB1Ztyf15fHxsPdqc73d0dISzszMqKGcAIQMABgkMGDhZlYE0RSJKuz6wN5wpOFxbgSXcwzC0BghTi1khiilbbgSBQcTl5SUODw8tEBSildakCFnV4YWzYbVarey8dAE19zP34XA4tFERvg4/Lz8PO8i4/byecI2NpmmsJ5prf3AyLhsDDFpjppVlmVUoiqII+/sHWC5XVk1ouVxa8MdAmL3QnBdB0rg0Hy4vL3F2doa3337bJrGzYhPn7jA/ngHjZDLpJMOzB5sjBFmW2XHCxofvByhLahPnkbieZwatbAQwcK+LVk3J3fcBWMOB+9+NUDC4Z1oXJ7RvNhuSnVXK5lWwQcJjikEvG+5BEEALYl7wOsdiA3wejyPOq2GnMo8TBsE8JgBYlU7OiWCj36X68LrL52qt4aF1tnJb9/b2yEiRoiN9zPkavuchCmjdYqPAlSrmnBE2KFwHgTtfdn/nNYrfg4sp+J0xJZLfl+sYYaeQm4PE+MCl/QGwawu/Gx4ProobzzE2Hnif4rEBwBpW3B6+1l+rofHi08/tIuAHPlGOtIb0JFabFfr9BGEgUZYZgkCirgtI6aPfP0QcJVCqwScffYhPPvkEGkC2TfHy2Qtst1vMZuTxr8zkKzKqYq3NSz08PMT9+/fxwYcfksffgEx+UQBVLj84OMDxwSGk7yM23pTG8CqFJD3zXr8PPwigtMJiPsc2TbHZrrBar5DnObbbrQ3BqkahLDUuLy4p/F7XyAxHsmoaZCas19gkadr0m6YLLBkwGNZLxzPLngVC+4amw9Y1HE+tqlt6kRlgFqhLzwIQ+gL98HwCI0wDY9Dc8hE9sGQmt4faLSCce+16+tlTwJOZAVWjGmsU3QSGO8D3GkNjF5Rzn/FnHc+4aB/WjSjwM7jRFrdrdjM73PPYynfbRO+omy/AHhVeuDrve9fg2InkuM/qAlA3QavTZsdAA7oGx3VGy02GDASJEbjXbXvlam0C+z3VVYjic3fflevFFcJQoHbafl2br7a39fC39SQ4V8HNOWGVJIbtDj3IecVKC5vzQuOnfY9UGLMrx2p/chRBa0s/4nHnmc1sd/wKYehOu/MX7f2UaizVi1WThKnhEMcxkl6CMAjtHNs/GCOOQ0tBCsMAo/EYvuejP+ib9YdpnB4mkwniODI0AWnnJAG6GHmeATB887zAYNA38tIE0kdj2uT7vR4eff45Tk5O6J0CWM5nCAIfURSbd0NzrK4bBEFk6Qxu8up6vQaAjuwi02KkJFlTNjAY1KZpCmVolVJKbLdb3L59G0+ePIHneZiMJuglPcvz53fA3H/WlWcPHwALkJh6OhwOLTApyxKeUSoqCpJV59yJIAhwfn5uaTCz2cyC9aIocHR0hM1mg9PTU6RpasERF2RjD/1yubQgzvc8BA59iKXQWVWJKj9vLajgxFn2dPM1B4MBLi8vOzz7/f19bLdbPH36FOPx2EqMchSH1Wvc/ISmaSyw39/fNwqKe0jT1EYl2LPM3mmOjrBaE6+HbtE6VqMC2iTvMAwxM9Qwt66EqwLEvHaWZN1utxBC2FoAHDVx5TfZW8/9H0URKtMmNnYYfJ2e3sJqtbbgtjQJ3q5zgA0wPoeAv4fc0H6UovofDHYBoktxwj17n3mNYC+4m2/g0scYrPI7odpfKcqSck6EEFgsFnZ/YmOOE415rGut0ZRkxPA7Alp5caa2sTHB+axMcWMjhnMd2EhkmVf+3U0u5iRyrvnB8194EqUxJtnBEASBjRgC6DhB3b/xPVwwz8/H44b3JU4kvy7RWWuNMAiQOMXp3L3X830otMa+1g5lSRB9m9/Ner3uAHOO+nI/cdSDAb/LpmAnAkdZ+TuualRd19bIccUP+NnZuHTFBdxcGo4usWHR5tG0eJkFGHj+87MwNkzTFMPh0BpsbGyyUcN/53f2o7/zY3zR8foRjU8/tzw7KSTKikLMURyhNxwAQqMXh2iqDKvlHFWZmZBPTLUjjAXFnkXVKORpjjAM0CiFLE1NKK5GlheQIkDc7xPnCcT7lkKi1xuiqo03ua6x3aZUiK6ssFoukacp6qbBYjbDbDbD5eUl1us1lusttmmKpqmtUgZNQgklJOqmoYreUux0vkspES3qFRK1bhMh+bDgS7MHHDZ3AdpUbmbwJdoaAp6UgAQaRQO8C74VoBpIgc6gsYNZC3AlXE7UtcBPkqeaBzZbzTSRQzMZGjRNl+4j0HLrd73QLnh0vfAEwrqJptcl/O6CT/e+rvHR9nn7PZe6BQHLI99NsOKwBfdR17NPCezuwsXn7oLiFlBfr051fZvdfrze8+8C9OuA9xWDyznHNTJ2Qe5NRoZj5tifDECp7bvGpnOuaqVp3ee97hk6f5fdXITr/r0bGSPger0RJXZyTNzDjSq4Rrj5FFwTgp6vgedJNA3Xdega0jZqq2GjMr7nGdDrEZ1RtJEvWnw94jELAc9s3kopnJ7espSKW7dP4HkCB/sHAKiGw+nJqVGCq5CmG9y6dQuj0cg+B1E3fGiQqhHXWGB6UZpmSLdEz4DZDKUgdabLiwv0en0biXU3qbhH1BROpO0lPRQlbZQM6kimtbKJjEEQIDB9ZSs4G8M8zwt4Xmg9pFVVWcENN/GSN2P2vkZRhLOzMyv7yuCoKAoUVQEhhU30FULg8vISk8kEo/4IL168sJu3K5fJQID5xM+ePbOynPv7+3j06JEtksdgBgAWRhoVgI2wcGSYj8lkgpcvX1pPKdO+tNZW6YgLk3HSJFMRjo6ObJ+VRQFpgAoDEgaMLGu5WCwsLUwIYb3lXMNBSmmTmDmywN5+1wnCyols6DF/mwEhe5HZ08zAmdWZODLEFDE2eNy+d9WneOwyOGNFHgCWpsPn8j7B7WW6kbsWuf8xqGWgaB116Mp1MgjamkgGv1eOdNGYLTEyCo283zPY1Vpbg261WmE4HFpqk+93E3fZAN1sNphOp1BKYW9vDxcXJH/MlD02BhhsuspBrieagS5VuSYj0PXgc7+w2pE7Fi2AVm3+HxtuDHA5qjOZUN0YjtBxn7ORxWuBGyHgz9M0tWOAlaY4ssHrA+Vc1NAC2Gw2du9mQ5XXNzeXgMeDK5/qzg8AHRoTv2tev9lAcD38VUWVz5MotrLHnufZaKbSmgwiE/3k/mEDBUrbCCK/G5dCzLlJ3C43EZuxFo9vjugURWGNBXbI8NxlyhXv82w4c1+wseDmdrBxyFEXHg+8N/J5LjZko8qdS9xGjgbxPsuRSX5HHGksiuK1IhqvnQyeGKlZfnA/ihEYney0LJGmWwxHPURhD714ghfPniJdp9hun2NyeIjh3h7KhpITyzxDkRWYL5bYbrfYbLdkJOQ5xqMxaiWw3hb2JbH3I81SQHlI05Y6tV6t8cGHH9BCV+Soq9K22Q0pNZqBmgAnIjeNqaYqBAAC6qg534C40S6e4YWOJpy28pSuZW3pOqDEZ61NsjNaioRQJoABY9goMiSsuoy5jLaViY1xpurOwKVB5KFuNLSu7fXheFLpupyT0tj+AGAmDHuCDbXFNIBYGleBN2+67sLgGmbXebCvi1y4x02g1Y1S7F6P2+qCb/6c+6wF0TtGjXNffn98uAsIH60X/Ppq3tcd9rMdY+F1Dncx4PflPosLit3v32Qs7T63+cT+VWtW6+oaGjavRXclgnf7x33/rtHjftfNd9ltV9dwcvJIAHQLzbnP1UZ1uu9KmEid7lyTFlCTlwQFzxPwNSVvU36UWXzDAJQXRAWtPd/DcDgEtKaaDAcHgBDYPzxA0zR48603sZgvMBgO8PbbbwNKo5ckqMoKVV3h9PTUboZhGCDLiMbCNIpfvv8+9iZ7iJMYUlKEgbTpBaqiQa/fR54VGI9H8ITAfDqF1hpFnkNKiWF/CF96UAYgXRq1mSiKMBwM6B00DVLjRfU9D3EcochpfWXpSHLWkKev3x9CConnz16gaagw28HBEcqiwHa9Mh7x0kQrOBG49WAvFgvrjWYwOR6PrdITqwodHh5aRSAeD2xAsed1sjex4Oby8hJHR0d2w93f37e0ESGEBfeuU0UIgVu3btk6Db7vm8KwAws6uTqyUsrKwHLOBQO5r3zlK3j06BE+++wzmwzJjrPtdoujoyMLTvmZucYBr5sMAtbrNakJmiiF7/uWdgPAgl0hWpoEAxIGFgwUGNAzX5sNkCiKkGUZJpOJpXxxsVkppY0EsYeaeeB1XVsDk6XfpZQYDAY4OTmxY3m5XNo9gOlgXM+BPfL8uyt5yuCE32lVVRaUMoDlvY3XPPaSu9Fzfi8MGtlgGo/HFghKKfHgwQNbBI8l7tmYW6+31oPMUq4sv8/GlRuRIs97hbJsLEBerVYdA5LUoGgsHxwc2BweV4qU+4j71R2P7JXm6BNHGDh6w++PpXq5/W69CGiNOIws+GfvNtPHOB+EOfxJklhFLza2GOxyFIvpRm5tFVY54s+4/ewZz7IMnu+j0apD4XMBtNa6UyARgE2uZ2cE739sRPC6zv1ZVZWlxQVBYOtrcFSAIwXcVp5jgJFI9kg8iMcbj0cG/r2Y5HJd+WOO3vBaw+OXvf98fQbubnTFrc/Ca51bNdylgA6HQ2uY8Ocu44Hbw99nfObuu2z4sLoZR77YeHONL87R4HvwWsPtZOzJY2XXKXnT8doRje06R6Ma6zGra5PwCY1KKzS1AhqNOi9RZhmePHqMf/b/+CNML86QjIYI+wOkRYnNeovtcoNtmiEtKqw3G9RVbXh9Ed58803cuvMQWUXgJUvb0B95IbZoqsIm5223Wzx//hyz6RSNqqCcxC8hhIlQMMiiBFXfay10pRpA15ACNnm16xl3aTcOWNYa0C2lpOu5NxQo3XoVnA6HcLjl9B2TuAkJpXc8/tZ4aKB0O9FckNUoCSlbz4A7ID2flMJoAXFlZI1xBWEt2/bZDVUL7XPxc7ggkz9rAa+yWHDX++4aErtDzjUsdmlXYkcWyG0n9XPXOLEAXXH17WtyGoS+0p7rohK77bvJ0LgO+DsN7nz/VdGN3Wu7bXQNDTcKcJ2Bdq0xd+UvV49dL6I9d8dgcz9327J7HTjt2c1jYG8TL2IdQ0O3C6kbMm+rw/M1WyOf+oiIcWwYtt8RJjE1AoRGv58AQmMw6GPYG8OTHg4PD9E0Dd544w2Mx2MAGqNBD0VZ4vT01HrrxqMxlqsFalUbcNWz3ikadxq+AZXshWSqThQFWK0WtGB7NFcH/QE22w1WyzXu33+AqioBCEvBATR8P0AUxRiPR0b5KEFVlQjDCJ7nI0l6+PDDD7G3N3Eq2uaWvqO1tlQZStbcwAtJzCMKQzx79gyj0Qiz+Qy9pId+f2wTTHmjFELA9yTiKEBR5NAa1sMnpcTLly+tkovneVgulxYgcjSEKykzb5258FxzgYEGA5ikn1gaKfOBeXNONymiMLK5F/yTOfxMaUmSxIJiroXBnuc7d+5YYKW1hmfy9zj5nAEoJ17neW43YU5YZcNpNBp1gDSNIVigyO+TjYLGeGy11rbIXVmWtmCbm5vAXlT2bDM1h3+yYhWDT24L00lc+oQL0rTWlidfVRVu3bpl3zk71Pr9vo3INU2D6XRqo0FE7dnaKAODR84b4Crou2CFo17sXWeDjSM6bPS4/c10L55LPK7LsrRGRNM0ODo6soUVkyRBZdrMScpcY4EMWYoIAG3ewnXVurXWNuG8aWqUJXmiOfLEOQmcP8GSxNLk4bBzkJN4eSzxGsFGgkv/YYMiTXO7TjKn3s3D4WexbBNJap2BR3ig1+thvV7bccjzzqVQuV52F9gDsGPapbdxtIEBKz8X34OPoigQRCE8YzyxIeBGAvg983NwRIcdB+Px2D4XA2YeYxyZcnOGuE1sCPDeWdc1pO46JC1mkxJlXdkIiwv0ORKSpmnHOcE5T7x+AK1qUxiGWK1WHcOBjU0eC3t7e3acum1RSlmhhF6vZx0VbEizwcLRMJah5jWe3y/PRT6XxTe4ze477tDwjYOEx6EbhePICq87Ukr0+338jd/+DXzR8dqGxv/7X/wJNlmOqlLIihLbdYr1aoXNeousotyFsiyQbraYT6dYLpZItxt40CibBtL3IQTVYZAguUFWUWIg0TQKQeDj8Pg2bt9/A0JIY0XnCMIQvuehKlOUOWXfCyd0PJ1OsV7OIYUAlAYXgqZOl5bvyy+2tThrSKEg0NYHIN62NFVrjVdZcOVagL3bTVVaqhWBWgJBVERQWroU5wS0CVna/l8IYdVH4CSpKqXsPQFA6QaUiiFtG2mwaAjhww9Cu8jwBiU9D7bSsomSKEUStqzB7QLW7r8rKFUTpUw7z6EJcDOw09qAfZPeygsz97UUslOrQIPBcbdvwOmx9m98xbaP7P3QGn18rdagYKvS9A2EkYE10RaTPauUMkZcex+iyRlZY+28J+Px3zU0do9dw8A93OeHpid0AfwXeQd4zLoGhfv93fN3v2c/4yiZa9DSAOwsQG37hbHnRPurMtQzAIHnw0pBayeHBgJStrku3agFUQWlJ4muKAR8n/JHpOfZd717ru8Lk8vgW1lplskMQ1oAD/b34fmeBQ0PHjxAr5fg4OAQUURgSKNBz2zaRcZefPK+LpZLQGucnJygLHNkWYbz83NMTJ2Gvlmwy6qwgJjBc1XVGI9GuLi8oEVfUD5blmaY7E3M5u5bnfu6qtHr9xH4PjbbLcbjic1nGPSJKrTerAENBEGIIGw500yziMIIjfHED4dDFEahyC2oxDKNUgj0jOJPHEcQZlNigNEYj9jZGT2vJ9uE3qIoUDc1yiK3AJNBM1E8NnYzZlDHxjFvVIPBAKvVym6i6/Uae3t7ePnypb0e5xcA5NHcplsMh0Nb+MvKTJqqu5vNxuYVLBaLjuIPG0mLxQIALCfd5d27Tik4AJw9gEKIjnE0n88x4PwPAwatUSwlPANEPNNvrLhjEyy1xjZNEZiozNHRka2lwZ5ZjvYwqGFDBiDgx55JBlhM9zg8PMRms7FREj7YgNlNOGWwzBxvXkPY489zmWtB8HX5eQACbgy8GBwDsICG8yvYCeZ5Ppq6jfiwymQcxXYsMqhWSqFuGmRpiqquMTBzlI0qBkIcMclzUjhqDB2mlyTQsvXQt8n/Deq6Qi9OrIIX0cV8aK2QZTmk71nA3zRUGNHzPJyenqIsC3qOpkFZEh1tNBrD80hC+P/D2p89S5Kt2X3Y8immE2c+mVlVd+wBMIEmEwgKaBAzYKT4d+hFr/pzJNFMAl8k0gwG6EFmfJBEkYShQaAbaDQaMAKk1I3uvvfWvVWZecY4Mfm09bD9t315VDUq2+yGWVZlnhPh4b73N6xvfcOOp0UHVVWZQGPMiBSDnEu73V6LxVycyB5Cr8ViqRDGs67oISqKctKD45mOwyFO5SQbeXd3l/xcGIhQt6WRuCiHM1D2OjuDLBjGffdjafX5+Xna48Fja7t9TWU8BOQxgF+oro9JhgC9ZRkniHpgQFYDW0fmQhrPRAHIS0oN/0zjgv13GSRoASAvhtG4BLRN08Rx4CHEQRqhT2sWydo+ESPcI7pTHyMGjSVwcQ3zvNByuVCuTF9//XUiFuhxgBCl7JNgqmkardfrybQuaSRtIWUIBllPenuQZTJTBIsEjCHEIxVeXl7S+pPZeXl5mdgBz0BxDgt+BQxANoyzYVarVbI3UsTXv9QD+/53/9v/vf7opz9Xp1J9KJRnpbI+bpqyQvtjnPfdh3ZgGg7q2lZ5FuLM8yaeZ4Fza9pGbd+kyGgxjw4zz3PNF2cqqnH0HM6gLEvVx53aJioXmwVgKrJMubLJBkX2M1evNo1DHQF/jDZnZZ4WDWEhQg5tPOQl+qFhEkzPadVxtGQ/OJDeljId1ZBFoMbI2q7vFDJY59NpM5mKvLR/jwx+URY27nKcHR4/H0E1wgowy/M8Bl2DUYIZS4FIPh09y588z9SHWn0/1vWd/vHPOSj/k1h7fufv8eeMf4/XOa2xPwXw8fPjd1IOx7keeZ4rUzxTwF+n5T2nz9/1rfq+ETX7p0GYZwq+EUhk04biP2kN/BUZcMt22fVPP/ttvSanawOjDptP4JsycbI1y8ZkSwghHQCYPsSbvuW7+F2eZcMcq3jmwqTpTLmKYiai3KIoEyNT5LFsEEO5XCw1m8+0mC9UzUq9e/dW8/k8lcnUda0vvvhCVVXo/CKCCk45hrmhRpzRmYfDIRl/GEPqjSkL4ARl9OP29jYebmmAilri19dXbbdb3d3dJcCC4YdpZAT3er1OQBWH9fbt28TK0XTaNE0apQk7yUhRHA6lNmdncaz2ZrNJJQ8c7EUzIsAD1hh2yw/M8lGSzrD1fZ8aWbfbrd69e6eXl5dUDoCDhFX3fgv2gSCCsaQAyaZp9PHjR/3Kr/xKOi/h4eEhjbO9urrS119/nRg41x2CEvbEyxDQX1jzr7/+Wl988UUKVHjvw8NDkk2yHm/evEkMJD0vV1dXCZh4uQxOmwZzABN6xyFyTBEio/Pu3Ts9Pz+nQNazGl4Ow8nIPAcy6w2y9/f3ur29Teu8Wq0SQHt5edFisdDFxUUaJ8zz53me2NDUn7NYJD0ArAPueCbWFwYZwEzGhoZXytj8mRzkoZcSU2ukPJuWkVDqwohVAhkHmx4AerkU4NvL5WB5zy8udGzqtDeAo8UiHoRbFWP9v2cxlMXJmFwLkMbULuwJgBuQx14QZBGksE6SUqaQscKsZd/36QRwrsF5G26ffIqV93vgezyoJQDBvng2A1sIiQBpUuVjOZIz9Mpi9Qr7LI2l2J5V4PdZFscyk8kCd7B2ZBwSYTKMzKUsh+vyPDDrZFZ2u13KVOBHfKISNsQnbGHP8WUEKwQvBDJ+z5SbweYD0IuiUOiDXp6eFEJINp8MGRkjXl79URTjAYvYV+SyKIoU6LB+7BuvCeY1vQDbeAbRK1x4DtbbgxvWZyzJzye65oM8nKjv+/6XO3Xqv/tvflv/1d/7v+vD46uOtXQ8tuqaWnmWqUnOqouMaSYdD3vN5zPVwyF6MGJt0w6gJqTehbIotBhSmnmWqeulrh2beRCK2GjU6njcS4Mg93087C3Pc83KSj0H9hW5ur5Nwta2tbquTZMUfPOLbIz4MaR8Z8l5b32Mevu+GxhdMg5D6YeyOH62B7RNsyddN5x30QcpzxJbGGvkBxAHgLZsDMJZzoaDsIZpNdmQRSBz8G3AXIonBjhTTeByClglWRAiKevVda0YjwujT0A0MvEa71+n5UThW3/ngUY2ZIh4L8/tz8N9j+n/8TszC9oom8nzeGjaKVDmvgiocA5jANWr65txA+wzp4HDqdpMAw1JiVH65vvGiyhmN74lkCF7NH5QQxAxfNACVD4b/84Y12nWI8qanxlx8hx2tkjKsqVyp5jRU0YDdOzpKYtCZZYNBzXNElj68Y9/HBnIi3MtFxGEX1xeJAd0fnam9dlKP/zhD2M6uirHtHcIOr9YK/RB210EN7vtUEY0ZKKur68TuGGUpafd0TcmzZBizvM8OVicmjdH4iiom66qSufn56lulQkjm80mjVp9eXlJ5zIAOlh7n5ADuwXDTrkPfQbUw9OAvN1uUykS5VA8I1OaeF6m/EjS4+NjkgUOA6Okhmk/X3zxhWAdAccAJ6+X5rkpgQFUA8Qp+/BJLZRoAYY4nXiz2eju7i6VaZGVoTQA5my1WqWzFAgGsPMABerOHx8f1XWdPvvsszShhSDHHTUZDpq/yfLA3DEe9fb2VhcXF3r//n0qE6FEF9BFMIW8wgLy99RgOoBbpmuRwaEBlPMh2ANJur6+VgghHeZ2fX2ddJR9YO0AMYAEb9R89+5dmkTFvgKSAVo0XmMPsQMAP4IPSSkIvbq6SjaTLItPxvKSDew1MgOQCUFaLlYJuLBHHvBKSj0w+CrYX7I8s9lsEnwByLjfoojjU0Oepf4b9iplCjTqKcwwgK2cx/X14NczygQHZAMd1Dp4pKEWPcZPIH8xUxv3hMCQ/QYUspY8A4B4uVzq/v5+wjJTbw92gnxg/DH356drY3skaVHNJveZgLmCjs049tSfBxKsLMs0rej5+TkFBpQC8mxkiggWfYoTp6m7zpH9IhAlOEAmKFXySVjOyEtK/ok9ZW0pD+Q+PHAjW83+83NKMI+Hg+rDMe0zgTp+xAE6dgECm/eTMWa8MuTB2Av8zV5G/t91XbpvghfXPdZ7JJDzFAAhk/z8FGvhA7AJkP7cm9uRX2pG4+dfPun/+l/9A/327/wbdVqo7WIDc1Fkmi3mCqFXXccUYF7kur//qL7rxCG4bduIyUYaRLfvu3QgHUIpBTXHTrNy3GAWIMsyFWWurmviZ4dmZkDDarFSWcSTKpumVh86lWWhtm3U1EfVx0PaDP7EBskIrDabTQIpCEhZjDWyEzAYItiLjmuptm3SNeNm9SryPJ7z0QME+2RcMMxta+Nn8/jvajbU/rVdYpuLvBLlQX0/nlwem2LDwFCP95mAfBizFThIngODyP0Q/ca17tX1J6Nbk9SMpw+HPqQ+iQlNLmk8/TlteSqVGvGt1/LH4Ol0/GwIYcgqTWv/FWJDfghB/RDIgc/zbDoOL14/myiS9M0Dafq+UTgZ9RoC8vrN0qmQsl2n5VJDMN2f9n2EyV8zuz7/9/UhmPLrKZtmTjyDpxBLBePvx3KyeJ3xfadG6/QPzqyqSp2tl1osllqvz3R1da2yLPT555/re198L/YcDeAGefzxj3+k/WGvNrSaVUON/qxSkRcD4xqUa2xyp2QgOqw2BQDL5VJd1w6gtFfb9rGEaAClACgcF+wpQAMnjsOhgQ2WHOaQA8eY6nJxcaGu6xLYy7JMX3755QQUhxDr2wHp7D1pbQAz16KRme9br9eTul9YcBhngO9isdDDw0PSbUlar9fpfbNZPJSNufP7/T7VrJNVQP/bttUXX3yhDx8+pHGlZCRw5Pycg9UAr/RXwJKy3jTFtm2bDm9bLpc6Pz+PQC+MPRaUMxGIoHsEIoArggaAJmNmsVMAQ89m3d3dJaa+6+IBb7CQAEyAKH93Jpafn8oLQIU9Ihs1ElhjUyjBCYw+rDNgH9bUa8yZaPTw8JBABmw3tpyxooAL5Bawdzwe9fj4qHfv3qW9ZKztx48fJSmtA2wm+sNzA0jpKWBdYC4BNEwZGom/sYSFe8Xe+enE6CQEEIFTWZYp6PYeAP5NZom99EZbJyG5RwLwLItlx3U7ZkZg7ynZuTq/SD4PGQ4h6FjXKmdVIgbQ+d1ul/aUvUDHCX4BaARyDj65FtkhrunZOe9hQL884CCbCl7yHjXYd0r+kEsGTyArHpB55rRpGhXKEskAqG7bVkFBhyFQYV+5huMinwTFvTOxiTXb7/eTKViAZMArwRvrAUHgk4/AMr52XdelrAP+kUwXpVzIpcNeADd6z7Ng05mCR6CT9L8slYVxbDdrzr2cBjz4W7JSBPqQKRBi2DD8FQEjNokAgEALG4vseF+d2zAvLeNn7IVnQLjO8XhMY5Z5PmSWwDHLMv3Hf+Ov6Ltenz51alHoz/0v/ox+5/f+Z7WtpKJQVsTege1uL2UxpdQ2rfquVTVE8otZrNFkhjHKcTwetFzOxbHyXddrNqsU+qDlUirC2CgqaTRmimd3eKYghKAiy1W3QYf6qK5tFMesNmraY2TAm1r9YKTdwbVtqyKLbD0bSM1pCEFt06eZ+dJY1x6yWMbUtJ364dj6ruulYW59luVD3XuuohgOOCyLxGAXRal4AGKuvo/To5Tlw7MNSjYbU1kEZnFzaRzrFIZ5+F07MkIY9r7vNSurtH6sF0KDMnlKk2Cv66TQR8DuwN+zI3meq8/6yc8mZWnF9LA+pXaAaaPzaYYjs0xE3/dKOFscqkY2JY+OK0jS8Pfhrdwf1zh9eRDCc5OtkU4bl6eMmb/8vj1oiXKSqyynWZVJ8BPGcxT8Wt/IbpjxyPNMXdcqL6brNvZIFAp9nJYU+qBy6Fcoy0p5rlh+l+WazWepmXGxWOj25lZXV5cqy0qfffZO89lcv/prvzoAvrmWy4WqKtZTt00znMdw0LyqVJRxkk+maMzef3ivssy1Ol/pcIxTcPYvsQZ/sVhoMZ/r8T6Onv78889VloU2m91QhrTQbrfVcrlSWRbabl8Hh3HUfL5KQI5afIAw2QsPkp6HSXb0XwAWHx8fE6ilZAEw7Q2sZDmen591e3ubwI9nEB303d3dKc9j3xjAnGD+5uYmgW/ApAcoP//5z3V1daWzs7PJPXz48CGWli4WiYnlpGYYShwh6wIjejweU1M25S9d1+n6+jqBnefn5wRC1+t1+g6flsT0E5w290+tsTtBMgBt26bGZkBRlsUyJ9bef351dZX6C2azmT58+DAEmt1kogxAk/IAyusAbNTSw2ACZCACFotFsnfPz89p6ha6iQ3DNzw8POju7i71Avo9se9ehoKMU8ZB8/l6vU6NrdwroJSMFQ6ejA4ZEQA4z3d3d/eN5tu7u7sUbAIwAIUEeJTYoS/SmNmglILn4XvPz89TJgUw/jKMAWateGaCBj9XwoPcuI+xvwGgzZQyzupYLpeJ2aWp3INBgBl6ToCEbPH34/GoLM/VhT4RF5AMWZZpPgR6nLdBBiI11F/FsktkHl2TNClTARzynNgYwCIBJtchQ4KtOg1+sQkOpJFnDgYEQHPgpU/MAhgC4rE/2CnukbMa+M7D4SANOGq/3+v6+vqkgXvsccLWehkSAQnPwX4B8AHNyFhd17q9vU0BO3YAnUFnuTZrypr5pC0nTtF5DxgIDpzFjz4xXo+DRdfr9aTqA6zKOGbsKNjRz9iAfIFIIaOBLWDtCe4hy/DdlKWi97yX/SPI8qwFzwe28yAIu42suuxhB7BRBA6Q3+gXcuWBku8PGbZPeX1yRuPl4VE/+fJB//n/5e/rq49b1X1Q3x91PO5VFvNBEOfa7bYqijgG7lgftRoWNssztU2rooyL0dS1MgXNZpVeX7eazarB+EoKQV3TpUa34/E4jtPKRmavbhr1gwEuylIKsaG0LOMo2KDYQH087qWmVpHlk8gSo7V7fUnCwAaNqauQjAZKOgLKKZAmMo+v8UA3jyjrgVHwmnsMVl6UOp40KSbh7lst5tUEIPVdzDpo6EsB7E+yEGEEqg6UEdJvY7jj88QymxCmPQdE0H4NV3R/nb7Xs1N8jtfYaP0n9wX431N2g9X+1nKwMPn9n/SaBBHZyfcNzz8tXbJnPy1x4nPZ9B5DCOMBgvSzKAZVvMf3iL3wPY3GZ6Y4knkMjtwQF0WuL774XGVRar6IfQ7f//73hybdaKzW5+e6vrrS09OTsjzT+myti2E85X5/GBj5pepjre1up5eX5zQKE5CHETstIWAEYFDQ2flZYv1gsefzuZbzpRSkDx8+aPPyorKsdHEZgcwYaEwn2kTgulbTREMHAKdUxk9wxgF+/fXXms/nuru7S+DHyxouLi60Xq/105/+NAUJ9/f3w30sEzAF3NOPQbkNzoRzDebzeeqHAJwTCFC6UlVVcvrU1Tu4ZR0BLD/72c9SaQR27/r6Wq+vr4nBpDSEulrYZ6+BpkcgNX4bWH56ekrvoW7/6uoqORLAOkwmtpj30iRY13UaDyvFzAsyLCk1iK/Xaz0+PqZrUlpBQzhOERDujvHp6Um3t7cJvGLPYde9n+TDhw+JPKJ0BHaOMjrkAbsuTcsscPjem+HA0kkWL1tAT9gHwNwf//Ef68/+2T+bsiMAHJrBHUiu1+sEJpE1wMJ6vdbXX3+dwDhTj2im90wlmQFsMM9LUJdqzgdbQs+JpPSdBA6AXWwU5V9SBJV8v58sjZ+tqkqzaq62HTMS6BpZJw+SYNl5D3rNGpDl8mlUZM7quo6Z7bJIjbTOKH/x+RfaDA2u+EvWre06nV9eTJpssQUAMX7m4I81xZ+QrQTwE/CQdTzNItMTgAyyfug1+0SwD4nA9zG9DbsA7vBDAvk8gN8nFTV1naZVkTkk23R+caEujL0dPjLZM3tOIPDsBMzoCwE1pIFPWCMAR8bQM395eSYvwLCXB7E/nlUjGCDIBNewHugpAa5XefD+oohT5ObVLNKS5qOdaCHre1q2xPdgzx1TsA58BptCRspJE9abv/M+7yHjXtAdx2nYATKV4ET8Br7dS1fRWw+S/vrf+Rv6rtenBxofv9LuWOi//n/+lv673/wXqttej88fVZaZ5tW5pDAoWaeqispYN7Xm1aBo3Tj1abvdqm0a9W2jIKkqy2HqT69ZFefYN02tsqyGcqxYMjKbVQpZptk8ZkLKqkzC1badinymPC+V5b2KQtrtNqqbvR4fHxTqWlk/HrMuSX3XRcjXj3WYNFjiKKr5MGWjbpTlQ2psoOZDyFVVGL9Ooe9VVuWQtRiYnKEvRCFu+GG/j5FwMT1Cvu975WWlto/TkPLB8ARJTV2r72qVhdSSkRBNvJHJD39Cn0QxzNiHrY9GbdoI7Z/BocDIh9CPk5Ls+ihslg3TuDTW8vk1PWORRC1TlIcUEI2N9DHjkY89CDbZygH9NCiaPnf8+xhceJAzXHUi2x5ohOCVWd7f8M2+DP+ZPytG4jRzE0JIGZ14Bss0e0OAB+PXtm1qMru5udHz85Our2/0K7/yA7377K2uri718PCo73//+1osFkOpzFars2XaGxoM57OZZvOZ3n/9tdbn5zoeDwk8XZyfa7/daTGfqxwAsKR0IOZ6faE8j+D36fFR/TAXvSwrzRfzdFotDqqua11eXer55SWxLReXF1rMF3p+edG8nOl1MzL+zozO56UOx0OqE+f5N5uNbm5uUg8Cv2Niz/X1tcqy1MvLSzqXAUeME7m8vNTPfvazxMCzR0yBury8TKVKRVGk0geMMOctkL6GJQVsn5+f6w//8A/TvfAMklI5EuAJhwKzBlMO6EbuCA4YpYrueUkTp2njmPwsAUCQlzg4ICYwIjtDBggmnlGmAAiyH3yeAI7sBswejo/3nwYS0liy4L0UlHvRgHt+fj4pGdhsNhOSBIDddZ1ub28nQRCZAvZMUiq7AHzBPsL8wfwTPFdVnMt/f3+fZMkDOMAD12Y/2Yux7y0bpn0tUokeh9O5rpMRJpgFjBMs0DvBugF+KMuidCaeDr9Izcv0SRA0UaIGoGDNsZnopGc6AEYA6q6Lk8QAyD5kAUDJOgL2zs8vdDyMc/0lJVlzew0rL2mcGmTZAgIY9oKeIW8cLstS28M+3aP3W1Rlqb6NPThkfFLZZVmqbsczF/zQOu9jIuBzHaA/AtaX6VhZliWb8PXXX0+CHnwGjPrT01OyOWRbsFeMLgb8wUK77/MSaUD7brdLQZgTg/QW8VyX6/N03wDX3W6nLM/Va8xcuJ9Hfsn2Yk+Q5aqqEmnEGqR9GJh9cBnN99g4bA92k+CEICzLMt3e3k7e46SB64f7aMpbWWsCujSlT2M/p6RJUJ4A/oD5uH+CCHQG+fTJV05I4xud6IVwQnfwp/gQSi65Lwgu5AObQUDpwZgHTWTM0Qm3Y+gq/2ctZrN5bENoxrN9sizTX/mbf/UbuOj09cmBxte/+CNl+Vr/8//35/o//xd/T88ve9Vto65v1Rwbdd3IxMe+i6Djca+2OUSwSn1+CJHRCPFQOJqwqjKeEJ5nmep6qE20el6FYSRoKHR5daP15aWW5+dSVahaLdSFoKLPVWaFDoe9np+fhoOvenVtq3B81fPDRx33BxV5pjwEdU287079kGkh5d6r62KfxawqtZjP1bTtZAxqFIo+BR1dF5vE82JILR6OypSl5yiKOHavaZpUmQMbXpRDOq9XGuyaF7mYUlUWpZq+UTs0t2f5CLKz4aSJbAgICECG7VUIsW4+y2LjuALBRFCRh9T0m5j04b99F3shui5O1SpnMzVdJ6lXmY1GDLBQldFgdH1k7qMhjeeWREModV0zSZFGIQ7qujggYNLJAEDPC+UqFRTUd30KOvI8Vx7+fZmKLK4NCjxM/Rob9afR/aT0aDhoEUVN6dkQlBfjYUsEFFG++zTqOM+yeFARqem+j1NOhtLA8/Nzrc5Wur25Ul5Iq+VK88VcoQ/60Y9/FM9ruLzU2dmZFvOF5ot4iisTks4vznU4HmxKx0Eaeh4KOzcCfQx9UFDQ5vVVIQRdXV9p87JJzYTL5VJnq5VeX1+TkzoeD1qvz9U2rY6HQ2S0BjmWpPkwiQRWG0MqKdXjHg4HHetai/lcq4EtpwzgsDvEIHwo7SuHUZAh9Hp9fU0n8cLSOWvkaeL379/HmuXBMbdtq9ngXKrBISwHJhIjDvB8fHycOGsACSCFpmxJk0ZfL3GhgZcgwM+fuLy8VFmWaR48a+QlBOwTzppn43oOIF3mvHEa51zXdfo3ztybpP1EZp4rOpDpPH6cufexeXMwgR5gAmeeZfHkboAb/3dmnwk3jMMlEwFYYgQj90nZ0SkTSuZMUiq7wXmS6fLJWq7nUgTLDw8PiZH1TDfvd/AB0Ej+anDsAF4CUkBI0zQ6O1urPjZDH82jsizXfD4b5OpV1WzsAyEAip9tYxA/i0HisT7iGGIgNwQGs9lceR4BWlGWOh+AbtdRPtvp7GytLJOen19SALzf71TXjaqBBFydnQ1EUeyzRC73AwBtm0aLxVLZ0II3m0XwSZnRYrFQBdgcdOb8/GKw2Z26vtf29VXr83gQpJ+b4BPevJ4cQAio4j1eopJIusHid10cF10WhXb7vUIfdHEes6Ch75UPgfHV1aW6rtNuf1BRjqNXF8N5CVkmlXmhru9UlVE2NJA2X331lbrQp4wlOutlcz76k5Km/X6fzktpmmbS00FpHAEyE9CYrOSZDN6HX3MiJa5BN1kvB4qUcH78+DEFQpAhKcAGqwxnbpVVpUzSbihTLctSd3d3qUTRSTWyTmRmCWS82sB9J+tFRpXsHf6DwM8z/gx1IHPLffP8ngnFruPHnWABWBP0Yy+RPb6X/WWt6WmYz+fq2k7F8Bmuz9+RUeQcO8QzYzMIDrDxfgYLz0NGkWw0RAP+1m1XIq2HYCNmE8dydvRkPl/oeDwoz8czrPCRlIrH4yWOQ5k/PTALxX7rToxw/qt/67sDjU/u0eiCFNqj5vNCZd6rPu5Ut5360Ot4GEd6eQpqv9uqrXcT442g5Xmutm7VNsOIvWEeddycTHUdwd7xsEtOLMtyzaqFNi+xN6BYzuMY3LZTVhYqynhWR1aWOru41NnF5VCb/Kpj10h5qWPbqQhBeQgKfQx42tCrC0FSq8PxOPQERMDWto22+73GCUIhRYGxx6IYwX2WKRyHPoV+cMiH4yDA8c9ssRjanePBgQh+XOOgEGKPBGuxrGbKMqmoD8phzIdZ22SICklZNtb390OWgP/meZzspYxsRfx3/N5vpuviNKsuTtQqy7g2mVRVZWy6DnFIUcikIi+UqY9jjst42nKW5WnC1nyYKBQbgGMA1fdBeTYYsTxXCJ2atk4d0H6wYJlX0ccGKSvixK2CKJ3eFsU+CmlsjsaYSFGBymw8pDGelD72L5ANQsbiho4lTFkWJ6pVw4jWvCjS9+V5pqoqdXd3q5uba8UTkme6e/NGr5uNfvjDH+hivU7Gqe87LZex1OT65kpNc1TXRYND3axPR4n1vb2++mo7gJtMT08Pms0juxB7ER5HIz8A7Fk1sPC7barv74YZ6U+Pz4OB2+sHP/hhNNh9kLJc88Uy9QlE57RRH0JiCjGS+6GsgKYwJhzBUpIhAAQfDgethxIfgod5Pkv2oOs6vX37Ro+Pj4mZplacteG78jxP2QlGPkrS2XqtP/qjP1Lbtvq1X/s1PT4+6u7uTocB0FI+8Pj4qB/+8IfJThEowUjR+0FJEvXE9CDA3iFPPM/19XVi/G5ublJz6vX1dWLrpXF8tqRJQHhxcZGmyOBwLi8vJ6Bf0qQkgwPmKMe4urpKa0VfBoFb3/d6//79pJ8FIC3pG5OrYKZhtyiHOAUNj4+PKXNBsEAQROkTwQkAgvIsz4JRQuOOmLWZz+e6v79Pn/MyCT4L8wvQ8jICDtiDSSzLUpeXl2PZyJCN8V4JDxqQk+PxmMpXmSgFa8zPWdfta+w1ikwuGbRcTROD4Xhuz1jagI/s+6DD/qDQjwfSoX+rwXb0fZ8yRG/evNX9/b22212aBvX09DSArrjmBMQ+3SZ+b6U8yxMjfH19k87uWC6Ww3OPwX/XtXp+5oTp5RjEBWkxXwxrMR7oJWVq6kZVNdP2dZuCZyoHyCRhs0+z4JACBP7IHYHndrtVXkVQPV/MUzA7ZixzdcOedG0856ZtBiAces2KcWQvctl3nWZllUoWyUQ9PjzEk9SH0bfc91hmnaVeJ8Aj2UsyVNw/h0CiU2PJ9TgYh4wqNskJCBj0U2zla4dcoV/oJDqMHjARTQPy2A6sOHJCYM36kx3ARmVZlgIAdNYDewJI72+C6KDfB10iE4oOeXlR0zRp2AA2iJHfWZZN7HXCoEMm0zOs+CmIH+wfpAGgm+/h/tBz/NBsWUl9SBUyHtB4uSIT9rg2mQTsJ9my0/4MAlBJKQvi5Wk+QIGAC1s9VsqMWHIklcqUofAsC6WkHhRFOaPcLkw+F4P9TwshPjnQ+MXPf66+r7R9bfWDH3ym3/93f6igCBTzolA9RLDceHSMzTcOJUMh4u/iyNgQ4mm6krRcrdQzYaas4rkTw1kQXdeqbvfqdrUO3U5HNfrs+z/ScrmQ8jgBIDlPRvMNgr1Tp+PhoJAV2r28xCxH6CXl3yhzGV+5OkXWv5wt0pkHeTGeZ8BBgv3wDFwhdJEdH2b+DBsf4hTREBucCTC4Vq8YbJwyAGQM8jD2gzRZPN+jaRtl6lWW8bvInoQ+lqqFYUhTXhSqyhFsZ3mutikUNBycFuJUon4oHSqqmJ3pQ5C6LmZt+jhJS0OAnClIfaY8K6SQD985TDcKQzanaZPDKfKZ4iF60mI2V5ZpyHjkyrOj2mbI2BQh9UMUeaEsm47JzYcghkb0oiiGM1ziuRR9Hhvmy6JMWYaxX2QI+rLYiF1Wlfqu03K1GkDXXGdnEWzc3Nzq+vpKRR7Hs66HU6DfvX07plGrSkWR6/r6Ul3Xp0lJVVXp8elJ86rS+iw63peXeB7CfDbT5vVVz88PE3bUGRBvrsRQw+Yqy9QMYDHP43x/Jtd0bTzYqixLPT4+ShrPjcHY4LRhDzFAlNEA4JomHvR2eXmZnBTMC8w0aV3um9/DfsMyUw/sRhVjDoPV931i8gCrl5eXyTCvhj1q2zbV+C+Xy3jo2BCk3dzcJGC2XC7VDCy/FB34u3fv0uQZ7tVBACw47E48oKtOdovD0gBmeZ7rzZs3kxQ1DpUSJr77lGgBQEjjVCDOQvDaePaL0gIArzP6+/1er6+vaXIeAULTNGlMKkAcULtcLrXZbPTy8pLG0LInlBB4BpJJThFkjqwbIFtSyrzQW3d7e6vNZpNKwshgPD4+pv3MsiwFd2SNcJzeE0eQBwsbQpx89NVXXyXwjazxHmTu888/136/18PDg25ubtJaOMD58ssv04QcZwQfHx9T0IWM8918B9mCPM/T+SNSJg0lRfQ3EZRW1TjaFNDBej89Puru7k0KWvx9NG/iY8misebI7vn5eVo35Hu9Xk+yUmQkHJw8Pz+ng9riKfQx2GWAAsAIeUa/sSWAUC/3AQARTABOWUfwAXqFTjorTVkXAJvPrFYrZUWhdphWB2D28rhmCESxI+v1Wrv9XkVZJKA7mRRmtegE7fy7bSNBgH041Ul8DYEG2Ue/ZwIsf/6+75Odh4UHUAKEAfIE5N5nUJpv974LbB/jlLmeB80+/CGEkMolyXxSxuZEgU+gK8tSP//5z1MgBKmBvaPBH7nzbOopBvKmewA9+kGAhAwsFotkj1ln7AK2xkuD8H8AdGQLm8H38vc8z1PfH2sTQkgyUZWl6qaeyCnX5mfoNL8nKHBil7UiYwqJ4dkpZBP77H1CyBXZMOSO/qK2Ha+PvmM/uD42ht9hQ7Eh3oODHiLXn/L65EDj8vxSdRN0fX2uv/23/qr+0W/+D9psN2raXk3dpk3iJohci1kseyJKGutOI2AibX081iNLXATNF3ET27YZIqmYIs36VvVxr7yrNT9bqT0eNb+eScVsKDVqFYyl6vpebehVLVe6efOZbt8EPT886OPXXynPpKooUjag62KzLYYuz3O1fRtZ9wGcF3lk1Uvf5DyOoi2GgCPPsiGSJCvSqSjyxJaErhtA/LC4Q/9G03UKKbVGg22poEwhk/qh7yAoqC8rzecLqaljg/wglHk1U5cNZx0EDRFnvI+QxfNFQhcN/tnqXGUVjehyuVBVVkN5WoifLUtluVSWhZ6eHtX3ner9Tq8fP2g31IQnZQnxYMbhcYa1C8l4VNVMWVkpdByKFPtamM5VFXNVxVjbCIubDWsdlTw6b76zLIZsjGIAVGS58myYTpEHrddnQ8Bwo7OzszT5Z7lcqKxK/eqv/MpQGtarLErN5pVmszLVyvZ9Nxi7mMHYvL7odbPR7d2d8iye4dAPGYSn5/uh5n2mssr0un1WlvV6fPyg+rjSZvMyGMlObTtTUWQpdQobzVpxiBtpVViytCbFOEv8+vo6gYC3b9/qOEwPgV2mX4FDyfI8nvi63W7TxCEHtxh0Rqqer9d6GdL9lOVwKB4MEiCGeyEgotG47/t01oGDaJwLz3lzc6Of/vSn8hGaXlrA8xPk3d3dqSgK/eIXv1A5AB2m1QBCYrA7Gvv9fp8OpqO/4XA46Hvf+14qAwJAUwbFv6+urpIj4x69ZIFnns1mqV6bEg8yEOhMCLFuuCzj7HnKtDy7yPMuFovJqdaARNg2HApN6wAj7hVAieNgXCzPQRkYDD/2G/YQgErmgoMIcU4AFRg5gAyB6dPTU1p/Aszb21u9f/9et7e3qQyD+/YyMeTl7RDcs24euFFqRZ/B61AiWFXVZMzr3d2dJCXwwBrTiO09MHmep76Xm5ubBOCwPey3s4o+DSlmsxZJn5bLZXqW2Kjcq6pGJptAI4SQAmUybOgI//Z6eHpZCDK8tAvAQK07wSAlOWQVAF+Awu12m0oMAaAuG8gWQAcG30EW5Ss+yYcABqKCYJLsmfdi+DOzL9J4fgN2gQx/3/fpfBvA0G6306wok71DBmPJTatDfUwBMc/JOOqubpI8UdJCuczBMmir1SrZEgLXVE42YB6IB4JU7Cbrzn054VSWpa6urrTdbpMeoVfOunspENck6MMeseYEILzHS0XRUWQRffLSHoCyZxPpUeFayBeBHSAVPSALhY2GwaehHDY/+bpsnEiHbXTwS/M1gJdrnJJ3/ty8jwyFl28SBPgkM/QX/XdQTnbde0S8b8KzKKwjvSVeCui2hT4fD8rZGw9QeAawN//nPfG5I7713hKCJu8n4Z68zwZyEBlmz1kjyJ1PeX1yj8a//Ve/J+WFgkodjp3+3t//f+j/9f/+h2q6TFkWS3AAiGPqS8pCM4naHJi26XyJMaqXpDyLI195Lwau73spiyNr86LSfHWu5dmV/syf+w90eXmrvCoVMln9/+hU1PdqjrWO+53221e9Pj/rsNtpVpYKfTzLAyNHj0ZR5Oo1ZAYs2iWoyIsipb9hy7OMCqAsAe6u61LfRd91sQl+WCscHKnRoiqSgHLSdVlWsZKniFOF+K5iGB+b5RHozOYzzWdzlYMD2+/2Cn2p5WKV6qL7EGJ9vaTF2Xw4NDFmDNL3dkFNk6ksKmV5UKZe9x8/SOoUmqM+/vHvq4Xllca60SwWhUVwFdPW0tDTMmROijw6ynhadexviGtTJIPJXkd5iGe1BCk1dpZlqbPVSrOq0HI517t3n+l73/tCIUir1VI//vGPtXl9GdjpMn2mKivt9rvk9LMsytrl1WWa1PP09JCMMs2vNFPOl3O9f/+13r59q5eXF0kx9fvu3TttNq8qijwBTBiM181Gq8VCdX0cxkgu9Pq6GWpTX1TXkUUGzHDwEDpDGQl6UFWVNq+vqVfEU9jH41Fvbm8Tq8iY1Ofn5zhRaACbf/zHf6y7u7uhdvwpnUHw9PSkzWajt2/fJkZltVrpYThnAsfy5Zdf6u3bt0l3l8ulfvKTn+j6+jqBDsAvh0XBVtPQ6/0SVVUlkIA+4LzJPOCYxh6SY5KXqqrUdp3qZjy9WlI6/KnvOl1eXCT2jxIXmHn23kuOYGSdie26Lp1hAXjHSXmPBk4X4OXsM9kBytMw8AB1bCFOGZaOP4BL1oGab7JCAB3qeLk+o1UpG0Ce1ut1OqAOx0avDoAAEMb9enahKIoUuLHfsMN+v4AW7uE0gCTA80CJfUYHcMzYd++h4Luvr6/1/Pys3W6ni4sL0cxKME+A8vr6mhpj2RsvoSAjgm0HDJydnemrr77SeiiHxPZBGiA3IQTNqrnqukl6SEAQQUahph1PskffpXigXdO0KVvggBQghl/jeyELPMgjSCzLMk0pI9NBWeLZ2Vn6HGwpwxF4bnRCGplngA4ACJDL71hXSemeJCU2G/AiKfUvQEqcstEEF1yDe+i6OG1y87rRfACMfGaz2cR7L6sUmAOWm6bRfLFQ1/eazUeQRwDQta1CNx1Xy7NmeaZ6IDvcNrAnMOvYcNbAZch7l7xkDAad7B+YCPtPNma/36eeMb4XAEhg5s3ErLGDdAJCDyr4OUEvfpigF7nmmdB/ShS5PqCfoIRMHAE8Oo3vImjFBnDvDmzJ5iBLfpgkpBz6wtAN1hrbwb4QPEJw0PPBnnqA4kEwmICfL+bzVDqFH6CMigCMKWCe8YAowA66/rDn3qDu9pD78zXHXiEnNNKPuHTcE0lpgh3y7QGKyzp7yAt/6HY9z3P9xl/7S/qu1ycHGv/yt/+ZLi7PY3BQzPVPfut39X/4P/5dvW5rFeVyEkTg8PIsqGuPKU3Me4qiUNO26sIAxrPcDnILqkpGl2WazWJ5Vt/12u93Wi4XwySnmYpqrj7LdXVzp8+/9z3N12tlZWxkAvQyTq7IK7V1o75tVe93enp80GG7VS7Fno3czjcYMgB9HxSGw/CoR+vaNk1Eik6A3oU+NSkXRexrQCiLvEjRX9u1sVRoyHBcnF/EJuEQm43r42FITyPQQ2TZNOoVwXyWD6cyD6xcMzQGHw57lUPEvN/tpCzT68ur5tVsMq3g7OxMbdfqcHjVfj9OgsmyTF1PhqoazkXIddi96rDfKM+kvq1VDE3pTM/q+k7z2Xw4nLAdlGqsPa2qmeI5K8P4yGo2lCitdayPKotKm81WeREVYrlYDhHzUmdnS93e3ejq6kpv3rzRm7s3yvJM29etqjIe79e2rRZLyjdoWpqlsoax/KORlKkavv/lZaO6Pg4GeyGaoDgpFHBFUFjMiqTYAOxYtlWo75VAV54XquvjUBM+02G3HaayNCrLIgGrw+Go1epsUh7BidQoPQAUUJ9lmc6G2fM4KL738vJSRZbpF7/4RQquAJSz2UyHwVkvFgvd39/r888/Tw14d3d32mw2aYzramgOv7291W44MAwG3oNBHAnAH6B5dXWll5eXZBibpkkTsHA42AsagJnbTcp/vV5PDjUqikLX19eTEizWqu375Pj6fhw7mee5joeDvv7qK33xxRfJBjlLB5sXQpj0R5CKZp0lJYfihArlSAAHZ1y7rksTk7AHgF7S6rF59jwFWbCMOGIMf1VVaXoVjhVm+PHxMU1okqZgD/BOaVqe5ykLBiPLGQaUaRFIAwwomWEt3AGdnZ0lIATo5n6kyKZyeB/PCFOIjpL1QQ+wSez1aYBYVdWk6RYZIxDkZ/wdMOHA1YNK+ohg/jisEWAMQwtY9zWF3TwF3svlSnlWJJ3ypvg8z9S0Y9nFw1D/H7N1Mx32hwRgkAlsGbpDsOlyQ7ADIwtRgr8ioGT/CGb5LuScvedFwOolfQ58mN5FqQ3fxz1iiwgQJSWZZ5+5XspEtuPBuugy4A1g1ratuhC0XC0nmZIQ4uCZeTVOBON56rpWXhTqhl5Hyi/R26osFbpvNjBHP7NUr1G3PQAjE0EWE0DGs3HOB9kOntcnPHnAgA57NpYsBsCdtfDAwDGYZ1MJLrzfANtNWY0TO+i67x97iO0j2PI+I7JC3BOkBc9NwO6lO9g0dB9ygt9dXl6m7+G7sS1exup2KAWVg/yTUWRNTkcBuw6z9r5WPphgNpupKspYsj34FN4LQch1mRxIUIgPxh5kWTY5lwT7QeABGUcJL/LA+mNzWQ+XdypaXDbRMS9TQ87x6dJYai0pkTAEMOx3WZafFGh8culUWURWRHmmrOz0/S8+0831lTabX8QG4ey0B6OVFFQWueomOs5jXasoSlVFodurG2XWSMJnoyLFg9lCH5uRefBYJpOpyEtpABddkPqm0/tf/ELVeq3Z2Sqxe1LsTej6oRYw65XlQUU11/nFlapypr5tlYdezaCA8/liWOxSyqQmDApT5upC0HxI1SlIs0XQcrFQXuRazBfpIMGiKFXXTWz4LqvJpIK2a7U8W6ao8uXlRfvBIHf1Ublio+2xPqpru6QkWS81x1o0P0cDHxnUrq6lfmxO64cTvZumUaZaZTkKZJ7luleIp5YPk4rKolBexSkns9lMxXmc4pNn0mfv3qg57jSfFbq8GA4+m6+kLB56tFgsIjs+n+vi4lxhyP6s15EdipOeclVloawYR3sC0uMs+VJVOVPTMLWB0rOgujmKEce3N1dqu73ykOv5+YMuL9Yqi1zH+iBlsTfhcDhovozRfp7lOltGNnS726UemjwLqg97ZepVFUUcRND3Q79NpbbplGeF8izXahkBdqagIo/9GNvXvd69e6vdfq++C0Mf0Fxt22s+X6XDzY7Ho15fd3p5etLl5aWur2/105/+VOfn51oslqqqeXLEMCfPz8/6/ve/n0DmbmC3PC1/GBwOTcq73S6dJdHWtX70ox/p/fv3qSwHB51lme7u7iYp5MvLy8SGwhSTwWFSEvrJOQt8/uXlRdSD06zL8wDqMHA4Uc67YBwsJV/YjHfv3iVdL4oisYCnKXCMNY6yttQ1jh1j3tR1OqCLMgSYIgIaABTXhQXzLAZMEUFICCEForBKNPQDACh7Y114H0YbRhHjXdd1KhUAXOEYiyIeNnhxcTHI1mtypoBUnA6AXVLan8fHxxT0IFOU0Xhpq/fqYH9w8AALJumwTgB9ylyRO86O4flhTLFhkpLjxjbgxHivB6V8H4E3gAEG/nA4qu+7NLmH3p7ZbK6ua5N9drBE2SKnw7++vsYSnKaNjdLDsAbuic/weWQQprVt2jh9sGn19HSfskuwkE3T6Gy9mrCGnD0CkVEURTokD7u+WCxSxsntZ12PB7Kdn5+nhnYPdMkSEohII7Dw4OtwOOj8/FzPwxkTEAzsE/0qBHmuJ3wngezhcEjlajwXIA49BBDhE8jQ+dQi5IdsEWAVGa/KImVxeX/TNLFkexgV7jXy6EyvTOfn50m/OPW97zqdn60TsTKfz22scgR/9Ml4mQnPSLBA1gEbxvvBSIA+ArPTvgdKkHhOLz1EL9BNavMJ0NlX5Kssy8lBig5qybCQ4fTxsk5yeODigRbZJt9bAiVsMUMt+G4Hs/SmIYesD0EEJZOeUYBE6Lou9T8h15C6+DKIG0roICxOM2+erSCw83ViMEHCl0NzNGuD3qIP2DLkw2UdvMyzoLMevI9lUWP/MDLsxI/fv5NgcX1bhZAlUgTfha3l5T4JmSJI9N4Xl3mIj095fXJG45/99j8dShR65Xml3bbRf/l/+wf6nX/xr9X2sd+g74NClisvygHYZ8qrLJUh4YjKYaRcnoVhwlGvro1Tjtq21WK+VFkMQKXtVZazYfRrpuPxoOXZIp6EXYwNPMuzMx3Vq1qt9MUXX6iqSu0Ylxeket9qMVvq/v6D6uNBs1mlqir1snlRn8fyqLP12ZAxGQBAValUnprDjkOj2LE+xslLXRSAzcuLZvM4bejp8Um77VYFTd9Dmny336rvW/VdkPqhEafrdTge0hqobzUbgoKijEA39htkmpe5ijxO9sBZLJYLna1WCn2n+SKe9Eyker6Oh4XNF7kuL9ZaDsbk8vJSRZ5ruVppVo0TLEIIur29TYoWFIYzTTJtX1/FBK71+bleNq9aLGIjaZHnygZGKwphPPcjt3rOkRUZJq4MwhsVO6hpIsDj5GQMDMa0aWKPx3K5HBj/UiFEJdrvd8P9a8j2ZMNJvgflwynYZVUNIxljSnW33WqeGifjPXVtG+enD/XmEbyttdm8qKkbna1HY3asa93e3OhY18M45nh/x2OtxWKcnx7B2C45OYwooG82m6X6XZ/Es1gs9LLZ6HVgB3HCzWAgw7BHMH2SkuMGPMOok6auqkqL2Xj2ST2wKTBsi+VS79+/TzKCw1utVnoZxg8664RR5O842sfHx9QPU83nqYxqMfROVLNZrC0M48QNMgqvr6+SRvYEUEY2ADCF04ERDSFMHL0D0u12OwS6ZWp+hqHC6VIqggPHQVBfTsCEET8dn+iZCt7nmQevocaQe6mWl8bw7Pzd09zRcXTp2TH63ozLewjUmMjk8+gJfNq2TSypl4IQuOKQAZsEHg8PDwlI4Iz2+4OKvFAxHBTZ1BGUtF0cL7zb7Yd96ZVljNMOms9n2rxuUvDkgYxnCGBHpRiE1seh6XOxSGc0LeYLdV2r9fo8BmFloaYeA8PFYq6ui+Uy29dtAkZVVaptu0l9d9s2yTZmWW4lBZmOx1pNMwYD2+1Oq9VSx2MtDeQSjC7gAvYSmxhCzJRnWZbKdunn874XB+eUQZKpINMJMKM3RBrPD/DmTWy018IDBJH5xWKRSlB4fu4BPXDiD+D7/PycAvbD4ZCCG8AlMkjwT8DgDDnyBvj3QMkbbJFFsoJ9H7TfR1BPdr3ton8ty5hdBiwDlgg4gmJvYZZlarsu+vosS/YJG0HT9GIZR+nTf8Izea8O6+018dgN1g+gR2Dg5VaU33hGxf00VQkAf0ryCMal2F/GGmMj8zxP/gZ5Bj/hkwGyyIdnl7Gz6CW2yIkLZCuSjWvd398nm0fmk+wYdpiMLiCbLBPXw6Z5oOklZ9LIsBNsEFzhHwlguU/sKcMPnCDHBuNf+S4PECKJKxVZnoi5+/v7VCa8Xp9rNpurro86HMYD9AhW83zM3Hqp7my2sL7AMJAi7VA5U0z6mJiEGPV3HE8eD7+e3jN/RwbZe8ck2F9kjp+PdnBqC5CXv/a3f4nnaPzsZz+xaCmXwkx/+Ac/0//pP/8v9Lxt1fUasgydlqul8qKMU5r6Xrv9EP0riyBdEbSGvkvNx0Sd9fGoTr2yqlCeFZrN5iqKUn0vHQ+1ylmh2byKLFOWa75Y6LDf6+bmVufXd5otVlqfrWMt5ZBB6ftOeVEpKBs2rdNiMdfhOIzNq2K9XN3UMTjIpbZt1Da16m1scmvqRk3bpGkPfduq3W/TgS2utKHrpC7OKY9lUpmKIhr6qszVt42uLi/1ve99L7F5sU7/UlKn1SoGPNdX17ocHH7X1Lq7vlHd1Km84+rySs0wBWO+mKmpm1R7HBuYFnp4+Ki6ic1uP//5z/XmzZsEqBBaTqb97LPPkqJTenDaXNo08Tvevn2bJnxguGBwYRK//vprvXv3LqWPMb4YaIwshg0j9PDwoHfv3qnrYqMm3+W1kygCZSiUJ1AyRLQNC0gJirO37FlVVbq4uEjAkPthfj+Ajb4F7p1yChwMBlRSOliJUiGcNw3VONksy/T1118nFhmDHOuH5ymtSrkTIJF94Bo4YQDgYhEPnvM09mrow/jss8/0k5/8JPVlLFcr/eqv/Vqq3ad34+XlRZ9//rnaIeuQAlxrdDwtO6H2tut7tcP3Avz3+702m42aulYwhpagqyxLffjwQW/evEnMID/nu7wpmpQ0IIp1uLm5UdM0acIQjbA0/vV9n/oysD2+XwQPfD+pfk5yJuOBzOOcMfr8HjbN664pd4J9JfAjMKFUzJ0xDpVafi+loCcFMIIjoO8FcIFjZT+ogyfwgmnjWbD1BK8EKuwFIx9TBmy3V123yWkfj8cUCKKvgDaeOdqVoKA+NUXC1jENyFludCa+LwxjU6sJ4AYQwuA7c0rZH8/K81KeQ4aQ93ppx8PDQwL/ZNK8h0YawZqzz7C62BUcNFkM119sG1kYmG1k5Xg8JuYeXScYh/nl85TVhBBS3xekD/Yd4MPau6zA0KJnZH2oqUfXeRYH0tI4OY+SEXqXIETIcOEzvf6b5wAkjcxufFFqN07oGQNrv24MBON9+4GAyCPfhbwD1inB8rKoVGtflsrLsWyMPYaR59rImH+fl/agr8hMCCEdagfQhcggaKDkheZ1Dn18fHxMso3v5/P0Znj2kfvBf8HCIztOEGLzkSd/ZrfHIYRkU/37CW6xnQR72LRT+82+s7fIJ1kuyoggqbxkCrvjgZuk5NexqWQPyDKg7yHEHgtsKlUFrLv3W3RdpyLPNRvOD5PGSYpR1s+1XK4SdvDsUhxLPz3QFZmT8tS/4WVysbRxzEoglyMhOx5iyfUgC3xvsV2j7owTtzwolcbDKVlnsmx8P5jub/4nv8STwR8e7tV1NPgVCn2pX/z8Xn/37/6X+p/+3ddqh8PqsiIe2LdYzdW3ncqQ6XiIZwVwY0VRqOt77Yf0K0ICg9NlnYpFJWmY/92PDS2L1UKr1WIwisN4RKY+ZXO9bvZaLpdJKagLbzOp7Ts1Ta3DYa/d7lW73WtMx3WF+rbT/rBT33fqukZSUNe2KjOp78Y00uFwUF4UykKnKq9VVqVubm709s0bZVk8pXI+m6ksMp2v1/r+D743TKySvvjiM+23r+q7mFJ2BuDy6jLW95cRyDw+PaoflHo2m2k1P1Nbx2lV+10EbOcXF3HEWt0onto4lgxEpqpTlsXDCBHI8/Nzffz4MQEIZygkTcb8AWiqqtLDw0MCGTh9N6SeBg4hjgH1SSUYK5TBx6PCfm23W93e3iYHtVqt9LOf/SxNEsIwYJApF/FazM1mk8Du5eVlAlsfPnzQzc2NVquVvvzyy4GJjEzN5eWlPn78KHoAttttKiHB0WH0SHOTNXC2FxBHmZGDzKIoUg087IDXw2MI4wngz5oNJRJ3d3epNhwAenNzk4A36XVALCVSlDvA3LdNo3pIrwMqCH4Wi4UuhgknNHjBdIYQ9PL0lEAFwQFzyHkuZAAD9OHjR2kw6jineFjWlQ77vc6HII71cObT2SUCYIIFShEwkjyryx37Np/P9fLykgJGQDHMad/HEp/7+/ukGxhaZOd4PKYzMWgu5oApSYm56/s+nVHggMMnbSUme3ilHi4riSBI9lIFQDFlVt5bgCz1fZ9A3M3NjT58+JDACUE0ThmZZh1xIoBh/nhQ46l0PsOfCNCCmnpkFbEjrDvBHE6dQLLvO1WzsRSK9cAZIveUChEAHQ/1kB0vJz0KgNKyLJNusu5e5+y2C//DmvA9khLoRrbm83kCIovFQu/fv1fTNLq5uUnPBRCBYPFyMAAS+4+uUR7I3gLQACKSkq7AoHoZA/eIPMCyA2wlTRpeWQ9sCjYXPeZzrK+XeQEUGdXrwQXXZH0JGjzY8qDC9xTZ9EAKuXW7ACgcvy+b2F7uJa7Z2FDMd5LtITiSxtJtD3bR4Uk5Up4rZGNvAPuN7MCoE9jxfQxS8DJI5LFt21TWxL5RtgPY49qcrUHmg/XyIMZLxfA9BLJ8J76MBniCEUg5HyWOPcU/EPhTGub7h9ySCQDIk0lBprAlyIj3iiDPDCzwzASTuMg4s05kRpiKRxBDZnaz2ej8/HyiL6wTz+8BKviEFzqMLQohqMhiphwd9TKmvo/nTZxm0KI9bJKeE/BDXDw/v2i1GqcZupzN59Ff+JCIUS+nE6dc73lmZJjfud3jGZEVt4OeMUUnkIGiKPR3/rO/re96fXKPRttGkN73ncoyV1FmUtZJeaf98ain5xctz5ZxJG3XSrkUT9aOBwJVs0rLq3OtVmcqy0KH41GfX15Kigf8xF6HYjhBeaa+xQEfFEIUxmN9lNRrt9vqsG/Ud1GJNptNnCj0vFFo46nPu/1ebdOqLOP5FdvtRk1Tq+0a5VmmtovjdIs803Je6Wy11Bc3a4VQ6PLyTre316rro5azOCLx+upa1zfXWsznWiyXKopMZT6mpPM802K+iCNhJSn0w3r1qmbxtPKqbNWVvS5v3qgaDrLLQq+2Pur54SFOXsoL7Xd7dU2n3Xanq6tLNW2r/WGnIsu13cRnvrw6V55L1SxXCOVQXlRpsThXPIFbsech61UPhyJiuDGAHMJ0fn6eWK/NZpMc93w+Twc/IagA+IeHh+RsYf9xODhe0pwYqK6LNeCw48zvx1ACLjF+Hz9+TApIc2ZVVSlIe3x8TMw12RhmgOd5rvv7+3R/BJ+bzSadK3A4HPT27duUGbi8vEylB6QNuSd3mKT36WsgmKVxW9JkrVkbHAxBAorqThRjSx/G09NTOmzr5eUlGU6MrwcuAOcQgt69e6e6rlMTXd/3agfGvm3bycSSpmlSjft2u02ghyBpPbDs6BrvwVCxvxillA2y9HpZlnr37l0EamdnwwjosUynaZrEHl1cXKSm+Nvb25RpAbx2XZcYyvV6nc4LkaQ3b96keuiXl5fEZnnpB/sC6++lSQAZgkdKesjwvX//Pk3yoYYbVtvBESwQzhVGjHu/vLxMzoQyO9bKwQMsno+wZa/5Q3aBF6SAT1WCvZQ0AQswkAnADwwWa8bPud7z83NycKzJdrtVnuVaLmPWxwEhDs0dJuV6h8NBs3mVQBmkAM7Ry6Vgb3HYZTkt3ZOmtd+wfZTdeXDBs1EWQLaJdfcJWV4qxPQt1o2gnz4XSSm7SfkHMgCQJ6AC8IUQEnAgk4r9IAAgu0CQ4SQAtgCyxUETJSk8szQ9lMyzww6oHaygB5558AyL13w7eAFU5Xmeekr4PMGeA3TuAfvodhQA559BBuMajCys29h4T30q6/Lr8XnW7/r6OskIgRC6gMzleTzMtbEMPoF2XY/n9fBegjLYeIIM1oo+FD8ZGkDNdTwAQ27JZEG2rdfrlPVw4MozQkJBWL28vKReHnBBOhuiqlL5D3rrZXRkqAhkyBBQQsWe0MNTluOZSsg9ANsDYXSNDCtBsZOx2FaCHIgMrk0wwDXfvHmT9Onq6irJNXoaQuy1IWtOFhWdfH5+Tr4XshQZns/nysL0bCJ0O8pErMQhIKB3KT7nOEHQgTx+CfyB7SYAjeeJcUZdawFoo7KsEoEB6el2xDPKni13cgk9w/5zLdc17DhDJlxe/32vT85o/P7v/4GkfgC3M7VNr5fnnf7+P/iv9Xv/9qdq26Dzq0utVmdq2lZN16qaz1XMK+VFnvoHXl9fpRCnRKiQXjevCcB0fQwSwiHo5f2z+hCDitfXzeAsouN4fHoc01eUL+S5svaoMo/CvFqNTeHz2Uxvr650uT7TfDHXcrnQ2dlKRZHr8y8+0/pqoV6dVqtYhlXO4tSkPMu0HBxQkReDwnP+Q6a27RMjcXV1pdgEXuuw36sqSx0Oe63XZ2q7Rm1LTXel42GsnwshngLb973yotC+js2gCkHPLy/qu06rszMVeVDXjQcmEXVGwNCpKmcqq1JlUahu4rjL4+Gol81zSvfjzBBkZzpCiKeVUgeP4nz48EHH41Hf+973kgK7U4O1KIoiZUtWBkzdYHz48CEZMNhpaWyywjAh8C8vL4khpnyF8xUoH2MdKCkgowEwjSzBcwIlGFaAAIYUB+0lYJw6yrkWOAV3ZjgPaj09G3B9fT1xABhG/s7nUWB3fC+bje6GEiLv42AMLoaC0hKMFKATJnA+9Ensdjst5vN43og54tS0fDyqsJIPHHLXdZoNoNmfYbfbpYBwv9/r6ekpBXrr9TpOlTOmHGBTlmXq0ZCUgoRT54Lhd/YVx8ae3d/fp0AOmcSckS0jQATgcm0PLCRNjKzXzHLNtm11fX2dnA1OD6cF2KRsKxlYK1Uhg9b3vW5vb5Njvr+/T0ElpQgEBx58wFBS64yTZO+dlZPGkkaAEM7aAxZPnxfFOOWMzAo/55kJnLgfxmLOqjgtycdVnp+fp9JBJytYl3g/ZeyvGOSw7/u09oBdyAoyAG3barU80+FwTIyxZ18p6fTMIZkobAP7z33xchBLdpC1xabBhgIS9sOhfF5uReaQffcyJzJjXmrCuro98ACAgMVLMPg+9gWdBtzhm7Bd2C3sP+uJvCLrPKf3HjGJz4cDAHoJJABj6BL2kz3n5cCVdeGeyATzjNhmZ2idWY1rowk4ArTGZyySPOOPkBXAHWWTyAX7jW8kY7pYxImXrwMh4rKCTYojzCObj7wVRZGAPGvs/RtOtPHcBBFt2yZCELsMAcHfnYFmffERZBOQN4Jo9tf309l97g3byx5gg3wU7dPTUyoD9BIm9gEd8sCdDLCkNA7cg/SiKCb3hs1GBvxQQv7PixJUdMsnB3rJI+/FTt7d3SUQj61if1mXSearbVUfxr4jvi8SBKuJ3IE3IM+zTEnusSOx7C+O/Ue/kMGIe8YTwPFp4AgpTz6UZ3Sf4GVWnl1xW8C+IUsEKV7SCOnl2dO//Nd/Q9/1+lOUTsUD24pSms0qhT5T0wT9/u//RP/on/yuXjY7bfdH1cdOTSdV1Vxf/vzn2h3HqS7b7Vavr6+D4wxS1qhtWh2OR/VdpwNK0EmLvFI8oK3XxUVk75XFA8TOh8kI8/lMP/zhj/T27dvoTMqgIo9G582bN3r37l0Eh9utzmbMPN6rD/GchxB6KQvqQqe2a3S2WupYH1TNKjVNrcV8odCNJ4QuFnM1TatYklTo2IzCVxTxsL52UJLRsZeS+qGXImg+X2q3PSbw1QwnZ3dtq9lgoPLhfIy+67VcDYcBlaWOxwgog6T12ZnqptFiPtfheEi1mxgC2PvD4aDPP/88gRacMICfU4UvLy/TzwHtAC4YjtlsnK3vLA99K/wb5XTgXhSF1uu1/vW//te6vb1NwI3zEihboZSIz+Z5roeHh1Syg3Hs+14PDw8pBYlBwUFfXV0lAOBlYOwXBpiafIw/gQPXI6hxhtTPXcDJUEZB1sXZRIwBwN4PM0KRYVVQ+CzPdTYw515HCjvBPrG+DgpYw8VikbJVTdPoYsisUHONccuyTMe6Tk39yC5sUmZZHdLTPsccA4VxbppGQUoTs3A0ANemrrW0PgcvtWHtyrJMhwICXG5ublKZCb/HwZCpAtg72+XODdYwzdmfj3PjYZ3duXRdHFLw+PiYyqfcSXddlxrJCYIhTijTQgbevHkzYYgBwRww1/d9Ko1AX93Iz2bxDBLKGp6eniYggz/otj8vcu6lCTToes+Sl3OxN8yjh6VEpmBE43oVKouxbwcHx3c4K0s2IwLdTPvDLgExejwcsCKTsG9lUaqq5knu0HkcK+OSYZLjlLfYC0TvBusN6PUyFIIG3oO94P/IOj0uDuK5x+RgDWQBLv13/PHyVT7P87Af7CHywTWk8bwo7pP9Q4aRCcAxQJHfAwP4PX+8tNHLBbH/ZAyRoa7r0oQhyAI+gx4QTJMJhDChn4AyHcAS981eoXeUmsFbsDaSkt3Bz3tgADAEVFJqCxNPFgBdxaYul0v1IajpxmZoSDAyPFdXV2nv0Cn2FL+MzrH2fBaZAwR7AMN6scecOcTvsGWeFcNvQDbg09gjMj2nJTzsAYGR2xWeDZ1mnenl9ICQ7IeTVGS/U4ZISnb8lP1nvfAz3COyhc0mKw1JxXMgc4Bn+ncg4Mi2cT+QNEzdYtw7B1t6WePhcFDXtKrKsS8R+YzrH4dIYEuwt3F943lfXs7KZ9t2zMp4mVfEGOMQHeR11N2RwPHsl5PDLltONLifHHHp2OPipAL7xGfquv7lNoN//dV7KQs6Hndqu1aZcnWttFiu9Yd//FP90R/9TD/78mt9/Pisjx+f9eHjo143G4U2Op1qAG/b7VbVbKZZlWs+j0D3888+0/n5uT58/KgvPv9ct7dXOlvNtFgutNtt9OMf/0ghxMlKF+u1joejQj92ygNA0+FzikddAHhmVaW2jYt4rCM7OKsKvWxeotMqFyqLSq+vG5VloTxXNFCS8lANB/TF8qQsy1VWQzqxHJl3DoPKskxNG4Ony8uLYapUUFHm2u92WiwX6vtOccrJOErscDjos7dv1XWNMmWJPTkejrEnRKWaJkyMxagYlY71MYE0KRpdSnoYgYrh4pwFwK0zRRhawDsslpdJoaCe+ialjxFCqbMs9q189dVXk3pQQI2PrKPEhPISshaAiO12q37wKpQjYaiJ5AmELi8vUy8H7O/d3d2kdMjPhsCA5Hnc93pYY5SRNUVRST8TLPB91POT3aC3AFDJ82IopBGcY0DLsownvZPuDEFlVaW9oIZXGkt9MNwYBUYGsofV4MRmA+iBoQRIbO2sh7ZtJ2P8ZgNgwAhx75RLEbxeX1+nw6RCCCoNHC/mc328v1c+yEPoxxPFCSxWq1ViAQm6AI55nuvNmzd6enpKTCTjgOshCwggJyMFY4ozZJ0JagAZi8VSz09PSa8JwH/+85/r7u4uOQR0pOu64SyYqKOppGAWv6du4kSar776SlmW6Wx1prKKz0OJIvcxm821222HjE2ptm1SluKwP6goC11dXattmzS6NZ443afSC9jOeArseOBcWcbzfYqySKAhAqQ4vpsMSzyNhj6kXMfjeAIuY2F5+ZSsMVAdan+zcdIcNek0b/reFEU8eyf0QfNFLDtlTwe3lPYrgrF2kMtOWRb3YPOynYBQ9BcnSGaGIN5LLLA9ZBicCcZGOtiWIoPKKc2MbIWVvbi4SHqIXhF0uqPHFnkfhze9evB5mnHx7JBnpT2LBbDAN3h5i0RQwveMTdWsGcB+ZEmnh+MRpLI+6JADEl9nGkcBOJ5p4F45yJCMpTfQc++UHCIPBPP8v+9j+RT6Xpal9TSMU67YY/7vthPgPwLUTE1TxwE3bav54Bu6vlfTjYfw+fQvstqctULJG30P+DEH4Oy5T+TitVws02Sy+Xyu0Ieop01k/5u2SXYw9CFlBufzudqmVduN5VPY0iyL/azIz3wxT/cwkgajncyHQEqSSiMhvEcgyk8uzohCnyIOmCsM55V45o6hLff3cYokwRx75eRf1/UKYSzHy7I8ZQQocaJ3j+ujG96sX+RF8guS4plmeZw8xl6il6EPart2JOKG4NDJo1kZzxrDnoJHuEcfSzs+S2w9iNig1nw+nm8W7zl+zgMi9qrvOy2Xi7Q2HhR23XhYH+Qq+gHJ6hl+D9z8hR3Cjjj5gY7wOXDTf/SX/8I3rvON635qoPEv//nvaLvbKXbLVzoeD2qbVlfX1wohCuF6fa7jodaHodm4azs9PjykdGKWZbq/v1cfet1cX6sYIuI+9AncnJ2dDRM3DoPgRWXPh82mFhCGASWA3bq4uJgwYhjtuh4P34rnXsyHsypYuDgJqyziSaMw/PWxSZF1NLC9jsehLq8iVd4pz+Pm77ZbLZcr9SEMCjSW2lADeLY+iwFEnml/OCgfFMcnD7GRZRHHBHddr7IolQ2O6+kpjtGtGyYLFIml9vpwn2DA6FNPgSNIHz9+TMESgQXMHeCK0qHb29tJcx/rj9FhrVF+BB2Hi3PEURH0UIYAgNjtduoH58QEJi8NOl+vdRzkAcbTm46pHeb7bm5ukhECoBwO8eRqGNDHgeUBrCRmtWlUDI6RNfEMB8qJY+FANMAsZVo+yYVyAy/f8XIq1ojT3JnQVg+se9t18ZT3LI5jdDATwVwsKdzv9zrWtbqhnIF7ZL9gtehVads4QpextAQrpKNxChhxAqvFYqGzs7NURrVYLDRfLPT89DQ65AHEvw7BCc8IWNvtdnp9ff3GeRpdFyeQ4QwpB2QfyrJMh02RPZU06aegPpz9a5pGi/lSVTVTXuR6foplhquzlfa7vV63rzpbnSXwiSPJ81wvL89q206z+cyyM+WkHtsze5yroExaLVfDvZYDAJ+rLONo2MPxoNVylbKEXdelww8ZMdm2jTabV9X1UYvFUuvztfKMWttWZTkwwUWubDh8dEzHD6Ogc28I7FRV4/knfYgn1C8Gtpg9yrJsYOUa5XmhpuFMkCytqfchsG5ZninLC1VVGYPnPFffh0j05HmcEpiNh075mMWiKAZiS4ONblUOB6Ri07y8A6Dh9eLcE/sC6PFyJmna+OtAm+e4v79Pjt0PeeO69D2d1uqzdoAHB+cw+Xy/yxo/41rYLXSA63sWzsEcZZcR5MRAtq6Pw/CQ2VCqtNJ+v0s2FLBHsEHA42wx9f5O0pA1Oc3mcF9eRuIZHA+8IGIA4BcXF6k8kIAQkI7+xkBknHz09PSYzlWoqplC0CTTmOe5NpsXywTPUoCJvd8f9uo1ZmurqlI/ZOpWq5WUhYkPI8sYMUijEOJ143MflGW5Fot4cC1DWvrh3KsQYlPxfNC7tmkTO59lmWbzWRx/3/dpdO/hGEdJExgej0d1fQSCZVEqKAbt67N18nF930/KBtmPqqpUN7WqdEBwlLe6ib2sxVCS1tS1sjz2kB6OB5XFUE5bxlLtbpBNJuEhEzHLc6mqqvTw8Jj0cb1eJz/I3rtcQCKxr+AY/FXXtToex8xpGnrSthM/66N5u5pD7IZM6XyW7Egf+nRQcNd1atomjj3OMy0XyxQAlWW00WE4pgG7SuCIznq5FnLu9xoDgZj5IChI1QBhlC8nPiTp7Gyluh6zk1F2o02nnw8iCKLBMxueoXQ7R/DgAYZnR/Cb3JtXr/yF3/gP9V2vTw40/tW/+F09Pz8nwfb0Ewbz1Fhz6e12m+qb8zxPNfOSEgtE0yvMCqCUhlSMDYwBf6eJlZpZymEoZ2EyAiwJ5Qk0vOKUSIFmWWwOvLq6StEpZzvgXDj0BccMsKGsgrpzAiHex3f6WE8CGCbDsLkYW5jBLMvSKDsCCoA/JQCff/55MvZZFg8jgqHBwcIgA+BQXhwH9ZyAUb4DAO8HQrGHTHUA5DElKoSgjx8/JuF+fHxMU6UAj7vdThcXF6mvA4CdxuENANune9Cv0XedjsOe1UOjM1kGjKqz73x+TG9GBbu8vEzyxYnuKCa1rX3XqbSMBsqKo4GNOlXYw+GQxrUyMhHGl6CFPeDevKkcB+5npABM0EPKUQggcdghhJQaZk8IInHgfAcG+PX1NQVofd+ncz28br7rujQ6l8lOAKeiKNJ0ntvbW/3sZz9LxhWANpvN9OHDB11fX6cTpJFnmBN3PIxDDiGkcjkcFWwn+4zsLpfLydhcbBIMIDLTteMoP6aVSJpMXXHGb7vdpobzth0b8gjGT2uvCY6ZEoSTxYYho34GAcDMQa2XxBDM13WdrsWZAp7CB0jgqE6fxx2Gl8GcpuWRZdaRa3utL0E18ogvWCwWClkELpQQ4ZTbtlWueDYQ9sDJiLZtJyl85F1SymIS/DnL7v0eO6un5xqw7NwPgY3XgSPX19fXappG19fXur+/TzYSAODZB/yIExmSEjmGvHjWAuCHXSHb5mV0XAufwPu9BAy7g59BX/ABUj6uOQRfyoiPWUBAKM8BmGV9kBWyxfweWfYRzCPbOj0VndJH33NkkXtyggBQ7NkHSk5ZS8/CQGrG+59Pymawndy7Z8Ow9fv9Xp3GUbAELvEzcWT9brdLE532+/3Q63Gpsow9QmTyGKsOrgGXuI2YlZXmxpxjM5Ar9NFLq9BzbLj3U/FM9Hj4JCyu8/Lyknw8Pid+bizNRR4j/siHwC18AwBnea5DHf0VPVP4OdbIy7pSwDbcNwErVQqsEwQee8w6QCKg/z58gzVB5/ncrJqpGwJoAmVsDboDzsIHYGOQGy8thUiF+PQ1oXrES72kcRKa95QhV+iykxLYP7ct2K7j8ZiCNPCGN2azTx4suK8fM9azSYDkmUTWzitXwDjYqKIofrmBxu/+s38+SYcCVNhwDAgsjzf7Nk1s3Ly+vk710VdXVwn8w2J7+hcBxbi0bZtSZCwiYBZl9Hp9NtfTqJ6+k5TKbLjPuq51fn6emoyp+354eEilSGQJvDyDZmaCDEpOCCrYbHohMMjO5FCqQjDCc6OMCBkAtWni1CgPLHCuTFvw2f+kc31CEulcyr+8BhEjSw1ylsW62cvLy9Rj4Gk4AAzlTnwGowhbzlSo29vbBBxgFgEJj4+Puru7i2PsunjWiiR9/fXXury81GeffRbLzQYZ7LpucoARTDd7AMhmjXg26s8Bs3XTaD/8m7p7KRrb3Xarcrg2zhD5o7SGvQT0Y8Q8qAa0dV2XgAQOjsAaeXWA6D0YfCfgBTbtlGHs+9iQ/vHjx1TC9IMf/CClxT9+/Jj6SNgv5MEDB6YY8d7tdqv9fp8IhJubG202G71//z4ZX+4N3YVMYDQvpWcQFoBlSAZ6KMjA3N/f6+3bt3p5eUmN+tTOAr4x3tT7v3//Pk138mEDyOrxeNRycZbAJ86CAMUBNi8cAYEswTHOCVBELTaAUBoNOcGRl7YABna7XbpnB63ehE7WxGtmsQ3oMPLIfXqNMUEtBAQy6GUp2CvkBrvsz00JIk7b5XuSti/LVG7COiU73McMHWvk2QhAKOvJv71OGXCGnXEQQ50/gS79RQ4yWBcIHeqoF4tFCrwA3NhZ9AWAjcwRwOLYT0tMkCPWzjOYp+w/78PJs3b0z+F3Xf4gMDyARF6bpktgDyAHeFqtFknWkCu33WQtySQShDqwlTQBd16q8fDwkHSGZ2YN8QFcF932vQWo+lkQZL/IhnrmA1B1PNbpLAN0Ah2CTGLfsSUJI2h8JsB63I9ch8M+4R3JyimHM7/IktOf5EEtMkP/Wd/3yiUV+XiPvI+XB9XoJfvrvoz7RRa8ZPf19XUCovkdPQ5VVQ37M8oB/oySyrIchwcge0VRaH84qKjKiR0mWMG3Y+fRR8cHLpd8r/tlaRy4gT/mevg69AbbAT4jO9L3vbp6PDiQ4B9Zxl/yTBAnkA7IBRUzTl5gA7wPEL0E23pmAd2hDAtfj/4io5B74BDuDZlEt1O59Qn2dSKF4JZ7xj5hd8BK3Au6hR1EBh1nIqf/4V/68/qu1ycHGr/3O//iGwwOkTs3REkLQNWjKoSZKJemPG82xPDBuGLImKPvzXAIHErtRp1NoVzDU64EHABT7hMhQcDZIL6L8ZRN06SZzKSqACcEO84G73Y7bTabdHAYJSB3d3f6yU9+ou9///vpmVBinB+ZGb4fwATDi3KNaeAq/R9hOlXkwyEeqPfhw4e0Tjc3N3p6ekrO+6uvvlLXdfriiy9SaRCC63V+GBNnvTwIRBE4LdpZYxwlMhBCSEEdY+Uo/3l4fEyHAFKGJEnLoaayquLkC4AXe8b3kLGhxpng7/7+PjXwzedz1U2jYpAHAi+cXQhBa2MYKfPr+z6dd+FBB9kHGIi2bdPJ5xgS2B0MYwghgTo+P5/PU1DorCCnM/N5jDhZFAwzzh298wBCUpoeJWky+hhDg3FjPzFo6DWgAoYTJpiDGikjAeixHoCh6+vrlOHEuJ+fn+vp6SkdxEjm8unpSW/evElgg6AEgwqQxNnQiIqNeHx8nEwyOTs7U9eOGTL2qyhiMzfpe4InPufsuafEceIOsjzz6Wltd5QeJDnZgvH3QAfHAGsGK+XT0OgDwrl5fwYZMUgBnIZnIgA1yBtyhFw78+bOB8foexJC7Jlr+5ERx3aUZRlLUg7HlEnFSfI+rokDhaTxrCTy6MDbs4ueBcCG4WTJUJwyfDy7BwOAM+wr74N4OpUFsouAGN5zyqbyOV7O8PM8nv0gK8c604jra8JzIy+LxSoBVJ49y7JBR4IuLs4nbD96KimRYtgYt/UM8/AMmI/rxqcWRZHKxPq+n0xXY7qg4wZk3QGSEyF8lsDUe69YsxiwZVouV0mvWFfKa7BngOOqqtT1ndp+HF3LZKJ4X0FXV5cKIej+/j5VOkhxnHzXxfUnQ8k9ot/IDDgpz3OFrlOe5RNfgXyxxwTD+HKXGfYdWQXAs9dgHmwEa81n2fPZrJKGsitsFPsZvyOCaghX5FR5pt7IL67tfaET4qEYewN8T8Fsz8/Pyb6jb565xBfxrDwD+ABfhx5WVRUPVj7WyQahf7ywO/wfP8z9UUGDnOBT/TNuP7FJPIPjJMhk5JDgBJkkMOA9TlqAadgbvpOfnVZHEEyDFQkYuK7Lm9sbrsn3etYYmwam/KVmNP75P/2txNxjQDAubGZRjHP/AWfUXnPjPhqL68zn83QuA5uBk2bOPgZ1s9kkBvv29lb/7t/9O33++efJ2MC0rtfryWQBFonfEVCUZZkchbMPbAZC4Y2MOFUPWjab2Nfh5x7gXPxaZVkmcMu/UZqui/XYTEchdUWzLMDu8fExgT+yGxh8BywYcElJUQAQ7uDYv6qKI2gRJsAVABqDilJwbwBvjADROmVtLy8vaTwgoAf2Is/zNIUKwefazQD8i0GwAS8pbW6OELAI4+cBF0aMcpXj8ajPP/887Q9zyFerlTbD83igTOahb8dpI56penh40Pn5+YSRALCTHQshHgJHA/Sp7sBilmWZJhax3+wx++hGByDGXhVFkQ6IS45ASsAEAy4plerB0JCdOx6PqWSRteAMAdYSow7I8QyGn0sAqCAY8QAFmef9BPboGsE1oJ2MGnsDk40O4Vy+LWPAZ/jOEGJGarc9TJxZXccRwjw7zBffg2GHWWQtCQo8G+V/vMwC9htmFcbPWW2CCycQpBF4O7vO86N3yAgMMYCtLMsUjJGldScOiOG6bp+RdXdE7A37xFrhG7D5WZ5L+bgHfLbrOoWuV991k2s76MZp4rApP0oObFh3yg9c3wFpBFnYFxwvfXgu/9JYosWzEDz5dbFR2NvTch5nS7EZ+Eh0l7XwfhKIDa6LHjJ9zdl8Bk14EysgCjYZu5Bl40hy7pVgs67HfjsHL/gKfue2pKqqZKfwnQSyrDX2mpJWfC4+lBJi7ht54XvRS/bdibzNZpMyUIA1CEuvEqjrRovFmFlAZjxYpuyQMt48z9WG8RwlCJCu67Ren4nhBafTo+bzhcpylAMnaAC1BBoQn3meq2/aNF3JMRD7iO1BByFs2EOIAdbVASw67GDSs10A1Ei8rFJzsmO1uJczNc2oA15e3HRt6h/kmT1rSgAB3vGgi3tyX8X6gW+4Pw8sWHtkxu0d5aQ+ma3rOjWHYyI3Cao9Q+w+CTvCunPv4Cm+k711kgGdYx15LzKAnnmgiM2H1HVCjmsA+LFLBBYEz9gWMJDrE3vj98reI5fsBX7Yy9XcfjmZP5vN9Of/4v9K3/X65EDjH/5//ltdXFykciLSfzgqWFgUEOeOM4X18NQSC5bneSrRATRTeoBxads2gVpJqUH79fU1lW7M5/FgmoeHh7QQABMHfKRKyTC4oFPaxUE4GAoMJ7PuUQbYQ2+wZlMxUEVRTM6W8APmECIcAJmc07Qef+/7Pt2fCxng0Fl99gSh9ElRNPayX3mep/3tui7VADLqDYbdmQbvV8AYcDAOgLfrOt3c3Gg2n6fRv9J4dgaOCQBFTS7PUFZVnDSlMVDlGT++f58Yf5wd++kGjgPSqAcluwKzyB4cj0d1g3KfZguyLFPbxHHC79+/VwhBd3d3KRBFCZFbGJ+zs7PEinv9o586jl6gM+wBh0h5SpM+m9VqpV/84hcT9vHq6iqVrnGwHkFvWcZmVpwno1r5fgJgSmE8i+X13Pzd5e7i4iKtrZeeENR3XZfKFHlGUv0Admbuz+fzSUDLCew4KowkrCky37atvvzyy9S7wfs8GGDt6fNaLpfabQ+T7CYlIhh775U4JSQIQKWxNtnZOZwaThdH6YZaUgJMp4w064NTOGWzAIE+rYZg1zN7HqicghbWheAE+8x3uz3j/j3o51n90Dlnh9HhxWo5+XzKQA+Bhl8LGXGg5J91Rpc95f6QF38P++Y9Mf5sXvKF3HEfMHnoM8QJwJB9xjZVVZWy86cMNfuHrPD/08yLB52+Fk5+OIvKZ9hr7Dd2LNqPRvOhFwbfJWkoTTwk+QHwIA+QGW5PTwGKywOfIVBg3Tj4klLe5XKZsoysH/sIIbFer/X8/DyZIMbaEGyyb6yjE2SAY/dVfA5wuVwuU0ko/WxZnuk44BBsDq+qKpXnWQqs0eHIQi+1Xp+nMiXW0jMw7sdTsNDFoR38mzV0wM+1sPeshweG+Ctk0vXcZYtyVPYL7BP/TE9MZ3/zvFDbdt8YXlDXtfKiUN02KTgno8DIfTJ7+DBvREe2PUhmjdALAmPPBEOKUNqEfnkTNjgg9RUc6yRn3NdpYI0sQdC4LWONfBgKgSpyALEEpgEDg4/QCc/sOnhHr5x04lkgCrCL2C7sBP6VNfRr8XMPFsB+vgb8HBKRwATcxR6hh33f62/+J39D3/X6UwUad3d3ur+/19XVVXLwT09PSQEuLy8nNcpt2+rjx4+pMQrjRokUzpXyKwfLCKKXl8BaEXRgMAFeGKYsy1Jak0X1+dUAQEppECZprAU8BcSnLGpVVTo7O0ujN/eHg85Wq3hQWTutXeZ5Xl5e9PbtW202r4nx77ox3RfH9I0TTKJjLJTnY6TM7PzLy8sJOwiTQdkHaW5+RxM5Rp+yElKdpGUx1u5gGKcZp15Fx00vCgAdo8L6YjzozWCtcHwwjd5sRbBFFirL4vkOi+VS67OzWDIxZE/m87lehz4KlP7y8lJ1HU9oRbb4u++Dg0Vqe2ezmbq+V9t1yrMsHp5oI1+zLJP6cTRvnk97kwDugGOco5cpeNkRWTOmIbkTxYATTDZNk4B8UcRSwqZpJnX7sNl93096b3CmlMwAgrxUBccBCMGoAOgxmsxu5zlYd8DTtz0rf2dWOkyopAkQo+GZ8qK+71Uf6zgeOpvO1Ye5inIZyxkwlH3fJ92m34o6bIKYPB/rZV83MRjz8gbK1HhGZAAjTOkOvQCscZ7Hsy0gFZARgCZODMIEXUPWvSTRy3P4mQMeGCdnm7k+MsZnyL6dBjHuxNgrMlA4cWdiIzjPxGSrEMYzJnx9cNCpubLIleeFjvUxjejMskx916s+HjVLWYdxFGu0QdN5+PzuFOTyfs9q81wAetYfW3/K5LmT5t5PARegAL32NTwlmTyQYV15Dg9qsAXoy8iSxxG03H/TtJLGbC+6yr7QD+BgE78XnyX2FzDmnfUKgSEMbSo/mspHnJgUgobeu2mwjI6wvqcBEYCcrCYZ31M7wvch4x6wnJZ0ekl0xA/rIeM0Bt4vL5sB4FaT/SBTSRY7y+PBvMj64XDQ/rDXbCgVlJT6BOL91AnglWWUge12pziBrVLXTVnmLIuH/XZ9p0xSXhQ6Ho4qy0JhWIdCIygGP7FHkHEA5vPz81SCC3DEPiIHEBeJ6VdQnkUbzdQ3B+BZnms22JugQS+68awKZZnKIo6ZVSZlytT1vaqyVNu1OhyOqubj2GVkAV+LrkAiY7/xDYBZ7JATrNh8BhE5qcLnyPrgj/k5djYF+MdapQXPeZ6r7bpkf4qy1Hyw9S+bjfI8UzaM2qZaYrmKo4SxJWBBsBeygW4gA05+gJmQZZ4b0t1tBWvo5DbBODbL7bPbMCemCBbwtaeZCSczkV2CGnwNz+JkbwhBf+mv/kV91+uTA41/8o9+M6U/OcnWnTAL6JEgzA+KCrPnjNzpJuEk2CyCDYwnwJWgww2512Y74MDh+wvGmu8F+HtjD4uJENOg+vXXX+vm5kbKx1M5vcRgPpvpZQh4Xl5edHFxkTa374PystJ+v1OeF+ma2+1WZ8uVqrJU0zY2bi4b1iDOxeacCYIlT0UToR8Oh0nZFNfA+VAvjgAj+DxLWZZ6eX5NBg+j9/j4KGVSUYwpdKZqACCJ+CmTomEdZpz9pzzBnezr62uaTsap0DQBfu/739fD/b2k6JAIJGazmZ6fnxM7iOxg9ABbPjYXZoD1YW0AbCicN5MyeQRAwXtXq1WSDYy9NDased0/AIYMC/vOZBjukYbgU3aFQJyyG0Aecgwzz33z/Ki4s0Y+5YvaXYwfz+VGy6/FMwISMKS+vhh67glHclo2B6hn4pyUKc8K1U2trh1HZq5Wq8RWRxktNJ+P04XIuLHfm81GyuIsegiRvu91eXmZdJJ1AWDxXE3TTMrVeHZncbA1BAmnvQs4WGQJO1MMAawbemwRjeLYK2QY5lIaHQo6z54i886kesreWSzPKrBf7nRwUoAF5CA6sm+eHty2lGJOR9SO7HgMTJATz8Zg29FJbFoErIXi6PDR+WKruT9fFydInLnEZqDjXkbnvoU15+cu614iwzrxfdhe1tjLjLxnDxLG95F1QOaiY4/nNrVtm8i7MbM9lv1x37Czx2OcDAgBhI/EFpA1RqdGwmd8H/7IbaKDPxjbOKJ1bMLlHCFYfoJVfAx2BV2mvMN7mbgOMs++kSH14A8yJQYTs0kQCdPMHpGVZn/qulYfeoXhPcvlMg2yQG+RC/zMaAeD6MOQxqEG3UBQFVmewGGex3M3QgjKLdhER7E1+GcInzGo16RhmEDjNMj0LH7TNJrN5ynDsFgs0mHA9fEYzwbLx94ugCf2lfth/SiN9eAR24+ceQ3/aUCOjGErvP+Lf2NzkIVTkgaMQ3CKfoG7sPvsB3Lu2QPe27Wd8mI8qBIMAHh2P4ccOGFWDMGJFM9nyzU23jvZ5ffJ2nlGlb3zIN2fdbVapV5gtzn88ayINJLNyBTBHXuJ/nv2A7LV/Zr7es+usp5FUUx6h8uy1F/9W39F3/X65EDjf/y9f6XX11c9PT3p9vY2PQQ3hDB5YMAD42hhbGDPqbkG5BNBwzjAfkhjTdx2u00gG6OJoacXAAPEtVCMEMa0t6f6QwipThOBJ/r+tpTe8XjU+vw89Q7A5nt/Smt1nRiwi4sL7fYHNW03aTqVhmbvPFcWlPo92FhJ+vDh6+HwrqsEer1cAmYUB8EeMJGDMijKuVBCarc5CG0+n6trOx2P4+FVPqL35eVFy1UsV7q/v0/K5CUz1AkSzCCUdV2ndaZOHNnwkiyMhwMqd/o4VhRwt9tNGPOqqlIZGM9KsOhlNMhb13V6+/at9vt9KoGjfMiDubqu09hjrkfPBXtNaRPP62weTq7runT4HAwi5XcE8AB3nI87ANhIACu/Rw8J1r3WF1kDHPE7eq48YMe5cl1YNoAbpXQjIBxT+gAcassJ2GmsbttWt7e3KeB4eHhITmuxWOjleaOrq+ukl5QBASCqqkrsLY4Ix0RgwwhnH9bQ933K9GH4AUne88D9ExRTisE+kN0E2PEcOH5PZXMtbJcbdBxwnueTemfsKs7SAwPPUjjABnhiY7kmsiRNgRsBBgCJe0VXHIQ7SxbvY3w2ZCPKSswsnWY1oqzFQ/1cFwGsAAj0h5/Fe47nfvC8p+CM97EOrJ3Xc3MvrBflTawxNs9r4k9LG0YGu5yAWPqWeAG0PEPnWUoHVBAWE/uf1iJOMMJWo1dxHcYgBtn3IJL7Rlch2ygzJmM49j7EshjkDbvl5Sd8V9u2aSJUvM/4HD5y01lX7D7yByni/W3cK0CLvg2GxxwOh1RuRbbOew3j+uYqinICPk+zK9hN9reqKvXZKDc0b9NXiL130tN1j79jO9qhkmFWVhO23gN45JTnQM+8r4l7Z/2dtXYAjb4SGLG+T09PUpapKAsth0CAgMOZcl97QLCTE6ekBHrpvgA5cMKW+8MHoVPgObASPsOHbPgekZly7OGBDLaMNUTGXObcBkECuS5z3042sBb4ZK7jwSH2flZWyk12sSf4VnCZYzVkgJ+zljyDZ9bd9vK83gPlwVVZjmdFgbuRYc9wSJr4TvwR5K9XLnCvEGmQw6fr+7f/N39L3/X65EDjt/7x/5BKBR4eHhJLgDHCqPnEE4/QPKrjJgk8qLkD+BCssAlnZ2dpYgwMOoYZFp3SnKurq1TygtE/DTZYZE/lAcKfn58TiGJTURKarXHey6GsipImWKmLiwsdhoPH3r59m4Kqi4sLNW2raraYOC0MS1WW0pCWIzDIsmyoG+80X8zTYXQcHkXwhWAC7NyoAoYIRpg8xc+++uorSUosel3X2r7u01rS7BtCiIfVhC6NDqUZlIALsPuHf/iHk8ZdHNbhcNDd3V0q3fJImXtGsVi3LMsm5R/0PFBexMQvphQ1TRNPnw5jExPACOXCqXtqlxIyDC6sAsaI8cRkGQBaXhbI2Oa2bVPZDutDBshZglSWpZFp8jIyjC9TsPwzWZalcwJSPXw5HlAJ6+mMCFNU+DcGCYeEw8H4oK+ACYwjwQSGtSxLXV1dpR4HgiDW11PIvpYYs5El71QW4yAEzJPXOWOIuRc3xHyPr4UbZbdXsN1+b9gGWFYcl9dqf1s/BmvJd7FvODP0h3V31hLZJ1jju5DZU0cHiMLoe6AhjY7HHXICV/10wpTX83qw6YE9/44nc4/lLc72xbr1sSyJ74wguVAIf3LpkzOoADiClyzTZA9Pn8mzl56NYP+RBfwJa+p9G2NgM7Kynkl0ffO1ARA5sOj7sXQRGfWAkefE1vk6E1zPZnMdj3UKSDx70fftJFhy/QHAun/FbnrwxPOyrrvdXvG05WxyzxBNEIg+iSjLpLZtJqQd/XVd16UgzLNWgEbW2DNLkiZnVElK0/AceJ7q8VdffaWzs/MkRzTNgwGcHMFesp5NPwJTbJbLjZ/3wXqwhw4OE5bZxwNOXTZ9X5FVAKz/Dl0gIGQ9APDcF+uF3R2zhk2Sp7Is1WejfQeDUVromVDWAhDpttrJJmfPXVckTSbenZIXvk6UWLsP9pIhrsczY9MAwL4HHkBgK6mk8OdjvbgP9ynYSses/j4nbjzgTkSVMhX5mMF3O4sfBRu4DwIHnwaA7o/dJqPffA6yjGfGl6Br4EmOS0Df+G4nk6L+79J6ICcQ/6wzg47wR/7+v/Of/W191+tPdTI4BoC0OICWSMpZAK95xekizDwAJR4e1Z2mOYl+v/rqK3322WeJnaFGDeXwpmfuB9aKEi+EWppGh3d3d/rqq6+ScNGDUFVVSg+iwM/Pz4l1OTaNnp6e9MUXXyTHQ2qwyMZ0KIFUVNBewdKrx+NRHz580MePH/XF55+rPhyTkQYIRYZsrqZtJk7SDQgAmyDIWW2U0YF7VcUJU5S2nJ+fq65rvXnzRh8+fNCsijPBAUus1/n5uQ7HXQK+gE2APs301JZyECF7eXd3J2lsXGvbNp3ijYJ4PwkKeH5+nhg5SZPpZTD8yF5szFuke+YZvSwP5cSAITfINE6b4MSboZw9d5Y9NRNm4xQIymEALfv9XsdjPEcEw8R7T40BGRECOhz42OBZT5w0IItroNqABDJrfhYO4IHRfRhAAEtib4ZsEIYXXQMUs85uA3CcOCBP5zogJ+MRP5erqcemYAcqp9cNIUyYWHTFAz8MPuDjtMTI9QjblHoLsrEMicwK90HARmYNJ4+MeKkUz4xuuqw7GPCaa+/RcLDK3nottztp1gSZ8kCF9Tllynh53bykiXONdmehopiuH88c+zU0kV8Yy67rledjzS9yRaDOdzmYj989lmh56asHZF6OhCN2RhJAxDqwx9gLgANgmevxDOgtMsKUJMAG9+FML8/m34fP9ACE58SHAo7j2Q/jfuIX47pHvcY+sg/OmCLXzgCzr4Bmvmu/P6goxgwf73ddR76RoXhPbRrzSkBD+Sdrgy5ABvpIXmSIjE5ZlsmeIueuHw60kHcGyNzc3Cr2N47jlQm2D4dD2kOImjzPpSxTXo5BlQ8ScSKKEi90wSs0XG/LslSR5QKCca/sH/bIh2kgy7zfAa3b8W8Lsh0HUCXANKqu6xSyTPlwsCDY4/X1NZXIndoF30fk3TM233ZPgFCy9pBL9FPgp+g3RY59Ep77KA9mCKZcnr20ye2XB8j4H/w4OoId43kcO/DsXJs9AJ84YcHal2Wp5WKhvh3H/Pqz8Ayn+8vvsDH8fcz+jlUdvhaOESDAHEPzO7d3/MxL6MFHYNL7+/tRfi1hgP3w84U8+HIy76/8zf9Y3/X65EDjd37rtyfMoQcMAMG6rhPgZUSkR/MwGgASgJmnwHGiAFGMNO9hw8qyTNHg8/NzSvfwPq/TdQeNQ8ER4mRwzmQTALQYZlKcP/3pT/Urv/IrsawrH9PrGO900NNwDzgADFfdNArKdXV1pT/4gz/Q5eVlmgKRZ5maYz0BUghrUeQ61od0XzA8ZIW8bA1hIBBww0+AsFgsdH9/PwFFgNvlcqnDvk6GgqkclDpleUh17ZwwijE7OzvTw8ODrq6uEmglssYoffbZZ+nANtg/podRq3t9fT1RJL4LWWAiiDexO+uLchFceubBwQSGmeuSrucF6+CKTeDEJCtAZN/36fwFppp5RsdBOi+Ard8XCuxpeTc+7jTdgPN5DI47Nc8uIstuRLuuS4yeFFkq+jQA2M4gO8viqXbuGxnls541grBwED7qaaau7SfPis4DXLzWlDX0e2DNnCXyoIxsEevkDs3ZJA+GnCVzZ+PNxtgCACu25nA4pMMJkUlK5vgscnLqSLw8gj/YhFMW7BSQcL/YIc+GEZB4IEXWBWB/mgWJcjKCQHQuDto4qCjyb+hXlPcgSqf8msiaO3uY+ag7hcpyHE/M+o6BT2T2YMFZYzLFp4CKwMSfU1IiCngv9wExwJ6TwQcs0WvgGXDkz/fq8fFRi8VCFxcXyTfxzA72Rl9XDlmgMNHl+Pyxd8UBBYDW7T//RgbYQ86kgeWPe1Smmm3sJufXUM7pMh73P9f19VXSJ8Yme8aM4MpBK+/36W6eCccWY5ew586O+7pFUmmV1tUnX7puY0s2m00s/8pzFVWZfIcz/awf38v/2R+/Hs8TQoiNxmEs6UEOIao8+KP3AjkAFDPVi3twgpaqi9Pvl8YJeay7irEXwGXBg24nIhzLsU/IsttC9x/8//SEaoJB7C2BNGTYWPKWpYydZ0e5Z2w+No215Hs9SHKsh2x4RvrbcKQTG+5n0Du3E5595bNVWaoqRj3m/6yRExb+fb42p/Dbs3Dud9EjfBmf9e9k/dEh37PTAJq1o4IIwh974vjjNFPqQfRqtdJ/9Jf/gr7rVX7nO4YXBhdgBsMGWGEzKA+hxhJh8odkQTj4BQPnI/9gnU6ZGjbfjQ5GmCZaZ7QxWIAomBxKr3DslEL4bG9ntnFUpNSPx6MOw4bz7JSOtU2TRjYitDA6x7pWMTiKL774IrE9eZ5L/ciQ5Xmujx8/Tsplymq8X08LEpjAcpPlIK3mTprmbw5JIxpGOTjfgzXFOMCC53muxXKWDAxBAN8nSd/73vcSwIJZYvpTVY2jgDG4rDX9Dg6m2E+MLfvQNPH8Esb0MgULJWKiGHLqRm+xWKQD/ggU/HR45BCDBoNNMOcNax6gzWazdCo7zsKBncsKDDtjH3HwGBdv9qbnA+fpZT1uSPM8T+NkMdwYEPYfI0JQzr3hYADzXgeNDjijy5o6o8p7MIpSrH3measqjof2cgBnseL+Fuq7kelFtgEwnmZn/fk+nAbv8ZS/gy1nSR1YVlWV5NTXhPexJzwzDtKzGp4BArRcXFykunNpOnzg2wIKSu14r//fQTAy4zaVwNWnjWGXucdTJpxgwfuiTjNCo73NJiUM9K+0baMsG0EFOhWzBrHnwNlCX38vleVnMYs3ZpG4L56Hdcbhca8eKKGbrItnc/AbrBf+zYPZoihSiSlBIraZMmIHz9LIrnow6uO3vcQK+fEANMrSOCTAmUnXY7dp3nvGaOy2bVPWFdshKZFLrGm8z7HMkIDp8fEx2Wvsn4OusoyHhiI3yNzFxUWSnxDCZFw5OsEeuz3n/VVVpUmP3J/LigeqY48aZX1jSZOXNpLpR9awCSHPksxgC7FJADZ0rKqqVKbKC4Du/Q3qx5IX6tqZHsgauR12wgAbddrzAFnHd2PX2UNpPH+D92A3kUNsC2tKgOVgmucmSELG2Te3+fh6SB72iawS4NjvzbOznl0AAxKwY29g2J2kovSY++a+HGgD1PGPHoxT5gW+wRahV75e7it4RnS9KApVZaX+JJvhdsJxleurE/UeTLjf9sAGu8HevLy8JCIWTO1r7fYVG0PWjnt1uUWGTkln9ojrYVf8Xj719ckZjX/9u/9SLy8vury8nBj3uBHl4FwrZcq03W2H1MxCTVNruVylRdvtOAsj1vT2fRiUOagsKzUDK1SUY2pyFN5es1mVynJm1Uzr8/UA9Jo49aEsB6eXaTFfqJpV6rteQUFt06oPQZmkooyApmlbvW42Wp+f67Dfqw8hTo3avGg+G8qdeg5HiYu9mC9UlKXef/gQhaks1DaxUa5pGylI+91Wq9WZ6npMBedZrmNdK8uLVGLUNK2+//3v6XW71cX5uQ67sfkXIBIN1EEXF+fqQx/X+3jUYrlQVTHPGUcb2SYHcLz/cDxquVxou90pBMoTMs1m1TgKMM/1stnosI/jQxnrtlqtdH9/r6oqNV/M0n2RtnX26mwYRQt7FhUvZl3OzxkVmGu/32l9FmdQN22jvo9KvV6f6atffKXZbKar6zhK+erqSs/Pz5NDCb18AccEMEYRSB17wOqMMdkRT2WisE3TTAwngBfFxqlhqPb7yHLG4EJqhwOOFstFWuu2jXsk4dxy9V2nZgDmniHBIGRZXC90JLGDIWh/2CtTprIqFZsiC7XtGCQdj2NpUTRkIyOIUXSHLymxqehzH3pJmfqhprmpG1Wzyhx7rzzepBg1+/KyUVWWKqtSh8NRi/lc/cCie3CUZSMDWNeNZtVMsXl4ZLZwuG4Q+R2OE6DoAMYDDwwn1yID6QYYsIVs9Unvx14PgC7GWxpZKGef0AWeF1vmWSHPOAACPBvEe/lunC/XZQ2RPxySA29GGTvpgC2GAACUAcglpRIKtyMStb1jMBf3ohsAeJYyNQ4U4jjh0VGzNt7jgBzUNaffcjZPMxBHy0GHx8l5PIfLMPcEmILwinZwLN/C+TO8gmt6doVrOyDvOhrNc52drbTb7UVvCrLh0+8ITACXECwALjIGlHfG34U08pxnQz6apk72vevi+sxm80F2ShVFqcNhnzJUvGezedV6fZZKjqJtqTSbVer7sZEdOwnhArMJaEYui2Ic9hKJoIPOztbDc5Vq205NU0/K89jrEGJmJupAPwQacTJZnOJXDcHpTEwyG1lqJlfGyVzRzs0TGcJaOzlCNgH9SgRj16oa9KEo4rjZvu+VZ7mUKZVGnmaeEqNdjY3PeZ6ryAtlgLiW6WKdQh8m2WRl056kvuviyOfBjitIWZ4lbLQbdBR7hix0XaeijH4l6laQgnSsa+VlMQGKHqQBwqWxhGeaNZseyImdZAiHE0AejI0+ZuzRQq+oPuC6EIU8D7JHXwY+F51wf8u98x0Qi+Nkz/HwOdYZcpY18Iwi++KZDd7nwNwDj67rFPpe2YBjFUa7VjdNmjLGPbhfyotCXdsqyzMBOTJJWR5L7/I8V900ygYbrixOMuU567pOBAjPBGHkGAYbCVYbiYyxyuj0M57d8zVkXd3H4Hd+qeNt/8ff+1dJ8djk+KdQ23RpI4lcMUIIKw+AQMOUxPnd4xkHfP7x8UFlWaWpMYz0JMiA+cZ5eyrKo1miQ0/HuSL5BCNS7QgI0W8UlNhfAasBw+Ab7ac5Nk2ctECpEmwh6WspKv/Ly8s3QJSPWkunJtdHna3OBoc8GhqMFeVTf1IUy33C3PNinjgBgqf7nGWtqjgh6OLiQofjLgWcMJpeekS0zP31g0Jut+PEHikaufV6nU46r6pq8rumabQ+P1Mcc9lPZooDBubzeRq7zPrxnfxpmiYFE15/jiF25WP9APzsE6lX5JZrpDRyOzo3Z0jJMiCbyCGK7AaZ9/hECGQsy5QCdvQK+QZoO1MrjSN4AZBB8d/06ZBJic9axACiqky3p+djnDqDVBPcd8qUTRh99ujm5iaxO+gAgNOzop4K5/cAUU+fn9a2smaUTRBA5vk4qxxD76waOurBiLOdCXxYxsQzNlwHQ+7BiYMIruP6Crj1YCbO369S8Ms9AK5jgDo6PPbUATcZL2ksI/ESMmQFoICuOGuHHnv5iNsiSlOcVfSSKHfUyEuW5ZrNxpPrkYVoP2aqqjGxjl7EvS8TA4xtHUs9Rhn1wDnL8lR+5PZfokl+lGlky7Ol2ALXv76PoHy/30+CEtbHMz6sS9tCbEzHCSNj7tA9CI77OzZlEix65ov185IGMmH4Au83QUZZP67BaG5s/GKx0IcPH5JN9wEDfLbrulSmzJ7znYDhqqpSuRjPxtqy7xErlNJgNxyQYZvBBB6UOzvu4BEwtVwuU/05rDvBPkGUyyj/xi7PZjMd61q9poG3s73IG+vuWVQYaX8WgvzlcqkiL9SHfnKgI+uLj2FP8jxOoexPWGrWvM/GjCM66evjtgg98f2UlIgGrwJBzhx8e1APccd12S/2yvEHpd3YaM9Ul2U5OauKsamQdU4IOGaTlKolnADE/pGtGXVxJA0cl7Jf/OHnHrDir9xfQA45KXRKeNSHo3ojndw+VPN4Zhf3z724TPq6Y6f6ZsQvkJFuM/kez0xjV9yXeYCF3rgOYB+QHey66w32pSiKX26g8f/7t/9T2nRnQw+Hgxbz1QQsYSQQPmfF3BijHA5CCBDcCOBQ6Y5n0WCQECSEC7COclPKgMADqrlX7vO04c1TgDAbXdelKU/cH4o/m83SxAgvneBFw1ZVVbq6ukrgGcVeLBZp8gbCTtraG+mPx2Nq3nWgyTOu1+tUKga7D9MGeMTgX11dpRpnSka8ZhIQhZGo61r7w1ZdF0t6vCSEe+Jem6axE7Cl+tikSU6UoCGsXsKxWCz08PAwMGlLHY77SbmHOwUMuUfczg5ySA3Nk2VZpjHIAD6u6yCIEhD21pkNn0YSA9K9mnqcTvH8/DwJJjEA/B4HeTo9xpUfI4vB8QkkAGj23WujpXHqkAf/klQ3hyRnyH1imbNxBDHXdUYPneS5KImgJAe55L3oDE4MQ43zOc0I+Tp4YMg9ISen7BT7gDPiO9xwew277yVri76zpqwJn5E0cSoEmp4lw17xdw9s/OfYHV5jaUA8Q8QDGO5Nmk5pYo9ZI3dy6J8Hw+wJawOAPQ1qPPhGHj1Q4XpuawGQbjurqkpDEKLdKNX3376+9HYgA57ej0ztWIrn6ypFVtuZ5jEgnGaA3LZnWUhnn5yOOg4hWCagm4xzrKp5ki8+w7AGJs2xv/wuTmUaS8ayLEs25XQfWON4xsulYl9LXH9sObpzOBxS2bGklEWijw39gcQKIaQ+CO6DfXKdIVjlmVkX9t37ibDDHlw7a+5g29/HH/AB2XIH7Owbe8rr1D87duCevbwVgIbtgdX1AMKZ5iQjeZb6LymZouTWAx7XeQdm3L/3QjjpgC4R9HkJJMEaz5FZKRbfCx5o+mlT8yl5gP0cM0nTfjqIsuQfhj42JzOwOewn6+kZRPQL38LEIh8+w56hv6wdJBRZM9YNu8OAFvw330swzfurqppMcPLAiufl3zwbpJwTkDy7y7/7NnQA+fU1pKR5Pp+rrRuFfmzOdpvXhV5ZPg7SAJMhU/wcmUg+rh1JJDJMp36BrAcYzgMEDzaQbV7IpxNG+AXWyUkgD7g/pRn8k3s0eLlBAcCjODCpRGg4ef7tTBkLw2YhmABaz4r0fa+np6fkRNn85+fnZGQAqEy/QSgcJOHkAKLcA/fnEaRHh9wzioXB8ft+fX1Njob7ol4VAydJNzc3aRwuxgTwyybiTHg/yshhPbBcPPe3/R926zSC99QjCgR7lqLx4Zm/zfmWZZkyCPSTcOAc8sA6Ophtm1b7/TGtK6Afh+EHsiETbdvqWB/TGjkrh8whD8hlWY7niaAkt7e3en5+TkaBgIv9R5ml8WRpAjcUEnDrgQnrx3fz3IBJN2h8D2w/Lxggbw7mPpFN9sDZemf7cQAYIPo0CLbSGOV+rG0/NU596NN+nTLWHkw/PT2l9SHo4d65bwwSWTZn7dgvBxWS0gAGWDXXc4w/+48hxPGgK84KIt/sFcyaryFOnn8DZN04O1DwIAC75ICFZwZAxszsYxrjK2lCRGAX4vPkWi7HA7A4OC3e42im/dmpo+ceuC+GbbBW1IZzn26XeS7fF2f2+Qy2Dl1z8AyQ8ZpfCJ74+mYGBHmJPxvZOwdvVTVPwAF7xHP2/XSQAeAj1nqffat+x5+NB0Z6AMUhjtgxnjnen/T6uk33AbCiRBRb9vj4mPZW0tDnND6rr62ktP/IfJZlw8TBXH3fpOfCn7F2BPDIAcx43/dpFHsIcUAL+0NQir1x8MQ6uW+kj80DcvTagwXPBiOf/Bt9dTlhHdAtRpL7eqPL2DPXST7LewBlrA2EBLbBfazvDdkuvhP72rat8qxQXhQTPBLCOLLbQRkv902nYPY0yHD/6FkQxxzYklyx6dj9iK+XN6dD7mATyTj7WU18F/fEurB+yAYlf2SOeJ8DX9aA6/uLdQOHUCJ4GpTisyG3XEa7bnrgJJNGsTc+KY57cRl1P3lKcDhBSyac3s+pDZpWufDs6AB7wpqn4GggE7zfI43ebccAGX/B3jvx4aVNWRbbAvDFkeDcTTIzTjzzdye6XYfx514J4n7wNGhjv+in4r0erPz7Xp8caDiL6unoqJiaLAjCwmJSZuRsHMIOQ1gURTqzAEOB0gG+EUgEYrlcpulDs9ksNTpj6Jj84wviKT4WH8XwOkQ2BSfAPfEclHnxzKwNTpbPk/aGuWGkKKVgZBNoIsawMwaWa3KveZ6nhlWMowsKTtQzKlk2NrJLY3mONB3BRlkMjommd2e+sizT6mxcE96PguCE1+v1hEVYLldaLrtJlsTT+mRiuA9X4Kbpk2H0gM+n5mBUeL4sy9IhcF4b7ewK34PBxmC5kXVlc8U/HA4p/V0UufLBKcEy7Pf71N/CtTFGHsA4s8N9weJ4CpN95gVrz3qOJX5Zyv4BZnlmglSAMPdZlZXKcnQisBrIIk4OR7vdbiUppahhMPm7M+vshYN31rMYnHkIIQ0U4DmSgSrLiYFk32HfPP2L/BOYs56Ab0DkaSqYfxMoc2/YHb7vNMBDJykbwXZ5+jv2NY2HFuLMIQrIBqxWi7T32KGiKJJ8ZcN5EqvVKjGGp6fGsq+ejgeIku1crVZ6fn6esFcAVcoICahYBwc5gAOCLNbN9/n0Hvo+JKd7Wr6VZUpT/wCFfDf9GF7uE23JUm07HibpshNJhNFZO4hmvwBprn+ATUAp8k+5Jn5hvV6naUxVVaWzgsqy1MXFRcqSkBHM82+OGGcdCQKRV56RwI/74p4ZI4oMYgcBWPwM2+ABqMu712Bj30IIKTh0Bhs7hh0lYGdaEPbFv8ODQi9DgTBgXbFJHiycZgs8owYAxdchpx6kuB47eMenYztDCEnusAkET8d6rHxgXZEh7sXtMdft+7FvCzvlpJKvAXaaoNt7MOjPCSGoOYwEwcQH5rnaenqwIt+JHYfoZE3BC+giIJ2sA/aeP+5PnShw0B1CSCQp2Xzuye0nuuvZZuwZcu8BALax67rUZ0aJFZgOoA65h+7c39+nQ43ZC9YEfTs/P1dVVansG9nxgJVnd/zoWM8PHwT448/6rlcXlKousIlxXVrtbNgB+oztxRZ7AB8/O47DZ2+4JmvGvfX9WM2DD+R53OY54eXZbz8o0T/jvtu/87tef6pmcBSWGyc6ns+Wycg8Pz/r5uZmEtk7qPcosijiSZyATRSPxSRCRBF5YN8Qd6gIBEqCgmEsHZwA0HxknB+QV5blhBHAIKAgODWYb2dZYIQ4pA8GEeXD2MBM0cgUQkizxE/Xz9PPrNepIPJ9BBkotUfpGG4mSvR9n5yms3k4TIJFHF2e55rNx2lHOCNnPbkfaRzfmmW5urafKLDPqGft+TwNaEWZK4SxVIp7xqFQguUpXs9w+Jg35Oc0pY0R9GufBiXIJ/svjX0eRV6o66Z17p4C5Tkd6HtGxHsQuEdYImeecBCsGQYJh+ipUU/rIkfK+rSurHMysiomAR57Kk3nggOUnRDgntyJnAI7HKk7ZfSV+0XPAS7OfHoGxH/HZ9kj7sODWPbBGxm5pgNiSjO5T57FgR3f6X9YB2TDGUtIFQfQPBOsbcxKxCZZ1hN5jDZmJykkR+uMMXp5mj3zDB2y03XjIYsE58iXM2roFDbXg3Be7Ievvwe9rCmAIMvGTICzi33faT4fWWz2NerG2Cy+3cZyzfFE+igvXA9CKMr3PIHHKWOXabGYp2DfwRVrA8AjcORV12NTM7/D1ngGmLWJwfNcdX2c2Bp0BV/EVDaXkyyLh+h5mZavmdtlst9+7pADBLcP6DJ20/cRfea+nF1nHQigWB/W1W2h2ywP2B2s8/dTWeL3DqLImnuWAP1yX+NBDDLDqH0YYO7HyapTglSS8iJX249TxLy8zdlcJ2KwGfTnwZI76QCh4VjBQR14xYOpXJmOA4ucZVnCIiEEHeqjNBBqbrd4Hs++4W/bNpaNA9gvLi7S4b8EP07WolN9338DvBMQApI3m80kwwYQZZ3QG2yFZ+mRc/cPELTgIj9/w3EjJdoEw45B2ad/82/+jYqi0GeffZZ0AD3Crp4e0Om4lRH9DKOBbGI/3N81TSOFoDIfx8piJ/u+V6+QAg3HA+gg13dZ67pOVVGqGewaa+g2mXXzz0oj5uP6rCHycHrOCX7An8txD3YeefmUHo1Pzmi4w0Eh+T/CRGQJG4JzcuWSxv4FFsAF0MEzqV8PKthMf2AWAGdDD4A7ZACFNB6aQ0oaUH6aqbm6ukpgEMDKuR+nwJcTPVl8wBX34O8H6CEoAMgQYorRwS7353WEDpZZF+rlAUw8K59DgAmu+D4MA47ZjSbf74wEikstr9d+ngLeiQJqZHn4LM6QfglYY4xSlmWaVaVet68JsPNdgE1KURzgeqoXxXNAxP0hS6y/Bxzch78XPXBllqS6qXU8NBPw5uVJpIAxrASiHpDwfvbUz6Ah6Ka8DSPMHvqwBYyE7xlrleVjraWnsGOwNNZk4qjd6HMt9tyfg/tC7gnQ3fk764lTcfbK+x08k8SeOjjHiXpghTF3g+7Gkfd5Vuw0OMXx+Hd8WzYMHYZoIQB3VohsBGDPASAsE6RJZNYOYtoWe0CvRWXz/gGDHjgBKFgHWHj6o7ynxAGIByHcD0ATJ+iy7mCANUYHqqpKZTcOOKOMjZ8HFE8zHtO6akoM5/PY//P6+ppAAz1t8XpFmmznI7O7btpI7MGlpDTthr2RRqCc5zFjTjZSoo58nPZG8AJAQAdh+rG7Xddqt9tqtVqle0NG2Tf3ZUzIWi7PJkw1+4L/AHg7m4/tdMDsPpUX6+6+Ed3zIA99Os3y+rh1dBk7hg0ly8S1CIiwHawDZB79I+gPz+qEIPoHqPRn4OdO2hCwQ9j45EHXfSdHkJM8L1QNfgAdoFfS9d7XFx1aLBZpjQgc+75PGXCyuE6EeXaUwIh7KrJs8kyOYy4Wc9XNeMim+1SXA2wKdmk+n0+mMaK3PM+pzQYE+9qBBZP/KGKZFMQr+0q2BJvO78iesu7SOBqbcjqytpAjngkC64EfGNRAhtaxR57n+vVf//V0PQA2wQLPSxWG6zj6Qbka9tInW+JfnfCqylKhGyfcYefQUTKC+HAnifgMJNJisVDbNMqGvi2ynS6Hjk1YJ8/Kkg3FrpxmPd0vsR6sndsO1t/tz6e8PjnQOByOylGOQ2xGrkOtwhhDByTH4zGdEQFL5vX01D+6M3ThYUE4Dfo0WOE9BBbr9VoPDw+Tn/sUFkCSG7L7+3vNZjOdn59P0vMJ5A4BEQ4a8ATTstlsUlkYRoZ7cZYFEOkRZdd16RAbr5nEOPA9RNA8v9fgofA4Zz9Hgu/FoSEUbdtODksiuufFZz2bMhrgIU0/MK9FnutwwODkms0KhT6OO+66TmVR6ngcTopfzLTf7ZNDxEnTjMV6ozzcx+vrUX0YRhP3vYKkrosz+5umVehjGrksK4W+Vx+CQhgyKkEKQWLGupQNUz+CuraVNNRLhzhVRiGoHA7g6fo4CSjPCzFqsWsJgjPtdvvBaO1Fwyr3DuiDnSuGdQhBiiN8c7Vtp7pupEza7naKzZ9Kyh0SOMjUtkzSKJVlvaoqjnnMsjhyk/cBVOMY3DH7lYBl6JRJ2h/2CYgVxVDG2I9sNPriThwZWK1WkyAMoINuwJgR8HkG0rOJBBFe0uDNmg6yiqKYZMJYI8oeyLg5g+jkAvqBDrhuutEFpHv5IWsCeeFO8zTTBJDyMk0cg2eWkA0vSYz3AvNZKs8znZ2t1HW9imLsq3A75XvDfTgDDTvKC2ZXGsuwcKKcGs8+eDBIsMUz4VjzPJ8MKWA9/fA7notAgUAgXre2wNBPkY+feXx8TAGWNyNipyjjISAE2M1mYw8doGacqDcy7mHQ+w8fPgz7Uerm5kZ5XmizedXxeBAjo5EPAhpkxTMaHBiYGkLbduixO6qum6Huecx0AeDbthtIrKXqOo6K7bqRxJGUSCv23AMM9jbLsnTeEf7Ie3PQWc/oeZYfufDsgmdRPJhxMAoQRde9XMZ1EPkPYcyo8zMvReIagDYYbWe5+awk1U2joixU9pXyIhfj9hfLpbrhXpxAA4s4IOd38d+NghGFgEKAmQfGyLSToW3bJr+93W5TcE11BMSKM9PojO95nseRuaEf5dVZ9qAxgMLXnE4LQz68HIjTnk8zNejwKfngvsTLvdh31he5Z9+en58lKZVsSrFHDZ2EfKOaAz2FuD0t+yEo8l4Zyt8og3Kf5HiObAXBppdyeukSeul74yQb94p9dUzq8tXUdRxTrDi2VlkmZVLbtcqLcZiC3yv358+MTuL7PJDAh3AvBH+Or/I8nonFuRvoFUG4Z9AhEPHLPP/pd7EWf5rXJ5dO/d4//5eJ1SDdA/gEfGB8nSnFKBN8OJPKDfNvFhJlQtBJL8PscMtEttQIElxgtDzzAhBBuPkuUpwstjtEN740q8JQA45cqYtinIDEGmFUUF6e0zeTz8JKoPwucKw7f8cYu5NgPxxEOUPI97CuPqud7zo/P9dsNtPDw0PaL/bWldTZXwwL9+NsCHvgQQSK68rEOlA2xvp6qlYa2Rlncdz5tW2bSuVYR/YfwMA1T7MYAFaeFaNNJstLYQCoOC3WGNDH90Q2d1oPzXe2faf5YpHOIlksFvr48WN0btVMcAXIm+sNL75nZJxHht7TrrCUzlb4/mHoHUA78899eLZEGssNnYXxPXXZxJF6szSMI01mMCteuufBCevo7KQz6G7O2rZNtsP1iveiJw4cHAyxvu5wcET8DJLFM06sG8+PA3C5d5aR++E66DpAkWs5u+Q6RlOuO2CCnhDCZLILoMD1P4SxWZOXs9vsLf/3wROw+d5Q6/bPr+GECnZHiuewYJ+wi4B29MqZOBrI6eE4PUyuKKpJPxwlIoAyB/pensG901fn72maJoEMl8e6rnV5eTnpm8PvOXiQlNhZv9Zut0sgkHWtqiqRQdSecx0vtYCgQyfdNgBYGPda1/Wk7IPn8NG5AAqXdYJ/AlbGodIrBAEHqCY7wZri/5G5i4uLJINOOLidQRdYJ/aM85LAHsnm952KchxnPGFnm3bS1O3ZTnSi78fqBj63PewnlRbIB+uKfSSY+rYqA/QBLOFN+O7fWHue3dnvXNk3/AC2rZiNfSXuf7imByHsad/3en5+Tljo48ePury8TDgBQoFMNWvv2SjuhWoJHzSA3BRFkWSY3+G/XAb5O1gOex5CmJT5ss48nweK3A92z3Elz+L+bbvdJpzEPXiPkGMEx13824lf1gd957n4fvYHm+qEOZ+ndAtdA6sSxIFbGAxAfxNr5YG+NE7OggR3/fP1kcaphwQobvtdN0/lE9vTtq3+1n/6N/Vdr08ONP7V7/xeekCiWsCAbyoCyOLgLGiQJquRbiAbSyn4fJ6PdYE4EhTchYEFQPBgHnDWbrwkTbIqnjIuzUg5CMch8TsCBVKhzqbxLLy8P8IFh82WRmfgZSoYIcAnP+d7HAg5q4wj9zSnGxePhE+F3cGAOzUMFwwvBhRjWRRFGm/KvuNEeHau7yns02CL52PvuS+Mh7PFHmhwfW+44vdcg3/7AIFT487+eJreDaQPGWDvWCeMOY4G2RoDr3jYnSsqz19WlZRPJ0Gw/2VeRDYkG9PpNMW5Y/YgIt5jZIfRUT94DeAgaWJMWWsMorNgHng5U8/zSUrG1BtdWV8H07Bl6ALT25y5cnKAdeblhpDvwNADvjzIyrIsGXE+Q1kXpATA30HVqV44cPfMhJMJqafIAldk1/UBGeZ9Xg7ooN6DYFg/bIaPVHW2Fn0gSCG74I3FvjfexA1b6NkXngFG0LMbngWC3KFcJM/zBGqRTTLWzpBGRr1R1/VpQhmsJk7UgfRsNtPLy4s+//xzHY8HzWYRkFM+FSfcxCxmnsdMN8BkPp9P+sA8KCWzzrqz19iY08w2AQ96gMy7DcI+eFDuQb/bTMq0kFcPfN2n8D1u+7guPTX8HT/A/fJM7CHBxcvLS9J7zsdg7WGVGeeOjML0I8+ASlhPJ7OcbCDoxQYge/h73ud9W9y7+zHviYSwkQFwnjHLMs3LcR/BI23bpvHyMN2+3mVZ6mnzkmwK944usq7S2C/jzDg+hXX097st9CCGPfDgq+s6qY8HCLOvgMK2bZVX5fi+4eU2hvVh3aXxXC5khPvFthFcvb6+Jty12WySzcQnzmYzbTab1Bd6PB6HbOD4/Mg5GQcnJbquS9kL7pV/Uzbs+4I/m81macKnN/yji1mWpQly3AP6hGzib/f7fZrSxgt7xr34XiFb+EFs77dhsL7vU3YH3TkejxPdJIBzII9MuXwURcQCZVGoLEYf4UGtYxnHeC439AJxX+Av7g9C1bMqHiSil+gh+/GX//pv6Lten1w69fDwkAwEoJ76MTaal0ef/N1TMN4MDqBz8OnKecpCsPEYdo8asyxLAYpH186ordfrxBhhCGazWWJ2nC3xMZlXV1dp0R3MO5NEbR9Gw1kylMyzHwiCg2WMiCsoBv90ljGOi+ueBg84PhTMywucBXPjxl7wYu0lpXUCfGCcXFlQfjcgKGgEFmOE7ulYDIizFO4guTdXXM8u8H04UJQFxYfZQ2F87SUlY8bLa2UxTp4Z4f9eJ++GZvx/l4ycg/vZbKYu9BPAQDBXVZWOTaM8m07U8vVGhjxon81m2u2mjZeAffaae0DmvMeGDBaM8yk7zV5K49QcB/kOxNDn078D2mFnHcC5k2LfXVcwvugJ10Rv2QPXd8+AAt4B07wPPfbeKdcl7he7gMy6/fJspQdonjH0um2AJUYb2+HsGvtNWVMIITH1rBlTXgj0AAvn5+fpfXwnDpy9cvvJ+TYEPjDT9IK4Hnp2DBkkAOJ+HWi7HsHg4zcOh2MaK9s0sZETW4nT8/LSq6urgdiJ+sv4b0pw4/3Wk6wYjDb23Mefo1+nmVYP+j0zC3hCB5xRBvQ5+eYBuesfenVKcJyyjp5ddD+52+3U9/HwV8/Eui0D1PnAEkgx9P/q6irZHR+bynfSX+Jg1m0xtsP3GB/vIMhZaHy4M8GUHDqYdb8CKEYPPMvRaTr5keCvqip19UhEsB7r9Tpd04MiSpzzYpxS59kI9N6JHu7V95d7wXdzv+y5ryWy6aDWA7CyGEubWFvWph+yCadlLi6b/gyeXXKCgeyJA0jwD7KELfLeDiZBee+gpKSL/Bv8gmxhzzwAzbIs9WJx/3wvL/f32AiANLoGviCIhHx2nfNADL3nWdkfdJ71xk/Rv+W9iW4bPCOPjngPHzqFzUBuAP2Ql/hX9iEWbGcTvOCElWd43DciF+4XWR90ijIyv0f2k9974Mq1vMzvu16fnNH4x//9b04E1ReXB5jP5+lEUE+xs8k4HXfYbCQLzCFDBBjeQ+ABDMLoDo/vkKaH1LjBR2k9sHG2hMXnWnwnwNTTXzhSFt1rHnlOZ7H4PjfAp/fgTskZftaa++D5HZjzdxTYU60YHoytlxE4g8ln3Kh5yZaDC2d2qfd2BeOznrGCXToN0Pp+TGlK03nsFxcX6vs+MZTS9OwLZ5l9fVzZpGmGB8DE+vMzjIcbWjfCHpxwDYAXDg2wFoFlPFnYZZLrH44HFUP5FU4+gdg813bzmgyzg19AkDMMowzFkaGA5lMH5sGpl4J4/T6652uJA8eRtm07mfaFLjiTwrX4Gfd7yqSfBhk4f0CdZwncXrAf3AtZU0Ara+RZCUmTfoTTLBovfu/AAQN7mtEBRLhT57qsBWWX1NDj9HzNvBzSU+cEcugvZ2zc3NykoIkSUho7WV+AjoMKgBNr55mpl5cX3d7eJkcHkHawzXOxN/yc4IYSF/YM54dehBB0eXmp5+dntW2nth17f3a7XToUkrImgh13ovF8irGR1OWj74O6bjqOkxn8DsiQR+QMHUcGPcCGQPHn5jM+Kc2dNDYEYPltJafoBbLgQb6XskhKxB6ggqy7gyb2jAALu8KeIbt1XafM0fF4TBk51gOQ5QQJgTI2A3Ku67qUEUKeHHRjR7fbrcqyTCSjZ7awP/QOsAZMZXS9d583m810bMdJjo4tijyerA0odhYWmWHded5EamQjK++4wLOGbmNZF/oRnLV23OCEjO+3B/9ua0LXK8+mVQ1d16ntOpWz6WGvHjA4oUGJJJlOfu9AFzuEjoB9+Dllf47J3J9xv6wf10FHfD08MPHAAr+G3Djxipw5QejZBXTMswDIgmPEUzLI/SdrgXx5Vp01gbwAy/q9MU6W58QGMgaXV1EUaR/4TkoqfdokMsceqA/pEEAwmNtWL0nmdx58nMqJk71O5mGr/OX2jr1B33+pB/bhHGHymPaTIi4DuZR4OBuOIPA+B+EY8bSg+uZ0DIwRjoWNO2124vvcYfNyY3UaAKBkNJr5AWrSFOR7usyzGw6QiGKdTXUB8HIGgCqfxQhjiAAEKIQrAPfA2vV9nxpZicQ9mPF6bmk6Do21Y/2dgWdf+DuAXdIkU4ACA0rJNLkD9vsm2GGdPHjhGrvdLt2HO3Ffc2dUWCeCFQ+U3Hm4s8cguWF0JsZZS+TMr4dxRabquk6MSlFMnxNjGzRm5/h5ev6TciKckAcElIF5bXyeZ8rzcUywB0eekaF526/pwBB5Q4/9UDCyhqwZcncK/tEN9u6UcYNlA0RiPAHXp/vpATnMPffDOnjQTLmM16H6nnuQwb65nIUwjlVkPbk3gLvXtrp941WWZSotgOnDFiBXV1dXen5+Tr/jDyV7BCEvLy8KIR5Aib2sqvHMDdg0l1fff28oJksBYK3rOh0IyrWxI4Ab9oe9AXBQfgAwJsCDaaQcw20ve55lWTp0kHslCD5lT5FJ7qHrRpIkhNiPEJv2lwrBwNrwO2TbCZ5TmXCbQjAG4+zTgpDvBGqLb/ac8Qd9b5pGj4+PSQ4Aag5CuE8PDrlPzyjhq5ydhgHG97jNA1Swd4BIB5XIuPtyD05YP56Ln1HlUFXVJLPm/RysLf7T9QxG1sktrvvy8pKCTbdVIYSk7735J4J1fEdox3IgSmROx43neZ7KSSQpaByRiz+g78/3yUk5Z/NZcweSrBs2BzlmTTwgwRbt93vNq1maLOX2ajGfq1dIPsTBOc9J1otJTiGEVBIFXgKg4ovBPZDFBGheUul2HF/uRJzbd/TPyWRfBypjKFVyecY+EWzT/4svcn3zig/3MeiqEyLokmeXWHP3a47L/OesB/aF/7u+ZVksf/efE8SfBjvIOvfBPaJnKQDuepVGhHp2hwwx9+I4hvvBP7CuLr+OfbynxANfXqfE66e8/lTjbf1UQAdFeT7WgTm4x4jCTJ2CPDbNS3iI9E7BHYoPY8J3I6Cn4FuaGkV+x7PgrHwzcdx+HRyqNAY1Dmr5OZvkYMgVECFyMMffvRwFgWQ9T4Mxj+KdScFQOJDgO5xx98/w3c7yu+ATqDjb4hkm7gV5wDH6d7HnXvt8ygx7UOkBju+r368DcDfmbgRPWQ830m4wPPhkDxwk+B6xH76GV1dXEwDlysx3H4/NZIoGf++7XjOrlwSs5HmurCx1tlylIIPfc78ABQAsowVdTnnmsixTfTpribH27IDrpgeBOCSuKY39EsikGzb2BAPN/QAq+a7TQI1r4/wd1OFAWSPYFAfbfJ8bQuTGa8OdjYR1chbXwQBjFl1nQgjp5w7AuXd0gnXEucPaEZRTH+965CM6syxLp+U+Pj4mB8CahDAeSorcAiK4P0aNPj8/p1N2CQrQD4Csj9ZmnbHbZ2dnqQfAy0WY+uL21m24FCfNABa9wXY2m2m1ihPrcHTcH9kyQIHbuWjPgqQiMYYEmg5QANEe+AFckEGCOvwNP3cd4oVtYf+YROZlc+5LXBawYzc3N0neAcX0vwDekW0+j+6/vLzo8vJyEnwBvk7JE57JKwiQUWeb2S+3n+gmuoRfQU6wuzC1yCOBIfIMmINMQx5DGEvzIIJcZ9zO5XmeSp08q8azZVkm5XEC06nvbdtWeRjLf7ku9oT1Rp5Zu91+ry70aUoUe4U99ADF/Zx/R9d1qdoBXwDQ5t+nQBgb6qXSzfGoshhLWHl2SWq7cRQ5sspZFmSOsEmUz/kRBU7eIjvYAPasOQlyKGckOPax0k7qgCHYU7JGfJ9n7pBN7hscgQ4w2MWzD070OFCWxolS6DFyjGw4CQ0u4X6qqkqVFXz3crlMk7IcnJOlPh6PadLoKa714J7ndFnD3jiJcJqdwW7xea7Pujv56iQI8gTxzYGkpwE913Nyj3txDHt6Lx7ofdfrk0unfus3/+nEefrfMcJ+c2x43/eTYMEXGuEkJexOwIWBcyykEeDwXc4C4FSYw3x9fZ1A9ykrewqovs3x+B+PajHSXpoiTRu8MKzu7JyhdaPvYNmDIoSOTcUoAwIAWnyfg1uesel6qWu1Kit16lWHVn0vzcuZsr5X0/fqGKsaqSF1CkPj0bSE5vLyUpLSTHAYCZeB1MxsQDKCsXIwvIWOx3pi7Mbek6C6Hkui4kF9UlWxDqOTGA3LWMqAfCCbyBf764rCHpyWMrDfsHzcJzILMGTvcABRNsapZyH0w+9a1fXI9LpBni8WqptaVTWTQlDQmLrMs1yy7/MyIAJRniUCttXwTGOZ3GlplRsiZ0gdKDrIGhmNEaSMuh6b3NEVaRwEEe8jmzDCAINTWcXA4ZR5JsAIBAc6xzXcMTkzSGbAyzd5Rp99zr6/vIyNjtGZRrk6O1uraepkjLmujzeczcgQSFnGpLh+Yv8ISpCfWNo09nQ4KDk7OxucXKbN5jXZRnQKtvt4PCgEDZmMMQNAwMWp1Gdn8RA3DnOr6+OgT1VyhATHbdvq5eUlOsy+j3MZQ4jP2MdR0fP5XEVZxNGNGlm4shx6daqx2Ri9Qbf2+33ak6KI46jjGs1SsIidbts2jRzHnwASxkCyU98DtGZDQ/cyjZF2wIPNdBvg5zw40PMgzokpMmjoh5MvEGmAPnwen2UNnOhg33k/NklSChKdTOGz7vwd6PsfJ4n8+whcnY13RtMZXvc5yLP3ebBn+E3WyrMP6KiXk3r2Aj936mPxm07csW/cjwOvLox150U+TnsKISg3EMV7/ABAnht713VDWVI1rHPXR5lv2pQx2h/2E0KSe/JSMHw1foqyGidMkQn20ku4UoBaN2qHYI3zsdKaleP5SuwteIBhMmQ6PRPs/gHM40SeA1mICmQZe+5A1jMy2ChsM+CcPfcM6enwAvcj7If3WeCHAcuOBcBt+A30mnXmeb0xHZ/kJDX7B150YgXATuXCYrFQMwQTZVnqsD9ImbRYDJNNNTb5s0eSJv7wlJhzTOo+N4SgWVWpyPOUxeo7qyIwEpG9dMKdffWgh4DMAw3sJa/TbAd+ln0qikJ/8a/8r/Vdr0/OaDiLi4I74PWaM0AaNfU8iAMDZ5URuFPDxoNQ00nmwCNTNgZhornq3bt36vuY4oKVw2E4E+Hg32uk2SyAK5vIojuz5U7kNAhDwNk0wJjfs6elcVKsq2/qKXvi0S335ky1skxt3mvW91qrU6FemlcKIZM6qe6kl77TMQ/KQqYiKyXlCgNYLQchQzipyc2yLJ3Q6w6B9QBQuyEoihg0tG0EqExjKopSfR/Utt0AlCpL/+YD8AvKMhxDriwba16dSWSdWBv2EWPKs3DPbdumE0VhFpEFAhSCOW/QokQjy7LkQA+HcdrW4XBMJ4kyOAHwgLOq61pd2yoLUgvIDvE0UcAYe84z8HJnwPOMpXq9ynIMfnDoziCxvn7oEnrrGZ7RoUdgyO8jqNbgtMZAezq+ukz/9kDO9Rz5BSzBACH7ZD9gjWFN6QcCMHnKnD4BgimvS0Y/eY4Qgs7PL4Y9lKRMfS/NZgu17Vjq2fd9Kk+q61p13SjPC9V1O3mu6ERjMO0gFycTWe7Ys9P3QcfjIclECNLj45M+fvyoH/zgB7q8vBpYs3WasjLK5ioBm6IY5YCSSMDZdrsbfkapSDXIY6G6bsS5K00Tg4PLy6uoR3mhsor7V85myUlkWaam7ZQVA/gfZAfHBEmwXFaDM82dmsq4AAEAAElEQVSV50Va57j+I0GDLBAIsc9e5+w+hj2Lf6QsK8QZNZEpHzNs6DyBAHKEA/eg1gMKQKgTZtwD/uS0/8T7zZBf9Oc06OczAHCfXONMIUAdcIbeA9wAUsiB2wjIB77H/TZ9TKfEijPj7ivRGWdg/Z6caZZG8oWAhGCE7/DSEfbViTtn57km9+GlLV5BsFwu1dQDmVllKvJI0iwGoIweeuYEG+fAEQDbbLc67GKmaL1ea7PZxGdvW+1CkPIxew1I9fvmZ2AJ5A7igPc5WG+aJo0H9mx+34xVCOw5Mqkwlts6VoCchehhb/GRyDGy5JkXD0Dw56e22QkjJlIR2HhQz/ecBiPcp7/HM1qsIY3m4B7kn/eEELTdblPjPnrg+IN7J8BB9hzEu5whBz64wIlUfE0Iw1lcfVAWpHo4Z67rOoWu02xWqRme14k7D0i9fzWEbw4R4fvT/vCdsuqYTAqZJqX6brckpdKzU+Ic+fSM/On6oGvIt9thJya+6/XJgQbGBKXE2XvDHALBzSNwAApv+OOaznqxuc7gNM04zcQZckCjAzHS7iEEffXVVwnQ4Lhg4U8j1REgHiaGl+/zwMijw1MDiTPzxWfTT5kzdwwIbp7nyTAi9CGMY9kQdBjuU0ZeGoER9zQ/tgr3T3qTzXVRzJSXQcVypeNmpz9ojlrfXqjtjprPFypCrmPXaTYvtShLhW6ss+S7WUuyUAR/AF/fb3fGcT+/2SjsGRwUzw0Tz+RB1ZghG50Q3+GyQFYJh833+nCBuq5TyZEbML8Xgo08z1PTpDs/xuHt9/s0apM1oSyBgODUwPEzSkWcyfw2hXf9YM2o5Y/3PI515f0AcjdqyCXyhkHmvhy0ZNn0DJDT7AJrw5qWZTnU3u4mgMlllefBDkBMrNfr9Cw4LZyZB7vU+i6XyzTaFJ1cr9eJjfO0vgcbDvS6rktZUPabXhfYOJ+SN58vxEGJXIs1lirV9TGxk9jD+OzlRE8pI9putyn1fnNzk9aZVDfO3u0M+1RV4wQ0J1ui7R37pwA4TN0DiGZZpoeHB11cXIx2sKknfRXOkBH8YePJVDR1oyIfp8G8vr6m4MfLl5xBx9lh76ZBy3iuBgE/pR+UdfA5B9bSeGI3wBK/gp4DonCaDuKwGdwrz+rOFXvMHwfxp46XIJVn4WcOOty34GN9fyDynp6e0nUcGGL7PPsNg+zXwIa6vvq+oIcONnw6DmvtYAkZQfeReV480+l39f1YUumZJOTKyQ7W3nuMALysAfuLb8TeYPOQM9cdromd4SwU9A3Az3cRLNTtKFfcLwEd9+pZHQAZsoA9coKI+0FX0nd1vRaz6fk87kPYCw+W2AvkBBvPkAYnQ5Hn08y/2xT+jnyzP03TTLLO6InjOfacNfdAGhnwTBn/5z6wVY4NvdTeS08hKXhu1hObTg8ZMoesu0112+y2wOUUXFOWpZTHa/g0zq7rVM1n6i1QYM39O/ku/jhWcXLAy834jOsdfoF15/+eJXK7y799EInbJd93rgMenZksssaf8vrk0qnf/se/9Y0gAuX1m/W0IAvs5xBMWe7xbAgUCEPlC+tG2I0LRqLv+4nCErk6sELRvSbQwY4zLv5v32jP2LjzREBO03/cI4IuTZvUsyxLjtPrZllbJhEw+xoh9NSfR+MuSCHECQXl/lV/8N/+pu7/6e/pts80r2Y6u7rU5dt36v/8n9Piz/xQr2q1WKwUuqBdfdT84lyrWaXXofkUx8X+IpQeXCD4rDnriiGL9zxG056eY39dcJED9o+98UBDGhtDuTf2FEPBfWEInclyucNRwWJhSLkf9tjrZEcHW6qqRmPJM7rcOjDHkeAwCLzPzs6S4cV4OmDmfjw49vGIAE93JM7geRkGjomAFQOJDLPmcQ+mgRKy4LqGAZ9mMbqJczpt8kYnWAeYLWTM7z3PY6+D/47roEPIm4Mufs7eIw/jvPAslQeQVh8d5pg5JCs1lgicpX+7zsVSprg+8eT4wyTAmc+Xen19TT0P1ANzDQBNlKtiArLLMp62e3l5qa7rdH5+riwL6QAuSJyiKAZ5GW01stv3vS4vL5MOIBM4/qqq1IYRjKGDfL8zsd4A3HedumY8w8DLarh/B+duEwFi2DYHwYAMtxWspTOOngUGrKMvXAOggR31xn4cL8AMMAEjSaB6OgIW/aEszIMy9oPAx8s/nGhyUOjMsQc47tu4vtt7L8Nw+XE943MOHrArADf3j7zHM8KAPff32DQn0vhOnt1lCfmI5W6xt2yz2aiqqmQDkRPKoNq2TTXxDpAAWWSk8VWM5eXnqRTJsmSbzSbpJmXB3qPgRE9i4UPMaHiGHBlm/Zwlxv77ujkYPwWyHmD1fa9cmWbVOIHRA4GQxdOmIarYM+yVk1Ue3Dn+wi9lWZamgnH/nkGCxGUvPDAiyGKN3R6CnVgjP8MB/IOcYn8c1HqGgWAHnd7tdhN/4QR1245Tn1g7AlsCK67vftEDd7CPpFQ25SB7PpspC+NBzTxz0zQqZ5WOg5ziG5Er31/8Bz4euQF/uOxxffY43UtRqO86ZZpOlHIc4vbFG+dP5RD5Y51c1z2wcV3/jb/2l/Rdrz9V6RQC4CPIWJTkpNppU7ZHlSww10OYPQV5+sA4JZQMIDGbzbTdbtO1ECLfEM8AuBK6kfYRvDiMU8OAc/DIGaeGoaU230EgDDjOyqNIXyecHhvHGrPZrvBE2QiqO0/SwDzb/nDQtpzp/myt5ld/pPeHg7LFTL/6v/wPdPbrv642y3VsG3VF0LGulYdMeZbreDioPeyVnTDPXssOk85++Lp6NgAA1PejcXHZcMZjNpvpV3/1V/Xll1/q4eFhErW73KCscbpSkSZXIEeAZgwgztKneCVDPgBnb1I+HQqA0fHPAjKi4o/X4vMYMeSce3fjy/UoGXGmfrVa6fr6WqvVSg8PD+m8BM/GsDcOuHyNcWg8P+voJXieXudeCYRgaEIYm0rdwZIB5N6pGfdA8DT4A7A6k8W6+EnVnAHhLCBBFfLPzwlexjK2w6RMxu0KNgobhu1wQAX4OBx2Sd8ofaMW/3CYMo/sa9PEE5g5nwBdqKpK2+1Ox2MzGUXI80PIwKq6bjDeGYdVlrGJPQL0Jk0EdLLmlAF21tlHrvIzbK6yTCGb1gtjp3mhU8jc8XiU+qGG+CRYAEw6MVTXdcpeSbIerdF2O0FE8IXO+JpJmtTCO9DARnMNL+vBwTuZ4MGCkwOUpGVZNhlV6QG6Z0X4PGuBzBFUelaQ95EpdWDqz8/fnZFkPVkDt0/smfdyAZzQd+wjOuy+qO/7CaHgwYlnHJwoZE9O9wFguFgsJgf7IcOz2SydB0HwyvpSLomcOqDt+ziOmXHITLg6Ho96fn5ONgef5KXRlLCyNsjfaTaLn+Frq1ml3AgsbIyXnSJn2Dhf11N85ESF60LSL5NRZBN/1w4N69vtNuEHTqenb8vxk9sU1wP8jQebfD/ZNO9b9c+5v8eOAJxDCJPJedg8x3i+F05YI3tOGDqB6SQG3+t74PLswxZ8j0dybiz39oCM9zk+9XXsuzgd0gN+sEPbdd/QGccBTmSAZ3k+z/RBvv5J5Hh8hqDQB2X5GOCdBkzoKnYDG+G4hvXhvk9titsk34tPeX1yRuMf/jf//cTQOVOGwLAxAAF+jmHB4MJmYEgQbD4/n88TS+cRuRsEaWQR3Mk4qPfPca9kDzx97OVb3AvghedDuRy8wcYQ6boTcCab70A5XNBQIp6Le0U4qan1FKADX+7ZBYayprbt1GWVymOns65T0x61L4O0mCsLmcq6VpgVOhZSaIO63VHzxVLVeqWurhX60WGw356RoE/DnYxnOZCDkaWfZnZcdgBaP/rRj1SWhf7oj/44ATUHCC4Ds9no2HG4OGVnftiDU0ftRoD98yDJg10ct9clsh/ROYwg3gNN2FxKfjwbyDPhSJwRYu2appkwuhgkvodAnTWpqukkCIJB1tF149RweT0uehlPLZ6CFRwDjD6MsTNkMYXdTeQX0LlarbTdblMQ7sykB0kADJwn6wG4IyNA0JNYRwsgZ7N4QBfgGv3o+14XFxeq63byWXfGIXzzvA5+13XjyFQcU5TTXPHU6nhyLnsUAetCdd2kdXh5eZGk1M9Dwyj3i71CNwik3LlmmdS2TVozSgfi945s8mlgAehyomCz2ej84kJd6NP3M1bWg1ovKUSGFaTFbDaRS+4HWw3w9h4ZWDPPdGMXvfcBPXX94oUL47qUK3rmzDNVzvrzO2ks4YOdJDBGDp3gcdDlARClk8gF601pxXTwwHgv9B65jWUd6QshIDg/P5+QYe7jfE2czeTvDqB4scbYSM+oOFjx5+F7fb+dVXcgyv8BbE9PT1qv12ltHfChn6w9e0o20wcYcMaGZzUASKdZKd9f7C1/wCboAuyyNy6n62RSUY1NtO7zeC+EALaRF7+HmGH4ATYSmeF6RVEoVyaFsQ/1+fl5rBDIx/KhkdAbS4ucXMCeu19kXdAtL4N3IoY1wkYB8D0op5ndz+lgL/i8y/Wp/LKe6GnbxiEW6A6YzHWQIJr1RB632+2E4Pn/0/Znv5IlW34mtmwPPpwpIjLz3roAQRT50HwhIFLqiURLFATor9YDBXQJIhtodgOUAL4VCFwQvKzKzIgzu/ue9GD+mX17R1RlXIByIPPE8eO+t9myNfzWby2zjR6bpHSMJ6lGRw2yu64rBATyKsfJN01+zknzdQt7pBSX8esqoHGl9dEEkBM2JwroILKFlJznOWJeIjZYgnVyYmc7MDbFv9lXbDG3x2Nc/D1PBv+zHtjHC4GiGCglk7AjtTI7ScG5mHkjuNhBsggwxEzO1Q6AlAEeyoKiodAPDw+r3xkXzNU8zyUoWKD8h8BxGCiwHStjtON3gsQiepOoky2MhvnBdHOajF9mLGALI6KyXWkXaRhjHt5j7paIQxdNdNGPEfMyxbhrY+ya6KaI/dRE23bxPg4xj0McDpVNcMvadpOvldcgeM08pliWKOvrQMb3MRDmgry938Dsc0r5ZCoDZpgMWBXkjk6wpn6QFcZPsMPReX5unbJesJE3b2ivJWQcHfoP6MUBEFRdHUSPkRlyQjdTSvH29lZaAUj23PY0TWMcj4dyAokrFlxvOxd00IGJOWf9q5UHA06TAK40sDYQdQA/2MrL5VLm7QeFYRu0i9l+sFGCw/Pzc/nbNE3l6dCAOW/gZ3yABxi/zHLnE1U4mnOappKcvb29rOaIzY5jPkUtpVQSyJpctzFNY1lbEsv9fh/7/SHe3+uJbbQ5ARwM0AEiBEf0GnKFxOJ0eo9pqrqKXuZE8D12u32p/BgYU2F4e3srFZOiA+26Wu0EAzkgV2xzv9vFcF63/Rg8oX+uTPACeKB7rmJY9vhtruWKJXpgP0K/vfUWf4JfdT84Ok4cAPzYZiJqYLZf9P4PrretEBjwAcp4OX6Y2cXn8X0nNU7A0Hu3DRMLABDYDr9fLpfV8fDI22ttMIl/ZHwQDFvA5CqREznHSqpw2A+6a3sjUYWtJwkBzKMPth/+jpy2TDYyIj7CIDPG5+fn+PjxY6kumuBK6dqq1NWnybNGdDSQNBiIudLl5No2smXVSfCH8yXa672oDEZc42jjAztS8a3M36CTyivjhZhkPbYkF3ZvUoN/cz18E/HldDqVtmODe+spNsC1SPidBFje7khg7PyE7DWxuyx1vwjfJR7YhvE7yJ4xcSSwscu2IlTWbV5ivvoUqkfF/iMimlqxso8zqYXMkYXtnPEbCyIr4iTXb1OKcagHAnAdV/XxLVzLrXXcc9siHxErzOP740//qz+wD+NxiYogaueC0jMoO0aDYoz47e3tq0XcZk44TQceBALLy/1xgASLbCgpLpch3t9P1xaI0xUMIbD3Ygg+uaXrKsv2LaXHAVuBMFa34VQmdF25casPoN7JlrN9Mnjed5BlHfjuOI7R9X2MaYkhpoi+i9Q1cZmGaK9H3B72h4g2xTROMVzGaCLLKeY5+t0uOJoVmTLnvDYRp1N9yBJH0GbFXJ9bviyVKbMDsiPi2i4TV2BXN/gBurPsp+A0Kk6wOp3O12SlniRmJjTLbI7dbl/WeBynwp5dLjBVbTRNdZBZf+rpHGtWtZYRuQ6OmwSBNb65uSltQQDVw+EQNzc3RcY5mTupVaaN8zmz8PmBX7elkkGAqmxRTVgACzg5qmqASsaYA8McXQcooz1uXAEltygRFDjxA1nQxpeTiLcrCMtzOR6Z+xhdl09o6vv6gC8CMHaNA8wy6K66mOJ8vpTELifh9bx72F/aKF5eXuLXX3+Njx8/FoBfgf8+Xl7eStsX7GBOIPtomrsyb1qnSBD2+7qfiwCFzGH1vnx5jPv7+8inMfXx+cuXSKnJfd7LEg8fPsT5co6bm9t4e30tzBmMLskFiWVElL5kxrpERLfbxa7fRdu1ka56usQSbd/HzbXnnfnN8xypbWKZ5xjnvGlxmue4DNfW07TePEzSY6BkgE3yWNi4ps1tA7FEEymm+dpy2l3bXWKJpmvzcw8iHz/KmLctVNguPm3L9hEcsS8D/C0pwXeyXq/tw0maCSv0CbbR93RMKsG+rftPDJjsM7gWNmnCihgRUU9u5Ho8Md1zoK3EyRv6415wdJeXP8/zVVwFcCxak0W17YRKBKB/2x5dSZhl5evxgQBB4hokAfZHmyLVbEC9H9aGDTghxP8g9/PlHOdrUtc2WZeato2mbaNPKdp5jn6/i/Hq6+4fHqLp2khNE8fbbNO7ri96nFKKeZwitRFNpEhNirZpI+Yl2q5uPHd1Ft/LCVbgk7Im8xKX0zmfQphSNF0Try8vMQ5jTuCH+swOJ4zTVI9PJX5SeUB/vCZ8zwQtNoMusw+G9THJRzKBDmEnPngAn2x8iP5ANmGLyIlru7tlm3QSx4iP8zwXf2m8iQwgDLFxP3yXdWFe6Cq+BTxb4vE0RZOamJcrlr2SFLEska7JnW2+ba+nQS0R47xEalOkiGibJqZximmpfowxb0lp1nobE/k8fgc/Pc+1zdIVGWSNbzG2Qid8T2zXJJn9oYl+J0+/9fqz92iY+YmIUs4nGPFZBoUTYMIALwTCIvG9bdsKrKw3uDl4kFE783Mg4dr53/kY1ctlWDmnpsEZZMCVj2VMsSzrzVMEalc/mBcGgUKY6TfjYxbGbDaAmySF7/N55Oz78DkewEVwsJK1TRMpmpjniPFtjD5dz/GOMd7er+C9aWKOJgOQJkWzNDFPc5zPl2KkyxIlqGWg2MVuV5mOt7f3IgvkvCwRbRsxjlO8vb0VAIZM0BcbAbrDXNA5DM5JCclFRG1D4OhVgk6WWRtNA4PDKVdd+XxuN0qRj86tiXJ2hLvr+uX/0Ff0PTuX9d4iniBLexGOz07DG5uHYSgP4+I6bZuPqs1J1qk4kfv7u9jvj0VPhmGIu7u7eHx8jN1uV548TEvRw8PDikl01cfM5bJUvcsADQdS+7DpMUcnkS/JsFnOfP0s52ma4v39FKfTuYCHceSEq3zUa0r1VDIHZoJetn90P8Xt7Z02My+x23WlV5k9DrR2caKSK6k40E+fPl31921lW9kW65nnt7e3JYk8Hm/icKinXRFQ8VHPzy9XwDFF07Tx6dNDZm77Ppq2jcPNsQSIm/425mWJ27u7SFF17+Xlpeg9CThjBIS1bRtLpNgfch902d+Rsi7fX9d+fzzEkuJ6LGcG+W3fxRIR0zzH+1m+pa1g2+1PtlGDSVebx2mKOXKv8EXVjdP5HM1VHyKlGEZtOr4CN+7FnPENVAIBFgYbEDl81yyy/agrEU4u0FvvdTD7zlhIrEg20MdtdYEA7+9jKySszKvfABSDecYPIRAR5fhQYh4nODpuuArkXn9iLveizcnVk/P5XPwIex4MULYVWmx/HMd4fn4uyb19C/sx0BHiOPKA1aaiVsmSuo4GplzLlSdkjA1juxERXd9FpBS7/T7mZYnzqT607vXL5zKmpmlimMZoujb6/W51tHlK6arTTfS7XaSImMdaQYspItol+q6L1DTRKqlFvyBmSfiscymlSEvEMs+xzHO0XRc3h/wsnDZVNj2iHnqA3XVdfc4Tfpu4SaLJ+pvZZuxgOVdEfHhFjed1vdB5gLzbekkWvReJa/hAG2Kc96yQXJhYAv9h65Au2C++kf0gjIuX7Z974uPRQ4heYhfYrtjGPMc414RumqaIeYlxqAkVHScm10lM9lfftczXWNtGjMLH6KsPGLL/dRKCDSJzZJJSiliqnrBOlWSvG7jRHeNS4y6ve427644TE91OkP6+13cnGigFgN4LhxH57xHr0hA/XX5DgVwJsOKbdeWa2zYA/0QwJARmWnHkBIstmI+I8jAjVyKG4bxi8ZgvbVnc1wENxfH+AkrTKAfzNVuDE3GQMjtnxpsghLN3IPF1c7Uhyxq2AvCdUm2D81ycnCF31taMBZ9zSRaFpd/cT15mnbZsAokXf0c2MB5m/txvzbh4UY43IwCDiHExXxs3CRD3suxdVn14uI+2bePLly+lvzafXtFHSu2qfQj9paSK0TMXZHN/fx8PDw/x66+/Bs98ycG6iQ8fHuLp6emrE23GcYjf//4v4vPnz0V/cbic8vTp06fo+76c3W5dxKEOw/DVA5G2yZ836uG82LRt9pQKHvbXNOuHNwFYqUBywgnvY3dUbxzIcOBt25SKZEQNbHm8Wefu7u5KkkHPO7pK9YXvXC6XeHi4+YrMqA66HvtHkMsM8E3xXQRI5ptSKn3jJDiA5Lbvouvr05L52+l0itRkwA0ARTboktlRxjQMQ9zf38cSS3z+/Dn/e1lWrCT+pjJf6/0F6IEBNt/Dx0A2IDv+hvwZE7q3LPUJ5fZ1VI4AC/jKZZrL2Pl+Tbiz/d7f3xcf5CSI3nDk4SdOE3ewZeJC27ZfPbDPwROf6liEXby8vBR9NWPq/UYmFfgMvtPJPT5rm/w6biFH1q7v++JT+Q7VIOyLuaNnyJRNxAZlyI3vkSg4GcHX3d7elgoIeMBMOPPlJ+tkuXLvrqv9806ykDPJFHMlvpmFByTidww8u66LZV5imNf7c/gbPs3zdheCk+hclb0ejb/fl75873nLr9o2bH+LrkXUNkF05fq1Ms/39/dVQgjbjkx52GvTZFKw2JAImq7ryj4v1hOZMW8/W4x5uFURu2WDPsRdRH0uA/LHrrynCl3GNhzfOWEMeW/bh/EPTuDBTybLWCe3/JkEpuJqXUbPXKFzEpFJsfeKK+NauUq1NYu2NtaR2EVSSSKJ/7G/3u12MY9DTHPd4+RDA9B/7MYEP5iH8dtvdc3adziOm8DYkrm8xxj5nfUntllvHVv+/1LRYAAGt23bFiaBBbPio0xMestcAP4sVARlxeA7ZlZwOhG1jwwHkVJtV6nCbL4Z+FLKR7uVRevqfomm+fp0EYLylkVjfDh8gBaO32dVY1g4WozTzhLjiIgCGAGGWyaMn4yP6zEGg/M8zyiVHIMHBwtkD/PCmhGgAOEvLy+rtXq9toHs9/tyKoaZKoNODGBbueC+2zKoWYqSzUdtX0DeyML65qoX8oeJQDbuWcZ5ZYcwx+PjY7nO+qSfzNb6VCQz0S8vLytwB0NuoEzl4ePHj9c9CqcCDtCPChwyW/j29lbYsvv7+/gv/+W/xG6XN3Azzz/96U9lzVgvvlMYtZTi9fWtBCmctQMPcmTteDlZMzCjZ912jIPC1iKibLxk3waVHD5P+0U+laY+M8RJaV7XWNmTK6zWMcafx5qf+O1Tv7xOTZOPOjYI/fTpU+QnYU+lPcvtBLBhyIMnXDMW9s50Xbd68Ns8TuUYS4L309NT0fctMUJgent/i+PxGB8/fizyt71hZ2a4DCgBC/h4M/3MA/BldtO+gr8DULGdw+FQYgO64DUhedt19WFQ2/gAMIK13Lb00LJFQsxGTcbHd2gngQCIWFchsX+TEvg4/sY1DWSIAX5gGf6bRN+bc9FZPrcsywp4ed7ouFlw4qznxjrf3t6W75odZs0BcI7L9u0GXP7cfr9fVUbRQwgKEkuvhYki+xknZ1R5+KzBCwmRQS1jRAe8d4Wf+BvAYH9d4/f39/jw4cMqsTAhyjowT/sSJ/qXyyXatGbFC2aY51iiVhbc2859uTd6luVZH4LoSopZaAPLEoM3p8PxffSBMVhXibPb5+Gge05G8f2VBFo/98uJ1rIspcWTyoWTF5PB6AT2y/U+fvxYbI4xMF9iMrHXhOR2Mz36aXIYv8bnkC3zRkZ8L+K677RpIy11jw9r5oSUJAiZ4BPwAwbu+bNjpKaS9SQ7JpUYG3N0t1DtQqgVjLarByJZJzhQx3tZTH6g/9zHSQkvPmfiy9XZ73l992bw/+f/41+vHJ+drFkKD8jMDQbpEjNgmL9vA52zJRTCxsYio4goNUYNQ5CdYVoFERbC4Mjj5NW2Tex2a5DOHK2gBihbxsJshtk4evU9JhbWTKmv7yqHAxPXcYb+re89Pz8rQ64GAOjGoSNLX4P/bm9vy0Y5mAzWessYWZYGKDhGHAPGhALbWBifExUCCtdz8oljYYzMESfAfZAL38MpwIqjr5Qqx/FSgKDLtNmpZhB1f39fTslwWdllVrdh4JDZhAb4PBz2EbEUXV6WpZTe+34Xb2/vqwdMNU1z3VjZRtuuH0j34cOHsi7ojtvrskNan9rFvLm+K0QEJGzU+mtmC7BppuSXX34pLQteP1ikvDciFYBjvxDRrBywA+Q8TzEMtcIH0Gez6eWST3MiuGaZRvCUea6Hnmb7qEdHYwv4lJTWG+1YW57J4TljG8M4lg2C2CJr4k2fPEuAuTuwutweEXG4OcZeT7Yn6YEcgS2E+SeRx1eZvYWd41q0Khng0dIFwHRFwJUT9JoEku8bPND/3rXrfQ3ooP2oK+mssQOtCZrj8Vhay5x4kmATEwC7JObsFaQSxrUj4npCWZ4L/o6xOg5S3TVxxdzcboVeEcMMMCBY8Bk+MOHt7a1UFFgHKqSAQVc6iD+ukKELZkgNrAGiLy8vcTgcVtUsV5LtDwzaTVBhT+iGARJJhIExuu2xOA5V0rASmgaxjhcppYgmn0qxPRXP8d8xhX/zk3UoSXCkWKZpNQ/0eYklLtJ/+0auaX3AD/dt7vdnfE40jAlYR9ag3+8C8Obk3AktsZB7+vr4PXwl9uG4xbqhVyZNWTcTaMaF6Aj3xaYZF5939Wjrn7YYClv2++5S4H78h81xb+M87mviwslYSim6totpqCdioV/ohAkYZMnL5LeTkLfrfkvm7PWyj+eajJV1RkboWEREG+tTxFg76yfvkcxZb7jPdi2xA59w5WSkaZr45//9P4vfen13ovFv/uf/dzEMgiMT4CSXbUbEoFlIGzBG45J2xLq0aMEhHIIMTmhb0UCYbuMApGwdlhcXpbYTzAzcUIDb1gExJm/49vwtA/rGmSMMIGwP48fY7Zxw2LClPAE1ombZtNeYLSH5I6t11p7HUk9dYFyszTAMhfXwGpAIuM1oywA54bQscD5OOlFwgDHyjKgVMgd21tMsccS6fYvWBnTB6+4+SnT47e2tgCHvyWFNsoNJ8fr6smL9CcB53buiDzCoBmUAZwACn8PJwPaSrB2PhxiGWlK1M0upibe3etwlY85Pfe5iWeayR4N5oCvM+3w+x+vra2GgUqrHT6I3PgIVO0afSIDcysh6sNYuV7N2gKbdLh/5e3d3V+6RE4tcnUC/kHd2kLnlj/e8GXCaKjPrdgs226O7yIF9KPlggDwWnn+BHA6H3YpxwyZ+/fVz9H3dPAi4JaiQ2JkBWpYlTudz9Pv1k5bRxX3fx8vzS2GfcO783O7ZgBiYljmGMfen89TvrV0iR7OAyBAfs2X83L5jX4nu+AjZLaiglce278Bo4LvM+WhGA1ETQdjlFlzyb9YYP7bth+d6XMukDPZOK2BNMKs80E1XmgxobX+8ByvMWnFNmFe3A9oXcR0ATNfl9jta8QyGh2GI29vbVZsJesja2mezFrC8rop9+fJlFaMjahXbts2aogvYt0EQ32fdXImAhDDrvSXniA/4Sq6PHbjKsCUMIYoyYZHv/X6psRCChPugF6yVYx06zprTItqkJhZV15n7MAwxjGMsKco6b5NI1ph/E6sPu110bX0uE4AWvfBaM9eUUsyp6g+JiatnrvgjN9bJtkuMNUnkRAedZJ22yQCxDPLMSTOfQSfxD8Rs+wQTsZCZjscF/HdfH9vqKuaWkDRz73Yh26wTH2Q+z3P0XRfLVB/g6MTUyYsxBmtif+UxTssS4/VkQhOozAn/ZP3H1+A3sN+yDmPdCE4lCT3zOhP/GBt64TjgJORbsWSrR//tv/g/xW+9vrt1ymVYDJmb4UQJ+rQPsaje0AU7GlHZou1CEQy4NgLjqZ3OAM2QcQ2Eg1CzU1k/IwEl9EI456qbYKqC05dK/x2tLF4YxoQTYvG4Ztd1ZT8LYNgJEXJkHlybVh16hCOiOGwbgLNZDMJKa9YrolkpkRMvXjiAbeBy2ZGA6tI76+ffKbU7SXTGT1XBQdjjwxi2DAHj4G8GfX5gFc4Q+eDoCCTomYMHQXkYcvDjCbI4PFjgZcn68euvvxY20G1usPbMgcTI5W5kmRPKFJdLlsWXL18iIm8IPZ1OcXt7VyogzIV7PD09RdNUsEhyyjpERAH7nESUQVgFOX6IpQOKHSOgIyLKPLl2AZEbtjEiCgh3Qoae5GsswZO1Yc5gfTiEAL1mbbMezbHb9YXJZu0eHh7KtXH62FC2qfx9jgmubU1vcT6/r2y5bXOrT07ku8J8j2PeuP709FQYZ88fQHE8HqPbrVti0IXz6RQ//vhj6Z3Gd5EkOKFjf0/f9zFO2Yfe3t6uKrqQEd60O89zGRsB2ECNJJ22KpI02r2YL34S4A6jbgC1Dbj4Mt87A6Mh+q5bBS9O+cLGnfi72ms/j8/AvyEns7nEiOPxGPv9vrTNEW+4JuMkBmzHbZY4ola32b9kEgO54vfMLJv5NaMPIE6pnjToVhj8Bq1K6DdxEft0Gye+h7UATDsmujLlk6SQMUkcPsNzwhczdq7hU8lcwfC9IqIkhk4E8MG0mOLrTZxsSUrWiLG6MoL97na74peppCI3YjynADLG+/v7LN9IMU5TOdSC6/L91FZbQk5OfpAJoO14PEabcsKNvqADjjPEfD4zTVOkto0lvvaxjs1gLuzBPhkdNolkfGZ7IHEwGUs1wJVt1gc7NDBHvsuyFDKFmEIcYQ09Bnd9oL9b/0V8Q5+MC43PmJOrefYRToT4TvrGfRkbY4eMc+eC7RHZnc/nSG1NbhxjtySM94HxQvZu0crjrIkS3/ccKg5ePxPHa2qfxWeNwY3Z+Cz+6bde351onM9DpIRwrk8jXNi0V1twvCM+K3MXKeUTEvL38slOBGiU2OUqKy5OwwHADtqGCbgwg1EDXxPLwmLO0bZdjOMSw3AJ71UoDkOCxUniXGFAzVYYVDMegjY9h+5VjchndgOKDXBRSLNLKAOOe9tm9Pb2VioayIdECFALsLS8OFnqqsbRdVQ38u99vz4CMq9tbf2xEdu4cKLIECNlLt4/A9hC7ugSzImrFS5z4tT6Pp/Sgz6xLi57k8zRmjLPczw/PxcnA1DMx5Fe4suXL/HTTz+tTpOYpjHu7x/ieDzG09NzvL29xuUyZFtI+RkWqW3jMg5x93Aft/f3MVwukWINgOwICNIkYvT8z0tui2naNu4/PMTz83M8v77Gly+fY1lSfPjwoTjfL1++FH3tuj76nnP62Z+zq8B0HK/6vsR+f4zb2/YKhA7FKX+LhcEGzVoSfMy22lkaODnAmT2+vb0tAQr7ORx40m4+engcT7Hb9aWKwFGyfd+Xh+JlZnmI3Y79BvU0q+xPTrHfH6Jp0vX5Ers4nS5fgSjrKmAp+6AhpukUTVPPkQf4Ho/HeHx8jNvb269OH+Go7Jubm3h7f4vT5VwcNPt0sFt8CskRtm/2mWolbWDzUp9CTdB/fn5ePV8FkOMg63YDA4J5nvODn86XfBrONMWu6+P97S2WaY6u38XxNlehpmGMi9jmt7e3iG6JKSKGqCd3pZQiLUsMl0v0XRd9m/c0vb++xdPTUyyycc7iR7fRFVdEImIFRKh4cZACNsU6obvEpW0Vgs+TML++vpb2SfTXraAEYbc5sYb4pW2lAXCM3RBP/BwJ/Cb3MBFgm+MeVG4X6QD2yfXw8wAyt4tsx0R8MxDhJ0mm2+CQzTbpozXNcQs/vG1fJeHBbgxk3MHgxNEgfJ7zqWmxXDfWxxJNtCVuozfIFGC09VUAYN7znh53Chz2h+iaZkWAlLjY97GkDAKfnp5WJCR+khhlfDJPcwzjEG3XRhP5VLhIKeZliWnOyQ3g3QlHxLoViWuCPYwp5nle6QF6iTydyDmZIWm0LeKnnUCY/GV+1i10k3VGrr4escbko4GvKw4G+fgHd0h4XK4uUDlgvq6kbhOsPI45OhEx/hvjxJ7wL+fzOfIRgk3EPEfbtbGkuB7t3cUSS3Sq9LNWjhtuP/acuC+/g3HmZYppgcSY81G6c8WT7phAjk4yrKfYBvOyT0KWJoG+5/VnPBn8fy4TNZDPTj6DrGVZipMBOA7Dut+MCWUHXc8k5zM4VoIBzna7qYlFx2lty9QIx46J79OjynWOx9uS4BhwZHbjsnLuOG7G8fDwoOpHUz6H8eC8ScB4qisJlIOJFZi2FsbuazE/b9Y1I07WDSizE4jIjvDl5aWcJkIrC4rGWhHEzODlceYWFtaRNgQAFGCVvxsg2Fh5oUcuGbvKwfgdDF2pMGgg+fA50DCNsN3bRBS2+fPnz4Xp59rTNJU1YnyWyeVyiXGaIrW1Qsacm6bJ52en5rqZ+bxKlAmeBKCI2oZzGS7lvO3Hx8f48uVL/P73v8/HrHa7mK5HguIYaK+BZeQezNV7V9wWA8toO+Ez2CMMs/tJDYzcP458vDkcJsuf599mMLGjbfLuJB6Z4wg5KQ77Rec4dYU1NCPv1h4ACcnAzz//HD/99FMBFszXThm5Y8v07bvlyawQc14i4jzU1sjawjWVJ7t63pAF7+/vZR+BW0T7vo+m62Kasy786U9/ik+fPq30D/mySRqfiJ/zszvGMT/v4ubaEoiPcRCyn3NVi+vSsufWMfuPiIgvX74UufIMmV9++aVUPD1HGGAzoBA4ThLYD2ISg/kCLmy7yNkJuO0QsMS9SQTxydwL3weoiYiyptgL13aVGR0xuGJcfg7Czc1NOfnHBzSYoWTPBv6Ee7AusPfcgxgAEHcSZ+CKjmztMWJ9Kg7fRV+pvkOs8b7JPGyK9YFsKqxv+vphwHyW5Jh5DnN96B7Xxc9bz/EbVAepXvDiutsTioirTdPEMi/RqkrAnOZ5jrbvolGVAJ/lz+JHDIodA/kOSWgTKdqr/RhoRkRMyxzTXB+ci6928mCfuG1xAvwjW48ZEtOsNok7/pox4V+RH/GC7/F5E22suWXo5MPjsv/gd65hPMQ6OVFBl627TkKcaLCOzDUiVqdOsV7IurRCTbXVmLG0XRfn4Wsyw/rteRqToMOMy2uBDkDuMQ+PGTsuFZVlvc8D/eP6Jg3cfmf8yX2xfdv9v/i//I/xW6/vrmiwWAyYBc6KVMEAxwvi+JumW51TXB1dH8syF3BihTaoJ6BZ0ARcJk+VAadu42ZxrfQIEcbf7AZzYhFg2ugDNvAgsDpg8F0W3OwSAZ95MQ9v5ObaVi6Ch4Mmc0NRKI3zWQIbbQ8uKfIZ98ui7KxPRJTEa7fbrTYgdt0udrv9yvHZ8RBUvO8BGSCXlFIxONbo5eWlOEQCvdtw+Mm9aktN3ZTLCU8EOwN5HnhlRgP5wUibNeakhi0TgJMu4OQ6Bhw363pzcxNNSnHY1VONrLc4OkAzgHQYhjjeHGOa6zFyd3d35QQkOyhagC6XS0mk7LzRGzsNnIXLvSml8lwIM1usI7rjRBDnyBq5dY77OugRhGwLPqoTv4LzRGfY1M9a4CM4wpYxjuMYHz58iKZpSrsF4+NEHrOiBqfoEoCeNXl9fS1AE/LD9sK+DXykKwcA2Pf393h6eopxnuL55SV++OGHksRXUJ5KouEgRvWCPm1kQjCfliUi5STgp59+iogo/dzWR9YfO+Gn21AAU5ylj05vkxvWlzaUiCjECGtnFpH7Ydu0F3Vd3lx+e3sbv//970sy6/twfCk+GL1E9wncJFTokls9GS9jIXlBp7kvpEaOT5XZf39/L7IwYcY1mbOBHuQNTDSvrYzwXxAR+G3m48qC4xc6zvjMPjvRilgfFc78DPyJ17yIGz4IAeDjNivvWTGI9L6mbbsGa4DcnPgAkEzsOYZyXVeALpdLNH1XkhTslKTMFVquy54X1oPx4K9MKOH7SQ7HYYi0RPE3xJe2bWM6neJwc1zJkXlvuzTQAX46yYjQQyCbfPIRf3NyMC8RndaHdTX+IQZyTTPnTnaMUcBD+DuD2W3i7oMKiIngBid+yMDxy0ksMdoJBj7OFULHN7AZc+a6jtX4Bv4GVvIaEwuRg2V8OV+iTXWrAL4MvTLpYTJqGGubJ3t9wHqeJzriBNr3QB+8nk7QtwccuYplWfrf+BKwtbGZ7dqYdpuI4Tu/9/XdFY2/+tf/rxVzgaJkIaxBklnMZakTdNtMvlZtcWGiZrG7rislSk7xwNkQIFkoXwO2G6eP8m9PNKqL1q4WjUCY5xgrcFgEp8VDmTFwgzBanexIAYcOJCyqZWVjxsGOY+7XZtMfiuHA5eQGpQR4sW6uErAGBC3YT5Tdm7LHcYq+r0cMcg8cL4CNtbEDRcnNOqBPETVJZfwwTjgUs2RmFmlDQR44DzNDtJLwGfcMo3c4JoI1Djki4o9//OOqlYrPN00T4zRF26/35KAru34XSQGLgLzt+zabtCxLdLsuLtfN4ABiQOzldInT+6mw1+ia2Ug7cgIu+meGE73iezhdAhc2gr0YPCC3rQM0AEEegFIqDYwJnTGwNTu6ZdEJlNs2RLcUMj++gw6RRJ5Op/jDH/4Qr6+v8cc//jE+ffpUeuKZJ0GEDet+xg6+CXnis9w3yzqiw/Ocn0A8jHWPF2N6fX2NmOfo2spSO1gybirF+IPX19e4vb+Pm9tcgXO7BmtBSx5zi1ifrIefdkIf07qsznfwn4Dn8/lckiD3s+ODrXe8OFHLDCcACNkbnDMGkzIkaMxpWZZSuWUsBFBaSokRAAr8J8khtm+2lvdJ4GlVwk7sT6nkmDQweEJX3JqCzi/LUq7rNgp8kQkaZLK1SzOi2C3ry9idbKFP2JEriiRZ+EcDSwNl7uuN7wZtvCxnqgpUirBTM7/4FnQkIkqV2klISTqbFE2b9zfudrtSMWNcJN4Gy6yhN9QiJ5OSHtOy5CfZt2l9SEtphb2OxaQoa2KizMmSiSDGzJwvl0vs2q6sxxZ/LU32EcwNvUMvjSMiYpUQmCzaxgswigk+cIcBuZPHZVnK2PGPzA1MsE1mHQPBGFvbZ1zc13jRWMey9LyYOzaE3Fkz1od7GLT3fX99ON+wipMk7VwXPWUMy7JE07Uxyd65l6tJ+ARskjVCPoyfdbRs0VUSMGMKbLbIcF7v4XHcZK7bh1RaX7E11s8xoW3b+Jf/6l/Eb72+O9H4t3/1v3zFfNTgnwrzBNjmqMV5rieVeBN1dsKXwsI4sFrpnU3jeBEkoMZMGRUDgqfZOTMeGFoOPlVBp2kqDGV+rRUBFgVZ4Cxx2ltH7LHyfYAz2TCboDBgwATBwKwSCrBl0lBQNlEOwxAPDw/FoABgGO92jE5S7HidNLFOp9OlAEfWjJK5M3XvUcHgUVrWiXHj8F0NQnawyDgYt7fxAswZAF8ul1Kl8FqYyTdzZkDsrN8MKsbs0mXbtjGnr0/kuQ4k+rYrLJqBuQMYsidQ7w67mJf6BHkAxfl8juE8xDzVjcHIlXWmjIuNGqwZmADqWCuAY0St4JmVYr5mUXxN9Ne2whr7ydtOfmClb29vCyhED7Yb3tArZA7LCZtr5t1BkvExji3DCVuJ/VNlMACG5LCMqaCY9MBWSGh5fxiGmJclul09ttSJxDLPkZYoQHMc8/Np2DOEnZjl//LlS6S2iR9+/DHato2ff/65rBOJNSAEmaHrJOcGOPiTNipBYbAHUEePDTRMxDAv1sGtKOiTGV1v6t/GAAd9Egf0HT9KAAVYGuBj99ux40u5lu1rOxf+ThLD+uCb0FPAkP2dEy18Cr7n9va27DEyiCGR4ppO3J3U8+wK5gOowb/bTyIr9tIwL8Dh3wX0+YmesOZcG7l6nk5IfD2uYYCFXRrgsN5uQcMW+a7vE00+Oprx8z3sBFbcgJ94hr5wb2wXf8C6FR24XMrD0dBfjgFuujbOm44CV6msA7YrALwrOFSV+qZdsfi+zjhP5eheP/iR5BGd5vO2J9aBNUDn8KGuiBrAEhvwYXzepKZJIe7leGDZMWYITds9ts3cbdNb0Ms10SVXLCwD+xbrA/rqv0VEtE0bTdS9x8jE2Amb4O/LssSS8uNeXQHGho0nfX/7Kf6GnNyyZnxmnGR/ZeI+pnV745ZsZky+nvHq1nawxYi8L+qf/Xf/h/it13e3TjFBQLUXrOvqQjqDy8EhD/ju7m4FAnlIjRfKbC9BA8dLZgxjx8PKxnEsDzxyPz9A5f7+vgAjNrHhqLNRjtH3zeqeDobLMq2ecmtlMZhjQQiALKTBKf/BBgIqDZ7M7N3c3JTr4TwwcBIoOwTKdMuyxA8//LCqivhIUoIjzJJbGdi/4XlhQNl5rPu8eWKv25IwdBs418GISHq2LIw/C7jz8w/MrDtZIGH1fpm7u7sVgGdNuTasHcHWjLrBKcnhy8vLqoXGgL25VjRobwHsTNMU0daH+TlBNHCxTFJKcTwcY46aSNFacTwe43K6xDzlgMrxsIyZda7rVYNdRGVMXIVjAy7y9glNdkY4K4LLPOf9Th8/flydCOf9GA46XIs1ozqJXhq4eB6Xy6UE4i3D68TFCbkdLnqD/Bxw8AuQB05gm6Yp/oZAA/Djb67uOEnaJkR3d3f5abBtfQ82chzHiDk/hdYJ3Q8//FD8kucxjvW4zW6f7fjnn38u4I/1wT/SBmO2rO/7QmY4YW+bJtISZc4w/4AA7AaSh3sybmyfdbU/c4B7e3tbHdmJPrjqvN/vy9jxWRG5KoINs36AO3SbzyJj6wPJRNd1X1XKuT66DHnGevJdAzdiGL506zcZR9PU6uqy5AfE8cJmiLXY6rLk/XokCyYqGDPXRk7oIv6Q783zXAgE7BF5o+8mr/APJPH4WeyYZ62Ytfb4kZH3/3FvSBIOdgDobn2IN4lvffk0TbFEBWtmrfHbEHf2h8jb8Wk7XuIIr3oE7hKX8bIiMcAfS9RNzYyHBM8Vdn53PNoCuVKxbZpVMmsQnH/USgdrU4ncsayzGXfmZ99F/KON0Mm3fSL2hr5YhiUWNs0q2dn+3TIiZnpv0RZIOwH0tSPWm8i5PhjSpE2pOl1f6CqYjb3FzKd8J6WIWXt0FBOdNHk8EVFaWllX7oW9ESvQC8/TPjalenx3XfeaXPHT7ePb8UFkbTuH/q4qGN/xZ41f0QNizPe8vjvR8DGANpJxHKJp1mcBI2wSDVhLJpa/H8EDyXg58TDbCWihIuLMFieHArOw+/1+xXLCbgAoAFPZiedAwNN1vc8hop4XzgL7SZQYLgDDiRELhNHjaL2BKaI6OvZBOHhHRPzyyy8lUDooEEReX19XDPswDKvWBYAvVSF6KG9ublZH7fI9G78dCd87HHKgJBFi7lSDGAdyA5w3TROPj48liJjVcaIJAAegudUq4mum3CeAAJBoT3PrVkR98i/gieTCm4NxVMgZnbq7uyuVMtZ8WZaYlznm8esTK8yEsenWVRLumVIqcmND7DiPEam2rKBvp9Mp5nGOWCoQMesLSKKvnKoWMjMzxP4imGJkZNCO7Phc29bWQmTw+PhY9BvZLcuyshMHUfRxGPJG58fHx7i7uytVDTMmJB8Ge3bS+A1sA9kia8ZDEEZPAept2xagAJjwi5PJsB/IDnQYoBRRe6C3R40CuIdxiGmpraGujk3DEG1TE1eS2sfHxzgej3E4HOL29jZ+/fXX1f3uHh7ifDmXdUcHPB4qXIAQ1gfwgp0WcBH16bFub8Imza6bJcN+8K9+PgFxA52CeMIWYeiRickd1hobQpds1/hsfA1rZX203LZPbufa3yIxtmwt8+U9XutKeK2eGkigv8z77u6ukDvfYuyRo2VtIM+Y+Dv3ANC4xcxgNR+D3ZT4yTUN6CLqKTpOwhmXExsTAQb0zJP7Ymu20y2o4XfGbYIGv2O/N0VtJWOt+btbfbgv8RUfxDqS/DghwKaIHVQe8enDMMRf/MVf5JjfNnG7q7a3bdvBJ7EW7K2zvhgMZj1YP1QXXZ/nOT8ZfF5XcN31YXAI2cSYkTMYCGyDT3RM53diJTblNUZvDOyxEeNBEldkzBiwe/QYXWBc6KL9ErrhljBkb0LLCQ9z2a6J74vsuq6LaZxiUrcEn3U8NUYt4D9FjIozJp34vHXfSRDXRV9JnNFlE2xcywQ69yiVorYrFVRIPGI8awnett5bTttxbn3fb72+O9HY9jiiSCz64+Nj9H23Uu5xrL18ZlCygpyjadrIx84CPHgq9SUiavkOQEjZl/dgvAj8zsQIoLW1JLdIzfMSbZufG3C5DLHf76LrKLnCeLbRdU30fS3BM24YOBIdnBUL70ycz/F9A+gtAEbBkKkZHZTNzsRgFkdi5gqHk+e4j9vbm6s8xjgcjrEsczRNGx8/foq7u/vrHKIwaK+vb7HfH67AYr6ubT5ulDV3cIcBy7LuVscgmhX3eG1ArvogCwKay7NmZQA0yBbjAQyiB05cWRu3+gFCAMawCMjYvctOJLx2bZPPsl6mKeZxyv2zSz6xYhzH1fMRvN4OkDB55/M59of6wLNpmqLv+khLirSkWObao06gwNFRecFRchIV64L+ui8fOXnfRMQ6UOF4OHfeOo+DZjwRUZJWAIKZG9sp4wB4Ytfcc9sK5jYlAyuDX/wC90VX3eeNXuC83VoYsT4ykaodvgzg5MoPpAg6hl0MwxAvLy95k/2VYd7vdhFpiSZSLJGia5qYmyYu03UM8xyHm2MsKcXusI/bYz556OnpqdgBTD8PdaTnHZ+SUop85lmK3X4fbdtFGyn69rrmV93Kx9d2kVIT4yWDxWFctwDR1oA8eJbINoGFdXabEvYZkYMT/hg5sV48pwAWHr1is3jT1L1q+DeOoPW1iFWubtp+8UO01EBCuRKFTeIn7Ddg8klW0DFXHJgjc7DcACvs9+BIY9qgTCyYVcfW0H3rIuPExtEB7Ah95jvEIbca8z0zltiUq0rMlzFhp4xpC/YNBiFrAJlmXBmz52/AyT0Yj8HkqEr3MNWnWk+RYlpqF4YBNvpocMj1bEPMqbSjNE2kdF3zWPKzLNL10LhxLKdO8V0z9/j4rc24WriKKW3u8x+GMfpYIqYcY8ZpinR9VhJJIqCeddsmb+xfMX5C/lThXdHHxzlGuFpBXHKlyWSzSWM/Rdx48FvkIXgKu/TeDOsK+MgJg4kiYyM+862ftl8nyMxzYM/OPEVa5oiU4vamPotojoilSXEZx0gpYhyvzzLbjNcEn3XP7Z6Mm+QXebiCZIxJwmpS2xhlnvMxt+AtruHP4nPtV1hDy5zx4Ef+3Nd379H4d//2f1uBQ0AHTtonX5DN21GgpAA8M19mETK7+hrpG2wuAsVBw6q8vr6u2DqOgwSg5xLvMZorY3g+n0vvfjaKVIKAGSTuSfa83WRO0IGBdHsCDsoP2uIEGwIIn+U6ViJkSGUBZaNlirl5bHZqPCk4pao8sCWw/gAlAndKKZ6fn1dAnbngaAn87JvASRt42GmYCTMQ4UVg4j4kiHzfJedt4AEM2SAABU6E7BRhe7m3nZ7l1zT5uFb36mKwJI44V/SONfXZ+E6ymZ8dII6V8QN2j8djeTKq2XaAJvcyIMGZD8MQf/M3f7NK9HhIGSd7ARxJrggsDrwR66PskL3ngh34PfrGGSOfwSfwu5mX7UlOrAMgGr3h+1wDpwyopSJofxNR9y4xT4/ZjBT7o8yoIwfm7uTMv1MdMYNMZY1El+TKz4YZxzHGeYrxuk6055Rjlds2lrnqfESU560Mc91Dhf9kvY77Qwza1IlcsQ3W2+PlHuitCRT02skeOoecDeRI8PHV23YBA1y3VOJLLFv8OEkILTusI2vhtin0EQDFKXL4OD9sCj9EFZT2FbcEkaAYHPFy6y7r7DY992rzmcPhUB7KtQVUyJf15IVvY8x+3991JcbXxS6J07625TWOYzkGHjlvwZD9mtlj2G/sFZ1w+6mvt/XHzMfJjn2IfR3rYJ/owwaodvi66Mp23iYOty9ii+WI/CDWeA4L13Oc4H4QeYzbINKxyFV8J4hboGliiPGjc7YdZAXh5bgbURNU/Bx+ljnjI7FtV4i97shlS7giUyep4AX7drcD8h86QCXdscrrwdoyLz7n7hH0xD6QcTBWbNlVOvtPVyS978tJOHpBBQkfgB6ylsY1bqlyO7sxlWPAluhBBo5VKaXo0vo4YpMw9vfgbesa8ycG2weAl/67f/nffmUv29d3VzRcSgHU4qzIQHEUblkAXFo5MBAmQLWE7K1tu9jvc5bH8ZdmY33aiU+JILBzKhNVkNxnvYumact7bh86n9+LYyPrNptL8IPZZBEA48jBzJ8NCYfshAQWAWCEXBgbwbRpmsLcmckiseNe9KHyHoF/HIe4ubkt2TMK4iBBa8myLPHhw4fVvZyRM9fz+RwPDw8rRsMndZkJcqB237T1BCV3sHDAhLXxZww0AZiAN4zWwAoD894U72XAgZEs28j5vlsucG7MAf324QO0CWC87vN0QDA4wSk9PT0VPXBwtOM2k4t8np+fCyDjCFXkgYNgTA5mDgBcz0kyzsf6w++8sBeuiTN2YDR7iT754VgkKW6BQQcAh8iLuQM6Hx8fK9M012Ox0U+AgIMFc1+WJT5//hyHwyEeHh5KpZT5cL+3t7d4eHhYJSp28rBTgF/GQKAmUcWOarLbRaT6VGZ0ru/7mK/le2Rxc3NTAFtx5F19HgPJTFoiH8cp8mLrH9yCYN10HzR/M3PGfKmcAsrx8ejWPNfnFQCqAZpcj+qTqxneH0LixX+MOSJWSTO2SwD3oQVN05Rjkn0ddAE9wnbxxeibfZIZcOyDwL0sS2nlRHb+LGvGCWZOyq03rBNAhmuY9ODFNdArbIDPEIdN1CAbZOlqyjapNmDD95r5xtcblLldxDaP/+R9Yq79DPq79RfEEI+VpAhiAEBVkrlrJd+trk540eGtj8S2WSvvO3Occ9UOfcW+rKPowjZp2+4P3PpEdNLyQ9fdGkg84J6sneeDH8D/E1efnp4K9jJGQ3eYA98HA1oPWTfwyTbW2efjq0i60SV8MTHQ/onPuLPDRNcWF/B9vrcl/PxCh7eVNHwedosfMu7ivtxj61vwfV4X9B5Z8X37DxMA26TK2MFkrONxqURFimZzjW1i7iQKOwa3uaUS3bEdfO/ruxMNFoKbwrQSGDEUmAyUEsfPZlG3KsCymhnMAeYQ9/d35aQavkfgnaZpdVqHBYyjxAHVc5SXWJbsrO/u7uL19bXcbxynoFXLi8mCcX2ChkECRkvGx9NpXSkgqFOuBvQzZzO1lp8BJDICvH/8+LE4T86wxwETQPI4usCuuq4rfcQ4923Jfpqm+PTpU/zyyy+rdiauj2LDVJJwYWhugyKosOasCYmNHRpOFMMiwFIBMluHLJCHHSkgxW0QZh5dOWI8OG0H0G0lxeypS8jMASfjAE+1gPUjqR6GYfVQQMsMPYqoDhCHylgcJHkho5ubmwKYuYZL/7QuYE/WdeaBY+W0FoINdktAc5Jr3fQeBmRh5wy4aJpm9XR2dBQdIfg4eaB95nK5xIcPH1bjMRPoI3QBEt5bUhygkm6OufXhEU9PTyWRAdAgOzbRE7zQWXTKp+bQbuPq2TAM5Uz3w82xsJNUMsqTrscp5qt92Ma3VSgSbuaYIr7yPegEhIwrIZwUCPPPmjthA1jR14280QHr5pYZdsLjwO9E1ETW3/7t35b40Lbtqh2OII6PxTchEzPeDor4PI6jZe4GWdg5Osp/6B3+3pUHkhHvY0Gv7dctbwMT7gewckUZOzcIxOcRm5al7iFzMmLwhx35etuEBJvFFyF74p+r8HzHlRUDR+zXjK2rTQbg6I2JOvsKEkqSBnQFeTl5j4jSj+55GeAZ2CInxm1yh7hF7OBay7IUHbKvxtaczCEvEhH0ABsgvnJIAHZ/c3Oz2rfpZ5SRXBC30Bm350CWMB90iTVnDbz3yWSIdQ5f6cqMW634O77IYB0d4G+OM7Z7ft8mslzDbDv+2QkxYzPRyziQDVjVNo1MsD/mx7qx1sRY1s825GTIcZn3WcNtAujqpHXCiQUkF3Jz2xs+gHHaXzDGfVePA+Ze9osmI20XTsxdqTHZY9v/+17fnWigtABNFMuGhDMFJFjJSDo4650EhE2odnCXy6WcyGH2ap7n+Nu//dsClhGUFQ6jwUHWEnu7AisEz4iIm5v1U5sBp8zzfD6Xnf8oLApmlmea6jnJJDlmk2A7cUAAAwMy7s3vyBTFconarKs3RcH0ZKffR0RVFgyWFg2vHwbjNjKXC2mRmKapnITiexGEnASYAdqensF8YCKnaVrtBQJwWKcwOLNPrIed6baVw0ysHQXjYv3QOQdMHJIrMMwPfSM4+OQo5r4FELBPzN8swbcSqq3jIMmZpqmAr2ma4u7uLtq2jX/4D/9hGdOXL1/iw4cPxRb6vo+Xl5cSCF1+3bYNsEZOsp04oGsEMkCCAYvnxRpCICBnbM1OGB00k4ZtIGeAi8GcAz5zQ38gN8zo4IBZYz9B20dlR9R2EwAG97RjBugwxi3D5jYG/MFut4vUNtFd7ZyqGLJIaf3AO/R6WZZomxS7/aHM28xw1/UxjXVvCTpLYH15eSlVK8Zv+eBXnHy2bd0ThA92Sx8yxA7deoFv9LoDtCJqFZKNytgtbW+856SHiqbbXdG7pmnK4QLoqqsvgFbAGZWBLVOOL/FRsgan6JtBBbLxfhNszESF228YI0kpvspJEnJ2qxXr+/T0VHTajLIBHC/rrP0qf+O9LVuMn7RfNwiyvyXWMHbv1WBO1jUz+7yQH4dlsP6MyZVuPoc8l2WJaJtou7rn0e0wJoGQo1uzWCfrP2OdpikeHh4KGMae8Z8AVydmbP4meXal0Inxzc1NtG27ekCngfvDw0PRDZJeZMy10B8DZ1db+Txxl7Fbx/CN2yele+yOrU5W0AuvL9/HD6BLTdMUsnRLcDw/P5e45QouL8d124gxEmtjMsp6j1/mGt6/yPqic/zcgnrmasyAbvIZJ1gG946R6Cg6YxtHxvg/xzDrssm3FBFp/rr90n4DvLXVe65Fcux7MZ/vfX13ogFg9wK5Nw1HbdDHgC+XfAwqysSEMGwrQXZUzSoQuZT/j//xP44vX76sqitedAKFFyqPI60yYr6bWYT1E5rNauI4b29vy3v8BxvQ9338+uuvxcEBpCLqkWZWKuRmR42hw8ptQa6zejZ0AXK/1UJR5Z9inmvJGeAEwKUFw8/FACjg+HAGJHgo3+3t7Qq8AIodeLcMkTNjXxsG10HIzgW9M+BnTGZV0C0DEhuWDYZrkUDjSMxqMg4CoEGSr+EE1eDCjnu7qcuJuvdZYPzotAMNOgaQQN70lhNQ+e5PP/1UmBxkgY7xOSdWrC2B1eDQc4+o1UPv3SLougfcLSrbhNSJFbYCeHfyGRHlqd1u7fjy5UsB9FwT2yCwA3KptFBNw652u12pziFr1tvB3nYA+MRXbPcOtG3er2FG3sGEl9niSLWVCGA1TVNM4xT73fqhhstyPUlv18f7VT6ugCHPFOtn5CADWufwv6w7Y3IrBwAEUI48aFdBL/HfzNHsr4Gufbv9R0SOMxxJbhBrBtaneqEHrqovS93H9/r6ujpRDh9ARcdkCXNv27bsgbHstgAKwE2lCb0144edYr8Gs8gIW2S9+Qkg8ue3/of3zeZbzw3C8C9mQh1fiAsGVT6q3UyxbZfxOa5tEyoTZ+iI75VSKm0mTVPb3lhj5rKNH4BnX4fxppTick3m2rYtxFxEfLWhH/tEVsiFOeMjDLq4Jj7V+sOYTRICzpkjfhE/iVzw4SayvPcVPXM1/ubmpowPueDP7W95j/miB9yf9fLJdR4n9obOeMxbgnkrU5Oaxo/WTcYPKeCDQSDVWONt8urkCF/J/E0WMoZtJY7v48dYU3DQFmdYP3kfwnqLaU2iWRa8rLvYCf6Cv2+TE67r725bBPNFrseWb5IRJzBOkrEv+4atD0AX/qtXNJg0TgRHwaYZP4ANBXKbVETNxodhKEkJho4SZVbtPlKqG47IbiPqiSIEBys837ew7+7u4uXlJS6X2q+PEbLY41hLVgbECN79rNyPsVlxb29v43g8rk4X4Ym1Zrmaph4piZOBSaV1hvHYYbMGVootkLZzz3+rR8aSGMG60QM6jmM8PDyUdXYQd/bPmgIykDksfk3qKnuBXgBcUVT0AVn1fV+el2GDbtv6sEeuxX1vbm5KkHdw57pmg9BXft+2WdjIzNhFRAGrBHCchgEazpYxG5QA6lgrqnncx0AcB2cwypyxAa5FIsB3GBeOBN2cpil+/vnn0q7lPUZU3rg+FScSU5d2DWzcIgJzRIDs+351ZOJ+v/+KKWdc3ttDgLZ+IR9v9L69vS2B0BU+1oj1914V3q92UR84iP3t9/uyGRxfQFDGH2A/Zo0I9tiVfRZr5z0QrnAhk6zDbby+vRbQjN6kZQ0m0a/z+RzTUluQ7Av7vo8mpRiX2j9P0ubWTifLrMn7+3uxdfR8mqZysh1rvK3G+gnMDmroqatz2Av+GiAGqILJbNu2tHhxXR9i4T1t6MI4jsX+b29vV7oL+MDXYodc01UywILbwwB6vMezSAx20AsADu1x3J/54ysAjU4QPVb72YhY6Ti2DlmFnWBvZlPxVfaDrL2TPfTLpId9pishnKjmezFmJztd18WnT59WhAn26vjIepi0sh76EBMfroBe0KIN229f+uHDhxVYMulp2dPiir8w0UMSbuDN3Lkua8w6ofsmmNAPsNHd3V0hRtq2La3dJF/gDXQBPU2pEoO2Za+RQScgkQMv7APsb72fZAvSiTcmqPgdOe1EjCBb+1FsB7lAshrgkgRt2zmdmPIe8rSc0Wl030neNvl3ksxagi+5BrLydXjhh9zyy7UZM/dEZ/C39gcmOe0r+ayTN66ZUn46IDI1QZsin3zZtG3Esq6GGhcxZmNJ7o2eoX/+aZzy972++9Spv/rXfxV9Xx15vnkTTcONUnDmcwZN8/VvKZYF9pAsLpfDCdwsJqdBNU0b01SNmMCIQQFQDMxgsxgbBtm27fX0oEMMQy15W0AABbfjcP3399fiOOix3DLRGIQXGFCHA/XmVTs7OwUWFmUgqBMIABqu4mSQ2kbX0eN/iq7ro20xhsoIAjKQi1leAxVArFkUHLnnYUeM0yXZMRAtxhCxCmhNk0umHz58KECPpMEsgB05v5tlJjhUeVQ2irHjLOwAzHYwdpI4mFMzZFvWHz1AvjZU1pO1wgGZnWX8EZXhcCLGtS1X9N0BxEko+kMQwBmzuRxw9eOPP5YqFgCGAxYAcK5UoX+sGSABOZl19TzQJcb89vYW85w3ND8+Psb9/f1qbwGBaevcefoua+pndPBy8N62aPA7Osi/GZ+TzS0zy3dgr+0nrJ8kEK5+Odjjw9yCgawiZR86XC6x2+9jGsdITX5O0bxk97rb7XKwaGqLaVqWuFyG6No2UkMLRn5+yqtOGLMNOjF1QCbpZF+UfT1zcasd+uaE03ZgwsT3J6jZ3pCNqw9OqPGxrAP2Zx/OfySMZoYNEGwrjBcga1LLFZkt0cMcbCsGKYyfPTXbaiD3xhe4oukNv2YgLW/7MGyeuWJv1mVODLMPJZk22PCGYrOu1lV0gLhh/2o/9q01dnzj32ag3RJGIkNVkUNUuH9JXvsuUtPwBLtrHLwm9rGs4uuyLKuH0uHXHMfM3JusgoAhxnifjvdxGShyDa7jqnZElDlvkxC/rAPoFTKn/RGyhzht+aCXriJApuDDs9+coknNyk4qo51iXuav7ME2Qix2ddSECfpVYtwScT5frvceous4RfFyTZzrQTL5gIx8XL+T5KbNG57zgwvbGKcxHwXPWjQp5qkmUSYQs/7FFcc2Mc8TKhSpuVa3J22gblI06ZqQ9l2Mw/WgirZ2M4zjeP1M3RMcsURKTaQU5b1hHKLv6K7I/8vjnCNdT4lKTboeT9uWNem6NpYlMqbWOrRNGylF5D251yrKTIvcFClqrBun6ZqYzNG39eQvXugKNux9U1l31w+6/Jf/6n+M33p9d0Vjt6sbeGs/bI6AW8PKryXyBuy6s/7t7bU4V0ALE8MRmV358OFDqXQQNDAOZ4hcoyrPmsnJjip9JSDuu2W+K3isTyYFmAOCXKYnCDK20+lUWpJgwDB2AxGSKO7pgG8ntWXrmScBqu/rGfMVKNenPyMTWGqzIwQWNrkiF9aJNgsYco9rCzrMLpspA5ATBO04kREOijkBcDzXmsROq/VibDhXO3bWKBtITSjMlrmHH8AJY+s9P+gb64Z+AYS4P0GD+zFXgx+zlFwf27EcXSXhMwavyAcA4GQyIrN4JHOMfxzHciDCn/70p1iWJf7yL//yWvnLTxunzQB7J7DCPKEDrBE6QjBENmwcxoYsO5/I5HYmP6sDVnTbP0+CzL4U5mUwh50hO8uSPTXI2O0Q2LdZPlcLuJ/9nRNb7JykHBBjvWAtChMadQ05kjaWJZrURNd3cRnqgzzD/qbtor+u+83NTczTHLu+j7frCUtO2Bg7doff9rju7+/LZ5dlKUwi92NtqNy6Vcygyswk9o8/MIG0BWLcm43ryJQKMADp/v5+ZcOAbvTC62MyAP/L/LFLEoJpmlYPlXMlElvniFB8sit5zNt7sJx8mM20PdJyi9/hhc5F1N5xJ0nEUfy7CR8nUu7Px+62VW7W0RUatyoB0tlDgEwhEKZpKklBRHwFUlgjXryHv2NNIBTRv2+1PLPGOZmIWObaFrcsSwaFba0SW8787hPTtv6UWM7vJqhYe+RO1cEsP2M2QCOZ8oNsHSPwWY7xJl1MbKC7bpUmsS1+4vpye56TACcTEREpMpjGh3LPktSn9elITs4c7xif44M3WrOGmSAl+a37YSBN8VfI+nKp++FYq/OpniyXUhNNqvsYUkoRU30qObLjdxNV1suSYC8bsm9aIq5incZayfFn50QXRMUQ+XNNzLOS1lS7b/KaV8IeQstxjDGTqCxLivmaMKSUou3roxuc5KeUYl7qARSjyIsm1eSVNTdJzzpaRx1L7Mt+6/VnPEfjf80Lq97ZiFht6obxt7LhhAkALmNHrJ8k+/r6Wnqrcdxs3HYgYbEiKsgqyrDU898NNoehOgpn4RFRkgLAkB3OOA7XTHd9ZCdggaTLp0sZiDghwFnxjI/dbhevr6/x/v4enz59KkZr5Y6I8pwQJ1H8zOCyngA2jmN5wjLOGzkbdGxZYxhZ3mcOgDozI2Z3mBfXITHxWN32EFE3k+EYv8WqEaCQuQMlekDAsRG4pcPHuxpUOXFA3p4TQGK7mW8LXBz0qag4wKMzrKuTCp9o4yDLf96obUbOAMp2ZsDrTcjY6zboAR7HcYx//+//fTRNEx8+fIjz+RwfPnyIruvi97//fQH61hOCB3Jj7iQhEbFqy4uovb7MhyAF8PF3PTc/fLBt29XzLbauy8GRtXTLjoOzgY9tGzbfIHkYhnh8fCygxwHLQRZ74XfWzQ9GM8D1mtgm+RukwTjP0e/6lfMvVaausua0CfkkGvyA54w9wXJv9Y19DU5MLF/8A0kHFUXmCtBqmqYAU9Z1u05cn0QTmyB5MEGDjiFbEzQ8HwY/FhGrU7bQFZMM+AKvP/bB8bpmgyPWR2/bT1MdZm3Rh62PBPD4/tzb/qaCrq4c1e7KzzRN5ZQi67wBE1UaxsR7vg66so2nfqF3JkJ8pC7+iH/zfZ+SRJz3gSC0NbojwHiAtTWBxLrin5dlidTltSHZhiSxj+FVEvurjRpfmEwk1lCxZY74amTy9vZWfCY6vk3m0TsTIZYTMna8NqHkpJzE2PjAiZxjNLqPvNgYja/dYqVMbtRnepngHMcx5qWuP3qMzpDAsI+O73wLpILXLuf1QTeAXogGZLet2kPiOIEAjLtzwEmzkxPWBtkZF9iX2/a367a1k78LhOPTGLsxkOXCZ43vjKuctDn2oNOsFe+5U2KaxvKAR+O/JjUxy7dDSHiekBnb1nISnrZt/+tWNABG3BQhs4E3oh7/5oEzORTDztZ9eQiSp8CO41g2N1kBcJIoiTN3FBxGBCXOgSfFblf3VRi4eyPhFpTlz337GDPuicB5n7k4IcEQ2bNBUN6yazg2ACKs7ja4Xi6XwiydTpcV+GJNtuOwQ3GVwU4rogbmeZ7LUZsAChwpio7cvgXakRHjRx+Yv5NEJ2msA8DLyRqgw4qP7vkzPk3D+2NYM34ahHEdxghAxLGjMw5cW6aJMXM/Ow8cqdv82H9gYIEcDWgB5Ky92yqQCffjuE82MLJpPyJXHmhDQl/+6T/9p8VOliUf5ff4+Bivr6/Xhz6ma+m6spsEFes4tmCniB3ybAEOMkBPAFJtW58xgwwgKAB9Ji6QET7En0der6+vZS+Y+8hJUg1g0VHAISDcwd1kgStxTkBJDgykzdAC7rgfY8G3Il+C/TAMMccSffRfBcSIehISoNpr5D5r/sPefA0CakSUMSHfiHryHTaHr2De2I9bZZiD/SbrxjGs9r+MB5BomeCvbJeOKSRXfA7/6eczGRige/xOPMCGiG/MuzCcEStdRJZN06wOS2H8Ka2fN4DcYWgdyyJiBa7ww56DgaQrYugdBImrIMyBaic+Bh3mMxADBpCWkYEpJ0Ji8/xtG3N87DDjdRyissI4uKd7xq3HXIOkFlm1SxOX65rxkFPv+WDOEDwp1SO5IUdNdESsj0HHDq2rtiGuwb3QGQAxrLYPokAPTRowH3yPAa+PdsaWINrQIXcfYGvFh8y1EkHMwG9DGozjFCnyenL4TQXiKfpuX5IedJH9eCS17sJAPui5E6K2beN4bCOlutfImGG7l4nYaXKAGOdqufVwGx/th1lPJ6OMi7XhvtiD7cr+0WNzAmCfRTw01mJu6IQP30FWkDDM24mU9YhYCPmN/ozjEE37dWt1nvNY2g1tK9+yGeJe9lv1RDP7r7/v9d2JBswipRXYG1iYbfaFIbpf1NljRGWHCBQI1Iu7ZQUMmFgwFsHsqgFg/sy6X5oFtbGVzF1sQN/nctWWmdwqCuwSc6YkTUUAMIBxwhyy6JxwklKKL1++rBgUAA+BBUfE3A+HfVybvFfMPo6J5yE4QfJT3R0smGdhHS6XFQPiXl8SHSehdrguwbL2TiwNTm2oni9/Ry/QJ77LXPgeD+XiNDBABEDEzNA2ebU+EaBh3ACV6JrXhzlGxCoB8j3QQ1dwtqddsXYAs63zNdPEPHjxgCcMH2fqsTjh9Qk1fGe3y8/AeHh4KADn8+fP5ZktACjkZZDvdbWtIqfT6VQ2jLtNreu6sn7IATBJUEMODkjoI4mKZebg8fHjxwLAsB9fB3mQvBooolPotokNJxYG3vv9ftWzzzjQyS07hr6RMODDCIJd18V03ePGwwSRZUQ+I90VPkCT7Y+WDm9+5u/Mcev7+F5ElISSgO7Aw+8GpSTngJktMCGgGkihk6fTqTzMjjUx0WEixe0YgH3mwcEG3BO/BZjAT2Ab/ESH0HfkZGC/PUrXrCQEAu+hoySpjMlJDp8BUNrGnQjbHtwu5nUDiJhR9xxYW2TnPU0ppcIAY8P2H/x0UmWCguuzXvYH+FfHA8Zu2VoufqaQ29I8n2VZYrnmZtyT8VewVR/kh7/CNjl9iu+5soLd2lfadqwXBpgcmkCMpTJmxt5su22deBdR9yk52WPtbFtgDvyikyZkYUy13UPGuLq2Ky0/HIHO5wyQ8dG850Mv0FXkgo8xUEV+y5z3VbjSufWZXifGYczm6iR24b122JIPaLB+IjtjQhPH2IGxreM5emBbNamBDnIdE7b2sY4HTqr9npMR6/DWd3OvaZpiXpaY5Y98v5RS7A+V5LHebe9hYjPLYlnp/G+9/qzjbc3WMhlOfyH7ZcFoRQJQsSilhzJVdt0LykTtSPiuwalBLMwPAM4ZZgQl5Nquwj3MPBvcYmB5/LUEiFO6u7srTClHvjpYcE0MH0feNE1JLmwYXB8ww9GWgLKU6gMPOdcd55kTmmOcTudiQFZKkgyyXRs8wdZ9ec5gDeAMOpxI4ixpe7N+8LAhwCyA0qAI44+oe2Zgdl9eXrKSXgOiN+Ix//v7+9WpNSSDnDiEPrDRFL1xMHXww9go+zuzt945SaLczv4cfuezTi6QvTc2U6nwg5JYP65hvcKeSGJhXwFTAEL62d/f30twMaBFB4ZhiPv7+2IbEfWIzP/0n/5T/O53vyvBhLUEUDEfA0qc+ta+WUt+R6fYu8Lv7IviPfSI+9B6yPq8vLysqkAkLxG1ZWtZltXzdzjViL/j6ElWAa2fP39eHZ/rlh6CFnrEOjhpZf1MjDgpZU4GtVSgOD3o/Xwq4/71119XCWaar73KV380z3OpCrHWWyCH7Rk48TtyZDz4L35HPxkfv9MGenNzU8CPbTViva8MG0QGyN6b/LcVmQKIunrCDXaIPvDZLaPtKhbgCH+PjzUZwvrgO2nFQVboMT6Be6ETbmEwgHKM2FZ/p2kqBzJsAQZrYDLBYKzs0dEckI2PqMbfkMzzPKRxHAvjznV5bZlmrkWC7Go6yRI6iN54j5UTOlcIDABtF8RHxmeb4yf/Joa6Yr/9Nw/zSymVY5DRE+z+5uZmVYlnrdEJrsfau6qKXKgy+rkzEDXbOSAvVy64Pv7D+/tYF/wkXRlOKNFj7MVVE7AHcSalFOO07tfPVYdj3cMS6wcn4w9MLmLH1k3W03gmf3fd8uTYh52ga2AR1sFgHB9j4hj9wsaJMaw7PsKyNBbx9bfj8bzQacbgpAr5sB7EascH41T7C+sGOM+yqfi04j0nN8yhTW1chvPqmgWbx/VEKhF3xt2szba6lsdb9+98z+u7E41Pnz4V5WEABhFb9sefRUEI2A7WVi6ADwuf/5ZLPAbnyxIxz0vwIDorSS0P97Hb9dcz2S8rZ4vwuC/GAjBzBtq27PHIO/75DgqfN7yv+1vnuYKMrQJtDRSjHYah9FMzBubsRIf7APjIqGF/aBv48OFDaTsxa4mDTCkVQM81cTh2pIAOG5ZZ04hYPTXTPZoOik423TZiBnGea6sWgXC7Sd3rSAJm54seIF+MhNYZOxCCAU7QwAImicoUsmDjKBUomE+zgeM4lifXR1RHT8LBtfndSTq/07+M4zI7ih0wPq6D7AmSOH3eMzNkm/UeqC3bGhHx66+/Rt/38fHjx6I720TJyS265QDEewZFzIH7IuvL5bJKiB4fH0vp26ekMFYcP7btdk7m6mfIRERpYXTyyLMTYMBp5bxcLqtWJvwTukbQZq5uncAfYafMl7Xetj5ErJ/cjSxSsz66uwTcpolF4JLPcy23y9inGJTP8xx3d3dF3k5k7Z8gASCMWAvk//DwsGIhXUU14DZw9XhMoETUZyQgPwdtr7cZR+Ru1tABc1uR5r8tUcSYvE5bBhefxJqxF4Ug7fmZWeb7fIbnpiBPgyYTPAYwBpT46re3t3JPk23EBQMXQK0TSeIMcd1rhr+yvFgnYg7ywzZp0WS98Cl8jnFDLNA1sSxLzEoOl2WJt/f3aJumEGeAR9vjFszjp/ibExL0MyJWe/nM8uMf8RVb0me7n+bu7q7MFfnZ1rm2KxCXYSjPyCHR4XusMTIn4WXd8Ydck7XGzyALVzo4oCcRTy9r4qlt1627+OtIEW1biVtjN/s/V22I7egcbU6FBIjK7meZ+fSndXcB/3ZygW/gfh6PY6+TQnAFeoc9sUbGrfYRjjWsqb9nkO8KkLHcIjvgXiaCnKTYN+Xfs8TKPFNEv+sjlohhuMQ8zdFf9XnSPfBr2Dm2XRL7JVZrwIvPsmbgm5qE1mTme17fnWhYsdwHiCLgTBEUPX60nsBOMoH8uSamaYmmqT3y+/1RwffrBzZ5E092mG3M8xRd10dEE7vdIdqWyskcr69vkVITnI5FMgEYYHwAMCtRHucS00QPcIploQ2LExtyUpOd/xJt20fTtNG2faTUBkf+ZkVfYlly8pSPL2gK8z4M9fjMiCaGgadjs4G+siYYCCDz7q4rAIHAj7PiOxEVODI/O7OI+pAfAzIcG/I3WKa3lzXxCV0wW9YfgvLDw8OqemTnuyy1NaLruq+edusEycwL8z2dTnF/fx8R1ZgNdg0IkSHBj+DPdXiP188//xw//vhjfP78OR4eHsrJOzh7P0jx4eEhbm9v4/HxsVQ6cGI4PAADrSdmsUgwkSUPgUTvSSoiolTAGEtE1hXkjKyQqRMdkiTkhJ3y+z//5/88lmWJ//Af/kOcTqd4eHgohAHMJc9dYG2sOwZUbsvYOlLvXTKwRC8ByowNYMMpSRw0YSZtHMfSP5xSKsfyWhdZD6pHDppbZsn+Aj+G7AASAFJ8isfipBodNGFje4VIGIYh9v0uxmmMZskVjDQvsSxTpKaJw81tjMNQSAizWQ7MTlTtE7ou72nwXgLWymw4rCm6anbSbB5+iITB80ZHTA65dxkbJzgzZogVdNj2y1oC3PAlZtxd0fEaEIfQG2LcNimy/0CfzVZiYz6a24ms1zoiSiWZa7iyhs1bb5gnQM5x2C03rDtEBTGZOcEMm0xgPbke/zaxREszf0O/va7WO1eLGRvzImbh6yFg3t/fY5yn6K7j7ducQKeuja5pYlyyv9rvdnFznzsK5hSRunyC3OVyKc/pMBlDnDNAJSEbLkOM47Rai+EyRtu1K9t2zGBtHDMcI7ZxCX+Ffpwvl2iuOjFSYYtY+X8DziZdD9w4XSKWFLGkuJxrl8C2FbiuW+QT6HZ9tF0Xy5w3X6OviaNWo4m2bWJOlVnHBomNOTFJMU9LDMMYsVx9XtdGumK04TJG13fRd32cz5dY5lyxmKfcHhUpxTJHnsdVT6JZYl7maNpMJrfdLuYlt/vEkp8Bttv3heTpuz7meYm0pK9scgv68e/oqpMRYwJjUv5uDGRfxAuSx0SmsVXbtjGMYyyxxDJPMY/X9vl5iUhx3Zi95HmPUzRt1oV5mSMS5+tGTPMUbdPmY4UjJypNmyJSnuvp/T3GaYplzknGPE9Zt5Yrkb7M+W9tl0+omuaISHEZTmXOEH7gB8uRf7vVNaJW9bNsvm+PxnefOvX//d//P6vgb8cDG8lmT/fyOvNkcBFxBQZZuSlX8iKIOYN0FeJbSmYQiRHi3HjBttCjTaDAOXNthI6jNpNoZdsqsLNikiIHgGmqD8MC0PBdHDQZd0r52Qco8m5Xn42BUlc2dYzz1fnAXODgYOv9HeZjZoIgCTvNi7YoQAZjBUTC7KO4bt0xmHUmDXvlsnZhTqI+yI+/IVeMApBrfWR9nYy6EmJm4vn5uVwbvZ2mqZw4ZF1A/m61QLfGMbfE8aAy9NT66TKrf2eeyB7AB0BwTym6SDWFOdmhRlQm/NOnTytmyTpDsF2WvN/m4eFh9Z4ZZ9b1crnEL7/8UubKU8gjKhviDbysEfrYtnkDqQEXeso1GK8rnm43QubYDZUGJ9Teq8M4HFi6riutdfgLV+2cGHhPikFvxPohmREVoJEAoWtbmbrP3MDRCc523HyOao9bTbYMLT+tZyQBgFlkbLYbfXOJ3AEGP4CM3MJAIGastHg4oSVJoVJUgvHGT2ETgGsHO4gLdGqblNtXAA6RzbaVwzYDw2pgbSaZa7utCFk7sbVvQ0eQMS/Gg70DwkmS+74v5BzjYM+P/QLxFp9ggow14XeqUNY/3iceYq+QGegA8dTyQk/d1uO5tW27Ihv4vpNDX4vPLMsSwzRGiFDy9fHd9sFOdJxcmjUm6fI6lc3WqVbfuA8+r991ZRxmfF0ZNCAzmcC9Ic9KZe0aM9g/+PLyEl3Xxa5fn74YUdsGh0tNPMFThSzp1hUG/OU4jjEO9cQs/LPX0lgFfXXibB9F5YhYDz7xflj8IC2UrgC4OsKa5XuOEamOn7jP/Rx/3faek6O2xAhwg+MY4zLGM1Z0gmw73TL+vI/uQVLYN+PH7QfHaSrPNfL18+cjunZ9uqAPSzJmjqiVZctzhSmaJvb93x2rbEPYiitM/M0EC/cw6Wb9QT/bto3/6//9X8Vvvb67okFwYzFYSN4DXNL/yIlRPlGHBc5BoH7fm4eslEycewO+ADkG6SwSgc7ZLaxMRD0tAAYAoW8ZSgzKrDjvWzH4DjLYBinuybjd++8HQ93e3sbLy0s5j5y/V6auPriG9YigJak+1MX/OVDyHeRvsOy2K+Tadd2qX/h8Psfr62v8+OOPq/lS1XA5HKfmxA65u8+W99ADAq8ZFbML2/7JiJrkYoC01WBIgHTrGNf3pkbYataQ6oBBEY4PwEMChSNwQPLf7MRxEKyrwRrPmxjHcbU/hhObnDh/KwjjcH/99dfVUboRUUAqVaa+70tSyVhfXl5Wx1Y6oP/www8loZrnOf74xz/GPM/xu9/97ivAwE+AOzqGbrj/3/KgbRJ501JCxYG/Afz83Yi68Q7ghd47Wd2W4VkXM8oAMgII98AnWWcdcKiwECxIhvkO946oe9qcBG+rJa58bHWVQM+90TVkS6Bkri5748u8PlzbLX5myyFJvI/MVQsCIwEI/4Ru4z+w2aZpyqZvZGiZI0/ee3p6KjrNGByAvVna/t8+wyRARK1mAi64Pj4K5p21wDc6qUD26JLjlckMv+99HAYGPMTWB1e45crkFvKxLRgoooMkIgBhEgzGylobsNM+yJoiO8sPP8Raul3N9sJ1sSPIEmK1QUyXupjkx7iPEzvHb77vyg73AQdERLEr7JfWUtYI+bOOh8Mhur76DBIX1tBJNu142JoJVa8tfgD95nrDMEQstY3c7cRt20YsaeV3eD+z7RUcM/dsO02JceiCbRt5mwhGvuhPSqnYAFVhxswakBgzbycj6L6rp8ZjXdfF6XyK3a4e9sG6IV8TVyTfTdPEPM1xPq8r767gGSNYdvgpkyxeH3SacZowN+HhvTvYh5OSct15fe3iK9L6KF0SQXzSNtEwruSFDIu+JCcyNXE2sW17tGyQI/dwhcx/R/fsl7GN33p9d6LhvlIzBmaBELg355ohMujiPwbP5CxQZ9vOIu10Efi2KoJRuQffiQSsUsTXD3Thvg5O3rTI2M0qbgO2F8GfxdlzLTP/9FbzfZx+7q9f4qo75XsEvIga9AiOlMi9n4YARxDpum71oCXmT3BlTQA6nD7DZwD1BjkEemfEEZUpcEUFucIIs35s5t5+n3UiALPGEbkdgXambRsNgGzrVB1s2raNX3/9dZXFcw2YIW9k82Y/nLYTu5TS6mnnthWClIOydQMHYdbBAA5G3zo3DHlD93avAL3+yJW5Pz8/r9gT2jkMsl9eXuLu7m7F0tJD/PDwEH/1V38V/81/89/EH/7wh3IMLrqAvLcBFHsbhqFUkFx5srM3a4lPMLPHunEf1taBy37IjDPfZc7I15sGAUNOzBkHa2yWzM7awB3Qw7jwgQ6qJCYc9WsQbd03MGyaZvUwQ/QImdtu7LPQGZMWBpEw6NiIz+0H6GOfjA+A5soZ1QcSGpM2XAv78/sRUWxsmvKhFLRDOpkx++gEDZ/kGMJ6MzavJWvLeNyKyD23SZ6BPN/l4At8QkQ9OpbvOcHg1D7v7YLcImnGP7KWbs+DXGD8ED7opteUe1wul9V+D/vybesfsrfvQB5UJPGJyNxEg7sSSDIcCwAxBUMscyQlbGaR+R5jRQ/Yh2gA731PrAHXNHnUtXV8rMNutyvHgaIPVEC8L5L7eBO2542PJzYNw5BbX6624goGT3hmPZG9W6TBQADQ4/EYS9Tn+KCP2X7mmJf13jj0np/InVPeDKSJSVRk3F5s22WOXnODXK6JniG3EtPTusJiO+OFL3ULYSy10oH94oecvG6JIL5vvOf7MhdaiEwuMHf0Ht30WLf7Opao8+ce9d/rU/fQGx+2Yr9tfXTyXeJlrLsnWC/P09V771kEv7DextFbwppr4a/+qycaBvncDEO3UwX4RcTqbwzeTmNZaobswLpVbO6PA0agMBXb/l2UgUWgVQIDMwuHoDBuz5VFMMtgI6PEh6KgIDgSO1kDbINMl71xIIXpiKq8eQ9KPc6Qyki+dj31gGQD+UVUB+Mea5QRJ+qnNPP5reFiiHwOZ/iV0rfrDeCsixnqiBrkeBIv4JaghWy8KXpbzcJwzPw5yBkIEaAMRrZAm0BNxQPdhN1g3VkbHCgJDsCAhA6AWZPC9Xnc6IJlQtUEHSEoMS7vq9g+7I5rcB0DDuaC04Y8eHp6ipubm7KZlXm6Cujrn8/neHt7i9/97ndF1hy5ejweS3sSCSEg0M/CwE/YpzihcFsJ80Eelh1zM5OF7nFft9XQIsiaQjpsE2P0GuCVUiqte/SEcz8nbKyjgYQBWUSUk25IOszckUiS4JjhNjPHelpmZj2RiX0Q9sPnDSoAMHwOPcdnWHe37LXZWvw4/yZZNolkIoLvcW2TUAbP/s48z2V9GLN11EmB/YJZf/sfB0sCratDtkv8i5NZ6ye6a59un8I9/F3kzEZnTkFirIACwL4TRLfr+CF3JkVIHk0gGRRZrugD68g96E4gzrpCvO7ZXid4Tmz9jKJti27XdRHzFJMIIezPpCLJNTaJfviwEQgxr53Xa5py73tK6yN8S3vwmOJw3JfTotAj1g/bJ2a6dRLZog9FRwVotxikbWpbEbpbksOuX1W/WbdpmkqvvsFs0e1I0fW1wuO1wHa3HQX2ZU6o+S466bV38m2b2lYMvpXYj9MY/Vxb9yLWp5phiyYj9vt9pKjJh4G/CR3bvMeAnvI3vkcc4O9b8gV9RB+Yn7GfE+SmbWOaK5HCvPP3m1LFslxNVBvDmLwBO7gbIKXEbvES29FTMKnJU+bAT/yF/SXXJl5YjtgnvuJ7Xt+9R+N/+1/+XVnQtm0LwGFQKJkDEeD3crkUlhkDzMFjLCcLUVa3waAwCM3lQDOZdpBWICcMMLOMkQyOBQB8urpiQbNg3riLcZgpL4JNtbqzrdL4eyh4RG0/o9XEVYBhuMQw1Cfe4rizAeTN7ii8GTQMzKxYRE1gYNEMbkliMOQty+D5EQhxCrDeEVFadVhLWo4AHTgPgDKggUqFAzIy9P4Axm9Ail4A8s1uucK1ZdFtxGZCWH8DQeZKQlfXqLLzTsbZuE2Fw6el8Bm3n5iNWZalnMkO44H8HSD4O3/zNaxr7sMmISBA3t7elvXB5gxUCSIc4dv3fTw+PhadO51O8Zd/+ZcrhhVGFDvbskkEaRyXmUiXj9n7ZfKBIAHYceuE/Qh6gk3gJ2y7+B/LjeDuRHbLylGVsf6YmQT8Wbfxi04+sTeOufR9nCwdDof48uXL6mQx5I9dEHwNvvFryIukk3n6mTr4Q+aEziNbs16uHDpJcLuO/Sk6bJs1E24Z8/m2rc+ucDWA9XUrg22R6xqossYO4PZxrjyYbedeJh3wYTynhcTVa837JGuAHdhp6yHy5HcDfe/TsG83ked4y5oaZDghMkA12YbPJdmB4MC+uNbNzc3qwbBOFt2+hA1xfQNsfBt6uKQMjpkfQN3tOU6iec/+ifUkfnId5G59a5v6OcvveDxE065bY5ApBACJkkEu675N2CMixunrTo0CYsXqm8wcxzFS1MSK7/G6dsuU664/kyKWeogAuuw2GftJZI5/cJWPa25BZQHVTa3Suq3GxAPE7/qzbez266ddm4k3qW0sssy1AkIc9tpP0/robWNFY0Y/Lww5Mjb0xMmJCVhswXjBvjVv+l4//bvE98gneGGbjI/5Mgd8N/MjXriVqbRILzVWbOfj5IqkAh/c933BaKwBum2yAB3DDqwL/8P/9N/Hb72+u6KRT2pI0TS19SiDvCa6rjp3O+3cs3eOy/UINRaxafJxsbznM+8JnAYZEVGe11GdTURKFRiyCGbZzOTj9FwRIKBsv4PQ/dAnHB5JFvdl3iju09NT7Ha7Amh9TxTKi4YhODkCjGAoKBDK5cAxTXM0TTZaM3ZWXJSKxMRBF2Oz4jIm5B1RHZZPm2HeW+Dhpx9jJHwOx27niMN1CZpr8jcnHcgExxZRQamdPeDIrIR11MHcLCcO2UwIe41gPXgf1t6VAubAmm9l64czOtCZEfEmev4zM8T6cj/0x/bA7+gSAI3Eht5bQMyyLAVg4ADN5MCwkIjudrv46aefin5/+PAh9vt9/PLLL/Hx48eYpqmU5r0GTjBcKWIO6AWERUQ9WYvNndi6W4kgDww8kEVEFIfK3AgKu91u1apm0OSkhM+7UoMf5H2AE9Uw/jNrh34xT/SEFqXthmuPhc9tGWOCFjoOQMCOfKIINoL8DRbMcFJtbNvcVuJjjNE7J1e2JxIf+3QqQqwdSRo2aiCGH7Q/Rn95ATIM6lgrgwx+mnhw9RIw5GOesQ+qvYzZe4awXyczxD3v0TKRQJzA1oZhjL6HnVyibet+EIPnnNimlfxrclT9gRMI7rkli2xnJs3MpsIoewz9jgd2jnG6kiy12poPK0EX+h7QNV3jU1fAdtM00bRNPsloqYdkpLaN1Fz3RU1zOf3JB7HkCkA+1We4XKJpazKZKyYpIk7Xa3YRUZ8gbyDYNPVgACoT1XcskZrKRG9JoO7qE/A7WYfrSYHTNEXTtsFDdN+vtmcSgxa5eZ5jvoLPJS9qNALwTbM+DMf6vcwR48jehF2JU1kvL6uqLbYxz/ko62Ec4yR/OIxXn7jMMc1rdp/1wTbxEY6hYAP7BWRnWzNobdumVL5NCmDbjrMQcvm+WXecvO92fUSsjx/nWl3fxTxdY3osse8zmTMvc7RLW8hO6zqxwBVPTh2NqIA7Ip8ihSz42Xb5NDHa4SEWSDJMOHsPhp+pZQzI53g5acxyqnM2UeSHmHKNLQZ1goHvNRnYdfVoedaQxMrj+/te351oLEsqip8d+xKnEz2h6ycd04aSjXsfKVFivUTbdpFSRN/X3meATD1Gr2a1w3Apjp5+VJxZSnG9dwWX3pPh06dgXEkeWKzsfMbsXJIXsI+uy0fVmtGCVR3H8atTbnzOvxnLlFIBBzgjM3/MZ1tetKHlBW3ifB4iAiOqjKvBFwppEFAYEjFhJFsY0vF4XAVurksFZVKgiIjV2Onbdr+nnyIeEauxOdnBkaPoEeuSvhkJM2hcj3F1XVdO6mJ9MWbkzT1hoHAwbilxULGTM+vu6oGZPUCoAT735d7ek+FKE06fz+D42LOCA3FvP7JlTHzeD2sjcSDw3N3dlbYAdMag1pVK5MfGesaOTb6+vsYf/vCH8jT7z58/x/F4LBvLcdZbQIut8m+AOn9HXwF16AjJBja1fRAYQJSg53Ya/MswDF/pSUqpVHS2jBiAkiqOk1FshbVdnzW+PvmJn67aoGfIhyTDfd7Wd/ZUORBYb5kLrJX13fpvuwRouQ3PYN8JAIAa2aAjrgBhi25pdcLGC9sy89w0Tfzud7+Lp6en8jczfXzO68O13MJiu6OK5yTNviUiVqfGGWznyns92hcf6kAPMcB6wBJix74O185jYmPlEtNUyY1pmkuSZxJmv99FhqP1uQzZXiDJovgG5uukEl126wwJBfdhLm3bxsvra6Qmn0a13+/jMjxlgHo6xf6yi+V6oMsccyxpimGarlX3FJdxWunmbolo2y7atonUNtEqwVvm+nTvZVpinjJwGi5jzG1tnamtNBHLvMQ4TtEuEVPMMaQx2qa2Vc/zfP3MGPO0xG63z8flRn7YWNvUSjaHHFCBHMd8alPEFNN8Bc1LxG63j4gU45jX8XTm2M8U79dDR7KMmxjHSv40zboNqe93V61NBV+UcU/5xKKIJVLTxngdU5rmmGOJaGpVr2vaiNTENC8RV195uOKzZa5kTsVLV3t4f8vHzaaIyzhck76sWcNQHxLbdZUYHS450bXNY2sGtyaRSOjRQycrWW/r89WMc7aEodtnazIVMYzX42fbvB+CRHdZIrq+LYnsNF2rEk0bacmVoK5v43Qag0N22q5WKVLKD7LLH4565CyvtMS8TDGwJ6rtottl/921+OCsZ/tdH32XZZDi6/2Z4D4ng8zXGIHP4wu2HTSuthDTTdZj91uCa5tEEx9ZL9Zu6zeJ09tx/F2v7040PHEEkrPymtFGrJ92mxmaCogMAtySYoBMhePm5hg8uIWWnoh6MkIdl3sK674PBMyYAGLcg0XJzqv2rbIY1YHPYi3GUpZ9fX0tv/MiqBIQARV3d3dFERxsrUDImOQHdtZJyH6/L3sBUJzdLh8p/Pr6Gh8/foy3t7d4eXkp7CEGCkAFIHMNACgK/OXLl3KyFEDRQZN5Mj87GFgas/BmCdiE6JOg+J4NgeuyEZXA56SUcdD327b1Sdi8CHR2VqwP10RPXA1ibszBfeIp1b0mgF6X8SMiPnz4EI+Pj+V3M57WEycX7juGESWJob8a+TBWJ40AB+9vYuxmxytoqa0yBAWSTPbJkGx6XxGM/TDkB0yiHwZunz9/Lkn4zc1NfPr0qZAQjMdVMPTJoDWiPnfDrPS21OyEkGTfrRMAJ1ruSMy9/4T74odIpPg7MkPH8D9UBNBdwDBO2P7E1TUHfezKG6Z9TQNABwkqKU3TlIftcV/aWvAhPN0XOZosgMBhPhA1BEHuyeftr9FrV/+YP0GM99EZ64CPjGZM2DsyYt8fhNG20hZRNyqbiELOBGfmBzhycmgg4xZMfLJtFZ0gKSZ5YWwmRogvEesHweXv16TIP5ExRACV26w/U+SHxtaN/94rNM9RWii5Zt3jV3utt1Uk1mccx8LA5vcjtzPJ9yEbgBRzxWb3+8qg9n2/2jeSUorz5RKHw77IyVWvaZqj7/qVX0am1nvWCUA7z3M5yYdYxueRoZM9ksGaCKyfEdJ1XYl5kGjp2skxTmO8bw4JMLD24QxbQsq6jqyT5Ltek3z8a2HUU0Tf9evY0baxa+pegZSq/2NNIFhcuRundTutCRMeNmy7TSlF13bhDhJ8rvUbIOqKMmSHiQljEipYzIk1MZj1/jbLkEo5160k1hzXKZa2Rd+zVqLXRDfXsv5wXeSFz/c8sOk1AVUrP/gK5ARuNLDHJ1HVYK7V3mq8Bwswxmkc47g/lGOFI9YHNRGX8O/ci/G4MmJMa1LQRBD+34df/NbruxMNBANrv+5JrItiRdjt+qL4CADHiKHBgPPgOoAFfZmUoM2kIRj/PStnfXgewvGzGWwUKEEGAYcYx+ErEBdRAxbfNdBhHHxvGIZVT7pL8wYXgFm+w/sGtCQGTjJglGFu3Z5BEmfHhgwd/J2pEvwJqpdLfgYDDB5rBKAhaGxbpTAiWqMcaM00GkyllIqsdrtdvLy8rBJQgpB1gvYH2Gx0AOM2+EC+rBPJjRlorwXzA6yS8KIrEbUH1smq3ydgfvnypRi5TzEyU+x2KzMbvMf+FrM83NMBAFnjCHwfGFTWwsmMWTT0E9b25uYmbm9vV+xmRJTkhP9IoNnECqBg3Le3t/H09BTPz89xd3e3YlHRZcvRiR7z8XXRV9bIAcCskMEeeoR8XUHi+parx9F1XXm4l/XAVRKzPvgxn/7joGW78X3wjU6AIRGokFQ2tz4A0e0X3BOfh/9wMHOwYEwkVQbjThCwJwOIrR46GLPG6Bdr4MQeH7IlBvic+4CxbUAN93OCz3rjy7y/zX6XuVCphc1mLSKiJGWVna4bsr0GjMFrZDDgKqyBBrqa17yCG3wpc8av43Orn2tjHIegZTmlWgHMa3kobXK+53Z8JmFI5vAZ3g/SXHWd97FPbMCJkm2JE7VICsoG6sO68u2krlUCj73gU+d5LvuoTGSR/LsSblCJ/jhOY2cmnmjzxT9Y12ty2Mcwrg8dMIjld/SDtUcfu65bHSSCLkTECl8wdmwMm3VSaSDJvbDvlFJMYqrRp0IICICyhvn3/BQ/V1OR0ThO+Ql/UWOrAS/6DmjeymeNq67yXeaIqbZXuRXb8/fT5bmfk3psh+t6PWz/xgv4CmTL2O2jTIixJm6ZogKGf+L+tld0FL/E/SCU8S3IgPtGRNFLj8G+qpAoqbY+oVd8Bjxg3Gb/RCJOokvcADtwH16Wl+Pbb72+O9EwW7dd9KapRw26d/F8PsfpdI4ff/wxxnEsm+ZwhAamBMn39/c4HHJpDPYUJ++eMByyhdcoO46om1nNpi7LUnrM+UzEEsNQN77a4bft+uQDjBZ2F6dLWxaK0LZtaefwvgRAgReeBIVxPz8/F2YRVmAc66k9sMg8iZoxwOaQdJilsYIwT75HkkNAwnj6Pj9UCPYePeC6W1CHU0Mh7ezRH07cIXt2m9m2nxQmnRdOwMAJJ2Imy45lWZbCvPP3m5ubooOuoLC/huvSSoZDeH5+jnEc4+7urozHzCEyIBn35lCMGF26XC6lpWO325Ve+Lu7u1I+5R5UFmD0kLPnRPmf+duRstbYhpM/ejiRJ7pvJ0KgTnJo2Mnd3V0ZE+P9B//gH8Tb21vRfZ7u7uOAzVo6kXPy5wBDEOUzPhqXBBZ9qQTIsjoFj+862fFeKoNIJ9novVlq6x5yBfhHrE/c43PMxaw79725uSnAEvvx6XFmkkhCWA98EXM2WDGrhr9lLG5nA9TZbhm7wQJ+hOsyDr7L+plQQKcAsswFX2YQ7BbQiNrGh80QOPGjJprQF+zaQBM9Y03sx/gJSKLi5+d1wFQbwJgcwI4jovhPs9fY8xpw1XY+X5uKJs8ZMWgdhiFub++v1aCxtC+3bX2gKySBiRtiEDHHyaGPUeXzKeUHzGGr3p9jn2ymHHkRl5iruxyQPa2gJEnTNEXXdjEM3itR16X259cH+m376q2P1ilXnM0ko6++Ntf68uVLHI/HkoTjA5uUolfbLYmmWXn7KesdgM8nqHFdJ/fIw77M3RIR6yN8kYEJt5iXlY7j88/XudqXEZtzIlFBKHqQY8su5mndml0rKes1dmuP5WBQOs9z7tVKlbBwkmDClbmDHdBt7k1stT+1Xfu9+riAdes168T9TALbX5h0wCa4vsmdLcmEroIL8GtURPmdtTJ5RhynKo+O4CvBMG55ckLhuOeEkPvgOx8fH4t9kPiZlCdm4Aux5+95fXei4fYjG3F2LmNRfAKRWxJeXl6Ksex2u/JQq4gorT8oe55o7hVEEABdn6xiVh5lG4Yx9vva2gFYQTFpKxjHsbB+WXGaWJbad0gi0jRtaUN6fX0t17KioXg4aDbTlqPylH2ez+f49OlTAWFb5oVEzMcIWllx6sgZpQQM8DeU1oDQAAIQE/E1K0vwj4hr0ncoAcR9yGToGCxjwUjNBphJ4DPcg1aJT58+rcC8kwrPkaSLMeDgcLIEDTMfvJgfD8aKiHh5eYn7+/vSrvH4+FjYOLe5sS44qW37AZWLzCruV+Pi5Q1efMfrZIfkKiBy88vMyOVyiYeHh1VyhvMxc4UtYgO2qW0Cii5CDBgg4VANPLF3z+vp6Sl++umnVTLjDXauUHqtvV5UPvicnxpLkNyyTWa3DazQ0S2YRWcBc5VkaAsAB0gR6NCBiCjjIjg5KbAu+n6AItszzCn3tSMnWcHxk1SY6aJCgEwILszFh0K0bVvac1xpMajhPcbh6hp2TGBygoEuAdxJcEx8mFkG7HmtuKb90jTV5zo4gWANnBi7ChcRhWyC5HAMs4yd1Fp2zBXfz9zw+TzMkmvQskFlOKJuxKytV3U/AXJkXMjTxID1JIPvIZblmnD1uzidxkhpfRQ99yah9r455Gnm1WuUYn2iFb7NXQvMi5jC+8wDQFjaM2KtA7xy5XoXsVSsgY6jo2bwI2KFB8AAjAeQZF11ywvj9D4GPg954coXyeP5conliiVYZ1eUnAhbf/BPbgWEAGDsfNZjhPjbxhP8NFgHnz7PcwyXSwyX+uwnk11t08Ruv1slAiV5nnJrHvIA5BbSIGqF3vLE73o98clbUhC7zLqQq1hcy/7fIB97R7/AASZerFNOkvCzteKXY7iPHzfZgY0hd8c8J9rM1+QY/sGdFf68O1S2VRzayokzxB1ilZNlx93iw5Yqd+TH37fVeOTixI/Y7IoecW9bucCmTTj81uu7Ew1aIryALErfZ2Dz8vKyqmbkjLkysmRhKeW2HlcWEGhe1LVCmnXGGfvIO4w1nwiSr0fmioISaGwYPN12ntcPAGRzL4pEEoXCAcy2LSNknafTqfToEyReXl6Kk6ZKQAbJHFBYgw+UHxDLuDjyFOVCEbYGw1gxHmfy28DvBMLBDXngtAx8CZSsndcJudCOwPsGaTiL//yf/3N56NvNzU3pNSYocz/6EG08rLUDK7JgTjhhs7MGknzu4eFhlaQ+Pj6WZMRsNXJlHluwQLULvceGnKxvbcVsCoks8qF1juC6LHWzPQyh2TqDA+wPvbGDZA1gXJnft4KtD1FwkoB80QHmTnL+888/xx/+8IeiE8gNZ0hrnEEactwe0Wk9Y43NLNln8AKoDMOwOl0K4IUMmB+2Vv3buh2TtWaNAH++pxMABwUCoYOJGT2fgFP9YQWcDnzLspRkwdWsiHpUtit9Ly8vBXBG1EoVc3PQRGedgPJ51oIDAhxokR1yxPbxwcwjorZKbYkO2iXNJnK/Aoqutuw9Z9iCW0r5DmvvNeEnNkecYW2RjdcQBhJ7xL+ZXZ6mabV/ydc22NpWHfg7AZ7EBd18enqKy3nIG5uXJaZpjK7v80bdJcUw1uodMjNJwxicePrhZIBc1ulyeY/3K3ACCGK7Zt2ZM3oHVsB3YFcppZjGqZwUxbgY6/l0ipTWbX3WDewa/2XwhT7bR/BirtvEBcLRMsM2OA4f0F/wRiwxLzX+MA4Sa2yOsTJuJ1smF00sbVl5V0KQN0SlD24AkCL/fI16H67BPedY70uc53oIxfGwL74Dvc+6MESKtPLD7FVEp7mfSUJejreVza+ne5pEiYiVr+OF7O7v71fjdiWC9bYNTNNUjph3lQO5+IV/cyLBNdE9Yvq2Mm0yDn00rqJKTlyxjK3nJKSMdxzHQtZt8VbXdbHMS7TNukqHP+a66CD+yEQPa8c6mEThP8ddtwuayP37Xn/GqVNzvL6erix+iv3+EPnouHMMQxQm0ME0IpUMbxiGYryfP38uxuHMD9DBJiiUBPYYBcnPjKjsoTNIslaz8GYUURgDvIi4ZumMoYuI6znPVyfprI5Wp4jKpJjB9EK4tMxCL8sS5/OpXPN0eo+U8kP5DDhZ4IgoQYv3nQw9PDzEstSTAQgmJE0YlTNQOz5K0052DApwHn7eh1knDAxj8ilhyMTAZZt48GwJrvf6+rpSeNaV3wnyy5LLqW6fsAMy+MSh8x1YeuZskGfAToD1pifrJfNnjHZQxRGIhTPThU6if76WGVf2L+EQnDRaJtiIwSb3Zo3RLVcDpml9DK3X0U6mBrFqOwBZy57N5D/99FM0TRMfP36MX375pdgizo1gj0wAF8gVeblVYmu/fMbBjvXeti+xngZOzA3fwLqaheL72CIJIwCEdYfBxqk74XFyxjob+BJIsFHAtnWFtYP4IJDwPjLlHk74uT/3BGD5M65i4Y9pMQM4+m/YNv4A4sXld/sc/Ajkwdvb23XeEfmI1yXGcSixBFvCF5lBd+uIfZorNRGxSsTyaT/LlUB4Ku9vjyguZ9M3bbRtc/WNu8gbsdfHxvIyiVNBUhNNQ4tdbjHOviHHU5595LYpJ932kfi7lFI+irSpTzFmI/Q8z9H1fXSqfByuZNr5dLqe618flgth1zT5aNglIo6HQz7tqskbdVlL9MnjYC3xc/zcnnCGvJZlidSkmJVwsaZt28Y8zSub/NZJaY7z6C8VRRhv7x3AP+GjaJckjtrn2gdBBJzP55jmWpFPkWJ3qO1ZfN5trE3TRNs0uTMIEDqtgb/tkuNs+66L45UcxRbbtlntAXp/e4vuGou7to0pfGRp1jlsBj/p2NR1+YhXJ/u5WhHXDee1QuREj1Onuuuxren6b3zpvFxj4DzHPH9dmWvbfDgQJ5I2bd7Du/XVTrRZD3SK311NhRAwUQ1gZ/xcyy2l6BP667hr4ogDaRwLvO5ONhgPvtuYhM/wMElwnjsPfFDBtyqbTcoP+uNa6boOTdtE19Tj3Vl/1s4Eq3GDK1O8jGFIoN1ihd5Yt77n9WclGrtdF12H4nKkaD0pxc729vY2LhfKu5Wp8v4MJuifGeDsIj+grrIhTPp0OkdKzVXxztE0S6TEGeX1lCYLjnKfgRcsR1aoXfR9dRy5fLjEONYeW5SZQMQ9UFxXenDIKD3AOwfHJpomt3/c399fk5C4BrfKDEVEYS5YfK7vlhgYarMIJBBmXczuM26zW87YOaXHIA1D3Z7hjyEz77u7uxWwoYXMlRWehYAcDX4jYtUe475h/hZRn1oOiCapQfa0uSAfzr9vmmbVMuISoQGrAwhywCm9vr6uklQAiku4yNwJGcDUVTHsxYk2R8Pe3t5G3/clqYUJ3+7HcP871S+C8u3t7apn1qDAQY89QgBgry+6A0McUVkjdMjX5OVKx48//hhfvnxZ2Tn3dhIKGEUeTtoA4wbWOD4zTwZoXHfrJCPqZjpYGeZi8sD/ZuwmEWwLLsE7KcAOC+iYa/mfvzkpZw1hGQm0jAfbQkaMjbF7vm6dMQHicXtjLHpswOzqClWxLXmAnrJ2yMrkDMmr1+ZwOMblco7Lhc2xgIZ8dDlkiYEca2UWs7bftcGRoVwvt8VO8g8+EnmKfALUEk2Tv5/1YLn+Lbc4kXABfJYl4ny+rHwrySZruN3TgV/g5arglkCwrzaz2O9SIVbMJnZdF2+nq023bcQScbi5kg+pieNtPoxh16vCOs+R2q48VTiWJaYl4nS5Ar+mja5Zt9d47Tx24gZxp+u6QggxJ/wqunoZq2+MJR/1ahuCpINEQa8gQNDziPqMHNbAGMAA1ofYmChzu/IwDDHHHO/nXFVfRgHzro3pSjS0Tcp6c7VX9D2v5ZyBYErRd20Myxwploglnw6Vgj2ftWIVEbHMeR/IzfFwjRdzRJNiuIzXFvKcfPT99UnZuz7med3K03ZtdG19uCn4ZZ7n2B/yMb8RSxlPk9q8B0OVKa/VOI45QbwmydM4xfEmk4XjNKyImSY10bQpmiXFNOWnfxODUkqxP2TdjaXu/3I12xUAfBvxD1/lWEr8QydNvLhKb//v/Whm/l1dQ08eHh5W+Aas5CQVfQLcu6pD5enl5WVVYfU48SFgXGNLx5z5qnfNkrfTpJRivMrvVTiJsTrGsY4QTI7tEOH23967gg/iWsRPx8Xfen13ovHp06cVqMCYq0OvQaScMLHfxzx//QRHApUDHM6EydObjTNFIW5ubkvyAjgCIKOwZkVtMAAqGCy3UvnklWWpm62YM0HdQdrBg3vibGi18Weygg8xz1P89NNPZYEfHh5UXajnJbtqwtwsZzPcBghNU1tpWCuDXYMBKzXGCZNjhnie5/LQRIKJg8Ht7e3qjH8zUWah7FB8rCY/SXBcviMAuzTetm0pA/LaBrSbm5vVqWUR9cjUwsTM9UFOTnoInNsqAjJ1wMTAAbkw98hie/oTeshpLIwFduPm5mZV9jTwjqgMFnYDqPHhBJY34+M0CeslwNS2ZjCB7fF9Ei1AsveqkKC4gsjfHh8f449//GM0TRMfPnyIiNpHOs9zedKzkxUzUDhjAzh8jNeCpNP7g6wXBuHcv5byq6/wOpMIoHusudfGOs61TUoQEKlo8ll8HXrM9121QD+xHeTj5JLrW8/Yh4ZvYvyuuDBv9Be9xR7O5/PqOTFUA2mFMiDA3xLIn5+f4/b2Ntq2jQ8fPpQx+lQs2m0hYkimI2qVr+u6sv8EG3P/sBnI87kmZxX0TSv2Dv1x+yYyy7KqR01CiOGPiBff8oFmA/lpkGxfZZ/FtXyYAeuC/fm0R+bOSW7cm3G4ZcdJEGvIv7k+30U3TVQ5uTA4cjXHJztiayQDvG/yhuv7IAF0nPGwl4vvb30KsREdRg6sN7Hd+IJxAJCcqLNGTZMftuZ1cKKHf0SOjBefzPy9vvgpwLFbvrAX9Bo9sV1F5FYufvfJR4zDBASkAnZgXDVchhjGit2wVTof2HCMnN7e3srcvObeZ4K+LcsS41wrJX3fRzd15d5OoqdpijSm4luJXeiA9zM4TjJf7u02JuRhObprBvtnrQ2m+elkgv/wBRH1dKtSZWjqQQ6uUBuPmtS0PThOWG+Nr03g9113rRhVvTbRwbXw48Ytu91udWqbCRpjBsbvJMIJIZ/zHt/vef1Zz9HAyaFI26DMzdk/sNtVxpqTKNg30bZtYadpP8D573Z9SSJQcJ8r7pNLSHK2iYHBBQrqY/Z8EpXBNouOM0f5zYLyd5yZWU6UebuBi+tkYLRuncAB7XaVqaE9ABmjLIA03rODqRWZOl+3oRCIkLmdJ/J0CRMDIwHYzhNjHscxXl5eyrhgHXBw3qcAcKQ/mIrPly9fyjpjMFS0XBGy8dkROGD1fR83Nzfx+Pi4Kp3S68h8+enEh/Yhg21a1kjyuKf3/aAbMHkYs0+iiajM7vl8LnpPafZbT4Q2w2PgbTbPrAq2FVGdBbLhs+gC47Ajds8w7wGm7cj4LnKEdUYfWS98w8PDQ/yzf/bPYp7n+PXXX4uzvb29LWNHhw+Hw+pYWSeKb29vpTqFXLBVxkvrpBks/JDJBYKZ72HddmUEvXCiz34hVyvsl2wjBv74T4I1PsmBy0kyf8e3sYcJfwK4tK54ozlBP6V6EAI2jXzYM+NkHgDgNkr8C3pguVKtxO/e3d2VdbAeclJPDpRzNE2/kqHbuvDfMNZOkKmiQI4gb56u7bZPn+KG7vMTXULfTFYwnm1rBrqFnFk/7oGPQB4GF/zOGEwimYHEf9gG3WPtJHdZlhinqTyN2Ppi5hQiAz0xCLcMiKfbvZVUqCFoWMdtOwhjQldcTXRsxt+BHwDhJvMAZHwfn2wfiMyxMSdKJJrICvk7YXDCGOnraqd1Jul3+w0zyY4vXnvWru/70g4NScQLf8j83RpsksK+3y1sl8sQsayfK2NZcH+qpsY5+aTQU9EtfIfvze/8G5xBIozvJ/b5HtYV7xt04sJ68323vxMHjV2cVBogA8RNetLeuR0ncjaZDmm1xS+uQvCTVjsSDnQQLLddO1dj8L+O47xWZOuyjuHGaPYXJuV4uWpRcWglG9Bn3ttiYBOA2K8Tw996fXeiQbvGly9fymY4BgFAYPMfwOzt7TUiavZ0PB5X7BClfMqWZOJ+AqW/GxFxuQwlcKB8OEEDH4ABv7uH00HteDyWJxk7qGOYMAMoG3Pmug6kgEwfUWmnnR1OfiJmSikeHh6uDye8uSoY/80lyaBVCUXghYOmlQZ5eg6MFRmZceNl1iZizSRgzFasbasKbUOMxw6RI0gZP0a/DbSsV9M08fj4WJwQ1/SmdycNOFbmaQAKOKBsC1PK/HAgOBQcDXPDAHEGMC7MYbunIqIykFQnCC4+9cLr4QDC5wiYrAd6hN5iD9u19X6lbUWFa5iRRH7ImM9ZDugA9oWuAhK4Lj9JsvkbSd88z8Ue397e4scff4zT6RS//vprPDw8RMSaIQEg8zvjsq8AQBmcbeWNXPgeSR6tdYz55uZmBTbRP2SK3F25sG8CHG1lzjyoavgUOr6XUiqJZtvWfRJcn58mdrAHVzYZGwmM5QmYdmA04MNfcCy2KxUppXLQgllWAj73M9vo753P51KNIEnH9uZ5jh9//KnowOvra2lPYu/APNeWVYNXfDgsHeuW1662wXg82Bnfx9bReYAHsjYTW1jYDQnhgzP4rH2C18V+1ZUqg1DGyT0YE+vCOpilLuxmrIG8iTrep3rmBDSCPYpTASHEpG0cgPDDD9T9AfXQAHQWOzLg+1Zc4bvYK2vjhMb+aEssGEBzbeSDPplo4XfW2c+2QB5zfL3pt8SaqG1jbse2X8bvWI6+holKE4CO9ejBMAzFR5nocVWFqiNzjKWeuGmygyQD34Ye46OQtyvfEBDeg2b9dlLE2DiQYZskGLwaxFtGjBXM8q1KhH0kPsl2RgJt4Mwc8WPoJ3iSMdsOGQO6uJWpgT5jZo1NPDEObJaf2F3btqsT9Zi38VxKdS8k8rQ/dgzCXlyV8LOx8H38zTZpf4rsbJPbRP17Xn9WReNyuZRSuLMzDIeFSinpAV11hzsgyIKnQrHORis7S1BA6Ple1eGTEPj+MNoWGkfKAn7N0KaU4sOHD2XvAPckePK7AQ1jc8bJvLjO+Xz+KrliA5QdM8B5WSJ4YixODEV0WwsL7tL2stTyLc6C5MtyQkkMamHSkRNtIre3t6tNcU5WWDvutQWAbqlx4GRdSQr9QMf1xs2+nBTRNE08PT2VqgqVICdjjAMHP471PHnWD2fBBlB0z3tCzGxZf8wqOpjZyN3mt03g+BzJqNe+bdtVUlaAw1JPVgEswg5t2z6wSTN9yNmB2skq3yFQwIgAnEiEWFfswbYZsXaMBAXkBMg06MZG7+7uVmw0tsb1zYABGOZ5jh9++KG03LRtPYeciiXBumma0qZJ1bNpmvLsDwIHeuSA6UBCoIHhRz+Q8+vrawHjbp80uDUIAxhhPw5K/J25sL4kxbZVJ+r+3cm4q4NOjrgXukogRw7YOvqHrhD0XBnlO64qMFaALWvI+qLPEXmD6Pv7e1wul3h6eip6sCx1ky5EFLbtRJ6N6pUxrrI3CDBrx7x53wkgOu/1MkHjZGE7H4NPA050hvWxf+De+B8ABCDVcmb9mDuEX95XEKu1tP1YN/B/TjoZ7zb2oYtOyF2xrWtVT0x0Qu3Trhg3OmTdNwn2rVjHd7fkiXGB/TfXQW8NCAFPzNX7CCOuLP1Y25O2lb4U6ydUW47MC321HyFG0X6IfVv3sCWAPf7LOgtRxFq4alSSv1RBrYmQZVliXqbiM71nikTSrXjoO99nbUxOYBdOFvxsEcdWPmdymJ8QhX5+kluf7I/sq6cpVw7v7u5W+mjsgeyxTf6Or2R9+Bv65ViM3WPv4E3synvgTCxsK4NOkvGbkF/G09sEdpnXpxCixyQOmdyvj4qA3EIP/Hwb28t2jbi39wUiQ3wDsmE9fuv1Zz2wj4vj4AzEWAjALgFmnqOwiYBPZ+JMhICfhVD71bgWRgXjb5bGWSoCJ+gQaDnr3EnSNE2FHTTgRGFwFMwdo3UvqNkUAjGySCnF8/PzprVhjsMhVzze3t7KMxyywdZ2ExQXZ9B1XdkDwYv54XzNUpj1gT13udcActuiQSDCOBwccTToBO+bKaMKZHCN02c9YWbMLJzP55VhACIBrt6HQj/xMAxfgT/3tLMmsOmn0yl++umncjRsSqlUhGzYEVH0BplY59AhwC734N6AWhybGVl0hjVEtxi/e3Aj6pG+ZhwAyowJveZ7nPyEnttGfW0zFeiOK1ReE+TlZCBifSITlUN06XQ6xcPDw2r8JLLDMMRf//Vfx+9///tycpr3ahj0ck+SJpKralfLyoFiU4fDoRwtjS04IXTFjd9xxrBxBAzmatnzHknuFuA4mfDL4NzgCgLAgJL7o2P83UEAGQFg8MMRtbXA4NyMoMEfemg202uOf3NPPX6RtoSmqQ+1oiXC6+SK5M8//xwpNavKQG1fHUpibn+E/TNGxo8vwocaODjuELv4jqvVx+OxxAF85uvrawFABjFmKAF7yBsixe2EBtaM3fsQnJiaUcVfmOFHD9GLtm2jEYiwPKyr7vm2rXmDrKu9yMztdYBDx15XMrgm89iSTtghc3fSzudMwgCut8mjfZorcAZhfMbJB2vlsdg3n8/naPtqd+jOOI5xPBxif9WPLVHD2kNoejwkDvhE5Ec8QWeGYSiJCPaM7zLBY90ziCeuXs41qcUOkW2kWi2CPMF/e58QssIGX15eSqsRANutt/hM/mbSiTVm3f1wTcvRdsWYSEDQN+8/ub+/L3iUn+BFdB39oFqMnNAn+wh0Hrm6rcq+k/F/i3zDhhw7jBfRKZMz+FH8L/dDX/q+jzSv98HZdokVXkvICkgrz491xb7xf8b3jutOlvkcvux7Xt+daJhJwCkgmFxhiKvDzidD5WQhn7Dw9PQUDw8PK6Mw82LwgTISDAxq8qSWiOhWirllpFg8AyyyTxQQA0SINhorOoJHqVAYl5UwSjMPLDCLdrlcSitBHncTP/zwY8zzFPO8xM8//xJNk/uaMVgCBVkqBuANpsyPwIJzMbPIZwyQnfFH1DIbjtLPW3DyQ0Bh/V16Rz4OGjCZXC8iAzPWO6Lu6VmWpTzbhLlYZ9ANDORwOBSW0+DVrDAgx33w6KPBm9kx1jClVJ4CblYMnUQe6JCDLfrjvmOXvF2StC47uPL9LdvqwIrDoZKBfP05bMQnTljvzfYZVNOri72g56yV7W+ea/+4AQ7lYGSQUj2QYZ5zdeLDhw/le/v9Pj5//hy3t7fx+fPn0nLF36nyMUd8h2UGA+uNzJa12yhc6dsm1bzPvfzsC4I9OsmT3S1HkphPnz6VRNwspysOrAMvdMTPUtmCJwcEAixrArmDXmPbrCd2EVGPfsbHmeV2cDVwRp+dHDuB4AVIMfBFTrXC2Mey9FfZ8wDBOZalnkbjB2VuSR/bVfV3VJ+baBoq6XMcj/fFpwBOAA7YjOVxPp/L8ducRni5nGMcp6vvrs8nsI0DFNxak08KmktFgO94Eyk2QjJlvV2WfMLRsqQ4ny+RmiaGIZ8qtUSKSOt2Eu6Bjo9j3r9SgXVESvlhtfg1+7BKFtYxw566HdggBABHpdyxkjnYR2yTQCcMW3LF8Yv3XJnv+y6WiOvJR/lIWU4Yi4jrJu98PH6Jp3Mdd03g52hSF8s1tqN7xG/8WdM0qwd4Ei9NEvjAE8bJ+LF9A0CqrT4wAV+JLK2zxiC0Js7zHEss0bRNXAZORhuj74+RmhTHY463Ly8vK8KAe3j/JonF8/NzRNRWcSc7JhT5LnoD6YHfwK/abyArE5foBZ0xxj+HbyR6+B5IB7dCIm/WyNVb9J772Qeb8PELbLHFAhHxlUydeHM/bBK9BDuaAOO+2MQ4jpGWJfqubhw3huVe6KCrtxFR9jw7OeU7WxLR2Nyx0b7Jse57Xt+daPjF4HEqTUMWuETEFJcLGVm3KhsBIM3SEcAQOJOlHG7WPU96/VRYs3EYJgDNjCVCchD2eCLqE2X5Dg/Vg2UwIIVlYOHcX+csE2XEkZlJnOcss67rY78/xP39/cr4eJ4ESgq7bwbbQM/gnPnYCGDnkMMqgCnQuMxnhcaA2KgbEV+tDy+uT6Xo5uYmXl5eSjLhygPfN0hnfSKy8SJ7qjq3t7dFB6g6eJxmPMnozRJugwM6ATPNtQE0zIfrec8Gm8ipqrDezMEnz2yBotko1oE1oVrDC8fu8+L5PskU9sT+HzsUwBTrYDYGHTG4ZO7oUUQU8NF1XalCwHD7msgR/WF9XXWijWC/38fT01M8Pj7G58+f4+PHjyVBMzEBAQGod2KL3rvca/DDOpPomETw8yMcPLdseUq1+nV/f79KtlxFQ6eR5evr66qFhM9xfx8lTQA1IDEhYKfvjX/oP8w/MuF9Ah7B16d18VkOaHBig3/E7znZYR1tg66wwYC79cT+Ycui5XmmuFzO5fr4aMcGg1HG41OOKjvLqXJ95KNy62ZI2FyTUrWiXisjxKm2bWIcfXJZ3aDfddU/YINZvyLGESaXQ0fyM5SWpcYKxy8neVvGPaUUw7jEy+tzHI+HWKaIZWlUzagVIYAqoHAcK+OMfZ5OQ0zTGMvCEcD1+R3YP22xtK6uY3HdrA/oZvy0abiCA6BCp1lX7MTx0Qkp686/zQKzzkvUVux5mWK+tlcfbw6rxLFVVTpSE11qV/Nu2iaati9+9nCtZKO7Xbs+Upu4TlIF2EUGyMkyY02IESYq3d4bsX7KOXsnuDd75rBz7C8D7T5Op2yTp3OOhefL6Zow1ePSXW3ymhqM+pAfr3fEeo8Ga89nYPXbNu8/eH5+XiWRJq5ZV/wfdsEYsBUnu9sOGVr7tuSQMaLtjPjiSgLkDn4aO+TzTpbxDYyfcW7jNu/j97YxhbFuY7CJsZubm4h5Ls/M4Xvb5BaddAXICZF1i89j54zTpKBjBJ8ndvKZ73n9WYmGA3gVwhQ8eIggxX+3t7dlc7jZ1YjazsPk3IPctk0cj3crphLFe38/xc3N7VcnVKBs7pnzWBCKj9R1kCN5AJR0XRePj4/lATPMgc3eMOhmKlAekgUMzAHFxogh4vhRRhTalRGcNaVJgxGUA6X0SSfb6ghOE9AM4MBRehMsMksplX5rr6HZZeSOw2Q9+Wm22BUPGwJOxEEJmbDfAnbUTBAOxkcik4xcLpd4eXkppxs5sQWw++hDVwlgRgCIzBu9ZRyu/nBtrrdlhJ0MONAatBkUAjK4DsE8oia53qCNvNARxsL6oxu0gsHYIVcACuNxwDGLYSYFx4gewEThdJmTmamUUvzFX/xF/PLLLxERcX9/H4fDIf7jf/yPpU//hx9+iIh8tDb2ga4w/ojM1jj5JaiQWL2+vhYiAH/iVj63xHitCDgAevwUn+P70zSVp6CbRQMgbRnZZclVNbdX8PKxnQQKBzmzj96/Q8DzPq2INQPpUjl/d5B3gOM7zMMtFs/PzzrAYi5PHGddqG5hKwYi+CKS4Gma4uXlpfgl5mtCgmCIX4FEYC6uCG3JI+7rAzpMxNiOrQPIIetVrqIDRrGJ7CsrIHcVOdtSbc90wpzH18T5PBViB71gnPzu8UZEzAsPk1ufANl1bUzTXNoF8SvEDwMarp+B2hApLWXd8tjyc0KOx5vgIYP4ZM8B0gV7NkNvObKm+CgzodiIfSL4wokK9zPDS6wex/ycB38H2fFv7AI9YkzELOzIc/F13L7JdwCU3qQPKfn4+FhkRYIA4+/9jBFR9nexTw8chH0TF1JK5bkOxEnGjYz8gN6I2qaFnozjGL/++usq9mIX+HD02UDYLTcQLk4afA8IC+/ZxScSS40VmDNrwzXALvwbHLfdvG/g7UqB9Z3rGxshY9bdpDT41OQS90CvkJN9MqfgOfaavOaz/A0CkFjJ97mHSc9YIqa5dhah+7YjfmdN7fdZP+yf+2NL2+QlIlbxZOuf/5zXdycaZmsQXERc2afKJLOwZL9+mjUPUEMwDpw4JNphTqe3VdUDhwYbSQB1ywhjdM+nwRjAHgexrT4QIHkfw2OsPo3DLxbAfdE4A2fNW5aGhGVZlrKRaftsCHquDfydkLiMuW2V8fWdBDkr5Sfy99xRdIwFWbH+rAnzxZB8QgZO2oDAjImZ267rSuXohx9+KA/Gc6uBEyyvTURlU5Ev7BAPorGekQShmyQcJGo4EXTDoIY5wfYRgEly/JAqZEJLmJ0y8/b9cThuXQGc9X1f9Mkta+wl8KlbdhiurhyPx7i/vy/yduuYAYl1cBiG+PTpU7mPnS9A3f7BiZkd+DYRww5d5v1H/+gflf0zf/3Xf102fjNGgj0AgLkxXnTd+yt43/ripK6wlde5AQTMfEXUTckRtW/YSaB7a538Q05YJ+7v74s9mKElIAKkDbrMpkXUk2Zw/sjS4J8n0SIz2EAH/GmaymbsrutWiTN2ZIDI39H9H374IaZpKjJ5f38vfeEGnARuV2kgAJA3gZD4wnxIFmBL8UeWif0vPod1ybY9ra5tv45fRA+JRff399cYk1ZjNGCNiJVc8QcGcQa0eS6H4r9NcpjV5374y7ZtY4k5ur4+NBMbPp/HiJjj8+fPsSy53ZaYl08TWz+tGV+f/dMUXUfP9xLLEjGOU3RdPn7YrDE+c/symHfsdGLD77Y3EzhmZpkf/tOkJL6sgKiohw0QPyASDBi3LDV+yRUKdBLCzdW4LbBkbM/Pz4VoMAjn8xzdDqAD5PKZt7e3srcNYuPu7q58x0DP8dtknD+DrElgwWWOC8QQVw2wUbcuuzppphzQDpnDf74/9s+6MUbHQPbmYueMCfmiE07SWEP+ZmCPfTtOIQtsyOvtJA17BDdwZLvt2HjHmIx47X+jo8jBRCDXYdwG/ryMm29ubmIa6smSjqmM0UkXWAmdc+y1f2qaXOUlGfbfqO4Yozspt33/1uu7Ew0CIotM1pWBfw3eZtbNEDJYn+7AApDBoyBNU5UVhbSStG23CvrOeHFyOBD/9IKizCQD28yYwA7DiME50zNDaQNm3iwIBujsFscMQMRxAB64FzLiM1zTDmYcx8L+GrB++fIl2jb3CfPEbubt/Quvr68FMMIAA7C2TJhbziIq6CBo3d/fFydGogNT49OiuNa2Z501Op1O8fT0VKpMlhv6YJBYGcYKIrZy3zKLDmTImuTVQYP5cC3k7nW2A6U6gNPhfVdtrKtmNWHSAR5U0aiu4IzNVhBASUj4G3rP2qDvZhqdDKHDBNvD4RCfP3+OaZpKwsvczXiZnTb7bwaFv6PXnAJHYurKEPP/J//knxQZMH7afpom7/3iwZj4AVgqt7Y5eEI29H2/OokO+yOxs21bzwxOsGGCmA+PQFcM2n3kNvbDHguzS9zLgdvAloDAiS/bZB8dcvua5zDP86qFEmBGOxvz9glX+H7WchzHVStE13Xx9PRUZOTEe7uxmN/RZT9HYGujvOd2ClcJCOT4D+aFbfNC5yFHAE7oBvdy8sDRuRkUVh/A33NMWD9Hh5567uVNnRwfjI5Yx2Az0T2P37qXml77/GqV/HCAjEmlQuP7nM9TSbiIf9n37GOaxpim+fofpE0f0zRH36+rD46z6Nz278Qc1sdEgv2/wY99KDbv2Ml80T0n4YwDP2dfzzXRbVdlDKKQNWsEyHTfPCDv+fm5tH2SWAPWTCZCZpFEkPwZ97DBmmrhFpCjf/f390Vmjl1ch8QYe7MO+Dhp/O/d3V2ZI7IneUCmYB7/2wSkdZNrRERpVWYdkRMx06RlRK2U0z2CDW0fR7AsSzw+Phbdwna5N7YAdjGZarn532CgbUWYa0KobveYekwmbLhuRI1H24SJdXTiyHskBtvK7On9PZpUk3SuiR8zbsWnYjvEd5OsTviZJzrrti5IPOSCrFxV+Z7XdycaLjkZaHRdH09PzytG04wj/5ltB8jZSZgFPp8vMV+fMIlDhEVu2z7muWZVGDenMxjsY3xWZp8GEBEFkNjAWHT3tfH5l5eX1QbhrTN8fX1dlQabpilP9cTxRmRHBoiOWJ+GgzEAKGgTeX19XZX7cRIRUZIKG5nZwHXvcP0JkOWzKJMzbDMWlGY9bqonrDVrStB0hQC9QDYcp9c0TWlxYsw4SjauubRLYvD09FSCCIkb1/M4GZcrEhiRWQiuhWxIcpxg22H5icUYqBMit6Cwvqwx4zJjQhAlGBvgMW7Gimxx6Ga73FZhB0hLC095x1nxWRzm6+traWHyHquICjQB5tiHk+5t4h4Rq5PqSER932VZSrAcxzE+ffoUbVuPXyYBYSwfPnwo/sEsKePiPrxSqpt+SWjQc3TGz59APswXJ8upMCQaJGZmM9EHryl6xvW27DDO3AwYctwmspygh20BtG3bnFbmdWHu+AcfNw67yPi37RXYjIMUgIYHj22DmMGh44eZemRgdo+5IkcYRidf/I1eeNbTjKkTnnzfrx9gRkDF1r3ubCJflvVTnwFTWW+jJJXoYAYVlcDC//H3iBRtW9fMbUD4dvvSso5TRKTaYsRcsi8bo+vakkCxtvln+5VPq20mtBpPkfdsLNE2bURaIqXKpLt/3mCdmMrawIQyb3ym4xHx3xgBn8l9rBduybUPGscxur5W23zogP2vySyPE9/KeE0+8T5/wy8zV5J4dIk2Hyqy+Gt8+f39fdHXiPqcIboZeD4ZdmcW3iAVnUgplVYbbMR+HdslCWL+6JiTiG+t4bf2NdjX2i865pi08fcMqAG0tlWT1KzhthpgGzXIZX3wK66m2P/YB3NdcICTAMsYkhZ9sg9kDuiw/QiHppiYZV2cjPL9rb9FJvipvm2jbeqeNO/xcfxjLugQ5JsTRCdfyAdc79hte0Ferip9b6KRFqT6G69/+1f/pjBynDBSAVXd60DABSxg4CjaPM9xd3dXDJDFR0HywgzRtrUUhCLlQFFBsBUMheV9DJ/gg4MlW3SZF6U1g8QCGdhiNGYurMxfvnwpFQkeQoXjcID1AvJCHoB2nIErC2aTMBzkDTDAwH3qlVtvxrFuPgXIbHsKAbCu9DBugA16gNJ/q0z4+vpalNLnvZuVOh6P8fT0VGRDEse8CVIGrU6W+BwJgsdnMIHj53vWPVgg5oxD4+V2PAN3ZIjTIBByD5JDxrllBpzAeF25DvaFnphpwaZcOWPsBAj/HeezTUi8MQzywD2pnE9OgDIjErFubbGszSZGrBkcSAfsx8mx22ucWDJHQIrBN2NiLV3yx7aQucEi44qo1VXv/yEIsc8MWd3e3pYxIQsHRperkQNjcyLPT+wcfcTevMF8G8SRxXbvBtVDt+mYgXPlinmYoUevfK4962ZQiU/l7+i1qwMRUQ64oPrhRMasmckB35M1Y41pi8PG0J/D4VD2wyF/9L4E6r6PlJrVvgL7cftyQAdsX0pRDi6galKTlJqAb4Fa31f7YC7TlFun8C1uj+GeHM+MLhRfkfLJVbapLJ8pctvTvAJF6AN7TByHkfU81WqEfUOkOQ6HmhjzPWTJZ1kb1hBdsn0QL1g77mVb5HrczwB1K1tY+t1ud02Iakx1OytripwZO9UG5O4Yx71YM06OIsnxJmf87ZYNp40L3ST5sK6zhvapBuncz+QYn7tcLqXbgrli436ooll44hhxAfk4qYcA2doQOuGefa7B/SFFIR68zqyvfTpYirhif21f7Xv5Ok7GIKLwISSB+Cbk54TOLenMz0QV67Tb7crhBozDsZt7QFZvcSXr6vmAvUzQ8xkOluFeVMzmcYplrns5uDdkp9vcWH9iuJMPyxCbsN2jy/h4twtiZ8TdaZri//x/+5/it15/xmbwFKfTeXUE7OWSHXDTdGXyGLTZAgZo8GI2nsmRTWWF8FNYm0hpiGWJSClinqtAUEyEQrCxgyNg8VmYURg4txMBjB34DfpOp1NpNWLMtGLQ02unZ+AVUUv4BoZWXidpEbW1IqI+GRZFAOygzGZyIqK0ZZkdcpltWZZiQMwPJ801ncGbfed9t16dTqeS1Dw8PBSGz32cyJ/xUKUxUwXgtCPAAbjlC+Bu5UcvAH0ktmYNHLgIAGaYmSuyBXhsWyz4yZoiL+ZA9YB5AVS3QR15c6oYQMibzv05xuN2w4goffboLAme+3DNDll/XZVgrSLWz3HYltL9HVoOnp+fvwJtyIUE3RUZ3wv7NCgzYCEJ4HMGZwZPEbV/Gp23E/WcsEV0Euf//Py8Yn9vbm6+SnwgBbAHmHUYStuOk0kCDQdMOJEwIYFfapom5uv8TudTdG2bT9npuhinehpURERq2mjaJabz+Vpqb+L29uZaFYIhpuUttwRlOeaDPYZB95znyMw7LH/+rxJM1adHpOCo7hwT8oNVp+lL5I3LU0zTpVzn5uY2jsf8jJN67arj6K8TS9bSuukAXllMn48fV5Z+LmMbhrr5kXXxJn+D35TqKWVmoufy8Kw2uq6CDABwPp0tP5AQG75cqLRdZX25Ju/LEn3XxjxfSZSmjbbbxTguMY5zNE3EOF4PL2kiOJ51uFyiadtIqYm+72JZhhjH2mKEz8q2GhGRjzntOtrQzllWyxLLPF9lda08LHO0TW2xMkgygeBKoDsKUsrPa5jnqQDcru/ieHOM15fX6LrrgQNXe17mJcZpjF3fxzhOkZoUu3aXxzzP0Xd97HZ9vF8PJOm6NprmOof0dYwxoML3okfEWuwd/4FN39/fx/Pzc/FT2Lyrcujo1t8AxvHdx+OxVOPxZVwDf0Qc4xr45f1+X6r5+ChswgkYYBXijhjCe9zLVUcTFOiIASayJK7iB20zBtpN05ST+Gg5fHp6Kg9CXiXLS20vst908oY9GcBbt7gOfgESAPkSZ6y3rCeJBL9bRsQf/IxJJyeixpXbGGY/7oospDC4JCJW40IGTqhIIvb7fSz9HMPlUnw/CWWkum+ae3lPoFuhwDAlXqQ1YQvBjU1YJk6ekAHX+a3XdycaBKllYdP0qQBZWHwzdhgfJVICKZNzD3vEusUjZ4j7qxFcouuaGMf68CJafQwuMUQSFQNFPsdGczPfrmJwygkKej6fy0JHRDF+DH3LmrrsbtBpRgcF4rveJOzyGbIgKUIuAHUbnIET2TBJk5l7lzKtZC5Lu/0tpfyQO7cE4RgZA4YGcOIEjYjs/Pk+TDWtMTh4mNOtAU/TVPpZ2WjHfRk7xm2GBHbBBkN/bETdMI7BUbVxgmx2jjm6ZcmMBetiHcCJuGqFrC2Lt7e3FZuEwQNY7OzNerIWHotPMrGDw3HBrlk/kQ16ilw8duQMMGPtuBYPmUJGzI05o+/YuJ21T/2wDLmPGSTsAv302My28LuTfTNK/B25OGD4/PgPHz6s2CGSBnyPS8tcByBA+xUOnTVkPsuyxIcPH+J4PMbf/M3fFD+FH3PyHBExzlPMGv/5OqYmLbFEit2+Ptn+8ekp6+AS0TQp5mmKt7f6PIZKOtD6km2PNisAdERuYc260Fw/87bSFXxHRMR+XwmPHCuyfpxOY3AyE3PEZ1Dtq2uWQXv+dxNd18bxeKhAVazvVkddIZvnJZqmXdnjNC1xOLCXplvJGN/MemGr2GEFrfk5GtOU1wWSIqLuPXTFKcdA2MpMkqG/4xAxzylS6mIah2hSRNddmcMmRZeugK+lAhax3+/ifL5E29Cm2cUy52SqaZuYltoq6JatrIu1Ktj3x4jISVfb5mQJm8vr00a3NJGP5m1XMsG32BeZOJimKfpdH6fz+4oBj7QEic7N7bEQEk17vV7XlOSk69sr232twF914DJcoutyS9f+sC8+Z5ryyWWQjOiYSSkTNzzrAJY7r1NNOrBt7/fBNxKPXcX2M2vczmLAnFJ+eC+AeJqmsn/RVWxi7ziOpfXGyTXrkImC91U3AfNFx4ghnoMxyxZgEy8ZhwEmnRHuTCABoULw/v5ebJpYja0aiDtxdVXDVQrHD1pVTVS6AwOdfH5+LhjDeLO2CNZWZP5jbq5Cc21wCfdh3J6L8Qp+nPWmQwLb4H6sif0T+0DAUegV8lqWJcZpitPVz0zLHJfr0dmNYieyAftBjkOWoDuMz9Vrx1RX0E2sGWdZl37r9WedOuXFoazLghgc8ZmIuom7aZoCdpzNEtwvl0thAnMik9k+b2RCUABHKg0kETgelBVwYsUchqGAIxaQMaDgvO89BQYinz59iq7Lz/pwyR9lxEDNzBqoUnqdpmkVrDDwy+VSWg6QIUbNKTJWGsYI6+YNqm4B8YYzb8ofhqGcx325XIqiPz09Ffl1XRcfP34sTzqPiMLA4+hIBmi1YV1wKByPiyLj+EiszudzeYq0Ex70C3BAKZvxOyPn2jjoZVnKU7LtxNERnAL6wjyYF47DQMfs/HYdAEXeFA0rgw6bhZ+mKe7u7oruISdsi2vxN5wB43LLkJNlknwng04AcLhmpJDflr1gjowJXUM/acHxQ9VcfakAcP0kVFfX9vv9qlrKd0houda2KuENhQTKLTvHPSgTY8voAHPl5YQF1hJANc/1yF7v6zKZ4gSDZ2jwGeT39PS0Sm594hkApVZC1k9355V9aR2TWfq+7yMtS7RXHWfM9nvfYrhWjHTUfUPb9fL7+Cxs0KCNz6IrrIErPVwbG2euTVMfxGmiw8HdzCzrNE3Zd+931+c+9FfmdppyhSClSHEdf4pIkWKa55inKS7LkGsQyxJd3+VKzzAV3/D68hb91R6HyyUuqT7fY5kjmtTGPM3Bw/FyVSOKn0HGuz4/PC6vR34+1DBcom2bWJbMUsb1oWvTNEXbtXG+nGOcxuhSFykt0XbNleGM8uC5DObXhzuYAceX5LWrurR9+Fv2c22JUU7Q8aFN0xRQ571q6EVN8jKYfH19LW1LJr/YMO2E0gAVvXAlFntk/dm/w3dsu5AE+FZatx1HfSiDk06q7YBGZGSwjf5hW8zLp65Bgl4ul1Id9WZm1ooY4nYYCEB8CrrPGFzVxncjt22l38QMYzXh4nhGcmUc4lZmrokstwcZODmz7rP+JITgRuTAZxn/lmRjbe0r8KHeRI6um/hxUkwM5b/b29tS9bGv3uJa+2DjYhMV4FbjHK8xdkQMAJsxf7qDuKYrauiUK2rMhaSXk//ocri7u1vhVcvdz8ZCd7d6gizchWD9/a3XdycaBi+AQAwGRXBPMU7A2SJGzCIQHGHiAaKATj5PL6IVkHvAELsVy8ENgycowfS7AmPGYFlqy4uzNwfGrTLjTJkXY7BjcO8f48ORbNkKlMh7RHDUnJBjkAlwenx8XIEwKhGUS90/zvU5XQhHSXsK92A9Kd9GRGEvzAphON9KOAly255P3mfNDRqRP3Lxk7/NEqAjERVEOfmLiNVeEyek/gyBwK106BsBiTUzaAXsIm/W3POwXgJscTqMwYkVwdslbTMhXJv5G3z7abwEA4ABesQcXMlxJZBggw0buDg4RcTK7pyU0Btu5o//XPUhyQAEoQOMH71CDuuqZ02MbO/8jvxJ5pH36XQqB1KYxcROmafZbIMwVx/NeG0rEgQg5klAtnP3MdtOYPleBrBTtNGu9I3Pp5QiRT3dh7mklK5tKONK15CdSRbPDR/I51lXEjlAD2tcWOy+X8nKLBj2BchCt9Bx5EnCgt5H1MMnuI5JncvlEq+vr0VvAITDMMU0ag/CvG6zOF3qiTzopFnKzMA3MY2zgBZ7MVI+z36aSvUlyzhXcgp73Ha5PWiqySEyzhWn3G+d91bkRKPv80Pedod1cp2TjfEqzzaWZY7UpIjIP5uUrq1TS5GxHxZnMocx2B/TvsKaIleTHAZTtk+z4IVcS5UxR+chh6znxA58ALEYP4Su4xu3Ldf4Ea5nm3l9fY3b29sS+yPq3gp0jv/c0sl9qUoQT56fn8tmbmIEa21fwP62vu9LRZ51RP4QKiaMuAb2iU9ETxnj4XAox7474WB9aRGLyHGPSj6xB5yCPXHCJP7D+5/se51M4NOpZmDHEVE6NHgfObLuzBXfbJLLeMrVAOswRzYvy1JsH7mbDCTBJBEyGw/mRK/HcSwH9lAVYxz4FZNIVK7xkczBB3MQR/j7lpQhSaADhbZzZOrDkYjdJKeQOhG1rbpNKZrUlNMhwYdt28bDw0OJU9Z/Dt5x+7T9FC+PnaQfn7kl6f6u13cnGjgVgBoAhEFx1j3CYFHYFIRzQ/GpMlDGPJ/Pq03JKBCGjuLD/BEM/YArA1qAJOUvyqD0cvZ9Xx7kZQYFY8AhEJwdeN22ApgnyXCG7VI6hm2ARgA1eHEihHPiPxIcqhqAIYILFSOCBgrt5AbnxlGKzBvGc5vZ8j5OEyfD+fdk0TgrXmZ6kQ0ZNlUSO+CI+gDALXMOsPJeBYOj4/FYkqRvZeXMGf3B6VRAE6syNbrLWm0BIutonWuappTBOQEN+TAWwDFrY4bQeuaHyxmkb+3RP1k7HDlOA6eLTbg8j8zRQeZv5sSsnUulTjYAcW6jcxA2G8U4/f6WUTN77WP6uDafQT94mTwgOAD+0R2eKO9jcfkOpISrIwYE2D3y9Zw8Dt7n+ugY+kbgZF24B2tJECDI9M0ulqhtZZ53uvbre77IYeq63Osa6yPAt4ycGUf8JLri+ZkYwSdx323CZF8SEQUkOsh7Ld1y4uR4S2Cxntin2xCHYcg+/XAX76dzuWZuE+L4TPzwvPKHu1131ckUPLAufzdFSm04ni5LRD79cI627aJpINXyPsJ5zv+N4xjjNEW67lmBxJmmKSePbRdtCwDIyczd3U1E08RluMThkPeCeL2ahqpk3qOwLPM1yblERG2/Ic5h4+ieN8G6dQM79ylk2Cf+0rHYJJqrGCUhibqurkTYPk304F9o40AHWGeq7m6pdNsndsQGaKrI6Cj+Hb8P4PTeDqo3fm4T40CXIJSQJT7jouTVeIfkAF9i3wcYto+APEkpxdPTU4nzfP/t7a18n3W+XC7l6NyIuvHdiQykAv6H+MMct10S7LH0cfvEKvsR4rljHPMhrrA2zBkfhryYH2Pc7XblyHNXxud5LqSRfQI+G2wIGEbnLFPGh+9g/Rzjt4Qn+pXtrynxJGLdZUDc9z2Is67MuyULGc/zXI4wprJH0oa/dysbhD3zjiViXioZ6GqUCV1+dyJkohuizCQv8/Q6RawfCvxbr+9ONFgYlA3lRBG8R8HKDqBE8V0iaprcCw2I9tFuPv4VhaWc9PT0tGpvAQy7JOeEg/tyT05P4dpklAgPIGDAxLgAigaiGIuZQgNAAyCUy6wIpWlfk3m1bVs2sTmbxFD7vi+tRa5YRNSnaaOYEVGugXOMiJXxo5wOLnzP4HD72mb46AzfRfEdxEhQnTTgRJgj90dXDD4NODBgVysIZhyPyjr6IYgu9fpaZsnMBpmld6tKRAWC7OVBlmZLYbJZR0rfTkjMHCJTMw42eO/B4f7IDn0kAfKDydBTb7rnHt9K8Lmf14o1YM5OGqxHBvFci6TY4Hrr1CAgDLS4NwGbcTnA854ZGHySr2lm00HU7QZmg7mGgyhj9/iYL7aArPw+/omxIxNaQldMadtGairDjdyWZSktM9g442rbNpa5tq2QCBpAYlfWsW8ltFSfI+ox56wnc8Am8cH4WAdldIo14d7YEcAQIut8rg9YJdib6dv6Wb47jGMsS8TlMsQ816rf8Xiz0tuSrF319Xi8ibx52UeWY1dN7HZUQXJnU9/vYp7XDHhEbnki4UhR+9MhHw6HQ/Td7iobNiHnTd3zPMf+eIjmnGKa5jgeD7Es87UVYhf5qN0I9ljc3t5cx5NinquPw77RL+yJ9eGZJ9inwdxut4vb29vS845PNukAkNvuE7CPso/EP+NDnXBO01SeofCtSugwDHF7e7s6Mhcdwka24An7N7iMiGJbEFrES3yAk2t8Kj6P69OGDDHq+1ufkSX+xPJgvui6mWjsCDkRz8BFTvLQY2QDBvBBKga82+qWCVATdW5/ZTzEcCcqrB+2ROvutzAhmMKE0zZ2ELfxB2xqhyDymN3pwnh9PLnJT3RmW7UxqWFZME8noczBh8a4o+Xjx4+reI5/ZT5Ufvb7fTw/P5d1Z28Fib512ON6fn6Ow+FQTubsuvqA45hqjGJMELrGntixdcL3Q9dN5G2r+captq2/7/Vn7dEwM0hQQmENMH755ZcC1Glrcv80QQtnA+AhgFlRf/nll7JxEoX/9OnTCphwXZTXTJUzOBzM+/t7vL29lSckw4a7hGjF9z4QGyT3wxmiuIAs9ksQJHFmZKwkE1SKDNRp7XCg50xv9zQaPOCoKcO1bRtfvnyJlNJXJ0JEZDDGQ/FQIsrOd3d3xVnN81zYEoNIFNBlS8aEEqPssAYADD4PA2WHtE1WnAA5OUDnzLhM07RqBUP26AP/WV8jKkgB8DMe9547aDAvXpTICfAEaf6z43AgxGFtk3QDf7MLdoww6w4qNzc3JaFgE5iZB9YB2/VeK37yeSc06AZjsLN1EEaHGRtBwC+vQQV065Ns/Df0BZ+BjiBPZG6Qzwtnud/v4+7ubnUkJH4NXTPjyfw9J6ph/A3bRy8J/H6eBAHZwZU1BeSYGLGP4T79fhdJbDDPD7lcLnE51yDF2EridLUF5MaDw/gcDBnypk0Je0JGtC1ugws/vRYkcyYVXA2cpml1AIZ9keMKQZkkxowc+mgfxNo1TRux0G4J6MjVg+wLeDBmrgpUgiRv9B6GehhDXu82xjEnGikB3udoW46xht3NG+irPk2R0hzN9Zh2V8jmeY6393rs9eFwiKZNkY915/kVESktMU1sMu5imsa4XKpu1ZO+aMHrVsAEv4CfIx5F1IeJ4d/4HAku4/Xr9vY2Hh4eVlUB1opNzkUmURPotm0L851SrTo4CeI/Em1iLPd4e3srJxTaL3F/5ouvZx3Mmttf2gZYE+J8RJRDY2xP6LtjOfZv8oHx4U+9t4gKAWt2Op1KQk7XQCNbx/aOx2PpZHDViWSL7wC00RFX4K0TyAO7RiaWF7F/m1zAoiNPE5WO5diz/Tu66HvzWV5OzNj3xwtfz9jARybMqNqZyMJvmBRBdq5EuarF9UxaUcXBxvAThRS6Jk4Q6qyfZWHcgrwsZ1e5qWxP0xQPDw8lqcfWSjt6jAVnmRw2mbIlhLBxfjoe8XnL3jK0Tn3P67ufo/G//pt/VzI1FgBAgSLhGN7f3+Pjx49lQ5MDEkbiz5t1NLPs0hEKgZJZEA58GFpEFGZ8C1oRLMrMT+blhwmZ6SEDdXb49vZWFg3HZMBCgoSiTdNU+meRJZUJKg3OZFPK7ODT09NKCdy7ilzJtp+enmIYhvj06VPZFGTw7swZ5WZcHz58KO93XVc2zm3ZBweCx8fHYhQ4MTtcMwM4hy1TQBICEHRp15UpXq5EMP4tA9C2bTFUNoTbiXPPiChrhW4C5Bg74NMBxg7D7UYAb97jZQcK0+FTzMwWONlGV/g+1+TAhP1+X/owSUiRqR25HT3r4LYp1oV/O7g6kLrqQlscf0fvKf1uWWfWhTVEZlyTeeIMPUZszowd4zDgxNbQdXwPa+4qAt9njtZz27+rAA6e1gOAsXvbfQ/0wWzzNslCb3idz+dor3MZpzHu7+5LBRb+vG27KxjOpxvlPv4lYmEzbd4/sNvl50hURnkopIeTTTaYM8ZtIsX827YtBAa6wJry9GTW2rqLjm1/WlerD2I/T40hx+OhECZd1wfH9WY2d4q+P8SyRExjPbEsVwvqnp+myUcGx7LEEtdTmsb6nJh5WaJJ9WQ7gvAwDNfjVmuVD/00G3xd+ej6mpRaP73utGsh/6ZtYhjGmJc5uraNiBQfPnyI19fXeHl5KWuR40Bu83IFkCTNiUPTrp+UDnmV7Tb/bX9NSuc5b4yPlEkkWjre396jaZsKkq+xhblBmA3jGE2TSpxi/gam6BK6jh92ku2EA39mwtAn61iXvC50VtTnidS9GvYVfBaA7rVyl4DJVXwCmAAf5GqBW3rxKa6WO8Fjjo6bxCJiP7LcxlGPwQATf2uCynGfrg5X/LFxiE53pnA9xvzEKXdXnWCN0SPHRa+zyVHWFJxnP2PWHTLaVXB8Ap/BhkwwuTrMmiBj2+WWJNsCdeyf76MbxFvHkbZtywlcyNe4ktjsKpxjYESs8Mc0TTFPU+x3tVNinMbo2qu+Sg4mVF1xcSKMXpmkw/cxFxNttjH+Yz3+j//DP4/fev1Zm8ENYJgU4I2BYURkjGYXXYY0S2sBAJop+ZxOp7i/v1/1JiIIFtlMRtM0q2NWAWs4LdprKPu7/cJK4LIhBkMSg8JRugIUG2hiuDh0t0JVRqoCJydk/A4gMCNjhfyWEmDwBHmzi2wOg523ojMWDBFFdU+uHa/BkxOMiAokXcIDjDH2rbPs+7481dRAy88BwfEAsB1ccCKASQIWyaplaxYKmQGUDKTQIbMe2wTJiYv/ZmdIMGS+bBS0LkdU4G1nTADku3YA45ifjn17e/tVMmYAZNm5SuAxIXPkYn02MIhYtw8ZSJAkG0zjvNAj5szPrT9ZlqVsJCQBw0/gX3gfvUGXkCOsE3Nh3P47cnEl1WDYFQ9kZaaMtWXc9mckWOgoyTLvbQGJZcX62uEbTF3O55jGMWJZSnBZ5ukKSK+AfoqVDlaGcb4m8/X4R2wG/1jHXNsK8HkGWKwhJ9O5Left7a20h/JZ5Ild4nu4jisgXt/LZVhVz6ZpitfXt5im2tKBveTngjTRtllHT+d8YMUSc0zT1YfOWZbLfK2YFfLjHPMys9f7uiZTLHFNBtoU8zJE16fYNZBCsMMppmmJpllimsfYH2gTrXuykB8ETwb3lbyY5+oj0ng9ea2pScrb60ukiLi9Oa5sxXFvHLMekACM4xgXNh6vkpO+tOmN4xiXIZODL68vq2oD9tz3V6A/XmIZ2AyeYhiHmBedAtV3MU5jjONQ2Hkq88RqfAH7I02e4d/wVwZ0ECgQbPgdYiDV/mVZ4pdffim24ATMJB2MMMmxKyUmXGzH6KljDCdp8R0wkquD7tvn3sQZJ/PYADGCNlvin+1wv9+XtmPI3ePxGA8PD9H3fTk9ic/b1xBX8fOOFRFR9l9ib2Cxbazt+76cZoScsHEDdGx5mqZyQiH6BVbE96LvTs4hop10eY8EWAcwj49x3MNe+LcJVgN9qr7uUHDMYA0YH3EA/bG+uDJhXYU8Nl5ERoydMRZyY5pye1TT5ubMeY60ZPql39yblzG6E1Dkz99NlBifmWAl+TIu2BKpf9/ruxMNLxDPQvALIWKEW6Xh8yhC7WmtZ1i7Z5lkgABocMP3ST5QQq7pnfncj5IlL0qKEesnrFrB9vt97Ha7eHl5KQwtwZEMH8cB+2pmkiTDGbcTGpd32dB1PB6LsuM4eaiVS8xOYqgcEXC5vw3fyk5SYJluGQQAPrIhAURRcahsxLZsMQ73oVrBLXcnRwBeHwrgU3FwmG1bT7Zi7dFR/h1RH3iD4RK4XLbFkDAwJ40GR8jMFTd03oydg6N7biPWFTYzDdgAP9FhZO6qButcgrtaAFx2dwJnIItNodeAQoAfwNtgxuvkuXMfPm/9NkNlmQFK2aCJXpulxY6Qg0Eojo17Av5J/B2w7bzto9B9gp0ZetbAbA/vc6IMa8l93FJm4MD3CMpmlZx4APQZH7rM92y7DiTWX7Ng2+BlsoRrs3bo0/l8vvrE9SEH/rwDrxm/pmlW/hUgC3hgjugNnyPhcDJpgmerd+iKfefpdCpVZeyAzyM7tyBSafJ6dV2NT7Vql+JyqYm9v8faHQ55E+Y0L9G1TXR9H+3CZvxzSehSqpV25uWqqv0VY8D+TTBB4tkumYdjDzZE+0bbtpFkj/M8xy+//FLW4zLUTdPW/bu7uxInOdSFtWe9naiyljyThfjFRuVpqkec+8ATA01AY9u2pSrmDd6O1ejl7e1tSRi8r4zffeS3E2aAvDsctrZJrPNBJCYMIb4cU/f7fdkfeXd3VzCF2X0SQcZBTIuoJ7RhB+j6lvl2JeL29jZ2u118+fJlFc8B4FSeaddCz1hbPxQTXaWNzRVm6+q2Skm8QY/d9UDM4x7ovQkRk08mYNBJPkP3CGtHUkd89XMowFGcVAXAt11xD8bD+hAr+Tv+21jPfgq7xNeBkUxm++X5oQvI0QfvFEJ4Xu+XRA/x676OE0cT9PbrYAPL1i8nlybj0B3W9Xte351ofGvTKYZslhTFQxm8iRYjN1jBUBAcgieJwLESuLzXwwaHUr+8vBQHwlM5p2la7fSnwgFLwngul0t8+vSpKDYJijNQb+Z6eHhYAXQDDAcCgPS3wJmVD8V0RktQJbvFuMx+c0+OnWV+NgAUicSA++E4HdAtKwIVztstNB4fv+P8+b4dEkbiBIj1NUBCNtt2KQJp0zSro9m4PmACHYMV45p+IJv3b3hTH2tIsmpw50zfTgKguQXoTiR5b5t0uVLBZ2xXyMWJoStH4zjG09NTkT+6aMaMzxoIcxjChw8fSlLEvMzUG/xig05iHQQNJNEl7MZJm0GvnTcAA7CIM3eVzQAxIkoLDbZBcuIxABaQM77Ijt226w2Ynj/z8wkiEbHaX+UEDwCBk/axiCY0nPj6PeZO+R9QY5bNFRfmzvjxbb4+lQd8MXPAZzI/399z39rjtpJkwqAESMUN1srjJQZ4HRkD/g192Oq0yRPAKJ/jGugZ1/KcSDQN/Bzg+byDMDozTVM+7WW+Hgk91+cpxMIpefNX+pP1bz0PdMaJ+jbJp62FdhdAVa2Aj6vKEjEwNU0M19hpYMgafot4Yu0Oh0Ppk8dPENPtv7egxi0l6ImBqf02e8q8QRt5mUhwUtA0TXn2E0Qc/fCuYEJY8m9AqFuaeHVdVwApMvaabBN+4g/xgrlZ/4mRJkF4Eauw2ZeXl2ITrMM81/2RHJYAEDWxg4zZo2l9WpYlHh4eylxvb28LQYks6XLYbjY3jnCihB6aJOZvgHs2zOPTIM3w9SSVkGQ+KQ054ctMPvOsrdfX1xXBtSx5b+TLy0t5JoZtjMoWuucqP3OzrR4Oh5KE2f7N5KNX6LnJKXwPa0L8wZ5N0OL/8GPECmMMfIl9gwmmbeUNf0NSzBix44eHhxL3tqSO4xHyICa4mvNfPdFgIG4bwglE1GzKmSSK5n57jIEEAGMkQyI4IgA7Jgfgts2nMXEE3OPjYznVgkoEQYQy/jzPxRnRp8kimJ3z/gWfhIWiABowBFc2CAY4asDqlhEk6FrRXFEgOXJriAERysf1uCbj25bQmM/z8/OKZXcVAIdmltXG4MDNaQlmUxkf76G0rhgY0DEPl6PdChFRmWMzVQQg5My6Y6DbsvTWmHGMXJcgQAB26x/jNZPEWtnhoOcGJjgTAgnfIVjjEEh2CCLTNJWT1ZyUAjjtxJzQbVueuCf6ZFaQzxvA8zm/kLUTM9Z5ezABjgmZAtZx8ma4fJY893WSgv7gU5gjiTqbuwEMfIY1NbPtNgzWF9sjyfz48WNpnXt9fV0dT/zjjz+W99krxT3RM8Zum7LOGCR4rZCPfRvrYZYL+QBAeDl5sr5zfVdmGAvtk/g0bKL6qZpkEOg8l227mau3jIf1RS/sb1h39BsWmM/af/A+vtyA1joH4WHb47OAwO1+KAdY7N190QbK1jsS9Ty/FF23uyZq1ye5j/nI2Vi+3uSOH8LukYFPRdyyrQA7QK79KDbJennN2e/2/vYW76dTJCVZXONwOMS8eH9OtlWqEsRD/v329lZAKz7U5/6j2yZwOHTFCYr1FZDE2pGk8zefkOhDSdBJ/FNEFH8AWHfrB/HSZNB+v191RgAKTT45AdvtdqVVNaW8Fwn/glxdnTRBagxDFc5Jitvr8PXjOK4+S7y0z+Dz2MTW3tEDdM4s9jRNq2NxwUvbDfOsi/07drDFCXzeXQ8QudYz9NsVCsYIsCW5IO57DyeED3GB2LHtPDHJ7U3v+Dbfl3VkXRir/TrvERu5v5MM75kpdnb9PgQUiS8yYczGdyb1u7biYeM7EmTiveOxZe4kmIqh72l/6iSWfztem/z4ntef1ToFgIdxRaHMKJOdRsTKQdnoOVrPk+N3HBsKjkHBDAzDUDbVIGSSjsPhUPqjUS4cBgCH0zZgQ7zBiBItbLkTA5wSwMclUYMIfpLB25AJVM6Su64rpT+zuGZot4Gan8wTxSfZQX7H4zEeHx9XLMi3QBHG4p5W1hHQ4Pk5W962HhkYci+ztryc3bPufjqtHyq0zbr5txlXAxM/Ad0BGcfiigD3dhsHgX1rhAa/vM96ROQg6E1+6Af3xOidSDE272c5Ho/x66+/xrIsq8CKDqP33xoD8gNM+zQOMyDMhfnyeXRzW6XgHm3blgMG5nkusoZpx0lhd5Yp625H5vUxa+Skhnkyfr4DGDGoZH0IjMjedulKHPfgLHPPl/v9zd/8TZk/wdWMW8T6GRmXy6U8gRjW0tfG7vms7YT5uTJHMIfBw2eZpHGwc0uXK8hma12hRu+qb1hXMLCRbeJtO3f7iEGyK35eExMAyNC97nzGVVK3vTgBsp7gq5xMk3za5vgs82Y9nTCxt8DJJNeuc0wxjZwQdI68Cbr5Sre3Vaq+P0Y+SapWXxibKytOstF1QLF1vlan6rOs/FC3JSI+XQ9o4cGvGdBFnC95TPf390UfkFvTNEXv+r6Pn376qewBsB6YhEkpb15/f3+Pp6enVXLD57AnEjYz/oB1rufN4X5iMsnN3d1dWb+7u7sVPmB825ZD1tMtKsyb/7AXxofvI7Zjr9t9lvgW7uuTn/Ad8zzH4+NjOd2RsSIvH2nvWM983CGBbVB9YM0B8O7zJx4QK0n4HSOst+4yQSeZS0SUxwyQEBJLTB5zTYgpTsIDi7mygT/hHmAh6xBjRcdJfLAl3x+/YpKRtcY/sJeFtTN7T5yzXkbUZArfwHVpueIFPnQccyw3yWlfTLywT9zv9qtYYv+ADrMuxh2+nsktV3FMLG1xmX2SOwGIo9/z+u5EAxBLTxwGZsDgqgHBoW3bAsBw+NM0lX5njpxE6RASjMThcCglxYgoQBqggaL+8MMPcbnkZ2xcLpf4+PFjuZaVdQvyHaC9eLA0PpfZAe3z58+F5cRpslAAGBIgrsnJFygazg+ngZJ7rwo/XfYnYZnnuWx8x1BxeIwNAD+OYzFo1gaF8xoTXOwwkR2G4TGwrhiKQRBKzcuMtxMpM7yuGrE2Zt2/5cwxYFcqHJgNJixnHBVzZHzotttUGL+TE4Mq5MJ9GB/XApBHVDDkapXHsCxLqWaxLuiXNxYyT+Rm5tmAjXG7rQTb4Lq2V+TGWlKCdsIWEcWOI3LQIGFt2zb+9Kc/xfPzc/z+978vYMHrY0fItQjq1k10jb/bbgDLboHw+hBMDTpgR5EJdkSFDjaMzxKEuMf/r717WY4jSbIGrR4XgLiDWazMqpZu6f8dZhbzb+bpR0ZkLm/Qm+5VZ1VlkQQQAIi4uM8i+Jkf9+RUMkVqGS5CIQlEuJup6eXoUTXzDARVNWGksFZYNBtesyqVCbLgi5U0Z/aTrCWCJROyDHCAEH+VzLb2T1eSA+SddgGs5vpIJubEgX+LAVq2+FrPGAH2eqL3mdBVVZsnvZcMsA1AiV1lhY2P8zyggO1KzHLPE0AnZiXLaHyZDHrOCPoWtejGE8cWi1V13aKO77kYaqhDeat32nKuAztaLBbtjH16kfaWoJcdI36OYzm+34M+kfNyuazLr8lBVo/5Z/EmWd/U0wTDbHmz2UxO9OE78o3ki8WivU077dUftpzJMj3mH5fLZX348KF9N6tKWa3L9sXVanwzeBITWPAEq7lhuuu61oY19yWSZe8w4M/oggp1xrDD4dAqoH3f19PTU/MZ9JS96AARU9M3u+iEkxTFpzzdT/IkeaDzVTXZuC1h44eSaKSP4g2wbN28PRvInPfyJ25BzkpY2T9sNfcD9GbO8EsmEjMk4Z36Y20zeaTv1tp6VVWTn2dnIuqZ/JMulyTnfFYMFXszxmY85QPyd/yb+1nrTLgP/bRKm0mRsVlbVbT0rYntxFLrnmuYssh1MUfjzHn+1vXdiYbNgskiM9xs8aAYFqlqZE9NyuBUIQiTYqfzMnEK5LXzguD19XVdXV21jHq5XNYPP/zQAol+PouaoHkYhnY2t+f7f/bUpdJIUoAgCk3wFNC9MuvjOJ04lMpuYW0EJ5NhGCYbotP43EOg8DnPFLgShApMGDQJSmbV5kJW80qIErP7JjjK/lrBIMF36kcGJL83Z32kc4frXubiWf7tvPZk2XL+ydRluZsBSQg+f/7c5ko/BMQ5mOUIkoGlY8kCJYDnbJLZNVbjEgQzkctgnQkIwGBN9TWzPcHHOhonPRZkOGJjJyuAIBkUcsgqCRu4urpqz0s7oisCOvIinSwZ02XzIRtB/+eff67tdls3NzeTtoQcI98k2ADLmdQBR0iBJCdybeZHSNLZBKvJwFYdCYkMZOn0s+Vl7sj9PWe0/T8va5n2lGuWunn0QauvtrkL9hiorbYObCyPfRZM5+wXPfT8JFTIZ7Hw3oehqgCTxdfNs5f1+fNDvXt33tZLIpjsm3X1rEyo7D+zvqrHdIJd0cGqESTRj+fnTUt2ttu3OhzGfT9HAKO9T6tw1Wp5qMOhr/V6VX0/birvh0N13dhKena2btUuvt+b2JN1pW9ZJUsGmk/NRPCol8dnPT091WJxfLnf8/PxONzPj49HoCN2dct6fnmu9WpVq8P0lD2+FnHFp0tk0za+Rf5kwpsbgNPGrUc+U8xL3TGOfA6QPyeB3IfOOer3+vp6krSnDfHhwJa4mMQn1v7+/r42m019+vSpzfdbZM1isainp6eJr7V2sEFVtVMWc/+nfa1sT0z3ygB2xy7tSb29vW37M8Ws3G/Kz7D3jH+Z+GeCm4QgPUy9y6qupAX4zmSD7bIhCVISJpng8OUu656EtniWHS2ZdCMixAwxSQyjv8ZmDMZcNX3rd1Y8YFkyyvvRhTlwTyI121SNfxiG9k4OyZ24LImufvS15poV4hyThHyeyGdMT+KErq7Xx5NJc13ymTm/33P9rj0a2Z9KCD///HN7oR5nVVWTtzFTamBhtVrV/f19XV1dtZ47L5bL06AWi0VtNpvquq4eHh6akTGKL1++1N3dXSvlyuY4Dw5qvncBQKBkekS1OjCeBG/mkBuoUoEE+cvLy8b+JYAwN4ZIgeYlS8pNVplB5ma5m5ubSd8fZdrv95PKibUzFgkb9s9cJBw+e3Z21o4oBJopte8kEDIn30/QzclYO44hTzLJAMAYlFmTQeXA0snP2biqMYFKFsx36XHuPUhHIMnEIOd8c89NVgyyWmItU78w1pxfAn3PpbNkYG05o6qxxz2DJubXSWEPDw9NHr6fuohZFoDmTJaKZQIg405n9u7du3p5eZm0OmayySHRk77v6+PHj9X3fati6i++v7+vp6enNqbUJwA+g2/XdfXTTz81+9ntdq2XOR08ciSrUBJgAT9PXEkGiAwQDElWbLfbSeKWL//kf4DKrIRm0khf+cx8frbS0Xf3ycpTroX7f8tO6dzYT901mzgGvHUbf47XmMgzKyF+Rg9TT+hwVdXT0+MkcaHzqcf7/a4Oh33t92xnV4vFsrGndCFbCd/e3ur6+vpXlURr5J0T6/W6EUhpQ9ZoJMHsEVvVdvs2ATvb7dsk2RnZ8+ML/Y7H4nbVD19JhzrU8aDc42bxqqFeX6cgx/pUVUtijQ1YyKQrN7/yqWxdZbmq6ubmpvkU63V2fvS/NfS1WKyqH/p6fX2p9dcX8OXnk1CxRklIZBXJ+rDJ3C+RvtH3+Ub64zOZHGN++fLb29t6eXlplZ4EbOK5SiTZSPi77vgWdHqQRABm3ffMN5lwPnq73dbnz5+b3wbK+75vJ/eJWSopEl1x294W1QRrmW3CfHOSJbvd+E4stsyPO1qeD7YOb29vkxbwJHc87+Hhof7whz+08WX7Xraduv/l5WUjdXMfDBtCDCYRTWfyYAp4wnzpOduYJzRZnXP/HEMSY8YkSZYYG5PnJ4b1vIuLi9YWLFFOO01S+fb2tumny30SZ/m+z5ID/aFzqmLz+MUOX19fa1FdLYOsTzwrkZi3dIlZ7pckEN9bVZNOFHMZq7Sjn8+Ez/e+5/ruRMOiuDGA8OOPP7b/Z+/vzc1NSzYoECFXHfvZ9UUDdtn2kouai8WpUkzGzdEkIKsa2S8KlgE/BYXRkPiYTyYaxsDgGfmcxeb4EjBVjcmLzwFHlG673bYyNVmks6PAArXsP6tF87mnUqZxzxmgqpo4GjKwfpk4eF4aeW6clChx5sZSNX3Td94XiLi4uGgvHARG3ZeSc8S+61IpYESr1Wry1nJjy8QrQZXPnJ+ft5NWUqbJ+GdCUDW+cJBDdCUwYfjJQHCGkjxBWRuS7wmA6Qzcl81pjRDUgFF6QEcFDv3RxsvxSbg9C6ObslssFvXp06eWNCISVPyMlT0ZRwKYTF7z5UY+D9RYcz5Im1NVTfZKAdHsJBNXMuA/VOny95w0uevRzpJ9Bkk6I7BlP/RicWwbwVqaDyChfc4604msRCW77OI/EqwPw7Eqk4lDzsX9xrF31XUjs0xPgNtk7PitPEErg5MrQTld8+xhqIkeJxs395GZbANKknRyYwvaY+esJJv2OQy3+LXdblv1Q4J2XP8jGDBX98nEOSuER/mNByYAVEiKl5fnOj9/1+yHn1N1ZY/pz+hwypWvoiMqCpvNpgGETGC7rpvsqzj0h0kCaF2yewAJZu0Oh0Pb9MyHzu1xvx83SrM5YwYQM8FIP5D6YQxai+gdfX18fGxvHs9KtnsB1uSZ7YM+kzbLFsWwvJfN4PRbazQSJokPtkIOVdVO8ROHFotF3d3d1eXlZbNthI01kABZR1iJ7SE3s7qXp+1Z2yRkUkfhskziDodD/elPf2o+WxwXuxGWdJZ9f/nypTabzQSXWPMkgehRVsTZehI29EMMFs+sixiRJKyEQhxIMJxJ0pxs8ZqCjPn53NxTSdeGYZjsuaBfSWqanziSSWISNknqsWHfZTtzMjWxyWqxrPXXJInu8mXkm90tql7zVzmIC9+yy7m8k1hIcizX/Huu7040MovOPvEsk8rsOaHMyBKoCmpV1Zh/WZtJEQ52JlnXTEx8FvCXXXM6WnwsQt/3DdRwHlVj/5qKRI47z89fLBatlcA9yKaqWttTVTXmghOpGk93ARKyIpIsJgec7VVV49G8gl9uaHSajPlwgAAIliiDV1YzKC5ZZGAjv2QBkinODJk85sxNBqd8djLHNsZXTSsbGWSSpVGZyOSparppzH6HLAmSfYKIeQKVm9OSDa+qJkfOyNqSvfuxEWunZzdP3PH81I9hGCatR+4JQNLFZAWrqskCYzNne6qqnariHr6LgeH407aSgR6GoR4fH+vt7a1ubm7a2e0cYx7/6o/15ATJmtM0p7RxfoLzB8I4Z3NPoJ+sezKDQByZs4FM0hPQ5dplYkpmfGIG0OVy7FHPCgA7SiBHnhhg+uW+uQ50AVieJwjkQGaqL+SVwNXnj+1L1da9qiYbiLP/PefrHkBCzn+eZEvaD4d97XbTYzjnrQbzhOhIPBx70YE0Okwn5sk+mWWcyRYbOgl4ZfI1DNONx+zk7u6usc7JQGrJPRJUI8gnByDb/LKSQw+z3e9bbD/yay5/Y8sE2v352PPz88n7l9h5gsaqalVAhIDPzN9xI+bxU0nwpI1n61HG4UxQk+3lD/gsclytVm1sl5eX7QCZ3W432cBNh7Rwm3f6MmuSFa+q8X0R7Ort7a0eHh4a0UPmj4+P7f8SKz9nl8ZhXc395uam7cEwHjEr11AbWSYyaV+SKbqDhFNpYQ/2hEk2kqyFwTL2eet7JpiZMCcRat3oCFKHHeR9c13Ydt+PJ0JJUsQROA3usraZJAG9YhuSAD7LZJyusCe6fXZ21sipBOVd17X3mOmkyJZeV5J6qf8Z25KYyiTIvSR8Kl6ZwItr7CR9/aKmhxjwbUnisFlro1qS9p9YPHVDHBYHzE1ylt/PKvL3XL+ropEgIVlOEzRAC0XpsCFVY9kuAzcDwoYSemZdc9CJPZZ0YB92u13d3Ny0UnkKhsInIMqNRAKlhUmGtGosuzFiysvBA8mUFEhPlpT8gH/7NbRlpWNg7LmwDNvP04gWi0Vjo/f7fTuFK4EM5cuN/BIQRpSOwH3mrCEAm6xmslW+6+fkxyjJOw0gAXOC3fmGXjLN4D0/2cHzMmhnwE9D46AykagaN9/5I8CRWTIWGczJD/Dtum7CGjH+dIrGYfyMmONiO+bO6efaZ2DJRDFPS6MH870R7kk/2JZqIabefDCM1lMFb7FYTDY2p6yMIe0kj15UJa2qiS3mGqb+KPlbv/QXwzBuFs1EJStsWWXKpM1YyCnL2eSOBFitjm2GyZYBCXlqzTwJysTP74wrmWm2aQ5Zjk9gCyRj8+hDMvP8yPEeU+Dq855pHAlOrBU/mORDrgt95T/X63U70QjTljElq7XA0/G5x2qIJPL6+rrpDgBij4NNtDb7p48Wg7D0ZMcO6UvVCGx8FvDRO79ardrJQLm3RxU7GcGXl+cmd77eAQH8tLV3uIh5vr6+NjCaSVgSP+l3tGeS+dnZWWulPPR9rZarGmqYrG++eDfJv0wC5/dM0ifbZ/KEqwRpeSoQ4EjfPC/3KNDjYRjay2slejke+pKtT5IEsYOdkrPvJFMs7hiH7768vExarnPvD3/j74zRqW9JNkggbI5XScgKjESBvSFeJSowUBK3SQbS+WT+tdRmBUlMF1PcMysz9IrPFAskpQ8PD63iQRZZ3ci4pnNDdSZb4xAJMOHDw0OLTXyJ9WGXxm49k1kne+OR6GZF7/n5uWFN8ZE/4ufYSSb/9IWe5/yQqlkxyYpPkk98aB4Kw/7sPbEeWdEeqibx8O3trTabzeQAk6rp6W6SRvaXv8txwT98sbhBnxKb+X7K5beu7040LIQFz4ckCH5+fq67u7uJwXrD5OXlZd3f30+yPZNxL4ohmGXw5NQ5GMDj5uam7SfAEnBoeSoO4XLCNpYvl8t2kgOnOC8NVh2V7Obmpvb7fUsKMglyj9w0PwfRMnMKS7ESeKTDSpkDHD5nbJK+NLpsVcskwXPnIDNPviIDv8u19nuKybCsVwJ+c8oEr2o8ZYtcOKas/OTvAf503JmscEqe+y2dyqw+nTtAnH3FWQHIpBPYdm9OnjGnc/Esus5m6GEmOslaGtM8gcykKudm/ZPl950EqxzGnDn1DHPzXdf19XX73Wazqbu7u0mSwlFz3oCC9SAnoAx4pzPAqkDqs8AbO8oeVrZhnLe3t/X29tbeVpxlfGAx5eDveVKW5X5VAXrBCSdj7/P5Xgq25Tn8gmeQi8RTgMkWjrS1TMirxiopmaQOs4tkx7QHZUuWdaBTxkbvM0lO+0+/nOvLX6R8EUHHNqFDffz40qrh5mOcc2AyVk1HMNj3x1N76Kd2nlxvoBxYA2A9S/DMFkPzPMp0lI29fplQDcPwjfaesQ1u7jsBPTJP0speKL4lyZk8+ShbQRM85M+tTyayGFO+bbEe48ic8OFf0+/e3983MJh6IZli93xB2ke2kdze3k72m2CnrTHbkJSnLpNLkmpiNf3OGCu5Xy6P7Z8IFnJNcoK8Ades1qVNJW7I7otk2OnI/A/bIxexKqsF5+fnzX9IksnwcDi0NrvD4VDv379vn3t9fZ1UL1Q5ktiYg2Vr7uQslRAY6+Hhoe01g82SZBTL56ReJtPsjBz5nawQmRfZZZJKZxN3WQd+8+npqVWR8qTSrLJa+7QRMmVHmazTPTEo/U7GzyRZcv7ZCTInirJSZNxJxknk6KQxIGp97jD0tduOPi/3GRoPP8WvsTnjytgthpiPJDT9u9+5Bz+bhYLvub470UhWJcvRmdEeDsfe8Pl7I/IUhQx0HJSAcX193RbBvTm7qmPP7sPDQ6uYGE/VeGRostaEPpbHx3KekixB73a79gKwDKrGdnFx0d6zIUD5HZAxV0bzzNYFQVwFJIN/KqlFz4yUjDmuBAxkpcQsSctMlEGl3IzJPWXVyVBw1tl6ZH0pMyNKkJxAaM565LjcM1kI8qBfcxYqe9DT2at6TZiAqAhl8kJnOPMEoHNQSk6AHifgXuaIka2qiTGbC4OlM5xZjje/m0mlfz8/P7eAlY6MrAVO95XYZqnU2I3LM7O9IJMkwbvvx5de+kwGL4yigKyC57Mj2/vSknzlfwcE2O/BWbp3jtvzBe9sBQO2Eigb17wiYH5zxo+epgMXZHNfF/unr2SWybP5JBjLYMrXsG+yqxpbZOg6v5bA1e/SN4ws/fiWW/ZxlOto+xKDtLO8D7Y+yZEEDoJ6gre3t7d26h7AmWvH1yQh0/d92/fD1pfLX78MTYxQZTDOrFZZm+Vy2fbUOYlIoM3PH3vd17+SdfpMukNW5+fn9fnzQxtHApWjHe0n+yAAukxeM/nMpEEFZL8/vrBNHKiqyek5GTMALzE32+aGRdf8JH2j20DqxcVFO9J5t9u1920kyeLY2NfX15ZEJMhjQwB/gnh/s9ms/u33+9Y6NNdpPkBiQg8y1mali09n+9Z7bl9ZcU8/kskLvQZo+Ufv4sqYlrE7ZW39/I7Nuz/98lyVYmtoLjaW68unw2xY9UJ1y7jMCQCl9zc3N80vOvZ/v5+e0nV5edmeC0gn2YPUJGvPzXjP55sbHSYztuD/KpO+T25aT/MQDn/u7u7a+NL/ZuLnOUks0SnrY15VY/Usibxcv+wqyDYsMrau9JE9u497Z5LR9+PJX3k6Xdd1td+OlZokVpN0I3dzp++ukSAZEwX+M0kRn81uGDEyO5Kyo+UfXb/rPRoWimCw5lXVMlSsEoCBGfJ7E8mSlaCod5wToURVY68fwerLw1jmBq0ff/yxldX7vm+b5iwEJ4NxEMznASATDg6PsJMp8e9xQYc6Ho04AhEA9Pz8rCp67bIa5DkcGIe73W4b8wNQz9u+AGgMivXKfnhODUDNTchKokBMlpgpYr4ISeDJIM7pkUnVEfh58+rIVI7zT7Ypv5Ml1jT8ZOUZcTKXgnQGUbLlmK1vM4LVeGSgNc6gT2eqaiJzz0+mN+VNtwWdeSXAOLJEmQwaXQTG/K21Ipn6DHjmlKxLJn0CU56aklWMdNJVNdFFn8NyZMtKJnHr9boeHx8nrKmjITebTd3f30/Y5Pv7+7q5ualPnz41tteJcuv1urUm2bOVDFVVtaQl10YVlU+SePMFZJL2K8Bn5SEDtsTIWtBpuoMNt9bZmjKvXpBjJg2SUUEpE/dMipxJny2QgFYmluZxd3fXmOOj/KoWi662230tl8djZoehr9VqrMapKOAD6MH5+dlXYGbz5HGfgqNp93vM/VCXl0dA9OXLWx1PaDrU25u9A4s6HPpGMHVdVdctvib+TjQa33ouroxkyaKqVjUM9lYd9fnz5891d3fX1igTPLbBDq1HEgvILX8fgdq6bYLd7ewB6asKebGv5fK8zs/P6vX1S9nzwT7YHr0VpPmW+/v7pi9930+OjKfbyJH0WXQByz8nDsS4/XZXq8Wxz3u9Xle/7GuzeaqualK9YyMXFxdNhuRobyMdyhdmdl032eROt63Vu3fv2l4bxB3f33XH9pmsiCK1xBo2ap1szAYSgd2UcSbkYgF5JxHD5/I1OXbJehKH4iy7S1uma9k6li203yKx/H69XtfV1VWrzPIHxmj+l5eXtdlsWot4VrcSBMIj9Ah+yGq6uC6Ry9gnjmclI2NCngCWOEGnSCa+fKn4Anukz0I+eUY+OxP8rExIWPnzTCQymRaD6KnPJAFonZETWWGAHZJkz3iTCQDdI7/c11NVtVwsa1j01Q1Vw+H4ks1FHf3qfrurbqhaL1d1fXFZq6/36XfjS2jphb/pPtkYXxJs/J/4Ya4+l+2SiRX5lCRyEUvz/cP/6OqGtJR/cP0//+f/24xW2cc7MDg2oNPECAIonjOqXdc1pWSYFotyUj6G4lkMMNnkrLo4MQmTlEbedV3bTIXBzHFlKY0B2bjjZ+kssq1jZL1GZj4z5b4/nlRi7wSFYbTJrFIgvZ2cysj2jQqV8+C8AHOOnaIDz1UjeLq7u2uZNwXjyDebTWPU5wlZ9m1mWTGdJUU9Pz++jIo8OWrOLpO+7LNOIEfODN+apUNPVtDv/ZxxJcBI8JiMMx3w/WThMjHh0IyPAToVI6uAAjlmJk8KyvVLloiup45aX/pI7uZuXGwp25mwRe6HOTE2QP9f/uVfmmObs2/5XOtERzhXrPZ2u22nsVg7NpS6DGx7lkT27u6unaKTTLqWoL7v20EQ9/f3kwpCBnRn2/MjfBiwZC2yKuJvR2RmsM6/2XeetOPe1sz6YiPZZybe8yBgneiCP44gJrdMAJNZBzyskQCa5AQ9yYQybUYgSoCWexnIGXDb7XaTY2hfXl7bXh/3k2Dzc0n+YFiPycNZGzOgfWxf3bXnsDvje34eDyVJfZyzzfY/WdfX15dJ5TSrD4vFSCSlXzk7G1sOVQSwkVjbJEOS4EjGHWg3lwRWvpMEkQSEXJAz2a6TwCuZZiCoqqofhtodjpuC2b1qSvrurJhmy1qyuMmoj+9OGRnwrCxUHROcPG0uj/jNVkLyMJ8kaXIc4gdZWV82as3evXvXDrDIGG9+7jePhfQCCebnEsNkhP0uq6vGlRX39A9XV1ctRmY822w27ThVMevLly+NvGWL1imPDrcG9gZZH/5aLAG0rQV/kO+8YMNp69aaDYjduS8wZQIb2lvLxjMZsq7iAtmLY54NyGe85nvTbvjWOYGt/Yw85/49cWqSNonnVHuzEsyHZTKUCerZalXbt/EEMmPz7MQuMHTGde2ffGESfTlWcSQxUPqgjDESRvdP4pvOHQ7jizkzwflf/+f/Ur91fXdFQ5YHBFjY7LkEAgCOxeJ4BGbmMtlqlZl0Aug5mE3AYJG9DTuDZQrUfarGProsC0lA0hGmYyBYjryqJtk1RdCn6vtjdjk9dq2qq7MzL1A5tOQiN+QxuizfMlgAPN+yLjBbh2QWkpkyVsrO2AXdqqqHh4dJhurvw2E8KtUzyZCMAWWfZ/gZkDL7to7GAvg9PDy0e+YzVMWydYHTAkjS0VifefWHfDJwzIFaMkHzZKJqPGElS8PL5bIFzd1u104j0eOaFRMypLPmqT0OAEhnn0nonD33/dx0aa2G4binKCtKqf/J2invV1U9Pj7W3d1d+1wm3fncTHTJZ7PZTHTg/fv39enTp/aOjD/96U+tRTETLusmeGn7SPZGa17V+BIt+iFQ/vLLLw2cZKJlA6+9HNfX1y1p1erBoSpdp7zTt/F39ERwZHdVNQEG1hUIrBpL7SqzAtO8VG0N5uAfu2VO7J3OS27T3yYr5fmZYPB96UOrqoHPrNoC73n6Cl+WVR7A9O3trbXeYUbTDwAZKjk3NzetH13rHH9FFyQXkvSscFoL/hQIBvR8ng0YJ18jgTLft7fRJydQS1ae/SRJxEZU3FUk3BuQZGfac8k2yTBJt7XMam36EL5ltVrVp0+f6vb2tgHhBCB09exsPEiFbFPvsqc7fTuQmXtB7NUSX5O8WSwW7UWswG+y65kwJRGhpTIrD9bVmNm7JIm/siZ8ReobmWf1d7vdNlIvEyVzyE3ECaCTfHS/JJcyxtDxTG7Yk/iQhEzOx9qyYetXNe5H5c8lqqphdJUc6GnuA+HXjM34UtdV4JPYSVLQ9wFwskjwLw7xAQnuyRLWtL7p+1KX+eYjqfHSyDMJa3afZBcA35zkXRLlfEOCePqAGMjqRuqUZIuvS7D+duirQu8S92U7bJJAPkeei8WiVQWNDVbUApfdI3y2cbBv/i0ToSRH2T/5Jj7MePFb13cnGk73ELjnm7hSOQk6FZQTNzmK57u5GVl2KRgCWZmtCdIZ+Dglwp6XzgQDVRaKlE4oA0+2VGQQpxQUgHJawCPoXnxlWZ3B3H3tAV7Ufv/alMNz0/llAM4WmQzgyUgDVuaXYMJ9rIHnZXlUpSSBEKVPcMKJ5nPy2Rnk/F4bDUaK0qdjTtBOdySr1t53sqJGTnPjtG6CnLEkcyxxppd+nr+jm8adyQajJNt0wA4FyD8ZeDNh5fjd1xjToaRuZRVpri/+JBuSG8HSTrB91vfx8bEuLy9bEGTfQEZuYk8gzC4AjwRgbOH29raNZ71eTzb1CrCZHAGIvsdeq8YjtAEV40i2Cru5XC7r8+fPrXqVrZlZYq+qur+/bxWovM9yeXxR2ocPH9oaJYAla3aZ78+RLB0Ox42fNlpuNptWgWGTWTHAtiWzS3Zd100YZP4rq0xaMLIdQZCVrKdO8WNzokaiAuymbfznf/5n/dd//VctFov613/917q/v6/lctn2WHgnzlHO3WR/G33yLM9/eXlpLTTIAQA5q5g53jkryfbt7dhsNhP2Nf2EAI8JP7aQdRP5+G7Vr98UnH4gWfdkwTOYC9gJ5IdhaC94S10ybxXS9fr40kFg8vLysrUqz8dmjnnAgj/50tjD4VDrs7N6+5oEAUYqtznOTOjIjW8GJPmn7EKgm9aSPBL0IFXYVxIP1jXBIUBFTuLO09NTq8TQ4Zubm7Ymu91usnk9wTRg9enTp1a9zCN9vXgzk92u6ybVBrGQ7SMskpjhU+GPJBrINt+TUDUC4KziGAO5Z2U2ATY/YTy5Zj6TsYAfEotgtsPh0Nrz6LqYlmw7v6HLQbUuq0bWOG2F38ok2dyTOM2KS1W1OWW8ybmLr+w0Kw2ekdgiSe+Mo74nicsT4ZKEMxZ+7lsvTx6q6my9/pV/8Bn3SF+UlRx+wRizBTgxQfoUMnZ/yVR2EiTpagzwfhIk7pmJ429d39069X/9H/93AxiUK4GG0xOGYWgl5Mz+vWCGQVAMvxe8M+PODbsElJluOjNg9unpqf2fgqgQ5JnQnPHV1VVr7wDuMiBaECyKMSSAFZQwZMcF7RootEBHwHTWzkD2JysyjJGiuX8y4VXVvmsfijEytnQyfp5vT6f0HHkmhX4G0CfYmZcUBW+ggnwotYShaiydJ4NIB74FkrNiNc/CyY3TNkfrmEGOseZGOXLCvNCTZD+qxqNHgZp0dHRuPt4E2xJVpe7cyJaXAJR7lDgTuizp9IysNNBbDnTO/mTyP09Aq46VCBUQ90lQUjWWiq0Xe+C4JUCZ5D0/P9f19XV766oxJTuapWF/qn5d2k2bMx4BgD7MnX7VsUKTVdZsPaGryYYJ/plc0OW+n26GT6bL5llgRHKUlVNzTWZd73q2E3L4fCW2WqKdwNKcyCArcvn+Bzrhd9n2NW9hYsfmn20buf/NOFQrnp6e6u9//3v9/PPP9T/+x/9oLysbhml1bH7kpjGN/nMEGXQOUD7a0Eg+ABB04vhCwikZwibSXjxTgD0c9hNfl0lQ12mvem3rVFV1fn42IWPmLSs+l22OCc7pLrmzR3J2byyj9c8jOCXsyWCnzOig/UoJQrquq/0wvjA2q0vAYBJqdEVcWCwW7YV6KrmurBLws6njZ2dnbd9LMt3JEpu7uUk0yDhJhqenp0aQJDkJRJNvnviDmDLn7XY7STDEBWuRc8vkIjs7rNn19fWkMoIENTdEwGKxaO9lyWO1JW38AFtJn5XrYi4SEbbuM5kMJpidg0s+I4/adQAEf0ff7J+z1gA9/5ct7OyabibpmESe+JT2kj4p2+wzceA3s5qda2u9kYtklRU3MYCcEkMsl8uWeJEB+dIZPoWumq/1G4ahumGooR9PnoIJck2T4Mw4m2M2lmxbg02yEmJtEqdm0uF76e+TqCS3TProWN/39T//9/+tfuv67ooG54ahA9qwXgwk2UwnM2SZr6oaC0UoucFPqRwwopRANTYS0yNIAcvJuCcIMQfZtoUFKgh8/sI4xpQKPVdgDiqN7fn5tXbbXe0P+6qhqh/66qqrQ7+vm5vrXylWJlAUP5MeCpCtRqkQ5pcMt6TK54FA8gEOMylkxMnEcBSex8DTqypGlQAALflJREFUEFyUcRrAxyNsGaPAKWs2T3J59+5dM3rrz/gz0cm2Kmxc/syFVct9AAmotcAlaADUsuxqzMYggNGVDF7GmOX9Znir8UhE4NZZ5cmQWYOq8Vhg38NsmEfK0XPZYm5i8+y8F1YV87jZbGq/39ft7W3t9+ORm6vVqgFOz82qAgYk2zISNCVrQq5PT091fn7e3rXgu6nfkl+6R7czyPiOhAwrbjzW0M88P4/G1g6glcQ9+AQO1rP8vOoYMJ1+kuOaV0Xdh/37PDu01qoHqVMJPhOk5tvcsV6pc/PnZtJpHpmsClaqScZvX4Rx/vLLL5Pvd11Xf/7zn+vy8rI+fPjwdQ3Hsj2gl/Ekk1e+bhiOLUXGaLzixtG+hgZq+P1hqOr7Q/M1/GWCnJTf6IcW1XXTjZZV9ZWUGY+p9ay0bT4/2cH5ffKZCXqMk28H9lUXrT/gCJwAcPnG7Ew2jS8Te6x8MtHn5+f18jwScHyEKo94oALn9xIAfhMmQGQhJS4uLmqz2Ux86+EwHlmeOme84qCkng4iLrSa0TmVSL48v19V7aV05MzHac1zsW2VIvFN21batPVgI2Sc87BnFQaqqgbYD4fxJCLjTj/HlpLFV8HNdsxMTjP+pN2kPzWPfHEen4sQ9ju2yQ8nk03PxU76zsY9U0I6HkLx6xd3SnCSRJsn3mzLHOC9TBThsSSD/YweZbIphqU+i++ek3H88vKyHdNO1uzR9zOh4rPodEuQukUtZkRX+us5kUiWSQ7Ay+aQ96L/XkxoTFmpz+qu8dMHupBESeLTjIWZfP+j67sTDYxWKv28zJTlKxnXXLkIwEBz8Rnvfj9uCsxyl35AWbPAzSgofbaLUEhMWLZjVU371AAuQq0a94IwnoeHh/Y8x8MZ+36/r8+fP9enT59rGLqqry+bOhz2tVqt6/r6um5vbmuosdyVLWcWXsARkBLUUX5OKI1zDhISvGdC4vu5NrmGGXQEJcrF0aXTSaUnxznblNWeXOdsOaITQIaxAYm5LskQA2oJrMzDeFxkytDoE0eR60GHkvnJ0jI55/zzaOd5QpOHIiToyFLn+/fvmy5wrlmpska+M++Dnjtb/04min1qQ5L4+9zLy0s75UnrU9WRILi+vm73dJ77+/fv2/Popc/M2y+sUdr87e3txOnRqwxEmRikDOgDkJXM7svLywRQAwLJPvV936qtkiqsdT5D+wGdBlJyn4T2IPe2jpKITJYlyV3X/apHWmsI/8DGJRpV436IPN2KDrAdyeNcD8nPZnqbSukv28iDCrJyw2YE+T/+8Y91dnbW9vbs9/v68ccfW2J8fv6usZ6ZUFjLJKHyRBP+hP5ke9xxvOOeqayWvb1Ng2i2LAI0QLPnHRO0sZ0uAcJut23yn8fC1NdkWhMA+b9YiTkFxNmlP1l5ScCaoIAOOqRE7FUZc1jA09NT7Xa7urq6aoQeguL8/Ly2u22zQ/e27nQviSs+WZKSbTHZ7gL4a4dLP5uEi5iWpBtWmm4keZh6DBD5Y2+FMcAP4o247RnsP5n6TML59TxwxvxfX1/r+fm5YRL38Htz4wtUPSQyjowl20zE6LI553olYcS/Sp6N3z0liPSJ3yDnz58/N5uqqkkSyuaSMMpWvHkFLBMDYNU6it9kQ57zOMVP8ZeSSLLkqz3rw4cPraXfmrHLs7Oz2u33NfRTojbBeK6XdiixYvQJY/LIn2cCkH4/fRofw4/BpsdY9aWuLq+aPvFF9I3OGHeSo/x0H/NK35OdPH5fNR4YlLhIbM7kJRMwBHX6THbkM3zib12/63hb7B/H1XVd22iKaROotCoxDMFyfgxmZpUEJZhRrmwp+fLlSwM7HDNDlJQky7xarVrVwvOTVb2+vp4waf5vQ1oKeLk8vizocDj2KzK+p6enBtbv7++/thEcjzw8GsnyK8t2ZNuWy7MGKLDmxu3iQIAyYMCcGV+W6DPACYxpxJTT/ClgKiI2ChhhfHn/ZGAciZuJQgbFTADSSLEBVdVadOYBOqs3AgxDYmDaVQAqzjn75zPh8AyyyERBopHVlzkTbC8C+dM/dqGqkuCQTOaBiM6QRzI0yZ5KCDJAJ3ikOwn+6Equ7wicdq3XGwBOALDdbtsLrwTmruvq/fv3E4C+WIztFWzX2OZrloDZxb6VpwVi41wsFq31gE4Zn2DDv6zX69ay6bsC8bwiwe7SUfMB2dpmPa2Zlr1kMyUHqe/Jnp+dHY/YZXfGxC+5Hx9mPIJhJm/8MHbasaSqLypC9/f3kxNaXLmec9+RYA4ozMqN7yQx0XVd/fGPf2xgPWWUyfdxHsfjdI/zPw8A5k3Ryzo/P/o6TPput6+zMxXovt7eVK3Pq6qr9XpVj49PTZeWy9XERywWi5bEOUQjK5vZLpCJ/fFkQC+S3LaWRycCub/Pr1ZjBdyf49zGZCkB4LfAtcSdH+OD2H8mAZnAWDv2rvIIUN7f3zcWdr8/7r0Cvruuq/XZuvrwD9abzSSppdLi/09PT7VardreCH7148ePjfnc7/fNf2V8y/hB59OvsW3yoVsSfkRm+nUySYDPFtMHIgeNkY1bB2vk+ez4+vp6cipijo/+e76xsaVM2FQUvI/E3MV5uCPtfV5Nl5yMuj+etOn5eYRs2iZ/x0fzyxkr6IwKERLi+fm5PScJZPtyxD4JjFhMPvkdvlz7ugTMmuWeCQSnt4iTqfY0+rUIm6iq6g+H+vL2VhdxKEu2n7FhCX+OcU54ZTUyY9vV1VVrzxVb+OgkHFusP3/X/MI8TmcsspaIUffgo7N6ZDxe9yBJYxdwDrwgkUsiMJMwWIdN0N8kUxK7/9b1uxKNuZAFq6pq52QbgJ9xUMApwSbTxuEm+5RMI+NlcMpVz8/PTdkoRQIEzsIfgnUviYIAz3Fki4aSn3kaK8CfTG4a6DGQrCfO9chOX7S5ui+jZOzaCjgfoCKVgJwoBLCWvd2Atj8+zyllH2cyE5RZeZcckxknB+uZ7ARFd7571VhVSMY3FdjGbOPPDZacbH5XAKRzWSK09tZYsirJmOvTMAyNKUk5SbIy+OQ+BM83hyxlZrVCmx+2IAF5BkI6xoFk2ZY8k03IhFxAA6CSZfO9qmo2KOjkemVrBLlk8k//rQPAlHZsbayXMVVNT0wyB/LEjLqMPYEOO3v//n3zDZlAID1yzdg12VpfQIG82Z+5DsPQTqqi43SJniTQ4ae6rvtVspNJSdV4POYceAqmAmkmyvSeL0sbdIpXEgP0hgwwZTl+tqD9JRMKV+oZ2WIrJXHAxYcPH1rlwrGl+SzySvYSkMg1yk3CV1dXjdW8vLysp6enrzq1ry9fqn2/6nhakheWAtp8WgbXbDf0/5FEmB6AAWhJ6oz95eWlnaC0Xh8Tzc1m02IR29EOZzwPDw8TgsEY2S1/l0dQa1uiAxh1QDOTu5ubm+bbXl6Ob2O/v7+vqrFil4TF0WeNG9Wz6pYnZVkTAOjdu3d1cXHRjl4HftiQdc6jP/PwFrIHsuifjclpP+J22nSy14kxck0Rndpmsl2IX6HHKkH8qeckYQK4J36BAfjqJOnMOWUtttI3/2aLt7e3TQbW2bOdOEY35idWJuj7/PnzJD7RH593n+fn53a4D1k6iKDqeEiGOJ0VwPx3Ei5JWiCGMf7fqrzQezbODyyX03ZQMp13Kki+rZfWab8fvspmf5ju/5hXEdKG+P9MVgHs0WbGvT/mBltlq6f7IbCqvm5g/ypn8ssWskxi+D1xiZ6t1+tGnCCH+eKsiqa/FcsTEyaWZPfzNbVu7DR1+J+eaMz77PRd5uasBKIWQiDQb5utPn/961+bwWy321buzQUBOM/Ojuep23hGwRJUp5DsIVE5SbDNQb2+vjbHkIA7jVeQskgMlHJWHZ2L3sY0tAQKjCeBcmbWwzBMmPJ0dowrnWM61WSefvjhhzo7O6uHh4fmaKvGDUoJorOX3lx9xhjzu56b5dSq6THCmSgmIF4sFu0lTMkmZIUrv6ddAHNzOBwaKGVA1ryqJoaabTL5ew49jYwMkmX+FhtmLQXcLP9yLJlAkpt1TbYzWVcATuUKyGRHTl7K9rXc0CmpUPHjZNbr4+lOSQbs98e2RUHbHhhyl+Q6/jVPDMvkgJwzwHKmWXolJwBFIOfk2XMeASwpMm4+hDz7vp+cJOQzWXnIVpDsfU5b8QxsGR1+eXn5lX/BvPJRfpYVAeNLBjOrVMaVbGIyQ3xSskRpr9Y+k2SkiMoIAF1VTc7Wnt/Mao570nv6m+2lyIZMfpKtNhftB9lfnjIBSnLs6fvIgo3npuFhGFoFGYDe78fEkL08Pj62dasae6TTdjMYPz09Td52n0FTvKmaHmCS68Cu2QM/pfXD5wCbbGWQVKqQ9H3fqgKSK3K1b0vik61NdMrzdBSwGXGK3gJ99PT83Xl1X7/nUlFaLpe12WxakjQnlSRF9NO4+SF6729X6itfm4mUBDRPFKJ7SfIYI93hv5bLZdvPKUnxWQlFEkAJuPh6upf6bs8Mnb+5uZlsLPed3E+Ue6ToDl2gv+Rhb6HnA9v8VVZhsn3PGHe7Xas6zGXgD2Da933d3t7Whw8fWlUFdjFXckECwSuOu68aq6QIv7SNrKBUjcQHvaHz4q94IWFF5lhTep5JRVb1lstlHb7aMrkjYbfbbXURxxNMI8SrRpxgrmL0HGuk3+GftFKxB742caB57KN1j31I7Oc2k+Rxxir/93syJXc27w/74tPE8Iw/7jlv3+U7k3RNf/hb13cnGtnq0/fHEk0KjvA3m037t6MlLy4uJpsbE4w9PT21l3FRGEoi0SAk/6asHHSyhsmSC8QYGAyP4Jc9a+aQTozgfceiGlsurEXETFIii+NKJaEAj4+PrawtEUpHwrjyJVgcnuclW5LMrjkJ5sCBKxWqGUEAMfIV5FPW7uu5qbgJUs1XkDMH9yev3CiXpTmOB4NAtp6XDIN18m8OxZwFTI5FYkSnOPZkwDkk4CCBpjU3xmS6BAWOyxzsEZCca7+yBpmAAL4JyLTa2DNhDkrI2bqSgM1aeyEU8EieAuNqtaq//vWv9dNPP02Ck2en4+PEE2Tn+mVZnswyaXISTt/37d0Wmeyye/pIrpycv8kUswzI0OdseaKT5KKaxv4yOUuAvVwu276sJCPoaSaK9C0rLHQg2VvMbAYu30HgpA2xv2REgRJjFOTpU1U1ptsYkyTJRHCe5GRilARIEjBkmccuuy8gxU6y9dH6zVndZEaTXLF2R8A76lgGYX6HnmTrAoKIXPp+fIFhMpDsgT8wP1W0TCR3u11jY6uq6TI57ff7SQKUffDGkiSBdTGvqmqbOiVLiAp+YL1eN7CUenl7e1svLy/1+PjYdObTp0+tyizBXJ2Nx4F6rhh8f38/iVm+B9jwYdYx1z0rHMCPSqLYlJWvBFv2jlnjfJdL2m6SbflST7YiZlkLOl1VrSWOvSWYp3NipLU2lwTPqgZ8IP0zF2Sf+2k9Mrb1el339/cT/0bOVTWxmapqR5GbS7Y3eameODCfmyTc2P3x+bTFZMEvLi7aWqUPAPaTrE1iyNzz4BK4yxwllUnIIcwQT8blbfXa6bOqYgxwTNpX3t/LY/08wXImM/QmOypyfmzFZzKRSj+T8tjtdrU9vNV6tZokSvQgY5bvkI/Ymj4v/VvaEdnn/90rx2KtzTVJOX7Ez+brTOe+5/pdm8ETNAP5nK7FMihlb5k2o2P8VeMbcquq7u7uJoHOYlsIwAq7Q3Gy7UOwJDiLrSyYDgE40Uc3b29xTN6cNeXUqqYvb3OyRFYtMpOVSKQRAQs26hk/gOHkn0xq8pSD7BU2PvdJGQj2ZG0OlM9ngWgOPQGDnyWQSXabkQIPDDlZXEbEKDPoWJ/UMbrj3oJfMj7JNnC4mTCmUwCuBQfJJmcoeHD4yfoy5mSiBE6yS0POJHDeGue5GSg9K3vHOVjP8JkEzp8+fWpj/uWXX+qnn36qqnEvQrZpWbtkS+xtIpsvX760vnt6jEGjZ9m7XDUGxJx79ttmkMfeJXmAccw2rGRLsxUOu8VB0i3VMWA450dvHbGbb8dlc8rtWXXJljHjyqBgDckgN3HmfgsAMW0JWyfJtO4AL6bNMyRb6QMkkuaaATMDSLYyJImQJXGV6SQWJPAp29QrMsmXzGVLGL2Q5AiE9NPfZJJ2xGdm9TTtU1KYepLkDVDFf2SLQq5hVU1OkqGL4tVms2n3+uGHH8rmeeMwDwxysroAHD3Ltpps+zFucS8PwqCT1iH9q8Qt2XT+BWB1mhp9Afb2+32roGQ7ZfrXTPTshUviLZPgjOnGkQk7HcoN/Ykfkjy0Xklk3t7eNuY9QR+7Wa1Wrd/cv5GMyeSanzGqjlqnPEUpKzNICrJP4sWaeClp13XNttkUXdahkeRjEogIp77v629/+1trE9UODhP8+c9/ro8fPzbiSkwTI1KnkiBIf+l3xpQVNzbM9r7VfcEP5MmM9MUczcez6VaCXM8yXnIXL6xv7rukh1m5bUnQYtohws+QQb6GwfeS1EmdQW4nZmOHaftZkcsEN5Mq8n7b7mrRje/zSQA/xyDsHP5OYivxSa4ZHMovkHvqnGflcb2ZtKcfyKTG779VJflH13cnGpjVnDzlWi6XDSxna1Tf9203vwAK7PsewLdYLNo52D6b5faqowO5ublpxmtRMgMUWCQOyZ5SkMw29QHK/jMQV9WklSMBPSWxiQnQSOYqy1wJxjLYJhueLULJoFO8VEb3/fLlS2s5E2DIwWf0YmKtGa3Aw4HmqRIUjJEzmjmLbM4Z7DOZyg2v32JHycG95xUPgcafBJ6Ck0ugyXYsDinLz373/5fJZ9C2DlnSnBsdmc1bqPzhILMC5HtzJtvc05GmzMkLM/WHP/yhnp+f68uXL/Xjjz9O3rqdc8SWeC5wq30wgzR9SoY6A5f1Sma6qlp7ZDI8Kauu61pFQFDa749vhJfYSCTS5vSy2ugKXNCXDOYIAqCGnQpeWY1gn5g8a05eSSRY40zGgaK0AT356Z/4z0yckBOZgAK8Ahc9SUDM73p+BlD3YmNJBljjDFKCKhBEDq4E7cnWsYM5CydRwI7zp3wxnSGXZHazDZOPZjdAcVZvhqGaffAZ5nA4jHvLUlaq8j4LCBkzHcx2Gr754eHhVy0To12O1Ry2kPqdLKD554ELWi6yFUplOokffgz7LPbwd5LfZIOHYWibmOmG5Hq329Xl1VXVl9eJ7AG09INJmrgPMiEBOHvUTpOtXmLIxcVFq1CQcYJiP88WWMm2l31WjUy/hEt1h41n4kUfxRCxDWljPdzz9va2JQ7zqtt8j4v1VT3q+74dzOB0MS3NbE5yg3TC0HufRsqEn7i8vKybm5tm1/f395OXIKe+Vo0JasYCB5eIa7vdrvkrPtp8zBcZZ23oV8bheaLo//lKAutKLyVHfIPxWXe+A7GZ5NJ8M37DnMNQw376omV+MuNS1fguFLqTvon+5XeT+BYH6Rf5ZVVsTsRal4uLi+oPYzszm09b59PEArqW5Jf7wwr5DGNmO5lowHTWdrFYTHCo9UuC0D0y3mcs/a3ruxONZNWx7hwi58QBJztgoMpVmPVcEMxL1x03yznZ4vPnzy1jp1QYpgTeHOC8lJfOOYNA1QhG571nmRDkXLI6AGw8PDxMmB1MRjpdwTD71xNsA2KcpfIvZTGn9Xpdj4+Pk166qpr0jToVZbvdtp7JZAVz3gyQ4Rkz5cnyWyq0OVF082MIHFS2Z6QRMGY/q6pJVcl6ZQJhrLmJM1l4lQ8G/Yc//KExeZ6Frc+yOraKbmRg5WQAkKqxKpBOJJ2s5/i9d5RUVWOMzR8ozk1myuyCQAJfzzZHz8W4YLZzrTKx3u129fj42OabbYiCczr2p6enpl8SZ4CMDnkGW85ELgNlAhR6kG0ijkRNpyZgWX/giJ4lIw8wpvzJOXVRRTL1HWuWa08ns21znozSdSCWP0pyA5hNgiZbYzLRrBpbiehdMtAZBCU+AuTcvgTQTF6zbdEYrRkQmkmddiA90nx7MqHzwG0t+JlsnZFEJYvJh7DFZFVzjsnQsoHdbvq+oSPg7SfyUn3j3zMREWTZN78txogfCb6zyuU5m81T+33qf9cdT3xiC5lIzP27GOTKzbNHOSxqGKYvHlRlkTTmv61JypbPpDPAcA3jgQvpi6yXdb24uKgapi0wSIqMy+njFotFS/wx8V03tjPTowQwfIy5+6xuAOx51fjeiARB7Jd+iqupX1l1+vjxY6u42WCfpCOgKZHc7Y6nux0Oh0nL88PDQ7179669idxJW07kSuIhK+hJunkuvfV8STx9JH+2lfEYLiMTtsPnZmUmY21WOubx41v+1P/TR7H/vF/uZUziL4lVNjKvChjP4XBohLU4n1V1slksFlVBfrGJ3W5XQ9/XOioliQ8z+aYXSS6xzWxFS9IRgULO4s0wDK0K6DO73a7OVuP6z8F84hAEDDuoGnGpGGKNyS4rzeQ4158kOn1Oope+w1qbJ7m6byZEv3X9rlOnkg3YbDbNeSY7jhnnSBh1Mi0+r7ph0krSwC0nbNGqxtYGxsV4c3HTQJzwkgHAvTlWgUc/brZAAOkqL4yIYxDAXl9f29G3yQy4x36/b+fMY0Cvr6/bYnGwuYhAAEcuGJIdBc12g7u7uwkzxkB9xj2TrUy5MA6sgfFQUE4nq02ZFFgLjg0oxGT4HYeZgAoDksyjZwrwmTRZZ6e/SAyxBByZz2JP5u0YgvH81KLVajyuORmRqhEkJEOcrSbuP38TOHl968SiTMzcixysdTLIGaRXq1X9/PPPdXNz0wKZ9aSDjm6WBAlo9N4JIXStqhrbStYJkDNxGIahgQr6nmBbYMlSLRm/e/euPn782OS53+8nJ2UBSZmoZhBN4KeiAEzNP5fMDt+SG8nND+DAsPF5HLLKBL/DPrygjH/wc36FvQLA7DQrAZ6fyTgdSaefx3Ime8+2+A72R4/oUpINetXdW4BJYijBV/rkBJ8SASCGfiTBYi2AUvJN4oWuWf8MfJjU/f544tMRTCyralFVQ1VNjycmG62xqZOqLfwdcsKz2EAmeuZ+XP91DUNfV1fXX/3K8djdwyHfHzXUcnmovh9qvx/3YxwOfe12I4hbLo9n7F9cXNbxKOChlsvVBEjw7dmWCuCln8z4yR8mecberU8CXcz+25e3Oux2tey6qkPf2PmPr79ULbpaBeObrcPW3X4VLUN50AYfadxkejgc2rsRMuF2fCg92u12dX193fRyu902tj/xRVXVX/7yl5bsigPur/Kl91+CLPkWf1QDz87O6i9/+UtdXl626jHfZj1ubm7qT3/6U2Ps6fV+P75gMdvJk30/Pz9vLwuUzPlM6qZx8UOZPLiSRONr6UcmxRnbknTN6ibCMmNAtjXTzcQ+q9Wqzs/Oa78/1GHf12KxrK6OL9VcdIvqukUtV4s69EMd+qFW67M6HPY1VFe7/dd3hB36GqqrxWJZ/VC13e1r/dUGl8tlbXe76r4mGORPv5IA7hbjiU18Id+dYDkrF2SNWHadn59PXuiaBIrnDYe+9m/bWtZX/7b6mlge+toexqp9JnD5MlK+/FutwvCSuYgXmaglzhXr/Nx6IlNdSSzTdXidnmQCn7H0t67vTjQye14ux2PXqkawlMkE4Tl/3AQ5eW0AwCBH5bOSiWSQPXO5HPthM7tPJhWY4nDyd8mEEGS2DYwBoq/Hx8fmTDOxohQciCpP1x3LpZ67XC5bTzgHbvGr6lcsu/sn85YAjKKZE2dj0WXBDw8P1fd9O9pwXpXJdaN4fuaIyGRgzDXZk67rWgUmg1uW64ydEWZ1ibPE7Fuf3EuxXq/bi8ew7JxuAqwsQQJwTrnKYzhz3owRS0/eVdWcCz3haLICkEA2dcGVJ9pw5Flh4NQSVDVHNYx9sP4937jO1nxX4l5VLVjTU6f2YHm6rmvyBHBV6QTEdMy5ydaaZuLKZjnpbOtJPyEBEPTYigSBjL0Yc7k8vsSQPzFnIGG9Ht+foR2Df9G7jK3MVqosGyfLniwjP4DR9Oybm5sGntiH9c3AQFfZ8N3dXTsW1b3IkpyPLPmmtVskM8XvGR8CIdlrcsoqYLJ4ZMO+rLH19Bzrl6RA+uRMcOYsafoycSH7i8mer3KfTCATsPhd2tavk5LjuziOsenLpKqeVVv+h51nMp7Vb3sN+GPfXyymp/DkGtOld+8uGsAehrFSOWdS2XuSDefn79ozkyVOUit1liwWi8Wv2sv4tmwdysTDuPvdtt2f3z/OfVnnX21087aZVH5W63Ut1yOwlNyzLWMQ/7Lanftm6AMfDRdknE2cwFcYr0pK1x07IJB+q9Wq/v3f/73Znr+952q329XT01M7mldCne/iSZZXe9XZ2VmL5/QUyUJ/+YVkuvlh731If0dOVTXZXJ9+IZPm/D1fQO5zYsVaiiFsme+sqgkhQaesTVYpxKvEBkmofuvvw/6YYCcRctgfqvua1Kyi9e8og2k7rvFLJo/+4tASMOvj8ly25b7bqCgmpvQs9pb+JcmP9INV1fw/vc0EYL/fV/81afQZ7WLnX8E7okmyY+3MIWWQtsPW2Fe2CPIrSQynLaavmft7sdXvMjlOItl36FP65H90fXeiQYExKev1umVRMjvHiunLI+hhGCZHBQLjCbKzBYDj8WZf4I5hqKY4PUMQ5MA+ffo0Kd0lsEvjSzaTU5bBJgMBiFrIBMHGnpv7koHAYPrOt1ouMlBl2dN9yNC9cxN91cjsZ697AsUsLyYLn72m5O5+lNVzxsA5bgbNjdC+s1qNm2K1EwBiTkjSmsGQ+n5883OyJVnqnpe8k+FL9opBZ184kJMMkuQJo8X4bQZNhiZPRkoWx5iAPZf1y3bCTEIEMbKZMwPGIpBkuTgdDh3yPEkldo8zw5SRn88LJKom5ktXAUFjEQTN35ww34ItebqP+Wsjy4SBLQMw5K3ylLLLFpN0fpkwZBUhmfE5CyxREXw4+5SRU9CsAX8DsGWyabxzQGucTg6zJyxL1Kkj7As7CwRkkpdrAiBlgp9+gk0bBzY3TzlLH5Frh5RI4ifBsmeRHQDDhv1JPXB/dm8ObIXPzsqwdRPE3S8rKTlG4zQ292bz9giICXkka+6vs9aOA8Uou3ff942h9n/P4ufSlq0vfUGqZKVcMkmemeweDzIYQQb92263bQ8e21qv1+2Fei4n6hmPda8aAZqqDjs7X41JpPU5ynhZ/TC0TeIZ6wBj43bvH374obqua0da0+u//e1vkzhhzc/Pz9s+lbOz43sxfvnllwljLjn4+9//Xufn53V3d1dXV1ftOGCEQ+67sUYqsMYoyaBLkgMylaB0XdfIBnGF3qTNwSvGmYcTsGGfy2Ql3xpv3HTd94ZhmLynLEla68gu+Fz3h8WM3xxVuDLJtYbuQY/939/0F4bic4Z+OFYyum7iY3Kd3S/xSlYnxLERr3QTfyY+zEm/JOGGr/cVF2C/tCXJVXYM0OW0X7EIMUE/MjHe73bVDSNOSHLVvBND8h+5sR6uSAyU1alMIJKghAtShhkv+f20zfT9Y9JXzX+6B9/HNyZu+UfX76pozDcLp6ImKMgTGTabTWvJYOhODBE8swwINACIAmhu2tPu4XNZdk12X7JjH4MqgTKslhvBx7wou7laVNmpl0b5fSZKyU5LxA6HcZNTOjZA3BgYKvklQEpGUtCtGrNdBpnlOPdkKFliT6BrvBTVcyUTQAnQmi9ySnBujYFnLRn0Rs/7y8tL+yynbo5YWDLNJC57vvMNoeYg8CfQsE50Scn6w4cPE6Obg21gIR2LRCN7UgVyOuo788CcICSBh+fklY7C/9kZcJHJRq4b+/E5DiET4Fy7XP8cG/2nW+YiGCTL0vfHfm9rRH50I1sp870gw3DcqHp3d9d8TDI9kmZz0hPOhgRG6yAIO+IxdbrvxxNMJEWp/9Ysk1/P5Mv4hWTt58E3k/XUV74ydYePS3+VzD0fkCSLamf6ECAlqxDsJ4NGslbG6j7fClr0ApGEycog5H7mmwDFnNOuskpIpzKpTAIjy/vGkiX7jD0qynOWLkmX9Jv0O6sJySAeDscquwMvnMyU4M4akWsmYNh/80ywSDb8V/oIdsD/+q64eXa2bv4h7ZZvSfJMAkBmT09PEyYc2Oe7qqrNdbfb1eXFRQ1n55O4Zqzr9fGN4siNBEPmuFgcj27nl/hY8Y0cD4dDff78uVW23QcZ+f79+6o6xjfJCmDMH//bv/1be64EGYFgLOm/gLjcaGztM2G2JuIqGzb+BNtiAftItnl+ZCq/lrbHfuwBUZ2xRzXlOyd8JLvswfryVSoi+fmsqiXWSiIIVkDi5FonyMyYNfEL0QGR7cDb7baGbjwcIX2N+NGShGE84OLoD1ZVNTR84RSpBN8q+q7ValV9EE/8VFY8raOYlu1IfAnfQFdTd2DIL1++1LKbbpJ378QhyHp6lD5kTtaZQ+qhOJlYwvzJMtc09TkThsR8EmH31Gqb2DWrpub+W9d3JxoURyDnUBPUcJAGTBDZKsAglSxNKtlH7AjQgV0AFpIZUDnAKlRVUx5G9ve//33CjGEVJRzAb7LDjMqcbOylDBQOo9vKgodxIy+FwHQwFooHYDJ4imdu5D4H7+6T1Q/PomzAVma1mXR4sU9m/Qwlj9W0vllG9vxkfMjR5zhEFS/X4XBoewWyZxdbLfkEQKwBdrmq2pnj1nOeyVuffD8LOVtPR0jaC2APToKbYRga+LNGkl0ggi1kaZuj4uzNOytlZEvPOHNJqXnPmSV6zQFmKTSZswQ4QBIbdaXT2O/39dNPP9XT09Mkyei6riUluVkXIKQrCSiVtZ+fn9u7B7CH9LZq3G/V930DR2wfcMyKQzpL8qPn/IfkwxqQDQYwiQiBI1nwrDBgbDzbOLFRGNBsoQIsyIIeJIEh0bJmAoLfAQJ0ka9IezeeZOfpBx+cbFz2fs/Hmvqd7CSd4f/m/bzkmwEtW1ySUeUTEqzwWeSXc0/Q7XSlZBp3u13bW6QFL+0g28Xod4Im5EIebMCn8DdJ8tB3PsLaAJB0L6stqqwJ+shUbON3k9xwD+TMNFnZ1nK5mJA95+fn9eHDh8b+e07VrxMo+iixXa1WtRyGWq1X7f/2uS26RV18Zerzu8a7D1vht7P9kb+kUyoskr7ValWbzabOzs5+lfjf3t62tayq1kppfpnM8hPAEB/h3mJgnjhmDLe3t41M6/u+rVO2+mViz7bFGDEWKeazZJAkalZA+RV2lFWE3FeEKc/uB3rIh0kYXXlcd5JZ7DOTWnqG7CPfTBytVZIY/Fu2gJqLebDx/jAenpFxen84VD+MhDN9dS82lpjyaM/TigjckJWU3GcqyTj7ehgCO0li2pXjQGxlzM6EKP0sm2nxtRvfd2b9+CEYQTJNn8xJ/LNOmYylDOdJauIcuIg8PMNlrXNObDmrWNY/SYas9orlv3X9rs3gCXw4AA+S5WcCkKAmv5ObmkxST60+vKrxFAqBa7lctqoCw/acPPJPCZGTSJbll19+afeUmRpXMmmenwtNodM5zMuZuYHGJYhh032uakyygEf/Z2RZYs9xJYOVGWkGGsBDEBNgnIyhtU2iNmfQqsYgiMm1f+P29rbd2xj9++PHj00pOXFBl1Fki8J8szGjTbbPGmMUf/nll7b/h55oQ9ADqy+fQdNHgFPCSwcTOHCU6RTokSSFHnNyApkEC2jxfEbKKdChbM1T/cO+CjbJeEu+k41PZoN+JGi2tsAzWUvGtDzmvhY6Ra651hg/AVm7JEd1eXnZdDY3zAEGbCGdsXloeyBX96eTbDuTawDO/elaJnPWn12ZW8olq2OAR9pPyi91JJ2+MeVY2UqyrX4PxGZwMIbD4djqAGzTC3NGvHiO8ZlvJjgt8PfT9idgSMJGhvyOe2SCk1UFv/PMDNaZUGSA4gPYBFZbJUuw9Yzn5+fW+mMuyKFMKI72cpiARfrIjvhtiQf/tt/vJy+UlfAnaNeiNE/ShmFoe8nI/enpqRFMEgJxwBjEkkxYyEgFAvg96um+DocxbhhXjvPy8rL5f5URJN1ut5uQA13X1dn5+JLZqpEAqMV4vLvEbLs9nkj38dOnWq5Xv6pkdl3XDk3Il0Qi896/fz+JfToTbm9vW0sVAEf3JXf0nIyvr6+bb+Pzc/N1MvLL5bLdP1thyJvPFnvyYAs6nHoseUfa0S0xJxljep5thYlxMhFgnyorWZGZgu3pO8ayWpfEb7LYSYIlUDZ/+s4nIQ3TDufECx1LffT9o53u67AfAb94Zk77w9iubl3ShjyPfifJRLd0raxWq9Z2mNjh66AmiSIfpKUVbk3ZZCWCjNyb7Wcrp/EkwM/kYV4JyOQlycn8TuKx9J8p9yS7M6lIvy0uWEe6liQT4soapY4lAUwmc+LyH13fnWhgVpwOw1FbAMosAyc8Dk/QMsg5M27yVeMpJgRBGP5231QmjAQHkSw7J7Lf79tRczLezWYzORrUIlMUgp73qmvVSIaNonB0CQ4BGgaXwMJ9OSmtQXNFZvwCFiDmXsmEkbskQoBNJs1nsuUKYzIv0VFwIBBIOzs7a/st9Cj+8MMPVTWe+6/lYLfbtX03V1dXk5Ol+v7Yn6gPVoCQYDBI8nYaFCMRvHNTV54cJEmpqlaK5sSAuEwarLHn0vXX19fJZuAEVYw1GWmyI7NMCgUSnwHyyctn6b6EhMMEjLFXKgnmf3l5WZ8+fWrzATro1GKxqP/+7/9uTNzb21t9+PBhwm5JxNmecnPuAVIlzOqZsbG91FNOTyBbr9ftOXSO/XJ62epAJyVD7iMxMCY6n8kIgsJ4fN+6m6c58knmxO6TjWb7bFDSlOtkDkle8IP8hDWScGLW6UCSHCqP+q7JPRljege0SHaNo6omfkggImtgKq9hGFo7B1vjixIEsGv/TwBR9Wu2N8mgDGCqiyoGmcRla0m29X5Ld+a+nY6Tp88mc5jJfFaAc4zWTxLofnx0tqrxZ+afDHa2yySoZSdZZUzd9fJaJ52x7Tzas+/7dlACX9+IncWi+v5Qq68Vr//4j/+om5ub1l74xx/+0GK8+R5bXy/qMIwnHT4/P7cWWuuNcGNP79+/b/YhKaJzj4+Pk/iVJyNmJYNepY1JBvIY6fy9tUnwnckM/y5GsR1kIbCdn03Cle7zK+zQemalgI9IbCCeiY/sla7x/ZmI0h+/F4cTi2UinCA4AXD+nP9JMGmsSVrkvY3F75K05Ye7GjHOhIToxwM5PG9ue5k8sdEvX15b3MykJf10EkCeaY3mZN+8Y4Dc+WFzIptcY/4vu3MWi8Xx1Kl+JKfokXV1JW5I3EaPzSNJRnPKdc1kYZ6gZWXE/Nj0vBKT8SWJvEx26EsSZr91dcP3piSn63SdrtN1uk7X6Tpdp+t0na7T9Z3X9+3kOF2n63SdrtN1uk7X6Tpdp+t0na7fcZ0SjdN1uk7X6Tpdp+t0na7TdbpO1z/9OiUap+t0na7TdbpO1+k6XafrdJ2uf/p1SjRO1+k6XafrdJ2u03W6TtfpOl3/9OuUaJyu03W6TtfpOl2n63SdrtN1uv7p1ynROF2n63SdrtN1uk7X6Tpdp+t0/dOvU6Jxuk7X6Tpdp+t0na7TdbpO1+n6p1+nRON0na7TdbpO1+k6XafrdJ2u0/VPv06Jxuk6XafrdJ2u03W6TtfpOl2n659+/X/IyJbI417+2gAAAABJRU5ErkJggg==\n",
+ "text/plain": [
+ ""
+ ]
+ },
+ "metadata": {},
+ "output_type": "display_data"
+ }
+ ],
+ "source": [
+ "plt.figure(figsize=(10, 10))\n",
+ "plt.imshow(image)\n",
+ "show_mask(masks, plt.gca())\n",
+ "show_points(input_point, input_label, plt.gca())\n",
+ "plt.axis('off')\n",
+ "plt.show() "
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "41e2d5a9",
+ "metadata": {},
+ "source": [
+ "## Specifying a specific object with a box"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "d61ca7ac",
+ "metadata": {},
+ "source": [
+ "The model can also take a box as input, provided in xyxy format."
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 20,
+ "id": "8ea92a7b",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "input_box = np.array([425, 600, 700, 875])"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 21,
+ "id": "b35a8814",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "masks, _, _ = predictor.predict(\n",
+ " point_coords=None,\n",
+ " point_labels=None,\n",
+ " box=input_box[None, :],\n",
+ " multimask_output=False,\n",
+ ")"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 22,
+ "id": "984b79c1",
+ "metadata": {},
+ "outputs": [
+ {
+ "data": {
+ "image/png": "iVBORw0KGgoAAAANSUhEUgAAAxoAAAIYCAYAAADq/5rtAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjcuMSwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/bCgiHAAAACXBIWXMAAA9hAAAPYQGoP6dpAAEAAElEQVR4nOz9Wa8lS3agiX3LzH3vM0TEjTtn5s2RZCaZySRZTM5ksYpFVrO7utEPhW61BAgQ9Av0LkAQBEiAfoMeBDQg6UmAHlutQqO7WqqBYzLngTnnzTsPMZxpb3c3W3pYZubmtn2fiGxRECCEXcQ95+ztbsOyZWtey0RVlWftWXvWnrVn7Vl71p61Z+1Ze9aetX/A5v5/PYFn7Vl71p61Z+1Ze9aetWftWXvW/v+vPVM0nrVn7Vl71p61Z+1Ze9aetWftWfsHb88UjWftWXvWnrVn7Vl71p61Z+1Ze9b+wdszReNZe9aetWftWXvWnrVn7Vl71p61f/D2TNF41p61Z+1Ze9aetWftWXvWnrVn7R+8PVM0nrVn7Vl71p61Z+1Ze9aetWftWfsHb88UjWftWXvWnrVn7Vl71p61Z+1Ze9b+wdszReNZe9aetWftWXvWnrVn7Vl71p61f/DWPe2Df/zrv8U//k//Q57/5GtohB4PCMGBE8E701lijIQQUFU636EKqkqMkRgjAM45RIRxHAHYbreEEAB7Nn+f/xaR0kf+3TmH9x6AcRzL33n8GGPpR0QYw8QUAiEE+r4H4ObmBhFhs9kwDAMAfd/jvWeaJhs/Wp/DMDCOIyLCNE3cuXOHzWbDOI5M08SjR484Pz+n6zpCnBCJeO8ZhoHr62tEBO893jmmYSww8t6jqmw2G/bTnhe2p/zp7/0+2+dOie++z+N/+1VOxoD2sOn7AodpmnDOFbi2MOq6jhhjgV+GZb6fse97XNqzPBfn3OJnvRfOOXtehKix9O2cK/COMeKQAtvT09MFDuXx6nnUc8t7Vq/DpX91y2vqVbjZCBsVXnnto3z1v/pv2Sic3D2j7zt7BhCBPRNDp9z/+Kv82h/+Ju8/+ADf9Ui3xZ+eEjc9QQSiw0/wzje/z/tf+3vujkJA2XvFCYgqKsq0Ee79wmt88Y9+mwdXjxBRxHVEBKRDup6I49pv+MQ/+m1OT+4SgjKpsh93fPDoQ7ZOeO7Oc8j5KRIDlz/6Ke///bc4lQkEJhdRHxGNaPBcxA2v/PIX+fgvfIYoavPF4YPSB8ePvvVdpofv8Zf/x/8zdx9c8VhvCDFyGhyh8+n86cF5xAlB7fycbDdsNz2qIK7DO0cMA75zjPdO+Cf/8/+MHz14mzMVTtUTthv8dgPiiFOEMfLWT37GxcUFExHN5x0BAe8cfiP8wuc+g4gQI+A6EMMtVdApgio7p5zdu8uP/vVfcf2X3+E0RG5cYBLYug6GCbzj2iu/8Z//OeHOhq7rcJ0nAiEGphAYh4GwG7h68z1++O++zP3JQ4hMoriuQ3DsdjumKRCCEkJgmibGIZTfY7TzfP/+fU5OtogTMlpmGpNxs235u6hKrM5j/fyEsJsmXn/9dbbbLZvNppy5TdfjgN4Ld+/ewSOggRgDXmDsPS/88qd57hc/gbt7Ttdv8M7juo6N75EYCSGye/8hf/df/bfc34ETZecVnLANSiAyvXTOH/zn/wk3CFrR4kLXNSLDxLt/+Q3e/cb3UYHJCz6CD5GI4dfo4N4nP8of/sv/mHfiNRFhqx5X0agQArubG77+f//XnL53TR+UoIGhs/N6t98wjIHr/Vj4RNd1MyxZ0qeaBoYQFvOueQXOs/MTn/v938C/cE5/5w6bzRm+2yC9IFOk73vUOWSY+Jv/+r9j9+b7uADee8ZOkLunqBPCwyvisOPzf/glvvTHf8B7+0uuo/EIr4LHpxMQiVPg+uqa//q/+lc8enDFT99+h5tpZL8bmMaJj33kJU5PO37/93+LP/uzf8bV1SUhBLz3FZ1XxikSI/z0xz/hX/0//hvCOEGEje+5Nygvb895+ewu027PTiLx3il/8B/9KV/8g99DOm/4p9CrsHt4wY+++R2+/Zdf5mevv852s2UYB0h7pKo4ZMGP81xq3M3fZ7qe97im+cda7mON7+c5qCocOWP2uxQ+mt9ZO5c1P8zzzd/VfDJqXJzT9kznd+v+7TkBdYvPFvi6st6Mt/U8WtjU/dRrqXn+wTO4RR817637XMhZGK81OhVtzhVM1t7N74dKHqjnuTZubu28630JVPvRPFfvVZY9VA2+IKtwq3Eiv5/7zXJjPY81WOf9Kv07QSr608Km5rM1jukK35hx0+NkKX/ZeEqUiETFBQcIsYv80q9+js9+4bOM4rja3/Dhwwc8fO8D3vr+jxk/eMzzJ+dc7fY82l1zHUfGGNg6z3ObU877LZ757C7gZaBcxZn2vPwfvv/XB3vbtqdWNMAE+qgRjRAVFCHiEFFCQ2BUlf2wp/P9AqAt8tSbvHbI6k3Lm51/AoUYt60mBOM4Mkwju/2+COF937PZbNjtdqgq42gMTVW5f/8+AM55gsI0TUUpyExyHMcyblYisjLiO4f3JOFlous69vt9UnBs/K7rinKVBX1VY6YYXU1zcCgTzvkFIfLel/XVykaGS1aKZkSdYVkz7JZY1kpGfcjKnogUBMyfZYFIVZmGcYGEbf9P024jTgslJR2SGCLTfm8w3Q8zEczPhwAScU744O13ePToETc3N5ydebou7a9zRO9ABUEZdSIITBrBGQGWGBEURYkh8t6bb3F9cUnUgPcOjZEpanre2ZMu0jlhd3ON4hlC4GZ/xc31FT98/XW+8IUvcv/eGV4cJ2dbU2I04oAQIkqwcdWhIXB+dorDcEWEQmDHcWScTEHZ9BuiXhiEJAtcRqzqNu8rKAGi4iZH7zsQ0BhMgfIeojJe7/jpd76PvHDG4NK5jAE/TeA8MVgf/ekJ2zDhxpGYcFvEhteoTGPg4cOHPHfvPlNUJNr7iBCiwhQRhZGJ8/NzbvZ7xDs0RJJcYeceCCiTRB48fszp9nkUwSlJIYYYIE6KIkjfE50nIvafGONwsmRmrZDTKut2APLPn7/VTDLvX1wRfAr+KyCaBBnAYUKBc6A27w8++IDuoy9yen5CmAac80gMRB/x4ogxEDoh9I4YBR2nsv5JI+qFi5trHl1cEPoeSXhTn90hTHiFx+OOwZnSTVQkgERFHKZqiPD+B+/z6NFD9KxLSp8SKxiGZPTxJ1smf02nAlFAIyrGX0KiazUNKk1ZKBP1HpVHGvplgFbw8JOf/IQX/cc5ccImCq6b6ILHI6gIURQJkeiFYIiGqBKi4mLEdT04IQr8+Cc/5hd+4ws82l8Re1cUDSeZL0U0Rm5ubsygJba2EIJhUoxkAenrX/86n//8r7DdbtPaQHWa6bEKMSqPH1+QsBrnHeKESSJTB/sOONvwy1/8PL/zZ/+E05efBwQJ4MURhpGf/vDHfP0v/5Yffffv0esBorK7uZn5qzhU40KgbIXrmicfU7Bbvr72TP6+3een4Rs1D2z7q/FgoUhUQnH97FKgPaSV9XyyYnPb2mq5RoUilIYQDhSdVqZp198KeLcpcO2Mnpr/ylLuYkXAPBhrRajPRplW+WxlwDUlYJ7K4dqfpq3tdf3dGizqfW/HWsP3uckCB1rFr4VPMeSKzAJes8Zj+J8VXyem3MSoeN/hEDREMzhd3rB7dEncj/hotHgaRqZxYtzvmeJE0Mgkkeg2uI0DZWGYKTi5Atd2Xk/C/7r9XIrGzc2NCcFO0ABZh6wJRCZUZgVUAvMiskCe38nImCddP1czj7xxXdctiF29wXkT20OYNd4s8APldxHh3r17BdBd1zFNU2GC261pl13X4b0nhMAwDOX3rIBki9k0TUUZyR6FVlA3HJuRN8+l73t2496eT0Jc522+gqDRLOm5v/qw1gTzNqtI3p98GGpLVK2t19p7vae53fZ7JqTtAfx5Wmt5qltZd/qfJvhMo3mJukxg1IRVj1nluiQ4TePEsNsBhhthv7f1e88YJojO3js9YZDI5ASnikZwMSkZTstBHG5uCF5tFPGYPB9QcUSUoHuuLx7z/Iuv8uGDCx5eXrEfbxCE559/kUkVQekFrvY3qAYCSpgiAbMqERWfFCad9kgSMERnguA6j+886hynp6dM+ZxqJJPtliTkfQ0aESIiZgfrNFvhAhoVfGdwDpF4saO7d8q1jMSTE1wIiIDzWuD+3CsvsR9HwjCiCk5mq4+GYIJkgJubvTFf50jaAYqg0wSJdlw+fkyMBgmvcWFlUQcjkdEL4j0xKTFOFefMmjyOIzFGduOI225wp1uGYc8mE3YnOJetxgGY8a7+V8ZMZ/gYft7WRMzz21qrVJVQbc6hcF0p/hpNsDf7KM47phjY9D2u6wx3wkRXlHHDfRVwZye89OmP8+jvf8qZlyTFmqIxAHdfepn9YMYYZDYeFLrsHPtp5NVf/DQfvvEO7magi7Z1AoaPAkGU07t3GMeJ8XoC74m+X1j3spfo5U98jLfee4RMEx1qHkOV4rE4xsjELfekVc7WlMV6LSFG9tOIIxLCSOeEKUQ26lAgONBx4mOf/QzffPtdNmrKvaoxegUCkRFTrC+uLhnCANGjzhQNEUdU84Siiu86Nicn3NxMCRc80gn73R6S8qWqXF1dVd4Mv4BBiAbke8/do/OecYqJrwk7GbmUyC/9wif5/T/6I177hU8xdYJuOvoJ4hR486ev880vf4U3f/hjHr7zPjLOkQRZuBTncCIE++KogHibQejY2VhTBp/UROSAdi37OBRa6/6PCbql7/adI6PVuLW2lrYtPD1QPBotXWnHOAa3NeWk/TstoKzhSXOs15INc+S56fLdtb1bPF/NY8040K5tMXb9bLJlxgbOT8QVbQyRR2TL+vta6WwVjnrdNQ4VPHJihhWdIzvatbWwk0rJWFt/S8fy906SESatEQdhmgjDyHR9Qxgjj958h93lJeP1NW4M9DjCODINA14cG9fhNdI78y7HaEaotf1aUzTWzsrT8r+nVjREkiXcSTai4Z0nCJXVdHYrFSVCZ8G//l51DhvKz9cCcB5zjdnnvtYQuRaO898xmivUJ4Ug/8sKRh1udHJygoikcK4JjW5hYXDOsdlsUDUhJoc4bLfbMs9xGthsPOM4FoUmP5cZysnJycLrkEO3zMolwCy0mzCo+Gqd+WdLQPM7dShard3XikXN8GttPCtObRhTgXecXalt6MIUpsIkWyJYa+1rylDdV/nbHijrq8dMpxxQ+s0G1WhCgEamKQnNiUmZO1zYnp6Y5e5kYwJjxssYcL5DxSyad15+AblzwnQx0o0RMu46UCeMOvHSyx8lxAjevCriTEBTo3goilP44I2fcX56Ttc5zu+c8cr5y4Qw8cGHH9D1HZ0D2Q9cvP8ecRwZnZpSIxCTO96Lo3OOh++9y0sf/RhIh0Uvmo/FeY/fbhgvjMnEGM3ync8NS8K1IKRYKI14x+AdO+/ozKWCYB7MyTsmiXYuhgBbxz4EtuKQZCUOCr7rGSKc373LdH1D3/cmQMUcWANhCoh4QoiICp5M2AR14FzyUoWJd999l904mDJWECZZxYGpg/sffYXTO+fEdJaceEOLimG6riNu4ROf+yXe+ep3CbsJjSYEZgXecD2dqcpa1Qqpyu3K9pqwU2C+wlA0CbFrfVl/SZBPCKsy4/0+BPo7Z5w/d5eTO2dMTuicp+861HVIEoyjbTKf+9Kv8zM63vvuD/CTKeGDQDjpePVTH0eFIrjWtEBEEI3IyZbu1Rf41T/6Hb7z7/4GvdjZs6oWzueFHYFPfeoT7McB128WdGxhIPGeFz/+Mboh8ubffQvZV0qCQEi0sg6pbI0qa/jcfgcz7RtDQE48zz1/n/O7d5CuM2+ZE/NEppCTiDJK5P5HX+ELv/ObfPfffplOTAES74gOggjRC698/GNcXF8hW8NQTWc3xJAsjybAu87zhV/9Vf79v/trEHDeEYLRut1ux+nZHV588SWc8wzDiPcR54yOz7TYBLDnnnuOX/+N3+CrX/5KodEvvfIy/+Jf/Mf81pd+i03XmQfJgQTYPbrgG1/+Cn/7F3/FzcPHuDHQTRGnFv6sCYa1USkrxa2QW8/nmDJ4TABZOxstvrfnAw4Fn7aPVhhseePavNoxythRiyLbjlPLH62iZR7CFet8otFr7z/JWLGm1NQKdK285+ecc4R42MdijStw1ywHkOmRzvRmZQ41TWthv+blasdu92KBY7IMTT3W8noNBochVscE9xqva8NOqzAdg3/mKzGNWSsZa+dl0SeH56CMoevf5fddMhqZlVUZd3u++tdfJu4Dl1eXlh4wBVxUNl0PRM7OPCdi3n8VMww5mwQhhoVCXObPfOaOKbdPwt26/VwejYLEISYLfiDokvHWCoQqjMPAZrMpzKo+YG0cZxb884Kylpj7zM/XFm9VLWFIIrKI563zNU5OTorwXBOi7Jnw3nNycrJQPlrkzN6HaZoOciTA8h6sT2Ecp7JuFvChjJvnsd+bJ0N9ekBMMN50phBpGC1WviIqtWJQ91/Ptz00ay7C+qDmvaiJRP1OEfxdDj1pLCoAOj+7No9aqThG6FsCXudoHDAFNeukKcGOOAVUwYtZc4MqOGGIgeg7PvGpT3B6fgZdshY6D96B87jOg3r2IXDy3B0+/6Xf4Lv/+i+LshPCBOKYnNDfPee1X/gUru8sdtI7swKLQ1wH3uMwy+flB+/zzYtLPvKZz6L9lt1+x7br6V3HyfYEr8rNgw+5+fADTpxnchbOgzhc7yw8ZYKNd7z3xuv47Smf/OyvIC6J6En5D8FyEuqW8U1wizjbJdzBIwTXEe/e4e5HP8rFB+9zshf6aUJUuCbysS98jv7eHVzvONt6tPd00eG6Dro+ES9wAbb3nuPm8oIwTkQNBFWGOBFC5LVPfIztdmvn0XeIeFQMftGZN0KYCL1jFOVzX/g83/vxe0z7sQhxMSq+75Btx2c+/zm2p6fEfL6TpQkBcZ7oJkQDYz9y5xOvIY92vPOt79NhjCLnMGgS3m9jLrMF7DiRbYXbct44NJDMjHV+95CAz2piVLNCadY+th0vf+o1/Ev32Zye0G96vO/Mi+E8HQ7vHHsNTCgqkU/+6i/zxve+zynmhRhd5PO//Y/oXnqObrNhu92aR6ii1WDnbCKiZ557n/gIn/7lz/LDv/oqLhoOTSjXYeLTv/F5nv/4R5BtT7/dIs6TQ7HyerMCGk+Vj33+F7l84x0uf/qWjaMWPpiZeP1egdcThKd2/1QNb7TvePGjr3L/lZc5ef4+nGzB9Xjf4zpHH1Ju4cYTUNhPfOaXP8eHP3qT9372Fq7vEuwdQwx89FMf5/yF59icnCC9x236otShhociat6jCJ/69Kd49OiK1996m5D3O9HC7XbLF77wBTNKiS/fZR7ikifFOcc0THzxV7/I2faUL//Nl/mjP/oj/uRP/5S7d+8i5p+0vX18zU9+8EO++9Wv88Nvf5ewH9ioSwYYwXlJhhETlI3WJnjKrIC056AV4o4p3mv7sPb7be+s7e3y2Sd9f3hOW6PXgfDUvFMb3dp+yjmvxqrDUepn1+DUwm+NL9fP14bbWk7K77ZrPqZ01Z+JJFytvmvb2mcZJ9vv2pyHY/uzJhvArNy0OFbPud2zvAftfNdgW8+tlVfq947tzRo8juF5DSs4zHdZ7HH13LJZblVCMqYQ6Jygw8R4eU3YB3xQJEKHM8KuCt7RpYBvn1hGJCZDKPZzBTdqQB7jc+1ZuK09taKhySsQQiCqMowD3nd2HnVp2c5hUarBkjMr5cHWZkCurVyq5iHo+35xgNbcs1k5qIFQC975+6ykbDYbfNcV4pHHrEOpvPcljyLPxca2d/LntZIAsN/vOTk5Kc+M48hmu0V1ouu25fn8k6R8hRDYbCx5dRgGpjARJ4XtKS4R/Lx+Jw7nPSFMZZ21Bp3h1XqIMuz2VW4KLBG5VfxaJTA/X8O5VghrIlArXTWcb2MoLRHJ49WEpyUy87Omd5f99J3F94sxWVAikWEKhK3n5U98jOc//hFib96Hvt8y4SzhTUx5wjm63jOOE3dfeoGTe3fQB5c2pncEp+yJ/OpvfJHu/JSpSwlcLiUyg4W+OUfE4aJy4oWH11dMYWAIkf0wcPL8izhxnJ+dEW5ueP+nP6WbJvNaicdQTwi+RyV5OOLESed446c/4SOf/AybzR3LFxpGXH9qSk+M5PDGBSEQEBwQF3AGo0m9dDzynrNPvsYf/s/+p/z1v/pXPPzGt/AXN8gkPP+pj/OLf/TbPHj0gA2wVSFGh8djbh4LQSohfgTzsMTASy9/lAcffMD9l17k+vqa5154gWHcJ7j5haIhKQTLRc/WeaJObE9POLl7znRxkwijKZ9TDJw99zybu+cEBZdyL8BCxmJUxnFCp8AkkX2MoIHRMlKQkHJuRC08KyrgKi/njKM13poH97jV6ZilJ9OnNUayppwXemkrKkUYonWGiHD6/HO8/KmP89gFS1CeJnxI1lVvYUjqHCqKelO4Lx5/yBADJ9Gg1Z+e8MqnPsG1DwyjxfQ6vxJ7HAKKckNgHyYe7q9RL0SXCkQI+DunfPYffZHhpCOIKcFR5yIRrQFnEEU7YUyeQokRjZYYnsOnao9GEXQr5WtNYFzbE1U4f+l5PvG5X+TSWd5eH3scSpgGNDhO/AYX1IxozqA/qK03Cz+W+CpED5//9V/D3z+1ELzEY7SbrY5m4I4lzykivPqRV2camyyLCPzhH/4hr732sZTXOHuSYI4QyDDpfU/cRH7ti7/GP/3jf8prH/+4zSma5z7uR95//U1+8JVv8L1vfIvHl49xIdBH89k4J0wOohMkSZgOEt0sSEkdt9/m+/1/s7W4t/ZdNdGFXrAqON0yTpuUbZ7pdUWnnc9SrmHxzPIMHwrFa4rLmvB6oGSz5JFtAvb83Myz2/W2Y2Zc1PyfEdkSolzPRVUXuImu07waBmuyQLvOek0xhSk/SQFtv2u/vW28YwpM244px9aR/ahx6JhiN3ey/HOxH8f1ZVMSMlycQ4j03tORPMYh4pIMErGUNzC+iAoOTYqGI2KGnGNK09O02/azbU8fOuUc+93OBIkY6buNJVvGiG+IfBbUTdhdImDrBciCawihJE9P08R2uy3VoVrBt3Yd1hWT6mTtHB6VBXBjTgmhxVz9ZsWBk+2W3X6P956u60xwc44wTajGFPYkluw4RfrelIP93vI1drtdEfK7rgNRpiTw7nY7huTV6bqOmCyntbBehEMxOKsTuq5HRbiZBjqUOEacd4uDsbbxXectnKciYlnByHCqCVzt4akPSX62VvTKHshMMDO8bV+PC1Kt0tDiQz1+3YcTKQnF9Xxy0KsDvDfFbIyBDtAQic5c/4LgXcdA4PTeHWLn2A3X9F2P8z0hKuo7YgSJIESCWnjCKMKgkV6EGCZCZ14SFPrzc6IzLxc+Wy/FsiqcImJVImK0/rx3PHfnLoN4fNfjRHn++fs4VcabG4brK3QaLemr26T4VDUPRQqXUGAcdrhtn/J3DKabk60loo97eidMcUomZkW8hYIVJpKI+AENjBDFs9909K+8yD/+L/4z/u3NDTff/gEuBEYP3Dnl8oN3uKMOn6hYkDQLxZSEROVULWHVdZ5uu+HO8/dRjbx4/hJTqgCHOFTMA6Fo9ueiYUKi5bmgykjgcnfDRnTOzQkRFccYA/swIrqhw0MqVkGSFbxzaT+wqjtdZHQmPPbFM2BCaIgRX4VM5DC6bLErNK6B3Zoi3TKdtWfr5hDy0K0A4hPtISoaLazIpSyNhxePeefD9+HuGacieOxfJ5Yz5FNhgs5h+mCn3H/xRU7unBPev6Rzjuuba9754B30fEvfd3RZsHAuMTSScucsAb+zfeu2G0aNpBg9osA+BnYauNoPiPdsZYNTMZe9OBNoJXmqUYJA1EB3dkJQZSMOR0QMIrPhKgnxlvOQM1QWm1AU/YyP1VcGU4Gr/TWPLi8YtnB6xwxBEs2L4Tqj4SEGUG8M2jnw4E43BveoxCnSnZ4gXQedYwwTOik+RoIq0nnUQYh5v5XOOzSCqOPBgweM48Q0LcNeXn75JUC5ubnGN0VUVJWu7yykD+i7Da+++iovPv8ine8tIdSZD/Xygwe89aOf8oOvf4uffef7hOsdSDDjFelMJGWN9Jkdq6yoz3hYC9Fq/yuJqVK+SF6FVcw+bE8S6tYEVtI5hUMB53+ozlPzvTp5GQ7XsqZotErXTCOM3lO8o7PC1ioH7XprgfxY/7nVil+dnG7vL3lsy9tbGNgfeZ/Ln9TErg7/Wsh7a32twHqt1eufw1cjVMbN+tm1vhbKgj2weH6ttfmoWY5sFaZj8oqIFEW8/r42kq/tWxmD9fNitOu418T4jyZzmhV3QC331OVw3xkEhXeJgmRcT3xt4cJam8gtfM5gLcffb9pTKxpeHMP1zkorimFknAKu76ziToUENZAkMZX8WVt6tp549hrAeqJZvWEZUXLuQw6Vyr9n4bpYChX6rrNqH5OVvPTe0/U9iHK6PTErzzBalaIYrfqOd4zjnk46us62d5omxNmm5VCtrGTEGBFHCbGKMZa5ZOHBe1/K4k7TNCNmsnuMIhA9/uSU4e4J4eEVJ7gSg14LMSKSqly5BFPoXMr5kFx16JjFg4XSk+GV4Z8VidbaijTuvkJgdPF+7j8nytdEsV5He7iLZUnmeM/681nhEfpISZjeiyU0+xitUoxAH62STKdwdXHB3fi8ebicR6LQ+Q24HvEnSNfTqZqy4S2Z3J1uiQ+u8SoMEnlucMi24+LxJc+fPM8JnuidWfdT5SR8D111tKbAtN9x8+BD3Mkp1+PIlUZ8v+Xk9JRTmdA4Mm2gkw7NnjQRegE6IThLBOtcb1Xfxj0SN+ynkTBNnDnHcPWQ0+srpjgwaWBLb2EoTkv8rVnsl7ggqkwS6KJyEhynmxPkzhm/+Z/8R/x3P/sv2e6veHx5QRhHTp3jXDqmHsaNw2Eha3XpTEHpVAhXI3sZeO4LL/CT17/KZ3/xF/jwrXd54aUXCH1Ht+lNmXAOEfvn48TQwdR7+sncvfHEc/7yc1w/vkSngM/ilsL52SmqkW7jiS6m9ZnAFDXSeSHi2aR4WrfpOX3+HiMRVRNpFQudi5NZ01WtvOKkprBGZxXANuIrfGW1tQLCkpFLKfGan83NIbhoeKwdZt3P3kyUTlJ1PrNHFwZydnLGxjlCVDrFXOWpRGLEFMHoSTleAuLw2w1dvyX4awLK6cmGl+7f5f3pyjw9vrMqYICIT9ZutfyFENmoECKc372Hdh1xsLKLvu/onBDCyKQjfW80tZOOVCprpkRiOR8nYpXd7r38Mu9976d0o+DU4bVniBaaG1IYUBYiQobvKpfL3o68BybwmVFM2YhyfXnB9ux5nOtMefJWOhjvLa8h0RyP7YN2cP8jL/L+T99EJ6HXDZ3f0p+dczNNxN2ezeaEzjl65xDfIeKIPYj3xk/U9jiGwMuvPG9eT515lveOd955A9X73Dm/vyhC4nLoVOfpouf8zl1efPUV+pNt1mZMWNrt+dn3fsDX/v1f895PfsZwvWMME1Esv0/U1hOSfNDlnIIkLKmBb7Ysh2jejiTAmedDSljq7FlKwnMSvqJqKuu7sjsVT3mSYLoWmrEusK4L6sda/f0xD8XaGYX1cJH5+VjldmSjhNGKumzp2npqIbcWeoFFpELLN+v8glb5yn+2hot6rXXFzkVCdDKoIZQiD9lQW+/N7LE53m7b49rguphH82wdFXNMWdK08DXDz7G11wpH29a8Tcu16ALG9VyOrb2MJWK0flWpWOJz8ehaTTxTMFQhBi4vLlAcKt4KRSCgMYVQpX7F1BplmUvi85lfg0/z90IWFOHIlh5tT61oxBDsX4wWvztFuq5PRCtv9MwAJDF7tIpvTJubM95jc5jygmpPxtqhr0vi1iFNZtHvDiwG+b1clrYW/rM3JZegrS39UdUEm2TtMCXJKk+hdv/Hzc0NQIprnq3zIcx5HFnIVjWBL89nGIZFrgcoQwqrMkFBeP4jrzA8/hEn3i36X1g+ooUtZK9OXr+IoHGZ1FkTprzW+pDURKz1aJR/GScSHItSwnIv6z5bC059wNaIbW45L2SN8Ec1XEQjN9fXhBhSVRasjGWabxCzZt5/8QWGaeSs7+lcCSTCJwHIBJmEv6lk57brGUKkC8p2Aq9C6D0vfuI19teXnInAFHHe7oKw9Sam7AQRh0qkx9EpbH1PhzAOe4bdjv04sL95xHh1yUYDnXPJUuITkzJrcECYggKeYZx492dvsnn+eTZ37nD58AEn5+fobmS8umEaRvNaxJi8LJoqVK3nHwjQBaUbA+fdBlGP67e88MlP89IvfZaLi29x585dHB6ZFOkMvhItQdusMPYv9+oAN0auP/yQ7/6//orH77/P3/zoZ7z2yU/gX3qBDqFP4msOtxLU7h9w5tr1k1XbcuLY+I6bmJmnkdsxBDabE0uYj7NXoISCaMqLUIUQkSnixoiMkS6CTJYXFUJM/0J1RpYWVKmZoWrNCxZtDU9rZtwylXIeUsiQpu5jVPBSlKYDASg9F6IlSIzTxBAmxDkCEU+KyU046TB81qTMkKvxoajrCcHCzLx44jQh3op9oFr2NordmzGkULNus7H+MfxmjJx359zdnHB5fUN0I1F6ojdBuuZeAnN4oyr9yZZRI0NIHobQE2JkTHlH4j2+EoprmnBMmCh7Uu3NabdBJoV9gCnVgEzaj9cU/qiWYpH77VC2YvfV+KBWex5h0/ds+p7dNCKdFX4QFVyqOOWxUKYwxVQ1Jil7IeITrnbpDMgUeeH8HjJMxM2E9LNxSpLwfnp6ykdffY2z83OimjKvQZH9xMP3PuAbX/kq3/67r7L78DFd0KQMYLx4JZy6WDcbONYGsRafayv3k4T5Jz1zdL9WBDVDlXUBruYZcw6VW322nV9+5+BZebq5tzxs0Y/YzDXJf/Vc61CtHGq+ECqPCNX1WLfhf/3K0/TR/l6e43Yl4ra2Nq81b8GqcpeZcTX//FwbhVGM12J8oVasjtGGtXGfNN+2ZXreGsdb78iasmFewLnvOY3ALejVAczsCys9DxYhQ1YjNPEKFr7JTD8WsiNZAXm69S4UInvwKFzW2tMrGsl9bRstdN4bE0+hU75ixHbXhjFqi8FOVu60EM2IwrKUYz5oWVkADhKdVLVYetYs4S0C5X91InhG1ixY5JK1raJyc3ODz3Hvaa6zMGJjtApGjJEpjMB80dc+lVAVSXBLz+12u7LmcRzpO1eUGAUrkdr1hO2GKZjQlddZh0D5zpKCa201P5eVO1WdLyGsDmz+u35njUi3cIZDd62IfZaVv+yt0WoOa9aQDL82l6du9Tj1u9M04fuezXZrQla0C7DEjPdEhAkYQkhlXK0snO8thj1IJMiEXZkmBOyCvhADDCa4TZhA7cbI2PeMd0+RF++xv75gGy32XZOEEjHlRVI8gTorE6nJMt6fbJHY4XuPD4E47C1eMg6oRvAOJxYWpDN3wnmHkw7HhA6R7fYEh+Pm4prHHzxELq4Zd3vGy0vGmx0unauAyVI5qqk9G5noWK6u3fmBwMP9nseXF3zsS/+Ir3zne3SdR1MY2IjdieBwJaa7EEfM+jWpMk4Tj99+n+eCo7u45sFwxfSRVxmnkSkGy/FyFcGTJNw7U5CzgDsFs2wTleS0MOXBOW72e85DoKtwqnhL078olpMRo8IUStUrXLbICuNk+QmnXZeIsi7ucXBOjKY1Z6A9PzWuts+hWko21u/Z89j+axamLWxQoxruZIMNc9lHyy1RxjGwGwfG/QgIrrfKU9nCHApOJlhOE523ogcxyf/Xuz03+z1bPOHEFPauU7zMnmEV2/tRIzFMphylUsT5bqVeYdwNdimpOJyMdqlfD122zidjRUzrI9HIiJ2RDpeUjIkhjExTwHWe3kTymYkuQLsuDtV7oaiF200TDAP9FCAEyEaumAw0+R4czTl/EcaEN1jFKbwjpoTwm93ePEDe03WCF8WJwUQdxTtU8oZCsPs5JFh4ZZrffj8gCMN+pKfHu8547abjI69+hHv37uG6DYh5aGU/cf3+A775N1/me9/4Nh++9z6dCm4M5n1KVec0xmScXtLV2ww8cBhesgbXJyl5P287dnaeVmFZW8ex7+oQ7Py9CbnH19TOqYVBzZ8WMkhUkMPE4jVht+XH9Xe1nFQrK6vC7MrvbauNgHV/q2svMRf/cK1Wro4pVm1b0s2lQB9TCdinGTfLeT8PbtVz0Orz1jhaG6zX5LJ2n4tSn5WASv6tFSdTMlLfInjviNGbzJgMN3WrFfSf76zqARxbevHztKcPnVoI9snl5ZM7MHknXIq39jlePwTAWflATWJTTDG2bo59zouo4yQz4IdhOFA8clnYXKJWZPaC1Bu8hkBtHke+KTwL4XWfp2dn7IZ9mUsOk7L8D0HoChLkn3l+XSdljvW8Nv3GynrKXMEmfx+CJfI5EbOCdT1xs2HXdfj9jhOZkTQjsIhZypxfJmzn5txhjeTaYrXGRNqk1FZjF5jjdEUOSrvlELLs7ag1/DyXDJcMtzXNv8yhWVMhuAiu90w5hjvhoKJWeUEpgqQanScOI6N6cxh4mESZdKKTACqMZGEuMo0DO50YnOKcWTJvXMR/5AX2246baWKrCr5DxKTiACDJu6fmVdhMym430Y2K3012yZ0qvu8JZzCFHt95wjDiNRI1oOKJMltwFVAvTFGYRLm8vuT5O3fYKLz2yiv4aeLDGHj8/geM1zv6aTLhtdoz6+yQCU0aCc5udL64fMQ43NDducfDYc8nPv9ZutdeZnRWcWsIgV1nyd+dwKiWcI84QmKkcYpEEaKDxxePueq3jMMenHIzDlyHkRADGjyiMSkcSekVYY/F7gdMYdmFwCDKFCI+2ngaFec7Lq+uuD+MXN/s6E9O6HorURyzoocpf+rMQ7jbDzy6vmYnajutwuXlJRfX12iMbE+FKWpx3c+Mz9hs9nY4P5+1NYtoLRQUPNc5vr1lqKpY/oUqLo0XQrDKYuJtHQJjtKTv7HGVEHj84BFT59DdBOrROEHviL2iaiWEQ7pXZj8O6M2Obd9xrdE8nkG5enjF5dUF8S70/Q5xjq7v2TpBvC93smhU4jASdwMyTOYlCZHgOkLnmMLE5c0NVzc7q3biLOS0g6SczgpTUGXaDQyPrri5uCwwCqroNHEzDlzubtAY2Ww3M3MvZazXhZKaztR8IKoSHIwxsr+5IV5d06N0GtkC9Km0gYidQYxWTtPIzTgwOSVopN92SC+oduxi4Gq/JzhH9B4fha3LoWsR573lp2BGn/1ux8OLC6Y4sY8DijIR2cXA5X7PEIVzv8cHU4w/9YlP8NGPfITtZpuskA4dI8PVDd//6jf49t9+hUfvfsB4fcMmWhikTxcFqojFZTMrGS1e5s/WrMuzku1WFY36Z/vZmuh2m+W4FhhbXpBlh+Pi4JNDWFreWM/1gLfYLwfftfjWGjNruB6ucXnDdDuvek65tXy75cP1/A+NcMcVj9rA186/buXsJHqkstzzlr7VfT9pr+t2jPfXY9ymONV7mQ3AT1IgjuFvC8vbhOpszKplmHa/WiWj/m4Nb5RsdDrEy6IEi4VgOudKlUnry3iT5WLM+XWxGmcNJvVe1WkOzTUqM345WRjMnqY9fdUpQGOuJjXH8IdxRLwvl8tBEmRVLQ4eeyZGS2abSxZKuixrFpBrwlYf6lqxqK0s9T0U9WbN4UtzEnEGYi3w5mfzwa1dxcNgTEBEFjeD57/tKGsJjarfzWPl+eXwKPt9RGNcJRYCOKdM48g4Bc7OT9jce457H/0o8WdvIMO48CJkBpBD+jOS5KT2OjRqjSnXsG4/XyMYRbvmMEGqVjhqS0FeZ10lzLn5LpKs9LUhYfXYdVsc5BwSpElBc46olvvinQeXypACPkT0aseDDy7wXc+Lr76KP1PYbvFdT7wa6Hvw3YYpBIb9QLzeE272BhPTdhid8Cu/+gU2QeDxDVMSSjY+mmXUOcJ+YnPumcaRXRi5HPZcayTc2XLpI9HC3nHARjuL1d5PMExMo+A3Hu2CJTG7lAwPTNFyh7owcfHO2+wfXzAME3e2J9w72XLz7rs8ePNtwn7AZ2U2+0USnFSWe5qFu1EUlcjDt9/i5u23OD3tuOeEToQv/P7v8N2v/B37Dy+YrvbcDCPb0w0hKLrZEhG66FPVmogOE3EfOducMA0jl1dXjOPAtYwWN351wxQDLti9G/SKOFM4AoL2IEGRUYnjxDANeGfFESZN+QaSwkZ2I9Plju3JGegIQXAbsXLDzpIiXYiE3cTu8RUP3n6XRw8eMSnsVemwiwMvLq7YbFJxABwxWuhjth4Z9U80Ss0o0DKWNTytz16LzevKM1CJVZnO5DlM6ax47y0HZe/54PW3GVG2bOjPTvHbLd2m585zdzl/7i79iZUgvri4YPfhA/aPLrm5vCrrYVTef+MdHjx+yHT3hngVcJ153Tanpzz34gucnp3S+46bixs+fP89hocXyAeX+JDyyoiMClvxPHz/AY8ef8jJvTuEsxHvN3R9T9/33LlzB7/Z0PmOh48es3v4mJv3H/DgzXdgCihCTHTyanfD46tLHML5+Z1kaT7MzKjpTM304bDK1e5m4CYEwmPBScd4vac7O0HOJ7anwun5OZJuxQ4hsL++5vrigsePHqWQVk/n0x0wIXD94UMuHzwgng+wV3y3I55ObE9O6Da95YE5IU4Tu8srLh9fMDy+wU+RLvUXojLs9jy+uESYCNHxi7/0Gr/82c9x5/TM7n/CoSHCfuSdn/6Mv/rv/w3vvf4G1w8v7FZ2hT7DoCpo4EToxS+smsdo7EJR0Nvxu21LPnIoSNZjLJTvaq9aRafppOz7oTIx50zVwn9rzGrX2LZaIdVwvGz8sXW3QmottOX+14TstbYqhKbPWpxuP7d35oqZ7ThPowy0SpSuaHprwvhtvBuWRTLa9dZejdCsb02Qb9evTzH+2vyf9rlDJZMiIz4JT5bvHSpq8zvrcMwyq6qWpO58JrquT387LLuQ+d0VRbWso5ljjXP1u+VcFLnVDHjiXKErT2pPf4+GZqucuZJ9dCb09D09gobKBRcs38D7lOyG0KWYU9Rc6BZSUmuiS69AnaBch93klr/P/1ogZkWjPjD1Yahdj1lRqIGZFYghjCUUqHaJIZTE0TZZ2caeL8LLJXutQlFnybftPRyqTPn3BKjt6Rnd2SnDyZbN+Tk+XCwQrgj4cSpW/9rTMRPhQ4KQn6uJ06JkHYeHNe+/iJQExZYg5b4zLOvP6+8zbHIYXEsoW+ZQ91PmqCnHwrtFmJZ5nhJ+SCSKQ93Eg5+9zaOrx+we7fnB9B1e+dTH+eRnf4nohJvdnjtn55yenXF98Zibmx3D5RXjuw9x1wNOU4JahDuh4/J7b/Dw6z9g1zneD1d0AV58+WXuvfAC/dkpXJnn4oMP3+NxGLgJcPHxdzk5u5vKBipOHahnePCI3RsPCDdXbLoNp2f32Ny9y+ZkYwpkgvs0DEzjgB8Cvfa8tDknBkEfXjLs3uXx3/+Ax++8W25q1hT/LopVYvLLsqwzY8XMF7sRefCIr/3X/w2f+u1/hLiOdy5/wFYc8YNL3v/693nv3be4c/8O3sGd+/c4eeUFzu7cIVzu6b1nuLrh+r0PuH50xfs/fhO3Gxm6HSLw4r27vOC3XL3+Lvthz3Tn3JJot1v6zRa/PeH0/AwXLL9i/85D3n33bYYOdu8+gAjBS6q65AjjhF7v+fCNd+g/eGx5VtPE6Z0zzp+7x/0XX2C73fLonQf89Ac/5NGjRzz68AHj4ytOgoAK++SN7foe3/cMk13kN6XcrSLcVHhIOldrbY0pzTTjMLTzWMtMUzHBx6WQthCDefCiGW3Gx4Ep5Wb8+ME3wXm760EE74XTsxO2d85BhJurK4abHTpN6G7HSfQQIsPFFa9/+weEqFxO79L3PyZiiq3bbui2PduzU154/gWuHl/wwaOH6DByOsEm2HNTiHjXsfvgEd/9i79jkoDrekJM3sR05k9PTnjhhRfx3vPmm2+g42iVnPYjMgWGkGlhACfce/4+nfNst9sZxg18W6bewnUcxyKIjO98YIK4CDdvfYjb9mhnXncvHXfv3uX+/fuoKhcXF1xfX9N5x83jB5wEY+zX73yAO98Cgfcvf8jl5WMuuo67z90nquC7js6bonfnuXuM48CDDz7kg/feZxwstPMjcsIjVbzv2Z94oo5cvf2AV197mT/4vT/gY5/4JF4cvTicwrQfub645Lt/+xX+/qvf4MO330PHCYkWbqlOmFSLNT63nC0X3e1W42O4e8yy+7RCWv1uy4fhuPe8HWNNQL9NSK9/r/nQWrjw2nrWzuiTzuyxuc79H/cetO3YPNu51d8vCsXc0vcaz86f18J+68WKzfxLPxyjhk8W+J8Gj+qx6jCrY+022nDbO2s4+IS3eBIfODav4/M4/k42RAkme8YQCDGWy6Kzx8mUjup9WZ6DZqKLsYrcJWsmnfQMZmx2OcT8KdrP5dG4udmTYkOSpVQgxYGLWvyvSLbAzQnf5bK9tOgpTITJdK98ALPg2/fdzFzFxh2yFyCkcrnOzfApDDjVvVe1mFrN1ZRmG6FUgrRL3pTOd+xCMCtVjEzJCyGpLK+FrlvpwGEYUqJqut04Je7mA74fhhTLrnhnt+vaxtqcpikAQudcsRBogq3dXC441xODIuoM6ZxDO4ff9OCFEKIdeEyzVWYCmpWr2rMRYySGfDhJlllL5ixWU0mx6hrJt5u2yduQEufTTZIZXbNSVhPzcRwtn8fZxTKxVvgwYUnJIQpW2jdXCgsxWiheTLeAZSWlBEElbTptqu2VJwa7Ndeq80yMw5TmHRBxTIy88+M3ECdsw4YueC5+9A5ff/098I4wGTxEUvI+FirlQ6QLEJwnOiHs9/z3/6f/K6rK+eUeJbDbQqdw8fq7lhDfdYj3RAHdj2yi3anxV3/xA/C9WdtRdiIMvaOPA3p9QacWvoXvcBsTgBApZY2HaWQcRgQ42ZzSdxsrSztOxGHP/uba8lNCNGu+JAsSENRitdvQqdxcsPAO2U9897/7f/Ltf/+X4DvGIYDv8PuBh2pn990OYpjwm554Z8vLr7zCwwcPrIrNfmS4ukbHiBPPS+f30BDMM3O148d/9y1GQjqvQohmGRHf0ffJ8n33nGkYGN57yM04MDjlzgB9TNXEnBBjwKuwu7ji4u9/BFEsxcNZMrR4z9ndO5yfn3Px3gPGcWScRnqFTfD4YDfHBxG22xPzpoRg5yvdFeR9VxK0Yb7ZPJ+ZJzGmjOPphVnRqJ4pZ49AJKTE/RwKkuhP+jufQ58LMKjYjfHePMdOHFOIdoO3c/ghorsrrj64SKFGkT6ms9T1TJPhkqjDpQpfnXq6G6ueMykwjujNRLwY+ODdxyCwFVNcfUiWyM4jkyXYb1zHdD3SOUUZLWcgJYyLc+j1DZeP3iRG5ZTMDwzvxXWoREK0+vB3tpaPIGpVt4pjJ8HE4LMUjp2YRyTzA5+q/YxxQgE/aIIX6BDR3d4U186KL1x8eMnjH79lpbHT3g5xwntlIx0xKNPVDXHYIzFyFScEZVJ49OE1MSalSpW3RfB9RxgnywWJRre8CJ+58wLjuRK9J3aeuy8+xz/5k3/Kr/7mryFnW6tcFSJhnLi5uOZHf/89vvP1b/LW3/8AGaxmvgerlibpfo2sFJByWTQLJwKiq9Usi8CuVLS1prHrYStrlvbyXCN/rQm1Bfer746FFEnmA9Ueu8R7235rgbHOBXyS0rCYm8wFTbKXvlbG2vfWBHZYRkhAe9O6K7xbWAqGrZfnGEzqkM2Ddd6ifLdGwSftS+bbNe84pjgeSMoc4swxRamdZ93qsLM1IV4Snait+f9DFcUWzu0a6z1cCPRH3m2bwRyoQv5SL4XfZKWCvJf5jIhDU1iniDCME5uNyWVm+Da5SUs+jZKFzSyLLhdrY1SQowhX5PNTHjQ5T8RCnGPk8e76ifCEn0PRCCrcPbtr1Xg2nVU2USub51L5UrBKJTER+ZzPOVVaT/4eNBX7yBsEuZB8QBHv5hh17DKkWdsGnwR6VYsxN8abw0RM6M018adxSETMEsld5xlHE2gnHTk9PUFV2e32hGC3f4fJwqw6Z2UGp3GEaHdqEGNSDpK65RzDsC/EL4RA7ztzaQPjOEEQereh7zqiBGKw+vFWNUat9nqMiPj0bGeJq+NA5x1u45kEJiJ974njlEJDNOWwzESn9vIIChpAtbo/JBozEVuDT4w33ZmGE0oyZGvR8s4nQXm2gOTvnXMECUX5y/GS4pPnJnuwEuycn290n2KwC2VE0rqSwmoFoIsmHazYJaqki2hAo+fk5C5Cj0jAtOFcMjXBiA4fO5zaJVoi0EVFhwBM9BnPY0yHwmLSM7MdiUUBO7m8MYaQntsMJlwQrYpLHCdEAl2BjzPhb9zDZCF5KJxg1WxElDCBc5ZnEsdIvLkpMZIxhRluEbaJJ+nuhqDXZtlIypnTSKcWCz9U3kIFJicosdAZIVvKU6lUHJNasnU3KDINKENKsjZhxfILwCUrNTHS73c8/OCnpmyChVem8+E6hWi4p8GkD40RCZFN8rRNwepiITbeoMrw9odJyRdOVNmmczSpmkJh16YzZo9h0DmeVEwAkxCJDy55/OEFHsdGYxKMMQbR2b56DSBWDjCmM5/d4S56Rp0M45wHnZLAs2RkbaxzvntDJN1Qns6I80YffNoXagOBBtRbDkE0gktHYONcYhpzFbiagYWQLVhW9lUkJf/GyCQzW3GFAZlgE6dQbqYGhWCHIohaAnPhgGpVlEIsSlyhJQLRap3iO1dyTAQPcZY1i/ibvLhaeYpQTTfX2oNRpeQzdGEWLK3DRLNshPzWjJ8xomJhFyFb8KMiEQtR6h2oI4gUG4ZzSSCPgBiCiFhYY74zSlCc9NAJ6iJ9KpygouYtjVZS3Hi0Cfl5rhIiW1y6SEuJokQn+JhK6p5v+dXf/S1+90/+MWfP3cN3zs5qCMSbgct3P+Abf/Vl/v4rX2e4vLYCl0n4yPvuNOdhZOEm4wTlzJLpZYJWoQNSIYnmO0psDcmfvFAqbmvzMzPtqT8/Zum/LUevPMc8zdJfPFZENy8nmQiOxM/nz9qLgzMu3eZRWVtH2+/ynVj2J+9VKVOd5Jz8bh32nHlsq4DU47aRA+2c1z6vFY01haxWZNqV13sGWVadeXumbYu/V9oarGaZY5lv4RZKWmNcqDw5x7D0SR6Gts8Wd2uPSpnzkT6e7M2oc3lo1q6zUl3Dl6ScKliVBw+OFEqcvE1E1IESmZgvLs5hgLNSUc9Ey+V9IFacJT/RVqor8/FMqtx44YePHxysda09taIxxcjJySkalXFvCdp2gZNjSrdoi1g8eZxCSk52xWq9SBRPITtWAtcVYEtiphpDk8QsqeLLrHlJNLLpUvK25gvAoml9IZpQ0KUk4e3Wbu+2iwQdPsWaSRKqx2kohFYQ+q5PN3E7yzFJysM0WpiSSwQ6x0pv0jyG3Y4wTfTOxsg5GbYmE+g9pn2TEncA0IgXh3PmWdkPA1wrvfNMITLsBjQENn0P0UodojANQwoNOLyTwqz9zFW+Ko22HOgVy4JL1s98INqkwAX5rMKd2hCyNhG+tjQtiEN1yOu+VJVpGgzeddiadVbYplUJmvND8v4sD3xiqImImUGhJcAsCFVtycmGgWJlWBzYJITXcM3EIyoqsQiwuXJRJorZOoFaGcwaTtmKYcKhKzdD1zCuiV++EM2qWC1r1Wu17xQsyPtnSm/uV1XRlM+kOiuMihkPRGZPlJBunI9VScHKQpfbglnmZ5Lw01rmMtyzhTZf2FjgHQKkc3uwX2l93vsZ1o7F+1qejanCWCwXIiKkykgQg+2X3QQd8akqVgvLBf5y2OZz6RYCRc2wvfN0qR+7ODAnRudqfanalM4GlLLu9P0sgBmTrqEaajxJFndNCF/X91dVojadqybjhC7i/03XNLxx4pbv1esv8GLOeSmwmem6mi6azvZs7cvCspGvlFcWD1DMno0pETKFv6UFmOKbLg7MpMAq1GQl0cbMnQatzqzOl4jl3wuuJcZfw6/gYLRqb1lInkSJvWMSoN/wsc98ij/+83/OKx//KNGnMxUUPwoXH3zI9771Hb7xN3/H9YcPkSHYPSuyTAaeYdzgREXb1sJNWpqbP3vaXLm2LZ7J+1iN09Kj+r02zyH/vE1AfZr5tOs41k/NN+swx9xHG8Z0rL81mC6+L+NCjh7QCla5tXvQCrB1/3U4TKtAwJPLvD4tjFslr13z2t/tHtyWZ3HssxoP1nCnHue2vm57v32+NR7V7y1ya29Rc5+Eo8fGbs/oYl1l3Hl/FYsIGKNFdGSSJOkFM9HMfcZKFrCHk1G3zfxuWm2QcKSqjUq6p+3J7akVjX5r8eJehI2zG66jQiCmG0clhZ+Yi9A7Xzalk1ngDONkiogIpPxZSZc5ZUtvlyx4nesMlGLhNp5ZOPVJ+QjTWBSEEEbiZHdiuCQ1SAqnKVa0YEmn4zRYEg1mgQ7DZBddbXr6rmMcJ0Q8w7Cn63qcI4U+2S2y4gTne1RhmiK9c4T9nk1KCBaw0ARVNp1niCElsAbEQe98us11vrzuZLMpl6Fc39zw8OIB515gigw3N2wgrUOYxpHeW7iRCAyDldA9SBYXKYG6teXGOccQpkU+Sjm4MYdqrIdGsUJMMjLWCgTM79f5KHWYV55z62auhTON4cCdXIhQsehrEeJMM1+Wy7vNOtUK37C0sKSPyJbstqkml2fDFExQsXqsrTAdi1dsyTScc0VIrglZXkcL78VYlRDUEvQMl0yu6jGzMg9zqEANtxJK1xK+pNzkfaznkrTDxbzKnHXJII9ZgGqYZUWnZsoheeZMaTlkNPkMZBgXkTbPSSNTjEwpn6pWRaySnkAqdTqOk1m5JQsKS0EODsvP1s3OxmyDX2PknbOL7RQhqFmrJpRecgJeFpDrfpNVjCUei5Piec3j10JfEa7ThZ5CFpylhJumNy3sLXm2TNhP69BEu6HQi7WW52ZGgEMckgqmqqYszGc2Pa9alKmoFMNTHiD3E1P4gKIQYerMwych0odI9C4pO1rWYOO6ufy6ainbnJl3CNlbXmkqJKVzhb4IgqSS5NE5grdCEnuv3Hv5RX7/z/+Mz/3qr5g32hn8JSr7qxve/PYP+Lt/9xe899Y7SIg4JXlE5pvR6zNfw3I+s7NysabIt4J1SyfLO04W76z1k8eeMUYXtGJNWK9/X1vLk1pLt/KPY33cZmU+oJXoQnFr6dSTFI78TFvwpfo2kSujyWv914a7mu63sGqVofb72+bYttuUu3zAa8NjLUvkd1uvyxoPXlPwWhipUsLX29zNFqZL+KzfQXLs3Rre9ZyPGUdrgxnCwXuH8zlUrDKdu20fbmuSDOTZaNP3G3ZTTAaxWdMoZxkWFcNqPjHj+mxAWx9z/r8nAiPXE4Sn0zOeXtE4vXPHJhYiGiw5UaPV05e0ALPwu2SRotxGnDWwXPa2S3datJVC6svsOlJVFe+ZUnUOL0IU66dzHVGDhWeJMo0THkqZW8XhBfquNwakpiCcbLYpOftkQZQ3Pt0R4h0xRLb9xtZ3csIwjkyjcHK6sdt6U4zdbrdnGAemdNGfV+g780h478m2/2mccL2VMN3tdjjXMUVzT9tt5aZ42QVZFgd/fXPD1c1j/HaD7PZ2y2OIqVypYVLQiRjs3o6MQNM0lcsIVa0EqHdzsnWdWO/Vlb3p0h0pc3lftzhkUB3WLHtXikV9uNYqXmUBuo59rYnIGiOTjEcsiW8hJDEmwQIuLi8sFwWzFsWQQ2yWBKkWissYFeOOysF8siJhScgs+sxN63NQ9W1wD4u+asYfm7/LHCtQ3EZkb1tfTehs3KWiMs8xW3d1QUiNabhZCKSWJm3vAoeXY6qqlUOt8GahALEUZtbeL/ApFsYsZJtgl59wmLAsFU7m94pVilRaNsxmcNVo51rjos9a8TM5RgiTrTukZzNe5fMUYyznJ5cbrOeSfxexW8tzcvICnzXlq6Q8C+dT9aWouKg4Z9X+NFI8PfmejIxHxVuQJPe2YEPeg6w05P9iSOE1CbsXnglJY5qrbIaLzmFjee9ijbM1TlMJF2RGWDYC0czoKMxSFdtTyfRG0pxtguZRnmlT9jCXUo4qiPfcOGWvka0KXRAioVReM6VFy3ytDK035SsLKingMwYL0TVYZlzO89KDWP6o0XKWRBidciMRf++c3/3D3+O3/+gP8Ocn6f4dUyKmm4EH73/AX/3bf8fb3/4B8XLHJvUXxslKQHsLWWhpZW3IqZWN1jBTP7921pa4mteft2ldGF5vh5fBPk1be7Zey5rAZlrm7NlsvT01Laznn2lSPoN1cZma3q6N3fa55pHJ3x8oDUlxTU8AicdW9De/W1errNvaXra/5zN3W9hYC5fFvle8wA5jFc7cwLmF1xoc2nbAX5tnRNbfW8O5Mm9IZ3OFPzf4eqtSBQfrqPnKQnm5pb8WxmtyxdqaaiPBvKfGv82LkN5NY15dX7MPoxlFrONZaRBZ0OWD+YjdwVb+vkXZmNelBBfZR2WSJz8PP4ei8b/63/yvOTs/N2LsXbHedn1XLIrZI5EnnQVXyVndYqxCSZWnaqsUM+MyTdZu7L25vjFvRlZORNhst1xfX6Nq1vBpmuj7vliC+74rlq0s2Drnae+UGIY9Nzd7nBNubnbEdImYT4K3otzc3BCjcrLd2qVwMgtn4hzTOKULCucqSuK8VYcJId3+PSLJ8hvixPXNjjfffLMQAlOkDIZbb8nwY5jsboioTFc7NiFZb9XyXHIcNpXwlpG9VFlRRV1YHJK8N7kErvH8mRAWARNZMCSoDoTMloz8XiihNnb3ST4oa4S3WO116YHJY7QMsvWI5Hm6guPC6ckp/aZnuryyPAWNSDw86PXP8vZCCdD150SQQxpXvsv3d2RhvzAMADli2RJZrCl/X4hmdehrOK3Nr4ZtXca53JrqrMKVSVn1eGntzLiRL5q0PmYrUWZelgxm72ZL+G2CRz3fglscWuDWhIKipEQtl8stGKEk3UGy4rlyT0tSEEKcPXoxiZCKxbdaMt0y5lvUwqamGFCNdMm7mhOr27VlJV8bxaqChDGLap9rXDAPgRRvcUTsPpEk3KLQda6EK4lIUrQSDHNoTQpTncK0oAtLpT57FW3oXCwiJngZrc130cyV8CzUzX4XoVR7E2cJ2HXLq1O1EKslrUn3LEn2qliLjVI4w0hmJQXKTddFaU3wiRoJCJ0qQYXXH7zPj99/my985JOcdHcYNSyYsDReM+/mOSpquXoxh7Wa4j0rG1lfqjzIVYjn2Dl2Eonbnl/+zX/E7/7JH/P8qy/Z+Ul5awwTj95/wNf/+st862tfZ3+zw+9GtqTCJdEURuOt5m2KFd7VdPuYoFfjW21IqAXr+rkZW3VVaGufXRNm14SsY+2YwJVh2npkarpQC3tP09q+6v7qOdZruk3Qz/PM/dZ0p8aJWgGwPpo5yTotbMddo5N5bxfK3RFBvX6vXnNNw9vPVLXkXR7jPbXisYhYWBl7KUCvr09l+fkafh8Ycpi9ocdwqt3n284MrONL/W6maS1MaD4/xuNaWLdrXh2XmbYaXCIhTsVomXmMyx6hdl5J1g6q1OVwsxx5bK25BRft7i1Rep7OpfHUisYPf/yjIujny7WmdEDWwkIyMq0dPCPodnNt7q9cCIgxcu8cvus4Pzvj+vq6XLDX9T2np6fEEHj0+LGFTCWB2ydL/nW6fKsGb5imyrWUiLfOikot9PZ9X6zy4zgSQmCz2bDdbOg3m+KdyUh7fn7OfhgI04Tzns1mY5VYEOI0crrZcufOnVIa+NHFBSebbaoCVLkiscRFiTCEiWkCN450XZ+SaZnDRDKzSIiRrR/AwaHPwkBbRhY/r6G+LNH2rWMOK5j3zSaxjGktCmUl0GTPUhZ26z7WhNL28NdhRDn0qGY8MUb6rmOarNLZ9c0N4ziRrY0uWSXbMdYYR80EjjFIs4of6ScL4awQlPr/KwSwZlI1wZZUgjM/Xyty9fv1GlYZBBRcrshYnnaZG1DuuFkynVDAqMmoLSJ2aZzMfbUwVp3DZA7wR5fzbeG9FlesWHUiTbAplwZFq9fUsbQqLoi8JG1Es9W88mqZQTopH5T3LXSK4sGI0dY+hWCCOEumvAgnaEJWirIsjqDLO3TKjmhO1nXFUxtUixc4hyjV1QTFQYzTAc7WfWo1zxnP8t7X86ecHXHOilUcZAOS7tBZvitiShlyuJ/1/uWWrf8xRtBZgVetwrpssOrNlVAUmY+4Jmtf0GgV4qIyorxz+Zg3rx7xiTgxhIC6uSjF4RkSgluzYlu1P1WHSO3VICni85xqa+SOwGuf+0X++D/4U179hU+ZByOtwYsj7nZ8/6vf5Ot/8Td8+ObbSFC6pHxNknPNUr5Zho8NehCKlMdeo2//w5uw3LnmW5kNQceE2tvofCs4P4mm1Z/XwmE99AHerQjVx9pME5brPtYnzBcA3wb3BT3OoXdNy+8fu+Ct7WcNLguFZoXPtGOtCcJrxkH7uZx2Tc9b+GRZpCi1Dbxa2n9kseVwS4Xva/tYz7/2ONTrb9uaUlz3V4/TKl/1FFuF6FhrlZljyz+meEBl6NR0zQBKjELfd2x6n7zaUuRc51yKLNLZQJNkeIOVEpkVdSfHywYvFA2wIhjA2ebu0TXX7akVDbsd1uJbw2TEMMSwqKNrzHUOFck3epuQZJO1sJ5ZSO77flY+vF/0pQoXFxezppUsb48ePaqemS99qwEyjzsflBCm8nyx6DfIFEPkZrpJ851j/40IRMLlJScnJ5aMjc3ngw8/LGEmYAqPYEml3jturm+4ePy4VJ1xztN7T8CY7jQMSTA3AarrOnRyeFHC5TVdCJbPkUpZFoEBQ3QrWpEsopkjqSYNf/bq1EpBnaOR4VUzSVP4jCiKVAJz6l+pDng0pjuFOQHfOQtBQ+eyfhle9eV9RRDNY2Jwz+V3M82vvSf5vZCIkcaIs7JBtgbvbX6NpwCRFFp1hLHFiFbx5wkTk9CZQkMS4TTBkbIPIQl8koClKYE6UieW5h4TsTdJNoWOaAllmTd2yQhIFkaoPAg1IddU2hmh9qLkz4zRLVgo2Vk6kZLGCtVxSCFuVpkCTQmrIunm4wyrtElawdZ7fBKdDT4zA/CSbyyN9WTSOnPojuHwzDgqeMScwGZzEWASU4gkEcAp5WSpISAxGhwyXhj+2C3RJSQsrTmHCwUNKbTK9t9hXosQIuJn3Mnhht77UkI038oqUPJbDFcPBa2MFFHNWxzUSmF7BR+VvRPMhmI4I+kSSolm5fdCujzJ1huz4cX7BMOwFBTUkv8NX0nCfiwwDeNU5lwXVTCaOs3ejozHkpiZqzArzuvK75YPNIWfqSTr26xMwBxOmJWJ0meY5t8rxp2tcMm+WMLhxqjgHCEq17s919sTOp9ujS8yZSVwKOCXQkHGScG8Hzl/xVi0pFzDVOCgMwUhotx/9SX+g//4z/ncl36NIEBnNFemwMWHD/nW336Ft3/yOg/efo/p8gY/WWEQh6Rytdmr7NOqxCoCVpuYabLRgqWA1ApKNa+slYM2Fn0Bk3rPKmNJ2YMV4eugLYnpwbu3KQCtUero2Lo2wmFf7bt1q0OArfLWejKwyLKv2nvc9l0b4ubP5pymjNzFe1YZ5OpWw6pWJjIfbeFi/2T29Ob307ha7WWrWBTVOuNCziurWMOaoF/WX8+j6uuYAnRsnaysae3ZxZpjxPsq1Ld6b82AuIa/tz132zNrrcW5tefWFNTaaDXjTxbuIEckZN7cec/98ztz/1rRN3uE8kHiAxlGtSlpOYtZIZ6ps874k2XO7dMZNZ5a0fApBjmK4LtEgK0+YuWST8/6biEY+pT/kAGXK4NENUYgSfANcZnUa+/7qizrUnC2A5CIUb4zQmfNNrvy8wbEDGfvEe9RLKZak2Cu1bOZgcVUWjVirqjdzUC/3ZZSkjHGUsKyjD1Z6NJwNRCjlcQ9PT2lS+B2rg5hgM3GbnYU1+HF4/HghCGMhGFkurJEcEnzK+FD6XfvhE3XmSUhhTs4cawRca3mDSwQuiBF8gyJsEgSlySIlYovcRYGRVIYB8I0WKJ69vqAoGLwrW9LnUN6zP1nSo0JMZLujlhUaaoUkzzHKYyEMHF9+YjtxrP3ki4Pm+9aSdtrybFJGTQ4ZKUqW98hHR+U5Imhwg3Jwq4JqSW+G2aFT7I1NuU3pDDDSFwKX9HKO7uUXaxJoXFJCNN63oVuSPl/Ph/ZC5HnEdUUPOelCJ4aTbA0Y1oWLisPBsJIUs5o4r8VhKncRqr2YjkPYaZHBjs341kYQ1Jc3SJfRlFEo5X6TKVrszcoqqBqyc8xKbBF2U9zLIvFwjKdcxZ7r+kOCbW5FdqQjBZTlNkwknIiQmVhNCUzw0sITojRldwMjTHdHG5wVGYlwmWPrLM8r4xJInPssHe+eJfymcv4HJP/oDvpCVeXOI2EYEnhiidO6ZZ7IQmgAhEc6SLJkDEjbYaI3Z2S4DTDLCtzEZW4mGeGi+LJ5CAzs7LD4lOiuhbeJ7kaV8W1YtZ3i7JaspvQ7BojyxOJPid6YGRlFnCysj+TMqMTmvhBVtxzXyFV3RpEOfEnnATP1dUNl5t79JMNp5o8Bt6BmueoE4E4e3411cHOFbwkeRlUI3Z7lBUa8dE89MMQOHn+Dr/zJ3/Eb/7x73HnhedQSZ6/qAyXV/z029/j7/7Nv+fi3Q9gDAVYRTATwYsp42CVkWsheCGYaDYTzIaINk8DOPiZf88GuhIt0K2IA1pRHW2EQXfYb94y3yh/BS+KmFs9vyKk589rHtZ6tMo/ZDmvqtVe/Px9/Xfd3/yu4YHgUmSE4ewcXhiKYtcKvO34reepCI0VtKLOUFnbq7q1isvas9mTXBu9IBkjaoG1mnN+1j60fSId03xn2jFhmbyi3K9U4Wwi5XwuntdWgavCZHXGmqNGwRXly2it0Zs21Kpe51qftdKwNlY9Rv7eCYsbzJ/UZrlnPhNrCk1tcF/iTzK8OkrEjohyerJlgxnwXdpv4wQG+xBDpWfMSogK4GYjxbI5JMmrKlm2sOiB/FmrEN7Wnt6jwVyuNjNU70y4jRJT4qEmJuhKbobGOU5RxG7h3u13KZ7ZmHPJv6gIagZunRC1sDpUrrkWCVoky+9nTbFsqmPRT4xxvg8kCQ6eeY4iYmFbMbLb7cq8c0x+jocHGMehjH1zc8M4jpyenrLdbk0IqypAzQcgouKJajkb0zQSpoGemJ6fY/ChqiIV7XbsmlGsuVFrt6U4wUVXktBq929mPPndDMtSJcp1RSMuSlwF891uV25T3263s1LD8rDnPQ1ql6TlOWflJu9fXm/XzfdudEmxEjFl8frqinEYjLA58yJkpStWc4R04YwqzuXDKKQrrxYMpByqzM4rPpSFNXS2+kgl5xlcgl0Mpw7H7I0oVmAnTD7f/K04L6mSkithL61lBkjKkmNMd1OUePtoykTM9wglYmBx71ath/zPsIRiIMiCo2qlLMzryYsr1cGi3U3QWoNmwi6mmMWkfMR57IlIlFgpU1qtdfYoxUgxSmT1r5I1y3wtOdg+zMqwU7MGl5AzlBApAnTuX/O8Mq5X300KIUKIYvc7aLr4MCXQ5fNfnzFL+F5aJOuz0wp7ZSfE453jZHMC4pkiSLKub8Uh6ojBAOgcdq+HCGMJV0pKSF1usCiqM9wyLOYk64QnNcNQo0XSlA82+l7/pXO0lC5DJNJHlE2vvhJneSjZY1oXAZHUjyajgGiqSBiXMB2nYAphDKX4hnl7NXnehX0MnGzv8InXPsNGHbtRrbRsXjSz+uMUegedd8QppHPtGIfRPFUh4CTvX0ywFlQio3P4jfBLX/wif/af/ke88rFXkU2HRMvrGYeBB+99wHe+8jW++dd/h9tPSDwUdmcASYmvfppW09Ico74Wnrf2fFucoxZy6ufzzwUP4enmt+zs0JhxTJi8bf4LmrgiGGYY1JEOtQxwbKzCk+L8dz5bRfl0y+fr/o+taRZwK4+DLPto3137rqaxreA8C9uQlc66z58ntE6gFDhZe7q2ts9j/n/WFutuPl9T4Fr5JhsbWuUlP1OMc418+KT2JOWvfa5dy9pzFoo5hxQ/zVzyGrxzOE9iXsmwlWSSYkxk9n7msvcH/THLOIWhUq/BVEyUcidejV+1l+tJ7enL2/YbnEvKhMzabd9vbJqyTA7On9mEZ8LQdT2nYgKu9zMDruPU6woeGZnt1vB+0X8d6lMLxLm60X6/L7/XAsGalSRbd7KAXCs+eYw812maSsKsiBRhehiGonSIGPEeBlM49vs9+/2ek5MT+r4vfZyfn1tOR7JOT+PEzeU1U5hwOnLS+XITqsZpEQ42K1CTWcYrWOc11h6EaZqKwmQJp1qE0RaurTI3E+yccDUTsXLze/q973uur6/ZbDZF+ZLkHl54pKp+2/yRmhhkxaMOsatL4276nvvn93jD/YQYAlNQam4QQsXQxeKwTUhS82ZoraCGWVlgtrZHIIRlbGtIwrlLakoJYSNZ7iJ4NS9FZrBoTtJyBFX2GopVFk1lnNO67H49XRBPsAstcS7dTi/lTEY1id5CQ5IEnYTGGBWVWUGUBAstcJ6VKruTbcaj4uMR8g1x5jEqZqcMWygsR0i5FOBy/D9ZgQPSfs/uf1NOaoIY1QRq2xuF+hY4ZniS4K6Ay14y1G4yQpPwbcpCiFIE7xghVPGrxcqEBcZMKuVCJFVBgn2WNacsqNX0LYQKfzL8Ktp4jAEJVh5825+gkzGAXGEuBsOJwoxCoOsSHmbvVwq1yfto21vTRRtFM8jqeUgjNKoZlsrD1XO16hE1w3fG+bqPvN95LuWrKQl6wSBtF/0lw4Bo+XuBD0seyGSEi4AyhgBxwif0kAAupgpyAmebc2QMDGNglLnYiOlbMTFvZVJHJy6VMYcQBvsuRrxkj62iIeC8Xc5JJ7z2C5/kn/+n/4LPfPGX8RvD105tfR++/S7f+9a3+e7Xv8nl+x+yCYKbIurmCxYPBBmNZbFPI4RnPmUGh2n1mTW8a418t41RvE3ZM+DkoM+nEpYa0aQ1otzWVytAlnN35Jk855of1rytHnu2NmfP81JoLHKCBlr1u36uFfxz3/Vn5V4izRDRYvBr130YerX8vVU28ufOyaIoybxvrih6q7RIdVbcmuPfrrWWqW4TOJ9KsWnn8wRFtN6v+jOpPlt7vq06+TRzbRWBspe3LOuY8pjXWZ+32vD6pLnV9NxK6mdcrQ1xmjzhaS9r0l6MP7kISnNZZk1vE32PWcme0cLecy53+MT21IqGKRl5Fo6um4XFeRG26Fkwag+yWYOc63BExGlFJJe1itcOVO3eravptBp9/nd2drbQZOuNrQ9wEVg3m0WoUD23mjjld7KQlOdi8du5TJ6UPrJ7Oj/T9xYqtdvtCCFw9+5dRIRhGhn3Y1I0RjqJnDqXLnyLxZvUWmq8W16MN+/ZYe3y/FwI6QZvZpjUORAwV5TJfZhHYVYoaqWgVvgynIZhQETSeqHG+LrfGEMp2dYmma1ZJfJcs8LWdR3b7bbA36tjChNTjFk0KHCKGlNcPkAoxCmhblmPzBOd58lsGVh434J5IuZzMFd82EfILgJVYyhekxVRzQsRVdMFkjbeECa6OOdgIHOYg4igrrOSq4BotvqTQj0styUn9ipUhRFSUnPMyp25W6cQiC4WpWEmV1lBMotuRaNKHk7NsBekVcB13twCeRlpfYLggxSFNYdIlRcLQa3DJcySP8O4sQhrsuEIwGxpc05QnRbKQAym9IQYGUTLnhrdsrk4MU/hNE2MYcKp4jRZ25MVKc8t/xzHsQCoNQa0Z7E2AsRoJaqnYGGXTrVUlJs0EDXgXZfij01Q6TB89ip4cUWZdCkv44D1J6G9CPFVPsUy6VoQlcUlfgvljzkvJq9DRIrgmfetMLNM/4uymvc3wSLBNBtMCnwAopR1CLLET2f8xTugSwYhrCx3nEYLgVJl46y+mFNloxAISV+1/uKY+u88qoEpzt7UTedx3uNIgrY3Y5B0HTi48/x9/uTP/4wv/eHv0p1vib0gXtBhYtpPfO/LX+Prf/t3fPjOuzAGNlGsIl6MdhG7P7RO19bhp1Ey6u9rT3BLS9dajYu3JdvW85tfZtVKujbGgpfnfay+O6aA14pAK6i1BrX8XW3wqr2Ia0rK2hwN/im0u4muyN/n+ee+WjmkhlmrSC2rziWIJJpYr6mFQ8sX63/1/PKzMepBbiZQyjjXgnrZ29poRJJRtTrD1Xrb/eEJOFrDJL/beliW657XU8NkzUt1TOFdk/NyH+1cWqF/bb2Hc1yG860pme3v9bNr82ufreemFbxEmC+0jcucDgurzeVwk4KgczjazF8VzdUybVZl/wULM3Z20Z3RaJKxWNXGXlnXsfbUisZMVWrAy8yYXSZ2sTqgGXPzJVAzkEQ84qyf2nNwjPjUn7UHrHWHttp23UeNsCLCMFgeRd/3C+t6/VyNoHV4T30nhaoWb4jI8nCP41gExVxvP0arvT+OIx9++GG5O0FDtMpTYkIPImjMN9wuD14hFhpL6EPtGagJXVYMauJZt7XDmity1fdf5PWtEfF67zJByMrKZrsp88vzyDBF1Zh8VTkL4ORkvutkv9+XkK5WERLnePjwASFMjNNEGILF+qfQD+ecCQmpxGauo98qZiJCVJuDQvL6zMHqgTmsIL8fktDaWjcy84gCsfa6xVQsQCiKUcZX71OlMlUmlwoX5P0mK5KSiIMJbBnXwhQSg6RcdJTHizkcy1neUlGkZLBkVifsw2gnVeZzPjMjSyYWmWEyJctpETklu2hnk4jEGa/yzekiFtZEoMrhqaoNSVacjLYYjlhRhRCyMmBC5rwXeR7JUp0EYefsHgNNxes1PVxyt6IJ3AenQSPTGNPdNQEXA5Z0rfQC3rFQ7hfljCvlKAt+i1yMOnSTfJ4jU5wQB6fbjvvnZzze3eDUWeims9A+l4R4SbCV5LWRdKu4CJaxscLzrbAFhUEpsKgSVXY908n5wyUjnJ/JZyOpeKjLOWuV4SFdPOmLZyomfJTFpZrWX6OsqjAfrFrgEPCxXEIl0pU8PlOuHV0QJEYmgcmbXrKJllOUlYacx5Y90OKyIhrKvUvmmfNMKrjeEQTcScev/Pqv8if//E+5/8LzsOnwznIr4s3A2z/+KV/+i7/g7Z+8QbjaWfhktEIU0UHsXVGuMnwXAkuzd2t0qv459yGM4xwNsCZkr/Xj3FygoxVo2/1fbE/T11Kg/vnCU9o5Hft8TbhuDVhZiT8mA7T95PmWZ45qUCbLWLXIWZ5oIx4WvLkOL6q+S3aExOcP8wfqObb7fEwYXfJhFry+hWs2ctRh43Kw8qXm0cpepc+fY49vw4ljilb9dwvfNVmmfQeWURpr72b41XJbjRNrCku77mPwaeff/r7kBcv1t563Fg4ANzfXxXBmhXGcFQ1hptlUc8vnIsRUckLElAjVig9oiYxQzd7q9H+NhzzzCe3nUDRmy2LWyo3454VnRJf0bJM4s1AckoLSxBDWxLZVNGqLOSwJRh1rWm/A2iHP79ab+ejRI1588cWj7qw1LbzNC8nPZM+F9/PGZiWmCJOJKOXE0Ln8rAPn8OKJ0eJ4DcoUJMhj156XnIXZEs46hyV/duxgrr1fhMRmn3IIVHtwW5iDKVnjONL1XblALK+7lPITu9Rws9nMYyRmkV37eX9r2Jef4vBeOD09Y7q4wdKFKmE8JQbHlFScYmFALWSkZhg1blFVfPG+s3CNuolZAHIlptxCxWRFHLFKzM9KqqrSdx2xW+5xIQ7OwrFcRRzy7/Z3xmvAW+IyKM515CT3ltGY18UXgcy5uUzzWdwUpU3q9aX9ydbwci5SnL0e8UIiZnwo3pFqHpbHMJeVrv9FLEHXyhbX5x0E86rmz7KBIltxlsp3rgwm+FylybQrtFy8lhXChLupypwpeCmXJ4V/dU7oMYu0U1O8YpRyfosFNZ2BaZoYxxEROTjnNTzK+iyLj23f8ZmPf5SL6xurniTKRlyqTMYBjYrB8gWcc7OYICw8ADVO5/2ILGlBsWklb0aBfUsuUjnXmT66fAzInitFF30UxUJmI9jMF+Y677aWSqhqFY+CWoLz6woVwIhaiFKEkUjwll/jwxwGIFm5SPhoXj8rIpHh57sOVInOM7qeySkf+8VP8Xv/7I959ZOvEVyETWfK0KQ8+MkbfP8b3+Irf/PXXF9fsfEbXDDjkXPe9CbvGEVgCiXU8kAQkeXSbhPMaoNSCHHx95qAstZHK/ys8cwyt/x78/fBHj2l8FnP82nfaQWxuux4/r5WdG4T5OvnS9+J1q2tQ5Lu2+bAHBMED5SEWD9bnUk9FEhbpWq1vxV5yD6bZbDFvBYy29JoGWMsRQjaVuNUPZbB6+fb6wM+u7JemQn2qiD+JLzO/ddj1DJiLU/W0QJrONhGtpR1Z95fPVfDql5bO68lP1zKpccUq9qTZI8kPpgqwk77PaiaEVANAwQW9+4AUOhslokOcd1kTTOIROb8u2Li+/nsB0+vaMwItp4wltvaZq3FzIEgYmVgQ8ylAn1iRorI4ebU/a9pg7BUSNpyuYdzgO12y6uvvFLWZYER6WKkaKEttVJRr2cJFxbj1xYi53yBXX7UuzmvYbvJCdNpDeKI6qx85X7AYTHxpOfrOxWycOrcfGjauUmywmgpjZn1VVkefGwKJuympHDnk/Ux1fhOumRWlnLOxbGL98phDjHdzaElOSlil2FN48R887F5Cby35NcYR5xzpRTxAtYKEavO9dy95/j4Rz/KB2PEBTWLEfOehxisGpOby7YWQR0tXg+lSUaXWYC33GuTlmKGZS2MY4JUHQdqAn5DnN2JeS6SJ8Tml/pzKQxGWVh8c4ldTdaEHGpll9C5IsRpTNV4qtLMhlMCEvGdn63wSbFAsVK0kkP+mtj+JHjlOOJpmoqlOocZ1J6mDI9iLBDDaVcpfFMMwIYcE23wSrkwFTMpylcB8tLDONOWfK5cYdzO2157l5QNkUoYS3CJlQBcC+ZOiI5ynZGg9EnZcwhxqmJb1YRkl4plDPv9bAhIz9idQZWFNeNdArBzgsPCI0/6npPOM4wDAWWDQzR5ExIDzqEWsfflPMKsDFr52IqGVoxR82Jzsndad3auZ4WlXF4p9smck5F0z3SfiX2X7pXwmY6nkMV0Dm3NCuXMpPVoFeblmDfAZjDTG6Tsq6J0OpfelbJD1tPWeUvcDopXYUp75kSZ7DCkaEZ7N5fNdZhyIs48c50zfjA6x/2Pvsjv/OM/5FOf/yyy6VAviHj219c8fPs9vvvlr/H4jbd58Na76H7Pibmn8WIVBCOa+k1Ks5NScS6fMTSz8YyMmaYshU3bzkMhzYxV/oD25udbobRupcjDyphPYw2uP6tlgAOe1Ozw2lraNRaFyrlEH2c+Y56hw0sHa6HvmALT8u3y+coc8zet4WQNDmtrsa01pbbgfma4CadFDqM2asG65a+3NklnNZ+LWE4ZypJ21rgzVwypqG4jDNfrnflfxQBrGNRTWpnzoSLX9FeNU/Y8xqOwbodYe+8YPOt+67VZuCxl75PwYGeYJVyOKRlLRTHTv/wvv7+OW/N7c7+zsbBDcQwxsJ+mpDNoOWgikq4XyAr3nLNqMlfmUbPyIWC5f2ktIcsRktmWWC2RZq9va09f3raqsFQTpVpLbQ9dLZjXWmF9qGOMpZpHWaiLiMz3c9QW7LyRa8RtTdCt55N/1u5CTYRqfqcao/LK1AhUJz/nflpBO1s4SRarvt/MISuaYvNTrX/nzHqWhT8FxHm8V9gPxfOzuOiKGqmXjKl2G5MIWgipDGQhcHmNQIrnzMJkhkPn+5lJpAo9zs2ehfpffi5bmGslr3hxUj7FNI72bEjhZD55OKY6JC95GWS2PBaGk4QmgiU+jxpxnUfHgTvbTYpzr2JsJQngflYEazwoOAaMUa3CT9ors7gCKUk8M4iua8XfhOsoUWalMQpmrWYOvcsbM9/RAkGMkboOFAdBi/KIagr3AhGf+rSQs4RiZa9zkJ3IvJ9lH5yAmEJDKWGcFItCMOfzomrCZoyWY6Q5sT8piy6V7hXA+RURIo+tIEQIifCpeWpExMoe55CVaApWVvalwD4LvA5kLjXrcGiiHVZhTE19UxPqfGLkImoCnyjohMtCMZmwZlGVuQwvER8UT+VpzbHBZoqYBTBxJUQthmXoEOXMzUxQKvpTaI1mr4UiTHiNdBoSnGZlys5sQhoUn+efQZ9/DYdMQFUX97hqgm1L38h4F0OCUCpTvqCHJAVgDp/CWdqXJBzTqFYefBFGY0wwFzEozDbjYs2kyedjfrYozqTb5QuTLiwylfw1b5Ag+NSlJqVa05oKyMQlRcSnVB+PdsJehO2dO/zW7/82n/2932Rzfop0dleKV7h68Ijvfe3rvPvTn/H2z94g3OwJ4x6v0Gna/3wPAQl9Ufok9Imb77gplWG0QLO0mte1gvjMDx3eH3qt1wTEFieOCctrCkP5OzOWlXfafheKxDERvlE22t9john5szpHLuec1bQ897kmm6zJDEv4HAqxJQyLW6r4VH218omTLnleWmt8UsSExfN5He286+IuLdwOzjEw5+rVaz6igKb1zUpQOucNjtTwKML7IThWWw2XY0pGUYhq3vwUOG3rXMK9fudJSlotz5Q+oVRygoo/NPhdK4TteO26Cy1jhmVdXOdwfrMhrswpnfkowsOLS8IYkVSxsRgxUURhilp4HYD4lOcMZnRBsg27KB5U58o+T+GxUML+fg494+dJBhe6zuMqi9QsYNbCZr2ZifA7c+LMBGDuN2v4+Z08+TVBthUOc9+166t1aeb36+/zRjo335zYKhRlHF32Vbc14tX+vjYXqhyFtiKWWZ4F1ZCspiwuNsvKRm35sFK4y/yGpRKy/KzMTw4PSVEYUJzzZZxSrapiZBn24zgWITorGLVHJ1fVUlX2+33JZRnHkb7vDyr3LCxnHO5B/s57zxSzcma5D5vNhn1IuRtaEQ1v6kDLCOo9jTGVq2XOHyh7YhtU8h0y1hYhKd+dUO1hhnGXKkM4J1kLSNb99L6IXQCXFSixRGpRGNtbVqv8ApGc7DwTIOcpShqYpyJN3mxbSQg/TF6s4TArtK13Ju9x3rN807WIVEnn817VsF07w4fGgST65zNKJUOny5hYCV+kwskWV5KBGhGh8x5NBpN5Dku8MmgIzq8bNdq1tefK+fVQzpqWtbka+ZmD8EatLJEVzHKr88TKXFZCJOuzVcZLfa/NYwnfGSpt6NYMgyXMs9DiRJDkjZyF1YRtFb0t4zdGqLrV47WhercJEfmTdLQQpSgfqAmOVo1HoHMMXognHZ/79S/y2//kj7j7wn2CM/xzwO7imm9/+St868tfgWHi+uIilzCzM4GCMw+eT2e+xtU1AeqYgNIKwsd4iwmsyz3OBr6a/7V4Xj/3pLY8W7mk5lJgmuWAef4H7YhUWq+9hUGNJ0t6IWXd+bP8ThvGW/O6ti3gnOj12phPaq0c0QrP7RzL/Kop1WMe27NaTllTLm+jVSZYxgUtEBGOYlaDg7WssKbcLMas6Ndav207pgSsPdOusb5D7VZFZmXcGsfq50w3PD6ntbU/Da6s0dC2vxq2x9aT84v77Yau7yjKIYklijCQy1Ibb2/PRIyW/5cvT3XOWQhdsCJERj8yLbHLfQMmqx/f3WV7akWj63waNG/IoQYotRa8+JkJ6goTkNxPZelVSlhKfaBuZe6VpTq3/F1tYW+/V/ul/J2Jcn6+JtrHxs3IXSsMB4c7C06SbYCU6lMLBipJG51MNxexC9hCDLQhay1CiswhW4Xh3HKohDnErGZKMdp9HjUcsnBUC0gt7FsBaDFW9X0uA5wriI3Jw9Guxf5eCjFlDYmxOucQtdjq66sr4s3N4vbvlrkviEgrXAGC3bSMpL2I+WI8BRW8LC+AcrIkXu3eW3gHRakrLKc6P5mYibM7RYiKiSuHDMk5xxTDARMtsCqWCz0kBDLf/VDvYS1s1mcmwybnGKzl7fh0x0WOr88eOVQXoVui0OWE4EaIWKxR53jQ9gy1sFgIALaIeV8SA67xd5H42Agpt53d1luJLuFV40N+tzVs1M/Ufa2N1wqltzHGuZz2oTBStxbvW6GhjJf2LrdaGF47R23/7fzqPtaEn1aYamnIsfXbTe1LZlx7lldhgOGhy4qGMbGSizM5IfSOV3/p0/z2P/tjPvLpTzA5GLxLhQEiH7z1Ll/9i7/m7R/9hPHRJUyBOOytwAOCOE90pmhQnd8aL9f25jbh5OkEmfnujcV+Nud6DUe6ShE8ELRUD4xbZR2NcAxz2OihIeNJ8z/kZ/VnvqEbZdWZvnLIm+t+2nCbzOfyGMs1p+IZsjSsle+za/uWlucxGywP5Z8Z9+dQmOXncvBZ/W4bVXHs/C/pDQsFH5b8u+5hDrNcP/s13qydf5gVrGPrWJsrMhsq6vWthe7VsKIyetdzrvcit/bMFYG7irwpz1Xj3HaOjskcbWvnVY+V53Ebv6vn4Jzj/gvP87v/9B+zPT1hs9kY7BIcnfd02xNcirDJ97uBEFN1lXqMkJULVeI0sR/2qYCNN4OJd/h+g/guHYF/YEUjxrk+t2rekLkGvi283oDKZIRDJMeiHbE6LRJSHFEPQ6dsrEPLSY0cdd+tZrsm/Kuamz/HT2dCma302VXW5mm0yFGX282Ce/YCLA5rNX5ej6qWalS5Dr+qphj6+V6QmkXVd42sza8cTubbkDPsMqzyBXo18mahOu9phnEt0NQhHy08Wwt4S9DqPutn1nJLbC5zPsqiP63g4GC335e/Jd2aXLuZ1whFLaDMglZMIQ6ClWJWSBd0uXxFJilHIvGOWlDPY5UxijNTyk3DRgiYDw65H/NJ2rznZL7s0VhUNWnGofQZF90uCEHCqzrHJysHU5yrt+XPa6WkZf5FiE5dLxiqUkLwcunURShdJaTUOFPGWCHYNnbNfurCCyWA6ICRZVjmM90qBLmwxXoe2RqM5+drD03BYWXhIc2tfr7uu8XBdty1PLPW0l8/X+/FmqX6mGCw6L+B/8IL0ozVrqX9vqUTx/Cpfrb+u6Zzi+dCJFawP9iHarzl35LCzUBFiJ1j8sIkyr1XXuL3/vmf8qnP/xJse9h4RJVOHMOjS77ztW/wva99kwc/e5stjn6ysz2EiIhZFi2l3LyGdpGkO1hbW3mvxqljikj++TR78LThUy1/PIYXrYB2bPy1MVr6Lqn0Zv39bby9rGlF0M6wXJtre26fBnbz81IMQWsREibIrC5/Med2rBoHln3Pnuk1L0zdWhypeWtNT2peX8+njkCp4VjWXwvqHCoKB7BgScfqddZ91HvbwugAbqoguVT5EnZr+FXTunAkib+mYS1NaNewdgbyM2v0tIVPS/Pqz9aUnTXFou6z3tOWT3Vdxysf+wj/4n/yL4kpLy8rGZLWnYuWWn9qURJihWB8kjNiqlJV5BNRM5jYTFCt5GzF7kDSHJL15PZzJIMvE7qIcxhG8+DybxE0hnQhUxYW1ty32UV/yIiPHdqWqSyncWjVaFsR0lPVkVq4mqbpwNtRI1V+ds3K2x6oVlBuGUEer+u6Um7UOZfSAgTxrgiXtcei9CGW75AROSPkmkUwvw9YKEBFmMv6Ugxx64KvrbRrwke7zvaA1MQzj1ULEi0jiXG+rbvFgxgjEix0JyzGj4QAnuXN5u2et3gwz1GXh1WMVFpu3Zw0b0qJppj8+RwcrtsUWfF28WK1ZYbpGXdQu+m4fJa08tQW8fwi6Rbk2CicNnc5ut5DIm17UN87cVhFbA1eho+zUiDMeKOqJYyqhNNpJciWIJblPCxW+RAPjhHhhSKZxqv7yng6x3LHIpzYOTBPan3zfCv4AKV6VPlOZ4ac51H2O0Rwh8ymFSrr3+uz0yoCawLTsfDQtv9j7ZgQs/bcMYVg7f1j56wVnlo6etuZrL9bCI0N/bmNR7RzVBEro+wduw7k3gm/+Y//gF//0pfY3rtL9Fj/U2QzRV7//vf58r//S9574y3C1Y5eBURxviOEie12W11MKlZYIcXBZ49ibXhq51sLYbVBZw3Gt7X6/KpqCaethfHbhOy1/lp+VebNbIzKn9f91J6Nxd4jB8+3e31sPjWfzX3XeZC3vdPCu11nbmYsUERmz1gbypvLKrfvtmd3sRadY94PBNFG7oHZSFYLqLWA3PLU+vkiv6wIqnCLVV4p/HZNk2r3p75NvqWZRQ5p5IH8zNo5KPMRytmp19Tyu/bdFmsWNJulotDSnqPnzJj9z3Vu1lpN29f6qOWrFs71+avzg4FyR9vklEk0mTlypI4VO9GgizvYxHludjt8dGxTtIJUil2GvV3orIWvOhGiaDHUICCHdpHV9vTlbesqUDprnM419ZobjS0LiU6XglgNSADXhErl+uktQYKlJSYDT5dy2eJw1Qi2WEIWYHU579qDMsXQHHKlLh/axlqvxV7XRMEnIlALQrXgThbgBOqqKhrV4varg3Gb8NIenBlOS829JlYLT4Usk7lruNR9t6Ebea15TfmuiEyQgMIA19yUrRWmzuFp1yNOIBhj6Pu+hFPBoVJXE+wWPrMA6lDN1nXKP6zHKixpScSaAmlLvBYxwTRbWtIeNy+gGhHv8Q5Ercyx6pJ5Ffiw9ECR9ZJ5gDLWYp0rMJy/yef58G6LNdjnAbSyTvrkDRMopYyBKp8knato6JXfXDDQFTiWs8x8Ttv4YO8NDrWXIf9TXd4+vxTWmzsMFsJp2pdqnKxo1BOt98dKHa+fz2PMrD6PrbXy52FmT9tauEIV3sTtVqoavre1Y0LjGm28TZhuaVPBo6RU5z4X57GlfczbJc6UjKBK6OAXv/Rr/Naf/wl3X3kRXCo9C3RBefTWu3z3L/+OH3/n77m+ukb3I73CpuvAO4Y44XuPi7MXKFOJWOXMtQJOK3Tk+T4Jpk9qa4pgCXFslI0Mx1Ji/EhrhbXqmxUyVtGCysi14Iluyf/bvVrDTRuNQjdrup55/zF4HBP81/gYZPpnYW813yhzERY86ZgAehDKpEpddKZukcq4xTrMc59t/1mhVNUSimz0cC6jX/eR17YWAWJihxRjT1rhwfpamNRW9va7WsloeXLb52LNyYZVzzO/u+bREZHFdQn19y0cb6M3h+/PJWzXz8E8/3ZOa8+swac+I3U/9TlZC+3NvHocBhgnfJciJ7IymXhm9FIU/DG5NzYnW5NNcq0ftRLckIz+qvgKd7x3Fs4fI9551JEKoDwdHJ9a0di4fq4tr+kyDzGVpu/SYTeFOR38rGTMjCzGueqSE49zPmlNoDnhWRwuVS9JjxLCbMWPiVi5LPSJA7okaIQ03mxNUrUqMOTbbsmMZ7a+5jm2BMKI8Sbli1iJRBNaqtARmWvpZ6Spw4fqZ1SV6FwJ4YgxcnZ2VsHHbsgW5/CuQ0KEONilYULJa2hvgJWkddcHodZ8o8WykMuLalp/mILVis+CaTnAWohUrWSIzDkgNZFaCAFicYFFqINU2vPQUpxbbWlumXCGyxqDCAIuQDcZwqsKfYggMYW85ToJmvIeZitJtuJnGOWbruNK2Eteb1Ts8kSRRATtPgXvvFXXyQpDUhRLPwm/S6yjmY6MhKdkUQ2kcg5z3kcWvQ2OVdnWYvEhzSUW75sRmtkjU2RGnStjpR0uPKSrzqHhtZSQIkTIKd6qmipXZQX4UNCr1cKpsuDlnchTKBW3NMXbi1RezRnmmr5TjAA60hlVy6XJOEcWnpL3z/tcchdgzjHJqqJPgnWu9BZjIAYQ/MIqXM+jVE+qGHUp1FApJ6XkIWlP83nhcG21gFG3/F1+R6p/i9bMs513/TP/vipklIGzwKsz7PP+ViasDPNZMDi0DtY0qqypmc/s5U6DFwShKBIZDpI+jyGmcr9WDhmZvb5g50bUqk25/IFzBFW879gReP4zH+d3/oN/xid+5bMEl9bnTWkYH13x7k9+xl//63/Dh2++g4tK2O3mC/68szGyclaF32nM5b67RZ5hu7droXI13Oq/2z7W8SUL8wmulYdkUYWwarNyPwt3CKnweRKoC+JJ/aT9Xk3jYI7J4JHPx0JpqASlej1rwnX5KUWwOBA612h1/fsa32lhvQzrTX9XvNKetTW5dN6TCbA5c43hNeO3VAJ8hTPWxQzXmvfVc2sF+0J/KkWyhkt+v1UC5jWu04sgdiYtSngh0B3F19b4UOhqQ0dv25P2uRhnXl0/d5shxn5fCvOtLHFbP+1YZb7pfy7js42ywI28hvpnC6d6Pq0CVfPQY4pK5pHkcdMdGPubHTEKPnqmYaDznmEc2Ww2JlOJMCWZc5OSwsXNyoX3nckMITKFia7r0SRPFT7kOnQKXD68NIPopufO3bu3mKSW7emTwUWIOPCOqHbD8OLwK0UjygRPVcFZcsnMiJNQkFWFzIxcRo50syEUS2jnct6A0vWpBKHaJWrgQRPzrJedBDZ1njBGlIB4m2MWgDWHc5XNN8t7TO5Yl0I+THikuBXtApNglmcOCViLcHVIlZNZQakt+iJCNpQoWGnZcSROAReCMcxkgWoJbN93hOQ5yOMUpM7zSHJlFsRiFFRNeHb13tjEF+EmBaS6DM0qa8qfVQnew34/w6IhnFmpWOBXt0TF4iVp3OL1YQyi9Dg6FfZjAOc4dR2j7hnjhLC0qsFMROe+ZuZS15JebxaBXRinmCcOsoJgS52nW8U9pnHzd5mIJzWoEqpTCc4QF8wsKzD5GREpN4HWMM5lb0sFKE3rdEsGd2A5yYK6y1ZjiCwJtpNqTZps3y6FHTpX1pLX41OyoOUd6UIxqXHYAebiCAVPC8TTWkyhyFWoksKhihMtd4povQbSeFnwEqk3hqw4CLMi452Nke0/IrM7PgvdWbBXSYoSGV1mQQMS7WIe+0AYqvZ8sQ9Vy3SqZkj58xnD5nfr0uO18FT3XQv/ayFNqrkEbmJ+lWUXsaTc+gwWQaH873hrGbAmHHLl41Zwm+eQF6uF0VeFNYQU2ligYV5qTeex6xiIROfZ3jnnd/7J7/PLf/jb+LunTCJsxeMRhus9b3zvR/zgK9/gre/9iP3lNSow5AseUaTrmPIcytmYaWEIgT6H36aQu9rD2woUazhQ09x2z2ve0gpZ2UhSP9uGvx54VhJcszJR8N3+LJePaoPfLLltu9HFqJN/b8/e07QDBaHCvRr/1hTmGr55/fnzxfqrPuZ/bmk7yBZiyXDOBqRcLETKM2UuauEo5e4cIKf4KRTjjTBXS8qt5bnHFKQ6PK3+7hhsMj2rC7Us4C2YpTqHfmZjUCW85/fafajnulA6qrHXPLyra2Metx2vnXe7v+1n7VgtXrTft+cMqoIvFU2fxYT5uXzGDpUfFn/fppDUnqp6b2Os5OLCF0xOePjhA/5v/+X/hWEaOT8/59VXXy05xvfu3WOKwQzhiVdfXV1xc3PDNAUcc4RN3/eMw2BKa+ehs3DvzjnOtqeQZI8xTOzHgbv37jEOA//y136FJ7WnVjQmmQqz9yh9561UZDqAxVoogvQe1OLnVQQk3bBaAdmLIBrM0pwNJ0nIiWEqVkcRe++k6+YLo1LyZ754BMBtujKXvDFZaFQNTNNAiBNIVwmX4HyHxHQJV1JCphBNSAojfZKHxxDYbLaM6cbiqBCT0N8Sg4wcORa8FtBbRaFFPEtoSiFWMcWhJ/JUWy/qAzFNobgNa4bSxjPWwkUWWOtjUCs/XbrXI1sm6jwNmG/3zvHrAMM4st/tyhxzVa261QeqJYY1M84tVkx8lSilA+98KreYmZrOz9WEL4RADPO4fd8Xb0a7j21rhbS55O/SLX4gCKoeMHl71iw3benJYkXIeEGyoCThSZhlAw5wqJK3WBK2Gm4LGDYMuQ2Fc+JKXHLbX31b+IJoMyumLeOr8b1lVvPq5lYT8PxcG8den6V6/rWAUX+eYZ77q/E1f1bj6CrTXhEU6/a0uLTWjsEp/51bNvhknMzfH4vLr62PtaLRCjcZxmvz+nlbPfe6mQAbqW/3WGP0q7ASQUXK7bd1+GKnphRFgdALNxKJ2w2f+/Uv8nt/9iecv/wCgzfv8lY8ejPy5utv8MPv/j3f/9q3uH7/Adt8D0/y4NVnd3kZqwDLMNNQ8YUaBvXa2v18GhyqBY81nDSvhhwIn5lW18LL0wr7P89+L/fn6fu47QwUXDwS+tW+v8Zvjs1h7VlNMkY7/zVeXdPM+pl2n4GiqD1pze28boNNKwfcttY1gfdQSZNZkG3och110N4jVo+Zn1kLhYVD/vE0raUfa+8XgVyXnrbb3mnbOkyevi1yeXSpyN5WQa8e/9jnNU/Nf2fZzCk8/tnbhGnicYi8/rVv27Mx0vU97nQLWOXYru/ZbDacn51zstny4dvvJNnb8fo77/DwwYOiCE/J8I6me6hUOdlumaYJv+k5Oz3Fdx3/8n/5v3gibJ4+GVwsNosYIEa6rmfrLawlOo90HaAM494s/aIQI9MU6fquJK/OgAs4h13WlUQpu3zLcX1xwUnXcXp6it2YiykKYWLTb+hweO/YTxPjMBFVOT09JeIYx8AwDOzT7bwzUQ9MYSSEwJ07dxjH0RK/R8em2yDe0/cGjpOTHhEL9tCwZz8MdB72+2tudgNusy2Hqa3+BEuEq4l6q/Hnf/OhTrefMpe7y+54ScLzGjKuMbRWyGs1ZVVF5bCyEHAghNUx9FnZ2O12jKPBs+97O+jVoaoFmSKQV8JQVmTqcWthKbeFK5uK6NsLZb5d3zOFkDxjEIMiLJPlsnKw9Ab1xRVdw/M2hlULPoXhiVudf1YJavgt92wpcJRYTeeWaVFUrvOQk+TXQmVmQb1lWC0hrd+/zXMVZd6bhTVMcxGHdSZXr7nFp5Z5z8T00IKXyyi2Vqt2j+p+a69hu4etoLK2N62A165xjWkcU0bWmPFt79Xvr817QWsSHcpwqsds96JWKtZyBp6GobdwmR8+eHT13Xoc1+L4UwqMmXY5LJzBGQc25SN9FhBGD/tOeOHTn+R3//xP+MQv/gKhE4Z0gWOvQnx4yQ+/8R2+9ld/y4fvvw9joA+QAxdDCpXsZJm7VBsO2tr0xcjlZgvkWrjawujTeJ/WYNHykUP4Qj777ft1pavFHpMs2Q0dXhOYju3JwRwrS+9xYf7JbeGZb95Z9lvMLkdbDdP2Z/2MiCRz9eGca/pV/575WOZzmffVNKu+9C2/l8d8Gg/Gbcpo/dwxGtS2dSUNSnz/kdYq0DUO15c657EzN1qTgY4J9LJibGrXmFu9NzHmoL91HF6DxW24fYxezw8dKpDH5nxbP23+Rc2fFu9UuFEblcZh4OrhIz54771qTWmCIsa/8z4xG92sML2Vpt9uNwzDWAzHvrOKe6itcIx2hcDNfgciDDvh5tGjpz7LT61oPHj4gLt37nL/uefY9ht6Z26Vm+sd+2Gi73v2+xuub65xDq6uLtkPe/b7kdOTU+7evWvCXro9Vwl4D5dX1+zHgdOTc3Ad5+d3uXN2xumm5+TkJN3fYSW5LKQkcPH4AlB2u10ad8fjxx+CdAQ1q9I4DFxeXVZej0CIge1mw9XlBZvNhqurK05Pz9huzzg/u8PJSWLW+OTyVNQ7/GbDww8f8ODRBX2/5c5mW9z2a0iyCAupDl4RcpmrcsDsHYhq3gulK7F4QBE6s2P7wCoJBYFyCFJ9SGqhPr/vnF/cUFwTPucsvn2fSsZmIgJWgWcYBpxzxROQL+CLsrxzoFUgpiYxrW61EDsrh1Vsf2qLRHJVVMD3Hadnp1AEGI/EgKiUueZ5uhTi4/x68n+2FNR7WvahIvoHZUdXmEiMsRCjdQI371vLzIrKUP1Ned4O/1r8bT2no4S8EfLrtdU4MhO8Q2vs3NfcZytQ5TNQK5w1XGvBt+6jHaOGSxaW6osua5ivvZP7bgWXFk+zu3mNKbaf1f/qsVuB8tge5L7WFKF6zmvnZAHbal71uO3abptTu/f1sy1cW0VmsU9H1lvD6cBzWMkUt8Gqbs45KwCnglOhc8IUo122FyyEMnaOk5fu8/t/8kd89ku/gW4c6j2d2B0aw6Mr3v/Z23zv777OWz/8CbvLKzqNxClVHUqGk4zg2cvbWnZByRWKMu0osKn2pfYyt3vTCn1reLomeLR0Q5KAn+l37jP3n8dvQ7mysFQLxsc8yPXvazStzKv67EnvtuegbSJSBJ72HKYnFrrB0wiWLZwP6ODK80/DC9pnjwmsa+doAb+VMeGQ5re8ql1zO34OExWRZQXKhk7URuEWD+sxatxdC8U8Jmgfg2uZT5KEWnis0cjcTB5a4km7r7eFN7Vzb3lBHqP0pUujYkt76/5rGfDYmlo4HITCV+/V/DZqZDfuGHU6MCQQwaniZc5R1hjRMDGqEpKhc389lHf7rmfSYNAXk1+is39GYrTINS0MjrWnVjSEjt1u5CeP3sB7z6bf4DuPRkuYnqYrlEDfe3bDjgcXj3n48AEvPvc8u5srNE6cnJyw3++5uLjg5GSDeMtn6XzPbjciDvpu4kJ3XF5fMw7vMU0T4zShKcSEKTLu9lgCbGQcB7yHV155hX6j3Dk7t4TprafvYL8fODs7I4TIsB9M0YmKwxHGyF4GLq4G3vvgEWCCrLm/zVNyM16jwKbrOTs7o+tPiNOINhaujBhrLrL64Hrn0Mrikb0H5h0Zofd0Xcc4DuTYX0Mm24WaEBRPQwx4v7w9OjMmWLduiaTQA+eK8J7XnglYfQ/IOI4lDGyz2SwOQs08qZhibqpKSOWC28N4TJCaBRFZCNyLn5KZZ2SYRsZpSsXdMKUmuRbb29dz4mjLZOrx6zlmuK01+97+1Uyndh3nPTkQYmERn9taNWUxhnUmKCEosZrOkpEdembWwmJaRtISsHaNGV+zl9DmumQoC0HFLyu31GO2xH/xU2fJs2XsrVcr/12HsizgVb17jMnV/bXfHfuZ32nLW7fj1s8em89abPGTxs7viUhRruvPjsE399Pi/rF5r53PVlCr1yCN4HabgDnPOccbL9dxKywFLP7dDBExKuqFGwLxtIOTE371936H3/iD3+X8+XsWD+/Meud3I4/ffo8v/5t/zzs/ep14vWMaRlDwndit8RpLNZJcSn6h9C/WMt9XMI7jUmgWQZNiXHuN1+hODde2xO0xYbSGp312WNVo7Vxn3FVdCgq1cSGfr7pq0YE3pJn/jA+6qIzXPru6p096rqGHx5Sdlsas4W+73trQBrOSsTantfFa5bk+2zNeG11bE1xbYb7tP/eRaflRfnGEzixpVOZJy3LpM34kIbLBzzznmsav8fJagb0NlmtnoG23KSnrPNoBh5dL1v3U0RbHaMxtbY1v1OPUsFjbj6dpNd2u5bk1Oi5iCqP0qSBNSvImPeuYDZr5rNdzTL4n2ztvxtuQ7g3LK41YGGpUu6PMOYekGijqnm5NT61o/O/+t/97PvOZz3B29w6nZ6ecnp/Tbzecnpyx6c4IYaLrhBAGzu+c8Nxzd+k2G7x33Lt715JK+h7VyP3n7rHZ9uyGPYhnmgxBH19c893v/oAxTgzjzkKghoEwWTLLxcVjxus9u6trbq6vQBTn4Jc++wv8j/+L/xGnyQMyTVNSQBz37p7T9xticPT+xKyW3nN1dcW4D3z9a19l6np8tylKCCjb7ZZhHBl9Sr7VwCsvvsBvfOElvHM4IipucfiOCWtrxC0T8tmdbRqiVUOyakYiTVy/LK1atYuy7rdF9nZu9SHNSkLNRHK/Wajc7XZ470u9+LyOOqQqz+MYsVNMEGkVifqwtn0Z4ToUPsr8sTKVURXnPeId4zhBZ9ZHRQ88PPb7MpSnJVytspFeWqxrSUwOGUh5BrI8fhiyglluWBP2YgSkJCCbdyTta1XbuvxL8MihTPV4WSCeYXooENZK6gJeQsn/aZmpCV9LprkmeK9eXFkxwKUCYX22eFArTIVIVvdo1OOtMch2v+t+jgl99Vlq+11T3o6Nv9Za5aB+P3+/xmDa79bamiDW7vmxdT1pHbcx1Za+tGtdhwNFsGnP4wEdze+0c3LC5EC3Pa997pf47X/+z3n1Ex9n1EDwziqURXjw7nu8+8Mf88Nvfoc3f/hjOqtETHAWk+wUrJSZR5NHwydFKIcXHXgD1Iqd5DLeqjPNqfH6GGxqmNatFTBruBzCMCndahRlzcue+4Ql39BoXuE6pLWec91q5afur+Zl9rvQLmltjS0u5d/X2m3KU0svjsGrPgs17Vhb69OEAubW0qVjykD9TH3+68/bVsM8K4htqG+9tnY9bb8hBkSWVvWixGgsxLeFXd7jYwpcPcfa0Fl4YPXMMdqz6FPK/47Cpl1v4alH5lhg8ISSzre1JX+n5C4+CYdro8zPq3DMdPYQFsaHhZPOcyWg5MJIc4uSvJY6G2qyH9MnGUPTgmba4PDpcyfKFFMlT1WYYskVfdr29DeDj8qPf/hTXvnoR3jpI68S3cCp6wgy0IeUPKweL3ZZ0cdfeZVpfw/v5zJ7d5+7y/Z0C2qxxbt336f3HX0nnJycs9+PvPHWm4Aw7gd2ux3X19fcXN9wc3PDbrcDr5ycn/DcR17h3r173Lt7zsdefZnNySniPTe7PTc3O7abDc47XnjpJTabLQ8fXxL3A9f7azyBbtsxoOydA9+xSzkbCnRdz6AQnGMKASd2O+y4n+i7DZIE2Dge5mfUpQTz54sD2ggWWRCc8yJyaIgjToBzpVqFsLSgFGakZqHI5W/rQ5/Hz2PNhM3+F1PsnWiKsUwXy12mygTb7ZaTk5Ol9TYaPDKSQ5qf8+QyiySB16cL0RTFd10pK6pJcEa1WKsk/R4TLLquSyWFsQuwYhov0VjRSBgnJjUFbSOejfNMPhFQ5+ichTdoYsLiUqWa3NeCSR0SjHyw7TAurU7l2bQ5c9WqRBBSib5cQSNXJ8kCQek/70kwN6h3HhVfRR5r8dQgFEuuwUDKWnwaw1TlpJhKriTlmoRyMcUv70GDx4WYpedRq/gkzlfKgLlkNWkcIuAdaLS/s5KYK7BQEsrDvB8Jbhm3NJW4dRXsixqVAJKZWSsUtUJ1K0isMeD679bqHMNc4QiRhLMJTprOctpTSYwxe6jymb+NQbZzqAXLlqEcMp1DBakdT+qfagKza/D7mODaCkK51Yyy/U4ii7rkSqWAIKXaW129y6xp6+53l2hJgBIqJSlcygeHOGEUGDee89de5o///J/x8c/9IrLpGYg4BR8CNx8+4qff/yHf++a3ePDGW0y7PS4LhNYtUa30rVUscxVDXho5ui6HxNpixjGU6lKd94QYiSEV56hCauqQK4NfTXsSnpJpjS94JOTKgBkHZg7fKrgt62/Pc2tMqvlUDgur2zHloOUvh89KoaVtn+17xz5rleVsSGnXnHGo/qw2ZNQ8r1VA7Odcyhl1ZW/qsdq+898Hwj1m+MpCnIjhVilHWD3bCp5ZRmrPdat8r82n3adjNEfEwmey5xEOQ+Tyc+1Ya7Sm5ZVrc4blvtVhfGsKRIZjORMNza77aPfHBGwpckWWl+Y+lzBa83q047UK1HKe63xziV9LmK3BZ+37deXX1lZ/r6pJeTzBHBlGvxavLdad+mE+O7Y/OT9JURXUCSHLNdHOhBcrjRtjMIO8rBcMWWtPf49Gt2WcJn72+hsMU+DVj3/Mkon3I/1Jz/b0FB8jLkSYRkvIG+2ehgic3bnLyekZp2d3cM6x3Z4gbsP15QVhGrm8eMQ07nn3vXe4vLhhd7Xj+voGEeH09ITn7t3n059+ge29LbJxKI6u7/GquL5nDIHnn3+BYT9wefUW4jtOz8544823+chHP4LreuKw59WPvoJzwjvvvs/p3Tv47QlDVPCOgG2aE7OG4xweE4CnYV9qEXvJ++4QyfdqZDwwqSyX0a2tX3X8a23NLUqAmhU7xMgUMnFVQoyEqHR+eTjnMK3Dg1/HCufxWqLr3KyUFAUmMcoQAtvtdpEsnt/r/Zw3YzknUpA36vJgLSxlkksHG7IfxmtLEYqsX+Z645qF9VT+NQtOzpkALNi9I1MgilVf8Sm8IrHwFGaWppqE8DLXNAZJGFjEWku6Z6Fa14L4JqFz7sjmXW7HzjX+NQ8yK42acCcTEKu0lvCoEii09J2ZlpLjJAvRExB8ecSEIS3KbRbYa0J3EKrWNE1E2/6R3q8ekGpaxesSLSZScrEDDoTJJdHNlmEtSky+6X5BdGV+9yA0r7kZtx6jHa+2IrZrPVBuKhhk4bNmODFU1cdSGWxZYYTHYFtbAOt51ox7jYmXNTZrawW2XE57ZsTz2aGiGTUdaBWJts/bhIzcv02I+afM3xkarQsZ9RqDS6E9Kng8GiMbl/IknGPqPf7+HX7zj36XL/zel3CnW9zGvncxMjy+5O0fvc4Pvvltfvq9H6LDSBciLvUfmXMpvHN4N4eM1jltmb5nxmwWZaORwzCU8soZ3uKWl7CWW8MrWAuz8CNllAovSHQrK7b594av13uTnRo13c3nIZ+Pel7pgcW5WsPFY+O1+wUpzBcz8rR4Uj9b09Da09sKfLWw2vaRv88elFrBaMds8Xym60bPnHSZMSQlYV14Pybsl78zMUyGHiQbfo4L47dFQxxr9XOugnXdZw2jMm9Zwin/nj1ixxSHNeXnWGtz1gqe34JXyzYbBvPaao/ZmlK6Nqf83gKXVvavfr5ee42/a0p4Zumt4vCkc7PgM40cdBts1hQtEUvm1pjLW5Muza37WfKSTIOdE6LKLFuIGSTzpbsqYsUwynt5TId0KYrmKf0aP1fVqa53xCny8MGHTHHihZdf4s69uwQ5J6ij7zcm+EchqOPk/A5d73n33Xe5d+8e5+d32G63XF9fI+J54YWXeOH+fa4uH3N1fcPlzchbb75NwHH//vN89FOf5P795xaXxgVGcMoUFO86Tjc9u5tdIaR37tzhtddeA+Ds7IxxHHnn7XeIruP0dJOSg4XNZpOQJyU6J2KXKynlZD/TFg3AOTm66zoTmBuq3yJojehFcE3r6Pv+IJFrJpxZcUlMyzt0nC8tLISBZJmStZvPtXg41uaY1yEii+pcMUaGYUBESpJ3+16OiR9SzeVSdWqlicxVg0KMhwy3WncW2HIlqHotNVMqnyVBwS4ztHmfOYfZQNcPtuHyMlGzJtpx5TNIgm91AddhbP2SCIskN3fVX6tcZsbUwgPMakAVOtcy+JYJ2O+A5nyeNYawZCSLUCc9Lni3nx1jtjXOl71x7gBeyJIM1oQ6hwu2iXD17/Xc1yymLYyWwthSCTjAjScQ+7a1/azhztMw6Lym/PuxZ5+W2cMMr1poLriox1nEsXm0glC7H2vPrM29Fm5qgbjF8SExwk2APgqd2zLEgGy3jCeeT/zar/ClP/unnL18H+m8XdA3KXK959033+LbX/sGb/7oJ1w/eEwXFJ1Cqmx4SJ9rmlivLc+zDjFVtUIkIubFWNLuZXJsXkt7b9BtgnMrjC/gwuxZPQbf+vd6znXFvTUBvp3P07YDerBCS27rv8XpGp6LvlfGa99fw9m1MebPaiOXoFWO2Np818I9yzOCJdyu7OExulKfnTV6tqaAPA2NqgXzY+1wH8woRCNkr53nGt9vo3lJeDo437c324OsgB7w4pV12Xqz0Wo5h7JHi7U+eV9aHlvPIwvemX/X/d12fuu+W3it8du6aVwaBZ1LebXnZ3R9Xz5rjXDH9k6qPON6HvkZ13mcd0U+bGF6wNdvaU+taNx//j5XV9dMMXBzc81+2Bk6hEi3C2zPzthsJrwoo4PLmx0fe+VFwjTy8kuvcPH4is98+hznPX0X2GxO2DHQ+y1np6fc3Q/cDMrnP/8FtnfvIm5WLmYXt9D5DTEG+s4UGxD+36z9V69tSZImiH3mvvbeR1x9Q6bOSFlZlZVaVFZVqhKNZoM94PQLwQbBR3L4MuAQ4BP5Y4bs6QcCJAE2wGliZsBBT3dXixJZlZmVKrS8EVeee8QWa7kbH9zNl7ktX/ucqGoP3Djn7L2WC3Nzs8/Mzc232y04AkOfDo1rcHP79m1473G22QJINyRerC9w685dLJcrJLmYmEFStS6Xy6JcZIto3PLOk+AdONSgTU+ELlqASDua2aQt7zyQb3mOMQLKqy59lHHJYvPeI+a0vRZM2IPpWkiGEKobygXcb7fblPo3M65mJivQW4tLvrdjFcNAFLmkF24tAhmbTR1swRwg26NpJ2qxWABYjzssPL5TnWGJXAEO3bZuowKzDXBdhAihuh24FkgjD0zpg3GuUT+nfRItRWrnOin43P8ZPtTty3sSMhF45CmZ8zkwo9u0ZwxK3xRttXFox2JpkpRLLcTkpycHUoft9ZxOPLVoA3bdR8uzVkFoBWnB5BzAlosRdT1zykMrIivIdb/0uQALODQdbXvakVHVTTTecm7G1pxL1ZdWX1uK045zbnytZ9IHgGeCD4QupsQCW8dYH3R45lMfxff/6Ad44TOfQDhcoPeAj8Bix3j0xjt48Na7+Olf/gQXp2foL9ZYhHTWgiPAXZINOpxV36osY+66riS/sOtd5kK8wJJMQ2jekit6/DHGFF4IatJOrz/LX7pOW5jb8yZt6PVReA9TAGbnpSXb5+bP+5QWM6hEJpZnrd6w/Ck8X/WhGqfm/2Z39vZXv5/WMsolven8ggQ/jc+3dJ+mVZqviKjqbzn/Wn2Y22HVpcUj+8aov6/eZTa7dfqdHJVsvtNYQtfX0kGWT/fJl1Ypn+dwM60DLA/ZOSAC5gxFkeegtvzR9eodNo19rIEjulaKjVixxdLN8uFltLHfSz/XF2vw9euVPtlH37LDXeaj1tPp/UbWqwb+2MezulzZ0Pi9730XZ2dn+LM/+zMM5z367Rb33nkbTx49wvMf+yTW5xdYrFYAIg58YpLj42NwJsZyuUTXLTEMA3a7Ht4vsVisQHGAdx0OVh7Xr13H0dExAhz8okvnBdSkDX0PUL4QBg4cgYAIH4GuW6LrugrIPvvsswCAzXaLAyZ0ncOzd5/Do0cPAXK4e/duAomZAWWXQUB4IiwQhoCld/Be4lg9iNJWu534yhhRE1QmpqFY5HuxyCUGTs5NhJhiw9PZjfEgV9/3AFL/vKOy5S9KsMS9G2aw2aJijGXczIzFclm2BPU4gDFrg/wufdF00OMqz7h0rkAbEBZECQ2BaezoxMtKacswpmizcnGc9qZLfRaYSWiR7bcoXg2Si5ImQkBdjxWodmt3DmSW9jAudv0uUT6DsUco6r6VtsSbMwfqCNWWqsy77lOhQ2MMliZaIOv3iMa+C8/quYYBGhaI6jmrQJJ6xh5wt/Ng0yzPrTk7l8KLLcA4AcNmLoDRaTGnTOw7cyBmzjibtMe150+PraVw5Dtr5F8GImy7tu/CSxrQ2jnV87APwFJCDFhGAgeHQIR4tATduYFv//D38blvfAWrRVfud1kMwO7kDK++/AZ+/u/+HB+8+U462B3SOQ3JHJWAC0BuCv41LeU7mxIcqMGjcw4he/ssOLbFtkduDEVoKW0bVlraYACon7e8N0tT05cWn+rSkm9W7ln6zX0u/8Q7alOZ23613tfJRKbf7wdo+8Yn+iTtaDBA7edsf+33UQ7ToF6XUlr00XS1Wez0O5ftTthi16blrdYdVuR8Dr+bn0ddh8U2V+1X63dLV0072+4+PWtlTlmTSidJ/bof1hiarC0jvyeYAjVGaa3DluxsyVvt4NQ8QuSqOdP1CxYU3Wfrbc1BmsNa740OvIgcNVWFr+n5svy9r1zZ0PjWt7+FzXqNmzdv4F/8i38BT4QQBoTtFo8/eB83b9/BsNtit9vgadyBEHCwSsaEDH636/MCZAxDulPDgxGJAXJYrQ5xcHiE4FwyIFw+KA2dQjVPBnkwEtjuOoeuW+D4+Bq6zuPo6KgwRiJIgO88Pv7xj8Ej4rXXXsX5xQa0OEjhP8uDcplctbDzIdrFwsETm+w7ESBfMZxmXu9rgVMJakwXe/Kax2TIY2QU7zy2w5jpSUqVUjYDTK3sNUNp5tC3lRONjNX3PbbbLVymOWxsYy4xxnIQWVu82jCQdioBzwDT2G/NvJpG8r54Ca0ybCl8AmG1WjbA0tjnInQ5GSc6/KBeuFNhTkSwy7UOkUiDa4I7xmjMzpQ2mJNY4XnFNhG03Ox+eiYyIut4yzZYsd8DtbGg37FCRmdESWcy6kupCs1kh9KAWauEtJEhvwfl6bWeIw1i5HOdHKG1S6NBsOY3oumOUpOutj7UvDL3rubl1ny2PpO/54yL1nOt9SXPzSkhOw/aCTCniFuGxFVoVstpA8yIEFYe4dohPvWN38XXfvD7OLh1Ay5frNqFCDrf4IPX3sK9V9/AL/7qb9BfrIHdkC/LS97NwDEdgs/r0Lv6dmMtm/UOrPU0a+dNUcp7wJbmK0sTDY4/DFCbK4lf//71SNEGN9A2eDX/TftSe0lFfujdozmg0jRm3Nyh7r/7GCugWz5L8e76PK2dH91nCbOWSloAda7tFk3t2rBOlxa9WnPQqs++Y4Gz7OpYuTK3prWjR8trXXTWRAvuJ4aOfneP3NQyZ67o9ij3Yc6AsqVl5Ov2dR/1dzVQnxoS+/pr+z6ZP0bKNql5Vs3L0eEhPsi82HIItPgxScda/xa+kGZV3/XOrXx+Vdl1ZUPj7PwUF2fneOGF5/GZlz6Nl3/zMg5WRxj6HmFzgfvvrbELASmsieEowju5ATpmAohXI8D7Ab5bwDsPR+ns6Gp1gIPVAc53Wyy6DgBh2I33NzgQOteBKR+aDiF7yR2GfsBms8Ht27cAjIItncnwuH3jRiIKAev1GiFEnDx9iKHv0QdgN/RYLpdIMeKZKSPgfPYUIeUSToLSpX88FSyALMBx90EEqt2S0wtGDA1yDt45hCEAPG7LM4Z82JSKwGZOlqzDuIi0p1f6NQXgo4Eizw3DgNVqVb4TAQFMs2ZpAWhBzJwntgUs5dlKWKsy129ZDJ7SNj1zoutut0OIMcUVxtHQqIR3TudYz1VbgOt5LYe95ZBf9QzAPArvagGqzzR9Ur/qdmpPTfqnhYDdwtRzLO8HAza0wCrZdFS5LJaXaDxj01IqViALDSJzORStgeQwDPD5osd6q1avo7any7Zrx24VnTVEWkJRxtdqR2do2qewbdFGrB6fFfz2vgRbbwuISLGGfGte9BqzbcwBHXl2Tn7od21o5qxCBioD2NYP6PWVno0g9AuP57/wGXz9T36IW5/8CMh3WFAHP0T0YYeLJ0/x+l/+DL/6938FbHZYREYc0sWhSeZk2hDKPRqEUX4JfTRgsl5UO2bArGEFLKwMs7K+lmP1+m+twRbfo7G+576zpTVPc0XLd22ItWhi150OKLHOIrsGLJ9YoK1/1zS2fdo3Xt2e/q7i/WL05dj7mX5Y2ulzjjFEMNX8bR0Crf5dFbBZXWvH1qKlrTuNbbrDAci81fNjZcmcPNB9qLBQZnQrR5t8o+nspmvBjsfqgtTUuDa13h2TtUx1x5RG9V1kczpAcE0Z64ys1d/PzZ1tWz4veArCm1O+9N6DHE2cJ+Wn4ue6/RFf6PVU5JM6Z6nH0JKTl5UrGxr//J//N3j/vfexXl8gDAN22x2u37ie05du0fcRIUZcu34Nzz53B91iAeocUhhQQIp8SKnkjo4O0XUeoHQTtiOfUklSBGiAX3jAd9hut0mw+JRxxPuUUUeATOcchu0OwAKHh0e4du06lstlxSgHBwd45u4dMAH9bg1aLnHnmWdxcnKGDx6eIOx2iOB8i/mugCBH6aCfYwAxCRDPHgSC8z4JpsiAyi6UZycdEHT1YdWi2EIomWKEiSVsyYkyJErj7Dw4BJBb5SwBmbkjpzAyTulFwemgNTAKdgmjskV7mIjSZXf6cr4iLBhjP5EOuSUPXi30hfGstT4BbY4Qwxi6BJKD18nroQWyvSxQ00/qDiHAxZT1IBDQbQNWvsPg0jx05EuWKOd8qT9lYqo9s9rjGGIo+toaDY5QUsgh7yLlSzJBXqY/JRiQyCftFZ8oIAIYozCxW5RJ7IuglhixtBNlhay04cs0pMY5jbY6t2F/FsMA6l2jPMpIpD0jYFreRjTmruu6Mrcy76IE9K212jiROUrhU4kwkZM3WYzsZBSU3sORg5yK53ziReoPmb+RFRMV73cx7yZKs1Kear5aXm8PSme4tEIT+afkvBbY1gvWml9b5tacVhxSNODjPNclhTAAa2a7VFGam/yc5FWnVGH6qfsnPCS0y32JYESK8CAgZ4OLyGmmwVjAwXOiew9g3QHXPvIc/uCPf4xPfvELCIt0q7cnB+oD+vM1XvvJ3+De62/g/TffRthsEfoBIYayw6DnqMuKWNIVa/3Aip91nxko2aRI7T7L56Rop2neAsctAyLJC33BZaJF5r6UhhQoN7+L64GLAwL5Yq70RhYTSOqgBhW2bxbsy0Vec/xmweHc93bccwDagrsW2JsYu5ieZRufT/Ro1avXMSveSPIph2NyvRbJze8N6d1VXbekxhfnHUceZzOBA8CMSctKDdz0M63Q1JbBUc/xuKME4mqnixwQuI58kHYcEUIDyLb6NccLFrimyJD2+QPLG9UN6xiNPyr1JvwYaepASX1q71gX/kUlfptOKD221vqp6hcSN/Sq5UFpw/Kird8aN1WkSHq46rfULWH9E8chcwkdjYK9kJwv6fK9Qo3EGznRDxHBC9VUJISjlGp/bB9XKlc2NIY+XYJXsiURcHp6iuPjY3jnETl5xA8PDrHoFjg/v8CTk6fwSDH96YxGl0HigBB3AAI8eXRuiRAJZ2dn2O522EYG0wAQYbvbjSAROWsmCKBkHCAOCIGwyPVvNhsAKBmXvPdYrlbohy1CCNhsNrh16w6uXb+Dn/3tr7FcLHF+sUM5A5EFr8s5g/vdAHBSYAtaQRaxqJjCRDFtuY6Ke8zaJIIhxpz+M8aSqUnnM+cQMnAWpZa8wl23QreIAAaEPojpnhV9HWsvfWJOlw7Kjd7aczdavlxSL1bZqbj8D0ASmkNIh7d1TLIGhLpdMZ4q0ASaLEhJL1vgoFng2uuojYHSfmT0iIAnbM4usPA5bnsIcPm+B7HaZZeKmRExjfMtykd5Uqziy+RIACDW8z+Yy+PGOlIGKStwYoxlfm1oRfmp+iBAI51Pkr9M3yCGCcZdG6Lqaf3sHBigJNkLP0O9LyBSlIDcANyqQ9Zga2dhAiyASrlbepWfPNJv7GwyLAJCtvESQGYx3FR2uGLgFDBMRQNpemtF1goL3LcNTgntjXKLUvYkMZS08TRnSGj6aAXV4hXLdy3vc6OBEfjYPuTvZPfSab40wNyOu7kGsuGNyCBO/JivxQAoncFgR+g5ort9Dd/6/u/hC9/5OpZHx2Cku3A4RAzrNe699Q7++j/8OU7feBvY7bDL+kE7dLQ30rkUOotYG7CaNszprJSk3pbnWjHz4OTUkbNqznsMM0B8HwDXf2v6AUj36WD6OZCdW6Xf5YFZPtL90CDHglT5uQ9Eaj60INgWkduttq4CVG2bUO/pMe1rX9NXn7cp8xBTiHN9kWycINIWv7Ta8yLnOI9DvkMt23RdrTascWSf2Wf4ybzEnKjGkSs7rIWXqQ5zLTosO1RjjDXoV++2+MaWis55/HNj0u/osMVmiBiQXUbT98c13959u6y0eNIC+in9MdnB0t/b8dl29BppvWdlhegxy9uRI4ahL7rB0i6dTHCQiCiGyF5pc4w4GfvQ3rUoWOKKBoaUKxsab7/1FmJMWZxu37kD7z3u3bsHIkIfAkCEvg949OgxvAcePXiEG1/7WomHFQKVfy5juggQOsBRupdjuYQfAmIO8+i6rmRHYlYXHhFhsUC6WCQyHj55jFs3r+H2rRsAxtApAPAsl4URnF/AdQEXF1vcu/c+3n77bfQD4JZLHF4/hss7CzGm2w9Z3SLtHKVzG86lLXiqx1TiodWEaabgbCDoeDfNbJIaDzECpG5OlvrJJWONU6hTHIYCYrUClUxCFrhbC5oop0fzvlaqhom0EGwJIPuMbm9O4YiRVQQj1yFXtu92ccnvzjv0MeDgYJV2wGIs4VTiARnFfN4ZKMZ+aqPMhfFkyaKdi3OfK3phpl+nihZAdd5A01CPV/ezvLtfx6qSPX0jNpn0syXkLKhtAcryngmT0G2LJ0TXaX/Xn82BBwvIW3TRdcnvc2DoKnPYUqhW6es+62dE9lg+Tlh7WoetuwVEWyDe/q2fnTPuWmVufvcpzFb7rb7J8+lQNqULJpPgBJFDdMDWMehoic9+7cv4+g//AMd3byI6AiKhYyBut7g4OcUv/vKv8cpP/xZnDx9jyYxF50vSDqG5PbsjAFMnsdD01EaK5jObmadlJFQ3bDd4YY4m++hbnuN6LuaKrefDznPM4BKYhni1+tXiw8uKDR1tgbKW/LF91zxVn5OYAkI9X/rZETzVur0eaHsO5wymObpdlU5zHmw9dqlPj0nPhY4GSPys7mNC7TDhxudFZpDaPTZttwB8SyZpY6EKidxTrs5bKZJgX4hjC/O02rN/zzmPWn0TnGTDmW39l/G3xhaWd1p16DbEIOTIODw8mtRPJEllzM6N1rlmrHqH/T9lufoZjbMzHBwc4Ctf/Squ37iOi/UaZ5sLLLoFzp6eYbjYIA7Jy3729BwP7z9EGALcYrrIE2MnQ4O8A+DhugVefu11PD2/QCBCGCKWy2V1GC295xBDwK7fgbzDwns4T3jn3vv4xte+AuI67MZ7j81mg912l7xPQ4B3Hc7OHuGXv/wVHj8+wdOzc9x+5hlcz0YKczqz4bIw6jzBZcUSc6hRGkrbq6gXvWZCWXhawcnn3vscopRCCpIxlqxQ53M6RSRvfORYQqec8whhvPtD75LoxWMFcDrTkJS0vhW2MCnqRSXjaS0MHZbRijuX5228rhgtjDboEn7R507KAsgLRkLZnEqHPPqQRs8DkMK0Sr+UMKz6H0MlBOZKJei4zuIzFRjt1MeCJ1rAW363gjPG8ZIcq1CZefQ4KCrIL1aEzyl8LeBaArBVh1W0ROP8aj6/DGzNef60Mtf9tABffpd51fOk+aolSO08aH7TCsWCTt1X2V20a4Co3gXVc9sOA+DJ/BbloYBBa250fa0+7pt3TU+r2Gyfrgo6CQCYEt9SuumanUN0hLDwePbTH8N3/+Ef4fanPorBEzYAOhCWIPRnF3jj1y/jJ3/2H3H+4BH4fIuDyGDH2Ib6cKLupzbe5V8IITuJxudsLLamh+V9K+/s55ZOdv1anmnNoXw+ZzAkUcZV31v91XOzD7TLeOTzfUaNfsburLWMA90PS1srKy8DhHYeLouHl+8sH4/tAckZZZKWpDcn7++jRWvtTOb+it6hFr9ZMK3Hp/uhP5dEL/vklOY/IkLnHYbYTjIhz052+Br9quQjj97yD1t03wsd4/xas+vhMppZ+Wzn24L6iUymxClWHug6W3q11e+WY7iqyzgr5VnBe+v1Gs65yoE91pN26mIO50sx2zlk0qRj17Sbm2fBFVeR/VKubGg4Ity8eRMf++hHce3WTfzmlZfhlwssDg5wa7ECuac4eXQCB8JmvcG/+Vf/Bj/64Q9w++7tknaWmccYbQDglE+cvMPZ2QV++rc/x4AUb7boXPFWCTGTFz+AyIGcAxOhjwxyhF+98gruP7iPF565i91uVw42x5gyKqXbtsdMOD/5yV9jGEKJeV2ulsnD3PdwPsVZx5i2sMMQsBIgmb0BjtKBYyG2hCcVIJ7BhmYgCZ2SEuP0oFgK+SFESErbFCJE1UTnmNBcX7dYFEGmjYHdbjcBRXYhWaYsTGyUjxgxdjtRexCJxnsZxNreZyGXfjgNj6egVegn3poEKAmQg18MeJ+zZbHcsp6/QAK9tSct/bQpPi040HMk32salc+yIpHPa/Az7pLId614fE0jDVTnFrMWepqW+nvZuNZKTrerPbJzdWnDstQr31P6nxXYQnnnqKrH9ru1QyQ00/RqFUs7S6vLQLDwrv1M98PSWH8+p8gsYK14phEe2OIDGbf8beOpa1q1x7Zv3LpYR8Skz2buNd00H7c8jLI2IkeQ84hMIO8xgDB4wtGdW/jOH34Pn//mV8ByH4Zz8AGIFxvcv3cfv/npz/DqL36F/uk5aBeAIV1kGdVdOLqvdixWhrTmjZnLoe4WL9uxtuq/jO66D63+VGPgtoeWiCr90Zq3uR1mPYd2LRYaNPpi6acNo8vAo5UzVnfo9lv8remmf2+trdb3QHuHID0XwVzrszLHqdKqz9oZpWWDXgtE9d1V+jlELuu/NT691qyXfB8A1vVpw4IwXReCXxBrwFzGZsap9Z6VW3rcLWxQ+oPcZJyGK+siPGq/s2u2zCeN3+uxt2grz+1bn5pGrR30Vr/IUeET+4yVS1KflZPyng5ls/UVXRCm2CuEgEXnsd3mC0RVNAuAfN4rOXe8dwgxIuTQTAaDUGMbfba3tT7LWC6RdbZc2dBI6Wl3+J/+9f+Enhmn63McHB/CLzr4rsMz3QEcLXD6+AkQAz54/wP8+z/7d/jH/4t/XG6EFmaMMaWuJSZQPgvx81/8Ag8eP8GQhenQ77DbbtF16VC4TMDBYoUYGT0HLA+X6IcecbEEx4i/+slP8Kc/+mEl3ApoQ/KoxQis1xf41a9+jbPTc3DMd1UMAf1uB8pnFUTgO9+h65ZwWUi4fHtmCBHMU5AmC8beMF0mXzGY3XKNzGAX4fwinddQt5KTc0BO09iHAU4OnzHnNLxTxhZGsQI+xpgNPodhSCmC5RC9Zir5XS/mfQJDj8nuXmjQZGPcJe64pXSsgC/gkMY2+6EHkGJkUSlv+ZliN8dxzCwSGjMsWUEgv7e+S3Mz7xVwKtxMgwYRVFaIa3rOdLQJAIUsySjFqNgohVCphByTce0rWolU/SRUBqkt9hPhPQuk95WWorAAbe69liHfAoaXKSH7nn639V3Ly67fa4HD1ty3ANVVaKbft+tQA6cWeG4B1bm6rTKee945jyHmbFDeAYdL/PZ3vomv/P7v4fDmNYRsYBxEgLYB2yenePPXr+A3P/sZ3n/zTaAPcPleoeiAwTV2woyinwMKludHXm4fvLXjvQpYaYGJfe82gbTY8mrOmZMDSw7XWpCr/00dWPvPU8wBWalfA2vtgdV1jINA0Uk65NmOtdWP/xTlsvVeADlG95ZeLyHGKh4eGOlnw+Wu0o/UVu1A0WUfb7RAvh2j7n/5jlOIkTZi0nNq0JYmBMCsAXnGjtdGYwCj426yk2JBamPMmp/138zjBYNFTu5hkzmZRERjYoXG3F1mBFk6lmcbY7M002O24az6WUsDLTeIWidT5Dlgt6uPF4xGC6XjC0QpoZH3qc8xICj+0AZuq209HqGldoBdVq5saCwXSxweHmK93YI6j9t37uTYTkIMKcvK7du3gSHg9OQxQmD8y3/5/8Uf/PAPcfv2bTjny+HoGCOGfkDYDQA57ALjX/+bf5sOgjNjEWLyXAHq4jztlcnE7dMBmCFEcAj4+d/+Al//8pdx+/YtiLHBhSAp5MpRh//wH/8cJydPESPnW8VjBqwDEAOWyxUWzkPOaqy3ayw7j+ODZe6Ly4dua8/GkE/se++BHEIhE1ZyEDOX7TZ5R0K9fA4NA9LWZwgRMRLCbovt0GPRjYwdQ8h1pUxWeiFYwSQCVD6XG9Cl37JbpLOptJRXa7HZoheKFka6fa2QOQvEUd/XoEovRr0QxsXH6DoPBmMIAY4TIMmyNtcni52yPTCndFnshQp46cVn6Rlj1OfHZ0GnXZBEKexLFqwFAvtBzfQyqPJNTFmCJJNS4DgqUzU+3Q8rJG0/mHly7ifV1wbg5TPRajTSQvhNnm3Hgo4GoqaF5uerGAYyT63vJn29pC47xnTmfp5mVwmvkbrmwn+0bJHdPL0OWuBD12HDveQZC7btrtU+OlgZU+hRHpK1nGgEQkq5vOgQHOETX/wsvv3HP8LdT3wEu4XDxjE8OXTbiPjkDA/feBc//Y9/iXtvv42w24D6Hj6ndQzEYE8IDqAhZ9y7QmkZnJpGdmx2DlrA2oJyzW963i6j5+zvPJUZzMlpYflK8xtRfYfRnPFQ2iGUQ/CtsVlwPt7BNNUNpdDUGN0XzteiwWXPXuX9fe/moVfPlnM+DTlT31s13785A6B6Tiu8mTJnYMh3++Rf+k7OJ6L85CSwK9Bq9XxxXoqMm+mDHZ8GqhXfGHrtm9OWMaPfKw6viQerZXvU6ylyrTNaRkMF6hvruzW38kxr56wld6282Fe3/CuJdTBvY0lEjWBQ5xwW3SLRISJfEKp0So7+YIwRQ7rNJMIv17f/yQ2Nm8+9iNXBAVarVRJ24k3hdOHewAHUOdx67hkEYpyePMF7D57g//n/+n/jn/yTfwJmxo0bN7Ln3KEfBmx3OwTq8P/713+Ge49PUtqyMGC97dH5RQY3AczJ0CZKMYQMoOtSStxh1yO6lNnl/pNz/A//6t/iH/+jf4jdbg3nCCECkQjEARx6PDo7xV/9zU+xC4zV4QEu1hfgOCDsNoi7DdB1iM5hQACHCIZH5zw6eIR+yEK5w3jYuGHNQpR3zGnHQhZi2SI3i6mkt1106fJCDilVY+Ys5z1o6EFxZLqI5E0OMSYDCpS2RJF4S7ZHY0wX7MUhlJ0bZkYYhnTzIwOd88loWyyScRUivDq30QIUeuEIUB4PotVxixqg6kObYz3IXvd6y1bqaQGb9C+C4wC38FguOzgHOBLP2ZimrQbIDFCAHEgdDzEQ0qV7KaOaHbMFErXiVBOvChFVdVnPtQBV6aMd31zRoMjOCbr6sD6HmM/6UM5W1fZU2NICXROFh1rmayGdUtcmgw+MnCY6A1uiaidE09JVxl5KwMAs4IsrPmnNUUUL1e85QT4LlhrvlvXkHDgohSf9xchOcwpVUl2ShLQxikKX8Du9g7RPwelx2tICzvY7eb+1tuZAdXax5PSIrpJnlDfiPfKa9Q7RE/qVw+FHXsD3fvh9fOqLn0O36NIuBjO6yBjOz/DorXt486e/xJu/ehlPn5xATiIxGAM4pQd26XwFh8Rf9p4i3d9ZQ06DCcDc3zE/dkvrOeWrd+5t4gwbimINydJ3pLEWMCoAcIaPdf+0DNVyZZZnLjGY7dopazUJ27R+8/m3shxUnXPGjvTR9k+Hblg6SWnt5GjQptuy4HGkOcHRuHs9CaPMISfiDCwp7IGyW9MCxro9bZw6KAIpIxxAyY6nxya/N2XIzHireSVGSnwi8pRBOWc9ufGQdtUGc+mnZOImOHBIdWl+bRkEUvRzhNGI08/u42M9H3ruR/piJF7uNyBps1mla1b0yf8XsJ50M43rTc1ZS1/YtSt1suq77uuc/NR8MSdn5NnJ7n9Muly3J78vFwscrA7Q0y7tMjkCcZIb5Gvnn8sym0AYYuKRdE1FBoQxJdnRParWFSdn7lUdPcCHMDQOr1+Hdx7s0tkIJ7FdYMTYIyIPwBFu3b6NECPWF2f4i7/4K/zn//k/yYCb010V+fI+UMqx/tY77wDkUxhUSKlJpTjn8/XqCSz1ctglEHa7XZqQkCfOE95+911sdzskH3dEiACTR8cBjjxOnp5hs9mBGVgtV1gtlzi/6DPDpcxOfT8ArgOYMPC467KKPuXuJwLIIfJUcBaQQCjGRfpetmvTpGpLVc5SLLr6QLFeT0M/AK72sAF54RpQInVbD4Oue7vZIl1pn5WxWQBS/+SGb9RGhv4nC0Lf/q3p01qI6e/6Mw0cNODSbQMFoyV6IGJ5sMLu6UVJ56Yv75F3i1KlTAsBfQ2QOae8JkLStFGXemxVO0rZyHdCbyu8awNl6smeA5xFYEcuOyj6vZYim2t30g8jLFvnWSRMT+9qsYBVxSN1eN9Yf3UXDE3nyhqCmhebNG/8PffMHIi5rOwzEgvgESMz/wtZZthduzmAuM84bPV3TrHb9Wjn1L5fFLP8y4tQfx8dEDqHwRNwvMJX/+C7+NL3vouD4yPAZeAfImgY8PC9e3jn5Vfxy7/4awwn54ibbRoHjW2NsYCpX50FhbrthtGhS53Gmye0tqDUAtHaQbLfKLMyqwWaowF8zEYoZCNjbr7tpYm2H1fhWT12+3wr9j49F8HR0mCUqZYWrb7N7aBdaf0YQH/Zu5b2Wj7JOOVzK+PK85kf960PuwZbjrLyDqQPXG59bgHxlszVY9eAdHwupa9P72MCGluygUqPMMlUSOTQuTFVri5zskPTpDXXVs9Xut3wr9Wbtm8iUaM4b1DPRTnXiQZfqjWu8UtrfVc0zEd+5/pseUIXO7/WSNXzWeYcbTzEnKNxMuakTCPkd0Kc3qcmM+2dr/gOaIf+6r7Z/l+lXP2MRgYLZYHm2RTr0bl0U7ZzKUf97du34T2w3W4QY8T169fhXDrgvd1u0XmfPAV+kXY2xLOB5MFnllu9p9mTQghVWsMRWEQMQ9odOD4+BABcbLYIzEg7SgSCRxgiQh+wOV9je7FJd2bkS6TCkOLaXJeYOXrGQLHkfQ8xYAgRnZsqJL19rc8QyE/v/WgUqYmrremUirelHvRC1pmYmKgcZpRiz1NohTHG1jG6blGelXhLfQdGS/BJvTqNp10A8rtehC1BMgcUW4aF/jvt1GRjzjF2OQTOOQKieMZagI0yZsm0ZKUYwdlNMfVQSD1zHpl9ZU6BzD1X8VGj0ChLm3VUz0odAtR46oGZUxx2rib9ICqXmgGojQJMDVL5THP3ZW1VfIB2qmTdnj3TM8d3pS8zYMj2Wz6LSk7pz0vd2TvQApytsUqfO0WX1pmNv0uZG5v+bt/3ljfEAMjBnXBcZ68BEaIj7DywWxA+9bu/he/+yY9x9MxdoOtABHgmYBdw/vAx3nv9LfztT36Cp/cfAJse2PZwcBg4h/8RlV2T1ly1xicGrS42LlrLxDma2NICfi26jXdFhckzen3L73ZsKclHEUFXKvvW59+32DS/Y9+5eErngNgceAQSneyh0xZAL++iMr8m49N0tP3VbUu/YmSAx3DElkyZMxCs/GoByjlDoV3q0dm1N8d7+/hVh8NU8je9DMA1xzbfwzpt/1yx/eLshW+F+u4DrhZH6Hf+UxRrHJH5TH8312cxOjUukGcukyUtbGHrt/1t3esj+tS5dDHpth/vORNsY7FUxV+ECkzIGdp0brZNs79LubKh0XVdid/TE1AAbe5ViFwO1F47voaFT1mfdrtd+bzvexwdHiLGgB6j8eHEo8/pHIQOxfHZMBGCacJkKmC1GK2z7XaHdMdEyojQxx1iHBCGdKkXDyHdfBgCDq8do/NdCjfylH8HyBPS2ZmUUnbXbxFjyDGcVFLR2u3fGFPaMAHt8rmkxyWMoUUiUNPPFGtHzmEIQxVG4rzL90OMjF3AVBwXigYveueDKN0XIcyW6ObAPGb2Qq5DlKVlflu/1NMyFqxQ0eOdgu564ejFYAWrVVppN4MxDPmQpEuH5vV7lTJJHybMzeKdpdINymmLrdCx45v03y5g9X1roes69dg1v88rgnmgZesstHdUDK/W2HQfrloYXKUb1E4ByweV8AYA1waPc/QjoolQ1KXl1ZT5srssc8BIt9WiQ1lzKixxMqc8Py/W016PbwSXOnNbq7/WiGkZRBa8za2fVv3ybAsoMpB2frOSYgLYAdETonOIC4/bH38R3/qjH+Cjn38JceHSLjgA9AHbswu88/Lr+PVPfop7b76d7kza7tDlm9yZkqxjMfh57KP0w8oPCwjmwKaeJ8uXLWOmtas6kSeGb23GON1H59LFtdvtdtIfeSbpUjmrN87HXJkzvC0NdFuaZ/Rzc+tCy/qxPkzesUaVbkv3dxJC2uDLVt/tnAq9WPHIVdb2SDeUQ9/6Tqe5eWHmFIbqp+fu7FrTf7d22Oq+0mRsLdpJP+yup01gottpzvGHkPHl/Zw1S4eF2jmyPFZ+Gpross9xZMtcKFmRy+Zzy1dWVhb8pJ7Xz7R2Yco7zDn6eppl0OIETZ8WjaysaBVd74QGyiYomEZEJ08dI6Vvqj493lJHg78tLa5armxoaGtWJlwfIvbO5zjGceF3iw5HB4vKU87M+VbsBHz96hDLxSLdbJhjPSOnW7a1d3ez2Uzux5BFXLYP40jIdCP2Dr5bAZKhidKOC8cB3kU4DFi4AB62cOEAsd+hy894ADwMcBRGj3fnC1BNOw9t5R5CCtMSQ0nidUMISUjlG5flgLhMdpRzH5XgRAlrInAxuOqYXi4oxQo5qxRHxsopIpmrPrQUkl58luH053onRL7TzwGjolksFtUYJWyk9b5dxABy1jIG9xGBI7pFJy6GTNv6ng9pOwlaG9IVIWmFrdEzp/iqYjwHtcCSez0ayjNv884JIUuHkR5VN81Y2saYp/HSzJYR2BIimu7687lSKWQaY+h1e6Vvqm3tpbH1zwEkKa344H39s3XOtWmVaUUDjMrTvp+E+9Tgvgzg68OKNoTR0s+uR11fa+3NrW37XGv8lWLO3zmJde48IiLCwmHoCMd37+DL3/02vvTNr2F5tEIUUDJE8KbH+2++jV/8xU9w/413sD55ilW3BHYDFvm2cCYCeYeQaZivRS00EXq2+NUaCfJ3teOint1XrNdQFytTrIyUd/X5DGkzOcC2k7qkP2VcPF1vLYBkx2KBkv29BbauUqxcST+pRCHY8Kp9gMQ+P6cv7Pd2fm29Wo+1+qDbTr+HFPoyQwa9Fg01mm1oPVuHwU131OxYRYfr71rv2DnUu3dzYWhWHxARQHWWoX0yc+zn6OyRdWWfs3hDj99ikhYN5vSdpYH9Tj3UDBMax1fLVztGS9+5dsqaB1frvaVXWjLX0rwlyyxNOIMke0YUQHFgMEdgvUnvCWPTWKfFgURUzk1aXSXj07w2x2NXKVc2NEIRUIBE/wVOnn6KSIoXBOc8YpDtGyDGMLlafrPZIIR0IR+ruxYS4HMY+qHEoQuolsUnwlrf0ZAAKrDd6d2DAd536BYdhshIWxTA4dESBysPioRbNw6xpJtg1+H4xjXQcgl0Ht53wJBS3PkuZ/EA4WB1gJiNB+fHy/daExhjrHYzyuchlvfq3QzxanLzNs0YIxxNGTXGWHY6pOjv7cKUn96nHRTmaRyuDo2yC8X+vg+Q6ee0UKzipJHtNaNQWmPQCy+ECBdCOnNAwNnZeRGCepHod0pdsb70jkjASy30tXeLaGpIzZU5Aa5BChFNhKLt62WlpXDl84kSNEBLt2Oft+FHVxUwUq/1AAstdZn6n+ox6TL2Z/rsnJLcpyjs2K/SB8AAvD3ty3M2paelu+YnmgEZrWJpqdu1fW8piNa60N/ZeGFdEsQkUM7+FBYe8WiF3/rm1/D1H34fh8fHxVjwDGAXsX7wCG/86mW88vNf4sHb72FYb7DwHULYocvgJSJ5CGMOm+oaYLQly+aA0hxAB6ahaXYe9RwIIGvRcI5PWgAJqOdiH9Cw/W/9va8Pdof9MrnSMlbs59N30HR2tMYzB6T2FQ189tW5Twbo5+xP5xzA0yyGUqxz6rK51jqrtX6bMrl8Nt9/W4fsXrRCRC8rBWsYOszpdI25UvuojJRW/fLTgmVN3w+j41r1X1Zaa97qDw2gZUz6fWAMT58rjtLOq6ZHy7Gh67zqXOl+7tMx2hFfUvhfsh6KHEyfVDp6DPmcvqvn78MaHVc3NHLmJIBSxqKcNpOcS+FAOU1BiAExBnBk9P0OxITFYoEQUtrY9XqtRkElXV7f9/BI6bhGQ8MV4yNGRoyDSiHrMAz1reEBcYzpBaXQrL6H6xbw3mG72+LunVv4r/6r/xKnT56gvzjF0jscHt3ALkTce3AfN+/exXKxxLJbIg4DwAHM+bI/53B6epqMLHBOo9pWWMJ8MnnCgGlnApNn0veycxTLYUtxuhAIIQyVAVMEQq4vNT0ymQ6/kTAvDfqErvpZK2jmlHpLkWkwLp/bRTK3/dlSzuU5ZkC17/LhL3IETx5DHNIZDc5b25ExRM67FA4xBohp75xDkEPieVGKZwJAvjxQ9YNHUCxCXo9ZKL5PQbf4Yq7sU5yl7chIuRQaQFAJAS1AYkyXU+o5bnlhdFtznt0y9uRkmfRP/92m1zzQtfVohceg5nNT4MyZZaxiG5+XjFhEUzBzqSLgNPA52gltLwMBLdnBSDuYrJ8xr+t+6gxeTitTGusUTGjXqW5XXiQZX+6LnmtKQVOAIwTvMCwdXvjcp/HNP/khnv30J7B1hOA8OiK4PmJ3coZ7r72Jx+/ew29+/gs8vPcBeNtj2S0ARKDzCMzwjhCY0421VHuSRWlbA9YCGK34Qkjhsc5Pgf0ceK1ws+KdlofWzkFrHoW+Wt7ZmHm7VltzrGWx7fPcTmRLlu7b0bE2w6XyJ8vjqo5G/+bG03q2JQ/0+mFArVmtkwABS61iaTT2Y3rPk3UC6HFJiWqttMZn+bY1Fv23NaKltEB5U17sqWO+qOyJXKeLtUbBSP8kUyUFfrNWgx1k3kh9b8e4r89X5W1dHLkUEaP60CrVfKt6LV3n9JRgAlK7DBpbtfo9pwv2jUnzi0QV6TUtMmS92eD46HB8j5CcV5znkBQ9tKDLY4Byrhb9qLDQhwlxa5Wrh07FdMleGEK6NCj3kwQ4x4ghBGw2W+y2W6w3a4Rhh2fv3gTIpUsNB0Zkh65b4eTpBcARB8dHuHPzBhAGBDD6kC9/IYnpTyE2VLzVAb4okLSohyEka857HB4f5+cjEAPAaYeF0cE7RgyM06cPcf34AFs6wPriAi994qM4ODzE6Z8/xZMHHySgkDNfDTEmzzOnHZzFYoGjo6M8R2lSvPcFtImAiXH0ggtzpD5zAfcTpmTkbCvAamAMDtisCAsOOASB8/Mh72IIIIAyyhIjiJDIKfoyc7jUqFpYqbEwDGmXgRngmA7jO6oMIes90Vt4Nt5ZijCljn9tKmwG5DY5ci6l2Mv0EKHuKG3VM6d0yt45REmCGQmLxQFi12FwEcsYQOxBlA41pf6iGCuOPQh+bJuyR1kbbsXASPQjjCBoMsYYpwYKlCdW/14JC6oU576QjbpueSb3z4lAFLHe8lTXcyLzoneaKuCl+jsbWgeugPpcaSkunSyhZcTa92XckklM+H18nhHCUMI00+coPwWQtMA/cw3C54Rp+U4JcCnFo5U98q210RLUhc6RIbG2KYsKwBjrqtZEHpQ8S3mdyL1G46CUl658M7bj5JyZGosDwXGSrMEBcLnlELHwHZgdNguH7sW7+Paf/hCf/d3fhu86DIhwnuCGAdRHnN57gPdffRPvvvI63nn9DfS7FJYaly4pPU+AS/zDBOgbakWpSnY+ymfQUlipUrQyb04uZBU65zFHhh9HnfUUF4Ygob8JbWRO7xERqOvK3HCmM7nUW8p0mgvfa4HFFtiwskHAS8VzprQcCtoos+vN7uLUHVYSgyEJ+XI427TdJNOyw4enDok54+gykGKft2s0rV8NtqfvWVpWw9TgETXdm2CyBWSVMWz7LrKy8LA5TzFHm5iZc84B1QKi9rK0Vl8tDYocJQAly9VovBG5Mqfy/CjzUPCM8J7lzdaOXWvGW+ejJn1HzqRFBMop92UVp8D2JqEAcDlDp8cs+raA66zkNWgfeSxlY2BJz04jX8UYEXm81wKcsAgnN1529jDI+3yp8zQyojVPrXVuDWEd6aIxg3ME36UrJ9ghpf9Wco9ZZJwoQiXrM4aG8xgEqwqN5L0iD4wO+hDl6oZGH7AbUtgPGOmmwXyvw2a9Rt/32Gw2qc/OYblcYXl8hDu3b2O93uDiYoM7d57BcrlCCIwQIi7OT3FwdAxiwpNHT3B84yaYGIvlAiX/cz6ILYDGOz8KmAyGPUlaL8a142MwAN8tsQtbWVMY+gDnUuYTAuHx4ycA0n0Vr77xOj7+8U/g7rPP4nz9Zhov8hZY5xEHLnddSLaM5SLt7sjCsrHYwHiCX37XHq1C1+oATga7ADpKCpldWmiE0cui6wRz3v2RGqdKLSqwCLWwwKNhJAtCDozDjYq75XXTRoj9ThctaFtWsRU29nsNcidgl5KXK/FjXjKUQpII48VWBJXqljGZt6K0matx5+qK0SFGiw6JkX5Y5WHp0TbCRlBUf17XofvqXLp40nuH2nDj2TrST9kta05T9Z5+twWWigLCNORE/z67c0N1H+eMDGvY1GUKIpi5MmpjHM9w2X4me7umh93+nhtbbrBqW0qMDEYdGnlZmQNEcyF4ek6c7Zcp1PqDgC4rwqTA1XwQYeeSknGcwLwnB1p4REeIR0f4re9+HV/54fewvH0d8CnReccevB1w8fgE7776Ot769St479U3gX7AbpOyDPrOw0m4ShHiKEaTpkVLnshOj6zXQhszv3rtlHnMbWrjX76fA7jpvZrm6QuMlgvX/Snzoni/hEqGRprJmfnbB8o1aNFGhAbOH+bs0lzbLeBT9UF9Z+W0bjfGWBIc6M9aBlHLUBjXKZl60++tsBcp9QF21Z6xF1qGkf5O180zz2gAPedUs7otjarO6NQGyXXZp0OFJpqm9csjaCRSdTOX3QC7A5aTOVbjsP1sJevBHj62fa/GmeeHxTEiuh6AOFSn81UbSNOxZ0NF8LYqlh9b+lvaEQyod72IJgzV7EvN0yMWu1QOMJc7NCbzmtsIMV1MLREDyOsmMiejgWoeBusYASUz1Zh1P6p3P2S5sqEx5PsvEBkcAra7HhcX59hud3Cdx2q1wrVrx1gslogxIEaGd8D1G9cROeL6tRvl/gwigJzDervBxfkFbl6/gccPHsGhw2J5CJ/zE+tBMjK49WKVJk+uGDwEwBHjYLFADBHBdYhwWPolIkdstlscHx/DOYLzHRbLFYAA7AhPTk5wevYLxBhyGEKqX9oEUGXASv2pAzkqUGEEmA5RCZkBrGIYwXMKB6I4bldaASuldSCrgOZcvPMIYaiYehQUdeYrKQmsJV+gFcDyzwqiiWI3xfarFSctf9u6NdAuxlOMCBwQshCSS5QYAtLyNjd06Ej+p8hm+yFKZCIYUHsR7FzYOdc0as21XtRa2GoazG1X6svu5Oc4RzXNq/dQlzkgvRdgq88dXDmsq9+Td8TQnvYjCWVrYLQUawWaLgFfEq4k7+n5s2EMEtJoFZ2eq1mwxzy5j8Qa4/b9uXWxD0iMIZU0mZ+9/btSaRuCkQi9Y3QxGRkApTsxFg4f/9IX8fU//hFuf/T5tDPhCB0csBuwfvAY9998Cy//6td48O77OD95Ch8ZPITk+Vfr7O/ab2sIyO9W8dpdJPuOfdfOt8znHN3tnLUA6iyAUuUqh3Ftva11KmtEAxZrbNnv50oNEuvPq7EQVYJ0325sC2C1dMowDJN7hMq7XMs9O0ct4D9nPKR3uAJM9n27dsszDTkla9W2r/tlx1vrlrptPVeVQa2KvtjQ9rf1d+lX6kSzTmaxoKdrLdXHE16ygPnD8PKcISbYSuuRUX7sca7w1EEnc7NvHc71B8hLwLyrMdMcn6Tdh/06wK7ly8Kqbdu6j855LBaLhrxL0RxknHtgLkac1EvIBnhzH+rvV65saByvFji/uMCw26FzHh6Mw2WHm9eO4BZdzqbB2FycZu8FI3LA4eERwhBySINDCH2yTAm4fecOnHd49tlncO3wAGGzQdzswKsFdsMmUwDZkxwzUORyaZ4IJdlpODpc4trhAcAEJo9rN27DO4/zszM4vwDnTFHkPQgd4hBB3sNzPiPifTrkrQVB4y6GxAy10qyApGIw8eaUwjWoqZSiHKoXY4qRvbJUGEIYslLaPIJfexC3NKveK0xNrqpLAJgcMJedEBmbjVu1wlwX208rYG04jo2Ftopf11nonY2MEBm77a4C7wAjxHwPSwkccRKN2BY8qr0JSKExxGLiITdbozXYnQKeUn9pdn5bVY9fioSRWcE0zlO9ywagZHFjTAWcBSVlzOqZlhIR4SQ00X3QdemdPWD0UrUV3TwAzJVOlPc++tm1oo239J2fAL59YEz3WSsy2Unx3o9ngMyY5taJ/XtOYVvP9aySq5RZawyAeAU1nZNMICxDupwLDhg6h4OPPovf/5//KT72uZfQLZfoc6xNFxlxvcbjt9/He795FfdefR3vvv02HAhdTKEE5NIlp2KQXhUQFd5q8Kp+z3rSp+uvTfMWYLd/T8Bu43lydWikBTlalrTaaYKPBh5q8YNtr1Xs2vhwYGt03Oi6Eo/WO5otua3nahJSY2SsfKf1QEUbagM1yxMtg9+e7Rl/n+pw3Rf9ewF4qHcL7O3vluYtWkz6QbUOsfS0/dF9mgLLeh51u0RU3XBun89kbsrwtAuC6jMtS1uGh9THGOWalNYOYKmLHBijEVWfdQ1wVQIhY0AqntTnX1s0apWp/Kx5zspgacPyf8yYoaWrbNkb1qj7hhpb6v46R3mnZYBHxrmc5PTYN2f4KYc+y3wbXrI8rHui279KubKhce+dFGe76BbovM95ehn9Gjm96ALeOThmxO0uhTT5Djdv3sDdu3cRYwqXGk+2O6y3O4SB8fxzz+BwQYhhAw4BQ0wCLuQ7K4RJd9stQj54TuSwCUPeTmN432FYL3D31i2AHMgtAFrkXW6C9x2c60pccGSAyYntDOd9ynySlajY9rINpZWPjr2UfxbQyCSJl7XKMKMmqVJQNC5KPaldtyhtAKNy1V5v26ex/pohtJDUh8Nbnn39t/YqzAk4oQ2ACS1ayt32Scamt2CtstZtDmFA4LRzcX5xXgkVonwuQwAOdFq4toLRVLf9TvdzTL/XgsV6emKUGPt2/4W/WjSxwGVOEM0BEPluHNu8QGgpQWs42L5pACA8ZL0x+0DfBFyZz1uhFS3Q2aKT5T39Tg3OreCt57XVxyKQTV+K4gNP5mTf3FlFZGljv5vrV7uu9pwTpbHbtetzOJVzHgMIq7s38OXvfQtf+v53EK8fYPAEHwkdOfTrDU4ePsHu8Sl++Zd/jSfvvY/1yVP4CLBkUyMqfKfnyTog9Pea9sxakbYzBFkguQ982c9mD4ab+bI8ZOk8N48tGWjrFVrMGQp67LaPesf0qrs4+nM7ztZ6ae3USr+1gVXJGlsHpvyt5YvWG/J91bcMIC29WwBtbu5a/GbHPLeLNUcPO25d9Ny05k5+ElE6l4n23LXm8io7B1cBrpN5iyl0yqZmFixkdd5la21faa2pqg5DZ6C+VqFVn+2Tpv3cPNl3J31TfSDan+zmMhq01rLul57XlryoiGLa2263WCw6OOcBZnOeogS91U5S5iKf0z0p44BbsvbvU65saPwf/sv/fTY0OqwWS3S+w/HRIY6OjrHoOpydnWG5XGK5XJb7Ia7fuo2TzbYoXwmpSoMgbLcD3Mrh7p2b+L/8n/9PeObWDRAGgBw4H07xPhHu9PQUT56cYNcPWC5WGELAdrNBn28VH4YBYRjwkReeT3c0UAqdIhCc67BYeXAGhHAeqQsJQDIhXxA1LniiNjiriT5a8yKkBJAzjyFTklmrvG+EndyNMWFgl+IBZaeFYu2RHZmxrVDTM+MFSVYZxBgqY6Vifq5jAoH6kiS7MPW7AlpaxSozqRdIgl6nQrbj0b/HGNMZFhoNN+9c2aXhEkSNxE9R6C0+lsvLBLSqrcaWsLfAhTn3gsYzHZZ/5t5v9aXUaWg/BfQzh/MxAj/LC1ZQW+HS2qaPeZdR1oD17GhPf6sfrXY0r82FDdixt/hFnrM7PvV40+d2Te0DEMyJB3TdlQEeL++TrmtOOc0B1hatdF2Xbb2PdQKyPkRWAQB1HtvVAp/92pfxzX/wIxw/exvBAQsQXCC47YDtZounHzzAf/hX/xr90wusItCfbzBwxMApe57LoadO2lLgxK4T+5nuI5l11gIDmk/a68EAuwadtAGkn7EgxRrgRDQeADUgx9Zvi57/ii9mAMVVFH5rXe97/6r8qPsBZDqYUC0tEy1osuvBnoNqrdOxYVSeWdv/Of6w/FC/S5WMkWfmUpraevbNRUt3aX6xZ0qsM9O+O/f5nJzRdL9K/6Qf6czrqF+rULusy+bwgPzdrF/10zoVLY+WV9QWig0hbsmEMpeNndOrrhv5WT1PVNXZOntl5caIM+q6LX3suC/jq7kiuDPpWgDZsTle8CzOJcZ4vgWIIOR8I+l/jXWk+zt+ljDUh+nrlQ2NT3z0ORysVgnYDwMWXQcOEbvtUwxrxrDZ4vrBbZyd3MfFxQUWiwV22zUOn3kR3nfodxvEyNj1PWJgLFYrkPPwXQeAEcIW9++/haOlg+8W2IVkZUnGga7rcPPaEjF2ODw4wsHBQQY3Hs55LJdLuMUBdiHd5eE6Xy4UYhC6RVdAgs8X+FEOp0lSjMruh1h2ib7WEyMLAxlwjBOTGNHD+QiE2nOjmUtiDLXwAVKcHTyB4NIBx8jwcNj1O3SGCfYphRoE1xapDn+Ksb7QyoZWAYDvOoR8WzlBLQZOoVUEqsJGfK4nhlClGpaxz/W57/tqR0KHbOlSCVbHCENEiBGbfgf0u5SSGCkzl/cphA95vrzvADjEOECD/KpPDbAdYwSHkNJvmndG8F97V1tzYhWMtoU+TNELf6pMqeLJ8SWMQkbebdSpx9QqeoyinHQIoy6tXbb0Igr5LXDUvNjqFww/cIwIBkwJ6GkZJLquFmgd66nkriZUkR1pbGmHLMZYaJHapywryouwkz0qHhtWkohkQY01fMe1YMF6aldmODlSaMwmxOl/0hvXdehjBHuH5z79SXz5T3+Ej37xsxhWDmswDuCx2kb0T57inXfexhuvvY712Tk2D09w/vgEPjCcd9iFvvSDY5JzzvlsoLfD88rvwlO5T0nWYDIJVva1gLJ8J6BR88McsLFFg9AxbGPkZ6109wE7zXtzO36T2GymiVzYp9T36QP9uYzlwxRL5wIu81okpDTyBXCZ/sj4tVwXx5voDNv36brk5HFtAH0rbyegtAHGa/CFQmvR6y0AOCVMeo/SA5Pd8En/eWoAjMB5dJYRJWfFrGFVfiYBpZ2Bc8btPl6XcEnkHftRxI59L+JaQI8p1rhrkKnSqS3ZO5G3NCoJjZO0I7IJzHUlPBpHUtvcOprQWfqndqhbxrHtR92ncWyid9k4RaStFs/tMzzke5fn7datW7h79w7OT8+UPpE+jM5HwR0xRnBEivIR+s7wsW5TjBSRe1c1Nq5saDx9/128d3aGk5MneOWV32AYdmCOuFhfYOgHHB0d4+joCE+fPsXQD7h27Rr84Q38Z//0f4fVYQfq0hkJ363QDxu4yDjMh7Op63Dz1i0MF4+wwA5HK4c+AOuLC1w/uo7dboeLi1NcnJ1huz3DZtUhBMbT03M8enyKGAnkPJY3X8QP//gfpY2iIZ25IOeQgoS64v12visBNSFGOPYAXL4bhBA4nV8YwpAWPCIiU/6Xlp7Edo+hOAIsGICD3AidwG0Ac7oDA1yffdB3XQRwPoDJ2LoUpdj1AQxgcKiUtUy89x5xaOf8FoGqmUR+H4VeLQTkgOyqSzdtxz4d0OMQ1LNZMTIXpk4CLwA5pSQzg4cA+HxwLYYCCLXi1322YVctxahBaASwjIRdYBzcvpHA3bsfIBIB8ACn2+pBIshCUS4V7lVKSxbkZQfIbJiUDWeTegUIWvBbvldLuxWaJkVS0apJa845US00tRDrspoKyghk1QMN8nUdc6EudntbH1C0oS5VH5ESOUjdUq9WRFLHJLREeFcZTESkLhRt85PsGtqdF0B4ggovy3qulKqih6MRXHH+L4e6Zh6T/jK6zikDLDkqrNGZqs87AcX4CAWEJmeBjEkbIqmP49qWRBbJJl4w0HPA4BzYJ+9VFwmOGeCQwIrvsHWE/sZ1fONPf4Tf+va3cHC4wtAR3NLDDQF0MeC9X7yKt3/xa9x//108fPQQMSRnAjiHYMaILjtrOnJgl3exOZYzOnrtl/UDjAYQESJiATzzCrxtdOmkG8453L17FycnJ9jtdoUf9inufYBJey/NiyBOcrvodeEeQgmpLECcpiFPGsikdsbq9TMWmMjv9jNt3Oh2tVGzj66l7nE4E/Ce1REIXG6KH5/NFzCacVlaSr1z8zExPoxcbIU6zdXTMj5i7NOuWwZriUcBIg/moWq7akdkVpQd6zT+yAzKWTHTmdJ0f5NzqU5Jec+KJ5JuHY1sYnEAUHFoKAk9rhcaDa/W+C141TIVcTyn0eU0/iw3RGe/KxFATjtHMmBFGltyUhb4jsvSnFuQDgCRQ+VZKI4bkrVW83MZq5IXduyd8xBDmLOTcTQZ9hvsQp+5HS3903433QGKY/gSUqKiLNRyHVP93dSxM/2wz/f57DQkFXh6AGl3I8lnMU5Bacc5yiFXRrkXTy5KHWIEfJtWUo9OI3xZubKh8cH9d8HMODhc4Hd+97dxenqKYRiwWh3g6PAo7R6AMIR0J4MjwsVAuH79eom512CMOd8MHlOKWZDH6dkF7lxbJiYBY9tv4Tce2+0O680a799/HzFscbhaYrPdAUgXsq03awwD45MfuQ6U7byArvMyI+MCz3nu5QZzQIQIQJx2PySXtAAamVsNzmMGsC1QB8WUNvyDMsrVwLO2ZPMi9ynLscurnsFVtoXKqneEjroJKEtMMBWwBXCpLD1SZKFpANhSFPK5DhnTAsEuzCGEZMC5+oCWBQxSP1CHUrXKMAxYcAqXgpND0BL2VpabmbupN7S0613hF/3s6N2o3y9jMN7Sqk3Fe2IYFsOm9TxqoKC/K9+nD6p3xjIC5kkMdyVAR17OUqk5Zk0f/bcofudH4ar5QRdL70mP1fvyt+1HK1RNgzhLL6lDQoKsomsBHcsPI1VQgRwNFOy8yoVe1vut15A1qIB8uLahaKZhRvXvduyinGWHBUToooD5tCbYEYIHYucRFh0+8eUv4zt/+ke48dyzYO+wAOBDBF/0ePTeB3jtp3+Lt37xMrZPTxF2G8Q4ZuuKeX12XVcAl50DPX79WQE/NJ/+tVXq8U4v55L2Pvjgg73v2mJlxJxsmgPHwtjl3WxQ2zrm3tdyAWos+r4b4T29WzM1WttruLVGbPvW4GrRpzyPmperOUH9t14PrX7qNq2jI3euMvZHHDEFZbb/rTVejyklhQC3jUxdh/R1uoa1HEvrORkusTgwK89MLkV+Tb5RQ2/osdoAmZa5HWHLL26Sqr1uS8sb3d5IxyxTFKbRhWNMBhjVzxBRjjipns5tjjtA9sxjmvMZOul51/MiFFNtza3B1udz68HiFfud1d+2jhZNWk69Vh/td0+enODo4KAeez6/PDYoFZj6GtEdzrkJL7TGeNVy9fS26BFixHbTp5S2rsPJ0zXIbQGcAEipVLuuw9HREQ4OD3Dj5h0sFgv0w7YSksycb+xOnoS+j2DyeOud9/H0sINzEXBIF57gAWSrp1utQHEJIuDg6BBHR9fhn55jFx4jbnu88OILE4FHRInZKTN89lx47xFDnzL4EFVKW7Z3hcAWnBaGcG0vUpkoM0kiUCyjSJtVLKB3CEOyPnd9j8XMvDBz9rDG4jXUaT4duRKWIH0qApqmzCNGgCg3HbMq455s9avvLEMW8ECoQJ8uuv6WQaNpK+2nuzLkxuhEh4uLC0iIEKimp55HO1d6W38uPhpU97tWyBGk8jFrZaQ9F5ctTOuha/EcAPCeeiQ7GzB/u216EPVuBmrgposFCKOhUa8P4cEWsNo39laberyaFvpvDfiJqMSMW1ClwZpdy7q+CbBsgAgtiC1fJTpi9JKiXuuHh4eJRzE9gzLxiBlaW5mhgVbTaPIOPTE6dliEfGbCeew80HtC7wnPvvQJfONP/xgvfv4lUNchkoOPBPQDto9O8PYvfoM3f/0KTk9OcHF6CmLGbrcr4FnWq/yzfZeQI2tg6fG3eGQWyJv51zSytLGGzVVKCzzq+i4rLR7f18/ZtotRWM+z5ttWvfrzFrCRotfMhwmlmgMbTQCm2rdpp/Vzdg3OjVG/29p1bZUW0JvI0tKv0QOdnhl33eyzczzLQMER6dn5/rXWxGVj0J8VLDHTRsugmjOihA/EwavfUX+U1tp0n9FvVO88V/NvHp3TAxXdLUg28wrM70poo8m20dIFl5U5mrbendtNtfL9srabbRY9nHV1DmHMcX2XjsPWDyBFh1zyrNXR+8qVDY2f/PTnAKeD1bvdgDfffAeb9RZDH/D888/j9p07iPkGbebkZf/97/8YLa8yESkAnLxuy+UR3nrnA7xy9gSgAbthmxdTAjTireYhptAcEHy3ABPhwcNH6BZL/IP/7JnKs14s5xDRibPapTMQi8UC/W6bbqKOQMjp1ORQdsmy5I2FLpNMbaHZEkZA7aXXz1cgIpPK5ZuBC+gRmjmfgaRtA1V4glyOlIyQOjRGAyrK4WJWuGtGnwrkqedCntehM3YOpBc63tmC6tbv8oxOkSrKOHKKM2QCzs/PUzhO1nFO3TDUqrupyDCeO9FjTnMwPTwo42HmyuuoBSbL3krDgIhRLqNsAxBNc00PNs/UoHb6bglTy2uNaPReOe9K+ugYp3Xa/mgecc4hKP6w/LUP1IPaQncOKE2Uum0HSCFBubR2EGxbdlwt2kONq9muAbiybi2/MXO50HRufDq0ptU/C85bdZXvCGCXQj1TWKhD9A7bjrC6cxPf/cHv4wvf/jri9RW2xOgcgTc9dk8v8O5vXsH9V99EfHIOOrvA+v4jwBMGGndRhIaSu10+s04Jq8T1PIseINRG/L65mswPGrwFVPS6rNg51PVah9NVgble//J30yBUfS80a+hMW8dcvLgtGlhbnrQXj05AfwN02vaaoA2obphujbM1Nhs6q9sQB8qcXLH01Y5Nq2v17lCiDSdE4RxQHEa1vrN8bOchOanEyZDDVTRpaNQhUvSOlNSh25zSwBhrjiZ0lr5N5JIag82cJJ87YHLebaQEitEwlZdj6JTVj7poWQggh1ur3RXFw1pH6rGk3SFf9c+OW79T46upzNaySMtZ2+/W71fR2/adfaUlX8o6RwrZBU3BfVrLKeSyWstEJQmOc9PdSo1ptHwQva5Tktu5ueqYpFw9ve0HZwDnEJgQ4ReH6GKHi+0p3rv/CB88epqvi09K8ujoEM8+/xH0Q58PfwGOfF6AKaY5xpTmlpnAvkPEAn/9s18jxh0i6RjlcXudhwCXT9WHGNGHgNXhAT79mc9gsVyVS3+qiXBGQDCwWCyKQNBCRDz4RVGpRV4xmRMjYOqR2cd8wHSrbfyO4SjtIvQcSkrVsougbsTU9XXej6GOillijJVnCdBAINWtFZEUG8LSWlBzwkq3pQU+Zp7VdQs4bO0GTf4W5eGAMPR45tYtnD+9ADsH5nwrdEP5tMBHEVg8AoMWmJM5t8Auw8umwNc01n1JfeAqBELeadGm9bsF06k/rs1rag608KUMKNJ2/1S5WuGihaE0Y8Mi9LMT4dYAhbpPVd9mBLluo9BZtVH3cTqflk9b7SRBXPfTOgnmlDlMW3ZcmhZ6rvfFru8DEy2jJMUnA+w8tp1H8A5D5/Hbv/dtfP0Pv4drd28jeADOYQWANj3O33uAd371Ct597TW8/8ZbOGCHYb3FwBGRHQIYXu2KzhkE+vPWmQDpt/Z0C6i3dNX00+/PfaaBZYvf9GdzbbVoqj8T/mrxjW53vPx1OoetdV5ohSS/LM+2eK6a80bf9fvW2cU8pl0XR8llNNEGjvX4l3YJRe7tAyX2u7n5SmHKBGC6bu347T/pnx2bpS0zikxOj8SKl3SZC/GTepjH31ttaXDXkgktWsi7FX0a9LS/T+QkpsaLftYWrW/lOq9WCJz0xuqjplyVuUJ7Pdj1NeEjGnGXxQ8tHWlp1dTTs2UMubJh3HNzpH9vPWPLvjmo5EkS6bP1JUw7YlawOIZmjCKq56mF4cpFyKZ/LVm/r1zZ0NjulqljMQJIoU3sgIEB75Y43+xw8+YNdF2Hvu9x7eZdPPv8iwjDeH8EsxL2DKQDj8B2NwAHB3jxxU9gvflXcN5jN6Tbx51z6LLhMIQBK/LwRCBP2A479ENEdD2efe4FxAhEGuNXS+iIhNgQUogLJU9c2h5NB76t0C9CLqeH1f8SCKkJbL2nZL6rAN+coIQB5FAeAgWStYCy/dUKu/Qp8uQZlBja0ctjAZpVylJkPlugXQuhFqCXOvXhUNuWfQeow66ENvL3YrHA6uAAfHyEpyEAkHCq/Z7fpiKksV79XowRMdT9rEKTfDte1+4PWwNNYtz1P92upQnz6JnRn42KdWy0epfT/+Q93/m8VS5AvQ1srcKqBBHPGGyKZi1Qvz+6+GqlBSCKuT4DbFqlKYBzsd5QfealGo/mo8Z8WSCov7PKaC4sca6efYJ+SR0GR1gvgBe+8BK+/aMf4KMvfRrwDmGxQAwBbh2wfXKC9195A4/fehfvvPI6np48RrfosA0DBpedLj6d8Wl5zvVOi5UXrT5XIZHITg+MhkdLpjUBhylarlgaX6XY5+Z2j67KX0QErzzr+xwo+h3K56ws7VpAWXvFL+uLvCMXyNo1bh0GMHO4r+59NLHj1jTUgLAFsmRO89GjJi3sWpxrV+ssOx5XnHoy7Hq97xuP6jEE0lY0IyA5VNvzbmX/nLzYV5p6wnxveccWC2LtOoo0Z4ykt62cci7JjKjarfEBV+/p9+dCjQCJ+LhcHuixEjAbCmT5sRq7wYZXLbP1XeG91lzOzR8zp/tPaNSF5XuWZ9thhoQaj1WYxz77IfnRlisbGq++9g4iR3Sdw3LZYblcwHuHbnmIyA6rg0M8OTnF9evX4ZzH0dE1LJYrxMjgCHjvIJlmUqdT2IvvPDqfiPXSS5/BwfF1bNbn8IsVfARiiDg9X6fYYHI4jxFHqwMcXTtCCIwQGD4CH//4J9H3PZjGXQGhVrLy5FaN0ZvmvcMwFPcLgAweZR4J5RIbOXiqGTAlSJl61iLXlxnpRRNjLHnXLfBFjnOUDABSh/ceIMmskw5wxRwixswlNl12c6RN733yjkGHk+WsDFEA7jjHwzCMuydiHFEeqgKVxISu8yXsahQUbd4pRhRnD36IJaVfAqz1hW9zCieFxckWOsAhGY9DCNicX6DfDQgAPJLrRRtOen4SKFUhUqYt3YcRxE5vbBaB6LsO8vFoxKDMKfNUWCWQRdUuiVU2Ff149BhF5uZz6e92W4n+WbjnW33BsaSNzJsypq6pAah3CwmJV3UYgu2X5o/i2ebcvjRKIz2sCdIScFYx2bE6atPUlhZYseO3a7ulCLSHmGMsByxbdc0pclmzfd/j8PCwnvOsEGImF+vJkmcoxdRSTowQmdF3HsfPP4Pv/PEP8Zmv/jYWhwcYYoTvPPrtDhePT3D+wQO89YvfoH9yivtvvoPdeg3v0jgGjuBuDFPocmotTh9oMQk5p+RUv71zgKS85pRNKgIlxBYu1ZcOlwuAE49yoVJZ73LQveYJC1yhfmr6lt8mc6OLne8W0J/ju2ll9Z9ziloDq9RuffGpXl+Wj/aBrZYcaLUN5LucQijzlNZpIvy+uyUksUg1Zq5pNX+2rd6J0uOZkpL2ymm7LkX/idwRvWYNUSkSaUvU4rFp31ufEWGUa0l5KxYYZZvMn3aW6Pr2GRpWZhTTJutRYOT6WYNiTtfIQpsZ/xwfJV03Gr0uh0QxoxiIUoS/kEOKGe2zj1bW6rbHZBQ1ftH91n0svJXD4CkPVa9Py5d2nHq+9pWrgPHSvvob+TNqJAUp628GEyRaJvzkO48wDHAkUUPpwH27XxoHjkayfAeq1+lVx9cqVzY0Do8PS2YRIMchAui6RQIcIcD7BbbbLY6Pj/DMs89guViiH1LUoycPTw7OMQIB2z5DQiYsnYMj4O4zz+Da9Zs4vzgDhgEERt/vEIYe280aALDwHnfv3kKIA4bQA2DcuH4DH3vxo1j6JSJ5cOCkkANjsVyAhy28S6lXCOmCJUcOy+UK2+02xaPlmDSmdB5EjIsBnOIWkYVhZHBIRktEfVCvAhyYAt3qeyNcE019Pl8hACxNPhElSegIIIfOeWyzgPLOJeCuFIII92EYUj8DwDn1pHi8ORIi1f05PDxMFx+GIaW2k++BilkZSYAQEZxPRmPaRZFt/2mIF1Ha+qPI8EQlNRoDYHI5zKAB8NUZEuu965gRPTDECOrTQhy8g+9Tml1S6dmqBeIoXd6Y57sUJbWswCoxuEogpV0xMSZGgZjCS1RcMNVhIoUvaGxzX0iXNW7IuZKPWz8rBjxQe8QLvzEXKSex4JJO0YoPK1haikmMz5YQsllxmoaAWLFIqZ05K3uhQg0gZ3ag6k7X52HkOaM0KxBPCZRLQgWr3Cw/ljkwGk73j4CSgCGNTvWvjB2FDtIHMvwn7zhOACYQSl9TWGWEQ0ozTTHJj9h5bMDorh/jC9//Hr76B9/D6toRyCUZgAHYPD5B//gx3nnlVZw8eIQH797D5uQUcdsnkMsAeobHyM9ElFPWRjiqlgrAMT2bwUMyHBOg6ByBYwAJHbOjJXIERRaBhHTvyKBoy/A+rSNtRIwARKgo4FADf8uPBEHAaY6m/LzPINV1ad5ogc40lvbB+H0Ggb1PokrooXabte7QgLW1XuUd27blM7mw1nmpJ+svJKRoZbnIEnYpNl9CNZJepULxqg0DoKVOkXk2jE7TNMmSkRatsm/3XOsP+U7OciaeADinuYZLhm0IDWfNzNyVfhIBylAbcWCSc/pMjMy5BfSVHGnwo/7MkQbOXDzUAhJbcszWMQl7U59Pd7e4kqU1bVLYmRj+VVuU1jfRuKNP+RLd0etez1mLp23oX+JQVsxGVX12zkRMEI+yN4acJMjXdVe4jfdHXeg+WpnSorneWpHVMq66dv1arol80TwvGBaIAI0OWRR/wdyOVki4jQhEoq+lH6PDrDW+aV3z5cqGhgaxaYGMTJ7kUSJs36czGc8884x0sfqXmG3IixsgB3iXL4Vj4Pj4CNvtFn2/xna7Le1fu3YNfd/j1s0bcN7jYr1Od2A4h9Vqhes3rmN5sESI4wJzOr4sRjifBKF8v1wuAdQhXUI8ASpR3fQtAn48PDOmZdSH0MU7pCdET5h+TkpqEwUcUSZQjHG8+M4lj6HzDouuK32TPswpvuVyCWauDja2wjN2u12O1fVwbtpXDcS0Ahtjq6NwRFEQ9fjqzFSFzoRq4dTAenpI1Frz3ntcnJ5iwUlJyGGmlvKt6DNWjFbR/XXkysFtLQRT/1Mi4nEnaPQCiyKX36v4XiVXWkpsTjlYI0M/z5w8xEAdzjdXtxh7ehvVAnoLEsY6xv7rOltAqzUmCwD0WFvPXaZ4bTtST8he14mxABTjcQ5E6Nj1VpuWx6zingOw+pOyJiiFdNot7EApXaj0Ocnc5MUKMafZ9g6x8xiWHT75u1/Cd378Q1x/4TmQ9yBHcEzozy+weXKKe6+/iftvv4WThw+xPjvHbr3BZrtB53w+I2AMQk0zMxSq7Ln5cwR6TiwN50JU5gxK24Z8VntUp+E5+/oi63oEoNOiAb4Fxq0+XQY+WvUzcxZMUzAo31uem8hT9azWXdLn6mxXqyPSR67HoftCSn/YddUal362FSY1V8rcNerUbYpum5zPNPJMz8Ecn7bGNDfHmoe08WedFrbIs63D3voge2ss4pS6Ks330brimQ/xnl5nlg51AyjGieY7oqnBq3/uOw8n76d+TEYEbezoudbh9NIPkXdy8FnPddGNvH8ur1Im/Ud77OEKPNme74jtViVQSo3MLPBa70tbdb1XW59XLVc2NAAUC7xStAAWXQdyhO12gPdd3tU4RvFsZQMjRgHGgM9uMeZYDAaOETdv3sD5+RkWC5fqwKiIb9y4gdVyiYuLM4SYbgTebrcIHNEtl/m5dEle13W5vylunZyH97XAsecJWsaEWIplEqhWALLw5UIwIE3ePqYotDNCL93UKM1Q2UXxoPEwPDNiGFO6hhDg3RguZesNM0LdglC9ENOuynj+wCpWYLzJu6ZFfW+AfkZ7b/RP5xxiqIVq3d9RcEy8eIGTFzeDNPlcYslB9SLaB4DnShF8PBobE4AxQ9Mynua4MG55t75r/G373hLCzhFC4CbvkeFdoYn2VM0pv5ZSiI36Z2kwo+QnCiiHGOi2K2B0yZrS7Wka6fWoFauj6Za4VvganOlxzikyy6Py3T6DSICUU/0M6uxOFI8zpzAqx5RlhcfgCcEBw8Lj7ic+hm/9yY/x4hc+A1p0IHLwRAi7Hif3H2H75Cnuv/kO3nzlNbgYsD0/x3a9xvriAiBCzxGdc+XCTUu/3OMJPVtz3/Lg27V/2Xzq+bIguvVca+4t/eeAlJYvrTakPutwsSB0sk7M+twHaMc+K284poZ4a+wtmurx7DXiGrxp67OhTTHGFILZ4AXdh1Y/tY7YN0cir0MIKdB1pp9ats/xhpZtQtN5nqkdCbrd1o6KDntrvdMq+3jZOuPs9/psoF0j6SEAHJtQca+eYS5OP13/XP/n5lvr2SEEkJtmlNq3ZvfxUasf5pOJXBIekr5N1qmppzaIpsb7f4pixzvSZkxPb8e3bz6YgYv1RZY5EHAhb851YiJfx/r/7kZVq1zZ0Oi6bhZ4DMMAkMRCptsw5dI+AGAOiHmnYRh6DEMPv0zGydAPKZOUI3S+wwsvPocbN66DOe0SyLmD4+NjLJdLnJ+fYdf3GGLAZrtJhgAzVgcrADGd2fCuGBjMksc9xQFLfbXga6dwZWZlMmeGiHEiIGtGaXsiihcCKAcEpY5ReCUvYj8ERDcylqQu00J+XAC1EOz7fgQoMcIxiiFnFYc1TioF4OpFZrdS6z4IhQgh1vTQcbF28cv3XOKwqeIzq8Q0IHQub/kjhRLJbddpLDHtKijDR3ZgktAZgCsog1qBp23afYpb07cczHJ1NiFNc80fVlHpemseGd/Rv7dCKVoAQJ6vgCDlNInmuJwGjLY/QBbQxrsG1IrX7gjMAbiyjqj+zI6vRfPWOCvhqdasBWE6Pa+l7Vydum3L11Pj+3KBTZS2BebCYToGHFMKj4oEsEMPIJLDpgOOn7uDb3zvu/id734b7nCJoXMYCKBdwObpGbZPTvHea2/i4Vvv4uzhY2zOznF+cZbuEOK8c+Hl/IWVSZrW4zkJvSbl+dZ8aPrZQ+P7AEULENbrsS4toNr6nRR/6e9b/bHv6yJyTRdrZJMx2Gy9c7yUwkrrrDtaTrcMiBYtreyYkyUMNPtpx6jnQjuW5uakZXxpntFjtzLMfg8Viqo90zKeOZ7QdJuG3kyNWQCTG4/1OFrzt28ubH/0c9Z4k7HYOvV8WppagFwiG1yLhtM+aBqwGavdlRHZ3HL6aHlgZbeUlpHWkrvyvuwwtpyiLRmin7Gpm7XsEVqVOSfKoZvT9OL2bpE5mtoxt/RD6fcMiLd0997vdbAVHcEpY6Qjl87xImEje/p9bo1quo10RTVqiwPmsMVcubKhYYXMGCaSYtcRR0ODKF1Otd1tEULNcCmlrBxsSTdosqd06Dp70UMYIAfilstlORx5fn6O9WaNGAN2/Q59GOCdQ7foEMqB7YAQBzB3hUBdl84UyI6KZN2Qhal3MPTOhj6UVw5KzxC3YnpKsX+tRSK/t4BljBFD3rp35MvFbIwU29ip91wemzfeWAHqY+GyG6JLSznYrU15Ti9SEd56e7cwnaGH0DrGWFKvaV4QegvNrGJI9Y4xk1Uf8kpgZgQeEMgBbpzzxF5ToaPHb4WFLG67gMo8oVZIVhnpurQiXB6sKjqPz0XoA662Pf13xUszAiPRvL2boWk6GVeMYDd+VnnTlTKc9I9QDDaZl77vy30q2rgDauA956UVY1zatAL7MmVejUveTX9MxrGvWIV+VaF62TqbU4wgqs6XaGXqY4RngJgQQNgREFZLxIMlvvB7X8Y3f/SHuH7nNpgIAYALQNjucHb/IU7vP8Abv3oZ77/5NuJ6h+16DTBASrF674sDjIDi1dTgbBz/1AO9z3CwgMM+Z9cQ0DYuNK3sWmvRswXUWiB2DiS32myNW/orAKUCsZERMa3f8tSk/QbII6rD+DQgadUp77acDhUdqPxvLw01LaVeGH2g37U7gC26WmC2rw/6cz0uW1pgUeuVuVLP7zSUb05utPhqjp9avNMa59z6uKx+ouyowzQUaI7XKoDcqLvwExG4QQIN5Fvv2v7Zv+dkqpYpLbmi6xhpCQDt5y/TFzHUBmmVHXJy5qt2ZAFTp5LFRkWWe48QRiPHGswBPKlD9GgIQ0o2ouQMc3INSUh9xx2G3Q5yLsiOvZojwiR0asQ61ExUcxUd2CpXNjRsWk75F2M+IM0xe0RZdHq+YCRdtOa7ZIQsuyVAiXGHEFKoEDnEENB5B0nFRURYLpdpZ8Q5bDYbbDYbxMgYQkC3WKTwqRCKx37Xb+F9l0OlGCAGOU75n8PUkzDG406FhACUmCcyyjmMSwRWrqUCxnVYVV1qxZA9LhxBERj6bNyEkM+zjIeAhxDgiOA7Dwq1l7zy/BNVnrW5Ugl9tIW+zPeccCWSC8LGfogAannkq+1UFR6lQ/TSIetGfyIXweiIsFwssaCUdYFiyOFlVPohIQ993yNgqqxaCnCy8+BoMu45Wm42G3jvscjnY2wbuUYQ1cBJA4irLGqrrLUntKXI9RqWOQlRsk+NdersZbNAmYHIoeq/VmgWGOo27RhKvTwadPvASKtfdn3LGt6n1K9a5oDth61vDlCBuVj3Qifn8kFv5xA4IBIQlgvsVkvc+eyn8e1/8Md47jMvAo4xeA8EBnYB64cnePrBIzx860289fIrOH30BP16A46MgAi/WOTsUKnvPp8YFGMjDerD0WMuDKY1j3XYXtvpoT9rhcXMGQgfpkzX49WKtKtvm299z8zFaLN9nuUDoBlaremoaSmyXgOP1jst0JZewCRpxj7aij4jjknbN/rUApVz62ZOj9gyJwesETEH+q8it8eXUC7Cu4w3WnOr+1v+Rjpsb89X2L5andMCt/v6omX2ZXN5WZm0N2NIWKOg4gkzx1cB/lKnjaLQbbVALxFAzkOnc23pPflb5EpyWo7PD8NQpYAm13aOWL3dakPPCZB1Uw05K7oAtR7TdTgixEY76dhBiiQq+lX6BZ3kYV5u2jkkUCWD5uh41fKhdjRSZ0SBj95YAOAYseu3+eAl4eHDhyAiLLxPhgYlz/JytUQcegRmHK7SBXuOgEiSDYpBxFguV+i6DiEEXFxc4OLiokyY9x0IwGKxBNGAx48eY7PegNnh6NCnQ40AEAMQMziPKduJdylbCwOIYYAwpTacCtDLYPbi4qIAfMaUkYTwJRwl78yIJ10OiwMpNS0kRWs+pyKACEhMHoYAsEOIIX3vPRbLBVy/Q4jihBJvEpdUt4t8TiXboykBAaXQEeFtzv/2AQlSwYNtfgABAABJREFUqk4zZcvL1hIa2hCR9IfaUJW/5dko+RYaglK6WpSlKNTIxbr3jtBdO8K1u8/gyclTxA/uw/EYkpWZFs57BDnTkzOoSf9HoRNHD7jW+A3BoCkm3gMgnV85OzvD0dFRut/DKMay6FGDSz1mK9haoSzVnJm5sErGKuqqTzkMIobEby7TWYSb8HxLker1IEw2DEM51Gy9OhYUWMWjvUdzinKfkJvQBTPArUG7y8plwvqyQsn3UbJr5caTMZHpTJkXvfMpAx6SIUjLBbYEXHvhOXz7R9/HS1/7XeBohUgDiBmxHxDON3j81j3ce/kNnLx/H4/u3cOw3WJYb4rnimi8wdg7j2zZpQw2XHvgiVohkjUNNBho8hanNSgfpXpaM5KK3c3QP+V37UGf0HiPQZJ+n9Y3Z+Tsq6f8JJSL+YLSkVkgjMlHSl25XpH/QEUzohR+Kmtefyc7hXaNA7VzqdVXO48Vvzd4vwUsKsOAx93mOeNCz4mla0teJepQ+b82vWisuPyU1PNzxoSlqx1Ha37L54olrjq2y+SCxhj2/YoGNOUL+6wtOiwsxghWoVN67oVHc4v1MqTp2IpeBGNoGLPT9WUMJ5bdgnp3DSpcuiV77U56jQlIreO83gpbTI2dFkbRWEYwiN49kN+99ylLpUS8MBf8ZY05O29SB9E0eUTr9xhjSRyjaTj2t866WbcN9LsdvKfqPQDlHrW50up/SivK+RqC5JRqYcar6E3gQxgafd+nF7p0HwY5AMToh7543Yc+be0sFwu88vLL+NEffh++c/AEdLmTPPQ4WObdCAY6SjdO0tKDwLh/7x1cPzrEdojFAy3Zp+SgsoDs5aLDcrHCdtvjF7/4Fb79rW+BhwAeBlDnwSGAspETOXtpFx0iB8Q4YLs9A2EAMI0hlwkVZgkxhZREJehbAkGUiJ6UsshDKIYacp+opK0F2FEKiQoOkXO9jjC4ZIghZM8VZ08BkHIl53sJIicrJKbcs4hqd0giDZnFcz16e7WyyrNUxqKFuB6LvdG6/FRZv/TuBPM03r/QJwP1pqUN2RkbUxImtU5gWmCR5+mUA77wra9i+ewz+Nn//f+BQ0qKqFz0l8fkFx3Y5H4v/WW1lyNgwcyjHqsUeUvvRKxWKywWi+p5LXBaws8+2/o9f1D1ySpUy5+ASdfXEFQAo1Mxn4XHMu3ZtFfeN6Ff3vlED54CC13s2inP5LVjQYMdT0vBa0/5hG9rIlc/W2EVLXBhzw3oNkQRWi+Urj/dapPCm9hRykIcGMRApLxCmeBjXtuLBQYOCN0CODrAV/7g2/jtP/wOljevgR3BI4B2AcP5BZ7ef4T3X38Lj995H4/f+wAXT0/B2XERKWfgA6FDOlAOUEptTOMWOUCgGCF3CQgwT8MYDXI7Z3PzLDRI4XwjyWXndpyVNqDSn2ngYb/Xn1n+1EX3TWST/V47mrR803wgJfFDnse0753klKZbZEDAMAMSNizp4a3usIaBpUdrDdixtww+O845gNeSJbYdG0Z9lXWqaWff0QCSE1F0bXnnWjs0sqEGwJPLKelDBYxt+5rGOvxsjlatudf12LG12tL6LoWa7Zfvc/Nlgb1ur6kzqU6XXckh5nJ+I5GRi/4F0aROLjqR8n047fGLbrPFQb3D6SxgWsvpTKCdA/33LB9FgJwvu05gmqyX1rpt1W3XcyvUnUQdKpkpPkKbEEXan4awzxtV1fiotv2kL4Ir52gCEHb9DkfdAYAx2oMx4pMprygLDajkHpjQUT6rUfpMJeR2H7+2yofKOhVjwNnZBfp+B0aE98niS2A+MZpfLDD0PX7+s5/h3ffexa07twrocs7h/r37uHPnDkKM8D6FlTx68gTeEd59+y388pe/BAAcHBzg/Pwcm82mWpCRkydbe8qdc/jn//yf4/joCJ/73OdB+YK75WqFzXYHZsZ6s8FyuUDkiN1ui2HYYbPZwpppIqzSAkuhKFws73yOYggYhoCuS4xTpSwFUoiTulHcAj67za1DuSIDiJzuFYgppz0jhUotsqBg5jG3fWR0XR1Lr3cQ2CjoKsQqGxsWODHS4tqn0K2CLGPKhoYOdyieAUPnlnAXGtmwpil4TnMT+h3IoxyiX6/XiebJiqpoLPXqA+eTGHTRatqLdoWi+ye7JeknJuOoFm5DWbTGWwla03YNMK7uZbB9t4cli2DOAqlVr/YuF2NDYv4vabO1Pogo7eSp/lih1lISc9/ZsVi+s5+1+LtVbPjP3Bh1/QNzuViPGaCY1pljYAAjegLBYReBzqcMZ9E5PP+lz+G7/+hPcfe5uwirDtQ5EAPDeovto8d49N77eO03r+DtV14H9QFxuwMPARKGZs/KMPOEt2vQU8crzylIC0hawDf9BDTXarpIFXPz2wJSQn8rj7RsbZ0tahVrfIw0mOe3ircycCthiOIMcQ6eXNXHfWu4Mmx46qxp9VnaEXkvPGvHbuk4kS/ZuN9HH2vAMccJyNIe3BbQ0/2zcwdkILdnvlpGixQtg2xf55xiWh/WMsBNDoRfVjSd9p3LtOOw/ZHvdATAPnln+y6GAe15PoW82sscpsZOmcuZsdo+tWS5nAOQ51588UV88MEH2Gw2WCx83Q9M17W0oeV3NLqo9XvLgJHvNc4YMU/bOaH5dtSxI7/aosPlqzW9p0zlQhtvEdUt6v5454rTj1lk7uWlxWOCI67S36uWKxsa5+fnWbABq9USi2VXFvAQY7qsJo5C5NGjR/hn/+yf4X/7X/wX8F3EEHZYLhe4feduAoCRsd6twcw4PDjE2dkp/m//13+G7baH7zo8PTtLIUtZmMpZDRFu0rYs6gcPHuD/89/+S/wfv/Tb2O6ScUHOp2xUzNm7TPCuw9Bf4GK9nh1rAV4k2at8Mi76AVEJIO1F0Z4wQu3dbgk//TPIGQwat4y9IwwhGXfJmBngFQDQVi4wCk2bxk0YZgrUx4UiC0KDJgaXC4F0/boefSB8jPcf+6Y9BC36Son5ULQ2hmQnBBNwrhdFfj9GHBweoHMe3A9YUPYbG4Vn+28BphZiGrxfWrJk14u2gAMGyI07QLVRJ2ElbUFox7u3C6pOTeMPIxRk7eo4Yo4BEZTucHHTuGXtHQTGNcENU2MiqKk+J5M/nN35agEm248WmGgZGGNzbQC2TzloRXJZ0YAhUvqXW4Mnn41kxoKzAeI8QufRLzxuPvccvvWDP8DHv/IluOMVYs5EvD1fg3YBD9+7h3d//iu898ZbeHpyki7n7IeUWc+5fDHV9BxEy6jSdJwAUTNmuTdHK/LJOqp2zdo0t7KxBcxaoGyufzoc8zJjpcVHVsZYJVw5adT5Jsm+ZOtgyOVX8xfN2XGlMbiSsnyOb3UfNXBqndVo/a3HJTuQrT7Z+kZacDFitbxvzaMen9Sh1+tlcrYl++045vgFwCTcTI8txjE5zHgX1mxX9vbPyjbzVAaA+2WRpaXowqvI81Incwn3sf3KPakAvabdbIiuadauCf133cd6HfV9j81mk6NEYqG1fka/3zQQ4Sd0uQrP6b7qaBUYQD9HV/3M3PzJGtSyqMWbV1Adpc5x3NPvgBwuR+ksRsIdV6tc0MLfxXD4sO9c2dA4OjpCyRgFBiPktLb58DIn2OrcGAP869+8jL/6yV/jG9/4BpbLJZbLFYgcdv0ODMJyeYCLi3P0w4Bf/+o3ODs7x3K5wNOnp1ivN1WcnF4QevJEOIcQ8Ld/+7f4xS9+iS9+8bcwhIh+COgCo+s8Dg+Psd1usNttcXBwkA+WD2BO2lsrMD25KVyKc/YsQkqZSthsdunQOaVLtqpL+9xUgI4xhih/a2ESQ0C+5BfO0SRbif5d2unyYVFWsM6Ow9JLM3wM4w6Jbqdlqdv6AJRD7uM4CUTTg3kCAorxABOuwrWAqQSr6UcZD1I4lPfpEsPQD+icT+EpiUUrL4Wu2xocMgfk2ovHChXdV2YunZS6Kg8/TT1Ouk+s5kzeswrbth9jrIRjaStTTHbTJv00z2re2Gfc2FvbdWkBU+nfbDhcQ2CXPplnNHiy49UywXqO9BgrA5rr0AndB00DqxwskG71R9PU9pOIyg3MlEOogCQnezAO/ALMwIYI7uYxfud738ZX/vB76K4fgT2l3RAGNk/PcPbBI9x77U1cPD7B/Vdex/rpKSiWPDOpPVffh9Eak52L9HtbMQp9NP30HGqngq2/FZo29inFb1vgo+vdV4edFyunpnPVBhL6PctLLaNGr3VuPAMge+indEgyo5aNJbzOe2gnr04qommq+235Tb8j+lGvgcooN/xqxyt0sSFzti9XAcBaBuv6yzOcA3lm6tK8Yc/5ybis0WLbsPpddp8nu+mYOtGkvhYGsbpxQhPCRGbP0UrT2q4HSw/7e+EtjHrU3ruhx2FLKxQu1YsKY+ifUrSDqOh5ZuVpZ3zwwQfj2mkYL7Zty3vpw1pez2Edrde0nqjHJWGO9Zpp6U1Lu5YO0TJEj6Gm7bz8lXMYtk2g+DOr+qT/zJyOLnB6irJTKgyh0F/mSOpl5kkonB2/FZeWNpfxs5QrGxrOKUCuEvRyZHTe51hUAVfCZBF//Td/gy9+6bewXK2wGwaAgSEMGIaAMOwQI8P7Dn/2Z/8OwxDhXDoo3Q89uq7DYrGomIaZS7YpZsYu716kz4H3P3iAz30uwnfp1u9+CNhst/Cuywe6CYtFlz1N6QAsUzrA+u677+K5556rCCkeqRiTsTEMASGnru37oey0VEwX6y3i9P6YGUQzf+XxZC7xgKAxW9JysYRzPi32fE6DkA+UcmYatIWRVaKVIATKXFkhob1cLUUmn7eAiwVumgb24Kjupw4RGIVZBGG68McFl86mnD99itj3yRMY890Abupl0QtJC3AWSWoWjlVSUkcFZIkQeDo+Ma5sHWVOHFXtzSkpCyz083bh6+lvPd8am22vajM9WADJ7HNWCaYvZ5TWSA/NSzHG5lY6ML3wSbc9e/ZHyQ0bjtcC0XO0sM9Jv63ibr1frzfKuwzp+8AR1HkE77B2gOuW+OTvfBFf+dH3cevjL2LXEXbeYREZfjfg5MEj7E7O8OrPfok3fvMK4noLyqGhiQ7JEeIkyQSmvGznSwPJ1jh19rEW7wn9Z8dsgOh0nsYD5VpGyju6Hd3/qyi4dp/qz/QY9E+bZVGv+YksUHKmAjmIJQR1Mi4DNvTZreSomtLysiIGi6WN3XW09Ckx+qj11L55dW4apjk/x9PSkqtQHGsNBNuPGnhOQ0yuAoIK2DIOhsvkph4rgEv1IYCin+UzHe42azCoYuVkS1+WtUxUpUmtdC1NwbPud1Neq9+sDN5Ho7H+8e+qDaprn6tnwoNc06klF+xa1HVP+47ZbKK6v3ptybhqrDg9nzdDlMk8a4fa9PFi4gGYruFsw5asZmWrgvPunFoPNpQYM/Tm+oNZ2ly1fMisU+PfYniEHNrTapJAuHHjFpzrsN322UuQDnjHISIMEc4Rhhjwta99Ha/85jdlsvR2prQ/DAP6YSh3WojC995jsVjg7jPP4/Nf+CI2ux7Lg0P0Q8C2H5IAHgIOD1bw3qHvh0J0sSJXqxWeffZZOOcwDAMuLi7QLZYg8uj7LUJIBtCwCwATum4B5xboOj9RwnoiLCjV3wE188cYU8iDSzmTY/ZSJmOrEBW+60B5gZWsQHFGYDiAwwj8ZWE65wrgEcFXGwbTGd23iNK77fekWAEuRRuxTWPI1FH6gmQQcYx49u4zKXSvH9Jh8Qbo1uNvKUhHrhwan+t3U+lhXK92vqV/GvQWQzOiXIyox9Yar+6HfsrSS4egzSnMufMvM6oC0fRTlw8jbFp9tkpCx/O2nrWltdsxGYFRprquyzzGH6oocGjnBUiOOALgxaDtOgyeMHjg5ic/hm/9+Af4xBc+D3QegQieHfwmYDg5xdmDh7j35tt477U3cfbwMfymR1jv4EqWjanHS/O6Bo2XGX92DC1jSj8DTM/qWCNMr4/6/Wk/tJzRddizcK3+7x8bIAfdpbSMGf35vvrG32nCW0RUxflP+1eDhmrOTHvzddRzYHfuSkr1/L1NWe3yjrjE6Nv27FhNr6Bldos3WqVF53EO2s+3ZKAFTJrX5+SFjL0A8pmw3uTIS7rM8sFl/CD9Gfsnz2AC8j9M2ScDdbvpj4S9NI00EI7c3v39+5R99bXOrCR5xLOONlvm+ljpjgrTTddK6wxXbhiR55PV6L7V9dXp/OfGYWWKNqjtM44ITLVjp+gvY2do3tT1Ualv3HFt7eTMRRxctWg+v6xc2dAouxiUNFphYiSBKuQTQemdx/G16/jaN7+BPjJcCNhenGO5XGLXD9hcbODJY7PbYtF1+OwXvohnnn8BJ48eYbla4YjSuZDtdpvuPtBKhhLQ7zpfhOdytcL/7B/9I3TLJXbDgCcnJ1itVliuVgAR/GKJCIfQB4TQwzmPGEPyRgVCv+uxXC7Hm7Wzx0EyODGAPgzohx4pWwJK+60tt/HnmJpsjNedhmyI0QBWwBSUcucDoMigEFJ4GlFJs5a2xaaeYfldDiRar41uV/+rgB2mwkPXr3+WxVT+p61wTKxi3R4AeCKMl9dlzsoCUyL+0/N5xwCuGFs7Zgynp3Chx4N3304p9TiCeZqBpBLYeYHK9mGcWXwa4KednhSXnd39YKYxCwYwphOm0ZjQ9GqVlhHG6jv9GTMKeBzdF6Ox0zIuLPisnlPgp2yzjvgVslWdJ2SM7UTN63U/WU39vLK2/fPkUHKfMcAcyz0fumhw1QKl9rn59Tk9E1J4sxCVIPsDFThJxAGrXRjPgIdDJEJwjMCcUxYCXQQWnBwJg3foO4K7cwPf/sH38JlvfRX+2gF6EDwTlhHYPjnF6f2H+OC1N/HGyy/j/XfeA4UID0q3hAtwSUIBlJULkPmONNBJmY6IaoAvz4wGQw2cLUgZNR2rvznPlXVSSF31XOvf5Z1WiEpqd5xT58SDGxUoHT0wLeNO+lHWhvqUslyX238JecFCCKcM+30AkROvc5bdkNAFUElXOY5X9KgbqdQA07K2LG/Oj1HP4eiE0zLd0ljaygg40ZgyeLoCCNkHvse629+3jMkrhpZXdY98Pd0h37cLKp/Jv5ouErWReZcAQtYXhZfzroJLzlMI0CdxVUU1JAJo6gFnRo5UmOoFLa9aIN4atRVtYpIJThxxWSyIPEvqtUjvvP6nWbHsbnJkZCceyp1L+/iRs1BgtOVu5DhJVjNXqvHaNjDuNkiYoA6Rtoao7vco17jQJkODFN7KKCmU9RoS3UtU98/uyrbnbDyMX97jMTW2yOci2Shnmy2xZgqLqL9CzLoyf+Y0/xr9mGQVJ73Rpnj6f/4+Klr/XcrVQ6ck/SJGIJh+dwg5JCrPC7zv4LsO/8t/+r/CZz/3hXL4BwIQnYfzHWIEDo6OU/iRB/7p//p/g//mv/6v8ejR/QIg1us1iKiEKAnlRiGVFsKPfvgj/N7vfQ/d4qDa5QAT1usN+iHi6PAAPh+Sct7DRYcw9ImZVBxjiBGu8wj5ZtcIKiA0IoIREGKPJembqBMTloNnToSRUxhbJqod3+fy4vfOpW13l7Ij9dxjQQ6Lrks0LNiC0sV0sc7/rBcd89QIKgKYx/hdC8JGVZd7vofJJgqnAHfVNziA/ETxee+zcZVD8ICKNsJjWe2nRZwxrEdEzxHBL3CwWGAVA04+uAfvAI5U1VVlZVGG2ZxxUeggdKHM+FkKVRlXZCETCr1H70o6CzPn8dGKsIpTV9yi+5KwbboRfnxfhHTbQ6x/aroWIUsEdkmYRRLVKBIU6udohCgRUPGOBg36zIsWxC1DwK4D4U9CAj6dcwg83W+y87ZPYWka6DWr6VIBklCHSZEIOHk+B8C0vFpE6vwKON8R5ADn0XuH4fAAL33zK/jqH/0Aq2duIlCAiwEdA7TZ4ezxUzx85x7eeuVV3H/zHZw+epLSdjuXzmtkGefzXCQgYL1WKHwhBrFM2nTOKNOFJoBI03bUoXrNE4ikDm0s6GxJIx+25kdopW+/jhGlPg0cpQ8i/9Oc7/NGqt9V00GSa4hecwSSEKbICGpitVEwts1ZDrsyQjljUJwOSGfJRhkzdqAFSBKfTQ0y+V5/3jTwLQ8r2uk2qvdYQrbcOFYe04oLANXADaYvmibA9OxWawy6jM9NZYPVT7q9OUBud3daNLF6saaPrJm6W+lvAecAKMJ5MSBFximnqFpLCcvndOs55XMsdxzUdGrxsg3RapXyXhx31Thf7suyy0GoohnK8Dgb3YZf5KdT30u4HWNqbFR9N/SW31NoYnsco+6sdcP4bC3jrT6ztJtgGx4z1MmzvjgOM7bCGJIUQU2axHzPmT1fJsXqurpfMiapM/NQxnaUPywyzkY+sJgT2clD2XihUXrou461fqt0ZBEBdkeQAHIgptFQdLUxqmlxWfkQOxo1YClMb4SlxJq++OKL+PLv/A5WiwWOj46KYuz7dO9GOA7wfoGQPZb9boNPfvIT+MY3voH/8X/8H8DEOMiXnWlGCsYz773HcrnE177+dXTdAsvlMu1kLJflfIf3Hqen5wCla9rJLQAesNumXYZhCIXmwzCUy1sks4YsDGQBNISAwcTD6gl03mEIQ+m3fUbT0QpBJ4qKHYjSYe3FosvfAwAVmo8gqQZN+rAdlILQ1ngIARR50qcR0I7Czy5cveCsMrEMXW+bjp/rXRcr9Pcxb2mP04r05OAisD09x+mDR9g+PcN1Hrcg9TsFqO8pLSEl9GgJ1bn+yjN6J66lINg8X36q76ZgeuxHy0u5b0z2UCcnpJYNmP0Zn/ScJt5CMa4nisnVAtYKXAsEtKCudsgEfBHVkrPRvxbwsv23h4t121aQl/Xc8ALPCdtAQO8ICxAWgbDiZIBGAvrOYbvq8MLnX8LX/+hHuPuJjyE4AjGwiMCSPC5OTvHgnfdw77U3ce/Nt/Hw3geI2x4+96PruiJ3vPdwEC9ce60C0wOAmgfsuSIdOy7KeAy7EmN2qlTnDMkWjezn+uI3ey5Al0l8sZmPORroZ+fuAZC/rxIKMBeLPeHBxjO6WIBc64t5T7F+X68lu2b0eZM52boPGNlytTjy9vqYm5s5oN8CjLof5Xk3XfMtI2JfXVYn1Z+FMh9j3YCAXavjZ4v6WuS3vGfX5xw4nWCvS2hs+UEatzsopZ6MXXQ7RR5nB58YKYykgvkS54/QTvqgjQGuyTLBRJpG1U7CzLLQfGN50BaLT1oYba7MrRP7uWDh1pq7DOdcpdTvJ4PDe9FvORzMOMek/Q9bij7AlEevUj7UPRpWMcnvq2W6J0MAPpCyVN3/4D7uPuOwWq3gvMdi0aHzHZaHB1hjm3YMYkQIA4YwAMOQ7rpQyk0UX/GmKH+PHuzF+XmVXQFAUcwhBBwcHKLr0maic0AIhL5P7cYYsV5vAOQDmjoHckxGVgihgHY5I6KVq/7bLnrN9NYrYQ0NbWQIk/iuQxQQFsYDhpxjSYmoePvHbb1MBxqZxGbp0P2fMB/NL1Q9Vp0xRdpu0SG1O/Vmt4SJ7d8cqIsxZ5oaIlZugSfvJVDmAoM5pksO1RzkP2rp1ih2boqBQjXNxrAdN9l9kMOkli+qdrKobQlGMTQm/WAxuts0Er6142Ee88nr9xKP0NjmJcJZ00dAogCZOt9/e7t6bk51v+dAZOpq+24NSwsNNHR4lQbZ+pmW4N/HJnPCVoKsfCR0MYVg7jyw6YDjjzyPr/74B/jUV76E/sBjQymUyvcRfHqORw8e4t0338Jrv3kFj9+/j2G9TaFSjqrLH22IkfTCGkQaPMnvNgONHrs2GiWLXtWO4X87V9K/OXrtMwD0Z+NzFoq0M7LNGRlCq6sq2HFtzRsbLXCp+UzzVgSXcxpWFto+Cf2TgTKCqRYQb4WE2MPszDxJ62oNEDuu5vqb7G2PTiN9KVwL6F8FjMi6Fzm67z1LvxACHFIoog5FaQHVlgNF973lNGzJUQtmLb3mBwrItgGzfb52oMyBZNu+LfpznVygfhcFM+hS1kkDqNc/Ux0h74wgy599a8vOadlN2OM0snytx6D7NPeupYctc+FNzTBaJHpO70uj4pyTOuf4d4735nCjpUMLk8g7LreZkhyNhh/HCM6ypKV7NT6xMobZ6ESRO2TkwyUyVcqVDY3VaoXVaoWDgwN477FarVIFXYeF70qaOCHI0dFRTmmbDI/ddgsCsPAdhmHA0PfY9gN2Qw9GSs0FSqFSp6enOLp2XA6EFw88JSNDh42IMXFwcIDNeg3nF1Wmn91ul7cLfTpEjQgOsUxMP2wAEF5//XU8PX2Kz33+81islkLGZAyFfDt4YPT5cLkW2NrwSoq/FmzyU8YhuztNEMajcE+CNxliKWOWMB+gVUWIYbwB23r9HCBR7zpuMSmi6fakvCtFC+lq6xz1YpGzMjYueKx/3K6VYpm8pVD17xNBT4Q+BBATdhdrnD05gc/tDIHBmUi6P1KsMmwJpao9cIlTnCrrJIC1lxyo71lpgRM71lnwOgFzdR9tn+eKFTDVdwrUzQlzK5Bkt0/GWIdnJKNAAKs1QKX+lnFgFe04N1T1Q+hr39NzaRWtHXfLCCnC2tRn+dPSlojQMcEHl+Kjlx5nFBBvHuG3//A7+PL3vofF4SGGpQMvCBgC4nqD9ZMzvPJXP8Xbr7yKk4ePsF1vEh/HdMbK5bUtfa1AowqN1MBSyya909niNcvTmrZ12Mo0JtnOVWvHaA44pX7XAFHTU+Kg7ef6dzvvVglOvP1AvlB16jluARRmRglnMLTXvNei62UKubUemBkxDBDQ3SoWtLUAcgtsz/VBg6xq7MbQq+mNAhSt4at5rjUHtpR249QJptvV67yiG+o50XJBntOx83reWkXTzdJE03qi9xs8UeoUoxMEogiXw6JjFJfSSL/Wbqset11v+kxOS5ZpPS2v2jElQM0grudSlwSslUOKAfL7d+3sp1au67HL93os9h37rOY3vVsidJS+tUJ2pR1xHuv0+2ObaczyvnYwpkfaRtmEdupdO9YWP07mpqGLeZxMxBiw2/W1THF1OL29+NPKiHrHUtEhDyXGdDCwhW0vK1c2ND772c9WikgzOId6YQDJAHnhhRcQA2G5XIJWB+j7Hp1PZy1673Gx2cJ5j2HosVwtEbZbfOxjH0tnOjqHxWKBg4ODIjh2u125dl4rxtVqheeffx7H165jdXiUQgryd13X4ejoCEQdiBjM6QD4bhfKYokx4KMf/Sjubp/BarVKseAsqWzH2OeUrnSMwYwcq0vt9ATKz9ZE2Lhw/Z54REHJoEo3Q/TohwFLTl5jlthxIkAJE91eMbbm+sK5/2h5kUYml8WnzzjYRWS3fq/i7XTOlTs4pNhFbmlnDZPo8vkHOKwWC3S+AwEYQph3R9MIlmzfWnNV969dpQjeVrz/nACea2NfaQFd3W6rTju3LQUazdhb/W7NJXPNI5UiZyrphcUJYeuz3umW8q/6QrVaskDC0sUqHP2eBTJ2V48Mn7TmsdVfAuBch40Hdkcdnv/iF/CtP/kBbn/0BTB5wC3QMYMuemzOL/Duy6/g8Tv38MFrb+HJ/YfpTBMonRdwSPza+VlQw4n5KiBm6WbX1T7QaddBPT+jwaFBp27Php/oujQgqudo/N4q3RbAk781TVoeShvbP85QPadza7TvezCr9O2Y3rVi26zphupMyNxa1PRLn0/HXdZqI3zMygALXjQdWjwxK3+ynTHHK2J82f7bsi8kq+qHtKm7MCOTK/oo2rTlVO0Q0XwqdbR0jbyvIwXm6HhZ+Ko8K71L9Wter3Wjbrt63/BPc4fa0K3CBS4dXreOu1zjnnlM8lBM0CZ2adE+1docgxiI+ruW/LHjESq2+tnCE5ORGN5vtadqFAhVdN1Yx9yezLTf9u6YObmmQ1dlfufWpx3fMPTJeYyydAtbzenZlpEj444xn2V2DhFIDi+q67sKvgE+hKFxfHyMEAIWi7RjIDsF6exCWrxdl0KjQOmsQwgB3i0rL/4wDDg8PMQQAvq+x/LgAIvFAv1ui8VigY985KM4Pj7Grt+Vcxb1XQQoqchEaCwWi3ygfPSqh3wAKmRA65wszAHDboOTJ4/Q91u4bKEdHh7i8OgIb779Fn7161/hG9/8JspB6sh5F2aAY4wGT2SwazOMFM0oGpCJ8GqFC1Fe1C7FeJWD7S4M6d4PyzBmcWmhy7FeSEWIEcOhm/Hy1OBAPtcAR7cnceMyfruIdNHv6xhieymjzKP2zmnmJiL0iGBKl/YBadkHTrdk0ng2r1nmFJCdwwoMzFcGSSvbAlhzC5KIRu/QDL3m+jOn4FsAzc5Zqx85ycqVhIduI8aahq1i4+51G3uBzrSnFQjTRWRESzFrBbFPaFfzL5K6AeLHeUNxCsjnwXucu4hrn/wIfu8f/hgf/cJL8MsFiIGOOoQ+ANseJ++8h9d/8Uu8//ZbCLsddutt6udikZJREJWdW8L8jlda4+1Un7NUbPCENjxt2N/47H7jU38mfdChry3vcDpfFqvdmPH9cRG3xq1/b4XGtD6z3wOo5LH1AAqPk1mDc7KiAgZXVMLCt9Zwa43bvrePn+347Tq8rH5pw84ZMMpCK5NbYHPf39XnvN+zq/usdQXyGpTPW2mQtVzWc3SZXNTzYef6KkB7fAGlrxKtkL4WPmq3qdtu8d0c2Nb9sXXK363dvqvyrHOunHeyOr+SQQ1+K33eI/a1/NDvJXk3D5BbYNp+J9/rdubomlRBvYaKLHb715Jur+VEsWNt6far8Kn9nlyKYaE8AI117G6ENnDm6mQe9zYZ06MCVylXNjRu3LwDifVKC7lLE8BAP+zgQDhcHcA7h8ePHuUD1cB2t8bFxQVijLhz5w4iGN1ygfVmnU/Kh7wDkcC07xb4xCc/jT7ssFmvcX5+DuJ06PfZ557H8uAAb731VmJyTtt9u36LPvS4uewQhh7EEefn59jtety+fQtnZ2cAORwcHKDrOmzWO5ydr7FYJOIOMaR/IYCJsDo8Qh8ZHIFhu8Nuu8N2F9CHROrzdY8Y8yl/4RnKDEljqjIposDkvIjkN7cCkSNAXbLXPVFKa0sEeA+/XIK3WxApjxdROrtRCV3jOUwPT4RXjBEx9GlHJnOQ9N/e+9ASTFYA6HpbCzdN15i/XQs8aUdv7dntfyvAiAgIAKXYsGRIhgDilCWCcgpM0UNFpnMtwCfGgcsgEpyzSOW2ZJXxCDLHkr0bzHsFSpnnMh81SNX9sYdW6z7XoLkSoPKMrj7PLYFGoSmfkYQ5UTkTUo1srzBJ49ahc+UbRyl2es/unbx7FaOjUk5a6gFprK5Wqvqn5R9NM5fDHMXISlnckmxJZ6RkTIwATmvNJdp1cKCBQXDoidIh8Lu38I0f/SG+8M2vwh2vEAnw7OH7iLheY/30KV7/1a9x/uAx3nv9DZw+eYJF18F7h2WX5tU7X/U5hgDJBpX6LiEQBEmzWbyDjkYeV+O3ns+QeaSsqZh2FgrfU6IpE0Z6uEQxqGwxDAEUI9+VA7rAGIZGKVNbOUgK6Z+aUi+5XpCM9/wFUepHCcETPuYpX6G0FXOoZrqniSjtElmaWGDSCtcE0oaGrNn0jDKuiUv2uhC10dfg35m/tbGT6NdeB5eFLVgw1QLeU3qNv2R1kX5S/bzu86XAWvVBAx37ef33qFtqQ2LaRk2HWOYGxCgmMdfvWf3R6pP9nVlS0CLzW6q4ZWjaUvVfZFYRWknOJPnXDqfZN78tOui+l0h9opxNjMGBK8eWrlPCqh1quVmeJT3+vJu1x6Mv/WBmRA4lg5lEYYBlB2tmJ6QBvMvvKgOqXLdALsnyEPMdKMTlduxkFCR8JTSzDikp0zBnLlOm5UP6AON6Qb3exQFnsdAcz819ZkOt5kpkRuedShxEJRXxPh2uHUAFe2T5xggAkn5TyqfUuQ/j2HJlQ8P7Vcm8RM5hdZBeZTBo6IAhIg4R2+0GDz54iNXRIR4+fIwnZ09L9qjl+gL90x4fOzwAdR4L78vac+QRA0B+gRs372C32+D6tZvo/AOcnpxg2S1wenKCT929i5c+9Wn88je/wq7vMYQB5AmbzRoxDLj//kPEGHF0dITT01MsFx2ePHmMyBF37jwD3y0QQsTh8XUw99huLxBiwC4MCDHizrPPgLoFtrsBznmEvJPRB0YfkpLcbPucr7hOKVmAOidQJ8BZ774AKZREA+zCkH70YDoAu2GAixF9GLDsFghMoEhYkAeIMXBAAJeYY2Gc0p+syGGE6vg7ox92KU1mTjNbxlHkVDvuWSsE643TwEbGL59LaW1d275bg0B+l58eKQtCiAHOMZbOpRR8IqCydB/bHQVH03ABEpBU90ZEjqN+KIc+pK5RKWuh2FKSU5CtAaP9vE3Hsc6itaYLPoqRkSWg2tFy3kFnUivv5Tz0rR2guXFoA0WHRlWKFVNBqseQPpoK3lYYTFpTKD+zKSmdKqhI85JWmK2xiMJL/9LwBQiDkqHvclYozlqFHQBi+JD75DtsCegPlvjCN76Gr/3JD3D03N10l0uMWJFHON3g9NEJ7r3+Ot569WWcnZzi9MkTUIjoQPABIKSU2jI+R+NOhc9zI9nxUtfHM1t6boqckfEDE/omw4SEcYvTRk8/A0WuCOAsNwNwal/TthiMlNODu5wgQQwfncYzs2aQtZUUQFlWYrgI+ITweAjFSPHcBkRE+VZkGuuT3/Vt323DdwRdukQWXqVisEi8e6J3PhgNGmW48JyJn9fF9tue22sV/Z3ekWkZ1zp7mD3YX81zbRFlIDeKAwv6CmAyfbOAUIBLaOzCt+QKg+HITeZGxtg2TrgKpWEedZcYxCIPpD0LJm1I7timApGghGYRwdwjxnoHZ05GlrGRwHMuRjYjKlpPz0bY+bT1T3YkqKym0ZjPPyPzmGYZNKm7GN9mHVj5rWVx5bhSpdbXcZQrnJwHpT01VS3azQLkJNSKc0UuIHRecvClURNlavMom8Sgb2GL1lyK8W3HVun58uX4nDhEWmHNpeYZzGBpbd/Rn5fv88/lagVwvkg76xCRLS35Y89WF0ODCClludm9YM73s0wx3b5yZUND4ul1uJJzDiEGkCccXltiWG/x8P4DbHc7nK0v8MH9+4BzWF9sMoE8NusNnnv2BTBSuFLf7xBy3eebC8TIWB4cIMaAEAbcuHEL64sLxBgwcMSDhw/xu1/9Cp594Tn8d//9fw/nO4A8zi42eOvd97A+3+Lo6AhMDoGBp+fnCBE432xxsN3hgH3auQDh/sOHOD4+HNPbRmC73cJ3C2y3O8TQY9ilywL7XY9hCCA4bDYBYQiThb5YLBBCwGazKedEYozl4LwtIgBFGHvnEmP4LhkyPFr+lHcnRgDCxRvA4BweNioz7aUvQqRhELSYXAtibSRob5+EO0mxAgmYZlQQhdDadrPhCnohlUQAVjCyGGsBm/UGuHZzHMMe/td9tQe0dGkd3GrVVfoKwAoLS5OqPqAC91c5AKe/03M3zjWKkcFQ94QgYXF2OZxOeebEdNlX2lul6d4FTYvyTAaKrUOJljb1vGIyphY9bF/s9rbUYUGj7T9RrTyknUjAzgGO0yV8AgQIDAqEQ/ZYO2B9vMSdz3wS3/7jH+LZT3wMfrEAwoCOHGI/YHPyBI/fex/vvPI63nv7bZydnaDfbMH54j1XlPXUGSA/7TrVxYbqFcVJCQa0Yri1XJEi82Prq8OnAH1fhf4pcmMSBqppeomCl2da89j6W+rZp8xr0FOHEEx4yIxHCqVOTvoxAuga5Ou67Pj2tSUyVu/kzL1ny9xYgGk63jl5pH/fx3fCC9HU0wKuLcBo6y+0iDHJJ0N/DYLmaKDbaY1F00E7yOb6l2s1dXJZA1pOtWggfZoLeax20yajmRoP076N9djvGPXatuu1xVfFkDNOqEJzc1mQ6Drd0j5a2Plm0UszYNoW+WwuZEfXb/uTcNj4u7TfOktqaUTFQLy81GtkurZn+d7IpX3zpOmh1404lGJxprgRC1Abn1m6Vcb8nrb/LuXKhsZ6vcZqtSrnMpjTPRdHR0eIiNieX+D8/ByPHz/GZr1GAOPhw0d49sWPIHCP5WqFi/UWznk8PTvHZrvFwEAYAnabLRwBDx88giPCtes3AAAhDHjyaI3F8gB9P8B74MnJCU5OTvDpl17C7Tt38ODhI0QmPHnyFM4dYHV4hPuPHmN5eIS7zz6Hx48fI4AwhIghMB6fnuH99z/A6ekT3Lp1DYscPx2GiH6XDl3vdgOGIWUiCH1f0tkK6O13O2w2G+x2ByVvsUwaACyXS2w2m3LGRHuepAijayAdOSJyvpwuH9hKtyKnbVbvHCIPBfI4l+7rcM4nNIRaiDNzybClt+alEBycS8w9DEMlzK1Q1wtA5l94wSp6Gz40LpzaYCn9ICq7KhMlr4SHNYjkM+ccnE+GK3heMMwt+ppuI32qcAaipvAu9ZnPbVtN42OPkuP0x4zQoUa/5wSDEiRFwIuXhgqIQkNhXNaGKF1NI0sDu/tlgaGuV/ONBaX6ZwskgkeVp2m+T1gX80RNbDWvnL3UDHTkAUYKZ3QOF45w/LEX8LUffw+f+sqX4JYdQA4UGLQdUha0h0/w0z//Czx+7z4uTp6iH3qgS2Gg0QGI6VbjOSvPhkVo2sjftt/VWtlDs2TaTEHZXEk0TXKp1Rd93sqCbv28BWJEbVA5Po9mHVmTX4H/a6+15qvWTmuTDpQu4JMMakXmFMdQG8C3gJb9XvdFdh3Sgd3982H72TIGgDE0Qq+/ag5MX7Rh3gKH4xim7gm73lpy3uqGSmYo+TAXPiXft2jZMjg1sNROD70erJ4a+5vGOc6F/re/zAHLmvdl7LUMsPrtMj6Q58rvZq9B2moZahoTyA6BrQ/5W6FFrmRiZFzW1zYPtccxV8/cGrN3VrTmcy7sUPP+NBSt3tG4apHIgZZu2yerqvloyDcrUznPQwqPI2y3WxlV4anWurM0adF7r1yly+WTLlc2NM7Pz0FEOD8/x507d9IB7r7HwdFh9vYPePjwIbbbLTbbLa7fvIHtdof37t1H1y3gu01JIfboySn6oU9bXTEBeoSI87MzcIx47vkXEGLAdrPBnWeeRT+EdKYjBoQY8cabb+LTn/kMvv/DH+K//Zf/HWIE3n7nHj54cArXLeCdx8PHT4vwds6hW3Z48Ogpzs/X6PsBu90aZ+szHF//TLphuh+w3fbYDamNYQi4uLjA+ZMncH6JgR2GIaDnAIQe680am80KR0dHhUaixPq+x/n5eWVktASMLJAKOOT3mbIlPvSlbpKQBLnTI1+Wo4WoTH45p2GE6ChkAeIxA4XsvtjUvdIvYTphWJ1OV96x3uN6kbliWbdS+zKPuzIWJBJRtWNjAayIVtl1IxIPdC1M5rbfNUjSW8e6b+n36cVtgMDVqSCwQkLPMxGVPNwjjdSY0fYQjm20lSMjhUiBs5HpBJhls4IURGCkXY4chOSdhzUCpGg+LuPKlemD1uP8TYGnLVYBJ/7iSrBboGaFZWkzEWwyd7rvkzqBKra24kkGlpx2NIgTzw6UwrXctSN84fvfwZd+/9tY3rmOHgEuAqtACCfnePLwIX7z81/gvdffxMmDR1iSB/oeHcmt1jEd1svGgISuWTBg51fW6KUH9xqAU9NLcLqlkQbQspYkzDNTCJL0YE7xaaeKPjhp19M4nykcRa9rKSFMs7jJe3L+7DJlZ0Gb9WhaulnQSZR2kO09DVZx60srtTGj/57bOdV9LfHRBnhKuYrxoudhXFd1KGFr3HN12v5bQK9pNQew9XP6vWoHi9qGn6bxHN1adBojK6ft7lsjLXmVPkuGNpGA7qlDxrZR8VMDJCadTxPTpaVH7PcthwMgw24bgnOAEpDd7xEnSJKXsZ+ogC2F0diwckD3sQWUy9zT1EAFppksW/1t0cjiB3m2nO3iaZp++/s+gG35uYUpWvRtrY25umUce+e4okHeF8/JM3S4YowRjmsDqzVWeacVeWCxq1paVy4fakfDe19ius7Pz9F1HfrdDovFAvdPT/H06dPU2RDw0ksv4fHjxzjvH4M5Za3qug7Xjo9BtMFu2KFbdthtdzg7PcVmvcZuk+7a+OQnPoaPf+ITePXVV9F1HW7dvoMYAz54/x4WywUePXmE0/NzfOGLX8LJ0zX+5qc/x8nTc1y7sUS46NF1HZ6ePkUMAcfXruHatWtYcrIyh4TEEMnj/GKLR0+e4va1Q4SQjY2+R4iMIUTce+99vP3aa3jps59DtzxMOxuhx7JzOZY0TeDFxQUODw/BzOVil4uLC9y6davKmGUnV77Tyk/+i4zkKcvvDGHAMjMehZB2PxCrm1E1MxXFp5hkGkbClUBpKTS7iGz4QstokFJZ8ahTBlrBo5VJS3DP7gqFiAjG4FBC8CIzugY4uUyBxYZyGt/ZJxgA56dCzyou24eW8ii/pw8mbab3ACgBTzTmjgehbJ1ztmM0sAZEqbEaUjJw9fzouuf6aJWE/ukyKG/RQT/b8jJpYWvp1Prd/tSg3SrAiYDn0S9XgQ9muBhBziN2Dmti4OgQn/jSb+FrP/4Bjj/yDIJjMBOWAfCbHrvTNR6/+x5+/td/jXtvvYOw2WIJhxh28J3DECIopnAz56ic4+i6LsfQTvuhx2rH3lJE5ZnGelS1VTxU1z8azZa2wuvANIShDczal0cCOt0jAEzB+1jHHrDRkKtjB+pnxfCx61DTb9brqDCbNURkDFpWttbMnPJu0UbTufVeSz7a91s7gnOFQNVZw7l+jX1LfGLHa0HY3Fitrqr1TDvs9DIg1+ongJKlsdUf/bzm5wnPxuySIAciD8YY5jsHpC099ve53klvPSe/W53clGkzoVNXLW1dnO/BorzsGrtVf9+yTx/qndMWP+7TBfK9XEuwby226omYGgr6vZbzR3SxdTq0DLLW9/by6VbR2KYS51mWOVV/9az6XYq0p3f95su8DJorVzY0nn32WXSdx8HBYbqw72BV0twe+HSR30c+8iI269u4du0aPvGpTwJ+gWtuBUCEODDkBb1YLgFi+M7j2rVrODw8SGcPImOxXMH7Di++8CJOT5/iYLXCndu3cPPmTWy25wixx+Mnj/HCdouvf+MbuHHrLg4OjuEXK/iug/cdrl2/DgLQLfJN451DHyKWfpmI3DkAAx49eYy4uUDnPYYhguDAMYURPf/88zherXBweATyCxwdXwM4oHOMbjGmdD08PCxgDwAODg7w8Y9/HM65Kn+yVmpaaIzfJS+xI4cgYTtIWS9CSPd/MAi+67BwhN2wQyQGD7FSugKygDozlmaydB9HBtgqdlXncLaHvfXCai0YwKR/08xIdUDTdIsSE0NILwgLSK1V7vLFZqNRE6p6dJt2YZd2MLXUx2cZ4LYnmTBVCHZh6/aL0BKDwAhLSD9mgFy6z6DeYXDOpdoE4IOTl98IyDnDSV+mqI3jfYaGBWfSzxhrA1ietcKs0M8ILU2vuR0WABV4jI3v7TyXtojK+Z6cTmg690QYHMAdISw87nz6U/jaH/0QL3zus0CXstB0zMB2QFhv8OC99/Drn/0tzh4+xNN79+ECQJFAHOG9Q3AER75keiLQeMg6RsRsgGh6WO+7VRR6/lv02Vd0XfXcjcDZApu0mzHfloAvCzatEi48QgQ2h7qn81d7R6s0xsxNQ9WuG3vuQ/fdnkezQC5XWNGo5qWc8W4GhFiFPld0ncxtwKSftZ/J37JmWsC52Q9K/+QGc1vm+5+N5dg+g7DvYPvsDk9eF9LXufdbpfUsM1fnSDTPt4DUFPDlfwSk27yz15imstyC/8v6PQHV+nc1dsurdf/Q5le2pkYbTNtCQNqpaALozI8Sglj6095t0e1Y2ly1TGXTVNcA7XNqVvemz67c9N7xaAdY29BrG0Bt2dJua24c9vsiE2OEnJesNDzVOqWF54A018MwjE4vl84PtvpMJP+7ermyofHjH/1hakTiPdWg05VpAJgR8yHplEHFIYCKp1gGN4Sh9FOy+sS8Td51HZCzCDz3zC04RwjDAOfSCflh6BHikA5mOw/A4Vvf+N3ERNnjQJTAuTBmENBJCcTHyAAxhqEHEcMjA3XOOwnOYbPdAreuwX/kueTxl/CJoUcIA64dH8H7FGKwWq3KRIgXQC4atMyWQp9ivjZ+XKhOYlpAOVVnCiPxqVJg6EExgLlHJAfvOhAz4jDApyOqYI4gHg8/xSh3nKC0r3PkwwBiGyPfUvxNkJ+VW0vo6tKK4weSCCOXNDaJxyQbXQIEbR9iTHzjM50657DsFnmaHQjtrFYC7LU3n0pK0Kk3qy4j8ClbxpmvNG0sgIvlWZ6AWSv9KuHVNBCEdhKSlBQgURpD5Ho7uwUCWsB+3yE0LagExAAYw1cklXDeLSGX6UgjfBfFnepKw7bCr+WdbymxJvjK7Y9EQjEgHCf+SsYdSjYnMINzOkzPBJfz+AcwBiKcO49rzz+Lb/34B/j07/423GqJgSIcGBQDXB+xvv8I7732Bl7+5S9x7733Uoao3QAHQteldegXfkzgABR55DufjQs0i95hmgMxLeN5/H0Mychckng9Jv7R74xtRRD5IkPSGTSRIQzm+r2WId1Srnp+dR+ToSFzKeGOY9ij5l8dLhlDHI1q8RzKOqD6vRa/W4Bg5Zq8V5SyAcBjvfM7pq3npf9TEKT+YbojZz2NbaOsDTz3yWWO3LzdOa2VJEkkXbs4VEZ5Vtdrf1rZJT91PH01pmx8M+fziLJmeJQd1gBr0UK373ztkLG76i0APr6fQn7FgaPXkpVR9buJryVUR8LlRxhIRR60boDX+tjKOq1zLR1af0uxO1wtR1/BBcCUNrnnzmUnqMyfwha6n3Nrq1oP+XvBQuMr4w6bxiFzRkol/1i3K4YrQ9xvLf3R0q/MKuuWkidWvk3GVOpp82dLn7cwkZab++oQGaRlr+y0FbqhLZukXuENMTJKG6q9Odk2V68tVzY0bt++URaqFZR68JYwujMpuxMDWKgFsyh1SYwYM8E5rya2Q98nAwMELBZLdB2Xi/pagk5ijZOCGy/yA0brDVipBTumPVssFgjxCLvtNt3hoVKDxZj6sugcKO8A7HY7MHM5AK4Vohyy1rQpsdaUQPLIk6PnUPLYE2WhFBPAEa9KyLnhPRxcziQUYmbW5N4tMa9WeLSEjJ3LOSZvKW0ZUytMrLSLKWNWwjONDGJ8FbFM46Vw8k5pOx+m9eQAvvyCLt2OPCag14K1llLWiLDen2mDek4IavwbKGcmRAG12msp55ruI33GStLZBlJ902tC6rCAQ37OretCNwOK5HeXjeI0VtkZGVOmWtpouaS9r+OYp3SdA1d6PBNxR1nAChgSo5UgYchpDJHzu+nukugdegL8tWN87Xvfxpe/912srh0g+MQoB0zYna9xcvoYT95+Dw9eeQtv/eplbM4vUopWoSEBgQB4SndWQBmBWXH1fQ8iyucg0q5GS3i3lJulgwV2lIFReVx9Frg2YLR3Nj1PCCGqHYy2opEdKlFu1ps+p5A1eJbJkn7GyHBuCt41DbRREUUhSv8a77RAaYueFsxbAClt63mRZqfKf/y81f/WLs/Yh+Q00DS0IRj6c91/O047ZguYiKjIzklhZHg21sPqfAKbPs3p/jkANZWvqVE1lRgNjBEw6TnS9GgBuJb32c5lS8aOdJJnFA14P/gSs55BWTy7nOVZ6x0BhorYmPLZHGC3Y7f9Fz3T1GNAk5f0fDVlLajgDn3287L3WyC5tM/JyUyk52c6F0Adtt3irfS8/jfyiGSdsrSsaGZkVmnbjXOyD7BXdFW6rmXk7ZtX26eqXjMG59J5TLl7Z7FcYOEdzs9Ps8tmugPUwhYaRzNnx0pjqII+9uGsVrmyoSHC0Xqt9GTJwg751m/mlJlKBsk8ghnZ8pEByiT2fT+Jx2sBL2YuWz3yN9E0X7BMRuuQpdTf97uiNMsBqBw7jUx0eb/rupSuloAhG0a73W5Sv4xPLwhmLnNnFaCMTaAwkYPLlqojQh8jmFO/ogC7zMAc2wunBTQrZYQ2U7c+s3227dmwsH2C2Ap8xFi8ZC3BMdcXT4RhCGBKt7U/fXqSgQ5no6xRmIunrlXmxp6/rNq3dNF8W94tc1q/N6fk9HN7+2L6W/7GKB/mlPyUxtMQgBZYkjrswfAWOCYZe0OhaR4Uuo1rdD60oUWLOWBe/Z0vakPMa1n7FtmBvMPgCP3KY90RPv5bn8d3fvgD3HruWbADIjE6Bng3YPv0DKePn+Ddd9/CX/3bf49uFxAutmOoWFbCc0B7bi60TBIa2/lvgjP1rpXLWrnq8EidgKI1J7odHUqpn2cePX5yAakFAPscFfpni0dt2Jwdq5Yz9m/97L4dSiubNe3quqe7ffZZPf65tnSbrXHZtafHNgdyJnd+mBA72wfm8fxeeYamjpNWv1tF97El++14rQ5p0aB1lsY6ZWx2LD0+3YbeaW+tE91ua+yWN22be0vFM/WYmyF/mPKBlQ/y7j5PN5ddoLqvrbrq7jJAbUekHhKRmFKAVaR27dvSkgWaZ8vaN4aX/N7i67n65z5vvW/1mqwRCWFv6UWLt+pnRiPS8rLlx6uWyzAXAJycnMAT4H03YqA4vg+gcoDrsVdzRvM77ckImflyplzZ0NAEaS1eUV46TaoYG1p56thNq4xSaFK9AyCTLulPdRt6C7alCDXzjPSrt6916lqtOLuuS4ZGHAGAPqAjl8RoD54YKQDK2CVbUtlFSebghKbMyQyPIWJgBntfLo6Ti7NiTOluHQhe7c6QEQxWIGnaVFuujYViaWfrnYKZOkRptpjvqn5hXjHCxIDquQ45fIpz9YeHRzk0bWha42Ucajx2nLOCbM/Y7DsVSJkZX4vugDKuZ+g1t+Vdfk+VNpVVRYMZBdqK37yKgp20YwCnNrpbYG2uLeHZFsi2wrsFOED5RmoAHadcZJJRttz27Bw2nrB47jZ+/0d/gJe+8jtgTwic6d0P2F5ssHl0godvv4c3XnkFb7z2KmiIGPoBnfOIhBLfbMcnfdIxzTaO3hpv+v2W7N03HwIma7Ozpqn+3cpzvbsldLdzRZScQjKvmm/0O1ZB23myxRka2rme8+xXa07x2T6ZNAd4dT/F+A2hdrRZuWfpOlf0Orbtyffg8bZoC05a/GH7sa9d+y4RTTyUhWYkYY7z7en5bfVxjl+b4KYxjvrnfmNHjxUY9eacvGzxpP5c02yOn1v1jkZF3UcJQav62JAVwneWn+2YZ9cSA9W2LabzK0DaOkhLX5VMkDo5Oz5TGv4UdUGOipGq18WcrtNtteatjEkNpyUL9O92bvbN+dz60LpG10s0hgw2d/1MHQXfonZot9Zuy1Bo1al/t1hBsHGR20Q4OjzEk+22hJ9J1imtR217Vu9zlNDnmn5gBtP0/cvKh7gZ3E+2IeV3KfK5xHppA0ODdPlcwo705Mr7AKrdCnlGE1ZPnmUUeU8rdCGmGBJi+CwWXTm7oFO1WmDAnMIdFvmAOWj0+C2Xy9KuGBXynY1J3bcz1HUOYRfAGA88yjPO+bzLkheloYGuX/4W2o/gQ6WyhEOk/ecxdN+sUtHzavnCbuPLYrWKxefb4SU21wrgFCfuq/7rfjjvyiU1wi+SMtMaKenL2ntnF7nm8aqvzHXYkylCD61gnXOTvROrdK0SaYEoy+fST/tZwpUuHwyb3sFgaafHrOu1wnoOKNjvNIAKmXaX5TfXijeNqb2DOadsLgNfQhfivNPAABOhR0TwQICDO1ri81/7Cr7y/e9hefsGdp5A3oGGgP7iAuunp3j07vt44xe/xv0338XTx4/hnQMxp2x1MYI6n9LgqjWo+5XWPCHG6UWfdiya1i1A04pbnspCmdvp3LVAsvyuPcU2A5ydF6voxnFOPa7Sjg090p+1dp3l3Rbo02Owv1/2zD4gJO3pfrbqJRLPXtsJZ+sUXbAPXKfvU5VzckGe13Le1mN3Nlr0sGC2Bab2AR07Nr0GLT+29EurzjqMT7dd+3qsA83WTURJd+51Yk1/b8m81hq0dcm/NLdiqAH4//P2p8+SHFl+KPY77hGRmXetfQVQVdgbQG8z04OejT3L47xFJtHsUdSzp7/t6YNM0jOZPkgyoxn5hkayh7NwONMr0I3GvlYBVaj1rpkZi/vRh+PHw8Mz8tbFkJTDCvfezAjf/fjv7CHYwUmwbIy+5+ula6oYJV/LnK57ljDn6dqna5xniicSgYzecTmNMsYgZpKUl4bvZhhi3drn9F6fWclcHfjKfG3G9lIOktdh07E7La9zDAs9bS/kdDt8ivyjtA/r9vm6kp/lwWfeB1+kVEgEqEmk7yQgUL4HIoZK6HWcH0ODPRvblooirnna2dDyjTQauYor/U41Az4BGAr8XAIE80vJOTdQ42jnNX67MQZlWQ7qGQN06whqvrCqYUhD0zH37eqG1/H6TszAmqYZvGuMQeu6wSJoe9qvnJinC5P+HQEaSTg+Y40kBiP5XyQMJtTnRKKQm2jk9eYSIyUI0SyD/QpBGSvpOyepfNPx6Pyl85nuyaHkwA/WIK1Lzdd0b6Xce2H6JFp17bBcLkCkkbaGMdcjEQLBGkKXZTbXfT1GMHvivf6y0jrSdY/1ZWYw695fIZQjfdC5G/RrAFyG6/A0jZN+lpvq5GPK52msv+m7higkETpZiqQ/07wszKv9H+v7mPRprP+SmNKAHYew0EBjgbYgXHzpBfzuH/8IF5+5LsyCMZh4gq87HD95hId37+H+na/wxYef4PjJPlzdhIzegAPDiesuqkATTACfOaOR0iHtc/r7aeYpXW89V2n+hnX7Mc7DCN3Ws5326aTQijmAyIVEufY5pYcpuBgrOa1M2xnryxj9GRvr0+Y1H9/47/07A3DCvfQyfye/A9JLPqdz6Typ8/O6oqYPuVBtrO9jbYztE603m6GV59fN8zozt7Q/J8231pEz0WPvrKzByHjX9eO0z6Tt5+MfO0dpvzQqYF7lU+n9mvtUy9h6jzESAHpBJVbv5PTcpowx0Qlrln1uaFVz+bSSjjfPH7ayT7OxpQKMk3BHai667g7M1/okOnfSMyeNkzUCQFZfOldPtU6gIQM59qzOlWhcCW3boW1bKP3wzkehRXrOczo7MgqkA4jzDBLfo29YvrHpVHrJxS6NXDIDsJ5cZmPENwV8VVWJiVASsWkMrI9dJvq7gs8xVVe6yVPtBRFFhkd/ei/hdrU+bUO1GgBWtCv5nK0SQ47c5brDY40Rh03dkGR6RiSYC1GcS2CduCS3ndaia2jIngjk0jnL/x5jLPR3BSuDzb0mTrj3Hi4kHkwJ4GDt3YhkBEMi2XUt2qaN9FB+jlwK4WdZlqMXUE5ctE9EBPh1h3LYd61LPh9moB3bk2Nt5nXn5y0HKzopDj0Ry+sYa0s/yy+tsXfzvoztmYGkcYRpS+vIpa49c9b3Y0XSsgb0EBBNJdSkTh3SYyhbInhj0FpgdvEc3vzR7+PG996AnU7RhchlaBzqvSMcPXqCB3e/xMcffIDl0TGO9w7gW4kmxQR4aRCm7Jn3wloYYwdmlSlzoSW3kX/axTcG/MeYiLF6xtrQuc/PLXOvNUzPW37W9TOlXWOAaQz8rCs90BkHBbrfc4Y3/T1tb2zvj+2fbwIe8r72oBhAEvJ37D4aA8S5RH5VILDKsKTAII0Ok89Deh8PBEtPGdMqqMaKRiDVPq1b27H5XmcmchLjOQbOhnO0Hryn9Wv7Y0IkGed6f6Ixuqn15vRLi/RZQuXrMp50Ak4yoxqrW4Wd6bPpGWBmwNDKvsnv17TEec60XP33/Y48aSxjTEDafr4P8jHH92lkTCPzkc6brPH6OwLohdsnlfysYU1934R+5OdBz/D42V8dW77P9HNjNAKs/CuKHnsbonh+9Z38PkjXIf2cgYGsI64VQWM2fKNyakYjbUyJWCpZVVOkITCQ3vSMh+iE48R6mQxrTJQW+64DkosnXwgAK6rDMaKdSzsVdOv7WoiECxyCQQsFqRJpkaItog+HGESwpoBGSLG238DW9IxY17Xi+R/bE3MaBeIpaCQDdC2DveZ6BIy1cJZDCGEjph8siisdtyUTTZN0fOn4U+mBMjcAwETwDPhgi642fQwEs6xx4pfXlRM/neuUUPuwH4hE2u0p4ZmJomP6yiEA4OKch31CABsT59Z6SJJFYjhilAyATEhYlzK4gWCyiZeArkscOwXVN/XrRSQRxlIH867T9QsEDmJKRyGcIphDlBSI+3EcW5gT5ii45DC/AxJDvVNxulf1OzYUiHEIpqQEwwAWJp41awW4a3QoLekZygnz6gWRgIGwJrp2StCMRlEJTnA6RkBBol5eAHReRsBN3o8cDKffaZ8MGRQhAEDtHbwJAMlIyFrbGXhr0MxKNLMCb7z523jjd38Hm2d30cKDnYf1QLd3gMWjPRw9eIJPP/gQjx49wOHhgQgGnIMt7ADkqe+HCbQPgcalF2qq4UU49/lFHsdhTW8vz16YcyIUZRVoj4fnDiHImswjKNIUBoHIAsTC5KG/mMZM4rQPKniIEkpkzuHpfvB9iGhOaT33OQsIwmTqPom0KN3e6M933JPeD9pK94Wa4sW7IRkHMNxL6biUNqX7Rn/PtXj5+30/AO4nXaSV1N+18dLX215e7H9PPo89JgJgZK1YEkOKAEo0oCqM0n7m2qAcDKVnJKehuoY9/ZD/eaXxSMdKA/rOGPZjDLTos2m/0vbXzXHav7T/Oc1L28/38xjwzBngtK514PBpAqD0s1xomtYvzwCADzQ41TZS+E61YfpiX/c6GpfORTr+lOEYYCAaB/3r1kM+GBfoxD4SSfJC7QN6OpSehTGtydha5XM3YIjX9HcMF8Z6WXLaBDCknjKhAbmPx0wbU2F43keJrjWcinhXmzAn+VmL/ernNN5HJHdzpPPJGNcJUsb+1s/0n4dHEfKtyZ2MgBWTPmdnU8eenulBWxr9FIIVg54mCoXz/XlSOTWjoVJ+leQDQ+1ECi51AEqke0DWf+5DLgn2PgxiyD3mdr6Ufa7/xi4O7VN62aumhXmooVCwnDJQuumqagLvnTg+WQsTzMHU6duadPrChc/isG2TzZ9LgcY2tVzKJEnnIBcOE8O7DiaYZbAbOqCDaOVS0nmKTE8CINLkgRxAIBkLglxuRu1J/arZUXootO9j6s90bdLCEEaqtGUEC7o2Yxe8rmmYWhAZwIW1iJ+TaDskrm9IAklgJwnjPDM8UmmwqjTFtp4SABDjePMQQER2mSWSQ0rgpI/SwbGLKi4slICGd8MQvZc1jgd8sJvWlwGDkv2t0g1pq98Dcrmthr/MiXcOIOI8JyBySJB0XhXM5P4H8hZR/7z+nmsr+vqGfXxaYTBaS9HJG51HYW0PwicVXFXg0rdewG/96R/h3NVL8OzhmFF6Qjuvsf9kD/v3HuDuJ5/jwZd3MT88xLJZRiFJqsWNl+iYpiGMIAW5g4sHawCPLhwLiPXeS/6NMKfOqZYX4W8Ha00PYpNLRWkRRsBKCiZ1XOm5S83dUq1kpKvhzK9I4ULfB4xVDmSSPsRzhYRJSH7X56BnML3Mw+c5YNIyBiaQ15HvoRMuTGYMHHm1//2Z96tr+tS9q+BMzo/QGhmX5pQaPJ2BgbG+5+cpfT63qeZ+9gfPDuYx7MWx/bNS/wgNz8+4fpeC5NG+jgDk9PccLOV3RjofIjRcnb8UpI2BppTpyffGOiuAcWAfxu8JKmRSJkNf9xp2m1Y1evm49Jkcu6SgMQXY6bhWgfAac7rBNh65j+WPvj7m4d2VzGc+77r2uXB41RqA4pyMrffJ/eZEE5d8xliZwzGwnP89dpIVT6TjXTEfzEgKgaIAJj9XqfWJztPYeUjbi/Mb23fY2DyDra0tHB8daIvhihj3C0zHPKBh2ZqCgrDHSKJOXiVRJ5ZvZDqVc6hjf+dmQCnR916cpMuyFOmdk7/FpkwGX1XVgJCnGzC99PUi1DYUvKcS9txROTXRSpkL7330CdF+qISeaNhuWtcYwc3nLIIS9LkmUmYp9kcJGxAksQYeKh118H64EQZAXbMbn+JQpz/T8epzxkiGbfa9Bih9Jh9TStRT4px/r9qg/LIYO+S5ujsyp8lPQM6x0YurY8znc3SdwyT0VwFfvj55m8PIOVh5TsbG8dLSPsaxGTGnGYMqRARiGqxJf5jRRxYbudDWlZPGstI2pW1TJLbW2qfa4offBqAuf3Zdv/MLPP1dH0/30hCcJODzNPNCQFdI2FrjCBNYsGOYqkBjCZNr5/DDP/4Rnn31RdCkBHtGaS3cssH88QEeP3iILz75FHdvf4knDx7CqBlV0kf9PWc40p850Bjb60TDPRDnMwE1urfato1+bmNmZmMXkO5j59yoD1d6PvVzpWuRXmb0I21P686llmn9K0KGETA49nna/5w2je3RvI30ks5/P/VeGilEoqUeE6CM9SPtd/qZfv60krLbY/WdxGykey2lX5qTSZ/JQWfav5QZScHZSSWnNWlfUjCsv6uwb0gXhiArvbvGxp+fzbwvT1urvP/533n7+fycZGOfm/rJe+O+VGk5zVyve2+wB7CqmU6f/c+pPy8Cdod/p0B+bL30ufwOiPPOvVN9fm5PWtf157wXPj9t/vOx5TQk9ikTHKWmavl+THELmZ45SJ8hooHlzUklnVM5V6JtOjw4gGsaAEEbs8ZX6CRaMmgj8h0c8RZhHOucVE7NaKSS/Pwga2dTs4D0Yk0lF6nJEHiojo2gEmIypAMcAzlpFCzth5oMpReCXqIabjZ1Us8Jm0aK6s2AOI49jdi07uKIF3ewm8ulhdrHXPIUGSoDcMcCkqwN8ncOWY3FsSed2/6SXyUCOh6injFLNSnGmMjgpX2JxJV5JVznOgCRamzyeYn9IjHzyM268stJP18n2RmT2mmsa2UMI1NCq2Bw7MJQouicw5hJhI6zdU7WAcHMJUThIGPA0TsCo5KMsXlOiXPOqOXjHhK4IaE6iQkAkFzo/XhzsJtLeCIoML1UaGyvp3OUXq7pOcnPgDDNQzvnvN+nATZ9PwjWm+ikDWJ0pYE5u4U3/vBNvPTb30c5m8IRwYLBncN87wD79x9i7/Y93Pn8C9y+fTtoWUMfeSiYSMPzruvrmElhCq7CzMX3uq7rL9osH0J6tig8P8jayr3GIe3H2J7Iz5v2cd2aI7k00/6kl20ujU77rLmR8u9OAlEn7fu0nTi+0VpWQfTYns3beHoZzuWwP2KiOFZfCqRW+7B6tvVZoqFgJ68zH0va1thnDI53h36WC+XSuY/WCcZErehYm2OfncTQpZ+PmfLlYxt8l9Uzxozq72u1yxjuj5xGpWWMHuf1rJuPpwFZnfMeZFM0GcyjkvV7Ykhnc3PAwb0Y1lxLPs51dFduM4ZoW4Z7d2xNY50YXnlp/1IBSTqvuUXHCr1Av+YnrcHTPkvbGNOg57TlaSD8afRrwFCM0M+iKOTuTjROeh+n76wbb04X4h4NKrK264bMigCilf7nGHLdvClTMQw+NOzTacqpGQ01mco3nG7iPqt3bz7DLNIvBfa6AeMF54aSdu8l+V01mcAm6dDTwY+BL5XOpkS0B56rNoNpFKx082n/NOFgClzT8fb9HS72mClRvoG0LW1/oP4Ew2qW4LARDRk41ww2VqrR0bbVBjcHO9pe2vfUbCK9jGPfkYTAzZi59EDp+2PPpuNnFgmF86sHKSf8+UHXelNn/Egogt2/JdGEzTZmQPi9aZtoBrKupAQnEkTTm5wMngXAPg332ft1GPT26enaM7NoMxJGcHAJEmKit3QucoZN+0eCQAAeZkvPAdQqcBmemzGGMF+L+Jn3AI3nhzgJEKbfrxLv4fquEqtVMJWPJd2PNpj9EQxcadBWBs98+1V8+0e/h60rF8AuXFzOY7l/hMX+IR7fu487H3+Kux9/jnq5hGdGYS1AwYEz/MvPQkrvUu1GGhEvnwN9PnXUy4GSCgvSsekestm5SNdxoFnL1i4HI2tBe7ZO6ThSMDgGEtO9rv1OtcN5v8ZAQw6A87Myts/yPZ5qXNKLO1+LsXkaO5tDEDsEKSrA0XUzZty3IP07B1x5u0Pgx0GIsSrMGT8vGN1Xg3FntCK/d9P+9uvrV8aQjyetawyo5ftg3V5cB2R7ICWmrakQMaUHqYBxIB0fmaN8/sfKSYDvaWWMTqXt5XX6kT49bT5yBmRwL3KA/iP0NTdbG6y999HkKO/PupIyG2P9yMF8ulYpPopzccI5SescO9/raE74Mtyd4+NYRzNSnKXPpVXCjJ+ptB85DlSTxHQ+xs7j2NyN4SNA7mlmD+M1pK2D58RCJaGNWnINz9h+A8KU6fyFT5QmnvZ8fKPM4Kk0OiW8aSbwtJPihGoGgFileCYseiopTC/uHKymErSVg5qp6VJQkEaWGpM45uF2tZ62bcN7Q6fqVPW7rj9pn3JioPXo3wNzJfZgw4ANPjE2IB0WBoTabgg6QzuGh8QtvzjHDkLar5Rw92uVSZRoKFFNy9j4tI9xHp6icMvbGut7TmiZGOh8lA64TsxFxqJKnHQgBvOTjC0lPhJJiILdf+Dqqef2RVkQNE96QMPaSbjdp19a6xiAASHwHrCKhJ8+tv5dIJ//dYRF34tnygzVzuuA4kl9Gba1fi9oP9N1PknqAoQoc9bCFQbbz1zC7//ZP8HFm8/CTEvRTLQeXNc43j/EfP8Qd7+4jS+/uI0nDx7BNUK3yqKIqmGG0FRraLAHxsCt9lHPRnqJppeq0iIFpTqWnrmnFf+X/IJK52CoJRnOcb4eqfQ0nbuceUj7k6533tYAACafr6M3QwA07G/e1zFAPQpeRsY8Rm/zPo/1K70zUoZpMF9Jv3NmiOgkprkvw/bHz5BosAIdGQFd+fzoHkmFR2qWpP2zxkY/l7R/aV3pfR4ZRRqe03x+9Pmx/ZWWXDuwbo7SMQ3mYw0tHNtX2r9UeLeurKMnpyljz2r/cxDNzAAPfeQG7wWJxhgTNAYsx8D2ytmSD1f6O4aT4vvh/hvDQ2N1hA/TFgff5//G5iunqfrPJ0kr07bz+cjnauzzfj7G52rdO6cpY++N0Z11ba5rb2xvjq3FWCnLEo3vQBzouONRWpKvy9g5ImMkEA+n7fV9yZUB68qpGY26rqNKxnu/Elko7WR6AecXrlymJu7P9BkF8kIUPbqOV7QS+YSkkvv0Quy1Kr20LffRyEsKbLRdrb9pmijFdM6B/VDlpW3oGM3IBTxmVtJ1XZ+0TpWQYS46Yglta22U3qcERucUPCREuZnX2GHWEvucPhPrX1V15+ZTOQOQq8QVYDknGQfyNR8DCjnIySVV8bCBQpQoAAQ418F7CW+a6F2FeK6sdijZ4fVYvehkAoLWCFp1kBgBUftEgfHg0B/dpt6HkZMycErz4i+DfULRUTQOrZ9X9O9zAspPGF76V9/7McKXfUeg6H/idU4j+Ag7djB/WUtESV85Sthopf1U0tT3Md9P/dzIM2RCpCcw6MwW3vi938Xzv/0GMKvQGoOi7mCbDs3eHHsPHmHv0SPc/vRzPL7/QOhXSAbpieCYewfypF9WI0rF+eyd6yisJzAEakQUzqyP47bWout8BKVajNEcOiTzY8Ts0nkNQU26EiACnOOk3ThVcb4iaAHHi4aBvi9hoVK6nWpj9PmU2dOzl4PAPCt4pLO6jxN6m4KA/NLMaZTMi+kjTQHRhK/ffiRRZUnOF4PjXBBE26zrlJy2SJfHgEHadvo30erZSMcO9HdBv3sx+D32jCj2i3koJIv1p2dlBGDkQqxUqJOeGS2p0C5nqMYECDGvFQFMPS3SudPzS5kwD4S4JiuMFJ4uAU3vlrS/6Xf5faG/5yAz3s2n5x1OXdYxVWPATWlg+GD0Pb03+r/lkvAjz6frfhIoTu/Xk5gVfRZI1jV0KGcQ87tf3zlNyfdjKkBJ92I8i9DrZoj98v2Qz08+N/04pcYIoLM5QGz15JEN1pcQQ7gr1snxVf5O8uGwjfDnSWu7bg36Hkt9ER+SmjKvujnk+2Gsn3GOXDBDjzRQ6hzD0OvKqRkNE7zN67qB9y7JCLtKoGVMIaSslZCsNly8hbGwIRxjxz0zkJo/gSQByWRSxTak6OSsmgToZI2p3sUxUiQ7iECd4uUrwDq8QxJyUEJ2yoEL1zzYM7qgVQBDwtYGxEckzqh6GaaLkB7YFKwTiZlPf+gkapUxAqcMAQYlCmthTQHP7QrzIJubwYEpENOf4AtRWLE7NxJgl1nCRxILEDHoD216UJgZ0Ig2noM0H2CWcLgAYMnAi9FQGDOBOIzfFBEJe+cAY2FgYjjM4b4K2bMpAFpwkCSLlJmIYFGgU4d4COgAA8Yx2BjAEgw8SlNI2MuQ1TLIiIN50hrCEZFLIBwswFVtVRFAP0MStKWiEUsm+vx0rkPnXGAyw3pqyNyCIuFko4dVLuUIbQkwnOyZIESIhFX7yyzhbCODEcLlsYLvACQUfKWFtO/cM0IsalByhIKC47GsagAagCfRrsm+S2KzM4O8gl6llP28diHkrSHqQacxkqWbCxAIhobMFpOTSGGsMy8CFc8ATAHvgIIIxhJcaVBXBs9+60X81h/9PrbPnkHnOtH8NS3cssaj+w/x6Ms93L1zF48fPkJX1xKlzAeaQQwLG88volbKw7ODpQIwSEwNOPQ7AYVgGAo0jBlOD4mRc2atnENbKp2Rf7JNpA9CyPuLSpiEoO1lFvaKgcImGhMDODh4cNS06ZgEKZi47t4QGIngIASnFImX+GTBC40HhQgoYT4YBt71AEgdApXbkV0oWdG9nk1jYnhFoQ+9cEn2sY9bxoR9rgIXYWoDPQjBEsD9bvbsQxCIsEMMgb0KAsTMRpgtZYYB1amayI9I4k6EMTFLiMjUdIRIaIEwLRLdz0j86CEAA0uo8HB3+UDPDBiWWGhK2PcwVuaUIKcstBGdtRNGg5lBMeRxmIYRs6EUMKW0fAyMp/+0nrQ+Zk78GY3QNSJwYQF0KNijYAfrDYim6NjBGdmLBh7WSyB2DlHP0ihmyvCmd/Sgf8n+RCJ8SPFPziCuA9Oyf3twmYK/FFilArH0mXUgPgfw44CXAkYJBFTvjFwooO+zgkgOZ6Q/V+AcDA/fT8cyEGDQyUxWCu4HppAQ8qHXolbJEge/30dxrXqmWPuVzmvaV21XaWmOhVb6PzKufI1zUJ6bIab9MDYYBJj+/or333By0dPpVewQ+0MKczKGbYRZUIZ8yEwLRvEBDFiykj8tGbeOR7FxKkxI54SC6TCzR+fETD0eoIzBz/fTuv0l3yW+XeiZUWOGwZCeVk7NaCig8t6jrvtB63dDwhZUNQiE0TNqV8uSFYAxiIR1jENjZhjbS0smk0lvcmWGId1yNXFKONK+ddwGkJo4KlEA5MBgQYEhcyGXoYngk73aXBcJABmC9fTfuug+6eHzXiKDeO9jm7EfFKSMGZEriiLOC9DjNSKKiXe0fr1A4xz5XgOThvTtzdSQ1KmHjaE5FfoDRtHPwHkvuT4CsVRumkg0D9p2agrH4VItChs1RxptZxA4AKsH2YYM6mwQ1YNQJskPCSDWHIpIUjg4TKb7UNuK89rXo3NsiwIbm5sgK8719WKJrm1lrVjJVV+rpaTucBEJOMRgHZmFuaB034TDDh4SwEGOCo9EKzMcq0EKSpQYhovFGnAgesLkhHEyMOVJEvo49D9k2NZwAtpzBbwGhEI1eNo3AJaBjoDW+sGZStfDBGYPRLE+UlbLAp0BOuNx9pnL+KM//CEuXbsKB0Z7fAw4j7ZusTw6xr0v7+Lre1/j7v37WC5rCXteAGRlLmAIjl0ARAAbE8Argdig4j5RY2FKWSMTxhLzrki3HDsYJhQk0eIUOAEEdIC1JRrXwZseSKV6q4INCrIwIccLkw/MAMn+DmeY2cOQjQxlwS5oO/1wL5EAZ6VhNmxdZaIdexmzZ9EKEoHD80oniUXgQ8aKdMy50AdZJ6uXetjYkngz7C0b7nHdz5SMmwAfOVIPGIDIh74wPMm3pfeyN+NekOKZwK2J+193t5wFj9hURKoUf0hOorBmspEFbBDgYYIghgLP3IOpEkFzRojgUc8mBcYBJPOmv1swiiDidx2j8wzywhYi5MEho3eMMClkqJcqpEWHmp3pdcA7jQxGhgJ4HAdnedF73gPwlnDp1nO49MJN/Oq9d7C1McWlrS0c3nuMr28/ErrNBHIhTxGsgGzqowwOQH6mTdExUKRt/bjGtOdxjZO7bMD05VqTjCnIAXA6H/lcriuntU2ncH6Ff1wNpLJSIl3nsL96M87VR9czT3LvrT4/9nuqKYqfE6IFiIZaXgdU46kMXU/ndh2ze1L/0zZOWo91a5Bq+/L3c+uN/ru8lqxvCQPM6Z7OsMkYUw8kGobM0mdsbERD37SU2cjnLG3XxPNteszIPuKbsXnP9+AoPg0+pj48L9Y8gDHrTcLGyjcKb9sFj/beUZoGnFa6wPrPcZ9IBIFjRhEkahkgB3oTDe8RQ+GmTEa+OdcBUf0ZOWdmsHMoy3IAsHUMudq2B7N2sIFyjUluNqDvK8eXc+xpH9P5UlDunJf4/MaAit70QKOGxL9T9V+m4syJ7uBwIHHkC5JXzZKtn+cq03RO8z2Rjik1EcvnLB1zP0dDcwwX1kfrSMN76lqkbXsObQWThbbrRJvheADQT7oU0vbzko5fMaP2O+3/crkUqarOA6UXxAlmW0DMMq0AsW9btIhp//P9nfY/fp6tR/wOIs0FEzxHOBmZRlAwNWEOwC4QKDYglOGZMB4O+jAPTDLOTIENLMPbADwJ0QyACwGOxAyYFBRKsZ5gfJ8oTLVRJjjddeRhtmf4/pu/g1uvfwuWGW5+jNY5dI1Hs2yx93gP+48P8NXtrzA/nsO1C0yCgK+whfhdhX3uglTckIEt9CIADFlYTMEcNIEImhhjQJbQcogypnuMxWTPkIWl5Dwwo2lbGFuhrAw6I/bHagqZ7TiQVUFKYHoY6Cyiml6BBCDmXtbJuuZAgsmBTCOL4hiWGRZGNH5gNKYVxkBuqKDN4wB+C9kbHkEwY4WZJdGy9Ge6z6vhvIMnGZO1BmxT8yMamJJK3oBwGbPMnSERNnSdiwymbNheIylCmMAUmZ7RYEWoLMIjk2+qQeH+mCXAikik8CYcXELwywLBkkjrde8rJxAZycAbMAPEvXmwCWeYyMC7DtbomVZNzKoJk2wp6vuG4bnnRAOYg5+Uxit90t89u8H3gxnJ9mG0BPAeRVXg2LV48Xe/j1s/+gGODvdg6yUefPwFPn/4V9hgoGwYxgGeDJwVTRllWnwt6b2n441MR8IMjYGg/F5Xq4p8jvKxjTEX+fw9bU5Ow1isvqf1a/9Xz2lu5pYXaXYc5I+1HU1cT/nOGLhUTJTvp3xtonl6kjw2rWcdoM7Bfm6qmD+/7n5+2lz8Y74bK/lY4r4+4fmxOzrHI2OM0BhaWM+UhPrkqdBOgjfD3fW0sY21038vLUQYRHLvnISbxso3MJ3qCaEyGWmSkchZJTb1zIy2btCwqGM3NzcDEOlzLKfEqDcJMDCU+Dxkl5RyU+nkpCZYOUfJ3APPlMtcp40Y3QDZRtMEgKpmTudG/g3Nu9J51DrSv40Rp5uyEJWP4z67p4JBMmZgExjfCxdTSnzT9Ugd1wdMhFk15UrnbpTDHel77nCf7pXc10Lbq+saVVXJHCWS8PRQqmTNGDOIZKP7wpIBm2ByYQ2KSgCx5/Adr+e6070Rmcwwj6PjJxFCgoYHXfaHg/cJI0Uhq3ckG6uSPflU2ZCwfkn1nkXaPMYs5fUMGB8MJSpxPgFQSMeucwNmkZ6zAAUihGzx3IfQBYNNi9i58B4AwAIumEgoOOtNT3wwHVJpL0n2Y2tgPDDj/vkwA1J/UPl7MNjInhcQa1EUhFdefh4v/s53QbMKi8UxuG7BTYdF53H/0R72Hu/h8YM9LOct6mWLwhSYlbuoChNpiw1AHmC05OLZMmpCyYA3BnNTgKMkmwYXKwcNnDGmz+XCjIaUIaFoskjGoDUGjghs+0hziDyDmNkYg6AlNeKbZSS8MIyJJne6Z2PGWhf65SRRqDIjbdugqw8B10nAhNbBdQ7oHCwTinYObtvAwEm9zjuhMUborCcB16L9IBiyIggBg6nPB+SYYUwB4zswe5QQzYwwq6IFVZ8EAL2JEiRiGDsHOEZpDSwBmq+uLgt4m+dYSSWwPS1MhRsGNoJx0mcBEANVR8LkMqIm1iBoIbjXAlhrw94UAZDwS2JWG2krSaZfMr22xRQ2mDzKPjOBznpv4NtONPn9QV6hC8aYYHu8Tlo4lFaP3VX5d0JD5Tyvo4f6fCqgqqxB13kcPniEX/zkp3jhd76H6e4ujvY8dm9dw4/+2X+DX/z7vwU/XoKcmG54NjAWMIlZdE7DUjCbrqveAdpnfTa9Q9PfV/y3Mhqp6z7AFhluyEHgujlJnx/4Eqx5l4iSyGH9Z+vWLZ0X/V1NCE9bYp38NPFW0sdkXGkf0uAWQJJjByPO/QR0yR23jllM2x271wbrA47zl/ZzbC+NMbJ52/k+yZ/J61/XXtp/2V+rz+VzsI7hyseV7td1fc/7C4gQz0L3+Ug4aubBPho7L2NYSbGMJqEmIpClUwtx03JqRiNlLNQcKQWWCnIj0SDC/PgYzbLB/sE+Njc30bYttnd20LoOW1tbMdO1lmgCRavSjpxIpBdLejC6roP3HlVV9U5tCECCelVUekGlxDW3H9V+pKFwUxCsMeN1bsqyDG2uOjilGzQ/bNbaoE6Xi5fZg6yBBQNNH6mry0BkSphTkJ8zGzqeYfQuAH6V6I2C4pGDkppCpc8URRGjdqVznTJo2mf1b/CJdCpvb5XZlHVovWRKdl0LQ5B6FPhgeCGNXQwrxCUZXz5GuaQRBUW634lEsuHB0S49oJIAvhljNF/3CNAzfBze0+/GGL0xIpmb660tNpji5ISPgUJBYARhBmQMOvaobacdEGClBMkDxokEzSRA2FgCdRYFJgCR+LYQwdrARBMHyXMvFfLeiwM1LLrQFhPEJMczds+ewauvv4rt87vYa2sczp9I3pumxeGjJ7h/eITjusXB/hG8I0w3NlDunkFRTdBWJXxRoKxKFGUJWBuYGqAsCUVZoKoqVGUJa8Uc0hYWVNiQw6Y317TWwJQFilkVGAETaQBRYApsbz9bFgWsCcIHY2GpiFJuNc8hArxheBMcboM2Q/dQ9IkI209M4ELuFxajMlYmCIB3Dk1do1seoVsuUR8eoT6a4+jxHvYfPsZi/wD28Ah+uYRvO7i2AzoHY8qwLxgMB2MNwCHwhzpcgGALC2OsjMMYgAwsALARvxYU8G0fXpyMDQxnCG5RJIlEwXAs57bzBFF3C1NSwYCd0g4B78we3jPIdPDsQNAw44Gx8Qx4C8VommRTaIYIqaB0UaMcEoGIYbkJjKH8LVoYK5pT2J7RNgXgg2Fa2AOGIPUFwQ9Zg7KownkBOj+HoRZWGSe/evfFs5sBkYENfdgzwDjIzcF3pBuZ9jgtOd2I9Nx7TI0Fd8BHf/MzPPjyAf70n/33uHD2Ig72H6K44vDmP/0RfvYXf43myQKWREPV+/Wtgk9F3Wnf+7uqZwy1X6lZtP5cN0atV+85/Xwsn1XOlKV1aMlBeP5sCrizb5M513UchuXVn2m/clMw5qFD+Lr+5HcbM/fCnzX3+TpmoOu6iO3S58bM0vV9zxzOzDjoz+czB7ijIJrWMyFpvfkarrvf87nT98Y0SicxHWl/VYgy9m5a1mGP3KKD9PzQkEFZt88HayNOdDDGoixL1PUS7AOmSjBLXtdJZ4AomFJ7ETQpTtF9lT9/Ujk1o6G+EHrwU7t+PRga/rbrOtR1DQLhP/z4x/jyqy9x49Yt/OAHP8DR8RG2d3fQtC0qO8x6q5PnvYMhO9gU6SZPD1T6TOoLsVgsIlFS6XcaSSotSjA0r4XWm9YZpZChpH1QYA/02h5Fl/kB0WfSjR7BP/ecpyEDD4oaDGOMmAQll48yUiYbU9qeEo60L5E4Jg7D+l36bHo4x4hb/ozOY5pTJWUA9TlrbTRhM8ZIFvTk/dxETtchtevVYq1F4zs479B2XfAcJvDqeR/t92C+IBL9fL2cc8GZefUiivsvMAaSjZMic6HNjBEtYVKCM2kwMSL1EQgmGWMXQl5H+i8d9solbwpwIu1iZYqI0PggeeUwliABNQzsOk2EF0CvSrks0JQyc8aaaDJCBHQgNLYEFRaeABhCa0Vr1xqCK8S/Rc9dVVUoyxKmKFBUFWxZCGNUWOyeO4vzFy+gZY/H7AAQNlWj6B02XYer5QTlZAZbViirCaqyEvPFwgKV9MNYI+uomVkJAqhVMxEcmUEi5S48xwWkADI5bJToc6BrxL3knAd7NLlYwKBI1zmaITEL48XDrZ3UQP1lAaBLzpyhsDb6bNjfmwCYLwjQYoJlwDcd2rrBo/v3sf/lXXz12ec4ePgYNF/CzZdwdQs0HUxTw1IH5ztJhsk+OJfK3gQZ8duwIWSvDWB7UgCdk7n2PiR8Y9EAWQtjLVqle+GS8/AxH41PLn3vPYw3MGFfRrCI4F8DBgXpHTuR2DMEHBNTvNhUQmghZ6uFxJcHERwFrZqeVT/raZDVABos+XPCuiktMgXBmiBwC8yKCZpVE/ZYUU4wnWzAFgbe7qFtazljrhNNk+swRmPlxxob9jV07aTCfaXxjh6jfyvvEdCRh20JO63B4sOvcPDJXWy/cBXTzS0c1ccozu3g5T/4LfzdX/wVqpZRsQ1gqde8DGhX6MsYPUsl8ekdkN7ruYQ9B2/rQHj6vd6fYwzL2Ls5vc3HlL/DHBy7MVzPtB8nAbQh+Fz9bqx/6T46Lfjr+9vXmaYbyOcmtUoYq4NH6ls3vvwuHzBXav41Mo4BKA/f59qv/Lm0//p8zjCd0NkV7VCcF0ODPbRuH+ZaxrSf+RgyiLGCRcaYL0Ok3njRd88EDXo6L2Nt5udwgCWYh4w+CcOc1neqOcQ3NJ0a6yQHFXsK4suyRNu2aNsWn3z8MW7cvInHjx7BGIOtza04KAXoYxwqs9i+TyaTFal4iuLSbOQ6QWVZRgmfSxYwJzQ6njRxnn6WHoTcfyOdk7Rf3nM0mQJ6ZiUlkKlqPmWEAAiA8yGqkFEmQxcZSTsJNx6AQB/RSWzA1f9CTY7G/DUoOjXSSh8DcorznF9wjFUCHbVQzkkEJmWaAjPlwp5xnkHOwdoi+GwbRLMFQzAwUSJmyMCQlbjaoBg9TCJ0SHQksgauabVjEgEnRBgLYmORPnAvGfYxRFt+svuz7oMpiYAYD4JE9EqfiwQ22NOLQ3x4IPzotQCqvu8l5GpA5IOZlAJ8JCFxEfY8xy72UnZQ7/8gxLk3S1TmABDpbUsGCMCIgWgN5ZnQ2UJAOFE0GAEROmtxZAuYEPigiMxBiWJjCrdRoZpMMJ1OURQFJpMJyrJEOZ3ATipMplPYSQkqCpjSoqgqlGWFsihhbNAEACjKUhxLocMwYEvBh4IBa9GCYUEo2cCGrOytIbTEIZKVrJVHf9kQMSovznLiII0YJYhIzBvkTgviVN3X5OGtBj7gaOqkfzMlRFnXhqUfdkC8h6GjmXy4PwmeVFMUoo9xcmGH+SdANEDZHtUflkPEKB5KmjwzWitmPJ4JjgEzLVFMSlzavokLL97E83/wJrrjBZZPDrB37wHuf/ElHnxxG3j4CF29xHK5ADsL9h2Udy6ohJp5mkBbrLFwxsAXJQAGFWU0G3Lega2BN2KKZAJTagIN9FZ8lFRYQmRCDH0Cl2Vgjnv6VRSF7EGeiNbC9IlTAQ70cAkTrODUf4QD8Nt0Di4IPWIgDWaADdBWcJ0bmC8wM8i1KLpFjDSmYF0ZTGWwjREmQzVnk2qG6WQT1hJQzVDXc3jfYrlcAM0C6AIUDVr4sP0kEhXzkMHU9WU9uUkJfVgP71ic+mk1o/sY8Iljt4QlHCZUoOoY7Dv8/K//Dm9e+m8xKafY3N7G8f4hFgXAWyXa/RoTJpAHGGa0HW0jjin5XvF4CnRy4VfOYOh9uI4JSO/8/J30+7zNsd/z+UrbS58xgcEWhkq/XwWJYyW/ozl7Pm83mi+GeemFllgBradhAPI5HDNhWxH46d4Mv6fNpi3mdefzlq/bSYzgmCZj7Gf+TopJUiw2lntrrP70b3YM0HignxyED9Z0zXjH6klLjj3jWigmpl7gz+Fz9hpSBoO9P8aQpn3wHCKGpviFEBTb/XNPmzctp0/Y5ySiT2FszCkhjXuQFfBTFiakKgcMMaaTEi+9+BLufnUXL738EramG5jaUgCj3C6h0wKcFIQVZbhcnIPvxNvRBqdgdhJ8MzIFAIrU18J7+K6L3LVOdtji6BkA3SCp6Um6IXRC+8yv6WLJwgw5xqIIJhHwcEFalRIqjVLlPfo6Q7vGELwTswDHDPKMyhAMdzATK86ntoB3TmxhHaMgi5YZgINnAdpkTNggYv8stv79RoowhhnsCMQmgPd+47KTsIwaIUkvfwDBdj8kO6TE1AkKjMXR1YRL37FHUVUh9GMJDydRY2Bhq4nwQ66B4RaKMn2wm9cVM7Ag9CYXjGDqYBh118BWYn4FMphQganzEo4VIk2tCfDGonTA1EnEI91DEaCHA2QD0+WjU2eiFiYbpfne+T6RHSDS0YxZE7DAYrEEBqMIjh6y8Wz4DwZBoh2k7Ebs/MlDpPomhM60FMxKLGAMfFGACyNg3BDYErwRUC97rUBZFiiKEqYsMN3agJlUKKYT2KqELQsUE9EekDWoJhUmkwmqqkIRTI1MUYg0OtSZ+oOIPT/FcxYvmzjEYGseAbzefyYx/0A8x8I0JUQngFuE8xMCg8LBgW1vI2uhQXwkLK6FXnDSoCPEMKkJaZdLUcMoAtEmuG84MCGDjnFwYFYQyPpE/JnqlfTy7avtw04O7y5COnmstCp8ZwbPDkYR/WnSNpmMMDzcP8/x+dBcaVCd2cRkdwNnblzBjd95Hc3RMR5++AXee/sdLO5+LeGAicXfxhKK2TY2NqaYTktMN2aoNjdQzTZAZYFqOoG1FpOJMJNFIfuPCtmvCGdLhCzB7IgAtReIQ1AO2FCMftZ/Hi5CF/FNmEe9vHXf9S/JNMi6mf6F+J6uA3tEJ33nJNOu9x5wHlw36NoWTduAWXwO62WNuu3QtB7sPHzdwtUNuHMwjlHaTcw2z6G0BD54jOV8H66Zg4720cyP4JYL8HKJou1g6iUo+NA47sRPxUv8ellfDqChl5Snu857BmtoMc9B2ho054yY2yQFPHGGRv7mAJKttWBD6KyHN8D+g7v46q13cP7Zc5g3eyiKCjuTCf7oD/8A7/7kbex/9RBTKoFEwJaCwlT7n96PakqWg7CUpqZMRdzruk8AueeN0BYNz50espMYnTEmIAeG6XM52E6fFeECVFwTmAw76nOQ17sCPpM+p/M4anaTnpWUQV1T4n0/8n4+HykwH5s7g+GaaQkeXaP1aj36LxW8KrOvzw+Ye2BlTwCr+3gwjxju/ZQRGPNRTTo85Jaykvcr7mFCjP4oQSXCfLBqdA18WnGCCzTpsNabji8dU8SWQJ/eAJLzzgQcmnc9X+tebiogyAfsq8GHUozDgS4TSWTENIH308qpGY3CWhS2QBfsadW+PpXqy3zJIbfWwnUOf/Lf/JkctHCRumA35rwDOQazgvw+H0DXDk1u0onp1Nwm+5dy21ESQoSyqgYcvzzT9WApOzg6lpxj1jLcULJEMtfKZGBlE2tbJgB/o7byQJTeAoi2wQjhPT07mbvCophVaA4OA4MkmiRrJAKO95J0jJnFsdEEpowMKhZJlAu29GIOIO6YnZX5dC7koFBu18gW7chFbYeaihAQ/R+iVBc0SCjoQ5hLPVQuMGwWnUTDIYNpYVFZj847wHkQldIGhQsSEsWHLQlQZAbYBYZCxlF5iykm8GyBSYHq7DnUF85gWbeYHi1RMWEOj8n1y+CtGVom+KXD8uAAi/lxXBddL2KgTLQectCECfMENIWEDO33QQDZQcoeL7Jexi3amWBiQdYKw6ymO2WBdlKJJqGQKGMC/iew0ylsVaGcVLCTCtVsimo6QTGdwEwrmImYGJmqEOZhUqGsKlRcoCSJFGTUjCP0tYSYNfgAvB0QgAxipJ78HJwk9Vh3NsKTynpGQh3wLSJixAAf9w/lf3L2MYXLK2BzSoDmWDURjGdlhQivPLFaUinzWGH0TE1ea2TS4zfD59ZhgpGZPunLWOtoNwfdD2se9gCMQXlmG8/89rdx8ZUXsPfgMdgzNrY2Zc/aAraaoioNbMECfo2FCyZglaGI/pkZbdNg/+AAHoyt7W1UVTX0RYh9WJXsAeN77DTfrczHKevU71dAAwOWbIT1afFGTLAsghO387AgoHVwHcGYEr5zaOYL7O89wvzgCfaePMLRwSEOnuyhmS+w2D9Ae3gsvnhtB1ocAU0DblvJ+cIMYoZlA5guAlgxNxWNLqyJWnwKQqZcKp3OxRgAHQORehcpX12B8Jt/+BnKtw2a5gAMA2sKbE12UB/MUXkL58SEVSXFuXlJKlXVdse2fgpAgd5cW7WqEXMkZsSjjMjIGNdpI8Y+H2MKBmA6AaqrwCsVmfXvpJYcY5Lt9Pd141k3NoSWBtRlpB3FcXlJ+5VKztfeDcqwJ1YTsR3CgMjneyDXRsWQ9iNzkAt7T2KiTirrGJLUFeCb1D22R3ohRu9no1Ygip0Y6xm8XCCwMq95m6RCdT1vHk3drWTuzs94/Il+v6uLhCU1h+53E510+Z1QTs1oqJo5B+H5wdSDVlUVrC0wxyJGQqrU9lpeBCDckzHil6F1pOZQutHruo6hTl1mlpPanKb9SJ9JOcM8okJKVHThcwlCOlZ9p98IoqdPBBDx+VQCInUC6uyZtimMkGgAPLEk43LChHREsFUVE6lZa0QdH/MnWKg9MVgvGQAg+MKjg4NXEyDuGRmAQexRFIAtxOSJiAETGBYwVNMUOW5h1XX5AhOpEjMSJi7kAzG2Ny+wRICRiEdkDEqDEGOeRYKPQuK7GAr+EAHIoBNH02AK5VDEuPPWTAEQOvZwxsOcu4Dt772OBXc4/Nl72GiBRWlx7vXX0JzfQVsUqA8XuLC5hZ3tbSwWC3H6VfTlGV3bSr6AIP0kY9C1Lep6iR0jtuDGBP8CkGgMStEiEAid67BcLmGNwWQyRVVNUVUbmEwnmEwnqKZT2LJAWZaSdbooUFQlikq0DiACh6hDhOA3EYCgB8Sh1gdzmYjc+4zmOhQxfwraBBEPwYSwvwKGEXNJseLDkTOhv4+dd/l7KNVbLT3s7c/GP45YPa38466dtOTX80lPjo+BwxlNq4yXZvxf2l765dP6duqH/9GFCWhKgjmzgXNbUzx5vI8D54NvBWEKj01rMa0KGCN7zJGYO8KHHBHMmC/mePz4Mc6ePYvpdBaEK71/Wk9LRQIMnAycVi/yk6Wk68ppGZSh5I/A1Ed0GzwnWTfh0MnZLEjMdUthKh0YxBbl7iYuXtlAYZ4TOsOMtu3QLhsc7x3h6Mk+Hn/9EA/ufo3F3TtYPnqA9vAI1Dj4uoGvW8B5lIYAdJIUkjxg1acKgR4PgUoOVsecX582D7qmvpNEfWgZZsnY4KAxh0eDQxgHVFShpTRfzKpNfHp3ppqBnLbkn6d/D5mhVbOs/5ySA+qx73O88J/T9knMkCbjzPuzjkGKfcz6m76XMkNj5j3pmNf5ZJxmHNoRxvqzm69p/M4MfQXG5vlp/RoD7WNn4mnjWleIqHeQXim92Vzah5yByN/NAwiNzX/e18HaIgnokjOEybNRa4RVOhHXhAUXiM/MyQK2p5XTm04lA06dmZ1zsElEJo02RESSB6G0MDb4QVgjKniW7M/wYmYFlugjynSAOUooNEqR934Q9UolJcb0oU9TO8VcipISudyhPB/nmEot3+T9z5QAqIqRo+03uFc7gpVoMJgdvAvMlDVBU+HhXBsdi51rASrApoCBgXUE8oQSIeIXd/COYcjDkoNE+zchk3JwzAahA8EUkrXYa6hKECon2gxrLay3YtIUbN8jgFSmhBFU0xYoJHykMhIMYQzFlk/WgkzvY0EhmpbTubYGriwAW4Ith3kwMRM2h03NAMgJwNH5tszonINzHk9Ki7YiwHk03uHefIHZ9euwFYHmHssHT2AmU3S7Z7CcTODLCmW1haWv0TRzsGH4rkVRlJhUFYqiBMwMNkjjJtUEs9kMVchQX02n2NzaEmf2oM2z1krmdvRSxN7gJYyDBdiHD6M6WQ86IN93OmYCSudROsES/YWDWIlmESeiLBeFE11ZYPA4cL9EhI5CyOTQD6QXVVJDTojXX2iUvTkGhlcvYebhsycByvSZtQT3BALYj2/1/RWpTvYzfW4APryEk1U6orTIey+SKhpK6nrJXxBKJECK0YM/Strrg0oM5yiXgKXfrwKeVZX78PvVIudZdqgtCbDAj3/8Nzg4brBz5hwuXjiLl1+4gcvnz2BSGVhDIfdKuOBksnF4dISd3V3MNjagEbTGpM25lO5pe+FpwO9pJY/8c5r6QWFs1AuS4u5mj8L1UkGQARsOZz7k/GCIDxEMGi/BDLhkoCIU0wnOnZnh0s0reN69Ctd6dEcHeHL/Hr6+/SXufvI5Ht75CkeP9sBNi2J+DNM1AHew8DGMrDQibec5EPI5Ogm4DBi48LcP9L8wBq5zmNpC2uNSNKQAnGdJSuklWiLgkEurc6Fk3rd0fVSguU4bktbLoe6xYCHp+MbGPiY8TD8/6bylfT/pmdjJpJykeRmuwfgzJ7YVaNQ6ejfGGI3NywrdW3NWmXtTp5SRESHj6c/w4G/PSKNc5OsxBuBTjDfW53Vj0zLKhHNiXpvRGcVF+XyEVuSJ7PP8Lh27c9J9nCbezOcrr0eCYgzbSbFsbsKoSWAVY+vzkUEZTJqMyKtmbg2ztq6cmtGYTqcwxmC5XA6Aug46ZT700It9uJhJWSNhtqwm4NLJ8V38TobAsIWFLcoVNbuAbzeYQNVy6N/rEvhoH7XfAxOrMB4NjatZqcfqSDlOE7VSHkURHJjhwSHsIlicH8XEmeC7TjYtqcZGHI4tyhBBxaMIzFbT9aEbHTNsOYGxJQwEyDe1OCcXpoBHEyLqpKH8AIBRdQUmrgyOpggXEgAiLLkRx80Qkpd871ROVjK8Sk6KkJjLSQ6B2lJ0kiYy8R0fmCwxpep9OhhAB4Maos1QR1JhegyIGEQsDseFhS3L4BxcwBUFUJSYTCbR0diGCDaYWJjComKS3Aw727A7G6BZBXz3ByhRoDQW1c42mtKCYVAw4GYOVOqaakhRhDj7Yc0CQICqFMmgo5DYkIdSB+MBypI+ypuiMTIB/IfqIjBmGjw8oMlEgCsGX8f3HEoEA40I8k64gmINKwYKzJGWp5qJk4hHerHKflpzERJAxIM5HNTTxy4Y1pGNpCfEYQRKYJXoB3bNh+zYzImURiUxwTbaOSdqbCTBLICByl8lPZHQq8NwuLyVdhSZJicCINNrl1JhDAXGT9rmEOZUmA6GOOuXkwqFLcKZ6GKSOxFG2Ci0iO0mbasztf4T29px4D3ONPZ/W+ckrwcZnN3ZQbNo8PDrJzg6clgczbEzmWK7KFBuzzApSzHhMQQXVJ2GSM5vKXltum6YL2FYxiV2Y309CSinz+Ylpd/D/bvGvj2vFwBTHyYyfd4CqDxFDSJCYkMA0TxCQYfsw9AX14E0eQ0kiSYMwUwMiukWLp5/AVe/9RK+vagx3zvAV5/fxgfv/AaHH32O4/sP0al/h/cog8DEmdV1zX/PGYoxQDl4B2LCChIHUQMSzbcx6IwRk1nv4Qlw3IEtiWWo7+tKz1baXo4hwEOJ7jqAltYFIPH1XJUIp+ubmk8DQ+1tOgc5YM33UF6exrT29MqsfD42zmTyR+vL287XkCE+AExjJj2cmZGvMjzr/l7LzIdtHYUtGbjOGcn077zu+HeypjnzuI5xXcc0jtW/sveyz/KxjjE6Pgj0UouZvh9q4bKemdR38u/WlTFmQz8Xs3yhN8vlEpOiN4VXAX0+Bgr32mi9KjMi0qgyUSg6uH9PoN1p+UZRp4wxmEwmICLUdR0a4YF2IXUaKmwJYh+b4aAG1IGV0xChpiwHYXOb1qHpPCaTSX/5J8RA29O+5IQp1b6kBG1M2pESKP1bxxYv7WwxeoLpB5suEjkgmjUhad85D0MOcC0oJOejgjCpDCg4VnfeYd7UaJ0HQiZiA4PZ2Qs4fLQvJkqe0bUdvOtkjsxMpPPOQeLGJwCqszBkYaiP9w8ItlvAwU4m4KKA966PTFIYGNvHy7fWYDqZCtixBr4qYALYrxT4GwNrCxRWnIzJGJH0W3EihrVwFPwFDGBsAQZQTCuUhUVBBFgBSLYoxKzIGngrkngFfwMJVwCNGrEH4W82QEsGBVnYzsEbgIyA/soDbEp4F5A9UQB7wq0vC4qHT/aGmPwYZhS+Ux4NxC4eRkeMZbXGpwcMk1wAUaNBQOEJhetdOm2yxzpidImqImUmrAPKkQPOBHSGe+1JVgqPAbMRTwP3RCS2N0IgV6QvnPYqE16x+LPkl7g+lyYsHSNWeu7Ts6+2ozk9SM9ff9ZcBPTIHHx1TdPLJxUiKA3Tv51zASz3AScM9+akzrkYIMN1HstlI8nxwKjrBm3biqAGjK6r4ToxJd3a2sLly5fhnMO8rdEE+9pr165hd3d3oNUgN25+ku5RpXFyFg1s0ScO1H+nKoxgVudhigKXr17Dux/dw8It0FGHLx88wJUr5zGbVdIuQmQr0ovJ4OOPP8aVK1dw5cqVSAfzfSVlXPK6bk+cBPjS57Tk7a2zSX9anUgCX6R1OgCdznsCrIlCyAPqWXyOTuosQThcOHd6jAwDcBJswBZCj2cVtqYX8Oq1S3jxt7+Dw/tP8O7P3sKdDz7E/Y8/RXd4BNO0ILIgX4O51wLkTq7r/A5PKlbsXeEg0RDFNgNwkHxFxBLRrSDAsYOHJsPsy6pfTj+PA/8R3/tm5mXdniBlgJJ7YR0jfdo6889OAwLHygCI/eOqWCkn7e3Bc+jpWg789d0U1+S04WlM+4ABSXMorTHNy+n1SaBen0+l62N4Lmdk07rGxjw2/nXj7b+neM+PPcNY1U7lc5FrE9QSAhhaB2mdeR25hY0+l861IfEBJe8CRpF60vQGK4y7jGrQXhpKuv9KiLyYrPdz8V+F0ZiUBWYTSYK3XFpMq1ISQ7WtOAWH56qqQt00mG1uCijuWsxms9hxZpHOee8x3ZjBdR26Tpx8p5MpmBnHiwUOjxcorMFsNoNzDoeHhyE7obgLVGWB6XSCwhbJYMNmS6eQJQoSJYseN6hOIno/DmMM2raNIEP8ISTejYDxPp/DZFoJs6CEPFyoXSMZclnHSyLl297cRGEYk4J7aWX4v2Q8NwAsurbFUdMCJNFZmrrB0jXozmyhtAWm0ylmIQcJM8NUFRAijKgvDABxPN6ewlvCbDYTMzNboJpISFIqJyirCSaTKoAyG5OVwYQkLSTSbs2USzDw8YBn4BIQhknH5odEVtyPgwDEGsk4HPYFcc8AMeTyZmaU7DDRcL3MEn8+4lwTLnoGQkQqCzH/ciZoWizBGwdnPcBO2vElQlws6V6IWgJmTNrewb0fVLjQyIUzp8RSv2ZMXEYow7CJCYW38TMdnzAcFp6SYLhEQHBGt54ldGk6t+GcO8Ng03sCcEITKhfwikpR41wRXPCJie3FChgdp39mFzD39qaqJtcBea8gTT5Iv9OoPcw9gUrPHFZ+D3PEounzzqNtWyyXS9T1Em3TQu35OfRT501ygPCAiGvtru0leC5EpPPB/EnH2rYtuq5D23Xo2hZd8NPxzqFuGnjvUQWBiOucRLYLTIb3HsvlEs45tE0H13gcz+c4OjxC0zZYLBYivPAdCD0zU1UVXnrpJTzzzDPwlrB1ZgfMjHt3v8ZsNsP169dw9epVWCtMtxB3P2AKNQiDbh8KoQgl9wRgrUFR2CAMsFEoAIxL9wBh1BGSKjoGrj33DGr+KdquhW2B+/t7eDI/xvb2DDCQhNnewIVNRZ7QuA7vf/ghLl6+DGLuNaXZ5aTCqqFUlOPng3uXFUAFSXq/8fr1VqAR9+1ApxD3agQjkRkIu5d1d6lPkd4V4TPdbyR/tQTUkOBw1hgg5BwxRNEfTZgJDY4RWnIGxAYMDxCDCjFBBTEqskDbAUTR2s7BgSvC5NnL+M6VP8PlV1/EF2/9Gnd/8z4OvroHzBeg2sB0HeCcJPACwyGYR4DgmAfOuRI9TXuEaCo1ALMA2FDwHRQ6Epl6MIxnWAbgGaWVaH1iHbbqN4mk/jGQT9Q7kKcgKDV77O/LNMGuD35940C032fDkvdvRZCS7alvWgagWidzzXNjUmUBg6drN2ck1Qw5/y4H+KlwFlhlONKyToOgd+UY+FQz7XXztx7g99/pmVNa5zHUWqV1rWMu8r6lgud8z4wxqixd6J3VAxNCJvYwbW04HoxrZVZMALN21zFM+fzrPWTCmk8mEzGfP8GUMDIo2TyOafOQ9oGfzmCNlVMzGjulaBC8L9BUosbvXIe6adEFjq2pG0yqEjNjUFUlNjc3MT86hCVgY0OSIS0WC1hiHNdLtIXBYrEEkWTUnk4lQlTXNuBJgbKw2JxV8M5jamRgT/b3UU1nmEwnKA2BvaiFoi+AzIvkWmAPBwG1RCUAgkOQdBqLfu5Yb+kI3JumAcAwxCD4KL0kAJMqZA8miThalsJstG2LpmlgWKQ9RVWg8R08e1RW3J03CoNKKHNs18Ohg0ThslShgjj8tmEshalw/Y1XcOnCOezs7mJjYyNIz3TMlOx1ikSNQDFkamT0oEzhiiFNUnjlNwV2gmEpXk69g4DOfRJXeWWP94SDw8EwOv8azSlpMEANOJi+Lr0RQz/iDx/GG1ooWJgC5U9s10f6QpAi9mcksUc0CFdzD2IR+9jvrwF9DB7XSnzEZCq8SgSnhzf7vyFCkUhgYi4UknC2aaSkgUQkdCBVZSqg9x1BlkAmUHMIMDNciAYGRsi9EswemNERYhg+7xMzsGBbLsRG/XIQmXClwHE69AyGiUqJkTJwms3CGAvSxJwhrI1jQuc8Dg8OsffkCer5QoAbAAlb6uOmjPkRKNgke/VtgGgSuhauc1gsW4gZu8d8vohEtK5rtI1HXTeo6xp1vUTXiTDh+PgYi0WNtu3gug5N02BZ12jbBoBkpa+bBm3TirQnrJ9jAXdqytXvF1kzSvYREeEn73yEsixRGYurly7i2995Hd/61iuoTImP3v8AH773Hp67cQvXrj+Dja2ZgLzAccrlQiGBXaAoIaIesZjjOMdoO4YxLoSbFZMqa5IQ20hBl5fE6TDCcbDBma1NWN8ADuCW0SyWODpaoL1AKD1Q6IUbGFwm4MYzN/Cv/tW/wu//8PeDWr+/qLxPoG3gkpmB+fxYGD7XinBlcQh40SZ1XRejFTrn0SwdOheESIRgyjmUarMXHzSV7jrn4WDlZ2Imqueb2YmmloZaIAOKYa9BITSl9yErvGZJF6GYJp6syhLTqQhxqqqMwioxaaNo5uDZwVqA21b82iCaTLJlZAiNoRDhTyL3lSXh5ss38exz1/H4B7+Fjz/4GJ++/xGOP7kD/3gfxdExCreE4yUa49ChRdmIsGvJHo6EKSo8gTyjNgLsXcJ8aqQcBZFqKsiBOS+Cf5FnF0xmlX6TcJ6J5UKfnb0HUvKdrFM0uYHQKJjex0D5ohhNOtQjzejdNsy3sA78pBrMuO4Z8F5lgrH271wqPtZerJNppf7TFELPbKQS8nUairj3MQTF6xiwk7QK+bjz9/M5H9eODDVrcg7dAGgDqZWI7jvoNS2MPQLQ597SZGy+c+3HihQ/A+npvKbPDeY/cONy7wUMZeT+gU+C7CR03YQzIIJmEx2qU0yRt58zu2N9yvdwZBg4ZAcIlj5d18Ij+Dwn7xm9qxkgP1zv1TlNvvcirIiY6il7Py+nZjQsAVVhURQT8IyDBK/A1uYmHIskYrFcAAC6tkNRWEynU2xOJ7h//z4ODw7ALEBgYzZDWVWYL2scHx1K7P5SNCT7+wdo6hq729vonENVFDAlwRpC2zQ4s72N6cZG6FUw7yEh+ERi0iXmOkrc5LLxMGK65Hr/jAhSyMff+wgZMvFFUQaTItlQVXAaJkKQrktuERDQSYOBcSrg2MOA0baNgLyihDUTRFCt/zyBnYATbxh126JpOky2tvHCiy/i8uWLsAXBWoOts2cGJkRj6vB0+1Aq2ViBuk8v6VYa31h04p9jX0YJD5/8CmW/jPV4tE80/L2/Lk8+GGrGEA84UU4T1rbP3NdPZKBsAPOQruhly8xwajbCQWOAAPw9h6Rd6sQlwKw3JZJ/Cpb0GfmM0AWzIQX64vjl46XFoWNxH7BgSufSMJi9E4XhoOYNe7AsQyZvb1GZAgi+GGRMX28ABrl0RmeaSOZCcx6wZ3TO4+DoGF/cvoPHjx6jsBbTagJiYFJVaOsa9XKJZb1E2wr414urDTkO6rrGYrFA0zQ4PDxEUzdoHXB8dBw1C3VTB/Dq4DpG17kITGlwrsQ8Mm685Bw5cKJK7neXRobLL3QtBokUzXu0rsF8WaM0Fnv7h/josy/wl3/zt/jBD34Lv/0738PuzjY+/PhTfPTJp7h56xaeee46prNpjBQG6s810PdFpFzClFCQbHnP0ZxMrCCHIcLjftZ1YgBM2NneRlkadCyS8q7rsH9wgGXdYFIIEJdHTXxvd3cHznV48uQJdnZ2BvPQ0ywGvMXDB4/x7rvvicYkSNiuXbuKSbmJRb1E2zSwxQRlMYVxDvAtyoIB7qJ0U5hsEQi1bRv2uKhbjKADtK6DA6FtHZhJmNzQn651cJ5hjObP6TVPMY9NAMZN04JItPeVLVA44PDwQM6KNVjMF0miVIeNjY3A5Imv2fb2NiYbU2ztbGJ7axPTWYlqIsIqYwmOSTKskxOmJIBqYwGiVoA8GVTTEldvPIMrz17HG7/1Xdz+4GN88qvf4OFHn6F9+Ah0fAxTL2Fag8a4uGfYOzjjouYqpV0rUW4IPZ1WAVMGLiUBZr4Dn15yYDhWhn0hqHQ1NW9MAdqY6c4YYEvHMNb+SczIOk3JGCMSfzcENRsf82PI6+iZL/T33xoJt7alZjhyL7hIy/J+p2D/pLKufyvmmxjXTknXV8e8rt6x4Dvhy16DJYAmPjuWgFJLLuQa01ycxJzq2MJfER8MMdHgDfTN9/d8Og5EOtIzgukY1o1ljCEeMH5qUcHAfD4XpiiEvB4wMml3szGvnIMRZjbM1jdmmk/NaEi4Whs32XQ6xWKxCM0ywB5VcMzemE7je8fHxyiDs7FIDWtsb29HNbMlMSna2toCEWE2qbA1m2JjYwPMjPl8js3NTVRlAbBHUZaoqslg4xojuQ6stbEPurkdgKoo0THQtKJOtlbjboeoMZ0LPhMljKFgRiFMUVO34qCJkGmaJbEeQVTFxhi4TiJtubYV8w7vMa2mmFQVmq4BWoDYobAVVGSvknvyAMGgRIkGHq0HyBZ4/qUX8ezN52FLi65t4BqPsxmTAZwuXOHYJtbyTbjS/1JFJf8ATjzoUlT6GfZ9AuyG3tT/5fpFCWEfSOH01g1dEuYgxmGI0lbttzIAPXOBEGSgz1rvlVgzx4yennmYZHHwD+g48VMIFfsAXEE21qmN6qqbwACBc3AqzJGCf/VjAORse9ehaVssl3M416LrWhSFxc7WNs7tnMH2zg5sSLIp/h6IEqBUcpWDCvndx3n+6su7ePvX74JBmJYVPDnsPznA7c+/wFd3v8KTR3uYzxeYH8/RdR0610XTJc8hf0tCwGWONI+LapU4SJuCzTkPVcfEvbMkhSzeFAl1T2w7ZsBSP6f6fpB+D8eo+6fH8Eqs5TvAQaKuNY3D/P5j3P83/x5/99Of4w//8A/wO7/1PRhivPve+/j4k0/x/As3ce36NUw3ZnHd+pJf+v3eUWBWFBbeEXwwq1KgqdGhwmtAYJjKssR0MsH+fCHzDKHLdVOjm5UhFHP/KiBS7Oeffx7vvvsu3nzzzUEG2XS+267Dv//xX+Po8BDHx3M0jZitbm19iCuXrgJMODo6wsHhYTBjEy3T/HiOzjl0QWvVdi26VnLsNE0rJrnOwXsXxQydc2h9C4TLXcNXU/iuaboo8VMNuSHRClNZDPx2rLUoigIVWcys+BlOZzNMqgrMjNnGBrY2tzGbbaDzBbxfouu6eGcihDCvqhJbWxs4c3YXFy6ew/lzZ3FmdxubGzOURQEHJ4EDjIakdtHvxpGBNZLf6syFXWye/z5ufPdV3Pv8Nj556x18+av30N19BL9/CM9LoG1RtIwSDE8erXGSUNWXcY7SkktaxyLXjIG13gRttYwB0hxEadv6/BjjkN5/+tlAg3BCe4O+rmF08vtoTIp8mnfytk56f+zddC61r3kwnrxOYyQZXD436bvrHLfXlTFwftKzkeYAwYyz90UYa/u0cyJCSuqFPsmYgPFwsDkoTyX3qR9I3v+0/rExKtOj7cck1txjFq1jsN/QC+HW34t9O6nWR+nPuBO/TIvktyO09XJlD+Rj+CbMQv+e3HOn2QtavrEzeLphdYJLa2CsQVkER+Qw6fv7+yAjPgPMAtwPDg4ip24tgdmhaZZwXYWNzU3UtUziwcEejBEnZO86sHcoCnGalnb6tPEMhJCkMqnL5VI6HSeC0TlOpF16gVbBuVNU2qqm986hDNlri0oczovgvNy2TbAPljCrnevCxgeauokmKV1Xw5DD1mSCs5vnUNdLkfz5kHCJCATTg0omOE/ApMKrb7yMydYOlm2HrmnRtQ02ZpMYYSst32Sj/GM31moZSkoiIRy0tfrWSURNwc7qAQUy38L+IHOvoj8ts5X+rpdn+n7qgKzPxHcTe/j04tXP0lwzegZkOGq2xeIXgODY7H1vasTBzIP7yaQEjPb9Fwli571EawvSETUbs55QIDUlCNoSFgZCNSDyUs/8K+Pb+ycJ6GyaVrKXE0DBx6MsLZbHx/joi6/QdB3OX7iAW88/j3Pnz6EoS9gQaW5MIqJFLh0hud4D9+5+jX/4h5/iwsUrOD5aYH/vEO+++y5+9atf4fGTJ2Guxa49zn+ipfFJlJIoafViXqiRz8Bi3y++QQZB7AOwqJidk/pCKncwXMIshflkjSkeTEdkB/ZjhEQh0z6mTLWGNe6f7fsFY8Agcbxlj2bZYX7vIf4///Jf4yc//Rn+6Z/9CV5+8QXUTY23fvlrfPrJ53jxpRdx/doVTCYTqc8Qegd9MbXJwU0Eh5bALExGUeg7Yb8lDLw4FzOK0qJzLTov2rJlXWPZNMIsGyS53qU45/Dyyy/j3/27f48333xzsA/SM3V0NMfDh48xnU7x+edf4oMPP0LXSoLRsrLouhad61Z8apq2lrq8gi/JXxHPYwrOwFCTPTYJgAtzL0eBALZBq9iD2AiE0/U14nuhfnYKXsQHzkYzLmsKFEWF3d0z4isT/OOm0xmmkxkuXLiE3Z0d7B/cx50v74FZ/IA2N0pcvngBFy9ewPXr13D27C42tzZhg68EFQYtd2AwiqKAL0R6bYsKGztbeO7br+LSCzfx5Hd/G5/+7B18+tY7OPryC/iDQxgm2LaB61pwYUDWBNPI/n4Yc05N7/10b+eAPc49rT6Trn9af/p9au4zplVYxxSkQVvyPudt5n1Jx7BOU3ESE5EC2dR8L50/mZdhH1I/k3w+IpBM53Wk7fzuSttM68wBczpXuVVEOtdjc5MD3HweYn9D/3NQrP1NJfk5oM6DAii4BhTv9WPJ+69zmoaGzfuXWoSMMWTpnOdC7bgW2d5PmWS9c/M1SNvJ53HdHtVn02hhK/s0eb9zDjsbW1jOj+OeexqTMWY+ls+X7keP9edpXTm96VSizdBOlGUZJEYioVf1YOc7dHWDSVkBxqCaTNA0Dfb392N22KoSR+rz586JY/VkAvYeRchX4DuH+XyO0pgogSrLEo5lUmXMhLoWJ8zOWpRlBWtFw+BcFzg7G65zL0CJOKgVLTrXoChKbFSzcCAYYHFm1s0rIW+BNmRElwg0HQCGDX4WJpiMeO9Q2AK2LDCZVJiWFaqgviogwKjrgkO7LcLbkuuidR12z1/AhWvX4W2JxgV7766DIWA2m4466pxGGqHlJKCfP5eXwXupRzMy4VU8TL30V0GtIU0kmMAtJmh05tBSYvMYTI1SOhKJL8QG28vh8yEcsTBuwqAwElDDKtVVgIpVyX9KWMLAlNkxxoC7Pl+I83344/RyXpWQKHgL0hESjZgl8XFQ/yaVhCtYAhO64EOh8+i9h+s6tM6BQejaFm3XBgY3jLER5tQYg7KUcLxd18V9q3+3bSuau7aFcw7LZY3joyMsQ8S1/f09sPJzrifIZVXg/Pkz+M53v4PLFy7BG4OvHzzAX/3VX+O5G8/h1vPP4/z58zBFL7VKL4lkIXW10dQNfvOb9/DMM8/h3t0HePxoH2+//Tbee+991E0tHh1BySKaAQrOPVmW7UQYL/ydDdvUZhL3RIUcQKQPZlCpqjxu3bROeQi9OR7i3GsT/TfU73dWHiC5cAd72kODDRMZFEEIUtcOn31+B/+3//v/itdf+xb+9I9/hJdfehWPHz3EL3/+Fr68cwc3bjyHq1evRs2xAGAx8NL92Q9X97sBac4dB2lfo9wRxfycDInNTuThvYvOwOKfV4d5pzDWId04e/YcFosFjo6OsBHNXTNGnz0mswkuXrqM2We38eVXd9G1stieGnhuRs08orBBL3eiYDIieYmQzPuAQiUBEYarQEidypSJJSIQM4osjHMERST/iCgyGKGDso5Fif3jxzHiWYwKRhUsldjc2sRstoHd3R2cPXcWuzs7cN0G5sdf4tPPbsP+/C1s72zhxo1nce3qVVy6eA47u1sgY+ChZsFivktNAyoLUGVRbc5w5eVbuHLzWbz6e9/H5//pZ/jo52/h8Kt76A4PwcslLLFEqZH46yuAKQfTY0xFClYVIEbGLgOsY2CKuQ+Nn393mihZQ3CXaiNXmY283XX36BgIS+djzIlY74AxYA4oQ/z08eQAV8O85s7aOYOTjkHuj+E5O2mcYyBYS2qilDML/burEZGGDMfq51pHqgVImcW8P+l3Hozc/2TMsmMs5YK2n2vnxvbL2O95G2NMl/4+xigDCInw+vHlTGk+j3mdaV+MCSKesL+MNZhNp9jZ2cHeo4crfTnNnsjL2Ln3/F/JdEp8H+zANlIAnEicve9g2IpdWOvQdjVmG5uAEdvTjY0NtG0bQ9ISQaJK7WwBIBTWAARsbYqjszMt5schgZ33qKqJXIDWiC0tGcAy5uok2IpmoTATeNdhWoXQuEHdXnuAicR3o+gjVLRtA24R67bWwhqLzomZVVWYyHnXdQ1UBRCyU7MTB0uVghVlAe88OtfBGBLTKnCYG99fcuGS9ABaAL6wuPTMTeyePYfWAcumA5Mk2HPssbExjaBRQ/uOSYr+a5Z+kwHgVae6/pnh3+pwSoTgJDsMTapOgMx9NniwXPQuOHumGzoC6tCWmCrxChHJ+6WAPyX2qTRpHXMVLxcyYA0IEJgF9X2I7Ya177ouhpWTkMYW3nP0JRCGtYMLTq5dJw7HIAq/O8BIuDoXIrsRRNvgvEdTtzg+EmmFZ0bbNFgulzg8PETdSoSk5XKJ5XIZNHYM5x3qukbTNHEMdd0IeJQBDqQiGr2sKitJNkaEoixgLOH2w7v42W9+Be88bt24id/7gz/AtWvX8cnHn+LOl1/hjTe+jWdvPIONmUQ/S3PS6LwKMJWfh4eHuHbtOg4PD3Hnizv47JPb+OyTz9G2HTzkXEpIBor9JMjl7QPzploEZcoGjr4mCVAgi933JWgj88/lT+rV9Ck+JSCV+lvq6xgyGkMHOxF38OBvZgVYDiShK2Lb1mieAoe67vCLX7yNjz76GH/wez/Ej/7oj/D8jVv4+uHX+OUv38bt21/i+cDk9RqOEIs0FD0X3jnAa4JND/GTkXw2DIk2pbQquOPi8pXLuPP1fYAA5z0677FYLiU6V1UEkLUqMb1y5Qpu376NV155ZUV7yMyYzqaopiW2tjfw3I1nUVbi80Nk4WHBVA3mst9HcsGKFgdRgq7aqZShG6yrSfjNwVrzCm3QVwmI2ou4cFCmlILvA4d7IJgCMgcfHIZvxISrj6YEGF4A3mP/UPIVEUkUsslkgp2tHVy6cBFXrl7B+fPn0B0c4dEvf4W3fvUOzu/s4Pq1K7j+7DO4cvUyNrZnIAY6dPDEMN4BnQEbQjEpwQXh4o2ruHL1f8BLb/42fvPzX+DTt9/B3mdfAftz2KaG5yMZzRrGIp0Pnat0jVf+9VM0WnIQr8l5c21A+my8K9aAmzEG4yQpcT6m/9JlBfjSkC6MMv/J35HZ6HxMvrsO6I8V/ThnjsYAZ8psjAHQPDJR/pz6QKV3r0q/V/u16l+g+GpdaONcK5HP7YCpyeYzZ8LS+tL+jP0+9l5e9xiTMLYug2fN8Fzle1d/z03kxs5jnJfORaHu0fExyrKI9+S6fqR1j+3B9J1h/w0MryZgPamcmtEYi1+fcoWeGew6Mf8xhM3NLdiigONe4lFWZdAyGNE4BDtXveyZxW7VGglbSiT2uYD4hAR8grZtUJYSw306nYgqLZg7eHbYmM1iKNzCWjRtDUuFJL4zYuZFoGDmZADfBamdMAVEjK3NGaqqjFJUAOi6Kfb29gIzUsB1EvVmY1Okdd55LJYLVKbEpCrEvrfr+vCOVhZetCQMbwpUWzu48twNlNUM82WL5aIGFQVgGa5rYa3BbGMm9Ufw1JuJ5UX3R09o0m8zxiAwPSvkgHvJkPzZ+xswiwSUeZVQx72RSINZx45eqqD7KDo2By2DmiyoiZFnr2LgMJ5c2uFj8jxEJidR34N7B+UwTpWEOKf90IABwTk4hIWMDIDzEsGhc3BtF7UlCGNpmkZymqjfhXNB09ChLAp4z+g6eU7zs3gv0Y+aYE7Xdi0WiwUODw8jI7Koa9Thd2FSRAuhsnTuUkmRwWRSgYxBQx62LFFNJjFAgq0KbMx2sBns0YkkV0kZHFaryQTLVqKsuYSYEqmkRC4NMoSqLLB7Zhez2RTHB4f45L338b/8L/8X/JMf/Qjf+/73cfvOHfzs57/Asqnx0ou3MJlUyR5QKbQBorkG0LYdzp49i//4t/8Jd+/excHhvgBYEBgSsYjDZaZ8Oof9EDai/Oo5mjUO9mZGRNNdmz42BCYEa4ugCaHBOaHsRQFXgdlgID1ROfCyei6hY9G93wFJbhYi6TcRSehOFj+Uw8Nj/Nt/+2O89cu38Gd/8if4nTd/G03b4KuvvsTDhw9x9epV3LhxAxcvXggMEAHCosEagk/mUCIydTLWop8Z5RcoLJAxBttbm6EeH84dY7Fcou2CEzW4H1tyR7z66qt455138PLLr0ThAClTABYfhe0NLJZLXLl+HWcvXMTBwVGILjMbMi/AQONHasJJif+RTm4G7MYWfwAOoIzGUCjBocNpuFDvNTFhOE/BwT5GV4phnSVKmkpWNSGs9x7EDZp6jmW7CHSPcDyXkOSPHj3G7Ttfonq3xM72Ni5euoArVy7j+Vu30HYe773/ET746GOcPXcWV5+5huduPIfzF8/DTywMHGznUBDQtbUcs6pAW1XYvHUFv/vsf4tX3/wdfPwPb+OTf3gLe3fuwh8xuK1h2MX1dRT2sddtPQxxqXOs661nwAfVYwqm1pV14DD/e0z6m4PjMUn4adrXchJgSoHu8L3U78qA4NeDL040nznTIURjBVDqbajaobToXaqh7KNZUbIWkRKxavlpQJvyeVBzo3Rucwl6Ph8RA1LftvZPz/g4a4/YZi4xzz/X7yLwhoBdEaKFEPCcnP1kTEqPx/ZTrqVR5kjPPAUBk+ehb0l8ligKFAaBUOI6rMx0+NxE5lEZwNyHbYy5GAsApHer0Hept2kkpDoR9fOTCNTS+2jduYkCOyQmygk+43yen1JOzWgAMhlFknEwSqhkGuCCbTcRoawKAftGACFDpLgL18Us41Uxi4OKC+gJprAoywm2t3fgnMN0OkVd13C+Qec8lk2DzU0TAFMZJ6oIwEBUuH2eiUk1BZFE4ykLSTYHCOAnS2gDd2aNgSVgOq2wMatkYdE7jFtY1PMaRVlid2cGG/J+lGUZxzGdTuC6FkWQbnUsjlkOAFw4zNZi6YDN3V08c+tFkKmwOK5xeHgsYM4YwDlY+JB7o0jGQxEkpFKktMjir0rw5VeVJDM630l8dC82+77fPfCdSyuMoUQBEjP1APwis6CPGplnJAfCC5qPPg56gLUQKBJaZTq8U8KpBmY9setcF6IUSc4DFy7xJiRHc66Dcw045GIAxGSqbmrRMJgKIBMiD3nRLATThs530dRIzY2Wy6UkZIOPeRTquo7Mtzh51jg+Po6aibqWv+XSLcKaCYNZViXKogTDSfz9ooiHvygKTCcTFBub2A4ajelshkLjyzOjrCYoSzE1rJtGbMOLAt45uBDml0hMOTQPhGtlwquqxHJZo67nIn0FMJtOMT86jvPadl2UzLZdK87U3Ku2bz3/PBaLBS5fuoBX3/g27t27h3/5r/8Ch4sGv//7v4fPPv0Cb7/9Lqwtcev5mxKGmj2YO6iJEJkCRCEnTlXi/teP8fnnX2H/8BDlRoFyWsIta8mAzgAMo6CQeyBcnABgQtQctibNqdYzIEG4MACYyR96ifSXc1JFAAADBkMejm3Efa9nEcNrlcN5TMnxUCIMWFhwyIOTCnM0RKJSWBkOoW47fPX1Q/y//t//X/z9T3+CP/uzP8Prr7+GJ3uP8fnnX+DBgwe4efMGnr15A9s7G/C+Q2mDNJCtnH/DcIGx6XwHCtobQyZqiWSYoku6eP4MCkMo4GAgZlaLukPTAq4j2GIcDF2+fBl/+Zf/AfWyxWRahbMopqeyRA7PXLuKt97+EJeu3sAzt17Gr9//NYAOzBYE1RgLuGcvRobwQQsdogEiAUNq/qV+NSnodTy0ydZFYgCcmvgl6ymXdR+m0nDPgGm+DBtMfL1zYOdAGm/ShLqcR2G9aJOYYWmCWTWLtMazR9d2Mbxv29RYLoHjwz08fHgXH3/0Ht5+6+e4dPkSbt16HrduPY+9wwW++umv8fYvP8Bzzz2Hm88/g2eeuYqtrQ105MC+g7GABYPYgcigtBUuXLuMc//9n+GVN38Lv/yHn+PTf/gFDu/chdk/gF0uwNzAUwtPQEEWCGZz4aDBcBlORxeZC5kSZfxWQRLQ+3mqQEZBE2VrlwOfFNimWKE/Q+NSWf3+JMn/WB0p0E7LUAKsuAUgksACTA6qmc/fkWRqiH5gDI6+PmCAqb9/B+AXQ9+FIe3o5yKX0lvIvas5lVK65LJ2VJOQMxgrY0iez7Ua6d+DOnh8btO+jzGHaV16XuPzqbRE50LHaIZzFWm4MngJsB4kmgYFVjEVUMn/0neGaxOMLQOTkX6udJ8SWZgKMoiGPlFSRe+kn89tPv7YTsKQKqRSul2WJZrFPBG69Pceh36rJnZs7plIXWAFx0MsC2T+VxmUp5VvzGgoF6gLVRTFYKPqhMSNYkxcuo3NTXjn0HYdplWFtm1jkjidTFXDEUnikcVigclkgslkguVyCaYOJRjH87mAzq4LoQMLlLaI0iNrJaFf23bY3tmOkUnU4bawFuV0KuCOPDwL6CmsQVXYhKMOS2RkY5ch+paCQzGdSiYeEEbGO3QsDEbrPcrJVKRxzmHZepy7dAXXbz4PB4uDwyPsPz4QG2sQbn/xBZ599llYY4MmZ6iiy52+xpgNLZLXggXnewZ7tfkUKbn6NMhn6u/ge84+gKReA8ExIlJ0ktINTABZI86bzg+IoHcuOMMzmlbMd7zzcU3azsG5TiLGBJCvl5FextaaaIKk0oE2XM5qJtRnaZbkbsqALOtl8E3oMF/UOD5eACC4zmFZ16iX4ufgfIsmahISqUMYf1mVKMsqOuaXRYHpdIaqmmI22wQRRXt00U4wqqkw1JKbBdje3kbbtlgs5pKxPKxpKk3S89Y5j+PjeTS7Em2MHH59PjJgXQd2GEhP00tc/06d26La1q9KBeO7ZmjL++TJzwEA777LeOGFG3jppZfw2muv48c//jF2d3fx8ssv486dO/jNu+/h3PlzOHd2V/aCV22XB0E0S2VpcO7cOfz0J2/hwf2HMAVw7ZkrODxcYlE7ONaEZ16YDAWPSC4qQFQF2YWWjiMt6cVH0S9i1TTBu1WThbR+BZr6WezLyLN523m9RGJCY0y/VqJ9QwC9ITEZEYy1YO+xWDb46OPP8MUX/1e89tqr+PM//6d48cWXcPv2F/jNb97D3fsP8Nrrr+Ly5XOSFwEUtERDR9R0r3vvg2O6jokBMphtbIg2OO4n0UQt6xq8OYOEix3Osfcek8kEm5ub2Nvbw6XLFwczRGHJbj1/C//m3/4N2M7wwosv4u7Dr9H6Gr71QKRXwzj7aXCSFamkX51vZfZSwJECWxl3sdY8xwTfg9x01ZBK8kMgEe9B4UwVZQFrQxTDuoGD5D0h3XdkYEwBCu3ZyqH0HuQlmlbT1Oi6Fu2yxny5xP7hIe49+BofffIxtje38Owzz+Hmc7dw5fJVvP/+e/jwow9w9eplvPDCLTx34zrOnpUEkF3bwTRe7qXCgwuPoqywfeks/vB/+FN89wffxzt//1N88Pc/xfGdr2CO5yjqGtY7dMYFhskEZkNAMbwAPp2PwVlbw2jk+GAFuI08r2udn6GT7ry8pDQwb0+/+yb+IIM+AsI2cJQbB6a3/xbh3tMhqC+LloGwQ/s60n9gNddBTuMG9DuAw5QGpc/rHTEGZHMtzrrxC8hflXDH82FEcBGl6SOgfYxRHPssHUPat7Sv6yJEEUkgBZ333J8G1If8HdwDI3Wl/VmZf/kj6TcFJiNhKLJax9ZuHXO8jglOxVvsGU1dizDEknI9K3Xl2p5hez3OE18+ZTJ6rKj08zTl1IwGWXHyJterrBx7EHtRr4ZOqse9Z45JdtKDoyqv+UJUxltbmxJ7PkTjKaiA65KDZyWOedd14mRdWFQ0HXB+bXBorZc1OEiajTHirMiM6VR8HMgYEIstYFFKEiUyBLYmqjWnlYTRVWAJCNHQxdjd3Y3j9N5HUxNjDFzoS1mWaL04c9eBmWIQ6kYWf3P7DK5cewbOA/O6xvHRHJPJFJNJhb/8D3+Jmzefg/ceW1vbg8O0zhk8l3T0zwio6xkLscX2LpgmdaI5UCfh1DwO3JszRVOn4DfhQwSvpmnQNBLuVJ2LW/YxwZkyC5rTwYXsy0rYNQIYjMGyaVAvl2jaNtrtLpdLdOGZumkwn8/hnYNnxv7+PjplCLjP7NwTatGsSPQXGyUdZVmiCMyCSGYI061tbJ+t4DoHU4jDM5FkiLfGSIb10H9DJsSnFjOjsigwmU7hun4NlPGR3A4deO8gakeICF9++VWc0851aAMDkmpyAMQ8GcwilXVOQnWS6UPY9iFrGcaoU6VKVYYSn0iQzZDAEkTCrWcgJ8CMgN0CoY4EmYGPPvwEy2WDV155GRcuXMCPf/zvceXKZWzvbGH/YA/vvvc+3vzd3xEpFCdSqCRDdmEq3L9/H01TY2u6gfPnL+De3UeYHi4wX7bSl6Q/MlccI3bp98jOhdKBvIxdqPm50jM+VgaAgFelsHlb+fPr2ksvHJ0bjVymicm8Zp4OQSa891jWLX751q/x4cef4I/+6PfxJ3/yxzg6OsbXD+/j7//+p/jed9/Ac89dhzUEEAc1ey8cUqYGQIymxCxSVwpn8czuGdFmm34cbdtFc8DcvCOd+1deeQWffPIJLl+5FJ5RmZ9I+XZ3t/Hss8/iq3sPMdnYEVPRmkXr0vYhHQdgyxCgCUuVUWAxf7Jys0MTmipjxOwlopiI/mDJBtOAkPtEJh9pIkOEnnoDMAjGloPof6TrxRZFIea6ynAEt0OUVYWqLMFOaGMUEHiGYQ2B7UBOmBTyHUpjUVQTABw1HHWzlBxL+3s4OjrCo8eP8f5772F3Zxc3nruJ5248j8WnX+D9Dz7CtetX8Nq3XsFzN57FxYvnYFjMP5uO0RUOZBsREpYlNq+dxw//2Z/j5R98B7/5jz/FR//p56jvPgIWc8AfAewiXZJzH0xlEsCf7+l1AHUMYKYlB6pj50Q/Wwe+03KSHbmeM7330nYHDGpyblcYHO4lyomMGz2TET4nEccNoicxR1++dfQj728+rycB0vzd+FkAvum8pcKGpzFwKRgWrDBcyxVmCMNn1gl+xkq+B9J1GJsvvWPz/qqAIWdSVFiwTiD0jy2Kecf2kgQe6YU8OcOSMxx5vfreuj5GTRkS9mNsvoiGvmeD9nrcq5hetWsyh99sjk6v0QgJ7CBBmSTahnPwZKIqxZDYhGlkEumsD1oNQmHFoXnDWuGIvFxknkVqSiB4QGK7AzEEaB3Apg3PGhs6EWzHKit5NdQkS8+46xwYjKOjI2xZg6Is4HzQbISFms6mMFZMT5xzaJ2DAQMJ6HNeojg472CLAj7U4ZkDqG5RlKLhaNsWEz9BvVgCBLz77ruYTqfY2d5BURRY1g1+8Oa3YOwErZcMxkQGrnW4c/8Ojo6OMJlIKNuq6k2ytKQEcYyopxtQE705p47VgPMdmlqA8PJoicODw8goLOs6Ata2bcTkJjAGbQD+AnYtuq5DXS+xXNbioN91OJ7PMV8ugwmPR9eK70HXdbDGoF4ucXh0BBcu4rZrsVwsJSFWkIrI+Fjs4ymYlgStl4zVhPmpYK2YzU0mwjSIhqxAWZVgSEQn53xM3th1IiG2hSAA5zgm6vKNSHe6tgWWwSzK9cyAdx4c+q0+J6JxEIDmui74lCBy+3ENRrLC9o5evURdNTVS0kNMIkFk6Td7kZIJE6/42sA50RWkxAKRyEOAGSVNgGCMjapRscNGIII2mKsE8KmSdgJgVCruYMni3t2vce7cOVy/fg0///nP8P777+K73/sels0G7tz5Eq+//ho2NyZIkwBKFu+eCC+XS9R1jV27HddTeAlC6xw0/i6rpNBQAJaBFCSzpeNfp+I/6VLMyzop29iZzJ/T39Nzug5M5GBG+6bviHmNAzHBQXwihNbJunXe4eDwGP/6L/4tPvjoE/yLf/F/xOUr1/Ho0UP8w09+gdlsE5cunhPejIbzMXBY9xwjEMlek2dns2k0m7WJFmS5XMreL4qgtu+1ZHqJXr/+DH719l/gh7/3ZmBAdH5Ew2Ut4VvfegW/ef8vcMZOsb21i6Zr4bp2ZV6jRI8ovE1Rs9xrBeNo4IKmToOIMBCPlkei+Yr1BaYkpbOGJG8KCOrHF3qEgigmYSRrgklwEYI6tIDXBIBiEmyMwdRYwBh0QTjhvIuBIZg9qGvRNcsQ3dDDAJhtVqimM3TdUvIqdR2Ojo8xP57j6PgIDx89xG/e/QBXrlzFrVs3UdcNvvjiDq5du4qXXnoeL996FleuXIQli65leNeidS0K12BazNBZi51nr+KH/+P/Dq/89vfx67/+CT57623Q/S/RLZcwTQELj4I9vG/FrCKxcU8FfwpC1gE3BfgngcfTgL5U+HZSGZOK6++5dUBad9q3dcwOggAnzcAcN5mOC+PmSOn48nnMn0mfSxmsHKSO/UzHARJWyI/MecpIjf3L+6Wf+6wP2lb0Zcp9G0bmO/8un5+xMa+rK9dKipC079N4ZMg1fVK7o6TktHpsb4ytxYAxpKFlwbr5Sc9KWocKogZ9CfTMFBLIpV7MxZ0hC9Jx0n24MnoBBAGbpRrGIbP/tHJqRuO9999D13W4ePEiiqJAURRomiaYNc2CraxBXdfonMN0Ik7aDEZRlth78gSfff45tre2cObMGWxubsK1HebzOR4/fixSszNn4mRUkwqz6UwkDomqsZpN5Qyj3zwqFUgPqXfRiw3GGHx9/770vSrBnnF8fIyDgwPUTYNqYxrMnSQErqi3BVA2rcejh49w8+ZNAVfOoSzLgb2pZy/jDqD8/oMHKGyBpm1x9+v7OHvmDB492cPFixfx/AsvY7q5i5Y96k5s6h89eoI7n32Bv/tPf4d/8T/9c1y/fj1c6mbtJhjjdPPPBBRLfg7vCPP5Eo8fPcajR4+xv3+A5WKJxXyO+XyBw6NDLBYL7D15gqYRM6LOOcyPj7FYLmSjOQk5rJYJTV0LuC+KGPLVeXFQU78VZpZoKsFpjY3FbFsy5RqSoADVZAJj7cBEyhiLuq7Rtg2sFadlNT2SsLYc/SGWdSNzHwgbEaHp+tCenjma7LH38NHDUSS3Lmh4QGKjGZ2uuA8TyMwhUk8SqUo1BkASGUSfR9zLJmEmxDyNAhPYO1hJSSMUcYKetT4B+JTYpCNaXGoVBI00lBJUZoTw033RZG+GCKUR0x2Oanz5nSEAKiVoEfjKLoP3wL17X+OFF25gOp3g408+wrfeeB1FVeHo+BgHB4fY2JgFs52hvbAxBk3dhmhYiKGvRWrM4cFUqmhlHvTSG0gOh+dh7FLS7/JLLb+sxy759P303dyGPH8u1UR+EylQvFiIAGPhOzEHNDBgdjGHB1FIiMVivvPBhx/j//G//j/xP/3P/zM2NndxdHiIX//6ffzxH/8BjGUALqioRiR/EOBrEMJMB7MQEXxUsMZGHzfnHerlEm3XYuItxoZGJJnFAWAxn6MKwQHi5iYJtvDii7dARJjPF9jZOYOv73/d94l5sI4y32KS2zP9Yd8CwggHCapqBUXgnJqVIAJBhMs0xL8DmOMFTcps6aZlBPamZ9616J2ggpHOEDo1Ew3MiwHA7GA8YAsbTX11XM45cNNiSQaeFwAx2HXCZNoSpTEoi6n0MZhX1U2NpnVYLB2Ol0t8efcrnDl7Bjdv3sR8WePzL27jvSuX8frr38KNm8/g0pULKErRjrnOowWASQlfFqDC4tyLz+GfPHsVr/3we3j/r/8WH//6Pcwf7sEdz2HbBtaKwKpn/nOmYHVfrdv3Om59JjVlW/deCtjWnbn8vfycj9WZ93ns+xVwGaQ9K/1kZWQYzA4w/b2R04MUwOf/8v6nv+chXnMQrX1acd7Gelq3bh7WMRsqGEzrGvRzpI6xkjN9OYMzVscYfV0PfDkC5ZQREZPJgewltmMy3758rvI9mzp0ax3jfyvNGY41r1dL7pM0nHv0tCgIHdXk/uCJapz69wfM6QlXkUaElN/ztRMFwmnMDbWcmtFgeLz/4XsAMW7cvIHNzU0sl0tsbGzCUC95L6oSTdPEBS0CaDBlgbptcHV3B3fufoXZZIorly/DscdscwNHR0donTAek8kEprAogkR/sVxGW7Kqa1FNp1F9rT4aDKB1XUy5LtJ4kZ61roOtSnzx5R20TYMmmPlcuHABZ8+fw8b2FjrnUJVFwGke+/tPsPfkCc6eu4jNrS0cLxdomkZ8JgoLciJVbJsWIOnHwcEBjo6OUBQFNjY28dW9u9ja3UHtOpRlid2zZ/D8Sy+hcSxW6p5w9959GADnzl3ASy++hEuXLqNpGmxtba2o8PtNsJ6LXJXYGDRLhwcPHuLTTz7F4eExlvUSX399H++99y4+/+JzLJdLAXdlCWuMOB+HubfW4tyly7BWgP+12QzWlr2vhecY+aJu6hAtSCT8PU4O5leuN8FatH1GXz44hHcd2hDmVU3SvKq0SbhpNZWKifFUCxJMtMaAXyRg3DMGTEJArl9/Ft4x5k2I/EJBS6BJwCghYGDACuFM4kMEoIKQLR69NIviExie6ESyF+y0xwoljwoWSqQSRv2kRhhOK2cVCPbjpn8u3UopIyTjoyB9stEckIyYjHHQdkg2Y81JYWHIAa4F4PHkyR6WyyuYbczw5MkjHB0eYrq5g7KscHB0hMu4JIwJy/+UITPGoGmWwZbXB2YyDTucMD0JNo4XGPcq6sH8jUiJxspJl9NJzMb/P4uq2otqAmLxZWINexnsZ0WiFS49AJ9+dhs//vFf4c///M9RllPs7R9jPq+xtV3CGNWkDS+3OBeRuUbYEyYwfyVsWYivRqBNTdNESTzzathJ7yW885UrV3D33j3cunUzMNsKHCQ0+ubWDl568QW8/9FtbGxsYjKdoZ7PV/oXnSajHEnONoJEkkBg1b4BQxBLFPeZ9yHIRBAEEAExapT38F2Hjl18R82EAuch7Rkb/L2FKVNhmAj7LayZRBtp33XR9w0Qpt8aIDQJY0TrYgzQeY9iMsWsKOXvrkXTLNF1LeAsmBhEIWb+rMJ0MkPbNGi7DodH+5gvLI7mR3j06BF2d3dx/fp1HB4s8fnte7h54zpe/daLeP7WM7hy9SKYGA01ML6DbUUb3NoGZVHi8qu3cOnms7jx/id466/+Hvfe/QDd44fgY4b1BtQ1axhz1TSOM+3pmo7tvxxkyj5ZLwFP39fP89+1vtOA0jGQv64PqyV9xgBgWFsGLeEq86R0aswJ+Kkt0dBXSc/byp2QgXSTgO2T2hsDwWmJbY18LfeHiQz9aUq+NjnzkjNQpylx7YIdfxrlKY6de8uCtD2lgakPzeg4w+eqQX8aABeT9L5/uZD8m4wrtp+8ymDxEw1CEkrmNR1filPysQs9HQ83rO0PGO6nlFMzGmfOXcCf/Ok/xe7uDpgRwhoSPBOqqopqMmuBaVH2OS/CRFy4eAm/d+Yc2rbBw4eP4QFMN2Yga7BFBCbg+OgYZ86dxcUAbFUq3gUzluVygXldA7aAB6EsC9iyipuHgt2uZ0bnGaYoUFUTzDa34L3H2XPnA6gSIGyMJDXzJCYnZTUFgeFdhwuXrmC6sY3N2SbqpsFscyvYkbcwJuQTcU7MeKzk3fAQ+/m9vT0sl4/x9f37ePJkD7PpFDdu3MS1a8/i668f4NzFZ3B0dIjj+QKXL12CJYt/8/P/Dc8/fwtFETKSF+JXMNjccU1z9ZcfHAwBC/Je3Th88tkX+OSTT9HUDZ48kWRov/rVr+HJ46VXXsaVy5dRVRWaupZQrd7BgYMPRoO67cBNi7qucXg8R9c5NE0dwq3Kpus6F3JIyCXeNI2EimU1MZKLVkyMhnkvNF5uv8kpMifxQEGFR7KfUqcuBUOGSCRHNrj4hjkqCgpMRD+XTdvhzO5ZXLhwCR98+CEW8wXELj049KuIAKE7+kvojRAm6ZU0ayIQUQAMBBBCpl+7cHblWROZGwBxbwIYfJYXY4rBxRQJGwEcbMkjDJPpCdq3HDgjPqfMycbWNq5du4Y2+Mo8fvQYT/b3o/qfWXQSkscmXFheNEL1skFhCyzrFvfufY2bz+/CGCNBHJI5CVg2rK9E49rYmEnEq6ZDvVzAFiL5DfA5znMOINJ9kZYx0HGa8rRnxy66MXOHFJzkn50kQRxri6CEHQATyqKCI9PPPXtxMDYmAHeJMPSbd36D1157DZcvXsLSdTg4nGNz6ywkb8aatpl1thHQkVyGAHzXoJoKvQv8NeqmwbJpsdE5kKFoPjW41OBx89YNfPjhB7h588agOeecoG32+M63v4Vf/PId7FQXsDnbRLNYhJ4kUkyNNiacpoRCV1NFBVtBIACiKNygYN6p91EvUQTYhKgqTNKX0mJSbcJ1TsJEOh+YK4BYfXJMJAcyU/3YVUBhrUVRTEFMIuBqGukPGIYZXdME7Wwf5lt8GKVjRSk+MZPpBBt+hrZtUR8v0DUdOEQMY+9gbQU7LTEhoct13WJZL1E3NY4Xczx+8gTbW2dw5fIVLOoFPvvsM9y68Rxee+1lvPDSC9i+dAbGeRSuga9rlJUFCgM3m6KpClz7zst45qWb+OQX7+JXf/O3uPvRB2j29lHMDdC0MPCiTYOTuWeOOlaluiEhOyT/an8ecmGAgu5U07OOgdD9ld4lJ5lSjWkP1tGHHOiOaU2CuCPspTxDDmAsxeAzBmmAhWFeixzQj9GOsbGk/WHWdgOdwJDG6DMitOnzNqxrI5+rMc1C/EnoI1amdQByH3uCG3l3bDz6TArWc9p6EjOa9jPto37unOvvasUaWXsDhge88tnYPOX7KhV+9Ugi1A9K0zAB4BjtL7nREAUnYSyOubcE0Hl3ettT7KvrXGRg2PtBNFHGsP+J4iL2m+PfPn7JEGsORhDEwkeLj9OUUzMaF688i6ZpwUYyepcAqpmYr8wbFxPdgRkeHkxWsmCrBBQEUxhUpsS3v/t9HBzsYe/oSCIBNQ1a7/H8Ky9hZ3sHMBbGVuDgKFdBFnq2sxvDurZtC1MEM4rQR50z7z02d6aJaROHQy8HzBKhCCFv+4RfwjQZYwFj0XpGMdmCY4Oy2oD1HteuiZN23TSoJpUcniAZK4oKtvM4e3EL1XQDi2NJQnbr5gsoqwkuXriEd955H6++/m3s7++DjMHmbIb5fI7FYoFlu8TFK5fgvcPW1rZIwsDQSDMSsE49//vM1boJYsx3FhmbaAWAL+7cxWe376DuOty5+xXefvttfP7559g5v4tX33gDzIxHe/t4cP8+lscLNIsF2rZB4xp0XTuI/R6dxYOOrv9dN2noZ9KvWFaIqawYEYFMOZAo9DbcyTODi4gQQymyfp/t+bTp0KAeOvIeZIHaM+zmBma7Z1A7AEySsT1eXv1BIgAF+kZWiGX6Z7o4K18iOdhh7ahXa+fdT+eQ4nMsITRHLgnRTAwJpQgoaNgjJRpRIiIZoI+PD7C/P8VkMhEAUxAohFQmHX8EWOJ31TEAeDgHWDuBdwscH85hmVESwTdtiKzT98E7QHhFD8k1UAJs4DqR/p49swEiB0MVPBuIZ8Lw8lkH0scunnXPfJN3c1A0xjCkl/JpbcjT9/MxcQDTCOcMASTbokQR9oxEN5N8PdYQCmPhug71vManH3+Aq5fPwhqDw/05rl69AM+dOExn7cR/XiIwMcK6e49ZWWB7WsEzoTRGfKrJo3Ed6s7D67mnVGIW6gbj8uWL+Pu//7vABAUmBnqpOcDVePnWczizOUG9WGBaTgEve0+sM4YmiBzottKllD5wkF4yQjJFQ4j5UmEiowsikA1MAxiGGI46mMkMsAWmdoJqYxtHB0dYtgtMTAEKNM8EzaELUr+U2QCLJr20ZRAyMIqK4NsOy7aWxK+MyECmwMgwQ0+99wy0HmQLlGWJybTCmdkmmnoRQ24vFovAZEkdk8kGytL3wTnCv+VijoODx7h3bwdXLl7B4UGNjz++ixee/xyvvH4Lr7z6EnZ3toCC0NUNSm/FMb00aMsK5WyCl37/u7jxxov49U/ewlt/+bdYfvYlzMERisUSRC0IHbx1YqoWA8T0lIwSuqjrlTu2KtOu5tBDgVomWME4UF/HTAz3yHrAGEHaKeiGgjHPksVbE0h6BWlG7mrHFmmo19QHRH+uoyv5eUp6LbsuoffKZBCFoPocwj9rrGXCUGiUtNlH2lwtKROnazBkdvzKPMexEA0YK/08X9uUVqZ+HWlU03XRsFLmQ98fmy2EOzcSAeaYI2eMBhOEfhDRIMpjfl/nwSq8D8KfQdvytxfJWN/3YL4lPseInElqCg4WC5p4BYBFMBHGwmx6WWZRiIAkzFkM7x3u/GgiSgDIgGyShDsOXZmSZI1I54YANhFrn6acPuqUsbCFcjwUN1A5maBtWxwdH2NzczNsCpHUmkLDBULUNx7ofIv9/X18ff8eiCTE6osvvhgduduuQ2XLwaXeX/4iVQIwiPwB9NxYChAGBCw4kOtnKjHxITpKWWo+DkTnJmbJzC1hZyUhSrtciuTQWJB3gxjKFPxUtnd2Ma1KnD17DkQWi0UNUxTonMfm1hZsWcYEbV3X4a233sLW9jY2Njf6vmTzz9wv+irx1ezaAhIEhAOL+QJ37tzBxsYG3n33Xbz//vt48OABdnd38cqrr+D+g4d4//338fDBA4n/3slGF9tsP2iTqDeXMCQqwqJQxKzzHgwJEolB7GnGDKikFgknjuS7sZITQ2NsJJpSU1rJ6ru6P4wxYIeY1KbzDiAJdUtGnc6FOGvfomyiH/LI+qT9Hx+DMmVa8khPeZ2jc0FyscELEeklFtLHdYA4vbRyqRBBHOettbh3T+zj5Yww2Nuk6V4zRJTGxhcmtCpLeM84PDwEWOpomjbW1XWdAEgAaudprcV0OoExBl2IZDSpqngxIFmBXKp2kkRu3T76JuW0jEp+SY0BnJMkemNtjUlc83aMkeAI3hlJLOklmIVI7zzufvUVjg4PsTHbxdGR5nUxIH/SHu33SGpXLtHbbNCciNSZvfinyZ4z0Q46H+N0KszrwcEBdnd3kzEJXei6DltbO3j++Rt4652PsLW5gbIo4bs2gAKOIEFAuIsRUzRqjAsR6QDEC3PYF2HS9DL3XiInGoiGunMObCysEcft1knwj+3zZ1E2U8wPDuCZUXgP8iYyBr0mQ8KjCwNuMK0m2Nvbx+HhYfQvU02961y8N1Lw3HUdjO2j5DEH3zRmUFXBWopz2XWSk6ppGiyXCzgns0NEKMtS2glhsdtmiaZdousazI+O8OD+17hw4SKOjvfx2e2P8dGHH+O1117B8y/cxJkzW2hqhjEOpmsBx0DJoGKCYjbBm3/8+3j19Vfxs7/+j3j3Jz/H8Vdfwx4eo6wbbDQNfAEsqQGZEDnPKBVlGDawQRCWRghKaXtq7jYmxc6j9azLKK3r/03NksbO6RgT0P8dhCg+076lQiKp5Bu1f4onwz+VPPPgc2kz9WtbvWu1rTxFgXR3yDCMaRlEYNWvzYpT88j9DgyZvXVMX7439D1NsXASszEQnIyNaWRt87GFAazc2fpO/l7O8Gpd6efMLAmcs/fGokhx9n7PSI5ghbjeFDBgoPMja6JFTHI92PVamDhnONmvKj2LpynfgNEQ4qudUNDm2KOaTDBfLvDl3a8wmUyws72DMomYxMx4/Pgx5sdztG2Doixx8eJFHBzu4/y5a5hMZjH6VFFUIOovrFxlpUQjJS56CPTzHEilUq+co46cHDMmk0lsR/ODLBZL2KIUaT0BZTWBWy6xrOsYzUjrLMsy2CQLA+Y6D2MKPNl7gJ///Bf45//8n6MsSxweH+P4+DjkUljgyy+/xA9/+ENYa/voLmsyq+ZSGnXGUsm1FuccvvrqK1y6dAl//Tf/EV988QUODg7gvceNGzfw6NFj/Pxnv8Dh4RGsMaiKCigogsd+kwkRJagkoL+0c4JMMDHzsO6Zfq/2bIW8I1JaZgZiRt6+xf6thGgzYhKz9Lt0f8T3aPU7ZX4AySRf18vgm1MFs4UgtcjmW8tpXZ++6YWm63jSoR0F2OCBNFcEhv2FMAiOkF8AGUG2RCiKEtHRlght24UwqLIHVvqE5JwZg6ZpUVUSUW4ZnIQlDHIdzaSIREIEzTLvJcLY1tY2yrJE5yQi2u6Z7ewMDMeez0k+72PEdd2zWsYujm8CUAZzM8JgjLWx7vN1F2TOwOhPG8yZ2kZMAziYUR0fz3E8n2Nz4wzmIfeQSMrs8KDFhvt1Tds3xuD8+fO4v3eEsihj7iN2nZhcdh24Kgd7Lh//M888gzt37mBnZyc2Rkzwnew/7xp8/3tv4GdvvYONjS1MJxVcU4PJ93bSYR9KzhsPayyathlKxkn2l0oLUwGUGrgwEJ3GXevABcMbScoqQSo8yJbogqmW3ZhiqyywODhAvVjCeIMCRqwfjUoZhempigJFYdB2Le7evYuNjQ1MJhMAiCaJQL9H9Q7S4rxEFwuTBwrMRlEUoKJPRGuMwebmJmazWcg5dYy6qSUpYBDqGGODI79FXS+xqOeomyUWy2McHO3j0eNdXLp8GfP5Ap99fhsvvfQ83vj2a7hx4zlsblSAc+hcC9d4tLbFdDaF9w4bl8/iD//H/z1e+t3fwk9+/B/w6c/egvt6D+XBAgW3KEhoujFAxx28YXhiOfdueIflQRvSKDvp/knPfhQU+vXZuHMad5Lg4SRQuo7JWHkme35Ig2j8vI2Uk4DvKhOktHncB68XPIngbKytdC6f1occTOfMgtYXMZnp5yVfh5SRTLGavpvO4xiIz+vM91L6TC6wScc49l1ecg3UuvdyxkA/W7nb17yXl5P23rACqBxllFFOMV1/JvxKxLDYl+z9sXswZz5PKqdmNDzSfAocNo/auwJVVeH69etwzuHg4AC0oBidqWkaTKZTnDt3DgDwZO8J9vf2cPbceZw5ezYMQCMiuADqx5PIpFKPlKsa27D6rqq84uWYMBi6Adq2HUid9HB6LwYbxoSY9mQwmU6DyUINoFfTlWUZgDOjbcTetppMce78eXzv+9/HhQuXcHh0jKPjZbRbV6f0a9euoSxLTKezwETpQRsemHTzRhAZOF3F0d5L2Mmu63C8XOLTTz/F4eEhmBlnz55FURT4+KOPUM8X2JzO4tz4yGmTaGoi4AB6gqYEi3rsGTcoEFVOHKxWM+FAJI+M5C/ZYf1Akw0e/y8SmbQMsp5nB3XtwSQKKj9GXYuNdFWVUMMvXvMux3+cEAmKPzQTcRDVjzJLyQfpIEK3aLA39bOVfnBk89HzfUNG4GkX1QrxYg3DK0yGZzEbM6aIDL/WO6g7vC6aCB/MYvowo3ruVOJtQohsFuE3OLSj2smiLFDXS9R1g9lsGiPZwYX4SpQ6tp8ghVozd08rY4RUx5fXmYOJsXfG9lGqUU2fP82FsvaSBcIlI9Gh4FXF79E0NQ4PD3H+rIu5ZsT/JT2LSR/khhlclvr7bDYF9o5CtKSg6bAWdd2g6xyYi1jPqvTM4/r163jrrbfwxhtvJM6YBhTM9og8XnjxJrY3Z1jWS2xtbGJ+cAgb/aEQJXaF0RDnjNLKniMggGyh/2VZBu1H74QtWekDfeP+0vUhO3fhGb7tQEUBBw82BqYswSQM8XZZoj46Qn14FJIgGpS2QGEMDDEohFw3MPCuG9LphLFQplsl+zpvsp7SP2YGnAeFPS+mq2bA4CuDNZlMUFUluq7DYrGMPnQcCBfZArONTZRtyMnRLtG5FnW9wOHRMb7++j6uXLmCg4NDfP75Hbzw4gv4zre/hRvXLmEytYBlwLQ4cg7FxGLCHhXNcPHZ6/jv/s//J3zx/e/il//ub/D1ux+C9/Zh5gzyDuQdjBfn+ZY7UPBVSPs+GHsCGNPPU+GJzhswZDjSOcnPUi7USevNNSLr6OVa4VX8TOjUaP4e7mn0mPlPWuc6ny/tb1+3fjcEmPFDUHQ6lnHwyv2W7s+cMVvnl5ADdwZifiUdX/9w70ydv5cDdf0+BfU5aB/rU9rnfA7TunKGdmyOV/8e35dp23kfUyZpjOnAyP019vdJeCa/i/qxi8BUmb18jvP5N6bHyoN9J40O1iPtV86YPq2cntEINxOzJDcyYXeTMaJ+tmLrRWDsnjkjETRIgNsGb/Qqbc84f/48yqqSC7es0LYNmAyYwkKOXFLDUJ3D0G45p6aEW9/VxHApOND6UklYDgCIEDIzL7C9vQ0yejAlHpoxFuobkToni60bwZYFdnbP4Be/fBs/+MHv4vD4CHXdoWmlf3rx37hxA1tbWyhDEsG0rANMqeoYiXJSkj8xFosFzp8/h7/+l/8b5vN5HNvZs2cxn8+xv3+AqpzAxihD6BkGENRLSLddts37X5Mv5BC54WOKxXnl8aycBAx1ffPPV6VP2o/8cOXzaIxmRmUUhWRkX6cm1eI4kZylBx2ICSpje6O9XB1V2q90TXOCPxif1hkQZqyfeRAuNyXUeRlc3AmYR1h7sTU/mWlR8KZOZ23bYntnE4CYgGhm7aZp0LYtZjMx9wAjmBhIFVVVYnt7C9PpFPv7e5jP5yHksYkgkXoLxQHxO4006mllHUN30mcD6c8pLo302bUMZLL2Y/Ws6xOH/UYQRoMdwVuPrhNJ+MHBgURx8x7z+RzT2VS8csfqV3oyAi7OnDmLO/efRF8JYwzgHZq2gXMdnC9P3G9nz57FUfDLixd3MLdkZrDvsLUxxQsvPIef/uI9VEGrHC+0bI4o2Q/GGHG4DYkn9Y5QO+fwpEjUpUeIGWUDAwvv0S2W4I5hqgo0IfiiAGwAo0buu92LF1BcOI/H975Gs6xRNADBw5YFYAmuEzqo+z+V0kZmQwNjJCYkOs+u87BF2OeB2RDzsN6cNa1P76+iKGGMhbUlum6GuhY/jrppoqa9KA3KskLXCpOxaGrUHWNRL7F/dIAzu7u4engNe4eH+OKL23jjlVfw2rdexrXrV0DWw3EHBwffeBjrgbKAnVR44buv4bkXb+Hdn7+Nt/7yb/Dkg0/hj45QNDVMC8A7FMzwphdQpfdtHho0Lek9PwYq0/OVn6EcrKbz/bS60jU5iUasB33ZcyPvp/R9rP95SYG25CECyPSCLh8iJtpChIF+MNb+XsoxUz72MeHtOgYhH3vyweC7de+O0cv8mZQ51D4+re40EeNJwiKtL21jyEiNM6zpcznNTveamhePjXlsD42VsX2Zrktqoqb5v0SAuOoLlJ6Jtfco9+ZT+RiVtq5LiDtWTp+wDz3AiQ0C0Qa0rKokLGbgJnVg2vHQQVtMsLGxISFovUfnPIoAmAS0DNWARBRDmqr0c526NDWh0klUtbVOpGoeVPIKiEZGL6x+UYCdnV3M53Ps7e9LfoiiCOIDCkn+urih+/6IU/lsOsNyWWNnZwdVVeHoaA7vZeOpBkVzkzAzZtNpNIHgE4F3dkjUsIklXruOa75Y4tNPPkHTNNEHZTKZ4N69e/DeoyAr5k7wkugNPSjmgGRJ6x8QkNRpuQc6K7aYCeBmAPCrxEnnKy74yCPrzyDFF06CmuNE0aBtxeFd94qYT6WMZkYAMymblpilW/fOU4jGafp4ElH/z4PVfRkSXbHj1X/axoo2ZtDXkcsgah48OtehKCjYkC+xsTHN2g6hHSsb/DSm4ODHUZWagbnPoszEOJkhzfs3Pt5/DGMydhmO0aAUEI1JfJTGPI1BOg2TkX6nmjYiMQt0xoCMR+ccFvM52qYBbRIODw9x9vx0dBrjZZtk/04vmXPnzsF1H4o2I4yBQqLMtm3BfgoqxoGaRhLa3NzE3t4ednd3o3aLmEBw4icGi+9+5w387d/9AhuzbWzMZjhoW9jUJIII5Pv4/UoFiCho3jvReABiuqFzFOgjQhJNDyDYO4EoKGO9g3cNfMcgNuApYGwBsIGtLOzEwpYltjc2cOXKVRzcv4+7n36Ktq3hJyUMSSRFTVXCzH0I9njBS7SYGFwjB75giGJGxmatDbmJqjCOYZQlCoySc5orQJiJqhL/yfligflyEbRIDoBHURpYU8BVHZqmwXxxhGVt0TQ1Dg4P8eDhQzy+dAWPHh7gk0++wHdefxWvvvYidi9swxOjoVYYIGdQuhJlKf4b3/knb+LGqy/i13/7U/z6b/4T6rtfwx3sg7oaIBPXLaevqXYj3TciS6EVYctJZ2YdQ6+fp2B9DFDn+3fd3/kYNEDJKJjO+pmah60TLIyNr2dIeiNA71k0YOAo0VM/TXlW8UEyjoTZS+f+abQzZzq0pLRw9O48gVF8WsnfO2me1q3n02h/Xn/6brorc4Ynb2dsvCkNfdoaf5MyoBsZM7QM/qfpZzmzIKRwOI5+fwznKzdJ033zX5zRYGAQGpBJwKf3jGoyjUwEIC60RCQhX5lRFgWc92jqRkC0D+YUOvlQ9bWHtxoaz0QuTcB5EeKJtyhLyVCbMh35BkwnSP5WMCUHT/9WYq7mQPJZX0fnPWazGTx7HBzsg0DY2NxEYSW8rbUGRWHipWFiYh6P2WwDf/VXf40XXnghZK0mybi9rENuEKCuF5hMClSTApNpJY7YzFFarfsnZzxSwsBq1MOiku+6FkVZ4r1f/grzZR18R0Qi2XUeT57sB8dBhBnuzZ0GC94bUg3g/GBTB4CTSvO1CMPEsa4BI7LmwNHI7+nYB0QEyvD2sJiDhBLx0lplgXxgbCQcb4uiNBJ/kfspWEcUUsnHOqKRSg/SfiZP9D8SQphLGnIiNSAWAXOvLBlOB6hXzgohzlPO1owxG2mbakrZtl2UgtRtg9a1IFvCeUZTdwAkESPDh2FTFAowPLa3N0J4TxmcNbp2aiJEQWCBqC1d6c+ay2jdWq2TLI2BlPxyGdsHY5Kxsb7kdZVlGYUp4dOkX+NSvCFADY+F7PFEFq5rYWiCxUJyBxlrMJ8vAS6RXp+Dy4fCaQ/7Aei1zNvbW+i6ts/bwQxjDbqmRd116LyH8RywO0GVhERiTlIUBa5fv47bt2/j7NnzMdQkw0PSDzpY8njpxedxbncbx0cNNqZTHB8ehvvEAxoJjjhGMaI4RRwib0l/03MzjJsP6ISJAEQ7itAfB+eCOYHvYAFwVYFIwqlXsyk2dzZwZmOK566cwbdefBY/+fu/x+OHD9HUC2xtbGNaTmGLApOQP6prqfdZI4BI/Becc/1ZZqAqSzADk6qCLSxKW/TLAQ4JCleBFMAh0amaNeg5ADY3NmCLEk1bS9hxJ0EDyMr706JEOZlgsVjgeHGMpmuwbOZ4/OQhLpy9gsODPdy7dxcff/opvv29b+O555/D1s4MddGAGkbbNqjKBkVVwZYlNi+ewe/9H/4cL3/3dfzk3/4Yn/zibbRP9sGLJWxbw7RNXC/PHLKMmyjqYkqWhAUJpGAvFwiO+aTlZYxxzs9hXl/6+YAOJ3Syv10oBifQZ4cgTISTaRspo5iWdX8PAbQN5oY5s6Oa4sCAJO8Jo83BbHWV3qXmaGPzN0br5F2ZjBW6pnOUvDPALae4nyLYHzHfyX9X2pv2TU2InlaUZuvPiBt1INkcpPfxNynKPDOG6zLGHD21nmRuUpTDABZ1DU8EnzC/gAghEDCj9xyFyApF1HdWLDxMTFYaZjvWz0QilD0l43R6Z3BIqMAoZQid9+xhUMD5Dl0jl1lhC4nvHZyMDRF859DWNbq2RbcU573pbAoXQl+yC3DXSTg/9oALIfsM2XAJWDDJRui6rveJSCYf6DdnqtUQbh7oOgdr+2g54pfKIaELDWzS2TMKCdiOrY0JqsLg8PAARwdPcPbMWZRFFRfQlDaaaQGMqpoEpqjEzs4OlsuFZA9vW7DzMOTx+RdfYGdnB1vbG5hMCzAlG1cDHEeuB4NxDsABMxDCfzIBjWsAY/HOu++DmVCW4mBvbYX58SEO9o8BFPBad8YRg1lCwGaHPXLBg+7oFqRV4BvmXOowMYdE/4D+6B+UzS5mEQRZG88joEjZI5ZNnwJkDu0RsDJPRATHFKTjjKaeY2N7G2xEAtnnEFgP1NdJL/LvFBwnn/Rjjod7eDmN1Zn3xXBg4lgP/XDe87rG+r8ikdL5j/+LPY7Llp8vGU4f4aJ1kqTRFBbOO8ybOUy5A4bFsunAniAzrGYSFEzXLCaTEhub05BLQy7ujc0ZHj9Zhv0gzGP0oxmwvqsX4YAIj4z3aUxi/uwYwzcaQjHZb2OXRs6I9P5dlYQDp/x8qxBlvM8UNoJoFcP8MgUa14A9oWkkr40xwPy4BngCYAnG6uWt60/E/z/a/uvZkiTP78Q+7h7iqKsy86bOrCxdWaqrqmcGYmYWMwPMQBCzWAAEDDAu9o00W/KFZnziv0Fb4wuNDzQS2LXlLgCuwMgWmNZdrUt06azKyqzUVx4Ryt354O4RceLGuXmrZ+Az2XXPOREe7h7uv9/v+5MgrLtGOAvVcDSkKiuwFmmFi52QEo2lNIbSSqR12ZcApN/j9bnTmkuXLvOjN3/sSucYgRHBd9xgMRidsz7Z5Nknr/LjH7/DYDAmlhGlLp0uwAtrtRrKC9R4sKykJIoTSl0dEU5kC4BYawmJ1517nucXAkcbjMUWhSskWhawNkIoQeytzoNEcWojYRhJ4o1Nfv/v/y7v/OIt3v35L9nbs2yMI0YjxebGGg8fPkRXhQMB/rwooRiMhxiTsr+/j5IRUaS4eOECB3t7rI8nrv5QVTnwrbXXXDu+EObQBru6ExPi5u320CCJiCNBHCvyXFKUJZXRviinREnNRCW+MGBGns2oyowyLzg43OXCuQvsT2d8/OkXvPryK7z0ynNcfGKTJIlBWYqqpLIaVeUM7AARJ2w/eZ4/+K/+GZ+89go//dp3uP/hTczuIzAzImkwZQG4zF/aapQAwn4T1gMst9ea+MHmHB2hRyvOcPvsdgPNu5r4dqB+r/AXaEkggc3XXiBb1oavGmN3vEf4Rg8ta89ZylbcUqf/sC+MsSjZKGOhxdtayou2YL1qrN21aAv1dATv+lrvUtsuGNcGNH3P6lvzNt09zhrcpcndtW+Prw3w2uvfdrGq6aFsnhfmvQoYtOfXNze3d/rlhz5lVt/adJ/VKKMc37RC1CUaNO7sKBGAQ13Fxm/eAJcDyGhkizqLXe3p4MdBkLlaAt5j2omBxp07dzhz5szSYuzt7TEejTHKFQrSRhMnzvwaRcpri1xk+3Q6xVrL1uaWL7LkhOKgaVpeNE9MTROspXzKv0jFaF25+hs+g0ffiw/fN8FTweJiMUbjArcai4axGmGaDAxhXI43ifretbU17t27x4OH9zl9+mwjIMtmo2pt2NzYZDabcfXqVea+wm0URRituX//Abe+uM3hdMoLL7xAmqbEUYzszTTVCBztdlRz4DaOsYaq0jx4uMudO3c9sDKMxyOMsRxOp8xmM6QQaFp73raf5kGX/779nfVjCU9vNCj4+Xe1F7K+ZmlWPYco+FxLvO+pv64WdKGVuq0BI1aEsdlaA+FAyDII7QYwWQt5njNeW6/fm13p3vWrt3qJWyCjy4jaxBSOrs+S9tziXYnatKIflHTbKgb9ZRhje2KiJlLCp1f1PujWZ8pZV2hgPnfF1wJtClYK4zW0kVIkoUBnpTn0WmwlJVo6ARMjeulaW8vU567UZeTd+5a03Z3f2muyqp/us9rXh776WqBRUkpXW6HzrCWN4THPQ/gCleE6AQKXdaosK/Isq2PaFosFVVkRp8el/FxmyGHvxVHEIsuARjAJDDsvCleTSIb4nqOxBwDj8ZjZbO77dJbfRuihdp379V9/g+9+9ydE3s12b2+vScjh16QN4duCgktA4lKX13vDDyW4YBnTZFwJ4CpUn3fAXXhXKospSorDGVUlECJiPIgxeoBUDhzHQlDFkl/7jTd48olrfP/bb/Lo/n2yfMhkMubCuQuOJwmBUJLYx54IATuPdsizjPPnzjObz5xrrrXE3nUwKNXa8+wTRroB0d2zba2zHKbKJTOx1pLlObP5HF1qQPjkJSlJElEWXjGmZxRlzmx6yIMH97h84TK7uw/5+NP3ef2rr/DCC8+yffa0q3ouKuJYocspgyQBpRgMhrz061/hmWee5q3v/Ii3v/sDHn52i3I6xVqBMhVSl8TGBdNbzy+spAaRAZwhVp2P5bn20bWugHrcOvUpEWr6zGoacNx5t8bXd+GoBaYbpNzuq319u+/AH7vPDtdEUeQszC3QEd5x18X5JPFu7fGFf3UAuG0UCqGfIFetAi19IGDV2nVpezcg/Dh+133mqmu7QK2+zvPXL8MXj7OsfZn2uD6W9jLL6yKEK6Qd4uGMbSwpQC1DLe0tuZy5L9BDcPGpTTu6Rx/XTgw00jTm7t07nD59isVCe0E/R6oJeZ4REFVR5MznU+7du8dnN2+yyAq++vrrDNMhGxvrGKuxWtdAI4xbV676qgsud0G6waVKVxXKOBNYUVl0pTFY8rLwpm6fy1xKhLWuWqLRSKX8Ann0JSwqCqnXtLMsyFDczqcJrZzUHF6CKTWlr3Lt6gCUZPmC+/fvM5/PmEzWiKKINB3WJsckSX38hq5jP4qi4M6dO3xx+zbz6YzD2ZTReMz58+dJkgSpQiGpxxOyo8JMIIrGraOKeO+X71GWVUeYyXj08KG//xgTnQAhVJuNO8Lmqduy04rbvsuaFvd9XerEBg1Ki0j2AQ3w/trU/wK4WbougEkvdNfeqv4mtyJOom2Py3j3PR1MF7iAfBUpF2OkC18EZ/VB6hKk9vcn1V6t+q6teeteu0Rca8ASHr48vj4m2n3eiYAEtN5d03/9NwFkOuKkK+c+GGKXguskCBYebIdOrXX3uQKcTsAZTyZI6epBLBYLxuMRiL1aAF1CGc12qufU/tfWBnYZTHu9g+98d036Pnfnf1wLjHEV4wx9toNh2zUolsfUZhHHPDOMU4Tz2ihYtNY+zXDk6pTEzo30yDnkKFMO45hMJq5mh9FImTZnEMizjKosMWnsgU+tN6vn7P5J1tfX2dvb5fTpbbQOgd4Ci/SpZTXPPPsU6+sTptMFaero6ZJrmV3OZhOaMRZbVVjj+Ek7kBxrsaKV7jbMz9+ra4HJA/vIJTShskhbYfSMaVkR2YqtUcJilrGWJghhXXyRLjl/8Qx//w9/n3d+8Ut+/tO3qPYKJuM1hsMhWIHQDsRo4yzQk8mE8XiMEC5+JoqiOttaiGsJyRRC8dT2PuoDwUG4DAq3cF0cx1TWVSIXQnBmfY1od48sy8mzzNE+60CqHEjieMDcp8wty5JKF8znU06fOk2WL7h77wEff3ST1994laeeusra+ogi10TSkhULRBKhraVKDcnmgK/+/d/mmdde5odf+y6//PGPmd65i1jMUbkgsgJpfbSgJ3G2ZVHzKKOe+8qYjh7aGYT5Nm0MgaztsxZ+657bZS15o1Ts0vI+OtJu3e+11vX5bytGu7S7zcOW5sXy+Qr/DXNwSrkmSQ1IItlYi9r3raJVfXSvHZMqZcgitux+1IzxqOttfZ89eXrUNk/rWgy663IcYGoDpfb8Vj+44X8nEazb67TSsvHYXk7WlgHRsiug6HzuA3bW2qUYDat1E19trZerurAUT0tZ6vdx7cRA48aNG9y8edPHGiiiSDEcjhgMBggUUgmm00P29/cwVqN1xWg0xuK0dZFS7O3tOdDg08yKSNWazaLwoMG6NIJxnDgNltG1OTI821qL9MWi2mnV2pkrXLVc96KLosDSBIhb4wBHtsjIC+e3GgoGBo2a03L66tAi1G9wzE1XmsPDA27c+NiBjGTAqVNnXO73wYDXX3uDLHMuH3me8+DBA+7cucPe3h6L2RxdVYwmY15++WWElK5mh1xddKh5v8uagDZhdGBAkWUzitLy8cefAKJea7B1kUBXIyQG1WgllwQ1ACuxNK5yxqNbpSSiR+sfUvu5jeyEHd8RVgQrxdFD6CbjfLqdBoQm45H1LiFLAqXrE8AaryUUDUAzoZJ6cMloEf9GK+aIsJSSLMvRlSZNErJFcURL+qtoJpYP9bJE3EfMH2e2DuOotcu+R+Mv/TIjPMKs/pKalyAIC0GTDEK4cWaLhdOoeBoQAImUoaqocwky3n8/ilwxuCAYD4fD5jlSYrVZApZCLpvJ+87GKrCwiqn3zS8IJqsI+Um0ZN1ndBm88Ps4WHCXBSCzZCk8Ln0nOFDm4igcTczzwtMzRwsd4Bgge321l4WWo6AtWCJcU75qdbAKaW2Qob5Qa77NOYTz58/zxRdfcObMWS+oBPcn0MZiRcFkssYL15/ne9/9cW3Rdm6prhlfRTf0W9MwY2p6Es5KABkEZUZ4B8FK69fJWQdtTUuEtlhfGFAY6z8bDu6V3KwKBgI20iHEMEoTVJoSxworLK//xqtce+oaP/zuj7h75y6lLhgP1xgmA0zlLOYychaWoHUMYw2xh2FfhM8hiUi7QvHj9l24T2ufHcwLEVJKkiRhbX2NwXCEsZr93T2KIsNUFVJESKUYTiSmqijyjCzPKMqCvMg4OJxyavMss9mMmzdvcv3F53n99Ve4cuUSIlUIodF5RYmgtIYojkmimPHFs/zuP/tDnnr1eX709W9y6+1fovf2EfMMrHbB4qZyQFVYbChIavuVU935dgXO9j5uW3yOo7l9aVAb3mgR3hNilf9/V7hrnrEsGHeBzqq5dIXi+hprvVKwEcCXXEVb59eNtRvXdZRm9s2j/bkvxiIoEbt9ONnhKA3sE4L7hP9VgKCvnzC2vsKD7fH0WY+616ziCe2xdLOVHlmTHtq8/N6W92bfc1a1vv0qOu8xz/Mlebjv7NTuiILmPdXAhVoeX7Vnvkw7MdDIsjlnz55hZ2eH06dP12OSUuCsZ86/eDo9JB0kjEZDxuMRKkr45JOP/GLA4eEhH77/AaWueOHlFxnV1cRBSeW0y7HLsOGYYtEIRxaXilTIOj4jZPQA75rU1mCJdrYqB1rCBsmyjDzLiWJ3T5qlTpOknFAUCiTFccRwOHBpE7VjYlZatNVIabFWo03JdHoISDY3tkjTITs7j7hx4wa3bt3i4cOHLBYLsixjfW2N8+fPEScJly9fdlVea4vG8gYMG6Lbjm5iJ6SUpSHLCvYPZjx48NBp0DyQKYqC/f19pHKFtyyCyjT1DoLVIwgkxoagIdcECkTzrOXxuCsaYuM2bk2Alq6j7rH9V+M7itNyO+ePJZNsuLr/IDptqRLeAmL1EY13WFfHaBTGusJyxhoHXFtIve71MYe+ry0JpMeAjL53e9zzlq73gokVtvXV8t7pu7ePYB/bRPhPPzNv/nTCuDaayFdVzv3ZlSgWiwVaG6JYIPzeCutUVhUbGxusr60TeQ1ulmWMx5M6scKR+YAPjG1eWd+Zedz56QYPdhn9cWBhFVDpvofjBIn2e7G2yTCU53ktPLTB6iom2YazNgB9f33oy2lxhXN/silLB+QELYok62trdSyAm5Abc1VVntYarJVeU9Zo9NprcfHSBb733R/Ugl+gewJVpxAHzVe/+hrf+osfoLUmTdOaJocUyTVAYVlxYbVx6Zo77oYhC1S9jngFSeBjLZcxIRqLiVASbUDFMbJyFvnDe494f56hZzlXr11kkA4YSIUQinQ4oChK1k5N+L2//7t88tEN3vrZW0wXB1gMiUox1mAqU1uEtJ9TEJYqr5BrB+YGATm4DbfrFvQJjuGd15pmLygHAVcAw9GQ2BjiKGI4GLC3u8d8NnOxhD52JYpjoighzzLKImORZVSVZTHP2Nt/yP7+GXZ3d7n1+W3eeON1Xnr5Bc6cWXe7UgvyRUVVGqqowiSCJI554pVnufTkZX755k/50df/gnuffQ6Hh6g8R8kYaSpXX0UA0mKaUij1HIOSsQseVmnJuzSwjyZ2++9zRzP2KE1pv6Pez61bHCDXS1l7VtHivrE1PKz/utpa03rsSWj9cYDrcQJmH2g4Tuh+HO/r28vdcfWtdQBb3aDu9u+rgESbltRnpOPOfhz/PI5XnJTXtxUn3fv69kIjZyz3u5w9tVnHLlC0gS7TJNcI/xuAaSMD4mRCa7vC3GPbiYHGZDKhKAvW19dI03QJzQuh0LpCCMtg6FLJrq1NiKIYhESJiPFo7DXpkiSJkUaRDlJOnT7t4jk8Io1U5FPgRiRJjBBrWJqsIQKJFAqpJGVREidxYw0QLiBOChcDErQ2FtCmJJEJWlcgIqSSpGmC8j6x2phaMzeKRgxHwzp3eTBhh8rRIZB9mJ5xAeORs+oMh0OeeeZZDg72+c53vsPDhw+ZTqcURcH6+jrXrl1jOBggLAxGQ06dOkUSO+AkpauoHNpJtAvNRnOiepZlRFHMxx9/QqWdiVxF1D7gZVkyGo2d0GiXTZBtU6aTtyUu3LrJSw8C7UHF0TMiW/8NY2o2ZHdbtrWiS99bILhttYTY/tbST1oLPqCfWgBZJpCN5lhgMbWGUAjnfy7Esln5V21tM7Sxxhcc+8u1tnb5y0Ofv7q2TBwboSxou4OVMS8Ll1LV760sy3xslCuUJpe0cJrhcEDsYzSEcNbLwXCMlArQR5yHhLuw2Wkn1Ar1MYo+4X0ZAKwGK30AojuOVQy6CzJCeszgUhGULN2Kvk3c2fFNeDekoshrK20UJWSLBYjNx95/dLwCpaI6I1MYu1KKzCtnjHEFQB1/bisZmjUYDceucnxZorzLKDbE3xikEpRVzrPPPsnW1haHh4cMh8MlLSK4fPFunh13l9b7XGL+4FP3eoHIr5HF0f9QJ0N5Oih939ZYl8yrKps9U2oWpeW9X7zPw0ePeOnl57h4+QzpMEZIQTJIIaoo8oKrz17h/MWzfPDuh3z8wSdMhpBGEbZyYLmOHTMGWzmf97IsnTtWS+gIz27Hx/QlO+gKPPU/vwbWGJRX1GljqbSLAXGuixFJnDKfzX2MhsYaV0Q3HYxckpMsoygWGJ1TlHPmixl7e3vMZgsePtzjgxuf8PpXX+HZZ55mMhoSSTCVoZKGrDygSr2r8VrKq7/3mzzx4vN8/5vf5sPv/ZDFnbvYPIfSIv1+aHhcPSkI7+gE56DZv8vn8HFpXXt5cItuHaf1Pul4+pQZbX7cpT/NHuhSxOb3k2ZaOsnY+ujgUUG94bndvdr2829/3/e5GyuypLA7Rojvjim4rXdj744rzLhqTN2td9LWBV6/Suu++/aadJU3zUXL4zXaNAqTlgIs0APL8j5sFL5Ngp327xZctsEvOacTAw0VRaRCOHejPHdF+WrUJCgrQWINp06fYW9vhyQdMBqNQUju37tPkg5YW18niiKeevYZ9g8PWVvfrAPTwBNfY0kGPg2maTa7rOsb4AVzWZuAA7MLAEVKCS0fTPAp8oxGydiDBYVMnOuWMRahXLR+nCTOP82b3ZVsqs4qFYGQGG0YDEcINEIoJBGJStjcOMPaeI3/8d/+O25+/hlFUTCZTHjm2aucO7tNWRUYbSiKisuXL9faS+lSXyFDAalWW8VAlg+JQ52LrECqmI8+/pTFYoGMEkcYpSLPS7I8R6qIqvKCm9cSuWxAwp8qT+BEm8gsE3vhhYhmXEsDRgR0bINm1fv+trUDHXletP6QRxhn/5osk1oXd1MfRJo5Cf8wpwGlnrsQUJUlGIuSyrvmLBP5Ve+hjwC2CUAQEoq8YFV7HAE6Tkg90tqah78kA3Tddd6OaL5v5u5ynYVAZLeX3FpiDLooKIsSEsU8yymqijiJ6/3jBD4XqJjECUmaECdOkM2zisFIIYRLe1o7vQhH6GoC2BlvlwmGd7KcBKCfQfcx/O76dZ9zEuDSt1/6hBjhrVOVF2hdquvjtbP1s6HRTgnh0oO2hOjpfEZelsSDAYezDGecFQQM3Mx19T4RwKUL53i4s0uk1t3ZsiB90c+y0s5qgNOeO5VDowgJvSipWNvYYO9gn9OntxydN609ZQy2qtjc2uLZ567y5ps/RsohSZo44QFTuwp034X1TDAwTAdCaT5ZHH2qGbZ7qDCCKmxz4ayjIS5ISOncq4wF77LlLCAlVghu3rjF4f4+zz5/jaefvcb65prby0ogUhAUSFK+8tVXuXrtCj/6wY84mB0yHo4RFkxuqKqyFvyBusZPrVkV4ZkgVESUgKhc7REXu+GD5GnW0QnkzTsQQfeDE8YQAoxL315VLqYqHaSucG6siBaJB4QFunJ70ViIhyOSYUpVOK+AajGjqErm2YLdg112D3e4//Ahn392h9dfeYXLF8+jlIXIUqKpbE5lClSckMYD1i6c4ff/2T/mpVeu8/0//Rq33/+IancfmWWIYkGkQ05F5y7q6LhBIhwYkU7BFKwPfdrc7tlpA7D2d+091dZ+13TP2qUsRH0uNO3+as26aAuey2n3+2jDcQBo6Uy25hGEa3BnsCm66+mlaPPy4/lL6K89LoSoj3IzVr/nrPDpm7sRnMv0rg3Q+gL02y28y6WzLZeT/3TXe5WyKMyjq6xoz7f9zFbPdGli3zOO7JOe+XQG3Fqjpl+pVA2kneyyLO9QA4Lmnpru+/hSiQDjPEOMBWldYelQH0mj/T727vE1Lw7zBYvBiDo6pYmnxu0tYYLHysnaiYGGFK4y6vr6JovFwglkQoGEylREsbMSnBKnOZxOvdCbMByOGE/WSAZDZJwQScXVJ5+i0oY4aSwjQgS3qGbjGeFiJNw69qeeCyCjvcnChmofQPei/LNaL0kKgfELL2SEUAppLQifeUpbpIiwxqVFFSJCynCt03ZFIkLJhCefeJpbN7/gzR/8CBnBa6+/xtmz2wgJebFA6xIhnGvY6TNniOPYzclSxwz0CYR9qHjps7AuXaG2zKdzvvjiPnlZEnmPUllpFnnuhAshAOkLA4f0vw2gcP6nTUrL5UPZjQnpCFoERicIbhMuJbJndp192Z1pOFQhBKQWnI9c6cfbll8IKDsgCe8n7tPYtqvqCuEYlMHF8mAsaRx7AXZ1erpVrU1g2nuuTr/8JYX8Vc/+y4GF1X30afoa7fBxT3DpOh1xdte7YHAXx2N1hZISKSJKk1NUJSOUr3GiPK0TWGNIB86/fTCI2ds7JFtUXBiOnVApNIIInx6iXs+Ad9vno+/vPm1cFwiE/y5pb3rAZN+69YGKPrB6XB9O5tOd8R17a+dV+DnjY1gsXvhybp6zxYxSVwgZMVuUGC2wQnoFQOiiGw/VGbu1bKxNuHP3rnerURhtkZFCCJ8yVRvi8F5toAMuaXRo2lq2z57l3v17bG5tuFHLBjhaa31WtYrX3rjOd777LeZZTBzH5NK5jBjdz9CFCK6bfsgtZRW4HQvLe8d6UCSdXN7wCxmsLBZRu4N5FyRrEEisrsAIDnYP+NmP32bn4S7PvfAs5y+eJU1d/ArKUirHZ9Y2J/z+P/g7fPD+x7z79nuMkxQVK6fwQJAXpQvWpqFbTrHmxmKERAgPpoSiokQaS1VpsLrmlZ7Uhf+pQUIQDoJiTqomDXilXcr4OIldDIwSRKmiKGIWi4WjlY5dYbUgScdIlZBlC7IiQ9uKRTllOttnNp0xP1hw+7M7/NpXX+O5566xsTFC1SqgCrSh1BoiSxwNuPzyC/yjJ5/g7e/9mJ9+/dscfHYLpgcI5ijj5meFQdvO2SPQ+qPAvutC076v7cPeZxnpKg7CarblhzZtaFtIjtAgLNaWLm2/dnFsjbLFy/A9gn83XWub1jgvC5aeAyFWTnlA0EpdfgxN71OSLK3JkqC5PJ7Acgn004MN42m1aF3fBVNtntl+dhtoHccLwz3tdTtaQLl5/qoMW13As8QbRMPbwnfdeJguaF1ab5b3ZhtkHFEY+d/bcuqRuXNUdjI4uiA8ojQWZJJAlAEKgQszsCKsu0EYkCLyzzTLgeFAndazvYaE4YslV9THtS9VGTxo4IMfaXAnEnZZYxhFEWtra1gL+/v7LBYLTp8+XfskGuMqk8ZJulQmvlvSvPui2sw79BU+B9/d9gt9HGIXnQ3URb4AtmqYf59voPR5yCeTNSZrE77+Z19nscjYPn+KK1cue7OVQWuX9SPPC86dO8tgMPDWjOMrnnY3b5/wYnFBnkkc8/NfvMt8Pq/dycJ/syz3WjMnALjUwf39gaj939tZcbpr1zvuIOfX/z2K3B/XugSgr616fn1QV9wjpbNIGf9ZV9onK4hccLFZbRY/aTPG1Fliut10tSGrCGmflqu3BeFBHIVj3fseN6c+YhJaYc8AAQAASURBVAnhvfWM0YM2WmeyKiviOKlrAITrXLrbEiGG1HKwf6Y2hiRxWduCRbKqKpIkBawT+LSn949hkuG/fYyzuxbd77oZfdo+2t31WZVGt6st7Hvfq1r7XJ2UgHfnGO41UGcQ0Vozn80oigKE8MHgAQD0j6P939CMtWxtnfIZxBpBLvK0OC+KOotUEEA8a6LtKmmM4eLFi/zoRz/i+eefpyW6EXaGta4Q3AvXn2M8HpEtMsbjxAtWTnsqkUfW+7j5tIXNXhBeC3xNJp1QlKoywb3NBycb69LnWuutR65A4icf3+Dho4e8cP15nnjiMqdObyBQDFIXJyeE29vPv/gCV69c48ff/wEP7zygWOQYC/PFjKosWFsbU3krhcJb6YV3mfEoyQpBhKIsc1z9ibZyZnVT3hXYWuuzNjZ0PvD24XBIFLkMZeHzYrFgPp+7KvDWKQykikgHI4oyJy8z5zJZahZZzt7eHvfv3eXunVu8/NILvPb6K1y5epnhKMX64ry6KqmiGaUqiZIBg9GYv/a7v8Nzz77IT775bd76/veZ7TyC+QGqLIi0ITEGg0BLiw5r4a3zjQsw3uW5ETBX0d4+AXFJcG/FgbjduSyLtGlC1wpyhJ6KEFvRiIsnPfPLsk3zkpfdnm0tyPYJ4d3r2/32rVOzYA1Ibc+nAfDNPcYnZOjysO48++hq96x2r1slxLc/L8V+dfp8nNIoyAhLoFX0zLcz5r7ntdd/pby0YhzH/X6kH09nVbBgY8mF4Su/9mvkVcmDvV0O9vcp8ozFbIYpc2xVYbTFlM6mYViuV+aaqglKe18IIREiAlMR9RR37GsnBhrz+bwmPN1Um4GZLRYLZrNZ03mkyDLLaDSqUaAQzq2kKJpgtsaqcVTzIFvMMnxuH+ImgLkRJtrZB9oAIfRbC5x+Q8ZRVLthhWtCP7K1iZYIB1CVGiWdierSxcvs7R3wwx++SVWVPP/cc0glkDZYDyKshSQZcPnylTrOpWs+bLc+wrjqusViQRyPeOutt8iyDBn5FIlKMZvNXNEpQjpPQZ7lhLze3bVxNOyon2S7tb9riI1fmM4B7M7lV20nOYTNf4M2smlBsA00UQgHqIqiIB0461KlzdI++FXG3X5PIW9/Xz+rTPwne+7qtTjJ/auAzJHP4X8fuwweaOgKSLA+O1tZliCSWnCUwlVht74IV6hgnCQJcRwzGU/YebRLWZaUZeHnslycqnliI5SuYkBdJtUmmH3r1Lev+wDMqvUM7XHpIvvG2v2ufX3f91360O4rCBwu+5JlNp87oAEUhQPBceR9/REI1Rb2VysSxuMhBwcHPrvUsvbTZTqpvO88NQMU4ui6rq2tkWWZD3puCxVtoa3i9Oktnn7mGj//2XuOrslgHXGgpEsT+wSZvne6yuIkPIgxPhC6rhkkpHOvDN9jsdr7nytB5SuvYwT7uwf89Cc/49HDRzz77FOcOXOG0XhE5PydEH6tolTxm7/12/yb/9e/pswqpBQkg4TBaMB0Pkd64G11hfSZjqxfViGdl4HWFUgQkcJUptEet/5r21/g3KCd5TGugVOfYBcs7kK4pCqj0cgry3Ky2QxTVQhACckwjoirmDxfkBcuw1xZulT3e3s77O/vc+v2Hb76xuu8+OJ1zmxvQmSw2mJ1gYkqClNS6QqbDFm7corf+Rf/kCe+8hzf+fo3ufPOO4jdA8QsI6pKjBBo4eI+ItO4GIbC8SFjTnsLt89MVxg8juavipfoXt9Hh7rCtRQCI7zVzYOk7jlepZxYPpM+tXQrs2Kz36lDJbt7vz3XPqVSHx/oowNieWH9f6HtVnVEHj5GGG/3u+r8ht+6MSh9iqY+WaHrttXX+kCDFUfBTBdArHpm+7q+tVxF1/sUWn30zPfiipn6/9MCDIZnXr7Oq3/t14m31sjmM8osZ3Z4yBe3b/Hg1ufcv3Ofg90pO492PE13/DrPM6yVQLB2gLAOyGAt2lpUnKJ6xr+qnRhofPTRR4zHY4wxzOdzrl69ymAwYDgaMs/mWGvJssx1GkU8ePAAV406Ik1TDg8PGY/HpGna+BHaRivWRZsBXITfwmchRJN5hGXNYxs86E6MRnszLG2isFitDB7ta1waRVH3HzJbCSGJogRTGTbWNlhf3+AH3/kBDx8+4tSZLa5cvURI5xmsB0ZbNjY2am1RO43l4zZg34YMY9Q+v/re7i4PHjx02mDlMndJ4VLsLhaL+uCHgoeOyPX5SS5rqsP3fVqE44T/xwGDVW2V0NVeq+MEPiEal4fwry1gVNbVF9G28tagktFILYGQ7vO7c+0bW9hvbQDRN76+v/ueAf3FmvBTq8smdpjpqjH2jaU93rYgXv/zz+qOMzzXehNWA0xcJXpjbZ3lLYqjOsMXAp+qNgx8mflHkaKqnOIgiiKSJKEsMydIWFuDxTYQ6q50d488Trjvzq0NSk7SjntO3zvua20a2E6l23fuuib79rjBM1FrQbpK2Ma4tXfB2i69t3tG82yEaMXBGYxZ3tNuLwg2NjZ96nC9tHeSJEYXLgbNjdu7ufn+ukjVWuu15BmTyZj2MgVwqU1FqhJeeuk67779AXjLiBQKK4/G59T03TTViNvvsO2q0X6/bn7ULlFSNtnrXLC2xbZcVELqXCfPubpNIaZNKYWxhsUs55MPP+NgZ5+nnnmaq09eZbI2RihJlMZoISgWOW+98x7TWYY0AhlBURZsb51hfm9eu5EZQS1BW4wDH9bH9AjnGmesqy0lpav9YfGaeH++nLWmCQgXQjjQLxrA1l7D9l4aDocURVHz7SiKGMQJi9mcPM/cs41GRQmpcAkDyrKk8pazPM9YLObM53MO96fc+vwOr73+Kk8/fZXByGWYstalEV6YKdrkDOKE0WDAta88y/lnr/KLb3yXX3zzu+zduImdTkFXaCpP3kWtGAvubc7TwmJtE2fQnduq87WKv6wSuvsE41XXGtMCA4Tz9Xge2if4t3l1OIuOjjR+++1+VgnuXZmoj+45C+Iqft+S28KzWi6u9VUr+HmzNmYJBPUJ/Uu0/zE03hUtLDva+KN9dO9bAg0eDPbR8a6yoo9/9+2lPmDSlXn6+u0qwpt+bQ2sDRaNcwP9H//9v+M//uSH/K0//HtcvnKZR4/ucbizA2guPv0EX/nrv8HG9lmM1szncw4ODil1xY1PPuH+/R0qrbh35w7TwyllljM9PMRqH6/sk3O0i4ke104MNNbW1hiNRhweHhLHsatmHcdUZeU9p5sNOx6PARgMBmRZwaNHj7h79y6TyYRz585x6tQpXzivWdS2W9IyA3DXBJ/SwITD922m3N1AbYGjC27qZn0wuGgQ5NImME5gCii6qipvKZAYJEpJrly5SllUfPtb38Voy8svv0IUN4Hyxhc8qKqSs2fP1W5nx/mFNsM7HikHTWKapvz8Z+/UFZXdmrmUvg5kOEGiqjRlUbb6XGa8jkh4wiLlEZep7hiWvu8Z50kR70nbSQT+1a0RhmvgIYSz9gi3x8pCL5mI+55/smetGEEP4ez233cGjgNtQdjuu+a4Mf6q76YmhmGdwlExhqIsXGCqpa5Jk3jm6tKqhl4aH1SttQcoMcPRCLBUWhPHSV1QzwlwuqU9s72gsI/prwKuJ5njqvtOAuKOY2Z9n9tAr/t7lzYe99xgiZVKIYVzTcsWC8BlIbG4lLeT8cA/xLkFBcGl21+7DQbDOkbL/W68BTmi0AvKUB1eypY/+1GgZK3l/Pnz3Lt3j9HoqZpGByHZWoutSiod8epXXubf/o//M7rSYINyZoUiwzoBp2/tu9e3+YMDZ971xUJQwFQWjNA+1bYXYgUI6TMlauNi/ACrFEVeOosIbvwP7u5yePg2j3Z2efq5p9g8s0mUKNI05s0f/JC3f/wuIH1V3pK8cslWojgmSROXItoKyqoiTVPWN9Yx1rJYzD0IcVllnKFQEicxUeRiw4o8p/SJBYRoBW8GuiM8CHyMEB5cpoNQ4ZKjCCYyIklTZvMpZZEjhEWqiETGxLGlLDKKfIY2JfZQs8gWTA+n7O/vcffOXV599WVee/1lzp3fcskjcsF8sUCKBekgYjFIGQ3GREnCX/u7f4dnX3qZb/3Pf8Tb3/4OzKZQGhdPWR+JQAkF+NScq4rrhXaSNKLtoGjRQ3O6rSskd+m849suRi2knBY9WvP2MwJdaAr8uXssfbUtwrOPKl1WjbcNwvssHtaylMxlub/mpHe/Oo4ndfl42wul67J6XFulzAlZRPuCx1eNI3zf8I8wmf7Wfa9tuTT83gcs+u6Boy65X5ZnSSGIpGA8GjNeW+f2Zzf59je/ybnz59jf32V+eIA1mkhKzpw7x+b5Czz33HO8+aMfMRqNSJKE6298hd/cPkeUjpkeHDI9OKTKC+59cYeH9+8jowhtfXbJPD/R2E4MNK5du4ZSiq2tLR48eEDlCV8cx9jKLWCapr4wl6uUqpRiNHI50A8ODsjznE8//ZSDgwMuXLhIkjpGVwt9LY1wO4grLH7X1aSdZSJ81079F75rH/jQX+jTMcUVLj7W1n7OZdnOAOKsFBaYjCecOnWKGx99yqeffcpoNObK5SvO7826oFcpFAZNkgzY2Ngg8qlU+yw5zaOXtSN9v4X1cH60MR98+CFaV7WAZowlz3IODw99jnsfo0Eo4tQIFkvP8YTlSBBZ5/l/1SDipK0Nsr5c84xIOCEYYb0bg0vD6oTa5uA8jkD/Ku04oXOV5uY4kPFX0f6q+hfCueRVVeXqwuAKcSapE3ayReY0jbrN1Kmvj6LIZ+tyoDzLFsSRc9+wVf0QnDvLMnPrW6/Hzes/1bo+Dhge17oKEzhq5j+u7xqsBN9Zv0RFWTrtnjVIISlri2a4JtBJjsgM7ZYkEaPRCJeq2Na4LyhidBVSSja2pjaACefWGMP29jbvvP0uTz/1rJs3snalc/y9oqpKLl28wIULF7jxyS2iaODqAlVF3d8ys/ZqrxOsfzhnXYFjSUjEF2sV0hUtdWYF77YiqEyTQlO6pHVOcSUFCJetaj7L+PCDj3i4+5Bnrz/L9vltTp/e5PyF8/y0eguERAjFYJjw+ldf5tlnn+VP//jPEEoyGo2cy5sxVFXF4WzqlHTujRFFcZ2KXUpFpBwwD4HeZMENzFlekG1rpahT94b5d4WitqLPFep1qUOLvMAIl8lGSEGWKfLCFwkzLuQ+SUFFlsV8SpYvMMZw/0HJdP+AnQe7TA+mJHHMvXvrvPLK83x64wv+4hvfJS8OEbIijhVxkjJIR5w+v83FC+d59j/7G0STAW/+yZ8i9yvS0mnPpXKeBkZTa9ItLLk+9+yAel+259oV/oKyw8kbRxT1R+7v++8ybV9OjtAW1FfRjqMZmrx1pJXNallI7QdFXTDZp7jrU+SJzr1Lyt0whRWtbx1WXdeW107S2kAqrEFYh1A0uTuGvnF05xzkM2fQ+HLCfndduyC2K1f8ZfiF69R5NzhS7tyosumM0dqEtWTA9MEjyumUjY11TFFy4dIFNjc2yMuCWAg++eBDitmce7dvMxqNuPnJJ0TDEacvXCKbL9hcW+fc6W3KYkGkYGNjwqUrlzmcTjEtRfRx7cRAIxkMMFozWV8nThIqXRHFMYs8Q0WqSS+rQhVThVQRojKMxmPGkwlFUXB4eMj+/j43Pv2Ua9eedJXFxbKmrpvvGFpWD6Dy5uxQKwMf4OsIiwuas14DJaREIDq1DER9UKVULnWe9ysOmgZXE8CiPUNzB90RCGPcIdZUXDh/HqstP/z+m8ymU178jeuMJilFufAbSCOFq2p74cJF4jiu3a9CocFfpbUPFkTs78+5fesu4DQDIU1vls8pygVnz25z7dpTvPvue0wP5uSlxidCc/1Y6xlpWPB+whL+ro+JtUuBYP8pW/sQtz/3AZ/abcN/QjhzsjNd+4wJSASuXoFSgihq1wBZrfHoMqLub0v31j02hEAIEfjDEfeP9hz7NCHWulGL9jMENUHsYyR9c+iu17Fzaf1vaE4RgK+X4K7TANIFilkjybMSaytv3ZPkmcEa6a70kbfWZ8DQumCyNmAwcIXkjK//MB4PebSz754nJcZqLww36xvG2ico/lW3Ve+p21Yx11V7pyvwrjLLP06LutQP1rlP2Qq0pvAxFFGSkhUaLSTGVijRvF1374p1ExYpLEmSUlaQYpFCI4RBiRitDUVZuTNmQ19hHy+voRCCtbU1Dg4PsNbWiTzae85aha5gPBry/PPPceOTzwlBz913saodtxfaa6WNs5ZZ4+mgbTLrKeEsFKGAaOOyKJBKEpvIu13h3HWMj0GSltJaF/9iLDsP9vnF7B2uPfkEPHOVS+cu8vTTT/Huz9+DJGWcpOwfHFBYzdVnn2R+OCWbzZlMRszyjMtXrnDu0nmkFJRFycHBAQ/u34cpCCmR1tM3K10NK1WSCsizzIEf/2brfYu7TwtTv1/j8tfQOmJLQmxQyEgpfQyWRCjhCu0WKYtsQZlrIqlwhi/D2nrEYj5lkc3QUUlV5SzyQ3b27pLlh/z1v/k3mC1KPv34Mza21vmDP/jPKco5xpYY69x8dw+m7E0P2Nk/pJQRkyeeJL91i2J3F+W0YsRCumK6AnJboaX1xUGbop/S0yxrXdBsVRmXGc/LCc4zw9VysdafIbwrkDzK6ZZAaXDXC+c3WCfDQgqBw3xNPAkIX6+lnzb0ZUkKcUruuYKgHbBGgJU1j2kraNsa9u5ZaLucW5ws4OKm3L5v74O2taPux58Pwko55rQkaK8EMJ3z2aWVq3hYN6ao3V+fi9Eq5dPjhHwp5VL2Oa0d32vz99BP9x21QdOqRBR9So6urNW3fu1mvWwRqhQIY9HznIO9few4RVSG9XTE9pmzGKu5f+8eWTZHSsG9e/cxFkqtyfKS2Sxntsj4yhuvo3Bn/M//7Ousr61htcVUmkhFbJ857WI6qorf/cN/uHL9QjuxpCukwBoXs5CXztd3c2sLFUfedWeAMebIhlZRhLTO9SEI2UmScO/efe7cucO1a9eWnyMas1n3kLmDIFwdCOE0Rk7TBNZrCoQ/VELQ+BzjNVA2vNDG9C6EK98eQEbDaCUIQxTH9UF2KQQFLn2YIEljTp8+w+HelJ/86EeMxgNeeOlZRGRRJvJaP0PurSFnzpxpqqCfMFq/3dobN2zeoihRMuGTjz9gNl0ghKxN21q7CrLnz29z/cXrXLx4Eazle9/7Uc0UkaIhpu1Nv+LgQyt7g1+XJguaWDp4v0o77r4jQry1deauEB9U99P+SwBCYaxFCAVUrSvcGoIliiW10aOjcWg/vz2e4wS/+h7RFt0sIiSlbjDNkTk+Vkj2goI9xr+3bzxf9hp3Eprvl+ZsLa7Oha1zqBvjyZ5QgHTZaIo5g3STqnSM0aXmXGZgxlaMJymbm+u4zDwli2xGkiZO2FOKymi0DZtttUbopBqi4wDCSVo3FmdJ6GgJsb/KeNp/H8ccu0ysea7FSovwxdJ0VVLmGUZXCDkkyytX7TrIYZ4mHqeZxDoX0tOnt1lkJaMNi5UarEEKp02vygqtjasH4d+zG1urGz/mKIqIVMRsNqvrziwxYqEoS0NZal599VX+6I/+FGMqlIqIYse6ukW5atXCY+jIkTNtvTawlgmXE54EwdwI76suwvGVvm6HrdMKC+tdqqwAaRC+No8sITvM+eS9G+zv7PDsc086f3oMKhYICePxhKIqKUzJV15/FUrNmz/6EckgZvviWfb2d7lx4xPSNGU8HnPl2hW01nz++ecUeYawEmukTzscodAMREqlDEVeLrmSWBtoUeB5zsrh0YgTikUT69he02DhUJFC69gBRaWQUUQRlZRFia4ihEixumQ4mhBHMVm2oCwLBjamOJjzi7d/xsF8wa/9td/kzu3POLu9wbmLZ7DCMhjERJEAYSlzw/1HB7z7/g1++dld9rRCjiboPGd9fUQ5m2PnBaookBYS4wVe7eciZE1vtM+4JgglOASufhT1Wvjt27jZiqMgoysg10Au/NbdlTbQRi9/+P4RqwXJLh1YVkg0LlKuNXNsH+RVKV3b+7/OOoZ1buHW1oAoCO9BKdlWhLh7WuC703fXY6MvScYq7X6fwm0Vjex+dxIlxHFp7Os5C7Fczy30bxwgE20LYQ8fOrEyb4UiqQ0Ww/VHgYq7x3iln7IuF4BUkt3FnMEgIc1yMq2prEVEiqzI/DMFRanRCJLBiIc7+zzYO+Bnb71bF1M9nC2I0yHnzl1wzykq9vZnWGs5ODg4dn6hnRhohE0TNkocxxhjavepGlh4E3oACtIHaocFHAwGfpPCgwcPuXXrFmfOnHFMx2tKusx62c0p+Cg2Cx/6bweyHudW0/1d+lSJfZUjTVnUhEEphSvo5gpUXXviGhLBW7/4OYeHBzz19JNsb58BaYikoqqaw7q+vs5kMkYpWRPpk6x5n+DZ3tB5nqHUiHfeeYeycnnQg8tTiF+5cvUKUaR49OgRyq+zrlyNEEf82sTq6ME7XkjqkZb/ilufoBW+b7u0ta8Vrf8NhD+YQqVsfJQFuMrJvu6FFP35ofvW5MsKkl+m9YGq8HlpJLXWzb+JjjbkP2mrwSa1VauqmuA7XWlX3dqfybwoqKqKKF4WwsO/8XjiaIAPUpVScurUKT788KZTAjwmPiHM/aRB3H33t101261vTY/Tln/Z1gdQVl3XHkef0NwWnhFOw1qWJVmW1Yqg4OYiW0Y8IXxApup/fpjvuXPbfHLzHlqvEdmGjrpq5mUtdHXv7f7t+jrHgwcPuHz58pG5CKAsK7TRPPvc05w5c4pHD/eJosTtkS/ZumvXVmr1nZt6PVvfOXtcv0AYBM1wbxe4hWflueXunbtMZwcc7DuQFccx29vbvPTSi9hIMEhTbnz2KU9cucrv/d3f57vf+x6f3bzJiy++QJYtmE6nANy6dYs0TXnqqSdZzA+5+fktz6uVt3pGoCRSOOcKWxRuSN7lyQbFhxUIX/ArKJGCDLOKngSZILhUBZ/4alShS+OsGIspVWFRuAD7JElYzOfoskAJyWIx59HOI771rf+IrTQfvl/x1JN/wnA45MyZ08Rx5JMZLLj74BHvffQZX9y+g5nPGOQLotLwB//0H5NEkh98/T8yvXWH6GDBcF4SFZoiKtHCoK0v+IfABOHQ9GfbkkLSxIICBHcnnxymo9xpALLbIYEs2lphFSwqy6BbCBeQL1hNr45TPhxLe1p7+jiF2BIf84WDu3QtfA4JdrrWVssyqFolNIfnnaR16WCXX3SftWpu7fiVk7qgdq9dBfZEa9bdM9KWRY97Vmht2bqPJnWzJbafJYWoi4qCr1okXVIGWzn51Xm3uILOPtmgU9hLQZSkThkSOaWtkmJpLOvra8xmM5RSTMYT8nmGLTVFWdY1zx7XvhTQCFH8bbTX/jukla1rY4hlM5YQorZsuFiFmOl0yu3btzl//nx977EbR1cIcTR/endzHA2qafSy4dDU2Vu80Bl+W8p8oCKca4f2B8xdmCYpZ8+cJZtlfP+7PwAL11+8TlZkqFgQe+uIs6pUDoDAUhD4KqFildZheT5NJdD9/R2++OKLel6D4ZBKV8xmMy+4uTXKsozDw0Of7Sq4B+DnvmxaP67Vm97aoANrDewoKDpuDu3fuge6bw36mN2RCqbLV9S/qRboFaIJ7qx81q44VMutGcLyHvsy7aTXr5pXnwajuaZ/z1hWrUH/mB53rXvHHMmvXRNbD1CDQOJogDtXcRxTVqVPnqDAWqqyxGgDiawFsLCP3T0Rg8Gwfk+z2QwpY/Ama8vjNX9dgb3LaI+7d2luQqwELOH6IIw8bo2/zF7oC049rgXGD8t5/H2PBPHXWlfUM9BX46p3Qu026v3GH7MnpFSsra2xt/c+2xdPETL+uBibmKpqtOaiRjH9mjtrLWfPneXjjz7h6tWrS5Zsd72bS1lkrG+sc+XqJe7de4isEkxLM99e4/p/7dH93QUTbWDW9x6bfS448jasJVjWAi1xFhFR/1x599u+FOzaavZ2DzEGzl+4xLUnroCtuHHjE7Iyw0oYr60xzxdM7874rd/5Ld5++21++e67PPfcc9y8eZPpdEpVVT6r4JyrV8/zyisv8f4vP6LIXAB7KMoqpHQ1sKypM/EsFeiyzuVLm8rH87n3MBgPa0Xi4wJVA2/XkYYURoOELBtwsL/PYjFDyRQwjMeS7PAQ4xURRZEhs5h8kTM9mPI//U9/xNbWKbbPnCOOE7IsZ3q4x8F8ysP9Q/KiIMKwFivGUcKP3/kl/6f/83/NEy+/yPf+9Ot89sOfo28/QkznoCrnseA10FYItJBYa0iWLADtsy+RPkFCiBlyekHr3KHUURdetxOoz09zflefp5r/2/5r+vhh33dHFAxQp2Rtf9fO4LnqHYb3LISoY1PaY22fixpwGNs7zZMoYtrP66MR3c9tmak7plX9r1q7Nt1s/94Gcd21Dc9sZ3Tre14bcHTpS7ev9rPb2VOBI7WcYNmSLgLzbel7rXGOnkWREyUxKMnhfM5Hn9zAWsP6xhrj8cCFDGiwWnM4mzOdL8izkiRJETTnuRQaISQPHtxnY2ODJE3ZuHSJqqqYtspZHNdOXhm8neZQNJrD9t/thWwHXXevCZt0MpkwHA55+PAhDx8+5OrVqyuFn3BPNxtBnxDRPUjt58dxvDRON7nl+9upcaV0MRl17IYPAj937hyRiPjgkw+4ceNTzl+4wNlz22RlhrICg6otN3EUs7m55cd/dGztz31tiYC0EG6I+P/444+Zz+d+g7l1qqqSoijY3Nys0yFmi4y9vb06KFRIWWs+hCe6pudddg/D0nvpHfFfvq0iho8bTzMuf3C734sQLdH0p43BaEOcOE2pFUcJT7ePVWPtfnfcGLt9tpn5lwEF/gKwR90Nj3ve45rzMz6qnW46ad6/tYFpNJnZrHXB4ItsQbrusuW4YNqjmmNrXQKJNEkYDAYYU5BlOdvbmw6cazB6WUPUnWMXVPStw6p17a5HH8hYlaHmpGe4fd5X3ddlbid5T4FetRNouO2wfI7n8zllUQKQ5ZnXeC8XsgqPC/TyKFOD06dPs1gsaj1mCDZ22uqZdxuyRFI06tvOWoS5bWxssLe3t0TX6utwTLOscowpeeWVF/nZT95GCIFqpThfWjcv+PSd3S4vgP532m5hT+swLuE3fVg86+/1oM3SWL6tFZR1XRG5VJDWWhDW0d39vQNuR1+QJpIin5GXGaPJmKd++zdRScIiX/DxZzd47voL7D54xE9/+lNeeuklZrMZ9+/fR2tNkibcv3+fy5ev8vJLL/Pzn75DkZfkWY4SkAyGlGVJLAZUxqCxCJ9lS+vS0Q5rWF9f58rlZ4iiiJ/97OdUVVnzzL41DXML+y9kDjMYpJIMBiPSJGU2nXK4v09Z5igJo/GY6f6B35cz4nRIWZXkZc6t27fY2dnls89uE0UJ1kJZZhS6JDcaK9zeKnKLGY/47KNPeXj3EWevXOYf/pf/gg+vX+fNP/469z/8mOpAIyqBskCpkVgUYH1MSzgiXeWE9LGmLqtakOIal89ehYV0sWgNuAbn3rSM34UHqEGJI4PKqyPPrNqPYd3btKK7j9tJcdp7vc0f+oT0VTJU+7/tvmqaJpr90BWgu/Sj77dV82zzxO79bTrSLWfQ7r8LkLogon1tmw718Zrl5/QrJ47jMV35pS3TruIPXYDVfp7/y1/fKLCdFbtitLlJKSW51kT+t/uPdtnUG75ekOPR2rvbjydjjIU4jmoFg5MNhS/6XJEOBqTJgBTYPnuu9/1125eKRm4XzSvLsp5sO9K/zaD6Xl74XimX9UgpxWAw4ODgwBHCMLnWooZAQTfpRuvWBjtNfYvlA+QC1BVKNDnqw3iCdcHKZW1Ne8N2BTe3ORRXLl+hKjVv/vBHVGXF008/ze7eDoP1FCkijBHkixwQnD17zoMv5XxyTyCc9B2C9m/W2rp44ttvv8V8PgfREABduXc1Gg0ZDgaEirLz2dzNIQTNByIAtTWj73knFZj/sq1LFPqIU5eYrRynbb5v/6v9cltaz7IqSdPBSlDTHt9xrUtUj1u7IKh9aVDQvlTg/aw73AyO9NklZI99TvsZnZgI4QUrrHcvqNfXXZMkCVk2YzFf1HE0unKCiJBRXbcmjKOqKgaDIUnqr7VNNqp6XGGT9rQukT8OJD6OuX3Z31b93icIrLqvy+CP2w997ej1nl56ZYcxhjzLKEqX3KIqq5YF7Pi9V4/RPYiNjQ2qqmz5pLv74zjisNLkRc54mC6BjFVMMk1SAMqyXKor5C7yNNhWlFXGq195icEwZT4tiVW0ws3NKYfazzwp/VpJkwW1q5Zu0SXnDLNc5yb4bUshiaUCKWoLQjtFOkIQJwkh09bDh4+4fOkscRxz4cI26WjggqxTRRINsUpw5+5ttta2+PVf/3W+8Y1vcPbsWZ555hmyLOPg8ICqlDx88IgXnr/Egwc77DxwSqXRcMDmmQ3W19dBCrRJKavKVx63iEizsbHBCy+8wGQyAQHTwymnzm6xv3O4pF1tg9rAl4NFOAhMEtEUNjQGjEWpmPF4nTxfUJZzjE+PWVYV8/mUZDjCoKlszizfp9CZ55cRWNDGoq3BSLe+NlIoFVHZivlizgfvfcDWuW1korj+N77K5Wev8cNvfou3vvkd5vcfoadzYlsitXZuZJ1tv/y+20Jk0Nwb/7fC2moFf3IJY9z+tTgXqyAkglN7NfGhbnPSJPPwbZWSrf3b4+jDl7mu/tf5LezZIDcBS4AyfA40ZIkt9Zy9trzWx+cDb2+P6QhNaI2tvf59WUZXzTWMrz2ubjra9vV9gGzVWnYV4d3f+57RvrYP1K16/tL6tdfGujiboqqIBAxG4/o7KRU2y1hklVc2u71ukUjlZO9B7GrfIRtrqIupE+zt7XH61LY/B5Yz29vHrkloJw8GbwnpUeQC+IqiqIFBaH0MtU8wdHnKm3iP4XBYL17YXPUgo6j+zblvN1q2NqDpYyZh8yolvaa/0YIF31JU8/0SknQP8JlxGi3FuXPnUFLx8O4j3n7rHU6dOsVwNOTeg/uwa5isjTg13mSQDinLinPnziE8PlJqOQ7luFiNVWBDeIBQliW7u3t88cUdL5Qpkjj21R1zlIoYDkcMh0PyPPOmrinGaGfo7wis7Wf2gQ06l9fr/eVkomNbe136zI5hbOHakwGgQOjD/Y4hCFzMhjEuXeNoOF7KFf7lnrF8TzfWqP9CCC5HbYAe+jhx80Ag7PX/lG1pTy65MjUMQ2uN8v7aFgeIB0mFRNYF3drvMKxVksSsra0xHo958GjfVT0muF/qrpPeicb6uODDk7bl8/dXH5Pzq7Y2YzoyTylRrf2U57mve4Sv4O60YHYpOUL/M6y1YF3M3WTi8q2395rWGuXPTlUGwdMl2ej23Wac1ho2NjZ4+PAhZ8+e7VlX565SVQXnz5/l4sXzfPDe56Aa2r+054X/H/urx+qEMdb/9a4hxrhieTJyAnIo5hpqUTgFjvD8yT07UgolJdqYIy6eWltHgzxYz7IFk8mA7TNn2J8eUFYV0hpUrBjIAZFSTKeHpHHCP/gHf58/+7M/52tf+xoXLlzg7NmzbKxvUZWG/+H/+2+5d/uRswAimZsC1D6TyYTNzU12dnYYjYacPXuOyfqYaOCsuZubGyglGQ1H7E932TyzwaMHe8TG1DEYztWp8O5xLgNc41Zsa6CBdUXEsKB9ra0oSogiRZFLSgFFklBpjdYVRZERxRIhK4zNqYx2/MkX9qwqF6CMdHtKaJf6NorGMIy4u3ufosyRWkAaMz69ye/943/I089e5+v/9n/h0YcfIw4OiIoMawqsMTj7RrNvghuwXQIa3jIgQmKZxs1QCKcwdRaP4KYYLBqN5UPUgei27ldK6YG0wJlV+hV7j1OcrGpdAXkVzQvvLVglRUt+6ypK+oBC7bUi+/tvA4m2ojmMp2uZ6c61z0LfHkP4vm1haT/7JE2Io5mq+u5/XH99yvX2eProUdvjp6qqOk65e++q99cngymlGmtwWRFJt7OFzwSbpAMEAmMqRCRI0pSqLF1GNvDZN1vz8XXkQnyxNZZSOxdMy8li5U4MNKqqQmtd++1FUcR8PmcymSCkImQ7coEpqn75wlrAeKLUxHRYGwrXiroQYJZlpGnqD3CDZIMwbp1qzmkEam9cWxO1IEAGdB7Skllra4bbTvUGrqhLHMfMta/ESnjx/nlCBO9b/3I0F85eAi346U9+wt7+Dm+88QbaljXymx0sKA9LVJRwavM0cTwiigcgBFI1h649r8dqTHHraHF+4ZUusQg++PATDucLrM/bp1RMmeccHkyRyvm8DwZD5vOM+TTDmkAgKiSqpQV3DLM7lj50f+w4jyGIqzQ1fVrdZp/0a96PJca4DAwh85/73WsbhfOnNqJxhxDS+TPGcYRSgsLqmpm4rsNYVxOevvm0CaHwz+laI0I/XeLW1fbUz8TPi+AqQvMOu2CwA8h+FcD0uO+FZ8rW+orgxmV0UVGMUIoyLxjECZFwZ15b4/aqk1vdWdAaqzUSiGNBkkiUiCgWJeNhArYg8lnDpDvYS3EjtrOG7fUPWuT29+05dJlM+C5cG+hdiE0Lvz/uLKz6vQ+8t5l5+95VmrFVzCvQ3PC3E4AkwiqslujSYLVGWBfzUlUam7Rl8yAILe+XtoAAhjRSDCKIrCAyESGKIYojhHTVra13CwqbvE7p2dnrUijOnTvHvXv3OH/+fK3MCiDEWkBGaG0ZDiTPPPs0H75/B21BqKa+ihBOcXJUL3v0va96b+076/1lLNZnqbfCuvTK2tbVsAkWdlt5XicQ2vFDdAXSkMQxTz71HDc//5z9/QN05ao3G1vV1jtrLXv7hqoa8NO39rn21DUe3HvAKX2ayWRCEieQxlRCUZQF+4e7/L1/8Pv82Z9+nQ9++RGP7u5h0Xz22edYDbYCYwVSRVQW8sxZKZ5//jnKKuf1r77GE9eukKQxi+wQYzTnL1zwvNNy8fJ5PvnwU+58es8LcZqqKqmqgqrS7sz6VNPWu4lhGxdcIXCxEUJQmpJ8sWA8GnHx4kUOD6cc7kdobZjNM4S1lNmcQbqOtbjc/C1a7Qi6ctkNPXi1RkMcMRgmTNZHCIHLuiVdtsV0kJIkMc9+5Tk2t/4lP/3WD3j3e2+Sf3GPeD5DVSWFqSiEpUATxTGiMiiNyygUi4aeWurYG5/Ph2CdMN4cIbxwJ0S4PgCvQJ4FQkT1uXYyiLP8yNZ+bNMj/0VtNXTDCXJP+N1vUxwYDt93lSJ9n9uJe2peseTaHR4U3sVREFTzuLA6HfelOptVxw1zlTDe/dxHp9vXtMFHu982De3zUAl/G7NcZqAdt9EGSN1+wvqENekClTbvh2V3/KPWoOVnh/l16fwqHu7kVAhODUa4EhDWCmxWECEosahYESUxQkt0WTnarVyGOiEiELbOHCelIo5dxseFyZDS7ZeyzIlihVSSclE2LqWPaV8qRqM92eFwyGw2cwuI0+C438KL0rWQ1tzrPofz20ZuSZKws7PDcDhkc3Ozdrdov2BXQRiiSGGMWApok62XIIQTKqWQNdJu9xWCOEPGjPoFeubc9j02PihMWIE1lq2NU0xG6+zu7PCjN99kMEi5eOk8s8WsDiZWKkJXFQrJ5SvXUCpBqchtAmMQ0eqsWH1Ewf2A13wYjHXaL4vk3V9+6NINW4sSEhVF6Pmc2WzBfL7gpZdf4t69BywWGffvP3L+xlrjCKUiUCdLY/o+kWD6JYXWMJ+TXve4MTyuL8PyWhqtGQxcgci8yOr0lKHleY42mihSCNk+uKufvwoE9X4OoKD9WyvIoe++4wSi8C/03d77q8Z73Ofe54R9eOx9ovlnl/3ftXepsNpQ5DlJkrrPnducVtAQRYrxaMBkMvRKPifAxrGiLEAJAb4omhBHlnNpfH3EPvy+CiD2tXbyiy4Q/su2vow37dZluKsYc/v6pXuE08QqGSGsRJeaIssdrbYCXVVYq1g2bfZrFiEobgxJEnFmax0qjdU4JY4IYKlxFQp7om21647XWsvZs2f56KOPjgQ9CmmxWmINVKWjWa++8jJ/+sffc3WclNsIQnhdtGxnwjm6bsc20f3oBRPrMxb5eAa0j/uSwgEdwEpBmsaMJ0MuXrzIweGc27fuIaVga2OMVAohnRsrCA4ODymLEuXPixYu6DhNBlx94inuPbzPx5/exhjDqa0tnnzySXZ2d8myBa+++iLD0RCNYffggN/5vd/j+9EPee/tDx1PqFwVDCeMG6TUjMcTrNFUZcmZM6eodMYXdz7n6rULPhZBsLOzx9lz550yTCqGI8Uzzz3H2z/9gDt37qKksyioOAGp0abCGF9bylqqUmO1t/AgiVXE008/xZ07tzic7lKUC7KdQw6mu0ipnPVLSYRyWW6qsqQqSqQBtPV0RLstZCwOPXm2owRCKSKl2NhY4/z2NgKX7ERFyr0r3DsrlWbj8ja/+V/8Pa6/8RW+9f/7D9x995fo/UOiRYauCmKv+LQCiLwcQFXHaFtAW7cjlJC1LCCU25tO+eMBurdkhGPYnMej/vdCCHQNHo7SZ2u9Mmypr0Dn24qB1n7nKH1aRfP6NOxL1y2Nefm6rrfBcbSqS4dX0YG2wN7+vk9x1zfuQKPb6xzc40OCg+6zVvHN9vftfpeVfv2KvS7d7N7bByja4+6LqWnPs/238JvNemAP7m8jcPu4rBDWKcwqYzBV6ax5unLu9drJv3meU5YlSZK47FKTCesbmz5MoqrHdXBwwOVLT4Bwrp+5z373uPalYjTaC2KMqVPVhs/tBegKrO1Fa/8e3Jc2NzdJ05SiKJjNZggh6v67Lk/tTdKHsLvj6DtodXyGtXU18/Bb+zowzldUSCpjuHTpEtZaPrlxg89v3eLJp54kimNkoTDWm8ZxmySOYy5fvuzWQEqkammiO+N7fHMmWAlUWmMM3L93n1u3brmAPxUzGKRY64J7oigiWyzY3d3j7LmzfPe73wfraoFo7YWAdu8r1ir81n7/x46y8+5P0rprfyLBoOe+1i/u/1vrvJQNrWOmBlc5GfAA1wf+1+bwX73Vez9knXHfnvjek65FX+t7b18a7LlPvYBI0Gjr8NY+LP6sitqXV3ulgyUI7k02F6zTooTxDYYDBumgHn+cxCRxTCZcTRohvWUK0au97s69PeaTAIXuWrWZzEnexePW/FcBfG1m1Cc499E8KWVNh4LipSgKprOp165Fdb2hcFYsBmvlMUoE4eIPjODcubPszxYMxuN6DFJK0iR1KU619oGujSvJqjYcDp1Q1cniZW0QqFwqxrKqeOrpa2xurvHg4Q7gszxJuaSJPW59H5c5qdsCcNahpoCUzoUgjkgHA0qt0QIG4wFPPPMEV65dpagMydYGX3x2k6ysuHjmLHfvPWBnZxen+ZcoFWMtaBucbQzTWc5nn91GYzn07+lgf86DB3suTbSSZEXOb//ub6GEZZAIyspy/eWX+cXPfokpQRJR6RKpIEkjrly6yKmtU9y9e5eqzDl/9ixpqvizP/8TLl48z7nz58hNxeUnrlHh0rxjnRX/8HBGnlfMpq6qd5qmrK1NmEzWSMcDtHKWhSLPiYRw53Q+Z29nj9nhlChV/KN/8oesT9b48IP3KcuCyfqIw8N99vf2me4f8id//CcgJHlRkpZFLUuIsMctWGvACC+OWyQKa51iYnNrg60zZ3wRYU1lNJUxKO0AYpIqClUhU4XdGvO/+d//7/jZt7/HT77+HzG3HqEWGRQ51mi0hTICbTXK6OAAhcHxb4QDZVK3XfXEkkVwFY3o4/m1bOSBcr9yKVhFju7TPrqySphvj+M4PrvyPFingO269Qg//yVVhV2WcdrP68qE3bGdaCzHNCHEksdK12rTdQELLtrh3q7s0icXfZlxdffEqr5PMi9YUYcEcYS6unOkqfKcLMtI1iYURc7O/V2KoqDMcvIsJ/FZHoui8HEYDhKcPu0sqSEeu21kmM2mKFWQps5qeJJ2YqAREGwjrDlzkLGWSIglwb+L4PpQabg//BZiPeI4Zj6fM5vNaoYZJllVLvVeAAlxHHfMT8tuEN0sVd0XrrVLr9c3vjBH5w7mnjEaDdnY2CDLFnz/+99HCMHzLzzP4WyKd+4EXKEUKQTbZ7ZJ06ROMSulRMkm/qRrOjuuBbczl2rXAYU33/wRs9ncoXVcQHyWLVgsMg+e4Ft/8S2ElAyHQ+LYZfCQ3g2lkR7d2GuzYWedlsfh1ypIAUfGeXLh78sCiva9j7u21kZ1NAUNeGhpLPxBc66BreCzADY6e6PJsf74OdTXEQRzsUSVVxGvri9sPYbW/3T386r1+bKAZVlrs9yWz3b3fTZ7OooUCLx7iav3kqahKBtu//gxGW3qczgejxlPxoBgfX2d4WDoq9zP/PzdGegK3ydtj1unbmv70Hb7OG4f9q15lyaGRBX9Qc1HhYb2XLvgov3M+rNsBBi8FmsxXzjXlDjyZu/gnuJOhu9oqe/6Wf7dWQuDwYhPb93h1JkztZBvrSvQmi0WnrZT943oD9YHJwykacp0OmVtbS08GWs1Tgx3wD/PczY21rl8+Sz3H9wHEhfs7gujhsJafWvzq7TgWqG90KmiCBXHWGGRSiGVAq1dxXphOHX2NJU02ASuPf8Eg2HMrY9vkFUVKkkoKw3G71vjApzBYqWzBM1nC7Is9+WrHQ8x2nBYzRBSEkVw7+4DHtx7yJmzrvirtoY//ZM/YTGfEZsEIdw4LRVXrl7i3OktIhUxGiZMpzmTYUykTlHmBTc+/IgXnn+BSinu3r3L1StXXEVoIbh98yb/3b/577l/+6GrhoxzM97f22U4HLJx5hTnrl3mzKmzICy6yJke7JGO1rhw5RxFVnB4cMg3vv0XrE/G/LN/+k954uo1EDkH0x0O96fMZwveeuct7ty6AxK0rpzIVL93v69Mk2TCvRe3RQeDlO3tbSbjCSqOAYE2xvmb+8xnmJg4EYhYUmHYLeb8zT/8e1x+7ll++B++xo2fv031cJeoKFBApZ21T2EQxrmfCSQWA6EWSZAtAvAH8All2qEKXfrQFTJrDwKaGMKl8yFC8PnxdL7LI9q/9Sk+wvi7/a3qP8yxj+ZadwF9yqi+uba/P2LBbM1jFf3sjrMN2ML3ATy0/4V+25n5wndtJWSfu3ZXmd6ee5AP2mvS18eqNQjr0J1T+/tuqxVJ7eeukMXKqqIoCihyprMpDx89QpcltnL0OS8rkiQhjuPammGty1C4t7fHaDSqnxHG98GHH1CVlq1TWyRJ0jvGbvtSweDB7aj9YCmWF7VvsbtZqdpoNix+QFLBlanWhvZsgHa2i1D8zmWdslhb1QCkbw5hI4YXH76PIuc/GQrAhes0hjRJUURcOHcBa+HOnbu8/8H7bJ7eIk5TsqpACNtgDSkR1vDkU0/W2XScQLF8CPt8Dh/XrBVkWcF8tuD99z/EGsf0G9QNpa/cLqRAWkUUxzXIcPUIBFhRB345TYUrVNdN69Ztq+Im6nlATZT61v+IMNT5LqxLX5DYSdepTzhu/+qK2Si0dsxMSdxhxAHdNiFpWyCkbIhSd/zt1iZsS/vMZ6NxgXetxepp3X6X5tACqicRtLsame5zjn+fq5llAGJNP6J2VXQCqaUovBuN0a7ibCsuRirlGHhLmE+ShDRNkVJwcHDAbDZjMpmw8yhD6ybznfUWviNr07N+XWbW985WrVv7vycFlifdt6uYfZ+Aclw/3XuXmJh1rmohhi3LM8qqYiAH3nXKeBe+IOwsr8/S80QD8i5cvMDP33m3Bu+B8SVxzPTwEF1VjTJCrF47izsvZ8+e5dGjR6ytrVGD0SBoWqdZrqoSIS2vfOU6P/v5Ow2tEsKP+6jWtLt+j3NX6/5WXyMlUZI4n2a/pk6D7gocWqNdQHMliQcDpIXLl86zMRiyv7uP9GlMhXWKDmMqVDj8xoOxEDjvXZKEdP+QziVZWIWUilsf3eDM5jpREvO9b32LB7dukhKBKUA5kC8iyWJ+wDQRPPf005TZnMP9R0RSEUnJOB2QqoSHd++zdfEc9+7eYfvUKeLxhHyR8T/8t/8dt258irKxP+dQlDkIqLIZWXbIwcEjFlcu8/z15xlujDm1tcaj3YfsH+xzeusUp7Y33bvThj/75jdQUnLt6gVefeV5RsMhkYx4+eWXuHnjM8d7ixyBs3aGHCkhEYsjGy6jmOPNgvFkwObmOoPRiMlkHStcjGJ4L5QVUQVSg9CGrfU1fvnuL9mYbHL1+vOcfuISv/j2D/jF177F4ae3MQdzImOwpkAYgRSOL1aldgrCsIdChktv4dMhtpEOfew5l/20pOE04Tfqb0TtBdEVxNvXrwIIx/3e11aNvaH0yzKMEA4UG7F8ZsJvgRf2ZY9q88lV/K5vPO0zHlrb0tKVI7p0ti3jtBVJfdaa9jOP0DBr69d23Fp35Ztu3+3nP+49LiVdCGADvAteayzCAfSicC5RkTFsbmxQ6srJuNbx9ihOSAcDoihiOBzW7ykEpnctPnEck+cli2yK3GfJ0+i49qUsGkH4N8ZFnDtzriJJBjVQaAc5d7WBYeO1rQVhYdpIs52BKixoG+C0hdDwOcsyhHAAoizLenODM813x9IOxA6uWX0xColKHNIjYmNzE2M0P/7xj5lNZ7z62qvM5jOqqkTFkfOTkxKpJMMkZcvXzmiaaNOTY4nSEVQtpNdASqrKcOvWbaaHU6RyVcrH4xFlWTKdTp2vqgdgRmuGw6HXjDhf2NrX1doalQdi1mgojo4pjLnzy5HPJ8FM7f76/u5ed1wfvb+5Cx4zBmoGEUBtHCfNWJaIf3NN1xc0jKWrsWjvXSkEo/HYFa0rQvL2fmLSvr/bLPhia/0Esbs+bU3MUj92WRPTJ3w/TqgNOvBwWbh+sVhw5swZ4ijGWpdqWUnhhYjAXJYeBP63yXjC2to6SinyIqcoCpI4PuLytmq+7bmFvx93fXtNHjfvkyoEHnfvEhhoEfK+8awCUt3PfWNzNR0saZqSps61Er+3axeDIKvTrNkyrhXNdxaEhO0zp5oYHNsolyJfcyEkD5E+AUIbkC6NmwZo/PKXv+Spp55qAu9rIO6ARFkWaFNy/fpzJElEkTuLkLHLjDis6RIzPmYtV7XA66wFFSmEcjF/Sii0tVTGBYQLA5FQbI5H7O7ssH94wGg8YZAMSSJFmc9YHO4R2cofYEiFcXEA1llurHEgBAOuFoPAeqBhhcAIQSUlslDc/fgTbo4HlGXOW9//PmZRuoB/AVIm/OE/+icczqf8xTe/wXTnAbt374BQzKaH7O/usLu3x2I+pyoKfv7Tn/K3zv1tbFUw3X3EWhzxra//OR+/+44Pelf+Pfk9gKUSkmKqKPYfUe494otPPuT13/h1nrn+PBtbmxRVzr37d6hkxdbGKYQVlEXJh+9/yNf//E+hyDl/7jzXX3ieUZIiMEgbLAJesK7BqfFIMwjc3k1EWDY3N9jYWGc0HqOimMPpjPHaGla4GIqyMiykQZcVMZrYSK5cuswv332P1954g2Q84K//wd/imeee4yff+A7vvflz5o8OXKB4foA1GmEMMjLoqkJYQ6TkkpuTxseCKuce6+psrD7HXdArhGjcxOgoSDp99LnNhH7a1x2RHVpnou1W1P6tLU+1W1tZFpKptBNs1DJDa4zQuCyFM3kc+Op+135u+DvIjWG8bZeoVck8wvWBB7djH/pARNetKlzb5en1Z+/G272uPY/2M/rm2df3cWCkD4z5HpbX1X9blg5YDCzEScLFixedu6nxCU5kVGe6Gg5drR2tNUmS1OsY+EYYw+bmBoPBECGcS+tJ2omBRl1R1pg6xV1Ib6tUXL9QOBrZ316Y7oJ2kVx7M7W/b6eBbW/ytnY5ilwmiwA2wuYMgUAhwDwsYPs53QMIjrlILGVRsr614UzHj/Z58803GY1GnDt3jr39XRcc6AO1pfdNv3ztCtZaoiiug86VOpr+tyvk9R12oDbTauMY+Pvvf0BgwM6NLKEoSg4PD6kqjZSKNElJpEOhRV5RVS2BxmupsAFmLD/7VxOoap3H0nt6XGsThFXmwpVP7BzUVdqI1fc7S0VVVRitlwo6uj7DhcvaiaBJCJ2sWrd6P1tnjlSixRS8JmsVqGiPo/4bR+Daz16aT2dN2gLX0bnb7hfthzYd9m2F1hl069LVvCxbCUXcKAr6tlb4bTBImUzGJEmKNdbVZBiPiaPYFRbrTpaWPGr9ei59PqYFJrmE/9t7uD3Qo+vc10T3Q1vT1Dgnhcc3YLfNWDn6Ho8+sRlnm57Ve0UQMnMyGo/ZGI+REu9m6VqT+QafV8lgjcGIJqnH0jnyYM9ay3g8wVjr3V2a8+f4gaoVN6taV+BaX19nsVjUn4/uTfefosi5eOk829tn+OLWfSIVYUQJrbPUdm1sP8+dg/Z3NHtEtNc0bP9wj+cFyp07l+JRO9AhBQqIhWD3/gOkMFzc2uLe3XtMK0NlYDGfUyxmxMIwnR76F28wtnTZq6zBmMrP2QISKWTtsovwIE5FFCjygz1+Ot3l4cP7zA+nRCKiLA02lfzu7/0+b3z1ZdLxiCevXeLf/Zv/nrt37oBwwZsP7t/j9hdfsLezw500JR0N2Ll/j4vbZzjc3WEgBD/94Q+oFguX5QmfZjy4nXrQo42hsob5ziPS9TW+dXjI/QcP+Ou//ducPn2GrTMb3Lt7l939XS5dvMygsrz0yss8vHWHd3/yc27d+IKf/PDHTEZDqCpUHDsPhShCWIsSwqUPthZrXaXjcIKsdQkkTp065WhDnCCE5Kc/+zmvv/4GySAF4crgzUxFoQ2xgAGKdDCgMpb7d+9x4ewmRBHbT17mdy/+Ey68/CLf+uNvcPujG5QUXDh3lkvnzvD+W7/AljnKaqQVKK2QPqUx+Loo0rlYSWjRQ2+Rqb87au0UAqddFtSWRVp0QGNRUjkAZp0Vd1nAtq3rA19f7T7oMlytsOiGMdRj8wqgIIh3hP8lkEKPO0+PS9jS444I27J+ejv+ruHry0qz5v6eqfQAh+CNcGR+HcV3nxKoTy5bpaBr/97Xuvd0x9G9fxUAWXpuRzEkcPKwKJzL6TrOfbmy1is7nedPpQ27u7ukacpTTz21tAaNG3RUWzrKsiRSjeJbyv8EFo3w0oKmKk1dsSVXALapAq51Gzw0m7PrlnNEcOsIL2HCbdcpa6njOcqyIsQuRJHLoBSARRBag+knaNgCYgNYW1tzL8OCkqrm/NY4X+NYRmjjcoBvbZzCaMHbb7/Lo4cPeeml62hKULVY7eZqNFZIrl55EhAoJZAKhPTB3NJl2RCCjvZjOUD7iFZWgJCSxaxiNi355MZtDBKtS8aTCVJGGFNSFBqswhpJFKUIFWF9dSLn9hDMbV6DEYiLtQiLS+IrcFqh7hh8k0IsJ6qh2eer5NL2vMJ77e6vVe3LgJ4wZuMJ/NE+3FylUEhvAcNYKA2m1CTD1MtoHgQjkB6UGeHTCNYSbotY2OXn1PubZUE4pM20re8ep+3omaQvIGYxHiiFZuwyaAwEowvijmiS6jPoPoeiztY/q96lNszVn1UhHFMX7uxIoTCVxlSaSAqktc6lRLkUlJV1Pu3OXSSo0gUaqKwlSiLGa0NUJLBWYyrL+mTd5+Z34w5ODNYax/CxdYXfwCwdrWrRmIaDufmFP4U/d0GYX1rzqIYttn5jnkbQaM3aPsFC+AWqZYYgBNiQ480/xj3LZQsJI2pRkrB3xLKFsGZ4fp7tHP1SWoQIsQ0gtGQ4HHH1yiUO9/ed6wuW9cnY7enKYrWPBbDufm0NyioEsn7/tdCNrec3Ho8ZJSm6LBFaI41GWkWsIiIZUeQl2mi0zz/bFmCW9rVxqWKDIinP88Z9MWjTpSv6Zo1CV4L1tTHXX3ie2zfvg/F7W2a4VL4xQuIW1Vpf8RZ/7H3NivrR7pr6vIkKRKPUgRKB43WDJMYKZ3kwpXP3M9YiseiiQoshh/fvcu/eHV547lnmD+9TFiUGXIapskBUh5T5js8G5bT1oQaHrEGGozEGwGdWwoKwEmwFIqIqc+7f3kXriiR2loxKwrWXnuGrf+tvoIWmKDNeeuVFnvy//l/49//Dv+XN7/0AlQhu3rrBnS/uUJZz9vcfMtYTvvYnf05VlAzimFhJvvj8FpjSC7UaFSmXXcm26iYIgcGloZ0dHlJWmo/fepficMF/9vu/x+nzZ3jy4tPkp3M+/+wm586eJ0kVW2vrCK0xVUmpSxazQ6wN2f4klXGurJEQvqanSyFbq0n8MimVsLF5mnQwRghJmg555xe/ZBBPeOnlF4mTyFmbZHCTluQVkFiuPPEkv3zvXc6c/irW5CgscRrx+t98haevX+Otn/yc7379O3z+2edEnOOFv/13EVaTJAKdZeSHcx+7UzGbTRkOh4wnI+58dIPi4Z6jpRaEsQjvFmd9Nsuw+5yC1GvYDSivMLSergU6FUt/8uyyO661FuV7E1agfSyc8gJJJXTDix3iIZIKK5VTxmonT1i/36wHOKG2lAjKV+ncw4R1cVIhyhEpfalKR5+UCLGdARjWhKx19h2/Usrd60CkQAjrgbWo10oIB2TdMXAKZHdOnQs6NW30Vi9PCwPta/O/ttzZl+68qyBfFaR+1Ariaqw5xZ9tQBzLbKR7f1vW7VpjVgGyPsVJu8kQ++v5v5AO9EZSwbyA3CU7ePfDD9jf3UdZ2FrbJI0jDmdT1jc2KM5lLs2zcBkJS12RA8lggGe/IAQKiamMrxF0MgjxpbJOlWVJFEU1wKhjJbTzNw3MQogg/EhCdpmgZerTmjvN/9GhtNFo+3rXZ1MRPAAQWkg+BIuHftI0XQJLWZYdfblekEE4YdppcizD4YgkTsnmOT/43g+IlOKpp57k4PDAbxThn+WY/MbaButrm2gdtFQ+p7FtuSAQDkcX9Tfjb28m492mylJz+4t7HB7OqSp3oOMkwVrBwcEhglDPwOXKN9qBC2g0An2aldDCUQnCztL61L93BNV6/Ee6W9nafZ7U8nHSfo0XxDjmYApPAIPgJ4CyKEiHY++Opo/giUa+DkJpu7/wfdM/1DLnUbBUo48vP7/WaBB4V6rQpFgiOO2xdJtoNh7NarTOQrjONteqVpxK0Jpb4RiMEAIlJVXliv9E0gGUqiyokqqR5wlCsqcRnqEYa0kSXxBukLBYzJnP55zaOgMYVCRdXI0PDrW2SW8d9m3N1EQA19ZrG4Mw6WlEoBMiqkF3XUCrXqAAVoPbVkBZAqOdYBBFiiSJvQLDnXMnIHejW8LtjXuisLa13KJzaavooxEIoZo+OvMNzFbiNO2gkAKUsLz2yotIKZkd7mO05tTmKdYn6+zv77nYMxnhqqK1ALAVNchoNqpjpsq7QsVxxPr6hGw2x2yto6RwMcxCkESJoz0tkFKDqK5WEPcupZRsbW2xu7vL9va2n1PQDPsUn1ZSFBXaGF68/jzf/Np3scYSSRdL56RhhbAhqJhmXta6OAkPLoz1WnoT3EI0Gg80TGO5r6oSoSSVmde8pnZd9DOTAqrCUi7mHOzs8NbPfsqlCxeRkRcOJewf7JHNZ8QRLo6gdHWQrAmuQM3eEx6ACKOxGF/4zu3BSlowlqrymWCQWCWRg4jrr75CVVbk8wU21rz587fY3dnh9PZpxpMR1lhuf36TR48eYaqSN157lbPnzvP2ex+y+/AROh1wdvu0E568QqbSuo4lsWHdarDrtNxKSUyl2d/ZI5K3+LP/9U948SsvMxoOmU1n3Lt7l/94++scHBzw6IsvqMoCXZWOP6L9OTYIETkeIly8YDijTjHRimvzPG5zc6vmOVVVsZjn/PAHb3L50iW2t08RS+n0GdoBTivBGleBPklTbtz8nIsXLxCLEmsqrFGMJgm/+Tt/k9dfe43bt+7ywXsfs7+3z2A84NatT6nKguEgZTxe52/+xq9x8eJF8iLj8GCfnXv32b17nyovMWWJKTW2KKnKkqIofR0S7V1wnUvLfL5AVYbUZzoM1wTFbWQNwrj9YLWh0q6aO7aTMEQrB16N9e8vaiiKMX7Purpm0nq4EARsr0YR1iJ8nS1hBZGvym59imeNryZmPT0N7EMYrPTj9EHzIiif8EqLQOOEdS6B1tbKzEBbqkDLpQNGjfzhFTge1LhCoKHOVUNb+lpbhmz/3fUiOE4e6SoPa3oivHujEDV7YEklteyS1R3XsmWqn0+3n9d1/Vq2Cot6T+BpNMIp5cuyYHpwgFofY62zdMjKkmcZUqTEcURVlWRFzjiNMVZzeHDAg9v3nBt+HBHFMelw4M+mZTQaceb0aeLorzjrlBCi9ttq16Fom6faGaLcZ9XSih1dxG7QbNdEFJ7bdneytaDH0r3tGI9utfJ2X+E+KaVL++Ur3Bqtl36rkSaCzc0tpJDcuvkpn3zyMRcunCcdJCQ6otQlcRwzGqRgYTqdce2Jp6gqB8oCgAqWhJNq5/s2e1W5VKEff/wxVeXcSNI0IY4TDg+nZFnu193V7BDCmbjD3+G99PV/ZK1o5GDZEswAp40+QevOddlkvPyOV/12XOse/EaDL2rN/kn7AUGRFwjhqvlWRTAJNmORQRaFWmvuBI2Tjbfbvoylpn1G2ut1RNPh/1d0tDJYe2ScNRDp6cfd0hV/WXaRxPraBd43GUAKkiRuaWFogIkNyR6aObUtmlprkjRmPBkxSAfs7e5RVSUbm+tEkSDzCoZgrar1bw5LHBHtQ2YYX5KjtZgtWiBkzRSO8ivP1APQCIDK1wkAizAaYTQyWHSdHqnWnDfgFC/8Gt9N53ntC+mCe9WqTNy4qjmFgHPXxNczkB54xEnEX/+N17j+wvP88Ic/coJdVfHC8y/4miaKza11WjrKI89ulBG1RIG1IiRF4syZM9z64g7ntI9jkKq2dM9mM++ymrgEASsOY1DsaK3Z3t7m3r17nDt3rmXFXrZ0Bqv0M88+yWQy4PAgYzBQlJV1EZG2BJNhTVVnKXQA0L9DUxJiIhrLEI6B+tUOwjRao6whkjFp5IRUt1cbVxKEK3AlhHPriiOJRDh3qbIgaSm4wr/gvhYARleRE4A/Fqz2ArL/LBRHhMxKaybrE7749DNiK9ja2uLbf/EXPHrwkN/93d9ldjhlMZszGg7Z2dkhzzLWJhP+1X/5r3j/gw/5D3/yNcbjERcvXmBrfb2uVxV4YreieVDS4N0jpYpwBXsthwcz4sE+f/5Hf0KeZVSF41O6LF12sjq5S7BYNO81Uv3iSOP9gCsopiRRHIEUZD4lbhQZ8jzjzp27fPzxJ6yvj0kHCQSli23crLXWXL58mXff+hlntrex1hLFCmMs6SDBWst4bczzLz7Lcy88R1mWlGXJIptTFjmFf+bW1gZSCSghXUtZu3SGq9Grjs5ZJ2KLWup0IE1rjdHtWNeCqLIo7ZK4FEVBUZaURUlVFohSo4uCPMvcOKqKPM8p8pyydP/NZnOKLEMYS5UX5IscaQSmcrVTrAkWuJCCXNfV2zEWGfiKdQ5qRhuEce5rwjjaYICi5QbW1ioaYWkosq09NrCuTohFePrs/nbKN+nAfbBIC4lQDnAYgMrWGbxCWnOCpVaoI8HffYrTtrzTdglaJRu2+dEq+SjIh22+1QUM3X4f1/qU6b2K0R6wBF7ZaC0K6WRu0ViXpBAkwxRtK2yZM0wjFlPn8rqoCipKBqMho40Js3yOTBSLLGN+OCWWEdFw4txqpaRY5AghGUxGqEHCo8N9tra2Hjs/+JKVwUOsQS2cG2f2bcdPtBcPmvRsfZaM0LovqA0awmZpXmTTZ6hUHvroCtNtNFkHJraeX2ewaQGe9guXSmK0ZG2ygTWWH/3wTawxPH/9OQ5nhz4yX7G+PmY4GFIUmiLXXL54laIo69RfUrry7d0sU911qH00YWmtwnV5npNnGZ999hlV6awlp06dpigr5vM5eZ4hRKg54g9Oa03bgnlXuD/SWnJQXaE3MGW7+gCtApXHHd4wnu7nx4KhHkDqhnf0vqNCdBByGhcVZ6FzglJZVK5iZksEC4J3na3LC++176rX8vlBhLvaNLl3nqGvvjEfR3CW51NLs8uWifZYlqVJ/x6Xfzgynp6zGjS7SChNjvYFtiIlSeOYNE2QSvgAZEVVaYTQS++ouxZBgyykZX19zKlTp7h58yaLRcbW1iaTyYjpzq7TONsmc5oTDFlKKxnGH4RBXevs3FyFEHXV+LCXZcv3uWYeRF4z5Ak73pKKQNrIZRCzBlMJhImcm13oxwvv0h8aa63LrkWj81LCFRfD+gJrtltHImS2KVHKu6UaX2EWv5bCEEVOIE/SmNOntnj6mad54/U3GCQRP/zBD9nffcDhwS6vvvoav/bGa9y6fYvXXn+VJI0QtTWq2SvBwiOsOLKeIbOYtZonn7zCZ5/fRFcWIVQN4JIk4eDgoElfvsKa0W3b29u8//779X6Qqp/GVFXJ9rnTnLtwhoP9T4mjAdMip8gWVLnB6DnY5cxwTiEASmgHjuWyVtECSjhLlPTETxiDtq5Cn9AuC4s1lkr7VLrCaV/zrMRGkbNYqIgXnn+OyWTEz37+C3KftrkdiFtVFVaI2uWiXm9Pi6xpCtBah01xbhp4YN/iC0IQRzFnt7eR2vLFpzf51te+wfTggDOnTvPp+x+RZQuX3riqmB4ckGUZg8GA//t/89/w0cc3qAzYyrC/u8fegwd1ZW4pxBEX2tCklMgoIlIJSAUoPMxl79Eui8WspolKSJTBW4+C4iHEEwkPUgwiauTXNu9WStVgUEiJihSjyRhtjEuDX2mqynLlyhVu3rzFe+/9kudfeIY48dZKmj6bqsyCwXDCp5/e5MqVy8iqcppd7QTlRMbOnVoACtI4IR074OL2TihAbEgYYLFE1qJDdirt6Y+boXuvnuaGgxY8M6SQ3oWwUdLW/LLyboO2mUnYT8ZUzlW7MpiihEqj85I8yzEGqqKkyAv3L3Mp74ssYzE7YHpwSFWUHpgsyBcZuqrQVYmtKmyl3fmvNIT97tMcgwPAWOcipoiRVmNwgF55V1uLc5U1wtE653VpwXiPDSGprA6aLrQxaBM8Epr6O0I69yob3MutWpIRu0rK7ueQ7EeIJpC9zefCmneF/fpNdfZ/1/rRVszUz5XBlcseuaYNatp9dK0bXX7U5Z/tJhC1HIsQzr3MWHRVks0OSYRmFEk2kpQiUuR55SqAK8n5s9ucPXcOJaSz+BaumngyGhKnSe1iF4Lfn3/xOlvbp/nWd77DjZuf9Y6n204MNNramKDVDAEi7d+7SK+dZaqdmissfFi4drGmxgVrmUEF9yFrde0bHVrb1609hvazQ9C304BETCYTn9UmQfhA4LAZhXACzPrGOkJGPLr7kLd//gvW1sacPr3Jw70dlJRsTMZsrU9cTnVTcG77PJPROtliWj8nbKp6/q01Xd7UTpoP37WRqzFOY/P557ec6du4AkpKRZTzjMPDQ0KGlGaNwdrl99N+n922JLgv/4Joa4FpMfBOP92AsCUt2AnQfXscq4DpqlYf5p4+Vj6LBnS41MaizpzTBg7WOheItjZHtYVmp56sLR3NmI6fW/f77nddDUu4blVq1DZ4aO5pfmvPvG9Z+7JstC9cOote6DfGoKTTBD/9zFPs7j6iLEu2trYwtmA+n7G5tYGKFOvr6y52wi4/0xhDpSuMrpisjXjm2ad4++13ePRoFyHhjTe+wh9/7etIawh5cFyxM+kqhnurw5E96QWm2qogXchmDQzRuBoywvslB4YjEaQeCPi+/SLWYNs64dSU7p5YxmhdIKXT2Lp5aX+OQUUOrDSWpeBO6mK5QvaPoMxJ05Q4jhmPE9bWnZUnHQzY3NhgNB4TRZGvJXDaFS/b3CKKBXu7e9y5e5ef/OJj3nvvPfZ2d/jKV17mn/6Tf8TTz1zl+ReukQxTprMpYH0dDOH3DFgRtGbLNNWtuqyB0rnz2zgZyfpaC+6aJElqXqGNcRmbxHLK6iWFhxe0R6MRVeVcSly2rGU3h0DLq6piOLI88/w1PnjvY6zWFIs5ZT4HI1BCu7iOAOtaVhFnzfBuXYTz5ARA0wJW7pwbrHX7wyUX0bXbhgqWfK3d30ZjjWZjfcK5s2e4d/cui9mMdDSu4wKDZc/Vv2iAfBCkrXWxgTYyDtyIQAMc3wpVryUWERRskeLytSe4+tQ1pFD88p13SVWEGI7J5wvuffEFg8GAqiiJlCL3Yz44OOCHP/gBCEU6XmcxnxMB9+58gTAuiYm1zg0j0Jp24S4Vxe6fjBAycmsnIiyCMi9rf3W3sM7qZhFY6Vxv4jh2bmnCnRF/pFqJU5q0mmEPSuUE/yiJiZOEoiyptKYoS6wVpOmAOI65desWBwcHTCZDhIqX9lyjZLScv3CJd955m9NnziKEE2il9O5gQrnvhM845rXFrmaK9e/GycPCA1NpBZJW0hqsK/YnxJILbTgnMtAxBUjpga4DrwTQOayDQKGmQI01TgofTG6sr6qusQgqIZx6JaRONhartXcXdJYOU2mEtQ5wFCXGGopsQbHIqIqCbDpnPp0yPTiknGfMDmYc7u+ji4oiy7DaYKrKZVEsncuW0Q7sSB+HZykRVC5JTqU9zXSucEJaImGc14V1Y5fWF2gW1tOhyoEM26LvUCt02uDB0YjlRBCBbvQpw9t84rhkKUvK55bXTvuatmwJnmW0mFybL3Vl5rZc3P591d9dkGQDgAu8Tog69k9YWOztY/Kc1AgmccLa6bNU65q8LMltRVJosgc7pHFCHEVEi5x8MYc0ZWNzjVJXZHlOkZVsnzvLC08+SWngb/3mb/Nn3/jakXXraycGGoEAtK0LTqMmlqwF7RbWqC0sdxes+xLDs9rpzMLnxWJBmg4QQi3d203R1gY37fF3QU4URZRlSZ7npElSp8UNhUsQgs1TpzEGfvaTnzE9OODV115mni0QEtZGE+cLmkiMtlhteeLaNWaHC9JBtBSzEp6rVAgGP5nw3GaueZ7z7rtN/niXjqyoTa5VVXmhyVUw1brtztEPDHpby5oB1ITRCWZOIGuvZR/aP+45jwM5q+49ydiD4GDtMuDoG18AY0K4OeV57ghXsI6Fgme4gHDjhUTXha2tAhDEtNazWpq5Xon+S7ST7JX6HNnm2WEcNYNbeqmNls1a5y8Ly8S11qK0bgyWB2udhsuIygfnWS5fvszZs2d4+PAep0+d4vy5be7du01ZOuve2bNnfarpyuWpb1khhRDoSpPlc86dO8PFi5e4ePESn9x4n89v3uR3fvc/4+NPbvDBhx+5824lWkDw69aEzEOd9RDCA5HlNQk7XAjjGZl7l5F070sIMLpwlgkZhD63wAKwkfH+6Y4WDQYD71pqiWLBcDQiSRKS2GW6G09GrI1HJFHsi2fGTCYTJpOJP8sx49EIJWMsMBgMGQwGPrvfnDSNKUvtM8pJ0jShLCuKwlkvZ7Mp7737Pru7j7h58yY3b95k59EhSZLwW7/1W/zBH/wdXrj+DOfPb1Lpkt2DQ7QuPX31y+LxhjUWjXYgwridLaUDGdTxXoZTp7ZYX1tzLh1FBWNHZ5M0RipFnuee/jTvpM0H3H5afmfj8ZjFYsF4PPY1WY4ya+d6VPHii8/xJ//L18izOcNBQrHYRznnD0wrNqODOwkuYBYftCukE6iFalkrjStqJZzm1VqotLd8qCYLi1NAyLomSRxFnDl9ivfefYeyLCB31r8Q4B74J94dwYHFAcPhsHZNns0WBCE9z/Pakp9lC7LZ1CUV8Aql89tneOKJJ0BI7t65w50vvkApRew160ZrDvYPfJyHj+fyAojRhiRNsFpTFSWZzDjYP2CYDsBrp01HuAp8WvlA0CB8KxFjUS6oVzr3QY/eap9xgwtWTpKYqiooirzOaATO6yCOHMgYj8fM5/OG9nlAGqcJW6dO8dzzz3Pq9GmEcgLeYn6A1hVpmnJwcMjuzg7b26dJVHyE5ocmVUSSDrn/4BGbmxsY61wlBcLFLnnaoCKJQCFljBAKi67pgStw6FyGpBUo25AY4TX1Dmh45Ypo4qrqPSmpCYygyfIkACtlreIIcRG1kiQklfH7QUlV76sCAwE4IZ11MBL+OkHsiZqT5USdXEQY47PLOUBgvZsXxlk4jdZUeUGZFRRZzmx/n/l0zmKWsbezy+HeAbODQ8oso8wL8jwjL3JM5VzAhLbYyvVXmQKLO2doA5VGGlu7c7l1rUAarK2w1iW+sCzzjXZT6qicB41M2ZZVu8rphkYsC/9tXti9r90aGU8tZ4ZsPaMLEkLrs1a0v+sqiZeVkIE2N7zeet40GgyIIl/s+tEupRV+n7h4G4VhdrBgZi2Rioh9UiQrwCaK+w8eoSLlYoOk4P6jHb4/zdk4e4Hf+J3f4uUXrnOS9qWCwbtZa2prgWp85tomLfdyG1TZh8jC567mKrzs9st1GnyFUtGSK9Aqc1L75bTT5raflSQJi9m8Tq2olHL+mIsFSTpAqYhiXvCTH/+YSEVcu3aNw+KAJI3Z3NxgMh5jKSmFJokTzp09z3yek9ioHoO11JpSRxgaAeXImGmE13C/EG6jFEXJRx994jTCSiKloCgKXx3cFRUyxqN9XICo08CdAFwc02qFuPXaFNNvaeg9RLbVQee67szbT1wGpQEQdO4IQnXgRUf6ac0g7DV/GoXACTKecEshfDV1Q5zEHhCGjC8ClcjmWiVrEBNcHJQQlKWuK7IfM/klM4f1mtWlyVnbgKSaca1+h0d9NoPE2KyL6Oyr8AxovQ/hnnTk/bQ+Sv8+3NDcCxiPx7x4/QVeeeklvvmNrzOfz3j5xRdRSlKWJZUpOX/uHFevXmnAqgixXQ0ystYym805vXWG06e3+LVf+zUePbrDX3zrWzz55NP8H//r/wP/6//yH3j7rXcocs1smpEXFRaJkcIFerfmZLzmWrVYNTi3iSiKiZRESifcjMdjBoNB7Rq2trZGmqYkSUySxpw6tclgkLoqqknEZGPIaDSqXTdHIycoWiMwxjHuKI4x1ilIiiJHYMAK8rzwQZ9VLTjv7e5x/859kiQhz3Om00PnamItuzsHlGVFVWkX9LpYMJ/PkVJSlpbDwynGuABTrSuUkownY776xl/jja++zvXrz3L+winOXziLtSXT2T5FUTqNq7VOqLLNObPgLBGmyfQXdlHYjWCJk5gLFy/w8OEBRVHUNDkEyIcUt+4dH80qZ+3y+TDGsL29zcOHDx0A884S/oUuAeaqzLh27Srr6xP2HjxgPBoz3X/gAqmlPwWeYbY3srWynopo9R20gGBJktQVYvPuLFIpRF0Q1iJV5GpbYL1SwnWzmM1dIbw4ZTadoVRUF75y57FJCOIyXgUNqOD551/gySev8fVvfAMZKTY2t4jjmNlsVp/t27dvoSKFsg3QGA6H3L9/nwrDF7fvkPviXIVx9Wekd1+LE5cC1k1VLNUL0sb5wO/sPMJYTWUhVpIoijHCUxMf7ySNE6TiJCVSAwfSUAipQCgPwgRWhPoXTnC3JgBzp4WfzaYkUeTWWDqXQOuzxA0GQ86fP8+9e/cQQpIkCaPxiLX1NbbPn+P8hQtcvHiRtfU1R7dnC3Z2dlwWSmPJsowHDx7w1NPXSMWoV8kYqOSVq1d5//33eeOrr2NCAjoEVnuZRBqXZQyBFKZWqrjfrHfF8jRMeBzefON5jajBQHjfrR2JrJpsj3i+HQCJtIKwicO7q8+LDXVwAk9z1kYhBEZ6+ch6b45gXfKKSOMD8K0QPsDNjTFC1H04lxnr9k0sXdprYqJRQmJhiOAUlzAKjLQ+mBxsWVEVBbrSlJkhX1TooqBc5MynM6b7B8wOpxwe7jCbHVJlBfPdfcp55u7NSmxeYCpNWeZABWi0dvFVRgeFnwcEPqMXQWHUUmgE+mOsQSjndi8IwMNbAZzf6hJtCry3thz1uOAHN7ygUI5CIcf6HR91q+oqe7tK9y6g6AKS9m/NfTR7JNynnVU9Ef7dy8gX64wQInJWaGupvDJAgIvLsV5GthaRVwhpsLbACk8nlOKLd99jPs2xf/03GMR/xZXBq6payuLUNvso4XxXtTHOVQhcOj6zrJEKrR1MHharDRran9uL7UzyLLlvLaHNUNTOI7bgEe0OoDtYUjoTrsY6f2chiBMHLsajiS9E6ALYNjc2SS289f773Lx9i2tPXEUmikhLzmxucOHUJioWZEWFtJK19Q1KbbwSx1VxBeF8blVIbnkUZC03f2isM7xanDtUWZXs78/Z3V0QJQnDsUQlUFhBnpdgFXEcoyt3sLS2GH1Ui3Oi5tcSf2+Tj6YW45bGXr+jeoZtIde7ExECxuqHtNbA0GT28UTT55QNlabDb0u+9lZSW2vCumF9Zh+FS4nkR9uqX+Gyy/jK71XhAoatpdIlSsFomPDUU5d54/XXGA4G4FMuTiYTV0iuLPn3//7fM50vUFHE2toYoQyLecXD+yVUAoTBmNL7mSuvdcALd6YumqM8I8eEvOz4MQcfaQgoqwElLaYpQAWNO86VSXjhp37tgXF5k38bxDk/ZItUYun8DQYDlFREcYQSktFoxGg0rLW5o9GI0TBlfX3I6VOnuP/gAX/+x3/E7u4ui/mCU5ubfPzxhyxmGc8+/zyvvPQMp0+PvYQkCWmplQypiJ0wmi005Zrm6WcvMZvvs7v/a3zn29/jX//r/5Z/8r/9z/lX/9U/RRT/BQc7e3zwwYe8d+NjDrIFhpg4HjAej0mSmEE6qF1cNtYGDIcDojgiiROSJGY8du8yjSVJ3CRt0N70bo2lKDVZnjkByLsM53nOYpFRlCXzA5e5brGY14kYhJFkc83B9JCidBaDoiyYzmZkswXKujXOgs90kRNFEUVRUeRFzczclnBCbuzdL601KBURx5ELDtewPh6yvb1Fkqasra0xHo/Y3t52/85ssHVqkwuXzrO2NmE+z5jNZmR5ia5dfwz4mC5wQFJLl1a1MhJRgYoV0iczcUzf+8pbycWLF7l755HLgqR9tic0cRqzWGRU1qcn7dMthKeKxlKxvb3Ne++953K6W9252HVirEUXkrOntrl65QI79+4hZAoyRQhNHAnyMq+LFS51YWzzYA8wQgYq7S0WRe75kzDEkSSKJHHklPNVpSmLqdMAC4EVEcLGgEKXguFgnflMMzusKHPQyhX2A4W20hfAUyhcpiOhLaYyPPvM8xwcTpkvKpI4YXZwWJ9RcEUwq7xEicQPWzJIE4yN2N+d8uyzz5LPDbODHCG8ZS7UdhI+1bkMrjmC1PPSvHRxUaUuWeQZcZwQIX3GuIaiSxmhcbE4cRSTRANSMUKFIobKFReUQvjMZ44OyTjCSEFlXAD8opiDrRC5AXIqFKXUFEpTlsJlfhqOuHzpoo9DVMgoIUkVSTrEGiizEqshVSlCCHazPR4+3CFfVOSLnMVsznQ2RWM8j+/P6mOtZjQcYoxmPp0xGA7ABoWNdjhJByHcYoVPpy89X+tgZ+HdwkQQ/IMFI5B12ycNCbTViKDgqQm3uy+8BWBJwSeEaPiyxQmawjQKWFlzYoQwrV5AhCQXgX83P6BbvD0oPRs9Q+DmDXhqzhK14s1ZW0AkCpnEjDeGTl7r3B+AqNWGwge4L+YLDvb3mT7c43Bnn/nhlPneIdO9fYpFhs4LqsWMMs8xZYUtNVIbTKV9bquF441GO/dE65SulYCF0q6opZV1Nk5JSKJRESQYgUTaYIUTGNGse5+Lfl/tie577rN+wNHsoqL1QkR709gmfsP0XItoKVWsS7sdoIeUCQbjzqgPwgcvNwRXYRHGpOv3aK1P/CSli6tButgjW6H1DBMZolHKSdqXitGQUlIURY3cAlNU0nToedjAjZDbrsTdfkHBHattEelqINqfg4WkLeTWpl3pciy769xhauIivMuDZ9gh64gF4ihybhvZAqWcFmlr6xRrkzWEsXz7W99CKclTTz9FlmeMxyO2NtZJU+8zqhRFCadObTObz1Eq9hpb5xqglGCZ2hzDdb2a3rI87ziJuf/gAVlWMk5S1tYm7O7tEMXDOtDJ9SFqzZvwRZ/6TIm9j18ixEFsh+Wd3xC6gNhtPWZqQvLlmmj9wxF7vwbG12SpfTJbvTtNRAjcNQQTdjPUFihpzaSGv+3sMbhMDFhLmsYIa/n9v/O3GQwSyjwniWPWxmsYa6hMyY1PP+be/XtIJdk+d4asWHDn1iMePZzSFNVwAr5LTxroqg+8FZYQiCuhScEqWmfEVC52QOD9WNtgHNpF1dI0XYqbGgwGDAaDWoCO45jRyPkwx3HMYDCoLYRSSlQkm+X3z6lKX3RNG4oid77mPqh0Pt3n0YMZ2WLKbDZjf//AJSvIc65fv86jR4+4e/cu6+tr/Mt/8S9Y31wnUoKirJpdIrwuAukEUeGyouzvHbB95jSXLp1Hqb9GHKV873vf5//9//z/8PHP3+df/uN/ymsvvM71J1/kD6qCDIMVGXmxqOlKWYagSEueSxZZ4YU1zXT/gHtfPGKxWJDl87rie3ALWywW7t7KmdrzPKf0GvtKO82r1ssumnXsl1JOaDUahEBFEdK7gwgksVB13NZgkNZWEhXBaDQgSVy6wXQwYDQcOa2U1+jGcUwUxQyHA0ajEUmaICPJeG3s3W8GRJEiimLfj8QYwXyRcfvOA+bzhatmba3TVFuoUwRb53KhPMgYpDEiSVDSuwoGAUpS0xUhFRcvXuDHP/4FeZ61agNY0kFaW1qXha2jrghtrry5uclsNvPnp42W2wop91kpwYsvPscvfvoTR5cna1TFHKktAysR3rprWjEaSjS0CuP/8oC+VMuCoEFjTQlGgVWuLkwUIb0QFxhzlDrtbZqmXLqyRVHuIuScKMmJYwl1TZIKcFmwlI0QJnYgTCu+960fcHA4JREDZKWQPsWwEE6xZhYVQ7np3WBckoLJcILSCZGQ6HlMNFecH2w711yckCql12jHae0WppQiTVMGgwHWCCI7RGhBdapAWUEkXFKHJFKgQApFpGKkd5VK0wFRmiAHic+sKEmSmCiJnJUQ51MfJTEiish1ye7BPlmRMzc5KhaU0zmHj3bI8oxpueDe3g63731KZTI2z4wYraVMNtfIczBGUlKxv5ix0CVZVVIKC7FiY91VBh9Pxvz8J99jMZ+hdcl0dugKLBoDqqcAJE1NhSeuXuXmzZu88MILPdeJlo7N87tWfZ6lK+1ysHFD64/niEGWFEFG8fzUGSBaHC9c5xVMttVvfY/no7ZlKQ7P8LNZAv3dObSxk7tnGdwsrUtz5dKznOxjWgK4rM8MUPOukEjFactAjgeMxwM2Lmw7cCwjx0K1xRaGfJ4xOzhkdrjLgzt3Odzd42Bnl9nuPtO9A7L5HFvkmKqizAsXHF9WWK0R1jDWnj/gEjqghAPfVqMFNbBC4Gp4KB/PZ44vStdndQh0Naxbb+xj5/76+7q/9t47uvJL7l6wRGPB7xOaZE3GWFf7pu6nSWRTW4V807aRj20nNMJazebWBlEa9wDn/nZioDEcDgHqjFPtCQXRrRtw41yEmvLvXVeptrWim2Gq7TolRJMtIqSJhWVQAg2wCZ/baflEXSRP1IE7wYRtDMSxi9EQQnL69BmSOCVNB9y+9QUffvgh6+trnDq9AWhOn95kbW3N1VvQGkQEwlXgzXJN1PLHDYdM4F2ZLHX10FUuX+0WrkmSxJuHS0ajEQCz2YzxJPZ+226jpUmMrnK/5rbWNLTX9nGtBg6ttWyAHTjU6wJnoUV0LQ1Fa3qjORq28317/7TXQiz97s6e1za0Dp31mn8XOdnuF0KdkuU+w58WGbQUeGZgoTJeSIpj7t69wx/9h/+AEJZsPqcqKyI5YJHNyYuMSheksULFksP9XSaTdSIpkRhUABLWW6VVo7kQQtbCfeRrD6RJQpImpInT0A2GDiTEcYIA0jR1Put+z6hIOreIINRqvZzf3lLHHllclp48y6l0yWKRMZsbqodV7b7jBGZdgwjj925Ib2mqRhAPfq61cK4NZeFiGdI05cUXr3PmzBl+8Yufsbm5wT//5/+cK1cuo40hK3IvPDb7rE2kHeiLqErN7u4BL7zwPIKIX//1iHNnz/GzH/6C99++wf/ts/8H1y5dIctz9uaHZFVBVc0oyxyj3VzqtKZASUSpfeCuarS6AgHRMhWP49ifOUuEi9cZDgcM0nG916MoYjAcEixukVIMBgPvSiVQUpMOnXVFRF7wiJyw5iwqQUCL/H1D4kSgIuHrFCUM0oEfp3Nhkd5XO1IKqZR7N8KiLVTa1O9xUeQUs0OXt78EXVlKXXmLnSvipY0hRE5Y/x6CVKuUJI4Uo2GKHhqMcQkyZOKybLWD+C2Wrc0NRqMBeZH72J0G+OKF5ODOEN5xc36Xuahz6XHPWywWDIbpkpBW0yBA2xIRGV557Tr/7t8qhDFMJhvs72hkbjCyEbyiFmmRLfe6NrkweP/u1k9aa6QoEEqRKGchM8J68B801xIVJ8hEUBUl+SymnKSk0RkGAwXKFbCNopjFfEGVuhiJUTokUSnGB16PkjHjrS2SJCVSmijqJJsQwd3WuS2lacLaZI3xZOI0lUIg3rhOFEWMhyOG6Yg4iol9wHYknRtwUEY4JYQiTiKIDZFywCxSCiUkiYqIEheY7u5xKWytcXWbjMXHD/gMWdJlaZRBMyqsF2wseZWzs3dApSuksPz/WfuvbkuOLL8T/JmZux91ZehABBABBJAQKSpVZWZRdLEE2V2zSA45NUN2c/ph1urPMvMwn2DWmueeh169umc4q8Uim2QJVmVWVlWqQkKLQASA0DeuPMLdzWwetpm5ud9zA0ANHStw7z3HhbmJbfu/xX+PjUa1HrtscA7m9Yq7D+7zf/u//195vP+YTz76hM8/vU9RjhiNNphMN9AjA1rmcmstx/M5T/ef8oMf/ICN6QYPHjzg4cP7sj4Kxfnzu1JlPBurdSEoIGxnH3zwQY/F8m97DPNQcyXyrCOumbgM8y00GcUY6E2hb7sFeTr0ZvCU8KzTCvHps7rndb/7DPd3+wyQctji+2o91B0cMeo+b19O0tHNI41bLCSkR4u8sa3D6ILRZMRk5zKbxWWe//7XUVaMYO1ixfHBIXsPn7D/8CmP7z9k/8lTDh4/YXk85+TwCLdYMJmPcLaVorG+CSxZkrDvdShKGfQOp5RUIfT0PFfRqP1FhlsBUn1998voX7kx9dnjefbRy1mG5EHygSxI6Q7gRSKGs9qSdOscGOGpyvIrte0rVQaPD4ybdV4Rd9jAHAwMlfscXEDXoZ1yvp62LA5WXFQ5OOk6sj8BIsuHovOipER2csGgKcsR3sGqrrlw/hJKaX7845+wXM755jdfx9qa3XPbAjJC/GLrPR5NUYxpHRCEb5+Stztyi/xpJf609a7rZ89iscA5R1WVPHx4n6ZpwskiBIpCQsCcl9AgqfTbKbfee+q6PjVO657fWTKi8MsZQGISZxQoilidOoIoUWD6Lls5X36m2ML03KEi0lk/citmrPbsvU9lgFAkTxYQoqT6HjF5pkZo8uQ8rQUIJOuPt7i2Zff8eQ6f7vPTv/iLQIkpzyv1VMIESsXm1pSNjU28smxsbNA28OILL/DSjVtYK8pIWRVMJmOMKcGL96+qKgGoraWpl7hWGGlaK5z/zjoBBqsVTdNineXw8Jinew9o2niOpa5rmqYlhtREIoOocOZgOwJu69qeBT4XmDbQJefWuHiP3OMYx0jWJxSmYnNrm62tDTY3N9jf32dv7wk3b97k93//9/jhD3/IaDTmZH5C07RCGR2ZULL7xXHXSvICF4slcMgrX3uFc+d2mU6nvHD9Bg/vPeTux5/w6MFDFsslBydHUjTJVhg9oyjFYxBZm4pC4/UyJWhPxuNkwa/GY6abM4oELqQuzWg0piwMhRLlczQaURgBBmVZoo1mOp0wmYyT0lkUEq5VFgUSmAnaaDDCZuSihSvUmhDjmQ9rKY5DNzbWCXhoVzWtXdFan0Bg27SJk7+1HgKdpNSNsJKI6HyqrOxVeAYkjnWXKQo+LuqwJo2Bum2pm4Z6PBJg4kZMlBaFVOkQTmAlT+PqJe5++jnLwPUfWYO06mQ+XS32wTrvK1bWWra2tjg6OmIyHSf50Jt/SHx609a88spL/Ff/539BoTSXLlzk/Xfe5+033+Rw/6Bjm1ExURaiF9NES3FgkSqKUmo0BCpyYwymKGibVhTWspDcrWDRKYqC8WhEWY2ZzjbT2O9s7zCuKr719W9QjCqpqouiKkdS28eJrByNDFUpzy2rUgwHoY1GKUptMNqEKuI6yIwW61Wqdt00jeRsFAYctNphW4fU7pXkdk0RvEo6XaO1ls+iN8tafCv9vKwFkCtvKbTQn7ZNkxTg1XIpAHflsctozJO5GTWytrVhjnoa19K0LSdz8Ry2tJK/0XqJxfcGqzSHJyc8P3kNDu9y0sw52T9kwTEH/gnjccnmuQtUY8m3aNWCVVEw39tnvnfIdHOTd99+m+VyzsZsyvb2Dt/+9rfFY0te06e/96b6PsDVq1e5e/cuN2/ePAUKckNI3LvWfR/vGz/LlbRng42Bhy87otrZyeaQR+V9R9FNt0/2PRt5+wJk8R7r1ivJnqgvrFFwVdeO4WfKSiRBAh8q6jlRpnRtiZEJqGA1D+1TKCH3iMUwlZfaK8B8vsB6KMqKUT2iqAxFqFdTKkNZacaXdrlx9RIvKXFL2rrmZP+Ip4+f8OjefR7fe8CTj+5ysLfH/PAANT/B2Ba7XFLgaD1o70Mld0CLgUB0i05xz/W6+Pe6uRBrBw2Nafl8iEcv2odng+Lhc9L9Te5x8L3vvFKB9SxE89gApOjP1/gz/31oCJR3E3IK51znff6C4ysV7MsfHC17q1UtbBFl2QMJ4SLIzs/RYN4p3vuOmz/vIN8vnpe3Zaj8RPQGJPDT6zxkgx0uevkuS8wOSutstsFiseJnP/8FZVVw7foVtPFMpyOKQtJLrRcB7pxiPNmkaSRZRhmV1nl/ckZwdNpTMHy/HGTIRJRNOxahklhriRHf3dnh+PgEhWKxaNBalAXhtw8KXBZWE62MOR1b3o99b0MnxPrnxPtG8NdR96qQ3yG39uROuVwgdn3uO9QdjZ9KCVd38DiYkPvjHMJapEPlUiLgCXkeqlvkIImpkFuqCfSEiqooYNth2wajoBpVPH/9eV5++WUuXbjAxQvnmY7HNLV4iDQjwHMyP2JRn4ByrOoly+UK27hQGEwEY1PXocBSkwCEDV6CJgjQtqnFtR/G29qWpm4SUI2ehhgKF5P7ZU75xA4Sk90k7jQbozjvI2lDSPqL4xCTQ73zga2nC8tKc1OpsKHFUDwV1ogoZUUxDqGHjpOTOVeuXOYb33iDb37rm3z9jW9w6dJF9g8lrEqoOfssGkNQE2eW95LkXNcNu7s7fOf8OfYP9zl/bYcbrz0n1uO6prU2jLew4CgldQW0iRVbPVUBhYkEFSrkOVQyJwpDUZZUSYnUFMaE5Nku6TBujgIYQ02LAAhcUKYXds68BttabBhv6614HKwUp3I+jq3vclM8gAFfEEMO8n+ti4GfhPHOo3QlptiTr9EAEL0wIXnv8WHspZCl79ZrthmGu2O0p07F7mw334DpeCRzB58s2C+9dJOPPr6daFyd98l6HilRdVmkZ3VyJbRf9+fDlStXePLkCZevXgZ/mqkQvCQtO8fmbMatl2/x9Mk+u7uX+f1/+Ar//P/4f6Kul8znc1n7hXj/lKKLt/ZCCyoCRWo9FMqkeP7O0ychuTF2Pcrz2C+rpqF1sYIEIUfBM5tssKyXoSCZYn4yD2sX6lUNXqOcliRoazFK1mdTNyxPoG0Uq+WS5XKZZGdd1yybBq0N1llWq1CszhjxuNZCseqsFyuwkuTPtrHCqBWAn9Ld/lmogtIWycvqQ2KoVip9F53DsaxEWRaUkwIzUUymY0ZVxXgywhQhDl9JvoYKa9AWltqIYeTENxzWc5q2oTAWpQqs90y3L3Hpe9fYP9nnrU/e4a2P/obj1WOadkW7POHgkccU42RYiTrAHfURripRQKVha3vGf/Pf/F+4deslGgfe9pXu4RqKSt7Nmzf5yU9+wq1bt3rySeRmpn8oRQwwGiqMufI39GwM75kfnTcjC5npvk3rdPh3P8zJn7om+7bbcwn5Utla7BTSMNTJqLdeic7vC4RCf339oOsL17suJ6axqU6Q6mSBEp2vBIkQ0AZVWeaLJbptUaYIxed0qJGkaJTk4mm9wpnogdOUF8ZcvfQ8115/AVAsV47DvT0e3fmUT999n0ef3GX/3gMO955Ao9CNFF4tQKqwK4vTJPDVH6/TACJ/f43KdJ7TwG2dcdf7br/JyzLkBr+190DkWZ6qsG7MhoWXT+t03e9DcJ7eNRij2lbovlt7tkckP74y61TuhQAROs52LiWtdQId+DUW/QyIrENT8T7Dc/vgQp26DgT9ZysydZRYtXyXCDh8dgjLEW+dZjrdoKpG/Nl//HMeP37M1772EtWo5MLFHWazMcZE+t0G7wtWtWe6OcahxOKn+wPUJa1Hyt5no9Vh+4uiwHlJlATY3z9gOply99M7bG2f5/rz1/n1m7+WaqJtm8bKeQ/Bgirx3bL5R2abfAKfXjSe6JbNQZw0TIS3Ckqn0qB0CBVCrBHxvrni6yJwNF1/EARftOYa09FLFqVsWnETFMujoaokt6A0Qh8q14inZzKdoJSwcRlTMJtOqZsarTTjidCFHp2c4AK5gfKO1XKBdwK+7n5yh08+vg14vG3Bu5S74RpH0zZYLwqidZbWhe9al1h/RBHpx+93nr/cU9CBtlzoRw9M7OO8r+J8leqosaKEpzQFqujXtonWty5uOCiHg4Q2vEfbUAQu+z4KFrQSZjklOQcRtBVFRTUas7u7zYUL57h2/QrPP3+Ny1cucuOFF7h8+QonJwuOj46FlQgfvHCiHOfrMP7Uqm/BOzk5YrGYS/jSdMyLN64LKQSetm2i0QznW1GElFQN7qxvGlyBokv6dYHNSaz+NhQS8zStxdo6AYHaWQGGQeFO6wSx6sd1IZa8sEKckD9I8SkndA5e5ooLn7tgtZMk86CYIZS9Mi98yivwXqzCTnXWrqFSkUIYTm16ASQQ3jVrb6o0nvo/yAEnSbxFFi4X300pFdhrCql6HNiCLl2+iCl08GjUVHYUwFxJXddC0MFp+Z7anx3OOS5fvsydO3eSAjbcc0RmFDStFPi68eKL/Oyv/z/8+D/+jMVxw/bmNpsbG9J3tVjwXQCKbegTHcCFMOQ0gdYxsNIoacd8sUgGgtaqZKiSys7BYt+ApQozWgWxKfPK+gaHDeOmadvo4dV4xig/EkXMW4rgXY0J3H01svPaq7KUXJpAoRn3LAWMLRhEQTNag5b1NB5pCl1hjBjzisIEQ4HGlBrGlqKU2i1lUVKNKqrRiEIVjIox43FFUUi/jMcl4+mY0U6F3oLpxoSqKhmNymDISOpnX/G2wUhiHe2yxTmbjCE+EDAUeozThl+99y7/7f/7f+DdD9/m8cO71ItDmtZTuyYZooqiwFRiMNjc2eXK5Yu88bWX+Mf/+H/Ha6+/xrJuoXWpMGM+f3qGjfCzqiomkwlHR0dsb2+fAsS5TM2JRfLjNIhe/93pCyXxluCd75/pex90RljEIqr6n6+5RD7KvRjJ2Nfpnd4HsoNguBN9qzMRquz/6VcflWrfUySjEWaoTMu66r226BKWADBCsUMPTgfyCaPY2tpic2uLpm5o2lAYMBQ7DLQDWBXCgZIYlbloYr0ZY/ClYuvaeS5ev8Q3f/hd6uM5jz+/z5/90R/x/i9+SbN/QLlqcHULNrSNTravAxi5Up5/Z7MXHbJCxnvl18fPYiRcvNc6nTufC3Hw8v0i/17rfrhrNOiGbl7DBUjvfYY6duyLoyMJz9WDNp11fGmgEeMXc89FZ9mWh0crUFRstO64mqFLvlrHZZxPzHwQ4ud91053Tc8y4UmKlVaqUwI4PQDiyYgdHh2UsrFtbmzR1pY//dM/BeC1115lMhmxu7vNaDTCWYRKD2Tie5NibZ11qYiZpx/T13lnTomS/t9ZW2NfF6bg2nPX2N7e4unTp1x7/hL7+wccHx2wu73LrVsv8tZbb6ONErc4wpQTQzJbKwCkbuog9DO6XdUVvCGEc6i4WOlP8FxoR8UhjXVYl/nYFpH6OMTwSnx6mbw74/GE0agI1HVC1zibzULIj6MqC4zRzOdzmrbFaKEfXa5WuMZTmFJ41BfzwOKzxNoOcD0MymTuHbBOvAeyr1vatsHbNhTFGuGco14tiWAjKVthXK2LbmuVrNxiBRSAFFmloouxjyvj3yoIQZ2FdXR9ChKjrXS0zBNiK6OSq4J13uBdB+C0ipZ7kwBttBaVgaI3xlRHqmijNKUuxQIaAGkELNpIJV6tNZPJhI2NGVtbW8w2Ntja3mFnd5et7S02N8eMJyWbWzM2NmZ4D0/3D9jbe8qqXqWwHdncNCoGvgZLTFwEOm3iMRnN07Y1q4MV+um+hLwYaacJCpZCBbrRzhiSgAGBHDHIkgjYfLRWO5WeI4ChA8VWde7xXDkWkGRSyFGUcyrMBaKi6VwKmXIRXNpAExiU6MjSpJVNBgofvB0x78bpri/weR9FkJVUu147vSdd58LadekeMVwrnd0pH05qLNi2CTSVTQBkDmyL9xMmaoTSDq0E4D939QrHRydd7R4rDISrxbwHhNZuuGH4o0VvMh3TNHXIQ8kMSlHRCTLLOU/bOs6fv8Dv/M7v8uP/+Jc8ur/PkzuHHN6rWa6WITdJZIF1Dh+Wmvbyrwij6ZyDQgd2QJJxKBm2lCRCy5qUNVwWmqK0qDLkTinJ6cFDaQxFpSkr8Y6Z4FGIeTZOg9IGY4R5bVQaRmVJWRjK0oisLEuKsqQsRKEuykLcCrqjj48e76Is0DOh4a5KExLCPYVRlKZAKyEoSftJYXpJzUUleYZGhxpVYU5jCIx0EGtraBOKwSF1G3xQWWScQtFYOpY8pRTGawrAMMLZEO+v5Dpn66BkeVrnOPzoKc9/4wVmz5/n6GCf+dEBrV0FmS15PFUluU6bs00ubO/y6q2X+J3f/i20kr1OPHmB+SrtY3ltBJ3NfTlef/013nn3HX70wx/1vusp8arTd+S7daB5cOM1in//a58xSvX32HhdT38JN3TPsCYPgU1HEENgYzqtE0WPhidXpLs3GuZzdO2lK0AZPrPWdfIsvk8ENpnOmrdSSpcptPdY7SiVFu+FD+QThZa0Cae6kEwv7Yr5HsK/oiSEXSvcqg4EDpaJ8awWc1pTSl7VxoidV27w/env8+2/+wPe/etf8N5f/YKTBw9RtUTqYH2ICpC56rvmpzHKFfP4GS4yf3XnRWTXGaw6uTcc7zw0K+qrZ4ZpRYPgYOyTcT4CGB9ZzOTc3HuFz/I5BvcH0UXifhqLPK6Wq1Nr6KzjK4VO5QX7IsVs0zQoU0gxs0KszI7QybpDebkVNQrx+Hevo9coslFp6JRaldzXzjnKshSFy1o0QlFpEtOECL+2CXHTKihkwaLqvKP1FqOET95QsDXd5JMP73D3gztcurLNxQu77GxvUpoR3oLCYQy0GFwrDCvWO0ot8am2NTSlp9RK+P2D5UGHIi7CM6QTC0jWycRYxz4wgaIouXDhPN/+9rf4o//wZ9Qnnhev3+LzO3cYFQUvvvgSv/d7/4C3336Hz+89YLFcAUH5xVG3Kxpby4RSnqIq0V6LBTNaSsM011qjCnqAsdvUJInZGJM8JHFBVKMxRTlO46iUJNJKuJfQKMY5ZNuWVV1TGIVrGwihQPOjE+aHx4xGYw4PD7HNEmtriU8OYSo2G3u5lw0WY5esssn6mEKPOlekDYpfXEYuuHcLrTt6PuIijIqRB+VRRlGWQQkPVkGhw+soa1I1+GBxNFoUeq3EM4APDD+REjKzWOTKTSfEJJxJwlEUOEWhRRkpiiIpu0VgiqnKMtSAqJJCa4xiPBNr5db2JrPZjLKoJCdhPGY8nVBWFdOJsBmNxxIfPxpVlKMitbMqi2SNF0VWSWKoc1jXslo0HB08YLGqWTSN5AzEvkjT3Au3nidU3s43qb4BIG0mBEDROnxjUasmzTsAiyaE1CaLUheWRggX8Qk0pjBK9KlxjpY8621aE3EOpeuyMcvjjuPY5nMwHh5QRoCSD0I7gQGlRG2LhhEVABmSjyAAJAAe3RkEfGYBTeApvI+zacvo/VR4cCopYAJGwmakvFgM8bQ2enrmrGpP03iwDucV1ivGfsRYe5Tx3Lj5Aj/5879kMtnEFBVjJGm5PToS2lvlA5WxzYBSUExDYFJuHJtMK1arJbPpBrEad/4qGotGUS+XTMcjXnn9RS5e2eXdd95n8dizs3me/acH3L79CXVTE7dwAdKBsrY0VFUh4ZXKo4wLyn0RwgILRlVFUZW4kKifiByC0a0oC8qqCDk8pgPoSWZGL2MMmc33gXxjD/uiHmS1+dzwxtmHAhvDUgIRRbd+Om8Y2edJkQgaR5yHpL3Ah/UQfnOB2c8F2Re0RrlNMDRhQpXirmkus6a3LEWGpzVIYIIUJXjv4IT3PriLcmNmk4qiGDPb3sb7FoIRszAlk9GYsqjYmE4YuYabN56ntY6mqUMumqdI+ldUyGz33l50FB8WoQcuXdzlzb+ZY9sl5WgSlDSd2tmNQZiLwWgin2cAP7klRJ7INX050EcefQ9LPjZton3vXyP3OMPCPfg7t7YT5Fp+Tvedwpuhp7O7rg+wut9dmgNyiOEnGEnpK6yRlFehojUzzEeCp1ehnaLwLdobVKFofZP0Oesdzhq81dhW5LRCY+OcDvJUanDKM6KsXWqfvJvWNaAkx0kXimJrxmu//ff52m/9Pf7j//Jv+Pivf4rZf8xIOVzwNLcBKMj6JgrpniE5jl1UzOVdez0jntTQf3lCvAr9GscrypChR244xsnIm56QjVGUH+r0dYquboqnK8wrwFcWfbrMOQkH8x7jYKOcSuj6mjatO74S0MiTR3PXSo62cuapIbIadlRu3crvmyfH5M+IltlI5xrBh3MuWbDjRIjekEjFC5lFLAjb9LsXK7cxitl0xng05k/++I9xtuW1114FPJubW0ExK/E4jk+OURiaesn2zhRPx3IltQzWJ/Qo1SFXa10PdA3tHnl/V5Vmtjnie9//DX7967d5+PABL714C+dqPvnoI7CWl19+hT/8Z/+Uh48ec/uTTzg8PmG5bAIrlUosRskT5FwQlF2sdrQUFCMp6hP7OlpLnXMQvEwxZ0QUO8u8qUHtk5Q170LSsuQdWC9tiSFkdd2E+/nOihoKN5VlyXK5FIuJ6yP7TPPsFFMVhV2G8sPPMuR3xAEYZR6XfB4bY9BePAZdrHHclKJ3pqu+WsT8mSDU4j1ywGCUoQy5A6Yw4ZxCcgIKgw/MF8YUVMFSN55MArWpWO7LYL2fTCdsbW4wnYwYjUdUZcl4PGEylUrTVVlSlobJZExZFcF2ESyw2uA8ySInSnq0vFtWrSSet21L07QsWwkhOl7OwahO0aALAYxgMvZrJGOQtSteBrG+qQTsZZY7cDbds8dW5yFaRdO8JChLvjMwRKueDSEYPlQId3FTjCAGARjE7zLl39PNn6Gl3flQPyat18hQ1yVux2ssNsm33E1+ev1nm0D3UfhbGKTyc7sp2xkBcqXBex/ogemfmykOwx0mQo2kCzGQw3jwDaiu71tnOVnME2XwTt2ybS3b3oFyjKm4fPEi87kUTrPOsXteY0wZvA6yptHRG316H4Buk5XwqYs8efKE2XQzeT9z5UYrg1bipTw+PmZzc5PtnS1+6+/+kMJJboK1Dmt/RNx+xVIboqcDvbQyEhcuc6QDxFEpB9EnbASSxH2pN4qDPu9/J68XwhtUiMpI/S3/olzFihzLn9Ef0/6Rf+TVWd/7np6oeu8xVE77bc/Hami9P0vHGN4331fI8oasJ8ikUAC1KHj3vdusVh5UwagylKMSi7DxGQLAMwWFkbwM5R1GWXZ3d1kuV8SdXetOX0gtVl0oXtc+H5cDoLhx4wVuf/IxX3v168lglDGCyr6Wp0jBYNyzGXAGeMi/O6vveu3LxyObXqcZpNYDgTh/nAshm2s8E9kLZvUY0t0iZDrVDPmj//5xnmsVV12QXVHu+FBAL1wX2+pCHRKLRBJ463AFvXw752LoYl8nyPssV9Kj51wpFXIzQbdKPIlG0zYN586d58mTx/z0pz9n99wlfvSP/hHPXbrEX/wv/xPL/T1G3koxOxX6QAm40kEHWgcGhuObz45kAMjOHx7D8Vt3z9Rvz/B0nHX//HqlcplzRtt8l+PpnKNeLhl9yWJ98BWARvQsxKTtOHFz9AVdqM+woc65RB03TJTKXU/rwEVu4fe+S0BOCWzZ+TmyjGFeAgD6zAGd5TjGuIoreTqd8vjJY37xi58zm0659fLLTKdTyrKibYVG9Ny5HY6OjoXxBYntLcqKmBcR27UegfKFk6w7V967bVuU9ly6vMvjR0/5gz/4h/z3//3/yCe37/C97/yA2x+9w4cfvMvewwfcuf0xk+mUajShXi1paqH5tG3LSbDU5rkD3vteqEZUlsuR9N3h4SHL5TIppM56vPVdfHumfFnbgJeiXTEfI8Z8O4Jr1nUMUkkhJ1hXM6WvrpcUhcZZydtQRcfFHRdGuEsW5tB9L8XNTFKEY56KKP86VKntxskUhsIUeNtPnI9zKG46McelLAthjClLTKEwI1Jo0XQqReOqakRVVhQhMXY6nTKbzRiNxO2vghdiMpkEr1zMQxGLqouJmUaHUAexbqNaFC5L6u9q2rSu5WB1gJ13YYXeExiKDKkysZXQggiQbbaNREU6KcaxJox3afOJ/aZCyE8O2kShDzAneDXtgEYvbmYSipZ9noGg2IYIOASfdBumIlgklZaq4CoqbbI5d1XHVdd2FUGpCt7P07G0YXICniEYjb9Hb23sr3y9Put41sbS28h7SlIfxPXPWf+87jFnKDR5M3r3kbEjKZzyncOxbBvmB5anJwu29g+4eGGbSxe22d6cMZ1MmM2mPN3bC/O6YjwVSua6ibH1sZCk6z0vvlbeNxcvXuSjj+7w4s1bPY92/u4R6LatZT6fU1Wy8Vm/ognWRm980sajQq+UChzzHt/k86zq6vUMAJuPY5TL7/S/XK4n+Nb97mN3ipISw2RyTd1HEBz7Y+3vpxUNl+cdqv530WqJUkGjP93PDO/rGcyYXHmN58vfZ+YaDu4RvXEeH/rdBdVVobSR4qxKY63mg9t3cISYeqVBGQozpigqNFL0ViHKvnNSW+jyc5cpyyKsfzcILVyfT5H3Q762b926xb/79/+e19/4VurDPJIjB/1f9TgLCKxrVydTIE6y0+Ofh0meBnfD+6V5qzl1Xm7sTGWgkn7W5YIM2zn8fSgThxf6sAZEpnUeNwAsaZ05PLax1Dovc0AAeesZn4ZgY2j08QHwawfWKbRVKQx7srHBjRdvcPuTe7S14+Xf+C7zxvPX//Z/pTh4iG8tJrU5hOlmfRzbmM+TZ8r6rJ35efl9coA4zHXOn7GuH4bjs+74ou/XtRtkBS7mi7Suv8zxlTwaeahMfLD3Ei40pLrNAUC8/llWvxwg5L/ngyf5GronPIZgJR+U2Ja8YnY8ejHXSlidPDCejPnzP/kzDg6e8v3vf5+yKNnY2OTHP/4LxuMRb7zxGmLYNSzmc6rRjLZ1lJWhdVLJ25j+pIhWslx4rJuIim4S5n3UNA0ox+bmlAsXtvGv3uSf/bN/wr/+1/9ffv7zX/C933iNf/S7f59f/erXvPnWrzk6WeC9eBmsE/58F8KO4oanVAgv8b43uaWw2xRdFayWK+aLefLUaC3hQYUq0xjHcCABa1UoKkfIJZBnaKVSkbB+IrIU9lGEvIE188EEthildGdhghTGIIXqOi9BWVapnzc2ZgEgihWtqiScSHsoTcFoPGI8GodaCAVFaZhOKzY2Z8ymM0wMnSglTGI8ktoIo/EIHWKZq6qiGld47UM7VW/ORgWrs7DLIcm5ku/hrKV2Da7JwsGkrHvf6kynLHWCVvWUkmjhjvH90ZYr8ZU6hTEka4iX8LLIEhO9BHKdQ9jOfKYsCRhQIURHa0IyX987phDyBRU2lb5xRKW9RdrTJkXNBctvHlOc1kweJyR3DSBHSXEuJVVPrRsoZh68E2ua8nET95nyF5Tr8JLRy4E6LYhVBCp6/aaSbwjDTSR+lu6TrfdTikdPUTitRKRr+l2S7h2ttwGJDSyh+b27a5IBRnXWX6y4zEXBUqALlvWK1XLOwdMn7O9tc/XyeZ67epWNjU3u3vmMajRmNJmitGwv9aqRopVoepmJPaW8O4wxbG9vc3BwQDR8nPaIy3vF8LLlckVdN5LoXITxUEMQ2CnHEcj2wISvu3ELT0igwKk09xN+iLLa+yS/4jqMSmAXBij/V6je2OVhgvn909wke4cvUHC9iuPcVwCVQmLXB+fHWjK9uacGoVvZM7WK9Yaj7Mguy6+KRoDwIlLPKQILkTFC0CJAQmmN0gUf3LnLk71jymoq0VyRWVB5vCvwSIibz2SbbS03b97EGMnzk3ypsL7XdNepPXewDquqYnt7hwcPHnDp0qW15+U/e/0/+Kwz9Hw1YDK8Lr88Gm7yf1/kKenrOusBQs94F2VZZpSRjyIhCYNn5pdFw1BmQKCb1y5zB3nnJew2rqOs/AEuhKy1kRjhdGLyOvka3zU3ZqfQZB0K3fqQo6U1jgZlxdB47bnncKrg44/u8osPPuLmN77LzacHfPJn/xY1P6FyUn3cStUdnKIXBrVOjuegMW9/XtgxP4ZjOgSJZ+0DQ90pf/4wGX3d/fPzh2sib3scz6ZuAmvfl5vbXxpotIGlJ99ccx7qvEHrOu+shTpEgRFQeC8eifzz6NFY94wIMNYtunWbeW4RE9o/z2Q8wWjDj3/850xnU974+hsopbl/7wHvvfc+3/3utxmPJzR1i3eK4+MFL5x/jsW8Qay+LUUpoTV5MqFSarDBq16bU3uy9xkO9nLZUJQFN1+8gbWf8M1vvcpkWvHv/t2/52/efJPP797h69/8Ji+8+BKLZc3e06ccHR+zXK1YLBbUq5rVapXCYyLlqvc+/R3b1zYtrm7QxjAbz3qgoCwrcGQVd7uxkAJ1YnWKrmvJExDAUFXCFS+MUiWjSphQUF6qIY/GvZyDyXTCaFziXAtKBU/AiCIkA4/HYzY2NtBaQPBsNgu5ByVVJUXVylKePxpVCfCMq4rxKORRKIM2RYo5dmoJhPj6TOB39TsiTW2kHl2wms+xNvCTB8tdnNMgCnBUbjtBLALaQbpXrCSqO/7Bbi5HxdmDp8A5lbxDubCJhdhQRbJmeheTkluclEPuCX7vJWtIJeYKMiXM4YIlMT+UJ9Rr6K3CtDYVwkueMyh161JJsUelkmcsEii03gmrV0Q12XNNIhHtllH6WyP0mqHGQD9RMiRrB1DWXUtmBfbpcaISdfG+p2QW/bDGoQAfbgapudGSN1AUYpLdUOHr+rpjKxtuLOvc8B0Izc7tKZTSD1opof+Mm7F3IbZfjAMaJXTdiAfAOo9SLT6weyk8jx894WBvj4Onh9hQ32U+nzNbLDCFMCQt5ovgdQuxzbG/E1jo959zjtFICuTVdd2jpk6yJiqtdGvHOcnjUq0BPaBS93ENydXOujQV5KcD1XIatoX+kmz6NC99kuc+U85Vf5mkOXx6TOmN2VmWxRykcOq8TrGLP3z3jNCmuBaHgFS2pADGhlbn3nkdcHbdh5zqp95+HEFeaJfqKLMxI2wL9x8+5t79BxydLEKKrebx/iG6nICOOWG58Uko5VUQnFqDc5bJZMT29s5apW1oJ3gWWIgRG9ZaXv3a1/jVm29z5cqVHuHMunU2vM86RX8oE4bHcF33zw05Ziqu65yt0LHO2LHu+d0/8Yp3oUV9oFHEqAB5NB2wiFgx8+pmCCOX+7039b6Tbdn7eaJ3Ory7c7RZHl2LRBJ6bzMD8WmF+FmyNzd6h19kTjmJknDeSgHlkGc5GY24dukC8+M59x4c8v5n97n1vR+xePqQe2//Gn18yFiH0N0ItgY6Zl9X7e8d+ffD+Tr8fR1AWXfuWdcOnxn/zs9fB4y+6EhjbC1t0zCqvlz41JcGGrFBefKvhCV1MdZ9as2z75MPRrxfXsU7LoBYbK9/TRfPPRyQIXgZekjyjbdrj8M2ktC6s7PL4eEhT5485vnnr3Hl8kVUYfjjP/4TLpy/wEsvvczly1cAz+HRCUoJZ4kxIR5eqR7ASAPpfca4M1AMM+Qt8rvvDu0Ow8nxiunU8PIrL3L79l1eVjd47tp/xc9++tf8zS9/yY//4q84WSzQWhIxy2qENpq69Xht0OWItl4FelbJL3DWURaGqhx3TzKFJC0rhYkJz1qq/SrE4hlZiGIo3Xg8ZmNzAxVcnbPpjMlUvm+ahkJrZpMRo2ok3oHJmPFoLEWVCk01qqSycqhpIOFJJUqbxDISx62sCoyOCrsAtMJotC6DQiPWdpmjQag5G6poCxCo2xj2VXdx/t7jlaVpJdE4hlFEZXxogE2KjAOFyeZhfK4XABqSa7vv4xwQg0CkWnXOCctTDCcYKinhOutarOvaE9ufgtCCNykK/Qg0vBKPW/4uyYIawqhAAESy/Hux2uRzUmoxOPA60aTG/nBEz44ESMjabpMyLffQtDbM/+S9kJ/Wu8BbLh2tMgu476lEXViW9HULtWg2MQG3C3tSKB89aZnhQw/XGAl8gTB0DGNwwyndnOC0opAf/b8FqEb5OfQO5654st+HQCPKPBfiqWPuyNDiF6/JZZFSEjKmXEh0teLN8tZ1BU+dpQ41MZSX/Clpn2W+nIfwwRLXtqyWS+7e/ZRPPrnNaFTwG9/+Dk3bUDcNo6alHFXUjVSAju+ZvVg2xVWv/UrB7u4uBwcHidZ7/aYYQiOV3C+BfNsfn363ilXd2zgfOsKA9Up/DubCOBKbrjrrPV3F3fh+fZWxD5Lz+58NOPI+On309jJFzwPhU+v660hlQCB1zZpHi/xQZzRr+OEArHgS2ImV7LU23P3sIb9+5yMeP3ki7dMGj0aZAm0KTAohVQE35f3iu3/Ko5Tl2vXrVFUhVOREeZaNTm+v76/Xdf3ovWdnZ4flcsnJyYnsec8ACuvumf9+lj7U9zL0Fb/hvh/3Cu87w1I8PwfTXYhRvo5U/3Ml8jxGC/SJSMCoTvZGkBC/62Ty2YAqzpr4tU7RHBDHJP7uC7J3c1hr0l5Qt8Io17YqMd7ZGDETyhHk77YufCj2g7UWwhgqH8I349xEDGKFgma5ZGsiYGM02uSTewc8PF7wzX/wBxzuH1Pf+Qi/OsEol1j8vkhZH+q5eV+t80Csu/6sPeWs6/Lzc4bXdfc7CySvcxZ0f4hH42D/gOpL5ml8aaDRq16YNcIUXdz3sDNjg4cAIB4xf6IrSreec3h4r7jAIhjpgMRpwZIWZfh/t+FmCh9S2Xc6nfHw/j1++KMfcuXiZbZ3t/no4495443XefnlW7RNw7vvvseD+/e5/+Ahv/G9H7GqG7QRXv/IUx4tp95FvmcR2FGwD4VS1+5c8vcPUfocR0fHTKcTXnjhGufObfPo4RN+5/f+Ad/97nf59LPP+ezzz9jb22f/4DAUM5NCT9G9L6wLDq0MlTFsbmwwHk/C2InyM5ttMBqP8V5YYmKI0ng8ZjweC4PRaMRsNqMopGLydDZjPK7AWKqR5CdE12sZ2JCwrVBAZrk6uZUlF5oRyHqM/Ms2j9VqSWKToi9w47+87oFoEd3ci8oZEKrmxs1XYb0mhfMLPAiX655yKOfrtKn1rd9daBCelJ/QE0xeApOs7wCE8w7tSRziAVuE720nkL1NdIIJuAaPi1YmvmBcNV0Ylera1V+nPr6w/GWDBctHgbaOpcSh0OIhoa9E2RiPTfdcm1UDjxH63neMNN1a5FQdmg4UdesYSGsrjVaaO9LmWPwJ55HQrsGGjsNngG74TE1MHo3KZNdfQ2AgG2B4vu8266E8jN3sAWW7cIVTikk0PCBVrAl9FDNnYv5OmInByiT1HeqmEa+kszhnsW0rxSMbqTh/cnzM4vAYF9aItVYKgIZcLLwVWtimCV7KwDJXGup6gcczGk+QuHrHcrWiaWomk4KdT3Z4/oUb1HUtgL5p0CgWyxWT6ZhSR2W4r4IPD2sdV69K4b4rV65k+0Y3r/tdq4PMbYnhNWnxhPHpWMAkjCuBjEBxTArxIckMvA+0n2H+xI/DO3hkncRQUReeuS70rhdqlD1GAMog3Db//lm2u541M/ZLvp7XABgVwuCCfOsBoBzXJP1+PQByznXX5kAm7N+S66txDqzX/PXPf8kHH9+jcSXoSuZ4KPxpigKUxmih+/V0NZj64smL2HUtGs/NF64GQNzP+0mt9OsU+jg1uvcSq7lO6/qFF17gs88+5cUXX0r9Kd/RAfL0GN+bi9GoFD2OcR767Gee75YbDqR9+UQh2R7TGohzI+yBss0KiBDlO/R/ZD7TJgMbhHpD0SPQgRCFCzVNYptIXrHYlx3Y6OtZHbjplk7/6MBQ7LuYUynvqxNxj/eeovQhckDo65u2xbathIHbzvPhvJME8kAQolVXvDS2BSQiQ9ixbApl11pJIVMNtW2ojGdpF1w6v4sua+Y13HtwwH5R8f3f+X1+/D/8v3DtkgJZy411vbHOAV7+Wd4/+dgOc5WzDu36LN8X4lJLgK0vQ+MpibY6TJV1oPdZ4Oas7ztdWpLpnWsZj/4TA418MSjVJdLWTYMaFH+KL3QW8Mjvl8fsx2vy/IyIyHKQ0sVvr0+WyZOUuwngJWE0UADaPLTCw6SaMK5KRmXFP/7H/3uauuHBg/tcf+Eav/sPfoePP/6Yt379Fh9/9DGFKbh04Spbu+c4PlkwGengjizQaJQrMGhKUwbFT0v4DEHJp2vbuvg5n214sq7Dd+Hc+XyJMYbJZMqLL23iWqkS+9rXb7FcLqnrmnrVMF8saOuaNlTnjfkXJlTLVkoLtelICuB5hC+5Go0wJm5ECLtSCGlS2vQEZvxpnSScixD1iWrTe+FcblarEO/cAcXY92KR7QOMuMB8EHi5shwPRwSesaWke8R+jFbwbE/A5ptpvhHIzOi+Se/X30jWM4V1G3ofUDiE+KJTjmOYkCOyBolElKJi0kfO6S7xOWtDtIgTBYnqhLUDVqHkEvStJgDG605hVt04eA/adwnWfRYRj829Cvm74RBS1iyeF/AqAp8uZCKn+9OqC4GKm3ECSj6CO58pA3FjEgARc1OSbFHxnYIFK23IHtW2KOeDItjF5gMorWl02CzCEClF4t4vkLne2o6mMM7taMUeGgwg0jTK+TacKwXWPD4UcIuyrwkhi/ViQbta0bYtq9VKasI0DYv5HG1bXKjzUtc1bdtKxWjvIYR+Nm0T6sjU1CtherO1hALV9Uoqudqc8cemd+gnz4ryEeuwlIXUcmgbj9FTdrbPifJSGIqqDFSZnnO729T1HOtq6nZF61oaJ+Qhy7Zl7hq2lKXUGu1Eg3EY+ouTXjsuXDjP++9/gOc1GctMcXD+dAiCyIEieDOC9yjMC+ujJbSjgozKCIXEbItiFQGktNHHSYGidU7yV/BB+/PBW9ApT0oF1rnoNenpEEPFoIt3zw0pcsQx6UK81vVR77uoGCZNND2JPtjIwGw4cd0z1n3WASAVkrOjDMru4eUzo+XZrdP85c9/xfufPETpEboMdRF0bm3v1gboVCE5LiRD9CIFD5aHndmYCxszvG+T9zQNV/auSZL5/ud4k8mZ/ELPtWvP8dOf/pSbN1/EJc+XR0Iqg0zOIHMsqRSkcUZB3bd4r7OC5/cfHs51YaW58irGzDgHJC9UG40x0dJvgo5meiFo8l33HKXi/FKJjj1XkIdtzWZHH1zlg5/uHedFBwI7HTGMATHvROZADH0t6PrEedEt2laIbZK3I3rKvezxzjqhAw77QYcxJeROq6ANWC/efS/1qJyzeA2NMmhVYBvY2NxgVDxmWsLRyZJiZ4ubf+c3+eh/+9+olhoamwpsxjWc77fDdIDc4zwEIXl/KW9Tw2MXKVQC9Vm3YYg0/QqlitT9KhuzVE8uH7k1wCNv17rf8za2tqW1jvsPPmdy9cqauXH6+EpAIwcF/aRveh2cn59vBr2YWfoKW75h55N73WDEBZyDlqHinocwDfNI8muk/gZsb2/hnOOtt97iYP8AZ2FzY8bv/t7fl81YG773/d+kbRxN03Ll2jW0NjRNw+ZmEaokdp6fmBwYayJEBhxBgi5tmv2FrNJnHZqNMDW8s9Zo5YWCdLkKXgqpqCmsRxtJifGeUFukS1I0RuOJ4SYyAdus8rG1lsVqIc9LSnhcOCGWnLxOgdwk1rggFP9LbR8q6iq+WhdKE7SBADpc2PA7Ad6bF+QqcM4GM5wvMUwlWlm6Brhs9x9apsnemWyMolLhs5+5spCv5FRALb6rza1qUVkFS6BQpWu7WMy8KJat7VVVju3zvrOY5hSBwUaf0RMOgVm27SZQoFJYn/SjS5tNGi9ySlKXtleP6oBg+j72TRB4WTt8BAfepc5x4Zk5AMj7PK4bDzRtm6zSkWI3Cez4bnG+BECnEPCSxszHcZU5GqlT+/HKPigMLsKykEfShYxGEJvLtvi5dZZ6VVM3dcp/Wi6WNIs5zXLBfDGnqRsWiwUnJyc4Zzk5PqapV2kttq14IwBa36Y+je8sRehi/LawwuRjrZVGe5XWbVOvcE6Axu7uLrsXzjOeTBiPx2xubhLZzsbjMdPJTMKjRiOmITwSJA9qPJpKlegwJYRe9ojbtz9gtaopgizQJnLky8o5mc9xfieANJlTyZSS1rhcEd9jMpmmIrDD+R9Yp0/tO7I3xb2kWxf4YL0Na3O5XITCpmHdhfj8qiwpTCheZwyutdRtC5F4QqlQOK4LiVRKSEo6eRfmziAUa6iw5YrI6c9d75x1x1lGvP5JYaV+BWvms4780uGe3j1Dpe3L4/nk7l3ufvo5pqgoyxGwns1tqODmbU5zBcnrwnueu3oZo5WwPyYNzHOK9jW1Pdc/FJwCq/E7x2hUURQFx8fHjKoxOWulgNHgy436S5QpiUkpNqczyMXr057juz49C2jEop+5fpQAg4qeMB2AhqIoIoGKOSXXsuZm49m1z1okTDIZu3p0gOEG2bt1N+nt5dG4R9wb6YxO1nZeEa275PLuJ+nmSsm7GlVQGKlc75xj5KQocdM0Qb5arG1pW03r2mS4dDbOSwkPsK6vPMf+0VqBUbG6mVBn0/LC89f57O7PmG5tsb885trr32b/9ucc/PotqsKDtWSQYC2YODWPh2DEOVA6zT/FegAQa0LFPtYh5CH3g3Zmg3x4VPe3j/NXZK53nk72np57Z8kJo5TkaNQNNpaV+ILjK+doDDtOOsCcCmHKwUi8tudFYH2HDmPt8utjzYzoTekpGoP2tVkH5N6QoQVSvCGywWqtuHTpEov5gqa2fO3VVzk5mWO0oSwrqtGIK9euYa1jY2ubZdsmRpR4z5jYOgRM3d9daMVpsCHCL75XVLbid7KAmqR04LuQjW6NqmQN8iDKv888BXKK9FGIm4/xj967TkGLSle4IIa4AVKAMLY5KKwxH6JHJxheMD4jfqboU8NFoBGVhJw2MaqZvdMjEAubex9odAWUuo2ljwR8tjxzq3Q+L/IG9Oafj8nUqeH0hWQQAj6zamS3S4UCc8W706HC3wEdad19lb1fwgDhl0RTjMfmQl8N19hgh8i7xdveebk1qE9j2YUACh9IPq86IRuVgaElToCMI+a7u2zORY9dmjdpI5awFxvmG9DlnXjS/I+bb/56TSPsGG3TslgsaJsGgjywbUu7XEoxSGtpmpamqWlC2JFtVsFd31LXjWxmjYQmxTye2E5Z+3HTs2Jtsy4lmFrbgnUY73rXGCNyrAiFEAFhTzMapxTVqMKZMcW4xGipAD0ajVKtmXI0oRqNEiNglI3GGJSHxWLBwf5Tbn/4IQdP9/DWcfXaVb71mz9ktrUpeVZGCi+ZpJjEgpHCNJc2Rw+lLsWqr6Vw5aiqmEwnfPD+eywWK8ZK6ldE6spI1HByMse2FlVW5OuG3lbZn5/eezY2ZhweHrKzs0N+nC1fw/pJFgoV5pXm+PCIvUePOTk+ZrlcsljMA1vViuViiW2aVFhzOpuxs7Mjxfy0oXaws7PN9evXGE/HYU4qJETPJqtxp2yoAEazlbNG2V8HJHLl94tAwd8GQHwpgPKFNwFH/z7dfb1UZkZTt453P/iIcjRG6xIXiESGicjrfvbaGO+LhE5ppbh85TJNW9OFJcf50N/jz3pvvO31dfdqDt+2XLt2jdu3b/PKy6+GcQ5AJsi0aNQRgwuBzahT3H1K2va9+ZmD4fhafrCPxcO5jnh86KFWqKQol2WBNhLSEtfwkNp32D/xswTuIh14AAvpZxoBn+1R3agMRyt+n4xw8ia9dxADcGQuPA06yd55eJ0OBWvLkL9rnU31uupW0VpHi6XNSEV81t85QJaxEL1Le4XxFu0bKi11st54/RX+5u3bbF66yKFtefXv/B5/ee8h/ul9jHM9XSI/8rU7HDdC96mwj/Z1k87gNgQoZz3ji9Zv/m3SKHzoB2IfnK5zB6xdHziPNorHDx7y/JXLz3x2PL4y0IgvlyueUflXqh/qlC+aPLwpV6RtKP6WV1Q9NTD0J1yuNOdty8FDBD3x/j0lqKf4eEajEfsHB4yqMTdu3ODC+YsYLQjaWymzPpttYJ3nynPXOJkvWCyXWOsYjUZJ0ZNwI6FazducAygdlEePSqxPebt8pNlE6iNAZO7xtMFaml/jrCgucbp7T1qoccOLnorUP8HS26NCzWlPFaQQmwgUvMe4mFAmeQ0i3LPQHidCOoPJcfC638ORJ9n6ADR6wje+T7CPxOkQKY7F3dpnUPKQ3MJ9oR3mbkDybqBU956X/RnpH10QVC7kSeTXRUGhA3WeKLFRQMfnZfeP/eZko4p9LePgu5MIbtHMIwcqVfyNil9UwiGEBeXrLjtXrGj9NRMVQbm4G1OZnXF9QOsidW3INwn3jcp/nD8x5lbiZiXEIK7Vbr2BonMPp74eGAu898maHZX1er6kresUQtSTKa1lfnzMcrnCWst8MWe5WHB4eMhquaJerahXdZpT8Tli5e88JD4DiNAGi2GYo4pkgYpG1FxhMsZQViVlqLNCYTBGmNRMESpNj0pGkQTBGMbjEWVZUY5K+RcKNJaFUEiXVQkKTAAScQxitWwVGHqijHEhP8ZZUQOXiwUnR4d45fnVzw/Eo4pn++JFimpMWZUyNqIZiFzynewibOYmsE/paoRRQr5QFBKWsbm5hUfjrKJtnPwLZAtGa5TWrFY1q1WNG1UUoSKzJ/dod/Myn6NXrlzlyZMn7Ozs9MGE78vVfN64EBbmQiFQjeLTu5/x87/6Gfc+vcO777zDwcEBi8UiWUWVLMA0T5NSozVeKcrxjK+9+jW+95vf44c/+gHbuzuo4NXqxsOE0A9RELUxmaJ29nEWQFj3eV8Z65+z7rMvc9919/gSjc7Ee1/hEW+Tw2vDp/cesli1WF2AlzDcofdiqFAN6eljG7XWBLI6NmYzNjZm4C3WukSTmrcnXteJ7ExpSvJzTV8pmVfb2zu8++573HrpZazNqtMTw1zBhj0veUsH81M+D4YFuu+gI52QHKE+KIkyVgdTdM9bmeVexPxWU0SWrhwYdH3XB+Xu1OfJGKsywJP21tCHGfDovPryeW7U6n0Xrwt9ka8rAxjdhXKleRGsUGfVadFahbyxItzbMCoLrHOsmpq6aahXDa21tI2lbQNLJH09FEj6oVcGE8IUCxRtXVMUBRcv7nDuwYyjxYLJxjZ+x3D929/m9h//Gyn8a9cr/M9cgz56alRgziNOCAnvz+6R7y1DQ31fjx0aXPtAJ30W2+a9sHAFnX0oO4bX5s/USuPbhv0ne2w8fnL2e2bHV0oGHwqk1EAvA1aWJUVR9DpkKBjjMUSx+X3PRILyKfnCy4FEzlyVC6y2bVMNhuFkiNa/P/2TP+Xv/72/z3d+49tU5YjPPr3Hgwf3GRWaD977AIeidVDbltY5LBLKUYZCfdHSGxcBnI7Xi8BKkoPXWeTi+5HOjexF1iM1F1KeikvKo/K5WOliUiNijRWRU2VkgrCJfRjDVqKwC2Oaci2SMIrJ1J3DME1QBCQp+iEE8V2SAA2HbMzxc7EodF6OTBjnlo3Qrzoo7509pVtkHQ1tjnOCtTH2t/KpbMLw6OYeKKdCvrdKyfQ5hkrD5T112wblPPZJ6Bd1WnlK/8L1Ucnr3j2OkXzsfATn2fyIgFN1eQcxFCTv+56Q8U7cw1oS5qTAnxRUVBnzVlw3WusAZLsxjVXmIxCIsf4AtbU0TY1znrZe0dRLVqulrE3nhObU2ZCvIRXivfOYwmBMEaz7klNwfHzCwcEBx8fHYqmqa5qTOc2yTh6C5L0KLmgJfxFPVgxNSH3tcuYvCZVBK3whdWCkAGOBMUX6vRqVFCFkpigKRuNxqL4+opxME81yURSURSE1WooCXZgeJWvyhBmNMkbytILcSRNKx1XUGQogeBlQkuejxBpsfEei4QceREWQDUi2kR6NcUpz49YrvPfeB9TzOa1VbGzuYn1WdbcnQeT/UX6YoiQW4GzxRFe/5NNotCkoioq29ZgW6lUb2N2inDfUy5rFYoWdTSV8XfWX31AZip/t7u7y1ltvcevWrf7a6QHC7nyhngzANsT6Hx0c82/+p3/LO2+9zaeffMTJyXEKT4trSPeMIaq31mSDPmD/yWPufXaXul7w7e99h3Pnd+U9lA3zV7ZT21qUMrRt01cksuOreBHWKTDrrl+XE/lVnze8/pnXDZSSuJdHZcYpz6f3HuBNRe4lW+e5GFquT30PQVGVsbp6VdgfhfBAk3FNkO+t6wyScu+zAZfkizjxEmjN4dERs+kGTSPjGXNEHQSigE4xz0lBYujucI5Ku2NoJ5CICXJgInPcKJH7EVDE/jHGiIczGCBy5TQvijs03oTuSbIw9lGkq/fp3A6QRLnS660163WdUhoNiOm8sN8pBUZBaYyEYqp+uLvSQuW7zvCsw9qMS1QpCXcyRlOUhlFT0pQNTWNZLRtq3VA3LU0r4a/R6NrpiAqrdNibutBgfItXnjfeuMV//POfMR5V7M2PuPLaqzx47x3qu3fQrE7Ns3X90eun7PzYhg4Q96Mj8vUedfAcHHbP6YD70DvRYySkAxxxQM4yUKzXv2WrKrzCt5aN2cap79cdXxpoxIbkynld14DkCAxfaBjilCsw+Uud9TLPEqh5W+Jz4mf5+W3bdmEEA+EV2xQH77d/+z/j8OCIuq7ZmM149OgRZVFy6eJ5prMpJ8sVrYd2Psc1NU75pDCI8iWWz6IoktI4HPQYw03GDd3VK4C+0tx5IbxHnu27UKlOpqoB0ECsEiF/wma5ELny7ZxPjEFdrGAXvhSZWDqQBFHU+FgNOsSGR4QsdvDBxprASw6B5LDRsxDoJSNI6F+eKeQqtiFsWF53ZCcRTCSFvFO2BZjGe4eSO953lUl7fRfmpJivU2547JfY0zlriCfQM/uoKkbhJ/0zZCfKBcVQaAwBQhsS7JXqwtNy0JYsUb17k86R9SUbkfExJ6S/ATV1jW3qxNyhkBwAayXXYLVYpiTkuq5TsrK3lma1TF6HWEOhrmuWiznONrQxxIhOAc7gZBqnNAfpQiTzitDpXcKm2sXXyvoux6NUWFGqrHeGBbG8i4KwXC359O6nHB0d4bzj8sUrfO/73+Pc7i5bW1uYABpMUbCxucXGxgbz+Zyjo6OkyGpT0EZK1PAe0bjg8HiTCXkf8qrCzzCQYTPtkwoIZhCFNy+mppXpqHi1RiNrUBuDyzaNeD4q1MjQUJqKqrZsecP151/k9ocfYIqRzKMQ3x3QTSeLfZTJIkdsK3Op8Q2NbSm0ptCKUVHQqoaNyZRzu+f59JPPcc4n74VthQGqMAajC06OT2h3ttChf1ySCesTT7WGzc1NCXlr29453kHuAU2yCk/bNhLqVrccPT3mL3/yV9z+8Db3P7vPyWJBG+SnKiS3jajU6c6QkOf7KKAqRL4/3XvEhx+8y40Xr7O1PeXCxQs0tuXg4CjkzdVMp1NG1SQB3C9z6DMASVw38RgqBUOF4m9zPEtZPOs8eeBpUKOCMUah2D8+ZP/wGFQIC4xhg3SyZ7hn53tO9mSgMyo6LLvndoTgwNVYW5DCULP7wvo+6e69HmgI8YCs9cuXL3Pv88+5fv2FzoCFCkA+yLNsD8R1gCG9R1TcEyCRHkjKZg40Mp1BAU5JpEQeEhl/z4211oYaOJGkQJleP3S/q2jL6gMNHTzUEYDQhXfFtnRohr5lPH3pOlkiF3aU8qEdbdsmOVNqhS8s1hZJ4Y4hiLGeYw98JF0xeqU6gAVZXmxVhrpdjqqsaJqWxapmWbfJEx7liRgmFMqagGAc2goI8l7jihpdaL7z6k1++otf8o3vf58773/A6z/6z/jZw/8RY+vT6+ILDkVn1NBKRf6XtfM0N5jH+T8kUMqPIfuq9z7TDzvKfjEkO7zupx6kNub7wbD93mFQbM422Nr4Tww02qYNSYEQJ2tk28hDlPJGphd9hvDKF0v3skM01t+QY4hAXKjW2l7V6Px5XVVr2VCjshs9McYUXHvuGsrDnY8/4e2338Lokl/98le8/PLLnD+3g3Were1tdFGy2ba89/77TGYbrBar9K7OOUyoVh0HdWjpgcDOlBcByjwGEWik98ti0F0I1+isA1FNY1Bst7NGxLNyxVP6JIQ7hfkeE0ajIBW6wCBUAwDpxigkFWvQMZfAZ8pOliyWj2fsk/i7h7RRdQKcYHlOp3ZxwPmkD++mQhhPPubDhKwUsx8XkwcMp5g84vmtl/kWr4vYJtWOCG/gB5KhpwTlAkKRqGhj+yCERXnE905/HcRnKLqY71j/w4fcAuccTduEhHHb3TtsIC7LE2itZbmY41crmtWK+UJC/+qmpqlrCSuqheXIeQfOYxuLa6WmiHUNTZt54Vxsv5eEuF4oow/ASPorUiarwDKjlArrRDwBRVlSlSXaaIpCQEI1GlGEyu1VVTGZTCjLEgodePYLKcAY8geKUrwIOqw9CS/smK48Hq81TdPyZG+PcmuTn/3VX6K8Zrwx4+atW+zs7gQaSCWFHosSbSqKskS3DqcXYtBwNiQViuKZQGl4d600GBPko0ry0fsIwxWYTLGM8iMzPojxQ+ahx6VQJo+ETyolrn7rM7pw318nbWvx2iBOrgJMyTe+8z0uP/c8V69cYbGsMYVJTC4QQ3803nebepTrTd2gCyM1cZVYWseFYWdzhikUL710g9sffcRiWbOYr1guxYponaUsFabQHJ8cCx34uArzJKNHzRWxsO5sCEFUSrFYLCSUNSpHNgBqD/tP9zk6OsK2DabQYKTvxuWIjY0Rz79wlcsXzvPJx7f52S//midPHtNkTHxFUVCVFVXwZIk3a8RkMqGqKqrCcPXSeS5duczlq1f5O3//71JNRjx68oSd7V2c01TlBqvlisePbvPxR3f4xje+EcX5miNu4t0nsk+p7PxOduYhJM6GfKQUgpvflb6sHsSld4fP/t//LimV8UzfnRuVvPS0wf3jtQK8DZ/fe0BrLT5GQ/jglvMdcQveh5oGqt9XvjPaxA9ciATYmFWMRyPqeoVyEg4ZSTRERq7XJdLd4n6bYbvOohyeZSX/cmNji7fuvM2ly1cBCS204ZbJwBP7yQs9bNwvUrvivpM9R+o6+bTXdQYi0tzQWgcq2qg8wpBBKso3gne4k0QdI1N6btpk+6FaUcdyCGuT65SGcC8fdKezD5W9m4RLhh1MaUzwoCulKEJOqxiyPDUebTsm0wQqrE990IGQ8I9g7NaxEGumYGt5ZiTDKQpHZSuKqqRYtaxWhTClrghUuU7kubdgRLmx3tHg8VqhV44SuHhukyvnt/jgnTe5cP4KZbnJuRsvcvTeEdoKlboNdXO0V6dAeGR/kn6yab5bZwMlbwBt2p/q51wmpnUdjTQqzp8gP8IHSd9SgM49ieE54af3gWY4M4gO8Uvu/wAJbXPOMRmPuHju3DNmRXd8BY+GuMCds+iwQhUdRV30DuSItbOodsrzEITkXoXh63UCObO09wBJt5nnCmP+7Dg5xdIQus15QhYXk9GEcVGCh6+/8Tr7+/ucv7TLt7/zDQDMyHCyWvDo6Z7EgjpQrcUul5gsfj4ulOjRsN6hvesjSOcC0AhxvTZyDkUrgk4x9tbGHA05nG+7JHO5qJucacL1NxD5o9/XPv0uynoMjxJLaFTWPcbHTUOHegLBy6HAIf1p6QQf6U1iC8LkdXGD6ZQGAsjr2uiIHOZR6ekdSU537EG58E4CVXUgQAd6S61Nx3se2tu6tlv0dALeK6i9T0BDebmPDtYaSxeW42PIUTbX+m32Xd9meTXRS9W2LbZucLWAhVW9CgltLU1d49oWVwuhwXIZvAatpW5qbFtjrdCgeh8YUKwjFSWMAKG1GaOYRTUNzrU03mIJVjCJy8IZjQ+gqFAF2kHh5c2bKnPda0VZFSmcyBhNVY0Yj0ch7KiU/IOqxBdCgxqLLxotOQyFMcFlLiQM6XsjibfLuslkgg/sQw2rVRPmh4ALHyxTAKYyiR89B/LRyuVNSYvhxBZcu6F5/9fvYZdzQDOeboAqGE0mjKpRCo+YLxqao7nkO6gStCRcurZFKfEYdvItgARdALqnMCpi0l1YM0rRxo3Ii6fDeYU2whnvrELrIhRxlIrdWgmvvFLROBHyrLxQ2EZF1Tkb+kThbCHhnk1NYx1NMWbr+g1WhWHv8ATvfTLQeOfkd61RWkK6jOmsY9oYnNMYX6ANFNpSaM9zVy/w/e9+C6M8r71yk//uv/vX7B/XzOcNq8ZR25aNSmNWnkWz4rheYsYl0bptVEYsAb09wjuZi1vb2+w9fcrFixc745Lz4BS3P/yEX/38V3zj629w84XrbG/NqKYGU5pE1PHo8ef8o3/5T7FNy/6TA/afPKVpJTcjesOlMFsURyIbR6ORtMm2eN+wXDUcHc351c/f5OhkycPHj3n48ClKT2htIzlcytHYhq3tC1y//hzet0nmdfshKcY/ExeiDKDwdPJC5lZ+oiiJrLHUR6/6KfkZH9D/ICm3fW9KX7mPNNg5YJZ2RZrg2LYAGpUiEG/yeO8p2iisbyVMUYeCoi5adeX6Dmx2ilPelPgYeWbLhd1dXGBz04BzTTKY5ZZ0UAiFqYdMzsdHOcWpvST0DAbNsrYU1Yz5ynI8X2GKAge0IXQ0GfhCiLPyFq2sgBEHziss9ABfp8N0YVVRgZSmq6Q8l6WmNPQKkMYOcs7RkuXfuWgoDB6EVChPjE4+zAHnZE+L4KY7HBZPje2gZKB2c94LRXjYiHOrefRq6DTFPN4YcMLyZIwORkmhNNdGo8sC703ScdoQHdCGiuUqRHULcBVPrwmJ7uAplMUYh8+My5rA+BmpyFXnzTbGSw5LVVGMCsxyiS4Uy+WSpnHQyD6oEPDplBjWfaExCrRuWeqSl197jT/5kz+n3ahZec/z3/sWv7j7HuPDE4x3NMZhtWZsNdgufC0bfPGso4N32+GdeOjiWose3jQXIIW2icZNT24Q5IYOhhu8IkKaaCT1oUN91HhU9Cr6kJdm0L5jWMx1oohV0pxQCmsUrYdmsUDVNV/m+NJAYxj/mRRs+uEgwyMugjwZOh6d26/zhqw7xELX9tqQPy+PXYuby9AdG8MB8nY456jKktVqhVZC73jp0iVBa5OJoHNTMJtNBJmbgoP9w0A/ahOIEeEhQsRaF9pKsC7F+gGyyIWuThQClwq+AAi3fRQ+efK293Kd9X1rff4z9tPpfuwzcuTgL107AH6CbsOGr1WwwMQJ2iWxAan+Qd7XueIdE2yVis8JC2LQ9lzRyA/rfYqBzYVy3Kc7od1BB1kcKillkf4zWQJUthDpQAzIFhleErzHOk8TNrW6WaXCZzGJNP4eXbLxXyyOZpsGggcihgPF89u6pl0FV26yrlhsa1MxNa1CPgOdAtRiJXQvVDxNYx/eQkBvVzMjWn/KcYnWJVXoC9u2zA+OsHVDqz27589z9frzzGYbTEZjtmabTCZT1EhThJAkAe+SiNe5s8XCGi0kEUdaNajRoBW2FQrR6XTKbDrrcqfCPcuqom5tqP0gSnM5GkuO1KLBI7UdBAyAKSucdajAyFSYAm2k4nWs7dJaYQdpnacajdjZPcelK1f57JPbWGVYNg6rGhaNBY5jJ4IuU5K714YmsmN5UKpIOp0kqeYECX3Kv44Kd0AMkNYKeBe8GHRw3QbWKq2cJO25ftKe99A4QAsI0EqSZfHivWlsTVWNaJ1GmTFlyF0oi4JpYSTHxBTBWNAldysl4EWFhFOCQmN0IV4kHJWB6bhgOhphgI3JjN/6rR8ymW7y//h//rcsFwtWy2UypozHE5bLBfPFgtlkIiAmgORohOmULegU4Zbz5y9w//59Ll68lGRZ2zZoVfDHf/qn/Oynf81P/vzPmU0qRqOSrZ1znLtwge3tbcqi4KOPP+azO3vgoaAQwF6vqGtZuwCLxZy2FWYxWds21TQxWlZSXbesmhaUgLFVXfP40ROqcSU1DMqC0WTEaFxy/doVrl65JLqzgo4W1Kf1ke+WKjMU9b/NAIkH7ztFJK77JCvdkNWx9xf9owMaak0IVNcOly611mVtceQ0skkxVLLfHB0fsVgsiMZCkgLdWVfXGWiilba3r4WWKCQ5entri8VygXeNKFhO9uBePkZ6p8x6H+/rAa1SWHFPyQ/P06gUtjkajXi6v8/W1haNc4kgAcKwxrBP1/WpJzAABuzn/Wk9aZ3RNBpHjZEaMx4lwF+plJcoHofIetbf/0TfknCgCKIi6Uz09iiv1wANiR6osQw2RgFenhR5kYy3sQ9kZNKO2rp8fklUgVM+i4KwxHoZ0YAcHya/x6KBXZ9Y23Zef+1xVlirkpdD+fA3PQNzCq9UirLUaD2iLAxVWVAWhuVyyZIVrg3EIHg8CqeUrNWwZ9XUjMdTXnvtVd597wMuXbrK7OI5LnztFk9+8SbTWjNyisaHNZKKAmY6a9bX3rtsvT/7iN5slc3R4djl4cX9UEuysT79PAUpvLPv2STdq2dk8DKHtFIcHBzQ/KcGGsOchhguFV05QwUzb/iwU+ILxAkxXHBJAGYLr4fu1oCV+Oy8s3vhNF6shPn1Wos1VmUhFpEqTWKxDXtPn6L0gQgPB8tljTLiCoyJlHFQAIlJR4SAMGSoNMguxCs639WdiJYG70Nyme/AWbSUSjVon5TIZHk71eedcB0eeR/n/ZJ1ZDxRhFqUjr67vmOlyCZyskzJX5H9QKkOMGWN6IGe3mYaC+3EyZx9I8pyF7OO94HVSPIOksDyPvHhe+dTeERTCx1p0zSSBFpLJeOmbpLFXzwALcoLEGhCjLm1jrZpJMSoXgroiPSn1iYh2YZn5jk3PloMknu7C9lShLkf5qM2JlVu11pTlBqlq+QlG41GITnR4AyUk1HIR6hS+EcREpGLLLFZlMdQGdaYwBTlsE3LydMDPnznXd57623wcO7CRb73wx9QjEdoU2ICF3sy0PcssGkXwuE792+cfwoMAYhqSWouy5LlckU1mWCqMaqocEGBxoFbLWmPFixWKxaLhYRLoTg6WYb5J/d2rcU3UhMihk/ZxlG3Dd7XHT1zPi+VECoYXUA54satr/F0/4jdi1dZOUW9bIN3NoYPOTwNUVGKMk9+V2DJ5p3t7Lq+xWdFH1FZiAii0KdwRFRQtL3UWG9risKkDVTWabDK6qz6tHMSNkDwNBUVBNkctTJTFKAdSosiaZQO/xRVUVAWPo2JMZK8PpmMmIxHGGRTl/C1cQoH9Xi8gUIbZtMx25sbTKoKPDS1w+P42muvcv35a9z57B6L+QmulZCO0WiMMSXz+YJms0WpMoxPZ8U7bbCAtrVsbW3z3nvvB2UtyNEANm7fvs2Dhw8xSjEuNdvbm7z93kdobZhMJoDi+PiIv/jJX4kCF5Us51MeUhyHSGEavYRR3khNEiNzyDkBD1phvaWpawqjMIUR1rCqZHtnm0cP70v4YpgD3aupZHTp7YpR5vmYq9ObQt1p7rRs/9sc6yz5686KTorenhq2hmFDkyKkHI/3nkhIVCrOGYNB4zv1rba9Zw7Okd+lf0ZVhVKKum5wVjy7WpXBQdaB1UjQEsN6474RBZnH9+oH9Z4LwaouJBZbm9s8ebxHVY1RWoms913su7OBmtsbvNNSHFI5PBarghfc+US0NwQb8chzzoqiCB4Ag/gSxCLdZlEOWpvMe9vtgzaGH0egkUCX7yIMfN/DAwQvTz4v42/Bq4p4JmwrXggbCubhlFjmM2OBJKgrtBHDVNyjupxZC7iwH0ajtYqtRmtHyqsMemAMlXLBcKbamNMRc1eklkgk0JAQqy582kSDW2F6YMMozXLZJr3Pe7mv8IVYrNJo7XBty/Vrz/Hpp59yePiUeQXP/cY3ePjhx/iDEyrbohS0RvLjjOt00uEhOXKOyNR41tF5d09HA/Xv1/fk5IcEm512BOTnDvXwoVG691zv8SEnaGjcOOv4Sh6NPOk0b1hMhsqV3hwM5J2Qv0T8bojC5KsONDRNk0DOsHPyxJh8UHMkqaPLdgBaRKETWjQyRdVDsAjAqq1Babz1NK3FWuGvTzGyPeU9KOMtoMR9nL9bLN7lvOsNULS+yAYn755bfVzY3KIiHudL158ZEBj087pDNgt/ijdbNtYQGrTmPuJRUAmJ+wBKSD9BcEXnpYleGwlF6pLjgFRNWuILuxwEZ6UNbdviGwkxsm3LalXTtFIt+ej4mHa5oq2b4AJtUrKys5Y6FfNpeyFE3jt8SFD2rnNfewQUNSHmFxUs1YHFSPYolRQ5neYixNoWxoiVWKtus9Cl/ItgoQh5PGVVMRpVgQq1TCFHRSHhRzrmHQSLsg4sIzFeW6zXEdS4OIwxIlBeITGgSahJ6yXAoUSsGJPJBraF27fv0jYryqqimkzwRQFFgdcFFkVh+owxEnJShA0iBquF+i1keQvB8iGbn8Vb0MWIZeOY13P2jxaisEWqYyfxsiiN1iWrVogenA1UhwF4k+SDuKhBvF650SFtqijwBussjWul1kXdcP7KNX77H17GTEfsHy2zadwxkUTFPiyaAA6TqpSuieujLAvEsNklbsaxIlg2S2NQhUq0ry6wRxXGQ9xwtcLonMAi0MRmhhmQjXNkDMpLCFRVCTAdjUZUVYkpETrdsmRUVmxMZlRlyXhkcIWs+aKICkCY2M6jU/5DFq6KKN+tr8N3iuXJnJPDY/BKgLxtmEw3uHT5Am+/9x7zk3nI9fGoUjzCq+WKppGQJU0MuOnkVKc0df1qTBHqXTRJzrkgc+J8X9UrppMNXnv9NX7xq1/y+PEjDo/kneaLBVVZ4ZzFYBLDTgzPipuwdHdm0JEeQXkFLnhFESDgtUqKVmkKqBVqqVFGc3RyxO/+/u/iCDk1Yf7EcMt4RIeAiHadasmgVPIERvCx/vDk36js/+nbuAR6+RQJ4yVrabpmAD58dsf8d7lPl+OW7uFlSe4fHYpnEYXB4JUo/akvBkYv+cOnsVcpjCRrs/NMJ5NQ78aivJQ89W3d0yny9/Co5MmOYC5KrKiOr0sY19lHo9GYu3c/ZWdnF1MWWA2RChkbQhitlbv6gta1gMP6Bqdcyr9SdMQ4OXDLDRlVVaU9Qhst8l8F+e2aTrYqha9tygHJDXSRqTJnjYzf+SyE3Qd9pfMigVcmyWTbWlarpZA7zOcsT06YL+aslitW9Sqd0zYt3vaNzZ2OpVJ4fQQbZVkyHo+ZTEZMp2M2NjaYTCZMp9NgHBAjglKy74lXWWPD2mm1AAEdPK7aaLRzGKfRVsBZ4XzoP53keJHtYaXRmNEIE4xgxqzQ2rNcOsDhvUTGNK3MF43BmpaqKHjj9Vf58x//hMnuJtXuLudfeZnDn7+JqVuM1rRlMBi2pyu6x99jXkRv+q8BJbnBPOqb69bOKc9gprvFiu9pXbAeWORpAENyil5EUpBT08kkEEJ98fGVQ6eioI8x2853gnrYoHUIadgpZynD+ecpcdr3J3OeQJt7KWKICnT8w4XRPUU8t1CiZHG2wToggyOKQJtoOGM/SAEq2YC6DTEK72RZbyzORWVV7tu2khzpgnstbnhRGY95JLFNoqSF/lBkHMu516Cj8kwbT97PcfNc08/JZZ6eEbxTrovXQ4kbOd3L92NKY55KDPVRVvoxFjdrY6jQakmzmgtYCOFGUYi1tkkCsG0b5vMFi8WcxWKJai2+tSnvIIYl2bbFty49Nwe5cQxQXd2NwhipWKyVsMvEPgiKswIpxOYaHJL8P55MGI1HjEN15CrUP4g5CVFoFkUpFs2QzCyVk0NCmta4MsS8hzlFXAsqKqtxTst8NEajTCGu/ZAU3LYtLgirUmm8MjgXkrcxSQOIgDT3BjrvqQqDQQuXeBi7ZXvC1vkLTLa2OTnaR5Ul1XiCMxplxJugkMTOfN2IhtIl4sW5YH202kVF3yWggVIEVuSwOcrcltAD8VLI2MWxid6iDpDnfZVv1s51VXqdc8mLIt6sFq2qEJ5WS66T9XinUKqARZuoaCUO2hBrVMRq0lpLrklkEVNAGbyZ1lqqYGXVWoUB6CyT3gvrkjYSB1uZyH+vg8epoKpKRmOFQkIKylJCyFLNAZDieKOKooihoYbJeMykCHz0hdwzWZCVBy8KT9sKKYDWGmyDtw1tCPVqVj4ppEnOWXoJtT6YsB0eryRPTWwzWoyjMSQUS+sVFy6eZ7k6YbUQOuK2tvgxFEVFs1ywWCzFS6AIGWD9TXK4VxTGUJUjjo/mUh3YO6yS+XE+sD7hHXtPn3Ln0zvUzQl1c5xZ46ToolIarx0tYF2b5mr3PHeqHdEbFeeuV2CKElOW8nspcftKSYx5QcELL93i69/+LnUr8zLKZOddUGB92jeT+M3EcyQaCE/MLNJh2XFalg+PZEDJ5GJ3f5XGfOgNH24T/rQOHu4Bkr+R7TPh2kVdSzFYRTDwReKDkGMwqNwdD9mPh17vcKmzaAXjUUXdrIKRQwxA2qlOpsrZmZwI8kmRPFRJV/GnjXPd83JgpkLBTgEPPuSt6OAhbFuh7G7aFc7XSB0OS+ssbci3EaCxnt0nz3nIFbx4XWu9gDone34MYXJWxisCiu6ajmAmD+f1YQ5aXBouH/bztm1Z1Q2L+Yrj4+NEKx5rGPm2hYwWNldM8RI4lSdud+1wKCcGzMhAGK9vGqlV4ZxLhpLxeMzW1ha7u1ucO7fLbGODqpIioZ4Yri7siFE+xtwykbMKYyzWGCEdiaFVWqOCcSEaOAut0GUZ6lkoTKHQBpYLoWi31oNXOOXwJoThqhUXzp/juecuc+fBA7zWvPCtb/Kz9z5g3DqKkOQ/dFL0yJKSPpV7Ovsy7yy9OJ836wzK69Z7Pr+H3+efx7l3lg6fzrdQmSKEDH6xLIKvWLAvbuxxQnXIuH9evliGyChZ6AfnDY+cziy+bEf3OswB8Kld8Rn5/aNCEK2E8fvoIYkF8VxYiN55qqoCpUICuKWLjdXCu5iUezmslWrHsUKoR9G0kf5WKg63bYjjVoGSN3OrqrDpphocxHjF3HJKNjlVjzYuvqdWKiQpRzRLr0/y843u6OGstTTBYui9x+CpV6uUn2DbluOTY57uPeXo4JDFcsH21jYXLlxgVYtwWi6W1M2K5XLBYrFIBbFWq5q2WeGaVaJJjfHn0YIX25jnpuRAEDqKPwBdaIoqCBJjemEgxhh01eUURHYjrZRY7UdlsOCIkF3VNSfHx/zNr/6G9kSKtL3+jW/y3PXrTDdnTKZTTFmiInVxBhLycBbnXVIKQpNxDgrVeeLyEKOozKk4tYK1xehCEqeVbAcC7LulKolkOrBJiOUmW2BhznQWJe1DiI0XMGBVYNooCqqNGeevXOXo+JBqPCZ61p1vwYn1rCWzvIV56QIVrrMdVbDSkTTA4ZVKuTxKqV4+iXNgfeeti2MvSnXHU59CiyCs1Uw5y4SyUhK/LPOlAC1nmaJE6wpjJsHa2Ahw0xp0hVIFpdIBaEjYVHTPG6PDuA0sR1oc0UZ3OVp5O0oDpe42zslkjDGF5KSMCmZjSYA3RoCCvJfM52SNzNaoyDfR7Dujgoyx957WN8Jq1nh8nSkZzmFCH9vgkbOhL4UxLIZuCShUyaghStLQexItpmgVktRJVlAX7m2txa9WXL16Ce8dJ8cnLE4WNLUo9WVZspyfsJgvKYtS1q5yXbXaNIVPG0am0xlPnz7l/PnzAiBpWSyWvP76G/zkz37CydERCs87774L3lIECl/JJ+oIOVZ1G/YterkzAuh72n5GzWkxIa/LI6ExpQKtCzZ2zrF7bped3V2uPHeN5194kRdu3KQYTcUwEkMpwx4T5bLznUW9e2QAtookR4a5kT4wL32pw5M8jMNLfAA6fVCz5tb+jD06scrlFmxRKE8Wc3k3rTMgqcQzpITwJH/n7g8X1hvhXt1XRgtFtIaQVxP3M1Fk47vm74ePoXY+u6cP15L23nR+dr2h30ZjDKvVSkgoIhhSDrSm0JrZbMZiNWe5WuB88s+nMN5I7DLUX6JBIu5tuX7ivNRnsrbtjDoQgIMP4UodgxWQ6kTYjLQk/rTRmOfqVAx1FVgIlyGfyrWiy8T+EpIWh9YFSmmqxPo3YjIZU5YV08kIrci88iZ5ErRRKC3vb9sW5wUgnJycMJ8vOT4+5uTkhJOTE9q2ZX9/n729PT75RPbtyWTC5uYmFy9e5MKFC0ynU4qR3LduazH8OvH4toWncArtDIUHFYosFiGsShmZR0T9Nci4siqZaaiqEGqs5iyXEhEh+bjSdtElNG2z4rVXX+Heo8cs5ysuXthl5+bzzN98l6lTGFSaX6fmOIRomM4ILB79zluey9wcdCQYvQZI5MdZYGN47XAPzT0uub54ChwjxucmlIL4MseXp7e1bVKSkmJv+t6DuDnlC2YdqBgKzyEbVd4JuSBbd156+SDo4iIpTJEW3BCwxPvqoFS0QWnyoZCb0+ALARNaSOuD5wFZOERFqFv4IniC0SYAANvaJPxivoB0gJLEsbgJBHCgkboQ2nTUhQk8BSFh2zYJjLquaa1ltaxTmFDbtiyXouwL4mywbbRMtJkQc7hWkpLrlbhBl8tVugetZbVc4bwTS3/TsFhJPQXXtKfQd4qP7XkLunGRHAub4sFNUVAUY4mx15qyqKhGI8rgJYhMRJQGU4nXYDwaoY1mVEl+gi5COFGMzwwW56IoxV0YlKKehUDFOFQfmJrEQ3J8csynT54w/+BDlCk4d/EiuxcvBIBhUKYQoEG2HSnwShREr8RKZKDnqtZaUdDVeREWsnB5LFiYz/mwQXrbzVPvwSjTWam8zEMpnOZJXoAwCdO8xNO2DqUVdWs76j4nXqC6aaiXK155/XWev36dnd1d9vYOKcpK2hiUSYtPoYI5KFSyeHvAXlzeCrSmtm2SCXkRKecVXnVVlEUmGJQyaBXDwwTIta1lPB6jtVDAkmRMsA5FL5A2IXE53i/IIcAohdHyQkp5Sa7UBd4rxqqrs1MGMKqNxPFPJuJBiPO3KoXutjAao126Joa8aa0ZlVAanzxcKsgP7z3atyjXJGtss1rRBPkmYW2dtytZXZ0YMIhWXhc9EKLINUr36JM7a5oCGxQSL9bljqUGjBUV0GX3jJufxYPyKBuppuMzxZARyS8IyncM+WnrlrZ1jEcztFLM58ccz4+DJ8mGfjYsVg3VqqUwIeRQd8puziyoiNZ9xfb2DntP9tja3qFpW1ShmS9W7J4/zx/+y3/Jn/7JH3N8dMBicYKr62SlBVDGMZ/PwXtsI+BhMhmDVrRtE3ou5mjEjgSlTPAgKXAhTAWD0RVej/jmd77HP/s//HPGGyLHrHU0jWW6tcWiboJM7KzJ+ZgmAdmJkqCaOlCxUGu+V/pMmT4DGKj87y4ZWEFiZEuXRfndvyiIn8x4RRfCpboPw7nJBR+eobFty3JVJ7mvlAqgVq7L25/Lk9jiCHr7gEf+qEaV7H118E7FvTzWMMpARLxOHFK5LO2UsFQV2g+KnHkJM42HGKhGHBwcsbm1kRTEstC88MINrly6yJXL5zk4PGS+PGFZNyyXLR/evsOjJ0/xPuZidWOSQq+QPIJc2cvb1Lqwbuk8MEkO+M7YGOdU9EC4ACw84m1sQ05h27Ysawl9cpGAJNZnUEUg5Qizx1sm4xGFMYyrSiz/0sMSMmUbFJrjozl1M8cHEDEaSd6rgBwZ2fiMUSXhwuPRiPPnd3n++evMZjOKogQ8i8WCp0/3uXfvHo8fP+L46Ij794958OA+Wms2NjY4f+kc15+/zubmpsjOVgxxhXXYQlOYYLzVnUe/8MJmJWFSncyXOkeR3KQADHiDUhJR4a1LHlvlLE0joG86nvDCc9f44O6n7M9PeOVbv8Ev3/8E2y6wksCHSRu9SkZd70MYMZIYr9J+47p5G5ZItD/mCzt9FsdiABZOgZS4cjv1p1vPqr/6k4FXBYaqTB/pA3XJzZhVFePJiC9zfHmPhrQgxY5a73oLdwgSYtx17IRc0A7dPkMPxABApXOHnZl/J79HJoTQUcGaYgLDgQiwzuVXlGXwYoS8jPAfClFqPGiJDQhl3sB4i/E27LESe+qVVFhunaM0FbZuUNaiISUYRfflarVKeRrLVWAxCtXCvfeJtm+xWKRz67qmWSyxTcNyucLaNoQSBXDRtOLqC8LEtjYBC+Xa0Cdx9vqw+VmJHY1KBCQLHgCNxIXq0mDKAl0UMv7GUI10ykfI8w6KsqSazpJ1ZjQaMR6PJcRoFLisQ4JyWZapqrIoo114jnh7wlgHwJDPgW6ixXGWYxgPmbZvH3IFglVRXKcapRxYy6Sc4nzBjZu3ePDxbYyB2WxKUZaookSXJSidQogIcyVPb3RBSVNI5fJujqqowslmEfpZh7A8KVoY14Ykz3nf4m2XWJ9vjnGTwmf0uVG4hJAfR8dS5rwXGkfvUVbhrXCYi2s4JMI3DqoZR0tL0TYo1QEEtMKF/IiYfJ28Sgiw0iqEhGlJOC/LAoeiKELRzpRMHOhmtQkKZMydkn/GFBiVFWbyHhPnRwAvEWQkauEAYCrtMYH7T04VJbEsCjZGMJuMUpJ8BAzKe0YGAbdVSVkUXVu9RxmxiLdNQ9O2KRE1zrX8kHESWlnvPG1tsXXdUwJ0FG6enjwEoVTMLdw+OyfahaMV2ofNG8Q75cjul8nOXEbHteNwRPa7XtujZ1EpOvMI+HwDjJ/6br5GBdZbL+w/rWN3c8bGZIP5cs58ecyqXdC2C4pijNIFjYVlbTGFJKsXxoT11IWBOCegvFDgXcvWxg6f3P6UunW0zuNXjsWypfFw82svc/3ll1g1tSidq5Wkz4a9arGY80d/9Ef8/Gc/w3iPMZ4//MM/5JNPPuH9Dz5gMZ/TtDXi8RruRR6tS8kTFFMJmIIrzz/PP/sX/4JiVFG7LoSzKAuhjm6W2bzoG7i8D4nEa0CC98LHn3K+7en9czjvuj86L0Ay7PkwlsoNLz3ziAaPqIzEv6NHMzf8DQ+Ja2/RwbhCAKRyXc8ORXdC6ALfzS/oDFXei1x1SHirHF1I5Vmh1Xkb80Tl/LokV+mvnQ6IeQplGE9GHO4fMJtN8UqUxMoU7G5Nuffph6xOHjEej9Ao7t+5gxmNuXL5PI+fPMaFZG7Cu8Tlq7ROCfO9GhJZu20GgmyIlYqECEOA4b1PngrtRRm0eFZtw6pphBrdusRCpZUkRY/KCttI3h1OxqgqDZ4WhUUpy6gwTMcTptMZo9GIjY2Z0E8XBdPZmP2DPeq6ZjabSrVoJV7stoXVyrL3RL6fzqYcHR6xv7fPk8dPmS8WAlCS92KDnZ1dvvnN15nNvofWmkePHnHnzh0+++wzDg72eXq0z+07d9nY2ODatWtcvnyZ6XRK21oKFcJICwk/RTusB+uMhDpqR1GIx0MS1TXKaQFZKEalQU0lskQrWC5WAuaCR14FPcBpzyu3XuKzB/dp6pbdC5eZbp+nre/jXI3R4rlPczwi7WhkDoBepl/0IJEMjAlgeHpRLnH5iBFG9Yya6wz16dHhDj67Pjca9q5JelN3fdRzJHJBylygPc7H9fjs4yuxTsWY45xJKI/ryoVhnjMxtH73X6r/jKRwZdbJU66brENzL4ezrieU1aAj8yPVBfCeQhvapkEBpZH8C+3FNXR8dEzbNBwfH/N074DDwyPG4wmT8YS9J09YLJYslysa60Bp5osly/kiAYZlqGor7dSSLd2EnI1gcWhD2I0oKVkitJOk8ViIx2f9E9lqRPmwRPrEmExZlhLLjJZFV9d1cM8hOQRGYfSIcVWFsepyVo6Pjjl6ug94ZtMpL7/6NaYbG4wmY8bTKZOxJG2Nx+MU366iV8Z04STREhx/V5HSjv7G60KQ83B+RDTuEaVbNh6dbSL96G6jTS/mtgsNCSw/BopMiEuytFxTFobnrj5HNZ7igWI0oSjHeKNBmdCO02xn0fXeCZUswdx3SmG+eacqxzjQYd5nG6IID1HEewqGD1a4wMAVw7XE4hD7LnJyq1QXQwULRelFmCpVYIxHchAKinKELwRMFqYDfDrkLKBKsSASgUI3viqjuc1/OucZhyJ9MTm+kw0mAYoo1EzIeShcTRGKTZVl0SXVh7BHAYky1tHrNZlOmE5gXJmUTBnnYWEKjJMY4pg8L5qLAu9QLhIDSJ2OpNwAMZRGKbHILTOFpn90gJYwVztlKZNBA2UzP7xSnXJJZrn0oGPK9FBphc6j5iMo6L5zPaDRgXWZb92z880KyJj0T7d1qPQm+W89trbgLK21nD93jsM7hyxO5tSrJau6piyl8GIbjCQOkUeRujJ/P+kvhdOG1rXMJhMOjg7DdfKddVJwz4Y9YDwey8Y8Goe5Im3b3D3PP/8X/yVeF/zqpz/GW8vjvT3+1X/9X9M0NXfu3OXho4cslyfJMNQ2DfPFHK01y+WKDz/8kL2n+xSm5MLlq/yX/+pfUY2qlIMR531Zlj2ldjhm6TPXzYfeeYBXPmWLDPews4xsAN6pU+PSzSh7as496zjV3mw/fdYRc1rgi889dahhtk74OPwvKtZnAa6z+jr/Pj/yuPl1hgMIxoGgUM/n85DbpJA8DMebv/wVB08e8vjhfcaTiguXL3CyqNm5cIndC1cwWlEvVzhVxLv1npGPU1xbqQJ6ll8RZVAOMNYBDecESBD2hsZalvVKwia97GCmCLI0WK2VD94i22KqQOlbGba3dtne2mRjNmM23mBcTpKHqG1qWtsyny85OT5gtbK0rWf/8VOsfZyAhlCzu6Q/rpYrJpMJz115jrKqxIipNE3bsljMOTw85MMPPuKtZklZlezu7nDu3Hlee+PrfPf7v8nJfM6dO3d57/33OTjY592jIz784AMuX77M89efZ2drA20NJhSqNSEHxAWDldWxX21gqZKEez30bKfQfU29ajovke08Q5PxiFs3b/L2R++zP57w0re/wdv/4SFVLUQtNrCTghjjqqpkMpmwPDyhXdUdJbJy9Ivq9edgnBusmffJ+J4ZYodge3j+unn+VY44b10AiF/m+NJAYxi6FP9F93TMkRha0OICWJePkXdG3jk6FIzK7zP0guSf55upDspmzpK1Dqg0TcPe3h6bm5u4pmVxdMLdu3f59LNPeXD/AXt7e9SrFaumpiorANrWUZQV21s7TEYjxkE5+vSzz9k/PJT4X48kjtUtkZUn5mkAwlLhunf1KlDdeg9aLB/RSqiDsgcSThVBQxEUwqqqKKuSqpJKyaPgPbBtK5Yf77FKYwopkFWUBUoRithIgbCylKRTHXIdrLU8fviQv/6LP8c5x9b5Hd741jeYbmxQTUbookQp8UTEjTF0Mh6f3IFZZ4faJhDjfVUc9zg2HrxXvXooaYMIfZTGMPFvIzmFOXULiLVcZ14v71E+C+WLiyRT5KIQKasR3/jOD/AeivEGJ6sWXRQiKL24qvP3inkKWmX3CwqneE9cZBIUK5TvkqNlobpgxY6bISlHSNaASQqgtDlWuQ8en+D5ibS48R6aDvD5YDmTJOGM6lZFBd+Ie7sQtznZWtNKciaUj5SvgwUsTsM0DxRd/pAObTEZcInjWmhDgcEH1pgIgKvKsDGacH5zzDRYxqpRJfH8xiRPDulZ3dh7Pw/KlMX7FmUVWKhXDmW73CypR+G6KaO6ekCxnbEfo2LgA5BTGR/96Y7oZFAMlSK7p8y9CBhcumc8LAMFKVmUOstSrox256n+59k9bPo8B1cZG1e8R+/efpCrO1T9+uszeg1cMIa41rJardje2paQzKbl+OiYjc1tZtOtQCXehMRQqRjuvQ8sZiEfJT1TNuIYL++8k0J7vmPt9yqynZG80pgSAvFB7KOiKvjnf/gveP7KZX7y53/Gn/3kL/jLn/08FeUTJa1NtOPOOwmTQAqmlZVQIr/8yqv84Ee/xfbOOUlC111YZBznuq57Y9uTZz4aJlxvrEQMyjg5MVeemj9fqBR43b8/2XzOKZe/4Bju4Wf9PUxc7p77twAZcpNTVtbkyQ6f5Tl8wzav+5nrAEMwkffRWUDDefBK9AkpkOpCPpiEhE3HMxamYmO0weHhU+4u51y4dBVb1xJq5EIRQedx9EO/O32nM87Fgsd5G78q0PDeh6iGNsgEKJQwoqGiEQ6Z523MP9DsbG1y+fI5dnd2mU1n4sldNRzsH/D4831W8xVHx8fUdc1yuWS1WrFaSo5H20gIcmtbmrrpjGC0QcZLmKTWhqoqqcqK0WQcEsCFdGVzY4Pd3XO8dOMGelxxspjz5Mke77z3Pm+/8x5b21ucP3+eq1ef443XX+fg4IA3f/1r7t65y2effsbnn33OxXPnuHHzJtu7u5LHWRSYtqQsWnwIsbZO01ghhTGF1BIqC9Mbj8je5z0oliyXy2QwjmNUFIZbN29w+/6nHNQnvPjaS7z90x9T1DXKt7TB2CmGMfHYV2XFoj1Eu+hpJHi1JITK41O+TW7Ed85hBImkuTHUs3rhf4O5fBbwWHd8MfiQfaIKebBf5vhKQCMKl3wR5y+X/56/VG6pzu+Xf6eCQhq+TbG6+bVq0JlRgc+VrOEizgVPvDa2+5e//CWPHj1Ce3j86BGf3rnLRx98gAKmkynbW1tcuXKVjc0NqqqiaSzOSqViBRjXcnx8xLlzOxSVcMTromR//5CFkrCnspKiX1UAAePJBF1oTAjTqCKrUVlQjSdUo0moliwUlePxRKy0VYkpA/VpSmDVIZ+jQFijpRMWyyVHR0csFwthe2rqxPjQtjXWtRljBJRlhdHhemvZuXSFarrByfwEr0uKyRRVVahyhCpKlK6EwTcsojSmeHwWR+9dDOsAoUspEiAhKqWqc8vZsNlqE92LXpB6tr58zxCogiIfNwUXdfYUumfzRDkXQ8ZcLznOWstquaRuGi5ffxHv4cnBAm1WxFKc2oQEbHlL8Z4MvAnR0+BFOkFqq0KF3AMVXacqhiJ1XOBxjuuYLEan+JscqBsdwogyj0AEEH4EXvcS/WP4UqPF8jFkOfHeo3vKZ25V9hgicLfklds1Dm1XyesQaXrLsqTQOhWzSmtWhbAmr3C1rNuNzU1mGxM2N2aMJxWFFrDardsW2hbbIkwwPo48AZCHudPj8w6KZ1D8o5LlssmT5JEJ40QHYLqx6wBgByQILuj1wthn4SuxjxNIkFaQwDXd+7gh0IgAI3uP7vPOW+bxxBicoTLqYiszJTa+QTLkZDIzekDyVzv1nuldpE068IBGb5FrxRNw5fIV9p7s0TYNq8WSerUSA1BYKyK3C9rWpneJNWlS/yiwWAyKZV1jipKj42PGs2miyHUhwVSZvO6IIfHzRRDiFaYa85/9zu/zgx/+Fvfu32Nvb4+Dg8NkQVZKAM/GxozxeIzSmulkws7OLtV4RDUao40U/LPeo4P3O3Z5rrAOFfS1v2dCLQeQQzA53NP6cyQfrNNzMhoUoo/kixSN4T59lgK+bk9PyswX1AY489nPuMrTBw1ntfkswJErW9B/r0RqsxbMdRTPJycncr2zOCdW+PPPPceNa9dYzeeczA8pJgaUofGKJtTSgsjQ171dBBdFMPDkIAHotTMHFXnkyPCz/PfUn0oxKksB5iGHrrWt5F86y/ndc7z04ktcOH8OZx1Hh4fsPTrgk8PPOdo/4PjohMODQ44ODzg6PuD4+CiBjKYOdalsDXTel3wf7vpTpb1eCBpM2rPi3pEobqcTqtmMi1cvc/nyZV65dQvwPNnb49M7n/DpJ5+wtbXJ1avP8Zvf+z4/+sEPef+993jrrbd4/PgJT/aesrWzzUu3XmJrexvTtLRlgTVSzqCwOhhbNcZbCutwViWPRgz9NkZq8cTSCMvlstfPTV0zmY555eZNPr5zG70949zN53n69IDCyf4X1x8OlIHlsRSxlMrtOlDPduHTIq/6OmucD+vWbmdsi5EEHWPUs44vBhN9HT1eE/dx7brQ1C9zfGmgAf0wqEjbOmxMRHxN0yTax+E9coGcA4AcwETQcJYnI7duJCESrEtDmq7o4YhWgahgfec730nX7pzb5dq1a3jvOdo/wNYN9z77HP/gPpevXKFtLZ99do+N2QYvvvgSdV3z8MHnPHz4iFdefZXv/Ob3GY2nTGczCenRFUrpEP5RpIIyqihwRiUlIFoPJXFLwmWiQhAVzLD9dgo89Coue1fg6Xj3q3LG+c0L1PWKxfERTShQJ1VvV6FQVUvb1qnYUB2Ah9cKXU3Y3LnAorYUoym6nOBNhVWFTBnXWdV7Qh6xcAqFasgxiNtHCCeJSkowfIf2+2R9xWcbSrTq0t9Iujkj9JouhKClxFcfq4SqnhCOCpd1kn/iXJc0J4nhmraV+VMWUihJB8FTFAafcgk6z12cS3HeaWN6ljmJ2jJpA46ECkYbeavobQhKOF4U6AQ8ZMKnehjyoMzqrkjKm9Ia7UuwYX02wuttUtEsh0PyUpIwU0o8TKEAT1o33oc4VY8isDWhmFZlEsA7WzN2N0tmGzPKoqAoyhQqp6GLuQ4vEr0QYuHLCjWpYO23K5RX3VxgIBBzra73nSJki6TPe9Xrle2UY9/NoaBlZ/AqO7z0V9/y310TQ93kVXx6b6nz0bf0+jBYzru0rofvdpZSCtGRk7TZZN31yY6fd0/3t+2/Ue+ZIkPXK6s5ZeGzNiStNW0MV1XQWItrWw6PjtjZ3ebpkyc8fviIS1cusVwtQ5Vt8Q7XtTAHyVoireOedVlJ7opHsaxXKC0/y8lYZD8ZcYaK8gcxufh0i7AU5YPWe4rxlBdevMWNl17uge1Y1yR5JVPfKPE2e2isE+nVMyaeDgnuX0/vszRWWSOdP7vPe3NhoPj3j5gNdvpaz2mQsvYOa5XtZzxxAH5iO3Lw9WWsqM88V6lTIGoduFj3ey6jh2FXuZFz2I5ctoglvquGXRgTiBTgo7t3KAvDuCrBW/yyZb6sWbVeIHIxpm1WcqdBgkpHnNPXVfrGhG6/G8qIdaAjf9+yLMFLsU6A+ckJhwcH7J7b5mtvvMbVq1dp65r9pwe8+9bb7D/d5+neAU8eP2b/6VMO9vc5Pj5mcTJntTqhtcsUNtSF+HpQLdrI3tu2tpPxABTgTezK3l5plOyvyXAcC+8VBVQF1dtjxuMxm5ub7Ozs8OKLL/LizRcpqzGPHz/m3bff5rO7d7lw4QLXr13jtVdf5YMPP+KXv/oVe3v7HBz+igsXLvDCzRtsbs6wRmOaRnI0CkNRaIrSUGiHL0i5pt77HgtYVVWpf+ss784rT9OsePHqczx+8IDHh/s89/or3HvrHSbGSyJ5NtZea6rJlPlqiTehPpaXiAtEgwvMdH1Amnv1hmtg3V4S53D+ey8fKZtHw/Py+RVBVz6v5DtpjPc+Rdx80fGVgEbe4GGD8pePCb7PElpRqCQrSA/B920bQ4UuX2C5dwO64l/xOqDnbs3vFat/eyUKwmg64bN7n1Og8W3L/QcPKMcjrly5wuHBAfPjY/7gP/8DLl66zOHhAbc/vcPNV1/l7/3O7/LyK1+TpGGgacHrUXAl2mggxYRwGe+7jVEUX0ehFbiQHBss2S57F8I9ODVBBB1HC7hS4ItCqvEWBePRlNWqYblaUNcrqrbOgMYCZ1vaEO7gQ7hA21ouXr7GfNmyfe4Sqwas9lKkynm8azDGdVSt2eZpPSlEJLdsAChHt4lnyoxDFP98vOI7et/dPyrc3vvgvowhdi4pkEp3FMHey5wwJjBpKFHgrS5TTGMENwIEtFSZ9ZLsZ4zC6E5R8YHib2gt6Hsk4thEFBW/C88L/SXeljDP01TvqkgHQzhx085XkbfBkyKXSHiUMlK7xR+Dk7ogRmlwkhtToplpRLgWIT8pMTZpqqpIG9/pf7I+YxJ/WUY2Jo/ykcnMYhtLLOEnm3OmIGRAQ+KqLA4BrC7ylYdQQ1Hk5QVzxWoIal3mXYFm7XkQQO/w+nxepc/indcduWc1Wt+7e/UV+NMKnYCf04pn7wmdgTuBGg+QMUvpwLYT1xG92g/D9z79fhGId4xfPuuG8PuZQEO+V2HiiTdDpRC9WETv+PiYyXiCbS33Pv+cF166Qb0SZrxqMkmy19oWAYhqoAzKsyJY9ChWqxWbW5uczOeMZ7OUFKVVeHbmq9G+YzgjAx0QSBu0GEQIe4ENDDU4eZY4Vrrke1TIBwvWPB8yM0Sud6yKwz1pHdBIxjnVJWauO++s41nf9Yw3g/NSqOYgpOqr3H/tMweGxvAHmi9v7UyXDe7Zb1j/mbkMznNGz2pf/D2+3zDsa3hePLRCmCDDmLVNw2g0kjmMD7lVimXTQFsL6yAFTkNjFS0KUxVYW6Po57Z2hltFnk81BKvDcKn4/TrglMBL2Adt27K3t8fiZM5LL97kt37zBxSjgsePH/HmL/+GvcePefL4CY8ePWJ/7wlPn+5xcnLManFCXS+x7QoCeUzrhERk6LWT56pkyO3tj77pvIvIukvX0KUnRwOeCtEadqlQR+Ipf3QPRqMRH7zzFpubW1y4/ByvvvY6zz//PAD379/n/v37XLhwgWvXnuef/JN/yptv/Zr33nuPzz//nL2nT7l58waXL18Ie1hBURaYVlNZQ2EsvnW96uWpaKKWf+PxOL1SLCDduJaCggmK6+cu8s7t93nlpRtUl8/hj+YYr2iaOhlla60pxga1NQXbSuHg1qIcFF4oldssxzPq2lHZPwtsD4HEuuOZujind711xv3+DZHQudXqzGfmx5cGGlFZzwHCUKgOwYM2Mbyk4+u2QZkoiiIol2KZjsXpfLD8imIgG0hkjYqx1Ym2kOCm9R6lImuJC8pd5OCXe0UFX8cEHYWwPoRlUK9WfPbJHerVitp5FscnABjvKXXB3uPHfPe73+Wb3/om1XhM3dTceOVFLj93DVONODqeU+qCQhViXUdhlabUBboohQFGiZXX+M6a5fBo5QLlJsI1HgfbVF3fZmMRrZGdKir/TzUclEIVoiEXylCOxpSrkuVyyXK1wASgYWzFql6hdIPyJlhpG1wDF567ybkrzzPbmPH0cE45KjHlMmh4sbBckawX0V1uoyAKilUcI9WZFpOVPioBIhQDC1EYl3iOid9lgDItrECJGgVd2qpUpEsN91Mx2d0kjxAJMHSCTsBGrOYsFm2FR2lRLH2kqc1rRiRFunOxa6Ujigw6WyggGCwWqEArqhxSlSECJReKQPrEGZ8oGGUi4L2nVA1aecqyCMnPJePxiMlkwmSqGI8Mo3LE5saMsigZVRWjsqJUTnxmvU0uCCr6Mb+y3mzILSHRIEqomcPaWmgTybyLA6Uu5nVEfi6iQUE5YtI8gW0tYtIImCMQ6Fl6yZiZTgldC94l62f+tVdGFEcygeuDry0/LyqWvmt/XKl9YHI6dMrZjmCgp/rnigMRaIf292S3rIe4yfQ2BaVCMufpDSAqvOuO6EGRu8frOkW+f5/uHU/fL1fCCPLV0zYh9M9JTQgb2PhWTcvu7g6zjRkHT/aYHx6zWqxomwY/Fs54UwSjke8IEDpjU+ipKNOBVdNQVCOePHrI7vnzFGFPcGG8Yp5GhPMDzfTUGyWOe2QPECIRHTxSMQRIwIhzgYqHCDyIkzX0axeKeDpZOTfKxb/l2g7PibEhtl8NxiUfp2G4wlnnnX7fsLqeoYzEd5AL8vdbdyJ0xh01+CpZSToQJn901/Zv01vP3fyMJ/q0rvP3iauq65M4h/pAPzcQ5IpuBPP5XOlCUbL2h7k1m02ZzxdSbyg0q7XCRea9R3mF8QSSl844oJSXIrHZ3h4t5t5LTo6ii+SQOjYRuIZwqEhrndZx1L9kr/POJcY8UxjquubB4ye4tuXlWy/z8ku3aJYrPv7oNvfvfc6jhw949PA+jx8/YP9gj5PjI5bLOW1T09Q1zrXgJectenZttjbChp5FFnSWd2ddNneyMVNAAlSi6/ncWh7SWItWdCahjJYwYNuuWC41h4dPuXfvHu+98zabm5u89OIt3vj6G5zbPcfTx495+PAx5y9e4MWbL/LiSy/x5ptvcvvOJ7z//gc8ffqUGzdfkGK7bUNZFlhbUBSWWjWMrJCLFKag9J7COYx2lIXU4hmPKvCOhQolHbyicZ7WeZ577jk+uvMxShd88+/8HR59dJv6+FhISJo61H4BZxSTnUuMRlOU89jFivmTPdqjAwql0G0dqszHaR89zyTZHNdLVwgzYzSMu2i2tyulUEb3i7CG/UfT7YtJ9tAdwpA5WM/BHF4vFswPj/gyx1dmnUpu5mzDi5aoUzFdziWKRWO68A6QSRYr3Lm0aMKrqm7Tl42m+10RWYDk3a0Nxe+CEidc06KctaFNSmebRli8Wku137ZtuXrpMhfOnePpg0d8dvdTNjc3WR7PsdYym85YzOc47/nNH/4mN195iaIai8vetczrlqPlCl0WGFNiKFDeSpVYpVFFhfNa2GFi4mxmMTRKobVPcnWYUA8DfST0b7Ts5+dqE4RxNg7ae8oStK6oSs10UkkYQ12zckA5RjcNqpQ8DlY1TlX4ahPlHV45fKFovadtWgFraoxSJhTaCjkEhKJ5hekJ8RRqpFSwYEeQkhexyxKQM2uIfNdZ3uNGkTxgpguXiX2XrtUdE1acvyoIvzJkKuchEmmeZxtMbpk2WiVWF68zJS/sHw4HsXJ7FAxW3KtRwfZRcBCsFXiER1hiNJUTBbxQirFRzEYlm5u7zGYzptMp0+mE8bhic6QYlSrl60SPigA6qQadOiXt1SHt3HmUcgmYp/frXjQB1jKIh86aJrU8XGTecJ7GGZq2TS716Fa3rUN7HWqWxDA6gtCMFuEwR4JiIX3eeX+GsdNeK5zKFYe+QpGTQPQULm+z8+L/ui7qHZ40L7pnhy/OOLrCb6IKOJO1y/XLsp1luc7l6bPi4oeK4v8/1u+1oIYhN06mlKvoOfXdJogPCpWCVtF6h9cSInrh4iU+ef9djvcPWc1X2KYRC7H2eCuyweMDlXhXITx5a4JYjPkr5XjEYhmMHdGwEJNtM9zm8GcXhcvO82Eud+8Zvc9pV00hcsp3pAEJ+NMZMeL91sctZzI6GDKkWFh3Rkyml2f0iwfmc1FFoBLHI3+1wTj2QWn09H7x0QPca+Zc/qyhwSJ8mWR6+o7US6f3M7I+p5tvwyMHNH0AoZLMzddIZ/zM29wBC6UiuB8mzse9S4m+4QHnKMqSVduIjJQTReZkb2ZDt/mQB6gQJUvoq7t9Oe9Tl2o99ZPpY96TT0MRdKfwT4Uib0ZLnQ/xdHvuf36fg6MDvvOd73DjhRvsPX7Cr37xcz779FMePXjIwZOnPHp4n6PjfRbLA+pmgXMNtm3RFBJKG/Y/hZA0CHYMwZi+A8RE1rvAjNcNEL3xl3EejHxaRHJ9VKCdFZOe1hbtNG3QC7QNeS2qZdGsWB7t8/TRA/7m53/NlStX+dZvfJurN27y9MkT9vaecOnyZb75za/z8tde5uOPP+aTO5/ywUe3uX79OXZ2NvG01G0r4e1a0XhL2TZUZcUYj3OG0pQhvKlAa8VkXKAoqRuPVQpUQa0Vo9GIKxcvsThZsHXpMn/5k7/Cn5xAKzmGhRGmz9FswvTSVS587Q22t85TecPJw4fce+/XHN//DPV0D2NrwIrOoZSYO5UUrFShj5Ka5z2BvDLMcXrbftQTDarzOsskDLqo6MpFts+S6eMKUr5sGCrJEVaapm6o50u+zPGVksFzRc45l1xI+Wf5T21M77MIVuRvi8rrEgwFB31BOfSgROtRsgoM4hWH4VNDpTxZbkN8/s7OLjdu3GC2ucl0OqOtW7xSHJ4cc65tOHfhAtV4gjFlStY+PDxAqQKtWkyhQBdYL252p8AXCpRGQtGj5V+Tm1HXeYfydz/r7/z86NYdepu87xTf0hhKY/ChWI51jnnTsqwFbdd1Q9s01KNaBJ+Pyb/h3ZTQwXnnKM1IvAOqc9XGBGajuqT+nO4Ulam/sa3x2kzw5qBV/umU8H0qwWlQZTbFzSvwKtK8htyTlL8BXhVh7+gsl2luBKzWQdu4ifjsN/npsmtc3OnkAWHFC82gDwV8lHfpn8FRaENZFUw2xkzGI7Y2Zmxvb7GztcnmRsVo5CliRXDVKYfGd3Ho8nyPWJ/i+unmSE+p7llXB2B2oLT3xmmweftIc+2hcprIqBWry7e2Fea1VgqY1W1La0NND0dX/yMWikuhf7JKogB1Xiq+2niuJtUEWbde+pbKfLGsV1Dyd+2dPvhs3d9nnePwYHXPInrWvZ5lfV4nC54dn7/+Pmd/uf49xLBz9v2G7Upzw3deregZOHfuHO/XDQcHh6xWq1R9uBd3rDSxYNlQjg8VMqVUCPHsvLfr3jPstWu/U9n/n3UMDT0qkz1DQ1vv/s8Agr13ob80o5yOf3QeqJB3oeIcV70Ln+WhGO6jX/b4KuevW2+e9fM8KvbDz/NnntVfz2xDrll9xSPuT6fXikp7k5bYVGazGccnJyJgg9zPlefhLYZGw2cl6K7LwRj2RW7kjbK9CHUwcJ6Dg0Pu3rnLrVu3+O3f/m329/f567/8S25/9CGPHt5n78kj9vf2OD48ZLXMWPqI+XLdWJpMd4t73Fm2lqFelusf64xCw/6PfZfe3Tm8b7Mclk7OFIEF0pjgSanBtpbbt29z5+5dts+f51vf+Q63Xr7Fg/uf8+jRA3Z2d7l65TIXL18Dc2AEAAEAAElEQVTmsxBKVZSGyXSc2lvooGcUHtd6sB5XVqiR6kIxlaYoNOPJCG0UjQOnhHhCacONmzd56803eeH6NRo8R/M5rq4D0NBMZhOcq5hOd2DjMnbjHNOdc1x9+etcfeVVPnvn19z78a+onzwGfwB+IYn2XlMgRDqK0/uXj+1jvTFqXX/nY/WsMVw73k4iL5rlis/u3D3zWfnxlXI02rbt0VWmQQpcxXVdp9+BULHZ9F4gxue6YFkdAoO8M3Jq3A5hrRfy6wBFbF8M+cg7Nn+P/adP+fTOXapqxO//w3/Ip3c/5dL3L/GXP/0pzWrF1evXuXjpMs463n3vPZxXwjClNOPJlHOXLlOUJbhQTAcXGFPEspHCcWLbntHHQ2vMWUdP6AwA2RCMRQU4JZIXBQVQVCNmkwnOe2zb0qaqol4K3AR7otIh3h5hjTHEgjbRit4l+cbCYjlVrQpAKKfN7FujuvCUXGEMPUKKlx6Ot4Ke5S8PDU2aXtoT8IFiyEcLke4sRBE0RH7704ssgohwdyWJ0h1TT3hX77NzxdqlcYxHJZuzKZvTMVuzERuzKbPZBpPxhKoqGVWlWPi9p9DgfB3AUigcqfLNUOFcNkd81ydDXXSdovssC+W6z4ZAIx6KCDLFE1GGAnneC71i01jqumZVNyxWNXUTwGxrBXiE9aKMOGPREsiiQx9KW7MKwCYLITvV2iAA1yoN/XcaKpH97wOUjM8IP3sC3A/6IYRveo/UQLBnA4JnKv9/i/P+Nod0r+1t7p0197RH46x29YFGWEOBwrNpGq5cuUzTNBwdHTKfz1ktVymGO1pw8/t+0Rw0xqQQhDM3wWdK19P3POu7nqyBXvJ/fu2XHachkFfQ82znhw6haeFKJP08+JKUxun1e+C69/mq7cyV4rR/PON9hkmmyQrK6f0ovs9QY/0y8mid4W3dOH7VdbPWwIJKFl8p8CrEHVVVsdrbO7VHndVPp2TEGR6NYVsi4M4/z/9FxXJUjNBKcjk/fP8DyqLkD/6L/4K6rvmrv/gpH3/8EQ8efM6Tx/c5OnjK8fEBq+UcZwO5R1bLyFoXQn778z8BHE4bcYaA+yyQfdb4rAOpXV86vO+MyfHa1WqFUZqyKACFVi1FUVEU0LaWRw8e8Mf//t/xs7/6Kd/57ne59bVXePLoAYcH++jRCKNgVJYc7h9QaMNsNgmh0OK5cq3DGyeVz2lpjUEpjxJWCsnXKQopJNp6WhvCch1s755jurGBU5oXX3+Vj7VidbJgUhRUZUE1rpivlhzOFxzNV/iqZmQds8mEnZsvsHNpl1vbr/DJz37Bowdvcnx4B13XeCuU9d6YpP+uY2DrGQO/QH8cHkMQu87IE50FGsn/9K3jcO/pl7r/lwYaJtRYKIoiJV+lMu6uozbLz5E5fHryCVruJxXlLxN/H4IPpVRy6cbnDdsxBBwRBQ8HJgEP51jVNY8f7aGUYXNzh8OT92gfPESXFVcvXmQ8nWKKioOjE54enkh1TecwRcl0POW5S1epkIQfqxyNg0UjbkgXEqjjm2jUIDzntDI3/P0s4dlbwIO/43U6AyLR5yr3j9bEoJgVXSVXj6J1MSQpWtTkYoXkreisXUOL0jq6wFNCKHNfW++SIBvOh5DpfKoPUrt91heKlETsfSFJxpCoYSM48b4J1pxOqdQRQOAl3IlOeMqmG3nAh7H+MQ8hWD7xFIWSiqtVyeZsxsZ0wtbGlNmopNSeyijpbiVhgAqP9nUAGg5aT3fH0KcqsxANBEp8/6i85Qpkr8/9emUp9c2a3/N+OC24uvhsFax7ykgvFEZTlQXjcclyVTMeVyzrhuWqZrVqWCwFgDjnaRqpkK60AW+lQJ2KYXXZe7p8vvszFDXXO0fm+5dXPnpn9pRN3/tSlHUZC+U65SnOhbM22XX9/EVWqLM29OHvw+eddS8J2+sqEfeupz/z1ikGQ8MRhBASpVJ4yGq1YjqdorXm6OiYk5MT6qYOz+iKOsb7PCtJORqnOvrzzqg8PHJZlCtm6/ohf6fhs7+oX4eAZNg3ZynKQwUyvWMmLxX05tqpMKSBnHxWm5+leH8RWMkVj2dds/Zd18xtOc+Hvaefz3nWPrgO+MXvO49BF2501jh9lX4h34t81w/T6fTUM4a6y1BW5nukyg2mz3i3oYclv1/btoxGIwlT1or9p3t8+MGHfOONr/PizZu8+847fPjhh3z+6V0eP37I071HHB7u0dQLcC0eG6o5q1BfKuZGmrTuz5q7nYHgNFNo/tmZvXrGvrKuL/PzhyBOKWiaGqGMF9ZIa6WyuS4KXOt5+uQx/+Hf/Vve/Jtf8v0f/CYv3XqZ+XzO1vYO9arGec/i8BjjpdCnw2HrFq0UrW5odI3RhuViSTkqKQpJCDcGykCcgiowgSkLpSmrMc89/wL3793j2s0X+Z//5/+VerHENw2zyZhbr7zMbGuD7Y0Jdr6PGxfYekJda3a2J+zsnGNcXqYsNIc/eYgvl8z3H6EXDbaJpQJO7/lDPTj/fh0AHu4fX7QuhjI/5mBppdjY2DhzvPPjK4VORSv10AUYPyvLMoGQmDSqi9PhUZLZr3obTf7dWQq43KOzLuUu+CGKi9fFuPF8Q42ASAcUa1RB07T84pe/4Lnr1/jBj36ENppXXnsNjacqK7QuqBspbCP6hca1LbOq5ODePf7qJ3/B4mTOdDrla2+8wdUXX2KFpzEeqwAVMhp6ysp65Bi/yz87axOLiudZ1/Vcuz17n+RGmKBZJCracLrR3XlysYKUlRGYVlSmpAQptQ7wdHdJCCudr1Eh1awPVvLjrE1BK99pG75rh7x1FueceR2UAqNbYp6AD+0wReD1VsI+UZUl1WhEWRSYopAqoonCtOP+7wBHjJf9/7H3Z82yJHliH/Zz94jMPPs5d626t9ZeqtfpmR4AQwwGAE2AzEQjRRkl0mhGM5kW6lV6lD6AHvSoLyDRZCaZCTSKEgSBBgEiMSs2DWbpZbq7urvWe6vuevZzconF3fXwd4/wiIzMk7e6BtKDvPvWyczw8N3/++IZ5Zo814yyjPEoJ1NCdBut0VhUQ5QGBitogTTgnTg1W69IM5E3jtWBOfLeh7+R7/BxFTuMULp28dquQ943rXlnbwlmBfEdFcwDg/mTUx6TabQe4yZjJtFUr6xZzBdM5wWzRcm8rPGVbaKhNRbwKhItTYekh2QVTvORaWzuRTdy1bp5r0SUA8sRjevo3cf0Xq+KmrU85uVnr4K0+++sak8I2eV2m742IEzj534UwHRvyrJkf38f771oM4qCxXzBbDZja3encbRPBUZp20N9KaVCEi0f/PuGcYTrbVanrXB/UpyzitFrCEJYgk3x/RQH9cPz9uF2R4jWQ+qRUSPcofbMyzx9CKHsle5ELxs2+1kuq4QK/Wc3lTjHvl/muv7S3+Tfcps3xf1fNf6hszz07k1rlBL4Ys4Z2wftaUz+5vM5UVgXx9KHKf12lVKQBDTx3ndokn5Jz2SfKdna2hLC1ns++fgjLi8u+O2//tvUZckf/sEf8OjTRzx7+jnnZ884OzthPptSVxLxyiiFKC1iPqi4dsFnTiGa5WTsaUlNwfom6+nYX6UMwWKZ77L2JBajfchPEs0wJQO5rmt0JVEVtZHw9C+ePeGf/D//EQ8fPuTWrXs458mynLqyTKdzrHXcvX+XW/duo1ASuliJAHprMkEZwf/Oi4+ndTV1VZKPcg4PjjA6Yz6fs7U9YWdnm52dHUymefdrX+dv/bf+Dlen55SzKcfHL3n/lx/gjeLW7af8zt/+u1Bto+2CrWyP+7f3ONodw4HhnnuD7+a/zQ9+f4a6nGHUNfhCosatiByXMnpDTOy6+5+GsF21f6n/ow15wJxWHNw+2mifXynqlHOO8Xi8xBEpJapyay3j8ZiyLJtBpVLIFLj3JxwvXT9UXR9IRISWctdxbLF++vu6y9DmVoCnT5/x67/+fQ6ODuXaaYX3jjxocop5idFZQxR67xllYCrPf/MP/is++slPuTw9wzvHv/7d3+erv/Gb/Lf//f+A7Og2tQKvHA7V8Ud4FQDfX5M4j4bR6D1ri2+QVro2IhG2CTCjBTzeS9hSeStpqkeMBiK5YeJoEXdfWgEtk+XbBlYyF00Vn4yiaa+1SxQ8LHVM8AXRWlSqxqR+IhnaaPF5sFYiJwQnamMkgWJmDLlp++oyu2BdyLbe8YdQKK3IdCahY41mlEuW69wY8iw6uVpiPCLXzEL8efBensUIbYALGa7j3J0P+VW8fI7EtPddyV4MX7oEMBTBxCloElUXRa87i0P3Pd3CtF6HIQ6mTDo68I9EMuTHjmqUs7M1YTovuZoXXE3nTOcFtW+TPDZ7HEwZxJl1NZPQn3C7RmKH3O7lZvfuVYj5/ueUEOyvz7o2Nx3Xq8KODhKPa/oFSweOJDAoPQzWWkajEVor5vMZ0+triqKgrErGbqt7Z+nGau8jxZSoybNMzCe2spVr0ITdHhp7r911c2rGwzKf2cdj6biHmJjBsPCdMTcQPOCIOK44Hxm8hSYRWGyv69eyllf8lcrQPNO/Kawe2hnV3N/1zP4mpWVy1p/kDgPRW5jUx3MlgRyEOwohyCS4w7LWIv5LaY3OWY57ODDnofmn+Sbiuud5jlISQvbP/+zPuHt0yG/9tb/Go08+5dGnn/Ls6VOefP6Ey4szrq+fsphPwRE05UjkOpGqNZr8GKoZouVCNy9CQx/0I4utmP/Q+q8qNzMlw/6rEn3Uo9CBIQmm8VgyEyJgaYUyBqU1VVXy0Ycf8Pjjx+DFTMzoDO9Fk/P5o88Y7U/Y291lMh4zmUzYGo05Ojzi4NZtDveO2N/fZ2t7QhaS/ikF49GIrfEEoXwcZV2iQjJCpQ07u/t8/uhzxtrwzjtf4fWHD/nhj3/EJ58+Jvvjf83f+Xf+XTkvTtrCK6ptx9abu0xObmF2jkCdoFkAc6ySgALrzstNZWjN03QCq+qmsEtpReWEnh0lYX/XlVfQaAhB5pwkWYqdG6OpnSXLR3glDtSjyURsaV2M19519tMh+pLyBPtmwLX25kprvA232/W4slSi2zvg4kQUBxwkq4FI6QB+H0zBnEUrTWUrxltj7t6/CyqEcVMhuZp3ZCZjlI0bggkCjaw8z3/2S84eP0bNpuzmkjW2vpry83/5r3n55Dn/7n/yn3Dn3XdYOI/XGue1RPckiRQQ/rdOmrCWEOwdnqW6Q6/6RLIU308Zvw6y7x1QlZou9XJlNNJ630jowiTjf1AqiX7gxdgiHbJKqiucREzoEZgqaA8yo8iyHGOyJvZ1lhmUsejAaESiWoCjRtV0NUvE+XlUEw0KfJAgxLnXgZgnMGpGi1me0ZqtkWKUZyERkJgOCZEsxUXHZ5VKknzo27U24PGcQsvU4vG2btbZ4TsZ0SU1m2/uRtTuLAGVkAXbhbmm662TscY70zBcqnvPUiSjVftbC+wS5tB5iTLkxd8iyww6gzzLGW0ZJls5k3nG9iTj6tpwNp0zLSqctcJsWRfGp3AhH8lNjHr3d9/Z7FXAc+j5KmlxH/H16ywRXj1GbdV4VxFfN33elPFo94zGREJFJmEVYZ7KGZroPATiOQ15LsIZCYSgsb4mH43QxlCWC4rFNGQULtkO0XG094zGE8qqorRlqw1r9tg3TLmEuLSM8xGuqtFbDMK1xiSzQ8z2pejLxG7KsMc5NsIsUmlhzL4rGoZ45peli63kN5oKyzsxEaeMSeBVmsNGtPDW1ok5smvGX3kXwowihJbzaB0jA1U4bzEmWAuosCINrA/vqSDhSaLkCUwb2v+wt4lgR767BqamcL2BXSvuh09gTzw7LS5Zljz1UVTcvq6uXua0KkBA/D1lxFpho12qHwU4RElYeE9r1dIraphoW3X3+2d1OVrXsImatCUMttYwu77iT//kT/j2t77F0d4RP/7hX/D5Z495+vljCVV7dsp8eoV104Bbu75QKrTXmII2UfzkvFiXRGELzIfSIS+KWh5bn7leFTFvaF79sly3vb/pMxvmpZTgY6V0oBDE9w8vUTC9qwPOydBKUZUleNA6o6oKvFdolVHVJYt6xvz6islkwmQ0xhjDy+fP2drdZ2vvgIODA27dusXBwT77+/vs7e2Sm5yiKCWnlFaM8y1ZK6O5nhV869e+x9Vsxi9+9jMevvMmuJpvld/kj//8B/zyo19w+4evcXB0gPf3+OTjz3nz/l1GuyNqk5Hdv8veO2/y9MNfknsrSWeVEZfNgTVtGNJ0PZ1rwh63NMXymsd76EIdOfrhzqzYH6PAViXjrMuYriobMxpam8Z0KkX2QgjJ4mrvQ7Ij+esRtaO1qYpVgLUPBF08IipMriFOUE08Zu/Fr0OhsMTMz7Y53B2ES2KykAA+rXSTSE6k+a5Ro3vv2DvcJR+LSi0zMcSmzMt739jtN3SzApONePH0GcwLMu+FczAG7cFby9mjR/wX//v/Hf+d//g/4qvf+x4LJypZ5UOeCHwjpfUQCKI+g7G8Fx3AkUpN2hptK6r5T7NGsd2VQDFpW54PqMgDoumebN8QMJruwfZJ3Qjw4xPdIC/f7mF4qpVnnKlw/iRvhAlI2SiL0W1M8nSMtfKBIA/IhbjKjkaIk6yJSEQUJsYtBLy31L4WggqFJWTwVJK8bpRnjEcjskwzzmCUJ8EPlLAr1ssqtCGcW4KtRXZDvkWiCYkES4v4wPm6Yz7RBe6t5qOD1AFs61/S2WfE76YlGAJDFjlA1UeC7bk0Ojk7dllrEH+X3yTkLQZ0rhiRkY9yCdm7s8Xu1ojJ9oSz6znT6ZT5vMZ6CZEdjCVpEyOqJSlOKuVt+o4M1IaM+6rfhxiUV2N41iNZ2FwqNTSedWVI8KDS/e49u7lPgVkNDaXaPBYiuVV4p9ne2WVrZ5uLi1PmsyvKshC/HO/x1jHODPfu3ObRZ59LMtNoPhSHoXRjHimaU8MkH1EtCtS+MEhDCVq1Vs35b/ep3av0u9Rvo+OldzEyAGnbce+jtjwNdhLrxe/Wtia+Kdyta8lNIPloaqqqbPqNeAvVgwtBC9kIeaxDyD+N8opMicBP6+DYagzOQ+2spJcJfr4NI5bAYiITNbDnOt3kdpYd+J2WFI53f48kTFcw0RciLpdo7tf7NR1PMpb2/i9LwrtjXh5j830JTwXNsVIUpYSB18m+p7B7aWzhe8xp0yEKu0i6Kal1h1KwPZlgjOH0+Jh/+S/+Bf/Wv/VbuMryZ3/ypzx78oTj4xecnDxlenXOYnGFc9H8NDH7i8wRHrxtzlgKR6NQq7MmYZ2cdZ26KezrMx79/e/fnc1KSgv13gn+JB7C2U2ijCq5Ky4w9d7VWGfJc4/RI1BQBwYEBY5a4EjpcHWFcg4fzNoKY7i8voaXL9BaktWORiN2dnbY3d3l8PCQo8ND9g/2OTq6xf7+Ptvb2xIQxSjIc37jt/4qr735gNdv3+K9t9/m//if/We88+br/PzjTzg/fcF8esXl+SULZfCV4XBnl5Nyzu79e+y99QC9t0V17bE4XOVwthVgpOvrE42p61kFxVwl9Pe6f15Dnea4JDAhvYOKkBTVOs5fHm+0m6/kDJ4C7kbKG0IalmW5RDBpramqqnMoG2COD8mt5GjrVDUnsyQKZTzJhWf5IsdxicmFQwUJTu1sw1hopeXwBaLPORsAtgUnESWcc8JYuLicDX/X6av57BzXlxfsTCYsvNgla2VwXuL9505hT874R/+nv8ff+R/M+dZf/y1K74UzjW0E3w1NwCNp5KQVUUkCNZ/U79Xz/cqblU2kov16NxFgbd116nIfuKdwmJX46ozynHGumIzkmEapXyxamWaHhBtvQ85aYUmHJxDTsidzEIkaFHV8IONx+EYaqZRo8/JcHL3HuSTDM0YxMukljsxgnHNkGBwx7n5LCLnmWUocRSl8fAZyHuJ9Se9al9GIgH4A4asYTKEFKLEYUkSsAk2jIhXZWb6WqYsM5TKBL8xIYFZozdS09qhatJqyn8JATibyd7y9zc7OgovLEReXOdfzBbNFQW1tk29jSAOQlk3P8U1lVcSdZQLmi/U35Ov2ZZV1Gpd4Jl+1rfR+p7A8tilnsjVF2dreYrK9xcWlYjqdUSwWlGVBWZaNSep0Ou3YFve1NCowMD7kmchHo8BcmBAnYpnhTAnYVGrej5gYn/frRkFVVVVLDrBp++2cu3BNBQaoLwQbgpXp+sV+Gw13h5iWdo33aGvJjGF7a8Lezi77+3sS1MQ6yqqmrCqKsmJRlszmc+poMnPDln9Z92YTxvdX6WsI/7/qGNaOKRLk4Xex5IjaAdfJzTTEiPYJaqWUmOrQ+iT1CUVoz3+8V1prxnlGpg3HL17yB7/3h/zO7/wOF6dXfPjBh5y8fMrJiTh8X12eUtcFUIv7Ug90rVqPftSwVXXj+U2J3CHGo2+K1hegbVpWC3xgiCPt+y1Ec/o8zwEoy4LMEMLjAkFTFf/G8Ozx7kZ60LlC8gJpzWIhr7x8KWuQZSMU4ps8DiZXe3t7HB0dcXTnNgdH++zt7bC1NaEsCi4uL7lz+w5Pnzxly2T4oqCYLygqx+fPT5nONdcHFjfKuHp6zs7uLW69/ibPnj2RwEJWIu51kj0G+FPXljzPlxi8Pu3d96tLcVyfCRk6y/1y+WUn7Isl7bgJnaraS9dmD7bNxPqDbXJr0B5EE7MuQ9Bm2IanNQNRo/olXbToMCNAok34JhNAbOqVtKmMwTs5WALo20vfn3faF96jncWVJfV8TuY9WyYjMzlV7bC5wViFrTzV1ZTf/S//PqWt+PW/+TconIS/jVyFRomk14XEb0trHvtNf0zHmR6u+Cx+73Klr1K+COGTEiND0SL6LUaitDUdCEl5sow8z9DKoZsEeQ7bOGIL09hlV4RZ8BBTCyW/B4BHIKAbsRWJeZTCNj5FHu9sYA4g05o804xGOVuTEaM8l3CuxjR0uEg6g2u7ikyCxyPaNNGutOP3BKbEhQzYUaLkwfqQlTtJluOcC9nuYzjeNpMsxKsoplkt85SuQztO6JrHKboStpbwoyFyxIGV5JkPYY7lxTYJY2yn6iBPpaLPhvAuwmyEvIuIlmhLKzIFk1wIqdPLa9TFNdPZAltVHaK0Tzj2CUjiXt8QdWpI+tasxAqiaFNCpk9spmVdXowvQoj1hUBfJkF2EzxUgEFhA0FrjEEDh7du8fmTz5hOp8xmM+pKgnPkRuDvbDpbYtqGiBMVCO+tyYTnz5/z4I03QNEg1/7+A0tEUHqPVu1Ln0iq67oZUx+upcTX0PhDi43kOBKaMjbTZOrtO1XrJBRqJIaUVmQmY8toDnZ3uHP7iLt3bnPr1j4Kz3w+5+yy4MXxKTjPwhb42mK8QpuMSrVnbYkITgKw9Pd16D7cVG56Z8hplXbGS+VVJOF9RvWmeit/V+33mG9JK81kMukQ2ylhPcRwrgoM0P2tmysins/JZEIGHL94wR/94R/xW3/1r/HiyXM+/eRTXr58ycXFE87OXzK7vsS5Eq0ceBsElIbVK9qd7zoGoz8fwXG2824K4/t1Y1kX/SiWm/YsqUk6t35/KRMfmQdjDGVZYG3NeLwFIQSN4DPBQ0qZYLIoObjyPBc+xNVor7DeNzjQWqjLgiwbUxUL5tMrlFIcvzA8yjImW9uYPGN7e8zB4R63Dw/4/N49tra3wFoe3rnLs8ePefzxJzg/YV4Z5m7ColbsHezhlMOQc/DaAx6bjBEGSca7Aq57OlY+/TvWZ8BSmNbfk/Q8D9JxLoQFcr4vg1xZXikzeLxgketrJDe6e9C8F4l0XcvCRA4sJviLz6u6XbiYxEtpjTGZSF+D9MAF052yLNmebDXZh1POP6qcldbYuoaQDbyygiiyLJPcFqEtjw951RxlUTAeT9qxuPTAt1x87Ku5cGVJMZvhq5KJNoy0JjM5pa9xWmGcovaWyiqq6ZQ//L//Q7T3/Prv/DYVUDoXMokGu2QdNDJLwHJZKxAZjCH4G4nBqCm4CUSvI0j6lzf9bQj4DyFdH5jRZg7hb8tUGDKjJdt6QKpCvDq8q6ls3Wk/dtFdm5SQiBXa9ZBn4fLorGFI4vrEcVZeiBrvPTgxo8tVMJMaG8ajEaMsIzcGo0R05BG/nj6REpkXpzy1tWFAoZ6LWocek+yihgOcTxI5gaiEI3OBC8+6mpEIPGNGahXHEk5ZsljdM4APDEUkzlWzhKlpSfpXKTFtaxI02pTgizbN0pTyEqfd25pMa4xSaO3R2uFcqKtkHKNMofWYLMvJ8hF5Pub0/JyrqylVVXfG0J6D5bPXSA17hOLQme0TqUNEaypBSn9bRwRF2LHJXVnV96rxet+u/U220WnbWika480bxt+HRem6x/trrQXnMSGvTlFV4B3GKA5uHYGicQSvagmooJXAvKIslvpqg0vQEnwaMqXZ3t4WZ3Cjsb6rERhay6G1WAW/0nOQItt1mq1VaxZxjKyX/C4hekWLZxNTlBj1xYS8U8KIK3SIgGOMmG1kxpApGBlNXVuePnvG8fELNJ7LqwvOryum85KqrgUmxfF7hdctDO6sj2/NZfrrNqQZepWy6l4OMYNSkSW4lL6XMorr+lt1L9N7m7YzFBTAJpngwaHRYX+EZGrNyJfnmZ6h1G+tTwy3RGB3jtZaYTKM4ezFS/7w9/6A7373Ozz57DGfPXrE6ckZF+enXFw9ZTq7RBz2xBwvYkRPV6i3jvnblJEbWs80Cln83mc4NnK6T+oPnZukFn0Gqt9un8GJtJvJxH6wrguybESMBCrvxCiUgjXruqIxyRIZsOQbi2dIiWilLstAr8SoYoLU53ZKlhmqxYz59JrjZ085f/GCf+fv/l3efONNPvv8M8gy3v/Jj/nsxRmvv/1tKr0NWU6tM3a3J1in2Lt/n/HhIdX1eYPLI6zoCkDo/N43JQc6ZqZDdygVeKTme8s4zJNpESRdnl+u3M+0vBKjEZmL9J9wt7qzACCIJQ48JvqLDEIDwL2YT3kPtq5RCjI0RVlgTB5FtGg0VV1zdn7G+N6oM650sa11eCthMhWKLM+DqsyH0GByCGKfLjiDmyxrVGwtYI0ERWy76xOilMI7iy0LsJaRUgROBuMRKlEr7DiDyrHtoJjO+aO//w8xKH7tr/81vNGUtsYqg1IO1ZjXpMCrmSmqgx9WS2GjlCSCGhW1RSsA71AZYipWAdZ140g/e+8QB0qFMRkxj4fRQrDqoM3xNrg3C8WcttjBQ5GAjiUdl+uZnaXnxDXSjB5jgJekf15S+2VaMTaayShjazIiHwnCzzNhMlRDeIoDWsqw+HDWXJDyxnoxGzaBwfReiUYjUWU657BeMm971yYFbJ77cJ7DeYlMetSAxCXxRFtymVNwoArr0YbrlbouMBiRsUic2SMjEDVO4V2lJTxy4yOjdZItHoxRDfOitWmighFykSglNsgmU825iJJDbTRjLSGHR5lmbCA3Gcen5x3kNnTO+uczzR/SRf7dc7Pq7EI3c+8QwlxFhPWR+CbEWp+oS5FCyjC18Lf7bNUcmjZV6gW1PKY+EbKqpDDR2+DB5KXtyllsXXFweIDznmKxoFgUEp0wMMyaEBBEdQnaOGeVIkvvsc424c+ttR3d7zrt0FBZBfvWwbtY+iYGWdai0Y5kV7chpeN7EWFrnZEG/8iyrJlbpmVNq7JqBGhlUTC3TpxYncVoieygEzhUeS+JMPHEKEchz1hnfJ35+RCmvFnmLiEcf1vH1K8rHYZ/4L3OOienchVjvglTnEpzh57H0jHDTfY0+nIGyg6jTcOggyS3JVhA9NuLNFAqDCDOLsHrfUbFB4FRVVVMJhPyPOfy4pLf/6e/z9e/+nWeff6E50+fcH5+wuXFGefnJ8wWlxI5kkh+x/ULBq2vsFevwkT26/YtWFKCNd3/vpnhUFs3j1kYgU3GG9d/SEgOlZg+6daft70DDudq6lqCGWVZDkqSydpmbnEMEff7kOxX41SNUQ5chrVgbcV4lHF2fsanjx7xtffe46NPPuaNh69xMSt4+uRT1GSf8d4RF4sx5jpnlGXcu33E0es7/PxfHHL+eff813XdnDETrHLiGq9j2NbBydhen8lIn4EwWdZJEKC9LzuPRtqpc65JymeyjNq14WW16KAa+9aY6C9qM+IFc95T2ZpMZeEwWIzJgkmRarQY1jlqLwjt8OiIsqzkTASAHccVmQllNCrYCde2DqFAe8SHbRfdK4LmpZ1bWVR4H8PJLSMbFQGOtZLF1ToOdnYpigJvPb5W5ECBB6PIlCEvakZOMZsu+P1/8F+hgO/8zl+ndE5ioyuJzhNDoHqWw/J5v1pK1C3iT9C+65r3U7TTv8s9QRdKxX58Ut8Tc4n0CX18f1wQL6RWaQc+tCOmdxLiLdrAhr4iU+HpEEUdQqrxWOjN3gswipCjj1wlg/EAI4TDBRvXLBMfjMnYMMkzJnmGChJGFc4rPjIZ4JxuNCQdZpqQIZ5W5RyZCQltqxvmoa7rRhNRO0ftWkYmajqi+ZQjrltkOtySlqTL9ACuXa+u0RlIKLRWGyF/A+PgW4TRmEMGpsIEX4ssz4WhiMyjUZgs9cPQrRRGexymMZ1yPmo3AGXQJkMH39fMwM44Iz/YweRjdJZzfHzS2uBmGVkuQgkXz2My/760cvmcdAmUzpL07nwfgA8xOv3Sl2KuKpsKAdI2+gzJqjrrxnXT+/3f+/OJa5ZnOSOdgc4Yaygqw+z6nL39fbTWFGVJUQqj4Rr1PQ3TE+F95646SwyprTwo5zvZwVMfkXXE7Lr1GJLspoxcf79bR97UJFB1JInRNryqSrI8RkprJYp1XRMTfVprsdayWCwaokj7NqhGtB3XSktiMi032HiPxhCSNAn8NDXeeFQgNH0D54ggV9aAaAokggA9cERuEiptWtYx5Tcxxv2yKXGZtrXqnXQP+/b9AkJ8bBBQAb44nHUNkTfkY7W7u4tSitls1n2u2siJ6T0SwWybU2Y8HjMajVgsFvzu7/4ud+7c5eXzlzx9+ojrq1OuLk+5OD9msZgKblQaHwSmneiTK4SSm67jFyl9e/+he3dT3ykzshoOrX5/6Dy1hHNN9AlUKgiadWAIg/AxEBx4Qr4IL1Gq2vueEZkdoZEijo0EeqBfnAUftM3W4qymrmqePX/Ot7/5LUyWUZQF3/nON7j4s78gyxxFOcUvRoyznOk042LiqeZXHL12h6v3DdW8m3OoPb8W09Oar4JhKRO4SqvRxwuR7mu0GgGWmCg83KBszGjUtdiMZ0FjUVdC/KMDaaw0Xmkqa8GD9WLCYlDUHpTJxO+iQzQbXLAoUcrgHVSlSKrELj/RksT3lBBn2muR3niRgEoK+Uqc070QSSLphaq2GJ1htGmIOu8cxmRYJ1yq4DNPXZdcXV6glWZra4uiKlDokCgKtnd2iNLroqooywWZ9+yNckxVUjuPNYB3jFAY58i8qMQX1jJG4a5m/N4/+IdYo/jmX/8tSuXwWJHoeiVIlSiKClJhguNtuAsdR2fvGwc1OSTSf4wsEyVnSiUAFFB0yfSUDWi6DxJ+731bIYT9bYU+PmkgBXYquaBhFI1QVaI/Ra1WBOQxy6vQIFHS05oPdYqSOTS9JmdLfvPNl5SIQHVNjjrcupbcF+PRiMlkxCjPyHONMoRoFlB7FSI5BCbD+6Y9OVuJ9gFwIfRijEJjbdC+BUAWieb4jrVWJMIhMo13kv3UBYbeu5SJcOFuyv2sLc2apY7k4PG+9Q9ZWspmX7oSSKPEzMmEqHNExiHLhXlQAshNUaKNlqSHRmO0CuF/BbALo+Ew2lAbj1FViB4WkiQ1Gg2L8TFeOBijUV7ijN82GaNM4asZJ+dXeESooGuFzpG46Y0QIABl7wPRRSO59V6kuMq04l7nLK2Wp40S065PT4rmfdAQhdMXP4Ym+8TUTQg2Jfz7BH1ap+1+aA+X/RQG6/V+X9VW2uaqupHIzk1IwgrUtqZ2Nc4rDvZvk6kcqppytqBcFEKoqRAIxImWs79GWkvwjmZOTuCECZGglGo1bHFc6ZjT0iVekjOuWjiDogkZnUoFu1qIZZ/DjrDLi0S6rmuKQpgqjwshaHXDOMh7shMRRjnfniHVgdFyHq0TzjsmxXRecu0oJaZWXoXjqFpBXgwhbpRBqbA+QQbTrGsgogWWqiDAcw1Mcsl+d4h435MbLRXf9jX01EdTToHrrValvUjpe7rXd2d/OzgndiBtmzDnJYFYM1/V1I2iKR9pGgKDGxqOAQm0B+NjpDXf9h9gy3w+75gPpYMzIceLQjXh8p0H6zxGZ2yNxriq5l/90R/hi4KFnvHZ40+ZXp8wnZ5xdXXGfHEl6+bbeSZ8ZJji8jr1178Z1RdkPPpMeYpb+g7vN/WV3qebx+jwvZxe8liRaq+j4EzwXvStCNqNURivE0d9EyJZJdy40LEC0cjzDLHcsaHdqLGKY4s7IOOyWHAlxhkMEmCotp7zi2tUptm/vcf19RW7uzv8d/+9f48PHp+g8bjaMi8q5mPPydmcF1cv0DpnUZVobwM+8y0OC8xNHXN7+ZbJUwHGmIaO8o27gPcEU/2WoW4Ex05OqPPRf1hhslzgo1J440Sr6qGYzgb3s19eIY+GZE2OA1YKuaROAJwKqlrvJfpSlucUZYkrxAY3z3PQOvhlCKGWmywQX+0BjQggDd9pgwZFKUVtCVKhVuJtncW5CqU90BJW8a/3khhNayOMhQ2OtjIZCZmaZXjvKBYLFvMpRmsyA1dX4lW/t3eA97Czs4uzFqWVaEzqmkwpVF1jQo4F8FjvMF5jrCcPc2KUYauKbW2YLhb87j/4f7B7dMAb3/wGzohmxXiJchEZjXh0o91uOBNNVm6IgLZFpDQzj0irNa9Ir6enDVnWudTQ5OaLYKzbriN1sO3AgKSd1j45Ap9EsxTH7hzKSyjGFlD55PIuj28Vsdwty4Arfk+BYh9YZipjlOWM8hFZlqONAiMaJ+883nqs7RIvkhagdeJrtBnOCbPgxUcjMhfOyZmOPhe2tuLkHrQW1llxBk8RfmBAamtFaxa1G06i4xAIfudV4ljeyGiaJWnwdH/5fLrmSXg8X2GQWNwmk4hqBHWyMZpcK/I8a5lJHTUa4neTBbtzqS85TkzQZGTGkGlDZhxZkI5EoZBSra113JuRVhxsjVAP7mPxnJ1dyzrjUcZjMmEYsiwLced1I32MZ68vyY8SzToSgaHvJtJ0T/qjtdxNndykhmCBVqvSO2/rtARD57Tve9BnPFYR1aukiJ33I4IceGfo3VXIPz3nMadG5Sy1s5JPyFpu377HZLSFLecSYWW+oK7qFunRvctdqaiYv45GI7SHuqzYmkwaAUae5x0GPWUO0tJoEUDOX2aanDuROUhDqfclgKkAIN65oZLCpf77MVlmK+wYoMDD96iNiN/aZ14sNSAhqGxzWxtGAjmTJjCB4pi/mlnsEIhJMJeo8U/rpedBR9MvNYA/4tg9aGOW2yCey6xh4tYxv9EsyCfrJD20vmfd+xHf6gyoGWDDxnjfJJlv6hKcXcMWqWRPjdISAESLZlvpVtQVQzT3tWTNvMPAVKB/IOTzqlwQZo7QSvGTn/wFn3zwIa/dv8fjR59weXVGsbjk8vqc+ewKHyw82nkGxqI/z94YVpV1uPQmjdbQXIfaHWIkht4ZErAM99//3jUtl7akXkuzBkuXgBOa8NWeJtdGHx7J+y4IvFXyW7+v1BoDUMKkiOBYUVU1WmmupnOup1fcu3uHFy+e8+z5C/7d3/rbHJ/9GS7LWAQh2WxRkukRjz78lDczQ+kcufcimgjknle+EYg5hAmAGIGTRrjrrO/MSwVhRcqoNtYkyQUTPBiCwFiHzkdYPHWwjFDA8bMXS3s1VDY3nQrAsblIQVposixIVB0mC7ku6rAxOgtZHKEsK6qqCipmqKo62H4bqqpugL4NRLwybd4OqW+bBXLOdrKBN3aBPiWehbu1Tgg58dgvsFYIkQhMy2LB/s5E3g+LvVgsGOW5qPyLAmNCNloj5iFNLqTayQYgPiY6cNAa0WiLNYrCehgFwYk1ipkrmLgMpnP+6d/7L/nv/6f/Ew7ferPlNmklLtGHL/4bEg81Mez7vyemBTeVFLl2EdlwXbiZ4N8EiMR1T10q0np9wqnvoLiuDCH+PpMRf1NKkWcZ+ShjPB6R55IEUOFxtccryeDZZYgAH6WHXR+LSGBY50Q7YSWZkHPCJNhangliD9qISBR7R+1ryeFhXfM8Rq7SaPBxHZQky/TBjwKP6THuMXKV8XnDbPQBtU0lreGuK4LUlBKPSGRk7nL9lYYaR1WZjnmUCSZmVcJomKzG6MhoKDIj5jY2y0LuGiPMgfLYWgj3PMuazOLaiBTJKM32ZMLbb7zBfP4x80VF5WpGVuFKx9HRYcdGugpEberUBoSkaF1TtpTpbIjBgTOldNfHIS09/rhzr9Yh/P6Z7p/PmxB0v51mrFFyvQKBr3sf2qyxq/ptJZhAwmJ5BJEfHOwzHo+5ml1TFItG4u+cQ5lgNuXcEqEpbYvQylrLyORypirRhBVFKdrCAfjWhxnpOjpvoeqOP2oJ5dx05zUEJ/owZdW6dgj4nlnJEsE8wMCtK6vgY7oGHUkzy35GQ/2lzKP3HmVWSKX9MpHZjClxgB8aY/8sDu390vl2vmFOunWFwBxiwttOl6bQGc/gO733Fe2aOueCNFm0co0/R8Ko9uc0dG8inKpr8cswWvHi+TP+8A//kAevvcaTzz/j6vKKxWLKdHrFfHZNQxQ6H4mEblnPU6yc/1BZxzisE56kZ2zdHdlUk3LTXVjHnPTva+q0Hn3MRKBXi+l+b9wg96auhyM+DcJmedCMwTuHD8KOsig4fn7Cm2+8w09+/D7GKa7Pz6kXV3z9O1/lw+M5uckoZ1ecXi04fvGM+3e38TrDIsxtvM+Sby6MVXWAiTAWWosGIuB8H+5stH7Bt/hcTMDSeQVPnyjw0lBWBSoXnOyctHtxerZ2b2LZmNEoywqTiUP3aDSiCsgiRxy/syyjruokOZ8gBet9oxqvqrrZtMzkQcroG3+PmDnYA2VViapSx40UO3+xR7fNhYfW9jW2rVQIH+jbiCExWk3c/H50hCj+dU7sZbVSTZz38XjC9vYOBAJO7CqdJHcJUh/ro4mXOOARTF7woJVDWUfmFWPtqLWlLEt2zYT5ySn/+O/95/z3/qf/Iya3b+O0Cs6SYqZmFOiAo/yqi6lUpB6bg58imqHSv0y9py3wHHhvCFm0Q1kGTpFTjpKhJSTu6TAaQxEq4ud44fu/D/XfJ976UsZIeEYJ/Gg8ZjzKyQOTGcclPtROQneG7mxsw0VGwzYmeZGQck40W7Wrqa1rGHBn5X3bMBlC6ERi2HmPo8b6eomQ0kZjvJgvQdYgwBYJWzxdojmORYc43H21ukg7xJMEpUL0r7igCJQhaEoi8MIL0MNS1x6lLNYatJYcB+Lwb7DGoY1FlTXGSNjizEio4Lr2GF1jlDAkeZ4HJiTYuvvoVE7IDi+atCzL2Rpp3nn7DX750SfU1jf7cXl5FSLDtKptrVVHMNE5eyvOrdKqc9+GTSHWl3XSvqGS3sl1WoZN/RHWIvkVfa/TYAz10dYTzXQKh5RSjMdj9g/2uTh9SVEUzOdzalsjmaWzBnTFfjuOpOGY1nWNr0Wgo7WYtFZVhUr8flIN0DLD0sKBoXlHprKfWbpDqPfg5SpGJP2t30Y6t3XjXF7b1bB9aK/S36Pwwqg2GeE62B3HJ8xQEDgM4BHv/OBZky+wirr/4jip28YmTDOrh7GyHTkLNFrfVobdDQfukSR2xFxgXnCmU7LHWZY1vkSr+s7znNlsRp4bRqOccrHg9373d9nd3ub89ITrq0vm82sWxZT5NDh+R2GTMviBpdqEKH+Vsml7N53dL9r+F60LXaEixKhvbbSmJummznBOLG2GmFRPy5iYRDuX9rM0Th+1Bq0PZe08ZVXy/PkLfuPXv4d3cH1xLaF6XMnr9/b58HiKrRY8+egjPn7/R/jFCd+591cZ7+4xv54KTPTtqfQejBbT0pQhRimxvMAFbWZkJLzE5iUxR4z6woQsUHgxVyUk4Ubhc8PR3dscHhzy4S9+iXWanC85M7jzYMsYU1xR10JY15VEnaqqNPqJEFtVXbcEODFTqjjUOOeDL0YEnqaJuiGbnzeaDq1141webeSiHVqq2m6WyNNIca2leS9ytBHYxcRP8rtICeq65tatW+zt7lJby5tvvtmYT8XDKbGUg/OQCs6+RmOdR3uPreo2mpatqZ2XDK1GobQn0w5bV7jaMdZbXD55zD/+z//P/If/6f8MPx6LGUZu8FoHqUW7/f0Sicx27ZcR4CalT4RH9ck6qcSrAZllRNut19U09IFEWvdVgFqKfFNzpz7ClqgvIpWPDKWtI4cn6tMySNXwXc2FmMsoMeGz7e/CTIi9upytoBVxra1o1LpJm75hNJQWv4gs+DzoxLY3U6qJNKNVmwDTOY+zFTFkc4yW4Z1DjpQnN3LP8lGIshb8OCaTUWMCVVU1dV1hraMqK+bzYNqFChG7TGB0hKkOZCEg/icKFRzZa6zzqFo1YTpr6zHaU+cmMBkyz9wYqjpoNvIMY8B6ydBqtCHLFUY7jAFtRQt2uLfH6/fv8tmTpyhl8F5RljXGxDNEYDS657V/VgZ/9zTmUJEhTZ/332/bEAf5TcqNY+iVPoG5CWMwSFj0ml8HJ9YRhcvjbjU6EeEZk3FwcMBnSlOVFUVRUAeBE4oQ818NrnGUVjc9+Nb2ez6fMdneauDBKs1tKsX0/Yl35hgQ7QrCfYiJ6NcdIvTTZ93fl89PnxFeVTbdr/QsW2c7a7GOCW7mCh2U02cmVpOsq1Z6mEneiPhVNEu2NH8/ML7wu2f1OFcxXT55yXv5j+iK233USuOVmP9FoSSqdfCOezoUcSk+K8sSpRSjPEd5x09+/GOePXnCwd4upyfHlIs5dbVgMbvG2gqFA+8kCMBqkmAt/PgyGJH+fRjqvw+bNoFvm5Y+TbIKFvf/+t79TgUAWvvG2qV/N+J7kX7pw6mUdmrm7cQyx3kx2Yq5g8qy5PzqgtHWCJPnfPTxJ0yvr7F1yfZkhDZgq5LHH/+c0+eP2MprTs9OscpQexWk2F14Yq3DxJxscf4B+Xkfc12oIEgPY44L0q5qc34FdtNkG1dZDnkG4zHf+q2/xv7uHo+fPue6OsG7De4ur5KwT2kWiznj8YiirEQ9qg1FsQj25y2jIcBMiCnrxaE1Iola2cZsYWu8FSI7BSKldpRVCUphMsPV1XUThUEyjINSpgMsuwhGtU6gpA5JuknsZJOxyvvBtriuUSE8aJSae+cwIeyttGUaCThe4TV4Y9i9dcDtgwMuj09ZLK6bd2vvhMFQHoK9XmZhSxtUDtO6oraiKnv6/o/5V//4H/Fv/wf/EVNb4XOD9aLlUfGgrNueGwiCTeo3dTvYffV7KcFzU3+ptGCZWfAdINBH5qsIssGxr/g8RBhEoBAze0bi2VqxMRezNbmwznuK8DfViID8VlvbmELFc1bXdeN7Ee8DXuFcywjHZHsCHMQZWYhvJ8kKEyKkOb91iavFBEVrJfkmsozbh4dkWnN0dMhoNGZnZ5vJZNLYbKokVrjJIrISzdk4D7lxUCHeeES4Ilgo65qryyuOT884PTvn7PyCRVlK9KvQhlYG51Qg+l2wwQ932wtR6WqL0610aZTnou2xjsw6jDJUlQ25A2JuAUdmPeQW7WBsPEYZtPa8ducWl+dnXF2XSAQW0S56fGPC1fptDZ/RQea1d847524dMd+ndTY4u0Nl1Z3qI9kUufXrxjKEIGOMlVVjXTWWlaX/auA4qrLk1tEtvHfMF3PquqKsygbhxdf6PinxbqkgOCIw0grx94uS+j78WRpWjzFMSeA+DFKsN3cZfm+4rHo3ZUi7R6qdx6bmrv3S17o1fXmIgStivVWMRt9xvvshnQeN+eDyeizby8cyxKjHMaxcV7++zXQO687wuqhyg30OPG7vWuJrE19xjtFo3NzL1IdoiPksy7LJj3J5fs4//2d/xGQy4uXL59iyoKpKFvMZxWKGMYgGxQfA7BX0BBrrhHBfRnkVZmEIxg61s2m/m8xriNlPhTPpvUhhpwRoaEN1d328Ws3EELxd1a+HJoKkDk5AXgudcHZ9SuELfuOvfJ+fv/8hf/DP/hmT3W1KW4VwuxXV4hrjCrZDBDKnMirnm/2XuSXMDiHktY/+tAF+Kh2EOVKi5U/7fmcBExoQlM4C45zx4J13effb30TdOkJt7fAbf+Nv8If/9J8ym0032sONGY3r6ZSyLCnC5UgXWJCYaSYivzvGo7EQ6l4c7kbjMTs7O8Lxe8BLjo2qqiQ/QUyhrhT5eNRkZU2jfnScMpMD5L2oMvPRSBiHoLbMc7HtHY1HjfmE1mKqQeA8tavZ3toG7ykWBcp7JpMt8nwEWrG1tY3WhtFoIjHTvUivvVJs7+/y27/5m5w+esR8PqOYFVTlQkxhNPhci3mMFzUUDnQl9p0+1yxcgbE1WV3xp3/we7z77d/g9W98lYV3OK+xxORWNJqNYfvwCMBX7eAaEQjLgECpGE2pJ5GIANinfQ5ImHrdyPhV58LGdlODhr70bx3A6v++iujoMxtpSMos5FBppQOxb4eyEBxncEClol9FmgsmOGTbutFmxPk51zp5C4PhidEvIo4yWR7GohtzNYVCuxID2NoyX8yDn5Fib2+P27cPOdjbYXdvl62tLYw2VHVFsSioy4pyUVBOp1yfnUrkm+A4XtUeZyXsc1wDHfY68xajRLMzGo3IsoydnR12d3cYbWt2dnc5eP0ub7/xAOcVs/mcs6trnpydcnJ6xsX5FYtFTQzp1wD1aLwcvnkfEh/ZOmhgRCtjtaUODuG5EwYjBoGIn70O5lrOM9EZShsypXj74UN+/sEjrGulTyJVAqejZKZ3HnuIZ4lQiS/0kFT8zay4R0p12Zp1SHUoPOZQ6SOy9G6sZt6Xbd/Tz7o3/qU+5BPR7jx8g95dTVpoPqnkq/OO27dvA1BVFWVVUZVVKy1LmNFYP3XUbbrwnqhxENOpujPHTZmN2OfQHIYIhnXtNfN9RcJpqL2UwOkzAel+r8sBkxJWnXEqiTy1CWPWf9ayg0NmJSt+X6PRSOcb+xtc5xvoynRu8kO6qb3RN1d6talZp80bxpDW7+Pira0tZrNZY5bTyT2WNBkDeBgjRqH//J//M2azKaVWVEWBtxV1VbKYTwHbEoYhMlpc+6H5LOHsXhliDKX+q5ztdYyf6twz39zjOGaSZ2lf6+iX1WVozENwUSmWfo9Mo7Xd+9PMWzX/6TAaqQnVEHMjtIFAtvhOPA/Xs0vOr085n17w45/9hK9VNW+9+w7zRSH9OkuegVaWrXGGNpp8a4uidpCYjnfOodao4LaQRpMymjainQIffU1YvncyvxjoyeCd4rWHD3nv29/m9sMHmL0drusS4zxXRcGsqrBusw3bmNH43je/00hf4wGPJhutLbM4h0sCkdax22jT2LnFhF82JNVrVJI0govhDQyPZCG6TEYKQPrIN/71SkJlamgIdxlnBjZnnG0BsL1t8U6Tj7fRVkIvTibCNKE0eT6WUfucSmeUzvIv/+KHvHHnNtXeNkVd4w52mVcV+WjEKDBP23nO9eUli6sr5tfXZFqT15qJhdJVkClYTPkX/+jv8x++9z/H+pzcGdkg43GJAMMHTjV+S0v/7gsib6t1kWy3rrQrn1SwMWziM8e1TPgN76HDJvglGN+MydO99KlUTe5BOsAg2fP0p7dMGOC7r4XfPC3R2S+Rec2ynDwfo3WOdxqUxioZi3eSRbRJpgfUvgraCd+YSVkrEaIqH+PKyhhsLYmUfPSaDgBNApCpEHENtM7RCiRcnmgrZrMp9WLByGQcHhzw9psPg3ZiTFkWzGZz5vM55xfPqaqSqpJAC7a22MWcsiiaEJu2roNNPJRFRVnVzT1Oma5cG3GCz3LGkwnj0Yh8lMu515CPcra2ttna2mJvb5+9vT129/f45lu7ZF/9CtPpjBcvjzm/uOLl8UsWZY0lI9M5aDGpkmMh2k6NQWOaPDm19mgDxjtqPJnPyLxDhyhSxlkMIfysqXEZGO3I8ozx9oTDgz1Ozi7C+VWgQnhUH4/FMhJJ4caSFBiC6VTKMMlBU0STz3Br0jPJkqBxdUnPZp846LXZfy9GbFfJb/16Ooy3GVf47OTgtTSaJ8lzExxNleo8R2zJEpZR9WzEBUabBoZINLzSOfZv3ZIgkVVBvZhRzae4qgQ7Dppx1Uwm0xL9z7kkAlicT/BfU0YxvbpGkkxqPK02JE1UmgytaX89T7CZj8ByfqMV7yX9idO77xI7nQH2BEhLtLti+STEdgQ+pwk4oT/XNupRv/gUhqv2cyALh99PCP0lxq2//APMxBJDE4iy9NeNSBjfm9Iw7zvY7yrcoCJyi/WDQCYlIhsBKC0+0UoLNWPrBjcZpXj99dd5/vQ51gFGUXuL02LGqpTj+MUxP/rBn+NtTWlrlLJU9YJFcYW1BUr5kLc2CSKQcvNDcxw4jr553hdwyFNBVV0mt9tQNGUUP74YPr0NsyrtRAYs1dB5hBj2LoZMbqiCdGSd8cTfb7qTNz1v9zn69EbBU+v/i/chIqpF66hJNzgHWmUtrIuaQdn4IJiMZ7xdM621OFIrgYNGGcnS5TzFrGZ6Oef+a3eZFVcU9YyqLvn88RN2R7eo9QKrNF4biqKmrCqsUUydFbPpZLUkOqJYF9XWIcFgNJOtLR4+fMh8tuDy9FyiXgUXhDwI/+fFAhs0OaJJiWshUU2/9t632NndZbqo2JtXUF1TlQWfnz/iJ3/8x9hZgbebaV83D28LTdznqHVQiFOrCdoBwVU6OKwI8FNhh7x1crSsx2uJEEWwY1fGiL8pHfjV2I/Hyw5Ie2E9JNu3aw62hMaNB6ILSJyO4QtpU7NEVZSFSB4oZVA6YzYvRPVZObTK5MAFHBYBe60U7GyRH+6i79zmzXffZjpd4Dzcfe01tra3OTo6ZHp1zc72Ds+ePUN7y8/+5E85/ewJ509fgIJyMcVnGnzNZx++z6cf/oL73/o1GZcCpyORn6Ii3/7XJ5dtGN+tAEkJqluq1CKcjnbBdwkOOiNadrbsjCBhCvu2utFmOy16Bdedfu7ssYu5PRQ+SSoY63YJSx38c4KZX2CauhqX4PfgHAIuhEhPw1yKj4bD6eD873xAVK5BQnFio1Eucam1JlMaZxwoR1UWTGfXlMWM3e0t3nxwl1sHtzAqY76YMb2+4uXLpywWc8qypFwUFPOC6+trri4vmU5nXF9fc319zWJ6STGfN+aJ0TEd6JgNNoxeRBw6YzTKyXPR/OUhrOhkMmEyFuZi/2Cfg4MDDg8P2dneYWd3m/FWzs7uNgeHhxzsi8/EO2++zouTU569PGc2m+N9QExefE+U92GthZF3yuNUyHhuRZskTvQGbTWZC6ZUTsIR+lz8MbIMnKpRTnHr6JCLqysJ+qBNg4w90aZ6WYUez/aQZqM5TwM3R0BX15+o1eBsXtKzqxr4GZns9plO4F+s25deNgxF/73kWfO71h3H1raaLFobgGOYGVtVYj4BhQITfNe859ad2+RZTm1rymJBWcxxITllB/D4YGYQ7oiObUmjzTiyLKOuqyCA6jOKoXIo7V0OY1xrU7zePKdTcwWT2oFXPWLQmGWTi3Xtd+r05tUpCW3f3aPlNm6cXsK9Rny+qtpKxk31mCaG12uJ+aB9bzUuGR7M0DiGVndQG9EsT0o8xDvZnjHo2uHHLYl3NQ8hUrWW5HnGGMbjMUWxaP0TlcLZaMoocOkPfu/3KedzskzjbIXCUpZzFosZXUHG+g1cYmCH6vqufKPRKjZruNrHQfkUzmky05r0puRvykzL+9KxVhof4D/Qkby3uDx+by0e1pVNBANtnVazsrwGwefQW6q6BJVjsphXKZpw+kZgmmop4kKnMCjmsRKNlfRZ11WIeAonL8947xvvYYyY7xdFwdnpOdv37gqtmeeSk806rq+nZCHMfhR+Aq2Td2hfm3BWNcwWM84uzjjcP6ScjLHWMpmMJJGuyXDOYmrdhNHXaJTRQaMstOazl8+xz57gnGP75+8HxstRzK5x5ZzJ3vZG6w+vwGhUbtkuzPvgJF47ISCUIsbgb9Qw3mEQ3wkdkgFpdCMx90oTQUyTZKghCmU54/lTKjIZvmFCYl9xcxuc5dvD2tQJyb9CjFJsCJdpy6pRcXrvGY/HXF5eYoyhXEgekCYiUGLDWpucgwcP+eq7b5IFpDcpLS9fHvP4w/e5ffs2v/32A5xx2O1tdkb32dvaYuEq3v3a1/h//V//Psbn+IVHeYvRUFQFP/qTP+Xf//avU3iHDZmYtOlLIbpEyqZlSNV6U71XaX9dSaVB6+xl+32vGmefMOzW6wLltG8I2i2dZpd37dnyqZ9P9KPwWFt2ohc1TAkSoUF89QIQCP1l2kDwFRDnbh3ycThm03Pm82tGec5bDx+yt7uLd46ry0sef/ops+sZZbng8vKCi8tzTo6POb844/r8gsVsxmw2C6aHJXVtsXWNtWWzDhEwtNGsWilxypELktFN2OeoGlbBEdtoQ56LhiPPxJ9lNB6xv3/A0dEt7t+/z+GtWxweHbK7L8zI3fv3uH//AecXVzx5+pTZvAihruUyqyRBV2ZMlEk3mtA47jgmHaRhRgf/Dx/9rYIZnM7Z2dnh+vo6JC6LIZMb4LHmZCYE/gb28RE598/U0Dlcd3fWOcYORTdJ6w4lwxqqt6pfPTCuRtuoxC8nZaJu6tPjm5gVjbQ3EFsHBweMJxOm87mYT5UVVcyu3GOi4vtRspwKO+LYd3Z2cC9aOBLHtSpM6ipzo35dZ1fDw6H3hzTn3b66WqZ+/Vcjkr54WXc+v2h/X2QuQ6Xz/mbL/0r9fZFxCXhctpbo4q/kcLadoZRia0uCFIxGI5xzXF5eNvybC4E/8iwnN5rPP33ML97/GUYrXF3hncW5mqJYSHZp/Mbw5IuW9I447zv3NxXOKL+Mi6M/broYMWyvlOXEfc1z1WcyEpzqWmag2/4rHJKkDMGFvlAppQdi7p3M5Cvbi0xH2uYQM62U6tCXVVlyPZ0x2dpiNB6DgrIoOTk5g70CrzT5aIzJM0bjEUW5YOdgn629bbJoyh3SKpjgM2x9BYFxlYS6BozjYnqOGnl2R9sYY9jSk2ZM++YAHwQ70VzaBAGkxUNItuu9ZzKZcPfeXXa2t9ne3WZ7Z4vd3V329nY3Wv+NGY1FWYYFbDl4RctQxGRdkcBvD5dq6vtgw65DvFYV4kC7uiYawdgmfJvqXPgoTfcI9+msbceRPO8fIAgSSOXQTgWNiJdIPIhUoS7LJsdHPHBlWTIajSjLkvF43HEwj2recTbm7t3XycbbZLlmvijw44xsewudZ3z+9Ann11dooyldTYlj5i357UN2Do/QO1s4Z9FGzBkkrrzjk5/9lOryCj/exmpDk4dQ+0RK/uplCMEsSUbjriUXpXuZdHPBhpBMSnitQkI3SbaGpKmrxr+qXz8oteiqvVNNjfdiMuKxCTPZRpeSbLnV4BjiPdBKgTEo7yWnCiokusskvKS11EXBxdk5zjnu3bvDd77xHsWi4PjlMcdPTphdT7m8uOTi4pRnzz7j/OyUy8sLrqdXLBbCWNTFHOU9dVUt7Y/1tskWquo4vyhlaRarkcS0BLOiCFFQvJd3mz3yqgkBLPktcpRWjLIJmZmQ5zmT7S0Oj464d/8+9x+8xhsP3+Dw1hG379zha++8jVeeTz55zMnZRZvdWYt5E0GKggrSdNcy9JF4UwJ4wh0V5iPLDN5LpDBtMiaTSYgQF7WTsjs+0VSlSHXV+UvPzNDndWXwfNzQT//Zq9zvFN6lkrahZ7CZT0Oa3DC+e9OYBPwOz30y2RImcDZjsVhQVSU2BtxomMG2fmduvd+9l3Do0+vrhpFJCaJ+G+vWfGis6Vxvgk+btrnq3VVr+irt39TWqrpDcH9o3pvs/VAZIsA2uWeblE33dx1DCMt8QvJmAxfj+3Ed0nDKUfgX69V1RVWZhsGIWmVrbaMyiEEwtFJQO/7f//xfUBUFo5GY6Ti8aK4Xi0DvfDHCel1ZumPp3aErKGhgplr2H2r9ZQ1RIyDrpknzMqgkuW+E59J2a8XQP5OZGeERgrrV7ootStreunITvG2fL/t0xP3TKqMvX1nVbup32gm80XMgt7Xj8uISZz0H+4cYnVGUFS9evMAcXZJlY5QKa6oVKtP8x//Jf0x5fR1M/0WzoVwU1HiUFhyaZRmTLcHJKNXQuY3gSrWacxH2iTVSHnxVZX9MCHQkhpM6CAWzXCwyrKubs1zbemkdhsrGjEZRVo3kKSUAtNYSDcGCtSV5nuE9IYuiD5qMoLFIkSA0akkbQx2qNiN4CgT6Wg4VtCBKxXBd7eGQi6EbqZ110r/XQBmAhdZNoj2lFK5qNRqpNLWua8qqZHt7uxlLc0A9jDFQWcb5iKPbh4Di8uISVdSYgzkfnpxx/vwl919/TfJoKI31Hj+ZkKuM7YMDrmYzySga8h9kCubHJ5x+/pTDr3wVqxUGWnM04nnZXEp1U0n3E+js01LdVE//CqXPNPSBXfpsSDLZf2fVfFsAsgw8UmlxRBY+SEsaJzvlcK7uAJz++0PIt8mS6z2ZyTABOGe55HSYXU85PTnBaM3XvvpV9nb3eP70OT//8Qecn59xeX7B8ctjzk5OOH55zMXlS2bzc/HBKEusq/E+BDMI+u+UIesiVZlXZJrboQbpfvNO93cVNAzxb5gOYi4vZxSgqkToUOUVI1NybR36MuPk9CWPP/uEyU+3uHPnLq/du8+bb73Faw8ecOfuPV5/7TXefPiQR48/5/j0lMlkQpZnknjNR1tXjVfdJHrxblZoJIa4Jfp8RWKTrJK8MyGBqA+IXSkV8vG02GKIIB06Y0Pf+2d4iCHfRNsQ34nv64HxDfWZ9jt0B7q+T8vnI36PEtZ+u3gQmqJ71m8iBiPySutrrQOR5djf3+fZyxcURUFRFJRl2ZzldBrdIBHLksFI7OkQ9jx99iowY1nYAZsCtkFhVkJAbfLuJvVuHvMXh/mbjGHTdtaVdcKtJUbYr7+b69pcNZ4hBifOXYSZA2upuu/2747QPYFA123kSuc8RVF0zGqb/lUQonrRchulePH0KR9/8AFGgbcW70UrLUyGwygx6eWGNV41/nWs1FARhqJ9Jwpeo+Au9btIz4/81vd/0wlD0DIQnf0dgH3N/UeI6SYDu5LAQTKlYZPWTee4qsT5xL2L9KBSWbMFnfd9F6+kpWNiF96J7da1pSgqZrM5WSb55OrKcn5+ydGiZGd3Alp84ITUdXzla+82edviudUIXShguwZCuHvvGnjWCEBJ1l+pQD9AFMpZa8lHo8aPxgtAl/6MDoaMTuhXW6OdI1cK1UvouqpszmjUVpgBF4kSRV2UMgkvTuB4j3ayGWWIld5wxFFdFm3vwj/CgfVKUYWEYn1E3XLO8lY0w8J3CZIsy3BBgmAAjCT/K8qKNK+IiZ49gQnJEyI+JunzXoCGojXziUAECMQLzMs5Otcc3hJfjNxotrKcejzB15azk1MevPEGla3JTEZpLVk+QnvNrTu3uX7+XAgsL1F1DArmC148esStr36NKiHsvf9iCOKmy/VFJFY39dUnzOPfIUna0JjS+puOLyVGUiuIIWJFGFRxghE+VnwDvK8aU6O2f7gJaMeneZYLItEaozTX0ytOT07ITMavffs7lGXBy2fP+fGzH3Ly8piTFy85Oz3h7PSE62vJ/losFtR1gXM11taA+DZoDcpbottkWKWGaFTht6i1I8yrXaB0pKr78xrAHfmO2I9H7l3pS5ySfBtoBXOFMprJZMLlxSlPHz/iZz/9C157/QFvv/0ub73zDnfu3uPBG2/y2uv3+ejjTzg/O+Xg8JDM6JB3xGFCuN7UTBFC7hEncCVzBmfEDC0fBbMdrRmNRtT1IjkTy3cmNbf5ssomZ3SoThxXlDitIpZXEZd9QvTLvMtD41jVd3Mwes+dc2AtR0eHQIg8VZaUVSmmCflo6Wo1+zXAJETGMgvCAlgO1zpEWPbHtY7JHIKxKwUvCbG1CVxOYeBf5l5tWvrrtkxAts/6v/WfrWrvL7Os29tVeyiCTNXSIAMlZXLTdqtK7Ox14wemJKCBa0OHRya6O5bWnzUzGbnS/Pmf/BnlfEGWBWbFOeqyoCoLCfbgbzbj7M89zDT+f3CdhvxnVJxH0la8a96H5IRJacL8A0oZVCSwImPU4BpPEy2zL8RBL21AIzxw7ftKtSZazkX89+Xdo5Qoj4xkhF1iRmUxJlu64z68vE7IkdIRTbteTKVm01lIBC00Zr0omC9KJtswnmyJY76SfFLHxy8YVx7tg/WLB+8kX9ZsNgOtyLXCKE3txO9zlI8AmsS/dQwa41xgGuHhw4dMJhN+//d/H4DtnR1sXWOU5PCyVnKBVVXdrMnB3g6v3b3N1dUVH3/8Cf/j7//6jWu8MaNRews+JhqTGNFeg8lzXFVTlmIbroKJhY0cndbYuu6ESo27qwMDAq1JkkMW0nfUUCYwFDWRAyvLsiOB7xOwKbEoWoqghvQeE5xxhYnwlHVFFRx1jDFMZ1OU0hRlifZwdnbWSPIjEDFao7SloKKgxmzn1NeSM8Mbz7ws0KOc44sznFFUVtasmldkOqNaFNy9e4/P1M8azt97L3b8Hp58+ohvK6idJfOqY/cYJY+p5GVTCdA6QLy6gU2eL0ve+mPo71Hq+LdqrGu77UnGOtFgvFoCYnHukTmFaD4V/IG8R7Jqu4YYbYFF/3s7ZwXogEAyY9CArSyff/4ZSsHXvvJVyqLkJ3/xFzx7+oQXz59z8vKY6fUFVxcnXF5dUFcLysUMfI1SXnwPyAGHMWFeIY+AV6qV6fhWKidCB9UBxCphNFKmo8s8+TD3gXMUEEZcH5RqGA+8D5oWDy7YdVqo6wKjM6p8zmI+Znp1xeNHj7j78/f5+nvv8ZWTU+6+/oC333oL6yw//8UvUEaztbODDjk2UkQWNZoxCzvEqCEh+pd3+MyHxIZdTadSApCdajVZr8TAeh8lIp2fVyHxTRjo9J30TA61t65dRddp/MstA3eY1OlzuV66tvG71hqdZdy7dx8FFMVCGI1S/J18CsgYmnsXHsQ7XgUtdJ/JuGkqS+sYvkah16pxDBOtw3PvSj0HhvMlE+CrCP0vUtJ59KNrhd42bicM7hXe6tbsb9W6qTXiE6UadKRUhI1xk9MGok9RC8NbPDTMvERGo6NJQywkCESwS/xG0/cFhDmMkXClZyen/OynPyEzGTF8rXOW+XwexhQ1IWrwJq4tkUmP006j5zUgP8EZ0IG16Z3q5lVpcSykvhjBaf4VYVGaEHX5XdW7Y5IvyloFyoqWvSHie2+uwPs3jke12sbWRL5G65wgR48tEhduCC70GfYULkSNxmJRMJ8v2NnZYTYrA5rRzGZT9g9vSYAkxK+4qi1/9Ae/z4sf/Zy9fEKxKLB1hbdezLHrWnK0ZRlFWSwdd+usJCJWSiIOEgU2mvv37vBbv/VbnH34iM8++6zBu9prtNWt03tgkrXWbG2P+WRLWIcXL17cuK7wKpnBbS1RA5zFWUsllAfTokQj5lNbkwnFouTo6IjxSHJQaKO5uLxgOp0mxFvwnvcO5WzXHlDrYMYSk21JgrOyqFFao1Wwm48ct5bDXtcWhxWZbrhkVVGE3Bq5XAXvqcoapzVmMhEti3N4bVjUNcbWOOWZLua4kGl4e5SxmM0YjSU/x8X0iqurK7T33DrYYZQZVO1QpSfXI6z3VN5RAftHtxiNtyRkY71gokdcFVfo3RHXtmL3/h1GuztwnFHbCmsVOaLVePH5Y3wxJRuPccpgFY06UcQVN0vY+r/FEhmVCCQaYtVHYKtIhSmdt33SR/xPvPDSWVI1OEzFSxt9B3z7vBlfGO46Z9w+o9IvXTOnrjOtAA1Q3mPrOvTcOnz75nL6DqBoMtB7jw/JExuC30uYUW1AZ1qijjjF6fExp8enfPWdr+C94yc//Amff/44aC5ecn52zGx6zXx+RVnMKcuiBarxbmgFSJAFD210y1TiGP+juusYbezFhGrFOSFhUKBBkCtWnhSwxv2z3gaFatfU0VqHsxV4z7xaYHRGPs+ZzS95+fIJH/z8F3z3O9/n+r2vcef+PX79O9/i2fELPn/6hP39I3KdUzsr7RqDQ+GVwijQAW6IeZQAvhrJyZHleTMSWTXbLFzc36HcEsNIqEVwKTu8xHMkSGSolW50J9X525wv+bHb7NJwhoilbvv9Nr4MUtYT7YDjt7gKfkmLofDi1Op8I9A0WoHJuPv6AzyeqphjyzlVOUfC06bhgD04ybAstsjtuWunKVpoW1cSShfxt2vWUMUgAMkadGiqLhPQgVbhPi8xTKgQgtd3wK+gQBfwmUP3moflfWzHMERAJu/1mIc+8fKXUYY0fzKDCBuGT1SHrwp5UEQiH09L8JNamnELt5Rv71u/TkM3dwQlrZCkY7Kfwka6EaNIrDGkvWT3VXoYAt4KAg6lJG+WQvC0WFOEtkJgGe3as5GOr9k3LEZBnhvA8v77P+H6+pKJkSRrOPG5q+pCUDJa/kkIw+7S+OVzFbUrbUk0tkm0qMgUBHQfdQYh54OSQD2RyA/0QN8EaBleOtJNUCqepfCs2ZruqH3P6qY9ATox35QRtnA7+ohKFFAXtOAtHB++H3043xe2pvNLf7fOol2B923QoqRS+16cW0KjRA2RDoLBwG3igdp5ZvN58IsQUzlchS6ucEpBNiZTFnTOwmb4ecnVi2csolCUlq5y4QzGCJjetUJDrU0bXZ/WXFopja3h80dT/uHTz8UXpqrwWosg04FyLaOhtcbWQWNXXXN22QZH2qRszGjko+1gbyuooQoag0xneDQ6VxS1kBzHZxfgvRDnWtREHjAmp45O2EYyE1vvQEniNNE+1MyLEtAhHXwAeDqnrCogJPHKJBqABXQm8forWyaSTEURkpwpB84Jo2TR1NZDWZPlKiTus5RVxWQyxtqay8tLnMqYbG1Ta4RL1MINlmWJDXkInJMkZ7asJWyvdUyvp1xdX1PaGqdEXWoTR3KtxKTG4ti7dchke5vReML1QtRfCkOWGS7OT5lfXaKyI1SWBYf7eCniQQ9/X4GiaC5Tejf6l9N3f+sDiPRwLWkpEqlA+sw5lyCTPiPkAjJZfjf2l0rY0r77Gpr4r0mAR8tkJNPrjC1FPKsATgQWAb9IH0qFs6hAi7T2kw8+5s7hLb759a/z0Qcf8vHHH3Fy8oLz81POz06YXl9QLGZU1YKyWBAjKHXXOKxDRMQkz1Ocs3Lf2/dWS3KW0f76klJvyXpDo3FMq0bfK+ccFRVVXVIUC3F0nJecvjzlgw/f57vf+x5vvfsO9x8+4Jtf/yYfffQxWT5isrNDWYtmUxkDKLQPiD12433IEG2anBFtdLioFRENTzyDkXGMYX5vlnQlxG7zH5Lvywir8/YAYbiEcHtt9bpp6iz9vmrsK+7ZRmWpYx8I+LTZPiW/3GdHCppl3Ll3D2My6rqkqiTrceuP0W1CJeNun/lOncl43BCoTY6DUGHJNCT91OEzfOdZv6+OQ2fwEwo1Qz80a9N2lMKOoSvaEnlfpKzbzyXTlB5c7D9bpzlribYOFc9GyMb7NgBMQnC1nbd9NTB3MGKYVNa6JXqT17t1k5fieejD/Yjz1NJLA1OLgF6lcLQr7Y/CuSDPxyiF6zEwsThrJWAOYhXxgx/8OcaIuW6cW1GINsMHAZH3Cp8S8Umzq+BNq0lKf28J5MgAKKWaCENpm43fSsTH6Q0ZOC9D+NpHKQPLBP7qEnRPHTjStpfO1yfBSQTe10uwJB3bUFkntOxqIsR0qLYVRmdEK4g45mTC3dkktEyDG8N36xxVVbEoCkYjCSdfqxq8x1ZzTGbwSuGdZVGU5EbcFHAW61prnVYL1frReDzW2xaGYdFKcrz4BDZ6V6OATBlc6Zos5spHsaFCeQnrr5SEXY6MdFl5Kic+28PiteWyMaNxejEFpQJijxcOFk4WyJhMCHAf0px7B/MCZVRyCFSr7g7AY7FYMJmIl3xVVRRlQbGoMEYyhStgPp+zu7uLtZb5YsEozzFZyIGQ2Ftbb4Ux8ZIwLWZ+ns6nmGDWEsdSuZp6usBby1h7bh8eYOua3Bi+9Y1vMCvFWWek4fmTz9jZmlDYmv3dHepSkujEi7pYtOYAEl7TYzLD1vY2h4eHQbqnqK34uUQJ+c72FtkoZzKZoC7AeyFm93Z3OC0WzK6vOLh9RxxwXJthVM52/0IOb3gfodyEfIZ+7xP3Q2WVzXvsbyhcZ4rQXfK531/qWNWX9PWJmlcpre9PCGrQ8wlYLkELB2SZITdZCC+nePbiGc+ePOXrX/0q08sr/vk/+wNePn/J6ckLTs9fcH5+xmI+pSzm4CWEoXdt4IJ1az70/cswveivZfrb0Dlb1e/QmqXSr8gQxH+2shTFnFlxxbMXz3jnK1/jO7/267z59jt89d2v8NmTJ1yen7N/eEQdibygCdV6+YzWdU2mFFbFDLptVLG+NDhGfYnj/rJ9NTYpmzIlr7rHfxln5FX6SBn1+E9rjfFweHBAPsqxVUFVhWSSAR722xoigtPvWmvyPO/s5Zdd+jBzlYZ4EwfwoeITLdtQnxu3kxByfxn7/UXLJtqXVcxOv4hQJ0qUpTQmgwPM3Lp+v4hWKBVyifBzGRdpLUEsotltnFfEK857RlmOUornT5/y7MlTxtpILrG6orZC+0TTXRGO6KhbWRp/n4BflswPMwX9s9LXvHzRsoqWeJWyam79OsKQyPfIcLRj2LzPVHjR764/doE12SCV1dLDy/B8Fe1knWOxWLC1NWlpHDQ2BDJpzdI8ZSXCbaXElyfOu8sQJYKdcObkIc3v6d9m4pHuUr2UA2FRxLpNGA5jBAdL+kVhHTY9MZv7aJCFRQj+EnU7KJEO1u3nIP6Sgy2X0xNjI3ugbjkhZZiVNcaG5xjMSBa5CtqJbLLFohaJwHh7m6qqqSqLMUKouTpoGKyEvFRKY52ntqJKQo1YFBU+jFHMs6qwUB5bLijKkjw7QGPJ8212UXDnNr6uuH10iHeO6XTK/v4e4/EI7yy5FgK6qiqKoiALIcJsXeOAytZ4JX4WXiGhwIIULssyJvmIbDQiyzO8dXitcYRoWK7m/PiYgzffiUHdJNxaEp4yXkyNWkpHHOusktz6KNoZkJIMlS/yLAUaKfBYupgqKNd9a8fY1zj0P6f10ou2ihDqvBumPUQk9W3lO+9rmlwOuTHkWUZdVfzi/V+gjeYrb7/Nh7/8BU8fP+b89ISTly85PXvJxdUJxWKOrasgCXWIyYXpMFJfhGDpr/fQb6uYhnR9+s83GcvQ2vbbGGIKZvaaspozqQuKuuB6OuXZ02d841vf4Rvf/AZvvv0mt/QhHz96xO1799s+kPue9hmBqnUWV3XtoyNjEceaSpgmkwmLxeJLQ7D9cJD9NVq3fje1ven4vuwztEqwsWlp19wxHo85ODjg9OULyrKQMLchmWT0QRoSinQlme2+RpgbiYyhsL2vurd9uJr2u7nJ3Xp42E5u8/fScax7vq69L3bGuwhiFaxIx9esYSJB79dJv/f3ddUcbAyBfcN8OmPo4ZKbGJtVc1p1nzvClETbEuFS+q5EHwTtPD/+8x+iQzCZiIfLcoG1Elmw7WA5ie0mZ0DGvfybjGvZpLh5f0B7MXT/+uuwClcP9bEOx6wLO57uaWayJWauwQO2WjoDm/af/p7SA5GO8s5JMliWlRh9PJeuWXo3xFRWYWsb4FcYt6+bflxIUOs9GCOhb7XS1LVkBk/XI/Y5lJcsXceI99JnWomhXEwySbAcUEo0b8ZHIahQoFkmz6136OBjt2nZmNE4P7+UhQ9qmlSXH1WL6aGUQYjNbkzOJIsTJy5/I/HcIZyb7629efwdJHJJNIOI0WkkVKJke/ZJeLKykBCjtbXUQeUUtS4qELjOixooywzaiaOpNiEbuBkxyTKUVtw+OmoiWmWjHKPaRCcAeR60MOGA1iGC1XyxaBzkJRxwq9UZb0+orSUzhsohDFJZsbM95vjZE952lspK7oKueWDvwgzcmZuAkkL2M71Q8dk6gn2oraG+h4BygzjSQ6pUM7c+09C/LP0++r+35whIbDv7Y9G9fmKdJspGcimj7aNynskoZ5RL4rrp1RV/8aMf88bDh1R1zZ/88R9zdvKSs+OXnB2/4PLinNn8mkU5xXkbMmI3KFjuAO0YbiqbEAs3EUBDDGefiOoj/5v6vYmw7u+982JOWJQLnJdEaS+f11xfXnB5fsz56Td4+913ee+rX+HDTz7l1t27eJQkBjXL9sLGSLzxSIBGlfqqMULXLOZXJfhX3ZVVZZM16re/qs3+778K09R/f904N31XKxXM6zS7O7u8fP4Uax1VyF3krGsiAqZ7elN/8Y72NVKyfpszZqu+94nfIRgyBJNWjXldvZvu/qr9X0c4v8q4boL1/X1ZxxDIZ4ia+1WMa3znpiAISggG+pqL+Hlo5frwYRUOGcInQ+MEiHkV0ra6cFPoFaU0podHY12TGWbXUz7+xS/JUBJBSIl51GIxD8FuhLmQiEwdV/bBNVoHe/r7FmmquHopzdXMneG1Gyrrzu0Q0zG0/5u2131v2YIitt2aUy37D6xuf/mc9u+99zFVw/C41jEtfTglQncxn9re3kcpFWjAjKquEaI+a0IoR/9JuQtt221Qm+U+03kM/c2yjExpRggzYbRprJS0kYhTukOLK0wmGp26rlmUpURh/bLD286n181n68Tuy2SSNdhFp9Uw6TzP0UrCadlgK220XBwfFsi7oIYMKdjFd0EIhswYFkWQNkLIsxEcQo0hNwqL+F3YygapmAmRpEKW8hCObDTKAYU1mqLsHgaRhnkyxNE7z3OMA+WlDRe0MCZobRUS+Wo6vQLvGeVZ41vinEjttNaMx2PquibPc+bzOVdXV9y+fZu6rsV5vZbxeq0YTSaNQ6gxYptXFgVkcPz8WXD4UUKMswKo3IBX0wO2rmxC7H4ZpY/EVz3/okAuvttw7gPhklNANGQ+swSAFUxGI0aZ7PnJ8Uve/9n7vPPW2zx/+oxHn37C+ckJpycvOD895uryjGoxl9ByQVrRONxH5/s4PbU5YfCrlD4C6WuEUqA5RPStK0OAug/w2qJxjuDQXcgZr0tsveD9n5acnJxwfHzMN779Lb7+9fd49Nnn7OzuNllKI0KpQ9K3KCWKCbSqqlpLgHnvJSTgl1T6QpYvUl7l/VXI+ss6L1/6uQNMlnEYQtxaK9K8qizXwq5VxAog5qaqK4Dq9virldT8YN169wnXOOYbmTQRfa9s599kedU7fiMjvaLtofeHYMVQi13DKRpUqFAMxbt4FcYu9d1aNQatJVP0eDzuwM7uKMWfZEjTro0IRT/57DMuTs8kl1fQxFZ1HQKCpJOLvhutMOomJr8Lv3Xn95SpSJmNpXY3PHpDTMIQHGzm39P4rtrvm+7Q0DjStnQIDtTHa78KTBMmw2K1JcvaaJVp2ZThb8crQrHd3R0JYe9FQG2DUD6a6BljxLnbJ0msWaZhUlgZ4WEUmnrV5ryLz7MsI9OGcdBaxL6iKZpWNPlLWiZOnuW5YTQ21FsZVVlttIYbMxpvv/FA8koEQjhK58U20SaHRzIL1lWFzbQ4SRnDKM/RxjQLFSWONmgaTLC7lYlklNUYfPs8htfaCmnbvXMsFkUwWQoiMadCVnEtCZ2UYjwZU1U1DkdVR9WQSB6yLAuZEyUihAmLiW21L0rROKoJZymOxiCc3WQyaZJQ7e/vk+V5AFyGnR0hjoqiwGhDaSW2satqlIHaWvb39zFGGLa6dtS1MDC2qjk9PsZWNSqbYJ0jy9QSArwRoSWlIz1KCd1euVmqmqiz+vUidGz4otV1G2C0os+h+n3EtLp0tRVp/Sjx6Lcd18c5GxL1tBdzPBozysWp6vHjxzz57HPeeP0hP/3JT3n29AnXF+dcXpxx8vI58+kVVTEDL458Siu0Mh2HeL96WW4smzIlq4BhCpAisErXdl2b6ySgaUkRy7DUJWh0vKeuS3E2o6a2jqqyXF9Puby+Yr4o+M73vsejx4/Z2T3A6Exgh2kBp7WWzLShhzuIjG7kmfT8rJqfvBdf6D7rvtMi7S7i/KKE4tAeJmdlZemdqd77X2QMfSY76WbNMJJ1Tqp7JLvs/fuvoZXsU1mWzOdz0WjkK0bSI0jS9c/zvAlxHpFwbwrNKHxvXJuUqIWRaflmbkMSZt9IHCE17YvP4zP5nc7vsa/OuHpnrLuvr3K2+kBmxbv9gxPlV8l8oIc/0oPZJ1y973S1dIaTtWngbqyw4rCrSGQ11VoVh9zxtt4q3BDbcHTvchQWpvW8a/fbhbplWUrGZej1IZ+d9xIUJp1HODsxUtXPfvpTvBVaJpp2F8U8nKHEnCrg53UMaMzY3Iy7d7qHhG1xXmnVNpTrssZhJQPo/UrgolTCR3uaMLYpnknH2J9fszdr+vAJbaGUDo71npgqIGo2hnB9v+9N+foYuEU1kcBU83cVTkxxTWoaJr87RqMxmcmoK3nfuuijIXiurirS84WL2dKTtQzLpIO/pzEm5N0yOGeprCSzjTQxwa7CO0flHMrJ90wcF4Llj0Mnc9KRychy8kyTaUU+HrE9mWy0dhszGvsjS6UR4mkyakFXOAyR6YhZfI0Zh3PSOpC3CVA0+SRilzyoJCOjoXGuQo8MSoHJxrLIIWO33PyC0daYKsuoxsEXobZsbW11DrIgoop8O8c7i9EZWXAwr61t7CmxNTu5R/tKDo82eBsPcRe4GmMYjUYyFwXj8ZhysaBclFRVzWiyRW0dY2vQZoxS19jaM87HVEXJ1mhMYSvGkzH19TV72ztkaHZH22S+pPBip2krx+LiHIoZajQGleG96RzoeHEz3R6gFinKJXC+JbME/vsAoFpgehPRvgSEmwsegHwKDENoywb3RHjbyGba0GsR2qXRqDq40NPHUA13772XKF29C91KpnyQRCxHyNKo4FycvBuYAO9tOALiiKdQ5OOM8STHuJpf/uIXXF/OOdi9xZ/88Z9zdXXOxdkLphfPOT09YTGfUVeVzDdA27hGKWPVANAvLmgZLOuAePzeB/h9R7abEMFN/ca6q5gW7+UMOA8+wgutoarRbo71ntpX2F9U1HVJXZd899d+jSdPnnOwf4QxkpQIrUFLIqeqrMizjN3tHQkAMZ1SFEVy1rrjimfE2hqlsqVxtsRf993WXCKdW4oPX4UQ7G9+t91mBEs4vs+4bcoJrOu7HUNLXAwwtOkZSM9JAmfCICXEqRLzEIzh9r27VNaivKIuKuyixlUWJu0ZXCbQl88VgMZQzApBkooAJ3w7/hiKur9XCTnWn12fUIvrrNuW5QyE2h0mpiHOW/OUft+tNJkOEaV8FNCEs6nbA9XeoVdjXiVMd9NzOKMprFZNvYFtThah/agjQI9EXhrSNFQWmNk9s0LEJicuCgNipBtoxAENTiaC/7AuykR2WurFcMOhve7cW66us6Nh3DFynQ8DX4JrnfckFZ2zjrooxSxKOSFsScyNY4st/4NEAHJkWpFpKIsZn3zyITpTeC22+NZXzIsp6CCZbnQ3w+e/W3RnnC3jBSpozSPzoDp5M5RklG56ipzgMmHfmV+63ipomZqIYvHe9TQout1DnZmw9/IegUh24Rw0jvPhbDTt9LawZTJaDY3WJgkFLL9lmQ75NmJerC4D0G11FdPU1o8+IFmWh3daPdsmgr5W6CZ3x9qa0SgX5hKHx4YoiSGfnFOUZS1z0Q4dzq4CCdWs5AQYrcgQRiMLAn0dkkqWdYXKFA8ePODF8+fYqhLNWxh3oSLc8xC1E15wc6SRoqWS0QZjDBOt2R2NmyBOm5SNGY3xCCajHKVV44AnnLD4NEQHFm3GKMTOy1mPQlPVFXVV47xDq3HDcaVSVBsYiSzTaD0iMy0RJJs6orYSqcfWFq1qRhOD3hk1UpEsywIH63DOS14DpfDeko8km2wjxTWm0Uwob8gziYUe0YgLUhnhxruc9qQxd/JUC0mQcnRwAN4zGuWUiwXTcsFiPuPq+oKd7S1q5VC5xo4UCxSjsWJ6OpcQqbVnT+egLc5IAkG8ppjNcLWE9I0XeUgqIAAuIoEuYvI9AkCrNskh3ATIhkvcs6E2hHNPtA4pYoWBsSPkfMKQpKAlRYtdGkd15tVve51WZojwbP7hm3wf3kmI5jzPwcPPfvI+11dTNBn/+o//mOurC64uT7k4e87s8pjZbNYSsX3o2A5yYEU324ebGMJVxP7gmg+01ZF8+fa8bRKZ6VWYkFVjlGTtjhpJ/um8w34gpgXeOf7KX/lrfPDBx9y6c0dCVUeiM4SFdiFgQzSrASSyl1nlcNoSi1/kHqyaz+bzv6nfFpmuK19s6JvMua/hauEHdOfaR9UNQRIIZ+cct2/fCUm3LN55yqJshFCDjEUPdqmmYUJOp5boVeFh4y9IjC+/PO/udRy+qCl8a85/QoAGGqkRqDRQN4TqHiy9yaQEacQyw3Ct+3eTkvAx4d2+aU0yph64Ghxvw2AkBGsHHqcCrRQPtf0PN9tlVjqwqmHiEuYt1Gs0pgPa0qTTDuHf626gerdf1T5Aa01Zlmxvb8lPial4Z95pX0FTEyXJL54/5+z0lJHRQlgGYjMNf9r5S3/s/TXt1kgd8I02HUFSWqcvrOzX6WtRUmYjJllO8UoU2vQtLRomYeDg+kBf9TXIKjIwiZapr6WOGiat+2da/BlSP8smD9a6c3JDaZgMZbHOkqksIUiGGbO+oK3XYEPzGmMYj0YUi3nwBRVBp9HCxDgndMh4awtvgvBdKXxdN1ZBOoTDtUpRaY8eG8x4hNOKuvT40vLpk6fiu1zLmYyMpqZnRh3G51yAn6HEqGp4T6YU11nO9vYWu7t7G63hxozGZNIl1OWfxiOEvNajsHDRhlphtaiHsizDjTVVWZHl4lBirUMbUXrK5ogjTBbMrTQhfnasq8UZxdqKcZ7J5Ve6YUQk2JVFmxjBpxstRCFZg7UKNp3eNdy11hH9iFmUtS5I89YfIo9nb2+Pzz99zM7WFtZbjPJkOGwxY351gS3mHN69TTmb4qqSSjuqagG25vizJ+jTC1gUGOvQrpeVs6qZXV2ze+s+NgUoS0Rjiz430U4MEZ7rSpd4H3bKTv+2qsFfLQrMqnE0bZEwIqrLuA6pMiMhHRM/DdXx4dIpYDwaicmfUvzkhz/m+uySxbzgk48+Yja74vrqjIvLEy7PjrFVsQT0hvroz2OT8kXbGGI0+kik3966+q8y9qF6rfQ3yFB658Vai1dh7WpPsfBcesWHH/xStJ4o3vvGt/n86VPuv/YA8NQhwVtMAupC2MAm94oxQRjSJWTbs+K+0J0YnBdffL36Zd35+TdZOkIEGCDcl+sNFeccBwcHjf8a0MmlMRQmViSx3XaiaWaWRpsiSjIZJF5SYcWqsgqmxc+DEkvAh7OsBt4b7GfNs3gGXcIM3SQg6MPEod+H+nnl4nu8RYIeVfJ87QQ3GMsQw9kSmsOE3NAaLTErv2JRSjGdTtnd2+38tu7uR2fd0UiEoR9++KHAuMik+GButeGiLa/VsG9h9FnrEPxr4H/6fIggV4Fuwndt/ft10jCzKS6On6M1S6zvA6G+Cvf0329NvNrxRxovyzLG4xGLYtGse1cgHqwVvkC5aX1WvZOWzprQMi9ai3m/O58GwYmTYEPBNFhp0d5n+Qid5WgXhCxKo42ETbbO4RQ4BSWeb3zrPd791jepjOL42Qt+8Ud/zGI+w9bBKshJnimcJ1OJ70YzNoIbgiTj9SFpsPWiodM4rm1FZgsmdbHRemyesM+A0k5kCpE49yJ9dk6hlNgXqihV9xaj48YoyeKaK5SWTTfGI6k02sOeG1DKhaywQgSIM7ZumGKdGSCEs/SWNnlL5KoF6bTcbuB0K9eodLVSkhTFR6YoMk8uME2COrzvcnV9SYDWEmrt+MVz/uLP/pTbt29xfX3F7HqKfXEO19fc3d9FvTjh9OUJzlpGmWF+PaUoC375o7/APjvFzubis4GoEI0xWO+oyorTlyfsvfkVlG5FM+khToHK0DhvQlRDv61iFMJTSPZsFUMx1Hd8tgQwpXKnzf5Y+uMDQtzyNoTpqhCUfWArzJJ8+t88+l9wWZ92x0grXUNBXYn0wO947Njivy+aPNdI1L4kYnCZt/3/zTb/0kuUhIXPSvFL9QN+r/yHjH4uGib7gRUmopG0Es7QshR73xzxv3r4v21bT85tFGbEskq63v38q81u3f3ol7UM25r2NmHq+5LCVfU3JdqGCAbvveQB8p5RULdXlYSgLIqCsiw70VM6Y+h1J1BZBEUx0VWUpCoV3w227qgWprwiPIz1VhHBS++qVgfb2YNem10iiY0JzC9S+nuaRhXsjjM1PevhDlTrU0Zc/1VFNfSASPu7OGLwjd54hs7hEOEZS8eHJpl3e15DW4P4o7v6nb6V6poIhudlWTIajVczngNzjYR5XVs+/vhjskyce1GidYsavaGyCo+vEmildy5K9ofmNxTooL+Gsb0o+IwBa9K+4jtat20Orc1Q2wJ7zcawNH1P6a5jeWQqbt26TVWXnJ2dNf7EUROV5xl17RvT/u4Yh/cy/k3rRlglKRugH4lgHdzt7nPLKEdz8KqucHWFVr7xO7bOU1SWynqoHVjJF+espSjL5mzXOFxm8JMR9x+8wcHduyyUZzzZYfbhM3785z8I50Lwo7MW4SesOJ7HgE0+TClTWKXRmUGPc1SeMZqMsd4zmRhuH0m0rHfeeWej/duY0TCKEEdYQwzT6kUjYJRIlTIdbdY8PsavTyUPQBb8A0R93vpJKGjMlLTSjc2vUsLl6eZgB06weU/szXwIgxtBfuP0EjY9zRQdk54oJbbh0RbXeYshvZw0zM4SwMNjEbu1el7wr37/D7l3cMDWeMQHP/kZXBVghTFTeJSXkI5ZDXnlcZmirktG1qOdpdAemylccER3OLy1nB2f8FUUzveJZcJcxPE8liFE19IJy4TFOsYjAvJVXHwfMXRUtANjTYFFJ8mOh/SyrwvZtjTeyID2/AzahDfdvuNL8eNlfcq5PRmcX6fEJd74xvz/yxcvwyRYTUXBPKbsaf9uUPpSvXgW+urhtH7/c0qcrWIu1xH3qwimobJOct2fxyZ9rmt786Li/2/sN80NExFplhkODw8pQ/6SlNGAXvQ33zIWsetm3N4zHo+5uLhoYHOLuEXTHd8TX6nViL8vjBiSlEfpYx+mNfvofcJspH19Ue2G6sDszpONiJjl34YI+cj4RKZsiYGlzbpOg4+jeWVittQbklYap4ZNc/tS6/5Y+2daxt2d/7rz27kbwTKCgbn3h91lsJb7iYzG9vZ2p/4q5j6eGRPMXabX1zx9+hSlxGLDI5E3XdBsvGoRBqr7vUOjsHpcQ3PrrwG0TNI6uCX71RLgKV4XZkIvfW4ZxGQuA/2nfbbnTiTr/TwaWZYxm884ONhnb2+Ply9fcn5+3rwXaY6hKE1DVyqOJWVMIlNT17XMcyjcWTLudbA3rllcG5mPl1xbToKbRNP+yjqu53PmZYldSERFay22rkWb4RxeaawGV1b89Ec/ZWE9pYKf//RnnLz/EUVVY70FFGglzIpW+JFBKc94LFGuiqLk3r27vPXVr3L74es8fPNNbt+/y2R7C2U0DtjeGpEb1VnDm8rGZFOzqUrho2e7i+nJWw4pHqRWpd1y7JEnToF6uoGpI2/TV8I4+LBBeN1kKWyIYe+E6UgklF3gKm0oRWAmgirOueBEBHVdNfb4EM2qAlBdumBggUzBVpZzfHbJp588Rtc1s9Nz8hJhyJSowRSeTEHmNbnPKCvHltFQ11hn5ZB4F+zRLdqIk/fzp0/RXhybUF1gET97v7lsLH13kxjmQ4hhSBK0ad/xUqXfhYpY/+7yOwhy161J1NA80vEtxbPuIBfNgTlqkKlS4gC4WCzQSoVQrMLoRueyZtBR3PeqpT/nTdt4lf6+6Nj+DZZkOztFRao2fgv7nGUZeTBHUNHpF5Y464v6FB/i0sdAFfK429EqpPBFy02E/6vemU2Zl03q/5sqXeJBcMJoNOLhw4d89MEHLBYLFoui0W7Aiqg08W8QRnhopLWz2Uy2ujf31LBD9Q6/6126VGo7NP74ORVcpPun1WrY1e87reYUg/fS+8Bh/YqXdogpatrv9Nftqs+ECPaT3yTMvAiGOsvl27+qabQ9633GoT/OoXX9Vc9x590Nrlt/fdK9iwR0miByqY/YVW99hdHQvHjxgtlsxiQkmwORLseoSJvMdFnK3v/enmeN7mj60zIUiSllBlrhbOvnEWm74TPVajW6Ar1uvqw+4ytWJ93Ih0OMfv9vxOMpPVHXtSQBrUru3LnDgwcPMMZwenqaWDrohtlYBYOH1iWuoVKqE6FMAhKole+uKo1wIsxFmBkR5NdVQV2VZMESx2SZMCVoTqsiJHUMmhzlhKE3AhM9YMuSP/vhj/jRz39O5RD8V5eMtnO0GbO9s8Ob77zFO1/5Cnfu3WX/1hFaa/b399Fac3F+zltvv814ewczmTSkmVIK6xxlWXB9dcliUXVyyN1UNmY0JPa/pEjXxog3vwsSLqVxIUU6DXgS52qtMlCRKBOJPSHXtdFZkHhJWz5uHqJ1aBzBVbClxqO0YWRk8auqIs9jQpFWxRc3M96J5rMKUZjC90YjE9prL0ULOaOvx5I0CAFGCjg4OOB8NEaNt3njrbv85PwHQLjMTrQZ3tngtANTKlDC2GTBL0N7K9kYtQENdUgQt5jOQvzk6CQYewZUV6XZ3a9Qt/PQJ3NrGboWeHS/R1+FLqBKo5n0JEi9i5aGLWyexO8u2Kb6dDxtnT4zk5rISLhYhXUR6fXsPIPMSAun2ACjPMuCuVMrcYrlwBzxv37z/4AZZexsbbGYzvm//Rf/F6gtpy+PmV1f42zJfH7FfH5BUcxwdY1CMnh6Fc7nGulMv6yS4Kys38wvqdsecqCr2ekA8LjCEWivGdcS0lWqOU+xz+bE9JDH0ryiNCiOJwDZOJf+3VJeomtok6G0QWlNluWYLMPoEZPJDodHR3z9W9/kb/ytv831bMZrrz+kdqKd8IAJzOf/8qP/Ied1q62KwgqRBnbHoGTxBtb/1Tm11URdoi7fkIHoRLnqXZX29VZwEx/LPsXx03kxTL81hVEJsyeDSwfSNT0C8KqFHivOcDs0JXAWyLKcu3fv8ov332c6nWLriqossHUNo3EbojbcYRlfu/5RWKRVRmYM1taBcGjzqbjE966zWJ2SnLfQn9xd3XkjBYu+cZZszbLi+/FsD1G0KTHWTC9tOx1VaEOlG7JijZf6geV7By3cDBseJfx4H5guH2BYC4vliof5eYgRoTKj094ajNT+1p6tOHffZPTu4h0fxtT4uKjkTKUtej/4e2NyHUeX9Bm1XwkJyNLe9Bms5RrNXBo/TyUJepfrqcF7rZRq8mU8+vRTWXNrw33yeGfxNkYhYk3pEvdDTEZcBx+iEXn8IAPdH3cccwd2pGZSzjVnPTVzj3+dFaJ/NB4xmUzY3d1le3ub8XjcRBFVSlFVFUVRYK3j6uqKi4sLFouC2tatr21YbxdCvKZCzpQJSR28429lKQFErFE8f/6chw8f8uD1BzjrOL84D3hQIpvGZHlRG9OW9fg4ZWzi+VqH5/s0Y/KAKPzSSmODhY33jqq2WFuhcNQe7h4e8fLkDKc1HO7w+v37jMdjHjx4ELKF15RlyfHxCWVRok3GZLLFeLLN7du3GW9P2L+zz97RAUdHR0y2tzF5hvVtJCkZi8Fozfj2Ptd1xWx+xdhVksgvDLuuJRjT3mQb5SUo0+xqs3xUmxuCKMleCDSZrb2TiCKZVnhfI4lMovRZPte2WjrQrVRApMMAo5EQgeCFOETjU8doL4igBUfRvto1TIZUbWOaxz4apqKBRwpjhAGSAyuHoa4dMpxU6t11IEovpbGKzDoO7t5hYjL29g/YvnuEHmfU8zIcII8iQ+tM5qQUaIf2SFgzoxFdkGaCADSrNcpVgKa4vMBjUdkoMC2gVUAKnpCbpJvOqHspWwCIb99DSfSCdt3i/Ah7GJ3UFLheluV0PVyUEfomgkG8jNF8LY4JEO2RjwBZsqOnBHG6ed5LmDcBcsk4PYEwiFoq3QC8aBtsooZDa+qqQiP+NLW1WGXRqqvRAcgzw9ZohLGe3/3H/w31rOLq7JRidg31nLq+piyvca4K6kpBpH0kMQR8hgjyzvP+BgyUZl1XIBAPDVGXdDbc1uCv3bF2kZr4K2lFQ2hJSZypk+g8/fmmNsEpgdpH0h4FSoJMaOSMWmfxtYdMM19M8eeeTz/+mJ2dHX7j+9/n7OULDu+9LoIE1ybwTGeuFXitG42nUy2t0Wg6kn9d4iS1bw8M3crV24wpWadF6f+uw1hS4qpbN4xV0dzFhhlZMbQUPrY75ZP5x5+6J0XGLb853/aTUJcofKM50MqjcaAlgue923exVY2zFdbOcfUCZWuUrds47xEmRWYo9BH9/UChlTglKm/D+sgEDTG3QN+kKq5luhwpMQ/e1c10tNK00krf/s+nfj1x3RPGpickSTrrfNT9vuN3H3YhhclJ3aX9YbheNFdr3lMp8RhgZJxC3wYxXgwfCPkYNnSJC0jPoU8c90O+IOcE5waY1OwHch8jQ9B0mk67t46d+9aBPSyHR4+MFQHJNuDKt9PwHpPi+d49aCiFMEZrXYisqah7YeE79E1YlbquUc6jPWgPzz/7nJFSwS9VfEytq7F12az3soAimIZr05z9yFTEyy7PdeezomuJ0NcUrROA4INPbFzhiE8U6CyYLjkLXpJmvnbnNe7du8fO9nbQNhtQQavSMCfSfnRGvvfgDgpFVTkuL6549vQZp2en7XoajfaezGjKssL7iFfC3Uf8I02AFZG2qcsSk+d4B0+fPOPOnTu8/voDiqJkvph36E9ro2/nau1GLKmgtaO1CecqTY7Yz0mVMkzNuwnst85iqwrxac5wZoIBqtqyyHd58+tf57PPPuTh197lb/87f5vDW4c45wLTZtne3kYpoZdjv1kQqCpEC2GdFSaBBG7LVmM9gS6qcR7JOeccRkM5vcZZS1mWZFkWghpoDrb3yfOczMPk6EuOOtWqeBJu1kuyjzrYyUYJk1xO13k3VcelmyYhvWQxRDrVvRQpkZLnOXVZQeBqoxO3jIdOVIPI+caxxr/xAlVVldgTRkZD0r+nnO6Q1FUeAE4Sq2zv7aJNhq/LoGXJqbUAaOWDuj7UF8RLiImMZEYHDCGygxLGyWiDx3B1foGtK7TaYil6fo/4SddNnrfItq3f5dAlypaEBE41Gd3slwMceXyyIvTpSmlKhMQr5jIsFR8gmHxLcMW6jRo6ufCuFz4TH8+qbaQoseRZTqY0P/rhj/jZT35CpjSL62u0slR1yXw+pSyLrgNfh4B4NbOYlAnYhDyNwGqISE17HWJqNiN/b+67/1tUffeR2iopX7/01yvV0kTGKt7Tuq5QITno2ekJH37wAbu7e7z19lvYqsTkI7wVfBRVyd22289DeRvUmv3orGn47+CcVLsX66SJbFCnuQsD4xkaV6e9pXPY1Yl2rlePaFz+1ukwIeuT+gnc7UqTkyg43nF06xYo2cu6LsVHwwapt/dEbcn6lZMw4iIt7Y6kP+ul9VnT6rA2q/usA3N9+KvWwKp2ICvHEdjr5EG749217DIarzQ3fIdBHXxpCcwLw9iXLqcjjyXF292mIqEZfhfioCF2VoXO7p/57lz90m99yXM7tmEiOwq6lsaswjHsEed1XTEejzp9LeGqMLd0/lppyqLk2dOnDd8DGu+rJqFcV9B3E/6QE6CUQsfw/Mmh68Pam9pL97XJPB2EXZ09D0yDtZZbt27x8OFDbt++zWg0wpgMYwxZllFVIoSrq4rC1iglNIZEhZowGo2Cc3zNYl6SZyOOjo6oqoqXL1/y+PFjFosF4yxrfCH6Z6u/9ulncdgfURQFV1dXaK158803efToEYtivmQ2JR/Xw+D0zERBn7UWo/Pm3WX4wODv8fxLmwprHZW1aJ2hTMZkaxfvPcViASi2tycYA/l4jAU+efQIlOLOnTts70oEtDowHqdnZ9Qh7O1isZA8Ut5z584dbt++TVVVjdZJMo9rnBeafLFYMJ/PmUwmzXwb/zmlKKuK7Z0dAC4uLxvGI6Xn15VX8tGI/6Ljj0itNTbYrMe4wOnGR2lhtG1LiYeUcIoqrZjRMdaDllGJUUZS9VW0ERsiavqAKD0EfS41zkXGGN/vHpwl4k6JidNoZ4tsMqKazXj99df5IMtY6GgKJlnKlY+A3kvSFS8SW5EuuYDAw1p6h9EKHULylouC8c6aywZd6RwB5qEa2DcoAffLTlUg0pi+r0tabgrx1mVYBsY7sEdD4S1vKlHalM6nP95UAxCZTwlC0EqC5CUY5TmX5+f8k3/0j/HWsagKvLdUdsF8MWVRLBpA+v+tsnQGB+b8b7LvNDzsECOSEimr2kn3vo8kI0wQqZVDaYWtK2bTKafHx3z4y19ydHjI5XTOV7/2HjrTFGWF1+vXY0h4sI4hWseEdMa8ttcvWHw07RlGZsP3Zpms7Lgrp3fHJ0zYK/HJy2s1JEWNBLlzlp2dHfJMkrTWdf1K96mP9MuyXIIjr0pkrZrPkNQ3xX/dya1uZ9P+vki56Rz8ZcKEV4HVKe3QZ+xXrfkqfDX0bN1YVq2JV8uS/aF6sRRFQZZlgchcllpDDy4owfUAl5eXXF9PA5yLhG4b3EYpDWpZsi70vV4SmMZ5pdmhl8ayiQAj6c+E1AWs8Nu01rK7s8u7777Lvfv3yPOcPM8py5Lp9ZS6FvpPchhFJ2qNUp6qKimKK+azOWUl0vG9vX3u3LrN7du3Abi6ugLgzp07vHz5kiePHwcTKhc0OskaK43WXcFiLDF09mg04urqitFoxN7eHrdv3+L45JiqqgbD7G5yhlJ6yTnXERCswyXp3/bMy/moarFcycdbaDNCGUlqWBVzJiNDFrSlB4eHfP29b1BURQMzdfCVrqqK8cSzf3DQiSgmpmumocPj2MuyxFpLlqmQfFD2P89zosbHGMPW1lZjYpY6+Wutm99TH5x15ZU1GpEoaD9L1IRUqtwBxIp2YxJg3QfYaeQRpdps4v1D0DqZt85KkQlRSpz2hFDWLQOR2FjGvrpRiVpJX1VJ5sco1UiZmg5gVEBIRDXZ2caMR0yLguMXL8GGEYbzFN/tSp2dZEZW4R8i2fLBKVw5kZTVVcXZySkP7tylThym+n4TPZFY59MqoDOk8YmHqr0McbyrpdOrLmkfsawqXxwhymXt9zFE1HYcga3HoCS7ZtOSMH7/9J/81xTTeXjmqOqCqpozm1934v7/KqU5S3RJlHWEzro1WiWVT/vqt7kpkRKEWyuQmTwfCjOZlm7unS4ATu/u0HgirBmNRthKEr2hNVVVMJ9d8/zZU37+/s/4zve+x8vnT7h95y5GB8fVjtS+O/YhIUQX1gShQO8s+bAgnZy8fUbcb5YMc9NzPygVW9OO+FapFiwEoscPSAaTx4MM1Kp12rR4L75SNrw3mUyYTCYsKlH911UlZiYDhOfQGGKbZSnakGa+CT5Zdd76bSyvw2oGYchRvSUUh9tctU9DZ7DTnzwcfDY0h6F9uelsrao7tNabjH0Vw7dqDYYch/v1hgQV8bchGL8JfFtqZ4U0u8HZYe+vrq7Y2dlZOgdpWFcfvhPeyYLP0NOnT4Ww06mAI4bObxmOVeudBkIZml8quF135letVaolbygi3woAAb7y7ld4+Oab7O3tYYxhOp1ycnxKVdUN41XXlrOz8xAJTuiz8XjEaJQzHk/YvbuP9zCfz7g4v+Tzx5+T5zn379/n9ddf5+joiLOzM/I85/X793j06adh7dI1V3hsg3fSe69UMBsKPhhZlnF2doa1lv2DffarfV6+fAl0LWtSnL7qvPefWyvmY9GneB1cTOk1OXNifuk9zBcF+WQLpcc4lzHZ3sUYzeX5KTvjHGzN3s4O2mSUdc18sQgBi0RLuCgkj4WzrtEqKaUaxjjuYRTq5HneJJxGiVleelaqqmro7/l83sytLMuGrs7znCzLJCjLl50ZPA6gv+AesYdPNytqJVAtQIlqsLjg8SDEhYhtxn7iZWnVi3LQcpMRM0/HolQbxzm2G99vQqKFNlLAEN8VqUF7YLMso64t/bC26bxBYb3DKtDjEWaUk49GfPzRR9RlCVpJtsbgq6CU2C42yEnTZsMOgnUXv7hA5ADeOq4uL6mrWpKXJCUl+OKYWnOpdm1WlfUMyDKjsQmx229/HRIbGsNNkoUOoe+X46qnXHYfkUXmUoV+o/Qjlo8//Iif/PDHZNrgvJdM9L5mNr/E+fpXYjIGAZHqOlVvSij027kp4laKNNchoOG1b00M0ufyeT3xEZn9obGlgHwVUI/14robLZyNszXKO6bX1ygUnz1+xP3791Am4+6d22TGcFNypqF1GELUQ8TcKuLkVfpa9/tAxTVmJMtjbHyVIpcYn6c8VPp+yD1EOscVYxuM/sbyXU/reNp91qr15amqiirJcNtvow870j4XiwWj0WgpD8HQuNN7O6R1G/q+6o7FOutg2aqzlZa17/vlYBhNHam4tp2b2l/3+/Id36zuJiWFExEHrzKd2qSsYiBvYhibd3332arzrJRisViwu7srNIHRnfeaMxPMTGIr0dn32bOn2LrG5K1UWASyYjblXOsHsTTHNXNKhalD4+60k5zrPhORwrY0FGwU8Hzzm9/k3v37ZGPREpyfn1OWJVdXV1xfXzOfFyHITxAghwigzlmyzDRR4ra3tzk8POTOnTvcunWHnZ1tnj19yk9+8hM++OAD3nrrLb7+9a8Lw3F8zNtvv83R0S1+/vNfUBRlCAAhiZ776xBNfGJAiWhxUxRFAyuOjo6YTqfM5/Ml4dY6HJQ+76/h0L1etwdKSd42Vws98fLlCdu7eyg9oawVt27fARSXZydkyvH+T36ErSsmW9vMFgXzouJ6tqAsy0ZoI/kvqo51j1LigA+ttirSPN57MWELzuSRUY1RpCKdFOFrFYRB5+fnXFxccO/evabupjDgFaJO9R25lxdx4KVG5ZVOILaTSgw6eRVoica+6Ut/TOnfyGj01Tx9zUlfAtsk6HMtIBJA4Dt9d4CwguiEjvHs3zpk9slj6qoWZ6qgefHe4VXWIHEHVIiTWAQizstvNYoQSKlBJkopzk5Om/H2AaB8bhmOdZEmbjoUXQKr+3va9yaHq08YrLp86bhuksZAF+G7sFj999M2IqHaN5XD+zYOfCj/9T/5J2gvzJ2tLR7HdHpFbUuqurxxbH+ZZRUBsIowXvUu3ExwpAx6f7+77/oGoA/1FVW7N61Z2kd/LvF7WRSMszzAExv2taIsC85OTvjwl+/z5ttv8+nHH/POV7+G85vZjm5a0rMlZherJtOdz5dyXnzXVXXdGIHG9yg67qvAbDReKz4CGZoxqsjMeKhvgLM3nbEh5OuCY3BMDOW9ZLS1thYfvZ7Z7VBJz0Vd10uIbgg+pWd5aKyblP6YUvwhwSCW7+amcHKoRMbsld7Z8I5v+nxVnSEBwauUFCdsgo++6BoOleU9Wc00pfjKGMPV1RV37txJebylO64Ck+GD1iPi4vPziy5ziO9afmwsb+jh/YH3IvMxBE/7c0uFCk3bYb7OOfb39/nud7/L4eEhlXU8e/aCs7Mzzs7OmE6nDSE7Hm8xHo3Q2jT0VmzTubq5/4t5wefXT/j8s6fs7GxzeLhHlmXM53POz8+5urri5cuXvPfee7zx4HUuQh6M73//+7z//s+5OL8UGnLJWzVZm0SIIYn68sBo5IzGOXfu3OH58+fNGPvM701nuoMHkrVL3x1iNlomQ1IrjEY54Dk9O+Otr7zH6dmMrILd/QOss0yvr9gxJddlyc7WNrdv3SLPR5hcSPa+64CmDZUcz0EsZVk2JmN5njc+JrW1ONfut1KqaSNqQbz35HmOUop79+5x//79pu00L8lNZXNGw/k2g7brHt7OggcEIosrYnsJDQh1LVm3JRyuI4YlTDcjlpSASRfNOtuG6IOGWPS0mxkdgtKxReYjcrIpEBPVnIy3KAu2trYboj0ewBiWk4C0I1jyJti37WwzPtznYHTEk6spfj4TxYTR1CHpH4SU7ipE5UDh8NQBuVfEiBYOpyXqVlnX3Lp1hFFSRxFCPKbqzhD5KIbB7RIRsAqgpg776fq3rEsfyMuYVwP/PrDu9p0yRI3NpUqf+V5dkR778FU++zgMtFK4oBmS7QmROXS7Bu3ZTJKIEbQVyZyrquLzzz5jQhYuW82iuKYo5wFYdqVVS5SmSiTH8WzGR02V5Qgg6edVBPvQ9+XSMp1DRG7/t2EGJSIyGnMWlCLP8g7iJKj9I8E3ZPoErRnleDxeOQdZEzrjTp/FPavqGqM0GtXcRe08ZbmgKDNevHjB0a3b/OAHf84bb72NzkYr1qk/hpsJsiUmzvfI/rB0IjgY6Ce9j533fHvZAlPQH2tzD1fs/9K6ex8isEXtC+2dSQayJM1TLfKiOUc0ek0fvsh7iqV19PGu9ccXiBdtwEA+ytna2eby+gpvPVVZhch1AoM7jtXNkH2Az4GQ81E45JukVn2iIfYdo0UlI6KBNf3lVum8+mexDTMs99Q351Yplu7VKgJvleClQxj2xjSw2k37faKyXyfte+jz0Hv9McfSN+FZJ9xIxzjU3qp3b2oz1AodNC+lX7p3RUXckI5HNbhiaJ7p+GMpioKtra2wP8n58skQUtyoQBuJqnh6ekyeGdKztWRi3sxnqdHuzFN45DxOucHztgrXKKWCBDwJ6tA7i7W1HB4e8t3vfpeDg0Om11OePHvGyekpZ2fnaCXRpbb2djBmhMkmGJOTZZqqKvns8SNqW3Kwv8+9+69JMrmqwtqaqixYLGbMZlOuLs/Ex6Csmihp0+mUH/zgB5ydnvDNb3yD0XjMs2cv+Oa3vsVHH33EyxfHkFptNHAz0FM9Rr+2NapSFMGX5OjWEQcHB41QWqq31go3CQiadYy0SLKn7bstzdHuR8w1osizjHw0RinNa6+9zle++nVO/+ynHNy5xXg8oZpfU8yvMabkjft32JqM2NvfpiYETLI2aHdsMOGSoEPWxgiuIxaLBVdXVxTBj20ScLC1tskOLjBffotMo9Y6+NkI7s3zvBHqbG1tdaxFhvKxrCqbh7cNCCwS7FqpEGpVS5QX60C3BL3zEl0p0xmVrYK/s8fWjtHINEA6dfjuJ0VKL0/jKO4cLhDUkfOKSNIGNVB0VBmPxx1zrbSvrircEh3Ara1wrg6IWlHZwD8HosuHC+qDD0XpHCOr0bf2Ofz2V7i/t891uWD0YsKzp0+ZzwvKWuz5BERJmGDrwSoovafWitp7jPJkeHIzwqmMQmvsZMzDtx+glfgVGCXcq6ZlOpQ2yQXoIiWVEBj9ZxGlxTkRLolv5pvUVHFfXK+VljiNbaXfBRhH5Bt/U017QDBb84n5WttGJL5cNCXz7f65oDGKw+ggeyJhlA5Tfq+cp3Y149GomWJRLMi1xztw1FjmzItzPAXWRfOMxNSJbkl/V+1iNIvQnGu6GUE3kQouMQ7K04R1xjRrG5PXAWByVDbuIqseUHDOoep5S0gmRQCKaPmKomgY7yh1jnOIvlqp5DiOsx/UoX3WJz4I928YscZSOUue5SEXjhAK3lYsFjMuLjKePn3Ooqz54Jcf8vVvfrvXTjjbS4SN7uxFH+n2x9B+TphCwslQbcSkSDBqpVqfDeiE4vSJ/5gPdQcWoLM/UZjTPG4YAxqTQPDgguYlYSB0jLITCPB4mpuQ08HxMMjrSSPRNYR+kxehHV/TeeRVAxxpkqw6h8JjnUUZw87ePur5SzQSerq2pbSrY59p+2k3QjHKWQSFQ8Vw5rTChPWlBxcSWJPuaRILPa5G9xkCw5xz9E04h0pfGn2TtD4FW5tqR1b5Sq1jLFad9b7mIb0b64jY/l1Z57/V0QSsI5QDAa6IYVxp9sZHoinevM642noNMdp87wQYXmJw+vOPZkSo1NfSt+cyjECD0CdGgYGqXjC9uhCy1FtQEXY5onlnR8DQmQtLzEaHUQvMU99Ede3+AtqGcSuFNy38izh1Z3+Pb//ar7F/cMTp2QWPHj3mxfFzqrpmZCYc7e6hjcerjPH2PVS+h5mM2JrkGFVzenHN6fFTLi4vePDuN9ndv0ddlni74OXzzzh79jnbW4at0Q7OgvIZJiR+vnvnHh7Pp48/4/J6yve+9z0evPkGjx8/5p2vvovX8OzZM2F2jKGurYS59bLhKvq4ahrmxbqaxWKOd57JZIvtrR2m1zOqUnJ4oDOcK5fWamj9YjGZQXwt4jmJ4YdbWJIeeecsoNHao7IdDg7v8trr9/lbf+tv8fJqwc6de2zt3Wesc04+/xitSnZ2JmRZxsM37lG7axaFxbnWrzE6dUfNRp7njPWYk9PzYEpmyLIRs9kM0BRFwc7ODlU9ZzQaMR6PUco3TvwxIJP3nsVi0XExiBqRNOFhpLMfvj24RJ2yOaORLPwq7j9KH1P1XWqKBEmEGe+bRCVp3YZ5GOhrFTCIEUw0qklgAjSOKilj0XUCj+P2aJ01RKvYGC6bXnQvMNROGBtXenb39nny0cfsb+3gRzmzssIqAybDeYutA2GkNZXJqfFMy5LCOWqlqYFMazIFI2MYjSbsHt3id/7m7/D05JT37j/A+OXwpoNSoxV7txZZJRKORkKUZL3sOJd2X2x6XCuD6o2x77C5+j1BGB3aY8Xl74euG0KMEWkA5D2HMIWEMXSuZj6fUtdlABBCkK6aYF+D0S8pwb2ZxG4VcRvmpAEMShnU7n28Upijd8lf/26Dl/T+Q/TO0dJ6xLjokXi1Z5/iy+umTv3yl9QvfgFXzyHmpFDtPPrai5TJGCJarLWNf1ZKtDZnpkekrCKSWgmV7QR5iH0Ui4Lj45fk4y3++I//FV997xstjvabEKDDJd23dp/9yjuW0NmxAbk3qiEfmnY767gCrg6uyUCfg2NJ3o1ai5UvqpbgUb2HmxKwKXWsdVeDLESAONHfunWLj/mQqqzET6OqaKOXLc+oL8ToM4b9Z4E6X7s2w8UnnfVfTp6RwKUe47AKZw2VVQyACh30YeNNDHGs07cE6LfTZyY2Yaxvupv9MfS1LUP4qt/eumf9euu+J7dsabxt3a7Eud9Oip+i32gDP3Uc48ohSg9aNWFDI9PucR08lY4njrm/rv39ds6J069ertefb+yjaSMsS8PPxHpKAmiMJ2O++91f4+DgkJcvT/jkk085OTkF49ne22F3vE+xmPP86SNq57l9r+S7v/m30OMd8BZbLfjGr32fl8/v4+qK0dYepbWYLCcf5dx97SHHJ8+4np1j9IS9nQMRvjohWi8vL3nw4AGHR4c8evSIP/3TP+U3fuM3ePDgAU+fPuXdd9+lrmuOj4+pCfRc6oOlNDYIDCJRbK2VUK9OIoDt7u6yu7tLWZYURdGhV9ed135xvjXtT1MtxD1Ki/dypg4PD3nj7a/xm3/1r/K1r3+F2/fu8fmPfsadu3fwZgu9qHjy2acY5XnzjYdcnJzy/e//JtbW1LXDmLwZ32g0auiZ+Pf6WnD5eDxu8PXh4WEzl8Viwfb2NsYY5vN5o8FISz9NQLRIiCZYqS9I3891VXml8LawHC0iLm3fMSkFvkvhRXubmbYdv3ectugC0LTtdFHqqjXj6PezfLHbeenehZ1NZ2xv7zRRIdLSHDylyI3GWYuvK0bjCeeX1/zFxSXb2zuogz22RyPUbM52lqOVZjSaMN7ZJtueMNnbw4zH+FGOnozJt7fY3dtna2uLSTZmkk/Y2d/HZRknV9dokwVcN+x0OVRuBsjddUjb9fLCQJs9CUzn4XpmY2gMfcSyDjHHekPERZ/oSDVW/T6ddYxHeYfpVEBd1Sg0dV0ym12LVMR7jDaSzLEhhNaPM9VY9ImjVc7RN5XmrmRjzP1vMPrK30Tv3ENvHwVCTkmiy4bKbSVe7dpEQ7QgedEabr3Tjst7svvfESqquMTXBW5+QfnRH1Gff466eLpEdKaChaG9dM41jEa7H5CelC4cWM14inzCLjGpwsyUzK6vGVnH5dU1n378MendHYoatGkZIvTVmvC5Cb0tZqbIyqfs6BLzuIJovIkQXDfWIeJwkxLf68Pn/lhuugP9osN52N/fb8YVGdEhWN3vO/6VPa+X7lcsEWqvgyk3waFuvfVEaXx/1Xq86h708dUQIzM0t77mcGgdh8azql76fWh+fZqg33cfVq9ipPuMT780v6zYs1VzGZrbqnVYt0dlWTIej0OQheVz3eKQ/iGB2XyGTXM5+WX8kN63ofXuj1tgtQg8Uq1Gf01Wzc+LVKFVQoYISFlu+Pa3v8OtW7c4OTnlgw8+5OzsnK2tbUZbE/LtXbYm+3h9ReE/w2vH+dUZNXWIAjijKub4umJr/45kj0Zj6xJvfciEXvH6W+9ycfaCva1tRibH5DlVVVAUc46PT1FK89Y7b/KVr3yFTz75hB/+8If85m/+Jm+88QaPHj3ivffeo6oqrq+vl/eb5fMoWkewutUC7O7uNlL6NNjQqwik0t0eggd9xnVrawutNdPpNU+fPeXBWw/JZzPGWxO2NZSV5fz8JScvPuftN25xeLDHnYMD7t2/z7PnL7i8nLO/f8jW1ha7IYdGigOVUo2pUzxP0aLHGMNkMpFQuOEsx1wYZ2dnnJ+fs7u729Dwqc9GFNzfunWL2WzW5NtY5w/cLxszGnEiqVS2idI0yhvOv5NHw7UOiJEgiW1577CubmL3DjEXsY94CKLqJtaJoWzj9yzLMAnRk76bAr94MdMDGU2lAE7PTjk9PefBg4fNOJYAltZE75CPP/qI+3fu8q3vfY+drS1GxuB/669QlRV5PmJnZxdjJDu4NkZyZaCoQbKA5znOSNZwZTJGOkM5sM7jHOwfHuKRrKLpGG4q65BNf07rfuu0OVSnB9xWIZRN2l9Vt4+EGuKa7mXuEyzt/gYH1NqiQOwks4yyqoKtiJKwqHVNWc1BtRo335NcDpUUeQzNZ0jqtG5NUuThUKid24ze+W1G7/x11GgnBBuIjB8SfxuFqOODCU/MBtwIzRT44DeFQnmFTD4gu4RB0VuHYvKyc5etu1/Dl3PKT/4l1af/Cnf5TLL+rkDcfUIjAq42SIOYfd1U+mcpth/D7MU+nHPUVUlVFiJlUoYf//gH8GtdZBMlMf0++vvSfl9BOLLaGVwpkdrHvYkVvYr9pO13Ceih37vjWf686t0+4TI0zv73m8YydAeG+lw1fq8UeM/eriSlso3vXr3U9yo4EkvMMhzvSWfMr85L3tCfx/tlZiOWvhPpqrveZ5bSsopAHGIqBpmrAYK6fx/7JsPr9jGdW7/PIeYgJdSG8O0mOGH1GsCmm/r/Ye7PYi1b0vw+7Bexhj3vM+fJzDvknauqq6sH9txNkTRlEaZgSIJl0zIEC5ol2IYfRPjN8otfBPjFgP1gGrL8YkO0IBsGQT9RhkxJJKu72dVjTbfumHPmmffZ05oi/PBFxIq1zz6ZWdUk7HWR95yz9xpixfDF9/+G/3cbCNv2vFe1Jz7HM041TRPk7tb20849/938ek5RlqSJY2NSIv/ifetVoHfzfYLuZQ2a7ljGgCU+OgpvTObjjUZKgbK88+673L//FpcXV/zk08+4uLhiMBhK7Zv+lN74mPH4gLtvDxjvH3N6+pTRaJer6xXLZsl0PGJ/75hBr0eWaFKtsUj1bVNbmrqmrtZcXZ0yngwp5nM0sDMcUFcl89mM5XLBxfklFsPHn3zMhx9+yGeffcYf//Ef86u/+qvcu3ePhw8f8vHHH/Mnf/InNHUtJBOqNVJthsrjetsbNaqqYjweM51OWa/XLFdL1x03KZc35V285zS3gJLbQHlZliwWC4w658svvmQ4GfMXfv3XGQ1HlPWScrnixz/4QxQl3/rGh4x6OffuvMXu7h6VWTKdZo4RVSJ4PGDwe5vXvb1O7f/5ehpeXvo12uv1sNayu7tLlmWcnZ0F9qk8z5nP58FQeHR0RJZl7O/vh/yi18no+PipWKfijToOd4rDouLzlVKYKNQixNYbQ11XpFnSOT+eJPHi2mYx8feMqWyV29ittWHzipmu4g2gFY4SP2et1wkUw+GI+fVcXKZJtyBgELzGkPYybCMWj6OjO9y//xar9RqDoTYVTSMbqVUKoxIaK8qftAcXJS05FqnSGCU5HMZZ0HQqBXQSK0pkCG24RYDe9vdt43mbYNo8Ospq+0l0s1c/e9smvGk52NycNzewbYBRdIo3sODYlh2pMQ1ZkpAlKaZuqMoSnOfQNoa6kWQ1izDitPdy8enRhurvu7nxvw7pv8l3SmtUb0Jy+CH5t/46yfgOOOCgQqKv42wHkk5uo3J4oZtMD87tb9tEVmwbBmSjd8TNW1ysvckH9D76b5F/9FdoTj+j+vy/on72p2G9bWOH85YU/32Xfo/o93hdbrfoxkcsRP1zrbU0TSWAS8HnP/kJ5tub7uttyverlI9XgfQOvu6CyehyFclE0Ze6nq43XbtvKtDj829b29s208733FjhP/WxqSwpCEQhA+e6x9qOR+NVsmhT4ao3PNfheXhL7e2yYFs747bG57Xfv/l63gbYbgMj/rxt8+9VCuPrzr3tnG33fBMQu3mf2/bjbce2PfhVx43zYkMJrx7P+B1e1V/xefERsyb5cxaLBcPhcCuA9H9b6yw+zljpDZnrYu1kqitYjN8z2ms3n/fKviDSszb03DcBvNba1kgFqERTNw3D8Yj33n+fxXzF559/yfm5eDIm4wnj8ZR8tEd/5z7TnbtUpuHgfkY22qVaV4yHO9zbnzIe9Uk1VMWK9fKKdVlSlGK0S3VPammMBkwn71BWh8xnV1ycnrNazsmyHKUTri6v2JlOODs9Q2nFz/3cz/H+++/z2Wef8Sd/8if88i//Mnfu3OHFixd8/PHH/PAHPxDNyL1jYw2athi03yM8CPFsVH5M+/0+q9WyLcmw0Xfb5lC7Xm/K8c4+sGUsyrKkvrikKsSbQpLyycffwqzXfPHDP2N29pxvffIeD965R7lc8fFHH7K3t4fOdlEq4eXLE87OzphOpyFJO27XtvDsTYCRJEmoGu7XZq/X4+23326rgQPTqUTY5HkegJJSqpM4/k+8Mrgkjii3oTehOEiSJBRVeYOu1nd4TEEYKyBS8KP1TsTXbno2XrUQ/f1a5UUFoOGLt8QAJr7npvVF624yutY6CIZtvMtShj5hZ7rD48dPePDe+5BlNC6ZHG2o6walE7QWlIlOMFo23swqbAPK0Fon/CRxFlChqLQRALndqnjb3/HxOuuRP5INBT6c8RqHxOvu+7pjc65sW8jhWSi06i722zZtP97GGIa9IVma8oM/+34EeOS6olxLzYymwnsH4s1jky0knqvxv239cdu7ds5RmuTOx/S+9c+jp/dQaR+U9zv46wAk8dtqhTJt1oAAWbeJWK9wWbFeWQc8lGdAUSjnc7QOcIhiLNco96yQeO3amt35hPTgA+oXP6T4/t/FXD+/9X1iw0GcOL6tH/y1tykk8Wd+TQYlxjTUZUWS5lhgMb+mririVCuphvpqkddNqnzlqZ12tSCjjYMG0PE91GuXz5/7+GmsTP+kj9vkktroyNFoFBS6qmqpF18FwDYPG8UOv/K8n0EG/TTHZju3GVDeRMl+leL+pn2yeb/YKLJpqInv96by6qd9p817vu6azXb9ecfuNmC12a7brvM6wGKx4K233pLzFR0Lw7b3ESVXFN3lculknshSY2xgB/rzHrft+68bE/90pSQvQ2nFJ9/4BmmW8/XDh7x48ZJ+f8DOzg7WwNnZGXdHO+wdTqkMXK9WXF6dkiWGt959l1F/gDEF5y+ecX76nMX1OU25QiG1QlAaYzRpNiDPe0ymI+7cOWR3b4/9w0MuTk55+ewZed5Dq4T5bM5kb8zZ2RlffvklH330EW+//TZffvkln3/+Od/4xjdYLpekacqdO3c4efkSp/fLjhbN9za6pTVMVVXFaiUJ0ZIEnQc973V91537+kYi/uaci/c7H8bU0xmJTphfXfPZD3/C3nifR18/4uGnP+bte0f80i9+G60M49GQDz/8gCTNsLqmKiuGwyEvX77k8vKS0WjUeaaXPTGw9x4J3wavw/jDRwT58KjRaBS8H0VRdOrfKdXmQPuogsFg8Mr+8sdPnaMRx4Btfgc3rUKeajRGT15x9QtOKSVZ/K5wXtNIeEviCqdZi/vckOdZm2kfqA2dcuSsCkprUsf92ziL57ZAjdaV3ApfoQtTTKcTqqok6/VlAlpCYSuHj0mclWJ/b5/v/qPv8vY779DLMygMFy9P2Ds4JEkyrJK6GhgbwIJQdWphT2ksymqUEosHChqPRp0CKKxLbSJvdz3ELoUN21vEnmLD/72S6QVTMHi391MqKJpy2/BL97yNVuhwjX/oxmbhwWZ4KC4Uxba3tzb8FEtR/EbSA1p7KylBUcZXqfcCQ0Xtds9OlCLPMhSK3/vd78K328Y3TU1dlQFEWrznQJTxprppZe+yl706ofk2ECQNVejDD+n//L9EsvuWAwbunm4N3egTL1z9Bujnvx+70CbaSeMu9cn97Wf+Cou1uh1nB97D5dZ9mGQkd7/D6PjbNC9/yPpP/u+Y+Rmewg88hbGKNtmWLGLTKtn2nYqes/2ILTX+fsZaatOQG4NKNNZT9iWEPomp+doxadlC4r/95NSh88JH0n8xNoTgvlfxhzFAj9r9TwsIbCrq2xS3diOMlUuiv4P5GG/iiI8208SBVkt0Pu130TMsbgK4eZ7mmYAu65gCm8ZRoHefLW3uPj1udH8wcLftMhRZdfvc8f2xqSzHPzf7rPvm3cMvofbc6PzoHlq3v4d7Kro/o3eL+z/ulmjU3MvGbfFy3X/Q3id+p835cNthAau6UQoia8G6HVVZL2fdmm93FdciK2LZKghyZXtoX3hN24695Wb/Wz+dwo5mw0B4Gdn2UndNhOd1N7x2DSgcU2Mr340xjMfjVs7GPr9YTnrZqqSIcaIVZVF2xncb2Gp/jd/Wf3dzfELIuu5as18HzLTWjgK/1QIADg+OuHN0zNXlFY8fPyZJUkbjCVVtePTwEdbCy4srxnfu09ghl5dzhuMBb909ILWG85ePef7kIcvFDGjQtiLRRn53089qUKaiWle8vL7k9MVTRpMp7777gDt37jAZDHj25AnFesVysWA0HlCUa54/f87e7h7Hd45ZLBZ8/vnnHB0dcXR0xFdffcU777zD+fk5TSXP8npWmF9hHbbGYp/cf3197diaUsqqEL3MeTbeBOT68+O6bTLHJHhWKaE4TnSC0jqEJN07fou33nqXnf0Dxju7fPH5F/zwz77Pg3v3+fYvfMzhwQ7z2Sm/9Gu/jk4VdVODFdBWFAV37hyxXhcsFvMotFFobYuioGkahsMheZ67yu0NSeJTCjTGePao9h19OYj1ei1gqNdjMBhgjGE2m4XP0jSl3++H/nlTY8BPBTRi4bC7u8tqtdqadR4EmnZUjE5LMV5b0gpldVCEcAoGyrE6qESK3imFCtSQCVmaopAF3FHemjbG3FNJ6tRVgXZuwqqWQnpws/y8tf7dfFiDoTHw9PljiqrhcP+IUW+MRlM1JbapSHupVChWmsGwz/z6ir/1v//fcf/4Lk8ePuL85JTf+Wf/2/zWP/vPsahqEut4rBoDRmE11FYsrCqVpa9tJPzd+Hkvi8KSYL0U5Obu5I4u5mj3LDYFt9+k3Fh5ARiujc7rjG28sUaPtVYsl7Ztmae37NQgcffsXIuVmiOuTTYoafK511E6V/i92t3bKypKOeJCG23C7r2qumLQH5AmmtMXL3j09Vct0ADWZUHtGCrqWuYByqCUUz5t10rS9kl3LDbBxu2L0W1mO28x+JX/EXrn7ZCYp6xuQXY8DE6QuW6QcVLOM6FUEOwedMQbsNc5LAhCU7h38htx4s73f7v+DRt6rMSItw2dk937BfTe+xSf/heYh9/F1IWbJ7EbuRWIxmxutF2lzk+XNzmCB1RrrDUUVckwTcFGnlEI+VxxqJUHYd3xcQqStShjUUmyAep9n/rulFwXBSTucxsZDIIS5G+95dhmwb2NMajTjDftpJtP7DSmXZoxOPDNVp3rGuvnt89D2VDM3XnWdpV00BhlMImiNxrQG/apyxJMDU0tOT8WlCPuNgDGy7COpoZSYIwS2Yirgh6ASWwtvm185TMBqnGorurItrhPtsMMeeMW+Ha93tZ2QwT9+WBdXHwrD4kUemOkv/y9jDNttfSu/l5dORQSlTsKtxIKeiIgZ6N8rNBOJ7MiOW1QmA7QcCTjbt+QsbJgolBqN3E87Ty0RjOUddDJ3cfLoHB0e9mLcGnSxj7kv3fyzYO8Lvh1NPCuq0U/kC898MPtiaKQev+vUEH7aAgfHSHKmeSXdoxKLsfPuLboxpIpRQpY5xk3djNnMJaNG/uy/zAa402P1DYPlR/LVxo0lFTPNihkuijeeec9TK149PApxbpgPN2jP9zBoCB5CU2NUinFvOB6tWR354C7d48w5TUPH/6Q02ePwBmfTWOoTNNpl9YNaZqRJJAmCb2+VJxeXl7yw4sL7r/1Fu+/9x7vPniA0pqLywuSVJEs51xfXvL1l18xHU+4f/8+57NLfvTjH/Pbv/Xb7O8fcHZ2xr37b/Hw64doz0ClvExWbs65rDknC+J9QMBCGhhKlZJcmrqqQ4hQ3J/x3pEkOoT/K6WwRvZmrRPSBPq9jMFgSJr3SLOcxlh++7d/h9/+S3+Fs4tLnj1+wh/83j/m6cOH7E53+M63PmF/b8hyMWNn94Dxzh5nV+coJQxTWZYxnY4piiLkXSyXSxaLJaDIspydnZ1QH2S1WrvooZb4RuSdyBcJcuhG/PgoIF95XCnF3t4eQAAxHqz9UynY529Y1zW7u7shZvH6+jp0fJwgYowJvLx+sLYle8dHsA5v7J/+2tjt06XLdILRdkOi4muT6JmbNKjWKXQe6QKBmeDzP/0+P/7Bp2Qq58G77/H2u28BlqqqQUvCk2oMH330Ef+X//of8P0/+hOn/Gr+63/wXb75F34D1etTY9HWghWFME0TkjRFW01wwSlIVMuk1UkwFq0vcENvs6S/7tjYr+Uz3ye3WJk2r3vtM6LfYy9FfBOvA8dXqRh8dFFI59gmVGNBECuS8ed+gaRpglaKH3z/zyiKIjzAIgtJFlnl8+TwtSnEOtKNR3xVn7/Oi6HE3EH+rX+e/MN/RkKkXDsCC5qVTT3s/bad70EHgqCkxCBAhK1sggFYOCVaBLCKcGa7wSvlR8PjkFbzknkoSNArO9obB/IR/e/8C9hP/irm4iuKP/i/Ql10NsafNoHsVs087kPojHnTNBIO4PshOrwQ3dygt1sXVVug9EabO5DrxtH1mHQn+6tA6W398tN4QLrg7iaAkc/Db7d8/tqnECDFa9ZAx7rsNuper0eWpayLNVVVhw3MW8w3n7F5Pwk/aW7QMuKvaP8X3Wuz/UQgIz6nC6xUpxk339UvSxln7Qxl7Rg4XS5S6/3K8WMj7egwRqEj5Rn3e/yO0XyNv3BrOng2tP97A7jbbu8Em8SG/LWAVWZzGYWbGDwRiwdD4I0UJkogaD09KvQPRAao0Hy10S4bft5Ygx35RchbM1HtF+/RCfiJtgZNUErj+7kbJk4B84qUV+qapiFJNdvmAXhZ6Kmq5TOvrLLxLpvHrctoQ3Z4D4usFev2h264+ua6e9Uxnkw4ODjg6mrGsxcv6fVH5KMd+tN9dg+OOLz3HvPZJaPxhHVt2dnZ4e69O5Traz770R9zdfYIZWqaSqzksrYHQbH1rEU+J8BbxHu9Hj0ttR2ePX3Karnkgw8+4N1330VrxdnlOb3egHpQsVrOefbsGW8/eEeSwb98yOPHj7l//z6z2Yzj42OeP38uRm/rZJJqZVOsK0HrCffKdK/XY12sSNOUvb09/upf/av87b/9t0PkTtcw1Q5IzNwk+QpppOdaqqZhdXlFY8SwcPfufd5+8IDlaskPv/9n/OEf/AF1seaDD9/mGx9/zMHeBEOJtXDv3n0uL686enOWZezt7TEej5lMJCl8NBrTNM+Zz5do3QSPhA8rjueL14MAlssl6/UapWxIi5B0hjS849XVFcPhkKqqQnXwuq6DnhTr4K87fiqPhjGGPM9DbFiapp0Ytc2XimPD/D1i5XBTeHiQ4K0JvqPiUIv4p4/5bq+tad32cnjwoHXSARjxxPFsUzFAkRyUjOPje/zk4ic8efyQ3/vuP2b/cJ9/7q//s+we7aGzlDzNyJXmnQfvcnx8zOOvH1JVDaQpv/Ybv8VwNGVdOfo0JHTKWEtRNejG0hjI0ow8TwR9q9vBWDzRXydIflpr521c+Zv3e93E2qZIvongi+fGjXtGO+OmxTD+LFY4N88NC0NL9dI//uM/dNVa26coRZRHYEmSTMbDCy17k5Uibsfm+7zibUnu/yL97/wL6OGBgAJahcA6i4wEBPpQHtXypssDwr02GtN+pwDvPdhQlIUBCG8SFEBiLdYBDW/pC/3pN0+D81TSWjRpx08Ppuj+z6P/2n/I+rv/Mfb8q61jtqmA/rRHvLnCJtFETZpkoW1+s9hk0HnT574OyG/07Bu1/U2NA5vXvXGbXiEn4inyqmf8NPd8k0MphUaTZRlZlrNGhXAA0zSv7bnWQtoWn+pY4+GVoMA1ItJtWyu+hDuozvWd9kTgJQbP1slzE60z64D8JuBxAaEBaPj9KEkSYo9GACG3vH/HiLH1FTc8/uGF/X1b2BMr4fEz/PNvGxORSyb0AVHh1I0Tab3w0s/W+Ods5mv59Srd18rybvtVsLK0SbltsdIYPACmDRlRSqGd3DCNGEzquqau6uDVqOuKqq4AUTKvr6+BNrlbKXmf7XuVGMuUbgubVlUdvxnWeVo3ld83OTYt634Yu7rMKwxbW4779+8D8PjxY4yFfLRDPt5lsHtEf3rI3vGQY9Pw/PkLktry1tv3WS1mfPbDP+Xy9AnUK6dwJ1IMb9iCDNlzdcjnrWsJ4/GRMP3BIFCuXl5e8umnn/LJJ59w7959lus1q+WCfq9PtV7z/PkLju4ec7B/yMunL/jyyy+l3sbuLicnJ9y/f5+vv/66U/R0sy9i3aQDQpQYoaqq4vz8nE8//TQo5PFa97+nacp0OmU6naKUYj6fO9rcOpqvijTNGAxHTKZTJtNdhuMJP/70U373d3+X05MX7E4HfPNbv0g/T3jn/l3u3j3mydNnvPvuzzGdTh1wiWqEaA1IDmbTWLJMQqOOj++RZRdcXV4xv16yLtZopZlMxqF/lRI2Kp0k9PKc0VAzmUxIUx15O5QLt6qo65rVasX19TVN09Dr9RgOh4Gi13uG4nyPVx1vDDS80l8UBU+ePGE8HksieFmGyR4DDg8E/KKIBzimpPVHjMi9AInRZJz4CQTXjUdbXujGwCN+ZqK71skY3SVJSwfmlREBVT329/bp9Qb0ewPKsuLzz7/g468+4rgumOxOmYzGoBKyPOcXf/mXePniBXsHB/zGP/NX+It/5S9hgX6v5/YcsbgY2gVgjKWsKpTW6FRT25v5L5uWns2+e5UV46Y1M1ZWXw0u/Pmbi3Xb/V+nhMTfb26CxgnoTQuWfNe14MX32gwv2dxg4989SNZK8eTJY07PTtxmGb+HbARZltIiG6czRO3bxoy2+e639oPWZO//RXq/+C/jYzlx7kzZsi0YI3k9SgQLViKfW4Bhw8boHhaBC9U1X/rYcGNdord8H6CNbi1+AMqFM3hroXGuaFwLvYfEh8VJClBrQfLxzSodMvjtf4/qi39A+YP/V3hA7LLe2j/RfNtmEY//3vReydoVoJFnbaJwXbdJ6PG930TRf/V56uZvlk6Njduu/WnBzuvauHnf24Bcq4xsv/5Vx6aR5nXXh3UZLwUlxCLj8YjL0xMal0tT102k9aob94l/etm9OY/a7+NwH4gVWA+sw2VRRXpvcJJ7hMvCMzc98h6AG2ccaO9jA8DfCAZy68rlXiDXNdZ2coFarBO1J4ij9jOvwMUVe33fBA/JhgLaIa/w99btnPCU2I0x6ER35kmnLxpDkrYKSsB5jrpaPjPOgyHyxwTAH7NLyhuLIUfhXZEtO+O28CChIa8dK6Cn+/TvvV6vKYpCPBiVpSgKVqtV8EosFgvSJEHTFhzLcwG/eZ6jE0WWSRG2J0+ecO/evaCLSF+1SmjctwqXO6gI7S+KIjpPQmuEBCeScVu8d+0YdcOmYmNposRQtgla/JhsC2vxepLFkiQpd46OKIqC8/PzEJc/Go0YjScMRhPSPOfi7JzFquSjDz5AmZqvP/8Bl6ePsPWK0aCHMZblck1ZFtR1wWAwCPOpKEq09qCrCv1YliWNkZo6viaDz8H45je/ydvvvM1XX3zB9WLBbHbNYDTg5OSUd957l8OjI548fszz5885Ojri9PSUg4MDHj16JPvRbTrPlp9JkpBlGU1TM5vNMMbwve99L8ylzb3dK9gXFxecn184HVLC7vf2dsjyDKUgz3v0sgFZr4fWMJ9fsVov+ZGpOdjf4RsfP+DOnSPG4xHjQY+iXHJy9oIHDx5wdHQc5lRd2+ClkL2uZDa7dtu8C63WivW6JEnEGzEajty6aLi+noc9crVai86e56RpSq+fY4wlTbu5Jl6uDIdDrLUsl0tOT0958eJFAFp5njMYDKiqivdvzLKbxxsDjaqqWo+D1pyenoo7Rcvi6YT5RJN9c5C2KYXxsQkwtjH8+Db4zPetG4A78jwPRVk22+av9YAjtngqpVgslyRpn9FoArx0C6SiLGo0EjJlqppKGxpb8+u/81u8/d673L13j72jYyBDqR5NFM9saUKYkn8/ay3W1DSNcqj45gRXetMq3R5vYtm8+YXv8G7fx++/7di2iDfHKT53m0K1OU882Nj83jql4DURNOH+mxYd/zMmL0jSlB/96AdUVelCY9p7NKbaaOvtAGzbO237vXNe2mPwm/826dFHARB4hd4nLfqgJS9IAJSOPC+2+70POeuOV9RnThlSamM788AqDoORxm7Mjei+sZJmiZ4t53lFLVyW9Mg/+auo/oT1H/ynHY9n3C+bFqPb5t6bzDGvaMW5Y96z6l3KP4034Y3OU4DtGgNed92rAJT/fhM4v6p9b9JOv04l72t7e17V/696hzc4W9rplLE8FwWlciwmfn/xuMDSzm1/xO2K46dvtrdV2tm4R9v2TTDTnV9at/eQtdYNC/bPbIwJIMMbumJg1Vokb8rveKnFiZmxAWTzEAp3+T2e556WUiy0ouQHLwXgOQ4ULeA2SC6CB0yhdcqFXVkVntUxbKCQfC4VZALGorQiceFaWIu1LQmLtQ11VaGo0TphXRTCNmYaTGNCeI1/r+vra+qmFvOLNSyXK8AzQxq39wvnvzeC+jAYsfYrhqMRvaxHopOgUAKkqSi+ibLCimQlabdV6CXfJk0lFOjly5e3GpfiPccihhbJdxRdSaqCR/uR9fOx1TUstjM1OvN54/PbZOSrDDSb56EU1lim0ynD4ZBHT55QNzWTyYhRnjDupUwGOaN+zqoomc8uOdzfY9TLePzljzh/8RBlVgyGOf3BiIvzC1brFQB1XQZGJ51oB+SFTtUX2PPW8aquub6+Zm9vLxiLr66uePjwIR989CGHB0fML2esi5L+cMjJySl37t9nb2+PZ0+f8ujRI+7du8dkMmE2m7Gzs8Pl+cUNI4iX/dv0UF+MMc9zxuMxl5eXN/TFzTFp9U2xuhkrynqapezuTklTxSDvM+wPyXo98l6f4WjM/sERd+/eZdBPsE3F7u4YrROurgTg3Lv3Nr3egKvLa9eXdZA1/pn9fh9rJOfYWAkR1jpBqxTtjIbCsCULXozzsFyuKIqC8XiEtbBaFVzNroCGwaDPcDgMzoPNOTQYDHjrrbdC38WRRJ6t6nXHT52j4QfMexcSldywmviGdqkiby7QzcUSBtbasMDi58ZKirdmde+jXLJWG4/m6bmMtwq7QYvBhdZpB9j4zq6rmgTDcDAky3solTh6rwqMZZj3GeY9lsslSisaLL/467/qBD1Ym2DqhkxlrmyNBatIneFOlDxnuTEGbMPDh1+7OMUN12or8/+pHJuL8OZ32xXprcBDNIXw9+a9WivY7W8Uj+kNgGXbr153hGRhJMbRNA0/+tGPbjAf+XO3Hhvvsg08bW874fzk8EP6v/jfF0Ypr6y7fdoaI3Uz3IcqKATu4YqwobdGPxsUfvFauD73z7bhf1GS6GZ/R4pCp8ECTMArWQ5NhHu7vy2BDrfd/KzsoVaUArCk7/wquTFUf/Sf4QkXfD/9rBb9TSttvH5FOWkVo6apWS6XIZY2vsc/jWPTaxNP11c9c3Na37o6VPfcmH3rdfcMt9iyGd+2Hl93j1uBNX6cTAtIlYQaHRzs86kx1I7XviiL1tDjPZxm05fZHtto00N747m/RZ5132p7u0FtvMct/eQXslzSyXXrtq0LeCId/mbLXiEXdeyNkbvK3DfWFWNrCVE6GS8+nMUrwu7zQNDibTouz8SHGvv3MI2hrCpXW0j21vVawkWaxlAWBdfzuZuD1sWAFyHmW2L0hTVSdAfZyz0TT5II3f1wOKTX6zGdTknTzCVh6yhMO2mNLEF+KKdkxbmcErZDxGwZGyfBomnwZAJaC7jyniXjEtwPDw959uzZVh2mnQIRAAM806MFVqtVAC+AC7MzYT790zi2GfiCrkTbdzs7uwCcnpyiUAwHPZr1jB/88RMmj57wi7/62xg0Tbnmzv37lIsZzx9/AfWS8SgnzcSIWjYNxjYoBWVVU1YFOpkwyIf0e0OSJAvKvA/FyfOc/mDAfD7n+vqayWRCnucYY3j58iW7+/scHBxweXbO6cuXYBWr5ZqryyvuHO6zs7PD+fk5i8WC3d1drq5m3Llzh/PTsy0sUN217JVlpRTr9Zr+QHK9YoP1Nv3AH/5+aZpilKUs1zSNoSoLvvOdbzOdjhhmOdPRmNF4Qn8wQOkUqxT9/gBrSsrKcnVxhrWa6c4+7z34gLzXZ72qAkgQcgkdeW8JnjlhfiKc03oRbfg8Dv8Sdq2c0WgY7p2mfZJUwHbsRNBad/ow1qFi5kZo2aped7x56FSaYI0UXGpc7J11FikdBIfXQbxCLwrqZtx8AAnOWuGLWgWFyHbDImJrQpqmotQ3rrqmJbhEJfnNb+6OvceFpdS12/ydUtQ4961OUkzTBR6Ji9cDjSkLRqMBw1GfJBMtr6oqbAO9rEdTG4qyEuGcVFxdz7l75xiFYr2uIE+oG0MokWMtNL5CqI/rFd3MNJa7d+92FIaOUvaK8QnWEjbteWz8JrtKCx68G7/dEHEWvHZH29yst981VkTtxjX+e++4NcYGyxfKCXh/vvJWMWE+sf4Otm2nKNtd4WGsZw9xc8B7wKyVSuA64fLsnJfPn8tbm6bzLr5AX/dQUa9FO3LcGxEQ2abYJPd+nuFv/JuoJAu9Jow5yvHzSsHIEF+qdNSxugUZ+DAUG/paKa+xWAdwW6YlycPwSocoblgXQqXctrgJGjc2o9AHN5Sr+PMofEIpJK8lCWNlrSJ799fROqH43t8G285/bjzLt/bm73LKTSu/3zhEVojS4fO1QNb0xYvn3H/nbQxO6UX7vPZXrytu+d62wMuT5/jZYazMOb2hrHqwZrGgOjMZq8xNR1K0nj24aNsjVzfWPT/6vn2ciu7h2qvaBOXwZhsKe5A5N/rCv7P8ExYiWozrlGCLCixwFodvlcIiVelN07C/f4RF3Pur5ZrlckXdNORW8tgcKpN38u3ySf5K0R8NaaxY5cNeEPdzaLO3GHdlxValUXXfXaHDpr+hSrq9TvYuE92/47HTQmserZYOCJL7uBo10XP1jZ5v5Y43Svh9sW5q562QK8NachPFJ8gaU4fEe+MIE4qiYL1eU1vZ05fLJVUlNaDqumG9XpKmWtgetaauKpI0pd/vkeoMaxS9vEfe65EkCTvTXQbDoRCdRHW2PDhIdEKaaqlqrX2IVjeM2hqCZVbGye9DTs64uRFyaoLcE8OLD13KUgnP0ViSNHFGD0OaeXkubFzQFuhrJb2XxWIA1JFctcZAINRye6f3xCHtbeoGbIo1hvly7uawwdJgHU1pmkb1F3jFEQmgG4pvDDi3KMVbwYYz2BprOTg8oChL5vM5WZqSKsXJ86dczpacnF4w3dnj3lvvsjeZMB7kfPHwU+bzK/K8x3g8YbkumM8Xof+8XpWmGZYEdMLu4RF3ju+xf3AA1jJfLPj6q6+4vLwk0wmTieQ4pGnCaDSil2XMi4qnT57wrZ/7FofHd5gvlzR1xXx5zfnJGUcHh+zuHXJ6dsWLl2e8//77JGnOaDwlSdNukj+tzrmZo+erhK+WK3r9PkoJFW2jG9IkwTZNYE29KS+EYcsYl2NFTZ5mHO7u8vbb99HW0M9ysjyj1x8yGA5YrtZcXJyxLtYorch7A+7fvc/de29TFo1QIaMCu5nXk/NcQFrspS/LxuXG5CSJpqpquvuplrXm9GipOaQisJ7JHEwa1uum837GmJCnERv6Y0PLbUae244392h4JU8R2CxQhPATGxhxND6s2wvVOL/CexO01iReoTKtouIt4n5ieIQVrCsqoszFT25D3TQkgRVIBK2xIhgynThFvht6VVZtSEXlPB9ZnovC6uPZG8N41Gc46mOVozsFtErQWY9EK3p1w3K5pFhXvHj6gjt7d8h0xiBLKOuaRnlhZLweHwY1tpR492/snm9B1mtoxBzQiO8tP52ItgRhLKf7372i2HYd1gYPkJwRAxE6Am5D5Y5+dt3B8ecyd2zQdVQrptu+UGK9115p81TJ0Tv4fAAfcGSjOaotNK4fGtPQSzMynfDVp59hyoosTVp2Ivf0tj/cfTflulOyYiXZX+vn7uaR3v95Br/2r4NO5c5ucUjyqDxH6aTVLrVyTDKqHTy/n7r3dPoi1hpMsJbZMAdEQXNnh/nVggzxViha932Iq0D55HOvpDqFz/dHbBWzipb+NihQCl/B3N9bKSS5/Z1fw8xeUH76/46+2wwFeJXgagFGLBe8XJExagCNsa1QVtby6LNPee/BO1gLdWNQVkKITLSubnpY3LvFoA4/9p6T3D/Xfa80KJF1Yvtt76cE3mwowu23VnVBoR837WTRtp6xVgl5AMpRaLbfaVRUh6jblna8NhjnaMd3u9e5TaDGAyllA8hsgUdLb2oxjtteSRhpbTg4PEYnKU1jWK9EYalqQ9XYgLNb2ai8SJf2GsNkZ5fZ1RW1N1hsggvbDdP1ZShveC19yJLC2S1azU4rl+StPeiw4mVRjrXI1XwR66gff5wRS9aMMRKe5D3sWmuvLoc5YaxPRpd7mVoIUXDzum4amqZ2oWYV8/kc3LnL1UqSPVHUtWU+X6C1dmFCkiOQ5zl5moWwI2EGykjSlCTJSfOcNMs4OGq9B4lOSDNNmhqpT6BaBR9rBRDYNmIhVuRuzFG8AUj+0oBtapHvCiePDKAhUUFmSB96+j8PJm/uK95DAC1jn7WQ5xIilCSglOm0L0xhN9rWGNEX/JpzdMCr5TVVuaKpJKxLabCmCYBXqRZUKwW2qWiqmjwdslyvmM0unRGswdpaDCC2cdtAC5A2j9Yb2s4W/5lX+rZXB9vo+00FWSlUokmVZjQasVouKdYFw+GIJM3RaR/LijRJGA16rJcLju+/w3q94PTsGXXTMJnskGZDmvmapioZ9HoMB05vQZFmGf3BiG99+9t8+Mk3QbeVqPu7+7z94cdcXl7ywz/8I5azS8qyYL1a0s8zUp2TJzmzy0uuZjOm+wf0Ts4oVgvyqmAxm1HVlsnOAUn6mJOzK977IKU/nLJeLRkOhyxciFa8t8S6VizTmqZhtV6T5r1gSBE5aMEakaFR/3UMCqrBGki1Jk1yRr0+o7xPjuibZd2wXBdwNW/zppRiMJry3ocfcf/+W1hruby8ZLlcMZ1OWC3XaC0he571sKpKCfFDSI2SpPXqiUfRF+Iz4Typm5E4z68YMoV4Y0WWZbx48ZKjo0OmOyP29vbCHrper8P+6uea76dYT/X77puSGrwx0AhhCTc2n3bzjVFOvIC84hwrZ6Lsywle4YsnQow+/SBprcWb4DYS796Jk99iZcAL9qurK5aLJYcHB6H9WmvW63VIKPfP9rG/klxmGORD6rphd3fHxbdZ1usClAz6cDRkXVSMRklwQV1cXXH/zj1Hk6qhRoRzsFqpTj+0XektN9uV1jc9OuxfyU1qt5ZBoxtvHI/PplfltvZsQ7SvO9cr2O3n3fkT7uP+p1Vr/emcsxUI4CwQsllXztWfJAmmMXz6k0/FWhFZ+n0btr/rTz8Ofi4l977N8Df+TXCFlZRSkCQtaPebDW0Cod/AAtxxnWB8KJO1TpGzQSFVygMKIiDWjdNW4LRNH9pmaPn043kZUEyrKHY6ScVIh1gx80pqeAbgk9k913z+jb9GdfIZ9uLLG/3lN/k3nftxIrg0r3XzbrJhfP3VV/wld40yTmFMVGctvvlxc73cPEV1GFD8YW69xm7M525I6O2PiWvGd9eejb63lmhMNp78iveIv2uNFTfff3P9bnozQ6scoN4/2CfPezR1RVmVzGYz1qs1w/EkSk7uysx4nHd393ny5DlVLfuAKIs3493jx8aW11juyQkK00i+oXVz3zQWlEYb7bxGOijcpgGf5KrcvbUgEkfpWaNoJKyorKhr4bav6ypQwhsjSsRisQj7WV1LhfssycjyLKzpvJfT7w9IUgHHg8GQrN/jYDwhy3IXWqRc/oG0M01F7milQtRkUMD8mCiF3VhHbcI2aNW0g+gVcQU6VdgQmgFJCtbqG/u8fO99D16796FDHsiHxoUHyW8hwwNrWw9lkNV+vOOHedIHY0TGG4uhHfcYiW9S8BoXzkVHdzhl0E/BSg5RonxIi5NbziAj+7uiWK8pywoFPH36hKuLixDW1kQGEd8vfm6+iRSKlecwJm9wdL15ouzGdRisNUJtmvf41i/9GmVVMxxNOT6+x5Onz5mOB5y8fMb1bEaWpQyHA5qmZjFfoIBEp6SZhEfpLKfXH/Dtn/8O7773Po2Fqm5ItSu0jGW9LBgNRvzmb/0Wf/iPf5fGlFycn7FarZiMc5I0pVmtePHiBd/81pGESVUShleuS8qiYDzdodfvc3l5SVXVDAYDrmdXTCdTFvP51j1k22fWWpq6CZSt1roaKng6dC87/fmEP5SyJFrqUWit6OU5i8WSy8srkf9JSlXVGNPQ7w+4f/8dHjx4wL233yHN86CoHxwcBJ1MKrGf8+zZM+eFECNEVZUopRkMhjRN3dGpvT7r81xkvbh1ZCVqI0m0C6eS+Xf37jHTnQl5noQaU7PZTAzmRRFYtTwlvLU25NKVZSkMVlqzWq148OFHr52DP1WORpwE0k56Z4mg3Wxaa3zrcowHOrBj+O+cya1xloI0y6mrulW8nWJmawmP8vGYZVmGDvdJjp7mzrfDWqECmy/mjCdjPC3cqpBMfoOlqKTjsEosbzJEGCzrsgSr2Ds44M69u/z4s88oyjLIq16vT5K0imSeJ8znC9a7pViPraMPw0KzRZmOkbKFxgm/bcVQNpXg2xSEm26+m8/z4xCP2yZq747zTQXwNpDxpu60bffa9o5eSbhNyekqWl7BUm7sm5AIWDc1z54+izbSm2j8zwPw4mMryHBehrDxup/BkhwUezd+2inpqLAJ32Qo8ULFWb+CohR8Gv7NXMfY8GyIwAX+ts47o/3G3G77KmpbC0Y86JDLu2Pkv1LtH2mP4e/8+xS/+3/EnH3ZMRC0c6edC23f3Txia1Use9qYUhte6+T0lMViQT4aurAN5UDZzzbet60J339x+zave8Vd3XW+1W0Menvv7traWnE6etamq/u2dwEnD6wlUdvjk72etv07+4q/bQC1sjZhNBpx584Rz548oa5rrmYz5os507098rRdM/G4xpuqTjLeffc9fvjDT/nGN75BmibB9utDutpx8OCiBbJKJaFtomRK2AeokAwqm7t4JRaLVTh37ZRJvw8VxcoB25ZRMcsyl4+QBkaXfr/vqDF3glfBv6cPNWq9pi2dalhySkUeOKdIGCtJtwDUQj3tw46dIh6orH2fuoJqSjuLvy8w6W6rNTS2QaHQQcMigCxZogalGmeXkHv6+hGWOOy2vR4be9zlnzG1/1LGyUTSrQME/Xnt/OoCGPe5icC8dTOicUUDvbzy426iRFa3z9h2ktM0lqdPvubw8Ij1+trleFjAFWZUCtM0AtaMwRiYza4xBorVij/4/d+nLNakaUZVGeq66RhNX2UNtr7tm93oZYrlNd5YOt+FUgFKgrh9ATixYLu/e30md+5xeHCEVprF9Yw8T8kSxWJ2SVGsGA8HKGu4urqkqSq5Lk1JM1c/I8t578EHvPfgA1AuJ0ZpDMbl84LVNoTv/dIv/zK/+91/yNXVBUVZMjSGNEtJqoTLS/F27OzscHrygjRJKayEX+3s7TMajXj58iXz+ZxeryeezumUZ8+e3tqvvj86+4VL3Bc9IaeyBWmWMR6PHaOZpW5qt6+4/SlsfZZEKw4P9/nOL/4Cewf7DIdD0qzPaDhhPB4z3ZkKE5SCfq/PYrGkcflMTdNwdnaGtZIkf3BwwHQ65s7xL7BYLDg9PaEsSwbDIVma0+v1uLi4xFrLarWkaRoGg4FLH5A1kuc9qRemlSs2qdFJQpIqJuMJQ7cHyvvXQT4dHR1hrVA6z+dz5vM54/EYaMmgfHXwLMtCTZQ3Od4YaPjDbyAtpZ5YKHySVTdMiqD0+2sDKEgSGtNaHbVT8LXW1KaBVPIuyqIMC6VpGlKlqUtZ6E3TBMQlrh2wpiHv5TSNLOwsE8vO/uEhtTVop+/U1pBYJ3QTARymqZ3QEKtY4z5LkpREK955913ee/99dvb3mOzsYBqhxj3YP5R4NmvIUilSeL1csrMzpalq0iRxAknAVEx4smmpjyl8u0wJ7TW3KfPblJqY4So+p2NxfIUit6mk/LRAIr53vMBfCbg2PvfKzabi5O3RMRzzwMTn/0Drap7NZsGaCF13YPy+f16woY8+EZARcjJwsb0Ss62txPKGGH4lkMA6LSzUspAecP93Xr7QNOMRVfjMb0Dx7hQ24oBiXCias2pacJXUwXqmnWD4854W5ZSW8DZSebUtQ+6qucs13soo7ZE2CwAS5V9nA/q/9DdY/1f/W6iKW+fTzbnWhqhtWqT9WokND5HuxHw+5+zsjPvjkQDNxlkvf4ax3rxi0wMWy7yf9a7+Pdu/t4OFbjhIu8ZvWOw37rMpB+K+3oxl7h43qTRvu3f8bkopF+tuaawlVYp79+7z5OFDl1gsiZ7H9+4R5tQWWRHkZJqys7+PUYof/eRTjo4OhY7R5Tw1TU1RlCHW2TSGdbEOCoW1VmKiVdtGXAK0DzkQr4AYrzydo5clkocgPPdKEUIVII5nJvRtO15dj0vQiSPLvA9VDSGlUSRBstEfOvO1HcIT0EqUYVInR6RwRTAa+KrU3vsjl8salvwmUZ68acSvO010jbJYExWjk81bEs2954hWblsryqUKBg93D2vwBBFKJY5VS8KhUW1QrSd5ifvTGyW8J9g4ueqBujUuTyqamyYQE0j74yRyr1M0jQDV1WrFV199wd27R5y8fI6xRlghjdR88ZS6dSU5mmVZURQVSZLy8sUJf/zHf+Ta0WCVdeFvWxglN1ZL6DNcTp7qfu5/3wQs29aiBxjt/DNY1SbxrtdrN5c1WZaTZD1UkqKw1HVFv5+jVcNiPkOZBmsaLi/OWVxfY40hTWR+ZKlYuKfTCR99/HFodJomEtKjFFZLm7RSYBQqScgSxXvvv8fTZ4/EW1FV5JkUkPM5RKPRmDRJWKzXGCP0xEopBoNBqMvha7uJt6UJdUximRTLko7RwgGiJMndvmi5f/8+f/M/+A+4OD/n5cuXPHnyhNPTU05OToQRra5ddEHD/sE+/5P/2f+U73zn23zx5Rekacrh/jFJmocxytKU2sm5ZbkGRVDWd3d3O+NUlAXGGtI04f79+xSeoa0WdrbhsI8xlsGgh6fy9kBAwHBFr5c7ooWMNOuys7Uefw/wbZgL1gpBw/7+fjjPmLZoZVyIsWmaYCx53fHGQKPL0tRW6JYB7JZm94fWKgIB3Q3NT/igGGiJ/aybGqwm0Zm71sfEijXXNCKQfaJKkiSUZUme5xRFjTDmOABjFWUhdLE+1txzbgPYVNxmxhjyXk+EVdOIZ0U5NgqbYmzNqiq4c3zMO++8w0cff8R4Mha3moF+f4BSqq2AiWW2uKY36JGnGU1dk2pNYy1W61eQF95UzOF2y+g2sPAqpW3bz/h41bXbAMO2+7zKerrtu9dbrbvvFoMwohxQv6m5pdP+bS15lqITzaNHj2iaGq22MUzdVJLexHt040h79H/xv9cmfvu+s059CBZ8XyfDb+XRc32GsiCsoHYEx4BT3F/pOre29VqoKFSC6Frr82Ta2Hr/Q7l7uBOcQu4tOX48JMbatigDt+M70NLGZsvlrj0amByT/tq/weof/i2S6D2Ue96mcaIFmq2cuW28goLquwIZ72fPnvH2+w9CWL61tpMz8SbgPbxj9N22kNLbfr/9uLm+/ee2NbJG3/vftq+nzd/jz24D036e/qzHrcaCzjxy8cRVxTvvvMMf/P7vhdCFq9kVy+WKvD+MrPTde/txbWxNYw37h7vs7E25vp5xfnlO09QkVpF5xiKXmJyPcg6yw7CZxxu7z0czGmfxbWWSX4aejcm6/S9mZXExkGEtuZ4O/yIpTZLGtO22nUvR+CcqGmxrCV2hvPGk9ZopExlvqIJhwB/WvYdtxLAh1atNqGANVrwX3ojTqADOxJjTtr6x3jDmmK2cl6E7pxwwcT+No721RuoPJEo7hkXr9nQrwEhJ5IE3ThpXTbm1PN80CgWDSSQjYo+mMcJq5gsAexbKyrFnmaoMtTisbUNDLLBYrrm4uKCXZXz+k886c9DYhroS/aMoCy4uLijWhSvaJom0FxdXlJWr5+MAjgcm1toOQHjVsblMwzrgZu5B3DfxufFn/nOvINYuSkXrBKwhVTV5YlHW0NQFw36OaSrKYoVQpAtlb7Feg21YLy2DyQRLQ6+XcnC4x3DYc3T8iZtbOAIDb2FPMKmirkrSLOP+22/RHwxYrdYUZUGaSihg2dQud2GHNM14efqS6WjIcrGQWkku/Gg+n3N0dOTARfrGeQMBbCQtQ+CD9x7w9OkTyqJgb2+Pd96+j1ZCKKCUoixKZtczKWi3WKCsZTQe8cGHHzKcjPnFX/olPv30Uz778nPuHd9nZ3dHCpSmGTmQZSnrYk1jmlCPYr1eU1WV06trynIdxmk0Gjk64AHKAaJ4v4nnUayTt3q2AIqmqWiaKlzjwYIPt6qqiqurK/r9fgBtMSW0j7DxwMN7YP+J52h4mthgWXGu4MFgwOXljKqsQqEqHxsqHdIKojgvwBiDSsXeUDc1to6skY0iSVpvR5qkFKWznigRvGVZhtgycIiuEcHmefMbx+6UpClWSyJd0zSueJmiqSrXcbIZ1K6yo7VWaoSgMbYBa2iMJTEN777/Hod3jqiNQWNCEvlyuQxUdmVdUdmalycn3Du+6xLSEqeA/SzWTrYKlJ/m2j/P8ToQ87Pes1UmfybDcrc/YuVSRcqmbXN5vvrqK7dZyzUxi4O/3896+Hvm3/rr6MlxeKlgbNRixQlKDE4Bi7xWrVbj7qf8+W18sQonEv3mznHWRsEDCu/I8CAi1CazFuUVgPaRnTaIN8yDCVE4BCu0ioQK1hDlrnFN0f6hrRos4+J8UNYlrB1+xOC3/j2q3/9PoPF1EeTsGFTGwMbam1V1b7PSx6+klOLx48f8mgM+3rrbBWBvOv7bQYUk+nZVy9sO/57du0YsNL6N1luiCT+950quvsmwEgOxzTa2z78N4KtXrMUwm7d/e8uzbxxWNq67d48l5MFtesvFktVqybjeIdNtWNH2Z1mUttSN7AOT6YjpzliAbaPQKtk4vx2zJJHESd/WzNGfoxqgdjlcfg4aN6VTSVz2qFiJdV7pOHfR91H0op0xtgGUd1NrbAj3USCKuGmTlzvhyn5R+nUXZIwNYUh+jigVfR/JjoBbXBO0bVo7gVZoa1BGPJDGey3c89td2WKbFmhsWo/9EedsGGMwofaAwRYNxuVeWCN7t1dk6qqWGiUutMVaoZsvyiLURWrqRqp4W5yBUvqxrupAu2ubJiRrNw7g+LZq33NWvDxFIUDj5PSUp89f8P7777O/v89ysQwWXU92Y41mcb3g4aNHPHnyxBECCHhKtFR6T5DCgkYpV3Kka1FvKbBfJS9UZ+5Gn7oaZl1wv2nQvaE3qPbZ1oqXyTrjkVYWyiVNcU2WZqimIu3lGNNQlgWJFnBeFmusbTBNzWpZ0WAlQiRVHBzsYW3NcDCgsZaqajBKoY14KIr1iuuy5Orqkl4+EIYmLTTC5+cXMuZROxeLOUppKaJrcePaBB3UWiE88LqpV35fZfDc7C/TGJTztrx8+ZK6qpmOdyjWa3p5Qpo0NLUlzTKyTHN4sCO6Z1FRlRXD0ZDVaolKE/J+n4+/+Q0evFfy7OlTVus5WT6lapyBIlP0VO7olyXcaWdnJwIM4skQj2pbfFrWtr7hlfB5xvFn3nvRGuN9QT4dDHW+MLHoyNIXh4eHoe9iYOGpxGNdylrLyhFR3H/3wSvmrxxvDjSsoqm9wmHZ39tnOpnQVDXNwHBRXEAjiogxzvtghc7NOoaXuhaXY1mUGBRJk7bejmjHr+sGqEjcQiyrGoUwfdTWoDAUVUWGiyG1HkSIVaRpGtIkDQoGdQnaoHSUH1KKkinAA8qiCUqWuEENiU6wStixqqqhahqO7hyS5QlFsYasT1FVrNZVoLirqlIEY2NZ1StOXp6wM5mgM0nWU41zQQfDV2SJ8Jai8JUNn3vrWnxJuwHJWUCgCvYCVW3E9MaFobzbWP61Y/0qxT8olht/eyuUt6jFIMK/Q/ucNiHRC5W2D7rP8tvjVu+NVxU9patX1L1yZg0J0Es0CYZnTx+hkPmolMyZ+IntM7a/vHfL+37rTFqlSN//HfIP/xJeAYiVWawo5t6CLn3U6SBQUWyzIqp/4U7wm4rrWL9BSK5HiFCX+9uN84MV1Cn7rn3tnPK5IITv/DwVILJtkFxpsehaX8TI30qe4VCOUghDkVjPlErI7nyD5K/8Lyj+8D+lOf3SzaPWCxpvlpvj9PpNOjqM4ezFC3Axwz7qSyn/7l1ldHOP6gKL7kbeDV2IFb0wFd3c1G1rbzTdQ7nNr+We/m8/FaJV3N7IPxDx/Ch1M8crvCduTCPQFR4cL353TwsoG1EwR/eLLmzvrbyXrF3DSilRlDVgFePdPaF9vL5mfnXJcjFjtVxgTI1SGUolrqK0udEXWvk+A1ySrvfIKO3H10/CSCFz8kJjwcs/I8arRLm7G6lS7sMvrQVlK1kPtgV6/hHKhQCrCGD7bvL9av39/Dp1YUN+v1HWU6x2jQryeyvTJTk7Yk8MiEWhtM9NiWRvNKw+vjx4fsNzpLE+zNZPfgnVNEGWtutRcsdM0xbxhbaAoDfmGWNoHJ9/W73b0DSGolhTlGtAqKiNsTR1jW2cJ8IZgYwRD4FKEuqIw98ryxKyrYKXKYlAojEGUzchDM7nryjEq5O6SsrimTAslws+++xzrq5mHB4ckmcZZyenpFnKdDpFK4VOpMJ1VVUUZYFWisR7eYwQbHhvdVlXwr8hlG9uDhD6PoCAm8Ig+j76m2jvU61M3jQa3Obt9WMn80JC5NptwjK7OOf7f/pH9PsDfu03fpMk6+MpnJWWSulJktBYQ+Pu1VhD1TSkVc317FrWlpIxLUsheaiqkqurWWBLqqqapq4YTndIlULlPQb9oeiP1mCdhw1EF0zTjH5/yN7uPk1dSL6NEmOF0mKoTtKENMuEiUtrrGOCC+9P1xDVNUwZmrrCJgnroqSqK9599x3efvc+VbmmrtaSl1XXjMdjdCLPStOMfGDkfaoKvV6TpKmrqj3g7bffZj6fMxgMwhz081JpTeLmrG+LrCMpsCeGEJm7UuleksFHo1GnhpAP55Q+S0PYGECWJVirub6+oliv2dndFZ3aM8RZSNMeILkjMt9c4nmigne3KkuXZ1S68MB1kIPL5ZI3Od68joaWl6urirfu3mPYG5CphCRR7I7GTIYjqqbherlkNl9Sm8YpWY2wMCgVsuXFWptQ1G1cmU/QFMEi1RNM4psnMbd+YjWeY9gqmkpiJAGq2lA7oJGnkDolwDRCRZamflBl6uGeV9cSKuVDsIxj8qlsDY5iTKOoixpz0bAznVLVJRbFsijp50OMqWmM7AnWQJrmVGXB08dPUG/dZzTo0+vl+L09bCJsCCBaodG1dHsBFQuhNvEXtT3UQEUx1ZsAwiuecn77O2FRRjvV1kOF/gz6sqUj4OJn+fAfryDEd48Bku+TjhqzxUpqsdjIY+YVatc0rGlIlSLB0hRrLs9fYqwwgki8bcXN42YNk/C0Dnjyf8tnenqf/i/9y6IcBQVeagLooCEK65PI9WhzCQPjwYlpnwlo/71PRFPxmHmFiDBPnCHTEdXKFyGMyimVyp3oN5+2WnSriCgHWPy8DLDF3T/QUvt+V0rabi1tNYDo2e7/8bOtUujxEb3f+HdZ/oO/hb38MsR/+jEIfPOqnZ/tGNH5riu0o/OamovTU9bXc4aTqYQxYpHZcXOOSx8mNz73bwBtLH4chmc8gNGt4hvaZzWdR91cJjfaEADcLRd05qjyves/6z7PTzHA0RK7e9Aqm0AYL/mOds4qJAci3C+6oVzYfZbHlyDKKQaJkJVw295oxGg8Yn5xwsnLS3q9jA8/+oCqXNHrCf2qVfI+XlH3yE0pi3bg2a815WWPahAacuW8a9JOqdXjQIS7VZhRxopS3XalPNODxyaaJQ5oGCzaWpRt6U79tSr63WLBMQ+JorEZH23DavHjYfEgyAhTnTES1kuNwlcLbhzQcM9WOO+QMO3F3l5lcTmRAp685980jfvOhHUX/zOmoa4bFyMuYMGCGNaa2lnEJfSibiQhfF0Ucn1dByBiceyQVkK1vEfJeyfSNMXWDS1Qlp5LneJmHKrL8xwf+iMKVx68DXEYibd4SzK+t9KmGNMCj7quSBLNel2wXK7ZO9jncnbN7Pqag8N9sixlMOgHa/lg0Gc4GjG7vma1gmZWM5oMmeyMOTk5lZwdElAJjZFcJBvyQh1g9/Ig+hfW2ZZDufELHm4nD+Xam0Bj0yBzw8tkwRpFVTWuZokOc/Dly+csri6YXVzwR9/7Hr/y67/pqrdbklT6LkkSRqMx1+ZaxtbWWCsVwNM0py5lPBOdsJjPqauS1XxBqhTj0YjxeETq8lgHvb4UNHaUtgrlqKAJa8MGyu6E3d0DitWcylrqpqE2ddjsdJLIMtcJQk5s0Iic8KRm2zxt4slRpI5WXlnRmH7y6Y959vwx9+4eY0xGkjrjFxpjFZdX1/R6PUbjMdO9YScnxDTiIez3BwwGw2A4a3O32hwcG/IuPSW2eMziuhVap9T1iiQheCyyLAu/A+I5Mk3Y90oHDtIkYWeyw3nVcPLihN3dXfr9PmenZwyHI9LUhKrq67WEbA0GEqZ1dnrCcrmkrmuyLAsUxfi1bEy45nXHm9PbViVZmvHegwccHR5yfnpGUwnyzBKNMgatM/LdXa6v51xfXdAbDrAoysopDpGmm2YaqzQgng6l23LmXkR7ujnvhTDIHtJYX5RLOMaLtVynHXWoMchnWQZWaO60hqqpQKlgLTVNgy+c1tSl8JVXa3TiaHStxShJnEqThKooKVVJVdV88P4HXF5ds14t0aQu1hFQ2tUXUKxWa/74T/9Ukn3cxEnShG3K7KbL8wbqdkgjdkMH5VvH3o5XAYPu4ZWkQOsWuRzjdrzuHj/NM/0Rxwlu3m/jCbSARm0997aQGR9LqJQUBVqv1y63w2KbmxSoXkGXOXfTAhL3fedIMka/9e+iVBIsJz5sQQdF0VuvCIqKCkqC22j8c1S7Afk1ExQ9Z030eRY3rPtOg1Ja08syiQ/NhCozCC8HNuqmoSor6qamKkqqumlDOJRYepTym6QooKHGh7VCT+OUpGC59TkotODXFcqlrZAn7yPhLc6ym/QY/s6/x/of/R9QJz+5sWluC/3peju6m8jm2GolOVRnZ+eMpjuivDhw2k3K35gQtzxfodh00Qev48Z8bC2XvBq333JoRbeoe9QU460P8WG9xXcDCLQnSB5Q9C7tN9F4ESlE2nnC9C0v4C+M2uiVdbSEZVjXYIujHEVxcLDPi0dfMxz0mc0uWS3nVOslTb9HloisVDRoK0XG8InqQt/RMbyEBaxaY1IAawp8LYwt3ejGrQ2ljI0IQmgQvZshgB9jLSqSxZvr0XuQzZZz/PdKdZPE/boTfOKAs8sdTLAuIdklZJomeH0qp9j7xNDaKfs+YdkDgqqswr5qbOPyB6pODHbcD/5epmnzQ6qqdIqct+DLNGwccCgr8Rb7OPQkkVxH40BFrycFyIbDfmCvSbUQvmgHJFAEGk2LIs1S8rznJ1ton9Zp1O/SljgEJMuysJ8LQ6TQCieJZjgc0O9XjEaiR+zu7nL37j329vYAQliO954sl1Kr4fnz56zX66juQJwv0d3XvTE1zLUNuWJ8xc8thzf+3GaNv+3YBBzx375MABDyHJqmYTgccWItVmnGkwlpllKWa3Si6PXyAD59EnZRFGRZRr/XZzQaMxwNOTk54d0HD1DAwd6+3Puwpt/vO2+S5IUopVz+qoDY2WyG9w5Le2QOpmni1o8YitfWkug09LN/B6k7kYo38g2OeC02piExHqBKf9VNTZ7l7O7u+oAJoM2DGI/HMjcT3762/IK8B4AK3gX/U75TIWQ/ifJD3Oigg+1A+mM0GjEYDIKXb71eB52tcuH/ElIm61/ylQtmsxcMBgOG/QFFUfLs2XMWiyW7u7s0jeHs7Izlch3ut16vg4divV7T62WsVqtgDFitVkynU8qy5OTkhPPzc9I05V/6G3/jtf39xkDjg3fflTg003B5foZC3KJ53qOpxIJijEFnGcPRkPPLC9ZFiVEpSqU0XpF1QtHUEl/rLXDGCD+vL25kbMuA4QWGQjwPLUOEgAifi2Gp8DHcyshmqhBe5LKsxD1mJavfD5JMHhuYDHynhuQyDMPhgMl4QpokpDrhJz/6lLt37jIcDHgxO6VpNFmehyReYywJlourGSjN5dUVeU+KIlmlSZKuUhw2nw3hEB+bbtH4M7vl/NuU/63P3bjvtvPi572qjbfdI/6sFci3P6N9Vqss3fZOm0I1/ploST48OTkJ8wZwgLQLGOT7dnOI7ynzwVsS29hpnST0fu6/ixrsdsbQ+naJhh0UTW+hCmOtxMIr9lHxCFhDyHcKypP7XSFgo9UT3fOU5DLleY/RaER/0BcmECXJbhJfGzosUjQs1jQSdljXYt1bLVguV6LE+D0wPFuFfd4ZYvA2OuvAh/88fpav/9EhLRJNFCl8ZlHZgOHv/Pss/97/Gr2adfraj098xBvo6wCvXyMvXr7gvQ8/lPGMYrYDYIk07PYVNkGPRquWfrqbGBwBM9+e0CHRTW8cwVSwpfEhAM/fPRwxlhAFx7RhQze0l/beMQjZVL6Dch6usi5ax3bvGPe3snRDtURTto42RweAbKhNReqqt08mI7JeJhvieMxqeU2xmmPHA5TNXBHWRmoeeIudCi8rHjc/ht7Sq014h1a/s67ORbLRRv8eFmujUEp3f+t/RgpMa3iQ84zLE/BJzzY6z9/DW/O9Z8JaXBiRKA9Sa8MRlfi8wBBu1IRKvVgbQIP/HLrg2hsLrF/frh21M/bFhpPGNJDIGLcsWt5bLuHDKgpNqmvxCOc6YzR0ypZSDIbDtlfdPqq1dhECbWiVVlLQzRu4Mve7zMmuNyJY75WEaPT7g1AFWaiDxQurVYqn+G5pO50BzVgSnaEyaXtTN6zXBVVdgou2KIqSsqxZzFesVgV37hzz/PlLrLFcXV2FRNwkeUZZlVRNw8XFhTOMeq9MV1bFho7O+noFANh2xN7GWA55y3VcY6pzXSTX2lyQ9vAAyYOGsiw5ODjgV3/jtxgMRrz74AEGxfX8AqVgOhkH0OdBgzfk9Xt90kSTKOXqYSzo93OGY2GLsn4s3Nj0nFfKY/mrqytOT08744cbe194Mhh+jTB7ilFPo9AMByMUUidLq1sF7I2x8B6w4Jl2ifw+1O/07JS7947R6LYmjevrfr8v10Weh/iePnzO72Hx3BZdQjyLEk0jsli2eh3Wda/XCwQFq9Uq8l5UARSUZSnAviy4upq52hsCkMuyZLlY0Mt7VFXF6ekp1loODva5vpainw8ePGAwGPD3//7fd4n6abhfmiZBvqSp0HSfn58zGo1CpfLBYPDK/vbHm+dolA22kSJGVkv107I2GCpMY6hrQ5KlVLUh7w9Rac5iuULn3mqZ4NdeVVnq1UoWgxt8iyRxiV4mG4Kxnq6rQatawmvcJMjznLIoHJuBIEOhNWzIshTTNCyqJaXr8NoNmAK0c6V6BoqqErfWaDjqWEZw7qzVsqBYluRpilaK6/ya7//ZD/jgow8pioKz8xnjyS46S1wymCZTDc9fnjAcjbmaXTMcDqXq9w3GkvYwprUobx4+pi5WrHxS1LYrNj0Tm99te/42j4B/1ub32+5x23233X8bteyr2vq6I17s/l5N00AmQu3ly5eyKbnQOx8C4m9vLUGYbbQ6fL8NpGX3f4H8o78M2tVp9aa9EO6hQ9K1hKar9qFO+VTOSug0eZSKlBx8krcKRuO4cjJY8l6PnekO/UFfwIar+ptlklBmrEsu3chFkFh25Z4hyZbDUc1OI1aL5XLF9fUscK17h4mhdUc7fTLc138W3PrYTr6IABP5WzmQpZz1x2JRaZ/8V/7HrP7h30JhItf+9uNN5o0HGcpaTl6+DOd7707IOzDddqJuWh/9l14J2myHB2S+H3xMeGsU2FQ0/H0ji2WL3txzLR1O7I3NMijMyhIbRzshYXYzQCy6x+atN/rSz2sFUc7XzftvJqZbBy6VTBq3Hix5qrC2AVuTporReESSaEajAZia5fySajLA5ilJ1kMrS0ODUQ219YyCeAyP9SDCSqy/jKkD643kGWgNtrZAutVbaUwDqg4KnKc/9uNhTBPkg+wdTVBc67puefYb4zwE8r2/T9M0FGURlIimdmDDhT8preSaqgJTO1AmylicB4ElKCc2DsnQoihprUNCrM9Z0DpBJ0mg7syzluqyrCqSntBfeqpP7b6Te3vLsSyIuq7p9XKUSkL9KKwoIkVZYBqfkCpMPT60S/rNdMCMn6nSr/J+o9EIEGNdWZUugRvq2rBeS/+vVktJ4FVKaloZOV/qmxTUdUNRSK0TUcQk58PHl5elxOFLLpAmTTOsiTwRVii/faXlszPVrlMl9b+M8WDGh3h6m5C9sbdtMw7KO5ob54V18wZHHDrlZfq2e94wxClRRMWjNAzAsG4ajvYPOT4+ZjAaBUBm6pKdnQl5Ll6NyWTCZDLh4cOHFEUBVsLo6rpEl4rPPv0xf+FXfgXlSgdYIEuljlWik6BQAzR1wxdffMHc1ZXwYW2+9MF4PMaXKpD51zDM8jAntE7I8x7rdUFjLIa2KF0HW9lWXm0CPF8Lzuubmc54//33+ejDjxgOB6yXBculEAJ4RialFInP/XH/vDfQWkuayvt5w7UnU5ICg6K8Z5kPgfJzs3D5S05ndaRGw+GQ8/NzqqoiSaTK+nw+Z7FYRCGO4qFIdMLs+pr5/JrlYgkKRoORAyYLyrIiy1KOj4/5+OOP+frrr0PNDE/hLeFxQ/r9HtPpFG+U9+9ydnZGVVVkWcb5+fkbzdU3BhpKJSiVcT1foZKCJE2ojaFarJFlqTBFw3y55OtHj6gcd3JixdvRNMIQIejWItzerRUmAAqXOGXctDCmEppZrcWVt15jm5rSxYwmro5GkiThnsvFirqqhE3EJXsrFIlKnLtZhFSW5iQqo5c5wVbUFEUR3L3GGqySfJHaGIrlGqwl1Qk/+LPvM92ZYq3m2dNn9IbX5IMBWT8nTTWDJOX585cc7O/x4uSUPO8xHI4YjQSIpGkaJkhshbGdPt9u7eh4XIxLIH61YWSrkvzq8X51vOdtVppXPXfb39uee/Me27+7KTDavz0wSxLZOM/OzoB2E4iLT7qrXf+3ligJhWmV567yp0h232Lwq/8qRBW9Yy8TTknxOaJC19hSYVpwiRSixStvDbW2vZd1CXzQVdiReOX9vT0Gw2GwLCWJpnYWqtV6Fax6WksooigcLuyqceEoVmgi+4MB/X6O0v2gUEwmY9arNRfnF6yKVQfs2k5/gOPMDO/fGvJb9izfds8Pr6J+9UqdOviQ/q//6xS/95/cmAvxEXvGtL45N+L2aS300t6qI7lbLa3nhhFfwsQ8cNiYdzFwuPEzhOu4527O5wjHtPOpRQe+p7rry4ENtgHeJtxUYn7jXIJXhBHEGIG2r7b5QeIGW7v9nmpjfXiPlwdNvl/Ew6yoTUPTFPR7Offu3eP6+oo8E6/1YnbBaWLRtmEymooC5cJoVQidUpL3oLXkF0QhSh4US+3nCmMqR0ziiT5aT4FxycriUSid8th6MANNal1R1c6rgIQySe0kea43+oQwX+NCAvGhunLfxjEbopy31cksXydKO/CvEzFqJWkiim8iBbjSTMJ4k6iooZ9jWdJVfHzF9Lpp0JkklSoQq6dS1FXNXi+nadqw2evra3KVMhiOJMIgeDKkvxbrFXnWoz8ckiRZuydoTWoUjWowtqIqS1n3WkIWjTFOkWooVuugTDVNw2K5ELpYN/cr93lRFDQOvJVFhTVtbLjf/1rvc2u88eMHrYVZEnSHQTkzpsHiEpcbr99EdOMexaKCUuxEJY2JPFqOjEE5AfIqY9s2z7vWEvMfK8Gb5/ojfqcbMmlDDt3+e7tOVqtVCK31QGNVFJR1zdDpW2maUBQrptMJo9GI2WzGYrHg4OCA/f19Xrx4IWF01udfGR49esj+/p7UHNvZcx4IRS/LwzsqJbk8X375JT/84Q+pXPE/rxf5JPDBYEBRFCxXSy5OT1AYhoMhoKTwXWMZjSZCjbsuUNSOKcmvrbiXujqQ/6ldrmtd1cEIvDPdYW9/LzCWrVYrrq+vAULBusb1oQ/Lns1mDAYDjo+PWS5XWCv1m8qyDOFP8/ncFW40PH/+PIyp92D4+6dpKiAOXBjUjMvLS+q6Zj6fs3KGel90UZGEsK0sy0iTnDStubi4wDY40JJQlkvqumG9LvnTP/0+6/WS6XSKp7oNIW5KkWUSdjiZTML3s5kk9c/nc6EgLqOil6843hhozBclSZrQkFCsSoyqKCrJV8jSPmVdc3V9zbOXLymqmizviX1rXTs6wUay8wPLlICN2E3mO7mxhrKWuNC2cJKmKd31dSWunSzF1BV1VYnLp2kYjYaMRiOur2bUZSmfG4tFk9BQ2YrGNJhaGCm8ZUUjylc/lyIoyiq0VUJNZyWm3zQNVVGytpaiWPN3/+7f5fjeW/T6UxbFJf2qZtAMyVJNDbw8eYnWkDm303g8EpfvhrvNb2qxNnubIIkFkac068KT7jVeabnhplWxZb1VjMPfthXWWwWWu95GllLFTWEaFvTG37e917Z3iA9vcdr8btMlKqDBumKLmsvLSyTsrgkWBu8R8K2XWOBbgJDd6AedMPrVfxWVD9ncEywepOCqe7vOsXYj1j7esNw11jo2HPF0tEnyeI2TJEnY2dtlZzIh6+X08h7WCs3farUmy9LAggZQm0YIrXBDrEWBSXOJMZXPRWhez2foJGE8njAajyOBP2Q+n3N+fk5Zld7/EPU/AUB5z0C79fv+k44IemA8hi5+V26jye59m+b+L1A9/qPt47E5PLYbr78V/FrL+fk54gFNaIyEGSXbwK1S2LBOIXYybIYydOeuhS35DzZovx6QtMvNW3vbe4ZeC+2O0FgHCMTJ2f6+oR20DEVtGzbPc39HHyRboIZvv9bR/WLDSOBOdofZkDvB2mrkSwWr+YxeL+P+/fs8fSpMcKapWK8WnFZrZufnMg+HUsn2ej7n/OyM2eya1aoURdVRnBpjqHwYTOEAgq1BNezsjjk+PiRJNSppQ95ilrymbiDK4egYcgCLCRtwzDIWtjJ8PoHkhOV5QppmIewoS9N2LQNpqun1sgDyEid7JJcBkiQN3PoeGFtrqeoigJs2fl3mc+rCipeLBcYaBslAqiwnYrhDQ1FVJGRopWmUZw9KqGt5vzTtgdUsFwWr1YqyErBRVzXL1ZLVcsmTJ8+xVhKKi1LGwYd4NHXNuhDPhqeLD8QORuauB2XtvHMJ6q2gkPfyOSGAtgmeGjgGAU3TtIYa5YGBcgUUY2+oCoxXxlikuGK3zpcPedFKk2phWZJQkki+YCWYz3kzrG3XOEqFXI14n74NBGx+/qbGv03P/W333XY48Q8oLi4uuHv3LuPxmNlsRllWrIqCVVEwtYY0TRmNhlxdXvDOW29zfHzMbDZjNpu52g4SLles1xitHFuRJlml/P7v/x7rYsVHH37C7u4+vV4vrJ2yLFmv13z+xZd873vf4+zsTICIU7S95Xw8GTMajbi4uOLk5UuuLy/Zm05ctWrFarkiTVMGw6EjIDDU1ToAbBUL2dv6w1pHDCPnpyrD2oavvv6KFy9esLszpSgK+v0+q9WKi4sL6rpmOp2yXC5pXFj2YDBgZ2eH8/NzBzqusVY8dIvFgs8+k1os/X6f3d19Hj16hLWWi4sL3nnnHebzeWjP1dVVoKjt9XrMZjPOzs64vr5GKcVisQj95A3Vq+XazQeh7hbvxFDmulKURUXeE6Ij0zQsHJV4mkoonL9vVVUunK6mqqS9HlQAoS98yOPx8fEr+9cfbww0/uTLr+jlPTIXc1lWjqHJWprVgrIsWaxWlD5Z2zq6PNO6IEXo1FjrEJZOUYiQl02mIUstOtHkWUq/l7tkbWFxEnNMhk6sMDsld1B8ZQABAABJREFUCVolIU5R9kLDznTEdDrl+uqSxXxBVVRYpVGpo6Jz1T2rqkRpSI1yhZgUwhokG79SioQUlKXRwnBlkIqZFkuzhq++/oos6zMcTzhSx2S6hiRFpSnz+TXl3i51VfD82Yrd6Yjd6YQ8STBKk+UZRon73GJD0tvWBQES7+wtok6pMsqG3/3Rcc86K7F0jbcZ4UDCq0Y8ottsTaThh3XUeFZiF4JN1StJm23ympryPxVhYRh3A6taa64XSsq2/EVB2fO6aWsHiu7nFYVGlMhU5sbVbEZLBdrQeM75VlPCboR+3Dyss8Jr0sMPSfYfEFi9PODyeqbFhQ2IadcDDBsskD5cyqKsy8+wtEw6zurp8YV7S4aDAYeHh/T7PfJe34GoC4pK3NIA63XBerlyYYGlK0CpXMV7Z6FTCq0TslTT6/XoDwcM+n0GA6k6ej2bcdkYJuMxo/GAqqzRiaLf73F+fi5CT7t54ECneGD8K9tgYdfa55Q4hYDYQ6OlD1Q015RFJSn97/xLNM9/gHUKy+aG6hXZ2+pqdA/xJC1XcxbLaya7u9jaYNEB8G0iRk85qsM50Xd4z55n2fKfu+m5AeL9eCqXae0hl8gsH17mkrRte6/OvHMfxuA9GCbiZ4W/6/CJt6jj5pPMORu8M5vGCFGy24Jo/r4mSBN5qrdXxJ4EYz2gEFkJbU5U7RKVq7rk6vKSLE3IJxn37t3lxYvnLJdrUYa0RtkZDx9/zXK55uTklJcvz1ivCrdfEOabdbHagAubqEWup5qDg30Jf10JyUfWF6uq1kmgbjamod/vSz+5jVsnCYn7maYJylHHKUVQAowxJDoNhg0/D421wbjUGBPCJjwQD6xOLl+jl/dIQ52AhsuLC/r9Pv1+X9ZPFMqUpX2KQuKyK8/6ZgHjmHiqmqZJWK1Kri7OUQi4uLi6DJ4AH5YhOR9QlU2gbI09BqaRPBE/57yRxzi5TTRvOivNGGclNgFk+imjHamAJyMIRkc3R2VOysk+rFO89i6DzSvw2sszCVXryoZ2RXgvU1yo1z/XhufKyrFWjB3GGmoUifMQ+R3Ue8Q8Bav8ax+qgVQLi12Qs/5rF88fezICKLDdNnd+82vPvV+YYy6/zLpne6NiOD96f/++ASDToLTianbOO++8xf7+HpeXl6xXC+r1gvV8xjliwR7kCS9enGHvHXN8fIdHjx4ym824uDhnNBq6MHXFbH5FY6wLA9T0BwNmsxkPv3rEN775LQ4ODkJc/4sXL3j06BHPX5ywXK1ZrwvSNKOXD8FqmlphdJ/D47dJ04zLsxOqQnIUssGAwc4OdWNYzucMhkPSfo+zyyu0ypjP5qEavMLLrlZeeYOO75O2/8Vzd3z3iMvLc6QC+ZKyKCnWBVVZSShf3bBcLkP9n/2DA9599wFVVQWykfPzc1arFavVmg8++ICmaZjNpMifBwm9vMfh4RHvP3hAr99j0O9TFGsuL6948eyZm9Oas7PTkEOjtdTC6PV6okNXJdZIaGS/L+FjaSY6QL+f0+v3qZuKPEnFI1uWZFlKXUlhz7t3j6nqEp0osjwnbeReVV1KbQ+lQoidlwtpmjKfzxkOh1RVFbw8rzveGGg8OruShqYpiRILTZZlgirzjLzXo2ksBk2SJi5cKQkKdEtv2Lp1dSJAI/GWCCvWf2zj4tolDs4AtYs/tSpDp2Bq4azWaNIkDUnk0NDUJavlNVrD4cEBV+czFoulTDhlSXsZymhUJhR3ppQkOREsurVmWQO4YiUo0jynamoaW7qiSpY81RhTMZ+dUxULPvzwQya7+8xm1ywXM0wjMaLL1Yonjx9xsLtDP7tHoiwqS4gZUkSCeEU8UnqUbPBN4FoXZdZ6wava+FIfboOSTdMr453/25ZerXPY+FdFN3O3bYs01ytnmwqRAxmbSVlWBUsKrg3WMdBYZUPysxecFrEapegumU27ZwXqVQ8y2m9kM9CJWKXqWoSGf4FYeb+1A7Z9FwxXiv53/kXa6tyqTd6OhJzj2wsWt/btwSd+d4OKWi+BcuPr0YvWCdPplL39fbJcXJyrxZLlciUgvjEsijXr9Urimp3VTiWSq4GypIinxCrtivEZyrKhWM+5uroiSVNHQThmMp5gLSwW18wXM/Z29phOxyxXa5SWMKvT01OMaqRHA5BQnW7UThkPziPlfSEqDII4OhwvtL/Yghrsk7zzq9RffbczEpueBA9YA1axN8Mp/NwsyzWz2SWjnTEWZ8bSBIW7e7j8Cj9i7h2s/84K0UB8lVaKJMiO7uHstG5c3Rr04xzkgHuGW1uhOyJFzyv/XrPvhIm57ySPpg436IRkKJcPZlqKR4iYkYI1X9aRV4yttSFhMmZRakwTPreIZ229XjOfX1OVNVVdkaZJFLsuRoTj42P6/QFpkpFlYj09OXnJ1dWVhE80a6qq5Pnzl5ycnGONpixqmkbyPHw9G1EmK7RKyLKUvK/pD3IODw/Z399nOp2GcNjheBzCgbZZkGPPemCK0RIq5Q0snoGrqivZv3zBLBdqlTpQX7m8Dg9MrJVY5ySVdWnLhropKcqaxUpqMqzXBetVyfVMjHftRi9EDWUh+SDWWJbLZZgXkofockSinA7v2RUsYltvbwyEN4xUnTBAfB5lPMfFqLdtjlvrqHrdumhBrzscePXnxgC5JTHw8z0uhGi6Bgzbrht/v3j9d7ZPBbHHsJ03uiNLZM93dL21AYowzzf7Kf67Vew1iRaAsUm1ixagGTxkkTEt9PXWPan7rDjk11erljbYzs+NXu/ISx+3OptdUdUlk+nYMXOVlKs5zx6v+a9+8inGGD755BM+/PBDTk9ecu/uW9y7d5fVasnV1aUQAyhIMwHtSapFZngmtMbw7PlzTs/OyXOxgK/Xay4vLwXEjMZcL9YkScrAhUPVlaGuLePdPXZ291mvVqyW1+zv7XA9X9AbjckGA2Yn59RlzcHxMUZrlus1eZYxv5qJN1VZB/ja+RX0HrvJBKbcs2uePn2KMSU6GfPpj3/MoD9gMV+yWCxCqFlRFOJtTBLGkzH37t0L/Xx5eYVSmt3dPQaDgidPngR2ssViwfX1NdYY7t+7z/nZWfCoeeYnH6bYetiUC/8X77FB6lokSULmwsyyvIdViryXhoTx5WpBmiUMBz1ms2uyLCHPh1R1SV2XVFWBMUN2dqesVitAcqq8UaQo1uRZHnIz+v1+kDNKCTmDUsqFpL/+ePM6GsmAbDSSmMa6Jsv7ZGnKYH+KSiQkxVhLLx+RpEmLuK1Q1yolQlbcvRasIVOQpUmgl+znPek8I4nlFxdXiKNd0csyUJo8UxTlkrSXSlKckVjeLNUMhzlNU4hnZJDLBLm8ZJD3UdZweXUl5eatRQMaTZbkJH2E7tQn3DkGhUQpGuMYFZWhqY0o+6mW+6DBEOJly3XFT378GUopZrMZTVXx2ac/5s7hAWVZkGcJz59OGfYVBweHoGp02kMYFOKkO29paZUurRRKJ07RsY7XEhIHBiJDaKv0KXlH+UsUemH9kpj28Dj/fSykTPRlfAQtXcUFoNujU74gstDEOABwyAhrnXUrbG6tIuWtEZvP6GKwVoGKNwRrrcQya81ysWS9WgWs4DeiuHjh6w4voJRSqN6YdPetVjH11tXonUWRdrSPYT9WLVDy76/CaOMaBT4nw/dzotnb22NnZ5f+YADKcnl5gUYoF1fLpbivDSRZQpJlaJ2iVQpakyaa5XLOqlgJ6cFoKlzmFiRPqgZTYkzN1WzG5eyK0WjE/u4ek8mUxtScX1zQHwzY290j1SmJTkmztBNnKrUI5D26yeJuXJT/2kENPwGVS4gPaklLG5t/479D+dXvEsIso7GOFYRXHl5xt2CamqpcozHkiUKhSZ1nFVqLqQALz17U1vTwr+SHOwlOKz/u4p3wuQRbGuKe5BV5P8+7dT98m703IUI4Dii0oTydc6N/NJJkK0nDwhKIs8qWrvKycSQBPpencZtaNwZeYqbFyifxyEopBsMBuXOh+/wF0wjQKIqKZ09fcHExo2kqPvr4fXZ2dhgMBozHY6bTKVmWS95BmpAZTZJClt8lyxMXC17R6w3Y3z8kz4acn1+xWl0EymoPsrRuGI36jCcj9vZ22d0bs7MzJU0ToU1NhaFIimlJPPp4PAyKf0xTbK0N7Do+zKMpDXkuoR8GyfmT+gJgmgZjSiwEq+Z6LfHiaZ6yWCxYLJeYpqGsJOGzKiuaxlKWFeu17FfeYuirYfsxjRVdb0CJQ1rj0CplWpKRGx6qSEZ1Abpi0yPYTsFg9ujOTf/9BkD58xwKQmE7f/iQq3idb8qAuC9uC1naDDHyltlNpT9WQjfBmL+n/84rgd0+aHNCYlpTMZCKTI/X1Z+n33zC/23Hppey8y5Wvl+v11xfXzOd7kT5FyuUEg8gSvHVVw/51rd+jouLS/b3Dnnvvfc4OzujLEvm8zn9fp9er0+/16esKvq9jDzvk+d9B2oti8WS9Trh+vqauq6EnEBblosVNJb+aES/P8AYS1FVpFnGW2/dp5fnvHz2GGstvX6f5bpk/0CqV19cXGCBg6MjVk6JH6BYzBcuRPEmmI7nfXyILJaCzhKtYvjOd77D9fU1s6sZVSlsTPv7+1xfXzMaCWnQ2hlUTk5OGI/HQRFfLpcURcHV1VUAJj6nAiQk8IsvvpCwr8GgMze7hBNSvyLPc3Z2dpz+nAbANplMSNOU5XIV5lssz87OzujlOXVVsVgs6PV6gfrWy32tdbjPer0OdMfGGTI8e5wPNR+NRoxGIy4vL8P8fqP5+kZnAdPpLgphpkl6UtVQK+X46GsJYdIiiJvakKUpfh00jv5v0MukojaWPIFPHrzDRx99xGQ0pu8y3vu9PihNaQz/4B/8Qx49foJOU5JUgEYv02CH7O3tMxlNKJYF1lju37vHvXuH5L0EY2oW8wXf/e7v89UXj/jyy4ecnZ9zcn7K+x98IGwZSpEnqVNIU7CWytEHxgnqWS+jMRVVBbUpyfs5iUmkqmhl0VYKAzaNwTYNVd2QJJrxsEc/36cqCy7OTqjKgsTWPHmcMxhAmlh2dg/pJym+loeKBISiZV6ANtK6tWxGQVbBmtwuHTp/RRZ1ZUkSv3HYjmBvL7CtNX37HtNx7d74xhtOuu4OYreltyZ5JpT2Nk4B67Q+3NCd79tkw/OVEiXXOkVWWamRooD1ekldFqG9wjd9s4bH6w4vDNI7n4DOgnUWK8QHAr4k5tlb6MRr4+pe+A61EZy0LX2ha3xk2bagFUdHdxiPxwwGfdZF6dhuDLOFsEWIVy+jlylMolFpjk5ylJJ1o7Wmmi+dlc4wGCcMJzuYRsItkqZmNTuhKmvyXo4ClvMlq+WayWTMwcE+B/sHXF3NeP7sGQeHR4wnY3SiuHfvHs+fv6BxTBoexAV13bbvo9rXFwuNBwwudEw5ZUgKbDoVpz9BT44xV09vKAzdDdRP1u2bt88AscbSuORFay1pqsi0n5veu+rnUVuR2vql4n6xpm7bYHyFdPFTeSrTMIZyYlhXHUDgvAbGAQIPrmNlx4ex+FwEaJNiRRS0Vuz4mtyZoqXQlPxee4VW6c6y9tc0rnJ6vDHHxdsWy7njWrcU5SAaC+u8JKBVhmksn332JfPrBUmiuHfvLvfvvc10OhXOe52F4lxCWVoiBV3h4GCf0WjI5eUVq1VBUytWy7JjJW6MIdGaXr/HaDTgnXfvMxmPKKuS8XhEr9dzXvc8bJ5C/9xHqZqqMs7LoKlKAQHr9Zq6Eg+MBwaL+Zx1UbJelS7HsGa9Xgd++W5iMtE4tHH/cRKvsR4wKjoFc4IoaS3TCkBJdID3Am6ovmIEQ9HUhkS1yu/mGohDbuL1s6mExvknRLIpvp+13pN+Y5n5ZuHDVvz5P4tiHVdN3gQaXpnaBBeh7VuO4XDIL/zCL/CHf/iHwSIbK+zx/WOgsQmoOn208eKboUr+/konWKU6LEHbvEqv6594/OJ5deNw+7Zf1/48pVpiBa01T58+ZXd3j7t37zKbzVitVuzs7LC/f0BRlLz99tvs7uxRlQ2PHj3iww8/5OOPPw7Jz+v1mtFowGQypShKeq6mRprmYEWHKV1Ing+3kfwYYcgbj8dSIsFa1mVBg+Xu8TF7ezsUxYrT05coIxZ/nWYcHB5RLFdcnF/Q6w85ODpmvlxSlitsVTsvS5xc3+0Wnx+0GYbrPdcWSHTC1dWVqxOSB1A1m80oigKlJJ9hMBxgrCjkL1++DMBgPp+Hfl+tVkGB9/1froswf0uXR+yTrf188Ynx8Rzp9XoBSKSpGDE8yYFBoTwbq0s+X61WlGUVcip8+3Z2dlyFc01ZFQEMxYAiyzNs09aPEZph6StP7uBZuN7keGOg0UtckTydBg/EoNcTi46Vyoy9Xg+tFJVrbLleYk1Df9xHaUWiFYPjfXZ2JkxHA1RdUs6vsJmmagqefv0FZVny9jvvcO/td/jk/XdoyhWroiDP+wyGQ6aTEdiG9XLF//M/+7/xxWdfYBrLwf4Bf+2v/VX+4l/8DXr9jL3JhDzR/PEffY+vvnzEyekL0Ir51SU/9/PfYTCcYBqpYIlCSsrnUm2xKkspfoRFmVqSIxONSVPWjbiuq6pCG+jnfXppgk0TylKYNapacgCWyyWrxZxitSLPU4pBj/OzEx5lBmUted6j1+ujXI2DoDtjhRlLi3Lif3qGIGUJcaktMBHh4pPW2kUUBU25e8eW2e7RQhJfYMsLpq61tbUmdne+1v6l3LOJYnFjV3sr0F27TVujQmsd7b8RILIEhg6/EbYtb3+xVrjtdQZNU3F+eoJpasnP2bAKbkVRW46wwaUZvW/+dWeFxxUj067fLb7Gr97s3GCNtls+k3EL8cz+OwVHh4dMplP6vR6r1Vosx1XF+fk5RW1Ik5w8y1FYFvNrStMwHE3Yv3NImg5QSYKyljtac34iIG6yt0+vPwKnDJi65Or8BWVVUzUN08mUxIUQXs3mrFZr7hwdsbOzw3K55MXz59w5PmY8HmOs5e69uzx/+gxjmhb7tXr/hrRXATV7xd3nEcvf7pdQlDBh+Av/IuXv/p+oa3Ujzrrd2CX+e1toCMQeKQu2QZkKUwm7TS8ZBQ+X3yCsFcYiD3xDjQIfkmIrfLhV4zIJm6Z2ScWu6rLz8ja1FEWryirM3cBO1Pi2WhpTu7j/JKy7+F2augnes21KnFd0k0SMQMu6FuNQ1Gcyx4SZzCcnx+uONEFZQny6zw0Qpc+wWi85PT1lNpvx3nvv8cknnzgAgIuDb1CkrJYl1jbOu924e0hoahuiCpiGWmuUSpyVX2or5Xmffq+mKmEwsPR6K7SeBWIRhWI6nXB4eECaacqi5KKuMU3Nel2SJlehn+u6FnneGKpGRfkIhtVKQio3QUOMANrqxO5TJeEM63XRUSCCgmNDXUGwCoWrCG5p72v9nPcKju0sky4trJOV+MJwSSsmbCsyNJpY0Q3zPrrPpvV+GyjpzBV7U6HephTHAEcr8VZuApjbnhUUYEwbQrsBMPz1IbE8rNP2vTa9BZttLMuS1WoV6EX9vPfKVXydBznbQMs2QCPnms5c8J43X2/BuGt9fk+7B73ZEe614cnZBFxa6J86bevsreEazfn5ObPZNdPphJ2dHS4vLyl6Fe+8/YDd3V3effddsqzHwcEhDx8+5OnTp9y9e5fVasWPf/xjrq+vWSwWkg/p6jgFkNE01I3UjJDmatI0p2nEmDEa9EmcAltWJUVVsX9wyPFb90kSxcMvH4ocW60oypL9o3skacbJyQnFquDdB+/TH4559uSENFGcPH7q33ij5yJSB9cvceikzFlHFOMMRUop8cBU4qX1feevmUwmVLUo/cvlMnixZrNZx9ijtSRb+zwL3/c+xMnnP/jvPYWwD2HyCr2fs358/T63Wq2EZct5XH2ok8/DMsZQuJop0BbFrqqKNEuxyP0PDw85PT0NoLVyNe38Gthk6ez1evR6vcCM9brjjYFGnlQCMDJECWkaBlmGymRON01FhmyGu46beXLnLnvTETu7U3Z2phwc7LkKpA1XF+ckSvHF559zfvqSLEnJHIK7OHnJ9dUl4+mEb3z4Hmfn52R5j8ViSaIsqc74f/zd/5zf+0e/CyhMYzk7OePrzz/n9PkLfv03f4UkS/i1X/sVPv3JZ9RNTZbjkpEMX372GfffepfdvX0XS5qKcq0l5yPJUqzbTJqiwDQiiBILGVDVNWWxpikr5qbh2dPaCbDSDbSr2OqS4LWSELG96Zjd6YTf/I3f4o/+6I/Y3T1gOBwBRsKi8JYgp3hrz3il2qTuCCQobx42XrXHWaHawwdqBMETwMHNzcNab9n1CzIS+p17yv+3A43Y8kX429lpO+d2LPdGknUlFjGKjPe3dM9pQ1sk+e6mPi/QpGlqBv0+eZpQrFfyXlZJ5VpPi/kzeDT0+A7J9G5rFQwt8BU9naKsnLBX0TjR7X4xcquQdBzfDSUUezvTKb08Z7laUdcVq+WKy4tLDJos65PmPZI0Y71asHYKpbGiqFUNVOtCClWaivHOLtYqVuuSVdEEpSBLE8aTHa4c/3jeH4YNuK4r6rri6bNnHJYH7O3vobTm5YsX3Dm+w3g8ARTHx3d4/vyFA8CxFT8eGxW8GrH3IVbrULhK4wK6rLXovQckvRFZVoS49FgR8BtwR+G7oRwRPGJZolkvrimrAmsViW65zq21oZpy1ZQS5mIkyTZUXHYCvHZVbYWfvMQay2A4EGtQpKR4hcMrTD5J1If/yNu7RFilqFWNDyazJi7qJDWA/LWJTrDKulykJBRX88/UqpuQmrjEZlCUdeXaJSDZK1uixEOaZjTus9AvjWG9KvjRDz91obGa7/z8L5JlGYvFgmJdkyQZSmvyXkaWJaxWK5SCoqi4vLyiLCvG4ypsotKnQmValCVrRxe5ckmiy4XkHDW1sB75TbyqK87OTrm+nrk1ZYNRxhtbFJLMqBOxECoUJGkAlNDKL0nUNYEwIVr1+DC39hOZb8KkIzPby892vvm6R16x92ugnect3YYiktQRcQIdAadQIUektZ77+hqtAWYrgNjQvV6lkIe/t4D19ndAbw/dUaqVY/H63LyPXw+BctwKG2T8Dtv++Wvjn/Hvm94Xf6xWK773ve8F67HWOhSuu2Hhjrw+P+2xeb0nw1CoEPri15ufG1vwzCuPTUNDDEJkX+6+z21H0zS8fPmCjz/6hmOVuma1WpOmC7Is5+JC8il6vT5HR0c8e/aMNE157733APj0009ZLRc0TU1RlBTrinm2QgXvGlR1W21eqFtdJe9UPHxFuaZBsX90wLsP3mM4HvH4q6949vQxNJ6MQHHv/ttUjeXJ48ekacb9t95huS65uLxikiWcnT0PWoGXn9JH3ZpgndwZcAZME87ViWY6nYb+TNOkY8DyinyaZZ08GR8e5ZPeveXfgzzvQbOKoIPkrnihr6/jz/WeDuiG23nvhwcMfrxjgKGUUNz6c7TWHXBdlmXwYiSZDqGwcTiub1OWZQFoeODk5+82EH7b8cZA48H9A7eZiem9KkvSJGU6HpNo6+JhB6FBg0GfqizpZQkP7t9htV7y+KufMJtdkaUJSiecnV1iGqHPdOONMZbLqwsm4yGJNlS1YToeUrh7XV/NePnylB//+CfoJKMqKuqqFvq9xvDdf/SP+fZ3fp60l/Bn3/8+e/u7VE1Jr5dLOJcyLJcLnjx+TLGuuHvvHhbZuPygKqU4Oz9jdnlJvVhSrl2Rn6qgaSqxXBqp4Gqd5dXnFRjrij3hpIf7ZxtLnqX8K3/jf8jB4QGNsXz55Rfs7u2ykylSnTo2FcfmgcVE1Ua9gm2scWDE12NQYFMUifMM2M7mZL3CYomkmQcV8ebpLWNu81WCsnWSoJS9IdC3CfrIl+FPjPa3DU6njWfb6L2sbcM6unBCRcJZQdNae+PPrZU4+TTRZGnC1dUlWGGIsbpNBmzB1OsXjBcm+Yd/OSjA8iwPjOQ2Up3YK9iKkKChuu8bfvPj6Ddf1zfDwYC9gwN6feERr6uK5XLJxeUliUrI0x5Jb4DO++S9nOFohE4TmqJkMt7h+npBbYR/P88TBr2xi42VML3ah/qVpYT1pRm7e4dkecawP6S2hmK1QlcFphLShNOzM+qm5s6dO1gsL09ecnTnmPFoiDENhwcHrk6Fe5Ooe22kfITuCGAtvDggyeqtx8pi0wFmeh99+WUnnj62kvpYaC8wO/MVZwFtGtJewnJxzcW5ZrVaUFYli/k0CHcfT1us18Iy0rTAW/jZE5rGoBDA4K1Kvv5OU9f0BrnIBC0bS5JlKCBJM9I0dx5KgnfC0zEaa1ySX9YmrLpN0csXrbVb923IhFAUu6R7Z820clGYhlKs1FlTXX6cD0O0dnNNSNK8dbJMvAENRVFhbcLxnfvkvZwHDx6wmK9pzIL59Tx4TtbFmmdPn3I9n6G0xRjFZ599zqNHEm8db/pCt9hWqffzpg0RkfeSdruwr6ZBmQajfOJtCp55yiisbcL7ZGnf9XcS2LBaq75ulfPmphesu/5jpVyAjY7Ck32/BRAJIddCKSebbcuoFIdNCZuSBPdppdpsHRGMrUHGPxzvaQirJ/Tnre13CewdT8cG2NhyVQuQNoGLUh263k3QoqJnxOd4I0Gs2AQga53nyZjOtduA021gYtvf8ec+5jwG0LFM2by+S5H7Zkes9Lf/NERemRiMvOketPmM2z6P3+V1QElrzYsXL3jw7nvs7e1xcHDIyckJq9WaXm/F5eUVWZZzcJAwHA45Ojri8eNHNKbhwYMH5HnOF198zuXFBVoLRbSEfRtXIyppw8ecAuzbJNZ8kXFHR0e8/d4DBqMxj5485uHXX/Lk0SNGowGD/oDj+2+T93o8ff6C5XLJO/cesLd3yNcnz6ibhrOrM0xdo3Tu3qz14jRN16Mbe3bAzS/vLQTu3bvH7u6uMD0pjTW2rS/h1tH5+TmNMWQ2C2DZK+fr9TrMm16vF+RdqHavVMiH84q7UorBYBA8GH5eeqNWHEbV9Uopl9dlg1fFy0h/nzzNAr2wX3NZljEej9nZnZKkSagF4iN8fMK5NV39xHuThbhiHcDQ6443Bhr/3F/6TUGnZcnl5aUs2qoObvOyLEkTzWA4Zu3i0t66dwzK8IMf/ZlDe744SYlOhJ/aGS5lwLUIxCzNeO/DD8nznMViyen5ueP7HXJ455Bnz57QyyVJpipF6a9qcSF99vVPeHH2nLffvs/F6TnnZ6dkSRoGeb1agq2wDZyfPcGYJbsHd+gPhzS1xOd+9dXXvHz5kjRJ6KUpGAm5UEjGvzG1UwxaS6P3Myg3wX0CJtZiEwEdXz18xH/8n/yf+da3PuKDDz7g7PSEp48fkaeawWAoglu7zQkkSboRd543AmtLiOX2djBrq2ApVVin20rnascwRCRERbGzgew1KCa2taopa9DWon10u41Cqbwi1wESuE01EnTOVOMZEzyn/A1B6Baf03rQtq2Kq5WbGO4BXolXDhlp1W7YrYXSAoZeloI1XF1cilJoHd2vtQ48bYSE4WuZ3CacNTobRpdEsfvKTWTlZ4HHmJ6tyFsf27Rn/HX+XPcqSZpycHTEcDikMYZiXTi2jitSnZBlOWnWQ/cG5KOJJKqahp0dRVkWGBSDfo/RaES/nyPTz9Fphk0zQeseWo2wxlBUJcvFgsViyWy5oJf36Q8mpEnObL3AGmGluLi4QGvN/sEBTWM4efGS+/fvSaymtazWa65n126s/Ht3ezR0By7MT7mZbMEGhoFWGQdL+v5fpv79n4S5H1dlhaiIlfX2rPAkFD6noaEoG/70T/+MyXRI09SOZrtNAvXzUhKgCxeOlYQNUixQUk1YKwVaU1QNf/THP2Rvb58PPnzAzv405AnkeU6W51gjVZE9cUQLVD1TXBSeo6M4cG9JtwT5aRFqb6U11qjw3t4IkaSSI2SseAIaY7C10GhXNBL2syqc4tWwXC6YXV+zXq2FWKAoKIp1cOmvHGtKWVSsVuuw+T199IJ/9N/8brD2S46GxRhXoVtJ2JSERRkWi2VHPijlPFzWhnWpXe6fwgRjfaI11tSBA08phfE0qWrTa9AymlljUakny3AsQ9YGj4EwhqnAjOaNwJurX6ahCn+piFjby/tgW7CezUjTKEWDxqLxphMdintqqRMh6IJEWVAGS40iB1IsjXs3AkDSbnZrVwl8U5Fs5WsEflCtLAovZdt9RqnAVuXlldaiZDTWizYd2YacXI8UuLjf/Hmxfm6tRAwYI0Y3lfj8PEMLrW7K3TdVmF91+Gtj67JUDO8Cmfjcbd9t3u91z+zM88QVNTZtfoRXNC02ckBs9oMzFXo5qnzIT+utjEFYG47lz7/5PvKt/15yaL/68nO++c2f4+7duyyXwrIkYXpyzmo15+Gjr6mqkrt37/Ls2WPKcs39+/cYjoY8e/aCJ0+eOAYjSHChl47oBu2UXBqaRuanJmEwmnJ475j942OSLOHLr75iPpuBC0tKeyPy8S537j+grmueP3lE0h9y9733WVUVs5NzdvI+nz56jtYpJhTc9fM+CpF28y38xBsbhCjDWIVSltFoIKHuxYrhaMigP+Di4rJjyFquF2id0OvvBU+G9yh4MB1b/2OwofFFPOU8730oy1Jyedy4GaVAJ/R6fXxIJgibZFyLpm4aEi2FS/uDASDeFaWF1ChPUtIkpW5qVKIwvZpqtSYZT5hdXEnKg1WkJNjaslgsUFqxLJc0taQKtDnDsvaNEdllmjcL/3tjoPHwyy+w1kqBl2FfqnZWDavlIvAGD4dD7t69y9HREXme8+z5M05OXwbE6C0giasU6YWicagJ7RUuxeVsxnQ6ZTQZM55OGAwG1HXN9WIhSqKr6pkkGqWElq5uStblirJagzKcnLxwKE1ieJVCqpNbSVq0Vc3VpWyOO7t7jIYjnj57zvLqinGvJ3GVRtgItErIhkO0EspPrHFJTd1DCja1SkTjYhSVTrheLPkv//7/h3/03f+Go6Mj/rV/7V/j8ePHjMdD7tw5JstSdNK11LTCP7J6m5ZD2y8mWSTuX1BmFdYol3AaAQ2n3JuO8IkFXKtAOzzRClsHorwQ3SaEYwEbzsNiGkIBRN8GCVloKROttWhX3MqDLRvdO+m461W3X6wFl4ydaiVJ71YYmrwV0tLmnGzApHDPzfdxXQJpj/T4W04vlufElk6UihQZAvByAcsRMHOjoyLYobxabNnf32c8mZDohMV8RlFWIugSoa9rqopK1ezsDsh6fcqqplgtsVXJcDxhujMlSzRNXbNazFgvFpRVERKBQfo7TRLyPKc/GNAb9Nnb22E6mTBfrJhfz6mqmjzLKNYlVV0yHA5IdCoFlnTCzs6Uqiw4OT3l7p07lFnOwcEBxXrtqE7dq/v+o90QfQK49LgbC/+dSpCIbTcBlSI5eI9C50AZxjxODnYTIChKLd1we4iHTvPFl18yGvfJ85w8z0KlVz+X8zyn1+szngxdfQVCqIVPihv0RyiVoFXK9fWa2WzOxeWc1XrF3Xt/kV5vIOEBSQJWoXVKGrnJRRbKiIvXMKGpTWvFcmuhLIoQytW4EISqrtpaCJUwkHimE19Reb1eUzsPjadjjOsk1JWlKNqqrt5tv+kh9P22afndlEld67UYPHDrmggAiqjxntgwMZzC69j1lISwKu3BQ7u+NVbAqPFzIHVtsPiq5copb34phzBMh1z8zGgVRvcuN2ZM+Dpqg1egnUlGJSh82CuRLBPvSZplzlhiSDzpgJdzznpomqb1NtpE6lApBSTOayKyOUk0vXRAXTte/TQJoV7iAYe6bgIoiUPEvGy94XlQN40/WLd+PAALhA6xVyHepzodBXST1ttnSpjmgwfvsLOzww9+8AOaBmySCRGAbUJoUcw49brjTUHINi/IqzwD3ba/yXO7HvfOWon6q+vNaCmI2++8AS6+tw/N296eTYOLaeyN76JbhV/8nvrixXPu3r3Hzu4hb731Fl9//TWLxYLEUcT/5LMf8+KF5EDMZlf89m//NhcXZ8znM+6/9S4fffwxh0dHnJ2dhTpLVVVRGyECMo0AcKsUSZYxHk843DtiZ/+AfDhgsV7xxZefYUoJwU+1ZndnD9I+733wCVk+4OsvP8M0hvvvPmD/8IgnXz+Cpub69JJisSDRUm8lvJ0VY6I3WnrQ4UssyDk+SdQbOqxLcLb0+j1XFFRC4NdrKYY7Hk84Pj7m8vKKohCWOW+IU87A0dSy1/j8DT824k1JgpfCe1f8/lKUFVipRyI1ScQYk2WZKzjZoKwzNDnQk7rk+jQR8ossTdFAsS6oqxqViKGrripMYyjX4rXPs5zlcuny+pJQdNPTlHv9xXtyvGHDAyRr21yT1x1vXhl8PkcpePbsGb1eznA4YjKZ0Ov12NnZCRUDJ5MJZ2dnXFycS4VQJ/xrlxFvrQ1uIG9hiN1YIPH1L1++5PHjxySJuOy8BaCxNsSzGdPG1CZaY5IEYy3rdek215qqrClLV0ncDax3X1oryYdlZRkMBvTyjMloyGLQp6zKTrKWJIfiKq0mCLjrLvrNGHHPiewnvY9rXixKquol/8V/8V8yHPawNKR5wnQyluJQqkXOTh93VibHX74NfFjrNgS18X03qc0LPessWh4EQLwht/9H9sWwSP218X/R/kKIFUZCIvy9jRXGG9833uWmra9uHllkVEpC4tqfAS7eXGtQEXMVUeVmXPx6NCRCvWa5vp6htVMMEHacbRuI9OUtm5aCZPcdVDbwJwcB5hdkyD/wfa1wrFIEq5V8rbo3jkBevz9gb29P4t5ncxpjHZWcFNUpq4rlfA56zXC6h0pyVssViYKjO4cM+n2qquTs4pL57EroBN34xaDJKkVjoVguuL66RKWawWDE3t4euzsTRoMBZ5eXrNYLeoOcciaUpePxEFNZzk7PyLOU6WTKqavWPBqPaeqa/YMDXjx/5izLfirJO/q57IU7vg+d1Uv0GXeS9dz5CtI+VrX0nU00l1plym/G/mhnctN4er4x/f7AsZ3kpGkia7/XY71ed+K3xUIlirmEJgpYthbqeilsQEZiXu/dv8/52QWgOHl5jlKpY1kRr4nkXGnWRctYJJvUytENQlmIR3Xlii1aLGUhCesmYqqJDRCe2CBmdAvWM62dR8Sv/bjvtfM+dMNU4t9jD89mSEa7XghjEltWO9+h8V7JCDdIG53FdBO8+BCDeD3HicJGOy9pyEF5M2XzZz/8Go1lhAKbgM0Qpc2iaJynpCZNpJJ6L0sZ9PuMRwP6eUZRlizmKzG8GIvWOdbCYDBiPJ6Q5Rn7B3tMJhMODvbYP9h3Cs6ID97/mK++fsjf+Tt/h0ePHkl1YreX1Y2E8UrVbqlxEO8FXv61llmxLjd1G54a9mOk7oPWsYIbFnOnH/ycauO7N6nD29yE6e6Iv/k3/+ccHB7xH/4v/1d8/fVjF46tMZTBcBMTGPz/8vipPCluXbb0y3TXq/t7E5wb24bHxd9vf0TbrzoypsQApx3r1x8xi9Wnn37Kr/zqPru7O5TlPZ48ecJisULqgwhtbdM0jMdTdnZ2GQxGnJy85Mc//jG7uwccHgr97f3790PdiaKQSBODQiVinc97fXr9AXkilKqPvv6M2WwmLHIqYXZ+QVHUGJ3w4QcfMBqPuLi45OXpObs7+3z0wcdcnl9wdXnBeJDx2Y++AC1lFLoAeCMcTnFDhuEu8YaOJEk4Ojrk+vqa4WiAtdYlU8NwMJDw2vWa07KiKiuWyxW1Y4KqSlfg0vV+Ywz9Xg/l6s75/InN0EFrrQMSDZluC1AbY2hsQ6o0tmrAuCgTN7zGNB1qbK011boIemflckSu6+ugM4uHQgwVz148B1oa6ZhwYeTqae3u7JL38kCtu7u7y3Q6ZTAYMBwOmU6nbzTP3hhoGFMDivVairXEzD1+IQ0Gg5B4IswHLa2a78jYxeeFiU+IAb9gNEXhXft1SIzRWuIcR6NR23GOAtZXYbXGcnV5hbWayXjKeiWVyIVh5DrQk/l211VNsq55YuGdd991rn5C3Ydg/XfhU2mSkqUZRfQu2zZYL7A9qGqFjQJS6kbx+3/wPXZ2Rlwvr8n6KR99+AHDfl/od90hscbt777v5BnafdYV+PHEgdZtJ22FWAht/r0pBG+4XINi2FV44mvbORMpP1a8Ti7gAWNrB1jaOHtpvjBuWVxyrztHK4220nc+xl0gkw7FGpMkRQFlVWFsTZIolqulixUnKF2hXa+wVrX9E1nj3v5lSYC0FpzVMnS8s/jhQwwCdlAuzhFiIUjo9og5ScHBwQFpmlKVJXXTcHV1RVU19AcDkixntSqwSgRVUzcsF9f0ej0OD/ZINFxdnnNxdkpZlc4jZDGeU9zYAJA8tahY1i22rrieXbKYX7Ozs8vuwQGHh7tcXcCiKdBJRuqSja1V1HXJ6dkpb99/i53phLPzc/pO+KAU16MRi+uFm5QbG5+fc5sbqs8vclTACgGW1n2nj75B8/D3glzw8dYyTk0AGt4iGG8oSaqZTnfo96Wq6npduZ9QloYsKyiLEot1DCSGui5BOUYiRy9buaTwum6oK5fEXIgxAxTrYsXf+3svXLu6tTJEwaNV8PFVlsUyr5VnRSNS2jZCMBwYs+BywRqnnMWKjZ93IoKtjddm/LPNbwmGED8U0fPjw8cAQxym08be+zZ0wItbp+0UcF5NXD5xJ/+hfWaSJK6CtJgrEh3lbmmJTd5sg3ZJ3cZ5fcFXmN7uv7wNOG07r22bex/Em66pgQZUDapmNMq5/9Y9vvVzn/DgwVuMRkPef+8B9+4eUxYrHj9+jFaZ/EtEXowGU3Z2DhmPdkOSqQ/xWTtmmZPTUy4uTtnZGfOv/Cv/AwaDAfPFnLKQcOaXJ6c8evSYp8+ecn5+znq9pior6kZo2+u66YQJai11oqzxOVH4mUXwDin/7hBCP61Fat20VlpfADL2Mm4Cx9FoxL/1b/0b/Ppv/AUg4d/5d/5t/qP/6H/D1eUCrRISnVLb6sb8eZ334f9fDq+kxcQU4NdSgw+dinOUoLsr3NApgkzb/u6bAGObIr3NQBD3sV9Dy+WCn/zkR3z88SccHu5TVRUvXrxgPl8wGPR56/5bZHnOvXv3WMyXDAYD7t69x/X1kpPTM05PTxkOh+zu7jKZTBiPx6AMOpGCy2Ul4UlVbbi8mnF9cUaxWlLWBZfn5+zv7nO9qlkt1xS15d33PmTv4JDlcslXXz+kNxjx8Te/jakbnj95wmiQ8/WXP6au1yga0DpUnI/fVfK/2sKqcX/EieFaKyaTCVprynJFY4Q4JlGZ5KgpkTmL62WUNxE9zBVbFi9Q6rx0zkuLMDVNJxPxJCtCuJTPDcyyDFM6HUm1DIslwuzkAYX3TPv38OeFAqNuXOu6Js1StA/XxZL1eozynDRJGI6GpGnK/ftvMRj0qauazLFePXjwgCMXvu3zkLNMCEJQijSR3JuiLHmT442BhhR4kxoErsh3uwkbQ1WVQquopeiOJDXboAR2PRaipHte4M1NzReWihdByxCkAqWgvpEAqgDN1dU1y+WKsqr57LPPefHiRP4u12FQ/LOqqkJV4rI9PXnBYDCkrkusrWXDsglaOW8FNhQV6ioJN2kF/WdxMpn3OrirMdYwu77mRz/+VGKiK8PhwQHj8VjCqLR3n+mwgfoE1Fgp8ElAHnR4C2+apGGMgpXFugAi1SpCyo+Xm47xvW87YuXHmJaxJ164HYCD49VxlvVMaxcq4K2qcp54vrIADlEWrR0LmNXYpiEhilNFAYmzIMikl3CTiqoqWSyumc1mbiylFcGK6+ZT1/rTVdr8oZKE3oNfD1Z6AUmtEuPnpjOchOJ0YF1BDSsJp36eW4P11eytnD/o9Rn0e+gkYT67FsvnYkGW99BpSvb/pe7Pgi3LzvtO7Lf2vM987nzz5pxZhRpQADETBAlAIkFRpEjNEtVqtlvd0TYd4QiHI/zisB2OcPSbHhS2ww6Hw08dUlh2uy1KsiipJZqyKBIgJoogCgVUVVbON+985rPnvfywhrPPzawBLcpib+BW3nuGPa71rW/4f/9/ELG12yZdLhXWX0AchWxsbkBdcXJ8zHwyVkxq2riunAcdmGojVNWlGr+oZmJH6ObgquLi/IxlsmR3b4+NYR/Phdl0ge/5KpNSKUckT3MuRiO2NjcIAp+Li3N2d/fIspzNjU2Wi2UjkLVmXgfbQs8CCWbR0/fC9s+YIEU/O+/KJ8kffMNSIUOTkaOy12kc7dVYrVks5kDFaFTZ+aHeuxxQ19qgX2rCNee+tvCvPmAyuKtA3Ib/+jIEdfl8T5f6r6MhZo1s5SrFqWNU8/dqtJnG8NW1qOtqNiSbjMmLHJU12BnrTv7qWp6HSZnvXv7si/4241uY/emg2zpZjupJWrfxCoLqIvBdd3U/TV+GI5COgVatFlUzFupyhWNeEQbogETwXEBltmYm2txP40hDU+kZyjLHcVyGGx2uXtmgrgt6/RZB6PAzX/4Cg2GXIHCJYk8nrkacnl5o9qtzDq7copYO8/lML+ZLJGMcxwcZglSQK8+tiWOPPJNsbw1pdzpW3dw4h1KiWXx8hHAs+2Gt+wTPzk6Zz1WGebGYc3ExIkkSJpMxf/RH3+f46FzDMtQ6UVYVjqfHVA2O26icaxvuaAVslZhTsC4wr68SZEIIPE/RZ/71X/3r/MW/9CvUdU0Qhnztaz/HH3z3D/kHv/GPKIsKF4e6Wq2bwNqY+JO+NemoFXHEOmsQjZ6K59Acdrp/MFsYrOaOGd/NAN++L9Ypkm31pJEYNMnb5jGPjp/R6ba5sn/Azs42IDg7u2AxX1K3QhzHYzKeUhZKF6PT6ag+riTRUCuXo6Mjnjx5AoDr1qi8qUOaldTSpawkwnGJXAfXgacP7pMkCygrqtpDCp9rt19i/8oBWZry6NEjpICbd1+i1RtweP89yixhslxyfn6E60gErqoONm/dC5MIz99QY6Mcx+H2nTskSUIU+WR5qskl1L4MTMjTlN1BGELTbrlQgEqSe7WtAlRVqhLhVcVyNqeoSrJGj1Ce59YndnEtMUWapji6h8P3PGvvPP27oZ81dqvX67Gzu0u322FnZ5coitjZ3QF3pY8BCobla6FVU80XQliqWiGEZaUyoL4oVMUAldeXFHVFXYEf/jFDp2zjszDVDfA8xfihBm+FpMYxXe91qRxfsVqQXrRwGYe0SQEptfMBq8Fiv4diQkmShLIoV5MHNXHiVouvf/0b/N7v/S6AKsFVWExzk4/Y1VGZ63iURc58NiPwfTzHobDMEKCcBWmdSsPGZLoV10uW2Ncu/26cU4C6Fto5hiTJeeuH93j65JjQ9zR2PLABlRFv8Tylxuy5HiB05Oxao+xqLRPzWfU9nXlyVfnO9TzdQK3gZjb7ojP1xhA1FR9flNk0zecWuqEuUD0jx7F9HGaTKGfaPHvP820WTJoAoCEkZJpvhVAq7M3AbRVYufpcTCSvxsB4PCZPS2azKaenJ+R5pntlFHxLcfqbpsyPMvpBCCXyuGIZMxl582zRmhqrQomhNBR6sipnWt8N3RQq61prXdQMhgP8IKQscqq6Zj6bIYSL5wd4fkAQhLS7Pbq9HjP93tbWBnVZcnR0SLKYI3QDsEThOF3XRSIJgxDhOqtzlVI1B+c5eZYDNY7r4ToqYM2ShMPHT9jb36PX71NXsJgnBJ5PEITUdYXjlkwnE9odBaM8OT1lo8gJ45CyLGi32ywWCwwMVpgIDO1UC4GwEAvT32Iy32ruqXmvg9O9V3H9kCpPX/B8Vr+rMbTK/CtHNGM8zuz7q5VdZfTRi40JItdiI54PLIwTtXLuV9luU8mV9r/CjjVH/2ICMJ0a0D/NC1r9Wq/9ue6INL+1sldqU6mR9aRBM/PZvF/NYOvDMseXkyjN5MplJjAppW3uFoCU6zTEfqRFqrQtM4tgEARsDzfodrq4uord7nTwtW2LOm2GmxtEUURZlhwfH/P48WNGozE/fPNHnB6fEni+5rpXjoEUglqsMs/NBJcQ4jmu+LX7IlULuKpcVHg+3Lx1jf/xr/8tXv3YdQ4Pn9AftCmrjIvRCY8fP+DRowfEUcCtW7fwHEGWJXQ7bXzXoxWFVLWL50hm8wmT8ZzhYI8qqxDCRwKDwZAoakEtGQ66eK5P7Xo4hqVR33fT01CUBlLsm1IEjuuyu7tlJ0hVlbRiVXUUQvDg/gO+//0f8PDhQ6uPkqQJ3U6Xe/fe4+JiZCuHru7pcrVdCYPQohGiKCKKIgaDAXErxnM9NjY36Ha7XLlyhddee439/X2Wiymj+QwhBEVe8cu/8kt857vf5tGjx8gKRL2uFWF+/n1XM/449m/GUFNzxzh0EqEy7g1f4P0YrUxlyMwd8/nnz3GFKli/DkV93WRXuuxzNee6/XEEZVXw8OF9WnGbbrfP3u4evhdxdn7KfD6hKAryvGCxWNJut5nN5jx8+Ihnx0c4jsPdu3d56aWXLN5fVgmt2CNudSkrODub4Dg+de2QZwmPHj4iS1IG/T5ZWeJGLa7d/Bj9jR3mScb9d9+lKgvu3H2Jnd0rHJ6csVhMcJ2MB++9gxAKaYNlp6zX7kszsFpLcDSCPKHXGtd1acUxcRzjuiAJkJWkziRlUSFrJRqq6GBhNp2jcj0rgoE0y8g1asbaE6Hsv0Wa+D4SaedTt6t6kDudDr1unzRJmUwnOI5Lv9/n5s0bXL16zYobdzod6ko926qu8D2fKI6sz2f0moIgACGYTCc6ESYJw0hTnMPFxQjP91gmSzzPo91pk+cFaZoQxTFVsmQ43CDLUlxPtQw4nqu0ReqKuBV/5HnzkQMNWJVuqkpJsrvuKsMTx1Gj6UXYCH5VWl0PJmA1oUwZyGYna2mbApuRvyqBSVUOEkIrJKuGa0c4eH5Iu9Umy1KyLNFQGoeyWhnj5sBzHMWFHvohAFmWcnF+ppQtjfOBYk1wdKCRpktbljcR5osc8ebWLCVLqSBEqulb4WmVI+Ywn6XMdUAneD7IclxXLR7NxRBNidgoxxqn1kw4kMi6Vs69dtpWToCz5tSY11Rjk3lVrP3u+x4mO452bkzT52UjZjMI+rPG4BkDLITA811837XYeNOc6/s+rufojJrmtHZdgjDEdRzN4GPgYyZD4zKbzQiDiCePn3Lv3nsq+57ngLDBpufp8foCQ/8i4+9s3gYv0udhKkCXHE8praK1ydJTryoaxuCYJ6eawBWO3tMNcp7rMZtNlT5DkhBowxAEAVGrjeM4zJOcspbs7W8h65qT4yOSmWJ6KspcaUVoStWyKlWQhSCIQq2vYJrSBJHnI1wF1ULDGdV3BXVZcnz4jL1rB/QHA/K8osgKrT6a4giXosqZjids7+wQRzEX5+fs7O7iuA6dbpf5fG7HiB4+a9n8Nc+4cX9sPAa28oVwcfpXkefvPbfAcsnhbgb15pm6rkmKNB67rpyZhZZ6Nd/W9/nigNtkwlZHW1VLVFxl9iPsvDYXt6qsmCDm+QDnua2R/FD/FdCEC5gpJ5TekakSre1Tst4s30jWoMPiy85J0+luwjlNokPNWQ8/COh1u9y+fZsoigmCgF63xaDbYWND9R4Z5qpWK6bd7zLcGOL7nl0nlPaGw6fe+IQKiEu1QFf1CpaC56qkiSMo9MInhEOe5/zgez/irTff4r337nP//ntMJhOl5p2m1MI4GcKOBfN8jV21lZFa6s8pMhDPESog8gRf+MlP82u/9jfY2uzx+PEDnjx5xNZyg4ODfRwcvviTP81illCVFWfHU37qi18AKXny6BHLZU62ELRaHU7Pz5Q9EgEP3n1Ep7PFlYMrCCF59OA9gjAiTXJOTs64ffsu7eEG/eEmvu9phXZotdoqWHYc/MBfC/aMjTOJuFpDjsuq4uz0hJ2dbb7ylS+RZZ+1Tbwvf+xjRGHI8fEJjx89A5SWQLvdZnNzUyk5V4WiHm21LAzQaFJIpO4dUertjutyfn7CfD4hCiMuzi+Yz+fMplNqar74xc9xMTphMl3iuR5NOEizuvFRA+H/kJut7LsKjWCy2sJVlP6XE3hG6+BFgYDveSBXVbfL65IQznP3Qu1nFcg0j9X8t+lbrL5ryCgKfvDWD/j4658kDGLVHC2g3Y441/14WZazXCbKOe73OB+dY2ycYSZ0XSXK99lPvUFZCY6OTjl6ckxRpqRpSZam+G7AcDAkLTL6W0P2brxM2Nlktsx4+ughALfv3GFnb5+z0YiLiwv6ocO9H71LXWUIUaP6pFzAAVGwIkNYBRqOY9AP2LW4GbwJoZAyWZaxOJriulCUOUVaQCGssJ7xWRRUv0LKyiasB4MBTgNK5Hke169fp9Pt4nserXabKAxxA6U11Ov1uHHjBlevXiUMQ6SUhFFMGMfaD1ZVfQVTUoQJRVnaPgspJWmSWlr0ulLJ2jxTkMm8rmjFMa1227YgpFmKV6mApN1pU5QlcauF67oUmmFqPJkgHIe41cJ02Sap6hs09r6qKlguLVnKh20fOdBQsChBUahVyzX0tI1VTAhHN1OuRJHqWkEa1OCvaFIhmqhPZfjUQiFlrei6xGpSmkZy4whYrLNUbB0CxdriCEGn02IxlySLhCxJCYJIwSAuTbaV0XJwvUCpc9eSZZqyyCZ4fkAYBjgSAt/HdQXz+YwkTfW6rpTO3zfIWPNyVk6BEHqhBrsA2PORIHCwiBft4FvfVcOO69pgY9X1502aXcmayrasmjCrZhl6BZtq2i/jxEhhyuQNZ6Oun4OUOFoDwDh2phV81TSu96t/7HU2+k3UJPcUjZs2dmgHyZyDyc55nkfg++p3jWV2dUVDInWFSgW0k8mUra1ter0e0+lTe09cF1RT+eWAYgUfu2yEHK2UbNh0pFxVNExQLIRAmMxn01M21JnSOHD62RqH1nXodDq4nq/Eyaqa+WKOcBVLi+86xFFEGHpkhaIY3drcJHA9Lk5PWM7HICRlUeD5AbFuWiuyjKLIkUCtqVwVC47KeFVVpR25EnT2rawqirLE93yEgLIsOD16xpWDawyGfU6OT6hqyXIxR1YlUStmsVjSz3I67S5nZ2dUlWpqz4sCL/Api0KPDD0OzP2z0JfmXNCf0vdL3acV3t7r71OevavmgVQwJgXX8LSt0UGBs3q2AkFZSh2QOqs52Eh4SKmICYQdwZcCBsxCtc6oI4SpV+kRVINXOVQOlLr/QErNLi+gkpUdP9ZuOFibotj0TBiqq4uOa++Tg9CMJD51Da6QOF4zPNM9JlLhwo0on+upJIXrqmC8KGqqsrZCTwqaqIINTfwIJoEhVnGK0GQMrufi6XH7yquv8uUv/zQ3b90giiJ6vR79fl/bDKmqKvUKSmCqlVVVMZ1NOTo+5ujoGT2d2YvCkP5gwGg6IfADqromTRLKstLrkKrSFWVhq2sqy7qgrmu2dzd46WO/ZPHMy+WS8/Nz7t+/z5OnTzg+PmY2mzGfL5hOp+RZRlEqnRGTdez1eoRRRJam1GXB1b0dfvKLX2AwaOMHDq+99jLLZEYyvyCIPIYbQ5BwenzG5sYuTx8c8VNf+CoIBUk4fDamzHOuXX2ZP/ze95guMoIILi4U3GR3d5/9/Q7UDqWEi9GEMGjRHwxxnDk7ex5xu4UfxDhugJSCbm+o2W7U2Pc8VbVeLpdEgWLMefLgEYl2CLJMKZmra87Z3dslmc159uwZ0+mMIAhYLhb8P/7e/41+v88n3vgkD969x8HBFfpbW0S+z3I2w+0oyNbFqaI03d7e5qWXXuLk6MjCMbIs5zvf+TZbW1vcf+8+/UGfxWLBfLZgMBjaSr0QMOgO+OU/++f4h//4nzKbJ+j8C4UswQNRCxts/kne1NzRPo+h/jXrAipI9X0f1/XwPJc0LSnKXBdwBaYR3hE1QRDwhS98ngcPHvP4yaGeg3oV1ct5LZ4n07E2RTNzNv0TtWZhWSiblSq7D03aUOYlP3jz+9y5c4ckScmynDAK2dvbZz6fWVapNE3xg4Dt7R3bhHx2dma1gapBl7OLOaPRhHfefpfxZEZZ1pRFRV5J8qoibvW4desKW7v71MLn9OKCZ0+eEcUtrt++y3Bjg7OLMyYXp3TcmvfefpMsWah75azWbNBw90aA0QzeXLGqcAspcQ2zk/kuBYfPnqB0eBwFkSprPFQy1vM84jCiFbcYDocUVUm336PX6+H7Pl/96leZTqc8evSIXq/HxsaG0pySijI2iiLtS7iW8c9xHGaLJQstCdHr9fFmM/JC9Sq1Wi081yXLc8pC9RC2223KotAoDUUyUugKkiFlEqGgLApbWTLBQbfbfa7Hw+hhhGGI4zjs7u4q7S4NuS/0fppQQMPS+FFJGz5yoCGEinSbD7d5kCYGbJ3NpImHXWXF1vFzq31cxhOabJljGwFV45nU01o46r26UnS3Ld3U4jiu0hBwPNI0WcNQN0uxZVlSVCVx4BO4AV4YkRcFVS1J8wIPSJMEKSulYFmpJmNDvfh+gcYLkuL2YoX27mXj2o0jYcp4H7ape+Pa+2WULU3DPMb9aUy0JmVg/ZwCrslwoIO41d9rPTQ2I43eZ7OxTdrmfBqfsb/rL0spFZe6DiaEUNi/sqgso5cQWINhsgmXjaZqd3kxNtzAIy4uRmtwsLquFfxMs6B80LYai+Bu3VbnbgMzpUNimitVwKuhUWuiicYRbQYuq/dMBrrd6eB6HslS9TXkaYavK1iTyYSylsRtVa0LgoBOu81iMePiQgnklUWFH0a04zbCESRpqnGgK0q/slSVyFpKS8FXVxVlWSCF4uNutVrK8SoKgjDAcR3SNOH8/IytnX3anbZis6pK6rIglC3qCqazOdtb27iex2w2ZzDo4/sJ7XZbkTOwdkvUfWkmKhpZ+lVEYr6hFV9kjXfzp6ne+dcga1TPlMoeUlc4QtHwhaFPqx1z6hWUVGs9ACZ50bQBzcTD6lmtGl1NCVxokgYbMDc9cDv+KqRTIYWPQFHbCmo8UeNIgZT+KtusK0suaswr7QIVyDqssuzCqfB8oUvsbeIwxndD4rjFoN/RQaqroJGupxm1fIJQJWSiOKLT7hDHitEsDCPOzyY8ePCQBw8fcP/+fZ4dHjIajcmLnEJTsyrnSNhgxfNcPF9l2G7cuMnnv/B5fvILX+DKlSv4gU+SJrbiUNelLe3XdY3nugpSo5+F4ziEUUiv3+PatWtIKUmShDzPmU5VRe/Z0RGTyRRQhCHKSTNwSccuouYZhWGooFRVwfnFKb7vc3FxQRRFXL9xlTt3b2GqqYD9rlmgDRVlXddWgb4sS6o8R5YJ168dUFY5y+Wc3/qXv8WXv/JlKlkynSzZ3Nzl5o0bPHjvPnXpMr5YsL11wHg6xXEcPvbyxwmjiD/4znc5fHbOSy9DWtRcv/US7XYXWUOn06Xd6iCFx3BzTqfTYbFY0uoMAeh2e7hhC9cL9JpXITE9j45SsS9LfK0efH56xsXZGePRmNlsRp7n/MRP/ARFllNXFbnW5xn0BnRaHaJIZawf+o84fnbMbx3/S77//R8wHA45ODjg8ePHbG1tadpmh62tTXZ3dzk7OSVLlKjt06cqofOlL32JYX/A6fEJN2/cYDQaEYcRk9GEsiiIoojpZEK32yVLU7a3tvnspz/Fv/m9r6tMveMjEVSyRtaldsI/Gmf/f6htbT1t/K5QDEqrwUC3bZWmrjUhgJpzjgDf8/nJL3yO1159hd29fc5+85+RLBJM4kqnX+y+m+QvBtbW3NZgkfrc1tZR66yoRIypihRFzjvvvM3169fxfJf5fKEqlL0+nU6XxWKh2aXS545vKjqT6ZTDoxPF/Jkp51glDHyibo/dnR02N7fx/IDZMuPs/ITpbM7mxiZXDq4RxjFHR89IZmM8mfPw3R+RLeeNHjZ933UvWhMZ88JnpK/fJCdVAlOwta1ofaMootPpcOvWLfb39xmPRgy6Pdqttk0+BBp5USEJIsVWWNc1w+GQuN2iN+hbuDtA4AcEkepHllLieT5xq43QSQghhKYnVz2ZRotDCMF4NCKKIhINbwLJ2empRYQMh0NCz6Oi1kiD3H7fBAMmAPQ0/GndD1Q+9nw+x3EUCZOx4YaF0dOaVdPp1O4jjuM1SvgP2z5yoGEu3ETBpuveNOGZRdy7tKg3B70JRsyFmAs2g8M4k04jSjc3yERXoG5cp9Pm/PScMPBwXNWgKhwH3/eIooBWK6aqTPnbWcN+rg08obK9RVEQ+IEWIpMs04xkuaTKcwLf09UDQZanuvrywYEGazZHrL3e/POjPigjbmaOaT1UVHS5ubXJ3bt3OT094cGDhxpHqJwwmy2VK4dXiEZPjKwxPre9LgMpMGV4/Z5sBGorZWFb01rTuVg5kiaAWje+5t41A9fm60042OWsjYF6NA1lM4g1nzUTyDgiQRDgaCiSqaY9X9m4tAnwd1/Xn1MZcV3ysecDDQSLzcajjLqOTuTl13We3HU9fC9A1ooFLUszpToaBGR5rgXTcjq9Pnmes7W1Q13ljM7PLO2p63m04jZ+GJJlCWWe47iOcmDN89YN+K6nsk2e55FnGWme6Wy3S11VxHHMYrm0c0/gMJ3O6PYGdDsdkvmUVtxisZjbysR8PqffHxCGIfPZjOHGAM/1aMctxuOJCrdk47oblR3sMNEl7ab/bqtikhoH/LbKuskKx63xPEG7E3Jlf5tr1w44uLLP5tYmG5tD/reL/z3jekqzQmUC7jzPbVa1OSabz7PJrnQ5QfE8jEEnLkSNdCsEPg4urqhx6pROIBVEUyqT67mecsIrQV4UtAYC4aZUpdQOtQoOfD8k7vT5S3/1r6syfLtLp9tF2UGHOIxwhLDJmNPTU2azGb7vU5Q5vu/TarUU7lgna4qiYO/KPj/x6TfU4pLnnJ6c8OzoiLfeeovJbKrgiXpB2dzYwPU84jii1VJY/OFgQNxq6funnm2r1bJz1bCC+b5vnSuzsBqnHla4ZZN1Mxm0LMsoq9o2Kpp5bRkNwVKrm32Y/jRHSLvQDwYD+/2zszNGoxHL5ZKtrS06nY7FR4dhaPdnPm+SXMvFjCyZKRYdYDIZ0d94RFH5XLt+m6vXX6YVxbiuS6+zQEjJ5z77M+RFztOnZ7z8sZdxcGlFPT71qc8zn2XcufM6Ozu7KqEjBb4X6ASdZJkkbG7v4boek1nC22/fI89zPvfZzxG4FUWeUNeV7S1aLpfM5zPSTDXkDgcDdra2qMuSzY1Ndnd22drasokbs55ubW3pRvQVm9jVa9d4/eMfZzGf853vfId+f8DJySnb21vcvn0L1/W4desW3/72N+n1ety+fZt79+4xGo1ot9vcunULx3GYTCaW+nKxWFCWJZPJBM9zOTx8queVy/n5Ob7vc3h4SKsVcPvWAQ8ePaZOawLfpSiVoo50HFa6IP/935q2Rq1AKlEa+C53bt3k1s0bxFHI7vYWN69d5d1371Hoqs6L7oCFFPI8/f1z/gerNdecw+qc1hOQVVVx//59tnd2GAyGmgWxsP04Gxsbqhk8y7TYZ05RlFSZPlfHYbLMCIIQL4hpRzG93oBOp4MXxjiuzzzLmJxcMJsvCKOYm3fusDHYIE0Sjg4fUxUpZTrl0cN3KfOl9TVedE+b8Pjn/DJ9ry/fEyEEf/Wv/jVee+1VhBC6R0P5slVZMp/N2draIooi0jRlPp9TpAXtTpvpdEqr1VprrjY2ynEcoihS8GEgjmOd4FS+TpqmWoU9IYoiC90yPrVZnxQtrrMiW9LPuygKptMpaaqQO1EU0Wq1bAFAva6+b36v65rxeEwURUip7GSSJPi+bxMtNlh0VMV6uVza/jnDLGtZYD/i9mP1aLiuS5ZltNvtNaevSatlHrjrKgxtk9LWRFbNiNMsHs3FvZI1vivsjTbc9lmeUUuYzWcqoIgDfM+lrktNu+UQt2KFY6sKXNc0FKt+ChfXlozM+fq+j+uoslpR5FRFQX84VGIri7keMArT6/surueQJIv3n8iwysg2ttVnnjcTa9kGxIsnCRIpSxxXqV1HUcS169d5+eWXufvSHXb399RA1YP3wYMHfPvb3+H0+Ew1B0mJguuu7nuzIuG6JrrVzwqnEVysTlvKGqEDC6OMbHCkhk9ImuvVAc7lwMEeX+Mmm0FEsyGzeW9fmH3WmaIX3cumk7iqrmlola5oXM78vN9mxzWN69YVHFXl0CXvxvHXJZrQ1HvakYY1Y+kHHlVdMplOQJcyBQ6uo3ogBKqZvy5LPEfQikPmswlLLRwppSSOWwRBCEiyNEMIR0H/BEokyXHoD4f0ej0VbAmVEV0s5hwfHSlcplBQOD8ICMtKNYHppvuyrrk4P2f/ygGdTpu6KolbsaJ1LQpKzfLl+4EW+yuU5owRLFNSa5cWiWYmTd0V60foAAahgjQTWuO4+L6H5wh8X/IzP/15/uwvfo1ON6TVCinLygrXCVVdp6oqgoZtsgQIlxab5vi5vF0OYJuvN8dkLV2k4+NIB1fk+Cx59ZUhv/rXvkq7I6mlakgPw9AG1ufn5/SGPfKyZDyaUlcO/d4msna5ceMug403OLj6BskyxfVDparsCiVSWueqr2ex5PT0BClhY2NDlfnjWFXahK4m6/sfui6KXaukrgVllbGxNWRnf5tXXn0ZL1D9UfP5nMlkQqQpt7MsxfNWzaXj8QWtVoswDJVQVBBaAag4Vo2C4/GYs7MzikZgZ+a1qVSa7FsURY3+iFor28c6sdSh3+9bB2C5XHJ4eEhVKSGtLMuYzWYMBn3FWqcZVNI0tcHDlStX2N/ft72Cxrk29kEJdWGTEmbzgoB2dxcjarV39Ra/8hevqaAozwk8D9dx8FwPR6iAri49qrLi3r3HvPrqJxkOh8i65t233+LxoyOWi5wgaJOkGWen5yRJSrfTU45CJfgX/+SfIoTgc5/7HFGrwzd+/7eJ211VfdSZzPPzc05PT3nppZd0YKZw2Ml8gYeg2+2x1IkWI6i7XC7Z3t5WhBl5roMzn/fee08FSr0eZVny5MkT7ty5g5SSW7duEgQB3/3ud+l2u0hZ8nM/97M8evSQb37r90FKprMpW5tblijl6ZMnLBYLPM+j2+2yWC5JlkvKsqIoSp2lTQnDkDxXAp91XnBwsMNg0OOtH77DbJ5SV1Ldz1o8Z/ub2wuTfX+CtstJtrWKKqr/0/dcfuITn+DO7VvUVcV4dMFiseQLn/00J8+eMZsvqKRaW8z6c7nK31wnLyfyVuuvXPvM6j3Bilhl/X4eHx2xWCTs7u5QFAVJsiTPM4LAxw8jWt0eg41NHFcrytcK/107LsLzCcNI21zXOtrjecJkdkqe57TabW7euk2v10VKOD89JkuWOFSMz444O3oCVYZDBeL5ik3zvl72cewzYN3OmzXgxs2bfP7zn7OJFVPlNEFCu9Oh1W4TBD5JmoIQtNptfN+n1+9b57wsS+v4m4x/kiS2krFYLLQ9GlDXyuYNh0P6/b5FWBjH3lRUjY1SFV2XyWRiG8hNhVcRYqjAbjKZ6KRf3/reRaGIWVzXfS7ogRUpkpRyTdn87OzM2o3ZbGapf43PrvrsWh9p/P8Y0Cm1MHQ6nbVJbkoxZhCvidU0JpO5Yc3mcFOlMA6fDUokaxe04nlX0JzhsM9/9Dd/ldHFCFnVfPOb3+KHb75FVde0WrHV4KiqUrNx5CtaXlbRv8ELD/sD1UkvJXmeMr64YDqbU1clQhpnXILOlFVVYQWRXhRovCDOWHuPFzgzZuCbUuBaxkOoQKc/6HFwcMAbb7zB3bt32dzc1E2A6oBFURLFAVev7bOzu8nH33iN5Tzl+OiEx48eczG6YLFYUJWVwukWOUWugry8yBVdGrr5slaTsKpXvM6G5lE6684V2kFV11c9dz/0hWAIAazBk0oAsXmdlxeQZmBo/jaBp+c6VPUqQGney8uO44tIANR35Nr3muey3mBvqjrmP/rCDdyt8X3TmqE/of5jhNN0Rslm8BF4vk9VKtaYwPfISzXmheMy2NikXVf0ul2kFERxjJA1s9lM9cxUlVayDkEIksWCoshV/4rr4riqiXNvd5ewFamhZ6oEUhLGEYPBkMOnT7Sjqox1qEUry6ok8Hxc4bBcLsizhFa7w2w2U6wZvmKyqaVSIu32VAY6SRLiOMQVAt/zKYr8cuil759swKT0+2IVdBhGJmlhSjV+4LLZ7/JX/tIv89nPvkEcedQoikBZVTgSm2Qwt785Jk2m6XLw8NzCdCm4bY6Py/DP1eYhpI/vZHT8OV/70x/nz/3SG3Q7GXWdUUvF1iYcJd5Z1zW9do+8rjm9GCNEyubGFkkyoSzg5Pg+k6nDYLhPWTgUSULUbtHuthACAjdASFW1bHU6eJ5Hb9DX1+laW5fnuYVqGR0aTzM9hXFkmwUvxiPG4zGe5zVgMoq1qdPpIIRi8FOOksPjx084ODggSXKEs+TRo0dsbm7a++x5Skm+12BWMdVrc/8MLOqyyux4MrXVSFOhME6A67rs7+/bOWoWXalZ18xjbLLuGPvTpL0165VZ34wdzrJMZ/sVTfh8nthzXSyUqq76O0RWNUmS43s1V/av8s//2T9lY7hBmqW89uob/NH3fsD+/j6TyYQ/+IM/oNMZkGcF9+69x3KhSEuWi4RvfuNb3Lx1i1Yr5tbNW9y/f59/9dv/SlUKbt7ivXfvUVcl7XaLk6Mj8jyn2+3yzW98Q8NyFNpgd3uHKi+4fu0aVVny9OlTVZFqtVgsFuzu7nJwcMBoNOLNN99kb2/f3qs333zTVqaKouD111/jW9/6ls5utvmJn/gkUkq+970/5NnRM5bLBY7jaN2OxD7zs/NTiqJgY2OD8WSke30UJKfb7TCZTPT8CqjrijgOcZyAqipBCj75iY/zzrv3eXZ8inA8ZF4jXcfC3f77vpkAQEoFCfU9h5fv3uHundsIAb7nUGQZLjWx7/KpT36cf/N7v68deEclspzn7ZD1I3jeN7EJt8btW7dhOin7omSK4zCfT1ksZmxvbxNFIfP5nKoqWKYZbhCvsZLZLRDUZUFWKh8xzypbufPCiJ3dPTptlawoi5yLsxOyJMV3oExmHD19SLqY4ohKVbZYR0c01/dVj976ey8ifTG2YDAY8HM/+7M6EFIVV+OTLhYLhhsbAKRFxmQ+RSAYbA5VRdZxbCUgDEPNBCnY3NzUIqwqIdz0ZVU1cZVcMT6osYmmutDv94l1U7hR6wZJt9u1dsok/ZUtxQYOBtJk5uL169eZzWY2AReGoYWHNtEiWZbZgGO5XNLv96nrmjRNbaDShP6Za/wo248h2KcezMbGBlIq3HgzcDCZqmZp+7JYnRkAZvEwD/Qyq0ITmtUctL1ul/5wwNHxMd1uh2G/jxBw48ZVkl/8eR48eML1G7f4b//bf0FVK7adulLNWULLKZr9mWOXZYnvevyNv/6rJFnKb//2/5fxdEqR57pZF9C4bTWQHVt6NoHGH8emSqgqoDDZftdx2dzc5OrVq7z++stcv3lAu9UCYaAXJVJW4Aili6Cd6aquKfJcVYCqkrt37/Dyyy+RJIkN2kzj5HQ65eLiwmLyVNauIJmlzDQm7/z8QuOhc+bzxZqRNMdUz7pG0nToVxlqiYIWGQyh7/ukWWq/eznIMBMlDEO74CscY2avoShKdS8aTUovClbMmDJj0WQBrLq07U953tG0+5MghLMKFE1AiMQgqew3RcOuaUfaVIXMZwGrs2HgIcIR1BKq0gRSHlE7Zm+4SS1rTk9P2WhtUOSFEsPT5+wHypHPlwvyLFUc29rB7HR77F+5ohhMaFSA6no1tgVcvX4dPwi4uDhXxlxK/CBQjWKOh3BURWU+nbGxuYnrKxEj4WgxRUeQ5RldlC5ClqZ0u23cwKfVbjMe5WtxhK1lGLVnG6yBkEJr9umAw4wgqZyVK1d2+Z/8+n/OtSs7UOcErkuSlVRljUPAfLLQDFPqm65u5G/2GpmfH4en//0qmOswiBLfydndEPy1v/gz/ORnD3DFFKmrsY4XgSyR5YoJL0sSaidmMRP4bp+yCJC1y3w2p9OC+fKIb3/rXzPcuMpkmnNw/QZXwgMqSqQrCLxAMYd4HqPRiCRJbaZJSqkqvLViBvK1M1+WhQ4IUxbLBU+ePOHg4Cr9wYCdnR0cx7X87qvkkKqWeb6iOHaEh7Pt0e9vaKhWwSuvvGLtvqkYf+Hzn7eMRIb1LYqiNUisWXDN4hoEAds7u0jZSECxgkeo5+paWwBY++Vom6DU1zMb1JiAxUALzJpm4FwAnU5HVQWSxCasDD60qioW0zl+4HE4vtBMeQHpUglulXnB6GLEO++8TbfT4Z1775LlGV/5ylc5Pz/j5OSUe/fucffuHe7fv8fh4VPSNOP119+gKiu6nYizk0PyomA8mdButZBVydHhU7a2thj2uioRVJXEnTbLZIlAsr21qbLMacpwuMFiNueHb73FYjaj3+tz9+5dvvXtb7NYLpnNZpqWdMbDhw/59re/Q7+vAtOf+Zmf4fXXX7cVqdlsSlWXfPozn+Ldd9/l6rUDjo4OGY1GnJye4LoOVVWyWKS02zFJohyXOI555ZWPaSGy1DpWy+WSoBMShhG1rNTfoQ+ozG8rivBDX+H34xZXr17l7Xff4Xt/9CY1Hnmxgl6bsfDfVyjVKvBVRB+vvfoxbt28ia5XkGcpyWKB7wpmkwtuXLvKw6tPuP/wUAGm6xq3Afu9XNlobk3fS2lNOC/8nHntheunAJXTk5ycHCs4se8reGcckOY5ruuSZIr10HEdgiAkjiLiuAUoSvvAD3FdH8/zEUI5rslyyXx8QVXmBJ6LqDOePnxAOh9DlRMKSYWkAmrh4dJI5Gm73uw7oPFe8/dVRX2VbP4Lf+Ev8Eu/9EtMphe4ulm/ef3zxZxa+yKFtl3z5YKdnR3GoxGF9mUM7KjdbhPHMYDVFTE2zlQLwjCyFVQDazLXkSQJnufRarVI05TZbIbjmPNS1VtTDTdU/qp6Elp/vNVqWXvmOA6Hh4dr0CcDHTaBg+d5qnLTbiOltD0nxi8z/rr5EULBNVuareqjbB850DD9FRcXF8CK1tAMYoMzM05fqbn8mw+8WfUwUZSJkIzRV9nGmM3hJmdnZ/Y9Q/91fn6usMY6Q5LnOa7jcOv2LV7/+CcoS9VUtb29zZvff5MnT57iOOiKhlijUDUOp+vB6ekx/8Nf/3V+7mtf47/6r/4uv/2v/hVlVasynVxdRy1XTFFrg9gsSHoyrhwkFPRDCLuf1TDW5U8doUskvh+wtbXFxz/+Oi/dfYmtrS329/epZMbF6FTTNCb2fvm+jx8GpJlqxivygrzIqcqS84sL8mXJ7u4+Ahhr3GxZljbSLooC3/cZDAYWT52mKVWvwr95E0BpLejF9/T0lCRN8D11HxGCTC/wrusStyOVuWy3ieKYzc1Ner0ufhCyvbPDd7/7Xf7u3/27fO5zn6MsS37/93/fDmYzPoIgYDDos7GxSb+vGquklJycnPDgwQPCMOT8/NzCtcwzMMHEizLQzR/fc+m0289l2D8McyiRUK+a7E0y3ibb9bM2T5ZLrzW/YwIvB7EqfUojfKgEDGsBnh/geg5FpjIavu8xny0oK6Va6umG8aJUi3pVVopCz3Xwg4C93V18z0cKDZ1xlL9u9DyEEMhKHXd7d4c0TcjynFqq56Do8ySuVJWFJFmC2CTSvRiBphh1hCBPc0Wj7LoW/uUIhyAMkEKYlu5LDfPrkIKVcKSaQVKItWqQ9GNEe4OLi3OmF6ekyzlpsmA8npDnJbPpnLOzC9I0Y/GLS2hpAVCkzeYL+UEViecDTjOG5HPPVvUsqZ4TcB3w3ZI7Nzr8R3/tS9y+7uHIM0QtKQsX4bmUUi02ZtzOF3PqSpLXSghqMr6gliPiqE1eJJycPmH/4HXG41N+6kt/ml5/nwqPWkikqHGkQ1XUFEVFEMRsbChF2vFkynw+A7Bl9sVioR3Njk3wqIUuY2trVwdkDq7j43oeRV7iOoIwiqy9pqt6ikAFAIOBcsClpgU2lQdTKajrmixN2drYRDjC9qYY59/CDnTSwFQcpKl6VxVlVREGAUtNe1uWpYIbVhV5pitZaGcgL5jPptR1Ze1ZURTEUcxCZ989z1M6TDrg6HQ6NuMXBAGHh4eEYUiSJGxsbCAQzCdzPM8hCH2kLEmzBYeHT2l3Okgp1HmUFcliwenpM4LggCRZsFim/MEffJder8doNFLBt+uyXMzod2I2Bz0mFydsDDe5cuMqjx495uTijPF0yvGzp7TbbTqdLnm65Gw6BQFVXXNxca5tnrrPCgYVs5wvVaa5LFnM5nz+c5/j6PAZO7u7zGYzzs7O+M3f/E0+8YlP8NZbbxHHMXfv3qHd7nBycoyUsL+/R1UpdqrFcsZodEFR5Pz+73+dPM81JE+oPsiytKw7Rhl6Op1a2GVZlqpqrslTikI9r+FwgBBK3Kzf72HWzDTNCcJAieaWGS/dvcXW1oBvfff7HB6e4DirplrVs1GjOKlXE/P5WfoffmuuS81Kaa/X4wuf/zS9TpskWVJXHlEQ4Pkeg0Gf8fkFlSsZT4/pdbv4gU9d1Fan6nKe80VV2rV1zS5aL97W+yJNlVm56Gp9rS1de1HknF+c44UJG1t7DIYDqrIiyzOyNCPPM+Rc0Zx7ng8I6qpQiRUpKfMSKcF3HWSRksynPDo5JlkuCGSOUxcIaUiGBBKXGsHKtZWWecmeGzTW48YYcByENMr1yi71el1eevkuo/EFRZEymUwsSsT3PZU0dx0y7SMt5gsdQAWcnZ3heytKbpNsH4/GFEWpqiHDgXbkfYLAtz0eQjicn19Y39nz1LFMst5xHDuXXNe1wtZKFFvZx+l0avuiwjAkyzINa1RFgMVioeh2tb27rO1ixoRJ8phET7O/o9VqMZ/PV6rler0wmjmG4eqjbD8Gve2qefgyTEXWUJVKnVF9psZzAwSOzaAa6lpwKEtDv1pRVRIhVpUNIRR7z/n5ub1Y0ziT57nt2XAcRx1TOBRlhesHVFScj87o9lt88Uuf5dOf/QSz2ZSjoyMuRhfcunXT4swAK3AiZcHZ6Rn/9T/4e/zSL/4Kv/af/g1+/1tfZ7lMKU2W3KalUUNddaBrq6aqEVKnaqUE4TpIw8+PwgM7UtHfuZ6HH/haUE1hqYUj2Bz0uX51n92dXfr9ngqsTo9JFlOKumSeqEztfDFH6ug3imPacYzjqIZ4c59cz6UddeiEgjxN6PZ63LpxXZewBf1+n1a7Y9U9Advo4zgOgeOSJoplK8syEv37dDplNpuzXC4bJb4I13XZ2t4i6kR0u13FehOEFraSZwV5UjA6O2V/Z5tf/at/hTwveO/tt4k7LVyNCd/Y3NQNmhG+pnsFxccetyKC0CNuhfgzl7wqqMqVQJKJ/JsG3VTOjKPkug6h6zBot/D1WLPBCrUBSK2N79Ufahw3DbWlAZWGlrSRrW8EGCtzbYq/Ok8vHKpa2qJwVZZ2TLlC/TgIZFUReD5SKL0XakUZ6gY+da2yEGVRgCMoNPRqY9gnDH0Mla+iUhDgKMHI2lRmHGHljja3tnjy9Cmu1glxXJe6KvHcAIQyuqb8Op9NV/ZACIqqpJKKRWWZZBZPXFZS64koYy+lxKrkoko8Qk8vQ+uqONF1KOgI7VSA64UcnS34P/+f/q/q+oVLVapsveu6tFot2u0O/f42nveAgpI4ivjqV36K3/mdf0NepDhhpEUlJQ6rSpcZM5erFpcDDweJEBWFDKlliOtCIBLaQcIXP73PL//ZV+m0C6pkQSULpeoqJLIsqasS6dRUVGRFyXSRkGU1eVYyHuUslyVpluP7NXGrA0EbWQ94/bVPkSxrorjECzwELq4TIOoaN1ixMJkmPRWkD9aaf4VwGQ43kFKrwNcKElHq8WLmkCOU/kq73bIimp7nqEVdQE2N57m4nlp8XKkSP1GsqgECVLVL37PA9UkXGb7nUoocT4+pPM/UONfBctLI1jmOw2w6o6wqFgtFQ3v16lXKslQLq4PN2s3nc+tQXVxc2N9VH4pyRC6k+vx4fEFVVcznc7vgqsXWZXwxZnt7S0EJD58qhz1dEkcR/f6AIPBZzOfUdcWwO8A/cDk7V30q+9v7FGXJk8eP8YKQspZ8+tOfZTqbsb29xWKxoCgUm1sYuriOoKwl48mIZJly79499vb2KYqSh48eoaCDNf1+j7LMqOsCz4PZfK4b9AcsFgsmk4lNOCErzk6PEcJhOp3Qbrf51ne/xRe/+FO8+tpreL7P1s42v/M7v8Nwa8jXfuHn6LQ7LKYz5rMJR0dHHB4e8sYbb1BqEdBFMiPXkApH1LRbIcvlnG63i+c5tOKOgjsh6fUULG5jMKTISpZFwnBjg+VCZXvLqEQIh8APGY/H9LsDalnjex55WrC52QdRWyrQ+XxGupjSbUX86Z/5Iu/ef8j3vvcmS1lTlAYCWINMUXSuzqUgY5Xx/5OwNQMM3/fpdru8+sortKKIPF2SpynzaU6R55SV8i2yoiYvKmqU3k+706XQaJJmUuZy0uRFwYbrugh3dU8M4sDoTiAFUhYYjaiqajSNSwdqBwcPiaSWaqX0BMii5PzZY8Ynh8Sxtr9xS1Uu4ohUQ4pc1wMdIOZFTpVmJPOZDkwTfR4VrgQpBBUeCMOs6eAKcCQIscqsV1WTQAZ7beqP5j2ocXD0tUlcDz7z2U/w8svXmc6mVFVJr9dluZzz8OFD+v0+g8FQZ+7bOL5DHMYgYD6ds7u7S1UV1LVCtiRJymQ8x/dDwlDgugFFUWrNmRopVVKgqiRQWQp645eYYME497u7u7b6a/yZ5TJluVyyt7dHELgMh5vEcWyD++VyyWKhkA7b29uUZcloNLIBgknsmyBBzWHPVlSSJKHb7TIej+35AFYU1VRMptMpUagr0vlKAPuDth+7onH5p65U44/JZKlMA/YhN7PMJsNlSuhmAjQhDKZ0IzX9qrnRTd7fJkOVigh9jo9PGG4MGG4MmM4mSCRxK2QwvMrO7raNBJtYNIXLLZA17GztsFym/MPf+A0+8can+MynPsPXv/4NFf1KEzC41FJSVKoBECks1t84s0EQqChPKP2NdqvFoNdX0alQWWYn8Chy1Sxrzr+qSnrtFkWaUlcl4/HYih2VpU8la1qagnB//4qF23ieR7sV0YpjxQQxHBI01HWFEKrcFkVrSuDqXivj1XwmBmoQOA4bG0MV1evJqgT0PH3/ldZCLaWiZAVc37Oc/qY8Z5pCESVplrGxuUkUx7z00kts7+xw7717fPmrX6Hb7/F3/s7fYTqd2vMuNRtYnuf0+30tFCis0VQl4FV/EGArZCZSb445IVRTdLsV0m23CYP1RibHEbbnAxpVK+N46hjEGHijqaE/ot+Utukbk403u6z1Z/QX1NpQW+eprGpkoQy9owNUpBLuKXIFSVTMVAVKcUEdPM8ya0iEdvxrWdPrmkyhNP/XQbMSWBQOekHTQU5V0YpbeEKViX2tuaH2pypvpXaWFRRLMJ1MWCaKxraWperv0VlnlWV2tQaOWRSFXQRWAfoqC2nDPk2valJ2Qv/PERDHLb7y2S+DrPEcj1as2INef/017ty9qzDEYcgX/vFXSJKEdqfDr/+P/gv+8A//LRcjpZLqOQrPX5QljiPWbFWzebIJubNjQghk5eA4Hor4Z8nmsOYXf+7TfOFTuzickpcq26pIFlyEkNSVpmqWUJQO86VkNJYcPpuymEmmkww/iPCDiE53wPbOTb74xS9x/ebrZIWrHcgZjpfi+gFR1EJoKA2oREMQBvbcLXOKtk9hqAJ/x3FxMAQOIFyV0SrKUvXVeS6Bzm4JHexVZWUXPM9dkWoYesY8y/B9134uCAJGY0XNWGUFVW7YpRQcyXFXlUbP89X4qUrms0w3DBc8OzxEOKriN7o4B1nTarU0RAeWywWj0Yh+v89ymRDHkYVBKcpNRZkrpaTb7ZGmCUHgs1zMKfIMz1UCd1meMZ+lbAwHuA7MpmP2dndIel3LBHP49DF1XdPvK+a3yWRCkiScnZ3T7nZJlkrnQ+G0FV1knpc8ePCQ4+Nj7t69bfnrz87PKIuMfr9rbVmWZXz3u9+lLCtqXO2kKPHOK1f2QSjorpSSViumKFQFc3t7S2cw57TilUJ3EPiMx2OOjo743d/9N5S1pCwrrl27yl/+y3+Jt9/5Ec+ejRldXJAnGctlwnw+JwxD/uiPvkcQ+MxmU9qdSK2ROuhRgY2jjtdqM5/NbHArhGAxV87WYq4QDodPD609N4w3UtaKREKvKe22gtY8e/aUwXCg7HBVMhgMNNzXYzaf88Yrd3GpuP/gCefnY5ZJhusKqgrNhihV8fNymv9PwNaEboZhyObmJlEUcXJ6yvnpM5WlF5o901TkUVChGmF7Wh1X0UwbqYHLldfm8V6UMGm+f/lvBIr23NB5mwq8sddSJ4ZQCTtsgqbCcdR3l/M58+nMrpHSEdQaseG6DgauW1U1Tr3SR1JmVe1LrQYe0ianTaLXpPEMU6apaH2UB6AJMaoK1xX89Je+xJ//879Mlqlk9vlyRLcb6wrfXZWMcQRhGFFVtU4M1kRhhOt0Ub0sUgviVgwGfYWmqeHi4kyLDHc4PT2zSJ9Wq4Xneaq/UvuxaZpadInph5NSMp1Orf+b57ll8Ds4ONCwxpntaZNSqYWb6u1gMLCXbRq5DQy21+updV73YZmg15BvGL88DEPb1A7Y/rg0Tel2u5Y443Jf3fttP1YzeHPhnc/n9mQBy02+hhWslaiScW4NPt6oYV4OPsxWVaoBWTUIFarMVhQ6uw2VhmX1ej22trY4OTkhjiKqsuTx8RFxHLO9tcVyueRMQ2zyTOFoO92uYmGqpc1+DdpdJtMp4/GU8/Mx/+j/+V+yt7fPoN1jkS6QmAqIy9bWNp12GwnE7cgOHuOojMdjBv0erTggz1T2LgpCWq0Y3/Vo97q0B336gz5RGBHpaoAjHNpxi8Dz17jmDWbZC3zFHuSuRAxt0FArIas0TW2PjAkw9I22oixpklDVFVEU43uBHdxmM8ZwPldYXsdzG0FZCVLBlRzPIysV84DQYmCOaxi6HFzXI88VL7RqLg1od7qUsubW3Tscn5+xvb/HX/nVv0ayTNjf36ff7zOfz9cCB4NbNAGcCejCMGSZpKuGOla41yZus/meaiIPGA6H7OxsskzLS2Xk52nvzP0zlSm1rQQJzaJmlUvWEHRNnJRc+ddmH0IgcaxQDpVValQZhjRh+mjK3v6+DkrV94xjCdg5YYIQVRpQTC2ub7jCG88Wlfmp6lVAgpSURa5w944gjELmZ/P1/gV9LUIHp17gI5G2ObOua2rZcHp1D4gZD8IEXebeIexuV6Vu8xT0vRSryo8wwYiEbqfDr/yFX+bawR5bm5u0ohaO74MULBNFyztbprY5sK4r2q0Wf+orX+H/9Rv/mLqSSNfBwaGsFXXgZehe89qbY0wtyC6O42mV6Ip+1+Uv//kv8tpLPWo5RgpfO/c+pcZSG5KFxSJnPE5ZLh2Wy5CHDyecn2W4XogfdkkLh76/xdXrn+Kll16j279L1NoiQlKUFX4QUNUSx/UwlJi1Pq8gVA5dVdd4JrCr1WeklJR6sfF9H0eqsZPnOWGwgrYJBKPzc+I4XutlcBxH2eGqJklOFKa+3UbqxSfLUso8I00zzs7O2N7eYj5f4LoOURgT+SFJonqssjxVr2uletMAaShxV+X/uc3WR1HEe++dA5Isy5GysoxXT58+0fAC1ZxoKCJ7vR5FkevAsaYsC/Ii0eO+oqxyslxh1oPA43vf+0N2d3ctDbZhaTFrVq/X4/j4mW08f/z4IdPZnCu+6n9SMLQE1xUMBn1OTs64evUqcRzx5ps/wHFguDG06+dsNiHPczrtns5MxiwWCdRC2zqlnbJcLml3WrZ34uTkhOFwqJ031dDaarWoSgjDyDbzT6dTOp0OWZbxD3/jN5BSNWJ/4Sc/z7vvvk2WJYAS9lICnZIw9HWlZMRg2F8T/DLOj0lKTSYTu+4vl0uKomA2m9Hp9Miz0lJqmn5OtR7VlFWJp4NbKUuSROkz+PqzK2iHoNfrkyYJ2xsDlosFL92+wf7ONotlyjvvvsejR49JcpdCV67+ZAClnt+Mr9Ptdul2u4C6Z2VZKruvbagRqLWEObXU2k3rva7KJn34cY3P9TzzFM+tdSYJ1fzMyi+rdWXcvGHWRkOfLnUiV1UfpE7OqqqzThSVqwDHtYZfVe4sIkAHDlLUrC+Y0t4bVcWo187//e75mt1GnVur1eJXfuXPc/v2S5yfnxJFIXHcRgglphiGcHExUrBJIYDa+qxnZ2eWxSlNl4RRQFEUtOICKWFzc4tlMrOsfbDqB3n69KlFkBjn39ip8XjMZDKxcCfTe2GY+fb3920/hwpsBjaJZHrJzHM2WhxRFNnkRhRFNqBwHEU/baBZvu/b3lkhBHt7e8znc4bDoSVtaDaEe77PUvtkF0dHHz4I+TEDDQM1Ojs7Yz6fa3zWClIEq0WpCWdpUggajJhxUAwu1pRnqkpls0I/0GqwavFZLBZ0Oh0qsBngbqdDVZZsbmzQ7XY5Pn7G3u6eyhClGbPpjFqzHfh+yGw6J/dzjo9OLH/wfDbnMH3Kcp6Q5wUCh3Yc04piPvOzn2aZL0mThCiO2Bhu0Ov3cISjBMuEZHtnh4ODAyWiphlVHj28T7JQeD8HoVhAypJ23MINA0oXjYkLyHMlmuT7PoEX4gqFeV9RAesGdkfx7ZuAodnjUhU5oFgMOp2OjYonkwntnlqo0jQFRxC1V5GsqMVa04/hkq/rmlYcIhCq96NQNIiu54FQzbVFUYCATrejn6tqNDYQDkUV19JBQUwt1fdOL87Jq5JFssQLfLr9Pt1ebw0HaMaN+TcMQ46Ojtje3iYIAl577TXeeecdJrM5rhaHNGPPbGbcABaDCGqh3d7eYGtng+WyRDQqGMammeqH3Z8XQtC278laabaYioNx7k0+3jrVorFjjWtdNY0LDcUCpGrgl1KRABgo12KxoKwqHj9+zMHVA4WhB1UdECpgEAh8X2lwVEIpPHuuSxCGNsApZU2WpAqm4Ho2c6ZgdOZ3NaccAa7jWGfNjA198Woh0J8RwiGKo9W5o/alrk5fL3rxEDpKsfBDU2HBBmwNpBnmLkl7XInQFLlhGPDKx14mCl3SdMF4dI7rh8qp14azmbhwHIeN4ZC/8pf/Kr/1W7/DZLpEVspZV9DJlX3qdDoMBgObtTZjuVkVQ0hcHxwhiUOXQafFN373D3nvBx6bGy16GyrjE8WhzuIpppUkkcxnAWenCRcXC90g3SIINnBDBy8Q1NJlkUm+/s0/5Lvfu0en3ePajX1+6Zf+DAcHB+r5eo4N6Cp9zUJAXanAv9S2N8uUPkqn01EipJp+MQwjPG2XTROgZUSpKvIsYzwa8ejRI/b29q0D5LouWZ7Zpsbjo0PKqqLf7zMZj/E9VzujkqosCAKPLM04n82hhigKOb84p9NpMR5PLetJnud0Oh2bPTMJE9/3aLVjLfAliFuKE/7K1p4Sq5NSVzt7CMdhuViQpImtqhwdPVNsWkVule6zPFOQsHqlGp5lKb1uT9P0+nb8mOs0zs90OuXw8FD3NChtEj8I1DkWJecXZ7TiFq1WTKfb5t6996gq1VelGjRTHCHY3BxS5jl1XXJ+ds5ykXLlygHb2zuk6RMm0ymeH9DtKkrNOI4Io4C6jmyQY/RR8jxnZ2dHQVqnqpH04OCAJ0+esLGxoSCVGnpcFDl5nvD9P/pDglBRwwO4jlpLT09PSbME13Xo93vUVUVV1QwGA05OTmyvnFERLvXaavDphrgDHHyvtGyUxiEaDAY8e/aUvEg1c1FkoXKGZtcwBLV0Y2qW5niej0uN7wjidps8SWhvDrl68FMcHZ/yo3cfcP/RE+aa/rU2heYfAzX1YU3lH+bUfpT9O46iGTbUpeZ1UesKs15HzfGEgFpIC1+8fB5CuO973k0UyWW9MuM7vOiamoxVz+9bBXIqfmiqjq+SSlKCcCRo38IRNU6TAUWC0Ek3KVykVCk6Vc3QiSgbcKxXY5rBlknUPXcNzeX8UsXGQPxu377NP/9n/5yHDx9ycX5Or9fj1VdfpyxndLs9fd4ey4WqmHm+gmTHUczjx080Je2AOFaJ4sl4rO1YxsXFGUpUurbVgiBQwYiB7Zu5cHR0ZCsHpl/4/Pwcz/O4ceOGDehnsxnj8dj22gkhODw8pNfrsbm5SZIk9Pt9iqLg6tWrnJ+f0263LaTUVDsMZbepVMRxTJoqOJYRSzUkOcvl0gYo5nPm/pelYmhFCPrD4QvH3+Xtxwo0AGs49vf3dZa7spy6TXYDM7FMpNRqtVaZsXpFc9rsxjclu+FgSK/d0f0AU3rDIf1ulzhu0e12mc6m9Ht95Tj5Pr1uj8Nnh8ymqjk1y3JmsxlVVSlHOct48uQZT54+5emTp/i+z8bGBnfu3mFzY5PtjW12tndVdrTVwvMUftIPfNWK0WiQMtcmNMZWgmUyMZmGra0NHCpOT07otNsUeU6v36MuK0UXqysWJttmFW8dQaajytlsph4uqoKT5zmZvo9K+TewGDvPdcjShJOTE65cuaKcaj3I8ywnbrV007tu1NdRblVW9rmZRcSqvTvq+QVRpLRJioKiULjquiwsbjpJElzHpd1pqwZx4ZLnmXJ+pSEKSFEwEo/JxYg8TVXFab5Q99hx8FstNjc3ee+999ZgcWZhMywMcRzz67/+6/zmb/4mRyenzGbzNfzg5fFqxqypbqjMr0MQOEgCmK+N8heOeREPEXFf9xtdNm7aoXactQACwx4mpRY9RFc11jP5UFPp4MVzXUoc23BummSNuSyrEuE4eJZCWrnrcStGuI7qm/E8Vf1AKMIEz1MLmSMQUlWckEobQGFiQQS678BR0DJbMTGBT1Wvrdkm21jXFe1uF8d1ybKcWi8CVV0rxjYk1KhrkCvGD9aCC629IlnBppq1o+Y91w5EURQ8PTwkXc4JA59Ou4tXOsStNq7rkKcrdVRQldVH959yfHxKu9VhOplTl7nKtDXgAca2NRvlmrZstUhLWi2HNz7+cTYHQ4SsCF0o0gXzZUZWeZydK3XsWhaKJtsBWbvIeoDrbjPc8MjyQkMXS3AqClkiaih1H1WaL5gvZ4Qtl95gg7ys+OH3v0+v02FzQ0EkPc8n1YuEwvGuRJdMhtn3fas1UVUVoda7MPc40dA3Y8em05m9/vvvvWfL9/P5nNliZkvsZiE1FdAw8G1j8MOHCrYzGAyIwpiqqCxqTogWg0GfnZ0tHRAcK52kLG1w0HsUZcbJieKNn81U8mA4HHJ2dkxV1RoilbC3t0tdr+AGJjju9VWSxfUcmwhSWHBJHCtHudtts1gs8H2PKwd7RGFEkiZqcU1Swsio6yrGlmUy5/DwCZ3Oy/T6HSbTGaPROd1uj93dHaqq0ot4RK/XYzKZs7Ex1GujogGXEnZ2d3Ed2Nvb4+T4jKIomUymNik0Pj5hOOxTliU7O1skyRI/8CwXvxFhDMOQZ8+eWTIO0/B9dnZmsdjvvP0OAoiimFJWLOczskRVlMqyJIgizi/OiFuRZaVCSP391OK5TVCqgrTSBhyXodBVKRkOh4xGI+tYmWTiq6++xmI5w/d8yqoijiPbZxeFsfUDTo5PbbJDCIGvImlm8wWu73F6dh/X88lL1ah75coVJpMp0/mCvCjIC8VCtyov//vbPmoQsra+Nl/H9BQClonVVLefDzCa+/ugYzcd7Saz52V/pumwK+bLdVavVZCzbi+lXcQkKypBoYIHgYIPyZVQ8NpWS01XqwN53dQvzbohzfr2/LWYe/Uc9Mv+vvqcqUYr31K98YMfvMW7777L7/3eN5BSEoQhd+/8WwaDPr1enyhSzGi+77G5uUmeK3hTWSmilboSPHjwhDAI6A8EQdDGdQRJkrFYJERaLbwoyjXBOyEEi8WCMAx58uQJ3W53zcfZ3Ny0vRtGk8MwV5nkx3g8ptVqKZXyMLRJmtlsxmg0sgnqIAiUvVoumUwm9LXeh0G5mCSP8dkNo6whWoiiyAbEBt5lVMOllHi+D44g1X0cH7Z95EDDnICU0uKyFNWoh5SKLtFEzoZ1xDAYwYppagVhUYbbVDTyPKfdbitHOm4xn0zZGA65dnBAXhScnp5yfnam1DM9n1B/Zz6dcXJ0zPHxMWEY8Hg+t2JO8/lcRZN5gXA8PvnGJ/mFn/8FPvGJTzAcDokiRTMWBCFlpeBHZVUgNCayrkvtHCo8YFlVuI7C9QrhIKsVf7Pve3bgu66HxGH/2nXlpOnKjfBcOq0YqfnrHcfRGWBp76NsqXvcarfXmpvNgDTBjMkWGehUK47sonPjxg37HKQjrCO+0APHDLIyU2wsppLQzExJZ9U/U9dKpdrzfRbLhRXyajYBT6ZTHOFQFZVdgGCFFe+2u7jCoRVGVFnO1mCD5XTG5uYmvh9QyZrtnZ1Gk9eqmdRUNQxNXJIk/PRP/zT/zT/4DdI0s87VB2V3zEJYFAp24fsOCBfmje8Ix0J1mpvrGnE37QALQ8WqGvKa7FVCaqYkc2zzu7bHJkOv30QIB9/1yIocNCOGMFm9VosoCtnc2sYLfIs39zRVraOrKkIICx2sDBSqKsnyQgnmuS6tVludQG3IDSRCT38rtKgDi2SZ4DgCz1OyjcJk21BBk6mYSYmFTEldHcnzXMEd7fVfWlxlraGIpqIjVvdEiAb1rdT0v6aRXt1Cgeox6HUHDLsDZrM5ve42nhsiEWRJyuhizuPHT0jTDByYTmf8b/7X/yWj8YgkSwjDgKquCEKXshbUtbBQxCzLWCwWdsyY+Wac9yAI2NoYcuNgj8DzmC9mOpASFLliApMkIBVERCBxPaVDYTjw2+0uvhdSljlCVDiu0q1xRUitM7eO55FmKWHo80u//Ofww5hlsuDevXsMe11a0aucL+YI4eD5Pqdnp1ycX9DutHEdh7KsKMsCx3GZzRSBg7Hdvu+RLhPmcwVZ6XQ7nJ+dKi2GvMTzAhKt3F0UBcONobVDva7KjvX7XdIkJYpDBv0B49BXGiZIlgsV/G9tblCVFcvFHCFcAp1UOD8/ww9UELdYLHUQYzDHQjEOAVGksvpKjEqq80oWbG9vk6YZk8nYVt2klOzv79kMflvbzyhSdmg+X+jmc6nHtk8cu9ppj1WArm1LnmcsFqrput1uW+dgPFHN4nmeW9HYl166Q1XDcpnw9OlTgsCnKFykjIiikMlkzuPHj6lrFdQo6mAlrJVnqi/i2tUbuK7H0dEx4/GEwXDIcGOT6XSClLWC+FIzGPSt/TZNmwoeVui+xhUjTVVVliHScR2qvABZIYSnBGodh+lkQl7kRBoC7Xmu7o+obJMtSMss0263OTk5YXt7G6PSbWyvsb+TyQRHuJSlsgAmYxoEAePx2CIW1nWoVE9LkiRrTrBKTrkKElop8oJaSnAgyVIc7bxlVUlWVNZhcmuJU9WKme0jljX+XSsWH7Z9WMXEaAdZfOpH2M9HPeVmsGD+NRXaJjuclOA663Cq9WBj1XRt2M7U56SFuiJNn4WhF0H/fvl8WAUZ6B8BUlcDNNhKf57GscUqQSbW+1AMPOry+Zv1x+gKGV9WveZQFBXvvnNP2R99DYpxSjntlRbDcz0X13FtJUFKyfXrV7l58yY7u9t0ux2EIwjDmDyfc3FxYau0JuE+m80sHN6wfRpyCkVWMWY4HK5YPHXvrdE5MsllVzM7mmsry5LHjx+zu7trgwITVJq+LSGE1b4Iw9D6x71ej36/z7NnChZqCCZMZUNqX6Tb7SrbUNeUctVv9FG2HyPQKPFcVzFIuC5xFJOmGalmQjL6Bq1WyzbkplqhGKkWlFbcUhoAiyVZmtuSqXn4YRgxGU85Pz7FkZAlKeky4a233iLLctrtFuPR2A4Q07Vf5AVZnuF5qrQfBAHb29u88rFXGAwGXLlyhVa7y9bmtsryF7ltcnVdl6zMQECWldRSGdkgULSisha4wkXUCpfuuOp6pFw5oOqGB1gWCOUNmVmFKwRRq60aMLVDVetmV89bTdgm3Mxk5VRQ5mHYotTgWWXn67pSzrF+6K1WiydPn3Jw5YpiDEJqhpkVfbDFX5dqspm/syxjNBopfQskQaiqJhsbG7iOSyUr+r0+3W6Xvb09qrLC8z0VLAkl2JYsEovrOz095fHjxypLt1ji1ArjuJjO+e1/+Vtsbm4oEoEwJGzFTMZj0JNDVgqe5Ljr+PgwDBmNRnzh81/gtVde5Zvf+paljbM2WEDTBjfLyFYbwHUJnKBhrdU9UuZ03VgZDL+0ZW3znrNykM2xdOZdrRcr46tXVZ3px35GooICAGpj+NU48TX+ut/vkWaKstg0/DqOSy1Vj4UqoKgG3MVySS0EdVkxn8+IWxGKwUmXrBvaJoDl2TIVlyxNqeqKVhwjHIc8y1fjulZOs+f75Klieqnr2gYZsqwV935R0u51EUIFxGVVKoY2IXQwx+o+N6BU6CDNvmJ+t9UQA0cTSviprJhOUt568xu8+857PHr0iLPTUybTiXJw/uMldJTtOj4+RVIRhQH9YZ87L93i81/4An/37/19zs4UZXZV15RFwXQyVSQQVUnge7zyyit85atf4a0f/ICf+Zkv88Wf/ALTiwve/MH3+N1/869JiyVZkeOHkWKyqmvdYI6FgwohKWSOEJJ5WtKKOjiOYnzyHYGQHlIqeE9ZKViNJ1z29/ZwheAHb34fgeTm9et879/+WxzA91wuRiPiuMUyWTKdTOl02qQmWNLsLsaWGKG7uqotMUSaJjx+/Ii7d+4QBQFxFLGYJ3Q6bQ2LUg3AF6MRvu9RSZVpq6ua6XRCoKGWURCQZQntdoft7W0m4zFZnrO5saHYqSqFw/Y8h7gVI/EtZLTdbtmAIEtTK+I5m01ot1s2o2Zwyb7v0m5tWAXiMAxI0tTaNhMcCiFoxS0eP3msYK1VBaImTRNAkmYJvX5P9dJ5nmJ302Pt8NkzXbkp8DzFStXv93QyRuGvR6Mx5xcXtDs9kiQhTRN6va6tfvm+EivMMgVpGm70uTg/o5Y1ZZHTitXifzEa0WmrAK7UAUIUx4DSOwoCH+FAmqom4q3NLUajEWVRMh6NSZKE6XSKrB06nS6D/oB+r0eaZpyeniAAz3coypyt7U0Nk3PpdnsIB7KioNPpMJ1MSdKEJEnWEj79Xp/ZbEotJXEU8+D+A61CXpBl+YpEpCzp9ftMp3NFbFFLrSavkmiq18NF1tj1r6qrBjTREBj4lLovZDafKThR7SmdHNehrCtm8yllXVFXFVmZU+kqcFnVSJN1x1lbBz5se7+qwb//zaRlVlVqdWy4fPjL5/hB57f67DrlbXNrii3rj647746wzHzKB1EL1wrapCn/DbuoTkwZmJVcCzhWdr+2VRsDC6vNIrCqXl+qYqxXVxq9wM1rE89/zyQ7Aa0npBkXEVRFjRCS2Wxu3/dcV0Oj1Rpf10Lb6oqqyhmP5zx7dooQgrd++A6B7+F5Dltbm9y+c4t2u8XVa1cYDvu2WtxqtSwsUyUkAs1Ep9BA3W53JRCq+6tgtX6YYN0kUYwf0+l0GI/HlgHUyEyY5HCWprh6f6YiYWxkGEVMp1Pr//V6PWUzNQrHkDgMBgNNMKEIn3AUSZFKDH20+fHRoVPSpcwlvqdYlga9DbK0hMphNLpgPldNv5ubm5b3d7lc4vmhbTieCpW1qMpKZ5ta+E5MJWvyvOKtR28rjYfAZ9jtcFae4Xkuy5kqJ8+nc6QjkMKxeLJ2u0272+PKYMhg2GdjY8je7h7dXpcwCAFFJzuZTMnrkrKQliNZlbbaNkvr+6sufkffTNdmyldiepWmnnO0k2cWNv1lPZl034CUlLoJtrYTQxsBsTK4JpusBreBkdRIKtUjLI2kmWI2NQ+4qlfiVbgOveGAH/7wh9x/+ICbN25w9eCqmpQROqNfqH6KuiDJUkBwfHxMkijlWwPjch0XF5dsmTGWY5XV9Hy8sMEd7WqlXUfz4nsSv+cSx0ol85VXPsb161c5Ozvj9OiY82cnVEXGpz/5Cc6Oj3jtYy9zcHBABZxNxgSOh+8o5ho1RqRy7h2V6RYSXOFQFSWOEPzCL/w8b775ffIso/Q8irLS91bh4i8HG47jkBcFQnjIChx/tRAJAZ4XUMlyzaDZZ1pXqiQsJVJYeblVICGx4nN2dXAc9bBM8KEPJEDvQwUmWZrR6fc09KjC8TwqWessuMLcm/FVlgW+H+gsuXoOeZYRt2I836cuS2ohqJyKycUF3W6bOIpBCtTpGxpARVMqpKSSSs9DIDg5PQcU20auCRgMta1E9Tr5rss8L3Clgy8cVPFU4jpKqKmSDq6nNBnqssZX1EzKwFPbhQSpnq3+uq3+WBgBq/umFt0aqpKTZ4/5n/7P/ufUZUWRFRR5QVnXFFWpsfvrwpGuK/izv/JVxpMJv/qrf53bt2/T7XYIw4j9vV3yrOAf/qN/zPf/6AdUVU0YRoRhQKfr8/rrr/Of/ed/i4ODA0otGFbXNYP+ATfvXCPLE779nW/DbK6qhKVqdBWAcHyC0NcwnxSXQDmqcYjnKNYuz9fNeFmBdLR4nW6mdF2PbrvDxekJ7XZbZYsdwQ/e/AHz6YzXP/5xAi9grAU166Kgygs8BJv9Ib7vWgexKAr67QHT2ZQ8SwjbbaazCa7j0IpDjo+e2YbdPMsZDAeKAcdRAUqZZSxmqiFS1pLA89je2OLRo0cq2RN4QE2RpSxmSq8nTRacnRYW5gngEODImrooKNJUsezpvr0oilRTbFEwHA45evqUMtOaP9JD1A6+ExJ4EXEUcvfOLYqyZDqb4YcKilPkBb24h9JwEVRVwZ2bN3l6+ERlJF2II183QEryZKHIMYIOnhNSFhUbwyGtVszx8SFxNEDWFfP5hG63x2Kx0HTBOaenRyyXXZXBzHKbPc3SlOFgaJvQF4s5e/s7OI4kCD3KqsB1Q2oE7e6A5WLJe/cfkaaqF67TbZOmiVZgD8lzxZIY+CGRvyQRKdPpzI43KSV1LkmSOYvpjFBXIFzHIQ4jmyDPi5zz8xGe6xJGEZ6nUAdB6HF0eESR50ip+lhcR4uilgXPxDOQSouq0jDUolSVSZOcMUHJZLKkolbiatqJtRz+UlJXAqRLXUvtLCl2qfPzc7wgUPTvOlsLWGw4BoJj/UmBaQ62dhhQ9PhYqvl/1+2PK/j4oADBJHJqQ5YhVjb6gy/igxiX1Pq0Okzz91VvRxM9oAgfKoRuJBTaZmuHBMcVtl9L2Wahzbh6Piq54tjjqWsxeifSOu8qOQqWVrdxqdY3unTta8GDpj83FTF1IQZy9eKgxHEUgkEa/6zB7uUInXxxXYTjKj/NrDt1rfr5HEdDoNXRC7MmawKWrChZPjni8VNlq12nZHOry/b2NnEc89WvfpXd3V1L3qAqy76FpZpzMegSA/U0VYskSRBCWNj8xcUFBwcHLJdLxWoVBAy0f+NqgoZA99Ua0gzT9G0CHuvrmcqNTrwbggfTw2fgkcJ1qUERjdQVy/lc9Yjt7n7AOFTbRw40Bn3VDT+fzxmPJ/zhH37PsgH5vs+rr77K7du32dnZwfM8bSTVgDQwKsNgoWBTLdWU2FCFfvToEaenp5RFju8JW/7xPZ8oVgxPo/GETren+fLbtnNeReaVpUCVUpIXBYeHh1xcXPATn/7UWlOwGYDNaLgZ3duJV6+YtsyEAaEw15UuXhhnExWBIhTMRDVMqzI1aGy7MMFCbaNZgwt3XXfNOTZRu4EMGceymaFvljfNMa5fv87jx49BCA4Pn3J2esb29rbN6K8YwBTTi1GO3N3dtQ3/zabsLMtYzBfEcUwQBPb7KouX2gxYVVV43qrKk+eqynX16lVeunMXoRuQPVfBQix3v4StrS1+/mtf48F797n37ru4+p6Wea5YrYxRcBxbWvzJL3yBW7dukiRvqUVM5pau14G1soZ5xrbUWFW0W579jAnCcNYNu5SSenlGvbzAaW2pTIgWvBON7ItqrdCZd9P4LW3ZQpeXm/mqlXhfmqX03QEOglJjn838KYuyoRTukiyW9AZ9BfcrS5xaKXKrzHJFoaloK131Onp2xNWrB4pWWZpqjZbO04wmpvIy1kI/CibjKBpdoZzhWl9Pu9OmlpI0UU2jRamICOq6JoxCOh2FW4/iFlUttUCXxgdjsmHmTqhXzWK2VhUyd0kHHIaKVaZz8rOnPFVlHxsgVVQ2I+Z6Sh3arEFRFPG//F/9L0iWS3xfjd+yKplORnz6059EIPjYyy/x6PET0kTBQXu9Ltu7A5VxqytOj49xNLPbcrGg3e6Q5RlvvPEGm5ubfPvb3+LxkyfquCgnzyjw1lWB53rkucrohkFIXdW0WrHOmNWEUYBSUK7wfdUkGUUxN2/cIFku8FyHIs9YJgnj8YhXX32Vi4tz6rJAVhVpslRNf3nOxWhEUeR0ux27iCnoYY6n6THzPMNzXdvAqdB6SgvB4HJd19M9ExFSKqYmIVxaGvIqhCDwFTU3skY4WFisweeLMNR9Y2qum4SGOacsywjD0MIDfN+3AlYf//jHyYucx48ecXT0jNu3b2sb71JVLmlaq4XV8/Acn063q5R0a4fA80k0K0xdl9y+fVOxEJ6dqMZbPS9ND8vx9JibN+6wOJ0jaxVoXtm/wmQ6AQRBEHFxMVLKwPM5m5ubfOpTn1ZwpwslELmzs022XCrK96Jgc2OD/Sv7tNstNjYHeJ7P2dk5VV1SFBVpkhHHMc8Oj6hqBZ+taqW102q16PZ6pEmqg72Sw2fPuDgbWcrdJEkYDobMFyrI9f2AulI04oY0pK5rlkmC47oqKaXnnoJJORamWesgydgtQwxgM8TSwCTV+pPlBVleWZIBRb+q+zVr1Ve2RqCgbamsBUJ4a+vWbKHgGTJN1drZ6OG8DNuxdtkCLJV9aDICmldM9fOPe/vvArN6UXDywftRNnDVC7Gexf8IR2StkrB2/OdFbc1nzLM39/45xr3Lp6gPpfwjEGKdDWptDMh6rfrxYQHbCysW6GBSYKuWlwOL5t+WwaxRIWlWPJu9m7X5t2oGcFprpK4VNLThy/WHba5d26XT6XDjxg2SRJEchGGE7zkM+j3d45FbP7UsSzY2NuzxYcVy6HmehaQbFjdTkTE+j/EbDw4OkFL1Qg0GA3AUpXwURSuqe41ykFJa+Kch+zF9HFVVWdhwkiS26mHsx2KxUD6A9tOVEK9a32yF4yNsHznQWC6XbG9vM5vN2N/fp9PpsL+/j+/7ykH1fb2Q+2tRkeMYBVoP31fYsiAM9CLsWJiQlJKXX36Ju3fvUFUFwlGRviOEarw2xqxQWWvj2AJrk8I45eY8Njc3ARiPRmxvb2v4iw6APAWXMDoZjkBDSwyVmsK715XCCFd1rXmuNWWZVH0bJvIz2aUojgmi0Dbi9Ho9yzsspVTYUljRk6VKfTnUD85MABPZrjCU8rkfG6CIFSdyv9+n1+upe1OUdDtdS59mZObN9wBu3LhhB7qJXs0ANM1CJuiTUtpgw7ApGG5m1byX28lhBMQMhthB9R94nnK2TBN0qXmdo36P//jX/ib/9J/8pppQeU4pa3ItGjifz+n3+1y/fk1hqKOQr375yzx6+JCyrFRDsuCFEFeL1yyUGqlxasQlY1zrMWXuZ13X1FUJRWZfN9keUzo22TPTLyEb+0N/SkpsRsS40UI7xkWeI2twfZVx8QMFK0FnA1UVwyMIQ5I0oS8GtNot1WujM85GnT0MA4o8J8tKiiJXlJ9VyZWDA+JWS8VAtSoPGbwrUtH5nZ2d4XquGudlSVmqMSF0qVw4Dv1+3zbizuZTkmRBK45BSvwgxHE9wCFudXS2c8VUhb4PjiMwL4lLjoBkFfg0X1OLo4OIe9Ddox4/U+rR+v66gUO328EPPPI849d+7W/yf+z+X7goR8RxxPjinMViYRtTDeNdVakxPhpN8FxBGMB8PsH3at59+5jNzQ0mEwXFMtz3s9mM87NTer2ewtFGAWWRk6eKGEEVsio7jxSmNsBQ/ZpjVpVhOKoIdPVVvV7qRaSP40BZFZyendhG9M2tDaq6YDwZ4UqpmIlaEZKaZbKg1YoIwz7L5RzHgd3dHUs1rfoOWnZuj0YjKx5m5rjC9KoFqd1WZfYkWdq+nbIq1PhxBL1+hzt37rC/v8fFxTn379/n7OzMjv0wDFks5tbWGRtlxKjMMQ12fzKZ2GRHFAcKKrS9QX/QpZYVfuCSpEvKqtS2CtxAkV/kRUEYRVRpQV5mlFVBjQqCksmSuq7Y3t7h3r17GPVfx3EBoWx24OO6gslkrOggA4/Dw2csl0vCqEUct1gsFrTbbZIkU/TgQYQsKxwp8YTA1wwto7NTRtMFJ6enqu+jLLh69QApBdNZAlIync6YLxLCuE2eFwR+QF1rWHBRUSZq0a+KSs8hl7QoWSSZUlkPIk4vRiAUbBU0YUTDWco14YjRsbHVemeVRZdSsR4ZByTPc4SjaJLTQonHmb6Nulb2oqxqwLWwzTURX231pBSs8PkSKQ0UspHJ1vbIcZTYXq2duRc1TV/ezHr077O/4scPEP74t3/X4z1/DeuBg1kbm2Q95ntNgp/mv2vn1EwSvSB4MZvZf/MYH3VrHs9xG4Fr4/k3gzJgfZxLlR1sJmdXQdD6ta5dmw6gTF9EMwEbhh6vf/xlfuEX/gyu67JcLonjmPl8TprkdFrK75rP51qEeEV2YPqSAZ1UXFVYTPXB2EYDbTLVhb29PYbD4crfjCIqKWm325pAaWY1M0zAMhqNbAB5WYnc+Dmw0iEzpBbGDzTK4Uq4U2gfI1tJKHzI9pEDjS9/+ctEUWQjXoPnB/UQct1kYh7+SmCv0E6pRxj6GnakHHmT4K+06Ikp3UhUI2ipedGNAVQKsoL5bG77DZpBhWrOVU63GRT9fh/XdVksFix082PTiVdGuFnGbDqe6xMlDHz7XSmlpWT1PI/BYGAj0NlsRlkr59lEsma/ppHWPFjPdQn1ecCKHcLc4yY9oDm/pu7F5Ylh3jfPwNd88K1Wi42NDepaNRdOJhOWy2MtALhvqx1GaA9YO6Z5NoB1EJIksbSYnU6Hdru1ot3UnzcDNQgDSh2pT2czJppT+t69e8xnM/rdHq+8/DLb21v8/J/5mqKCQ1AhQffCmDGg2GkSZF3z+c99hn/yT/7fqrHJ95C5ClIvG1dj5Mz4A3CVathzY/1Fhl1oUTelprwyVjQXOiFo+s0mwJDaSUYaFpRGHwJQlCooUCQDAj8IEAKNQa45Pj6mKiv6PUXjmWUZ3U6HWYP1K0kSXSKN1PzSFZGiKLkYjSmrkn5/QKfT1f1EyhmZzWZcjC5IkoxOp01RKA2bpca8u76vskG1qmYEYchyphqgVQOqbsxzHUt3LYTCxpelEh8sikKrpGtdDEuHvYo+pM4+KtjDevghjREGcDyErwQxXU/gOqq3Zjho85/+rf8BdVWxTBZ85jOfxLvnQalwt++8/bauvJXMZnOmU8Xtv1wuNCd6ohePiMAPkDJnb3ePKAzwNzcoi1LB7pBsbgyZTWecnZ5SloqmezqZEAa+RjOo4EplA41QlcR1Q12iLnUTndS2ryTPV8QJoNj8er0u4/EIhGC+mBPHEe12hzAM2NhQ0Jz5ZEy/30NKSbfbJUkUxj4MQ/r9rl1IiyJnY0Mp3SrKbBXwDIdDbY8qa4cHg76e27lmj5Nsb29paIxS8q3rmk6nw+3bt1gs5jx9+oRr167x0ksv8eabb/K9733PalGkaYZG81BVFUdHR5Yy0TTYG/rFbrfL6ekpt2/fZjafcnj41DIWNSuyrbiDQNErhy3F1GJYz3Ad8jxFuA6O5yCES5XXLOYzZpM5r7zyKu+++y7LpeKkXywUleOVvX0uLs5J05TFYmGrNpPJlFrO6PcVo9bji0MFd+x2WC4WyKpUNLCTCXfu3OXi/ALf95kuU0ajCUVZ0G53uP/gsaJLdlw+9alPIWXNd77zXXw/QAhF1RyGMWWZadIKqSu0lWYVU3PEiKqppIda9LW3pLVsKuuom7WmlqoGYJ7xykFTAYE0dNzSaPOofdV67BpYihDGodNVW7WHFZu3rvA2q5arpIx2+JqQH6ma1Wtp9i/WnNv3c1o/yFb/u26Xj/N+x/iw82m+/yLo1OVKweXP/PEHGKvXL59n88ewf8KKxtYEBy96LhZe9YJjvt81NYOC962YvGAfl4Ofy8cz19Y8f/MZVzewN5O0q9/FC89NOI7qq9R/K9ikos4/PxvxT3/ztzg7nfCLv/hnyfMUbycgimKioIXreBY6FcexTfY6jmMRJuY8wPQwOfacTUJGSlVtNDbzwYMHPHv2jL29PVsRTrLMft/YLZNMM3bTVENAJYAMG1az39n4beY6DSGRUQkPggDHdel0OhbO9VG2jxxotFot+2BM4/eVK1esIMjR0RFJknD9+nVOTk6Yz+dsb28Rt2IQkqourfPgeqraIW1gAlLWVFWhgw9BkRfkWW4DDYDJaEy707XnZG6maphTdJ1ZltooMEkSyw7gCKHE6nRDJEKQmgqMJ6wDYAIJUxEwUbFAUBWqJOWimmibGgNmcLuuy3BjCI2JaSavclS14rE+J9c2apaqstKI+Jtq65ejdXNuze1FEb7rONZRM0ws5toWi4R79+5xdHRkKSsXi4XlcgbFNGIClMViYWFSRrHdwOKOjo50xWqlm2ImyGg0UlnRNOHo6JgbN65z7do14jhWAjUoRyhbJrx77x3S5ZLx+EKpYMuaNM8s2wFgqydVUXDn1m2+9MWf5PjkRE8MVON0xVoQYc4nL3JFf6izds/Pk+cXCpXF05A63VMgDe5UgCE8ELZUv8rWrVVMGrVmo7oB6n4laUIUt/A9D1mqjEelDdpsOqOuK9I0ZXdnh8l4zO7OLj2tP1JLSV3qfUTRqolewwkFkjTLyU/PGJ1fWKckzTLyIkfWklaro5xi4TBfLqhrZehc4VDVFY7rsLW1BVJR7Hm+S+AHVKoMiOe6eH6gGnyDgCD0mc1UtiPLc3W90jTCa/fEohvWgQ+icYf0QNZBndHrqPBDhV1st0I2hn02tza5d+9HfO1rP4fnOezvbVG+vaLpdR3odtq6h8Jlb3cHIQT37z9gc3ODJ08eM51OSJYLDg4OyPOEhw/v4zgKKpRrmKPBjxsKQmPIDdOS7/ko7PFKubYo8rUx5WkWqrI0CvYqePY1DEnN1RauqyBuZVlY3QbPc+l0FINYu92iSJerYGc60SxEqlKD0IJ+UlLLivl8inAE0+lcqXvXNXEc4biqwuh5qnx+enYCQBB4tNoRWZYTxSFCOLTbHfb2dq397/Z6nJ+d8ezZM8ty9NM//dPcuHGDr3/960wmEzY3N2zix3Ecul2luN1utxmPxxRFQRRFdDoder0ee3t7aoy5HsIzNNkeTx4fcutWhJQ1YaBsmev5hBKlSdRgMnLcAFnXJMuE+WLGfK4oe0VV8/TpIfv7V/jBD37AZDJlPp+zv79L3ApZLOdsbmwyHA55660f4vsBnheRpDnj8UwzeTns7OxweHiooVeqQlbjULx9j16vx/loxHSxpKwqJWJ4PkLW0Ol0+amf+hKTyZhv/P7Xmc8XIAWu69FqtTk5ubBrYVk2Kwm6Yl/XVNV61vgyROmy/QK1XjUMUcMW1RjthsubROs6GLumYgg1fXVgYOasPZ6UplTZ2E9j/9ZGrrZ6zWlddyxftO590PZ+jv6Ps/13dfCbSb8PCkL+Q1ZJ1KFfXHVont/lIKD5r7lO+3m94w8LGJpOdDNYaJ7H+wVda/dMJ+9eNAcMJKl5Lc0qxouu12zNIMT+XqteOZNkNTZMJV8Fi3nJN77+BxxcucFPfOqTpElFEKis/3w+X6OhNQmVJgIlSRI6HaVFtlgsLPyprmu63a6FWxmfyvd9KyiqNJFCPM9jfn5u4U5VVdlAAhR02GjugPLlTUXF+HC9Xs8KDJo+DqNoboIQw2AlgEQz333U7SMHGmoRVNGOobszzrUQghs3bmgM7JmlqUvSlCRdWuraTqfTWGQrHC3YUlWVxe5mWYbvushaNZFWEpI84/T0lPfeu8drH3+Dl156mYvRiIcPH9Lr9SwMZnt7i6LIreKm4zgcHR2pTGUQ4DYiN4MLVvhiiecIkKpZ6dHTp2RpyubGBpnODBl61dlsilKPjPA83wYQJrNv1JZni8VacGYoxfRIp8wL/MCnzA31mmI1clytnKkH9uWo90UT4kU4SvOvgYU1J4rZXNflxo0bBGGoHA+dySjKkmS5tNSFzYDKZMOaDURhGLKxsUFVqcy8CT48z1PCZVHEZDzBFQ4He/u4OIzPLxijJsHm1gat1hbHz4741re+iZCKX35jMGRzZ5taB58m6DIToMpzhIRev8eP3n6bH7z1I5ZJaqPv5tbMGhRFQZokGNrW99vM/a2rivTt/w/xZ/+TNUO9YtjQWhmsL6GmYdw0OZs1ttFKrr4rBMlySa+vmsSyRGkJTMcKrxkGilVHSkkURyRpSpZn9Pt90uWSyXSqIE+laoYN/ECNaddFuOr5uRqnWtaSulT0s0VeaL9A4HgulW46K6uKwA/s+K7rmv5wSKvVYr6YkRc5cRgpuE1ekGYZ/Y7WsMhTOp2uCvrznKLIqavKJDoVr7pAKVY7Rk/dVDqwwaEJxg2Ll6p0SMim9JwJ/8mv/2f823/7Hf7UV36Gne0tPNcj0mXl5XLOZHxug8i6rpnPpmRZTpIsAcH5+RlRFHN2OmYxWzKZjFkmC+JWpPRvul0dPDokSzWXp5MJxyfHDPoDwiikyDOS5YLFYonQFVqoFFOLQNs65awJ88D1fPU9TycWQFLhegLHBc9TehLXrt0mbiloUOApDvX5fKrVaiVJssB1Fdud16g0zmZT2ztXywrPU81+nU7bLpJGf+Hk5MTO4zTTleOqxDFwvEyNs06no3UyQnq9AdevX6fVavH977/Jd77zbcVM1O+TZcr2TqdTXn75ZX72Z3+Wb37zm0rZur2iRc7zXFXiXNcumnmec3Z2RqfTYTQaaZvnMhopHY3y5IKyLPne9960In2gGFEOrl/DcV02NjfY3tnF95VYZbfXoSwLnj17wqNHD5lNp/R6XTaGQzY2NvnlX75rYXFxHFFXGT//8z9Hvz9ke2uHf/7P/wUPHjzi/HzEZKogCL7n8+Uv/5SipSy/Tau1oKhrnj17xtnoGXX9lIODAzzP451798mKnKKsGE/nCFzieMF//d/8Q6azMXVVUCtZd/WvPFPz0XleJ6Cua111cG2Q0HQIHcdQbq9s18rCqGO8n9stm1hTKZ//3Pt8sZnmWndcG0XLF23v995HjAs+asXhj2t7v+N92HE/6P3/fwUW77e9yNE324vgT010A7Du0Eupbdz77++yj7KiSH//qktzMz6PQVc0Aw2z76Y/2vzeqnK3YqBav44VxKrpbwkh9BqvhS0bAYLneQhH4Psu168fMBwOcBwoyoQgbCGEy87Ojj1Hg6QxQnxGj0YIYZ16A+k1gYmpRBiIk9EYMjB880zOz88t4Ybx0Q0trkpsefa6TZLWvGcCmKZfb87XJNlNpcTQvSOlhf5/VAjcRw40zENp/mugPaY5zTilQRBoDYCIWhYoLvBzPM+15ZY4auN5vr3Z8/mc2Wym6MCimF6nS6fTxvN90uWSJ48fUxUls8mUmebc3traJAhCfQOVgmKWpRb/a7jfpVQ4+KxSmcayrMiCTJemCgQFYRAQhgFRGHL7xjVAUhUZo/NzlaXUA6MuCmbjEXHUoqdFUBZpysOHj7l67brCJCcJQRhYByMI1MDJspw8yynSjLIsmE2nnJ6ccHJyxGuvvsqdl1+mriuVyROmTFjZyg0oI66EZ4RVqJayeuGElVKCbi60eWKdeXccxQ7VasUslwl1XWlGqgpTSjSUk+oequNWlXYQG46/EIJlonDHjoMt9+V5I+hzHaIwIk0SxUZSlgoihHJ4acX0h33+4l/6i5wen/Ds2TM2d7YQjiCKVE9PVVc4jkuWpiR1zXQ8YXwxIskyPvHGJ3jvvQcslok2Duvr1sooqvNL0tSyCDXuGFwKF2xVI5vbTDsIy0Zmmqvtwq4DD+PlmnNQ2Xx1XgJoSIQDkCQpRZbjxy08zeftaSdQNXEFdLpd2p0OVV1zdnbG/v4VhpubZEVBslwq6seyVM6iEMStjur78TUXPYKyyCkK1TDuCEeLRirWjXkyRwp0kOHpLBWEcczm1hZlXXFxrrCeVVlRVlIlDByHVqulGtdrSX8wpCiUhkS6VI49JtuJ1sqw993gtrGVFv3A9JBV9kG1Vgk8B/70V75Ev9/mK1/5KaTMOTp6DLXKuBwePsbzPVVh0GXisix59OgRUtYsl4nFpyrHuaegQLLmypUrRFFAp6MYnoIg1D0WLnmesru7w2h0ge+7Slnb89jf2+PR48eaf94hMKrkYkUp7fuq16yu61Ug5Qg84eksVYAjBI7rgqxpacE30+dmz1dnqVSVcKyyWUKQV5US0qwlN27epDo5JY4i/NBVYn5FjlM7epwlLJcLVLN/aRerwA9xHcUUFsch02lpRZ5AL7KOYDwaURYFnu9RlgX9vsqEJcvEio2+9957usIZsLOzw9tvv630IQYD0jSz1dCLixG5piNPksQ2LPq+r7N7MBxucX5+omypoxZbRzgsFgme75EXBVdv3OBnf/ZnGWwMFdSoVKMqyzNc12FvZ4+X7rysxkKasbOzw8WFsutXD25SFAXHx0fUdc73v/8mReFQ5PDqq29wejomy2pe6m/heh7j0Yjf/cY3efvtt2nFMfMkY9G4prqueHZ6rpqvK1XtdzTkV0pBkhUaQVnhCE23KYygp8Bx3AbsWDtSNjurEkcWWijWrRbGBl1aClQBYr3B1ZoeIXWg0QhK1ioMl7K+NIsWzZJGwzHlgzbRiEIuf/L9oTNyLQBqVI3Nnl540JXFXhniDzy5xmnJ5/8Uq+tvnptYew7Gfqn/NK9Urr70vqfyvveuYRY/8HPmEOZrL/jgh0PBJEZs1zjoL6p6rJKcOphg1Zxti9Gs9wB8WIDVrDqswbMaydXajuVmstVVcgN2VKoHtoJECV0Z10uLDXaMP7si/rns5xqWtk67TbfXU0idKObg6j63b99ge3sTP3BptyNFuOE7CHyrV2au30Bba917qYRJla0zgqtNIh6TVAVYLBYAFmpqEtxZljEYDOj2+3Yfpuph9mGuy0D7m0lb857Zd7MJ3fSlwCqoKYqCVhzjuUpo24hAf9j2kQMN85CllGuCJyZKMu+pZtFqddOkx8Ywot/foCpL2u2e0nWQK5VxU4re29tTN8F1tXFWkJr+1iaf/txn7bHSdEkcR1oksKSqirXzMgGGuVGm7FPLnDjuWJqvuqpodzt4suD87ISTxQLqiqosOD87ZWO4we9/89sslkv+1Ff/FJubmwRhQD+KmM8njJdjwrhFVkg2ul2KtCAMOnS7MX7gUZQljnDI8gpH+Aoa5ka0e23S5YLAD2iFAY/vv8sP/+gPSJYz3vjMZ6nKDM/zraq0Ya8pSmn7VPT0U5zkKExts0Ro/8VMHte+bgaOupcJ06lqHoqiCMdR+HBjQM2/anIoPH4lHWazGXmeW0EahSGMQAsnmUFsInVTGTi4dkAQhEikbvR3tB4JhKiSnBsGDHe2cbTAlytcW5USwmGWT5mMJ1R1zfb+FSbjCV/90z/Hm2+9TfKHf0SeVcg8pWzojVgj5UBeVORVTaYdUbs5UlH7XRr3juNQnt1HljnC9VdW3PrFTSOqnWn7m96P+bBQvOK2moFO/9WSdJEQBDFBGFOWNXGrw3w6pXYrgihU9IJCKYHPZzPOz8/Y3t5ic2uT45OK3Ch3akOWLJaURU4QKjpcaTLqgQ+1xBcOjhdSV5XCeaOYazwj4FhVOL7H5t6eUuM9PkZWFUEYkmWKTaqqpVaDDhhPJsRxmzCOmY2nOCj9nFWW1OiONBwW/Yu9V0Ksx2DaYde3G+foD9j4VIfp6IR2OyYMAoIw1roGFyzmEw4ODmxQY56LEKpa0G4rikBjo9qdgF4/skkSY3iVk696E0xfU11XvP76a5yenrKzucVkMlEGWQhCXfEF7RgKoeg6G4bc/OsHquJk6A0916XU48xkpnrdrtIIyDOyPFeaFUGgejT8gDzNWc4TotBhuZizubnNZz7zObwg5LWP/wSPHz3i8Pghaamxtb7HbDxRzdx5oaqygQ84FEXJdDIDKeh029RVTRSFWgPBRVH+hkwmY6q8Il0ulHZNlhFHEe0ownE9lscJ6VI1SZ+fXVDXNc8Oj5Rit+NyejqirmvyQvUpqKqzoKpnOMJBIhTFaxRz9dp1nh2fcXJ+RtyKWc7mVHVFpp16U9W8ev0mr73+BlHU5vxkpM5ZuMynM05PT1ks5mzv7DCbznj8+DFFIRmPxgwGAx4+eMhcN6rnRcHToyNOT08Vk5XratjVHAkUAptFtb2Io5kdoyufWzv6VQVC9YeUldR1O9WsbeEccmVE1K+SyjRKWx/LaA6orZaqhwqdbbXsSyaOZ+WMvv+2Xn3Azq7VHGxua5USGtlwa1cv7f6jZutf5C03EhDrH2246qq8+YG7WX3QJHy0o7y2X3npsy889Mpm2XNrRC3PJarebx/NFz7s/jx/XrJ5zBd+rrmtV7wuQ7aaQedlmJFKbK6/vtrn8/CjtUqHo5JX6+P30lhqGPcVMc8L7oBU51nXZu4I7TNoBilWgU6TRa7ScgHW5q5VI3zKUlXrQQXtQaDsvFoflMRBv98njmMODg4YDnvsX9m2TFE7OzuWMMckTYs8pRX3KfMa34+RVa1Zb1dVk6IorGClYYIyKJ48z20frUlYGKiT6cEwc67TWTEJdjodNjY2FDJHJ7UMuqe5Gf+32dRtAiqTFAZsct4EO6bK0axomUpPnuc42nf/KNtHDjTSNLXOexiG9iaah90ccKbppEnJ6gMiEmsRoznx5oRo7lc4Al8EDLTjY2i/lsulbXi0QYTGr5kbZprhPM+z3f6i3SZNVQOg7/vEvZ5irikFYavLxXhGHEWMR1PyCh48PuTOSy8xmUz53a9/nStXrvCxj31MUTVKyXw+ZyuMyfKMCo/AdUnShDpRToaCUhXM5zPbVOl5Hk7LA88jCBQT15/7lT/P+dkpv/N7v0vU6XHl4IC6XtDv96FWEXwtV0FEs5lPGXw1YZvlTBvpCxclnFY/d589L6DTDgiCFsfHxzx7dsLW1haLhVLfXS6XhKGaeHWt8N5VXVPqJvvmIBZCUJUlnivsYLXwrQYuU0rDNZ+RZZkuDfrUdaV7YaDX79Pt9WwQWuiARmVVHfwwYLCxgecph22+ueDw8Bm/9mu/xv/u4v9AUT6gpqbS/TrNbExdK+rOLMtI0svNTM9nymyQUqZKdM71V1UOu/pKu/A3FyOlG7G2M9YWdPMpnTKbTBV1sxsoQxiEIa6vaFGFEKSuwJvP6XZ6it1isWA0GtEfDEDC6fkZeZLhOB7CUYtGmilRLWEUx0FnV0E1dKrsuuN5eI66v8YZ8gOPnd094ihkPL5gPp/iOY5iWMqVQJfjunR7A2ogK0r2NrcoS0U7muvqoqM1OFZ+grAFDHU6q+XfVt8ano3KYkmErOmy4Mb1l5EyJ/Q8qrIkitTYODi4wsOHDxFC0Ov1cC4cqFcCmEZVtWkb5poLXEH/Kuv8dzodjAp9k4I6ilSzuFLH7j9HUb0KarENztIGPVpbp8HQY2zkKvDPuHHjBrFufm7LDjU1s/mcPC9UP1oYcXpyzt7ePmmSMF8s6XZLrhxc5fDomOXFBVevXmW41eMP/uC7pMuEXBY4rkeWFbqnoCTNcgI/xFDqRpFq4C9zRd4Qhp5Sea9hNJqovqQaLsanamzLmlbcYrGYU5Q1aVZQlgVRpFjIcg1jBRVEmLlotCiEtieVFTVUsIjD4zO63S5bWzvcufMxpJScB+c8uP+AxWKh2F1aMYEf8L0/eosnT48I/EAFEmWB56hsW7JMrIOm+moKkLrZ2FHN8AJhnZlCwz8qbYtscg2oxIscNzOJm477pWqAjUHWoUvrGfoXbOK5X9aOfflYNObTB+7uha9/eGAgxCo7aq9f/6yVV+x+P3yfz19/IzB4YYniA4KB99kuw2jWji9f/Ln328dlh73xgdUpve9uxPMX/KJjNhIkLzqHjwobe7/PvR9UqfFN3u8ZvN/Ya/olTfax97uGDzrPy+/Z940vIQ0pzcqXbMKlXO3bGJhTs8fW80J8X/VCRVHE9vYWGxsbDIdDoiigP+hz8+ZNy9Y0GAxIkiVCqGTRfD630H+AVium1NVm01thfDPj0BsYFGB7eJv9akIIC6MyNtBA8E0TtoFPGYip6Q0sioKtrS0FadLXa6okhtjHQKBMf6FhnGq1Wup+at/58jM0xzVwKePTmedixAU/rEJlto8caERRZCsKxlE1QYWpIhjMfhPXb0ovl0tvzfKQeQjNzURglwMRo7BoGlbMMQ2Vqik3mUXLUqvqLKWnBUzMzQ2iCOG0CFo9Nnf2oZZcvXGL0fk5eZ5RZBlbuzn7V6/T7XaoagnSwXXADWPORmNcPySIfJZJghdIwEG4PlmagIAgaFmFRuF4zJeJqtr4Pm4Q4jmw12rzZ/pDvvXtbxFGMfv7+xgUrPJjjVLl6p6aiYRYcVMLoRrbDa0aNVRlRafT1s2knlKejSKQihHGQM2KvObsdEQYhTw7PLEO2Wy6VLCSuAVCUtalfV5Nw5JlGbIqrGZKHMf2+ZmynoHJmcnnuq5tWF3M53Q6Hc7PznBdl36/TxhFBFGkaG5zxbwQd9rkWYZAsJgvkLLm7t07OI5LkvwX/O2//bepZEVeFnYcrAKwijwvWC5TlovkkvFcH/O2DAzUVUn27E3CG59V0B+dOREaxoZUz8BUDWzIouPAVV5GHwv9pglFpKAsCuaLGT1f0dcu5gva3a6Cq1QVbl6SzJd4QqnnBlrxU0rJxsYGnu9xfjFmPp0BQosu1koETV/gKtAE19H4U2GgZurZArTabTa3txSd62TM5OJCsU2VBd1On6osKaqaja0tvCDkfHSOH0a02h0WyyUImI7H6tg2gSAbib1VJtQs0Dre0vHYpRI4AkHFKxsFw0EPISpErSgLpWZRSpKEmzdvrnHwGxvj6lKvsWXGPoVhyHw+t+x1TUfKVENNIsXwiu/s7pAtlaCa0QYyc9IsgqssUWmNu1n8bGNvWdmslRFeUuqsDrPZ3C4WrU6bRPcejcdTyqJiPB7zox+9w/b2kDBsMZ3N+b///b/Ppz/zWV56+RV+9MO3uHn3Jj//87/Ab/2Lf0G6TKgrNc4c4VLUGUJAki71XFD2yWj/GO2ToihJs5S6qgjDiDTN9JxSTe51LcnyjLKsCaOYuqo5O1dMS8Zul2Wlk/yVtRkq+VFSVTogN069XnCPji54990nlGWNp7WRlgvV3FjLmsUiVxDBp8fPzVWc1ZyXctXAqdYcNRPrWikAG20kiUSK1RpU1lUjcX3ZQV3P6n6Ys3d5zXuR0/dBAcSflM04SoYR8cdxNF60fRTn/t91aybdLmfpm/jy5zP4vPBzH7q9T3OKCTo/yvm+3+s/zrgw6/OHjdEXHEknoXRlvmGv37/68IKQUTRXOr2G1u/3mfffp/mI665gWmYMGkfdOO/GyR4MBjbbf+XKFS4uLmi327z66qtEkeonLUslFJnnOWEYkOUp/z/i/vxZsiTNDsOO+91jf/vLzMqs6qV6epbGjDANYBYMMJgBJUCEaCYTZRJhECkzgYRIyKSftPwVMooiAWIRaJARosihBpRAkBQBGEhgegYDcVb03lVd1VW5vyX2uPt1/fD58esR+TI7GxhR0Vad772IuItfv37P+b7zna/ICwRhgLLaIk4CLJbXGGQDwErCtNbuO1VVIYljZGlqnfw6e5wibdpsNk7i5PeroNqGWY31eu0yGV3XIcsypxZhnzg+y1jXQuVOnue4urrCaDyWoKStefMJmi8H4xzi84j3MwD37OPY+zW4NBFiBobX7geZkz+QdMqXTJG5sSIegHvokn35vsOHk4qg/3CBJftaLBZ7kS+llHN4mUwmrnmcf7L+xeDvhwPBtBOzH0pptAjQwUCHCQKtMIgTjCYzmeQWeFE6VFWl86RfLG5wdnGGNBuiaYEoStEZQOsQgOidfUKmtYZRBi1km4FW0pgOIiGbzAL89E//DAaDgZN9KUbBlUS+e1mH/+Aye4sYJ3DbtoiDGIv1wuqQXzo3riRJsFkXTq4hcoTMpiID7Iq+U/hqtcZy+U1bd5NAhT1Y4yQUBh6iU/0E5/zghOY4TCaTPSatYFCXhUT2O4PJaIzxeOxAShiHgAGqUiQXYRhY1yfZp/g9CxH5qZ/6g/iTf/JP4D/8pV9yBgZO6mAY3SxR1y3yvAACL+IFDYP9iEwfoe6Qf/VvIXn0kwJ9bXE1jLEReZH8OKnWHbFCkg95V7vvwthiYaWxms8xHA4RJSnCRGo1BsMhdtuNbUKnsFwscGsLZkeTMRQUmrbF6ckJzs/PMBwNsZgvURUFTKeglZZungpyBN7DUFmS11iQFycJprMZJjOx0p3f3mC7XEIZg6oqcXJ8jLoxqJsGg+EQk8kRyrpGUdS4d/8eWmNQFgWaqpJmYxbsSSd0j2oZ938wWlv7W8muyHhYO2DYXh9KAVffwOe/eA+b9RKz6UjcyKoOcZyi6RqsVivXB2A0Grlz1EqKhlerFaIowsuX0r11OBy6BwjJ8GKxwGg0csGToihckIWuHHVVYZhJH5PtdrtX6CjZpwCSjmdDPCn2lT4UIeq6cU5C67U0QJXaKOD09BxKBTBGurPP53Ost1ukWYrbmwWePXuOo6NjLJdrXF7ex3Jl99+1+MbXv47f+s3fwS/8/M/jj/zCL+Ar/+BXcO/BA/zwF38Uv/arv4oXz54j3+2knkNL1qosxRGsqYWAt63t+Gz6HkGdjXLJKYp9IryIvNQFtWjbudz7xlijAblvOiMmBHRqq5taAH7HLigEN3SOoX233GNdUbpnAx2SWrsuN50Qfgm0CEttTOf6Ibn517ZWsksCKmTJJ7XSTd4+q4yxjTdtUOEtMd7bRm0P//Y2D+zfK/D9tq+7jpGBrMPjeR3peNsI/Ou+d5hNeDUr8Xbjdtfn7pJ9HGZA+jnUH8/rSWGfkdk/5ruxiL99f1tvIhtver3pHP33DoO3+xvR7p4Qt0W734Mx9AuwHbbxjv+ubSvVy+4Y7IKSHi7y3r4qgw2WJQAzxtg2apaGz9LfJ8syvP/++xiNRjiyhiV00AzDELvdDoPBALvdFlqLcUye56iLArt8bd0sK0RRiMlUOnEPhyOLZ9hAWTvCQLmsUgp10yC2gWuOCa2xx+PxXh8xZgN8gK61NB9m9iDLMnRWLcJaDjpJMWuytSZD/H7btlivVhiMRnuBsu1267AwlT980cDHH+Pb21vbV6onRnQa5XOPf6PRDxMKn/385944L4EfgGhsNhsPdO1PKP5OpsnJB8A2pGIjKgFxhyfunwRTQkxFcbvMVNDO6/Dm97fD12EUg+DBn+yd6dB2gFFeIZORzvIGxpIGAAEQhgoqjBEmLYbTI5zduxTNX5xI/wEllpFahTBGu8ZogHHuMkpBosyQ7oquTkXJBZ9OxvKM89KBSgF107qQAJ2TCOQNOkRR6JyxSMiKokCNBgoBkiRDmmQwBgiDBlGY4PRUbpA4jrFYLAAYsbgstihK8ZaPwshGCkQGlucNdBTs3UR+H5Mo6NODfVSxd3tgZNFPbSpjoOMEaSLX+7BASa4dkIQhVGdQ5UKQqNtlBqUqa4RhhH/pT/9P8e0PPsBXfu3XXDaLxFhrhe12h7IssVqtgSM3W+SfOzLXAjwAVSzQLZ9Az95x18VAyWTRynYjP1y40Wc4BE3Zz3hFipa0mK5DbTqslgtMj04xSAdYVUukw4Ho03c5AIUuDNA2NToDbDcbHB8do8xzPHn6FEfHx5hOhYjnux222x2KXYG2bXpNrD0GuX/s3EkzDIcjTMYjhKFkDK9urlBVJdI4hmlbjEZj6CBEsV1DhSGOT0+hdIDF/AqjyVi09Fspmp9fX/cDqbpeRrL34PbvTys0s2kg447RjrExSG6+ji+8/8cwGCQo8i2SKIEJFPJdifVu7WRRu93OXm8rVTIGt7e3To86HA6d21CSJI5886HGdYyyKWMM5vO5u1erqkKeSDfjb33rO5jNJk7W6aegOZe59jVNg6KQguzCuohJk0sh44vFEml6JU2QDBDFkXy2LNHBINAhVqsNzs/voWkavHjxEtvdDl/68S/h6sVL5HmJz3/ufVxfXaFYr/En/+SfwmqzhobCH/2jKb730Uf4pf/ol7BaL5FXOXQg9UKBDnFxcYnx+AQfffQRNrvcNraU+UIjC+nRIAGXru27RBtLOjrv5z3QY5uz8uVHiPeLlOXFdUPb+5778CVnvjSng3Vk4m1sb0kcHIf0aujBoGQ25Cdm1YSL23vTP068CvR+UOD3tpmQ34vXm6LM/7Tg3wdJP8h33vb9vSlzx7PbHHzvbY7jbTNF/rkdbtc/lu9PdPr3ffDt1/H5GRZ/TnDbr9O9v+l8XznmO47PJx13ETcSCve79vdl+ntA9UFd1/vM9EFeP3ijlEEUEQuI7frQ9nsKwxCTyQSz2RSj0Qij0QhxHLsmy9PpzL0/sVLqpmmdY51Irv1iZzYlTbDZrDAajTAej6xsSCPNxCo7z3dI0wR5vrP1Dy2qsnP92ZbNEqPhyDar1SiK0oH9oihcjR8srtntdtZ1r3SEgGtcnufOrtb1vrEvgv04jh1O9rPn/hxigJwBfHb2dkH+snRtJ3gd2O9js9k4jMTgK7fTtq0bb5HuFi5DwywG5Vd+9p7PwrdprAn8AESDD0ymYXzAwJ/5gObfDi3DCPSZNiKx8Hsz0MWKUgbKejgQlEXdddNzX4eyLP9n7pfHq7WG7mxqu5Uusl3bIIltTwhoLwBs9X8h5T4BdCRMHFqAk1iJBkI8AmW98P3aFCEb0jHdWN28BSdNh6IoHRAnYKmqSsAoJHq4XC6dFKmqKmSDFKenMllWqxWyLMPl5SXyXY6uARbzBfJdgd5ZqrOSDpH+bHdy7EGgEScBBsMpzs9PbKfc0JK7wEX7Om8x5U0lN4ZkJljQBMBda6X6budAv+gVRSF9IwJ28JSIeJZlaNpGikbrxhamRmhQoiykM26LDkYbBEGIMIzRtLVrbPVn/+yfxYurK3z44Yd7Nz4ArFdr5Lscy8UKZubPkTffA6ZtsPv1fw+jP/5/AHSE1hIHEhH4TX9AzNxnO5SN3AK4w3jFcIZhuZgjG4iH9mA4xHa7wWA0AkyHumQh2ARlVSKJE0vAY2w2W1y9fIEkTTGZzjCejDGajNE2LaqyRt3UaOsarZFC/FBrhMw+xjECpVE3NW5ubrFdr6C0xiBKYNChKKUp2GK5Rqc0Tk/OEEYJ5re3CAKN09MT1HWFqiiwW69RV5Uf27PEATA2Sqz8MfDHX0nGx0iIC0zfm6bG56Y1kjiCVsBoMIBWAdoGqMMWbdM6NxLWWThAaR+CbDI6mUxcFKosS7x8+dL9jVGj4XAIY8TQ4sWLFzDGuCLkNE2hlRDq3//7fwLfts0A1+s1mqZD28icLKtSxt5qXQncKdeRTBvT4oAKNdrG4Prq1s3XpmmQDTNsd1vkeQlA4+nTZ1gt19htc6zzHHlZ4b1HD/HHf/Gfw3uPHuEf/epX8Nf+6l/FT//8L+Bn/vAfRhiGKIonePL4Gb7w/hfx8fc+RtU1CMIQZVlhvVpjtS7w/MUcH338RKRSdr1nNpCGElW7LzcxZMuKNUs+UFPuuvq3lvFmhsg+99dpZSeHdsSTJMIDjYc35x42M/CMlPZf1ozBbcTt27isGvpP9Pv6p+QEbxNx///363USojeB+H8WkvT6775K5N4E7P9pj+F12OF12/Xxzj55OPyeFP/73+P942/SJxrAq5K6N2U03kQ09j7r/e2Q2L4uWyRv+sfvZ2jEitsPANKKleqU0WiENE1xfHzspD/n56cYDgfYbNaYzWY4PT3FxcWFi8qzp45/HlmW4cmTJ3tupiyoVkphvZbM9enpKcqydNH1IAhwdHSEIAgwHo8tzqncel6WJSaTiatBGAwGNmOjEQQRgiBG23bWAENGsa5Liz0kc5FlmQuuFnmOwFOE8Jym0+lex2y/NQQzLVz/icdY+8xnlV+GkCSJa27K68XsB49nY1sRAHAkhaSDzfpms5lzufJx2HK5dHOLWJuBYBqkMJicpqnLwPg47/u9fiDp1KF7CoHjYc8HfsYnGBzIoihwdXW1x+58hs0sRtu22O4kaji0AACA8xJmwYwvlfIXAf7rS3T8weN76OTB37aN6JDjCGkidpNKNgpjvCgEw2yw3uVKoq1dEEGjTyOGkT0uI5pirQ20MmjqGk2Zw0BccDqIPGi93mCz2WK9Wrumg23bWTlLjJ21qWRWZ5ANMBpLl+DRaIjhYAAohUGWWctfjSiM0FSdK15lgVEUx+LzH4l1mzEGOtAItEZzwLppy9lZUC14MZDiXCWyJzYFbOoKN1dXqKoK4/FYyEWaoShyC7hFEpMkiT2eBloHCAON9U4IlkhPgKLIRdJT1YiC0KYRb11xcV7kyEYD7MqdtVkW8ibSqghRoPC/+Ff+Zfyb/9b/SSRExmrFjcFyvcV8vkaSrjxyIdIeBzsOo45KrmOzfoF2/RzB7KG4ggVi9auMAC3lOof3mRD5uu0fQXmGbJy7tsBanGqMAW6ur3B5/x0ENttQ5DsMhmNsu5X185eFL4oTbNZrpNkAo9EYVV2gLAtcvXiOMIoxyIZIBymSQYqBGkjAV0OkW7ZZV900yLcbbDdblEWBupLtZ2mC2pK8qpJ+ANAaR0cnSAdDrLdbFFWBew8eAJ3BZrOGaWqsl3NRnbzyQBYAyGg0o8iWwXo6ZmXrWpT7Dhbfw0988TPggBoobLZbBCpCGNjarDiRe2AwwHw+B9p+LXj69CkGg4HT2A4GA3FDgsJ0MkEURqiKEloppHGCUAcoygqL+RJXVy+x3mzcQ1XbeqmyEuKy3Wyxy3NIw9AaVdEgjCK0TSvkys6JIAhk3JURmY5SUEpshKE16s7g+vYWxgBNI7UScRSh7loYJVaoxnRI0hgXlxd4/OQpNtsc829/gG9969uYjIZ45/ISbVMjz7f41idP8V/8nb+H0XCEDz/4AN/59ncAG5wo2xqNlUMpCIkgGepgZU2OLIi7XdO1PUlQymURjJFifeg+A6U90GggDQP5OtSrd+gcYe/QWWcauua5Lzn3Pf/+5PZ9UqGUAo2nD6CrzCW1/1m3A3Mom/Rn7j/7S6nDSPUbghyHgYg7fn+FDO3vzPtaPx7ylg8gLffCPjh1oRK3X+X24+5f1R/33SDWi4K7rb6ePBzs2XLMnmSy8m2fbLwapedRktjT8cst5UodgGhmzQiuuSQpKDthGOxXSu7f/nzg/cwsBT/b16aJzr8PhN5FGu4Gbeo179vj7Iyb73ufMcZlJHSg3d86I89r/l1u2/1MFf9jhiGMQkzGY2SD1NU9MPM7GAxwfHyEOE6gFDCbHe31D2uaCpvNWvqjRZED/FEU4fT0FJvNRpQXVsUynU5xdXWFJEkwHA6d45IPgEejEZIkcfIkpZRb02laRGw6Ho+9QugBtpscWoVQEFUHm6wqFQCmRZQmgAX7m83GrVtZmqJtGkS2y7f0pZKAHWsviK9Wq5XLBqRp6jArr49fW0zSUVUV1uu1w00kqTyPxva44rkFgRh1UDYdMgtvpb5NXSOw5jpxFON6eY2qqjCbzoSU6f1eIm3bomkbr9cbBGNlUndXV7KvIhdpGLM3fu+NN73emmgwZcJmaCQbfmMPAE7zdXhDNY1oqFkfwO9RYuBr+NNMrBONgjvxwUgijHVVOxbrS2z8zIq/TaakeMw+EXG/tzU0INkHuw+Sp6YTfV1gXUqYjsrzHErbuhEvY8GMzWq9RNs2jq0L0UpRFyW2q60FJztXoGqvLaCkSywMkGUxhoMBJpMJtrsN8nzrmOnIavI4KWG7EGdJ6ghUqDXCVCNNQzfJ2dujaRpw/WFdTGW12BwzZlOY4iMzptygaVoABmEQou1aoDNIwxDrxQJZHGO33eKqqqTXRycpSwI82iBvNhskSYwg1I7N73Y7VGWFMJJ+DduNdKG8ublx5FIWpho3N1I4HoQBirxAGEWoygoKBmmW4Q/+xO9DVRR4cXULA9GS56XBJ49fYDCa7T20tKJR8N0vQ2D+4X+F8Mt/RsiBjcC7Brr2gdUpK/3A3uPM4mj7JDIdAO0+YOinrxTKqsDtzTWOTk4QJym6DijLHOPpEXablZyrEYlI23Zo2g6RrevZrHao6hqj8QibusViuZAMRhDIw1BrOebOoO3oFKIQByHassRqvkAHg9nxTABu1aBqWigd4ej0FFk2xG6XY71Z4/jsFGEcYrdeA02Dm6uXVuJi7zMSh72B5KiovQejGysv0iyEo0P2/Ndx8VNfxvx2gd1O+i3ESYxhprFazRHHEWbTGeqmEdvCNAW2fcRuOp1hPr9FnheYzaa4vb1FXdXItzu0jbgsMTKX73bY5QWMCXB7eyuyvLpGXd8CxiBJU6x3W/vwMy6dL+egYRCga+Tams42djRKcKxjV9aJyeKdzmZIqhbouhYijzYo6wKdaREnMUobJetgcLO4xa7YYlfk6GxGtlpscL38wA2zenaL8KvfACCGEG0ngQuROPUuYMKSG7eGyt90n5U7BPXe3/bIpCUe+uA74Cm7f3pisAdsDQkwd7zv1NS6efM6VO59td/THkg3OJBqMSAAwHT72zYH2/3BX6pH8XbLPVbcB7lsrNq/y+M3e7/7h+SD+H2S4P1M4Hh4ZK+JbmvtyXlgAFez5t+vPoDeb4K2N4e8w/UJncF+4BKw2QLvGQ5uxwFfLxPlrarGGzfZpnxWjqEDlCWxUL0UyBD491IfpfZtejWbuR4QAloc3zWWMFRSsDdK15MTG2STMd6XRSsVePvoSZJSCoGOXJBPWeDYMdNrFBD0Tepc0zxlBRBGjlfqLpUNDgJhqBHHEUIri9Za4+TkBPfvX+Ls/AgXF+eYTKYYDDKnMAmDUGzSbY+vsqwshlNYrdZ48uQxHj58iLLcoa4F7FMyRDwxHo9RliXG4zHWa7Gbps4f6CPwdGEiQF+tVq7XDnHPdrt1uJJ1GQTnV1dXGI/He66AjP6HYYj1eu2i8VVVIRpHaBuRHZlWMI5WEaaT4Z5Kp65rwTHbLZjtZqSfBglaa1c/4uNgqmc4d4iz6PLEUgEqeLTWbqxISOIocXNDa42qrFGWtcXIBjvbhwhd54K/UEpuA6PQ1Z24MELvOVONRiNsCmvznffETSmFOIix2q6c7KrrOsRhjDRO9xy1vt/rrYmGdKRVTu602WxcF1iSBspkyrJ0dqQE/VVVoSgKnJ+fYzgcugi7nzbrug7L5RLapuWoQ2NxilzcCIHuNWL9Tda5rAcnFwlNn/qn80gfAdFaI7JpKInsB2h4oasKy9XKtYbnPtI0dXUSrMTnZIuiyGreZRKu12t3nJvNBnVZw7QdkkGK8WxivxO6xYg3G6MoTFEeH0/Rtg34oO1TX/1iaUxn7ShFGhXHkdVUt+gfCNJoCzJlUVcVojhyNxMMsC3Esz7fSUHSs2dPEUYRRsORyG9sMdFqtUJVlhiORtbhSjIQg8EATx4/xnq9xsXFBb7zne/g8vICOlB48VKI2uMnn0IphZubG2y3GysxA6bTKebzOfI8l7EMIlvoXbkbmwQLkPkwHo9d7Q4195PxCFXd4g/8oZ/GD//oj+H/8tf/r3j6/CW6QiIEt7c3+M53vgPzMx7wYLO9V8KL9m37IO22V4BxpRWSnYPtDG6lQQI6+4fhKy8LmnwXJhcitPtfrxaI4ggDANkgtQt8gdFkhiDcYbPdoClKxJE0QKyjEGVeYLVZOYB4/8F9GAh4bRspQC52Mp+HoxHiMALiWCRNXYfdbY7WdEiiCGg61K24SyXZANOjU0RJgrwohGQcH2M0GmKzWqGuSqxu504ytZ8p2geMdjCJjhxsUIfvM1Je7XAR57i5ukKoO2w2G0ynUxgDRFEIY4Dj2TFur26xWC5RVCXKukJz0gChXJ+PPvoYZVWhbRp897sfuQd717TOQYdrUBRFWK7W6Dpli5xbGzmEPOyV1HbxHmTzw850tsA4lBoGa4PIcz8EYbLdzgGvzt6jpjMuksVoJSNXWin8g3/4aw5Y1C0jsfu24XYPbk3kvg8zvpyLh+DpbSU/h1KWQ8DL8z8Etv7Lh8FvB+3v+NSbg8Gv/f0VYHxnVPmf8qVeodjudRdYPYwqH77Pf/1j3iMnPiC+4/27tnfX33wC4JiRoUzOB/0SlqEjUE8CeymQr3KQF+XU/fu+Yw8lJQz0cTtd12e0KMMEgECHkjGzhf0KYn7BiIVB6zIMPdsV0O/WbJfq8EdD33kdZHz6n/1Miuk6SAbEWpe+QoAZ8BRHQHcdfbILsz8PoGwzUNh11CAK2Ii4c2MSWzt9bRnGaDR0WYHT01McHR1JN/u2wcNH78DYgOVgOETbNjg6OkZZFthuVw7LMZPQti2W2yWOjo5cawFmFuTatNI0bjx2kiFRJ1SutUCSJA6IJ0niSAPPlUCdNbpd17mCaAY9KS2aTCZ7xcwkJcwWzGYzZxTkkx2p35DMgt9YWgGobAB5PB5jsVg4mRQl6sw6TCYTLJdL5waVZZlrpsdAFWtk/cLqp0+fYjqdOlIFYK+ompiG48VtOKepqkZRlciyAZRSrnCb0ihtTW14zZgUEJIZOinZZrNx5M5XFXHcuc+6rl3tIkkVx5u1iD1W/f6vtyYadDra7XZYr9dYLBaO9bB4xPfa9TVgHCzafu12O5dt4Gd5Y11cXMAYg8iIFMl0BpvVGo0tvgHgtGv83mw2c9th2q5tWyyXS6Rp6i4eFzF/sTbGoG0aBDbVxah9XdfY5Ttr4SiRbAUrX+gkVZWlMc5OpJELVF/Br610hnUNfgRGGlQxcgMEQegucKgCsQ2tatuoT8GYAPluJ0TALkJS+FwiSVOXhhMddoEwELvSPM+R5+KQY2w0hNkoYyR9WtmeIpvN2jp8MZ25Rtd1uLm5wdXVFQBYu9kZyrKQjEjbCBNeb9A0tZWVxNAQ54VPP/0Ejx8/wW//9m/hJ37iJ/Dy6iXCUGM0GuHFixdYWQKXZRnSVKRe1KwfHc0wm02lMOz4FFEYudQpAEeKmqZy2k1O+jAUx5/b+Vx08ssVHj58gP/x/+h/iP/4l/8mPv30MTqbwZnfXou8xb460wFvAAa8KYuXHyKrdtDJ0IUp+4eKEoclA/tA6x2oSOTkcUzdbi8k2oulWqel+e21a0iUJCINqooC2XCMMIqxWa+lFiDo0LQNlAbSJEXTNojiCFVlM25BIOORb3B9cy1zuW0xm03RVh1qKzEMoxCjYAilA+RlBaUDTI5OMRpPAa2x2exQFAVOTk8xGgyx22zQVBU2qxV2u6099v7BbnAQYbZhfYW+47E3yDI2CuhaQ0iCbv0Up9MM29UGUQD8+Jd+HF3X4eXLl/j000+xXq8xzMaIogRVXaEDsNqs0UyFaNR1jW9/+7vSQFP3HWDZCNAn9UEQoGoMoCI0XY26kXsfkMXeOSKpvumlX09hjETGO5thlDlN4OcDLlt7Ytekzs4/BkU608fTlbIRPx3ZuQZUdSVgyRYjcDv+664Is5uH3stff33g52/nrtfbkhEC+te9vh8oftPr8Ltvc0yvk+68Corf/L3v/3r95w9JgQ9qX0ce/ON7Exm56+fDOow3/byXffDWRGYWlM3C+mviPqnQe9vl/ALgCImf0QgC7cCPH+3nnDbGoGuxtw0CNt6DcdRbUTMzLuqD1mVp+v94jrISk/T4L5Kqw2uolNpbt4zyavQCyagIxtB797wbOwWXeSBhOczK7GdQWoShPNeCQFweCWjHowFOT0+RJgnee+893Lt/H5PxGG3X4uT4CG1HxUCKINAIQ+nrsNut3TnWTY00i7Ba3zrg2QdyJIpPskIbbjo/EehSIkRQyiwDcR/B6W63QxzHzhGTypCmaTAcDlFVlT3exJ0n96GUcsHE9XqNKIpcUzullMOWAJzj4Hot50l8OLR91Ojq5GqAqwqB1q7gnHIngn26gLKvhV9LQRcqP9BDjElzHgA4OTlxMjD/vuB9w+PhOfBeItErylJwoc18k+wZI6qE3XqzZ23LYzUG0GEfPKA8drvdunHh9eO9QzMVOl758q40TZ0ahXUab/N6a6LBmyAIAhRF4UgFGSJBLJkPmY5fQO6zV1/240cTOdkbm5XgwFR2+2SYAFxh5mAwcGyWoJ2TiJkU3py8uKzdqKoKpWXOWmtXbD4ajTCbzRAoS5bCwEUYXGTbRiMVBHhrHdgIrUHTVjBt77altEZTC/irrQRLUqN9pqWBQlfbZmJRhBtrYZplGZaL3OnhtNYSQV4uENsuj50xWMznmM1mWK5WjpCEQYD5fC6NsWzBvVIKpycneP7sGfJ8hyAMkKUZ1usVPvroA0Q25ff06TO8++4jfOlLvw9PnjzGer1BGGq0TQ2tDLIkwmhwam3fVsiLHJ/93Bfwm7/5m/j6N74GpYB3H72LJI1RNxHiOEKebzGdji25uLQp3BB5vkMcR+5GWq9X0Bq4vb1GVVY2NRpAuogLuYiTCErBdsg+F6tgZVBWosPcbNYwAKq6wbsP7+NP/0/+RfzN/+Q/wUcffwwFhapuXNQZgPjo35V9OHh1bYPyo68g++H/Xh9VIpg0Rmwx3Ub7f5UNrRHLuMCcjb4pA2eV61TVXYvbm5c4gkE2HCEIIySDIfLdDjqOcXRygjLfYbddo6wq6EAaGsZKCpY3m51oNZUA212+c3MYAPJceiSYVixuu06hMQqmNcgmY4wnU0TxAE3TYrlYAgDOLs6RxhHy7QZ1mWO7XmG9XAAQcsDmr45jw7quGblblAXZ3gcEQLuMUgcRCMmHou/+XdyOasSqxZ/4534Rv/O7X8PApsF/6Id+BB9+97u4enGLn/3Zn8Tl/XsYDIdY77b4T7/7FTv4CmXVWskfrRhtfYQSWVFd12jaXGSAdmFv2v1Gk/06ZXumYD8izvPrbVtxMBBq7884CHh06AMpe8DTElRZb2gRTDMJuH2/AlI80HwX4Xjd5/i6C1gfZkTeFBl33znIZ921v9/TTMIP8PpBCMoPvG0Ab9rq68bOt/gE9p0UAewB6jdd09eB1zdlOXzC4CQ6zqZdA8bLXKj9udLLmN1RAIANIjGwop2MyXj3fxhESOL+WQ4YF5El6G8aAd3sl1DXNa6urqG1wnA4ciYyALBcLgFbhxYE4jZkDMHdq+SSkiviADmffaLh7kv019WRn6CXSmnduytKkE/WvDAMoQONtmkdUH7w4AG6rsV8cYPRSOQ+5+fnmE7EXjwIgNPTU6eY+MxnPmNrXXNs1ktbeJy74KpE3FfIi43gtRAwqAGEaDuDuu6gA+WCqpvNBmmaWvOLDkmcYjQa9dlaixu01tjZgmPfpIdF0pwvJAxHR0f49NNPAcA1QJ1MJm4uEryy7o09IObzOabTqZMOsS8FrwlrAxy+sViFEXhfws9aULZJYECWNRtUzCSxNP4lLh0Oh86FkLUaw+HQBXOJeTku/v26s0Fhki7iTGYYfPBeVZW7j6fTKVarlcs0ZFnm3AhlTipk2cApXFgfwaA4x9MFQ22txmazhULvbsp5x3oPHiPPgWPK82J2i+dK4sS/vy3RUOYtV1hpAgbXSt3vR0FJkd8Xg7Ipv4Dcd6QiGfGjbhxEBUihi1LIiwJlUaC0Ufyj42OMxmN3on66lQyQmkBefC7UeylJLuSMopo+ZUsyIrIPWTzaxlou2sh7WZROOxmGoY0wSgamqsWXmeMlzcQKOy4KndXckQjRAWG33Tp93ng8xm63Q13VqOsKeV6isYAoDKUjctM21r5VyETPtLkYSLQniWOsbVMyrTXm81sMBgOMR0OkSYLEEhhOKHY9DoIAT58+kezILkc2GGA6ncCYBkVeSNQ8inB9fW1JWobRaII8L/DixQtoGyXIsgxJEmMyGWO73WC5XOL6+sbpKtNUsmDMcG23G3CBj6MYpoPTMI9GI1Sl6AXjRDqK8wYd23lRVSWUDqGgsMtzDAYDp3P84IMP8A/+4VfwO//kq9hsc2z/fA0zAbACwn97AJj2reQbwewdTH/xfwsV2mIoI/IkKRbk3IF7SPsP1f4nZdUJfeRQKaJ0AnD3f5jMpAgbOpTu3V0HrYDYOn7luxxFKfcKTGdJbGDlBELCFOAK+anT77oOaITkIAqRDDIMJ1OEkVyXYifORoNsgMl0ggCiU23rEpvVwj7Uebh+DsMGESyRYoSPD2sXASVbt+Mm96Idv2qL0X/zb+Inf9+P4A//zE/hP/9P/zZevnyJ2WyGn/3Zn8Unn3yCL3/5y4jjDGma4eX1NZI0gQ5D/G9e/u9QZzWCjcb9v34O0xnrZCbgxVhpSN3UCLRkAo0F8/J+HwjpTOf6QPRXxF5L40HpA/C3J2dSff7KfY/khXBceR/2v/iaWamM1F0wqvY6ovG2r7u+c7jNu8jIGzMW7tq++XNvSzbuAth+rd6bXv+/IDSvz/hwFZDXq9K212/PJxqH2YjXZWD8Z+H3O8Y3jYP/TOb6JTNXJL0E8K/2HPIkV/vvSHYeBl3rb1O+02c3+B5cFhGwARnXk8bfn7xH0EiM4VtuyrY6Rxz64vEOXIv4zOfYxUmMrmu8Y7QFuCygNb2rJiU8gJANHUh0/fLyngWCLY6OjnB6eorhUMxblNI4Pj7CYDC0Ut8Yu13vdAcAi+USaZIgL3YIgwCR7QoNiD13WZRSc6f6WlgWSD958tj1mWHwNAxDPH/+HHVd4+zsHMZIr60kjqXdQBDg6dNngIGTJknAT3Af3ZqMMQ7gsrkc95MkiYvi01ZVnv2Ji4iTSFKFQMzR1392rsZBnuWVk6sTIxII04mJxdhurbZ4lKSTEi72rFitVq9I8wJ7DUl8uF8/IM3jJU4sigLj8RjAvlyf50pyRmLALA5lW+yvQfzHc2PzVmZPeD51JdLnPM8d1uF51E3pyAsz8zRfaurOmQgxwE3SwMC/MWZP8UKpG7fFjAtLJyg7M8bgD/3hn3rtWuLG+AchGj5Qb5oGn3zyiZNCnZ2dueIQ1kZEUSSFvTYLQYZEZsXKfF4UV9NhrJwpCGFMhzRJkaQJRsMhVBBIlb3NTvgkgzddoDVqb0D9BZif8bMoyvtuTzJED2+aCnEUoWlqF0lXShyjqrpCEgtrXq/XwrS1EAlG229v52i7FtvNRrIaVYWmFIel+WKBIJBtLpeijWSxWZZl+NznPofr62vb40Jht8sxmUzAiJJfd8LeJKdnZ05T3jQ1qqq2WkOZREVRuEm/3awRhSGKspQxsySnqiqEkfXwzwssFtJEbjgaIQw0skHibioZN9vhuKqRZSO3kDx79gz37t1HEGhkWYq2lSjIfD7Her2B1sr2AZGHSpZlePTwkZOIdV0HbcEqQSLJCAD7cJEHBWVY8pBREvlPEqyWS4xGQ3cDLRcL1G2L3/ndr+Lv/v1/gKf/s1uYMYCVQvDvZFBd+4ozTf/g3JcDZJdfwPDn/tdQYQzTGSt3Ue46wrD5mJAHFmdJ5gJSzMeaDjlAV9Fg3EPOuM8baAyGY4ymM3kQK0oijLhtRUKumrZGXVWoywpVVUvGwoinubHfk20zABAhSlLEWYY4SRGEti6mqJDvcoRxgMl0KgtVXWG3WQFdi8XNFYpitwee7eiAzdZc9JDkiWB7H6lbrtH3YBAc0KH+lf8zBsUzvPPgEre3cxR5aZ3QOP8VBoOhEPKmke1ohbKu8fxfeYlu3EGvFY7+0jEA7NU5BUEgBcYM0PoZBhiogD1cDrIWBlbd7Q5/b668LZaVoIqdG6ofk0NSymxU//LAK7BHgP5ZX3cRid9LovHfxjG+6fV7QTTefhu9bPIH+d4hgTjMRhxmK/g6JDJvI5d63f4ZHJF/7XqBAH6NxSGh2CcorxIbWRP77foqB/9c/KzK/tzb34/fv4HZBh8XCMlonOw4cBlxBSjlpLfT6dQFXqQ53ATT6diZzpycnLjtPnr0CMbWPQ6HA1dnEIQh0ixxGYvZ0QxZljmzmKIosFqvMJvNsNls9uQos9kYQaCcWUNlDVTCIMR6vUGWiRU3o+ysf0VnsNvliOO+FnQ6nWGxmKNpakxnUyyXSxf01DpA23bI0gEq21DzxYsXiKII77zzDrquw+PHn2A8HrvsgzHG1Rp0nTRwm0wmLgtBQE8JM3GdUsr1nCCg9Wt3KREiySORoFSI7lR8rygKB+xJRjgmJBwE0n4d52azwWq1wtnZ2d6cYl3eeDyW6L6dR36QmufPJq/M3gwGA3Gk8soDGHQ/vL94nnTI4lg4B0ML+P1aYpLG9Vok7SQJVdkTaJIUjllVFUjSxB0/a0UCHSDPS+fgxXMrrGye426McWPH4xwOBTfRDpeZGNYls9b6j/13f+GN6wnwg0inlI0qg3Iohct7lyjyXEBN06CuK5iuEx0/pB5hdjRz31FaezIOuZCj4UCirqpPYZpWelnc3NzgV3/11/GZz3wW9+5dIo0jqE4chqoih6Y8qxVtdNuKd74JAinM0hpVWaBtOwTeJPObuOV5gaGdtFVVQhrAtEiSFJ1psV5Ioy42dxHWJ7aTi+USWosPcZKk2Gw2ODs9xe38FkWZoyrFsqysSmSpgGAFas/hPJDjOEJbN5ienCBOYmx3O0zGY7x4/gJJkuCdB++4xbSsKqR2wrRdh4EtRqqbBoDBzfVL5LtcJlaaYLddI99tMDuaYTFfoKprlGUuKS/TIc+32O12OJrN0LQ1dKdg0OHq5XPHxk1nUJY5TNciiiMMhymGAxmzrusQRxG6tkWNGm1bI45TPH36TCZ21+L5y+cIwwBJmqAoSlvA22G7LSwJybDZrKGg8PTpU4RhgPF4giRN0HYt6qpBVZZouw4319fi2T0eYzDIAEhxGDs9V1Ul6ctAI99tMTuaYrvZIIlj1GWFui7Rmg4/+ft/HJeXl/g/hn8Vte3UHhkhCJ3tFNJ50Xii0d7aUaF8+SHi7/0jxJ/7I4DSAj4V4NEFWygMwChXKE4yaYyCar0sBvyMABcrPqBFUrTbiETq6OQEURChC6QZWtu2yEshwYEOkGYjDIe2s7KROc3It9LK1QBpLfeTUYHIzKoK290adVEjiWKcHB0jHkhTo81qiXy7RlnsUGw3MF0r47FHzEz/n5KzsQHRHpCzhgXKc6XyQIsBgA7Vd/4ezPx7KAPgg+9+BHHo6kEFjJCK1Y4FiC2UzTh2pjf0NADqVgIFfh1O29S2r4ctrPRknPIBa09ryQWvG2HX617sXg3sg79DgGzI+V7B6GrvQSeWyPtk14EwKzd7O5rxCoN+9XUAEA0OiZRy11IugZu4b9jmXb/vjyKzSPt/w6tjo2wU3GUMlSOK/Sl44NS7Z/19+1+h5l7us4PteB+U46H7T3/eynvPmP5vbyYavG+8G8MRSrvWKC3245C5LfOhc2CZ4KDf7j756DMMqq8tcmfvDa5HGoyBI/DG2HsDnG8Benljb5/KMexM7+RIRyd3HUwnhdvuojJbyMJv/x4U05K2bSzA7wmI/+IzXGtpChdFMdjI7Z13HuL4+AhAhyCUqP79+/dxcnKCzWaD8Xgsz4UkwWg0QlEWjlBI4ENkQKwBaTup+RykGeIwcg036ZLYtjW2mwphHCJLU9RViaaW5/9gOEBdVfYza2kWt8uxy3eIwhBhqHF9fYUgDNHZ6P5wOESgFWbTKbIsQ9t1qMoC7PMlwdgWVVXbImUxUZH6iCGOjmZQSuHJ46cYjUYYDod2zaxxezu3wDzFw4cPASisVisMBhnee+89tG3rCpevr68BSICSNQwMNPvR/qOjIyc1Ivj3QSklSfP53EXdWXPB7fMzq9XKAd3dbuf6Fwle62srjDF7kiZmnkjgUlvDOhqNXLSedrfsmcTvnZ2ewpi+PgGAkzGVZenGj5kIv+k0G7+SKDC7Ecex61Ke5zlOTk6wWq3cd+mc5UuQKEkjmSN58Rv0MQtnvAVTByJ/b23gkZBhMBgAShxTi1L+GCcJ0jRBWVVuuTfGoG5qQImtLQxcg0I+b5llkdrOGVgT/TavtyYaRbFzzLXrOqxWK7x8+VJSM9bqTKQ1U4xHI/lsEKBj5J0+3Nb6ra4raRBmmRknL+UVTV1hNB7gF37x57FcLvG9Tz7C2dk5ZrMp6lpIjd85XIiMpGiLsm/Qxsm3zQtoSGv2PM8RJwmyNMV6tcJWAbvdFnQ6ACR1GYWRLX5WLh0YhmLlulwssVptXCaHrgaVzRjEQYzBZID7l/fdhFRKYbvdoKpKlw2gfGo4mmC73SKOE6RxirbpsFyuxMkhL6GUQRRLau2jjz5wWaRmMpHF20ZjylJ6dpTlDm1bwZgGSmnc3lzh9vZWIgLQMF1jIz4tRqMBqrpEHEfOfQBdi0CJq0+aZghDSRUmUYgk6m3dCOxHwxGqokIUarR1haPpEebzOV5WLwAl5xLtJE27q0oEWiEKJROxXq1kjuWFk8ydnZ4hDEK8vLnCeDzBfL5A27VIswy7nfTOODs7BdBnqrj4MwWtVIzGLlJFUcDAYHZ0jMXyGnGs8N6j+8hWGWqsEWiFDECtNRoLVLWyHv/udQDCTIf8G/8F4s/8DKAipzs2lhTAARgSCPnNgUtl/07gBkhxoaMp7CUggIVRxLaucP3iOcaTCcbjKVQoHVeDTjIodV3ZBnvi1BJobYvBIxDcK6XEH7vt0FQlukaKmsNArvdsdoQoFHvh3XYjvRm2G2yWCzRNBWX1yMa7p2V1s+etANiGawZwWUOX0QCzG+jBvB0IpYDme/8I7bf+NpQCykauRxAoKLQw7AStFHCoEmkJyPaJS2taHPZJsHzG+2qfzfSlZXKtzd4M6BwwuyPy7E0Tzh/3fefT35NSdzRexNYvJhVQv09YJKOj3HF8P/7Qg0//w6/5kn/8dxaGKw8nvxpZ39+fvcienp/nBff/+/v1aNprjs/eEd618o95jzAeHJf23H4OJUqma3vCr/yaA5mbrx1iSxYM57Tbpg0sGBb/9tdVIUAUJU76QNkEpbQAXOa/rmu0sMDOMKop64HWPVd5VW7F49bQKuoHGMadk9Qh9KbeBrJm0LnJ9LZ4e9dawbruedkI9mSC0ugMrNSCc1jb53RPRqQxmqwjcZygbgq7TY0gUIhMhCTto7Bt02IwHOL4+BiDLIMOApyenuDsdIqzsxPcv38fQRDi6dOnePjwobNnTdMU6/XagTpKfbM0xHQ6lWxAoJDvNoIVtpJxODs7c0CUz8XGkoCqrlxEN0oimMogtpKYIAiw3Wwc4O0sMKvKCk1dIwwCLOZzHB+LkUxVNDg7uXBYJS8K1FWFqmhQmkaMMbQU4Qc6AIyy/bZKJ3G6vb2xxcSS2Xj8+DHiOMb5+bnLnrStyLgoxxFipi3JEMXBZHLinqPb7dbVZFDp4Ef5jTHOfIdAmVkXkgwCbQJlAvnRaAQqN0gyqqpyNqrMltDIZ7vdOjWGUsoGd/u5MRgMcHt764A5e2oQU1JCttvt9hye2JOKwWfKskikiC1JjFjjmiTJXs1rmqZ7wJzHTxdM4iTWNvs9Nmj3S1LrSwGNMa6eYpCpPRLEYw50gNV2BRglhAgKdd2iyEu0TYc4CRHFVvZUlWi7vswhjATXyXwIUBQ7RJHcpzwmrlG73a7Pptk1htK57/d6a6LBRcxvhDIejwFjoKGs5WzrLjwntgoDZ03KlGZRFNisN5jYycYiGRYhhYFGoBQW8wVmsxm26w2+8iu/gjAI8eU/8GUczY6c7i7NUtRVhdFojPVmjZubazx5/BhBEGI0GiKKYjx//hzKtqpfLBauXTzt08YjuVkGg4FjbEmSILDRjq7rnN7w6OhIBn27QxgGeO+9dxGGAZqmRZal7gYTrd0WVSUdrfkAMUas5/wbmVERTmTqGMkaxU95iK4TUnJ2doZf+ZVfcZGBruvcpOMCwGgD079pmuLo6MhFc7Isw3x+62RF/qK13W4xnUraVdgsnDyLi05d1y5Fx5tuOByiahtUtgBru93i/OIM2+0KSmnM5wtMpxNk2cCleqnrLEtfchfj008fSzF+oLHZrDCZju1ikSBJHiAItCWaCmVZAJDF5+TkGFk2sLUsgZO0DYdDfPrpp7bot0W+K1GWlSumzbIMP/nlH8PXvv0tLFelzQQQ8vsFkPv3RLm+RvH1/wzJj/wPAMUCTc/NyD3AlSsG998h5urxnwsxgPKFVxCObey3Xi5tKnuKbMCIlcIgS6GgrTWrLPJ1U9kIpaU9SkBXGARIkxjBKEYYRq6GqG0aLFcboGvRVRWqIsdqvUTXtlbtRRCj9vweRSLRI0YBFnBF7vbP7hz97xjTAV2HLp+j+sbfhsK+Yw0JpSMSByDSfzELwf11r/nsXTKSQ/mHH7R40/fvkg/5QOxNEp/D7/rnfdfn9kDfa7b5e/G6SwLzg3+un/dv/TIAoLyoeU8KlFIekOZ7e3uH9r7nWD1kzvsSWf+aELT70qH+ur25vuLu05NMQhiGSK2so6oqGBhEUYIwjFxUnDpsf64x8NXXOiroIIRWvGcABTqUeVkM0/dO0FrbPkb98cvc6uyzRzKir54PSRxeGXeSMA6xq02DBB3AyDJqKK1cjUFdN5iOxkiSGMfHx1aqEuPk+Bir9Rr375/jwYP7e3r107NT1LUAo5vrawnspSnKosDINjcr861VI8gz6vLyAoBxAJcAtqoq3N7euuh7VVV49uwZRqMR2raBMSHiOEKanjhnIoLys7Mz14iNz1natBI7hGEoTUBV7xg0m81QFMVefcJms8HDhw+RJAlub28dgBa9/gZhEAIRXMaKLp0knpvNxkXqg0C6NfP8+KxnxJwA26+D6GsrjAueai2OkLvdztVX+DUJeZ672gnK4dkXgw1SKUOjIxJBP/tBGGNwenrqCAvt/2mn6tdHKNX37aqqykmIeP7sicHsD4vaBTBHrs51tVq5VgS8lpvNxtkBc4xD3bsyjUYjt22SiTiOnY3tZDLBYrEAi99ZL8L7d7VauYwE5yAARzgYSCBBYl8Pzl/WLlPaBMDWpjZuHCgXIx4/OTlxWJoZiPF4DAODwSB16wjvf97HeZ47skBzJZIvEgpiSyYZmE1hpudtXm9NNMq8ENmT7otb6QPfNftuDGzOd3R8hK7s0DYNylxuFhixZnz65FN8VFT47Gc/i2fPnuH09BSr1UqAfVNjt95gl++Q73ZYzOf4zLvv4Wtf+xq6pkVT1zBdi/VqiauXL1yh73a7xWAwwOnJKebzOT795FNst1u8++67QCfs+/z83LVvB8SdYjYduxTQxkYi6AfNwp3ZbIbr62sH3H/sx34MZVni+fPn7uZl2nc6nQDomx9RKqS1coy2aRq8ePECeZ7jc5/7nNMe8sbmDQcA0+kENzfXqJvS6Sd/5Ed+BN/61regtcbFxYUjRMYYx9xZaERCQBJC5p0kqSOEtKzL8xzz+RyRDtyE5iJJj2raxPEmoqNCGIUIAKyWt+g6gyCIkO9yu+Ap15XZmJ1LmQq4FetcelLTdQGQ/i1lmWM6nbkCMq01FouFPf4OSZJBKeD29tbqUCUyUOQFjAFWqzWWy5Wtk1G4vr7CaDTGyckxrGoKSgFf/vKX8PC9B3j+/CV++3e+ivU2R10bGNtcDardA3bGSGfQ3bf+HuIv/vetPMF4Pu5wn3MRTvmDRGWJhY3tEu3xGJfHUH0uhJanFv4CUDBNjfnNtTiQJQm0DhHFiXVZs9FSRZlBZ6VKssUo1BgMMqkd6oCq2KFtaksmDNqmxm6zQbnbwLQiJ9N2v358t9e+AsxKsGt03yQLMPCakinYKDCk0ZtlXJ3psP2H/zZUvtobP//f38vXm7bpg9F/2pevC37d/g/fexPB8L/j/3u4z7d53ZmN+T7H9qbX67YBtT9ftCe5OTxVtXffvGZ7eLX4+y6ic/exKygVgH17Dr+rdW8AQDCu2Ejz+7wOSadWGlqHgFEoSza26rfPZ4x/LX1HKV8mAbDYuy9ihjG2nqp1AODODJPZl/D5GR85v/1zINEOAo0w8LMggI5sJNTauDeN1OUNBgNX+xfHEY5PjnBxcYHxZILJeIzz83PUdY3j42MYI9p4X4bTti3CSDlAmCSxtdLfIAo1gAb3758jy1IrEWqRJBpN02Kz3rhnOusf2AuBgGwwGODy8hLvvPMOdrudk0Xxucgu2Iw0397e4uLiwgGvIAgwHo8xGo2wWq1QliVOT08xnU4BwNU3xnHsdP/Mrq9WK1xdXeGdd95xGILHSpdLZgScVMuSS9Y1zOdzl2GZTCZ713k+n7vCXD77SUJohEIrUgZRx+OxA8J81vp1GJyLdIxiZoByHvZSi6LIERmSopubG+cMxkxSFEWObKRpiufPnzvnJEqWKHEi4SExI9hmBmk0GmG73bo6DrpthaFks6Iownw+dyBYa+2ICQOkdGtSSqHIc8ne21qUuq6du1TXdZhOp44EMPrPInAALutCPESZlY+1iJN4LQ5NC3hP+kXlvlMUAxLHx8cO51EVQzcwYtokSXBzc+OyIpTe8ju+WxazS0wG8FoBClVZ27ofqWHabrduLSrL0s3dt3m9vXRqu7PuSsJ2OAhaa7S1OOAslgtMxhNJQekAVVGg6Wrc3Nw4NsvX/ctLfPej7+Hq6gpVVWGxWODly5d4+PAhQiVa/SgMsV6ucO/+fURhhGE2wPc++ggP3rmH8/ML1OgQhRqj4UCyKW2LKAiRxgmiIMS9y0ts1lK0w3qDtm2xXq9dOq0sC3Rd4wgGF5qyLJ2PM28y2qyRbAAG5+enMAa4vr6yk6eCMZ3VK0qjobZtoDUQRTEa2yAMEBDNG4APRlqrcVJIyjHBxcUF2q5Bnu+w2Wzwk1/+MtI0xWKxcMflEwMWqTE9SxZLQiOLhWQC2HyGbL6ua7x49gyblxs8ePAA0+nURn1ad7P5zWIASZO3XYeulULgtm3wvY8/wcNHDxAEsq+myRHoADpiw8UIaSqRvcEgs1ZzmbvhojBBU7eYzY6R5zsbWUjEMWs8QVlWiMIYrekQ6ADHR6co8gqr1TV2tnNzEITSUbxrURZC1LpWY7FYY7vdob1oAStfTtMY40GG8ec+g/uX9/H8xTW+88FHuLqeo6gqtEqja5s9EGOMQVsV2P3Gf4DRH/yXbZSvj6K6B36vpHj15lT7D3tj+i/QKnZPz23/QBtVBaBrDMq2RgdJsetAY5BJ4ZoOA9CpUSmFtpMmVk1VYNs10jwKCm3ToMhzVGWBrqmtRMpAKV/+0wMPkgo5WuvU5LI5FphwnOyR+sPB8+mczEyh+trfgtlceZzs9STjENjty548EP3KN1//OgTX/6wZg9dJig5/9o/5B9nfm47vLhLS//767AzXRj+DdPgZf9937b8H6/Y+cN+HF/02e6TjkDwxin947I7Qup9fPY/+XDrL6xkIk3vNz3O4z7oIPbcTuH3RIlK2bc8PkEaOztChH1vB9bL+87a1IwM2vPPnqz/ODKYQuDISKUCxsc+lPirpAgpB4Maj63r3KY4lI5E+mZBzkf3GSYzxqHd0BAwm4xHeffcRAOBzn/0cwkie/bPZFHVToSxFWfCZz7yHMIwwn98iTRKEkchPmlqisFEc4fj4GOv1BqbrsF4tEEZSXBuFEZSSLMvpyTHW6zVevnhugdUMbdNgs9mibWp8+slLHJ8cYzKRaHqaJKjK2M230WjkzvXs7Mx1kiZQiuPY9YRYLpeSEfHcdujqyP/m1jLe74zM4GOe5w5XjMdjHB8fO5JxdnaG29tbqa9opZ/FJ598guFwiJOTkz0cQTUAsx3MliilXM+Chw8f7vWA8FsEEOjTIShN01cKtJmVaJoG5+fnDryzvsAPHJKcUAZGSREJURAEuLi4cKCYGYbhcOgyM/ws59rp6anrzdA0DY6Pjx1WCcMQR0dHbm6u12vnqkRiR8LN6zgej3F9fY3BYOAAMNURJBMAHGD311YSHrlPOiTjMYzFNk7NYu8VkicSYpIUzo+6rh125P3GOhEATi7lN7BmfQhNkIjXSPz8c+C+us6gaVvUVe2wHMeT40Y8FgQBHj586EgITQ+YwWEtDQBHgJjB4Vzq2s4FgRnEiK1DGe8TFq6/zeuticZ3P/wQURSjKMV3fzQaIc0y6RZtLcPW6zXyoxzn5+fYbbf4+OPvIkrkYnzzW9/EO++8g5MTSUtut5JyvLm5wcOHD/H1r38dq9UKn/nMZ4TU2El1cnKCv/nLv4x33nkHP/ajP4rz81PkxQ43N1cy6TayiA0HQ9fPgQvN+lpsT1Pb4ZB6TVbXywIuDwnWWPCGYjqSC4LffIaLfhhqaZIGOU5mD4yRAjTVGrStLQxK5ObLshR13WI8HuOzn/0s5vO5swdlymsymbibXly5SlRViTDSLh356Sef4Pz83BEAFjYxsgHANSsEgNVqhbZtvUYuxk12RoGcY0MY4vOf+7ybfHQHo8aS58/FhFGUXZ7j6maO1XKLQEdYLpcYL0Y4OpogiUUeVRalayIE5CiKBForXF21bvIWRekemsYYDAYZqrpGoLWdc0OrnZX0sPitBy59PhgMsNvlAIwrJKzrCoA4d9V1ayMWKbqzDgikCPof/Ne/ilAHgNLQQYjp7ARffP/zmI5fYL3dYlOVWFu3CaYdCWDKj/8xknf/AKKLL7rF1W/A5hynLMpxbkNe4RaMBS3qDhjo0IoUkct3PZAGC6gMANWhaxU26yV227VEVgONIAjtPJZMg4EstE3bAk2Htm0ka2IMwOyDMei8ZIwDVC4zYY+l64uvASZt/OPbfzGT0Z9/B7N8DPX4H0PrXosq27rbyUZ2v58xeBPo5rZe997b/v11r7uA/eHrTe/fFZW/6zuHANUH1n5NhU/SDgnBofb+kKT5+zx0M7rre288J7Wf0eDfBRzyd5kzfh3D4VC97jhwIJ3q6yAApQNvfihxenPf4nfl+93B/pQl5lppdB284zW21gPoVCf3rfLlVV6Nxh3nzTEOAuWNw/6Y8+HuSy9kDAI0DTMd+49vGT/WoLR75wb0zxdGR+U7LYLQ4POf/xz++T/1p/Dee+8J0Ygi1HWDJOiLdW9urpGmKc7PL6A0oAKFFy+eW/38zmYGMrduRNaU5fTkGJvNRgqibW1DU1codjvAqq3rh6YAAQAASURBVAGCIECgNZqqxmK+QBSGqMoK5U5qJJIohg4CnJ+eiSuOqmGaDsvtErHtpbXb7Zxs5fOf/7zrVJ3nOVarlQvqEZxxbBlkY2H9zc0NiqLAxcUFlsulk/4QgGutXVaE2f2u67BcLlEUBeq6xmq1cjIaYwzu37+PJ0+eWDlwgJubGyc9IeagfJkRZMp1fDtWKhA2mw0uLy8dmKTqgNkNyrt4TnRL4lhQcsQgLO8v4gu/PsAY47pEEzQTtG63W1RVhfPzc0c6uF+CYY4bsyWAZCcoQTo5OcFisXC4hBL20WgkZjq2n8rt7a2T1ZGg5HnuskG+jT2zJOwSvlwupTB/MECSJHtOSmw3QPkS1SC8J5mVmEwmDmORZBFs836lLItjwKyB3/ODzzbWiDD4S/zD/XOuUcKXxLFoCew9TNnacDhEEATO5t/fd9e1jpDSLYuYhPth40MATkpXd7WbcwD2PscsEteUt3m9NdG4vb5xGrjRaIQ0TmCaFug6bNZrLBcLiRhEEfLRCG3TII4iJEmIo9kEtzcnGA0yhFrh4+9+CKMCxEmG5XKJ1WqF5XKJq6srO3gZPv7ODY6OjvDtb34Lf/DLfwBf//rX8eTxE2x3awwGCQAB7UczYfxNXUGpDuPRSCZt1+HFixc4OztDlmW4vLzEarVyqaeLiwvX4bzrWucKAMDpLkk+yK63ts8Fsxlt10ApY4FRA6UNMutZXVUVRuOhW9R4EcuqxHAwdjavTFnRYeP29tZ1X6R289mzZ6iqAheXZ45EcXFjdoLpQ7JgfoZSJC40dHGQaEu614FzvV6jaRpsNxt0jURIjo6OXKqTFnGbzUbOxYvIAFLMfXtzC4UQ49kMxgAvnr+E1kCSRGiazmZ1JEIlZG7joifClAu7wBX2RjHIdxVy62IBM4eymkiljLNi4/gCvZ88oy8AUJSl6wRd12Jx2jQt6s81QCQRwPntFpFWSLMUF/eOce/iHLOjI9RNjedX13hydYvtboeXL19CKYWPP/64j/p2LbZf+UsY/eH/JYKzL0DqNbo9mNG7FtkaCQISAgxN6GNfDLt6xZs9C9F8EyQfvnOTNUqG6QxatGg7aYLpemhw84ab7DMTzLx0EEtc608q+7Pev8rQgpc9J3jMAim1JULG4yT7p+VZxirA1BXyr/xFoN65BddPB/ebv5ts3EU0zMG//228vh/wvis78KbMwA+yzX3QClBi8yphUa+M2WFE/U3k7q7jv+u9fh++197+S4gFa/oaG2CwPRUOgPphNuVwX/7vJL0k9u7vd8ixXJbCO0aeey9l2u/HJP8CvpvT6879rvcpq+U+OM+l3sGSIruNOIltNlACJ3709HBMXj3GV0mp/3uSJvijP/8H8Iu/+AtIsxTr9dzasnZAB4SZBPAmkyG6tkZZlVgubnF6fopPnnyKuqpwfn6G8WSCZ8+eSdY5jABjMMgkcrtdb7BarwGIAUWgA0RhhDqQbL1SGovFEoEOsNY7TIYik0UUoCpbaKVRlFLDWVcSRFmvdm6OpgPtgoRz2+T28ePHrlaBz1FmIAiwj4+PnYKBwJj6fspmGN1umgYvX750ALjrOjx9+tRZjy4WCyff5rOXYJD1CiQ0BIisc10sFpjP5w5bLJdLB5Z9UhjbXhoElldXV2jb1hVYX1xcuIjz7e0tGLQkMPetY0mImLEgQOc4EUAz+s3zY9SbBdOz2czVdfDFmhVAunOzazgAN9aUdU8mE1eXSlUGo/xizRvt1cTwxflPcsH91nWNi4sLN45VVTkyQikVCd3e+duGfyTjbADoB7LoCCWy7cTdR36tBF+8lpQX0VSA2RWSGj97CcC1h1BKuSbT3M92u3NzifWsDBDzmcm5SvKVpinarrEZSjjnVK4hnJ+83i7jiV46zLnD+4bSPr959vd7vTXROD87RxLHtqirRl2KVk4ZwLQtTo+PkSYRYFo8efqJ6NQB7HZr7JIdTo5OUBYlTGsQKIkaAz2DYorryZMneP9zn8PkaIrVdo2qrvDr//jXpS39aIjhaABxUpLFuCgqrFYr22DOWMeIAE1jMJ/f4vz8DLe3N0izDFVZoKkr6zKQi3NVEkMHEsHhIgXA1UgMhxmMsY3v0hiB1siLHF3bIUlCRFFsMwIRqrISqYgR+87VciVOTl7hThzFUOgk+m4tN9tGmvK1nUGSJsgGGba7DepGWPP5xRmapkLTVI6YiOTA2M7aEeZzqVmQ4vaxkL4kBlBLJqoooZT0TNjtckzGE4Rhr9OLwhCj4RBXV1dYLVdorQvRYrHC5eUFRqMxPvjgu0iSGHEqKcrpbCY1OXbi5UWBUIXYbnMU8RZVWaAsdjCddETP0gydFyGY30jH8qqSFHjbtWD3b2OAqizRdECel4DqU7EKSjJJxN0e4AmDAGEYCfFTCkq36NoWnelJSRTLjVw1PcZvuw5PX9wCpkUYhXj84ga/8btfRVmWqOoKbdeh7hSatpcjGGPcPIdWQFtj8yt/EcOf/dcRXnwRSmkoAiZFcE39tsXvHsmwCQuJ7gIiWyIlUICDzB4QcUzBve0VkftyDmNA2mOMJRMOoPYOR+B37bEZJQeqlHU/4rHYfRtuzw9N29crEMtXXtm6DKMA01TY/fpfQ5uvAWU8cNcD5e+XiegtZV8H2n0C4suq1BuIiP/OgSmo6X/WNmrfj8Gr35LvHAB3RSapvETR4bb8awu4bBj2f3eAWiaOM3m6m2hg/zoRfNrtSNGirD0iC/LsmJV2e+/PpZfh9NODRFhBeqpod6xSs8YTls7RgY3EN7xvoVC3rbtf/EuiFHwTq4NjkQ8JUOs7Qbtsg81K8HiNze4BChq0WA3ce2kqPZzy3RaNDR70zKW/ZlorNK00+9Q6cPers33ldXXXpEMYBkiS2NX4hWGEyXSCqqxwcXGOi4tLpGmCo6MjPHr0CIvFEl/96rfwX/6Xf9dbC/upQbtq466X3NNyzZQ0qkQn9zI6vPPOffwL/8I/j9/341/AdrdFXZZIogijQSYSJyPGJbe3N9A6gA7EKbCqS2w2a6RxjPFoiLqucP3yJQZZimgyhmklOBEGAaqygjHA6ckpmqbBer3BYDDEcDBEnhdo6sZZ5LdKYzgaW5ltiyRNsN1sEcfW5tMYDAcD1I003SwtKBsNBlBa49mzZ5hOJlLMGwRYr1bSHdkWHNMIxVjAT7XC7c2NA2IEUjoIZM1k0C4IsLRZCkb26STEjP7JyQkmk4kjL3RPMsa4/hwslKZ8hgCRkXfep1wDmTUnWWBEeTabYbvdYblc4fLy0st+tcjzDcqyxMXFBW5ubhEEgbWWlQLmKAwwGA5hvBqAyj47GwtQa1vszfqQ0NbXZqlkM7Ikg7auoSLRzRx4Z/E2b5HcRs611hKVVwrb3Q4D2/eK+5za2hOllNejSwrxmQ3xC7v5GSo16NDGvma+01gcx67fUNu12BQbJGkCBSXF9zpEXTNDoQHTuWBo27bQKhDzGCtzLssKdVVBaeVAv9gMT9wx7LY7lEWF6WzqlvM0zbDdbDCdzLDLpbYi0IHtyRYjsM148x1dqUqkSYogDADTN9njvGF2gZkoystIHhicqKsGRVdiNBSDpKYWkm+M6RUkAqagtVgfl0VPklkUTyLGOcw5+/1eb000Li7uieVaVaFtOlxdXeHq6honx0cINLBaSWYAymCbb5GmCaIwQqACNJVcwGEmjGhbbhGnGYIgxGQycex2Pp8DkGLx4XSMJEtRlAXqpsbx8RFGo6FtrT5yJ2yXWCgl0pAoIkCeo64rDIeSKpPCqwTSZXuLKAoA60m+2+0wLwpXz1CWpRvM1WqJOIlcOopazSgKUeYF0BkkkUyykU3rGdvVOLVR+mE2cBNhu90i0FKI27aNALuuRl0VVicfoKkriFe69D+oyhKDQYLCNAjTFFEcuQgXjGj1sySDMgoaGvkul07mETDKhtjlOdAB66VkcD755BMAwP37l1CQ/iHL5QpRJFGApqGLiELTdHj+/KWLrCwWK2zzHdIstQXwAW6ur6Ww0SjUhbVhbDt0TYOjoxlOTk9xe3uL21tZ6IqiQJKmCLRGNshw7/IBjo+PkGYp7t9/gKF9cOR5jqYzSNKh00pWlRDLx48f43e++k9g4BfQNW7h6TuNGhttsdFzAB0kakp/dC7u20Z0kappgaKSBw3HGBbg7EVY+3Q2t422we7X/hIGP/3nEF58EbDgxXjAjxzAyTuUArre/tXfnrIEhVkA+aIAGWWBeo98LWB1plc288Cf0YMS7ySAjkXaNgPhTkbxQAUk81gh35Hdirbadft1RMm6bLlsCxzQ6rxouWkr5P/4r6F98Q0n21LeGPSH+fpof8+1elD/Ci/xuxa/BnDvvzgQe3/hl7Avz7E1B3dRFkcUXk3t+JFxR/q8VHxPsuwcUH3Gwt+G8s7dcVL0Ufk7z+Cu87YEsqob20PG1kioPjugvEdGTyYApTohOAfEHwBMJ0XRJIxN05NhY6Q5q1KtOwgZTunF0Kfd9o9ZvyGQJkPNeoXOReu6rpV5qXpXKqUUOlvjpS3ZEKcmOb6mbqSvk2kRhZLZkD4aVoqk+87WaRKjdVIgjdlsiuEoFf11KJKT8WSM2XSGyXSEk5MjjMcjV+irtfRkYjflHfshJQmyLMXNzRC//uv/DQIdoDYCNNz4cH2xfagkQkrZpgFag0BJf4yTsxl+8vf/OH7mZ38Ko9EQdVmjrVrXt2B5u3IRzMVyIf0dug5FWTgNOyUtQRE4oKWg0DWdc1C8ub225yzuklEcIk4iVHWJXb5FFIcYjaUmcZfvMD2eOtlMnESI4gh1U+Ly8gJFUWC5XKJuJaIeqwhlXcKgdVmLJI5dB+umrgFjUNu+U3Vd48g6QC1svwm+mqbBFsB0OpWfralMHMfSn8rO0djKsJe2GJwqAcqz2HzYrxVgsfX19bWLAEvfqI0rSGdGS2uN+XzuGh9T8sJMArMc0+nUBkFHLiPEWA9x0GgUYz5fWIJSI8sGGI2kaVwaR9IQOY6hlWS6tVJI4hgrazVPG97tZgMYg7OTUyc5VkZhtVy5Neri4hxQxgJyIZjGGtukdm4QU7WNdPkeWYm3VtLssCxL3Fxf91mqLENoI/rz+Rzj8djNMwJeyrl5DQG4sWVRNrFfkiTIYmmgaDqDOIphWumZtdwuXTanLHeuxiXQIZq6dXUT4oal92pjjJVH+/06RE6eIRzadgFVgyKXbtp5W8AYhfV64wIFresxI2tPpDRgpL4rDMQierNYvTKvSN6YLfOfG5Rp5XmOsmQNSIz5fGnrmAKYDkiSfUey4XAo+257yRWvnb+Pfq39Pc5ovP8jX3TSk/V2i9/+zd/EfD5H0dbQjbjmBK5YKgK7UIZBjPlcmt6xIKiua2zzAid2Ig4HQ2w3G9y7vMR0PEEYStOXthbdJBvRiDsTrejY5j1AlqWgW0hZisTmi1/8IgA44kBHI778waLuj39nxL2qKuTFFmM9RtfZRmjpwGowNyh2kmKcTieQ3iAtgiBC1zUWUJfoutZeIBb2NSgKSV2JVZloH5fLJWCAwWCIrhapUwCNLJKC8OXNEsNBiqapESUShSgL0XgWZYm2qrDMd7aIJ0QQBrh5+RLX1+LElOc5yqpEVVb49NNPcHV1hcEgw+nZKSbjiWPXMMB2t0UUhqib2rWbDwNbwxHHiKIEl+f38GM/9mPoug638znqqsJ8vsRv/dbviENHmuJLP/7juP/gAZq6xoNH7+Hd997Dg/sPoAONyWSCwWCIsioxSDOsVmtnkXdzc4PFYoHdLsf17S1uF3NcXV1hsVyiqRsslwvkeY5tkdsIRYfOS58SoPkPE94UxgIoo7o3ynL2NNN2QfC11K9Epr0brqsr5L/1H2L0i/97qCj1ov8WMIFdMuQ3RwQIOJV6JWLL70GZ/rsutOx/Bn1U20YoSDD6RoLE5SQ9B2DYw8TGbdQ7R5IXC8YlEu5tn+PjEw8jNtgkGcZ0aG4/QfX/+fdgipUHoN9u4ToYGPgym++3+B3KbF6/0X47fZG7nE+g30Ze1BOJu+xR9wjCwfFQUiS/vj678/p9AySfSvUz4K7vOZLIb3VCKLRiEaUAVMXsxN7x6v48VE9GXYYDSmzP0JMkgqqu6yxR692SeI7ynp2tSu+9518L/3y0zUw4UmuDI74kIAyYCZSPtF0H8cozCDWsgYesJUGgkUYxuq5FGoju+vj4GMPhELPZzD3sHz16hJOTE1xcXqBtWmeoEYQacRIgTaTej5FKkU20mExEknt0dISyLPHixQvcv3/fjc9yucBwOMBiMcftbYfVao3nz58iCBXiJHTRdp6/1GU0tvZDZBJJmmI0HCKLUrz33rv4oR96H+++9w7SNMJyNcdieevkHWVZYjqd4vnz586UhNF7SmFOTk4QBAGur6+dwxLlGJS5MArK4msWB/M5zLWZkpau6zCZTEArUzoZaa2xXq/xzW9+E+fn53tafz53GXhiETQdeqjBp1KCunlmNZgx4JyiDSqdffy+WcxehGGI1v6tKAosFgtp9ud1rGZkG4DLXhAMsuhWa+3GjAHT9XqNzWaD4+NjAHC1lL6kie6OtK0Nw9hZoFLiwmOWgv3ZnhsUJWFRoFBVcj/QvcmvH2AGhOcsc0FqIunCxetDuVhZ9Q36xEVyCq21qw1lUz/2ZvAzEb7EiHUYHfqGjL6rFa+XL/nyLf45TqPRyNWesjal3JV715wkhdJtysT4edZnSKuCnSsA51hDGaueaVy7BNjjDoPeMIlr0G63c2t3lmXuviA5ZabCb1HA/Uld83avuJ9SSQYFeC9RTkXCwc/yXuZYcg1mbS7H03/O+PIornd8Mav6Nq+3JhpV11i2rDEYD/Hf+YNfxre/8x3sNhvoprHSlAKm6xDoCGEgN1aRl3j58qUr0h2Px3j33XcRRBGKukbbtYjiAEezKW5vbzEaDRBa94SqKHFycuIm4Fe/+lX88A9/EXEcuUFlT4ymqSEFwZWLEvipPF5QahNZnU+NGmsZuHiv12ubqixwdHSEwWAgtSm2MctgNsC8u4VSwG6XI00zlGWB3U5coWrbS4L6tiAI0DYtwihCXVe2qK92es7hcIjNegNtNJ4mibB+60SxWq3QtQ2iOEQSJ5hMJ4CVBWy3W1RNhcVyge1mKw93pdyi2tRAVdUo8gJVXSGKYkxGU1RFjfFkgtVig/nNCgZAZm92pRWqrkGSpMjSIYIwgFYaWZYiTlL89M/8HH7u5/8Ylje3uLm5xhe/OMDs6Ajf/fC7uP/wPRgDnJ2dWeYtY311dYNvfutD/JOvfgM310IkOiMNX/JdgTwvnK6Q17YzBp1ppVO351RjjKS3oa3zi1EwynpPm05kOYr/sLN2D6hNx4jfqy8fyB2CH+7/le+A2Qcbse86tOuX2H7lL2D4s/8GVCR6Tm0BncsEHIAzyRp4gN7dxH0BuHIsYX///P/eApc69X3GYLxflb8BpgVcNqUnH+6MSYK8fWul2LnLZtg6sJ8IvOi2HJttgNe1yH/7l1B/9KsIA72vK+9TNHvj/aYFbY+wfb/P3vHeXX8zXpRYPhPsZbPeDPa/3z7Uwd/umFMWwMvck2JkAmytvLoAd5nuGicvE3FAdJwEzn3HzWJIO5PO1R/0ZKonc/559fvsszB+DYF0iYbLivLeo905bL8atx0DBEoyDdDK3Tdun/ruxxYzPqHWLtLo5oQl3QYNwkjAngKQpAkGgyHGoyFOT2fI8xwP7t9HmmU4Pz+HVgoXlxdswI5Hjx5ht9uiaeRhTYBEnXyQRUiSAAY1Pv30I5ycHuG7NzfI0hSdMa6Y9OL80gEAHyQ+fvwYx8dSPM1IPSCkYTbT+MU//sfw/PkVFou5yHZtgevZ+RmiSCFNEiitcHx0jNFoJFLXKMFkNAZgsNttUZQ7WRuVAdA64Nx1HR4/fgxAJGPX19euBmE8HmO5XDptfttK92hamNIohPUKBHKj0chp7QlCCZ5p8+pblpMscGxoccrMgO+Q4/e8IgAmaKPFKa8NAeODBw8wn88d+GMPBoLttm2dht13/KKuv7VFu8fHx267JJa+ln8+nztyQ+zDBnY0MPFrHXjf3NzcOKtd3i++fIrgXMZjsOeKSZtVFhkTSN7e3rqxjKIIdZm7c2PNBMfS78zNcZW5YaCgHW4C4PpLwEkVjSMQnLfMZgC9wxGvuV+DQJJCt0zjmSFQzsZjJcDlXGDDP8rLWEfjBwbjKIaO9F6Bc5+lUI4I+7UdvGacHySwHP84iVx/EUrafXeyoihdVoCNC0kgaNLDMSFJYcaG22CROMkQ5wVrPnjvcJx4HnxxDvgKIN8xioXm/L5fE0R5n79v7oPE6Pc8owGtAS1AziggHQ7w+37ix1HscuTrDa5fvsDzZ0/RNbWA0jSDArDdiK/y5eUlTk9P3WRYLJeYzKZYrVaIj4/RNjU0DG5vrnF99RJ5WSCNE+mZYQyKPMezZ89wfDzDdDq2N0CO7XbtNJKrVd+NMwgCvHz50vk5cyG8d++ea7biuyTUde2iMlwsuK3d7tme3VxRFPLftu8HURQFrq+vcXQ0QzYQstR1xlmd8WLHsXgUt11ro78dyrLCYr6CVhqmlXQi2XPbdbh6+VKaqmn2MZGIKtP+remwK3Kwy6pcrgBhGCBLR9CtQpIFGE1mSJIER0cz/NiXfgJ11yFOEoRBgLPTMyTWGUssUeWhxZtqs9lgvV5jmxf4rd/+Gn71134Dy5UU8Bd5gdF4hMViibKusN3u3OJljLgv1XUDg313FRYrm85iWC1NpvxMAtU7QOtkTFAKSgdCRCgnckQA/ec8SU3fsE3tRTX81+tunLsKLw+/t3+r2Pqjqw+x+Yf/DkY/9+ehgl5/a0znHbInV/LkL4zIOtrgshc9EGeNh1EkCB65IHGAN5Z2XFhma/zzsVFebs81F/SJhTfGUJ4si9KpO0hQ3zXcbtt0KP/J/wPd935NylraXrrmE7vDv/kR/bvG/PB6aHufeFPDO9VXt3/4kr8fRu/3iQGPxz9uOaz9ngX8jF9w5y/8fWZkb2/9to1CoD2J1AE/8QnuHXzG/aADbe2n7bE5+RePQ+oPhGDc3UPkrjHrxyFw5+lbSvrz95Wiw66T/jGWgPM9raV3jYDSw74Pck8YGLdeGAOEoTx0x6MMxsoARuMxTk9PnZtPmsW4d/+eRD61uNhFUYSz0xPUdY7OiKHIS2tMkqapa2q6XC5xffMCk8kUOlBYrefQgaztcRJhtytt4CwDVIxH776D5XKBs7NTF1kcDu9DKYUsHWK93jqwzS7Om80Gs9nMRemDIMCLFy9wcnKCzWaD6XSML3zhfYShyI4//fRTqV8cDrHdLDCbTVx0dbla4eT0HVRlic12IRkfSy66rrHN6RLX/JbuSmmaOvkQCcP19TVOTk6ctGg8Hu+544RhiPV67cApn729RXvsCADBMX/2jU8YMaXro1IKR0dHuLm5wXK5dFbsjNZuNhsnt8qyzLk8+cXDzMIQhNFKlo5SBLTs5eCDVlezYef07OgIoQ1K8j7YWCdCgmdiDuIQmuiwI3me57i+vsZkMnHXlZ9hJon31WKxwGQycW5BElRtrPNR37eB4JDnRhtZRtQJdHe7HcbDbM/EhRIcRrRns5m3hso45XmBspBmwQScVH5AGbSV7IuRegJUzmECWOIokgVmfwigOd7QvdMl1xQ/y0DSxoZ/JDhJkrgMBIG/MQY60EjCxO2T85LjwAwIAIcBCbApiSIu5HkqDaRp4hk5dJ6ML3Vrll+ozTEjiSDA97MyQRC4LtzcF4vTi6Jwyg8SJdoT87r4zQnp2EWCymvOcWYWxc/88j9aN5PYG2PcPGVQmPj3+72UeUtKslyv9qrTCcQDrRHYB+v3vvshnnzyCeqyQBJH2K43+PCj76IsSzx8+NBNwtlshuuba+R2wDfbLRbzOR49eoSXVy9xenaObDjAdDzBdrPBb/3Gb+KDDz5AGAR4//3PQiljnR96p5KmadF1BrudTEYWAtFJgjc92Sdvgu126zIfvPicFOv12jW+0Tpwk01rhd12h8jqHyeTiSM7RZFbLKxQFLmb9L0Dkjpg+OyyzSimFO5prRGEAbJUxqwscteoJ4kTzGZThFGEQGscn54hs13W0zTFdDKxadKBrVGQ5kCm65Bmqbt2qzzHze0tqrLEarnEbpejLAtcXV1js15jtV5ju93YTFDpvmeg3SRlgbOCBY0ETyBetsCqI3DdB/SU2nDMlFIu2qqUglGdkxw5hyfvZjicvPuRVOUWr72XB5bWf24BMzZQa4XhX5z0JOgA5L7pxeO46/Nd2yI6+zyGP/fnocIEBlKcpRittlkGZXqUrjTlTh7IJwHg9rW2QL8HcXKefb1AXxDcg253YXwyZw6+Z+UqXvy+JyckIBaUKtWPFzcPdyb7FqVdW6P83V+G+eQfAd4acjCaruMwH3Z+5PdOYqBIxvrId9d1yP+Ntbu2g784sR/t589hvUMPYhkdZxdp0+/GXY67gbgcg7/49vIlZTdijNRVKQ904645RoJiayV4n+xn43x2Zw6+rvZ+3r93uB2/cFjOmed9N7kzr2zX2+MrY6JUX6jvF/i7MYcRZZWd8dJJ3s5F1QHaIIkTaSypFEJrvx3YBmDvvvuuk++cnpxgPBljlKUo8h2ywQCj0RCTsTjvzOdzFHW5Z88oQEhkrWUlEVX2Jrq5uXHdjxnZ54MbwJ51JzXjjF7K968BSCfhru3QWhltHCeoqwZdJ4CYwIPBpSRJcHUlfZlOT09xc3PjgNHWyh+Oj4/Rti0Wi4VtalqiLcWyO8syXF1d4eTkBPP5HJPJBDc3N5hMJs5NiRF4kfUkDhhSXkOtPu8/kpcHDx64zL+vGCAgnM1m2Gw2DjwTM9CwxbdX9+3WfZkryQbdiEajkXNjJPbg+zxeSluurq6cXp6EwZeOsIdDFEWOzN3e3mI6nbosEsEwySEzDl3XYTyZoKwqJwGSrJFkcejWxOcUg5tsLOfmtTE4OTlB10lGn7Kx7XbrLFQpddJaO6JBiRGzK03TOft5Zk+Ia/x1jMFUcWWqoGFcozwCar+Zr58hKcvSRuljwKg9GROxTRRHKIqdk/DQNYoElkAYgJOOsRdXUYibGMkhydbadsCu69r1Panr2mXFaEdLaTzJAQE57+2mabBYLMQsyGal/SwRATPvQ5LizBaqO9MFez2NMS6TKTVfncN+lJHJNQgRR32Xbx6vL/XivKSszB8XZnA4lw5lSsx6BEHgsCuzIZwzlCZS6sbx8B2y/CwZMR1Jir8fzhNmroiF0zTFz/3CH8H3e7010VgsJR0aBIEUPxojUWrTIY5S0MBweXuDJ9/7Hp49eYLNeo2zy3N873sf497lPbx4/hywi9HN7Q2ub67QNA2+9rWvYbfb4Ud/9EcxGIgMJx2OkEQxFvM5TNfhb/2//hYePXyIy3tnGA5T96BgsU/TNGgbkZhw0LfbbZ+Ks8xNKeXSqryppctojO12Zy3QCE6Vc98o8gJB2F/Uuq4RQDnSws7gXCB4fHx4GGMQhCG0Esu5o6Mj93CZTqcIwxCj8RhnF5cYDIfIsgxZliIKQzR1Axigbhpstls0Ns3O1Ndqm2Ozy7FerbFYzHFzfSOa06Z2RXtFnru0LwCxdjWwwJdgSgCHaFGlQYwPd7XWaDuRM/if7yxw0tatwV9QfWBjoFxzK5fTMIBUL78K7N1iCR7nq83U9icvCYuP2+6Y3qYHM6t/be7A6OQvHzli4t8Wr8t0uOP1PnfXvgBAHb+H8R/5X0GFKTrDHhXu5OwZwrlYKWEi7vx9YmDsH5W9flDayy7Im/6xMALcj7pL9JA+MEa/P/bq1X27X212QlnS4bIqbvB7kmFMh271FLtf/StALrKFztxt0QlLdPai3h4xuCvCLhvZb+4GALt/fdWTyH93+uq1AVxh7/5YkWiIc9HhfBRZTq9l3X/1RKPPFPTn6kf0+fvhvv3f5bOv/v2uMTiUA76OEPgZlcMMQ5+Ved1++ntH3jfe51+1h3XbsHOD3xHSAQRokcShZE/jCPfu3cdkPIaBwQ/98OehA43T01NbnBtBKSuJ7VqMRkOEYYRPP/3UracwBlEgkr62abDdbZEmQhI22x1ubm9w/8E7WK/XTrpRFDnSJIUOQ9RVBSiFKLTdeEPp77C2wHm9WqEoSjx8+I7YXKap1MVFofR/iIUIhZG4ELKYeDgc4fTsFN/98LuYzWZQSjmAzAJw6q0JFBiBTtPURTFPz06wWC5QFAUePXrkegMYY5CvN0iT1IECWIDS1DXOzs8cuRCwIW5UVVmibgTQ+1Fukgjq65ntIGgieNztdjg7O8PNzQ222y3u3bsHoJfV8LnLqC2/zwJpyqH8OgjffhPo5SS0SSXJ4TykfGU0GuHm5gZ1XePs7AxN0+DFixdYLpc4Pj52/arYLM6XorApmx+IpNadBKfrJBNd2vd9OQzBd5IkLvNCfMHgpW/56mOG5XK517drPB6760AwSXnMbrdztTQ0bGGmgLJwEkXOIRKoIAiQpSniKERVle6YSVwAOEBKEsGfy6JEGMbuOCj5luCpQRDqvW7eXB/88+Z8AnoLbQDuecusRxAEqOoahc32sT6BZMiXPPH7BPB+TQ3Pr6oqDAdD1FUNmL4DOr9H1QaJtu/YRLJHIM5/u65DVZcui8q5StOftukz+WmaYrPZuDl1WAfB+cH5zHnHz3NeEPAT9wFwvS1IDInvendS7dYDni+3RwJDgkllj09aeU/y2Dg+fs+OtyEaby2dMl1rwYF0EtaBRqABY6QpSGhTd8dnF5geneDdz72Pb337W/jow2+iaWt86xtfgzKdxTslnj17huVyjaZpEYcRVDZAVZbomhZlVQJao7N6ySgI0XQ1Fqs50jSC6SZQWqGpG6xWW0zGYwAB6rJA29jJokNMx1OUVeVAunRLbZGjQhjEePz4GeqqhmkVulYueFW9sJOwtel7YbUGdEexMhyLqZKk7xaeZRnu3buHy/v38fDdR+iMwXg8dh1Kh8MhsiRDqCVSslytsFqucHNzLZGHXY6XV3NsP36CJ0+euGjCYj7HzXyOjdV2Mt3YMv2lNOpWujkS51GjrK1eWWmNtmldbFqi4rYY2I8cdx3qtnOAVSnYxnMQpyFjAOsiJNFHG8W0ThMG0qSwh1k9aDVdK6DJSLErSUZH7RSIuXtgGygNWFcNmD6r0S9m/Z46RlzZY8IA8GQ77qV7EN+/ejcoHQR2LO04KQPTChlyYIkECgTtr8px9sDd7cfY/spfQPaT/xKC8SWI4k3XOQkUrSllv509D0VnUICSKAXhZizQ5d/swSgFKNP3EgDPzHArNgtijGvH4X5XjFpr9xXFDzhC0bnjB0zfT4Of7fcIU+1QffD3UX/r77gdsf7mcIx4HRyZAsmp9rqGqL2x5iTTSru57INht1Vl/8/Na3lAHrZ38KmiYOO7shYBOgR731GWRAcqAMw+YZPtGPfJINgnF8wm7GcmmM1QYP93Nzfs+2EQwID6W6axlSOAEsFs4IqkVU86WfegrVyx82xbef+KzbSfV5MMlp+dkXkiGbog1C5yysjwcDhAHCfO4z+KQpydnTmgcf/eBUaDTFxmwr6Wo20aDEYpVCC9Fyorba2bAkGo0DYtqiKAiRp85t2HmM8X2G42AvKzFFESA8YgCEJAifXsZDJG23bQUIiCEPcuLiUCHkTiLtUI+NhsNnj06BGyLMOHH36Io6MjXF7cw4sXL5CmAxwfn2K7zVGWNSaTmc2AJAjDCFFobVJbgyiK0bYdqlqaolLmUJYldtutk6icnZ5isVhIfYkFS/PbW2v4USDQGg/u3xd5b1HiaDrD8L4E0Oq4xma1kXo+aJd5TpIUw2GG0XCMm9sbKCXvSZfrGlVVu5lGIsBmYwQpgKy3rJtghHm73eLly5cONG02GycLYeS3KApnJMJny7Nnz7Ber/Hw4UNXpMvgHztwU29P0MwMyaFKwY/wEhje3Ny4rMKnn34q+zUGYRRhs90CmsSqQRhFWK7W2Gy2GA7FDGa5WuGebYJXlDUyHWCXF8gLIVlXV1fS+bvIcXR0hKqq8PLlSwf6eKwuiGUzJqPRCNvt1kl/ptOpNTvZOYJHEkYgx8j4bDZDXTcuerxarTEcjpGmYkHNDA+BI7NPVVGizWrEUYwoCJFlKXa7XJogFgWmkwkWyyUUFAbZUNZYLetiU7cYZEMsyiXarsAgGyCKYmgd7El0WAwehoHtMJ4ijlPkux2UFrLeGaAoK0fIROo1Ql7kbq60RqTgXdehblqUlbWwTam+4NqjURQ5qkrWNBKu3a7wLLOV3OM6QBjGqKoVkiTFdrdDsc2dGcHR0ZEb57quMZ3NACWklYqKuq7d8541VFSmCKmJXEaUEX5jhGxo1TlpGwAHygnsAbjfSQLqunZGBSRV/D6D137Bum836xeAa933I2HwwndSZeCbUjPOV//cmMnza4i4HrD32tta2wI/QEbj5YtnFsQad2JBGEJDoyprtE0t0Z9QahCSNAFg8OL5U3zrd/8J/vFXvoLJMINRBnlVYLPbYbuW4mz6j5NNhVEIHUin5yKXopebmxsEQYCT42N0bW0fWnKikkVQMK0wvbZpLTkA2qYBFNB1QjaA3lWkba3zkOFDXCOwD0kDWAcDIAxCjCdjxHGM4WCI0WiE84tznF2cYTKdIk2k8d10NsNgOIAOQlwv55jP51ivN7id3yLPczx58gQvn73Ebp27juBVWbl0GSxYarvWIZ6mlWxGp4DG9JF2TiKxWPQKYUGpUs/O/RSpD9R5PfcmhAU+2qun8MEzFxjKphiB72VU/TEeRqEPMwX8zF2vPoodOC35YZS+M/tOU/yeD6a43z35lO6B4+pfvYUZd1BrhfFfPt47dl9/KN83e8fhg0l/XLkvd7xeZF5HCdKf+lcRnL0vgNqNr3a5BRbGGpu1UN7xuiLe/oL7KRUYrfpaCcrV+LYHZpnRMIw0O2qAnmD03ETOAX5hff9Zt2/lyatg0FVbbP/rfwvd6pnTEL8uM3SYzbrrfUqj+Fm/iPyubNj6X5v31/avzCxxk/8UxDrVqM6dhH9vKaWgPTLhF08DQOdlGVwdhpY6Fbrz+cWIckxC+tmngRK6fsMeQYFcd6mXsFInpffGXUiH2Av7coleokR+bZwcivsLtLIPjYF7mHGt6LoaR0dHYk9ppRLjyQRaAeenJxiPJ1BK1s933nkAGGAyHUPpTjTn2y0GmciWGEWeTmdWPjNx3Yt53eI4duvh+fl5r5vvGsSJ6LGLorBZ3gwvX77EIB1YABS54tz5fI7FYoF33nmAx4+fuOgsff1nsxkAuC6/fPgyWq6CvlcBCyHX6zWyLHPNvhjhYxR+tVq5Zq9+jYK/5hK8M9qd5zmiMJRrbMfAd48iWOADXizdJarOAlX69VN+Q2065RG0Z10sFu768rvcByVhJBBaa1xdXeHo6AhhGGK1WiGKImdw8oUvfMHJgHmsp6enuL6+dsXi1NWTrGRZhsVigffff9+9z4JoP+LKjAcLpWmhS+ek1WrlmsfO53OsVivcu3cPSilXT8KCfGrUZQ7tS5/8aHUcpy7KSznzbrdzTe5ubm5c9oZEa7FY4OLizNntUppzenrqCstHoxHyPHfHdHx87J4n3P+LFy/Qti3Oz89dEfxoNHLSL9aYrNcbtG2317OAQJBZJpJYPm/TNMXzp88QR5HL7NCNiQTNv4a06uV2mR3wtf2UntFilXUStFrlttl1m1mjvCygLbh1yo6AxKRvhgjAFbNTicL6BWZE2CyQWQCCbBru8PxZqMzrHccxqrJ0LqYcCwL6oijQWmWHUmova6GVRmDJHN+jIxmPxc8Q+88sZl3oHAX0zk3M0rFGi2PDIA3XAN/cgE5qvF+Z2SFu5rUC4MyA/GMxxuzVIzNzwUwcx5y1Sf6zhD9T0gXAydl+8U/8cXy/11tnNJqihDRTkwdf17VQrUHTSmQ+igKMRkMEqFHWBcq8RpaNcHJ0hp/+mT+KECG++Y2vIwgUVJiiKIBRliCNMtRNg+1mi04Bxa5C2+aoClnQ4yQGDPCFz/wQ5vM5tqsNyqro2ZxWtnleAgXtmvEEgXTvNkYi8kEQugfTdDpFNhggjmJMpmPoqGd6w9EIo9EIgyzD8dEJsmwMGIXZ0RGCMEBZFKhK6VR9vZjjer7Ay6uPcH19jeVyKV0+lwssbAFV27Zo2kYiZnz4NL0nfmOjFZJh0GiN6OS06htcKb1fvOPSuIbyhD5Cys6xSZJa/V3jZTZ60OPXOzDSqVTfKA3dPvjyf2aKEXZsHcjrzB4Y8793SFgO/3Z4kzpi4AjMfgTcgXO1X3DLV9u0Nkq7n2UA9qPWhy/e6IzW+MdCYsbrQKIH7KeCfVBtbLrdkZOmQv6Vv4DgwU8g+fF/ESoa9iTDyxRITwlItqBjDNtYh6c+xkwg6caOvxslwN8lPLxouPG/qw7kUfskg4kOuQ4ewbhj3z4Ra57+Dorf/L+hqwo3Frx+d5GJ/et7mEFQ3t89smSLj/tLy6g9DrahoFUEBW2/I/0QAEBpZnH2awmUUlDGzzzsb9PPmOxlT5QUXft/Jzn3z11BLmV/fv44GEcqjO1TEoYaQdATR4kASnBCQeq52NsjTRIkaYIkkULmKIpwdHQszcqMLZIeZHj07rs4sSCobhpkaSrNSLsWJ8fHWG/W1qtfHl6m62Dafr2qLDjdrNdI0t7i9Mg2H2OHY6UUlsuFk7MSuMznc9e7gQW9lM1UVYVsmGG727ooMTXMvB9p9cmoLiU5L1683NOXp2nqou8EHrxv+V7TNOg8mRCJy8XFxR4INca4Lslt27oCadYZ0ITk/PzcRbTZQOzs7MwB0dACQgIAggQeW5IkexILyUTIZ1kES8nUxcWF663AmsM4jrFerx34JYBgkelut3MZBD4fWG/Rtq3bjlIKDx48wHa7dQExPxJLi9flcumIEC1RCeSiKMKLFy8QhiGOj48dqTHGuG0SwI5GIwf0/Ua+7FnBZnUEXiSAt7e3robBt/FMrdMS/0aAe3x8guVy5dyESAgpVSqKwu2HdREkyl3XYbVa4eXLl3j//fcdISc5pesRz3O1WqGqKrc9yqZIFE9PT12NRtu2OD4+xmKxAEBpjJAC9oigZIlzcDqdOhJA4P7wnXf2nonU6gNw14RzczqdujWKuICRbhJrzltmvkajkbt/KEPk9eRnWBjf2vvVv/+yLMN6vXaf5/dJfAjESTYYNGXQgS5h7MTOniQ+SCapMUayWkkU97InC9BZG6G02rM+5r7DIEAUxa6WiDULJMm+hTElRiQltJz1s1X8tygKN79ZJ+FjC9YnkWTwXCgtDILeMZW1LcQdfpaDv/NYOOd4b1J213Wd7blR7mVdmL3itfax51vmKAD8AERDtQpNVaPT0jm5qOSBoAONsigQBhnKfIt1lSOKNJqmRFPuMByeIk0y/PQf+Rmc3zvFhx9+CAPg7HyH50+eYbvd4vb2FlAtoDpAddKwLtTougZtI1GTd955IP0dkmO0gpwcCwSkc/nJyQnOT06hwxCpncytBXpKi5/5YDhEGEXoTIfFfI7tbofNdoXVeoWiKHB1s8A3v/2haEHbDlVlcH11Len3pkFuNZJ12yK3ab3WFUkLgGjbfWAsgEHZzIkFSBDtdUPLTytBkB4PBnXXQRlKXADT9dFb/wbqATejmfw8IDiJDePM3o0gCwqLQXmVmaqzrkO89gfg8K5IvnzbuIg2F7nD6L+/Tf9nn0D4bBoGe9vwv8e/HWZq5PNqL9vSn+HhsfipgX4R9o+J2Qx+xl+QOQZ+vcFe7UEfVu7PAUDz6W+ifvZ1xJ/7OSTv/wJMPOjJBGxmSr7gztsAMDbzReDrcllKWEFftm1Jgp/V4I8uC8Jx9bI9lnw4vsJjAEBLXj9r0WdEFEzXor39GOWHv4L2yW85cnN4zd5US+BfC0D10jzFWgXlzl1rFqTzhDx50MEaqFXsiDQzB8aY3r2t66B1fyzuflLU6ir3PSggsIv4IVFWysqdus5lphDAkeUgFIJAqRddk5Tt4ZCmKbJBhjiK3YPj+GSKNI2dBCmOI0ymU4RBiOFoaNcfyjgDzGYzpGliZQIyVxioSBJx6wOs3rwoMR4Nrb10AaVaHB2PUdY7HB2N8fH3voeLiwt5eAFYzm8RRSGSJLXXRiNJQzRN5QAZC2uzLNsDIiwIBaRxKR/ytENN09TpsXe7HdbrNTojIHO73SLLMnz66afugTvIBk7nT+nBYCB/40N0MhETAMp5/CjgeDx2dpTGGMSefz2vKyOHL1++3JPBEGw/fvwYZ2dnWCwWuLy8dBavRSG26IyWn52dYblcumgqr61IY2oXySdoYdSfBbZ0OuR58fvT6RTX19e4urpyOvvj42Nst1s8ffoU0+nUkZfhULLxdLMhIWAmYL1eO/v21Wrl3luvpdErI8uMjBL0EXgy8EKSQsLD/lVaa5fJIClljwgWuxOE+YWwdMFar9d7fT2YfVJK3CAJkNioLUkS1PaYKFkD4Misu1+1xmg0wnq9dlFbzjFmTHitRCYkGaWRDUoyI8XngO+MNZmIwQijxQTSBKskNYyWn5+fy1y0Y7Ld7lBVfc0J5wBfzAZQ6uLXjIzHY+R53jtYtr19P7dDgx7/GvH5x2J4Xg/OCQCO7HD8+czLsszd/7Ku9faqxCDGGAeiSWh4boz413XtgLhvi8xrRikTs4b+M5mEiu5NvLezJHVjxnlVFAUCe0yM1BOoiwSql6xyjgBwRIQZTAYo3Pd035OC14jSQmIU3i88dr7PceD2mIXkOXGd5ff8WhoGO7hf/zoR/9GcgNfCv4Ys0B+Px46ocI3kve+rQ159dt/9emvp1NPvfs9NYq00qlpu8iRNMBiPAGUwSGO0dY7Vco66yi0bS6V3hGXxSikoiM1isSsQxxHarkO+29lUXIO8KKFVhHQ4FM0TJMKrlcZgMEbd2IvUNNhud9KIrqqxWi5R7HZo2haL21vc3t7i+voa6/Uay/UW290Obdu4yI1cQI1OaTRtKx29dV+gI4MvBdF2uLzIr0Zj9l11eCGMMQ7UGSulYCTZ74oMe5MAQKA1oIG2a9wF7MF3B3QttOqj5Zw0bduiMwrshMuMhstWaAHJLADiBBcGTobfom335T4Kpod7dxANH4T7xIcdQrmA31Xw+zrC4I9f//4+aPSlW1BwOvLDAitqfvwb3u0LUsCulMLmz/XF4OO/fPwKAeozL/vOVYfj8UrWxItc38X+/d9VnCF672egJ5eI3vn9gBZdOeej4zid6esy7J/gv+8TDzkB7sz7W9/RGurV7IIfWZfztyPW9Rp+GV9jv9/B1DmaT38D9Uf/EN36pTgqKeU6ZnMs7/rZT8322bm77YdZs3K4DW6HL87F6//5Y3SjFnoT4Oyvv+e+Z0yLINBoW/Z12CfEvMe0JVpd14ldtZU9NW0D2PnNOR6GEvnSSiHQ2kWCLi/vuajyvfsXCAKFk+MTANLD4fLi0jrB1djtNrh3754Dx31UN4SBuBqxxwJB6W6XY7cVeQYsONBK3Jmur64wGAxdJpbRxLIskQ4SB9yyLMMgG6CsSgesfPDGQsYoihDZsXIdnG0UuChKBEHs0vh1XTvDDb/wkg9PRvKSJMGLFy+cLSfBUVmWKOsSSitX6KuUwvX1NWazGSbDCZ49e+ZANCUhlCFwn8PhEE+ePHG2nMfHx/j4449dkzzKWQBgsVo5sJ5lmeuFwPcBAZvPnz93AImyL4JJyR4dOdtNRrO7rsPZ2Zkbs6osoZVyx8/jZjFvGIZYLBZOFqaUcs3P2MNBa+2KmAl4CPQJYrquc86JBNrUb8dxjM1GOhTf3Nw4qRmjxHRnYmaIEjGCVH/sffcpzl2CVTryAHAyHX6XzwkeL+VG/lru/8fMg5+F4Ytg1nfX2VqgzevKiLDM2QoT69DI5z0LiI0xjpysViuMx2MnbQrD/cJdEtDNZoObmxt0XYejoyNcXV1hNBo5yR6j4SQyvnOQr8E3RgJ+ksHYOZLICD7HhW5H/lzkuKjOuHuAEjkCThLu2Uz6xmy3W0eqeA+RbPA9AB4mEnDLOcDsFWWGXB+k5qKBUb0FcF/XEbr1za8l4Hzw7VP9+wPoiQLHzncvJKjnOHBbWilkSeoIchAEzlmqMwYq0C77yfEhQUFnXNaV18aP6pMg8Lj8QmxiLc5vnyiQLDATx3uXwJ8ZEBIajgWJvl/bweADpVicD3w28ns+NmSAxb+XeIxd17mMJgAnseI18u1zf0+lU5m1muWJh0mKKMtwdHSEXVVht9tiPBkgiQcYpDM8e/IYu/UO2+1TzE5PMT46QtVKcWJV5CjzEvPFEtvtFpvtVkhCUWA6maLpFNbb0l2kW1sYt8t3QBdgt+ulU+vVGt/69rdkoSsLNHXljpmTQWuN1kXGFViI3LYCOgRdCVBHY4Gh7Rbr45n96Llx9pRcqLh9ADCQwmdjOifhkRvZJm6UBfNavOTBQmn5spWw9ARHwWZ4vIkrkyhA0xoY07jt91Fe2O2yJqV14wHA3jCMBFsnGXsAgd4nOzx+Pz3HSecTs0PA7T8s7gKPHNd9sNmTmLuO4RDEyzj4Tjjyrh+Z3Nuft9/+tU+c/Pf6KPjrO4kfvtx73nm99rNNieaDvw9jDMrf/iXo088jfviT0OdfBOIhtA6EqKq+1NrVS3TwsgrGk0uZXhJlGa9RCoppZfeenW6OOLh0hyWJ8rvpvyXf6VqYfI3yO38P9cf/CKYu+lqZPZLcO5m9bux86ZsUafdzcb/RnD8Pei3r/rWSuoY9IgcWWdqxQYcgUAiNFG9LfZRdfOMIUhckDa2DMMB4PAaMkZ4MJyeAUjg+PUHbtvjs5z6LxXyB0XiE999/H+gMBlmGuqpRNzUuLy/dwzCOI+S5yFgoo/jGN7+Jo9kR0iyF1pJhEG96hbpsMRgOUeQlptMJAqUwv7mReVLIeI+HY4Q6QGcB0rV1m0mSBGMrbzBti52NwodBgDRNUBayvtI6UoI1lOaMoZXG0yfPnDTj5OQMVVliu15ZP/fKZitYCJy4xm6LxcL1NyCYnE6nLrPBiPLp6alzBOJ8IIFihG92NHPg5vr6GmdnZ+6Be3x87LTiSikH7v2gilIK9+7dQ1EUWK/XCMPQNoYdOdBJCU7Xdc4GljUXBHKf//zn8fHHH+Ojjz5yxZAMnG23W5ydnTlwynP2ezb4IGC9XouboI0eMrNAS1mCXUZnfWkGgQWBAgE9MzUkIIwEz2YzF9VltkJr7TJBjG5SotE0jSOYzEww4n9xceHm8nK5dM+AFy9eOLMTknzaulLWQhkOwQmvKbNQBMXMrnD94drhFyADcNeFoJGEaTqd7slt3n33XdcEjxb3JHPr9dZFfSm1o/0+yRXJcR95r1FVrQPIq9Vqj0CKG5TM5ZOTE1fD40uVOEYcV38+MirNGiJmIBjB9yU7zGD4wFjZtT6NEwf+mX1jdoP1INTwM/PI+4gSJKWUy2JRbsRrNxgM9uRfjJj7lsB5niMIQ7Sm23MH9QG0MWavQSIAV1zPYATxFUkEnxUcT2Y/SIApLWQdBS17eay8xwBrkRyIeRDnG+cjgf8gFbtc3/6YUk2uNZy/jP5z+wTuvjyKGVU/E+Z3Ded2m6ZxfW38LJwv0+bx8PN7sm1775D40N2M2QmSN598UWLJfXCt4XESe3KuvGWe4u0zGtt1gbZrXcSsaWQx7WBQmw5t0wGtQVNUqPIcn378Cf7f/9nfxs3VC2STMeLhCLuywma9xXa5wXaXY1fWWG82aOrGFuQl+OxnP4t7D95DXgt4zXd92kiiEFu0delSeEwR397coO1qdF7hl0RVhVQQmnbGIAx6ht51LWAaaAVnubkfGfdlNx5YllSFm5z7kXuJ7PPve6kmY6A6boepKFu4CY3OHET8HXlo0Zn+RvNBVttpaN1HBvwJGYTiFCYLiG8ja8kVlGO2/bkDpmsA9OfF8/BBuK+FlH87hwX9G2GPHNwxOX1i4Uux5Irty2z845Rx3icnjth0TIHeYYmq+nPwC4aH/+7sTkLQg+a7iYYfDff/tb/sff77ZTe8D8OoAProEeLP/zxUdoRg9g7Y36KntG6gvB/38hq9UurwWyQh/iZc0s70v9gNmLZCO/8emqsPUD/+TXSrF35d/d55knDw90O5FKNNXMT2iIbZr3fpry2lcNxmT/Llnhc5F4nh0z/9Adphg2Ab4v3/55eQZQmgDIbDDFAGo9EQ48EUgQ5wenqKtm3xmc98BtPpFIDBZDRAWVW4vLx00brpZIrlaoGmayy42q8tMJ1BaEElo5B0iUuSCKuVNAvVtiP6aDjCZrvBarnGo0fvoq4rANLNWB6sBmEYIUlSTKcT63yUoa4rxHGCIAiRZQN8+9vfxtHRzOtoW7hGbsYY5xYjcowNgljMPJI4xpMnTzCZTHA7v8UgG2A4nLoCUz4olVIIA400iVCWBYyBi/BprfH8+XPn5BIEgavP8IsU2USL2nVKONhzgUDDNagaZpJ9tICU4DsIAuw2OyRx32zObzrXti0mk4mTWxEUsxcGI88PHjxwwMoYg8DW71ESRADKwuuiKNxDmAWrJE6TyWQPSMscggOKvJ4kBa2N2BpjXMO6qqpcwzZGDLlmMEI/tNbnXde5f+lYRfDJY6F2u7ch3QdpxoiTE8HavXv33DVnQG04HLqMXNu2uLm5cdmgLMtc9sSP6rLYlV3QD8EKs16MrpOwMaND0uOPN5uV8V7ivK6qypGItm2dRE0pyYTV9phZpMweC0JkJSMAwD0D7+rWbYxxBedt26CqJBLNzBPNBDabDeq6dpbE2tbhMDjIIl7OJa4RJAm8XhxPyVgVbp2kFTBlTr4zmFObaHHrjALBA4PBQCSIXV8I7xN5zg2CWR/YA3BzmoCW5JJjBsCdF/fBV1mWiJIYgSVPJAJ+JsCXVBL4Ev+s12tMp1N3XgTMnGPMTJFwMBMDwBEBYsGmaaDNfkDSYTatUTW1y7D4QJ+ZEDZzZHCiaRqX9fFJC7PGbBwJ9F3PSUC01jg6OnLz1D+WruucvHAwGLhABYk0CQuzYbSh5hrP6+tnWBj0YRbID47zGesHg0lw/f0w+JEkiVt3KMP6Q3/4p14FAQevtyYa/9Xf+VVs8gJ13SEvK2zXO6xXK2zWW+S11C5UVYndZov5zQ2WiyV22w0CGFRtCx2GUEr6MGiI3SBdlAgk2rZDFIU4Pb+P+48+A6W0ZdEFojhGGASoqx2qQqrvlZc6vrm5wXo5h1YK6Axrme2ga3TWRpUXtmecDbTqoGCc7CgIpHGedK21qSUbTVYWjRnToa0rJ7USUAubKZFGfIcOPdznHuxTykZulZW19KCb+wSAzrTQgYAtHqNMFgOlQoRR7BYZPqB0EEC6NsPhxq7rrLSl16oD+1kF+blG1zUiKTPeeRgB3AR2xgJRq9x3CzPHWiu916vAoNf3+2PTo1n+TfWA2o6R2x960sdt9YSCrNKODYRsumyLHKzcZEph+WdfWqKhMfkrpwCsrbED2xyPV4nG4csnUz655Nm5LRpbWN35Bf2vjw4YY6QTejJG/JmfgYolyhRMHyI4etjvwc4hl9nweEV/7sb97Eaew6ZYX9DCdNL7orn9GN3qBdqnvyvZsXoL03aOskRBCGcFbbxma1DQuq912c9aiFRQB1rkYUohDKWZpQ4Cd60PvxuGytYyhM5WmjaZcSwL4MnxMYJQFs6/cf/fxzbYYKZn+Mvv/1UkiYAhgxYD+9Au877ANggCLJZLwEiBbVUVyPMcL1++xMz2aRjaBbuqSweICZ7rusF0MsHV9ZUs+kojjELkuxyzo5l9uIfO576pGwyGQ0RhiM12i+l05jTAo6FIhdabNWAgBYlx5KKKlFkkcYLWRuLH4zFKq6f2GyrRplErhYHV/qdpAmUfSgQYrY2IvXgh5xvo3pmlLEs0bYOqLBzAJGhmkSofxgR1DEzwQTUajbBardxDdL1e4+joCM+fP3fbY30BIBHN7U66ULPxl7OZrGon/ZHi3mNXmEzHH5IkFtaybwGBpH+vkhjzocsIoFJqjxzN53OMbGFlZMGgI8VaI2Cxph03Ou64AktjsN3tENmszNnZmeulwcgssz0ENSQygAA/RiYJsCj3OD09dcXCfgaRBMYvOOV9xcJwghNGMTlWAFzBLrfL8wEEuBF4ERwDfXdlFm33tQ8h2qbP+NBlMrXmJSTsBDNN2yLf7VA3DUb2HiWpIhBixqQoxOGotXKYQZbB6D5CTzlS07RomhqDNHMOXiIXC2FMhzwvoMPAAf62laL3IAhweXmJqirlPNoWVSVytMlkiiAQC+EwDCDNGEMHGiUjEth5Dux2OdI0QRwn9pw7pGkGY/peV6whCoJwr9eFn+lgfQezkaenp/36bgOh/loqgYvQ9kDJMRwyWGDtvrteWj0ej901tk9sbLcbJ+MhIRcCn6KqSjeHCHrDUBxEfWLArAbXOmYugL4nCoE8AFcrxPpJRv/9OUjSQoCcWmtcEtq6rsUO3EhdXmc6N2YSrO1cYITHyHunKgWDigROxlDrAFmWQkPhxYsXLrDAXicMiFL2STJV17UzCvAzEH6mheTJDzSwTolzmZkpkkUSRmOkpcJqtXLjz8wOa2z8ehlmoFhXxucKg77MhrE3zGAwcOsNIPj697SPxt/4G/93fPzpU7QI0ZkAWoVQnVw0qAB5KX7fnRFmXbVAF6YQf84WRV0J6NUaQaBRmxaN7ZSqtUaaJEDQAVpjvV3jgw++7SYNHwZhGKIqd2hqubl4sQjWgiCEhkKHDqGLHsvxiw1ka4lA684rDEPEYeQGjZOF9ridtZc1CpawmL7mQon7Fvs3tGQ3WlkgLD8ro5zdbNu1dls2q2ClK53NkAQ6tJvo+z90XYcgDD27y947XIiPgGrnuRz0Lgfoels/Rly7TsAeI8Kc6FyYNO1yvQev/x+MAL9A83sywg7sos9EdDLg8re9rIM7PfAKcTv+Pnls/feYHvaBOS0SpWhXBxoKIYJgP9zuZ6u09rItgJs/fVPAw/qb/d4MrxCJA6Jw+LvZ/7Ctr9CuBmkviwW8si2tAJMv0HzjP3d/r6Bg7HxQUFDT+9DjS/d7z938bb9KZvYSG0qhufoAJl8AXbuXG3FEytaJaCV0JdDiJe7XDxloBEHsWEwQhC4iE2hAoZdyZGmGOImRJimiOMTFxTmSJHEymaqqcP/+fURRgPFEQAW7HDNyQ404i2iLosAvf/gfY1tJb4XLixOnN64qg7qqEGYZ1pulRJF2a5ycnCAIgKIo8fzFU7cQX967xGazsVKS2AGW1YqNtzoXxWdh7Gg0tuBRPPsHg14+cn0tzdfqpoMxCm0HTKdH7lpEUSRgNIoQhpEUqQYBsjBzD3dAIolVLRKm4+MjO/5ibc1rXjc1BsO+YdZ221seEuymNnq+tdHlwSDD0WwqZKhpsNtt3AOSDjskH1xnKBmJogjL5dLJTwjSaQGa5zmm0ylub2+xXC6RJAkePXqEFy9eOCkIteZd12E6mWIwGIg7UidrQ5qkiEIpuDw5OXFR86IonKsRI+G8VwnKCKzPzs5cBJI1LzPrlkUydzSbOXlMZOVNmSVxdN1RSrkmcmVZYhzHGFsXJjaJq+28ZFYj9oDE8+fPXVExzwOAi9yS6D1+/BgnJyd7ayAdkVar1Z4jjF8nQe21bztLp62qqlwU3m/2pZRy5MBvaEf5EuU4XD/9wmZu3486E7SIHSgQ2drAIJBjiMIYi8XSWaxGUej6gcg5Zhh6BFAyPqmN1A5hDIQcaKn9lIxfjTQboLQZwjA0aJoWeS7AOE0SREGI0BKfQTawEeAA0SRGWVeutoPznXbGjCKTZLN415jAAWKut0JepEEu0B44ofVuWF2nXFZks9na826wXK7c/PUDGwSbzHIwUwNgDxPxPiAJ5Lxruw5D60hXliXiRO7TKOzlSFdXV+67UKJekSBLjYp6/pB9ahq09vkaBIFIPosCddMgML0bFYMPjI77hddcW9gLhUDZt1Ruba0vyTHnCAExM390U/MdmwyA0JIXbRQSG4QheeH9QgLg1qMkFidBe++xvqSqaqxsEIOklITQvw8PZU+0rCW+ZZaOGVcSHd+ymNiFAQRm80gaWMPGa+67WflyPN6XfvdvboMkBOjJW57ne9lmAO64+PPbvN6aaPzpP/Nn8B/8R7+Mq/kGZQWUZYO2rmCUQt020HEs/R9UaDXcDbLhAFVZQAVy8LR5VbbAuoMCdCCR9yhGAHFhKZsGbbHek1fwAkdxLP0TlELXtEAQQtmLEYURuqZFFAmZabvGTbamqdC2Mik5ON0ByOON4GQQxthIK2A6Yb0S7ZWIPTMOQRBKBKFt+oJy12ZLSEbb2sJeEKQHFrgyWm7sRIbFgn09hDEGYWwbYVm3GmWzCC5zoF+1jm3bFhr7MitfpuK//FSajAdtjBsvok/wr7woyaGzE6VeZv/c7Hv8l39yhAs+sA7c92XbrLUJ7PHDbVd5pE1rFoBJ07QDcZEjMHdJtACxDPW7lPPtPZLljvFV5yR+Xilmnthxff9z7mcZeLdt5R+vMnucQBJHmikRy1EN0NZu7nQ3H6G9/hgK+31FZDfanRu357/va6CUsmXXjlhJRg+KBdBy3cMgQKiUbdQkgGQwGOC9996TCORkjCyVB+FkOnFzbzwcYjQc4NGjR5KOjsI+7W0MxpMRTGew3Uk0cLe1MiKbiaKbj1IKi8XCPWSprSXocUTVGKdPJtnwrS79JmGMyrMubDweu4gtOyP7MqTVaoWrqytMJhOMx2Pxjs9z9x8foLe3tw4UENj5D1jq4andpStTFEUOhFISxAiU7xrCMWBmgJkeRh75gFmv17h//74Dj3RfAuC05rS7pJtK0zQ4OjpyoHo+n78i+/CjYrTBNMa4B950OnVRZ2ahaSVJiQT1+nRgIhng9SHxI9C9ublB27a4vLxEmqa4f/++671AqQazBCxeN8ZgMplgs9m4yDyJRdNI/4nb21t3LsPh0B0bAAfYGXkkoCEIZzSXlq51LU3n/No2EmVGBlmkzdqPxWLh+lnwHqWF7GQycUCWQINg8enTp1BK4eLiAtfX1+58OVdoy8v6RkrfeF15fH5Rui8Ho0MR6zqYCSAQDoLAWbz6wUESOr58ByhGgIE+cwLA1cBwnWbWzS9YJeHjfeQHzeI4xnKxgNHKZTz4TOR5MTDH+5n/KqXc/eRLfihd4/66rnPado7BeDyGX8/AglpeL4I2gnmCW2aGkiTB6empq7fhNaL8jsfiEx8/ysxIP7fJv5Oc+AYBvLasxwCAyNa3MarugC0MamvRz+Pm9wjuwzB0bkXL5dJdE0oB/WtAUsk6EQZQJpOJ2yflUJxLnGNct/0aDHaqJkHnM57zzg9ekEBw/fQL8knMGLzi9eO+ObeSJEFp1zrOaf94SFw4z5ml4XrDc2LmiD1ZuA8el48XiON4TG3bunWMxI33HmuIuD2OoxD5yOFpX67mK1r8IAevLe+7tm1dds0P2r/p9dZE44d++Av4/Bfex+1vfB1JmCJIpIA5CBTiNIExHapKUoA60Li5uUbXtkhsLUXc1KCzEezU7brWNaTrFwojRZBZvBcVdowuSqAD6UYug2jcwj9IBwgD6VRZ1xU60yIMAzRNjboqUZWFs1TjZJMCSYF41DLypges3t0OvIs6W5BvFBCGEnFpmhpo1J4jQaBtVFlphFEAYzqEcbg3cZumddITpeX3KLbav8b2zdAKgY5AeVBnCY/SUsSktbFy+j6r4U8aLi682fjyFxm/WEnGukPbtXtyJWX/J4japvVs7wzq4olglVLW2anvF/CqVAre9uRzLHL2yZBkMF7V/sNIQb4xBl0r42E6oOlaaOvC5Y8Fx46/790kpj9Dv1cEj1WpV7MM9hAc2dknLsper8Ni9FeJBzM5fWYIYBMLkilAQWmR97HvwyGZkE9pR4KkYJrZmZ4YyoOrNzLgsfv/9Q+zEMNRhjTNMBoNMZsdIQwD3Lt3Dw/uP5CaIwtuZFsa7733LvIiR2MaxNa7PIojBDqwDdwMNBipaRCGEYwRu9q2bTCfXzvwLB2YS7Rth6bpEEWxc+NhRJHRJC7ih1phBbiCN+rHB4MBVquVS2vHcewiVVEU4fT01PUcUErhyZMnDrQTqKzXa1esxwcYF24WUU4mE7Rti+vra6fp54OA9py8NxeLxSuFzJQHEQgDcPIgP3XOiJ5SyoEIkiQnQ2kafOlLX8LV1ZWzKyUR4HpH2RF7MASBOOowos2H3Hg83nN6aprGNW/Lsgzj8Rjr9dqdB91oxJ433gsiNY00xmMfCJ4Xx4bXwc9wa61xenrqgCrB1ng8dgW8SikX6ecc4Tly34wKM1pMgEQgRQBO8MNtcZ1k5I/j3bZiK8qIJB/qABzh4rOEBdfj8Ri3t7cOaNDml5/bbDYYDoeObDKiyGMsy9L1/MiyDM+fP8d0OsXR0RGur6/3wDuj9Lx/uA4SwDGq6XceBmDrBXaOaPhF4iRhPFauS7zODAAEgQSA/Kgz7xVGYSmH4r1B8E3gw2vR/X+Z+7NmS7b1PA97R3azWf2q2u05AAiQYliyQ5RkNhYlkVTI1i9x2OF/4Aj7h9g38pV1ZV36xo0sWpBESmwEMtTYIggQwDln711Vq59ddsMXI5+Rb859qF1wIByeERVVtdacOTPH+Jr3e79mjOlwSPZBUs425HKQ9Vpt3+XAlADn+++/lyTdXl1neeLvtm11altVpzoTA9jD/X6f99TPGyFwZa+ddEFnyTpAIhBUck1Ky7iG22WCU56dDEsIQV9++WXGRnwGvSQbcHt7uwh2CPi9zIjemWEqSXRb1vf9FGgkUsv7TzLWmewt64It9Swl30cGMGdXJuBKUIoe4IOYVAbTz3fyrF7iRsCArvK8fmI7949c+/1hL5Bf7AX3QLCbMnFVzmJQwuYjZj3g9mlNrGM61ygu+pLwQ6wT98h6QJjxooeF9ZxLFMtMIICtvbQMOaP0zfcQ+T2dTtn2sp5eass1P+f1+VOn1qX+xf/Bv6C//3v/L/W9pLJUKFPvwG5/kEIy2n3Xaxx61ZNDWjepRnOzmpuiEpA/arNZiWPlh2FU09SKY9RmI5WxWDx8NmZKZ3eggLmRLxRq+6hje9LQd0pjVjt1/SmBxK7VOAy5dg0H1/e9ypBYc091YeT7bswz86U5+xFDKmPq+kHjdGz9MIzijIMQUqothEJlOQlLVab6/JhKSYqp5GQc0/QohWJ6tsm4NdWiryMHJIHGsSGVhCkdUEdWgsBiHMdcFoZCcj2UiffBTBLsDYMUR6kI5QJ4Y9BwsmMYFz9blKWVdmp4hIVflhVhAOf/a8Hsj+OYm5TT/+nJmLIpMeSeDEbaBs1jcLnG+SuDf4t7yNborAGd8adeOuXywH17vXaSk0JVtcyaLIKDOJ+j4NfKAa19x2xEQ+orKpfrNvdIlIpjmpYUx5SRS4CqToFckfpmmlWTmxnX67Xe3b/T7e2NqqrW119/pVWz0u/8+d+ZQOJKm81adZ3qqfuum85jOGpV1yqnST4A+h8+/KCqKrS92up4SlNwDi+7DPzWq5UeP6XR0998842qqtTr635iG9fa73fabLaqqlK73dvkME5arbbZMQK2MeB9P88dx0H5euI0y7LU4+NjZjTHcdT19bVCCJkxBGRxDsDz87PevXuXwRDrHmPMpyeXZWooB5B5qUnbtrq/v8/gGzDpIOmXv/ylbm9v85kJ3MOHDx+yU6dmm5OaAZw4QtaFLMfpdMpN2X3f5xrfu7u7XDtO+RKZCL7DpyWRzcFpc/+ATHeCDOno+z43NnuZDaASkoef397e5v6Cpmn04cOHHET6RBkYNpw15XVMK6KWHmcJQ4nDBxytVumUbqZuoZvYMHzDw8NDDjoJmLgn9t2zZMg4gInm88vLywwKuFdAKQ38yCwZHVhvADjP9/79+x81375//34R/B0OhwwKCVDIUKEvknJQQSkFz8P3kqVjDGzf9xnQe+BHORb9O162RiCa9jH1N1ALz5QyThAna4LukZ30YIZnZP0BeZTYkQEJRaEhzuUpBO4hBK2szIXeH0lzQ/1tqrlH5r1chGtwD6yF2xjA4mq1WgQTgE8vO2QfsOEQD6wv8sw5JwDop6enPByAMkWAIUEo9gc7xT1S7sV3Ho9HacJRh8NBd3d3Zw3cc48TttbLeCiX4znYL3o1mFKEjLVtmwNFtwPojPcM0Y9EczeBEpgFf0kAQjCID53LzOcpT5AMIQQ9Pz9nQoXfgR8IlAkAMi6cGsXLifylUZ2gh4wGtoC1J7iHGMJ3cw4Nes972T+CLIJuxwie5WM/sdvIqssedgAbxQQ3yG/0C7mi2uB8f8ZxXJyN9N/3+uxAowy9fvu3fqYv373Tdx93U63/oNPpoKpcJXDTlDpNs+nrstapPSmWlbbrrUIR1He9ymqafBAKhZjmFHdqtdmkQCROZTdDP+RGt9PpNI/TCjNr33adxskAl1UlxdRQWk2H/UUNKspSp9NB6lqVochAgQ3puk77t5fFZAycDiUpIYSpbGrMKSlAaVFUE+ufTh9HkKQxOweivrqu1U7RYAjzxmN0i7LS6axJsV4lBY5jr/W6ngFSN2ocUtYhlTLNJ3suWPtuPsDHgbJnCxCgGbjOJTIxzmvB+iwZ8dLYcqmqfnyewWI99eNpVazXdGcLufMSJVeu84xHCBY8iKTHDMJ/XbDx616LxvUpGEgN5al87nz9/KRtb7zWWZYjxjgfIKiY3x40v8f3CBn1PU3Gp1EayTyf9u6GuCwLffvtN6rKSqt16nP4+c9/PjXpJmN1eXWlu9vbdFBaEXR5canraTzl4QDLuFF7arXb7/Xy8qw4DqqrQkPfaeg7vRxTdmCMhfpTp3RydZmZo7brVXd1BuOwm+M4Ko7S7e29um7Q99/9oKqqdX1zrTQ5rVJVNaqqWs/PrxqGqKaptVptptNNE0D91a9+lctubm9vc2kO5TXTouf9BxC7sebQrT/+4z/OQO3Tp0+5bASABPOILsOyA2Jvbm603+9zlsADA2S2rut8kFzf93p6etJ6vc6lUN9+++3CgQNYKCeidELSYqxrXde6vb1dsOtMGYkx5slX9AhgSwEsHDbHfeHkeH7KMSgbATTAuAFU2V/Gw1KCxmckZQB9eXmZz57A6fn5FWQr0AtOxe66Tj/88IPevXuX9+bl5WXhFCVlpvzp6SmTR5ycjS1mrcgiYdclZVCBfFCnD5Pn41irqtLdNCgAv8S6wApSx388HvXP/tk/01/8i39xUQJCWRT+Dsb83bt3GUwCXAhELy8v9f3336tpGl1eXub6fprpARbu57BHAGyCOsAMDCXPJ83nErBuTFTCXpGZIEikR8bL0vj+ruvU1KucrUAvWR/uZbfbZbBHGRCkCPcEaAT0ESg48RAlFVWZy/H8s+/ff6HX5+cs56z5ep3O/SJTiI4TpBIY8jOuB1vNZwCPBF8EDejN5eVlDjawD33fTxnfORvEtfh+ADjBGHuC7q3X60wuwJCfl58D7imronyna9s8rYq1JHt7dX2tIY45qGZIga+JA3H2iz32MijuYb/fL+SM9WEfpDlQ9ZeXgvHCTmMH2R9wlJcJAejxy5APyCrXP6/yILDJGeAxjZDn+xhMEGPMgTLyy/qzj04y8Zz4LydfwQTcn5MmPmSCLJQTMbzQR18/9BdbBzGDj4NAYCIeRAG4hLX/M89oaDzp/f21/pV/+X+o/8fv/gOFftTj815VFdRUjaSo/dteMY6pF2GMClEaJ8EZh3nq0263U991GvvUcF1XVWqIHkc1dZpj33WtqqrW29vrtCkJcMQQtN5sFUKhq7rK0XDfDyqLRkVRKRSjylLa71/Vdgc9Pk4R4DguhGwchowRPd2JwHddp3o1TdloO4UiKQmNtjEWqmuMX5rUU9XVlLWYmJypL0QxKUM/DCrGuTkbITocDiqqWv2YpiEVk7E8nk7q2lbj0GpfSj0ZiUlJQlGIE8d7C1JQoqIoFTOAnaf+EOHz8uifz9JnkCp65hKqopgPmgoh5AlEZFL8moVNfMqfL8skDzkg4kxxMh7FHG/8aLKVX3tW4KIoz55n2US+7KmwAMfimrQnXpnl/Q1SLH5dI/UyM4MRYH3PAy0yOukMluUzxTgHrBgOGnBTY+mT7u7u9du//Rv66usvdXt7o4eHR/385z/Xer2eGnB32l5s8t6Q1l81jZpVox++/16XV1c6nY66uFxPk0CCHh4+aL97UZUbTI/5QMyb6+u0vgp6e0mnNa9Wq5SRKYrMlsUY82jNm9sbPb+kAL4IpbbbC61Xaz2/vCiMJ7297rVqtqrvp7R9OyiEqKCT2rbXOB7UdUN+/sTmbXQ4PGYDye8od6mqSo+Pj/O5DGHO2gHY/+RP/iQz8I+Pjzk4oNzk9vZWDw8PuRzHy0U4EZpJNYD1rut0c3Ojq6sr/cEf/IHu7u5yaRQGn8zROM4nB/d9r0+fPmUwwr3iMKUEkDnYiSwDrBRNkUwkgQ2nR4GAoe/7nIaHeYT9Wq3SaeMEhJTP9H2vt7e3/CwOOHG+Pl0KGb++vl6k/2FPPWNKUzZgQFIGaDSRM6Hq6uoqyxalXIBM1vTt7U0vLy969+5d/k7K5BgRSS09mRz2jpIumD8PJpmSw/rycxhEr1t2phT5Yt0Av23b6rd/+7cVY8xTXPb7fQbB9B5hiyj5IaMEu8ieeo8M793v93p5edHt7a1Wq1We7MPzU/JEFgUgQwkFciLN/RpzmW+fwTPgg0CMz5HVAjwDSnN588VWp+M81x+54UA3/o98SFroEc9AZg8ASSAMCOS7d8f5TAaCgtQH86ixH3JfDus+jqO2VaXWWF0H15S+kCHhpHjuC9sP60vQyfcSVBEcePkhpZWUhqJjZFmKIvX20M+ADUEnkAXIC2f72WPvoSHAJzCPUl539Ad88vLyolFz5oIA3snCRU/HFGRruiZ7C4ni2QrWADtBVgvGHVtGZoDAlT149+5dfg9EDd/NmhDU8Zk09GKbyQiCDII5nsGDLsB2Lhvrh0zGEPz5mSsAfK7vQyq8z8K/x8kt9pbsNIQOdgDdoOyMbPpc3VDkIAh9JnCDvGLd8HPcg9s5sExdN0rnyLSLLNHnvD470Dh0RxXVpf7iv/Cb+n/+7t9Ruz+oDoWGrtfL2wcNwwxyd0MvxajT6aCn7pjAKvX5MU1/UEyHwjVNo+PhJTVyj6Pa/qi2TRt0GOZ50kWIGrpBMZZqNpe6vLnR5upKqkvV27WGGFWOhapQ6ng86Pn5SWO1VVWvdd9cKZ7e9PzwUafDMY2CjVFDTKNohxBUVKWKoky8ehGkWKhqatVVpfVqpaqscsvyOE51neOgvk1nRwxDahKPMRmv0/GkoBSYHPfz+Miu63JlDmx4WU1O6niaQHuanKSodHZJWWksSh2HXjGGafoUJzyniUQh0ny+BL9DlEJZp7Gl0z4UZSqHKooJ+BbzSafA/XFIQG0cp7NHmmYKckZVYdSpX85Gr6s6ZZc0jbQN6T7H6T1FkIahmwF46KUh5gAllIuCqfkZ6lKlakVFjcM4Bx1Fkfql43kPxLS2MagIVf6+YRxSdqKgv0Q/+lxSnlIctIiiZoMdY1o7CxDT78ccYKfMRUgHFcEojqPqqlI9lQZeXV1pe7HVu/tbFaW03Wy1Wq8Ux6jf+nO/lc5ruLnRxUUC56t1OsX1w4cPGsdRV9dXOp6O2XkfDsdJMtPY1kIpGJdSRmtdJ2P76eODiqJS06x0Ora6vrrVp/aThkG6u0+jMUsV2u2POp2Oury8UlWnEpOr62ud2pPW2wSIV9MkEkCEg4HtdqvXl1e1x5NObav1aqU4RD0/pRR1URZqmkr90KquUvnDZptA6/GU2NGrq6scJMEmvb6mAREEGmQGNpuN+mFQ1/cKRaHdVDbiGS/KKihPoqmZIB+j+/T0lA03DgvHDujACVBiAFN4PB51dXWVsx83Nzfy5mWMN8ECJRHInjs6UtXjOOYGS5c5UvpSCva++OKL3ONA6QUBSQhpJr2fyAy49d4FAhSCCcrTuHfIGMAB//ZzABgJC6ihDAcnDcPPOFyAPpmCjx8/5kBntVrlw8xYC0qMyJzRbE1mgvVhv4qiWIBYmP7j8bg4wIo9AeDg8GFF2S+AogN2ssxkpslMXVxcSrFQs2n09PSoVbNRU6dyoKEfLAs5s+MpMEl9S1eXqU/j1J502J8mPxPVnrpJ71YahzgB63RA4+Fw0OXFtU7HTof9URcXlwqSunbQ5V1qtB36UZrOvkq+ttGqWavvUp8lctm2vYYhpkqEda26ahSj1NS1+m5Q1/Z6+PSYyiHX2+k6zdR3cj35t0FNs9bu7U2XV1ca+vk5yeogR8gacglwhL1Frrwev+s6jZLKutbusNf24kLr7Ub7w0GnrtP97W1az1CoWW+mQPxGwzBoPxx1aE8alNZwvVprfzikzHxRahgH1VWtu+sbaQqiv/vuu3x/BH/IBjLn40YpqSGLiF5gEwCdzuaTDSFriu4XRZH1CwBJoOVg0scQQ6ziBzebjT5+/LgYKUtwtl6v0/TQstQwEYCDYl5P9OL9+/e5RJEgz7PJyD+kSd/3OUNx7jspM6qqKtskbDH67PpHZhH7PwxDLkfl+QmUyEiQqUOf2Rd8lZ+M7o3a/E3AXRRF7iFbrVYaFFROAR52RUpBCTKKrfXyMDIarBnZSsgpHy2NnkCSIGN8D70drJGfcYFP6TrK2ZlSGjUMqbkfgjY9/3R47YRCY0zn5ZVTlisFUWtJYSLih0y0/9TrswONIUqxP2m1KlUVo9rTXm0/aIyjTseU0icS4gEP+536dp/BAVE2StO3vfouNQ910zzq9KBBbZvA3um4z6AhhEJNvdbrS+oNKDcrlXWKLENVphGwoVCoKl1c3+ji+maqTX7TaeikotKpH1TGqCJGxTEFPH0cJ8VKGYTUE5DY+L7vJuDCBKGYGYE8BUmUywTF09SnMCaA0x1PE+BJf5r1emo3TgcHernWEKNiLATjPgyDNnWjEKSyPaZxolPA0HVdzhCVkkKwevScJZh6WgqpKtMY4vSe9P/0vUulKopimmaVRmSmkz0TuK/rKjVdxykWC2lSU9CYJjZV6bTlEIrpxPOo1TRRKDUAh6mRP6oIUVVdT83cg7q+zaUufrBgVdRJ7KMUyjRxq6QEjN4WpSyLNJ9SPrOlE/sZ5kMa00npqX8hg1GhbFM2Jc4lTCGk4QP1NKK1KMv8fUURVNeV3r9/p/v7O6UTkhu9/+ILvb2+6jd/8zd0PZU2JMZr0GaT5lHf3d+q606p52ICR4AgHFlyNqO++w5jFfT09KBmtVLfdxO4e8yp6j7G1KRWJ1C42+/mJtlpRvrT4/PEfhz0G7/xm+kwrjFKodBqvcnlGane9VWjlT5gJA+TM8XIMuEIlvLl5UU3Nze57OR4POpyOn2ZA9pWRZPtwTAM+vLLL/T4+Kh3797pcDhkkOo1udiOm5ubPPKTAOfi8lJ/+Id/qL7v9ef//J/PwSqcGwb/8fFRv/mbv5ntFA6edDm9H5wWTRkLbC0gGHniee7u7jLjd39/n894uLu7y6c0S/P4bGluOCQb8OnTp8x00xTsPQOSMqvctm0+YI5yjNvb28VUlt1ulwO3cRz1ww8/LPpZYOck5Wd6fHzMTgvWjXXHIWNriiKdLQEzGkLIk3B2u10ugyDzgzMfhkG30/hYHD8gDRnzDO1qtcpTpjhV3UsKKPHwOnQaSeu6zgfswUhXVZXL7QCs570SnpFAThhPys9vb28zUObnrOvuLfUaJaAC0CjUdb2ayRYgD4DC5EOjjoc0zrdt29wL03WdtpPtoMQolb99qU+fPmm32+dpUE9PT1Pwk9acgPj5+TmX3aTvrVVMZbzjOOru7j6XxWzWm+m5xyxDw9Dr+ZkTpjdzFjtK69V6WosZ7EhBXduprhvt3tL97vf73DhPQIzN9swwWSwaYJ1FJ0Ow2+1U1AngrtarHMzOwK7QMO3J0KdzbvpuAsJxVFM2OaDJU5mGQU1V5wEDgMvHh4c0catr8z0ARPGhlLUx5hZwDmvM/XMIJDo1l1zPg3HIPjhwPg+Kz7GVrx1yhX6dg2qfyEbmK0raTaw4ckKfButPvxI2CiLHB1Z4YE8A6f1NBBU+Lvj29jaXVaFDXE9KwJphA9igy8tLvb6+KoSwsNcZg9owBzJE+CnIMewfWQ2CGr7HG7jx40VRqNnU0jhnbjKunfwDNpZzj7g2xIsHG5J+1J9BACrNmTxsEqV+HqSu13MfNPiHqZfeEyZV07/n5yKQITgkC5fkjEMc4+JzKaj7Mw40fvXLX2oca+3eev3Gb3ytf/JP/0BRCSgWZal2imC58eQYux8dSoZCpN+lkbExptN0JWmz3WpkwkxVp5nwY5wUulfbHzTsWx2HvU7q9PXPf0ubzVoqqgRGcZ6UIkyCvdeg0/GoGErtX1409L3SAWzFj8pc5lehYSrqqZq1IspTDlnQOUhwnJ6BK8RhKudRAvtp42OaIhpTg7P3g0ipS2GIfvL13MhaV7WKODdWd6GTotT1nYLGBJqVSqvKskwHrsVxOrMjZTHqagbboSjUd6WipoPTYlQIo8apdKisU9N9PgcjSMM4JpA/BchBURqDilBKsZi+M10nxGkCQ9dnh1MWjcaprnHdrBSCpoxHoSKc1E/9JKGMuR+iLEqFsByTW0xBDI3oZVlOZ7ikM07GIjXMV2WVswxzv8gU9AXlwC3tadD7L+61Xq90cZHAxv39O93d3aos0njWy+kU6K++/DKXh1R1rbIsdHd3o2EYJ2OaDMHj05NWda3Li82Ufk6TfFZNo9e3Nz0/P2QjjsNgf7y5EkMNa6wQ1E1gkZIaJtcMfTrYijIiaZ6uhbHBacMeYoCcIUeXFVKdJk7KyyEAd7wwUl4KRFMzjJ8bVYw5p5aO46jb29tc/rHdbvNoUUocMOSPj4+ZYd5sNtpPQdr9/X0GZlmHpqxFXdf66quvdDqdMqMIIwgI2Gw2mWkchmE6oKvNdgsWHGBGNgEGimuQ0fCSo3OiBQAhKTv06+vr3JwIyGC/SMs7S8n3HQ4Hvb296fX1NTsJyj8ZkwoQB9RuNhu9vr7q5eUlz1hnT8haYBvphwC8+OQWQLakRWnB6XTSu3fv9Pr6mkdcksF4fHzM+xlCyMEdZUE4Tu+JI8jz2mSmLAG+kTXeg8x98803OhwOenh40P39fV4LBzi/+MUvcsmcM4KPj4856ELG+W6+gxIzSgkhOXQ45Ob6YRhyUFrXVWYSAR2s99Pjo96//2JR/8/7aN7Ex1J2xJoju4wOxn/QM+MTZCjJcXDy/Pycxx2nU+hTsMsABYAR8ox+ew8HwSR2DQBEMAE4ZR3BB+gVOglg5DP4RTJr2XaUZTrHYWK3JeXyuN1up24KRLEjl5eX2h8OKqsyA12+m2lC2EGCdv7f93MJF3roOomvIdAg6+b3TIDlzz+ajaIsBUAJEAbIE5Dz3dh0bDB9F4BHKWUrKQtkPwiufPhDjDGf/A4b72O52VsCRDIuv/zlL3MgBKmBvaMUCrnjnpxkxVZ7071nCnhGD7LoR8EWEYwTUGBLPCBM5Nl8zgTPNeODObsMi++lXjHGLBN1Vant2oWccm1+hk7ze4ICJ3ZZK4YfQGKgM+i+92hwzx5gUmKF3JFV6/v5+ug79sOzhfgF9sVtL3rpWV7k+nNenx1o3FzdqO2i7u6u9Lf+5l/Xf/y7/6led6/q+lFd2+dN4iZyfWdTSHE+HZYasqJIgIlJIqdTO7PEZdRqnTax7zvRbD1KCmOv9nRQMbRaXWzVn05a3TVS2UylRr2isVTDOKqPo+rNVvdffK13X0Q9Pzzo4/ffqQhSXZY5GzAMqdkWQ1cUhfqxn8amTocNFolVr3yTi5BT4eNUOpMiSbIig8qyyGxJHIYJxE+LO/VXdMOQelDW65TNOaUJHXEapTtOfQdRUWNVpzRW16YG+Ukoi7rRMI01DVFTxJnuI4Z0vkgcksG/2KbSGElpqlCVsgepTEjTIYFSVZWppnUc1B72evv4Qfup4TArS0wN/NPjTGsXs/Go60ahqhWHpPgKqa+F6Vx1uVJdrvKawuKGaa2TkifnzXdW5ZSNUQqAylCoCNN0iiLqcjqQ6P7+XhcXF3nyz2azVlVX+p3f/m39r37/f6GH4UFXV1f63/5v/tdqmipPnxjHYTJ2KYPx+vait9dXvXv/XkVIZziMUwbh6fnTVP7RqKqD3nbPCmHU4+MHtaetXl9fJiM5qO8blWXIdbew0azV9fV1djZMQmIqRd/3CpNs13Wtu7u7DAK+/PJLnabpIbDL9CswIrUoUuPfbrfLE4cc3GLQHx4eFGPU1eWlXqbzCDjrgX4FGCRADPdCQES98TiO+awDB9E5yJue8/7+Xn/8x3+ceyIw7M7aUKJSVZXev3+vsiz1q1/9Kh/ERBOes16UBgLsX15ecn8DzW4/+9nPNAxDdm6S8mQn/n97e7tovqMmPNmOIT8z/SPUZ3taHJ2JMeaSgaurKzVTycl5yp6yAz/VGpAI2+ZlGkwQkZTvFUCJ43iemmB5jhhTbwcMP/Yb9hCASuaCme84J4AKjBxAhsD06ekprz8B5rt373JjN2UY3LeXiSEvX07BPevmgdvFxUUOxOjZQAZvbm7UNI0+fvyo9+/fS1IGD6wxjdiwxTDFNFXf399nAIftYb+dVfRpSCmbtc76tNls8rO0bauoUXU9M9kEGjHGHCiTYUNH+D+MKeCcA/uQvXlSUMx+EFApKTfhklUAfAEKd7td7gEBgLpsIFsAHS/zAWRRTumTfAhgICoIJsmewTBXBvQB5HxvXr/JLpDhH8d0kCABc647L6ts75DBt7c3DUOvY3vKATHPyTjqoe2yPFHeslqtNPSDjpZB22632ZYQuKKzYB6IB4JU7Cbrzn054VRVlW5vb7Xb7bIeoVfOurPHDux9+Az/prQT4FjX6Xweghl0FFlEn7DNTr54NpEeFa6FfBHYAVLRA7JQ2GgYfC9tQp+wMUykwzY6+GXKHYCXa5yTd/7cvI8MhZdvEgT4JDP0F/13UE523ftIkBV0kEwE60h5FrYTncW2MH7bg3L2xgMUniFn7mNcvCc9d8K3XtZG0ITNJajHn7iuUV2B/8FmsjZ8z0+9PjvQ6E69QlGqPR10fbXRX/nLf0n/l//r31Y/cFr1XMvOQ4SQ2MSiKDIrCIAaY1Q/jOrHVvvjKUf1UjoVexznTnxOuh7HND527NOBcof9Ub/6xa90eX2nm5uNirpSDKsctVVNSp1vLrbSOKo7tTod9lIoVVaNjvu9mqpSHNNZHhi51ACdzgOpylpjHMXZBSpKjf2QwHxZK46poTyUpcZpOtEYNZ0OLsWikMpBo4LKZqUwDBr7LgHzccgO7tBOTYVVqRgKRQVVzUZFEVRVdarkKdNUIZj5chofG4qp1nrVaNWsVE0O7LA/KI6VNuttroseY0z19ZLWF6v0bNMZDijGOER1XVBV1gpFTBmTYycpGZnD4wdt1pOj11zXt2oqRTGKdW6qLoqgoCl1V5fT/nRKzead+i6VIyWnijHhwMJBZZHKwLbby3mKznarpi612az01Vdf62c/+1YxStvtRn/uz/05vb69TOx0lT9TV7X2h312+mFqitcgPfVP+l/+v//n03rM6fngZ2iYksfpfeOYMjLpAEOJcyqSwkv5pHHP6sWYf6fpukWRenLGyDjf+TOSpD9OPwuaTlu3F/caY0yBsBmeEIpcYsfLG7xyuZxlG93h+HsU0/CB/HlN1ZwhLK6ZWUquURTSf6e8lmNKT6WANC1aCuT/cZHXI19nHKfnDiSi8nAC1ghBi1OQz+o8tA+TPQn6+c9/ntk/ehG++OKLDExxxDg8b5bFblG2Q98G7CIOjACZszl8CglBpZeEAJpg+M7rnQEux+NRr6+vGcgy6WUYBj08PORGdxwSZ3148MFoVS/TgL384YcfFmyyAxmfbuPgiuyCl5oBrHCCgDiySJIyAxpj1Ndff50zPwR41CsDnmi6d6abDAsMntd/851kJmiQBngCQJjMhbMnwJC0aDJGJwBG1OkziACGMU9bm5j8zWYzTVjqcgaNbEbSnZBL8VgznmOz3qrr+pwtcEAKOPfeqO12m8kCSjsoq4KtJzhNRMsm13tfXFzkz3ngwDQvz+DwAhTjZx0EOjsMe80zE9Ai62RQyXZxHTJb7Cl7BGh0sFhWlXZvr1qt1/ryyy8zcH59fU1BSjUPVnC5urq61jCOalYpkGEtxnHUaOUq6DSfq+s0kAYWmPtlipSX5nnpD9lXSgMJTCltIkAlIKTkZq4A6TPhdJiyZJvNJpfoYDvQVwJxAlXKz8BZlA8h23yeQBFb4xOjkAOeCf0nKMH+YJuwi+gq/U/Zt056TNkiJJH3pBDgO+mCHLD+7A36wrhv+mE84KZagEZwMjtkE3gGZBN588MS8aHr1UphslkAcX4PGbderxc2Db8BoPdgBL/JvbAPnrXCjxDosA9eGsY6Jxs2j0eWlHti0EHkCxlEZvmbgIhSX+Qd/+CZ/P++12cHGqdjq+ubK/Vj1NXVRv/Sv/QX9R/97d9Vu2tVTMrMpiOgcYyT4s8pLx5m6HtJQWNMZzUoRJWcSlk1udymaVJ51jiMOhz22myupklOjcp6pTEU+vTDRzX1SqvLS4WqTIagTg3EVZyaPYta/SipbFTWa8Vyr1hU6kapjImxblaTk1VQVU+nXxdRZaDJKDX4lk0SplPXTQB96kMIKUiir6GBZS3mkYj90KdSoSnDcX11nZqEY2o2bk/HSZDqSZmmyLLrNCpNowrFdCrz5Ay7EyebHlRNEfNhv1cZar3t3hTbTv3xkA1SeXGhfuj19OlXOhx2eU9CSGN8U4aqns5FKHTcv+l4eFURpLFvVY7UF04H/ZVRq2aVmr/HXmW5VlnOtad13SidszKNj6ybqUTpUqf2pKqs9fq6m5qEG23Wmyli3ujiYqN37+91e3urL774Ql+8/0KhCNq97VRX6Xi9vu+13lC+kUDv9fWXGaQd9q+TUeskBbWng9brlV6mCUqSNGrUh/bD56rD8vV5h2P+/9fLiYjz+/91z/P/zXt+6uf/P3qFotAPP/ygb7/9NoMOWNFU0jafrRPCXHuMw8KmSX5eyXxq6nmJBIw6TpsJLjgVnC7pbDJFzuzhZCmXoERuu93mMxIIoIdh0OPjYwaRfp+UcQC2b29vdX9/r8fHx5wVobmTjMHd3V1mySkFwrkBWgEbqbfmy+yYKFegpl+a2VRARV3XOTBiPXIG3EopWF9e+/1+UbrFi33kvqoqjZyl9IHnYk0BfV5KQB8RZWr7/T6fNyJpEQj97Gc/y8GIO31nWMdx1Hqz1nZ7kYcDENikzwUVZcjXeZjq/5umyT1RP/zwQy7l4/lZZ+TYZcRBG4wsAI419dIy1pumZsAPQN8JB1hML+nzAIg1o9RGmptiX19fF2sFkCaQvri4yIEagArQRYYA8Ax4Y7/b00lVVS96PQDcMsLFM49932s8HDTEUS+vL7n8Er2idIpnpPyl6zqtNxs1TbFg3aV54iPP6KVGzlbn8qx6PhMmf6/1FwHikFtAKvaGwJh18elVyDnAmrXHHiEnBPCMH6cklcyY9yk4WcKaIveeMcW2EUiRgUZOeEbXVWytX4NgGpDrI6Sx0+glsu+H8pVlmftgkP+3t7f87FVV5f4fCAmCI5fBruvy+SXIACRQUMjHNbDe6CSBIPac7BDAXpqDP4JKMnmSco8kgfO5LcR3kG3woAAsPuPIuR+HoJnzjHwteV4PpvidkzmseSYgP+P12YFGVVbpuPgiKFSDfv7t17q/u9Xr669Sg3A478HoJUVV5TRTv651aluVZaW6LPXu9l7BGkk8Oo0xsb1xTM3IPHgqkwkqi0oKQf04aojS2A364Ve/Un15qeZim52YlHoThnEyNGFMgUO90tX1reqq0dj3KuKoLkeP68nhV1KQujilxKtCQ4z5pHNFqVlHbdZrFWWh9WqdDxIsy0pt26VAp6rzxInVaqV+6LW52OQo9+XlRQemFLQnFUqNtqf2pKGfj3oPo9SdWtH8nFiwxKQNbZvGCYf51PAceapVVc0nnxah0Ccl5jtMpzNXZamirrVqUjRcXm1UN42KIH391RfqTnutmlI314mFrVZbKaRDj9brtd6/f69mtdL19VXKBsVUtjSO4zTpqVBdlQrlbPxgXNPEiEp11ajrMNaUnkW13UnpxPmod/e36oeDiljo+fmDbq4vVZWFTu1RCqk34Xg8arVJzFARCl1sUvnCbr/PPTRFiGqPBwWNuqtucwZh/nt5OniMkUEMs5xOWbmcJ8jKOh/wl+zJfPhPZv4x3spzwrIODMZCeWYA9t5zGTgh3hOmrEPUXMJYmBGhpE1MgJtexZRl4ed+OjsPFczBaEoijMZMiYykpV3HYczX40M4Le6NrhnuxjMv/N/Z1HwPvHd6rvwens0yHdfFdQadPgEE5vfy8jIDKECnO1LYSpgiehJijNY03y4ANWAIFpLAgvdJc2mTp/0Z8UojOSAD8PH4+Kjr62udTqc0Jayc57cDttzpSNLV1ZVWq1UOLhygEIB4aav36mB/cPBkeJikwzrhhClzpUeAs2N4ftg5ae4dAtxjGwAcPhJ3ziTOtdr8m/KhtB8npfOdTjlzlaZtrTQMfbbPXoJC2SLTvd7e3lIJTtenRulhZhEB4xyMyHpTCrTZbNLnykJ91+vp6dPirAbKyy4ut9lJJ2LkOss0tdgckofNSdOdUgbO7WfbzgeyXV1dZeAEGPZmXLIu6BF2guwXk9MYv8sZHuwT/SrM4nc94TuLIg0IOB6PuVyN54KpRg8B8fgEMoE+tQj5cYDuJzHXVZl7Q3h/13WpZHsaFe418pndVjrhHv1iqt04DLq6uMxBIBPvkm1KNpk+GS8z4RkJdpgQRGmMZ4jRJWSGZ+QalNrQG4T+Q3x45hn5IwBhPbk3gng/SNFBrY855kwWHy9LgOBBqgdaEAW+t5QfEmQx1ILvdjBLbxpyyPrA4EMUeEYBez4MQ84K+iQpz9AA1imhI9jyEixpzpRxH+encHtgEpIDzAEiAT7rg530jJbLevab07Ogs57Vxv8z5IbreNYbv8X9I1ezjU2TSiGy8F3YWl7uk5ApglnvfXGZpxTvc14hnnvxf87rv/jP/06KzoZRRVFrv+v07/8f/wP9/X/wj9WPqd9gHKNiKFSUEzMVgoo6nZhdlrMjqqqUyilCnCYcjRr6NOWo73utVxtV5TTXvB9VVY3iKEUFnU5HbS7W6STscm7g2Vxc6KRR9Xarb7/9VnVdac+4vCi1h17rZqNPnz6oPR3VNLXqutLL64vGIjVOX1xeaLNZqx8mAFDXqlRkhuM0NYqd2lOavDQkAXh9eVGzStOGnh6ftN/tVNL0HYKqqtT+sNM49hqHKE2ZnnEYdTwd8xpo7NVMQUFZlSrCNOWlCFpVhcoiTfbAWaw3a11st4rjoNW6ybOh27bV1WU6LGy1LnRzfanNZExubm5UFoU2262aep5gEWPUu3fvsqJFxelMk6Dd25uYwHV5daWX1zet16mRtCwKhYnRSkIodW2bAjxjXxKzMk1cmYQ3KXYaszYMQz452RskE4BJPR6bzUYPDw+q60oxJiU6HPbT/U/N3UWYTvI9JtYwFNMBTLX2+0MqodjttMqNk+mehikNT715Am+Xen19Udd2uricjdmpbfXu/l6ntlURaHxsdDq1Wq/n+ekJjM1pU4wooK9pmly/65N41uu1Xl5f9TaxgzjhbjKQlCvB9EnzRCXAM8wDpSV1XWvdzGeftBPDQSp/vdnohx9+yDKCw9tut3p5elJVVbl21JtB+TeO9vHxMffD1KtVTjmvp5RuDdMY54kb1Ae/vb1JmtkTQBnZAD+vA0DkUzMczOCodrvdFOhWufmZEhuc7maz0cvLS3bgOAjqywkQMeKAHvYUB+UHtZF5IFCAZcKQs/aAae6bZ+ffEBI4BRyzHwboLBTvgbSBWYP1pjQGBpNpNrBjlBhxSB4sPWw6I2cBEjijw+GosihVTgdFdu10QOLQa7Nea78/5JLDEBinHbVaNXp9e83BkwcyzqB6c/84jmpPU9Pnep3PaFqv1hqGXpeXVykIq0p17RwYrtcrDUMql9m97TIwqutK/XSmwpxVmscQh1Bkh14UQadTq66bg4Hdbq/tdqPTqZUmcglG19lwB+QxxkxcULZLP5/3vTg43263ebypT7UBmNEbIs3nB3jzJjbaa+EBgsg8ZSWst+sUeuDEH8D3+fk5B+zH4zEHN4BLZJAhAwQMlIOhA33fZ/DvgZI32CKL9LKMY9ThkED9MA5aNYnQG4c0JKVtTxksA5YIOKJSb2EIQf0wJF8/ERjorqTcNL3epFH69J/wTN6rw3p7TTx2g/UD6BEYeLkVZYbONLufHscx+yjISogN9OXt7S2vMTayKIrsb5Bn8BM+GSCLfJRlmckY7Cx6iS1y4gLZSmTjZT4AVVI+vJOMFnY4jUO+yiCbjBrXw6Z5oOnVM9JcPkSwQXCFfySA9bIySXn4gRPk2GD8q5dnsQ+JxFU+BPpwOOjTp095eMnl5ZWaZqW2Pel4PC2CGClVg0CYeJaradbWFxgnUqRXjFJdl4s+JiYhJv2dz+BomnrC3PM9829kkL13TIL9Reb4uVcjuS1AXv6Nv/XX/7lxA6/PDjT+5E/+yKKlQoqN/uD3/0T/u//9/0HPu17DqCnLMGiz3agoq1RfPY7aH6boXyGBdCXQSn+Dp4ja00mDRoW6VBFKNc1KZVlpHFP5VtWUalZ1YplCodV6rePhoPv7d7q6e69mvdXlxaVCATOU6tSKslZUmDZt0Hq90vE0jc2rU7NO27UpOCikvu/Ud63aXWpy69pOXd/laQ9j36s/7BQn8OBKG4dBGjrVdTWVSQWV5XQCeFVo7Dvd3tzoZz/7WWbzyrLU/f2NpEHbbQp47m7vdDM5/KFr9f7uXm3X5vGXtze36qYpGKt1o67tFrXHm81aDw8f1Xap2e2Xv/ylvvjii0Xam/rS5+fnXDONAFEq4M2lXZe+48svv8wTPryGlbMK+r7X999/r6+++iqnjzG+fioqBgsj2batHh4e9NVXX2kYUqMm38V7XRFopKY8gXISom1YQMounL1lz+q6zgch+f0wvx/AxiQI7p2GNxwMBlRSPrju7e0tT3TyhmqcbAhB33///aIm9OLiYqofXuW06nq91qdPnzJIZB+4Bk4YALher/Xw8JCbG7uu03a91tPTk77++mv90R/9kdbT/zfbrX7nz/95PT8/5zKIp6cnvby86JtvvlE/NZrnANcaHfk/ZSeU1gzjmM626OaTUQ+HQ+o1aFtFY2gJuqqq0ocPH/KZEBhGABqgGeDFSdeAKNaB04mZMETdM41/4zjmvgxsj+8XwQPfT/0289rJeCDzOGeMPr+HTaOnY7Va5TGQXhoUQsiBCTXF7oxxqDS0eikFQwIAI16igM74gVnsB1NZCLy8rMiDKoJXAhX2glp0/n3YH9S2fXbap9MpB4Loq5evAJZT/mlclFxQrsU9AhLQmfS+OI1NrReAG0AIg+/MKWUFPCvPS+lF27aLQ/+wF5Q2Af4pOQHE8YxeGw37DKuLXcFBk8Vw/fWaawgjwAjPCXPvtfFeosLnmcoTYzqIMZd7GEAA+LD2LiswtOgZWZ/9fp+fkaABZp79k+bJeZRkvb295cZhSnO8jARdgFjgGuiAwxSGH8wTeubA2q+bAsF0336WCvLIdyHvgPWqqhajWkMIubynrCoV1Xx+BHsMI8+1kTH/PnTXy3+8b2G32+WMqjT3lBA0UH5H8/put9N2u9Xj42OWbXw/n6c80rOP3A/+CxYe2XGCEJuPPPkzuz2OMWab6t9PcIvtJNjDpp3bb/advUU+yXJdXFxkO+D6zHpzb8iopOzXsalkD8gyoO8xplG12NQQwqLsMcsAmbGiUFPVWf8JupOsX2mz2Wbs4NmlNJa+WvQ+IHNSkZvHwWn4kM1mzkoglzMhW+UsO9eDLPC9xXb5dCu+x4NSSdnus85k2fh+MN3f+Hf+Lf3U67MDjYeHTxoGTjktFcdKv/rlJ/17/96/r//2n36vfkzjUEMZ1A+91tuVxn5QFYNOx3RWADdWlqWGcdRhSr8iJDA4QxhUrlNt2d3d3TTqNDmY9Xat7XY9GcVpPCJTn8JKb6+pERKl4NCvPkj9OKjrWh2PB+33b9rv31I6bkgN3ofjXuM4aBg6SVFD36sK0jjMaaTj8Zia0+OgumhV1ZXu7+/15RdfKIR0SuWqaVSVQVeXl/r5b/xsmlglffvt1zrs3jQOKaXsDMDN7U2qha4SkHl8etQ4zI1K29WF+jZNqzrsE2C7ur5OI9baTk2zUt/PJQOJqRoUwqiymtmLq6srffz4MQMIZyik+eTg82kYDw8PGWTg9N2Qeho4xjQG1CeV+CQSFJrmUtiv3W6nd+/eZQfFSc40OGEYMMiUi/BzUtyA3Zubmwy2Pnz4oPv7e223W/3iF7+YmMjE1Nzc3Ojjx48qyzLXZVNCgqPD6JHmJmvgbC8gLoSQm2UBmdSFAxwwAE3T5Bp4QPLz87OaqUTi/fv3osENAHp/f5+BN+l1QCxNoJQ7wNz3Xad2Sq8DKgh+1uu1rqcJJ9SiwnTGGPXy9JRBBcEBc8h5LmQAA/Th40dpMuo4J06tPh4OupqCONbDmU9nlwiACRa8th5D6ge/UfIBkH15eckBI6AY5nQcU4nPp0+fsm5gaJGd0+mUz8S4vr5WXacJLe6wyXxwRoEDDp+0dd5UCwj2kgiCZC9VABRTZkUAgwMDZAPi7u/v9eHDhwxOCKK9hI9rOZgGDPPHgxpPpfMZ/iSAFtW1yxprZ3MJ5nDqBJLjOKhu5lIo1gNniNxTKkQAdDq2U3a8yvYIGwegQjdZ93rqX+O+eXntNPaEewF0I1ur1SoDkfV6rR9++EFd1+n+/j4/F0AEgsXLwQBI7D+6RsMrewtAA4hIyroCg+plDNwj8gDLDrCVlJtMAdbeM4TNRY/5HOvrZV4ARZrbPbjgmqwvQYMHWx5U+J4imx5IIbduFwCF8/eFhe3lXtKazZNy+E6yPQRH0lwS68EuOrwoRyoKxaAciLLfyA6MOoEd33c8HhelNdgDbBFlTewbZTuAPW/8x18D0rk/9sxLxfA9BLJ8J76MBniCEUg5HyWOPcU/EPhTGub7h9ySCQDIk0lBprAlyAi+kp/h5wkYIDuZxEXGmXUiM8JUPIIYMrOvr6+6urpa6AvrxPN7gAo+4YUOY4tijCpDypSjo17GNI7pvInzDFqyh13WcwJ+iIvn5xdtt/M0Q5ez1Sr5Cx8SMevlcuKU6z3PjAzzO7d7PCOy4nbQM6boBDJQlqX+7X/3b+mnXp/do9H3CaSP46CqKlRWQQqDVAw6nE56en7R5mKTRtIOvVRIMY6p/CYUqptam9srbbcXqqpSx9NJ39zcSEoH/KReh3I6QbnR2OOAj4oxCeOpPUkatd/vdDx0GoekRK+vr2mi0POrYp9Ofd4fDuq7XlWVzq/Y7V7Vda36oVMRgvohjdMti6DNqtbFdqNv7y8VY6mbm/d69+5ObXvSpkkjEu9u73R3f6f1aqX1ZqOyDKqKOSVdFEHr1TqNhJWkOE7rNapu0mnlddVrqEbd3H8hGshDHNW3Jz0/PKTJS0Wpw/6goRu03+11e3ujru91OO5VhkK71/TMN7dXKgqpbgrFWE3lRbXW6yulE7iVeh7CqHY6FBHDjQGkYfPq6iqzXky3IRDh4CcEFQD/8PCQnS3sPw4Hx0uaEwM1DKkGHHac+f0YSsAlxu/jx49ZAWnOrOs6B2mPj4+ZuSYbwwzwoij06dOnfH8En6+vr/lcgePxqC+//DJnBm5ubnLpAWlD7skdJul9xnwSzDLiU9JirVkbHAxBAorqThRje5wcxNPTUz5s6+XlJRtOjK8HLgDnGKO++uortW060C2XRkyMfd/3i4klXdflGnem0RAcHA4HXdrkjtfX1/weDBX7i1HK2SBLr1dVpa+++ioBtYuLaQT0XKbTdV1mj66vr6cSuVrv3r3LmRbA6zDMk24uLy/zeSGS9MUXX+R66JeXl8xmeekH+wLr76VJABmCR0p6yPD98MMP+cA8arhhtR0cwQLhXGHEuPebm5vsTCizY60cPMDi+Qhb9po/ZBd4QQqQHWG/eY+DBRjIDOAnBos14+dcj0k1BCBFMY2BDYU2m5T1cUCIQ3OHSbne8XhUs6ozKIMUwDl6uRTsLQ67qpale9Ky9hu2j7I7Dy54NsoCyDax7tgPz+pIyiNQWTeCfvpcJC1G3aLX2EmAoQc9McYMHMikYj8IAMguEGQ4CYAtgGxx0ERJCs8sLQ8l8+ywA2oHK+iBZx48w+I13w5eAFVFUeSeEj5PsOcAnXvAProdBcD5Z5DBtAYzC+s2Nt3TmMu6/Hp8nvWj2dgz3ugCMlcU6TDXzjL4BNptO0+P470EZbDxBBmsFX0oBMMOqLmOB2DILZksyLbLy8uc9XDgyjNCQkFYvby85F4ecEE+G6Kuc/kPeutldGSoCGTIEFBCxZ7Qw1NV85lKyD0A2wNhdI0MK0Gxk7HYVoIciAyuTTDANb/44ousT7e3t1mu0dMYU68NWXOyqOjk8/Nz9r2QpcjwarVSiMuzidDtJBOpEoeAgN6l9JxdXlMH8vgl8Ae2mwA0nSfGGXW9BaCdqqrOBAakp9sRzyh7ttzJJfQM+8+1XNew46vVKv/5nNdnZzT+yT/5fUnjBG4b9d2ol+e9/k//wf9Zv/ff/LH6Purq9kbb7YW6vlc39KpXK5WrWkVZ5P6Bt7c3KUZtthuplN5e3zKAGcYUJMRj1MsPzxpjCire3l4nZ5Ecx+PT45y+onyhKBT6k6oiCfN2OzeFr5pGX97e6ubyQqv1SpvNWhcXW5VloW++/VqXt2uNGrTdpjKsqilTyVMI2kwOqCzKSeE5/yGo78fMSNze3io1gbc6Hg6qq0rH40GXlxfqh059T013rdNxrp+LMZ0CO46jirLUoU3NoIpRzy8vGodB24sLlUXUMMwHJhF1JsAwqK4aVXWlqizVdmnc5el40svrc07348wQZGc6YkynlVIHj+J8+PBBp9NJP/vZz7ICu1ODtSjLMmdLfKScG4wPHz5kAwY7Lc1NVhgmBJ5pGDCDzHXHEDC7vWmaXFLgEyIo8Xl+fs6gBMMKEMCQ4qC9BIxTRznXAqfgzgznQa2nZwPu7u4WDgDDyL/5PArsju/l9VXvpxIi7+Ngpj+GgtISjBSgEyZwNfVJ7Pd7rVerdN6IOeLctHw6qbSSDxzyMAxqJtDsz7Df73NAeDgc8qjAu7u7VDvd9xqMKQfYVFWVezQk5SDh3Llg+J19xbGxZ58+fcqBHDKJOSNbRoAIwOXaHlhIWhhZr5nlmn3f6+7uLjsbnB5OC7BJ2VY2sFaqQgZtHEe9e/cuO+ZPnz7loJJSBIIDDz5gKKl1xkmy987KSXNJI0AIZ+0Bi6fPy7LMwTKZFX7OMxM4cT8cUtbUjaqqyaU12ANKB52sYF3S/VSpv2KSw3Ec89oDdiEryAD0fa/t5kLH4ykzxp59paTTM4dkorAN7D/3xctBLNlB1habBhsKSGDcqJdbkTlk373MicyYl5qwrm4PPAAgYPESDL6PfUGnAXf4JmwXdgv7z3oir8g6z+m9R0yG8uEAgF4CCcAYuoT9ZM95OXBlXbgnMsE8I7bZGVpnVtPaaAGOAK3pGcssz/gjZAVwR9kkcsF+4xvJmK7Xa/VDr7eJEHFZwSZtt9vM5iNvZVlmIM8ae/+GE208N0FE388T3LDLEBD82xlo1hcfQTYBeSOIZn99P53d596wvewBNgidQ68oA/QSJvYBHfLAnQywpHwGhwfpZVku7g2bjQz4oYT8zYsSVHTLJwd6ySPvxU6+f/8+g3hsFfvLuiwyX32v9jj3HfF9iSDYLuQOvAF5HoKy3GNHUtlfGkmPfiGDCffMJ4Dj08ARHC+BrYVI4369zMqzK24L2DdkiSDFSxohvTx7+tf+zb+qn3r9KUqn0oFtZSU1Ta04BnVd1D/5J3+k//g/+4d6ed1rdzipPQ3qBqmuV/rFL3+p/Wme6rLb7fT29jY5ziiFTn3X63g6aRwGHVGCQVoXtdJZBaOurxN7r5AOELuaJiOsVo1+8zd/S19++WVyJlVUWSSj88UXX+irr75K4HC300Wzmo6LP2iM6QC9OJ2PMcRB/dDpYrvRqT2qbmp1Xav1aq04zCeErtcrdV2vVJJU6tTNwleW6bC+flKS2bFXksaplyJqtdpovztl8NVNJ2cPfa9mMlDFdD7GOIzabKfDgKpKp1MClFHS5cWF2q7TerXS8XTMtZsYAtj74/Gob775JoMWnDCAn7F+Nzc3+eeAdgAXDEfTNNlpOstD3wr/RzkduJdlqcvLS/3jf/yP9e7duwzcOOyIshVKifhsURR6eHjIJTsYx3Ec9fDwkFOQGBQc9O3tbQYAXgbGfmGAqcnH+BM4cD2CGmdI/dwFnAxlFGRdnE3EGADs/TAjFBlWBYUPRaGLiTn3OlLYCfaJ9XVQwBqu1+ucreq6TtdTZoWaa4xbCEGnts1N/cgubFKwrA7paYJEwCFGE+ASlbKKPi8c4Nq1rTbW5+ClNqxdVVX5UECAy/39fS4z4fc4GDJVAHtnu9y5wRoyZx8Gi71hz3Euw5CGFDw+PubyKXfSwzDkRnKCYIgTyrSQgS+++GLBEAOCGYc7jmMujUBf3cg3TRoVSlnD09PTAmTwB93250XOvTSBBl3vWfJyLvaGefSwlMgUjGhar1JVOfft4OD4DmdlyWYkoBt0OO4zEKPHwwErMgn7VpWV6nqV5Q6dx7G+vLzkZll6RegFoneD9Qb0ehkKQQPvwV7wN7JOj4uDeO4xO1gDWYBL/x1/vHyVz/M87Ad7iHxwDWk+hJD7ZP+QYWQCcAxQ5PfAAH7PHy9t9HJB7D8ZQ2RoGIY8YQiygM+gBwTTZAIhTOgnoEwHsMR9s1foHaVm8BasjaRsd/DzHhgADAGVlNrCxJMFQFexqZvNJo0eHuZmaEgwMjy3t7d579Ap9hS/jM6x9nwWmQMEewDDerHHjG7ld9gyz4rhNyAb8GnsEZme8xIe9oDAyO0Kz4ZOs870cnpASPbDSSqy3zlDJGU7fs7+s174Ge4R2cJmk5WGpOI5kDk/J8OzwGTbuB9IGqZuvb6+ZmxyXtZ4PB41dL3qau5LRD7T+qchEtgS7G1a33Tel5ez8tm+n7MyXuaVMMY8RAd5nXV3JnA8++XksMuWEw3uJ2dcOve4OKnAPvGZtm3/bJvBv//uBylEnU579UOvoEJDL603l/qDf/bH+sM//BP9yS++18ePz/r48VkfPj7q7fVVsZ9mZk/gbbfbqW4aNXWh1SoB3W++/lpXV1f68PGjvv3mG717d6uLbaP1Zq39/lV/7s/9lmJMk5WuLy91Op4Ux7lTHgCaD59TGpkJ4GnqWn2fFvHUJnawqUu9vL4kp1WtVZW13t5eVVWlikLJQEkqYj2d+p3Kk0IoVNVTOrGamffLy8ssAF2fgqebm+tpqlRUWRU67Pdab9Yax0Fpysk8Sux4POrrL7/UMHQKCpk9OR1PqSdElbouLozFrBi1Tu0pgzRpniP99vamd+/eZaNZVZV+9atf5f4Gd36AQYQTEIQB88kWDtAxcm5wUeoQUt/Kd999t6gHBdT4yDpKTCgvIWsBiNjtdvmwN8qRMNRE8gRCNzc3uZcD9vf9+/eL0iFquJ0ZLIq07+20xigja4qikn4mWOD7qOcnu0FvAaCS58VQSDM4x4BWVZVOeifdGaOqus57QQ2vNJf6YLgxCowMZA/ryYk1E+iBoQRI7Oysh77vF2P8mgkwYIS4d8qlCF7v7u50OBwy41EZOF6vVvr46ZOKSR7iOJ8oTmDBIUo4RQeORVHoiy++0NPTU2YiOXixnbKAAHIyUjCmOEPWmaAGkLFeb/T89JT1mgD8l7/8pd6/f58dAjoyDMN0FkzS0VxS0KTvabs0kea7775TCEEX2wtVdXoeShS5j6ZZab/fTRmbSn3f5SzF8XBUWZW6vb1T33d5dGs6cXrMpRewnekU2PlQvKqqNA6pRwvQkABSGt9NhoVxxskJFjqd5hNwGQvLy6dkzYHqVPsb5klz1KTTvOl7U5alhnFQHKNW61R2yp5ObinvVwJj/SSXg0JIe/D6sluAUPQXJ0hmhiDeSyywPWQYnAnGRjrYlhKDyinNjGyFlb2+vs56iF4RdLqjxxZ5H4c3vXrweZ5x8eyQZ6U9iwWwwDd4eYtEUML3zE3VrBnAfmZJ50CGe5WU1wcdckDi60zjKADHMw3c63a7zVl0MmTYL+6dkkPkgWCev8cxlU+h71VVWU/DPOWKPeZvt50A/xmgBnVdmwbc9L1Wk28YxlHdpA+AYoJUstocjEjJG30P+DEH4Oy5T+TitVlv8mSy1WqlOMakp11i/7u+y3YwjjFnBlerlfquVz/M5VPY0hBSPyvys1qv8j3MpMFsJ4spkJKkykgI7xFI8lOoquYsvwTAXynGcREkUR5dVZU+fUpTJAnm2Csn/4ZhVIxzOV4IRc4IUOJE7x7XRze8Wb8syuwXJKUzzYo0eYy9RC/jGNUP/UzETcGhk0dNlc4aw56CR7hHH0s7P0tqPUjYoNVq1WQ7nu45fc4DIvZqHAdtNuu8Nh4UDkPMwQDkKvoByeoZfg/c/IUdwo44+YGO8Dlw07/21/7VH13nR9f93EDjv/x7f1+7/V6pW77W6XRU3/W6vbtTjEkILy+vdDq2+jA1Gw/9oMeHh5xODCHo06dPGuOo+7s7lVNEPMYxgxsOpWrb4yR4SdmLabOpBYRhQAlgt66vrxeMGEa7bduZdS8LrVer6awKFi5NwqrKSq9vr5nhb09djqyTgR11Ok11eTWp8kHFdNjgfrfTZrPVGOOkQHOpDTWAF5cXKYAogg7Ho4pJcXzyEBtZlWlM8DCMqspKYXJcT09pjG7bMVmgzCy114f7BANGn3oKHEH6+PFjDpYILGDuAFeUDr17927R3Mf6Y3RYa5QfQcfh4hxxVPmgqqkMAQCx3+/TCerDkCcweWnQ1eWlTpM8wHh60zG1w3zf/f19NkIAlOPxqJubm8yAPk4sD2AlM6tdp7KYTwzFIZPhQDlxLI+Pjzm1SRaDjATPRrmBl+94ORVrxGnuTGhrJ9a9H4Z0yntI4xgdzCQwl0oKD4eDTm2rYSpn4B7ZL1gtelX6Po3QZSwtwQrpaJwCRpzAar1e6+LiIpdRrddrrdZrPT89zQ55AvFvU3DCMwLW9vu93t7e9NVXX+Xf81zPz8/ZGVIOyD5UVeovwkkRcHs/BfXh7F/XdVqvNqrrRkVZ6PkplRluL7Y67A96273pYnuRwSeOpCgKvbw8q+8HNavGsjPVoh7bM3ucq6AgbTfb6V6rCYCvVFVpNOzxdNR2s81ZwmFII48hM5KD6fT6+qa2PWm93ujy6lJFoNa2V1VNTHCZTqAuimDp+GkUdOENgYPqej5AcIzpEMP1xBazRyGEiZXrVBSluo4zQUJeU+9DYN1CERSKUnVdpeC5KDSOMRE9RZGmBIb5EEAfs1iW5URsabLRvap6CqAmm+blHQANrxfnntgXQI+XM0nLxl8H2jzHp0+fsmPnkDf3K/Q9ndfqs3aABwfnMPl8v8saP+Na2C10gOt7Fs7BHGWXCeSkQLZtT9PwkGYqVdrqcNhnGwrYI9gg4HG2mHp/J2nImpxnc7gvLyPxDI4HXhAxAPDr6+tcHkhACEhHf1MgMk8+enp6zOcq1HWjGLXINBZFodfXF8sENznAxN4fjgeNmrO1dV1rnDJ12+1WCnHhw8gyJgzSKcZ03fTcR4VQaL1OB9cypGWczr2KMTUVrya967v5tO0QgppVk8bfj2Me3Xs8pVHSBIan00nDmIBgVVaKSkH75cVl9nHjOC7KBtmPuq7Vdq3qfEBwkre2S72s5VSS1rWtQpF6SI+no6pyKqetUqn2MMkmk/CQiZTluVFd13p4eMz6eHl5mf0ge+9yAYnEvoJj8FfD0Ot0mjOneehJ3y/8rI/mHdpugUWaVZPtyBjHfFDwMAzq+i6NPS6CNutNDoCqKtnoOB3TgF0lcERnvVwLOfd7TYFAynwQFORqgDjLlxMfknRxsVXbztnJJLvJptPPBxEE0eCZDc9Qup0jePAAw7Mj+E3uzatX/tW/+q/op16fHWj8o3/wD/X8/JwF29NPGMxzY82ld7tdrm8uiiLXzEvKLBBNrzArgFIaUjE2MAb8myZWamYph6GchckIsCSUJ/ix9t4HEEJqDry9vc3RKWc74Fw49AXHDLChrIK6cwIh3sd3+lhPAhgmw7C5GFuYwRBCHmVHQAHwpwTgm2++ycY+hHQYEQwNDhYGGQCH8uI4qOcEjPIdAHg/EIo9ZKoDII8pUTFGffz4MQv34+NjnioFeNzv97q+vs59HQDsPA5vAtg+3YN+jXEYdDrOJ+ACeGHbURb+z+fn9GZSsJubmyxfwwRaUExqW8dhUGUZDZQVRwMbda6wx+Mxj2tlZCKML0ELe8C9eVM5DtzPSAGYoIeUoxBA4rBjjDk1zJ4QROLA+Q4M8NvbWw7QxnHM53p43fwwDHl0LpOdAE5lWebpPO/evdOf/MmfZOMKQGuaRh8+fNDd3V0+0Rp5hjlxx8M45BhjLpfDUcF2ss/I7mazWYzNxSbBACIzQz+P8mNaiaTF1BVn/Ha7XW447/u5IY9g/Lz2muCYKUE4WWwYMupnEADMHNR6SQzBfNu2+VqcKeApfIAEjur8edxheBnMeVoeWWYdubbX+hJUI4/4gvV6rRgScKGECKfc970KpbOBsAdORvT9fIqvy7uknMUk+HOW3fs99lZPzzVg2bkfAhuvA0eu7+7u1HXpZOJPnz5lGwkA8OwDfsSJDEmZHENePGsB8MOukG3zMjquhU/g/V4Cht3Bz6Av+ACpmNccgi9nxOcsICCU5wDMsj7ICtlifo8s+wjmmW2de0ewTQQd7DmyyD05QQAo9uwDJaespWdhIDXT/a8WZTPYTu7ds2HY+sPhoEHzKFgCl/SZNLJ+v9/niU6Hw2Hq9bhRVaUeITJ5jFUH14BL3EY0Va2VMefYDOQKffTSKvQcG+79VDwTPR4+CYvrvLy8ZB+Pz0mfm0tzkceEP4opcJsPoOV6oSh0bJO/omcKP8caeVlXDtim+yZgpUqBdYLAY49ZB0gE9N+Hb7Am6Dyfa+pGwxRAEyhja9AdcBY+ABuD3HhpKUQqxKevCdUjXuolzZPQvKcMuUKXnZTA/rltwXadTqccpIE3vDGbffJgwX39nLFuFgGSZxJZO69cAeNgo8qy/LMNNP7hf/H3FulQgAobjgGB5fFm365LjZt3d3e5Pvr29jaDf1hsT/8ioBiXvu9zioxFBMyijF6vz+Z6GtXTd5JymQ332batrq6ucpMxdd8PDw+5FIksgZdn0MxMkEHJCUEFm00vBAbZmRxKVQhGeG6UESEDoHZdmhrlgQXOlWkLPvufdK5PSCKdS/mX1yBiZKlBDiHVzd7c3OQeA0/DAWAod+IzGEXYcqZCvXv3LgMHmEVAwuPjo96/f5/G2A1DPjX6+++/183Njb7++utUbjbJ4DAMiwOMYLrZA0A2a8SzUX8OmG27Tofp/9TdS8nY7nc7VdO1cYbIH6U17CWgHyPmQTWgbRiGDCRwcATWyKsDRO/B4DsBL7Bp5wzjOKaG9I8fP+YSpt/4jd/IafGPHz/mPhL2C3nwwIEpRrx3t9vpcDhkAuH+/l6vr6/64YcfsvHl3tBdyARG81J6BmEBWIZkoIeCDMynT5/05Zdf6uXlJTfqUzsL+MZ4U+//ww8/5OlOPmwAWT2dTtqsLzL4xFkQoDjA5oUjIJAlOMY5AYqoxQYQSrMhJzjy0hbAwH6/z/fsoNWb0MmaeM0stgEdRh65T68xJqiFgEAGvSwFe4XcYJf9uSlBxGm7fC/S9lWVy01Yp2yHx5ShY408GwEIZT35v9cpA86wMw5iqPMn0KW/yEEG6wKhQx31er3OgReAGzuLvgCwkTkCWBz7eYkJcsTaeQbznP3nfTh51o7+Ofyuyx8EhgeQyGvXDRnsAeQAT9vtOssacuW2m6wlmUSCUAe2khbgzks1Hh4ess7wzKwhPoDrotu+twBVPwuC7BfZUM98AKpOpzafZYBOoEOQSew7tiRjBM3PBFhP+1HoeDxkvCNZOeV05hdZcvqTPKhFZug/G8dRhaSymO+R9/HyoBq9ZH/dl3G/yIKX7L69vS1ANL+jx6Gu62l/ZjnAn1FSWVXz8ABkryxLHY5HlXW1sMMEK/h27Dz66PjA5ZLvdb8szQM38MdcD1+H3mA7wGdkR8Zx1NDOBwcS/CPL+EueCeIE0gG5oGLGyQtsgPcBopdgW88soDuUYeHr0V9kFHIPHMK9IZPodi63PsO+TqQQ3HLP2CfsDliJe0G3sIPIoONM5PRf+St/ST/1+uxA4/f+/j/4EYND5M4NUdICUPWoCmEmyqUpz5sNMXwwrhgy5uh7MxwCh1K7UWdTKNfwlCsBB8CU+0RIEHA2iO9iPGXXdXkmM6kqwAnBjrPB+/1er6+v+eAwSkDev3+vP/qjP9LPf/7z/EwoMc6PzAzfD2CC4UW55jRwnf9GmM4V+XhMB+p9+PAhr9P9/b2enp6y8/7uu+80DIO+/fbbXBqE4HqdH8bEWS8PAlEETot21hhHiQzEGHNQx1g5yn8eHh/zIYCUIUnSZqqprOs0+QLgxZ7xPWRsqHEm+Pv06VNu4FutVmq7TuUkDwReOLsYoy6NYaTMbxzHfN6FBx1kH2Ag+r7PJ59jSGB3MIwxxgzq+PxqtcpBobOCnM7M5zHiZFEwzDh39M4DCEl5epSkxehjDA3Gjf3EoKHXgAoYTphgDmqkjASgx3oAhu7u7nKGE+N+dXWlp6enfBAjmcunpyd98cUXGWwQlGBQAZI4GxpRsRGPj4+LSSYXFxca+jlDxn6VZWrmJn1P8MTnnD33lDhO3EGWZz49re2O0oMkJ1sw/h7o4BhgzWClfBoafUA4N+/PICMGKYDT8EwEoAZ5Q46Qa2fe3PngGH1PYkw9c/04M+LYjqqqUknK8ZQzqThJ3sc1caCQNJ6VRB4deHt20bMA2DCcLBmKc4aPZ/dgAHCGfeV9EE/nskB2ERDDe87ZVD7Hyxl+nsezH2TlWGcacX1NeG7kZb3eZoDKs4cQJh2Jur6+WrD96KmkTIphY9zWM8zDM2A+rhufWpZlLhMbx3ExXY3pgo4bkHUHSE6E8FkCU++9Ys1SwBa02WyzXrGulNdgzwDHdV1rGAf14zy6lslE6b6ibm9vFGPUp0+fcqWDlMbJD0NafzKU3CP6jcyAk4qiUBwGFaFY+Arkiz0mGMaXu8yw78gqAJ69BvNgI1hrPsueN00tTWVX2Cj2M31HAtUQrsipiqDRyC+u7X2hC+KhnHsDfE/BbM/Pz9m+o2+eucQX8aw8A/gAX4ce1nWdDlY+tdkGoX+8sDv8jR/m/qigQU7wqf4Zt5/YJJ7BcRJkMnJIcIJMEhjwHictwDTsDd/Jz86rIwimwYoEDFzX5c3tDdfkez1rjE0DU/6ZZjT+3t/5u5m5x4BgXNjMspzn/gPOqL3mxn00FtdZrVb5XAY2AyfNnH0M6uvra2aw3717p3/6T/+pvvnmm2xsYFovLy8XkwVYJH5HQFFVVXYUzj6wGQiFNzLiVD1oeX1NfR1+7gHOxa9VVVUGt/wfpRmGVI/NdBRSVzTLAuweHx8z+CO7gcF3wIIBl5QVBQDhDo79q+s0ghZhAlwBoDGoKAX3BvDGCBCtU9b28vKSxwMCemAviqLIU6gQfK7dTcC/nAQb8JLT5uYIAYswfh5wYcQoVzmdTvrmm2/y/jCHfLvd6nV6Hg+UyTyM/TxtxDNVDw8Purq6WjASAHayYzGmQ+BogD7XHVjMqqryxCL2mz1mH93oAMTYq7Is8wFx2RFIGZhgwCXlUj0YGrJzp9MplyyyFpwhwFpi1AE5nsHwcwkAFQQjHqAg87yfwB5dI7gGtJNRY29gstEhnMuvyxjwGb4zxpSR2u+OC2fWtmmEMM8O88X3YNhhFllLggLPRvkfL7OA/YZZhfFzVpvgwgkEaQbezq7z/OgdMgJDDGCrqioHY2Rp3YkDYriu22dk3R0Re8M+sVb4Bmx+KAqpmPeAzw7DoDiMGodhcW0H3ThNHDblR9mBTetO+YHrOyCNIAv7guOlD8/lX5pLtHgWgie/LjYKe3tezuNsKTYDH4nushbeTwKxwXXRQ6avOZvPoAlvYgVEwSZjF0KYR5JzrwSbbTv32zl4wVfwO7cldV1nO4XvJJBlrbHXlLTic/GhlBBz38gL34tesu9O5L2+vuYMFGANwtKrBNq203o9ZxaQGQ+WKTukjLcoCvVxPkcJAmQYBl1eXojhBefTo1artapqlgMnaAC1BBoQn0VRaOz6PF3JMRD7iO1BByFs2EOIAdbVASw67GDSs10A1ES8bHNzsmO1tJeNum7WAS8v7oY+9w/yzJ41JYAA73jQxT25r2L9wDfcnwcWrD0y4/aOclKfzDYMg7rjKZObBNWeIXafhB1h3bl38BTfyd46yYDOsY68FxlAzzxQxOZD6johxzUA/NglAguCZ2wLGMj1ib3xe2XvkUv2Aj/s5Wpuv5zMb5pGf+kv/8v6qddnBxp/+//+H+r6+jqXE5H+w1HBwqKAOHecKayHp5ZYsKIocokOoJnSA4xL3/cZ1ErKDdpvb2+5dGO1SgfTPDw85IUAmDjgI1VKhsEFndIuDsLBUGA4mXWPMsAeeoM1m4qBKstycbaEHzCHEOEAyOScp/X49ziO+f5cyACHzuqzJwilT4qisZf9Kooi7+8wDLkGkFFvMOzONHi/AsaAg3EAvMMw6P7+Xs1qlUf/SvPZGTgmABQ1uTxDVddp0pTmQJVn/PjDD5nxx9mxn27gOCCNelCyKzCL7MHpdNIwKfd5tiCEoL5L44R/+OEHxRj1/v37HIiihMgtjM/FxUVmxb3+0U8dRy/QGfaAQ6Q8pUmfzXa71a9+9asF+3h7e5tL1zhYj6C3qlIzK86TUa18PwEwpTCexfJ6bv7tcnd9fZ3X1ktPCOqHYchlijwjqX4AOzP3V6vVIqDlBHYcFUYS1hSZ7/tev/jFL3LvBu/zYIC1p89rs9lovzsuspuUiGDsvVfinJAgAJXm2mRn53BqOF0cpRtqSRkwnTPSrA9O4ZzNAgT6tBqCXc/seaByDlpYF4IT7DPf7faM+/egn2f1Q+ecHUaH19vN4vM5Az0FGn4tZMSBkn/WGV32lPtDXvw97Jv3xPizeckXcsd9wOShzxAnAEP2GdtU13XOzp8z1OwfssLf55kXDzp9LZz8cBaVz7DX2G/sWLIfnVZTLwy+S9JUmnjM8gPgQR4gM9yengMUlwc+Q6DAunHwJaW8m80mZxlZP/YRQuLy8lLPz8+LCWKsDcEm+8Y6OkEGOHZfxecAl5vNJpeE0s8WiqDThEOwObzqulJRhBxYo8OJhd7o8vIqlymxlp6BcT+eg4UhDe3g/6yhA36uhb1nPTwwxF8hk67nLluUo7JfYJ/0Z3liOvtbFKX6fvjR8IK2bVWUpdq+y8E5GQVG7pPZw4d5Izqy7UEya4ReEBh7JhhShNIm9MubsMEBua/g1GY5477OA2tkCYLGbRlr5MNQCFSRA4glMA0YGHyETnhm18E7euWkE88CUYBdxHZhJ/CvrKFfi597sAD28zXg55CIBCbgLvYIPRzHUX/j3/m39FOvP1Wg8f79e3369Em3t7fZwT89PWUFuLm5WdQo932vjx8/5sYojBslUjhXyq8cLCOIXl4Ca0XQgcEEeGGYQgg5rcmi+vxqACClNAiTNNcCngPicxa1rmtdXFzk0ZuH41EX2206qKxf1i7zPC8vL/ryyy/1+vqWGf9hmNN9aUzfPMEkOcZSRTFHyszOv7m5WbCDMBmUfZDm5nc0kWP0KSsh1UlaFmPtDoZxmmnqVXLc9KIA0DEqrC/Gg94M1grHB9PozVYEW2ShQkjnO6w3G11eXKSSiSl7slqt9Db1UaD0Nzc3att0Qiuyxb99HxwsUtvbNI2GcVQ/DCpCSIcn2sjXEII0zqN5i2LZmwRwBxzjHL1MwcuOyJoxDcmdKAacYLLrugzkyzKVEnZdt6jbh80ex3HRe4MzpWQGEOSlKjgOQAhGBUCP0WR2O8/BugOeft2z8m9mpcOESloAMRqeKS8ax1HtqU3jocNyrj7MVZLLVM6AoRzHMes2/VbUYRPEFMVcL/v2moIxL2+gTI1nRAYwwpTu0AvAGhdFOtsCUgEZAWjixCBM0DVk3UsSvTyHnznggXFytpnrI2N8huzbeRDjToy9IgOFE3cmNoHzICZbxTifMeHrg4POzZVloaIodWpPeURnCEHjMKo9ndTkrMM8ijXZoOU8fH53DnJ5v2e1eS4APeuPrT9n8txJc+/ngAtQgF77Gp6TTB7IsK48hwc12AL0ZWbJ0wha7r/reklzthddZV/oB3Cwid9Lz5L6CxjzznrFyBCGPpcfLeUjTUyKUVPv3TJYRkdY3/OACEBOVpOM77kd4fuQcQ9Yzks6vSQ64YfLKeM0B94vL68TwK0X+0Gmkix2KNLBvMj68XjU4XhQM5UKSsp9Aul+2gzwqirJwG63V5rAVmsYlixzCOmw32EcFCQVZanT8aSqKhWndSg1g2LwE3sEGQdgvrq6yiW4AEfsI3IAcZGZfkUVIdlopr45AA9FoWayN1GTXgzzWRUKQVWZxswqSEFBwziqrir1Q6/j8aR6NY9dRhbwtegKJDL2G98AmMUOOcGKzWcQkZMqfI6sD/6Yn2Nnc4B/alVZ8FwUhfphyPanrCqtJlv/8vqqoggK06htqiU22zRKGFsCFgR7IRvoBjLg5AeYCVnmuSHd3Vawhk5uE4xjs9w+uw1zYopgAV97nplwMhPZJajB1/AsTvbGGPVX/vpf1k+9PjvQ+M/+49/N6U9OsnUnzAJ6JAjzg6LC7Dkjd75JOAk2i2AD4wlwJehwQ+612Q44cPj+grHmewH+3tjDYiLENKh+//33ur+/l4r5VE4vMVg1jV6mgOfl5UXX19d5c8cxqqhqHQ57FUWZr7nb7XSx2aquKnV9Z+PmwrQGaS4250wQLHkqmgj9eDwuyqa4Bs6HenEEGMHnWaqq0svzWzZ4GL3Hx0cpSGU5p9CZqgGAJOKnTIqGdZhx9p/yBHeyb29veToZp0LTBPizn/9cD58+SUoOiUCiaRo9Pz9ndhDZwegBtnxsLswA68PaANhQOG8mZfIIgIL3brfbLBsYe2luWPO6fwAMGRb2nckw3CMNwefsCoE4ZTeAPOQYZp775vlRcWeNfMoXtbsYP57LjZZfi2cEJGBIfX0x9NwTjuS8bA5Qz8Q5KagIpdqu1dDPIzO3221mq5OMllqt5ulCZNzY79fXVymkWfQQIuM46ubmJusk6wLA4rm6rluUq/HszuJgawgSznsXcLDIEnamnAJYN/TYIhrFsVfIMMylNDsUdJ49ReadSfWUvbNYnlVgv9zp4KQAC8hBcmQ/Pj247ynFXI6ondnxFJggJ56Nwbajk9i0BFhLpdHhs/PFVnN/vi5OkDhzic1Ax72Mzn0La87PXda9RIZ14vuwvayxlxl5zx4kjO8j64DMJceezm3q+z6Td3Nmey77475hZ0+nNBkQAggfiS0ga4xOzYTP/D78kdtEB38wtmlE69yEyzlCsPwEq/gY7Aq6THmH9zJxHWSefSND6sEfZEoKJppFEAnTzB6RlWZ/2rbVGEfF6T2bzSYPskBvkQv8zGwHo+jDkOahBsNEUJWhyOCwKNK5GzFGFRZsoqPYGvwzhM8c1GvRMEygcR5keha/6zo1q1XOMKzX63wYcHs6pbPBirm3C+CJfeV+WD9KYz14xPYjZ17Dfx6QI2PYCu//4v/YHGThnKQB4xCcol/gLuw++4Gce/aA9w79oKKcD6oEAwCe3c8hB06YlVNwIqXz2QrNjfdOdvl9snaeUWXvPEj3Z91ut7kX2G0OfzwrIs1kMzJFcMdeov+e/YBsdb/mvt6zq6xnWZaL3uGqqvTX/+a/rp96fXag8V/93j/S29ubnp6e9O7du/wQ3BDC5IEBD4yjhbGBPafmGpBPBA3jAPshzTVxu90ug2yMJoaeXgAMENdCMWKc096e6o8x5jpNBJ7o+9el9E6nky6vrnLvAGy+96f0VteJAbu+vtb+cFTXD4umU2lq9i4Khajc78HGStKHD99Ph3fdZtDr5RIwozgI9oCJHJRBUc6FElK7zUFoq9VKQz/odJoPr/IRvS8vL9psU7nSp0+fsjJ5yQx1ggQzCGXbtnmdqRNHNrwkC+PhgMqdPo4VBdzv9wvGvK7rXAbGsxIsehkN8jYMg7788ksdDodcAkf5kAdzbdvmscdcj54L9prSJp7X2Tyc3DAM+fA5GETK7wjgAe44H3cAsJEAVn6PHhKse60vsgY44nf0XHnAjnPlurBsADdK6WZAOKf0ATjUlhOw01jd973evXuXA46Hh4fstNbrtV6eX3V7e5f1kjIgAERd15m9xRHhmAhsGOHswxrGccyZPgw/IMl7Hrh/gmJKMdgHspsAO54Dx++pbK6F7XKDjgMuimJR74xdxVl6YOBZCgfYAE9sLNdElqQlcCPAACBxr+iKg3BnydJ9zM+GbCRZSZml86xGkrV0qJ/rIoAVAIH+8LN0z+ncD573HJzxPtaBtfN6bu6F9aK8iTXG5nlN/Hlpw8xgVwsQS98SL4CWZ+g8S+mACsJiYf/zWqQJRthq9CqtwxzEIPseRHLf6CpkG2XGZAzn3odUFoO8Ybe8/ITv6vs+T4RK95mew0duOuuK3Uf+IEW8v417BWjRt8HwmOPxmMutyNZ5r2Fa30JlWS3A53l2BbvJ/tZ1rTHMckPzNn2F2HsnPV33+De2o58qGZqqXrD1HsAjpzwHeuZ9Tdw76++stQNo9JXAiPV9enqSQlBZldpMgQABhzPlvvaAYCcnzkkJ9NJ9AXLghC33hw9Cp8BzYCV8hg/Z8D0iM+XYwwMZbBlriIy5zLkNggRyXea+nWxgLfDJXMeDQ+x9U9UqTHaxJ/hWcJljNWSAn7OWPINn1t328rzeA+XBVVXNZ0WBu5Fhz3BIWvhO/BHkr1cucK8QaZDD5+v7t/5nf1M/9frsQOPv/if/aS4VeHh4yCwBxgij5hNPPELzqI6bJPCg5g7gQ7DCJlxcXOSJMTDoGGZYdEpzbm9vc8kLRv882GCRPZUHCH9+fs4gik1FSWi2xnlvprIqSppgpa6vr3WcDh778ssvc1B1fX2tru9VN+uF08Kw1FUlTWk5AoMQwlQ3Pmi1XuXD6Dg8iuALwQTYuVEFDBGMMHmKn3333XeSlFn0tm21ezvktaTZN8aYDquJQx4dSjMoARdg9w/+4A8Wjbs4rOPxqPfv3+fSLY+UuWcUi3ULISzKP+h5oLyIiV9MKeq6Lp0+HecmJoARyoVT99QuJWQYXFgFjBHjickyALS8LJCxzX3f57Id1ocMkLMEuSxLM9PkZWQYX6Zg+WdCCPmcgFwPX80HVMJ6OiPCFBX+j0HCIeFwMD7oK2AC40gwgWGtqkq3t7e5x4EgiPX1FLKvJcZsZskHVeU8CAHz5HXOGGLuxQ0x3+Nr4UbZ7RVst98btgGWFcfltdq/rh+DteS72DecGfrDujtriewTrPFdyOy5owNEYfQ90JBmx+MOOYOrcTlhyut5Pdj0wJ7/p5O55/IWZ/tS3fpclsR3JpBcKsZ/fumTM6gAOIKXELTYw/Nn8uylZyPYf2QBf8Kaet/GHNjMrKxnEl3ffG0ARA4sxnEuXURGPWDkObF1vs4E102z0unU5oDEsxfj2C+CJdcfAKz7V+ymB088L+u63x+UTlsOi3uGaIJA9ElEIUh93y1IO/rrhmHIQZhnrQCNrLFnliQtzqiSlKfhOfA81+PvvvtOFxdXWY5omgcDODmCvWQ9u3EGptgslxs/74P1YA8dHGYsc0gHnLps+r4iqwBY/x26QEDIegDguS/WC7s7Zw27LE9VVWkMs30Hg1Fa6JlQ1gIQ6bbaySZnz11XJC0m3p2TF75OlFi7D/aSIa7HM2PTAMC+Bx5AYCuppPDnY724D/cp2ErHrP4+J2484M5ElYLKYs7gu53Fj4IN3AeBg88DQPfHbpPRbz4HWcYz40vQNfAkxyWgb3y3k0lJ//d5PZATiH/WmUFH+CN//7/97/4t/dTrT3UyOAaAtDiAlkjKWQCvecXpIsw8ACUeHtWdpzmJfr/77jt9/fXXmZ2hRg3l8KZn7gfWihIvhFpaRofv37/Xd999l4WLHoS6rnN6EAV+fn7OrMup6/T09KRvv/02Ox5Sg2WY06EEUklBR0VLr55OJ3348EEfP37Ut998o/Z4ykYaIJQYspW6vls4STcgAGyCIGe1UUYH7nWdJkxR2nJ1daW2bfXFF1/ow4cPauo0ExywxHpdXV3peNpn4AvYBOjTTE9tKQcRspfv37+XNDeu9X2fT/FGQbyfBAW8urrKjJykxfQyGH5kLzXmrfM984xelodyYsCQG2Qap01w4s1Qzp47y56bCcM8BYJyGEDL4XDQ6ZTOEcEw8d5zY0BGhIAOBz43eLYLJw3I4hqoNiCBzJqfhQN4YHQfBhDAktmbKRuE4UXXAMWss9sAHCcOyNO5DsjJeKTPFerauSnYgcr5dWOMCyYWXfHAD4MP+DgvMXI9wjbl3oIwlyGRWeE+CNjIrOHkkREvleKZ0U2XdQcDXnPtPRoOVtlbr+V2J82aIFMeqLA+50wZL6+bl7RwrsnurFWWy/XjmVO/hhbyC2M5DKOKYq75Ra4I1PkuB/Ppu+cSLS999YDMy5FwxM5IAohYB/YYewFwACxzPZ4BvUVGmJIE2OA+nOnl2fz78JkegPCc+FDAcTr7Yd5P/GJa96TX2Ef2wRlT5NoZYPYV0Mx3HQ5HleWc4eP9ruvINzKU7qnPY14JaCj/ZG3QBchAH8mLDJHRqaoq21Pk3PXDgRbyzgCZ+/t3Sv2N83hlgu3j8Zj3EKKmKAopBBXVHFT5IBEnoijxQhe8QsP1tqoqlaEQEIx7Zf+wRz5MA1nm/Q5o3Y7/uiDbcQBVAkyjGoZBMQQV08GCYI+3t7dcInduF3wfkXfP2Py6ewKEkrWHXKKfAj9Fvyly7JPw3Ed5MEMw5fLspU1uvzxAxv/gx9ER7BjP49iBZ+fa7AH4xAkL1r6qKm3Wa439PObXn4VnON9ffoeN4d9z9neu6vC1cIwAAeYYmt+5veNnXkIPPgKTfvr0aZZfSxhgP/x8IQ++nMz71//G/0Q/9frsQOPv/93/fMEcesAAEGzbNgNeRkR6NA+jASABmHkKHCcKEMVI8x42rKqqHA0+Pz/ndA/v8zpdd9A4FBwhTgbnTDYBQIthJsX5x3/8x/rt3/7tVNZVzOl1jHc+6Gm6BxwAhqvtOkUVur291e///u/r5uYmT4EoQlB3ahdACmEty0Kn9pjvC4aHrJCXrSEMBAJu+AkQ1uu1Pn36tABFgNvNZqPjoc2GgqkclDqFIua6dk4YxZhdXFzo4eFBt7e3GbQSWWOUvv7663xgG+wf08Oo1b27u1soEt+FLDARxJvYnfVFuQguPfPgYALDzHVJ1/OCdXDFJnBikhUgchzHfP4CU808o+MgnRfA1u8LBfa0vBsfd5puwPk8BsedmmcXkWU3osMwZEZPSiwVfRoAbGeQnWXxVDv3jYzyWc8aQVg4CJ/1NGjox8WzovMAF681ZQ39HlgzZ4k8KCNbxDq5Q3M2yYMhZ8nc2XizMbYAwIqtOR6P+XBCZJKSOT6LnJw7Ei+P4A824ZwFOwck3C92yLNhBCQeSJF1AdifZ0GSnMwgEJ1LgzaOKsviR/qV5D2K0im/JrLmzh5mPulOqaqaxxOzvnPgk5g9WHDWmEzxOaAiMPHnlJSJAt7LfUAMsOdk8AFL9Bp4Bhz58716fHzUer3W9fV19k08s4O92ddVUxYoLnQ5PX/qXXFAAaB1+8//kQH2kDNpYPnTHlW5Zhu7yfk1lHO6jKf9L3R3d5v1ibHJnjEjuHLQyvt9uptnwrHF2CXsubPjvm6JVNrmdfXJl67b2JLX19dU/lUUKusq+w5n+lk/vpe/2R+/Hs8TY0yNxnEu6UEOIao8+KP3AjkAFDPVi3twgpaqi/Pvl+YJeay7yrkXwGXBg24nIhzLsU/IsttC9x/8fX5CNcEg9pZAGjJsLnkLOWPn2VHuGZuPTWMt+V4PkhzrIRuekf51ONKJDfcz6J3bCc++8tm6qlSXsx7zN2vkhIV/n6/NOfz2LJz7XfQIX8Zn/TtZf3TI9+w8gGbtqCCC8MeeOP44z5R6EL3dbvWv/bV/VT/1qn7yHdMLgwswg2EDrLAZlIdQY4kw+UOyIBz8goHzkX+wTudMDZvvRgcjTBOtM9oYLEAUTA6lVzh2SiF8trcz2zgqUuqn00nHacN5dkrH+q7LIxsRWhidU9uqnBzFt99+m9meoiikcWbIiqLQx48fF+UyVT3fr6cFCUxguclykFZzJ03zN4ekEQ2jHJzvwZpiHGDBi6LQetNkA0MQwPdJ0s9+9rMMsGCWmP5U1/MoYAwua02/g4Mp9hNjyz50XTq/hDG9TMFCiZgohpy60Vuv1/mAPwIFPx0eOcSgwWATzHnDmgdoTdPkU9lxFg7sXFZg2Bn7iIPHuHizNz0fOE8v63FDWhRFHieL4caAsP8YEYJy7g0HA5j3Omh0wBld1tQZVd6DUZRS7TPPW9dpPLSXAziLlfa31DjMTC+yDYDxNDvrz/fhNHiPp/wdbDlL6sCyrussp74mvI894ZlxkJ7V8AwQoOX6+jrXnUvL4QO/LqCg1I73+t8OgpEZt6kErj5tDLvMPZ4z4QQL3hd1nhGa7W1YlDDQv9L3nUKYQQU6lbIGqefA2UJffy+V5Wcpizdnkbgvnod1xuFxrx4ooZusi2dz8BusF/7Ng9myLHOJKUEitpkyYgfP0syuejDq47e9xAr58QA0ydI8JMCZSddjt2nee8Zo7L7vc9YV2yEpk0usabrPucyQgOnx8THba+yfg66qSoeGIjfI3PX1dZafGONiXDk6wR67Pef9dV3nSY/cn8uKB6pzjxplfXNJk5c2kulH1rAJsQhZZrCF2CQAGzpW13UuU+UFQPf+Bo1zyQt17UwPZI3cDjthgI0673mArOO7sevsoTSfv8F7sJvIIbaFNSXAcjDNcxMkIePsm9t8fD0kD/tEVglw7Pfm2VnPLoABCdixNzDsTlJResx9c18OtAHq+EcPxinzAt9gi9ArXy/3FTwjul6Wpeqq1niWzXA74bjK9dWJeg8m3G97YIPdYG9eXl4yEQum9rV2+4qNIWvHvbrcIkPnpDN7xPWwK34vn/v67IzGP/6H/6VeXl50c3OzMO5pI6rJudYKCtrtd1NqZq2ua7XZbPOi7fechZFqescxTsocVVW1uokVKqs5NTkL76imqXNZTlM3ury6nIBel6Y+VNXk9ILWq7XqptY4jIqK6rteY4wKksoqAZqu7/X2+qrLqysdDweNMaapUa8vWjVTudPI4Shpsdertcqq0g8fPiRhqkr1XWqU6/pOitJhv9N2e6G2nVPBRSh0aluFoswlRl3X6+c//5nedjtdX13puJ+bfwEiyUAddX19pTGOab1PJ603a9U185xxtIltcgDH+4+nkzabtXa7vWKkPCGoaep5FGBR6OX1VcdDGh/KWLftdqtPnz6priut1k2+L9K2zl5dTKNoYc+S4qWsy9UVowILHQ57XV6kGdRd32kck1JfXl7ou199p6ZpdHuXRinf3t7q+fl5cSihly/gmADGKAKpYw9YnTEmO+KpTBS267qF4QTwotg4NQzV4ZBYzhRcSP10wNF6s85r3fdpjyScW6FxGNRNwNwzJBiEENJ6oSOZHYxRh+NBQUFVXSk1RZbq+zlIOp3m0qJkyGZGEKPoDl9SZlPR5zGOkoLGqaa5azvVTW2OfVSRblKMmn15eVVdVarqSsfjSevVSuPEontwFMLMALZtp6ZulJqHZ2YLh+sGkd/hOAGKDmA88MBwci0ykG6AAVvI1pj1fu71AOhivKWZhXL2CV3gebFlnhXyjAMgwLNBvJfvxvlyXdYQ+cMhOfBmlLGTDthiCABAGYBcUi6hcDsiUds7B3NpL4YJgIecqXGgkMYJz46atfEeB+SgbTn9lrN5uok42kw6PE/O4zlchrknwBSEV7KDc/kWzp/hFVzTsytc2wH5MNBoXujiYqv9/iB6U5ANn35HYAK4hGABcJExoLwz/S7mkec8G/LRdW2278OQ1qdpVpPsVCrLSsfjIWeoeM/r65suLy9yyVGyLbWaptY4zo3s2EkIF5hNQDNyWZbzsJdEBB11cXE5PVelvh/Ude2iPI+9jjFlZpIOjFOgkSaTpSl+9RScNmKS2cxSM7kyTeZKdm6VyRDW2skRsgnoVyYYh171pA9lmcbNjuOoIhRSUC6NPM88ZUa7nhufi6JQWZQKgLie6WKD4hgX2WSFZU/SOAxp5PNkxxWlUISMjfaTjmLPkIVhGFRWya8k3YpSlE5tq6IqF0DRgzRAuDSX8CyzZssDObGTDOFwAsiDsdnHzD1a6BXVB1wXopDnQfboy8DnohPub7l3vgNicZ7sOR8+xzpDzrIGnlFkXzyzwfscmHvgMQyD4jgqTDhWcbZrbdflKWPcg/uloiw19L1CEQTkCJJCkUrviqJQ23UKkw1XSJNMec62bTMBwjNBGDmGwUaC1WYiY64yOv+MZ/d8DVlX9zH4nT/T8bb/1e/9o6x4bHL6U6rvhryRRK4YIYSVB0CgYUrS/O75jAM+//j4oKqq89QYRnoSZMB847w9FeXRLNGhp+NckXyCEal2BIToNwlK6q+A1YBh8I320xy7Lk1aoFQJtpD0tZSU/+Xl5Ucgyket5VOT25MutheTQ54NDcaK8ql/XhTLfcLc82KeOAGCp/ucZa3rNCHo+vpax9M+B5wwml56RLTM/Y2TQu5288QeKRm5y8vLfNJ5XdeL33Vdp8urC6Uxl+NipjhgYLVa5bHLrB/fyZ+u63Iw4fXnGGJXPtYPwM8+kXpFbrlGTiP3s3NzhpQsA7KJHKLIbpB5j0+EQMZCUA7Y0SvkG6DtTK00j+AFQEal/9OnQyYlPWuZAoi6Nt1eno9x7gxyTfA4KCgsGH326P7+PrM76ACA07Oingrn9wBRT5+f17ayZpRNEEAWxTyrHEPvrBo66sGIs50ZfFjGxDM2XAdD7sGJgwiu4/oKuPVgJs3fr3Pwyz0ArlOAOjs89tQBNxkvaS4j8RIyZAWggK44a4cee/mI2yJKU5xV9JIod9TISwiFmmY+uR5ZSPajUV3PiXX0Iu19lRlgbOtc6jHLqAfOIRS5/Mjtv0ST/CzTyJZnS7EFrn/jmED54XBYBCWsj2d8WJe+h9hYjhNGxtyhexCc9nduyiRY9MwX6+clDWTC8AXeb4KMsn5cg9Hc2Pj1eq0PHz5km+4DBvjsMAy5TJk95zsBw3Vd53Ixno21Zd8TVqikyW44IMM2gwk8KHd23MEjYGqz2eT6c1h3gn2CKJdR/o9dbppGp7bVqGXg7Wwv8sa6exYVRtqfhSB/s9moLEqNcVwc6Mj64mPYk6JIUyjHM5aaNR/DnHFEJ3193BahJ76fkjLR4FUgyJmDbw/qIe64LvvFXjn+oLQbG+2Z6qqqFmdVMTYVss4JAcdsknK1hBOA2D+yNbMuzqSB41L2iz/83ANW/JX7C8ghJ4XOCY/2eNJopJPbh3qVzuzi/rkXl0lfd+zU2M34BTLSbSbf45lp7Ir7Mg+w0BvXAewDsoNdd73BvpRl+WcbaPx3/81/mzfd2dDj8aj1arsASxgJhM9ZMTfGKIeDEAIENwI4VLrjWTQYJAQJ4QKso9yUMiDwgGrulfs8b3jzFCDMxjAMecoT94fiN02TJ0Z46QQvGrbqutbt7W0Gzyj2er3OkzcQdtLW3kh/Op1y864DTZ7x8vIyl4rB7sO0AR4x+Le3t7nGmZIRr5kERGEk2rbV4bjTMKSSHi8J4Z64167r7ARsqT11eZITJWgIq5dwrNdrPTw8TEzaRsfTYVHu4U4BQ+4Rt7ODHFJD82RVVXkMMoCP6zoIogSEvXVmw6eRpID0oK6dp1M8Pz8vgkkMAL/HQZ5Pj3Hlx8hicHwCCQCafffaaGmeOuTBvyS13THLGXKfWeYwjyDmus7ooZM8FyURlOQgl7wXncGJYahxPucZIV8HDwy5J+TknJ1iH3BGfIcbbq9h971kbdF31pQ14TOSFk6FQNOzZNgr/u2Bjf8cu8NrLg1IZ4h4AMO9ScspTewxa+RODv3zYJg9YW0AsOdBjQffyKMHKlzPbS0A0m1nXdd5CEKyG5XG8devL70dyICn9xNTO5fi+bpKidV2pnkOCJcZILftIcR89sn5qOMYo2UChsU4x7peZfniMwxrYNIc+8vv0lSmuWQshJBtyvk+sMbpjJcbpb6WtP7YcnTneDzmsmNJOYtEHxv6A4kVY8x9ENwH++Q6Q7DKM7Mu7Lv3E2GHPbh21tzBtr+PP+ADsuUO2Nk39pTXuX927MA9e3krAA3bA6vrAYQzzVlGipD7LymZouTWAx7XeQdm3L/3QjjpgC4R9HkJJMEazxGsFIvvBQ9047Kp+Zw8wH7OmaRlPx1EWfYPUx+bkxnYHPaT9fQMIvqFb2FikQ+fYc/QX9YOEoqsGeuG3WFAC/6b7yWY5v11XS8mOHlgxfPyf54NUs4JSJ7d5d99GzqA/PoaUtK8Wq3Ut53iODdnu80b4qhQzIM0wGTIFD9HJrKP62cSiQzTuV8g6wGG8wDBgw1kmxfy6YQRfoF1chLIA+7PaQb/7B4NXm5QAPAoDkwqERpOnv87U8bCsFkIJoDWsyLjOOrp6Sk7UTb/+fk5GxkAKtNvEAoHSTg5gCj3wP15BOnRIfeMYmFw/L7f3t6yo+G+qFfFwEnS/f19HoeLMQH8sok4E96PMnJYDywXz/3r/obdOo/gPfWIAsGe5Wh8euZf53yrqsoZBPpJOHAOeWAdHcz2Xa/D4ZTXFdCPw/AD2ZCJvu91ak95jZyVQ+aQB+SyqubzRFCSd+/e6fn5ORsFAi72H2WW5pOlCdxQSMCtByasH9/NcwMm3aDxPbD9vGCAvDmY+0Q22QNn653txwFggOjTINjKY5THubb93DiNccz7dc5YezD99PSU14egh3vnvjFIZNmctWO/HFRIygMYYNVczzH+7D+GEMeDrjgriHyzVzBrvoY4ef4PkHXj7EDBgwDskgMWnhkAmTKzj3mMr6QFEYFdSM9TaLOZD8Di4LR0j7OZ9menjp574L4YtsFaURvOfbpd5rl8X5zZ5zPYOnTNwTNAxmt+IXjS68cZEOQl/Wxm7xy81fUqAwfsEc85jstBBoCPVOt98Wv1O/1sPjDSAygOccSO8czp/qS3t12+D4AVJaLYssfHx7y3kqY+p/lZfW0l5f1H5kMI08TBQuPY5efCn7F2BPDIAcz4OI55FHuMaUAL+0NQir1x8MQ6uW+kj80DcvTagwXPBiOf/B99dTlhHdAtRpL7eqPL2DPXST7LewBlrA2EBLbBfazvDdkuvhP72ve9ilCqKMsFHolxHtntoIyX+6ZzMHseZLh/9CyIYw5sSaHUdOx+xNfLm9Mhd7CJZJz9rCa+i3tiXVg/ZIOSPzJHvM+BL2vA9f3FuoFDKBE8D0rx2ZBbLqPDsDxwkkmj2BufFMe9uIy6nzwnOJygJRNO7+fSBi2rXHh2dIA9Yc1zcDSRCd7vkUfv9nOAjL9g75348NKmEFJbAL44EZz7RWbGiWf+7US36zD+3CtB3A+eB23sF/1UvNeDlf++12cHGs6iejo6KaYWC4KwsJiUGTkbh7DDEJZlmc8swFCgdIBvBBKB2Gw2efpQ0zS50RlDx+QfXxBP8bH4KIbXIbIpOAHuieegzItnZm1wsnyetDfMDSNFKQUjm0ATMYadMbBck3stiiI3rGIcXVBwop5RCWFuZJfm8hxpOYKNshgcE03vznyFELS9mNeE96MgOOHLy8sFi7DZbLXZDIssiaf1ycRwH67AXTdmw+gBn0/NwajwfCGEfAic10Y7u8L3YLAxWG5kXdlc8Y/HY05/l2WhYnJKsAyHwyH3t3BtjJEHMM7scF+wOJ7CZJ95wdqznnOJX8jZP8Asz0yQChDmPuuqVlXNTgRWA1nEyeFod7udJOUUNQwm/3Zmnb1w8M56lpMzjzHmgQI8RzZQVbUwkOw77Junf5F/AnPWE/ANiDxPBfN/AmXuDbvD950HeOgkZSPYLk9/p76m+dBCnDlEAdmA7Xad9x47VJZllq8wnSex3W4zY3h+aiz76ul4gCjZzu12q+fn5wV7BVCljJCAinVwkAM4IMhi3Xyfz+9hHGN2uuflWyEoT/0DFPLd9GN4uU+yJRv1/XyYpMtOIhFmZ+0gmv0CpLn+ATYBpcg/5Zr4hcvLyzyNqa7rfFZQVVW6vr7OWRIygkXx4xHjrCNBIPLKMxL4cV/cM2NEkUHsIACLn2EbPAB1efcabOxbjDEHh85gY8ewowTsTAvCvvh3eFDoZSgQBqwrNsmDhfNsgWfUAKD4OuTUgxTXYwfv+HRsZ4wxyx02geDp1M6VD6wrMsS9uD3muuM4921hp5xU8jXAThN0ew8G/TkxRnXHmSBY+MCiUN8uD1bkO7HjEJ2sKXgBXQSkk3XA3vPH/akTBQ66Y4yZJCWbzz25/UR3PduMPUPuPQDANg7DkPvMKLEC0wHUIffQnU+fPuVDjdkL1gR9u7q6Ul3Xuewb2fGAlWd3/OhYzw8fBPjjz8Zh1BCVqy6wiWldeu1t2AH6jO3FFnsAnz47j8Nnb7gma8a9jeNczYMP5Hnc5jnh5dlvPyjRP+O+27/zp15/qmZwFJYbJzpeNZtsZJ6fn3V/f7+I7B3UexRZlukkTsAmisdiEiGiiDywb4g7VAQCJUHBMJYOTgBoPjLOD8irqmrBCGAQUBCcGsy3sywwQhzSB4OI8mFsYKZoZIox5lni5+vn6WfW61wQ+T6CDJTao3QMNxMlxnHMTtPZPBwmwSKOrigKNat52hHOyFlP7keax7eGUGjox4UC+4x61p7P04BWVoVinEuluGccCiVYnuL1DIePeUN+zlPaGEG/9nlQgnyy/9Lc51EWpYZhWefuKVCe04G+Z0S8B4F7hCVy5gkHwZphkHCInhr1tC5ypDDmdWWds5FVuQjw2FNpORccoOyEAPfkTuQc2OFI3Smjr9wveg5wcebTMyD+Oz7LHnEfHsSyD97IyDUdEFOayX3yLA7s+E7/wzogG85YQqo4gOaZYG1TViI1ybKeyGOyMXtJMTtaZ4zRy/PsmWfokJ1hmA9ZJDhHvpxRQ6ewuR6E82I/fP096GVNAQQhzJkAZxfHcdBqNbPY7GvSjblZfLdL5ZrzifRJXrgehFCS71UGj0vGLmi9XuVg38EVawPAI3Dk1bZzUzO/w9Z4Bpi1ScHzSm17WtgadAVfxFQ2l5MQ0iF6Xqbla+Z2mey3nzvkAMHtA7qM3fR9RJ+5L2fXWQcCKNaHdXVb6DbLA3YH6/z7XJb4vYMosuaeJUC/3Nd4EIPMMGofBpj7cbLqnCCVpKIs1I/zFDEvb3M214kYbAb9ebDkTjpAaDhWcFAHXvFgqlDQaWKRQwgZi8QYdWxP0kSoud3ieTz7hr/t+1Q2DmC/vr7Oh/8S/DhZi06N4/gj8E5ACEh+fX1dZNgAoqwTeoOt8Cw9cu7+AYIWXOTnbzhupESbYNgxKPv0X//X/7XKstTXX3+ddQA9wq6eH9DpuJUR/QyjgWxiP9zfdV0nxaiqmMfKYifHcdSomAMNxwPoINd3WRuGQXVZqZvsGmvoNpl1889KM+bj+qwh8nB+zgl+wJ/LcQ92Hnn5nB6Nz85ouMNBIfkbYSKyhA3BOblySXP/AgvgAujgmdSvBxVspj8wC4CzoQfAHTKAQpoPzSElDSg/z9Tc3t5mMAhg5dyPc+DLiZ4sPuCKe/D3A/QQFABkjCnF6GCX+/M6QgfLrAv18gAmnpXPIcAEV3wfhgHH7EaT73dGAsWlltdrP88B70IBNbM8fBZnSL8ErDFGKYSgpq70tnvLgJ3vAmxSiuIA11O9KJ4DIu4PWWL9PeDgPvy96IErsyS1XavTsVuANy9PIgWMYSUQ9YCE97OnfgYNQTflbRhh9tCHLWAkfM9Yq1DMtZaewk7B0lyTiaN2o8+12HN/Du4LuSdAd+fvrCdOxdkr73fwTBJ76uAcJ+qBFcbcDbobR97nWbHz4BTH49/x67Jh6DBECwG4s0JkIwB7DgBhmSBNErN2FNO22AN6LWqb9w8Y9MAJQME6wMLTH+U9JQ5APAjhfgCaOEGXdQcDrDE6UNd1LrtxwJlkbP48oHiZ8VjWVVNiuFql/p+3t7cMGuhpS9cr82Q7H5k9DMtGYg8uJeVpN+yNNAPlokgZc7KREnXk87Q3ghcAAjoI04/dHYZe+/1O2+023xsyyr65L2NC1mZzsWCq2Rf8B8Db2XxspwNm96m8WHf3jeieB3no03mW18eto8vYMWwoWSauRUCE7WAdIPPoH0F/eFYnBNE/QKU/Az930oaAHcLGJw+67js5gpwURal68gPoAL2Srve+vujQer3Oa0TgOI5jzoCTxXUizLOjBEbcUxnC4pkcx1yvV2q7+ZBN96kuB9gU7NJqtVpMY0RveZ5zmw0I9rUDC2b/UaYyKYhX9pVsCTad35E9Zd2leTQ25XRkbSFHPBME1gM/MKiBDK1jj6Io9Bf+wl/I1wNgEyzwvFRhuI6jH5SrYS99siX+1QmvuqoUh3nCHXYOHSUjiA93kojPQCKt12v1Xacw9W2R7XQ5dGzCOnlWlmwoduU86+l+ifVg7dx2sP5ufz7n9dmBxvF4UoFyHFMzchtblcYYOiA5nU75jAhYMq+np/7RnaELDwvCadDnwQrvIbC4vLzUw8PD4uc+hQWQ5Ibs06dPappGV1dXi/R8BrlTQISDBjzBtLy+vuayMIwM9+IsCyDSI8phGPIhNl4ziXHge4igeX6vwUPhcc5+jgTfi0NDKPq+XxyWRHTPi896NmU2wFOafmJey6LQ8YjBKdQ0peKYxh0Pw6CqrHQ6TSfFrxsd9ofsEHHSNGOx3igP9/H2dtIYp9HE46goaRjSzP6u6xXHlEauqlpxHDXGqBinjEqUYpSYsS6FaepH1ND3kqZ66ZimyihGVdMBPMOYJgEVRSlGLQ49QXDQfn+YjNZBNKxy74A+2LlyWocYpTTCt1DfD2rbTgrSbr9Xav5UVu6YwUFQ3zNJo1IIo+o6jXkMIY3c5H0A1TQGd85+ZWAZBwVJh+MhA7GynMoYx5mNRl/ciSMD2+12EYQBdNANGDMCPs9AejaRIMJLGrxZ00FWWZaLTBhrRNkDGTdnEJ1cQD/QAddNN7qAdC8/ZE0gL9xpnmeaAFJepolj8MwSsuElieleYD4rFUXQxcVWwzCqLOe+CrdTvjfchzPQsKO8YHaluQwLJ8qp8eyDB4MEWzwTjrUoisWQAtbTD7/juQgUCATSdVsLDP0U+fSZx8fHHGB5MyJ2ijIeAkKAXdPMPXSAmnmi3sy4x0nvP3z4MO1Hpfv7exVFqdfXN51ORzEyGvkgoEFWPKPBgYG5IbTvpx67k9q2m+qe50wXAL7vh4nE2qht06jYYZhJHEmZtGLPPcBgb0MI+bwj/JH35qCzntHzLD9y4dkFz6J4MONgFCCKrnu5jOsg8h/jnFHnZ16KxDUAbTDaznLzWUlqu05lVaoaaxVlIcbtrzcbDdO9OIEGFnFAzu/S/ztFIwoBhQAzD4yRaSdD+77Pfnu32+XgmuoIiBVnptEZ3/OiSCNz4zjLq7PsUXMAha85nxaGfHg5EKc9n2dq0OFz8sF9iZd7se+sL3LPvj0/P0tSLtmUUo8aOgn5RjUHegpxe172Q1DkvTKUv1EG5T7J8RzZCoJNL+X00iX00vfGSTbuFfvqmNTlq2vbNKZYaWytQpCC1A+9inIepuD3yv35M6OT+D4PJPAh3AvBn+OrokhnYnHuBnpFEO4ZdAhE/DLPf/5drMWf5vXZpVO/9/f+y8xqkO4BfAI+ML7OlGKUCT6cSeWG+T8LiTIh6KSXYXa4ZSJbagQJLjBannkBiCDcfBcpThbbHaIbX5pVYagBR67UZTlPQGKNMCooL8/pm8lnYSVQfhc41p1/Y4zdSbAfDqKcIeR7WFef1c53XV1dqWkaPTw85P1ib11Jnf3FsHA/zoawBx5EoLiuTKwDZWOsr6dqpZmdcRbHnV/f97lUjnVk/wEMXPM8iwFg5Vkx2mSyvBQGgIrTYo0BfXxPYnOX9dB8Zz8OWq3X+SyS9Xqtjx8/JudWN4IrQN5cb3jxPTPjPDP0nnaFpXS2wvcPQ+8A2pl/7sOzJdJcbugsjO+pyyaO1JulYRxpMoNZ8dI9D05YR2cnnUF3c9b3fbYdrle8Fz1x4OBgiPV1h4Mj4meQLJ5xYt14fhyAy72zjNwP10HXAYpcy9kl1zGact0BE/TEGBeTXQAFrv8xzs2avJzdZm/52wdPwOZ7Q63bP7+GEyrYHSmdw4J9wi4C2tErZ+JoIKeH4/wwubKsF/1wlIgAyhzoe3kG905fnb+n67oMMlwe27bVzc3Nom8Ov+fgQVJmZ/1a+/0+g0DWta7rTAZRe851vNQCgg6ddNsAYGHca9u2i7IPnsNH5wIoXNYJ/glYGYdKrxAEHKCa7ARriv9H5q6vr7MMOuHgdgZdYJ3YM85LAntkmz8OKqt5nPGCne36RVO3ZzvRiXGcqxv43O54WFRaIB+sK/aRYOrXVRmgD2AJb8J3/8ba8+zOfhcKP/ID2LaymftK3P9wTQ9C2NNxHPX8/Jyx0MePH3Vzc5NxAoQCmWrW3rNR3AvVEj5oALkpyzLLML/Df7kM8m+wHPY8xrgo82WdeT4PFLkf7J7jSp7F/dtut8s4iXvwHiHHCI67+L8Tv6wP+s5z8f3sDzbVCXM+T+kWugZWJYgDtzAYgP4m1soDfWmenAUJ7vrn6yPNUw8JUNz2u26eyye2p+97/c3/6d/QT70+O9D4R3//9/IDEtUCBnxTEUAWB2dBgzRZjXwDYS6l4PNFMdcF4khQcBcGFgDBg3nAWbvxkrTIqnjKuDIj5SAch8TvCBRIhTqbxrPw8v4IFxw2W5qdgZepYIQAn/yc73Eg5KwyjtzTnG5cPBI+F3YHA+7UMFwwvBhQjGVZlnm8KfuOE+HZub6nsM+DLZ6Pvee+MB7OFnugwfW94Yrfcw3+7wMEzo07++NpejeQPmSAvWOdMOY4GmRrDrzSYXeuqDx/VddSsZwEwf5XRZnYkDCn02mKc8fsQUS6x8QOo6N+8BrAQdLCmLLWGERnwTzwcqae55OUjak3urK+DqZhy9AFprc5c+XkAOvMyw0h34GhB3x5kBVCyEacz1DWBSkB8HdQda4XDtw9M+FkQu4pssAV2XV9QIZ5n5cDOqj3IBjWD5vhI1WdrUUfCFLILnhjse+NN3HDFnr2hWeAEfTshmeBIHcoFymKIoNaZJOMtTOkiVHvNAxjnlAGq4kTdSDdNI1eXl70zTff6HQ6qmkSIKd8Kk24SVnMokiZboDJarVa9IF5UEpmnXVnr7Ex55ltAh70AJl3G4R98KDcg363mZRpIa8e+LpP4Xvc9nFdemr4N36A++WZ2EOCi5eXl6z3nI/B2sMqM84dGYXpR54BlbCeTmY52UDQiw1A9vD3vM/7trh392PeEwlhIwPgPGMIQatq3kfwSN/3ebw8TLevd1VVenp9yTaFe0cXWVdp7pdxZhyfwjr6+90WehDDHnjwNQyDNKYDhNlXQGHf9yrqan7f9HIbw/qw7tJ8Lhcywv1i2wiu3t7eMu56fX3NNhOf2DSNXl9fc1/o6XSasoHz8yPnZByclBiGIWcvuFf+T9mw7wv+rGmaPOHTG/7RxRBCniDHPaBPyCb+9nA45CltvLBn3IvvFbKFH8T2/joMNo5jzu6gO6fTaaGbBHAO5JEpl4+yTFigKktV5ewjPKh1LOMYz+WGXiDuC/zF/UGoelbFg0T0Ej1kP/7av/lX9VOvzy6denh4yAYCUE/9GBvNy6NP/u0pGG8GB9A5+HTlPGch2HgMu0eNIYQcoHh07Yza5eVlZowwBE3TZGbH2RIfk3l7e5sX3cG8M0nU9mE0nCVDyTz7gSA4WMaIuIJi8M9nGeO4uO558IDjQ8G8vMBZMDdu7AUv1l5SXifAB8bJlQXldwOCgiZgMUfono7FgDhL4Q6Se3PF9ewC34cDRVlQfJg9FMbXXlI2Zry8Vhbj5JkR/vY6eTc0899DNnIO7pum0RDHBWAgmKvrWqeuUxGWE7V8vZEhD9qbptF+v2y8BOyz19wDMuc9NmSwYJzP2Wn2Upqn5jjIdyCGPp//G9AOO+sAzp0U++66gvFFT7gmesseuL57BhTwDpjmfeix9065LnG/2AVk1u2XZys9QPOModdtAywx2tgOZ9fYb8qaYoyZqWfNmPJCoAdYuLq6yu/jO3Hg7JXbT863IfCBmaYXxPXQs2PIIAEQ9+tA2/UIBh+/cTye8ljZrkuNnNhKnJ6Xl97e3k7ETtJfxn9Tgpvut11kxWC0sec+/hz9Os+0etDvmVnAEzrgjDKgz8k3D8hd/9Crc4LjnHX07KL7yf1+r3FMh796JtZtGaDOB5ZAiqH/t7e32e742FS+k/4SB7Nui7Edvsf4eAdBzkLjw50JpuTQwaz7FUAxeuBZjkHLyY8Ef3Vda2hnIoL1uLy8zNf0oIgS56Kcp9R5NgK9d6KHe/X95V7w3dwve+5riWw6qPUArCrn0ibWlrUZp2zCeZmLy6Y/g2eXnGAge+IAEvyDLGGLvLeDSVDeOygp6yL/B78gW9gzD0BDCLkXi/vne3m5v8dGAKTRNfAFQSTks+ucB2LoPc/K/qDzrDd+iv4t70102+AZeXTEe/jQKWwGcgPoh7zEv7IPqWA7LPCCE1ae4XHfiFy4X2R90CnKyPwe2U9+74Er1/Iyv596fXZG4z/5j353Iai+uDzAarXKJ4J6ip1Nxum4w2YjWWAOGSLA8B4CD2AQRnd4fIe0PKTGDT5K64GNsyUsPtfiOwGmnv7CkbLoXvPIczqLxfe5AT6/B3dKzvCz1twHz+/AnH+jwJ5qxfBgbL2MwBlMPuNGzUu2HFw4s0u9tysYn/WMFezSeYA2jnNKU1rOY7++vtY4jpmhlJZnXzjL7OvjyiYtMzwAJtafn2E83NC6EfbghGsAvHBogLUELNPJwi6TXP94Oqqcyq9w8hnEFoV2r2/ZMDv4BQQ5wzDLUBoZCmg+d2AenHopiNfvo3u+ljhwHGnf94tpX+iCMylci59xv+dM+nmQgfMH1HmWwO0F+8G9kDUFtLJGnpWQtOhHOM+i8eL3DhwwsOcZHUCEO3Wuy1pQdkkNPU7P18zLIT11TiCH/nLGxv39fQ6aKCGlsZP1Beg4qAA4sXaemXp5edG7d++yowNIO9jmudgbfk5wQ4kLe4bzQy9ijLq5udHz87P6flDfz70/+/0+HwpJWRPBjjvRdD7F3Ejq8jGOUcOwHMfJDH4HZMgjcoaOI4MeYEOg+HPzGZ+U5k4aGwKw/HUlp+gFsuBBvpeySMrEHqCCrLuDJvaMAAu7wp4hu23b5szR6XTKGTnWA5DlBAmBMjYDcm4YhpwRQp4cdGNHd7udqqrKJKNntrA/9A6wBkxldL13n9c0jU79PMnRsUVZpJO1AcXOwiIzrDvPm0mNMLPyjgs8a+g2lnWhH8FZa8cNTsj4fnvw77YmDqOKsKxqGIZB/TCoapaHvXrA4IQGJZJkOvm9A13sEDoC9uHnlP05JnN/xv2yflwHHfH18MDEAwv8GnLjxCty5gShZxfQMc8CIAuOEc/JIPefrAXy5Vl11gTyAizr98Y4WZ4TG8gYXF5lWeZ94DspqfRpk8gce6Ax5kMAwWBuW70kmd958HEuJ072OpmHrfKX2zv2Bn3/Mz2wD+cIk8e0nxxxGcilxMPZcASB9zkIx4jnBdWPp2NgjHAsbNx5sxPf5w6blxur8wAAJaPRzA9Qk5Yg39Nlnt1wgEQU62yqC4CXMwBU+SxGGEMEIEAhXAG4B9ZuHMfcyEok7sGM13NLy3ForB3r7ww8+8K/AeySFpkCFBhQSqbJHbDfN8EO6+TBC9fY7/f5PtyJ+5o7o8I6Eax4oOTOw509BskNozMxzloiZ349jCsy1bZtZlTKcvmcGNuoOTvHz/Pzn5UT4YQ8IKAMzGvjiyKoKOYxwR4ceUaG5m2/pgND5A099kPByBqyZsjdOfhHN9i7c8YNlg0QifEEXJ/vpwfkMPfcD+vgQTPlMl6H6nvuQQb75nIW4zxWkfXk3gDuXtvq9o1XVVW5tACmD1uAXN3e3ur5+Tn/jj+U7BGEvLy8KMZ0ACX2sq7nMzdg01xeff+9oZgsBYC1bdt8ICjXxo4Abtgf9gbAQfkBwJgAD6aRcgy3vex5CCEfOsi9EgSfs6fIJPcwDDNJEmPqR0hN+xvFaGBt+h2y7QTPuUy4TSEYg3H2aUHIdwa15Y97zviDvnddp8fHxywHADUHIdynB4fcp2eU8FXOTsMA43vc5gEq2DtApINKZNx9uQcnrB/Pxc+ocqjrepFZ834O1hb/6XoGI+vkFtd9eXnJwabbqhhj1vfR/BPBOr4j9nM5ECUy5+PGi6LI5SSSFDWPyMUf0Pfn++SknLP5rLkDSdYNm4McsyYekGCLDoeDVnWTJ0u5vVqvVhoVsw9xcM5zkvViklOMMZdEgZcAqPhicA9kMQGal1S6HceXOxHn9h39czLZ14HKGEqVXJ6xTwTb9P/ii1zfvOLDfQy66oQIuuTZJdbc/ZrjMv8564F94W/XtxBS+bv/nCD+PNhB1rkP7hE9ywHwMKoyItSzO2SIuRfHMdwP/oF1dfl17OM9JR748jonXj/n9acab+unAjooKoq5DszBPUYUZuoc5LFpXsJDpHcO7lB8GBO+GwE9B9/S0ijyO54FZ+WbieP26+BQpTmocVDLz9kkB0OugAiRgzn+7eUoCCTreR6MeRTvTAqGwoEE3+GMu3+G73aW3wWfQMXZFs8wcS/IA47Rv4s999rnc2bYg0oPcHxf/X4dgLsxdyN4znq4kXaD4cEne+AgwfeI/fA1vL29XQAoV2a++3TqFlM0+Pc4jGqsXhKwUhSFQlXpYrPNQQa/534BCgBYRgu6nPLMVVXl+nTWEmPt2QHXTQ8CcUhcU5r7JZBJN2zsCQaa+wFU8l3ngRrXxvk7qMOBskawKQ62+T43hMiN14Y7Gwnr5CyugwHGLLrOxBjzzx2Ac+/oBOuIc4e1IyinPt71yEd0hhDyabmPj4/ZAbAmMc6HkiK3gAjuj1Gjz8/P+ZRdggL0AyDro7VZZ+z2xcVF7gHwchGmvri9dRsupUkzgEVvsG2aRtttmliHo+P+yJYBCtzOJXsWJZWZMSTQdIACiPbAD+CCDBLU4W/4uesQL2wL+8ckMi+bc1/isoAdu7+/z/IOKKb/BfCObPN5dP/l5UU3NzeL4AvwdU6e8ExeQYCMOtvMfrn9RDfRJfwKcoLdhalFHgkMkWfAHGQa8hjjXJoHEeQ643auKIpc6uRZNZ4thCAVaQLTue/t+15FnMt/uS72hPVGnlm7/eGgIY55ShR7hT30AMX9nH/HMAy52gFfANDm/+dAGBvqpdLd6aSqnEtYeXZJ6od5FDmyylkWZI6wSZTP+REFTt4iO9gA9qw7C3IoZyQ49rHSTuqAIdhTskZ8n2fukE3uGxyBDjDYxbMPTvQ4UJbmiVLoMXKMbDgJDS7hfuq6zpUVfPdms8mTshyck6U+nU550ug5rvXgnud0WcPeOIlwnp3BbvF5rs+6O/nqJAjyBPHNgaTnAT3Xc3KPe3EMe34vHuj91OuzS6f+7u/+nYXz9H9jhP3m2PBxHBfBgi80wklK2J2ACwPnWEgzwOG7nAXAqTCH+e7uLoPuc1b2HFD9OsfjfzyqxUh7aYq0bPDCsLqzc4bWjb6DZQ+KEDo2FaMMCABo8X0ObnnGbhilode2qjVoVBt7jaO0qhqFcVQ3jhoYq5qoIQ2KU+PRsoTm5uZGkvJMcBgJl4HczGxAMoGxajK8pU6ndmHs5t6TqLadS6LSQX1SXbMOs5OYDctcyoB8IJvIF/vrisIenJcysN+wfNwnMgswZO9wAEk25qlnMY7T73q17cz0ukFerddqu1Z13UgxKmpOXRahkOz7vAyIQJRnSYBtOz3TXCZ3XlrlhsgZUgeKDrJmRmMGKbOupyZ3dEWaB0Gk+wgLRhhgcC6rGDicMs8EGIHgQOe4hjsmZwbJDHj5Js/os8/Z95eXudExOdMkVxcXl+q6NhtjruvjDZuGDIEUApPixoX9IyhBflJp09zT4aDk4uJicnJBr69v2TaiU7Ddp9NRMWrKZMwZAAIuTqW+uEiHuHGYW9ueJn2qsyMkOO77Xi8vL8lhjmOayxhjesYxjYperVYqqzKNbtTMwlXV1KtTz83G6A26dTgc8p6UZRpHndaoycEidrrv+zxyHH8CSJgDyUHjCNBqpobuTR4j7YAHm+k2wM95cKDnQZwTU2TQ0A8nXyDSAH34PD7LGjjRwb7zfmySpBwkOpnCZ935O9D3P04S+fcRuDob74ymM7zuc5Bn7/Ngz/CbrJVnH9BRLyf17AV+7tzH4jeduGPfuB8HXkOc687LYp72FGNUYSCK9/gBgDw39m4YprKkelrnYUwy3/U5Y3Q4HhaEJPfkpWD4avwUZTVOmCIT7KWXcOUAte3UT8Ea52PlNavm85XYW/AAw2TIdHom2P0DmMeJPAeyEBXIMvbcgaxnZLBR2GbAOXvuGdLz4QXuR9gP77PADwOWHQuA2/Ab6DXrzPN6Yzo+yUlq9g+86MQKgJ3KhfV6rW4KJqqq0vFwlIK0Xk+TTTU3+bNHkhb+8JyYc0zqPjfGqKauVRZFzmKNg1URGInIXjrhzr560ENA5oEG9pLXebYDP8s+lWWpv/yv/4/1U6/Pzmg4i4uCO+D1mjNAGjX1PIgDA2eVEbhzw8aDUNNJ5sAjUzYGYaK56quvvtI4phQXrBwOw5kIB/9eI81mAVzZRBbdmS13IudBGALOpgHG/J49LY2TYl19U8/ZE49uuTdnqhWC+mJUM4661KBSo7SqFWOQBqkdpJdx0KmICjGoDJWkQnECq9UkZAgnNbkhhHxCrzsE1gNA7YagLFPQ0PcJoDKNqSwrjWNU3w8TUKot/VtMwC8qBBxDoRDmmldnElkn1oZ9xJjyLNxz3/f5RFGYRWSBAIVgzhu0KNEIIWQHejzO07aOx1M+SZTBCYAHnFXbthr6XiFKPSA7ptNEAWPsOc/Ay50BzzOX6o2qqjn4waE7g8T6+qFL6K1neGaHnoAhv0+gWpPTmgPt5fjqKv/fAznXc+QXsAQDhOyT/YA1hjWlHwjA5Clz+gQIprwuGf3kOWKMurq6nvZQkoLGUWqatfp+LvUcxzGXJ7Vtq7btVBSl2rZfPFdyoimYdpCLk0ksd+rZGceo0+mYZSJG6fHxSR8/ftRv/MZv6ObmdmLNLvOUlVk2txnYlOUsB5REAs52u/30M0pF6kkeS7VtJ85d6boUHNzc3CY9KkpVddq/qmmykwghqOsHhXIC/5Ps4JggCTabenKmhYqizOuc1n8maJAFAiH22euc3cewZ+mPFEIpzqhJTPmcYUPnCQSQIxy4B7UeUABCnTDjHvAn5/0n3m+G/KI/50E/nwGA++QaZwoB6oAz9B7gBpBCDtxGQD7wPe636WM6J1acGXdfic44A+v35EyzNJMvBCQEI3yHl46wr07cOTvPNbkPL23xCoLNZqOuncjMOqgsEkmznoAyeuiZE2ycA0cAbLfb6bhPmaLLy0u9vr6mZ+977WOUijl7DUj1++ZnYAnkDuKA9zlY77oujwf2bP7YzVUI7DkyqTiX2zpWgJyF6GFv8ZHIMbLkmRcPQPDn57bZCSMmUhHYeFDP95wHI9ynv8czWqwhjebgHuSf98QYtdvtcuM+euD4g3snwEH2HMS7nCEHPrjAiVR8TYzTWVxjVIhSO50zNwyD4jCoaWp10/M6cecBqfevxvjjISJ8f94fvlNWHROkGLQo1Xe7JSmXnp0T58inZ+TP1wddQ77dDjsx8VOvzw40MCYoJc7eG+YQCG4egQNQeMMf13TWi811Bqfr5mkmzpADGh2IkXaPMeq7777LgAbHBQt/HqnOAPG4MLx8nwdGHh2eG0icmS8+m37OnLljQHCLosiGEaGPcR7LhqDDcJ8z8tIMjLin1alX/PSkL8JK12WjoooqN1udXvf6/e6ky3fX6oeTVqu1yljoNAxqVpXWVaU4zHWWfDdrSRaK4A/g6/vtzjjt548bhT2Dg+K5YeKZPKiaM2SzE+I7XBbIKuGw+V4fLtC2bS45cgPm90KwURRFbpp058c4vMPhkEdtsiaUJRAQnBs4fkapiDOZv07hXT9YM2r50z3PY115P4DcjRpyibxhkLkvBy0hLM8AOc8usDasaVVVU+3tfgGYXFZ5HuwAxMTl5WV+FpwWzsyDXWp9N5tNHm2KTl5eXmY2ztP6Hmw40BuGIWdB2W96XWDjfErearUWByVyLdZYqtW2p8xOYg/Ts1cLPaWMaLfb5dT7/f19XmdS3Th7tzPsU13PE9CcbEm2d+6fAuAwdQ8gGkLQw8ODrq+vZzvYtYu+CmfICP6w8WQqurZTWczTYN7e3nLw4+VLzqDj7LB3y6BlPleDgJ/SD8o6+JwDa2k+sRtgiV9BzwFROE0HcdgM7pVndeeKPeaPg/hzx0uQyrPwMwcd7lvwsb4/EHlPT0/5Og4MsX2e/YZB9mtgQ11ffV/QQwcbPh2HtXawhIyg+8g8L57p/LvGcS6p9EwScuVkB2vvPUYAXtaA/cU3Ym+weciZ6w7XxM5wFgr6BuDnuwgW2n6WK+6XgI579awOgAxZwB45QcT9oCv5u4ZR62Z5Po/7EPbCgyX2AjnBxjOkwclQ5Pk88+82hX8j3+xP13WLrDN64niOPWfNPZBGBjxTxt/cB7bKsaGX2nvpKSQFz816YtPpIUPmkHW3qW6b3Ra4nIJrqqqSinQNn8Y5DIPqVaPRAgXW3L+T7+KPYxUnB7zcjM+43uEXWHf+9iyR213+74NI3C75vnMd8Ghjssgaf87rs0un/vP/5O/+KIhAef1mPS3IAvs5BEuWez4bAgXCUPnCuhF244KRGMdxobBErg6sUHSvCXSw44yL/9832jM27jwRkPP0H/eIoEvLJvUQQnacXjfL2jKJgNnXCKGn/jwad0GKMU0oqA5v+v3/8Hf16e/8nt6NQau60cXtjW6+/ErjX/oXtf4XflNv6rVebxWHqH170ur6Stum1tvUfIrjYn8RSg8uEHzWnHXFkKV7nqNpT8+xvy64yAH7x954oCHNjaHcG3uKoeC+MITOZLnc4ahgsTCk3A977HWys4OtVNezseQZXW4dmONIcBgE3hcXF9nwYjwdMHM/Hhz7eESApzsSZ/C8DAPHRMCKgUSGWfO0B8tACVlwXcOAL7MYw8I5nTd5oxOsA8wWMub3XhSp18F/x3XQIeTNQRc/Z++Rh3leeMjlAaTVZ4c5Zw7JSs0lAhf5/65zqZQprU86Of64CHBWq43e3t5yzwP1wFwDQJPkqlyA7KpKp+3e3NxoGAZdXV0phJgP4ILEKctykpfZViO74zjq5uYm6wAygeOv61p9nMEYOsj3OxPrDcDjMGjo5jMMvKyG+3dw7jYRIIZtcxAMyHBbwVo64+hZYMA6+sI1ABrYUW/sx/ECzAATMJIEqucjYNEfysI8KGM/CHy8/MOJJgeFzhx7gOO+jeu7vfcyDJcf1zM+5+ABuwJwc//IezwjDNhzf49NcyKN7+TZXZaQj1TulnrLXl9fVdd1toHICWVQfd/nmngHSIAsMtL4Ksby8vNcimRZstfX16yblAV7j4ITPZmFjymj4RlyZJj1c5YY++/r5mD8HMh6gDWOowoFNfU8gdEDgRjSadMQVewZ9srJKg/uHH/hl0IIeSoY9+8ZJEhc9sIDI4Is1tjtIdiJNfIzHMA/yCn2x0GtZxgIdtDp/X6/8BdOUPf9PPWJtSOwJbDi+u4XPXAH+0jKZVMOsldNoxDng5p55q7rVDW1TpOc4huRK99f/Ac+HrkBf7jscX32ON9LWWocBgUtJ0o5DnH74o3z53KI/LFOruse2Liu/9V/46/op15/qtIpBMBHkLEo2Un1y6ZsjypZYK6HMHsK8vyBcUooGUCiaRrtdrt8LYTIN8QzAK6EbqR9BC8O49ww4Bw8csapYWipzXcQCAOOs/Io0tcJp8fGscZstis8UTaC6s6TNDDPdjgetasafbq4VPc7v6UfjkeFdaPf+R/9S7r4C39BfSh06jsNZdSpbVXEoCIUOh2P6o8HhTPm2WvZYdLZD19XzwYAgMZxNi4uG854NE2j3/md39EvfvELPTw8LKJ2lxuUNU1XKvPkCuQI0IwBxFn6FK9syCfg7E3K50MBMDr+WUBGUvz5WnweI4acc+9ufLkeJSPO1G+3W93d3Wm73erh4SGfl+DZGPbGAZevMQ6N52cdvQTP0+vcK4EQDE2Mc1OpO1gygNw7NeMeCJ4HfwBWZ7JYFz+pmjMgnAUkqEL++TnBy1zGdlyUybhdwUZhw7AdDqgAH8fjPusbpW/U4h+PS+aRfe26dAIz5xOgC3Vda7fb63TqFqMIeX4IGVhV1w3GO+Owqio1sSeA3uWJgE7WnDPAzjr7yFV+hs1VCIphWS+MneaFTiFzp9NJGqca4rNgATDpxFDbtjl7Jcl6tGbb7QQRwRc642smaVEL70ADG801vKwHB+9kggcLTg5QkhadO0y7AAEAAElEQVRCWIyq9ADdsyJ8nrVA5ggqPSvI+8iUOjD15+ffzkiynqyB2yf2zHu5AE7oO/YRHXZfNI7jglDw4MQzDk4Usifn+wAwXK/Xi4P9kOGmafJ5EASvrC/lksipA9pxTOOYGYfMhKvT6aTn5+dsc/BJXhpNCStrg/ydZ7P4Gb62bmoVRmBhY7zsFDnDxvm6nuMjJypcF7J+mYwim/i7fmpY3+12GT9wOj19W46f3Ka4HuBvPNjk+8mmed+qf879PXYE4BxjXEzOw+Y5xvO9cMIa2XPC0AlMJzH4Xt8Dl2cftuB7PJNzc7m3B2S8z/Gpr+M4pOmQHvCDHfph+JHOOA5wIgM8y/N5pg/y9Z9HjqdniIpjVCjmAO88YEJXsRvYCMc1rA/3fW5T3Cb5XnzO67MzGn/7//YfLQydM2UIDBsDEODnGBYMLmwGhgTB5vOr1SqzdB6Ru0GQZhbBnYyDev8c90r2wNPHXr7FvQBeeD6Uy8EbbAyRrjsBZ7L5DpTDBQ0l4rm4V4STmlpPATrw5Z5dYChr6vtBQ6hVnQZdDIO6/qRDFaX1SiEGVW2r2JQ6lVLso4b9Sav1RvXlVkPbKo6zw2C/PSNBn4Y7Gc9yIAczS7/M7LjsALR+67d+S1VV6g//8J9loOYAwWWgaWbHjsPFKTvzwx6cO2o3AuyfB0ke7OK4vS6R/UjOYQbxHmjC5lLy49lAnglH4owQa9d13YLRxSDxPQTqrEldLydBEAyyjq4b54bL63HRy3Rq8RKs4Bhg9GGMnSFLKexhIb+Azu12q91ul4NwZyY9SAJg4DxZD8AdGQGCnsw6WgDZNOmALsA1+jGOo66vr9W2/eKz7oxj/PF5HfxuGOaRqTimJKeF0qnV6eRc9igB1rXatsvr8PLyIkm5n4eGUe4Xe4VuEEi5cw1B6vsurxmlA+l7Zzb5PLAAdDlR8Pr6qqvraw1xzN/PWFkPar2kEBlWlNZNs5BL7gdbDfD2HhlYM890Yxe99wE9df3ihQvjupQreubMM1XO+vM7aS7hg50kMEYOneBx0OUBEKWTyAXrTWnFcvDAfC/0HrmNZR3pCyEguLq6WpBh7uN8TZzN5N8OoHixxthIz6g4WPHn4Xt9v51VdyDK3wC2p6cnXV5e5rV1wId+svbsKdlMH2DAGRue1QAgnWelfH+xt/wBm6ALsMveuJyvE6Synpto3efxXggBbCMvfg8xw/ADbCQyw/XKslShIMW5D/X5+XmuECjm8qGZ0JtLi5xcwJ67X2Rd0C0vg3cihjXCRgHwPSinmd3P6WAv+LzL9bn8sp7oad+nIRboDpjMdZAgmvVEHne73YLgQY6dpHQfT1CNjDrIrqoqExCsVx4nXxTpnJPixyXsCkFt/+MsoONKl0cngDxg80ABGWRtISXHcZTGKJ1hCfbJAzvXA8em2De3FeeY2+/HcfHnnAz+pzqwjxcLimAglDyEG1IXZg9SMC7OvOFc3ECyCTDEPJxnOwBSDvAQFgQNgb6+vl78n/uCuRrHMTsFX1D+sOAYDATYDSv36IbfAyQ20ZtEPdhCaXg+mG6myfjLGQvYQkkz2xUaha7X2B00VlFaVypUqe6lMQ7qm1J9VagapNVQqCwrHfpOY99pvZ7ZBC9ZO2/ydeF1ELxkHoNiVN5fd2R8HgXhWVhv7zdw9jmENJnKATNMBqwK645MsKd+kBXKj7PD0PnzeemUywWNvKmhfU4hY+iQf0AvBgCn6tlB5Jg1Y52QzRCC9vt9LgUg2POyp2Hotdms8wQSz1hwvfNnQQbdMfHMSf7mzIMDTicBPNPA3kDUAfxgK9u2zc/tB4WhG5SLuf6goziH19fX/LthGPLp0IA5b+Dn/gAPMH6J5U4TVRjNOQxDDs72+7fFM6KzfZ+mqIUQcgA5B9elhqHPe0tguVqttFqtdTjME9socwI4OEAHiOAckWvIFQKL4/GgYZhlFblMgeBBTbPKmR8HxmQY9vt9zphkGSiX2WoPMFgH1hXdXDWNutOy7MfBE/LnmQleAA9kz7MYvvbYba7lGUvkwO0I9fYut9gT7KrXgyPj+AHAj+uMNDtmt4ve/8H1zjMEDvgAZbzcfzizi83j8x7UeACG3HvZML4AAIHu8P+2bRfj4Vlv32sHk9hH7g+C4RwweZbIAzn3lWTh0B9k1/WNQBW2niAEMI88uP7we9bpnMlmjfCPMMjc4+vrq25vb3N20QmuEKZSpWo+TZ49oqKBoMGBmGe6PLh2HTln1Qnwu1OrcvouMoPS5EcLH9gRsm3l+R10knnlfiEm2Y9zkgu9d1KDf3M9bBP+5Xg85rJjB/cup+gA1yLg9yDA19srErh3/obsdWI3xrlfhM/iD1yHsTusPffESGDHLucZobxvY9Q42RSyR1n/JamYM1Zu45zUYs1ZC9dz7t+xIGuFn+T6ZQjqu3kgANfxrD62hWt5aR3feV4iL2mBefz7sad/5gf2oTyeosKJunFB6LkpN4wOilHi/X7/o008j5wwmu54WBBYXr4fA4izSIoS1LadDofjVAJxnMAQC3bIiuCTW6pqZtl+ndBjgF2AUFYvw5mZ0GXmxkt9APUebHm0TwTPz93Jsg98tu97VXWtPkR1GqS6UqgKtUOnchpxu16tpTJo6Ad1ba9CaZ00jqqbRoxmZU155rQ30vE4H7LECNokmMu55THOTJkbIDdEXNvTxDOwmxv8AN1p7QcxjYoJVsfjaQpW5klizoSmNRvVNKu8x30/ZPasbWGqShXFbCCT/MzTOZas6pxG5DoYbgIE9ni73eayIIDqer3WdrvNa5yCuaOVypQ6nRILnw78usiZDBzUzBbNAQtgASNHVg1QyT0mxzCqqgBllMf1C6DkJUo4BSZ+sBaU8aUgYj+BsPQsmw3P3quq0oSmup4P+MIBo9cYwLQG1SSLQadTmwO7FITP8+5hfymjeHt708PDg25vbzPAn4H/Sm9v+1z2BTuYAshaRXGZn5vSKQKE1Wru58JBseawek9Pz7q6ulKaxlTr8elJIRSpzjtGXd/c6NSetN1eaL/bZeYMRpfggsBSUq5L5l6jpKpp1NSNyqpUmOQ0Kqqsa22nmneebxxHhbJQHEf1Y2paHMZRbTeVnoZl8zBBjwMlB9gEj5mNK8pUNqCoQkHDOJWcVlO5i6KKqkznHiiNH+Wez0uo0F1s2jnbh3NEvxzgn5MSfCbJ9VI/PEhzwgp5gm3073SflJ19OfefOGBym8G10EknrPAR0jy5ketxYro/A2UlHrwhP14Ljuzy8vdzvopnAdwXLcmiueyETASg/7w8eiZh4sLWYwMBgvg1SAL0jzJFstmAej+sDR3wgBD7w7qf2pNOU1BXFkmWirJUUZaqQ1A5jqpXjfrJ1l1dX6uoSoWi0OYi6XRT1VmOQwga+0GhlAoFhSKoLEppjCqrufHcs7PYXiZYgU/ynoxR7fGUphCGoKIqtHt7U9/1KYDv5jM7PGAchnl8Kv6TzAPy43vC55ygRWeQZfpg2B8n+QgmkCH0xAcPYJMdHyI/kE3oIuvEtb265TzoxI/hH8dxzPbS8SZrAGGIjvvhu+wLz4WsYlvAs9kfD4OKUGiME5adSArFqDAFd67zZTlNg4pSP0aFMihIKotCQz9oiLMd457PSWn2+twn8n7sDnZ6HOcyS8/IsNbYFsdWyIR/J7rrJJnbQyf6PXj6qdefukfDmR9JOZ2PM+K93BRGgAcGeLEgbBKfOy9bgZX1Bjd3HkTUHvm5I+Ha6d9pjGrbdgvjVBQYgwS40ljGoBiXzVM4as9+8FwoBALhTL8zPs7COJsN4CZI4fO8n3X27+F9HMCFc3AhK4tCQYXGUer3veowzfFWr/1hAu9FoVFFAiBFUBELjcOo06nNShqjslNLQLFS08xMx35/yGvBOscolaXU94P2+30GYKwJ8uJKgOzwLMgcCudBCcGFNJchMHoVp5PWrFRRwOAw5arK70/lRkFpdO4cKCdD2Ez7l/4gr8h7Mi7L3iJOkKW8CMPnRsMbm7uuy4dxcZ2yTKNqU5B1zEbk6upSq9Umy0nXdbq8vNTz87OapsknD1NSdH19vWASPevjzGWMs9wlgIYBmeuwqTFHJllfgmFnOdP10zoPw6DD4ajj8ZTBQ98z4SqNeg1hnkrmjhmnl/Qf2Q+6uLi0ZuaopqlyrTI9DpR2MVHJM6kY0Lu7u0l+9wvdSro4zzy/uLjIQeRms9V6PU+7wqFio15f3ybAMagoSt3dXSfmtq5VlKXW2012ENv6QmOMuri8VNAse29vb1nuCcC5R0BYWZaKClqtUx107u8ISZavpr1fbdaKQdNYzgTyy7pSlDSMow4nsy3lDLa9/Ml11MGkZ5v7YdCoVCvcWnbjeDqpmORBIajrrel4Am58F8+MbSATCLBwsAGRw2edRXY76pkIDy6QW+91cPadeyGwIthAHs+zCzh4/zy6QsDKc9VnAMXBPPcPISApjw/F5zHB0f2GZ4G81h+fy3dR5uTZk9PplO0IPQ8OUM4ztOh+3/d6fX3Nwb3bFvoxkBH8OOsBq01GbSZL5n10YMq1PPPEGqPD6K4kVXUlhaBmtdIYo07H+dC63dNjvqeiKNQNvYqqVL1qFqPNQwiTTBeqm0ZB0tjPGTQNksqouqoUikKlBbXIF8QsAZ/LXAhBIUpxHBXHUWVV6f9D27/9SJZs+ZnYsn1xj3tkVtWpcwCCaPKBfCEwzdHcSIxEQYD+aj1QwLQgcoDhDEAJ4FuDwAHBw+6qzIx7uPu+6MH8M/u2ZXZXHoByoCoyPNz3Nlu2Lr/1W8tsX13kZ+H0qbLpEfXQA+xuGOpznvDbxE0STdbfzDZjB8u5IuLDK2o8r+uFzgPk3dZLsui9SFzDB9oQ47xnheTCxBL4D1uHdMF+8Y3sB2FcvGz/3BMfjx5C9BK7wHbFNpYlpqUmdPM8RyxrTKeaUNFxYnKdxGR/9l3rco61fcQkfIy++oAh+18nIdggMkcmKaWIteoJ61RJ9rqBG90xLjXu8rrXuLvtODHR7QTp73t9d6KBUgDovXAYkf8esS0N8dPlNxTIlQArvllXrtm2AfgngiEhMNOKIydYtGA+IsrDjFyJOJ0OGxaP+dKWxX0d0FAc7y+gNI1yMF+zNTgRBymzc2a8CUI4ewcSXzdXG7KsYSsA3ynVNjjPxckZcmdtzVjwOZdkUVj6zf3kZdapZRNIvPg7soHxMPPnfmvGxYtyvBkBGESMi/nauEmAuJdl77Lq3d1t9H0fX758Kf21+fSKMVLqN+1D6C8lVYyeuSCb29vbuLu7i0+fPgXPfMnBuov7+7t4fHz86kSbaTrFzz//Pj5//lz0F4fLKU8fP36McRzL2e3WRRzq6XT66oFIbfLnjXo4LzZtmz2lgof9dd324U0AViqQnHDC+9gd1RsHMhx433elIhlRA1seb9a5m5ubkmTQ846uUn3hO8fjMe7urr4iM6qDrsf+EeQyA3xVfBcBkvmmlErfOAkOILkfhxjG+rRk/vb+/h6py4AbAIps0CWzo4zpdDrF7e1trLHG58+f87/XdcNK4m8q87XdX4AeGGDzPXwMZAOy42/InzGhe+tan1BuX0flCLCAr1znpYyd79eEO9vv7e1t8UFOgugNRx5+4jRxB1smLvR9/9UD+xw88amORdjF8/Nz0Vczpt5vZFKBz+A7ndzjs9rk13ELObJ24zgWn8p3qAZhX8wdPUOmbCI2KENufI9EwckIvu76+rpUQMADZsKZLz9ZJ8uVew9D7Z93koWcSaaYK/HNLDwgEb9j4DkMQ6zLGqdluz+Hv+HTPG93ITiJzlXZ89H4+33py/eet/yqbcP2t+haRG0TRFfOXyvzfHt72ySEsO3IlIe9dl0mBYsNiaAZhqHs82I9kRnz9rPFmIdbFbFbNuhD3EXU5zIgf+zKe6rQZWzD8Z0TxpB32z6Mf3ACD34yWcY6ueXPJDAVV+syeuYKnZOITIq9VVwZ58pVqq1ZtLWxjsQukkoSSfyP/fVut4tlOsW81D1OPjQA/cduTPCDeRi//dbQbX2H47gJjJbM5T3GyO+sP7HNeuvY8v+XigYDMLjt+74wCSyYFR9lYtItcwH4s1ARlBWD75hZwelE1D4yHERKtV2lCrP7ZuBLKR/tVhZtqPsluu7r00UIyi2Lxvhw+AAtHL/PqsawcLQYp50lxhERBTACDFsmjJ+Mj+sxBoPzPM8olRyDBwcLZA/zwpoRoADhz8/Pm7V6ObeB7Pf7ciqGmSqDTgygrVxw37YMapaiZPNR2xeQN7KwvrnqhfxhIpCNe5ZxXtkhLPHw8FCusz3pJ7O1PhXJTPTz8/MG3MGQGyhTefjw4cN5j8J7AQfoRwUOmS18fX0tbNnt7W38l//yX2K3yxu4meef/vSnsmasF98pjFpK8fLyWoIUztqBBzmydrycrBmY0bNuO8ZBYWsRUTZesm+DSg6fp/0in0pTnxnipDSva2zsyRVW6xjjz2PNT/z2qV9ep67LRx0bhH78+DHyk7Dn0p7ldgLYMOTBE64ZC3tnhmHYPPhtmeZyjCXB+/Hxseh7S4wQmF7fXuPy8jI+fPhQ5G97w87McBlQAhbw8Wb6mQfgy+ymfQV/B6BiOxcXFyU2oAteE5K33VAfBtXGB4ARrGXb0kPLFgkxGzUZH9+hnQQCIGJbhcT+TUrg4/gb1zSQIQb4gWX4bxJ9b85FZ/ncuq4b4OV5o+NmwYmznhvrfH19Xb5rdpg1B8A5Ltu3G3D5c/v9flMZRQ8hKEgsvRYmiuxnnJxR5eGzBi8kRAa1jBEd8N4VfuJvAIPjeY3f3t7i/v5+k1iYEGUdmKd9iRP94/EYfdqy4gUzLEusUSsL7m3nvtwbPcvyrA9BdCXFLLSBZYnBzelwfB99YAzWVeJs+zwcdM/JKL6/kkDb53450VrXtbR4Urlw8mIyGJ3Afrnehw8fis0xBuZLTCb2mpBsN9OjnyaH8Wt8Dtkyb2TE9yLO+067PtJa9/iwZk5ISYKQCT4BP2Dgnj87ReoqWU+yY1KJsTFHdwvVLoRaweiHeiCSdYIDdbyXxeQH+s99nJTw4nMmvlyd/Z7Xd28G/3/+P/71xvHZyZql8IDM3GCQLjEDhvl7G+icLaEQNjYWGUVEqTFqGILsDNMmiLAQBkceJ6++72K324J05mgFNUBpGQuzGWbj6NX3mFhYM6W+vqscDkxcxxn6t7739PSkDLkaAKAbh44sfQ3+u76+LhvlYDJY65YxsiwNUHCMOAaMCQW2sTA+JyoEFK7n5BPHwhiZI06A+yAXvodTgBVHXylVTtOxAEGXabNTzSDq9va2nJLhsrLLrG7DwCGzCQ3weXGxj4i16PK6rqX0Po67eH192zxgquu688bKPvp++0C6+/v7si7ojtvrskPantrFvLm+K0QEJGzU+mtmC7BppuTXX38tLQteP1ikvDciFYBjvxDRbRywA+SyzHE61QofQJ/NpsdjPs2J4JplGsFT5rkeeprtox4djS3gU1LabrRjbXkmh+eMbZymqWwQxBZZE2/65FkCzN2B1eX2iIiLq8vY68n2JD2QI7CFMP8k8vgqs7ewc1yLViUDPFq6AJiuCLhygl6TQPJ9gwf634d+u68BHbQfdSWdNXagNUFzeXlZWsuceJJgExMAuyTm7BWkEsa1I+J8QlmeC/6OsToOUt01ccXc3G6FXhHDDDAgWPAZPjDh9fW1VBRYByqkgEFXOog/rpChC2ZIDawBos/Pz3FxcbGpZrmSbH9g0G6CCntCNwyQSCIMjNFtj8VxqJKGldA0iHW8SClFdPlUivZUPMd/xxT+zU/WoSTBkWKd58080Oc11jhK/+0buab1AT889rnfn/E50TAmYB1Zg3G/C8Cbk3MntMRC7unr4/fwldiH4xbrhl6ZNGXdTKAZF6Ij3BebZlx83tWj1j+1GApb9vvuUuB+/IfNcW/jPO5r4sLJWEophn6I+VRPxEK/0AkTMMiSl8lvJyGv5/2WzNnrZR/PNRkr64yM0LGIiD62p4ixdtZP3iOZs95wn3YtsQOfcOVkpOu6+Of/w1/Gb72+O9H4N//L/7sYBsGRCXCSS5sRMWgW0gaM0bikHbEtLVpwCIcggxNqKxoI020cgJTWYXlxUWo7wczAnQpwax0QY/KGb8/fMqBvnDnCAML2MH6M3c4Jhw1byhNQI2qWTXuN2RKSP7JaZ+15LPXUBcbF2pxOp8J6eA1IBNxm1DJATjgtC5yPk04UHGCMPCNqhcyBnfU0Sxyxbd+itQFd8Lq7jxIdfn19LWDIe3JYk+xgUry8PG9YfwJwXveh6AMMqkEZwBmAwOdwMrC9JGuXlxdxOtWSqp1ZSl28vtbjLhlzfurzEOu6lD0azANdYd6HwyFeXl4KA5VSPX4SvfERqNgx+kQC5FZG1oO1drmatQM07Xb5yN+bm5tyj5xY5OoE+oW8s4PMLX+8582A81yZWbdbsNke3UUO7EPJBwPksfD8C+RwcbHbMG7YxKdPn2Mc6+ZBwC1BhcTODNC6rvF+OMS43z5pGV3cj2M8Pz0X9gnnzs92zwbEwLwucZpyfzpP/W7tEjmaBUSG+JiW8XP7jn0luuMjZFtQQSuPbd+B0cB3XfLRjAaiJoKwyxZc8m/WGD/W9sNzPa5lUgZ7pxWwJphVHuimK00GtLY/3oMVZq24Jsyr2wHti7gOAGYYcvsdrXgGw6fTKa6vrzdtJugha2ufzVrA8roq9uXLl02MjqhVbNs2a4ouYN8GQXyfdXMlAhLCrHdLzhEf8JVcHztwlaElDCGKMmGR7/12rLEQgoT7oBeslWMdOs6a0yLapS5WVdeZ++l0itM0xZqirHObRLLG/JtYfbHbxdDX5zIBaNELrzVzTSnFkqr+kJi4euaKP3JjnWy7xFiTRE500EnWqU0GiGWQZ06a+Qw6iX8gZtsnmIiFzHQ8LuB/+PrYVlcxW0LSzL3bhWyzTnyQ+bIsMQ5DrHN9gKMTUycvxhisif2Vxziva0znkwlNoDIn/JP1H1+D38B+yzpMdSM4lST0zOtM/GNs6IXjgJOQb8WSVo/+u3/xf4rfen1365TLsBgyN8OJEvRpH2JRvaELdjSiskXtQhEMuDYC46mdzgDNkHENhINQs1PZPiMBJfRCOOeqm2CqgtOXSv8drSxeGMaEE2LxuOYwDGU/C2DYCRFyZB5cm1YdeoQjojhsG4CzWQzCSmvWK6LbKJETL144gDZwuexIQHXpnfXz75TanSQ646eq4CDs8WEMLUPAOPibQZ8fWIUzRD44OgIJeubgQVA+nXLw4wmyODxY4HXN+vHp06fCBrrNDdaeOZAYudyNLHNCmeJ4zLL48uVLROQNoe/v73F9fVMqIMyFezw+PkbXVbBIcso6REQB+5xElEFYBTl+iKUDih0joCMiyjy5dgGRDdsYEQWEOyFDT/I11uDJ2jBnsD4cQoBes7ZZj5bY7cbCZLN2d3d35do4fWwo21T+PscE17am1zgc3ja23Pe51Scn8kNhvqcpb1x/fHwsjLPnD6C4vLyMYbdtiUEXDu/v8eOPP5beaXwXSYITOvb3jOMY05x96PX19aaiCxnhTbvLspSxEYAN1EjSaasiSaPdi/niJwHuMOoGUG3AxZf53hkYnWIchk3w4pQvbNyJv6u99vP4DPwbcjKbS4y4vLyM/X5f2uaIN1yTcRID2nGbJY6o1W32L5nEQK74PTPLZn7N6AOIU6onDboVBr9BqxL6TVzEPt3Gie9hLQDTjomuTPkkKWRMEofP8JzwxYyda/hUMlcwfK+IKImhEwF8MC2m+HoTJy1JyRoxVldGsN/dblf8MpVU5EaM5xRAxnh7e5vlGymmeS6HWnBdvp/6akvIyckPMgG0XV5eRp9ywo2+oAOOM8R8PjPPc6S+jzW+9rGOzWAu7ME+GR02iWR8ZnsgcTAZSzXAlW3WBzs0MEe+67oWMoWYQhxhDT0Gd32gv63/Ir6hT8aFxmfMydU8+wgnQnwnfeO+jI2xQ8a5c8H2iOwOh0OkviY3jrEtCeN9YLyQvVu08jhrosT3PYeKg7fPxPGa2mfxWWNwYzY+i3/6rdd3JxqHwylSQjjnpxGubNqrLTjeEZ+VeYiU8gkJ+Xv5ZCcCNErscpUVF6fhAGAHbcMEXJjBqIGvi3VlMZfo+yGmaY3T6Rjeq1AchgSLk8S5woCarTCoZjwEbXoO3asakc/sBhQb4KKQZpdQBhx322b0+vpaKhrIh0QIUAuwtLw4WeqsxjEMVDfy7+O4PQIyr21t/bER27hwosgQI2Uu3j8D2ELu6BLMiasVLnPi1MYxn9KDPrEuLnuTzNGasixLPD09FScDUMzHkR7jy5cv8dNPP21Ok5jnKW5v7+Ly8jIeH5/i9fUljsdTtoWUn2GR+j6O0ylu7m7j+vY2TsdjpNgCIDsCgjSJGD3/y5rbYrq+j9v7u3h6eoqnl5f48uVzrGuK+/v74ny/fPlS9HUYxhhHzulnf86uAtNpOuv7Gvv9ZVxf92cgdFGc8rdYGGzQrCXBx2yrnaWBkwOc2ePr6+sSoLCfiwuetJuPHp6m99jtxlJF4CjZcRzLQ/Eys3yK3Y79BvU0q+xP3mO/v4iuS+fnS+zi/f34FYiyrgKWsg86xTy/R9fVc+QBvpeXl/Hw8BDX19dfnT7CUdlXV1fx+vYa78dDcdDs08Fu8SkkR9i+2WeqlbSBLWt9CjVB/+npafN8FUCOg6zbDQwIlmXJD346HPNpOPMcu2GMt9fXWOclhnEXl9e5CjWfpjiKbX59fY0Y1pgj4hT15K6UUqR1jdPxGOMwxNjnPU1vL6/x+PgYq2ycs/jRbXTFFZGI2AARKl4cpIBNsU7oLnGprULweRLml5eX0j6J/roVlCDsNifWEL/UVhoAx9gN8cTPkcBvcg8TAbY57kHldpUOYJ9cDz8PIHO7SDsm4puBCD9JMt0Gh2zapI/WNMct/HDbvkrCg90YyLiDwYmjQfiy5FPTYj1vrI81uuhL3EZvkCnAqPVVAGDe854edwpc7C9i6LoNAVLi4jjGmjIIfHx83JCQ+ElilPHJMi9xmk7RD310kU+Fi5RiWdeYl5zcAN6dcERsW5G4JtjDmGJZlo0eoJfI04mckxmSRtsiftoJhMlf5mfdQjdZZ+Tq6xFrTD4a+LriYJCPf3CHhMfl6gKVA+brSmqbYOVxLDGIiPHfGCf2hH85HA6RjxDsIpYl+qGPNcX5aO8h1lhjUKWftXLccPux58R9+R2Ms6xzzCskxpKP0l0qnnTHBHJ0kmE9xTaYl30SsjQJ9D2vP+PJ4P9LmaiBfHbyGWSt61qcDMDxdNr2mzGh7KDrmeR8BsdKMMDZtpuaWHScVlumRjh2THyfHlWuc3l5XRIcA47Mbhw3zh3HzTju7u5U/ejK5zAenDcJGE91JYFyMLEC09bC2H0t5ufNumbEyboBZXYCEdkRPj8/l9NEaGVB0VgrgpgZvDzO3MLCOtKGAIACrPJ3AwQbKy/0yCVjVzkYv4OhKxUGDSQfPgcaphG2u01EYZs/f/5cmH6uPc9zWSPGZ5kcj8eY5jlSXytkzLnrunx+durOm5kPm0SZ4EkAiqhtOMfTsZy3/fDwEF++fImff/45H7M67GI+HwmKY6C9BpaRezBX711xWwwso+2Ez2CPMMzuJzUwcv848vHmcJgsf55/m8HEjtrk3Uk8MscRclIc9ovOceoKa2hG3q09ABKSgV9++SV++umnAiyYr50ycseW6dt3y5NZIea8RsThVFsjawvXXJ7s6nlDFry9vZV9BG4RHccxumGIecm68Kc//Sk+fvy40T/kyyZpfCJ+zs/umKb8vIurc0sgPsZByH7OVS2uS8ueW8fsPyIivnz5UuTKM2R+/fXXUvH0HGGAzYBC4DhJYD+ISQzmC7iw7SJnJ+C2Q8AS9yYRxCdzL3wfoCYiyppiL1zbVWZ0xOCKcfk5CFdXV+XkHx/QYIaSPRv4E+7BusDecw9iAEDcSZyBKzrS2mPE9lQcvou+Un2HWON9k3nYFOsD2VRY3/T1w4D5LMkx8zwt9aF7XBc/bz3Hb1AdpHrBi+u2JxQRV7uui3VZo1eVgDktyxL9OESnKgE+y5/FjxgUOwbyHZLQLlL0Z/sx0IyImNcl5qU+OBdf7eTBPrFtcQL8I1uPGRLTrDaJO/6aMeFfkR/xgu/xeRNtrLll6OTD47L/4HeuYTzEOjlRQZetu05CnGiwjsw1IjanTrFeyLq0Qs211Zix9MMQh9PXZIb12/M0JkGHGZfXAh2A3GMeHjN2XCoq63afB/rH9U0auP3O+JP7Yvu2+3/xf/mf4rde313RYLEYMAucFamCAY4XxPF33bA5p7g6ujHWdSngxAptUE9As6AJuEyeKgNO3cbN4lrpESKMv9kN5sQiwLTRB2zgQWB1wOC7LLjZJQI+82Ie3sjNta1cBA8HTeaGolAa57MENtoeXFLkM+6XRdlZn4goiddut9tsQByGXex2+43js+MhqHjfAzJALimlYnCs0fPzc3GIBHq34fCTe9WWmroplxOeCHYG8jzwyowG8oORNmvMSQ0tE4CTLuDkPAYcN+t6dXUVXUpxsaunGllvcXSAZgDp6XSKy6vLmJd6jNzNzU05AckOihag4/FYEik7b/TGTgNn4XJvSqk8F8LMFuuI7jgRxDmyRm6d474OegQh24KP6sSv4DzRGTb1sxb4CI6wZYzTNMX9/X10XVfaLRgfJ/KYFTU4RZcA9KzJy8tLAZqQH7YX9m3gI105AMC+vb3F4+NjTMscT8/P8cMPP5QkvoLyVBINBzGqF/RpIxOC+byuESknAT/99FNEROnntj6y/tgJP92GApjiLH10uk1uWF/aUCKiECOsnVlE7odt0140DHlz+fX1dfz8888lmfV9OL4UH4xeovsEbhIqdMmtnoyXsZC8oNPcF1Ijx6fK7L+9vRVZmDDjmszZQA/yBiaaVysj/BdEBH6b+biy4PiFjjM+s89OtCK2R4UzPwN/4jUv4oYPQgD4uM3Ke1YMIr2vqW3XYA2QmxMfAJKJPcdQrusK0PF4jG4cSpKCnZKUuULLddnzwnowHvyVCSV8P8nhdDpFWqP4G+JL3/cxv7/HxdXlRo7Mu+3SQAf46SQjQg+B7PLJR/zNycGyRgxaH9bV+IcYyDXNnDvZMUYBD+HvDGbbxN0HFRATwQ1O/JCB45eTWGK0Ewx8nCuEjm9gM+bMdR2r8Q38DazkNSYWIgfL+Hg4Rp/qVgF8GXpl0sNk1GmqbZ7s9QHreZ7oiBNo3wN98Ho6QW8POHIVy7L0v/ElYGtjM9u1MW2biOE7v/f13RWNv/rX/68Nc4GiZCFsQZJZzHWtE3TbTL5WbXFhomaxh2EoJUpO8cDZECBZKF8Dthunj/K3JxrVRes3i0YgzHOMDTgsgtPiocwYuEEYrU52pIBDBxIW1bKyMeNgpyn3a7PpD8Vw4HJyg1ICvFg3VwlYA4IW7CfK7k3Z0zTHONYjBrkHjhfAxtrYgaLkZh3Qp4iapDJ+GCccilkyM4u0oSAPnIeZIVpJ+Ix7htE7HBPBGoccEfHHP/5x00rF57uui2meox+3e3LQld24i6SARUBu+77NJq3rGsNuiON5MziAGBB7fD/G+9t7Ya/RNbORduQEXPTPDCd6xfdwugQubAR7MXhAbq0DNABBHoBSKg2MCZ0xsDU72rLoBMq2DdEthcyP76BDJJHv7+/xhz/8IV5eXuKPf/xjfPz4sfTEM0+CCBvW/YwdfBPyxGe5b5Z1RIeXJT+B+DTVPV6M6eXlJWJZYugrS+1gybipFOMPXl5e4vr2Nq6ucwXO7RqsBS15zC1ie7IeftoJfczbsjrfwX8Cng+HQ0mC3M+OD7be8eJELTOcACBkb3DOGEzKkKAxp3VdS+WWsRBAaSklRgAo8J8kh9i+2VreJ4GnVQk7sT+lkmPSwOAJXXFrCjq/rmu5rtso8EUmaJBJa5dmRLFb1pexO9lCn7AjVxRJsvCPBpYGytzXG98N2nhZzlQVqBRhp2Z+8S3oSESUKrWTkJJ0dim6Pu9v3O12pWLGuEi8DZZZQ2+oRU4mJT2mdc1Psu/T9pCW0gp7HotJUdbERJmTJRNBjJk5H4/H2PVDWY8Wf61d9hHMDb1DL40jImKTEJgsauMFGMUEH7jDgNzJ47quZez4R+YGJmiTWcdAMEZr+4yL+xovGutYlp4Xc8eGkDtrxvpwD4P2cRzPD+c7beIkSTvXRU8Zw7qu0Q19zLJ37uVqEj4Bm2SNkA/jZx0tW3SVBMyYApstMly2e3gcN5lr+5BK6yu2xvo5JvR9H//yX/2L+K3Xdyca//av/tevmI8a/FNhngDbHLW4LPWkEm+izk74WFgYB1YrvbNpHC+CBNSYKaNiQPA0O2fGA0PLwacq6DzPhaHMr60iwKIgC5wlTrt1xB4r3wc4kw2zCQoDBkwQDMwqoQAtk4aCsonydDrF3d1dMSgAGMbbjtFJih2vkybW6f39WIAja0bJ3Jm696hg8Cgt68S4cfiuBiE7WGQcjNvbeAHmDICPx2OpUngtzOSbOTMgdtZvBhVjdumy7/tY0tcn8pwHEmM/FBbNwNwBDNkTqHcXu1jW+gR5AMXhcIjT4RTLXDcGI1fWmTIuNmqwZmACqGOtAI4RtYJnVor5mkXxNdFf2wpr7CdvO/mBlb6+vi6gED1oN7yhV8gclhM218y7gyTjYxwtwwlbif1TZTAAhuSwjKmgmPTAVkhoef90OsWyrjHs6rGlTiTWZYm0RgGa05SfT8OeIezELP+XL18i9V388OOP0fd9/PLLL2WdSKwBIcgMXSc5N8DBn/RRCQqDPYA6emygYSKGebEObkVBn8zoelN/GwMc9Ekc0Hf8KAEUYGmAj923Y8eXci3bVzsX/k4Sw/rgm9BTwJD9nRMtfAq+5/r6uuwxMoghkeKaTtyd1PPsCuYDqMG/208iK/bSMC/A4d8F9PmJnrDmXBu5ep5OSHw9rmGAhV0a4LDebkHDFvmu7xNdPjqa8fM97ARW3ICfeIa+cG9sF3/AuhUdOB7Lw9HQX44B7oY+Dk1HgatU1gHbFQDeFRyqSmPXb1h8X2da5nJ0rx/8SPKITvN52xPrwBqgc/hQV0QNYIkN+DA+b1LTpBD3cjyw7BgzhKbtHttm7rbpFvRyTXTJFQvLwL7F+oC++m8REX3XRxd17zEyMXbCJvj7uq6xpvy4V1eAsWHjSd/ffoq/ISe3rBmfGSfZX5m4j3nb3tiSzYzJ1zNebW0HW4zI+6L+8r//b+K3Xt/dOsUEAdVesGGoC+kMLgeHPOCbm5sNCOQhNV4os70EDRwvmTGMHQ8rm6apPPDI/fwAldvb2wKM2MSGo85GOcU4dpt7Ohiu67x5yq2VxWCOBSEAspAGp/wHGwioNHgys3d1dVWuh/PAwEmg7BAo063rGj/88MOmKuIjSQmOMEtuZWD/hueFAWXnse3z5om9bkvC0G3gXAcjIulpWRh/FnDn5x+YWXeyQMLq/TI3NzcbAM+acm1YO4KtGXWDU5LD5+fnTQuNAXt3rmjQ3gLYmec5oq8P83OCaOBimaSU4vLiMpaoiRStFZeXl3F8P8Yy54DK8bCMmXWu61WDXURlTFyFYwMu8vYJTXZGOCuCy7Lk/U4fPnzYnAjn/RgOOlyLNaM6iV4auHgex+OxBOKW4XXi4oTcDhe9QX4OOPgFyAMnsF3XFX9DoAH48TdXd5wktQnRzc1NfhpsX9+DjZymKWLJT6F1QvfDDz8Uv+R5TFM9bnPYZzv+5ZdfCvhjffCPtMGYLRvHsZAZTtj7rou0RpkzzD8gALuB5OGejBvbZ13tzxzgXl9fN0d2og+uOu/3+zJ2fFZEropgw6wf4A7d5rPI2PpAMjEMw1eVcq6PLkOesZ5818CNGIYvbf0m4+i6Wl1d1/yAOF7YDLEWW13XvF+PZMFEBWPm2sgJXcQf8r1lWQqBgD0ib/Td5BX+gSQeP4sd86wVs9YePzLy/j/uDUnCwQ4A3daHeJN468vneY41Klgza43fhrizP0Tejk/teIkjvOoRuGscp+OGxAB/rFE3NTMeEjxX2Pnd8agFcqVi23WbZNYgOP+olQ7WphK5U1lnM+7Mz76L+EcboZNv+0TsDX2xDEss7LpNstP+3TIiZnpvUQuknQD62hHbTeRcHwxp0qZUnc4vdBXMxt5i5lO+k1LEoj06iolOmjyeiCgtrawr98LeiBXohedpH5tSPb67rntNrvjp9vF2fBBZbefQ31UF4zv+rPErekCM+Z7XdycaPgbQRjJNp+i67VnACJtEA9aSieXvR/BAMl5OPMx2AlqoiDizxcmhwCzsfr/fsJywGwAKwFR24jkQ8HRd73OIqOeFs8B+EiWGC8BwYsQCYfQ4Wm9giqiOjn0QDt4REb/++msJlA4KBJGXl5cNw346nTatCwBfqkL0UF5dXW2O2uV7Nn47Er53cZEDJYkQc6caxDiQG+C867p4eHgoQcSsjhNNADgAza1WEV8z5T4BBIBEe5pbtyLqk38BTyQX3hyMo0LO6NTNzU2plLHm67rGsi6xTF+fWGEmjE23rpJwz5RSkRsbYqdliki1ZQV9e39/j2VaItYKRMz6ApLoK6eqhczMDLG/CKYYGRm0Izs+1/e1tRAZPDw8FP1Gduu6buzEQRR9PJ3yRueHh4e4ubkpVQ0zJiQfBnt20vgNbAPZImvGQxBGTwHqfd8XoACY8IuTybAfyA50GKAUUXug26NGAdyn6RTzWltDXR2bT6fou5q4ktQ+PDzE5eVlXFxcxPX1dXz69Glzv5u7uzgcD2Xd0QGPhwoXIIT1AbxgpwVcRH16rNubsEmz62bJsB/8q59PQNxApyCesEUYemRicoe1xobQJds1Phtfw1pZHy239sntXPtbJEbL1jJf3uO1rYTX6qmBBPrLvG9ubgq58y3GHjla1gbyjIm/cw8AjVvMDFbzMdhdiZ9c04Auop6i4ySccTmxMRFgQM88uS+2ZjttQQ2/M24TNPgd+705aisZa83f3erDfYmv+CDWkeTHCQE2Reyg8ohPP51O8fvf/z7H/L6L6121vbZtB5/EWrC3zvpiMJj1YPtQXXR9WZb8ZPBlW8F114fBIWQTY0bOYCCwDT7RMZ3fiZXYlNcYvTGwx0aMB0lckTFjwO7RY3SBcaGL9kvohlvCkL0JLSc8zKVdE98X2Q3DEPM0x6xuCT7reGqMWsB/ipgUZ0w68XnrvpMgrou+kjijyybYuJYJdO5RKkX9UCqokHjEeNYSvG29t5zacba+77de351otD2OKBKL/vDwEOM4bJR7mmovnxmUrCCH6Lo+8rGzAA+eSn2MiFq+AxBS9uU9GC8CvzMxAmhtLcktUsuyRt/n5wYcj6fY73cxDJRcYTz7GIYuxrGW4Bk3DByJDs6KhXcmzuf4vgF0C4BRMGRqRgdlszMxmMWRmLnC4eQ57uP6+uosjykuLi5jXZfouj4+fPgYNze35zlEYdBeXl5jv784A4vlvLb5uFHW3MEdBizLetgcg2hW3OO1AbnqgywIaC7PmpUB0CBbjAcwiB44cWVt3OoHCAEYwyIgY/cuO5Hw2vVdPst6nedYpjn3z675xIppmjbPR/B6O0DC5B0Oh9hf1AeezfMc4zBGWlOkNcW61B51AgWOjsoLjpKTqFgX9Nd9+cjJ+yYitoEKx8O589Z5HDTjiYiStAIQzNzYThkHwBO75p5tK5jblAysDH7xC9wXXXWfN3qB83ZrYcT2yESqdvgygJMrP5Ai6Bh2cTqd4vn5OW+yPzPM+90uIq3RRYo1UgxdF0vXxXE+j2FZ4uLqMtaUYnexj+vLfPLQ4+NjsQOYfh7qSM87PiWlFPnMsxS7/T76fog+Uoz9ec3PupWPrx0ipS6mYwaLp2nbAkRbA/LgWSJtAgvr7DYl7DMiByf8MXJivXhOASw8esVm8a6re9XwbxxB62sRq1zdtP3ih2ipgYRyJQqbxE/Yb8Dkk6ygY644MEfmYLkBVtjvwZHGtEGZWDCrjq2h+9ZFxomNowPYEfrMd4hDbjXme2YssSlXlZgvY8JOGVML9g0GIWsAmWZcGbPnb8DJPRiPweSkSvdprk+1niPFvNYuDANs9NHgkOvZhphTaUfpukjpvOax5mdZpPOhcdNUTp3iu2bu8fGtzbhauIkpfe7zP52mGGONmHOMmeY50vlZSSSJgHrWrU3e2L9i/IT8qcK7oo+Pc4xwtYK45EqTyWaTxn6KuPHgt8hD8BR26b0Z1hXwkRMGE0XGRnzmWz9tv06QmeeJPTvLHGldIlKK66v6LKIlItYuxXGaIqWIaTo/y6wZrwk+657bPRk3yS/ycAXJGJOE1aS2Mcqy5GNuwVtcw5/F59qvsIaWOePBj/y5r+/eo/Hv/u3/vgGHgA6ctE++IJu3o0BJAXhmvswiZHb1JdI32FwEioOGVXl5edmwdRwHCUDPJd7L6M6M4eFwKL372ShSCQJmkLgn2XO7yZygAwPp9gQclB+0xQk2BBA+y3WsRMiQygLKRssUc/PY7NR4UnBKVXlgS2D9AUoE7pRSPD09bYA6c8HREvjZN4GTNvCw0zATZiDCi8DEfUgQ+b5Lzm3gAQzZIAAFToTsFGF7ubednuXXdfm4VvfqYrAkjjhX9I419dn4TrKZnx0gjpXxA3YvLy/Lk1HNtgM0uZcBCc78dDrF3/zN32wSPR5SxsleAEeSKwKLA2/E9ig7ZO+5YAd+j75xxshn8An8bualPcmJdQBEozd8n2vglAG1VATtbyLq3iXm6TGbkWJ/lBl15MDcnZz5d6ojZpCprJHoklz52TDTNMW0zDGd14n2nHKsct/HulSdj4jyvJXTUvdQ4T9Zr8v9RZy0qRO5Yhust8fLPdBbEyjotZM9dA45G8iR4OOr23YBA1y3VOJLLFv8OEkILTusI2vhtin0EQDFKXL4OD9sCj9EFZT2FbcEkaAYHPFy6y7r7DY992rzmYuLi/JQrhZQIV/Wkxe+jTH7fX/XlRhfF7skTvvaltc0TeUYeOTcgiH7NbPHsN/YKzrh9lNfr/XHzMfJjn2IfR3rYJ/owwaodvi66Eo7bxOH7YvYYjkiP4g1nsPC9RwnuB9EHuM2iHQschXfCWILNE0MMX50zraDrCC8HHcjaoKKn8PPMmd8JLbtCrHXHbm0hCsydZIKXrBvdzsg/6EDVNIdq7werC3z4nPuHkFP7AMZB2PFll2ls/90RdL7vpyEoxdUkPAB6CFraVzjliq3sxtTOQa0RA8ycKxKKcWQtscRm4SxvwdvW9eYPzHYPgC89N//y//uK3tpX99d0XApBVCLsyIDxVG4ZQFwaeXAQJgA1RKyt74fYr/PWR7HX5qN9WknPiWCwM6pTFRBcp/1LrquL++5fehweCuOjazbbC7BD2aTRQCMIwczfzYkHLITElgEgBFyYWwE067rCnNnJovEjnvRh8p7BP5pOsXV1XXJnlEQBwlaS9Z1jfv7+829nJEz18PhEHd3dxtGwyd1mQlyoHbftPUEJXewcMCEtfFnDDQBmIA3jNbACgPz3hTvZcCBkSzbyPm+Wy5wbswB/fbhA7QJYLzu83RAMDjBKT0+PhY9cHC04zaTi3yenp4KIOMIVeSBg2BMDmYOAFzPSTLOx/rD77ywF66JM3ZgNHuJPvnhWCQpboFBBwCHyIu5AzofHh4q07TUY7HRT4CAgwVzX9c1Pn/+HBcXF3F3d1cqpcyH+72+vsbd3d0mUbGTh50C/DIGAjWJKnZUk90hItWnMqNz4zjGci7fI4urq6sC2IojH+rzGEhm0hr5OE6RF61/cAuCddN90PzNzBnzpXIKKMfHo1vLUp9XAKgGaHI9qk+uZnh/CIkX/zHmiNgkzdguAdyHFnRdV45J9nXQBfQI28UXo2/2SWbAsQ8C97qupZUT2fmzrBknmDkpt96wTgAZrmHSgxfXQK+wAT5DHDZRg2yQpaspbVJtwIbvNfONrzcoc7uIbR7/yfvEXPsZ9Lf1F8QQj5WkCGIAQFWSuXMl362uTnjR4dZHYtuslfedOc65aoe+Yl/WUXShTdra/YGtT0QnLT903a2BxAPuydp5PvgB/D9x9fHxsWAvYzR0hznwfTCg9ZB1A5+0sc4+H19F0o0u4YuJgfZPfMadHSa6WlzA9/leS/j5hQ63lTR8HnaLHzLu4r7co/Ut+D6vC3qPrPi+/YcJgDapMnYwGet4XCpRkaJrrtEm5k6isGNwm1sq0R3bwfe+vjvRYCG4KUwrgRFDgclAKXH8bBZ1qwIsq5nBHGAu4vb2ppxUw/cIvPM8b07rsIBxlDigeo7yGuuanfXNzU28vLyU+03THLRqeTFZMK5P0DBIwGjJ+Hg6rSsFBHXK1YB+5mym1vIzgERGgPcPHz4U58kZ9jhgAkgexxDY1TAMpY8Y596W7Od5jo8fP8avv/66aWfi+ig2TCUJF4bmNiiCCmvOmpDY2KHhRDEsAiwVILN1yAJ52JECUtwGYebRlSPGg9N2AG0rKWZPXUJmDjgZB3iqBawfSfXpdNo8FNAyQ48iqgPEoTIWB0leyOjq6qoAZq7h0j+tC9iTdZ154Fg5rYVgg90S0JzkWje9hwFZ2DkDLrqu2zydHR1FRwg+Th5onzkej3F/f78Zj5lAH6ELkPDekuIAlXRzzK0Pj3h8fCyJDIAG2bGJnuCFzqJTPjWHdhtXz06nUznT/eLqsrCTVDLKk66nOZazfdjG2yoUCTdzTBFf+R50AkLGlRBOCoT5Z82dsAGs6OtG3uiAdbNlhp3wOPA7ETWR9bd/+7clPvR9v2mHI4jjY/FNyMSMt4MiPo/jaJm7QRZ2jo7yH3qHv3flgWTE+1jQa/t1y9vAhPsBrFxRxs4NAvF5xKZ1rXvInIwY/GFHvl6bkGCz+CJkT/xzFZ7vuLJi4Ij9mrF1tckAHL0xUWdfQUJJ0oCuIC8n7xFR+tE9LwM8A1vkxLhN7hC3iB1ca13XokP21diakznkRSKCHmADxFcOCcDur66uNvs2/YwykgviFjrj9hzIEuaDLrHmrIH3PpkMsc7hK12ZcasVf8cXGayjA/zNccZ2z+9tIss1zLbjn50QMzYTvYwD2YBVbdPIBPtjfqwba02MZf1sQ06GHJd5nzVsE0BXJ60TTiwguZCb297wAYzT/oIx7od6HDD3sl80GWm7cGLuSo3JHtv+3/f67kQDpQVoolg2JJwpIMFKRtLBWe8kIGxCtYM7Ho/lRA6zV8uyxN/+7d8WsIygrHAYDQ6yltj7DVgheEZEXF1tn9oMOGWeh8Oh7PxHYVEwszzzXM9JJskxmwTbiQMCGBiQcW9+R6YolkvUZl29KQqmJzv9MSKqsmCwtGh4/TAYt5G5XEiLxDzP5SQU34sg5CTADFB7egbzgYmc53mzFwjAYZ3C4Mw+sR52pm0rh5lYOwrGxfqhcw6YOCRXYJgf+kZw8MlRzL0FELBPzN8swbcSqtZxkOTM81zA1zzPcXNzE33fxz/8h/+wjOnLly9xf39fbGEcx3h+fi6B0OXXtm2ANXKS7cQBXSOQARIMWDwv1hACATlja3bC6KCZNGwDOQNcDOYc8Jkb+gO5YUYHB8wa+wnaPio7orabADC4px0zQIcxtgyb2xjwB7vdLlLfxXC2c6piyCKl7QPv0Ot1XaPvUuz2F2XeZoaHYYx5qntL0FkC6/Pzc6laMX7LB7/i5LPv654gfLBb+pAhdujWC3yj1x2gFVGrkGxUxm5pe+M9Jz1UNN3uit51XVcOF0BXXX0BtALOqAy0TDm+xEfJGpyibwYVyMb7TbAxExVuv2GMJKX4KidJyNmtVqzv4+Nj0WkzygZwvKyz9qv8jfdathg/ab9uEGR/S6xh7N6rwZysa2b2eSE/Dstg/RmTK918Dnmu6xrRd9EPdc+j22FMAiFHt2axTtZ/xjrPc9zd3RUwjD3jPwGuTszY/E3y7EqhE+Orq6vo+37zgE4D97u7u6IbJL3ImGuhPwbOrrbyeeIuY7eO4RvbJ6V77I6tTlbQC68v38cPoEtd1xWytCU4np6eStxyBZeX47ptxBiJtTEZZb3HL3MN719kfdE5fragnrkaM6CbfMYJlsG9YyQ6is7YxpEx/s8xzLps8i1FRFq+br+03wBvtXrPtUiOfS/m872v7040AOxeIPem4agN+hjw8ZiPQUWZmBCGbSXIjqrbBCKX8v/xP/7H8eXLl011xYtOoPBC5XGkTUbMdzOLsH1Cs1lNHOf19XV5j/9gA8ZxjE+fPhUHB5CKqEeaWamQmx01hg4r14JcZ/Vs6ALkfquFoso/xbLUkjPACYBLC4afiwFQwPHhDEjwUL7r6+sNeAEUO/C2DJEzY18bBtdByM4FvTPgZ0xmVdAtAxIblg2Ga5FA40jMajIOAqBBkq/hBNXgwo673dTlRN37LDB+dNqBBh0DSCBvessJqHz3p59+KkwOskDH+JwTK9aWwGpw6LlH1Oqh924RdN0D7haVNiF1YoWtAN6dfEZEeWq3Wzu+fPlSAD3XxDYI7IBcKi1U07Cr3W5XqnPImvV2sLcdAD7xFe3egb7P+zXMyDuY8DJbHKm2EgGs5nmOeZpjv9s+1HBdzyfp7cZ4O8vHFTDkmWL7jBxkQOsc/pd1Z0xu5QCAAMqRB+0q6CX+mzma/TXQtW+3/4jIcYYjyQ1izcD6VC/0wFX1da37+F5eXjYnyuEDqOiYLGHufd+XPTCWXQugANxUmtBbM37YKfZrMIuMsEXWm58AIn++9T+8bzbfem4Qhn8xE+r4QlwwqPJR7WaKbbuMz3GtTahMnKEjvldKqbSZdF1te2ONmUsbPwDPvg7jTSnF8ZzM9X1fiLmI+GpDP/aJrJALc8ZHGHRxTXyq9YcxmyQEnDNH/CJ+Erngw01kee8reuZq/NXVVRkfcsGf29/yHvNFD7g/6+WT6zxO7A2d8ZhbgrmVqUlN40frJuOHFPDBIJBqrHGbvDo5wlcyf5OFjKGtxPF9/BhrCg5qcYb1k/chrFtMaxLNsuBl3cVO8Bf8vU1OuK6/27YI5oucjy1vkhEnME6SsS/7htYHoAv/1SsaTBongqNg04wfwIYCuU0qombjp9OpJCUYOkqUWbXbSKluOCK7jagnihAcrPB838K+ubmJ5+fnOB5rvz5GyGJPUy1ZGRAjePezcj/GZsW9vr6Oy8vLzekiPLHWLFfX1SMlcTIwqbTOMB47bNbAStECaTv3/Ld6ZCyJEawbPaDTNMXd3V1ZZwdxZ/+sKSADmcPi16SushfoBcAVRUUfkNU4juV5GTbovq8Pe+Ra3Pfq6qoEeQd3rms2CH3l97bNwkZmxi4iClglgOM0DNBwtozZoARQx1pRzeM+BuI4OINR5owNcC0SAb7DuHAk6OY8z/HLL7+Udi3vMaLyxvWpOJGYurRrYOMWEZgjAuQ4jpsjE/f7/VdMOePy3h4CtPUL+Xij9/X1dQmErvCxRqy/96rwfrWL+sBB7G+/35fN4PgCgjL+APsxa0Swx67ss1g774FwhQuZZB3u4+X1pYBm9CatWzCJfh0Oh5jX2oJkXziOY3QpxbTW/nmSNrd2OllmTd7e3oqto+fzPJeT7VjjthrrJzA7qKGnrs5hL/hrgBigCiaz7/vS4sV1fYiF97ShC9M0Ffu/vr7e6C7gA1+LHXJNV8kAC24PA+jxHs8iMdhBLwA4tMdxf+aPrwA0OkH0WO1nI2Kj49g6ZBV2gr2ZTcVX2Q+y9k720C+THvaZroRwoprvxZid7AzDEB8/ftwQJtir4yPrYdLKeuhDTHy4AnpBizZsv33p/f39BiyZ9LTsaXHFX5joIQk38GbuXJc1Zp3QfRNM6AfY6ObmphAjfd+X1m6SL/AGuoCeplSJQduy18igE5DIgRf2Afa33k/SgnTijQkqfkdOOxEjyNZ+FNtBLpCsBrgkQW07pxNT3kOeljM6je47yWuTfyfJrCX4kmsgK1+HF37ILb9cmzFzT3QGf2t/YJLTvpLPOnnjminlpwMiUxO0KfLJl13fR6zbaqhxEWM2luTe6Bn655/GKX/f67tPnfqrf/1XMY7Vkeebd9F13CgFZz5n0LSc/5ZiXWEPyeJyOZzAzWJyGlTX9THP1YgJjBgUAMXADDaLsWGQfd+fTw+6iNOplrwtIICC23G4/tvbS3Ec9Fi2TDQG4QUG1OFAvXnVzs5OgYVFGQjqBAKAhqs4GaT2MQz0+L/HMIzR9xhDZQQBGcjFLK+BCiDWLAqO3POwI8bpkuwYiBZjiNgEtK7LJdP7+/sC9EgazALYkfO7WWaCQ5VHZaMYO87CDsBsB2MniYM5NUPWsv7oAfK1obKerBUOyOws44+oDIcTMa5tuaLvDiBOQtEfggDOmM3lgKsff/yxVLEAMBywAIBzpQr9Y80ACcjJrKvngS4x5tfX11iWvKH54eEhbm9vN3sLCEytc+fpu6ypn9HBy8G7bdHgd3SQfzM+J5stM8t3YK/tJ6yfJBCufjnY48PcgoGsImUfejoeY7ffxzxNkbr8nKJlze51t9vlYNHVFtO0rnE8nmLo+0gdLRj5+SkvOmHMNujE1AGZpJN9Ufb1zMWtduibE07bgQkT35+gZntDNq4+OKHGx7IO2J99OP+RMJoZNkCwrTBegKxJLVdkWqKHOdhWDFIYP3tq2mog98YXuKLpDb9mIC1v+zBsnrlib9ZlTgyzDyWZNtjwhmKzrtZVdIC4Yf9qP/atNXZ8499moN0SRiJDVZFDVLh/SV7HIVLX8QS7cxw8J/axbuLruq6bh9Lh1xzHzNybrIKAIcZ4n473cRkocg2u46p2RJQ5t0mIX9YB9AqZ0/4I2UOctnzQS1cRIFPw4dlvztGlbmMnldFOsazLV/ZgGyEWuzpqwgT9KjFujTgcjud7n2IYOEXxeE6c60Ey+YCMfFy/k+Suzxue84ML+5jmKR8Fz1p0KZa5JlEmELP+xRnHdrEsMyoUqTtXt2dtoO5SdOmckI5DTKfzQRV97WaYpun8mbonOGKNlLpIKcp7p+kU40B3Rf5fHucS6XxKVOrS+XjavqzJMPSxrpExtdah7/pIKSLvyT1XURZa5OZIUWPdNM/nxGSJsa8nf/FCV7Bh75vKurt90OW//Ff/U/zW67srGrtd3cBb+2FzBGwNK7/WyBuw687619eX4lwBLUwMR2R25f7+vlQ6CBoYhzNErlGVZ8vkZEeVvhIQ922Z7woe65NJAeaAIJfpCYKM7f39vbQkwYBh7AYiJFHc0wHfTqpl65knAWoc6xnzFSjXpz8jE1hqsyMEFja5IhfWiTYLGHKPqwUdZpfNlAHICYJ2nMgIB8WcADiea01i5816MTacqx07a5QNpCYUZsvcww/ghLH1nh/0jXVDvwBC3J+gwf2Yq8GPWUquj+1Yjq6S8BmDV+QDAHAyGZFZPJI5xj9NUzkQ4U9/+lOs6xp/8Rd/ca785aeN02aAvRNYYZ7QAdYIHSEYIhs2DmNDlp1PZHI7k5/VASva9s+TILMvhXkZzGFnyM6yZE8NMnY7BPZtls/VAu5nf+fEFjsnKQfEWC9Yi8KERl1DjqSNdY0udTGMQxxP9UGeYX/TDzGe1/3q6iqWeYndOMbr+YQlJ2yMHbvDb3tct7e35bPruhYmkfuxNlRu3SpmUGVmEvvHH5hAaoEY92bjOjKlAgxAur293dgwoBu98PqYDMD/Mn/skoRgnufNQ+VcicTWOSIUn+xKHvP2HiwnH2YzbY+03OJ3eKFzEbV33EkScRT/bsLHiZT787G7tsrNOrpC41YlQDp7CJApBMI8zyUpiIivQAprxIv38HesCYQi+vetlmfWOCcTEetS2+LWdc2gsK9VYsuZ331iWutPieX8boKKtUfuVB3M8jNmAzSSKT/I1jECn+UYb9LFxAa661ZpEtviJ84vt+c5CXAyERGRIoNpfCj3LEl92p6O5OTM8Y7xOT54ozVrmAlSkt+6HwbSFH+FrI/Huh+OtTq815PlUuqiS3UfQ0opYq5PJUd2/G6iynpZEuy1IfvmNeIs1nmqlRx/dkl0QVQMkT/XxbIoaU21+yaveSXsIbQcxxgzicq6pljOCUNKKfqxPrrBSX5KKZa1HkAxibzoUk1eWXOT9KyjddSxxL7st15/xnM0/re8sOqdjYjNpm4YfysbTpgA4DJ2xPZJsi8vL6W3GsfNxm0HEhYrooKsogxrPf/dYPN0qo7CWXhElKQAMGSHM02nc6a7PbITsEDS5dOlDEScEOCseMbHbreLl5eXeHt7i48fPxajtXJHRHlOiJMofmZwWU8Am6apPGEZ542cDTpa1hhGlveZA6DOzIjZHebFdUhMPFa3PUTUzWQ4xm+xagQoZO5AiR4QcGwEbunw8a4GVU4ckLfnBJBoN/O1wMVBn4qKAzw6w7o6qfCJNg6y/OeN2mbkDKBsZwa83oSMvbZBD/A4TVP8+3//76Pruri/v4/D4RD39/cxDEP8/PPPBehbTwgeyI25k4RExKYtL6L2+jIfghTAx9/13Pzwwb7vN8+3aF2XgyNr6ZYdB2cDH9s2bL5B8ul0ioeHhwJ6HLAcZLEXfmfd/GA0A1yviW2Sv0EaTMsS427cOP9SZRoqa06bkE+iwQ94ztgTLHerb+xrcGJi+eIfSDqoKDJXgFbXdQWYsq7tOnF9Ek1sguTBBA06hmxN0PB8GPxYRGxO2UJXTDLgC7z+2AfH65oNjtgevW0/TXWYtUUfWh8J4PH9ubf9TQVdQzmq3ZWfeZ7LKUXWeQMmqjSMifd8HXSljad+oXcmQnykLv6If/N9n5JEnPeBILQ1uiPAeIC1NYHEuuKf13WNNOS1IdmGJLGP4VUS+7ONGl+YTCTWULFljvhqZPL6+lp8JjreJvPonYkQywkZO16bUHJSTmJsfOBEzjEa3UdebIzG17ZYKZMb9ZleJjinaYplreuPHqMzJDDso+M73wKp4LXjYXvQDaAXogHZtVV7SBwnEIBxdw44aXZywtogO+MC+3LbfrturZ38XSAcn8bYjYEsFz5rfGdc5aTNsQedZq14z50S8zyVBzwa/3Wpi0W+HULC84TMaFvLSXj6vv+vW9EAGHFThMwG3oh6/JsHzuRQDDtb9+UhSJ4CO01T2dxkBcBJoiTO3FFwGBGUOAeeFLtd3Vdh4O6NhC0oy5/79jFm3BOB8z5zcUKCIbJng6Dcsms4NgAirG4bXI/HY2GW3t+PG/DFmrTjsENxlcFOK6IG5mVZylGbAAocKYqO3L4F2pER40cfmL+TRCdprAPAy8kaoMOKj+75Mz5Nw/tjWDN+GoRxHcYIQMSxozMOXC3TxJi5n50HjtRtfuw/MLBAjga0AHLW3m0VyIT7cdwnGxjZtB+RKw+0IaEv/+yf/bNiJ+uaj/J7eHiIl5eX80Mf07l0XdlNgop1HFuwU8QOebYABxmgJwCpvq/PmEEGEBSAPhMXyAgf4s8jr5eXl7IXzH3kJKkGsOgo4BAQ7uBussCVOCegJAcG0mZoAXfcj7HgW5Evwf50OsUSa4wxfhUQI+pJSIBqr5H7rPkPe/M1CKgRUcaEfCPqyXfYHL6CeWM/bpVhDvabrBvHsNr/Mh5AomWCv7JdOqaQXPE5/Kefz2RggO7xO/EAGyK+Me/CcEZsdBFZdl23OSyF8ae0fd4AcoehdSyLiA24wg97DgaSroihdxAkroIwB6qd+Bh0mM9ADBhAWkYGppwIic3ztzbm+Nhhxus4RGWFcXBP94xbj7kGSS2y6tcujuc14yGn3vPBnCF4UqpHckOOmuiI2B6Djh1aV21DXIN7oTMAYlhtH0SBHpo0YD74HgNeH+2MLUG0oUPuPsDWig9ZaiWCmIHfhjSYpjlS5PXk8JsKxFOMw74kPegi+/FIat2FgXzQcydEfd/H5WUfKdW9RsYM7V4mYqfJAWKcq+XWwzY+2g+znk5GGRdrw32xB9uV/aPH5gTAPot4aKzF3NAJH76DrCBhmLcTKesRsRDyG/2ZplN0/det1XnOU2k3tK18y2aIe9lv1RPN7L/+vtd3Jxowi5RWYG9gYdrsC0N0v6izx4jKDhEoEKgXt2UFDJhYMBbB7KoBYP7Mtl+aBbWxlcxdbMA45nJVy0y2igK7xJwpSVMRAAxgnDCHLDonnKSU4suXLxsGBcBDYMERMfeLi32cm7w3zD6OiechOEHyU90dLJhnYR2Oxw0D4l5fEh0noXa4LsGy9k4sDU5tqJ4vf0cv0Ce+y1z4Hg/l4jQwQARAxMxQm7xanwjQMG6ASnTN68McI2KTAPke6KErOO1pV6wdwKx1vmaamAcvHvCE4eNMPRYnvD6hhu/sdvkZGHd3dwXgfP78uTyzBQCFvAzyva62VeT0/v5eNoy7TW0YhrJ+yAEwSVBDDg5I6COJimXm4PHhw4cCwLAfXwd5kLwaKKJT6LaJDScWBt77/X7Ts8840MmWHUPfSBjwYQTBYRhiPu9x42GCyDIin5HuCh+gyfZHS4c3P/N35tj6Pr4XESWhJKA78PC7QSnJOWCmBSYEVAMpdPL9/b08zI41MdFhIsXtGIB95sHBBtwTvwWYwE9gG/xEh9B35GRg3x6la1YSAoH30FGSVMbkJIfPACht406EbQ9uF/O6AUTMqHsOrC2y856mlFJhgLFh+w9+OqkyQcH1WS/7A/yr4wFjt2wtFz9TyG1pns+6rrGeczPuyfgr2KoP8sNfYZucPsX3XFnBbu0rbTvWCwNMDk0gxlIZM2Nvtt22TryLqPuUnOyxdrYtMAd+0UkTsjCmaveQMa6hH0rLD0eg8zkDZHw07/nQC3QVueBjDFSR37rkfRWudLY+0+vEOIzZXJ3ELrzXDlvyAQ3WT2RnTGjiGDswtnU8Rw9sqyY10EGuY8LWPtbxwEm133MyYh1ufTf3muc5lnWNRf7I90spxf6ikjzWu/YeJjazLNaNzv/W68863tZsLZPh9BeyXxaMViQAFYtSeihTZde9oEzUjoTvGpwaxML8AOCcYUZQQq7tKtzDzLPBLQaWx19LgDilm5ubwpRy5KuDBdfE8HHkXdeV5MKGwfUBMxxtCShLqT7wkHPdcZ45obmM9/dDMSArJUkG2a4NnmDrvjxnsAZwBh1OJHGWtL1ZP3jYEGAWQGlQhPFH1D0zMLvPz89ZSc8B0RvxmP/t7e3m1BqSQU4cQh/YaIreOJg6+GFslP2d2VvvnCRRbmd/Dr/zWScXyN4bm6lU+EFJrB/XsF5hTySxsK+AKQAh/exvb28luBjQogOn0ylub2+LbUTUIzL/03/6T/G73/2uBBPWEkDFfAwoceqtfbOW/I5OsXeF39kXxXvoEfeh9ZD1eX5+3lSBSF4iasvWuq6b5+9wqhF/x9GTrAJaP3/+vDk+1y09BC30iHVw0sr6mRhxUsqcDGqpQHF60NvhvYz706dPmwQzLede5bM/WpalVIVY6xbIYXsGTvyOHBkP/ovf0U/Gx++0gV5dXRXwY1uN2O4rwwaRAbL3Jv+2IlMA0VBPuMEO0Qc+2zLarmIBjvD3+FiTIawPvpNWHGSFHuMTuBc64RYGAyjHiLb6O89zOZChBRisgckEg7GyR0dzQDY+ohp/QzLP85CmaSqMO9fl1TLNXIsE2dV0kiV0EL3xHisndK4QGADaLoiPjM82x0/+TQx1xb79Nw/zSymVY5DRE+z+6upqU4lnrdEJrsfau6qKXKgy+rkzEDXtHJCXKxdcH//h/X2sC36SrgwnlOgx9uKqCdiDOJNSimne9uvnqsNl3cMS2wcn4w9MLmLH1k3W03gmf3fb8uTYh52ga2AR1sFgHB9j4hj9wsaJMaw7PsKyNBbx9dvxeF7oNGNwUoV8WA9iteODcar9hXUDnGfZVHxa8Z6TG+bQpz6Op8PmmgWbx/lEKhF3xt2sTVtdy+Ot+3e+5/XdicbHjx+L8jAAg4iW/fFnURACtoO1lQvgw8Lnv+USj8H5ukYsyxo8iM5KUsvDY+x24/lM9uPG2SI87ouxAMycgfY9ezzyjn++g8LnDe/b/tZlqSCjVaDWQDHa0+lU+qkZA3N2osN9AHxk1LA/tA3c39+XthOzljjIlFIB9FwTh2NHCuiwYZk1jYjNUzPdo+mg6GTTbSNmEJeltmoRCNtN6l5HEjA7X/QA+WIktM7YgRAMcIIGFjBJVKaQBRtHqUDBfJoNnKapPLk+ojp6Eg6uze9O0vmd/mUcl9lR7IDxcR1kT5DE6fOemSHbrPdAtWxrRMSnT59iHMf48OFD0Z02UXJyi245APGeQRFz4L7I+ng8bhKih4eHUvr2KSmMFcePbbudk7n6GTIRUVoYnTzy7AQYcFo5j8fjppUJ/4SuEbSZq1sn8EfYKfNlrdvWh4jtk7uRReq2R3eXgNt1sQpc8nmu5XYZ+xSD8mVZ4ubmpsjbiaz9EyQAhBFrgfzv7u42LKSrqAbcBq4ejwmUiPqMBOTnoO31NuOI3M0aOmC2FWn+a4kixuR1ahlcfBJrxl4UgrTnZ2aZ7/MZnpuCPA2aTPAYwBhQ4qtfX1/LPU22ERcMXAC1TiSJM8R1rxn+yvJinYg5yA/bpEWT9cKn8DnGDbFA18S6rrEoOVzXNV7f3qLvukKcAR5tjy2Yx0/xNyck6GdEbPbymeXHP+IrWtKn3U9zc3NT5or8bOtc2xWI4+lUnpFDosP3WGNkTsLLuuMPuSZrjZ9BFq50cEBPIp4et8RT329bd/HXkSL6vhK3xm72f67aENvROdqcCgkQld3PMvPpT9vuAv7t5ALfwP08HsdeJ4XgCvQOe2KNjFvtIxxrWFN/zyDfFSBjuVV2wL1MBDlJsW/Kv2eJlXmmiHE3RqwRp9MxlnmJ8azPs+6BX8POse2S2K+xWQNefJY1A9/UJLQmM9/z+u5Ew4rlPkAUAWeKoOjxo/UEdpIJ5M91Mc9rdF3tkd/vLxV8v35gkzfxZIfZx7LMMQxjRHSx211E31M5WeLl5TVS6oLTsUgmAAOMDwBmJcrjXGOe6QFOsa60YXFiQ05qsvNfo+/H6Lo++n6MlPrgyN+s6Gusa06e8vEFXWHeT6d6fGZEF6cTT8dmA31lTTAQQObNzVAAAoEfZ8V3IipwZH52ZhH1IT8GZDg25G+wTG8va+ITumC2rD8E5bu7u031yM53XWtrxDAMXz3t1gmSmRfm+/7+Hre3txFRjdlg14AQGRL8CP5ch/d4/fLLL/Hjjz/G58+f4+7urpy8g7P3gxTv7u7i+vo6Hh4eSqUDJ4bDAzDQemIWiwQTWfIQSPSepCIiSgWMsURkXUHOyAqZOtEhSUJO2Cm///N//s9jXdf4D//hP8T7+3vc3d0VwgDmkucusDbWHQMqt2W0jtR7lwws0UuAMmMD2HBKEgdNmEmbpqn0D6eUyrG81kXWg+qRg2bLLNlf4MeQHUACQIpP8VicVKODJmxsrxAJp9Mp9uMupnmKbs0VjLSssa5zpK6Li6vrmE6nQkKYzXJgdqJqnzAMeU+D9xKwVmbDYU3RVbOTZvPwQyQMnjc6YnLIvcvYOMGZMUOsoMO2X9YS4IYvMePuio7XgDiE3hDj2qTI/gN9NluJjflobieyXuuIKJVkruHKGjZvvWGeADnHYbfcsO4QFcRk5gQzbDKB9eR6/NvEEi3N/A399rpa71wtZmzMi5iFr4eAeXt7i2mZYziPd+xzAp2GPoaui2nN/mq/28XVbe4oWFJEGvIJcsfjsTynw2QMcc4AlYTsdDzFNM2btTgdp+iHfmPbjhmsjWOGY0Qbl/BX6MfheIzurBMTFbaIjf834OzS+cCN92PEmiLWFMdD7RJoW4HrukU+gW43Rj8MsS558zX6mjhqNbro+y6WVJl1bJDYmBOTFMu8xuk0Raxnnzf0kc4Y7XScYhiHGIcxDodjrEuuWCxzbo+KlGJdIs/jrCfRrbGsS3R9JpP7YRfLmtt9Ys3PANvtx0LyjMMYy7JGWtNXNtmCfvw7uupkxJjAmJS/GwPZF/GC5DGRaWzV932cpinWWGNd5limc/v8skakOG/MXvO8pzm6PuvCsi4RifN1I+Zljr7r87HCkROVrk8RKc/1/e0tpnmOdclJxrLMWbfWM5G+Lvlv/ZBPqJqXiEhxPL2XOUP4gR8sR/7tVteIWtXPsvm+PRrfferU//f/+P9sgr8dD2wkmz3dy+vMk8FFxBkYZOWmXMmLIOYM0lWIbymZQSRGiHPjBdtCjzaBAufMtRE6jtpMopWtVWBnxSRFDgDzXB+GBaDhuzhoMu6U8rMPUOTdrj4bA6WubOoUh7PzgbnAwcHW+zvMx8wEQRJ2mhdtUYAMxgqIhNlHcd26YzDrTBr2ymXtwpxEfZAff0OuGAUg1/rI+joZdSXEzMTT01O5Nno7z3M5cci6gPzdaoFuTVNuieNBZeip9dNlVv/OPJE9gA+A4J5SdJFqCnOyQ42oTPjHjx83zJJ1hmC7rnm/zd3d3eY9M86s6/F4jF9//bXMlaeQR1Q2xBt4WSP0se/zBlIDLvSUazBeVzzdboTMsRsqDU6ovVeHcTiwDMNQWuvwF67aOTHwnhSD3ojtQzIjKkAjAULXWpm6z9zA0QlOO24+R7XHrSYtQ8tP6xlJAGAWGZvtRt9cIneAwQ8gI7cwEIgZKy0eTmhJUqgUlWDc+ClsAnDtYAdxgU61Sbl9BeAQ2bStHLYZGFYDazPJXNttRcjaia19GzqCjHkxHuwdEE6SPI5jIecYB3t+7BeIt/gEE2SsCb9ThbL+8T7xEHuFzEAHiKeWF3rqth7Pre/7DdnA950c+lp8Zl3XOM1ThAglXx/fbR/sRMfJpVljki6vU9lsnWr1jfvg88bdUMZhxteVQQMykwncG/KsVNbOMYP9g8/PzzEMQ+zG7emLEbVt8HSsiSd4qpAlw7bCgL+cpimmUz0xC//stTRWQV+dONtHUTki1oNPvB8WP0gLpSsAro6wZvmeU0Sq4yfucz/HX7e95+SoLzEC3OA4xriM8YwVnSDbTlvGn/fRPUgK+2b8uP3gNM/luUa+fv58xNBvTxf0YUnGzBG1smx5bjBF18V+/LtjlW0IW3GFib+ZYOEeJt2sP+hn3/fxf/2//6v4rdd3VzQIbiwGC8l7gEv6HzkxyifqsMA5CNTve/OQlZKJc2/AFyDHIJ1FItA5u4WViainBcAAIPSWocSgzIrzvhWD7yCDNkhxT8bt3n8/GOr6+jqen5/LeeT8vTJ19cE1rEcELUn1oS7+z4GS7yB/g2W3XSHXYRg2/cKHwyFeXl7ixx9/3MyXqobL4Tg1J3bI3X22vIceEHjNqJhdaPsnI2qSiwHSVoMhAdKtY1zfmxphq1lDqgMGRTg+AA8JFI7AAcl/sxPHQbCuBms8b2Kaps3+GE5scuL8rSCMw/306dPmKN2IKCCVKtM4jiWpZKzPz8+bYysd0H/44YeSUC3LEn/84x9jWZb43e9+9xVg4CfAHR1DN9z/b3nQNom8aSmh4sDfAH7+bkTdeAfwQu+drLZleNbFjDKAjADCPfBJ1lkHHCosBAuSYb7DvSPqnjYnwW21xJWPVlcJ9NwbXUO2BErm6rI3vszrw7Xd4me2HJLE+8hctSAwEoDwT+g2/gOb7bqubPpGhpY58uS9x8fHotOMwQHYm6Xt/+0zTAJE1Gom4ILr46Ng3lkLfKOTCmSPLjlemczw+97HYWDAQ2x9cIVbrkxuIR/bgoEiOkgiAhAmwWCsrLUBO+2DrCmys/zwQ6yl29VsL1wXO4IsIVYbxAxpiFl+jPs4sXP85vuu7HAfcEBEFLvCfmktZY2QP+t4cXERw1h9BokLa+gkm3Y8bM2EqtcWP4B+c73T6RSx1jZytxP3fR+xpo3f4f3MtldwzNyz7XQlxqELtm3kbSIY+aI/KaViA1SFGTNrQGLMvJ2MoPuunhqPDcMQ74f32O3qYR+sG/I1cUXy3XVdLPMSh8O28u4KnjGCZYefMsni9UGnGacJcxMe3ruDfTgpKdddttcuviJtj9IlEcQntYmGcSUvZFj0JTmRqYmziW3bo2WDHLmHK2T+O7pnv4xt/NbruxMN95WaMTALhMC9OdcMkUEX/zF4JmeBOtt2Fmmni8DbqghG5R58JxKwShFfP9CF+zo4edMiYzer2AZsL4I/i7PnWmb+6a3m+zj93F+/xll3yvcIeBE16BEcKZF7Pw0BjiAyDMPmQUvMn+DKmgB0OH2GzwDqDXII9M6IIypT4IoKcoURZv3YzN1+n3UiALPGEbkdgXamto0GQNY6VQebvu/j06dPmyyea8AMeSObN/vhtJ3YpZQ2Tzu3rRCkHJStGzgIsw4GcDD61rnTKW/obvcK0OuPXJn709PThj2hncMg+/n5OW5ubjYsLT3Ed3d38Vd/9VfxT/7JP4k//OEP5RhcdAF5twEUezudTqWC5MqTnb1ZS3yCmT3Wjfuwtg5c9kNmnPkuc0a+3jQIGHJizjhYY7NkdtYG7oAexoUPdFAlMeGoX4No676BYdd1m4cZokfI3HZjn4XOmLQwiIRBx0Z8bj9AH/tkfAA0V86oPpDQmLThWtif34+IYmPznA+loB3SyYzZRydo+CTHENabsXktWVvG41ZE7tkmeQbyfJeDL/AJEfXoWL7nBINT+7y3C3KLpBn/yFq6PQ9ygfFD+KCbXlPucTweN/s97Mvb1j9kb9+BPKhI4hORuYkGdyWQZDgWAGIKhliXSErYzCLzPcaKHrAP0QDe+55YA65p8mjo6/hYh91uV44DRR+ogHhfJPfxJmzPGx9PbDqdTrn15WwrrmDwhGfWE9m7RRoMBAC9vLyMNepzfNDHbD9LLOt2bxx6z0/kzilvBtLEJCoybi+27TJHr7lBLtdEz5BbielpW2GxnfHCl7qFMNZa6cB+8UNOXlsiiO8b7/m+zIUWIpMLzB29Rzc91nZfxxp1/tyj/nt76h5648NW7Letj06+S7yMbfcE6+V5unrvPYvgF9bbOLolrLkW/uq/eqJhkM/NMHQ7VYBfRGz+xuDtNNa1ZsgOrK1ic38cMAKFqWj7d1EGFoFWCQzMLByCwrg9VxbBLIONjBIfioKC4EjsZA2wDTJd9saBFKYjqvLmPSj1OEMqI/na9dQDkg3kF1EdjHusUUacqJ/SzOdbw8UQ+RzO8Cul77cbwFkXM9QRNcjxJF7ALUEL2XhTdFvNwnDM/DnIGQgRoAxGWqBNoKbigW7CbrDurA0OlAQHYEBCB8CsSeH2PG50wTKhaoKOEJQYl/dVtA+74xpcx4CDueC0IQ8eHx/j6uqqbGZlnq4C+vqHwyFeX1/jd7/7XZE1R65eXl6W9iQSQkCgn4WBn7BPcULhthLmgzwsO+ZmJgvd475uq6FFkDWFdGgTY/Qa4JVSKq179IRzPydsrKOBhAFZRJSTbkg6zNyRSJLgmOE2M8d6WmZmPZGJfRD2w+cNKgAwfA49x2dYd1v22mwtfpx/kyybRDIRwfe4tkkog2d/Z1mWsj6M2TrqpMB+way//Y+DJYHW1SHbJf7Fyaz1E921T7dP4R7+LnJmozOnIDFWQAFg3wmi23X8kDuTIiSPJpAMiixX9IF15B50JxBnXSHe9mxvEzwntn5GUduiOwxDxDLHLEII+zOpSHKNTaIfPmwEQsxr5/Wa59z7ntL2CN/SHjyluLjcl9Oi0CPWD9snZrp1EtmiD0VHBWhbDNJ3ta0I3S3J4TBuqt+s2zzPpVffYLbodqQYxlrh8Vpgu21HgX2ZE2q+i0567Z1826baisG3EvtpnmJcautexPZUM2zRZMR+v48UNfkw8DehY5v3GNBT/sb3iAP8vSVf0Ef0gfkZ+zlB7vo+5qUSKcw7f78rVSzL1US1MYzJG7CDuwFSSuwWL7EdPQWTmjxlDvzEX9hfcm3iheWIfeIrvuf13Xs0/vf/9d+VBe37vgAcBoWSORABfo/HY2GZMcAcPKZyshBldRsMCoPQXA40k2kHaQVywgAzyxjJ4FgAwKerKxY0C+aNuxiHmfIi2FSrO22Vxt9DwSNq+xmtJq4CnE7HOJ3qE29x3NkA8mZ3FN4MGgZmViyiJjCwaAa3JDEYcssyeH4EQpwCrHdElFYd1pKWI0AHzgOgDGigUuGAjAy9P4DxG5CiF4B8s1uucLUsuo3YTAjrbyDIXEno6hpVdt7JOBu3qXD4tBQ+4/YTszHrupYz2WE8kL8DBH/nb76Gdc192CQEBMjr6+uyPticgSpBhCN8x3GMh4eHonPv7+/xF3/xFxuGFUYUO2vZJII0jstMpMvH7P0y+UCQAOy4dcJ+BD3BJvATtl38j+VGcHci27JyVGWsP2YmAX/Wbfyik0/sjWMufR8nSxcXF/Hly5fNyWLIH7sg+Bp849eQF0kn8/QzdfCHzAmdR7ZmvVw5dJLgdh37U3TYNmsm3DLm831fn13hagDr61YG2yLXNVBljR3A7eNceTDbzr1MOuDDeE4LiavXmvdJ1gA7sNPWQ+TJ7wb63qdh324iz/GWNTXIcEJkgGqyDZ9LsgPBgX1xraurq82DYZ0sun0JG+L6Btj4NvRwTRkcMz+AuttznETznv0T60n85DrI3frWd/Vzlt/l5UV0/bY1BplCAJAoGeSy7m3CHhExzV93ahQQK1bfZOY0TZGiJlZ8j9e5W6Zcd/uZFLHWQwTQZbfJ2E8ic/yDq3xcswWVBVR3tUrrthoTDxC/28/2sdtvn3ZtJt6ktrHIutQKCHHYaz/P26O3jRWNGf28MOTI2NATJycmYLEF4wX71rzpe/v07xLfI5/ghW0yPubLHPDdzI944Vam0iK91ljRzsfJFUkFPngcx4LRWAN022QBOoYdWBf+x//5f4jfen13RSOf1JCi62rrUQZ5XQxDde522rln7xDH8xFqLGLX5eNiec9n3hM4DTIiojyvozqbiJQqMGQRzLKZycfpuSJAQGm/g9D90CccHkkW92XeKO7j42PsdrsCaH1PFMqLhiE4OQKMYCgoEMrlwDHPS3RdNlozdlZclIrExEEXY7PiMibkHVEdlk+bYd4t8PDTjzESPodjt3PE4boEzTX5m5MOZIJji6ig1M4ecGRWwjrqYG6WE4dsJoS9RrAevA9r70oBc2DNW9n64YwOdGZEvIme/8wMsb7cD/2xPfA7ugRAI7Gh9xYQs65rARg4QDM5MCwkorvdLn766aei3/f397Hf7+PXX3+NDx8+xDzPpTTvNXCC4UoRc0AvICwi6slabO7E1t1KBHlg4IEsIqI4VOZGUNjtdptWNYMmJyV83pUa/CDvA5yohvGfWTv0i3miJ7QotRuuPRY+1zLGBC10HICAHflEEWwE+RssmOGk2tj3ua3Exxijd06ubE8kPvbpVIRYO5I0bNRADD9of4z+8gJkGNSxVgYZ/DTx4OolYMjHPGMfVHsZs/cMYb9OZoh73qNlIoE4ga2dTlOMI+zkGn1f94MYPOfENm3kX5Oj6g+cQHDPliyynZk0M5sKo+wxjDse2DnF+5lkqdXWfFgJujCOgK75HJ+GAra7rouu7/JJRms9JCP1faTuvC9qXsrpTz6IJVcA8qk+p+Mxur4mk7likiLi/XzNISLqE+QNBLuuHgxAZaL6jjVSV5nolgQazj4Bv5N1uJ4UOM9zdH0fPET37Wx7JjFokVuWJZYz+FzzokYnAN9128NwrN/rEjFN7E3YlTiV9fK4qdpiG8uSj7I+TVO8yx+eprNPXJeYly27z/pgm/gIx1Cwgf0CsrOtGbT2fVcq3yYFsG3HWQi5fN+sO07ed7sxIrbHj3OtYRximc8xPdbYj5nMWdYl+rUvZKd1nVjgiienjkZUwB2RT5FCFvzsh3yaGO3wEAskGSacvQfDz9QyBuRzvJw0ZjnVOZso8kNMuUaLQZ1g4HtNBg5DPVqeNSSx8vj+vtd3JxrrmoriZ8e+xvs7PaHbJx3ThpKNex8pUWI9Rt8PkVLEONbeZ4BMPUavZrWn07E4evpRcWYpxfneFVx6T4ZPn4JxJXlgsbLzmbJzSV7AMYYhH1VrRgtWdZqmr0658Tn/ZixTSgUc4IzM/DGftrxoQ8sL2sXhcIoIjKgyrgZfKKRBQGFIxISRbGFIl5eXm8DNdamgzAoUEbEZO33b7vf0U8QjYjM2Jzs4chQ9YlvSNyNhBo3rMa5hGMpJXawvxoy8uScMFA7GLSUOKnZyZt1dPTCzBwg1wOe+3Nt7MlxpwunzGRwfe1ZwIO7tR7aMic/7YW0kDgSem5ub0haAzhjUulKJ/NhYz9ixyZeXl/jDH/5Qnmb/+fPnuLy8LBvLcdYtoMVW+TdAnb+jr4A6dIRkA5tqHwQGECXouZ0G/3I6nb7Sk5RSqei0jBiAkiqOk1FshbXdnjW+PfmJn67aoGfIhyTDfd7Wd/ZUORBYb5kLrJX13fpvuwRouQ3PYN8JAIAa2aAjrgBhi25pdcLGC9sy89x1Xfzud7+Lx8fH8jczfXzO68O13MJiu6OK5yTNviUiNqfGGWznyns92hcf6kAPMcB6wBJix74O185jYmPlGvNcyY15XkqSZxJmv99FhqP1uQzZXiDJovgG5uukEl126wwJBfdhLn3fx/PLS6Qun0a13+/jeHrMAPX9PfbHXaznA12WWGJNc5zm+Vx1T3Gc5o1u7taIvh+i77tIfRe9Erx1qU/3Xuc1ljkDp9NxiqWvrTO1lSZiXdaYpjn6NWKOJU5pir6rbdXLspw/M8Uyr7Hb7fNxuZEfNtZ3tZLNIQdUIKcpn9oUMce8nEHzGrHb7SMixTTldXw/cOxnirfzoSNZxl1MUyV/um7bhjSOu7PWpoIvyrjnfGJRxBqp62M6jynNSyyxRnS1qjd0fUTqYl7WiLOvvDjjs3WpZE7FS2d7eHvNx82miON0Oid9WbNOp/qQ2GGoxOjpmBNd2zy2ZnBrEomEHj10spL1tj5fzTinJQzdPluTqYjTdD5+ts/7IUh01zViGPuSyM7zuSrR9ZHWXAkaxj7e36fgkJ1+qFWKlPKD7PKHox45yyutsaxznNgT1Q8x7LL/Hnp8cNaz/W6MccgySPH1/kxwn5NB5muMwOfxBW0HjastxHST9dh9S3C1STTxkfVi7Vq/SZxux/F3vb470fDEEUjOymtGG7F92m1maCogMghwS4oBMhWOq6vL4MEttPRE1JMR6rjcU1j3fSBgxgQQ4x4sSnZetW+VxagOfBFrMZWy7MvLS/mdF0GVgAiouLm5KYrgYGsFQsYkP7CzTkL2+33ZC4Di7Hb5SOGXl5f48OFDvL6+xvPzc2EPMVAAKgCZawBAUeAvX76Uk6UAig6azJP52cHA0piFN0vAJkSfBMX3bAhcl42oBD4npYyDvt++r0/C5kWgs7NifbgmeuJqEHNjDu4TT6nuNQH0uowfEXF/fx8PDw/ldzOe1hMnF+47hhEliaG/GvkwVieNAAfvb2LsZscraKmtMgQFkkz2yZBsel8RjP3plB8wiX4YuH3+/Lkk4VdXV/Hx48dCQjAeV8HQJ4PWiPrcDbPSbanZCSHJvlsnAE603JGYe/8J98UPkUjxd2SGjuF/qAigu4BhnLD9iatrDvrYlTdM+5oGgA4SVFK6risP2+O+tLXgQ3i6L3I0WQCBw3wgagiC3JPP21+j167+MX+CGO+jM9YBHxnNmLB3ZMS+PwijttIWUTcqm4hCzgRn5gc4cnJoIOMWTHyybRWdICkmeWFsJkaILxHbB8Hl79ekyD+RMUQAldusP3Pkh8bWjf/eK7QsUVoouWbd41d7rdsqEuszTVNhYPP7kduZ5PuQDUCKuWKz+31lUMdx3OwbSSnF4XiMi4t9kZOrXvO8xDiMG7+MTK33rBOAdlmWcpIPsYzPI0MneySDNRHYPiNkGIYS8yDR0rmTY5qneGsOCTCw9uEMLSFlXUfWSfLdrkk+/rUw6iliHMZt7Oj72HV1r0BK1f+xJhAsrtxN87ad1oQJDxu23aaUYuiHcAcJPtf6DRB1RRmyw8SEMQkVLObEmhjMen+bZUilnOtWEmuJ8xRL26LvWSvRW6Kba1l/uC7ywud7Htj0loCqlR98BXICNxrY45OoajDXam813oMFGOM8TXG5vyjHCkdsD2oiLuHfuRfjcWXEmNakoIkg/L8Pv/it13cnGggG1n7bk1gXxYqw241F8REAjhFDgwHnwXUAC/oyKUGbSUMw/ntWzvrwPITjZzPYKFCCDAIuYppOX4G4iBqw+K6BDuPge6fTadOT7tK8wQVglu/wvgEtiYGTDBhlmFu3Z5DE2bEhQwd/Z6oEf4Lq8ZifwQCDxxoBaAgabasURkRrlAOtmUaDqZRSkdVut4vn5+dNAkoQsk7Q/gCbjQ5g3AYfyJd1IrkxA+21YH6AVRJedCWi9sA6WfX7BMwvX74UI/cpRmaK3W5lZoP32N9ilod7OgAgaxyB7wODylo4mTGLhn7C2l5dXcX19fWG3YyIkpzwHwk0m1gBFIz7+vo6Hh8f4+npKW5ubjYsKrpsOTrRYz6+LvrKGjkAmBUy2EOPkK8rSFzfcvU4hmEoD/eyHrhKYtYHP+bTfxy0bDe+D77RCTAkAhWSyubWByC6/YJ74vPwHw5mDhaMiaTKYNwJAvZkANHqoYMxa4x+sQZO7PEhLTHA59wHjG0DarifE3zWG1/m/W32u8yFSi1sNmsRESUpq+x03ZDtNWAMXiODAVdhDTTQ1bzmFdzgS5kzfh2fW/1cH9N0ClqWU6oVwLyWF6VNzvdsx2cShmQOn+H9IN1Z13kf+8QGnCjZljhRi6SgbKC+2Fa+ndT1SuCxF3zqsixlH5WJLJJ/V8INKtEfx2nszMQTbb74B+t6TQ7HOE3bQwcMYvkd/WDt0cdhGDYHiaALEbHBF4wdG8NmnVQaSHIv7DulFLOYavSpEAICoKxh/j0/xc/VVGQ0TXN+wl/U2GrAi74Dmlv5bHHVWb7rEjHX9iq3Ynv+fro893NSj+1wXa+H7d94AV+BbBm7fZQJMdbELVNUwPBP3N/2io7il7gfhDK+BRlw34goeukx2FcVEiXV1if0is+AB4zb7J9IxEl0iRtgB+7Dy/JyfPut13cnGmbr2kXvunrUoHsXD4dDvL8f4scff4xpmsqmORyhgSlB8u3tLS4ucmkM9hQn754wHLKF1yk7jqibWc2mrutaesz5TMQap1Pd+GqH3/fbkw8wWthdnC5tWShC3/elncP7EgAFXngSFMb99PRUmEVYgWmqp/bAIvMkasYAm0PSYZbGCsI8+R5JDgEJ4xnH/FAh2Hv0gOu2oA6nhkLa2aM/nLhD9uw2s7afFCadF07AwAknYibLjmVd18K88/erq6uig66gsL+G69JKhkN4enqKaZri5uamjMfMITIgGffmUIwYXToej6WlY7fblV74m5ubUj7lHlQWYPSQs+dE+Z/525Gy1tiGkz96OJEnum8nQqBOcmjYyc3NTRkT4/0H/+AfxOvra9F9nu7u44DNWjqRc/LnAEMQ5TM+GpcEFn2pBMi6OQWP7zrZ8V4qg0gn2ei9WWrrHnIF+EdsT9zjc8zFrDv3vbq6KsAS+/HpcWaSSEJYD3wRczZYMauGv2UsbmcD1NluGbvBAn6E6zIOvsv6mVBApwCyzAVfZhDsFtCI2saHzRA48aMmmtAX7NpAEz1jTezH+AlIouLn53XAVBvAmBzAjiOi+E+z19jzFnDVdj5fm4omzxkxaD2dTnF9fXuuBk2lfbnv6wNdIQlM3BCDiDlODn2MKp9PKT9gDlv1/hz7ZDPlyIu4xFzd5YDsaQUlSZrnOYZ+iNPJeyXqutT+/PpAv7av3vponXLF2Uwy+uprc60vX77E5eVlScLxgV1KMartlkTTrLz9lPUOwOcT1Liuk3vkYV/mbomI7RG+yMCEWyzrRsfx+YfzXO3LiM05kaggFD3IsWUXy7xtza6VlO0au7XHcjAoXZYl92qlSlg4STDhytzBDug29ya22p/arv1efVzAtvWadeJ+JoHtL0w6YBNc3+ROSzKhq+AC/BoVUX5nrUyeEcepyqMj+EowjFuenFA47jkh5D74zoeHh2IfJH4m5YkZ+ELs+Xte351ouP3IRpydy1QUn0DkloTn5+diLLvdrjzUKiJK6w/KnieaewURBEDXJ6uYlUfZTqcp9vva2gFYQTFpK5imqbB+WXG6WNfad0gi0nV9aUN6eXkp17KioXg4aDbTlqPylH0eDof4+PFjAWEt80Ii5mMEraw4deSMUgIG+BtKa0BoAAGIifialSX4R8Q56bsoAcR9yGToGCxjwUjNBphJ4DPcg1aJjx8/bsC8kwrPkaSLMeDgcLIEDTMfvJgfD8aKiHh+fo7b29vSrvHw8FDYOLe5sS44qbb9gMpFZhX3m3Hx8gYvvuN1skNyFRC5+WVm5Hg8xt3d3SY5w/mYucIWsQHbVJuAoosQAwZIOFQDT+zd83p8fIyffvppk8x4g50rlF5rrxeVDz7np8YSJFu2yey2gRU62oJZdBYwV0mGvgBwgBSBDh2IiDIugpOTAuui7wcosj3DnHJfO3KSFRw/SYWZLioEyITgwlx8KETf96U9x5UWgxreYxyurmHHBCYnGOgSwJ0Ex8SHmWXAnteKa9ovzXN9roMTCNbAibGrcBFRyCZIDscwy9hJrWXHXPH9zA2fz8MsuQYtG1SGI+pGzNp6VfcTIEfGhTxNDFhPMvg+xbqeE65xF+/vU6S0PYqee5NQe98c8jTz6jVKsT3RCt/mrgXmRUzhfeYBICztGbHVAV65cr2LWCvWQMfRUTP4EbHBA2AAxgNIsq665YVxeh8Dn4e8cOWL5PFwPMZ6xhKssytKToStP/gntwJCADB2PusxQvy18QQ/DdbBpy/LEqfjMU7H+uwnk11918Vuv9skAiV5nnNrHvIA5BbSIGqF3vLE73o98cktKYhdZl3IVSyuZf9vkI+9o1/gABMv1iknSfjZWvHLMdzHj5vswMaQu2OeE23ma3IM/+DOCn/eHSptFYe2cuIMcYdY5WTZcbf4sLXKHfnx97Yaj1yc+BGbXdEj7rWVC2zahMNvvb470aAlwgvIooxjBjbPz8+bakbOmCsjSxaWUm7rcWUBgeZF3SqkWWecsY+8w1jziSD5emSuKCiBxobB022XZfsAQDb3okgkUSgcwKxtGSHrfH9/Lz36BInn5+fipKkSkEEyBxTW4APlB8QyLo48RblQhNZgGCvG40y+DfxOIBzckAdOy8CXQMnaeZ2QC+0IvG+QhrP4z//5P5eHvl1dXZVeY4Iy96MP0cbDWjuwIgvmhBM2O2sgyefu7u42SerDw0NJRsxWI1fm0YIFql3oPTbkZL21FbMpJLLIh9Y5guu61s32MIRm6wwOsD/0xg6SNYBxZX7fCrY+RMFJAvJFB5g7yfkvv/wSf/jDH4pOIDecIa1xBmnIsT2i03rGGptZss/gBVA5nU6b06UAXsiA+WFr1b9t2zFZa9YI8Od7OgFwUCAQOpiY0fMJONUfVsDpwLeua0kWXM2KqEdlu9L3/PxcAGdErVQxNwdNdNYJKJ9nLTggwIEW2SFHbB8fzDwiaqtUS3TQLmk2kfsVUHS2Ze85wxbcUsp3WHuvCT+xOeIMa4tsvIYwkNgj/s3s8jzPm/1LvrbBVlt14O8EeBIXdPPx8TGOh1Pe2LyuMc9TDOOYN+quKU5Trd4hM5M0jMGJpx9OBshlnY7Ht3g7AyeAILZr1p05o3dgBXwHdpVSinmay0lRjIuxHt7fI6VtW591A7vGfxl8oc/2EbyYa5u4QDhaZtgGx+ED+gveiDWWtcYfxkFijc0xVsbtZMvkoomllpV3JQR5Q1T64AYAKfLP16j34Rrcc4ntvsRlqYdQXF7si+9A77MunCJF2vhh9iqi09zPJCEvx9vK5tfTPU2iRMTG1/FCdre3t5txuxLBetsG5nkuR8y7yoFc/MK/OZHgmugeMb2tTJuMQx+Nq6iSE1csY+s5CSnjnaapkHUt3hqGIdZljb7bVunwx1wXHcQfmehh7VgHkyj857jrdkETuX/f6884dWqJl5f3M4ufYr+/iHx03CFOpyhMoINpRCoZ3ul0Ksb7+fPnYhzO/AAdbIJCSWCPUZD8zIjKHjqDJGs1C29GEYUxwIuIc5bOGIaIOJ/zfHaSzupodYqoTIoZTC+ES8ss9LqucTi8l2u+v79FSvmhfAacLHBElKDF+06G7u7uYl3ryQAEE5ImjMoZqB0fpWknOwYFOA8/78OsEwaGMfmUMGRi4NImHjxbguu9vLxsFJ515XeC/LrmcqrbJ+yADD5x6HwHlp45G+QZsBNgvenJesn8GaMdVHEEYuHMdKGT6J+vZcaV/Us4BCeNlgk2YrDJvVljdMvVgHneHkPrdbSTqUGs2g5A1rJnM/lPP/0UXdfFhw8f4tdffy22iHMj2CMTwAVyRV5ulWjtl8842LHebfsS62ngxNzwDayrWSi+jy2SMAJAWHcYbJy6Ex4nZ6yzgS+BBBsFbFtXWDuIDwIJ7yNT7uGEn/tzTwCWP+MqFv6YFjOAo/+GbeMPIF5cfrfPwY9AHry+vp7nHZGPeF1jmk4llmBL+CIz6G4dsU9zpSYiNolYPu1nPRMIj+X99ojicjZ910ffd2ffuIu8EXt7bCwvkzgVJHXRdbTY5Rbj7BtyPOXZR26bctJtH4m/Synlo0i7+hRjNkIvyxLDOMagysfFmUw7vL+fz/WvD8uFsOu6fDTsGhGXFxf5tKsub9RlLdEnj4O1xM/xsz3hDHmt6xqpS7Eo4WJN+76PZV42Nvmtk9Ic59FfKoow3t47gH/CR9EuSRy1z7UPggg4HA4xL7UinyLF7qK2Z/F5t7F2XRd91+XOIEDovAX+tkuOsx2HIS7P5Ci22PfdZg/Q2+trDOdYPPR9zOEjS7POYTP4ScemYchHvDrZz9WKOG84rxUiJ3qcOjWcj21N53/jS5f1HAOXJZbl68pc3+fDgTiRtOvzHt7WVzvRZj3QKX53NRVCwEQ1gJ3xcy23lKJP6K/jrokjDqRxLPC6O9lgPPhuYxI+w8MkwXnuPPBBBd+qbHYpP+iPa6XzOnR9F0NXj3dn/Vk7E6zGDa5M8TKGIYF2ixV6Y936nteflWjsdkMMA4rLkaL1pBQ72+vr6zgeKe9Wpsr7M5igf2aAs4v8gLrKhjDp9/dDpNSdFe8QXbdGSpxRXk9psuAo9xl4wXJkhdrFOFbHkcuHa0xT7bFFmQlE3APFdaUHh4zSA7xzcOyi63L7x+3t7TkJiXNwq8xQRBTmgsXn+m6JgaE2i0ACYdbF7D7jNrvljJ1TegzSMNT2DH8MmXnf3NxsgA0tZK6s8CwE5GjwGxGb9hj3DfO3iPrUckA0SQ2yp80F+XD+fdd1m5YRlwgNWB1AkANO6eXlZZOkAlBcwkXmTsgApq6KYS9OtDka9vr6OsZxLEktTHi7H8P971S/CMrX19ebnlmDAgc99ggBgL2+6A4McURljdAhX5OXKx0//vhjfPnyZWPn3NtJKGAUeThpA4wbWOP4zDwZoHHd1klG1M10sDLMxeSB/83YTSLYFlyCd1KAHRbQsdTyP39zUs4awjISaBkPtoWMGBtj93zdOmMCxOP2xlj02IDZ1RWqYi15gJ6ydsjK5AzJq9fm4uIyjsdDHI9sjgU05KPLIUsM5Fgrs5i1/a4PjgzlerktdpZ/8JHIc+QToNbouvz9rAfr+W+5xYmEC+CzrhGHw3HjW0k2WcN2Twd+gZergi2BYF9tZnHcpUKsmE0chiFe38823fcRa8TF1Zl8SF1cXufDGHajKqzLEqkfylOFY11jXiPej2fg1/UxdNv2Gq+dx07cIO4Mw1AIIeaEX0VXj1P1jbHmo15tQ5B0kCjoFQQIeh5Rn5HDGhgDGMD6EBsTZW5XPp1OscQSb4dcVV8nAfOhj/lMNPRdynpztlf0Pa/lkoFgSjEOfZzWJVKsEWs+HSoFez5rxSoiYl3yPpCry4tzvFgiuhSn43RuIc/Jxzien5S9G2NZtq08/dDH0NeHm4JflmWJ/UU+5jdiLePpUp/3YKgy5bWapikniOckeZ7muLzKZOE0nzbETJe66PoU3ZpinvPTv4lBKaXYX2TdjbXu/3I12xUAfBvxD1/lWEr8QydNvLhKb//v/Whm/l1dQ0/u7u42+Aas5CQVfQLcu6pD5en5+XlTYfU48SFgXGNLx5zlrHfdmrfTpJRiOsvvRTiJsTrGsY4QTI7tEOH23967gg/iWsRPx8Xfen13ovHx48cNqMCYq0OvQaScMLHfx7J8/QRHApUDHM6EydObjTNFIa6urkvyAjgCIKOwZkVtMAAqGCy3UvnklXWtm62YM0HdQdrBg3vibGi18Weygp9iWeb46aefygLf3d2pulDPS3bVhLlZzma4DRC6rrbSsFYGuwYDVmqMEybHDPGyLOWhiQQTB4Pr6+vNGf9mosxC2aH4WE1+kuC4fEcAdmm87/tSBuTVBrSrq6vNqWUR9cjUwsQs9UFOTnoInG0VAZk6YGLggFyYe2TRnv6EHnIaC2OB3bi6utqUPQ28IyqDhd0Aanw4geXN+DhNwnoJMLWtGUxge3yfRAuQ7L0qJCiuIPK3h4eH+OMf/xhd18X9/X1E1D7SZVnKk56drJiBwhkbwOFjvBYknd4fZL0wCOf+tZRffYXXmUQA3WPNvTbWca5tUoKASEWTz+Lr0GO+76oF+ontIB8nl1zfesY+NHwT43fFhXmjv+gt9nA4HDbPiaEaSCuUAQH+lkD+9PQU19fX0fd93N/flzH6VCzabSFiSKYjapVvGIay/wQbc/+wGcjDoSZnFfTNG/YO/XH7JjLLsqpHTUKI4Y+IF9/ygWYD+WmQbF9ln8W1fJgB64L9+bRH5s5Jbtybcbhlx0kQa8i/uT7fRTdNVDm5MDhyNccnO2JrJAO8b/KG6/sgAXSc8bCXi++3PoXYiA4jB9ab2G58wTgASE7UWaOuyw9b8zo40cM/IkfGi09m/l5f/BTg2C1f2At6jZ7YriJyKxe/++QjxmECAlIBOzCuOh1PcZoqdsNW6XxgwzFyen19LXPzmnufCfq2rmtMS62UjOMYwzyUezuJnuc50pSKbyV2oQPez+A4yXy5t9uYkIfl6K4Z7J+1Npjmp5MJ/sMXRNTTrUqVoasHObhCbTxqUtP24DhhvTW+NoE/DsO5YlT12kQH18KPG7fsdrvNqW0maIwZGL+TCCeEfM57fL/n9Wc9RwMnhyK1QZmbs39gt6uMNSdRsG+i7/vCTtN+gPPf7caSRKDgPlfcJ5eQ5LSJgcEFCupj9nwSlcE2i44zR/nNgvJ3nJlZTpS53cDFdTIw2rZO4IB2u8rU0B6AjFEWQBrv2cHUikydr9tQCETI3M4TebqEiYGRALTzxJinaYrn5+cyLlgHHJz3KQAc6Q+m4vPly5eyzhgMFS1XhGx8dgQOWOM4xtXVVTw8PGxKp/Q6Ml9+OvGhfchgm5Y1kjzu6X0/6AZMHsbsk2giKrN7OByK3lOa/dYToc3wGHibzTOrgm1FVGeBbPgsusA47IjdM8x7gGk7Mr6LHGGd0UfWC99wd3cXf/mXfxnLssSnT5+Ks72+vi5jR4cvLi42x8o6UXx9fS3VKeSCrTJeWifNYOGHTC4QzHwP67YrI+iFE332C7laYb9kGzHwx38SrPFJDlxOkvk7vo09TPgTwKV1xRvNCfop1YMQsGnkw54ZJ/MAALdR4l/QA8uVaiV+9+bmpqyD9ZCTenKgXKLrxo0M3daF/4axdoJMFQVyBHnzdG23ffoUN3Sfn+gS+maygvG0rRnoFnJm/bgHPgJ5GFzwO2MwiWQGEv9hG3SPtZPcdV1jmufyNGLri5lTiAz0xCDcMiCetnsrqVBD0LCObTsIY0JXXE10bMbfgR8A4SbzAGR8H59sH4jMsTEnSiSayAr5O2Fwwhjp62qndSbpd/sNM8mOL1571m4cx9IODUnEC3/I/N0abJLCvt8tbMfjKWLdPlfGsuD+VE2Nc/JJoe9Ft/Advje/829wBokwvp/Y53tYV7xv0IkL68333f5OHDR2cVJpgAwQN+lJe2c7TuRsMh3SqsUvrkLwk1Y7Eg50ECzXrp2rMfhfx3FeG7J13cZwYzT7C5NyvFy1qDi0kg3oM++1GNgEIPbrxPC3Xt+daNCu8eXLl7IZjkEAENj8BzB7fX2JiJo9XV5ebtghSvmULcnE/QRKfzci4ng8lcCB8uEEDXwABvzuHk4HtcvLy/IkYwd1DBNmAGVjzlzXgRSQ6SMq7bSzw8lPxEwpxd3d3fnhhFdnBeO/pSQZtCqhCLxw0LTSIE/PgbEiIzNuvMzaRGyZBIzZitW2qtA2xHjsEDmClPFj9G2gZb26rouHh4fihLimN707acCxMk8DUMABZVuYUuaHA8Gh4GiYGwaIM4BxYQ7tnoqIykBSnSC4+NQLr4cDCJ8jYLIe6BF6iz20a+v9Sm1FhWuYkUR+yJjPWQ7oAPaFrgISuC4/SbL5G0nfsizFHl9fX+PHH3+M9/f3+PTpU9zd3UXEliEBIPM747KvAEAZnLXyRi58jySP1jrGfHV1tQGb6B8yRe6uXNg3AY5amTMPqho+hY7vpZRKotn3dZ8E1+eniR3swZVNxkYCY3kCph0YDfjwFxyL7UpFSqkctGCWlYDP/cw2+nuHw6FUI0jSsb1lWeLHH38qOvDy8lLak9g7sCy1ZdXgFR8OS8e65bWrbTAeD3bG97F1dB7ggazNxBYWtiEhfHAGn7VP8LrYr7pSZRDKOLkHY2JdWAez1IXdjC2QN1HH+1TPnIBGsEdxLiCEmNTGAQg//EDdH1APDUBnsSMDvm/FFb6LvbI2Tmjsj1piwQCaayMf9MlEC7+zzn62BfJY4utNvyXWRG0bczu2/TJ+x3L0NUxUmgB0rEcPTqdT8VEmelxVoerIHGOtJ26a7CDJwLehx/go5O3KNwSE96BZv50UMTYOZGiTBINXg3jLiLGCWb5VibCPxCfZzkigDZyZI34M/QRPMmbbIWNAF1uZGugzZtbYxBPjwGb5id31fb85UY95G8+lVPdCIk/7Y8cg7MVVCT8bC9/H32yT9qfIzjbZJurf8/qzKhrH47GUwp2dYTgsVEpJD+iqO9wBQRY8FYptNlrZWYICQs/3qg6fhMD3h9G20DhSFvBrhjalFPf392XvAPckePK7AQ1jc8bJvLjO4XD4KrliA5QdM8B5XSN4YixODEV0WwsL7tL2utbyLc6C5MtyQkkMamHSkRNtItfX15tNcU5WWDvu1QJAt9Q4cLKuJIV+oON24+ZYToroui4eHx9LVYVKkJMxxoGDn6Z6njzrh7NgAyi65z0hZrasP2YVHcxs5G7zaxM4Pkcy6rXv+36TlBXgsNaTVQCLsENt2wc2aaYPOTtQO1nlOwQKGBGAE4kQ64o92DYjto6RoICcAJkG3djozc3Nho3G1ri+GTAAw7Is8cMPP5SWm76v55BTsSRYd11X2jSpenZdV579QeBAjxwwHUgINDD86Adyfnl5KWDc7ZMGtwZhACPsx0GJvzMX1pek2LbqRN2/Oxl3ddDJEfdCVwnkyAFbR//QFYKeK6N8x1UFxgqwZQ1ZX/Q5Im8QfXt7i+PxGI+Pj0UP1rVu0oWIwradyLNRvTLGVfYGAWbtmDfvOwFE571eJmicLLTzMfg04ERnWB/7B+6N/wFAAFItZ9aPuUP45X0FsVlL2491A//npJPxtrEPXXRC7optXat6YqITap92xbjRIeu+SbBvxTq+25InxgX231wHvTUgBDwxV+8jjDiz9FNtT2orfSm2T6i2HJkX+mo/Qoyi/RD7tu5hSwB7/Jd1FqKItXDVqCR/qYJaEyHrusayzsVnes8UiaRb8dB3vs/amJzALpws+Nkijq18zuQwPyEK/fwktz7ZH9lXz3OuHN7c3Gz00dgD2WOb/B1fyfrwN/TLsRi7x97Bm9iV98CZWGgrg06S8ZuQX8bTbQK7LttTCNFjEodM7tdHRUBuoQd+vo3tpV0j7u19gcgQ34BsWI/fev1ZD+zj4jg4AzEWArBLgFmWKGwi4NOZOBMh4Gch1H41roVRwfibpXGWisAJOgRazjp3kjTPc2EHDThRGBwFc8do3QtqNoVAjCxSSvH09NS0NixxcZErHq+vr+UZDtlga7sJioszGIah7IHgxfxwvmYpzPrAnrvcawDZtmgQiDAOB0ccDTrB+2bKqAIZXOP0WU+YGTMLh8NhYxiASICr96HQT3w6nb4Cf+5pZ01g09/f3+Onn34qR8OmlEpFyIYdEUVvkIl1Dh0C7HIP7g2oxbGZkUVnWEN0i/G7BzeiHulrxgGgzJjQa77HyU/ouW3U1zZTge64QuU1QV5OBiK2JzJROUSX3t/f4+7ubjN+EtnT6RR//dd/HT///HM5Oc17NQx6uSdJE8lVtat140CxqYuLi3K0NLbghNAVN37HGcPGETCYq2XPeyS5LcBxMuGXwbnBFQSAASX3R8f4u4MAMgLA4IcjamuBwbkZQYM/9NBsptcc/+aeevwibQldVx9qRUuE18kVyV9++SVS6jaVgdq+eiqJuf0R9s8YGT++CB9q4OC4Q+ziO65WX15eljiAz3x5eSkAyCDGDCVgD3lDpLid0MCasXsfghNTM6r4CzP86CF60fd9dAIRlod11T3ftjVvkHW1F5m5vQ5w6NjrSgbXZB4t6YQdMncn7XzOJAzguk0e7dNcgTMI4zNOPlgrj8W++XA4RD9Wu0N3pmmKy4uL2J/1oyVqWHsITY+HxAGfiPyIJ+jM6XQqiQj2jO8ywWPdM4gnrh4PNanFDpFtpFotgjzBf3ufELLCBp+fn0urEQDbrbf4TP5m0ok1Zt39cE3L0XbFmEhA0DfvP7m9vS14lJ/gRXQd/aBajJzQJ/sIdB65uq3KvpPxf4t8w4YcO4wX0SmTM/hR/C/3Q1/GcYy0bPfB2XaJFV5LyApIK8+PdcW+8X/G947rTpb5HL7se17fnWiYScApIJhcYYizw84nQ+VkIZ+w8Pj4GHd3dxujMPNi8IEyEgwMavKk1ogYNorZMlIsngEW2ScKiAEiRBuNFR3Bo1QojMtKGKWZBxaYRTsej6WVII+7ix9++DGWZY5lWeOXX36Nrst9zRgsgYIsFQPwBlPmR2DBuZhZ5DMGyM74I2qZDUfp5y04+SGgsP4uvSMfBw2YTK4XkYEZ6x1R9/Ss61qebcJcrDPoBgZycXFRWE6DV7PCgBz3waOPBm9mx1jDlFJ5CrhZMXQSeaBDDrboj/uOXfJ2SdK67ODK91u21YEVh0MlA/n6c9iIT5yw3pvtM6imVxd7Qc9ZK9vfstT+cQMcysHIIKV6IMOy5OrE/f19+d5+v4/Pnz/H9fV1fP78ubRc8XeqfMwR32GZwcB6I7Nl7TYKV/rapJr3uZeffUGwRyd5srvlSBLz8ePHkoib5XTFgXXghY74WSoteHJAIMCyJpA76DW2zXpiFxH16Gd8nFluB1cDZ/TZybETCF6AFANf5FQrjGOs63iWPQ8QXGJd62k0flBmS/rYrqq/o/rcRddRSV/i8vK2+BTACcABm7E8DodDOX6b0wiPx0NM03z23fX5BLZxgIJba/JJQUupCPAdbyLFRkimrLfrmk84WtcUh8MxUtfF6ZRPlVojRaRtOwn3QMenKe9fqcA6IqX8sFr8mn1YJQvrmGFP3Q5sEAKAo1LuWMkc7CPaJNAJQ0uuOH7xnivz4zjEGnE++SgfKcsJYxFx3uSdj8cv8XSp464J/BJdGmI9x3Z0j/iNP+u6bvMAT+KlSQIfeMI4GT+2bwBItdUHJuArkaV11hiE1sRlWWKNNbq+i+OJk9GmGMfLSF2Ky8scb5+fnzeEAffw/k0Si6enp4ioreJOdkwo8l30BtIDv4Fftd9AViYu0Qs6Y4x/Lr6R6OF7IB3cCom8WSNXb9F77mcfbMLHL7BFiwUi4iuZOvHmftgkegl2NAHGfbGJaZoirWuMQ904bgzLvdBBV28joux5dnLKd1oS0djcsdG+ybHue17fnWj4xeBxKl1HFrhGxBzHIxnZsCkbASDN0hHAEDiTpRxu1j1PevtUWLNxGCYAzYwlQnIQ9ngi6hNl+Q4P1YNlMCCFZWDh3F/nLBNlxJGZSVyWLLNhGGO/v4jb29uN8fE8CZQUdt8MtoGewTnzsRHAziGHTQBToHGZzwqNAbFRNyK+Wh9eXJ9K0dXVVTw/P5dkwpUHvm+QzvpEZONF9lR1rq+viw5QdfA4zXiS0ZslbIMDOgEzzbUBNMyH63nPBpvIqaqw3szBJ8+0QNFsFOvAmlCt4YVj93nxfJ9kCnti/48dCmCKdTAbg44YXDJ39CgiCvgYhqFUIWC4fU3kiP6wvq460Uaw3+/j8fExHh4e4vPnz/Hhw4eSoJmYgIAA1DuxRe9d7jX4YZ1JdEwi+PkRDp4tW55SrX7d3t5uki1X0dBpZPny8rJpIeFz3N9HSRNADUhMCNjpe+Mf+g/zj0x4n4BH8PVpXXyWAxqc2OAf8XtOdlhH26ArbDDgbj2xf2hZtDzPFMfjoVwfH+3YYDDKeHzKUWVnOVVujHxUbt0MCZtrUqpW1GtlhDjV911Mk08uqxv0h6H6B2ww61fENMHkcuhIfobSutZY4fjlJK9l3FNKcZrWeH55isvLi1jniHXtVM2oFSGAKqBwmirjjH2+v59inqdYV44Ars/vwP5pi6V1dRuL62Z9QDfjp03DFRwAFTrNumInjo9OSFl3/m0WmHVeo7ZiL+scy7m9+vLqYpM49qpKR+piSP1m3l3fRdePxc9enCvZ6O7Qb4/UJq6TVAF2kQFyssxYE2KEiUq390Zsn3LO3gnuzZ457Bz7y0B7jPf3bJPvhxwLD8f3c8JUj0t3tclrajDqQ3683hHbPRqsPZ+B1e/7vP/g6elpk0SauGZd8X/YBWPAVpzsth0ytPa15JAxou2M+OJKAuQOfho75PNOlvENjJ9xtnGb9/F7bUxhrG0MNjF2dXUVsSzlmTl8r01u0UlXgJwQWbf4PHbOOE0KOkbweWInn/me15+VaDiAVyHMwYOHCFL8d319XTaHm12NqO08TM49yH3fxeXlzYapRPHe3t7j6ur6qxMqUDb3zHksCMVH6jrIkTwASoZhiIeHh/KAGebAZm8YdDMVKA/JAgbmgGJjxBBx/CgjCu3KCM6a0qTBCMqBUvqkk7Y6gtMENAM4cJTeBIvMUkql39praHYZueMwWU9+mi12xcOGgBNxUEIm7LeAHTUThIPxkcgkI8fjMZ6fn8vpRk5sAew++tBVApgRACLzRm8Zh6s/XJvrtYywkwEHWoM2g0JABtchmEfUJNcbtJEXOsJYWH90g1YwGDvkCkBhPA44ZjHMpOAY0QOYKJwuczIzlVKK3//+9/Hrr79GRMTt7W1cXFzEf/yP/7H06f/www8RkY/Wxj7QFcYfkdkaJ78EFRKrl5eXQgTgT9zK55YYrxUBB0CPn+JzfH+e5/IUdLNoAKSWkV3XXFVzewUvH9tJoHCQM/vo/TsEPO/TitgykC6V83cHeQc4vsM83GLx9PSkAyyW8sRx1oXqFrZiIIIvIgme5zmen5+LX2K+JiQIhvgVSATm4opQSx5xXx/QYSLGdmwdQA5Zr3IVHTCKTWRfWQG5q8jZlmp7phPmPL4uDoe5EDvoBePkd483ImJZeZjc9gTIYehjnpfSLohfIX4Y0HD9DNROkdJa1i2PLT8n5PLyKnjIID7Zc4B0wZ7N0FuOrCk+ykwoNmKfCL5wosL9zPASq6cpP+fB30F2/Bu7QI8YEzELO/JcfB23b/IdAKU36UNKPjw8FFmRIMD4ez9jRJT9XezTAwdh38SFlFJ5rgNxknEjIz+gN6K2aaEn0zTFp0+fNrEXu8CHo88Gwm65gXBx0uB7QFh4zy4+kVhqrMCcWRuuAXbh3+C4dvO+gbcrBdZ3rm9shIxZd5PS4FOTS9wDvUJO9smcgufYa/Kaz/I3CEBiJd/nHiY9Y42Yl9pZhO7bjvidNbXfZ/2wf+6PLbXJS0Rs4knrn/+c13cnGmZrEFxEnNmnyiSzsGS/fpo1D1BDMA6cOCTaYd7fXzdVDxwabCQB1C0jjNE9nwZjAHscRFt9IEDyPobHWH0ah18sgPuicQbOmluWhoRlXdeykal9NgQ91wb+TkhcxmxbZXx9J0HOSvmJ/D13FB1jQVasP2vCfDEkn5CBkzYgMGNi5nYYhlI5+uGHH8qD8dxq4ATLaxNR2VTkCzvEg2isZyRB6CYJB4kaTgTdMKhhTrB9BGCSHD+kCpnQEmanzLx9fxyOW1cAZ+M4Fn1yyxp7CXzqlh2GqyuXl5dxe3tb5O3WMQMS6+DpdIqPHz+W+9j5AtTtH5yY2YG3iRh26DLvP/pH/6jsn/nrv/7rsvGbMRLsAQDMjfGi695fwfvWFyd1ha08zw0gYOYrom5Kjqh9w04C3Vvr5B9ywjpxe3tb7MEMLQERIG3QZTYtop40g/NHlgb/PIkWmcEGOuDP81w2Yw/DsEmcsSMDRP6O7v/www8xz3ORydvbW+kLN+AkcLtKAwGAvAmExBfmQ7IAW4o/skzsf/E5rEu27Xlzbft1/CJ6SCy6vb09x5i0GaMBa0Rs5Io/MIgzoM1zuSj+2ySHWX3uh7/s+z7WWGIY60MzseHDYYqIJT5//hzrmtttiXn5NLHt05rx9dk/zTEM9Hyvsa4R0zTHMOTjh80a4zPbl8G8Y6cTG363vZnAMTPL/PCfJiXxZQVERT1sgPgBkWDA2LLU+CVXKNBJCDdX41pgydienp4K0WAQzuc5uh1AB8jlM6+vr2VvG8TGzc1N+Y6BnuO3yTh/BlmTwILLHBeIIa4aYKNuXXZ10kw5oB0yh/98f+yfdWOMjoHszcXOGRPyRSecpLGG/M3AHvt2nEIW2JDX20ka9ghu4Mh227HxjjEZ8dr/RkeRg4lArsO4Dfx5GTdfXV3FfKonSzqmMkYnXWAldM6x1/6p63KVl2TYf6O6Y4zupNz2/Vuv7040CIgsMllXBv41eJtZN0PIYH26AwtABo+CdF1VVhTSStL3wyboO+PFyeFA/NMLijKTDLSZMYEdhhGDc6ZnhtIGzLxZEAzQ2S2OGYCI4wA8cC9kxGe4ph3MNE2F/TVg/fLlS/R97hPmid3M2/sXXl5eCmCEAQZgtUyYW84iKuggaN3e3hYnRqIDU+PTorhW27POGr2/v8fj42OpMllu6INBYmUYK4ho5d4yiw5kyJrk1UGD+XAt5O51tgOlOoDT4X1XbayrZjVh0gEeVNGoruCMzVYQQElI+Bt6z9qg72YanQyhwwTbi4uL+Pz5c8zzXBJe5m7Gy+y02X8zKPwdveYUOBJTV4aY/z/9p/+0yIDx0/bTdXnvFw/GxA/AUrm1zcETsmEcx81JdNgfiZ1t23pmcIINE8R8eAS6YtDuI7exH/ZYmF3iXg7cBrYEBE58aZN9dMjta57DsiybFkqAGe1szNsnXOH7WctpmjatEMMwxOPjY5GRE+92YzG/o8t+jkBro7zndgpXCQjk+A/mhW3zQuchRwBO6Ab3cvLA0bkZFFYfwN9zTNg+R4eeeu7lTZ0cH4yOWMdgM9E9j9+6l7pR+/xqlfziAjImlQqN73M4zCXhIv5l37OPeZ5inpfzf5A2Y8zzEuO4rT44zqJz7d+JOayPiQT7f4Mf+1Bs3rGT+aJ7TsIZB37Ovp5rotuuyhhEIWvWCJDpvnlA3tPTU2n7JLEGrJlMhMwiiSD5M+5hgzXVwhaQo3+3t7dFZo5dXIfEGHuzDvg4afzvzc1NmSOyJ3lApmAe/9sEpHWTa0REaVVmHZETMdOkZUStlNM9gg21jyNY1zUeHh6KbmG73BtbALuYTLXc/G8wUFsR5poQqu0eU4/JhA3XjajxqE2YWEcnjrxHYtBWZt/f3qJLNUnnmvgx41Z8KrZDfDfJ6oSfeaKzbuuCxEMuyMpVle95fXei4ZKTgcYwjPH4+LRhNM048p/ZdoCcnYRZ4MPhGMv5CZM4RFjkvh9jWWpWhXFzOoPBPsZnZfZpABFRAIkNjEV3Xxuff35+3mwQbp3hy8vLpjTYdV15qieONyI7MkB0xPY0HIwBQEGbyMvLy6bcj5OIiJJU2MjMBm57h+tPgCyfRZmcYZuxoDTrcVM9Ya1ZU4KmKwToBbLhOL2u60qLE2PGUbJxzaVdEoPHx8cSREjcuJ7HybhckcCIzEJwLWRDkuME2w7LTyzGQJ0QuQWF9WWNGZcZE4IowdgAj3EzVmSLQzfb5bYKO0BaWnjKO86Kz+IwX15eSguT91hFVKAJMMc+nHS3iXtEbE6qIxH1fdd1LcFymqb4+PFj9H09fpkEhLHc398X/2CWlHFxH14p1U2/JDToOTrj508gH+aLk+VUGBINEjOzmeiD1xQ943otO4wzNwOGHNtElhP0sC2Atm2b08q8Lswd/+DjxmEXGX/bXoHNOEgBaHjwWBvEDA4dP8zUIwOze8wVOcIwOvnib/TCs55mTJ3w5Pt+/QAzAiq27nVnE/m6bp/6DJjKehslqUQHM6ioBBb+j79HpOj7umZuA8K325eWdZwjItUWI+aSfdkUw9CXBIq1zT/7r3xabTOh1XiOvGdjjb7rI9IaKVUm3f3zBuvEVNYGJpR54zMdj4j/xgj4TO5jvXBLrn3QNE0xjLXa5kMH7H9NZnmc+FbGa/KJ9/kbfpm5ksSjS7T5UJHFX+PLb29vi75G1OcM0c3A88mwO7PwBqnoREqptNpgI/br2C5JEPNHx5xEfGsNv7Wvwb7WftExx6SNv2dADaC1rZqkZg3baoBt1CCX9cGvuJpi/2MfzHXBAU4CLGNIWvTJPpA5oMP2IxyaYmKWdXEyyvdbf4tM8FNj30ff1T1p3uPj+Mdc0CHINyeITr6QD7jesdv2grxcVfreRCOtSPU3Xv/2r/5NYeQ4YaQCqrrXgYALWMDAUbRlWeLm5qYYIIuPguSFOUXf11IQipQDRQXBVjAUlvcxfIIPDpZs0WVelNYMEgtkYIvRmLmwMn/58qVUJHgIFY7DAdYLyAt5ANpxBq4smE3CcJA3wAAD96lXbr2Zprr5FCDT9hQCYF3pYdwAG/QApf9WmfDl5aUopc97Nyt1eXkZj4+PRTYkccybIGXQ6mSJz5EgeHwGEzh+vmfdgwVizjg0Xm7HM3BHhjgNAiH3IDlknC0z4ATG68p1sC/0xEwLNuXKGWMnQPjvOJ82IfHGMMgD96RyPjkByoxIxLa1xbI2mxixZXAgHbAfJ8dur3FiyRwBKQbfjIm1dMkf20LmBouMK6JWV73/hyDEPjNkdX19XcaELBwYXa5GDozNiTw/sXP0EXvzBvM2iCOLdu8G1UO36ZiBc+WKeZihR698rj3rZlCJT+Xv6LWrAxFRDrig+uFExqyZyQHfkzVjjWmLw8bQn4uLi7IfDvmj9yVQj2Ok1G32FdiP25cDOmD7UopycAFVk5qk1AS8BWrjWO2Ducxzbp3Ct7g9hntyPDO6UHxFyidX2aayfObIbU/LBhShD+wxcRxG1stcqxH2DZGWuLioiTHfQ5Z8lrVhDdEl2wfxgrXjXrZFrsf9DFBb2cLS73a7c0JUY6rbWVlT5MzYqTYgd8c47sWacXIUSY43OeNvWzacNi50k+TDus4a2qcapHM/k2N87ng8lm4L5oqN+6GKZuGJY8QF5OOkHgKktSF0wj37XIP7Q4pCPHidWV/7dLAUccX+2r7a9/J1nIxBROFDSALxTcjPCZ1b0pmfiSrWabfblcMNGIdjN/eArG5xJevq+YC9TNDzGQ6W4V5UzJZpjnWpezm4N2Sn29xYf2K4kw/LEJuw3aPL+Hi3C2JnxN15nuP//H/7n+O3Xn/GZvAU7++HzRGwx2N2wF03lMlj0GYLGKDBi9l4Jkc2lRXCT2HtIqVTrGtEShHLUgWCYiIUgo0dHAGLz8KMwsC5nQhg7MBv0Pf+/l5ajRgzrRj09NrpGXhF1BK+gaGV10laRG2tiKhPhkURADsos5mciChtWWaHXGZb17UYEPPDSXNNZ/Bm33nfrVfv7+8lqbm7uysMn/s4kT/joUpjpgrAaUeAA3DLF8Ddyo9eAPpIbM0aOHARAMwwM1dkC/BoWyz4yZoiL+ZA9YB5AVTboI68OVUMIORN5/4c43G7YUSUPnt0lgTPfbhmh6y/rkqwVhHb5zi0pXR/h5aDp6enr0AbciFBd0XG98I+DcoMWEgC+JzBmcFTRO2fRuftRD0nbBGdxPk/PT1t2N+rq6uvEh9IAewBZh2G0rbjZJJAwwETTiRMSOCXuq6L5Ty/98N7DH2fT9kZhpjmehpURETq+uj6NebD4Vxq7+L6+upcFYIhpuUttwRlOeaDPU4n3XNZIjPvsPz5v0owVZ8ekYKjunNMyA9WnecvkTcuzzHPx3Kdq6vruLzMzzip1646jv46sWQtrZsO4JXF9Pn4cWbplzK206lufmRdvMnf4DelekqZmeilPDyrj2GoIAMAnE9nyw8kxIaPRyptZ1kfz8n7usY49LEsZxKl66MfdjFNa0zTEl0XMU3nw0u6CI5nPR2P0fV9pNTFOA6xrqeYptpihM/KthoRkY85HQba0A5ZVusa67KcZXWuPKxL9F1tsTJIMoHgSqA7ClLKz2tYlrkA3GEc4vLqMl6eX2IYzgcOnO15XdaY5il24xjTNEfqUuz6XR7zssQ4jLHbjfF2PpBkGProuvMc0tcxxoAK34seEWuxd/wHNn17extPT0/FT2Hzrsqho62/AYzjuy8vL0s1Hl/GNfBHxDGugV/e7/elmo+PwiacgAFWIe6IIbzHvVx1NEGBjhhgIkviKn7QNmOg3XVdOYmPlsPHx8fyIORNsrzW9iL7TSdv2JMBvHWL6+AXIAGQL3HGest6kkjwu2VE/MHPmHRyImpc2cYw+3FXZCGFwSURsRkXMnBCRRKx3+9jHZc4HY/F95NQRqr7prmX9wS6FQoMU+JF2hK2ENzYhGXi5AkZcJ3fen13okGQWlc2Tb8XIAuLb8YO46NESiBlcu5hj9i2eOQMcX82gmMMQxfTVB9eRKuPwSWGSKJioMjn2Ghu5ttVDE45QUEPh0NZ6Igoxo+ht6ypy+4GnWZ0UCC+603CLp8hC5Ii5AJQt8EZOJENkzSZuXcp00rmsrTb31LKD7lzSxCOkTFgaAAnTtCIyM6f78NU0xqDg4c5bQ14nufSz8pGO+7L2DFuMySwCzYY+mMj6oZxDI6qjRNks3PM0S1LZixYF+sATsRVK2RtWby+vm7YJAwewGJnb9aTtfBYfJKJHRyOC3bN+ols0FPk4rEjZ4AZa8e1eMgUMmJuzBl9x8btrH3qh2XIfcwgYRfop8dmtoXfneybUeLvyMUBw+fH39/fb9ghkgZ8j0vLXAcgQPsVDp01ZD7rusb9/X1cXl7G3/zN3xQ/hR9z8hwRMS1zLBr/4TymLq2xRordvj7Z/uHxMevgGtF1KZZ5jtfX+jyGSjrQ+pJtjzYrAHREbmHNutCdP/O60RV8R0TEfl8Jjxwrsn68v0/ByUzMEZ9Bta+uWQbt+d9dDEMfl5cXFaiK9W111BWyZVmj6/qNPc7zGhcX7KUZNjLGN7Ne2Cp2WEFrfo7GPOd1gaSIqHsPXXHKMRC2MpNk6O90iliWFCkNMU+n6FLEMJyZwy7FkM6Ar6cCFrHf7+JwOEbf0aY5xLrkZKrru5jX2irolq2si7UqOI6XEZGTrr7PyRI2l9enj2HtIh/N229kgm+xLzJxMM9zjLsx3g9vGwY80hokOlfXl4WQ6Prz9YauJCfD2J/Z7nMF/qwDx9MxhiG3dO0v9sXnzHM+uQySER0zKWXihmcdwHLndapJB7bt/T74RuKxq9h+Zo3bWQyYU8oP7wUQz/Nc9i+6ik3snaaptN44uWYdMlHwtukmYL7oGDHEczBmaQE28ZJxGGDSGeHOBBIQKgRvb2/FponV2KqBuBNXVzVcpXD8oFXVRKU7MNDJp6engjGMN2uLYG1F5j/m5io01waXcB/G7bkYr+DHWW86JLAN7sea2D+xDwQchV4hr3VdY5rneD/7mXld4ng+OrtT7EQ2YD/IccgSdIfxuXrtmOoKuok14yzr0m+9/qxTp7w4lHVZEIMjPhNRN3F3XVfAjrNZgvvxeCxMYE5kMtvnjUwICuBIpYEkAseDsgJOrJin06mAIxaQMaDgvO89BQYiHz9+jGHIz/pwyR9lxEDNzBqoUnqd53kTrDDw4/FYWg6QIUbNKTJWGsYI6+YNqm4B8YYzb8o/nU7lPO7j8VgU/fHxschvGIb48OFDedJ5RBQGHkdHMkCrDeuCQ+F4XBQZx0didTgcylOknfCgX4ADStmM3xk518ZBr+tanpJtJ46O4BTQF+bBvHAcBjpm59t1ABR5UzSsDDpsFn6e57i5uSm6h5ywLa7F33AGjMstQ06WSfKdDDoBwOGakUJ+LXvBHBkTuoZ+0oLjh6q5+lIB4PZJqK6u7ff7TbWU75DQcq22KuENhQTKlp3jHpSJsWV0gLnycsICawmgWpZ6ZK/3dZlMcYLBMzT4DPJ7fHzcJLc+8QyAUish26e788q+tI7JLP04jpHWNfqzjjNm+71vMVwbRjrqvqF2vfw+PgsbNGjjs+gKa+BKD9fGxplr19UHcZrocHA3M8s6zXP23fvd+bkP45m5nedcIUgpUpzHnyJSpJiXJZZ5juN6yjWIdY1hHHKl5zQX3/Dy/Brj2R5Px2McU32+x7pEdKmPZV6Ch+PlqkYUP4OMd2N+eFxej/x8qNPpGH3fxbpmljLOD12b5zn6oY/D8RDTPMWQhkhpjX7ozgxnlAfPZTC/PdzBDDi+JK9d1aX24W/Zz/UlRjlBx4d2XVdAnfeqoRc1yctg8uXlpbQtmfxiw7QTSgNU9MKVWOyR9Wf/Dt+x7UIS4Ftp3XYc9aEMTjqptgMakZHBNvqHbTEvn7oGCXo8Hkt11JuZWStiiNthIADxKeg+Y3BVG9+N3NpKv4kZxmrCxfGM5Mo4xK3MXBNZtgcZODmz7rP+JITgRuTAZxl/S7KxtvYV+FBvIkfXTfw4KSaG8t/19XWp+thXt7jWPti42EQFuNU4x2uMHREDwGbMn+4grumKGjrlihpzIenl5D+6HG5ubjZ41XL3s7HQ3VZPkIW7EKy/v/X67kTD4AUQiMGgCO4pxgk4W8SIWQSCI0w8QBTQyefpRbQCcg8YYrdiObhh8AQlmH5XYMwYrGtteXH25sDYKjPOlHkxBjsG9/4xPhxJy1agRN4jgqPmhByDTIDTw8PDBoRRiaBc6v5xrs/pQjhK2lO4B+tJ+TYiCnthVgjD+VbCSZBrez55nzU3aET+yMVP/jZLgI5EVBDl5C8iNntNnJD6MwQCt9KhbwQk1sygFbCLvFlzz8N6CbDF6TAGJ1YEb5e0zYRwbeZv8O2n8RIMAAboEXNwJceVQIINNmzg4uAUERu7c1JCb7iZP/5z1YckAxCEDjB+9Ao5bKueNTGyvfM78ieZR97v7+/lQAqzmNgp8zSbbRDm6qMZr7YiQQBingRkO3cfs+0Elu9lADtHH/1G3/h8SilS1NN9mEtK6dyGMm10DdmZZPHc8IF8nnUlkQP0sMaFxR7HjazMgmFfgCx0Cx1HniQs6H1EPXyC65jUOR6P8fLyUvQGQHg6zTFP2oOwbNss3o/1RB500ixlZuC7mKdFQIu9GCmfZz/PpfqSZZwrOYU97ofcHjTX5BAZ54pT7rfOeytyojGO+SFvu4ttcp2Tjekszz7WdYnUpYjIP7uUzq1Ta5GxHxZnMocx2B/TvsKaIleTHAZTtk+z4IVcS5UxR+chh6znxA58ALEYP4Su4xvblmv8CNezzby8vMT19XWJ/RF1bwU6x39u6eS+VCWIJ09PT2UzNzGCtbYvYH/bOI6lIs86In8IFRNGXAP7xCeip4zx4uKiHPvuhIP1pUUsIsc9KvnEHnAK9sQJk/gP73+y73UygU+nmoEdR0Tp0OB95Mi6M1d8s0ku4ylXA6zDHNm8rmuxfeRuMpAEk0TIbDyYE72epqkc2ENVjHHgV0wiUbnGRzIHH8xBHOHvLSlDkkAHCm3nyNSHIxG7SU4hdSJqW3WfUnSpK6dDgg/7vo+7u7sSp6z/HLzj9mn7KV4eO0k/PrMl6f6u13cnGjgVgBoAhEFx1j3CYFHYFIRzQ/GpMlDGPBwOm03JKBCGjuLD/BEM/YArA1qAJOUvyqD0co7jWB7kZQYFY8AhEJwdeN22ApgnyXCG7VI6hm2ARgA1eHEihHPiPxIcqhqAIYILFSOCBgrt5AbnxlGKzBvGs81seR+niZPh/HuyaJwVLzO9yIYMmyqJHXBEfQBgy5wDrLxXweDo8vKyJEnfysqZM/qD06mAJjZlanSXtWoBIutoneu6rpTBOQEN+TAWwDFrY4bQeuaHyxmkt/bon6wdjhyngdPFJlyeR+boIPM3c2LWzqVSJxuAOLfROQibjWKcfr9l1Mxe+5g+rs1n0A9eJg8IDoB/dIcnyvtYXL4DKeHqiAEBdo98PSePg/e5PjqGvhE4WRfuwVoSBAgyY7eLNWpbmeedzv36ni9ymIch97rG9gjwlpEz44ifRFc8PxMj+CTu2yZM9iURUUCig7zX0i0nTo5bAov1xD7dhng6nbJPv7iJt/dDuWZuE+L4TPzwsvGHu91w1skUPLAufzdFSn04nq5rRD79cIm+H6LrINXyPsJlyf9N0xTTPEc671mBxJnnOSeP/RB9DwDIyczNzVVE18XxdIyLi7wXxOvVdVQl8x6FdV3OSc4xImr7DXEOG0f3vAnWrRvYuU8hwz7xl47FJtFcxSgJSdR1dSXC9mmiB/9CGwc6wDpTdXdLpds+sSM2QFNFRkfx7/h9AKf3dlC98XObGAe6BKGELPEZRyWvxjskB/gS+z7AsH0E5ElKKR4fH0uc5/uvr6/l+6zz8XgsR+dG1I3vTmQgFfA/xB/m2HZJsMfSx+0Tq+xHiOeOccyHuMLaMGd8GPJifoxxt9uVI89dGV+WpZBG9gn4bLAhYBids0wZH76D9XOMbwlP9CvbX1fiScS2y4C473sQZ12Zd0sWMl6WpRxhTGWPpA1/71Y2CHvmHWvEslYy0NUoE7r87kTIRDdEmUle5ul1itg+FPi3Xt+daLAwKBvKiSJ4j4KVHUCJ4rtE1HW5FxoQ7aPdfPwrCks56fHxcdPeAhh2Sc4JB/flnpyewrXJKBEeQMCAiXEBFA1EMRYzhQaABkAol1kRStO+JvPq+75sYnM2iaGO41hai1yxiKhP00YxI6JcA+cYERvjRzkdXPiewWH7ajN8dIbvovgOYiSoThpwIsyR+6MrBp8GHBiwqxUEM45HZR39EESXen0ts2Rmg8zSu1UlogJB9vIgS7OlMNmsI6VvJyRmDpGpGQcbvPfgcH9khz6SAPnBZOipN91zj28l+NzPa8UaMGcnDdYjg3iuRVJscN06NQgIAy3uTcBmXA7wvGcGBp/ka5rZdBB1u4HZYK7hIMrYPT7miy0gK7+Pf2LsyISW0A1T2veRuspwI7d1XUvLDDbOuPq+j3WpbSskggaQ2JV17FsJLdXniHrMOevJHLBJfDA+1kEZnWJNuDd2BDCEyDoc6gNWCfZm+lo/y3dP0xTrGnE8nmJZatXv8vJqo7clWTvr6+XlVeTNyz6yHLvqYrejCpI7m8ZxF8uyZcAjcssTCUeK2p8O+XBxcRHjsDvLhk3IeVP3siyxv7yI7pBinpe4vLyIdV3OrRC7yEftRrDH4vr66jyeFMtSfRz2jX5hT6wPzzzBPg3mdrtdXF9fl553fLJJB4Bcu0/APso+Ev+MD3XCOc9zeYbCtyqhp9Mprq+vN0fmokPYSAuesH+Dy4gotgWhRbzEBzi5xqfi87g+bcgQo76/9RlZ4k8sD+aLrpuJxo6QE/EMXOQkDz1GNmAAH6RiwNtWt0yAmqhz+yvjIYY7UWH9sCVad7+FCcEUJpza2EHcxh+wqR2CyGN2pwvj9fHkJj/RmbZqY1LDsmCeTkKZgw+NcUfLhw8fNvEc/8p8qPzs9/t4enoq687eChJ967DH9fT0FBcXF+VkzmGoDziOucYoxgSha+yJHVsnfD903UReW803TrVt/X2vP2uPhplBghIKa4Dx66+/FqBOW5P7pwlaOBsADwHMivrrr7+WjZMo/MePHzfAhOuivGaqnMHhYN7e3uL19bU8IRk23CVEK773gdgguR/OEMUFZLFfgiCJMyNjJZmgUmSgTmuHAz1nerun0eABR00Zru/7+PLlS6SUvjoRIiKDMR6KhxJRdr65uSnOalmWwpYYRKKALlsyJpQYZYc1AGDweRgoO6Q2WXEC5OQAnTPjMs/zphUM2aMP/Gd9jaggBcDPeNx77qDBvHhRIifAE6T5z47DgRCH1SbpBv5mF+wYYdYdVK6urkpCwSYwMw+sA7brvVb85PNOaNANxmBn6yCMDjM2goBfXoMK6LYn2fhv6As+Ax1BnsjcIJ8XznK/38fNzc3mSEj8GrpmxpP5e05Uw/gbto9eEvj9PAkCsoMrawrIMTFiH8N9xv0ukthgnh9yPB7jeKhBirGVxOlsC8iNB4fxORgy5E2bEvaEjGhbbIMLP70WJHMmFVwNnOd5cwCGfZHjCkGZJMaMHPpoH8TadV0fsdJuCejI1YPsC3gwZq4KVIIkb/Q+nephDHm9+5imnGikBHhfou85xhp2N2+gr/o0R0pLdOdj2l0hW5YlXt/qsdcXFxfR9Snyse48vyIipTXmmU3GQ8zzFMdj1a160hcteMMGmOAX8HPEo4j6MDH8G58jwWW8fl1fX8fd3d2mKsBascm5yCRqAt33fWG+U6pVBydB/EeiTYzlHq+vr+WEQvsl7s988fWsg1lz+0vbAGtCnI+IcmiM7Ql9dyzH/k0+MD78qfcWUSFgzd7f30tCTtdAJ1vH9i4vL0sng6tOJFt8B6CNjrgCb51AHtg1MrG8iP1tcgGLjjxNVDqWY8/27+ii781neTkxY98fL3w9YwMfmTCjamciC79hUgTZuRLlqhbXM2lFFQcbw08UUuicOEGos36WhXEL8rKcXeWmsj3Pc9zd3ZWkHlsr7egxFZxlcthkSksIYeP8dDzi85a9ZWid+p7Xdz9H43/7N/+uZGosAIACRcIxvL29xYcPH8qGJgckjMSfN+toZtmlIxQCJbMgHPgwtIgozHgLWhEsysxP5uWHCZnpIQN1dvj6+loWDcdkwEKChKLN81z6Z5EllQkqDc5kU8rs4OPj40YJ3LuKXMm2Hx8f43Q6xcePH8umIIN3Z84oN+O6v78v7w/DUDbOteyDA8HDw0MxCpyYHa6ZAZxDyxSQhAAEXdp1ZYqXKxGMv2UA+r4vhsqGcDtx7hkRZa3QTYAcYwd8OsDYYbjdCODNe7zsQGE6fIqZ2QIn2+gK3+eaHJiw3+9LHyYJKTK1I7ejZx3cNsW68G8HVwdSV11oi+Pv6D2l35Z1Zl1YQ2TGNZknztBjxObM2DEOA05sDV3H97DmriLwfeZoPbf9uwrg4Gk9ABi7t933QB/MNrdJFnrD63A4RH+eyzRPcXtzWyqw8Od9P5zBcD7dKPfxrxErm2nz/oHdLj9HojLKp0J6ONlkgzljbBMp5t/3fSEw0AXWlKcns9bWXXSs/WldrT6I/Tw1hlxeXhTCZBjG4LjezObOMY4Xsa4R81RPLMvVgrrnp+vykcGxrrHG+ZSmqT4nZlnX6FI92Y4gfDqdzset1iof+mk2+LzyMYw1KbV+et1p10L+Xd/F6TTFsi4x9H1EpLi/v4+Xl5d4fn4ua5HjQG7zcgWQJM2JQ9dvn5QOeZXtNv9tf05KlyVvjI+USSRaOt5e36LruwqSz7GFuUGYnaYpui6VOMX8DUzRJXQdP+wk2wkH/syEoU/WsS55XeisqM8TqXs17Cv4LADda+UuAZOr+AQwAT7I1QK39OJTXC13gsccHTeJRcR+ZNnGUY/BABN/a4LKcZ+uDlf8sXGITnemcD3G/Mgpd2edYI3RI8dFr7PJUdYUnGc/Y9YdMtpVcHwCn8GGTDC5OsyaIGPbZUuStUAd++f76Abx1nGk7/tyAhfyNa4kNrsK5xgYERv8Mc9zLPMc+13tlJjmKYb+rK+SgwlVV1ycCKNXJunwfczFRJttjP9Yj//2f/zn8VuvP2szuAEMkwK8MTCMiIzR7KLLkGZpLQBAMyWf9/f3uL293fQmIggW2UxG13WbY1YBazgt2mso+7v9wkrgsiEGQxKDwlG6AhQbaGK4OHS3QlVGqgInJ2T8DiAwI2OF/JYSYPAEebOLbA6DnbeiMxYMEUV1T64dr8GTE4yICiRdwgOMMfbWWY7jWJ5qaqDl54DgeADYDi44EcAkAYtk1bI1C4XMAEoGUuiQWY82QXLi4r/ZGRIMmS8bBa3LERV42xkTAPmuHcA05adjX19ff5WMGQBZdq4SeEzIHLlYnw0MIrbtQwYSJMkG0zgv9Ig587P1J+u6lo2EJGD4CfwL76M36BJyhHViLozbf0curqQaDLvigazMlLG2jNv+jAQLHSVZ5r0WkFhWrK8dvsHU8XCIeZoi1rUEl3WZz4D0DOjn2OhgZRiXczJfj3/EZvCPdcy1rQCfZ4DFGnIyndtyXl9fS3son0We2CW+h+u4AuL1PR5Pm+rZPM/x8vIa81xbOrCX/FyQLvo+6+j7IR9YscYS83z2oUuW5bqcK2aF/DjEsi7s9T6vyRxrnJOBPsWynmIYU+w6SCHY4RTzvEbXrTEvU+wvaBOte7KQHwRPBveVvFiW6iPSdD55ratJyuvLc6SIuL663NiK4940ZT0gAZimKY5sPN4kJ2Np05umKY6nTA4+vzxvqg3Y8ziegf50jPXEZvAUp+kUy6pToMYhpnmKaToVdp7KPLEaX8D+SJNn+Df8lQEdBAoEG36HGEi1f13X+PXXX4stOAEzSQcjTHLsSokJF9sxeuoYw0lafAeM5Oqg+/a5N3HGyTw2QIygzZb4Zzvc7/el7Rhy9/LyMu7u7mIcx3J6Ep+3ryGu4ucdKyKi7L/E3sBibawdx7GcZoScsHEDdGx5nudyQiH6BVbE96LvTs4hop10eY8EWAcwj49x3MNe+LcJVgN9qr7uUHDMYA0YH3EA/bG+uDJhXYU8Nl5ERoydMRZyY55ze1TX5+bMZYm0ZvplbO7NyxjdCSjy5+8mSozPTLCSfBkXtETq3/f67kTDC8SzEPxCiBhhqzR8HkWoPa31DGv3LJMMEAANbvg+yQdKyDW9M5/7UbLkRUkxYvuEVSvYfr+P3W4Xz8/PhaElOJLh4zhgX81MkmQ443ZC4/IuG7ouLy+LsuM4eaiVS8xOYqgcEXC5vw3fyk5SYJm2DAIAH9mQAKKoOFQ2Ylu2GIf7UK3glruTIwCvDwXwqTg4zL6vJ1ux9ugo/46oD7zBcAlcLttiSBiYk0aDI2Tmihs6b8bOwdE9txHbCpuZBmyAn+gwMndVg3UuwV0tAC67O4EzkMWm0GtAIcAP4G0w43Xy3LkPn7d+m6GyzAClbNBEr83SYkfIwSAUx8Y9Af8k/g7Ydt72Ueg+wc4MPWtgtof3OVGGteQ+bikzcOB7BGWzSk48APqMD13me7ZdBxLrr1mwNniZLOHarB36dDgczj5xe8iBP+/Aa8av67qNfwXIAh6YI3rD50g4nEya4Gn1Dl2x73x/fy9VZeyAzyM7tyBSafJ6DUONT7Vql+J4rIm9v8faXVzkTZjzssbQdzGMY/Qrm/EPJaFLqVbamZerqvZXjAH7N8EEiWe7ZB6OPdgQ7Rt930eSPS7LEr/++mtZj+Opbpq27t/c3JQ4yaEurD3r7USVteSZLMQvNirPcz3i3AeeGGgCGvu+L1Uxb/B2rEYvr6+vS8LgfWX87iO/nTAD5N3h0Nomsc4HkZgwhPhyTN3v92V/5M3NTcEUZvdJBBkHMS2intCGHaDrLfPtSsT19XXsdrv48uXLJp4DwKk8066FnrG2figmukobmyvM1tW2Skm8QY/d9UDM4x7ovQkRk08mYNBJPkP3CGtHUkd89XMowFGcVAXAt11xD8bD+hAr+Tv+21jPfgq7xNeBkUxm++X5oQvI0QfvFEJ42e6XRA/x676OE0cT9PbrYAPL1i8nlybj0B3W9Xte351ofGvTKYZslhTFQxm8iRYjN1jBUBAcgieJwLESuLzXwwaHUj8/PxcHwlM553ne7PSnwgFLwniOx2N8/PixKDYJijNQb+a6u7vbAHQDDAcCgPS3wJmVD8V0RktQJbvFuMx+c0+OnWV+NgAUicSA++E4HdAtKwIVztstNB4fv+P8+b4dEkbiBIj1NUBCNm27FIG067rN0WxcHzCBjsGKcU0/kM37N7ypjzUkWTW4c6ZvJwHQbAG6E0nea5MuVyr4jO0KuTgxdOVomqZ4fHws8kcXzZjxWQNhDkO4v78vSRHzMlNv8IsNOol1EDSQRJewGydtBr123gAMwCLO3FU2A8SIKC002AbJiccAWEDO+CI7dtuuN2B6/szPJ4hExGZ/lRM8AARO2scimtBw4uv3mDvlf0CNWTZXXJg748e3+fpUHvDFzAGfyfx8f8+9tce2kmTCoARIxQ3WyuMlBngdGQP+DX1oddrkCWCUz3EN9IxreU4kmgZ+DvB83kEYnZnnOZ/2spyPhF7q8xRi5ZS85Sv9yfq3nQc640S9TfJpa6HdBVBVK+DTprJEDExdF6dz7DQwZA2/RTyxdhcXF6VPHj9BTLf/bkGNW0rQEwNT+232lHmDNvIykeCkoOu68uwniDj64V3BhLDk34BQtzTxGoahAFJk7DVpE37iD/GCuVn/iZEmQXgRq7DZ5+fnYhOsw7LU/ZEclgAQNbGDjNmjaX1a1zXu7u7KXK+vrwtBiSzpcmg3mxtHOFFCD00S8zfAPRvm8WmQZvh6kkpIMp+UhpzwZSafedbWy8vLhuBa17w38vn5uTwTwzZGZQvdc5WfudlWLy4uShJm+zeTj16h5yan8D2sCfEHezZBi//DjxErjDHwJfYNJpjayhv+hqSYMWLHd3d3Je61pI7jEfIgJria81890WAgbhvCCUTUbMqZJIrmfnuMgQQAYyRDIjgiADsmB+C+z6cxcQTcw8NDOdWCSgRBhDL+sizFGdGnySKYnfP+BZ+EhaIAGjAEVzYIBjhqwGrLCBJ0rWiuKJAcuTXEgAjl43pck/G1JTTm8/T0tGHZXQXAoZlltTE4cHNagtlUxsd7KK0rBgZ0zMPlaLdCRFTm2EwVAQg5s+4YaFuWbo0Zx8h1CQIEYLf+MV4zSayVHQ56bmCCMyGQ8B2CNQ6BZIcgMs9zOVnNSSmA007MCV3b8sQ90SezgnzeAJ7P+YWsnZixzu3BBDgmZApYx8mb4fJZ8tzXSQr6g09hjiTqbO4GMPAZ1tTMttswWF9sjyTzw4cPpXXu5eVlczzxjz/+WN5nrxT3RM8Yu23KOmOQ4LVCPvZtrIdZLuQDAOHl5Mn6zvVdmWEstE/i07CJ6qdqkkGg81zadjNXbxkP64te2N+w7ug3LDCftf/gfXy5Aa11DsLDtsdnAYHtfigHWOzdfdEGytY7EvU8vxTDsDsnaucnuU/5yNlYv97kjh/C7pGBT0Vs2VaAHSDXfhSbZL285ux3e3t9jbf390hKsrjGxcVFLKv352RbpSpBPOTfr6+vBbTiQ33uP7ptAodDV5ygWF8BSawdSTp/8wmJPpQEncQ/RUTxB4B1t34QL00G7ff7TWcEoNDkkxOw3W5XWlVTynuR8C/I1dVJE6TGMFThnKS4vQ5fP03T5rPES/sMPo9NtPaOHqBzZrHned4ciwteajfMsy7279hBixP4vLseIHKtZ+i3KxSMEWBLckHc9x5OCB/iArGj7Twxye1N7/g235d1ZF0Yq/067xEbub+TDO+ZKXZ2/j4EFIkvMmHMxncm9Ye+4mHjOxJk4r3jsWXuJJiKoe9pf+okln87Xpv8+J7Xn9U6BYCHcUWhzCiTnUbExkHZ6Dlaz5PjdxwbCo5BwQycTqeyqQYhk3RcXFyU/miUC4cBwOG0DdgQbzCiRAtb7sQApwTwcUnUIIKfZPA2ZAKVs+RhGErpzyyuGdo2UPOTeaL4JDvI7/LyMh4eHjYsyLdAEcbinlbWEdDg+TlbbluPDAy5l1lbXs7uWXc/ndYPFWqzbv5txtXAxE9Ad0DGsbgiwL3dxkFgb43Q4Jf3WY+IHAS9yQ/94J4YvRMpxub9LJeXl/Hp06dY13UTWNFh9P5bY0B+gGmfxmEGhLkwXz6PbrZVCu7R9305YGBZliJrmHacFHZnmbLudmReH7NGTmqYJ+PnO4ARg0rWh8CI7G2XrsRxD84y93y539/8zd+U+RNczbhFbJ+RcTweyxOIYS19beyez9pOmJ8rcwRzGDx8lkkaBzu3dLmCbLbWFWr0rvqGbQUDG2kTb9u520cMkl3x85qYAECG7nXnM66Suu3FCZD1BF/lZJrk0zbHZ5k36+mEib0FTia5dp1jinnihKBD5E3Q3Ve63VapxvEy8klStfrC2FxZcZKNrgOKrfO1OlWfZeWHuq0R8fF8QAsPfs2ALuJwzGO6vb0t+oDcuq4rejeOY/z0009lD4D1wCRMSnnz+tvbWzw+Pm6SGz6HPZGwmfEHrHM9bw73E5NJbm5ubsr63dzcbPAB42tbDllPt6gwb/7DXhgfvo/Yjr22+yzxLdzXJz/hO5ZliYeHh3K6I2NFXj7S3rGe+bhDAtug+sCaA+Dd5088IFaS8DtGWG/dZYJOMpeIKI8ZICEklpg85poQU5yEBxZzZQN/wj3AQtYhxoqOk/hgS74/fsUkI2uNf2AvC2tn9p44Z72MqMkUvoHr0nLFC3zoOOZYbpLTvph4YZ+43+03scT+AR1mXYw7fD2TW67imFhqcZl9kjsBiKPf8/ruRAMQS08cBmbA4KoBwaHv+wLAcPjzPJd+Z46cROkQEozExcVFKSlGRAHSAA0U9YcffojjMT9j43g8xocPH8q1rKwtyHeA9uLB0vhcZge0z58/F5YTp8lCAWBIgLgmJ1+gaDg/nAZK7r0q/HTZn4RlWZay8R1DxeExNgD8NE3FoFkbFM5rTHCxw0R2GIbHwLpiKAZBKDUvM95OpMzwumrE2ph1/5Yzx4BdqXBgNpiwnHFUzJHxodtuU2H8Tk4MqpAL92F8XAtAHlHBkKtVHsO6rqWaxbqgX95YyDyRm5lnAzbG7bYSbIPr2l6RG2tJCdoJW0QUO47IQYOEte/7+NOf/hRPT0/x888/F7Dg9bEj5FoEdesmusbfbTeAZbdAeH0IpgYdsKPIBDuiQgcbxmcJQtzDgSAiNowUrBUsGhteXZVygkzwhZVkztiPWUsIFidkDnAAIfyVmW3aP3mZHEDetgvAqteHZKIlDvg3MYCWLXwt96gAe9zovRO6iCjzRO9JBrANgBJ25QobPo77AQqwXRIz73kC0BGzzDIyPieD3KeCvi66VE8c67ohUuoiP+dijTXm4KnetmWvA3bUdV05Yx+9sL0Z9GLHED95LPn5HugTcu77Pq7OyYGrx/hn4o1ZX+upwTC2/Pz8vDnRB9/hJ5J3XVeepm175T9s2ckyeox/7Ps+fvrpp/JdV5VcrXP74jDUJ4ObmIAFN1j1humUUmnDan0JyTLPMMCfoQtUqB3D5nkuFdBlWeLp6an4DPQUe6EDhJhq38wLneAkReKTT/cjeSJ5QOcjYrNxm4QNP2SiEX0k3gCWWTeeng3IbHv5jVsgZ0lYsX+wVesH0JuW4SeZMGYw4W39YW2dPKLvrDXrFRFFftzbiSj3xD/R5WJyjs8SQ4m9jrGOp/gA/w3/xvVYayfc87Kt0jopYmysLVU0+1ZjO2Ip6+41tCy8LsyRcXqev/X67kSDzYJmkTFct3igGCxSRGVPmRSDowqBMFFsOy8mjgLx2HmC4M3NTVxfX5eMuu/7+OGHH0ogoZ+PRTVoXte1nM3N/fndPXVWGpIUQBAKjeBRQK7lrA/HyYlDVnYWlo3gyGRd182GaBsf1yBQ8DnuSeAyCCUwwaCRoDirZi7Iqq2EUGLmugZH7q8lGBh8Wz8ckPg7c6aPtHW4XIu5cC/+zXntZtk8fzN1LndjQCQEX758KXNFPwiILZjFEZiBRcfMAhnA42zM7DJWxkUQdCLnYO0EBMDAmtLXjO0RfFhHxokeE2RwxIwdWQEIzKAgB1dJsIHr6+tyP9sRukJAh7ywk0XG6DLzQTYE/T/96U9xPB7j9vZ205bgMeKbCDaAZSd1gCNIAZMTXpv2CEl01mDVDGxEJiQcyOz03fLSOnJ+tow2v/vFWtqevGbWzeyDhrNtnsQeA2qjrAM25mOfCaYt+4Uecn8TKsin63juwxoRAJPuvHn2Kr58eYiLi31ZLxJBs2+sK/dyQsX+M9aX6jE6gV2hgxEVJKEfLy/PJdk5Hg8xz3XfTwYwtPfRKhwx9HPM8xLjOMSy1E3lyzpHSrWVdLcbS7UL38+T2M26om+ukpmBxqc6Ecx6me/19PQUXZcf7vfyko/D/fL4mIEOsSv18fL6EuMwxDBvT9nD10Jc4dNJZG0b3yJ/nPB6A7BtnPXwPYl51h3G4fsA8lsSiOugcxz1e3Nzs0nabUP4cMAWcdHEJ6z9hw8f4vn5OT5//lzm+y2ypuu6eHp62vha1g5sEBHllEXv/2RfK7ZHTOeRAdgddsme1Lu7u7I/k5jl/ab4Gezd8c+JvxNcE4LoofXOVV2SFsC3kw1sFxsiQTJh4gQHX86LdTehTTxzR4uTbogIYgYxiRiG/jI2xsCYI7ZP/XbFAyyLjHw9dKEF7iZS3abK+Nd1Lc/kILkjLpNEx1J9LXN1hdhjIiFvE3nHdBMn6Oo45pNJvS6+p+f357z+rD0a7k9FCH/605/KA/VwVhGxeRozSg1YGIYhPnz4ENfX16XnjgfL+TSoruvi+fk5Ukrx8PBQjAyjeH9/j/v7+1LKJZvDeeCg2r0LAASUjB5RWh0wHoM35uANVFYggvzV1VVh/wwgmBuGiAK1JUuUG1k5g/Rmudvb203fH8o0TdOmcsLaMRYSNtg/5kLCwWd3u105ohDQjFLzHQMh5sT3DbpxMqwdjsEnmTgAYAyUWc2g4sDs5Fs2LqImUGbB+C567L0HdgQkmTDInq/33Lhi4GoJa2n9grHG+Rnoc190FhmwtjijiNrj7qAJ88tJYQ8PD0UefN+6CLNMAGqZLCqWBkCM287s4uIiXl9fN62OTjZxSOjJsizx6dOnWJalVDHpL/7w4UM8PT2VMVmfAPAOviml+P3vf1/s53Q6lV5mO3jIEVehSIAJ+D5xxQwQMoBgMFlxPB43iZsf/on/AVS6EuqkEX3FZ/r+bqVD37mOK09eC67/LTtF52o/dSo2kQPeWMbv8TIm5OlKCO+hh9YTdDgi4unpcZO4oPPW42k6xTxPMU3Yzim6ri/sKbrgVsLD4RA3NzdfVRJZI545MY5jIZBsQ6xRJcHYIzbE8XjYgJ3j8bBJdip7nh/ol4/FTbGsZ9Ih5sgH5ebN4hFrvL1tQQ7rExEliWVsgAUnXd78ik/F1qksR0Tc3t4Wn8J67fbZ/8a6RNcNsaxLvL29xnh+AJ8/b0KFNTIh4SoS64NNer+EfSPfxzeiP3zGyTHML7787u4uXl9fS6XHgI14TiUS2ZDwp5Sfgo4emAiAWed7zNdMOD76eDzGly9fit8GlC/LUk7uI2ZRSSHRJW6zt4VqAmvpNmF8s8mS06k+Ewtbxo9ztDw+mHU4HA6bFnCTO9zv4eEhfvzxxzI+t++57ZTrX11dFVLX+2CwIYhBE9HojA+mAE8wX/Qc22gTGlfnuL7HYGKMMZEkkxgzJu5vDMv9Li8vS1swibLt1KTy3d1d0U9eXMc4i+/zWeSA/qBzVMXa+IUdvr29RRcpepH1xrMkEm1LFzGL65kEwvdGxKYThbnUKm318074+N73vL470WBRuDAA4eeffy6/u/f39va2JBsoEEKOyP3s9EUD7Nz24kX1YuFUUUyMG0djQBZR2S8UzAHfgoLRIPFhPk40GAMGj5G3LDaOz4ApoiYvfA5whNIdj8dSpkYWdnYoMIGa7N/VonbuVkobd8sARcTG0SAD1s+JA/ezkXvjJIkSzpyxRGyf9O3rAiIuLy/LAwcBo1wXJccR811eVAowomEYNk8tZ2xOvAyq+Mx+vy8nrVimZvydEETUBw7iEHkZmGD4ZiBwhiR5BGXakPgeAdDOgOtic7RGENQAo+gBOkrgoD+a8eL4SLi5F4yuZdd1XXz+/LkkjRAJVPwYK/bEOAxgnLz64UZ8HlDDmuODaHOKiM1eKUA0duLEFRngP6jS+e84aeROj7ZL9g6S6AyBzf3QXZfbRmAtmQ9AgvY51hmdcCXK7DIv/IfB+rrmqowTB8+F69Wxp0ipMsvoCeDWjB1+yydoOTjxMihH17j3usZGj83GtT7SyTZAiSQduWELtMe2rCQ2zedguIlfx+OxVD9I0PL6ZzDAXLmOE2dXCLP86oEJACpIitfXl9jvL4r94OeoumKP9mfosOWKr0JHqCg8Pz8XgOAENqW02VcxL/MmAWRd3D0ACcbazfNcNj3jQ1t7nKa6URqbY8wARCcY9gPWD8ZAaxF6h74+Pj6WJ4+7ks21ANbI0+2DfMY2iy0Sw3wtNoOj37RGQ8KY+MBWkENElFP8iENd18X9/X1cXV0V24awYQ1IgFhHsBK2B7np6p5P22NtTchYR8FlTuLmeY4//OEPxWcTx4ndEJboLPb9/v4ez8/PG1zCmpsEQo9cEcfWTdigH8Rg4hnrQowwCUtCQRwwGHaS1JItPKbAMd/39Z5KdG1d182eC/TLpCbzI444STRhY1IPG+a72E5LphqbDF0f4zlJQnfxZcjX3S1UvdpHORAXvmWXrbxNLJgc85p/z+u7Ew1n0e4Td5mUzB4n5IzMQJWgFhGF+SdrY1IIB3bGrKsTEz4L8Ce7xunQ4sMiLMtSQA3OI6L2r1GR8Lh9fn7XdaWVgGsgm4gobU8RUZgLnEhEPd0FkOCKiFlMHLDbqyLq0bwEP29o5DQZ5oMDBIDAEjl4uZqB4iILBzbkZxbATLEzZOTRMjcOTr63mWM2xkdsKxsOMmZpqEw4eYrYbhpjv4NLgsjeIKJNoLw5zWx4RBQ54oxYW2TP9bAR1o6eXZ+4w/2tH+u6blqPuCYAEl00KxgRRRYwNi3bExHlVBWuwXdhYHD8ti0z0Ou6xuPjYxwOh7i9vS1nt+MYffwr/7Ge/7/27mRJbiRJE7DClwhGMDZmsTKrWrql+x1mDtOXefqREZnlDfrSfepamCRjJSPcHZgD+Bl+gJxMpkgeHSIUkhHugJmaLr/+qmbgBMma0zSntHF+gvMHwjhnc0+gn6x7MoNAHJmzgUzSE9Dl2mViSmZ8YgbQ9XrqUc8KADtKIEeeGGD65b65DnQBWF4mCORAZqov5JXA1efH9qVq615Vsw3E2f+e83UPICHnv0yyJe2Hw752u/kxnMtWg2VCNBIPYy86kEaH6cQy2SezjDPZYkMnAa9MvoZhvvGYnVxfXzfWORlILbkjQTWBfHIAss0vKzn0MNv9vsX2I7+W8je2TKDdn489PT2dvX+JnSdorKpWBUQI+MzyHTdiHj+VBE/aeLYeZRzOBDXZXv6AzyLHzWbTxnZ+ft4OkNntdrMN3HRIC7d5py+zJlnxqpreF8Gunp+f6/b2thE9ZH53d9f+L7Hyc3ZpHNbV3C8vL9seDOMRs3INtZFlIpP2JZmiO0g4lRb2YE+YZCPJWhgsY5+3vmeCmQlzEqHWjY4gddhB3jfXhW33/XQilCRFHIHT4C5rm0kS0Cu2IQngs0zG6Qp7otsnJyeNnEpQ3nVde4+ZTops6XUlqZf6n7EtialMgtxLwqfilQm8uMZO0tevan6IAd+WJA6btTaqJWn/icVTN8RhccDcJGf5/awif8/1myoaCRKS5TRBA7RQlA4bUjWV7TJwMyBsKKFn1rUEndhjSQf2Ybfb1eXlZSuVp2AofAKi3EgkUFqYZEirprIbI6a8HDyQTEmB9GRJyQ/4t19DW1Y6BsaeC8uw/TyNaLVaNTZ6v9+3U7gSyFC+3MgvAWFE6QjcZ8kaArDJaiZb5bt+Tn6MkrzTABIwJ9hdbugl0wzey5MdPC+Ddgb8NDQOKhOJqmnznT8CHJklY5HBnPwA367rZqwR40+naBzGz4g5LrZj7px+rn0GlkwU87Q0erDcG+Ge9INtqRZi6s0Hw2g9VfBWq9VsY3PKyhjSTvLoRVXSqprZYq5h6o+Sv/VLfzEM02bRTFSywpZVpkzajIWcspxN7kiAzWZsM0y2DEjIU2uWSVAmfn5nXMlMs01zyHJ8AlsgGZtHH5KZ50fGe8yBq897pnEkOLFW/GCSD7ku9JX/3G637UQjTFvGlKzWAk/jc8dqiCTy4uKi6Q4AYo+DTbQ2+6ePFoOw9GTHDulL1QRsfBbw0Tu/2WzayUC5t0cVOxnBp6fHJne+3gEB/LS1d7iIeX769KmB0UzCkvhJv6M9k8xPTk5aK+Wh72uz3tRQw2x988W7Sf5lEri8Z5I+2T6TJ1wlSMtTgQBH+uZ5uUeBHg/D0F5eK9HL8dCXbH2SJIgd7JScfSeZYnHHOHz36elp1nKde3/4G39njE59S7JBAmFzvEpCVmAkCuwN8SpRgYGSuE0ykM4n86+lNitIYrqY4p5ZmaFXfKZYICm9vb1tFQ+yyOpGxjWdG6oz2RqHSIAJb29vW2ziS6wPuzR265nMOtkbj0Q3K3qPj48Na4qP/BE/x04y+acv9Dznh1TNiklWfJJ84kPzUBj2Z++J9ciK9lA1i4fPz8/18PAwO8Ckan66m6SR/eXvclzwD18sbtCnxGa+n3L5teu7Ew0LYcHzIQmCHx8f6/r6emaw3jB5fn5eNzc3s2zPZNyLYghmGTw5dQ4G8Li8vGz7CbAEHFqeikO4nLCN5ev1up3kwCkuS4NVo5JdXl7Wfr9vSUEmQe6Rm+aXIFpmTmEpVgKPdFgpc4DD54xN0pdGl61qmSR47hJk5slXZOB3udZ+TzEZlvVKwG9OmeBVTadskQvHlJWf/D3An447kxVOyXO/pVOZ1adzB4izrzgrAJl0Atvuzckz5nQunkXX2Qw9zEQnWUtjWiaQmVTl3Kx/svy+k2CVw1gyp55hbr7ruri4aL97eHio6+vrWZLCUXPegIL1ICegDHinM8CqQOqzwBs7yh5WtmGcV1dX9fz83N5WnGV8YDHl4O9lUpblflUBesEJJ2Pv8/leCrblOfyCZ5CLxFOAyRaOtLVMyKumKimZpA6zi2THtAdlS5Z1oFPGRu8zSU77T7+c68tfpHwRQWOb0KHev39q1XDzMc4lMJmqphMY7Pvx1B76qZ0n1xsoB9YAWM8SPLPF0DxHmU6ysdcvE6phGL7R3jO1wS19J6BH5kla2QvFtyQ5kycfZStogof8ufXJRBZjyrettlMcWRI+/Gv63ZubmwYGUy8kU+yeL0j7yDaSq6ur2X4T7LQ1ZhuS8tRlcklSTaym3xljJffr9dj+iWAh1yQnyBtwzWpd2lTihuy+SIadjiz/sD1yEauyWnB6etr8hySZDA+HQ2uzOxwO9ebNm/a5T58+zaoXqhxJbCzBsjV3cpZKCIx1e3vb9prBZkkyiuVLUi+TaXZGjvxOVojMi+wySaWzibusA795f3/fqkh5UmlWWa192giZsqNM1umeGJR+J+Nnkiw5/+wEWRJFWSky7iTjJHJ00hgQtT53GPravUw+L/cZGg8/xa+xOePK2C2GmI8kNP2737kHP5uFgu+5vjvRSFYly9GZ0R4OY2/48r0ReYpCBjoOSsC4uLhoi+DenF3V2LN7e3vbKibGUzUdGZqsNaFP5fGpnKckS9C73a69ACyDqrGdnZ2192wIUH4HZCyV0TyzdUEQVwHJ4J9KatEzIyVjjisBA1kpMUvSMhNlUCk3Y3JPWXUyFJx1th5ZX8rMiBIkJxBash45LvdMFoI86NeShcoe9HT2ql4zJiAqQpm80BnOPAHoEpSSE6DHCbiXOWJkq2pmzObCYOkMZ5bjze9mUunfj4+PLWClIyNrgdN9JbZZKjV24/LMbC/IJEnw7vvppZc+k8ELoyggq+D57MT2PrUkX/nfAQH2e3CW7p3j9nzBO1vBgK0Eysa1rAiY35Lxo6fpwAXZ3NfF/ukrmWXybD4JxjKY8jXsm+yqphYZus6vJXD1u/QNE0s/veWWfYxynWxfYpB2lvfB1ic5ksBBUE/w9vz83E7dAzhz7fiaJGT6vm/7ftj6ev31y9DECFUG48xqlbVZr9dtT52TiATa/PzY6779StbpM+kOWZ2entbHj7dtHAlURjvaz/ZBAHSZvGbymUmDCsh+P76wTRyoqtnpORkzAC8xN9vmhlXX/CR9o9tA6tnZWTvSebfbtfdtJMni2NhPnz61JCJBHhsC+BPE+5vNZvVvv9+31qGlTvMBEhN6kLE2K118Otu33kv7yop7+pFMXug1QMs/ehdXxrSM3Slr6+d3bN796ZfnqhRbQ3OxsVxfPh1mw6oXqlvGZU4AKL2/vLxsftGx//v9/JSu8/Pz9lxAOskepCZZe27Gez7f3OgwmbEF/1eZ9H1y03qah3D4c3193caX/jcTP89JYolOWR/zqpqqZ0nk5fplV0G2YZGxdaWP7Nl93DuTjL6fTv7K0+m6rqv9y1SpSWI1STdyN3f67poIkilR4D+TFPHZ7IYRI7MjKTtafun6Te/RsFAEgzWvqpahYpUADMyQ35tIlqwERb3jnAglqpp6/QhWXx7GMjdo/fjjj62s3vd92zRnITgZjINgvgwAmXBweISdTIl/Tws61Hg04gREANDT05Oq6LXLapDncGAc7svLS2N+AOpl2xcAjUGxXtkPz6kBqLkJWUkUiMkSM0XMFyEJPBnEOT0yqRqBnzevTkzlNP9km/I7WWJNw09WnhEncylIZxAlW47Z+jYj2ExHBlrjDPp0pqpmMvf8ZHpT3nRb0FlWAowjS5TJoNFFYMzfWiuSqc+AZ07JumTSJzDlqSlZxUgnXVUzXfQ5LEe2rGQSt91u6+7ubsaaOhry4eGhbm5uZmzyzc1NXV5e1ocPHxrb60S57XbbWpPs2UqGqqpa0pJro4rKJ0m8+QIySfsV4LPykAFbYmQt6DTdwYZb62xNWVYvyDGTBsmooJSJeyZFzqTPFkhAKxNL87i+vm7M8Si/qtWqq5eXfa3X4zGzw9DXZjNV41QU8AH04PT05Asws3ly3KfgaNr9HnM/1Pn5CIg+f36u8YSmQz0/2zuwqsOhbwRT11V13epL4u9Eo+mt5+LKRJasqmpTw2Bv1ajPHz9+rOvr67ZGmeCxDXZoPZJYQG75ewRq27YJdrezB6SvKuTFvtbr0zo9PalPnz6XPR/sg+3RW0Gab7m5uWn60vf97Mh4uo0cSZ9FF7D8S+JAjNu/7GqzGvu8t9tt9eu+Hh7uq6uaVe/YyNnZWZMhOdrbSIfyhZld1802udNta/Xq1au21wZxx/d33dg+kxVRpJZYw0atk43ZQCKwmzLOhFwsIO8kYvhcvibHLllP4lCcZXdpy3QtW8eyhfZbJJbfb7fbev36davM8gfGaP7n5+f18PDQWsSzupUgEB6hR/BDVtPFdYlcxj5xPCsZGRPyBLDECTpFMvHlS8UX2CN9FvLJM/LZmeBnZULCyp9nIpHJtBhET30mCUDrjJzICgPskCR7xptMAOge+eW+nqqq9Wpdw6qvbqgaDuNLNlc1+tX9y666oWq73tTF2Xltvtyn300voaUX/qb7ZGN8SbDxf+KHufpctksmVuRTkshFLC33D//S1Q1pKb9w/Z//+X+b0Sr7eAcGxwZ0mhhBAMVLRrXruqaUDNNiUU7Kx1A8iwEmm5xVFycmYZLSyLuua5upMJg5riylMSAbd/wsnUW2dUys18TMZ6bc9+NJJfZOUBhGm8wqBdLbyalMbN+kUDkPzgsw59gpOvBcNYGn6+vrlnlTMI784eGhMerLhCz7NrOsmM6Sop6eji+jIk+OmrPLpC/7rBPIkTPDt2bp0JMV9Hs/Z1wJMBI8JuNMB3w/WbhMTDg042OATsXIKqBAjpnJk4Jy/ZIlouupo9aXPpK7uRsXW8p2JmyR+2FOjA3Q/4d/+Ifm2JbsWz7XOtERzhWr/fLy0k5jsXZsKHUZ2PYsiez19XU7RSeZdC1Bfd+3gyBubm5mFYQM6M6250f4MGDJWmRVxN+OyMxgnX+z7zxpx72tmfXFRrLPTLyXQcA60QV/HEFMbpkAJrMOeFgjATTJCXqSCWXajECUAC33MpAz4Lbb7WbH0D49fWp7fdxPgs3PJfmDYR2Th5M2ZkB7bF/dteewO+N7fJwOJUl9XLLN9j9Z10+fnmaV06w+rFYTkZR+5eRkajlUEcBGYm2TDEmCIxl3oN1cElj5ThJEEhByQc5ku04Cr2SagaCqqn4YancYNwWze9WU9N1ZMc2WtWRxk1Gf3p0yMeBZWagaE5w8bS6P+M1WQvIwnyRpchziB1lZXzZqzV69etUOsMgYb37ut4yF9AIJ5ucSw2SE/S6rq8aVFff0D69fv24xMuPZw8NDO05VzPr8+XMjb9midcqjw62BvUHWh78WSwBta8Ef5Dsv2HDaurVmA2J37gtMmcCG9tay8UyGrKu4QPbimGcD8hmv+d60G751SWBrPyPPpX9PnJqkTeI51d6sBPNhmQxlgnqy2dTL83QCmbF5dmIXGDrjuvZPvjCJvhyrOJIYKH1QxhgJo/sn8U3nDofpxZyZ4PzXf/0v9WvXd1c0ZHlAgIXNnksgAOBYrcYjMDOXyVarzKQTQC/BbAIGi+xt2BksU6DuUzX10WVZSAKSjjAdA8Fy5FU1y64pgj5V35+yy/mxa1VdnZx4gcqhJRe5IY/RZfmWwQLg+ZZ1gdk6JLOQzJSxUnbGLuhWVd3e3s4yVH8fDtNRqZ5JhmQMKPs8w8+AlNm3dTQWwO/29rbdM5+hKpatC5wWQJKOxvosqz/kk4FjCdSSCVomE1XTCStZGl6v1y1o7na7dhqJHtesmJAhnTVP7XEAQDr7TEKX7Lnv56ZLazUM456irCil/idrp7xfVXV3d1fX19ftc5l053Mz0SWfh4eHmQ68efOmPnz40N6R8ac//am1KGbCZd0EL20fyd5ozauaXqJFPwTKd+/eNXCSiZYNvPZyXFxctKRVqweHqnSd8k7fxt/RE8GR3VXVDBhYVyCwaiq1q8wKTMtStTVYgn/sljmxdzovuU1/m6yU52eCwfelD62qBj6zagu85+krfFlWeQDT5+fn1nqHGU0/AGSo5FxeXrZ+dK1z/BVdkFxI0rPCaS34UyAY0PN5NmCcfI0EynyfnyefnEAtWXn2kyQRG1FxV5Fwb0CSnWnPJdskwyTd1jKrtelD+JbNZlMfPnyoq6urBoQTgNDVk5PpIBWyTb3Lnu707UBm7gWxV0t8TfJmtVq1F7ECv8muZ8KURISWyqw8WFdjZu+SJP7KmvAVqW9kntXfl5eXRuplomQOuYk4AXSSj+6X5FLGGDqeyQ17Eh+SkMn5WFs2bP2qpv2o/LlEVTWMrpIDPc19IPyasRlf6roKfBI7SQr6PgBOFgn+xSE+IME9WcKa1jd9X+oy3zySGk+NPJOwZvdJdgHwzUneJVHONySIpw+IgaxupE5Jtvi6BOvPh74q9C5xX7bDJgnkc+S5Wq1aVdDYYEUtcNk9wmcbB/vm3zIRSnKU/ZNv4sOMF792fXei4XQPgXu5iSuVk6BTQTlxk6N4vpubkWWXgiGQldmaIJ2Bj1Mi7GXpTDBQZaFI6YQy8GRLRQZxSkEBKKcFHEH36gvL6gzm7ksP8Kr2+09NOTw3nV8G4GyRyQCejDRgZX4JJtzHGnhelkdVShIIUfoEJ5xoPiefnUHO77XRYKQofTrmBO10R7Jq7X0nK2rktDRO6ybIGUsyxxJneunn+Tu6adyZbDBKsk0H7FCA/JOBNxNWjt99jTEdSupWVpGW+uJPsiG5ESztBNtnfe/u7ur8/LwFQfYNZOQm9gTC7ALwSADGFq6urtp4ttvtbFOvAJvJEYDoe+y1ajpCG1AxjmSrsJvr9bo+fvzYqlfZmpkl9qqqm5ubVoHK+6zX44vS3r5929YoASxZs8t8f45k6XAYN37aaPnw8NAqMGwyKwbYtmR2ya7ruhmDzH9llUkLRrYjCLKS9dQpfmxJ1EhUgN20jX//93+v//iP/6jValX/+I//WDc3N7Ver9seC+/EGeXczfa30SfP8vynp6fWQoMcAJCzipnjXbKSbN/ejoeHhxn7mn5CgMeEjy1k3Uw+vlv19ZuC0w8k654seAZzATuB/DAM7QVvqUvmrUK63Y4vHQQmz8/PW6vycmzmmAcs+JMvjT0cDrU9OannL0kQYKRym+PMhI7c+GZAkn/KLgS6aS3JI0EPUoV9JfFgXRMcAlTkJO7c39+3Sgwdvry8bGuy2+1mm9cTTANWHz58aNXLPNLXizcz2e26blZtEAvZPsIiiRk+Ff5IooFs8z0JVRMAziqOMZB7VmYTYPMTxpNr5jMZC/ghsQhmOxwOrT2ProtpybbzG7ocVOuyamSN01b4rUySzT2J06y4VFWbU8abnLv4yk6z0uAZiS2S9M446nuSuDwRLkk4Y+HnvvXy5KGqTrbbr/yDz7hH+qKs5PALxpgtwIkJ0qeQsftLprKTIElXY4D3kyBxz0wcf+367tap//U//ncDGJQrgYbTE4ZhaCXkzP69YIZBUAy/F7wz484NuwSUmW46M2D2/v6+/Z+CqBDkmdCc8evXr1t7B3CXAdGCYFGMIQGsoIQhGxe0a6DQAo2A6aSdgexPVmQYI0Vz/2TCq6p91z4UY2Rs6WT8PN+eTuk58kwK/QygT7CzLCkK3kAF+VBqCUPVVDpPBpEOfAskZ8VqmYWTG6dtjtYxgxxjzY1y5IR5oSfJflRNR48CNeno6NxyvAm2JapK3bmRLS8BKPcocSZ0WdLpGVlpoLcc6JL9yeR/mYBWjZUIFRD3SVBSNZWKrRd74LglQJnkPT4+1sXFRXvrqjElO5qlYX+qvi7tps0ZjwBAH5ZOv2qs0GSVNVtP6GqyYYJ/Jhd0ue/nm+GT6bJ5FhiRHGXl1FyTWde7nu2EHD5fia2WaCewNCcyyIpcvv+BTvhdtn0tW5jYsfln20bufzMO1Yr7+/v6+eef6y9/+Uv9y7/8S3tZ2TDMq2PLIzeNafKfE8igc4DyaEMT+QBA0InxhYRzMoRNpL14pgB7OOxnvi6ToK7TXvWprVNV1enpyYyMWbas+Fy2OSY4p7vkzh7J2b2xjNY/j+CUsCeDnTKjg/YrJQjpuq72w/TC2KwuAYNJqNEVcWG1WrUX6qnkurJKwM+mjp+cnLR9L8l0J0ts7uYm0SDjJBnu7+8bQZLkJBBNvnniD2LKnF9eXmYJhrhgLXJumVxkZ4c1u7i4mFVGkKDmhghYrVbtvSx5rLakjR9gK+mzcl3MRSLC1n0mk8EEs0twyWfkUbsOgODv6Jv9c9YaoOf/soWdXdPNJB2TyBOf0l7SJ2WbfSYO/GZWs3NtrTdykayy4iYGkFNiiPV63RIvMiBfOsOn0FXztX7DMFQ3DDX008lTMEGuaRKcGWdzzMaSbWuwSVZCrE3i1Ew6fC/9fRKV5JZJHx3r+77+9b//t/q167srGpwbhg5ow3oxkGQzncyQZb6qaiwUoeQGP6VywIhSAtXYSEyPIAUsJ+OeIMQcZNsWFqgg8OUL4xhTKvRSgTmoNLbHx0+1e9nV/rCvGqr6oa+uujr0+7q8vPhKsTKBoviZ9FCAbDVKhTC/ZLglVT4PBJIPcJhJISNOJoaj8DwGnobgoozzAD4dYcsYBU5Zs3mSy6tXr5rRW3/Gn4lOtlVh4/JnLqxa7gNIQK0FLkEDoJZlV2M2BgGMrmTwMsYs7zfD20xHIgK3zipPhswaVE3HAvseZsM8Uo6eyxZzE5tn572wqpjHh4eH2u/3dXV1Vfv9dOTmZrNpgNNzs6qAAcm2jARNyZqQ6/39fZ2enrZ3Lfhu6rfkl+7R7QwyviMhw4objzX0M8/Po7G1A2glcQ8+gYP1LD+vGgOm009yXMuqqPuwf59nh9Za9SB1KsFngtR8mzvWK3Vu+dxMOs0jk1XBSjXJ+O2LMM53797Nvt91Xf35z3+u8/Pzevv27Zc1nMr2gF7Gk0xe+bphGFuKjNF4xY3RvoYGavj9Yajq+0PzNfxlgpyU3+SHVtV1842WVfWFlJmOqfWstG0+P9nB5X3ymQl6jJNvB/ZVF60/4AicAHD5xuxMNo0vE3usfDLRp6en9fQ4EXB8hCqPeKAC5/cSAH4TJkBkISXOzs7q4eFh5lsPh+nI8tQ54xUHJfV0EHGh1YzOqUTy5fn9qmovpSNnPk5rnottqxSJb9q20qatBxsh45yHPaswUFU1wH44TCcRGXf6ObaULL4KbrZjZnKa8SftJv2peeSL8/hchLDfsU1+OJlsei520nc27pkS0ukQiq9f3CnBSRJtmXizLXOA9zJRhMeSDPYzepTJphiW+iy+e07G8fPz83ZMO1mzR9/PhIrPotMtQepWtVoQXemvl0QiWSY5AC+bQ96L/nsxoTFlpT6ru8ZPH+hCEiWJTzMWZvL9S9d3JxoYrVT6ZZkpy1cyrqVyEYCB5uIz3v1+2hSY5S79gLJmgZtRUPpsF6GQmLBsx6qa96kBXIRaNe0FYTy3t7fteY6HM/b9fl8fP36sDx8+1jB0VV9eNnU47Guz2dbFxUVdXV7VUFO5K1vOLLyAIyAlqKP8nFAa5xIkJHjPhMT3c21yDTPoCEqUi6NLp5NKT45LtimrPbnO2XJEJ4AMYwMSc12SIQbUEliZh/G4yJSh0SeOIteDDiXzk6Vlcs7559HOy4QmD0VI0JGlzjdv3jRd4FyzUmWNfGfZB710tv6dTBT71IYk8fe5p6endsqT1qeqkSC4uLho93Se+5s3b9rz6KXPLNsvrFHa/NXV1czp0asMRJkYpAzoA5CVzO7T09MMUAMCyT71fd+qrZIqrHU+Q/sBnQZScp+E9iD3to6SiEyWJcld133VI601hH9g4xKNqmk/RJ5uRQfYjuRxqYfkZzO9TaX0l23kQQVZuWEzgvwf//jHOjk5aXt79vt9/fjjjy0xPj191VjPTCisZZJQeaIJf0J/sj1uHO+0ZyqrZc/P8yCaLYsADdDseWOCNrXTJUDY7V6a/JexMPU1mdYEQP4vVmJOAXF26U9WXhKwJiiggw4pEXtVxhwWcH9/X7vdrl6/ft0IPQTF6elpvexemh26t3Wne0lc8cmSlGyLyXYXwF87XPrZJFzEtCTdsNJ0I8nD1GOAyB97K4wBfhBvxG3PYP/J1GcSzq/ngTPm/+nTp3p8fGyYxD383tz4AlUPiYwjY8k2EzG6bM65XkkY8a+SZ+N3TwkifeI3yPnjx4/NpqpqloSyuSSMshVvWQHLxABYtY7iN9mQ5zJO8VP8pSSSLPlqz3r79m1r6bdm7PLk5KR2+30N/ZyoTTCe66UdSqyYfMKUPPLnmQCk30+fxsfwY7DpGKs+1+vz102f+CL6RmeMO8lRfrqPeaXvyU4ev6+aDgxKXCQ2Z/KSCRiCOn0mO/IZPvHXrt90vC32j+Pquq5tNMW0CVRalRiGYLk8BjOzSoISzChXtpR8/vy5gR2OmSFKSpJl3mw2rWrh+cmqXlxczJg0/7chLQW8Xo8vCzocxn5Fxnd/f9/A+s3NzZc2gvHIw9FI1l9YtpFtW69PGqDAmhu3iwMByoABc2Z8WaLPACcwphFTTvOngKmI2ChghPHl/ZOBcSRuJgoZFDMBSCPFBlRVa9FZBuis3ggwDImBaVcBqDjn7J/PhMMzyCITBYlGVl+WTLC9CORP/9iFqkqCQzJZBiI6Qx7J0CR7KiHIAJ3gke4k+KMrub4TcNq1Xm8AOAHAy8tLe+GVwNx1Xb1582YG0Ferqb2C7Rrbcs0SMLvYt/K0QGycq9WqtR7QKeMTbPiX7XbbWjZ9VyBeViTYXTpqPiBb26ynNdOyl2ym5CD1Pdnzk5PxiF12Z0z8kvvxYcYjGGbyxg9jpx1LqvqiInRzczM7ocWV67n0HQnmgMKs3PhOEhNd19Uf//jHBtZTRpl8j/MYj9Md538aAMybotd1ejr6Okz6brevkxMV6L6en1WtT6uqq+12U3d3902X1uvNzEesVquWxDlEIyub2S6Qif14MqAXSb60lkcnArm/z282UwXcn3FuU7KUAPBb4Frizo/xQew/k4BMYKwde1d5BChvbm4aC7vfj3uvgO+u62p7sq0+/IP1ZjNJaqm0+P/9/X1tNpu2N4Jfff/+fWM+9/t9818Z3zJ+0Pn0a2ybfOiWhB+RmX6dTBLgs8X0gchBY2Tj1sEaeT47vri4mJ2KmOOj/55vbGwpEzYVBe8jMXdxHu5Ie19W0yUnk+5PJ216fh4hm7bJ3/HR/HLGCjqjQoSEeHx8bM9JAtm+HLFPAiMWk09+hy/Xvi4Bs2a5ZwLB6S3iZKo9jX6twiaqqvrDoT4/P9dZHMqS7WdsWMKfY1wSXlmNzNj2+vXr1p4rtvDRSTi2WH/6qvmFZZzOWGQtEaPuwUdn9ch4vO5BksYu4Bx4QSKXRGAmYbAOm6C/SaYkdv+16zclGkshC1ZV1c7JNgA/46CAU4JNpo3DTfYpmUbGy+CUqx4fH5uyUYoECJyFPwTrXhIFAZ7jyBYNJT/zNFaAP5ncNNAxkGxnznVkp8/aXN2XUTJ2bQWcD1CRSkBOFAJYy95uQNsfn+eUso8zmQnKrLxLjsmMk4P1THaCojvfvWqqKiTjmwpsY7bx5wZLTja/KwDSuSwRWntrLFmVZCz1aRiGxpSknCRZGXxyH4Lnm0OWMrNaoc0PW5CAPAMhHeNAsmxLnskmZEIuoAFQybL5XlU1GxR0cr2yNYJcMvmn/9YBYEo7tjbWy5iq5icmmQN5YkZdxp5Ah529efOm+YZMIJAeuWbsmmytL6BA3uzPXIdhaCdV0XG6RE8S6PBTXdd9lexkUlI1HY+5BJ6CqUCaiTK958vSBp3ilcQAvSEDTFmOny1of8mEX4cKKgAAJG9JREFUwpV6RrbYSkkccPH27dtWuXBsaT6LvJK9BCRyjXKT8OvXrxureX5+Xvf39190al+fP1f7ftV4WpIXlgLafFoG12w39P+JRJgfgAFoSeqM/enpqZ2gtN2OiebDw0OLRWxHO5zx3N7ezggGY2S3/F0eQa1tiQ5g1AHNTO4uLy+bb3t6Gt/GfnNzU1VTxS4Ji9FnTRvVs+qWJ2VZEwDo1atXdXZ21o5eB37YkHXOoz/z8BayB7Lon43JaT/idtp0steJMXJNEZ3aZrJdiF+hxypB/KnnJGECuCd+gQH46iTpzDllLbbSN/9mi1dXV00G1tmznThGN5YnVibo+/jx4yw+0R+fd5/Hx8d2uA9ZOoigajwkQ5zOCmD+OwmXJC0Qwxj/b1Ve6D0b5wfW63k7KJkuOxUk39ZL67TfD19ksz/M938sqwhpQ/x/JqsA9mQz094fc4OtstXT/RBYVV82sH+RM/llC1kmMfyeuETPttttI06Qw3xxVkXT34rliQkTS7L75ZpaN3aaOvy7JxrLPjt9l7k5K4GohRAI9Ntmq8/f/va3ZjAvLy+t3JsLAnCenIznqdt4RsESVKeQ7CFROUmwzUF9+vSpOYYE3Gm8gpRFYqCUs2p0Lnob09ASKDCeBMqZWQ/DMGPK09kxrnSO6VSTefrhhx/q5OSkbm9vm6OtmjYoJYjOXnpz9RljzO96bpZTq+bHCGeimIB4tVq1lzAlm5AVrvyedgHMzeFwaKCUAVnzqpoZarbJ5O859DQyMkiW+VtsmLUUcLP8y7FkAklu1jXZzmRdATiVKyCTHTl5KdvXckOnpELFj5PZbsfTnZIM2O/HtkVB2x4YcpfkOv41TwzL5ICcM8Bypll6JScARSDn5NlzHgEsKTJuPoQ8+76fnSTkM1l5yFaQ7H1OW/EMbBkdfnp6+sq/YF75KD/LioDxJYOZVSrjSjYxmSE+KVmitFdrn0kyUkRlBICuqiZna89vZjXHPek9/c32UmRDJj/JVpuL9oPsL0+ZACU59vR9ZMHGc9PwMAytggxA7/dTYshe7u7u2rpVTT3SabsZjO/v72dvu8+gKd5UzQ8wyXVg1+yBn9L64XOATbYySCpVSPq+b1UByRW52rcl8cnWJjrleToK2Iw4RW+BPnp6+uq0ui/fc6kordfrenh4aEnSklSSFNFP4+aH6L2/XamvfG0mUhLQPFGI7iXJY4x0h/9ar9dtP6ckxWclFEkAJeDi6+le6rs9M3T+8vJytrHcd3I/Ue6Rojt0gf6Sh72Fng9s81dZhcn2PWPc7Xat6rCUgT+Aad/3dXV1VW/fvm1VFdjFXMkFCQSvOO6+aqqSIvzSNrKCUjURH/SGzou/4oWEFZljTel5JhVZ1Vuv13X4YsvkjoR9eXmpLuJ4gmmEeNWEE8xVjF5ijfQ7/JNWKvbA1yYONI99tO6xD4n90maSPM5Y5f9+T6bkzub9YV98mhie8cc9l+27fGeSrukPf+367kQjW336fizRpOAI/+Hhof3b0ZJnZ2ezzY0Jxu7v79vLuCgMJZFoEJJ/U1YOOlnDZMkFYgwMhkfwy541c0gnRvC+Y1GNLRfWImImKZHFcaWSUIC7u7tW1pYIpSNhXPkSLA7P85ItSWbXnARz4MCVCtWMIIAY+QryKWv39dxU3ASp5ivImYP7k1dulMvSHMeDQSBbz0uGwTr5N4dizgImxyIxolMcezLgHBJwkEDTmhtjMl2CAsdlDvYISM61X1mDTEAA3wRkWm3smTAHJeRsXUnAZq29EAp4JE+BcbPZ1N/+9rf66aefZsHJs9PxceIJsnP9sixPZpk0OQmn7/v2botMdtk9fSRXTs7fZIpZBmToc7Y80UlyUU1jf5mcJcBer9dtX1aSEfQ0E0X6lhUWOpDsLWY2A5fvIHDShthfMqJAiTEK8vSpqhrTbYxJkmQiuExyMjFKAiQJGLLMY5fdF5BiJ9n6aP2WrG4yo0muWLsR8E46lkGY36En2bqAICKXvp9eYJgMJHvgD8xPFS0Tyd1u19jYqmq6TE77/X6WAGUfvLEkSWBdzKuq2qZOyRKigh/YbrcNLKVeXl1d1dPTU93d3TWd+fDhQ6sySzA3J9NxoJ4rBt/c3Mxilu8BNnyYdcx1zwoH8KOSKDZl5SvBlr1j1jjf5ZK2m2RbvtSTrYhZ1oJOV1VriWNvCebpnBhprc0lwbOqAR9I/8wF2ed+Wo+Mbbvd1s3Nzcy/kXNVzWymqtpR5OaS7U1eqicOLOcmCTd2f3w+bTFZ8LOzs7ZW6QOA/SRrkxgy9zy4BO4yR0llEnIIM8STcXlbvXb6rKoYAxyT9pX39/JYP0+wnMkMvcmOipwfW/GZTKTSz6Q8drtdvRyea7vZzBIlepAxy3fIR2xNn5f+Le2I7PP/7pVjsdbmmqQcP+Jny3Wmc99z/abN4AmagXxO12IZlLK3TJvRMf6q6Q25VVXX19ezQGexLQRghd2hONn2IVgSnMVWFkyHAJzoo1u2tzgmb8macmpV85e3OVkiqxaZyUok0oiABRv1jB/AcPJPJjV5ykH2Chuf+6QMBHuyNgfK57NANIeegMHPEsgku81IgQeGnCwuI2KUGXSsT+oY3XFvwS8Zn2QbONxMGNMpANeCg2STMxQ8OPxkfRlzMlECJ9mlIWcSuGyN89wMlJ6VveMcrGf4TALnDx8+tDG/e/eufvrpp6qa9iJkm5a1S7bE3iay+fz5c+u7p8cYNHqWvctVU0DMuWe/bQZ57F2SBxjHbMNKtjRb4bBbHCTdUh0DhnN+9NYRu/l2XDan3J5Vl2wZM64MCtaQDHITZ+63ABDTlrB1kkzrDvBi2jxDspU+QCJprhkwM4BkK0OSCFkSV5lOYkECn7JNvSKTfMlctoTRC0mOQEg//U0maUd8ZlZP0z4lhaknSd4AVfxHtijkGlbV7CQZuihePTw8tHv98MMPZfO8cZgHBjlZXQCOnmVbTbb9GLe4lwdh0EnrkP5V4pZsOv8CsDpNjb4Ae/v9vlVQsp0y/WsmevbCJfGWSXDGdOPIhJ0O5Yb+xA9JHlqvJDKvrq4a856gj91sNpvWb+7fSMZkcs3PGFVHrVOeopSVGSQF2SfxYk28lLTrumbbbIou69BI8jEJRIRT3/f197//vbWJageHCf785z/X+/fvG3ElpokRqVNJEKS/9DtjyoobG2Z73+q+4AfyZEb6Yo7m49l0K0GuZxkvuYsX1jf3XdLDrNy2JGg17xDhZ8ggX8Pge0nqpM4gtxOzscO0/azIZYKbSRV5P7/satVN7/NJAL/EIOwc/k5iK/FJrhkcyi+Qe+qcZ+VxvZm0px/IpMbvv1Ul+aXruxMNzGpOnnKt1+sGlrM1qu/7tptfAAX2fQ/gW61W7Rxsn81ye9XoQC4vL5vxWpTMAAUWiUOypxQks019gLL/DMRVNWvlSEBPSWxiAjSSucoyV4KxDLbJhmeLUDLoFC+V0X0/f/7cWs4EGHLwGb2YWGtGK/BwoHmqBAVj5IxmySKbcwb7TKZyw+u32FFycO9lxUOg8SeBp+DkEmiyHYtDyvKz3/3/MvkM2tYhS5pLoyOzZQuVPxxkVoB8b8lkm3s60pQ5eWGm/vCHP9Tj42N9/vy5fvzxx9lbt3OO2BLPBW61D2aQpk/JUGfgsl7JTFdVa49Mhidl1XVdqwgISvv9+EZ4iY1EIm1OL6uNrsAFfclgjiAAatip4JXVCPaJybPm5JVEgjXOZBwoShvQk5/+if/MxAk5kQkowCtw0ZMExPyu52cAdS82lmSANc4gJagCQeTgStCebB07WLJwEgXsOH/KF9MZcklmN9sw+Wh2AxRn9WYYqtkHn2EOh8O0tyxlpSrvs4CQMdPBbKfhm29vb79qmZjscqrmsIXU72QBzT8PXNByka1QKtNJ/PBj2Gexh7+T/CYbPAxD28RMNyTXu92uzl+/rvr8aSZ7AC39YJIm7oNMSADOHrXTZKuXGHJ2dtYqFGScoNjPswVWsu1ln1UT0y/hUt1h45l40UcxRGxD2lgP97y6umqJw7LqttzjYn1Vj/q+bwczOF1MSzObk9wgnTD03qeRMuEnzs/P6/Lystn1zc3N7CXIqa9VU4KascDBJeLabrdr/oqPNh/zRcZZG/qVcXiZKPp/vpLAutJLyRHfYHzWne9AbCa5tNyM3zDnMNSwn79omZ/MuFQ1vQuF7qRvon/53SS+xUH6RX5ZFVsSsdbl7Oys+sPUzszm09b5NLGAriX55f6wQj7DmNlOJhownbVdrVYzHGr9kiB0j4z3GUt/7fruRCNZdaw7h8g5ccDJDhiochVmPRcE89J142Y5J1t8/PixZeyUCsOUwJsDXJby0jlnEKiawOiy9ywTgpxLVgeAjdvb2xmzg8lIpysYZv96gm1AjLNU/qUs5rTdbuvu7m7WS1dVs75Rp6K8vLy0nslkBXPeDJDhGTPlyfJbKrQ5UXTzYwgcVLZnpBEwZj+rqllVyXplAmGsuYkzWXiVDwb9hz/8oTF5noWtz7I6topuZGDlZACQqqkqkE4knazn+L13lFRVY4zNHyjOTWbK7IJAAl/PNkfPxbhgtnOtMrHe7XZ1d3fX5pttiIJzOvb7+/umXxJngIwOeQZbzkQuA2UCFHqQbSKORE2nJmBZf+CIniUjDzCm/Mk5dVFFMvUda5ZrTyezbXOZjNJ1IJY/SnIDmE2CJltjMtGsmlqJ6F0y0BkEJT4C5NK+BNBMXrNt0RitGRCaSZ12ID3SfHsyocvAbS34mWydkUQli8mHsMVkVXOOydCygd1u/r6hEfD2M3mpvvHvmYgIsuyb3xZjxI8E31nl8pyHh/v2+9T/rhtPfGILmUgs/bsY5MrNs6McVjUM8xcPqrJIGvPf1iRly2fSGWC4hunAhfRF1su6np2dVQ3zFhgkRcbl9HGr1aol/pj4rpvamelRAhg+xtx9VjcA9rxqem9EgiD2Sz/F1dSvrDq9f/++VdxssE/SEdCUSO524+luh8Nh1vJ8e3tbr169am8id9KWE7mSeMgKepJunktvPV8STx/Jn21lPIbLyITt8LlZmclYm5WOZfz4lj/1//RR7D/vl3sZk/hLYpWNLKsCxnM4HBphLc5nVZ1sVqtVVZBfbGK329XQ97WNSkniw0y+6UWSS2wzW9GSdESgkLN4MwxDqwL6zG63q5PNtP5LMJ84BAHDDqomXCqGWGOyy0ozOS71J4lOn5Pope+w1uZJru6bCdGvXb/p1KlkAx4eHprzTHYcM86RMOpkWnxedcOklaSBW07YolVNrQ2Mi/Hm4qaBOOElA4B7c6wCj37cbIEA0lVeGBHHIIB9+vSpHX2bzIB77Pf7ds48BvTi4qItFgebiwgEcOSCIdlR0Gw3uL6+njFjDNRn3DPZypQL48AaGA8F5XSy2pRJgbXg2IBCTIbfcZgJqDAgyTx6pgCfSZN1dvqLxBBLwJH5LPZk2Y4hGC9PLdpspuOakxGpmkBCMsTZauL+yzeBk9e3TizKxMy9yMFaJ4OcQXqz2dRf/vKXury8bIHMetJBRzdLggQ0eu+EELpWVY1tJesEyJk4DMPQQAV9T7AtsGSploxfvXpV79+/b/Lc7/ezk7KApExUM4gm8FNRAKaWn0tmh2/JjeTmB3Bg2Pg8Dlllgt9hH15Qxj/4Ob/CXgFgdpqVAM/PZJyOpNPPYzmTvWdbfAf7o0d0KckGveruLcAkMZTgK31ygk+JABBDP5JgsRZAKfkm8ULXrH8GPkzqfj+e+DSCiXVVrapqqKr58cRkozU2dVK1hb9DTngWG8hEz9zH9d/WMPT1+vXFF78yHrt7OOT7o4Zarw/V90Pt99N+jMOhr91uAnHr9XjG/tnZeY1HAQ+1Xm9mQIJvz7ZUAC/9ZMZP/jDJM/ZufRLoYvafPz/XYberdddVHfrGzr//9K5q1dUmGN9sHbbu9qtoGcqDNvhI4ybTw+HQ3o2QCbfjQ+nRbreri4uLppcvLy+N7U98UVX117/+tSW74oD7q3zp/ZcgS77FH9XAk5OT+utf/1rn5+etesy3WY/Ly8v605/+1Bh7er3fTy9YzHbyZN9PT0/bywIlcz6Tumlc/FAmD64k0fha+pFJcca2JF2zuomwzBiQbc10M7HPZrOp05PT2u8Pddj3tVqtq6vxpZqrblVdt6r1ZlWHfqhDP9Rme1KHw76G6mq3//KOsENfQ3W1Wq2rH6pedvvafrHB9XpdL7tddV8SDPKnX0kAd6vpxCa+kO9OsJyVC7JGLLtOT09nL3RNAsXzhkNf++eXWtcX/7b5klge+no5TFX7TODyZaR8+bdaheElcxEvMlFLnCvW+bn1RKa6klim6/A6PckEPmPpr13fnWhk9rxeT8euVU1gKZMJwnP+uAly8toAgEGOymclE8kge+Z6PfXDZnafTCowxeHk75IJIchsG5gCRF93d3fNmWZiRSk4EFWerhvLpZ67Xq9bTzgHbvGr6iuW3f2TeUsARtHMibOx6LLg29vb6vu+HW24rMrkulE8P3NEZDIw5prsSdd1rQKTwS3LdcbOCLO6xFli9q1P7qXYbrftxWNYdk43AVaWIAE4p1zlMZw5b8aIpSfvqmrOhZ5wNFkBSCCbuuDKE2048qwwcGoJqpqjGqY+WP9eblxna74rca+qFqzpqVN7sDxd1zV5AriqdAJiOubcZGtNM3Fls5x0tvWkn5AACHpsRYJAxl6MuV6PLzHkT8wZSNhup/dnaMfgX/QuYyuzlSrLxsmyJ8vID2A0Pfvy8rKBJ/ZhfTMw0FU2fH193Y5FdS+yJOeRJX9o7RbJTPF7xodASPaanLIKmCwe2bAva2w9Pcf6JSmQPjkTnCVLmr5MXMj+YrLnq9wnE8gELH6XtvV1UjK+i2OMTZ9nVfWs2vI/7DyT8ax+22vAH/v+ajU/hSfXmC69enXWAPYwTJXKJZPK3pNsOD191Z6ZLHGSWqmzZLFarb5qL+PbsnUoEw/j7ncv7f78/jj3dZ1+sdGH54dZ5Wez3dZ6OwFLyT3bMgbxL6vduW+GPvDRcEHG2cQJfIXxqqR03dgBgfTbbDb1z//8z832/O09V7vdru7v79vRvBLqfBdPsrzaq05OTlo8p6dIFvrLLyTTzQ9770P6O3Kqqtnm+vQLmTTn7/kCcl8SK9ZSDGHLfGdVzQgJOmVtskohXiU2SEL1W38f9mOCnUTIYX+o7ktSs4nWv1EG83Zc45dMjv7i0BIw6+PyXLblvi9RUUxM6VnsLf1Lkh/pB6uq+X96mwnAfr+v/kvS6DPaxU6/gHdEk2TH2plDyiBth62xr2wR5FeSGE5bTF+z9Pdiq99lcpxEsu/Qp/TJv3R9d6JBgTEp2+22ZVEyO8eK6csj6GEYZkcFAuMJsrMFgOPxZl/gjmGopjg9QxDkwD58+DAr3SWwS+NLNpNTlsEmAwGIWsgEwcaem/uSgcBg+s63Wi4yUGXZ033I0L1zE33VxOxnr3sCxSwvJgufvabk7n6U1XOmwDltBs2N0L6z2UybYrUTAGJOSNKawZD6fnrzc7IlWepelryT4Uv2ikFnXziQkwyS5AmjxfhtBk2GJk9GShbHmIA9l/XLdsJMQgQxslkyA8YikGS5OB0OHfI8SSV2jzPDlJGfzwskqibmS1cBQWMRBM3fnDDfgi15uo/5ayPLhIEtAzDkrfKUsssWk3R+mTBkFSGZ8SULLFERfDj7lJFT0KwBfwOwZbJpvEtAa5xODrMnLEvUqSPsCzsLBGSSl2sCIGWCn36CTRsHNjdPOUsfkWuHlEjiJ8GyZ5EdAMOG/Uk9cH92bw5shc/OyrB1E8TdLyspOUbjNDb3ZvP2CIgJeSRr7q+z1o4DxSi7d9/3jaH2f8/i59KWrS99QapkpVwySZ6Z7I4HGUwgg/69vLy0PXhsa7vdthfquZyoZzzWvWoCaKo67Ox0MyWR1meU8br6YWibxDPWAcbG7d4//PBDdV3XjrSm13//+99nccKan56etn0qJyfjezHevXs3Y8wlBz///HOdnp7W9fV1vX79uh0HjHDIfTfWSAXWGCUZdElyQKYSlK7rGtkgrtCbtDl4xTjzcAI27HOZrORb442brvveMAyz95QlSWsd2QWf6/6wmPGbowpXJrnW0D3osf/7m/7CUHzO0A9jJaPrZj4m19n9Eq9kdUIcm/BKN/Nn4sOS9EsSbvhyX3EB9ktbklxlxwBdTvsVixAT9CMT4/1uV90w4YQkV807MST/kRvr4YrEQFmdygQiCUq4IGWY8ZLfT9tM3z8lfdX8p3vwfXxj4pZfun5TRWO5WTgVNUFBnsjw8PDQWjIYuhNDBM8sAwINAKIAmpv2tHv4XJZdk92X7NjHoEqgDKvlRvAxL8purhZVduqlUX6fiVKy0xKxw2Ha5JSODRA3BoZKfgmQkpEUdKumbJdBZjnOPRlKltgT6BovRfVcyQRQArTmi5wSnFtj4FlLBr3R8/709NQ+y6mbIxaWTDOJy57vfEOoOQj8CTSsE11Ssn779u3M6JZgG1hIxyLRyJ5UgZyO+s4yMCcISeDhOXmlo/B/dgZcZLKR68Z+fI5DyAQ41y7XP8dG/+mWuQgGybL0/djvbY3Ij25kK2W+F2QYxo2q19fXzcck0yNpNic94WxIYLQOgrAjHlOn+346wURSlPpvzTL59Uy+jF9I1n4ZfDNZT33lK1N3+Lj0V8nc8wFJsqh2pg8BUrIKwX4yaCRrZazu862gRS8QSZisDELuZ74JUMw57SqrhHQqk8okMLK8byxZss/Yo6K8ZOmSdEm/Sb+zmpAM4uEwVtkdeOFkpgR31ohcMwHD/ptngkWy4b/SR7AD/td3xc2Tk23zD2m3fEuSZxIAMru/v58x4cA+31VVba673a7Oz85qODmdxTVj3W7HN4ojNxIMmeNqNR7dzi/xseIbOR4Oh/r48WOrbLsPMvLNmzdVNcY3yQpgzB//0z/9U3uuBBmBYCzpv4C43Ghs7TNhtibiKhs2/gTbYgH7SLZ5eWQqv5a2x37sAVGdsUc15bskfCS77MH68lUqIvn5rKol1koiCFZA4uRaJ8jMmDXzC9EBke3ALy8vNXTT4Qjpa8SPliQM0wEXoz/YVNXQ8IVTpBJ8q+i7NptN9UE88VNZ8bSOYlq2I/ElfANdTd2BIT9//lzrbr5J3r0ThyDr6VH6kCVZZw6ph+JkYgnzJ8tc09TnTBgS80mE3VOrbWLXrJqa+69d351oUByBnENNUMNBGjBBZKsAg1SyNKlkH7EjQAd2AVhIZkDlAKtQVU15GNnPP/88Y8awihIO4DfZYUZlTjb2UgYKh9FtZcHDtJGXQmA6GAvFAzAZPMUzN3Jfgnf3yeqHZ1E2YCuz2kw6vNgns36GksdqWt8sI3t+Mj7k6HMcooqX63A4tL0C2bOLrZZ8AiDWALtcVe3Mceu5zOStT76fhZytpyMk7QWwByfBzTAMDfxZI8kuEMEWsrTNUXH25p2VMrKlZ5y5pNS8l8wSveYAsxSazFkCHCCJjbrSaez3+/rpp5/q/v5+lmR0XdeSktysCxDSlQSUytqPj4/t3QPYQ3pbNe236vu+gSO2DzhmxSGdJfnRc/5D8mENyAYDmESEwJEseFYYMDaebZzYKAxotlABFmRBD5LAkGhZMwHB7wABushXpL0bT7Lz9IMPTjYue7+XY039TnaSzvB/y35e8s2Ali0uyajyCQlW+Czyy7kn6Ha6UjKNu92u7S3Sgpd2kO1i9DtBE3IhDzbgU/ibJHnoOx9hbQBIupfVFlXWBH1kKrbxu0luuAdyZp6svNR6vZqRPaenp/X27dvG/ntO1dcJFH2U2G42m1oPQ222m/Z/+9xW3arOvjD1+V3j3Yet8NvZ/shf0ikVFknfZrOph4eHOjk5+Srxv7q6amtZVa2V0vwymeUngCE+wr3FwDxxzBiurq4amdb3fVunbPXLxJ5tizFiLFLMZ8kgSdSsgPIr7CirCLmvCFOe3Q/0kA+TMLryuO4ks9hnJrX0DNlHvpk4WqskMfi3bAE1F/Ng4/1hOjwj4/T+cKh+mAhn+upebCwx5WjP84oI3JCVlNxnKsk4+XIYAjtJYtqV40BsZczOhCj9LJtp8bWb3ndm/fghGEEyTZ/MSfyzTpmMpQyXSWriHLiIPDzDZa1zTmw5q1jWP0mGrPaK5b92/abN4Al8OAAPkuVnApCgJr+Tm5pMUk+tPryq6RQKgWu9XreqAsP2nDzyTwmRk0iW5d27d+2eMlPjSibN83OhKXQ6h2U5MzfQuAQxbLrPVU1JFvDo/4wsS+w5rmSwMiPNQAN4CGICjJMxtLZJ1JYMWtUUBDG59m9cXV21exujf79//74pJScu6DKKbFFYbjZmtMn2WWOM4rt379r+H3qiDUEPrL58Bk0fAU4JLx1M4MBRplOgR5IUeszJCWQSLKDF8xkpp0CHsjVP9Q/7Ktgk4y35TjY+mQ36kaDZ2gLPZC0Z0/KY+1roFLnmWmP8BGTtkhzV+fl509ncMAcYsIV0xuah7YFc3Z9Osu1MrgE496drmcxZf3ZlbimXrI4BHmk/Kb/UkXT6xpRjZSvJtvo9EJvBwRgOh7HVAdimF+aMePEc4zPfTHBa4O/n7U/AkISNDPkd98gEJ6sKfueZGawzocgAxQewCay2SpZg6xmPj4+t9cdckEOZUIz2cpiBRfrIjvhtiQf/tt/vZy+UlfAnaNeitEzShmFoe8nI/f7+vhFMEgJxwBjEkkxYyEgFAvgd9XRfh8MUN4wrx3l+ft78v8oIkm63283Iga7r6uR0esls1UQA1Go63l1i9vIynkj3/sOHWm83X1Uyu65rhybkSyKReW/evJnFPp0JV1dXraUKgKP7kjt6TsYXFxfNt/H5ufk6Gfn1et3un60w5M1niz15sAUdTj2WvCPt6JaYk4wxPc+2wsQ4mQiwT5WVrMjMwfb8HWNZrUviN1nsJMESKJs/feeTkIZph0vihY6lPvr+aKf7OuwnwC+emdP+MLWrW5e0Ic+j30ky0S1dK5vNprUdJnb4MqhZosgHaWmFW1M2WYkgI/dm+9nKaTwJ8DN5WFYCMnlJcjK/k3gs/WfKPcnuTCrSb4sL1pGuJcmEuLJGqWNJAJPJkrj8peu7Ew3MitNhOGoLQJll4ITH4QlaBrlkxk2+ajrFhCAIw9/um8qEkeAgkmXnRPb7fTtqTsb78PAwOxrUIlMUgl72qmvVSIaNonB0CQ4BGgaXwMJ9OSmtQUtFZvwCFiDmXsmEkbskQoBNJs1nsuUKY7Is0VFwIBBIOzk5afst9Cj+8MMPVTWd+6/lYLfbtX03r1+/np0s1fdjf6I+WAFCgsEgydtpUIxE8M5NXXlykCSlqlopmhMD4jJpsMaeS9c/ffo02wycoIqxJiNNdmSWSaFA4jNAPnn5LN2XkHCYgDH2SiXB/M/Pz+vDhw9tPkAHnVqtVvWf//mfjYl7fn6ut2/fztgtiTjbU27OPUCqhFk9Mza2l3rK6Qlk2+22PYfOsV9OL1sd6KRkyH0kBsZE5zMZQVAYj+9bd/M0Rz7JnNh9stFsnw1KmnKdzCHJC36Qn7BGEk7MOh1IkkPlUd81uSdjTO+AFsmucVTVzA8JRGQNTOU1DENr52BrfFGCAHbt/wkgqr5me5MMygCmuqhikElctpZkW++3dGfp2+k4efpsMoeZzGcFOMdo/SSB7sdHZ6saf2b+yWBnu0yCWnaSVcbUXS+vddIZ286jPfu+bwcl8PWN2Fmtqu8PtflS8fq3f/u3ury8bO2Ff/zhDy3Gm+/Y+npWh2E66fDx8bG10FpvhBt7evPmTbMPSRGdu7u7m8WvPBkxKxn0Km1MMpDHSOfvrU2C70xm+Hcxiu0gC4Ht/GwSrnSfX2GH1jMrBXxEYgPxTHxkr3SN789ElP74vTicWCwT4QTBCYDz5/xPgkljTdIi720sfpekLT/c1YRxZiREPx3I4XlL28vkiY1+/vypxc1MWtJPJwHkmdZoSfYtOwbInR82J7LJNeb/sjtntVqNp071EzlFj6yrK3FD4jZ6bB5JMppTrmsmC8sELSsj5seml5WYjC9J5GWyQ1+SMPu1qxu+NyU5XsfreB2v43W8jtfxOl7H63gdr++8vm8nx/E6XsfreB2v43W8jtfxOl7H63j9huuYaByv43W8jtfxOl7H63gdr+N1vH7365hoHK/jdbyO1/E6XsfreB2v43W8fvfrmGgcr+N1vI7X8Tpex+t4Ha/jdbx+9+uYaByv43W8jtfxOl7H63gdr+N1vH7365hoHK/jdbyO1/E6XsfreB2v43W8fvfrmGgcr+N1vI7X8Tpex+t4Ha/jdbx+9+uYaByv43W8jtfxOl7H63gdr+N1vH7365hoHK/jdbyO1/E6XsfreB2v43W8fvfr/wHCtEErWM5QoQAAAABJRU5ErkJggg==\n",
+ "text/plain": [
+ ""
+ ]
+ },
+ "metadata": {},
+ "output_type": "display_data"
+ }
+ ],
+ "source": [
+ "plt.figure(figsize=(10, 10))\n",
+ "plt.imshow(image)\n",
+ "show_mask(masks[0], plt.gca())\n",
+ "show_box(input_box, plt.gca())\n",
+ "plt.axis('off')\n",
+ "plt.show()"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "c1ed9f0a",
+ "metadata": {},
+ "source": [
+ "## Combining points and boxes"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "8455d1c5",
+ "metadata": {},
+ "source": [
+ "Points and boxes may be combined, just by including both types of prompts to the predictor. Here this can be used to select just the trucks's tire, instead of the entire wheel."
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 23,
+ "id": "90e2e547",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "input_box = np.array([425, 600, 700, 875])\n",
+ "input_point = np.array([[575, 750]])\n",
+ "input_label = np.array([0])"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 24,
+ "id": "6956d8c4",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "masks, _, _ = predictor.predict(\n",
+ " point_coords=input_point,\n",
+ " point_labels=input_label,\n",
+ " box=input_box,\n",
+ " multimask_output=False,\n",
+ ")"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 25,
+ "id": "8e13088a",
+ "metadata": {},
+ "outputs": [
+ {
+ "data": {
+ "image/png": "iVBORw0KGgoAAAANSUhEUgAAAxoAAAIYCAYAAADq/5rtAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjcuMSwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/bCgiHAAAACXBIWXMAAA9hAAAPYQGoP6dpAAEAAElEQVR4nOz9Wa8lS3agiX3LzH3vM0TEjTtn5s2RZCaZySRZTM5ksYpFVrO7utEPhW61BAgQ9Av0LkAQBEiAfoMeBDQg6UmAHlutQqO7WqqBYzLngTnnzTsPMZxpb3c3W3pYZubmtn2fiGxRECCEXcQ95+ztbsOyZWtey0RVlWftWXvWnrVn7Vl71p61Z+1Ze9aetX/A5v5/PYFn7Vl71p61Z+1Ze9aetWftWXvW/v+vPVM0nrVn7Vl71p61Z+1Ze9aetWftWfsHb88UjWftWXvWnrVn7Vl71p61Z+1Ze9b+wdszReNZe9aetWftWXvWnrVn7Vl71p61f/D2TNF41p61Z+1Ze9aetWftWXvWnrVn7R+8PVM0nrVn7Vl71p61Z+1Ze9aetWftWfsHb88UjWftWXvWnrVn7Vl71p61Z+1Ze9b+wdszReNZe9aetWftWXvWnrVn7Vl71p61f/DWPe2Df/zrv8U//k//Q57/5GtohB4PCMGBE8E701lijIQQUFU636EKqkqMkRgjAM45RIRxHAHYbreEEAB7Nn+f/xaR0kf+3TmH9x6AcRzL33n8GGPpR0QYw8QUAiEE+r4H4ObmBhFhs9kwDAMAfd/jvWeaJhs/Wp/DMDCOIyLCNE3cuXOHzWbDOI5M08SjR484Pz+n6zpCnBCJeO8ZhoHr62tEBO893jmmYSww8t6jqmw2G/bTnhe2p/zp7/0+2+dOie++z+N/+1VOxoD2sOn7AodpmnDOFbi2MOq6jhhjgV+GZb6fse97XNqzPBfn3OJnvRfOOXtehKix9O2cK/COMeKQAtvT09MFDuXx6nnUc8t7Vq/DpX91y2vqVbjZCBsVXnnto3z1v/pv2Sic3D2j7zt7BhCBPRNDp9z/+Kv82h/+Ju8/+ADf9Ui3xZ+eEjc9QQSiw0/wzje/z/tf+3vujkJA2XvFCYgqKsq0Ee79wmt88Y9+mwdXjxBRxHVEBKRDup6I49pv+MQ/+m1OT+4SgjKpsh93fPDoQ7ZOeO7Oc8j5KRIDlz/6Ke///bc4lQkEJhdRHxGNaPBcxA2v/PIX+fgvfIYoavPF4YPSB8ePvvVdpofv8Zf/x/8zdx9c8VhvCDFyGhyh8+n86cF5xAlB7fycbDdsNz2qIK7DO0cMA75zjPdO+Cf/8/+MHz14mzMVTtUTthv8dgPiiFOEMfLWT37GxcUFExHN5x0BAe8cfiP8wuc+g4gQI+A6EMMtVdApgio7p5zdu8uP/vVfcf2X3+E0RG5cYBLYug6GCbzj2iu/8Z//OeHOhq7rcJ0nAiEGphAYh4GwG7h68z1++O++zP3JQ4hMoriuQ3DsdjumKRCCEkJgmibGIZTfY7TzfP/+fU5OtogTMlpmGpNxs235u6hKrM5j/fyEsJsmXn/9dbbbLZvNppy5TdfjgN4Ld+/ewSOggRgDXmDsPS/88qd57hc/gbt7Ttdv8M7juo6N75EYCSGye/8hf/df/bfc34ETZecVnLANSiAyvXTOH/zn/wk3CFrR4kLXNSLDxLt/+Q3e/cb3UYHJCz6CD5GI4dfo4N4nP8of/sv/mHfiNRFhqx5X0agQArubG77+f//XnL53TR+UoIGhs/N6t98wjIHr/Vj4RNd1MyxZ0qeaBoYQFvOueQXOs/MTn/v938C/cE5/5w6bzRm+2yC9IFOk73vUOWSY+Jv/+r9j9+b7uADee8ZOkLunqBPCwyvisOPzf/glvvTHf8B7+0uuo/EIr4LHpxMQiVPg+uqa//q/+lc8enDFT99+h5tpZL8bmMaJj33kJU5PO37/93+LP/uzf8bV1SUhBLz3FZ1XxikSI/z0xz/hX/0//hvCOEGEje+5Nygvb895+ewu027PTiLx3il/8B/9KV/8g99DOm/4p9CrsHt4wY+++R2+/Zdf5mevv852s2UYB0h7pKo4ZMGP81xq3M3fZ7qe97im+cda7mON7+c5qCocOWP2uxQ+mt9ZO5c1P8zzzd/VfDJqXJzT9kznd+v+7TkBdYvPFvi6st6Mt/U8WtjU/dRrqXn+wTO4RR817637XMhZGK81OhVtzhVM1t7N74dKHqjnuTZubu28630JVPvRPFfvVZY9VA2+IKtwq3Eiv5/7zXJjPY81WOf9Kv07QSr608Km5rM1jukK35hx0+NkKX/ZeEqUiETFBQcIsYv80q9+js9+4bOM4rja3/Dhwwc8fO8D3vr+jxk/eMzzJ+dc7fY82l1zHUfGGNg6z3ObU877LZ757C7gZaBcxZn2vPwfvv/XB3vbtqdWNMAE+qgRjRAVFCHiEFFCQ2BUlf2wp/P9AqAt8tSbvHbI6k3Lm51/AoUYt60mBOM4Mkwju/2+COF937PZbNjtdqgq42gMTVW5f/8+AM55gsI0TUUpyExyHMcyblYisjLiO4f3JOFlous69vt9UnBs/K7rinKVBX1VY6YYXU1zcCgTzvkFIfLel/XVykaGS1aKZkSdYVkz7JZY1kpGfcjKnogUBMyfZYFIVZmGcYGEbf9P024jTgslJR2SGCLTfm8w3Q8zEczPhwAScU744O13ePToETc3N5ydebou7a9zRO9ABUEZdSIITBrBGQGWGBEURYkh8t6bb3F9cUnUgPcOjZEpanre2ZMu0jlhd3ON4hlC4GZ/xc31FT98/XW+8IUvcv/eGV4cJ2dbU2I04oAQIkqwcdWhIXB+dorDcEWEQmDHcWScTEHZ9BuiXhiEJAtcRqzqNu8rKAGi4iZH7zsQ0BhMgfIeojJe7/jpd76PvHDG4NK5jAE/TeA8MVgf/ekJ2zDhxpGYcFvEhteoTGPg4cOHPHfvPlNUJNr7iBCiwhQRhZGJ8/NzbvZ7xDs0RJJcYeceCCiTRB48fszp9nkUwSlJIYYYIE6KIkjfE50nIvafGONwsmRmrZDTKut2APLPn7/VTDLvX1wRfAr+KyCaBBnAYUKBc6A27w8++IDuoy9yen5CmAac80gMRB/x4ogxEDoh9I4YBR2nsv5JI+qFi5trHl1cEPoeSXhTn90hTHiFx+OOwZnSTVQkgERFHKZqiPD+B+/z6NFD9KxLSp8SKxiGZPTxJ1smf02nAlFAIyrGX0KiazUNKk1ZKBP1HpVHGvplgFbw8JOf/IQX/cc5ccImCq6b6ILHI6gIURQJkeiFYIiGqBKi4mLEdT04IQr8+Cc/5hd+4ws82l8Re1cUDSeZL0U0Rm5ubsygJba2EIJhUoxkAenrX/86n//8r7DdbtPaQHWa6bEKMSqPH1+QsBrnHeKESSJTB/sOONvwy1/8PL/zZ/+E05efBwQJ4MURhpGf/vDHfP0v/5Yffffv0esBorK7uZn5qzhU40KgbIXrmicfU7Bbvr72TP6+3een4Rs1D2z7q/FgoUhUQnH97FKgPaSV9XyyYnPb2mq5RoUilIYQDhSdVqZp198KeLcpcO2Mnpr/ylLuYkXAPBhrRajPRplW+WxlwDUlYJ7K4dqfpq3tdf3dGizqfW/HWsP3uckCB1rFr4VPMeSKzAJes8Zj+J8VXyem3MSoeN/hEDREMzhd3rB7dEncj/hotHgaRqZxYtzvmeJE0Mgkkeg2uI0DZWGYKTi5Atd2Xk/C/7r9XIrGzc2NCcFO0ABZh6wJRCZUZgVUAvMiskCe38nImCddP1czj7xxXdctiF29wXkT20OYNd4s8APldxHh3r17BdBd1zFNU2GC261pl13X4b0nhMAwDOX3rIBki9k0TUUZyR6FVlA3HJuRN8+l73t2496eT0Jc522+gqDRLOm5v/qw1gTzNqtI3p98GGpLVK2t19p7vae53fZ7JqTtAfx5Wmt5qltZd/qfJvhMo3mJukxg1IRVj1nluiQ4TePEsNsBhhthv7f1e88YJojO3js9YZDI5ASnikZwMSkZTstBHG5uCF5tFPGYPB9QcUSUoHuuLx7z/Iuv8uGDCx5eXrEfbxCE559/kUkVQekFrvY3qAYCSpgiAbMqERWfFCad9kgSMERnguA6j+886hynp6dM+ZxqJJPtliTkfQ0aESIiZgfrNFvhAhoVfGdwDpF4saO7d8q1jMSTE1wIiIDzWuD+3CsvsR9HwjCiCk5mq4+GYIJkgJubvTFf50jaAYqg0wSJdlw+fkyMBgmvcWFlUQcjkdEL4j0xKTFOFefMmjyOIzFGduOI225wp1uGYc8mE3YnOJetxgGY8a7+V8ZMZ/gYft7WRMzz21qrVJVQbc6hcF0p/hpNsDf7KM47phjY9D2u6wx3wkRXlHHDfRVwZye89OmP8+jvf8qZlyTFmqIxAHdfepn9YMYYZDYeFLrsHPtp5NVf/DQfvvEO7magi7Z1AoaPAkGU07t3GMeJ8XoC74m+X1j3spfo5U98jLfee4RMEx1qHkOV4rE4xsjELfekVc7WlMV6LSFG9tOIIxLCSOeEKUQ26lAgONBx4mOf/QzffPtdNmrKvaoxegUCkRFTrC+uLhnCANGjzhQNEUdU84Siiu86Nicn3NxMCRc80gn73R6S8qWqXF1dVd4Mv4BBiAbke8/do/OecYqJrwk7GbmUyC/9wif5/T/6I177hU8xdYJuOvoJ4hR486ev880vf4U3f/hjHr7zPjLOkQRZuBTncCIE++KogHibQejY2VhTBp/UROSAdi37OBRa6/6PCbql7/adI6PVuLW2lrYtPD1QPBotXWnHOAa3NeWk/TstoKzhSXOs15INc+S56fLdtb1bPF/NY8040K5tMXb9bLJlxgbOT8QVbQyRR2TL+vta6WwVjnrdNQ4VPHJihhWdIzvatbWwk0rJWFt/S8fy906SESatEQdhmgjDyHR9Qxgjj958h93lJeP1NW4M9DjCODINA14cG9fhNdI78y7HaEaotf1aUzTWzsrT8r+nVjREkiXcSTai4Z0nCJXVdHYrFSVCZ8G//l51DhvKz9cCcB5zjdnnvtYQuRaO898xmivUJ4Ug/8sKRh1udHJygoikcK4JjW5hYXDOsdlsUDUhJoc4bLfbMs9xGthsPOM4FoUmP5cZysnJycLrkEO3zMolwCy0mzCo+Gqd+WdLQPM7dShard3XikXN8GttPCtObRhTgXecXalt6MIUpsIkWyJYa+1rylDdV/nbHijrq8dMpxxQ+s0G1WhCgEamKQnNiUmZO1zYnp6Y5e5kYwJjxssYcL5DxSyad15+AblzwnQx0o0RMu46UCeMOvHSyx8lxAjevCriTEBTo3goilP44I2fcX56Ttc5zu+c8cr5y4Qw8cGHH9D1HZ0D2Q9cvP8ecRwZnZpSIxCTO96Lo3OOh++9y0sf/RhIh0Uvmo/FeY/fbhgvjMnEGM3ync8NS8K1IKRYKI14x+AdO+/ozKWCYB7MyTsmiXYuhgBbxz4EtuKQZCUOCr7rGSKc373LdH1D3/cmQMUcWANhCoh4QoiICp5M2AR14FzyUoWJd999l904mDJWECZZxYGpg/sffYXTO+fEdJaceEOLimG6riNu4ROf+yXe+ep3CbsJjSYEZgXecD2dqcpa1Qqpyu3K9pqwU2C+wlA0CbFrfVl/SZBPCKsy4/0+BPo7Z5w/d5eTO2dMTuicp+861HVIEoyjbTKf+9Kv8zM63vvuD/CTKeGDQDjpePVTH0eFIrjWtEBEEI3IyZbu1Rf41T/6Hb7z7/4GvdjZs6oWzueFHYFPfeoT7McB128WdGxhIPGeFz/+Mboh8ubffQvZV0qCQEi0sg6pbI0qa/jcfgcz7RtDQE48zz1/n/O7d5CuM2+ZE/NEppCTiDJK5P5HX+ELv/ObfPfffplOTAES74gOggjRC698/GNcXF8hW8NQTWc3xJAsjybAu87zhV/9Vf79v/trEHDeEYLRut1ux+nZHV588SWc8wzDiPcR54yOz7TYBLDnnnuOX/+N3+CrX/5KodEvvfIy/+Jf/Mf81pd+i03XmQfJgQTYPbrgG1/+Cn/7F3/FzcPHuDHQTRGnFv6sCYa1USkrxa2QW8/nmDJ4TABZOxstvrfnAw4Fn7aPVhhseePavNoxythRiyLbjlPLH62iZR7CFet8otFr7z/JWLGm1NQKdK285+ecc4R42MdijStw1ywHkOmRzvRmZQ41TWthv+blasdu92KBY7IMTT3W8noNBochVscE9xqva8NOqzAdg3/mKzGNWSsZa+dl0SeH56CMoevf5fddMhqZlVUZd3u++tdfJu4Dl1eXlh4wBVxUNl0PRM7OPCdi3n8VMww5mwQhhoVCXObPfOaOKbdPwt26/VwejYLEISYLfiDokvHWCoQqjMPAZrMpzKo+YG0cZxb884Kylpj7zM/XFm9VLWFIIrKI563zNU5OTorwXBOi7Jnw3nNycrJQPlrkzN6HaZoOciTA8h6sT2Ecp7JuFvChjJvnsd+bJ0N9ekBMMN50phBpGC1WviIqtWJQ91/Ptz00ay7C+qDmvaiJRP1OEfxdDj1pLCoAOj+7No9aqThG6FsCXudoHDAFNeukKcGOOAVUwYtZc4MqOGGIgeg7PvGpT3B6fgZdshY6D96B87jOg3r2IXDy3B0+/6Xf4Lv/+i+LshPCBOKYnNDfPee1X/gUru8sdtI7swKLQ1wH3uMwy+flB+/zzYtLPvKZz6L9lt1+x7br6V3HyfYEr8rNgw+5+fADTpxnchbOgzhc7yw8ZYKNd7z3xuv47Smf/OyvIC6J6En5D8FyEuqW8U1wizjbJdzBIwTXEe/e4e5HP8rFB+9zshf6aUJUuCbysS98jv7eHVzvONt6tPd00eG6Dro+ES9wAbb3nuPm8oIwTkQNBFWGOBFC5LVPfIztdmvn0XeIeFQMftGZN0KYCL1jFOVzX/g83/vxe0z7sQhxMSq+75Btx2c+/zm2p6fEfL6TpQkBcZ7oJkQDYz9y5xOvIY92vPOt79NhjCLnMGgS3m9jLrMF7DiRbYXbct44NJDMjHV+95CAz2piVLNCadY+th0vf+o1/Ev32Zye0G96vO/Mi+E8HQ7vHHsNTCgqkU/+6i/zxve+zynmhRhd5PO//Y/oXnqObrNhu92aR6ii1WDnbCKiZ557n/gIn/7lz/LDv/oqLhoOTSjXYeLTv/F5nv/4R5BtT7/dIs6TQ7HyerMCGk+Vj33+F7l84x0uf/qWjaMWPpiZeP1egdcThKd2/1QNb7TvePGjr3L/lZc5ef4+nGzB9Xjf4zpHH1Ju4cYTUNhPfOaXP8eHP3qT9372Fq7vEuwdQwx89FMf5/yF59icnCC9x236otShhociat6jCJ/69Kd49OiK1996m5D3O9HC7XbLF77wBTNKiS/fZR7ikifFOcc0THzxV7/I2faUL//Nl/mjP/oj/uRP/5S7d+8i5p+0vX18zU9+8EO++9Wv88Nvf5ewH9ioSwYYwXlJhhETlI3WJnjKrIC056AV4o4p3mv7sPb7be+s7e3y2Sd9f3hOW6PXgfDUvFMb3dp+yjmvxqrDUepn1+DUwm+NL9fP14bbWk7K77ZrPqZ01Z+JJFytvmvb2mcZJ9vv2pyHY/uzJhvArNy0OFbPud2zvAftfNdgW8+tlVfq947tzRo8juF5DSs4zHdZ7HH13LJZblVCMqYQ6Jygw8R4eU3YB3xQJEKHM8KuCt7RpYBvn1hGJCZDKPZzBTdqQB7jc+1ZuK09taKhySsQQiCqMowD3nd2HnVp2c5hUarBkjMr5cHWZkCurVyq5iHo+35xgNbcs1k5qIFQC975+6ykbDYbfNcV4pHHrEOpvPcljyLPxca2d/LntZIAsN/vOTk5Kc+M48hmu0V1ouu25fn8k6R8hRDYbCx5dRgGpjARJ4XtKS4R/Lx+Jw7nPSFMZZ21Bp3h1XqIMuz2VW4KLBG5VfxaJTA/X8O5VghrIlArXTWcb2MoLRHJ49WEpyUy87Omd5f99J3F94sxWVAikWEKhK3n5U98jOc//hFib96Hvt8y4SzhTUx5wjm63jOOE3dfeoGTe3fQB5c2pncEp+yJ/OpvfJHu/JSpSwlcLiUyg4W+OUfE4aJy4oWH11dMYWAIkf0wcPL8izhxnJ+dEW5ueP+nP6WbJvNaicdQTwi+RyV5OOLESed446c/4SOf/AybzR3LFxpGXH9qSk+M5PDGBSEQEBwQF3AGo0m9dDzynrNPvsYf/s/+p/z1v/pXPPzGt/AXN8gkPP+pj/OLf/TbPHj0gA2wVSFGh8djbh4LQSohfgTzsMTASy9/lAcffMD9l17k+vqa5154gWHcJ7j5haIhKQTLRc/WeaJObE9POLl7znRxkwijKZ9TDJw99zybu+cEBZdyL8BCxmJUxnFCp8AkkX2MoIHRMlKQkHJuRC08KyrgKi/njKM13poH97jV6ZilJ9OnNUayppwXemkrKkUYonWGiHD6/HO8/KmP89gFS1CeJnxI1lVvYUjqHCqKelO4Lx5/yBADJ9Gg1Z+e8MqnPsG1DwyjxfQ6vxJ7HAKKckNgHyYe7q9RL0SXCkQI+DunfPYffZHhpCOIKcFR5yIRrQFnEEU7YUyeQokRjZYYnsOnao9GEXQr5WtNYFzbE1U4f+l5PvG5X+TSWd5eH3scSpgGNDhO/AYX1IxozqA/qK03Cz+W+CpED5//9V/D3z+1ELzEY7SbrY5m4I4lzykivPqRV2camyyLCPzhH/4hr732sZTXOHuSYI4QyDDpfU/cRH7ti7/GP/3jf8prH/+4zSma5z7uR95//U1+8JVv8L1vfIvHl49xIdBH89k4J0wOohMkSZgOEt0sSEkdt9/m+/1/s7W4t/ZdNdGFXrAqON0yTpuUbZ7pdUWnnc9SrmHxzPIMHwrFa4rLmvB6oGSz5JFtAvb83Myz2/W2Y2Zc1PyfEdkSolzPRVUXuImu07waBmuyQLvOek0xhSk/SQFtv2u/vW28YwpM244px9aR/ahx6JhiN3ey/HOxH8f1ZVMSMlycQ4j03tORPMYh4pIMErGUNzC+iAoOTYqGI2KGnGNK09O02/azbU8fOuUc+93OBIkY6buNJVvGiG+IfBbUTdhdImDrBciCawihJE9P08R2uy3VoVrBt3Yd1hWT6mTtHB6VBXBjTgmhxVz9ZsWBk+2W3X6P956u60xwc44wTajGFPYkluw4RfrelIP93vI1drtdEfK7rgNRpiTw7nY7huTV6bqOmCyntbBehEMxOKsTuq5HRbiZBjqUOEacd4uDsbbxXectnKciYlnByHCqCVzt4akPSX62VvTKHshMMDO8bV+PC1Kt0tDiQz1+3YcTKQnF9Xxy0KsDvDfFbIyBDtAQic5c/4LgXcdA4PTeHWLn2A3X9F2P8z0hKuo7YgSJIESCWnjCKMKgkV6EGCZCZ14SFPrzc6IzLxc+Wy/FsiqcImJVImK0/rx3PHfnLoN4fNfjRHn++fs4VcabG4brK3QaLemr26T4VDUPRQqXUGAcdrhtn/J3DKabk60loo97eidMcUomZkW8hYIVJpKI+AENjBDFs9909K+8yD/+L/4z/u3NDTff/gEuBEYP3Dnl8oN3uKMOn6hYkDQLxZSEROVULWHVdZ5uu+HO8/dRjbx4/hJTqgCHOFTMA6Fo9ueiYUKi5bmgykjgcnfDRnTOzQkRFccYA/swIrqhw0MqVkGSFbxzaT+wqjtdZHQmPPbFM2BCaIgRX4VM5DC6bLErNK6B3Zoi3TKdtWfr5hDy0K0A4hPtISoaLazIpSyNhxePeefD9+HuGacieOxfJ5Yz5FNhgs5h+mCn3H/xRU7unBPev6Rzjuuba9754B30fEvfd3RZsHAuMTSScucsAb+zfeu2G0aNpBg9osA+BnYauNoPiPdsZYNTMZe9OBNoJXmqUYJA1EB3dkJQZSMOR0QMIrPhKgnxlvOQM1QWm1AU/YyP1VcGU4Gr/TWPLi8YtnB6xwxBEs2L4Tqj4SEGUG8M2jnw4E43BveoxCnSnZ4gXQedYwwTOik+RoIq0nnUQYh5v5XOOzSCqOPBgweM48Q0LcNeXn75JUC5ubnGN0VUVJWu7yykD+i7Da+++iovPv8ine8tIdSZD/Xygwe89aOf8oOvf4uffef7hOsdSDDjFelMJGWN9Jkdq6yoz3hYC9Fq/yuJqVK+SF6FVcw+bE8S6tYEVtI5hUMB53+ozlPzvTp5GQ7XsqZotErXTCOM3lO8o7PC1ioH7XprgfxY/7nVil+dnG7vL3lsy9tbGNgfeZ/Ln9TErg7/Wsh7a32twHqt1eufw1cjVMbN+tm1vhbKgj2weH6ttfmoWY5sFaZj8oqIFEW8/r42kq/tWxmD9fNitOu418T4jyZzmhV3QC331OVw3xkEhXeJgmRcT3xt4cJam8gtfM5gLcffb9pTKxpeHMP1zkorimFknAKu76ziToUENZAkMZX8WVt6tp549hrAeqJZvWEZUXLuQw6Vyr9n4bpYChX6rrNqH5OVvPTe0/U9iHK6PTErzzBalaIYrfqOd4zjnk46us62d5omxNmm5VCtrGTEGBFHCbGKMZa5ZOHBe1/K4k7TNCNmsnuMIhA9/uSU4e4J4eEVJ7gSg14LMSKSqly5BFPoXMr5kFx16JjFg4XSk+GV4Z8VidbaijTuvkJgdPF+7j8nytdEsV5He7iLZUnmeM/681nhEfpISZjeiyU0+xitUoxAH62STKdwdXHB3fi8ebicR6LQ+Q24HvEnSNfTqZqy4S2Z3J1uiQ+u8SoMEnlucMi24+LxJc+fPM8JnuidWfdT5SR8D111tKbAtN9x8+BD3Mkp1+PIlUZ8v+Xk9JRTmdA4Mm2gkw7NnjQRegE6IThLBOtcb1Xfxj0SN+ynkTBNnDnHcPWQ0+srpjgwaWBLb2EoTkv8rVnsl7ggqkwS6KJyEhynmxPkzhm/+Z/8R/x3P/sv2e6veHx5QRhHTp3jXDqmHsaNw2Eha3XpTEHpVAhXI3sZeO4LL/CT17/KZ3/xF/jwrXd54aUXCH1Ht+lNmXAOEfvn48TQwdR7+sncvfHEc/7yc1w/vkSngM/ilsL52SmqkW7jiS6m9ZnAFDXSeSHi2aR4WrfpOX3+HiMRVRNpFQudi5NZ01WtvOKkprBGZxXANuIrfGW1tQLCkpFLKfGan83NIbhoeKwdZt3P3kyUTlJ1PrNHFwZydnLGxjlCVDrFXOWpRGLEFMHoSTleAuLw2w1dvyX4awLK6cmGl+7f5f3pyjw9vrMqYICIT9ZutfyFENmoECKc372Hdh1xsLKLvu/onBDCyKQjfW80tZOOVCprpkRiOR8nYpXd7r38Mu9976d0o+DU4bVniBaaG1IYUBYiQobvKpfL3o68BybwmVFM2YhyfXnB9ux5nOtMefJWOhjvLa8h0RyP7YN2cP8jL/L+T99EJ6HXDZ3f0p+dczNNxN2ezeaEzjl65xDfIeKIPYj3xk/U9jiGwMuvPG9eT515lveOd955A9X73Dm/vyhC4nLoVOfpouf8zl1efPUV+pNt1mZMWNrt+dn3fsDX/v1f895PfsZwvWMME1Esv0/U1hOSfNDlnIIkLKmBb7Ysh2jejiTAmedDSljq7FlKwnMSvqJqKuu7sjsVT3mSYLoWmrEusK4L6sda/f0xD8XaGYX1cJH5+VjldmSjhNGKumzp2npqIbcWeoFFpELLN+v8glb5yn+2hot6rXXFzkVCdDKoIZQiD9lQW+/N7LE53m7b49rguphH82wdFXNMWdK08DXDz7G11wpH29a8Tcu16ALG9VyOrb2MJWK0flWpWOJz8ehaTTxTMFQhBi4vLlAcKt4KRSCgMYVQpX7F1BplmUvi85lfg0/z90IWFOHIlh5tT61oxBDsX4wWvztFuq5PRCtv9MwAJDF7tIpvTJubM95jc5jygmpPxtqhr0vi1iFNZtHvDiwG+b1clrYW/rM3JZegrS39UdUEm2TtMCXJKk+hdv/Hzc0NQIprnq3zIcx5HFnIVjWBL89nGIZFrgcoQwqrMkFBeP4jrzA8/hEn3i36X1g+ooUtZK9OXr+IoHGZ1FkTprzW+pDURKz1aJR/GScSHItSwnIv6z5bC059wNaIbW45L2SN8Ec1XEQjN9fXhBhSVRasjGWabxCzZt5/8QWGaeSs7+lcCSTCJwHIBJmEv6lk57brGUKkC8p2Aq9C6D0vfuI19teXnInAFHHe7oKw9Sam7AQRh0qkx9EpbH1PhzAOe4bdjv04sL95xHh1yUYDnXPJUuITkzJrcECYggKeYZx492dvsnn+eTZ37nD58AEn5+fobmS8umEaRvNaxJi8LJoqVK3nHwjQBaUbA+fdBlGP67e88MlP89IvfZaLi29x585dHB6ZFOkMvhItQdusMPYv9+oAN0auP/yQ7/6//orH77/P3/zoZ7z2yU/gX3qBDqFP4msOtxLU7h9w5tr1k1XbcuLY+I6bmJmnkdsxBDabE0uYj7NXoISCaMqLUIUQkSnixoiMkS6CTJYXFUJM/0J1RpYWVKmZoWrNCxZtDU9rZtwylXIeUsiQpu5jVPBSlKYDASg9F6IlSIzTxBAmxDkCEU+KyU046TB81qTMkKvxoajrCcHCzLx44jQh3op9oFr2NordmzGkULNus7H+MfxmjJx359zdnHB5fUN0I1F6ojdBuuZeAnN4oyr9yZZRI0NIHobQE2JkTHlH4j2+EoprmnBMmCh7Uu3NabdBJoV9gCnVgEzaj9cU/qiWYpH77VC2YvfV+KBWex5h0/ds+p7dNCKdFX4QFVyqOOWxUKYwxVQ1Jil7IeITrnbpDMgUeeH8HjJMxM2E9LNxSpLwfnp6ykdffY2z83OimjKvQZH9xMP3PuAbX/kq3/67r7L78DFd0KQMYLx4JZy6WDcbONYGsRafayv3k4T5Jz1zdL9WBDVDlXUBruYZcw6VW322nV9+5+BZebq5tzxs0Y/YzDXJf/Vc61CtHGq+ECqPCNX1WLfhf/3K0/TR/l6e43Yl4ra2Nq81b8GqcpeZcTX//FwbhVGM12J8oVasjtGGtXGfNN+2ZXreGsdb78iasmFewLnvOY3ALejVAczsCys9DxYhQ1YjNPEKFr7JTD8WsiNZAXm69S4UInvwKFzW2tMrGsl9bRstdN4bE0+hU75ixHbXhjFqi8FOVu60EM2IwrKUYz5oWVkADhKdVLVYetYs4S0C5X91InhG1ixY5JK1raJyc3ODz3Hvaa6zMGJjtApGjJEpjMB80dc+lVAVSXBLz+12u7LmcRzpO1eUGAUrkdr1hO2GKZjQlddZh0D5zpKCa201P5eVO1WdLyGsDmz+u35njUi3cIZDd62IfZaVv+yt0WoOa9aQDL82l6du9Tj1u9M04fuezXZrQla0C7DEjPdEhAkYQkhlXK0snO8thj1IJMiEXZkmBOyCvhADDCa4TZhA7cbI2PeMd0+RF++xv75gGy32XZOEEjHlRVI8gTorE6nJMt6fbJHY4XuPD4E47C1eMg6oRvAOJxYWpDN3wnmHkw7HhA6R7fYEh+Pm4prHHzxELq4Zd3vGy0vGmx0unauAyVI5qqk9G5noWK6u3fmBwMP9nseXF3zsS/+Ir3zne3SdR1MY2IjdieBwJaa7EEfM+jWpMk4Tj99+n+eCo7u45sFwxfSRVxmnkSkGy/FyFcGTJNw7U5CzgDsFs2wTleS0MOXBOW72e85DoKtwqnhL078olpMRo8IUStUrXLbICuNk+QmnXZeIsi7ucXBOjKY1Z6A9PzWuts+hWko21u/Z89j+axamLWxQoxruZIMNc9lHyy1RxjGwGwfG/QgIrrfKU9nCHApOJlhOE523ogcxyf/Xuz03+z1bPOHEFPauU7zMnmEV2/tRIzFMphylUsT5bqVeYdwNdimpOJyMdqlfD122zidjRUzrI9HIiJ2RDpeUjIkhjExTwHWe3kTymYkuQLsuDtV7oaiF200TDAP9FCAEyEaumAw0+R4czTl/EcaEN1jFKbwjpoTwm93ePEDe03WCF8WJwUQdxTtU8oZCsPs5JFh4ZZrffj8gCMN+pKfHu8547abjI69+hHv37uG6DYh5aGU/cf3+A775N1/me9/4Nh++9z6dCm4M5n1KVec0xmScXtLV2ww8cBhesgbXJyl5P287dnaeVmFZW8ex7+oQ7Py9CbnH19TOqYVBzZ8WMkhUkMPE4jVht+XH9Xe1nFQrK6vC7MrvbauNgHV/q2svMRf/cK1Wro4pVm1b0s2lQB9TCdinGTfLeT8PbtVz0Orz1jhaG6zX5LJ2n4tSn5WASv6tFSdTMlLfInjviNGbzJgMN3WrFfSf76zqARxbevHztKcPnVoI9snl5ZM7MHknXIq39jlePwTAWflATWJTTDG2bo59zouo4yQz4IdhOFA8clnYXKJWZPaC1Bu8hkBtHke+KTwL4XWfp2dn7IZ9mUsOk7L8D0HoChLkn3l+XSdljvW8Nv3GynrKXMEmfx+CJfI5EbOCdT1xs2HXdfj9jhOZkTQjsIhZypxfJmzn5txhjeTaYrXGRNqk1FZjF5jjdEUOSrvlELLs7ag1/DyXDJcMtzXNv8yhWVMhuAiu90w5hjvhoKJWeUEpgqQanScOI6N6cxh4mESZdKKTACqMZGEuMo0DO50YnOKcWTJvXMR/5AX2246baWKrCr5DxKTiACDJu6fmVdhMym430Y2K3012yZ0qvu8JZzCFHt95wjDiNRI1oOKJMltwFVAvTFGYRLm8vuT5O3fYKLz2yiv4aeLDGHj8/geM1zv6aTLhtdoz6+yQCU0aCc5udL64fMQ43NDducfDYc8nPv9ZutdeZnRWcWsIgV1nyd+dwKiWcI84QmKkcYpEEaKDxxePueq3jMMenHIzDlyHkRADGjyiMSkcSekVYY/F7gdMYdmFwCDKFCI+2ngaFec7Lq+uuD+MXN/s6E9O6HorURyzoocpf+rMQ7jbDzy6vmYnajutwuXlJRfX12iMbE+FKWpx3c+Mz9hs9nY4P5+1NYtoLRQUPNc5vr1lqKpY/oUqLo0XQrDKYuJtHQJjtKTv7HGVEHj84BFT59DdBOrROEHviL2iaiWEQ7pXZj8O6M2Obd9xrdE8nkG5enjF5dUF8S70/Q5xjq7v2TpBvC93smhU4jASdwMyTOYlCZHgOkLnmMLE5c0NVzc7q3biLOS0g6SczgpTUGXaDQyPrri5uCwwCqroNHEzDlzubtAY2Ww3M3MvZazXhZKaztR8IKoSHIwxsr+5IV5d06N0GtkC9Km0gYidQYxWTtPIzTgwOSVopN92SC+oduxi4Gq/JzhH9B4fha3LoWsR573lp2BGn/1ux8OLC6Y4sY8DijIR2cXA5X7PEIVzv8cHU4w/9YlP8NGPfITtZpuskA4dI8PVDd//6jf49t9+hUfvfsB4fcMmWhikTxcFqojFZTMrGS1e5s/WrMuzku1WFY36Z/vZmuh2m+W4FhhbXpBlh+Pi4JNDWFreWM/1gLfYLwfftfjWGjNruB6ucXnDdDuvek65tXy75cP1/A+NcMcVj9rA186/buXsJHqkstzzlr7VfT9pr+t2jPfXY9ymONV7mQ3AT1IgjuFvC8vbhOpszKplmHa/WiWj/m4Nb5RsdDrEy6IEi4VgOudKlUnry3iT5WLM+XWxGmcNJvVe1WkOzTUqM345WRjMnqY9fdUpQGOuJjXH8IdxRLwvl8tBEmRVLQ4eeyZGS2abSxZKuixrFpBrwlYf6lqxqK0s9T0U9WbN4UtzEnEGYi3w5mfzwa1dxcNgTEBEFjeD57/tKGsJjarfzWPl+eXwKPt9RGNcJRYCOKdM48g4Bc7OT9jce457H/0o8WdvIMO48CJkBpBD+jOS5KT2OjRqjSnXsG4/XyMYRbvmMEGqVjhqS0FeZ10lzLn5LpKs9LUhYfXYdVsc5BwSpElBc46olvvinQeXypACPkT0aseDDy7wXc+Lr76KP1PYbvFdT7wa6Hvw3YYpBIb9QLzeE272BhPTdhid8Cu/+gU2QeDxDVMSSjY+mmXUOcJ+YnPumcaRXRi5HPZcayTc2XLpI9HC3nHARjuL1d5PMExMo+A3Hu2CJTG7lAwPTNFyh7owcfHO2+wfXzAME3e2J9w72XLz7rs8ePNtwn7AZ2U2+0USnFSWe5qFu1EUlcjDt9/i5u23OD3tuOeEToQv/P7v8N2v/B37Dy+YrvbcDCPb0w0hKLrZEhG66FPVmogOE3EfOducMA0jl1dXjOPAtYwWN351wxQDLti9G/SKOFM4AoL2IEGRUYnjxDANeGfFESZN+QaSwkZ2I9Plju3JGegIQXAbsXLDzpIiXYiE3cTu8RUP3n6XRw8eMSnsVemwiwMvLq7YbFJxABwxWuhjth4Z9U80Ss0o0DKWNTytz16LzevKM1CJVZnO5DlM6ax47y0HZe/54PW3GVG2bOjPTvHbLd2m585zdzl/7i79iZUgvri4YPfhA/aPLrm5vCrrYVTef+MdHjx+yHT3hngVcJ153Tanpzz34gucnp3S+46bixs+fP89hocXyAeX+JDyyoiMClvxPHz/AY8ef8jJvTuEsxHvN3R9T9/33LlzB7/Z0PmOh48es3v4mJv3H/DgzXdgCihCTHTyanfD46tLHML5+Z1kaT7MzKjpTM304bDK1e5m4CYEwmPBScd4vac7O0HOJ7anwun5OZJuxQ4hsL++5vrigsePHqWQVk/n0x0wIXD94UMuHzwgng+wV3y3I55ObE9O6Da95YE5IU4Tu8srLh9fMDy+wU+RLvUXojLs9jy+uESYCNHxi7/0Gr/82c9x5/TM7n/CoSHCfuSdn/6Mv/rv/w3vvf4G1w8v7FZ2hT7DoCpo4EToxS+smsdo7EJR0Nvxu21LPnIoSNZjLJTvaq9aRafppOz7oTIx50zVwn9rzGrX2LZaIdVwvGz8sXW3QmottOX+14TstbYqhKbPWpxuP7d35oqZ7ThPowy0SpSuaHprwvhtvBuWRTLa9dZejdCsb02Qb9evTzH+2vyf9rlDJZMiIz4JT5bvHSpq8zvrcMwyq6qWpO58JrquT387LLuQ+d0VRbWso5ljjXP1u+VcFLnVDHjiXKErT2pPf4+GZqucuZJ9dCb09D09gobKBRcs38D7lOyG0KWYU9Rc6BZSUmuiS69AnaBch93klr/P/1ogZkWjPjD1Yahdj1lRqIGZFYghjCUUqHaJIZTE0TZZ2caeL8LLJXutQlFnybftPRyqTPn3BKjt6Rnd2SnDyZbN+Tk+XCwQrgj4cSpW/9rTMRPhQ4KQn6uJ06JkHYeHNe+/iJQExZYg5b4zLOvP6+8zbHIYXEsoW+ZQ91PmqCnHwrtFmJZ5nhJ+SCSKQ93Eg5+9zaOrx+we7fnB9B1e+dTH+eRnf4nohJvdnjtn55yenXF98Zibmx3D5RXjuw9x1wNOU4JahDuh4/J7b/Dw6z9g1zneD1d0AV58+WXuvfAC/dkpXJnn4oMP3+NxGLgJcPHxdzk5u5vKBipOHahnePCI3RsPCDdXbLoNp2f32Ny9y+ZkYwpkgvs0DEzjgB8Cvfa8tDknBkEfXjLs3uXx3/+Ax++8W25q1hT/LopVYvLLsqwzY8XMF7sRefCIr/3X/w2f+u1/hLiOdy5/wFYc8YNL3v/693nv3be4c/8O3sGd+/c4eeUFzu7cIVzu6b1nuLrh+r0PuH50xfs/fhO3Gxm6HSLw4r27vOC3XL3+Lvthz3Tn3JJot1v6zRa/PeH0/AwXLL9i/85D3n33bYYOdu8+gAjBS6q65AjjhF7v+fCNd+g/eGx5VtPE6Z0zzp+7x/0XX2C73fLonQf89Ac/5NGjRzz68AHj4ytOgoAK++SN7foe3/cMk13kN6XcrSLcVHhIOldrbY0pzTTjMLTzWMtMUzHBx6WQthCDefCiGW3Gx4Ep5Wb8+ME3wXm760EE74XTsxO2d85BhJurK4abHTpN6G7HSfQQIsPFFa9/+weEqFxO79L3PyZiiq3bbui2PduzU154/gWuHl/wwaOH6DByOsEm2HNTiHjXsfvgEd/9i79jkoDrekJM3sR05k9PTnjhhRfx3vPmm2+g42iVnPYjMgWGkGlhACfce/4+nfNst9sZxg18W6bewnUcxyKIjO98YIK4CDdvfYjb9mhnXncvHXfv3uX+/fuoKhcXF1xfX9N5x83jB5wEY+zX73yAO98Cgfcvf8jl5WMuuo67z90nquC7js6bonfnuXuM48CDDz7kg/feZxwstPMjcsIjVbzv2Z94oo5cvf2AV197mT/4vT/gY5/4JF4cvTicwrQfub645Lt/+xX+/qvf4MO330PHCYkWbqlOmFSLNT63nC0X3e1W42O4e8yy+7RCWv1uy4fhuPe8HWNNQL9NSK9/r/nQWrjw2nrWzuiTzuyxuc79H/cetO3YPNu51d8vCsXc0vcaz86f18J+68WKzfxLPxyjhk8W+J8Gj+qx6jCrY+022nDbO2s4+IS3eBIfODav4/M4/k42RAkme8YQCDGWy6Kzx8mUjup9WZ6DZqKLsYrcJWsmnfQMZmx2OcT8KdrP5dG4udmTYkOSpVQgxYGLWvyvSLbAzQnf5bK9tOgpTITJdK98ALPg2/fdzFzFxh2yFyCkcrnOzfApDDjVvVe1mFrN1ZRmG6FUgrRL3pTOd+xCMCtVjEzJCyGpLK+FrlvpwGEYUqJqut04Je7mA74fhhTLrnhnt+vaxtqcpikAQudcsRBogq3dXC441xODIuoM6ZxDO4ff9OCFEKIdeEyzVWYCmpWr2rMRYySGfDhJlllL5ixWU0mx6hrJt5u2yduQEufTTZIZXbNSVhPzcRwtn8fZxTKxVvgwYUnJIQpW2jdXCgsxWiheTLeAZSWlBEElbTptqu2VJwa7Ndeq80yMw5TmHRBxTIy88+M3ECdsw4YueC5+9A5ff/098I4wGTxEUvI+FirlQ6QLEJwnOiHs9/z3/6f/K6rK+eUeJbDbQqdw8fq7lhDfdYj3RAHdj2yi3anxV3/xA/C9WdtRdiIMvaOPA3p9QacWvoXvcBsTgBApZY2HaWQcRgQ42ZzSdxsrSztOxGHP/uba8lNCNGu+JAsSENRitdvQqdxcsPAO2U9897/7f/Ltf/+X4DvGIYDv8PuBh2pn990OYpjwm554Z8vLr7zCwwcPrIrNfmS4ukbHiBPPS+f30BDMM3O148d/9y1GQjqvQohmGRHf0ffJ8n33nGkYGN57yM04MDjlzgB9TNXEnBBjwKuwu7ji4u9/BFEsxcNZMrR4z9ndO5yfn3Px3gPGcWScRnqFTfD4YDfHBxG22xPzpoRg5yvdFeR9VxK0Yb7ZPJ+ZJzGmjOPphVnRqJ4pZ49AJKTE/RwKkuhP+jufQ58LMKjYjfHePMdOHFOIdoO3c/ghorsrrj64SKFGkT6ms9T1TJPhkqjDpQpfnXq6G6ueMykwjujNRLwY+ODdxyCwFVNcfUiWyM4jkyXYb1zHdD3SOUUZLWcgJYyLc+j1DZeP3iRG5ZTMDwzvxXWoREK0+vB3tpaPIGpVt4pjJ8HE4LMUjp2YRyTzA5+q/YxxQgE/aIIX6BDR3d4U186KL1x8eMnjH79lpbHT3g5xwntlIx0xKNPVDXHYIzFyFScEZVJ49OE1MSalSpW3RfB9RxgnywWJRre8CJ+58wLjuRK9J3aeuy8+xz/5k3/Kr/7mryFnW6tcFSJhnLi5uOZHf/89vvP1b/LW3/8AGaxmvgerlibpfo2sFJByWTQLJwKiq9Usi8CuVLS1prHrYStrlvbyXCN/rQm1Bfer746FFEnmA9Ueu8R7235rgbHOBXyS0rCYm8wFTbKXvlbG2vfWBHZYRkhAe9O6K7xbWAqGrZfnGEzqkM2Ddd6ifLdGwSftS+bbNe84pjgeSMoc4swxRamdZ93qsLM1IV4Snait+f9DFcUWzu0a6z1cCPRH3m2bwRyoQv5SL4XfZKWCvJf5jIhDU1iniDCME5uNyWVm+Da5SUs+jZKFzSyLLhdrY1SQowhX5PNTHjQ5T8RCnGPk8e76ifCEn0PRCCrcPbtr1Xg2nVU2USub51L5UrBKJTER+ZzPOVVaT/4eNBX7yBsEuZB8QBHv5hh17DKkWdsGnwR6VYsxN8abw0RM6M018adxSETMEsld5xlHE2gnHTk9PUFV2e32hGC3f4fJwqw6Z2UGp3GEaHdqEGNSDpK65RzDsC/EL4RA7ztzaQPjOEEQereh7zqiBGKw+vFWNUat9nqMiPj0bGeJq+NA5x1u45kEJiJ974njlEJDNOWwzESn9vIIChpAtbo/JBozEVuDT4w33ZmGE0oyZGvR8s4nQXm2gOTvnXMECUX5y/GS4pPnJnuwEuycn290n2KwC2VE0rqSwmoFoIsmHazYJaqki2hAo+fk5C5Cj0jAtOFcMjXBiA4fO5zaJVoi0EVFhwBM9BnPY0yHwmLSM7MdiUUBO7m8MYaQntsMJlwQrYpLHCdEAl2BjzPhb9zDZCF5KJxg1WxElDCBc5ZnEsdIvLkpMZIxhRluEbaJJ+nuhqDXZtlIypnTSKcWCz9U3kIFJicosdAZIVvKU6lUHJNasnU3KDINKENKsjZhxfILwCUrNTHS73c8/OCnpmyChVem8+E6hWi4p8GkD40RCZFN8rRNwepiITbeoMrw9odJyRdOVNmmczSpmkJh16YzZo9h0DmeVEwAkxCJDy55/OEFHsdGYxKMMQbR2b56DSBWDjCmM5/d4S56Rp0M45wHnZLAs2RkbaxzvntDJN1Qns6I80YffNoXagOBBtRbDkE0gktHYONcYhpzFbiagYWQLVhW9lUkJf/GyCQzW3GFAZlgE6dQbqYGhWCHIohaAnPhgGpVlEIsSlyhJQLRap3iO1dyTAQPcZY1i/ibvLhaeYpQTTfX2oNRpeQzdGEWLK3DRLNshPzWjJ8xomJhFyFb8KMiEQtR6h2oI4gUG4ZzSSCPgBiCiFhYY74zSlCc9NAJ6iJ9KpygouYtjVZS3Hi0Cfl5rhIiW1y6SEuJokQn+JhK6p5v+dXf/S1+90/+MWfP3cN3zs5qCMSbgct3P+Abf/Vl/v4rX2e4vLYCl0n4yPvuNOdhZOEm4wTlzJLpZYJWoQNSIYnmO0psDcmfvFAqbmvzMzPtqT8/Zum/LUevPMc8zdJfPFZENy8nmQiOxM/nz9qLgzMu3eZRWVtH2+/ynVj2J+9VKVOd5Jz8bh32nHlsq4DU47aRA+2c1z6vFY01haxWZNqV13sGWVadeXumbYu/V9oarGaZY5lv4RZKWmNcqDw5x7D0SR6Gts8Wd2uPSpnzkT6e7M2oc3lo1q6zUl3Dl6ScKliVBw+OFEqcvE1E1IESmZgvLs5hgLNSUc9Ey+V9IFacJT/RVqor8/FMqtx44YePHxysda09taIxxcjJySkalXFvCdp2gZNjSrdoi1g8eZxCSk52xWq9SBRPITtWAtcVYEtiphpDk8QsqeLLrHlJNLLpUvK25gvAoml9IZpQ0KUk4e3Wbu+2iwQdPsWaSRKqx2kohFYQ+q5PN3E7yzFJysM0WpiSSwQ6x0pv0jyG3Y4wTfTOxsg5GbYmE+g9pn2TEncA0IgXh3PmWdkPA1wrvfNMITLsBjQENn0P0UodojANQwoNOLyTwqz9zFW+Ko22HOgVy4JL1s98INqkwAX5rMKd2hCyNhG+tjQtiEN1yOu+VJVpGgzeddiadVbYplUJmvND8v4sD3xiqImImUGhJcAsCFVtycmGgWJlWBzYJITXcM3EIyoqsQiwuXJRJorZOoFaGcwaTtmKYcKhKzdD1zCuiV++EM2qWC1r1Wu17xQsyPtnSm/uV1XRlM+kOiuMihkPRGZPlJBunI9VScHKQpfbglnmZ5Lw01rmMtyzhTZf2FjgHQKkc3uwX2l93vsZ1o7F+1qejanCWCwXIiKkykgQg+2X3QQd8akqVgvLBf5y2OZz6RYCRc2wvfN0qR+7ODAnRudqfanalM4GlLLu9P0sgBmTrqEaajxJFndNCF/X91dVojadqybjhC7i/03XNLxx4pbv1esv8GLOeSmwmem6mi6azvZs7cvCspGvlFcWD1DMno0pETKFv6UFmOKbLg7MpMAq1GQl0cbMnQatzqzOl4jl3wuuJcZfw6/gYLRqb1lInkSJvWMSoN/wsc98ij/+83/OKx//KNGnMxUUPwoXH3zI9771Hb7xN3/H9YcPkSHYPSuyTAaeYdzgREXb1sJNWpqbP3vaXLm2LZ7J+1iN09Kj+r02zyH/vE1AfZr5tOs41k/NN+swx9xHG8Z0rL81mC6+L+NCjh7QCla5tXvQCrB1/3U4TKtAwJPLvD4tjFslr13z2t/tHtyWZ3HssxoP1nCnHue2vm57v32+NR7V7y1ya29Rc5+Eo8fGbs/oYl1l3Hl/FYsIGKNFdGSSJOkFM9HMfcZKFrCHk1G3zfxuWm2QcKSqjUq6p+3J7akVjX5r8eJehI2zG66jQiCmG0clhZ+Yi9A7Xzalk1ngDONkiogIpPxZSZc5ZUtvlyx4nesMlGLhNp5ZOPVJ+QjTWBSEEEbiZHdiuCQ1SAqnKVa0YEmn4zRYEg1mgQ7DZBddbXr6rmMcJ0Q8w7Cn63qcI4U+2S2y4gTne1RhmiK9c4T9nk1KCBaw0ARVNp1niCElsAbEQe98us11vrzuZLMpl6Fc39zw8OIB515gigw3N2wgrUOYxpHeW7iRCAyDldA9SBYXKYG6teXGOccQpkU+Sjm4MYdqrIdGsUJMMjLWCgTM79f5KHWYV55z62auhTON4cCdXIhQsehrEeJMM1+Wy7vNOtUK37C0sKSPyJbstqkml2fDFExQsXqsrTAdi1dsyTScc0VIrglZXkcL78VYlRDUEvQMl0yu6jGzMg9zqEANtxJK1xK+pNzkfaznkrTDxbzKnHXJII9ZgGqYZUWnZsoheeZMaTlkNPkMZBgXkTbPSSNTjEwpn6pWRaySnkAqdTqOk1m5JQsKS0EODsvP1s3OxmyDX2PknbOL7RQhqFmrJpRecgJeFpDrfpNVjCUei5Piec3j10JfEa7ThZ5CFpylhJumNy3sLXm2TNhP69BEu6HQi7WW52ZGgEMckgqmqqYszGc2Pa9alKmoFMNTHiD3E1P4gKIQYerMwych0odI9C4pO1rWYOO6ufy6ainbnJl3CNlbXmkqJKVzhb4IgqSS5NE5grdCEnuv3Hv5RX7/z/+Mz/3qr5g32hn8JSr7qxve/PYP+Lt/9xe899Y7SIg4JXlE5pvR6zNfw3I+s7NysabIt4J1SyfLO04W76z1k8eeMUYXtGJNWK9/X1vLk1pLt/KPY33cZmU+oJXoQnFr6dSTFI78TFvwpfo2kSujyWv914a7mu63sGqVofb72+bYttuUu3zAa8NjLUvkd1uvyxoPXlPwWhipUsLX29zNFqZL+KzfQXLs3Rre9ZyPGUdrgxnCwXuH8zlUrDKdu20fbmuSDOTZaNP3G3ZTTAaxWdMoZxkWFcNqPjHj+mxAWx9z/r8nAiPXE4Sn0zOeXtE4vXPHJhYiGiw5UaPV05e0ALPwu2SRotxGnDWwXPa2S3datJVC6svsOlJVFe+ZUnUOL0IU66dzHVGDhWeJMo0THkqZW8XhBfquNwakpiCcbLYpOftkQZQ3Pt0R4h0xRLb9xtZ3csIwjkyjcHK6sdt6U4zdbrdnGAemdNGfV+g780h478m2/2mccL2VMN3tdjjXMUVzT9tt5aZ42QVZFgd/fXPD1c1j/HaD7PZ2y2OIqVypYVLQiRjs3o6MQNM0lcsIVa0EqHdzsnWdWO/Vlb3p0h0pc3lftzhkUB3WLHtXikV9uNYqXmUBuo59rYnIGiOTjEcsiW8hJDEmwQIuLi8sFwWzFsWQQ2yWBKkWissYFeOOysF8siJhScgs+sxN63NQ9W1wD4u+asYfm7/LHCtQ3EZkb1tfTehs3KWiMs8xW3d1QUiNabhZCKSWJm3vAoeXY6qqlUOt8GahALEUZtbeL/ApFsYsZJtgl59wmLAsFU7m94pVilRaNsxmcNVo51rjos9a8TM5RgiTrTukZzNe5fMUYyznJ5cbrOeSfxexW8tzcvICnzXlq6Q8C+dT9aWouKg4Z9X+NFI8PfmejIxHxVuQJPe2YEPeg6w05P9iSOE1CbsXnglJY5qrbIaLzmFjee9ijbM1TlMJF2RGWDYC0czoKMxSFdtTyfRG0pxtguZRnmlT9jCXUo4qiPfcOGWvka0KXRAioVReM6VFy3ytDK035SsLKingMwYL0TVYZlzO89KDWP6o0XKWRBidciMRf++c3/3D3+O3/+gP8Ocn6f4dUyKmm4EH73/AX/3bf8fb3/4B8XLHJvUXxslKQHsLWWhpZW3IqZWN1jBTP7921pa4mteft2ldGF5vh5fBPk1be7Zey5rAZlrm7NlsvT01Laznn2lSPoN1cZma3q6N3fa55pHJ3x8oDUlxTU8AicdW9De/W1errNvaXra/5zN3W9hYC5fFvle8wA5jFc7cwLmF1xoc2nbAX5tnRNbfW8O5Mm9IZ3OFPzf4eqtSBQfrqPnKQnm5pb8WxmtyxdqaaiPBvKfGv82LkN5NY15dX7MPoxlFrONZaRBZ0OWD+YjdwVb+vkXZmNelBBfZR2WSJz8PP4ei8b/63/yvOTs/N2LsXbHedn1XLIrZI5EnnQVXyVndYqxCSZWnaqsUM+MyTdZu7L25vjFvRlZORNhst1xfX6Nq1vBpmuj7vliC+74rlq0s2Drnae+UGIY9Nzd7nBNubnbEdImYT4K3otzc3BCjcrLd2qVwMgtn4hzTOKULCucqSuK8VYcJId3+PSLJ8hvixPXNjjfffLMQAlOkDIZbb8nwY5jsboioTFc7NiFZb9XyXHIcNpXwlpG9VFlRRV1YHJK8N7kErvH8mRAWARNZMCSoDoTMloz8XiihNnb3ST4oa4S3WO116YHJY7QMsvWI5Hm6guPC6ckp/aZnuryyPAWNSDw86PXP8vZCCdD150SQQxpXvsv3d2RhvzAMADli2RJZrCl/X4hmdehrOK3Nr4ZtXca53JrqrMKVSVn1eGntzLiRL5q0PmYrUWZelgxm72ZL+G2CRz3fglscWuDWhIKipEQtl8stGKEk3UGy4rlyT0tSEEKcPXoxiZCKxbdaMt0y5lvUwqamGFCNdMm7mhOr27VlJV8bxaqChDGLap9rXDAPgRRvcUTsPpEk3KLQda6EK4lIUrQSDHNoTQpTncK0oAtLpT57FW3oXCwiJngZrc130cyV8CzUzX4XoVR7E2cJ2HXLq1O1EKslrUn3LEn2qliLjVI4w0hmJQXKTddFaU3wiRoJCJ0qQYXXH7zPj99/my985JOcdHcYNSyYsDReM+/mOSpquXoxh7Wa4j0rG1lfqjzIVYjn2Dl2Eonbnl/+zX/E7/7JH/P8qy/Z+Ul5awwTj95/wNf/+st862tfZ3+zw+9GtqTCJdEURuOt5m2KFd7VdPuYoFfjW21IqAXr+rkZW3VVaGufXRNm14SsY+2YwJVh2npkarpQC3tP09q+6v7qOdZruk3Qz/PM/dZ0p8aJWgGwPpo5yTotbMddo5N5bxfK3RFBvX6vXnNNw9vPVLXkXR7jPbXisYhYWBl7KUCvr09l+fkafh8Ycpi9ocdwqt3n284MrONL/W6maS1MaD4/xuNaWLdrXh2XmbYaXCIhTsVomXmMyx6hdl5J1g6q1OVwsxx5bK25BRft7i1Rep7OpfHUisYPf/yjIujny7WmdEDWwkIyMq0dPCPodnNt7q9cCIgxcu8cvus4Pzvj+vq6XLDX9T2np6fEEHj0+LGFTCWB2ydL/nW6fKsGb5imyrWUiLfOikot9PZ9X6zy4zgSQmCz2bDdbOg3m+KdyUh7fn7OfhgI04Tzns1mY5VYEOI0crrZcufOnVIa+NHFBSebbaoCVLkiscRFiTCEiWkCN450XZ+SaZnDRDKzSIiRrR/AwaHPwkBbRhY/r6G+LNH2rWMOK5j3zSaxjGktCmUl0GTPUhZ26z7WhNL28NdhRDn0qGY8MUb6rmOarNLZ9c0N4ziRrY0uWSXbMdYYR80EjjFIs4of6ScL4awQlPr/KwSwZlI1wZZUgjM/Xyty9fv1GlYZBBRcrshYnnaZG1DuuFkynVDAqMmoLSJ2aZzMfbUwVp3DZA7wR5fzbeG9FlesWHUiTbAplwZFq9fUsbQqLoi8JG1Es9W88mqZQTopH5T3LXSK4sGI0dY+hWCCOEumvAgnaEJWirIsjqDLO3TKjmhO1nXFUxtUixc4hyjV1QTFQYzTAc7WfWo1zxnP8t7X86ecHXHOilUcZAOS7tBZvitiShlyuJ/1/uWWrf8xRtBZgVetwrpssOrNlVAUmY+4Jmtf0GgV4qIyorxz+Zg3rx7xiTgxhIC6uSjF4RkSgluzYlu1P1WHSO3VICni85xqa+SOwGuf+0X++D/4U179hU+ZByOtwYsj7nZ8/6vf5Ot/8Td8+ObbSFC6pHxNknPNUr5Zho8NehCKlMdeo2//w5uw3LnmW5kNQceE2tvofCs4P4mm1Z/XwmE99AHerQjVx9pME5brPtYnzBcA3wb3BT3OoXdNy+8fu+Ct7WcNLguFZoXPtGOtCcJrxkH7uZx2Tc9b+GRZpCi1Dbxa2n9kseVwS4Xva/tYz7/2ONTrb9uaUlz3V4/TKl/1FFuF6FhrlZljyz+meEBl6NR0zQBKjELfd2x6n7zaUuRc51yKLNLZQJNkeIOVEpkVdSfHywYvFA2wIhjA2ebu0TXX7akVDbsd1uJbw2TEMMSwqKNrzHUOFck3epuQZJO1sJ5ZSO77flY+vF/0pQoXFxezppUsb48ePaqemS99qwEyjzsflBCm8nyx6DfIFEPkZrpJ851j/40IRMLlJScnJ5aMjc3ngw8/LGEmYAqPYEml3jturm+4ePy4VJ1xztN7T8CY7jQMSTA3AarrOnRyeFHC5TVdCJbPkUpZFoEBQ3QrWpEsopkjqSYNf/bq1EpBnaOR4VUzSVP4jCiKVAJz6l+pDng0pjuFOQHfOQtBQ+eyfhle9eV9RRDNY2Jwz+V3M82vvSf5vZCIkcaIs7JBtgbvbX6NpwCRFFp1hLHFiFbx5wkTk9CZQkMS4TTBkbIPIQl8koClKYE6UieW5h4TsTdJNoWOaAllmTd2yQhIFkaoPAg1IddU2hmh9qLkz4zRLVgo2Vk6kZLGCtVxSCFuVpkCTQmrIunm4wyrtElawdZ7fBKdDT4zA/CSbyyN9WTSOnPojuHwzDgqeMScwGZzEWASU4gkEcAp5WSpISAxGhwyXhj+2C3RJSQsrTmHCwUNKbTK9t9hXosQIuJn3Mnhht77UkI038oqUPJbDFcPBa2MFFHNWxzUSmF7BR+VvRPMhmI4I+kSSolm5fdCujzJ1huz4cX7BMOwFBTUkv8NX0nCfiwwDeNU5lwXVTCaOs3ejozHkpiZqzArzuvK75YPNIWfqSTr26xMwBxOmJWJ0meY5t8rxp2tcMm+WMLhxqjgHCEq17s919sTOp9ujS8yZSVwKOCXQkHGScG8Hzl/xVi0pFzDVOCgMwUhotx/9SX+g//4z/ncl36NIEBnNFemwMWHD/nW336Ft3/yOg/efo/p8gY/WWEQh6Rytdmr7NOqxCoCVpuYabLRgqWA1ApKNa+slYM2Fn0Bk3rPKmNJ2YMV4eugLYnpwbu3KQCtUero2Lo2wmFf7bt1q0OArfLWejKwyLKv2nvc9l0b4ubP5pymjNzFe1YZ5OpWw6pWJjIfbeFi/2T29Ob307ha7WWrWBTVOuNCziurWMOaoF/WX8+j6uuYAnRsnaysae3ZxZpjxPsq1Ld6b82AuIa/tz132zNrrcW5tefWFNTaaDXjTxbuIEckZN7cec/98ztz/1rRN3uE8kHiAxlGtSlpOYtZIZ6ps874k2XO7dMZNZ5a0fApBjmK4LtEgK0+YuWST8/6biEY+pT/kAGXK4NENUYgSfANcZnUa+/7qizrUnC2A5CIUb4zQmfNNrvy8wbEDGfvEe9RLKZak2Cu1bOZgcVUWjVirqjdzUC/3ZZSkjHGUsKyjD1Z6NJwNRCjlcQ9PT2lS+B2rg5hgM3GbnYU1+HF4/HghCGMhGFkurJEcEnzK+FD6XfvhE3XmSUhhTs4cawRca3mDSwQuiBF8gyJsEgSlySIlYovcRYGRVIYB8I0WKJ69vqAoGLwrW9LnUN6zP1nSo0JMZLujlhUaaoUkzzHKYyEMHF9+YjtxrP3ki4Pm+9aSdtrybFJGTQ4ZKUqW98hHR+U5Imhwg3Jwq4JqSW+G2aFT7I1NuU3pDDDSFwKX9HKO7uUXaxJoXFJCNN63oVuSPl/Ph/ZC5HnEdUUPOelCJ4aTbA0Y1oWLisPBsJIUs5o4r8VhKncRqr2YjkPYaZHBjs341kYQ1Jc3SJfRlFEo5X6TKVrszcoqqBqyc8xKbBF2U9zLIvFwjKdcxZ7r+kOCbW5FdqQjBZTlNkwknIiQmVhNCUzw0sITojRldwMjTHdHG5wVGYlwmWPrLM8r4xJInPssHe+eJfymcv4HJP/oDvpCVeXOI2EYEnhiidO6ZZ7IQmgAhEc6SLJkDEjbYaI3Z2S4DTDLCtzEZW4mGeGi+LJ5CAzs7LD4lOiuhbeJ7kaV8W1YtZ3i7JaspvQ7BojyxOJPid6YGRlFnCysj+TMqMTmvhBVtxzXyFV3RpEOfEnnATP1dUNl5t79JMNp5o8Bt6BmueoE4E4e3411cHOFbwkeRlUI3Z7lBUa8dE89MMQOHn+Dr/zJ3/Eb/7x73HnhedQSZ6/qAyXV/z029/j7/7Nv+fi3Q9gDAVYRTATwYsp42CVkWsheCGYaDYTzIaINk8DOPiZf88GuhIt0K2IA1pRHW2EQXfYb94y3yh/BS+KmFs9vyKk589rHtZ6tMo/ZDmvqtVe/Px9/Xfd3/yu4YHgUmSE4ewcXhiKYtcKvO34reepCI0VtKLOUFnbq7q1isvas9mTXBu9IBkjaoG1mnN+1j60fSId03xn2jFhmbyi3K9U4Wwi5XwuntdWgavCZHXGmqNGwRXly2it0Zs21Kpe51qftdKwNlY9Rv7eCYsbzJ/UZrlnPhNrCk1tcF/iTzK8OkrEjohyerJlgxnwXdpv4wQG+xBDpWfMSogK4GYjxbI5JMmrKlm2sOiB/FmrEN7Wnt6jwVyuNjNU70y4jRJT4qEmJuhKbobGOU5RxG7h3u13KZ7ZmHPJv6gIagZunRC1sDpUrrkWCVoky+9nTbFsqmPRT4xxvg8kCQ6eeY4iYmFbMbLb7cq8c0x+jocHGMehjH1zc8M4jpyenrLdbk0IqypAzQcgouKJajkb0zQSpoGemJ6fY/ChqiIV7XbsmlGsuVFrt6U4wUVXktBq929mPPndDMtSJcp1RSMuSlwF891uV25T3263s1LD8rDnPQ1ql6TlOWflJu9fXm/XzfdudEmxEjFl8frqinEYjLA58yJkpStWc4R04YwqzuXDKKQrrxYMpByqzM4rPpSFNXS2+kgl5xlcgl0Mpw7H7I0oVmAnTD7f/K04L6mSkithL61lBkjKkmNMd1OUePtoykTM9wglYmBx71ath/zPsIRiIMiCo2qlLMzryYsr1cGi3U3QWoNmwi6mmMWkfMR57IlIlFgpU1qtdfYoxUgxSmT1r5I1y3wtOdg+zMqwU7MGl5AzlBApAnTuX/O8Mq5X300KIUKIYvc7aLr4MCXQ5fNfnzFL+F5aJOuz0wp7ZSfE453jZHMC4pkiSLKub8Uh6ojBAOgcdq+HCGMJV0pKSF1usCiqM9wyLOYk64QnNcNQo0XSlA82+l7/pXO0lC5DJNJHlE2vvhJneSjZY1oXAZHUjyajgGiqSBiXMB2nYAphDKX4hnl7NXnehX0MnGzv8InXPsNGHbtRrbRsXjSz+uMUegedd8QppHPtGIfRPFUh4CTvX0ywFlQio3P4jfBLX/wif/af/ke88rFXkU2HRMvrGYeBB+99wHe+8jW++dd/h9tPSDwUdmcASYmvfppW09Ico74Wnrf2fFucoxZy6ufzzwUP4enmt+zs0JhxTJi8bf4LmrgiGGYY1JEOtQxwbKzCk+L8dz5bRfl0y+fr/o+taRZwK4+DLPto3137rqaxreA8C9uQlc66z58ntE6gFDhZe7q2ts9j/n/WFutuPl9T4Fr5JhsbWuUlP1OMc418+KT2JOWvfa5dy9pzFoo5hxQ/zVzyGrxzOE9iXsmwlWSSYkxk9n7msvcH/THLOIWhUq/BVEyUcidejV+1l+tJ7enL2/YbnEvKhMzabd9vbJqyTA7On9mEZ8LQdT2nYgKu9zMDruPU6woeGZnt1vB+0X8d6lMLxLm60X6/L7/XAsGalSRbd7KAXCs+eYw812maSsKsiBRhehiGonSIGPEeBlM49vs9+/2ek5MT+r4vfZyfn1tOR7JOT+PEzeU1U5hwOnLS+XITqsZpEQ42K1CTWcYrWOc11h6EaZqKwmQJp1qE0RaurTI3E+yccDUTsXLze/q973uur6/ZbDZF+ZLkHl54pKp+2/yRmhhkxaMOsatL4276nvvn93jD/YQYAlNQam4QQsXQxeKwTUhS82ZoraCGWVlgtrZHIIRlbGtIwrlLakoJYSNZ7iJ4NS9FZrBoTtJyBFX2GopVFk1lnNO67H49XRBPsAstcS7dTi/lTEY1id5CQ5IEnYTGGBWVWUGUBAstcJ6VKruTbcaj4uMR8g1x5jEqZqcMWygsR0i5FOBy/D9ZgQPSfs/uf1NOaoIY1QRq2xuF+hY4ZniS4K6Ay14y1G4yQpPwbcpCiFIE7xghVPGrxcqEBcZMKuVCJFVBgn2WNacsqNX0LYQKfzL8Ktp4jAEJVh5825+gkzGAXGEuBsOJwoxCoOsSHmbvVwq1yfto21vTRRtFM8jqeUgjNKoZlsrD1XO16hE1w3fG+bqPvN95LuWrKQl6wSBtF/0lw4Bo+XuBD0seyGSEi4AyhgBxwif0kAAupgpyAmebc2QMDGNglLnYiOlbMTFvZVJHJy6VMYcQBvsuRrxkj62iIeC8Xc5JJ7z2C5/kn/+n/4LPfPGX8RvD105tfR++/S7f+9a3+e7Xv8nl+x+yCYKbIurmCxYPBBmNZbFPI4RnPmUGh2n1mTW8a418t41RvE3ZM+DkoM+nEpYa0aQ1otzWVytAlnN35Jk855of1rytHnu2NmfP81JoLHKCBlr1u36uFfxz3/Vn5V4izRDRYvBr130YerX8vVU28ufOyaIoybxvrih6q7RIdVbcmuPfrrWWqW4TOJ9KsWnn8wRFtN6v+jOpPlt7vq06+TRzbRWBspe3LOuY8pjXWZ+32vD6pLnV9NxK6mdcrQ1xmjzhaS9r0l6MP7kISnNZZk1vE32PWcme0cLecy53+MT21IqGKRl5Fo6um4XFeRG26Fkwag+yWYOc63BExGlFJJe1itcOVO3eravptBp9/nd2drbQZOuNrQ9wEVg3m0WoUD23mjjld7KQlOdi8du5TJ6UPrJ7Oj/T9xYqtdvtCCFw9+5dRIRhGhn3Y1I0RjqJnDqXLnyLxZvUWmq8W16MN+/ZYe3y/FwI6QZvZpjUORAwV5TJfZhHYVYoaqWgVvgynIZhQETSeqHG+LrfGEMp2dYmma1ZJfJcs8LWdR3b7bbA36tjChNTjFk0KHCKGlNcPkAoxCmhblmPzBOd58lsGVh434J5IuZzMFd82EfILgJVYyhekxVRzQsRVdMFkjbeECa6OOdgIHOYg4igrrOSq4BotvqTQj0styUn9ipUhRFSUnPMyp25W6cQiC4WpWEmV1lBMotuRaNKHk7NsBekVcB13twCeRlpfYLggxSFNYdIlRcLQa3DJcySP8O4sQhrsuEIwGxpc05QnRbKQAym9IQYGUTLnhrdsrk4MU/hNE2MYcKp4jRZ25MVKc8t/xzHsQCoNQa0Z7E2AsRoJaqnYGGXTrVUlJs0EDXgXZfij01Q6TB89ip4cUWZdCkv44D1J6G9CPFVPsUy6VoQlcUlfgvljzkvJq9DRIrgmfetMLNM/4uymvc3wSLBNBtMCnwAopR1CLLET2f8xTugSwYhrCx3nEYLgVJl46y+mFNloxAISV+1/uKY+u88qoEpzt7UTedx3uNIgrY3Y5B0HTi48/x9/uTP/4wv/eHv0p1vib0gXtBhYtpPfO/LX+Prf/t3fPjOuzAGNlGsIl6MdhG7P7RO19bhp1Ey6u9rT3BLS9dajYu3JdvW85tfZtVKujbGgpfnfay+O6aA14pAK6i1BrX8XW3wqr2Ia0rK2hwN/im0u4muyN/n+ee+WjmkhlmrSC2rziWIJJpYr6mFQ8sX63/1/PKzMepBbiZQyjjXgnrZ29poRJJRtTrD1Xrb/eEJOFrDJL/beliW657XU8NkzUt1TOFdk/NyH+1cWqF/bb2Hc1yG860pme3v9bNr82ufreemFbxEmC+0jcucDgurzeVwk4KgczjazF8VzdUybVZl/wULM3Z20Z3RaJKxWNXGXlnXsfbUisZMVWrAy8yYXSZ2sTqgGXPzJVAzkEQ84qyf2nNwjPjUn7UHrHWHttp23UeNsCLCMFgeRd/3C+t6/VyNoHV4T30nhaoWb4jI8nCP41gExVxvP0arvT+OIx9++GG5O0FDtMpTYkIPImjMN9wuD14hFhpL6EPtGagJXVYMauJZt7XDmity1fdf5PWtEfF67zJByMrKZrsp88vzyDBF1Zh8VTkL4ORkvutkv9+XkK5WERLnePjwASFMjNNEGILF+qfQD+ecCQmpxGauo98qZiJCVJuDQvL6zMHqgTmsIL8fktDaWjcy84gCsfa6xVQsQCiKUcZX71OlMlUmlwoX5P0mK5KSiIMJbBnXwhQSg6RcdJTHizkcy1neUlGkZLBkVifsw2gnVeZzPjMjSyYWmWEyJctpETklu2hnk4jEGa/yzekiFtZEoMrhqaoNSVacjLYYjlhRhRCyMmBC5rwXeR7JUp0EYefsHgNNxes1PVxyt6IJ3AenQSPTGNPdNQEXA5Z0rfQC3rFQ7hfljCvlKAt+i1yMOnSTfJ4jU5wQB6fbjvvnZzze3eDUWeims9A+l4R4SbCV5LWRdKu4CJaxscLzrbAFhUEpsKgSVXY908n5wyUjnJ/JZyOpeKjLOWuV4SFdPOmLZyomfJTFpZrWX6OsqjAfrFrgEPCxXEIl0pU8PlOuHV0QJEYmgcmbXrKJllOUlYacx5Y90OKyIhrKvUvmmfNMKrjeEQTcScev/Pqv8if//E+5/8LzsOnwznIr4s3A2z/+KV/+i7/g7Z+8QbjaWfhktEIU0UHsXVGuMnwXAkuzd2t0qv459yGM4xwNsCZkr/Xj3FygoxVo2/1fbE/T11Kg/vnCU9o5Hft8TbhuDVhZiT8mA7T95PmWZ45qUCbLWLXIWZ5oIx4WvLkOL6q+S3aExOcP8wfqObb7fEwYXfJhFry+hWs2ctRh43Kw8qXm0cpepc+fY49vw4ljilb9dwvfNVmmfQeWURpr72b41XJbjRNrCku77mPwaeff/r7kBcv1t563Fg4ANzfXxXBmhXGcFQ1hptlUc8vnIsRUckLElAjVig9oiYxQzd7q9H+NhzzzCe3nUDRmy2LWyo3454VnRJf0bJM4s1AckoLSxBDWxLZVNGqLOSwJRh1rWm/A2iHP79ab+ejRI1588cWj7qw1LbzNC8nPZM+F9/PGZiWmCJOJKOXE0Ln8rAPn8OKJ0eJ4DcoUJMhj156XnIXZEs46hyV/duxgrr1fhMRmn3IIVHtwW5iDKVnjONL1XblALK+7lPITu9Rws9nMYyRmkV37eX9r2Jef4vBeOD09Y7q4wdKFKmE8JQbHlFScYmFALWSkZhg1blFVfPG+s3CNuolZAHIlptxCxWRFHLFKzM9KqqrSdx2xW+5xIQ7OwrFcRRzy7/Z3xmvAW+IyKM515CT3ltGY18UXgcy5uUzzWdwUpU3q9aX9ydbwci5SnL0e8UIiZnwo3pFqHpbHMJeVrv9FLEHXyhbX5x0E86rmz7KBIltxlsp3rgwm+FylybQrtFy8lhXChLupypwpeCmXJ4V/dU7oMYu0U1O8YpRyfosFNZ2BaZoYxxEROTjnNTzK+iyLj23f8ZmPf5SL6xurniTKRlyqTMYBjYrB8gWcc7OYICw8ADVO5/2ILGlBsWklb0aBfUsuUjnXmT66fAzInitFF30UxUJmI9jMF+Y677aWSqhqFY+CWoLz6woVwIhaiFKEkUjwll/jwxwGIFm5SPhoXj8rIpHh57sOVInOM7qeySkf+8VP8Xv/7I959ZOvEVyETWfK0KQ8+MkbfP8b3+Irf/PXXF9fsfEbXDDjkXPe9CbvGEVgCiXU8kAQkeXSbhPMaoNSCHHx95qAstZHK/ys8cwyt/x78/fBHj2l8FnP82nfaQWxuux4/r5WdG4T5OvnS9+J1q2tQ5Lu2+bAHBMED5SEWD9bnUk9FEhbpWq1vxV5yD6bZbDFvBYy29JoGWMsRQjaVuNUPZbB6+fb6wM+u7JemQn2qiD+JLzO/ddj1DJiLU/W0QJrONhGtpR1Z95fPVfDql5bO68lP1zKpccUq9qTZI8kPpgqwk77PaiaEVANAwQW9+4AUOhslokOcd1kTTOIROb8u2Li+/nsB0+vaMwItp4wltvaZq3FzIEgYmVgQ8ylAn1iRorI4ebU/a9pg7BUSNpyuYdzgO12y6uvvFLWZYER6WKkaKEttVJRr2cJFxbj1xYi53yBXX7UuzmvYbvJCdNpDeKI6qx85X7AYTHxpOfrOxWycOrcfGjauUmywmgpjZn1VVkefGwKJuympHDnk/Ux1fhOumRWlnLOxbGL98phDjHdzaElOSlil2FN48R887F5Cby35NcYR5xzpRTxAtYKEavO9dy95/j4Rz/KB2PEBTWLEfOehxisGpOby7YWQR0tXg+lSUaXWYC33GuTlmKGZS2MY4JUHQdqAn5DnN2JeS6SJ8Tml/pzKQxGWVh8c4ldTdaEHGpll9C5IsRpTNV4qtLMhlMCEvGdn63wSbFAsVK0kkP+mtj+JHjlOOJpmoqlOocZ1J6mDI9iLBDDaVcpfFMMwIYcE23wSrkwFTMpylcB8tLDONOWfK5cYdzO2157l5QNkUoYS3CJlQBcC+ZOiI5ynZGg9EnZcwhxqmJb1YRkl4plDPv9bAhIz9idQZWFNeNdArBzgsPCI0/6npPOM4wDAWWDQzR5ExIDzqEWsfflPMKsDFr52IqGVoxR82Jzsndad3auZ4WlXF4p9smck5F0z3SfiX2X7pXwmY6nkMV0Dm3NCuXMpPVoFeblmDfAZjDTG6Tsq6J0OpfelbJD1tPWeUvcDopXYUp75kSZ7DCkaEZ7N5fNdZhyIs48c50zfjA6x/2Pvsjv/OM/5FOf/yyy6VAviHj219c8fPs9vvvlr/H4jbd58Na76H7Pibmn8WIVBCOa+k1Ks5NScS6fMTSz8YyMmaYshU3bzkMhzYxV/oD25udbobRupcjDyphPYw2uP6tlgAOe1Ozw2lraNRaFyrlEH2c+Y56hw0sHa6HvmALT8u3y+coc8zet4WQNDmtrsa01pbbgfma4CadFDqM2asG65a+3NklnNZ+LWE4ZypJ21rgzVwypqG4jDNfrnflfxQBrGNRTWpnzoSLX9FeNU/Y8xqOwbodYe+8YPOt+67VZuCxl75PwYGeYJVyOKRlLRTHTv/wvv7+OW/N7c7+zsbBDcQwxsJ+mpDNoOWgikq4XyAr3nLNqMlfmUbPyIWC5f2ktIcsRktmWWC2RZq9va09f3raqsFQTpVpLbQ9dLZjXWmF9qGOMpZpHWaiLiMz3c9QW7LyRa8RtTdCt55N/1u5CTYRqfqcao/LK1AhUJz/nflpBO1s4SRarvt/MISuaYvNTrX/nzHqWhT8FxHm8V9gPxfOzuOiKGqmXjKl2G5MIWgipDGQhcHmNQIrnzMJkhkPn+5lJpAo9zs2ehfpffi5bmGslr3hxUj7FNI72bEjhZD55OKY6JC95GWS2PBaGk4QmgiU+jxpxnUfHgTvbTYpzr2JsJQngflYEazwoOAaMUa3CT9ors7gCKUk8M4iua8XfhOsoUWalMQpmrWYOvcsbM9/RAkGMkboOFAdBi/KIagr3AhGf+rSQs4RiZa9zkJ3IvJ9lH5yAmEJDKWGcFItCMOfzomrCZoyWY6Q5sT8piy6V7hXA+RURIo+tIEQIifCpeWpExMoe55CVaApWVvalwD4LvA5kLjXrcGiiHVZhTE19UxPqfGLkImoCnyjohMtCMZmwZlGVuQwvER8UT+VpzbHBZoqYBTBxJUQthmXoEOXMzUxQKvpTaI1mr4UiTHiNdBoSnGZlys5sQhoUn+efQZ9/DYdMQFUX97hqgm1L38h4F0OCUCpTvqCHJAVgDp/CWdqXJBzTqFYefBFGY0wwFzEozDbjYs2kyedjfrYozqTb5QuTLiwylfw1b5Ag+NSlJqVa05oKyMQlRcSnVB+PdsJehO2dO/zW7/82n/2932Rzfop0dleKV7h68Ijvfe3rvPvTn/H2z94g3OwJ4x6v0Gna/3wPAQl9Ufok9Imb77gplWG0QLO0mte1gvjMDx3eH3qt1wTEFieOCctrCkP5OzOWlXfafheKxDERvlE22t9john5szpHLuec1bQ897kmm6zJDEv4HAqxJQyLW6r4VH218omTLnleWmt8UsSExfN5He286+IuLdwOzjEw5+rVaz6igKb1zUpQOucNjtTwKML7IThWWw2XY0pGUYhq3vwUOG3rXMK9fudJSlotz5Q+oVRygoo/NPhdK4TteO26Cy1jhmVdXOdwfrMhrswpnfkowsOLS8IYkVSxsRgxUURhilp4HYD4lOcMZnRBsg27KB5U58o+T+GxUML+fg494+dJBhe6zuMqi9QsYNbCZr2ZifA7c+LMBGDuN2v4+Z08+TVBthUOc9+166t1aeb36+/zRjo335zYKhRlHF32Vbc14tX+vjYXqhyFtiKWWZ4F1ZCspiwuNsvKRm35sFK4y/yGpRKy/KzMTw4PSVEYUJzzZZxSrapiZBn24zgWITorGLVHJ1fVUlX2+33JZRnHkb7vDyr3LCxnHO5B/s57zxSzcma5D5vNhn1IuRtaEQ1v6kDLCOo9jTGVq2XOHyh7YhtU8h0y1hYhKd+dUO1hhnGXKkM4J1kLSNb99L6IXQCXFSixRGpRGNtbVqv8ApGc7DwTIOcpShqYpyJN3mxbSQg/TF6s4TArtK13Ju9x3rN807WIVEnn817VsF07w4fGgST65zNKJUOny5hYCV+kwskWV5KBGhGh8x5NBpN5Dku8MmgIzq8bNdq1tefK+fVQzpqWtbka+ZmD8EatLJEVzHKr88TKXFZCJOuzVcZLfa/NYwnfGSpt6NYMgyXMs9DiRJDkjZyF1YRtFb0t4zdGqLrV47WhercJEfmTdLQQpSgfqAmOVo1HoHMMXognHZ/79S/y2//kj7j7wn2CM/xzwO7imm9/+St868tfgWHi+uIilzCzM4GCMw+eT2e+xtU1AeqYgNIKwsd4iwmsyz3OBr6a/7V4Xj/3pLY8W7mk5lJgmuWAef4H7YhUWq+9hUGNJ0t6IWXd+bP8ThvGW/O6ti3gnOj12phPaq0c0QrP7RzL/Kop1WMe27NaTllTLm+jVSZYxgUtEBGOYlaDg7WssKbcLMas6Ndav207pgSsPdOusb5D7VZFZmXcGsfq50w3PD6ntbU/Da6s0dC2vxq2x9aT84v77Yau7yjKIYklijCQy1Ibb2/PRIyW/5cvT3XOWQhdsCJERj8yLbHLfQMmqx/f3WV7akWj63waNG/IoQYotRa8+JkJ6goTkNxPZelVSlhKfaBuZe6VpTq3/F1tYW+/V/ul/J2Jcn6+JtrHxs3IXSsMB4c7C06SbYCU6lMLBipJG51MNxexC9hCDLQhay1CiswhW4Xh3HKohDnErGZKMdp9HjUcsnBUC0gt7FsBaDFW9X0uA5wriI3Jw9Guxf5eCjFlDYmxOucQtdjq66sr4s3N4vbvlrkviEgrXAGC3bSMpL2I+WI8BRW8LC+AcrIkXu3eW3gHRakrLKc6P5mYibM7RYiKiSuHDMk5xxTDARMtsCqWCz0kBDLf/VDvYS1s1mcmwybnGKzl7fh0x0WOr88eOVQXoVui0OWE4EaIWKxR53jQ9gy1sFgIALaIeV8SA67xd5H42Agpt53d1luJLuFV40N+tzVs1M/Ufa2N1wqltzHGuZz2oTBStxbvW6GhjJf2LrdaGF47R23/7fzqPtaEn1aYamnIsfXbTe1LZlx7lldhgOGhy4qGMbGSizM5IfSOV3/p0/z2P/tjPvLpTzA5GLxLhQEiH7z1Ll/9i7/m7R/9hPHRJUyBOOytwAOCOE90pmhQnd8aL9f25jbh5OkEmfnujcV+Nud6DUe6ShE8ELRUD4xbZR2NcAxz2OihIeNJ8z/kZ/VnvqEbZdWZvnLIm+t+2nCbzOfyGMs1p+IZsjSsle+za/uWlucxGywP5Z8Z9+dQmOXncvBZ/W4bVXHs/C/pDQsFH5b8u+5hDrNcP/s13qydf5gVrGPrWJsrMhsq6vWthe7VsKIyetdzrvcit/bMFYG7irwpz1Xj3HaOjskcbWvnVY+V53Ebv6vn4Jzj/gvP87v/9B+zPT1hs9kY7BIcnfd02xNcirDJ97uBEFN1lXqMkJULVeI0sR/2qYCNN4OJd/h+g/guHYF/YEUjxrk+t2rekLkGvi283oDKZIRDJMeiHbE6LRJSHFEPQ6dsrEPLSY0cdd+tZrsm/Kuamz/HT2dCma302VXW5mm0yFGX282Ce/YCLA5rNX5ej6qWalS5Dr+qphj6+V6QmkXVd42sza8cTubbkDPsMqzyBXo18mahOu9phnEt0NQhHy08Wwt4S9DqPutn1nJLbC5zPsqiP63g4GC335e/Jd2aXLuZ1whFLaDMglZMIQ6ClWJWSBd0uXxFJilHIvGOWlDPY5UxijNTyk3DRgiYDw65H/NJ2rznZL7s0VhUNWnGofQZF90uCEHCqzrHJysHU5yrt+XPa6WkZf5FiE5dLxiqUkLwcunURShdJaTUOFPGWCHYNnbNfurCCyWA6ICRZVjmM90qBLmwxXoe2RqM5+drD03BYWXhIc2tfr7uu8XBdty1PLPW0l8/X+/FmqX6mGCw6L+B/8IL0ozVrqX9vqUTx/Cpfrb+u6Zzi+dCJFawP9iHarzl35LCzUBFiJ1j8sIkyr1XXuL3/vmf8qnP/xJse9h4RJVOHMOjS77ztW/wva99kwc/e5stjn6ysz2EiIhZFi2l3LyGdpGkO1hbW3mvxqljikj++TR78LThUy1/PIYXrYB2bPy1MVr6Lqn0Zv39bby9rGlF0M6wXJtre26fBnbz81IMQWsREibIrC5/Med2rBoHln3Pnuk1L0zdWhypeWtNT2peX8+njkCp4VjWXwvqHCoKB7BgScfqddZ91HvbwugAbqoguVT5EnZr+FXTunAkib+mYS1NaNewdgbyM2v0tIVPS/Pqz9aUnTXFou6z3tOWT3Vdxysf+wj/4n/yL4kpLy8rGZLWnYuWWn9qURJihWB8kjNiqlJV5BNRM5jYTFCt5GzF7kDSHJL15PZzJIMvE7qIcxhG8+DybxE0hnQhUxYW1ty32UV/yIiPHdqWqSyncWjVaFsR0lPVkVq4mqbpwNtRI1V+ds3K2x6oVlBuGUEer+u6Um7UOZfSAgTxrgiXtcei9CGW75AROSPkmkUwvw9YKEBFmMv6Ugxx64KvrbRrwke7zvaA1MQzj1ULEi0jiXG+rbvFgxgjEix0JyzGj4QAnuXN5u2et3gwz1GXh1WMVFpu3Zw0b0qJppj8+RwcrtsUWfF28WK1ZYbpGXdQu+m4fJa08tQW8fwi6Rbk2CicNnc5ut5DIm17UN87cVhFbA1eho+zUiDMeKOqJYyqhNNpJciWIJblPCxW+RAPjhHhhSKZxqv7yng6x3LHIpzYOTBPan3zfCv4AKV6VPlOZ4ac51H2O0Rwh8ymFSrr3+uz0yoCawLTsfDQtv9j7ZgQs/bcMYVg7f1j56wVnlo6etuZrL9bCI0N/bmNR7RzVBEro+wduw7k3gm/+Y//gF//0pfY3rtL9Fj/U2QzRV7//vf58r//S9574y3C1Y5eBURxviOEie12W11MKlZYIcXBZ49ibXhq51sLYbVBZw3Gt7X6/KpqCaethfHbhOy1/lp+VebNbIzKn9f91J6Nxd4jB8+3e31sPjWfzX3XeZC3vdPCu11nbmYsUERmz1gbypvLKrfvtmd3sRadY94PBNFG7oHZSFYLqLWA3PLU+vkiv6wIqnCLVV4p/HZNk2r3p75NvqWZRQ5p5IH8zNo5KPMRytmp19Tyu/bdFmsWNJulotDSnqPnzJj9z3Vu1lpN29f6qOWrFs71+avzg4FyR9vklEk0mTlypI4VO9GgizvYxHludjt8dGxTtIJUil2GvV3orIWvOhGiaDHUICCHdpHV9vTlbesqUDprnM419ZobjS0LiU6XglgNSADXhErl+uktQYKlJSYDT5dy2eJw1Qi2WEIWYHU579qDMsXQHHKlLh/axlqvxV7XRMEnIlALQrXgThbgBOqqKhrV4varg3Gb8NIenBlOS829JlYLT4Usk7lruNR9t6Ebea15TfmuiEyQgMIA19yUrRWmzuFp1yNOIBhj6Pu+hFPBoVJXE+wWPrMA6lDN1nXKP6zHKixpScSaAmlLvBYxwTRbWtIeNy+gGhHv8Q5Ercyx6pJ5Ffiw9ECR9ZJ5gDLWYp0rMJy/yef58G6LNdjnAbSyTvrkDRMopYyBKp8knato6JXfXDDQFTiWs8x8Ttv4YO8NDrWXIf9TXd4+vxTWmzsMFsJp2pdqnKxo1BOt98dKHa+fz2PMrD6PrbXy52FmT9tauEIV3sTtVqoavre1Y0LjGm28TZhuaVPBo6RU5z4X57GlfczbJc6UjKBK6OAXv/Rr/Naf/wl3X3kRXCo9C3RBefTWu3z3L/+OH3/n77m+ukb3I73CpuvAO4Y44XuPi7MXKFOJWOXMtQJOK3Tk+T4Jpk9qa4pgCXFslI0Mx1Ji/EhrhbXqmxUyVtGCysi14Iluyf/bvVrDTRuNQjdrup55/zF4HBP81/gYZPpnYW813yhzERY86ZgAehDKpEpddKZukcq4xTrMc59t/1mhVNUSimz0cC6jX/eR17YWAWJihxRjT1rhwfpamNRW9va7WsloeXLb52LNyYZVzzO/u+bREZHFdQn19y0cb6M3h+/PJWzXz8E8/3ZOa8+swac+I3U/9TlZC+3NvHocBhgnfJciJ7IymXhm9FIU/DG5NzYnW5NNcq0ftRLckIz+qvgKd7x3Fs4fI9551JEKoDwdHJ9a0di4fq4tr+kyDzGVpu/SYTeFOR38rGTMjCzGueqSE49zPmlNoDnhWRwuVS9JjxLCbMWPiVi5LPSJA7okaIQ03mxNUrUqMOTbbsmMZ7a+5jm2BMKI8Sbli1iJRBNaqtARmWvpZ6Spw4fqZ1SV6FwJ4YgxcnZ2VsHHbsgW5/CuQ0KEONilYULJa2hvgJWkddcHodZ8o8WykMuLalp/mILVis+CaTnAWohUrWSIzDkgNZFaCAFicYFFqINU2vPQUpxbbWlumXCGyxqDCAIuQDcZwqsKfYggMYW85ToJmvIeZitJtuJnGOWbruNK2Eteb1Ts8kSRRATtPgXvvFXXyQpDUhRLPwm/S6yjmY6MhKdkUQ2kcg5z3kcWvQ2OVdnWYvEhzSUW75sRmtkjU2RGnStjpR0uPKSrzqHhtZSQIkTIKd6qmipXZQX4UNCr1cKpsuDlnchTKBW3NMXbi1RezRnmmr5TjAA60hlVy6XJOEcWnpL3z/tcchdgzjHJqqJPgnWu9BZjIAYQ/MIqXM+jVE+qGHUp1FApJ6XkIWlP83nhcG21gFG3/F1+R6p/i9bMs513/TP/vipklIGzwKsz7PP+ViasDPNZMDi0DtY0qqypmc/s5U6DFwShKBIZDpI+jyGmcr9WDhmZvb5g50bUqk25/IFzBFW879gReP4zH+d3/oN/xid+5bMEl9bnTWkYH13x7k9+xl//63/Dh2++g4tK2O3mC/68szGyclaF32nM5b67RZ5hu7droXI13Oq/2z7W8SUL8wmulYdkUYWwarNyPwt3CKnweRKoC+JJ/aT9Xk3jYI7J4JHPx0JpqASlej1rwnX5KUWwOBA612h1/fsa32lhvQzrTX9XvNKetTW5dN6TCbA5c43hNeO3VAJ8hTPWxQzXmvfVc2sF+0J/KkWyhkt+v1UC5jWu04sgdiYtSngh0B3F19b4UOhqQ0dv25P2uRhnXl0/d5shxn5fCvOtLHFbP+1YZb7pfy7js42ywI28hvpnC6d6Pq0CVfPQY4pK5pHkcdMdGPubHTEKPnqmYaDznmEc2Ww2JlOJMCWZc5OSwsXNyoX3nckMITKFia7r0SRPFT7kOnQKXD68NIPopufO3bu3mKSW7emTwUWIOPCOqHbD8OLwK0UjygRPVcFZcsnMiJNQkFWFzIxcRo50syEUS2jnct6A0vWpBKHaJWrgQRPzrJedBDZ1njBGlIB4m2MWgDWHc5XNN8t7TO5Yl0I+THikuBXtApNglmcOCViLcHVIlZNZQakt+iJCNpQoWGnZcSROAReCMcxkgWoJbN93hOQ5yOMUpM7zSHJlFsRiFFRNeHb13tjEF+EmBaS6DM0qa8qfVQnew34/w6IhnFmpWOBXt0TF4iVp3OL1YQyi9Dg6FfZjAOc4dR2j7hnjhLC0qsFMROe+ZuZS15JebxaBXRinmCcOsoJgS52nW8U9pnHzd5mIJzWoEqpTCc4QF8wsKzD5GREpN4HWMM5lb0sFKE3rdEsGd2A5yYK6y1ZjiCwJtpNqTZps3y6FHTpX1pLX41OyoOUd6UIxqXHYAebiCAVPC8TTWkyhyFWoksKhihMtd4povQbSeFnwEqk3hqw4CLMi452Nke0/IrM7PgvdWbBXSYoSGV1mQQMS7WIe+0AYqvZ8sQ9Vy3SqZkj58xnD5nfr0uO18FT3XQv/ayFNqrkEbmJ+lWUXsaTc+gwWQaH873hrGbAmHHLl41Zwm+eQF6uF0VeFNYQU2ligYV5qTeex6xiIROfZ3jnnd/7J7/PLf/jb+LunTCJsxeMRhus9b3zvR/zgK9/gre/9iP3lNSow5AseUaTrmPIcytmYaWEIgT6H36aQu9rD2woUazhQ09x2z2ve0gpZ2UhSP9uGvx54VhJcszJR8N3+LJePaoPfLLltu9HFqJN/b8/e07QDBaHCvRr/1hTmGr55/fnzxfqrPuZ/bmk7yBZiyXDOBqRcLETKM2UuauEo5e4cIKf4KRTjjTBXS8qt5bnHFKQ6PK3+7hhsMj2rC7Us4C2YpTqHfmZjUCW85/fafajnulA6qrHXPLyra2Metx2vnXe7v+1n7VgtXrTft+cMqoIvFU2fxYT5uXzGDpUfFn/fppDUnqp6b2Os5OLCF0xOePjhA/5v/+X/hWEaOT8/59VXXy05xvfu3WOKwQzhiVdfXV1xc3PDNAUcc4RN3/eMw2BKa+ehs3DvzjnOtqeQZI8xTOzHgbv37jEOA//y136FJ7WnVjQmmQqz9yh9561UZDqAxVoogvQe1OLnVQQk3bBaAdmLIBrM0pwNJ0nIiWEqVkcRe++k6+YLo1LyZ754BMBtujKXvDFZaFQNTNNAiBNIVwmX4HyHxHQJV1JCphBNSAojfZKHxxDYbLaM6cbiqBCT0N8Sg4wcORa8FtBbRaFFPEtoSiFWMcWhJ/JUWy/qAzFNobgNa4bSxjPWwkUWWOtjUCs/XbrXI1sm6jwNmG/3zvHrAMM4st/tyhxzVa261QeqJYY1M84tVkx8lSilA+98KreYmZrOz9WEL4RADPO4fd8Xb0a7j21rhbS55O/SLX4gCKoeMHl71iw3benJYkXIeEGyoCThSZhlAw5wqJK3WBK2Gm4LGDYMuQ2Fc+JKXHLbX31b+IJoMyumLeOr8b1lVvPq5lYT8PxcG8den6V6/rWAUX+eYZ77q/E1f1bj6CrTXhEU6/a0uLTWjsEp/51bNvhknMzfH4vLr62PtaLRCjcZxmvz+nlbPfe6mQAbqW/3WGP0q7ASQUXK7bd1+GKnphRFgdALNxKJ2w2f+/Uv8nt/9iecv/wCgzfv8lY8ejPy5utv8MPv/j3f/9q3uH7/Adt8D0/y4NVnd3kZqwDLMNNQ8YUaBvXa2v18GhyqBY81nDSvhhwIn5lW18LL0wr7P89+L/fn6fu47QwUXDwS+tW+v8Zvjs1h7VlNMkY7/zVeXdPM+pl2n4GiqD1pze28boNNKwfcttY1gfdQSZNZkG3och110N4jVo+Zn1kLhYVD/vE0raUfa+8XgVyXnrbb3mnbOkyevi1yeXSpyN5WQa8e/9jnNU/Nf2fZzCk8/tnbhGnicYi8/rVv27Mx0vU97nQLWOXYru/ZbDacn51zstny4dvvJNnb8fo77/DwwYOiCE/J8I6me6hUOdlumaYJv+k5Oz3Fdx3/8n/5v3gibJ4+GVwsNosYIEa6rmfrLawlOo90HaAM494s/aIQI9MU6fquJK/OgAs4h13WlUQpu3zLcX1xwUnXcXp6it2YiykKYWLTb+hweO/YTxPjMBFVOT09JeIYx8AwDOzT7bwzUQ9MYSSEwJ07dxjH0RK/R8em2yDe0/cGjpOTHhEL9tCwZz8MdB72+2tudgNusy2Hqa3+BEuEq4l6q/Hnf/OhTrefMpe7y+54ScLzGjKuMbRWyGs1ZVVF5bCyEHAghNUx9FnZ2O12jKPBs+97O+jVoaoFmSKQV8JQVmTqcWthKbeFK5uK6NsLZb5d3zOFkDxjEIMiLJPlsnKw9Ab1xRVdw/M2hlULPoXhiVudf1YJavgt92wpcJRYTeeWaVFUrvOQk+TXQmVmQb1lWC0hrd+/zXMVZd6bhTVMcxGHdSZXr7nFp5Z5z8T00IKXyyi2Vqt2j+p+a69hu4etoLK2N62A165xjWkcU0bWmPFt79Xvr817QWsSHcpwqsds96JWKtZyBp6GobdwmR8+eHT13Xoc1+L4UwqMmXY5LJzBGQc25SN9FhBGD/tOeOHTn+R3//xP+MQv/gKhE4Z0gWOvQnx4yQ+/8R2+9ld/y4fvvw9joA+QAxdDCpXsZJm7VBsO2tr0xcjlZgvkWrjawujTeJ/WYNHykUP4Qj777ft1pavFHpMs2Q0dXhOYju3JwRwrS+9xYf7JbeGZb95Z9lvMLkdbDdP2Z/2MiCRz9eGca/pV/575WOZzmffVNKu+9C2/l8d8Gg/Gbcpo/dwxGtS2dSUNSnz/kdYq0DUO15c657EzN1qTgY4J9LJibGrXmFu9NzHmoL91HF6DxW24fYxezw8dKpDH5nxbP23+Rc2fFu9UuFEblcZh4OrhIz54771qTWmCIsa/8z4xG92sML2Vpt9uNwzDWAzHvrOKe6itcIx2hcDNfgciDDvh5tGjpz7LT61oPHj4gLt37nL/uefY9ht6Z26Vm+sd+2Gi73v2+xuub65xDq6uLtkPe/b7kdOTU+7evWvCXro9Vwl4D5dX1+zHgdOTc3Ad5+d3uXN2xumm5+TkJN3fYSW5LKQkcPH4AlB2u10ad8fjxx+CdAQ1q9I4DFxeXVZej0CIge1mw9XlBZvNhqurK05Pz9huzzg/u8PJSWLW+OTyVNQ7/GbDww8f8ODRBX2/5c5mW9z2a0iyCAupDl4RcpmrcsDsHYhq3gulK7F4QBE6s2P7wCoJBYFyCFJ9SGqhPr/vnF/cUFwTPucsvn2fSsZmIgJWgWcYBpxzxROQL+CLsrxzoFUgpiYxrW61EDsrh1Vsf2qLRHJVVMD3Hadnp1AEGI/EgKiUueZ5uhTi4/x68n+2FNR7WvahIvoHZUdXmEiMsRCjdQI371vLzIrKUP1Ned4O/1r8bT2no4S8EfLrtdU4MhO8Q2vs3NfcZytQ5TNQK5w1XGvBt+6jHaOGSxaW6osua5ivvZP7bgWXFk+zu3mNKbaf1f/qsVuB8tge5L7WFKF6zmvnZAHbal71uO3abptTu/f1sy1cW0VmsU9H1lvD6cBzWMkUt8Gqbs45KwCnglOhc8IUo122FyyEMnaOk5fu8/t/8kd89ku/gW4c6j2d2B0aw6Mr3v/Z23zv777OWz/8CbvLKzqNxClVHUqGk4zg2cvbWnZByRWKMu0osKn2pfYyt3vTCn1reLomeLR0Q5KAn+l37jP3n8dvQ7mysFQLxsc8yPXvazStzKv67EnvtuegbSJSBJ72HKYnFrrB0wiWLZwP6ODK80/DC9pnjwmsa+doAb+VMeGQ5re8ql1zO34OExWRZQXKhk7URuEWD+sxatxdC8U8Jmgfg2uZT5KEWnis0cjcTB5a4km7r7eFN7Vzb3lBHqP0pUujYkt76/5rGfDYmlo4HITCV+/V/DZqZDfuGHU6MCQQwaniZc5R1hjRMDGqEpKhc389lHf7rmfSYNAXk1+is39GYrTINS0MjrWnVjSEjt1u5CeP3sB7z6bf4DuPRkuYnqYrlEDfe3bDjgcXj3n48AEvPvc8u5srNE6cnJyw3++5uLjg5GSDeMtn6XzPbjciDvpu4kJ3XF5fMw7vMU0T4zShKcSEKTLu9lgCbGQcB7yHV155hX6j3Dk7t4TprafvYL8fODs7I4TIsB9M0YmKwxHGyF4GLq4G3vvgEWCCrLm/zVNyM16jwKbrOTs7o+tPiNOINhaujBhrLrL64Hrn0Mrikb0H5h0Zofd0Xcc4DuTYX0Mm24WaEBRPQwx4v7w9OjMmWLduiaTQA+eK8J7XnglYfQ/IOI4lDGyz2SwOQs08qZhibqpKSOWC28N4TJCaBRFZCNyLn5KZZ2SYRsZpSsXdMKUmuRbb29dz4mjLZOrx6zlmuK01+97+1Uyndh3nPTkQYmERn9taNWUxhnUmKCEosZrOkpEdembWwmJaRtISsHaNGV+zl9DmumQoC0HFLyu31GO2xH/xU2fJs2XsrVcr/12HsizgVb17jMnV/bXfHfuZ32nLW7fj1s8em89abPGTxs7viUhRruvPjsE399Pi/rF5r53PVlCr1yCN4HabgDnPOccbL9dxKywFLP7dDBExKuqFGwLxtIOTE371936H3/iD3+X8+XsWD+/Meud3I4/ffo8v/5t/zzs/ep14vWMaRlDwndit8RpLNZJcSn6h9C/WMt9XMI7jUmgWQZNiXHuN1+hODde2xO0xYbSGp312WNVo7Vxn3FVdCgq1cSGfr7pq0YE3pJn/jA+6qIzXPru6p096rqGHx5Sdlsas4W+73trQBrOSsTantfFa5bk+2zNeG11bE1xbYb7tP/eRaflRfnGEzixpVOZJy3LpM34kIbLBzzznmsav8fJagb0NlmtnoG23KSnrPNoBh5dL1v3U0RbHaMxtbY1v1OPUsFjbj6dpNd2u5bk1Oi5iCqP0qSBNSvImPeuYDZr5rNdzTL4n2ztvxtuQ7g3LK41YGGpUu6PMOYekGijqnm5NT61o/O/+t/97PvOZz3B29w6nZ6ecnp/Tbzecnpyx6c4IYaLrhBAGzu+c8Nxzd+k2G7x33Lt715JK+h7VyP3n7rHZ9uyGPYhnmgxBH19c893v/oAxTgzjzkKghoEwWTLLxcVjxus9u6trbq6vQBTn4Jc++wv8j/+L/xGnyQMyTVNSQBz37p7T9xticPT+xKyW3nN1dcW4D3z9a19l6np8tylKCCjb7ZZhHBl9Sr7VwCsvvsBvfOElvHM4IipucfiOCWtrxC0T8tmdbRqiVUOyakYiTVy/LK1atYuy7rdF9nZu9SHNSkLNRHK/Wajc7XZ470u9+LyOOqQqz+MYsVNMEGkVifqwtn0Z4ToUPsr8sTKVURXnPeId4zhBZ9ZHRQ88PPb7MpSnJVytspFeWqxrSUwOGUh5BrI8fhiyglluWBP2YgSkJCCbdyTta1XbuvxL8MihTPV4WSCeYXooENZK6gJeQsn/aZmpCV9LprkmeK9eXFkxwKUCYX22eFArTIVIVvdo1OOtMch2v+t+jgl99Vlq+11T3o6Nv9Za5aB+P3+/xmDa79bamiDW7vmxdT1pHbcx1Za+tGtdhwNFsGnP4wEdze+0c3LC5EC3Pa997pf47X/+z3n1Ex9n1EDwziqURXjw7nu8+8Mf88Nvfoc3f/hjOqtETHAWk+wUrJSZR5NHwydFKIcXHXgD1Iqd5DLeqjPNqfH6GGxqmNatFTBruBzCMCndahRlzcue+4Ql39BoXuE6pLWec91q5afur+Zl9rvQLmltjS0u5d/X2m3KU0svjsGrPgs17Vhb69OEAubW0qVjykD9TH3+68/bVsM8K4htqG+9tnY9bb8hBkSWVvWixGgsxLeFXd7jYwpcPcfa0Fl4YPXMMdqz6FPK/47Cpl1v4alH5lhg8ISSzre1JX+n5C4+CYdro8zPq3DMdPYQFsaHhZPOcyWg5MJIc4uSvJY6G2qyH9MnGUPTgmba4PDpcyfKFFMlT1WYYskVfdr29DeDj8qPf/hTXvnoR3jpI68S3cCp6wgy0IeUPKweL3ZZ0cdfeZVpfw/v5zJ7d5+7y/Z0C2qxxbt336f3HX0nnJycs9+PvPHWm4Aw7gd2ux3X19fcXN9wc3PDbrcDr5ycn/DcR17h3r173Lt7zsdefZnNySniPTe7PTc3O7abDc47XnjpJTabLQ8fXxL3A9f7azyBbtsxoOydA9+xSzkbCnRdz6AQnGMKASd2O+y4n+i7DZIE2Dge5mfUpQTz54sD2ggWWRCc8yJyaIgjToBzpVqFsLSgFGakZqHI5W/rQ5/Hz2PNhM3+F1PsnWiKsUwXy12mygTb7ZaTk5Ol9TYaPDKSQ5qf8+QyiySB16cL0RTFd10pK6pJcEa1WKsk/R4TLLquSyWFsQuwYhov0VjRSBgnJjUFbSOejfNMPhFQ5+ichTdoYsLiUqWa3NeCSR0SjHyw7TAurU7l2bQ5c9WqRBBSib5cQSNXJ8kCQek/70kwN6h3HhVfRR5r8dQgFEuuwUDKWnwaw1TlpJhKriTlmoRyMcUv70GDx4WYpedRq/gkzlfKgLlkNWkcIuAdaLS/s5KYK7BQEsrDvB8Jbhm3NJW4dRXsixqVAJKZWSsUtUJ1K0isMeD679bqHMNc4QiRhLMJTprOctpTSYwxe6jymb+NQbZzqAXLlqEcMp1DBakdT+qfagKza/D7mODaCkK51Yyy/U4ii7rkSqWAIKXaW129y6xp6+53l2hJgBIqJSlcygeHOGEUGDee89de5o///J/x8c/9IrLpGYg4BR8CNx8+4qff/yHf++a3ePDGW0y7PS4LhNYtUa30rVUscxVDXho5ui6HxNpixjGU6lKd94QYiSEV56hCauqQK4NfTXsSnpJpjS94JOTKgBkHZg7fKrgt62/Pc2tMqvlUDgur2zHloOUvh89KoaVtn+17xz5rleVsSGnXnHGo/qw2ZNQ8r1VA7Odcyhl1ZW/qsdq+898Hwj1m+MpCnIjhVilHWD3bCp5ZRmrPdat8r82n3adjNEfEwmey5xEOQ+Tyc+1Ya7Sm5ZVrc4blvtVhfGsKRIZjORMNza77aPfHBGwpckWWl+Y+lzBa83q047UK1HKe63xziV9LmK3BZ+37deXX1lZ/r6pJeTzBHBlGvxavLdad+mE+O7Y/OT9JURXUCSHLNdHOhBcrjRtjMIO8rBcMWWtPf49Gt2WcJn72+hsMU+DVj3/Mkon3I/1Jz/b0FB8jLkSYRkvIG+2ehgic3bnLyekZp2d3cM6x3Z4gbsP15QVhGrm8eMQ07nn3vXe4vLhhd7Xj+voGEeH09ITn7t3n059+ge29LbJxKI6u7/GquL5nDIHnn3+BYT9wefUW4jtOz8544823+chHP4LreuKw59WPvoJzwjvvvs/p3Tv47QlDVPCOgG2aE7OG4xweE4CnYV9qEXvJ++4QyfdqZDwwqSyX0a2tX3X8a23NLUqAmhU7xMgUMnFVQoyEqHR+eTjnMK3Dg1/HCufxWqLr3KyUFAUmMcoQAtvtdpEsnt/r/Zw3YzknUpA36vJgLSxlkksHG7IfxmtLEYqsX+Z645qF9VT+NQtOzpkALNi9I1MgilVf8Sm8IrHwFGaWppqE8DLXNAZJGFjEWku6Z6Fa14L4JqFz7sjmXW7HzjX+NQ8yK42acCcTEKu0lvCoEii09J2ZlpLjJAvRExB8ecSEIS3KbRbYa0J3EKrWNE1E2/6R3q8ekGpaxesSLSZScrEDDoTJJdHNlmEtSky+6X5BdGV+9yA0r7kZtx6jHa+2IrZrPVBuKhhk4bNmODFU1cdSGWxZYYTHYFtbAOt51ox7jYmXNTZrawW2XE57ZsTz2aGiGTUdaBWJts/bhIzcv02I+afM3xkarQsZ9RqDS6E9Kng8GiMbl/IknGPqPf7+HX7zj36XL/zel3CnW9zGvncxMjy+5O0fvc4Pvvltfvq9H6LDSBciLvUfmXMpvHN4N4eM1jltmb5nxmwWZaORwzCU8soZ3uKWl7CWW8MrWAuz8CNllAovSHQrK7b594av13uTnRo13c3nIZ+Pel7pgcW5WsPFY+O1+wUpzBcz8rR4Uj9b09Da09sKfLWw2vaRv88elFrBaMds8Xym60bPnHSZMSQlYV14Pybsl78zMUyGHiQbfo4L47dFQxxr9XOugnXdZw2jMm9Zwin/nj1ixxSHNeXnWGtz1gqe34JXyzYbBvPaao/ZmlK6Nqf83gKXVvavfr5ee42/a0p4Zumt4vCkc7PgM40cdBts1hQtEUvm1pjLW5Muza37WfKSTIOdE6LKLFuIGSTzpbsqYsUwynt5TId0KYrmKf0aP1fVqa53xCny8MGHTHHihZdf4s69uwQ5J6ij7zcm+EchqOPk/A5d73n33Xe5d+8e5+d32G63XF9fI+J54YWXeOH+fa4uH3N1fcPlzchbb75NwHH//vN89FOf5P795xaXxgVGcMoUFO86Tjc9u5tdIaR37tzhtddeA+Ds7IxxHHnn7XeIruP0dJOSg4XNZpOQJyU6J2KXKynlZD/TFg3AOTm66zoTmBuq3yJojehFcE3r6Pv+IJFrJpxZcUlMyzt0nC8tLISBZJmStZvPtXg41uaY1yEii+pcMUaGYUBESpJ3+16OiR9SzeVSdWqlicxVg0KMhwy3WncW2HIlqHotNVMqnyVBwS4ztHmfOYfZQNcPtuHyMlGzJtpx5TNIgm91AddhbP2SCIskN3fVX6tcZsbUwgPMakAVOtcy+JYJ2O+A5nyeNYawZCSLUCc9Lni3nx1jtjXOl71x7gBeyJIM1oQ6hwu2iXD17/Xc1yymLYyWwthSCTjAjScQ+7a1/azhztMw6Lym/PuxZ5+W2cMMr1poLriox1nEsXm0glC7H2vPrM29Fm5qgbjF8SExwk2APgqd2zLEgGy3jCeeT/zar/ClP/unnL18H+m8XdA3KXK959033+LbX/sGb/7oJ1w/eEwXFJ1Cqmx4SJ9rmlivLc+zDjFVtUIkIubFWNLuZXJsXkt7b9BtgnMrjC/gwuxZPQbf+vd6znXFvTUBvp3P07YDerBCS27rv8XpGp6LvlfGa99fw9m1MebPaiOXoFWO2Np818I9yzOCJdyu7OExulKfnTV6tqaAPA2NqgXzY+1wH8woRCNkr53nGt9vo3lJeDo437c324OsgB7w4pV12Xqz0Wo5h7JHi7U+eV9aHlvPIwvemX/X/d12fuu+W3it8du6aVwaBZ1LebXnZ3R9Xz5rjXDH9k6qPON6HvkZ13mcd0U+bGF6wNdvaU+taNx//j5XV9dMMXBzc81+2Bk6hEi3C2zPzthsJrwoo4PLmx0fe+VFwjTy8kuvcPH4is98+hznPX0X2GxO2DHQ+y1np6fc3Q/cDMrnP/8FtnfvIm5WLmYXt9D5DTEG+s4UGxD+36z9V69tSZImiH3mvvbeR1x9Q6bOSFlZlZVaVFZVqhKNZoM94PQLwQbBR3L4MuAQ4BP5Y4bs6QcCJAE2wGliZsBBT3dXixJZlZmVKrS8EVeee8QWa7kbH9zNl7ktX/ucqGoP3Djn7L2WC3Nzs8/Mzc232y04AkOfDo1rcHP79m1473G22QJINyRerC9w685dLJcrJLmYmEFStS6Xy6JcZIto3PLOk+AdONSgTU+ELlqASDua2aQt7zyQb3mOMQLKqy59lHHJYvPeI+a0vRZM2IPpWkiGEKobygXcb7fblPo3M65mJivQW4tLvrdjFcNAFLmkF24tAhmbTR1swRwg26NpJ2qxWABYjzssPL5TnWGJXAEO3bZuowKzDXBdhAihuh24FkgjD0zpg3GuUT+nfRItRWrnOin43P8ZPtTty3sSMhF45CmZ8zkwo9u0ZwxK3xRttXFox2JpkpRLLcTkpycHUoft9ZxOPLVoA3bdR8uzVkFoBWnB5BzAlosRdT1zykMrIivIdb/0uQALODQdbXvakVHVTTTecm7G1pxL1ZdWX1uK045zbnytZ9IHgGeCD4QupsQCW8dYH3R45lMfxff/6Ad44TOfQDhcoPeAj8Bix3j0xjt48Na7+Olf/gQXp2foL9ZYhHTWgiPAXZINOpxV36osY+66riS/sOtd5kK8wJJMQ2jekit6/DHGFF4IatJOrz/LX7pOW5jb8yZt6PVReA9TAGbnpSXb5+bP+5QWM6hEJpZnrd6w/Ck8X/WhGqfm/2Z39vZXv5/WMsolven8ggQ/jc+3dJ+mVZqviKjqbzn/Wn2Y22HVpcUj+8aov6/eZTa7dfqdHJVsvtNYQtfX0kGWT/fJl1Ypn+dwM60DLA/ZOSAC5gxFkeegtvzR9eodNo19rIEjulaKjVixxdLN8uFltLHfSz/XF2vw9euVPtlH37LDXeaj1tPp/UbWqwb+2MezulzZ0Pi9730XZ2dn+LM/+zMM5z367Rb33nkbTx49wvMf+yTW5xdYrFYAIg58YpLj42NwJsZyuUTXLTEMA3a7Ht4vsVisQHGAdx0OVh7Xr13H0dExAhz8okvnBdSkDX0PUL4QBg4cgYAIH4GuW6LrugrIPvvsswCAzXaLAyZ0ncOzd5/Do0cPAXK4e/duAomZAWWXQUB4IiwQhoCld/Be4lg9iNJWu534yhhRE1QmpqFY5HuxyCUGTs5NhJhiw9PZjfEgV9/3AFL/vKOy5S9KsMS9G2aw2aJijGXczIzFclm2BPU4gDFrg/wufdF00OMqz7h0rkAbEBZECQ2BaezoxMtKacswpmizcnGc9qZLfRaYSWiR7bcoXg2Si5ImQkBdjxWodmt3DmSW9jAudv0uUT6DsUco6r6VtsSbMwfqCNWWqsy77lOhQ2MMliZaIOv3iMa+C8/quYYBGhaI6jmrQJJ6xh5wt/Ng0yzPrTk7l8KLLcA4AcNmLoDRaTGnTOw7cyBmzjibtMe150+PraVw5Dtr5F8GImy7tu/CSxrQ2jnV87APwFJCDFhGAgeHQIR4tATduYFv//D38blvfAWrRVfud1kMwO7kDK++/AZ+/u/+HB+8+U462B3SOQ3JHJWAC0BuCv41LeU7mxIcqMGjcw4he/ssOLbFtkduDEVoKW0bVlraYACon7e8N0tT05cWn+rSkm9W7ln6zX0u/8Q7alOZ23613tfJRKbf7wdo+8Yn+iTtaDBA7edsf+33UQ7ToF6XUlr00XS1Wez0O5ftTthi16blrdYdVuR8Dr+bn0ddh8U2V+1X63dLV0072+4+PWtlTlmTSidJ/bof1hiarC0jvyeYAjVGaa3DluxsyVvt4NQ8QuSqOdP1CxYU3Wfrbc1BmsNa740OvIgcNVWFr+n5svy9r1zZ0PjWt7+FzXqNmzdv4F/8i38BT4QQBoTtFo8/eB83b9/BsNtit9vgadyBEHCwSsaEDH636/MCZAxDulPDgxGJAXJYrQ5xcHiE4FwyIFw+KA2dQjVPBnkwEtjuOoeuW+D4+Bq6zuPo6KgwRiJIgO88Pv7xj8Ej4rXXXsX5xQa0OEjhP8uDcplctbDzIdrFwsETm+w7ESBfMZxmXu9rgVMJakwXe/Kax2TIY2QU7zy2w5jpSUqVUjYDTK3sNUNp5tC3lRONjNX3PbbbLVymOWxsYy4xxnIQWVu82jCQdioBzwDT2G/NvJpG8r54Ca0ybCl8AmG1WjbA0tjnInQ5GSc6/KBeuFNhTkSwy7UOkUiDa4I7xmjMzpQ2mJNY4XnFNhG03Ox+eiYyIut4yzZYsd8DtbGg37FCRmdESWcy6kupCs1kh9KAWauEtJEhvwfl6bWeIw1i5HOdHKG1S6NBsOY3oumOUpOutj7UvDL3rubl1ny2PpO/54yL1nOt9SXPzSkhOw/aCTCniFuGxFVoVstpA8yIEFYe4dohPvWN38XXfvD7OLh1Ay5frNqFCDrf4IPX3sK9V9/AL/7qb9BfrIHdkC/LS97NwDEdgs/r0Lv6dmMtm/UOrPU0a+dNUcp7wJbmK0sTDY4/DFCbK4lf//71SNEGN9A2eDX/TftSe0lFfujdozmg0jRm3Nyh7r/7GCugWz5L8e76PK2dH91nCbOWSloAda7tFk3t2rBOlxa9WnPQqs++Y4Gz7OpYuTK3prWjR8trXXTWRAvuJ4aOfneP3NQyZ67o9ij3Yc6AsqVl5Ov2dR/1dzVQnxoS+/pr+z6ZP0bKNql5Vs3L0eEhPsi82HIItPgxScda/xa+kGZV3/XOrXx+Vdl1ZUPj7PwUF2fneOGF5/GZlz6Nl3/zMg5WRxj6HmFzgfvvrbELASmsieEowju5ATpmAohXI8D7Ab5bwDsPR+ns6Gp1gIPVAc53Wyy6DgBh2I33NzgQOteBKR+aDiF7yR2GfsBms8Ht27cAjIItncnwuH3jRiIKAev1GiFEnDx9iKHv0QdgN/RYLpdIMeKZKSPgfPYUIeUSToLSpX88FSyALMBx90EEqt2S0wtGDA1yDt45hCEAPG7LM4Z82JSKwGZOlqzDuIi0p1f6NQXgo4Eizw3DgNVqVb4TAQFMs2ZpAWhBzJwntgUs5dlKWKsy129ZDJ7SNj1zoutut0OIMcUVxtHQqIR3TudYz1VbgOt5LYe95ZBf9QzAPArvagGqzzR9Ur/qdmpPTfqnhYDdwtRzLO8HAza0wCrZdFS5LJaXaDxj01IqViALDSJzORStgeQwDPD5osd6q1avo7any7Zrx24VnTVEWkJRxtdqR2do2qewbdFGrB6fFfz2vgRbbwuISLGGfGte9BqzbcwBHXl2Tn7od21o5qxCBioD2NYP6PWVno0g9AuP57/wGXz9T36IW5/8CMh3WFAHP0T0YYeLJ0/x+l/+DL/6938FbHZYREYc0sWhSeZk2hDKPRqEUX4JfTRgsl5UO2bArGEFLKwMs7K+lmP1+m+twRbfo7G+576zpTVPc0XLd22ItWhi150OKLHOIrsGLJ9YoK1/1zS2fdo3Xt2e/q7i/WL05dj7mX5Y2ulzjjFEMNX8bR0Crf5dFbBZXWvH1qKlrTuNbbrDAci81fNjZcmcPNB9qLBQZnQrR5t8o+nspmvBjsfqgtTUuDa13h2TtUx1x5RG9V1kczpAcE0Z64ys1d/PzZ1tWz4veArCm1O+9N6DHE2cJ+Wn4ue6/RFf6PVU5JM6Z6nH0JKTl5UrGxr//J//N3j/vfexXl8gDAN22x2u37ie05du0fcRIUZcu34Nzz53B91iAeocUhhQQIp8SKnkjo4O0XUeoHQTtiOfUklSBGiAX3jAd9hut0mw+JRxxPuUUUeATOcchu0OwAKHh0e4du06lstlxSgHBwd45u4dMAH9bg1aLnHnmWdxcnKGDx6eIOx2iOB8i/mugCBH6aCfYwAxCRDPHgSC8z4JpsiAyi6UZycdEHT1YdWi2EIomWKEiSVsyYkyJErj7Dw4BJBb5SwBmbkjpzAyTulFwemgNTAKdgmjskV7mIjSZXf6cr4iLBhjP5EOuSUPXi30hfGstT4BbY4Qwxi6BJKD18nroQWyvSxQ00/qDiHAxZT1IBDQbQNWvsPg0jx05EuWKOd8qT9lYqo9s9rjGGIo+toaDY5QUsgh7yLlSzJBXqY/JRiQyCftFZ8oIAIYozCxW5RJ7IuglhixtBNlhay04cs0pMY5jbY6t2F/FsMA6l2jPMpIpD0jYFreRjTmruu6Mrcy76IE9K212jiROUrhU4kwkZM3WYzsZBSU3sORg5yK53ziReoPmb+RFRMV73cx7yZKs1Kear5aXm8PSme4tEIT+afkvBbY1gvWml9b5tacVhxSNODjPNclhTAAa2a7VFGam/yc5FWnVGH6qfsnPCS0y32JYESK8CAgZ4OLyGmmwVjAwXOiew9g3QHXPvIc/uCPf4xPfvELCIt0q7cnB+oD+vM1XvvJ3+De62/g/TffRthsEfoBIYayw6DnqMuKWNIVa/3Aip91nxko2aRI7T7L56Rop2neAsctAyLJC33BZaJF5r6UhhQoN7+L64GLAwL5Yq70RhYTSOqgBhW2bxbsy0Vec/xmweHc93bccwDagrsW2JsYu5ieZRufT/Ro1avXMSveSPIph2NyvRbJze8N6d1VXbekxhfnHUceZzOBA8CMSctKDdz0M63Q1JbBUc/xuKME4mqnixwQuI58kHYcEUIDyLb6NccLFrimyJD2+QPLG9UN6xiNPyr1JvwYaepASX1q71gX/kUlfptOKD221vqp6hcSN/Sq5UFpw/Kird8aN1WkSHq46rfULWH9E8chcwkdjYK9kJwv6fK9Qo3EGznRDxHBC9VUJISjlGp/bB9XKlc2NIY+XYJXsiURcHp6iuPjY3jnETl5xA8PDrHoFjg/v8CTk6fwSDH96YxGl0HigBB3AAI8eXRuiRAJZ2dn2O522EYG0wAQYbvbjSAROWsmCKBkHCAOCIGwyPVvNhsAKBmXvPdYrlbohy1CCNhsNrh16w6uXb+Dn/3tr7FcLHF+sUM5A5EFr8s5g/vdAHBSYAtaQRaxqJjCRDFtuY6Ke8zaJIIhxpz+M8aSqUnnM+cQMnAWpZa8wl23QreIAAaEPojpnhV9HWsvfWJOlw7Kjd7aczdavlxSL1bZqbj8D0ASmkNIh7d1TLIGhLpdMZ4q0ASaLEhJL1vgoFng2uuojYHSfmT0iIAnbM4usPA5bnsIcPm+B7HaZZeKmRExjfMtykd5Uqziy+RIACDW8z+Yy+PGOlIGKStwYoxlfm1oRfmp+iBAI51Pkr9M3yCGCcZdG6Lqaf3sHBigJNkLP0O9LyBSlIDcANyqQ9Zga2dhAiyASrlbepWfPNJv7GwyLAJCtvESQGYx3FR2uGLgFDBMRQNpemtF1goL3LcNTgntjXKLUvYkMZS08TRnSGj6aAXV4hXLdy3vc6OBEfjYPuTvZPfSab40wNyOu7kGsuGNyCBO/JivxQAoncFgR+g5ort9Dd/6/u/hC9/5OpZHx2Cku3A4RAzrNe699Q7++j/8OU7feBvY7bDL+kE7dLQ30rkUOotYG7CaNszprJSk3pbnWjHz4OTUkbNqznsMM0B8HwDXf2v6AUj36WD6OZCdW6Xf5YFZPtL90CDHglT5uQ9Eaj60INgWkduttq4CVG2bUO/pMe1rX9NXn7cp8xBTiHN9kWycINIWv7Ta8yLnOI9DvkMt23RdrTascWSf2Wf4ybzEnKjGkSs7rIWXqQ5zLTosO1RjjDXoV++2+MaWis55/HNj0u/osMVmiBiQXUbT98c13959u6y0eNIC+in9MdnB0t/b8dl29BppvWdlhegxy9uRI4ahL7rB0i6dTHCQiCiGyF5pc4w4GfvQ3rUoWOKKBoaUKxsab7/1FmJMWZxu37kD7z3u3bsHIkIfAkCEvg949OgxvAcePXiEG1/7WomHFQKVfy5juggQOsBRupdjuYQfAmIO8+i6rmRHYlYXHhFhsUC6WCQyHj55jFs3r+H2rRsAxtApAPAsl4URnF/AdQEXF1vcu/c+3n77bfQD4JZLHF4/hss7CzGm2w9Z3SLtHKVzG86lLXiqx1TiodWEaabgbCDoeDfNbJIaDzECpG5OlvrJJWONU6hTHIYCYrUClUxCFrhbC5oop0fzvlaqhom0EGwJIPuMbm9O4YiRVQQj1yFXtu92ccnvzjv0MeDgYJV2wGIs4VTiARnFfN4ZKMZ+aqPMhfFkyaKdi3OfK3phpl+nihZAdd5A01CPV/ezvLtfx6qSPX0jNpn0syXkLKhtAcryngmT0G2LJ0TXaX/Xn82BBwvIW3TRdcnvc2DoKnPYUqhW6es+62dE9lg+Tlh7WoetuwVEWyDe/q2fnTPuWmVufvcpzFb7rb7J8+lQNqULJpPgBJFDdMDWMehoic9+7cv4+g//AMd3byI6AiKhYyBut7g4OcUv/vKv8cpP/xZnDx9jyYxF50vSDqG5PbsjAFMnsdD01EaK5jObmadlJFQ3bDd4YY4m++hbnuN6LuaKrefDznPM4BKYhni1+tXiw8uKDR1tgbKW/LF91zxVn5OYAkI9X/rZETzVur0eaHsO5wymObpdlU5zHmw9dqlPj0nPhY4GSPys7mNC7TDhxudFZpDaPTZttwB8SyZpY6EKidxTrs5bKZJgX4hjC/O02rN/zzmPWn0TnGTDmW39l/G3xhaWd1p16DbEIOTIODw8mtRPJEllzM6N1rlmrHqH/T9lufoZjbMzHBwc4Ctf/Squ37iOi/UaZ5sLLLoFzp6eYbjYIA7Jy3729BwP7z9EGALcYrrIE2MnQ4O8A+DhugVefu11PD2/QCBCGCKWy2V1GC295xBDwK7fgbzDwns4T3jn3vv4xte+AuI67MZ7j81mg912l7xPQ4B3Hc7OHuGXv/wVHj8+wdOzc9x+5hlcz0YKczqz4bIw6jzBZcUSc6hRGkrbq6gXvWZCWXhawcnn3vscopRCCpIxlqxQ53M6RSRvfORYQqec8whhvPtD75LoxWMFcDrTkJS0vhW2MCnqRSXjaS0MHZbRijuX5228rhgtjDboEn7R507KAsgLRkLZnEqHPPqQRs8DkMK0Sr+UMKz6H0MlBOZKJei4zuIzFRjt1MeCJ1rAW363gjPG8ZIcq1CZefQ4KCrIL1aEzyl8LeBaArBVh1W0ROP8aj6/DGzNef60Mtf9tABffpd51fOk+aolSO08aH7TCsWCTt1X2V20a4Co3gXVc9sOA+DJ/BbloYBBa250fa0+7pt3TU+r2Gyfrgo6CQCYEt9SuumanUN0hLDwePbTH8N3/+Ef4fanPorBEzYAOhCWIPRnF3jj1y/jJ3/2H3H+4BH4fIuDyGDH2Ib6cKLupzbe5V8IITuJxudsLLamh+V9K+/s55ZOdv1anmnNoXw+ZzAkUcZV31v91XOzD7TLeOTzfUaNfsburLWMA90PS1srKy8DhHYeLouHl+8sH4/tAckZZZKWpDcn7++jRWvtTOb+it6hFr9ZMK3Hp/uhP5dEL/vklOY/IkLnHYbYTjIhz052+Br9quQjj97yD1t03wsd4/xas+vhMppZ+Wzn24L6iUymxClWHug6W3q11e+WY7iqyzgr5VnBe+v1Gs65yoE91pN26mIO50sx2zlk0qRj17Sbm2fBFVeR/VKubGg4Ity8eRMf++hHce3WTfzmlZfhlwssDg5wa7ECuac4eXQCB8JmvcG/+Vf/Bj/64Q9w++7tknaWmccYbQDglE+cvMPZ2QV++rc/x4AUb7boXPFWCTGTFz+AyIGcAxOhjwxyhF+98gruP7iPF565i91uVw42x5gyKqXbtsdMOD/5yV9jGEKJeV2ulsnD3PdwPsVZx5i2sMMQsBIgmb0BjtKBYyG2hCcVIJ7BhmYgCZ2SEuP0oFgK+SFESErbFCJE1UTnmNBcX7dYFEGmjYHdbjcBRXYhWaYsTGyUjxgxdjtRexCJxnsZxNreZyGXfjgNj6egVegn3poEKAmQg18MeJ+zZbHcsp6/QAK9tSct/bQpPi040HMk32salc+yIpHPa/Az7pLId614fE0jDVTnFrMWepqW+nvZuNZKTrerPbJzdWnDstQr31P6nxXYQnnnqKrH9ru1QyQ00/RqFUs7S6vLQLDwrv1M98PSWH8+p8gsYK14phEe2OIDGbf8beOpa1q1x7Zv3LpYR8Skz2buNd00H7c8jLI2IkeQ84hMIO8xgDB4wtGdW/jOH34Pn//mV8ByH4Zz8AGIFxvcv3cfv/npz/DqL36F/uk5aBeAIV1kGdVdOLqvdixWhrTmjZnLoe4WL9uxtuq/jO66D63+VGPgtoeWiCr90Zq3uR1mPYd2LRYaNPpi6acNo8vAo5UzVnfo9lv8remmf2+trdb3QHuHID0XwVzrszLHqdKqz9oZpWWDXgtE9d1V+jlELuu/NT691qyXfB8A1vVpw4IwXReCXxBrwFzGZsap9Z6VW3rcLWxQ+oPcZJyGK+siPGq/s2u2zCeN3+uxt2grz+1bn5pGrR30Vr/IUeET+4yVS1KflZPyng5ls/UVXRCm2CuEgEXnsd3mC0RVNAuAfN4rOXe8dwgxIuTQTAaDUGMbfba3tT7LWC6RdbZc2dBI6Wl3+J/+9f+Enhmn63McHB/CLzr4rsMz3QEcLXD6+AkQAz54/wP8+z/7d/jH/4t/XG6EFmaMMaWuJSZQPgvx81/8Ag8eP8GQhenQ77DbbtF16VC4TMDBYoUYGT0HLA+X6IcecbEEx4i/+slP8Kc/+mEl3ApoQ/KoxQis1xf41a9+jbPTc3DMd1UMAf1uB8pnFUTgO9+h65ZwWUi4fHtmCBHMU5AmC8beMF0mXzGY3XKNzGAX4fwinddQt5KTc0BO09iHAU4OnzHnNLxTxhZGsQI+xpgNPodhSCmC5RC9Zir5XS/mfQJDj8nuXmjQZGPcJe64pXSsgC/gkMY2+6EHkGJkUSlv+ZliN8dxzCwSGjMsWUEgv7e+S3Mz7xVwKtxMgwYRVFaIa3rOdLQJAIUsySjFqNgohVCphByTce0rWolU/SRUBqkt9hPhPQuk95WWorAAbe69liHfAoaXKSH7nn639V3Ly67fa4HD1ty3ANVVaKbft+tQA6cWeG4B1bm6rTKee945jyHmbFDeAYdL/PZ3vomv/P7v4fDmNYRsYBxEgLYB2yenePPXr+A3P/sZ3n/zTaAPcPleoeiAwTV2woyinwMKludHXm4fvLXjvQpYaYGJfe82gbTY8mrOmZMDSw7XWpCr/00dWPvPU8wBWalfA2vtgdV1jINA0Uk65NmOtdWP/xTlsvVeADlG95ZeLyHGKh4eGOlnw+Wu0o/UVu1A0WUfb7RAvh2j7n/5jlOIkTZi0nNq0JYmBMCsAXnGjtdGYwCj426yk2JBamPMmp/138zjBYNFTu5hkzmZRERjYoXG3F1mBFk6lmcbY7M002O24az6WUsDLTeIWidT5Dlgt6uPF4xGC6XjC0QpoZH3qc8xICj+0AZuq209HqGldoBdVq5saCwXSxweHmK93YI6j9t37uTYTkIMKcvK7du3gSHg9OQxQmD8y3/5/8Uf/PAPcfv2bTjny+HoGCOGfkDYDQA57ALjX/+bf5sOgjNjEWLyXAHq4jztlcnE7dMBmCFEcAj4+d/+Al//8pdx+/YtiLHBhSAp5MpRh//wH/8cJydPESPnW8VjBqwDEAOWyxUWzkPOaqy3ayw7j+ODZe6Ly4dua8/GkE/se++BHEIhE1ZyEDOX7TZ5R0K9fA4NA9LWZwgRMRLCbovt0GPRjYwdQ8h1pUxWeiFYwSQCVD6XG9Cl37JbpLOptJRXa7HZoheKFka6fa2QOQvEUd/XoEovRr0QxsXH6DoPBmMIAY4TIMmyNtcni52yPTCndFnshQp46cVn6Rlj1OfHZ0GnXZBEKexLFqwFAvtBzfQyqPJNTFmCJJNS4DgqUzU+3Q8rJG0/mHly7ifV1wbg5TPRajTSQvhNnm3Hgo4GoqaF5uerGAYyT63vJn29pC47xnTmfp5mVwmvkbrmwn+0bJHdPL0OWuBD12HDveQZC7btrtU+OlgZU+hRHpK1nGgEQkq5vOgQHOETX/wsvv3HP8LdT3wEu4XDxjE8OXTbiPjkDA/feBc//Y9/iXtvv42w24D6Hj6ndQzEYE8IDqAhZ9y7QmkZnJpGdmx2DlrA2oJyzW963i6j5+zvPJUZzMlpYflK8xtRfYfRnPFQ2iGUQ/CtsVlwPt7BNNUNpdDUGN0XzteiwWXPXuX9fe/moVfPlnM+DTlT31s13785A6B6Tiu8mTJnYMh3++Rf+k7OJ6L85CSwK9Bq9XxxXoqMm+mDHZ8GqhXfGHrtm9OWMaPfKw6viQerZXvU6ylyrTNaRkMF6hvruzW38kxr56wld6282Fe3/CuJdTBvY0lEjWBQ5xwW3SLRISJfEKp0So7+YIwRQ7rNJMIv17f/yQ2Nm8+9iNXBAVarVRJ24k3hdOHewAHUOdx67hkEYpyePMF7D57g//n/+n/jn/yTfwJmxo0bN7Ln3KEfBmx3OwTq8P/713+Ge49PUtqyMGC97dH5RQY3AczJ0CZKMYQMoOtSStxh1yO6lNnl/pNz/A//6t/iH/+jf4jdbg3nCCECkQjEARx6PDo7xV/9zU+xC4zV4QEu1hfgOCDsNoi7DdB1iM5hQACHCIZH5zw6eIR+yEK5w3jYuGHNQpR3zGnHQhZi2SI3i6mkt1106fJCDilVY+Ys5z1o6EFxZLqI5E0OMSYDCpS2RJF4S7ZHY0wX7MUhlJ0bZkYYhnTzIwOd88loWyyScRUivDq30QIUeuEIUB4PotVxixqg6kObYz3IXvd6y1bqaQGb9C+C4wC38FguOzgHOBLP2ZimrQbIDFCAHEgdDzEQ0qV7KaOaHbMFErXiVBOvChFVdVnPtQBV6aMd31zRoMjOCbr6sD6HmM/6UM5W1fZU2NICXROFh1rmayGdUtcmgw+MnCY6A1uiaidE09JVxl5KwMAs4IsrPmnNUUUL1e85QT4LlhrvlvXkHDgohSf9xchOcwpVUl2ShLQxikKX8Du9g7RPwelx2tICzvY7eb+1tuZAdXax5PSIrpJnlDfiPfKa9Q7RE/qVw+FHXsD3fvh9fOqLn0O36NIuBjO6yBjOz/DorXt486e/xJu/ehlPn5xATiIxGAM4pQd26XwFh8Rf9p4i3d9ZQ06DCcDc3zE/dkvrOeWrd+5t4gwbimINydJ3pLEWMCoAcIaPdf+0DNVyZZZnLjGY7dopazUJ27R+8/m3shxUnXPGjvTR9k+Hblg6SWnt5GjQptuy4HGkOcHRuHs9CaPMISfiDCwp7IGyW9MCxro9bZw6KAIpIxxAyY6nxya/N2XIzHireSVGSnwi8pRBOWc9ufGQdtUGc+mnZOImOHBIdWl+bRkEUvRzhNGI08/u42M9H3ruR/piJF7uNyBps1mla1b0yf8XsJ50M43rTc1ZS1/YtSt1suq77uuc/NR8MSdn5NnJ7n9Muly3J78vFwscrA7Q0y7tMjkCcZIb5Gvnn8sym0AYYuKRdE1FBoQxJdnRParWFSdn7lUdPcCHMDQOr1+Hdx7s0tkIJ7FdYMTYIyIPwBFu3b6NECPWF2f4i7/4K/zn//k/yYCb010V+fI+UMqx/tY77wDkUxhUSKlJpTjn8/XqCSz1ctglEHa7XZqQkCfOE95+911sdzskH3dEiACTR8cBjjxOnp5hs9mBGVgtV1gtlzi/6DPDpcxOfT8ArgOYMPC467KKPuXuJwLIIfJUcBaQQCjGRfpetmvTpGpLVc5SLLr6QLFeT0M/AK72sAF54RpQInVbD4Oue7vZIl1pn5WxWQBS/+SGb9RGhv4nC0Lf/q3p01qI6e/6Mw0cNODSbQMFoyV6IGJ5sMLu6UVJ56Yv75F3i1KlTAsBfQ2QOae8JkLStFGXemxVO0rZyHdCbyu8awNl6smeA5xFYEcuOyj6vZYim2t30g8jLFvnWSRMT+9qsYBVxSN1eN9Yf3UXDE3nyhqCmhebNG/8PffMHIi5rOwzEgvgESMz/wtZZthduzmAuM84bPV3TrHb9Wjn1L5fFLP8y4tQfx8dEDqHwRNwvMJX/+C7+NL3vouD4yPAZeAfImgY8PC9e3jn5Vfxy7/4awwn54ibbRoHjW2NsYCpX50FhbrthtGhS53Gmye0tqDUAtHaQbLfKLMyqwWaowF8zEYoZCNjbr7tpYm2H1fhWT12+3wr9j49F8HR0mCUqZYWrb7N7aBdaf0YQH/Zu5b2Wj7JOOVzK+PK85kf960PuwZbjrLyDqQPXG59bgHxlszVY9eAdHwupa9P72MCGluygUqPMMlUSOTQuTFVri5zskPTpDXXVs9Xut3wr9Wbtm8iUaM4b1DPRTnXiQZfqjWu8UtrfVc0zEd+5/pseUIXO7/WSNXzWeYcbTzEnKNxMuakTCPkd0Kc3qcmM+2dr/gOaIf+6r7Z/l+lXP2MRgYLZYHm2RTr0bl0U7ZzKUf97du34T2w3W4QY8T169fhXDrgvd1u0XmfPAV+kXY2xLOB5MFnllu9p9mTQghVWsMRWEQMQ9odOD4+BABcbLYIzEg7SgSCRxgiQh+wOV9je7FJd2bkS6TCkOLaXJeYOXrGQLHkfQ8xYAgRnZsqJL19rc8QyE/v/WgUqYmrremUirelHvRC1pmYmKgcZpRiz1NohTHG1jG6blGelXhLfQdGS/BJvTqNp10A8rtehC1BMgcUW4aF/jvt1GRjzjF2OQTOOQKieMZagI0yZsm0ZKUYwdlNMfVQSD1zHpl9ZU6BzD1X8VGj0ChLm3VUz0odAtR46oGZUxx2rib9ICqXmgGojQJMDVL5THP3ZW1VfIB2qmTdnj3TM8d3pS8zYMj2Wz6LSk7pz0vd2TvQApytsUqfO0WX1pmNv0uZG5v+bt/3ljfEAMjBnXBcZ68BEaIj7DywWxA+9bu/he/+yY9x9MxdoOtABHgmYBdw/vAx3nv9LfztT36Cp/cfAJse2PZwcBg4h/8RlV2T1ly1xicGrS42LlrLxDma2NICfi26jXdFhckzen3L73ZsKclHEUFXKvvW59+32DS/Y9+5eErngNgceAQSneyh0xZAL++iMr8m49N0tP3VbUu/YmSAx3DElkyZMxCs/GoByjlDoV3q0dm1N8d7+/hVh8NU8je9DMA1xzbfwzpt/1yx/eLshW+F+u4DrhZH6Hf+UxRrHJH5TH8312cxOjUukGcukyUtbGHrt/1t3esj+tS5dDHpth/vORNsY7FUxV+ECkzIGdp0brZNs79LubKh0XVdid/TE1AAbe5ViFwO1F47voaFT1mfdrtd+bzvexwdHiLGgB6j8eHEo8/pHIQOxfHZMBGCacJkKmC1GK2z7XaHdMdEyojQxx1iHBCGdKkXDyHdfBgCDq8do/NdCjfylH8HyBPS2ZmUUnbXbxFjyDGcVFLR2u3fGFPaMAHt8rmkxyWMoUUiUNPPFGtHzmEIQxVG4rzL90OMjF3AVBwXigYveueDKN0XIcyW6ObAPGb2Qq5DlKVlflu/1NMyFqxQ0eOdgu564ejFYAWrVVppN4MxDPmQpEuH5vV7lTJJHybMzeKdpdINymmLrdCx45v03y5g9X1roes69dg1v88rgnmgZesstHdUDK/W2HQfrloYXKUb1E4ByweV8AYA1waPc/QjoolQ1KXl1ZT5srssc8BIt9WiQ1lzKixxMqc8Py/W016PbwSXOnNbq7/WiGkZRBa8za2fVv3ybAsoMpB2frOSYgLYAdETonOIC4/bH38R3/qjH+Cjn38JceHSLjgA9AHbswu88/Lr+PVPfop7b76d7kza7tDlm9yZkqxjMfh57KP0w8oPCwjmwKaeJ8uXLWOmtas6kSeGb23GON1H59LFtdvtdtIfeSbpUjmrN87HXJkzvC0NdFuaZ/Rzc+tCy/qxPkzesUaVbkv3dxJC2uDLVt/tnAq9WPHIVdb2SDeUQ9/6Tqe5eWHmFIbqp+fu7FrTf7d22Oq+0mRsLdpJP+yup01gottpzvGHkPHl/Zw1S4eF2jmyPFZ+Gpross9xZMtcKFmRy+Zzy1dWVhb8pJ7Xz7R2Yco7zDn6eppl0OIETZ8WjaysaBVd74QGyiYomEZEJ08dI6Vvqj493lJHg78tLa5armxoaGtWJlwfIvbO5zjGceF3iw5HB4vKU87M+VbsBHz96hDLxSLdbJhjPSOnW7a1d3ez2Uzux5BFXLYP40jIdCP2Dr5bAZKhidKOC8cB3kU4DFi4AB62cOEAsd+hy894ADwMcBRGj3fnC1BNOw9t5R5CCtMSQ0nidUMISUjlG5flgLhMdpRzH5XgRAlrInAxuOqYXi4oxQo5qxRHxsopIpmrPrQUkl58luH053onRL7TzwGjolksFtUYJWyk9b5dxABy1jIG9xGBI7pFJy6GTNv6ng9pOwlaG9IVIWmFrdEzp/iqYjwHtcCSez0ayjNv884JIUuHkR5VN81Y2saYp/HSzJYR2BIimu7687lSKWQaY+h1e6Vvqm3tpbH1zwEkKa344H39s3XOtWmVaUUDjMrTvp+E+9Tgvgzg68OKNoTR0s+uR11fa+3NrW37XGv8lWLO3zmJde48IiLCwmHoCMd37+DL3/02vvTNr2F5tEIUUDJE8KbH+2++jV/8xU9w/413sD55ilW3BHYDFvm2cCYCeYeQaZivRS00EXq2+NUaCfJ3teOint1XrNdQFytTrIyUd/X5DGkzOcC2k7qkP2VcPF1vLYBkx2KBkv29BbauUqxcST+pRCHY8Kp9gMQ+P6cv7Pd2fm29Wo+1+qDbTr+HFPoyQwa9Fg01mm1oPVuHwU131OxYRYfr71rv2DnUu3dzYWhWHxARQHWWoX0yc+zn6OyRdWWfs3hDj99ikhYN5vSdpYH9Tj3UDBMax1fLVztGS9+5dsqaB1frvaVXWjLX0rwlyyxNOIMke0YUQHFgMEdgvUnvCWPTWKfFgURUzk1aXSXj07w2x2NXKVc2NEIRUIBE/wVOnn6KSIoXBOc8YpDtGyDGMLlafrPZIIR0IR+ruxYS4HMY+qHEoQuolsUnwlrf0ZAAKrDd6d2DAd536BYdhshIWxTA4dESBysPioRbNw6xpJtg1+H4xjXQcgl0Ht53wJBS3PkuZ/EA4WB1gJiNB+fHy/daExhjrHYzyuchlvfq3QzxanLzNs0YIxxNGTXGWHY6pOjv7cKUn96nHRTmaRyuDo2yC8X+vg+Q6ee0UKzipJHtNaNQWmPQCy+ECBdCOnNAwNnZeRGCepHod0pdsb70jkjASy30tXeLaGpIzZU5Aa5BChFNhKLt62WlpXDl84kSNEBLt2Oft+FHVxUwUq/1AAstdZn6n+ox6TL2Z/rsnJLcpyjs2K/SB8AAvD3ty3M2paelu+YnmgEZrWJpqdu1fW8piNa60N/ZeGFdEsQkUM7+FBYe8WiF3/rm1/D1H34fh8fHxVjwDGAXsX7wCG/86mW88vNf4sHb72FYb7DwHULYocvgJSJ5CGMOm+oaYLQly+aA0hxAB6ahaXYe9RwIIGvRcI5PWgAJqOdiH9Cw/W/9va8Pdof9MrnSMlbs59N30HR2tMYzB6T2FQ189tW5Twbo5+xP5xzA0yyGUqxz6rK51jqrtX6bMrl8Nt9/W4fsXrRCRC8rBWsYOszpdI25UvuojJRW/fLTgmVN3w+j41r1X1Zaa97qDw2gZUz6fWAMT58rjtLOq6ZHy7Gh67zqXOl+7tMx2hFfUvhfsh6KHEyfVDp6DPmcvqvn78MaHVc3NHLmJIBSxqKcNpOcS+FAOU1BiAExBnBk9P0OxITFYoEQUtrY9XqtRkElXV7f9/BI6bhGQ8MV4yNGRoyDSiHrMAz1reEBcYzpBaXQrL6H6xbw3mG72+LunVv4r/6r/xKnT56gvzjF0jscHt3ALkTce3AfN+/exXKxxLJbIg4DwAHM+bI/53B6epqMLHBOo9pWWMJ8MnnCgGlnApNn0veycxTLYUtxuhAIIQyVAVMEQq4vNT0ymQ6/kTAvDfqErvpZK2jmlHpLkWkwLp/bRTK3/dlSzuU5ZkC17/LhL3IETx5DHNIZDc5b25ExRM67FA4xBohp75xDkEPieVGKZwJAvjxQ9YNHUCxCXo9ZKL5PQbf4Yq7sU5yl7chIuRQaQFAJAS1AYkyXU+o5bnlhdFtznt0y9uRkmfRP/92m1zzQtfVohceg5nNT4MyZZaxiG5+XjFhEUzBzqSLgNPA52gltLwMBLdnBSDuYrJ8xr+t+6gxeTitTGusUTGjXqW5XXiQZX+6LnmtKQVOAIwTvMCwdXvjcp/HNP/khnv30J7B1hOA8OiK4PmJ3coZ7r72Jx+/ew29+/gs8vPcBeNtj2S0ARKDzCMzwjhCY0421VHuSRWlbA9YCGK34Qkjhsc5Pgf0ceK1ws+KdlofWzkFrHoW+Wt7ZmHm7VltzrGWx7fPcTmRLlu7b0bE2w6XyJ8vjqo5G/+bG03q2JQ/0+mFArVmtkwABS61iaTT2Y3rPk3UC6HFJiWqttMZn+bY1Fv23NaKltEB5U17sqWO+qOyJXKeLtUbBSP8kUyUFfrNWgx1k3kh9b8e4r89X5W1dHLkUEaP60CrVfKt6LV3n9JRgAlK7DBpbtfo9pwv2jUnzi0QV6TUtMmS92eD46HB8j5CcV5znkBQ9tKDLY4Byrhb9qLDQhwlxa5Wrh07FdMleGEK6NCj3kwQ4x4ghBGw2W+y2W6w3a4Rhh2fv3gTIpUsNB0Zkh65b4eTpBcARB8dHuHPzBhAGBDD6kC9/IYnpTyE2VLzVAb4okLSohyEka857HB4f5+cjEAPAaYeF0cE7RgyM06cPcf34AFs6wPriAi994qM4ODzE6Z8/xZMHHySgkDNfDTEmzzOnHZzFYoGjo6M8R2lSvPcFtImAiXH0ggtzpD5zAfcTpmTkbCvAamAMDtisCAsOOASB8/Mh72IIIIAyyhIjiJDIKfoyc7jUqFpYqbEwDGmXgRngmA7jO6oMIes90Vt4Nt5ZijCljn9tKmwG5DY5ci6l2Mv0EKHuKG3VM6d0yt45REmCGQmLxQFi12FwEcsYQOxBlA41pf6iGCuOPQh+bJuyR1kbbsXASPQjjCBoMsYYpwYKlCdW/14JC6oU576QjbpueSb3z4lAFLHe8lTXcyLzoneaKuCl+jsbWgeugPpcaSkunSyhZcTa92XckklM+H18nhHCUMI00+coPwWQtMA/cw3C54Rp+U4JcCnFo5U98q210RLUhc6RIbG2KYsKwBjrqtZEHpQ8S3mdyL1G46CUl658M7bj5JyZGosDwXGSrMEBcLnlELHwHZgdNguH7sW7+Paf/hCf/d3fhu86DIhwnuCGAdRHnN57gPdffRPvvvI63nn9DfS7FJYaly4pPU+AS/zDBOgbakWpSnY+ymfQUlipUrQyb04uZBU65zFHhh9HnfUUF4Ygob8JbWRO7xERqOvK3HCmM7nUW8p0mgvfa4HFFtiwskHAS8VzprQcCtoos+vN7uLUHVYSgyEJ+XI427TdJNOyw4enDok54+gykGKft2s0rV8NtqfvWVpWw9TgETXdm2CyBWSVMWz7LrKy8LA5TzFHm5iZc84B1QKi9rK0Vl8tDYocJQAly9VovBG5Mqfy/CjzUPCM8J7lzdaOXWvGW+ejJn1HzqRFBMop92UVp8D2JqEAcDlDp8cs+raA66zkNWgfeSxlY2BJz04jX8UYEXm81wKcsAgnN1529jDI+3yp8zQyojVPrXVuDWEd6aIxg3ME36UrJ9ghpf9Wco9ZZJwoQiXrM4aG8xgEqwqN5L0iD4wO+hDl6oZGH7AbUtgPGOmmwXyvw2a9Rt/32Gw2qc/OYblcYXl8hDu3b2O93uDiYoM7d57BcrlCCIwQIi7OT3FwdAxiwpNHT3B84yaYGIvlAiX/cz6ILYDGOz8KmAyGPUlaL8a142MwAN8tsQtbWVMY+gDnUuYTAuHx4ycA0n0Vr77xOj7+8U/g7rPP4nz9Zhov8hZY5xEHLnddSLaM5SLt7sjCsrHYwHiCX37XHq1C1+oATga7ADpKCpldWmiE0cui6wRz3v2RGqdKLSqwCLWwwKNhJAtCDozDjYq75XXTRoj9ThctaFtWsRU29nsNcidgl5KXK/FjXjKUQpII48VWBJXqljGZt6K0matx5+qK0SFGiw6JkX5Y5WHp0TbCRlBUf17XofvqXLp40nuH2nDj2TrST9kta05T9Z5+twWWigLCNORE/z67c0N1H+eMDGvY1GUKIpi5MmpjHM9w2X4me7umh93+nhtbbrBqW0qMDEYdGnlZmQNEcyF4ek6c7Zcp1PqDgC4rwqTA1XwQYeeSknGcwLwnB1p4REeIR0f4re9+HV/54fewvH0d8CnReccevB1w8fgE7776Ot769St479U3gX7AbpOyDPrOw0m4ShHiKEaTpkVLnshOj6zXQhszv3rtlHnMbWrjX76fA7jpvZrm6QuMlgvX/Snzoni/hEqGRprJmfnbB8o1aNFGhAbOH+bs0lzbLeBT9UF9Z+W0bjfGWBIc6M9aBlHLUBjXKZl60++tsBcp9QF21Z6xF1qGkf5O180zz2gAPedUs7otjarO6NQGyXXZp0OFJpqm9csjaCRSdTOX3QC7A5aTOVbjsP1sJevBHj62fa/GmeeHxTEiuh6AOFSn81UbSNOxZ0NF8LYqlh9b+lvaEQyod72IJgzV7EvN0yMWu1QOMJc7NCbzmtsIMV1MLREDyOsmMiejgWoeBusYASUz1Zh1P6p3P2S5sqEx5PsvEBkcAra7HhcX59hud3Cdx2q1wrVrx1gslogxIEaGd8D1G9cROeL6tRvl/gwigJzDervBxfkFbl6/gccPHsGhw2J5CJ/zE+tBMjK49WKVJk+uGDwEwBHjYLFADBHBdYhwWPolIkdstlscHx/DOYLzHRbLFYAA7AhPTk5wevYLxBhyGEKqX9oEUGXASv2pAzkqUGEEmA5RCZkBrGIYwXMKB6I4bldaASuldSCrgOZcvPMIYaiYehQUdeYrKQmsJV+gFcDyzwqiiWI3xfarFSctf9u6NdAuxlOMCBwQshCSS5QYAtLyNjd06Ej+p8hm+yFKZCIYUHsR7FzYOdc0as21XtRa2GoazG1X6svu5Oc4RzXNq/dQlzkgvRdgq88dXDmsq9+Td8TQnvYjCWVrYLQUawWaLgFfEq4k7+n5s2EMEtJoFZ2eq1mwxzy5j8Qa4/b9uXWxD0iMIZU0mZ+9/btSaRuCkQi9Y3QxGRkApTsxFg4f/9IX8fU//hFuf/T5tDPhCB0csBuwfvAY9998Cy//6td48O77OD95Ch8ZPITk+Vfr7O/ab2sIyO9W8dpdJPuOfdfOt8znHN3tnLUA6iyAUuUqh3Ftva11KmtEAxZrbNnv50oNEuvPq7EQVYJ0325sC2C1dMowDJN7hMq7XMs9O0ct4D9nPKR3uAJM9n27dsszDTkla9W2r/tlx1vrlrptPVeVQa2KvtjQ9rf1d+lX6kSzTmaxoKdrLdXHE16ygPnD8PKcISbYSuuRUX7sca7w1EEnc7NvHc71B8hLwLyrMdMcn6Tdh/06wK7ly8Kqbdu6j855LBaLhrxL0RxknHtgLkac1EvIBnhzH+rvV65saByvFji/uMCw26FzHh6Mw2WHm9eO4BZdzqbB2FycZu8FI3LA4eERwhBySINDCH2yTAm4fecOnHd49tlncO3wAGGzQdzswKsFdsMmUwDZkxwzUORyaZ4IJdlpODpc4trhAcAEJo9rN27DO4/zszM4vwDnTFHkPQgd4hBB3sNzPiPifTrkrQVB4y6GxAy10qyApGIw8eaUwjWoqZSiHKoXY4qRvbJUGEIYslLaPIJfexC3NKveK0xNrqpLAJgcMJedEBmbjVu1wlwX208rYG04jo2Ftopf11nonY2MEBm77a4C7wAjxHwPSwkccRKN2BY8qr0JSKExxGLiITdbozXYnQKeUn9pdn5bVY9fioSRWcE0zlO9ywagZHFjTAWcBSVlzOqZlhIR4SQ00X3QdemdPWD0UrUV3TwAzJVOlPc++tm1oo239J2fAL59YEz3WSsy2Unx3o9ngMyY5taJ/XtOYVvP9aySq5RZawyAeAU1nZNMICxDupwLDhg6h4OPPovf/5//KT72uZfQLZfoc6xNFxlxvcbjt9/He795FfdefR3vvv02HAhdTKEE5NIlp2KQXhUQFd5q8Kp+z3rSp+uvTfMWYLd/T8Bu43lydWikBTlalrTaaYKPBh5q8YNtr1Xs2vhwYGt03Oi6Eo/WO5otua3nahJSY2SsfKf1QEUbagM1yxMtg9+e7Rl/n+pw3Rf9ewF4qHcL7O3vluYtWkz6QbUOsfS0/dF9mgLLeh51u0RU3XBun89kbsrwtAuC6jMtS1uGh9THGOWalNYOYKmLHBijEVWfdQ1wVQIhY0AqntTnX1s0apWp/Kx5zspgacPyf8yYoaWrbNkb1qj7hhpb6v46R3mnZYBHxrmc5PTYN2f4KYc+y3wbXrI8rHui279KubKhce+dFGe76BbovM95ehn9Gjm96ALeOThmxO0uhTT5Djdv3sDdu3cRYwqXGk+2O6y3O4SB8fxzz+BwQYhhAw4BQ0wCLuQ7K4RJd9stQj54TuSwCUPeTmN432FYL3D31i2AHMgtAFrkXW6C9x2c60pccGSAyYntDOd9ynySlajY9rINpZWPjr2UfxbQyCSJl7XKMKMmqVJQNC5KPaldtyhtAKNy1V5v26ex/pohtJDUh8Nbnn39t/YqzAk4oQ2ACS1ayt32Scamt2CtstZtDmFA4LRzcX5xXgkVonwuQwAOdFq4toLRVLf9TvdzTL/XgsV6emKUGPt2/4W/WjSxwGVOEM0BEPluHNu8QGgpQWs42L5pACA8ZL0x+0DfBFyZz1uhFS3Q2aKT5T39Tg3OreCt57XVxyKQTV+K4gNP5mTf3FlFZGljv5vrV7uu9pwTpbHbtetzOJVzHgMIq7s38OXvfQtf+v53EK8fYPAEHwkdOfTrDU4ePsHu8Sl++Zd/jSfvvY/1yVP4CLBkUyMqfKfnyTog9Pea9sxakbYzBFkguQ982c9mD4ab+bI8ZOk8N48tGWjrFVrMGQp67LaPesf0qrs4+nM7ztZ6ae3USr+1gVXJGlsHpvyt5YvWG/J91bcMIC29WwBtbu5a/GbHPLeLNUcPO25d9Ny05k5+ElE6l4n23LXm8io7B1cBrpN5iyl0yqZmFixkdd5la21faa2pqg5DZ6C+VqFVn+2Tpv3cPNl3J31TfSDan+zmMhq01rLul57XlryoiGLa2263WCw6OOcBZnOeogS91U5S5iKf0z0p44BbsvbvU65saPwf/sv/fTY0OqwWS3S+w/HRIY6OjrHoOpydnWG5XGK5XJb7Ia7fuo2TzbYoXwmpSoMgbLcD3Mrh7p2b+L/8n/9PeObWDRAGgBw4H07xPhHu9PQUT56cYNcPWC5WGELAdrNBn28VH4YBYRjwkReeT3c0UAqdIhCc67BYeXAGhHAeqQsJQDIhXxA1LniiNjiriT5a8yKkBJAzjyFTklmrvG+EndyNMWFgl+IBZaeFYu2RHZmxrVDTM+MFSVYZxBgqY6Vifq5jAoH6kiS7MPW7AlpaxSozqRdIgl6nQrbj0b/HGNMZFhoNN+9c2aXhEkSNxE9R6C0+lsvLBLSqrcaWsLfAhTn3gsYzHZZ/5t5v9aXUaWg/BfQzh/MxAj/LC1ZQW+HS2qaPeZdR1oD17GhPf6sfrXY0r82FDdixt/hFnrM7PvV40+d2Te0DEMyJB3TdlQEeL++TrmtOOc0B1hatdF2Xbb2PdQKyPkRWAQB1HtvVAp/92pfxzX/wIxw/exvBAQsQXCC47YDtZounHzzAf/hX/xr90wusItCfbzBwxMApe57LoadO2lLgxK4T+5nuI5l11gIDmk/a68EAuwadtAGkn7EgxRrgRDQeADUgx9Zvi57/ii9mAMVVFH5rXe97/6r8qPsBZDqYUC0tEy1osuvBnoNqrdOxYVSeWdv/Of6w/FC/S5WMkWfmUpraevbNRUt3aX6xZ0qsM9O+O/f5nJzRdL9K/6Qf6czrqF+rULusy+bwgPzdrF/10zoVLY+WV9QWig0hbsmEMpeNndOrrhv5WT1PVNXZOntl5caIM+q6LX3suC/jq7kiuDPpWgDZsTle8CzOJcZ4vgWIIOR8I+l/jXWk+zt+ljDUh+nrlQ2NT3z0ORysVgnYDwMWXQcOEbvtUwxrxrDZ4vrBbZyd3MfFxQUWiwV22zUOn3kR3nfodxvEyNj1PWJgLFYrkPPwXQeAEcIW9++/haOlg+8W2IVkZUnGga7rcPPaEjF2ODw4wsHBQQY3Hs55LJdLuMUBdiHd5eE6Xy4UYhC6RVdAgs8X+FEOp0lSjMruh1h2ib7WEyMLAxlwjBOTGNHD+QiE2nOjmUtiDLXwAVKcHTyB4NIBx8jwcNj1O3SGCfYphRoE1xapDn+Ksb7QyoZWAYDvOoR8WzlBLQZOoVUEqsJGfK4nhlClGpaxz/W57/tqR0KHbOlSCVbHCENEiBGbfgf0u5SSGCkzl/cphA95vrzvADjEOECD/KpPDbAdYwSHkNJvmndG8F97V1tzYhWMtoU+TNELf6pMqeLJ8SWMQkbebdSpx9QqeoyinHQIoy6tXbb0Igr5LXDUvNjqFww/cIwIBkwJ6GkZJLquFmgd66nkriZUkR1pbGmHLMZYaJHapywryouwkz0qHhtWkohkQY01fMe1YMF6aldmODlSaMwmxOl/0hvXdehjBHuH5z79SXz5T3+Ej37xsxhWDmswDuCx2kb0T57inXfexhuvvY712Tk2D09w/vgEPjCcd9iFvvSDY5JzzvlsoLfD88rvwlO5T0nWYDIJVva1gLJ8J6BR88McsLFFg9AxbGPkZ6109wE7zXtzO36T2GymiVzYp9T36QP9uYzlwxRL5wIu81okpDTyBXCZ/sj4tVwXx5voDNv36brk5HFtAH0rbyegtAHGa/CFQmvR6y0AOCVMeo/SA5Pd8En/eWoAjMB5dJYRJWfFrGFVfiYBpZ2Bc8btPl6XcEnkHftRxI59L+JaQI8p1rhrkKnSqS3ZO5G3NCoJjZO0I7IJzHUlPBpHUtvcOprQWfqndqhbxrHtR92ncWyid9k4RaStFs/tMzzke5fn7datW7h79w7OT8+UPpE+jM5HwR0xRnBEivIR+s7wsW5TjBSRe1c1Nq5saDx9/128d3aGk5MneOWV32AYdmCOuFhfYOgHHB0d4+joCE+fPsXQD7h27Rr84Q38Z//0f4fVYQfq0hkJ363QDxu4yDjMh7Op63Dz1i0MF4+wwA5HK4c+AOuLC1w/uo7dboeLi1NcnJ1huz3DZtUhBMbT03M8enyKGAnkPJY3X8QP//gfpY2iIZ25IOeQgoS64v12visBNSFGOPYAXL4bhBA4nV8YwpAWPCIiU/6Xlp7Edo+hOAIsGICD3AidwG0Ac7oDA1yffdB3XQRwPoDJ2LoUpdj1AQxgcKiUtUy89x5xaOf8FoGqmUR+H4VeLQTkgOyqSzdtxz4d0OMQ1LNZMTIXpk4CLwA5pSQzg4cA+HxwLYYCCLXi1322YVctxahBaASwjIRdYBzcvpHA3bsfIBIB8ACn2+pBIshCUS4V7lVKSxbkZQfIbJiUDWeTegUIWvBbvldLuxWaJkVS0apJa845US00tRDrspoKyghk1QMN8nUdc6EudntbH1C0oS5VH5ESOUjdUq9WRFLHJLREeFcZTESkLhRt85PsGtqdF0B4ggovy3qulKqih6MRXHH+L4e6Zh6T/jK6zikDLDkqrNGZqs87AcX4CAWEJmeBjEkbIqmP49qWRBbJJl4w0HPA4BzYJ+9VFwmOGeCQwIrvsHWE/sZ1fONPf4Tf+va3cHC4wtAR3NLDDQF0MeC9X7yKt3/xa9x//108fPQQMSRnAjiHYMaILjtrOnJgl3exOZYzOnrtl/UDjAYQESJiATzzCrxtdOmkG8453L17FycnJ9jtdoUf9inufYBJey/NiyBOcrvodeEeQgmpLECcpiFPGsikdsbq9TMWmMjv9jNt3Oh2tVGzj66l7nE4E/Ce1REIXG6KH5/NFzCacVlaSr1z8zExPoxcbIU6zdXTMj5i7NOuWwZriUcBIg/moWq7akdkVpQd6zT+yAzKWTHTmdJ0f5NzqU5Jec+KJ5JuHY1sYnEAUHFoKAk9rhcaDa/W+C141TIVcTyn0eU0/iw3RGe/KxFATjtHMmBFGltyUhb4jsvSnFuQDgCRQ+VZKI4bkrVW83MZq5IXduyd8xBDmLOTcTQZ9hvsQp+5HS3903433QGKY/gSUqKiLNRyHVP93dSxM/2wz/f57DQkFXh6AGl3I8lnMU5Bacc5yiFXRrkXTy5KHWIEfJtWUo9OI3xZubKh8cH9d8HMODhc4Hd+97dxenqKYRiwWh3g6PAo7R6AMIR0J4MjwsVAuH79eom512CMOd8MHlOKWZDH6dkF7lxbJiYBY9tv4Tce2+0O680a799/HzFscbhaYrPdAUgXsq03awwD45MfuQ6U7byArvMyI+MCz3nu5QZzQIQIQJx2PySXtAAamVsNzmMGsC1QB8WUNvyDMsrVwLO2ZPMi9ynLscurnsFVtoXKqneEjroJKEtMMBWwBXCpLD1SZKFpANhSFPK5DhnTAsEuzCGEZMC5+oCWBQxSP1CHUrXKMAxYcAqXgpND0BL2VpabmbupN7S0613hF/3s6N2o3y9jMN7Sqk3Fe2IYFsOm9TxqoKC/K9+nD6p3xjIC5kkMdyVAR17OUqk5Zk0f/bcofudH4ar5QRdL70mP1fvyt+1HK1RNgzhLL6lDQoKsomsBHcsPI1VQgRwNFOy8yoVe1vut15A1qIB8uLahaKZhRvXvduyinGWHBUToooD5tCbYEYIHYucRFh0+8eUv4zt/+ke48dyzYO+wAOBDBF/0ePTeB3jtp3+Lt37xMrZPTxF2G8Q4ZuuKeX12XVcAl50DPX79WQE/NJ/+tVXq8U4v55L2Pvjgg73v2mJlxJxsmgPHwtjl3WxQ2zrm3tdyAWos+r4b4T29WzM1WttruLVGbPvW4GrRpzyPmperOUH9t14PrX7qNq2jI3euMvZHHDEFZbb/rTVejyklhQC3jUxdh/R1uoa1HEvrORkusTgwK89MLkV+Tb5RQ2/osdoAmZa5HWHLL26Sqr1uS8sb3d5IxyxTFKbRhWNMBhjVzxBRjjipns5tjjtA9sxjmvMZOul51/MiFFNtza3B1udz68HiFfud1d+2jhZNWk69Vh/td0+enODo4KAeez6/PDYoFZj6GtEdzrkJL7TGeNVy9fS26BFixHbTp5S2rsPJ0zXIbQGcAEipVLuuw9HREQ4OD3Dj5h0sFgv0w7YSksycb+xOnoS+j2DyeOud9/H0sINzEXBIF57gAWSrp1utQHEJIuDg6BBHR9fhn55jFx4jbnu88OILE4FHRInZKTN89lx47xFDnzL4EFVKW7Z3hcAWnBaGcG0vUpkoM0kiUCyjSJtVLKB3CEOyPnd9j8XMvDBz9rDG4jXUaT4duRKWIH0qApqmzCNGgCg3HbMq455s9avvLEMW8ECoQJ8uuv6WQaNpK+2nuzLkxuhEh4uLC0iIEKimp55HO1d6W38uPhpU97tWyBGk8jFrZaQ9F5ctTOuha/EcAPCeeiQ7GzB/u216EPVuBmrgposFCKOhUa8P4cEWsNo39laberyaFvpvDfiJqMSMW1ClwZpdy7q+CbBsgAgtiC1fJTpi9JKiXuuHh4eJRzE9gzLxiBlaW5mhgVbTaPIOPTE6dliEfGbCeew80HtC7wnPvvQJfONP/xgvfv4lUNchkoOPBPQDto9O8PYvfoM3f/0KTk9OcHF6CmLGbrcr4FnWq/yzfZeQI2tg6fG3eGQWyJv51zSytLGGzVVKCzzq+i4rLR7f18/ZtotRWM+z5ttWvfrzFrCRotfMhwmlmgMbTQCm2rdpp/Vzdg3OjVG/29p1bZUW0JvI0tKv0QOdnhl33eyzczzLQMER6dn5/rXWxGVj0J8VLDHTRsugmjOihA/EwavfUX+U1tp0n9FvVO88V/NvHp3TAxXdLUg28wrM70poo8m20dIFl5U5mrbendtNtfL9srabbRY9nHV1DmHMcX2XjsPWDyBFh1zyrNXR+8qVDY2f/PTnAKeD1bvdgDfffAeb9RZDH/D888/j9p07iPkGbebkZf/97/8YLa8yESkAnLxuy+UR3nrnA7xy9gSgAbthmxdTAjTireYhptAcEHy3ABPhwcNH6BZL/IP/7JnKs14s5xDRibPapTMQi8UC/W6bbqKOQMjp1ORQdsmy5I2FLpNMbaHZEkZA7aXXz1cgIpPK5ZuBC+gRmjmfgaRtA1V4glyOlIyQOjRGAyrK4WJWuGtGnwrkqedCntehM3YOpBc63tmC6tbv8oxOkSrKOHKKM2QCzs/PUzhO1nFO3TDUqrupyDCeO9FjTnMwPTwo42HmyuuoBSbL3krDgIhRLqNsAxBNc00PNs/UoHb6bglTy2uNaPReOe9K+ugYp3Xa/mgecc4hKP6w/LUP1IPaQncOKE2Uum0HSCFBubR2EGxbdlwt2kONq9muAbiybi2/MXO50HRufDq0ptU/C85bdZXvCGCXQj1TWKhD9A7bjrC6cxPf/cHv4wvf/jri9RW2xOgcgTc9dk8v8O5vXsH9V99EfHIOOrvA+v4jwBMGGndRhIaSu10+s04Jq8T1PIseINRG/L65mswPGrwFVPS6rNg51PVah9NVgble//J30yBUfS80a+hMW8dcvLgtGlhbnrQXj05AfwN02vaaoA2obphujbM1Nhs6q9sQB8qcXLH01Y5Nq2v17lCiDSdE4RxQHEa1vrN8bOchOanEyZDDVTRpaNQhUvSOlNSh25zSwBhrjiZ0lr5N5JIag82cJJ87YHLebaQEitEwlZdj6JTVj7poWQggh1ur3RXFw1pH6rGk3SFf9c+OW79T46upzNaySMtZ2+/W71fR2/adfaUlX8o6RwrZBU3BfVrLKeSyWstEJQmOc9PdSo1ptHwQva5Tktu5ueqYpFw9ve0HZwDnEJgQ4ReH6GKHi+0p3rv/CB88epqvi09K8ujoEM8+/xH0Q58PfwGOfF6AKaY5xpTmlpnAvkPEAn/9s18jxh0i6RjlcXudhwCXT9WHGNGHgNXhAT79mc9gsVyVS3+qiXBGQDCwWCyKQNBCRDz4RVGpRV4xmRMjYOqR2cd8wHSrbfyO4SjtIvQcSkrVsougbsTU9XXej6GOillijJVnCdBAINWtFZEUG8LSWlBzwkq3pQU+Zp7VdQs4bO0GTf4W5eGAMPR45tYtnD+9ADsH5nwrdEP5tMBHEVg8AoMWmJM5t8Auw8umwNc01n1JfeAqBELeadGm9bsF06k/rs1rag608KUMKNJ2/1S5WuGihaE0Y8Mi9LMT4dYAhbpPVd9mBLluo9BZtVH3cTqflk9b7SRBXPfTOgnmlDlMW3ZcmhZ6rvfFru8DEy2jJMUnA+w8tp1H8A5D5/Hbv/dtfP0Pv4drd28jeADOYQWANj3O33uAd371Ct597TW8/8ZbOGCHYb3FwBGRHQIYXu2KzhkE+vPWmQDpt/Z0C6i3dNX00+/PfaaBZYvf9GdzbbVoqj8T/mrxjW53vPx1OoetdV5ohSS/LM+2eK6a80bf9fvW2cU8pl0XR8llNNEGjvX4l3YJRe7tAyX2u7n5SmHKBGC6bu347T/pnx2bpS0zikxOj8SKl3SZC/GTepjH31ttaXDXkgktWsi7FX0a9LS/T+QkpsaLftYWrW/lOq9WCJz0xuqjplyVuUJ7Pdj1NeEjGnGXxQ8tHWlp1dTTs2UMubJh3HNzpH9vPWPLvjmo5EkS6bP1JUw7YlawOIZmjCKq56mF4cpFyKZ/LVm/r1zZ0NjulqljMQJIoU3sgIEB75Y43+xw8+YNdF2Hvu9x7eZdPPv8iwjDeH8EsxL2DKQDj8B2NwAHB3jxxU9gvflXcN5jN6Tbx51z6LLhMIQBK/LwRCBP2A479ENEdD2efe4FxAhEGuNXS+iIhNgQUogLJU9c2h5NB76t0C9CLqeH1f8SCKkJbL2nZL6rAN+coIQB5FAeAgWStYCy/dUKu/Qp8uQZlBja0ctjAZpVylJkPlugXQuhFqCXOvXhUNuWfQeow66ENvL3YrHA6uAAfHyEpyEAkHCq/Z7fpiKksV79XowRMdT9rEKTfDte1+4PWwNNYtz1P92upQnz6JnRn42KdWy0epfT/+Q93/m8VS5AvQ1srcKqBBHPGGyKZi1Qvz+6+GqlBSCKuT4DbFqlKYBzsd5QfealGo/mo8Z8WSCov7PKaC4sca6efYJ+SR0GR1gvgBe+8BK+/aMf4KMvfRrwDmGxQAwBbh2wfXKC9195A4/fehfvvPI6np48RrfosA0DBpedLj6d8Wl5zvVOi5UXrT5XIZHITg+MhkdLpjUBhylarlgaX6XY5+Z2j67KX0QErzzr+xwo+h3K56ws7VpAWXvFL+uLvCMXyNo1bh0GMHO4r+59NLHj1jTUgLAFsmRO89GjJi3sWpxrV+ssOx5XnHoy7Hq97xuP6jEE0lY0IyA5VNvzbmX/nLzYV5p6wnxveccWC2LtOoo0Z4ykt62cci7JjKjarfEBV+/p9+dCjQCJ+LhcHuixEjAbCmT5sRq7wYZXLbP1XeG91lzOzR8zp/tPaNSF5XuWZ9thhoQaj1WYxz77IfnRlisbGq++9g4iR3Sdw3LZYblcwHuHbnmIyA6rg0M8OTnF9evX4ZzH0dE1LJYrxMjgCHjvIJlmUqdT2IvvPDqfiPXSS5/BwfF1bNbn8IsVfARiiDg9X6fYYHI4jxFHqwMcXTtCCIwQGD4CH//4J9H3PZjGXQGhVrLy5FaN0ZvmvcMwFPcLgAweZR4J5RIbOXiqGTAlSJl61iLXlxnpRRNjLHnXLfBFjnOUDABSh/ceIMmskw5wxRwixswlNl12c6RN733yjkGHk+WsDFEA7jjHwzCMuydiHFEeqgKVxISu8yXsahQUbd4pRhRnD36IJaVfAqz1hW9zCieFxckWOsAhGY9DCNicX6DfDQgAPJLrRRtOen4SKFUhUqYt3YcRxE5vbBaB6LsO8vFoxKDMKfNUWCWQRdUuiVU2Ff149BhF5uZz6e92W4n+WbjnW33BsaSNzJsypq6pAah3CwmJV3UYgu2X5o/i2ebcvjRKIz2sCdIScFYx2bE6atPUlhZYseO3a7ulCLSHmGMsByxbdc0pclmzfd/j8PCwnvOsEGImF+vJkmcoxdRSTowQmdF3HsfPP4Pv/PEP8Zmv/jYWhwcYYoTvPPrtDhePT3D+wQO89YvfoH9yivtvvoPdeg3v0jgGjuBuDFPocmotTh9oMQk5p+RUv71zgKS85pRNKgIlxBYu1ZcOlwuAE49yoVJZ73LQveYJC1yhfmr6lt8mc6OLne8W0J/ju2ll9Z9ziloDq9RuffGpXl+Wj/aBrZYcaLUN5LucQijzlNZpIvy+uyUksUg1Zq5pNX+2rd6J0uOZkpL2ymm7LkX/idwRvWYNUSkSaUvU4rFp31ufEWGUa0l5KxYYZZvMn3aW6Pr2GRpWZhTTJutRYOT6WYNiTtfIQpsZ/xwfJV03Gr0uh0QxoxiIUoS/kEOKGe2zj1bW6rbHZBQ1ftH91n0svJXD4CkPVa9Py5d2nHq+9pWrgPHSvvob+TNqJAUp628GEyRaJvzkO48wDHAkUUPpwH27XxoHjkayfAeq1+lVx9cqVzY0Do8PS2YRIMchAui6RQIcIcD7BbbbLY6Pj/DMs89guViiH1LUoycPTw7OMQIB2z5DQiYsnYMj4O4zz+Da9Zs4vzgDhgEERt/vEIYe280aALDwHnfv3kKIA4bQA2DcuH4DH3vxo1j6JSJ5cOCkkANjsVyAhy28S6lXCOmCJUcOy+UK2+02xaPlmDSmdB5EjIsBnOIWkYVhZHBIRktEfVCvAhyYAt3qeyNcE019Pl8hACxNPhElSegIIIfOeWyzgPLOJeCuFIII92EYUj8DwDn1pHi8ORIi1f05PDxMFx+GIaW2k++BilkZSYAQEZxPRmPaRZFt/2mIF1Ha+qPI8EQlNRoDYHI5zKAB8NUZEuu965gRPTDECOrTQhy8g+9Tml1S6dmqBeIoXd6Y57sUJbWswCoxuEogpV0xMSZGgZjCS1RcMNVhIoUvaGxzX0iXNW7IuZKPWz8rBjxQe8QLvzEXKSex4JJO0YoPK1haikmMz5YQsllxmoaAWLFIqZ05K3uhQg0gZ3ag6k7X52HkOaM0KxBPCZRLQgWr3Cw/ljkwGk73j4CSgCGNTvWvjB2FDtIHMvwn7zhOACYQSl9TWGWEQ0ozTTHJj9h5bMDorh/jC9//Hr76B9/D6toRyCUZgAHYPD5B//gx3nnlVZw8eIQH797D5uQUcdsnkMsAeobHyM9ElFPWRjiqlgrAMT2bwUMyHBOg6ByBYwAJHbOjJXIERRaBhHTvyKBoy/A+rSNtRIwARKgo4FADf8uPBEHAaY6m/LzPINV1ad5ogc40lvbB+H0Ggb1PokrooXabte7QgLW1XuUd27blM7mw1nmpJ+svJKRoZbnIEnYpNl9CNZJepULxqg0DoKVOkXk2jE7TNMmSkRatsm/3XOsP+U7OciaeADinuYZLhm0IDWfNzNyVfhIBylAbcWCSc/pMjMy5BfSVHGnwo/7MkQbOXDzUAhJbcszWMQl7U59Pd7e4kqU1bVLYmRj+VVuU1jfRuKNP+RLd0etez1mLp23oX+JQVsxGVX12zkRMEI+yN4acJMjXdVe4jfdHXeg+WpnSorneWpHVMq66dv1arol80TwvGBaIAI0OWRR/wdyOVki4jQhEoq+lH6PDrDW+aV3z5cqGhgaxaYGMTJ7kUSJs36czGc8884x0sfqXmG3IixsgB3iXL4Vj4Pj4CNvtFn2/xna7Le1fu3YNfd/j1s0bcN7jYr1Od2A4h9Vqhes3rmN5sESI4wJzOr4sRjifBKF8v1wuAdQhXUI8ASpR3fQtAn48PDOmZdSH0MU7pCdET5h+TkpqEwUcUSZQjHG8+M4lj6HzDouuK32TPswpvuVyCWauDja2wjN2u12O1fVwbtpXDcS0Ahtjq6NwRFEQ9fjqzFSFzoRq4dTAenpI1Frz3ntcnJ5iwUlJyGGmlvKt6DNWjFbR/XXkysFtLQRT/1Mi4nEnaPQCiyKX36v4XiVXWkpsTjlYI0M/z5w8xEAdzjdXtxh7ehvVAnoLEsY6xv7rOltAqzUmCwD0WFvPXaZ4bTtST8he14mxABTjcQ5E6Nj1VpuWx6zingOw+pOyJiiFdNot7EApXaj0Ocnc5MUKMafZ9g6x8xiWHT75u1/Cd378Q1x/4TmQ9yBHcEzozy+weXKKe6+/iftvv4WThw+xPjvHbr3BZrtB53w+I2AMQk0zMxSq7Ln5cwR6TiwN50JU5gxK24Z8VntUp+E5+/oi63oEoNOiAb4Fxq0+XQY+WvUzcxZMUzAo31uem8hT9azWXdLn6mxXqyPSR67HoftCSn/YddUal362FSY1V8rcNerUbYpum5zPNPJMz8Ecn7bGNDfHmoe08WedFrbIs63D3voge2ss4pS6Ks330brimQ/xnl5nlg51AyjGieY7oqnBq3/uOw8n76d+TEYEbezoudbh9NIPkXdy8FnPddGNvH8ur1Im/Ud77OEKPNme74jtViVQSo3MLPBa70tbdb1XW59XLVc2NAAUC7xStAAWXQdyhO12gPdd3tU4RvFsZQMjRgHGgM9uMeZYDAaOETdv3sD5+RkWC5fqwKiIb9y4gdVyiYuLM4SYbgTebrcIHNEtl/m5dEle13W5vylunZyH97XAsecJWsaEWIplEqhWALLw5UIwIE3ePqYotDNCL93UKM1Q2UXxoPEwPDNiGFO6hhDg3RguZesNM0LdglC9ENOuynj+wCpWYLzJu6ZFfW+AfkZ7b/RP5xxiqIVq3d9RcEy8eIGTFzeDNPlcYslB9SLaB4DnShF8PBobE4AxQ9Mynua4MG55t75r/G373hLCzhFC4CbvkeFdoYn2VM0pv5ZSiI36Z2kwo+QnCiiHGOi2K2B0yZrS7Wka6fWoFauj6Za4VvganOlxzikyy6Py3T6DSICUU/0M6uxOFI8zpzAqx5RlhcfgCcEBw8Lj7ic+hm/9yY/x4hc+A1p0IHLwRAi7Hif3H2H75Cnuv/kO3nzlNbgYsD0/x3a9xvriAiBCzxGdc+XCTUu/3OMJPVtz3/Lg27V/2Xzq+bIguvVca+4t/eeAlJYvrTakPutwsSB0sk7M+twHaMc+K284poZ4a+wtmurx7DXiGrxp67OhTTHGFILZ4AXdh1Y/tY7YN0cir0MIKdB1pp9ats/xhpZtQtN5nqkdCbrd1o6KDntrvdMq+3jZOuPs9/psoF0j6SEAHJtQca+eYS5OP13/XP/n5lvr2SEEkJtmlNq3ZvfxUasf5pOJXBIekr5N1qmppzaIpsb7f4pixzvSZkxPb8e3bz6YgYv1RZY5EHAhb851YiJfx/r/7kZVq1zZ0Oi6bhZ4DMMAkMRCptsw5dI+AGAOiHmnYRh6DEMPv0zGydAPKZOUI3S+wwsvPocbN66DOe0SyLmD4+NjLJdLnJ+fYdf3GGLAZrtJhgAzVgcrADGd2fCuGBjMksc9xQFLfbXga6dwZWZlMmeGiHEiIGtGaXsiihcCKAcEpY5ReCUvYj8ERDcylqQu00J+XAC1EOz7fgQoMcIxiiFnFYc1TioF4OpFZrdS6z4IhQgh1vTQcbF28cv3XOKwqeIzq8Q0IHQub/kjhRLJbddpLDHtKijDR3ZgktAZgCsog1qBp23afYpb07cczHJ1NiFNc80fVlHpemseGd/Rv7dCKVoAQJ6vgCDlNInmuJwGjLY/QBbQxrsG1IrX7gjMAbiyjqj+zI6vRfPWOCvhqdasBWE6Pa+l7Vydum3L11Pj+3KBTZS2BebCYToGHFMKj4oEsEMPIJLDpgOOn7uDb3zvu/id734b7nCJoXMYCKBdwObpGbZPTvHea2/i4Vvv4uzhY2zOznF+cZbuEOK8c+Hl/IWVSZrW4zkJvSbl+dZ8aPrZQ+P7AEULENbrsS4toNr6nRR/6e9b/bHv6yJyTRdrZJMx2Gy9c7yUwkrrrDtaTrcMiBYtreyYkyUMNPtpx6jnQjuW5uakZXxpntFjtzLMfg8Viqo90zKeOZ7QdJuG3kyNWQCTG4/1OFrzt28ubH/0c9Z4k7HYOvV8WppagFwiG1yLhtM+aBqwGavdlRHZ3HL6aHlgZbeUlpHWkrvyvuwwtpyiLRmin7Gpm7XsEVqVOSfKoZvT9OL2bpE5mtoxt/RD6fcMiLd0997vdbAVHcEpY6Qjl87xImEje/p9bo1quo10RTVqiwPmsMVcubKhYYXMGCaSYtcRR0ODKF1Otd1tEULNcCmlrBxsSTdosqd06Dp70UMYIAfilstlORx5fn6O9WaNGAN2/Q59GOCdQ7foEMqB7YAQBzB3hUBdl84UyI6KZN2Qhal3MPTOhj6UVw5KzxC3YnpKsX+tRSK/t4BljBFD3rp35MvFbIwU29ip91wemzfeWAHqY+GyG6JLSznYrU15Ti9SEd56e7cwnaGH0DrGWFKvaV4QegvNrGJI9Y4xk1Uf8kpgZgQeEMgBbpzzxF5ToaPHb4WFLG67gMo8oVZIVhnpurQiXB6sKjqPz0XoA662Pf13xUszAiPRvL2boWk6GVeMYDd+VnnTlTKc9I9QDDaZl77vy30q2rgDauA956UVY1zatAL7MmVejUveTX9MxrGvWIV+VaF62TqbU4wgqs6XaGXqY4RngJgQQNgREFZLxIMlvvB7X8Y3f/SHuH7nNpgIAYALQNjucHb/IU7vP8Abv3oZ77/5NuJ6h+16DTBASrF674sDjIDi1dTgbBz/1AO9z3CwgMM+Z9cQ0DYuNK3sWmvRswXUWiB2DiS32myNW/orAKUCsZERMa3f8tSk/QbII6rD+DQgadUp77acDhUdqPxvLw01LaVeGH2g37U7gC26WmC2rw/6cz0uW1pgUeuVuVLP7zSUb05utPhqjp9avNMa59z6uKx+ouyowzQUaI7XKoDcqLvwExG4QQIN5Fvv2v7Zv+dkqpYpLbmi6xhpCQDt5y/TFzHUBmmVHXJy5qt2ZAFTp5LFRkWWe48QRiPHGswBPKlD9GgIQ0o2ouQMc3INSUh9xx2G3Q5yLsiOvZojwiR0asQ61ExUcxUd2CpXNjRsWk75F2M+IM0xe0RZdHq+YCRdtOa7ZIQsuyVAiXGHEFKoEDnEENB5B0nFRURYLpdpZ8Q5bDYbbDYbxMgYQkC3WKTwqRCKx37Xb+F9l0OlGCAGOU75n8PUkzDG406FhACUmCcyyjmMSwRWrqUCxnVYVV1qxZA9LhxBERj6bNyEkM+zjIeAhxDgiOA7Dwq1l7zy/BNVnrW5Ugl9tIW+zPeccCWSC8LGfogAannkq+1UFR6lQ/TSIetGfyIXweiIsFwssaCUdYFiyOFlVPohIQ993yNgqqxaCnCy8+BoMu45Wm42G3jvscjnY2wbuUYQ1cBJA4irLGqrrLUntKXI9RqWOQlRsk+NdersZbNAmYHIoeq/VmgWGOo27RhKvTwadPvASKtfdn3LGt6n1K9a5oDth61vDlCBuVj3Qifn8kFv5xA4IBIQlgvsVkvc+eyn8e1/8Md47jMvAo4xeA8EBnYB64cnePrBIzx860289fIrOH30BP16A46MgAi/WOTsUKnvPp8YFGMjDerD0WMuDKY1j3XYXtvpoT9rhcXMGQgfpkzX49WKtKtvm299z8zFaLN9nuUDoBlaremoaSmyXgOP1jst0JZewCRpxj7aij4jjknbN/rUApVz62ZOj9gyJwesETEH+q8it8eXUC7Cu4w3WnOr+1v+Rjpsb89X2L5andMCt/v6omX2ZXN5WZm0N2NIWKOg4gkzx1cB/lKnjaLQbbVALxFAzkOnc23pPflb5EpyWo7PD8NQpYAm13aOWL3dakPPCZB1Uw05K7oAtR7TdTgixEY76dhBiiQq+lX6BZ3kYV5u2jkkUCWD5uh41fKhdjRSZ0SBj95YAOAYseu3+eAl4eHDhyAiLLxPhgYlz/JytUQcegRmHK7SBXuOgEiSDYpBxFguV+i6DiEEXFxc4OLiokyY9x0IwGKxBNGAx48eY7PegNnh6NCnQ40AEAMQMziPKduJdylbCwOIYYAwpTacCtDLYPbi4qIAfMaUkYTwJRwl78yIJ10OiwMpNS0kRWs+pyKACEhMHoYAsEOIIX3vPRbLBVy/Q4jihBJvEpdUt4t8TiXboykBAaXQEeFtzv/2AQlSwYNtfgABAABJREFUqk4zZcvL1hIa2hCR9IfaUJW/5dko+RYaglK6WpSlKNTIxbr3jtBdO8K1u8/gyclTxA/uw/EYkpWZFs57BDnTkzOoSf9HoRNHD7jW+A3BoCkm3gMgnV85OzvD0dFRut/DKMay6FGDSz1mK9haoSzVnJm5sErGKuqqTzkMIobEby7TWYSb8HxLker1IEw2DEM51Gy9OhYUWMWjvUdzinKfkJvQBTPArUG7y8plwvqyQsn3UbJr5caTMZHpTJkXvfMpAx6SIUjLBbYEXHvhOXz7R9/HS1/7XeBohUgDiBmxHxDON3j81j3ce/kNnLx/H4/u3cOw3WJYb4rnimi8wdg7j2zZpQw2XHvgiVohkjUNNBho8hanNSgfpXpaM5KK3c3QP+V37UGf0HiPQZJ+n9Y3Z+Tsq6f8JJSL+YLSkVkgjMlHSl25XpH/QEUzohR+Kmtefyc7hXaNA7VzqdVXO48Vvzd4vwUsKsOAx93mOeNCz4mla0teJepQ+b82vWisuPyU1PNzxoSlqx1Ha37L54olrjq2y+SCxhj2/YoGNOUL+6wtOiwsxghWoVN67oVHc4v1MqTp2IpeBGNoGLPT9WUMJ5bdgnp3DSpcuiV77U56jQlIreO83gpbTI2dFkbRWEYwiN49kN+99ylLpUS8MBf8ZY05O29SB9E0eUTr9xhjSRyjaTj2t866WbcN9LsdvKfqPQDlHrW50up/SivK+RqC5JRqYcar6E3gQxgafd+nF7p0HwY5AMToh7543Yc+be0sFwu88vLL+NEffh++c/AEdLmTPPQ4WObdCAY6SjdO0tKDwLh/7x1cPzrEdojFAy3Zp+SgsoDs5aLDcrHCdtvjF7/4Fb79rW+BhwAeBlDnwSGAspETOXtpFx0iB8Q4YLs9A2EAMI0hlwkVZgkxhZREJehbAkGUiJ6UsshDKIYacp+opK0F2FEKiQoOkXO9jjC4ZIghZM8VZ08BkHIl53sJIicrJKbcs4hqd0giDZnFcz16e7WyyrNUxqKFuB6LvdG6/FRZv/TuBPM03r/QJwP1pqUN2RkbUxImtU5gWmCR5+mUA77wra9i+ewz+Nn//f+BQ0qKqFz0l8fkFx3Y5H4v/WW1lyNgwcyjHqsUeUvvRKxWKywWi+p5LXBaws8+2/o9f1D1ySpUy5+ASdfXEFQAo1Mxn4XHMu3ZtFfeN6Ff3vlED54CC13s2inP5LVjQYMdT0vBa0/5hG9rIlc/W2EVLXBhzw3oNkQRWi+Urj/dapPCm9hRykIcGMRApLxCmeBjXtuLBQYOCN0CODrAV/7g2/jtP/wOljevgR3BI4B2AcP5BZ7ef4T3X38Lj995H4/f+wAXT0/B2XERKWfgA6FDOlAOUEptTOMWOUCgGCF3CQgwT8MYDXI7Z3PzLDRI4XwjyWXndpyVNqDSn2ngYb/Xn1n+1EX3TWST/V47mrR803wgJfFDnse0753klKZbZEDAMAMSNizp4a3usIaBpUdrDdixtww+O845gNeSJbYdG0Z9lXWqaWff0QCSE1F0bXnnWjs0sqEGwJPLKelDBYxt+5rGOvxsjlatudf12LG12tL6LoWa7Zfvc/Nlgb1ur6kzqU6XXckh5nJ+I5GRi/4F0aROLjqR8n047fGLbrPFQb3D6SxgWsvpTKCdA/33LB9FgJwvu05gmqyX1rpt1W3XcyvUnUQdKpkpPkKbEEXan4awzxtV1fiotv2kL4Ir52gCEHb9DkfdAYAx2oMx4pMprygLDajkHpjQUT6rUfpMJeR2H7+2yofKOhVjwNnZBfp+B0aE98niS2A+MZpfLDD0PX7+s5/h3ffexa07twrocs7h/r37uHPnDkKM8D6FlTx68gTeEd59+y388pe/BAAcHBzg/Pwcm82mWpCRkydbe8qdc/jn//yf4/joCJ/73OdB+YK75WqFzXYHZsZ6s8FyuUDkiN1ui2HYYbPZwpppIqzSAkuhKFws73yOYggYhoCuS4xTpSwFUoiTulHcAj67za1DuSIDiJzuFYgppz0jhUotsqBg5jG3fWR0XR1Lr3cQ2CjoKsQqGxsWODHS4tqn0K2CLGPKhoYOdyieAUPnlnAXGtmwpil4TnMT+h3IoxyiX6/XiebJiqpoLPXqA+eTGHTRatqLdoWi+ye7JeknJuOoFm5DWbTGWwla03YNMK7uZbB9t4cli2DOAqlVr/YuF2NDYv4vabO1Pogo7eSp/lih1lISc9/ZsVi+s5+1+LtVbPjP3Bh1/QNzuViPGaCY1pljYAAjegLBYReBzqcMZ9E5PP+lz+G7/+hPcfe5uwirDtQ5EAPDeovto8d49N77eO03r+DtV14H9QFxuwMPARKGZs/KMPOEt2vQU8crzylIC0hawDf9BDTXarpIFXPz2wJSQn8rj7RsbZ0tahVrfIw0mOe3ircycCthiOIMcQ6eXNXHfWu4Mmx46qxp9VnaEXkvPGvHbuk4kS/ZuN9HH2vAMccJyNIe3BbQ0/2zcwdkILdnvlpGixQtg2xf55xiWh/WMsBNDoRfVjSd9p3LtOOw/ZHvdATAPnln+y6GAe15PoW82sscpsZOmcuZsdo+tWS5nAOQ51588UV88MEH2Gw2WCx83Q9M17W0oeV3NLqo9XvLgJHvNc4YMU/bOaH5dtSxI7/aosPlqzW9p0zlQhtvEdUt6v5454rTj1lk7uWlxWOCI67S36uWKxsa5+fnWbABq9USi2VXFvAQY7qsJo5C5NGjR/hn/+yf4X/7X/wX8F3EEHZYLhe4feduAoCRsd6twcw4PDjE2dkp/m//13+G7baH7zo8PTtLIUtZmMpZDRFu0rYs6gcPHuD/89/+S/wfv/Tb2O6ScUHOp2xUzNm7TPCuw9Bf4GK9nh1rAV4k2at8Mi76AVEJIO1F0Z4wQu3dbgk//TPIGQwat4y9IwwhGXfJmBngFQDQVi4wCk2bxk0YZgrUx4UiC0KDJgaXC4F0/boefSB8jPcf+6Y9BC36Son5ULQ2hmQnBBNwrhdFfj9GHBweoHMe3A9YUPYbG4Vn+28BphZiGrxfWrJk14u2gAMGyI07QLVRJ2ElbUFox7u3C6pOTeMPIxRk7eo4Yo4BEZTucHHTuGXtHQTGNcENU2MiqKk+J5M/nN35agEm248WmGgZGGNzbQC2TzloRXJZ0YAhUvqXW4Mnn41kxoKzAeI8QufRLzxuPvccvvWDP8DHv/IluOMVYs5EvD1fg3YBD9+7h3d//iu898ZbeHpyki7n7IeUWc+5fDHV9BxEy6jSdJwAUTNmuTdHK/LJOqp2zdo0t7KxBcxaoGyufzoc8zJjpcVHVsZYJVw5adT5Jsm+ZOtgyOVX8xfN2XGlMbiSsnyOb3UfNXBqndVo/a3HJTuQrT7Z+kZacDFitbxvzaMen9Sh1+tlcrYl++045vgFwCTcTI8txjE5zHgX1mxX9vbPyjbzVAaA+2WRpaXowqvI81Incwn3sf3KPakAvabdbIiuadauCf133cd6HfV9j81mk6NEYqG1fka/3zQQ4Sd0uQrP6b7qaBUYQD9HV/3M3PzJGtSyqMWbV1Adpc5x3NPvgBwuR+ksRsIdV6tc0MLfxXD4sO9c2dA4OjpCyRgFBiPktLb58DIn2OrcGAP869+8jL/6yV/jG9/4BpbLJZbLFYgcdv0ODMJyeYCLi3P0w4Bf/+o3ODs7x3K5wNOnp1ivN1WcnF4QevJEOIcQ8Ld/+7f4xS9+iS9+8bcwhIh+COgCo+s8Dg+Psd1usNttcXBwkA+WD2BO2lsrMD25KVyKc/YsQkqZSthsdunQOaVLtqpL+9xUgI4xhih/a2ESQ0C+5BfO0SRbif5d2unyYVFWsM6Ow9JLM3wM4w6Jbqdlqdv6AJRD7uM4CUTTg3kCAorxABOuwrWAqQSr6UcZD1I4lPfpEsPQD+icT+EpiUUrL4Wu2xocMgfk2ovHChXdV2YunZS6Kg8/TT1Ouk+s5kzeswrbth9jrIRjaStTTHbTJv00z2re2Gfc2FvbdWkBU+nfbDhcQ2CXPplnNHiy49UywXqO9BgrA5rr0AndB00DqxwskG71R9PU9pOIyg3MlEOogCQnezAO/ALMwIYI7uYxfud738ZX/vB76K4fgT2l3RAGNk/PcPbBI9x77U1cPD7B/Vdex/rpKSiWPDOpPVffh9Eak52L9HtbMQp9NP30HGqngq2/FZo29inFb1vgo+vdV4edFyunpnPVBhL6PctLLaNGr3VuPAMge+indEgyo5aNJbzOe2gnr04qommq+235Tb8j+lGvgcooN/xqxyt0sSFzti9XAcBaBuv6yzOcA3lm6tK8Yc/5ybis0WLbsPpddp8nu+mYOtGkvhYGsbpxQhPCRGbP0UrT2q4HSw/7e+EtjHrU3ruhx2FLKxQu1YsKY+ifUrSDqOh5ZuVpZ3zwwQfj2mkYL7Zty3vpw1pez2Edrde0nqjHJWGO9Zpp6U1Lu5YO0TJEj6Gm7bz8lXMYtk2g+DOr+qT/zJyOLnB6irJTKgyh0F/mSOpl5kkonB2/FZeWNpfxs5QrGxrOKUCuEvRyZHTe51hUAVfCZBF//Td/gy9+6bewXK2wGwaAgSEMGIaAMOwQI8P7Dn/2Z/8OwxDhXDoo3Q89uq7DYrGomIaZS7YpZsYu716kz4H3P3iAz30uwnfp1u9+CNhst/Cuywe6CYtFlz1N6QAsUzrA+u677+K5556rCCkeqRiTsTEMASGnru37oey0VEwX6y3i9P6YGUQzf+XxZC7xgKAxW9JysYRzPi32fE6DkA+UcmYatIWRVaKVIATKXFkhob1cLUUmn7eAiwVumgb24Kjupw4RGIVZBGG68McFl86mnD99itj3yRMY890Abupl0QtJC3AWSWoWjlVSUkcFZIkQeDo+Ma5sHWVOHFXtzSkpCyz083bh6+lvPd8am22vajM9WADJ7HNWCaYvZ5TWSA/NSzHG5lY6ML3wSbc9e/ZHyQ0bjtcC0XO0sM9Jv63ibr1frzfKuwzp+8AR1HkE77B2gOuW+OTvfBFf+dH3cevjL2LXEXbeYREZfjfg5MEj7E7O8OrPfok3fvMK4noLyqGhiQ7JEeIkyQSmvGznSwPJ1jh19rEW7wn9Z8dsgOh0nsYD5VpGyju6Hd3/qyi4dp/qz/QY9E+bZVGv+YksUHKmAjmIJQR1Mi4DNvTZreSomtLysiIGi6WN3XW09Ckx+qj11L55dW4apjk/x9PSkqtQHGsNBNuPGnhOQ0yuAoIK2DIOhsvkph4rgEv1IYCin+UzHe42azCoYuVkS1+WtUxUpUmtdC1NwbPud1Neq9+sDN5Ho7H+8e+qDaprn6tnwoNc06klF+xa1HVP+47ZbKK6v3ptybhqrDg9nzdDlMk8a4fa9PFi4gGYruFsw5asZmWrgvPunFoPNpQYM/Tm+oNZ2ly1fMisU+PfYniEHNrTapJAuHHjFpzrsN322UuQDnjHISIMEc4Rhhjwta99Ha/85jdlsvR2prQ/DAP6YSh3WojC995jsVjg7jPP4/Nf+CI2ux7Lg0P0Q8C2H5IAHgIOD1bw3qHvh0J0sSJXqxWeffZZOOcwDAMuLi7QLZYg8uj7LUJIBtCwCwATum4B5xboOj9RwnoiLCjV3wE188cYU8iDSzmTY/ZSJmOrEBW+60B5gZWsQHFGYDiAwwj8ZWE65wrgEcFXGwbTGd23iNK77fekWAEuRRuxTWPI1FH6gmQQcYx49u4zKXSvH9Jh8Qbo1uNvKUhHrhwan+t3U+lhXK92vqV/GvQWQzOiXIyox9Yar+6HfsrSS4egzSnMufMvM6oC0fRTlw8jbFp9tkpCx/O2nrWltdsxGYFRprquyzzGH6oocGjnBUiOOALgxaDtOgyeMHjg5ic/hm/9+Af4xBc+D3QegQieHfwmYDg5xdmDh7j35tt477U3cfbwMfymR1jv4EqWjanHS/O6Bo2XGX92DC1jSj8DTM/qWCNMr4/6/Wk/tJzRddizcK3+7x8bIAfdpbSMGf35vvrG32nCW0RUxflP+1eDhmrOTHvzddRzYHfuSkr1/L1NWe3yjrjE6Nv27FhNr6Bldos3WqVF53EO2s+3ZKAFTJrX5+SFjL0A8pmw3uTIS7rM8sFl/CD9Gfsnz2AC8j9M2ScDdbvpj4S9NI00EI7c3v39+5R99bXOrCR5xLOONlvm+ljpjgrTTddK6wxXbhiR55PV6L7V9dXp/OfGYWWKNqjtM44ITLVjp+gvY2do3tT1Ualv3HFt7eTMRRxctWg+v6xc2dAouxiUNFphYiSBKuQTQemdx/G16/jaN7+BPjJcCNhenGO5XGLXD9hcbODJY7PbYtF1+OwXvohnnn8BJ48eYbla4YjSuZDtdpvuPtBKhhLQ7zpfhOdytcL/7B/9I3TLJXbDgCcnJ1itVliuVgAR/GKJCIfQB4TQwzmPGEPyRgVCv+uxXC7Hm7Wzx0EyODGAPgzohx4pWwJK+60tt/HnmJpsjNedhmyI0QBWwBSUcucDoMigEFJ4GlFJs5a2xaaeYfldDiRar41uV/+rgB2mwkPXr3+WxVT+p61wTKxi3R4AeCKMl9dlzsoCUyL+0/N5xwCuGFs7Zgynp3Chx4N3304p9TiCeZqBpBLYeYHK9mGcWXwa4KednhSXnd39YKYxCwYwphOm0ZjQ9GqVlhHG6jv9GTMKeBzdF6Ox0zIuLPisnlPgp2yzjvgVslWdJ2SM7UTN63U/WU39vLK2/fPkUHKfMcAcyz0fumhw1QKl9rn59Tk9E1J4sxCVIPsDFThJxAGrXRjPgIdDJEJwjMCcUxYCXQQWnBwJg3foO4K7cwPf/sH38JlvfRX+2gF6EDwTlhHYPjnF6f2H+OC1N/HGyy/j/XfeA4UID0q3hAtwSUIBlJULkPmONNBJmY6IaoAvz4wGQw2cLUgZNR2rvznPlXVSSF31XOvf5Z1WiEpqd5xT58SDGxUoHT0wLeNO+lHWhvqUslyX238JecFCCKcM+30AkROvc5bdkNAFUElXOY5X9KgbqdQA07K2LG/Oj1HP4eiE0zLd0ljaygg40ZgyeLoCCNkHvse629+3jMkrhpZXdY98Pd0h37cLKp/Jv5ouErWReZcAQtYXhZfzroJLzlMI0CdxVUU1JAJo6gFnRo5UmOoFLa9aIN4atRVtYpIJThxxWSyIPEvqtUjvvP6nWbHsbnJkZCceyp1L+/iRs1BgtOVu5DhJVjNXqvHaNjDuNkiYoA6Rtoao7vco17jQJkODFN7KKCmU9RoS3UtU98/uyrbnbDyMX97jMTW2yOci2Shnmy2xZgqLqL9CzLoyf+Y0/xr9mGQVJ73Rpnj6f/4+Klr/XcrVQ6ck/SJGIJh+dwg5JCrPC7zv4LsO/8t/+r/CZz/3hXL4BwIQnYfzHWIEDo6OU/iRB/7p//p/g//mv/6v8ejR/QIg1us1iKiEKAnlRiGVFsKPfvgj/N7vfQ/d4qDa5QAT1usN+iHi6PAAPh+Sct7DRYcw9ImZVBxjiBGu8wj5ZtcIKiA0IoIREGKPJembqBMTloNnToSRUxhbJqod3+fy4vfOpW13l7Ij9dxjQQ6Lrks0LNiC0sV0sc7/rBcd89QIKgKYx/hdC8JGVZd7vofJJgqnAHfVNziA/ETxee+zcZVD8ICKNsJjWe2nRZwxrEdEzxHBL3CwWGAVA04+uAfvAI5U1VVlZVGG2ZxxUeggdKHM+FkKVRlXZCETCr1H70o6CzPn8dGKsIpTV9yi+5KwbboRfnxfhHTbQ6x/aroWIUsEdkmYRRLVKBIU6udohCgRUPGOBg36zIsWxC1DwK4D4U9CAj6dcwg83W+y87ZPYWka6DWr6VIBklCHSZEIOHk+B8C0vFpE6vwKON8R5ADn0XuH4fAAL33zK/jqH/0Aq2duIlCAiwEdA7TZ4ezxUzx85x7eeuVV3H/zHZw+epLSdjuXzmtkGefzXCQgYL1WKHwhBrFM2nTOKNOFJoBI03bUoXrNE4ikDm0s6GxJIx+25kdopW+/jhGlPg0cpQ8i/9Oc7/NGqt9V00GSa4hecwSSEKbICGpitVEwts1ZDrsyQjljUJwOSGfJRhkzdqAFSBKfTQ0y+V5/3jTwLQ8r2uk2qvdYQrbcOFYe04oLANXADaYvmibA9OxWawy6jM9NZYPVT7q9OUBud3daNLF6saaPrJm6W+lvAecAKMJ5MSBFximnqFpLCcvndOs55XMsdxzUdGrxsg3RapXyXhx31Thf7suyy0GoohnK8Dgb3YZf5KdT30u4HWNqbFR9N/SW31NoYnsco+6sdcP4bC3jrT6ztJtgGx4z1MmzvjgOM7bCGJIUQU2axHzPmT1fJsXqurpfMiapM/NQxnaUPywyzkY+sJgT2clD2XihUXrou461fqt0ZBEBdkeQAHIgptFQdLUxqmlxWfkQOxo1YClMb4SlxJq++OKL+PLv/A5WiwWOj46KYuz7dO9GOA7wfoGQPZb9boNPfvIT+MY3voH/8X/8H8DEOMiXnWlGCsYz773HcrnE177+dXTdAsvlMu1kLJflfIf3Hqen5wCla9rJLQAesNumXYZhCIXmwzCUy1sks4YsDGQBNISAwcTD6gl03mEIQ+m3fUbT0QpBJ4qKHYjSYe3FosvfAwAVmo8gqQZN+rAdlILQ1ngIARR50qcR0I7Czy5cveCsMrEMXW+bjp/rXRcr9Pcxb2mP04r05OAisD09x+mDR9g+PcN1Hrcg9TsFqO8pLSEl9GgJ1bn+yjN6J66lINg8X36q76ZgeuxHy0u5b0z2UCcnpJYNmP0Zn/ScJt5CMa4nisnVAtYKXAsEtKCudsgEfBHVkrPRvxbwsv23h4t121aQl/Xc8ALPCdtAQO8ICxAWgbDiZIBGAvrOYbvq8MLnX8LX/+hHuPuJjyE4AjGwiMCSPC5OTvHgnfdw77U3ce/Nt/Hw3geI2x4+96PruiJ3vPdwEC9ce60C0wOAmgfsuSIdOy7KeAy7EmN2qlTnDMkWjezn+uI3ey5Al0l8sZmPORroZ+fuAZC/rxIKMBeLPeHBxjO6WIBc64t5T7F+X68lu2b0eZM52boPGNlytTjy9vqYm5s5oN8CjLof5Xk3XfMtI2JfXVYn1Z+FMh9j3YCAXavjZ4v6WuS3vGfX5xw4nWCvS2hs+UEatzsopZ6MXXQ7RR5nB58YKYykgvkS54/QTvqgjQGuyTLBRJpG1U7CzLLQfGN50BaLT1oYba7MrRP7uWDh1pq7DOdcpdTvJ4PDe9FvORzMOMek/Q9bij7AlEevUj7UPRpWMcnvq2W6J0MAPpCyVN3/4D7uPuOwWq3gvMdi0aHzHZaHB1hjm3YMYkQIA4YwAMOQ7rpQyk0UX/GmKH+PHuzF+XmVXQFAUcwhBBwcHKLr0maic0AIhL5P7cYYsV5vAOQDmjoHckxGVgihgHY5I6KVq/7bLnrN9NYrYQ0NbWQIk/iuQxQQFsYDhpxjSYmoePvHbb1MBxqZxGbp0P2fMB/NL1Q9Vp0xRdpu0SG1O/Vmt4SJ7d8cqIsxZ5oaIlZugSfvJVDmAoM5pksO1RzkP2rp1ih2boqBQjXNxrAdN9l9kMOkli+qdrKobQlGMTQm/WAxuts0Er6142Ee88nr9xKP0NjmJcJZ00dAogCZOt9/e7t6bk51v+dAZOpq+24NSwsNNHR4lQbZ+pmW4N/HJnPCVoKsfCR0MYVg7jyw6YDjjzyPr/74B/jUV76E/sBjQymUyvcRfHqORw8e4t0338Jrv3kFj9+/j2G9TaFSjqrLH22IkfTCGkQaPMnvNgONHrs2GiWLXtWO4X87V9K/OXrtMwD0Z+NzFoq0M7LNGRlCq6sq2HFtzRsbLXCp+UzzVgSXcxpWFto+Cf2TgTKCqRYQb4WE2MPszDxJ62oNEDuu5vqb7G2PTiN9KVwL6F8FjMi6Fzm67z1LvxACHFIoog5FaQHVlgNF973lNGzJUQtmLb3mBwrItgGzfb52oMyBZNu+LfpznVygfhcFM+hS1kkDqNc/Ux0h74wgy599a8vOadlN2OM0snytx6D7NPeupYctc+FNzTBaJHpO70uj4pyTOuf4d4735nCjpUMLk8g7LreZkhyNhh/HCM6ypKV7NT6xMobZ6ESRO2TkwyUyVcqVDY3VaoXVaoWDgwN477FarVIFXYeF70qaOCHI0dFRTmmbDI/ddgsCsPAdhmHA0PfY9gN2Qw9GSs0FSqFSp6enOLp2XA6EFw88JSNDh42IMXFwcIDNeg3nF1Wmn91ul7cLfTpEjQgOsUxMP2wAEF5//XU8PX2Kz33+81islkLGZAyFfDt4YPT5cLkW2NrwSoq/FmzyU8YhuztNEMajcE+CNxliKWOWMB+gVUWIYbwB23r9HCBR7zpuMSmi6fakvCtFC+lq6xz1YpGzMjYueKx/3K6VYpm8pVD17xNBT4Q+BBATdhdrnD05gc/tDIHBmUi6P1KsMmwJpao9cIlTnCrrJIC1lxyo71lpgRM71lnwOgFzdR9tn+eKFTDVdwrUzQlzK5Bkt0/GWIdnJKNAAKs1QKX+lnFgFe04N1T1Q+hr39NzaRWtHXfLCCnC2tRn+dPSlojQMcEHl+Kjlx5nFBBvHuG3//A7+PL3vofF4SGGpQMvCBgC4nqD9ZMzvPJXP8Xbr7yKk4ePsF1vEh/HdMbK5bUtfa1AowqN1MBSyya909niNcvTmrZ12Mo0JtnOVWvHaA44pX7XAFHTU+Kg7ef6dzvvVglOvP1AvlB16jluARRmRglnMLTXvNei62UKubUemBkxDBDQ3SoWtLUAcgtsz/VBg6xq7MbQq+mNAhSt4at5rjUHtpR249QJptvV67yiG+o50XJBntOx83reWkXTzdJE03qi9xs8UeoUoxMEogiXw6JjFJfSSL/Wbqset11v+kxOS5ZpPS2v2jElQM0grudSlwSslUOKAfL7d+3sp1au67HL93os9h37rOY3vVsidJS+tUJ2pR1xHuv0+2ObaczyvnYwpkfaRtmEdupdO9YWP07mpqGLeZxMxBiw2/W1THF1OL29+NPKiHrHUtEhDyXGdDCwhW0vK1c2ND772c9WikgzOId6YQDJAHnhhRcQA2G5XIJWB+j7Hp1PZy1673Gx2cJ5j2HosVwtEbZbfOxjH0tnOjqHxWKBg4ODIjh2u125dl4rxtVqheeffx7H165jdXiUQgryd13X4ejoCEQdiBjM6QD4bhfKYokx4KMf/Sjubp/BarVKseAsqWzH2OeUrnSMwYwcq0vt9ATKz9ZE2Lhw/Z54REHJoEo3Q/TohwFLTl5jlthxIkAJE91eMbbm+sK5/2h5kUYml8WnzzjYRWS3fq/i7XTOlTs4pNhFbmlnDZPo8vkHOKwWC3S+AwEYQph3R9MIlmzfWnNV969dpQjeVrz/nACea2NfaQFd3W6rTju3LQUazdhb/W7NJXPNI5UiZyrphcUJYeuz3umW8q/6QrVaskDC0sUqHP2eBTJ2V48Mn7TmsdVfAuBch40Hdkcdnv/iF/CtP/kBbn/0BTB5wC3QMYMuemzOL/Duy6/g8Tv38MFrb+HJ/YfpTBMonRdwSPza+VlQw4n5KiBm6WbX1T7QaddBPT+jwaFBp27Php/oujQgqudo/N4q3RbAk781TVoeShvbP85QPadza7TvezCr9O2Y3rVi26zphupMyNxa1PRLn0/HXdZqI3zMygALXjQdWjwxK3+ynTHHK2J82f7bsi8kq+qHtKm7MCOTK/oo2rTlVO0Q0XwqdbR0jbyvIwXm6HhZ+Ko8K71L9Wter3Wjbrt63/BPc4fa0K3CBS4dXreOu1zjnnlM8lBM0CZ2adE+1docgxiI+ruW/LHjESq2+tnCE5ORGN5vtadqFAhVdN1Yx9yezLTf9u6YObmmQ1dlfufWpx3fMPTJeYyydAtbzenZlpEj444xn2V2DhFIDi+q67sKvgE+hKFxfHyMEAIWi7RjIDsF6exCWrxdl0KjQOmsQwgB3i0rL/4wDDg8PMQQAvq+x/LgAIvFAv1ui8VigY985KM4Pj7Grt+Vcxb1XQQoqchEaCwWi3ygfPSqh3wAKmRA65wszAHDboOTJ4/Q91u4bKEdHh7i8OgIb779Fn7161/hG9/8JspB6sh5F2aAY4wGT2SwazOMFM0oGpCJ8GqFC1Fe1C7FeJWD7S4M6d4PyzBmcWmhy7FeSEWIEcOhm/Hy1OBAPtcAR7cnceMyfruIdNHv6xhieymjzKP2zmnmJiL0iGBKl/YBadkHTrdk0ng2r1nmFJCdwwoMzFcGSSvbAlhzC5KIRu/QDL3m+jOn4FsAzc5Zqx85ycqVhIduI8aahq1i4+51G3uBzrSnFQjTRWRESzFrBbFPaFfzL5K6AeLHeUNxCsjnwXucu4hrn/wIfu8f/hgf/cJL8MsFiIGOOoQ+ANseJ++8h9d/8Uu8//ZbCLsddutt6udikZJREJWdW8L8jlda4+1Un7NUbPCENjxt2N/47H7jU38mfdChry3vcDpfFqvdmPH9cRG3xq1/b4XGtD6z3wOo5LH1AAqPk1mDc7KiAgZXVMLCt9Zwa43bvrePn+347Tq8rH5pw84ZMMpCK5NbYHPf39XnvN+zq/usdQXyGpTPW2mQtVzWc3SZXNTzYef6KkB7fAGlrxKtkL4WPmq3qdtu8d0c2Nb9sXXK363dvqvyrHOunHeyOr+SQQ1+K33eI/a1/NDvJXk3D5BbYNp+J9/rdubomlRBvYaKLHb715Jur+VEsWNt6far8Kn9nlyKYaE8AI117G6ENnDm6mQe9zYZ06MCVylXNjRu3LwDifVKC7lLE8BAP+zgQDhcHcA7h8ePHuUD1cB2t8bFxQVijLhz5w4iGN1ygfVmnU/Kh7wDkcC07xb4xCc/jT7ssFmvcX5+DuJ06PfZ557H8uAAb731VmJyTtt9u36LPvS4uewQhh7EEefn59jtety+fQtnZ2cAORwcHKDrOmzWO5ydr7FYJOIOMaR/IYCJsDo8Qh8ZHIFhu8Nuu8N2F9CHROrzdY8Y8yl/4RnKDEljqjIposDkvIjkN7cCkSNAXbLXPVFKa0sEeA+/XIK3WxApjxdROrtRCV3jOUwPT4RXjBEx9GlHJnOQ9N/e+9ASTFYA6HpbCzdN15i/XQs8aUdv7dntfyvAiAgIAKXYsGRIhgDilCWCcgpM0UNFpnMtwCfGgcsgEpyzSOW2ZJXxCDLHkr0bzHsFSpnnMh81SNX9sYdW6z7XoLkSoPKMrj7PLYFGoSmfkYQ5UTkTUo1srzBJ49ahc+UbRyl2es/unbx7FaOjUk5a6gFprK5Wqvqn5R9NM5fDHMXISlnckmxJZ6RkTIwATmvNJdp1cKCBQXDoidIh8Lu38I0f/SG+8M2vwh2vEAnw7OH7iLheY/30KV7/1a9x/uAx3nv9DZw+eYJF18F7h2WX5tU7X/U5hgDJBpX6LiEQBEmzWbyDjkYeV+O3ns+QeaSsqZh2FgrfU6IpE0Z6uEQxqGwxDAEUI9+VA7rAGIZGKVNbOUgK6Z+aUi+5XpCM9/wFUepHCcETPuYpX6G0FXOoZrqniSjtElmaWGDSCtcE0oaGrNn0jDKuiUv2uhC10dfg35m/tbGT6NdeB5eFLVgw1QLeU3qNv2R1kX5S/bzu86XAWvVBAx37ef33qFtqQ2LaRk2HWOYGxCgmMdfvWf3R6pP9nVlS0CLzW6q4ZWjaUvVfZFYRWknOJPnXDqfZN78tOui+l0h9opxNjMGBK8eWrlPCqh1quVmeJT3+vJu1x6Mv/WBmRA4lg5lEYYBlB2tmJ6QBvMvvKgOqXLdALsnyEPMdKMTlduxkFCR8JTSzDikp0zBnLlOm5UP6AON6Qb3exQFnsdAcz819ZkOt5kpkRuedShxEJRXxPh2uHUAFe2T5xggAkn5TyqfUuQ/j2HJlQ8P7Vcm8RM5hdZBeZTBo6IAhIg4R2+0GDz54iNXRIR4+fIwnZ09L9qjl+gL90x4fOzwAdR4L78vac+QRA0B+gRs372C32+D6tZvo/AOcnpxg2S1wenKCT929i5c+9Wn88je/wq7vMYQB5AmbzRoxDLj//kPEGHF0dITT01MsFx2ePHmMyBF37jwD3y0QQsTh8XUw99huLxBiwC4MCDHizrPPgLoFtrsBznmEvJPRB0YfkpLcbPucr7hOKVmAOidQJ8BZ774AKZREA+zCkH70YDoAu2GAixF9GLDsFghMoEhYkAeIMXBAAJeYY2Gc0p+syGGE6vg7ox92KU1mTjNbxlHkVDvuWSsE643TwEbGL59LaW1d275bg0B+l58eKQtCiAHOMZbOpRR8IqCydB/bHQVH03ABEpBU90ZEjqN+KIc+pK5RKWuh2FKSU5CtAaP9vE3Hsc6itaYLPoqRkSWg2tFy3kFnUivv5Tz0rR2guXFoA0WHRlWKFVNBqseQPpoK3lYYTFpTKD+zKSmdKqhI85JWmK2xiMJL/9LwBQiDkqHvclYozlqFHQBi+JD75DtsCegPlvjCN76Gr/3JD3D03N10l0uMWJFHON3g9NEJ7r3+Ot569WWcnZzi9MkTUIjoQPABIKSU2jI+R+NOhc9zI9nxUtfHM1t6boqckfEDE/omw4SEcYvTRk8/A0WuCOAsNwNwal/TthiMlNODu5wgQQwfncYzs2aQtZUUQFlWYrgI+ITweAjFSPHcBkRE+VZkGuuT3/Vt323DdwRdukQWXqVisEi8e6J3PhgNGmW48JyJn9fF9tue22sV/Z3ekWkZ1zp7mD3YX81zbRFlIDeKAwv6CmAyfbOAUIBLaOzCt+QKg+HITeZGxtg2TrgKpWEedZcYxCIPpD0LJm1I7timApGghGYRwdwjxnoHZ05GlrGRwHMuRjYjKlpPz0bY+bT1T3YkqKym0ZjPPyPzmGYZNKm7GN9mHVj5rWVx5bhSpdbXcZQrnJwHpT01VS3azQLkJNSKc0UuIHRecvClURNlavMom8Sgb2GL1lyK8W3HVun58uX4nDhEWmHNpeYZzGBpbd/Rn5fv88/lagVwvkg76xCRLS35Y89WF0ODCClludm9YM73s0wx3b5yZUND4ul1uJJzDiEGkCccXltiWG/x8P4DbHc7nK0v8MH9+4BzWF9sMoE8NusNnnv2BTBSuFLf7xBy3eebC8TIWB4cIMaAEAbcuHEL64sLxBgwcMSDhw/xu1/9Cp594Tn8d//9fw/nO4A8zi42eOvd97A+3+Lo6AhMDoGBp+fnCBE432xxsN3hgH3auQDh/sOHOD4+HNPbRmC73cJ3C2y3O8TQY9ilywL7XY9hCCA4bDYBYQiThb5YLBBCwGazKedEYozl4LwtIgBFGHvnEmP4LhkyPFr+lHcnRgDCxRvA4BweNioz7aUvQqRhELSYXAtibSRob5+EO0mxAgmYZlQQhdDadrPhCnohlUQAVjCyGGsBm/UGuHZzHMMe/td9tQe0dGkd3GrVVfoKwAoLS5OqPqAC91c5AKe/03M3zjWKkcFQ94QgYXF2OZxOeebEdNlX2lul6d4FTYvyTAaKrUOJljb1vGIyphY9bF/s9rbUYUGj7T9RrTyknUjAzgGO0yV8AgQIDAqEQ/ZYO2B9vMSdz3wS3/7jH+LZT3wMfrEAwoCOHGI/YHPyBI/fex/vvPI63nv7bZydnaDfbMH54j1XlPXUGSA/7TrVxYbqFcVJCQa0Yri1XJEi82Prq8OnAH1fhf4pcmMSBqppeomCl2da89j6W+rZp8xr0FOHEEx4yIxHCqVOTvoxAuga5Ou67Pj2tSUyVu/kzL1ny9xYgGk63jl5pH/fx3fCC9HU0wKuLcBo6y+0iDHJJ0N/DYLmaKDbaY1F00E7yOb6l2s1dXJZA1pOtWggfZoLeax20yajmRoP076N9djvGPXatuu1xVfFkDNOqEJzc1mQ6Drd0j5a2Plm0UszYNoW+WwuZEfXb/uTcNj4u7TfOktqaUTFQLy81GtkurZn+d7IpX3zpOmh1404lGJxprgRC1Abn1m6Vcb8nrb/LuXKhsZ6vcZqtSrnMpjTPRdHR0eIiNieX+D8/ByPHz/GZr1GAOPhw0d49sWPIHCP5WqFi/UWznk8PTvHZrvFwEAYAnabLRwBDx88giPCtes3AAAhDHjyaI3F8gB9P8B74MnJCU5OTvDpl17C7Tt38ODhI0QmPHnyFM4dYHV4hPuPHmN5eIS7zz6Hx48fI4AwhIghMB6fnuH99z/A6ekT3Lp1DYscPx2GiH6XDl3vdgOGIWUiCH1f0tkK6O13O2w2G+x2ByVvsUwaACyXS2w2m3LGRHuepAijayAdOSJyvpwuH9hKtyKnbVbvHCIPBfI4l+7rcM4nNIRaiDNzybClt+alEBycS8w9DEMlzK1Q1wtA5l94wSp6Gz40LpzaYCn9ICq7KhMlr4SHNYjkM+ccnE+GK3heMMwt+ppuI32qcAaipvAu9ZnPbVtN42OPkuP0x4zQoUa/5wSDEiRFwIuXhgqIQkNhXNaGKF1NI0sDu/tlgaGuV/ONBaX6ZwskgkeVp2m+T1gX80RNbDWvnL3UDHTkAUYKZ3QOF45w/LEX8LUffw+f+sqX4JYdQA4UGLQdUha0h0/w0z//Czx+7z4uTp6iH3qgS2Gg0QGI6VbjOSvPhkVo2sjftt/VWtlDs2TaTEHZXEk0TXKp1Rd93sqCbv28BWJEbVA5Po9mHVmTX4H/a6+15qvWTmuTDpQu4JMMakXmFMdQG8C3gJb9XvdFdh3Sgd3982H72TIGgDE0Qq+/ag5MX7Rh3gKH4xim7gm73lpy3uqGSmYo+TAXPiXft2jZMjg1sNROD70erJ4a+5vGOc6F/re/zAHLmvdl7LUMsPrtMj6Q58rvZq9B2moZahoTyA6BrQ/5W6FFrmRiZFzW1zYPtccxV8/cGrN3VrTmcy7sUPP+NBSt3tG4apHIgZZu2yerqvloyDcrUznPQwqPI2y3WxlV4anWurM0adF7r1yly+WTLlc2NM7Pz0FEOD8/x507d9IB7r7HwdFh9vYPePjwIbbbLTbbLa7fvIHtdof37t1H1y3gu01JIfboySn6oU9bXTEBeoSI87MzcIx47vkXEGLAdrPBnWeeRT+EdKYjBoQY8cabb+LTn/kMvv/DH+K//Zf/HWIE3n7nHj54cArXLeCdx8PHT4vwds6hW3Z48Ogpzs/X6PsBu90aZ+szHF//TLphuh+w3fbYDamNYQi4uLjA+ZMncH6JgR2GIaDnAIQe680am80KR0dHhUaixPq+x/n5eWVktASMLJAKOOT3mbIlPvSlbpKQBLnTI1+Wo4WoTH45p2GE6ChkAeIxA4XsvtjUvdIvYTphWJ1OV96x3uN6kbliWbdS+zKPuzIWJBJRtWNjAayIVtl1IxIPdC1M5rbfNUjSW8e6b+n36cVtgMDVqSCwQkLPMxGVPNwjjdSY0fYQjm20lSMjhUiBs5HpBJhls4IURGCkXY4chOSdhzUCpGg+LuPKlemD1uP8TYGnLVYBJ/7iSrBboGaFZWkzEWwyd7rvkzqBKra24kkGlpx2NIgTzw6UwrXctSN84fvfwZd+/9tY3rmOHgEuAqtACCfnePLwIX7z81/gvdffxMmDR1iSB/oeHcmt1jEd1svGgISuWTBg51fW6KUH9xqAU9NLcLqlkQbQspYkzDNTCJL0YE7xaaeKPjhp19M4nykcRa9rKSFMs7jJe3L+7DJlZ0Gb9WhaulnQSZR2kO09DVZx60srtTGj/57bOdV9LfHRBnhKuYrxoudhXFd1KGFr3HN12v5bQK9pNQew9XP6vWoHi9qGn6bxHN1adBojK6ft7lsjLXmVPkuGNpGA7qlDxrZR8VMDJCadTxPTpaVH7PcthwMgw24bgnOAEpDd7xEnSJKXsZ+ogC2F0diwckD3sQWUy9zT1EAFppksW/1t0cjiB3m2nO3iaZp++/s+gG35uYUpWvRtrY25umUce+e4okHeF8/JM3S4YowRjmsDqzVWeacVeWCxq1paVy4fakfDe19ius7Pz9F1HfrdDovFAvdPT/H06dPU2RDw0ksv4fHjxzjvH4M5Za3qug7Xjo9BtMFu2KFbdthtdzg7PcVmvcZuk+7a+OQnPoaPf+ITePXVV9F1HW7dvoMYAz54/x4WywUePXmE0/NzfOGLX8LJ0zX+5qc/x8nTc1y7sUS46NF1HZ6ePkUMAcfXruHatWtYcrIyh4TEEMnj/GKLR0+e4va1Q4SQjY2+R4iMIUTce+99vP3aa3jps59DtzxMOxuhx7JzOZY0TeDFxQUODw/BzOVil4uLC9y6davKmGUnV77Tyk/+i4zkKcvvDGHAMjMehZB2PxCrm1E1MxXFp5hkGkbClUBpKTS7iGz4QstokFJZ8ahTBlrBo5VJS3DP7gqFiAjG4FBC8CIzugY4uUyBxYZyGt/ZJxgA56dCzyou24eW8ii/pw8mbab3ACgBTzTmjgehbJ1ztmM0sAZEqbEaUjJw9fzouuf6aJWE/ukyKG/RQT/b8jJpYWvp1Prd/tSg3SrAiYDn0S9XgQ9muBhBziN2Dmti4OgQn/jSb+FrP/4Bjj/yDIJjMBOWAfCbHrvTNR6/+x5+/td/jXtvvYOw2WIJhxh28J3DECIopnAz56ic4+i6LsfQTvuhx2rH3lJE5ZnGelS1VTxU1z8azZa2wuvANIShDczal0cCOt0jAEzB+1jHHrDRkKtjB+pnxfCx61DTb9brqDCbNURkDFpWttbMnPJu0UbTufVeSz7a91s7gnOFQNVZw7l+jX1LfGLHa0HY3Fitrqr1TDvs9DIg1+ongJKlsdUf/bzm5wnPxuySIAciD8YY5jsHpC099ve53klvPSe/W53clGkzoVNXLW1dnO/BorzsGrtVf9+yTx/qndMWP+7TBfK9XEuwby226omYGgr6vZbzR3SxdTq0DLLW9/by6VbR2KYS51mWOVV/9az6XYq0p3f95su8DJorVzY0nn32WXSdx8HBYbqw72BV0twe+HSR30c+8iI269u4du0aPvGpTwJ+gWtuBUCEODDkBb1YLgFi+M7j2rVrODw8SGcPImOxXMH7Di++8CJOT5/iYLXCndu3cPPmTWy25wixx+Mnj/HCdouvf+MbuHHrLg4OjuEXK/iug/cdrl2/DgLQLfJN451DHyKWfpmI3DkAAx49eYy4uUDnPYYhguDAMYURPf/88zherXBweATyCxwdXwM4oHOMbjGmdD08PCxgDwAODg7w8Y9/HM65Kn+yVmpaaIzfJS+xI4cgYTtIWS9CSPd/MAi+67BwhN2wQyQGD7FSugKygDozlmaydB9HBtgqdlXncLaHvfXCai0YwKR/08xIdUDTdIsSE0NILwgLSK1V7vLFZqNRE6p6dJt2YZd2MLXUx2cZ4LYnmTBVCHZh6/aL0BKDwAhLSD9mgFy6z6DeYXDOpdoE4IOTl98IyDnDSV+mqI3jfYaGBWfSzxhrA1ietcKs0M8ILU2vuR0WABV4jI3v7TyXtojK+Z6cTmg690QYHMAdISw87nz6U/jaH/0QL3zus0CXstB0zMB2QFhv8OC99/Drn/0tzh4+xNN79+ECQJFAHOG9Q3AER75keiLQeMg6RsRsgGh6WO+7VRR6/lv02Vd0XfXcjcDZApu0mzHfloAvCzatEi48QgQ2h7qn81d7R6s0xsxNQ9WuG3vuQ/fdnkezQC5XWNGo5qWc8W4GhFiFPld0ncxtwKSftZ/J37JmWsC52Q9K/+QGc1vm+5+N5dg+g7DvYPvsDk9eF9LXufdbpfUsM1fnSDTPt4DUFPDlfwSk27yz15imstyC/8v6PQHV+nc1dsurdf/Q5le2pkYbTNtCQNqpaALozI8Sglj6095t0e1Y2ly1TGXTVNcA7XNqVvemz67c9N7xaAdY29BrG0Bt2dJua24c9vsiE2OEnJesNDzVOqWF54A018MwjE4vl84PtvpMJP+7ermyofHjH/1hakTiPdWg05VpAJgR8yHplEHFIYCKp1gGN4Sh9FOy+sS8Td51HZCzCDz3zC04RwjDAOfSCflh6BHikA5mOw/A4Vvf+N3ERNnjQJTAuTBmENBJCcTHyAAxhqEHEcMjA3XOOwnOYbPdAreuwX/kueTxl/CJoUcIA64dH8H7FGKwWq3KRIgXQC4atMyWQp9ivjZ+XKhOYlpAOVVnCiPxqVJg6EExgLlHJAfvOhAz4jDApyOqYI4gHg8/xSh3nKC0r3PkwwBiGyPfUvxNkJ+VW0vo6tKK4weSCCOXNDaJxyQbXQIEbR9iTHzjM50657DsFnmaHQjtrFYC7LU3n0pK0Kk3qy4j8ClbxpmvNG0sgIvlWZ6AWSv9KuHVNBCEdhKSlBQgURpD5Ho7uwUCWsB+3yE0LagExAAYw1cklXDeLSGX6UgjfBfFnepKw7bCr+WdbymxJvjK7Y9EQjEgHCf+SsYdSjYnMINzOkzPBJfz+AcwBiKcO49rzz+Lb/34B/j07/423GqJgSIcGBQDXB+xvv8I7732Bl7+5S9x7733Uoao3QAHQteldegXfkzgABR55DufjQs0i95hmgMxLeN5/H0Mychckng9Jv7R74xtRRD5IkPSGTSRIQzm+r2WId1Srnp+dR+ToSFzKeGOY9ij5l8dLhlDHI1q8RzKOqD6vRa/W4Bg5Zq8V5SyAcBjvfM7pq3npf9TEKT+YbojZz2NbaOsDTz3yWWO3LzdOa2VJEkkXbs4VEZ5Vtdrf1rZJT91PH01pmx8M+fziLJmeJQd1gBr0UK373ztkLG76i0APr6fQn7FgaPXkpVR9buJryVUR8LlRxhIRR60boDX+tjKOq1zLR1af0uxO1wtR1/BBcCUNrnnzmUnqMyfwha6n3Nrq1oP+XvBQuMr4w6bxiFzRkol/1i3K4YrQ9xvLf3R0q/MKuuWkidWvk3GVOpp82dLn7cwkZab++oQGaRlr+y0FbqhLZukXuENMTJKG6q9Odk2V68tVzY0bt++URaqFZR68JYwujMpuxMDWKgFsyh1SYwYM8E5rya2Q98nAwMELBZLdB2Xi/pagk5ijZOCGy/yA0brDVipBTumPVssFgjxCLvtNt3hoVKDxZj6sugcKO8A7HY7MHM5AK4Vohyy1rQpsdaUQPLIk6PnUPLYE2WhFBPAEa9KyLnhPRxcziQUYmbW5N4tMa9WeLSEjJ3LOSZvKW0ZUytMrLSLKWNWwjONDGJ8FbFM46Vw8k5pOx+m9eQAvvyCLt2OPCag14K1llLWiLDen2mDek4IavwbKGcmRAG12msp55ruI33GStLZBlJ902tC6rCAQ37OretCNwOK5HeXjeI0VtkZGVOmWtpouaS9r+OYp3SdA1d6PBNxR1nAChgSo5UgYchpDJHzu+nukugdegL8tWN87Xvfxpe/912srh0g+MQoB0zYna9xcvoYT95+Dw9eeQtv/eplbM4vUopWoSEBgQB4SndWQBmBWXH1fQ8iyucg0q5GS3i3lJulgwV2lIFReVx9Frg2YLR3Nj1PCCGqHYy2opEdKlFu1ps+p5A1eJbJkn7GyHBuCt41DbRREUUhSv8a77RAaYueFsxbAClt63mRZqfKf/y81f/WLs/Yh+Q00DS0IRj6c91/O047ZguYiKjIzklhZHg21sPqfAKbPs3p/jkANZWvqVE1lRgNjBEw6TnS9GgBuJb32c5lS8aOdJJnFA14P/gSs55BWTy7nOVZ6x0BhorYmPLZHGC3Y7f9Fz3T1GNAk5f0fDVlLajgDn3287L3WyC5tM/JyUyk52c6F0Adtt3irfS8/jfyiGSdsrSsaGZkVmnbjXOyD7BXdFW6rmXk7ZtX26eqXjMG59J5TLl7Z7FcYOEdzs9Ps8tmugPUwhYaRzNnx0pjqII+9uGsVrmyoSHC0Xqt9GTJwg751m/mlJlKBsk8ghnZ8pEByiT2fT+Jx2sBL2YuWz3yN9E0X7BMRuuQpdTf97uiNMsBqBw7jUx0eb/rupSuloAhG0a73W5Sv4xPLwhmLnNnFaCMTaAwkYPLlqojQh8jmFO/ogC7zMAc2wunBTQrZYQ2U7c+s3227dmwsH2C2Ap8xFi8ZC3BMdcXT4RhCGBKt7U/fXqSgQ5no6xRmIunrlXmxp6/rNq3dNF8W94tc1q/N6fk9HN7+2L6W/7GKB/mlPyUxtMQgBZYkjrswfAWOCYZe0OhaR4Uuo1rdD60oUWLOWBe/Z0vakPMa1n7FtmBvMPgCP3KY90RPv5bn8d3fvgD3HruWbADIjE6Bng3YPv0DKePn+Ddd9/CX/3bf49uFxAutmOoWFbCc0B7bi60TBIa2/lvgjP1rpXLWrnq8EidgKI1J7odHUqpn2cePX5yAakFAPscFfpni0dt2Jwdq5Yz9m/97L4dSiubNe3quqe7ffZZPf65tnSbrXHZtafHNgdyJnd+mBA72wfm8fxeeYamjpNWv1tF97El++14rQ5p0aB1lsY6ZWx2LD0+3YbeaW+tE91ua+yWN22be0vFM/WYmyF/mPKBlQ/y7j5PN5ddoLqvrbrq7jJAbUekHhKRmFKAVaR27dvSkgWaZ8vaN4aX/N7i67n65z5vvW/1mqwRCWFv6UWLt+pnRiPS8rLlx6uWyzAXAJycnMAT4H03YqA4vg+gcoDrsVdzRvM77ckImflyplzZ0NAEaS1eUV46TaoYG1p56thNq4xSaFK9AyCTLulPdRt6C7alCDXzjPSrt6916lqtOLuuS4ZGHAGAPqAjl8RoD54YKQDK2CVbUtlFSebghKbMyQyPIWJgBntfLo6Ti7NiTOluHQhe7c6QEQxWIGnaVFuujYViaWfrnYKZOkRptpjvqn5hXjHCxIDquQ45fIpz9YeHRzk0bWha42Ucajx2nLOCbM/Y7DsVSJkZX4vugDKuZ+g1t+Vdfk+VNpVVRYMZBdqK37yKgp20YwCnNrpbYG2uLeHZFsi2wrsFOED5RmoAHadcZJJRttz27Bw2nrB47jZ+/0d/gJe+8jtgTwic6d0P2F5ssHl0godvv4c3XnkFb7z2KmiIGPoBnfOIhBLfbMcnfdIxzTaO3hpv+v2W7N03HwIma7Ozpqn+3cpzvbsldLdzRZScQjKvmm/0O1ZB23myxRka2rme8+xXa07x2T6ZNAd4dT/F+A2hdrRZuWfpOlf0Orbtyffg8bZoC05a/GH7sa9d+y4RTTyUhWYkYY7z7en5bfVxjl+b4KYxjvrnfmNHjxUY9eacvGzxpP5c02yOn1v1jkZF3UcJQav62JAVwneWn+2YZ9cSA9W2LabzK0DaOkhLX5VMkDo5Oz5TGv4UdUGOipGq18WcrtNtteatjEkNpyUL9O92bvbN+dz60LpG10s0hgw2d/1MHQXfonZot9Zuy1Bo1al/t1hBsHGR20Q4OjzEk+22hJ9J1imtR217Vu9zlNDnmn5gBtP0/cvKh7gZ3E+2IeV3KfK5xHppA0ODdPlcwo705Mr7AKrdCnlGE1ZPnmUUeU8rdCGmGBJi+CwWXTm7oFO1WmDAnMIdFvmAOWj0+C2Xy9KuGBXynY1J3bcz1HUOYRfAGA88yjPO+bzLkheloYGuX/4W2o/gQ6WyhEOk/ecxdN+sUtHzavnCbuPLYrWKxefb4SU21wrgFCfuq/7rfjjvyiU1wi+SMtMaKenL2ntnF7nm8aqvzHXYkylCD61gnXOTvROrdK0SaYEoy+fST/tZwpUuHwyb3sFgaafHrOu1wnoOKNjvNIAKmXaX5TfXijeNqb2DOadsLgNfQhfivNPAABOhR0TwQICDO1ri81/7Cr7y/e9hefsGdp5A3oGGgP7iAuunp3j07vt44xe/xv0338XTx4/hnQMxp2x1MYI6n9LgqjWo+5XWPCHG6UWfdiya1i1A04pbnspCmdvp3LVAsvyuPcU2A5ydF6voxnFOPa7Sjg090p+1dp3l3Rbo02Owv1/2zD4gJO3pfrbqJRLPXtsJZ+sUXbAPXKfvU5VzckGe13Le1mN3Nlr0sGC2Bab2AR07Nr0GLT+29EurzjqMT7dd+3qsA83WTURJd+51Yk1/b8m81hq0dcm/NLdiqAH4//P2p8+SHFl+KPY77hGRmXetfQVQVdgbQG8z04OejT3L47xFJtHsUdSzp7/t6YNM0jOZPkgyoxn5hkayh7NwONMr0I3GvlYBVaj1rpkZi/vRh+PHw8Mz8tbFkJTDCvfezAjf/fjv7CHYwUmwbIy+5+ula6oYJV/LnK57ljDn6dqna5xniicSgYzecTmNMsYgZpKUl4bvZhhi3drn9F6fWclcHfjKfG3G9lIOktdh07E7La9zDAs9bS/kdDt8ivyjtA/r9vm6kp/lwWfeB1+kVEgEqEmk7yQgUL4HIoZK6HWcH0ODPRvblooirnna2dDyjTQauYor/U41Az4BGAr8XAIE80vJOTdQ42jnNX67MQZlWQ7qGQN06whqvrCqYUhD0zH37eqG1/H6TszAmqYZvGuMQeu6wSJoe9qvnJinC5P+HQEaSTg+Y40kBiP5XyQMJtTnRKKQm2jk9eYSIyUI0SyD/QpBGSvpOyepfNPx6Pyl85nuyaHkwA/WIK1Lzdd0b6Xce2H6JFp17bBcLkCkkbaGMdcjEQLBGkKXZTbXfT1GMHvivf6y0jrSdY/1ZWYw695fIZQjfdC5G/RrAFyG6/A0jZN+lpvq5GPK52msv+m7higkETpZiqQ/07wszKv9H+v7mPRprP+SmNKAHYew0EBjgbYgXHzpBfzuH/8IF5+5LsyCMZh4gq87HD95hId37+H+na/wxYef4PjJPlzdhIzegAPDiesuqkATTACfOaOR0iHtc/r7aeYpXW89V2n+hnX7Mc7DCN3Ws5326aTQijmAyIVEufY5pYcpuBgrOa1M2xnryxj9GRvr0+Y1H9/47/07A3DCvfQyfye/A9JLPqdz6Typ8/O6oqYPuVBtrO9jbYztE603m6GV59fN8zozt7Q/J8231pEz0WPvrKzByHjX9eO0z6Tt5+MfO0dpvzQqYF7lU+n9mvtUy9h6jzESAHpBJVbv5PTcpowx0Qlrln1uaFVz+bSSjjfPH7ayT7OxpQKMk3BHai667g7M1/okOnfSMyeNkzUCQFZfOldPtU6gIQM59qzOlWhcCW3boW1bKP3wzkehRXrOczo7MgqkA4jzDBLfo29YvrHpVHrJxS6NXDIDsJ5cZmPENwV8VVWJiVASsWkMrI9dJvq7gs8xVVe6yVPtBRFFhkd/ei/hdrU+bUO1GgBWtCv5nK0SQ47c5brDY40Rh03dkGR6RiSYC1GcS2CduCS3ndaia2jIngjk0jnL/x5jLPR3BSuDzb0mTrj3Hi4kHkwJ4GDt3YhkBEMi2XUt2qaN9FB+jlwK4WdZlqMXUE5ctE9EBPh1h3LYd61LPh9moB3bk2Nt5nXn5y0HKzopDj0Ry+sYa0s/yy+tsXfzvoztmYGkcYRpS+vIpa49c9b3Y0XSsgb0EBBNJdSkTh3SYyhbInhj0FpgdvEc3vzR7+PG996AnU7RhchlaBzqvSMcPXqCB3e/xMcffIDl0TGO9w7gW4kmxQR4aRCm7Jn3wloYYwdmlSlzoSW3kX/axTcG/MeYiLF6xtrQuc/PLXOvNUzPW37W9TOlXWOAaQz8rCs90BkHBbrfc4Y3/T1tb2zvj+2fbwIe8r72oBhAEvJ37D4aA8S5RH5VILDKsKTAII0Ok89Deh8PBEtPGdMqqMaKRiDVPq1b27H5XmcmchLjOQbOhnO0Hryn9Wv7Y0IkGed6f6Ixuqn15vRLi/RZQuXrMp50Ak4yoxqrW4Wd6bPpGWBmwNDKvsnv17TEec60XP33/Y48aSxjTEDafr4P8jHH92lkTCPzkc6brPH6OwLohdsnlfysYU1934R+5OdBz/D42V8dW77P9HNjNAKs/CuKHnsbonh+9Z38PkjXIf2cgYGsI64VQWM2fKNyakYjbUyJWCpZVVOkITCQ3vSMh+iE48R6mQxrTJQW+64DkosnXwgAK6rDMaKdSzsVdOv7WoiECxyCQQsFqRJpkaItog+HGESwpoBGSLG238DW9IxY17Xi+R/bE3MaBeIpaCQDdC2DveZ6BIy1cJZDCGEjph8siisdtyUTTZN0fOn4U+mBMjcAwETwDPhgi642fQwEs6xx4pfXlRM/neuUUPuwH4hE2u0p4ZmJomP6yiEA4OKch31CABsT59Z6SJJFYjhilAyATEhYlzK4gWCyiZeArkscOwXVN/XrRSQRxlIH867T9QsEDmJKRyGcIphDlBSI+3EcW5gT5ii45DC/AxJDvVNxulf1OzYUiHEIpqQEwwAWJp41awW4a3QoLekZygnz6gWRgIGwJrp2StCMRlEJTnA6RkBBol5eAHReRsBN3o8cDKffaZ8MGRQhAEDtHbwJAMlIyFrbGXhr0MxKNLMCb7z523jjd38Hm2d30cKDnYf1QLd3gMWjPRw9eIJPP/gQjx49wOHhgQgGnIMt7ADkqe+HCbQPgcalF2qq4UU49/lFHsdhTW8vz16YcyIUZRVoj4fnDiHImswjKNIUBoHIAsTC5KG/mMZM4rQPKniIEkpkzuHpfvB9iGhOaT33OQsIwmTqPom0KN3e6M933JPeD9pK94Wa4sW7IRkHMNxL6biUNqX7Rn/PtXj5+30/AO4nXaSV1N+18dLX215e7H9PPo89JgJgZK1YEkOKAEo0oCqM0n7m2qAcDKVnJKehuoY9/ZD/eaXxSMdKA/rOGPZjDLTos2m/0vbXzXHav7T/Oc1L28/38xjwzBngtK514PBpAqD0s1xomtYvzwCADzQ41TZS+E61YfpiX/c6GpfORTr+lOEYYCAaB/3r1kM+GBfoxD4SSfJC7QN6OpSehTGtydha5XM3YIjX9HcMF8Z6WXLaBDCknjKhAbmPx0wbU2F43keJrjWcinhXmzAn+VmL/ernNN5HJHdzpPPJGNcJUsb+1s/0n4dHEfKtyZ2MgBWTPmdnU8eenulBWxr9FIIVg54mCoXz/XlSOTWjoVJ+leQDQ+1ECi51AEqke0DWf+5DLgn2PgxiyD3mdr6Ufa7/xi4O7VN62aumhXmooVCwnDJQuumqagLvnTg+WQsTzMHU6duadPrChc/isG2TzZ9LgcY2tVzKJEnnIBcOE8O7DiaYZbAbOqCDaOVS0nmKTE8CINLkgRxAIBkLglxuRu1J/arZUXootO9j6s90bdLCEEaqtGUEC7o2Yxe8rmmYWhAZwIW1iJ+TaDskrm9IAklgJwnjPDM8UmmwqjTFtp4SABDjePMQQER2mSWSQ0rgpI/SwbGLKi4slICGd8MQvZc1jgd8sJvWlwGDkv2t0g1pq98Dcrmthr/MiXcOIOI8JyBySJB0XhXM5P4H8hZR/7z+nmsr+vqGfXxaYTBaS9HJG51HYW0PwicVXFXg0rdewG/96R/h3NVL8OzhmFF6Qjuvsf9kD/v3HuDuJ5/jwZd3MT88xLJZRiFJqsWNl+iYpiGMIAW5g4sHawCPLhwLiPXeS/6NMKfOqZYX4W8Ha00PYpNLRWkRRsBKCiZ1XOm5S83dUq1kpKvhzK9I4ULfB4xVDmSSPsRzhYRJSH7X56BnML3Mw+c5YNIyBiaQ15HvoRMuTGYMHHm1//2Z96tr+tS9q+BMzo/QGhmX5pQaPJ2BgbG+5+cpfT63qeZ+9gfPDuYx7MWx/bNS/wgNz8+4fpeC5NG+jgDk9PccLOV3RjofIjRcnb8UpI2BppTpyffGOiuAcWAfxu8JKmRSJkNf9xp2m1Y1evm49Jkcu6SgMQXY6bhWgfAac7rBNh65j+WPvj7m4d2VzGc+77r2uXB41RqA4pyMrffJ/eZEE5d8xliZwzGwnP89dpIVT6TjXTEfzEgKgaIAJj9XqfWJztPYeUjbi/Mb23fY2DyDra0tHB8daIvhihj3C0zHPKBh2ZqCgrDHSKJOXiVRJ5ZvZDqVc6hjf+dmQCnR916cpMuyFOmdk7/FpkwGX1XVgJCnGzC99PUi1DYUvKcS9txROTXRSpkL7330CdF+qISeaNhuWtcYwc3nLIIS9LkmUmYp9kcJGxAksQYeKh118H64EQZAXbMbn+JQpz/T8epzxkiGbfa9Bih9Jh9TStRT4px/r9qg/LIYO+S5ujsyp8lPQM6x0YurY8znc3SdwyT0VwFfvj55m8PIOVh5TsbG8dLSPsaxGTGnGYMqRARiGqxJf5jRRxYbudDWlZPGstI2pW1TJLbW2qfa4offBqAuf3Zdv/MLPP1dH0/30hCcJODzNPNCQFdI2FrjCBNYsGOYqkBjCZNr5/DDP/4Rnn31RdCkBHtGaS3cssH88QEeP3iILz75FHdvf4knDx7CqBlV0kf9PWc40p850Bjb60TDPRDnMwE1urfato1+bmNmZmMXkO5j59yoD1d6PvVzpWuRXmb0I21P686llmn9K0KGETA49nna/5w2je3RvI30ks5/P/VeGilEoqUeE6CM9SPtd/qZfv60krLbY/WdxGykey2lX5qTSZ/JQWfav5QZScHZSSWnNWlfUjCsv6uwb0gXhiArvbvGxp+fzbwvT1urvP/533n7+fycZGOfm/rJe+O+VGk5zVyve2+wB7CqmU6f/c+pPy8Cdod/p0B+bL30ufwOiPPOvVN9fm5PWtf157wXPj9t/vOx5TQk9ikTHKWmavl+THELmZ45SJ8hooHlzUklnVM5V6JtOjw4gGsaAEEbs8ZX6CRaMmgj8h0c8RZhHOucVE7NaKSS/Pwga2dTs4D0Yk0lF6nJEHiojo2gEmIypAMcAzlpFCzth5oMpReCXqIabjZ1Us8Jm0aK6s2AOI49jdi07uKIF3ewm8ulhdrHXPIUGSoDcMcCkqwN8ncOWY3FsSed2/6SXyUCOh6injFLNSnGmMjgpX2JxJV5JVznOgCRamzyeYn9IjHzyM268stJP18n2RmT2mmsa2UMI1NCq2Bw7MJQouicw5hJhI6zdU7WAcHMJUThIGPA0TsCo5KMsXlOiXPOqOXjHhK4IaE6iQkAkFzo/XhzsJtLeCIoML1UaGyvp3OUXq7pOcnPgDDNQzvnvN+nATZ9PwjWm+ikDWJ0pYE5u4U3/vBNvPTb30c5m8IRwYLBncN87wD79x9i7/Y93Pn8C9y+fTtoWUMfeSiYSMPzruvrmElhCq7CzMX3uq7rL9osH0J6tig8P8jayr3GIe3H2J7Iz5v2cd2aI7k00/6kl20ujU77rLmR8u9OAlEn7fu0nTi+0VpWQfTYns3beHoZzuWwP2KiOFZfCqRW+7B6tvVZoqFgJ68zH0va1thnDI53h36WC+XSuY/WCcZErehYm2OfncTQpZ+PmfLlYxt8l9Uzxozq72u1yxjuj5xGpWWMHuf1rJuPpwFZnfMeZFM0GcyjkvV7Ykhnc3PAwb0Y1lxLPs51dFduM4ZoW4Z7d2xNY50YXnlp/1IBSTqvuUXHCr1Av+YnrcHTPkvbGNOg57TlaSD8afRrwFCM0M+iKOTuTjROeh+n76wbb04X4h4NKrK264bMigCilf7nGHLdvClTMQw+NOzTacqpGQ01mco3nG7iPqt3bz7DLNIvBfa6AeMF54aSdu8l+V01mcAm6dDTwY+BL5XOpkS0B56rNoNpFKx082n/NOFgClzT8fb9HS72mClRvoG0LW1/oP4Ew2qW4LARDRk41ww2VqrR0bbVBjcHO9pe2vfUbCK9jGPfkYTAzZi59EDp+2PPpuNnFgmF86sHKSf8+UHXelNn/Egogt2/JdGEzTZmQPi9aZtoBrKupAQnEkTTm5wMngXAPg332ft1GPT26enaM7NoMxJGcHAJEmKit3QucoZN+0eCQAAeZkvPAdQqcBmemzGGMF+L+Jn3AI3nhzgJEKbfrxLv4fquEqtVMJWPJd2PNpj9EQxcadBWBs98+1V8+0e/h60rF8AuXFzOY7l/hMX+IR7fu487H3+Kux9/jnq5hGdGYS1AwYEz/MvPQkrvUu1GGhEvnwN9PnXUy4GSCgvSsekestm5SNdxoFnL1i4HI2tBe7ZO6ThSMDgGEtO9rv1OtcN5v8ZAQw6A87Myts/yPZ5qXNKLO1+LsXkaO5tDEDsEKSrA0XUzZty3IP07B1x5u0Pgx0GIsSrMGT8vGN1Xg3FntCK/d9P+9uvrV8aQjyetawyo5ftg3V5cB2R7ICWmrakQMaUHqYBxIB0fmaN8/sfKSYDvaWWMTqXt5XX6kT49bT5yBmRwL3KA/iP0NTdbG6y999HkKO/PupIyG2P9yMF8ulYpPopzccI5SescO9/raE74Mtyd4+NYRzNSnKXPpVXCjJ+ptB85DlSTxHQ+xs7j2NyN4SNA7mlmD+M1pK2D58RCJaGNWnINz9h+A8KU6fyFT5QmnvZ8fKPM4Kk0OiW8aSbwtJPihGoGgFileCYseiopTC/uHKymErSVg5qp6VJQkEaWGpM45uF2tZ62bcN7Q6fqVPW7rj9pn3JioPXo3wNzJfZgw4ANPjE2IB0WBoTabgg6QzuGh8QtvzjHDkLar5Rw92uVSZRoKFFNy9j4tI9xHp6icMvbGut7TmiZGOh8lA64TsxFxqJKnHQgBvOTjC0lPhJJiILdf+Dqqef2RVkQNE96QMPaSbjdp19a6xiAASHwHrCKhJ8+tv5dIJ//dYRF34tnygzVzuuA4kl9Gba1fi9oP9N1PknqAoQoc9bCFQbbz1zC7//ZP8HFm8/CTEvRTLQeXNc43j/EfP8Qd7+4jS+/uI0nDx7BNUK3yqKIqmGG0FRraLAHxsCt9lHPRnqJppeq0iIFpTqWnrmnFf+X/IJK52CoJRnOcb4eqfQ0nbuceUj7k6533tYAACafr6M3QwA07G/e1zFAPQpeRsY8Rm/zPo/1K70zUoZpMF9Jv3NmiOgkprkvw/bHz5BosAIdGQFd+fzoHkmFR2qWpP2zxkY/l7R/aV3pfR4ZRRqe03x+9Pmx/ZWWXDuwbo7SMQ3mYw0tHNtX2r9UeLeurKMnpyljz2r/cxDNzAAPfeQG7wWJxhgTNAYsx8D2ytmSD1f6O4aT4vvh/hvDQ2N1hA/TFgff5//G5iunqfrPJ0kr07bz+cjnauzzfj7G52rdO6cpY++N0Z11ba5rb2xvjq3FWCnLEo3vQBzouONRWpKvy9g5ImMkEA+n7fV9yZUB68qpGY26rqNKxnu/Elko7WR6AecXrlymJu7P9BkF8kIUPbqOV7QS+YSkkvv0Quy1Kr20LffRyEsKbLRdrb9pmijFdM6B/VDlpW3oGM3IBTxmVtJ1XZ+0TpWQYS46Yglta22U3qcERucUPCREuZnX2GHWEvucPhPrX1V15+ZTOQOQq8QVYDknGQfyNR8DCjnIySVV8bCBQpQoAAQ418F7CW+a6F2FeK6sdijZ4fVYvehkAoLWCFp1kBgBUftEgfHg0B/dpt6HkZMycErz4i+DfULRUTQOrZ9X9O9zAspPGF76V9/7McKXfUeg6H/idU4j+Ag7djB/WUtESV85Sthopf1U0tT3Md9P/dzIM2RCpCcw6MwW3vi938Xzv/0GMKvQGoOi7mCbDs3eHHsPHmHv0SPc/vRzPL7/QOhXSAbpieCYewfypF9WI0rF+eyd6yisJzAEakQUzqyP47bWout8BKVajNEcOiTzY8Ts0nkNQU26EiACnOOk3ThVcb4iaAHHi4aBvi9hoVK6nWpj9PmU2dOzl4PAPCt4pLO6jxN6m4KA/NLMaZTMi+kjTQHRhK/ffiRRZUnOF4PjXBBE26zrlJy2SJfHgEHadvo30erZSMcO9HdBv3sx+D32jCj2i3koJIv1p2dlBGDkQqxUqJOeGS2p0C5nqMYECDGvFQFMPS3SudPzS5kwD4S4JiuMFJ4uAU3vlrS/6Xf5faG/5yAz3s2n5x1OXdYxVWPATWlg+GD0Pb03+r/lkvAjz6frfhIoTu/Xk5gVfRZI1jV0KGcQ87tf3zlNyfdjKkBJ92I8i9DrZoj98v2Qz08+N/04pcYIoLM5QGz15JEN1pcQQ7gr1snxVf5O8uGwjfDnSWu7bg36Hkt9ER+SmjKvujnk+2Gsn3GOXDBDjzRQ6hzD0OvKqRkNE7zN67qB9y7JCLtKoGVMIaSslZCsNly8hbGwIRxjxz0zkJo/gSQByWRSxTak6OSsmgToZI2p3sUxUiQ7iECd4uUrwDq8QxJyUEJ2yoEL1zzYM7qgVQBDwtYGxEckzqh6GaaLkB7YFKwTiZlPf+gkapUxAqcMAQYlCmthTQHP7QrzIJubwYEpENOf4AtRWLE7NxJgl1nCRxILEDHoD216UJgZ0Ig2noM0H2CWcLgAYMnAi9FQGDOBOIzfFBEJe+cAY2FgYjjM4b4K2bMpAFpwkCSLlJmIYFGgU4d4COgAA8Yx2BjAEgw8SlNI2MuQ1TLIiIN50hrCEZFLIBwswFVtVRFAP0MStKWiEUsm+vx0rkPnXGAyw3pqyNyCIuFko4dVLuUIbQkwnOyZIESIhFX7yyzhbCODEcLlsYLvACQUfKWFtO/cM0IsalByhIKC47GsagAagCfRrsm+S2KzM4O8gl6llP28diHkrSHqQacxkqWbCxAIhobMFpOTSGGsMy8CFc8ATAHvgIIIxhJcaVBXBs9+60X81h/9PrbPnkHnOtH8NS3cssaj+w/x6Ms93L1zF48fPkJX1xKlzAeaQQwLG88volbKw7ODpQIwSEwNOPQ7AYVgGAo0jBlOD4mRc2atnENbKp2Rf7JNpA9CyPuLSpiEoO1lFvaKgcImGhMDODh4cNS06ZgEKZi47t4QGIngIASnFImX+GTBC40HhQgoYT4YBt71AEgdApXbkV0oWdG9nk1jYnhFoQ+9cEn2sY9bxoR9rgIXYWoDPQjBEsD9bvbsQxCIsEMMgb0KAsTMRpgtZYYB1amayI9I4k6EMTFLiMjUdIRIaIEwLRLdz0j86CEAA0uo8HB3+UDPDBiWWGhK2PcwVuaUIKcstBGdtRNGg5lBMeRxmIYRs6EUMKW0fAyMp/+0nrQ+Zk78GY3QNSJwYQF0KNijYAfrDYim6NjBGdmLBh7WSyB2DlHP0ihmyvCmd/Sgf8n+RCJ8SPFPziCuA9Oyf3twmYK/FFilArH0mXUgPgfw44CXAkYJBFTvjFwooO+zgkgOZ6Q/V+AcDA/fT8cyEGDQyUxWCu4HppAQ8qHXolbJEge/30dxrXqmWPuVzmvaV21XaWmOhVb6PzKufI1zUJ6bIab9MDYYBJj+/or333By0dPpVewQ+0MKczKGbYRZUIZ8yEwLRvEBDFiykj8tGbeOR7FxKkxI54SC6TCzR+fETD0eoIzBz/fTuv0l3yW+XeiZUWOGwZCeVk7NaCig8t6jrvtB63dDwhZUNQiE0TNqV8uSFYAxiIR1jENjZhjbS0smk0lvcmWGId1yNXFKONK+ddwGkJo4KlEA5MBgQYEhcyGXoYngk73aXBcJABmC9fTfuug+6eHzXiKDeO9jm7EfFKSMGZEriiLOC9DjNSKKiXe0fr1A4xz5XgOThvTtzdSQ1KmHjaE5FfoDRtHPwHkvuT4CsVRumkg0D9p2agrH4VItChs1RxptZxA4AKsH2YYM6mwQ1YNQJskPCSDWHIpIUjg4TKb7UNuK89rXo3NsiwIbm5sgK8719WKJrm1lrVjJVV+rpaTucBEJOMRgHZmFuaB034TDDh4SwEGOCo9EKzMcq0EKSpQYhovFGnAgesLkhHEyMOVJEvo49D9k2NZwAtpzBbwGhEI1eNo3AJaBjoDW+sGZStfDBGYPRLE+UlbLAp0BOuNx9pnL+KM//CEuXbsKB0Z7fAw4j7ZusTw6xr0v7+Lre1/j7v37WC5rCXteAGRlLmAIjl0ARAAbE8Argdig4j5RY2FKWSMTxhLzrki3HDsYJhQk0eIUOAEEdIC1JRrXwZseSKV6q4INCrIwIccLkw/MAMn+DmeY2cOQjQxlwS5oO/1wL5EAZ6VhNmxdZaIdexmzZ9EKEoHD80oniUXgQ8aKdMy50AdZJ6uXetjYkngz7C0b7nHdz5SMmwAfOVIPGIDIh74wPMm3pfeyN+NekOKZwK2J+193t5wFj9hURKoUf0hOorBmspEFbBDgYYIghgLP3IOpEkFzRojgUc8mBcYBJPOmv1swiiDidx2j8wzywhYi5MEho3eMMClkqJcqpEWHmp3pdcA7jQxGhgJ4HAdnedF73gPwlnDp1nO49MJN/Oq9d7C1McWlrS0c3nuMr28/ErrNBHIhTxGsgGzqowwOQH6mTdExUKRt/bjGtOdxjZO7bMD05VqTjCnIAXA6H/lcriuntU2ncH6Ff1wNpLJSIl3nsL96M87VR9czT3LvrT4/9nuqKYqfE6IFiIZaXgdU46kMXU/ndh2ze1L/0zZOWo91a5Bq+/L3c+uN/ru8lqxvCQPM6Z7OsMkYUw8kGobM0mdsbERD37SU2cjnLG3XxPNteszIPuKbsXnP9+AoPg0+pj48L9Y8gDHrTcLGyjcKb9sFj/beUZoGnFa6wPrPcZ9IBIFjRhEkahkgB3oTDe8RQ+GmTEa+OdcBUf0ZOWdmsHMoy3IAsHUMudq2B7N2sIFyjUluNqDvK8eXc+xpH9P5UlDunJf4/MaAit70QKOGxL9T9V+m4syJ7uBwIHHkC5JXzZKtn+cq03RO8z2Rjik1EcvnLB1zP0dDcwwX1kfrSMN76lqkbXsObQWThbbrRJvheADQT7oU0vbzko5fMaP2O+3/crkUqarOA6UXxAlmW0DMMq0AsW9btIhp//P9nfY/fp6tR/wOIs0FEzxHOBmZRlAwNWEOwC4QKDYglOGZMB4O+jAPTDLOTIENLMPbADwJ0QyACwGOxAyYFBRKsZ5gfJ8oTLVRJjjddeRhtmf4/pu/g1uvfwuWGW5+jNY5dI1Hs2yx93gP+48P8NXtrzA/nsO1C0yCgK+whfhdhX3uglTckIEt9CIADFlYTMEcNIEImhhjQJbQcogypnuMxWTPkIWl5Dwwo2lbGFuhrAw6I/bHagqZ7TiQVUFKYHoY6Cyiml6BBCDmXtbJuuZAgsmBTCOL4hiWGRZGNH5gNKYVxkBuqKDN4wB+C9kbHkEwY4WZJdGy9Ge6z6vhvIMnGZO1BmxT8yMamJJK3oBwGbPMnSERNnSdiwymbNheIylCmMAUmZ7RYEWoLMIjk2+qQeH+mCXAikik8CYcXELwywLBkkjrde8rJxAZycAbMAPEvXmwCWeYyMC7DtbomVZNzKoJk2wp6vuG4bnnRAOYg5+Uxit90t89u8H3gxnJ9mG0BPAeRVXg2LV48Xe/j1s/+gGODvdg6yUefPwFPn/4V9hgoGwYxgGeDJwVTRllWnwt6b2n441MR8IMjYGg/F5Xq4p8jvKxjTEX+fw9bU5Ow1isvqf1a/9Xz2lu5pYXaXYc5I+1HU1cT/nOGLhUTJTvp3xtonl6kjw2rWcdoM7Bfm6qmD+/7n5+2lz8Y74bK/lY4r4+4fmxOzrHI2OM0BhaWM+UhPrkqdBOgjfD3fW0sY21038vLUQYRHLvnISbxso3MJ3qCaEyGWmSkchZJTb1zIy2btCwqGM3NzcDEOlzLKfEqDcJMDCU+Dxkl5RyU+nkpCZYOUfJ3APPlMtcp40Y3QDZRtMEgKpmTudG/g3Nu9J51DrSv40Rp5uyEJWP4z67p4JBMmZgExjfCxdTSnzT9Ugd1wdMhFk15UrnbpTDHel77nCf7pXc10Lbq+saVVXJHCWS8PRQqmTNGDOIZKP7wpIBm2ByYQ2KSgCx5/Adr+e6070Rmcwwj6PjJxFCgoYHXfaHg/cJI0Uhq3ckG6uSPflU2ZCwfkn1nkXaPMYs5fUMGB8MJSpxPgFQSMeucwNmkZ6zAAUihGzx3IfQBYNNi9i58B4AwAIumEgoOOtNT3wwHVJpL0n2Y2tgPDDj/vkwA1J/UPl7MNjInhcQa1EUhFdefh4v/s53QbMKi8UxuG7BTYdF53H/0R72Hu/h8YM9LOct6mWLwhSYlbuoChNpiw1AHmC05OLZMmpCyYA3BnNTgKMkmwYXKwcNnDGmz+XCjIaUIaFoskjGoDUGjghs+0hziDyDmNkYg6AlNeKbZSS8MIyJJne6Z2PGWhf65SRRqDIjbdugqw8B10nAhNbBdQ7oHCwTinYObtvAwEm9zjuhMUborCcB16L9IBiyIggBg6nPB+SYYUwB4zswe5QQzYwwq6IFVZ8EAL2JEiRiGDsHOEZpDSwBmq+uLgt4m+dYSSWwPS1MhRsGNoJx0mcBEANVR8LkMqIm1iBoIbjXAlhrw94UAZDwS2JWG2krSaZfMr22xRQ2mDzKPjOBznpv4NtONPn9QV6hC8aYYHu8Tlo4lFaP3VX5d0JD5Tyvo4f6fCqgqqxB13kcPniEX/zkp3jhd76H6e4ujvY8dm9dw4/+2X+DX/z7vwU/XoKcmG54NjAWMIlZdE7DUjCbrqveAdpnfTa9Q9PfV/y3Mhqp6z7AFhluyEHgujlJnx/4Eqx5l4iSyGH9Z+vWLZ0X/V1NCE9bYp38NPFW0sdkXGkf0uAWQJJjByPO/QR0yR23jllM2x271wbrA47zl/ZzbC+NMbJ52/k+yZ/J61/XXtp/2V+rz+VzsI7hyseV7td1fc/7C4gQz0L3+Ug4aubBPho7L2NYSbGMJqEmIpClUwtx03JqRiNlLNQcKQWWCnIj0SDC/PgYzbLB/sE+Njc30bYttnd20LoOW1tbMdO1lmgCRavSjpxIpBdLejC6roP3HlVV9U5tCECCelVUekGlxDW3H9V+pKFwUxCsMeN1bsqyDG2uOjilGzQ/bNbaoE6Xi5fZg6yBBQNNH6mry0BkSphTkJ8zGzqeYfQuAH6V6I2C4pGDkppCpc8URRGjdqVznTJo2mf1b/CJdCpvb5XZlHVovWRKdl0LQ5B6FPhgeCGNXQwrxCUZXz5GuaQRBUW634lEsuHB0S49oJIAvhljNF/3CNAzfBze0+/GGL0xIpmb660tNpji5ISPgUJBYARhBmQMOvaobacdEGClBMkDxokEzSRA2FgCdRYFJgCR+LYQwdrARBMHyXMvFfLeiwM1LLrQFhPEJMczds+ewauvv4rt87vYa2sczp9I3pumxeGjJ7h/eITjusXB/hG8I0w3NlDunkFRTdBWJXxRoKxKFGUJWBuYGqAsCUVZoKoqVGUJa8Uc0hYWVNiQw6Y317TWwJQFilkVGAETaQBRYApsbz9bFgWsCcIHY2GpiFJuNc8hArxheBMcboM2Q/dQ9IkI209M4ELuFxajMlYmCIB3Dk1do1seoVsuUR8eoT6a4+jxHvYfPsZi/wD28Ah+uYRvO7i2AzoHY8qwLxgMB2MNwCHwhzpcgGALC2OsjMMYgAwsALARvxYU8G0fXpyMDQxnCG5RJIlEwXAs57bzBFF3C1NSwYCd0g4B78we3jPIdPDsQNAw44Gx8Qx4C8VommRTaIYIqaB0UaMcEoGIYbkJjKH8LVoYK5pT2J7RNgXgg2Fa2AOGIPUFwQ9Zg7KownkBOj+HoRZWGSe/evfFs5sBkYENfdgzwDjIzcF3pBuZ9jgtOd2I9Nx7TI0Fd8BHf/MzPPjyAf70n/33uHD2Ig72H6K44vDmP/0RfvYXf43myQKWREPV+/Wtgk9F3Wnf+7uqZwy1X6lZtP5cN0atV+85/Xwsn1XOlKV1aMlBeP5sCrizb5M513UchuXVn2m/clMw5qFD+Lr+5HcbM/fCnzX3+TpmoOu6iO3S58bM0vV9zxzOzDjoz+czB7ijIJrWMyFpvfkarrvf87nT98Y0SicxHWl/VYgy9m5a1mGP3KKD9PzQkEFZt88HayNOdDDGoixL1PUS7AOmSjBLXtdJZ4AomFJ7ETQpTtF9lT9/Ujk1o6G+EHrwU7t+PRga/rbrOtR1DQLhP/z4x/jyqy9x49Yt/OAHP8DR8RG2d3fQtC0qO8x6q5PnvYMhO9gU6SZPD1T6TOoLsVgsIlFS6XcaSSotSjA0r4XWm9YZpZChpH1QYA/02h5Fl/kB0WfSjR7BP/ecpyEDD4oaDGOMmAQll48yUiYbU9qeEo60L5E4Jg7D+l36bHo4x4hb/ozOY5pTJWUA9TlrbTRhM8ZIFvTk/dxETtchtevVYq1F4zs479B2XfAcJvDqeR/t92C+IBL9fL2cc8GZefUiivsvMAaSjZMic6HNjBEtYVKCM2kwMSL1EQgmGWMXQl5H+i8d9solbwpwIu1iZYqI0PggeeUwliABNQzsOk2EF0CvSrks0JQyc8aaaDJCBHQgNLYEFRaeABhCa0Vr1xqCK8S/Rc9dVVUoyxKmKFBUFWxZCGNUWOyeO4vzFy+gZY/H7AAQNlWj6B02XYer5QTlZAZbViirCaqyEvPFwgKV9MNYI+uomVkJAqhVMxEcmUEi5S48xwWkADI5bJToc6BrxL3knAd7NLlYwKBI1zmaITEL48XDrZ3UQP1lAaBLzpyhsDb6bNjfmwCYLwjQYoJlwDcd2rrBo/v3sf/lXXz12ec4ePgYNF/CzZdwdQs0HUxTw1IH5ztJhsk+OJfK3gQZ8duwIWSvDWB7UgCdk7n2PiR8Y9EAWQtjLVqle+GS8/AxH41PLn3vPYw3MGFfRrCI4F8DBgXpHTuR2DMEHBNTvNhUQmghZ6uFxJcHERwFrZqeVT/raZDVABos+XPCuiktMgXBmiBwC8yKCZpVE/ZYUU4wnWzAFgbe7qFtazljrhNNk+swRmPlxxob9jV07aTCfaXxjh6jfyvvEdCRh20JO63B4sOvcPDJXWy/cBXTzS0c1ccozu3g5T/4LfzdX/wVqpZRsQ1gqde8DGhX6MsYPUsl8ekdkN7ruYQ9B2/rQHj6vd6fYwzL2Ls5vc3HlL/DHBy7MVzPtB8nAbQh+Fz9bqx/6T46Lfjr+9vXmaYbyOcmtUoYq4NH6ls3vvwuHzBXav41Mo4BKA/f59qv/Lm0//p8zjCd0NkV7VCcF0ODPbRuH+ZaxrSf+RgyiLGCRcaYL0Ok3njRd88EDXo6L2Nt5udwgCWYh4w+CcOc1neqOcQ3NJ0a6yQHFXsK4suyRNu2aNsWn3z8MW7cvInHjx7BGIOtza04KAXoYxwqs9i+TyaTFal4iuLSbOQ6QWVZRgmfSxYwJzQ6njRxnn6WHoTcfyOdk7Rf3nM0mQJ6ZiUlkKlqPmWEAAiA8yGqkFEmQxcZSTsJNx6AQB/RSWzA1f9CTY7G/DUoOjXSSh8DcorznF9wjFUCHbVQzkkEJmWaAjPlwp5xnkHOwdoi+GwbRLMFQzAwUSJmyMCQlbjaoBg9TCJ0SHQksgauabVjEgEnRBgLYmORPnAvGfYxRFt+svuz7oMpiYAYD4JE9EqfiwQ22NOLQ3x4IPzotQCqvu8l5GpA5IOZlAJ8JCFxEfY8xy72UnZQ7/8gxLk3S1TmABDpbUsGCMCIgWgN5ZnQ2UJAOFE0GAEROmtxZAuYEPigiMxBiWJjCrdRoZpMMJ1OURQFJpMJyrJEOZ3ATipMplPYSQkqCpjSoqgqlGWFsihhbNAEACjKUhxLocMwYEvBh4IBa9GCYUEo2cCGrOytIbTEIZKVrJVHf9kQMSovznLiII0YJYhIzBvkTgviVN3X5OGtBj7gaOqkfzMlRFnXhqUfdkC8h6GjmXy4PwmeVFMUoo9xcmGH+SdANEDZHtUflkPEKB5KmjwzWitmPJ4JjgEzLVFMSlzavokLL97E83/wJrrjBZZPDrB37wHuf/ElHnxxG3j4CF29xHK5ADsL9h2Udy6ohJp5mkBbrLFwxsAXJQAGFWU0G3Lega2BN2KKZAJTagIN9FZ8lFRYQmRCDH0Cl2Vgjnv6VRSF7EGeiNbC9IlTAQ70cAkTrODUf4QD8Nt0Di4IPWIgDWaADdBWcJ0bmC8wM8i1KLpFjDSmYF0ZTGWwjREmQzVnk2qG6WQT1hJQzVDXc3jfYrlcAM0C6AIUDVr4sP0kEhXzkMHU9WU9uUkJfVgP71ic+mk1o/sY8Iljt4QlHCZUoOoY7Dv8/K//Dm9e+m8xKafY3N7G8f4hFgXAWyXa/RoTJpAHGGa0HW0jjin5XvF4CnRy4VfOYOh9uI4JSO/8/J30+7zNsd/z+UrbS58xgcEWhkq/XwWJYyW/ozl7Pm83mi+GeemFllgBradhAPI5HDNhWxH46d4Mv6fNpi3mdefzlq/bSYzgmCZj7Gf+TopJUiw2lntrrP70b3YM0HignxyED9Z0zXjH6klLjj3jWigmpl7gz+Fz9hpSBoO9P8aQpn3wHCKGpviFEBTb/XNPmzctp0/Y5ySiT2FszCkhjXuQFfBTFiakKgcMMaaTEi+9+BLufnUXL738EramG5jaUgCj3C6h0wKcFIQVZbhcnIPvxNvRBqdgdhJ8MzIFAIrU18J7+K6L3LVOdtji6BkA3SCp6Um6IXRC+8yv6WLJwgw5xqIIJhHwcEFalRIqjVLlPfo6Q7vGELwTswDHDPKMyhAMdzATK86ntoB3TmxhHaMgi5YZgINnAdpkTNggYv8stv79RoowhhnsCMQmgPd+47KTsIwaIUkvfwDBdj8kO6TE1AkKjMXR1YRL37FHUVUh9GMJDydRY2Bhq4nwQ66B4RaKMn2wm9cVM7Ag9CYXjGDqYBh118BWYn4FMphQganzEo4VIk2tCfDGonTA1EnEI91DEaCHA2QD0+WjU2eiFiYbpfne+T6RHSDS0YxZE7DAYrEEBqMIjh6y8Wz4DwZBoh2k7Ebs/MlDpPomhM60FMxKLGAMfFGACyNg3BDYErwRUC97rUBZFiiKEqYsMN3agJlUKKYT2KqELQsUE9EekDWoJhUmkwmqqkIRTI1MUYg0OtSZ+oOIPT/FcxYvmzjEYGseAbzefyYx/0A8x8I0JUQngFuE8xMCg8LBgW1vI2uhQXwkLK6FXnDSoCPEMKkJaZdLUcMoAtEmuG84MCGDjnFwYFYQyPpE/JnqlfTy7avtw04O7y5COnmstCp8ZwbPDkYR/WnSNpmMMDzcP8/x+dBcaVCd2cRkdwNnblzBjd95Hc3RMR5++AXee/sdLO5+LeGAicXfxhKK2TY2NqaYTktMN2aoNjdQzTZAZYFqOoG1FpOJMJNFIfuPCtmvCGdLhCzB7IgAtReIQ1AO2FCMftZ/Hi5CF/FNmEe9vHXf9S/JNMi6mf6F+J6uA3tEJ33nJNOu9x5wHlw36NoWTduAWXwO62WNuu3QtB7sPHzdwtUNuHMwjlHaTcw2z6G0BD54jOV8H66Zg4720cyP4JYL8HKJou1g6iUo+NA47sRPxUv8ellfDqChl5Snu857BmtoMc9B2ho054yY2yQFPHGGRv7mAJKttWBD6KyHN8D+g7v46q13cP7Zc5g3eyiKCjuTCf7oD/8A7/7kbex/9RBTKoFEwJaCwlT7n96PakqWg7CUpqZMRdzruk8AueeN0BYNz50espMYnTEmIAeG6XM52E6fFeECVFwTmAw76nOQ17sCPpM+p/M4anaTnpWUQV1T4n0/8n4+HykwH5s7g+GaaQkeXaP1aj36LxW8KrOvzw+Ye2BlTwCr+3gwjxju/ZQRGPNRTTo85Jaykvcr7mFCjP4oQSXCfLBqdA18WnGCCzTpsNabji8dU8SWQJ/eAJLzzgQcmnc9X+tebiogyAfsq8GHUozDgS4TSWTENIH308qpGY3CWhS2QBfsadW+PpXqy3zJIbfWwnUOf/Lf/JkctHCRumA35rwDOQazgvw+H0DXDk1u0onp1Nwm+5dy21ESQoSyqgYcvzzT9WApOzg6lpxj1jLcULJEMtfKZGBlE2tbJgB/o7byQJTeAoi2wQjhPT07mbvCophVaA4OA4MkmiRrJAKO95J0jJnFsdEEpowMKhZJlAu29GIOIO6YnZX5dC7koFBu18gW7chFbYeaihAQ/R+iVBc0SCjoQ5hLPVQuMGwWnUTDIYNpYVFZj847wHkQldIGhQsSEsWHLQlQZAbYBYZCxlF5iykm8GyBSYHq7DnUF85gWbeYHi1RMWEOj8n1y+CtGVom+KXD8uAAi/lxXBddL2KgTLQectCECfMENIWEDO33QQDZQcoeL7Jexi3amWBiQdYKw6ymO2WBdlKJJqGQKGMC/iew0ylsVaGcVLCTCtVsimo6QTGdwEwrmImYGJmqEOZhUqGsKlRcoCSJFGTUjCP0tYSYNfgAvB0QgAxipJ78HJwk9Vh3NsKTynpGQh3wLSJixAAf9w/lf3L2MYXLK2BzSoDmWDURjGdlhQivPLFaUinzWGH0TE1ea2TS4zfD59ZhgpGZPunLWOtoNwfdD2se9gCMQXlmG8/89rdx8ZUXsPfgMdgzNrY2Zc/aAraaoioNbMECfo2FCyZglaGI/pkZbdNg/+AAHoyt7W1UVTX0RYh9WJXsAeN77DTfrczHKevU71dAAwOWbIT1afFGTLAsghO387AgoHVwHcGYEr5zaOYL7O89wvzgCfaePMLRwSEOnuyhmS+w2D9Ae3gsvnhtB1ocAU0DblvJ+cIMYoZlA5guAlgxNxWNLqyJWnwKQqZcKp3OxRgAHQORehcpX12B8Jt/+BnKtw2a5gAMA2sKbE12UB/MUXkL58SEVSXFuXlJKlXVdse2fgpAgd5cW7WqEXMkZsSjjMjIGNdpI8Y+H2MKBmA6AaqrwCsVmfXvpJYcY5Lt9Pd141k3NoSWBtRlpB3FcXlJ+5VKztfeDcqwJ1YTsR3CgMjneyDXRsWQ9iNzkAt7T2KiTirrGJLUFeCb1D22R3ohRu9no1Ygip0Y6xm8XCCwMq95m6RCdT1vHk3drWTuzs94/Il+v6uLhCU1h+53E510+Z1QTs1oqJo5B+H5wdSDVlUVrC0wxyJGQqrU9lpeBCDckzHil6F1pOZQutHruo6hTl1mlpPanKb9SJ9JOcM8okJKVHThcwlCOlZ9p98IoqdPBBDx+VQCInUC6uyZtimMkGgAPLEk43LChHREsFUVE6lZa0QdH/MnWKg9MVgvGQAg+MKjg4NXEyDuGRmAQexRFIAtxOSJiAETGBYwVNMUOW5h1XX5AhOpEjMSJi7kAzG2Ny+wRICRiEdkDEqDEGOeRYKPQuK7GAr+EAHIoBNH02AK5VDEuPPWTAEQOvZwxsOcu4Dt772OBXc4/Nl72GiBRWlx7vXX0JzfQVsUqA8XuLC5hZ3tbSwWC3H6VfTlGV3bSr6AIP0kY9C1Lep6iR0jtuDGBP8CkGgMStEiEAid67BcLmGNwWQyRVVNUVUbmEwnmEwnqKZT2LJAWZaSdbooUFQlikq0DiACh6hDhOA3EYCgB8Sh1gdzmYjc+4zmOhQxfwraBBEPwYSwvwKGEXNJseLDkTOhv4+dd/l7KNVbLT3s7c/GP45YPa38466dtOTX80lPjo+BwxlNq4yXZvxf2l765dP6duqH/9GFCWhKgjmzgXNbUzx5vI8D54NvBWEKj01rMa0KGCN7zJGYO8KHHBHMmC/mePz4Mc6ePYvpdBaEK71/Wk9LRQIMnAycVi/yk6Wk68ppGZSh5I/A1Ed0GzwnWTfh0MnZLEjMdUthKh0YxBbl7iYuXtlAYZ4TOsOMtu3QLhsc7x3h6Mk+Hn/9EA/ufo3F3TtYPnqA9vAI1Dj4uoGvW8B5lIYAdJIUkjxg1acKgR4PgUoOVsecX582D7qmvpNEfWgZZsnY4KAxh0eDQxgHVFShpTRfzKpNfHp3ppqBnLbkn6d/D5mhVbOs/5ySA+qx73O88J/T9knMkCbjzPuzjkGKfcz6m76XMkNj5j3pmNf5ZJxmHNoRxvqzm69p/M4MfQXG5vlp/RoD7WNn4mnjWleIqHeQXim92Vzah5yByN/NAwiNzX/e18HaIgnokjOEybNRa4RVOhHXhAUXiM/MyQK2p5XTm04lA06dmZ1zsElEJo02RESSB6G0MDb4QVgjKniW7M/wYmYFlugjynSAOUooNEqR934Q9UolJcb0oU9TO8VcipISudyhPB/nmEot3+T9z5QAqIqRo+03uFc7gpVoMJgdvAvMlDVBU+HhXBsdi51rASrApoCBgXUE8oQSIeIXd/COYcjDkoNE+zchk3JwzAahA8EUkrXYa6hKECon2gxrLay3YtIUbN8jgFSmhBFU0xYoJHykMhIMYQzFlk/WgkzvY0EhmpbTubYGriwAW4Ith3kwMRM2h03NAMgJwNH5tszonINzHk9Ki7YiwHk03uHefIHZ9euwFYHmHssHT2AmU3S7Z7CcTODLCmW1haWv0TRzsGH4rkVRlJhUFYqiBMwMNkjjJtUEs9kMVchQX02n2NzaEmf2oM2z1krmdvRSxN7gJYyDBdiHD6M6WQ86IN93OmYCSudROsES/YWDWIlmESeiLBeFE11ZYPA4cL9EhI5CyOTQD6QXVVJDTojXX2iUvTkGhlcvYebhsycByvSZtQT3BALYj2/1/RWpTvYzfW4APryEk1U6orTIey+SKhpK6nrJXxBKJECK0YM/Strrg0oM5yiXgKXfrwKeVZX78PvVIudZdqgtCbDAj3/8Nzg4brBz5hwuXjiLl1+4gcvnz2BSGVhDIfdKuOBksnF4dISd3V3MNjagEbTGpM25lO5pe+FpwO9pJY/8c5r6QWFs1AuS4u5mj8L1UkGQARsOZz7k/GCIDxEMGi/BDLhkoCIU0wnOnZnh0s0reN69Ctd6dEcHeHL/Hr6+/SXufvI5Ht75CkeP9sBNi2J+DNM1AHew8DGMrDQibec5EPI5Ogm4DBi48LcP9L8wBq5zmNpC2uNSNKQAnGdJSuklWiLgkEurc6Fk3rd0fVSguU4bktbLoe6xYCHp+MbGPiY8TD8/6bylfT/pmdjJpJykeRmuwfgzJ7YVaNQ6ejfGGI3NywrdW3NWmXtTp5SRESHj6c/w4G/PSKNc5OsxBuBTjDfW53Vj0zLKhHNiXpvRGcVF+XyEVuSJ7PP8Lh27c9J9nCbezOcrr0eCYgzbSbFsbsKoSWAVY+vzkUEZTJqMyKtmbg2ztq6cmtGYTqcwxmC5XA6Aug46ZT700It9uJhJWSNhtqwm4NLJ8V38TobAsIWFLcoVNbuAbzeYQNVy6N/rEvhoH7XfAxOrMB4NjatZqcfqSDlOE7VSHkURHJjhwSHsIlicH8XEmeC7TjYtqcZGHI4tyhBBxaMIzFbT9aEbHTNsOYGxJQwEyDe1OCcXpoBHEyLqpKH8AIBRdQUmrgyOpggXEgAiLLkRx80Qkpd871ROVjK8Sk6KkJjLSQ6B2lJ0kiYy8R0fmCwxpep9OhhAB4Maos1QR1JhegyIGEQsDseFhS3L4BxcwBUFUJSYTCbR0diGCDaYWJjComKS3Aw727A7G6BZBXz3ByhRoDQW1c42mtKCYVAw4GYOVOqaakhRhDj7Yc0CQICqFMmgo5DYkIdSB+MBypI+ypuiMTIB/IfqIjBmGjw8oMlEgCsGX8f3HEoEA40I8k64gmINKwYKzJGWp5qJk4hHerHKflpzERJAxIM5HNTTxy4Y1pGNpCfEYQRKYJXoB3bNh+zYzImURiUxwTbaOSdqbCTBLICByl8lPZHQq8NwuLyVdhSZJicCINNrl1JhDAXGT9rmEOZUmA6GOOuXkwqFLcKZ6GKSOxFG2Ci0iO0mbasztf4T29px4D3ONPZ/W+ckrwcZnN3ZQbNo8PDrJzg6clgczbEzmWK7KFBuzzApSzHhMQQXVJ2GSM5vKXltum6YL2FYxiV2Y309CSinz+Ylpd/D/bvGvj2vFwBTHyYyfd4CqDxFDSJCYkMA0TxCQYfsw9AX14E0eQ0kiSYMwUwMiukWLp5/AVe/9RK+vagx3zvAV5/fxgfv/AaHH32O4/sP0al/h/cog8DEmdV1zX/PGYoxQDl4B2LCChIHUQMSzbcx6IwRk1nv4Qlw3IEtiWWo7+tKz1baXo4hwEOJ7jqAltYFIPH1XJUIp+ubmk8DQ+1tOgc5YM33UF6exrT29MqsfD42zmTyR+vL287XkCE+AExjJj2cmZGvMjzr/l7LzIdtHYUtGbjOGcn077zu+HeypjnzuI5xXcc0jtW/sveyz/KxjjE6Pgj0UouZvh9q4bKemdR38u/WlTFmQz8Xs3yhN8vlEpOiN4VXAX0+Bgr32mi9KjMi0qgyUSg6uH9PoN1p+UZRp4wxmEwmICLUdR0a4YF2IXUaKmwJYh+b4aAG1IGV0xChpiwHYXOb1qHpPCaTSX/5J8RA29O+5IQp1b6kBG1M2pESKP1bxxYv7WwxeoLpB5suEjkgmjUhad85D0MOcC0oJOejgjCpDCg4VnfeYd7UaJ0HQiZiA4PZ2Qs4fLQvJkqe0bUdvOtkjsxMpPPOQeLGJwCqszBkYaiP9w8ItlvAwU4m4KKA966PTFIYGNvHy7fWYDqZCtixBr4qYALYrxT4GwNrCxRWnIzJGJH0W3EihrVwFPwFDGBsAQZQTCuUhUVBBFgBSLYoxKzIGngrkngFfwMJVwCNGrEH4W82QEsGBVnYzsEbgIyA/soDbEp4F5A9UQB7wq0vC4qHT/aGmPwYZhS+Ux4NxC4eRkeMZbXGpwcMk1wAUaNBQOEJhetdOm2yxzpidImqImUmrAPKkQPOBHSGe+1JVgqPAbMRTwP3RCS2N0IgV6QvnPYqE16x+LPkl7g+lyYsHSNWeu7Ts6+2ozk9SM9ff9ZcBPTIHHx1TdPLJxUiKA3Tv51zASz3AScM9+akzrkYIMN1HstlI8nxwKjrBm3biqAGjK6r4ToxJd3a2sLly5fhnMO8rdEE+9pr165hd3d3oNUgN25+ku5RpXFyFg1s0ScO1H+nKoxgVudhigKXr17Dux/dw8It0FGHLx88wJUr5zGbVdIuQmQr0ovJ4OOPP8aVK1dw5cqVSAfzfSVlXPK6bk+cBPjS57Tk7a2zSX9anUgCX6R1OgCdznsCrIlCyAPqWXyOTuosQThcOHd6jAwDcBJswBZCj2cVtqYX8Oq1S3jxt7+Dw/tP8O7P3sKdDz7E/Y8/RXd4BNO0ILIgX4O51wLkTq7r/A5PKlbsXeEg0RDFNgNwkHxFxBLRrSDAsYOHJsPsy6pfTj+PA/8R3/tm5mXdniBlgJJ7YR0jfdo6889OAwLHygCI/eOqWCkn7e3Bc+jpWg789d0U1+S04WlM+4ABSXMorTHNy+n1SaBen0+l62N4Lmdk07rGxjw2/nXj7b+neM+PPcNY1U7lc5FrE9QSAhhaB2mdeR25hY0+l861IfEBJe8CRpF60vQGK4y7jGrQXhpKuv9KiLyYrPdz8V+F0ZiUBWYTSYK3XFpMq1ISQ7WtOAWH56qqQt00mG1uCijuWsxms9hxZpHOee8x3ZjBdR26Tpx8p5MpmBnHiwUOjxcorMFsNoNzDoeHhyE7obgLVGWB6XSCwhbJYMNmS6eQJQoSJYseN6hOIno/DmMM2raNIEP8ISTejYDxPp/DZFoJs6CEPFyoXSMZclnHSyLl297cRGEYk4J7aWX4v2Q8NwAsurbFUdMCJNFZmrrB0jXozmyhtAWm0ylmIQcJM8NUFRAijKgvDABxPN6ewlvCbDYTMzNboJpISFIqJyirCSaTKoAyG5OVwYQkLSTSbs2USzDw8YBn4BIQhknH5odEVtyPgwDEGsk4HPYFcc8AMeTyZmaU7DDRcL3MEn8+4lwTLnoGQkQqCzH/ciZoWizBGwdnPcBO2vElQlws6V6IWgJmTNrewb0fVLjQyIUzp8RSv2ZMXEYow7CJCYW38TMdnzAcFp6SYLhEQHBGt54ldGk6t+GcO8Ng03sCcEITKhfwikpR41wRXPCJie3FChgdp39mFzD39qaqJtcBea8gTT5Iv9OoPcw9gUrPHFZ+D3PEounzzqNtWyyXS9T1Em3TQu35OfRT501ygPCAiGvtru0leC5EpPPB/EnH2rYtuq5D23Xo2hZd8NPxzqFuGnjvUQWBiOucRLYLTIb3HsvlEs45tE0H13gcz+c4OjxC0zZYLBYivPAdCD0zU1UVXnrpJTzzzDPwlrB1ZgfMjHt3v8ZsNsP169dw9epVWCtMtxB3P2AKNQiDbh8KoQgl9wRgrUFR2CAMsFEoAIxL9wBh1BGSKjoGrj33DGr+KdquhW2B+/t7eDI/xvb2DDCQhNnewIVNRZ7QuA7vf/ghLl6+DGLuNaXZ5aTCqqFUlOPng3uXFUAFSXq/8fr1VqAR9+1ApxD3agQjkRkIu5d1d6lPkd4V4TPdbyR/tQTUkOBw1hgg5BwxRNEfTZgJDY4RWnIGxAYMDxCDCjFBBTEqskDbAUTR2s7BgSvC5NnL+M6VP8PlV1/EF2/9Gnd/8z4OvroHzBeg2sB0HeCcJPACwyGYR4DgmAfOuRI9TXuEaCo1ALMA2FDwHRQ6Epl6MIxnWAbgGaWVaH1iHbbqN4mk/jGQT9Q7kKcgKDV77O/LNMGuD35940C032fDkvdvRZCS7alvWgagWidzzXNjUmUBg6drN2ck1Qw5/y4H+KlwFlhlONKyToOgd+UY+FQz7XXztx7g99/pmVNa5zHUWqV1rWMu8r6lgud8z4wxqixd6J3VAxNCJvYwbW04HoxrZVZMALN21zFM+fzrPWTCmk8mEzGfP8GUMDIo2TyOafOQ9oGfzmCNlVMzGjulaBC8L9BUosbvXIe6adEFjq2pG0yqEjNjUFUlNjc3MT86hCVgY0OSIS0WC1hiHNdLtIXBYrEEkWTUnk4lQlTXNuBJgbKw2JxV8M5jamRgT/b3UU1nmEwnKA2BvaiFoi+AzIvkWmAPBwG1RCUAgkOQdBqLfu5Yb+kI3JumAcAwxCD4KL0kAJMqZA8miThalsJstG2LpmlgWKQ9RVWg8R08e1RW3J03CoNKKHNs18Ohg0ThslShgjj8tmEshalw/Y1XcOnCOezs7mJjYyNIz3TMlOx1ikSNQDFkamT0oEzhiiFNUnjlNwV2gmEpXk69g4DOfRJXeWWP94SDw8EwOv8azSlpMEANOJi+Lr0RQz/iDx/GG1ooWJgC5U9s10f6QpAi9mcksUc0CFdzD2IR+9jvrwF9DB7XSnzEZCq8SgSnhzf7vyFCkUhgYi4UknC2aaSkgUQkdCBVZSqg9x1BlkAmUHMIMDNciAYGRsi9EswemNERYhg+7xMzsGBbLsRG/XIQmXClwHE69AyGiUqJkTJwms3CGAvSxJwhrI1jQuc8Dg8OsffkCer5QoAbAAlb6uOmjPkRKNgke/VtgGgSuhauc1gsW4gZu8d8vohEtK5rtI1HXTeo6xp1vUTXiTDh+PgYi0WNtu3gug5N02BZ12jbBoBkpa+bBm3TirQnrJ9jAXdqytXvF1kzSvYREeEn73yEsixRGYurly7i2995Hd/61iuoTImP3v8AH773Hp67cQvXrj+Dja2ZgLzAccrlQiGBXaAoIaIesZjjOMdoO4YxLoSbFZMqa5IQ20hBl5fE6TDCcbDBma1NWN8ADuCW0SyWODpaoL1AKD1Q6IUbGFwm4MYzN/Cv/tW/wu//8PeDWr+/qLxPoG3gkpmB+fxYGD7XinBlcQh40SZ1XRejFTrn0SwdOheESIRgyjmUarMXHzSV7jrn4WDlZ2Imqueb2YmmloZaIAOKYa9BITSl9yErvGZJF6GYJp6syhLTqQhxqqqMwioxaaNo5uDZwVqA21b82iCaTLJlZAiNoRDhTyL3lSXh5ss38exz1/H4B7+Fjz/4GJ++/xGOP7kD/3gfxdExCreE4yUa49ChRdmIsGvJHo6EKSo8gTyjNgLsXcJ8aqQcBZFqKsiBOS+Cf5FnF0xmlX6TcJ6J5UKfnb0HUvKdrFM0uYHQKJjex0D5ohhNOtQjzejdNsy3sA78pBrMuO4Z8F5lgrH271wqPtZerJNppf7TFELPbKQS8nUairj3MQTF6xiwk7QK+bjz9/M5H9eODDVrcg7dAGgDqZWI7jvoNS2MPQLQ597SZGy+c+3HihQ/A+npvKbPDeY/cONy7wUMZeT+gU+C7CR03YQzIIJmEx2qU0yRt58zu2N9yvdwZBg4ZAcIlj5d18Ij+Dwn7xm9qxkgP1zv1TlNvvcirIiY6il7Py+nZjQsAVVhURQT8IyDBK/A1uYmHIskYrFcAAC6tkNRWEynU2xOJ7h//z4ODw7ALEBgYzZDWVWYL2scHx1K7P5SNCT7+wdo6hq729vonENVFDAlwRpC2zQ4s72N6cZG6FUw7yEh+ERi0iXmOkrc5LLxMGK65Hr/jAhSyMff+wgZMvFFUQaTItlQVXAaJkKQrktuERDQSYOBcSrg2MOA0baNgLyihDUTRFCt/zyBnYATbxh126JpOky2tvHCiy/i8uWLsAXBWoOts2cGJkRj6vB0+1Aq2ViBuk8v6VYa31h04p9jX0YJD5/8CmW/jPV4tE80/L2/Lk8+GGrGEA84UU4T1rbP3NdPZKBsAPOQruhly8xwajbCQWOAAPw9h6Rd6sQlwKw3JZJ/Cpb0GfmM0AWzIQX64vjl46XFoWNxH7BgSufSMJi9E4XhoOYNe7AsQyZvb1GZAgi+GGRMX28ABrl0RmeaSOZCcx6wZ3TO4+DoGF/cvoPHjx6jsBbTagJiYFJVaOsa9XKJZb1E2wr414urDTkO6rrGYrFA0zQ4PDxEUzdoHXB8dBw1C3VTB/Dq4DpG17kITGlwrsQ8Mm685Bw5cKJK7neXRobLL3QtBokUzXu0rsF8WaM0Fnv7h/josy/wl3/zt/jBD34Lv/0738PuzjY+/PhTfPTJp7h56xaeee46prNpjBQG6s810PdFpFzClFCQbHnP0ZxMrCCHIcLjftZ1YgBM2NneRlkadCyS8q7rsH9wgGXdYFIIEJdHTXxvd3cHznV48uQJdnZ2BvPQ0ywGvMXDB4/x7rvvicYkSNiuXbuKSbmJRb1E2zSwxQRlMYVxDvAtyoIB7qJ0U5hsEQi1bRv2uKhbjKADtK6DA6FtHZhJmNzQn651cJ5hjObP6TVPMY9NAMZN04JItPeVLVA44PDwQM6KNVjMF0miVIeNjY3A5Imv2fb2NiYbU2ztbGJ7axPTWYlqIsIqYwmOSTKskxOmJIBqYwGiVoA8GVTTEldvPIMrz17HG7/1Xdz+4GN88qvf4OFHn6F9+Ah0fAxTL2Fag8a4uGfYOzjjouYqpV0rUW4IPZ1WAVMGLiUBZr4Dn15yYDhWhn0hqHQ1NW9MAdqY6c4YYEvHMNb+SczIOk3JGCMSfzcENRsf82PI6+iZL/T33xoJt7alZjhyL7hIy/J+p2D/pLKufyvmmxjXTknXV8e8rt6x4Dvhy16DJYAmPjuWgFJLLuQa01ycxJzq2MJfER8MMdHgDfTN9/d8Og5EOtIzgukY1o1ljCEeMH5qUcHAfD4XpiiEvB4wMml3szGvnIMRZjbM1jdmmk/NaEi4Whs32XQ6xWKxCM0ywB5VcMzemE7je8fHxyiDs7FIDWtsb29HNbMlMSna2toCEWE2qbA1m2JjYwPMjPl8js3NTVRlAbBHUZaoqslg4xojuQ6stbEPurkdgKoo0THQtKJOtlbjboeoMZ0LPhMljKFgRiFMUVO34qCJkGmaJbEeQVTFxhi4TiJtubYV8w7vMa2mmFQVmq4BWoDYobAVVGSvknvyAMGgRIkGHq0HyBZ4/qUX8ezN52FLi65t4BqPsxmTAZwuXOHYJtbyTbjS/1JFJf8ATjzoUlT6GfZ9AuyG3tT/5fpFCWEfSOH01g1dEuYgxmGI0lbttzIAPXOBEGSgz1rvlVgzx4yennmYZHHwD+g48VMIFfsAXEE21qmN6qqbwACBc3AqzJGCf/VjAORse9ehaVssl3M416LrWhSFxc7WNs7tnMH2zg5sSLIp/h6IEqBUcpWDCvndx3n+6su7ePvX74JBmJYVPDnsPznA7c+/wFd3v8KTR3uYzxeYH8/RdR0610XTJc8hf0tCwGWONI+LapU4SJuCzTkPVcfEvbMkhSzeFAl1T2w7ZsBSP6f6fpB+D8eo+6fH8Eqs5TvAQaKuNY3D/P5j3P83/x5/99Of4w//8A/wO7/1PRhivPve+/j4k0/x/As3ce36NUw3ZnHd+pJf+v3eUWBWFBbeEXwwq1KgqdGhwmtAYJjKssR0MsH+fCHzDKHLdVOjm5UhFHP/KiBS7Oeffx7vvvsu3nzzzUEG2XS+267Dv//xX+Po8BDHx3M0jZitbm19iCuXrgJMODo6wsHhYTBjEy3T/HiOzjl0QWvVdi26VnLsNE0rJrnOwXsXxQydc2h9C4TLXcNXU/iuaboo8VMNuSHRClNZDPx2rLUoigIVWcys+BlOZzNMqgrMjNnGBrY2tzGbbaDzBbxfouu6eGcihDCvqhJbWxs4c3YXFy6ew/lzZ3FmdxubGzOURQEHJ4EDjIakdtHvxpGBNZLf6syFXWye/z5ufPdV3Pv8Nj556x18+av30N19BL9/CM9LoG1RtIwSDE8erXGSUNWXcY7SkktaxyLXjIG13gRttYwB0hxEadv6/BjjkN5/+tlAg3BCe4O+rmF08vtoTIp8mnfytk56f+zddC61r3kwnrxOYyQZXD436bvrHLfXlTFwftKzkeYAwYyz90UYa/u0cyJCSuqFPsmYgPFwsDkoTyX3qR9I3v+0/rExKtOj7cck1txjFq1jsN/QC+HW34t9O6nWR+nPuBO/TIvktyO09XJlD+Rj+CbMQv+e3HOn2QtavrEzeLphdYJLa2CsQVkER+Qw6fv7+yAjPgPMAtwPDg4ip24tgdmhaZZwXYWNzU3UtUziwcEejBEnZO86sHcoCnGalnb6tPEMhJCkMqnL5VI6HSeC0TlOpF16gVbBuVNU2qqm986hDNlri0oczovgvNy2TbAPljCrnevCxgeauokmKV1Xw5DD1mSCs5vnUNdLkfz5kHCJCATTg0omOE/ApMKrb7yMydYOlm2HrmnRtQ02ZpMYYSst32Sj/GM31moZSkoiIRy0tfrWSURNwc7qAQUy38L+IHOvoj8ts5X+rpdn+n7qgKzPxHcTe/j04tXP0lwzegZkOGq2xeIXgODY7H1vasTBzIP7yaQEjPb9Fwli571EawvSETUbs55QIDUlCNoSFgZCNSDyUs/8K+Pb+ycJ6GyaVrKXE0DBx6MsLZbHx/joi6/QdB3OX7iAW88/j3Pnz6EoS9gQaW5MIqJFLh0hud4D9+5+jX/4h5/iwsUrOD5aYH/vEO+++y5+9atf4fGTJ2Guxa49zn+ipfFJlJIoafViXqiRz8Bi3y++QQZB7AOwqJidk/pCKncwXMIshflkjSkeTEdkB/ZjhEQh0z6mTLWGNe6f7fsFY8Agcbxlj2bZYX7vIf4///Jf4yc//Rn+6Z/9CV5+8QXUTY23fvlrfPrJ53jxpRdx/doVTCYTqc8Qegd9MbXJwU0Eh5bALExGUeg7Yb8lDLw4FzOK0qJzLTov2rJlXWPZNMIsGyS53qU45/Dyyy/j3/27f48333xzsA/SM3V0NMfDh48xnU7x+edf4oMPP0LXSoLRsrLouhad61Z8apq2lrq8gi/JXxHPYwrOwFCTPTYJgAtzL0eBALZBq9iD2AiE0/U14nuhfnYKXsQHzkYzLmsKFEWF3d0z4isT/OOm0xmmkxkuXLiE3Z0d7B/cx50v74FZ/IA2N0pcvngBFy9ewPXr13D27C42tzZhg68EFQYtd2AwiqKAL0R6bYsKGztbeO7br+LSCzfx5Hd/G5/+7B18+tY7OPryC/iDQxgm2LaB61pwYUDWBNPI/n4Yc05N7/10b+eAPc49rT6Trn9af/p9au4zplVYxxSkQVvyPudt5n1Jx7BOU3ESE5EC2dR8L50/mZdhH1I/k3w+IpBM53Wk7fzuSttM68wBczpXuVVEOtdjc5MD3HweYn9D/3NQrP1NJfk5oM6DAii4BhTv9WPJ+69zmoaGzfuXWoSMMWTpnOdC7bgW2d5PmWS9c/M1SNvJ53HdHtVn02hhK/s0eb9zDjsbW1jOj+OeexqTMWY+ls+X7keP9edpXTm96VSizdBOlGUZJEYioVf1YOc7dHWDSVkBxqCaTNA0Dfb392N22KoSR+rz586JY/VkAvYeRchX4DuH+XyO0pgogSrLEo5lUmXMhLoWJ8zOWpRlBWtFw+BcFzg7G65zL0CJOKgVLTrXoChKbFSzcCAYYHFm1s0rIW+BNmRElwg0HQCGDX4WJpiMeO9Q2AK2LDCZVJiWFaqgviogwKjrgkO7LcLbkuuidR12z1/AhWvX4W2JxgV7766DIWA2m4466pxGGqHlJKCfP5eXwXupRzMy4VU8TL30V0GtIU0kmMAtJmh05tBSYvMYTI1SOhKJL8QG28vh8yEcsTBuwqAwElDDKtVVgIpVyX9KWMLAlNkxxoC7Pl+I83344/RyXpWQKHgL0hESjZgl8XFQ/yaVhCtYAhO64EOh8+i9h+s6tM6BQejaFm3XBgY3jLER5tQYg7KUcLxd18V9q3+3bSuau7aFcw7LZY3joyMsQ8S1/f09sPJzrifIZVXg/Pkz+M53v4PLFy7BG4OvHzzAX/3VX+O5G8/h1vPP4/z58zBFL7VKL4lkIXW10dQNfvOb9/DMM8/h3t0HePxoH2+//Tbee+991E0tHh1BySKaAQrOPVmW7UQYL/ydDdvUZhL3RIUcQKQPZlCpqjxu3bROeQi9OR7i3GsT/TfU73dWHiC5cAd72kODDRMZFEEIUtcOn31+B/+3//v/itdf+xb+9I9/hJdfehWPHz3EL3/+Fr68cwc3bjyHq1evRs2xAGAx8NL92Q9X97sBac4dB2lfo9wRxfycDInNTuThvYvOwOKfV4d5pzDWId04e/YcFosFjo6OsBHNXTNGnz0mswkuXrqM2We38eVXd9G1stieGnhuRs08orBBL3eiYDIieYmQzPuAQiUBEYarQEidypSJJSIQM4osjHMERST/iCgyGKGDso5Fif3jxzHiWYwKRhUsldjc2sRstoHd3R2cPXcWuzs7cN0G5sdf4tPPbsP+/C1s72zhxo1nce3qVVy6eA47u1sgY+ChZsFivktNAyoLUGVRbc5w5eVbuHLzWbz6e9/H5//pZ/jo52/h8Kt76A4PwcslLLFEqZH46yuAKQfTY0xFClYVIEbGLgOsY2CKuQ+Nn393mihZQ3CXaiNXmY283XX36BgIS+djzIlY74AxYA4oQ/z08eQAV8O85s7aOYOTjkHuj+E5O2mcYyBYS2qilDML/burEZGGDMfq51pHqgVImcW8P+l3Hozc/2TMsmMs5YK2n2vnxvbL2O95G2NMl/4+xigDCInw+vHlTGk+j3mdaV+MCSKesL+MNZhNp9jZ2cHeo4crfTnNnsjL2Ln3/F/JdEp8H+zANlIAnEicve9g2IpdWOvQdjVmG5uAEdvTjY0NtG0bQ9ISQaJK7WwBIBTWAARsbYqjszMt5schgZ33qKqJXIDWiC0tGcAy5uok2IpmoTATeNdhWoXQuEHdXnuAicR3o+gjVLRtA24R67bWwhqLzomZVVWYyHnXdQ1UBRCyU7MTB0uVghVlAe88OtfBGBLTKnCYG99fcuGS9ABaAL6wuPTMTeyePYfWAcumA5Mk2HPssbExjaBRQ/uOSYr+a5Z+kwHgVae6/pnh3+pwSoTgJDsMTapOgMx9NniwXPQuOHumGzoC6tCWmCrxChHJ+6WAPyX2qTRpHXMVLxcyYA0IEJgF9X2I7Ya177ouhpWTkMYW3nP0JRCGtYMLTq5dJw7HIAq/O8BIuDoXIrsRRNvgvEdTtzg+EmmFZ0bbNFgulzg8PETdSoSk5XKJ5XIZNHYM5x3qukbTNHEMdd0IeJQBDqQiGr2sKitJNkaEoixgLOH2w7v42W9+Be88bt24id/7gz/AtWvX8cnHn+LOl1/hjTe+jWdvPIONmUQ/S3PS6LwKMJWfh4eHuHbtOg4PD3Hnizv47JPb+OyTz9G2HTzkXEpIBor9JMjl7QPzploEZcoGjr4mCVAgi933JWgj88/lT+rV9Ck+JSCV+lvq6xgyGkMHOxF38OBvZgVYDiShK2Lb1mieAoe67vCLX7yNjz76GH/wez/Ej/7oj/D8jVv4+uHX+OUv38bt21/i+cDk9RqOEIs0FD0X3jnAa4JND/GTkXw2DIk2pbQquOPi8pXLuPP1fYAA5z0677FYLiU6V1UEkLUqMb1y5Qpu376NV155ZUV7yMyYzqaopiW2tjfw3I1nUVbi80Nk4WHBVA3mst9HcsGKFgdRgq7aqZShG6yrSfjNwVrzCm3QVwmI2ou4cFCmlILvA4d7IJgCMgcfHIZvxISrj6YEGF4A3mP/UPIVEUkUsslkgp2tHVy6cBFXrl7B+fPn0B0c4dEvf4W3fvUOzu/s4Pq1K7j+7DO4cvUyNrZnIAY6dPDEMN4BnQEbQjEpwQXh4o2ruHL1f8BLb/42fvPzX+DTt9/B3mdfAftz2KaG5yMZzRrGIp0Pnat0jVf+9VM0WnIQr8l5c21A+my8K9aAmzEG4yQpcT6m/9JlBfjSkC6MMv/J35HZ6HxMvrsO6I8V/ThnjsYAZ8psjAHQPDJR/pz6QKV3r0q/V/u16l+g+GpdaONcK5HP7YCpyeYzZ8LS+tL+jP0+9l5e9xiTMLYug2fN8Fzle1d/z03kxs5jnJfORaHu0fExyrKI9+S6fqR1j+3B9J1h/w0MryZgPamcmtEYi1+fcoWeGew6Mf8xhM3NLdiigONe4lFWZdAyGNE4BDtXveyZxW7VGglbSiT2uYD4hAR8grZtUJYSw306nYgqLZg7eHbYmM1iKNzCWjRtDUuFJL4zYuZFoGDmZADfBamdMAVEjK3NGaqqjFJUAOi6Kfb29gIzUsB1EvVmY1Okdd55LJYLVKbEpCrEvrfr+vCOVhZetCQMbwpUWzu48twNlNUM82WL5aIGFQVgGa5rYa3BbGMm9Ufw1JuJ5UX3R09o0m8zxiAwPSvkgHvJkPzZ+xswiwSUeZVQx72RSINZx45eqqD7KDo2By2DmiyoiZFnr2LgMJ5c2uFj8jxEJidR34N7B+UwTpWEOKf90IABwTk4hIWMDIDzEsGhc3BtF7UlCGNpmkZymqjfhXNB09ChLAp4z+g6eU7zs3gv0Y+aYE7Xdi0WiwUODw8jI7Koa9Thd2FSRAuhsnTuUkmRwWRSgYxBQx62LFFNJjFAgq0KbMx2sBns0YkkV0kZHFaryQTLVqKsuYSYEqmkRC4NMoSqLLB7Zhez2RTHB4f45L338b/8L/8X/JMf/Qjf+/73cfvOHfzs57/Asqnx0ou3MJlUyR5QKbQBorkG0LYdzp49i//4t/8Jd+/excHhvgBYEBgSsYjDZaZ8Oof9EDai/Oo5mjUO9mZGRNNdmz42BCYEa4ugCaHBOaHsRQFXgdlgID1ROfCyei6hY9G93wFJbhYi6TcRSehOFj+Uw8Nj/Nt/+2O89cu38Gd/8if4nTd/G03b4KuvvsTDhw9x9epV3LhxAxcvXggMEAHCosEagk/mUCIydTLWop8Z5RcoLJAxBttbm6EeH84dY7Fcou2CEzW4H1tyR7z66qt455138PLLr0ThAClTABYfhe0NLJZLXLl+HWcvXMTBwVGILjMbMi/AQONHasJJif+RTm4G7MYWfwAOoIzGUCjBocNpuFDvNTFhOE/BwT5GV4phnSVKmkpWNSGs9x7EDZp6jmW7CHSPcDyXkOSPHj3G7Ttfonq3xM72Ni5euoArVy7j+Vu30HYe773/ET746GOcPXcWV5+5huduPIfzF8/DTywMHGznUBDQtbUcs6pAW1XYvHUFv/vsf4tX3/wdfPwPb+OTf3gLe3fuwh8xuK1h2MX1dRT2sddtPQxxqXOs661nwAfVYwqm1pV14DD/e0z6m4PjMUn4adrXchJgSoHu8L3U78qA4NeDL040nznTIURjBVDqbajaobToXaqh7KNZUbIWkRKxavlpQJvyeVBzo3Rucwl6Ph8RA1LftvZPz/g4a4/YZi4xzz/X7yLwhoBdEaKFEPCcnP1kTEqPx/ZTrqVR5kjPPAUBk+ehb0l8ligKFAaBUOI6rMx0+NxE5lEZwNyHbYy5GAsApHer0Hept2kkpDoR9fOTCNTS+2jduYkCOyQmygk+43yen1JOzWgAMhlFknEwSqhkGuCCbTcRoawKAftGACFDpLgL18Us41Uxi4OKC+gJprAoywm2t3fgnMN0OkVd13C+Qec8lk2DzU0TAFMZJ6oIwEBUuH2eiUk1BZFE4ykLSTYHCOAnS2gDd2aNgSVgOq2wMatkYdE7jFtY1PMaRVlid2cGG/J+lGUZxzGdTuC6FkWQbnUsjlkOAFw4zNZi6YDN3V08c+tFkKmwOK5xeHgsYM4YwDlY+JB7o0jGQxEkpFKktMjir0rw5VeVJDM630l8dC82+77fPfCdSyuMoUQBEjP1APwis6CPGplnJAfCC5qPPg56gLUQKBJaZTq8U8KpBmY9setcF6IUSc4DFy7xJiRHc66Dcw045GIAxGSqbmrRMJgKIBMiD3nRLATThs530dRIzY2Wy6UkZIOPeRTquo7Mtzh51jg+Po6aibqWv+XSLcKaCYNZViXKogTDSfz9ooiHvygKTCcTFBub2A4ajelshkLjyzOjrCYoSzE1rJtGbMOLAt45uBDml0hMOTQPhGtlwquqxHJZo67nIn0FMJtOMT86jvPadl2UzLZdK87U3Ku2bz3/PBaLBS5fuoBX3/g27t27h3/5r/8Ch4sGv//7v4fPPv0Cb7/9Lqwtcev5mxKGmj2YO6iJEJkCRCEnTlXi/teP8fnnX2H/8BDlRoFyWsIta8mAzgAMo6CQeyBcnABgQtQctibNqdYzIEG4MACYyR96ifSXc1JFAAADBkMejm3Efa9nEcNrlcN5TMnxUCIMWFhwyIOTCnM0RKJSWBkOoW47fPX1Q/y//t//X/z9T3+CP/uzP8Prr7+GJ3uP8fnnX+DBgwe4efMGnr15A9s7G/C+Q2mDNJCtnH/DcIGx6XwHCtobQyZqiWSYoku6eP4MCkMo4GAgZlaLukPTAq4j2GIcDF2+fBl/+Zf/AfWyxWRahbMopqeyRA7PXLuKt97+EJeu3sAzt17Gr9//NYAOzBYE1RgLuGcvRobwQQsdogEiAUNq/qV+NSnodTy0ydZFYgCcmvgl6ymXdR+m0nDPgGm+DBtMfL1zYOdAGm/ShLqcR2G9aJOYYWmCWTWLtMazR9d2Mbxv29RYLoHjwz08fHgXH3/0Ht5+6+e4dPkSbt16HrduPY+9wwW++umv8fYvP8Bzzz2Hm88/g2eeuYqtrQ105MC+g7GABYPYgcigtBUuXLuMc//9n+GVN38Lv/yHn+PTf/gFDu/chdk/gF0uwNzAUwtPQEEWCGZz4aDBcBlORxeZC5kSZfxWQRLQ+3mqQEZBE2VrlwOfFNimWKE/Q+NSWf3+JMn/WB0p0E7LUAKsuAUgksACTA6qmc/fkWRqiH5gDI6+PmCAqb9/B+AXQ9+FIe3o5yKX0lvIvas5lVK65LJ2VJOQMxgrY0iez7Ua6d+DOnh8btO+jzGHaV16XuPzqbRE50LHaIZzFWm4MngJsB4kmgYFVjEVUMn/0neGaxOMLQOTkX6udJ8SWZgKMoiGPlFSRe+kn89tPv7YTsKQKqRSul2WJZrFPBG69Pceh36rJnZs7plIXWAFx0MsC2T+VxmUp5VvzGgoF6gLVRTFYKPqhMSNYkxcuo3NTXjn0HYdplWFtm1jkjidTFXDEUnikcVigclkgslkguVyCaYOJRjH87mAzq4LoQMLlLaI0iNrJaFf23bY3tmOkUnU4bawFuV0KuCOPDwL6CmsQVXYhKMOS2RkY5ch+paCQzGdSiYeEEbGO3QsDEbrPcrJVKRxzmHZepy7dAXXbz4PB4uDwyPsPz4QG2sQbn/xBZ599llYY4MmZ6iiy52+xpgNLZLXggXnewZ7tfkUKbn6NMhn6u/ge84+gKReA8ExIlJ0ktINTABZI86bzg+IoHcuOMMzmlbMd7zzcU3azsG5TiLGBJCvl5FextaaaIKk0oE2XM5qJtRnaZbkbsqALOtl8E3oMF/UOD5eACC4zmFZ16iX4ufgfIsmahISqUMYf1mVKMsqOuaXRYHpdIaqmmI22wQRRXt00U4wqqkw1JKbBdje3kbbtlgs5pKxPKxpKk3S89Y5j+PjeTS7Em2MHH59PjJgXQd2GEhP00tc/06d26La1q9KBeO7ZmjL++TJzwEA777LeOGFG3jppZfw2muv48c//jF2d3fx8ssv486dO/jNu+/h3PlzOHd2V/aCV22XB0E0S2VpcO7cOfz0J2/hwf2HMAVw7ZkrODxcYlE7ONaEZ16YDAWPSC4qQFQF2YWWjiMt6cVH0S9i1TTBu1WThbR+BZr6WezLyLN523m9RGJCY0y/VqJ9QwC9ITEZEYy1YO+xWDb46OPP8MUX/1e89tqr+PM//6d48cWXcPv2F/jNb97D3fsP8Nrrr+Ly5XOSFwEUtERDR9R0r3vvg2O6jokBMphtbIg2OO4n0UQt6xq8OYOEix3Osfcek8kEm5ub2Nvbw6XLFwczRGHJbj1/C//m3/4N2M7wwosv4u7Dr9H6Gr71QKRXwzj7aXCSFamkX51vZfZSwJECWxl3sdY8xwTfg9x01ZBK8kMgEe9B4UwVZQFrQxTDuoGD5D0h3XdkYEwBCu3ZyqH0HuQlmlbT1Oi6Fu2yxny5xP7hIe49+BofffIxtje38Owzz+Hmc7dw5fJVvP/+e/jwow9w9eplvPDCLTx34zrOnpUEkF3bwTRe7qXCgwuPoqywfeks/vB/+FN89wffxzt//1N88Pc/xfGdr2CO5yjqGtY7dMYFhskEZkNAMbwAPp2PwVlbw2jk+GAFuI08r2udn6GT7ry8pDQwb0+/+yb+IIM+AsI2cJQbB6a3/xbh3tMhqC+LloGwQ/s60n9gNddBTuMG9DuAw5QGpc/rHTEGZHMtzrrxC8hflXDH82FEcBGl6SOgfYxRHPssHUPat7Sv6yJEEUkgBZ333J8G1If8HdwDI3Wl/VmZf/kj6TcFJiNhKLJax9ZuHXO8jglOxVvsGU1dizDEknI9K3Xl2p5hez3OE18+ZTJ6rKj08zTl1IwGWXHyJterrBx7EHtRr4ZOqse9Z45JdtKDoyqv+UJUxltbmxJ7PkTjKaiA65KDZyWOedd14mRdWFQ0HXB+bXBorZc1OEiajTHirMiM6VR8HMgYEIstYFFKEiUyBLYmqjWnlYTRVWAJCNHQxdjd3Y3j9N5HUxNjDFzoS1mWaL04c9eBmWIQ6kYWf3P7DK5cewbOA/O6xvHRHJPJFJNJhb/8D3+Jmzefg/ceW1vbg8O0zhk8l3T0zwio6xkLscX2LpgmdaI5UCfh1DwO3JszRVOn4DfhQwSvpmnQNBLuVJ2LW/YxwZkyC5rTwYXsy0rYNQIYjMGyaVAvl2jaNtrtLpdLdOGZumkwn8/hnYNnxv7+PjplCLjP7NwTatGsSPQXGyUdZVmiCMyCSGYI061tbJ+t4DoHU4jDM5FkiLfGSIb10H9DJsSnFjOjsigwmU7hun4NlPGR3A4deO8gakeICF9++VWc0851aAMDkmpyAMQ8GcwilXVOQnWS6UPY9iFrGcaoU6VKVYYSn0iQzZDAEkTCrWcgJ8CMgN0CoY4EmYGPPvwEy2WDV155GRcuXMCPf/zvceXKZWzvbGH/YA/vvvc+3vzd3xEpFCdSqCRDdmEq3L9/H01TY2u6gfPnL+De3UeYHi4wX7bSl6Q/MlccI3bp98jOhdKBvIxdqPm50jM+VgaAgFelsHlb+fPr2ksvHJ0bjVymicm8Zp4OQSa891jWLX751q/x4cef4I/+6PfxJ3/yxzg6OsbXD+/j7//+p/jed9/Ac89dhzUEEAc1ey8cUqYGQIymxCxSVwpn8czuGdFmm34cbdtFc8DcvCOd+1deeQWffPIJLl+5FJ5RmZ9I+XZ3t/Hss8/iq3sPMdnYEVPRmkXr0vYhHQdgyxCgCUuVUWAxf7Jys0MTmipjxOwlopiI/mDJBtOAkPtEJh9pIkOEnnoDMAjGloPof6TrxRZFIea6ynAEt0OUVYWqLMFOaGMUEHiGYQ2B7UBOmBTyHUpjUVQTABw1HHWzlBxL+3s4OjrCo8eP8f5772F3Zxc3nruJ5248j8WnX+D9Dz7CtetX8Nq3XsFzN57FxYvnYFjMP5uO0RUOZBsREpYlNq+dxw//2Z/j5R98B7/5jz/FR//p56jvPgIWc8AfAewiXZJzH0xlEsCf7+l1AHUMYKYlB6pj50Q/Wwe+03KSHbmeM7330nYHDGpyblcYHO4lyomMGz2TET4nEccNoicxR1++dfQj728+rycB0vzd+FkAvum8pcKGpzFwKRgWrDBcyxVmCMNn1gl+xkq+B9J1GJsvvWPz/qqAIWdSVFiwTiD0jy2Kecf2kgQe6YU8OcOSMxx5vfreuj5GTRkS9mNsvoiGvmeD9nrcq5hetWsyh99sjk6v0QgJ7CBBmSTahnPwZKIqxZDYhGlkEumsD1oNQmHFoXnDWuGIvFxknkVqSiB4QGK7AzEEaB3Apg3PGhs6EWzHKit5NdQkS8+46xwYjKOjI2xZg6Is4HzQbISFms6mMFZMT5xzaJ2DAQMJ6HNeojg472CLAj7U4ZkDqG5RlKLhaNsWEz9BvVgCBLz77ruYTqfY2d5BURRY1g1+8Oa3YOwErZcMxkQGrnW4c/8Ojo6OMJlIKNuq6k2ytKQEcYyopxtQE705p47VgPMdmlqA8PJoicODw8goLOs6Ata2bcTkJjAGbQD+AnYtuq5DXS+xXNbioN91OJ7PMV8ugwmPR9eK70HXdbDGoF4ucXh0BBcu4rZrsVwsJSFWkIrI+Fjs4ymYlgStl4zVhPmpYK2YzU0mwjSIhqxAWZVgSEQn53xM3th1IiG2hSAA5zgm6vKNSHe6tgWWwSzK9cyAdx4c+q0+J6JxEIDmui74lCBy+3ENRrLC9o5evURdNTVS0kNMIkFk6Td7kZIJE6/42sA50RWkxAKRyEOAGSVNgGCMjapRscNGIII2mKsE8KmSdgJgVCruYMni3t2vce7cOVy/fg0///nP8P777+K73/sels0G7tz5Eq+//ho2NyZIkwBKFu+eCC+XS9R1jV27HddTeAlC6xw0/i6rpNBQAJaBFCSzpeNfp+I/6VLMyzop29iZzJ/T39Nzug5M5GBG+6bviHmNAzHBQXwihNbJunXe4eDwGP/6L/4tPvjoE/yLf/F/xOUr1/Ho0UP8w09+gdlsE5cunhPejIbzMXBY9xwjEMlek2dns2k0m7WJFmS5XMreL4qgtu+1ZHqJXr/+DH719l/gh7/3ZmBAdH5Ew2Ut4VvfegW/ef8vcMZOsb21i6Zr4bp2ZV6jRI8ovE1Rs9xrBeNo4IKmToOIMBCPlkei+Yr1BaYkpbOGJG8KCOrHF3qEgigmYSRrgklwEYI6tIDXBIBiEmyMwdRYwBh0QTjhvIuBIZg9qGvRNcsQ3dDDAJhtVqimM3TdUvIqdR2Ojo8xP57j6PgIDx89xG/e/QBXrlzFrVs3UdcNvvjiDq5du4qXXnoeL996FleuXIQli65leNeidS0K12BazNBZi51nr+KH/+P/Dq/89vfx67/+CT57623Q/S/RLZcwTQELj4I9vG/FrCKxcU8FfwpC1gE3BfgngcfTgL5U+HZSGZOK6++5dUBad9q3dcwOggAnzcAcN5mOC+PmSOn48nnMn0mfSxmsHKSO/UzHARJWyI/MecpIjf3L+6Wf+6wP2lb0Zcp9G0bmO/8un5+xMa+rK9dKipC079N4ZMg1fVK7o6TktHpsb4ytxYAxpKFlwbr5Sc9KWocKogZ9CfTMFBLIpV7MxZ0hC9Jx0n24MnoBBAGbpRrGIbP/tHJqRuO9999D13W4ePEiiqJAURRomiaYNc2CraxBXdfonMN0Ik7aDEZRlth78gSfff45tre2cObMGWxubsK1HebzOR4/fixSszNn4mRUkwqz6UwkDomqsZpN5Qyj3zwqFUgPqXfRiw3GGHx9/770vSrBnnF8fIyDgwPUTYNqYxrMnSQErqi3BVA2rcejh49w8+ZNAVfOoSzLgb2pZy/jDqD8/oMHKGyBpm1x9+v7OHvmDB492cPFixfx/AsvY7q5i5Y96k5s6h89eoI7n32Bv/tPf4d/8T/9c1y/fj1c6mbtJhjjdPPPBBRLfg7vCPP5Eo8fPcajR4+xv3+A5WKJxXyO+XyBw6NDLBYL7D15gqYRM6LOOcyPj7FYLmSjOQk5rJYJTV0LuC+KGPLVeXFQU78VZpZoKsFpjY3FbFsy5RqSoADVZAJj7cBEyhiLuq7Rtg2sFadlNT2SsLYc/SGWdSNzHwgbEaHp+tCenjma7LH38NHDUSS3Lmh4QGKjGZ2uuA8TyMwhUk8SqUo1BkASGUSfR9zLJmEmxDyNAhPYO1hJSSMUcYKetT4B+JTYpCNaXGoVBI00lBJUZoTw033RZG+GCKUR0x2Oanz5nSEAKiVoEfjKLoP3wL17X+OFF25gOp3g408+wrfeeB1FVeHo+BgHB4fY2JgFs52hvbAxBk3dhmhYiKGvRWrM4cFUqmhlHvTSG0gOh+dh7FLS7/JLLb+sxy759P303dyGPH8u1UR+EylQvFiIAGPhOzEHNDBgdjGHB1FIiMVivvPBhx/j//G//j/xP/3P/zM2NndxdHiIX//6ffzxH/8BjGUALqioRiR/EOBrEMJMB7MQEXxUsMZGHzfnHerlEm3XYuItxoZGJJnFAWAxn6MKwQHi5iYJtvDii7dARJjPF9jZOYOv73/d94l5sI4y32KS2zP9Yd8CwggHCapqBUXgnJqVIAJBhMs0xL8DmOMFTcps6aZlBPamZ9616J2ggpHOEDo1Ew3MiwHA7GA8YAsbTX11XM45cNNiSQaeFwAx2HXCZNoSpTEoi6n0MZhX1U2NpnVYLB2Ol0t8efcrnDl7Bjdv3sR8WePzL27jvSuX8frr38KNm8/g0pULKErRjrnOowWASQlfFqDC4tyLz+GfPHsVr/3we3j/r/8WH//6Pcwf7sEdz2HbBtaKwKpn/nOmYHVfrdv3Om59JjVlW/deCtjWnbn8vfycj9WZ93ns+xVwGaQ9K/1kZWQYzA4w/b2R04MUwOf/8v6nv+chXnMQrX1acd7Gelq3bh7WMRsqGEzrGvRzpI6xkjN9OYMzVscYfV0PfDkC5ZQREZPJgewltmMy3758rvI9mzp0ax3jfyvNGY41r1dL7pM0nHv0tCgIHdXk/uCJapz69wfM6QlXkUaElN/ztRMFwmnMDbWcmtFgeLz/4XsAMW7cvIHNzU0sl0tsbGzCUC95L6oSTdPEBS0CaDBlgbptcHV3B3fufoXZZIorly/DscdscwNHR0donTAek8kEprAogkR/sVxGW7Kqa1FNp1F9rT4aDKB1XUy5LtJ4kZ61roOtSnzx5R20TYMmmPlcuHABZ8+fw8b2FjrnUJVFwGke+/tPsPfkCc6eu4jNrS0cLxdomkZ8JgoLciJVbJsWIOnHwcEBjo6OUBQFNjY28dW9u9ja3UHtOpRlid2zZ/D8Sy+hcSxW6p5w9959GADnzl3ASy++hEuXLqNpGmxtba2o8PtNsJ6LXJXYGDRLhwcPHuLTTz7F4eExlvUSX399H++99y4+/+JzLJdLAXdlCWuMOB+HubfW4tyly7BWgP+12QzWlr2vhecY+aJu6hAtSCT8PU4O5leuN8FatH1GXz44hHcd2hDmVU3SvKq0SbhpNZWKifFUCxJMtMaAXyRg3DMGTEJArl9/Ft4x5k2I/EJBS6BJwCghYGDACuFM4kMEoIKQLR69NIviExie6ESyF+y0xwoljwoWSqQSRv2kRhhOK2cVCPbjpn8u3UopIyTjoyB9stEckIyYjHHQdkg2Y81JYWHIAa4F4PHkyR6WyyuYbczw5MkjHB0eYrq5g7KscHB0hMu4JIwJy/+UITPGoGmWwZbXB2YyDTucMD0JNo4XGPcq6sH8jUiJxspJl9NJzMb/P4uq2otqAmLxZWINexnsZ0WiFS49AJ9+dhs//vFf4c///M9RllPs7R9jPq+xtV3CGNWkDS+3OBeRuUbYEyYwfyVsWYivRqBNTdNESTzzathJ7yW885UrV3D33j3cunUzMNsKHCQ0+ubWDl568QW8/9FtbGxsYjKdoZ7PV/oXnSajHEnONoJEkkBg1b4BQxBLFPeZ9yHIRBAEEAExapT38F2Hjl18R82EAuch7Rkb/L2FKVNhmAj7LayZRBtp33XR9w0Qpt8aIDQJY0TrYgzQeY9iMsWsKOXvrkXTLNF1LeAsmBhEIWb+rMJ0MkPbNGi7DodH+5gvLI7mR3j06BF2d3dx/fp1HB4s8fnte7h54zpe/daLeP7WM7hy9SKYGA01ML6DbUUb3NoGZVHi8qu3cOnms7jx/id466/+Hvfe/QDd44fgY4b1BtQ1axhz1TSOM+3pmo7tvxxkyj5ZLwFP39fP89+1vtOA0jGQv64PqyV9xgBgWFsGLeEq86R0aswJ+Kkt0dBXSc/byp2QgXSTgO2T2hsDwWmJbY18LfeHiQz9aUq+NjnzkjNQpylx7YIdfxrlKY6de8uCtD2lgakPzeg4w+eqQX8aABeT9L5/uZD8m4wrtp+8ymDxEw1CEkrmNR1filPysQs9HQ83rO0PGO6nlFMzGmfOXcCf/Ok/xe7uDpgRwhoSPBOqqopqMmuBaVH2OS/CRFy4eAm/d+Yc2rbBw4eP4QFMN2Yga7BFBCbg+OgYZ86dxcUAbFUq3gUzluVygXldA7aAB6EsC9iyipuHgt2uZ0bnGaYoUFUTzDa34L3H2XPnA6gSIGyMJDXzJCYnZTUFgeFdhwuXrmC6sY3N2SbqpsFscyvYkbcwJuQTcU7MeKzk3fAQ+/m9vT0sl4/x9f37ePJkD7PpFDdu3MS1a8/i668f4NzFZ3B0dIjj+QKXL12CJYt/8/P/Dc8/fwtFETKSF+JXMNjccU1z9ZcfHAwBC/Je3Th88tkX+OSTT9HUDZ48kWRov/rVr+HJ46VXXsaVy5dRVRWaupZQrd7BgYMPRoO67cBNi7qucXg8R9c5NE0dwq3Kpus6F3JIyCXeNI2EimU1MZKLVkyMhnkvNF5uv8kpMifxQEGFR7KfUqcuBUOGSCRHNrj4hjkqCgpMRD+XTdvhzO5ZXLhwCR98+CEW8wXELj049KuIAKE7+kvojRAm6ZU0ayIQUQAMBBBCpl+7cHblWROZGwBxbwIYfJYXY4rBxRQJGwEcbMkjDJPpCdq3HDgjPqfMycbWNq5du4Y2+Mo8fvQYT/b3o/qfWXQSkscmXFheNEL1skFhCyzrFvfufY2bz+/CGCNBHJI5CVg2rK9E49rYmEnEq6ZDvVzAFiL5DfA5znMOINJ9kZYx0HGa8rRnxy66MXOHFJzkn50kQRxri6CEHQATyqKCI9PPPXtxMDYmAHeJMPSbd36D1157DZcvXsLSdTg4nGNz6ywkb8aatpl1thHQkVyGAHzXoJoKvQv8NeqmwbJpsdE5kKFoPjW41OBx89YNfPjhB7h588agOeecoG32+M63v4Vf/PId7FQXsDnbRLNYhJ4kUkyNNiacpoRCV1NFBVtBIACiKNygYN6p91EvUQTYhKgqTNKX0mJSbcJ1TsJEOh+YK4BYfXJMJAcyU/3YVUBhrUVRTEFMIuBqGukPGIYZXdME7Wwf5lt8GKVjRSk+MZPpBBt+hrZtUR8v0DUdOEQMY+9gbQU7LTEhoct13WJZL1E3NY4Xczx+8gTbW2dw5fIVLOoFPvvsM9y68Rxee+1lvPDSC9i+dAbGeRSuga9rlJUFCgM3m6KpClz7zst45qWb+OQX7+JXf/O3uPvRB2j29lHMDdC0MPCiTYOTuWeOOlaluiEhOyT/an8ecmGAgu5U07OOgdD9ld4lJ5lSjWkP1tGHHOiOaU2CuCPspTxDDmAsxeAzBmmAhWFeixzQj9GOsbGk/WHWdgOdwJDG6DMitOnzNqxrI5+rMc1C/EnoI1amdQByH3uCG3l3bDz6TArWc9p6EjOa9jPto37unOvvasUaWXsDhge88tnYPOX7KhV+9Ugi1A9K0zAB4BjtL7nREAUnYSyOubcE0Hl3ettT7KvrXGRg2PtBNFHGsP+J4iL2m+PfPn7JEGsORhDEwkeLj9OUUzMaF688i6ZpwUYyepcAqpmYr8wbFxPdgRkeHkxWsmCrBBQEUxhUpsS3v/t9HBzsYe/oSCIBNQ1a7/H8Ky9hZ3sHMBbGVuDgKFdBFnq2sxvDurZtC1MEM4rQR50z7z02d6aJaROHQy8HzBKhCCFv+4RfwjQZYwFj0XpGMdmCY4Oy2oD1HteuiZN23TSoJpUcniAZK4oKtvM4e3EL1XQDi2NJQnbr5gsoqwkuXriEd955H6++/m3s7++DjMHmbIb5fI7FYoFlu8TFK5fgvcPW1rZIwsDQSDMSsE49//vM1boJYsx3FhmbaAWAL+7cxWe376DuOty5+xXefvttfP7559g5v4tX33gDzIxHe/t4cP8+lscLNIsF2rZB4xp0XTuI/R6dxYOOrv9dN2noZ9KvWFaIqawYEYFMOZAo9DbcyTODi4gQQymyfp/t+bTp0KAeOvIeZIHaM+zmBma7Z1A7AEySsT1eXv1BIgAF+kZWiGX6Z7o4K18iOdhh7ahXa+fdT+eQ4nMsITRHLgnRTAwJpQgoaNgjJRpRIiIZoI+PD7C/P8VkMhEAUxAohFQmHX8EWOJ31TEAeDgHWDuBdwscH85hmVESwTdtiKzT98E7QHhFD8k1UAJs4DqR/p49swEiB0MVPBuIZ8Lw8lkH0scunnXPfJN3c1A0xjCkl/JpbcjT9/MxcQDTCOcMASTbokQR9oxEN5N8PdYQCmPhug71vManH3+Aq5fPwhqDw/05rl69AM+dOExn7cR/XiIwMcK6e49ZWWB7WsEzoTRGfKrJo3Ed6s7D67mnVGIW6gbj8uWL+Pu//7vABAUmBnqpOcDVePnWczizOUG9WGBaTgEve0+sM4YmiBzottKllD5wkF4yQjJFQ4j5UmEiowsikA1MAxiGGI46mMkMsAWmdoJqYxtHB0dYtgtMTAEKNM8EzaELUr+U2QCLJr20ZRAyMIqK4NsOy7aWxK+MyECmwMgwQ0+99wy0HmQLlGWJybTCmdkmmnoRQ24vFovAZEkdk8kGytL3wTnCv+VijoODx7h3bwdXLl7B4UGNjz++ixee/xyvvH4Lr7z6EnZ3toCC0NUNSm/FMb00aMsK5WyCl37/u7jxxov49U/ewlt/+bdYfvYlzMERisUSRC0IHbx1YqoWA8T0lIwSuqjrlTu2KtOu5tBDgVomWME4UF/HTAz3yHrAGEHaKeiGgjHPksVbE0h6BWlG7mrHFmmo19QHRH+uoyv5eUp6LbsuoffKZBCFoPocwj9rrGXCUGiUtNlH2lwtKROnazBkdvzKPMexEA0YK/08X9uUVqZ+HWlU03XRsFLmQ98fmy2EOzcSAeaYI2eMBhOEfhDRIMpjfl/nwSq8D8KfQdvytxfJWN/3YL4lPseInElqCg4WC5p4BYBFMBHGwmx6WWZRiIAkzFkM7x3u/GgiSgDIgGyShDsOXZmSZI1I54YANhFrn6acPuqUsbCFcjwUN1A5maBtWxwdH2NzczNsCpHUmkLDBULUNx7ofIv9/X18ff8eiCTE6osvvhgduduuQ2XLwaXeX/4iVQIwiPwB9NxYChAGBCw4kOtnKjHxITpKWWo+DkTnJmbJzC1hZyUhSrtciuTQWJB3gxjKFPxUtnd2Ma1KnD17DkQWi0UNUxTonMfm1hZsWcYEbV3X4a233sLW9jY2Njf6vmTzz9wv+irx1ezaAhIEhAOL+QJ37tzBxsYG3n33Xbz//vt48OABdnd38cqrr+D+g4d4//338fDBA4n/3slGF9tsP2iTqDeXMCQqwqJQxKzzHgwJEolB7GnGDKikFgknjuS7sZITQ2NsJJpSU1rJ6ru6P4wxYIeY1KbzDiAJdUtGnc6FOGvfomyiH/LI+qT9Hx+DMmVa8khPeZ2jc0FyscELEeklFtLHdYA4vbRyqRBBHOettbh3T+zj5Yww2Nuk6V4zRJTGxhcmtCpLeM84PDwEWOpomjbW1XWdAEgAaudprcV0OoExBl2IZDSpqngxIFmBXKp2kkRu3T76JuW0jEp+SY0BnJMkemNtjUlc83aMkeAI3hlJLOklmIVI7zzufvUVjg4PsTHbxdGR5nUxIH/SHu33SGpXLtHbbNCciNSZvfinyZ4z0Q46H+N0KszrwcEBdnd3kzEJXei6DltbO3j++Rt4652PsLW5gbIo4bs2gAKOIEFAuIsRUzRqjAsR6QDEC3PYF2HS9DL3XiInGoiGunMObCysEcft1knwj+3zZ1E2U8wPDuCZUXgP8iYyBr0mQ8KjCwNuMK0m2Nvbx+HhYfQvU02961y8N1Lw3HUdjO2j5DEH3zRmUFXBWopz2XWSk6ppGiyXCzgns0NEKMtS2glhsdtmiaZdousazI+O8OD+17hw4SKOjvfx2e2P8dGHH+O1117B8y/cxJkzW2hqhjEOpmsBx0DJoGKCYjbBm3/8+3j19Vfxs7/+j3j3Jz/H8Vdfwx4eo6wbbDQNfAEsqQGZEDnPKBVlGDawQRCWRghKaXtq7jYmxc6j9azLKK3r/03NksbO6RgT0P8dhCg+076lQiKp5Bu1f4onwz+VPPPgc2kz9WtbvWu1rTxFgXR3yDCMaRlEYNWvzYpT88j9DgyZvXVMX7439D1NsXASszEQnIyNaWRt87GFAazc2fpO/l7O8Gpd6efMLAmcs/fGokhx9n7PSI5ghbjeFDBgoPMja6JFTHI92PVamDhnONmvKj2LpynfgNEQ4qudUNDm2KOaTDBfLvDl3a8wmUyws72DMomYxMx4/Pgx5sdztG2Doixx8eJFHBzu4/y5a5hMZjH6VFFUIOovrFxlpUQjJS56CPTzHEilUq+co46cHDMmk0lsR/ODLBZL2KIUaT0BZTWBWy6xrOsYzUjrLMsy2CQLA+Y6D2MKPNl7gJ///Bf45//8n6MsSxweH+P4+DjkUljgyy+/xA9/+ENYa/voLmsyq+ZSGnXGUsm1FuccvvrqK1y6dAl//Tf/EV988QUODg7gvceNGzfw6NFj/Pxnv8Dh4RGsMaiKCigogsd+kwkRJagkoL+0c4JMMDHzsO6Zfq/2bIW8I1JaZgZiRt6+xf6thGgzYhKz9Lt0f8T3aPU7ZX4AySRf18vgm1MFs4UgtcjmW8tpXZ++6YWm63jSoR0F2OCBNFcEhv2FMAiOkF8AGUG2RCiKEtHRlght24UwqLIHVvqE5JwZg6ZpUVUSUW4ZnIQlDHIdzaSIREIEzTLvJcLY1tY2yrJE5yQi2u6Z7ewMDMeez0k+72PEdd2zWsYujm8CUAZzM8JgjLWx7vN1F2TOwOhPG8yZ2kZMAziYUR0fz3E8n2Nz4wzmIfeQSMrs8KDFhvt1Tds3xuD8+fO4v3eEsihj7iN2nZhcdh24Kgd7Lh//M888gzt37mBnZyc2Rkzwnew/7xp8/3tv4GdvvYONjS1MJxVcU4PJ93bSYR9KzhsPayyathlKxkn2l0oLUwGUGrgwEJ3GXevABcMbScoqQSo8yJbogqmW3ZhiqyywODhAvVjCeIMCRqwfjUoZhempigJFYdB2Le7evYuNjQ1MJhMAiCaJQL9H9Q7S4rxEFwuTBwrMRlEUoKJPRGuMwebmJmazWcg5dYy6qSUpYBDqGGODI79FXS+xqOeomyUWy2McHO3j0eNdXLp8GfP5Ap99fhsvvfQ83vj2a7hx4zlsblSAc+hcC9d4tLbFdDaF9w4bl8/iD//H/z1e+t3fwk9+/B/w6c/egvt6D+XBAgW3KEhoujFAxx28YXhiOfdueIflQRvSKDvp/knPfhQU+vXZuHMad5Lg4SRQuo7JWHkme35Ig2j8vI2Uk4DvKhOktHncB68XPIngbKytdC6f1occTOfMgtYXMZnp5yVfh5SRTLGavpvO4xiIz+vM91L6TC6wScc49l1ecg3UuvdyxkA/W7nb17yXl5P23rACqBxllFFOMV1/JvxKxLDYl+z9sXswZz5PKqdmNDzSfAocNo/auwJVVeH69etwzuHg4AC0oBidqWkaTKZTnDt3DgDwZO8J9vf2cPbceZw5ezYMQCMiuADqx5PIpFKPlKsa27D6rqq84uWYMBi6Adq2HUid9HB6LwYbxoSY9mQwmU6DyUINoFfTlWUZgDOjbcTetppMce78eXzv+9/HhQuXcHh0jKPjZbRbV6f0a9euoSxLTKezwETpQRsemHTzRhAZOF3F0d5L2Mmu63C8XOLTTz/F4eEhmBlnz55FURT4+KOPUM8X2JzO4tz4yGmTaGoi4AB6gqYEi3rsGTcoEFVOHKxWM+FAJI+M5C/ZYf1Akw0e/y8SmbQMsp5nB3XtwSQKKj9GXYuNdFWVUMMvXvMux3+cEAmKPzQTcRDVjzJLyQfpIEK3aLA39bOVfnBk89HzfUNG4GkX1QrxYg3DK0yGZzEbM6aIDL/WO6g7vC6aCB/MYvowo3ruVOJtQohsFuE3OLSj2smiLFDXS9R1g9lsGiPZwYX4SpQ6tp8ghVozd08rY4RUx5fXmYOJsXfG9lGqUU2fP82FsvaSBcIlI9Gh4FXF79E0NQ4PD3H+rIu5ZsT/JT2LSR/khhlclvr7bDYF9o5CtKSg6bAWdd2g6xyYi1jPqvTM4/r163jrrbfwxhtvJM6YBhTM9og8XnjxJrY3Z1jWS2xtbGJ+cAgb/aEQJXaF0RDnjNLKniMggGyh/2VZBu1H74QtWekDfeP+0vUhO3fhGb7tQEUBBw82BqYswSQM8XZZoj46Qn14FJIgGpS2QGEMDDEohFw3MPCuG9LphLFQplsl+zpvsp7SP2YGnAeFPS+mq2bA4CuDNZlMUFUluq7DYrGMPnQcCBfZArONTZRtyMnRLtG5FnW9wOHRMb7++j6uXLmCg4NDfP75Hbzw4gv4zre/hRvXLmEytYBlwLQ4cg7FxGLCHhXNcPHZ6/jv/s//J3zx/e/il//ub/D1ux+C9/Zh5gzyDuQdjBfn+ZY7UPBVSPs+GHsCGNPPU+GJzhswZDjSOcnPUi7USevNNSLr6OVa4VX8TOjUaP4e7mn0mPlPWuc6ny/tb1+3fjcEmPFDUHQ6lnHwyv2W7s+cMVvnl5ADdwZifiUdX/9w70ydv5cDdf0+BfU5aB/rU9rnfA7TunKGdmyOV/8e35dp23kfUyZpjOnAyP019vdJeCa/i/qxi8BUmb18jvP5N6bHyoN9J40O1iPtV86YPq2cntEINxOzJDcyYXeTMaJ+tmLrRWDsnjkjETRIgNsGb/Qqbc84f/48yqqSC7es0LYNmAyYwkKOXFLDUJ3D0G45p6aEW9/VxHApOND6UklYDgCIEDIzL7C9vQ0yejAlHpoxFuobkToni60bwZYFdnbP4Be/fBs/+MHv4vD4CHXdoWmlf3rx37hxA1tbWyhDEsG0rANMqeoYiXJSkj8xFosFzp8/h7/+l/8b5vN5HNvZs2cxn8+xv3+AqpzAxihD6BkGENRLSLddts37X5Mv5BC54WOKxXnl8aycBAx1ffPPV6VP2o/8cOXzaIxmRmUUhWRkX6cm1eI4kZylBx2ICSpje6O9XB1V2q90TXOCPxif1hkQZqyfeRAuNyXUeRlc3AmYR1h7sTU/mWlR8KZOZ23bYntnE4CYgGhm7aZp0LYtZjMx9wAjmBhIFVVVYnt7C9PpFPv7e5jP5yHksYkgkXoLxQHxO4006mllHUN30mcD6c8pLo302bUMZLL2Y/Ws6xOH/UYQRoMdwVuPrhNJ+MHBgURx8x7z+RzT2VS8csfqV3oyAi7OnDmLO/efRF8JYwzgHZq2gXMdnC9P3G9nz57FUfDLixd3MLdkZrDvsLUxxQsvPIef/uI9VEGrHC+0bI4o2Q/GGHG4DYkn9Y5QO+fwpEjUpUeIGWUDAwvv0S2W4I5hqgo0IfiiAGwAo0buu92LF1BcOI/H975Gs6xRNADBw5YFYAmuEzqo+z+V0kZmQwNjJCYkOs+u87BF2OeB2RDzsN6cNa1P76+iKGGMhbUlum6GuhY/jrppoqa9KA3KskLXCpOxaGrUHWNRL7F/dIAzu7u4engNe4eH+OKL23jjlVfw2rdexrXrV0DWw3EHBwffeBjrgbKAnVR44buv4bkXb+Hdn7+Nt/7yb/Dkg0/hj45QNDVMC8A7FMzwphdQpfdtHho0Lek9PwYq0/OVn6EcrKbz/bS60jU5iUasB33ZcyPvp/R9rP95SYG25CECyPSCLh8iJtpChIF+MNb+XsoxUz72MeHtOgYhH3vyweC7de+O0cv8mZQ51D4+re40EeNJwiKtL21jyEiNM6zpcznNTveamhePjXlsD42VsX2Zrktqoqb5v0SAuOoLlJ6Jtfco9+ZT+RiVtq5LiDtWTp+wDz3AiQ0C0Qa0rKokLGbgJnVg2vHQQVtMsLGxISFovUfnPIoAmAS0DNWARBRDmqr0c526NDWh0klUtbVOpGoeVPIKiEZGL6x+UYCdnV3M53Ps7e9LfoiiCOIDCkn+urih+/6IU/lsOsNyWWNnZwdVVeHoaA7vZeOpBkVzkzAzZtNpNIHgE4F3dkjUsIklXruOa75Y4tNPPkHTNNEHZTKZ4N69e/DeoyAr5k7wkugNPSjmgGRJ6x8QkNRpuQc6K7aYCeBmAPCrxEnnKy74yCPrzyDFF06CmuNE0aBtxeFd94qYT6WMZkYAMymblpilW/fOU4jGafp4ElH/z4PVfRkSXbHj1X/axoo2ZtDXkcsgah48OtehKCjYkC+xsTHN2g6hHSsb/DSm4ODHUZWagbnPoszEOJkhzfs3Pt5/DGMydhmO0aAUEI1JfJTGPI1BOg2TkX6nmjYiMQt0xoCMR+ccFvM52qYBbRIODw9x9vx0dBrjZZtk/04vmXPnzsF1H4o2I4yBQqLMtm3BfgoqxoGaRhLa3NzE3t4ednd3o3aLmEBw4icGi+9+5w387d/9AhuzbWzMZjhoW9jUJIII5Pv4/UoFiCho3jvReABiuqFzFOgjQhJNDyDYO4EoKGO9g3cNfMcgNuApYGwBsIGtLOzEwpYltjc2cOXKVRzcv4+7n36Ktq3hJyUMSSRFTVXCzH0I9njBS7SYGFwjB75giGJGxmatDbmJqjCOYZQlCoySc5orQJiJqhL/yfligflyEbRIDoBHURpYU8BVHZqmwXxxhGVt0TQ1Dg4P8eDhQzy+dAWPHh7gk0++wHdefxWvvvYidi9swxOjoVYYIGdQuhJlKf4b3/knb+LGqy/i13/7U/z6b/4T6rtfwx3sg7oaIBPXLaevqXYj3TciS6EVYctJZ2YdQ6+fp2B9DFDn+3fd3/kYNEDJKJjO+pmah60TLIyNr2dIeiNA71k0YOAo0VM/TXlW8UEyjoTZS+f+abQzZzq0pLRw9O48gVF8WsnfO2me1q3n02h/Xn/6brorc4Ynb2dsvCkNfdoaf5MyoBsZM7QM/qfpZzmzIKRwOI5+fwznKzdJ033zX5zRYGAQGpBJwKf3jGoyjUwEIC60RCQhX5lRFgWc92jqRkC0D+YUOvlQ9bWHtxoaz0QuTcB5EeKJtyhLyVCbMh35BkwnSP5WMCUHT/9WYq7mQPJZX0fnPWazGTx7HBzsg0DY2NxEYSW8rbUGRWHipWFiYh6P2WwDf/VXf40XXnghZK0mybi9rENuEKCuF5hMClSTApNpJY7YzFFarfsnZzxSwsBq1MOiku+6FkVZ4r1f/grzZR18R0Qi2XUeT57sB8dBhBnuzZ0GC94bUg3g/GBTB4CTSvO1CMPEsa4BI7LmwNHI7+nYB0QEyvD2sJiDhBLx0lplgXxgbCQcb4uiNBJ/kfspWEcUUsnHOqKRSg/SfiZP9D8SQphLGnIiNSAWAXOvLBlOB6hXzgohzlPO1owxG2mbakrZtl2UgtRtg9a1IFvCeUZTdwAkESPDh2FTFAowPLa3N0J4TxmcNbp2aiJEQWCBqC1d6c+ay2jdWq2TLI2BlPxyGdsHY5Kxsb7kdZVlGYUp4dOkX+NSvCFADY+F7PFEFq5rYWiCxUJyBxlrMJ8vAS6RXp+Dy4fCaQ/7Aei1zNvbW+i6ts/bwQxjDbqmRd116LyH8RywO0GVhERiTlIUBa5fv47bt2/j7NnzMdQkw0PSDzpY8njpxedxbncbx0cNNqZTHB8ehvvEAxoJjjhGMaI4RRwib0l/03MzjJsP6ISJAEQ7itAfB+eCOYHvYAFwVYFIwqlXsyk2dzZwZmOK566cwbdefBY/+fu/x+OHD9HUC2xtbGNaTmGLApOQP6prqfdZI4BI/Becc/1ZZqAqSzADk6qCLSxKW/TLAQ4JCleBFMAh0amaNeg5ADY3NmCLEk1bS9hxJ0EDyMr706JEOZlgsVjgeHGMpmuwbOZ4/OQhLpy9gsODPdy7dxcff/opvv29b+O555/D1s4MddGAGkbbNqjKBkVVwZYlNi+ewe/9H/4cL3/3dfzk3/4Yn/zibbRP9sGLJWxbw7RNXC/PHLKMmyjqYkqWhAUJpGAvFwiO+aTlZYxxzs9hXl/6+YAOJ3Syv10oBifQZ4cgTISTaRspo5iWdX8PAbQN5oY5s6Oa4sCAJO8Jo83BbHWV3qXmaGPzN0br5F2ZjBW6pnOUvDPALae4nyLYHzHfyX9X2pv2TU2InlaUZuvPiBt1INkcpPfxNynKPDOG6zLGHD21nmRuUpTDABZ1DU8EnzC/gAghEDCj9xyFyApF1HdWLDxMTFYaZjvWz0QilD0l43R6Z3BIqMAoZQid9+xhUMD5Dl0jl1lhC4nvHZyMDRF859DWNbq2RbcU573pbAoXQl+yC3DXSTg/9oALIfsM2XAJWDDJRui6rveJSCYf6DdnqtUQbh7oOgdr+2g54pfKIaELDWzS2TMKCdiOrY0JqsLg8PAARwdPcPbMWZRFFRfQlDaaaQGMqpoEpqjEzs4OlsuFZA9vW7DzMOTx+RdfYGdnB1vbG5hMCzAlG1cDHEeuB4NxDsABMxDCfzIBjWsAY/HOu++DmVCW4mBvbYX58SEO9o8BFPBad8YRg1lCwGaHPXLBg+7oFqRV4BvmXOowMYdE/4D+6B+UzS5mEQRZG88joEjZI5ZNnwJkDu0RsDJPRATHFKTjjKaeY2N7G2xEAtnnEFgP1NdJL/LvFBwnn/Rjjod7eDmN1Zn3xXBg4lgP/XDe87rG+r8ikdL5j/+LPY7Llp8vGU4f4aJ1kqTRFBbOO8ybOUy5A4bFsunAniAzrGYSFEzXLCaTEhub05BLQy7ujc0ZHj9Zhv0gzGP0oxmwvqsX4YAIj4z3aUxi/uwYwzcaQjHZb2OXRs6I9P5dlYQDp/x8qxBlvM8UNoJoFcP8MgUa14A9oWkkr40xwPy4BngCYAnG6uWt60/E/z/a/uvZkiTP78Q+7h7iqKsy86bOrCxdWaqrqmcGYmYWMwPMQBCzWAAEDDAu9o00W/KFZnziv0Fb4wuNDzQS2LXlLgCuwMgWmNZdrUt06azKyqzUVx4Ryt354O4RceLGuXmrZ+Az2XXPOREe7h7uv9/v+5MgrLtGOAvVcDSkKiuwFmmFi52QEo2lNIbSSqR12ZcApN/j9bnTmkuXLvOjN3/sSucYgRHBd9xgMRidsz7Z5Nknr/LjH7/DYDAmlhGlLp0uwAtrtRrKC9R4sKykJIoTSl0dEU5kC4BYawmJ1517nucXAkcbjMUWhSskWhawNkIoQeytzoNEcWojYRhJ4o1Nfv/v/y7v/OIt3v35L9nbs2yMI0YjxebGGg8fPkRXhQMB/rwooRiMhxiTsr+/j5IRUaS4eOECB3t7rI8nrv5QVTnwrbXXXDu+EObQBru6ExPi5u320CCJiCNBHCvyXFKUJZXRviinREnNRCW+MGBGns2oyowyLzg43OXCuQvsT2d8/OkXvPryK7z0ynNcfGKTJIlBWYqqpLIaVeUM7AARJ2w/eZ4/+K/+GZ+89go//dp3uP/hTczuIzAzImkwZQG4zF/aapQAwn4T1gMst9ea+MHmHB2hRyvOcPvsdgPNu5r4dqB+r/AXaEkggc3XXiBb1oavGmN3vEf4Rg8ta89ZylbcUqf/sC+MsSjZKGOhxdtayou2YL1qrN21aAv1dATv+lrvUtsuGNcGNH3P6lvzNt09zhrcpcndtW+Prw3w2uvfdrGq6aFsnhfmvQoYtOfXNze3d/rlhz5lVt/adJ/VKKMc37RC1CUaNO7sKBGAQ13Fxm/eAJcDyGhkizqLXe3p4MdBkLlaAt5j2omBxp07dzhz5szSYuzt7TEejTHKFQrSRhMnzvwaRcpri1xk+3Q6xVrL1uaWL7LkhOKgaVpeNE9MTROspXzKv0jFaF25+hs+g0ffiw/fN8FTweJiMUbjArcai4axGmGaDAxhXI43ifretbU17t27x4OH9zl9+mwjIMtmo2pt2NzYZDabcfXqVea+wm0URRituX//Abe+uM3hdMoLL7xAmqbEUYzszTTVCBztdlRz4DaOsYaq0jx4uMudO3c9sDKMxyOMsRxOp8xmM6QQaFp73raf5kGX/779nfVjCU9vNCj4+Xe1F7K+ZmlWPYco+FxLvO+pv64WdKGVuq0BI1aEsdlaA+FAyDII7QYwWQt5njNeW6/fm13p3vWrt3qJWyCjy4jaxBSOrs+S9tziXYnatKIflHTbKgb9ZRhje2KiJlLCp1f1PujWZ8pZV2hgPnfF1wJtClYK4zW0kVIkoUBnpTn0WmwlJVo6ARMjeulaW8vU567UZeTd+5a03Z3f2muyqp/us9rXh776WqBRUkpXW6HzrCWN4THPQ/gCleE6AQKXdaosK/Isq2PaFosFVVkRp8el/FxmyGHvxVHEIsuARjAJDDsvCleTSIb4nqOxBwDj8ZjZbO77dJbfRuihdp379V9/g+9+9ydE3s12b2+vScjh16QN4duCgktA4lKX13vDDyW4YBnTZFwJ4CpUn3fAXXhXKospSorDGVUlECJiPIgxeoBUDhzHQlDFkl/7jTd48olrfP/bb/Lo/n2yfMhkMubCuQuOJwmBUJLYx54IATuPdsizjPPnzjObz5xrrrXE3nUwKNXa8+wTRroB0d2zba2zHKbKJTOx1pLlObP5HF1qQPjkJSlJElEWXjGmZxRlzmx6yIMH97h84TK7uw/5+NP3ef2rr/DCC8+yffa0q3ouKuJYocspgyQBpRgMhrz061/hmWee5q3v/Ii3v/sDHn52i3I6xVqBMhVSl8TGBdNbzy+spAaRAZwhVp2P5bn20bWugHrcOvUpEWr6zGoacNx5t8bXd+GoBaYbpNzuq319u+/AH7vPDtdEUeQszC3QEd5x18X5JPFu7fGFf3UAuG0UCqGfIFetAi19IGDV2nVpezcg/Dh+133mqmu7QK2+zvPXL8MXj7OsfZn2uD6W9jLL6yKEK6Qd4uGMbSwpQC1DLe0tuZy5L9BDcPGpTTu6Rx/XTgw00jTm7t07nD59isVCe0E/R6oJeZ4REFVR5MznU+7du8dnN2+yyAq++vrrDNMhGxvrGKuxWtdAI4xbV676qgsud0G6waVKVxXKOBNYUVl0pTFY8rLwpm6fy1xKhLWuWqLRSKX8Ann0JSwqCqnXtLMsyFDczqcJrZzUHF6CKTWlr3Lt6gCUZPmC+/fvM5/PmEzWiKKINB3WJsckSX38hq5jP4qi4M6dO3xx+zbz6YzD2ZTReMz58+dJkgSpQiGpxxOyo8JMIIrGraOKeO+X71GWVUeYyXj08KG//xgTnQAhVJuNO8Lmqduy04rbvsuaFvd9XerEBg1Ki0j2AQ3w/trU/wK4WbougEkvdNfeqv4mtyJOom2Py3j3PR1MF7iAfBUpF2OkC18EZ/VB6hKk9vcn1V6t+q6teeteu0Rca8ASHr48vj4m2n3eiYAEtN5d03/9NwFkOuKkK+c+GGKXguskCBYebIdOrXX3uQKcTsAZTyZI6epBLBYLxuMRiL1aAF1CGc12qufU/tfWBnYZTHu9g+98d036Pnfnf1wLjHEV4wx9toNh2zUolsfUZhHHPDOMU4Tz2ihYtNY+zXDk6pTEzo30yDnkKFMO45hMJq5mh9FImTZnEMizjKosMWnsgU+tN6vn7P5J1tfX2dvb5fTpbbQOgd4Ci/SpZTXPPPsU6+sTptMFaero6ZJrmV3OZhOaMRZbVVjj+Ek7kBxrsaKV7jbMz9+ra4HJA/vIJTShskhbYfSMaVkR2YqtUcJilrGWJghhXXyRLjl/8Qx//w9/n3d+8Ut+/tO3qPYKJuM1hsMhWIHQDsRo4yzQk8mE8XiMEC5+JoqiOttaiGsJyRRC8dT2PuoDwUG4DAq3cF0cx1TWVSIXQnBmfY1od48sy8mzzNE+60CqHEjieMDcp8wty5JKF8znU06fOk2WL7h77wEff3ST1994laeeusra+ogi10TSkhULRBKhraVKDcnmgK/+/d/mmdde5odf+y6//PGPmd65i1jMUbkgsgJpfbSgJ3G2ZVHzKKOe+8qYjh7aGYT5Nm0MgaztsxZ+657bZS15o1Ts0vI+OtJu3e+11vX5bytGu7S7zcOW5sXy+Qr/DXNwSrkmSQ1IItlYi9r3raJVfXSvHZMqZcgitux+1IzxqOttfZ89eXrUNk/rWgy663IcYGoDpfb8Vj+44X8nEazb67TSsvHYXk7WlgHRsiug6HzuA3bW2qUYDat1E19trZerurAUT0tZ6vdx7cRA48aNG9y8edPHGiiiSDEcjhgMBggUUgmm00P29/cwVqN1xWg0xuK0dZFS7O3tOdDg08yKSNWazaLwoMG6NIJxnDgNltG1OTI821qL9MWi2mnV2pkrXLVc96KLosDSBIhb4wBHtsjIC+e3GgoGBo2a03L66tAi1G9wzE1XmsPDA27c+NiBjGTAqVNnXO73wYDXX3uDLHMuH3me8+DBA+7cucPe3h6L2RxdVYwmY15++WWElK5mh1xddKh5v8uagDZhdGBAkWUzitLy8cefAKJea7B1kUBXIyQG1WgllwQ1ACuxNK5yxqNbpSSiR+sfUvu5jeyEHd8RVgQrxdFD6CbjfLqdBoQm45H1LiFLAqXrE8AaryUUDUAzoZJ6cMloEf9GK+aIsJSSLMvRlSZNErJFcURL+qtoJpYP9bJE3EfMH2e2DuOotcu+R+Mv/TIjPMKs/pKalyAIC0GTDEK4cWaLhdOoeBoQAImUoaqocwky3n8/ilwxuCAYD4fD5jlSYrVZApZCLpvJ+87GKrCwiqn3zS8IJqsI+Um0ZN1ndBm88Ps4WHCXBSCzZCk8Ln0nOFDm4igcTczzwtMzRwsd4Bgge321l4WWo6AtWCJcU75qdbAKaW2Qob5Qa77NOYTz58/zxRdfcObMWS+oBPcn0MZiRcFkssYL15/ne9/9cW3Rdm6prhlfRTf0W9MwY2p6Es5KABkEZUZ4B8FK69fJWQdtTUuEtlhfGFAY6z8bDu6V3KwKBgI20iHEMEoTVJoSxworLK//xqtce+oaP/zuj7h75y6lLhgP1xgmA0zlLOYychaWoHUMYw2xh2FfhM8hiUi7QvHj9l24T2ufHcwLEVJKkiRhbX2NwXCEsZr93T2KIsNUFVJESKUYTiSmqijyjCzPKMqCvMg4OJxyavMss9mMmzdvcv3F53n99Ve4cuUSIlUIodF5RYmgtIYojkmimPHFs/zuP/tDnnr1eX709W9y6+1fovf2EfMMrHbB4qZyQFVYbChIavuVU935dgXO9j5uW3yOo7l9aVAb3mgR3hNilf9/V7hrnrEsGHeBzqq5dIXi+hprvVKwEcCXXEVb59eNtRvXdZRm9s2j/bkvxiIoEbt9ONnhKA3sE4L7hP9VgKCvnzC2vsKD7fH0WY+616ziCe2xdLOVHlmTHtq8/N6W92bfc1a1vv0qOu8xz/Mlebjv7NTuiILmPdXAhVoeX7Vnvkw7MdDIsjlnz55hZ2eH06dP12OSUuCsZ86/eDo9JB0kjEZDxuMRKkr45JOP/GLA4eEhH77/AaWueOHlFxnV1cRBSeW0y7HLsOGYYtEIRxaXilTIOj4jZPQA75rU1mCJdrYqB1rCBsmyjDzLiWJ3T5qlTpOknFAUCiTFccRwOHBpE7VjYlZatNVIabFWo03JdHoISDY3tkjTITs7j7hx4wa3bt3i4cOHLBYLsixjfW2N8+fPEScJly9fdlVea4vG8gYMG6Lbjm5iJ6SUpSHLCvYPZjx48NBp0DyQKYqC/f19pHKFtyyCyjT1DoLVIwgkxoagIdcECkTzrOXxuCsaYuM2bk2Alq6j7rH9V+M7itNyO+ePJZNsuLr/IDptqRLeAmL1EY13WFfHaBTGusJyxhoHXFtIve71MYe+ry0JpMeAjL53e9zzlq73gokVtvXV8t7pu7ePYB/bRPhPPzNv/nTCuDaayFdVzv3ZlSgWiwVaG6JYIPzeCutUVhUbGxusr60TeQ1ulmWMx5M6scKR+YAPjG1eWd+Zedz56QYPdhn9cWBhFVDpvofjBIn2e7G2yTCU53ktPLTB6iom2YazNgB9f33oy2lxhXN/silLB+QELYok62trdSyAm5Abc1VVntYarJVeU9Zo9NprcfHSBb733R/Ugl+gewJVpxAHzVe/+hrf+osfoLUmTdOaJocUyTVAYVlxYbVx6Zo77oYhC1S9jngFSeBjLZcxIRqLiVASbUDFMbJyFvnDe494f56hZzlXr11kkA4YSIUQinQ4oChK1k5N+L2//7t88tEN3vrZW0wXB1gMiUox1mAqU1uEtJ9TEJYqr5BrB+YGATm4DbfrFvQJjuGd15pmLygHAVcAw9GQ2BjiKGI4GLC3u8d8NnOxhD52JYpjoighzzLKImORZVSVZTHP2Nt/yP7+GXZ3d7n1+W3eeON1Xnr5Bc6cWXe7UgvyRUVVGqqowiSCJI554pVnufTkZX755k/50df/gnuffQ6Hh6g8R8kYaSpXX0UA0mKaUij1HIOSsQseVmnJuzSwjyZ2++9zRzP2KE1pv6Pez61bHCDXS1l7VtHivrE1PKz/utpa03rsSWj9cYDrcQJmH2g4Tuh+HO/r28vdcfWtdQBb3aDu9u+rgESbltRnpOPOfhz/PI5XnJTXtxUn3fv69kIjZyz3u5w9tVnHLlC0gS7TJNcI/xuAaSMD4mRCa7vC3GPbiYHGZDKhKAvW19dI03QJzQuh0LpCCMtg6FLJrq1NiKIYhESJiPFo7DXpkiSJkUaRDlJOnT7t4jk8Io1U5FPgRiRJjBBrWJqsIQKJFAqpJGVREidxYw0QLiBOChcDErQ2FtCmJJEJWlcgIqSSpGmC8j6x2phaMzeKRgxHwzp3eTBhh8rRIZB9mJ5xAeORs+oMh0OeeeZZDg72+c53vsPDhw+ZTqcURcH6+jrXrl1jOBggLAxGQ06dOkUSO+AkpauoHNpJtAvNRnOiepZlRFHMxx9/QqWdiVxF1D7gZVkyGo2d0GiXTZBtU6aTtyUu3LrJSw8C7UHF0TMiW/8NY2o2ZHdbtrWiS99bILhttYTY/tbST1oLPqCfWgBZJpCN5lhgMbWGUAjnfy7Esln5V21tM7Sxxhcc+8u1tnb5y0Ofv7q2TBwboSxou4OVMS8Ll1LV760sy3xslCuUJpe0cJrhcEDsYzSEcNbLwXCMlArQR5yHhLuw2Wkn1Ar1MYo+4X0ZAKwGK30AojuOVQy6CzJCeszgUhGULN2Kvk3c2fFNeDekoshrK20UJWSLBYjNx95/dLwCpaI6I1MYu1KKzCtnjHEFQB1/bisZmjUYDceucnxZorzLKDbE3xikEpRVzrPPPsnW1haHh4cMh8MlLSK4fPFunh13l9b7XGL+4FP3eoHIr5HF0f9QJ0N5Oih939ZYl8yrKps9U2oWpeW9X7zPw0ePeOnl57h4+QzpMEZIQTJIIaoo8oKrz17h/MWzfPDuh3z8wSdMhpBGEbZyYLmOHTMGWzmf97IsnTtWS+gIz27Hx/QlO+gKPPU/vwbWGJRX1GljqbSLAXGuixFJnDKfzX2MhsYaV0Q3HYxckpMsoygWGJ1TlHPmixl7e3vMZgsePtzjgxuf8PpXX+HZZ55mMhoSSTCVoZKGrDygSr2r8VrKq7/3mzzx4vN8/5vf5sPv/ZDFnbvYPIfSIv1+aHhcPSkI7+gE56DZv8vn8HFpXXt5cItuHaf1Pul4+pQZbX7cpT/NHuhSxOb3k2ZaOsnY+ujgUUG94bndvdr2829/3/e5GyuypLA7Rojvjim4rXdj744rzLhqTN2td9LWBV6/Suu++/aadJU3zUXL4zXaNAqTlgIs0APL8j5sFL5Ngp327xZctsEvOacTAw0VRaRCOHejPHdF+WrUJCgrQWINp06fYW9vhyQdMBqNQUju37tPkg5YW18niiKeevYZ9g8PWVvfrAPTwBNfY0kGPg2maTa7rOsb4AVzWZuAA7MLAEVKCS0fTPAp8oxGydiDBYVMnOuWMRahXLR+nCTOP82b3ZVsqs4qFYGQGG0YDEcINEIoJBGJStjcOMPaeI3/8d/+O25+/hlFUTCZTHjm2aucO7tNWRUYbSiKisuXL9faS+lSXyFDAalWW8VAlg+JQ52LrECqmI8+/pTFYoGMEkcYpSLPS7I8R6qIqvKCm9cSuWxAwp8qT+BEm8gsE3vhhYhmXEsDRgR0bINm1fv+trUDHXletP6QRxhn/5osk1oXd1MfRJo5Cf8wpwGlnrsQUJUlGIuSyrvmLBP5Ve+hjwC2CUAQEoq8YFV7HAE6Tkg90tqah78kA3Tddd6OaL5v5u5ynYVAZLeX3FpiDLooKIsSEsU8yymqijiJ6/3jBD4XqJjECUmaECdOkM2zisFIIYRLe1o7vQhH6GoC2BlvlwmGd7KcBKCfQfcx/O76dZ9zEuDSt1/6hBjhrVOVF2hdquvjtbP1s6HRTgnh0oO2hOjpfEZelsSDAYezDGecFQQM3Mx19T4RwKUL53i4s0uk1t3ZsiB90c+y0s5qgNOeO5VDowgJvSipWNvYYO9gn9OntxydN609ZQy2qtjc2uLZ567y5ps/RsohSZo44QFTuwp034X1TDAwTAdCaT5ZHH2qGbZ7qDCCKmxz4ayjIS5ISOncq4wF77LlLCAlVghu3rjF4f4+zz5/jaefvcb65prby0ogUhAUSFK+8tVXuXrtCj/6wY84mB0yHo4RFkxuqKqyFvyBusZPrVkV4ZkgVESUgKhc7REXu+GD5GnW0QnkzTsQQfeDE8YQAoxL315VLqYqHaSucG6siBaJB4QFunJ70ViIhyOSYUpVOK+AajGjqErm2YLdg112D3e4//Ahn392h9dfeYXLF8+jlIXIUqKpbE5lClSckMYD1i6c4ff/2T/mpVeu8/0//Rq33/+IancfmWWIYkGkQ05F5y7q6LhBIhwYkU7BFKwPfdrc7tlpA7D2d+091dZ+13TP2qUsRH0uNO3+as26aAuey2n3+2jDcQBo6Uy25hGEa3BnsCm66+mlaPPy4/lL6K89LoSoj3IzVr/nrPDpm7sRnMv0rg3Q+gL02y28y6WzLZeT/3TXe5WyKMyjq6xoz7f9zFbPdGli3zOO7JOe+XQG3Fqjpl+pVA2kneyyLO9QA4Lmnpru+/hSiQDjPEOMBWldYelQH0mj/T727vE1Lw7zBYvBiDo6pYmnxu0tYYLHysnaiYGGFK4y6vr6JovFwglkQoGEylREsbMSnBKnOZxOvdCbMByOGE/WSAZDZJwQScXVJ5+i0oY4aSwjQgS3qGbjGeFiJNw69qeeCyCjvcnChmofQPei/LNaL0kKgfELL2SEUAppLQifeUpbpIiwxqVFFSJCynCt03ZFIkLJhCefeJpbN7/gzR/8CBnBa6+/xtmz2wgJebFA6xIhnGvY6TNniOPYzclSxwz0CYR9qHjps7AuXaG2zKdzvvjiPnlZEnmPUllpFnnuhAshAOkLA4f0vw2gcP6nTUrL5UPZjQnpCFoERicIbhMuJbJndp192Z1pOFQhBKQWnI9c6cfbll8IKDsgCe8n7tPYtqvqCuEYlMHF8mAsaRx7AXZ1erpVrU1g2nuuTr/8JYX8Vc/+y4GF1X30afoa7fBxT3DpOh1xdte7YHAXx2N1hZISKSJKk1NUJSOUr3GiPK0TWGNIB86/fTCI2ds7JFtUXBiOnVApNIIInx6iXs+Ad9vno+/vPm1cFwiE/y5pb3rAZN+69YGKPrB6XB9O5tOd8R17a+dV+DnjY1gsXvhybp6zxYxSVwgZMVuUGC2wQnoFQOiiGw/VGbu1bKxNuHP3rnerURhtkZFCCJ8yVRvi8F5toAMuaXRo2lq2z57l3v17bG5tuFHLBjhaa31WtYrX3rjOd777LeZZTBzH5NK5jBjdz9CFCK6bfsgtZRW4HQvLe8d6UCSdXN7wCxmsLBZRu4N5FyRrEEisrsAIDnYP+NmP32bn4S7PvfAs5y+eJU1d/ArKUirHZ9Y2J/z+P/g7fPD+x7z79nuMkxQVK6fwQJAXpQvWpqFbTrHmxmKERAgPpoSiokQaS1VpsLrmlZ7Uhf+pQUIQDoJiTqomDXilXcr4OIldDIwSRKmiKGIWi4WjlY5dYbUgScdIlZBlC7IiQ9uKRTllOttnNp0xP1hw+7M7/NpXX+O5566xsTFC1SqgCrSh1BoiSxwNuPzyC/yjJ5/g7e/9mJ9+/dscfHYLpgcI5ijj5meFQdvO2SPQ+qPAvutC076v7cPeZxnpKg7CarblhzZtaFtIjtAgLNaWLm2/dnFsjbLFy/A9gn83XWub1jgvC5aeAyFWTnlA0EpdfgxN71OSLK3JkqC5PJ7Acgn004MN42m1aF3fBVNtntl+dhtoHccLwz3tdTtaQLl5/qoMW13As8QbRMPbwnfdeJguaF1ab5b3ZhtkHFEY+d/bcuqRuXNUdjI4uiA8ojQWZJJAlAEKgQszsCKsu0EYkCLyzzTLgeFAndazvYaE4YslV9THtS9VGTxo4IMfaXAnEnZZYxhFEWtra1gL+/v7LBYLTp8+XfskGuMqk8ZJulQmvlvSvPui2sw79BU+B9/d9gt9HGIXnQ3URb4AtmqYf59voPR5yCeTNSZrE77+Z19nscjYPn+KK1cue7OVQWuX9SPPC86dO8tgMPDWjOMrnnY3b5/wYnFBnkkc8/NfvMt8Pq/dycJ/syz3WjMnALjUwf39gaj939tZcbpr1zvuIOfX/z2K3B/XugSgr616fn1QV9wjpbNIGf9ZV9onK4hccLFZbRY/aTPG1Fliut10tSGrCGmflqu3BeFBHIVj3fseN6c+YhJaYc8AAQAASURBVAnhvfWM0YM2WmeyKiviOKlrAITrXLrbEiGG1HKwf6Y2hiRxWduCRbKqKpIkBawT+LSn949hkuG/fYyzuxbd77oZfdo+2t31WZVGt6st7Hvfq1r7XJ2UgHfnGO41UGcQ0Vozn80oigKE8MHgAQD0j6P939CMtWxtnfIZxBpBLvK0OC+KOotUEEA8a6LtKmmM4eLFi/zoRz/i+eefpyW6EXaGta4Q3AvXn2M8HpEtMsbjxAtWTnsqkUfW+7j5tIXNXhBeC3xNJp1QlKoywb3NBycb69LnWuutR65A4icf3+Dho4e8cP15nnjiMqdObyBQDFIXJyeE29vPv/gCV69c48ff/wEP7zygWOQYC/PFjKosWFsbU3krhcJb6YV3mfEoyQpBhKIsc1z9ibZyZnVT3hXYWuuzNjZ0PvD24XBIFLkMZeHzYrFgPp+7KvDWKQykikgHI4oyJy8z5zJZahZZzt7eHvfv3eXunVu8/NILvPb6K1y5epnhKMX64ry6KqmiGaUqiZIBg9GYv/a7v8Nzz77IT775bd76/veZ7TyC+QGqLIi0ITEGg0BLiw5r4a3zjQsw3uW5ETBX0d4+AXFJcG/FgbjduSyLtGlC1wpyhJ6KEFvRiIsnPfPLsk3zkpfdnm0tyPYJ4d3r2/32rVOzYA1Ibc+nAfDNPcYnZOjysO48++hq96x2r1slxLc/L8V+dfp8nNIoyAhLoFX0zLcz5r7ntdd/pby0YhzH/X6kH09nVbBgY8mF4Su/9mvkVcmDvV0O9vcp8ozFbIYpc2xVYbTFlM6mYViuV+aaqglKe18IIREiAlMR9RR37GsnBhrz+bwmPN1Um4GZLRYLZrNZ03mkyDLLaDSqUaAQzq2kKJpgtsaqcVTzIFvMMnxuH+ImgLkRJtrZB9oAIfRbC5x+Q8ZRVLthhWtCP7K1iZYIB1CVGiWdierSxcvs7R3wwx++SVWVPP/cc0glkDZYDyKshSQZcPnylTrOpWs+bLc+wrjqusViQRyPeOutt8iyDBn5FIlKMZvNXNEpQjpPQZ7lhLze3bVxNOyon2S7tb9riI1fmM4B7M7lV20nOYTNf4M2smlBsA00UQgHqIqiIB0461KlzdI++FXG3X5PIW9/Xz+rTPwne+7qtTjJ/auAzJHP4X8fuwweaOgKSLA+O1tZliCSWnCUwlVht74IV6hgnCQJcRwzGU/YebRLWZaUZeHnslycqnliI5SuYkBdJtUmmH3r1Lev+wDMqvUM7XHpIvvG2v2ufX3f91360O4rCBwu+5JlNp87oAEUhQPBceR9/REI1Rb2VysSxuMhBwcHPrvUsvbTZTqpvO88NQMU4ui6rq2tkWWZD3puCxVtoa3i9Oktnn7mGj//2XuOrslgHXGgpEsT+wSZvne6yuIkPIgxPhC6rhkkpHOvDN9jsdr7nytB5SuvYwT7uwf89Cc/49HDRzz77FOcOXOG0XhE5PydEH6tolTxm7/12/yb/9e/pswqpBQkg4TBaMB0Pkd64G11hfSZjqxfViGdl4HWFUgQkcJUptEet/5r21/g3KCd5TGugVOfYBcs7kK4pCqj0cgry3Ky2QxTVQhACckwjoirmDxfkBcuw1xZulT3e3s77O/vc+v2Hb76xuu8+OJ1zmxvQmSw2mJ1gYkqClNS6QqbDFm7corf+Rf/kCe+8hzf+fo3ufPOO4jdA8QsI6pKjBBo4eI+ItO4GIbC8SFjTnsLt89MVxg8juavipfoXt9Hh7rCtRQCI7zVzYOk7jlepZxYPpM+tXQrs2Kz36lDJbt7vz3XPqVSHx/oowNieWH9f6HtVnVEHj5GGG/3u+r8ht+6MSh9iqY+WaHrttXX+kCDFUfBTBdArHpm+7q+tVxF1/sUWn30zPfiipn6/9MCDIZnXr7Oq3/t14m31sjmM8osZ3Z4yBe3b/Hg1ufcv3Ofg90pO492PE13/DrPM6yVQLB2gLAOyGAt2lpUnKJ6xr+qnRhofPTRR4zHY4wxzOdzrl69ymAwYDgaMs/mWGvJssx1GkU8ePAAV406Ik1TDg8PGY/HpGna+BHaRivWRZsBXITfwmchRJN5hGXNYxs86E6MRnszLG2isFitDB7ta1waRVH3HzJbCSGJogRTGTbWNlhf3+AH3/kBDx8+4tSZLa5cvURI5xmsB0ZbNjY2am1RO43l4zZg34YMY9Q+v/re7i4PHjx02mDlMndJ4VLsLhaL+uCHgoeOyPX5SS5rqsP3fVqE44T/xwGDVW2V0NVeq+MEPiEal4fwry1gVNbVF9G28tagktFILYGQ7vO7c+0bW9hvbQDRN76+v/ueAf3FmvBTq8smdpjpqjH2jaU93rYgXv/zz+qOMzzXehNWA0xcJXpjbZ3lLYqjOsMXAp+qNgx8mflHkaKqnOIgiiKSJKEsMydIWFuDxTYQ6q50d488Trjvzq0NSk7SjntO3zvua20a2E6l23fuuib79rjBM1FrQbpK2Ma4tXfB2i69t3tG82yEaMXBGYxZ3tNuLwg2NjZ96nC9tHeSJEYXLgbNjdu7ufn+ukjVWuu15BmTyZj2MgVwqU1FqhJeeuk67779AXjLiBQKK4/G59T03TTViNvvsO2q0X6/bn7ULlFSNtnrXLC2xbZcVELqXCfPubpNIaZNKYWxhsUs55MPP+NgZ5+nnnmaq09eZbI2RihJlMZoISgWOW+98x7TWYY0AhlBURZsb51hfm9eu5EZQS1BW4wDH9bH9AjnGmesqy0lpav9YfGaeH++nLWmCQgXQjjQLxrA1l7D9l4aDocURVHz7SiKGMQJi9mcPM/cs41GRQmpcAkDyrKk8pazPM9YLObM53MO96fc+vwOr73+Kk8/fZXByGWYstalEV6YKdrkDOKE0WDAta88y/lnr/KLb3yXX3zzu+zduImdTkFXaCpP3kWtGAvubc7TwmJtE2fQnduq87WKv6wSuvsE41XXGtMCA4Tz9Xge2if4t3l1OIuOjjR+++1+VgnuXZmoj+45C+Iqft+S28KzWi6u9VUr+HmzNmYJBPUJ/Uu0/zE03hUtLDva+KN9dO9bAg0eDPbR8a6yoo9/9+2lPmDSlXn6+u0qwpt+bQ2sDRaNcwP9H//9v+M//uSH/K0//HtcvnKZR4/ucbizA2guPv0EX/nrv8HG9lmM1szncw4ODil1xY1PPuH+/R0qrbh35w7TwyllljM9PMRqH6/sk3O0i4ke104MNNbW1hiNRhweHhLHsatmHcdUZeU9p5sNOx6PARgMBmRZwaNHj7h79y6TyYRz585x6tQpXzivWdS2W9IyA3DXBJ/SwITD922m3N1AbYGjC27qZn0wuGgQ5NImME5gCii6qipvKZAYJEpJrly5SllUfPtb38Voy8svv0IUN4Hyxhc8qKqSs2fP1W5nx/mFNsM7HikHTWKapvz8Z+/UFZXdmrmUvg5kOEGiqjRlUbb6XGa8jkh4wiLlEZep7hiWvu8Z50kR70nbSQT+1a0RhmvgIYSz9gi3x8pCL5mI+55/smetGEEP4ez233cGjgNtQdjuu+a4Mf6q76YmhmGdwlExhqIsXGCqpa5Jk3jm6tKqhl4aH1SttQcoMcPRCLBUWhPHSV1QzwlwuqU9s72gsI/prwKuJ5njqvtOAuKOY2Z9n9tAr/t7lzYe99xgiZVKIYVzTcsWC8BlIbG4lLeT8cA/xLkFBcGl21+7DQbDOkbL/W68BTmi0AvKUB1eypY/+1GgZK3l/Pnz3Lt3j9HoqZpGByHZWoutSiod8epXXubf/o//M7rSYINyZoUiwzoBp2/tu9e3+YMDZ971xUJQwFQWjNA+1bYXYgUI6TMlauNi/ACrFEVeOosIbvwP7u5yePg2j3Z2efq5p9g8s0mUKNI05s0f/JC3f/wuIH1V3pK8cslWojgmSROXItoKyqoiTVPWN9Yx1rJYzD0IcVllnKFQEicxUeRiw4o8p/SJBYRoBW8GuiM8CHyMEB5cpoNQ4ZKjCCYyIklTZvMpZZEjhEWqiETGxLGlLDKKfIY2JfZQs8gWTA+n7O/vcffOXV599WVee/1lzp3fcskjcsF8sUCKBekgYjFIGQ3GREnCX/u7f4dnX3qZb/3Pf8Tb3/4OzKZQGhdPWR+JQAkF+NScq4rrhXaSNKLtoGjRQ3O6rSskd+m849suRi2knBY9WvP2MwJdaAr8uXssfbUtwrOPKl1WjbcNwvssHtaylMxlub/mpHe/Oo4ndfl42wul67J6XFulzAlZRPuCx1eNI3zf8I8wmf7Wfa9tuTT83gcs+u6Boy65X5ZnSSGIpGA8GjNeW+f2Zzf59je/ybnz59jf32V+eIA1mkhKzpw7x+b5Czz33HO8+aMfMRqNSJKE6298hd/cPkeUjpkeHDI9OKTKC+59cYeH9+8jowhtfXbJPD/R2E4MNK5du4ZSiq2tLR48eEDlCV8cx9jKLWCapr4wl6uUqpRiNHI50A8ODsjznE8//ZSDgwMuXLhIkjpGVwt9LY1wO4grLH7X1aSdZSJ81079F75rH/jQX+jTMcUVLj7W1n7OZdnOAOKsFBaYjCecOnWKGx99yqeffcpoNObK5SvO7826oFcpFAZNkgzY2Ngg8qlU+yw5zaOXtSN9v4X1cH60MR98+CFaV7WAZowlz3IODw99jnsfo0Eo4tQIFkvP8YTlSBBZ5/l/1SDipK0Nsr5c84xIOCEYYb0bg0vD6oTa5uA8jkD/Ku04oXOV5uY4kPFX0f6q+hfCueRVVeXqwuAKcSapE3ayReY0jbrN1Kmvj6LIZ+tyoDzLFsSRc9+wVf0QnDvLMnPrW6/Hzes/1bo+Dhge17oKEzhq5j+u7xqsBN9Zv0RFWTrtnjVIISlri2a4JtBJjsgM7ZYkEaPRCJeq2Na4LyhidBVSSja2pjaACefWGMP29jbvvP0uTz/1rJs3snalc/y9oqpKLl28wIULF7jxyS2iaODqAlVF3d8ys/ZqrxOsfzhnXYFjSUjEF2sV0hUtdWYF77YiqEyTQlO6pHVOcSUFCJetaj7L+PCDj3i4+5Bnrz/L9vltTp/e5PyF8/y0eguERAjFYJjw+ldf5tlnn+VP//jPEEoyGo2cy5sxVFXF4WzqlHTujRFFcZ2KXUpFpBwwD4HeZMENzFlekG1rpahT94b5d4WitqLPFep1qUOLvMAIl8lGSEGWKfLCFwkzLuQ+SUFFlsV8SpYvMMZw/0HJdP+AnQe7TA+mJHHMvXvrvPLK83x64wv+4hvfJS8OEbIijhVxkjJIR5w+v83FC+d59j/7G0STAW/+yZ8i9yvS0mnPpXKeBkZTa9ItLLk+9+yAel+259oV/oKyw8kbRxT1R+7v++8ybV9OjtAW1FfRjqMZmrx1pJXNallI7QdFXTDZp7jrU+SJzr1Lyt0whRWtbx1WXdeW107S2kAqrEFYh1A0uTuGvnF05xzkM2fQ+HLCfndduyC2K1f8ZfiF69R5NzhS7tyosumM0dqEtWTA9MEjyumUjY11TFFy4dIFNjc2yMuCWAg++eBDitmce7dvMxqNuPnJJ0TDEacvXCKbL9hcW+fc6W3KYkGkYGNjwqUrlzmcTjEtRfRx7cRAIxkMMFozWV8nThIqXRHFMYs8Q0WqSS+rQhVThVQRojKMxmPGkwlFUXB4eMj+/j43Pv2Ua9eedJXFxbKmrpvvGFpWD6Dy5uxQKwMf4OsIiwuas14DJaREIDq1DER9UKVULnWe9ysOmgZXE8CiPUNzB90RCGPcIdZUXDh/HqstP/z+m8ymU178jeuMJilFufAbSCOFq2p74cJF4jiu3a9CocFfpbUPFkTs78+5fesu4DQDIU1vls8pygVnz25z7dpTvPvue0wP5uSlxidCc/1Y6xlpWPB+whL+ro+JtUuBYP8pW/sQtz/3AZ/abcN/QjhzsjNd+4wJSASuXoFSgihq1wBZrfHoMqLub0v31j02hEAIEfjDEfeP9hz7NCHWulGL9jMENUHsYyR9c+iu17Fzaf1vaE4RgK+X4K7TANIFilkjybMSaytv3ZPkmcEa6a70kbfWZ8DQumCyNmAwcIXkjK//MB4PebSz754nJcZqLww36xvG2ico/lW3Ve+p21Yx11V7pyvwrjLLP06LutQP1rlP2Qq0pvAxFFGSkhUaLSTGVijRvF1374p1ExYpLEmSUlaQYpFCI4RBiRitDUVZuTNmQ19hHy+voRCCtbU1Dg4PsNbWiTzae85aha5gPBry/PPPceOTzwlBz913saodtxfaa6WNs5ZZ4+mgbTLrKeEsFKGAaOOyKJBKEpvIu13h3HWMj0GSltJaF/9iLDsP9vnF7B2uPfkEPHOVS+cu8vTTT/Huz9+DJGWcpOwfHFBYzdVnn2R+OCWbzZlMRszyjMtXrnDu0nmkFJRFycHBAQ/u34cpCCmR1tM3K10NK1WSCsizzIEf/2brfYu7TwtTv1/j8tfQOmJLQmxQyEgpfQyWRCjhCu0WKYtsQZlrIqlwhi/D2nrEYj5lkc3QUUlV5SzyQ3b27pLlh/z1v/k3mC1KPv34Mza21vmDP/jPKco5xpYY69x8dw+m7E0P2Nk/pJQRkyeeJL91i2J3F+W0YsRCumK6AnJboaX1xUGbop/S0yxrXdBsVRmXGc/LCc4zw9VysdafIbwrkDzK6ZZAaXDXC+c3WCfDQgqBw3xNPAkIX6+lnzb0ZUkKcUruuYKgHbBGgJU1j2kraNsa9u5ZaLucW5ws4OKm3L5v74O2taPux58Pwko55rQkaK8EMJ3z2aWVq3hYN6ao3V+fi9Eq5dPjhHwp5VL2Oa0d32vz99BP9x21QdOqRBR9So6urNW3fu1mvWwRqhQIY9HznIO9few4RVSG9XTE9pmzGKu5f+8eWTZHSsG9e/cxFkqtyfKS2Sxntsj4yhuvo3Bn/M//7Ousr61htcVUmkhFbJ857WI6qorf/cN/uHL9QjuxpCukwBoXs5CXztd3c2sLFUfedWeAMebIhlZRhLTO9SEI2UmScO/efe7cucO1a9eWnyMas1n3kLmDIFwdCOE0Rk7TBNZrCoQ/VELQ+BzjNVA2vNDG9C6EK98eQEbDaCUIQxTH9UF2KQQFLn2YIEljTp8+w+HelJ/86EeMxgNeeOlZRGRRJvJaP0PurSFnzpxpqqCfMFq/3dobN2zeoihRMuGTjz9gNl0ghKxN21q7CrLnz29z/cXrXLx4Eazle9/7Uc0UkaIhpu1Nv+LgQyt7g1+XJguaWDp4v0o77r4jQry1deauEB9U99P+SwBCYaxFCAVUrSvcGoIliiW10aOjcWg/vz2e4wS/+h7RFt0sIiSlbjDNkTk+Vkj2goI9xr+3bzxf9hp3Eprvl+ZsLa7Oha1zqBvjyZ5QgHTZaIo5g3STqnSM0aXmXGZgxlaMJymbm+u4zDwli2xGkiZO2FOKymi0DZtttUbopBqi4wDCSVo3FmdJ6GgJsb/KeNp/H8ccu0ysea7FSovwxdJ0VVLmGUZXCDkkyytX7TrIYZ4mHqeZxDoX0tOnt1lkJaMNi5UarEEKp02vygqtjasH4d+zG1urGz/mKIqIVMRsNqvrziwxYqEoS0NZal599VX+6I/+FGMqlIqIYse6ukW5atXCY+jIkTNtvTawlgmXE54EwdwI76suwvGVvm6HrdMKC+tdqqwAaRC+No8sITvM+eS9G+zv7PDsc086f3oMKhYICePxhKIqKUzJV15/FUrNmz/6EckgZvviWfb2d7lx4xPSNGU8HnPl2hW01nz++ecUeYawEmukTzscodAMREqlDEVeLrmSWBtoUeB5zsrh0YgTikUT69he02DhUJFC69gBRaWQUUQRlZRFia4ihEixumQ4mhBHMVm2oCwLBjamOJjzi7d/xsF8wa/9td/kzu3POLu9wbmLZ7DCMhjERJEAYSlzw/1HB7z7/g1++dld9rRCjiboPGd9fUQ5m2PnBaookBYS4wVe7eciZE1vtM+4JgglOASufhT1Wvjt27jZiqMgoysg10Au/NbdlTbQRi9/+P4RqwXJLh1YVkg0LlKuNXNsH+RVKV3b+7/OOoZ1buHW1oAoCO9BKdlWhLh7WuC703fXY6MvScYq7X6fwm0Vjex+dxIlxHFp7Os5C7Fczy30bxwgE20LYQ8fOrEyb4UiqQ0Ww/VHgYq7x3iln7IuF4BUkt3FnMEgIc1yMq2prEVEiqzI/DMFRanRCJLBiIc7+zzYO+Bnb71bF1M9nC2I0yHnzl1wzykq9vZnWGs5ODg4dn6hnRhohE0TNkocxxhjavepGlh4E3oACtIHaocFHAwGfpPCgwcPuXXrFmfOnHFMx2tKusx62c0p+Cg2Cx/6bweyHudW0/1d+lSJfZUjTVnUhEEphSvo5gpUXXviGhLBW7/4OYeHBzz19JNsb58BaYikoqqaw7q+vs5kMkYpWRPpk6x5n+DZ3tB5nqHUiHfeeYeycnnQg8tTiF+5cvUKUaR49OgRyq+zrlyNEEf82sTq6ME7XkjqkZb/ilufoBW+b7u0ta8Vrf8NhD+YQqVsfJQFuMrJvu6FFP35ofvW5MsKkl+m9YGq8HlpJLXWzb+JjjbkP2mrwSa1VauqmuA7XWlX3dqfybwoqKqKKF4WwsO/8XjiaIAPUpVScurUKT788KZTAjwmPiHM/aRB3H33t101261vTY/Tln/Z1gdQVl3XHkef0NwWnhFOw1qWJVmW1Yqg4OYiW0Y8IXxApup/fpjvuXPbfHLzHlqvEdmGjrpq5mUtdHXv7f7t+jrHgwcPuHz58pG5CKAsK7TRPPvc05w5c4pHD/eJosTtkS/ZumvXVmr1nZt6PVvfOXtcv0AYBM1wbxe4hWflueXunbtMZwcc7DuQFccx29vbvPTSi9hIMEhTbnz2KU9cucrv/d3f57vf+x6f3bzJiy++QJYtmE6nANy6dYs0TXnqqSdZzA+5+fktz6uVt3pGoCRSOOcKWxRuSN7lyQbFhxUIX/ArKJGCDLOKngSZILhUBZ/4alShS+OsGIspVWFRuAD7JElYzOfoskAJyWIx59HOI771rf+IrTQfvl/x1JN/wnA45MyZ08Rx5JMZLLj74BHvffQZX9y+g5nPGOQLotLwB//0H5NEkh98/T8yvXWH6GDBcF4SFZoiKtHCoK0v+IfABOHQ9GfbkkLSxIICBHcnnxymo9xpALLbIYEs2lphFSwqy6BbCBeQL1hNr45TPhxLe1p7+jiF2BIf84WDu3QtfA4JdrrWVssyqFolNIfnnaR16WCXX3SftWpu7fiVk7qgdq9dBfZEa9bdM9KWRY97Vmht2bqPJnWzJbafJYWoi4qCr1okXVIGWzn51Xm3uILOPtmgU9hLQZSkThkSOaWtkmJpLOvra8xmM5RSTMYT8nmGLTVFWdY1zx7XvhTQCFH8bbTX/jukla1rY4hlM5YQorZsuFiFmOl0yu3btzl//nx977EbR1cIcTR/endzHA2qafSy4dDU2Vu80Bl+W8p8oCKca4f2B8xdmCYpZ8+cJZtlfP+7PwAL11+8TlZkqFgQe+uIs6pUDoDAUhD4KqFildZheT5NJdD9/R2++OKLel6D4ZBKV8xmMy+4uTXKsozDw0Of7Sq4B+DnvmxaP67Vm97aoANrDewoKDpuDu3fuge6bw36mN2RCqbLV9S/qRboFaIJ7qx81q44VMutGcLyHvsy7aTXr5pXnwajuaZ/z1hWrUH/mB53rXvHHMmvXRNbD1CDQOJogDtXcRxTVqVPnqDAWqqyxGgDiawFsLCP3T0Rg8Gwfk+z2QwpY/Ama8vjNX9dgb3LaI+7d2luQqwELOH6IIw8bo2/zF7oC049rgXGD8t5/H2PBPHXWlfUM9BX46p3Qu026v3GH7MnpFSsra2xt/c+2xdPETL+uBibmKpqtOaiRjH9mjtrLWfPneXjjz7h6tWrS5Zsd72bS1lkrG+sc+XqJe7de4isEkxLM99e4/p/7dH93QUTbWDW9x6bfS448jasJVjWAi1xFhFR/1x599u+FOzaavZ2DzEGzl+4xLUnroCtuHHjE7Iyw0oYr60xzxdM7874rd/5Ld5++21++e67PPfcc9y8eZPpdEpVVT6r4JyrV8/zyisv8f4vP6LIXAB7KMoqpHQ1sKypM/EsFeiyzuVLm8rH87n3MBgPa0Xi4wJVA2/XkYYURoOELBtwsL/PYjFDyRQwjMeS7PAQ4xURRZEhs5h8kTM9mPI//U9/xNbWKbbPnCOOE7IsZ3q4x8F8ysP9Q/KiIMKwFivGUcKP3/kl/6f/83/NEy+/yPf+9Ot89sOfo28/QkznoCrnseA10FYItJBYa0iWLADtsy+RPkFCiBlyekHr3KHUURdetxOoz09zflefp5r/2/5r+vhh33dHFAxQp2Rtf9fO4LnqHYb3LISoY1PaY22fixpwGNs7zZMoYtrP66MR3c9tmak7plX9r1q7Nt1s/94Gcd21Dc9sZ3Tre14bcHTpS7ev9rPb2VOBI7WcYNmSLgLzbel7rXGOnkWREyUxKMnhfM5Hn9zAWsP6xhrj8cCFDGiwWnM4mzOdL8izkiRJETTnuRQaISQPHtxnY2ODJE3ZuHSJqqqYtspZHNdOXhm8neZQNJrD9t/thWwHXXevCZt0MpkwHA55+PAhDx8+5OrVqyuFn3BPNxtBnxDRPUjt58dxvDRON7nl+9upcaV0MRl17IYPAj937hyRiPjgkw+4ceNTzl+4wNlz22RlhrICg6otN3EUs7m55cd/dGztz31tiYC0EG6I+P/444+Zz+d+g7l1qqqSoijY3Nys0yFmi4y9vb06KFRIWWs+hCe6pudddg/D0nvpHfFfvq0iho8bTzMuf3C734sQLdH0p43BaEOcOE2pFUcJT7ePVWPtfnfcGLt9tpn5lwEF/gKwR90Nj3ve45rzMz6qnW46ad6/tYFpNJnZrHXB4ItsQbrusuW4YNqjmmNrXQKJNEkYDAYYU5BlOdvbmw6cazB6WUPUnWMXVPStw6p17a5HH8hYlaHmpGe4fd5X3ddlbid5T4FetRNouO2wfI7n8zllUQKQ5ZnXeC8XsgqPC/TyKFOD06dPs1gsaj1mCDZ22uqZdxuyRFI06tvOWoS5bWxssLe3t0TX6utwTLOscowpeeWVF/nZT95GCIFqpThfWjcv+PSd3S4vgP532m5hT+swLuE3fVg86+/1oM3SWL6tFZR1XRG5VJDWWhDW0d39vQNuR1+QJpIin5GXGaPJmKd++zdRScIiX/DxZzd47voL7D54xE9/+lNeeuklZrMZ9+/fR2tNkibcv3+fy5ev8vJLL/Pzn75DkZfkWY4SkAyGlGVJLAZUxqCxCJ9lS+vS0Q5rWF9f58rlZ4iiiJ/97OdUVVnzzL41DXML+y9kDjMYpJIMBiPSJGU2nXK4v09Z5igJo/GY6f6B35cz4nRIWZXkZc6t27fY2dnls89uE0UJ1kJZZhS6JDcaK9zeKnKLGY/47KNPeXj3EWevXOYf/pf/gg+vX+fNP/469z/8mOpAIyqBskCpkVgUYH1MSzgiXeWE9LGmLqtakOIal89ehYV0sWgNuAbn3rSM34UHqEGJI4PKqyPPrNqPYd3btKK7j9tJcdp7vc0f+oT0VTJU+7/tvmqaJpr90BWgu/Sj77dV82zzxO79bTrSLWfQ7r8LkLogon1tmw718Zrl5/QrJ47jMV35pS3TruIPXYDVfp7/y1/fKLCdFbtitLlJKSW51kT+t/uPdtnUG75ekOPR2rvbjydjjIU4jmoFg5MNhS/6XJEOBqTJgBTYPnuu9/1125eKRm4XzSvLsp5sO9K/zaD6Xl74XimX9UgpxWAw4ODgwBHCMLnWooZAQTfpRuvWBjtNfYvlA+QC1BVKNDnqw3iCdcHKZW1Ne8N2BTe3ORRXLl+hKjVv/vBHVGXF008/ze7eDoP1FCkijBHkixwQnD17zoMv5XxyTyCc9B2C9m/W2rp44ttvv8V8PgfREABduXc1Gg0ZDgaEirLz2dzNIQTNByIAtTWj73knFZj/sq1LFPqIU5eYrRynbb5v/6v9cltaz7IqSdPBSlDTHt9xrUtUj1u7IKh9aVDQvlTg/aw73AyO9NklZI99TvsZnZgI4QUrrHcvqNfXXZMkCVk2YzFf1HE0unKCiJBRXbcmjKOqKgaDIUnqr7VNNqp6XGGT9rQukT8OJD6OuX3Z31b93icIrLqvy+CP2w997ej1nl56ZYcxhjzLKEqX3KIqq5YF7Pi9V4/RPYiNjQ2qqmz5pLv74zjisNLkRc54mC6BjFVMMk1SAMqyXKor5C7yNNhWlFXGq195icEwZT4tiVW0ws3NKYfazzwp/VpJkwW1q5Zu0SXnDLNc5yb4bUshiaUCKWoLQjtFOkIQJwkh09bDh4+4fOkscRxz4cI26WjggqxTRRINsUpw5+5ttta2+PVf/3W+8Y1vcPbsWZ555hmyLOPg8ICqlDx88IgXnr/Egwc77DxwSqXRcMDmmQ3W19dBCrRJKavKVx63iEizsbHBCy+8wGQyAQHTwymnzm6xv3O4pF1tg9rAl4NFOAhMEtEUNjQGjEWpmPF4nTxfUJZzjE+PWVYV8/mUZDjCoKlszizfp9CZ55cRWNDGoq3BSLe+NlIoFVHZivlizgfvfcDWuW1korj+N77K5Wev8cNvfou3vvkd5vcfoadzYlsitXZuZJ1tv/y+20Jk0Nwb/7fC2moFf3IJY9z+tTgXqyAkglN7NfGhbnPSJPPwbZWSrf3b4+jDl7mu/tf5LezZIDcBS4AyfA40ZIkt9Zy9trzWx+cDb2+P6QhNaI2tvf59WUZXzTWMrz2ubjra9vV9gGzVWnYV4d3f+57RvrYP1K16/tL6tdfGujiboqqIBAxG4/o7KRU2y1hklVc2u71ukUjlZO9B7GrfIRtrqIupE+zt7XH61LY/B5Yz29vHrkloJw8GbwnpUeQC+IqiqIFBaH0MtU8wdHnKm3iP4XBYL17YXPUgo6j+zblvN1q2NqDpYyZh8yolvaa/0YIF31JU8/0SknQP8JlxGi3FuXPnUFLx8O4j3n7rHU6dOsVwNOTeg/uwa5isjTg13mSQDinLinPnziE8PlJqOQ7luFiNVWBDeIBQliW7u3t88cUdL5Qpkjj21R1zlIoYDkcMh0PyPPOmrinGaGfo7wis7Wf2gQ06l9fr/eVkomNbe136zI5hbOHakwGgQOjD/Y4hCFzMhjEuXeNoOF7KFf7lnrF8TzfWqP9CCC5HbYAe+jhx80Ag7PX/lG1pTy65MjUMQ2uN8v7aFgeIB0mFRNYF3drvMKxVksSsra0xHo958GjfVT0muF/qrpPeicb6uODDk7bl8/dXH5Pzq7Y2YzoyTylRrf2U57mve4Sv4O60YHYpOUL/M6y1YF3M3WTi8q2395rWGuXPTlUGwdMl2ej23Wac1ho2NjZ4+PAhZ8+e7VlX565SVQXnz5/l4sXzfPDe56Aa2r+054X/H/urx+qEMdb/9a4hxrhieTJyAnIo5hpqUTgFjvD8yT07UgolJdqYIy6eWltHgzxYz7IFk8mA7TNn2J8eUFYV0hpUrBjIAZFSTKeHpHHCP/gHf58/+7M/52tf+xoXLlzg7NmzbKxvUZWG/+H/+2+5d/uRswAimZsC1D6TyYTNzU12dnYYjYacPXuOyfqYaOCsuZubGyglGQ1H7E932TyzwaMHe8TG1DEYztWp8O5xLgNc41Zsa6CBdUXEsKB9ra0oSogiRZFLSgFFklBpjdYVRZERxRIhK4zNqYx2/MkX9qwqF6CMdHtKaJf6NorGMIy4u3ufosyRWkAaMz69ye/943/I089e5+v/9n/h0YcfIw4OiIoMawqsMTj7RrNvghuwXQIa3jIgQmKZxs1QCKcwdRaP4KYYLBqN5UPUgei27ldK6YG0wJlV+hV7j1OcrGpdAXkVzQvvLVglRUt+6ypK+oBC7bUi+/tvA4m2ojmMp2uZ6c61z0LfHkP4vm1haT/7JE2Io5mq+u5/XH99yvX2eProUdvjp6qqOk65e++q99cngymlGmtwWRFJt7OFzwSbpAMEAmMqRCRI0pSqLF1GNvDZN1vz8XXkQnyxNZZSOxdMy8li5U4MNKqqQmtd++1FUcR8PmcymSCkImQ7coEpqn75wlrAeKLUxHRYGwrXiroQYJZlpGnqD3CDZIMwbp1qzmkEam9cWxO1IEAGdB7Skllra4bbTvUGrqhLHMfMta/ESnjx/nlCBO9b/3I0F85eAi346U9+wt7+Dm+88QbaljXymx0sKA9LVJRwavM0cTwiigcgBFI1h649r8dqTHHraHF+4ZUusQg++PATDucLrM/bp1RMmeccHkyRyvm8DwZD5vOM+TTDmkAgKiSqpQV3DLM7lj50f+w4jyGIqzQ1fVrdZp/0a96PJca4DAwh85/73WsbhfOnNqJxhxDS+TPGcYRSgsLqmpm4rsNYVxOevvm0CaHwz+laI0I/XeLW1fbUz8TPi+AqQvMOu2CwA8h+FcD0uO+FZ8rW+orgxmV0UVGMUIoyLxjECZFwZ15b4/aqk1vdWdAaqzUSiGNBkkiUiCgWJeNhArYg8lnDpDvYS3EjtrOG7fUPWuT29+05dJlM+C5cG+hdiE0Lvz/uLKz6vQ+8t5l5+95VmrFVzCvQ3PC3E4AkwiqslujSYLVGWBfzUlUam7Rl8yAILe+XtoAAhjRSDCKIrCAyESGKIYojhHTVra13CwqbvE7p2dnrUijOnTvHvXv3OH/+fK3MCiDEWkBGaG0ZDiTPPPs0H75/B21BqKa+ihBOcXJUL3v0va96b+076/1lLNZnqbfCuvTK2tbVsAkWdlt5XicQ2vFDdAXSkMQxTz71HDc//5z9/QN05ao3G1vV1jtrLXv7hqoa8NO39rn21DUe3HvAKX2ayWRCEieQxlRCUZQF+4e7/L1/8Pv82Z9+nQ9++RGP7u5h0Xz22edYDbYCYwVSRVQW8sxZKZ5//jnKKuf1r77GE9eukKQxi+wQYzTnL1zwvNNy8fJ5PvnwU+58es8LcZqqKqmqgqrS7sz6VNPWu4lhGxdcIXCxEUJQmpJ8sWA8GnHx4kUOD6cc7kdobZjNM4S1lNmcQbqOtbjc/C1a7Qi6ctkNPXi1RkMcMRgmTNZHCIHLuiVdtsV0kJIkMc9+5Tk2t/4lP/3WD3j3e2+Sf3GPeD5DVSWFqSiEpUATxTGiMiiNyygUi4aeWurYG5/Ph2CdMN4cIbxwJ0S4PgCvQJ4FQkT1uXYyiLP8yNZ+bNMj/0VtNXTDCXJP+N1vUxwYDt93lSJ9n9uJe2peseTaHR4U3sVREFTzuLA6HfelOptVxw1zlTDe/dxHp9vXtMFHu982De3zUAl/G7NcZqAdt9EGSN1+wvqENekClTbvh2V3/KPWoOVnh/l16fwqHu7kVAhODUa4EhDWCmxWECEosahYESUxQkt0WTnarVyGOiEiELbOHCelIo5dxseFyZDS7ZeyzIlihVSSclE2LqWPaV8qRqM92eFwyGw2cwuI0+C438KL0rWQ1tzrPofz20ZuSZKws7PDcDhkc3Ozdrdov2BXQRiiSGGMWApok62XIIQTKqWQNdJu9xWCOEPGjPoFeubc9j02PihMWIE1lq2NU0xG6+zu7PCjN99kMEi5eOk8s8WsDiZWKkJXFQrJ5SvXUCpBqchtAmMQ0eqsWH1Ewf2A13wYjHXaL4vk3V9+6NINW4sSEhVF6Pmc2WzBfL7gpZdf4t69BywWGffvP3L+xlrjCKUiUCdLY/o+kWD6JYXWMJ+TXve4MTyuL8PyWhqtGQxcgci8yOr0lKHleY42mihSCNk+uKufvwoE9X4OoKD9WyvIoe++4wSi8C/03d77q8Z73Ofe54R9eOx9ovlnl/3ftXepsNpQ5DlJkrrPnducVtAQRYrxaMBkMvRKPifAxrGiLEAJAb4omhBHlnNpfH3EPvy+CiD2tXbyiy4Q/su2vow37dZluKsYc/v6pXuE08QqGSGsRJeaIssdrbYCXVVYq1g2bfZrFiEobgxJEnFmax0qjdU4JY4IYKlxFQp7om21647XWsvZs2f56KOPjgQ9CmmxWmINVKWjWa++8jJ/+sffc3WclNsIQnhdtGxnwjm6bsc20f3oBRPrMxb5eAa0j/uSwgEdwEpBmsaMJ0MuXrzIweGc27fuIaVga2OMVAohnRsrCA4ODymLEuXPixYu6DhNBlx94inuPbzPx5/exhjDqa0tnnzySXZ2d8myBa+++iLD0RCNYffggN/5vd/j+9EPee/tDx1PqFwVDCeMG6TUjMcTrNFUZcmZM6eodMYXdz7n6rULPhZBsLOzx9lz550yTCqGI8Uzzz3H2z/9gDt37qKksyioOAGp0abCGF9bylqqUmO1t/AgiVXE008/xZ07tzic7lKUC7KdQw6mu0ipnPVLSYRyWW6qsqQqSqQBtPV0RLstZCwOPXm2owRCKSKl2NhY4/z2NgKX7ERFyr0r3DsrlWbj8ja/+V/8Pa6/8RW+9f/7D9x995fo/UOiRYauCmKv+LQCiLwcQFXHaFtAW7cjlJC1LCCU25tO+eMBurdkhGPYnMej/vdCCHQNHo7SZ2u9Mmypr0Dn24qB1n7nKH1aRfP6NOxL1y2Nefm6rrfBcbSqS4dX0YG2wN7+vk9x1zfuQKPb6xzc40OCg+6zVvHN9vftfpeVfv2KvS7d7N7bByja4+6LqWnPs/238JvNemAP7m8jcPu4rBDWKcwqYzBV6ax5unLu9drJv3meU5YlSZK47FKTCesbmz5MoqrHdXBwwOVLT4Bwrp+5z373uPalYjTaC2KMqVPVhs/tBegKrO1Fa/8e3Jc2NzdJ05SiKJjNZggh6v67Lk/tTdKHsLvj6DtodXyGtXU18/Bb+zowzldUSCpjuHTpEtZaPrlxg89v3eLJp54kimNkoTDWm8ZxmySOYy5fvuzWQEqkammiO+N7fHMmWAlUWmMM3L93n1u3brmAPxUzGKRY64J7oigiWyzY3d3j7LmzfPe73wfraoFo7YWAdu8r1ir81n7/x46y8+5P0rprfyLBoOe+1i/u/1vrvJQNrWOmBlc5GfAA1wf+1+bwX73Vez9knXHfnvjek65FX+t7b18a7LlPvYBI0Gjr8NY+LP6sitqXV3ulgyUI7k02F6zTooTxDYYDBumgHn+cxCRxTCZcTRohvWUK0au97s69PeaTAIXuWrWZzEnexePW/FcBfG1m1Cc499E8KWVNh4LipSgKprOp165Fdb2hcFYsBmvlMUoE4eIPjODcubPszxYMxuN6DFJK0iR1KU619oGujSvJqjYcDp1Q1cniZW0QqFwqxrKqeOrpa2xurvHg4Q7gszxJuaSJPW59H5c5qdsCcNahpoCUzoUgjkgHA0qt0QIG4wFPPPMEV65dpagMydYGX3x2k6ysuHjmLHfvPWBnZxen+ZcoFWMtaBucbQzTWc5nn91GYzn07+lgf86DB3suTbSSZEXOb//ub6GEZZAIyspy/eWX+cXPfokpQRJR6RKpIEkjrly6yKmtU9y9e5eqzDl/9ixpqvizP/8TLl48z7nz58hNxeUnrlHh0rxjnRX/8HBGnlfMpq6qd5qmrK1NmEzWSMcDtHKWhSLPiYRw53Q+Z29nj9nhlChV/KN/8oesT9b48IP3KcuCyfqIw8N99vf2me4f8id//CcgJHlRkpZFLUuIsMctWGvACC+OWyQKa51iYnNrg60zZ3wRYU1lNJUxKO0AYpIqClUhU4XdGvO/+d//7/jZt7/HT77+HzG3HqEWGRQ51mi0hTICbTXK6OAAhcHxb4QDZVK3XfXEkkVwFY3o4/m1bOSBcr9yKVhFju7TPrqySphvj+M4PrvyPFingO269Qg//yVVhV2WcdrP68qE3bGdaCzHNCHEksdK12rTdQELLtrh3q7s0icXfZlxdffEqr5PMi9YUYcEcYS6unOkqfKcLMtI1iYURc7O/V2KoqDMcvIsJ/FZHoui8HEYDhKcPu0sqSEeu21kmM2mKFWQps5qeJJ2YqAREGwjrDlzkLGWSIglwb+L4PpQabg//BZiPeI4Zj6fM5vNaoYZJllVLvVeAAlxHHfMT8tuEN0sVd0XrrVLr9c3vjBH5w7mnjEaDdnY2CDLFnz/+99HCMHzLzzP4WyKd+4EXKEUKQTbZ7ZJ06ROMSulRMkm/qRrOjuuBbczl2rXAYU33/wRs9ncoXVcQHyWLVgsMg+e4Ft/8S2ElAyHQ+LYZfCQ3g2lkR7d2GuzYWedlsfh1ypIAUfGeXLh78sCiva9j7u21kZ1NAUNeGhpLPxBc66BreCzADY6e6PJsf74OdTXEQRzsUSVVxGvri9sPYbW/3T386r1+bKAZVlrs9yWz3b3fTZ7OooUCLx7iav3kqahKBtu//gxGW3qczgejxlPxoBgfX2d4WDoq9zP/PzdGegK3ydtj1unbmv70Hb7OG4f9q15lyaGRBX9Qc1HhYb2XLvgov3M+rNsBBi8FmsxXzjXlDjyZu/gnuJOhu9oqe/6Wf7dWQuDwYhPb93h1JkztZBvrSvQmi0WnrZT943oD9YHJwykacp0OmVtbS08GWs1Tgx3wD/PczY21rl8+Sz3H9wHEhfs7gujhsJafWvzq7TgWqG90KmiCBXHWGGRSiGVAq1dxXphOHX2NJU02ASuPf8Eg2HMrY9vkFUVKkkoKw3G71vjApzBYqWzBM1nC7Is9+WrHQ8x2nBYzRBSEkVw7+4DHtx7yJmzrvirtoY//ZM/YTGfEZsEIdw4LRVXrl7i3OktIhUxGiZMpzmTYUykTlHmBTc+/IgXnn+BSinu3r3L1StXXEVoIbh98yb/3b/577l/+6GrhoxzM97f22U4HLJx5hTnrl3mzKmzICy6yJke7JGO1rhw5RxFVnB4cMg3vv0XrE/G/LN/+k954uo1EDkH0x0O96fMZwveeuct7ty6AxK0rpzIVL93v69Mk2TCvRe3RQeDlO3tbSbjCSqOAYE2xvmb+8xnmJg4EYhYUmHYLeb8zT/8e1x+7ll++B++xo2fv031cJeoKFBApZ21T2EQxrmfCSQWA6EWSZAtAvAH8All2qEKXfrQFTJrDwKaGMKl8yFC8PnxdL7LI9q/9Sk+wvi7/a3qP8yxj+ZadwF9yqi+uba/P2LBbM1jFf3sjrMN2ML3ATy0/4V+25n5wndtJWSfu3ZXmd6ee5AP2mvS18eqNQjr0J1T+/tuqxVJ7eeukMXKqqIoCihyprMpDx89QpcltnL0OS8rkiQhjuPammGty1C4t7fHaDSqnxHG98GHH1CVlq1TWyRJ0jvGbvtSweDB7aj9YCmWF7VvsbtZqdpoNix+QFLBlanWhvZsgHa2i1D8zmWdslhb1QCkbw5hI4YXH76PIuc/GQrAhes0hjRJUURcOHcBa+HOnbu8/8H7bJ7eIk5TsqpACNtgDSkR1vDkU0/W2XScQLF8CPt8Dh/XrBVkWcF8tuD99z/EGsf0G9QNpa/cLqRAWkUUxzXIcPUIBFhRB345TYUrVNdN69Ztq+Im6nlATZT61v+IMNT5LqxLX5DYSdepTzhu/+qK2Si0dsxMSdxhxAHdNiFpWyCkbIhSd/zt1iZsS/vMZ6NxgXetxepp3X6X5tACqicRtLsame5zjn+fq5llAGJNP6J2VXQCqaUovBuN0a7ibCsuRirlGHhLmE+ShDRNkVJwcHDAbDZjMpmw8yhD6ybznfUWviNr07N+XWbW985WrVv7vycFlifdt6uYfZ+Aclw/3XuXmJh1rmohhi3LM8qqYiAH3nXKeBe+IOwsr8/S80QD8i5cvMDP33m3Bu+B8SVxzPTwEF1VjTJCrF47izsvZ8+e5dGjR6ytrVGD0SBoWqdZrqoSIS2vfOU6P/v5Ow2tEsKP+6jWtLt+j3NX6/5WXyMlUZI4n2a/pk6D7gocWqNdQHMliQcDpIXLl86zMRiyv7uP9GlMhXWKDmMqVDj8xoOxEDjvXZKEdP+QziVZWIWUilsf3eDM5jpREvO9b32LB7dukhKBKUA5kC8iyWJ+wDQRPPf005TZnMP9R0RSEUnJOB2QqoSHd++zdfEc9+7eYfvUKeLxhHyR8T/8t/8dt258irKxP+dQlDkIqLIZWXbIwcEjFlcu8/z15xlujDm1tcaj3YfsH+xzeusUp7Y33bvThj/75jdQUnLt6gVefeV5RsMhkYx4+eWXuHnjM8d7ixyBs3aGHCkhEYsjGy6jmOPNgvFkwObmOoPRiMlkHStcjGJ4L5QVUQVSg9CGrfU1fvnuL9mYbHL1+vOcfuISv/j2D/jF177F4ae3MQdzImOwpkAYgRSOL1aldgrCsIdChktv4dMhtpEOfew5l/20pOE04Tfqb0TtBdEVxNvXrwIIx/3e11aNvaH0yzKMEA4UG7F8ZsJvgRf2ZY9q88lV/K5vPO0zHlrb0tKVI7p0ti3jtBVJfdaa9jOP0DBr69d23Fp35Ztu3+3nP+49LiVdCGADvAteayzCAfSicC5RkTFsbmxQ6srJuNbx9ihOSAcDoihiOBzW7ykEpnctPnEck+cli2yK3GfJ0+i49qUsGkH4N8ZFnDtzriJJBjVQaAc5d7WBYeO1rQVhYdpIs52BKixoG+C0hdDwOcsyhHAAoizLenODM813x9IOxA6uWX0xColKHNIjYmNzE2M0P/7xj5lNZ7z62qvM5jOqqkTFkfOTkxKpJMMkZcvXzmiaaNOTY4nSEVQtpNdASqrKcOvWbaaHU6RyVcrH4xFlWTKdTp2vqgdgRmuGw6HXjDhf2NrX1doalQdi1mgojo4pjLnzy5HPJ8FM7f76/u5ed1wfvb+5Cx4zBmoGEUBtHCfNWJaIf3NN1xc0jKWrsWjvXSkEo/HYFa0rQvL2fmLSvr/bLPhia/0Esbs+bU3MUj92WRPTJ3w/TqgNOvBwWbh+sVhw5swZ4ijGWpdqWUnhhYjAXJYeBP63yXjC2to6SinyIqcoCpI4PuLytmq+7bmFvx93fXtNHjfvkyoEHnfvEhhoEfK+8awCUt3PfWNzNR0saZqSps61Er+3axeDIKvTrNkyrhXNdxaEhO0zp5oYHNsolyJfcyEkD5E+AUIbkC6NmwZo/PKXv+Spp55qAu9rIO6ARFkWaFNy/fpzJElEkTuLkLHLjDis6RIzPmYtV7XA66wFFSmEcjF/Sii0tVTGBYQLA5FQbI5H7O7ssH94wGg8YZAMSSJFmc9YHO4R2cofYEiFcXEA1llurHEgBAOuFoPAeqBhhcAIQSUlslDc/fgTbo4HlGXOW9//PmZRuoB/AVIm/OE/+icczqf8xTe/wXTnAbt374BQzKaH7O/usLu3x2I+pyoKfv7Tn/K3zv1tbFUw3X3EWhzxra//OR+/+44Pelf+Pfk9gKUSkmKqKPYfUe494otPPuT13/h1nrn+PBtbmxRVzr37d6hkxdbGKYQVlEXJh+9/yNf//E+hyDl/7jzXX3ieUZIiMEgbLAJesK7BqfFIMwjc3k1EWDY3N9jYWGc0HqOimMPpjPHaGla4GIqyMiykQZcVMZrYSK5cuswv332P1954g2Q84K//wd/imeee4yff+A7vvflz5o8OXKB4foA1GmEMMjLoqkJYQ6TkkpuTxseCKuce6+psrD7HXdArhGjcxOgoSDp99LnNhH7a1x2RHVpnou1W1P6tLU+1W1tZFpKptBNs1DJDa4zQuCyFM3kc+Op+135u+DvIjWG8bZeoVck8wvWBB7djH/pARNetKlzb5en1Z+/G272uPY/2M/rm2df3cWCkD4z5HpbX1X9blg5YDCzEScLFixedu6nxCU5kVGe6Gg5drR2tNUmS1OsY+EYYw+bmBoPBECGcS+tJ2omBRl1R1pg6xV1Ib6tUXL9QOBrZ316Y7oJ2kVx7M7W/b6eBbW/ytnY5ilwmiwA2wuYMgUAhwDwsYPs53QMIjrlILGVRsr614UzHj/Z58803GY1GnDt3jr39XRcc6AO1pfdNv3ztCtZaoiiug86VOpr+tyvk9R12oDbTauMY+Pvvf0BgwM6NLKEoSg4PD6kqjZSKNElJpEOhRV5RVS2BxmupsAFmLD/7VxOoap3H0nt6XGsThFXmwpVP7BzUVdqI1fc7S0VVVRitlwo6uj7DhcvaiaBJCJ2sWrd6P1tnjlSixRS8JmsVqGiPo/4bR+Daz16aT2dN2gLX0bnb7hfthzYd9m2F1hl069LVvCxbCUXcKAr6tlb4bTBImUzGJEmKNdbVZBiPiaPYFRbrTpaWPGr9ei59PqYFJrmE/9t7uD3Qo+vc10T3Q1vT1Dgnhcc3YLfNWDn6Ho8+sRlnm57Ve0UQMnMyGo/ZGI+REu9m6VqT+QafV8lgjcGIJqnH0jnyYM9ay3g8wVjr3V2a8+f4gaoVN6taV+BaX19nsVjUn4/uTfefosi5eOk829tn+OLWfSIVYUQJrbPUdm1sP8+dg/Z3NHtEtNc0bP9wj+cFyp07l+JRO9AhBQqIhWD3/gOkMFzc2uLe3XtMK0NlYDGfUyxmxMIwnR76F28wtnTZq6zBmMrP2QISKWTtsovwIE5FFCjygz1+Ot3l4cP7zA+nRCKiLA02lfzu7/0+b3z1ZdLxiCevXeLf/Zv/nrt37oBwwZsP7t/j9hdfsLezw500JR0N2Ll/j4vbZzjc3WEgBD/94Q+oFguX5QmfZjy4nXrQo42hsob5ziPS9TW+dXjI/QcP+Ou//ducPn2GrTMb3Lt7l939XS5dvMygsrz0yss8vHWHd3/yc27d+IKf/PDHTEZDqCpUHDsPhShCWIsSwqUPthZrXaXjcIKsdQkkTp065WhDnCCE5Kc/+zmvv/4GySAF4crgzUxFoQ2xgAGKdDCgMpb7d+9x4ewmRBHbT17mdy/+Ey68/CLf+uNvcPujG5QUXDh3lkvnzvD+W7/AljnKaqQVKK2QPqUx+Loo0rlYSWjRQ2+Rqb87au0UAqddFtSWRVp0QGNRUjkAZp0Vd1nAtq3rA19f7T7oMlytsOiGMdRj8wqgIIh3hP8lkEKPO0+PS9jS444I27J+ejv+ruHry0qz5v6eqfQAh+CNcGR+HcV3nxKoTy5bpaBr/97Xuvd0x9G9fxUAWXpuRzEkcPKwKJzL6TrOfbmy1is7nedPpQ27u7ukacpTTz21tAaNG3RUWzrKsiRSjeJbyv8EFo3w0oKmKk1dsSVXALapAq51Gzw0m7PrlnNEcOsIL2HCbdcpa6njOcqyIsQuRJHLoBSARRBag+knaNgCYgNYW1tzL8OCkqrm/NY4X+NYRmjjcoBvbZzCaMHbb7/Lo4cPeeml62hKULVY7eZqNFZIrl55EhAoJZAKhPTB3NJl2RCCjvZjOUD7iFZWgJCSxaxiNi355MZtDBKtS8aTCVJGGFNSFBqswhpJFKUIFWF9dSLn9hDMbV6DEYiLtQiLS+IrcFqh7hh8k0IsJ6qh2eer5NL2vMJ77e6vVe3LgJ4wZuMJ/NE+3FylUEhvAcNYKA2m1CTD1MtoHgQjkB6UGeHTCNYSbotY2OXn1PubZUE4pM20re8ep+3omaQvIGYxHiiFZuwyaAwEowvijmiS6jPoPoeiztY/q96lNszVn1UhHFMX7uxIoTCVxlSaSAqktc6lRLkUlJV1Pu3OXSSo0gUaqKwlSiLGa0NUJLBWYyrL+mTd5+Z34w5ODNYax/CxdYXfwCwdrWrRmIaDufmFP4U/d0GYX1rzqIYttn5jnkbQaM3aPsFC+AWqZYYgBNiQ480/xj3LZQsJI2pRkrB3xLKFsGZ4fp7tHP1SWoQIsQ0gtGQ4HHH1yiUO9/ed6wuW9cnY7enKYrWPBbDufm0NyioEsn7/tdCNrec3Ho8ZJSm6LBFaI41GWkWsIiIZUeQl2mi0zz/bFmCW9rVxqWKDIinP88Z9MWjTpSv6Zo1CV4L1tTHXX3ie2zfvg/F7W2a4VL4xQuIW1Vpf8RZ/7H3NivrR7pr6vIkKRKPUgRKB43WDJMYKZ3kwpXP3M9YiseiiQoshh/fvcu/eHV547lnmD+9TFiUGXIapskBUh5T5js8G5bT1oQaHrEGGozEGwGdWwoKwEmwFIqIqc+7f3kXriiR2loxKwrWXnuGrf+tvoIWmKDNeeuVFnvy//l/49//Dv+XN7/0AlQhu3rrBnS/uUJZz9vcfMtYTvvYnf05VlAzimFhJvvj8FpjSC7UaFSmXXcm26iYIgcGloZ0dHlJWmo/fepficMF/9vu/x+nzZ3jy4tPkp3M+/+wm586eJ0kVW2vrCK0xVUmpSxazQ6wN2f4klXGurJEQvqanSyFbq0n8MimVsLF5mnQwRghJmg555xe/ZBBPeOnlF4mTyFmbZHCTluQVkFiuPPEkv3zvXc6c/irW5CgscRrx+t98haevX+Otn/yc7379O3z+2edEnOOFv/13EVaTJAKdZeSHcx+7UzGbTRkOh4wnI+58dIPi4Z6jpRaEsQjvFmd9Nsuw+5yC1GvYDSivMLSergU6FUt/8uyyO661FuV7E1agfSyc8gJJJXTDix3iIZIKK5VTxmonT1i/36wHOKG2lAjKV+ncw4R1cVIhyhEpfalKR5+UCLGdARjWhKx19h2/Usrd60CkQAjrgbWo10oIB2TdMXAKZHdOnQs6NW30Vi9PCwPta/O/ttzZl+68qyBfFaR+1Ariaqw5xZ9tQBzLbKR7f1vW7VpjVgGyPsVJu8kQ++v5v5AO9EZSwbyA3CU7ePfDD9jf3UdZ2FrbJI0jDmdT1jc2KM5lLs2zcBkJS12RA8lggGe/IAQKiamMrxF0MgjxpbJOlWVJFEU1wKhjJbTzNw3MQogg/EhCdpmgZerTmjvN/9GhtNFo+3rXZ1MRPAAQWkg+BIuHftI0XQJLWZYdfblekEE4YdppcizD4YgkTsnmOT/43g+IlOKpp57k4PDAbxThn+WY/MbaButrm2gdtFQ+p7FtuSAQDkcX9Tfjb28m492mylJz+4t7HB7OqSp3oOMkwVrBwcEhglDPwOXKN9qBC2g0An2aldDCUQnCztL61L93BNV6/Ee6W9nafZ7U8nHSfo0XxDjmYApPAIPgJ4CyKEiHY++Opo/giUa+DkJpu7/wfdM/1DLnUbBUo48vP7/WaBB4V6rQpFgiOO2xdJtoNh7NarTOQrjONteqVpxK0Jpb4RiMEAIlJVXliv9E0gGUqiyokqqR5wlCsqcRnqEYa0kSXxBukLBYzJnP55zaOgMYVCRdXI0PDrW2SW8d9m3N1EQA19ZrG4Mw6WlEoBMiqkF3XUCrXqAAVoPbVkBZAqOdYBBFiiSJvQLDnXMnIHejW8LtjXuisLa13KJzaavooxEIoZo+OvMNzFbiNO2gkAKUsLz2yotIKZkd7mO05tTmKdYn6+zv77nYMxnhqqK1ALAVNchoNqpjpsq7QsVxxPr6hGw2x2yto6RwMcxCkESJoz0tkFKDqK5WEPcupZRsbW2xu7vL9va2n1PQDPsUn1ZSFBXaGF68/jzf/Np3scYSSRdL56RhhbAhqJhmXta6OAkPLoz1WnoT3EI0Gg80TGO5r6oSoSSVmde8pnZd9DOTAqrCUi7mHOzs8NbPfsqlCxeRkRcOJewf7JHNZ8QRLo6gdHWQrAmuQM3eEx6ACKOxGF/4zu3BSlowlqrymWCQWCWRg4jrr75CVVbk8wU21rz587fY3dnh9PZpxpMR1lhuf36TR48eYaqSN157lbPnzvP2ex+y+/AROh1wdvu0E568QqbSuo4lsWHdarDrtNxKSUyl2d/ZI5K3+LP/9U948SsvMxoOmU1n3Lt7l/94++scHBzw6IsvqMoCXZWOP6L9OTYIETkeIly8YDijTjHRimvzPG5zc6vmOVVVsZjn/PAHb3L50iW2t08RS+n0GdoBTivBGleBPklTbtz8nIsXLxCLEmsqrFGMJgm/+Tt/k9dfe43bt+7ywXsfs7+3z2A84NatT6nKguEgZTxe52/+xq9x8eJF8iLj8GCfnXv32b17nyovMWWJKTW2KKnKkqIofR0S7V1wnUvLfL5AVYbUZzoM1wTFbWQNwrj9YLWh0q6aO7aTMEQrB16N9e8vaiiKMX7Purpm0nq4EARsr0YR1iJ8nS1hBZGvym59imeNryZmPT0N7EMYrPTj9EHzIiif8EqLQOOEdS6B1tbKzEBbqkDLpQNGjfzhFTge1LhCoKHOVUNb+lpbhmz/3fUiOE4e6SoPa3oivHujEDV7YEklteyS1R3XsmWqn0+3n9d1/Vq2Cot6T+BpNMIp5cuyYHpwgFofY62zdMjKkmcZUqTEcURVlWRFzjiNMVZzeHDAg9v3nBt+HBHFMelw4M+mZTQaceb0aeLorzjrlBCi9ttq16Fom6faGaLcZ9XSih1dxG7QbNdEFJ7bdneytaDH0r3tGI9utfJ2X+E+KaVL++Ur3Bqtl36rkSaCzc0tpJDcuvkpn3zyMRcunCcdJCQ6otQlcRwzGqRgYTqdce2Jp6gqB8oCgAqWhJNq5/s2e1W5VKEff/wxVeXcSNI0IY4TDg+nZFnu193V7BDCmbjD3+G99PV/ZK1o5GDZEswAp40+QevOddlkvPyOV/12XOse/EaDL2rN/kn7AUGRFwjhqvlWRTAJNmORQRaFWmvuBI2Tjbfbvoylpn1G2ut1RNPh/1d0tDJYe2ScNRDp6cfd0hV/WXaRxPraBd43GUAKkiRuaWFogIkNyR6aObUtmlprkjRmPBkxSAfs7e5RVSUbm+tEkSDzCoZgrar1bw5LHBHtQ2YYX5KjtZgtWiBkzRSO8ivP1APQCIDK1wkAizAaYTQyWHSdHqnWnDfgFC/8Gt9N53ntC+mCe9WqTNy4qjmFgHPXxNczkB54xEnEX/+N17j+wvP88Ic/coJdVfHC8y/4miaKza11WjrKI89ulBG1RIG1IiRF4syZM9z64g7ntI9jkKq2dM9mM++ymrgEASsOY1DsaK3Z3t7m3r17nDt3rmXFXrZ0Bqv0M88+yWQy4PAgYzBQlJV1EZG2BJNhTVVnKXQA0L9DUxJiIhrLEI6B+tUOwjRao6whkjFp5IRUt1cbVxKEK3AlhHPriiOJRDh3qbIgaSm4wr/gvhYARleRE4A/Fqz2ArL/LBRHhMxKaybrE7749DNiK9ja2uLbf/EXPHrwkN/93d9ldjhlMZszGg7Z2dkhzzLWJhP+1X/5r3j/gw/5D3/yNcbjERcvXmBrfb2uVxV4YreieVDS4N0jpYpwBXsthwcz4sE+f/5Hf0KeZVSF41O6LF12sjq5S7BYNO81Uv3iSOP9gCsopiRRHIEUZD4lbhQZ8jzjzp27fPzxJ6yvj0kHCQSli23crLXWXL58mXff+hlntrex1hLFCmMs6SDBWst4bczzLz7Lcy88R1mWlGXJIptTFjmFf+bW1gZSCSghXUtZu3SGq9Grjs5ZJ2KLWup0IE1rjdHtWNeCqLIo7ZK4FEVBUZaURUlVFohSo4uCPMvcOKqKPM8p8pyydP/NZnOKLEMYS5UX5IscaQSmcrVTrAkWuJCCXNfV2zEWGfiKdQ5qRhuEce5rwjjaYICi5QbW1ioaYWkosq09NrCuTohFePrs/nbKN+nAfbBIC4lQDnAYgMrWGbxCWnOCpVaoI8HffYrTtrzTdglaJRu2+dEq+SjIh22+1QUM3X4f1/qU6b2K0R6wBF7ZaC0K6WRu0ViXpBAkwxRtK2yZM0wjFlPn8rqoCipKBqMho40Js3yOTBSLLGN+OCWWEdFw4txqpaRY5AghGUxGqEHCo8N9tra2Hjs/+JKVwUOsQS2cG2f2bcdPtBcPmvRsfZaM0LovqA0awmZpXmTTZ6hUHvroCtNtNFkHJraeX2ewaQGe9guXSmK0ZG2ygTWWH/3wTawxPH/9OQ5nhz4yX7G+PmY4GFIUmiLXXL54laIo69RfUrry7d0sU911qH00YWmtwnV5npNnGZ999hlV6awlp06dpigr5vM5eZ4hRKg54g9Oa03bgnlXuD/SWnJQXaE3MGW7+gCtApXHHd4wnu7nx4KhHkDqhnf0vqNCdBByGhcVZ6FzglJZVK5iZksEC4J3na3LC++176rX8vlBhLvaNLl3nqGvvjEfR3CW51NLs8uWifZYlqVJ/x6Xfzgynp6zGjS7SChNjvYFtiIlSeOYNE2QSvgAZEVVaYTQS++ouxZBgyykZX19zKlTp7h58yaLRcbW1iaTyYjpzq7TONsmc5oTDFlKKxnGH4RBXevs3FyFEHXV+LCXZcv3uWYeRF4z5Ak73pKKQNrIZRCzBlMJhImcm13oxwvv0h8aa63LrkWj81LCFRfD+gJrtltHImS2KVHKu6UaX2EWv5bCEEVOIE/SmNOntnj6mad54/U3GCQRP/zBD9nffcDhwS6vvvoav/bGa9y6fYvXXn+VJI0QtTWq2SvBwiOsOLKeIbOYtZonn7zCZ5/fRFcWIVQN4JIk4eDgoElfvsKa0W3b29u8//779X6Qqp/GVFXJ9rnTnLtwhoP9T4mjAdMip8gWVLnB6DnY5cxwTiEASmgHjuWyVtECSjhLlPTETxiDtq5Cn9AuC4s1lkr7VLrCaV/zrMRGkbNYqIgXnn+OyWTEz37+C3KftrkdiFtVFVaI2uWiXm9Pi6xpCtBah01xbhp4YN/iC0IQRzFnt7eR2vLFpzf51te+wfTggDOnTvPp+x+RZQuX3riqmB4ckGUZg8GA//t/89/w0cc3qAzYyrC/u8fegwd1ZW4pxBEX2tCklMgoIlIJSAUoPMxl79Eui8WspolKSJTBW4+C4iHEEwkPUgwiauTXNu9WStVgUEiJihSjyRhtjEuDX2mqynLlyhVu3rzFe+/9kudfeIY48dZKmj6bqsyCwXDCp5/e5MqVy8iqcppd7QTlRMbOnVoACtI4IR074OL2TihAbEgYYLFE1qJDdirt6Y+boXuvnuaGgxY8M6SQ3oWwUdLW/LLyboO2mUnYT8ZUzlW7MpiihEqj85I8yzEGqqKkyAv3L3Mp74ssYzE7YHpwSFWUHpgsyBcZuqrQVYmtKmyl3fmvNIT97tMcgwPAWOcipoiRVmNwgF55V1uLc5U1wtE653VpwXiPDSGprA6aLrQxaBM8Epr6O0I69yob3MutWpIRu0rK7ueQ7EeIJpC9zefCmneF/fpNdfZ/1/rRVszUz5XBlcseuaYNatp9dK0bXX7U5Z/tJhC1HIsQzr3MWHRVks0OSYRmFEk2kpQiUuR55SqAK8n5s9ucPXcOJaSz+BaumngyGhKnSe1iF4Lfn3/xOlvbp/nWd77DjZuf9Y6n204MNNramKDVDAEi7d+7SK+dZaqdmissfFi4drGmxgVrmUEF9yFrde0bHVrb1609hvazQ9C304BETCYTn9UmQfhA4LAZhXACzPrGOkJGPLr7kLd//gvW1sacPr3Jw70dlJRsTMZsrU9cTnVTcG77PJPROtliWj8nbKp6/q01Xd7UTpoP37WRqzFOY/P557ec6du4AkpKRZTzjMPDQ0KGlGaNwdrl99N+n922JLgv/4Joa4FpMfBOP92AsCUt2AnQfXscq4DpqlYf5p4+Vj6LBnS41MaizpzTBg7WOheItjZHtYVmp56sLR3NmI6fW/f77nddDUu4blVq1DZ4aO5pfmvPvG9Z+7JstC9cOote6DfGoKTTBD/9zFPs7j6iLEu2trYwtmA+n7G5tYGKFOvr6y52wi4/0xhDpSuMrpisjXjm2ad4++13ePRoFyHhjTe+wh9/7etIawh5cFyxM+kqhnurw5E96QWm2qogXchmDQzRuBoywvslB4YjEaQeCPi+/SLWYNs64dSU7p5YxmhdIKXT2Lp5aX+OQUUOrDSWpeBO6mK5QvaPoMxJ05Q4jhmPE9bWnZUnHQzY3NhgNB4TRZGvJXDaFS/b3CKKBXu7e9y5e5ef/OJj3nvvPfZ2d/jKV17mn/6Tf8TTz1zl+ReukQxTprMpYH0dDOH3DFgRtGbLNNWtuqyB0rnz2zgZyfpaC+6aJElqXqGNcRmbxHLK6iWFhxe0R6MRVeVcSly2rGU3h0DLq6piOLI88/w1PnjvY6zWFIs5ZT4HI1BCu7iOAOtaVhFnzfBuXYTz5ARA0wJW7pwbrHX7wyUX0bXbhgqWfK3d30ZjjWZjfcK5s2e4d/cui9mMdDSu4wKDZc/Vv2iAfBCkrXWxgTYyDtyIQAMc3wpVryUWERRskeLytSe4+tQ1pFD88p13SVWEGI7J5wvuffEFg8GAqiiJlCL3Yz44OOCHP/gBCEU6XmcxnxMB9+58gTAuiYm1zg0j0Jp24S4Vxe6fjBAycmsnIiyCMi9rf3W3sM7qZhFY6Vxv4jh2bmnCnRF/pFqJU5q0mmEPSuUE/yiJiZOEoiyptKYoS6wVpOmAOI65desWBwcHTCZDhIqX9lyjZLScv3CJd955m9NnziKEE2il9O5gQrnvhM845rXFrmaK9e/GycPCA1NpBZJW0hqsK/YnxJILbTgnMtAxBUjpga4DrwTQOayDQKGmQI01TgofTG6sr6qusQgqIZx6JaRONhartXcXdJYOU2mEtQ5wFCXGGopsQbHIqIqCbDpnPp0yPTiknGfMDmYc7u+ji4oiy7DaYKrKZVEsncuW0Q7sSB+HZykRVC5JTqU9zXSucEJaImGc14V1Y5fWF2gW1tOhyoEM26LvUCt02uDB0YjlRBCBbvQpw9t84rhkKUvK55bXTvuatmwJnmW0mFybL3Vl5rZc3P591d9dkGQDgAu8Tog69k9YWOztY/Kc1AgmccLa6bNU65q8LMltRVJosgc7pHFCHEVEi5x8MYc0ZWNzjVJXZHlOkZVsnzvLC08+SWngb/3mb/Nn3/jakXXraycGGoEAtK0LTqMmlqwF7RbWqC0sdxes+xLDs9rpzMLnxWJBmg4QQi3d203R1gY37fF3QU4URZRlSZ7npElSp8UNhUsQgs1TpzEGfvaTnzE9OODV115mni0QEtZGE+cLmkiMtlhteeLaNWaHC9JBtBSzEp6rVAgGP5nw3GaueZ7z7rtN/niXjqyoTa5VVXmhyVUw1brtztEPDHpby5oB1ITRCWZOIGuvZR/aP+45jwM5q+49ydiD4GDtMuDoG18AY0K4OeV57ghXsI6Fgme4gHDjhUTXha2tAhDEtNazWpq5Xon+S7ST7JX6HNnm2WEcNYNbeqmNls1a5y8Ly8S11qK0bgyWB2udhsuIygfnWS5fvszZs2d4+PAep0+d4vy5be7du01ZOuve2bNnfarpyuWpb1khhRDoSpPlc86dO8PFi5e4ePESn9x4n89v3uR3fvc/4+NPbvDBhx+5824lWkDw69aEzEOd9RDCA5HlNQk7XAjjGZl7l5F070sIMLpwlgkZhD63wAKwkfH+6Y4WDQYD71pqiWLBcDQiSRKS2GW6G09GrI1HJFHsi2fGTCYTJpOJP8sx49EIJWMsMBgMGQwGPrvfnDSNKUvtM8pJ0jShLCuKwlkvZ7Mp7737Pru7j7h58yY3b95k59EhSZLwW7/1W/zBH/wdXrj+DOfPb1Lpkt2DQ7QuPX31y+LxhjUWjXYgwridLaUDGdTxXoZTp7ZYX1tzLh1FBWNHZ5M0RipFnuee/jTvpM0H3H5afmfj8ZjFYsF4PPY1WY4ya+d6VPHii8/xJ//L18izOcNBQrHYRznnD0wrNqODOwkuYBYftCukE6iFalkrjStqJZzm1VqotLd8qCYLi1NAyLomSRxFnDl9ivfefYeyLCB31r8Q4B74J94dwYHFAcPhsHZNns0WBCE9z/Pakp9lC7LZ1CUV8Aql89tneOKJJ0BI7t65w50vvkApRew160ZrDvYPfJyHj+fyAojRhiRNsFpTFSWZzDjYP2CYDsBrp01HuAp8WvlA0CB8KxFjUS6oVzr3QY/eap9xgwtWTpKYqiooirzOaATO6yCOHMgYj8fM5/OG9nlAGqcJW6dO8dzzz3Pq9GmEcgLeYn6A1hVpmnJwcMjuzg7b26dJVHyE5ocmVUSSDrn/4BGbmxsY61wlBcLFLnnaoCKJQCFljBAKi67pgStw6FyGpBUo25AY4TX1Dmh45Ypo4qrqPSmpCYygyfIkACtlreIIcRG1kiQklfH7QUlV76sCAwE4IZ11MBL+OkHsiZqT5USdXEQY47PLOUBgvZsXxlk4jdZUeUGZFRRZzmx/n/l0zmKWsbezy+HeAbODQ8oso8wL8jwjL3JM5VzAhLbYyvVXmQKLO2doA5VGGlu7c7l1rUAarK2w1iW+sCzzjXZT6qicB41M2ZZVu8rphkYsC/9tXti9r90aGU8tZ4ZsPaMLEkLrs1a0v+sqiZeVkIE2N7zeet40GgyIIl/s+tEupRV+n7h4G4VhdrBgZi2Rioh9UiQrwCaK+w8eoSLlYoOk4P6jHb4/zdk4e4Hf+J3f4uUXrnOS9qWCwbtZa2prgWp85tomLfdyG1TZh8jC567mKrzs9st1GnyFUtGSK9Aqc1L75bTT5raflSQJi9m8Tq2olHL+mIsFSTpAqYhiXvCTH/+YSEVcu3aNw+KAJI3Z3NxgMh5jKSmFJokTzp09z3yek9ioHoO11JpSRxgaAeXImGmE13C/EG6jFEXJRx994jTCSiKloCgKXx3cFRUyxqN9XICo08CdAFwc02qFuPXaFNNvaeg9RLbVQee67szbT1wGpQEQdO4IQnXgRUf6ac0g7DV/GoXACTKecEshfDV1Q5zEHhCGjC8ClcjmWiVrEBNcHJQQlKWuK7IfM/klM4f1mtWlyVnbgKSaca1+h0d9NoPE2KyL6Oyr8AxovQ/hnnTk/bQ+Sv8+3NDcCxiPx7x4/QVeeeklvvmNrzOfz3j5xRdRSlKWJZUpOX/uHFevXmnAqgixXQ0ystYym805vXWG06e3+LVf+zUePbrDX3zrWzz55NP8H//r/wP/6//yH3j7rXcocs1smpEXFRaJkcIFerfmZLzmWrVYNTi3iSiKiZRESifcjMdjBoNB7Rq2trZGmqYkSUySxpw6tclgkLoqqknEZGPIaDSqXTdHIycoWiMwxjHuKI4x1ilIiiJHYMAK8rzwQZ9VLTjv7e5x/859kiQhz3Om00PnamItuzsHlGVFVWkX9LpYMJ/PkVJSlpbDwynGuABTrSuUkownY776xl/jja++zvXrz3L+winOXziLtSXT2T5FUTqNq7VOqLLNObPgLBGmyfQXdlHYjWCJk5gLFy/w8OEBRVHUNDkEyIcUt+4dH80qZ+3y+TDGsL29zcOHDx0A884S/oUuAeaqzLh27Srr6xP2HjxgPBoz3X/gAqmlPwWeYbY3srWynopo9R20gGBJktQVYvPuLFIpRF0Q1iJV5GpbYL1SwnWzmM1dIbw4ZTadoVRUF75y57FJCOIyXgUNqOD551/gySev8fVvfAMZKTY2t4jjmNlsVp/t27dvoSKFsg3QGA6H3L9/nwrDF7fvkPviXIVx9Wekd1+LE5cC1k1VLNUL0sb5wO/sPMJYTWUhVpIoijHCUxMf7ySNE6TiJCVSAwfSUAipQCgPwgRWhPoXTnC3JgBzp4WfzaYkUeTWWDqXQOuzxA0GQ86fP8+9e/cQQpIkCaPxiLX1NbbPn+P8hQtcvHiRtfU1R7dnC3Z2dlwWSmPJsowHDx7w1NPXSMWoV8kYqOSVq1d5//33eeOrr2NCAjoEVnuZRBqXZQyBFKZWqrjfrHfF8jRMeBzefON5jajBQHjfrR2JrJpsj3i+HQCJtIKwicO7q8+LDXVwAk9z1kYhBEZ6+ch6b45gXfKKSOMD8K0QPsDNjTFC1H04lxnr9k0sXdprYqJRQmJhiOAUlzAKjLQ+mBxsWVEVBbrSlJkhX1TooqBc5MynM6b7B8wOpxwe7jCbHVJlBfPdfcp55u7NSmxeYCpNWeZABWi0dvFVRgeFnwcEPqMXQWHUUmgE+mOsQSjndi8IwMNbAZzf6hJtCry3thz1uOAHN7ygUI5CIcf6HR91q+oqe7tK9y6g6AKS9m/NfTR7JNynnVU9Ef7dy8gX64wQInJWaGupvDJAgIvLsV5GthaRVwhpsLbACk8nlOKLd99jPs2xf/03GMR/xZXBq6payuLUNvso4XxXtTHOVQhcOj6zrJEKrR1MHharDRran9uL7UzyLLlvLaHNUNTOI7bgEe0OoDtYUjoTrsY6f2chiBMHLsajiS9E6ALYNjc2SS289f773Lx9i2tPXEUmikhLzmxucOHUJioWZEWFtJK19Q1KbbwSx1VxBeF8blVIbnkUZC03f2isM7xanDtUWZXs78/Z3V0QJQnDsUQlUFhBnpdgFXEcoyt3sLS2GH1Ui3Oi5tcSf2+Tj6YW45bGXr+jeoZtIde7ExECxuqHtNbA0GT28UTT55QNlabDb0u+9lZSW2vCumF9Zh+FS4nkR9uqX+Gyy/jK71XhAoatpdIlSsFomPDUU5d54/XXGA4G4FMuTiYTV0iuLPn3//7fM50vUFHE2toYoQyLecXD+yVUAoTBmNL7mSuvdcALd6YumqM8I8eEvOz4MQcfaQgoqwElLaYpQAWNO86VSXjhp37tgXF5k38bxDk/ZItUYun8DQYDlFREcYQSktFoxGg0rLW5o9GI0TBlfX3I6VOnuP/gAX/+x3/E7u4ui/mCU5ubfPzxhyxmGc8+/zyvvPQMp0+PvYQkCWmplQypiJ0wmi005Zrm6WcvMZvvs7v/a3zn29/jX//r/5Z/8r/9z/lX/9U/RRT/BQc7e3zwwYe8d+NjDrIFhpg4HjAej0mSmEE6qF1cNtYGDIcDojgiiROSJGY8du8yjSVJ3CRt0N70bo2lKDVZnjkByLsM53nOYpFRlCXzA5e5brGY14kYhJFkc83B9JCidBaDoiyYzmZkswXKujXOgs90kRNFEUVRUeRFzczclnBCbuzdL601KBURx5ELDtewPh6yvb1Fkqasra0xHo/Y3t52/85ssHVqkwuXzrO2NmE+z5jNZmR5ia5dfwz4mC5wQFJLl1a1MhJRgYoV0iczcUzf+8pbycWLF7l755HLgqR9tic0cRqzWGRU1qcn7dMthKeKxlKxvb3Ne++953K6W9252HVirEUXkrOntrl65QI79+4hZAoyRQhNHAnyMq+LFS51YWzzYA8wQgYq7S0WRe75kzDEkSSKJHHklPNVpSmLqdMAC4EVEcLGgEKXguFgnflMMzusKHPQyhX2A4W20hfAUyhcpiOhLaYyPPvM8xwcTpkvKpI4YXZwWJ9RcEUwq7xEicQPWzJIE4yN2N+d8uyzz5LPDbODHCG8ZS7UdhI+1bkMrjmC1PPSvHRxUaUuWeQZcZwQIX3GuIaiSxmhcbE4cRSTRANSMUKFIobKFReUQvjMZ44OyTjCSEFlXAD8opiDrRC5AXIqFKXUFEpTlsJlfhqOuHzpoo9DVMgoIUkVSTrEGiizEqshVSlCCHazPR4+3CFfVOSLnMVsznQ2RWM8j+/P6mOtZjQcYoxmPp0xGA7ABoWNdjhJByHcYoVPpy89X+tgZ+HdwkQQ/IMFI5B12ycNCbTViKDgqQm3uy+8BWBJwSeEaPiyxQmawjQKWFlzYoQwrV5AhCQXgX83P6BbvD0oPRs9Q+DmDXhqzhK14s1ZW0AkCpnEjDeGTl7r3B+AqNWGwge4L+YLDvb3mT7c43Bnn/nhlPneIdO9fYpFhs4LqsWMMs8xZYUtNVIbTKV9bquF441GO/dE65SulYCF0q6opZV1Nk5JSKJRESQYgUTaYIUTGNGse5+Lfl/tie577rN+wNHsoqL1QkR709gmfsP0XItoKVWsS7sdoIeUCQbjzqgPwgcvNwRXYRHGpOv3aK1P/CSli6tButgjW6H1DBMZolHKSdqXitGQUlIURY3cAlNU0nToedjAjZDbrsTdfkHBHattEelqINqfg4WkLeTWpl3pciy769xhauIivMuDZ9gh64gF4ihybhvZAqWcFmlr6xRrkzWEsXz7W99CKclTTz9FlmeMxyO2NtZJU+8zqhRFCadObTObz1Eq9hpb5xqglGCZ2hzDdb2a3rI87ziJuf/gAVlWMk5S1tYm7O7tEMXDOtDJ9SFqzZvwRZ/6TIm9j18ixEFsh+Wd3xC6gNhtPWZqQvLlmmj9wxF7vwbG12SpfTJbvTtNRAjcNQQTdjPUFihpzaSGv+3sMbhMDFhLmsYIa/n9v/O3GQwSyjwniWPWxmsYa6hMyY1PP+be/XtIJdk+d4asWHDn1iMePZzSFNVwAr5LTxroqg+8FZYQiCuhScEqWmfEVC52QOD9WNtgHNpF1dI0XYqbGgwGDAaDWoCO45jRyPkwx3HMYDCoLYRSSlQkm+X3z6lKX3RNG4oid77mPqh0Pt3n0YMZ2WLKbDZjf//AJSvIc65fv86jR4+4e/cu6+tr/Mt/8S9Y31wnUoKirJpdIrwuAukEUeGyouzvHbB95jSXLp1Hqb9GHKV873vf5//9//z/8PHP3+df/uN/ymsvvM71J1/kD6qCDIMVGXmxqOlKWYagSEueSxZZ4YU1zXT/gHtfPGKxWJDl87rie3ALWywW7t7KmdrzPKf0GvtKO82r1ssumnXsl1JOaDUahEBFEdK7gwgksVB13NZgkNZWEhXBaDQgSVy6wXQwYDQcOa2U1+jGcUwUxQyHA0ajEUmaICPJeG3s3W8GRJEiimLfj8QYwXyRcfvOA+bzhatmba3TVFuoUwRb53KhPMgYpDEiSVDSuwoGAUpS0xUhFRcvXuDHP/4FeZ61agNY0kFaW1qXha2jrghtrry5uclsNvPnp42W2wop91kpwYsvPscvfvoTR5cna1TFHKktAysR3rprWjEaSjS0CuP/8oC+VMuCoEFjTQlGgVWuLkwUIb0QFxhzlDrtbZqmXLqyRVHuIuScKMmJYwl1TZIKcFmwlI0QJnYgTCu+960fcHA4JREDZKWQPsWwEE6xZhYVQ7np3WBckoLJcILSCZGQ6HlMNFecH2w711yckCql12jHae0WppQiTVMGgwHWCCI7RGhBdapAWUEkXFKHJFKgQApFpGKkd5VK0wFRmiAHic+sKEmSmCiJnJUQ51MfJTEiish1ye7BPlmRMzc5KhaU0zmHj3bI8oxpueDe3g63731KZTI2z4wYraVMNtfIczBGUlKxv5ix0CVZVVIKC7FiY91VBh9Pxvz8J99jMZ+hdcl0dugKLBoDqqcAJE1NhSeuXuXmzZu88MILPdeJlo7N87tWfZ6lK+1ysHFD64/niEGWFEFG8fzUGSBaHC9c5xVMttVvfY/no7ZlKQ7P8LNZAv3dObSxk7tnGdwsrUtz5dKznOxjWgK4rM8MUPOukEjFactAjgeMxwM2Lmw7cCwjx0K1xRaGfJ4xOzhkdrjLgzt3Odzd42Bnl9nuPtO9A7L5HFvkmKqizAsXHF9WWK0R1jDWnj/gEjqghAPfVqMFNbBC4Gp4KB/PZ44vStdndQh0Naxbb+xj5/76+7q/9t47uvJL7l6wRGPB7xOaZE3GWFf7pu6nSWRTW4V807aRj20nNMJazebWBlEa9wDn/nZioDEcDgHqjFPtCQXRrRtw41yEmvLvXVeptrWim2Gq7TolRJMtIqSJhWVQAg2wCZ/baflEXSRP1IE7wYRtDMSxi9EQQnL69BmSOCVNB9y+9QUffvgh6+trnDq9AWhOn95kbW3N1VvQGkQEwlXgzXJN1PLHDYdM4F2ZLHX10FUuX+0WrkmSxJuHS0ajEQCz2YzxJPZ+226jpUmMrnK/5rbWNLTX9nGtBg6ttWyAHTjU6wJnoUV0LQ1Fa3qjORq28317/7TXQiz97s6e1za0Dp31mn8XOdnuF0KdkuU+w58WGbQUeGZgoTJeSIpj7t69wx/9h/+AEJZsPqcqKyI5YJHNyYuMSheksULFksP9XSaTdSIpkRhUABLWW6VVo7kQQtbCfeRrD6RJQpImpInT0A2GDiTEcYIA0jR1Put+z6hIOreIINRqvZzf3lLHHllclp48y6l0yWKRMZsbqodV7b7jBGZdgwjj925Ib2mqRhAPfq61cK4NZeFiGdI05cUXr3PmzBl+8Yufsbm5wT//5/+cK1cuo40hK3IvPDb7rE2kHeiLqErN7u4BL7zwPIKIX//1iHNnz/GzH/6C99++wf/ts/8H1y5dIctz9uaHZFVBVc0oyxyj3VzqtKZASUSpfeCuarS6AgHRMhWP49ifOUuEi9cZDgcM0nG916MoYjAcEixukVIMBgPvSiVQUpMOnXVFRF7wiJyw5iwqQUCL/H1D4kSgIuHrFCUM0oEfp3Nhkd5XO1IKqZR7N8KiLVTa1O9xUeQUs0OXt78EXVlKXXmLnSvipY0hRE5Y/x6CVKuUJI4Uo2GKHhqMcQkyZOKybLWD+C2Wrc0NRqMBeZH72J0G+OKF5ODOEN5xc36Xuahz6XHPWywWDIbpkpBW0yBA2xIRGV557Tr/7t8qhDFMJhvs72hkbjCyEbyiFmmRLfe6NrkweP/u1k9aa6QoEEqRKGchM8J68B801xIVJ8hEUBUl+SymnKSk0RkGAwXKFbCNopjFfEGVuhiJUTokUSnGB16PkjHjrS2SJCVSmijqJJsQwd3WuS2lacLaZI3xZOI0lUIg3rhOFEWMhyOG6Yg4iol9wHYknRtwUEY4JYQiTiKIDZFywCxSCiUkiYqIEheY7u5xKWytcXWbjMXHD/gMWdJlaZRBMyqsF2wseZWzs3dApSuksPz/WfuvbkuOLL8T/JmZux91ZehABBABBJAQKSpVZWZRdLEE2V2zSA45NUN2c/ph1urPMvMwn2DWmueeh169umc4q8Uim2QJVmVWVlWqQkKLQASA0DeuPMLdzWwetpm5ud9zA0ANHStw7z3HhbmJbfu/xX+PjUa1HrtscA7m9Yq7D+7zf/u//195vP+YTz76hM8/vU9RjhiNNphMN9AjA1rmcmstx/M5T/ef8oMf/ICN6QYPHjzg4cP7sj4Kxfnzu1JlPBurdSEoIGxnH3zwQY/F8m97DPNQcyXyrCOumbgM8y00GcUY6E2hb7sFeTr0ZvCU8KzTCvHps7rndb/7DPd3+wyQctji+2o91B0cMeo+b19O0tHNI41bLCSkR4u8sa3D6ILRZMRk5zKbxWWe//7XUVaMYO1ixfHBIXsPn7D/8CmP7z9k/8lTDh4/YXk85+TwCLdYMJmPcLaVorG+CSxZkrDvdShKGfQOp5RUIfT0PFfRqP1FhlsBUn1998voX7kx9dnjefbRy1mG5EHygSxI6Q7gRSKGs9qSdOscGOGpyvIrte0rVQaPD4ybdV4Rd9jAHAwMlfscXEDXoZ1yvp62LA5WXFQ5OOk6sj8BIsuHovOipER2csGgKcsR3sGqrrlw/hJKaX7845+wXM755jdfx9qa3XPbAjJC/GLrPR5NUYxpHRCEb5+Stztyi/xpJf609a7rZ89iscA5R1WVPHx4n6ZpwskiBIpCQsCcl9AgqfTbKbfee+q6PjVO657fWTKi8MsZQGISZxQoilidOoIoUWD6Lls5X36m2ML03KEi0lk/citmrPbsvU9lgFAkTxYQoqT6HjF5pkZo8uQ8rQUIJOuPt7i2Zff8eQ6f7vPTv/iLQIkpzyv1VMIESsXm1pSNjU28smxsbNA28OILL/DSjVtYK8pIWRVMJmOMKcGL96+qKgGoraWpl7hWGGlaK5z/zjoBBqsVTdNineXw8Jinew9o2niOpa5rmqYlhtREIoOocOZgOwJu69qeBT4XmDbQJefWuHiP3OMYx0jWJxSmYnNrm62tDTY3N9jf32dv7wk3b97k93//9/jhD3/IaDTmZH5C07RCGR2ZULL7xXHXSvICF4slcMgrX3uFc+d2mU6nvHD9Bg/vPeTux5/w6MFDFsslBydHUjTJVhg9oyjFYxBZm4pC4/UyJWhPxuNkwa/GY6abM4oELqQuzWg0piwMhRLlczQaURgBBmVZoo1mOp0wmYyT0lkUEq5VFgUSmAnaaDDCZuSihSvUmhDjmQ9rKY5DNzbWCXhoVzWtXdFan0Bg27SJk7+1HgKdpNSNsJKI6HyqrOxVeAYkjnWXKQo+LuqwJo2Bum2pm4Z6PBJg4kZMlBaFVOkQTmAlT+PqJe5++jnLwPUfWYO06mQ+XS32wTrvK1bWWra2tjg6OmIyHSf50Jt/SHx609a88spL/Ff/539BoTSXLlzk/Xfe5+033+Rw/6Bjm1ExURaiF9NES3FgkSqKUmo0BCpyYwymKGibVhTWspDcrWDRKYqC8WhEWY2ZzjbT2O9s7zCuKr719W9QjCqpqouiKkdS28eJrByNDFUpzy2rUgwHoY1GKUptMNqEKuI6yIwW61Wqdt00jeRsFAYctNphW4fU7pXkdk0RvEo6XaO1ls+iN8tafCv9vKwFkCtvKbTQn7ZNkxTg1XIpAHflsctozJO5GTWytrVhjnoa19K0LSdz8Ry2tJK/0XqJxfcGqzSHJyc8P3kNDu9y0sw52T9kwTEH/gnjccnmuQtUY8m3aNWCVVEw39tnvnfIdHOTd99+m+VyzsZsyvb2Dt/+9rfFY0te06e/96b6PsDVq1e5e/cuN2/ePAUKckNI3LvWfR/vGz/LlbRng42Bhy87otrZyeaQR+V9R9FNt0/2PRt5+wJk8R7r1ivJnqgvrFFwVdeO4WfKSiRBAh8q6jlRpnRtiZEJqGA1D+1TKCH3iMUwlZfaK8B8vsB6KMqKUT2iqAxFqFdTKkNZacaXdrlx9RIvKXFL2rrmZP+Ip4+f8OjefR7fe8CTj+5ysLfH/PAANT/B2Ba7XFLgaD1o70Mld0CLgUB0i05xz/W6+Pe6uRBrBw2Nafl8iEcv2odng+Lhc9L9Te5x8L3vvFKB9SxE89gApOjP1/gz/31oCJR3E3IK51znff6C4ysV7MsfHC17q1UtbBFl2QMJ4SLIzs/RYN4p3vuOmz/vIN8vnpe3Zaj8RPQGJPDT6zxkgx0uevkuS8wOSutstsFiseJnP/8FZVVw7foVtPFMpyOKQtJLrRcB7pxiPNmkaSRZRhmV1nl/ckZwdNpTMHy/HGTIRJRNOxahklhriRHf3dnh+PgEhWKxaNBalAXhtw8KXBZWE62MOR1b3o99b0MnxPrnxPtG8NdR96qQ3yG39uROuVwgdn3uO9QdjZ9KCVd38DiYkPvjHMJapEPlUiLgCXkeqlvkIImpkFuqCfSEiqooYNth2wajoBpVPH/9eV5++WUuXbjAxQvnmY7HNLV4iDQjwHMyP2JRn4ByrOoly+UK27hQGEwEY1PXocBSkwCEDV6CJgjQtqnFtR/G29qWpm4SUI2ehhgKF5P7ZU75xA4Sk90k7jQbozjvI2lDSPqL4xCTQ73zga2nC8tKc1OpsKHFUDwV1ogoZUUxDqGHjpOTOVeuXOYb33iDb37rm3z9jW9w6dJF9g8lrEqoOfssGkNQE2eW95LkXNcNu7s7fOf8OfYP9zl/bYcbrz0n1uO6prU2jLew4CgldQW0iRVbPVUBhYkEFSrkOVQyJwpDUZZUSYnUFMaE5Nku6TBujgIYQ02LAAhcUKYXds68BttabBhv6614HKwUp3I+jq3vclM8gAFfEEMO8n+ti4GfhPHOo3QlptiTr9EAEL0wIXnv8WHspZCl79ZrthmGu2O0p07F7mw334DpeCRzB58s2C+9dJOPPr6daFyd98l6HilRdVmkZ3VyJbRf9+fDlStXePLkCZevXgZ/mqkQvCQtO8fmbMatl2/x9Mk+u7uX+f1/+Ar//P/4f6Kul8znc1n7hXj/lKKLt/ZCCyoCRWo9FMqkeP7O0ychuTF2Pcrz2C+rpqF1sYIEIUfBM5tssKyXoSCZYn4yD2sX6lUNXqOcliRoazFK1mdTNyxPoG0Uq+WS5XKZZGdd1yybBq0N1llWq1CszhjxuNZCseqsFyuwkuTPtrHCqBWAn9Ld/lmogtIWycvqQ2KoVip9F53DsaxEWRaUkwIzUUymY0ZVxXgywhQhDl9JvoYKa9AWltqIYeTENxzWc5q2oTAWpQqs90y3L3Hpe9fYP9nnrU/e4a2P/obj1WOadkW7POHgkccU42RYiTrAHfURripRQKVha3vGf/Pf/F+4deslGgfe9pXu4RqKSt7Nmzf5yU9+wq1bt3rySeRmpn8oRQwwGiqMufI39GwM75kfnTcjC5npvk3rdPh3P8zJn7om+7bbcwn5Utla7BTSMNTJqLdeic7vC4RCf339oOsL17suJ6axqU6Q6mSBEp2vBIkQ0AZVWeaLJbptUaYIxed0qJGkaJTk4mm9wpnogdOUF8ZcvfQ8115/AVAsV47DvT0e3fmUT999n0ef3GX/3gMO955Ao9CNFF4tQKqwK4vTJPDVH6/TACJ/f43KdJ7TwG2dcdf7br/JyzLkBr+190DkWZ6qsG7MhoWXT+t03e9DcJ7eNRij2lbovlt7tkckP74y61TuhQAROs52LiWtdQId+DUW/QyIrENT8T7Dc/vgQp26DgT9ZysydZRYtXyXCDh8dgjLEW+dZjrdoKpG/Nl//HMeP37M1772EtWo5MLFHWazMcZE+t0G7wtWtWe6OcahxOKn+wPUJa1Hyt5no9Vh+4uiwHlJlATY3z9gOply99M7bG2f5/rz1/n1m7+WaqJtm8bKeQ/Bgirx3bL5R2abfAKfXjSe6JbNQZw0TIS3Ckqn0qB0CBVCrBHxvrni6yJwNF1/EARftOYa09FLFqVsWnETFMujoaokt6A0Qh8q14inZzKdoJSwcRlTMJtOqZsarTTjidCFHp2c4AK5gfKO1XKBdwK+7n5yh08+vg14vG3Bu5S74RpH0zZYLwqidZbWhe9al1h/RBHpx+93nr/cU9CBtlzoRw9M7OO8r+J8leqosaKEpzQFqujXtonWty5uOCiHg4Q2vEfbUAQu+z4KFrQSZjklOQcRtBVFRTUas7u7zYUL57h2/QrPP3+Ny1cucuOFF7h8+QonJwuOj46FlQgfvHCiHOfrMP7Uqm/BOzk5YrGYS/jSdMyLN64LKQSetm2i0QznW1GElFQN7qxvGlyBokv6dYHNSaz+NhQS8zStxdo6AYHaWQGGQeFO6wSx6sd1IZa8sEKckD9I8SkndA5e5ooLn7tgtZMk86CYIZS9Mi98yivwXqzCTnXWrqFSkUIYTm16ASQQ3jVrb6o0nvo/yAEnSbxFFi4X300pFdhrCql6HNiCLl2+iCl08GjUVHYUwFxJXddC0MFp+Z7anx3OOS5fvsydO3eSAjbcc0RmFDStFPi68eKL/Oyv/z/8+D/+jMVxw/bmNpsbG9J3tVjwXQCKbegTHcCFMOQ0gdYxsNIoacd8sUgGgtaqZKiSys7BYt+ApQozWgWxKfPK+gaHDeOmadvo4dV4xig/EkXMW4rgXY0J3H01svPaq7KUXJpAoRn3LAWMLRhEQTNag5b1NB5pCl1hjBjzisIEQ4HGlBrGlqKU2i1lUVKNKqrRiEIVjIox43FFUUi/jMcl4+mY0U6F3oLpxoSqKhmNymDISOpnX/G2wUhiHe2yxTmbjCE+EDAUeozThl+99y7/7f/7f+DdD9/m8cO71ItDmtZTuyYZooqiwFRiMNjc2eXK5Yu88bWX+Mf/+H/Ha6+/xrJuoXWpMGM+f3qGjfCzqiomkwlHR0dsb2+fAsS5TM2JRfLjNIhe/93pCyXxluCd75/pex90RljEIqr6n6+5RD7KvRjJ2Nfpnd4HsoNguBN9qzMRquz/6VcflWrfUySjEWaoTMu66r226BKWADBCsUMPTgfyCaPY2tpic2uLpm5o2lAYMBQ7DLQDWBXCgZIYlbloYr0ZY/ClYuvaeS5ev8Q3f/hd6uM5jz+/z5/90R/x/i9+SbN/QLlqcHULNrSNTravAxi5Up5/Z7MXHbJCxnvl18fPYiRcvNc6nTufC3Hw8v0i/17rfrhrNOiGbl7DBUjvfYY6duyLoyMJz9WDNp11fGmgEeMXc89FZ9mWh0crUFRstO64mqFLvlrHZZxPzHwQ4ud91053Tc8y4UmKlVaqUwI4PQDiyYgdHh2UsrFtbmzR1pY//dM/BeC1115lMhmxu7vNaDTCWYRKD2Tie5NibZ11qYiZpx/T13lnTomS/t9ZW2NfF6bg2nPX2N7e4unTp1x7/hL7+wccHx2wu73LrVsv8tZbb6ONErc4wpQTQzJbKwCkbuog9DO6XdUVvCGEc6i4WOlP8FxoR8UhjXVYl/nYFpH6OMTwSnx6mbw74/GE0agI1HVC1zibzULIj6MqC4zRzOdzmrbFaKEfXa5WuMZTmFJ41BfzwOKzxNoOcD0MymTuHbBOvAeyr1vatsHbNhTFGuGco14tiWAjKVthXK2LbmuVrNxiBRSAFFmloouxjyvj3yoIQZ2FdXR9ChKjrXS0zBNiK6OSq4J13uBdB+C0ipZ7kwBttBaVgaI3xlRHqmijNKUuxQIaAGkELNpIJV6tNZPJhI2NGVtbW8w2Ntja3mFnd5et7S02N8eMJyWbWzM2NmZ4D0/3D9jbe8qqXqWwHdncNCoGvgZLTFwEOm3iMRnN07Y1q4MV+um+hLwYaacJCpZCBbrRzhiSgAGBHDHIkgjYfLRWO5WeI4ChA8VWde7xXDkWkGRSyFGUcyrMBaKi6VwKmXIRXNpAExiU6MjSpJVNBgofvB0x78bpri/weR9FkJVUu147vSdd58LadekeMVwrnd0pH05qLNi2CTSVTQBkDmyL9xMmaoTSDq0E4D939QrHRydd7R4rDISrxbwHhNZuuGH4o0VvMh3TNHXIQ8kMSlHRCTLLOU/bOs6fv8Dv/M7v8uP/+Jc8ur/PkzuHHN6rWa6WITdJZIF1Dh+Wmvbyrwij6ZyDQgd2QJJxKBm2lCRCy5qUNVwWmqK0qDLkTinJ6cFDaQxFpSkr8Y6Z4FGIeTZOg9IGY4R5bVQaRmVJWRjK0oisLEuKsqQsRKEuykLcCrqjj48e76Is0DOh4a5KExLCPYVRlKZAKyEoSftJYXpJzUUleYZGhxpVYU5jCIx0EGtraBOKwSF1G3xQWWScQtFYOpY8pRTGawrAMMLZEO+v5Dpn66BkeVrnOPzoKc9/4wVmz5/n6GCf+dEBrV0FmS15PFUluU6bs00ubO/y6q2X+J3f/i20kr1OPHmB+SrtY3ltBJ3NfTlef/013nn3HX70wx/1vusp8arTd+S7daB5cOM1in//a58xSvX32HhdT38JN3TPsCYPgU1HEENgYzqtE0WPhidXpLs3GuZzdO2lK0AZPrPWdfIsvk8ENpnOmrdSSpcptPdY7SiVFu+FD+QThZa0Cae6kEwv7Yr5HsK/oiSEXSvcqg4EDpaJ8awWc1pTSl7VxoidV27w/env8+2/+wPe/etf8N5f/YKTBw9RtUTqYH2ICpC56rvmpzHKFfP4GS4yf3XnRWTXGaw6uTcc7zw0K+qrZ4ZpRYPgYOyTcT4CGB9ZzOTc3HuFz/I5BvcH0UXifhqLPK6Wq1Nr6KzjK4VO5QX7IsVs0zQoU0gxs0KszI7QybpDebkVNQrx+Hevo9coslFp6JRaldzXzjnKshSFy1o0QlFpEtOECL+2CXHTKihkwaLqvKP1FqOET95QsDXd5JMP73D3gztcurLNxQu77GxvUpoR3oLCYQy0GFwrDCvWO0ot8am2NTSlp9RK+P2D5UGHIi7CM6QTC0jWycRYxz4wgaIouXDhPN/+9rf4o//wZ9Qnnhev3+LzO3cYFQUvvvgSv/d7/4C3336Hz+89YLFcAUH5xVG3Kxpby4RSnqIq0V6LBTNaSsM011qjCnqAsdvUJInZGJM8JHFBVKMxRTlO46iUJNJKuJfQKMY5ZNuWVV1TGIVrGwihQPOjE+aHx4xGYw4PD7HNEmtriU8OYSo2G3u5lw0WY5esssn6mEKPOlekDYpfXEYuuHcLrTt6PuIijIqRB+VRRlGWQQkPVkGhw+soa1I1+GBxNFoUeq3EM4APDD+REjKzWOTKTSfEJJxJwlEUOEWhRRkpiiIpu0VgiqnKMtSAqJJCa4xiPBNr5db2JrPZjLKoJCdhPGY8nVBWFdOJsBmNxxIfPxpVlKMitbMqi2SNF0VWSWKoc1jXslo0HB08YLGqWTSN5AzEvkjT3Au3nidU3s43qb4BIG0mBEDROnxjUasmzTsAiyaE1CaLUheWRggX8Qk0pjBK9KlxjpY8621aE3EOpeuyMcvjjuPY5nMwHh5QRoCSD0I7gQGlRG2LhhEVABmSjyAAJAAe3RkEfGYBTeApvI+zacvo/VR4cCopYAJGwmakvFgM8bQ2enrmrGpP03iwDucV1ivGfsRYe5Tx3Lj5Aj/5879kMtnEFBVjJGm5PToS2lvlA5WxzYBSUExDYFJuHJtMK1arJbPpBrEad/4qGotGUS+XTMcjXnn9RS5e2eXdd95n8dizs3me/acH3L79CXVTE7dwAdKBsrY0VFUh4ZXKo4wLyn0RwgILRlVFUZW4kKifiByC0a0oC8qqCDk8pgPoSWZGL2MMmc33gXxjD/uiHmS1+dzwxtmHAhvDUgIRRbd+Om8Y2edJkQgaR5yHpL3Ah/UQfnOB2c8F2Re0RrlNMDRhQpXirmkus6a3LEWGpzVIYIIUJXjv4IT3PriLcmNmk4qiGDPb3sb7FoIRszAlk9GYsqjYmE4YuYabN56ntY6mqUMumqdI+ldUyGz33l50FB8WoQcuXdzlzb+ZY9sl5WgSlDSd2tmNQZiLwWgin2cAP7klRJ7INX050EcefQ9LPjZton3vXyP3OMPCPfg7t7YT5Fp+Tvedwpuhp7O7rg+wut9dmgNyiOEnGEnpK6yRlFehojUzzEeCp1ehnaLwLdobVKFofZP0Oesdzhq81dhW5LRCY+OcDvJUanDKM6KsXWqfvJvWNaAkx0kXimJrxmu//ff52m/9Pf7j//Jv+Pivf4rZf8xIOVzwNLcBKMj6JgrpniE5jl1UzOVdez0jntTQf3lCvAr9GscrypChR244xsnIm56QjVGUH+r0dYquboqnK8wrwFcWfbrMOQkH8x7jYKOcSuj6mjatO74S0MiTR3PXSo62cuapIbIadlRu3crvmyfH5M+IltlI5xrBh3MuWbDjRIjekEjFC5lFLAjb9LsXK7cxitl0xng05k/++I9xtuW1114FPJubW0ExK/E4jk+OURiaesn2zhRPx3IltQzWJ/Qo1SFXa10PdA3tHnl/V5Vmtjnie9//DX7967d5+PABL714C+dqPvnoI7CWl19+hT/8Z/+Uh48ec/uTTzg8PmG5bAIrlUosRskT5FwQlF2sdrQUFCMp6hP7OlpLnXMQvEwxZ0QUO8u8qUHtk5Q170LSsuQdWC9tiSFkdd2E+/nOihoKN5VlyXK5FIuJ6yP7TPPsFFMVhV2G8sPPMuR3xAEYZR6XfB4bY9BePAZdrHHclKJ3pqu+WsT8mSDU4j1ywGCUoQy5A6Yw4ZxCcgIKgw/MF8YUVMFSN55MArWpWO7LYL2fTCdsbW4wnYwYjUdUZcl4PGEylUrTVVlSlobJZExZFcF2ESyw2uA8ySInSnq0vFtWrSSet21L07QsWwkhOl7OwahO0aALAYxgMvZrJGOQtSteBrG+qQTsZZY7cDbds8dW5yFaRdO8JChLvjMwRKueDSEYPlQId3FTjCAGARjE7zLl39PNn6Gl3flQPyat18hQ1yVux2ssNsm33E1+ev1nm0D3UfhbGKTyc7sp2xkBcqXBex/ogemfmykOwx0mQo2kCzGQw3jwDaiu71tnOVnME2XwTt2ybS3b3oFyjKm4fPEi87kUTrPOsXteY0wZvA6yptHRG316H4Buk5XwqYs8efKE2XQzeT9z5UYrg1bipTw+PmZzc5PtnS1+6+/+kMJJboK1Dmt/RNx+xVIboqcDvbQyEhcuc6QDxFEpB9EnbASSxH2pN4qDPu9/J68XwhtUiMpI/S3/olzFihzLn9Ef0/6Rf+TVWd/7np6oeu8xVE77bc/Hami9P0vHGN4331fI8oasJ8ikUAC1KHj3vdusVh5UwagylKMSi7DxGQLAMwWFkbwM5R1GWXZ3d1kuV8SdXetOX0gtVl0oXtc+H5cDoLhx4wVuf/IxX3v168lglDGCyr6Wp0jBYNyzGXAGeMi/O6vveu3LxyObXqcZpNYDgTh/nAshm2s8E9kLZvUY0t0iZDrVDPmj//5xnmsVV12QXVHu+FBAL1wX2+pCHRKLRBJ463AFvXw752LoYl8nyPssV9Kj51wpFXIzQbdKPIlG0zYN586d58mTx/z0pz9n99wlfvSP/hHPXbrEX/wv/xPL/T1G3koxOxX6QAm40kEHWgcGhuObz45kAMjOHx7D8Vt3z9Rvz/B0nHX//HqlcplzRtt8l+PpnKNeLhl9yWJ98BWARvQsxKTtOHFz9AVdqM+woc65RB03TJTKXU/rwEVu4fe+S0BOCWzZ+TmyjGFeAgD6zAGd5TjGuIoreTqd8vjJY37xi58zm0659fLLTKdTyrKibYVG9Ny5HY6OjoXxBYntLcqKmBcR27UegfKFk6w7V967bVuU9ly6vMvjR0/5gz/4h/z3//3/yCe37/C97/yA2x+9w4cfvMvewwfcuf0xk+mUajShXi1paqH5tG3LSbDU5rkD3vteqEZUlsuR9N3h4SHL5TIppM56vPVdfHumfFnbgJeiXTEfI8Z8O4Jr1nUMUkkhJ1hXM6WvrpcUhcZZydtQRcfFHRdGuEsW5tB9L8XNTFKEY56KKP86VKntxskUhsIUeNtPnI9zKG46McelLAthjClLTKEwI1Jo0XQqReOqakRVVhQhMXY6nTKbzRiNxO2vghdiMpkEr1zMQxGLqouJmUaHUAexbqNaFC5L6u9q2rSu5WB1gJ13YYXeExiKDKkysZXQggiQbbaNREU6KcaxJox3afOJ/aZCyE8O2kShDzAneDXtgEYvbmYSipZ9noGg2IYIOASfdBumIlgklZaq4CoqbbI5d1XHVdd2FUGpCt7P07G0YXICniEYjb9Hb23sr3y9Put41sbS28h7SlIfxPXPWf+87jFnKDR5M3r3kbEjKZzyncOxbBvmB5anJwu29g+4eGGbSxe22d6cMZ1MmM2mPN3bC/O6YjwVSua6ibH1sZCk6z0vvlbeNxcvXuSjj+7w4s1bPY92/u4R6LatZT6fU1Wy8Vm/ognWRm980sajQq+UChzzHt/k86zq6vUMAJuPY5TL7/S/XK4n+Nb97mN3ipISw2RyTd1HEBz7Y+3vpxUNl+cdqv530WqJUkGjP93PDO/rGcyYXHmN58vfZ+YaDu4RvXEeH/rdBdVVobSR4qxKY63mg9t3cISYeqVBGQozpigqNFL0ViHKvnNSW+jyc5cpyyKsfzcILVyfT5H3Q762b926xb/79/+e19/4VurDPJIjB/1f9TgLCKxrVydTIE6y0+Ofh0meBnfD+6V5qzl1Xm7sTGWgkn7W5YIM2zn8fSgThxf6sAZEpnUeNwAsaZ05PLax1Dovc0AAeesZn4ZgY2j08QHwawfWKbRVKQx7srHBjRdvcPuTe7S14+Xf+C7zxvPX//Z/pTh4iG8tJrU5hOlmfRzbmM+TZ8r6rJ35efl9coA4zHXOn7GuH4bjs+74ou/XtRtkBS7mi7Suv8zxlTwaeahMfLD3Ei40pLrNAUC8/llWvxwg5L/ngyf5GronPIZgJR+U2Ja8YnY8ejHXSlidPDCejPnzP/kzDg6e8v3vf5+yKNnY2OTHP/4LxuMRb7zxGmLYNSzmc6rRjLZ1lJWhdVLJ25j+pIhWslx4rJuIim4S5n3UNA0ox+bmlAsXtvGv3uSf/bN/wr/+1/9ffv7zX/C933iNf/S7f59f/erXvPnWrzk6WeC9eBmsE/58F8KO4oanVAgv8b43uaWw2xRdFayWK+aLefLUaC3hQYUq0xjHcCABa1UoKkfIJZBnaKVSkbB+IrIU9lGEvIE188EEthildGdhghTGIIXqOi9BWVapnzc2ZgEgihWtqiScSHsoTcFoPGI8GodaCAVFaZhOKzY2Z8ymM0wMnSglTGI8ktoIo/EIHWKZq6qiGld47UM7VW/ORgWrs7DLIcm5ku/hrKV2Da7JwsGkrHvf6kynLHWCVvWUkmjhjvH90ZYr8ZU6hTEka4iX8LLIEhO9BHKdQ9jOfKYsCRhQIURHa0IyX987phDyBRU2lb5xRKW9RdrTJkXNBctvHlOc1kweJyR3DSBHSXEuJVVPrRsoZh68E2ua8nET95nyF5Tr8JLRy4E6LYhVBCp6/aaSbwjDTSR+lu6TrfdTikdPUTitRKRr+l2S7h2ttwGJDSyh+b27a5IBRnXWX6y4zEXBUqALlvWK1XLOwdMn7O9tc/XyeZ67epWNjU3u3vmMajRmNJmitGwv9aqRopVoepmJPaW8O4wxbG9vc3BwQDR8nPaIy3vF8LLlckVdN5LoXITxUEMQ2CnHEcj2wISvu3ELT0igwKk09xN+iLLa+yS/4jqMSmAXBij/V6je2OVhgvn909wke4cvUHC9iuPcVwCVQmLXB+fHWjK9uacGoVvZM7WK9Yaj7Mguy6+KRoDwIlLPKQILkTFC0CJAQmmN0gUf3LnLk71jymoq0VyRWVB5vCvwSIibz2SbbS03b97EGMnzk3ypsL7XdNepPXewDquqYnt7hwcPHnDp0qW15+U/e/0/+Kwz9Hw1YDK8Lr88Gm7yf1/kKenrOusBQs94F2VZZpSRjyIhCYNn5pdFw1BmQKCb1y5zB3nnJew2rqOs/AEuhKy1kRjhdGLyOvka3zU3ZqfQZB0K3fqQo6U1jgZlxdB47bnncKrg44/u8osPPuLmN77LzacHfPJn/xY1P6FyUn3cStUdnKIXBrVOjuegMW9/XtgxP4ZjOgSJZ+0DQ90pf/4wGX3d/fPzh2sib3scz6ZuAmvfl5vbXxpotIGlJ99ccx7qvEHrOu+shTpEgRFQeC8eifzz6NFY94wIMNYtunWbeW4RE9o/z2Q8wWjDj3/850xnU974+hsopbl/7wHvvfc+3/3utxmPJzR1i3eK4+MFL5x/jsW8Qay+LUUpoTV5MqFSarDBq16bU3uy9xkO9nLZUJQFN1+8gbWf8M1vvcpkWvHv/t2/52/efJPP797h69/8Ji+8+BKLZc3e06ccHR+zXK1YLBbUq5rVapXCYyLlqvc+/R3b1zYtrm7QxjAbz3qgoCwrcGQVd7uxkAJ1YnWKrmvJExDAUFXCFS+MUiWjSphQUF6qIY/GvZyDyXTCaFziXAtKBU/AiCIkA4/HYzY2NtBaQPBsNgu5ByVVJUXVylKePxpVCfCMq4rxKORRKIM2RYo5dmoJhPj6TOB39TsiTW2kHl2wms+xNvCTB8tdnNMgCnBUbjtBLALaQbpXrCSqO/7Bbi5HxdmDp8A5lbxDubCJhdhQRbJmeheTkluclEPuCX7vJWtIJeYKMiXM4YIlMT+UJ9Rr6K3CtDYVwkueMyh161JJsUelkmcsEii03gmrV0Q12XNNIhHtllH6WyP0mqHGQD9RMiRrB1DWXUtmBfbpcaISdfG+p2QW/bDGoQAfbgapudGSN1AUYpLdUOHr+rpjKxtuLOvc8B0Izc7tKZTSD1opof+Mm7F3IbZfjAMaJXTdiAfAOo9SLT6weyk8jx894WBvj4Onh9hQ32U+nzNbLDCFMCQt5ovgdQuxzbG/E1jo959zjtFICuTVdd2jpk6yJiqtdGvHOcnjUq0BPaBS93ENydXOujQV5KcD1XIatoX+kmz6NC99kuc+U85Vf5mkOXx6TOmN2VmWxRykcOq8TrGLP3z3jNCmuBaHgFS2pADGhlbn3nkdcHbdh5zqp95+HEFeaJfqKLMxI2wL9x8+5t79BxydLEKKrebx/iG6nICOOWG58Uko5VUQnFqDc5bJZMT29s5apW1oJ3gWWIgRG9ZaXv3a1/jVm29z5cqVHuHMunU2vM86RX8oE4bHcF33zw05Ziqu65yt0LHO2LHu+d0/8Yp3oUV9oFHEqAB5NB2wiFgx8+pmCCOX+7039b6Tbdn7eaJ3Ory7c7RZHl2LRBJ6bzMD8WmF+FmyNzd6h19kTjmJknDeSgHlkGc5GY24dukC8+M59x4c8v5n97n1vR+xePqQe2//Gn18yFiH0N0ItgY6Zl9X7e8d+ffD+Tr8fR1AWXfuWdcOnxn/zs9fB4y+6EhjbC1t0zCqvlz41JcGGrFBefKvhCV1MdZ9as2z75MPRrxfXsU7LoBYbK9/TRfPPRyQIXgZekjyjbdrj8M2ktC6s7PL4eEhT5485vnnr3Hl8kVUYfjjP/4TLpy/wEsvvczly1cAz+HRCUoJZ4kxIR5eqR7ASAPpfca4M1AMM+Qt8rvvDu0Ow8nxiunU8PIrL3L79l1eVjd47tp/xc9++tf8zS9/yY//4q84WSzQWhIxy2qENpq69Xht0OWItl4FelbJL3DWURaGqhx3TzKFJC0rhYkJz1qq/SrE4hlZiGIo3Xg8ZmNzAxVcnbPpjMlUvm+ahkJrZpMRo2ok3oHJmPFoLEWVCk01qqSycqhpIOFJJUqbxDISx62sCoyOCrsAtMJotC6DQiPWdpmjQag5G6poCxCo2xj2VXdx/t7jlaVpJdE4hlFEZXxogE2KjAOFyeZhfK4XABqSa7vv4xwQg0CkWnXOCctTDCcYKinhOutarOvaE9ufgtCCNykK/Qg0vBKPW/4uyYIawqhAAESy/Hux2uRzUmoxOPA60aTG/nBEz44ESMjabpMyLffQtDbM/+S9kJ/Wu8BbLh2tMgu476lEXViW9HULtWg2MQG3C3tSKB89aZnhQw/XGAl8gTB0DGNwwyndnOC0opAf/b8FqEb5OfQO5654st+HQCPKPBfiqWPuyNDiF6/JZZFSEjKmXEh0teLN8tZ1BU+dpQ41MZSX/Clpn2W+nIfwwRLXtqyWS+7e/ZRPPrnNaFTwG9/+Dk3bUDcNo6alHFXUjVSAju+ZvVg2xVWv/UrB7u4uBwcHidZ7/aYYQiOV3C+BfNsfn363ilXd2zgfOsKA9Up/DubCOBKbrjrrPV3F3fh+fZWxD5Lz+58NOPI+On309jJFzwPhU+v660hlQCB1zZpHi/xQZzRr+OEArHgS2ImV7LU23P3sIb9+5yMeP3ki7dMGj0aZAm0KTAohVQE35f3iu3/Ko5Tl2vXrVFUhVOREeZaNTm+v76/Xdf3ovWdnZ4flcsnJyYnsec8ACuvumf9+lj7U9zL0Fb/hvh/3Cu87w1I8PwfTXYhRvo5U/3Ml8jxGC/SJSMCoTvZGkBC/62Ty2YAqzpr4tU7RHBDHJP7uC7J3c1hr0l5Qt8Io17YqMd7ZGDETyhHk77YufCj2g7UWwhgqH8I349xEDGKFgma5ZGsiYGM02uSTewc8PF7wzX/wBxzuH1Pf+Qi/OsEol1j8vkhZH+q5eV+t80Csu/6sPeWs6/Lzc4bXdfc7CySvcxZ0f4hH42D/gOpL5ml8aaDRq16YNcIUXdz3sDNjg4cAIB4xf6IrSreec3h4r7jAIhjpgMRpwZIWZfh/t+FmCh9S2Xc6nfHw/j1++KMfcuXiZbZ3t/no4495443XefnlW7RNw7vvvseD+/e5/+Ahv/G9H7GqG7QRXv/IUx4tp95FvmcR2FGwD4VS1+5c8vcPUfocR0fHTKcTXnjhGufObfPo4RN+5/f+Ad/97nf59LPP+ezzz9jb22f/4DAUM5NCT9G9L6wLDq0MlTFsbmwwHk/C2InyM5ttMBqP8V5YYmKI0ng8ZjweC4PRaMRsNqMopGLydDZjPK7AWKqR5CdE12sZ2JCwrVBAZrk6uZUlF5oRyHqM/Ms2j9VqSWKToi9w47+87oFoEd3ci8oZEKrmxs1XYb0mhfMLPAiX655yKOfrtKn1rd9daBCelJ/QE0xeApOs7wCE8w7tSRziAVuE720nkL1NdIIJuAaPi1YmvmBcNV0Ylera1V+nPr6w/GWDBctHgbaOpcSh0OIhoa9E2RiPTfdcm1UDjxH63neMNN1a5FQdmg4UdesYSGsrjVaaO9LmWPwJ55HQrsGGjsNngG74TE1MHo3KZNdfQ2AgG2B4vu8266E8jN3sAWW7cIVTikk0PCBVrAl9FDNnYv5OmInByiT1HeqmEa+kszhnsW0rxSMbqTh/cnzM4vAYF9aItVYKgIZcLLwVWtimCV7KwDJXGup6gcczGk+QuHrHcrWiaWomk4KdT3Z4/oUb1HUtgL5p0CgWyxWT6ZhSR2W4r4IPD2sdV69K4b4rV65k+0Y3r/tdq4PMbYnhNWnxhPHpWMAkjCuBjEBxTArxIckMvA+0n2H+xI/DO3hkncRQUReeuS70rhdqlD1GAMog3Db//lm2u541M/ZLvp7XABgVwuCCfOsBoBzXJP1+PQByznXX5kAm7N+S66txDqzX/PXPf8kHH9+jcSXoSuZ4KPxpigKUxmih+/V0NZj64smL2HUtGs/NF64GQNzP+0mt9OsU+jg1uvcSq7lO6/qFF17gs88+5cUXX0r9Kd/RAfL0GN+bi9GoFD2OcR767Gee75YbDqR9+UQh2R7TGohzI+yBss0KiBDlO/R/ZD7TJgMbhHpD0SPQgRCFCzVNYptIXrHYlx3Y6OtZHbjplk7/6MBQ7LuYUynvqxNxj/eeovQhckDo65u2xbathIHbzvPhvJME8kAQolVXvDS2BSQiQ9ixbApl11pJIVMNtW2ojGdpF1w6v4sua+Y13HtwwH5R8f3f+X1+/D/8v3DtkgJZy411vbHOAV7+Wd4/+dgOc5WzDu36LN8X4lJLgK0vQ+MpibY6TJV1oPdZ4Oas7ztdWpLpnWsZj/4TA418MSjVJdLWTYMaFH+KL3QW8Mjvl8fsx2vy/IyIyHKQ0sVvr0+WyZOUuwngJWE0UADaPLTCw6SaMK5KRmXFP/7H/3uauuHBg/tcf+Eav/sPfoePP/6Yt379Fh9/9DGFKbh04Spbu+c4PlkwGengjizQaJQrMGhKUwbFT0v4DEHJp2vbuvg5n214sq7Dd+Hc+XyJMYbJZMqLL23iWqkS+9rXb7FcLqnrmnrVMF8saOuaNlTnjfkXJlTLVkoLtelICuB5hC+5Go0wJm5ECLtSCGlS2vQEZvxpnSScixD1iWrTe+FcblarEO/cAcXY92KR7QOMuMB8EHi5shwPRwSesaWke8R+jFbwbE/A5ptpvhHIzOi+Se/X30jWM4V1G3ofUDiE+KJTjmOYkCOyBolElKJi0kfO6S7xOWtDtIgTBYnqhLUDVqHkEvStJgDG605hVt04eA/adwnWfRYRj829Cvm74RBS1iyeF/AqAp8uZCKn+9OqC4GKm3ECSj6CO58pA3FjEgARc1OSbFHxnYIFK23IHtW2KOeDItjF5gMorWl02CzCEClF4t4vkLne2o6mMM7taMUeGgwg0jTK+TacKwXWPD4UcIuyrwkhi/ViQbta0bYtq9VKasI0DYv5HG1bXKjzUtc1bdtKxWjvIYR+Nm0T6sjU1CtherO1hALV9Uoqudqc8cemd+gnz4ryEeuwlIXUcmgbj9FTdrbPifJSGIqqDFSZnnO729T1HOtq6nZF61oaJ+Qhy7Zl7hq2lKXUGu1Eg3EY+ouTXjsuXDjP++9/gOc1GctMcXD+dAiCyIEieDOC9yjMC+ujJbSjgozKCIXEbItiFQGktNHHSYGidU7yV/BB+/PBW9ApT0oF1rnoNenpEEPFoIt3zw0pcsQx6UK81vVR77uoGCZNND2JPtjIwGw4cd0z1n3WASAVkrOjDMru4eUzo+XZrdP85c9/xfufPETpEboMdRF0bm3v1gboVCE5LiRD9CIFD5aHndmYCxszvG+T9zQNV/auSZL5/ud4k8mZ/ELPtWvP8dOf/pSbN1/EJc+XR0Iqg0zOIHMsqRSkcUZB3bd4r7OC5/cfHs51YaW58irGzDgHJC9UG40x0dJvgo5meiFo8l33HKXi/FKJjj1XkIdtzWZHH1zlg5/uHedFBwI7HTGMATHvROZADH0t6PrEedEt2laIbZK3I3rKvezxzjqhAw77QYcxJeROq6ANWC/efS/1qJyzeA2NMmhVYBvY2NxgVDxmWsLRyZJiZ4ubf+c3+eh/+9+olhoamwpsxjWc77fDdIDc4zwEIXl/KW9Tw2MXKVQC9Vm3YYg0/QqlitT9KhuzVE8uH7k1wCNv17rf8za2tqW1jvsPPmdy9cqauXH6+EpAIwcF/aRveh2cn59vBr2YWfoKW75h55N73WDEBZyDlqHinocwDfNI8muk/gZsb2/hnOOtt97iYP8AZ2FzY8bv/t7fl81YG773/d+kbRxN03Ll2jW0NjRNw+ZmEaokdp6fmBwYayJEBhxBgi5tmv2FrNJnHZqNMDW8s9Zo5YWCdLkKXgqpqCmsRxtJifGeUFukS1I0RuOJ4SYyAdus8rG1lsVqIc9LSnhcOCGWnLxOgdwk1rggFP9LbR8q6iq+WhdKE7SBADpc2PA7Ad6bF+QqcM4GM5wvMUwlWlm6Brhs9x9apsnemWyMolLhs5+5spCv5FRALb6rza1qUVkFS6BQpWu7WMy8KJat7VVVju3zvrOY5hSBwUaf0RMOgVm27SZQoFJYn/SjS5tNGi9ySlKXtleP6oBg+j72TRB4WTt8BAfepc5x4Zk5AMj7PK4bDzRtm6zSkWI3Cez4bnG+BECnEPCSxszHcZU5GqlT+/HKPigMLsKykEfShYxGEJvLtvi5dZZ6VVM3dcp/Wi6WNIs5zXLBfDGnqRsWiwUnJyc4Zzk5PqapV2kttq14IwBa36Y+je8sRehi/LawwuRjrZVGe5XWbVOvcE6Axu7uLrsXzjOeTBiPx2xubhLZzsbjMdPJTMKjRiOmITwSJA9qPJpKlegwJYRe9ojbtz9gtaopgizQJnLky8o5mc9xfieANJlTyZSS1rhcEd9jMpmmIrDD+R9Yp0/tO7I3xb2kWxf4YL0Na3O5XITCpmHdhfj8qiwpTCheZwyutdRtC5F4QqlQOK4LiVRKSEo6eRfmziAUa6iw5YrI6c9d75x1x1lGvP5JYaV+BWvms4780uGe3j1Dpe3L4/nk7l3ufvo5pqgoyxGwns1tqODmbU5zBcnrwnueu3oZo5WwPyYNzHOK9jW1Pdc/FJwCq/E7x2hUURQFx8fHjKoxOWulgNHgy436S5QpiUkpNqczyMXr057juz49C2jEop+5fpQAg4qeMB2AhqIoIoGKOSXXsuZm49m1z1okTDIZu3p0gOEG2bt1N+nt5dG4R9wb6YxO1nZeEa275PLuJ+nmSsm7GlVQGKlc75xj5KQocdM0Qb5arG1pW03r2mS4dDbOSwkPsK6vPMf+0VqBUbG6mVBn0/LC89f57O7PmG5tsb885trr32b/9ucc/PotqsKDtWSQYC2YODWPh2DEOVA6zT/FegAQa0LFPtYh5CH3g3Zmg3x4VPe3j/NXZK53nk72np57Z8kJo5TkaNQNNpaV+ILjK+doDDtOOsCcCmHKwUi8tudFYH2HDmPt8utjzYzoTekpGoP2tVkH5N6QoQVSvCGywWqtuHTpEov5gqa2fO3VVzk5mWO0oSwrqtGIK9euYa1jY2ubZdsmRpR4z5jYOgRM3d9daMVpsCHCL75XVLbid7KAmqR04LuQjW6NqmQN8iDKv888BXKK9FGIm4/xj967TkGLSle4IIa4AVKAMLY5KKwxH6JHJxheMD4jfqboU8NFoBGVhJw2MaqZvdMjEAubex9odAWUuo2ljwR8tjxzq3Q+L/IG9Oafj8nUqeH0hWQQAj6zamS3S4UCc8W706HC3wEdad19lb1fwgDhl0RTjMfmQl8N19hgh8i7xdveebk1qE9j2YUACh9IPq86IRuVgaElToCMI+a7u2zORY9dmjdpI5awFxvmG9DlnXjS/I+bb/56TSPsGG3TslgsaJsGgjywbUu7XEoxSGtpmpamqWlC2JFtVsFd31LXjWxmjYQmxTye2E5Z+3HTs2Jtsy4lmFrbgnUY73rXGCNyrAiFEAFhTzMapxTVqMKZMcW4xGipAD0ajVKtmXI0oRqNEiNglI3GGJSHxWLBwf5Tbn/4IQdP9/DWcfXaVb71mz9ktrUpeVZGCi+ZpJjEgpHCNJc2Rw+lLsWqr6Vw5aiqmEwnfPD+eywWK8ZK6ldE6spI1HByMse2FlVW5OuG3lbZn5/eezY2ZhweHrKzs0N+nC1fw/pJFgoV5pXm+PCIvUePOTk+ZrlcsljMA1vViuViiW2aVFhzOpuxs7Mjxfy0oXaws7PN9evXGE/HYU4qJETPJqtxp2yoAEazlbNG2V8HJHLl94tAwd8GQHwpgPKFNwFH/z7dfb1UZkZTt453P/iIcjRG6xIXiESGicjrfvbaGO+LhE5ppbh85TJNW9OFJcf50N/jz3pvvO31dfdqDt+2XLt2jdu3b/PKy6+GcQ5AJsi0aNQRgwuBzahT3H1K2va9+ZmD4fhafrCPxcO5jnh86KFWqKQol2WBNhLSEtfwkNp32D/xswTuIh14AAvpZxoBn+1R3agMRyt+n4xw8ia9dxADcGQuPA06yd55eJ0OBWvLkL9rnU31uupW0VpHi6XNSEV81t85QJaxEL1Le4XxFu0bKi11st54/RX+5u3bbF66yKFtefXv/B5/ee8h/ul9jHM9XSI/8rU7HDdC96mwj/Z1k87gNgQoZz3ji9Zv/m3SKHzoB2IfnK5zB6xdHziPNorHDx7y/JXLz3x2PL4y0IgvlyueUflXqh/qlC+aPLwpV6RtKP6WV1Q9NTD0J1yuNOdty8FDBD3x/j0lqKf4eEajEfsHB4yqMTdu3ODC+YsYLQjaWymzPpttYJ3nynPXOJkvWCyXWOsYjUZJ0ZNwI6FazducAygdlEePSqxPebt8pNlE6iNAZO7xtMFaml/jrCgucbp7T1qoccOLnorUP8HS26NCzWlPFaQQmwgUvMe4mFAmeQ0i3LPQHidCOoPJcfC638ORJ9n6ADR6wje+T7CPxOkQKY7F3dpnUPKQ3MJ9oR3mbkDybqBU956X/RnpH10QVC7kSeTXRUGhA3WeKLFRQMfnZfeP/eZko4p9LePgu5MIbtHMIwcqVfyNil9UwiGEBeXrLjtXrGj9NRMVQbm4G1OZnXF9QOsidW3INwn3jcp/nD8x5lbiZiXEIK7Vbr2BonMPp74eGAu898maHZX1er6kresUQtSTKa1lfnzMcrnCWst8MWe5WHB4eMhquaJerahXdZpT8Tli5e88JD4DiNAGi2GYo4pkgYpG1FxhMsZQViVlqLNCYTBGmNRMESpNj0pGkQTBGMbjEWVZUY5K+RcKNJaFUEiXVQkKTAAScQxitWwVGHqijHEhP8ZZUQOXiwUnR4d45fnVzw/Eo4pn++JFimpMWZUyNqIZiFzynewibOYmsE/paoRRQr5QFBKWsbm5hUfjrKJtnPwLZAtGa5TWrFY1q1WNG1UUoSKzJ/dod/Myn6NXrlzlyZMn7Ozs9MGE78vVfN64EBbmQiFQjeLTu5/x87/6Gfc+vcO777zDwcEBi8UiWUWVLMA0T5NSozVeKcrxjK+9+jW+95vf44c/+gHbuzuo4NXqxsOE0A9RELUxmaJ29nEWQFj3eV8Z65+z7rMvc9919/gSjc7Ee1/hEW+Tw2vDp/cesli1WF2AlzDcofdiqFAN6eljG7XWBLI6NmYzNjZm4C3WukSTmrcnXteJ7ExpSvJzTV8pmVfb2zu8++573HrpZazNqtMTw1zBhj0veUsH81M+D4YFuu+gI52QHKE+KIkyVgdTdM9bmeVexPxWU0SWrhwYdH3XB+Xu1OfJGKsywJP21tCHGfDovPryeW7U6n0Xrwt9ka8rAxjdhXKleRGsUGfVadFahbyxItzbMCoLrHOsmpq6aahXDa21tI2lbQNLJH09FEj6oVcGE8IUCxRtXVMUBRcv7nDuwYyjxYLJxjZ+x3D929/m9h//Gyn8a9cr/M9cgz56alRgziNOCAnvz+6R7y1DQ31fjx0aXPtAJ30W2+a9sHAFnX0oO4bX5s/USuPbhv0ne2w8fnL2e2bHV0oGHwqk1EAvA1aWJUVR9DpkKBjjMUSx+X3PRILyKfnCy4FEzlyVC6y2bVMNhuFkiNa/P/2TP+Xv/72/z3d+49tU5YjPPr3Hgwf3GRWaD977AIeidVDbltY5LBLKUYZCfdHSGxcBnI7Xi8BKkoPXWeTi+5HOjexF1iM1F1KeikvKo/K5WOliUiNijRWRU2VkgrCJfRjDVqKwC2Oaci2SMIrJ1J3DME1QBCQp+iEE8V2SAA2HbMzxc7EodF6OTBjnlo3Qrzoo7509pVtkHQ1tjnOCtTH2t/KpbMLw6OYeKKdCvrdKyfQ5hkrD5T112wblPPZJ6Bd1WnlK/8L1Ucnr3j2OkXzsfATn2fyIgFN1eQcxFCTv+56Q8U7cw1oS5qTAnxRUVBnzVlw3WusAZLsxjVXmIxCIsf4AtbU0TY1znrZe0dRLVqulrE3nhObU2ZCvIRXivfOYwmBMEaz7klNwfHzCwcEBx8fHYqmqa5qTOc2yTh6C5L0KLmgJfxFPVgxNSH3tcuYvCZVBK3whdWCkAGOBMUX6vRqVFCFkpigKRuNxqL4+opxME81yURSURSE1WooCXZgeJWvyhBmNMkbytILcSRNKx1XUGQogeBlQkuejxBpsfEei4QceREWQDUi2kR6NcUpz49YrvPfeB9TzOa1VbGzuYn1WdbcnQeT/UX6YoiQW4GzxRFe/5NNotCkoioq29ZgW6lUb2N2inDfUy5rFYoWdTSV8XfWX31AZip/t7u7y1ltvcevWrf7a6QHC7nyhngzANsT6Hx0c82/+p3/LO2+9zaeffMTJyXEKT4trSPeMIaq31mSDPmD/yWPufXaXul7w7e99h3Pnd+U9lA3zV7ZT21qUMrRt01cksuOreBHWKTDrrl+XE/lVnze8/pnXDZSSuJdHZcYpz6f3HuBNRe4lW+e5GFquT30PQVGVsbp6VdgfhfBAk3FNkO+t6wyScu+zAZfkizjxEmjN4dERs+kGTSPjGXNEHQSigE4xz0lBYujucI5Ku2NoJ5CICXJgInPcKJH7EVDE/jHGiIczGCBy5TQvijs03oTuSbIw9lGkq/fp3A6QRLnS660163WdUhoNiOm8sN8pBUZBaYyEYqp+uLvSQuW7zvCsw9qMS1QpCXcyRlOUhlFT0pQNTWNZLRtq3VA3LU0r4a/R6NrpiAqrdNibutBgfItXnjfeuMV//POfMR5V7M2PuPLaqzx47x3qu3fQrE7Ns3X90eun7PzYhg4Q96Mj8vUedfAcHHbP6YD70DvRYySkAxxxQM4yUKzXv2WrKrzCt5aN2cap79cdXxpoxIbkynld14DkCAxfaBjilCsw+Uud9TLPEqh5W+Jz4mf5+W3bdmEEA+EV2xQH77d/+z/j8OCIuq7ZmM149OgRZVFy6eJ5prMpJ8sVrYd2Psc1NU75pDCI8iWWz6IoktI4HPQYw03GDd3VK4C+0tx5IbxHnu27UKlOpqoB0ECsEiF/wma5ELny7ZxPjEFdrGAXvhSZWDqQBFHU+FgNOsSGR4QsdvDBxprASw6B5LDRsxDoJSNI6F+eKeQqtiFsWF53ZCcRTCSFvFO2BZjGe4eSO953lUl7fRfmpJivU2547JfY0zlriCfQM/uoKkbhJ/0zZCfKBcVQaAwBQhsS7JXqwtNy0JYsUb17k86R9SUbkfExJ6S/ATV1jW3qxNyhkBwAayXXYLVYpiTkuq5TsrK3lma1TF6HWEOhrmuWiznONrQxxIhOAc7gZBqnNAfpQiTzitDpXcKm2sXXyvoux6NUWFGqrHeGBbG8i4KwXC359O6nHB0d4bzj8sUrfO/73+Pc7i5bW1uYABpMUbCxucXGxgbz+Zyjo6OkyGpT0EZK1PAe0bjg8HiTCXkf8qrCzzCQYTPtkwoIZhCFNy+mppXpqHi1RiNrUBuDyzaNeD4q1MjQUJqKqrZsecP151/k9ocfYIqRzKMQ3x3QTSeLfZTJIkdsK3Op8Q2NbSm0ptCKUVHQqoaNyZRzu+f59JPPcc4n74VthQGqMAajC06OT2h3ttChf1ySCesTT7WGzc1NCXlr29453kHuAU2yCk/bNhLqVrccPT3mL3/yV9z+8Db3P7vPyWJBG+SnKiS3jajU6c6QkOf7KKAqRL4/3XvEhx+8y40Xr7O1PeXCxQs0tuXg4CjkzdVMp1NG1SQB3C9z6DMASVw38RgqBUOF4m9zPEtZPOs8eeBpUKOCMUah2D8+ZP/wGFQIC4xhg3SyZ7hn53tO9mSgMyo6LLvndoTgwNVYW5DCULP7wvo+6e69HmgI8YCs9cuXL3Pv88+5fv2FzoCFCkA+yLNsD8R1gCG9R1TcEyCRHkjKZg40Mp1BAU5JpEQeEhl/z4211oYaOJGkQJleP3S/q2jL6gMNHTzUEYDQhXfFtnRohr5lPH3pOlkiF3aU8qEdbdsmOVNqhS8s1hZJ4Y4hiLGeYw98JF0xeqU6gAVZXmxVhrpdjqqsaJqWxapmWbfJEx7liRgmFMqagGAc2goI8l7jihpdaL7z6k1++otf8o3vf58773/A6z/6z/jZw/8RY+vT6+ILDkVn1NBKRf6XtfM0N5jH+T8kUMqPIfuq9z7TDzvKfjEkO7zupx6kNub7wbD93mFQbM422Nr4Tww02qYNSYEQJ2tk28hDlPJGphd9hvDKF0v3skM01t+QY4hAXKjW2l7V6Px5XVVr2VCjshs9McYUXHvuGsrDnY8/4e2338Lokl/98le8/PLLnD+3g3Were1tdFGy2ba89/77TGYbrBar9K7OOUyoVh0HdWjpgcDOlBcByjwGEWik98ti0F0I1+isA1FNY1Bst7NGxLNyxVP6JIQ7hfkeE0ajIBW6wCBUAwDpxigkFWvQMZfAZ8pOliyWj2fsk/i7h7RRdQKcYHlOp3ZxwPmkD++mQhhPPubDhKwUsx8XkwcMp5g84vmtl/kWr4vYJtWOCG/gB5KhpwTlAkKRqGhj+yCERXnE905/HcRnKLqY71j/w4fcAuccTduEhHHb3TtsIC7LE2itZbmY41crmtWK+UJC/+qmpqlrCSuqheXIeQfOYxuLa6WmiHUNTZt54Vxsv5eEuF4oow/ASPorUiarwDKjlArrRDwBRVlSlSXaaIpCQEI1GlGEyu1VVTGZTCjLEgodePYLKcAY8geKUrwIOqw9CS/smK48Hq81TdPyZG+PcmuTn/3VX6K8Zrwx4+atW+zs7gQaSCWFHosSbSqKskS3DqcXYtBwNiQViuKZQGl4d600GBPko0ry0fsIwxWYTLGM8iMzPojxQ+ahx6VQJo+ETyolrn7rM7pw318nbWvx2iBOrgJMyTe+8z0uP/c8V69cYbGsMYVJTC4QQ3803nebepTrTd2gCyM1cZVYWseFYWdzhikUL710g9sffcRiWbOYr1guxYponaUsFabQHJ8cCx34uArzJKNHzRWxsO5sCEFUSrFYLCSUNSpHNgBqD/tP9zk6OsK2DabQYKTvxuWIjY0Rz79wlcsXzvPJx7f52S//midPHtNkTHxFUVCVFVXwZIk3a8RkMqGqKqrCcPXSeS5duczlq1f5O3//71JNRjx68oSd7V2c01TlBqvlisePbvPxR3f4xje+EcX5miNu4t0nsk+p7PxOduYhJM6GfKQUgpvflb6sHsSld4fP/t//LimV8UzfnRuVvPS0wf3jtQK8DZ/fe0BrLT5GQ/jglvMdcQveh5oGqt9XvjPaxA9ciATYmFWMRyPqeoVyEg4ZSTRERq7XJdLd4n6bYbvOohyeZSX/cmNji7fuvM2ly1cBCS204ZbJwBP7yQs9bNwvUrvivpM9R+o6+bTXdQYi0tzQWgcq2qg8wpBBKso3gne4k0QdI1N6btpk+6FaUcdyCGuT65SGcC8fdKezD5W9m4RLhh1MaUzwoCulKEJOqxiyPDUebTsm0wQqrE990IGQ8I9g7NaxEGumYGt5ZiTDKQpHZSuKqqRYtaxWhTClrghUuU7kubdgRLmx3tHg8VqhV44SuHhukyvnt/jgnTe5cP4KZbnJuRsvcvTeEdoKlboNdXO0V6dAeGR/kn6yab5bZwMlbwBt2p/q51wmpnUdjTQqzp8gP8IHSd9SgM49ieE54af3gWY4M4gO8Uvu/wAJbXPOMRmPuHju3DNmRXd8BY+GuMCds+iwQhUdRV30DuSItbOodsrzEITkXoXh63UCObO09wBJt5nnCmP+7Dg5xdIQus15QhYXk9GEcVGCh6+/8Tr7+/ucv7TLt7/zDQDMyHCyWvDo6Z7EgjpQrcUul5gsfj4ulOjRsN6hvesjSOcC0AhxvTZyDkUrgk4x9tbGHA05nG+7JHO5qJucacL1NxD5o9/XPv0uynoMjxJLaFTWPcbHTUOHegLBy6HAIf1p6QQf6U1iC8LkdXGD6ZQGAsjr2uiIHOZR6ekdSU537EG58E4CVXUgQAd6S61Nx3se2tu6tlv0dALeK6i9T0BDebmPDtYaSxeW42PIUTbX+m32Xd9meTXRS9W2LbZucLWAhVW9CgltLU1d49oWVwuhwXIZvAatpW5qbFtjrdCgeh8YUKwjFSWMAKG1GaOYRTUNzrU03mIJVjCJy8IZjQ+gqFAF2kHh5c2bKnPda0VZFSmcyBhNVY0Yj0ch7KiU/IOqxBdCgxqLLxotOQyFMcFlLiQM6XsjibfLuslkgg/sQw2rVRPmh4ALHyxTAKYyiR89B/LRyuVNSYvhxBZcu6F5/9fvYZdzQDOeboAqGE0mjKpRCo+YLxqao7nkO6gStCRcurZFKfEYdvItgARdALqnMCpi0l1YM0rRxo3Ii6fDeYU2whnvrELrIhRxlIrdWgmvvFLROBHyrLxQ2EZF1Tkb+kThbCHhnk1NYx1NMWbr+g1WhWHv8ATvfTLQeOfkd61RWkK6jOmsY9oYnNMYX6ANFNpSaM9zVy/w/e9+C6M8r71yk//uv/vX7B/XzOcNq8ZR25aNSmNWnkWz4rheYsYl0bptVEYsAb09wjuZi1vb2+w9fcrFixc745Lz4BS3P/yEX/38V3zj629w84XrbG/NqKYGU5pE1PHo8ef8o3/5T7FNy/6TA/afPKVpJTcjesOlMFsURyIbR6ORtMm2eN+wXDUcHc351c/f5OhkycPHj3n48ClKT2htIzlcytHYhq3tC1y//hzet0nmdfshKcY/ExeiDKDwdPJC5lZ+oiiJrLHUR6/6KfkZH9D/ICm3fW9KX7mPNNg5YJZ2RZrg2LYAGpUiEG/yeO8p2iisbyVMUYeCoi5adeX6Dmx2ilPelPgYeWbLhd1dXGBz04BzTTKY5ZZ0UAiFqYdMzsdHOcWpvST0DAbNsrYU1Yz5ynI8X2GKAge0IXQ0GfhCiLPyFq2sgBEHziss9ABfp8N0YVVRgZSmq6Q8l6WmNPQKkMYOcs7RkuXfuWgoDB6EVChPjE4+zAHnZE+L4KY7HBZPje2gZKB2c94LRXjYiHOrefRq6DTFPN4YcMLyZIwORkmhNNdGo8sC703ScdoQHdCGiuUqRHULcBVPrwmJ7uAplMUYh8+My5rA+BmpyFXnzTbGSw5LVVGMCsxyiS4Uy+WSpnHQyD6oEPDplBjWfaExCrRuWeqSl197jT/5kz+n3ahZec/z3/sWv7j7HuPDE4x3NMZhtWZsNdgufC0bfPGso4N32+GdeOjiWose3jQXIIW2icZNT24Q5IYOhhu8IkKaaCT1oUN91HhU9Cr6kJdm0L5jWMx1oohV0pxQCmsUrYdmsUDVNV/m+NJAYxj/mRRs+uEgwyMugjwZOh6d26/zhqw7xELX9tqQPy+PXYuby9AdG8MB8nY456jKktVqhVZC73jp0iVBa5OJoHNTMJtNBJmbgoP9w0A/ahOIEeEhQsRaF9pKsC7F+gGyyIWuThQClwq+AAi3fRQ+efK293Kd9X1rff4z9tPpfuwzcuTgL107AH6CbsOGr1WwwMQJ2iWxAan+Qd7XueIdE2yVis8JC2LQ9lzRyA/rfYqBzYVy3Kc7od1BB1kcKillkf4zWQJUthDpQAzIFhleErzHOk8TNrW6WaXCZzGJNP4eXbLxXyyOZpsGggcihgPF89u6pl0FV26yrlhsa1MxNa1CPgOdAtRiJXQvVDxNYx/eQkBvVzMjWn/KcYnWJVXoC9u2zA+OsHVDqz27589z9frzzGYbTEZjtmabTCZT1EhThJAkAe+SiNe5s8XCGi0kEUdaNajRoBW2FQrR6XTKbDrrcqfCPcuqom5tqP0gSnM5GkuO1KLBI7UdBAyAKSucdajAyFSYAm2k4nWs7dJaYQdpnacajdjZPcelK1f57JPbWGVYNg6rGhaNBY5jJ4IuU5K714YmsmN5UKpIOp0kqeYECX3Kv44Kd0AMkNYKeBe8GHRw3QbWKq2cJO25ftKe99A4QAsI0EqSZfHivWlsTVWNaJ1GmTFlyF0oi4JpYSTHxBTBWNAldysl4EWFhFOCQmN0IV4kHJWB6bhgOhphgI3JjN/6rR8ymW7y//h//rcsFwtWy2UypozHE5bLBfPFgtlkIiAmgORohOmULegU4Zbz5y9w//59Ll68lGRZ2zZoVfDHf/qn/Oynf81P/vzPmU0qRqOSrZ1znLtwge3tbcqi4KOPP+azO3vgoaAQwF6vqGtZuwCLxZy2FWYxWds21TQxWlZSXbesmhaUgLFVXfP40ROqcSU1DMqC0WTEaFxy/doVrl65JLqzgo4W1Kf1ke+WKjMU9b/NAIkH7ztFJK77JCvdkNWx9xf9owMaak0IVNcOly611mVtceQ0skkxVLLfHB0fsVgsiMZCkgLdWVfXGWiilba3r4WWKCQ5entri8VygXeNKFhO9uBePkZ6p8x6H+/rAa1SWHFPyQ/P06gUtjkajXi6v8/W1haNc4kgAcKwxrBP1/WpJzAABuzn/Wk9aZ3RNBpHjZEaMx4lwF+plJcoHofIetbf/0TfknCgCKIi6Uz09iiv1wANiR6osQw2RgFenhR5kYy3sQ9kZNKO2rp8fklUgVM+i4KwxHoZ0YAcHya/x6KBXZ9Y23Zef+1xVlirkpdD+fA3PQNzCq9UirLUaD2iLAxVWVAWhuVyyZIVrg3EIHg8CqeUrNWwZ9XUjMdTXnvtVd597wMuXbrK7OI5LnztFk9+8SbTWjNyisaHNZKKAmY6a9bX3rtsvT/7iN5slc3R4djl4cX9UEuysT79PAUpvLPv2STdq2dk8DKHtFIcHBzQ/KcGGsOchhguFV05QwUzb/iwU+ILxAkxXHBJAGYLr4fu1oCV+Oy8s3vhNF6shPn1Wos1VmUhFpEqTWKxDXtPn6L0gQgPB8tljTLiCoyJlHFQAIlJR4SAMGSoNMguxCs639WdiJYG70Nyme/AWbSUSjVon5TIZHk71eedcB0eeR/n/ZJ1ZDxRhFqUjr67vmOlyCZyskzJX5H9QKkOMGWN6IGe3mYaC+3EyZx9I8pyF7OO94HVSPIOksDyPvHhe+dTeERTCx1p0zSSBFpLJeOmbpLFXzwALcoLEGhCjLm1jrZpJMSoXgroiPSn1iYh2YZn5jk3PloMknu7C9lShLkf5qM2JlVu11pTlBqlq+QlG41GITnR4AyUk1HIR6hS+EcREpGLLLFZlMdQGdaYwBTlsE3LydMDPnznXd57623wcO7CRb73wx9QjEdoU2ICF3sy0PcssGkXwuE792+cfwoMAYhqSWouy5LlckU1mWCqMaqocEGBxoFbLWmPFixWKxaLhYRLoTg6WYb5J/d2rcU3UhMihk/ZxlG3Dd7XHT1zPi+VECoYXUA54satr/F0/4jdi1dZOUW9bIN3NoYPOTwNUVGKMk9+V2DJ5p3t7Lq+xWdFH1FZiAii0KdwRFRQtL3UWG9risKkDVTWabDK6qz6tHMSNkDwNBUVBNkctTJTFKAdSosiaZQO/xRVUVAWPo2JMZK8PpmMmIxHGGRTl/C1cQoH9Xi8gUIbZtMx25sbTKoKPDS1w+P42muvcv35a9z57B6L+QmulZCO0WiMMSXz+YJms0WpMoxPZ8U7bbCAtrVsbW3z3nvvB2UtyNEANm7fvs2Dhw8xSjEuNdvbm7z93kdobZhMJoDi+PiIv/jJX4kCF5Us51MeUhyHSGEavYRR3khNEiNzyDkBD1phvaWpawqjMIUR1rCqZHtnm0cP70v4YpgD3aupZHTp7YpR5vmYq9ObQt1p7rRs/9sc6yz5686KTorenhq2hmFDkyKkHI/3nkhIVCrOGYNB4zv1rba9Zw7Okd+lf0ZVhVKKum5wVjy7WpXBQdaB1UjQEsN6474RBZnH9+oH9Z4LwaouJBZbm9s8ebxHVY1RWoms913su7OBmtsbvNNSHFI5PBarghfc+US0NwQb8chzzoqiCB4Ag/gSxCLdZlEOWpvMe9vtgzaGH0egkUCX7yIMfN/DAwQvTz4v42/Bq4p4JmwrXggbCubhlFjmM2OBJKgrtBHDVNyjupxZC7iwH0ajtYqtRmtHyqsMemAMlXLBcKbamNMRc1eklkgk0JAQqy582kSDW2F6YMMozXLZJr3Pe7mv8IVYrNJo7XBty/Vrz/Hpp59yePiUeQXP/cY3ePjhx/iDEyrbohS0RvLjjOt00uEhOXKOyNR41tF5d09HA/Xv1/fk5IcEm512BOTnDvXwoVG691zv8SEnaGjcOOv4Sh6NPOk0b1hMhsqV3hwM5J2Qv0T8bojC5KsONDRNk0DOsHPyxJh8UHMkqaPLdgBaRKETWjQyRdVDsAjAqq1Babz1NK3FWuGvTzGyPeU9KOMtoMR9nL9bLN7lvOsNULS+yAYn755bfVzY3KIiHudL158ZEBj087pDNgt/ijdbNtYQGrTmPuJRUAmJ+wBKSD9BcEXnpYleGwlF6pLjgFRNWuILuxwEZ6UNbdviGwkxsm3LalXTtFIt+ej4mHa5oq2b4AJtUrKys5Y6FfNpeyFE3jt8SFD2rnNfewQUNSHmFxUs1YHFSPYolRQ5neYixNoWxoiVWKtus9Cl/ItgoQh5PGVVMRpVgQq1TCFHRSHhRzrmHQSLsg4sIzFeW6zXEdS4OIwxIlBeITGgSahJ6yXAoUSsGJPJBraF27fv0jYryqqimkzwRQFFgdcFFkVh+owxEnJShA0iBquF+i1keQvB8iGbn8Vb0MWIZeOY13P2jxaisEWqYyfxsiiN1iWrVogenA1UhwF4k+SDuKhBvF650SFtqijwBussjWul1kXdcP7KNX77H17GTEfsHy2zadwxkUTFPiyaAA6TqpSuieujLAvEsNklbsaxIlg2S2NQhUq0ry6wRxXGQ9xwtcLonMAi0MRmhhmQjXNkDMpLCFRVCTAdjUZUVYkpETrdsmRUVmxMZlRlyXhkcIWs+aKICkCY2M6jU/5DFq6KKN+tr8N3iuXJnJPDY/BKgLxtmEw3uHT5Am+/9x7zk3nI9fGoUjzCq+WKppGQJU0MuOnkVKc0df1qTBHqXTRJzrkgc+J8X9UrppMNXnv9NX7xq1/y+PEjDo/kneaLBVVZ4ZzFYBLDTgzPipuwdHdm0JEeQXkFLnhFESDgtUqKVmkKqBVqqVFGc3RyxO/+/u/iCDk1Yf7EcMt4RIeAiHadasmgVPIERvCx/vDk36js/+nbuAR6+RQJ4yVrabpmAD58dsf8d7lPl+OW7uFlSe4fHYpnEYXB4JUo/akvBkYv+cOnsVcpjCRrs/NMJ5NQ78aivJQ89W3d0yny9/Co5MmOYC5KrKiOr0sY19lHo9GYu3c/ZWdnF1MWWA2RChkbQhitlbv6gta1gMP6Bqdcyr9SdMQ4OXDLDRlVVaU9Qhst8l8F+e2aTrYqha9tygHJDXSRqTJnjYzf+SyE3Qd9pfMigVcmyWTbWlarpZA7zOcsT06YL+aslitW9Sqd0zYt3vaNzZ2OpVJ4fQQbZVkyHo+ZTEZMp2M2NjaYTCZMp9NgHBAjglKy74lXWWPD2mm1AAEdPK7aaLRzGKfRVsBZ4XzoP53keJHtYaXRmNEIE4xgxqzQ2rNcOsDhvUTGNK3MF43BmpaqKHjj9Vf58x//hMnuJtXuLudfeZnDn7+JqVuM1rRlMBi2pyu6x99jXkRv+q8BJbnBPOqb69bOKc9gprvFiu9pXbAeWORpAENyil5EUpBT08kkEEJ98fGVQ6eioI8x2853gnrYoHUIadgpZynD+ecpcdr3J3OeQJt7KWKICnT8w4XRPUU8t1CiZHG2wToggyOKQJtoOGM/SAEq2YC6DTEK72RZbyzORWVV7tu2khzpgnstbnhRGY95JLFNoqSF/lBkHMu516Cj8kwbT97PcfNc08/JZZ6eEbxTrovXQ4kbOd3L92NKY55KDPVRVvoxFjdrY6jQakmzmgtYCOFGUYi1tkkCsG0b5vMFi8WcxWKJai2+tSnvIIYl2bbFty49Nwe5cQxQXd2NwhipWKyVsMvEPgiKswIpxOYaHJL8P55MGI1HjEN15CrUP4g5CVFoFkUpFs2QzCyVk0NCmta4MsS8hzlFXAsqKqtxTst8NEajTCGu/ZAU3LYtLgirUmm8MjgXkrcxSQOIgDT3BjrvqQqDQQuXeBi7ZXvC1vkLTLa2OTnaR5Ul1XiCMxplxJugkMTOfN2IhtIl4sW5YH202kVF3yWggVIEVuSwOcrcltAD8VLI2MWxid6iDpDnfZVv1s51VXqdc8mLIt6sFq2qEJ5WS66T9XinUKqARZuoaCUO2hBrVMRq0lpLrklkEVNAGbyZ1lqqYGXVWoUB6CyT3gvrkjYSB1uZyH+vg8epoKpKRmOFQkIKylJCyFLNAZDieKOKooihoYbJeMykCHz0hdwzWZCVBy8KT9sKKYDWGmyDtw1tCPVqVj4ppEnOWXoJtT6YsB0eryRPTWwzWoyjMSQUS+sVFy6eZ7k6YbUQOuK2tvgxFEVFs1ywWCzFS6AIGWD9TXK4VxTGUJUjjo/mUh3YO6yS+XE+sD7hHXtPn3Ln0zvUzQl1c5xZ46ToolIarx0tYF2b5mr3PHeqHdEbFeeuV2CKElOW8nspcftKSYx5QcELL93i69/+LnUr8zLKZOddUGB92jeT+M3EcyQaCE/MLNJh2XFalg+PZEDJ5GJ3f5XGfOgNH24T/rQOHu4Bkr+R7TPh2kVdSzFYRTDwReKDkGMwqNwdD9mPh17vcKmzaAXjUUXdrIKRQwxA2qlOpsrZmZwI8kmRPFRJV/GnjXPd83JgpkLBTgEPPuSt6OAhbFuh7G7aFc7XSB0OS+ssbci3EaCxnt0nz3nIFbx4XWu9gDone34MYXJWxisCiu6ajmAmD+f1YQ5aXBouH/bztm1Z1Q2L+Yrj4+NEKx5rGPm2hYwWNldM8RI4lSdud+1wKCcGzMhAGK9vGqlV4ZxLhpLxeMzW1ha7u1ucO7fLbGODqpIioZ4Yri7siFE+xtwykbMKYyzWGCEdiaFVWqOCcSEaOAut0GUZ6lkoTKHQBpYLoWi31oNXOOXwJoThqhUXzp/juecuc+fBA7zWvPCtb/Kz9z5g3DqKkOQ/dFL0yJKSPpV7Ovsy7yy9OJ836wzK69Z7Pr+H3+efx7l3lg6fzrdQmSKEDH6xLIKvWLAvbuxxQnXIuH9evliGyChZ6AfnDY+cziy+bEf3OswB8Kld8Rn5/aNCEK2E8fvoIYkF8VxYiN55qqoCpUICuKWLjdXCu5iUezmslWrHsUKoR9G0kf5WKg63bYjjVoGSN3OrqrDpphocxHjF3HJKNjlVjzYuvqdWKiQpRzRLr0/y843u6OGstTTBYui9x+CpV6uUn2DbluOTY57uPeXo4JDFcsH21jYXLlxgVYtwWi6W1M2K5XLBYrFIBbFWq5q2WeGaVaJJjfHn0YIX25jnpuRAEDqKPwBdaIoqCBJjemEgxhh01eUURHYjrZRY7UdlsOCIkF3VNSfHx/zNr/6G9kSKtL3+jW/y3PXrTDdnTKZTTFmiInVxBhLycBbnXVIKQpNxDgrVeeLyEKOozKk4tYK1xehCEqeVbAcC7LulKolkOrBJiOUmW2BhznQWJe1DiI0XMGBVYNooCqqNGeevXOXo+JBqPCZ61p1vwYn1rCWzvIV56QIVrrMdVbDSkTTA4ZVKuTxKqV4+iXNgfeeti2MvSnXHU59CiyCs1Uw5y4SyUhK/LPOlAC1nmaJE6wpjJsHa2Ahw0xp0hVIFpdIBaEjYVHTPG6PDuA0sR1oc0UZ3OVp5O0oDpe42zslkjDGF5KSMCmZjSYA3RoCCvJfM52SNzNaoyDfR7Dujgoyx957WN8Jq1nh8nSkZzmFCH9vgkbOhL4UxLIZuCShUyaghStLQexItpmgVktRJVlAX7m2txa9WXL16Ce8dJ8cnLE4WNLUo9WVZspyfsJgvKYtS1q5yXbXaNIVPG0am0xlPnz7l/PnzAiBpWSyWvP76G/zkz37CydERCs87774L3lIECl/JJ+oIOVZ1G/YterkzAuh72n5GzWkxIa/LI6ExpQKtCzZ2zrF7bped3V2uPHeN5194kRdu3KQYTcUwEkMpwx4T5bLznUW9e2QAtookR4a5kT4wL32pw5M8jMNLfAA6fVCz5tb+jD06scrlFmxRKE8Wc3k3rTMgqcQzpITwJH/n7g8X1hvhXt1XRgtFtIaQVxP3M1Fk47vm74ePoXY+u6cP15L23nR+dr2h30ZjDKvVSkgoIhhSDrSm0JrZbMZiNWe5WuB88s+nMN5I7DLUX6JBIu5tuX7ivNRnsrbtjDoQgIMP4UodgxWQ6kTYjLQk/rTRmOfqVAx1FVgIlyGfyrWiy8T+EpIWh9YFSmmqxPo3YjIZU5YV08kIrci88iZ5ErRRKC3vb9sW5wUgnJycMJ8vOT4+5uTkhJOTE9q2ZX9/n729PT75RPbtyWTC5uYmFy9e5MKFC0ynU4qR3LduazH8OvH4toWncArtDIUHFYosFiGsShmZR0T9Nci4siqZaaiqEGqs5iyXEhEh+bjSdtElNG2z4rVXX+Heo8cs5ysuXthl5+bzzN98l6lTGFSaX6fmOIRomM4ILB79zluey9wcdCQYvQZI5MdZYGN47XAPzT0uub54ChwjxucmlIL4MseXp7e1bVKSkmJv+t6DuDnlC2YdqBgKzyEbVd4JuSBbd156+SDo4iIpTJEW3BCwxPvqoFS0QWnyoZCb0+ALARNaSOuD5wFZOERFqFv4IniC0SYAANvaJPxivoB0gJLEsbgJBHCgkboQ2nTUhQk8BSFh2zYJjLquaa1ltaxTmFDbtiyXouwL4mywbbRMtJkQc7hWkpLrlbhBl8tVugetZbVc4bwTS3/TsFhJPQXXtKfQd4qP7XkLunGRHAub4sFNUVAUY4mx15qyqKhGI8rgJYhMRJQGU4nXYDwaoY1mVEl+gi5COFGMzwwW56IoxV0YlKKehUDFOFQfmJrEQ3J8csynT54w/+BDlCk4d/EiuxcvBIBhUKYQoEG2HSnwShREr8RKZKDnqtZaUdDVeREWsnB5LFiYz/mwQXrbzVPvwSjTWam8zEMpnOZJXoAwCdO8xNO2DqUVdWs76j4nXqC6aaiXK155/XWev36dnd1d9vYOKcpK2hiUSYtPoYI5KFSyeHvAXlzeCrSmtm2SCXkRKecVXnVVlEUmGJQyaBXDwwTIta1lPB6jtVDAkmRMsA5FL5A2IXE53i/IIcAohdHyQkp5Sa7UBd4rxqqrs1MGMKqNxPFPJuJBiPO3KoXutjAao126Joa8aa0ZlVAanzxcKsgP7z3atyjXJGtss1rRBPkmYW2dtytZXZ0YMIhWXhc9EKLINUr36JM7a5oCGxQSL9bljqUGjBUV0GX3jJufxYPyKBuppuMzxZARyS8IyncM+WnrlrZ1jEcztFLM58ccz4+DJ8mGfjYsVg3VqqUwIeRQd8puziyoiNZ9xfb2DntP9tja3qFpW1ShmS9W7J4/zx/+y3/Jn/7JH3N8dMBicYKr62SlBVDGMZ/PwXtsI+BhMhmDVrRtE3ou5mjEjgSlTPAgKXAhTAWD0RVej/jmd77HP/s//HPGGyLHrHU0jWW6tcWiboJM7KzJ+ZgmAdmJkqCaOlCxUGu+V/pMmT4DGKj87y4ZWEFiZEuXRfndvyiIn8x4RRfCpboPw7nJBR+eobFty3JVJ7mvlAqgVq7L25/Lk9jiCHr7gEf+qEaV7H118E7FvTzWMMpARLxOHFK5LO2UsFQV2g+KnHkJM42HGKhGHBwcsbm1kRTEstC88MINrly6yJXL5zk4PGS+PGFZNyyXLR/evsOjJ0/xPuZidWOSQq+QPIJc2cvb1Lqwbuk8MEkO+M7YGOdU9EC4ACw84m1sQ05h27Ysawl9cpGAJNZnUEUg5Qizx1sm4xGFMYyrSiz/0sMSMmUbFJrjozl1M8cHEDEaSd6rgBwZ2fiMUSXhwuPRiPPnd3n++evMZjOKogQ8i8WCp0/3uXfvHo8fP+L46Ij794958OA+Wms2NjY4f+kc15+/zubmpsjOVgxxhXXYQlOYYLzVnUe/8MJmJWFSncyXOkeR3KQADHiDUhJR4a1LHlvlLE0joG86nvDCc9f44O6n7M9PeOVbv8Ev3/8E2y6wksCHSRu9SkZd70MYMZIYr9J+47p5G5ZItD/mCzt9FsdiABZOgZS4cjv1p1vPqr/6k4FXBYaqTB/pA3XJzZhVFePJiC9zfHmPhrQgxY5a73oLdwgSYtx17IRc0A7dPkMPxABApXOHnZl/J79HJoTQUcGaYgLDgQiwzuVXlGXwYoS8jPAfClFqPGiJDQhl3sB4i/E27LESe+qVVFhunaM0FbZuUNaiISUYRfflarVKeRrLVWAxCtXCvfeJtm+xWKRz67qmWSyxTcNyucLaNoQSBXDRtOLqC8LEtjYBC+Xa0Cdx9vqw+VmJHY1KBCQLHgCNxIXq0mDKAl0UMv7GUI10ykfI8w6KsqSazpJ1ZjQaMR6PJcRoFLisQ4JyWZapqrIoo114jnh7wlgHwJDPgW6ixXGWYxgPmbZvH3IFglVRXKcapRxYy6Sc4nzBjZu3ePDxbYyB2WxKUZaookSXJSidQogIcyVPb3RBSVNI5fJujqqowslmEfpZh7A8KVoY14Ykz3nf4m2XWJ9vjnGTwmf0uVG4hJAfR8dS5rwXGkfvUVbhrXCYi2s4JMI3DqoZR0tL0TYo1QEEtMKF/IiYfJ28Sgiw0iqEhGlJOC/LAoeiKELRzpRMHOhmtQkKZMydkn/GFBiVFWbyHhPnRwAvEWQkauEAYCrtMYH7T04VJbEsCjZGMJuMUpJ8BAzKe0YGAbdVSVkUXVu9RxmxiLdNQ9O2KRE1zrX8kHESWlnvPG1tsXXdUwJ0FG6enjwEoVTMLdw+OyfahaMV2ofNG8Q75cjul8nOXEbHteNwRPa7XtujZ1EpOvMI+HwDjJ/6br5GBdZbL+w/rWN3c8bGZIP5cs58ecyqXdC2C4pijNIFjYVlbTGFJKsXxoT11IWBOCegvFDgXcvWxg6f3P6UunW0zuNXjsWypfFw82svc/3ll1g1tSidq5Wkz4a9arGY80d/9Ef8/Gc/w3iPMZ4//MM/5JNPPuH9Dz5gMZ/TtDXi8RruRR6tS8kTFFMJmIIrzz/PP/sX/4JiVFG7LoSzKAuhjm6W2bzoG7i8D4nEa0CC98LHn3K+7en9czjvuj86L0Ay7PkwlsoNLz3ziAaPqIzEv6NHMzf8DQ+Ja2/RwbhCAKRyXc8ORXdC6ALfzS/oDFXei1x1SHirHF1I5Vmh1Xkb80Tl/LokV+mvnQ6IeQplGE9GHO4fMJtN8UqUxMoU7G5Nuffph6xOHjEej9Ao7t+5gxmNuXL5PI+fPMaFZG7Cu8Tlq7ROCfO9GhJZu20GgmyIlYqECEOA4b1PngrtRRm0eFZtw6pphBrdusRCpZUkRY/KCttI3h1OxqgqDZ4WhUUpy6gwTMcTptMZo9GIjY2Z0E8XBdPZmP2DPeq6ZjabSrVoJV7stoXVyrL3RL6fzqYcHR6xv7fPk8dPmS8WAlCS92KDnZ1dvvnN15nNvofWmkePHnHnzh0+++wzDg72eXq0z+07d9nY2ODatWtcvnyZ6XRK21oKFcJICwk/RTusB+uMhDpqR1GIx0MS1TXKaQFZKEalQU0lskQrWC5WAuaCR14FPcBpzyu3XuKzB/dp6pbdC5eZbp+nre/jXI3R4rlPczwi7WhkDoBepl/0IJEMjAlgeHpRLnH5iBFG9Yya6wz16dHhDj67Pjca9q5JelN3fdRzJHJBylygPc7H9fjs4yuxTsWY45xJKI/ryoVhnjMxtH73X6r/jKRwZdbJU66brENzL4ezrieU1aAj8yPVBfCeQhvapkEBpZH8C+3FNXR8dEzbNBwfH/N074DDwyPG4wmT8YS9J09YLJYslysa60Bp5osly/kiAYZlqGor7dSSLd2EnI1gcWhD2I0oKVkitJOk8ViIx2f9E9lqRPmwRPrEmExZlhLLjJZFV9d1cM8hOQRGYfSIcVWFsepyVo6Pjjl6ug94ZtMpL7/6NaYbG4wmY8bTKZOxJG2Nx+MU366iV8Z04STREhx/V5HSjv7G60KQ83B+RDTuEaVbNh6dbSL96G6jTS/mtgsNCSw/BopMiEuytFxTFobnrj5HNZ7igWI0oSjHeKNBmdCO02xn0fXeCZUswdx3SmG+eacqxzjQYd5nG6IID1HEewqGD1a4wMAVw7XE4hD7LnJyq1QXQwULRelFmCpVYIxHchAKinKELwRMFqYDfDrkLKBKsSASgUI3viqjuc1/OucZhyJ9MTm+kw0mAYoo1EzIeShcTRGKTZVl0SXVh7BHAYky1tHrNZlOmE5gXJmUTBnnYWEKjJMY4pg8L5qLAu9QLhIDSJ2OpNwAMZRGKbHILTOFpn90gJYwVztlKZNBA2UzP7xSnXJJZrn0oGPK9FBphc6j5iMo6L5zPaDRgXWZb92z880KyJj0T7d1qPQm+W89trbgLK21nD93jsM7hyxO5tSrJau6piyl8GIbjCQOkUeRujJ/P+kvhdOG1rXMJhMOjg7DdfKddVJwz4Y9YDwey8Y8Goe5Im3b3D3PP/8X/yVeF/zqpz/GW8vjvT3+1X/9X9M0NXfu3OXho4cslyfJMNQ2DfPFHK01y+WKDz/8kL2n+xSm5MLlq/yX/+pfUY2qlIMR531Zlj2ldjhm6TPXzYfeeYBXPmWLDPews4xsAN6pU+PSzSh7as496zjV3mw/fdYRc1rgi889dahhtk74OPwvKtZnAa6z+jr/Pj/yuPl1hgMIxoGgUM/n85DbpJA8DMebv/wVB08e8vjhfcaTiguXL3CyqNm5cIndC1cwWlEvVzhVxLv1npGPU1xbqQJ6ll8RZVAOMNYBDecESBD2hsZalvVKwia97GCmCLI0WK2VD94i22KqQOlbGba3dtne2mRjNmM23mBcTpKHqG1qWtsyny85OT5gtbK0rWf/8VOsfZyAhlCzu6Q/rpYrJpMJz115jrKqxIipNE3bsljMOTw85MMPPuKtZklZlezu7nDu3Hlee+PrfPf7v8nJfM6dO3d57/33OTjY592jIz784AMuX77M89efZ2drA20NJhSqNSEHxAWDldWxX21gqZKEez30bKfQfU29ajovke08Q5PxiFs3b/L2R++zP57w0re/wdv/4SFVLUQtNrCTghjjqqpkMpmwPDyhXdUdJbJy9Ivq9edgnBusmffJ+J4ZYodge3j+unn+VY44b10AiF/m+NJAYxi6FP9F93TMkRha0OICWJePkXdG3jk6FIzK7zP0guSf55upDspmzpK1Dqg0TcPe3h6bm5u4pmVxdMLdu3f59LNPeXD/AXt7e9SrFaumpiorANrWUZQV21s7TEYjxkE5+vSzz9k/PJT4X48kjtUtkZUn5mkAwlLhunf1KlDdeg9aLB/RSqiDsgcSThVBQxEUwqqqKKuSqpJKyaPgPbBtK5Yf77FKYwopkFWUBUoRithIgbCylKRTHXIdrLU8fviQv/6LP8c5x9b5Hd741jeYbmxQTUbookQp8UTEjTF0Mh6f3IFZZ4faJhDjfVUc9zg2HrxXvXooaYMIfZTGMPFvIzmFOXULiLVcZ14v71E+C+WLiyRT5KIQKasR3/jOD/AeivEGJ6sWXRQiKL24qvP3inkKWmX3CwqneE9cZBIUK5TvkqNlobpgxY6bISlHSNaASQqgtDlWuQ8en+D5ibS48R6aDvD5YDmTJOGM6lZFBd+Ie7sQtznZWtNKciaUj5SvgwUsTsM0DxRd/pAObTEZcInjWmhDgcEH1pgIgKvKsDGacH5zzDRYxqpRJfH8xiRPDulZ3dh7Pw/KlMX7FmUVWKhXDmW73CypR+G6KaO6ekCxnbEfo2LgA5BTGR/96Y7oZFAMlSK7p8y9CBhcumc8LAMFKVmUOstSrox256n+59k9bPo8B1cZG1e8R+/efpCrO1T9+uszeg1cMIa41rJardje2paQzKbl+OiYjc1tZtOtQCXehMRQqRjuvQ8sZiEfJT1TNuIYL++8k0J7vmPt9yqynZG80pgSAvFB7KOiKvjnf/gveP7KZX7y53/Gn/3kL/jLn/08FeUTJa1NtOPOOwmTQAqmlZVQIr/8yqv84Ee/xfbOOUlC111YZBznuq57Y9uTZz4aJlxvrEQMyjg5MVeemj9fqBR43b8/2XzOKZe/4Bju4Wf9PUxc7p77twAZcpNTVtbkyQ6f5Tl8wzav+5nrAEMwkffRWUDDefBK9AkpkOpCPpiEhE3HMxamYmO0weHhU+4u51y4dBVb1xJq5EIRQedx9EO/O32nM87Fgsd5G78q0PDeh6iGNsgEKJQwoqGiEQ6Z523MP9DsbG1y+fI5dnd2mU1n4sldNRzsH/D4831W8xVHx8fUdc1yuWS1WrFaSo5H20gIcmtbmrrpjGC0QcZLmKTWhqoqqcqK0WQcEsCFdGVzY4Pd3XO8dOMGelxxspjz5Mke77z3Pm+/8x5b21ucP3+eq1ef443XX+fg4IA3f/1r7t65y2effsbnn33OxXPnuHHzJtu7u5LHWRSYtqQsWnwIsbZO01ghhTGF1BIqC9Mbj8je5z0oliyXy2QwjmNUFIZbN29w+/6nHNQnvPjaS7z90x9T1DXKt7TB2CmGMfHYV2XFoj1Eu+hpJHi1JITK41O+TW7Ed85hBImkuTHUs3rhf4O5fBbwWHd8MfiQfaIKebBf5vhKQCMKl3wR5y+X/56/VG6pzu+Xf6eCQhq+TbG6+bVq0JlRgc+VrOEizgVPvDa2+5e//CWPHj1Ce3j86BGf3rnLRx98gAKmkynbW1tcuXKVjc0NqqqiaSzOSqViBRjXcnx8xLlzOxSVcMTromR//5CFkrCnspKiX1UAAePJBF1oTAjTqCKrUVlQjSdUo0moliwUlePxRKy0VYkpA/VpSmDVIZ+jQFijpRMWyyVHR0csFwthe2rqxPjQtjXWtRljBJRlhdHhemvZuXSFarrByfwEr0uKyRRVVahyhCpKlK6EwTcsojSmeHwWR+9dDOsAoUspEiAhKqWqc8vZsNlqE92LXpB6tr58zxCogiIfNwUXdfYUumfzRDkXQ8ZcLznOWstquaRuGi5ffxHv4cnBAm1WxFKc2oQEbHlL8Z4MvAnR0+BFOkFqq0KF3AMVXacqhiJ1XOBxjuuYLEan+JscqBsdwogyj0AEEH4EXvcS/WP4UqPF8jFkOfHeo3vKZ25V9hgicLfklds1Dm1XyesQaXrLsqTQOhWzSmtWhbAmr3C1rNuNzU1mGxM2N2aMJxWFFrDardsW2hbbIkwwPo48AZCHudPj8w6KZ1D8o5LlssmT5JEJ40QHYLqx6wBgByQILuj1wthn4SuxjxNIkFaQwDXd+7gh0IgAI3uP7vPOW+bxxBicoTLqYiszJTa+QTLkZDIzekDyVzv1nuldpE068IBGb5FrxRNw5fIV9p7s0TYNq8WSerUSA1BYKyK3C9rWpneJNWlS/yiwWAyKZV1jipKj42PGs2miyHUhwVSZvO6IIfHzRRDiFaYa85/9zu/zgx/+Fvfu32Nvb4+Dg8NkQVZKAM/GxozxeIzSmulkws7OLtV4RDUao40U/LPeo4P3O3Z5rrAOFfS1v2dCLQeQQzA53NP6cyQfrNNzMhoUoo/kixSN4T59lgK+bk9PyswX1AY489nPuMrTBw1ntfkswJErW9B/r0RqsxbMdRTPJycncr2zOCdW+PPPPceNa9dYzeeczA8pJgaUofGKJtTSgsjQ171dBBdFMPDkIAHotTMHFXnkyPCz/PfUn0oxKksB5iGHrrWt5F86y/ndc7z04ktcOH8OZx1Hh4fsPTrgk8PPOdo/4PjohMODQ44ODzg6PuD4+CiBjKYOdalsDXTel3wf7vpTpb1eCBpM2rPi3pEobqcTqtmMi1cvc/nyZV65dQvwPNnb49M7n/DpJ5+wtbXJ1avP8Zvf+z4/+sEPef+993jrrbd4/PgJT/aesrWzzUu3XmJrexvTtLRlgTVSzqCwOhhbNcZbCutwViWPRgz9NkZq8cTSCMvlstfPTV0zmY555eZNPr5zG70949zN53n69IDCyf4X1x8OlIHlsRSxlMrtOlDPduHTIq/6OmucD+vWbmdsi5EEHWPUs44vBhN9HT1eE/dx7brQ1C9zfGmgAf0wqEjbOmxMRHxN0yTax+E9coGcA4AcwETQcJYnI7duJCESrEtDmq7o4YhWgahgfec730nX7pzb5dq1a3jvOdo/wNYN9z77HP/gPpevXKFtLZ99do+N2QYvvvgSdV3z8MHnPHz4iFdefZXv/Ob3GY2nTGczCenRFUrpEP5RpIIyqihwRiUlIFoPJXFLwmWiQhAVzLD9dgo89Coue1fg6Xj3q3LG+c0L1PWKxfERTShQJ1VvV6FQVUvb1qnYUB2Ah9cKXU3Y3LnAorYUoym6nOBNhVWFTBnXWdV7Qh6xcAqFasgxiNtHCCeJSkowfIf2+2R9xWcbSrTq0t9Iujkj9JouhKClxFcfq4SqnhCOCpd1kn/iXJc0J4nhmraV+VMWUihJB8FTFAafcgk6z12cS3HeaWN6ljmJ2jJpA46ECkYbeavobQhKOF4U6AQ8ZMKnehjyoMzqrkjKm9Ia7UuwYX02wuttUtEsh0PyUpIwU0o8TKEAT1o33oc4VY8isDWhmFZlEsA7WzN2N0tmGzPKoqAoyhQqp6GLuQ4vEr0QYuHLCjWpYO23K5RX3VxgIBBzra73nSJki6TPe9Xrle2UY9/NoaBlZ/AqO7z0V9/y310TQ93kVXx6b6nz0bf0+jBYzru0rofvdpZSCtGRk7TZZN31yY6fd0/3t+2/Ue+ZIkPXK6s5ZeGzNiStNW0MV1XQWItrWw6PjtjZ3ebpkyc8fviIS1cusVwtQ5Vt8Q7XtTAHyVoireOedVlJ7opHsaxXKC0/y8lYZD8ZcYaK8gcxufh0i7AU5YPWe4rxlBdevMWNl17uge1Y1yR5JVPfKPE2e2isE+nVMyaeDgnuX0/vszRWWSOdP7vPe3NhoPj3j5gNdvpaz2mQsvYOa5XtZzxxAH5iO3Lw9WWsqM88V6lTIGoduFj3ey6jh2FXuZFz2I5ctoglvquGXRgTiBTgo7t3KAvDuCrBW/yyZb6sWbVeIHIxpm1WcqdBgkpHnNPXVfrGhG6/G8qIdaAjf9+yLMFLsU6A+ckJhwcH7J7b5mtvvMbVq1dp65r9pwe8+9bb7D/d5+neAU8eP2b/6VMO9vc5Pj5mcTJntTqhtcsUNtSF+HpQLdrI3tu2tpPxABTgTezK3l5plOyvyXAcC+8VBVQF1dtjxuMxm5ub7Ozs8OKLL/LizRcpqzGPHz/m3bff5rO7d7lw4QLXr13jtVdf5YMPP+KXv/oVe3v7HBz+igsXLvDCzRtsbs6wRmOaRnI0CkNRaIrSUGiHL0i5pt77HgtYVVWpf+ss784rT9OsePHqczx+8IDHh/s89/or3HvrHSbGSyJ5NtZea6rJlPlqiTehPpaXiAtEgwvMdH1Amnv1hmtg3V4S53D+ey8fKZtHw/Py+RVBVz6v5DtpjPc+Rdx80fGVgEbe4GGD8pePCb7PElpRqCQrSA/B920bQ4UuX2C5dwO64l/xOqDnbs3vFat/eyUKwmg64bN7n1Og8W3L/QcPKMcjrly5wuHBAfPjY/7gP/8DLl66zOHhAbc/vcPNV1/l7/3O7/LyK1+TpGGgacHrUXAl2mggxYRwGe+7jVEUX0ehFbiQHBss2S57F8I9ODVBBB1HC7hS4ItCqvEWBePRlNWqYblaUNcrqrbOgMYCZ1vaEO7gQ7hA21ouXr7GfNmyfe4Sqwas9lKkynm8azDGdVSt2eZpPSlEJLdsAChHt4lnyoxDFP98vOI7et/dPyrc3vvgvowhdi4pkEp3FMHey5wwJjBpKFHgrS5TTGMENwIEtFSZ9ZLsZ4zC6E5R8YHib2gt6Hsk4thEFBW/C88L/SXeljDP01TvqkgHQzhx085XkbfBkyKXSHiUMlK7xR+Dk7ogRmlwkhtToplpRLgWIT8pMTZpqqpIG9/pf7I+YxJ/WUY2Jo/ykcnMYhtLLOEnm3OmIGRAQ+KqLA4BrC7ylYdQQ1Hk5QVzxWoIal3mXYFm7XkQQO/w+nxepc/indcduWc1Wt+7e/UV+NMKnYCf04pn7wmdgTuBGg+QMUvpwLYT1xG92g/D9z79fhGId4xfPuuG8PuZQEO+V2HiiTdDpRC9WETv+PiYyXiCbS33Pv+cF166Qb0SZrxqMkmy19oWAYhqoAzKsyJY9ChWqxWbW5uczOeMZ7OUFKVVeHbmq9G+YzgjAx0QSBu0GEQIe4ENDDU4eZY4Vrrke1TIBwvWPB8yM0Sud6yKwz1pHdBIxjnVJWauO++s41nf9Yw3g/NSqOYgpOqr3H/tMweGxvAHmi9v7UyXDe7Zb1j/mbkMznNGz2pf/D2+3zDsa3hePLRCmCDDmLVNw2g0kjmMD7lVimXTQFsL6yAFTkNjFS0KUxVYW6Po57Z2hltFnk81BKvDcKn4/TrglMBL2Adt27K3t8fiZM5LL97kt37zBxSjgsePH/HmL/+GvcePefL4CY8ePWJ/7wlPn+5xcnLManFCXS+x7QoCeUzrhERk6LWT56pkyO3tj77pvIvIukvX0KUnRwOeCtEadqlQR+Ipf3QPRqMRH7zzFpubW1y4/ByvvvY6zz//PAD379/n/v37XLhwgWvXnuef/JN/yptv/Zr33nuPzz//nL2nT7l58waXL18Ie1hBURaYVlNZQ2EsvnW96uWpaKKWf+PxOL1SLCDduJaCggmK6+cu8s7t93nlpRtUl8/hj+YYr2iaOhlla60pxga1NQXbSuHg1qIcFF4oldssxzPq2lHZPwtsD4HEuuOZujind711xv3+DZHQudXqzGfmx5cGGlFZzwHCUKgOwYM2Mbyk4+u2QZkoiiIol2KZjsXpfLD8imIgG0hkjYqx1Ym2kOCm9R6lImuJC8pd5OCXe0UFX8cEHYWwPoRlUK9WfPbJHerVitp5FscnABjvKXXB3uPHfPe73+Wb3/om1XhM3dTceOVFLj93DVONODqeU+qCQhViXUdhlabUBboohQFGiZXX+M6a5fBo5QLlJsI1HgfbVF3fZmMRrZGdKir/TzUclEIVoiEXylCOxpSrkuVyyXK1wASgYWzFql6hdIPyJlhpG1wDF567ybkrzzPbmPH0cE45KjHlMmh4sbBckawX0V1uoyAKilUcI9WZFpOVPioBIhQDC1EYl3iOid9lgDItrECJGgVd2qpUpEsN91Mx2d0kjxAJMHSCTsBGrOYsFm2FR2lRLH2kqc1rRiRFunOxa6Ujigw6WyggGCwWqEArqhxSlSECJReKQPrEGZ8oGGUi4L2nVA1aecqyCMnPJePxiMlkwmSqGI8Mo3LE5saMsigZVRWjsqJUTnxmvU0uCCr6Mb+y3mzILSHRIEqomcPaWmgTybyLA6Uu5nVEfi6iQUE5YtI8gW0tYtIImCMQ6Fl6yZiZTgldC94l62f+tVdGFEcygeuDry0/LyqWvmt/XKl9YHI6dMrZjmCgp/rnigMRaIf292S3rIe4yfQ2BaVCMufpDSAqvOuO6EGRu8frOkW+f5/uHU/fL1fCCPLV0zYh9M9JTQgb2PhWTcvu7g6zjRkHT/aYHx6zWqxomwY/Fs54UwSjke8IEDpjU+ipKNOBVdNQVCOePHrI7vnzFGFPcGG8Yp5GhPMDzfTUGyWOe2QPECIRHTxSMQRIwIhzgYqHCDyIkzX0axeKeDpZOTfKxb/l2g7PibEhtl8NxiUfp2G4wlnnnX7fsLqeoYzEd5AL8vdbdyJ0xh01+CpZSToQJn901/Zv01vP3fyMJ/q0rvP3iauq65M4h/pAPzcQ5IpuBPP5XOlCUbL2h7k1m02ZzxdSbyg0q7XCRea9R3mF8QSSl844oJSXIrHZ3h4t5t5LTo6ii+SQOjYRuIZwqEhrndZx1L9kr/POJcY8UxjquubB4ye4tuXlWy/z8ku3aJYrPv7oNvfvfc6jhw949PA+jx8/YP9gj5PjI5bLOW1T09Q1zrXgJectenZttjbChp5FFnSWd2ddNneyMVNAAlSi6/ncWh7SWItWdCahjJYwYNuuWC41h4dPuXfvHu+98zabm5u89OIt3vj6G5zbPcfTx495+PAx5y9e4MWbL/LiSy/x5ptvcvvOJ7z//gc8ffqUGzdfkGK7bUNZFlhbUBSWWjWMrJCLFKag9J7COYx2lIXU4hmPKvCOhQolHbyicZ7WeZ577jk+uvMxShd88+/8HR59dJv6+FhISJo61H4BZxSTnUuMRlOU89jFivmTPdqjAwql0G0dqszHaR89zyTZHNdLVwgzYzSMu2i2tyulUEb3i7CG/UfT7YtJ9tAdwpA5WM/BHF4vFswPj/gyx1dmnUpu5mzDi5aoUzFdziWKRWO68A6QSRYr3Lm0aMKrqm7Tl42m+10RWYDk3a0Nxe+CEidc06KctaFNSmebRli8Wku137ZtuXrpMhfOnePpg0d8dvdTNjc3WR7PsdYym85YzOc47/nNH/4mN195iaIai8vetczrlqPlCl0WGFNiKFDeSpVYpVFFhfNa2GFi4mxmMTRKobVPcnWYUA8DfST0b7Ts5+dqE4RxNg7ae8oStK6oSs10UkkYQ12zckA5RjcNqpQ8DlY1TlX4ahPlHV45fKFovadtWgFraoxSJhTaCjkEhKJ5hekJ8RRqpFSwYEeQkhexyxKQM2uIfNdZ3uNGkTxgpguXiX2XrtUdE1acvyoIvzJkKuchEmmeZxtMbpk2WiVWF68zJS/sHw4HsXJ7FAxW3KtRwfZRcBCsFXiER1hiNJUTBbxQirFRzEYlm5u7zGYzptMp0+mE8bhic6QYlSrl60SPigA6qQadOiXt1SHt3HmUcgmYp/frXjQB1jKIh86aJrU8XGTecJ7GGZq2TS716Fa3rUN7HWqWxDA6gtCMFuEwR4JiIX3eeX+GsdNeK5zKFYe+QpGTQPQULm+z8+L/ui7qHZ40L7pnhy/OOLrCb6IKOJO1y/XLsp1luc7l6bPi4oeK4v8/1u+1oIYhN06mlKvoOfXdJogPCpWCVtF6h9cSInrh4iU+ef9djvcPWc1X2KYRC7H2eCuyweMDlXhXITx5a4JYjPkr5XjEYhmMHdGwEJNtM9zm8GcXhcvO82Eud+8Zvc9pV00hcsp3pAEJ+NMZMeL91sctZzI6GDKkWFh3Rkyml2f0iwfmc1FFoBLHI3+1wTj2QWn09H7x0QPca+Zc/qyhwSJ8mWR6+o7US6f3M7I+p5tvwyMHNH0AoZLMzddIZ/zM29wBC6UiuB8mzse9S4m+4QHnKMqSVduIjJQTReZkb2ZDt/mQB6gQJUvoq7t9Oe9Tl2o99ZPpY96TT0MRdKfwT4Uib0ZLnQ/xdHvuf36fg6MDvvOd73DjhRvsPX7Cr37xcz779FMePXjIwZOnPHp4n6PjfRbLA+pmgXMNtm3RFBJKG/Y/hZA0CHYMwZi+A8RE1rvAjNcNEL3xl3EejHxaRHJ9VKCdFZOe1hbtNG3QC7QNeS2qZdGsWB7t8/TRA/7m53/NlStX+dZvfJurN27y9MkT9vaecOnyZb75za/z8tde5uOPP+aTO5/ywUe3uX79OXZ2NvG01G0r4e1a0XhL2TZUZcUYj3OG0pQhvKlAa8VkXKAoqRuPVQpUQa0Vo9GIKxcvsThZsHXpMn/5k7/Cn5xAKzmGhRGmz9FswvTSVS587Q22t85TecPJw4fce+/XHN//DPV0D2NrwIrOoZSYO5UUrFShj5Ka5z2BvDLMcXrbftQTDarzOsskDLqo6MpFts+S6eMKUr5sGCrJEVaapm6o50u+zPGVksFzRc45l1xI+Wf5T21M77MIVuRvi8rrEgwFB31BOfSgROtRsgoM4hWH4VNDpTxZbkN8/s7OLjdu3GC2ucl0OqOtW7xSHJ4cc65tOHfhAtV4gjFlStY+PDxAqQKtWkyhQBdYL252p8AXCpRGQtGj5V+Tm1HXeYfydz/r7/z86NYdepu87xTf0hhKY/ChWI51jnnTsqwFbdd1Q9s01KNaBJ+Pyb/h3ZTQwXnnKM1IvAOqc9XGBGajuqT+nO4Ulam/sa3x2kzw5qBV/umU8H0qwWlQZTbFzSvwKtK8htyTlL8BXhVh7+gsl2luBKzWQdu4ifjsN/npsmtc3OnkAWHFC82gDwV8lHfpn8FRaENZFUw2xkzGI7Y2Zmxvb7GztcnmRsVo5CliRXDVKYfGd3Ho8nyPWJ/i+unmSE+p7llXB2B2oLT3xmmweftIc+2hcprIqBWry7e2Fea1VgqY1W1La0NND0dX/yMWikuhf7JKogB1Xiq+2niuJtUEWbde+pbKfLGsV1Dyd+2dPvhs3d9nnePwYHXPInrWvZ5lfV4nC54dn7/+Pmd/uf49xLBz9v2G7Upzw3deregZOHfuHO/XDQcHh6xWq1R9uBd3rDSxYNlQjg8VMqVUCPHsvLfr3jPstWu/U9n/n3UMDT0qkz1DQ1vv/s8Agr13ob80o5yOf3QeqJB3oeIcV70Ln+WhGO6jX/b4KuevW2+e9fM8KvbDz/NnntVfz2xDrll9xSPuT6fXikp7k5bYVGazGccnJyJgg9zPlefhLYZGw2cl6K7LwRj2RW7kjbK9CHUwcJ6Dg0Pu3rnLrVu3+O3f/m329/f567/8S25/9CGPHt5n78kj9vf2OD48ZLXMWPqI+XLdWJpMd4t73Fm2lqFelusf64xCw/6PfZfe3Tm8b7Mclk7OFIEF0pjgSanBtpbbt29z5+5dts+f51vf+Q63Xr7Fg/uf8+jRA3Z2d7l65TIXL18Dc2AEAAEAAElEQVTmsxBKVZSGyXSc2lvooGcUHtd6sB5XVqiR6kIxlaYoNOPJCG0UjQOnhHhCacONmzd56803eeH6NRo8R/M5rq4D0NBMZhOcq5hOd2DjMnbjHNOdc1x9+etcfeVVPnvn19z78a+onzwGfwB+IYn2XlMgRDqK0/uXj+1jvTFqXX/nY/WsMVw73k4iL5rlis/u3D3zWfnxlXI02rbt0VWmQQpcxXVdp9+BULHZ9F4gxue6YFkdAoO8M3Jq3A5hrRfy6wBFbF8M+cg7Nn+P/adP+fTOXapqxO//w3/Ip3c/5dL3L/GXP/0pzWrF1evXuXjpMs463n3vPZxXwjClNOPJlHOXLlOUJbhQTAcXGFPEspHCcWLbntHHQ2vMWUdP6AwA2RCMRQU4JZIXBQVQVCNmkwnOe2zb0qaqol4K3AR7otIh3h5hjTHEgjbRit4l+cbCYjlVrQpAKKfN7FujuvCUXGEMPUKKlx6Ot4Ke5S8PDU2aXtoT8IFiyEcLke4sRBE0RH7704ssgohwdyWJ0h1TT3hX77NzxdqlcYxHJZuzKZvTMVuzERuzKbPZBpPxhKoqGVWlWPi9p9DgfB3AUigcqfLNUOFcNkd81ydDXXSdovssC+W6z4ZAIx6KCDLFE1GGAnneC71i01jqumZVNyxWNXUTwGxrBXiE9aKMOGPREsiiQx9KW7MKwCYLITvV2iAA1yoN/XcaKpH97wOUjM8IP3sC3A/6IYRveo/UQLBnA4JnKv9/i/P+Nod0r+1t7p0197RH46x29YFGWEOBwrNpGq5cuUzTNBwdHTKfz1ktVymGO1pw8/t+0Rw0xqQQhDM3wWdK19P3POu7nqyBXvJ/fu2XHachkFfQ82znhw6haeFKJP08+JKUxun1e+C69/mq7cyV4rR/PON9hkmmyQrK6f0ovs9QY/0y8mid4W3dOH7VdbPWwIJKFl8p8CrEHVVVsdrbO7VHndVPp2TEGR6NYVsi4M4/z/9FxXJUjNBKcjk/fP8DyqLkD/6L/4K6rvmrv/gpH3/8EQ8efM6Tx/c5OnjK8fEBq+UcZwO5R1bLyFoXQn778z8BHE4bcYaA+yyQfdb4rAOpXV86vO+MyfHa1WqFUZqyKACFVi1FUVEU0LaWRw8e8Mf//t/xs7/6Kd/57ne59bVXePLoAYcH++jRCKNgVJYc7h9QaMNsNgmh0OK5cq3DGyeVz2lpjUEpjxJWCsnXKQopJNp6WhvCch1s755jurGBU5oXX3+Vj7VidbJgUhRUZUE1rpivlhzOFxzNV/iqZmQds8mEnZsvsHNpl1vbr/DJz37Bowdvcnx4B13XeCuU9d6YpP+uY2DrGQO/QH8cHkMQu87IE50FGsn/9K3jcO/pl7r/lwYaJtRYKIoiJV+lMu6uozbLz5E5fHryCVruJxXlLxN/H4IPpVRy6cbnDdsxBBwRBQ8HJgEP51jVNY8f7aGUYXNzh8OT92gfPESXFVcvXmQ8nWKKioOjE54enkh1TecwRcl0POW5S1epkIQfqxyNg0UjbkgXEqjjm2jUIDzntDI3/P0s4dlbwIO/43U6AyLR5yr3j9bEoJgVXSVXj6J1MSQpWtTkYoXkreisXUOL0jq6wFNCKHNfW++SIBvOh5DpfKoPUrt91heKlETsfSFJxpCoYSM48b4J1pxOqdQRQOAl3IlOeMqmG3nAh7H+MQ8hWD7xFIWSiqtVyeZsxsZ0wtbGlNmopNSeyijpbiVhgAqP9nUAGg5aT3fH0KcqsxANBEp8/6i85Qpkr8/9emUp9c2a3/N+OC24uvhsFax7ykgvFEZTlQXjcclyVTMeVyzrhuWqZrVqWCwFgDjnaRqpkK60AW+lQJ2KYXXZe7p8vvszFDXXO0fm+5dXPnpn9pRN3/tSlHUZC+U65SnOhbM22XX9/EVWqLM29OHvw+eddS8J2+sqEfeupz/z1ikGQ8MRhBASpVJ4yGq1YjqdorXm6OiYk5MT6qYOz+iKOsb7PCtJORqnOvrzzqg8PHJZlCtm6/ohf6fhs7+oX4eAZNg3ZynKQwUyvWMmLxX05tqpMKSBnHxWm5+leH8RWMkVj2dds/Zd18xtOc+Hvaefz3nWPrgO+MXvO49BF2501jh9lX4h34t81w/T6fTUM4a6y1BW5nukyg2mz3i3oYclv1/btoxGIwlT1or9p3t8+MGHfOONr/PizZu8+847fPjhh3z+6V0eP37I071HHB7u0dQLcC0eG6o5q1BfKuZGmrTuz5q7nYHgNFNo/tmZvXrGvrKuL/PzhyBOKWiaGqGMF9ZIa6WyuS4KXOt5+uQx/+Hf/Vve/Jtf8v0f/CYv3XqZ+XzO1vYO9arGec/i8BjjpdCnw2HrFq0UrW5odI3RhuViSTkqKQpJCDcGykCcgiowgSkLpSmrMc89/wL3793j2s0X+Z//5/+VerHENw2zyZhbr7zMbGuD7Y0Jdr6PGxfYekJda3a2J+zsnGNcXqYsNIc/eYgvl8z3H6EXDbaJpQJO7/lDPTj/fh0AHu4fX7QuhjI/5mBppdjY2DhzvPPjK4VORSv10AUYPyvLMoGQmDSqi9PhUZLZr3obTf7dWQq43KOzLuUu+CGKi9fFuPF8Q42ASAcUa1RB07T84pe/4Lnr1/jBj36ENppXXnsNjacqK7QuqBspbCP6hca1LbOq5ODePf7qJ3/B4mTOdDrla2+8wdUXX2KFpzEeqwAVMhp6ysp65Bi/yz87axOLiudZ1/Vcuz17n+RGmKBZJCracLrR3XlysYKUlRGYVlSmpAQptQ7wdHdJCCudr1Eh1awPVvLjrE1BK99pG75rh7x1FueceR2UAqNbYp6AD+0wReD1VsI+UZUl1WhEWRSYopAqoonCtOP+7wBHjJf9/7H3Z8+yJGliH/Zz94jMPPs5d626t/bqrt57pgdAYxkCNJEyE4wUJUqk0YxmMi3Uq/Qo/QF60KMe9SLRZCaZiTSKEgQBBgEiMTsWDWbpZaq7urvWe6vufvaTSyzurofPPcIjMjJP3uoaSA/y7lsnM8PDd//2xTPKNXmuGWUZ41FOpoToNlqjsaiGKA0MVtACacA7cWq2XpFmIm8cqwNz5L0PfyPf4eMqdhihdO3itV2HvK9b887eEswK4jsqmAcG8yenPCbTaD3GTcZMoqleWbOYL5jOC2aLknlZ4yvbRENrLOBVJFqaDkkPySqc5iPT2NyLbuSqdfNeiSgHliMa19G7j+m9XhU1a3nMy89eBmn331nVnhCyy+02fW1AmMbP/SiA6d6UZcn+/j7ee9FmFAWL+YLZbMbW7k7jaJ8KjNK2h/pSSoUkWj749w3jCNfbrE5b4f6kOGcVo9cQhLAEm+L7KQ7qh+ftw+2OEK2H1COjRrhD7ZmXefoQQtkr3YleNmz2s1xWCRX6z64rcY59v8x1/aW/yb/lNq+L+79q/ENneejd69YoJfDFnDO2D9rTmPzN53OisC6OpQ9T+u0qpSAJaOK979Ak/ZKeyT5TsrW1JYSt93z6ycdcnJ/zN//G36QuS/7g93+fB5894MnjLzg7fcLp6THz2ZS6kohXRilEaRHzQcW1Cz5zCtEsJ2NPS2oK1jdZT8f+MmUIFst8l7UnsRjtQ36SaIYpGch1XaMriaqojYSnf/bkEf/k//mPuH//Pjdu3ME5T5bl1JVlOp1jreP23dvcuHMThZLQxUoE0FuTCcoI/ndefDytq6mrknyUc3hwhNEZ8/mcre0JOzvb7OzsYDLN21/7On/7v/FvcXlyRjmb8uLFcz741Yd4o7hx8zG//Xf+bai20XbBVrbH3Zt7HO2O4cBwx73Gd/O/yY9+b4a6mGHUFfhCosatiByXMnpDTOy6+5+GsF21f6n/ow15wJxWHNw82mifXyrqlHOO8Xi8xBEpJapyay3j8ZiyLJtBpVLIFLj3JxwvXT9UXR9IRISWctdxbLF++vu6y9DmVoDHj5/wG7/xAw6ODuXaaYX3jjxocop5idFZQxR67xllYCrPf/33/yEfv/8zLk5O8c7xr37n93j3N3+L/+a/9++THd2kVuCVw6E6/ggvA+D7axLn0TAavWdt8Q3SStdGJMI2AWa0gMd7CVsqbyVN9YjRQCQ3TBwt4u5LK6BlsnzbwErmoqnik1E07bV2iYKHpY4JviBai0rVmNRPJEMbLT4P1krkhOBEbYwkUMyMITdtX11mF6wL2dY7/hAKpRWZziR0rNGMcslynRtDnkUnV0uMR+SaWYg/D97LsxihDXAhw3Wcu/Mhv4qXz5GY9r4r2YvhS5cAhiKYOAVNouqi6HVncei+p1uY1uswxMGUSUcH/pFIhvzYUY1ydrYmTOcll/OCy+mc6byg9m2Sx2aPgymDOLOuZhL6E27XSOyQ273c7N69DDHf/5wSgv31WdfmpuN6WdjRQeJxTb9k6cCRBAalh8Fay2g0QmvFfD5jenVFURSUVcnYbXXvLN1Y7X2kmBI1eZaJ+cRWtnINmrDbQ2PvtbtuTs14WOYz+3gsHfcQEzMYFr4z5gaCBxwRxxXnI4O30CQCi+11/VrW8oq/VhmaZ/o3hdVDO6Oa+7ue2d+ktEzO+pPcYSB6C5P6eK4kkINwRyEEmQR3WNZaxH8prdE5y3EPB+Y8NP8030Rc9zzPUUpCyP75n/0Zt48O+eFf+2s8+PQzHnz2GU8eP+bRF4+4OD/l6uoxi/kUHEFTjkSuE6lao8mPoZohWi508yI09EE/stiK+Q+t/6pyPVMy7L8q0Uc9Ch0YkmAajyUzIQKWVihjUFpTVSUff/QhDz95CF7MxIzO8F40OV88+JzR/oS93V0m4zGTyYSt0ZijwyMObtzkcO+I/f19trYnZCHpn1IwHo3YGk8QysdR1iUqJCNU2rCzu88XD75grA1vvfUOr96/z49/+hM+/ewh2R//K/6tv/vvyHlx0hZeUW07tl7fZXJ8A7NzBOoYzQKYY5UEFFh3Xq4rQ2uephNYVTeFXUorKif07CgJ+7uuvIRGQwgy5yTJUuzcGE3tLFk+witxoB5NJmJL62K89q6znw7Rl5Qn2DcDrrU3V1rjbbjdrseVpRLd3gEXJ6I44CBZDURKB/D7YArmLFppKlsx3hpz++5tUCGMmwrJ1bwjMxmjbNwQTBBoZOV5+vNfcfrwIWo2ZTeXrLH15ZRf/It/xfNHT/l3/uP/mFtvv8XCebzWOK8luidJpIDwv3XShLWEYO/wLNUdetUnkqX4fsr4dZB974Cq1HSplyujkdb7RkIXJhn/g1JJ9AMvxhbpkFVSXeEkYkKPwFRBe5AZRZblGJM1sa+zzKCMRQdGIxLVAhw1qqarWSLOz6OaaFDggwQhzr0OxDyBUTNazPKM1myNFKM8C4mAxHRIiGQpLjo+q1SS5EPfrrUBj+cUWqYWj7d1s84O38mILqnZfHM3onZnCaiELNguzDVdb52MNd6ZhuFS3XuWIhmt2t9aYJcwh85LlCEv/hZZZtAZ5FnOaMsw2cqZzDO2JxmXV4bT6ZxpUeGsFWbLujA+hQv5SK5j1Lu/+85mrwKeQ89XSYv7iK9fZ4nw6jFqq8a7ivi67vOmjEe7ZzQmEioyCasI81TO0ETnIRDPachzEc5IIASN9TX5aIQ2hrJcUCymIaNwyXaIjqO9ZzSeUFYVpS1bbVizx75hyiXEpWWcj3BVjd5iEK41JpkdYrYvRV8mdlOGPc6xEWaRSgtj9l3RMMQzvyxdbCW/0VRY3omJOGVMAq/SHDaihbe2TsyRXTP+yrsQZhQhtJxH6xgZqMJ5izHBWkCFFWlgfXhPBQlPEiVPYNrQ/oe9TQQ78t01MDWF6w3sWnE/fAJ74tlpccmy5KmPouL2dXX1MqdVAQLi7ykj1gob7VL9KMAhSsLCe1qrll5Rw0TbqrvfP6vL0bqGTdSkLWGwtYbZ1SV/+id/wre/9S2O9o746Y//gi8+f8jjLx5KqNrTE+bTS6ybBtza9YVSob3GFLSJ4ifnxbokCltgPpQOeVHU8tj6zPWqiHlD8+qX5brt/U2f2TAvpQQfK6UDhSC+f3iJguldHXBOhlaKqizBg9YZVVXgvUKrjKouWdQz5leXTCYTJqMxxhieP33K1u4+W3sHHBwccOPGDQ4O9tnf32dvb5fc5BRFKTmltGKcb8laGc3VrOBb3/s+l7MZv/z5z7n/1uvgar5VfpM//vMf8auPf8nNH7/CwdEB3t/h00++4PW7txntjqhNRnb3Nntvvc7jj35F7q0knVVGXDYH1rRhSNP1dK4Je9zSFMtrHu+hC3Xk6Ic7s2J/jAJblYyzLmO6qmzMaGhtGtOpFNkLISSLq70PyY7kr0fUjtamKlYB1j4QdPGIqDC5hjhBNfGYvRe/DoXCEjM/2+ZwdxAuiclCAvi00k0iOZHmu0aN7r1j73CXfCwqtczEEJsyL+99Y7ff0M0KTDbi2eMnMC/IvBfOwRi0B28tpw8e8F/87/93/Lf+o/+Qd7//fRZOVLLKhzwR+EZK6yEQRH0GY3kvOoAjlZq0NdpWVPOfZo1iuyuBYtK2PB9QkQdE0z3ZviFgNN2D7ZO6EeDHJ7pBXr7dw/BUK884U+H8Sd4IE5CyURaj25jk6Rhr5QNBHpALcZUdjRAnWRORiChMjFsIeG+pfS0EFQpLyOCpJHndKM8Yj0ZkmWacwShPgh8oYVesl1VoQzi3BFuL7IZ8i0QTEgmWFvGB83XHfKIL3FvNRwepA9jWv6Szz4jfTUswBIYscoCqjwTbc2l0cnbsstYg/i6/SchbDOhcMSIjH+USsndni92tEZPtCadXc6bTKfN5jfUSIjsYS9ImRlRLUpxUytv0HRmoDRn3Vb8PMSgvx/CsR7KwuVRqaDzrypDgQaX73Xt2fZ8CsxoaSrV5LERyq/BOs72zy9bONufnJ8xnl5RlIX453uOtY5wZ7ty6yYPPv5BkptF8KA5D6cY8UjSnhkk+oloUqH1hkIYStGqtmvPf7lO7V+l3qd9Gx0vvYmQA0rbj3kdteRrsJNaL361tTXxTuFvXkptA8tHUVFXZ9BvxFqoHF4IWshHyWIeQfxrlFZkSgZ/WwbHVGJyH2llJLxP8fBtGLIHFRCZqYM91usntLDvwOy0pHO/+HkmYrmCiL0RcLtHcr/drOp5kLO39X5aEd8e8PMbm+xKeCppjpShKCQOvk31PYffS2ML3mNOmQxR2kXRTUusOpWB7MsEYw8mLF/yLf/7P+et//Ye4yvJnf/KnPHn0iBcvnnF8/Jjp5RmLxSXORfPTxOwvMkd48LY5YykcjUKtzpqEdXLWdeqmsK/PePT3v393NispLdR7J/iTeAhnN4kyquSuuMDUe1djnSXPPUaPQEEdGBAUOGqBI6XD1RXKOXwwayuM4eLqCp4/Q2tJVjsajdjZ2WF3d5fDw0OODg/ZP9jn6OgG+/v7bG9vS0AUoyDP+c0f/lVeef0er968wXtvvsn/8T/9T3nr9Vf5xSefcnbyjPn0kouzCxbK4CvD4c4ux+Wc3bt32HvjHnpvi+rKY3G4yuFsK8BI19cnGlPXswqKuUro73X/vIY6zXFJYEJ6BxUhKap1nD1/sdFuvpQzeAq4GylvCGlYluUSwaS1pqqqzqFsgDk+JLeSo61T1ZzMkiiU8SQXnuWLHMclJhcOFSQ4tbMNY6GVlsMXiD7nbADYFpxElHDOCWPh4nI2/F2nr+azc1xdnLMzmbDwYpeslcF5ifefO4U9PuUf/Z/+M/6t//6cb/2NH1J6L5xpbCP4bmgCHkkjJ62IShKo+aR+r57vV96sbCIV7de7jgBr665Tl/vAPYXDrMRXZ5TnjHPFZCTHNEr9YtHKNDsk3HgbctYKSzo8gZiWPZmDSNSgqOMDGY/DN9JIpUSbl+fi6D3OJRmeMYqRSS9xZAbjnCPD4Ihx91tCyDXPUuIoSuHjM5DzEO9Lete6jEYE9AMIX8VgCi1AicWQImIVaBoVqcjO8rVMXWQolwl8YUYCs0Jrpqa1R9Wi1ZT9FAZyMpG/4+1tdnYWnF+MOL/IuZovmC0KamubfBtDGoC0bHqOryurIu4sEzBfrr8hX7evqqzTuMQz+bJtpfc7heWxTTmTrSnK1vYWk+0tzi8U0+mMYrGgLAvKsmxMUqfTace2uK+lUYGB8SHPRD4aBebChDgRywxnSsCmUvN+xMT4vF83CqqqqlpygE3bb+fchWsqMEB9IdgQrEzXL/bbaLg7xLS0a7xHW0tmDNtbE/Z2dtnf35OgJtZRVjVlVVGUFYuyZDafU0eTmWu2/Ku6N5swvr9OX0P4/2XHsHZMkSAPv4slR9QOuE5upiFGtE9QK6XEVIfWJ6lPKEJ7/uO90lozzjMybXjx7Dm//7t/wG//9m9zfnLJRx9+xPHzxxwfi8P35cUJdV0Atbgv9UDXqvXoRw1bVTee35TIHWI8+qZofQHapmW1wAeGONK+30I0p8/zHICyLMgMITwuEDRV8W8Mzx7vbqQHnSskL5DWLBbyyvPnsgZZNkIhvsnjYHK1t7fH0dERR7ducnC0z97eDltbE8qi4Pzigls3b/H40WO2TIYvCor5gqJyfPH0hOlcc3VgcaOMy8dn7Oze4Marr/PkySMJLGQl4l4n2WOAP3VtyfN8icHr0959v7oUx/WZkKGz3C8XX3XCvljSjpvQqaq9dG32YNtMrD/YJrcG7UE0MesyBG2GbXhaMxA1ql/SRYsOMwIk2oRvMgHEpl5Jm8oYvJODJYC+vfT9ead94T3aWVxZUs/nZN6zZTIyk1PVDpsbjFXYylNdTvmd//LvUdqK3/g3/haFk/C3kavQKJH0upD4bWnNY7/pj+k408MVn8XvXa70ZcqXIXxSYmQoWkS/xUiUtqYDISlPlpHnGVo5dJMgz2EbR2xhGrvsijALHmJqoeT3APAIBHQjtiIxj1LYxqfI450NzAFkWpNnmtEoZ2syYpTnEs7VmIYOF0lncG1XkUnweESbJtqVdvyewJS4kAE7SpQ8WB+ycifJcpxzIdt9DMfbZpKFeBXFNKtlntJ1aMcJXfM4RVfC1hJ+NESOOLCSPPMhzLG82CZhjO1UHeSpVPTZEN5FmI2QdxHREm1pRaZgkgshdXJxhTq/YjpbYKuqQ5T2Ccc+AUnc62uiTg1J35qVWEEUbUrI9InNtKzLi/FlCLG+EOirJMiug4cKMChsIGiNMWjg8MYNvnj0OdPplNlsRl1JcI7cCPydTWdLTNsQcaIC4b01mfD06VPuvfYaKBrk2t9/YIkISu/Rqn3pE0l1XTdj6sO1lPgaGn9osZEcR0JTxmaaTL19p2qdhEKNxJDSisxkbBnNwe4Ot24ecfvWTW7c2Efhmc/nnF4UPHtxAs6zsAW+thiv0CajUu1ZWyKCkwAs/X0dug/XleveGXJapZ3xUnkZSXifUb2u3srfVfs95lvSSjOZTDrEdkpYDzGcqwIDdH/r5oqI53MymZABL5494w//4A/54V/9azx79JTPPv2M58+fc37+iNOz58yuLnCuRCsH3gYBpWH1inbnu47B6M9HcJztvJvC+H7dWNZFP4rluj1LapLOrd9fysRH5sEYQ1kWWFszHm9BCEEj+EzwkFImmCxKDq48z4UPcTXaK6z3DQ60FuqyIMvGVMWC+fQSpRQvnhkeZBmTrW1MnrG9PebgcI+bhwd8cecOW9tbYC33b93mycOHPPzkU5yfMK8MczdhUSv2DvZwymHIOXjlHg9NxgiDJONdAdc9HSuf/h3rM2ApTOvvSXqeB+k4F8ICOd+XQa4sL5UZPF6wyPU1khvdPWjei0S6rmVhIgcWE/zF51XdLlxM4qW0xphMpK9BeuCC6U5ZlmxPtprswynnH1XOSmtsXUPIBl5ZQRRZlklui9CWx4e8ao6yKBiPJ+1YXHrgWy4+9tVcuLKkmM3wVclEG0Zak5mc0tc4rTBOUXtLZRXVdMof/N//Adp7fuO3/yYVUDoXMokGu2QdNDJLwHJZKxAZjCH4G4nBqCm4DkSvI0j6lzf9bQj4DyFdH5jRZg7hb8tUGDKjJdt6QKpCvDq8q6ls3Wk/dtFdm5SQiBXa9ZBn4fLorGFI4vrEcVZeiBrvPTgxo8tVMJMaG8ajEaMsIzcGo0R05BG/nj6REpkXpzy1tWFAoZ6LWocek+yihgOcTxI5gaiEI3OBC8+6mpEIPGNGahXHEk5ZsljdM4APDEUkzlWzhKlpSfpXKTFtaxI02pTgizbN0pTyEqfd25pMa4xSaO3R2uFcqKtkHKNMofWYLMvJ8hF5Pubk7IzLyylVVXfG0J6D5bPXSA17hOLQme0TqUNEaypBSn9bRwRF2LHJXVnV96rxet+u/XW20WnbWika481rxt+HRem6x/trrQXnMSGvTlFV4B3GKA5uHIGicQSvagmooJXAvKIslvpqg0vQEnwaMqXZ3t4WZ3Cjsb6rERhay6G1WAW/0nOQItt1mq1VaxZxjKyX/C4hekWLZxNTlBj1xYS8U8KIK3SIgGOMmG1kxpApGBlNXVseP3nCixfP0HguLs85u6qYzkuquhaYFMfvFV63MLizPr41l+mv25Bm6GXKqns5xAxKRZbgUvpeyiiu62/VvUzvbdrOUFAAm2SCB4dGh/0Rkqk1I1+eZ3qGUr+1PjHcEoHdOVprhckwhtNnz/mD3/19vvvd7/Do84d8/uABJ8ennJ+dcH75mOnsAnHYE3O8iBE9XaHeOuZvU0ZuaD3TKGTxe5/h2MjpPqk/dG6SWvQZqH67fQYn0m4mE/vBui7IshExEqi8E6NQCtas64rGJEtkwJJvLJ4hJaKVuiwDvRKjiglSn9spWWaoFjPm0ytePHnM2bNn/N1/+9/m9dde5/MvPocs44P3f8rnz0559c1vU+ltyHJqnbG7PcE6xd7du4wPD6muzhpcHmFFVwBC5/e+KTnQMTMdukOpwCM131vGYZ5MiyDp4uxi5X6m5aUYjchcpP+Eu9WdBQBBLHHgMdFfZBAaAO7FfMp7sHWNUpChKcoCY/IookWjqeqa07NTxndGnXGli22tw1sJk6lQZHkeVGU+hAaTQxD7dMEZ3GRZo2JrAWskKGLbXZ8QpRTeWWxZgLWMlCJwMhiPUIlaYccZVI5tB8V0zh/+vX+AQfG9v/HX8EZT2hqrDEo5VGNekwKvZqaoDn5YLYWNUpIIalTUFq0AvENliKlYBVjXjSP97L1DHCgVxmTEPB5GC8GqgzbH2+DeLBRz2mIHD0UCOpZ0XK5ndpaeE9dIM3qMAV6S/nlJ7ZdpxdhoJqOMrcmIfCQIP8+EyVAN4SkOaCnD4sNZc0HKG+vFbNgEBtN7JRqNRJXpnMN6ybztXZsUsHnuw3kO5yUy6VEDEpfEE23JZU7BgSqsRxuuV+q6wGBExiJxZo+MQNQ4hXeVlvDIjY+M1km2eDBGNcyL1qaJCkbIRaKU2CCbTDXnIkoOtdGMtYQcHmWasYHcZLw4Oesgt6Fz1j+faf6QLvLvnptVZxe6mXuHEOYqIqyPxDch1vpEXYoUUoaphb/dZ6vm0LSpUi+o5TH1iZBVJYWJ3gYPJi9tV85i64qDwwOc9xSLBcWikOiEgWHWhIAgqkvQxjmrFFl6j3W2CX9ure3oftdph4bKKti3Dt7F0jcxyLIWjXYku7oNKR3fiwhb64w0+EeWZc3cMi1rWpVVI0Ari4K5deLE6ixGS2QHncChyntJhIknRjkKecY64+vMz4cw5c0ydwnh+Ns6pn5d6TD8A+911jk5lasY802Y4lSaO/Q8lo4ZbrKn0ZczUHYYbRoGHSS5LcECot9epIFSYQBxdgle7zMqPgiMqqpiMpmQ5zkX5xf83j/9Pb7+7td58sUjnj5+xNnZMRfnp5ydHTNbXEjkSCL5HdcvGLS+xF69DBPZr9u3YEkJ1nT/+2aGQ21dP2ZhBDYZb1z/ISE5VGL6pFt/3vYOOJyrqWsJZpRlOShJJmubucUxRNzvQ7JfjVM1RjlwGdaCtRXjUcbp2SmfPXjA1957j48//YTX7r/C+azg8aPPUJN9xntHnC/GmKucUZZx5+YRR6/u8It/fsjZF93zX9d1c8ZMsMqJa7yOYVsHJ2N7fSYjfQbCZFknQYD2vuo8GmmnzrkmKZ/JMmrXhpfVooNq7Ftjor+ozYgXzHlPZWsylYXDYDEmCyZFqtFiWOeovSC0w6MjyrKSMxEAdhxXZCaU0ahgJ1zbOoQC7REftl10rwial3ZuZVHhfQwnt4xsVAQ41koWV+s42NmlKAq89fhakQMFHowiU4a8qBk5xWy64Pf+/j9EAd/57b9B6ZzERlcSnSeGQPUsh+XzfrWUqFvEn6B91zXvp2inf5d7gi6Uiv34pL4n5hLpE/r4/rggXkit0g58aEdM7yTEW7SBDX1FpsLTIYo6hFTjsdCbvRdgFCFHH7lKBuMBRgiHCzauWSY+GJOxYZJnTPIMFSSMKpxXfGQywDndaEg6zDQhQzytyjkyExLaVjfMQ13XjSaido7atYxM1HRE8ylHXLfIdLglLUmX6QFcu15dozOQUGitNkL+BsbBtwijMYcMTIUJvhZZngtDEZlHozBZ6oehWymM9jhMYzrlfNRuAMqgTYYOvq+ZgZ1xRn6wg8nH6CznxYvj1gY3y8hyEUq4eB6T+fellcvnpEugdJakd+f7AHyI0emXvhRzVdlUCJC20WdIVtVZN67r3u//3p9PXLM8yxnpDHTGWENRGWZXZ+zt76O1pihLilIYDdeo72mYngjvO3fVWWJIbeVBOd/JDp76iKwjZtetx5BkN2Xk+vvdOvKmJoGqI0mMtuFVVZLlMVJaK1Gs65qY6NNai7WWxWLREEXat0E1ou24VloSk2m5wcZ7NIaQpEngp6nxxqMCoekbOEcEubIGRFMgEQTogSNynVBp07KOKb+OMe6XTYnLtK1V76R72LfvFxDiY4OACvDF4axriLwhH6vd3V2UUsxms+5z1UZOTO+RCGbbnDLj8ZjRaMRiseB3fud3uHXrNs+fPufx4wdcXZ5weXHC+dkLFoup4Eal8UFg2ok+uUIouek6fpnSt/cfunfX9Z0yI6vh0Or3h85TSzjXRJ9ApYKgWQeGMAgfA8GBJ+SL8BKlqr3vGZHZERop4thIoAf6xVnwQdtsLc5q6qrmydOnfPub38JkGUVZ8J3vfIPzP/sLssxRlFP8YsQ4y5lOM84nnmp+ydErt7j8wFDNuzmH2vNrMT2t+SoYljKBq7QafbwQ6b5GqxFgiYnCww3KxoxGXYvNeBY0FnUlxD86kMZK45WmshY8WC8mLAZF7UGZTPwuOkSzwQWLEqUM3kFViqRK7PITLUl8Twlxpr0W6Y0XCaikkK/EOd0LkSSSXqhqi9EZRpuGqPPOYUyGdcKlCj7z1HXJ5cU5Wmm2trYoqgKFDomiYHtnhyi9LqqKslyQec/eKMdUJbXzWAN4xwiFcY7Mi0p8YS1jFO5yxu/+/X+ANYpv/o0fUiqHx4pE1ytBqkRRVJAKExxvw13oODp73zioySGR/mNkmSg5UyoBoICiS6anbEDTfZDwe+/bCiHsbyv08UkDKbBTyQUNo2iEqhL9KWq1IiCPWV6FBomSntZ8qFOUzKHpNTlb8ptvvqREBKprctTh1rXkvhiPRkwmI0Z5Rp5rlCFEs4DaqxDJITAZ3jftydlKtA+AC6EXYxQaa4P2LQCySDTHd6y1IhEOkWm8k+ynLjD03qVMhAt3U+5nbWnWLHUkB4/3rX/I0lI2+9KVQBolZk4mRJ0jMg5ZLsyDEkBuihJttCQ9NBqjVQj/K4BdGA2H0YbaeIyqQvSwkCSp0WhYjI/xwsEYjfISZ/ymyRhlCl/NOD67xCNCBV0rdI7ETW+EAAEoex+ILhrJrfcixVWmFfc6Z2m1PG2UmHZ9elI074OGKJy++DE02SemrkOwKeHfJ+jTOm33Q3u47KcwWK/3+6q20jZX1Y1Edm5CElagtjW1q3FecbB/k0zlUNWUswXlohBCTYVAIE60nP010lqCdzRzcgInTIgEpVSrYYvjSsecli7xkpxx1cIZFE3I6FQq2NVCLPscdoRdXiTSdV1TFMJUeVwIQasbxkHek52IMMr59gypDoyW82idcN4xKabzkmtHKTG18iocR9UK8mIIcaMMSoX1CTKYZl0DES2wVAUBnmtgkkv2u0PE+57caKn4tq+hpz6acgpcb7Uq7UVK39O9vjv728E5sQNp24Q5LwnEmvmqpm4UTflI0xAY3NBwDEigPRgfI635tv8AW+bzecd8KB2cCTleFKoJl+88WOcxOmNrNMZVNf/yD/8QXxQs9IzPH37G9OqY6fSUy8tT5otLWTffzjPhI8MUl9epv/7NqL4k49FnylPc0nd4v66v9D5dP0aH7+X0kseKVHsdBWeC96JvRdBujMJ4nTjqmxDJKuHGhY4ViEaeZ4jljg3tRo1VHFvcARmXxYIrMc5gkABDtfWcnV+hMs3+zT2uri7Z3d3hv/3v/rt8+PAYjcfVlnlRMR97jk/nPLt8htY5i6pEexvwmW9xWGBu6pjby7dMngowxjR0lG/cBbwnmOq3DHUjOHZyQp2P/sMKk+UCH5XCGydaVQ/FdDa4n/3yEnk0JGtyHLBSyCV1AuBUUNV6L9GXsjynKEtcITa4eZ6D1sEvQwi13GSB+GoPaEQAafhOGzQoSilqS5AKtRJv6yzOVSjtgZawin+9l8RoWhthLGxwtJXJSMjULMN7R7FYsJhPMVqTGbi8FK/6vb0DvIednV2ctSitRGNS12RKoeoaE3IsgMd6h/EaYz15mBOjDFtVbGvDdLHgd/7+/4PdowNe++Y3cEY0K8ZLlIvIaMSjG+12w5losnJDBLQtIqWZeURarXlFej09bciyzqWGJjdfBGPddh2pg20HBiTttPbJEfgkmqU4dudQXkIxtoDKJ5d3eXyriOVuWQZc8XsKFPvAMlMZoyxnlI/IshxtFBjROHnn8dZjbZd4kbQArRNfo81wTpgFLz4akblwTs509LmwtRUn96C1sM6KM3iK8AMDUlsrWrOo3XASHYdA8DuvEsfyRkbTLEmDp/vL59M1T8Lj+QqDxOI2mURUI6iTjdHkWpHnWctM6qjREL+bLNidS33JcWKCJiMzhkwbMuPIgnQkCoWUam2t496MtOJga4S6dxeL5/T0StYZjzIekwnDkGVZiDuvG+ljPHt9SX6UaNaRCAx9N5Gme9IfreVu6uQmNQQLtFqV3nlbpyUYOqd934M+47GKqF4lRey8HxHkwDtD765C/uk5jzk1KmepnZV8QtZy8+YdJqMtbDmXCCvzBXVVt0iP7l3uSkXF/HU0GqE91GXF1mTSCDDyPO8w6ClzkJZGiwBy/jLT5NyJzEEaSr0vAUwFAPHODZUULvXfj8kyW2HHAAUevkdtRPzWPvNiqQEJQWWb29owEsiZNIEJFMf81cxih0BMgrlEjX9aLz0POpp+qQH8EcfuQRuz3AbxXGYNE7eO+Y1mQT5ZJ+mh9T3r3o/4VmdAzQAbNsb7Jsl8U5fg7Bq2SCV7apSWACBaNNtKt6KuGKK5ryVr5h0GpgL9AyGfV+WCMHOEVor33/8LPv3wI165e4eHDz7l4vKUYnHBxdUZ89klPlh4tPMMjEV/nr0xrCrrcOl1Gq2huQ61O8RIDL0zJGAZ7r//vWtaLm1JvZZmDZYuASc04as9Ta6NPjyS910QeKvkt35fqTUGoIRJEcGxoqpqtNJcTudcTS+5c/sWz5495cnTZ/w7P/w7vDj9M1yWsQhCstmiJNMjHnz0Ga9nhtI5cu9FNBHIPa98IxBzCBMAMQInjXDXWd+ZlwrCipRRbaxJkgsmeDAEgbEOnY+weOpgGaGAF0+eLe3VUNncdCoAx+YiBWmhybIgUXWYLOS6qMPG6CxkcYSyrKiqKqiYoarqYPttqKq6Afo2EPHKtHk7pL5tFsg528kG3tgF+pR4Fu7WOiHkxGO/wFohRCIwLYsF+zsTeT8s9mKxYJTnovIvCowJ2WiNmIc0uZBqJxuA+JjowEFrRKMt1igK62EUBCfWKGauYOIymM75p//Zf8l/7z/5H3P4xustt0krcYk+fPHfkHioiWHf/z0xLbiupMi1i8iG68L1BP8mQCSue+pSkdbrE059B8V1ZQjx95mM+JtSijzLyEcZ4/GIPJckgAqPqz1eSQbPLkME+Cg97PpYRALDOifaCSvJhJwTJsHW8kwQe9BGRKLYO2pfSw4P65rnMXKVRoOP66AkWaYPfhR4TI9xj5GrjM8bZqMPqG0qaQ13XRGkppR4RCIjc5frrzTUOKrKdMyjTDAxqxJGw2Q1RkdGQ5EZMbexWRZy1xhhDpTH1kK451nWZBbXRqRIRmm2JxPefO015vNPmC8qKlczsgpXOo6ODjs20lUgalOnNiAkReuasqVMZ0MMDpwppbs+Dmnp8cede7UO4ffPdP98Xoeg++00Y42S6xUIfN370GaNXdVvK8EEEhbLI4j84GCf8XjM5eyKolg0En/nHMoEsynnlghNaVuEVtZaRiaXM1WJJqwoStEWDsC3PsxI19F5C1V3/FFLKOemO68hONGHKavWtUPA98xKlgjmAQZuXVkFH9M16EiaWfYzGuovZR699yizQirtl4nMZkyJA/zQGPtncWjvl8638w1z0q0rBOYQE952ujSFzngG3+m9r2jX1DkXpMmilWv8ORJGtT+noXsT4VRdi1+G0YpnT5/wB3/wB9x75RUeffE5lxeXLBZTptNL5rMrGqLQ+UgkdMt6nmLl/IfKOsZhnfAkPWPr7simmpTr7sI65qR/X1On9ehjJgK9Wkz3e+MGuTd1PRzxaRA2y4NmDN45fBB2lEXBi6fHvP7aW7z/0w8wTnF1dka9uOTr33mXj17MyU1GObvk5HLBi2dPuHt7G68zLMLcxvss+ebCWFUHmAhjobVoIALO9+HORusXfIvPxQQsnVfw9IkCLw1lVaBywcnOSbvnJ6dr9yaWjRmNsqwwmTh0j0YjqoAscsTxO8sy6qpOkvMJUrDeN6rxqqqbTctMHqSMvvH3iJmDPVBWlagqddxIsfMXe3TbXHhobV9j20qF8IG+jRgSo9XEze9HR4jiX+fEXlYr1cR5H48nbG/vQCDgxK7SSXKXIPWxPpp4iQMeweQFD1o5lHVkXjHWjlpbyrJk10yYH5/wj/+z/5z/zv/kf8jk5k2cVsFZUszUjAIdcJRfdTGVitRjc/BTRDNU+pep97QFngPvDSGLdijLwClyylEytITEPR1GYyhCRfwcL3z/96H++8RbX8oYCc8ogR+Nx4xHOXlgMuO4xIfaSejO0J2NbbjIaNjGJC8SUs6JZqt2NbV1DQPurLxvGyZDCJ1IDDvvcdRYXy8RUtpojBfzJcgaBNgiYYunSzTHsegQh7uvVhdph3iSoFSI/hUXFIEyBE1JBF54AXpY6tqjlMVag9aS40Ac/g3WOLSxqLLGGAlbnBkJFVzXHqNrjBKGJM/zwIQEW3cfncoJ2eFFk5ZlOVsjzVtvvsavPv6U2vpmPy4uLkNkmFa1rbXqCCY6Z2/FuVVade7bsCnE+rJO2jdU0ju5TsuwqT/CWiS/ou91GoyhPtp6oplO4ZBSivF4zP7BPucnzymKgvl8Tm1rJLN01oCu2G/HkTQc07qu8bUIdLQWk9aqqlCJ30+qAVpmWFo4MDTvyFT2M0t3CPUevFzFiKS/9dtI57ZunMtruxq2D+1V+nsUXhjVJiNcB7vj+IQZCgKHATzinR88a/IFVlH3Xx4nddvYhGlm9TBWtiNngUbr28qwu+HAPZLEjpgLzAvOdEr2OMuyxpdoVd95njObzchzw2iUUy4W/O7v/A6729ucnRxzdXnBfH7FopgynwbH7yhsUgY/sFSbEOUvUzZt77qz+2Xb/7J1oStUhBj1rY3W1CTd1BnOiaXNEJPqaRkTk2jn0n6Wxumj1qD1oaydp6xKnj59xm/+xvfxDq7OryRUjyt59c4+H72YYqsFjz7+mE8++Al+ccx37vxVxrt7zK+mAhN9eyq9B6PFtDRliFFKLC9wQZsZGQkvsXlJzBGjvjAhCxRezFUJSbhR+NxwdPsmhweHfPTLX2GdJucrzgzuPNgyxhRX1LUQ1nUlUaeqKo1+IsRWVdctAU7MlCoONc754IsRgadpom7I5ueNpkNr3TiXRxu5aIeWqrabJfI0Ulxrad6LHG0EdjHxk/wuUoK6rrlx4wZ7u7vU1vL666835lPxcEos5eA8pIKzr9FY59HeY6u6jaZla2rnJUOrUSjtybTD1hWudoz1FhePHvKP//P/M//Bf/I/xY/HYoaRG7zWQWrRbn+/RCKzXftlBLhJ6RPhUX2yTirxckBmGdF263U1DX0gkdZ9GaCWIt/U3KmPsCXqi0jlI0Np68jhifq0DFI1fFdzIeYySkz4bPu7MBNiry5nK2hFXGsrGrVu0qZvGA2lxS8iCz4POrHtzZRqIs1o1SbAdM7jbEUM2RyjZXjnkCPlyY3cs3wUoqwFP47JZNSYQFVVTV1XWOuoyor5PJh2oULELhMYHWGqA1kIiP+JQgVH9hrrPKpWTZjO2nqM9tS5CUyGzDM3hqoOmo08wxiwXjK0Gm3IcoXRDmNAW9GCHe7t8erd23z+6DFKGbxXlGWNMfEMERiN7nntn5XB3z2NOVRkSNPn/ffbNsRBfpNy7Rh6pU9gbsIYDBIWvebXwYl1ROHyuFuNTkR4xmQcHBzwudJUZUVRFNRB4IQixPxXg2scpdVND761/Z7PZ0y2txp4sEpzm0oxfX/inTkGRLuCcB9iIvp1hwj99Fn39+Xz02eEV5VN9ys9y9bZzlqsY4KbuUIH5fSZidUk66qVHmaSNyJ+Fc2SLc3fD4wv/O5ZPc5VTJdPXvJe/iO64nYftdJ4JeZ/USiJah28454ORVyKz8qyRCnFKM9R3vH+T3/Kk0ePONjb5eT4BeViTl0tWMyusLZC4cA7CQKwmiRYCz++Ckakfx+G+u/Dpk3g26alT5OsgsX9v753v1MBgNa+sXbp3434XqRf+nAqpZ2aeTuxzHFeTLZi7qCyLDm7PGe0NcLkOR9/8inTqytsXbI9GaEN2Krk4Se/4OTpA7bympPTE6wy1F4FKXYXnljrMDEnW5x/QH7ex1wXKgjSw5jjgrSr2pxfgd002cZVlkOewXjMt37419jf3ePh46dcVcd4t8Hd5WUS9inNYjFnPB5RlJWoR7WhKBbB/rxlNASYCTFlvTi0RiRRK9uYLWyNt0Jkp0Ck1I6yKkEpTGa4vLxqojBIhnFQynSAZRfBqNYJlNQhSTeJnWwyVnk/2BbXNSqEB41Sc+8cJoS9lbZMIwHHK7wGbwy7Nw64eXDAxYsTFour5t3aO2EwlIdgr5dZ2NIGlcO0rqitqMoef/BT/uU//kf8m//+f8jUVvjcYL1oeVQ8KOu25xqCYJP6Td0Odl/9XkrwXNdfKi1YZhZ8Bwj0kfkqgmxw7Cs+DxEGESjEzJ6ReLZWbMzFbE0urPOeIvxNNSIgv9XWNqZQ8ZzVdd34XsT7gFc41zLCMdmeAAdxRhbi20mywoQIac5vXeJqMUHRWkm+iSzj5uEhmdYcHR0yGo3Z2dlmMpk0NpsqiRVusoisRHM2zkNuHFSINx4RrggWyrrm8uKSFyennJyecXp2zqIsJfpVaEMrg3MqEP0u2OCHu+2FqHS1xelWujTKc9H2WEdmHUYZqsqG3AExt4Ajsx5yi3YwNh6jDFp7Xrl1g4uzUy6vSiQCi2gXPb4x4Wr9tobP6CDz2jvnnXO3jpjv0zobnN2hsupO9ZFsitz6dWMZQpAxxsqqsa4ay8rSfzVwHFVZcuPoBt475os5dV1RVmWD8OJrfZ+UeLdUEBwRGGmF+PtFSX0f/iwNq8cYpiRwHwYp1pu7DL83XFa9mzKk3SPVzmNTc9d+6Wvdmr48xMAVsd4qRqPvON/9kM6DxnxweT2W7eVjGWLU4xhWrqtf32Y6h3VneF1UucE+Bx63dy3xtYmvOMdoNG7uZepDNMR8lmXZ5Ee5ODvjn/3RHzKZjHj+/Cm2LKiqksV8RrGYYQyiQfEBMHsFPYHGOiHcV1FehlkYgrFD7Wza7ybzGmL2U+FMei9S2CkBGtpQ3V0fr1YzMQRvV/XroYkgqYMTkNdCJ5xenVD4gt/8Kz/gFx98xO//0R8x2d2mtFUIt1tRLa4wrmA7RCBzKqNyvtl/mVvC7BBCXvvoTxvgp9JBmCMlWv6073cWMKEBQeksMM4Z9956m7e//U3UjSPU1g6/+bf+Fn/wT/8ps9l0oz3cmNG4mk4py5IiXI50gQWJmWYi8rtjPBoLoe7F4W40HrOzsyMcvwe85NioqkryE8QU6kqRj0dNVtY06kfHKTM5QN6LKjMfjYRxCGrLPBfb3tF41JhPaC2mGgTOU7ua7a1t8J5iUaC8ZzLZIs9HoBVbW9tobRiNJhIz3Yv02ivF9v4uf/O3fouTBw+Yz2cUs4KqXIgpjAafazGP8aKGwoGuxL7T55qFKzC2Jqsr/vT3f5e3v/2bvPqNd1l4h/MaS0xuRaPZGLYPjwB81Q6uEYGwDAiUitGUehKJCIB92ueAhKnXjYxfdS5sbDc1aOhL/9YBrP7vq4iOPrORhqTMQg6VVjoQ+3YoC8FxBgdUKvpVpLlggkO2rRttRpyfc62TtzAYnhj9IuIok+VhLLoxV1MotCsxgK0t88U8+Bkp9vb2uHnzkIO9HXb3dtna2sJoQ1VXFIuCuqwoFwXldMrV6YlEvgmO41XtcVbCPsc10GGvM28xSjQ7o9GILMvY2dlhd3eH0bZmZ3eXg1dv8+Zr93BeMZvPOb284tHpCccnp5yfXbJY1MSQfg1Qj8bL4Zv3IfGRrYMGRrQyVlvq4BCeO2EwYhCI+NnrYK7lPBOdobQhU4o379/nFx8+wLpW+iRSJXA6SmZ657GHeJYIlfhCD0nF38yKe6RUl61Zh1SHwmMOlT4iS+/GauZ92fY9/ax741/qQz4R7c7DN+jd1aSF5pNKvjrvuHnzJgBVVVFWFVVZtdKyhBmN9VNH3aYL74kaBzGdqjtz3JTZiH0OzWGIYFjXXjPflySchtpLCZw+E5Du97ocMClh1RmnkshTmzBm/WctOzhkVrLi9zUajXS+sb/Bdb6GrkznJj+km9obfXOlV5uaddq8Zgxp/T4u3traYjabNWY5ndxjSZMxgIcxYhT6z/7ZHzGbTSm1oioKvK2oq5LFfArYljAMkdHi2g/NZwln98oQYyj1X+Zsr2P8VOee+eYexzGTPEv7Wke/rC5DYx6Ci0qx9HtkGq3t3p9m3qr5T4fRSE2ohpgboQ0EssV34nm4ml1wdnXC2fScn/78fb5W1bzx9lvMF4X06yx5BlpZtsYZ2mjyrS2K2kFiOt45h1qjgttCGk3KaNqIdgp89DVh+d7J/GKgJ4N3ilfu3+e9b3+bm/fvYfZ2uKpLjPNcFgWzqsK6zTZsY0bj+9/8TiN9jQc8mmy0tsziHC4JRFrHbqNNY+cWE37ZkFSvUUnSCC6GNzA8koXoMhkpAOkj3/jXKwmVqaEh3GWcGdiccbYFwPa2xTtNPt5GWwm9OJkI04TS5PlYRu1zKp1ROsu/+Isf89qtm1R72xR1jTvYZV5V5KMRo8A8bec5VxcXLC4vmV9dkWlNXmsmFkpXQaZgMeWf/6O/x3/w3v8M63NyZ2SDjMclAgwfONX4LS39uy+IvK3WRbLdutKufFLBxrCJzxzXMuE3vIcOm+CXYHwzJk/30qdSNbkH6QCDZM/Tn94yYYDvvhZ+87REZ79E5jXLcvJ8jNY53mlQGqtkLN5JFtEmmR5Q+ypoJ3xjJmWtRIiqfIwrK2OwtSRS8tFrOgA0CUCmQsQ10DpHK5BweaKtmM2m1IsFI5NxeHDAm6/fD9qJMWVZMJvNmc/nnJ0/papKqkoCLdjaYhdzyqJoQmzaug428VAWFWVVN/c4ZbpybcQJPssZTyaMRyPyUS7nXkM+ytna2mZra4u9vX329vbY3d/jm2/skr37DtPpjGfPX3B2fsnzF89ZlDWWjEznoMWkSo6FaDs1Bo1p8uTU2qMNGO+o8WQ+I/MOHaJIGWcxhPCzpsZlYLQjyzPG2xMOD/Y4Pj0P51eBCuFRfTwWy0gkhRtLUmAIplMpwyQHTRFNPsOtSc8kS4LG1SU9m33ioNdm/70YsV0lv/Xr6TDeZlzhs5OD19JoniTPTXA0VarzHLElS1hG1bMRFxhtGhgi0fBK59i/cUOCRFYF9WJGNZ/iqhLsOGjGVTOZTEv0P+eSCGBxPsF/TRnF9PIKSTKp8bTakDRRaTK0pv31PMFmPgLL+Y1WvJf0J07vvkvsdAbYEyAt0e6K5ZMQ2xH4nCbghP5c26hH/eJTGK7az4EsHH4/IfSXGLf+8g8wE0sMTSDK0l83ImF8b0rDvO9gv6twg4rILdYPApmUiGwEoLT4RCst1IytG9xklOLVV1/l6eOnWAcYRe0tTosZq1KOF89e8JMf/Tne1pS2RilLVS9YFJdYW6CUD3lrkyACKTc/NMeB4+ib530BhzwVVNVlcrsNRVNG8eOL4dPbMKvSTmTAUg2dR4hh72LI5IYqSEfWGU/8/bo7ed3zdp+jT28UPLX+v3gfIqJatI6adINzoFXWwrqoGZSND4LJeMbbNdNaiyO1EjholJEsXc5TzGqmF3PuvnKbWXFJUc+o6pIvHj5id3SDWi+wSuO1oShqyqrCGsXUWTGbTlZLoiOKdVFtHRIMRjPZ2uL+/fvMZwsuTs4k6lVwQciD8H9eLLBBkyOalLgWEtX0a+99i53dXaaLir15BdUVVVnwxdkD3v/jP8bOCrzdTPu6eXhbaOI+R62DQpxaTdAOCK7SwWFFgJ8KO+Stk6NlPV5LhCiCHbsyRvxN6cCvxn48XnZA2gvrIdm+XXOwJTRuPBBdQOJ0DF9Im5olqqIsRPJAKYPSGbN5IarPyqFVJgcu4LAI2GulYGeL/HAXfesmr7/9JtPpAufh9iuvsLW9zdHRIdPLK3a2d3jy5AnaW37+J3/KyeePOHv8DBSUiyk+0+BrPv/oAz776Jfc/db3ZFwKnI5EfoqKfPtfn1y2YXy3AiQlqG6pUotwOtoF3yU46Ixo2dmyM4KEKezb6kab7bToFVx3+rmzxy7m9lD4JKlgrNslLHXwzwlmfoFp6mpcgt+Dcwi4ECI9DXMpPhoOp4Pzv/MBUbkGCcWJjUa5xKXWmkxpnHGgHFVZMJ1dURYzdre3eP3ebW4c3MCojPlixvTqkufPH7NYzCnLknJRUMwLrq6uuLy4YDqdcXV1xdXVFYvpBcV83pgnRsd0oGM22DB6EXHojNEoJ89F85eHsKKTyYTJWJiL/YN9Dg4OODw8ZGd7h53dbcZbOTu72xwcHnKwLz4Tb73+Ks+OT3jy/IzZbI73ATF58T1R3oe1FkbeKY9TIeO5FW2SONEbtNVkLphSOQlH6HPxx8gycKpGOcWNo0POLy8l6IM2DTL2RJvqZRV6PNtDmo3mPA3cHAFdXX+iVoOzeUnPrmrgZ2Sy22c6gX+xbl962TAU/feSZ83vWnccW9tqsmhtAI5hZmxVifkEFApM8F3znhu3bpJnObWtKYsFZTHHheSUHcDjg5lBuCM6tiWNNuPIsoy6roIAqs8ohsqhtHc5jHGtTfF685xOzRVMagde9YhBY5ZNLta136nTm1enJLR9d4+W27h2egn3GvH5qmorGTfVY5oYXq8l5oP2vdW4ZHgwQ+MYWt1BbUSzPCnxEO9ke8aga4cftyTe1TyESNVakucZYxiPxxTFovVPVApnoymjwKXf/93fo5zPyTKNsxUKS1nOWSxmdAUZ6zdwiYEdquu78o1Gq9is4WofB+VTOKfJTGvSm5K/KTMt70vHWml8gP9AR/Le4vL4vbV4WFc2EQy0dVrNyvIaBJ9Db6nqElSOyWJepWjC6RuBaaqliAudwqCYx0o0VtJnXVch4ikcPz/lvW+8hzFivl8UBacnZ2zfuS20Zp5LTjbruLqakoUw+1H4CbRO3qF9bcJZ1TBbzDg9P+Vw/5ByMsZay2QykkS6JsM5i6l1E0Zfo1FGB42y0JpPnj/FPnmEc47tX3wQGC9HMbvClXMme9sbrT+8BKNRuWW7MO+Dk3jthIBQihiDv1HDeIdBfCd0SAak0Y3E3CtNBDFNkqGGKJTljOdPqchk+IYJiX3FzW1wlm8Pa1MnJP8KMUqxIVymLatGxem9Zzwec3FxgTGGciF5QJqIQIkNa21yDu7d5923XycLSG9SWp4/f8HDjz7g5s2b/M037+GMw25vszO6y97WFgtX8fbXvsb/6//69zA+xy88yluMhqIq+Mmf/Cn/3rd/g8I7bMjEpE1fCtElUjYtQ6rW6+q9TPvrSioNWmcv2+971Tj7hGG3Xhcop31D0G7pNLu8a8+WT/18oh+Fx9qyE72oYUqQCA3iqxeAQOgv0waCr4A4d+uQj8Mxm54xn18xynPeuH+fvd1dvHNcXlzw8LPPmF3NKMsFFxfnnF+ccfziBWfnp1ydnbOYzZjNZsH0sKSuLbausbZs1iEChjaaVSslTjlyQTK6CfscVcMqOGIbbchz0XDkmfizjMYj9vcPODq6wd27dzm8cYPDo0N294UZuX33Dnfv3uPs/JJHjx8zmxch1LVcZpUk6MqMiTLpRhMaxx3HpIM0zOjg/+Gjv1Uwg9M5Ozs7XF1dhcRlMWRyAzzWnMyEwN/APj4i5/6ZGjqH6+7OOsfYoegmad2hZFhD9Vb1qwfG1WgblfjlpEzUdX16fBOzopH2BmLr4OCA8WTCdD4X86myoorZlXtMVHw/SpZTYUcc+87ODu5ZC0fiuFaFSV1lbtSv6+xqeDj0/pDmvNtXV8vUr/9yRNKXL+vO55ft78vMZah03t9s+V+qvy8zLgGPy9YSXfyVHM62M5RSbG1JkILRaIRzjouLi4Z/cyHwR57l5EbzxWcP+eUHP8dohasrvLM4V1MUC8kujd8YnnzZkt4R533n/qbCGeWXcXH0x00XI4btlbKcuK95rvpMRoJTXcsMdNt/iUOSlCG40BcqpfRAzL2TmXxle5HpSNscYqaVUh36sipLrqYzJltbjMZjUFAWJcfHp7BX4JUmH40xecZoPKIoF+wc7LO1t00WTblDWgUTfIatryAwrpJQ14BxnE/PUCPP7mgbYwxbetKMad8c4INgJ5pLmyCAtHgIyXa990wmE27fuc3O9jbbu9ts72yxu7vL3t7uRuu/MaOxKMuwgC0Hr2gZipisKxL47eFSTX0fbNh1iNeqQhxoV9dEIxjbhG9TnQsfpeke4T6dte04kuf9AwRBAqkc2qmgEfESiQeRKtRl2eT4iAeuLEtGoxFlWTIejzsO5lHNO87G3L79Ktl4myzXzBcFfpyRbW+h84wvHj/i7OoSbTSlqylxzLwlv3nIzuERemcL5yzaiDmDxJV3fPrzn1FdXOLH21htaPIQap9IyV++DCGYJclo3LXkonQvk24u2BCSSQmvVUjoOsnWkDR11fhX9esHpRZdtXeqqfFeTEY8NmEm2+hSki23GhxDvAdaKTAG5b3kVEGFRHeZhJe0lrooOD89wznHnTu3+M433qNYFLx4/oIXj46ZXU25OL/g/PyEJ08+5+z0hIuLc66mlywWwljUxRzlPXVVLe2P9bbJFqrqOL8oZWkWq5HEtASzoghRULyXd5s98qoJASz5LXKUVoyyCZmZkOc5k+0tDo+OuHP3LnfvvcJr91/j8MYRN2/d4mtvvYlXnk8/fcjx6Xmb3VmLeRNBioIK0nTXMvSReFMCeMIdFeYjywzeS6QwbTImk0mIEBe1k7I7PtFUpUh11flLz8zQ53Vl8Hxc00//2cvc7xTepZK2oWewmU9DmtwwvnvdmAT8Ds99MtkSJnA2Y7FYUFUlNgbcaJjBtn5nbr3fvZdw6NOrq4aRSQmifhvr1nxorOlcr4NPm7a56t1Va/oy7V/X1qq6Q3B/aN6b7P1QGSLANrlnm5RN93cdQwjLfELyZgMX4/txHdJwylH4F+vVdUVVmYbBiFpla22jMohBMLRSUDv+3//sn1MVBaORmOk4vGiuF4tA73w5wnpdWbpj6d2hKyhoYKZa9h9q/WUNUSMg66ZJ8zKoJLlvhOfSdmvF0D+TmRnhEYK61e6KLUra3rpyHbxtny/7dMT90yqjL19Z1W7qd9oJvNFzILe14+L8Amc9B/uHGJ1RlBXPnj3DHF2QZWOUCmuqFSrT/Ef/8X9EeXUVTP9Fs6FcFNR4lBYcmmUZky3BySjV0LmN4Eq1mnMR9ok1Uh58VWV/TAh0JIaTOggFs1wsMqyrm7Nc23ppHYbKxoxGUVaN5CklALTWEg3BgrUleZ7hPSGLog+ajKCxSJEgNGpJG0MdqjYjeAoE+loOFbQgSsVwXe3hkIuhG6mdddK/10AZgIXWTaI9pRSuajUaqTS1rmvKqmR7e7sZS3NAPYwxUFnG+Yijm4eA4uL8AlXUmIM5Hx2fcvb0OXdffUXyaCiN9R4/mZCrjO2DAy5nM8koGvIfZArmL445+eIxh++8i9UKA605GvG8bC6luq6k+wl09mmpbqqnf4nSZxr6wC59NiSZ7L+zar4tAFkGHqm0OCILH6QljZOdcjhXdwBO//0h5NtkyfWezGSYAJyzXHI6zK6mnBwfY7Tma+++y97uHk8fP+UXP/2Qs7NTLs7OefH8BafHx7x4/oLzi+fM5mfig1GWWFfjfQhmEPTfKUPWRaoyr8g0t0MN0v3mne7vKmgY4t8wHcRcXs4oQFWJ0KHKK0am5Mo69EXG8clzHn7+KZOfbXHr1m1euXOX1994g1fu3ePW7Tu8+sorvH7/Pg8efsGLkxMmkwlZnkniNR9tXTVedZPoxbtZoZEY4pbo8xWJTbJK8s6EBKI+IHalVMjH02KLIYJ06IwNfe+f4SGGfBNtQ3wnvq8HxjfUZ9rv0B3o+j4tn4/4PUpY++3iQWiK7lm/jhiMyCutr7UORJZjf3+fJ8+fURQFRVFQlmVzltNpdINELEsGI7GnQ9jz9NnLwIxlYQdsCtgGhVkJAbXJu5vUu37MXx7mbzKGTdtZV9YJt5YYYb/+bq5rc9V4hhicOHcRZg6speq+2787QvcEAl23kSud8xRF0TGrbfpXQYjqRcttlOLZ48d88uGHGAXeWrwXrbQwGQ6jxKSXa9Z41fjXsVJDRRiK9p0oeI2Cu9TvIj0/8lvf/00nDEHLQHT2dwD2NfcfIaabDOxKAgfJlIZNWjed46oS5xP3LtKDSmXNFnTe9128kpaOiV14J7Zb15aiqJjN5mSZ5JOrK8vZ2QVHi5Kd3Qlo8YETUtfxztfebvK2xXOrEbpQwHYNhHD33jXwrBGAkqy/UoF+gCiUs9aSj0aNH40XgC79GR0MGZ3Qr7ZGO0euFKqX0HVV2ZzRqK0wAy4SJYq6KGUSXpzA8R7tZDPKECu94Yijuiza3oV/hAPrlaIKCcX6iLrlnOWtaIaF7xIkWZbhggTBABhJ/leUFWleERM9ewITkidEfEzS570ADUVr5hOBCBCIF5iXc3SuObwhvhi50WxlOfV4gq8tp8cn3HvtNSpbk5mM0lqyfIT2mhu3bnL19KkQWF6i6hgUzBc8e/CAG+9+jSoh7L3/cgjiusv1ZSRW1/XVJ8zj3yFJ2tCY0vqbji8lRlIriCFiRRhUcYIRPlZ8A7yvGlOjtn+4DmjHp3mWCyLRGqM0V9NLTo6PyUzG9779Hcqy4PmTp/z0yY85fv6C42fPOT055vTkmKsryf5aLBbUdYFzNdbWgPg2aA3KW6LbZFilhmhU4beotSPMq12gdKSq+/MawB35jtiPR+5d6UucknwbaAVzhTKayWTCxfkJjx8+4Oc/+wteefUeb775Nm+89Ra3bt/h3muv88qrd/n4k085Oz3h4PCQzOiQd8RhQrje1EwRQu4RJ3AlcwZnxAwtHwWzHa0ZjUbU9SI5E8t3JjW3+arKJmd0qE4cV5Q4rSKWVxGXfUL0q7zLQ+NY1XdzMHrPnXNgLUdHh0CIPFWWlFUppgn5aOlqNfs1wCRExjILwgJYDtc6RFj2x7WOyRyCsSsFLwmxtQlcTmHgX+ZebVr667ZMQLbP+r/1n61q7y+zrNvbVXsogkzV0iADJWVy03arSuzsdeMHpiSggWtDh0cmujuW1p81Mxm50vz5n/wZ5XxBlgVmxTnqsqAqCwn24K834+zPPcw0/n9wnYb8Z1ScR9JWvGveh+SESWnC/ANKGVQksCJj1OAaTxMtsy/EQS9tQCM8cO37SrUmWs5F/PfV3aOUKI+MZIRdYkZlMSZbuuM+vLxOyJHSEU27XkylZtNZSAQtNGa9KJgvSibbMJ5siWO+knxSL148Y1x5tA/WLx68k3xZs9kMtCLXCqM0tRO/z1E+AmgS/9YxaIxzgWmE+/fvM5lM+L3f+z0Atnd2sHWNUZLDy1rJBVZVdbMmB3s7vHL7JpeXl3zyyaf8j37wG9eu8caMRu0t+JhoTGJEew0mz3FVTVmKbbgKJhY2cnRaY+u6Eyo17q4ODAi0JkkOWUjfUUOZwFDURA6sLMuOBL5PwKbEomgpghrSe0xwxhUmwlPWFVVw1DHGMJ1NUUpTlCXaw+npaSPJj0DEaI3SloKKghqznVNfSc4MbzzzskCPcl6cn+KMorKyZtW8ItMZ1aLg9u07fK5+3nD+3nux4/fw6LMHfFtB7SyZVx27xyh5TCUvm0qA1gHi1Q1s8nxZ8tYfQ3+PUse/VWNd221PMtaJBuPVEhCLc4/MKUTzqeAP5D2SVds1xGgLLPrf2zkrQAcEkhmDBmxl+eKLz1EKvvbOu5RFyft/8Rc8efyIZ0+fcvz8BdOrcy7Pj7m4PKeuFpSLGfgapbz4HpADDmPCvEIeAa9UK9PxrVROhA6qA4hVwmikTEeXefJh7gPnKCCMuD4o1TAeeB80LR5csOu0UNcFRmdU+ZzFfMz08pKHDx5w+xcf8PX33uOd4xNuv3qPN994A+ssv/jlL1FGs7Wzgw45NlJEFjWaMQs7xKghIfqXd/jMh8SGXU2nUgKQnWo1WS/FwHofJSKdn1ch8U0Y6PSd9EwOtbeuXUXXafyrLQN3mNTpc7leurbxu9YanWXcuXMXBRTFQhiNUvydfArIGJp7Fx7EO14FLXSfybhuKkvrGL5GodeqcQwTrcNz70o9B4bzFRPgqwj9L1PSefSja4XeNm4nDO4l3urW7G/Vuqk14hOlGnSkVISNcZPTBqJPUQvDWzw0zLxERqOjSUMsJAhEsEv8RtP3BYQ5jJFwpafHJ/z8Z++TmYwYvtY5y3w+D2OKmhA1eBPXlsikx2mn0fMakJ/gDOjA2vROdfOqtDgWUl+M4DT/krAoTYi6/K7q3THJF2WtAmVFy94Q8b03V+D9a8ejWm1jayJfo3VOkKPHFokLNwQX+gx7CheiRmOxKJjPF+zs7DCblQHNaGazKfuHNyRAEuJXXNWWP/z93+PZT37BXj6hWBTYusJbL+bYdS052rKMoiyWjrt1VhIRKyURB4kCG83dO7f44Q9/yOlHD/j8888bvKu9RlvdOr0HJllrzdb2mE+3hHV49uzZtesKL5MZ3NYSNcBZnLVUQnkwLUo0Yj61NZlQLEqOjo4YjyQHhTaa84tzptNpQrwF73nvUM527QG1DmYsMdmWJDgrixqlNVoFu/nIcWs57HVtcViR6YZLVhVFyK2Ry1XwnqqscVpjJhPRsjiH14ZFXWNsjVOe6WKOC5mGt0cZi9mM0Vjyc5xPL7m8vER7z42DHUaZQdUOVXpyPcJ6T+UdFbB/dIPReEtCNtYLJnrEZXGJ3h1xZSt2795itLsDLzJqW2GtIke0Gs++eIgvpmTjMU4ZrKJRJ4q44noJW/+3WCKjEoFEQ6z6CGwVqTCl87ZP+oj/iRdeOkuqBoepeGmj74BvnzfjC8Nd54zbZ1T6pWvm1HWmFaAByntsXYeeW4dv31xO3wEUTQZ67/EheWJD8HsJM6oN6ExL1BGnOHnxgpMXJ7z71jt473j/x+/zxRcPg+biOWenL5hNr5jPLymLOWVZtEA13g2tAAmy4KGNbplKHON/VHcdo429mFCtOCckDAo0CHLFypMC1rh/1tugUO2aOlrrcLYC75lXC4zOyOc5s/kFz58/4sNf/JLvfucHXL33NW7dvcNvfOdbPHnxjC8eP2J//4hc59TOSrvG4FB4pTAKdIAbYh4lgK9GcnJked6MRFbNNgsX93cot8QwEmoRXMoOL/EcCRIZaqUb3Ul1/jbnS37sNrs0nCFiqdt+v42vgpT1RDvg+C2ugl/SYii8OLU63wg0jVZgMm6/eg+Ppyrm2HJOVc6R8LRpOGAPTjIsiy1ye+7aaYoW2taVhNJF/O2aNVQxCECyBh2aqssEdKBVuM9LDBMqhOD1HfArKNAFfObQveZheR/bMQwRkMl7PeahT7z8ZZQhzZ/MIMKG4RPV4atCHhSRyMfTEvyklmbcwi3l2/vWr9PQzR1BSSsk6Zjsp7CRbsQoEmsMaS/ZfZUehoC3goBDKcmbpRA8LdYUoa0QWEa79myk42v2DYtRkOcGsHzwwftcXV0wMZJkDSc+d1VdCEpGyz8JYdhdGr98rqJ2pS2JxjaJFhWZgoDuo84g5HxQEqgnEvmBHuibAC3DS0e6CUrFsxSeNVvTHbXvWd20J0An5psywhZuRx9RiQLqgha8hePD96MP5/vC1nR+6e/WWbQr8L4NWpRUat+Lc0tolKgh0kEwGLhNPFA7z2w+D34RYiqHq9DFJU4pyMZkyoLOWdgMPy+5fPaERRSK0tJVLpzBGAHTu1ZoqLVpo+vTmksrpbE1fPFgyj94/IX4wlQVXmsRZDpQrmU0tNbYOmjsqitOL9rgSJuUjRmNfLQd7G0FNVRBY5DpDI9G54qiFpLjxek5eC/EuRY1kQeMyamjE7aRzMTWO1CSOE20DzXzogR0SAcfAJ7OKasKCEm8MokGYAGdSbz+ypaJJFNRhCRnyoFzwihZNLX1UNZkuQqJ+yxlVTGZjLG25uLiAqcyJlvb1BrhErVwg2VZYkMeAuckyZktawnbax3TqymXV1eUtsYpUZfaxJFcKzGpsTj2bhwy2d5mNJ5wtRD1l8KQZYbzsxPmlxeo7AiVZcHhPl6KeNDD35egKJrLlN6N/uX03d/6ACI9XEtaikQqkD5zziXIpM8IuYBMlt+N/aUStrTvvoYm/msS4NEyGcn0OmNLEc8qgBOBRcAv0odS4Swq0CKt/fTDT7h1eINvfv3rfPzhR3zyycccHz/j7OyEs9NjplfnFIsZVbWgLBbECErdNQ7rEBExyfMU56zc9/a91ZKcZbS/vqTUW7Le0Ggc06rR98o5R0VFVZcUxUIcHeclJ89P+PCjD/ju97/PG2+/xd379/jm17/Jxx9/QpaPmOzsUNai2VTGAArtA2KP3XgfMkSbJmdEGx0uakVEwxPPYGQcY5jf6yVdCbHb/Ifk+zLC6rw9QBguIdxeW71umjpLv68a+4p7tlFZ6tgHAj5ttk/JL/fZkYJmGbfu3MGYjLouqSrJetz6Y3SbUMm422e+U2cyHjcEapPjIFRYMg1JP3X4DN951u+r49AZ/IRCzdAPzdq0HaWwY+iKtkTelynr9nPJNKUHF/vP1mnOWqKtQ8WzEbLxvg0AkxBcbedtXw3MHYwYJpW1bone5PVu3eSleB76cD/iPLX00sDUIqBXKRztSvujcC7I8zFK4XoMTCzOWgmYg1hF/OhHf44xYq4b51YUos3wQUDkvcKnRHzS7Cp402qS0t9bAjkyAEqpJsJQ2mbjtxLxcXpDBs7LEL72UcrAMoG/ugTdUweOtO2l8/VJcBKB9/USLEnHNlTWCS27mggxHapthdEZ0QoijjmZcHc2CS3T4Mbw3TpHVVUsioLRSMLJ16oG77HVHJMZvFJ4Z1kUJbkRNwWcxbrWWqfVQrV+NB6P9baFYVi0khwvPoGN3tUoIFMGV7omi7nyUWyoUF7C+islYZcjI11WnsqJz/aweG25bMxonJxPQamA2OOFg4WTBTImEwLchzTn3sG8QBmVHALVqrsD8FgsFkwm4iVfVRVFWVAsKoyRTOEKmM/n7O7uYq1lvlgwynNMFnIgJPbW1lthTLwkTIuZn6fzKSaYtcSxVK6mni7w1jLWnpuHB9i6JjeGb33jG8xKcdYZaXj66HN2tiYUtmZ/d4e6lCQ68aIuFq05gITX9JjMsLW9zeHhYZDuKWorfi5RQr6zvUU2yplMJqhz8F6I2b3dHU6KBbOrSw5u3hIHHNdmGJWz3b+QwxveRyjXIZ+h3/vE/VBZZfMe+xsK15kidJd87veXOlb1JX19ouZlSuv7E4Ia9HwClkvQwgFZZshNFsLLKZ48e8KTR4/5+rvvMr245J/90e/z/OlzTo6fcXL2jLOzUxbzKWUxBy8hDL1rAxesW/Oh71+F6UV/LdPfhs7Zqn6H1iyVfkWGIP6zlaUo5syKS548e8Jb73yN73zvN3j9zbd49+13+PzRIy7Oztg/PKKORF7QhGq9fEbruiZTCqtiBt02qlhfGhyjvsRxf9W+GpuUTZmSl93jv4wz8jJ9pIx6/Ke1xng4PDggH+XYqqCqQjLJAA/7bQ0Rwel3rTV5nnf28qsufZi5SkO8iQP4UPGJlm2oz43bSQi5v4z9/rJlE+3LKmanX0SoEyXKUhqTwQFmbl2/X0YrlAq5RPi5jIu0liAW0ew2ziviFec9oyxHKcXTx4958ugxY20kl1hdUVuhfaLprghHdNStLI2/T8AvS+aHmYL+WelrXr5sWUVLvExZNbd+HWFI5HtkONoxbN5nKrzod9cfu8CabJDKaunhZXi+inayzrFYLNjamrQ0DhobApm0ZmmeshLhtlLiyxPn3WWIEsFOOHPykOb39G8z8Uh3qV7KgbAoYt0mDIcxgoMl/aKwDpuemM19NMjCIgR/ibodlEgH6/ZzEH/JwZbL6YmxkT1Qt5yQMszKGmPDcwxmJItcBe1ENtliUYtEYLy9TVXVVJXFGCHUXB00DFZCXiqlsc5TW1EloUYsigofxijmWVVYKI8tFxRlSZ4doLHk+Ta7KLh1E19X3Dw6xDvHdDplf3+P8XiEd5ZcCwFdVRVFUZCFEGG2rnFAZWu8Ej8Lr5BQYEEKl2UZk3xENhqR5RneOrzWOEI0LFdz9uIFB6+/FYO6Sbi1JDxlvJgatZSOONZZJbn1UbQzICUZKl/mWQo0UuCxdDFVUK771o6xr3Hof07rpRdtFSHUeTdMe4hI6tvKd97XNLkccmPIs4y6qvjlB79EG807b77JR7/6JY8fPuTs5Jjj5885OX3O+eUxxWKOrasgCXWIyYXpMFJfhmDpr/fQb6uYhnR9+s83GcvQ2vbbGGIKZvaKspozqQuKuuBqOuXJ4yd841vf4Rvf/Aavv/k6N/Qhnzx4wM07d9s+kPue9hmBqnUWV3XtoyNjEceaSpgmkwmLxeIrQ7D9cJD9NVq3fte1ven4vuoztEqwsWlp19wxHo85ODjg5PkzyrKQMLchmWT0QRoSinQlme2+RpgbiYyhsL0vu7d9uJr2u7nJ3Xp42E5u8/fScax7vq69L3fGuwhiFaxIx9esYSJB79dJv/f3ddUcbAyBfc18OmPo4ZLrGJtVc1p1nzvClETbEuFS+q5EHwTtPD/98x+jQzCZiIfLcoG1Elmw7WA5ie0mZ0DGvfybjGvZpLh5f0B7MXT/+uuwClcP9bEOx6wLO57uaWayJWauwQO2WjoDm/af/p7SA5GO8s5JMliWlRh9PJeuWXo3xFRWYWsb4FcYt6+bflxIUOs9GCOhb7XS1LVkBk/XI/Y5lJcsXceI99JnWomhXEwySbAcUEo0b8ZHIahQoFkmz6136OBjt2nZmNE4O7uQhQ9qmlSXH1WL6aGUQYjNbkzOJIsTJy5/I/HcIZyb7629efwdJHJJNIOI0WkkVKJke/ZJeLKykBCjtbXUQeUUtS4qELjOixooywzaiaOpNiEbuBkxyTKUVtw8OmoiWmWjHKPaRCcAeR60MOGA1iGC1XyxaBzkJRxwq9UZb0+orSUzhsohDFJZsbM95sWTR7zpLJWV3AVd88DehRm4M9cBJYXsZ3qh4rN1BPtQW0N9DwHlBnGkh1SpZm59pqF/Wfp99H9vzxGQ2Hb2x6J7/cQ6TZSN5FJG20flPJNRziiXxHXTy0v+4ic/5bX796nqmj/54z/m9Pg5py+ec/riGRfnZ8zmVyzKKc7bkBG7QcFyB2jHcF3ZhFi4jgAaYjj7RFQf+V/X73WEdX/vnRdzwqJc4LwkSnv+tObq4pyLsxecnXyDN99+m/fefYePPv2MG7dv41GSGNQs2wsbI/HGIwEaVeqrxghds5hfl+BfdVdWlU3WqN/+qjb7v/86TFP//XXj3PRdrVQwr9Ps7uzy/OljrHVUIXeRs66JCJju6XX9xTva10jJ+m3OmK363id+h2DIEExaNeZ19a67+6v2fx3h/DLjug7W9/dlHUMgnyFq7lcxrvGd64IgKCEY6Gsu4uehlevDh1U4ZAifDI0TIOZVSNvqwk2hV5TSmB4ejXVNZphdTfnkl78iQ0kEISXmUYvFPAS7EeZCIjJ1XNkH12gd7OnvW6Sp4uqlNFczd4bXbqisO7dDTMfQ/m/aXve9ZQuK2HZrTrXsP7C6/eVz2r/33sdUDcPjWse09OGUCN3FfGp7ex+lVKABM6q6Roj6rAmhHP0n5S60bbdBbZb7TOcx9DfLMjKlGSHMhNGmsVLSRiJO6Q4trjCZaHTqumZRlhKF9asObzufXjWfrRO7L5NJ1mAXnVbDpPM8RysJp2WDrbTRcnF8WCDvghoypGAX3wUhGDJjWBRB2gghz0ZwCDWG3Cgs4ndhKxukYiZEkgpZykM4stEoBxTWaIqyexhEGubJEEfvPM8xDpSXNlzQwpigtVVI5Kvp9BK8Z5RnjW+JcyK101ozHo+p65o8z5nP51xeXnLz5k3quhbn9VrG67ViNJk0DqHGiG1eWRSQwYunT4LDjxJinBVA5Rq8mh6wdWUTYverKH0kvur5lwVy8d2Gcx8Il5wCoiHzmSUArGAyGjHKZM+PXzzng59/wFtvvMnTx0948NmnnB0fc3L8jLOTF1xenFIt5hJaLkgrGof76Hwfp6c2Jwx+ndJHIH2NUAo0h4i+dWUIUPcBXls0zhEcugs543WJrRd88LOS4+NjXrx4wTe+/S2+/vX3ePD5F+zs7jZZSiNCqUPStygligm0qqpaS4B57yUk4FdU+kKWL1Ne5v1VyPqrOi9f+bkDTJZxGELcWivSvKos18KuVcQKIOamqiuA6vb465XU/GDdevcJ1zjma5k0EX2vbOdfZ3nZO34tI72i7aH3h2DFUItdwykaVKhQDMW7eBnGLvXdWjUGrSVT9Hg87sDO7ijFn2RI066NCEU//fxzzk9OJZdX0MRWdR0CgqSTi74brTDqOia/C7915/eUqUiZjaV2Nzx6Q0zCEBxs5t/T+K7a7+vu0NA40rZ0CA7Ux2u/DkwTJsNitSXL2miVadmU4W/HK0Kx3d0dCWHvRUBtg1A+mugZY8S52ydJrFmmYVJYGeFhFJp61ea8i8+zLCPThnHQWsS+oimaVjT5S1omTp7luWE0NtRbGVVZbbSGGzMab752T/JKBEI4SufFNtEmh0cyC9ZVhc20OEkZwyjP0cY0CxUljjZoGkywu5WJZJTVGHz7PIbX2gpp271zLBZFMFkKIjGnQlZxLQmdlGI8GVNVNQ5HVUfVkEgesiwLmRMlIoQJi4lttS9K0TiqCWcpjsYgnN1kMmmSUO3v75PleQBchp0dIY6KosBoQ2kltrGrapSB2lr29/cxRhi2unbUtTAwtqo5efECW9WobIJ1jixTSwjwWoSWlI70KCV0e+V6qWqizurXi9Cx4YtW122A0Yo+h+r3EdPq0tVWpPWjxKPfdlwf52xI1NNezPFozCgXp6qHDx/y6PMveO3V+/zs/Z/x5PEjrs7PuDg/5fj5U+bTS6piBl4c+ZRWaGU6DvF+9bJcWzZlSlYBwxQgRWCVru26NtdJQNOSIpZhqUvQ6HhPXZfibEZNbR1VZbm6mnJxdcl8UfCd73+fBw8fsrN7gNGZwA7TAk5rLZlpQw93EBndyDPp+Vk1P3kvvtB91n2nRdpdxPllCcWhPUzOysrSO1O997/MGPpMdtLNmmEk65xU90h22bt3X0Er2aeyLJnP56LRyFeMpEeQpOuf53kT4jwi4d4UmlH43rg2KVELI9PyzdyGJMy+kThCatoXn8dn8jud32NfnXH1zlh3X1/mbPWBzIp3+wcnyq+S+UAPf6QHs0+4et/paukMJ2vTwN1YYcVhV5HIaqq1Kg654229VbghtuHo3uUoLEzredfutwt1y7KUjMvQ60M+O+8lKEw6j3B2YqSqn//sZ3grtEw07S6KeThDiTlVwM/rGNCYsbkZd+90Dwnb4rzSqm0o12WNw0oG0PuVwEWphI/2NGFsUzyTjrE/v2Zv1vThE9pCKR0c6z0xVUDUbAzh+n7fm/L1MXCLaiKBqebvKpyY4prUNEx+d4xGYzKTUVfyvnXRR0PwXF1VpOcLF7OlJ2sZlkkHf09jTMi7ZXDOUllJZhtpYoJdhXeOyjmUk++ZOC4Eyx+HTuakI5OR5eSZJtOKfDxiezLZaO02ZjT2R5ZKI8TTZNSCrnAYItMRs/gaMw7npHUgbxOgaPJJxC55UElGRkPjXIUeGZQCk41lkUPGbrn5BaOtMVWWUY2DL0Jt2dra6hxkQUQV+XaOdxajM7LgYF5b29hTYmt2co/2lRwebfA2HuIucDXGMBqNZC4KxuMx5WJBuSipqprRZIvaOsbWoM0Ypa6wtWecj6mKkq3RmMJWjCdj6qsr9rZ3yNDsjrbJfEnhxU7TVo7F+RkUM9RoDCrDe9M50PHiZro9QC1SlEvgfEtmCfz3AUC1wPQ6on0JCDcXPAD5FBiG0JYN7onwtpHNtKHXIrRLo1F1cKGnj6Ea7t57L1G6ehe6lUz5IIlYjpClUcG5OHk3MAHe23AExBFPocjHGeNJjnE1v/rlL7m6mHOwe4M/+eM/5/LyjPPTZ0zPn3JycsxiPqOuKplvgLZxjVLGqgGgX17QMljWAfH4vQ/w+45s1yGC6/qNdVcxLd7LGXAefIQXWkNVo90c6z21r7C/rKjrkrou+e73vsejR0852D/CGElKhNagJZFTVVbkWcbu9o4EgJhOKYoiOWvdccUzYm2NUtnSOFvir/tuay6Rzi3Fhy9DCPY3v9tuM4IlHN9n3DblBNb13Y6hJS4GGNr0DKTnJIEzYZAS4lSJeQjGcPPObSprUV5RFxV2UeMqC5P2DC4T6MvnCkBjKGaFIElFgBO+HX8MRd3fq4Qc68+uT6jFddZty3IGQu0OE9MQ5615Sr/vVppMh4hSPgpowtnU7YFq79DLMa8SprvpOZzRFFarpt7ANieL0H7UEaBHIi8NaRoqC8zsnlkhYpMTF4UBMdINNOKABicTwX9YF2UiOy31Yrjh0F537i1X19nRMO4Yuc6HgS/Btc57korOWUddlGIWpZwQtiTmxrHFlv9BIgA5Mq3INJTFjE8//QidKbwWW3zrK+bFFHSQTDe6m+Hz3y26M86W8QIVtOaReVCdvBlKMko3PUVOcJmw78wvXW8VtExNRLF473oaFN3uoc5M2Ht5j0Aku3AOGsf5cDaadnpb2DIZrYZGa5OEApbfskyHfBsxL1aXAei2uoppautHH5Asy8M7rZ5tE0FfK3STu2NtzWiUC3OJw2NDlMSQT84pyrKWuWiHDmdXgYRqVnICjFZkCKORBYG+Dkkly7pCZYp79+7x7OlTbFWJ5i2Mu1AR7nmI2gkvuDnSSNFSyWiDMYaJ1uyOxk0Qp03KxozGeASTUY7SqnHAE05YfBqiA4s2YxRi5+WsR6Gp6oq6qnHeodW44bhSKaoNjESWabQekZmWCJJNHVFbidRja4tWNaOJQe+MGqlIlmWBg3U45yWvgVJ4b8lHkk22keIa02gmlDfkmcRCj2jEBamMcONdTnvSmDt5qoUkSDk6OADvGY1yysWCablgMZ9xeXXOzvYWtXKoXGNHigWK0VgxPZlLiNTas6dz0BZnJIEgXlPMZrhaQvrGizwkFRAAF5FAFzH5HgGgVZvkEK4DZMMl7tlQG8K5J1qHFLHCwNgRcj5hSFLQkqLFLo2jOvPqt71OKzNEeDb/8E2+D+8kRHOe5+Dh5+9/wNXlFE3Gv/rjP+bq8pzLixPOT58yu3jBbDZridg+dGwHObCim+3DdQzhKmJ/cM0H2upIvnx73jaJzPQyTMiqMUqydkeNJP903mE/FNMC7xx/5a/8NT788BNu3Loloaoj0RnCQrsQsCGa1QAS2cuscjhticUvcw9WzWfz+V/Xb4tM15UvN/RN5tzXcLXwA7pz7aPqhiAJhLNzjps3b4WkWxbvPGVRNkKoQcaiB7tU0zAhp1NL9KrwsPEXJMaXX5539zoOX9QUvjXnPyFAA43UCFQaqBtCdQ+W3mRSgjRimWG41v27SUn4mPBu37QmGVMPXA2Ot2EwEoK1A49TgVaKh9r+h5vtMisdWNUwcQnzFuo1GtMBbWnSaYfw73U3UL3br2ofoLWmLEu2t7fkp8RUvDPvtK+gqYmS5GdPn3J6csLIaCEsA7GZhj/t/KU/9v6admukDvhGm44gKa3TF1b26/S1KCmzEZMsp3glCm36lhYNkzBwcH2gr/oaZBUZmETL1NdSRw2T1v0zLf4MqZ9lkwdr3Tm5pjRMhrJYZ8lUlhAkw4xZX9DWa7CheY0xjEcjisU8+IKKoNNoYWKcEzpkvLWFN0H4rhS+rhurIB3C4VqlqLRHjw1mPMJpRV16fGn57NFj8V2u5UxGRlPTM6MO43MuwM9QYlQ1vCdTiqssZ3t7i93dvY3WcGNGYzLpEuryT+MRQl7rUVi4aEOtsFrUQ1mW4caaqqzIcnEosdahjSg9ZXPEESYL5laaED871tXijGJtxTjP5PIr3TAiEuzKok2M4NONFqKQrMFaBZtO7xruWuuIfsQsyloXpHnrD5HHs7e3xxefPWRnawvrLUZ5Mhy2mDG/PMcWcw5v36ScTXFVSaUdVbUAW/Pi80fok3NYFBjr0K6XlbOqmV1esXvjLjYFKEtEY4s+N9FODBGe60qXeB92yk7/tqrBXy8KzKpxNG2RMCKqy7gOqTIjIR0TPw3V8eHSKWA8GonJn1K8/+OfcnV6wWJe8OnHHzObXXJ1ecr5xTEXpy+wVbEE9Ib66M9jk/Jl2xhiNPpIpN/euvovM/aheq30N8hQeufFWotXYe1qT7HwXHjFRx/+SrSeKN77xrf54vFj7r5yD/DUIcFbTALqQtjAJveKMUEY0iVk27PivtSdGJwXX369+mXd+fnXWTpCBBgg3JfrDRXnHAcHB43/GtDJpTEUJlYksd12omlmlkabIkoyGSReUmHFqrIKpsXPgxJLwIezrAbeG+xnzbN4Bl3CDF0nIOjDxKHfh/p56eJ7vEWCHlXyfO0ENxjLEMPZEprDhNzQGi0xK79mUUoxnU7Z3dvt/Lbu7kdn3dFIhKEfffSRwLjIpPhgbrXhoi2v1bBvYfRZ6xD8a+B/+nyIIFeBbsJ3bf37ddIwsykujp+jNUus7wOhvgr39N9vTbza8UcaL8syxuMRi2LRrHtXIB6sFb5EuW59Vr2Tls6a0DIvWot5vzubBsGJk2BDwTRYadHeZ/kIneVoF4QsSqONhE22zuEUOAUlnm986z3e/tY3qYzixZNn/PIP/5jFfIatg1WQkzxTOE+mEt+NZmwENwRJxutD0mDrRUOncVzZiswWTOpio/XYPGGfAaWdyBQice5F+uycQimxL1RRqu4tRseNUZLFNVcoLZtujEdSabSHPTeglAtZYYUIEGds3TDFOjNACGfpLW3ylshVC9Jpud3A6VauUelqpSQpio9MUWSeXGCaBHV43+Xq+pIArSXU2otnT/mLP/tTbt68wdXVJbOrKfbZGVxdcXt/F/XsmJPnxzhrGWWG+dWUoiz41U/+AvvkBDubi88GokI0xmC9oyorTp4fs/f6OyjdimbSQ5wClaFxXoeohn5bxSiEp5Ds2SqGYqjv+GwJYErlTpv9sfTHB4S45W0I01UhKPvAVpgl+fS/fvA/56I+6Y6RVrqGgroS6YHf8dixxf9ANHmukah9RcTgMm/7/5tt/qWXKAkLn5XiV+pH/G75Dxj9QjRM9kMrTEQjaSWcoWUp9r454n95/3/Ttp6c2yjMiGWVdL37+deb3br70S9rGbY17W3C1Pclhavqb0q0DREM3nvJA+Q9o6BuryoJQVkUBWVZdqKndMbQ606gsgiKYqKrKElVKr4bbN1RLUx5SXgY660igpfeVa0OtrMHvTa7RBIbE5hfpvT3NI0q2B1nanrWwx2o1qeMuP6rimroAZH2d3HE4Bu98QydwyHCM5aOD00y7/a8hrYG8Ud39Tt9K9U1EQzPy7JkNBqvZjwH5hoJ87q2fPLJJ2SZOPeiROsWNXpDZRUeXyXQSu9clOwPzW8o0EF/DWN7UfAZA9akfcV3tG7bHFqbobYF9pqNYWn6ntJdx/LIVNy4cZOqLjk9PW38iaMmKs8z6to3pv3dMQ7vZfyb1o2wSlI2QD8SwTq4293nllGO5uBVXeHqCq1843dsnaeoLJX1UDuwki/OWUtRls3ZrnG4zOAnI+7ee42D27dZKM94ssPsoyf89M9/FM6F4EdnLcJPWHE8jwGbfJhSprBKozODHueoPGM0GWO9ZzIx3DySaFlvvfXWRvu3MaNhFCGOsIYYptWLRsAokSplOtqseXyMX59KHoAs+AeI+rz1k1DQmClppRubX6WEy9PNwQ6cYPOe2Jv5EAY3gvzG6SVsepopOiY9UUpsw6MtrvMWQ3o5aZidJYCHxyJ2a/W84F/+3h9w5+CArfGID9//OVwWYIUxU3iUl5COWQ155XGZoq5LRtajnaXQHpspXHBEdzi8tZy+OOZdFM73iWXCXMTxPJYhRNfSCcuExTrGIwLyVVx8HzF0VLQDY02BRSfJjof0sq8L2bY03siA9vwM2oQ33b7jS/HjRX3CmT0enF+nxCXe+Mb8/8uXL8MkWE1FwTym7Gn/blD6Ur14Fvrq4bR+/3NKnK1iLtcR96sIpqGyTnLdn8cmfa5re/Oi4v+v7TfNDRMRaZYZDg8PKUP+kpTRgF70N98yFrHrZtzeMx6POT8/b2Bzi7hF0x3fE1+p1Yi/L4wYkpRH6WMfpjX76H3CbKR9fVnthurA7M6TjYiY5d+GCPnI+ESmbImBpc26ToOPo3llYrbUG5JWGqeGTXP7Uuv+WPtnWsbdnf+689u5G8EygoG594fdZbCW+4mMxvb2dqf+KuY+nhkTzF2mV1c8fvwYpcRiwyORN13QbLxsEQaq+71Do7B6XENz668BtEzSOrgl+9US4CleF2ZCL31uGcRkLgP9p322504k6/08GlmWMZvPODjYZ29vj+fPn3N2dta8F2mOoShNQ1cqjiVlTCJTU9e1zHMo3Fky7nWwN65ZXBuZj5dcW06Cm0TT/so6ruZz5mWJXUhERWsttq5Fm+EcXmmsBldW/OwnP2NhPaWCX/zs5xx/8DFFVWO9BRRoJcyKVviRQSnPeCxRroqi5M6d27zx7rvcvP8q919/nZt3bzPZ3kIZjQO2t0bkRnXW8LqyMdnUbKpS+OjZ7mJ68pZDigepVWm3HHvkiVOgnm5g6sjb9JUwDj5sEF43WQobYtg7YToSCWUXuEobShGYiaCKcy44EUFdV409PkSzqgBUly4YWCBTsJXlvDi94LNPH6LrmtnJGXmJMGRK1GAKT6Yg85rcZ5SVY8toqGuss3JIvAv26BZtxMn76ePHaC+OTagusIifvd9cNpa+u0kM8yHEMCQJ2rTveKnS70JFrH93+R0EuevWJGpoHun4luJZd5CL5sAcNchUKXEAXCwWaKVCKFZhdKNzWTPoKO572dKf86ZtvEx/X3Zs/xpLsp2doiJVG7+Ffc6yjDyYI6jo9AtLnPV5fYIPceljoAp53O1oFVL4suU6wv9l78ymzMsm9f91lS7xIDhhNBpx//59Pv7wQxaLBYtF0Wg3YEVUmvg3CCM8NNLa2WwmW92be2rYoXqH3/UuXSq1HRp//JwKLtL902o17Or3nVZzisF76X3gsH7NSzvEFDXtd/rrdtVnQgT7yW8SZl4EQ53l8u1f1TTanvU+49Af59C6/rrnuPPuBtetvz7p3kUCOk0QudRH7Kq3vsJoaJ49e8ZsNmMSks2BSJdjVKRNZrosZe9/b8+zRnc0/WkZisSUMgOtcLb184i03fCZarUaXYFeN19Wn/EVq5Nu5MMhRr//N+LxlJ6o61qSgFYlt27d4t69exhjODk5SSwddMNsrILBQ+sS11Ap1YlQJgEJ1Mp3V5VGOBHmIsyMCPLrqqCuSrJgiWOyTJgSNCdVEZI6Bk2OcsLQG4GJHrBlyZ/9+Cf85Be/oHII/qtLRts52ozZ3tnh9bfe4K133uHWndvs3zhCa83+/j5aa87PznjjzTcZb+9gJpOGNFNKYZ2jLAuuLi9YLKpODrnrysaMhsT+lxTp2hjx5ndBwqU0LqRIpwFP4lytVQYqEmUisSfkujY6CxIvacvHzUO0Do0juAq21HiUNoyMLH5VVeR5TCjSqvjiZsY70XxWIQpT+N5oZEJ77aVoIWf09ViSBiHASAEHBwecjcao8TavvXGb989+BITL7ESb4Z0NTjswpQIljE0W/DK0t5KNURvQUIcEcYvpLMRPjk6CsWdAdVWa3f0KdTsPfTK3lqFrgUf3e/RV6AKqNJpJT4LUu2hp2MLmSfzugm2qT8fT1ukzM6mJjISLVVgXkV7PzjPIjLRwig0wyrMsmDu1EqdYDswR/6vX/w+YUcbO1haL6Zz/23/xf4HacvL8BbOrK5wtmc8vmc/PKYoZrq5RSAZPr8L5XCOd6ZdVEpyV9Zv5JXXbQw50NTsdAB5XOALtNeNaQrpKNecp9tmcmB7yWJpXlAbF8QQgG+fSv1vKS3QNbTKUNiitybIck2UYPWIy2eHw6Iivf+ub/K2//Xe4ms145dX71E60Ex4wgfn8X3z8P+CsbrVVUVgh0sDuGJQs3sD6vzyntpqoS9TlGzIQnShXvavSvt4KbuJj2ac4fjovhum3pjAqYfZkcOlAuqZHAF610GPFGW6HpgTOAlmWc/v2bX75wQdMp1NsXVGVBbauYTRuQ9SGOyzja9c/Cou0ysiMwdo6EA5tPhWX+N51FqtTkvMW+pO7qztvpGDRN86SrVlWfD+e7SGKNiXGmumlbaejCm2odENWrPFSP7B876CFm2HDo4Qf7wPT5QMMa2GxXPEwPw8xIlRmdNpbg5Ha39qzFefum4zeXbzjw5gaHxeVnKm0Re8Hf29MruPokj6j9ishAVnamz6DtVyjmUvj56kkQe9yPTV4r5VSTb6MB599JmtubbhPHu8s3sYoRKwpXeJ+iMmI6+BDNCKPH2Sg++OOY+7AjtRMyrnmrKdm7vGvs0L0j8YjJpMJu7u7bG9vMx6PmyiiSimqqqIoCqx1XF5ecn5+zmJRUNu69bUN6+1CiNdUyJkyIamDd/ytLCWAiDWKp0+fcv/+fe69eg9nHWfnZwEPSmTTmCwvamPash4fp4xNPF/r8HyfZkweEIVfWmlssLDx3lHVFmsrFI7aw+3DI54fn+K0hsMdXr17l/F4zL1790K28JqyLHnx4piyKNEmYzLZYjzZ5ubNm4y3J+zf2mfv6ICjoyMm29uYPMP6NpKUjMVgtGZ8c5+rumI2v2TsKknkF4Zd1xKMaW+yjfISlGl2uVk+qs0NQZRkLwSazNbeSUSRTCu8r5FEJlH6LJ9rWy0d6FYqINJhgNFIiEDwQhyi8aljtBdE0IKjaF/tGiZDqrYxzWMfDVPRwCOFMcIAyYGVw1DXDhlOKvXuOhCll9JYRWYdB7dvMTEZe/sHbN8+Qo8z6nkZDpBHkaF1JnNSCrRDeySsmdGILkgzQQCa1RrlKkBTXJzjsahsFJgW0CogBU/ITdJNZ9S9lC0AxLfvoSR6QbtucX6EPYxOagpcL8tyuh4uygh9E8EgXsZovhbHBIj2yEeALNnRU4I43TzvJcybALlknJ5AGEQtlW4AXrQNNlHDoTV1VaERf5raWqyyaNXV6ADkmWFrNMJYz+/84/+aelZxeXpCMbuCek5dX1GWVzhXBXWlINI+khgCPkMEeed5fwMGSrOuKxCIh4aoSzobbmvw1+5Yu0hN/JW0oiG0pCTO1El0nv58U5vglEDtI2mPAiVBJjRyRq2z+NpDppkvpvgzz2effMLOzg6/+YMfcPr8GYd3XhVBgmsTeKYz1wq81o3G06mW1mg0Hcm/LnGS2rcHhm7l6m3GlKzTovR/12EsKXHVrRvGqmjuYsOMrBhaCh/bnfLJ/ONP3ZMi45bfnG/7SahLFL7RHGjl0TjQEsHzzs3b2KrG2Qpr57h6gbI1ytZtnPcIkyIzFPqI/n6g0EqcEpW3YX1kgoaYW6BvUhXXMl2OlJgH7+pmOlppWmmlb//nU7+euO4JY9MTkiSddT7qft/xuw+7kMLkpO7S/jBcL5qrNe+plHgMMDJOoW+DGC+GD4R8DBu6xAWk59AnjvshX5BzgnMDTGr2A7mPkSFoOk2n3VvHzn3rwB6Ww6NHxoqAZBtw5dtpeI9J8XzvHjSUQhijtS5E1lTUvbDwHfomrEpd1yjn0R60h6eff8FIqeCXKj6m1tXYumzWe1lAEUzDtWnOfmQq4mWX57rzWdG1ROhritYJQPDBJzaucMQnCnQWTJecBS9JM1+59Qp37txhZ3s7aJsNqKBVaZgTaT86I9+5dwuFoqocF+eXPHn8hJPTk3Y9jUZ7T2Y0ZVnhfcQr4e4j/pEmwIpI29RliclzvIPHj55w69YtXn31HkVRMl/MO/SntdG3c7V2I5ZU0NrR2oRzlSZH7OekShmm5t0E9ltnsVWF+DRnODPBAFVtWeS7vP71r/P55x9x/2tv83f+7t/h8MYhzrnAtFm2t7dRSujl2G8WBKoK0UJYZ4VJIIHbstVYT6CLapxHcs45h9FQTq9w1lKWJVmWhaAGmoPtffI8J/MwOfqKo061Kp6Em/WS7KMOdrJRwiSX03XeTdVx6aZJSC9ZDJFOdS9FSqTkeU5dVhC42ujELeOhE9Ugcr5xrPFvvEBVVSX2hJHRkPTvKac7JHWVB4CTxCrbe7tok+HrMmhZcmotAFr5oK4P9QXxEmIiI5nRAUOI7KCEcTLa4DFcnp1j6wqttliKnt8jftJ1k+ctsm3rdzl0ibIlIYFTTUY3++UARx6frAh9ulKaEiHxirkMS8UHCCbfElyxbqOGTi6864XPxMezahspSix5lpMpzU9+/BN+/v77ZEqzuLpCK0tVl8znU8qy6DrwdQiIlzOLSZmATcjTCKyGiNS01yGmZjPy9/q++79F1Xcfqa2S8vVLf71SLU1krOI9resKFZKDnp4c89GHH7K7u8cbb76BrUpMPsJbwUdRldxtu/08lLdBrdmPzpqG/w7OSbV7sU6ayAZ1mrswMJ6hcXXaWzqHXZ1o53r1iMblb50OE7I+qZ/A3a40OYmC4x1HN26Akr2s61J8NGyQentP1JasXzkJIy7S0u5I+rNeWp81rQ5rs7rPOjDXh79qDaxqB7JyHIG9Th60O95dyy6j8VJzw3cY1MGXlsC8MIx96XI68lhSvN1tKhKa4XchDhpiZ1Xo7P6Z787VL/3Wlzy3YxsmsqOga2nMKhzDHnFe1xXj8ajT1xKuCnNL56+VpixKnjx+3PA9oPG+ahLKdQV91+EPOQFKKXQMz58cuj6sva69dF+bzNNB2NXZ88A0WGu5ceMG9+/f5+bNm4xGI4zJMMaQZRlVJUK4uqoobI1SQmNIVKgJo9EoOMfXLOYleTbi6OiIqqp4/vw5Dx8+ZLFYMM6yxheif7b6a59+Fof9EUVRcHl5idaa119/nQcPHrAo5ktmU/JxPQxOz0wU9FlrMTpv3l2GDwz+Hs+/tKmw1lFZi9YZymRMtnbx3lMsFoBie3uCMZCPx1jg0wcPQClu3brF9q5EQKsD43Fyekodwt4uFgvJI+U9t27d4ubNm1RV1WidJPO4xnmhyReLBfP5nMlk0sy38Z9TirKq2N7ZAeD84qJhPFJ6fl15KR+N+C86/ojUWmODzXqMC5xufJQWRtu2lHhICaeo0ooZHWM9aBmVGGUkVV9FG7EhoqYPiNJD0OdS41xkjPH97sFZIu6UmDiNdrbIJiOq2YxXX32VD7OMhY6mYJKlXPkI6L0kXfEisRXpkgsIPKyldxit0CEkb7koGO+suWzQlc4RYB6qgX2DEnC/7FQFIo3p+7qk5boQb12GZWC8A3s0FN7yuhKlTel8+uNNNQCR+ZQgBK0kSF6CUZ5zcXbGP/lH/xhvHYuqwHtLZRfMF1MWxaIBpP/fKktncGDO/zr7TsPDDjEiKZGyqp107/tIMsIEkVo5lFbYumI2nXLy4gUf/epXHB0ecjGd8+7X3kNnmqKs8Hr9egwJD9YxROuYkM6Y1/b6JYuPpj3DyGz43iyTlR135fTu+IQJeyk+eXmthqSokSB3zrKzs0OeSZLWuq5f6j71kX5Zlktw5GWJrFXzGZL6pvivO7nV7Wza35cp152Dv0yY8DKwOqUd+oz9qjVfha+Gnq0by6o18WpZsj9UL5aiKMiyLBCZy1Jr6MEFJbge4OLigquraYBzkdBtg9sopUEtS9aFvtdLAtM4rzQ79NJYNhFgJP2ZkLqAFX6b1lp2d3Z5++23uXP3Dnmek+c5ZVkyvZpS10L/SQ6j6EStUcpTVSVFccl8NqesRDq+t7fPrRs3uXnzJgCXl5cA3Lp1i+fPn/Po4cNgQuWCRidZY6XRuitYjCWGzh6NRlxeXjIajdjb2+PmzRu8OH5BVVWDYXY3OUMpveSc6wgI1uGS9G975uV8VLVYruTjLbQZoYwkNayKOZORIQva0oPDQ77+3jcoqqKBmTr4SldVxXji2T846EQUE9M109DhcexlWWKtJctUSD4o+5/nOVHjY4xha2urMTFLnfy11s3vqQ/OuvLSGo1IFLSfJWpCKlXuAGJFuzEJsO4D7DTyiFJtNvH+IWidzFtnpciEKCVOe0Io65aBSGwsY1/dqEStpK+qJPNjlGqkTE0HMCogJKKa7GxjxiOmRcGLZ8/BhhGG8xTf7UqdnWRGVuEfItnywSlcOZGU1VXF6fEJ927dpk4cpvp+Ez2RWOfTKqAzpPGJh6q9DHG8q6XTqy5pH7GsKl8eIcpl7fcxRNR2HIGtx6Aku2bTkjB+//Sf/FcU03l45qjqgqqaM5tfdeL+/zqlOUt0SZR1hM66NVollU/76re5KZEShFsrkJk8HwozmZZu7p0uAE7v7tB4IqwZjUbYShK9oTVVVTCfXfH0yWN+8cHP+c73v8/zp4+4ees2RgfH1Y7Uvjv2ISFEF9YEoUDvLPmwIJ2cvH1G3G+WDHPTcz8oFVvTjvhWqRYsBKLHD0gGk8eDDNSqddq0eC++Uja8N5lMmEwmLCpR/ddVJWYmA4Tn0Bhim2Up2pBmvgk+WXXe+m0sr8NqBmHIUb0lFIfbXLVPQ2ew0588HHw2NIehfbnubK2qO7TWm4x9FcO3ag2GHIf79YYEFfG3IRi/CXxbameFNLvB2WHvLy8v2dnZWToHaVhXH74T3smCz9Djx4+FsNOpgCOGzm8ZjlXrnQZCGZpfKrhdd+ZXrVWqJW8oIt8KAAHeefsd7r/+Ont7exhjmE6nHL84oarqhvGqa8vp6VmIBCf02Xg8YjTKGY8n7N7ex3uYz2ecn13wxcMvyPOcu3fv8uqrr3J0dMTp6Sl5nvPq3Ts8+OyzsHbpmis8tsE76b1XKpgNBR+MLMs4PT3FWsv+wT771T7Pnz8HupY1KU5fdd77z60V87HoU7wOLqb0mpw5Mb/0HuaLgnyyhdJjnMuYbO9ijObi7ISdcQ62Zm9nB20yyrpmvliEgEWiJVwUksfCWddolZRSDWMc9zAKdfI8bxJOo8QsLz0rVVU19Pd8Pm/mVpZlQ1fneU6WZRKU5avODB4H0F9wj9jDp5sVtRKoFqBENVhc8HgQ4kLENmM/8bK06kU5aLnJiJmnY1GqjeMc243vNyHRQhspYIjvitSgPbBZllHXln5Y23TeoLDeYRXo8QgzyslHIz75+GPqsgStJFtj8FVQSmwXG+SkabNhB8G6i19cIHIAbx2XFxfUVS3JS5KSEnxxTK25VLs2q8p6BmSZ0diE2O23vw6JDY3hOslCh9D3y3HVUy67j8gic6lCv1H6EcsnH33M+z/+KZk2OO8lE72vmc0vcL7+tZiMQUCkuk7VmxIK/Xaui7iVIs11CGh47VsTg/S5fF5PfERmf2hsKSBfBdRjvbjuRgtn42yN8o7p1RUKxecPH3D37h2Uybh96yaZMVyXnGloHYYQ9RAxt4o4eZm+1v0+UHGNGcnyGBtfpcglxucpD5W+H3IPkc5xxdgGo7+xfNfTOp52n7VqfXmqqqJKMtz22+jDjrTPxWLBaDRaykMwNO703g5p3Ya+r7pjsc46WLbqbKVl7ft+ORhGU0cqrm3nuvbX/b58xzeru0lJ4UTEwatMpzYpqxjI6xjG5l3ffbbqPCulWCwW7O7uCk1gdOe95swEM5PYSnT2ffLkMbauMXkrFRaBrJhNOdf6QSzNcc2cUmHq0Lg77STnus9EpLAtDQUbBTzf/OY3uXP3LtlYtARnZ2eUZcnl5SVXV1fM50UI8hMEyCECqHOWLDNNlLjt7W0ODw+5desWN27cYmdnmyePH/P+++/z4Ycf8sYbb/D1r39dGI4XL3jzzTc5OrrBL37xS4qiDAEgJNFzfx2iiU8MKBEtboqiaGDF0dER0+mU+Xy+JNxah4PS5/01HLrX6/ZAKcnb5mqhJ54/P2Z7dw+lJ5S14sbNW4Di4vSYTDk+eP8n2LpisrXNbFEwLyquZgvKsmyENpL/oupY9yglDvjQaqsizeO9FxO24EweGdUYRSrSSRG+VkEYdHZ2xvn5OXfu3GnqbgoDXiLqVN+Re3kRB15qVF7pBGI7qcSgk1eBlmjsm770x5T+jYxGX83T15z0JbBNgj7XAiIBBL7TdwcIK4hO6BjP/o1DZp8+pK5qcaYKmhfvHV5lDRJ3QIU4iUUg4rz8VqMIgZQaZKKU4vT4pBlvHwDK55bhWBdp4rpD0SWwur+nfW9yuPqEwarLl47rOmkMdBG+C4vVfz9tIxKqfVM5vG/jwIfyX/2Tf4L2wtzZ2uJxTKeX1Lakqstrx/aXWVYRAKsI41XvwvUER8qg9/e7+65vAPpQX1G1e92apX305xK/l0XBOMsDPLFhXyvKsuD0+JiPfvUBr7/5Jp998glvvfs1nN/MdnTTkp4tMbtYNZnufL6S8+K7rqrrxgg0vkfRcV8FZqPxWvERyNCMUUVmxkN9DZy97owNIV8XHINjYijvJaOttbX46PXMbodKei7qul5CdEPwKT3LQ2PdpPTHlOIPCQaxfDc3hZNDJTJmL/XOhnd80+er6gwJCF6mpDhhE3z0ZddwqCzvyWqmKcVXxhguLy+5detWyuMt3XEVmAwftB4RF5+dnXeZQ3zX8mNjeUMP7w+8F5mPIXjan1sqVGjaDvN1zrG/v893v/tdDg8PqazjyZNnnJ6ecnp6ynQ6bQjZ8XiL8WiE1qaht2KbztXN/V/MC764esQXnz9mZ2ebw8M9sixjPp9zdnbG5eUlz58/57333uO1e69yHvJg/OAHP+CDD37B+dmF0JBL3qrJ2iRCDEnUlwdGI2c0zrl16xZPnz5txthnfq870x08kKxd+u4Qs9EyGZJaYTTKAc/J6SlvvPMeJ6czsgp29w+wzjK9umTHlFyVJTtb29y8cYM8H2FyIdn7rgOaNlRyPAexlGXZmIzled74mNTW4ly730qppo2oBfHek+c5Sinu3LnD3bt3m7bTvCTXlc0ZDefbDNque3g7Cx4QiCyuiO0lNCDUtWTdlnC4jhiWMN2MWFICJl0062wbog8aYtHTbmZ0CErHFpmPyMmmQExUczLeoizY2tpuiPZ4AGNYTgLSjmDJm2DftrPN+HCfg9ERjy6n+PlMFBNGU4ekfxBSuqsQlQOFw1MH5F4RI1o4nJaoW2Vdc+PGEUZJHUUI8ZiqO0PkoxgGt0tEwCqAmjrsp+vfsi59IC9jXg38+8C623fKEDU2lyp95nt1RXrsw1f57OMw0ErhgmZItidE5tDtGrRnM0kiRtBWJHOuqoovPv+cCVm4bDWL4oqinAdg2ZVWLVGaKpEcx7MZHzVVliOApJ9XEexD35dLy3QOEbn934YZlIjIaMxZUIo8yzuIk6D2jwTfkOkTtGaU4/F45RxkTeiMO30W96yqa4zSaFRzF7XzlOWCosx49uwZRzdu8qMf/TmvvfEmOhutWKf+GK4nyJaYON8j+8PSieBgoJ/0Pnbe8+1lC0xBf6zNPVyx/0vr7n2IwBa1L7R3JhnIkjRPtciL5hzR6DV9+CLvKZbW0ce71h9fIF60AQP5KGdrZ5uLq0u89VRlFSLXCQzuOFY3Q/YBPgdCzkfhkG+SWvWJhth3jBaVjIgG1vSXW6Xz6p/FNsyw3FPfnFulWLpXqwi8VYKXDmHYG9PAajft94nKfp2076HPQ+/1xxxL34RnnXAjHeNQe6veva7NUCt00LyUfuneFRVxQzoe1eCKoXmm44+lKAq2trbC/iTnyydDSHGjAm0kquLJyQvyzJCerSUT82Y+S412Z57CI+dxyg2et1W4RikVJOBJUIfeWayt5fDwkO9+97scHBwyvZry6MkTjk9OOD09QyuJLrW1t4MxI0w2wZicLNNUVcnnDx9Q25KD/X3u3H1FkslVFdbWVGXBYjFjNptyeXEqPgZl1URJm06n/OhHP+L05JhvfuMbjMZjnjx5xje/9S0+/vhjnj97AanVRgM3Az3VY/RrW6MqRRF8SY5uHHFwcNAIpaV6a61wnYCgWcdIiyR72r7b0hztfsRcI4o8y8hHY5TSvPLKq7zz7tc5+bOfcXDrBuPxhGp+RTG/wpiS1+7eYmsyYm9/m5oQMMnaoN2xwYRLgg5ZGyO4jlgsFlxeXlIEP7ZJwMHW2iY7uMB8+S0yjVrr4GcjuDfP80aos7W11bEWGcrHsqpsHt42ILBIsGulQqhVLVFerAPdEvTOS3SlTGdUtgr+zh5bO0Yj0wDp1OG7nxQpvTyNo7hzuEBQR84rIkkb1EDRUWU8HnfMtdK+uqpwS3QAt7bCuTogakVlA/8ciC4fLqgPPhSlc4ysRt/Y5/Db73B3b5+rcsHo2YQnjx8znxeUtdjzCYiSMMHWg1VQek+tFbX3GOXJ8ORmhFMZhdbYyZj7b95DK/ErMEq4V03LdChtkgvQRUoqITD6zyJKi3MiXBLfzDepqeK+uF4rLXEa20q/CzCOyDf+ppr2gGC25hPztbaNSHy5aErm2/1zQWMUh9FB9kTCKB2m/F45T+1qxqNRM8WiWJBrj3fgqLHMmRdneAqsi+YZiakT3ZL+rtrFaBahOdd0M4JuIhVcYhyUpwnrTBL6UBv0eKc3MJU21HnU3AOl8LaCatGuX0DE3kkG58h4R6lznEP01Uolx3Gc/aAO7bM+8UG4f8OINZbKWfIsD7lwwvhsxWIx4/w84/HjpyzKmg9/9RFf/+a3e+2Es71E2OjOXvSRbn8M7eeEKSScDNVGTIoEo1aq9dmATihOn/iP+VB3YAFaQj/075I2VMMY0JgEggcXNC8JA6FjlJ1AgMfT3IScDo6HQV5PGomuIfSbvAjt+JrOI68a4EiTZNU5FB7rLMoYdvb2UU+fo5HQ07UtpV0d+0zbT7sRilHOIigcKoYzpxUmrC89uEAKr1LfQt+55B1mRYUdVzGz8/Xai740+jppfQq2NtWOrPKVWsdYrDrrfc1DejfWEbH9u7LOf6ujCVhHKAcCXBHDuNLsjY9EU7x5nXG19RpitPneCTC8xOD05x/NiFCpr6Vvz2UYgQahT4wCA1W9YHp5LmSpt6Ai7HJE886OgKEzF5aYjQ6jFpinvonq2v0FtA3jVgpvWvgXcerO/h7f/t732D844uT0nAcPHvLsxVOqumZkJhzt7qGNx6uM8fYdVL6HmYzYmuQYVXNyfsXJi8ecX5xz7+1vsrt/h7os8XbB86efc/rkC7a3DFujHZwF5TNMSPx8+9YdPJ7PHn7OxdWU73//+9x7/TUePnzIW+++jdfw5MkTYXaMoa6thLn1suEq+rhqGubFuprFYo53nslki+2tHaZXM6pScnigM5wrl9ZqaP1iMZlBfC3iOYnhh1tYkh555yyg0dqjsh0ODm/zyqt3+dt/+2/z/HLBzq07bO3dZaxzjr/4BK1KdnYmZFnG/dfuULsrFoXFudavMTp1R81GnueM9Zjjk7NgSmbIshGz2QzQFEXBzs4OVT1nNBoxHo9RyjdO/DEgk/eexWLRcTGIGpE04WGks++/ObhEnbI5o5Es/CruP0ofU/VdaooESYQZ75tEJWndhnkY6GsVMIgRTDSqSWACNI4qKWPRdQKP4/ZonTVEq9gYLptedC8w1E4YG1d6dvf2efTxJ+xv7eBHObOywioDJsN5i60DYaQ1lcmp8UzLksI5aqWpgUxrMgUjYxiNJuwe3eC3/43f5vHxCe/dvYfxy+FNB6VGK/ZuLbJKJByNhCjJetlxLu2+2PS4VgbVG2PfYXP1e4IwOrTHisvfD103hBgj0gDIew5hCglj6FzNfD6lrssAIIQgXTXBvgajX1KCezOJ3SriNnzPcvTeXSJZO37zh+idW6h8h+zm2yE3yTDSiXHRFUhOl8hcVgvs8cciUJifU378RxA0F1RT/OIcl/hLxZIyGUNEi7W28c9KidbmzPSIlFVEUiuhsp0gD7GPYlHw4sVz8vEWf/zH/5J33/tGi6P9JgTocEn3rd1nv/KOJXR2bEDujWrIh6bdzjqugKuDazLQ5+BYknej1mLli6oleFTv4aYEbEoda93VIAsRIE70N27c4BM+oior8dOoKtroZcsz6gsx+oxh/1mgzteuzXDxSWf9l5NnJHCpxziswllDZRUDoEIHfdh4HUMc6/QtAfrt9JmJTRjr6+5mfwx9bcsQvuq3t+5Zv96678ktWxpvW7crce63k+Kn6DfawE8dx7hyiNKDVk3Y0Mi0e1wHT6XjiWPur2t/v51z4vSrl+v15xv7aNoIy9LwM7GekgAa48mY7373exwcHPL8+TGffvoZx8cnYDzbezvsjvcpFnOePn5A7Tw375R897f+tgi4vMVWC77xvR/w/OldXF0x2tqjtBaT5eSjnNuv3OfF8ROuZmcYPWFv50CEr06I1ouLC+7du8fh0SEPHjzgT//0T/nN3/xN7t27x+PHj3n77bep65oXL15QE+i51AdLaWwQGESi2ForoV6dRADb3d1ld3eXsiwpiqJDr647r/3ifGvan6ZaiHuUFu/lTB0eHvLam1/jt/7qX+VrX3+Hm3fu8MVPfs6t27fwZgu9qHj0+WcY5Xn9tfucH5/wgx/8FtbW1LXDmLwZ32g0auiZ+Pfq6gqA8XjcaDwODw+buSwWC7a3tzHGMJ/PGw1GWvppAqJFQjTBSn1B+n6uq8pLhbeF5WgRcWn7jkkp8F0KL9rbzLTt+L3jtEUXgKZtp4tSV60ZR7+f5Yvdzkv3LuxsOmN7e4cYFSItzcFTitxonLX4umI0nnB2ccVfnF+wvb2DOthjezRCzeZsZzlaaUajCeOdbbLtCZO9Pcx4jB/l6MmYfHuL3b19tra2mGRjJvmEnf19XJZxfHmFNlnAdcNOl0PleoDcXYe0XS8vDLTZk8B0Hq5nNobG0Ecs6xBzrDdEXPSJjlRj1e/TWcd4lHeYTgXUVY1CU9cls9mVSEW8x2gjyRwbQmj9OFONRZ84WuUcfW1RGnPrHfLXfkD+6vdQWwfC/CglUm2vJNFl02cr8WrXJhqiRcmLCtoB0KNt9CvfCYSaYvLuv9HOwZaUD/+Mxfv/EBbnnTVNBQtDe+mcaxiNdj8gPSldOLCa8fQevLdLTKowMyWzqytG1nFxecVnn3xCeneHogZtWoYIfbUmfG5Cb4uZKbLyKTvaJ+ZWEY3XEYLrxjpEHG5S4nt9+Nwfy3V3oF90OA/7+/vNuCIjOgSr+33Hv7LnNf37FUuE2utgynVwqFtvPVEa31+1Hi+7B318NcTIDM2trzkcWseh8ayql34fml+fJuj33YfVqxjpPuPTL80vK/Zs1VyG5rZqHdbtUVmWjMfjEGRh+Vy3OKR/SGA2n2HTXE5+GT+k921ovfvjFh9DEXikWo3+mqyanxepQquEDIKpLDd8+9vf4caNGxwfn/Dhhx9xenrG1tY2o60J+fYuW5N9vL6k8J/jtePs8pSaOkQBnFEVc3xdsbV/S7JHo7F1ibc+ZEKvePWNtzk/fcbe1jYjk2PynKoqKIo5L16coJTmjbde55133uHTTz/lxz/+Mb/1W7/Fa6+9xoMHD3jvvfeoqoqrq6vl/Wb5PIrWEaxutQC7u7uNlD4NNvQyAql0t4fgQZ9x3draQmvNdHrF4yePuffGffLZjPHWhG0NZWU5O3vO8bMvePO1Gxwe7HHr4IA7d+/y5OkzLi7m7O8fsrW1xW7IoZHiQKVUY+oUz1O06DHGMJlMJBRuOMsxF8bp6SlnZ2fs7u42NHzqsxEF9zdu3GA2mzX5Ntb5A/fLxoxGnEgqlW2iNI3yhvPv5NFwrQNiJEhiW947rKub2L1DzEXsIx6CqLqJdWIo2/g9yzJMQvSk76bAL17M9EBGUymAk9MTTk7OuHfvfjOOJYClNdE75JOPP+burdt86/vfZ2dri5Ex+B/+FaqyIs9H7OzsYoxkB9fGSK4MFDVIFvA8xxnJGq5MxkhnKAfWeZyD/cNDPJJVNB3DdWUdsunPad1vnTaH6vSA2yqEskn7q+r2kZAA7QgqpQwxl+3+BgfU2qJA7CSzjLKqgq2IkrCodU1ZzUG1Gjffk1wOlRR5DM1nSOq0bk0a5KE06uY7TL7738Ucvd5loOLYUBJ/G4Wo44OuI2YDboRmCnzwm0KhvEImH5BdJNE8IZW2MB0qHzN666+Tv/ptZn/0v8VdPG7irQ8htj6hEQFXG6RBzL6uK/2zFNuPYfZiH8456qqkKguRMinDT3/6I/heF9lESUy/j/482u8rCEdWO4MrJVL7uDexolexn7T9LgE99Ht3PMufV73bJ1yGxtn/ft1Yhu7AUJ+rxh81aHu7kpTKNr579VLfq+BILDHLcLwnnTG/PC95TX8e75eZjVj6TqSr7nqfWUrLKgJxiKkYZK4GCOr+feybDK/bx3Ru/T6HmIOUUBvCt5vghNVrAJtu6iombKi/deNJ68SIU9baEORlxfhpz158dnV59f9h7s9iLNvS/D7st9Yezhgn5oyMyPFm3rxVt4au6uquqq5Wq0mTogAbsmTAFk3BMAFKFgXYkh+kB73YfvKDAD8Zth4EGPaLAZM0IdsEX2wJkFpks6u72TVX3SnvvTkPMccZ97iWH9aw1z5xIjOrWoS9L/JGxDl7WHsN3/r+3/D/yIuCOLJsTMLIv3DfehPoXX4fr3tphaQ9liFgCY+WwhuS+TiPlxAgNLdu3+bg4AbnZxd89ulDzs4u6PX6pvZNd0RnuMdwuM31mz2GW3scH79gMNjgYrJgXs8ZDQdsbe7R63RIIkksJRpTfVtVmrqqqMqMi4tjhmt98ukUCaz3e1RlwXQ8Zj6fcXZ6jkbx4IMH3L9/n4cPH/LTn/6U3/3d32V/f58nT57w4MEDfvazn1FXlSGZEI2RajlUHtvbzqhRliXD4ZDRaESWZcwXc9sdlymXl+VduOfUV4CSq0B5URTMZjOUOOXLL76kvzbkO9/7HoP+gKKaU8wXfPKrHyMo+PAr9xl0Uvav3WBjY5NSzRmNEsuIaiJ4HGBwe5vTvZ1O7f65ehpOXro12ul00FqzsbFBkiScnJx49qk0TZlOp95QuLu7S5IkbG1t+fyit8no8Pi1WKfCjToMdwrDosLzhRCoINTCx9YrRVWVxEnUOj+cJOHiWmUxcfcMqWyF3di11n7zCpmuwg2gEY4mfk5rpxMI+v0B08nUuEyjdkFAL3iVIu4k6NpYPHZ3r3FwcINFlqFQVKqkrs1GqoVAiYhaG+XPtAcbJW1i62MhUcLkcChrQZOxKaATaaNE+tCGKwToVX9fNZ5XCablo6WsNp8EN3vzs1dtwsuWg+XNeXkDWwUYjU7xDhYc3bAj1aomiSKSKEZVNWVRgPUc6lpR1SZZTWMYcZp72fj0YEN1913e+N+G9N/2ndYaGcVEuw/ofP2/j1y/gbChKGhngdI2ZtnkEEWt3EZh8UI7mR6s2183iazoJgxIB++InbfYWHslJaIzYvDX/2Pq44fockH5+E+pjr9AF7PWe4f94NZfqOi7sWt+D9flaotueIRC1MkUrTV1XRrAJeDzzz5DfX3Zfb1K+X6T8vEmkN7C120wGVwuAplo9KW2p+td1+67CvTw/KvW9qrNtPU9l1b4r30sK0sCPFFIz7ru0brl0XiTLFpWuKolz7V/Hs5Se7UsWNXOsK3hec33776eVwG2q8CIO2/V/HuTwvi2c686Z9U93wXELt/nqv141bFqD37Tcem80FDCm8czfIc39Vd4XniErEnunNlsRr/fXwkg3d9aazvxhL+PlJIsz6xMtQWLcXtGc+3y897YFwR61pKe+y6AV2vtwZIGRCSp6pr+cMDd995jNl3w+edfcnpqPBlrwzWGwxHpYJPu+gGj9euUqmb7ICEZbFBmJcP+OvtbI4aDLrGEMl+QzS/IioK8MEa7WHZMLY1Bj9HaLYpyh+n4grPjUxbzKUmSImTExfkF66M1To5PEFLwta99jffee4+HDx/ys5/9jN/+7d/m2rVrvH79mgcPHvDRr35lNCP7jrVWSJpi0G6PcCDEsVG5Me12uywW86Ykw1LfrZpDzXq9LMdb+8CKsSiKgursnDI33hSimA8efIjKMr746BeMT17x4Qd3uXNrn2K+4MH799nc3EQmGwgRcXh4xMnJCaPRyCdph+1aFZ69DDCiKPJVw93a7HQ63Lx5s6kGDoxGJsImTVMPlIQQrcTx/9Yrg5vEEWE39NoXB4miiLwsLtHVug4PKQhDBcQU/Gi8E+G1y56NNy1Ed79GeREeaLjiLSGACe+5bH2Rsp2MLqX0gmEV77IpQx+xPlrn2bPn3Ln7HiQJtU0mRyqqqjZJutKgTGSEkmbjTbRA1yAUjXXCTRJrATUUlToAIFdbFa/6OzzeZj1yR7SkwPsz3iy733rftx3Lc2XVQvbPQiBFe7FftWm78VZK0e/0SeKYX/3ilwHgMdflRWZqZtQlzjsQbh7LbCHhXA3/reqPq95VCBvQNNghGl0n2rhFcut3kYNtTMEV53dw1wFIhAAtBUI1WQMGyNpNRDuFSxvrlbbAQzgGFIGwPkdtAYdRjM01wj7LJ17btibXPgCtiQ9+C51dsPjR30cdfrRyboWGgzBxfFU/hGP4NsDq1qRXYlRNVZREcYoGZtMJVVkSplqZaqhvFnntpMo3ntpqVwMymjhoABneQ7x1+fylj1/HyvTf9nGVXBJLHTkYDLxCV5YN9eKbANjyoYPY4Tee9xvIoF/nWG7nKgPKuyjZb1Lc37VPlu8XGkWWDTXh/d5VXv2677R8z7dds9yuv+zYXQWsltt11XVOB5jNZty4ccOcL2hZGFa9j1FyjaI7n8+tzDOyVCnt2YH+ssdV+/7bxsQ9XQiTlyGk4IOvfIU4SXn85AmvXx/S7fZYX19HKzg5OeH6YJ3NnRGlgsliwfnFMUmkuHH7NoNuD6VyTl+/5PT4FbPJKXWxQGBqhSAkSknipEeadlgbDbh2bYeNzU22dnY4Ozrm8OVL0rSDFBHT8ZS1zSEnJyd8+eWXvP/++9y8eZMvv/ySzz//nK985SvM53PiOObatWscHR5i9X6zowXzvYluaQxTZVmyWJiEaJMEnXo9721915778lIi/vKcC/c7F8bUkQmRjJheTHj40WdsDrd4+vgpTz79hJv7u3z7W19HCsVw0Of+/XtEcYKWFWVR0u/3OTw85Pz8nMFg0Hqmkz0hsHceCdcGp8O4w0UEufCowWDgvR95nrfq3wnR5EC7qIJer/fG/nLHr52jEcaALX8Hl61Cjmo0RE9OcXULTghhsvht4by6NuEtkS2cpjX2c0WaJk2mvac2tMqRtSoIKYkt929tLZ6rAjUaV3IjfA1dmGA0WqMsC5JO10xAjS9sZfExkbVSbG1u8cM/+SE3b92ikyaQK84Oj9jc3iGKErQwdTVQ2oMFQ9UpDXtKrRFaIoSxeCCgdmjUKoCGdalJ5G2vh9ClsGR7C9hTtP+/UzKdYPIG7+Z+QnhF09zW/9I+b6kV0l/jHrq0WTiw6R+KDUXRze219j+NpSh8I9MDUjorKV5RxlWpdwJDBO22z46EIE0SBII/+9Mfwtebxtd1RVUWHkRqnOfAKON1ednK3mYve3NC81UgSCPofPPfIL33L4OMTdSS7R8hhF9Dl/rECVe3Abr578bOt4lm0thLXXI/wXPcDbWWzThb8O4v1+ZDLQQoTdTbZPCDv4uavmbx8/8X6vATYunAvJ1nfpNtyCKWrZJN34ngOauP0FLj7qe0plI1qVKISKIdZZ9xBvoxXR4/T4ksaP3tJqf0nec/Mv0XTEkB3n0vwg9DgB60+18UEFhW1Fcpbs1GGCqXBH+7Fptz9NIabzJNLGjVBOfTfBc8Q2MngBkI4jQxoEtbpsC6thTo7WebNrefHja62+vZ27YZirS4eu64/lhWlsOfy33WfvP24ZZQc25wfnAPKZvf/T0F7Z/Bu4X9H3ZLMGr2ZcO2OLnuPmjuE77T8ny46tCAFu0oBSNrQdsdVWgnZ+2ab3YV2yJtxLIW4OXK6tA+/5q6GXvN5f7Xbjr5HU37gXAysuml9prwz2tveM0aEFimxka+K6UYDoeNnA19fqGcdLJVmCLGkRQUedEa31Vgq/k1fFv33eXx8SHrsm3Nfhswk1JaCvxGCwDY2d7l2u4eF+cXPHv2jCiKGQzXKCvF0ydP0RoOzy4YXjug1n3Oz6f0hz1uXN8m1orTw2e8ev6E+WwM1EhdEkllfrfTT0sQqqTMSg4n5xy/fsFgbcTt23e4du0aa70eL58/J88WzGczBsMeeZHx6tUrNjc22bu2x2w24/PPP2d3d5fd3V0ePXrErVu3OD09pS7Ns5ye5eeXX4eNsdgl908mE8vWFFOUudHLrGfjXUCuOz+s22bmmAmeFcJQHEcyQkjpQ5L2925w48Zt1re2Ga5v8MXnX/DRL37Jnf0Dvv5bD9jZXmc6Pubb3/0eMhZUdQXagLY8z7l2bZcsy5nNpkFoo6G1zfOcuq7p9/ukaWort9dEkUspkCjl2KOad3TlILIsM2Co06HX66GUYjwe+8/iOKbb7fr+eVdjwK8FNELhsLGxwWKxWJl17gWatFSMVktRTluSAqGlV4SwCgbCsjqIyBS9EwLhqSEjkjhGYBZwS3mrmxhzRyUpY1sF2roJy8oU0oPL5ee1du/mwhoUtYIXr56RlzU7W7sMOkMkkrIu0HVJ3IlNhWIh6fW7TCcX/Gf/x/8DB3vXef7kKadHx/xLf/1f4Qd//W8wKysibXmsagVKoCVU2lhYRWyWvtSB8Lfj57wsAk2EdlKQy7uTPdqYo9mzWBbcbpOyY+UEoL82OK81tuHGGjxWa5uU3LTM0Vu2apDYe7auRZuaI7ZN2itp5nOno7SucHu1vbdTVISwxIU62ITte5VVSa/bI44kx69f8/TxowZoAFmRU1mGiqoy8wChEMIqn7ptJWn6pD0Wy2DjqsWoNcj+Br3v/k+Jd943G6Ww4UNaNiA7HAYryGw3mHES1jMhhBfsDnSEG7DTOTQYhCaw7+Q24sie7/62/es39FCJweYMWfrotQP6P/i7qOOH5D/+e7A4a23spg8d4FgdrtEIr2UF8+rDe0ClRGtFXhb04xh04BkFn88Vhlo5ENYeH6sgaY1QGhFFS6De9anrTpPrIoDIfq4Dg4FXgtytVxyrLLhXMQa1mvGunXT5ia3GNEszBAeu2aJ1Xa3d/HZ5KEuKuT1P67aSDhIlFCoSdAY9Ov0uVVGAqqCuwBpzhCXuVgDKybCWpoYQoJQwshFbBd0Dk9BafNX4ms8MUA1DdUPA2e6T1TDDvHEDfNteb63bIYLufNA2Lr6RhwQKvVKmv9y9lDVtNfSu7l5tOeQTlVsKtzAU9ARATgf5WL6dVmYFclohUC2gYUnG7b5hxkqDCkKp7cRxtPPQGM0Q2kInex8ng/zR7mUnwk2TlvYh972Vbw7ktcGvpYG3XW30A/OlA37YPdEopM7/a6igXTSEi44wypnJL20ZlWyOn7JtkbUmEYIY0NYzrvRyzmAoG5f2ZfdhMMbLHqlVHio3lm80aAhTPVshbJqd4Natu6hK8PTJC/IsZzjapNtfRyEgOoS6QoiYfJozWczZWN/m+vVdVDHhyZOPOH75FKzxWdWKUtWtdklZE8cJUQRxFNHpmorT8/NzPjo74+DGDd67e5fbd+4gpOTs/IwoFkTzKZPzcx5/+YjRcI2DgwNOx+d8/Mkn/P4Pfp+trW1OTk7YP7jBk8dPkI6BSjiZLOycs1lzVhaE+4ABC7FnKBXC5NJUZeVDhML+DPeOKJI+/F8IgVZmb5YyIo6g20no9frEaYc4SamV5vd//1/i9//wr3Jyds7LZ8/5iz/757x48oSN0Trf/PADtjb7zGdj1je2Ga5vcnJxihCGYSpJEkajIXme+7yL+XzObDYHBEmSsr6+7uuDLBaZjR5qiG+MvDPyxQQ5tCN+XBSQqzwuhGBzcxPAgxgH1v6FFOxzN6yqio2NDR+zOJlMfMeHCSJKKc/L6wZrVbJ3eHjr8NL+6a4N3T5tukwrGHU7JCq8NgqeuUyDqq1C55Au4JkJPv/5L/nkV5+SiJQ7t+9y8/YNQFOWFUiT8CRqxfvvv8//9Z/8Mb/8yc+s8iv5J3/8Q776ne8jOl0qNFJr0EYhjOOIKI6RWuJdcAIi0TBptRKMjdbnuaFXWdLfdizt1+Yz1ydXWJmWr3vrM4LfQy9FeBOnA4dXiRB8tFFI61glVENBECqS4edugcRxhBSCX/3yF+R57h+gMQvJLLLS5ckZ64SwfbxEefymPn+bF4O4Q+fBf4f0/l9Bdoat1/UsaNps6n7v18189zoQeCUlBAFG2JpN0AMLq0QbASwCnNls8EK40XA4pNG8zDw0SNApO1I0BfSEEES7X2Hwr/zHLH7yD1HPf2IUyWBs3mZFXerFN3/r1n0rT6M24QCuH4LDCdHlDXq1dVE0BUovtbkFuS4dbY9Je7K/CZRe1S+/jgekDe4uAxjzuf/tis/f+hQ8pHjLGmhZl+1G3el0SJKYLM8oy8pvYM5ivvyM5fuZ8JP6Ei0j7ormf8G9lttPADLCc9rASrSacfld3bI04yytoawZA6vLBWq9WzlubEw7WoxRyEB5xv4evmMwX8Mv7Jr2ng3p/l4C7rrdO94msSR/NaCFWl5G/iYKt7YdGAJnpFBBAkHj6RG+fyAwQPnmi6V2af/z0hpsyS983poKar84j47HTzQ1aLxSGt7P3jCyCphTpJxSV9c1USxZNQ/AyUJHVW0+c8oqS++yfFy5jJZkh/OwmLWi7f7QDldfXndvOoZra2xvb3NxMebl60M63QHpYJ3uaIuN7V129u8yHZ8zGK6RVZr19XWu71+jyCY8/PinXJw8RaiKujRWcrO2e16xdaxFLifAWcQ7nQ4daWo7vHzxgsV8zr1797h9+zZSCk7OT+l0elS9ksV8ysuXL7l555ZJBv/yCc+ePePg4IDxeMze3h6vXr0yRm9tZZJoZFOoK0HjCXfKdKfTIcsXxHHM5uYmf+2v/TX+3t/7ez5yp22YagYkZG4y+QpxoOdqyrpmcX5BrYxh4fr1A27eucN8MeejX/6CH//FX1DlGffu3+QrDx6wvbmGokBr2N8/4Pz8oqU3J0nC5uYmw+GQtTWTFD4YDKnrV0ync6SsvUfChRWH88XpQQDz+ZwsyxBC+7QIk84Q+3e8uLig3+9TlqWvDl5VldeTQh38bcev5dFQSpGmqY8Ni+O4FaO2/FJhbJi7R6gcLgsPBxKcNcF1VBhqEf50Md/NtRWN294cDjxIGbUARjhxHNtUCFBMDkrC3t4+n519xvNnT/izH/5ztna2+Bv/3b/Oxu4mMolJ44RUSG7duc3e3h7PHj+hLGuIY777/R/QH4zISkufhgmdUlqTlzWy1tQKkjghTSODvsXVYCyc6G8TJL+utfMqrvzl+71tYq1SJN9F8IVz49I9g51x2WIYfhYqnMvn+oUhTfXSn/70x7Zaa/MUIQjyCDRRlJjxcEJLX2alCNux/D6rDq010e779L71PyLauNk8m4apSFuLjAkIdKE8ouFNNw9wT1p+QPOdAJz3YElRdqFZ1iRoAInWaAs0nKXP96fbPBXWU0lj0aQZPxGBkF26v/1voT/877H4p/8pYnF6qa+WFdBf9wg3V1gmmqiIo8S3zW0Wyww67/rctwH5pZ59p7a/q3Fg+bp3btMb5EQ4Rd70jF/nnu9yCCGQSJIkIUlSMoQPB1B1/daeayykTfGpljUe3ggKbCMC3bax4ptwB9G6vtWeALyEVmVt5bkK1pm2QH4Z8NiAUA803H4URRG0WNhE+1WW3r9lxFj5iksef//C7r4N7AmV8PAZ7vlXjYmRS8r3AUHh1KUTabzwpp+1cs9Zztdy69V0XyPL2+0X3srSJOU6g1C76CKgmpARIQTSyg1VG4NJVVVUZeW9GlVVUlYlYJTMyWQCNMndQpj3Wb1XGWOZkE1h07KswjdDW0/rsvL7LseyZd0NY1uXuQrIrF4PBwcHADx79gylIR2skw436G3s0h3tsLnXZ0/VvHr1mqjS3Lh5wGI25uFHP+f8+DlUC6twR6YYXr8BGWbPlT6ft6pMGI+LhOn2ep5y9fz8nE8//ZQPPviA/f0D5lnGYj6j2+lSZhmvXr1m9/oe21s7HL54zZdffmnqbWxscHR0xMHBAY8fP24VPV3ui1A3aYEQYYxQZVlyenrKp59+6hXyZQ+SA0uj0YjRaIQQgul0amlzq2C+CuI4odcfsDYasTbaoD9c45NPP+VP//RPOT56zcaox1c//BbdNOLWwXWuX9/j+YuX3L79NUajkQUuQY0QKQGTg1nXmiQxoVF7e/skyRkX5xdMJ3OyPEMKydra0PevEIaNSkYRnTRl0Jesra0RxzLwdggbblVSVRWLxYLJZEJd13Q6Hfr9vqfodZ6hMN/jTcc7Aw2n9Od5zvPnzxkOhyYRvCj8ZA8BhwMCblGEAxxS0rojROROgIRoMkz8BLzrxqEtJ3RD4BE+M5Jt62SI7qKooQNzyogBVR22NrfodHp0Oz2KouTzz7/gwaP32aty1jZGrA2GICKSNOVbv/1tDl+/ZnN7m+//y3+VP/irf4gGup2O3XOMxUXRLAClNEVZIqRExpJKX85/Wbb0LPfdm6wYl62ZobL6ZnDhzl9erKvu/zYlJPx+eRNUVkAvW7DMd20LXniv5fCS5Q02/N2BZCkEz58/4/jkyG6W4XuYjSBJYhpkY3WGoH2rmNGW3/2qsYgPvkn/+/+2Z5EyLl1jJTNbtgalTF6PMIIFbSKfG4Ch/cZobxyAC9GyEjpOZK20TfQ23/tIXdlY/ACEDWdw1kJlXdHYFjoPiQuLMylAjQWpqUQvkP0Nur/zb7H4J/+pf0Dosl51LFv4l9dC+Pey98qsXQM00qRJFK6qJgk9vPe7KPpvPk9c/k3TqrHxJsD5pu9/nWMV+L4KyDXKyOrr33QsG2nedr1fl+FSEIZYZDgccH58RG1zaaqqDrRecek+4U8nu5fnUfN9GO4DoQLrgLW/LKhI7wxO5h7+Mv/MZY+8A+DKGgea+2gP8JeCgey6srkXmOtqrVu5QA3WCdrjxVHzmVPgwoq9rm+8h2RJAW2RV7h7y2ZOOErsWilkJFvzpNUXtSKKGwXF4zxLXW0+U9aDYeSP8oA/ZJc0b2wMOQLnimzYGVeFBxka8sqyAjq6T/feWZaR57nxYJSaPM9ZLBbeKzGbzYijCElTcCxNDfhN0xQZCZLEFGF7/vw5+/v7XhcxfdUooWHfCmzuoMC3P8/z4DwTWmNIcAIZt8J714xRO2wqNJZGwuwhy6DFjcmqsBanJ2k0URRzbXeXPM85PT31cfmDwYDBcI3eYI04TTk7OWW2KHj/3j2Eqnj8+a84P36KrhYMeh2U0sznGUWRU1U5vV7Pz6c8L5DSga7S92NRFNTK1NRxNRlcDsZXv/pVbt66yaMvvmAymzEeT+gNehwdHXPr7m12dnd5/uwZr169Ynd3l+PjY7a3t3n69KnZj67SeVb8jKKIJEmo64rxeIxSih/96Ed+Li3v7U7BPjs74/T0zOqQJux+c3OdJE0QAtK0QyfpkXQ6SAnT6QWLbM7HqmJ7a52vPLjDtWu7DIcDhr0OeTHn6OQ1d+7cYXd3z8+pqtLeS2H2uoLxeGK3eRtaLQVZVhBFxhsx6A/suqiZTKZ+j1wsMqOzpylxHNPppiilieN2romTK/1+H6018/mc4+NjXr9+7YFWmqb0ej3KsuS9S7Ps8vHOQKMsy8bjICXHx8fGnSLN4mmF+QSTfXmQVimF4bEMMFYx/Lg2uMz3lRuAPdI09UVZltvmrnWAI7R4CiGYzedEcZfBYA04tAukpMgrJCZkSpUVpVTUuuJ7/9IPuHn3Ntf399nc3QMShOhQB/HMmtqHKbn301qjVUVdC4uKL09wIZet0s3xLpbNy1+4Dm/3ffj+q45Vi3h5nMJzVylUy/PEgY3l77VVCt4SQePvv2zRcT9D8oIojvn4419RloUNjWnuUatyqa1XA7BV77Tqd3deAzL+DiJKzL219gq9S1p0QUtOkAANta25eet7F3LWHq+gz6wyJMTSduaAVRgGYxq7NDeC+4ZKmiZ4tjnPKWruMq0h2r5H5zt/i+wv/m8tj2fYf8sWo6vm3rvMMadohbljzrPqXMq/jjfhnc4TgG4bA9523ZsAlPt+GTi/qX3v0k63Tk3e1+r2vKn/3/QO73C2aadVxtLUKCilZTFx+4vDBZpmbrsjbFcYP325vY3SztI9mrYvg5n2/JKyuYdZa+2wYPfMWikPMjSWZaYlUz3HzyX5HS61MDEzNIAsH4bC3fweznNHS2kstEbJ914KwHEcCBrArTC5CA4w+dYJG3alhX9Wy7CBwORzCS8TUBohBZEN10JrtG5IWLSuqcoSQYWUEVmeG7YxVaNq5cNr3HtNJhOqujLmF62YzxeAY4ZUdu83nP/OCOrCYIy1X9AfDOgkHSIZeYUSII6N4hsJbViRtEnabRR6k28TxyYU6PDw8ErjUrjnaIyhxeQ7Gl3JVAUP9iPt5mOja5gojHBehH+0P79KRr7JQLN8HkKglWY0GtHv93n6/DlVXbG2NmCQRgw7MWu9lEE3ZZEXTMfn7GxtMugkPPvyY05fP0GoBb1+Src34Oz0jEW2AKCqCs/oJCNpgbyhU3UF9px1vKwqJpMJm5ub3lh8cXHBkydPuPf+fXa2d5mej8nygm6/z9HRMdcODtjc3OTlixc8ffqU/f191tbWGI/HrK+vc356dskI4mT/Kj3UFWNM05ThcMj5+fklfXF5TBp901jdlDbKepzEbGyMiGNBL+3S7/ZJOh3STpf+YMjW9i7Xr1+n143QdcnGxhApIy4uDMDZ379Jp9Pj4nxi+7LyssY9s9vtopXJOVbahAhLGSFFjLRGQ8OwZRa8Mc7DfL4gz3OGwwFaw2KRczG+AGp6vS79ft87D5bnUK/X48aNG77vwkgix1b1tuPXztFwA+a8C5GILllNXEPbVJGXF+jyYvEDq7VfYOFzQyXFWbPa9xE2WauJR3P0XMpZhe2gheBCyrgFbFxnV2VFhKLf65OkHYSILL1XCUrTT7v00w7z+RwhBTWab33vd62gB60jVFWTiMSWrdGgBbE13Bklz1pulAJd8+TJYxunuORabWT+v5BjeRFe/m61Ir1SqTaagv97+V6NFezqNwrH9BLA0s1Xbzt8sjAmxlHVNR9//PEl5iN37spj6V1WgafVbXeXC+KDb9D73t/xdVmE1TK0xrBkeeustYjhQgHsWrAbemP0017hN14L2+fu2dr/L0gSXe7vQFFoNdgAE3BKlkUT/t72b42nw202P232UG2UAtDEt36XVCnKn/3nCJ1fAga/ybFspQ3Xr1FOGsWorivm87mPpQ3v8S/iWPbahNP1Tc9cntZXrg7RPjdk33rbPf0tVmzGV63Ht93jKgui+90o6Xb6CBNqtL29xadKUVle+7zIG0OP83CqZV9mc6yiTfftDef+CnnWfqvV7Qax9B5X9JMIQI1o57q129YGPIEOf7llb5CLMvTGmLuaua+0LcbWEKK0Ml5cOItThO3nnqDF2XRsnokLNXbvoWpFUZa2tpDZW7PMhIvUtaLIcybTqZ2D2saA5z7m28ToG9ZIozuYvdwx8USRobvv9/t0Oh1GoxFxnNgkbBmEaUeNkcXLD2GVrDCX04TtEDBbhsZJ0EhqHJmAlAZcOc+SsgnuOzs7vHz5cqUO00yBAIABjulRA4vFwoMXwIbZKT+f/kUcqwx8Xlei6bv19Q0Ajo+OEQj6vQ51NuZXP33O2tPnfOt3fx+FpC4yrh0cUMzGvHr2BVRzhoOUODFG1KKuUbpGCCjKiqLMkdEavbRPt9MnihKvzLtQnDRN6fZ6TKdTJpMJa2trpGmKUorDw0M2trbY3t7m/OSU48ND0ILFPOPi/IJrO1usr69zenrKbDZjY2ODi4sx165d4/T4ZAULVHstO2VZCEGWZXR7JtcrNFiv0g/c4e4XxzFKaIoio64VZZHzzW9+ndFoQD9JGQ2GDIZrdHs9hIzRQtDt9tCqoCg1F2cnaC0ZrW9x98490k6XbFF6kGDIJWTgvcV75gzzE/6cxouo/edh+Jdh10oZDPr+3nHcJYoN2A6dCFLKVh+GOlTI3AgNW9XbjncPnYojtDIFl2obe6etRUp6weF0EKfQGwV1OW7egwRrrXBFrbxCpNthEaE1IY5jo9TXtrqmxrtETfKb29wte48NS6kqu/lbpai27lsZxai6DTwiG68HElXkDAY9+oMuUWK0vLIs0TV0kg51pciL0gjnqORiMuX6tT0EgiwrIY2oaoUvkaM11K5CqIvrNbqZqjXXr19vKQwtpewN4+OtJSzb81j6zewqDXhwbvxmQ8Ra8JodbXmzXn3XUBHVS9e4753jVintLV8IK+Dd+cJZxQzziXZ30E07jbLdFh5KO/YQOwecB0xrUwlcRpyfnHL46pV5a1W33sUV6GsfIui1YEcOeyMAIsselWjjJr3v/C2ijdtB8TZrmbOWQLQpGOnjS4UMOlY2IAPdhCYFGwjBZ86CKsDmYTilwyhuaBtCJey2uAwalzYj3weXlKvw8yB8QghMXkvkx0prQXL7eyT732D+R/979PSotXFfttCtnmvmlMtWfrdxGFlhlA6XrwVmTZ+9fsXBrZsorNKLdHntb15XXPG9boCXI89xs0NpM+fkkrLqwJpGg2jNZLRQlx1JwXp24KJpj7m61vb5wffN40RwD9te0SQo+zdbUti9zLnUF+6dzT/DQkSDca0SrBGeBU5j8a0QaExVelXXbG3tojHu/cU8Yz5fUNU1qTZ5bBaVmXdy7XJJ/kLQHfSptbHK+70g7GffZmcxbsuKlUqjaL+7QPpNf0mVtHud2btUcP+Wx04aWvNgtbRAkLmPrVETPFde6vlG7jijhNsXq7qy3gpzpV9LdqK4BFmlKp94ryxhQp7nZFlGpc2ePp/PKUtTA6qqarJsThxLw/YoJVVZEsUx3W6HWCZoJeikHdJOhyiKWB9t0Ov3DdFJUGfLgYNIRsSxNFWtpQvRaodRa4W3zJpxcvuQlTN2bvicGi/3jOHFhS4lsQnPkWiiOLJGD0WcOHlu2LigKdDXSHoni40BUAZyVSsFnlDL7p3OE4dpb13VoGO0UkznUzuHFZoabWlK4ziov8AbjkAAXVJ8Q8C5QileCTaswVZpzfbONnlRMJ1OSeKYWAiOXr3gfDzn6PiM0fom+zdus7m2xrCX8sWTT5lOL0jTDsPhGvMsZzqd+f5zelUcJ2gikBEbO7tc29tna3sbtGY6m/H40SPOz89JZMTamslxiOOIwWBAJ0mY5iUvnj/nw699yM7eNabzOXVVMp1POD06YXd7h43NHY5PLnh9eMJ7771HFKcMhiOiOG4n+dPonMs5eq5K+GK+oNPtIoShoq1lTRxF6Lr2rKmX5YVh2FLK5lhRkcYJOxsb3Lx5gNSKbpKSpAmdbp9ev8d8kXF2dkKWZwgpSDs9Dq4fcH3/JkVeGypkhGc3c3pymhqQFnrpi6K2uTEpUSQpy4r2firNWrN6tKk5JAKwnpg5GNVkWd16P6WUz9MIDf2hoeUqI89Vx7t7NJySJ/BsFgh8+In2jDgSF9bthGqYX+G8CVJKIqdQqUZRcRZxNzEcwvLWFRFQ5uImt6KqayLPCmQErdJGMCQysop8O/SqKJuQitJ6PpI0NQqri2evFcNBl/6gixaW7hSQIkImHSIp6FQ18/mcPCt5/eI11zavkciEXhJRVBW1cMJIOT3eD2qocDn3b+ieb0DWW2jELNAI721+WhGt8cLYnO5+d4pi03Vo7T1A5owQiNAScEsqd/Cz7Q4OPzdzR3tdRzRiuukLYaz30iltMmQ3ss+2k9AFHOlgjkoNte2HWtV04oRERjz69CGqKEniqGEnsk9v+sPed1muWyVLiOUFdjl8yYCMWwz+8D9ApH2vdLnFYZJHzXOEjBrtUgrLJCOawXP7qX1Pqy+itUJ5a5n2c8AoaPZsP78akGG8FYLGfe/jKhAu+dwpqVbhc/0RWsW0oKG/9QqUANGoSiYMEMOg1RnR/4N/n9n/53+L1k2IYBtovElwNQAjlAtOrpgxqgGJ0o1QFlrz9OGn3L1zC62hqhVCmxAiFayryx4W+24hqMONveMkd8+13wsJwsg6Y/tt7icMvFlShJtvtWiDQjdu0sqiVT2jtTDkAQhLodl8JxFBHaJ2W5rxWmKcoxnf1V7nJoEaB6SE9iCzAR4NvalGWW57YcJIK8X2zh4yiqlrRbYwCktZKcpae5zdyEbhRLppr1KsrW8wvrigcgaLZXCh22G6rgzlJa+lC1kSWLtFo9lJYZO8pQMd2nhZhGUtsjVfjHXUjT/WiGXWjFImPMl52KWUTl32c0Jpl4xu7qUqQ4iCnddVXVPXlQ01K5lOp2DPnS8WJtkTQVVpptMZUkobJmRyBNI0JY0TH3ZkmIESojgmilLiNCVOErZ3G+9BJCPiRBLHytQnEI2Cj9YGEOgmYiFU5C7NUZwByPwlAV1XRr4LrDxSgIRIeJlh+tDR/zkweXlfcR4CaBj7tIY0NSFCUQRCqFb7/BS2o62VMvqCW3OWDngxn1AWC+rShHUJCVrVHvAK0YBqIUDXJXVZkcZ95tmC8fjcyCddo3VlDCC6tttAA5CWj8Yb2swW95lT+lZXB1vq+2UFWQhEJImFZDAYsJjPybOcfn9AFKfIuItmQRxFDHodsvmMvYNbZNmM45OXVHXN2to6cdKnnmbUZUGv06Hfs3oLgjhJ6PYGfPj1r3P/g6+CbCpRdze2uHn/Aefn53z0458wH59TFDnZYk43TYhlShqljM/PuRiPGW1t0zk6IV/MSMuc2XhMWWnW1reJ4mccnVxw915Mtz8iW8zp9/vMbIhWuLeEulYo0+q6ZpFlxGnHG1KMHNSglZGhQf+1DAqiRiuIpSSOUgadLoO0S4rRN4uqZp7lcDFt8qaEoDcYcff++xwc3EBrzfn5OfP5gtFojcU8Q0oTsudYD8uyMCF+GFKjKGq8esaj6ArxKX+eqZsRWc+vMWQa4o0FSZLw+vUhu7s7jNYHbG5u+j00yzK/v7q55vop1FPdvvuupAbvDDR8WMKlzafZfEOUEy4gpziHyplR9s0JTuELJ0KIPt0gSSmNN8FuJM69Eya/hcqAE+wXFxfMZ3N2trd9+6WUZFnmE8rds13sr0kuU/TSPlVVs7GxbuPbNFmWgzCD3h/0yfKSwSDyLqiziwsOru1bmlQJFUY4e6uVaPVD05VWowze4zc5Wuxf0WVqt4ZBox1vHI7PslflqvasQrRvO9cp2M3n7fnj72P/J0Vj/WmdsxIIYC0QZrMuras/iiJUrfj0s0+NtSKw9Ls2rH7X32wcoo2bFmT0fNuEEBBFDWh3mw1NAqHbwDzcsZ2gXCiT1laR014hFcIBCgIg1o7TFmC1TRfapmj49MN56VFMoyi2OkmESIdQMXNKqn8G4JLZvb7QHZF+81+n+Ok/bHq4ZSV59xyBMBHcNK9x8y6zYTx+9Ig/tNcIZRXGSLTW4rsfl9fL5VNEiwHFHerKa/TSfG6HhF79mLBm/BLYDb7XmmBMlp78hvcIv2uMFZfff3n9LnszfassoN7a3iJNO9RVSVEWjMdjskVGf7gWJCe3ZWY4zhsbWzx//oqyMvuAURYvx7uHjw0tr6HcMycIVG3yDbWd+6rWICRSSes1kl7hVjW4JFdh7y0NIrGUnhWC2oQVFSVVZbjtq6r0lPBKGSViNpv5/ayqTIX7JEpI0sSv6bST0u32iGIDjnu9Pkm3w/ZwjSRJbWiRsPkHpp1xbLZ3KYSPmvQKmBsTIdBL66hJ2AYp6mYQnSIuQMYC7UMzIIpBa3lpnzffO9+D0+5d6JAD8r5x/kHmt8YDrHXjofSy2o13+DBH+qCUkfFKo2jGPUTiyxS8yoZz0dIdjul1Y9AmhygSLqTFyi1rkDH7uyDPMoqiRAAvXjzn4uzMh7XVgUHE9Yubm+8ihULl2Y/JOxxtA5hRdsM6DForQ22advjw29+lKCv6gxF7e/s8f/GK0bDH0eFLJuMxSRLT7/eo64rZdIYAIhkTJyY8SiYpnW6Pr3/jm9y++x61hrKqiaUttIwmm+cMegN+7wc/4Mf//E+pVcHZ6QmLxYK1YUoUx9SLBa9fv+arH+6aMKnShOEVWUGR5wxH63S6Xc7PzynLil6vx2R8wWhtxGw6XbmHrPpMa01d1Z6yVWtbQwVHh+5kpzsf/4cQmkiaehRSCjppymw25/z8wsj/KKYsK5Sq6XZ7HBzc4s6dO+zfvEWcpl5R397e9jqZqcR+ysuXL60XwhghyrJACEmv16euq5ZO7fRZl+di1otdR9pEbUSRtOFUZv5dv77HaH2NNI18janxeGwM5nnuWbUcJbzW2ufSFUVhGKykZLFYcOf++2+dg79WjkaYBNJMemuJoNlsGmt843IMB9qzY7jvrMmttpaCOEmpyqpRvK1ipisTHuXiMYui8B3ukhwdzZ1rh9aGCmw6mzJcG+Jo4Ra5yeRXaPLSdBxaGMubGSIUmqwoQAs2t7e5tn+dTx4+JC8KL686nS5REHefphHT6YxsozDWY23pw9BQr1CmQ6SsobbCb1UxlGUl+CoF4bKb7/Lz3DiE47aM2tvjfFkBvApkvKs7bdW9Vr2jUxKuUnLaipZTsIQd+9onAlZ1xcsXL4ON9DIa/8sAPH+P7hqDP/wPIOnhlXBh1C2BsxxjLdFuI27ieP34SaukI/wmfJmhxAkVa/3yipL3abhW2Y7R/tkQgAvcba13RrqNudn2RdC2Bow40GEub4+R+0o0fwhJcvv7qBc/pT5+2Jqrzdxp5kLTd5eP0FoVyp4mplT71zo6PmY2m5EO+jZsQ1hQ9puN91VrwvVf2L7l695wV3uda3UTg97cu722VlacDp617Oq+6l3AygOticTq+GSnp63+Tr/hb+1BrVmbMBgMuHZtl5fPn1NVFRfjMdPZlNHmJmncyNNwXMNNVUYJt2/f5aOPPuUrX/kKcRx5268L6WrGwYGLBsgKEfm2GSXThH2A8MmgZnM3XonZbOHPzawy6fahPF9YYNswKiZJYvMRYs/o0u12LTXmuvcquPd0oUaN17ShU/VLTojAA2cVCaVN0i0AlaGedmHHVhH3VNauT21BNSGtxd8VmLS3lRJqXSMQSK9h4UGWWaIKIWprlzD3dPUjNGHYbXM9OvS4m39KVe5LM04qkG4tIOjOa+ZXG8DYz1UA5rWdEbUtGujklRt3FSSy2n1GN5Ocuta8eP6YnZ1dsmxiczw0YAszCoGqawPWlEIpGI8nKAX5YsFf/PmfU+QZcZxQloqqqltG0zdZg7Vr+3I3OpmieYs3ltZ3vlSAMEHcrgCcsWDbvztd1q7ts7O9ixSS2WRMmsYkkWA2PifPFwz7PYRWXFycU5eluS6OiRNbPyNJuXvnHnfv3ANhc2KERKFsPi9oqX343rd/+7f50x/+My4uzsiLgr5SxElMVEacnxtvx/r6OsdHr4mjmFyb8Kv1zS0GgwGHh4dMp1M6nY7xdI5GvHz54sp+df3R2i9s4r7RE1JKnRMnCcPh0DKaaaq6svuK3Z/81qeJpGBnZ4tvfuu32Nzeot/vEyddBv01hsMho/WRYYIS0O10mc3m1Dafqa5rTk5O0NokyW9vbzMaDbm291vMZjOOj48oioJev08Sp3Q6Hc7OztFas1jMqeuaXq9n0wfMGknTjqkXJoUtNimRUUQUC9aGa/TtHmjev/LyaXd3F60NpfN0OmU6nTIcmhpfjqzDVQdPksTXRHmX452BhjvcBtJQ6hkLhUuyaodJ4ZV+d60HBVFErRqro7QKvpSSStUQm7yLIi/8QqnrmlhIqsIs9LquPeIyrh3QqibtpNS1WdhJYiw7Wzs7VFohrb5TaUWkrdCNDOBQdWWFhrGK1fazKIqJpODW7dvcfe891rc2WVtfR9WGGnd7a8fEs2lFEpsihZP5nPX1EXVZEUeRFUgGTIWEJ8uW+pDCt82U0FxzlTK/SqkJGa7Cc1oWxzcocstKyq8LJMJ7hwv8jYBr6XOn3CwrTs4eHcIxB0xc/g80rubxeOytidB2B4bv+5cBG1prOh/8KyZcKvzcZBcaGmNtYnl9DL8wkEBbLczXsjA9YP9vvXy+acohKv+Z24DC3clvxB7F2FA0a9XUYCupg3ZMO97w5zwtwiot/m1M5dWmDLmt5m6ucVZG0x7TZgOAjPIv4w693/+7ZH/yn1EdfeEuvHRcnmtNiNqyRdqtldDwEOhOTKdTTk5OOBgODNCsrfXyNxjr5SuWPWChzPtN7+res/l7NVhoh4M0a/ySxX7pPstyIOzr5Vjm9nGZSvOqe4fvJoSwse6aWmtiIdjfP+D5kyc2sdgkeu7t7+Pn1ApZ4eVkHLO+tYUSgo8/+5Td3R1Dx2hznuq6Is8LH+usakWWZ16h0FqbmGjRtBGbAO1CDoxXwBivHJ2jkyUmD8Hw3AuBD1WAMJ4Z37fNeLU9Ll4nDizzLlTVh5QGkQTRUn/IxNV28E9ACqMME1s5YgpXeKOBq0rtvD/mcrOGTX6TUZ6cacStO0lwjdBoFRSjM5u3STR3niMaua21US6FN3jYe2hlf2qEiCyrlgmHRjRBtY7kJexPZ5RwnmBl5aoD6lrZPKlgbipPTGDaHyaRO52irg1QXSwWPHr0Bdev73J0+AqllWGFVKbmi6PUrUqTo1kUJXleEkUxh6+P+OlPf2LbUaOFtuFvKxgll1aL7zNsTp5of+5+XwYsq9aiAxjN/FNo0STxZllm57IkSVKipIOIYgSaqirpdlOkqJlNxwhVo1XN+dkps8kErRRxZOZHEhsL92i0xvsPHvhGx3FkQnqEQEvTJikEKIGIIpJIcPe9u7x4+dR4K8qSNDEF5FwO0WAwJI4iZlmGUoaeWAhBr9fzdTlcbTfjbal9HZNQJoWypGW0sIAoilK7L2oODg74j/7D/5Cz01MODw95/vw5x8fHHB0dGUa0qrLRBTVb21v8z//9/wXf/ObX+eLLL4jjmJ2tPaI49WOUxDGVlXPzIgOBV9Y3NjZa45QXOUor4jji4OCA3DG0VYadrd/vopSm1+vgqLwdEDBguKTTSS3RQkKctNnZGo+/A/jazwWtDUHD1taWP0+ppmhlWIixrmtvLHnb8c5Ao83S1FToNgPYLs3uDilFAALaG5qb8F4xkCb2s6or0JJIJvZaFxNrrLmqNgLZJapEUURRFKRpSp5XGMYcC2C0oMhNLLiLNXec2wA6Nm4zpRRpp2OEVV0bz4qwbBQ6RumKRZlzbW+PW7du8f6D9xmuDY1bTUG320MI0VTARDOeTej0OqRxQl1VxFJSa42W8g3khZcVc+BSv4b9uOrcN933KoX+bdeuAgyr7vMm6+mq795utW6/WwjCCHJA3aZml07zt9akSYyMJE+fPqWuK6RYxTB1WUl6F+/R8rtE179Geu8PzPXmJlbhtuqDD/FzdTLcVh4812UoG4Tl1Q7vGLCK+xtd51o3XgsRhEoQXKu1b6N2nQjNuVq7l7AKubPkuPEwMda6QRnYHd+CliY221xu2yNBiw7p7/17iMd/Rvnz/9wrVcI+b9k40QDNRs5cNV5eQXVdgRnvly9fcvO9Oz4sX2vdypl4F/Du3zH4blVI6VW/X31cXt/uc90YWYPv3W+r19Py7+FnV4FpN09/0+NKY0FrHtl44rLk1q1b/MWf/5kPXbgYXzCfL0i7/cBK3763G9daV9RasbWzwfrmiMlkzOn5KXVdEWlB4hiLbGJyOkjZTnb8Zh5u7C4fTUmsxbeRSW4ZOjYmbfe/kJXFxkD6tWR72v8LpDRRHNK262YuBeMfiWCwtcZ3hXDGk8ZrJlRgvKH0hgF3aPseujaGDVO9WvkK1qCN98IZcWrhwZkx5jStr7UzjFlmK+tlaM8pC0zsT2Vpb7Uy9QciIS3DorZ7ujbASJjIA2ecVLaacmN5vmwU8gaTQEaEHk2lDKuZKwDsWChLy56lysLX4tC6CQ3RwGyecXZ2RidJ+Pyzh605qHRNVRr9Iy9yzs7OyLPcFm0zibRnZxcUpa3nYwGOAyZa6xZAeNOxvEz9OuBy7kHYN+G54Wfuc6cgVjZKRcoItCIWFWmkEVpRVzn9boqqS4p8gaFIN5S9eZaBrsnmmt7aGpqaTidme2eTfr9j6fgjO7ewBAbOwh6hYkFVFsRJwsHNG3R7PRaLjLzIiWMTCljUlc1dWCeOEw6PDxkN+sxnM1MryYYfTadTdnd3LbiI3zlvwIONqGEIvHP3Di9ePKfIczY3N7l18wApDKGAEIIiLxhPxqag3WyG0JrBcMC9+/fprw351re/zaeffsrDLz9nf++A9Y11U6A0TkiBJInJ8oxa1b4eRZZllGVp9eqKosj8OA0GA0sH3ENYQBTuN+E8CnXyRs82gKKuS+q69Nc4sODCrcqy5OLigm6360FbSAntImwc8HAe2P/WczQcTay3rFhXcK/X4/x8TFmUvlCViw01HdIIojAvQCmFiI29oaordBVYI2tBFDXejjiKyQtrPRFG8BZF4WPLwCK62gg2x5tfW3anKI7R0iTS1XVti5cJ6rK0HWc2g8pWdtRamxohSJSuQStqpYlUze337rJzbZdKKSTKJ5HP53NPZVdUJaWuODw6Yn/vuk1Ii6wC9ptYO1kpUH6da/8yx9tAzG96z0aZ/I0My+3+CJVLESibusnlefTokd2szTUhi4O73296KKWID75hi/HF/qW8sVEaK45XYrAKWOC1arQa29fCnd/EFwt/IsFv9hxrbTR4QOAcGQ5E+NpkWiOcAtA8stUG4w1zYMIoHAYrNIqE8NYQYa+xTZHuoY0abMbF+qBswSuihOS9HyCTlPInf9+OoTk7BJUhsNH6clXdq6z04SsJIXj27BnftcDHWXfbAOxdx381qDCJvm3V8qrDvWf7rgELjWujdpZo/E/nuTJXX2ZYCYHYchub518F8MUb1qKfzau/veLZlw5tNq7r1/dMyIPd9OazOYvFnGG1TiKbsKLVz9IIqalqsw+sjQaM1ocG2NYCKaKl85sxiyKTOOnamlj6c0QNVDaHy81BZad0bBKXI4cMjHVeyDB30fVR8KKtMdYelLdTa7QP9xFgFHHVJC+3wpXdonTrzssY7cOQ3BwRIvg+kB0et9gmSF03dgIpkFohlPFAKue1sM9vdmWNrhugsWw9dkeYs6GUQvnaAwqd1yibe6GV2budIlOVlalRYkNbtDZ083mR+7pIdVWbKt4aa6A0/ViVlafd1XXtk7VrC3BcW6XrOW28PHlugMbR8TEvXr3mvffeY2tri/ls7i26juxGK8lsMuPJ06c8f/7cEgIY8BRJU+k9whQWVELYkiNti3pDgf0meSFaczf41NYwa4P7ZYPuJb1BNM/W2niZtDUeSaGhmFPnE5I4QdQlcSdFqZqiyImkAedFnqF1jaorFvOSGm0iRGLB9vYmWlf0ez1qrSnLGiUEUhkPRZ4tmBQFFxfndNKeYWiShkb49PTMjHnQztlsihDSFNHV2HGtvQ6qtSE8cLqpU37fZPBc7i9VK4T1thweHlKVFaPhOnmW0Ukj4qimrjRxkpAkkp3tdaN75iVlUdIf9Fks5og4Iu12efDVr3DnbsHLFy9YZFOSdERZWwNFIuiI1NIvm3Cn9fX1ADAYT4bxqDbFp83alpe8Ei7POPzMeS8aY7wryCe9oc4VJjY6sumLnZ0d33chsHBU4qEupbVmYYkoDm7fecP8Nce7Aw0tqCuncGi2NrcYra1RlxV1T3GWn0FtFBGlrPdBGzo3bRleqsq4HIu8QCGI6rjxdgQ7flXVQElkF2JRVggM00elFQJFXpYk2BhS7UCEsYrUdU0cxV7BoCpAKoQM8kMKo2Qa4AFFXnsly7hBFZGM0MKwY5VlTVnX7F7bIUkj8jyDpEteliyy0lPclWVhBGOtWVQLjg6PWF9bQyYmWU/U1gXtDV+BJcJZivxX2n/urGvhJc0GZM4CGgpVJ2SWYnrDwlDObay9gtfc/yplwyuWS387K5SzqIUgwr1D85wmIdEJlaYP2s9y2+NK741TFR2lq1PUnXKmFRHQiSQRipcvniIw81EIM2fCJzbPWP3yzi3v+i2ctHK4Q/97fwdkvKQMWrVTG8XcWdBNH7U6CEQQ2ywI6l/YE9ymYjvWbRAm18NHqJv766XzvRXUKvu2fc2ccrkg+O/cPDVAZNUg2dJiwbWuiJG7lXmGRTlCYBiKjPXMrM8Ieft7AOQ/+vtWYWq8oOFmuTxOb9+kg0MpTl6/Bhsz7KK+hHDv3lZGl/eoNrBob+Tt0IVQ0fNT0c5N2bT2UtMdlFv+2tzT/e2mQrCKmxu5B2I8P0JczvHy74kd0wB0+QeHi9/eUwNCBxTMwf2CC5t7C+cla9awEMIoyhLQguHGpqF9nEyYXpwzn41ZzGcoVSFEghCRrSitLvWFFK7PAJuk6zwyQrrxdZMwUMisvJBocPJPGeNVJOzdlalS7sIvtQahS7MedLO23SOEDQEWAcB23eT6VWsPzW2/m83e7TdCO4rVtlHB/N7IdJOcHbAnesQiENLlpgSyNxhWF1/uPb/+OaaxLszWTX4Tqqm8LG3Wo8kdU3VTxBeaAoLOmKeUorZ8/k31bkVdK/I8Iy8ywFBRK6WpqwpdW0+ENQIpZTwEIoqoAg5/pyybkG3hvUxRABKVUqiq9mFwLn9FYLw6sa2kbDwTivl8xsOHn3NxMWZne4c0STg5OiZOYkajEVIIZGQqXJdlSV7kSCGInJdHGYIN560uqtLwbxjKNzsH8H3vQcBlYRB8H/xNsPeJRiYvGw2u8va6sTPzwoTINduEZnx2yi9//hO63R7f/f7vESVdHIWzkKZSehRF1FpR23vVWlHWNXFZMRlPzNoSZkyLwpA8lGXBxcXYsyWVZUVdlfRH68RCINIOvW7f6I9aoa2HDYwuGMcJ3W6fzY0t6io3+TbCGCuENIbqKI6Ik8QwcUmJtkxw/v1pG6LahilFXZXoKCLLC8qq5PbtW9y8fUBZZFRlZvKyqorhcIiMzLPiOCHtKfM+ZYnMMqI4tlW1e9y8eZPpdEqv1/Nz0M1LISWRnbOuLWYdmQJ7xhBi5q6pdG+SwQeDQauGkAvnNH0W+7AxgCSJ0FoymVyQZxnrGxtGp3YMcRriuAOY3BEz32zieSS8d7csCptnVNjwwMzLwfl8zrsc715HQ5qXq8qSG9f36Xd6JCIiigQbgyFr/QFlXTOZzxlP51SqtkpWbVgYhPDZ8sZaG5FXTVyZS9A0gsVUT1CRa56JuXUTq3Ycw1pQlyZGEqCsFJUFGmkMsVUCVG2oyOLYDaqZetjnVZUJlXIhWMoy+ZS6AksxJhFUeYU6q1kfjSirAo1gnhd00z5KVdTK7AlaQRynlEXOi2fPETcOGPS6dDopbm/3mwhLAohGaLQt3U5AhUKoSfxFrA41EEFM9TKAcIqnOb/5Hb8og51q5SF8f3p9WdMScOGzXPiPUxDCu4cAyfVJS41ZYSXVaHTgMXMKtW0aWtXEQhChqfOM89NDlDaMICbetuTycbmGiX9aCzy5vzVaSPrf/zsQJR5AuLYoB4aFvbcDjGG4kR8YB05U80xAuu9dIpoIx8wpRPh5Yg2ZlqjWfOHDqKxSKeyJbvNpqkU3ioiwgMXNSw9b7P09LbXrdyFM27WmqQYQPNv+P3y2S4iPb34XVWnKn/0D6rpoFQbyfPOimZ/NGNH6ri20g/PqirPjY7LJlP7ayIQxojGz4/IcN30YXfrcvQE0sfhhGJ5yAEY2iq9vn5a0HnV5mVxqgwdwV1zQmqPC9a77rP08N8UAS0ts70GjbAJ+vMx3NHNWYHIg/P2CG5oL289y+BKMcorCRMiacNvOYMBgOGB6dsTR4TmdTsL99+9RFgs6HUO/qoV5H6eoO+QmhEZa8OzWmnCyR9QYGnJhvWumnaZWjwUR9lZ+RiltlOqmK80z3Rqvg1ligYZCI7VG6Ibu1F0rgt81GizzkFE0luOjtV8tbjw0DgQpw1SnlAnrpULgqgXXFmjYZwusd8gw7YXeXqGxOZEGPDnPv6pr+53ycdfhP6Vqqqq2MeIGLGgwhrW6shZxE3pR1SYhPMtzc31VeSCiseyQ2oRqOY+S807EcYyuahqgbHoutoqbsqguTVNc6I9RuFLvbQjDSJzF2yTjOyttjFIN8KiqkiiSZFnOfJ6xub3F+XjCeDJhe2eLJInp9breWt7rdekPBownExYLqMcVg7U+a+tDjo6OTc4OEYiIWplcJO3zQi1gd/Ig+OfX2YpD2PHzHm4rD821l4HGskHmkpdJg1aCsqxtzRLp5+Dh4StmF2eMz874yY9+xO987/ds9XZNFJu+i6KIwWDIRE3M2OoKrU0F8DhOqQoznpGMmE2nVGXBYjojFoLhYMBwOCC2eay9TtcUNLaUtgJhqaDxa0N7yu6IjY1t8sWUUmuquqZSld/sZBSZZS4jDDmxQmLkhCM1W+VpM54cQWxp5YU2GtNnn37Cy1fP2L++h1IJUWyNX0iUFpxfTOh0OgyGQ0ab/VZOiKqNh7Db7dHr9b3hrMndanJwtM+7dJTYxmMW1q2QMqaqFkQR3mORJIn/HTCeI1X7fa+w4CCOItbX1jkta45eH7GxsUG32+Xk+IR+f0AcK19VPctMyFavZ8K0To6PmM/nVFVFkiSeohi3lpXy17zteHd627IgiRPu3rnD7s4Op8cn1KVBnkkkEUohZUK6scFkMmVycUan30MjKEpbpTDQdONEooUEjKdDyKacuRPRjm7OeSEUZg+ptSvKZTjG88xcJy11qFKYz5IEtKG5kxLKugQhvLVU1TWucFpdFYavvMyQkaXR1RolTOJUHEWUeUEhCsqy4t579zi/mJAt5khiG+sICGnrCwgWi4yf/vznJtnHTpwojlilzC67PC+hbos0Qje0V75l6O14EzBoH05J8rRugcsxbMfb7vHrPNMdYZzg8v2WnkADaMTKc68KmXGxhEKYokBZltncDo2uL1OgOgXdzLnLFpCw78Mjuv41ovWb1iIZWOCFrZtgNxqvlFtFRXglwW407jmi2YDcmvGKnrUmujyLS9Z9q0EJKekkCXEckUoTixnJBuiYTd4w61QKylpQVnUTwiGMpUcIt0kaBdTX+NDa0NNYJclbbl0OCg34tYVyaSrkmTaY8BYbnqIF6d3voQ5/Sf3sR5c2zeWxv+ztaG8iy2MrhcmhOjk5ZTBaN8qLBaftpPylCXHF8wWCZRe99zouzcfGcsmbcfsVhxS0i7oHTVHO+hAe2ll8l4BAc4LJAwrepfkmGC8ChUhaT5i84gXchUEb3TxDmrAMbRussZSjCLa3t3j99DH9Xpfx+JzFfEqZzam7HZLIyEpBjdSmyBguUd3Qd7QML34Bi8aY5MGaAFcLY0U32nFrQikbjyUYQoPg3RQe/CitEYEsXl6PzoOsVpzjvheinSTu1p3BJxY429zBCG0Tkm1Cpqq916e0ir1LDK2ssu8Slh0gKIvS76tK1zZ/oGzFYIf94O6l6iY/pCwLq8g5C76ZhrUFDkVpvMUuDj2KTK6jsqCi0zEFyPr9rmeviaUhfJEWSCDwNJoaQZzEpGnHTTbfPinjoN9NW8IQkCRJ/H5uGCINrXAUSfr9Ht1uyWBg9IiNjQ2uX99nc3MTwIflOO/JfG5qNbx69Yosy4K6A2G+RHtfd8ZUP9eW5IpyFT9XHM74c5U1/qpjGXCEf7syAYDPc6jrmn5/wJE2hrPh2hpxElMUGTISdDqpB58uCTvPc5IkodvpMhgM6Q/6HB0dcfvOHQSwvbll7r1T0e12rTfJ5IUIIWz+qgGx4/EY5x027TFzMI4ju36MoTjTmkjGvp/dO5i6E7HxRr7DEa7FWtVEygFUuzfWFWmSsrGx4QImgCYPYjgcmrkZufY15RfMewAI711wP813wofsR0F+iB0dpLcdmP4YDAb0ej3v5cuyzOtspQ3/NyFlZv2bfOWc8fg1vV6PfrdHnhe8fPmK2WzOxsYGda04OTlhPs/8/bIs8x6KLMvodBIWi4U3BiwWC0ajEUVRcHR0xOnpKXEc8z/4m3/zrf39zkDj3u3bJg5N1ZyfniAwbtE07VCXxoKilEImCf1Bn9PzM7K8QIkYIWJqp8haoagqE1/rLHBKGX5eV9xI6YYBwwkMgfE8NAwRBkS4XAxNiYvhFspspgLDi1wUpXGPaZPV7wbJTB7tmQxcp/rkMhT9fo+14RpxFBHLiM8+/pTr167T7/V4PT6mriVJmvokXqU0EZqzizEIyfnFBWnHFEXSQhJFbaXYbz5LwiE8lt2i4Wd6xflXKf8rn7t031Xnhc97Uxuvukf4WSOQr35G86xGWbrqnZaFavgzkib58OjoyM8bwALSNmAw3zebQ3hPMx+cJbGJnY76m/R+63/orU0EY+JCLJyFzm+P4VgLY+E19lHjEdAKn+/klSf7u8CAjUZPtM8TJpcpTRKGYs5QTNmYf05aaXY6Ob20a5hkrAJYKUUtSipZMylqLuohM5VyPnzAtIxY1IYVTrs90D9b+H3eGmJwNjptwYf73LXZW4Y1bdIio4liCp9phIjo/e7/BIoJ5dFDH3cajk94hBvo2wCvWyOvD19z9/59M55BzLYHLIGG3bzCMuiRSNHQT7cTgwNg5trjOyS46aXDmwpWNN4H4Lm7+yPEEkbBUU3Y0CXtpbl3CEKWlW+vnPurtI3W0e07hv0tNO1QLaMpa0ubIz1AVlSqJLbV29fWBiSdxGyIwyGL+YR8MUUPewid2CKstal54Cx2wr+s8bi5MXSWXqn8OzT6nbZ1LqKlNrr30GgdhFLa+2v3M1BgGsODOU/ZPAGX9KyD89w9nDXfeSa0xoYRGeXB1NqwRCUuL9CHG9W+Ui9ae9DgPoc2uHbGApPf0LxDZY19oeGkVjVEZowbFi3nLTfhwyIITaoq4xFOZcKgb5UtIej1+02v2n1USmkjBJrQKilMQTdn4Ers72ZOtr0R3novTIhGt9vzVZANdbDxwkoR4yi+G9pOa0BTmkgmiMS0va5qsiynrAqw0RZ5XlAUFbPpgsUi59q1PV69OkQrzcXFhU/EjaKXFGVBWdecnZ1Zw6jzyrQ9m6Gho7W+3gAAVh2htzGUQ85yHdaYal0XyLUmF6Q5HEByoKEoCra3t/nd7/+AXm/A7Tt3UAgm0zOEgNHa0IM+BxqcIa/b6RJHkkgIWw9jRreb0h8atijtxsKOTcd6pRyWv7i44Pj4uDV+2LF3hSe94VcZZk8hIowZT9LvDRCYOllSXClgL42F84B5z7RN5Hehfscnx1zf30Mim5o0tq+73a65LvA8hPd04XNOXwjnttEljGfRRNMYWWy2eunXdafT8QQFi8Ui8F6UHhQURWGAfZFzcTG2tTcMQC6KgvlsRiftUJYlx8fHaK3Z3t5iMjFFP+/cuUOv1+OP/uiPbKJ+7O8Xx5GXL3FsaLpPT08ZDAa+Unmv13tjf7vj3XM0ihpdmyJGWprqp0WlUJSoWlFViiiJKStF2u0j4pTZfIFMndUywq29stRUi4VZDHbwNSaJy+hlZkNQ2tF11UhRmfAaOwnSNKXIc8tmYJChoTWsSZIYVdfMyjmF7fDKDpgApHWlOgaKsjRurUF/0LKMYN1Zi3lOPi9I4xgpBJN0wi9/8SvuvX+fPM85OR0zXNtAJpFNBpMkoubV4RH9wZCL8YR+v2+qfl9iLGkOpRqL8vLhYupCxcolRa26Ytkzsfzdquev8gi4Zy1/v+oeV9131f1XUcu+qa1vO8LF7u5V1zUkRqgdHh6aTcmG3rkQEHd7rfHCbKnV/vtLIA3B4Pf+bcRgC4QNUnOmPR/uIX3StQlNF81DrfIprJXQavIIESg5uCRv4Y3G7crJik6asFm9ZsSCrdkTbm71GQ4HrN/dJ44iqrqirmpqVeDypZzgMNa6CKVgMp0wmXzCyfmE14XkdfIeZ8keWW5d1BYfKRp3tNUn/Ri4z7xbH93KFzHAxPwtLMgS1vqj0Yi4S/f3/z342f+D+smf2VCbNwCId5g3DmQIrTk6PPTnCyHaeQeq3U7EZeuj+9IpQcvtcIDM9YOLCW+MAsuKhrtvYLFs0Jt9rqbFib20WXqFWWhC42grJEwvB4gF91i+9VJfunktIMj5unz/5cR0bcGlMJPGrgdNGgu0rkFXxLFgMBwQRZLBoAeqYj49p1zrodOYKOkghaamRomayhEJuC4Sph0GyJhYfzOmFqzXJs9AStCVBuKV3kqlahCVV+Ac/bEbD6VqLx/M3lF7xbWqqoZnv1bWQ2C+d/ep65q8yL0SUVcWbNjwJyGFuaYsQVUWlBllLMyDQOOVEx2GZEijKEkpfUJsuL5lFHnqzjRpqC6LsiTqGPpLR/Up7Xfm3s5ybBZEVVV0OilCRL5+FNooInmRo2qXkGqYelxol+k31QIzbqaafjXvNxgMAGOsK8rCJnBDVSmyzPT/YjE3CbxCmJpWypxv6pvkVFVNnptaJ0YRMzkfLr68KEwcvskFksRxglaBJ0Ibym9XafnkRDTrVJj6X0o5MONCPJ1NSF/a21YZB807qkvn+XXzDkcYOuX2v1X3vGSIE0YRNR6lvgeGVV2zu7XD3t4evcHAAzJVFayvr5GmxquxtrbG2toaT548Ic9z0CaMrqoKZCF4+OknfOd3fgdhSwdoIIlNHatIRl6hBqirmi+++IKprSvhwtpc6YPhcIgrVWDmX00/Sf2ckDIiTTtkWU6tNIqmKF0LW+lGXi0DPFcLzumbiUx47733eP/++/T7PbJ5znxuCAEcI5MQgsjl/th/zhuotSaOzfs5w7UjUzIFBo3yniQuBMrNzdzmL1md1ZIa9ft9Tk9PKcuSKDJV1qfTKbPZLAhxNB6KSEaMJxOm0wnz2RwEDHoDC0xmFEVJksTs7e3x4MEDHj9+7GtmOApvEx7Xp9vtMBqNcEZ59y4nJyeUZUmSJJyenr7TXH1noCFEhBAJk+kCEeVEcUSlFOUswyxLgcprpvM5j58+pbTcyZE23o66NgwRBt1qDLd3Y4XxgMImTik7LZQqDc2slMaVl2XouqKwMaORraMRRZG/53y2oCpLwyZik70FgkhE1t1shFQSp0QioZNYwZZX5Hnu3b1KK7Qw+SKVUuTzDLQmlhG/+sUvGa2P0Fry8sVLOv0Jaa9H0k2JY0kvinn16pDtrU1eHx2Tph36/QGDgQEicRz7CRJaYXSrz1dbO1oeF2UTiN9sGLmsJL9FmK0SUFeBlzdZZX5d4LDqXu6SVR6VqyxEDphFkdk4T05OgGYTCItP2qtt/zeWKBMK0yjP7cGB7lf/BtHGbf81IdixDTdKkFV2LTDw3gGwiRQGmAhnDdW6uZe2CXzQVtgRpJFgL/uYe+KY7fUhOzs7dLsPWCwWjMdjzh4/spSLtZ1vlQ0DjBFS+O+MYIzZ2dnm+vVr3Lx5wHw+5+joOYcnv+LobM5DcYds46sQKs0tZRgsZ6Z//8aQ37BnubY7fngR9KtT6rRM6Hz7b1IffIv8J/8A5quFWegZk/Ly3AjbJ6Whl3ZWHZO71dB6LhnxTZiYAw5L8y4EDpd++nAd+9zl+RzgmGY+NejA9VR7fVmwwSrAW/ubmpjfMJfgDWEEIUag6atVfpCwwVqvvqdYsT6sT8O+nvOmGUrSStXUdU63k7K/v89kckGaGK/1bHzGcaSRumZtMDIKlA2jFT50Spi8BylNfkEQouQspab2c4lSpSUmcUQfjadA2WRl41EorPLYeDA9TWpVUlbWq4AJZTK1k8xzndHHh/kqjSNYMGvM3Le2zIYI6221MsvViTLKvqkqLIUNtdVY5V8QJyaMNwqKGro5lkRtxcdVTK/qGpmYpFIBxuopBFVZsdlJqesmbHYymZCKmF5/YCIMvCfD9NcsW5AmHbr9PlGUNHuClMRKUIsapUvKojDr3soZpZRVpGryReaVqbqumc1nhi7Wzv3Sfp7nObUFb0VeolUTG+72v8b73Bhv3PhBY2E2Cbp9r5wpVaOxicu1028CunGHYhFeKTZrzxhZG/liDJLCCpA3GdtWed6lNDH/oRK8fK47wne6JJOW5NDVvzfrZLFYGOrVJPFAY5HnFFVF3+pbcRyR5wtGozUGgwHj8ZjZbMb29jZbW1u8fv3ahNFpl3+lePr0CVtbm6bm2Pqm9UAIOknq31EIk8vz5Zdf8tFHH1Ha4n9OL3JJ4L1ejzzPmS/mnB0fIVD0e31AmMJ3tWYwWDPUuFmOoLL7nVtbYS+1dSD3U9pc16qsvBF4fbTO5tamZyxbLBZMJhMAX7Cutn3owrLH4zG9Xo+9vT3m8wVam/pNRVH48KfpdGoLNypevXrlx9R5MNz94zg2IA5sGNSY8/NzqqpiOp2ysIZ6V3RREPmwrSRJiKOUOK44OztD11jQElEUc6qqJssKfv7zX5Jlc0ajEY7q1oe4CUGSmLDDtbU1//14bJL6p9OpoSAugqKXbzjeGWhMZwVRHFETkS8KlCjJS5OvkMRdiqriYjLh5eEheVmRpB1j38oqSydYm+x8zzJlwEboJnOdXGtFUZm40KZwkqQu7PVVaVw7SYyqSqqyNC6fumYw6DMYDJhcjKmKwnyuNBpJRE2pS2pVoyrDSOEsKxIDcLqpKYIitEBqYajptInpV3VNmRdkWpPnGf/4H/9j9vZv0OmOmOXndMuKXt0niSUVcHh0iJSQWOvxcDgwLt8ld5vb1EJt9ipBEgoiF1rShifta5zScslNK0LLeqMY+791I6xXCix7vQ4spYLLwtQv6KW/r3qvVe8QHs7itPzdskvUgAZtiy1Kzs/PMWF3tbcwiJZ2ZONDr+jL0JsEECVdel/9G9Z1eulUr7ya6t62c7ReirUPNyx7jdaWDcfme/gkeZzGiZSCreIx76vH3Lqxwe7uA+qq5vTslOOHxwwGA19AUgpJlmeIwmyiVQ2djqDb7TJaH9LpdBAC6rrk6PiIR48fk3ZSbt++za07t9m9lnF+fM69izE/vviE190HFETO/xD0P40133oGmq3f9Z/pCK8HhmNo43ft7DYA8fqH8O1/k8U/+8/ehqNx7EChdW/FSZyenmI8oBG1MmFG0SpwKwTar1MaCzqNJTEEOsGVsCL/QXvt1wGSZrk5a29zT99rvt0BGmv1RZic7e7r20HDUNS0Yfk8+3fwQbSit137pQzuFxpGPHeyPdSS3PHWVmW+FLCYjul0Eg4ODnjxwjDBqbokW8w4LjPGp6cMh2sM+qaS7WQ65fTkhPF4wmJRGEXVUpwqpShdGExuAYKuQNSsbwzZ29shiiUiakLeQpa8uqohyOFoGXIAjfIbcMgy5rcyXD6ByQlL04g4TnzYURLHzVoG4ljS6SQe5EVW9phcBoii2HPrO2Cstaascg9umvh1M59jG1Y8n81QWtGLeqbKcmQMd0jIy5KIBCkktXDsQRFVZd4vjjugJfNZzmKxoCgN2KjKivlizmI+5/nzV2htEorzwoyDC/Goq4osN54NRxfviR2UmbsOlDXzziaoN4LCvJfLCQGkjnDUwCEIqOu6MdQIBwys/JBhTo7wjFdKaUxxxXadLxfyIoUktixLJpQkkC9oE8xnvRlaN2vcyeZlD8ZVIGD583c1/i177q+676pD0zC2nZ2dcf36dYbDIePxmKIoWeQ5izxnpBVxHDMY9Lk4P+PWjZvs7e0xHo8Zj8e2toMJl8uzDCWFZSuSRIuYP//zPyPLF7x//wM2NrbsPmPWQlEUZFnG5198yY9+9CNOTk4MELGKtrOcD9eGDAYDzs4uODo8ZHJ+zuZozVarFizmC+I4ptfvWwICRVVmHmCLUMhe1R9aW2IYc34sErSuefT4Ea9fv2ZjfUSe53S7XRaLBWdnZ1RVxWg0Yj6fU9uw7F6vx/r6OqenpxZ0TNDaeOhmsxkPH5paLN1ul42NLZ4+fYrWmrOzM27dusV0OvXtubi48BS1nU6H8XjMyckJk8kEIQSz2cz3kzNUL+aZnQ+Gutt4J/pmrgtBkZekHUN0pOqamaUSj2MTCufuW5alUQDUCAABAABJREFUDaerKEvTXgcqAN8XLuRxb2/vjf3rjncGGj/78hGdtENiYy6L0jI0aU29mFEUBbPFgsIla2tLl6caF6QROhVaW4QlYwRGyJtNpiaJNTKSpElMt5PaZG3D4mTMMQky0obZKYqQIvJximYvVKyPBoxGIyYX58ymM8q8RAuJiC0Vna3uWZYFQkKshC3EJBDC0eOZTSUiBqGppWG4UpiKmRpNncGjx49Iki794Rq7Yo9EVhDFiDhmOp1QbG5QlTmvXi7YGA3YGK2RRhFKSJI0QQnjPtdon/S2ckGAiXd2FlGrVCmh/e/uaLlnnZUYpxg0Csub12BAt9mYSP0PbanxtIld8DZVpyQtt8lpasL9FPiFoewNtGisuU4oCd3wF3llz+mmjR0ouJ9TFGqjRMZmblyMxzRUoDW145xvNCX0UujH5UNbK7wk2rwDSQ/P6uUAl9MzNTZswJh2HcDQ3gLpwqU0Qtv8DE3DpGOtng5f2Lek1+1wwAu+1jvkYP8uaZLy8ccfczGekaQpEXAyP+Xo8IjJeMxkOqasCtM/lUZGsV13kk6aMuh32dpcZ+dgj91ru+zs7FJVFY++fEyWfcKd27e4cXOf9Y0BnaNjnr3+I35Z3mHcf6+JSbeg03hg3Ctrb2GX0uWUWIWA0EMjTR+IYK4Z+iAEgnj3A4RMQFWXNlSnyF5VV6N9GE/SfDFlNp+wtrGBrhQa6QHfMmJ0lKPSnxN8h/PsOZYt97mdnksg3o2nsJnWDnIZmeXCy2yStm7u1Zp39sMQvDfQLHiW/7vynziLOnY+mTmnvXdm2RhhlOymIJq7r/LSxDzV2StCT4LSDlAYWQlNTlRlE5XLquDi/JwkjkjXEvb3r/P69Svm88woQ1Ii9Jgnzx4zn2ccHR1zeHhCtsjtfoGfb9rGagM2bKIycj2WbG9vmfDXhSH5SLrGqipl5Kmblarpdrumn+zGLaOIyP6M4whhqeOEwCsBSikiGXvDhpuHSmtvXKqV8mETDoh7Viebr9FJO8S+TkDN+dkZ3W6Xbrdr1k8QypTEXfLcxGWXjvVNA8oy8ZQVdR2xWBRcnJ0iMODi7OLcewJcWIbJ+YCyqD1la+gxULXJE3Fzzhl5lJXbBPOmtdKUslZi5UGmmzLSkgo4MgJvdLRz1MxJc7K0wMF47W0Gm1PgrewRwoSqtWVDsyKclyks1Oueq/1zzcrRlnJbaUWFILIeIreDOo+Yo2A1/5qHSiCWhsXOKPxBAriN5w89GR4U6HabW7+5tWffz88xm1+m7bOdUdGfH7y/e18PkKkRUnAxPuXWrRtsbW1yfn5OtphRZTOy6ZhTjAW7l0a8fn2C3t9jb+8aT58+Md7ys1MGg74NUxeMpxfUStswQEm312M8HvPk0VO+8tUP2d7e9nH9r1+/5unTp7x6fcR8kZFlOXGc0En7oCV1JVCyy87eTeI44fzkiDI3OQpJr0dvfZ2qVsynU3r9PnG3w8n5BVIkTMdTXw1e4GRXI6+cQcf1SdP/xnO3d32X8/NTTAXyOUVekGc5ZVGaUL6qZj6f+/o/W9vb3L59h7IsPdnI6ekpi8WCxSLj3r171HXNeGyK/DmQ0Ek77Ozs8t6dO3S6HXrdLnmecX5+weuXL+2clpycHPscGilNLYxOp2N06LJAKxMa2e2a8LE4McaHbjel0+1S1SVpFBuPbFGQJDFVaQp7Xr++R1kVyEiQpClxbe5VVoWp7SGED7FzciGOY6bTKf1+n7IsvZfnbcc7A42nJxemoXFMJIyFJkkSgyrThLTToa41CkkURzZcKfIKdENv2Lh1ZWSARuQsEdpY/9G1jWs3cXAKqGz8qRYJMgZVGc5qiSSOYp9EDjV1VbCYT5ASdra3uTgdM5vNzYQTmriTIJREJIbiThUmSc4IFtlYs7QCbLESBHGaUtYVtS5sUSVNGkuUKpmOTynzGffv32dtY4vxeMJ8NkbVJkZ0vljw/NlTtjfW6Sb7REIjkoiQIcVIEKeIB0qPMBt87bnWjTKrneAVTXypC7dBmE3TKeOt/+uGXq116PBXQTtzt2mLaa5TzpYVIgsylpOytPCWFGwbtGWg0UL75GcnODXGahQj22Q2zZ7lqVcdyGi+MZuBjIxVqqqM0HAvECrvV3bAqu+84UrQ/ea/QVOdWzTJ24GQs3x73uLWvD24xO92UFHjJRB2fB16kTJibbTG9fopX4uecuPGLV69eMHhq0Nrxa04fHHE0fEhRV6glSCJY+JOj8Ggj5TQkRKlBDURSpm5f3E+4+zknE8/f0in1+XWrVvcvnWLu7fvUNeKZ8+e8Ozpl3z44Ye8//491tYOGT59xseHj3i+84eG7MH3jX2ToBulVca980g4X4jwg2AcHZYX2l1sFfBVx7InwQFWj1X05XAKNzeLImM8PmewPkRjzVgSr3C3D5tf4UbMvoN232lDNBBeJYUg8rJjqd32OjOudg26cfZywD7Dri3fHYGi55R/p9m3wsTsdyaPpvI3aIVkCJsPphqKRwiYkbw136wjpxhrrX3CZMiiVKvaf64xBbSyLGM6nVAWFWVVEsdRELtujAh7e3t0uz3iKCFJjPX06OiQi4sLEz5RZ5RlwatXhxwdnaKVpMgr6trkebh6NkaZLJEiIkli0q6k20vZ2dlha2uL0Wjkw2H7w6EPB1plQQ49654pRppQKWdgcQxcZVWa/csVzLKhVrEwSnBp8zocMNHaxDpHcYSIYnRRU9UFeVExW5iaDFmWky0KJmNjvGs2+oosyylykw+ilWY+n/t5YfIQbY5IkNPhPLsGi+jG2xsC4SUjVSsMEJdHGc5xY9RbNce1tlS9dl00oNceFry6c0OA3JAYuPkeFkJUbQOGbtaNu1+4/lvbp4DQY9jMG9mSJWbPt3S9lQJyP8+X+yn8u1HspSXcaJKM3TORBmh6D1lgTPN9vXJPaj8rDPl11apNG3Tr51Kvt+Sli1sdjy8oq4K10dAycxUUiykvn2X8N599ilKKDz74gPv373N8dMj+9Rvs719nsZhzcXFuiAEExIkB7VEsjcxwTGi14uWrVxyfnJKmxgKeZRnn5+cGxAyGTGYZURTTs+FQVamoKs1wY5P1jS2yxYLFfMLW5jqT6YzOYEjS6zE+OqUqKrb39lBSMs8y0iRhejE23lShLeBr5pfXe/QyE5iwz6548eIFShXIaMinn3xCr9tjNp0zm818qFme58bbGEUM14bs7+/7fj4/v0AIycbGJr1ezvPnzz072Ww2YzKZoJXiYP+A05MT71FzzE8uTLHxsAkb/m+8xwpT1yKKIhIbZpakHbQQpJ3YJ4zPFzPiJKLf6zAeT0iSiDTtU1YFVVVQljlK9VnfGLFYLACTU+WMInmekSapz83odrtezghhyBmEEDYk/e3Hu9fRiHokg4GJaawqkrRLEsf0tkaISPpE5k46IIqjBnFrQ10rhBGyxt2rQSsSAUkceXrJbtoxnadMYvnZ2QXG0S7oJAkISZoI8mJO3IlNUpwysbxJLOn3U+o6N56RXmomyPk5vbSL0IrziwtTbl5rJCCRJFFK1MXQnbqEO8ugEAlBrSyjolDUlTLKfizNfZCg8PGyRVby2ScPEUIwHo+py5KHn37CtZ1tiiInTSJevRjR7wq2t3dAVMi4g2FQCJPunKWlUbqkEAgZWUVHW15LiCwYCAyhjdInzDuav4xCb1i/TEy7f5z7PhRSKvgyPLyWLsIC0M3RKl8QWGhCHABYZITW1rrlN7dGkXLWiOVntDFYo0CFG4LW2sQyS8l8NidbLDxWcBtRWLzwbYcTUG7TiEd7jWLqrKvBOxtF2tI++v1YNEDJvb/wo41tFLicDNfPkWRzc5Pd+gXfWXtNt7fBxx9/RBIlzGZzXj5/yfnJKXWliAc9umsjkqRPFHeJkoROJ+HVy2e8Pn1NkiYc3LpP0lujqjWqqijzObo6pywWPPzsMz779FNu3LjB17/+dd577x5FMecXv/iIa9f2+MoHX6XbGTDov6T76k94uPb7aGHmv6lFYN6jnSxux0W4ry3UcBNQ2IR4r5a0aWOdx2Q5HCFUEN54OMVdg6oryiJDokgjgUASW88qNBZTAywce1FT08O9khvuyDut3Lgb74TLJVjREPskp8i7ed6u++Ha7LwJAcKxQKEJ5WmdG/yjNkm2JmnYsARirbKFrbxsQowahp7abmrtGHgTM22sfCYeWQhBr98jtS50l7+gagM08rzk5YvXnJ2NqeuS9x+8x/r6Or1ej+FwyGg0IklSk3cQRyRKEsWQpNdJ0sjGgpd0Oj22tnZIkz6npxcsFmeestqBLClrBoMuw7UBm5sbbGwOWV8fEceRoU2NDUORKaZl4tGHw75X/EOaYq21Z9dxYR51oUhTE/qhMDl/pr4AqLpGqQIN3qqZZSZePE5jZrMZs/kcVdcUpUn4LIuSutYURUmWmf3KWQxdNWw3pqGi6wwoYUhrGFolVEMycslDFcioNkAXLHsEmynozR7tuem+XwIof5lDgC9s5w4XchWu82UZEPbFVSFLyyFGzjK7rPSHSugyGHP3dN85JbDdB01OSEhragykRqaH6+ov028u4f+qY9lL2XoXbb7PsozJZMJotB7kXywQwngAEYJHj57w4Ydf4+zsnK3NHe7evcvJyQlFUTCdTul2u3Q6XbqdLkVZ0u0kpGmXNO1aUKuZzeZkWcRkMqGqSkNOIDXz2QJqTXcwoNvtoZQmL0viJOHGjQM6acrhy2dorel0u8yzgq1tU7367OwMDWzv7rKwSnwPwWw6syGKl8F0OO/Dw8hiU9DZRKsovvnNbzKZTBhfjCkLw8a0tbXFZDJhMDCkQZk1qBwdHTEcDr0iPp/PyfOci4sLD0xcTgWYkMAvvvjChH31eq252SacMPUr0jRlfX3d6s+xB2xra2vEccx8vvDzLZRnJycndNKUqiyZzWZ0Oh1PfevkvpTS3yfLMk93rKwhw7HHuVDzwWDAYDDg/Pzcz+93mq/vdBYwGm0gwCTMdExVQymE5aOvTAiTNIK4rhRJHOPWQW3p/3qdxFTURpNG8MGdW7z//vusDYZ0bcZ7t9MFISmU4o//+J/x9NlzZBwTxQZodBIJus/m5hZrgzXyeY5WmoP9ffb3d0g7EUpVzKYzfvjDP+fRF0/58ssnnJyecnR6zHv37hm2DCFIo9gqpDFoTWnpA8ME9aSTUKuSsoRKFaTdlEhFJqG21EhtCgPWtULXNWVVE0WSYb9DN92iLHLOTo4oi5xIVzx/ltLrQRxp1jd26EYxrpaHCASEoGFegCbSurFsBkFW3prcLB1afwUWdaGJIrdx6JZgby7QjTV99R7Tcu1e+sYZTtruDkK3pbMmOSaU5jZWAWu13t/Qnu/apP3zhTBKrraKrNCmRooAsmxOVeS+vYZv+nINj7cdThjE178GcddbZ9GG+MCALxPz7Cx0xmtj6164DtUBnNQNfaFtfGDZNuOzu7PLqCv5YPaYsig4Oz8hy3M+e/KI589eECnBsDuklyYUSUQyWCfujJDJkG5vSJJEfP74JeNFichKdkXKjdvvk5eKLMupshmvvzhmNjGJYULA8+evefXqmLt37/Dbv/1Nfuub3+bhw8/5p//0j/nOd77De+/dJUmfIZ/9kIfDH1CrJm499DoZ6lrbf83rGwuNAww2dExYZcgU2HQXSeKb36H88k8uKQztDdRN1tWbt8sA0UpT2+RFrTVxLEikm5vOu+rmUVORWrulYn/RqmraoFyFdOOnclSmfgzNiX5dtQCB9RooCwgcuA6VHRfG4nIRoEmKNaKgsWKH16TWFG0KTZnfK6fQCtla1u6a2lZODzfmsHjbbD61XOuavOgFY6GtlwSkSFC15uHDL5lOZkSRYH//Ogf7NxmNRobzXia+OJehLC0wBV1he3uLwaDP+fkFi0VOXQkW86JlJa6VIpKSTrfDYNDj1u0D1oYDirJgOBzQ6XSs1z31m2ccxaRpFyEqylJZL4OkLAwIyLKMqjQeGAcMZtMpWV6QLQqbY1iRZZnnl28nJhOMQxP3HybxKu0Ao6BVMMeLksYyLQCEiQ5wXsAl1dcYwRDUlSISjfK7vAbCkJtw/SwroWH+CYFsCu+ntfOkX1pmrlm4sBV3/m+iWIdVk5eBhlOmlsGFb/uKo9/v81u/9Vv8+Mc/9hbZUGEP7x8CjWVA1eqjpRdfDlVy9xcyQgvRYgla5VV6W/+E4xfOq0uH3bfdunbnCdEQK0gpefHiBRsbm1y/fp3xeMxisWB9fZ2trW3yvODmzZtsrG9SFjVPnz7l/v37PHjwwCc/Z1nGYNBjbW1Enhd0bE2NOE5BGx2msCF5LtzG5McYhrzhcGhKJGhNVuTUaK7v7bG5uU6eLzg+PkQoY/GXccL2zi75fMHZ6Rmdbp/t3T2m8zlFsUCXlfWyhMn17W5x+UHLYbjOc62BSEZcXFzYOiGpB1Xj8Zg8zxHC5DP0+j2UNgr54eGhBwbT6dT3+2Kx8Aq86/8iy/38LWwesUu2dvPFJcaHc6TT6XggEcfGiOFIDhQC4dhYbfL5YrGgKEqfU+Hat76+biucS4oy92AoBBRJmqDrpn6MoRk2feXIHRwL17sc7ww0OpEtkidj74HodTrGoqNNZcZOp4MUgtI2tsjmaFXTHXYRUhBJQW9vi/X1NUaDHqIqKKYX6ERS1jkvHn9BURTcvHWL/Zu3+OC9W9TFgkWek6Zdev0+o7UB6JpsvuD/+Q/+Pl88/AJVa7a3tvlX/9W/xh/8wffpdBM219ZII8lPf/IjHn35lKPj1yAF04tzvvaNb9Lrr6FqU8ESgSkpn5pqi2VRmOJHaISqTHJkJFFxTFYb13VZlkgF3bRLJ47QcURRGGaNsjI5APP5nMVsSr5YkKYxea/D6ckRTxOF0Jo07dDpdBEywuUMO49FrZQJx9Ha/1RO+Gt8XGoDTIxwcUlrzSIKgqbsvUPLbPtoIIkrsOUEU9va2lgT2ztfY/8S9tkEsbihq70R6LbdqqlRIaUM9t8AEGk8Q4fbCJuWN79obbjtZWKSnE+Pj1B1ZfJzlqyCK1HUisNvcHFK9+v/uvFWgC1GJm2/a1yNX7ncud4arVd8ZsbNxzP77zQ3Tv8ZH6YpO1sbFNWc8+mU+WzGz37+S84nGd3eGqPhOomoefroSyZlwd7t+3zru79Nb+0aUdJFovhu0uHnf/5fUSvFex9+k63dG2gRUVc1xWLCw1/8kPOzKeOpiSsVUZeiKHn4+WOOjg753ve+y/vvP+DVq5f88R//Mb/3e7/HnTt3KOsvEK9+yKeDH6BtJWrtUZTvvKAjhEfNTnF3ecTmb/uLL0oY0f/Gv8bi1c+oi8WlOOtmYzfx36tCQyD0SGnQNUKVqNKw23SigfdwuQ1Ca8NY5ICvr1HgQlJ0iQu3qm0mYW1phMFWXbZe3royRdHKovRz17MT1a6tmlpVNu4/8usufJe6qr33bJUS5xTdKDJGoHlVGeNQ0GdmjklTNCsI7fChBHGE0Pj4dJcbYJQ+xSKbc3x8zHg85u7du3zwwQcWAGDj4GsEMYt5gda19W7X9h4mNLUJUQVUTSUlQkTWym9qK6Vpl26noiyg19N0OgukHHtiEYFgNFpjZ2ebOJEUecFZVaHqiiwriKML389VVRl5XitTmNLnIygWCxNSuQwaQgTQVCe2nwoTzpBleUuB8AqO9nUFQQsEtiK4prmvdnPeKTi6tUzatLBWVuIKw0WNmNCNyJBIQkXXz/vgPsvW+1WgpDVX9GWFepVSHAIcKYy3chnAXPUsrwCjmhDaJYDhrveJ5X6dNu+17C1YbmNRFCwWC08v6ua9U67C6xzIWQVaVgEac65qzQXneXP1FpS91uX3NHvQux3+XkuenGXAJQ39U6ttrb3VXyM5PT1lPJ4wGq2xvr7O+fk5eafk1s07bGxscPv2bZKkw/b2Dk+ePOHFixdcv36dxWLBJ598wmQyYTabmXzIyBRU9CCjrqlqUzPCNFcSxyl1bYwZg57xuAMUZUFelmxt77B344AoEjz58omRY4sFeVGwtbtPFCccHR2RL3Ju33mPbn/Iy+dHxJHg6NkL98ZLPReQOth+CUMnzZy1RDHWUCSEMB6Y0nhpXd+5a9bW1igro/TP53PvxRqPxy1jj5Qm2drlWbi+dyFOLv/Bfe8ohF0Ik1Po3Zx14+v2ucViYVi2rMfVhTq5PCylFLmtmQJNUeyyLImTGI25/87ODsfHxx60lramnVsDyyydnU6HTqfjmbHedrwz0Eij0gCMBCJhqCF7SYJIzJyu65IEsxluWG7mtWvX2RwNWN8Ysb4+Ynt701Ygrbk4OyUSgi8+/5zT40OSKCaxCO7s6JDJxTnD0RpfuX+Xk9NTkrTDbDYnEppYJvzn//gf8md/8qeAQNWak6MTHn/+OcevXvO93/sdoiTiu9/9HT797CFVXZGk2GQkxZcPH3Jw4zYbm1s2ljQ2yrU0OR9REqPtZlLnOao2gijSkABlVVHkGXVRMlU1L19UVoAVdqBtxVabBC+FCRHbHA3ZGK3xe9//AT/5yU/Y2Nim3x8AyoRF4SxBVvGWjvFKNEndAUgQzjysnGqPtUI1hwvU8ILHg4PLm4fWzrLrFmQg9Fv3NP9fDTRCyxf+b2unbZ3bstwrk6xrYhGDyHh3S/ucJrTFJN9d1ucNNKnril63SxpH5NnCvJcWpnKto8X8NT0aAJ2v/WtEo+uNVdC3wFX0tIqysMJeBONEu/uNkVv4pOPwbggYqTHfvh5x48Z1Do+PmM1nvD485KOff4QiZjjaoTfapr825OTVc04XGWioKxit7zIpYHJxSpFNqIsptx98iEZweDrm9ZmJjY2jiFEv5dbdB8znpgDV+vY+da2YzabMZ1Pmswn/9X/9T/j2ty/4xje+ThTF/Mmf/Anf/8H3uXfvHlp/zmx+zHN1zVhWHJgKXRuYuSj8tAq8EuE4CmylcQO6tNaI7ojk9u+SPPtz74IOFQG3AbcUvkvKEd4jlkSSbDahKHO0FkSy4TrXWvtqymVdmDAXZZJsfcVlK8ArW9XW8JMXaKXp9XvGGhQoKU7hcAqTSxJ14T/m7W0irBBUosIFk2kVFnUyNYDctZGM0ELbXKTIF1dzz5SinZAa2cRmEBRVadtlQLJTtowSD3GcUNvPfL/UimyR8/FHn9rQWMk3v/EtkiRhNpuRZxVRlCCkJO0kJEnEYrFACMjzkvPzC4qiZDgs/SZq+tRQmeZFQWbpIhc2SXQ+Wxj62sqwHrlNvKxKTk6OmUzGdk1pb5RxxhaBSWaUkbEQCgREsQeU0Mgvk6irbIJxKFUELsyt+cTMN8fY5mRhOOWMvLHeVdHIOt3cxM1ynIBzs6EhTqAl4ATC54g01nNXX6MxwKwEEEu615sUcv/3CrDe/A7I1aE7xkLcPCf0AoT3cevBU45rwwYZvsOqf+7a8Gf4+7L3xR2LxYIf/ehH3nospfSF6y5ZuAOvz697LF/vyDAEwoe+uPXm5sYKPPPGY9nQEIIQsy+33+eqo65rDg9f8+D9r1hWqQmLRUYcz0iSlLMzk0/R6XTZ3d3l5cuXxHHM3bt3Afj0009ZzGfUdUWeF+RZyTRZILx3DcqqqTZvqFttJe/YePjyIqNGsLW7ze07d+kPBzx79IiXL56Zzczuk/sHNylrzfNnz4jjhIMbt5hnBWfnF6wlEScnr7xW4OSn6aN2TbBW7gxYA6by58pIMhqNfH/GcdQyYDlFPk6SVp6M25tc0ruz/DuQ5zxoWuB1kNQWL3T1ddy5ztMB7XA75/1wgMGNdwgwhDAUt+4cKWULXBdF4b0YUSJ9KGwYjuvalCSJBxoOOLn5e5XncNXxzkDjzsG23cyM1bIsCuIoZjQcEklt42F7vkG9XpeyKOgkEXcOrrHI5jx79Bnj8QVJHCFkxMnJOao2fMl2vFFKc35xxtqwTyQVZaUYDfvk9l6TizGHh8d88slnyCihzEuqsjL0e7Xih3/yz/n6N79B3In4xS9/yebWBmVd0OmkJpxLKObzGc+fPSPPSq7v76MxG5cbVCEEJ6cnjM/PqWZziswW+Slz6ro0lktlKrhqa3l1eQVK22JPWOlh/+lakyYxf+tv/o/Z3tmmVpovv/yCjc0N1hNBLGPLpmLZPNCooNqoU7CVVhaMuHoMAnSMILKeAd3anLRTWDSBNHOgItw8nWXMbr7CoGwZRQihLwn0VYI+8GW4E4P9bYnTaenZOngvrZuwjjacEIFwFlA31t7wc61NnHwcSZI44uLiHLRhiNGySQZswNTbF4zzNkSj640CLBxTit1YNbY6sVOwBT5BQ7Tf1//mxtFtvrZv+r0eN6tzbhwccHJ6wnQ65eWrl3z00cd0oh7d/gbdzeukoy3Wtza4fuMGSbfD4uycO3fe59GjZ0xLQdpNWR912L2xSa/TIYpTKh2R5SVVUTC9OGdycUraW+Or3/ht1kYjru9dJy8KTo6PidNT6plkPp/wkx//lCzL+N73fhetFX/+Z3/Gd7//e7x39y6TX3xEvn6X44uFHVo3j+yvgfLhu8ODNf/igDDxzG7toE04zs3vop79eSuePrSSulhoJzBb8xVrAa1r4k7EfDbh7FSyWMwoyoLZdOSFu4unzbPMsIzUDfA2/OwRda0QGMDgrEqu/k5dVXR6qZEJ0mwsUZIggChOiOPUeijx3glHx6i0skl+SZOwajdFJ1+klHbdNyETMor82hHWmqnNRX4ammKl1ppq8+NcGKLWy2vCJM1rK8uMN6Amz0u0jti7dkDaSblz5w6zaUatZkwnU+85yfKMly9eMJmOEVKjlODhw895+tTEW4ebvqFbtOFhgfLfhIiY9zLttmFfdY1QNUq4xNsYHPOUEmhd+/dJ4q7t78izYTVWfdko5/VlL1h7/YdKuQE2MghPdv3mQST4XAshrGzWDaNSGDZl2JRMcJ8UosnWMYKxMci4h+M8DX71+P68sv02gb3l6VgCGyuuagDSMnARokXXuwxaRPCM8BxnJAgVGw9ktfU8KdW6dhVwugpMrPo7/NzFnIcAOpQpy9e3KXLf7QiV/uafhMArE4KRd92Dlp9x1efhu7wNKEkpef36NXdu32Vzc5Pt7R2Ojo5YLDI6nQXn5xckScr2dkS/32d3d5dnz55Sq5o7d+6QpilffPE552dnSGkook3Yt7I1oqImfMwqwK5NxppvZNzu7i43796hNxjy9Pkznjz+kudPnzIY9Oh1e+wd3CTtdHjx6jXz+Zxb+3fY3Nzh8dFLqrrm5OIEVVUImdo3a7w4dd326IaeHbDzy3kLgf39fTY2NgzTk5BopZv6EnYdnZ6eUitFohMPlp1ynmWZnzedTsfLO1/tXgifD+cUdyEEvV7PezDcvHRGrTCMqu2VEjavS3uvipOR7j5pnHh6YbfmkiRhOByyvjEiiiNfC8RF+LiEc63a+onzJhviisyDobcd7ww0/sYf/p5Bp0XB+fm5WbRl5d3mRVEQR5Jef0hm49Ju7O+BUPzq419YtOeKkxTIyPBTW8OlGXBpBGISJ9y9f580TZnN5hyfnlq+3z4713Z4+fI5ndQkyZSFUfrLyriQHj7+jNcnr7h584Cz41NOT45JotgPcraYgy7RNZyePEepORvb1+j2+9SVic999Ogxh4eHxFFEJ45BmZALgcn4V6qyikFjaXR+BmEnuEvARGt0ZEDHoydP+T/9n/8vfPjh+9y7d4+T4yNePHtKGkt6vb4R3NJuTmCSpGvjznNGYKnxsdzODqZ16S2lAm11W9O5Ukjjsg+EqFHstCd79YqJbqxqQiuk1kgX3a6DUCqnyLWABHZTDQSdNdU4xgTHKX9JENrFZ7UeZFAVVwo7MewDnBIvLDKSotmwGwulBhSdJAatuDg7N0qhtnS/WlvwtBQShqtlcoUQj3vE178eXBLE7lsggnCzwGFMx1Yk/P39eLrr3Ln2VaI4ZntnhweTBUWRcn52weHhER9/9CndtMdobZ3e2hbp1i7r+3dZ39hGVhkPPpCcX5xTIdnb3eBbN2+yvbVBJ9aoOicvS8qqQiOQokOaJERyn7oquZhc8OL5S549e8mjZy/YXN9m59od+t0RD3/5jKqs6fW7/OKXvyBKIr71rW+RFQV//sM/5a/81b/KV96/x/iT/4bF6K8wmczsWLn3bveo7w5smJ+wM1mD9gwDjTIOGrlxmyLqoZX1aARVWSEoYqWdPcs/CYHLaajJi5qf//wXrI361HVlababJFA3L00CdG7DsSK/QRoLlKkmLIUAKcnLmp/89CM2N7e4d/8O61sjnyeQpilJmqKVqYrsiCMaoOqY4oLwHBnEgTtLusbLT42h9hZSopXw7+2MEFFscoSUNp6AWil0ZWi0S2oT9rPIreJVM5/PGE8mZIuMhU1kzPPMu/QXljWlyEsWi8xvfi+evuZP/umfemu/ydHQKGUrdAsTNmXCohSz2bwlH4SwHi6t/bqUNvdPoLyxPpISrSrPgSeEQDmaVGFAQOM1aBjNtNKI2JFlWJYhrb3HwDCGCc+M5ozAy6vfTEPh/xIBsbaT9962oB2bkaQWghqJRuJMJ9KFXApp6kQYdEEkNAiFpkKQAjGa2r4bHiBJO7ulrQS+rEg28jUAP4hGFvmX0s0+I4Rnq3LySkqjZNTaiTYZ2IasXA8UuLDf3Hmhfq61iRhQyhjdROTy8xQNtLosd99VYX7T4a4NrcumYngbyITnrvpu+X5ve2Zrnke2qLFq8iOcoqnRgQNiuR+sqdDJUeFCfhpvZQjCmnAsd/7l9zHfuu9NDu2jLz/nq1/9GtevX2c+NyxLJkzPnLNYTHny9DFlWXD9+nVevnxGUWQcHOzTH/R5+fI1z58/twxGEGFDLy3RDdIqudTUtZmfkojeYMTO/h5be3tEScSXjx4xHY/BhiXFnQHpcINrB3eoqopXz58Sdftcv/sei7JkfHTKetrl06evkDJG+YK7bt4HIdJ2vvmfOGODIcpQ2njjB4OeCXXPF/QHfXrdHmdn5y1D1jybIWVEp7vpPRnOo+DAdGj9D8GGxBXxNOc570NRFCaXx46bEgJkRKfTxYVkgmGgDGvRVHVNJE3h0m6vBxjvipCG1CiNYuIopqorRCRQnYpykREN1xifXZiUBy2IidCVZjabIaRgXsypK5Mq0OQMm7WvlJFdqn638L93BhpPvvwCrbUp8NLvmqqdZc1iPvO8wf1+n+vXr7O7u0uaprx89ZKj40OPGJ0FJLKVIp1QVBY1IZ3CJTgfjxmNRgzWhgxHa/R6PaqqYjKbGSXRVvWMIokQhpauqguyYkFRZiAUR0evLUozMbxCYKqTa5O0qMuKi3OzOa5vbDLoD3jx8hXziwuGnY6Jq1SGjUCKiKTfRwqYzSaglU1qah+mYFOjRNQ2RlHIiMlszn/1R/81f/LDf8ru7i5/+2//bZ49e8Zw2OfatT2SJEZGbUtNI/wDq7dqOLTdYjKLxP7zyqxAK2ETTgOgYZV71RI+oYBrFGiLJxpha0GUE6KrhHAoYP15aFSNL4Do2mBCFhrKRK010ha3cmBLB/eOWu560e4XrcEmY8dSmKR3rTk/P8NZITVNzskSTPL3XH4f2yUIEXvlxigUZqyDkwNFxl0jsAHLATCzoyMC2CGcWqzZ2trgYPELrm0Mefz4CefnEz766BM6aZ+NjQ2y+ZxazPjgg2usbe9yMZ5zdviCajbhxu073Hv/HoNuh3wx4+jZQw5fPWd8cU6WZ57VwjFerI/W2bm2y9a1Hb72tQfce+8uT5++4tGjZ0xmCzbWBpydnTObXXB9/zrd7oCf/uRnxEmXBw/uMz4/58c/+pHJ2dg85DxekOeJpTq1r277wlmZAJ8AbnrcjoX7TkSYiG07Ad349rZgeurHPEwOthPAK0oN3XBzGA+d5Isvv2Qw7JKmKWma+Eqvbi6naUqn02W41rf1FfChFi4prtcdIESEFDGTScZ4POXsfMoiW3B9/w/odHomPCCKQAukjIkDN7mRhWbEjdcwoq5UY8Wya6HIcx/KVdsQhLIqm1oIpWEgcUwnrqJylmVU1kPj6BjDOglVqcnzpqqrc9svewhdvy1bfpdlUtt6bQwe2HVNAACNqHGeWD8xrMJr2fWECWEV0oGHZn1LtAGjys2B2LZB46qWC6u8uaXswzAtcnEzo1EY7btcmjH+66ANToG2JhkRIXBhrwSyzHhP4iSxxhJF5EgHnJyz1kNVG+IKKSO0jkwdKiGAyHpNjGyOIkkn7lFVllc/jnyol/GAQ1XVHpSEIWJOtl7yPIjLxh+0XT8OgHlCh9CrEO5TrY4C2knrzTMFSRxx584t1tfX+dWvfkVdg44SQwSgax9aFDJOve14VxCyygvyJs9Au+3v8ty2x721VoL+anszGgri5jtngAvv7ULzVrdn2eCian3pu+BW/he3p75+/Yrr1/dZ39jhxo0bPH78mNlsRmQp4j97+AmvX5sciPH4gt///d/n7OyE6XTMwY3bvP/gATu7u5ycnHB6espkMjHhPMoQAanaAHAtBFGSMByusbO5y/rWNmm/xyxb8MWXD1GFCcGPpWRjfRPiLnfvfUCS9nj85UNUrTi4fYetnV2eP34KdcXk+Jx8NiOSpt6KfzttjInOaOlAhyuxYM5xSaLO0KFtgrOm0+3YoqAmBD7LMpIkZjhcY29vj/PzC/LcsMxppX0YlVYmL09GTf6GGxvjTYm8l8J5V9z+khclaFOPxNQkMcaYJElswckaoa2hyYKe2CbXx5Ehv0jiGAnkWU5VVojIGLqqskTViiIzXvs0SZnP5zavL/JFNx1NudNfnCfHGTYcQNK6yTV52/HulcGnU4SAly9f0umk9PsD1tbW6HQ6rK+v+4qBa2trnJyccHZ2aiqEWuFf2Yx4p+Q4JTp0M7qjrisODw959uwZUWRcds4CUGvt49mUamJqIylRUYTSmiwr7OZaURYVRWEriduBde5LrU3yYVFqer0enTRhbdBn1utSlEUrWcskh2IrrUYYcNde9Msx4o4T2U16F9c8mxWU5SH/5X/5X9Hvd9DUxGnEaG1oikOJBjlbfdxamSx/+SrwobXdEMTS9+2kNif0tLVoORAA4Ybc/B+zL/pF6q4N/wv2F3ysMCYkwt1bacN44/rGudykdtXNA4uMiImIbPsTwMabSwkiYK4iqNyMjV8PhsRQr2kmkzFSWsUAw46zagMxfXnFpiUgufnb4clegLkF6fMPXF8LLKsU3mplvhbtGwcgr9vtcjP7iG9fK3n1/IiyrPnoo09ARKytb3A+mfLq6TOIu1y//w1kb51Xr17TjeC73/8O13e3mE7H/PxHP+bRFw9ZTCfGWqqV9xoJoBaC7PyMs5fPefypIOqm7B3c4Ksffp2vfnCX/f09fv7Ljzg8fcnW7jbj8Tlnp2Nu37lFWdb85Ec/YW3Y5/79+/z4xz/miy++4P69ezz/6V8w3flXeX14aC3LbiqZd2xwQzOxveImXQiaPUk77nxzk+jWd6kOPwMa9pBmbrtNPRy0ZibXtaPnG9Lt9izbSUocR2btdzpkWdaK3zYWKqOYm9BEA5a1hqqaGzYgZWJe9w8OOD05AwRHh6cIEVuWFeM1MTlXpkq7Yywym9TC0g1CkRuP6mK+8MK+yE3CugqYakIDhCM2CBndvPVMSusRcWs/7HtpvQ/tMJXw99DDsxyS0awX29MB+Lj0HRLnlQxwg2mjtZgugxcXYhCu5zBRWEnrJfU5KO+mbP7mh1ujoYwQoCPQCUZp0whq6ympiCNTSb2TxPS6XYaDHt00IS8KZtOFMbwojZQpWkOvN2A4XCNJE7a2N1lbW2N7e5Ot7S2r4Ay4994DHj1+wj/6R/+Ip0+fmurEdi+rahPGa6p2mxoH4V7g5F9jmTXW5bpqwlP9foyp+yBlqOD6xdzqBzenmvjuZerwJjdhtDHgP/qP/pds7+zyv/5f/W94/PiZDceWKApvuAkJDP5/efxanhS7Lhv6Zdrr1f69DM6VbsLjwu9XP6LpVxkYU0KA04z124+QxerTTz/ld353i42NdYpin+fPnzObLTD1QQxtbV3XDIcj1tc36PUGHB0d8sknn7Cxsc3OjqG/PTg48HUn8txEmigEIjLW+bTTpdPtkUaGUvXp44eMx2PDIicixqdn5HmFkhH3791jMDTGrsPjUzbWt3j/3gPOT8+4OD9j2Et4+PEXIE0ZhTYAXgqHE1ySYdhLnKEjiiJ2d3eYTCb0Bz201jaZGvq9ngmvzTKOi5KyKJnPF1SWCaosbIFL2/u1UnQ7HYStO+fyJ5ZDB7XWFkjUJLIpQK2UotY1sZDosgZlo0zs8CpVt6ixpZSUWe71ztLmiEyqideZjYfCGCpevn4FNDTSIeHCYDBgOByysb5B2kk9te7Gxgaj0Yher0e/32c0Gr3TPHtnoKFUBQiyzBRrCZl73ELq9Xo+8cQwHzS0aq4jQxefEyYuIQbcgpHkuXPtVz4xRkoT5zgYDJqOsxSwrgqrVpqL8wu0lqwNR2QLU4ncMIxMPD2Za3dVVkRZxXMNt27ftq5+fN0Hb/234VNxFJPECXnwLqs2WCewHahqhI0AYqpa8Od/8SPW1wdM5hOSbsz79+/R73YN/a49TKxx87vrO/MMaT9rC/xw4kDjtjNthVAILf+9LAQvuVy9YthWeMJrmzkTKD/aeJ1swANKVxawNHH2pvmGcUtjk3vtOVJIpDZ952LcDWSSvlhjFMUIoChLlK6IIsF8Mbex4nily7frDdaqpn/sOUKS3P6uSYDUGqzV0ne8tfjhQgw8dhA2zhFCIYjv9oA5ScCeesnX185ZLCLmiwWfPnzIdL5gc+caneEGr08u0DJBiIgiW/Di2WM2tzb4zre+QTeBzz/+Gb/46U8Yjy9s0IapzqxqQ07g4jgjGSEjOz+VoppPefTpxzx7/Ij7D77K137rW/zOd77GJx9/DNkJaadHr2s8enWtmc8u+MmPf8zOX/9r3L9/n5/97Gfs7e3xrbvbyEf/bya9HzCbZXZSLm18bs4tb6guv8hSAQsMsNT2u+Tmd8h/8n9HV01l44ZqsvZAw1kEww0liiWj0TrdrqmqmmWl/QlFoUiS3BQ6RFsGEkVVFSAsI5Glly1tUnhV1VSlTWLOjTEDBFm+4L/4L17bdrVrZRgFj0bBx1VZNpZ5KRwrGoHSthSCIYXvTZMLVlvlLFRs3LwzIljrcG2GP5v8Fm8IcUMRPD88XAwwhGE6Tey9a0MLvNh12kwB69XE5hOLtvxxz4yiyFaQNuaKSAa5W9LEJi+3QdqkbmW9vuAqTK/2X14FnFad17TNvg/Gmy6pgBpEBaJiMEg5uLHPh1/7gDt3bjAY9Hnv7h32r+9R5AuePXuGFIn5Fxl5MeiNWF/fYTjY8EmmLsQns8wyR8fHnJ0ds74+5G/9rX+TXq/HdDalyE048+HRMU+fPuPFyxecnp6SZRllUVLVhra9qupWmKCUpk6UVi4nCjez8N4h4d4dfOin1phaN42V1hWADL2My8BxMBjw7/w7f4fvff87QMS/++/+z/hP/pP/HRfnM6SIiGRMpctL8+dt3of/fzmckhYSU4BbSzUudCrMUYL2rnBJp/AybfW7LwOMVYr0KgNB2MduDc3nMz777GMePPiAnZ0tyrLk9evXTKczer0uNw5ukKQp+/v7zKZzer0e16/vM5nMOTo+4fj4mH7feN3X1tYYDocgFDIyBZeL0oQnlZXi/GLM5OyEfDGnqHLOT0/Z2thisqhYzDPySnP77n02t3eYz+c8evyETm/Ag/8vdX8ebNuV3/dhn7XnM59z5/vum6fGjAa60Wj0BPREUWyREimSokjRluLEYWyXXE6USJE1lBy5LEZJFCuKypGUKlkmSylRNFui2SRFskiR7Bk9oRtAN4A3v3fne8989rxX/lhr7bPPfQ+N1xZlURv1cKdzzt577bV+6zd8f9/vI49TZDm79+7RqHncuvEdsixCkINllYrz1XtV/V9zYdXqeFQbwy1L0Gq1sCyLJAnJC0UcYwtX9agJZXOm41mlb6JyMi22rKpAjq7S6Sotiqmp3WqpSrKghEuZ3kDXdSkS7SMJUfrHCYrZyQQUpjJt7sO8rhQY1c81yzIc18EycF0kru/T8Dwc26beqOM4DqdObVGrBWRphqtZr86dO8fq6ir1eh3Th+y6iiAEIXBs1XsTJwkPczx0oKEE3pQGgRb5nm/CRUGaJopW0VKiO6qpWZZO4GLFQjnphhf45KZmhKWqi2DOECRKSkHrvgZQAVgMh2Nms5AkzXjrrWvs7R2on5OofCjmXGmaIlJVsj082KNWq5NlCVJmasOSNpbQ1QpkKSq06CTcTytofldtJjNVB/1uClkwGo/59nfeUJjotGBleZlms6lgVJYpn1nlBmoaUKtOgXEeTdBhMryO7ZTPqMyySA0gEnNHSJjnpadj9bPf7qg6P0UxZ+ypLtyFAAfNq6NLma5laaiAyaqq16nKl1sGhwiJZWkWMGkh8xybCk4VAdg6g6AmvYKbpKRpwnQ6ZjQa6WeprqLM4ur5tJj9WXTazCEsC6ezWWbpVZA0d2LM3NSJk1KcDqQW1JCq4dTMc1kgxbyvQAqo+QEr6Q7NRpebN24zGAy5d2+bequNW2vQ7C7z7vVTHO3sEtTqIGBjtctTTz9FnkZ86XNf4PYbr0OWInLVWCmLAijK9WILpWYdp6muMIHn+biejSMs8ijktW9+nb3dHV740Id44rEr1Fy4df0OjVoLISFLMrIsoX884LXXXufpp5+i3W7z9a9/nQ9+8IOcGQw4OvwGb1iPnMiGqu8lxllTcwKz6ZmKi+mfMUGKeXbCQSxdJN99bWETV3MxL5+DcbTnc1UxaEFOv5+X60P97WRAXWiDfqIJ11z7wsY/f4HJ4M4D8TL817chKLL7e7rU/y0NMatkK+cpTh2jmp/ns800hs/vRd1XtSHZZEwe5KgswM5YdPLn93I/TMq89+RrH/Szmd/CfJ4Ouksny1I9SYs2XkFQbQSubc/H0/RlWAJpGWjVfFM1c6HI5jjmOWGADkgE9wVU5qhmos14GkcaqkrPkGUJlmXTW2py+tQSRZHS7tTxfIsPf+R5ur0WnmcT1ByduOpzcHCs2a+O2Dp1gUJaTCZjvZnPkAywLBekD1JBrhy7oFZzSGLJ6kqPRrNZqpsb51BKNIuPixBWyX5Y6D7Bw8MDJhOVYZ5OJxwf9wnDkOFwwDe/+S32do80LEPtE1meYzl6ThVg2ZXKubbhllbAVok5BetSdkbNd5MgE0LgOIo+80/9xJ/ih3/khyiKAs/3+eQnP8HXvvoNfunT/5IszbGxKPL5vgkszIk/7EeVjloRRyyyBlHpqbgPzVEu9+/OFgbztWPmdzXAL/8uFimSy+pJJTFokrfVc+7u7dBsNTi1ucXa2iogODw8ZjqZUdR9LMthOBiRpUoXo9lsqj6uMNRQK5vd3V3u3r0LgG0XqLypRRRnFNImyyXCsglsC9uCezdvEIZTyHLywkEKlzMXr7B5aos4irh9+zZSwPnLV6i3u2zfuE4WhwxnM46OdrEticBW1cHq0D0wiXD/gBobZVkWFy9dIgxDgsAlTiJNLqE+y8CEHE3Z7fk+VO2WDSmoJLlTlFWAPI9UIjzPmY0npHlGXOkRSpKk9Ilt7JKYIooiLN3D4TpOae8c/b2hnzV2q91us7a+TqvVZG1tnSAIWFtfA3uujwEKhuVqoVVTzRdClFS1QoiSlcqA+gJfFQNUXl+SFjlFDq7/BwydKhufhalugOMoxg81eXMkBZbpei8y5fiK+Yb0oI3LOKRVCkipnQ+YT5byfSgmlDAMydJsvnhQC6dWr/P5z3+Bz33uswCqBJdTYpqrfMS2jspsyyFLEybjMZ7r4lgWackMAcpZkKVTadiYTLfiYsmS8ncnvzfOKUBRCO0cQxgmvP7ta9y7u4fvOho77pUBlRFvcRwHx1WNPSB05GyXRtnWWibmtep9OvNkq/Kd7Ti6gVrBzcrsi87UG0NUVXx8UGbTNJ+X0A11g+oZWVbZx2EOiXKmzbN3HLfMgkkTAFSEhEzzrRBKhb0auM0DK1tfi4nk1RwYDAYkUcZ4POLgYJ8kiXWvjIJvKU5/05T5MLMfrKALllsGe5YwGXnzbNGaGvNCiaE0NER7ypnWo6GbQmVRIGwbIQt6XsqFWs5oPCaJE27evIllOzRaHVqdHq3uEmfOXeD8xcvcunUT2/F49pmnSMIZn//d32Z/+w4iTxThAeD7gWK9kAVLS8vYrqsdBYnUmZHBYMBwMIRZrrixgxquJejv7/Gv/9W/4gMf/hBXrl4lTeHuzV06zTadzhJZGpKlHm+88R1On97i/PnzvPzyy4xGI9bW1jhz/CZ3OEcoahgYrDARGNqpFgJRQixMf4vJfKu1p9b9PBHhdDbIdl+77/mIExuMVcn8K0c0ZjCIy7/Pd3aV0UdvNiaIXIiNuD+wME7U3LmfZ7tNJVeW/xflXLP0NyYA06kB/a96Q/Nvi4UfFx2R6rvm9kodKjWymDSoZj6r41UNtt4pc3wyiVJNrpxkApNSls3dApBykYbYDbRIlbZlZhP0PI/V3hKtZgtbV7EbzSautm1Bs0FveYkgCMiyjL29Pe7cuUO/P+Dbr36Hg70DPMfVXPfKMZBCUIh55rma4BJC3McVvzAuUrWAq8pFjuPC+Qtn+N/9zJ/j0XedZXv7Lp1ugyyPOe7vc+fOTW7fvkkt8Lhw4QKOJYjjkFazgWs71AOfvLBxLMl4MmQ4mNDrbpDHOUK4SKDb7REEdSgkvW4Lx3YpbAfLsDTqcTc9DWlmIMWuKUVg2Tbr6yvlAsnzjHqtrtaeENy8cZNvfes1bt26VeqjhFFIq9ni2rXrHB/3y8qhbdt4nqcqoraN7/klGiEIAoIgoNvtUqvXcGyHpeUlWq0Wp06d4rHHHmNzc5PZdER/MkYIQZrk/OAPfYqvfPVlbt++g8xBFItaEebfv+1qxh/E55s5VNXcMQ6dRKiMe8UXeDtGK1MZMmvHvP7+a5yjChbvQ1FfV9mVTvpc1bVe/rMEWZ5y69YN6rUGrVaHjfUNXCfg8OiAyWRImqYkScp0OqPRaDAeT7h16zY7e7tYlsXly5e5cuVKifeXeUi95lCrt8hyODwcYlkuRWGRxCG3b90mDiO6nQ5xlmEHdc6cfxedpTUmYcyNt94iz1IuXb7C2voptvcPmU6H2FbMzetvIoRC2lCyUxYL41INrBYSHJUgz/Rd2rZNvVajVqth2yDxkLmkiCVZmiMLJRqq6GBhPJqgcj1zgoEojkk0aqa0J0LZ/xJpovdhs55aLdWD3Gw2abc6RGHEcDTEsmw6nQ7nz5/j9Okzpbhxs9mk0OiEvMhxHZegFpQ+n9Fr8jwPhGA4GupEmMT3A01xDsfHfRzXYRbOcByHRrNBkqREUUhQq5GHM3q9JeI4wnZUy4Dl2EpbpMip1WsPvW4eOtCAeekmz5Uku23PMzy1WlBpehFlBD8vrS4GEzBfUKYMVGYnC1k2BVYjf1UCk6ocJARZlpJnquHaEhaO69OoN4jjiDgONZTGIsvnxrg68SxLcaH7rg9AHEccHx0qZUvjfKBYEywdaETRrCzLmwjzQY549aiWkqVUECLV9K3wtMoRs5iMIyY6oBPcH2RZtq02j+pmiKZErJRjjVNrFhwox9Jx3FLob+4EWAtOjfmdamwyvxUL37uug6H0RTs3punzpBErMwj6tcbgGQMshMBxbVzXLrHxpjnXdV1sx9IZNc1pbdt4vo9tWZrBx8DHTIbGZjwe43sBd+/c49q160hpeKdFGWw6jp6vDzD0DzL+or2BsB0dOJsK0AnHU8q5orXZGIp5RcMYHPPkVBO4wtE7VsG52ddYOtvj5s2bDMcj9vb36fSWqdXrtNod1jZP4Xg+2/t7zNKMj7z//RRZwstf+Cx7d29DljCZjfA8l3qtjmXZhFFEkqZIYdFZXsb1PGaFQyJcnHxAa3mVcxcv8r//8/8x/5e/8bPcvHmbZqOJY9nEkxmf+53f5YPf93GuvusRRv2IyXBCp9liNPBwHY/pLOTNN9/kueeeY3V1lW9+85s8//zz9LotNq5/geudD4HlzuePWMzmL3jGlfEp4zEoK18CiXvpIyRv/esyKK68ufIxJmGx+Ext2yRFKo9dV87MRksxX2+Ln/nggNtkwuZnm1dLVFxlPkeU69rc3LyyYoKY+wOc+45K8kP9X0AVLmCWnFB6R6ZKtPCZksVm+UqyBh0Wn3ROqk53Fc5pEh1qzTq4nke71eLixYsEQQ3P82i36nRbTZaWeriuWzJX1es1Gp0WvaUeruuU+4TS3rB45smnVMYwUxt0XsxhKTi2SppYglRvfEJYJEnCa698h9dffZ3r129w48Z1hsOhUvOOIgphnAxRzgXzfI1dLSsjhdSvU2QgjiVUQOQInn//s/z0T/9pVpbb3Llzk7t3b7MyW2JraxMLixfe/yGm45A8yzncG/GBF54HKbl7+zazWUI8FdTrTQ6ODpU9Eh4337pNs7nCqa1TCCG5ffM6nh8QhQn7+4dcvHiZRm+JTm8Z13W0QjvU6w0VLFsWrucuBHvGxplEXKEhx1mec3iwz9raKi+++EHi+L1lE+/Vd72LwPfZ29vnzu0dQGkJNBoNlpeXlZJznirq0Xq9hAEaTQqJ1L0jSr3dsm2OjvaZTIYEfsDx0TGTyYTxaERBwQsvPMdxf5/haIZjO1ThINXqxsMGwv8uj7Kybys0gslqC1tR+p9M4BmtgwcFAq7jgJxX3U7uS0JY942F+px5IFM9V/Vr1beYv9eQUaS89vprPPH40/heTTVHC2g0Ao6OjhiNxsRxwmwWKue40+aof4Sxcf1+XwemSpTvvc88SZYLdncP2L27R5pFRFFGHEW4tkev2yNKYzorPTbOXcVvLjOexdy7fQuAi5cusbaxyWG/z/HxMR3f4tp33qLIY4QoUH1SNmCBSJmTIcwDDcsy6AfKvbgavAmhkDJxHDPdHWHbkGYJaZRCKkphPeOzKKh+jpR5mbDudrtYFSiR4zicPXuWZquF6zjUGw0C38f2lNZQu93m3LlznD59Gt/3kVLiBzX8Wq1MBiIMTEkRJqRZVvZZSCmJwqikRS9ylaxNYgWZTIqceq1GvdEoWxCiOMLJVUDSaDZIs4xavY5t26SaYWowHCIsi1q9jumyDSPVN2jsfZ7nMJuVZCnvdDx0oKFgUYI0VbuWbehpK7uYEJZuppyLIhWFgjSoyZ9TpUI0UZ/K8KmNQspC0XWJ+aI0jeTGESixzlKxdQgUa4slBM1mnelEEk5D4jDC8wIFgzix2OZGy8J2PKXOXUhmUcQ0HuK4Hr7vYUkUDagtmEzGhFGk93WldP62QcaClzN3CoTQGzWUG0B5PRIEFpqYBOPgl76rhh0XhcHGqvtPqjS7kgWVbZlXYVbVMvQcNlW1X8aJkcKUySvORlHcBymxtAaAcexMK/i8aVx/rv5X3mel30QtckfRuGljh3aQzDWY7JzjOHiuq77XWGZbVzQkUleoVEA7HI5YWVml3W4zGt0rx8S2QTWVnwwo5vCxkxkkt3NKO8Lq+qWcVzRMUCyEQJjMZ9VTNtSZ0jhw+tkah9a2aExvcf5CQJIWJHHOnbt3sD1Bo+7TDDzWlrt0Ow36kzF7+0e85+lnaAU1XvnKF7l78w2QGdNoQqPdZXV1jdFwwGQ4ZDweIoucNAqZhRG1Rp3QX8NavYiMHRjv8R/9me/nQx96P//hn/1JfvZv/T+Zzqa0mi2EJQhnE77y2d/lxY9/P+967Apf+uKXibKCnXt3SNMZK+vr3L2zx+VLE86cvshXvvIVnnlGsry8ztmjY24VMbmuwJUutRm/EvpSXQv6VXq81DhV8PaWU84HRYlqWEQcbWt0UGDNn61AkGVSB6TWfA1WEh5SKmICUc7gEwEDZqNaZNQRwtSr9AwqwMktcgsy3X8gpWaXF5DLvJw/5fyyKG2KYtMzYaiuLlp2OU4WQjOSuBQF2EJiOdXwTPeYSIULN6J8tqOSFLatgvE0LcizohR6UtBEFWxo4kcwCQwxj1OEJmOwHRvHtmg2mzzy6KN85CMf4vyFcwRBQLvdptPpaJshVVWlmEMJTLUyz3NG4xG7e3vs7u7Q1pm9wPfpdLv0R0M81yMvCqIwJMtyvQ/ZSJT2kef5FEWus6xTiqJgdX2JK+/6VIlnns1mHB0dcePGDe7eu8ve3h7j8ZjJZMpoNCKJY9JM6YyYrGO73cYPAuIooshSTm+s8f4XnqfbbeB6Fo89dpVZOCacHOMFDr2lHkg42DtkeWmdezd3+cDzL4FQkITtnQFZknDm9FW+8corjKYxXgDHxwpusr6+yeZmEwqLTMJxf4jv1el0e1jWhLUNh1qjjuvVsGwPKQWtdk+z3ai57ziqaj2bzQg8xZhz9+ZtQu0QxLFSMlf3nLC+sU44nrCzs8NoNMbzPGbTKf/s5/8pnU6Hp558mptvXWNr6xSdlRUC12U2HmM3FWTr+EBRmq6urnLlyhX2d3dLOEYcJ3zlKy+zsrLCjes36HQ7TKdTJuMp3W6vrNQLAd1Wlx/8o3+Mf/HLv8p4EqLzL6QyA0dVOUyw+Yf5UGtH+zyG+tfsC6gg1XVdJZTq2ERRRpoluoArMI3wlijwPI/nn38fN2/e4c7dbb0G9S6qt/NC3E+mU9oUzcxZ9U/UnkXJQlmtVJWfoUkbsiTjtVe/xaVLlwjDiDhO8AOfjY1NJpNxySoVRRGu57G6ulY2IR8eHpbaQHm3xeHxhH5/yJtvvMVgOCbLCrI0J8klSZ5Tq7e5cOEUK+ubFMLl4PiYnbs7BLU6Zy9epre0xOHxIcPjA5p2wfU3XiUOp2qsrPmeDRruXgkwqsGbLeYVbiEltmF2Mu8lZXvnLkqHx1IQqazAQSVjHceh5gfUa3V6vR5pntHqtGm327iuy0svvcRoNOL27du0222WlpZYW1tDSkUZGwSBel62XTL+WZbFeDpjqiUh2u0OzniskoNSUq/XcWybOEnIUtVD2Gg0yNJUozQUyUiqK0iGlEn4gixNy8qSCQ5ardZ9PR5GD8P3fSzLYn19nTiOS8h9qj+nCgU0LI0PS9rw0IGGECrSrT7c6kmqGLBFNpMqHnaeFVvEz80/4ySe0GTLrLIRUDWeSb2shaX+VuSKVaeum1osyyYIPGzLIYrCBQx1tRSbZRlpnlHzXDzbw/EDkjQlLyRRkuIAURgiZa4ULHPVZGyoF98u0HhAUry8WaG9e1m5d+NImDLeOx1qbOxyvIyypWmYx7g/lYVWpQws7lPANRkOdBA3/3mhh6bMSKM/s9rYJsvmfCqvKb/Xb5ZSKi51HUwIobB/WZqXjF5CUBoMk004aTRVu8uDseEGHnF83F+AgxVFoeBnmgXlux2lMygE7pnn1LWXgZnSITHNlSrg1dCoBdFE44hWsyfzvxmHekPs02ydZ2d7hywrGBz1adRrUBS89Z1vE8YZG6dP0z8+oNtucmbrFLt3b/Dat75BkWfMZjPa3R6bm6exbYvDwwMGwwF5liIAx82YTafUanVqs33EjT1lnJKEj3/swwC8+OIH+Xv/r39IkiSMJ2M6nQ6e7XB0sMcrX/8q73n/Rzh95hS3r71JGM2IwwlLq+skScaNG7d4z3veQ63W4NbNO7zrkSt0uh1auzsM3CuLSXXjVFcTFZUs/TwiMe/Qii9a8bkoJMgc1TOlsocUOZZQNHy+71Jv1DhwUjLyhR4Ak7yo2oBq4mH+rOaNrqYELjRJQxkwVz3wcv7lSCtHCheBorYVFDiiwJICKd15tln3W9moOa+0C1QgazHPsgsrx3GFLrE3qPk1XNunVqvT7TRpNpvYjq2gkbajGbVcPF8lZIJaQLPRpFar0ev18P2Ao8MhN2/e4uatm9y4cYOd7W36/QFJmpBqalblHIkyWHEcG8dVGbZz587zvuffx/uff55Tp07hei5hFJYVh6LIytJ+URQ4tq0gNfpZWJaFH/i0O23OnDmDlJIwDEmShNFoRJqm7OzuMhyOAEUYopw0A5e0yk3UPCPf9xWUKk85Oj7AdV2Oj48JgoCz505z6fIFTDUVKN9rNmhDRVkUBbPZrNxI8yRBZiFnz2yR5Qmz2YTf+s3f4iMvfoRcZoyGM5aX1zl/7hw3r9+gyGwGx1NWV7YYjEZYlsW7rj6BHwR87StfZXvniCtXIUoLzl64QqPRQhbQbLZo1JtI4dBbntBsNplOZ9SbPQBarTa2X8d2PL3n5UhMz6OlVOyzDFerBx8dHHJ8eMigP2A8HpMkCe9+97tJ44Qiz0kiRYPcbXdp1psEgcpY33Jvs7ezx2/t/Sbf+tZr9Ho9tra2uHPnDisrK5q22WJlZZn19XUO9w+IQyVqe++eSuh88IMfpNfpcrC3z/lz5+j3+9T8gGF/SJamBEHAaDik1WoRRxGrK6u899ln+P3PfV5l6i0XiSCXBbLItBP+cJz9/66Ohf208r1CMSitBgPdLqs0RaEJAdSaswS4jsv7n3+Oxx59hPWNTQ4/82uE0xCTuNLpl/Kzq+QvBtZWPRZgkfraFvbR0llRiRhTFUnThDfffIOzZ8/iuDaTyVRVKNsdms0W0+lUs0tF953fVHSGoxHbu/uK+TNWzrFKGLgErTbra2ssL6/iuB7jWczh0T6j8YTlpWVObZ3Br9XY3d0hHA9wZMKtt75DPJtUetj0uOtetCoy5oHPSN+/SU6qBKZgZVXR+gZBQLPZ5MKFC2xubjLo9+m22jTqjTL54GnkRY7ECxRbYVEU9Ho9ao067W6nhLsDeK6HF/gVanmXWr2B0EkIIYSmJ0+YTqelFocQgkG/TxAEhBreBJLDg4MSEdLr9fAdhxwVnJrmcillGQyYANDR8KdFP1D52JPJBMtSJEzGhhsWRkdrVo1Go/IzarXaAiX8Ox0PHWiYGzdRsOm6N014ZhN3Tmzq1UlvghFzI+aGzeQwzqRVidLNAJnoCtTANZsNjg6O8D0Hy1YMLMKycF2HIPCo12vkuSl/WwvYz4WJJ6DIFZzGcz2WlpcVq04UE85m5EmC5zq6eiCIk0hXX757oMGCzRELv6/++LAPyoibmXOa7CWo6HJ5ZZnLly9zcLDPzZu3NI5QOWFltlTOHV6lAWEgEQXG5y7vy0AKTBle/01WArW5snBZ01rQuZg7kiaAWjS+ZuyqgWv191U42MmsjYF6VA1lNYg1rzULyDginudhOQobaapp91c23u6QmIy4LvmU1wMVBEuZjUcZdR2dyJO/x/BmZWz4qodoNpvRP+6TpimddovBYMDh4RHHgwnnL11mOBrz7HufI03GfOuVrxJHIWmcEgRNNtbP0O12OT4+ZDyelD0Zju1g2S6O7+MFATXfV9nbNGVra4NTW5sAbJ0+xZUrF7l16y7bOzvMZjOazQaO7XH9+nUuXH6UC+fOsnvnBmsbG2zfva3gEbbN7du3uXr1KsvLy9y8eZNHH3+EZrPJcrFLX14qA+nyviuVnXJo0SXtqv9eVsUkhUn96/G07ALHETSaPqc2VzlzZoutU5ssryyztNzjv5r+XQbFiGqFygTcSZKUWdXqnKw+zyq70skExf0wBp24EAXSzhG4WNjYosAqIpqeVBBNqUyuYzvKCc8FSZpS7wqEHZFnUjvUKjhwXZ9as8OP/NifUmX4Rotmq4WygxY1P8ASokzGHBwcMB6PcV2XNEtwXZd6va5wxzpZk6YpG6c2efezT6rNJUk42N9nZ3eX119/neF4pOCJekNZXlrCdhxqtYB6XWHxe90utXpdj5+q2tTr9XKtGlYw13VL58psrMaphzlu2WTdTAYtjmOyvCgbFc26LhkNoaRWN59h+tMsIcuNvtvtlu8/PDyk3+8zm81YWVmh2WyW+Gjf98vPM683Sa7ZdEwcjhWLDjAc9uks3SbNXc6cvcjps1epBzVs26bdnCKk5Ln3fpgkTbh375Cr77qKhU09aPPMM+9jMo65dOlx1tbWVUJHClzH0wk6ySwMWV7dwLYdhuOQN964RpIkPPfe5/DsnDQJKYq87C2azWZMJmOiWDXk9rpd1lZWKLKM5aVl1tfWWVlZKRM3Zj9dWVnRjehzNrHTZ87w+BNPMJ1M+MpXvkKn02V//4DV1RUuXryAbTtcuHCBl1/+Eu12m4sXL3Lt2jX6/T6NRoMLFy5gWRbD4bCkvpxOp2RZxnA4xHFstrfv6XVlc3R0hOu6bG9vU697XLywxc3bdyiiAs+1STOlqCMti7kuyL//x0KPBNq6CYHn2ly6cJ4L589RC3zWV1c4f+Y0b711jVRXdR40AiWkkPvp7+/zP5jvueYa5te0mIDM85wbN26wurZGt9tjOFR9GqYfZ2lpSTWDx7EW+0xI04w81tdqWQxnMZ7n43g1GkGNdrtLs9nE8WtYtsskjhnuHzOeTPGDGucvXWKpu0QUhuxu3yFPI7JoxO1bb5Els9LXeNCYVuHx9/lleqxPjokQgh/7sR/nscceRQihezSUL5tnGZPxhJWVFYIgIIoiJpMJaZTSaDYYjUbU6/WF5mpjoyzLIggCJpMJALVaTSc4la8TRZFWYQ8JgqCEbhmf2uxPihbXmpMt6eedpimj0YgoUsidIAio1+tlAUD9Xr3ffF8UBYPBgCAIkFLZyTAMcV23TLSUwaKlKtaz2azsnzPMsiUL7EMe31OPhm3bxHFMo9FYcPqqtFrmgdu2wtBWKW1NZFWNOM3mUd3cc1ng2qIcaMNtHycxhYTxZKwCipqH69gURaZptyxq9ZrCseUptm0ailU/hY1dlozM9bqui22pslqaJuRpSqfXU2Ir04meMArT67o2tmMRhtO3X8gwz8hWjvlr7jcTC9kGxIMXCRIpMyxbqV0HQcCZs2e5evUql69cYn1zQ01UPXlv3rzJyy9/hYO9Q9UcJCUKrjsf92pFwrZNdKufFVYluJhftpQFQgcWRhnZ4EgNn5A096sDnJOBQ3l+jZusBhHVhszq2D4w+6wzRQ8ay6qTOK+uaWiVrmiczPy83VHOayr3rSs4qsqhS96V8y9KNKGp97QjDQvG0tn/JqzkvPnmm8hCOUQ2Nr5XY5hPEUJhpJMwpObYnFpb4sb1N9m+exOKnCIvWF/fpNNdRsqM/vExtm2ztLyqmt6FwHU9rj72KJcvX6bdbuPZDnEc8/QTl9X1/f2/D//Jf8InPvlRfuEX/iVhFKlscC3AcVxmSco3X/kGL770EmdOb5GGYzY3NxgOR4zHY8IwZDwe02q1uHXrVsmms+rMuIZECLucH/PFUc2kqVEp/QipoFUIFVSY0BrLxnUdHEvgupIPf+h9/NEf+CTNlk+97pNleSlcJ1R1nTzP8Sq2qSRAOLHZVOfPyeNkAFv9fXVOFtJGWi6WtLBFgsuMRx/p8RM//hKNpqSQqiHd9/0ysD46OqLda5NkGYP+iCK36LSXkYXNuXOX6S49ydbpJwlnEbbrK1VlWyiR0iLBsR3G0xkHB/tICUtLS6UgoxIQ1dVkPf6+baPYtTKKQpDlMUsrPdY2V3nk0as4nuqPmkwmDIdDAk25HccRjjNvLh0MjqnX6/i+r4SiPL8UgKrVVKOgCpQPSSuBnVnXplJpsm9BEFT6IwoajQaBduCbzSadTqd0AGazGdvb2+S5EtKK45jxeEy321GsdZpBJYqiMng4deoUm5ubZa+gca6NfVBCXZRJCXM4nkejtY4Rtdo4fYEf+uEzKihKEjzHwbYsFdALFdAVmUOe5Vy7dodHH32aXq+HLAreeuN17tzeZTZN8LwGYRRzeHBEGEa0mm3lKOSC3/iVX0UIwXPPPUdQb/KFL/42tUaLLEuROpN5dHTEwcEBV65c0YGZwmGHkykOglarzUwnWoyg7mw2Y3V1VRFmJIkOzlyuX7+uAqV2myzLuHv3LpcuXUJKyYUL5/E8j69+9au0Wi2kzPjEJz7O7du3+NKXvwhSMhqPWFleKYlS7t29y3Q6xXEcWq0W09mMcDYjy3LSNNNZ2gjf90kSJSRaJClbW2t0u21e//abjCcRRS7VeBbiPttfPR6Y7PtDdJxMsi1UVFH9n65j8+6nnuLSxQsUec6gf8x0OuP59z7L/s4O48mUXKq9xew/J6v81X3yZCJvvv/KhdfM/yaYE6ssjufe7i7Tacj6+hppmhKGM5IkxvNcXD+g3mrTXVrGsrWifKHw34VlIxwX3w+0zbVLR3swCRmOD0iShHqjwfkLF2m3W0gJRwd7xOEMi5zB4S6Hu3chj7HIQdxfsamO60kfp3wGLNp5swecO3+e973vuTKxYqqcJkhoNJvUGw08zyWMFGV7vdHAdV3anU7pnGdZVjr+JuMfhmFZyZhOp9oedSkKZfN6vR6dTqdEWBjH3lRUjY1SFV2b4XBYNpCbCq8ixFCB3XA4ZDKZlAkYIZSmTqOh+rhOBj0wJ0WSUi4omx8eHpZ2w+ztpv/LQG7r9fpDzf/vATqlNoZms7mwyE0pxkziBbGaymIyA1ZtDjdVCuPwlUGJZOGG5jzvCprT63X4yZ/6CfrHfWRe8KUvfZlvv/o6eVFQr9dKDY48zzQbRzKn5WUe/Ru8cK/TVZ30UpIkEYPjY0bjCUWeIaRxxiXoTFmep6Ug0oMCjQfEGQt/4wHOjJn4phS4kPEQKtDpdNtsbW3x5JNPcvnyZZaXl3UToDphmmYENY/TZzZZW1/miScfYzaJ2Nvd587tOxz3j5lOp+RZrnC6aUKaqCAvSRNFl4ZuvizUIsyLOa+zoXmU1qJzhUCzcIHi9X9QhWfOLlYaPKkEEKv3eXIDqQaG5mcTeDq2RV7MA5TqWJ50HB9EAqDeIxfeV72WxQZ7U9Ux/9M3buBulfeXLRpUEEFGOE1nlMoMPgKPhCROmMwU28t4MsbzAxzH49HHn2CWxJw7f5GigLXVNcgybt+4QZ6mpHFIq9Wh1+uCkOxsbzMcDmg0Gop1qlbj1NZpXnjhBZbWl1WFoFB6M00pee97n0YOh4i/9JeQf+bP8NJLH+Tnfv6fs7SyzHA0YhaGtJttXBt2791heHzE1uktbt+6gRv4NA0DXJZxfHzMhQsKnrK3t8/q+pJq6icj0/0PJybFvBwmylACo3yo/iQpR18AFLiezXKnxY/+yA/y3vc+SS1wKFAUgTLPsSRlksEMf3VOmkzTyeDhvo3pRHBbnR8n4Z/zw0FIF9eKaboTPvmxJ/hjn3qSVjOmKGIKqdjahKXEO4uioN1okxQFB8cDhIhYXlohDIdkKezv3WA4suj2NslSizQMCRp1Gq06QoBnewipqpb1ZhPHcWh3O/o+7dLWJUlSQrWMDo2jmZ78WlA2Cx4P+gwGAxzHqcBkFGtTs9lECMXgpxwlizt37rK1tUUYJghrxu3bt1leXi7H2XEcFUhVmFVM9dqMn4FFnVSZHQxHZTXSVCiME2DbNpubm+UaNZuulEo0yzzGKuuOsT9V2luzX5n9zdjhOI51tl9VBCeTsLzW6VSp6qqffWReEIYJrlNwavM0v/5rv8pSb4kojnjs0Sf55iuvsbm5yXA45Gtf+xrNZpckTrl27TqzqSItmU1DvvSFL3P+wgXq9RoXzl/gxo0b/M5v/46qFJy/wPW3rlHkGY1Gnf3dXZIkodVq8aUvfEHDchTaYH11jTxJOXvmDHmWce/ePVWRqteZTqesr6+ztbVFv9/n1VdfZWNjsxyrV199taxMpWnK448/xpe//GWd3Wzw7nc/jZSSV175Bju7O8xmUyzL0rodYfnMD48OSNOUpaUlBsO+7vVRkJxWq8lwONTry6Mocmo1H8vyyPMMpODpp57gzbdusLN3gLAcZFIgbauEu/37fpgAQEoFCXUdi6uXL3H50kWEANexSOMYm4Kaa/PM00/w+5/7onbgLZXIsu63Q6Ufwf2+SZlwqwzfog3TSdkHJVMsi8lkxHQ6ZnV1lSDwmUwm5HnKLIqxvdoCK1l5eIIiS4kz5SMmcV5W7hw/YG19g2ZDJSuyNOH4cJ84jHAtyMIxu/duEU1HWCJXlS0W0RHV/X3eo7f4tweRvhhb0O12+cTHP64DIVVxNT7pdDqlt7QEQJTGDCcjBILuck9VZC2rrAT4vs94rNjUlpeXtQirSghXfVlVTZwnV4wPamyiqS50Oh1quincqHWDpNVqlXbKJP2VLaUMHAykyazFs2fPMh6PywSc7/slPLSKFonjuAw4ZrMZnU6HoiiIoqgMVKrQP3OPD3N8D4J96sEsLS0hpWQ4HC4EDiZTVS1tnxSrMxPAbB7mgZ5kVahCs6qTtt1q0el12d3bo9Vq0ut0EALOnTtN+APfx82bdzl77gL/6l/9BnmRkecFRa6as4SWUzSfZ86dZRmu7fCn/9RPEMYRv/3b/5rBaESaJLpZF9C4bTWRrbL0bAKNP4hDlVBVQGGy/bZls7y8zOnTp3n88aucPb9Fo670ExT0IkPKHCxBXswrRXlRkCaJqgDlGZcvX+Lq1SuEYVgGbaZxcjQacXx8XGLyVNYuJRxHjDUm7+joWOOhEyaT6YKRNOdUz7pAUnXo5xlqiUK8GAyh67pEcVS+92SQYRaK7/vlhq9wjHF5D2maYZq0zBx9ULBi5pSZiyYLUKpLl/0p9zua5edJEMKaB4omIERikFTlO0XFrmlH2lSFzGuBUmej3mhgWaPSCYrCiGaziV+vs7y5zoeefIosy/jKl1/m6aeeYjoec/fWXSwJspB0uy1FkbmzzeBoX7H/uCrTdObsBV762EeVQbJysjTRY5XRa7dotRrwcz8H4zHil3+ZMz/1U5y/eJY33rxOvdWgf9wn8Os4rkM0mXD75nWeePIpgkaDVD9HQ6fc7/e5cOEC9Xqdo6Mjzl04zcpSl+bOLfr1KwtxRFnLMGrPZbAGQgqt2acDDjODpHJWTp1a4z/7mf81Z06tQZHg2TZhnJFnBRYek+FUM0ypd9q2UwaO1Uyfqug9fJPp21UwF2EQGa6VsL4k+PEf/jDvf+8WthghdTXWcgKQGTKbM+HFYUhh1ZiOBa7dIUs9ZGEzGU9o1mEy2+XlL/8uvaXTDEcJW2fPccrfIidD2gLP8RRziH4GYRiVmSYpparwFooZyNXOfJapBEMYRkxnU+7evcvW1mk63S5ra2tYll3yu8+TQ5I4inFcF8/zsYSDterQ6SxpqFbKI488Utp9UzF+/n3vKxmJDOtbEAQLkFiz4ZrN1fM8VtfWkbKSgGIOj1DP1S5tAVDaL0vbBKW+HpdBjQlYDLTA7GkGzgXQbDZVVSAMy4SVwYfmec50NMH1HLYHx5opzyOaKcGtLEnpH/d58803aDWbvHntLeIk5sUXX+Lo6JD9/QOuXbvG5cuXuHHjGtvb94iimMcff5I8y2k1Aw73t0nSlMFwSKNeR+YZu9v3WFlZodduqURQnlFrNpiFMwSS1ZVllWWOInq9JabjCd9+/XWm4zGddofLly/z5ZdfZjqbMR6PNS3pmFu3bvHyy1+h01GB6Yc//GEef/zxsiI1Ho/Ii4xn3/MMb731FqfPbLG7u02/32f/YB/btsjzjOk0otGoEYbKcanVajzyyLu0EFlUOlaz2Qyv6eP7AYXM1c++C6jMbz0IcH1X4fdrdU6fPs0bb73JK998lQKHJJ1Dr81c+PcVSjUPfC1qQcBjj76LC+fPo+sVJHFEOJ3i2oLx8JhzZ05z6/RdbtzaVoDposCuwH5PVjaqR9X3UloT1gNfZ373wP1TgMrpSfb390Aoh7bZaOLWPKIkwbZtwjhR0HfbwvN8akFArVYHFKW95/rYtovjKNHZNE0JZzMmg2PyLMFzbEQRc+/WTaLJAPIEX0hyJDlQCAebSiJP2/Vq3wGVv1W/n1fU58nmP/En/gSf+tSnGI6OsXWzfvX+J9MJhfZFUm27JrMpa2trDPr9cg80sKNGo0GtVgModUWMjTPVAt8PygqqgTWZ+wjDEMdxqNfrRFHEeDzGssx1qeqtqYYbKn9VPfFLf7xer5f2zLIstre3F6BPBjpsAgfHcVTlptFASln2nBi/zPjr5p8QCq5Z12xVD3M8dKBh+iuOj4+BOa2hmcQGZ2acvizLFpqGYV66q7IcmAjJGH2Vbayx3Fvm8PCw/Juh/zo6OlJYY50hSZIE27K4cPECjz/xFFmmmqpWV1d59VuvcvfuPSwLXdEQCxSqxuG0HTg42OM//pmf4ROf/CT/5J/8HL/9O79DlheqTCfn91HIOVPUwiQ2G5JejHMHCQX9EKL8nPk01uVPHaFLJK7rsbKywhNPPM6Vy1dYWVlhc3OTXMYc9w80TWNYjpdyKD2iWDXjpUlKkibkWcbR8THJLGN9fRMBDDRuNsuyMtJO0xTXdel2uyWeOooi8naOe/48AKkODsIwVJjCKMR11DgiBLHe4G3bptYIVOay0SCo1VheXqbdbuF6Pqtra3z1q1/l537u53juuefIsowvfvGL5WQ288PzPLrdDktLy6oh2fOQUrK/v8/NmzfxfZ+jo6MSrmWegQkmHpSBrv5zHZtmo3Ffhv2dMIcSCcW8yd4k46kGGeacC28sJ1D5HhN4WQiazSbRICo3Y6MbkQtotNt4gc/4eIoU0GjVuX3jDtEsJE9zakFAkedMJkOO+32SKKJe6+qmvTYf+OAHaDSamg2lQNhWKRx47qzKZPKLvzj/+lM/xQsvPMfnk0dpXf+X9I8H5HmB66jNZndnh6ff/TRLy8vcvnWLju+XKqH9fr+cW0dHR1iWjeN6BL6LFMK0dJ9omF+EFMyFI9UKkkIsVIOKIsf3XY6PjxgdHxDNJkThlMFgSJJkjEcTDg+PiaKY6Q/MoK4FQM39W6pn5rs5KQ+CSC1UGatXKEzPCdgWuHbGpXNNfvLHP8jFsw6WPEQUkiy1EY5NJtVmY+btZDqhyCVJoYSghoNjCtmnFjRI0pD9g7tsbj3OYHDABz74MdqdTXIcCiGRosCSFnlakKY5nldjaUkp0g6GIyaTMUBZZp9Op9rRbJYJHrXRxaysrOuAzMK2XGzHIU0ybEvgB0Fpr2kpxkFQAUC3qxxwqWmBTeXBVAqKoiCOIlaWlhGWKHtTjPNfwg500sAE29JUvfOcLM/xPY+Zpr3NsgzXU7DcJNaVLLQzkKRMxiOKIi/tWZqm1IIaU519dxynrMKBCi5Mxs/zPLa3t/F9nzAMWVpaQiCYDCc4joXnu0iZEcVTtrfv0Wg2kVKo68hywumUg4MdPG+LMJwynUV87Wtfpd1u0+/3abVUZnA2HdNp1ljuthke77PUW+bUudPcvn2H/eNDBqMRezv3aDQaNJstkmjG4WgEAvKi4Pj4SNs8Nc4KBlVjNpmpTHOWMR1PeN9zz7G7vcPa+jrj8ZjDw0M+85nP8NRTT/H6669Tq9W4fPkSjUaT/f09pITNzQ3yXLFTTWdj+v1j0jThi1/8PEmSaEieUH2QWVay7hhl6NFopLj3tZOVJmlJnpKm6nn1el2EUOJmnU4bs2dGUYLne0o0N4u5cvkCKytdvvzVb7G9vY9lzZtqVc+GEiStwgjuX6X/7o/qvlStlLbbbZ5/37O0mw3CcEaROwSeh+M6dLsdBkfH5LZkMNqj3Wrhei5FWpQ6VSfznA+q0i7sa+Wm9eBjsS/SVJmVi67216Kka0/ThKPjIxw/ZGllg26vS57lxElMHMUkSYycWDRbLRzHBQRFnqrEipRkSYaU4NoWMo0IJyNu7+8RzqZ4MsEqUoQ0JEMCiU2BYO7aypJ5qbw2qOzHlTlgWQhplOuVXWq3W1y5epn+4Jg0jRgOhyVKxHUdlTS3LWLtI00nUx1AeRweHuI6c0puk2wf9AekaaaqIb2uduRdPM8tezyEsDg6Oi59Z8dR5zLJesuyyrVk23YpbK1EsZV9HI1GZV+U7/vEcaxhjaoIMJ1OFd2utncntV3MnDBJHpPoqfZ31Ot1JpPJXLVc7xdGM8cwXD3M8T3Q286bh0/CVGQBeabUGdVrChzbQ2CVGHpDXQsWWWboV3PyXOG3zcYnhGLvOTo6Km/WNM4kSVL2bFiWpc4pLNIsx3Y9cnKO+oe0OnVe+OB7efa9TzEej9jd3eW4f8yFC+dLnBlQCpxImXJ4cMgv/NLP86kf+CF++s/+ab745c8zm0VkJktepqVRU111oGurpqoRUqdqpaR06EylwrZtLKno72zHwfVcHNvGthWWWliC5W6Hs6c3WV9bp9Npq8DqYI9wOiItMiahytROphOkjn6DWo1GrYZlqYZ4M062Y9MImjR9QRKFtNptLpw7q0vYgk6nQ73RLNU9gbLRx7IsPMsmChXLVhzHhPr70WjEeDxhNptVSnwBtm2zsrpC0AxotVqK9cbzS9hKEqckYUr/8IDNtVV+4sd+lCRJuf7GG9SadWyNCV9aXtYNmgGu46pSMYqPvVYP8HyHWt3HHdskeUqezQWSTORfNeimcmYcJdu28G2LbqOOq+daGaxQGIDUwvye/6DmcdVQlzSg0tCSVrL1lQBjbq5N8Vfn6fX8zSRIKQhnMTJXLFa+7RIICx9BEUW06jUQkmH/EPKUosjw/RZpmnF0dEw4nWpK2im1Wo3HH7vK8lITrBSKAseykNJC2oK0KLhwZgM5nSJ+/dfVdf7aryGnU178yAf4bz/997EtB8fxiOMZQaAohUdjJei1vNzj9vVrkDukSYpt2czCkDTPcAOf3YM90kJQCJvi6Dqsntd9KidUclWTC0IvL0PrqjjRdShoCe1UgC1s7tza4b/7+/8IigJb2OSZytbbtk29XqfRaNLprOI4N0nJqAUBL734AX7v936fJI2w/ECLSkos5pUuM2dOVi1OBh4WEiFyUulTSB/bBk+ENLyQF57d5Af/6KM0Gyl5OCWXqVJ1FRKZZRR5hrQKcnLiNGM0DYnjgiTOGPQTZrOMKE5w3YJavQleA1l0efyxZwhnBUEtw/EcBDa25SGKAtubszCZJj0VpHcXmn+FsOn1lpBS9RnJQkEisiwtM1OWZWEJyDREx4hoOo6lNnUBBQWOY2M7avOxpUr8BDVVDRBAUalCeLZLNI1xHZtMJDi2TZFnJEmsrKmtqHfDSrbOsizGozFZnjOdKhra06dPk2WZ2lgtyqzdZDIpHarj4+Pye9WHohyRY6lePxgck+c5k8mk3HDVZmszOB6wurpCt9tje/uectijGbUgoNPp4nku08mEosjptbq4WzaHR6pPZXN1kzTLuHvnDo7nkxWSZ599L6PxmNXVFabTKWkak6Ypvm9jW4KskAyGfcJZxLVr19jY2CRNM27dvo2CDhZ0Om2yLKYoUhwHxpOJbtDvMp1OGQ6HZcIJmXN4sIcQFqPRkEajwZe/+mVeeOEDPPrYYziuy8raKr/3e79Hb6XHJ7//EzQbTaajMZPxkN3dXba3t3nyySfJsozd3W2m4ZhEQyosUdCo+8xmE1qtFo5jUa81FdwJSbutYHFL3R5pnDFLQ3pLS8ymKtubBRlCWHiuz2AwoNPqUsgC13FIopTl5Q6IoqQCnUzGRNMRrXrAxz78Am/duMUrr7zKTBakmYEAFiAjFJ2rdSLImGf8/zAc1QDDdV1arRaPPvII9SAgiWYkUcRkpJgAs1z5FnFakKQ5BUrvp9FskWo0STUpczJp8qBgw7ZthD0fE4M4MLoTSIGUKUYjKs8rTePSgsLCwkGiqMUF4AiQacbRzh0G+9vUatr+1uqqclELiDSkyLYd0AFikibkUUw4GevANNTXkWNLkEKQ44AwzJoWtgBLghDzzHqeVwlkKO9N/VAdgwILS9+bxHbgPe99iqtXzzIaj8jzjHa7xWw24datW3Q6Hbrdns7cN7Bci5pfAwGT0YT19XVyvQcLAWEYMRxMcF0f3xfYtkeaZlpzpkBKlRTIcwnk1Gq1kpBECFEGC8a5X19fL6u/xp+ZzSJmsxkbGxt4nk2vt0ytViuD+9lsxnSqGhNXV1fJsox+v18GCCaxb4IEtYadsqIShiGtliKgMdcDlKKopmIyGo0IfF2RTuYC2N/t+J4rGif/Fblq/DGZLJVpoHzI1SyzyXCZErpZAFUIgyndSE2/aga6yvtbZahSEaHL3t4+vaUuvaUuo/EQiaRW9+n2TrO2vlpGglUsmsLlpsgC1lbWmM0i/sWnP81TTz7De555D5///BdU9GuUibEppCTNVQMgUpRYf+PMep6nojyh9Dca9TrddkdFp8LC9TwsTzlnjuuU15/nGe1GnTSKKPKMwWBQih1lmUsuC+qagnBz81TJxuI4Do16QL1WU0wQvR5eRV1XCKHKbUGwoASuxloZr+ozMVADz7JYWuqpqF4vViWg5+jxz3Adl0JKwtkMCdiuU3L6m/KcaQpFZERxzNLyMkGtxpUrV1hdW+Pa9Wt85KUXaXXa/J2/83cYjUbldWeaDSxJEjqdjhYKFKXRVCXgeX8QUFbITKRenXNCKFasRt2n1Wjge4uNTJYlyp4PqFSthIVwPEwMYgy80dRQr0X/UZZN35hsvPnIQr9Gv0FKQOZk02Pa7TZRlDAdq6yrbSlBRCGhyDKmWrW+KAqm0wlUIGqD/oDhYKDWkhT88A//Ma5cuczT7343QU1lHMrgR4c4jm3T7bThF34BQoU/JwwRv/qrXPjRH+X/9OPvA55nNBpR6CqFomgsuHL1KhLJuVNr/IO/9w/Y399nc+sURawwpsKymM1C0rzAcTx6bsJemVUT5SYwD9DnWcgy7NP0qiZlJ8x/fhO/u86H3/MIyALHcqjXFHvQ448/xqXLlxWG2Pd5/pdfJAxDGs0mP/O//d/wjW98neO+Ukl1LIXnT7MMyxILtqraPFmF3JVzQghkbmFZDor4Z8Zyr+AHPvEszz+zjsUBSaayrYpkwUYISZFrqmYJaWYxmUn6A8n2zojpWDIaxrhegOsFNFtdVtfO88ILH+Ts+ceJU1s7kGMsJ8J2PYKgjtBQGlCJBs/3ymsvmVO0ffJ9Ffhblo2FIXAAYauMVpplqq/OsfF0dkvoYC/P8nLDc+w5qYahZ0ziGNe1y9d5nkd/oKgZ8zglTwy7lIIjWTYL9rvRaFDkGZNxrBuGU3a2txGWUp3uHx+BLKjX6xqiA7PZlH6/T6fTYTYLqdWCEgalKDcVZa6UklarTRSFeJ7LbDohTWIcWwncxUnMZByx1OtiWzAeDdhYXyNst0ommO17dyiKgk6nQ5IkDIdDwjDk8PCIRqtFOFM6HwqnregikyTj5s1b7O3tcfnyxZK//vDokCyN6XRapS2L45ivfvWrZFlOga2dFIfxeMSpU5sgFHRXSkm9XiNNFSxpdXVFZzAn1GtzhW7PcxkMBuzu7vLZz/4+WSHJspwzZ07zJ//kj/DGm99hZ2dA//iYJIyZzUImkwm+7/PNb76C57mMxyMazUDtkTroUYGNpc5XbzAZj8vgVgjBdKKcrelEIRy2722X9tww3khZkGgHxXVdGg0FrdnZuUe311V2OM/odrsa7uswnkx48pHL2OTcuHmXo6MBszDGtgV5jmZDlKr4eTLN/4fgqEI3fd9neXmZIAjYPzjg6GBHZemFZs80FXkUVKhAlD2tlq1opo3UwMnKa/V8D0qYVP9+8meEguKWdN6mAm/stdSJIVTCjjJBk2NZ6r2zyYTJaFzukdISFBqxYduWLu5rkeViro+kzKr6LLUbOMgyOW0SvSaNZ5gyTUXrYR6AJsTIc2xb8KEPfpA//sd/kDhWyeyjWZ9Wq6YrfJdVMsYS+H5Anhd61ywI/ADbaqF6WSSZ7gPudjsKTVPA8fGhFhlucnBwWCJ96vU6juMwHo9LPzaKohJdYvrhpJSMRqPS/02SpGTw29ra0rDGcdnTJqVSCzfV2263W962aeQ2MNh2u02e52Uflgl6DfmG8ct93y+b2oGyPy6KIlqtVkmccbKv7u2O76kZvLrxTiaT8mKBkpt8AStYKFEl49wafLxRwzwZfJgjz1UDsmoQSlWZLU11dhtyDctqt9usrKywv79PLQjIs4w7e7vUajVWV1aYzWYcaohNEiscbbPVUixMhSyzX91Gi+FoxGAw4uhowL/853+TjY1Nuo0202iKxFRAbFZWVmk2Gkig1gjKyWMclcFgQLfTpl7zSGKVvQs8n3q9hms7NNotGt0OnW6HwA8IdDXAEhaNWh3PcRe45g1m2fEU/MRkHk3Wz1KlDGxb9ViYHhkTYOiBLkVZojAkL3KCoIbreOXkNocxhpOJwvJajl0JyjKQCq5kOQ5xppgHhBYDs2zD0GVh2w5JonihVXOpR6PZIpMFFy5fYu/okNXNDX70J36ccBayublJp9NhMpksBA4Gt2gCOBPQ+b7PLIzmDXXMca9V3Gb1b6qJ3KPX67G2tswsyk6Uke+nvQMQzTXs5moFajUXJDSbWqlcsoCgq+Kk5Ny/Np8hBFIK1q0BrtsgCmNtuFWgtL+/z/Xr1/ngRz5MrVEv7yuK5vdtAivXdcnznE6nzV//63/poQ0AP//z9//8oz/Kn/6JH3nHt374A8/x//l7/4A4TUh0k2YURiAg00xnrjuH0RgIlCH2NUO0AD1jXqxXFY35RqScYo/GyhY/9Cd+kDNbG6wsL1MP6liuC1IwC2dkWcZ4FpXNgUWR06jX+eiLL/I/fvqXKXKJtC0sLLJCUQeehO5Vq7bVOaY2ZBvLcrRKdE6nZfMn//gLPHalTSEHSOFq594l01hqQ7IwnSYMBhGzmcVs5nPr1pCjwxjb8XH9FlFq0XFXOH32Ga5ceYxW5zJBfYUASZrluJ5HXkgs28FQYhb6ujxfOXS5rl7pm1fVCynJ9Gbjui6WVBCcJEnwPa+EtgkE/aMjarXaQi+DZVnKDucFYbivMPWNBlLPxziOyJKYKIo5PDxkdXWFyWSKbVsEfo3A9QlD1WMVJ5H6faBsj2mANJS48/L/pMzWB0HA9etHgCSOE6TMS8are/fuaniBak40FJHtdps0TXTgWJBlKUkaKvISmZPlCXGiMOue5/DKK99gfX29pME2LC1mz2q32+zt7ZSN53fu3GI0nnDKVfz2CoYWYtuCbrfD/v4hp0+fplYLePXV17As6C31yv1zPB6SJAnNRltnJmtMpyEUQts6pZ0ym81oNOtl78T+/j69Xk87b6qhtV6vk2fg+0HZzD8ajWg2m8RxzL/49KeRUjViP//+9/HWW28QxyGghL1cx0UIie+7ulLSp9vrLAh+GefHJKWGw2G5789mM9I0ZTwe02y2SeKspNQ0/ZxqPyrI8gxHB7dSZoSh0mdw9Wvn0A5Bu90hCkNWl7rMplOuXDzH5toq01nEm29d5/btO4SJTaorV384gFL3H8bXabVatFotQI1ZlmWQK0FLAwU2+1hRFGSF1Gzei72uyia983mNz3U/8xT37XUKubH4mrlfVoCodpGbhBlasFbqRK6qPhj4r6o660RRNg9w7NLwq8pdiQjQgYMUBYsbpizHRlUxioXrf7sxX7DbqGur1+v80A/9cS5evMLR0QFB4FOrNRBCiSn6Phwf9xVsUgigKH3Ww8PDksUpimb4gUeaptRrKVLC8vIKs3BcsvbBvB/k3r17JYLEOP/GTg0GA4bDYQl3Mr0Xhplvc3Oz7OdQgU23TCKZXjLznI0WRxAEZXIjCIIyoLAsRT9toFmu65a9s0IINjY2mEwm9Hq9krSh2hDuuC4z7ZMd7+6+8yTkeww0DNTo8PCQyWSi8VlzSBHMN6UqnKVKIWgwYoY9wuBiTXkmz1U2y3c9rQarNp/pdEqz2SSHsnzeajbJs4zlpSVarRZ7eztsrG+oDFEUMx6NKTTbgev6jEcTEjdhb3e/5A+ejCdsR/eYTUKSJEVg0ajVqAc13vPxZ5klM6IwJKgFLPWWaHfaWMIiyzMKIVldW2NrawvP80pGldu3bhBOFd7PQigWkCyjUatj+x6ZjcbEeSSJEk1yXRfP8bGFg2WJEt9aFLqB3VJ8+yZgqPa45GkCKBaDZrNZRsXD4ZBGW21UURSBJQga80hWFGKh6cdwyRdFQb2mtBaiOCJJFQ2i7TgoHLXCFCKg2Wrq56qoZg2EQ1HF1XVQUKOQ6n0Hx0ckecY0nOF4Lq1Oh1a7vYADNPPGfPV9n93dXVZXV/E8j8cee4w333yT4XiCrcUhzdwzh5k3QIlBBLXRrq4usbK2xGyWISoVjLKHRlc/ymuRUmPxDVRQabYIk2UR6qvJx5dOtah8sMa1zpvGhYZiQSjqNOKkfNYGbnjv3j3CKOTXfu3X+NgnPk6gq0O2Yy9UAw2VXRzHTGcz/tP/9C/wt3/2v6K71IVr1+DP/3k4OLh/UU+n8Npri7/79Kfh8cdBZywWjtVV+Lt/Fy5dYjKZ8tf+xs8SNGrK4dQGPdP4aaTUCrS6R0Koas8cfqgDB72JlhUeKtUh80gMrAnFiub7Ho+86yqBbxNFUwb9I2zXV069NpzVxIVlWSz1evzon/wxfuu3fo/haKbgabaBTs7tU7PZpNvtlllrM5erVTGExHbBEpKab9Nt1vnCZ7/B9dcclpfqtJdUxieo+TqLp5hWwlAyGXscHoQcH091g3Qdz1vC9i0cT1BIm2ks+fyXvsFXX7lGs9HmzLlNPvWpP8LW1hZSCA1jUnM71/csBBS5CvwzbXvjOAad7UpSJeY2Go3w/QBH22XTBFgyouQ5SRwz6Pe5ffs2GxubpQNk2zZxEpdNjXu722R5TqfTYTgY4Dq2dkYleZbieQ5xFHM0nkABQeBzdHxEs1lnMBiVrCdJktBsNsvsmUmYuK5DvVHTAl+CWl1xwp9a2VBidVLqamdbVdGmU8IoLKsqu7s7ik0rTbQjDXESK0hYMVcNj+OIdqutaXrdcv6Y+zTOz2g0Ynt7W/c0KG0S1/PUNaYZR8eH1Gt16vUazVaDa9euk+cq2FYNmhGWECwv98iShKLIODo8YjaNOHVqi9XVNaLoLsPRCMf1aLUUpWatFuAHHkURlEGO0UdJkoS1tTUFaR2pRtKtrS3u3r3L0tISURSV0OM0TUiSkG998xt4vqKGB7AttZceHBwQxSG2bdHptCnynDwv6Ha77O/vl71yRkU403urwacb4g6wcJ2sZKM0DlG322Vn5x5JGmnmoqCEyhmaXcMQZGxKHCU4jotNgWsJao0GSRjSWO5xeusD7O4d8J23bnLj9l0mmv61MIXm7wE19U5N5e/k1D7M51uWohk21KXm96JAKVTrfdScTwgohCzhiyevQwj7ba+7iiI5qVdm9o0H3VOVser+z1aBnIofqqrjRVkBkBKEJUH7FpYosKoMKFJBioUAKWykVCk6Vc3Qiagy4FisxlSDLZOou+8eqtv5iYqNgfhdvHiRX/+1X+fWrVscHx3Rbrd59NHHybIxrVZbX7fDbKoqZo6rINm1oMadO3c1JW2XWk0lioeDgbZjMcfHhyhR6aKsFnieCkYMbN+shd3d3bJyYPqFj46OcByHc+fOlQH9eDxmMBiUvXZCCLa3t2m32ywvLxOGIZ1OhzRNOX36NEdHRzQajRJSaqodhrLbVCpqtRpRpOBYRizVkOTMZrMyQDGvM+OfZYqhFSHo9HoPnH8nj+8p0ABKw7G5uamz3HnJqVtlNzALy0RK9Xp9nhkr5jSn1W58U7LrdXu0G03dDzCi3evRabWo1eq0Wi1G4xGddkfhO12XdqvN9s4249EYz3GI44TxeKwYfOKIJI65e3eHu/fuce/uPVzXZWlpiUuXL7G8tMzq0iprq+sqO1qv4zgKP+l6rmrFqDRImXsTGmMroWQyMZmGlZUlLHIO9vdpanaedqdNkeWKLlZXLEy2rVS8tQSxjirH47F6uKgKTpIkxHoclfKvV2LsHNsijkL29/c5deqUcqr1JE/ihFq9rpvedaO+jnLzLC+fm9lESrV3Sz0/LwiUNkmakqYKV11kaYmbDsMQ27JpNBuqQVzYJEmM63pl1iEMIw0jcRgeq4bl1ZUVZpOpGmPLwq3XWV5e5vr16wuwOLOxGRaGWq3Gz/zMz/CZz3yG3f0DxuPJAn7w5Hw1c9ZUN1Tm18LzLCQeTBZm+QPnvPl9IY2hPZF/lxJpWQsBBIY9TEoteoiuaixm8gHC2iZx9Ca1eo3peFqWkz3PK42FySo4tk0tqM2bc4G1tTUcx2F3d5dao8arr36b//y/+Mv8zf/6r3Lm0iXkP/pHiJ/6Kfjt336otX5f8AHwsY9R/MN/iHXqFN954xqf+Y3f4/Nf+DJnzp3DdT2Gg4FuzlU4dAtKVegojHSgUB0yE1xo7RXJQrdMWTuqjrl2INI05d72NtFsgu+5NBstnMyiVm9g2xZJNFdHBVVZvX3jHnt7BzTqTUbDCUWWqExbBR5gbFu1UU5dgyztlhp3Sb1u8eQTT7Dc7SFkjm9DGk2ZzGLi3OHwSKljFzJVNNkWyMJGFl1se5XekkOcpBq6mIGVk8oMUUCm+6iiZMpkNsav27S7SyRZzre/9S3azSbLSwoi6Tgukd4kFI53LrpkMsyu65ZaE3me42u9CzPGYRjSaDRKOzYajcv7v3H9elm+n0wmjKfjssRuNlJTAfU9t2wMvnVLwXa63S6BXyNP8xI1J0SdbrfD2tqKDgj2lE5SHFU46B3SLGZ/X/HGj8cqedDr9Tg83CPPCw2RCtnYWKco5nADkzhpd1SSxXasMhGksOCSWk05yq1Wg+l0ius6nNraIPADwihUm2sY4QdGXVcxtszCCdvbd2k2r9LuNBmOxvT7R7RabdbX18jzXG/iAe12m+FwwtJST++NigZcSlhbX8e2YGNjg/29Q9I0YzgclUmhwd4+vV6HLMtYW1shDGe4nlNy8RsRRt/32dnZKck4TMP34eFhicV+8403EUAQ1MhkzmwyJg5VRSnLMrwg4Oj4kFo9KFmpEFK/Pyrx3CYoVUFaVgYcJ6HQeSbp9Xr0+/3SsTLJxEcffYzpbIzruGR5Tq0WlH12gV8r/YD9vYOyMiWEwFWRNOPJFNt1ODi8ge24JJlq1D116hTD4YjRZEqSpiSpYqGrNon/2zoeNghZ2F+rv8f0FAIlE2uxEC096Bwne8ce9HdzVJk9T/ozVYfd6FqZ1y7CRhftpSw3McmcSlCo4EGg4ENyLhS8cBRS09XqQF439SvImAlMHgz7MmN1H/Sr/H7+OlONVr6l+sNrr73OW2+9xec+9wWklHi+z+VLX6fb7dBudwgCxYzmug7Ly8skiYI3ZXlO4PsUueDmzbv4nkenK/C8BrYlCMOY6TQk0GrhaZotCN4JIZhOp/i+z927d2m1Wgs+zvLyctm7YTQ5DHOVSX4MBgPq9bpSKff9MkkzHo/p9/tlgtrzPGWvZjOGwyEdrfdhUC4myWN8dsMoa4gWgiAoA2ID7zKq4VJKHNcFSxDpPo53Oh460DAXIKUsYRmKatRBSkWXaCJnwzpiGIxgzjQ1h7Aow20qGkmS0Gg0lCNdqzMZjljq9TiztUWSphwcHHB0eKjUMx0XX79nMhqzv7vH3t4evu9xZzIpxZwmk4mKJpMUYTk8/eTTfP/3fT9PPfUUvV6PIFA0Y57nk+UKfpTlKUJjIosi086hwgNmeY5tKVyvEBYyn/M3u65TTnzbdpBYbJ45qxh+dOVGODbNeg2p+esty6LQGh1mHGVdjbGiPJ03N5sJaYIZky0y0Kl6LSg3nXPnzpXPQVqidMSneuKYSZbFio3FVBKqmSlpzTPmRVHgeh6O6zKdTUshrzxXmeo0zxiORljCIk/zcgOCOVa81WhhC4u6H5DHCSvdJWajMcvLy7iuRy4LVtfWKk1e82ZSU9UwNHFhGPKhD32IX/ylTxNFcelcfbfsjtkI01TBLlzXAmHDpPIeYZVQnephRO9KB7isbqiGvCp7ldDVj/Lc5vs5zLUMJFQTtIXv+WSTjFrNwnUc3TSWc+rUKVZXV3n3e56l0Wqyu7en4BP12oKTZ9s2q6urigggVRoHe3v7/PP/8Vd56cUXePqJq/Cbv4n4W38L/vpfhwdsdm97OA78jb+B/Et/iTzL+dv/179LGKtgOdPQm6xQzEBCCEbDEbPJRDOeqzGKoooxkoWGIpqKjpiPiRAV6lup6X9NIz26RUZBXdqtLr1Wl/F4Qru1imP7SARxGNE/nnDnzl11XgtGozF//a/+TfqDPmEc4vseeZHj+TZZISgKUUIR4zhmOp2Wc8asN+O8e57HylKPc1sbeI7DZDomSzOkFKRJpqo4hCAVREQgsR2lQ2E48BuNFq7jk2UJQuRYttKtsYVPoTO3luMQxRG+7/KpH/xjuH6NWTjl2rVr9Not6sGjHE0nCGHhuC4HhwccHx3TaDawLYssy8myFMuyGY8VgYOx3a7rEM1CJhMFWWm2mhwdHigthiTDcTxCrdydpim9pV4519otlR3rdFpEYURQ8+l2ugx8V2mYIJlNVfC/srxEnuXMphOEsPF0UuHo6BDXU0HcdDrTQYzBHAvFOAQEgcrqKzEqqa4rnOq5HjMcDkqaRyklm5sbZQa/oe1nECg7NJlMdfO5xLJUX0itZmunvYbrODjatiRJzHSqmq4bjUbpHAyGqlk8SZJSNPbKlUvkBcxmIffu3cPzXNLURsqAIPAZDifcuXOHolBBjaIOVsJaSaz6Is6cPodtO+zu7jEYDOn2evSWlhmNhkhZKIgvBd1up7TfpmlTwcNS3dc4Z6TJ87xkiLRsizxJQeYI4SiBWstiNBySpAmBhkA7jq37I/KyyRZkySzTaDTY399ndXUVo9JtbK+xv8PhEEvYZJlyZk3G1PM8BjoZYbDkxnE1PS1hGC44wSo5ZSMLCbkiLyikBAvCOMLSzlucZ8RpXtpCu5BYeaGY2R6yrPFvWrF4p+OdKiZGOwjd5/cwn/Owl1wNFsxXU6GtssNJCba1CKdaDDbmTdeG7Uy9TpZQV6Tps9A2HvT3J6+HeZCB/idA6mqABlvp11M5t5oXJthZCJLEAja5vH4T3BldIePLqt9ZpGnOW29eU/ZH34NinFJOe67F8GzHxrbsspIgpeTs2dOcP3+etfVVWq0mwhL4fo0kmXB8fFxWaU3CfTwel3B4w/ZpyCkUWcWAXq83Z/HUvbdG58gkl23bLm0dqCTMnTt3WF9fL4MCE1Savi0hRKl94ft+6R+32206nQ47OwoWaggmTGVDSkm9rpL8ea72sUzO+40e5vgeAo0Mx7YVg4TOqkZRTKSZkIy+Qb1eL3HjURQjhBKhm05n1Gt10iRlOp0RR0lZMjUP3/cDhoMRR3sHWBLiMCKahbz++uvEcUKjUWfQH5QTxHTtp0lKnMQ4jirte57H6uoqj7zrEbrdLqdOnaLeaLGyvKqy/KniejZNknEWg4A4ziikMrKe52E7FrIQ2MJGFAWO52LZ6n6knDugasA9ShYIgVLM1qvEFoKg3lANmNqhKnSzq+PMF2wVbmayciooU404JgNsmgKVgciVc6wfer1e5+69e2ydOoVl2xRIzTAzpw8u8deZWmzm5ziO6ff7St8CieerqsnS0hK2ZZPLnE67Q6vVYmNjgzzLcVxHBUsC4igmnIYlru/g4IA7d+6oLN10hlUojON0NOG3f/O3WF5eUiQCvo9frzEcDEAvDpkreJJlL+Ljfd+n3+/z/Pue57FHHuVLX/5ySRtX2uATmP9qGbnUBrBtPMurWGs1RsqcLhorIQssWSCFUU01f7PmDrI5l868q/1ibnz1rqoCEShfI5El4UFRFPiBj2UraJ7rebzrkXdx6dIljgf9MnPd7XbLCpQxmo7j0G632d7dxnZUc+nNGzd4bW2FvYMjPvj8u2n95b+M/OhHET/5k3Dz5jsv+vPnkf/0nyLe/37u3LrD/+H/+Nd468YtfvIn/zRHx8egm6lVEKcw8NdvXCOJIrbOnsOxVXUxjkLF0CaEDuaYj3MFSoWcQ9RM+tv83gCpZDzCT46V8FOWMxpGvP7qF3jrzevcvn2bw4MDhqOhcnD+zAyaynbt7R0gyQl8j06vw6UrF3jf88/zcz///+PwUFFm50VBlqaMhiNFApFneK7DI488wosvvcjrr73Ghz/8EV54//OMjo959bVX+Ozv/y5ROiNOE1w/UExWRaEbzCnhoEJIUpkghGQSZdSDpmLiyVJcSyCkg5QK3pPlClbjCJvNjQ1sIXjt1W8hkJw/e5ZXvv51LMB1bI77fWq1OrNwxmg4otlsEJlgSbO7GFtihO6KvCiJIaIo5M6d21y+dInA86gFAdNJSLPZ0LAo1QB83O/jug65VJm2Ii8YjYZ4GmoZeB5xHNJoNFldXWU4GBAnCctLS4qdKlc4bMexqNVrSNwSMtpo1MuAII6iUsRzPB7SaNTLjJrBJbuuTaO+VCoQ+75HqPuWDPmESZLUa3Xu3L2jYK15DqIgikJAEsUh7U5b9dI5DhbzCtv2zo6u3KQ4jmKl6nTaOhmj8Nf9/oCj42MazTZhGBJFIe12q6x+ua4SK4xjBWnqLXU4PjqkkAVZmlCvqc3/uN+n2VABXKYDhKBWA5Tekee5CAuiSDURryyvKCrpNGPQHxCGIaPRCFlYNJstup0unXabKIo5ONhHAI5rkWYJK6vLGiZn02q1ERbEaUqz2WQ0VIxyYRguJHw67Q7j8YhCSmpBjZs3bmoV8pQ4TuYkIllGu9NhNJqQ5UoUVKnJqySa6vWwkQXl/pcXeQWaaAgMXDLdFzKejBWcqHCUTo5tkRU548mIrMgp8pw4S8g1uiDT1N2qQmot7APvdLxd1eDf/mEgvyaLb4KCeU7KHCev8btd3/y1i5S31aMqtqxfuui8W6Jk5lM+iNq45tAmTflv2EUR2g8yTdzVgGNu94uyamNgYYXZBObV6xNVjMXqyqJuSHlv4v73mWQnoPWE1DWDIE8LhJCMx5Py745ta2i02uOLQmhbnZPnCYPBhJ2dA4QQvP7tN/FcB8exWFlZ5uKlCzQadU6fOUWv1ymrxfV6vYRlqoSEp5noFBqo1WrNBUJ1fxXM9w8TrJskivFjms0mg8GgZAA1MhMmORxHEbb+PFORMDbSDwJGo1Hp/7XbbWUzNQrHkDh0u11NMKEIn9AkRSox9HDr4+GhU9ImSySuo1iWuu0l4iiD3KLfP2YyUU2/y8vLJe/vbDbDcf2y4XgkVNYiz3KdbarjWjVyWZAkOa/ffkPx8HsuvVaTw+wQx7GZjVU5eTKaIC2BFFaJJ2s0GjRabU51e3R7HZaWemysb9Bqt/A9H1B0ssPhiKTIyFJZciSr0lYDobOVrjvv4rf0YNplpnwuppdr6jlLatYWUaWBk3ox6b4BKcl0E2xRLgxtBMTc4Bo4lprcBkZSIMnJNUe9ccEKzeqlFsZcvArbot3r8u1vf5sbt25y/tw5Tm+dVosyoHRMlTJnShhHgGBvb49QMw8ZGJdt2djYxLOYgRyorKbj4vgV7mhbK+1amhffkbhtm1pNqWQ+8si7OHv2NIeHhxzs7nG0s0+exjz79FMc7u3y2LuusrW1RQ4cDgd4loNrKeYaNUcUzh9LZbqFBFtY5GmGJQTf//3fx6uvfoskjskchzTL9dgqXPzJYMOyLJI0RQgHmYPlzjciIcBxPHKZLRg0ABkek0/2EM1T2hku5eXmgYSkFJ8rdwfLUg/LBB/6RAL0Z6jAZDqb8a71dZI8J05SvHqNOM/IZEaYxERJhOe5gCScTml3O3j1gCiNyWXOcDRgbXWNZrOhVFVthzic8cbrr3Hx/GksmfEbv/E7PPuepzj/wgvIr38D8clPwJe//PYL/rnnKH7jN7A6HT79S5/h//F3/jsO+n3WNlYJajUmgyGBsGm6Ln0UJa3n2bieSyYTglYDYXnEUUwt8OgLlaEqKMqNBKmeLXo6y4WNA0oYGmbTLcgnR9y7d5f//L/4CxRZThqnpElKVhSkeaax+4vCkbYt+KM/9BKD4ZCf+Ik/xcWLF2m1mvh+wObGOkmc8i/+5S/zrW++Rp4XSlHd92i2XB5//HH+V//Rn2Nra4tMC4YVRUG3s8X5S2eIk5CXv/IyjCeqSpipRlcBCMvF810N84mw8ZSjWvNxLAcQOK5uxotTpKXF63QzpW07tBpNjg/2aTQaKltsCV579TUmozGPP/EEnuMx0IKaRZqSJykOguVOD9e1SwcxTVM6jS6j8YgkDvEbDUbjIbZlUa/57O3ulA27SZzQ7XUVA46lApQsjpmOVUOkLCSe47C6tMLt27dVssdzgII0jpiOlV5PFE45PEhLmCeAhYclC4o0JY0ixbKn+/aCIFBNsWlKr9dj9949slhr/kgHUVi4lo/nBNQCn8uXLpBmGaPxGNdXUJw0SWnX2ggsnUxKuXT+PPe276qMpA21wNUNkJIknCpyDK+JY/lkac5Sr0e9XmNvb5ta0EUWSqem1WoznU41XXDCwcEus1lLZTDjpMyexlFEr9srm9Cn0wkbm2tYlsTzHbI8xbZ9CgSNVpfZdMb1G7eJItUL12w1iKJQK7D7JIliSfRcn8CdEYqI0WhczjcpJUUiCcMJ09EYX1cgbMui5gdlgjxJE46O+ji2jR8EOI5CHXi+w+72LmmSIKXqY7EtLYqapeyIHZBKiyrXMNQ0U5VJk5wxQclwOCOnUOJq2oktOfylpMgFSJuikNpZUuxSR0dHOJ6n6N91thYoseEYCE7pTwpMc3BphwFFj09JNf9vevxBBR/fLUAwCcrCkGUIQ9UK3/0mvhvjktqf5qepfj/v7aiiBxThQ47QjYRC22ztkGDZouzXUrZZaDOuno9Krljl+dC9F6b6ZZx3lRyFkla3cqulb3Ti3hf2Y01/bipi6kYM5OrBQYllKQSDNP5Zhd3LEjr5YtsIy1Z+mtl3ikLTzVsaAq3OnmqYv+rFFMRpxuzuLnfuKVttWxnLKy1WV1ep1Wq89NJLrK+vl+QNqrLslrBUcy0GXWKgnqZqEYYhQogSNn98fMzW1haz2UyxWnkeXe3f2JqgwdN9tYY0wzR9m4Cn9PVM5UYn3g3Bg+nhM/BIYdsUoIhGipzZZKJ6xNbXv8s8VMdDBxrdjuqGn0wmDAZDvvGNV0o2INd1efTRR7l48WKJF1dGUk1IA6MyDBYKNlVXTYkVVejbt29zcHBAlia4jijLP67jEtQUw1N/MKTZamu+/EbZOa8i87ykQJVSkqQp29vbHB8f8+5nn1loCjYTsBoNV6P7cuEVc6Yts2BAKMx1rosXxtlERaAIpcigGqZVmRp0o5UwwUJRRrMGF27b9oJzbKJ2AxkyDn41Q18tb5pznD17ljt37oAQbG/f4/DgkNXV1TKjP2cAU0wvRjlyfX29bPivNmXHccx0orQZPM8r36+yeFGZAcvzHMeZV3mSRFW5Tp8+zZVLlxGaStexFSyk5O6XsLKywvd98pPcvH6Da2+9ha3HNEsSxWpljIJllaXF9z//PBcunCcMX1ebmExKul4LFsoa5hmXpcY8p1F3yteYIAxr0bBLqYMd7fwWUqpEjA4GS6fZouQWLxu/ZVm20OXlar5qLt43mU7wTtewJUzHM4JajfFoSBInzKZTopnit64HNXZ3drh85QrdXo+pZsQ5Ojqm21ENzIbJJI4VHe3nPvtZPvGJj2OJFl/+0lfJsozLly7CY49990DjscewOh1+/uf+GX/3v/3/kuq5d/r0GYqi4HD/QFFgTgYgc9IsYWlpidNnznHt2nVWVzfI8pzxZEwaqwqnGYE5tlf91mxmC1WhEpusxspQsSY3P082jbg324FCYukSe05eZsRsR6lDmz0oCAL+y7/yfyaczXBdNX+zPGM07PPss08jELzr6hVu37lLFCo4aLvdYnW9qzJuRc7B3h6WZnabTac0Gk3iJObJJ59keXmZl1/+Mnfu3lXnBU1PrB2IPMWxHZJEZXR9z6fIC+r1ms6YFfiBh1JQznFd1SQZBDXOnztHOJvi2BZpEjMLQwaDPo8++ijHx0cUWYrMc6Jwppr+koTjfp80TWi1muUmpqCHCY6mx0ySGMe2ywZO1YOrtBAMLte2Hd0zESClYmoSwqauIa9CCDxXUXMjC4RFCYs1+Hzh+7pvTK11k9Aw1xTHMb7vl/AAozSfpilPPPEESZpw5/Ztdnd3uHjxorbxNnluE0WF2lgdB8dyabZaSkm3sPAcl1CzwhRFxsWL5xUL4eG+arzV69L0sOyN9jh/7hLTgwmyUIHmqc1TDEdDQOB5AcfHfaUMPJmwvLzMM888q+BOx0ogcm1tlXg2U5Tvacry0hKbpzZpNOosLXdxHJfDwyPyIiNNc6IwplarsbO9S14o+GxeKK2der1Oq90mCiMd7GVs7+xwfNgvKXfDMKTX7TGZqiDXdT2KXNGIG9KQoiiYhSGWbauklF57CialnCekgiQpVkFZZlWzPJ9niKWGCWvnME5S4iQvSQYU/aru1ywUK+QCgUJpSwVCOAv71niq4BkyitTeWenhPAnbKe1yCbBU9qHKCGh+g0lW/AEf/3NgVg8KTr775ygbOO+FWMziP8QZWagkLJz/flFb8xrz7M3Y38e4d/IS9amUfwRCLLJBLcwBWSxUP94pYHtgxQIdTArKquXJwKL6c8lgVqmQVCue1d7NwnzNqwGc1hopCgUNrfhynV6DM2fWaTabnDt3jjBUJAe+H+A6Ft1OW/d4JKWfmmUZS0tLCz2WhuXQcZwSkm5Y3ExFxvg8xm/c2tpCStUL1e12wVJCpkEQlDZftQUo5IOBfxqyH9PHked5CRsOw7Csehj7MZ1OUbBKtWajKCr3t7LC8RDHQwcas9mM1dVVxuMxm5ubNJtNNjc3cV1XOaiuqzdydyEqsiyjQOuUVJee7+lN2CphQlJKrl69wuXLl8jzFGGpSN8SQjVeG2OWqqy1cWyBhUVhnHJzHcvLywAM+n1WV1eV06gXoe0ouITRybCEykqrqNc0KUlVckeq1+ZFOcktqfo2TORnsktBrYYX+GUjTrvdLnmHpZQKWwpzerIoopASXz84swBMZDvHUMr7/pUBiphzInc6HdrtthqbNKPVbJX0aUZm3rwP4Ny5c+VEN9GrmYCmWcgEfVLKMtgwbAqGm1k17yXl4jACYgZDbCEQlnJ0fM8nl4rBKdO8zkGnzZ/56Z/iV3/lM2pBJQmZLEi0aOBkMqHT6XD27BmFoQ58XvrIR7h96xZZlhPHCYXggRDXEq+ZKjVS49SIE8a40HPKjGe5uaZx+XuT7TGlY5M9U2XjeZdHadjQmRpttI0bLbRjHIUheeYRaHhHu93i+PBQwQK0Y9tqNun1euzv7/OuRx9hY2OdnXuK2GAyntDvKwek1+sxmSg13/F4yGg0IAxnfOxjH2Xz1CaddhuZ54hf+ZXvvuA/8xlknvPIo1fVGtYJgitXrhBHEcfHx9y+fZP9vbusb2wgZUGr3SOoNZHCZX3jNGmiqmeJ26oEdJqdpDCjdyLTB3PIWeV3anO0cLpnKe59nSLT6tF6fG3PotVq4noOSRLz0z/9U/y/W/+A46xPrRYwOD5iOp2WjamG8S7P1Rzv94c4tsD3YDIZ4joFb72xx/LyEsOhgmIZ7vvxeMzR4QHtdlvhaAOPLE1IIkWMoApZebmOFKbWw1A/m3PmuWE4yvF09VX9PtObSAfLgixPOTjcLxvRl1eWyIuUwbCPLaViJqoHSApm4ZR6PcD3O8xmEywL1tfXSqpp1XdQL9d2v98vxcPMGleYXrUhNRqqzB6GM93bYJPlKQhVgW13mly6dInNzQ2Oj4+4ceMGh4eH5dz3fZ/pdFLaOmOjjBiVOafB7g+HwzLZEdQ8BRVaXaLTbVHIHNezCaMZWZ5pWwW2p8gvkjTFDwLyKCXJYrI8pUAFQeFwRlHkrK6uce3aNYz6r2XZgFA223OxbcFwOFB0kJ7D9vYOs9kMP6hTq9WZTqc0Gg3CMFb04F6AzHIsKXGEwNUMLf3DA/qjKfsHB6rvI0s5fXoLKQWjcQhSMhqNmUxD/FqDJEnxXI+i0LDgNCcL1aafp6pKh7CJ0oxpGCuVdS/g4LgPQsFWQQktVp2lRBOOiEqDb0mLjtYWkIr1yDggSZIgLEWTHKVKPM70bRSFalLO8gKwVY5FzJmN5utVUXfP8fkSKQ0UspLJFqpCZllKbK/QztyDmqZPHmY/+rfZX/G9Bwh/8Me/6fnuv4fFwMHsjVWyHvO+KsFP9evCNVWTRA8IXsxhPr96joc9quez7ErgWnn+1aAMWJznUmUHq8nZeRC0eK8L96YDKNMXUU3A+r7D409c5fu//49g2zaz2YxarcZkMiEKE5p15XdNJhMtQjwnOzB9yYBOys8rLKb6YGyjgTaZ6sLGxga9Xm/ubwYBuZQ0Gg1NoDQuNTNMwNLv98sA8qQSufFzYK5DZkgtjB9olMOVcKcgTZRcRCmh8A7HQwcaH/nIRwiCoIx4DZ4f1ENIdJOJefhzgb1UO6UOvu9q2JFy5E2CP9eiJ6Z0I1GNoJnmRTcGUCnICibjSdlvUA0qVHOucrrNpOh0Oti2zXQ6ZaqbH6tOvDLC1TJm1fFcXCi+55bvlVKWlKyO49DtdssIdDwekxXKeTaRrPlcQz1rHqxj2/j6OmDODmHGuEoPaK6vqntxcmGYv5tn4Go++Hq9ztLSEkWhmguHwyGz2Z4WANwsqx1GaA9YOKd5NkDpIIRhWNJiNptNGo36nHZTv95MVM/3yHSkPhqPGWpO6WvXrjEZj+m02jxy9Sqrqyt83x/5pKKCQ5AjQffCmDmg2GlCZFHwvufew6/8yv+kGptcB5moIPWkcTVGzsw/AFupht03108adgHkN34XZ+WSVlOeGyuqG50QVP1mE2BI7SQrFVsqhllXWVqnOTq6yZlWG9txaHc62LZFHEWkScLnP/c5oijiypUrWLbNoN/n3Nlz3Lh+g/3dXTzfY2dnh83NzbJJTdGcZsxmM1577TWiKOQ9730vP/5jfwLxO78Dh4fVG4YrV+CNN+a/OzhA/O7v8syLL7K01OX2vW1OnTlFt9vl7u1bTGdTVX3UTc6O67G8skohlSrq+sYms3CGbVmEvUe1SrrWxSjpsOfRh9TZRwV7WAw/pDHCgLP5BOnr/xNS5NiOwLZUb02v2+DP/rn/kCLPmYVT3vOep3GuOZAp3O2bb7yhK28Z4/GE0Uhx+89mU82JHurNI8BzPaRM2FjfIPA93OUlsjRTsDsky0s9xqMxhwcHZJmi6R4Nh/ieq9EMKkmhsoFGqEpi274uUWe6iU5q25eRJHPiBFBsfu12i8GgD0IwmU6o1QIajSa+77G0pKA5k+GATqeNlJJWq0UYKoy97/t0Oq1yI03ThKUlpXSraJRVwNPr9bQ9yks73O129NpONHucZHV1RUNjlJJvURQ0m00uXrzAdDrh3r27nDlzhitXrvDqq6/yyiuvlFoUURSj0Tzkea7Y0bRDbhrsDf1iq9Xi4OCAixcvMp6M2N6+VzIWVSuy9VoTgUVQC/DriqmlMHbVtkiSCGFbWI6FEDZ5UjCdjBkPJzzyyKO89dZbzGaKk346VVSOpzY2OT4+IooiptNpWbUZDkcUckynoxi17hxvE0cxzVaT2XSKzDNFAzsccunSZY6PjnFdl9Esot8fkmYpjUaTGzfvKLpky+aZZ55ByoKvfOWruK6HEIqq2fdrZFmsSSukrtDmmlVMrREjqqaSHmrT194SRSVJpJaW1mSQqgZgnvHcQVMBgTR03BKtV6U+q9Bz18BShDAOna7aqk+Ys3nrCm+1ajlPyhjmvsWeAMtWGi2mP+Ake2X50v+FnP6T53m7c7zT9VT//iDo1MlKwX37zh94gDH//cnrrP4z7J8wp7E1wcGDnksJr3rAOd/unqpBwdtWTB7wGSeDn5PnM/dWvX7zGls3sFeTtPPvxQOvTViW6qvUPyvYpOpLPDrs86uf+S0OD4b8wA/8UZIkwlnzCIIagVfHtpwSOlWr1cpkr2VZJcLEXAeYHiarvGaTkDH7ubGZN2/eZGdnh42NjbIiHBq2R41AMeuoFFTVwYwJJHzfL9mwqv3Oxm8z92kIiYxKuOd5WLZNs9ks4VwPczx0oFGv18sHYxq/T506VQqC7O7uEoYhZ8+eZX9/n8lkwurqCrV6DYQkL7LSebAdVe2QZWACUhbkeaqDD0GapCRxUgYaAMP+gEazVV6TGUzVMKfoVOM4KqPAMAxLx8sSQmWOdUMkQhCZCowjSgfABBKmImCiYoEgT1VJygYKZFl9MNdiAp/eUg8qC9MsXiGUU2T0FywhsMtGzUxVVioRf1Vt/WS0bq6tejwowrctq3TUDBOLubfpNOTatWvs7u6WlJXT6bTkcgbFNGIClOl0WsKkTAOzgcXt7u7qitVcN8UskH6/r7KiUcju7h7nzp3lzJkz1Go1JVCDcoTiWchb194kms0YDI6RhSSTBVESl2wHQFk9ydOUSxcu8sEX3s/e/r5eGBDFCXnOQhBhrifR4nIma3f/Orl/o1DN6UqTwPRhSIM7FWAID0RZqp9n6xYqJpVas1HdAAvRu8Dt/TfYPJNRr9VIo0hh3Gch0SzkxvUbJEnC0cEhz7///Xzn29/m/e9/gUuXLtE/OkIgSKKY/f19VlZWcF0X3/eIolypwvsux8fH9Lodldn8xV+c3+7qKvzjfww/8APwK78Cf+7PzTU3fvEXsT76UT784ef5Z7/4yzz77LMURcF3vvMdGo0GrVabJHWRKHrjZqvNweExzXaLTrfN9ZvXmUYx2dK71P1K0wiv3ZMS3bAIfBCVEdITWQd188ZBz1fYxUbdZ6nXYXllmWvXvsMnP/kJHMdic2OF7I3MPEhsC1rNhu6hsNlYX0MIwY0bN1leXuLu3TuMRkPC2ZStrS2SJOTWrRtYloIKJRrmaPDjhoLQGHLDtOQ6Lgp7PFeuTdNkYU45moUqy4yCvQqeXQ1DUmu1jm0rjvksS0vdBsexaTYbgKTRqJNGs3mwMxpqFiJVqUFoQT8pKWTOZDJCWILRaKLUvYuCWi3AslWF0XFU+fzgcB8Az3OoNwLiOCGo+Qhh0Wg02dhYL+1/q93m6PCQnZ2dkuXoQx/6EOfOnePzn/88w+GQ5eWlMvFjWRatllLcbjQaDAYD0jQlCAKazSbtdpuNjQ0lOmc7CMfQZDvcvbPNhQsBUhb4nrJltuPiS5QmUYXJyLI9ZFEQzkIm0zGTiaLsFXnBvXvbbG6e4rXXXmM4HDGZTNjcXKdW95nOJiwvLdPr9Xj99W/juh6OExBGCYPBWDN5WaytrbG9va2hV6pCVmCRvnGNdrvNUb/PaDojy3MlYnjURxbQbLb4wAc+yHA44Atf/DyTyRSkwLYd6vUG+/vH5V6YZdVKgq7YFwV5vpg1PglROmm/gJIFziyyuS0qMNoNJw+J1nUwdk3FEGr56sDArNnyfFKaUmXlcyqfX9rI+VEsOK2LjuWD9r3vdrydo/+9HP9zHfxq0u+7BSH/Lqsk6tQPrjpUr+9kEFD9au6zfL3+4HcKGKpOdDVYqF7H2wVdC2Omk3cPWgMGknQSdvUwgU01CCm/L1SvnEmyGhumkq+C6STjC5//GlunzvHuZ54mCnM8T2X9J5PJAg2tSahUEShhGNJsKi2y6XRawp+KoqDVapVwK+NTqb1dCYoqTSQfx3GYHB2VcKc8z8tAAhR02GjugPLlTUXF+HDtdrsUGDR9HEbR3AQhhsFKAKFmvnvY46EDDaM8bIRFzIMxg37u3DmNgT0saerCKCKMZiV1bbPZrGyyOZYWbMnzvMTuxnGMa9vIosC1bXIJYRJzcHDA9evXeOyJJ7ly5SrH/T63bt2i3W6XMJjV1RXSdI5TtyyL3d1dlan0POxK5GZwwQpfLHEsAVI1K92+d484ilheWiLWmSFDrzoej1DqkQGO45YBhMnsK9XZgvF0uhCcGUoxPdPJklQ1ziaGes1SJWRbK2fadjnG1aj3QQviQThK89XAwqoLxRy2bXPu3Dk831eOh85kpFlGOJuV1IXVgMpkw6oNRL7vs7S0RJ5npGlSBh+O4yjhsiBgOBhiC4utjU1sLAZHxwxQi2B5ZYl6fYW9nV2+/OUvIaTil1/q9lheW6XQwacJuswCyJMEIaHdafOdN97gtde/wyyMyui7elSzBmmaEoUhQlhvaxTVY5oL92UHbyGzGGmrTLSUkjnDhtbKYHELNQ3jpsnZ7LGVVnL1XtvheOm9TCd36HQ69I+OWF9b5y2dhV/SkKlCFqytrrJ/fMTx8TGXL19mf3eXt958qwysx+MxrVaLosgIAh/XcxR9p+vwsY+9pC7sl35Jff3EJyj+h/8Ba2ODvb0D1j/1KYpvfAPrP/gP4Dd/U73u7/09XvroB/nGt95kY2ODO3fvMBwOWFta5vyFS/QHA/r9PmfOncbzffrDY86cPUtepAwHQ/bzFjmWalsBxasuUIrVltFTN5UOyuDQBOOGxUtVOlRzYafb4Kd/8sf5+te/wkdf/DBrqys4tkOgy8qz2YTh4KgMIouiYDIeEccJYTgDBEdHhwRBjcODAdPxjOFwwCycUqsHSv+m1dLBo0U4U2t5NByyt79Ht9PFD3zSJCacTZlOZwhdoYVcMbUItK1TzpowD1yvV9dxdGIBJKo6Y9ngOEpP4syZi9TqChrkOYpDfTIZabVaSRhOsW3FdudUKo3j8ajsnStkjuOoZr9ms1FukkZ/YX9/v1zHUawrx3mGpRvA4zgiTmKazabWyfBpt7ucPXuWer3Ot771Kl/5ysuKmajTIY6V7R2NRly9epWPf/zjfOlLX1LK1g2rrLQmSaL0d2y73DSTJOHw8JBms0m/39c2z6bfVzoa2f4xWZbxyiuvliJ9oBhRts6ewbJtlpaXWF1bx3V9kNBqN8mylJ2du9y+fYvxaES73WKp12NpaZkf/MHLJSyuVgso8pjv+75P0On0WF1Z49d//Te4efM2R0d9hiMFQXAdl4985AOKljJ7mXp9SloU7OzscNjfoSjusbW1heM4vHntBnGakGY5g9EEgU2tNuUXfvFfMBoPKPKUQsm6q6/yUPnp1v06AUVR6KqDXQYJVYfQsgzl9tx2zS2MOsfbud2yijWV8v7Xvc0bq2muRce1UrR80PF2f3vIuOBhKw5/UMfbne+dzvvd/v6/VGDxdseDHH1zPAj+VEU3AIsOvZTaxr395530UYwt+G5Vl+phfB6DrqgGGuazq/5o9X3zyt2cgWrxPuYQq6q/JYTQe7wWtqwECI7jICyB69qcPbtFr9fFsiDNQjy/jhA2a2tr5TUaJI0R4jN6NEKI0qk3kF4TmJhKhIE4GY0hA8M3z+To6Kgk3DA+uqHFVYktp7xvk6Q1fzMBTNWvN9drkuymUmLo3pGyhP4/LATuoQMN81CqXw20xzSnGafU8zyFuQ8CCpmiuMCPcBy7LLfUggaO45aDPZlMGI/Hig4sqNFutmg2GziuSzSbcffOHfI0YzwcMdac2ysry3ierwdQKSjGcVTifw33u5RSYcpylWnMspzYi3VpKkWQ4nsevu8R+D4Xz50BJHka0z86UllKPTGKNGU86FML6rS1CMo0irh16w6nz5xVmOQwxPO90sHwPDVx4jghiRPSKCbLUsajEQf7++zv7/LYo49y6epViiJXmTxhyoR56eyCMuJKeEaUCtVS5g9csFJK0M2FZZ5YZ94tS7FD1es1ZrOQosg1I1VelhIN5aQaQ3XePNcOYsXxF0IwCxXu2LIoy33V5mTLtgj8gCgMFRtJpuhbBZAmKdRrdHodfvhHfpiDvX12dnZYXltBWIIgUD09eZFjWTZxFBEWBaPBkMFxnzCOeerJp7h+/SbTWaiNw+K+NTeK6vrCKCpZhCojBifChbKqkaUmlQeIko1M6qpEubHrwMN4ueYaVDZfXZcAKhLhai35a9w7/A6Pne9Rb7axsKgFNcJZSK/TpdfrcebsGbbOnSbOU772ta/x4osv8tRTTzEcDdnb3cP1lf5BFIZYluDU1ha9Xod6vUZQC3jm2afhs59VsKm/9bfgL/5Fsjjh//Zf/9/59Kc/ww//8B/jL/yF/wzrN34DfvZn4a/8Ffjc53jufc/z/AvfJk4SXv3mt2jUG0RhTBwlRGGC6wZsbGwymUxI0pRHHn2U6WxKnqcMus8hck0DrCsZSijW3LzBbVPCP/QD01NW2QfVWiWwsykf++iH6XQavPjiB5AyYXf3DhQq47K9fQfHdVSFQZeJsyzj9u3bSFkwm4UlPlU5zm0FBZIFp06dIgg8mk3F8OR5vu6xsEmSiPX1Nfr9Y1zXVsrajsPmxga379zR/PMWnlElF3NKaddVvWZFUcwDKUvgCEdnqTwsIbBsG2RBXQu+mT638np1lkpVCQcqmyUESZ4rIc1Ccu78efL9A2pBgOvbihI5TbAKZbOVMvEUISyyNCs3K8/1sS0HISxqNZ/RKCtFnkBvspZg0O+TpSmO65BlKZ2OyoSFs7AUG71+/bqucHqsra3xxhtvKH2Ibpcoistq6PFxn0TTkYdhWDYsuq6rs3vQ661wdLSvbKmlNltLWEynIY7rkKQpp8+d4+Mf/zjdpZ6CGmVqVsVJjG1bbKxtcOXSVTUXopi1tTWOj5VdP711njRN2dvbpSgSvvWtV0lTizSBRx99koODAXFccKWzgu04DPp9PvuFL/HGG29Qr9WYhDHTyj0VRc7OwZFqvs5Vtd/SkF8pBWGcagRljiU03aYwgp4Co6GzEESU2VmVOCqhhWLRapX26cRWoAoQiw2upekRUgcalaBkocJwIutLtWhRLWlUHFO+2yEqUcjJV749dEYuBECVqrH5pAee1NRGKy9/GP/+Qfejt4VqMGeuTSw8B2O/1P+qdyrnb3rbS3nbsauYxe/6OnMK87YHvPCdoWASI7ZrHPQHVT3mSU4dTDBvzi6L0Sz2ALxTgFWtOpyEnpnfFeVcriZbbSU3UM5K9cDmkCihK+OUVU8V7Bh/dk78c9LPNSxtzUaDVrutkDpBja3Tm1y8eI7V1WVcz6bRCBThhmshcEu9MnP/Btqq+vByLUyqbJ0RXK0S8ZikKsB0OgUooaYmwR3HMd1ul1anU36GqXqYzzD3ZaD91aSt+Zv57GoTuulLgXlQk6Yp9VoNx1ZC20YE+p2Ohw40zEOWcs7dby6uahg7nU75s8qqOSz1AjqdJfIso9FoK10HOVcZN6XojY0NNQi2rY2zgtR0VpZ59rn3lueKohm1WqBFAjPyPF24LhNgmIEyZZ9CJtRqzZLmq8hzGq0mjkw5OtxnfzqFIifPUo4OD1jqLfHFL73MdDbjoy99lOXlZTzfoxMETCZDBrMBfq1OnEqWWi3SKMX3mrRaNVzPIc0yLGERJzmWcBU0zA5otBtEsyme61H3Pe7ceItvf/NrhLMxT77nveRZjOO4paq0Ya9JM1n2qejlpzjJUZjaaomw/IpZPHb5ezNx1FiGjEaqeSgIAixL4cONATVf1eJQQjm5tBiPxyRJUgrSKAxhAFo4yUxiE6kLISjynK0zW3iej0TqRn9L65GAjyrJ2b5Hb20VSwt82cIuq1JCWIyTEcPBkLwoWN08xXAw5KWPfYJXX3+D8BvfJIlzZBKRVfRGSiNlQZLmJHlBrB3R8rCkovY7Me8tyyLPMrK7X8E5/4G5FS/94qoR1c50+Z3+HPNioXjFy2oGOv0nLA6KVaIoo7O0RhSmbG6c4ea1t0i9hM5KF6fmkto5qxsr3L1xm29842u8573v4alnnuYLX/qicj6lR56mpEnC7vYOk8mY7lKHT33q+9Xc+drXkL//+4j3vY/bt+/xV//a3+aVV15nNpnx3//3/4xXX32T/+a/+S858xf/IvKllxAvv4z9gQ/wyBNX+Sf/+OfI4pjlbo+jo4GCZqUZly5epNns8J0332R17RS9lQ2uv/UmYSqZOV4lS2p0RyoOi/6mHCshFmMw7bDr4cbeeZmVy6cZ9fdpNGr4nofn17SuwTHTyZCtra0yqDHPRQhVLWg0FEWgsVGNpke7E5RJEmN4lZOvehNMX1NR5Dz++GMcHBywtrzCcDhUBlkIfF3xBe0YCqHoOiuG3Hx1PTUmht7QsW0yPc9MZqrdaikygCQmThKlWeF5qkfD9UiihNkkJPAtZtMJy8urvOc9z+F4Po898W7u3L7N9t4tokxja12H8WComrmTVFVlPRewSNOM0XAMUtBsNSjygiDwtQaCjaL89RkOB+RJTjSbKu2aOKYWBDSCAMt2mO2FRDPVJH10eExRFOxs7yrFbsvm4KBPURQkqepTUFVnQV6MsYSFRCiK16DG6TNn2dk7ZP/okFq9xmw8IS9yYu3Um6rm6bPneezxJwmCBkf7fXXNwmYyGnNwcMB0OmF1bY3xaMydO3dIU8mgP6Db7XLr5i0mulE9SVPu7e5ycHCgmKxsW8OuJkggFZRZ1LIXsT8u5+jc59aOfp6DUP0hWS513U41a5dwDjk3IupbSW7ggaWPZTQH1FHInDlLmygd2zKOZ+6Mvv2xWH2gXF3zNVg9FiolVLLhpV098fEPm61/kLdcSUAsvrTiqqvy5nf9mPkLTcJHO8oLnytPvPaBp57brPLaKlHLfYmqt/uM6i/eaXzuvy5ZPecDX1c9FiteJyFb1aDzJMxIJTYXfz//zPvhRwuVDkuJqS7O3xNzqWLc58Q8DxgBqa6zKMzaEdpn0AxSzAOdKotcruUCSpu7UI1wybIcT8sYFLIoaePV/qAkDjqdDrVaja2tLXq9NpunVkumqLW1tZIwxyRN0ySiXuuQJQWuW0PmhWa9nVdN0v8/c38aK1uWpYdh395njjnu/OaXmZVDVWV1DV3dXdXFnqo5dIsEKUM0JNOgSNukaIkSbNiABRugDRugDJgAwUGUpVZLAA3TIEXKJEW23CSbg8iu6m72XJVZlUPl9Kb77hBzxJnP3v6x9tpnR7z7Xr5qlmUFkPnuvRFxhn322ef71vrWt6rKNqxkJyhW8ZRlaetoOWDBUieuweB7rtdrnQR7vR729vZImWOCWqzucV+Mf92ibiZUHBQGYIPzTHY4y+FmtDjTU5YlpMHuz/N6bqKR57kF71EUbaUPbZGt+Z2LTlxL1gCAiMUWY+QDd28Id7tCCgQixMh4C7PtV5qmtuDRkgijX+MB42I43/dttb/odpHnubVgTAYDcq6pBaJOH9P5CkkcYz5bomyAD+8/wksvv4zFYomv/dIv4fr163j11VfJqlFrrNdrHEQJirJAAx+h5yHLM6iMQAZJqSqs1ytbVOn7PmTHB3wfYUhOXH/gD/4hTC4v8C++/jXEvQGu37gBpTYYDoeAIgavdEsi3GI+WvDphnXTmZbpCw9CSEMStsfZ90P0uiHCsIOzszOcnpLGf7Oh7rtpmiKK6MZTivTejVKoTZG9O4mFEGjqGr4n7GS18i1Hl6k1e80XKIrCpAYDKNWYWhhgMByiPxhYEloZQkNRVYkgCjHa24NvQOx6f4NHj07xR//oH8VfnP5lVPWHUFBoTL2OG41Riqw7i6JAlu8WMz0ZKWsJm0b98Lfg3fmyfc9qiw1i5uiN+SOob8TWxrD1QOdPmZDZRB5gsXgfeweHUBAY7O0hOe9jsV7Di3wEl5c4vdfFC7dfQHl0hPsPHuDNN9/Eq6+9Bgjg13/9NzA7nyPwO5BNjbopMZsuMZ8t8Nnv+wzt8N//9yEA/Nf/9d/Df/Qf/SWs1xk8z0ecJIiiEO99eB//0z/+H+B/87/+U/jX/+DvA37ohwAAN46GeHDvQ8Seh/VqgeVihjTLEcZd3P3Eq6gBzFYbfOXzX0CalVguV7hoeqi1oMAClIMThKuS2ir+ttk3B9lQFEtD6AZDscLNG9ehdYnI99HUNeKY5saNG9fx0UcfQQiBwWAAOZWAahtgcldVd21YGy9wkv41Fvz3ej1wF3rXgjqOqVicumMPn7CobkktbIGztqTH9NZxHHp4jWyJf4E7d+4gMcXPXd2DgsJqvUZZVlSPFsW4OJ/g5OQa8izDepOi369x/cZNPHp8hnQ6xc2bNzE+GOA3f/M3kKcZSl1Bej6KojI1BTXyokQYRGBL3TjuoK4r1CWZN0SRj7oiec9stqC6JAVM5xc0t7VCJ+lgs1mjqhXyokJdV4jjBNBUD0U6YSIRfC9yLwph1pPGNjUkWcSjs0v0+30cHBzhpZdehdYak3CCDz/4EJvNhtxdOgnCIMQ3vvltPHj4GGEQEpGoK/iSom1ZmlmARnU1FaBNsbGkYngBYcFMZeQfjVmLbHANQCOuAm58E7vAfScbYDnItnRpO0J/xUs88cPWvnf3Bed+eubmrvz7xxMDIdroqD1/899WesVu9+O3+eT5O8TgyhTFM8jAU167Mpqt/eurP/e0bewCducD7SE9dTPiyRO+ap9OgOSqY3he2djTPvc0qZLzTTztGjxt7rm4xHUfe9o5POs4d9+z7zOW0GxK02JJVy7lGWzDMie3xtb3IwQB1ULFcYzDwwPs7e1hPB4jjkMMR0PcvXvXujWNRiNkWQohKFi0Xq+t9B8AOp0Etck2c20FYzMG9CyDAmBreN16NSGElVHxGsgSfC7CZvkUS0y5NrCqKhwcHJCkyZwvZ0nY2IclUFxfyI5TnU6HxtNg591ryPtluRRjOr4u3Fzw4zJU/HpuohHHsc0oMFBlUsFZBNbsu7p+Tr3spt7c9BBfBPfFDGyXiHCHRS5Y4X2ylSqnm/ihZa1VTZTSNw1MeHDDOIaQHYSdAfaPrgFK4+adFzCbTFCWBaqiwMFxiWs3b6Pf76FRGtASngS8KMHlbA4viBDGAdIsgx9qABLCC6gjsgDCsGM7NArpY51mlLUJAnhhBF8CJ50uft9wjF/9tV9FFCe4du0aWAVLOJY7VbZjyjcSROtNLQQVtrOtGhTQ1A16va4pJvWp82wcA5ocYVhqVpUKlxczRHGE00fnFpCtlinJSpIOIDRqVdvr5S4sRVFAN5XtmZIkib1+nNZjmRzffJ7n2YLVzXqNXq+HyeUlPM/DcDhEFMcI45hsbktyXkh6XZRFAQGBzXoDrRU+8YmXIKWHLPuT+HN/7s+h0Q3KurLzoCVgDcqyQprmSDfZzuK5PedtGtjMx/LifcR1AQQJtImcCCNjg6ZroA2CtpTF8MA2LmP2BfMmUxEtoDpHeDub4otlhus3ruH+vQe4fvcO3vnWm1hvNggXAc7uP0LiReh2e+h1u/jgvfehlMKnX38dnU4X3/jGt3H/w/sQUiIKI0SqQbeT4MtfIsKwXq3wf/6//N/w8//tP0bgx+h3OzS3AgkNjbTMoasCf+W//H8hbRT+jX/tq4iiCJ985UUsJmd49zH1G0jTDGme4dOf/wF0Bnv47Te/if7eIa7duI3TR4/QNA3OvTvUgM0GELQT2GsjofyANnzL8LGdFDioW8ZrN/oYjwYQooFQZFmojYtSlmW4e/fulgc/rzGeSfXyWsbrUxRFWJt+JNwsyT60TDaUAynsK350fIQipYZq3BuI70l+CLZRotou7vzws4W9dWOjVtx4ibqzSqxWa/uw6PS6yEzt0Xy+RF01mM/nePvtd3F4OEYUdbBcrfE3/vpfxxe+/4t4+ZXX8PZb38bdT9zF7/29P4V//I/+EfI0g2ponknhoVIFhACyPDX3Aq1P3PunaZQ9/rzIoZoGURQjzwtzT1GRu1IaRVmgrhWiOIFqFC4n5LTE63ZdNybI39g1g4IfNZrGEHIG9eaB+/jxFN/5zgPUtYJveiOlGypuVFphsympnuTh2RP3KmR7z3PmvLXUpDtRKeoAzL2RNDS0aJ9BtWqcwPUuQN2O6n4c2Nt95l0F+p5FIP6H8mKgxI6I3w3QuOr1POD+X/XlBt12o/SuvvzJCD6u/NzHvp5SnNL29fj4433a37+becHP54+bo1fsyWQTTGbeWa+fnn24gjJuZX/4Gfq0zzx9m/wRz2tlWjwHGagzeGeQPRqNbLT/+vXrmE6n6Ha7+OQnP4k4pnrSuqZGkWVZIopCFGWOPMvh+R6KcoMw8jBfXKKTdAAjCZNS2u+UZYkoDJHEsXHyU+Y4Sdq0Xq+txMntV8FqG85qrFYrm8lQSiFJEqsW4T5x/CzjuhZW7mRZhouLC/T6fWrOZ2reXILmysF4DvHziO9nAPbZx2Pv1uCyiRBnYPjafTdz8ruSTrmSKWZuXBEPwD50mX25vsO7k4pB/+4Cy+xrPp9vRb6EENbhZTAY2OZx7sm6F4N/3x0ITjtx9kMIiQYeFDSkH8GTAp0wQm8wokmuCGyzdKgsC+tJP59PcHh8iDjpom6AIIihNCClD4D0zi4hk1JCC40GtE1PCmpMB5KQDUYevvzlH0an07GyL8FRcEGR71bW4T649NYixhO4aRqEXoj5am50yOe2aDiKIqxXuZVrkBwhMalID2nedgpfLldYLN4ydTcRhN+CNZ6ExMB9KNFOcJ4fPKF5HAaDwRaTFtCoipwi+0pj0Ouj3+9bkOKHPqCBsiDJhe97xvWJ9kl+z0REvvSlH8RP//RP4W/8zb9pDQys1EFzdLNAVTXIshzwnIgXJDS2IzI8v5RWQJmhev+/g//q7zONrkAEw2QztGijjlyweVW+hN6V9rvQplhYSEy7r+HR7Ffx4vV99MdDCE/g5NYtnN7/CMFiDV9IvJO9hTe/9S0orXH77h0IKZDlOT73uc/hB37oB3Dj9i28/e23MbuYQGlB/W7CAN/8xrfwZ/6Pfxanj86QdLpmDlJjrqIqUasGo/EYL736Mj7xyiv44OE5/g9/9i/gf/5v/SF8+lOvoduJ8cnXXkWa19jkGU5u3MRLL38Ss/UKl/MlfvRHfwRl02ByOcHZ5RLl/oEFe9QJ3aFa2v4PWkpjfwsibtqxA4YgEi0EcPFtvPjaNaxXC4yGPXIjKxXCMEataiyXS9sHoNfr2XGXgoqGl8slgiDA+Tl1b+12u/YBwmR4Pp+j1+vZ4Eme5zbIwq4cVVmim3SQpik2m81WoWNZVqDiQQ0huCEeFftSHwofVVVbJ6HVihqgUm0UcHBwBCE8aC0QRTFmsxlWmw3iJMZ0Msfp6WOMx3tYLFY4ObmOxdLsXzX49re+hd/8jd/GV3/8x/GjX/0qvvbPfxHXbtzAJ1/7NH7p61/H2eljZGlK9RySUuZFUUJDoK6IgDeN6fis2x5BykS56BTJPhFORJ6slBs0zYzufa1RlUw0SEZQK22d2qqa+quQJI4lGQB3CqbeFrQvaEDlhX02sENSY9blWhHhp0ALsdRaK9sPyc6/pjGSXSagRJZcUkvd5M2zSmuwg4HW6srePFe9njdqu/u353lgf6/A9/O+rjpGDmTtHs/TSMfzRuCf9r3dbMKTWYnnG7erPneV7GM3A9LOofZ4nk4K24zM9jFfjUXc7bvbehbZeNbrWefovrcbvN3eiLT3hFLK3FKEP67axha2cY7/qm0L0cru6D8Agnq40HvbqgxusEwBmD76plEzNXym/j5JkuDll19Gz/SZ4kbOnGVO0xSdTgdpuoGUZByTZRmqPEearYybZYkg8DEYUifubrdn8Aw3UJaWMLBcVgiBqq4RmsA1jwlbY/f7/a0+YpwNcAG6lNR8mLMHSZJAGbUI13KwkxRnTTbGZIi/3zQNVsslOr3eVqBss9lYLMzKH36xgY87xtPp1PSVaokRO43yc4//xkY/nFB48RMvPXNeAt8F0Viv13aAdicU/85MkycfANOQihtREYjbPXH3JDglxKko3i5nKtjOa/fmd7fDr90oBoMHd7IrrdAoQAunkElTZ3kNbUgDAA/wfQHhh/CjBt3hGIfXTkjzF0aoKuqa2ygFKXxoLY1LCD3C2F1GCMAzUWzPRNmoCQpd8OGgT884Jx0oBFDVjQ0JsHMSA3kNhSDwrTMWE7I8z1GhhoCHKEoQRwm0BnyvRuBHODigGyQMQ8zncwCaLC7zDfKCvOUDPzCRApKBZVkNGXhbN5HbxyTw2vRgG1Vs3R44suimNoXWkGGEOKLrvVugRNcOiHwfQmmUGREk1u1yBqUsKvh+gP/JH/m38M53voOv/dIv2WwWE2MpBTabFEVRYLlcAWM7W+ifKzLXBDzoWOr7v4bg1d8LjvZoCJosUphu5LsLN9oMB6Ep8xmnSNGQFq0UagF86L2E/fkHOD48wWq5wsHJCYoiw+zsDBKUOcpSss68f+8eXn/9dUwuLvFP/8k/wSc/8xm88spLODk5xNmjczx88BAPzi7wB//1P4aHDx+gro3EEazvrpB0OjjeP8Kt27dx584ddLtUDP1rv/IvsZhNcf+tt7E36iPPSvT7Y5w//AgyTvCZz38/fD/Et7/9Nm7fvYuja0d4fP8emirHB9URYAA3hGplJFsPbvf+NEIzkwbSZpzodiTgF02+hVde/gl0OhHybIMoiKA9gSwtsEpXVhaVpqm53kaqpDWm06nVo/L5kfVvZMk3P9R4HWPZlNYas9nM3qtlWSKLqJvx22+/i9FoYGWdbgqa5zKvfXVdI8+pIDvPcwP0C0vG5/MF4viCmiBpIAgD+mxRQEHDkz6WyzWOjq6hrmucnZ1jk6b4zGc/g4uzc2RZgU+89DIuLy6Qr1b46Z/+A1iuV5AQ+LEfi/HRBx/gb/5XfxPL1QJZmUF6VC/kSR/Hxyfo9/fxwQcfYJ1mprEl3V9sZEE9Gijgopq2S7Q2pEM5P2+BHtOclV9uhHi7SJlevG5Ic9/zPlzJmSvNUTCOTHwbm1sSO8dBvRpaMEiZDfqJs2qCvkTT0D1OPAn0vlvg97yZkO/F61lR5t8p+HdB0nfzned9f2vKXPHs1jvfe57jeN5MkXtuu9t1j+XjiU77vgu+3To+N8Pizgne9tN078863yeO+Yrjc0nHVcSNCYX9Xbr70u09INqgru19ptsgrxu8EUIjCBgLSEhPotvpGNdOH4PBAKPREL1eD71eD2EY2ibLw+HIvj8wUuq6bqxjHUmu3WJnbkoaYb1eotfrod/vGdmQRJyQVXaWpYjjCFmWmvqHBmWhbH+2Rb1Ar9sjnAmJPC8s2M/z3Nb4weCaNE2N615hCQGvcVmWWbta2/vGvBjsh2FocbKbPXfnEAfIOYDPnb1tkL8obNsJvg7c72O9XluMxMFX3k7TNHa8Sbqb2wwNZzFYfuVm7/lZ+DyNNYHvgmjwA5PTMC5g4J/5Ac1/27UMY6DPaSMmFm5vBnaxYikDy3p4IFgW9bRUp0ty3JvMvaGZaFhphDKp7Ya6yKqmRhSanhCQTjbU6P98lvt4kAExcUgCTr7vw5MeEQ9PGC98tzaFyAZ1TNemY6sBJ7VCnhcWiDNgKcuSwCgoerhYLKwUqSxLJJ0YBwc0WZbLJZIkwcnJCbI0g6qB+WyOLM3ROkspI+kg6c8mpWP3PIkw8tDpDnF0tG865fqG3Hk22qecxZRvKroxKDPBBU0A7LUWou12DrSLXp7n0HWD0OMOnhqFsXGrm5qKRqvaFKYGqFGgyKkzbgMFLTU8z4fvh6ibyja2+hN/4k/g7OIC77333taNDwCr5QpZmmExX0KP3Dny8fdAs76EWj6GHFxHY4gDExG4TX/AmLnNdggTuQVwhfGK5hmGhRjg0cUanWSEmzdu4v7De7h26xZUXdmC3rt37mI6n2I0GmN/bx+j0Qj379/Hr/3LX8bewT5efvlV3H3pNu68dAdplmMxX+L45k3b74FqrUL0+z0MhkMkgxE5YKzX+OZvfwP3PvgAoR/geLQP3ZT41rfeAYSPd977ALUI8PnP/wA6gxHe/OYbiMMAn//8Z7FeLTA5P8O75RHUyYtubM8QB0CbKLFwx8Adf0EZH00hLlhCV1d4aVghCgNIAfQ6HUjhoamBym/Q1I11I+E6CwsozUOQm4wOBgMbhSoK6j/Cf+OoUbfbhdZkaHF2dgattS1CjuMYUhCh/sIXPod3jA3xarVCXSs0Nc3JoizQGHlUW3SnrVyHMm2cFgeEL9HUGpcXUztf67pG0k2wSTfIsgKAxKNHp1guVkg3GVZZhqwocff2Lfzun/w9uHv7Nn7561/Df/mzP4sv//hX8cO/63fB933k+UM8fHCKV15+DR9+9CFKVcPzfRRFidVyheUqx+OzGT748CFJpcx6z9lANpQom225iWa2LLhmyQVqwl5X99bSzswg2ef2Oi3M5JCWeDKJcEDj7s25hc00HCOl7ZcxY7AbsfvWNquG9hPtvn6HnOB5Iu7//349TUL0LBD/r0KSnv7dJ4ncs4D97/QYnoYdnrZdF+9sk4fd71Hxv/s9vn/cTbpEA3hSUvesjMaziMbWZ52/7RLbp2WL6E33+N0MDVlxuwFAtmJldUqv10Mcx9jb27PSn6OjA3S7HTIlGY1wcHCA4+NjG5XnnjrueSRJgocPH265mXJBtRACqxVlrg8ODlAUhY2ue56H8XgMz/OMxbuy5KPb7aIoCgwGA1uD0Ol0TMZGwvMCeF6IplHGAINGsaoKgz0oc5EkiQ2u5lkGz1GE8DkNh8Otjtluawh+9vL6z3iMa5/5WeWWIURRZJub8vXi7Acfz9q0IgBgSQqTDm7WNxqNrMuVi8MWi4WdW4y1ORDMBikcTI7j2GZgXJz3ca/vSjq1657CwHG35wN/xiUYPJB5nuPi4mKL3bkMm7MYTdNgk1LUsGsAAADrJcwFM65Uyl0E+F9XouMOHr8HRQ/+pqlJhxwGiCOymxS0UWjtRCE4zAbjXS4o2qq8ABJtGtEPPCc7oiClhhQadVWhLjJokAuOAsmDVqs11usNVsuVbTrYNApaKYRRiNTYVHJWp5N00OtTl+Ber4tupwMIgU6SGMtficAPUJfKFq9ygVEQhuTzH5B1m9Ya0pPwpES9w7rZllMZUE140aPiXEFxcW4KWFclJhcXKMsS/X6fyEWcIM8zA7hJEhNFkTmeGlJ68D2JVUoEi6QnQJ5nUNr0G/F8k0akqLQUElmeIel1kBapsVkm8kbSqgCBJ/C/+GP/Nv7CX/qLKE30uK4pq7FYbTCbrRDFS4dcaBvjd+ePHQtB17GuK5Qffh3xZ/8wuYJ5ZPUrNAEtYTuHt5kQ+rrpH8HyDNo479oAa3Kq0ZB4Z9PF8WqB3miIvYMjnD8+xY3bL+BB8x7myyUG/R6uXbuOwXCEex/dw9HxCe7cvovFcorL2RS//PWvoTcY4vjkOg6Oj3BwfIDr165TsZzVuyoLrB8/fID79+5jPplgvVii1+1ivL+H1XqN2eQSy9UK6zSDkhE+9ZnP4eD4Oj568BAX8wl+4vd8FVANHnz0IWarFIvBC8Z9ZDdaTQCQo9EcRTYM1tExGwtcQ9eEBjD/CJ977QXwgGoIrDcbeCKA75narDCie6DTwWw2A5p2LXj06BE6nY7V2HY6HXJDgsBwMEDgByjzAlIIxGEEX3rIixLz2QIXF+dYrdf2oSpNvVRREnHZrDdIswzUMLRCmdfwgwBN3RC5MnPC8zySzAlNMh0hIIRP5y8lKqVxOZ1Ca6CuqVYiDAJUqoEWZIWqtUIUhzg+OcaDh4+w3mSYvfMdvP32Oxj0urh5coKmrpBlG7x97xF+/h/9Y/S6Pbz3ne/g3XfeBUxwomgq1EYOJUAkgsmQgpE1WbJA7na1alqSIITNImhNxfqQbQZKOqBRgxoG8mtXr66gLGFXUMaZhk0Y7Jes+557f/L2XVIhhAAbT+9AV5pLYvuzdgd6Vzbpztx/9ZcQu5HqZwQ5dgMRV/z+BBna3pnztXY86C0XQBruhW1wakMldr/C7sfev6I97qtBrBMFt1t9OnnY2bPhmC3J5Mq3bbLxZJSej5KJPTt+2aVciB0QzVkzBte8JAkIM2E42C8E3b/t+cD5mbMU/Nm2No10/m0g9CrScDVoE0953xyn0na+b31Ga5uRkCaIB3OfeozjPKp5kE52xQ3icobBD3wM+n0kndjWPXDmt9PpYG9vjDCMIAQwGo23+ofVdYn1ekX90YLAAv4gCHBwcID1ek3KC6NiGQ6HuLi4QBRF6Ha71nHJBcC9Xg9RFFl5khDCrulsWsTYtN/vO4XQHWzWGaTwIUCqDm6yKoQH6AZBHAEG7K/Xa7tuJXGMpq4RmC7fniTpsxTC1l4wvloulzYbEMexxax8fdzaYiYdZVnaHlhMaDkLwvXK3BqCcC8ZdQgI1E0Dn7PwRupbVxU8Y64TBiEuF5coyxKj4YhImdzuJdI0Deqmdnq9gTBWQnV3VUn7yjOShnH2xu298azXcxMNTplwMzQmG25jDwBW87V7Q9U1aai5PoC/xxIDV8MfJ2SdqAXsiXd6FGGsysqyWFdi42ZW3G1ySoqP2SUi9vemggQo+2D2weSpVqSv84xLCaejsiyDkKZuxMlYcMZmuVqgaWrL1oloxajyApvlxoCT1BaommsLCOoSCw0kSYhup4PBYIBNukaWbSwz7RlNHk9KmC7ESRRbAuVLCT+WiGPfTnLu7VHXNXj94bqY0mixecw4m8IpPmbGLDcgGY6G7/loVAMojdj3sZrPkYQh0s0GF2VJvT4UpSwZ4LEN8nq9RhSF8Hxp2XyapiiLEn7go6kbbNbUhXIymVhySQtThcmECsc930Oe5fCDAGVRQkAjThL84Oe+D2We4+xiCg3SkmeFxr0HZ+j0RlsPLSnYKPjqlzb9dfX6FCYUYiPwtoGueWApYaQf2HqcGRxtvqsVANkGWNlPXwjU174fvzp5E1+QC4z2j1HWGovJBe6++imcfvg+phfnSCqFqgHyvEKaUWO1ThTh4fsPsVyvcOvObRTrHO9++22SBYWhIWKmG31NRgllUUJCoJd0UEyn+M63vo0KDT752dfRaIV8lWK5KSDCLj79+e/H8ckNnJ6d4f17H+H7fvALiPodnN77ENVqjfeKI1NUa7KKTBy2BpJHRWw9GO1YOZFmoUHz+tHXcfylH8JsOkeaUr+FMArRTSSWyxnCMMBoOEJV12RbGMfApo3YDYcjzGZTZFmO0WiI6XSKqqyQbVI0NbkscWQuS1OkWQ6tPUynU5LlVRWqagpojSiOsUo35uGnbTqfzkFCw4Oq6dpqRXUpQgvCsZZdGScmg3eUyZCUDaBUA5JHaxRVDqUbhFGIwkTJFDQm8ynSfIM0z6BMRracr3G5+I4dZnE6hf/GtwGQIUSjKHBBEqfWBYxYcm3XUPqbbLNyu6De+dtWJNUQD7nzHfAp239aYrAFbA3p4Y/QndW+GjtvnobKna+2e9oC6Ro75JcDAgC02t623tnud/8SLYo3W26x4jbI5caq7bt8/Hrrd/eQXBC/TRKcnxk47h7ZU6LbUjpyHmjA1qy596sLoLeboG3NIedwXUKnsR24BEy2wHmGg7djga+TiXJWVe2MG22TPkvHoABhSCxEKwXSDPxbqY8Q2za9kpu57hACtji+aiyhWUnBvVFUS05MkI3GeFsWLYTn7KMlSUIIeDKwQT5hgKPiTK8WgNc2qbNN84QRQGg6Xqq7FCY4CPi+RBgG8I0sWkqJ/f19XL9+gsOjMY6PjzAYUP8lVpj4no8wCuGZHl9FURoMJ7BcrvDw4QPcunULRZGiqgjss2SI8US/30dRFOj3+1ityG6adf5AG4FnFyYG6Mvl0vbaYdyz2WwsruS6DAbnFxcX6Pf7W66AHP33fR+r1cpG48uyRNAP0NQkO9INYRwpAgwH3S2VTlVVhGM2G3C2myP9bJAgpbT1Iy4OZvUMzx3GWezyxKUCrOCRUtqxYkISBpGdG1JKlEWFoqgMRtZITR8iKGWDvxCCbgMtoCpFLoyQW85UvV4P69zYfGctcRNCIPRCLDdLK7tSSiH0Q8RhvOWo9XGv5yYa1JFWWLnTer22XWCZNLBMpigKa0fKoL8sS+R5jqOjI3S7XRthd9NmSiksFgtIk5ZjHRoXp9DFDeDJViPW3mTKZj14cjGhaVP/7DzSRkCklAhMGooi+x5qvtBlicVyaVvD8z7iOLZ1ElyJz5MtCAKql4hpEq5WK3uc6/UaVVFBNwpRJ0Z/NDDf8e1ixDcbR1E4Rbm3N0TT1OAHbZv6ahdLrZWxoyRpVBgGRlPdoH0gUKMt0JRFVZYIwsDeTNDAJifP+iylgqTT00fwgwC9bg9VXdliouVyibIo0O31jMMVZSA6nQ4ePniA1WqF4+NjvPvuuzg5OYb0BM7Oiag9eHgfQghMJhNsNmsjMQN1xp7NkGUZjaUXmELv0t7YTLAAmg/9ft/W7rDmftDvoawa/MAPfRmf/PTr+C/+6v8Djx6fQ+UUIZhOJ3j33Xehf9gBHtxs74nwonmbszvTD4G6gAwiehQ3DaiQHKaYGQZ0tg/DJ14GNLkuTDZEaB6w6/Gn8ebibXxKn+H46BgSwGI2wa2XXkHcGeDB/XvIyjlZBecZNp0OJpcX+OCDD6AE7ffHv/pVAqxFgTxNUVc1Lh6Ttv/WzVsY9/sQIw8q8KDKCg+/+RhlXWE0GECtc6yzDMuiwvjoGl57/fPojvZwdjnBhx9+hO/77Pfh9q0buPf++1hPL/Hm/SWaF79stfV8XmIHMJrBZHRkYYPYfd9E4NTsAW7GKSYXF/Clwnq9xnA4hNZAEPjQGtgb7WF6McV8sUBeFlTcvl8DPl2fDz74EEVZoqlrvP/+B/bBrurGOujwGhQEARbLFZQSpsi5MZFD0MNeUG0X34NKk7+70soUGPtUw2BsEPncd0EYbVdZ4KXMPaqVtpEsjlZy5EoKgX/+L37JAouq4Ujstm242YNdE3nfuxlfnou74Ol5JT+7UpZdwMvnvwts3ZcLg58P2l/xqWcHg5/6+xPA+Mqo8u/wJZ6g2PZ1FVjdjSrvvs//use8RU5cQHzF+1dt76q/uQTAMiPNMjkX9FNYhh2BWhLYSoFclQO9WE7dvu869rCkhAN9vB2l2owWyzABMrPQ0FCmsF9A0OdMxEKjsRmGlu0S6Ldrtk11uKMhr7wOND7tz24mRSsFyoAY69InCDAHPAU86XTGdsku9PY8gDDNQAGuqws8bkSs7JiExk5fGobR63VtVuDg4ADj8Zi62Tc1bt2+CW0Clp1uF01TYzzeQ1Hk2GyWFstxJqFpGiw2C4zHY9tagDMLdG0aahrX71vJEKkTSttaIIoiC8SjKLKkgc+VgTrX6CqlbEE0Bz1ZWjQYDLaKmZmUcLZgNBpZoyCX7FD9BmUW3MbSAkBpAsj9fh/z+dzKpFiizlmHwWCAxWJh3aCSJLHN9DhQxTWybmH1o0ePMBwOLakCsFVUzZiGx4u3YZ2mygp5WSBJOhBC2MJtlkZJY2rD14yTAkQyfSslW6/Xlty5qiIed95nVVW2dpFJFY831yK2WPXjX89NNNjpKE1TrFYrzOdzy3q4eMT12nU1YDxYbPuVpqnNNvBn+cY6Pj6G1hqBJimSVhrr5Qq1Kb4BYLVr/L3RaGS3w2m7pmmwWCwQx7G9eLyIuYu11hpNXcMzqS6O2ldVhTRLjYUjNY4RMPIFRamqJA5xuE+NXCDaCn5ppDNc1+BGYKhBFUduAM/z7QX2hYemrilNZaIQWnvI0pSIgFmEqPC5QBTHNg1HOuwcvucBQiDLMmQZOeRoEw3hbJTWlD4tTU+R9XplHL44nbmCUgqTyQQXFxcAYOxmRyiKHEJQ46ler4f1ao26roysJIQEOS/cv38PDx48xG/91m/ic5/7HM4vzuH7Er1eD2dnZ1gaApckCeKYpF6sWR+PRxiNhlQYtneAwA9s6hSAJUV1XVrtJk9636cC5OlsRjr5xRK3bt3A//jf+B/hb/2//zbu338AZTI4s+klyVvMS2kFPAMY2JsyzxBvLuCPbtkwZftQEeSwpGEeaK0DFRM5ehyzbrcVEm3FUo3T0jR5Ee8/+AV4voe9/X1Iz8dsMsHRzTtI+gM8+OgDzJZzlGWBPKcs297+HrI8ow7Xs6ldcDtJjAeX1OhPa6qneeWVV1BsKqRVhaIo0e8PEEcU+bmYLSGDEK+8/gXcfOETgB/iowenuLy4wOe+8AXcvnkdj+5/hOXkHO+eFyg+8fsteeBzsxIIOwaNPWfueOwMMn1dAKrRBEmUQv1r/wX2v/81bJZrBB7w2c98FkopnJ+f4/79+1itVugmfQRBhLIqoQAs1yvUQyIaVVXhnXfepwaasu0Ay40AXVLveR7KWgMiQK0qVDXd+wAt9tYRSbRNL916Cq0pMq5MhpHmNAM/F3CZ2hOzJikz/zgoonQbTxfCRPxkYOYaUFYlgSVTjMDbcV9XRZjtPHRe7vrrAj93O1e9npeMMKB/2uvjQPGzXrvffZ5j2t2Pu41nff+7P76nf36XFLig9mnkwT2+Z5GRq37ercN41s9b2QdnTeTMgjBZWHdN3CYVcmu7PL8AWELiZjQ8T1rw40b7eU5rraEabG2DARvfg2HQWlFzZpzUB43N0rT/8TnSSsykx30xqdq9hkKIrXVLC6dGz6OMCmEMuXXP27ETsJkHJiy7WZntDEoD36fnmueRyyMD2n6vg4ODA8RRhLt37+La9esY9PtoVIP9vTEaxYqBGJ4n4fvU1yFNV/Ycq7pCnARYrqYWeLaBHIriM1lhG252fmKgyxIhBqWcZWDcx+A0TVOEYWgdMVkZUtc1ut0uyrI0xxvZ8+R9CCFsMHG1WiEIAtvUTghhsSUA6zi4WtF5Mj7smj5q7Opka4DLEp6UtuCc5U4M9tkFlPtauLUU7ELlBnoYY7I5DwDs7+9bGZh7X/B9w8fD58D3EhO9vCgIF5rMN5M9rTUa1SBdrbesbflYtQak3wYPWB672WzsuPD143uHzVTY8cqVd8VxbNUoXKfxPK/nJhp8E3iehzzPLalghsgglpkPMx23gNxlr67sx40m8mSvTVaCB6Y022eGCcAWZnY6HctmGbTzJOJMCt+cfHG5dqMsSxSGOUspbbF5r9fDaDSCJwxZ8j0bYeDzUCYaKUDAW0rPRGg16qaEblq3LSEl6qpGEAaojASLUqNtpqWGgKpMM7EgwGQ2g9ZUHLWYZ1YPJ6VEVRZYLuYITZdHpTXmsxlGoxEWy6UlJL7nYTabUWMsU3AvhMDB/j4en54iy1J4vockTrBaLfHBB99BYFJ+jx6d4s6d2/jMZ74PDx8+wGq1hu9LNHUFKTSSKECvc2Bs35bI8gwvvvQKfuM3fgPf+vabEAK4c/sOojhEVQcIwwBZtsFw2Dfk4sSkcH1kWYowDOyNtFotISUwnV6iLEqTGvVAXcSJXIRRACGAyeQSh4dHZBUsNIqSdJjr9QoaQFnVuHPrOv7Iv/mH8bf/zt/BBx9+CAGBsqpt1BkASX6uyj7s3geqQf7Nv4Pej/wHlJrmbqWcjXDdOnT7rzChNcYyNjBnom9Cw1rlWlW19PHo8CeAD/4JXrhVI+4MsH98DednZ4j7Q3zqs5/H5PwRHj+8j+lygdAP0BuNMfKP4AUB7j14hMhIpgQUTk/PoDURXK2BiwsaX1Uo5FWFstHY1NQh9ujFF/HCi5/AYHSMdZrjve+8Cw3gS1/+EvYGPTx+cA+Xj+/j/fB1rG8d0tyEtp29LceGcV3TdLcIA7KdDxCAthklBRIICdQPfwPDQOH87BxSlfip3/OT+O1vvImOSYO/+uqn8N777+PibIqvfOX7cXL9GjrdLlbpBn///a+ZwRcoysZI/tiK0dRHCJIVVVWFuslIBmgW9rrZbjTZrlOmZwq2I+J8fq1tK3YGQmz9GTsBD4U2kLIFPA1BpfWGLYLZTAJ230+AFAc0X0U4nvY5fl0FrHczIs+KjNvv7OSzrtrf9zST8F28vhuC8l1vG8Cztvq0sXMtPoFtJ0UAW4D6Wdf0aeD1WVkOlzBYiY61aZeAdjIXYnuutDJmexQAYIJIHHyQVsaknfvf9wJEYfssh8nC0nkCgCCrc7/tl1BVFS4uLiGlQLfbsyYyALBYLEDZEwXPI7chrRncPUkuWXLFOIDOZ5to2PsS7XW15MdrpVJStu6KFOSjNc/3fUhPoqkbC5Rv3LgBpRrM5hP0eiT3OTo6wnAwgJASngccHBxYxcQLL7xgal0zrFcLU3ic2eAqRdyXyPI14TUf0KgA+GiURlUpSE/YoOp6vUYcx8b8QiEKY/R6vTZba3CDlBKpKTh2TXq4SJrnCxOG8XiM+/fvA4BtgDoYDOxcZPDKdW/cA2I2m2E4HFrpEPel4GvCtQEW37AM2ETgXQk/14JymwQOyHLNBitmopAa/zIu7Xa71oWQazW63a4N5jLm5XFx79fUBIWZdDHO5AyDC97LsrT38XA4xHK5tJmGJEmsGyHNSYEk6ViFC9dHcFCcx5PvbbZlX683EGjdTXnecb0HHyOfA48pnxdnt/hcmTjx35+XaAj9nCvsermyk8bNZrBuiy8inyjLptwCcteRismIG3XjQRQAFboI6g9Q5DkKE8Uf7+2h1+/bE3XTrcwAWRPIF58X6q2UJC/kHEXVbcqWyQjJPmjxaGpjuWgi70VeWO2k7/smwkgZmLIiX2YeL2omlptxEVBGc8dEiB0Q0s3G6vP6/T7SNEVVVqiqEllWoDaAyPepI3Ld1Ma+lchEy7R5MaBoTxSGWJmmZFJKzGZTdDod9HtdxFGEyBAYnlDc9djzPDx69JCyI2mGpNPBcDiA1jXyLEfdUBHU5eWlIWkJer0BsizH2dkZpIkSJKbr9GDQx2azxmKxwOXlxOoq45iyYJzh2mzW4AU+DEJoBath7vV6KAvSC4YRdRTnG7Rv5kVZFhDSh4BAmmXodDpW5/id73wH//xffA2//c03sN5k2PzpCnoAYAn4/3EH0M1zyTeE9DD40T8N//jT9AdN2noqFuS5A/uQdh+q7U/CqBPayKEQjNIZgNP/VJli/8HP4/bxAWTYQZrnUHWJwBPUdE8rnD9+jMvJJT1klULgBwh8H77nwRMSEA09es3Cosycb6oaugBqAKLXwejkBDdf/AS6gwEAgfPTC5xPZrh2cg2vfOIleKhxefoAs8tTvBd+Ckv/uB2XrRyGCSIYIsURPn5Y2wgos3UzbnQv0vip9/4Z9s+/hs9+5lP4XT/8Jfx//v7P4fz8HKPRCF/5yldw7949fPGLX0QYJojjBOeXl4jiCNL38b86/9+hSip4a4nrf/UIWmnjZEbgRRtpSFVX8CRlArUB8/R+GwhRWtk+EPay8LXUDpTeAX9bcibR5q/s95i8MBwXzofdLz5lVgpNdRccVXsa0Xje11Xf2d3mVWTkmRkLe22f/bnnJRtXAWy3Vu9Zr/9fEJqnZ3x4FaDXk9K2p2/PJRq72YinZWDcZ+HHHeOzxsF9JvP6RTOXJL0M4J/sOeRIrrbfoew8NFTjbhM28s+SHzfqz9uh+Az3pHH3BxM08Swo27XcpG0pSxza4nEFXov4mc9jF0YhlKqdYzQFuFxAq1tXTZbwAEQ2pEfR9ZOTawYINhiPxzg4OEC3S+YtQkjs7Y3R6XSN1DdEmrZOdwAwXywQRxGyPIXveQhMV2iA7LmLvIDv1LVyBL3f7+Phwwe2zwwHT33fx+PHj1FVFQ4Pj6A19dqKwpDaDXgeHj06BTSsNIkCfoT72K1Ja20BLjeX4/1EUWSj+GyrSs/+yEbEmUiyCoExR1v/qWyNAz3LSytXZ4zIQJidmLgY267VBo8y6WQJF/esWC6XT0jzPHMNmfjwft2ANB8v48Q8z9Hv9wFsy/X5XJmcMTHgLA7Ltri/BuM/Pjdu3srZEz6fqqTeS1mWWazD51HVhSUvnJln86W6UtZEiAPcTBo48K+13lK8sNSNt8UZFy6dYNmZ1ho/9Lu+9NS1xI7xd0M0XKBe1zXu3btnpVCHh4e2OIRrI4IgoMJek4VghsTMiivz+aLYmg5t5EyeD60V4ihGFEfodbsQnkdV9iY74ZIMvuk8KVE5A+ouwPwZN4sinO+2JAPk/lSXCIMAdV3ZSLoQ5BhVViWikFjzarUipi2JSHC0fTqdoVENNus1ZTXKEnVBDkuz+RyeR9tcLEgbycVmSZLgpZdewuXlpelxIZCmGQYG/AHbdSfcm+Tg8NBqyuu6QllWRmtIkyjPczvpN+sVAt9HXhQ0ZobklGUJPzAe/lmO+XxGDc56PfieRNKJ7E1F42Y6HJcVkqRnF5LT01Ncu3YdnieRJDGahqIgs9kMq9UaUgrTB4QeKkmS4Pat21YippSCNGCVQSKTEQDm4UIPCpZh0UNGwDNp4uVigV6va2+gxXyOqmnw2994A7/wT/85Hv3RKXQfwFLA+ysJhGqecKZpH5zbgCsaHKL3e/8MhB9BK23kLsJeR2huPkbkgYuzKHMBKubjmg7aqK1o0PYhp+3nVZGic/pLeHEsoYQHIanRGjQtZJ1uB54nkKUpVosllvM51ssVipRczqRo7AMZaJs/djpddPcPsXd0jN54H0mnhzKvMb+Y4ezxOeJhgpdefhn7e2NsVguc3n8fOtvgm7MA9c0fvgK0mCJ3zWBAt+SJwfY2Ujdco+3BoBWAcoPqF/8yumqBG9ePMZ3OkGeFcULj+S/Q6XSJkNc1bUcKFFWFx3/sHKqvIFcC4/9sDwC26pw8z6MCYw7QuhkGaAiPe7jsZC00jLrbHv7WXHleLEtBFTM3RDsmu6SUQKf7TQe8AlsE6F/1dRWR+F4Sjf8+jvFZr+8F0Xj+bbSyye/me7sEYjcbsZut4NcukXkeudTT9s/BEfrXrEXw4NZY7BKKbYLyJLGhNbHdrqtycM/Fzapsz73t/bj9Gzjb4OICIhm1lR17NiMuACGs9HY4HNpgDzWHG2A47FvTmf39fbvd27dvQ5u6x263Y+sMPN9HnEQ2YzEaj5AkiTWLyfMcy9USo9EI6/V6S44yGvXhecKaNZTGQMX3fKxWayQJWXFzlJ3rX6E00jRDGLa1oMPhCPP5DHVdYTgaYrFY2KCnlB6aRiGJOyhNQ82zszMEQYCbN29CKYUHD+6h3+/b7IPW2tYaKEUN3AaDgc1CMKBnCTPjOiGE7TnBgNat3WWJEJM8JhIsFWJ3Kn4vz3ML7JmM8Jgw4WAg7dZxrtdrLJdLHB4ebs0prsvr9/sU3TfzyA1S8/lzk1fO3nQ6HXKkcsoDOOi+e3/xebJDFo+FdTA0gN+tJWbSuFqRpJ1JQlm0BJpJCo9ZWeaI4sgeP9eKeNJDlhXWwYvPLTeyeR53rbUdOz7ObpdwE9vhciaG65K51vonfu9Xn7meAN8N0Vit6CCdBSEvCuRZhqosUZlUmmqoKyuTg8QU2yilKBXopJm0bsGYm8LUDfWymEwm+PrXv44XXngR166d0IJgHIaqsoI0QKBpSBvdNOSdz5OXLiJ1u/WcSeY2ccuyHF0zacuyADWAaRBFMZRusJpToy5u7kKsj2wn54sFpCQf4iiKsV6vcXhwgOlsirzIUBZkWVaUBZKYQLCAtpbv7IEchgHSNMPe/j7CKMQmTUlraQqg2EquaRoUZYnYTJhGKXRMMVJV1wBoUcjSjCZWHGG5IBnVaDzCfDZHaTIsVVUB2tSipCnGoxGKsoQUtODNZzPLxrXSCMIAYRAiCAMcHR3Yxctl91mWww8jhGGMDz74EFEUYW88wuXlBXzfQxRHyPMCQeBjuVyZBYJcGtbrFaKI0ra+76HfHyCKCcBXZY2yKNAohcnlJXl29/vodBIAVBzm6jxJC0qkt9vrYrNeIwpDlEWJxXKORitEUYKHj87w5+OfRZXUwFIg/o+70Lox2RPTF8A+UPlhuy1H6Lz4JSRf/GN0Ve3n6XPU0VoaTa+A8Wy1QBa6leJt6yy0cW7iID8RMa0JuMj5B7hbv4OD8RCNkdHkZYmsKOFJgSgK0e10EQUBhCZCVhYFGuPI5Hke/MCHZyIrYRyjCSIoDcznS8wmc2xma4y7Q9y9exfDkxGapsLDBx/h8YOPMDl7iJnqIfzsHwak5w6POQlDNOyYaUO0DNEQrLowxfAWWBuioTRUsUbxW38T4vQbCHwBqu2QgGhBBTSMLAFmLjYQJuOotMbqf7mC7muIlUD/P+mDpBGNc7Ca+nqYa+XKOPkqgomSyYDwGujat+6+ngb+dgHyFpByiAbQ1m/QZ9roLnbmH8n2th1znv56gkF/7PG7+3S3ozWDzXYsn7q93a8733OuRAsk3S1ecSgCwtawPHnv7GRgrNRse9/uV1hzT/fkznacD9LxsPuPvdHbj/B1EO3ZPZ1omAADh+XpA86YUnTf9zy6o1Rj5oPaAugcoXS3f9X1a7utwxkPd8Db7AETeK2FJQY03zy08kbtGmo5rkbCfnZ7riuQcQnvq7XYbus2lP2b5/lomtoA/JaAuC9+hktJSoEgCMGN3G7evIW9vTEABc+nqP7169exv7+P9XqNfr9Pz4UoQq/XQ17kllBQ4INkQFwD0iiq+ezECUI/sA032SWxaRooaPihjySOEccUlV+tVuh0O6jKEmmWWVyUpRnSLEXg+zg+OcTl5QU834cy0X0Ghr5H8nR+9jEIldJDUzdI0xwAAebZbIa9vT0oRXWOQgi88cYb6PV66Ha7NgC4XqcGmMeIohAUxNyg00mMgUxjC5cvLy+tyoGfsy1Way1Yx+OxxQIM/hmYArDEZDab2ag7B6RZcRIEAeI4xnK5tLgnTVP73sa4PQVBYEEzYzJuvsrYDiBpPffM4L+x3S0DfCYLh/v70LqtT+BMF2ch+LwZmPP8A2D3zWPC2Q2uV2Yr2/39fXtuUkrrnMWEgT/LYy1E2+Hb8zz4XvhEsFxrUtDUdWXqc0xfJimRFwUG/T45KCpFeFlrhFEEKQSKskTg9PTITIlBmqaABo6OjpDnuW3W3ev1bN+70WgErsv+nmY0Li/OLHNVSmG5XOL8/JxSM8bqjKQ1Q/R7Pfqs50FBbz3A+WLUVQWPtfZGc+c2taqr0k6GxWKBx48f4/DwCKPREFVVozI9JYCWFQsprK8xTyBOe5ZZDgm6cFmWIYwiJGZSSwGk6QbsdABQ6jLwA1P8LOxk832ycl3MF1gu1zaTwzdCt9vdqtDn4nQ+ls1mjbIsbDaA5VNaaxst4AKoxWJhfZWF0AhCSq09evTIZpEo8gAbjSmKApvNxmaOOEuhlMJ0OrUpN7pxyKaOitbbAqKqqrBZruwNGscJfJ/IBDXhObILBwP7breL6XSKMImgGmC1yjCbzUAGWkTUgoDStJyCLcvSOnrxjcsL4muvvQbf93F+foF+f4DTR6doFEVWeH83b94Ap795XrmpQFcy5z4Y5otLSvspif9w+eewFCt4a4nBX+qgEhq1qi3JUGgLhukRvf0w98MYw5/6PwHJvsUMWmtbjwHh2Eta0sDf578Ly1G0YGDEIKV1bbLwQEjoYoXB5Nfxylgg6Q9RK6CsFcKQIiHWhcMPEIQBojCC50XtMUmJsq5QVhX1aMlLNFWFOOlgb38PBweH6HV6yLMUy/kF0tUSDz96D/cXNcRLPw6vfwSD9cltRTr1FWYfcICbPQPOaLRI1YwHSce01lDlGvkv/mXo5SldW0McrNSSM5JPiczyApz+exsiGkuBzn/SefJzV3zXBW27pOBp+9r97lXbc6O1z9oef8bVeO9umx8Mu1KpZ722t8Pf+fjvflxh+NPOZ2t/AnD1/M+ffZFXXqTdaPdVAHQ3St6+17r9cMCLv+/Wa/E1aLfx9LFyo5/8O49zC9Jb6Q6RVQ9BEFnpA8smWEoLwGb+uecQZdxrkDqTjodAEd9Ou3IrXmMkpAycc9D2nKgOoTX1bokGn/uTRMmSbYmtcW7HXUBpOCTBlUa767RnXNqAMIxQ1bndpudRACOK2yhsUzfodLvY29tDJ0kgPQ8HB/s4PBji8HAf169fh+fR8/HWrVvWnjWOY6xWKwvqWOrLEuHVamXtWpumwWZDGYfDw0O7jvJzke1XmQywQxJr21nOzRFz/vtoNDJ1IwSAz8/Psbe3Z6VNJKkirJLlOSqr34etPVgb+bPv+7aXAUucuA7Vfe67OISfh4PBwDHvCeF50jqHNk2D4+Njuy2ei/yc343yA+2xue6ivP8so4AnA/swDG0PNQoo0ri4++MaBc5IcNZqs9lgs9lQTYVxrWKiwvfqdDq1Y8A9NRhTMonhrAuToKqqEPg+pHBkskaqxNvlLAvXfDDZc5tMDwYD2zmcswVMhEIje+N5zIXzLP86ODiwBfLu9lnxw3/rJD07zlwvwvfqbDazNr+8Lmw2GyMx97dkTzyH+FjyPLfPGs4OKaURBi1W41eSJFaGztj1d//073nq2mjXjuclGpPLcwvo+SHHK5OEMJazjR1MjrgL37OT3q2jWK/WGPR69iTc1u6+J9FUJebzBUajET766CP8/D/4efiejy/+wBcxHo2t7i5OYlRliV6vj9V6hcnkEg8fPIDn+ej1ugiCEI8fP4Ywrern87ltF8/2af1ex05Otg2LosiSBKWUTXeOx2MAwHvvvYfFYonPf/7z8H0Pdd3YoiNOcVLqlRrI8U2rNVnPMWBmaRf/zMfB0QeeHP1+F0rXdsH/xV/8RRwfH+P27dtQStlJ56b+uKCKnRQomrG23Ti5VgOA1QlyAzc0ZDXMY8EPsSRJsL+/b1NpvA9LmpoaRVFhOllgNpvh6PgQm80SVVVitVpjOBwgSTo21VtVpdl/aaIY5F4lhDCsmW0+pVmUI+uiQURToChyAAKLxQL7+3tIko6pZfGspC0IAty/f98U/ZYIgxBFUeL/Kn8GC6zQa7r40j/+DN58521jbQoocMVBWwDJmMY+/JoG3aMX0Pnq/x5CUtGj1qZ3umibNIHpgt3AdsSWiYiFNJq+b+8nODBBa/Oeglg+wPH0l3Dn5k3AC+D5ETpdIvp5liHNMitPbBqgMd3oFWgRjJIY3X4fUW9IUbTQR1UWyNINZtMJmjxHs5rj0fklJjd/N9DZN25oxjEDW20OwWasTKoIWIDIjQvWdgA693bQSiH/F38BmN8DgCfA9i6oe9pLa43s30uhBxpYCiR/Jbnyc1dKPHbAvRu0+Lh9Puu9J8Hr1d/dyvjuHKcL7J4GtJ91bN8t0dg9zuclNjtb2erc/VyPHA1suxe1pIAjem6WZ/uw3N8530B/kLJ9hu0SjbbvQSsdasft+eortl8CQtBDPTayDgYcQRDB9wMHgCu7hjKw4PN0ax0hNKQ5Rib5XCsIgAi/1kYqaeRJUkKr9vjdZzjZij95PdzrvDvuQhgyInh7DbZqH8y6yIsa1RgEqKraNFsLsbe3Z6QqIfb39rBcrXD9+hFu3Li+pVc/ODxAVVGAb3J5SYG9OEaR5+iZIFyRbYwaQRlXpdSa1XAQqyxLlGWJ6XSK8XhsP8c2q6yL52caOxMx8ByPx7YRGwfqoijCfD634N73fWoCKlrHIAbS/EwXguQ8o9EIURRhOp2CaxmjKMJ6TUXcDJD5+DnIws5EXOzsedStmc+Pn/UcMWciw3UQDOBXq9VWPQEHRRlk79YkLBYLWzvBUXauT+h0Ori4uNgaN7ZIDcMQm83GBkz5WjD45ywIExEmHEK0fbs4IMnmP2maWkMAVjKwRInrIXhslsulvZ96vZ51SmI7YCbIvmxdmbgYnntE8OfZuncwGGA+n4OL3zm4yfK66XRq5WUcnGbCy+fO580YgrEeE1X+OwdJqTaVetExluMghZsV4eyJzb5Ao9MhYsPZOSafPB+5zoaVM1VVmX5boXWf4nnPBAiADfj+8I995WNXwud2nSqynGRPsi1uZR94VW+7MXBzvvHeGKpQaOoaRZbaKEVZlXj08D4+yEu8+OKLOD09xcHBAZbLJV3kukK6WiPNUmRpivlshhfu3MWbb74JVTeoqwpaNVgtF7g4P7MMa7PZoNPp4GD/ALPZDPfv3cdms8GdO3cApdHpdHB0dGTbtwPkTjEa9i3g5hudJxVHKUajES4vLy1wf/3111EUBR4/fmw1g5z2HQ4HANrmR+T1T84B7gJ4dnaGLMvw0ksvWe0h39h8wwHAcDjAZHKJqi6sfvJTn/oU3n77bUgpcXx8bG8OrbW9GbnQiG8EJiF800RRbCMdbFmXZZSJCKRn2S4XcbFHNdvEcZaHIzh+4MMDsFxMoZSG5wXI0swseMJ2ZdY6tSlV36fMyHA4sp7U7LoAUP+WosgwHI7szSWlxHw+N8dPMighYBZtz95QeZZDa2C5XGGxWJo6GYHLywv0en3s7+9RBTQI/3/xi5/Brbs38PjxOX7rt9/AapOhqjS0aa4G0RJpoI3i5dP7CB59A9HNzwPQjo877Oe2AJ6JxgtLNkyXaO3GHAnCM6AA0MpF6DdybhnewuPeMR49fgPJ4h34TYFxv4/RaGjHMPYoG5blFQJPQGnqNN2LA1y/fgzpB9g0wGxyjnyzRlNm8KGwWc7x4OEjrPQA3is/DS8egnuCuKShjTDTO9Dado1um2QBGk5TMkNENJ2YkZ0oFO/8AqrL97ctJJ8Snf5evJ61TReM/k5fu9H3q/a/+95Vx7SbXXG3+zslAx+XjXnWcV/1eto2dkkmd1+m93e34X73KdvDk8XfVxHGq4+dwD/37dn9rpRtZLOVKcknjvOq127WSQoJKX1ACxQFN7Zqt8/PGPda8gOdwQhHdQEu9m6LmKE1PD+wFssMUNxxoV+2JXxuxofOb/scmMh7noTvuVkQQAa+BSpUY0d1eZ1Ox0bFwzDA3v4Yx8fH6A8GGPT7ODo6QlVV2Nvbg9Yk9WGwY7skBxRco6Li0FjprxH4EkCN69ePkCQxZrMZ6rpBFEnUdYP1am2f6QzCuRcCR2g7nQ5OTk5w8+ZNC5AYNwRBYLtgs9XndDrF8fHxFqjr9/vo9XpYLpcoigIHBwcYDocAYJUDYRha3b/WVLi9XC5xcXGBmzdvWgzBx8oul+zeY6VahlxyXcNsNrMZFpbV8HXmaLb77O8ZVQkboTDA5sBhv9+3QJifE24dhhvNd+ssuP6Be6lxpoAlRmmaYjKZWCLAmaQgoH5XfIyPHz+2zklaa3vMRVFY4sfkjJUrnEHq9XpWPcKBYbamffToEYIgwGw2s9F9KaVt1ldVlb23mIDkWYbAZFK4SJvdpZRSGA6HlsRy9J9JFgDbPoHxEKsyXKzFOImvxa5pAd+TblG56xTFAQmWxnG2RAhhg9SMaaMowmQyceoxW5kVZ2J4neHsEvcp42sFCJRFZep+hlsEE6DANM/d53k9d0bj/bfeMu5KlGpyI9pNVUMrhflijkF/QDdIWSKKQ9SqwmQygdYaBwcHdntKabz/wUc2ldfpdHB+fo5bt27BFwKPHjyw+7l2/TouLy8xm05xcXGOGzev4ejoGFVVmvQhuTukm8zqNMuyhOd7WK+oaIf3wZo9BolFkSNJYoTmYvJCUxSFTcNZv2JzgdhbmhZfss2jOgTfXOjYsNjG6ku10cZTN226OFzAzAuuUtREh+VbfPNSpKFGo2pkWQqtNV597TW8+cYbmM/n1v6OJzXfzDwJeBLyw4jZelHklqW6hS9EgpIAAQAASURBVE2z2Qxnp6dYr9a4ceMGhsOhzTbxZ3ksuJAfoB4jZVXj/HyKLCvx1rffwq3bNyA9bfblwZMe4phvogBxTJE90oeGqKra3nCdTgdRFKA/6CHLUhNZiKx/dl0rBH4ICMCTnl3Al8slUtO52fN86iiuGhQ5EbX1egOlFYLAw88e/y2svRR91cX/Nv/jmE4XgJDYbAo8PrvEu9/5ABeXM+RliUYoNE299dDWmthCMLyO4U/9GUC02Q+WAgEwBN2NrdJH+O7bBlgAR3DZKrbNgDCgb+UPZgcQgjB7c/421Lv/GNcGEW7dumW0ogJl2UB6HvKiQKMVhCcRxTERNgTI1mtcnJ1iOl+gSsbQ174fcnwL0vSD0ZqzFa30qS2c50JultoYYMKA0D1v/lmYbZoi+WZ2H/l/9+ehmtYy71kkYxfYuRF+rTXyP51BD0g6FT8lo3HVaxes/U6A+8dt+6rtP+/+dgnGVSCb/716/NysRvudXQLNQPdphISP46rjbcG6uQ/s99vswC6R2SVP292g3fEBdo//6eeizFTlQJi0I8Bz0n52qwu2kR3ZiSod4mnOD6BGjtbQYTfDQnUOTxAQ2TaZdceU33P/czXsLKGi/gLbxiUAR73pZ6Va9ynarmefYy6ZoHOh4w6jEP1e6+gIaAz6Pdy5cxsA8NKLL8EPfPOcGqKqSxQFKQteeOEufD/AbDZFHEXwA4r61xVlyIMwwN7eHlarNWUt8xx+QFH0wA9QNzU0FEZGyrRYzOF5HgbDIZq6xnq9sc+mvf291pUnjLBcri34ZRVCURQ4PDy0naQZKHEkuygKUygd2OcaP3f29/eRpqktyG0DZAS0OcKrlMJsNrPAc29vz/SvypAkCabTqS3+Pjs7s+CY+0Gw8oGLnz3Pw8XFha1B4GvLgUAGv/w9t0WAK9VhssaZhSAIsFwusV6vUdc1jo6ObGB1Y7pJ8zlZebgB3VwfwOSDgXC/37c/8xxj2Tg3dKMiZRq3k5MTGx3n7zBo930fPaNuobrZ1lWp0+lQY+CytMFYzm4sl0uL6bjmgwkeE5JdAM4yLV5LeP/azAHXWlbr1mKZCbHNgDjSKz5/3g9jI56TTM44eMxF9DzmZVlaYsgkg0khB1YBsneuyspiOT4frbUxCWp7YrgkpG5asyUAWz+7x8NZl6ZpoBoFzwssXuRMBxNaVu94nocv/ciXn7oW8+u5icYv/NzPIQhC5EUOZVhQnCTULdpYhq1WK4zHYxwdHVENx8UZgoguxltvv4WbN29if38fw+EQm02GNKNOkLdu3cK3vvUtLJdLfPnLX0a+SbGcUUpxNBrh537u53Dz5k28/ulPo6wKZHlqXKAENmtaxLqdLqT0rXuT53lYGdvTOElwdna2VWDEC0xd10jiCN1uZ6vDI18EZv28SLsWYb4vUTc1uKCXCYzWGnESm8IuUxgUhZCC9ZMN+v0+xuMxZrMZFouFvTEPDg4s2+WGNoBGWRbwgzYSxSlSLl7im5cnAgDbrBAAlsul1T5yB8403disCe8zCAJIIRCHkdUM80K2+9DjY+bjSLMMF5MZlosNPBng7bffxs1bNzAeDyCERlGUNkUYRbG9+aVs04ekWyzsQ1NrjU4noSJ2Kc2c6xrtrLRaVSk9mz7vdDpIUxo3Jnok0RLmmBuzaMf4W6/9A6RBjigP8JV/+jp86QFCQno+hqN9ZFmB08dnWG02WJcFVsZtQghhCSHLPJIXfhCdH/i3ISRlsJRubRDhaqhFmxFQWrf4RBNoYWU14BANJi3cQEtsFwBbvKFNNkXVqB+/BZx/C7JOEW7OEcUxkpiiLzLwobRCVlL0RpcNinAEcfgqgjs/CBFENmqqDRChrAMfEB8V/c62sHwyzwKh9qVNUbyi4svil38G3ux9FEVu5xlv66roeitxeVJGtEs0ElOj8XGE5V/19TvJujxt/1dGp6/4jDvOuzUV/P3da7Grvd8lJ+6YP2t8nnXs9rjF04mN+xHDXcF1DE9mO552HNvSqbYOApbM2oziFZXpTB6U3rVrpX1KIcHDqg2hoOdBWwuxPU5tjcbTz1vb722TsvbFQNKNfPK4PO26uEGxp90z/DnaXgM/UPjEJ17C7/8DfwB3794lohGQ1CnyKHiW5zkmk0vEcYyjo2OqE/EEzs4eY7PZ4ODg0ATmWtt4aI2yqhAauU+nS8Yc3W7X1pHxM4oAFUWvTx8/RmCePW33aSpm5WJpVgUURYnQ9NK6vLy0oOvOnTu2U3WWZVgul0iSxGbjORMAtGDTLfjN8xzHx8d4+PAh4jhGv9+3oJYNVLjfAjs5MglhAM5KB45sP3z4EOPxGJ7nYTKZoCgKSzA4c1IUhY0gs+xoMplYF6g4jm2d6cnJiQWTrDrIjJ0715GwNSwDYiZC3DuDxwKADXjymDC41FpbgsOSNgbZi8UCZVni6OjIEgnGTCzD6nQ6liTwmLO1/Xw+x/HxMebzucVPTII40u4CcpZ3cQaBrweALRt7BtDcJZxl4BS8jLaclIQ5d+0EYzm7wxkldrxiGRxfY77HGBOs12s7F9qaY9jj4vud70GuGeFzYrLHahQmJ1EUIfBDlGVl1w+2meU5tFwu7ZxjaST1SSOixG5ZHEhg1QsHbgF28pSoygpBENm5wAFxLgHgWg8hBH70J3/siXVo9/Xc0qnp5cT6J/d6PcRhBF03gFJYr1ZYzOcUMQgCZL0emrpGGASIIh/j0QDTyT56nQS+FPjw/feghYcwSrBYLLBcLrFYLHBxcWGiEgk+fHeC8XiMd956Gz/4xR/At771LTx88BCbdIVOJwIgkCQxxiPqUlhXJYRQ6Pd6NGmVwtnZGQ4PD5EkCU5OTrBcLm3q6fj42HY4V4pY9P7+vr0ZmZGyvpA1j9zHAtBoVA0htAHKNYTUSIzOsyxL9PrbN3Jd1yjKAt1O39q88qLJDhvT6dR2X+QF7PT0FGWZ4/jk0JIojgawzIrTh8ys+TMsRWJbtjSlzMB0OkWSxFsdOFerFdVorNdQNbHp8XhsU51sEceREZaRMSjMsxzTyRQCPvqjEbQGzh6fQ0ogigLKQASh8djeGM3i2pIYikTkJrPEUSONLC2RGRcL6BmEKaISQtvFlMeXb2COavADNS8K2wm6qsjitK4bVC/VQEARwNl0g0AKxEmM42t7uHZ8hNF4jKqu8PjiEg8vptikKc7PzyGEwIcffthGfRVQ3vt1hLd/EN7xJ2FrKJx7qHUtIgIh4TyUAdvoz36HA6tb2QsG+q62mghAGzcGpOcjuP5p4PrrgFZolEKqKszv/Rr1XoCGCDvwbn4BMDKtUHqWAGmYlnnsrcsHY1IYQrMFL/ec4GOmLVCQl60st9cS4YwFQJsv3/86mrO30UBbwulGo9rNPwmudoFyO97b//738XqebMTuZz8O0D/vNrdBK7ALgNt9iyfGzCUGfP9cBVSvOq6nkbd2H67X3vaLgSmB49o8vExPhR2gflU2yN2X+zvXDTGxt3+/Qo5lsxTYzlTyeNKYbvdjon+p5uPjzv2q91lWy/vgeU71DvQ93kYYhXSHam1qwNro6e6YPHmM29d49/cojvBjP/4D+Mmf/CriJMZqNTO2rApQgJ9QlHow6EI1FYqywGI+xcHRAe49vI+qLHF0dIj+YIDT01PKOvsBoDU6ian5W62xXK0ACIqUSg+BH6DyaoRhBCEk5vMFPOlhJVMMuiSTReChLBpIIZEXpFOvSgXVCKyWaRvU60gbYZ2ZJrcPHjywtQr8HM2yzBIEpZTNQMRxbIExqxgYrLHWv65rnJ+fW2mPUgqPHj2y0eP5fG7l2/zsZTDIWQUG3px56ff76Pf7mM/nmM1mFlssFgtbP6C1ts8wLip2sx9N09hg4/Hxsc3MTKdTCCEwGAyswsO1jmVCxBFzBsI8ThzF56g1nx93h2ZAPBqNKGq+IwNisrBarWzxMwA71gykB4OBjZRzPQmTCs44MRaLosjug+c/kwveb1VVOD4+tuNYlqUtqGYpFRfRb51/VdlCZw6gck0K36dcP0Wy7cjeRyyJcp9VfC1ZWcKmAm6dslufwuSDSYUQwhat8342m9TOJS4yZ4LMz0yeq0y+4jhGo1oHLHbp4jWE5ydfb5vxRCsd5rnD9w1L+9zm2R/3em6icXR4hCgMERgNW1VQakpoQDcNDvb2EEcBoBs8fHSPdOoA0nSFNEqxP95HkRfQjYYnKGoMwKbqWJLz8OFDvPzSSxiMh1huViirEr/yL38FURSh2+ui2+tA69ouxnleYrlcmgZz2jhGeKhrjdlsiqOjQ0ynE8RJgrLIUVdk6ZXnGTlXRSGkRxEcXqQAWCbZ7SbQ2jS+i0N4UiLLM6hGIYp8BEFodKEByoLsYaGp98FysUQYBiiMTrRpGoRBCAFF0feGenM0NTXla5Q2lsAJNukaVU2s+ej4EHVdoq5LS0xI56xNZ+0As9ncSMgU+r0+kb4oBFBRJiovIISE75OV7qA/gO+3Or3A99HrdnFxcYHlYommphtnPl/i5OQYvV4f3/nO+4iiEGFMjXmGoxHV5JiJl+U5fOFjs8mQhxuURY4iT6EVdURP4gRKt7rF2YQ6lpdlgTiK0KgG3P1ba6AsCtQKyLICMDe/EKT3rpvaBkpdwON7VHzfNDRHhGygmgZKt6QkCOlGLusW4zdK4dHZFNAN/MDHg7MJfv0bb6AoCpRViUYpVEqgblo5gtbaznNC1hrrr/8Mul/5d+EfvwYhJNVZcNSfQbmmgk6ydm1JhglyUnQXoP4ujluThcwOEIElIPw2SyPa3wEBSA9a+ghe/BGzjXbfwmq2NbS7SSYTmlzPtG4zGByC1mYstkLTaHex9XL1U1yXIYB68iGKb/5doGmgTeduBsy7INh9uSCLM1dPRpefPBqnvR626dlVB+x+0vmrbn+WFPp2xuDJb7Wyt63QO3hQeJviiW251xZws2Hu7xZQ08SxJk9XEw1sXycGn2gNHzgTK8y81iabRXN6+3tMhO39CFiyQL9Jm2kTEKZmjU+YOkd7xg2q5vsWAlXT2PvFvSRCwDWx2jkW+hABtbYTtC3mltJuk4dZGItjCbZY9ex7ccx2pBvUJnjQMpf2mkkpUDdkNi2lZ+9Xtn21c8ReEwXf9xBFoRMxDDAYDlAWJY6Pj3B8fII4jjAej3H79m3M5wu88cbb+If/8BectbCdGlT83ZLENmtCdryelKZOijKIN29exx/8g78f3/fZV7BJN6iKAlEQoNdJSOKkybhkOp1ASg/SEwh8D2VVYL1eIQ5D9HtdVFWJy/NzdJIYwaAP3VBwwvc8lEUJrYGD/QPUdY3Vak19ezpdZFmOuqqtRX4jJLq9PooipxqMOMJmvUEYkuwEWqPb6aCqqelmYUBZr9OBkBKnp6cYDgbkaGQUDXEcY71agXs39Pt9aAP4WWI1nUwsELOyYGMFaoN2noeFiRhz8zJ2XOSM/v7+PgaDgSUv7MzImQh+j2snXIDIkXe+T3kN5A7OTBY4ojwajbDZpFgsljg5ObEAs64bZNkaRVHg+PgYk8nUOmXNZlTAHPgeOt0utFMDUJpnZ20AamWkSlwf4pv62iSmyHYSJZDGNbSTdNDpJBa8c/E23yKZiZxLKRGZOoBNmqJjJEq8z6GpPRFCOD26FA4PD61kqqoqp46HPsNKDXZo475mrtNYGIa231CjGqzzNaI4goCA7/mA9FFVta3JglY2GNo0DaTwUBQluKFkUZSoyhJCii1nKSZOVVUh3aQo8hLD0dAu53GcYLNeYzgYIc2MGZD0TE+2EJ70UTc1sjQzmbUCcRTD8z1At032eN5wjQqrcDjLwOSBgxNVWSNXBXpdMkiqKyL5WutWQUJgClKS9XGRtySZM0eu9S/XZT3P67mJxvHxNVRmoje1wsXFBS4uLrG/N4YngeWSMgMQGptsQ+5BfgBPeKhLuoDdhBjRptggjBN4nm9twYqisGm1sirRHfYRJTHyIkdVV9jbG6PX65p0a8+esFliIYSE5/kIAgbIM1RViW63Y90c4jgCddneIAg8QCt4HnVvnOW5tZtjFyVKRy0QRoFNhbGcKgh8FFkOKI0ooEnWM24Z2nQ1jk2Uvpt07ETYbDbwJBD4Ek1TA0JAqwpVmUNDoKk91FUJaixEPT3KokCnEyHXNfw4RhAGNsIFTRr3JEogtICERJZm1Mk8AHpJF2mWAQpYLSiDc+8eOfpcv34CAeofslgsEQQUBahrdhERqGuFx4/PbWRlPl9ik6WIk9gUwHuYXF5SYaMWqHJjw9goqLrGeDzC/sEBptMpplNa6PI8RxTH8KRE0klw7eQG9vbGiJMY16/fQNc8OLIsQ600orhrC83KkojlgwcP8NtvfBMabgFdbReettMoO3eY6DkABYqasj86L+6bmtLEom6AvKQHDY8xDMDZirC2Dd1422hqpL/0n6Hz5T8F//g1wIAX7QA/5gAs7xBCAEpbsOhuTxiCwlkA+iIBGWGAuksoNIDWkddkHvhntKDEOQnAar1bm13zJT5QAsl8rKDv0G4VZW64268lSrTvNtsCC7RYUgZoNLN7yL/+fwcaInNUAP9klPxZ0f6Wa7Wg/gle4nYtfgrg3n7xQGz9hb8EV54jbB3KFZTFEoUnUztuZNxmJRz9fkuyzBwQbcbC3YZwzt1yUrRR+SvP4KrzNgSyrNje2dRIiDY7IJxHRksmACEUEZwd4g8AWlFRNBPGum7JsNbUnFWItj6ChpN6MWwRYueY5RVDbc9S071JH29tgJVqaF4KtnWlbSpNUXZpyIaUkiSMGqirmvo66QaBT5kN6qNhrGVl29k6jkI0hjR4nsRoNES3R72BAj9AkiToD/oYDUcYDHvY3x+j3+/ZQl8ppXX3IVekzGr6kyTGZNLFr/zKr8GTHipNQMOOD68vpg8VRUiNlazSQKPhCeqPsX84wvd/4bP44a98Cb1eF1VRoSkp0p2mKRbTpY1gzhdz6u+gFHIjaeTahaIo4OVtPwQBAVUrW98wmV6acyb9fRD6CKMAZVUgzTYIQh+9PsmP0izFcG9onR/DiGy5q7rAyQlZri4WC1QNRdRDEaCoCmg0NmsRhaG1h6+rCtAalek7VVUVxsYBaj6bbUXg67rGBsBwOLSuiwyiqpqiUU1dIzQy7IUpBmeVAMuz2N2PQTDLa5IkweXlpY0AU9+otS1I54wW16Bw42OWznEmgbMcw+HQBEF7NiPEsR7GQb1eiNlsbghKhSTpoNejpnFxGFBD5DCkdgBVBSkEojDEcrmkMakq+J6HzXoNaI3D/QMrORZaYLlY2jXq+PgIEKaGVRDB1MbYJjZzgzFVY6RcPSPxloKaHRZFgYmRvpH0PIFvIvqz2Qz9ft/OMwa8WZZt9aoAYMeWi7IZ+0VRhCSkBopaaYRBCN1oKCgsNgubzSmK1LovedJHXTW2boLcsKS9LlTIThkKNhRgG+Q4TuB3TbuAskaekcwpa3JoLbBarW2goNEKnvShNa09gZCAFlAK8L0ASmms58sn5hWTN86Wuc8NlmllWYaiKE2tUojZbGFqVzxoRfXELl7qdru0b8dimK+du492rf0eZzRe/tRrVnqy2mzwW7/xG5jNZsibCrIm1xzPnLDvB+AulL4X2oKpg4MDy4w2WY59MxG7HdJuXjs5wbA/gO9T05emojqFmVkYyJ2pB2rQx23ePSRJDHYLKQqS2Lz22msAYIkDOxrxyx0sttPjv3PEvSxLZPkGfdmHUjCFzKTPWy7XyFNKMQ6HA1DX8AaeF0Cp2gDqAq49K0uk8pxSV1TURNrHxWIBaKDT6UJVJHXyIJEEVBOymCzQ7cSo6wqB8UUuctJ45kWBpiyxyFKohqIUnu9hcn6Oy0tyYsqyDEVZoCxK3L9/DxcXF+h0EhwcHmDQH1h2DQ1s0g0C30dVV1YH6HumhiMMEQQRTo6u4fXXX4dSCtPZDFVZYjZb4Dd/87fJoSOO8ZnPfhbXb9xAXVW4cfsu7ty9ixvXb0B6ZOfX6XRRlAU6cYLlcoXZbAYpJSaTCebzOdI0w+V0iul8houLC8wXC9RVjcVijizLsMkzE6FQUE76lAGa+zDhm0IbAKWFeqYsZ0szbRYEV0v9RGTaueFUVSL7zb+B3k/+hxBB7ET/DWCCNYGFJQcGMGoDSHcjtvw9CN1+14aW3c+gjWqbCAUTDG5e1uJyJj07YNjBxNpu1DlHJi8GjFMk3Nk+j49LPDTZYDPJUOkE+Rv/DdWQqAbKRt6fb+HaGRi4MpuPW/x2ZTZP32i7nbbInc7Hk88jL2qJxFX2qFsEYed4WFJEvz49u/P0fQNMPttxvfp7liTytxQRCinYWpgAquDsxNbxyvY8REtGbYYDAvBMxkC2bkq22ByAkK1bEp8jvWdmq21eyef/ZB1KSx4cUqud3itm/HyPM4H0kUYpkFeehm8av3E/Dc+TiIMQSjWIPdJd7+3todvtYjQa2Yf97du3sb+/j+OTYzQ11S9WVQXPlwgjD3FEtpYcqSTZRIPBgCS54/EYRVHg7OwM169ft+OzWMzR7XYwn88wnSoslys8fvwIni8QRr6NtvP5U1PLGp5H8yaKIkRxjF63iySIcffuHbz66su4c/cm4jjAYjnDfDG18g6uD3j8+LGtP+DoPUth9vf34XkeLi8vrcMSyzFc8xSWHXM0mbfPchSuP3T7ELBJCTsZSSmxWq3w1ltv2QJmlqjwc5cDT1znwIW+rMFnpQTr5jmrwRkDnlNsg8rOPm7frK0eD+ZveZ5jPp9Tsz+nYzVHtgHY7AWDQa5vYAMWjkYLQRaj6/Uae3t7AGBrKV1JE7s7tn2yqGaSrx9n7NlOdTQabblBsSQs8ATKku4HLlBnYMoFyFzj4fu+mQtUE8n1Hnx9bE+PMrcF7uQiOYSU0taGlmWJ8Xhs+0W4mQhXYjSdkuW+QtuQ0XW14uvlSr64YJklcp7nodfrWQcyrl0p0mLrmjNJYek2y8T481xb4/s+0jS1tSk81hDaqGdq2y4B5rh9rzVM4jUoTVO7didJYu8LJqecqeA5bGtIhDB1zZsnajoYT7s9Xdx6I54LJEfPtmqTeQ22tblmPN3njCuPcpsQAm2d7vO8nptolKo2bFmi0+/i8z/4Rbzz7rtI12vIujbSFOpA6MkAvqlYz7MC5+fntki33+/jzp078IIAeVWhUQ2C0MN4NMR0OkWv14FvnA7KvMD+/r6dgG+88QY++cnXEIaBHVTuiVHXlSkILm2UwE3l8QVlbSIXC7FGjWsZePFerVYmVZljPB6j0+lQbUocUwHNqIOZmkIIIE0zxHGCosiRpinW6zWRqc3G6ts8jzp5+kGAqiKCVNeV1XN2u12sV2tILfHIFK33jE3acrmEamoEoY8ojDAYDgAjC9hsNijrEvPFHJv1hh7uovXbriugLCvkWY6yKhEEIQa9Icq8Qn8wwHK+xmyyhAaQmJtdSIFS1YiiGEnched7kEKSO1cU48s//CP4kR//CSwmU0wml3jttQ5G4zHef+99XL91F1oDh4eHhnnTWF9cTPDW2+/hm298G5NLIhJKK6xWK2QpdRVnXSFfW6U1lG6goOA61WhN6W1I4/yiBbQw3tNakSxH8D/CZgIYUGvl9IHZeblAbhf88P6f+A44+2Ai9kqhWZ0jf+PvIv7sH7YRb2kAnc0E7IAzyho4gN7exG0RduvytL1//n9rgcs69W3GoJ1fhbsBTgvYbEpLPuwZMwly9i2F4M5dJsNG3dC1SY1syZu0onm7ucDmn/0F6HxpJYV2vNsUzdZ4P2tB2yJsH/fZK9676m/aiRLTZ9r6Ffe4rv7+x+1D7Pztijnl9GARphiZAbYUTl2AvUxXjZOTidghOlYCZ79jZzG0ggFzbcau/cyTxKjdZ5uFcWsIqEs0bFbULYakG1jAyr/MYXuCMg2Qwt43dp/y6scWZ3x8KW2k0c4JQ7o1avgBgT0BagjX6XTR73VxcECOfzeuX0ecJDg6OoIUAscnVPwMDdy+fRtpukFdN7bQlkFE0zTwkgBR5EGjwv37H2D/YIz3JxMkcQyltS0mPT46sQDABYkPHjzA3t6eLdpkC9woijAaSfzk7/4JPH58gfl8RrLd1QqdTgeHR4cIAoE4iiCkwN54z/asCIMIg14fgEaabpAXKa2NQgNoLHBWSuHBgwcASDJ2eXlpaxD6/T4Wi4XV5jcNdY9mC1MuLuV6BQZyvV7Pau0ZhDJ4ZpdA17KcyQKPDVuccmaAwTpLiDjDwgDYFs4aKTRfGwaMN27cMI1k6XnBPRgYbLuulK75Cev6G6WsTS9vl4mlq+WfzWaW3DD24QZ2bGDi1jrwfTOZTKzVLt8vrnyKwTmNR8eCRs6U8L8srVGK+jrwWAZBgKrI7LlxzQSPJdvxchS/beimISAtbgLa/hJA2ySXCQTPW85mALCmOnzN3RoEJilc/K8Vu3TWVs7Gx8oAl+cCF6CzvIzraNzAYBiEkEHrtsT3FGNDJsJubQdfM54fTGB5/MMosA5jLGlnosyBZs4KcONCJhBs0sNjwiSFMza8DWXmG5Mhnhdc88H3Do8Tnwe/eA64CiCeG5zxYIMjvud4jFje5+6b98HE6Hue0YCUgCQgpwUQdzv4vs99FnmaIVutcXl+hsenj6DqikBpnEAA2KzJV/nk5MTasJZlifligcFoSF0p9/bQ1BUkNKaTS1xenCMrcsRhRD0ztEaeZTg9PcXe3gjDYd/cABk2m5XVSC6Xa8vCPM/D+fm59XPmhfDatWu22QoVJa+tto+jMrxY8LbS9NTqAblIO89z5Ju2H0Se57i8vMR4PELSIbKkVOv+wRc7DMmjuFGNif4qFEWJ+WwJKSR0Q+lEZs+NUrg4P0cchU4fE4qoctq/0QppnoG7rNLl8uD7HpK4B9kIRImH3oCaBI3HI7z+mc+hUgphFMH3PBweHNrupJ1OB9KnhxbfVOv1GqvVCpssx2/+1pv4+i/9OhZLKuDPsxy9fg/z+QJFVWKzSe3ipbWG0opsa7HtrqJB/Ra0MhhWStMMzgHaguFS0zamEgJCekREWE5kiQDazzmSGqVbyOFGNdzX026cqwovd7+3fasQkCre+0WI0S3EL3x5S86itXIO2ZErOfIXjsha2mCzFy0Q5xoPLZggOOSCiQOcsTTjwmW22j0fE+Xl7W11Nnc/A960I8ti6dQVJIhlVfzFZjNF/i/+MmS1gRJtga2bGXBJ3e7PzyJ87vWQ0rET3iVmV2x/90V/343ebxMDPh73uOmwtnsW8Gfcgjt34W8zI1t7a7etBTzpSKR2+IlLcK/gM/YH6Umops0GSCv/4uOg+gMiGFf3ELlqzNpx8Ox58kOrPZft8eDtaKWof4wh4PyelNS7hkDpbt8Huic0tF0vtAZ8nx66/V4CbWQAvX4fBwcHVFM2HCJOQly7fo0in5Jc7IIgwOHBPqoqg9JkKHJujEniOEavR0Wki8UCl5MzDAZDSE9guZpBerS2h1GANC1M4CwBRIjbd25isZjj8PDARha73esQQiCJu1itNhZsh2GIo6Mj28yNo/Se5+Hs7Az7+/tYr9cYDvt45ZWX4fskO75//z7VL3a72KznGI0GNrq6WC6xf3ATZVFgvZlTxseQC6VqhCHZi3PzW2oM27fORgzyuZv2/v6+lRb1+30LtJk4cBM47nzNEjCOhDIBYHDMP7vGJxwx5eZmQgiMx2NMJhMsFgvrOsTR2vV6beVWSZJguVyCpSxcsMtZGAZh3OdgsVjYQCNH/dkOl3GKrdkwc3o0HsM3QUm+D9bGiZDBM2MOxiFsosMdybMsw+XlJQaDgb2u/BnOJPF9NZ/PMRgMbH8vCqrWxvmo7dvA4JDPjW1kOaLOQDdNU/S7yZaJC0twOKI9Go2cNZTGKctyFHmJw8NDCzhtEzuh0ZS0L47UM0DlOcwAlnEUkwXO/jCA5vGGGSe387ebZWDStjL1N0xw2DqY5yZH5KUnEfmR3SfPSx4HzoAArdsbA2yWRDEu5PMUEtaqn9ffVsYX2zXLLdTmMWMSwQDfzcp4nmebEvK+uDg9z3Or/GCixDa3fF24hoWLvW0drrnf+FgZm3IgXNi1lP7jDvJM7LXWdp5yUJjx78e9nptoVHVboe8C8TAKkUQH2Ds4QBTHeHjvHqqCotOb1Rrvf/A+kiTBYDDA+fm5bX5XVSUe3L8PpRROT08xn81w+/ZtvPvO2zg4PELSJf3jZr3GyckJ1us1lsslLi8vMJmcG+eH1qmkrqlnRZrSZORCILdwi7MHnPXgTAZnPrjQiyfFarWiwjJTWEgEo4CUAukmReB5WK83GAwG2NvbRxwnyPMMRV6iFAJ5ntlJ3zogiR2GL000hKOYVLgnpYTne0jiBP3RGEWeodenYqkojDAaDeEHATwpsXdwiMT4UMdxjOFgYNKkHVOjQM2BtFKIk9heu2WWYTKdoiwKvPvhR0jTDEWR4+LiEuvVCsvVCpvN2mSCCvs9jda3mwucBSgFacEoGC9zl3gNCGUwcAvoBQS0YHisLdjgaLgWrWONVqZJndZGguNG3mmfSjMwF+1nldpCm/ygetbrKkD1vOydXwIa2a/+NQitEd75IYrsQptoIm8U0IJdZAxglQziHZDPBIB/3v2MYLkJjZWCNjUSZl4BTmE3LOkgNK7A4Jj2QXIVJ37fkpOt77RCLJZVbuVD+BqZOg61mSD9538Rfp1Cy21HKTvWQriXyj7gnxjbXZIEbEW+nyaLcxfT3XqHFsRydJy7SPM4ttuzndF35ghtw11WHfmStlzORPBb0I2r5pZDUIiQmt4kTNxEu32AZD9PGyNLdhzrWNbxt0THo6Jfc95Xk7sne184e7QkgLMhQrSF+rsF/nTMkpRVhhQrRaAAoPvCDySikPrsCCHgBwEC34dnGoCxjWkURTjY30d/0EcviZFnKZJOB71eF4M+Oe/MZjPkVWGjt3b/nsZms0RRUkT1wcMHCMMQ6/UKQgDL5cJG9ouiwHw+M99tJV95nlswwpKh9XoNz/PR7fagGoVGNciyHGEYYTqdQam2LwP3RmC5C0s1WGfOzw/PF1gsp9jb28N0doGqztEfdLDeLNCUBTarFZIkwTzLcOPkBNOLCwwGA0wm9G+SJIjjxAAFCUCi20225BOcfeAuwLzu379/Hzdu3LAghgtfWb7BzWSllDg4OLBa9yiKrGGL21vAtVtnZ0QAFkiyGxFb4HL2yO3dMB6PkSSJzSjxs7bX69kMiCsdqesae3t7W7b10+kUw+EQ6/V669nsNhRkgsMAb7VaWRDW7XYxn8+NHr6wzxe2VeWgGzfyA4BXX30VSinbEoDVCXy/M5hMksS6IbHEiLMrda0sIeLsCbteuW5FLMWhOtFtYMnky23ma7GdyUZEUYRerw9osSVjYovbIAyQ56kF/5xZYgLLQJgzBgziOfPB8jM+hn6/j5WRdHFfEz5GHj/u48EkgIPJDMj52td1jfl8juFwaJUN7ILFhAcgssjkLAxD20uDMwe8fa21Iztqtly4mAyRMkYjNPawfD1Y5cK2tjwvWVbGJIWvtetmxcFe99z5M5xNc0kDZ2OYFHCgg8edn488f/h+1Frb+5vPlQvt3Wwfr3Ufh6Psk0E/J3qaLygd6nkeSUG0pii1VgiDGAwHF9MJHn70EU4fPsR6tcLhyRE++uhDXDu5hrPHjwFBHaIn0wkuJxeo6xpvvvkm0jTFpz/9aXQ6JMOJuz1EQYj5bAatFP7ef/P3cPvWLZxcO0S3G9sHBRf71HWNpiaJCbPtzWbTpuLMReBJM5vNMBgMzORqEEUhNpvUNuJj4MfuG3mWw/PbCVJVFTwIS1q4MzhrIfn4ODOhtYbn+5CCLOd4ceHOi77vo9fv4/D4BJ1u19wsMQLfR13VgAaqusZ6s0Ft0uxMpJabDOs0w2q5wnw+w+RyQprTurJFe3mW2bQvLaQNKk0QsgVTNFlJi6pRNw3gwF0pJRpFcgb380pTQbo0bg0c0XfZMZMCbm5lcxoaoOplvQNoHHAIPs5tkONKI+BsTwgXt10xvQ3IBIDlvzOD7muIlcDgZ8aWmLi3xdMyHfZ4nc9dtS8IAbH3Anpf+p9BJmMoA1ItRtTm2NGCSCJbTp6Dty24pgOms7ghBTa7QG8+Ke1xMiG8TQGmDxyj3x578eS+7a9aW7DNnc23B7+1WFWbCYo3/z6qh78NaYpzFRNAZxzNgMF2RNftv26EbXt4+di2m7sBQPrvLu217f6nwyevDWALe7fHiomGb4jS9nwk4tQ8ZaFtiUabKWjP1Y3o8++7+3Z/p88+nUC4Y7ArB3waIXAzKrsZhjYr87T9tPcOva+dzz9pD2u3wfeB+Q6RDsBDgyj0KXsaBrh27ToG/T40NF795CcgPQKtVJwbQAgjiVUNer0ufD/A/fv37XoKrRF4JOlr6hqbdIM4IpKw3qSYTCe4fuMmVquVlW7keYY4iiF9H1VZAkIg8E03Xt+DJyVWJuq8Wi6R5wVu3bpJNpdxTHVxgY/5bI4gJCLkB+RCyMXE3W4PB4cHeP+99zEajSCEsACZC8DdXkKDwcBGoOM4tsDz4HAf88UceZ7j9u3bWBnplNYa2WqNOIotkIMBUnVV4fDo0AISijaTG1VZFKhqAvRulNttGsZylH6/D84kMHhM0xSHh4eYTCbYbDa4du0agFZWw89djtry97lAmgGhWwfh2m8CrZyEASLXXvA8ZPlKr9fDZDJBVVU4PDxEXdc4OzvDYrHA3t4e1UEC2Nvb28qgcPSWrwk/01nrzgRHKcpEF+Z9Vw7D4DuKIpt5YXzBBMW1fHUxw2KxsBkcKSX6/b69DpxdYcKXpqnTa4PWPCZzLAvnzA7PIZbheZ6HJI4RBj7KsrDHzGQCgCWHHCDln4u8gO+H9jg4aEvBUw3Pl1vdvHl9cM+b5xPQWmgDsM9bznp4noeyqpAb0sb1CUxEXMkTf58Dx25NDZ9fWZbodrqoygrQbQd0/h6TTs5cuY5NTCBcYsxAvawKm0XlucqmP03dZvLjOMZ6vbZzarcOgucHz2eed/x5nhecaWHcB8D2wNC6lcwBcNxJpV0P+Hx5e0y0mFSysod/5s9yXRE/Y8gkaWnH+ke++qP4uNdzZzS0agw4qMmhw5PwJKA1MTvfpO72Do8xHO/jzksv4+133sYH772Fuqnw9rffhNDK4J0Cp6enWCxWqOsGoR9AJB2URQFVNyjKApASyjCowPNRqwrz5QxxHECrAYQUqKsay+UGg34fgIeqyNHUZrJIH8P+EEVZWpBO3VIbZCjheyEePDhFVVbQjYBq6IKX5ZmZhI1J35MmUIPdUYRtsiYEEEV0MTl1e+3aNZxcv45bd25DGXbOHUq73S6SKIEviV0ulkssF0tMJpcQQmCdZji/mGHz4UM8fPiQrFXLEvPZDJPZDGuj7eR0Y8PpLyFRNdTNkXEea5Sl0SsLKdHUjY1NawqNmghr2wlYK4WqURawCkHaeq1BTkNaU1QcFKm0RavGaUJDo2kqtDCrBa1aNQSaNBW7MslQrJ0CY+4W2HpCAsZVA7rNRrSLWbsnxRFX7jGhATiyHfuSLYhvX60bFDWGcroiCw3dEBmyYIkJFBi0t6DSXWjt/TN5H5t/+GeRfPlPwj96BYzitVJWAsXWlLRfzk4I24MPLIkSIG7GBbr8N3MwQgBCt70EwGemeStOVkPa0zLb4ai1tF8R/AFLKJQ9fkC3/TT4s7zHpkT50a+g/MbfBhTdOzSNlJWyPQnURUumwORUOl1DxNZY8ySTQtq57IJhu1Vh/mfnNT0gd9s7uFSRsPGTZEIIDwre1neEIdGe8AC9TdhoO9p+0vO2yQV9lsmgs0UhyB7VbN/ODfO+73nQYP0tp7GFJYBSSmPZKMD3ss04mGyKNHJF5di28v1LNtNuXk1ACEMgzKDSPCHZl+dLGxXnyG+320EYRtbjPwh8HB4eWqBx/doxep2EXGacDvRNXaPTiyE86r1QGmlrVefwfIGmblDmHnRQ44U7tzCbzbFZrwnkJzGCKAS0huf5gCDr2cGgj6ZRkBAIPB/Xjk+oE7MXkLtUTeBjvV7j9u3bSJIE7733HsbjMU6Or+Hs7Axx3MHe3gE2mwxFUWEwGGE+nyMMI/h+gMA3NqmNRhCEaBqFsiqxXq+tzKEoCqSbjZWoHB4cYD6fmyJSAkuz6dQYfuTwpMSN69dJ3psXGA9H6F6nAFoVVlgv11TPB2kzz1EUo9tN0Ov2MZlOIAS9R12uK5RlZWcaEwFuNsYgBaB7lesmuA5is9ng/PzcgibK3HhW5sLyEDYS4WfL6ekpVqsVbt26ZYt0Ofg3m80wMq5QbuM77qztqhQ40NdmxQjsTSYTq0i4f/++DWj4QYD1ZgNIJlY1/CDAYrnCer1Bt0tmMIvlEtdME7y8qJBID2mWI8uJZF1cXFBWIs8wHo9RliXOz88t6ONjtUEsI3/r9Xq2yZ7W5BpFZiepJXhMwhjIcc0oqT/aRoLL5Qrdbh9xnNjmbRxh57EpigJlXqBJKoRBiMDzkSQx0jRDWZQo8hzDwQDzxQICAp2kS2uspHWxrhp0ki7mxQKNytFJOgiCEFJ6WxIdLgb3ffp7FMUIwxhZmkJIIutKA3lRWkJGUq8esjyzc6XRJAVXSqGqGxSlsbCNWX3Ba49EnmcoS1rTmHClae5YZgu6x6UH3w9RlktEUYxNmiLfZNaMgBsncoH1cDQCBJFWrl+rqso+77mGymYWPbLRp59bp1KtiWxIoay0DYAF5QzsAdjfmQRwVpBJBY8X0BbGuwXrrt2sWwAuZduPhIMXrpMqB75Zasbz1T03zqK4NUS8HnDvtee1tgW+i4zG+dmpAbHanpjn+5CQKIsKTV1R9MenGoQojgBonD1+hLe/8U38y699DYNuAi00sjLHOk2xWVFxNvuPM5vyAx/So07PeUapq8lkAs/zsL+3B9VU5qFFJ0pZBAHdENNr6saQA6Cpa0AAShHZAFpXkaYxzkOaH+ISnnlIasA4GAC+56M/6FMXxk4XvV4PR8dHODw+xGA4RBxR47vhaIROtwPp+bhczDCbzbBarTGdTZFlGR4+fIjz03Okq8x2BC+L0qbLYMBSoxqLeOqGshlKALVuI+08ichi0SmEBUuVWnbO14wnNIMnvp5bE8IAH+nUU7jgmRcYlk1xBL6VUbXHuBuF3s0U8GeuerVRbM+Re2xH6bmTr7uP9liFPTaOXtiXbIHj8k9OofsKYiXQ/5m9rWN39Yf0fb11HC6YdMeV92WP1yUfng/v5ucRf+7fBLzAGV9pcwtcGKtN1kI4x2uLeNsL7qZUjKTK/H1LowVwvQd/DXz9BUug+Hhh922D6Zodq7ThcO1n7b5FK6/STYX0l38W9eNv2cVva0yclwvmn/U+S434s24R+VXZsNW/M2uv7X8+MsSN/hMg61QtlD0J994SQkA6ZMItngZYooetzwtJdSosI3OLEemYiPRznwbK0NmrAbgZJdB1JwlSK5lyx51IB8nSXBlPK1Fifq2tHIr350lhHhod+zDjtUKpCuPxmOwpjVSiPxhACuDoYB/9/gBC0Pp58+YNQAODYR9CKtKcbzboJCRb4ijycDgy8pkBZrOZjXwy2OD18OjoqNXNqxphFNruyyyJOD8/RyfuGAAU2OLc2WyG+XyOmzdv4MGDhzY6y77+o9EIAMmcBoOBffhytFx4ba8CLoRcGSkSN/viCB9H4ZfLpW326tYouGsug3eOdmdZhsCnjsQ8Bq57FN8v/IDnDtpCCCuJYNkSy29Ym85yEbZnnc/n9vryd3kfXIPCBEJKiYuLC4zHY/i+j+VyiSAIrMHJK6+8YqVJfKwHBwe4vLy0xeKsq2eykiQJ5vM5Xn75Zfs+F0S7EVfOeHChNMuTWEq2XC5t89jZbIblcolr165BCGHrSVg+xRp1mkPKjqNbeE5R3NhGeVkylaapbXI3mUxs9oaJFnWyPrR2uyzNOTg4sIXlvV7PduhO0xR7e3v2ecL7Pzs7Q9M0ODo6skXwvV6PiK+RqtAYrNE0aqtnAQNBzjIxieXnbRzHePzoFGEQ2MwOuzExQXOvIVv18nY5O+Bq+1l6xharrryNMxw87pvNxmaNsiKH9Npu4py1IGLSNkMEYIvZWYnC9QucEWGZEmcBGGSz4Q6fPxcq8/UOwxBlUVgXUx4LBvR5nqMxyg4hxFbWQgoJz5A5fo8dyfhY3Ayx+8zirAvLxYDWuYmzdCy147HhIA2vAa65ATup8f3KmR3GzXytAFgzIPdYtNZb9cicueBMHI851ya5zxL+mYvyAVgr35/8qd+Nj3s9d0ajzgtQMzV68CnVQDQadUOR+SDw0Ot14aFCUeUosgpJ0sP++BBf/uEfgw8fb337W/A8AeHHyHOgl0SIgwRVXWOz3kAJIE9LNE2GMqcFPYxCQAOvvPAqZrMZNss1ijJv2ZwUpnleBAFpm/F4HnXv1poi8p7n2wfTcDhE0ukgDEIMhn3IoGV63V4PvV4PnSTB3ngfSULaxNF4DM/3UOQ5yoI6VV/OZ7iczXF+8QEuLy+xWCyoy+dijrkpoGqaBnVTU8SMHz5164lfm2gFZRgkGk06OSnaBldCbhfv2DSuZnlCGyHlzrFRFBuNX+1kNlrQwzcVAxLejp1Yaht8uT9zihFmbC3IU3oLjLnf2yUsu3/bvUktMbAEZjsCbsG52C645VdTNyZKu51lALaj1rsvvtE5WuMeCxMzvg5M9IDtVDCDBq21yfI449jUqD/6VazP3kL8pT8Jb3SrJRlOpkBpbYC+AFRbwwIpbUbJDM/WGQn+XVN9C4NNK0fiTI/9blv3QRvYJhmc6KDr4BCMK/ZtiVhTIfvln4U6f9vOse0I/5NXYPv67mYQhPN3hywJ1hnbT5q5jJ1tCEgRQECa71A/BAAQkrM427UEQggI7WYetrfpZky2sicCtsaA/87k3D13AbqU7fm546AtqeD6Ft+nWgL+IEUAKTghQPVc3NsjjiJEcYQookLmIAgwHu9RszJtiqQ7CW7fuYN9A4KqukYSx9SMVDXY39vDar0yXv308NJKQTftelUacLperRDFrcXp2DQf4w7HQggsFnMrZ2XgMpvNbO8GLuhl2UxZlki6CTbpxkaJWcPM9yNbfXJUlyU5Z2fntriZwQlH3xl48H3L79V1DeXIhJi4HB8fb4FQrbXtktw0jS2Q5iJdNiE5OjqyEW1uIHZ4eGiBqG8AIQMABgl8bFEUbUksKBNBn+UiWJZMHR8f294KXHMYhiFWq5UFvwwguMg0TVObQeDnA2vrm6ax2xFC4MaNG9hsNjYg5kZi2eJ1sVhYIsR1CwzkgiDA2dkZfN/H3t6eJTVaa7tNBrC9Xs8CfbeRL/es4GZ1DLyYAE6nU1vD4Np4xsZpif/GAHdvbx+LxdK6CTEhZKlSnud2P1wXwURZKYXlconz83O8/PLLlpAzOWXXIz7P5XKJsizt9lg2xUTx4ODA1mg0TYO9vT3M53MALI0hUsA9IliyxHNwOBxaEsDA/dbNm1vPRG4iB8BeE56bw+HQrlGMCzjSzcSa5y1nvnq9nr1/WIbI15M/w4Xxjblf3fsvSRKsViv7ef4+Ex8G4kw2OGjKQQd2CeOaB+5J4oJkJjVaU1YrCsJW9mQAOtdGCCm2rI95377nIQhCW0vEjlBMkl0LY5YYMSnhGhM3W8X/5nlu5zfXYrjYguuTmGTwubC00PNax1R2qGLc4WY5+Hc+Fp5zfG+y7I7rk/kc+TnF2Su+1i72fM4cBYDvgmiIRqAuKyhJnZPzkh4I0pMo8hy+l6DINliVGYJAoq4L1EWKbvcAcZTgyz/6wzi6doD33nsPGsDhUYrHD0+x2WwwnU4B0YCKhRU1rPMllKrR1BQ1uXnzBvV3iPbQEHKyLBCgzuX7+/s42j+A9H3EZjI3BugJSX7mnW4XfhBAaYX5bIZNmmK9WWK5WiLPc1xM5njrnfdIC9oolKXG5cUlpd/rGpnRSFZNg8yk9RpbJE0Aoml2gBWodoQyJwYggbTXtbH8hJEgUI8HjUopCFu4C2jVRm/dG6gF3BzN5M8DhJO4YZzeuhFoQeFiUL7KnKoTtpDY3af91BWRfPq2thFtXuR2o//uNt2fXQLhsmlobG3D/R7/bTdTQ58XW9mW9gx3j8VNDbSLsHtMnM3gz7gLMo+BW2+wVXvQhpW3zyFfIf2nfx7+4UuIXv9DkOPbLZmAyUzRF+x3NABtMl8MfG0uSxArcEvIBZj8MYo1P9osCI+rk+0x5MPyFT4GAGzJy9eYiQWEAKoM9fQemrM3UT56A9hctra+OzKmZ9USuNcCEK00T3CtQuu+JKURFfFN4sqDdtZAKUJLpDlzoLVu3duUgpTtsdj7SbBWV9jvQQCeWcR3ibIQRu6klM1MwYMly55PBIGlXuyaJEwPhziOkXQShEFoHxx7+0PEcWglSGEYYDAcwvd8dHtds/6wjNPDaDRCHEdGJkBzhQMVUURufWQXABR5gX6va+ylcwjRYLzXR1GlGI/7+PCjj3B8fEwPLwCL2RRB4COKYnNtJKLYR12XFpBxYS0X8DIQYctLgBqX8kOe7VDjOLZ67DRNqeBWE8jcbDZIkgT379+3D9xO0rE6f5YedDr0N36IDgYDALByHjcK2O/3bSGk1hph0PrX83XlyOH5+fmWDIbB9oMHD3B4eIj5fI6TkxNr8ZrnZIvO0fLDw0MsFgsbTeVrS9KYykbyGbRw1J898tnpkM+Lvz8cDnF5eYmLiwurs9/b28Nms8GjR48wHA4teel2u7ZImiPMTPSapsFqtbL27cvl0r63WlGjV44sc2SUQR8DTw68MElhwsP9q6SUNpPBpJR7RLALEIMwdrfhebHZbMgK3enrwdknIcgNkgESF9BHUYTKHBNL1gBYMmvvVynR6/WwWq1s1JbnGGdM+FqRTIgySj0TlOSMFD8HXGeswWAArbWNFjOQZrDKpIaj5UdHRzQXzZhsNinKsq054TnAL84GsNTFrRnh4nPrYNm09v28HXaJcq8RP/+4gJivB88JAJbs8PjzMy9JEnv/07rW2qsyBtFaWxDtGg64xdhcwBxF0ZYtMl8zljJx1tB9JjOhYvcmvreTKLZjxvMqz3N45pg4Us9AnSRQrWSV5wgAS0Q4g8kBCvs92fak4GvE0kLGKHy/8LHz+zwOvD3OQvI58TrL33NraTjYwft1rxPjv263awvzOajD15AL9Pv9viUqvEbyve+qQ558dl/9em7p1KP3P7KTWAqJsqKbPIojdPo9QGh04hBNlWG5mKEqM8PGYuodYVi8EAICZLOYpznCMECjFLI0Nam4GlleQIoAcbdLmidQhFcKiU6nj6o2F6musdmk1IiurLBcLJCnKeqmwXw6xXQ6xeXlJVarFRarDTZpiqapbeSGLqCEEhJ101BHb8epiAafCqLNcDmRX4lauyAd9kJorS2o00ZKwZFkbljGINRGxKUEJNCo2l7AFnwrQDWQoo2W86RpmgZKC3AnXM5o2GyFJJDMBUA8wYmBM8Nv0DTbch8B3cK9K4iGC8Jd4sMdQnkBv6rg92mEwR2/9v1t0OhKtyBgdeS7BVas+XFveLsvUAG7EALrP9UWg/d/Zu8JAtRmXrZdjHbH44msiRO5vor9b0XwhQQiihCJqI/gzg/CG9+FHN2E8PyW4yjd1mWYP8EU17MWSriD1YbJnb+1Ha0hnswuuJF1On8zYqrV8Nvx0A2qB7+J+v6vQc3uAVW2tT0h3YyAuPJnNzXbZueuth/mmpXdbfB2+MVz8fKPP4DqNZBrD4d/9a79ntYNPE+iabivwzYh5ntMGqKllCK7aiN7qpsaMPOb57jvU+RLCgFPShsJOjm5ZqPK164fw/ME9vf2AVAPh5PjE+MEVyFN17h27ZoFx21U14cGdcLlHgsMStM0Q7oheQYMOJCC3JkuLy7Q6XRtJpajiUVRIO5EFrglSYJO0kFRtq5JLnjjQsYgCBCYsbIdnE0UOM8LeF5o0/hVVVnDDbfwkh+eHMmLoghnZ2fWlpPBUVEUKKoCQgpb6CuEwOXlJUajEQbdAU5PTy2IZkkIyxB4n91uFw8fPrS2nHt7e/jwww9tkzyWswDAfLm0YD1JEtsLgd8HCGw+fvzYAiSWfTGYpOzR2NpucjRbKYXDw0M7ZmVRQAphj5+Pm4t5fd/HfD63sjAhhG1+xj0cpJS2iJkBDwN9112m1+vZCCgAq99mZywhSJrMUjOOErM7E2eGWCLGINUde36muvIeBqvsoAXAynT4u/yc4ONluZG7lrv/cebBzcLwi8EsR/WbpsHGAG2+rhwRpjlbWpcsft5zAbHW2pKT5XKJfr9vpU2+v124ywR0vV5jMplAKYXxeIyLiwv0ej0r2eNoOBMZ/t2VKTH4oz4ZCdbr1JJEjuDzuLCtvzsXeVyE0vYeYIkcA04m3KMR9Y3ZbDaWVPE9xGSD3wPgYCICtzwHOHvFMkNeH6jmooYWrQVwW9fh2/XNrSXg+eDap7r3B9ASBR47vl78Hq/jvD5XFXU+T6LYEmTP86yzlNIawpM2+8njwwQFStusK18bN6rPBIGPyy3EZqzF89slCkwWOBPH9y4Df86AMKHhsWCi79Z2cPCBpVg8H/jZyN9zsSEHWNx7iY9RKWUzmgCsxIqvkWuf+z2VTiX9ATZmUarrGn4UI0gSjMdjpGWJNN2gP+ggCjvoxCOcPnyAdJVis3mE0cEB+uMxyoaKE8s8Q5EVmM0X2Gw2WG82RBLyHMPBELUSWG0Ke5GmpjAuzVJAeUjTVjq1Wq7w9jtv00JX5Kir0h4zTwYpJRobGRfgQuSmMd1UhQBAQB21AVKmW6yLZ7aj59r0tNj1jefoPhU+a62shIduZJO4EQbMS2MNyoXS9GUjYWkJjoDJ8DgTlyaRh7rR0Lq222+jvDDb5ZqUxo4HAHPDcCTYOMmYA/DkNtnh43fTczzpXGK2C7jdh8VV4JHHdRtstiTmqmPYBfE0Dq4TDr3rRia39ufst31tEyf3vTYK/vRO4rsv+55LKJ72WWigoEgJihWqb/4dVEJA+x0Er/wkohe/AvgREQNzBrZeQsFmFQS0I5dqLWaZ8WohIDitbN8z0818TjsN85QlF9ruF1pDpVPkb/w91KffBJrqyixWS5JbJ7OnjZ0rfaMi7XYubjeac+dBq2XdvlZU17BFeMBFlmZsoOB5Ar6m4m2qjzKLbxiA6oKoobXne+j3+4DW1JNhfx8QAnsH+2iaBi++9CLmszl6/R5efvllQGl0kgRVWaGqK5ycnNiHYRgGyDKSsbCM4ttvvYXxaIw4iSElZRjIm16gKhp0ul3kWYHhcABPCMwmE2itUeQ5pJTod/vwpQdlANKlcZuJogh9I2/QTYPUROF9z0McRyhyWl8PDg7ooVcWjjSnDykkHj08tdKM/f1DlEWBzWpp/NxLk63gQuDINnabz+e2vwGDyeFwaDMbHFE+ODiwjkA8H5hAcYRvNB5ZcHN5eYnDw0P7wN3b27NacSGEBfduUEUIgWvXriHPc6xWK/i+bxrD9izoZAmOUgqTycT2N1itVhbIfeITn8CHH36IDz74wBZDcuBss9ng8PDQglM+Z7dngwsCVqsVuQma6CFnFpbLJQBYsMvRWVeawcCCgQIDes7UMAHhSPBoNLJRXc5WSCltJoijmyzRqOvaEkzOTHDE//j42M7lxWJhnwFnZ2fW7IRJfpqm9ncGoky4mGy6WSgGxZxd4fWH1w63ABmAvS4MGpkwDYfDLbnNnTt3bBM8trhnMrdabWzUl6V2bL/P5IrJcRt5r1CWjQXIy+Vyi0CSGxTN5f39fVvD40qVeIx4XN35yFFpriHiDARH8F3JDmcwXGAszFofh5EF/5x94+wG14Owhp8zj3wfsQRJCGGzWCw34mvX6XS25F8cMec5WtfU+d3zfTRabbmDugBaa73VIBGALa7nYATjKyYR/Kzg8eTsBxNglhZyHQVb9vKx8j0GmB4XHpkH8Xzj+cjAvxNTcz2WcLo9OHit4fnrWsXyfpgEMP7ijCqfA897fmbxduu6tn1t3CycK9Pm4+HPb8m2zb3DxIfdzTg7weTNJV8sseR98FrDx8nYk+fKc+Ypnj+jsVnlaFRjI2Z1TYupgkalFZpaAY1GnZcoswz3P7yHf/Df/hwmF2dIBn2E3R7SosR6tcFmscYmzZAWFVbrNeqqNgV5EV588UVcu3EXWUXgNUvbtBFFITZoqsKm8DhFPJ1M0KgKyin8EkKYDAVDJ3KM8r2WoSvVALqGFLCWm9uRcVd244BlTfoknpzbkXuK7PPft1JNWkMo3g6nokzhJiSU3on4W/LQQOn2RnNBVqMkpGwjA+6E9HxyCqMFxLWRNeQKrc92e+6AVjWA9rz4PFwQ7moh6V9lsaB7I2yRgysmp0ssXCkWXbFtmY17nDTO2+TEEhvFKdArLFFFew5uwXD3Px1dSQha0Hw10XCj4e6/5petzz8ru7G7bUvQ4j6CT/wEghe+AhEkVvm0daTC/XErr9EqpXa/xSTE3YRN2pnP1gU5R330L+1Hm9kD6KaNPl11PSlT48iJrpBP8XcZLFmiobfrXdpry1I43mZL8umeJzkXE8NHf+Q7aLo1vI2Pl//uZ5AkESA0ut0EEBq9Xhf9zhCe9HBwcICmafDCCy9gOBwC0Bj0OijKEicnJzZaNxwMsVjOUavagKvt2gKtNHwDKjkKyS5xURRguaRmodKje7XX7WG9WWO5WOH27TuoqhIAdTOmB6uG7weIohjD4cA4HyWoqhJhGMHzfCRJB++88w7G45HT0Ta3jdy01tYthuQYa3ghmXlEYYiHDx9iMBhgOpuik3TQ7Q5tgSk/KIUQ8D2JOApQFDm0ho3wSSnx+PFj6+TieZ6tz3CLFLmJFmvXWcLBDcsYaNgGVd2Eso8GkDL49jwP6TpFFLbN5tymc03TYDAYWLkVg2LuhcGR5xs3blhgpbWGZ+r3WBLEAJQLr7kHE0f9OYNRFAUGg8EWkKY5BAsU+XoyKWhMxFZrbRvWlWVpG7ZxxJDXAY7Qd431uVLK/suOVQw++VhYu93akG6DNK3JyYnB2rVr1+w154Bat9u1GbmmaTCZTGw2KEkSmz1xo7pc7Mpd0HfBCme9OLrOhI0zOkx63PHmZmV8L/G8LsvSkoimaaxETQjKhFXmmLlImTsyE5GljAAA+wy8qlu31toWnDdNjbKkSDRnnthMYL1eo6oqa0ksTR0OBwe5iJfnEq8RTBL4evF4UsYqt+skWwGzzMl1BrNqE0lunYFHeKDT6dieHwzaXSLPc4PBrAvsAdg5zYCWySWPGQB7XrwPfhVFgSAK4Rny5PbKYGLhSioZ+DL+Wa1W1P/CnBcDZp5jnJliwsGZGGC7DwqPj9TbAUmL2aREafrEMVli4M6ZEG7myMEJ7i/B6wfQujax9NAlDm7dkJQS4/HYzlP3WJRSVl7Y6XRsoIKJNBMWzoaxDTWv8Xx93QwLB304C+QGx/kZ6waDmeC6++HgRxRFdt1hGdYP/a4v4eNez000/tk/+jrWWY6qUsiKEptVitVyifVqg6yi2oWyLJCuN5hNJljMF0g3a3jQKJsG0vchBPVhkCC7QXZRYiDRNApB4OPg6Dqu334BQkjDonMEYQjf81CVKcqcqu+FkzqeTCZYLWaQQgBKcy2zGXQJZWxU+cK2jLOGFAoC2sqOPI8a51HXWpNaMtFkYdCY1gpNVVqpFYFaAkHURFBauRTHg3mfW7BPCOs+AqdIVSll9wkASjeQHoEtPkaaLBpC+PCD0C4y/ICSngfq2gyLG5UiC1v24HbB8fbPFZSqSVKmnfPQBLgZ2GkTFTfKfbsw81hLIbd6FWi0+n53bCwctn8TLaA2Y2T3h5b08bZaQsGs0owNiGzaSDsdLN1kQmDxJ84N0ZAY/OcHAIytsQXbPB5PEo3dl0umXHLJZ2e3qE1htXIL+j8+OqC8GCLqIXzpK4AkSZVaX6CZ30Nw6/vh738Csn9k90h8kucVkWZdLFE9+ga83gnk/ostz+B5vXqEavIBzenL99BcvAOdb7aaxGllpGcAAs+HtYLWbbZMQ0DKttZlO2tBUkHpSZIrCgHfp2aW0vPstd79ru8LU8vgW1tptskMQ1oA9/f24Pm0cP616/9PbLw1RnKEn3n5ZxFFBIY0GnTMQ7vI2gJbz/MwXywATQW2ZUmN1M7PzzEyfRq6ZsEuq8ICYgbPVVVjOBjg4vKCFn0h4Qc+sjTDaDwyD3ff+tzXVY1Ot4vA97HebDAcjqwGuNclqdBqvQI0qCAxDGxUkWUWURihMZH4fr+PwuipOfLIIACCakc6RvsfxxGEeSgxwGhMROzsjM7Xk60zS1EUqJsaZZFbgMmgmYtU+WHMoI4DE/yg6vV6WC6X9iHKzcoeP35st8f1BQBFNDcpdaHmxl/WZrKsrPSHinv3bGEyO/4wSeLCWu5bwEDSvVeZGPNDlyOAQogtcjSbzdAzhZWBAYOWFEsJj4s1zbix444tsNQamzRFYLIyh4eHtpcGR2Y528OghokMQMCPI5MMsFjucXBwYIuF3QwiExi34JTvKy4MZ3DCUUweKwC2YJe3y+cDEHBj4MXgGGi7K3PRdlv74KOp24wPu0zGxryECTuDmbppkKUpqrpGz9yjTKoYCHHGJM/J4agxcphOkkDLNkLPcqS6blDXFTpxYh28SC7mQ2uFLMshfc8C/qahonfP83BycoKyLOg8mgZlSXK0wWAIzyMLYd/3QM0YfQsaKSPimXkOpGmGOI4QhpE5Z4U4TqB12+uKa4g8z9/qdeFmOri+g7ORBwcH9jmnTSDUXUspcOGbHigZul0OFhi7b9VKq/v9vr3G5omNzWZtZTxMyInAxyjLws4hBr2+Tw6iLjHgrAavdZy5ANqeKAzkAdhaIa6f5Oi/OweZtDBAjo01LhPaqqrIDlxTXZ7Syo4ZBWuVDYzwMfK9UxaEQUkCR2MopYckiSEhcHZ2ZgML3OuEA6Is+2QyVVWVNQpwMxBupoXJkxto4DolnsucmWKyyIRRa2qpsFwu7fhzZodrbNx6Gc5AcV0ZP1c46MvZMO4Nww00+Xw8z/ve9tH4a3/tr+PD+4/QwIfSHqTwIf6/zP1Zr2Tbmp6HvWN20ax+rczdnaZalk3aFEmZjUVJJAXJ+hGGLg0b/gcG7B9i38hXlgFDEuAL37iRSbMokRSLZLEgSpaqWGSdbu+dufoV3eyGL8Z8xnwj9iF3llEwHAd5duZaETPmHONr3u/9mjGmTVMotTuked9jTJF1O0hjtVSazzlo37UJ9BaFyrJQFwf145Ajo+ViIZWjVBR63bzq93//v81CgzOoqkrtYau+S8rFZgHWyrJSoaBRo6rMCKf7T2MghykQGPJzVVWlpqrzoiEsjMcdp/GyMWgKWOLccxHS9C3ObxiIboowAeH09xBDHjc7jMN0rSmrMJWujFOGpCyq6RLz+Q/jOKqsKht3Oc8OT0Axgeo8c7mcpxxonMf6wbiOYwJ7MMIIOoapYFyuOV7/o5iAX1nwubTCU3pB0pyJGNOCp58dZR3y44kd4jr+ndzb/DnSww7MGZGYmnaLslBQpdOTkj1bVRSWbZGy/MyHAp723xyfzfCdQOIkUDj9dzx+89RfUeQepKMslr6b5SiKQrHfKQx7db/3f/7O+7qHf65DWj1ROheCpNWNyrtfS+vz8C80vn4jjX2S0WJu8MrfHYd03k260RQEEzxMAadCks8ipNxJWaRZ4t4/FFWoLBsR5ZZllRmZskjlYhjK1XKlZtFouViqbip9/vlnWiwWuUymbVt99dVXqutSF5cJVHDKMcwNNeI00e73e/2nf/Afa9OmsxW++Pwu1xu3bVTXtqpWK72+PScWafuqu7s7laW03x/09Tc/z4b4iy+/0Nvb21RK0mTA8vLCwVtjZvFpjD0/v5jAY5rZv17P5SMfP6bD17p+VIxBwyhdXd1Ma5xA2mZyrFVVpybVstSqWmXnLiUmse1SCdPt7c20/mm0NYF413dan80HZm0288hDwO5yYs83E7u8Xq90c32VgqG+13b7lh0kE3YIPrAzlIzUda3n5+dcfgJIZwTobrfT1dWVHh4e9Pz8rMVioR//+Mf65ptvcikItebjOOrq8krr9TpNRxqTbVgulqqr1HB5d3eXWfP9fp+nGsGEo6uAMoD1+/fvMwNJz8v1NC2LYO7m+jqXx9RTedNqCuKYuhNCyIfIHQ4HXTSNLqYpTBwS101ySVajMSDx9ddf56ZinkNSZm4J9H7605/q7u7uyAYyEenl5eVoIoz3SVB77WNnmbTVtm1m4f2wrxBCDg78QDvKlyjHwX56YzPXd9YZ0JLGgUr11BtYluke6qrR09NzHrFa11U+DyQ940pnFgCmjM9yYmrPFKNScFCk3k9OPl+u1jpMGcKqiur7dDL7crlMB0SWlaop8Fmv1hMDXKq+bHTo2tzbgbwzzhgWmSCb5t0YywyIsacpeEkH5ErDySS0eRrWOIacFXl720zP3ev5+SXLrxMbgE2yHGRqJB1hIvSAIBC5G8ZRZ9NEusPhoGaR9LSu5nKkDx8+5M8qpOqVRLJ0aqnnrzinptcw+deyLFPJ536vru9VxnkaFeQD7Lg3XmNbOAsFoOwjlYep15fgGBkBEJP5Y5qaT2yKkqopeCli0GIiYQhe0BcCgGyPFk2aJDjpHv0lbdvpZSIxCEoJCF0PT8ueGFkLviVLR8aVQMdHFoNdIBDI5hE00MPGnvs0Ky/HQy/5fu4dsm0uyS+yrnm2WVK+L/7+Ka9PDjT+p//Bf6D/4//pP9WHxzcdWulw6DV0rWII6oZeRdOk8x9CNbGevVZna7WHvUKZbp4xr2FqsB4VpKJMzHvdqFSawnLoew3716PyCja4bpp0fkIIGvtBKiuFaTPqqtbYD6rrFMwMY5+Fre9bDUMSShZnPAF5KEIug4hxYloTiztMpVaJ0Z0zDmVZJQZh6OeG8nzMVgoyhiFO5yEA0ssJuMKWx0mQNaHSuR8ixqiqmQ7CmqbVhCmLkDMHxXfr4odhUKHjMisvU/GXp9LSejDGuDdGH/AfjCU5nexEqVc8frbpd/yXH+WASw7Sy/z5dG16bcrp/pWvGyxoKwoawNKhaSfFRTmA+WUlWlIaGeqnlGfs7UFWvsfvTk7i/SGQeeLE9eP35b+nhc/XDn6/IfqSKCWOClIiJxVQFrXFdGBhloWXD+pfPkyyljJ3CoXiKIVpb9N9+HcXRwGGlDJ6CjRAp32vylJVCNNBTQmQrNdr/eqv/mpiIC8vtFomR3h5dZll7+LsTOdna/34xz9O6ei6mtPeMeri8lxxjNpsExu43UxlRFMmimk+IQQ9PT1lJ0ttLaAnB6ox5vpkgg0fdemHhMHK0xd2cXGRGVtORvYypJeXF3348EGXl5e6uLhIs+N3u/wHB/rw8JBBAcDOHSz18NTuMpWprusMQikJgoHyqSGsAZkBMj0wjziY19dXffXVVxk8Mn1JUq41Z9wl01T6vtfNzU0G1Y+Pj98p+3BWjDGYMcbs8K6urjLrTBaaUZKUSFCvzwQmggH2h8APoHt/f69hGPTFF19ouVzqq6++ymcvUKpBloDm9RijLi8v9fb2lpl5Aou+T+dPPDw85Gc5OzvL9yYpA3aYRwANIBw2l5GuXZcOnfPeNgJlmEGatOn9eHp6yudZoN+MkL28vMxAFqABWPz5z3+uEII+//xzffz4MT8vssJYXvobKX1jX7k/b0r3cjAmFNHXQSYAIFyWZR7x6uQgAR0vnwAFAyzNmRNJuQcGO03WzRtWCfjQIyfNmqbR89OTYhFyxgOfyHNBzKHP/DeEkPXJS34oXeP7xnHMte2swcXFhbyfgYZa9gvQBpgH3JIZWiwWevfuXe63YY8ov+NePPBxlhmmn2vyc4ITHxDA3tKPIUn11N8Gq56BraK6aUQ/983nAPdVVeVpRc/Pz3lPKAX0PSCopE8EAuXy8jJ/J+VQyBIyht32HgxOqiZAx8cjd05eEEBgP70hn8AM8or947uRrcViocNk65Bpvx8CF+ScLA32hmcic8SZLHwH9+V4ARzHPQ3DkO0YgRu6Rw8R12MdUyBfZzzt5Wpe0eIkB3uL3g3DkLNrTtr/q16fHGj89/70b+k3f+tP6eF3/qkW1VLlIjUwl2VQs1woxlFtm1KARVno/v6jxmHQYuqlaPpOTDbSJLrjOOQD6WZDEVMT5Ko5YoVzRFcvVJTpNPK0iDEb/vVyrapMJ1V2XasxDqqqUn3fqWsPag/7PFINYUsNkgniUcuI0ktTvfu08Jn5nUB+DFJVJcal7zupD0cTCcoivVehUFWXinFU1VRHgtv3Qy49CUX6d91MtX/9dG5GEVQWtSgPGqeAJxSpiako4lRbP2c1XGgwLigbLzcy3qyU1nrUMA5H5Uph+l9C1FNabzo7g7p4IogQwjTZaT4v4LulUrLrpffR5OzBUMpgfLf2XzE15McYNQ5pPeIo9eOgYprC5WvB2vHvIyWJ8xP6WRHcawjHWYY5qCOwOA3ewrRfp83o3w08yOTMmSGJQywIpqSgUKTyPs598MBy/tYiB0GpYZrszBwYJsc1DzLg3v3P7MwqnZ2vtFyudH5+puvrG1VVqS+//FI/+OoHqedoAjfpWoV+9Vd/Rbv9Tn3s1Uyzy+umVlmU0wFuUYVganpVVa0Y07jaYej1+Pgxg+d0AvNBwzCq70fVdZOn8cAowiZhxE9rhYOUG96oH1+v13p5eclp7aZpMlNV17XevXuXzxwIIehnP/tZBu0AldfX19yshwPDcNNEeXl5qWEY9PHjx1zTjyNgPCe6+fT09J1GZsqDAMKScnmQp85h9EIIGUQQJOUylL7Xn/2zf1YfPnzI40oJBLB3lB1xBkNZpok6MNo4uYuLi6NJT33f58PbVquVLi4u9Pr6mp+DaTRpPG9zRCL1fToYj3MgeC7Whn3wDHdRFHr37l0GqoCti4uL3MAbQshMPzLCM/LdsMKwxQAkgBQAHPDDtbCTMH+s9zCksaIwkjh1STngwpfQcH1xcaGHh4cMNBjzy/ve3t50dnaWg00YRe7xcDjkMz9Wq5W+/vprXV1d6ebmRh8/fjwC77D06A92EAAHq+knD0ua+gW2OdDwJnGCMO4Vu8Q+QwCUZSKAnHVGV2BhKYdCNwDfAB/2YhzT4ZDsg6ScbcjlIMul2r7LgSkBzjfffCNJur64zPLEf9u21aFtVR3qTAxgD7fbbd5TP2+EwJW9dtIFnSXrAIlAUMk1KS3jGm6XCU55djIsIQR99tlnGRvxGfSSbMD19fVRsEPA72VG9M4MU0mi27K+76dAI5X/ef9JxjqTvWVdsKWepeT7yADm7MoEXAlK0QN8EJPKYPr5Tp7VS9wIGNBVntdPbOf+kWu/P+wF8ou94B4IdlMmrspZDErYfMSsB9w+rYl1TOcaxaO+JPwQ68Q9sh4QZrzoYWE95xLFMhMIYGsvLUPOKH3zPUR+D4dDtr2sp5facs1PeX361KllqT/93/9T+p3f/X+r7yWVpUKZegc2250UktHuu17j0KueHNKySTWaq8XcFJWA/F6r1UIcKz8Mo5qmVhyjViupjMXRw2djpnR2BwqYG/lCobaP2rcHDX2nNGa1U9cfEkjsWo3DkGvXcHB936sMiTX3VBdGvu/GPDNfmrMfMaQypq4fNE7H1g/DKM44CCGl2kIoVJaTsFRlqpOPqZSkmEpOxjFNj1IopmebjFtTHfV15IAk0Dg2pJIwpQPqyEoQWIzjmMvCUEiuhzLxPphJgr1hkOIoFaE8At4YNJzsGMajnx2VpZV2anikl+O4rAgDOP+bgh3l+5tw9vRvejKmbEoMuSeDkbZB8xhcrnH6yuDf4h6yNTppQGf8qZdOuTxw316vneSkUFUdZ02OgoM4n6Pg18oBrX3HbERD6isqj9dt7pEoFcc0LSmOKSOXAFWdArki9c00iyY3My6XS93d3un6+kpVVeuLLz7Xolno13/j1yeQuNBqtVRdp3rqvuum8xj2WtS1ymmSD4D+2w/fqqoKrS/W2h/SFJzdyyYDv+Viocf7NHr6yy+/VFWVen3dTmzjUtvtRqvVWlVVarN5mxzGQYvFOjtGwDYGvO/nueM4KF9PnGZZlnp8fMyM5jiOury8VAghM4aALM4BeH5+1t3dXQZDrHuMMZ+eXJapoRxA5qUmbdvq9vY2g2/ApIOkn//857q+vs5nJnAPHz58yE6dmm1OagZw4ghZF7Ich8MhN2X3fZ9rfG9ubnLtOOVLZCL4Dp+WRDYHp839AzLdCTKko+/73NjsZTaASkgefn59fZ37C5qm0YcPH3IQ6RNlYNhw1pTXMa2IWnqcJQwlDh9wtFikU7qZuoVuYsPwDQ8PDznoJGDinth3z5Ih4wAmms/Pz88zKOBeAaU08COzZHRgvQHgPN+7d+++03z77t27o+Bvt9tlUEiAQoYKfZGUgwpKKXgevpcsHWNg+77PgN4DP8qx6N/xsjUC0bSPqb+BWnimlHGCOFkTdI/spAczPCPrD8ijxI4MSCgKDXEuTyFwDyFoYWUu9P5Imhvqr1PNPTLv5SJcg3tgLdzGABYXi8VRMAH49LJD9gEbDvHA+iLPnHMCgH56esrDAShTBBgShGJ/sFPcI+VefOd+v5cmHLXb7XRzc3PSwD33OGFrvYyHcjmeg/2iV4MpRchY27Y5UHQ7gM54zxD9SDR3EyiBWfCXBCAEg/jQucx8nvIEyRBC0PPzcyZU+B34gUCZACDjwqlRvJzIXxrVCXrIaGALWHuCe4ghfDfn0KD3vJf9I8gi6HaM4Fk+9hO7jay67GEHsFFMcIP8Rr+QK6oNTvdnHMejs5H+Va9PDjTK0OvXfuUH+uzuTl9/3Ey1/oMOh52qcpHATVPqMM2mr8tah/agWFZaL9cKRVDf9SqrafJBKBRimlPcqdVqlQKROJXdDP2QG90Oh8M8TivMrH3bdRonA1xWlRRTfXo1HfYXNagoSx0OO6lrVYYiAwU2pOs6bd9ejiZj4HTiRFeHEKayqTGnpAClRVFNrH86fRxBksbsHIj66rpWO0WDIcwbj9EtykqHkybFepEUOI69lst6BkjdqHFIWYdUyjSf7HnE2nfzAT4OlD1bgADNwHUukYlxXgvW55gRL40tl6rqu+cZHK2nvjutivWa7uxI7rxEyZXrNOMRggUPIukxg/BfFmz8stdR4/oUDKSG8lQ+d7p+ftI2H8xBld1jjHE+QFAxvz1ofo/vETLqe5qMT6M0knk+7d0NcVkW+uqrL1WVlRbL1Ofwwx/+cGrSTcbq/OJCN9fX6aC0Iuj87FyX03jK3Q6WcaX20Gqz3erl5VlxHFRXhYa+09B3etmn7MAYC/WHTunk6jIzR23Xq+7qDMZhN8dxVByl6+tbdd2gb77+VlVV6/LqUmlyWqWqalRVtZ6fXzUMUU1Ta7FYTaebJoD6i1/8IpfdXF9f59IcymumRc/7DyB2Y82hWz/5yU8yULu/v89lIwAkmEd0GZYdEHt1daXtdpuzBB4YILN1XeeD5Pq+19PTk5bLZS6F+uqrr44cOICFciJKJyQdjXWt61rX19dH7DpTRmKMefIVPQLYUgALh81xXzg5np9yDMpGAA0wbgBV9pfxsJSg8RlJGUCfn5/nsydwen5+BdkK9IJTsbuu07fffqu7u7u8Ny8vL0dOUVJmyp+enjJ5xMnZ2GLWiiwSdl1SBhXIB3X6MHk+jrWqKt1MgwLwS6wLrCB1/Pv9Xv/iX/wL/dZv/dZRCQhlUfg7GPO7u7sMJgEuBKLn5+f65ptv1DSNzs/Pc30/zfQAC/dz2CMANkEdYAaGkueT5nMJWDcmKmGvyEwQJNIj42VpfH/XdWrqRc5WoJesD/ey2Wwy2KMMCFKEewI0AvoIFJx4iJKKqszleP7Zd+/e6/X5Ocs5a75cpnO/yBSi4wSpBIb8jOvBVvMZwCPBF0EDenN+fp6DDexD3/dTxnfOBnEtvh8ATjDGnqB7y+Uykwsw5Kfl54B7yqoo3+naNk+rYi3J3l5cXmqIYw6qGVLga+JAnP1ij70MinvYbrdHcsb6sA/SHKj6y0vBeGGnsYPsDzjKy4QA9PhlyAdkleufVnkQ2OQM8JjKjvk+BhPEGHOgjPyy/uyjk0w8J/7LyVcwAffnpIkPmSAL5UQML/TR1w/9xdZBzODjIBCYiAdRAC5h7f/EMxoaD3p3e6k//6/9D/T//O1/qNCPenzeqqqCmqqRFLV92yrGMfUijFEhSuMkOOMwT33abDbqu05jnxqu66pKDdHjqKZOc+y7rlVV1Xp7e502JQGOGIKWq7VCKHRRVzka7vtBZdGoKCqFYlRZStvtq9pup8fHKQIcxyMhG4chY0RPdyLwXdepXkxTNtpOoUhKwuSiGAvVNcZvUBxHVXU1ZS0mJmfqC1FMytAPg4pxbs5GiHa7nYqqVj+maUjFZCz3h4O6ttU4tNqWUk9GYlKSUBTixPHeghSUqChKxQxg5yZhInxeHv3zWfoMUkXPXEJVFPNBUyEE+oNzJsWvWdjEp/z5skzykAMizhQn41HM8cZ3Jlv5tWcFLory5HmOm8iPeyoswLG4Ju2JV2bNQFWSYnFaUnVclsUfjMZp5ibGmDM66QyW42eKcQ5YMRw04KbG0ifd3Nzq137tR/r8i890fX2lh4dH/fCHP9RyuZwacDdan63y3pDWXzSNmkWjb7/5RucXFzoc9jo7X06TQIIeHj5ou3lRlRtM9/lAzKvLy7S+Cnp7Sac1LxaLlJEpisyWxRjzaM2r6ys9v6QAvgil1uszLRdLPb+8KIwHvb1utWjWqm+ntH07KISooIPattc47tR1Q37+xOattNs9ZgPJ7yh3qapKj4+P87kMYc7aAdh/+tOfZgb+8fExBweUm1xfX+vh4SGX43i5CCdCM6kGsN51na6urnRxcaE//MM/1M3NTS6NwuCTORrH+eTgvu91f3+fwQj3isOUEkDmYCeyDLBSNEUykQQ2nB4FAoa+73MaHuYR9muxSKeNExBSPtP3vd7e3vKzOODE+fp0KWT88vLyKP0Pe+oZU5qyAQOSMkCjiZwJVRcXF1m2KOUCZLKmb29venl50d3dXf5OyuQYEUktPZkc9o6SLpg/DyaZksP68nMYRK9bdqYU+WLdAL9t2+rXfu3XFGPMU1y2220GwfQeYYso+SGjBLvInnqPDO/dbrd6eXnR9fW1FotFnuzD81PyRBYFIEMJBXIizf0ac5lvn8Ez4INAjM+R1QI8A0pzefPZWof9PNcfueFAN/6NfEg60iOegcweAJJAGBDId2/285kMBAWpD+ZRYz/kvhzWfRxHratKrbG6Dq4pfSFDwknx3Be2H9aXoJPvJagiOPDyQ0orKQ1Fx8iyFEXq7aGfARuCTiALkBfO9rPH3kNDgE9gHqW87ugP+OTl5UWj5swFAbyThUc9HVOQrema7C0kimcrWAPsBFktGHdsGZkBAlf24O7uLr8HoobvZk0I6vhMGnqxzmQEQQbBHM/gQRdgO5eN9UMmYwj+/MwVAD7X9yEV3mfh3+PkFntLdhpCBzuAblB2RjZ9rm4ochCEPhO4QV6xbvg57sHtHFimrhulc2TaoyzRp7w+OdDYdXsV1bl+60/9WP+v3/67arc71aHQ0PV6efugYZhB7mbopRh1OOz01O0TWKU+P6bpD4rpULimabTfvaRG7nFU2+/VtmmDdsM8T7oIUUM3KMZSzepc51dXWl1cSHWper3UEKPKsVAVSu33Oz0/P2ms1qrqpW6bC8XDm54fPuqw26dRsDFqiGkU7RCCiqpUUZSJVy+CFAtVTa26qrRcLFSVVW5ZHseprnMc1Lfp7IhhSE3iMSbjddgfFJQCk/12Hh/ZdV2uzIENL6vJSe0PE2hPk5MUlc4uKSuNRan90CvGME2f4oTnoCJomhQUcgDCXgxRCmWtIqTG8RgT0I+KKoqYm34zkz79/zgkoDaO09kjTTMFOaOqMOrQH89Gr6s6ZZc0jbQN6T7H6T1FkIahmwF46KUh5gAllEcFU/Mz1KVK1YqKGodxDjqKIvVLx9MeiGltY1ARqvx9wzik7ERBf4m+87mkPKU4aBFFzQY7xrR2FiCm3485wE6Zi5AOKoJRHEfVVaV6Kg28uLjQ+mytu9trFaW0Xq21WC4Ux6hf+dVfSec1XF3p7CyB88UyneL64cMHjeOoi8sL7Q/77Lx3u/0kmWlsa6EUjEspo7Wsk7G9//igoqjUNAsd9q0uL651395rGKSb2zQas1ShzXavw2Gv8/MLVXUqMbm4vNShPWi5ToB4MU0iAUQ4GFiv13p9eVW7P+jQtlouFopD1PNTSlEXZaGmqdQPreoqlT+s1gm07g+JHb24uMhBEmzS62saEEGgQWZgtVqpHwZ1fa9QFNpMZSOe8aKsgvIkmpoJ8jG6T09P2XDjsHDsgA6cACUGMIX7/V4XFxc5+3F1dSVvXsZ4EyxQEoHsuaMjVT2OY26wdJkjpS+lYO/9+/e5x4HSCwKSENJMej+RGXDrvQsEKAQTlKdx75AxgAP+7ucAMBIWUEMZDk4ahp9xuAB9MgUfP37Mgc5isciHmbEWlBiROaPZmswE68N+FUVxBGJh+vf7/dEBVuwJAAeHDyvKfgEUHbCTZSYzTWbq7OxcioWaVaOnp0ctmpWaOpUDDf1gWciZHU+BSepbujhPfRqH9qDd9jD5maj20E16t9A4xAlYpwMad7udzs8uddh32m33Ojs7V5DUtYPOb1Kj7dCP0nT2VfK1jRbNUn2X+iyRy7btNQwxVSIsa9VVoxilpq7Vd4O6ttfD/WMqh1yup+s0U9/J5eTfBjXNUpu3N51fXGjo5+ckq4McIWvIJcAR9ha58nr8rus0SirrWpvdVuuzMy3XK213Ox26TrfX12k9Q6FmuZoC8SsNw6DtsNeuPWhQWsPlYqntbpcy80WpYRxUV7VuLq+kKYj++uuv8/0R/CEbyJyPG6WkhiwieoFNAHQ6m082hKwpul8URdYvACSBloNJH0MMsYofXK1W+vjx49FIWYKz5XKZpoeWpYaJABwU83qiF+/evcsligR5nk1G/iFN+r7PGYpT30mZUVVV2SZhi9Fn1z8yi9j/YRhyOSrPT6BERoJMHfrMvuCr/GR0b9TmvwTcRVHkHrLFYqFBQeUU4GFXpBSUIKPYWi8PI6PBmpGthJzy0dLoCSQJMsb30NvBGvkZF/iUrqOcnSmlUcOQmvshaNPzT4fXTig0xnReXjlluVIQtZQUJiJ+yET7970+OdAYohT7gxaLUlUxqj1s1faDxjjqsE8pfSIhHnC33ahvtxkcEGWjNH3bq+9S81A3zaNODxrUtgnsHfbbDBpCKNTUS72+pN6AcrVQWafIMlRlGgEbCoWq0tnllc4ur6ba5Dcdhk4qKh36QWWMKmJUHFPA08dxUqyUQUg9AYmN7/tuAi5MEIqZEchTkES5TFA8TH0KYwI43f4wAZ70p1kup3bjdHCgl2sNMSrGQjDuwzBoVTcKQSrbfRonOgUMXdflDFEpKQSrR89ZgqmnpZCqMo0hTu9J/07fe6xURVFM06zSiMx0smcC93VdpabrOMViIU1qChrTxKYqnbYcQjGdeB61mCYKpQbgMDXyRxUhqqrrqZl7UNe3udTFDxasijqJfZRCmSZulZSA0duilGWR5lPKZ7Z0Yj/DfEhjOik99S9kMCqUbcqmxLmEKYQ0fKCeRrQWZZm/ryiC6rrSu3d3ur29UTohudG79+/19vqqH//4R7qcShsS4zVotUrzqG9ur9V1h9RzMYEjQBCOLDmbUV9/jbEKenp6ULNYqO+7Cdw95lR1H2NqUqsTKNxsN3OT7DQj/enxeWI/dvrRj36cDuMa0zSqxXKVyzNSveurRit9wEjuJmeKkWXCESzly8uLrq6uctnJfr/X+XT6Mge0LYom24NhGPTZZ+/1+Piou7s77Xa7DFK9JhfbcXV1lUd+EuCcnZ/rn//zf66+7/Ubv/EbOViFc8PgPz4+6sc//nG2Uzh40uX0fnBaNGUssLWAYOSJ57m5ucmM3+3tbT7j4ebmJp/SLM3js6W54ZBswP39fWa6aQr2ngFJmVVu2zYfMEc5xvX19dFUls1mkwO3cRz17bffHvWzwM5Jys/0+PiYnRasG+uOQ8bWFEU6WwJmNISQJ+FsNptcBkHmB2c+DIOup/GxOH5AGjLmGdrFYpGnTHGqupcUUOLhdeg0ktZ1nQ/Yg5GuqiqX2wFYT3slPCOBnDCelJ9fX19noMzPWdfNW+o1SkAFoFGo63o1ky1AHgCFyYdG7XdpnG/btrkXpus6rSfbQYlRKn/7TPf399pstnka1NPT0xT8pDUnIH5+fs5lN+l7axVTGe84jrq5uc1lMavlanruMcvQMPR6fuaE6dWcxY7ScrGc1mIGO1JQ13aq60abt3S/2+02N84TEGOzPTNMFosGWGfRyRBsNhsVdQK4i+UiB7MzsCs0THsy9Omcm76bgHAc1ZRNDmjyVKZhUFPVecAA4PLx4SFN3OrafA8AUXwoZW2MuQWcwxpz/xwCiU7NJdfzYByyDw6cT4PiU2zla4dcoV+noNonspH5ipI2EyuOnNCnwfrTr4SNgsjxgRUe2BNAen8TQYWPC76+vs5lVegQ15MSsGbYADbo/Pxcr6+vCiEc2euMQW2YAxki/BTkGPaPrAZBDd/jDdz48aIo1KxqaZwzNxnXTv4BG8u5R1wb4sWDDUnf6c8gAJXmTB42iVI/D1KXy7kPGvzD1EvvCZOq6e/zcxHIEByShUtyxiGO8ehzKaj7Ew40fvHzn2sca23eev3oR1/o9//ZHyoqAcWiLNVOESw3nhxj951DyVCI9Ls0MjbGdJquJK3Wa41MmKnqNBN+jJNC92r7nYZtq/2w1UGdvvjhr2i1WkpFlcAozpNShEmwtxp02O8VQ6nty4uGvlc6gK34TpnL/Co0TEU9VbNURHnKIQs6BwmO0zNwhThM5TxKYD9tfExTRGNqcPZ+ECl1KQzRT76eG1nrqlYR58bqLnRSlLq+U9CYQLNSaVVZlopjKlWLUwVJUZaqqxlsh6JQ35WKmg5Oi1EhjBqn0qGyTk33+RyMIA3jmED+FCAHRWkMKkIpxWL6znSdEKcJDF2fHU5ZNBqnusZls1AImjIehYpwUD/1k4Qy5n6IsigVwvGY3GIKYmhEL8tyOsMlnXEyFqlhviqrnGWY+0WmoC8oB25pT4Pevb/VcrnQ2VkCG7e3d7q5uVZZpPGs59Mp0J9/9lkuD6nqWmVZ6ObmSsMwTsY0GYLHpyct6lrnZ6sp/Zwm+SyaRq9vb3p+fshGHIfB/nhzJYYa1lghqJvAIiU1TK4Z+nSwFWVE0jxdC2OD04Y9xAA5Q44uK6Q6TZyUl0MA7nhhpLwUiKZmGD83qhhzTi0dx1HX19e5/GO9XufRopQ4YMgfHx8zw7xarbSdgrTb29sMzLIOTVmLuq71+eef63A4ZEYRRhAQsFqtMtM4DMN0QFeb7RYsOMCMbAIMFNcgo+ElR6dECwBCUnbol5eXuTkRkMF+kZZ3lpLv2+12ent70+vra3YSlH8yJhUgDqhdrVZ6fX3Vy8tLnrHOnpC1wDbSDwF48cktgGxJR6UFh8NBd3d3en19zSMuyWA8Pj7m/Qwh5OCOsiAcp/fEEeR5bTJTlgDfyBrvQea+/PJL7XY7PTw86Pb2Nq+FA5yf/exnuWTOGcHHx8ccdCHjfDffQYkZpYSQHNrtcnP9MAw5KK3rKjOJgA7W++nxUe/evT+q/+d9NG/iYyk7Ys2RXUYH4z/omfEJMpTkODh5fn7O447TKfQp2GWAAsAIeUa/vYeDYBK7BgAimACcso7gA/QKnQQw8hn8Ipm1bDvKMp3jMLHbknJ53GazUTcFotiR8/NzbXc7lVWZgS7fzTQh7CBBO//u+7mECz10ncTXEGiQdfN7JsDy5x/NRlGWAqAECAPkCcj5bmw6Npi+C8CjlLKVlAWyHwRXPvwhxphPfoeN97Hc7C0BIhmXn//85zkQgtTA3lEKhdxxT06yYqu96d4zBTyjB1n0o2CLCMYJKLAlHhAm8mw+Z4LnmvHBnF2GxfdSrxhjlom6qtR27ZGccm1+hk7ze4ICJ3ZZK4YfQGKgM+i+92hwzx5gUmKF3JFV6/v5+ug79sOzhfgF9sVtL3rpWV7k+lNenxxoXF1cqe2ibm4u9Df++l/V3/7t/1yvm1d1/aiu7fMmcRO5vrMppDifDksNWVEkwMQkkcOhnVniMmqxTJvY951oth4lhbFXe9ipGFotztbqDwctbhqpbKZSo17RWKphHNXHUfVqrdv3X+jufdTzw4M+fvO1iiDVZZmzAcOQmm0xdEVRqB/7aWzqdNhgkVj1yje5CDkVPk6lMymSJCsyqCyLzJbEYZhA/LS4U39FNwypB2W5TNmcQ5rQEadRuuPUdxAVNVZ1SmN1bWqQn4SyqBsN01jTEDVFnOk+Ykjni8QhGfyzdSqNkZSmClUpe5DKhDQdEihVVZlqWsdB7W6rt48ftJ0aDrOyxNTAPz3OtHYxG4+6bhSqWnFIiq+Q+lqYzlWXC9XlIq8pLG6Y1jopeXLefGdVTtkYpQCoDIWKME2nKKLOpwOJbm9vdXZ2lif/rFZLVXWlX/+1X9P/8g/+53oYHnRxcaH/zf/6f6WmqfL0iXEcJmOXMhivby96e33V3bt3KkI6w2GcMghPz/dT+Uejqg562zwrhFGPjx/UHtZ6fX2ZjOSgvm9UliHX3cJGs1aXl5fZ2TAJiakUfd8rTLJd17Vubm4yCPjss890mKaHwC7Tr8CI1KJIjX+bzSZPHHJwi0F/eHhQjFEX5+d6mc4j4KwH+hVgkAAx3AsBEfXG4zjmsw4cROcgb3rO29tb/eQnP8k9ERh2Z20oUamqSu/evVNZlvrFL36RD2KiCc9ZL0oDAfYvLy+5v4Fmtx/84AcahiE7N0l5shP/vr6+Pmq+oyY82Y4hPzP9I9Rne1ocnYkx5pKBi4sLNVPJyWnKnrIDP9UakAjb5mUaTBCRlO8VQInjeJ6aYHmOGFNvBww/9hv2EIBK5oKZ7zgngAqMHECGwPTp6SmvPwHm3d1dbuymDIP79jIx5OWzKbhn3TxwOzs7y4EYPRvI4NXVlZqm0cePH/Xu3TtJyuCBNaYRG7YYppim6tvb2wzgsD3st7OKPg0pZbOWWZ9Wq1V+lrZtFTWqrmcmm0AjxpgDZTJs6Aj/hjEFnHNgH7I3TwqK2Q8CKiXlJlyyCoAvQOFms8k9IABQlw1kC6DjZT6ALMopfZIPAQxEBcEk2TMY5sqAPoCc783rN9kFMvzjmA4SJGDOdedlle0dMvj29qZh6LVvDzkg5jkZRz20XZYnylsWi4WGftDeMmjr9TrbEgJXdBbMA/FAkIrdZN25LyecqqrS9fW1NptN1iP0yll39tiBvQ+f4e+UdgIc6zqdz0Mwg44ii+gTttnJF88m0qPCtZAvAjtAKnpAFgobDYPvpU3oEzaGiXTYRge/TLkD8HKNU/LOn5v3kaHw8k2CAJ9khv6i/w7Kya57Hwmygg6SiWAdKc/CdqKz2BbGb3tQzt54gMIz5Mx9jEfvSc+d8K2XtRE0YXMJ6vEnrmtUV+B/sJmsDd/zfa9PDjS6Q69QlGoPO11erPSX/uKf0//1//a31A+cVj3XsvMQISQ2sSiKzAoCoMYY1Q+j+rHVdn/IUb2UTh0ex7kTn5OuxzGNjx37dKDcbrvXL372C51f3ujqaqWirhTDIkdtVZNS56uztTSO6g6tDrutFEqVVaP9dqumqhTHdJYHRi41QKfzQKqy1hhHcXaBilJjPyQwX9aKY2ooD2WpcZpONEZNp4NLsSikctCooLJZKAyDxr5LwHwcsoPbtVNTYVUqhkJRQVWzUlEEVVWdKnnKNFUIZr6cxseGYqq1XjRaNAtVkwPbbXeKY6XVcp3roscYU329pOXZIj3bdIYDijEOUV0XVJW1QhFTxmTfSUpGZvf4Qavl5Og11/UtmkpRjGKdm6qLIihoSt3V5bQ/nVKzeae+S+VIyaliTDiwcFBZpDKw9fp8nqKzXqupS61WC33++Rf6wQ++UozSer3Sr/7qr+r17WVip6v8mbqqtd1ts9MPU1O8Bumpf9L/4r/9n03rMafng5+hYUoep/eNY8rIpAMMJc6pSAov5ZPGPasXY/6dpusWRerJGSPjfOfPSJJ+kn4WNJ22bi/uNcaYAmEzPCEUucSOlzd45XI5yza6w/H3KKbhA/nzmqo5Qzi6ZmYpuUZRSP+d8lqOKT2VAtK0aCmQ/70ir0e+zjhOzx1IROXhBKwRghanIJ/VeWgfJnsS9MMf/jCzf/QivH//PgNTHDEOz5tlsVuU7dC3AbuIAyNA5mwOn0JCUOklIYAmGL7TemeAy36/1+vrawayTHoZhkEPDw+50R2HxFkfHnwwWtXLNGAvv/322yM22YGMT7dxcEV2wUvNAFY4QUAcWSRJmQGNMeqLL77ImR8CPOqVAU803TvTTYYFBs/rv/lOMhM0SAM8ASBM5sLZE2BIOmoyRicARtTpM4gAhjFPW5uY/NVqNU1Y6nIGjWxG0p2QS/FYM55jtVyr6/qcLXBACjj33qj1ep3JAko7KKuCrSc4TUTLKtd7n52d5c954MA0L8/g8AIU42cdBDo7DHvNMxPQIutkUMl2cR0yW+wpewRodLBYVpU2b69aLJf67LPPMnB+fX1NQUo1D1Zwubq4uNQwjmoWKZBhLcZx1GjlKug0n6vrNJAGFpj7ZYqUl+Z56Q/ZV0oDCUwpbSJAJSCk5GauAOkz4bSbsmSr1SqX6GA70FcCcQJVys/AWZQPIdt8nkARW+MTo5ADngn9JyjB/mCbsIvoKv1P2bdOekzZIiSR96QQ4Dvpghyw/uwN+sK4b/phPOCmWoBGcDI7ZBN4BmQTefPDEvGhy8VCYbJZAHF+Dxm3XC6PbBp+A0DvwQh+k3thHzxrhR8h0GEfvDSMdU42bB6PLCn3xKCDyBcyiMzyXwIiSn2Rd/yDZ/L/Va9PDjQO+1aXVxfqx6iLi5X+zJ/5Lf3Nv/XbajetikmZ2XQENI5xUvw55cXDDH0vKWiM6awGhaiSUymrJpfbNE0qzxqHUbvdVqvVxTTJqVFZLzSGQvffflRTL7Q4P1eoymQI6tRAXMWp2bOo1Y+SykZlvVQst4pFpW6UypgY62YxOVkFVfV0+nURVQaajFKDb9kkYTp03QTQpz6EkIIk+hoaWNZiHonYD30qFZoyHJcXl6lJOKZm4/awnwSpnpRpiiy7TqPSNKpQTKcyT86wO3Cy6U7VFDHvtluVodbb5k2x7dTvd9kglWdn6odeT/e/0G63yXsSQhrjmzJU9XQuQqH99k373auKII19q3KkvnA66K+MWjSL1Pw99irLpcpyrj2t60bpnJVpfGTdTCVK5zq0B1VlrdfXzdQk3Gi1XE0R80pnZyvdvbvV9fW13r9/r/fv3isUQZu3jeoqHa/X972WK8o3Eui9vPwsg7Td9nUyap2koPaw03K50Ms0QUmSRo360H74VHU4fn3a4Zj///VyIuL0/n/Z8/x/857v+/n/j16hKPTtt9/qq6++yqADVjSVtM1n64Qw1x7jsLBpkp9XMp+aeloiAaOO02aCC04Fp0s6m0yRM3s4WcolKJFbr9f5jAQC6GEY9Pj4mEGk3ydlHIDt6+tr3d7e6vHxMWdFaO4kY3Bzc5NZckqBcG6AVsBG6q35LDsmyhWo6ZdmNhVQUdd1DoxYj5wBt1IK1pfXdrs9Kt3ixT5yX1WVRs5S+sBzsaaAPi8loI+IMrXtdpvPG5F0FAj94Ac/yMGIO31nWMdx1HK11Hp9locDENikzwUVZcjXeZjq/5umyT1R3377bS7l4/lZZ+TYZcRBG4wsAI419dIy1pumZsAPQN8JB1hML+nzAIg1o9RGmptiX19fj9YKIE0gfXZ2lgM1ABWgiwwB4Bnwxn63h4Oqqj7q9QBwywgXzzz2fa9xt9MQR728vuTyS/SK0imekfKXruu0XK3UNMUR6y7NEx95Ri81crY6l2fV85kw+XutvwgQh9wCUrE3BMasi0+vQs4B1qw99gg5IYBn/DglqWTGvE/ByRLWFLn3jCm2jUCKDDRywjO6rmJr/RoE04BcHyGNnUYvkX0/lK8sy9wHg/y/vb3lZ6+qKvf/QEgQHLkMdl2Xzy9BBiCBgkI+roH1RicJBLHnZIcA9tIc/BFUksmTlHskCZxPbSG+g2yDBwVg8RlHzv04BM2cZ+RryfN6MMXvnMxhzTMB+QmvTw40qrJKx8UXQaEa9MOvvtDtzbVeX3+RGoTDaQ9GLymqKqeZ+nWtQ9uqLCvVZam761sFayTx6DTGxPbGMTUj8+CpTCaoLCopBPXjqCFKYzfo21/8QvX5uZqzdXZiUupNGMbJ0IQxBQ71QheX16qrRmPfq4ijuhw9LieHX0lB6uKUEq8KDTHmk84VpWYZtVouVZSFlotlPkiwLCu1bZcCnarOEycWi4X6odfqbJWj3JeXF+2YUtAeVCg12h7ag4Z+Puo9jFJ3aEXzc2LBEpM2tG0aJxzmU8Nz5KlWVTWffFqEQvdKzHeYTmeuylJFXWvRpGi4vFipbhoVQfri8/fqDlstmlJXl4mFrRZrKaRDj5bLpd69e6dmsdDl5UXKBsVUtjSO4zTpqVBdlQrlbPxgXNPEiEp11ajrMNaUnkW13UHpxPmou9tr9cNORSz0/PxBV5fnqspCh3YvhdSbsN/vtVglZqgIhc5WqXxhs93mHpoiRLX7nYJG3VTXOYMw//f4dPAYI4MYZjmdsnI5T5CVdT7gL9mT+fCfzPxjvJXnhGUdGIyF8swA7L3nMnBCvCdMWYeouYSxMCNCSZuYADe9iinLws/9dHYeKpiD0ZREGI2ZEhlJS7uOw5ivx4dwWtwbXTPcjWde+LezqfkeeO/0XPk9PJtlOi6Lyww6fQIIzO/5+XkGUIBOd6SwlTBF9CTEGK1pvj0C1IAhWEgCC94nzaVNnvZnxCuN5IAMwMfj46MuLy91OBzSlLBynt8O2HKnI0kXFxdaLBY5uHCAQgDipa3eq4P9wcGT4WGSDuuEE6bMlR4Bzo7h+WHnpLl3CHCPbQBw+EjcOZM412rzd8qH0n4clM53OuTMVZq2tdAw9Nk+ewkKZYtM93p7e0slOF2fGqWHmUUEjHMwIutNKdBqtUqfKwv1Xa+np/ujsxooLzs7X2cnnYiRyyzT1GJzSB42J013Shk4t59tOx/IdnFxkYETYNibccm6oEfYCbJfTE5j/C5neLBP9Kswi9/1hO8sijQgYL/f53I1ngumGj0ExOMTyAT61CLkxwG6n8RcV2XuDeH9Xdelku1pVLjXyGd2W+mEe/SLqXbjMOji7DwHgUy8S7Yp2WT6ZLzMhGck2GFCEKUxniFGl5AZnpFrUGpDbxD6D/HhmWfkjwCE9eTeCOL9IEUHtT7mmDNZfLwsAYIHqR5oQRT43lJ+SJDFUAu+28EsvWnIIesDgw9R4BkF7PkwDDkr6JOkPEMDWKeEjmDLS7CkOVPGfZyewu2BSUgOMAeIBPisD3bSM1ou69lvTs+CznpWG//PkBuu41lv/Bb3j1zNNjZNKoXIwndha3m5T0KmCGa998VlnlK8T3mFeOrF/yWv//Lv/90UnQ2jiqLWdtPpP/o//Cf6nX/4e+rH1G8wjlExFCrKiZkKQUWdTswuy9kRVVVK5RQhThOORg19mnLU972Wi5Wqcppr3o+qqkZxlKKCDoe9VmfLdBJ2OTfwrM7OdNCoer3WV199pbqutGVcXpTaXa9ls9L9/Qe1h72aplZdV3p5fdFYpMbps/MzrVZL9cMEAOpalYrMcBymRrFDe0iTl4YkAK8vL2oWadrQ0+OTtpuNSpq+Q1BVldruNhrHXuMQpSnTMw6j9od9XgONvZopKCirUkWYprwUQYuqUFmkyR44i+VqqbP1WnEctFg2eTZ027a6OE+HhS2Wha4uz7WajMnV1ZXKotBqvVZTzxMsYoy6u7vLihYVpzNNgjZvb2IC1/nFhV5e37RcpkbSsigUJkYrCaHUtW0K8Ix9SczKNHFlEt6k2GnM2jAM+eRkb5BMACb1eKxWKz08PKiuK8WYlGi32073PzV3F2E6yXefWMNQTAcw1dpud6mEYrPRIjdOpnsapjQ89eYJvJ3r9fVFXdvp7Hw2Zoe21d3trQ5tqyLQ+NjocGi1XM7z0xMYm9OmGFFAX9M0uX7XJ/Esl0u9vL7qbWIHccLdZCApV4Lpk+aJSoBnmAdKS+q61rKZzz5pJ4aDVP5ytdK3336bZQSHt16v9fL0pKqqcu2oN4Pydxzt4+Nj7oepF4uccl5OKd0apjHOEzeoD357e5M0syeAMrIBfl4HgMinZjiYwVFtNpsp0K1y8zMlNjjd1Wqll5eX7MBxENSXEyBixAE97CkOyg9qI/NAoADLhCFn7QHT3DfPzt8hJHAKOGY/DNBZKN4DaQOzButNaQwMJtNsYMcoMeKQPFh62HRGzgIkcEa73V5lUaqcDors2umAxKHXarnUdrvLJYchME47arFo9Pr2moMnD2ScQfXm/nEc1R6mps/lMp/RtFwsNQy9zs8vUhBWleraOTBcLhcahlQus3nbZGBU15X66UyFOas0jyEOocgOvSiCDodWXTcHA5vNVuv1SodDK03kEoyus+EOyGOMmbigbJd+Pu97cXC+Xq/zeFOfagMwozdEms8P8OZNbLTXwgMEkXnKSlhv1yn0wIk/gO/z83MO2Pf7fQ5uAJfIIEMGCBgoB0MH+r7P4N8DJW+wRRbpZRnHqN0ugfphHLRoEqE3DmlIStseMlgGLBFwRKXewhCC+mFIvn4iMNBdSblperlKo/TpP+GZvFeH9faaeOwG6wfQIzDwcivKDJ1pdj89jmP2UZCVEBvoy9vbW15jbGRRFNnfIM/gJ3wyQBb5KMsykzHYWfQSW+TEBbKVyMbzfACqpHx4Jxkt7HAah3yRQTYZNa6HTfNA06tnpLl8iGCD4Ar/SADrZWWS8vADJ8ixwfhXL89iHxKJq3wI9G630/39fR5ecn5+oaZZqG0P2u8PR0GMlKpBIEw8y9U0S+sLjBMp0itGqa7Loz4mJiEm/Z3P4GiaesLc8z3zd2SQvXdMgv1F5vi5VyO5LUBe/s2/8Vf/pXEDr08ONH760z+yaKmQYqM//IOf6n/7v/vf63nTaxg1ZRkGrdYrFWWV6qvHUdvdFP0rJJCuBFrpb/AUUXs4aNCoUJcqQqmmWagsK41jKt+qmlLNok4sUyi0WC613+10e3uni5t3apZrnZ+dKxQwQ6lOrShrRYVp0wYtlwvtD9PYvDo167Rdm4KDQur7Tn3Xqt2kJreu7dT1XZ72MPa9+t1GcQIPrrRxGKShU11XU5lUUFlOJ4BXhca+0/XVlX7wgx9kNq8sS93eXkkatF6ngOfm+kZXk8Mfulbvbm7Vdm0ef3l9da1umoKxWDbq2u6o9ni1Wurh4aPaLjW7/fznP9f79++P0t7Ulz4/P+eaaQSIUgFvLu269B2fffZZnvDhNaycVdD3vb755ht9/vnnOX2M8fVTUTFYGMm2bfXw8KDPP/9cw5AaNfku3uuKQCM15QmUkxBtwwJSduHsLXtW13U+CMnvh/n9ADYmQXDvNLzhYDCgkvLBdW9vb3mikzdU42RDCPrmm2+OakLPzs6m+uFFTqsul0vd399nkMg+cA2cMABwuVzq4eEhNzd2Xaf1cqmnpyd98cUX+qM/+iMtp3+v1mv9+m/8hp6fn3MZxNPTk15eXvTll1+qnxrNc4BrjY78m7ITSmuGcUxnW3Tzyai73S71GrStojG0BF1VVenDhw/5TAgMIwAN0Azw4qRrQBTrwOnETBii7pnGv3Ecc18Gtsf3i+CB76d+m3ntZDyQeZwzRp/fw6bR07FYLPIYSC8NCiHkwISaYnfGOFQaWr2UgiEBgBEvUUBn/MAs9oOpLAReXlbkQRXBK4EKe0EtOn/fbXdq2z477cPhkANB9NXLVwDLKf80HpVcUK7FPQIS0Jn0vjiNTa2PADeAEAbfmVPKCnhWnpfSi7Ztjw79w15Q2gT4p+QEEMczem007DOsLnYFB00Ww/XXa64hjAAjPCfMvdfGe4kKn2cqT4zpIMZc7mEAAeDD2ruswNCiZ2R9ttttfkaCBph59k+aJ+dRkvX29pYbhynN8TISdAFigWugAw5TGH4wT+iZA2u/bgoE0337WSrII9+FvAPWq6o6GtUaQsjlPWVVqajm8yPYYxh5ro2M+fehu17+430Lm80mZ1SluaeEoIHyO5rXN5uN1uu1Hh8fs2zj+/k85ZGefeR+8F+w8MiOE4TYfOTJn9ntcYwx21T/foJbbCfBHjbt1H6z7+wt8kmW6+zsLNsB12fWm3tDRiVlv45NJXtAlgF9jzGNqsWmhhCOyh6zDJAZKwo1VZ31n6A7yfqFVqt1xg6eXUpj6auj3gdkTipy8zg4DR+yWs1ZCeRyJmSrnGXnepAFvrfYLp9uxfd4UCop233WmSwb3w+m+2v/7r+t73t9cqDx8HCvYeCU01JxrPSLn9/rP/wP/yP9N//sG/VjGocayqB+6LVcLzT2g6oYdNinswK4sbIsNYyjdlP6FSGBwRnCoHKZastubm6mUafJwSzXS63Xy8koTuMRmfoUFnp7TY2QKAWHfvVB6sdBXddqv99pu33TdvuW0nFDavDe7bcax0HD0EmKGvpeVZDGYU4j7ff71JweB9VFq6qudHt7q8/ev1cI6ZTKRdOoKoMuzs/1wx/9YJpYJX311Rfabd40Diml7AzA1fVVqoWuEpB5fHrUOMyNSuvFmfo2TavabRNgu7i8TCPW2k5Ns1DfzyUDiakaFMKosprZi4uLC338+DEDCGcopPnk4NNpGA8PDxlk4PTdkHoaOMY0BtQnlfgkEhSa5lLYr81mo7u7u+ygOMmZBicMAwaZchF+ToobsHt1dZXB1ocPH3R7e6v1eq2f/exnExOZmJqrqyt9/PhRZVnmumxKSHB0GD3S3GQNnO0FxIUQcrMsIJO6cIADBqBpmlwDD0h+fn5WM5VIvHv3TjS4AUBvb28z8Ca9DoilCZRyB5j7vuvUTul1QAXBz3K51OU04YRaVJjOGKNenp4yqCA4YA45z4UMYIA+fPwoTUYd58Sp1fvdThdTEMd6OPPp7BIBMMGC19ZjSP3gN0o+ALIvLy85YAQUw5yOYyrxub+/z7qBoUV2DodDPhPj8vJSdZ0mtLjDJvPBGQUOOHzS1mlTLSDYSyIIkr1UAVBMmRUBDA4MkA2Iu7291YcPHzI4IYj2Ej6u5WAaMMwfD2o8lc5n+JMAWlTXHtdYO5tLMIdTJ5Acx0F1M5dCsR44Q+SeUiECoMO+nbLjVbZH2DgAFbrJutdT/xr3zctrp7En3AugG9laLBYZiCyXS3377bfquk63t7f5uQAiECxeDgZAYv/RNRpe2VsAGkBEUtYVGFQvY+AekQdYdoCtpNxkCrD2niFsLnrM51hfL/MCKNLc7sEF12R9CRo82PKgwvcU2fRACrl1uwAonL8vHNle7iWt2Twph+8k20NwJM0lsR7sosNH5UhFoRiUA1H2G9mBUSew4/v2+/1RaQ32AFtEWRP7RtkOYM8b//HXgHTujz3zUjF8D4Es34kvowGeYARSzkeJY0/xDwT+lIb5/iG3ZAIA8mRSkClsCTKCr+Rn+HkCBshOJnGRcWadyIwwFY8ghszs6+urLi4ujvSFdeL5PUAFn/BCh7FFMUaVIWXK0VEvYxrHdN7EaQYt2cMu6zkBP8TF8/OL1ut5mqHL2WKR/IUPiZj18njilOs9z4wM8zu3ezwjsuJ20DOm6AQyUJal/p1//2/o+16f3KPR9wmkj+OgqipUVkEKg1QM2h0Oenp+0epslUbSDr1USDGOqfwmFKqbWqvrC63XZ6qqUvvDQV9eXUlKB/ykXodyOkG50djjgPeKMQnjoT1IGrXdbrTfdRqHpESvr69potDzq2KfTn3e7nbqu15Vlc6v2Gxe1XWt+qFTEYL6IY3TLYug1aLW2Xqlr27PFWOpq6t3uru7UdsetGrSiMSb6xvd3N5ouVhouVqpLIOqYk5JF0XQcrFMI2ElKY7Teo2qm3RaeV31GqpRV7fvRQN5iKP69qDnh4c0eakotdvuNHSDtputrq+v1PW9dvutylBo85qe+er6QkUh1U2hGKupvKjWcnmhdAK3Us9DGNVOhyJiuDGANGxeXFxk1ovpNgQiHPyEoALgHx4esrOF/cfh4HhJc2KghiHVgMOOM78fQwm4xPh9/PgxKyDNmXVd5yDt8fExM9dkY5gBXhSF7u/v8/0RfL6+vuZzBfb7vT777LOcGbi6usqlB6QNuSd3mKT3GfNJMMuIT0lHa83a4GAIElBUd6IY2/3kIJ6envJhWy8vL9lwYnw9cAE4xxj1+eefq23TgW65NGJi7Pu+P5pY0nVdrnFnGg3BwW6307lN7nh9fc3vwVCxvxilnA2y9HpVVfr8888TUDs7m0ZAz2U6Xddl9ujy8nIqkat1d3eXMy2A12GYJ92cn5/n80Ik6f3797ke+uXlJbNZXvrBvsD6e2kSQIbgkZIeMnzffvttPjCPGm5YbQdHsEA4Vxgx7v3q6io7E8rsWCsHD7B4PsKWveYP2QVekAJkR9hv3uNgAQYyA/iJwWLN+DnXY1INAUhRTGNgQ6HVKmV9HBDi0NxhUq633+/VLOoMyiAFcI5eLgV7i8OuquPSPem49hu2j7I7Dy54NsoCyDax7tgPz+pIyiNQWTeCfvpcJB2NukWvsZMAQw96YowZOJBJxX4QAJBdIMhwEgBbANnioImSFJ5ZOj6UzLPDDqgdrKAHnnnwDIvXfDt4AVQVRZF7Svg8wZ4DdO4B++h2FADnn0EG0xrMLKzb2HRPYy7r8uvxedaPZmPPeKMLyFxRpMNcO8vgE2i37Tw9jvcSlMHGE2SwVvShEAw7oOY6HoAht2SyINvOz89z1sOBK88ICQVh9fLyknt5wAX5bIi6zuU/6K2X0ZGhIpAhQ0AJFXtCD09VzWcqIfcAbA+E0TUyrATFTsZiWwlyIDK4NsEA13z//n3Wp+vr6yzX6GmMqdeGrDlZVHTy+fk5+17IUmR4sVgoxOOzidDtJBOpEoeAgN6l9JxdXlMH8vgl8Ae2mwA0nSfGGXW9BaCdqqrOBAakp9sRzyh7ttzJJfQM+8+1XNew44vFIv/5lNcnZzR+//f/QNI4gdtGfTfq5Xmr//g/+b/od//rn6jvoy6ur7Ren6nre3VDr3qxULmoVZRF7h94e3uTYtRqvZJK6e31LQOYYUxBQtxHvXz7rDGmoOLt7XVyFslxPD49zukryheKQqE/qCqSMK/Xc1P4omn02fW1rs7PtFgutFotdXa2VlkW+vKrL3R+vdSoQet1KsOqmjKVPIWg1eSAyqKcFJ7zH4L6fsyMxPX1tVITeKv9bqe6qrTf73R+fqZ+6NT31HTXOuzn+rkY0ymw4ziqKEvt2tQMqhj1/PKicRi0PjtTWUQNw3xgElFnAgyD6qpRVVeqylJtl8ZdHvYHvbw+53Q/zgxBdqYjxnRaKXXwKM6HDx90OBz0gx/8ICuwOzVYi7Isc7bER8q5wfjw4UM2YLDT0txkhWFC4JmGATPIXHcMAbPbm6bJJQU+IYISn+fn5wxKMKwAAQwpDtpLwDh1lHMtcAruzHAe1Hp6NuDm5ubIAWAY+TufR4Hd8b28vurdVELkfRzM9MdQUFqCkQJ0wgQupj6J7Xar5WKRzhsxR5yblg8HlVbygUMehkHNBJr9GbbbbQ4Id7tdHhV4c3OTaqf7XoMx5QCbqqpyj4akHCScOhcMv7OvODb27P7+PgdyyCTmjGwZASIAl2t7YCHpyMh6zSzX7PteNzc32dng9HBagE3KtrKBtVIVMmjjOOru7i475vv7+xxUUopAcODBBwwltc44SfbeWTlpLmkECOGsPWDx9HlZljlYJrPCz3lmAifuh0PKmrpRVTW5tAZ7QOmgkxWsS7qfKvVXTHI4jmNee8AuZAUZgL7vtV6dab8/ZMbYs6+UdHrmkEwUtoH95754OYglO8jaYtNgQwEJjBv1cisyh+y7lzmRGfNSE9bV7YEHAAQsXoLB97Ev6DTgDt+E7cJuYf9ZT+QVWec5vfeIyVA+HADQSyABGEOXsJ/sOS8HrqwL90QmmGfENjtD68xqWhsdgSNAa3rGMssz/ghZAdxRNolcsN/4RjKmy+VS/dDrbSJEXFawSev1OrP5yFtZlhnIs8bev+FEG89NENH38wQ37DIEBH93Bpr1xUeQTUDeCKLZX99PZ/e5N2wve4ANQufQK8oAvYSJfUCHPHAnAywpn8HhQXpZlkf3hs1GBvxQQv7LixJUdMsnB3rJI+/FTr579y6DeGwV+8u6HGW++l7tfu474vsSQbA+kjvwBuR5CMpyjx1JZX9pJD36hQwm3DOfAI5PA0dwvAS2FiKN+/UyK8+uuC1g35AlghQvaYT08uzpX/m3/rK+7/XHKJ1KB7aVldQ0teIY1HVRv//7f6S//V/8I728brXZHdQeBnWDVNcL/eznP9f2ME912Ww2ent7mxxnlEKnvuu1Pxw0DoP2KMEgLYta6ayCUZeXib1XSAeIXUyTERaLRj/+8a/os88+S86kiiqLZHTev3+vzz//PIHDzUZnzWI6Ln6nMaYD9OJ0PsYQB/VDp7P1Sod2r7qp1XWtloul4jCfELpcLtR1vVJJUqlDNwtfWabD+vpJSWbHXkkap16KqMVipe3mkMFXN52cPfS9mslAFdP5GOMwarWeDgOqKh0OCVBGSednZ2q7TsvFQvvDPtduYghg7/f7vb788ssMWnDCAH7G+l1dXeWfA9oBXDAcTdNkp+ksD30r/BvldOBelqXOz8/1e7/3e7q7u8vAjcOOKFuhlIjPFkWhh4eHXLKDcRzHUQ8PDzkFiUHBQV9fX2cA4GVg7BcGmJp8jD+BA9cjqHGG1M9dwMlQRkHWxdlEjAHA3g8zQpFhVVD4UBQ6m5hzryOFnWCfWF8HBazhcrnM2aqu63Q5ZVaouca4hRB0aNvc1I/swiYFy+qQniZIBBxiNAEuUSmr6PPCAa5d22plfQ5easPaVVWVDwUEuNze3uYyE36PgyFTBbB3tsudG6whc/ZhsNgb9hznMgxpSMHj42Mun3InPQxDbiQnCIY4oUwLGXj//v0RQwwIZhzuOI65NAJ9dSPfNGlUKGUNT09PRyCDP+i2Py9y7qUJNOh6z5KXc7E3zKOHpUSmYETTepWqyrlvBwfHdzgrSzYjAd2g3X6bgRg9Hg5YkUnYt6qsVNeLLHfoPI715eUlN8vSK0IvEL0brDeg18tQCBp4D/aC/yLr9Lg4iOces4M1kAW49N/xx8tX+TzPw36wh8gH15DmQwi5T/YPGUYmAMcARX4PDOD3/PHSRi8XxP6TMUSGhmHIE4YgC/gMekAwTSYQwoR+Asp0AEvcN3uF3lFqBm/B2kjKdgc/74EBwBBQSaktTDxZAHQVm7pardLo4WFuhoYEI8NzfX2d9w6dYk/xy+gca89nkTlAsAcwrBd7zOhWfoct86wYfgOyAZ/GHpHpOS3hYQ8IjNyu8GzoNOtML6cHhGQ/nKQi+50zRFK246fsP+uFn+EekS1sNllpSCqeA5nzczI8C0y2jfuBpGHq1uvra8Ymp2WN+/1eQ9errua+ROQzrX8aIoEtwd6m9U3nfXk5K5/t+zkr42VeCWPMQ3SQ11l3ZwLHs19ODrtsOdHgfnLGpXOPi5MK7BOfadv2T7YZ/Juvv5VC1OGwVT/0Cio09NJyda4//Bc/0T//5z/VT3/2jT5+fNbHj8/68PFRb6+viv00M3sCb5vNRnXTqKkLLRYJ6H75xRe6uLjQh48f9dWXX+ru7lpn60bL1VLb7at+9Vd/RTGmyUqX5+c67A+K49wpDwDNh88pjcwE8DR1rb5Pi3hoEzvY1KVeXl+S06qWqspab2+vqqpSRaFkoCQVsZ5O/U7lSSEUquopnVjNzPv5+XkWgK5PwdPV1eU0VSqqrArttlstV0uN46A05WQeJbbf7/XFZ59pGDoFhcyeHPaH1BOiSl0Xj4zFrBi1Du0hgzRpniP99vamu7u7bDSrqtIvfvGL3N/gzg8wiHACgjBgPtnCATpGzg0uSh1C6lv5+uuvj+pBATU+so4SE8pLyFoAIjabTT7sjXIkDDWRPIHQ1dVV7uWA/X337t1R6RA13M4MFkXa93ZaY5SRNUVRST8TLPB91POT3aC3AFDJ82IopBmcY0CrqkonvZPujFFVXee9oIZXmkt9MNwYBUYGsof15MSaCfTAUAIkNnbWQ9/3R2P8mgkwYIS4d8qlCF5vbm602+0y41EZOF4uFvp4f69ikoc4zieKE1hwiBJO0YFjURR6//69np6eMhPJwYvtlAUEkJORgjHFGbLOBDWAjOVypeenp6zXBOA///nP9e7du+wQ0JFhGKazYJKO5pKCJn1P26WJNF9//bVCCDpbn6mq0/NQosh9NM1C2+1mythU6vsuZyn2u73KqtT19Y36vsujW9OJ02MuvYDtTKfAzofiVVWlcUg9WoCGBJDS+G4yLIwzTk6w0OEwn4DLWFhePiVrDlSn2t8wT5qjJp3mTd+bsiw1jIPiGLVYprJT9nRyS3m/EhjrJ7kcFELag9eXzREIRX9xgmRmCOK9xALbQ4bBmWBspINtKTGonNLMyFZY2cvLy6yH6BVBpzt6bJH3cXjTqwefpxkXzw55VtqzWAALfIOXt0gEJXzP3FTNmgHsZ5Z0DmS4V0l5fdAhByS+zjSOAnA808C9rtfrnEUnQ4b94t4pOUQeCOb57zim8in0vaoq62mYp1yxx/zXbSfAfwaoQV3XpgE3fa/F5BuGcVQ36QOgmCCVrDYHI1LyRt8DfswBOHvuE7l4rZarPJlssVgojjHpaZfY/67vsh2MY8yZwcViob7r1Q9z+RS2NITUz4r8LJaLfA8zaTDbyWIKpCSpMhLCewSS/BSqqjnLLwHwF4pxPAqSKI+uqkr392mKJMEce+Xk3zCMinEuxwuhyBkBSpzo3eP66IY365dFmf2CpHSmWZEmj7GX6GUco/qhn4m4KTh08qip0llj2FPwCPfoY2nnZ0mtBwkbtFosmmzH0z2nz3lAxF6N46DVapnXxoPCYYg5GIBcRT8gWT3D74Gbv7BD2BEnP9ARPgdu+tf/yl/4znW+c91PDTT+8T/4HW22W6Vu+VqHw1591+v65kYxJiE8P7/QYd/qw9RsPPSDHh8ecjoxhKD7+3uNcdTtzY3KKSIe45jBDYdSte1+Eryk7MW02dQCwjCgBLBbl5eXR4wYRrtt25l1LwstF4vprAoWLk3CqspKr2+vmeFvD12OrJOBHXU4THV5NanyQcV02OB2s9FqtdYY46RAc6kNNYBn52cpgCiCdvu9iklxfPIQG1mVaUzwMIyqykphclxPT2mMbtsxWaDMLLXXh/sEA0afegocQfr48WMOlggsYO4AV5QO3d3dHTX3sf4YHdYa5UfQcbg4RxxVPqhqKkMAQGy323SC+jDkCUxeGnRxfq7DJA8wnt50TO0w33d7e5uNEABlv9/r6uoqM6CPE8sDWMnMatepLOYTQ3HIZDhQThzL4+NjTm2SxSAjwbNRbuDlO15OxRpxmjsT2tqJde+HIZ3yHtI4RgczCcylksLdbqdD22qYyhm4R/YLVotelb5PI3QZS0uwQjoap4ARJ7BaLpc6OzvLZVTL5VKL5VLPT0+zQ55A/NsUnPCMgLXtdqu3tzd9/vnn+fc81/Pzc3aGlAOyD1WV+otwUgTc3k9BfTj713WdlouV6rpRURZ6fkplhuuztXbbnd42bzpbn2XwiSMpikIvL8/q+0HNorHsTHVUj+2ZPc5VUJDWq/V0r9UEwBeqqjQadn/Ya71a5yzhMKSRx5AZycF0en19U9setFyudH5xriJQa9urqiYmuEwnUBdFsHT8NAq68IbAQXU9HyA4xnSI4XJii9mjEMLEynUqilJdx5kgIa+p9yGwbqEICkWpuq5S8FwUGseYiJ6iSFMCw3wIoI9ZLMtyIrY02eheVT0FUJNN8/IOgIbXi3NP7Augx8uZpOPGXwfaPMf9/X127Bzy5n6FvqfTWn3WDvDg4Bwmn+93WeNnXAu7hQ5wfc/COZij7DKBnBTItu1hGh7STKVKa+1222xDAXsEGwQ8zhZT7+8kDVmT02wO9+VlJJ7B8cALIgYAfnl5mcsDCQgB6ehvCkTmyUdPT4/5XIW6bhSjjjKNRVHo9fXFMsFNDjCx97v9TqPmbG1d1xqnTN16vZZCPPJhZBkTBukUY7pueu69Qii0XKaDaxnSMk7nXsWYmooXk9713XzadghBzaJJ4+/HMY/u3R/SKGkCw8PhoGFMQLAqK0WloP387Dz7uHEcj8oG2Y+6rtV2rep8QHCSt7ZLvazlVJLWta1CkXpI94e9qnIqp61SqfYwySaT8JCJlOW5Ul3Xenh4zPp4fn6e/SB773IBicS+gmPwV8PQ63CYM6d56EnfH/lZH807tN0RFmkWTbYjYxzzQcHDMKjruzT2uAhaLVc5AKqqZKPjdEwDdpXAEZ31ci3k3O81BQIp80FQkKsB4ixfTnxI0tnZWm07ZyeT7CabTj8fRBBEg2c2PEPpdo7gwQMMz47gN7k3r175C3/5z+v7Xp8caPyTf/iP9Pz8nAXb008YzFNjzaU3m02uby6KItfMS8osEE2vMCuAUhpSMTYwBvydJlZqZimHoZyFyQiwJJQn+LH23gcQQmoOvL6+ztEpZzvgXDj0BccMsKGsgrpzAiHex3f6WE8CGCbDsLkYW5jBEEIeZUdAAfCnBODLL7/Mxj6EdBgRDA0OFgYZAIfy4jio5wSM8h0AeD8Qij1kqgMgjylRMUZ9/PgxC/fj42OeKgV43G63ury8zH0dAOw8Dm8C2D7dg36NcRh02M8n4AJ4YdtRFv7N5+f0ZlKwq6urLF/DBFpQTGpbx2FQZRkNlBVHAxt1qrD7/T6Pa2VkIowvQQt7wL15UzkO3M9IAZigh5SjEEDisGOMOTXMnhBE4sD5Dgzw29tbDtDGccznenjd/DAMeXQuk50ATmVZ5uk8d3d3+ulPf5qNKwCtaRp9+PBBNzc3+URr5BnmxB0P45BjjLlcDkcF28k+I7ur1epobC42CQYQmRn6eZQf00okHU1dccZvs9nkhvO+nxvyCMZPa68JjpkShJPFhiGjfgYBwMxBrZfEEMy3bZuvxZkCnsIHSOCoTp/HHYaXwZym5ZFl1pFre60vQTXyiC9YLpeKIQEXSohwyn3fq1A6Gwh74GRE38+n+Lq8S8pZTII/Z9m932Nr9fRcA5ad+yGw8Tpw5Prm5kZdl04mvr+/zzYSAODZB/yIExmSMjmGvHjWAuCHXSHb5mV0XAufwPu9BAy7g59BX/ABUjGvOQRfzojPWUBAKM8BmGV9kBWyxfweWfYRzDPbOveOYJsIOthzZJF7coIAUOzZB0pOWUvPwkBqpvtfHJXNYDu5d8+GYet3u50GzaNgCVzSZ9LI+u12myc67Xa7qdfjSlWVeoTI5DFWHVwDLnEb0VS1FsacYzOQK/TRS6vQc2y491PxTPR4+CQsrvPy8pJ9PD4nfW4uzUUeE/4opsBtPoCW64Wi0L5N/oqeKfwca+RlXTlgm+6bgJUqBdYJAo89Zh0gEdB/H77BmqDzfK6pGw1TAE2gjK1Bd8BZ+ABsDHLjpaUQqRCfviZUj3iplzRPQvOeMuQKXXZSAvvntgXbdTgccpAG3vDGbPbJgwX39XPGujkKkDyTyNp55QoYBxtVluWfbKDxj/7Lf3CUDgWosOEYEFgeb/btutS4eXNzk+ujr6+vM/iHxfb0LwKKcen7PqfIWETALMro9fpsrqdRPX0nKZfZcJ9t2+ri4iI3GVP3/fDwkEuRyBJ4eQbNzAQZlJwQVLDZ9EJgkJ3JoVSFYITnRhkRMgBq16WpUR5Y4FyZtuCz/0nn+oQk0rmUf3kNIkaWGuQQUt3s1dVV7jHwNBwAhnInPoNRhC1nKtTd3V0GDjCLgITHx0e9e/cujbEbhnxq9DfffKOrqyt98cUXqdxsksFhGI4OMILpZg8A2awRz0b9OWC27Trtpn9Tdy8lY7vdbFRN18YZIn+U1rCXgH6MmAfVgLZhGDKQwMERWCOvDhC9B4PvBLzApp0yjOOYGtI/fvyYS5h+9KMf5bT4x48fcx8J+4U8eODAFCPeu9lstNvtMoFwe3ur19dXffvtt9n4cm/oLmQCo3kpPYOwACxDMtBDQQbm/v5en332mV5eXnKjPrWzgG+MN/X+3377bZ7u5MMGkNXD4aDV8iyDT5wFAYoDbF44AgJZgmOcE6CIWmwAoTQbcoIjL20BDGy323zPDlq9CZ2sidfMYhvQYeSR+/QaY4JaCAhk0MtSsFfIDXbZn5sSRJy2y/dR2r6qcrkJ65Tt8JgydKyRZyMAoawn//Y6ZcAZdsZBDHX+BLr0FznIYF0gdKijXi6XOfACcGNn0RcANjJHAItjPy0xQY5YO89gnrL/vA8nz9rRP4ffdfmDwPAAEnntuiGDPYAc4Gm9XmZZQ67cdpO1JJNIEOrAVtIRuPNSjYeHh6wzPDNriA/guui27y1A1c+CIPtFNtQzH4Cqw6HNZxmgE+gQZBL7ji3JGEHzMwHW034U2u93Ge9IVk45nflFlpz+JA9qkRn6z8ZxVCGpLOZ75H28PKhGL9lf92XcL7LgJbtvb29HIJrf0eNQ1/W0P7Mc4M8oqayqeXgAsleWpXb7vcq6OrLDBCv4duw8+uj4wOWS73W/LM0DN/DHXA9fh95gO8BnZEfGcdTQzgcHEvwjy/hLngniBNIBuaBixskLbID3AaKXYFvPLKA7lGHh69FfZBRyDxzCvSGT6HYutz7Bvk6kENxyz9gn7A5YiXtBt7CDyKDjTOT0z/+lP6fve31yoPG7v/MPv8PgELlzQ5S0AFQ9qkKYiXJpyvNmQwwfjCuGjDn63gyHwKHUbtTZFMo1POVKwAEw5T4REgScDeK7GE/ZdV2eyUyqCnBCsONs8Ha71evraz44jBKQd+/e6Y/+6I/0wx/+MD8TSozzIzPD9wOYYHhRrjkNXOf/IkynirzfpwP1Pnz4kNfp9vZWT09P2Xl//fXXGoZBX331VS4NQnC9zg9j4qyXB4EoAqdFO2uMo0QGYow5qGOsHOU/D4+P+RBAypAkaTXVVNZ1mnwB8GLP+B4yNtQ4E/zd39/nBr7FYqG261RO8kDghbOLMercGEbK/MZxzOddeNBB9gEGou/7fPI5hgR2B8MYY8ygjs8vFoscFDoryOnMfB4jThYFw4xzR+88gJCUp0dJOhp9jKHBuLGfGDT0GlABwwkTzEGNlJEA9FgPwNDNzU3OcGLcLy4u9PT0lA9iJHP59PSk9+/fZ7BBUIJBBUjibGhExUY8Pj4eTTI5OzvT0M8ZMvarLFMzN+l7gic+5+y5p8Rx4g6yPPPpaW13lB4kOdmC8fdAB8cAawYr5dPQ6APCuXl/BhkxSAGchmciADXIG3KEXDvz5s4Hx+h7EmPqmevHmRHHdlRVlUpS9oecScVJ8j6uiQOFpPGsJPLowNuzi54FwIbhZMlQnDJ8PLsHA4Az7Cvvg3g6lQWyi4AY3nPKpvI5Xs7w8zye/SArxzrTiOtrwnMjL8vlOgNUnj2EMOlI1OXlxRHbj55KyqQYNsZtPcM8PAPm47rxqWVZ5jKxcRyPpqsxXdBxA7LuAMmJED5LYOq9V6xZCtiCVqt11ivWlfIa7BnguK5rDeOgfpxH1zKZKN1X1PX1lWKMur+/z5UOUhonPwxp/clQco/oNzIDTiqKQnEYVITiyFcgX+wxwTC+3GWGfUdWAfDsNZgHG8Fa81n2vGlqaSq7wkaxn+k7EqiGcEVOVQSNRn5xbe8LPSIeyrk3wPcUzPb8/JztO/rmmUt8Ec/KM4AP8HXoYV3X6WDlQ5ttEPrHC7vDf/HD3B8VNMgJPtU/4/YTm8QzOE6CTEYOCU6QSQID3uOkBZiGveE7+dlpdQTBNFiRgIHrury5veGafK9njbFpYMo/0YzGP/i7fy8z9xgQjAubWZbz3H/AGbXX3LiPxuI6i8Uin8vAZuCkmbOPQX19fc0M9t3dnf7ZP/tn+vLLL7OxgWk9Pz8/mizAIvE7AoqqqrKjcPaBzUAovJERp+pBy+tr6uvwcw9wLn6tqqoyuOXfKM0wpHpspqOQuqJZFmD3+PiYwR/ZDQy+AxYMuKSsKAAId3DsX12nEbQIE+AKAI1BRSm4N4A3RoBonbK2l5eXPB4Q0AN7URRFnkKF4HPtbgL+5STYgJecNjdHCFiE8fOACyNGucrhcNCXX36Z94c55Ov1Wq/T83igTOZh7OdpI56penh40MXFxREjAWAnOxZjOgSOBuhT3YHFrKoqTyxiv9lj9tGNDkCMvSrLMh8Qlx2BlIEJBlxSLtWDoSE7dzgccskia8EZAqwlRh2Q4xkMP5cAUEEw4gEKMs/7CezRNYJrQDsZNfYGJhsdwrn8sowBn+E7Y0wZqe1mf+TM2jaNEObZYb74Hgw7zCJrSVDg2Sj/42UWsN8wqzB+zmoTXDiBIM3A29l1nh+9Q0ZgiAFsVVXlYIwsrTtxQAzXdfuMrLsjYm/YJ9YK34DND0UhFfMe8NlhGBSHUeMwHF3bQTdOE4dN+VF2YNO6U37g+g5II8jCvuB46cNz+ZfmEi2eheDJr4uNwt6elvM4W4rNwEeiu6yF95NAbHBd9JDpa87mM2jCm1gBUbDJ2IUQ5pHk3CvBZtvO/XYOXvAV/M5tSV3X2U7hOwlkWWvsNSWt+Fx8KCXE3Dfywveil+y7E3mvr685AwVYg7D0KoG27bRczpkFZMaDZcoOKeMtikJ9nM9RggAZhkHn52dieMHp9KjFYqmqmuXACRpALYEGxGdRFBq7Pk9XcgzEPmJ70EEIG/YQYoB1dQCLDjuY9GwXADURL+vcnOxYLe1lo66bdcDLi7uhz/2DPLNnTQkgwDsedHFP7qtYP/AN9+eBBWuPzLi9o5zUJ7MNw6Buf8jkJkG1Z4jdJ2FHWHfuHTzFd7K3TjKgc6wj70UG0DMPFLH5kLpOyHENAD92icCC4BnbAgZyfWJv/F7Ze+SSvcAPe7ma2y8n85um0Z/7i/+avu/1yYHG3/p//Ge6vLzM5USk/3BUsLAoIM4dZwrr4aklFqwoilyiA2im9ADj0vd9BrWScoP229tbLt1YLNLBNA8PD3khACYO+EiVkmFwQae0i4NwMBQYTmbdowywh95gzaZioMqyPDpbwg+YQ4hwAGRyTtN6/H0cx3x/LmSAQ2f12ROE0idF0djLfhVFkfd3GIZcA8ioNxh2Zxq8XwFjwME4AN5hGHR7e6tmscijf6X57AwcEwCKmlyeoarrNGlKc6DKM3789tvM+OPs2E83cByQRj0o2RWYRfbgcDhomJT7NFsQQlDfpXHC3377rWKMevfuXQ5EUULkFsbn7Owss+Je/+injqMX6Ax7wCFSntKkz2a9XusXv/jFEft4fX2dS9c4WI+gt6pSMyvOk1GtfD8BMKUwnsXyem7+7nJ3eXmZ19ZLTwjqh2HIZYo8I6l+ADsz9xeLxVFAywnsOCqMJKwpMt/3vX72s5/l3g3e58EAa0+f12q10nazP8puUiKCsfdeiVNCggBUmmuTnZ3DqeF0cZRuqCVlwHTKSLM+OIVTNgsQ6NNqCHY9s+eByiloYV0ITrDPfLfbM+7fg36e1Q+dc3YYHV6uV0efzxnoKdDwayEjDpT8s87osqfcH/Li72HfvCfGn81LvpA77gMmD32GOAEYss/Yprquc3b+lKFm/5AV/nuaefGg09fCyQ9nUfkMe439xo4l+9FpMfXC4LskTaWJ+yw/AB7kATLD7ekpQHF54DMECqwbB19SyrtarXKWkfVjHyEkzs/P9fz8fDRBjLUh2GTfWEcnyADH7qv4HOBytVrlklD62UIRdJhwCDaHV11XKoqQA2t0OLHQK52fX+QyJdbSMzDux3OwMKShHfybNXTAz7Ww96yHB4b4K2TS9dxli3JU9gvsk/4cn5jO/hZFqb4fvjO8oG1bFWWptu9ycE5GgZH7ZPbwYd6Ijmx7kMwaoRcExp4JhhShtAn98iZscEDuKzi0Wc64r9PAGlmCoHFbxhr5MBQCVeQAYglMAwYGH6ETntl18I5eOenEs0AUYBexXdgJ/Ctr6Nfi5x4sgP18Dfg5JCKBCbiLPUIPx3HUX/t3/2193+uPFWi8e/dO9/f3ur6+zg7+6ekpK8DV1dVRjXLf9/r48WNujMK4USKFc6X8ysEygujlJbBWBB0YTIAXhimEkNOaLKrPrwYAUkqDMElzLeApID5lUeu61tnZWR69udvvdbZep4PK+uPaZZ7n5eVFn332mV5f3zLjPwxzui+N6ZsnmCTHWKoo5kiZ2flXV1dH7CBMBmUfpLn5HU3kGH3KSkh1kpbFWLuDYZxmmnqVHDe9KAB0jArri/GgN4O1wvHBNHqzFcEWWagQ0vkOy9VK52dnqWRiyp4sFgu9TX0UKP3V1ZXaNp3Qimzxd98HB4vU9jZNo2Ec1Q+DihDS4Yk28jWEII3zaN6iOO5NArgDjnGOXqbgZUdkzZiG5E4UA04w2XVdBvJlmUoJu647qtuHzR7H8aj3BmdKyQwgyEtVcByAEIwKgB6jyex2noN1Bzz9smfl78xKhwmVdATEaHimvGgcR7WHNo2HDsdz9WGuklymcgYM5TiOWbfpt6IOmyCmKOZ62bfXFIx5eQNlajwjMoARpnSHXgDWuCjS2RaQCsgIQBMnBmGCriHrXpLo5Tn8zAEPjJOzzVwfGeMzZN9Ogxh3YuwVGSicuDOxCZwHMdkqxvmMCV8fHHRuriwLFUWpQ3vIIzpDCBqHUe3hoCZnHeZRrMkGHc/D53enIJf3e1ab5wLQs/7Y+lMmz500934KuAAF6LWv4SnJ5IEM68pzeFCDLUBfZpY8jaDl/ruulzRne9FV9oV+AAeb+L30LKm/gDHvrFeMDGHoc/nRsXykiUkxauq9Ow6W0RHW9zQgApCT1STje2pH+D5k3AOW05JOL4lO+OF8yjjNgffLy+sEcOuj/SBTSRY7FOlgXmR9v99rt9+pmUoFJeU+gXQ/bQZ4VZVkYLPZKk1gqzUMxyxzCOmw32EcFCQVZanD/qCqKhWndSg1g2LwE3sEGQdgvri4yCW4AEfsI3IAcZGZfkUVIdlopr45AA9FoWayN1GTXgzzWRUKQVWZxswqSEFBwziqrir1Q6/9/qB6MY9dRhbwtegKJDL2G98AmMUOOcGKzWcQkZMqfI6sD/6Yn2Nnc4B/aFVZ8FwUhfphyPanrCotJlv/8vqqoggK06htqiVW6zRKGFsCFgR7IRvoBjLg5AeYCVnmuSHd3Vawhk5uE4xjs9w+uw1zYopgAV97mplwMhPZJajB1/AsTvbGGPWX/upf1Pe9PjnQ+C/+9m/n9Ccn2boTZgE9EoT5QVFh9pyRO90knASbRbCB8QS4EnS4IffabAccOHx/wVjzvQB/b+xhMRFiGlS/+eYb3d7eSsV8KqeXGCyaRi9TwPPy8qLLy8u8ueMYVVS1drutiqLM19xsNjpbrVVXlbq+s3FzYVqDNBebcyYIljwVTYS+3++Pyqa4Bs6HenEEGMHnWaqq0svzWzZ4GL3Hx0cpSGU5p9CZqgGAJOKnTIqGdZhx9p/yBHeyb29veToZp0LTBPiDH/5QD/f3kpJDIpBomkbPz8+ZHUR2MHqALR+bCzPA+rA2ADYUzptJmTwCoOC96/U6ywbGXpob1rzuHwBDhoV9ZzIM90hD8Cm7QiBO2Q0gDzmGmee+eX5U3Fkjn/JF7S7Gj+dyo+XX4hkBCRhSX18MPfeEIzktmwPUM3FOCipCqbZrNfTzyMz1ep3Z6iSjpRaLeboQGTf2+/X1VQppFj2EyDiOurq6yjrJugCweK6u647K1Xh2Z3GwNQQJp70LOFhkCTtTTgGsG3psEY3i2CtkGOZSmh0KOs+eIvPOpHrK3lkszyqwX+50cFKABeQgObLvnh7c95RiHo+ondnxFJggJ56Nwbajk9i0BFhLpdHhs/PFVnN/vi5OkDhzic1Ax72Mzn0La87PXda9RIZ14vuwvayxlxl5zx4kjO8j64DMJceezm3q+z6Td3Nmey77475hZw+HNBkQAggfiS0ga4xOzYTP/D78kdtEB38wtmlE69yEyzlCsPwEq/gY7Aq6THmH9zJxHWSefSND6sEfZEoKJpqjIBKmmT0iK83+tG2rMY6K03tWq1UeZIHeIhf4mdkORtGHIc1DDYaJoCpDkcFhUaRzN2KMKizYREexNfhnCJ85qNdRwzCBxmmQ6Vn8ruvULBY5w7BcLvNhwO3hkM4GK+beLoAn9pX7Yf0ojfXgEduPnHkN/2lAjoxhK7z/i39jc5CFU5IGjENwin6Bu7D77Ady7tkD3jv0g4pyPqgSDAB4dj+HHDhhVk7BiZTOZys0N9472eX3ydp5RpW98yDdn3W9XudeYLc5/PGsiDSTzcgUwR17if579gOy1f2a+3rPrrKeZVke9Q5XVaW/+tf/DX3f65MDjf/qd/+J3t7e9PT0pLu7u/wQ3BDC5IEBD4yjhbGBPafmGpBPBA3jAPshzTVxm80mg2yMJoaeXgAMENdCMWKc096e6o8x5jpNBJ7o+5el9A6Hg84vLnLvAGy+96f0VteJAbu8vNR2t1fXD0dNp9LU7F0UClG534ONlaQPH76ZDu+6zqDXyyVgRnEQ7AETOSiDopwLJaR2m4PQFouFhn7Q4TAfXuUjel9eXrRap3Kl+/v7rExeMkOdIMEMQtm2bV5n6sSRDS/Jwng4oHKnj2NFAbfb7RFjXtd1LgPjWQkWvYwGeRuGQZ999pl2u10ugaN8yIO5tm3z2GOuR88Fe01pE8/rbB5ObhiGfPgcDCLldwTwAHecjzsA2EgAK79HDwnWvdYXWQMc8Tt6rjxgx7lyXVg2gBuldDMgnFP6ABxqywnYaazu+153d3c54Hh4eMhOa7lc6uX5VdfXN1kvKQMCQNR1ndlbHBGOicCGEc4+rGEcx5zpw/ADkrzngfsnKKYUg30guwmw4zlw/J7K5lrYLjfoOOCiKI7qnbGrOEsPDDxL4QAb4ImN5ZrIknQM3AgwAEjcK7riINxZsnQf87MhG0lWUmbpNKuRZC0d6ue6CGAFQKA//Czdczr3g+c9BWe8j3Vg7byem3thvShvYo2xeV4Tf1raMDPY1RGIpW+JF0DLM3SepXRABWFxZP/zWqQJRthq9CqtwxzEIPseRHLf6CpkG2XGZAzn3odUFoO8Ybe8/ITv6vs+T4RK95mew0duOuuK3Uf+IEW8v417BWjRt8HwmP1+n8utyNZ5r2Fa30JlWR2Bz9PsCnaT/a3rWmOY5YbmbfoKsfdOerru8XdsRz9VMjRVfcTWewCPnPIc6Jn3NXHvrL+z1g6g0VcCI9b36elJCkFlVWo1BQIEHM6U+9oDgp2cOCUl0Ev3BciBE7bcHz4InQLPgZXwGT5kw/eIzJRjDw9ksGWsITLmMuc2CBLIdZn7drKBtcAncx0PDrH3TVWrMNnFnuBbwWWO1ZABfs5a8gyeWXfby/N6D5QHV1U1nxUF7kaGPcMh6ch34o8gf71ygXuFSIMcPl3fv/E/+ev6vtcnBxp/7+/857lU4OHhIbMEGCOMmk888QjNozpuksCDmjuAD8EKm3B2dpYnxsCgY5hh0SnNub6+ziUvGP3TYINF9lQeIPz5+TmDKDYVJaHZGue9msqqKGmClbq8vNR+Onjss88+y0HV5eWlur5X3SyPnBaGpa4qaUrLERiEEKa68UGL5SIfRsfhUQRfCCbAzo0qYIhghMlT/Ozrr7+WpMyit22rzdsuryXNvjHGdFhNHPLoUJpBCbgAu3/4h3941LiLw9rv93r37l0u3fJImXtGsVi3EMJR+Qc9D5QXMfGLKUVd16XTp+PcxAQwQrlw6p7apYQMgwurgDFiPDFZBoCWlwUytrnv+1y2w/qQAXKWIJdlaWaavIwM48sULP9MCCGfE5Dr4av5gEpYT2dEmKLCvzFIOCQcDsYHfQVMYBwJJjCsVVXp+vo69zgQBLG+nkL2tcSYzSz5oKqcByFgnrzOGUPMvbgh5nt8Ldwou72C7fZ7wzbAsuK4vFb7l/VjsJZ8F/uGM0N/WHdnLZF9gjW+C5k9dXSAKIy+BxrS7HjcIWdwNR5PmPJ6Xg82PbDn3+lk7rm8xdm+VLc+lyXxnQkkl4rxX1765AwqAI7gJQQd7eHpM3n20rMR7D+ygD9hTb1vYw5sZlbWM4mub742ACIHFuM4ly4iox4w8pzYOl9nguumWehwaHNA4tmLceyPgiXXHwCs+1fspgdPPC/rut3ulE5bDkf3DNEEgeiTiEKQ+r47Iu3orxuGIQdhnrUCNLLGnlmSdHRGlaQ8Dc+B56kef/311zo7u8hyRNM8GMDJEewl69mNMzDFZrnc+HkfrAd76OAwY5ldOuDUZdP3FVkFwPrv0AUCQtYDAM99sV7Y3Tlr2GV5qqpKY5jtOxiM0kLPhLIWgEi31U42OXvuuiLpaOLdKXnh60SJtftgLxniejwzNg0A7HvgAQS2kkoKfz7Wi/twn4KtdMzq73PixgPuTFQpqCzmDL7bWfwo2MB9EDj4NAB0f+w2Gf3mc5BlPDO+BF0DT3JcAvrGdzuZlPR/m9cDOYH4Z50ZdIQ/8vf/O//+39D3vf5YJ4NjAEiLA2iJpJwF8JpXnC7CzANQ4uFR3Wmak+j366+/1hdffJHZGWrUUA5veuZ+YK0o8UKopePo8N27d/r666+zcNGDUNd1Tg+iwM/Pz5l1OXSdnp6e9NVXX2XHQ2qwDHM6lEAqKeioaOnVw+GgDx8+6OPHj/rqyy/V7g/ZSAOEEkO2UNd3R07SDQgAmyDIWW2U0YF7XacJU5S2XFxcqG1bvX//Xh8+fFBTp5nggCXW6+LiQvvDNgNfwCZAn2Z6aks5iJC9fPfunaS5ca3v+3yKNwri/SQo4MXFRWbkJB1NL4PhR/ZSY94y3zPP6GV5KCcGDLlBpnHaBCfeDOXsubPsuZkwzFMgKIcBtOx2Ox0O6RwRDBPvPTUGZEQI6HDgc4Nne+SkAVlcA9UGJJBZ87NwAA+M7sMAAlgyezNlgzC86BqgmHV2G4DjxAF5OtcBORmP9LlCXTs3BTtQOb1ujPGIiUVXPPDD4AM+TkuMXI+wTbm3IMxlSGRWuA8CNjJrOHlkxEuleGZ002XdwYDXXHuPhoNV9tZrud1JsybIlAcqrM8pU8bL6+YlHTnXZHeWKsvj9eOZU7+GjuQXxnIYRhXFXPOLXBGo810O5tN3zyVaXvrqAZmXI+GInZEEELEO7DH2AuAAWOZ6PAN6i4wwJQmwwX0408uz+ffhMz0A4TnxoYDjdPbDvJ/4xbTuSa+xj+yDM6bItTPA7Cugme/a7fYqyznDx/td15FvZCjdU5/HvBLQUP7J2qALkIE+khcZIqNTVVW2p8i564cDLeSdATK3t3dK/Y3zeGWC7f1+n/cQoqYoCikEFdUcVPkgESeiKPFCF7xCw/W2qiqVoRAQjHtl/7BHPkwDWeb9Dmjdjv+yINtxAFUCTKMahkExBBXTwYJgj7e3t1wid2oXfB+Rd8/Y/LJ7AoSStYdcop8CP0W/KXLsk/DcR3kwQzDl8uylTW6/PEDG/+DH0RHsGM/j2IFn59rsAfjECQvWvqoqrZZLjf085tefhWc43V9+h43h73P2d67q8LVwjAAB5hia37m942deQg8+ApPe39/P8msJA+yHny/kwZeTef/GX/sf6/tenxxo/M7f+/tHzKEHDADBtm0z4GVEpEfzMBoAEoCZp8BxogBRjDTvYcOqqsrR4PPzc0738D6v03UHjUPBEeJkcM5kEwC0GGZSnD/5yU/0a7/2a6msq5jT6xjvfNDTdA84AAxX23WKKnR9fa0/+IM/0NXVVZ4CUYSg7tAeASmEtSwLHdp9vi8YHrJCXraGMBAIuOEnQFgul7q/vz8CRYDb1Wql/a7NhoKpHJQ6hSLmunZOGMWYnZ2d6eHhQdfX1xm0ElljlL744ot8YBvsH9PDqNW9ubk5UiS+C1lgIog3sTvri3IRXHrmwcEEhpnrkq7nBevgik3gxCQrQOQ4jvn8BaaaeUbHQTovgK3fFwrsaXk3Pu403YDzeQyOOzXPLiLLbkSHYciMnpRYKvo0ANjOIDvL4ql27hsZ5bOeNYKwcBA+62nQ0I9Hz4rOA1y81pQ19HtgzZwl8qCMbBHr5A7N2SQPhpwlc2fjzcbYAgArtma/3+fDCZFJSub4LHJy6ki8PII/2IRTFuwUkHC/2CHPhhGQeCBF1gVgf5oFSXIyg0B0Lg3a2Kssi+/oV5L3KEqn/JrImjt7mPmkO6Wqah5PzPrOgU9i9mDBWWMyxaeAisDEn1NSJgp4L/cBMcCek8EHLNFr4Blw5M/36vHxUcvlUpeXl9k38cwO9mZfV01ZoHiky+n5U++KAwoArdt//o0MsIecSQPLn/aoyjXb2E3Or6Gc02U87X+hm5vrrE+MTfaMGcGVg1be79PdPBOOLcYuYc+dHfd1S6TSOq+rT7503caWvL6+pvKvolBZV9l3ONPP+vG9/Jf98evxPDHG1Ggc55Ie5BCiyoM/ei+QA0AxU724Bydoqbo4/X5pnpDHuqucewFcFjzodiLCsRz7hCy7LXT/wX9PT6gmGMTeEkhDhs0lbyFn7Dw7yj1j87FprCXf60GSYz1kwzPSvwxHOrHhfga9czvh2Vc+W1eV6nLWY/7LGjlh4d/na3MKvz0L534XPcKX8Vn/TtYfHfI9Ow2gWTsqiCD8sSeOP04zpR5Er9dr/et/5S/o+17V975jemFwAWYwbIAVNoPyEGosESZ/SBaEg18wcD7yD9bplKlh893oYIRponVGG4MFiILJofQKx04phM/2dmYbR0VK/XA4aD9tOM9O6VjfdXlkI0ILo3NoW5WTo/jqq68y21MUhTTODFlRFPr48eNRuUxVz/fraUECE1hushyk1dxJ0/zNIWlEwygH53uwphgHWPCiKLRcNdnAEATwfZL0gx/8IAMsmCWmP9X1PAoYg8ta0+/gYIr9xNiyD12Xzi9hTC9TsFAiJoohp270lstlPuCPQMFPh0cOMWgw2ARz3rDmAVrTNPlUdpyFAzuXFRh2xj7i4DEu3uxNzwfO08t63JAWRZHHyWK4MSDsP0aEoJx7w8EA5r0OGh1wRpc1dUaV92AUpVT7zPPWdRoP7eUAzmKl/S01DjPTi2wDYDzNzvrzfTgN3uMpfwdbzpI6sKzrOsuprwnvY094ZhykZzU8AwRouby8zHXn0vHwgV8WUFBqx3v9vw6CkRm3qQSuPm0Mu8w9njLhBAveF3WaEZrtbTgqYaB/pe87hTCDCnQqZQ1Sz4Gzhb7+XirLz1IWb84icV88D+uMw+NePVBCN1kXz+bgN1gv/JsHs2VZ5hJTgkRsM2XEDp6lmV31YNTHb3uJFfLjAWiSpXlIgDOTrsdu07z3jNHYfd/nrCu2Q1Iml1jTdJ9zmSEB0+PjY7bX2D8HXVWVDg1FbpC5y8vLLD8xxqNx5egEe+z2nPfXdZ0nPXJ/LiseqM49apT1zSVNXtpIph9ZwybEImSZwRZikwBs6Fhd17lMlRcA3fsbNM4lL9S1Mz2QNXI77IQBNuq05wGyju/GrrOH0nz+Bu/BbiKH2BbWlADLwTTPTZCEjLNvbvPx9ZA87BNZJcCx35tnZz27AAYkYMfewLA7SUXpMffNfTnQBqjjHz0Yp8wLfIMtQq98vdxX8IzoelmWqqta40k2w+2E4yrXVyfqPZhwv+2BDXaDvXl5eclELJja19rtKzaGrB336nKLDJ2SzuwR18Ou+L186uuTMxq/94/+sV5eXnR1dXVk3NNGVJNzrRUUtNluptTMUl3XarVa50XbbjkLI9X0jmOclDmqqmp1EytUVnNqchbeUU1T57Kcpm50fnE+Ab0uTX2oqsnpBS0XS9VNrXEYFRXVd73GGBUklVUCNF3f6+31VecXF9rvdhpjTFOjXl+0aKZyp5HDUdJiLxdLlVWlbz98SMJUleq71CjX9Z0Upd12o/X6TG07p4KLUOjQtgpFmUuMuq7XD3/4A71tNrq8uNB+Ozf/AkSSgdrr8vJCYxzTeh8OWq6WqmvmOeNoE9vkAI737w8HrVZLbTZbxUh5QlDT1PMowKLQy+ur9rs0PpSxbuv1Wvf396rrSotlk++LtK2zV2fTKFrYs6R4KetyccGowEK73VbnZ2kGddd3Gsek1OfnZ/r6F1+raRpd36RRytfX13p+fj46lNDLF3BMAGMUgdSxB6zOGJMd8VQmCtt13ZHhBPCi2Dg1DNVul1jOFFxI/XTA0XK1zGvd92mPJJxboXEY1E3A3DMkGIQQ0nqhI5kdjFG7/U5BQVVdKTVFlur7OUg6HObSomTIZkYQo+gOX1JmU9HnMY6SgsapprlrO9VNbY59VJFuUoyafXl5VV1VqupK+/1By8VC48Sie3AUwswAtm2npm6UmodnZguH6waR3+E4AYoOYDzwwHByLTKQboABW8jWmPV+7vUA6GK8pZmFcvYJXeB5sWWeFfKMAyDAs0G8l+/G+XJd1hD5wyE58GaUsZMO2GIIAEAZgFxSLqFwOyJR2zsHc2kvhgmAh5ypcaCQxgnPjpq18R4H5KBtOf2Ws3m6iThaTTo8T87jOVyGuSfAFIRXsoNz+RbOn+EVXNOzK1zbAfkw0Ghe6Oxsre12J3pTkA2ffkdgAriEYAFwkTGgvDP9LuaR5zwb8tF1bbbvw5DWp2kWk+xUKstK+/0uZ6h4z+vrm87Pz3LJUbIttZqm1jjOjezYSQgXmE1AM3JZlvOwl0QE7XV2dj49V6W+H9R17VF5HnsdY8rMJB0Yp0AjTSZLU/zqKThtxCSzmaVmcmWazJXs3CKTIay1kyNkE9CvTDAOvepJH8oyjZsdx1FFKKSgXBp5mnnKjHY9Nz4XRaGyKBUAcT3TxQbFMR5lkxWOe5LGYUgjnyc7riiFImRstJ10FHuGLAzDoLJKfiXpVpSidGhbFVV5BBQ9SAOES3MJz3HW7PhATuwkQzicAPJgbPYxc48WekX1AdeFKOR5kD36MvC56IT7W+6d74BYnCd7zofPsc6Qs6yBZxTZF89s8D4H5h54DMOgOI4KE45VnO1a23V5yhj34H6pKEsNfa9QBAE5gqRQpNK7oijUdp3CZMMV0iRTnrNt20yA8EwQRo5hsJFgtZnImKuMTj/j2T1fQ9bVfQx+5090vO1/9bv/JCsem5z+lOq7IW8kkStGCGHlARBomJI0v3s+44DPPz4+qKrqPDWGkZ4EGTDfOG9PRXk0S3To6ThXJJ9gRKodASH6TYKS+itgNWAYfKP9NMeuS5MWKFWCLSR9LSXlf3l5+Q6I8lFr+dTk9qCz9dnkkGdDg7GifOpfFsVynzD3vJgnToDg6T5nWes6TQi6vLzU/rDNASeMppceES1zf+OkkJvNPLFHSkbu/Pw8n3Re1/XR77qu0/nFmdKYy/FopjhgYLFY5LHLrB/fyZ+u63Iw4fXnGGJXPtYPwM8+kXpFbrlGTiP3s3NzhpQsA7KJHKLIbpB5j0+EQMZCUA7Y0SvkG6DtTK00j+AFQEalf9OnQyYlPWuZAoi6Nt0+Ph/j1BnkmuBxUFA4YvTZo9vb28zuoAMATs+Keiqc3wNEPX1+WtvKmlE2QQBZFPOscgy9s2roqAcjznZm8GEZE8/YcB0MuQcnDiK4jusr4NaDmTR/v87BL/cAuE4B6uzw2FMH3GS8pLmMxEvIkBWAArrirB167OUjbosoTXFW0Uui3FEjLyEUapr55HpkIdmPRnU9J9bRi7T3VWaAsa1zqccsox44h1Dk8iO3/xJN8rNMI1ueLcUWuP6NYwLlu93uKChhfTzjw7r0PcTG8ThhZMwdugfBaX/npkyCRc98sX5e0kAmDF/g/SbIKOvHNRjNjY1fLpf68OFDtuk+YIDPDsOQy5TZc74TMFzXdS4X49lYW/Y9YYVKmuyGAzJsM5jAg3Jnxx08AqZWq1WuP4d1J9gniHIZ5d/Y5aZpdGhbjToOvJ3tRd5Yd8+iwkj7sxDkr1YrlUWpMY5HBzqyvvgY9qQo0hTK8YSlZs3HMGcc0UlfH7dF6Invp6RMNHgVCHLm4NuDeog7rst+sVeOPyjtxkZ7prqqqqOzqhibClnnhIBjNkm5WsIJQOwf2ZpZF2fSwHEp+8Uffu4BK/7K/QXkkJNCp4RHuz9oNNLJ7UO9SGd2cf/ci8ukrzt2auxm/AIZ6TaT7/HMNHbFfZkHWOiN6wD2AdnBrrveYF/KsvyTDTT+u//6v8mb7mzofr/XcrE+AksYCYTPWTE3xiiHgxACBDcCOFS641k0GCQECeECrKPclDIg8IBq7pX7PG148xQgzMYwDHnKE/eH4jdNkydGeOkELxq26rrW9fV1Bs8o9nK5zJM3EHbS1t5IfzgccvOuA02e8fz8PJeKwe7DtAEeMfjX19e5xpmSEa+ZBERhJNq21W6/0TCkkh4vCeGeuNeu6+wEbKk9dHmSEyVoCKuXcCyXSz08PExM2kr7w+6o3MOdAobcI25nBzmkhubJqqryGGQAH9d1EEQJCHvrzIZPI0kB6U5dO0+neH5+PgomMQD8Hgd5Oj3GlR8ji8HxCSQAaPbda6OleeqQB/+S1Hb7LGfIfWaZwzyCmOs6o4dO8lyURFCSg1zyXnQGJ4ahxvmcZoR8HTww5J6Qk1N2in3AGfEdbri9ht33krVF31lT1oTPSDpyKgSaniXDXvF3D2z859gdXnNpQDpDxAMY7k06ntLEHrNG7uTQPw+G2RPWBgB7GtR48I08eqDC9dzWAiDddtZ1nYcgJLtRaRx/+frS24EMeHo/MbVzKZ6vq5RYbWea54DwOAPktj2EmM8+OR11HGO0TMBwNM6xrhdZvvgMwxqYNMf+8rs0lWkuGQshZJtyug+scTrj5UqpryWtP7Yc3dnv97nsWFLOItHHhv5AYsUYcx8E98E+uc4QrPLMrAv77v1E2GEPrp01d7Dt7+MP+IBsuQN29o095XXqnx07cM9e3gpAw/bA6noA4UxzlpEi5P5LSqYoufWAx3XegRn3770QTjqgSwR9XgJJsMZzBCvF4nvBA9143NR8Sh5gP+dM0nE/HURZ9g9TH5uTGdgc9pP19Awi+oVvYWKRD59hz9Bf1g4SiqwZ64bdYUAL/pvvJZjm/XVdH01w8sCK5+XfPBuknBOQPLvLv/s2dAD59TWkpHmxWKhvO8Vxbs52mzfEUaGYB2mAyZApfo5MZB/XzyQSGaZTv0DWAwznAYIHG8g2L+TTCSP8AuvkJJAH3J/SDP7JPRq83KAA4FEcmFQiNJw8/3amjIVhsxBMAK1nRcZx1NPTU3aibP7z83M2MgBUpt8gFA6ScHIAUe6B+/MI0qND7hnFwuD4fb+9vWVHw31Rr4qBk6Tb29s8DhdjAvhlE3EmvB9l5LAeWC6e+5f9F3brNIL31CMKBHuWo/HpmX+Z862qKmcQ6CfhwDnkgXV0MNt3vXa7Q15XQD8Oww9kQyb6vtehPeQ1clYOmUMekMuqms8TQUnu7u70/PycjQIBF/uPMkvzydIEbigk4NYDE9aP7+a5AZNu0Pge2H5eMEDeHMx9IpvsgbP1zvbjADBA9GkQbOUxyuNc235qnMY45v06Zaw9mH56esrrQ9DDvXPfGCSybM7asV8OKiTlAQywaq7nGH/2H0OI40FXnBVEvtkrmDVfQ5w8/wbIunF2oOBBAHbJAQvPDIBMmdnHPMZX0hERgV1Iz1NotZoPwOLgtHSPs5n2Z6eOnnvgvhi2wVpRG859ul3muXxfnNnnM9g6dM3BM0DGa34heNLruxkQ5CX9bGbvHLzV9SIDB+wRzzmOx4MMAB+p1vvsl+p3+tl8YKQHUBziiB3jmdP9SW9vm3wfACtKRLFlj4+PeW8lTX1O87P62krK+4/MhxCmiYOFxrHLz4U/Y+0I4JEDmPFxHPMo9hjTgBb2h6AUe+PgiXVy30gfmwfk6LUHC54NRj75N/rqcsI6oFuMJPf1RpexZ66TfJb3AMpYGwgJbIP7WN8bsl18J/a173sVoVRRlkd4JMZ5ZLeDMl7um07B7GmQ4f7RsyCOObAlhVLTsfsRXy9vTofcwSaScfazmvgu7ol1Yf2QDUr+yBzxPge+rAHX9xfrBg6hRPA0KMVnQ265jA7D8YGTTBrF3vikOO7FZdT95CnB4QQtmXB6P49t0HGVC8+ODrAnrHkOjiYywfs98ujdfg6Q8RfsvRMfXtoUQmoLwBcngnN7lJlx4pm/O9HtOow/90oQ94OnQRv7RT8V7/Vg5V/1+uRAw1lUT0cnxdTRgiAsLCZlRs7GIewwhGVZ5jMLMBQoHeAbgUQgVqtVnj7UNE1udMbQMfnHF8RTfCw+iuF1iGwKToB74jko8+KZWRucLJ8n7Q1zw0hRSsHIJtBEjGFnDCzX5F6LosgNqxhHFxScqGdUQpgb2aW5PEc6HsFGWQyOiaZ3Z75CCFqfzWvC+1EQnPD5+fkRi7BarbVaDUdZEk/rk4nhPlyBu27MhtEDPp+ag1Hh+UII+RA4r412doXvwWBjsNzIurK54u/3+5z+LstCxeSUYBl2u13ub+HaGCMPYJzZ4b5gcTyFyT7zgrVnPecSv5Czf4BZnpkgFSDMfdZVraqanQisBrKIk8PRbjYbScopahhM/u7MOnvh4J31LCdnHmPMAwV4jmygqurIQLLvsG+e/kX+CcxZT8A3IPI0Fcy/CZS5N+wO33ca4KGTlI1guzz9nfqa5kMLceYQBWQD1utl3nvsUFmWWb7CdJ7Eer3OjOHpqbHsq6fjAaJkO9frtZ6fn4/YK4AqZYQEVKyDgxzAAUEW6+b7fHoP4xiz0z0t3wpBeeofoJDvph/Dy32SLVmp7+fDJF12EokwO2sH0ewXIM31D7AJKEX+KdfEL5yfn+dpTHVd57OCqqrS5eVlzpKQESyK744YZx0JApFXnpHAj/vinhkjigxiBwFY/Azb4AGoy7vXYGPfYow5OHQGGzuGHSVgZ1oQ9sW/w4NCL0OBMGBdsUkeLJxmCzyjBgDF1yGnHqS4Hjt4x6djO2OMWe6wCQRPh3aufGBdkSHuxe0x1x3HuW8LO+Wkkq8Bdpqg23sw6M+JMarbzwTBkQ8sCvXt8cGKfCd2HKKTNQUvoIuAdLIO2Hv+uD91osBBd4wxk6Rk87knt5/ormebsWfIvQcA2MZhGHKfGSVWYDqAOuQeunN/f58PNWYvWBP07eLiQnVd57JvZMcDVp7d8aNjPT98EOCPPxuHUUNUrrrAJqZ16bW1YQfoM7YXW+wBfPrsPA6fveGarBn3No5zNQ8+kOdxm+eEl2e//aBE/4z7bv/O73v9sZrBUVhunOh40ayykXl+ftbt7e1RZO+g3qPIskwncQI2UTwWkwgRReSBfUPcoSIQKAkKhrF0cAJA85FxfkBeVVVHjAAGAQXBqcF8O8sCI8QhfTCIKB/GBmaKRqYYY54lfrp+nn5mvU4Fke8jyECpPUrHcDNRYhzH7DSdzcNhEizi6IqiULOYpx3hjJz15H6keXxrCIWGfjxSYJ9Rz9rzeRrQyqpQjHOpFPeMQ6EEy1O8nuHwMW/Iz2lKGyPo1z4NSpBP9l+a+zzKotQwHNe5ewqU53Sg7xkR70HgHmGJnHnCQbBmGCQcoqdGPa2LHCmMeV1Z52xkVR4FeOypdDwXHKDshAD35E7kFNjhSN0po6/cL3oOcHHm0zMg/js+yx5xHx7Esg/eyMg1HRBTmsl98iwO7PhO/8M6IBvOWEKqOIDmmWBtU1YiNcmynshjsjFbSTE7WmeM0cvT7Jln6JCdYZgPWSQ4R76cUUOnsLkehPNiP3z9PehlTQEEIcyZAGcXx3HQYjGz2Oxr0o25WXyzSeWa84n0SV64HoRQku9FBo/HjF3QcrnIwb6DK9YGgEfgyKtt56Zmfoet8Qwwa5OC54Xa9nBka9AVfBFT2VxOQkiH6HmZlq+Z22Wy337ukAMEtw/oMnbT9xF95r6cXWcdCKBYH9bVbaHbLA/YHazz91NZ4vcOosiae5YA/XJf40EMMsOofRhg7sfJqlOCVJKKslA/zlPEvLzN2VwnYrAZ9OfBkjvpAKHhWMFBHXjFg6lCQYeJRQ4hZCwSY9S+PUgToeZ2i+fx7Bv+tu9T2TiA/fLyMh/+S/DjZC06NY7jd8A7ASEg+fX19SjDBhBlndAbbIVn6ZFz9w8QtOAiP3/DcSMl2gTDjkHZp3/6T/+pyrLUF198kXUAPcKunh7Q6biVEf0Mo4FsYj/c33VdJ8WoqpjHymInx3HUqJgDDccD6CDXd1kbhkF1Wamb7Bpr6DaZdfPPSjPm4/qsIfJwes4JfsCfy3EPdh55+ZQejU/OaLjDQSH5L8JEZAkbgnNy5ZLm/gUWwAXQwTOpXw8q2Ex/YBYAZ0MPgDtkAIU0H5pDShpQfpqpub6+zmAQwMq5H6fAlxM9WXzAFffg7wfoISgAyBhTitHBLvfndYQOllkX6uUBTDwrn0OACa74PgwDjtmNJt/vjASKSy2v136eAt4jBdTM8vBZnCH9ErDGGKUQgpq60tvmLQN2vguwSSmKA1xP9aJ4Doi4P2SJ9feAg/vw96IHrsyS1HatDvvuCLx5eRIpYAwrgagHJLyfPfUzaAi6KW/DCLOHPmwBI+F7xlqFYq619BR2CpbmmkwctRt9rsWe+3NwX8g9Abo7f2c9cSrOXnm/g2eS2FMH5zhRD6ww5m7Q3TjyPs+KnQanOB7/jl+WDUOHIVoIwJ0VIhsB2HMACMsEaZKYtb2YtsUe0GtR27x/wKAHTgAK1gEWnv4o7ylxAOJBCPcD0MQJuqw7GGCN0YG6rnPZjQPOJGPz5wHFxxmP47pqSgwXi9T/8/b2lkEDPW3pemWebOcjs4fhuJHYg0tJedoNeyPNQLkoUsacbKREHfk87Y3gBYCADsL0Y3eHodd2u9F6vc73hoyyb+7LmJC1Wp0dMdXsC/4D4O1sPrbTAbP7VF6su/tGdM+DPPTpNMvr49bRZewYNpQsE9ciIMJ2sA6QefSPoD88qxOC6B+g0p+BnztpQ8AOYeOTB133nRxBToqiVD35AXSAXknXe19fdGi5XOY1InAcxzFnwMniOhHm2VECI+6pDOHomRzHXC4Xarv5kE33qS4H2BTs0mKxOJrGiN7yPKc2GxDsawcWzP6jTGVSEK/sK9kSbDq/I3vKukvzaGzK6cjaQo54JgisB35gUAMZWsceRVHoN3/zN/P1ANgECzwvVRiu4+gH5WrYS59siX91wquuKsVhnnCHnUNHyQjiw50k4jOQSMvlUn3XKUx9W2Q7XQ4dm7BOnpUlG4pdOc16ul9iPVg7tx2sv9ufT3l9cqCx3x9UoBz71IzcxlalMYYOSA6HQz4jApbM6+mpf3Rn6MLDgnAa9GmwwnsILM7Pz/Xw8HD0c5/CAkhyQ3Z/f6+maXRxcXGUns8gdwqIcNCAJ5iW19fXXBaGkeFenGUBRHpEOQxDPsTGayYxDnwPETTP7zV4KDzO2c+R4HtxaAhF3/dHhyUR3fPis55NmQ3wlKafmNeyKLTfY3AKNU2pOKZxx8MwqCorHQ7TSfHLRrvtLjtEnDTNWKw3ysN9vL0dNMZpNPE4KkoahjSzv+t6xTGlkauqVhxHjTEqximjEqUYJWasS2Ga+hE19L2kqV46pqkyilHVdADPMKZJQEVRilGLQ08QHLTd7iajtRMNq9w7oA92rpzWIUYpjfAt1PeD2raTgrTZbpWaP5WVO2ZwENT3TNKoFMKouk5jHkNIIzd5H0A1jcGds18ZWMZBQdJuv8tArCynMsZxZqPRF3fiyMB6vT4KwgA66AaMGQGfZyA9m0gQ4SUN3qzpIKssy6NMGGtE2QMZN2cQnVxAP9AB1003uoB0Lz9kTSAv3GmeZpoAUl6miWPwzBKy4SWJ6V5gPisVRdDZ2VrDMKos574Kt1O+N9yHM9Cwo7xgdqW5DAsnyqnx7IMHgwRbPBOOtSiKoyEFrKcffsdzESgQCKTrthYY+iny6TOPj485wPJmROwUZTwEhAC7ppl76AA180S9mXGPk95/+PBh2o9Kt7e3KopSr69vOhz2YmQ08kFAg6x4RoMDA3NDaN9PPXYHtW031T3PmS4AfN8PE4m1UtumUbHDMJM4kjJpxZ57gMHehhDyeUf4I+/NQWc9o+dZfuTCswueRfFgxsEoQBRd93IZ10HkP8Y5o87PvBSJawDaYLSd5eazktR2ncqqVDXWKspCjNtfrlYapntxAg0s4oCc36V/d4pGFAIKAWYeGCPTTob2fZ/99mazycE11REQK85MozO+50WRRubGcZZXZ9mj5gAKX3M6LQz58HIgTns+zdSgw6fkg/sSL/di31lf5J59e35+lqRcsimlHjV0EvKNag70FOL2tOyHoMh7ZSh/owzKfZLjObIVBJteyumlS+il742TbNwr9tUxqctX17ZpTLHS2FqFIAWpH3oV5TxMwe+V+/NnRifxfR5I4EO4F4I/x1dFkc7E4twN9Iog3DPoEIj4ZZ7/9LtYiz/O65NLp373H/zjzGqQ7gF8Aj4wvs6UYpQJPpxJ5Yb5NwuJMiHopJdhdrhlIltqBAkuMFqeeQGIINx8FylOFtsdohtfmlVhqAFHrtRlOU9AYo0wKigvz+mbyWdhJVB+FzjWnb9jjN1JsB8Oopwh5HtYV5/VznddXFyoaRo9PDzk/WJvXUmd/cWwcD/OhrAHHkSguK5MrANlY6yvp2qlmZ1xFsedX9/3uVSOdWT/AQxc8zSLAWDlWTHaZLK8FAaAitNijQF9fE9ic4/rofnOfhy0WC7zWSTL5VIfP35Mzq1uBFeAvLne8OJ7ZsZ5Zug97QpL6WyF7x+G3gG0M//ch2dLpLnc0FkY31OXTRypN0vDONJkBrPipXsenLCOzk46g+7mrO/7bDtcr3gveuLAwcEQ6+sOB0fEzyBZPOPEuvH8OACXe2cZuR+ug64DFLmWs0uuYzTlugMm6IkxHk12ARS4/sc4N2vycnabveW/PngCNt8bat3++TWcUMHuSOkcFuwTdhHQjl45E0cDOT0cp4fJlWV91A9HiQigzIG+l2dw7/TV+Xu6rssgw+WxbVtdXV0d9c3h9xw8SMrsrF9ru91mEMi61nWdySBqz7mOl1pA0KGTbhsALIx7bdv2qOyD5/DRuQAKl3WCfwJWxqHSKwQBB6gmO8Ga4v+RucvLyyyDTji4nUEXWCf2jPOSwB7Z5o+DymoeZ3zEznb9UVO3ZzvRiXGcqxv43Ga/O6q0QD5YV+wjwdQvqzJAH8AS3oTv/o2159md/S4UvuMHsG1lM/eVuP/hmh6EsKfjOOr5+TljoY8fP+rq6irjBAgFMtWsvWejuBeqJXzQAHJTlmWWYX6H/3IZ5O9gOex5jPGozJd15vk8UOR+sHuOK3kW92+bzSbjJO7Be4QcIzju4t9O/LI+6DvPxfezP9hUJ8z5PKVb6BpYlSAO3MJgAPqbWCsP9KV5chYkuOufr480Tz0kQHHb77p5Kp/Ynr7v9df/vb+m73t9cqDxT37nd/MDEtUCBnxTEUAWB2dBgzRZjXwDYS6l4PNFMdcF4khQcBcGFgDBg3nAWbvxknSUVfGUcWVGykE4DonfESiQCnU2jWfh5f0RLjhstjQ7Ay9TwQgBPvk53+NAyFllHLmnOd24eCR8KuwOBtypYbhgeDGgGMuyLPN4U/YdJ8Kzc31PYZ8GWzwfe899YTycLfZAg+t7wxW/5xr82wcInBp39sfT9G4gfcgAe8c6YcxxNMjWHHilw+5cUXn+qq6l4ngSBPtfFWViQ8KcTqcpzh2zBxHpHhM7jI76wWsAB0lHxpS1xiA6C+aBlzP1PJ+kbEy90ZX1dTANW4YuML3NmSsnB1hnXm4I+Q4MPeDLg6wQQjbifIayLkgJgL+DqlO9cODumQknE3JPkQWuyK7rAzLM+7wc0EG9B8GwftgMH6nqbC36QJBCdsEbi31vvIkbttCzLzwDjKBnNzwLBLlDuUhRFBnUIptkrJ0hTYx6p2EY84QyWE2cqAPppmn08vKiL7/8UofDXk2TADnlU2nCTcpiFkXKdANMFovFUR+YB6Vk1ll39hobc5rZJuBBD5B5t0HYBw/KPeh3m0mZFvLqga/7FL7HbR/XpaeGv+MHuF+eiT0kuHh5ecl6z/kYrD2sMuPckVGYfuQZUAnr6WSWkw0EvdgAZA9/z/u8b4t7dz/mPZEQNjIAzjOGELSo5n0Ej/R9n8fLw3T7eldVpafXl2xTuHd0kXWV5n4ZZ8bxKayjv99toQcx7IEHX8MwSGM6QJh9BRT2fa+irub3TS+3MawP6y7N53IhI9wvto3g6u3tLeOu19fXbDPxiU3T6PX1NfeFHg6HKRs4Pz9yTsbBSYlhGHL2gnvl35QN+77gz5qmyRM+veEfXQwh5Aly3AP6hGzib3e7XZ7Sxgt7xr34XiFb+EFs7y/DYOM45uwOunM4HI50kwDOgTwy5fJRlgkLVGWpqpx9hAe1jmUc47nc0AvEfYG/uD8IVc+qeJCIXqKH7Mdf+bf+sr7v9cmlUw8PD9lAAOqpH2OjeXn0yd89BePN4AA6B5+unKcsBBuPYfeoMYSQAxSPrp1ROz8/z4wRhqBpmszsOFviYzKvr6/zojuYdyaJ2j6MhrNkKJlnPxAEB8sYEVdQDP7pLGMcF9c9DR5wfCiYlxc4C+bGjb3gxdpLyusE+MA4ubKg/G5AUNAELOYI3dOxGBBnKdxBcm+uuJ5d4PtwoCgLig+zh8L42kvKxoyX18pinDwzwn+9Tt4NzfzfIRs5B/dN02iI4xFgIJir61qHrlMRjidq+XojQx60N02j7fa48RKwz15zD8ic99iQwYJxPmWn2UtpnprjIN+BGPp8+ndAO+ysAzh3Uuy76wrGFz3hmugte+D67hlQwDtgmvehx9475brE/WIXkFm3X56t9ADNM4Zetw2wxGhjO5xdY78pa4oxZqaeNWPKC4EeYOHi4iK/j+/EgbNXbj8534bAB2aaXhDXQ8+OIYMEQNyvA23XIxh8/MZ+f8hjZbsuNXJiK3F6Xl56fX09ETtJfxn/TQluut/2KCsGo4099/Hn6NdpptWDfs/MAp7QAWeUAX1OvnlA7vqHXp0SHKeso2cX3U9ut1uNYzr81TOxbssAdT6wBFIM/b++vs52x8em8p30lziYdVuM7fA9xsc7CHIWGh/uTDAlhw5m3a8AitEDz3IMOp78SPBX17WGdiYiWI/z8/N8TQ+KKHEuynlKnWcj0HsnerhX31/uBd/N/bLnvpbIpoNaD8Cqci5tYm1Zm3HKJpyWubhs+jN4dskJBrInDiDBP8gStsh7O5gE5b2DkrIu8m/wC7KFPfMANISQe7G4f76Xl/t7bARAGl0DXxBEQj67znkght7zrOwPOs9646fo3/LeRLcNnpFHR7yHD53CZiA3gH7IS/wr+5AKtsMRXnDCyjM87huRC/eLrA86RRmZ3yP7ye89cOVaXub3fa9Pzmj8nb/520eC6ovLAywWi3wiqKfY2WScjjtsNpIF5pAhAgzvIfAABmF0h8d3SMeH1LjBR2k9sHG2hMXnWnwnwNTTXzhSFt1rHnlOZ7H4PjfAp/fgTskZftaa++D5HZjzdxTYU60YHoytlxE4g8ln3Kh5yZaDC2d2qfd2BeOznrGCXToN0MZxTmlKx/PYLy8vNY5jZiil47MvnGX29XFlk44zPAAm1p+fYTzc0LoR9uCEawC8cGiAtQQs08nCLpNcf3/Yq5zKr3DyGcQWhTavb9kwO/gFBDnDMMtQGhkKaD51YB6ceimI1++je76WOHAcad/3R9O+0AVnUrgWP+N+T5n00yAD5w+o8yyB2wv2g3shawpoZY08KyHpqB/hNIvGi987cMDAnmZ0ABHu1Lkua0HZJTX0OD1fMy+H9NQ5gRz6yxkbt7e3OWiihJTGTtYXoOOgAuDE2nlm6uXlRXd3d9nRAaQdbPNc7A0/J7ihxIU9w/mhFzFGXV1d6fn5WX0/qO/n3p/tdpsPhaSsiWDHnWg6n2JuJHX5GMeoYTgex8kMfgdkyCNyho4jgx5gQ6D4c/MZn5TmThobArD8ZSWn6AWy4EG+l7JIysQeoIKsu4Mm9owAC7vCniG7bdvmzNHhcMgZOdYDkOUECYEyNgNybhiGnBFCnhx0Y0c3m42qqsoko2e2sD/0DrAGTGV0vXef1zSNDv08ydGxRVmkk7UBxc7CIjOsO8+bSY0ws/KOCzxr6DaWdaEfwVlrxw1OyPh+e/DvtiYOo4pwXNUwDIP6YVDVHB/26gGDExqUSJLp5PcOdLFD6AjYh59T9ueYzP0Z98v6cR10xNfDAxMPLPBryI0Tr8iZE4SeXUDHPAuALDhGPCWD3H+yFsiXZ9VZE8gLsKzfG+NkeU5sIGNweZVlmfeB76Sk0qdNInPsgcaYDwEEg7lt9ZJkfufBx6mcONnrZB62yl9u79gb9P1P9MA+nCNMHtN+csRlIJcSD2fDEQTe5yAcI54XVN+djoExwrGwcafNTnyfO2xebqxOAwCUjEYzP0BNOgb5ni7z7IYDJKJYZ1NdALycAaDKZzHCGCIAAQrhCsA9sHbjOOZGViJxD2a8nls6HofG2rH+zsCzL/wdwC7pKFOAAgNKyTS5A/b7JthhnTx44Rrb7TbfhztxX3NnVFgnghUPlNx5uLPHILlhdCbGWUvkzK+HcUWm2rbNjEpZHj8nxjZqzs7x8/z8J+VEOCEPCCgD89r4oggqinlMsAdHnpGheduv6cAQeUOP/VAwsoasGXJ3Cv7RDfbulHGDZQNEYjwB16f76QE5zD33wzp40Ey5jNeh+p57kMG+uZzFOI9VZD25N4C717a6feNVVVUuLYDpwxYgV9fX13p+fs6/4w8lewQhLy8vijEdQIm9rOv5zA3YNJdX339vKCZLAWBt2zYfCMq1sSOAG/aHvQFwUH4AMCbAg2mkHMNtL3seQsiHDnKvBMGn7CkyyT0Mw0ySxJj6EVLT/koxGlibfodsO8FzKhNuUwjGYJx9WhDynUFt+d2eM/6g713X6fHxMcsBQM1BCPfpwSH36RklfJWz0zDA+B63eYAK9g4Q6aASGXdf7sEJ68dz8TOqHOq6PsqseT8Ha4v/dD2DkXVyi+u+vLzkYNNtVYwx6/to/olgHd8R+7kciBKZ03HjRVHkchJJippH5OIP6PvzfXJSztl81tyBJOuGzUGOWRMPSLBFu91Oi7rJk6XcXi0XC42K2Yc4OOc5yXoxySnGmEuiwEsAVHwxuAeymADNSyrdjuPLnYhz+47+OZns60BlDKVKLs/YJ4Jt+n/xRa5vXvHhPgZddUIEXfLsEmvufs1xmf+c9cC+8F/XtxBS+bv/nCD+NNhB1rkP7hE9ywHwMKoyItSzO2SIuRfHMdwP/oF1dfl17OM9JR748jolXj/l9ccab+unAjooKoq5DszBPUYUZuoU5LFpXsJDpHcK7lB8GBO+GwE9Bd/SsVHkdzwLzso3E8ft18GhSnNQ46CWn7NJDoZcAREiB3P83ctREEjW8zQY8yjemRQMhQMJvsMZd/8M3+0svws+gYqzLZ5h4l6QBxyjfxd77rXPp8ywB5Ue4Pi++v06AHdj7kbwlPVwI+0Gw4NP9sBBgu8R++FreH19fQSgXJn57sOhO5qiwd/HYVRj9ZKAlaIoFKpKZ6t1DjL4PfcLUADAMlrQ5ZRnrqoq16ezlhhrzw64bnoQiEPimtLcL4FMumFjTzDQ3A+gku86DdS4Ns7fQR0OlDWCTXGwzfe5IURuvDbc2UhYJ2dxHQwwZtF1JsaYf+4AnHtHJ1hHnDusHUE59fGuRz6iM4SQT8t9fHzMDoA1iXE+lBS5BURwf4wafX5+zqfsEhSgHwBZH63NOmO3z87Ocg+Al4sw9cXtrdtwKU2aASx6g23TNFqv08Q6HB33R7YMUOB2LtmzKKnMjCGBpgMUQLQHfgAXZJCgDn/Dz12HeGFb2D8mkXnZnPsSlwXs2O3tbZZ3QDH9L4B3ZJvPo/svLy+6uro6Cr4AX6fkCc/kFQTIqLPN7JfbT3QTXcKvICfYXZha5JHAEHkGzEGmIY8xzqV5EEGuM27niqLIpU6eVePZQghSkSYwnfrevu9VxLn8l+tiT1hv5Jm12+52GuKYp0SxV9hDD1Dcz/l3DMOQqx3wBQBt/n0KhLGhXirdHQ6qyrmElWeXpH6YR5Ejq5xlQeYIm0T5nB9R4OQtsoMNYM+6kyCHckaCYx8r7aQOGII9JWvE93nmDtnkvsER6ACDXTz74ESPA2VpniiFHiPHyIaT0OAS7qeu61xZwXevVqs8KcvBOVnqw+GQJ42e4loP7nlOlzXsjZMIp9kZ7Baf5/qsu5OvToIgTxDfHEh6GtBzPSf3uBfHsKf34oHe970+uXTq7/323z1ynv53jLDfHBs+juNRsOALjXCSEnYn4MLAORbSDHD4LmcBcCrMYb65ucmg+5SVPQVUv8zx+B+PajHSXpoiHTd4YVjd2TlD60bfwbIHRQgdm4pRBgQAtPg+B7c8YzeM0tBrXdUaNKqNvcZRWlSNwjiqG0cNjFVN1JAGxanx6LiE5urqSpLyTHAYCZeB3MxsQDKBsWoyvKUOh/bI2M29J1FtO5dEpYP6pLpmHWYnMRuWuZQB+UA2kS/21xWFPTgtZWC/Yfm4T2QWYMje4QCSbMxTz2Icp9/1atuZ6XWDvFgu1Xat6rqRYlTUnLosQiHZ93kZEIEoz5IA23p6prlM7rS0yg2RM6QOFB1kzYzGDFJmXU9N7uiKNA+CSPcRjhhhgMGprGLgcMo8E2AEggOd4xrumJwZJDPg5Zs8o88+Z99fXuZGx+RMk1ydnZ2r69psjLmujzdsGjIEUghMihuP7B9BCfKTSpvmng4HJWdnZ5OTC3p9fcu2EZ2C7T4c9opRUyZjzgAQcHEq9dlZOsSNw9za9jDpU50dIcFx3/d6eXlJDnMc01zGGNMzjmlU9GKxUFmVaXSjZhauqqZenXpuNkZv0K3dbpf3pCzTOOq0Rk0OFrHTfd/nkeP4E0DCHEgOGkeAVjM1dK/yGGkHPNhMtwF+zoMDPQ/inJgig4Z+OPkCkQbow+fxWdbAiQ72nfdjkyTlINHJFD7rzt+Bvv9xksi/j8DV2XhnNJ3hdZ+DPHufB3uG32StPPuAjno5qWcv8HOnPha/6cQd+8b9OPAa4lx3XhbztKcYowoDUbzHDwDkubF3wzCVJdXTOg9jkvmuzxmj3X53REhyT14Khq/GT1FW44QpMsFeeglXDlDbTv0UrHE+Vl6zaj5fib0FDzBMhkynZ4LdP4B5nMhzIAtRgSxjzx3IekYGG4VtBpyz554hPR1e4H6E/fA+C/wwYNmxALgNv4Fes848rzem45OcpGb/wItOrADYqVxYLpfqpmCiqirtd3spSMvlNNlUc5M/eyTpyB+eEnOOSd3nxhjV1LXKoshZrHGwKgIjEdlLJ9zZVw96CMg80MBe8jrNduBn2aeyLPUX/43/kb7v9ckZDWdxUXAHvF5zBkijpp4HcWDgrDICd2rYeBBqOskceGTKxiBMNFd9/vnnGseU4oKVw2E4E+Hg32uk2SyAK5vIojuz5U7kNAhDwNk0wJjfs6elcVKsq2/qKXvi0S335ky1QlBfjGrGUecaVGqUFrViDNIgtYP0Mg46FFEhBpWhklQoTmC1moQM4aQmN4SQT+h1h8B6AKjdEJRlChr6PgFUpjGVZaVxjOr7YQJKtaV/iwn4RYWAYygUwlzz6kwi68TasI8YU56Fe+77Pp8oCrOILBCgEMx5gxYlGiGE7ED3+3na1n5/yCeJMjgB8ICzattWQ98rRKkHZMd0mihgjD3nGXi5M+B55lK9UVU1Bz84dGeQWF8/dAm99QzP7NATMOT3CVRrclpzoH08vrrK//ZAzvUc+QUswQAh+2Q/YI1hTekHAjB5ypw+AYIpr0tGP3mOGKMuLi6nPZSkoHGUmmapvp9LPcdxzOVJbduqbTsVRam27Y+eKznRFEw7yMXJJJY79eyMY9ThsM8yEaP0+Pikjx8/6kc/+pGurq4n1uw8T1mZZXOdgU1ZznJASSTgbLPZTj+jVKSe5LFU23bi3JWuS8HB1dV10qOiVFWn/auaJjuJEIK6flAoJ/A/yQ6OCZJgtaonZ1qoKMq8zmn9Z4IGWSAQYp+9ztl9DHuW/kghlOKMmsSUzxk2dJ5AADnCgXtQ6wEFINQJM+4Bf3Laf+L9Zsgv+nMa9PMZALhPrnGmEKAOOEPvAW4AKeTAbQTkA9/jfps+plNixZlx95XojDOwfk/ONEsz+UJAQjDCd3jpCPvqxJ2z81yT+/DSFq8gWK1W6tqJzKyDyiKRNMsJKKOHnjnBxjlwBMB2m43225QpOj8/1+vra3r2vtc2RqmYs9eAVL9vfgaWQO4gDnifg/Wu6/J4YM/mj91chcCeI5OKc7mtYwXIWYge9hYfiRwjS5558QAEf35qm50wYiIVgY0H9XzPaTDCffp7PKPFGtJoDu5B/nlPjFGbzSY37qMHjj+4dwIcZM9BvMsZcuCDC5xIxdfEOJ3FNUaFKLXTOXPDMCgOg5qmVjc9rxN3HpB6/2qM3x0iwvfn/eE7ZdUxQYpBR6X6brck5dKzU+Ic+fSM/On6oGvIt9thJya+7/XJgQbGBKXE2XvDHALBzSNwAApv+OOaznqxuc7gdN08zcQZckCjAzHS7jFGff311xnQ4Lhg4U8j1Rkg7o8ML9/ngZFHh6cGEmfmi8+mnzJn7hgQ3KIosmFE6GOcx7Ih6DDcp4y8NAMj7mlx6BXvn/Q+LHRZNiqqqHK11uF1qz/oDjq/u1Q/HLRYLFXGQodhULOotKwqxWGus+S7WUuyUAR/AF/fb3fGaT+/2yjsGRwUzw0Tz+RB1Zwhm50Q3+GyQFYJh81KS3Y8AAEAAElEQVT3+nCBtm1zyZEbML8Xgo2iKHLTpDs/xuHtdrs8apM1oSyBgODUwPEzSkWcyfxlCu/6wZpRy5/ueR7ryvsB5G7UkEvkDYPMfTloCeH4DJDT7AJrw5pWVTXV3m6PAJPLKs+DHYCYOD8/z8+C08KZebBLre9qtcqjTdHJ8/PzzMZ5Wt+DDQd6wzDkLCj7Ta8LbJxPyVssluKgRK7FGku12vaQ2UnsYXr26khPKSPabDY59X57e5vXmVQ3zt7tDPtU1/MENCdbku2d+6cAOEzdA4iGEPTw8KDLy8vZDnbtUV+FM2QEf9h4MhVd26ks5mkwb29vOfjx8iVn0HF22LvjoGU+V4OAn9IPyjr4nANraT6xG2CJX0HPAVE4TQdx2AzulWd154o95o+D+FPHS5DKs/AzBx3uW/Cxvj8QeU9PT/k6DgyxfZ79hkH2a2BDXV99X9BDBxs+HYe1drCEjKD7yDwvnun0u8ZxLqn0TBJy5WQHa+89RgBe1oD9xTdib7B5yJnrDtfEznAWCvoG4Oe7CBbafpYr7peAjnv1rA6ADFnAHjlBxP2gK/m7hlHL5vh8Hvch7IUHS+wFcoKNZ0iDk6HI82nm320Kf0e+2Z+u646yzuiJ4zn2nDX3QBoZ8EwZ/+U+sFWODb3U3ktPISl4btYTm04PGTKHrLtNddvstsDlFFxTVZVUpGv4NM5hGFQvGo0WKLDm/p18F38cqzg54OVmfMb1Dr/AuvNfzxK53eXfPojE7ZLvO9cBjzYmi6zxp7w+uXTq7/+dv/edIALl9Zv1tCAL7OcQHLPc89kQKBCGyhfWjbAbF4zEOI5HCkvk6sAKRfeaQAc7zrj4v32jPWPjzhMBOU3/cY8IunTcpB5CyI7T62ZZWyYRMPsaIfTUn0fjLkgxpgkF1e5Nf/Cf/bbu/+7v6m4MWtSNzq6vdPXZ5xr/3J/W8k/9WG/qtVyuFYeobXvQ4vJC66bW29R8iuNifxFKDy4QfNacdcWQpXueo2lPz7G/LrjIAfvH3nigIc2Nodwbe4qh4L4whM5kudzhqGCxMKTcD3vsdbKzg61U17Ox5Bldbh2Y40hwGATeZ2dn2fBiPB0wcz8eHPt4RICnOxJn8LwMA8dEwIqBRIZZ87QHx4ESsuC6hgE/zmIMR87ptMkbnWAdYLaQMb/3oki9Dv47roMOIW8Ouvg5e488zPPCQy4PIK0+O8w5c0hWai4ROMv/dp1LpUxpfdLJ8fujAGexWOnt7S33PFAPzDUANEmuyiOQXVXptN2rqysNw6CLiwuFEPMBXJA4ZVlO8jLbamR3HEddXV1lHUAmcPx1XauPMxhDB/l+Z2K9AXgcBg3dfIaBl9Vw/w7O3SYCxLBtDoIBGW4rWEtnHD0LDFhHX7gGQAM76o39OF6AGWACRpJA9XQELPpDWZgHZewHgY+XfzjR5KDQmWMPcNy3cX23916G4fLjesbnHDxgVwBu7h95j2eEAXvu77FpTqTxnTy7yxLykcrdUm/Z6+ur6rrONhA5oQyq7/tcE+8ACZBFRhpfxVhefp5LkSxL9vr6mnWTsmDvUXCiJ7PwMWU0PEOODLN+zhJj/33dHIyfAlkPsMZxVKGgpp4nMHogEEM6bRqiij3DXjlZ5cGd4y/8UgghTwXj/j2DBInLXnhgRJDFGrs9BDuxRn6GA/gHOcX+OKj1DAPBDjq93W6P/IUT1H0/T31i7QhsCay4vvtFD9zBPpJy2ZSD7EXTKMT5oGaeues6VU2twySn+EbkyvcX/4GPR27AHy57XJ89zvdSlhqHQUHHE6Uch7h98cb5UzlE/lgn13UPbFzX//K/+Zf0fa8/VukUAuAjyFiU7KT646ZsjypZYK6HMHsK8vSBcUooGUCiaRptNpt8LYTIN8QzAK6EbqR9BC8O49Qw4Bw8csapYWipzXcQCAOOs/Io0tcJp8fGscZstis8UTaC6s6TNDDPttvvtaka3Z+dq/v1X9G3+73CstGv/w//jM5+8zfVh0KHvtNQRh3aVkUMKkKhw36vfr9TOGGevZYdJp398HX1bAAAaBxn4+Ky4YxH0zT69V//df3sZz/Tw8PDUdTucoOypulKZZ5cgRwBmjGAOEuf4pUN+QScvUn5dCgARsc/C8hIij9fi89jxJBz7t2NL9ejZMSZ+vV6rZubG63Xaz08POTzEjwbw9444PI1xqHx/Kyjl+B5ep17JRCCoYlxbip1B0sGkHunZtwDwdPgD8DqTBbr4idVcwaEs4AEVcg/Pyd4mcvY9kdlMm5XsFHYMGyHAyrAx36/zfpG6Ru1+Pv9MfPIvnZdOoGZ8wnQhbqutdlsdTh0R6MIeX4IGVhV1w3GO+Owqio1sSeA3uWJgE7WnDLAzjr7yFV+hs1VCIrhuF4YO80LnULmDoeDNE41xCfBAmDSiaG2bXP2SpL1aM222wkigi90xtdM0lEtvAMNbDTX8LIeHLyTCR4sODlASVoI4WhUpQfonhXh86wFMkdQ6VlB3kem1IGpPz9/d0aS9WQN3D6xZ97LBXBC37GP6LD7onEcjwgFD0484+BEIXtyug8Aw+VyeXSwHzLcNE0+D4LglfWlXBI5dUA7jmkcM+OQmXB1OBz0/PycbQ4+yUujKWFlbZC/02wWP8PX1k2twggsbIyXnSJn2Dhf11N85ESF60LWL5NRZBN/108N65vNJuMHTqenb8vxk9sU1wP8jQebfD/ZNO9b9c+5v8eOAJxjjEeT87B5jvF8L5ywRvacMHQC00kMvtf3wOXZhy34Hs/k3Fzu7QEZ73N86us4Dmk6pAf8YId+GL6jM44DnMgAz/J8numDfP2XkePpGaLiGBWKOcA7DZjQVewGNsJxDevDfZ/aFLdJvhef8vrkjMbf+r//zSND50wZAsPGAAT4OYYFgwubgSFBsPn8YrHILJ1H5G4QpJlFcCfjoN4/x72SPfD0sZdvcS+AF54P5XLwBhtDpOtOwJlsvgPl+P/Q9m+/kiRbfia2zN3jsq+ZWVXn9AEIoskH8oWAmqO5kRiJggD91XqggGlB5ADDEUAJ4FuDgwOCze6qytz3HeEX04PFZ/a5Z3ZXHoAKoGrnjh3hbrZsXX7rt5aZW9EwIubFWFFOempdAjTwZcxWGNqapmmOOe1iOM1xM88xTqd4G3LE8RAppxjO58j7Pk59RJ5yzK+nOByvYnd7HfP5HHlpAYP1dkWCfRoOMq5yoAeNpV9Xdqw7AK0///M/j2Ho4z/+x/+9AjUDBOvAft8COwGXoGzmhzXYBmo7AdbPSZKTXQK3+xJZjxIcGoh3ogmbS8uPq4HMiUBiRgjZjeO4YnRxSNyHRB2Z7HbrkyBIBpGjbWPruNyPi12WpxavwQqBAUYfxtgMWSlhzyv9BXReX1/Hy8tLTcLNTDpJAmAQPJEH4I6KAElPZR2VQO735QFdgGvsY1mWuL+/j/N5Wn3XwTjnr5/Xwd/muR2ZSmAqetpFeWp1eXIua1QA6zHO57HK4fHxMSKi7udhwyjjxV9hGyRSDq4pRUzTWGVG60C5b2OTt4kFoMtEwdPTU9zd38ecl3p/jpV1UuuWQnQ4csRxv1/pJePBVwO8vUcG1syVbvyi9z5gp7YvXoQwrku7oitnrlSZ9edvEa2FD3aSxBg9NMFj0OUEiNZJ9AJ501qxPnigjYW9R/axyJF9ISQEd3d3KzLMMc4yMZvJvw2geCFjfKQrKgYrng/39XqbVTcQ5SeA7cuXL3F7e1tla8CHfSJ71pRqpg8w4BkbrmoAkLZVKa8v/pb/wCbYAuyyNy7X66SIftc20Trm8VkIAXwjL/4OMcPhB/hIdIbr9X0fXaSI3PahPjw8tA6BrrUPNUKvtRaZXMCfOy4iF2zLbfAmYpARPgqA76Sczex+Tgdrwfet11v9RZ7Y6TSVQyywHTCZbZAkGnmijy8vLyuCBz02SekYT1KNjhpkD8NQCQjkVY+T77rynJPu6xb2SCnO09dVQONK66MJICdsThTQQWQLKbksS8SSIzZYgnVyYmc7MDbFv9lXbDG3x2Nc/D1PBv+THtjHC4GiGCglk7AjtTI7ScG5mHkjuNhBsggwxEzO1Q6AlAEeyoKiodD39/er3xkXzNWyLDUoWKD8h8BxGCiwHStjtON3gsQiepOoky2MhvnBdHOajF9mLGALI6KxXWkfaZxiGd9iGXLEcYguhthNEUueY9r3MQ1dDHPEYe6i74d4m8ZYpjGOx8YmuGVtu8nXymsQvGYeU+QcdX0dyPg+BsJckLf3G5h9TqmcTGXADJMBq4Lc0QnW1A+ywvgJdjg6z8+tU9YLNvKWDe2thIyjQ/8BvTgAgqqrg+gxMkNO6GZKKV5fX2srAMme257meYqrq2M9gcQVC663nQs66MDEnIv+tcqDAadJAFcaWBuIOoAfbOX5fK7z9oPCsA3axWw/2CjB4enpqf5tnuf6dGjAnDfwMz7AA4xfYbnLiSoczTnPc03OXl+fV3PEZqepnKKWUqoJZEuu+5jnqa4tieXhcIjD4Rhvb+3ENtqcAA4G6AARgiN6DblCYvH+/hbz3HQVvSyJ4Fvs94da+TEwpsLw+vpaKyZVB/p1tdoJBnJArtjmYb+P8bRu+zF4Qv9cmeAF8ED3XMWw7PHbXMsVS/TAfoR+e+st/gS/6n5wdJw4APixzUS0wGy/6P0fXG9bITDgA5Txcvwws4vP4/tOapyAofduGyYWACCwHX4/n8+r4+GRt9faYBL/yPggGLaAyVUiJ3KOlVThsB901/ZGogpbTxICmEcfbD/8HTltmWxkRHyEQWaMT09P8fHjx1pdNMGV0qVVaWhPk2eN6GggaTAQc6XLybVtZMuqk+CPp3P0l3tRGYy4xNHOB3ak6luZv0EnlVfGCzHJemxJLuzepAb/5nr4JuLL+/t7bTs2uLeeYgNci4TfSYDl7Y4Exs5PyF4Tuzm3/SJ8l3hgG8bvIHvGxJHAxi7bilBdtyXHcvEpVI+q/UdEdK1iZR9nUguZIwvbOeM3FkRWxEmu36cU09gOBOA6rurjW7iWW+u457ZFPiJWmMf3x5/+V39gH8bjEhVB1M4FpWdQdowGxRjx6+vrV4u4zZxwmg48CASWl/vjAAkWxVBSnM9jvL29X1og3i9gCIG9VUPwyS3D0Fi2byk9DtgKhLG6DacxoevKjVt9APVOtpztk8HzvoMs68B3p2mKYbeLKeUYY47YDZGGLs7zGP3liNvj4RjRp5inOcbzFF0UOcWyxG6/D45mRabMuaxNxPt7e8gSR9AWxVyfW55zY8rsgOyIuLbLxA3YtQ1+gO4i+zk4jYoTrN7fT5dkpZ0kZia0yGyJ/f5Q13ia5sqenc8wVX10XXOQRX/a6RxrVrWVEbkOjpsEgTW+vr6ubUEA1ePxGNfX11XGJZl7V6tMH6dTYeHLA79uaiWDANXYopawABZwclTVAJWMsQSGJYYBUEZ73LQCSm5RIihw4geyoI2vJBGvFxBW5nJ1xdynGIZyQtNu1x7wRQDGrnGARQbDRRdTnE7nmtiVJLyddw/7SxvF8/Nz/Prrr/Hx48cK8BvwP8Tz82tt+4IdLAnkLrruts6b1ikShMOh7eciQCFzWL0vXx7i7u4uymlMu/j85Uuk1JU+75zj/sOHOJ1PcX19E68vL5U5g9EluSCxjIjal8xYc0QM+33sd/vohz7SRU9z5Oh3u7i+9Lwzv2VZIvVd5GWJaSmbFudlifN4aT1N683DJD0GSgbYJI+Vjev60jYQObpIMS+XltPh0u4SObqhL889iHL8KGPetlBhu/i0LdtHcMS+DPC3pATfKXq9tg8naSas0CfYRt/TMakG+77tPzFgss/gWtikCStiREQ7uZHr8cR0z4G2Eidv6I97wdFdXv48z1dxFcCxaE0WtbYTKhGA/m17dCNh8srX4wMBgsQ1SALsjzZFqtmAej+sDRtwQoj/Qe6n8ylOl6Su74oudX0fXd/HLqXolyV2h31MF193d38f3dBH6rq4uik2vR92VY9TSrFMc6Q+oosUqUvRd33EkqMf2sZzV2fxvZxgBT6pa7LkOL+fyimEKUU3dPHy/BzTOJUEfmzP7HDCOM/t+FTiJ5UH9MdrwvdM0GIz6DL7YFgfk3wkE+gQduKDB/DJxofoD2QTtoicuLa7W7ZJJ3GM+LgsS/WXxpvIAMIQG/fDd1kX5oWu4lvAszUez3N0qYslX7DshaSInCNdkjvbfN9fToPKEdOSI/UpUkT0XRfzNMecmx9jzFtSmrXexkQ+j9/BTy9La7N0RQZZ41uMrdAJ3xPbNUlmf2ii38nTb73+5D0aZn4iopbzCUZ8lkHhBJgwwAuBsEh8b9u2AivrDW4OHmTUzvwcSLh2+Xc5RvV8HlfOqetwBgVwlWMZU+S83jxFoHb1g3lhECiEmX4zPmZhzGYDuElS+D6fR86+D5/jAVwEBytZ33WRootliZhep9ilyzneMcXr2wW8d10s0RUA0qXochfLvMTpdK5GmnPUoFaA4hD7fWM6Xl/fqiyQc84RfR8xTXO8vr5WAIZM0BcbAbrDXNA5DM5JCclFRGtD4OhVgk6RWR9dB4PDKVdD/XxpN0pRjs5tiXJxhPvL+pX/0Ff0vTiX9d4iniBLexGOz07DG5vHcawP4+I6fV+Oqi1J1nt1Ind3t3E4XFU9Gccxbm9v4+HhIfb7fX3yMC1F9/f3KybRVR8zlzk3vSsADQfS+rDpMUcnkS/JsFnOcv0i53me4+3tPd7fTxU8TBMnXJWjXlNqp5I5MBP0iv2j+ylubm61mTnHfj/UXmX2ONDaxYlKrqTiQD99+nTR39eVbRVbbGee39zc1CTy6uo6jsd22hUBFR/19PR8ARxzdF0fnz7dF+Z2t4uu7+N4fVUDxPXuJpac4+b2NlI03Xt+fq56TwLOGAFhfd9HjhSHY+mDrvs7UtHlu8vaH66OkVNcjuUsIL/fDZEjYl6WeDvJt/QNbLv9yTZqMOlq8zTPsUTpFT6ruvF+OkV30YdIKcZJm44vwI17MWd8A5VAgIXBBkQO3zWLbD/qSoSTC/TWex3MvjMWEiuSDfRxW10gwPv72AoJK/PabQCKwTzjhxCIiHp8KDGPExwdN1wFcq8/MZd70ebk6snpdKp+hD0PBijbCi22P01TPD091eTevoX9GOgIcRx5wGpTUWtkSVtHA1Ou5coTMsaGsd2IiGE3RKQU+8Mhlpzj9N4eWvfy5XMdU9d1Mc5TdEMfu8N+dbR5Sumi013s9vtIEbFMrYIWc0T0OXbDEKnroldSi35BzJLwWedSSpFyRF6WyMsS/TDE9bE8C6dPjU2PaIceYHfD0J7zhN8mbpJosv5mthk7WM4VER9e0eJ5Wy90HiDvtl6SRe9F4ho+0IYY5z0rJBcmlsB/2DqkC/aLb2Q/COPiZfvnnvh49BCil9gFtqu2sSwxLS2hm+c5YskxjS2houPE5DqJyeHiu/JyibV9xCR8jL76gCH7Xych2CAyRyYppYjc9IR1aiR728CN7hiXGnd53VvcXXecmOh2gvT3vb470UApAPReOIzIf49Yl4b46fIbCuRKgBXfrCvX3LYB+CeCISEw04ojJ1hswXxE1IcZuRIxjqcVi8d8acvivg5oKI73F1CaRjmYr9kanIiDlNk5M94EIZy9A4mvW6oNRdawFYDvlFobnOfi5Ay5s7ZmLPicS7IoLP3mfvIy67RlE0i8+DuygfEw8+d+a8bFi3K8GQEYRIyL+dq4SYC4l2Xvsur9/V30fR9fvnyp/bXl9IpdpNSv2ofQX0qqGD1zQTZ3d3dxf38fv/76a/DMlxKsu/jw4T4eHx+/OtFmmsb4/e//LD5//lz1F4fLKU+fPn2K3W5Xz263LuJQx3H86oFI2+TPG/VwXmzaNntKBQ/767r1w5sArFQgOeGE97E7qjcOZDjwvu9qRTKiBbYy3qJzt7e3Ncmg5x1dpfrCd87nc9zfX39FZjQH3Y79I8gVBvi6+i4CJPNNKdW+cRIcQHK/G2LYtacl87f39/dIXQHcAFBkgy6ZHWVM4zjG3d1d5Mjx+fPn8u+cV6wk/qYxX+v9BeiBATbfw8dANiA7/ob8GRO6l3N7Qrl9HZUjwAK+Ms9LHTvfbwl3sd+7u7vqg5wE0RuOPPzEaeIOtkxc6Pv+qwf2OXjiUx2LsIvn5+eqr2ZMvd/IpAKfwXc6ucdnbZNfxy3kyNrtdrvqU/kO1SDsi7mjZ8iUTcQGZciN75EoOBnB193c3NQKCHjATDjz5SfrZLly72Fo/fNOspAzyRRzJb6ZhQck4ncMPIdhiLzkGJf1/hz+hk/zvN2F4CS6VGUvR+MfDrUv33veyqu1DdvfomsRrU0QXbl8rc7z7e1tlRDCtiNTHvbadYUUrDYkgmYYhrrPi/VEZszbzxZjHm5VxG7ZoA9xF9Gey4D8sSvvqUKXsQ3Hd04YQ97b9mH8gxN48JPJMtbJLX8mgam4WpfRM1fonEQUUuyt4cq4VK5Sa82irY11JHaRVJJI4n/sr/f7fSzTGPPS9jj50AD0H7sxwQ/mYfz2W0O39h2O4yYwtmQu7zFGfmf9iW3WW8eW/79UNBiAwW3f95VJYMGs+CgTk94yF4A/CxVBWTH4jpkVnE5E6yPDQaTU2lWaMLtvBr6UytFuddGGtl+i674+XYSgvGXRGB8OH6CF4/dZ1RgWjhbjtLPEOCKiAkaA4ZYJ4yfj43qMweC8zDNqJcfgwcEC2cO8sGYEKED48/Pzaq1eLm0gh8OhnophpsqgEwPYVi6477YMapaiZvPR2heQN7KwvrnqhfxhIpCNe5ZxXsUhLPHw8FCvsz7pp7C1PhXJTPTz8/MK3MGQGyhTefj48eNlj8J7BQfoRwMOhS18fX2tbNnd3V38l//yX2K/Lxu4medf//Vf1zVjvfhOZdRSipeX1xqkcNYOPMiRtePlZM3AjJ512zEOCluLiLrxkn0bVHL4PO0X5VSa9swQJ6VlXWNlT66wWscYfxlreeK3T/3yOnVdOerYIPTTp09RnoQ91/YstxPAhiEPnnDNWNg7MwzD6sFvyzTXYywJ3o+Pj1Xft8QIgen17TWurq7i48ePVf62N+zMDJcBJWABH2+mn3kAvsxu2lfwdwAqtnM8HmtsQBe8JiRv+6E9DGobHwBGsJbblh5atkiI2ajJ+PgO7SQQABHrKiT2b1ICH8ffuKaBDDHADyzDf5Poe3MuOsvncs4r4OV5o+NmwYmznhvrfHNzU79rdpg1B8A5Ltu3G3D5c4fDYVUZRQ8hKEgsvRYmiuxnnJxR5eGzBi8kRAa1jBEd8N4VfuJvAIO7yxq/vb3Fhw8fVomFCVHWgXnalzjRP5/P0ac1K14xw7JEjlZZcG879+Xe6FmRZ3sIoispZqENLGsM3pwOx/fRB8ZgXSXObp+Hg+45GcX3NxJo/dwvJ1o559riSeXCyYvJYHQC++V6Hz9+rDbHGJgvMZnYa0Jyu5ke/TQ5jF/jc8iWeSMjvhdx2Xfa9ZFy2+PDmjkhJQlCJvgE/ICBe/nsFKlrZD3JjkklxsYc3S3UuhBaBaMf2oFI1gkO1PFeFpMf6D/3cVLCi8+Z+HJ19nte370Z/P/xf//XK8dnJ2uWwgMyc4NBusQMGObv20DnbAmFsLGxyCgiSo1RwxAUZ5hWQYSFMDjyOHn1fRf7/RqkM0crqAHKlrEwm2E2jl59j4mFNVPq67vK4cDEdZyhf+t7T09PypCbAQC6cejI0tfgv5ubm7pRDiaDtd4yRpalAQqOEceAMaHANhbG50SFgML1nHziWBgjc8QJcB/kwvdwCrDi6Culymk6VyDoMm1xqgVE3d3d1VMyXFZ2mdVtGDhkNqEBPo/HQ0Tkqss551p63+328fr6tnrAVNd1l42VffT9+oF0Hz58qOuC7ri9rjik9aldzJvru0JEQMJGrb9mtgCbZkp++eWX2rLg9YNFKnsjUgU49gsR3coBO0Auyxzj2Cp8AH02m57P5TQngmuRaQRPmed66Gmxj3Z0NLaAT0lpvdGOteWZHJ4ztjFOU90giC2yJt70ybMEmLsDq8vtERHH66s46Mn2JD2QI7CFMP8k8vgqs7ewc1yLViUDPFq6AJiuCLhygl6TQPJ9gwf634d+va8BHbQfdSWdNXagNUFzdXVVW8uceJJgExMAuyTm7BWkEsa1I+JyQlmZC/6OsToOUt01ccXc3G6FXhHDDDAgWPAZPjDh9fW1VhRYByqkgEFXOog/rpChC2ZIDawBos/Pz3E8HlfVLFeS7Q8M2k1QYU/ohgESSYSBMbrtsTgONdKwEZoGsY4XKaWIrpxKsT0Vz/HfMYV/85N1qElwpMjzvJoH+pwjx1n6b9/INa0P+OFdX/r9GZ8TDWMC1pE12B32AXhzcu6ElljIPX19/B6+Evtw3GLd0CuTpqybCTTjQnSE+2LTjIvPu3q09U9bDIUt+313KXA//sPmuLdxHvc1ceFkLKUUQz/EPLYTsdAvdMIEDLLkZfLbScjrZb8lc/Z62cdzTcbKOiMjdCwioo/1KWKsnfWT90jmrDfcZ7uW2IFPuHIy0nVd/PP//i/it17fnWj8m//5/1UNg+DIBDjJZZsRMWgW0gaM0bikHbEuLVpwCIcggxPaVjQQpts4AClbh+XFRantBAsDN1bgtnVAjMkbvj1/y4C+ceYIAwjbw/gxdjsnHDZsKU9AjWhZNu01ZktI/shqnbWXsbRTFxgXazOOY2U9vAYkAm4z2jJATjgtC5yPk04UHGCMPCNahcyBnfU0Sxyxbt+itQFd8Lq7jxIdfn19rWDIe3JYk+JgUry8PK9YfwJwWfeh6gMMqkEZwBmAwOdwMrC9JGtXV8cYx1ZStTNLqYvX13bcJWMuT30eIuel7tFgHugK8z6dTvHy8lIZqJTa8ZPojY9AxY7RJxIgtzKyHqy1y9WsHaBpvy9H/t7e3tZ7lMSiVCfQL+RdHGRp+eM9bwac58bMut2CzfboLnJgH0o5GKCMhedfIIfjcb9i3LCJX3/9HLtd2zwIuCWokNiZAco5x/vpFLvD+knL6OJht4vnp+fKPuHc+bndswExMOclxqn0p/PU761dIkezgMgQH7Nl/Ny+Y1+J7vgI2S2ooJXHtu/AaOCbl3I0o4GoiSDscgsu+TdrjB/b9sNzPa5lUgZ7pxWwJZhNHuimK00GtLY/3oMVZq24Jsyr2wHti7gOAGYYSvsdrXgGw+M4xs3NzarNBD1kbe2zWQtYXlfFvnz5sorREa2KbdtmTdEF7NsgiO+zbq5EQEKY9d6Sc8QHfCXXxw5cZdgShhBFhbAo9347t1gIQcJ90AvWyrEOHWfNaRHtUhdZ1XXmPo5jjNMUOUVd520SyRrzb2L1cb+PoW/PZQLQohdea+aaUoolNf0hMXH1zBV/5MY62XaJsSaJnOigk6zTNhkglkGeOWnmM+gk/oGYbZ9gIhYy0/G4gv/h62NbXcXcEpJm7t0uZJt14oPMl2WJ3TBEntsDHJ2YOnkxxmBN7K88xjnnmC4nE5pAZU74J+s/vga/gf3WdZjaRnAqSeiZ15n4x9jQC8cBJyHfiiVbPfpv/8X/MX7r9d2tUy7DYsjcDCdK0Kd9iEX1hi7Y0YjGFm0XimDAtREYT+10BmiGjGsgHIRanMr6GQkooRfCOVfbBNMUnL5U+u9oZfHCMCacEIvHNYdhqPtZAMNOiJAj8+DatOrQIxwR1WHbAJzNYhBWWrNeEd1KiZx48cIBbAOXy44EVJfeWT//TqndSaIzfqoKDsIeH8awZQgYB38z6PMDq3CGyAdHRyBBzxw8CMrjWIIfT5DF4cEC51z049dff61soNvcYO2ZA4mRy93IsiSUKc7nIosvX75ERNkQ+v7+Hjc3t7UCwly4x+PjY3RdA4skp6xDRFSwz0lEBYQ1kOOHWDqg2DECOiKizpNrVxC5YRsjooJwJ2ToSblGDp6sDXMG68MhBOg1a1v0aIn9fleZbNbu/v6+Xhunjw0Vmyrf55jg1tb0GqfT28qW+760+pREfqjM9zSVjeuPj4+Vcfb8ARRXV1cx7NctMejC6f09fvzxx9o7je8iSXBCx/6e3W4X01x86M3NzaqiCxnhTbvLstSxEYAN1EjSaasiSaPdi/niJwHuMOoGUNuAiy/zvQswGmM3DKvgxSlf2LgTf1d77efxGfg35GQ2lxhxdXUVh8Ohts0Rb7gm4yQGbMdtljiiVbfZv2QSA7ni98wsm/k1ow8gTqmdNOhWGPwGrUroN3ER+3QbJ76HtQBMOya6MuWTpJAxSRw+w3PCFzN2ruFTyVzB8L0ioiaGTgTwwbSY4utNnGxJStaIsboygv3u9/vql6mkIjdiPKcAMsa7u7si30gxzXM91ILr8v3UN1tCTk5+kAmg7erqKvpUEm70BR1wnCHm85l5niP1feT42sc6NoO5sAf7ZHTYJJLxme2BxMFkLNUAV7ZZH+zQwBz55pwrmUJMIY6whh6Duz7Q363/Ir6hT8aFxmfMydU8+wgnQnwnfeO+jI2xQ8a5c8H2iOxOp1OkviU3jrFbEsb7wHghe7dolXG2RInvew4NB6+fieM1tc/is8bgxmx8Fv/0W6/vTjROpzFSQjiXpxFmNu21FhzviC/KPERK5YSE8r1yshMBGiV2ucqKi9NwALCDtmECLsxgtMDXRc4s5hJ9P8Q05RjHc3ivQnUYEixOEucKA2q2wqCa8RC06Tl0r2pEObMbUGyAi0KaXUIZcNzbNqPX19da0UA+JEKAWoCl5cXJUhc1jmGgulF+3+3WR0CWtW2tPzZiGxdOFBlipMzF+2cAW8gdXYI5cbXCZU6c2m5XTulBn1gXl71J5mhNWZYlnp6eqpMBKJbjSM/x5cuX+Omnn1anSczzFHd393F1dRWPj0/x+voS5/NYbCGVZ1ikvo/zNMbt/V3c3N3FeD5HijUAsiMgSJOI0fO/5NIW0/V93H24j6enp3h6eYkvXz5Hzik+fPhQne+XL1+qvg7DLnY7zulnf86+AdNpuuh7jsPhKm5u+gsQOlan/C0WBhs0a0nwMdtqZ2ng5ABn9vjm5qYGKOzneORJu+Xo4Wl6j/1+V6sIHCW72+3qQ/EKszzGfs9+g3aaVfEn73E4HKPr0uX5Evt4fz9/BaKsq4Cl4oPGmOf36Lp2jjzA9+rqKh4eHuLm5uar00c4Kvv6+jpe317j/XyqDpp9OtgtPoXkCNs3+0y1kjawJbenUBP0n56eVs9XAeQ4yLrdwIBgWZby4KfTuZyGM8+xH3bx9voaeV5i2O3j6qZUoeZxirPY5tfX14ghxxwRY7STu1JKkXKO8XyO3TDEri97mt5eXuPx8TGybJyz+NFtdMUVkYhYAREqXhykgE2xTugucWlbheDzJMwvLy+1fRL9dSsoQdhtTqwhfmlbaQAcYzfEEz9HAr/JPUwE2Oa4B5XbLB3APrkefh5A5naR7ZiIbwYi/CTJdBscstkmfbSmOW7hh7ftqyQ82I2BjDsYnDgahC9LOTUt8mVjfeTooq9xG71BpgCjra8CAPOe9/S4U+B4OMbQdSsCpMbF3S5yKiDw8fFxRULiJ4lRxifLvMQ4jdEPfXRRToWLlGLJOealJDeAdyccEetWJK4J9jCmWJZlpQfoJfJ0IudkhqTRtoifdgJh8pf5WbfQTdYZufp6xBqTjwa+rjgY5OMf3CHhcbm6QOWA+bqSuk2wyjiWGETE+G+ME3vCv5xOpyhHCHYRyxL90EdOcTnae4gcOQZV+lkrxw23H3tO3JffwThLnmPOkBhLOUp3aXjSHRPI0UmG9RTbYF72ScjSJND3vP6EJ4P/z3WiBvLFyReQlXOuTgbgOI7rfjMmVBx0O5Ocz+BYCQY42+2mJhYdp7UtUyMcOya+T48q17m6uqkJjgFHYTfOK+eO42Yc9/f3qn509XMYD86bBIynupJAOZhYgWlrYey+FvPzZl0z4mTdgDI7gYjiCJ+fn+tpIrSyoGisFUHMDF4ZZ2lhYR1pQwBAAVb5uwGCjZUXeuSSsascjN/B0JUKgwaSD58DDdMI271NRGGbP3/+XJl+rj3Pc10jxmeZnM/nmOY5Ut8qZMy567pyfnbqLpuZT6tEmeBJAIpobTjn8VzP2354eIgvX77E73//+3LM6rCP+XIkKI6B9hpYRu7BXL13xW0xsIy2Ez6DPcIwu5/UwMj948jHm8Nhsvx5/m0GEzvaJu9O4pE5jpCT4rBfdI5TV1hDM/Ju7QGQkAz8/PPP8dNPP1VgwXztlJE7tkzfvluezAox5xwRp7G1RrYWrrk+2dXzhix4e3ur+wjcIrrb7aIbhpiXogt//dd/HZ8+fVrpH/JlkzQ+ET/nZ3dMU3nexfWlJRAf4yBkP+eqFtelZc+tY/YfERFfvnypcuUZMr/88kuteHqOMMBmQCFwnCSwH8QkBvMFXNh2kbMTcNshYIl7kwjik7kXvg9QExF1TbEXru0qMzpicMW4/ByE6+vrevKPD2gwQ8meDfwJ92BdYO+5BzEAIO4kzsAVHdnaY8T6VBy+i75SfYdY432TedgU6wPZVFnf9PXDgPksyTHzHJf20D2ui5+3nuM3qA5SveDFdbcnFBFXu66LvOToVSVgTsuyRL8bolOVAJ/lz+JHDIodA/kOSWgXKfqL/RhoRkTMeYl5aQ/OxVc7ebBP3LY4Af6RrccMiWlWm8Qdf82Y8K/Ij3jB9/i8iTbW3DJ08uFx2X/wO9cwHmKdnKigy9ZdJyFONFhH5hoRq1OnWC9kXVuh5tZqzFj6YYjT+DWZYf32PI1J0GHG5bVAByD3mIfHjB3Xikpe7/NA/7i+SQO33xl/cl9s33b/L/7P/2P81uu7KxosFgNmgYsiNTDA8YI4/q4bVucUN0e3i5yXCk6s0Ab1BDQLmoDL5Kky4NRt3CyulR4hwvib3WBOLAJMG33ABh4EVgcMvsuCm10i4DMv5uGN3FzbykXwcNBkbigKpXE+S2Cj7cElRT7jflmUnfWJiJp47ff71QbEYdjHfn9YOT47HoKK9z0gA+SSUqoGxxo9Pz9Xh0igdxsOP7lXa6lpm3I54YlgZyDPA6/MaCA/GGmzxpzUsGUCcNIVnFzGgONmXa+vr6NLKY77dqqR9RZHB2gGkI7jGFfXVzEv7Ri529vbegKSHRQtQOfzuSZSdt7ojZ0GzsLl3pRSfS6EmS3WEd1xIohzZI3cOsd9HfQIQrYFH9WJX8F5ojNs6mct8BEcYcsYp2mKDx8+RNd1td2C8XEij1lRg1N0CUDPmry8vFSgCflhe2HfBj7SlQMA7NvbWzw+Psa0zPH0/Bw//PBDTeIbKE810XAQo3pBnzYyIZjPOUekkgT89NNPERG1n9v6yPpjJ/x0GwpgirP00eltcsP60oYSEZUYYe3MInI/bJv2omEom8tvbm7i97//fU1mfR+OL8UHo5foPoGbhApdcqsn42UsJC/oNPeF1CjxqTH7b29vVRYmzLgmczbQg7yBiea1lRH+CyICv818XFlw/ELHGZ/ZZydaEeujwpmfgT/xmhdxwwchAHzcZuU9KwaR3te0bddgDZCbEx8Akok9x1Cu6wrQ+XyObjfUJAU7JSlzhZbrsueF9WA8+CsTSvh+ksNpHCPlqP6G+NL3fczv73G8vlrJkXlvuzTQAX46yYjQQyC7cvIRf3NysOSIQevDuhr/EAO5pplzJzvGKOAh/J3B7DZx90EFxERwgxM/ZOD45SSWGO0EAx/nCqHjG9iMOXNdx2p8A38DK3mNiYXIwTI+n87Rp7ZVAF+GXpn0MBk1Tq3Nk70+YD3PEx1xAu17oA9eTyfo2wOOXMWyLP1vfAnY2tjMdm1Mu03E8J3f+/ruisZf/uv/54q5QFGKENYgySxmzm2Cbpsp12otLkzULPYwDLVEySkeOBsCJAvla8B24/RR/u2JRm3R+tWiEQjLHGMFDqvgtHgoMwZuEEarkx0p4NCBhEW1rGzMONhpKv3abPpDMRy4nNyglAAv1s1VAtaAoAX7ibJ7U/Y0zbHbtSMGuQeOF8DG2tiBouRmHdCniJakMn4YJxyKWTIzi7ShIA+ch5khWkn4jHuG0TscE8EahxwR8cc//nHVSsXnu66LaZ6j36335KAr+90+kgIWAXnb9202Keccw36I82UzOIAYEHt+P8f723tlr9E1s5F25ARc9M8MJ3rF93C6BC5sBHsxeEBuWwdoAII8AKVUGhgTOmNga3Z0y6ITKLdtiG4pZH58Bx0iiXx/f48//OEP8fLyEn/84x/j06dPtSeeeRJE2LDuZ+zgm5AnPst9s6wjOrws5QnE49T2eDGml5eXiGWJoW8stYMl46ZSjD94eXmJm7u7uL4pFTi3a7AWtOQxt4j1yXr4aSf0Ma/L6nwH/wl4Pp1ONQlyPzs+2HrHixO1zHACgJC9wTljMClDgsaccs61cstYCKC0lBIjABT4T5JDbN9sLe+TwNOqhJ3Yn1LJMWlg8ISuuDUFnc851+u6jQJfZIIGmWzt0owodsv6MnYnW+gTduSKIkkW/tHA0kCZ+3rju0EbL8uZqgKVIuzUzC++BR2JiFqldhJSk84uRdeX/Y37/b5WzBgXibfBMmvoDbXIyaSkx5RzeZJ9n9aHtNRW2MtYTIqyJibKnCyZCGLMzPl8Pse+H+p6bPFX7oqPYG7oHXppHBERq4TAZNE2XoBRTPCBOwzInTzmnOvY8Y/MDUywTWYdA8EYW9tnXNzXeNFYx7L0vJg7NoTcWTPWh3sYtO92u8vD+cZVnCRp57roKWPIOUc39DHL3rmXq0n4BGySNUI+jJ91tGzRVRIwYwpstspwWe/hcdxkrtuHVFpfsTXWzzGh7/v4l//qX8Rvvb470fi3f/m/fMV8tOCfKvME2OaoxWVpJ5V4E3VxwufKwjiwWumdTeN4ESSgxkwZFQOCp9k5Mx4YWgk+TUHnea4MZXmtFQEWBVngLHHaW0fssfJ9gDPZMJugMGDABMHArBIKsGXSUFA2UY7jGPf399WgAGAY73aMTlLseJ00sU7v7+cKHFkzSubO1L1HBYNHaVknxo3DdzUI2cEi42Dc3sYLMGcAfD6fa5XCa2Em38yZAbGzfjOoGLNLl33fx5K+PpHnMpDY9UNl0QzMHcCQPYF6f9zHktsT5AEUp9MpxtMYy9w2BiNX1pkyLjZqsGZgAqhjrQCOEa2CZ1aK+ZpF8TXRX9sKa+wnbzv5gZW+ubmpoBA92G54Q6+QOSwnbK6ZdwdJxsc4tgwnbCX2T5XBABiSwzKmgmLSA1shoeX9cRxjyTmGfTu21IlEXpZIOSrQnKbyfBr2DGEnZvm/fPkSqe/ihx9/jL7v4+eff67rRGINCEFm6DrJuQEO/qSPRlAY7AHU0WMDDRMxzIt1cCsK+mRG15v6tzHAQZ/EAX3HjxJAAZYG+Nj9duz4Uq5l+9rOhb+TxLA++Cb0FDBkf+dEC5+C77m5ual7jAxiSKS4phN3J/U8u4L5AGrw7/aTyIq9NMwLcPh3AX1+oiesOddGrp6nExJfj2sYYGGXBjist1vQsEW+6/tEV46OZvx8DzuBFTfgJ56hL9wb28UfsG5VB87n+nA09JdjgLuhj9Omo8BVKuuA7QoA7woOVaVd169YfF9nWuZ6dK8f/EjyiE7zedsT68AaoHP4UFdEDWCJDfgwPm9S06QQ93I8sOwYM4Sm7R7bZu626S3o5ZrokisWloF9i/UBffXfIiL6ro8u2t5jZGLshE3w95xz5FQe9+oKMDZsPOn720/xN+TkljXjM+Mk+ysT9zGv2xu3ZDNj8vWMV7e2gy1GlH1Rf/Hf/R/it17f3TrFBAHVXrBhaAvpDK4EhzLg29vbFQjkITVeKLO9BA0cL5kxjB0PK5umqT7wyP38AJW7u7sKjNjEhqMuRjnFbtet7ulgmPO8esqtlcVgjgUhALKQBqf8BxsIqDR4MrN3fX1dr4fzwMBJoOwQKNPlnOOHH35YVUV8JCnBEWbJrQzs3/C8MKDiPNZ93jyx121JGLoNnOtgRCQ9WxbGnwXc+fkHZtadLJCwer/M7e3tCsCzplwb1o5ga0bd4JTk8Pn5edVCY8DeXSoatLcAduZ5jujbw/ycIBq4WCYppbg6XsUSLZGiteLq6irO7+dY5hJQOR6WMbPObb1asItojImrcGzARd4+ocnOCGdFcFmWst/p48ePqxPhvB/DQYdrsWZUJ9FLAxfP43w+10C8ZXiduDght8NFb5CfAw5+AfLACWzXddXfEGgAfvzN1R0nSduE6Pb2tjwNtm/vwUZO0xSxlKfQOqH74Ycfql/yPKapHbc5HIod//zzzxX8sT74R9pgzJbtdrtKZjhh77suUo46Z5h/QAB2A8nDPRk3ts+62p85wL2+vq6O7EQfXHU+HA517PisiFIVwYZZP8Adus1nkbH1gWRiGIavKuVcH12GPGM9+a6BGzEMX7r1m4yj61p1NefygDhe2AyxFlvNuezXI1kwUcGYuTZyQhfxh3xvWZZKIGCPyBt9N3mFfyCJx89ixzxrxay1x4+MvP+Pe0OScLADQHfrQ7xJfOvL53mOHA2smbXGb0Pc2R8ib8en7XiJI7zaEbg5ztN5RWKAP3K0Tc2MhwTPFXZ+dzzaArlase26VTJrEFx+tEoHa9OI3Kmusxl35mffRfyjjdDJt30i9oa+WIY1FnbdKtnZ/t0yImZ6b9EWSDsB9LUj1pvIuT4Y0qRNrTpdXugqmI29xcynfieliEV7dBQTnTR5PBFRW1pZV+6FvREr0AvP0z42pXZ8d1v3llzx0+3j2/FBZG07h/6uKhjf8WeNX9EDYsz3vL470fAxgDaSaRqj69ZnASNsEg1YSyZWvh/BA8l4OfEw2wlooSLizBYnhwKzsIfDYcVywm4AKABTxYmXQMDTdb3PIaKdF84C+0mUGC4Aw4kRC4TR42i9gSmiOTr2QTh4R0T88ssvNVA6KBBEXl5eVgz7OI6r1gWAL1Uheiivr69XR+3yPRu/HQnfOx5LoCQRYu5UgxgHcgOcd10XDw8PNYiY1XGiCQAHoLnVKuJrptwngACQaE9z61ZEe/Iv4InkwpuDcVTIGZ26vb2tlTLWPOccS15imb4+scJMGJtuXSXhnimlKjc2xE7LFJFaywr69v7+Hsu0ROQGRMz6ApLoK6eqhczMDLG/CKYYGRm0Izs+1/ettRAZPDw8VP1GdjnnlZ04iKKP41g2Oj88PMTt7W2tapgxIfkw2LOTxm9gG8gWWTMegjB6ClDv+74CBcCEX5xMhv1AdqDDAKWI1gO9PWoUwD1OY8y5tYa6OjaPY/RdS1xJah8eHuLq6iqOx2Pc3NzEr7/+urrf7f19nM6nuu7ogMdDhQsQwvoAXrDTCi6iPT3W7U3YpNl1s2TYD/7VzycgbqBTEE/YIgw9MjG5w1pjQ+iS7Rqfja9hrayPltv2ye1c+1skxpatZb68x2tdCW/VUwMJ9Jd5397eVnLnW4w9crSsDeQZE3/nHgAat5gZrJZjsLsaP7mmAV1EO0XHSTjjcmJjIsCAnnlyX2zNdroFNfzOuE3Q4Hfs9+ZorWSsNX93qw/3Jb7ig1hHkh8nBNgUsYPKIz59HMf4sz/7sxLz+y5u9s32tm07+CTWgr111heDwaIH64fqouvLspQngy/rCq67PgwOIZsYM3IGA4Ft8ImO6fxOrMSmvMbojYE9NmI8SOKKjBkDdo8eowuMC120X0I33BKG7E1oOeFhLts18X2R3TAMMU9zzOqW4LOOp8aoFfyniElxxqQTn7fuOwniuugriTO6bIKNa5lA5x61UtQPtYIKiUeMZy3B29Z7y2k7zq3v+63Xdyca2x5HFIlFf3h4iN1uWCn3NLVePjMoRUFO0XV9lGNnAR48lfocEa18ByCk7Mt7MF4EfmdiBNDWWlJapJYlR9+X5wacz2McDvsYBkquMJ59DEMXu10rwTNuGDgSHZwVC+9MnM/xfQPoLQBGwZCpGR2Uzc7EYBZHYuYKh1PmeIibm+uLPKY4Hq8i5yW6ro+PHz/F7e3dZQ5RGbSXl9c4HI4XYLFc1rYcN8qaO7jDgBVZD6tjEM2Ke7w2IFd9kAUBzeVZszIAGmSL8QAG0QMnrqyNW/0AIQBjWARk7N5lJxJeu74rZ1nneY5lmkv/bC4nVkzTtHo+gtfbARIm73Q6xeHYHng2z3Pshl2knCLlFHlpPeoEChwdlRccJSdRsS7or/vykZP3TUSsAxWOh3PnrfM4aMYTETVpBSCYubGdMg6AJ3bNPbetYG5TMrAy+MUvcF901X3e6AXO262FEesjE6na4csATq78QIqgY9jFOI7x/PxcNtlfGObDfh+RcnSRIkeKoeti6bo4z5cxLEscr68ipxT74yFursrJQ4+Pj9UOYPp5qCM97/iUlFKUM89S7A+H6Psh+kix6y9rftGtcnztECl1MZ0LWByndQsQbQ3Ig2eJbBNYWGe3KWGfESU44Y+RE+vFcwpg4dErNot3Xdurhn/jCFpfi1jl6qbtFz9ESw0klCtR2CR+wn4DJp9kBR1zxYE5MgfLDbDCfg+ONKYNysSCWXVsDd23LjJObBwdwI7QZ75DHHKrMd8zY4lNuarEfBkTdsqYtmDfYBCyBpBpxpUxe/4GnNyD8RhMTqp0j3N7qvUcKebcujAMsNFHg0OuZxtiTrUdpesipcuaRy7PskiXQ+OmqZ46xXfN3OPjtzbjauEqpvSlz38cp9hFjphLjJnmOdLlWUkkiYB61m2bvLF/xfgJ+VOFd0UfH+cY4WoFccmVJpPNJo39FHHjwW+Rh+Ap7NJ7M6wr4CMnDCaKjI34zLd+2n6dIDPPkT07yxwpLxEpxc11exbREhG5S3GepkgpYpouzzLbjNcEn3XP7Z6Mm+QXebiCZIxJwmpS2xhlWcoxt+AtruHP4nPtV1hDy5zx4Ef+1Nd379H4d//2f1uBQ0AHTtonX5DN21GgpAA8M19mEQq7+hLpG2wuAsVBw6q8vLys2DqOgwSglxLvVXQXxvB0OtXe/WIUqQYBM0jck+x5u8mcoAMD6fYEHJQftMUJNgQQPst1rETIkMoCykbLFHPz2OzUeFJwSk15YEtg/QFKBO6UUjw9Pa2AOnPB0RL42TeBkzbwsNMwE2YgwovAxH1IEPm+S87bwAMYskEACpwI2SnC9nJvOz3Lr+vKca3u1cVgSRxxrugda+qz8Z1kMz87QBwr4wfsXl1d1Sejmm0HaHIvAxKc+TiO8Td/8zerRI+HlHGyF8CR5IrA4sAbsT7KDtl7LtiB36NvnDHyGXwCv5t52Z7kxDoAotEbvs81cMqAWiqC9jcRbe8S8/SYzUixP8qMOnJg7k7O/DvVETPIVNZIdEmu/GyYaZpiWuaYLutEe049VrnvIy9N5yOiPm9lXNoeKvwn63V1OMaoTZ3IFdtgvT1e7oHemkBBr53soXPI2UCOBB9fvW0XMMB1SyW+xLLFj5OE0LLDOrIWbptCHwFQnCKHj/PDpvBDVEFpX3FLEAmKwREvt+6yzm7Tc682nzkej/WhXFtAhXxZT174Nsbs9/1dV2J8XeySOO1rW17TNNVj4JHzFgzZr5k9hv3GXtEJt5/6elt/zHyc7NiH2NexDvaJPmyAaoevi65s523icPsitliOyA9ijeewcD3HCe4Hkce4DSIdi1zFd4K4BZomhhg/OmfbQVYQXo67ES1Bxc/hZ5kzPhLbdoXY645ctoQrMnWSCl6wb3c7IP+hA1TSHau8Hqwt8+Jz7h5BT+wDGQdjxZZdpbP/dEXS+76chKMXVJDwAegha2lc45Yqt7MbUzkGbIkeZOBYlVKKIa2PIzYJY38P3rauMX9isH0AeOm/+5f/7Vf2sn19d0XDpRRALc6KDBRH4ZYFwKWVAwNhAlRLyN76fojDoWR5HH9pNtannfiUCAI7pzJRBSl91vvour6+5/ah0+mtOjaybrO5BD+YTRYBMI4czPzZkHDITkhgEQBGyIWxEUy7rqvMnZksEjvuRR8q7xH4p2mM6+ubmj2jIA4StJbknOPDhw+rezkjZ66n0ynu7+9XjIZP6jIT5EDtvmnrCUruYOGACWvjzxhoAjABbxitgRUG5r0p3suAAyNZtpHzfbdc4NyYA/rtwwdoE8B43efpgGBwglN6fHyseuDgaMdtJhf5PD09VUDGEarIAwfBmBzMHAC4npNknI/1h995YS9cE2fswGj2En3yw7FIUtwCgw4ADpEXcwd0Pjw8NKZpacdio58AAQcL5p5zjs+fP8fxeIz7+/taKWU+3O/19TXu7+9XiYqdPOwU4JcxEKhJVLGjluwOEak9lRmd2+12sVzK98ji+vq6ArbqyIf2PAaSmZSjHMcp8mLrH9yCYN10HzR/M3PGfKmcAsrx8ejWsrTnFQCqAZpcj+qTqxneH0LixX+MOSJWSTO2SwD3oQVd19Vjkn0ddAE9wnbxxeibfZIZcOyDwJ1zrq2cyM6fZc04wcxJufWGdQLIcA2THry4BnqFDfAZ4rCJGmSDLF1N2SbVBmz4XjPf+HqDMreL2Obxn7xPzLWfQX+3/oIY4rGSFEEMAKhqMnep5LvV1QkvOrz1kdg2a+V9Z45zrtqhr9iXdRRd2CZt2/2BW5+ITlp+6LpbA4kH3JO183zwA/h/4urj42PFXsZo6A5z4PtgQOsh6wY+2cY6+3x8FUk3uoQvJgbaP/EZd3aY6NriAr7P97aEn1/o8LaShs/DbvFDxl3cl3tsfQu+z+uC3iMrvm//YQJgm1QZO5iMdTyulahI0W2usU3MnURhx+A2t1SiO7aD7319d6LBQnBTmFYCI4YCk4FS4vjZLOpWBVhWM4MlwBzj7u62nlTD9wi88zyvTuuwgHGUOKB2jnKOnIuzvr29jZeXl3q/aZqDVi0vJgvG9QkaBgkYLRkfT6d1pYCgTrka0M+czdRafgaQyAjw/vHjx+o8OcMeB0wAKeMYArsahqH2EePctyX7eZ7j06dP8csvv6zambg+ig1TScKFobkNiqDCmrMmJDZ2aDhRDIsASwXIbB2yQB52pIAUt0GYeXTliPHgtB1At5UUs6cuITMHnIwDPNUC1o+kehzH1UMBLTP0KKI5QBwqY3GQ5IWMrq+vK2DmGi7907qAPVnXmQeOldNaCDbYLQHNSa5103sYkIWdM+Ci67rV09nRUXSE4OPkgfaZ8/kcHz58WI3HTKCP0AVIeG9JdYBKujnm1odHPD4+1kQGQIPs2ERP8EJn0SmfmkO7jatn4zjWM92P11eVnaSSUZ90Pc2xXOzDNr6tQpFwM8cU8ZXvQScgZFwJ4aRAmH/W3AkbwIq+buSNDlg3t8ywEx4HfieiJrL+9m//tsaHvu9X7XAEcXwsvgmZmPF2UMTncRwtczfIws7RUf5D7/D3rjyQjHgfC3ptv255G5hwP4CVK8rYuUEgPo/YlHPbQ+ZkxOAPO/L1tgkJNosvQvbEP1fh+Y4rKwaO2K8ZW1ebDMDRGxN19hUklCQN6ArycvIeEbUf3fMywDOwRU6M2+QOcYvYwbVyzlWH7KuxNSdzyItEBD3ABoivHBKA3V9fX6/2bfoZZSQXxC10xu05kCXMB11izVkD730yGWKdw1e6MuNWK/6OLzJYRwf4m+OM7Z7ft4ks1zDbjn92QszYTPQyDmQDVrVNIxPsj/mxbqw1MZb1sw05GXJc5n3WcJsAujppnXBiAcmF3Nz2hg9gnPYXjPEwtOOAuZf9oslI24UTc1dqTPbY9v++13cnGigtQBPFsiHhTAEJVjKSDs56JwFhE6od3Pl8ridymL1aliX+9m//toJlBGWFw2hwkK3E3q/ACsEzIuL6ev3UZsAp8zydTnXnPwqLgpnlmed2TjJJjtkk2E4cEMDAgIx78zsyRbFcojbr6k1RMD3F6e8ioikLBkuLhtcPg3EbmcuFtEjM81xPQvG9CEJOAswAbU/PYD4wkfM8r/YCATisUxic2SfWw85028phJtaOgnGxfuicAyYOyRUY5oe+ERx8chRz3wII2Cfmb5bgWwnV1nGQ5MzzXMHXPM9xe3sbfd/HP/yH/7CO6cuXL/Hhw4dqC7vdLp6fn2sgdPl12zbAGjnJduKArhHIAAkGLJ4XawiBgJyxNTthdNBMGraBnAEuBnMO+MwN/YHcMKODA2aN/QRtH5Ud0dpNABjc044ZoMMYtwyb2xjwB/v9PlLfxXCxc6piyCKl9QPv0Oucc/Rdiv3hWOdtZngYdjFPbW8JOktgfX5+rlUrxm/54FecfPZ92xOED3ZLHzLEDt16gW/0ugO0IloVko3K2C1tb7znpIeKpttd0buu6+rhAuiqqy+AVsAZlYEtU44v8VGyBqfom0EFsvF+E2zMRIXbbxgjSSm+ykkScnarFev7+PhYddqMsgEcL+us/Sp/470tW4yftF83CLK/JdYwdu/VYE7WNTP7vJAfh2Ww/ozJlW4+hzxzzhF9F/3Q9jy6HcYkEHJ0axbrZP1nrPM8x/39fQXD2DP+E+DqxIzN3yTPrhQ6Mb6+vo6+71cP6DRwv7+/r7pB0ouMuRb6Y+DsaiufJ+4ydusYvnH7pHSP3bHVyQp64fXl+/gBdKnrukqWbgmOp6enGrdcweXluG4bMUZibUxGWe/xy1zD+xdZX3SOn1tQz1yNGdBNPuMEy+DeMRIdRWds48gY/+cYZl02+ZYiIi1ft1/ab4C3tnrPtUiOfS/m872v7040AOxeIPem4agN+hjw+VyOQUWZmBCGbSUojqpbBSKX8v/xP/7H8eXLl1V1xYtOoPBClXGkVUbMdwuLsH5Cs1lNHOfNzU19j/9gA3a7Xfz666/VwQGkItqRZlYq5GZHjaHDym1BrrN6NnQBcr/VQtHkn2JZWskZ4ATApQXDz8UAKOD4cAYkeCjfzc3NCrwAih14twyRM2NfGwbXQcjOBb0z4GdMZlXQLQMSG5YNhmuRQONIzGoyDgKgQZKv4QTV4MKOe7upy4m691lg/Oi0Aw06BpBA3vSWE1D57k8//VSZHGSBjvE5J1asLYHV4NBzj2jVQ+/dIui6B9wtKtuE1IkVtgJ4d/IZEfWp3W7t+PLlSwX0XBPbILADcqm0UE3Drvb7fa3OIWvW28HedgD4xFds9w70fdmvYUbewYSX2eJIrZUIYDXPc8zTHIf9+qGGOV9O0tvv4u0iH1fAkGeK9TNykAGtc/hf1p0xuZUDAAIoRx60q6CX+G/maPbXQNe+3f4josQZjiQ3iDUD61O90ANX1XNu+/heXl5WJ8rhA6jomCxh7n3f1z0wlt0WQAG4qTSht2b8sFPs12AWGWGLrDc/AUT+/Nb/8L7ZfOu5QRj+xUyo4wtxwaDKR7WbKbbtMj7HtW1CZeIMHfG9Ukq1zaTrWtsba8xctvED8OzrMN6UUpwvyVzf95WYi4ivNvRjn8gKuTBnfIRBF9fEp1p/GLNJQsA5c8Qv4ieRCz7cRJb3vqJnrsZfX1/X8SEX/Ln9Le8xX/SA+7NePrnO48Te0BmPeUswb2VqUtP40brJ+CEFfDAIpBprvE1enRzhK5m/yULGsK3E8X38GGsKDtriDOsn70NYbzGtSTTLgpd1FzvBX/D3bXLCdf3dbYtgucjl2PJNMuIExkky9mXfsPUB6MJ/9YoGk8aJ4CjYNOMHsKFAbpOKaNn4OI41KcHQUaLCqt1FSm3DEdltRDtRhOBghef7Fvbt7W08Pz/H+dz69TFCFnuaWsnKgBjBu5+V+zE2K+7NzU1cXV2tThfhibVmubquHSmJk4FJpXWG8dhhswZWii2QtnMvf2tHxpIYwbrRAzpNU9zf39d1dhB39s+aAjKQOSx+S+oae4FeAFxRVPQBWe12u/q8DBt037eHPXIt7nt9fV2DvIM71zUbhL7y+7bNwkZmxi4iKlglgOM0DNBwtozZoARQx1pRzeM+BuI4OINR5owNcC0SAb7DuHAk6OY8z/Hzzz/Xdi3vMaLyxvWpOJGYurRrYOMWEZgjAuRut1sdmXg4HL5iyhmX9/YQoK1fyMcbvW9ubmogdIWPNWL9vVeF95tdtAcOYn+Hw6FuBscXEJTxB9iPWSOCPXZln8XaeQ+EK1zIpOhwHy+vLxU0ozcpr8Ek+nU6nWLOrQXJvnC320WXUky59c+TtLm108kya/L29lZtHT2f57mebMcab6uxfgKzgxp66uoc9oK/BogBqmAy+76vLV5c14dYeE8bujBNU7X/m5uble4CPvC12CHXdJUMsOD2MIAe7/EsEoMd9AKAQ3sc92f++ApAoxNEj9V+NiJWOo6tQ1ZhJ9ib2VR8lf0ga+9kD/0y6WGf6UoIJ6r5XozZyc4wDPHp06cVYYK9Oj6yHiatrIc+xMSHK6AXtGjD9tuXfvjwYQWWTHpa9rS44i9M9JCEG3gzd67LGrNO6L4JJvQDbHR7e1uJkb7va2s3yRd4A11AT1NqxKBt2Wtk0AlI5MAL+wD7W+8n2YJ04o0JKn5HTnsRI8jWfhTbQS6QrAa4JEHbdk4npryHPC1ndBrdd5K3Tf6dJLOW4Euugax8HV74Ibf8cm3GzD3RGfyt/YFJTvtKPuvkjWumVJ4OiExN0KYoJ192fR+R19VQ4yLGbCzJvdEz9M8/jVP+vtd3nzr1l//6L2O3a4683LyLruNGKTjzuYCm5fK3FDnDHpLFlXI4gZvF5DSorutjnpsRExgxKACKgRlsFmPDIPu+v5wedIxxbCVvCwig4HYcrv/29lIdBz2WWyYag/ACA+pwoN68amdnp8DCogwEdQIBQMNVnAJS+xgGevzfYxh20fcYQ2MEARnIxSyvgQog1iwKjtzzsCPG6ZLsGIhWY4hYBbSuKyXTDx8+VKBH0mAWwI6c380yExyaPBobxdhxFnYAZjsYO0kczKkZsi3rjx4gXxsq68la4YDMzjL+iMZwOBHj2pYr+u4A4iQU/SEI4IzZXA64+vHHH2sVCwDDAQsAOFeq0D/WDJCAnMy6eh7oEmN+fX2NZSkbmh8eHuLu7m61t4DAtHXuPH2XNfUzOng5eG9bNPgdHeTfjM/J5paZ5Tuw1/YT1k8SCFe/HOzxYW7BQFaRig8dz+fYHw4xT1OkrjynaMnFve73+xIsutZimnKO83mMoe8jdbRglOenvOiEMdugE1MHZJJO9kXZ1zMXt9qhb044bQcmTHx/gprtDdm4+uCEGh/LOmB/9uH8R8JoZtgAwbbCeAGyJrVckdkSPczBtmKQwvjZU7OtBnJvfIErmt7wawbS8rYPw+aZK/ZmXebEMPtQkmmDDW8oNutqXUUHiBv2r/Zj31pjxzf+bQbaLWEkMlQVOUSF+9fkdTdE6jqeYHeJg5fEPvIqvuacVw+lw685jpm5N1kFAUOM8T4d7+MyUOQaXMdV7Yioc94mIX5ZB9ArZE77I2QPcdryQS9dRYBMwYcXvzlHl7qVnTRGO8WSl6/swTZCLHZ11IQJ+lVjXI44nc6Xe48xDJyieL4kzu0gmXJARjmu30ly15cNz+XBhX1M81SOgmctuhTL3JIoE4hF/+KCY7tYlhkVitRdqtuzNlB3Kbp0SUh3Q0zj5aCKvnUzTNN0+UzbExyRI6UuUor63jiNsRvorij/K+NcIl1OiUpduhxP29c1GYY+co6CqbUOfddHShFlT+6lirLQIjdHihbrpnm+JCZL7Pp28hcvdAUb9r6porvrB13+y3/1P8Zvvb67orHftw28rR+2RMCtYZVXjrIBu+2sf319qc4V0MLEcERmVz58+FArHQQNjMMZItdoyrNmcoqjSl8JiPtume8GHtuTSQHmgCCX6QmCjO39/b22JMGAYewGIiRR3NMB305qy9YzTwLUbtfOmG9AuT39GZnAUpsdIbCwyRW5sE60WcCQe1xb0GF22UwZgJwgaMeJjHBQzAmA47m2JHZerRdjw7nasbNGxUBaQmG2zD38AE4YW+/5Qd9YN/QLIMT9CRrcj7ka/Jil5PrYjuXoKgmfMXhFPgAAJ5MRhcUjmWP80zTVAxH++q//OnLO8ed//ueXyl952jhtBtg7gRXmCR1gjdARgiGyYeMwNmTZ+UQmtzP5WR2wotv+eRJk9qUwL4M57AzZWZbsqUHGbofAvs3yuVrA/ezvnNhi5yTlgBjrBWtRmdBoa8iRtJFzdKmLYTfEeWwP8gz7m36I3WXdr6+vY5mX2O928Xo5YckJG2PH7vDbHtfd3V39bM65Moncj7WhcutWMYMqM5PYP/7ABNIWiHFvNq4jUyrAAKS7u7uVDQO60Quvj8kA/C/zxy5JCOZ5Xj1UzpVIbJ0jQvHJruQxb+/BcvJhNtP2SMstfocXOhfResedJBFH8e8mfJxIuT8fu9tWuVlHV2jcqgRIZw8BMoVAmOe5JgUR8RVIYY148R7+jjWBUET/vtXyzBqXZCIiL60tLudcQGHfqsSWM7/7xLStPyWW87sJKtYeuVN1MMvPmA3QSKb8IFvHCHyWY7xJFxMb6K5bpUlsq5+4vNye5yTAyURERIoCpvGh3LMm9Wl9OpKTM8c7xuf44I3WrGEhSEl+234YSFP8FbI+n9t+ONbq9N5Olkupiy61fQwppYi5PZUc2fG7iSrrZU2w84bsm3PERazz1Co5/uyS6IJoGKJ8rotlUdKaWvdNWfNG2ENoOY4xZhKVnFMsl4QhpRT9rj26wUl+SimW3A6gmERedKklr6y5SXrW0TrqWGJf9luvP+E5Gv9rWVj1zkbEalM3jL+VDSdMAHAZO2L9JNmXl5faW43jZuO2AwmLFdFAVlWG3M5/N9gcx+YonIVHRE0KAEN2ONM0XjLd9ZGdgAWSLp8uZSDihABnxTM+9vt9vLy8xNvbW3z69KkarZU7IupzQpxE8bOAy3YC2DRN9QnLOG/kbNCxZY1hZHmfOQDqzIyY3WFeXIfExGN120NE20yGY/wWq0aAQuYOlOgBAcdG4JYOH+9qUOXEAXl7TgCJ7Wa+LXBx0Kei4gCPzrCuTip8oo2DLP95o7YZOQMo25kBrzchY6/boAd4nKYp/v2///fRdV18+PAhTqdTfPjwIYZhiN///vcV6FtPCB7IjbmThETEqi0vovX6Mh+CFMDH3/Xc/PDBvu9Xz7fYui4HR9bSLTsOzgY+tm3YfIPkcRzj4eGhgh4HLAdZ7IXfWTc/GM0A12tim+RvkAbTssRuv1s5/1plGhprTpuQT6LBD3jO2BMs91bf2NfgxMTyxT+QdFBRZK4Ara7rKjBlXbfrxPVJNLEJkgcTNOgYsjVBw/Nh8GMRsTplC10xyYAv8PpjHxyvazY4Yn30tv001WHWFn3Y+kgAj+/Pve1vGuga6lHtrvzM81xPKbLOGzBRpWFMvOfroCvbeOoXemcixEfq4o/4N9/3KUnEeR8IQlujOwKMB1hbE0isK/455xxpKGtDsg1JYh/Dqyb2Fxs1vjCZSKyhYssc8dXI5PX1tfpMdHybzKN3JkIsJ2TseG1CyUk5ibHxgRM5x2h0H3mxMRpfu8VKhdxoz/QywTlNUyy5rT96jM6QwLCPju98C6SC186n9UE3gF6IBmS3rdpD4jiBAIy7c8BJs5MT1gbZGRfYl9v2t+u2tZO/C4Tj0xi7MZDlwmeN74yrnLQ59qDTrBXvuVNinqf6gEfjvy51sci3Q0h4npAZ29ZyEp6+7//rVjQARtwUIbOBN6Id/+aBMzkUw87WfXkIkqfATtNUNzdZAXCSKIkzdxQcRgQlLoEnxX7f9lUYuHsj4RaUlc99+xgz7onAeZ+5OCHBENmzQVDesms4NgAirO42uJ7P58osvb+fV+CLNdmOww7FVQY7rYgWmJdlqUdtAihwpCg6cvsWaEdGjB99YP5OEp2ksQ4ALydrgA4rPrrnz/g0De+PYc34aRDGdRgjABHHjs44cG2ZJsbM/ew8cKRu82P/gYEFcjSgBZCz9m6rQCbcj+M+2cDIpv2IUnmgDQl9+Wf/7J9VO8m5HOX38PAQLy8vl4c+pkvpurGbBBXrOLZgp4gd8mwBDjJATwBSfd+eMYMMICgAfSYukBE+xJ9HXi8vL3UvmPvISVINYNFRwCEg3MHdZIErcU5ASQ4MpM3QAu64H2PBtyJfgv04jrFEjl3svgqIEe0kJEC118h91vyHvfkaBNSIqGNCvhHt5DtsDl/BvLEft8owB/tN1o1jWO1/GQ8g0TLBX9kuHVNIrvgc/tPPZzIwQPf4nXiADRHfmHdlOCNWuogsu65bHZbC+FNaP28AucPQOpZFxApc4Yc9BwNJV8TQOwgSV0GYA9VOfAw6zGcgBgwgLSMDU06ExOb52zbm+Nhhxus4RGWFcXBP94xbj7kGSS2y6nMX58ua8ZBT7/lgzhA8KbUjuSFHTXRErI9Bxw6tq7YhrsG90BkAMay2D6JAD00aMB98jwGvj3bGliDa0CF3H2Br1YcsrRJBzMBvQxpM0xwpynpy+E0D4il2w6EmPegi+/FIat2FgXzQcydEfd/H1VUfKbW9RsYM271MxE6TA8Q4V8uth9v4aD/MejoZZVysDffFHmxX9o8emxMA+yziobEWc0MnfPgOsoKEYd5OpKxHxELIb/Rnmsbo+q9bq8ucp9puaFv5ls0Q94rfaiea2X/9fa/vTjRgFimtwN7AwmyzLwzR/aLOHiMaO0SgQKBe3C0rYMDEgrEIZlcNAMtn1v3SLKiNrWbuYgN2u1Ku2jKTW0WBXWLOlKSpCAAGME6YQxadE05SSvHly5cVgwLgIbDgiJj78XiIS5P3itnHMfE8BCdIfqq7gwXzrKzD+bxiQNzrS6LjJNQO1yVY1t6JpcGpDdXz5e/oBfrEd5kL3+OhXJwGBogAiJgZ2iav1icCNIwboBJd8/owx4hYJUC+B3roCs72tCvWDmC2db5mmpgHLx7whOHjTD0WJ7w+oYbv7PflGRj39/cV4Hz+/Lk+swUAhbwM8r2utlXk9P7+XjeMu01tGIa6fsgBMElQQw4OSOgjiYpl5uDx8ePHCsCwH18HeZC8GiiiU+i2iQ0nFgbeh8Nh1bPPONDJLTuGvpEw4MMIgsMwxHzZ48bDBJFlRDkj3RU+QJPtj5YOb37m78xx6/v4XkTUhJKA7sDD7walJOeAmS0wIaAaSKGT7+/v9WF2rImJDhMpbscA7DMPDjbgnvgtwAR+AtvgJzqEviMnA/vtUbpmJSEQeA8dJUllTE5y+AyA0jbuRNj24HYxrxtAxIy658DaIjvvaUopVQYYG7b/4KeTKhMUXJ/1sj/AvzoeMHbL1nLxM4Xclub55JwjX3Iz7sn4G9hqD/LDX2GbnD7F91xZwW7tK2071gsDTA5NIMZSGTNjb7bdtk68i2j7lJzssXa2LTAHftFJE7IwptruIWNcQz/Ulh+OQOdzBsj4aN7zoRfoKnLBxxioIr+8lH0VrnRufabXiXEYs7k6iV14rx225AMarJ/IzpjQxDF2YGzreI4e2FZNaqCDXMeErX2s44GTar/nZMQ6vPXd3Gue51hyjkX+yPdLKcXh2Ege6932HiY2iyzySud/6/UnHW9rtpbJcPoL2S8LRisSgIpFqT2UqbHrXlAmakfCdw1ODWJhfgBwzjAjKCG3dhXuYebZ4BYDK+NvJUCc0u3tbWVKOfLVwYJrYvg48q7ranJhw+D6gBmOtgSUpdQeeMi57jjPktBcxfv7qRqQlZIkg2zXBk+wdV+eM1gDOIMOJ5I4S9rerB88bAgwC6A0KML4I9qeGZjd5+fnoqSXgOiNeMz/7u5udWoNySAnDqEPbDRFbxxMHfwwNsr+zuytd06SKLezP4ff+ayTC2Tvjc1UKvygJNaPa1ivsCeSWNhXwBSAkH72t7e3GlwMaNGBcRzj7u6u2kZEOyLzP/2n/xS/+93vajBhLQFUzMeAEqe+tW/Wkt/RKfau8Dv7ongPPeI+tB6yPs/Pz6sqEMlLRGvZyjmvnr/DqUb8HUdPsgpo/fz58+r4XLf0ELTQI9bBSSvrZ2LESSlzMqilAsXpQW+n9zruX3/9dZVgpuXSq3zxR8uy1KoQa70FctiegRO/I0fGg//id/ST8fE7baDX19cV/NhWI9b7yrBBZIDsvcl/W5GpgGhoJ9xgh+gDn90y2q5iAY7w9/hYkyGsD76TVhxkhR7jE7gXOuEWBgMox4ht9Xee53ogwxZgsAYmEwzG6h4dzQHZ+Ihq/A3JPM9DmqapMu5cl9eWaeZaJMiuppMsoYPojfdYOaFzhcAA0HZBfGR8tjl+8m9iqCv223/zML+UUj0GGT3B7q+vr1eVeNYaneB6rL2rqsiFKqOfOwNRs50D8nLlguvjP7y/j3XBT9KV4YQSPcZeXDUBexBnUkoxzet+/VJ1uGp7WGL94GT8gclF7Ni6yXoaz5TvrlueHPuwE3QNLMI6GIzjY0wco1/YODGGdcdHWJbGIr7+djyeFzrNGJxUIR/Wg1jt+GCcan9h3QDnWTYNnza85+SGOfSpj/N4Wl2zYvO4nEgl4s64m7XZVtfKeNv+ne95fXei8enTp6o8DMAgYsv++LMoCAHbwdrKBfBh4cvfSonH4DzniGXJwYPorCStPLyL/X53OZP9vHK2CI/7YiwAM2egfc8ej7Ljn++g8GXD+7q/dVkayNgq0NZAMdpxHGs/NWNgzk50uA+Aj4wa9oe2gQ8fPtS2E7OWOMiUUgX0XBOHY0cK6LBhmTWNiNVTM92j6aDoZNNtI2YQl6W1ahEIt5vUvY4kYHa+6AHyxUhonbEDIRjgBA0sYJKoTCELNo5SgYL5NBs4TVN9cn1Ec/QkHFyb352k8zv9yzgus6PYAePjOsieIInT5z0zQ7ZZ74Hasq0REb/++mvsdrv4+PFj1Z1touTkFt1yAOI9gyLmwH2R9fl8XiVEDw8PtfTtU1IYK44f23Y7J3P1M2QiorYwOnnk2Qkw4LRyns/nVSsT/gldI2gzV7dO4I+wU+bLWm9bHyLWT+5GFqlbH91dA27XRRa45PNcy+0y9ikG5cuyxO3tbZW3E1n7J0gACCPWAvnf39+vWEhXUQ24DVw9HhMoEe0ZCcjPQdvrbcYRuZs1dMDcVqT5b0sUMSav05bBxSexZuxFIUh7fmaW+T6f4bkpyNOgyQSPAYwBJb769fW13tNkG3HBwAVQ60SSOENc95rhrywv1omYg/ywTVo0WS98Cp9j3BALdE3knGNRcphzjte3t+i7rhJngEfb4xbM46f4mxMS9DMiVnv5zPLjH/EVW9Jnu5/m9va2zhX52da5tisQ53Gsz8gh0eF7rDEyJ+Fl3fGHXJO1xs8gC1c6OKAnEU/Pa+Kp79etu/jrSBF934hbYzf7P1dtiO3oHG1OlQSIxu4Xmfn0p3V3Af92coFv4H4ej2Ovk0JwBXqHPbFGxq32EY41rKm/Z5DvCpCxXJYdcC8TQU5S7JvK70VidZ4pYrffReSIcTzHMi+xu+jzrHvg17BzbLsm9jlWa8CLz7Jm4JuWhLZk5nte351oWLHcB4gi4EwRFD1+tJ7ATjKB8rku5jlH17Ue+cPhSsH36wc2eRNPcZh9LMscw7CLiC72+2P0PZWTJV5eXiOlLjgdi2QCMMD4AGBWojLOHPNMD3CKnGnD4sSGktQU55+j73fRdX30/S5S6oMjf4ui58i5JE/l+IKuMu/j2I7PjOhiHHk6NhvoG2uCgQAyb2+HChAI/DgrvhPRgCPzszOLaA/5MSDDsSF/g2V6e1kTn9AFs2X9ISjf39+vqkd2vjm31ohhGL562q0TJDMvzPf9/T3u7u4iohmzwa4BITIk+BH8uQ7v8fr555/jxx9/jM+fP8f9/X09eQdn7wcp3t/fx83NTTw8PNRKB04MhwdgoPXELBYJJrLkIZDoPUlFRNQKGGOJKLqCnJEVMnWiQ5KEnLBTfv/n//yfR845/sN/+A/x/v4e9/f3lTCAueS5C6yNdceAym0ZW0fqvUsGluglQJmxAWw4JYmDJsykTdNU+4dTSvVYXusi60H1yEFzyyzZX+DHkB1AAkCKT/FYnFSjgyZsbK8QCeM4xmG3j2meosulgpGWHDnPkboujtc3MY1jJSHMZjkwO1G1TxiGsqfBewlYK7PhsKboqtlJs3n4IRIGzxsdMTnk3mVsnODMmCFW0GHbL2sJcMOXmHF3RcdrQBxCb4hx26TI/gN9NluJjflobieyXuuIqJVkruHKGjZvvWGeADnHYbfcsO4QFcRk5gQzbDKB9eR6/NvEEi3N/A399rpa71wtZmzMi5iFr4eAeXt7i2mZY7iMd9eXBDoNfQxdF1Mu/uqw38f1XekoWFJEGsoJcufzuT6nw2QMcc4AlYRsPI8xTfNqLcbzFP3Qr2zbMYO1ccxwjNjGJfwV+nE6n6O76MREhS1i5f8NOLt0OXDj/RyRU0ROcT61LoFtK3Bbtygn0O130Q9D5KVsvkZfE0etRhd938WSGrOODRIbS2KSYplzjOMUkS8+b+gjXTDaeJ5i2A2xG3ZxOp0jL6ViscylPSpSirxEmcdFT6LLseQlur6Qyf2wjyWXdp/I5Rlg+8Oukjy7YRfLkiPl9JVNbkE//h1ddTJiTGBMyt+NgeyLeEHymMg0tur7PsZpihw58jLHMl3a55cckeKyMTuXeU9zdH3RhSUvEYnzdSPmZY6+68uxwlESla5PEanM9f3tLaZ5jryUJGNZ5qJb+UKk56X8rR/KCVXzEhEpzuN7nTOEH/jBcuTfbnWNaFX9Ipvv26Px3adO/X//3/+fVfC344GNZLOne3mdeTK4iLgAg6LclCt5EcScQboK8S0lM4jECHFuvGBb6NEmUOCcuTZCx1GbSbSybRXYWTFJkQPAPLeHYQFo+C4Omow7pfLsAxR5v2/PxkCpG5s6xenifGAucHCw9f4O8zEzQZCEneZFWxQgg7ECImH2UVy37hjMOpOGvXJZuzIn0R7kx9+QK0YByLU+sr5ORl0JMTPx9PRUr43ezvNcTxyyLiB/t1qgW9NUWuJ4UBl6av10mdW/M09kD+ADILinFF2kmsKc7FAjGhP+6dOnFbNknSHY5lz229zf36/eM+PMup7P5/jll1/qXHkKeURjQ7yBlzVCH/u+bCA14EJPuQbjdcXT7UbIHLuh0uCE2nt1GIcDyzAMtbUOf+GqnRMD70kx6I1YPyQzogE0EiB0bStT95kbODrB2Y6bz1HtcavJlqHlp/WMJAAwi4zNdqNvLpE7wOAHkJFbGAjEjJUWDye0JClUimow3vgpbAJw7WAHcYFObZNy+wrAIbLZtnLYZmBYDazNJHNttxUhaye29m3oCDLmxXiwd0A4SfJut6vkHONgz4/9AvEWn2CCjDXhd6pQ1j/eJx5ir5AZ6ADx1PJCT93W47n1fb8iG/i+k0Nfi8/knGOcpwgRSr4+vts+2ImOk0uzxiRdXqe62Tq16hv3weft9kMdhxlfVwYNyEwmcG/Is1pZu8QM9g8+Pz/HMAyx361PX4xobYPjuSWe4KlKlgzrCgP+cpqmmMZ2Yhb+2WtprIK+OnG2j6JyRKwHn3g/LH6QFkpXAFwdYc3KPaeI1MZP3Od+jr9uey/JUV9jBLjBcYxxGeMZKzpBtp1uGX/eR/cgKeyb8eP2g9M81+ca+frl8xFDvz5d0IclGTNHtMqy5bnCFF0Xh93fHatsQ9iKK0z8zQQL9zDpZv1BP/u+j//L/+1fxW+9vruiQXBjMVhI3gNc0v/IiVE+UYcFLkGgfd+bh6yUTJx7A74AOQbpLBKBztktrExEOy0ABgChbxlKDMqsOO9bMfgOMtgGKe7JuN377wdD3dzcxPPzcz2PnL83pq49uIb1iKAlqT3Uxf85UPId5G+w7LYr5DoMw6pf+HQ6xcvLS/z444+r+VLVcDkcp+bEDrm7z5b30AMCrxkVswvb/smIluRigLTVYEiAdOsY1/emRthq1pDqgEERjg/AQwKFI3BA8t/sxHEQrKvBGs+bmKZptT+GE5ucOH8rCONwf/3119VRuhFRQSpVpt1uV5NKxvr8/Lw6ttIB/YcffqgJ1bIs8cc//jGWZYnf/e53XwEGfgLc0TF0w/3/lgdtk8iblhIqDvwN4OfvRrSNdwAv9N7J6rYMz7qYUQaQEUC4Bz7JOuuAQ4WFYEEyzHe4d0Tb0+YkeFstceVjq6sEeu6NriFbAiVzddkbX+b14dpu8TNbDknifWSuWhAYCUD4J3Qb/4HNdl1XN30jQ8scefLe4+Nj1WnG4ADszdL2//YZJgEiWjUTcMH18VEw76wFvtFJBbJHlxyvTGb4fe/jMDDgIbY+uMItVya3kI9twUARHSQRAQiTYDBW1tqAnfZB1hTZWX74IdbS7Wq2F66LHUGWEKsNYoY0xCw/xn2c2Dl+831XdrgPOCAiql1hv7SWskbIn3U8Ho8x7JrPIHFhDZ1k046HrZlQ9driB9BvrjeOY0RubeRuJ+77PiKnld/h/cK2N3DM3IvtdDXGoQu2beRtIhj5oj8ppWoDVIUZM2tAYsy8nYyg+66eGo8NwxDvp/fY79thH6wb8jVxRfLddV0s8xKn07ry7gqeMYJlh58yyeL1QacZpwlzEx7eu4N9OCmp113W166+Iq2P0iURxCdtEw3jSl7IsOpLciLTEmcT27ZHywY5cg9XyPx3dM9+Gdv4rdd3JxruKzVjYBYIgXtzrhkigy7+Y/BMzgJ1tu0s0k4XgW+rIhiVe/CdSMAqRXz9QBfu6+DkTYuM3aziNmB7EfxZnD3XMvNPbzXfx+mX/vocF92p3yPgRbSgR3CkRO79NAQ4gsgwDKsHLTF/gitrAtDh9Bk+A6g3yCHQOyOOaEyBKyrIFUaY9WMz9/b7rBMBmDWOKO0ItDNt22gAZFun6mDT9338+uuvqyyea8AMeSObN/vhtJ3YpZRWTzu3rRCkHJStGzgIsw4GcDD61rlxLBu6t3sF6PVHrsz96elpxZ7QzmGQ/fz8HLe3tyuWlh7i+/v7+Mu//Mv4J//kn8Qf/vCHegwuuoC8twEUexvHsVaQXHmyszdriU8ws8e6cR/W1oHLfsiMM99lzsjXmwYBQ07MGQdrbJbMztrAHdDDuPCBDqokJhz1axBt3Tcw7Lpu9TBD9AiZ227ss9AZkxYGkTDo2IjP7QfoY5+MD4DmyhnVBxIakzZcC/vz+xFRbWyey6EUtEM6mTH76AQNn+QYwnozNq8la8t43IrIPbdJnoE83+XgC3xCRDs6lu85weDUPu/tgtwiacY/spZuz4NcYPwQPuim15R7nM/n1X4P+/Jt6x+yt+9AHlQk8YnI3ESDuxJIMhwLADEVQ+QlkhI2s8h8j7GiB+xDNID3vifWgGuaPBr6Nj7WYb/f1+NA0QcqIN4XyX28CdvzxscTm8ZxLK0vF1txBYMnPLOeyN4t0mAgAOjV1VXkaM/xQR+L/Syx5PXeOPSen8idU94MpIlJVGTcXmzbZY5ec4NcromeIbca09O6wmI744UvdQth5FbpwH7xQ05et0QQ3zfe832ZCy1EJheYO3qPbnqs230dOdr8uUf79/rUPfTGh63Yb1sfnXzXeBnr7gnWy/N09d57FsEvrLdx9Jaw5lr4q//qiYZBPjfD0O1UAX4Rsfobg7fTyLllyA6sW8Xm/jhgBApTse3fRRlYBFolMDCzcAgK4/ZcWQSzDDYySnwoCgqCI7GTNcA2yHTZGwdSmY5oylv2oLTjDKmMlGu3Uw9INpBfRHMw7rFGGXGifkozn98aLobI53CGXyl9v94AzrqYoY5oQY4n8QJuCVrIxpuit9UsDMfMn4OcgRABymBkC7QJ1FQ80E3YDdadtcGBkuAADEjoAJgtKVyfx40uWCZUTdARghLj8r6K7cPuuAbXMeBgLjhtyIPHx8e4vr6um1mZp6uAvv7pdIrX19f43e9+V2XNkatXV1e1PYmEEBDoZ2HgJ+xTnFC4rYT5IA/LjrmZyUL3uK/bamgRZE0hHbaJMXoN8Eop1dY9esK5nxM21tFAwoAsIupJNyQdZu5IJElwzHCbmWM9LTOznsjEPgj74fMGFQAYPoee4zOsu1v22mwtfpx/kyybRDIRwfe4tkkog2d/Z1mWuj6M2TrqpMB+way//Y+DJYHW1SHbJf7Fyaz1E921T7dP4R7+LnJmozOnIDFWQAFg3wmi23X8kDuTIiSPJpAMiixX9IF15B50JxBnXSFe92yvEzwntn5G0bZFdxiGiGWOWYQQ9mdSkeQam0Q/fNgIhJjXzus1z6X3PaX1Eb61PXhKcbw61NOi0CPWD9snZrp1EtmiD1VHBWi3GKTvWlsRuluTw2G3qn6zbvM81159g9mq25Fi2LUKj9cC2912FNiXOaHmu+ik197Jt21qWzH4VmI/zVPslta6F7E+1QxbNBlxOBwiRUs+DPxN6NjmPQb0lL/xPeIAf9+SL+gj+sD8jP2cIHd9H/PSiBTmXb7f1SqW5Wqi2hjG5A3Ywd0AKSV2i9fYjp6CSU2eMgd+4i/sL7k28cJyxD7xFd/z+u49Gv/b//Lv6oL2fV8BDoNCyRyIAL/n87myzBhgCR5TPVmIsroNBoVBaC4Hmsm0g7QCOWGAmWWMZHAsAODT1RULmgXzxl2Mw0x5FWxq1Z1tlcbfQ8EjWvsZrSauAozjOcaxPfEWx10MoGx2R+HNoGFgZsUiWgIDi2ZwSxKDIW9ZBs+PQIhTgPWOiNqqw1rScgTowHkAlAENVCockJGh9wcwfgNS9AKQb3bLFa4ti24jNhPC+hsIMlcSurZGjZ13Ms7GbSocPi2Fz7j9xGxMzrmeyQ7jgfwdIPg7f/M1rGvuwyYhIEDe3NzU9cHmDFQJIhzhu9vt4uHhoerc+/t7/Pmf//mKYYURxc62bBJBGsdlJtLlY/Z+mXwgSAB23DphP4KeYBP4Cdsu/sdyI7g7kd2yclRlrD9mJgF/1m38opNP7I1jLn0fJ0vH4zG+fPmyOlkM+WMXBF+Db/wa8iLpZJ5+pg7+kDmh88jWrJcrh04S3K5jf4oO22bNhFvGfL7v27MrXA1gfd3KYFvkugaqrLEDuH2cKw9m27mXSQd8GM9pIXH1WvM+yRpgB3baeog8+d1A3/s07NtN5DnesqYGGU6IDFBNtuFzSXYgOLAvrnV9fb16MKyTRbcvYUNc3wAb34Ye5lTAMfMDqLs9x0k079k/sZ7ET66D3K1vfdc+Z/ldXR2j69etMcgUAoBEySCXdd8m7BER0/x1p0YFsWL1TWZO0xQpWmLF93hdumXqddefSRG5HSKALrtNxn4SmeMfXOXjmltQWUF116q0bqsx8QDxu/5sH/vD+mnXZuJNahuL5KVVQIjDXvt5Xh+9baxozOjnhSFHxoaeODkxAYstGC/Yt5ZN3+unf9f4HuUEL2yT8TFf5oDvZn7EC7cy1Rbp3GLFdj5Orkgq8MG73a5iNNYA3TZZgI5hB9aF/+F/+u/jt17fXdEoJzWk6LrWelRAXhfD0Jy7nXbp2TvF+XKEGovYdeW4WN7zmfcEToOMiKjP62jOJiKlBgxZBLNsZvJxeq4IEFC230HofugTDo8ki/sybxT38fEx9vt9BbS+JwrlRcMQnBwBRjAUFAjlcuCY5yW6rhitGTsrLkpFYuKgi7FZcRkT8o5oDsunzTDvLfDw048xEj6HY7dzxOG6BM01+ZuTDmSCY4tooNTOHnBkVsI66mBulhOHbCaEvUawHrwPa+9KAXNgzbey9cMZHejMiHgTPf+ZGWJ9uR/6Y3vgd3QJgEZiQ+8tICbnXAEGDtBMDgwLieh+v4+ffvqp6veHDx/icDjEL7/8Eh8/fox5nmtp3mvgBMOVIuaAXkBYRLSTtdjcia27lQjywMADWUREdajMjaCw3+9XrWoGTU5K+LwrNfhB3gc4UQ3jP7N26BfzRE9oUdpuuPZY+NyWMSZooeMABOzIJ4pgI8jfYMEMJ9XGvi9tJT7GGL1zcmV7IvGxT6cixNqRpGGjBmL4Qftj9JcXIMOgjrUyyOCniQdXLwFDPuYZ+6Day5i9Zwj7dTJD3PMeLRMJxAlsbRyn2O1gJ3P0fdsPYvBcEtu0kn9Ljpo/cALBPbdkke3MpJnZVBhlj2G354GdU7xfSJZWbS2HlaALux2ga77Ep6GC7a7rouu7cpJRbodkpL6P1F32Rc1LPf3JB7GUCkA51Wc8n6PrWzJZKiYpIt4v1xwioj1B3kCw69rBAFQmmu/IkbrGRG9JoOHiE/A7RYfbSYHzPEfX98FDdN8utmcSgxa5ZVliuYDPXBY1OgH4rlsfhmP9zkvENLE3YV/jVNHL86pqi20sSznKepymeJc/HKeLT8xLzMua3Wd9sE18hGMo2MB+AdnZ1gxa+76rlW+TAti24yyEXLlv0R0n7/v9LiLWx49zrWE3xDJfYnrkOOwKmbPkJfrcV7LTuk4scMWTU0cjGuCOKKdIIQt+9kM5TYx2eIgFkgwTzt6D4WdqGQPyOV5OGouc2pxNFPkhplxji0GdYOB7TQYOQztanjUksfL4/r7XdycaOaeq+MWx53h/pyd0/aRj2lCKcR8iJUqs5+j7IVKK2O1a7zNAph2j17LacTxXR08/Ks4spbjcu4FL78nw6VMwriQPLFZxPlNxLskLuIthKEfVmtGCVZ2m6atTbnzOvxnLlFIFBzgjM3/MZ1tetKGVBe3idBojAiNqjKvBFwppEFAZEjFhJFsY0tXV1Spwc10qKLMCRUSsxk7ftvs9/RTxiFiNzckOjhxFj1iX9M1ImEHjeoxrGIZ6UhfrizEjb+4JA4WDcUuJg4qdnFl3Vw/M7AFCDfC5L/f2ngxXmnD6fAbHx54VHIh7+5EtY+LzflgbiQOB5/b2trYFoDMGta5UIj821jN2bPLl5SX+8Ic/1KfZf/78Oa6ururGcpz1FtBiq/wboM7f0VdAHTpCsoFNbR8EBhAl6LmdBv8yjuNXepJSqhWdLSMGoKSK42QUW2Ft12eNr09+4qerNugZ8iHJcJ+39Z09VQ4E1lvmAmtlfbf+2y4BWm7DM9h3AgCgRjboiCtA2KJbWp2w8cK2zDx3XRe/+93v4vHxsf7NTB+f8/pwLbew2O6o4jlJs2+JiNWpcQbbpfLejvbFhzrQQwywHrCE2LGvw7XLmNhYmWOeG7kxz0tN8kzCHA77KHC0PZeh2AskWVTfwHydVKLLbp0hoeA+zKXv+3h+eYnUldOoDodDnMfHAlDf3+Nw3ke+HOiyxBI5zTHO86XqnuI8zSvd3OeIvh+i77tIfRe9Ery8tKd75znHMhfgNJ6nWPrWOtNaaSLykmOa5uhzxBxLjGmKvmtt1cuyXD4zxTLn2O8P5bjcKA8b67tWyeaQAyqQ01RObYqYY14uoDlH7PeHiEgxTWUd308c+5ni7XLoSJFxF9PUyJ+uW7ch7Xb7i9amii/quOdyYlFEjtT1MV3GlOYllsgRXavqDV0fkbqYlxxx8ZXHCz7LSyNzGl662MPbazluNkWcp/GS9BXNGsf2kNhhaMToeC6Jrm0eWzO4NYlEQo8eOlkpetuer2acsyUM3T7bkqmIcbocP9uX/RAkujlHDLu+JrLzfKlKdH2kXCpBw66P9/cpOGSnH1qVIqXyILvy4WhHzvJKOZY8x8ieqH6IYV/899Djg4ueHfa72A1FBim+3p8J7nMyyHyNEfg8vmDbQeNqCzHdZD12vyW4tkk08ZH1Yu22fpM4vR3H3/X67kTDE0cgJStvGW3E+mm3haFpgMggwC0pBshUOK6vr4IHt9DSE9FORmjjck9h2/eBgBkTQIx7sCjFebW+VRajOfBFrMVUy7IvLy/1d14EVQIioOL29rYqgoOtFQgZk/zAzjoJORwOdS8AirPflyOFX15e4uPHj/H6+hrPz8+VPcRAAagAZK4BAEWBv3z5Uk+WAig6aDJP5mcHA0tjFt4sAZsQfRIU37MhcF02ohL4nJQyDvp++749CZsXgc7OivXhmuiJq0HMjTm4TzylttcE0OsyfkTEhw8f4uHhof5uxtN64uTCfccwoiQx9FcjH8bqpBHg4P1NjN3seAMtrVWGoECSyT4Zkk3vK4KxH8fygEn0w8Dt8+fPNQm/vr6OT58+VRKC8bgKhj4ZtEa0526Yld6Wmp0Qkuy7dQLgRMsdibn3n3Bf/BCJFH9HZugY/oeKALoLGMYJ25+4uuagj115w7SvaQDoIEElpeu6+rA97ktbCz6Ep/siR5MFEDjMB6KGIMg9+bz9NXrt6h/zJ4jxPjpjHfCR0YwJe0dG7PuDMNpW2iLaRmUTUciZ4Mz8AEdODg1k3IKJT7atohMkxSQvjM3ECPElYv0guPL9lhT5JzKGCKByW/RnjvLQ2Lbx33uFliVqCyXXbHv8Wq/1torE+kzTVBnY8n6Udib5PmQDkGKu2Ozh0BjU3W632jeSUorT+RzH46HKyVWveV5iN+xWfhmZWu9ZJwDtsiz1JB9iGZ9Hhk72SAZbIrB+RsgwDDXmQaKlSyfHNE/xtjkkwMDahzNsCSnrOrJOku96Tcrxr5VRTxG7YbeOHX0f+67tFUip+T/WBILFlbtpXrfTmjDhYcO225RSDP0Q7iDB51q/AaKuKEN2mJgwJqGCxZxYE4NZ72+zDKmUc91GYi1xmWJtW/Q9WyV6TXRzLesP10Ve+HzPA5teE1Ct8oOvQE7gRgN7fBJVDeba7K3Fe7AAY5ynKa4Ox3qscMT6oCbiEv6dezEeV0aMaU0KmgjC//vwi996fXeigWBg7dc9iW1RrAj7/a4qPgLAMWJoMOA8uA5gQV8mJWgzaQjGfy/K2R6eh3D8bAYbBUpQQMAxpmn8CsRFtIDFdw10GAffG8dx1ZPu0rzBBWCW7/C+AS2JgZMMGGWYW7dnkMTZsSFDB39nqgR/gur5XJ7BAIPHGgFoCBrbVimMiNYoB1ozjQZTKaUqq/1+H8/Pz6sElCBknaD9ATYbHcC4DT6QL+tEcmMG2mvB/ACrJLzoSkTrgXWy6vcJmF++fKlG7lOMzBS73crMBu+xv8UsD/d0AEDWOALfBwaVtXAyYxYN/YS1vb6+jpubmxW7GRE1OeE/Emg2sQIoGPfNzU08Pj7G09NT3N7erlhUdNlydKLHfHxd9JU1cgAwK2Swhx4hX1eQuL7l6nEMw1Af7mU9cJXErA9+zKf/OGjZbnwffKMTYEgEKiSNzW0PQHT7BffE5+E/HMwcLBgTSZXBuBME7MkAYquHDsasMfrFGjixx4dsiQE+5z5gbBtQw/2c4LPe+DLvb7PfZS5UamGzWYuIqElZY6fbhmyvAWPwGhkMuAproIGuljVv4AZfypzx6/jc5uf6mKYxaFlOqVUAy1oea5uc77kdn0kYkjl8hveDdBdd533sExtwomRb4kQtkoK6gfq4rnw7qeuVwGMv+NRlWeo+KhNZJP+uhBtUoj+O09iZiSfafPEP1vWWHO5inNaHDhjE8jv6wdqjj8MwrA4SQRciYoUvGDs2hs06qTSQ5F7Yd0opZjHV6FMlBARAWcPye3mKn6upyGia5vKEv2ix1YAXfQc0b+WzxlUX+eYlYm7tVW7F9vz9dHnu56Qe2+G6Xg/bv/ECvgLZMnb7KBNirIlbpqiA4Z+4v+0VHcUvcT8IZXwLMuC+EVH10mOwr6okSmqtT+gVnwEPGLfZP5GIk+gSN8AO3IeX5eX49luv7040zNZtF73r2lGD7l08nU7x/n6KH3/8MaZpqpvmcIQGpgTJt7e3OB5LaQz2FCfvnjAcsoXXKTuOaJtZzabmnGuPOZ+JyDGObeOrHX7fr08+wGhhd3G6tGWhCH3f13YO70sAFHjhSVAY99PTU2UWYQWmqZ3aA4vMk6gZA2wOSYdZGisI8+R7JDkEJIxntysPFYK9Rw+47hbU4dRQSDt79IcTd8ie3Wa27SeFSeeFEzBwwomYybJjyTlX5p2/X19fVx10BYX9NVyXVjIcwtPTU0zTFLe3t3U8Zg6RAcm4N4dixOjS+XyuLR37/b72wt/e3tbyKfegsgCjh5w9J8r/zN+OlLXGNpz80cOJPNF9OxECdZJDw05ub2/rmBjvP/gH/yBeX1+r7vN0dx8HbNbSiZyTPwcYgiif8dG4JLDoSyNA8uoUPL7rZMd7qQwinWSj92aprXvIFeAfsT5xj88xF7Pu3Pf6+roCS+zHp8eZSSIJYT3wRczZYMWsGv6WsbidDVBnu2XsBgv4Ea7LOPgu62dCAZ0CyDIXfJlBsFtAI1obHzZD4MSPmmhCX7BrA030jDWxH+MnIImKn5/XAVNtAGNyADuOiOo/zV5jz2vA1dr5fG0qmjxnxKB1HMe4ubm7VIOm2r7c9+2BrpAEJm6IQcQcJ4c+RpXPp1QeMIeten+OfbKZcuRFXGKu7nJA9rSCkiTN8xxDP8Q4eq9EW5fWn98e6Lftq7c+WqdccTaTjL762lzry5cvcXV1VZNwfGCXUuzUdkuiaVbefsp6B+DzCWpc18k98rAvc7dExPoIX2Rgwi2WvNJxfP7pMlf7MmJzSSQaCEUPSmzZxzKvW7NbJWW9xm7tsRwMSpdlKb1aqREWThJMuDJ3sAO6zb2Jrfantmu/1x4XsG69Zp24n0lg+wuTDtgE1ze5syWZ0FVwAX6Niii/s1Ymz4jjVOXREXwlGMYtT04oHPecEHIffOfDw0O1DxI/k/LEDHwh9vw9r+9ONNx+ZCMuzmWqik8gckvC8/NzNZb9fl8fahURtfUHZS8TLb2CCAKg65NVzMqjbOM4xeHQWjsAKygmbQXTNFXWryhOFzm3vkMSka7raxvSy8tLvZYVDcXDQbOZth6Vp+zzdDrFp0+fKgjbMi8kYj5G0MqKU0fOKCVggL+htAaEBhCAmIivWVmCf0Rckr5jDSDuQyZDx2AZC0ZqNsBMAp/hHrRKfPr0aQXmnVR4jiRdjAEHh5MlaJj54MX8eDBWRMTz83Pc3d3Vdo2Hh4fKxrnNjXXBSW3bD6hcFFbxsBoXL2/w4jteJzskVwGRm19mRs7nc9zf36+SM5yPmStsERuwTW0TUHQRYsAACYdq4Im9e16Pj4/x008/rZIZb7BzhdJr7fWi8sHn/NRYguSWbTK7bWCFjm7BLDoLmGskQ18BOECKQIcOREQdF8HJSYF10fcDFNmeYU65rx05yQqOn6TCTBcVAmRCcGEuPhSi7/vanuNKi0EN7zEOV9ewYwKTEwx0CeBOgmPiw8wyYM9rxTXtl+a5PdfBCQRr4MTYVbiIqGQTJIdjmGXspNayY674fuaGz+dhllyDlg0qwxFtI2ZrvWr7CZAj40KeJgasJwV8j5HzJeHa7eP9fYqU1kfRc28Sau+bQ55mXr1GKdYnWuHb3LXAvIgpvM88AIS1PSPWOsCrVK73EblhDXQcHTWDHxErPAAGYDyAJOuqW14Yp/cx8HnIC1e+SB5P53PkC5ZgnV1RciJs/cE/uRUQAoCx81mPEeJvG0/w02AdfPqyLDGezzGe27OfTHb1XRf7w36VCNTkeS6tecgDkFtJg2gVessTv+v1xCdvSUHssuhCqWJxLft/g3zsHf0CB5h4sU45ScLPtopfieE+ftxkBzaG3B3znGgzX5Nj+Ad3Vvjz7lDZVnFoKyfOEHeIVU6WHXerD8tN7siPv2+r8cjFiR+x2RU94t62coFNm3D4rdd3Jxq0RHgBWZTdrgCb5+fnVTWjZMyNkSULS6m09biygEDLoq4V0qwzzthH3mGs5USQcj0yVxSUQGPD4Om2y7J+ACCbe1EkkigUDmC2bRkh63x/f689+gSJ5+fn6qSpEpBBMgcU1uAD5QfEMi6OPEW5UIStwTBWjMeZ/DbwO4FwcEMeOC0DXwIla+d1Qi60I/C+QRrO4j//5/9cH/p2fX1de40JytyPPkQbD2vtwIosmBNO2OysgSSfu7+/XyWpDw8PNRkxW41cmccWLFDtQu+xISfrW1sxm0Iii3xonSO45tw228MQmq0zOMD+0Bs7SNYAxpX5fSvY+hAFJwnIFx1g7iTnP//8c/zhD3+oOoHccIa0xhmkIcftEZ3WM9bYzJJ9Bi+AyjiOq9OlAF7IgPlha82/rdsxWWvWCPDnezoBcFAgEDqYmNHzCTjNHzbA6cCXc67JgqtZEe2obFf6np+fK+CMaJUq5uagic46AeXzrAUHBDjQIjvkiO3jg5lHRGuV2hIdtEuaTeR+FRRdbNl7zrAFt5TyHdbea8JPbI44w9oiG68hDCT2iH8zuzzP82r/kq9tsLWtOvB3AjyJC7r5+PgY59NYNjbnHPM8xbDblY26OcU4teodMjNJwxicePrhZIBc1ul8fou3C3ACCGK7Zt2ZM3oHVsB3YFcppZinuZ4UxbgY6+n9PVJat/VZN7Br/JfBF/psH8GLuW4TFwhHywzb4Dh8QH/FG5FjyS3+MA4Sa2yOsTJuJ1smF00sbVl5V0KQN0SlD24AkCL/co12H67BPZdY70tclnYIxdXxUH0Hel90YYwUaeWH2auITnM/k4S8HG8bm99O9zSJEhErX8cL2d3d3a3G7UoE620bmOe5HjHvKgdy8Qv/5kSCa6J7xPRtZdpkHPpoXEWVnLhiGVvPSUgZ7zRNlazb4q1hGCIvOfpuXaXDH3NddBB/ZKKHtWMdTKLwn+Ou2wVN5P59rz/h1KklXl7eLyx+isPhGOXouFOMY1Qm0ME0ItUMbxzHaryfP3+uxuHMD9DBJiiUBPYYBSnPjGjsoTNIslaz8GYUURgDvIi4ZOmMYYiIyznPFyfprI5Wp4jGpJjB9EK4tMxC55zjdHqv13x/f4uUykP5DDhZ4IioQYv3nQzd399Hzu1kAIIJSRNG5QzUjo/StJMdgwKch5/3YdYJA8OYfEoYMjFw2SYePFuC6728vKwUnnXld4J8zqWc6vYJOyCDTxw634GlZ84GeQbsBFhverJeMn/GaAdVHYFYODNd6CT652uZcWX/Eg7BSaNlgo0YbHJv1hjdcjVgntfH0Hod7WRaEGu2A5C17NlM/tNPP0XXdfHx48f45Zdfqi3i3Aj2yARwgVyRl1sltvbLZxzsWO9t+xLraeDE3PANrKtZKL6PLZIwAkBYdxhsnLoTHidnrLOBL4EEGwVsW1dYO4gPAgnvI1Pu4YSf+3NPAJY/4yoW/pgWM4Cj/4Zt4w8gXlx+t8/Bj0AevL6+XuYdUY54zTFNY40l2BK+yAy6W0fs01ypiYhVIlZO+8kXAuGxvr89orieTd/10ffdxTfuo2zEXh8by8skTgNJXXQdLXalxbj4hhJPefaR26acdNtH4u9SSuUo0q49xZiN0MuyxLDbxaDKx/FCpp3e3y/n+reH5ULYdV05GjZHxNXxWE676spGXdYSffI4WEv8HD+3J5whr5xzpC7FooSLNe37PpZ5Wdnkt05Kc5xHf6kownh77wD+CR9FuyRx1D7XPggi4HQ6xby0inyKFPtja8/i825j7bou+q4rnUGA0HkN/G2XHGe7G4a4upCj2GLfd6s9QG+vrzFcYvHQ9zGHjywtOofN4Ccdm4ahHPHqZL9UK+Ky4bxViJzocerUcDm2NV3+jS9d8iUGLkssy9eVub4vhwNxImnXlz28W1/tRJv1QKf43dVUCAET1QB2xs+13FKKPqG/jrsmjjiQxrHA6+5kg/Hgu41J+AwPkwTnufPABxV8q7LZpfKgP66VLuvQ9V0MXTvenfVn7UywGje4MsXLGIYE2i1W6I1163tef1Kisd8PMQwoLkeKtpNS7Gxvbm7ifKa825gq789ggv5ZAM4+ygPqGhvCpN/fT5FSd1G8U3RdjpQ4o7yd0mTBUe4z8ILlKAq1j92uOY5SPswxTa3HFmUmEHEPFNeVHhwySg/wLsGxi64r7R93d3eXJCQuwa0xQxFRmQsWn+u7JQaG2iwCCYRZF7P7jNvsljN2TukxSMNQt2f4Y8jM+/b2dgVsaCFzZYVnISBHg9+IWLXHuG+Yv0W0p5YDoklqkD1tLsiH8++7rlu1jLhEaMDqAIIccEovLy+rJBWA4hIuMndCBjB1VQx7caLN0bA3Nzex2+1qUgsTvt2P4f53ql8E5Zubm1XPrEGBgx57hADAXl90B4Y4orFG6JCvycuVjh9//DG+fPmysnPu7SQUMIo8nLQBxg2scXxmngzQuO7WSUa0zXSwMszF5IH/zdhNItgWXIJ3UoAdVtCxtPI/f3NSzhrCMhJoGQ+2hYwYG2P3fN06YwLE4/bGWPTYgNnVFapiW/IAPWXtkJXJGZJXr83xeBXn8ynOZzbHAhrK0eWQJQZyrJVZzNZ+1wdHhnK90hY7yz/4SOQ5yglQObqufL/oQb78rbQ4kXABfHKOOJ3OK99Ksskabvd04Bd4uSq4JRDsq80s7vapEitmE4dhiNf3i033fUSOOF5fyIfUxdVNOYxhv1OFdVki9UN9qnDkHHOOeD9fgF/Xx9Ct22u8dh47cYO4MwxDJYSYE34VXT1PzTdGLke92oYg6SBR0CsIEPQ8oj0jhzUwBjCA9SE2JsrcrjyOYyyxxNupVNXzJGA+9DFfiIa+S0VvLvaKvpe1XAoQTCl2Qx9jXiJFjsjldKgU7PlsFauIiLyUfSDXV8dLvFgiuhTjebq0kJfkY7e7PCl7v4tlWbfy9EMfQ98ebgp+WZYlDsdyzG9EruPpUl/2YKgy5bWapqkkiJckeZ7muLouZOE0jytipktddH2KLqeY5/L0b2JQSikOx6K7kdv+L1ezXQHAtxH/8FWOpcQ/dNLEi6v09v/ej2bm39U19OT+/n6Fb8BKTlLRJ8C9qzpUnp6fn1cVVo8THwLGNbZ0zFkuetflsp0mpRTTRX4vwkmM1TGOdYRgcmyHCLf/9t4VfBDXIn46Lv7W67sTjU+fPq1ABcbcHHoLIvWEicMhluXrJzgSqBzgcCZMnt5snCkKcX19U5MXwBEAGYU1K2qDAVDBYLmVyiev5Nw2WzFngrqDtIMH98TZ0GrjzxQFH2NZ5vjpp5/qAt/f36u60M5LdtWEuVnOZrgNELqutdKwVga7BgNWaowTJscM8bIs9aGJBBMHg5ubm9UZ/2aizELZofhYTX6S4Lh8RwB2abzv+1oG5LUNaNfX16tTyyLakamViVnag5yc9BA4t1UEZOqAiYEDcmHukcX29Cf0kNNYGAvsxvX19arsaeAd0Rgs7AZQ48MJLG/Gx2kS1kuAqW3NYALb4/skWoBk71UhQXEFkb89PDzEH//4x+i6Lj58+BARrY90WZb6pGcnK2agcMYGcPgYrwVJp/cHWS8Mwrl/K+U3X+F1JhFA91hzr411nGublCAgUtHks/g69Jjvu2qBfmI7yMfJJde3nrEPDd/E+F1xYd7oL3qLPZxOp9VzYqgG0gplQIC/JZA/PT3Fzc1N9H0fHz58qGP0qVi020LEkExHtCrfMAx1/wk25v5hM5CnU0vOGuibV+wd+uP2TWRWZNWOmoQQwx8RL77lA80G8tMg2b7KPotr+TAD1gX782mPzJ2T3Lg343DLjpMg1pB/c32+i26aqHJyYXDkao5PdsTWSAZ43+QN1/dBAug442EvF9/f+hRiIzqMHFhvYrvxBeMAIDlRZ426rjxszevgRA//iBwZLz6Z+Xt98VOAY7d8YS/oNXpiu4oorVz87pOPGIcJCEgF7MC4ajyPMU4Nu2GrdD6w4Rg5vb6+1rl5zb3PBH3LOce0tErJbreLYR7qvZ1Ez/McaUrVtxK70AHvZ3CcZL7c221MyMNydNcM9s9aG0zz08kE/+ELItrpVrXK0LWDHFyhNh41qWl7cJyw3hpfm8DfDcOlYtT02kQH18KPG7fs9/vVqW0maIwZGL+TCCeEfM57fL/n9Sc9RwMnhyJtgzI3Z//Aft8Ya06iYN9E3/eVnab9AOe/3+9qEoGC+1xxn1xCkrNNDAwuUFAfs+eTqAy2WXScOcpvFpS/48zMcqLM2w1cXKcAo3XrBA5ov29MDe0ByBhlAaTxnh1Mq8i0+boNhUCEzO08kadLmBgYCcB2nhjzNE3x/PxcxwXrgIPzPgWAI/3BVHy+fPlS1xmDoaLlipCNz47AAWu328X19XU8PDysSqf0OjJffjrxoX3IYJuWNZI87ul9P+gGTB7G7JNoIhqzezqdqt5Tmv3WE6HN8Bh4m80zq4JtRTRngWz4LLrAOOyI3TPMe4BpOzK+ixxhndFH1gvfcH9/H3/xF38Ry7LEr7/+Wp3tzc1NHTs6fDweV8fKOlF8fX2t1Snkgq0yXlonzWDhh0wuEMx8D+u2KyPohRN99gu5WmG/ZBsx8Md/EqzxSQ5cTpL5O76NPUz4E8CldcUbzQn6KbWDELBp5MOeGSfzAAC3UeJf0APLlWolfvf29raug/WQk3pKoFyi63YrGbqtC/8NY+0EmSoK5Ajy5unabvv0KW7oPj/RJfTNZAXj2bZmoFvImfXjHvgI5GFwwe+MwSSSGUj8h23QPdZOcnPOMc1zfRqx9cXMKUQGemIQbhkQT7d7K6lQQ9Cwjtt2EMaErria6NiMvwM/AMJN5gHI+D4+2T4QmWNjTpRINJEV8nfC4IQx0tfVTutM0u/2G2aSHV+89qzdbrer7dCQRLzwh8zfrcEmKez73cJ2Po8Ref1cGcuC+1M1Nc4pJ4W+V93Cd/je/M6/wRkkwvh+Yp/vYV3xvkEnLqw333f7O3HQ2MVJpQEyQNykJ+2d23EiZ5PpkFZb/OIqBD9ptSPhQAfBctu1czUG/+s4zmtFtuZ1DDdGs78wKcfLVYuGQxvZgD7z3hYDmwDEfp0Y/tbruxMN2jW+fPlSN8MxCAACm/8AZq+vLxHRsqerq6sVO0Qpn7IlmbifQOnvRkScz2MNHCgfTtDAB2DA7+7hdFC7urqqTzJ2UMcwYQZQNubMdR1IAZk+otJOuzic8kTMlFLc399fHk54fVEw/ltqkkGrEorACwdNKw3y9BwYKzIy48bLrE3EmknAmK1Y21YV2oYYjx0iR5Ayfox+G2hZr67r4uHhoTohrulN704acKzM0wAUcEDZFqaU+eFAcCg4GuaGAeIMYFyYw3ZPRURjIKlOEFx86oXXwwGEzxEwWQ/0CL3FHrZr6/1K24oK1zAjifyQMZ+zHNAB7AtdBSRwXX6SZPM3kr5lWao9vr6+xo8//hjv7+/x66+/xv39fUSsGRIAMr8zLvsKAJTB2VbeyIXvkeTRWseYr6+vV2AT/UOmyN2VC/smwNFW5syDqoZPoeN7KaWaaPZ92yfB9flpYgd7cGWTsZHAWJ6AaQdGAz78Bcdiu1KRUqoHLZhlJeBzP7ON/t7pdKrVCJJ0bG9Zlvjxx5+qDry8vNT2JPYOLEtrWTV4xYfD0rFuZe1aG4zHg53xfWwdnQd4IGszsZWF3ZAQPjiDz9oneF3sV12pMghlnNyDMbEurINZ6spuxhrIm6jjfapnTkAj2KM4VxBCTNrGAQg//EDbH9AODUBnsSMDvm/FFb6LvbI2Tmjsj7bEggE010Y+6JOJFn5nnf1sC+SxxNebfmusidY25nZs+2X8juXoa5ioNAHoWI8ejONYfZSJHldVqDoyx8jtxE2THSQZ+Db0GB+FvF35hoDwHjTrt5MixsaBDNskweDVIN4yYqxglm9VIuwj8Um2MxJoA2fmiB9DP8GTjNl2yBjQxa1MDfQZM2ts4olxYLP8xO76vl+dqMe8jedSanshkaf9sWMQ9uKqhJ+Nhe/jb7ZJ+1NkZ5vcJurf8/qTKhrn87mWwp2dYTgsVEpJD+hqO9wBQRY8FYp1NtrYWYICQi/3ag6fhMD3h9G20DhSFvBrhjalFB8+fKh7B7gnwZPfDWgYmzNO5sV1TqfTV8kVG6DsmAHOOUfwxFicGIrothYW3KXtnFv5FmdB8mU5oSQGtTDpyIk2kZubm9WmOCcrrB332gJAt9Q4cLKuJIV+oON64+aunhTRdV08Pj7WqgqVICdjjAMHP03tPHnWD2fBBlB0z3tCzGxZf8wqOpjZyN3mt03g+BzJqNe+7/tVUlaBQ24nqwAWYYe2bR/YpJk+5OxA7WSV7xAoYEQATiRCrCv2YNuMWDtGggJyAmQadGOjt7e3KzYaW+P6ZsAADMuyxA8//FBbbvq+nUNOxZJg3XVdbdOk6tl1XX32B4EDPXLAdCAh0MDwox/I+eXlpYJxt08a3BqEAYywHwcl/s5cWF+SYtuqE3X/7mTc1UEnR9wLXSWQIwdsHf1DVwh6rozyHVcVGCvAljVkfdHniLJB9O3tLc7nczw+PlY9yLlt0oWIwradyLNRvTHGTfYGAWbtmDfvOwFE571eJmicLGznY/BpwInOsD72D9wb/wOAAKRazqwfc4fwK/sKYrWWth/rBv7PSSfj3cY+dNEJuSu2ba3aiYlOqH3aFeNGh6z7JsG+Fev47pY8MS6w/+Y66K0BIeCJuXofYcSFpZ9ae9K20pdi/YRqy5F5oa/2I8Qo2g+xb+setgSwx39ZZyGKWAtXjWrylxqoNRGSc44lz9Vnes8UiaRb8dB3vs/amJzALpws+Nkijq18zuQwPyEK/fwktz7ZH9lXz3OpHN7e3q700dgD2WOb/B1fyfrwN/TLsRi7x97Bm9iV98CZWNhWBp0k4zchv4yntwlsXtanEKLHJA6F3G+PioDcQg/8fBvby3aNuLf3BSJDfAOyYT1+6/UnPbCPi+PgDMRYCMAuAWZZorKJgE9n4kyEgF+E0PrVuBZGBeNvlsZZKgIn6BBoOevcSdI8z5UdNOBEYXAUzB2jdS+o2RQCMbJIKcXT09OmtWGJ47FUPF5fX+szHIrBtnYTFBdnMAxD3QPBi/nhfM1SmPWBPXe51wBy26JBIMI4HBxxNOgE75spowpkcI3TZz1hZswsnE6nlWEAIgGu3odCP/E4jl+BP/e0syaw6e/v7/HTTz/Vo2FTSrUiZMOOiKo3yMQ6hw4BdrkH9wbU4tjMyKIzrCG6xfjdgxvRjvQ14wBQZkzoNd/j5Cf03Dbqa5upQHdcofKaIC8nAxHrE5moHKJL7+/vcX9/vxo/iew4jvFXf/VX8fvf/76enOa9Gga93JOkieSq2VVeOVBs6ng81qOlsQUnhK648TvOGDaOgMFcLXveI8ndAhwnE34ZnBtcQQAYUHJ/dIy/OwggIwAMfjiitRYYnJsRNPhDD81mes3xb+6pxy/SltB17aFWtER4nVyR/PnnnyOlblUZaO2rY03M7Y+wf8bI+PFF+FADB8cdYhffcbX66uqqxgF85svLSwVABjFmKAF7yBsixe2EBtaM3fsQnJiaUcVfmOFHD9GLvu+jE4iwPKyr7vm2rXmDrKu9yMztdYBDx15XMrgm89iSTtghc3fSzudMwgCut8mjfZorcAZhfMbJB2vlsdg3n06n6HfN7tCdaZri6niMw0U/tkQNaw+h6fGQOOATkR/xBJ0Zx7EmItgzvssEj3XPIJ64ej61pBY7RLaRWrUI8gT/7X1CyAobfH5+rq1GAGy33uIz+ZtJJ9aYdffDNS1H2xVjIgFB37z/5O7uruJRfoIX0XX0g2oxckKf7CPQeeTqtir7Tsb/LfING3LsMF5Ep0zO4Efxv9wPfdntdpGW9T442y6xwmsJWQFp5fmxrtg3/s/43nHdyTKfw5d9z+u7Ew0zCTgFBFMqDHFx2OVkqJIslBMWHh8f4/7+fmUUZl4MPlBGgoFBTZlUjohhpZhbRorFM8Ai+0QBMUCEaKOxoiN4lAqFcVkJozTzwAKzaOfzubYSlHF38cMPP8ayzLEsOX7++ZfoutLXjMESKMhSMQBvMGV+BBaci5lFPmOA7Iw/opXZcJR+3oKTHwIK6+/SO/Jx0IDJ5HoRBZix3hFtT0/OuT7bhLlYZ9ANDOR4PFaW0+DVrDAgx33w6KPBm9kx1jClVJ8CblYMnUQe6JCDLfrjvmOXvF2StC47uPL9LdvqwIrDoZKBfP05bMQnTljvzfYZVNOri72g56yV7W9ZWv+4AQ7lYGSQUjuQYVlKdeLDhw/1e4fDIT5//hw3Nzfx+fPn2nLF36nyMUd8h2UGA+uNzJa12yhc6dsm1bzPvfzsC4I9OsmT3S1HkphPnz7VRNwspysOrAMvdMTPUtmCJwcEAixrArmDXmPbrCd2EdGOfsbHmeV2cDVwRp+dHDuB4AVIMfBFTq3CuIucdxfZ8wDBJXJup9H4QZlb0sd21fwd1ecuuo5K+hJXV3fVpwBOAA7YjOVxOp3q8ducRng+n2Ka5ovvbs8nsI0DFNxaU04KWmpFgO94Eyk2QjJlvc25nHCUc4rT6Ryp62Icy6lSOVJEWreTcA90fJrK/pUGrCNSKg+rxa/ZhzWysI0Z9tTtwAYhADgq5Y6VzME+YpsEOmHYkiuOX7znyvxuN0SOuJx8VI6U5YSxiLhs8i7H49d4urRxtwR+iS4NkS+xHd0jfuPPuq5bPcCTeGmSwAeeME7Gj+0bAFJt9YEJ+EpkaZ01BqE1cVmWyJGj67s4j5yMNsVudxWpS3F1VeLt8/PzijDgHt6/SWLx9PQUEa1V3MmOCUW+i95AeuA38Kv2G8jKxCV6QWeM8c/xG4kevgfSwa2QyJs1cvUWved+9sEmfPwCW2yxQER8JVMn3twPm0QvwY4mwLgvNjFNU6ScYze0jePGsNwLHXT1NiLqnmcnp3xnSyIamzs22jc51n3P67sTDb8YPE6l68gCc0TMcT6TkQ2rshEA0iwdAQyBM1nK4Wbdy6TXT4U1G4dhAtDMWCIkB2GPJ6I9UZbv8FA9WAYDUlgGFs79dc4yUUYcmZnEZSkyG4ZdHA7HuLu7Wxkfz5NASWH3zWAb6BmcMx8bAewcclgFMAUal/ms0BgQG3Uj4qv14cX1qRRdX1/H8/NzTSZceeD7BumsT0QxXmRPVefm5qbqAFUHj9OMJxm9WcJtcEAnYKa5NoCG+XA979lgEzlVFdabOfjkmS1QNBvFOrAmVGt44dh9XjzfJ5nCntj/Y4cCmGIdzMagIwaXzB09iogKPoZhqFUIGG5fEzmiP6yvq060ERwOh3h8fIyHh4f4/PlzfPz4sSZoJiYgIAD1TmzRe5d7DX5YZxIdkwh+foSD55YtT6lVv+7u7lbJlqto6DSyfHl5WbWQ8Dnu76OkCaAGJCYE7PS98Q/9h/lHJrxPwCP4+rQuPssBDU5s8I/4PSc7rKNt0BU2GHC3ntg/bFm0Ms8U5/OpXh8f7dhgMMp4fMpRY2c5VW4X5ajcthkSNtekVKuot8oIcarvu5gmn1zWNugPQ/MP2GDRr4hpgsnl0JHyDKWcW6xw/HKSt2XcU0oxTjmeX57i6uoYeY7IuVM1o1WEAKqAwmlqjDP2+f4+xjxPkTNHALfnd2D/tMXSurqOxW2zPqCb8dOm4QoOgAqdZl2xE8dHJ6SsO/82C8w652it2EueY7m0V19dH1eJY6+qdKQuhtSv5t31XXT9rvrZ46WSje4O/fpIbeI6SRVgFxkgJ8uMNSFGmKh0e2/E+inn7J3g3uyZw86xvwK0d/H+Xmzy/VRi4en8fkmY2nHprjZ5TQ1GfciP1ztivUeDteczsPp9X/YfPD09rZJIE9esK/4Pu2AM2IqT3W2HDK19W3LIGNF2RnxxJQFyBz+NHfJ5J8v4BsbPOLdxm/fxe9uYwli3MdjE2PX1dcSy1Gfm8L1tcotOugLkhMi6xeexc8ZpUtAxgs8TO/nM97z+pETDAbwJYQ4ePESQ4r+bm5u6OdzsakRr52Fy7kHu+y6urm5XTCWK9/b2HtfXN1+dUIGyuWfOY0EoPlLXQY7kAVAyDEM8PDzUB8wwBzZ7w6CbqUB5SBYwMAcUGyOGiONHGVFoV0Zw1pQmDUZQDpTSJ51sqyM4TUAzgANH6U2wyCylVPutvYZml5E7DpP15KfZYlc8bAg4EQclZMJ+C9hRM0E4GB+JTDJyPp/j+fm5nm7kxBbA7qMPXSWAGQEgMm/0lnG4+sO1ud6WEXYy4EBr0GZQCMjgOgTziJbkeoM28kJHGAvrj27QCgZjh1wBKIzHAccshpkUHCN6ABOF02VOZqZSSvFnf/Zn8csvv0RExN3dXRyPx/iP//E/1j79H374ISLK0drYB7rC+CMKW+Pkl6BCYvXy8lKJAPyJW/ncEuO1IuAA6PFTfI7vz/Ncn4JuFg2AtGVkcy5VNbdX8PKxnQQKBzmzj96/Q8DzPq2INQPpUjl/d5B3gOM7zMMtFk9PTzrAYqlPHGddqG5hKwYi+CKS4Hme4/n5ufol5mtCgmCIX4FEYC6uCG3JI+7rAzpMxNiOrQPIoehVqaIDRrGJ4isbIHcVudhSa890wlzG18XpNFdiB71gnPzu8UZELJmHya1PgByGPuZ5qe2C+BXihwEN1y9AbYyUcl23MrbynJCrq+vgIYP4ZM8B0gV7NkNvObKm+CgzodiIfSL4wokK9zPDS6yepvKcB38H2fFv7AI9YkzELOzIc/F13L7JdwCU3qQPKfnw8FBlRYIA4+/9jBFR93exTw8chH0TF1JK9bkOxEnGjYz8gN6I1qaFnkzTFL/++usq9mIX+HD02UDYLTcQLk4afA8IC+/ZxScSS40VmDNrwzXALvwbHLfdvG/g7UqB9Z3rGxshY9bdpDT41OQS90CvkJN9MqfgOfaavOaz/A0CkFjJ97mHSc/IEfPSOovQfdsRv7Om9vusH/bP/bGlbfISEat4svXPf8rruxMNszUILiIu7FNjkllYsl8/zZoHqCEYB04cEu0w7++vq6oHDg02kgDqlhHG6J5PgzGAPQ5iW30gQPI+hsdYfRqHXyyA+6JxBs6atywNCUvOuW5k2j4bgp5rA38nJC5jbltlfH0nQc5K+Yn8PXcUHWNBVqw/a8J8MSSfkIGTNiAwY2LmdhiGWjn64Ycf6oPx3GrgBMtrE9HYVOQLO8SDaKxnJEHoJgkHiRpOBN0wqGFOsH0EYJIcP6QKmdASZqfMvH1/HI5bVwBnu92u6pNb1thL4FO37DBcXbm6uoq7u7sqb7eOGZBYB8dxjE+fPtX72PkC1O0fnJjZgW8TMezQZd5/9I/+Ud0/81d/9Vd14zdjJNgDAJgb40XXvb+C960vTuoqW3mZG0DAzFdE25Qc0fqGnQS6t9bJP+SEdeLu7q7agxlaAiJA2qDLbFpEO2kG548sDf55Ei0ygw10wJ/nuW7GHoZhlThjRwaI/B3d/+GHH2Ke5yqTt7e32hduwEngdpUGAgB5EwiJL8yHZAG2FH9kmdj/4nNYl2Lb8+ra9uv4RfSQWHR3d3eJMWk1RgPWiFjJFX9gEGdAW+ZyrP7bJIdZfe6Hv+z7PnIsMezaQzOx4dNpioglPn/+HDmXdltiXjlNbP20Znx98U9zDAM93zlyjpimOYahHD9s1hifuX0ZzDt2OrHhd9ubCRwzs8wP/2lSEl9WQVS0wwaIHxAJBoxblhq/5AoFOgnh5mrcFlgytqenp0o0GITzeY5uB9ABcvnM6+tr3dsGsXF7e1u/Y6Dn+G0yzp9B1iSw4DLHBWKIqwbYqFuXXZ00Uw5oh8zhP98f+2fdGKNjIHtzsXPGhHzRCSdprCF/M7DHvh2nkAU25PV2koY9ghs4st12bLxjTEa89r/RUeRgIpDrMG4Df17GzdfX1zGP7WRJx1TG6KQLrITOOfbaP3VdqfKSDPtvVHeM0Z2U275/6/XdiQYBkUUm6yrAvwVvM+tmCBmsT3dgAcjgUZCua8qKQlpJ+n5YBX1nvDg5HIh/ekFRZpKBbWZMYIdhxOCc6ZmhtAEzbxYEA3R2i2MGIOI4AA/cCxnxGa5pBzNNU2V/DVi/fPkSfV/6hHliN/P2/oWXl5cKGGGAAVhbJswtZxENdBC07u7uqhMj0YGp8WlRXGvbs84avb+/x+PjY60yWW7og0FiYxgbiNjKfcssOpAha5JXBw3mw7WQu9fZDpTqAE6H9121sa6a1YRJB3hQRaO6gjM2W0EAJSHhb+g9a4O+m2l0MoQOE2yPx2N8/vw55nmuCS9zN+NldtrsvxkU/o5ecwociakrQ8z/n/7Tf1plwPhp++m6sveLB2PiB2Cp3Nrm4AnZsNvtVifRYX8kdrZt65nBCTZMEPPhEeiKQbuP3MZ+2GNhdol7OXAb2BIQOPFlm+yjQ25f8xyWZVm1UALMaGdj3j7hCt/PWk7TtGqFGIYhHh8fq4yceG83FvM7uuznCGxtlPfcTuEqAYEc/8G8sG1e6DzkCMAJ3eBeTh44OreAwuYD+HuJCevn6NBTz728qZPjg9ER6xhsJrrn8Vv3UrfTPr9WJT8eIWNSrdD4PqfTXBMu4l/xPYeY5ynmebn8B2mzi3leYrdbVx8cZ9G57d+JOayPiQT7f4Mf+1Bs3rGT+aJ7TsIZB37Ovp5rotuuyhhEIWvWCJDpvnlA3tPTU237JLEGrJlMhMwiiSD5M+5hgzXVwi0gR//u7u6qzBy7uA6JMfZmHfBx0vjf29vbOkdkT/KATME8/rcJSOsm14iI2qrMOiInYqZJy4hWKad7BBvaPo4g5xwPDw9Vt7Bd7o0tgF1Mplpu/jcYaFsR5poQqts9ph6TCRuuG9Hi0TZhYh2dOPIeicG2Mvv+9hZdakk618SPGbfiU7Ed4rtJVif8zBOddVsXJB5yQVauqnzP67sTDZecDDSGYRePj08rRtOMI/+ZbQfI2UmYBT6dzrFcnjCJQ4RF7vtdLEvLqjBuTmcw2Mf4rMw+DSAiKiCxgbHo7mvj88/Pz6sNwltn+PLysioNdl1Xn+qJ440ojgwQHbE+DQdjAFDQJvLy8rIq9+MkIqImFTYys4Hr3uH2EyDLZ1EmZ9hmLCjNetxUT1hr1pSg6QoBeoFsOE6v67ra4sSYcZRsXHNpl8Tg8fGxBhESN67ncTIuVyQwIrMQXAvZkOQ4wbbD8hOLMVAnRG5BYX1ZY8ZlxoQgSjA2wGPcjBXZ4tDNdrmtwg6Qlhae8o6z4rM4zJeXl9rC5D1WEQ1oAsyxDyfd28Q9IlYn1ZGI+r455xosp2mKT58+Rd+345dJQBjLhw8fqn8wS8q4uA+vlNqmXxIa9Byd8fMnkA/zxclyKgyJBomZ2Uz0wWuKnnG9LTuMMzcDhhy3iSwn6GFbAG3bNqeVeV2YO/7Bx43DLjL+bXsFNuMgBaDhwWPbIGZw6Phhph4ZmN1jrsgRhtHJF3+jF571NGPqhKfc9+sHmBFQsXWvO5vIc14/9RkwVfQ2alKJDhZQ0Qgs/B9/j0jR923N3AaEb7cvres4R0RqLUbMpfiyKYahrwkUa1t+9l/5tNZmQqvxHGXPRo6+6yNSjpQak+7+eYN1YiprAxPKvPGZjkfEf2MEfCb3sV64Jdc+aJqmGHat2uZDB+x/TWZ5nPhWxmvyiff5G36ZuZLEo0u0+VCRxV/jy+/u7qq+RrTnDNHNwPPJsDuz8Aap6ERKqbbaYCP269guSRDzR8ecRHxrDb+1r8G+1n7RMcekjb9nQA2gta2apGYNt9UA26hBLuuDX3E1xf7HPpjrggOcBFjGkLTok30gc0CH7Uc4NMXELOviZJTvb/0tMsFP7fo++q7tSfMeH8c/5oIOQb45QXTyhXzA9Y7dthfk5arS9yYaKSPV33j927/8N5WR44SRBqjaXgcCLmABA0fRlmWJ29vbaoAsPgpSFmaMvm+lIBSpBIoGgq1gKCzvY/gEHxws2aLLvCitGSQWyMAWozFzYWX+8uVLrUjwECochwOsF5AX8gC04wxcWTCbhOEgb4ABBu5Tr9x6M01t8ylAZttTCIB1pYdxA2zQA5T+W2XCl5eXqpQ+792s1NXVVTw+PlbZkMQxb4KUQauTJT5HguDxGUzg+PmedQ8WiDnj0Hi5Hc/AHRniNAiE3IPkkHFumQEnMF5XroN9oSdmWrApV84YOwHCf8f5bBMSbwyDPHBPKueTE6DMiESsW1ssa7OJEWsGB9IB+3Fy7PYaJ5bMEZBi8M2YWEuX/LEtZG6wyLgiWnXV+38IQuwzQ1Y3Nzd1TMjCgdHlauTA2JzI8xM7Rx+xN28w3wZxZLHdu0H10G06ZuBcuWIeZujRK59rz7oZVOJT+Tt67epARNQDLqh+OJExa2ZywPdkzVhj2uKwMfTneDzW/XDIH72vgXq3i5S61b4C+3H7ckAHbF9KUQ8uoGrSkpSWgG+B2m7X7IO5zHNpncK3uD2Ge3I8M7pQfUUqJ1fZpop85ihtT8sKFKEP7DFxHEbWy9yqEfYNkZY4HltizPeQJZ9lbVhDdMn2Qbxg7biXbZHrcT8D1K1sYen3+/0lIWox1e2srClyZuxUG5C7Yxz3Ys04OYokx5uc8bdbNpw2LnST5MO6zhrapxqkcz+TY3zufD7Xbgvmio37oYpm4YljxAXk46QeAmRrQ+iEe/a5BveHFIV48DqzvvbpYCniiv21fbXv5es4GYOIwoeQBOKbkJ8TOrekMz8TVazTfr+vhxswDsdu7gFZvcWVrKvnA/YyQc9nOFiGe1ExW6Y58tL2cnBvyE63ubH+xHAnH5YhNmG7R5fx8W4XxM6Iu/M8x//p//o/xW+9/oTN4Cne30+rI2DP5+KAu26ok8egzRYwQIMXs/FMjmyqKISfwtpFSmPkHJFSxLI0gaCYCIVgYwdHwOKzMKMwcG4nAhg78Bv0vb+/11YjxkwrBj29dnoGXhGthG9gaOV1khbRWisi2pNhUQTADspsJicialuW2SGX2XLO1YCYH06aazqDN/vO+269en9/r0nN/f19Zfjcx4n8GQ9VGjNVAE47AhyAW74A7lZ+9ALQR2Jr1sCBiwBghpm5IluAx7bFgp+sKfJiDlQPmBdAdRvUkTenigGEvOncn2M8bjeMiNpnj86S4LkP1+yQ9ddVCdYqYv0ch20p3d+h5eDp6ekr0IZcSNBdkfG9sE+DMgMWkgA+Z3Bm8BTR+qfReTtRzwlbRCdx/k9PTyv29/r6+qvEB1IAe4BZh6G07TiZJNBwwIQTCRMS+KWu62K5zO/99B5D35dTdoYhprmdBhURkbo+uj7HfDpdSu1d3NxcX6pCMMS0vJWWoCLHcrDHOOqeyxKFeYflL/81gqn59IgUHNVdYkJ5sOo8f4mycXmOeT7X61xf38TVVXnGSbt203H014kla2nddABvLKbPx48LS7/UsY1j2/zIuniTv8FvSu2UMjPRS314Vh/D0EAGALiczlYeSIgNn89U2i6yPl+S95xjN/SxLBcSpeujH/YxTTmmaYmui5imy+ElXQTHs47nc3R9Hyl1sdsNkfMY09RajPBZxVYjIsoxp8NAG9qpyCrnyMtykdWl8pCX6LvWYmWQZALBlUB3FKRUntewLHMFuMNuiKvrq3h5folhuBw4cLHnvOSY5in2u11M0xypS7Hv92XMyxK7YRf7/S7eLgeSDEMfXXeZQ/o6xhhQ4XvRI2It9o7/wKbv7u7i6emp+ils3lU5dHTrbwDj+O6rq6tajceXcQ38EXGMa+CXD4dDrebjo7AJJ2CAVYg7YgjvcS9XHU1QoCMGmMiSuIoftM0YaHddV0/io+Xw8fGxPgh5lSzn1l5kv+nkDXsygLducR38AiQA8iXOWG9ZTxIJfreMiD/4GZNOTkSNK7cxzH7cFVlIYXBJRKzGhQycUJFEHA6HyLslxvO5+n4Sykht3zT38p5At0KBYWq8SGvCFoIbm7BMnDwhA67zW6/vTjQIUjmzafq9AllYfDN2GB8lUgIpk3MPe8S6xaNkiIeLEZxjGLqYpvbwIlp9DC4xRBIVA0U+x0ZzM9+uYnDKCQp6Op3qQkdENX4Mfcuauuxu0GlGBwXiu94k7PIZsiApQi4AdRucgRPZMEmTmXuXMq1kLku7/S2l8pA7twThGBkDhgZw4gSNiOL8+T5MNa0xOHiY060Bz/Nc+1nZaMd9GTvGbYYEdsEGQ39sRNswjsFRtXGCbHaOObplyYwF62IdwIm4aoWsLYvX19cVm4TBA1js7M16shYei08ysYPDccGuWT+RDXqKXDx25AwwY+24Fg+ZQkbMjTmj79i4nbVP/bAMuY8ZJOwC/fTYzLbwu5N9M0r8Hbk4YPj8+A8fPqzYIZIGfI9Ly1wHIED7FQ6dNWQ+Oef48OFDXF1dxd/8zd9UP4Ufc/IcETEtcywa/+kypi7lyJFif2hPtn94fCw6mCO6LsUyz/H62p7H0EgHWl+K7dFmBYCOKC2sRRe6y2deV7qC74iIOBwa4VFiRdGP9/cpOJmJOeIzqPa1NSugvfy7i2Ho4+rq2ICqWN+tjrpCtiw5uq5f2eM85zge2UszrGSMb2a9sFXssIHW8hyNeS7rAkkR0fYeuuJUYiBsZSHJ0N9pjFiWFCkNMU9jdCliGC7MYZdiSBfA11MBizgc9nE6naPvaNMcIi8lmer6LubcWgXdslV0sVUFd7uriChJV9+XZAmbK+vTx5C7KEfz9iuZ4Fvsi0wczPMcu/0u3k9vKwY8Ug4Sneubq0pIdP3lekNXk5Nh11/Y7ksF/qID5/Ecw1Baug7HQ/U581xOLoNkRMdMSpm44VkHsNxlnVrSgW17vw++kXjsKrafWeN2FgPmlMrDewHE8zzX/YuuYhN7p2mqrTdOrlmHQhS8rboJmC86RgzxHIxZtgCbeMk4DDDpjHBnAgkIFYK3t7dq08RqbNVA3ImrqxquUjh+0KpqotIdGOjk09NTxRjGm61FsLUi8x9zcxWaa4NLuA/j9lyMV/DjrDcdEtgG92NN7J/YBwKOQq+QV845pnmO94ufmfMS58vR2Z1iJ7IB+0GOQ5agO4zP1WvHVFfQTawZZ1mXfuv1J5065cWhrMuCGBzxmYi2ibvrugp2nM0S3M/nc2UCSyJT2D5vZEJQAEcqDSQROB6UFXBixRzHsYIjFpAxoOC87z0FBiKfPn2KYSjP+nDJH2XEQM3MGqhSep3neRWsMPDz+VxbDpAhRs0pMlYaxgjr5g2qbgHxhjNvyh/HsZ7HfT6fq6I/Pj5W+Q3DEB8/fqxPOo+IysDj6EgGaLVhXXAoHI+LIuP4SKxOp1N9irQTHvQLcEApm/E7I+faOOicc31Ktp04OoJTQF+YB/PCcRjomJ3frgOgyJuiYWXQYbPw8zzH7e1t1T3khG1xLf6GM2BcbhlyskyS72TQCQAO14wU8tuyF8yRMaFr6CctOH6omqsvDQCun4Tq6trhcFhVS/kOCS3X2lYlvKGQQLll57gHZWJsGR1grrycsMBaAqiWpR3Z631dJlOcYPAMDT6D/B4fH1fJrU88A6C0Ssj66e68ii9tYzJLv9vtIuUc/UXHGbP93rcYrhUjHW3f0Ha9/D4+Cxs0aOOz6Apr4EoP18bGmWvXtQdxmuhwcDczyzrNc/Hdh/3luQ+7C3M7z6VCkFKkuIw/RaRIMS9LLPMc5zyWGkTOMeyGUukZ5+obXp5fY3exx/F8jnNqz/fIS0SX+ljmJXg4XqlqRPUzyHi/Kw+PK+tRng81jufo+y5yLixlXB66Ns9z9EMfp/MppnmKIQ2RUo5+6C4MZ9QHzxUwvz7cwQw4vqSsXdOl7cPfip/ra4xygo4P7bqugjrvVUMvWpJXwOTLy0ttWzL5xYZpJ5QGqOiFK7HYI+vP/h2+Y9uFJMC30rrtOOpDGZx0Um0HNCIjg230D9tiXj51DRL0fD7X6qg3M7NWxBC3w0AA4lPQfcbgqja+G7ltK/0mZhirCRfHM5Ir4xC3MnNNZLk9yMDJmXWf9SchBDciBz7L+LckG2trX4EP9SZydN3Ej5NiYij/3dzc1KqPffUW19oHGxebqAC3Gud4jbEjYgDYjPnTHcQ1XVFDp1xRYy4kvZz8R5fD7e3tCq9a7n42Frq71RNk4S4E6+9vvb470TB4AQRiMCiCe4pxAs4WMWIWgeAIEw8QBXTyeXoRrYDcA4bYrVgObhg8QQmm3xUYMwY5t5YXZ28OjFtlxpkyL8Zgx+DeP8aHI9myFSiR94jgqDkhxyAT4PTw8LACYVQiKJe6f5zrc7oQjpL2FO7BelK+jYjKXpgVwnC+lXAS5LY9n7zPmhs0In/k4id/myVARyIaiHLyFxGrvSZOSP0ZAoFb6dA3AhJrZtAK2EXerLnnYb0E2OJ0GIMTK4K3S9pmQrg28zf49tN4CQYAA/SIObiS40ogwQYbNnBxcIqIld05KaE33Mwf/7nqQ5IBCEIHGD96hRzWVc+WGNne+R35k8wj7/f393oghVlM7JR5ms02CHP10YzXtiJBAGKeBGQ7dx+z7QSW7xUAO0cf/Urf+HxKKVK0032YS0rp0oYyrXQN2Zlk8dzwgXyedSWRA/SwxpXF3u1WsjILhn0BstAtdBx5krCg9xHt8AmuY1LnfD7Hy8tL1RsA4TjOMU/ag7Cs2yzez+1EHnTSLGVh4LuYp0VAi70YqZxnP8+1+lJkXCo5lT3uh9IeNLfkEBmXilPpty57K0qisduVh7ztj+vkuiQb00WefeS8ROpSRJSfXUqX1qlcZeyHxZnMYQz2x7SvsKbI1SSHwZTt0yx4JddSY8zRecgh6zmxAx9ALMYPoev4xm3LNX6E69lmXl5e4ubmpsb+iLa3Ap3jP7d0cl+qEsSTp6enupmbGMFa2xewv22329WKPOuI/CFUTBhxDewTn4ieMsbj8ViPfXfCwfrSIhZR4h6VfGIPOAV74oRJ/If3P9n3OpnAp1PNwI4jonZo8D5yZN2ZK77ZJJfxlKsB1mGObM45V9tH7iYDSTBJhMzGgznR62ma6oE9VMUYB37FJBKVa3wkc/DBHMQR/r4lZUgS6ECh7RyZ+nAkYjfJKaRORGur7lOKLnX1dEjwYd/3cX9/X+OU9Z+Dd9w+bT/Fy2Mn6cdnbkm6v+v13YkGTgWgBgBhUJx1jzBYFDYF4dxQfKoMlDFPp9NqUzIKhKGj+DB/BEM/4MqAFiBJ+YsyKL2cu92uPsjLDArGgEMgODvwum0FME+S4QzbpXQM2wCNAGrw4kQI58R/JDhUNQBDBBcqRgQNFNrJDc6NoxSZN4znNrPlfZwmTobz78micVa8zPQiGzJsqiR2wBHtAYBb5hxg5b0KBkdXV1c1SfpWVs6c0R+cTgM0sSpTo7us1RYgso7Wua7rahmcE9CQD2MBHLM2ZgitZ364nEH61h79k7XDkeM0cLrYhMvzyBwdZP5mTszauVTqZAMQ5zY6B2GzUYzT728ZNbPXPqaPa/MZ9IOXyQOCA+Af3eGJ8j4Wl+9ASrg6YkCA3SNfz8nj4H2uj46hbwRO1oV7sJYEAYLMrttHjtZW5nmnS7++54sc5mEova6xPgJ8y8iZccRPoiuen4kRfBL33SZM9iURUUGig7zX0i0nTo63BBbriX26DXEcx+LTj7fx9n6q1yxtQhyfiR9eVv5wvx8uOpmCB9aV76ZIqQ/H05wjyumHS/T9EF0HqVb2ES5L+W+appjmOdJlzwokzjzPJXnsh+h7AEBJZm5vryO6Ls7jOY7HshfE69V1VCXLHoWcl0uSc46I1n5DnMPG0T1vgnXrBnbuU8iwT/ylY7FJNFcxakISbV1dibB9mujBv9DGgQ6wzlTd3VLptk/siA3QVJHRUfw7fh/A6b0dVG/83CbGgS5BKCFLfMZZyavxDskBvsS+DzBsHwF5klKKx8fHGuf5/uvra/0+63w+n+vRuRFt47sTGUgF/A/xhzluuyTYY+nj9olV9iPEc8c45kNcYW2YMz4MeTE/xrjf7+uR566ML8tSSSP7BHw22BAwjM5ZpowP38H6OcZvCU/0q9hfV+NJxLrLgLjvexBnXZl3SxYyXpalHmFMZY+kDX/vVjYIe+YdOWLJjQx0NcqELr87ETLRDVFmkpd5ep0i1g8F/q3XdycaLAzKhnKiCN6jYGUHUKL4LhF1XemFBkT7aDcf/4rCUk56fHxctbcAhl2Sc8LBfbknp6dwbTJKhAcQMGBiXABFA1GMxUyhAaABEMplVoTStK/JvPq+r5vYnE1iqLvdrrYWuWIR0Z6mjWJGRL0GzjEiVsaPcjq48D2Dw+1rm+GjM3wXxXcQI0F10oATYY7cH10x+DTgwIBdrSCYcTwq6+iHILrU62uZJTMbZJberSoRDQiylwdZmi2FyWYdKX07ITFziEzNONjgvQeH+yM79JEEyA8mQ0+96Z57fCvB535eK9aAOTtpsB4ZxHMtkmKD661Tg4Aw0OLeBGzG5QDPe2Zg8Em+pplNB1G3G5gN5hoOoozd42O+2AKy8vv4J8aOTGgJXTGlfR+paww3css515YZbJxx9X0feWltKySCBpDYlXXsWwkt1eeIdsw568kcsEl8MD7WQRmdYk24N3YEMITIOp3aA1YJ9mb6tn6W747TFDlHnM9jLEur+l1dXa/0tiZrF329urqOsnnZR5ZjV13s91RBSmfTbrePZVkz4BGl5YmEI0XrT4d8OB6PsRv2F9mwCbls6l6WJQ5Xx+hOKeZ5iaurY+S8XFoh9lGO2o1gj8XNzfVlPCmWpfk47Bv9wp5YH555gn0azO33+7i5uak97/hkkw4Aue0+Afso+0j8Mz7UCec8z/UZCt+qhI7jGDc3N6sjc9EhbGQLnrB/g8uIqLYFoUW8xAc4ucan4vO4Pm3IEKO+v/UZWeJPLA/mi66bicaOkBPxDFzkJA89RjZgAB+kYsC7rW6ZADVR5/ZXxkMMd6LC+mFLtO5+CxOCKUw4bWMHcRt/wKZ2CCKP2Z0ujNfHk5v8RGe2VRuTGpYF83QSyhx8aIw7Wj5+/LiK5/hX5kPl53A4xNPTU1139laQ6FuHPa6np6c4Ho/1ZM5haA84jrnFKMYEoWvsiR1bJ3w/dN1E3raab5xq2/r7Xn/SHg0zgwQlFNYA45dffqlAnbYm908TtHA2AB4CmBX1l19+qRsnUfhPnz6tgAnXRXnNVDmDw8G8vb3F6+trfUIybLhLiFZ87wOxQXI/nCGKC8hivwRBEmdGxkoyQaXIQJ3WDgd6zvR2T6PBA46aMlzf9/Hly5dIKX11IkREAWM8FA8loux8e3tbndWyLJUtMYhEAV22ZEwoMcoOawDA4PMwUHZI22TFCZCTA3TOjMs8z6tWMGSPPvCf9TWigRQAP+Nx77mDBvPiRYmcAE+Q5j87DgdCHNY2STfwN7tgxwiz7qByfX1dEwo2gZl5YB2wXe+14iefd0KDbjAGO1sHYXSYsREE/PIaNEC3PsnGf0Nf8BnoCPJE5gb5vHCWh8Mhbm9vV0dC4tfQNTOezN9zohrG37B99JLA7+dJEJAdXFlTQI6JEfsY7rM77COJDeb5IefzOc6nFqQYW02cLraA3HhwGJ+DIUPetClhT8iItsVtcOGn14JkzqSCq4HzPK8OwLAvclwhKJPEmJFDH+2DWLuu6yMy7ZaAjlI9KL6AB2OWqkAjSMpG73FshzGU9e5jmkqikRLgfYm+5xhr2N2ygb7p0xwpLdFdjml3hWxZlnh9a8deH4/H6PoU5Vh3nl8RkVKOeWaT8RDzPMX53HSrnfRFC96wAib4Bfwc8SiiPUwM/8bnSHAZr183Nzdxf3+/qgqwVmxyrjKJlkD3fV+Z75Ra1cFJEP+RaBNjucfr62s9odB+ifszX3w962DW3P7SNsCaEOcjoh4aY3tC3x3LsX+TD4wPf+q9RVQIWLP39/eakNM10MnWsb2rq6vayeCqE8kW3wFooyOuwFsnkAd2jUwsL2L/NrmARUeeJiody7Fn+3d00ffms7ycmLHvjxe+nrGBj0yYUbUzkYXfMCmC7FyJclWL65m0ooqDjeEnKil0SZwg1Fk/y8K4BXlZzq5yU9me5znu7+9rUo+t1Xb0mCrOMjlsMmVLCGHj/HQ84vOWvWVonfqe13c/R+N//Tf/rmZqLACAAkXCMby9vcXHjx/rhiYHJIzEnzfraGbZpSMUAiWzIBz4MLSIqMz4FrQiWJSZn8zLDxMy00MG6uzw9fW1LhqOyYCFBAlFm+e59s8iSyoTVBqcyaZU2MHHx8eVErh3FbmSbT8+PsY4jvHp06e6Kcjg3Zkzys24Pnz4UN8fhqFunNuyDw4EDw8P1ShwYna4ZgZwDlumgCQEIOjSritTvFyJYPxbBqDv+2qobAi3E+eeEVHXCt0EyDF2wKcDjB2G240A3rzHyw4UpsOnmJktcLKNrvB9rsmBCYfDofZhkpAiUztyO3rWwW1TrAv/dnB1IHXVhbY4/o7eU/rdss6sC2uIzLgm88QZeozYnBk7xmHAia2h6/ge1txVBL7PHK3ntn9XARw8rQcAY/e2+x7og9nmbZKF3vA6nU7RX+YyzVPc3d7VCiz8ed8PFzBcTjcqffw5IrOZtuwf2O/LcyQaozxW0sPJJhvMGeM2kWL+fd9XAgNdYE15ejJrbd1Fx7Y/ravNB7Gfp8WQq6tjJUyGYRcc11vY3Dl2u2PkHDFP7cSyUi1oe366rhwZHDlHjsspTVN7TsySc3SpnWxHEB7H8XLcaqvyoZ9mgy8rH8OuJaXWT6877VrIv+u7GMcplrzE0PcRkeLDhw/x8vISz8/PdS1KHChtXq4AkqQ5cej69ZPSIa+K3Za/HS5J6bKUjfGRColES8fb61t0fddA8iW2MDcIs3GaoutSjVPM38AUXULX8cNOsp1w4M9MGPpkHeuS14XOivY8kbZXw76CzwLQvVbuEjC5ik8AE+CDXC1wSy8+xdVyJ3jM0XGTWETsR5bbOOoxGGDib01QOe7T1eGKPzYO0enOFK7HmB855e6iE6wxeuS46HU2OcqagvPsZ8y6Q0a7Co5P4DPYkAkmV4dZE2Rsu9ySZFugjv3zfXSDeOs40vd9PYEL+RpXEptdhXMMjIgV/pjnOZZ5jsO+dUpM8xRDf9FXycGEqisuToTRK5N0+D7mYqLNNsZ/rMd/8z/88/it15+0GdwAhkkB3hgYRkTGaHbRZUiztBYAoJmSz/v7e9zd3a16ExEEi2wmo+u61TGrgDWcFu01lP3dfmElcNkQgyGJQeEoXQGKDTQxXBy6W6EaI9WAkxMyfgcQmJGxQn5LCTB4grzZRTaHwc5b0RkLhoiiuifXjtfgyQlGRAOSLuEBxhj71lnudrv6VFMDLT8HBMcDwHZwwYkAJglYJKuWrVkoZAZQMpBCh8x6bBMkJy7+m50hwZD5slHQuhzRgLedMQGQ79oBTFN5OvbNzc1XyZgBkGXnKoHHhMyRi/XZwCBi3T5kIEGSbDCN80KPmDM/t/4k51w3EpKA4SfwL7yP3qBLyBHWibkwbv8dubiSajDsigeyMlPG2jJu+zMSLHSUZJn3toDEsmJ97fANps6nU8zTFJFzDS55mS+A9ALo51jpYGMYl0sy345/xGbwj23Mra0An2eAxRpyMp3bcl5fX2t7KJ9FntglvofruALi9T2fx1X1bJ7neHl5jXluLR3YS3kuSBd9X3T0/VQOrMixxDxffOhSZJmXS8Wskh+nWPLCXu/LmsyR45IM9CmWPMawS7HvIIVgh1PMc46uyzEvUxyOtIm2PVnID4KngPtGXixL8xFpupy81rUk5fXlOVJE3FxfrWzFcW+aih6QAEzTFGc2Hq+Sk11t05umKc5jIQefX55X1Qbsebe7AP3pHHlkM3iKcRpjyToFajfENE8xTWNl56nME6vxBeyPNHmGf8NfGdBBoECw4XeIgVT7c87xyy+/VFtwAmaSDkaY5NiVEhMutmP01DGGk7T4DhjJ1UH37XNv4oyTeWyAGEGbLfHPdng4HGrbMeTu1dVV3N/fx263q6cn8Xn7GuIqft6xIiLq/kvsDSy2jbW73a6eZoScsHEDdGx5nud6QiH6BVbE96LvTs4hop10eY8EWAcwj49x3MNe+LcJVgN9qr7uUHDMYA0YH3EA/bG+uDJhXYU8Nl5ERoydMVZyY55Le1TXl+bMZYmUC/2y29yblzG6E1Dkz99NlBifmWAl+TIu2BKpf9/ruxMNLxDPQvALIWKEW6Xh8yhC62ltZ1i7Z5lkgABocMP3ST5QQq7pnfncj5IlL0qKEesnrFrBDodD7Pf7eH5+rgwtwZEMH8cB+2pmkiTDGbcTGpd32dB1dXVVlR3HyUOtXGJ2EkPliIDL/W34VnaSAst0yyAA8JENCSCKikNlI7Zli3G4D9UKbrk7OQLw+lAAn4qDw+z7drIVa4+O8u+I9sAbDJfA5bIthoSBOWk0OEJmrrih82bsHBzdcxuxrrCZacAG+IkOI3NXNVjnGtzVAuCyuxM4A1lsCr0GFAL8AN4GM14nz5378HnrtxkqywxQygZN9NosLXaEHAxCcWzcE/BP4u+AbedtH4XuE+zM0LMGZnt4nxNlWEvu45YyAwe+R1A2q+TEA6DP+NBlvmfbdSCx/poF2wYvkyVcm7VDn06n08Unrg858OcdeM34dV238q8AWcADc0Rv+BwJh5NJEzxbvUNX7Dvf399rVRk74PPIzi2IVJq8XsPQ4lOr2qU4n1ti7++xdsdj2YQ5LzmGvotht4s+sxn/VBO6lFqlnXm5qmp/xRiwfxNMkHi2S+bh2IMN0b7R930k2eOyLPHLL7/U9TiPbdO0df/29rbGSQ51Ye1ZbyeqrCXPZCF+sVF5ntsR5z7wxEAT0Nj3fa2KeYO3YzV6eXNzUxMG7yvjdx/57YQZIO8Oh61tEut8EIkJQ4gvx9TD4VD3R97e3lZMYXafRJBxENMi2glt2AG6vmW+XYm4ubmJ/X4fX758WcVzADiVZ9q10DPW1g/FRFdpY3OF2bq6rVISb9Bjdz0Q87gHem9CxOSTCRh0ks/QPcLakdQRX/0cCnAUJ1UB8G1X3IPxsD7ESv6O/zbWs5/CLvF1YCST2X55fugCcvTBO5UQXtb7JdFD/Lqv48TRBL39OtjAsvXLyaXJOHSHdf2e13cnGt/adIohmyVF8VAGb6LFyA1WMBQEh+BJInCsBC7v9bDBodTPz8/VgfBUznmeVzv9qXDAkjCe8/kcnz59qopNguIM1Ju57u/vVwDdAMOBACD9LXBm5UMxndESVMluMS6z39yTY2eZnw0ARSIx4H44Tgd0y4pAhfN2C43Hx+84f75vh4SROAFifQ2QkM22XYpA2nXd6mg2rg+YQMdgxbimH8jm/Rve1Mcakqwa3DnTt5MAaG4BuhNJ3tsmXa5U8BnbFXJxYujK0TRN8fj4WOWPLpox47MGwhyG8OHDh5oUMS8z9Qa/2KCTWAdBA0l0Cbtx0mbQa+cNwAAs4sxdZTNAjIjaQoNtkJx4DIAF5IwvsmO37XoDpufP/HyCSESs9lc5wQNA4KR9LKIJDSe+fo+5U/4H1Jhlc8WFuTN+fJuvT+UBX8wc8JnMz/f33Lf2uK0kmTCoAVJxg7XyeIkBXkfGgH9DH7Y6bfIEMMrnuAZ6xrU8JxJNAz8HeD7vIIzOzPNcTntZLkdCL+15CpE5JW/5Sn+K/q3ngc44Ud8m+bS10O4CqGoV8GlVWSIGpq6L8RI7DQxZw28RT6zd8XisffL4CWK6/fcW1LilBD0xMLXfZk+ZN2gjLxMJTgq6rqvPfoKIox/eFUwIS/4NCHVLE69hGCogRcZek23CT/whXjA36z8x0iQIL2IVNvv8/FxtgnVYlrY/ksMSAKImdpAxezStTznnuL+/r3O9ubmpBCWypMthu9ncOMKJEnpokpi/Ae7ZMI9PgzTD15NUQpL5pDTkhC8z+cyztl5eXlYEV85lb+Tz83N9JoZtjMoWuucqP3OzrR6Px5qE2f7N5KNX6LnJKXwPa0L8wZ5N0OL/8GPECmMMfIl9gwmmbeUNf0NSzBix4/v7+xr3tqSO4xHyICa4mvNfPdFgIG4bwglEtGzKmSSK5n57jIEEAGMkQyI4IgA7Jgfgvi+nMXEE3MPDQz3VgkoEQYQy/rIs1RnRp8kimJ3z/gWfhIWiABowBFc2CAY4asDqlhEk6FrRXFEgOXJriAERysf1uCbj25bQmM/T09OKZXcVAIdmltXG4MDNaQlmUxkf76G0rhgY0DEPl6PdChHRmGMzVQQg5My6Y6DbsvTWmHGMXJcgQAB26x/jNZPEWtnhoOcGJjgTAgnfIVjjEEh2CCLzPNeT1ZyUAjjtxJzQbVueuCf6ZFaQzxvA8zm/kLUTM9Z5ezABjgmZAtZx8ma4fJY893WSgv7gU5gjiTqbuwEMfIY1NbPtNgzWF9sjyfz48WNtnXt5eVkdT/zjjz/W99krxT3RM8Zum7LOGCR4rZCPfRvrYZYL+QBAeDl5sr5zfVdmGAvtk/g0bKL5qZZkEOg8l227mau3jIf1RS/sb1h39BsWmM/af/A+vtyA1joH4WHb47OAwO1+KAdY7N190QbK1jsS9TK/FMOwvyRqlye5T+XI2chfb3LHD2H3yMCnIm7ZVoAdINd+FJtkvbzm7Hd7e32Nt/f3SEqyuMbxeIwle39OsVWqEsRD/v36+lpBKz7U5/6j2yZwOHTFCYr1FZDE2pGk8zefkOhDSdBJ/FNEVH8AWHfrB/HSZNDhcFh1RgAKTT45Advv97VVNaWyFwn/glxdnTRBagxDFc5Jitvr8PXTNK0+S7y0z+Dz2MTW3tEDdM4s9jzPq2NxwUvbDfOsi/07drDFCXzeXQ8QudYz9NsVCsYIsCW5IO57DyeED3GB2LHtPDHJ7U3v+Dbfl3VkXRir/TrvERu5v5MM75mpdnb5PgQUiS8yYczGdyb1h77hYeM7EmTiveOxZe4kmIqh72l/6iSWfztem/z4ntef1DoFgIdxRaHMKJOdRsTKQdnoOVrPk+N3HBsKjkHBDIzjWDfVIGSSjuPxWPujUS4cBgCH0zZgQ7zBiBItbLkTA5wSwMclUYMIfpLB25AJVM6Sh2GopT+zuGZot4Gan8wTxSfZQX5XV1fx8PCwYkG+BYowFve0so6ABs/P2fK29cjAkHuZteXl7J5199Np/VChbdbNv824Gpj4CegOyDgWVwS4t9s4COxbIzT45X3WI6IEQW/yQz+4J0bvRIqxeT/L1dVV/Prrr5FzXgVWdBi9/9YYkB9g2qdxmAFhLsyXz6Ob2yoF9+j7vh4wsCxLlTVMO04Ku7NMWXc7Mq+PWSMnNcyT8fMdwIhBJetDYET2tktX4rgHZ5l7vtzvb/7mb+r8Ca5m3CLWz8g4n8/1CcSwlr42ds9nbSfMz5U5gjkMHj7r/9fenSzZjSRZg1bcwZ3u9ImRzIjMkiqp/x26F/1v+ulbWqSHN6hN1aoiMyNJ+kj6HYBegJ/hAMHOYIjk8kKEQtL9XsBMTYejR9UMSdJksMuWrqwgJ1ubFWp6N/mGeQWDjSwT77TzbB9JkJwVv1yTJADIMHvdfSarpNn2kglQ6glflcm05DNtzmfN23pmwmRvQSaT7j3NsavjwQlBrzVugl79SreXVart9qLGk6Sm6ouxZWUlk2y6DhSnzk/VqeldVvlSt6Gq3n09oMWLX0dAV/W6G8d0fX3d9IHcVqtV07vtdlvv379vewBSD5KE6bpx8/rnz5/r4eFhltz4HHuSsCXjD6y7X24OzzcmS26urq7a+l1dXc3wgfEtWw6tZ7aomLc/7MX4+D6xnb0u91nyLZ6bJz/xHX3f1/39fTvd0VjJK4+0z1hvPtkhwTZUH6w5AJ99/uKBWCnhzxiReptdJnTSXKqqvWZAQiiWJHnsnogpJ+HBYlnZ4E88AxZKHTJWOi7xYUv5fH4lSUZrzT/Yy2Ltkr0X51Ivq6Zkim9wXy1XLvgw41jG8iQ50xeLF+kTz8/OZ7Ek/QMdti6JO/J+SW5lFSeJpSUuS5+UnQDi6Pdc351oALF64hhYAoasGggO6/W6ATAO/3g8tn5nR05SOkLCSLx586aVFKuqAWlAg6L+8MMPtduN79jY7XZ1d3fX7pXKugT5GaBz8bA0eS5zBrSPHz82lpPTtFAAjATIPZ18QdE4P06DkudeFX9n2V/C0vd92/jOUDk8YwPgD4dDM2hrQ+FyjQWXdJhkxzByDNaVoSQIotSuZLwzkUqGN6tG1iZZ9285cwaclYoMzAkmUs4clTkaH93ONhXjz+QkQRW5eI7xuRdAXjWBoaxW5RiGYWjVLOtCv3JjoXmSWzLPCdiMO9tK2Ib7pr2Sm7VUgs6EraqaHVeNQUPCul6v6+eff67Hx8f68ccfG1jI9UlH6F6CeuomXfP7tBtgOVsgcn0E0wQd2FEyYUcqdNgwnxWEPCMDQVXNGCmsFRbNhtesSmWCLPhiJc2Z/SRriWDJhCwDHCDEXyWzrf3TleQAeaddAKu5PpKJJXHg32KAli2+1jMmgL2d6X0mdFXV5knvJQNsA1BiV1lh4+M8DyhguxKz3PME0IlZyTIaXyaDnjOBvlWtuunEsdVqU123qvE9F0MNdSxv9U5bznVgR6vVqp2xTy/S3hL0smPEzziW8f0e9Imc1+t1XX5NDrJ6zD+LN8n6pp4mGGbLT09PsxN9+I58I/lqtWpv00579YctZ7JMj/nH9Xpd79+/b9/NqlJW67J9cbOZ3gyexAQWPMFqbpjuuq61YS19iWTZOwz4M7qgQp0x7Hg8tgpo3/f1+PjYfAY9ZS86QMTU9M0uOuEkRfEpT/eTPEke6HxVzTZuS9j4oSQa6aN4AyxbN2/PBjKXvfyJW5CzElb2D1st/QC9WTL8konEDEl4p/5Y20we6bu1tl5V1eTn2ZmIeib/pMslyTmfFUPF3oyxGU/5gPwd/+Z+1joT7mM/r9JmUmRs1lYVLX1rYjux1LrnGqYscl3M0Thznr91fXeiYbNgssgMN1s8KIZFqprYU5MyOFUIwqTY6bxMnAJ57bwgeHV1VW/fvm0Z9Xq9rh9++KEFEv18FjVB8zAM7Wxuz/f/7KlLpZGkAEEUmuApoHtl1sdxOnEold3C2ghOJsMwzDZEp/G5h0Dhc54pcCUIFZgwaBKUzKrNhayWlRAlZvdNcJT9tYJBgu/UjwxIfm/O+kiXDte9zMWz/Nt57cmy5fyTqctyNwOSEHz69KnNlX4IiEswyxEkA0vHkgVKAM/ZJLNrrMYlCGYil8E6ExCAwZrqa2Z7go91NE56LMhwxMZOVgBBMijkkFUSNvD27dv2vLQjuiKgIy/SyZIxXTYfshH0f/7559rtdnV9fT1rS8gx8k2CDbCcSR1whBRIciLXZnmEJJ1NsJoMbNVISGQgS6efLS9LR+7vJaPt/3lZy7SnXLPUzdEHbb7a5j7YY6C22jqwsTz2WTBdsl/00POTUCGf1cp7H4aqAkxWXzfPXtanT/f15s15Wy+JYLJv1tWzMqGy/8z6qh7TCXZFB6smkEQ/np+fWrKz273W8Tjt+xkBjPY+rcJVm/Wxjse+tttN9f20qbwfjtV1Uyvp2dm2Vbv4fm9iT9aVvmWVLBloPjUTwVEvx2c9Pj7WajW+3O/5eTwO99PDwwh0xK5uXc8vz7XdbGpznJ+yx9cirvh0iWzaxrfIn0x4cwNw2rj1yGeKeak7xpHPAfKXJJD70DlH/V5dXc2S9rQhPhzYEheT+MTa393d1dPTU338+LHN91tkzWq1qsfHx5mvtXawQVW1UxZz/6d9rWxPTPfKAHbHLu1Jvbm5afszxazcb8rPsPeMf5n4Z4KbhCA9TL3Lqq6kBfjOZIPtsiEJUhImmeDw5S7rnoS2eJYdLZl0IyLEDDFJDKO/xmYMxlw1f+t3VjxgWTLK+9GFJXBPIjXbVI1/GIb2Tg7Jnbgsia5+8rXmmhXiHJOEfJnIZ0xP4oSubrfjyaS5LvnMnN/vuX7XHo3sTyWEn3/+ub1Qj7OqqtnbmCk1sLDZbOru7q7evn3beu68WC5Pg1qtVvX09FRd19X9/X0zMkbx5cuXur29baVc2RznwUEt9y4ACJRMj6hWB8aT4M0ccgNVKpAgf3l52di/BBDmxhAp0LJkSbnJKjPI3Cx3fX096/ujTIfDYVY5sXbGImHD/pmLhMNnz87O2hGFQDOl9p0EQubk+wm6ORlrxzHkSSYZABiDMmsyqBxYOvklG1c1JVDJgvkuPc69B+kIJJkY5Jxv7rnJikFWS6xl6hfGmvNLoO+5dJYMrC1nVDX1uGfQxPw6Kez+/r7Jw/dTFzHLAtCSyVKxTABk3OnM3rx5Uy8vL7NWx0w2OSR60vd9ffjwofq+b1VM/cV3d3f1+PjYxpT6BMBn8O26rn766admP/v9vvUyp4NHjmQVSgIs4OeJK8kAkQGCIcmK3W43S9zy5Z/8D1CZldBMGukrn5nPz1Y6+u4+WXnKtXD/b9kpnZv6qbtmE2PA27bx53iNiTyzEuJn9DD1hA5XVT0+PswSFzqfenw47Ot4PNThwHb2tVqtG3tKF7KV8PX1ta6urn5VSbRG3jmx3W4bgZQ2ZI0mEswesU3tdq8zsLPbvc6SnYk9H1/oNx6L21U/fCUd6ljjQbnjZvGqoT5/noMc61NVLYk1NmAhk67c/MqnsnWV5aqq6+vr5lOs19n56H9r6Gu12lQ/9PX580ttv76ALz+fhIo1SkIiq0jWh03mfon0jb7PN9Ifn8nkGPPLl9/c3NTLy0ur9CRgE89VIslGwt9141vQ6UESAZh13zPfZML56N1uV58+fWp+Gyjv+76d3CdmqaRIdMVte1tUE6xltgnzzUmW7PfTO7HYMj/uaHk+2Dq8vr7OWsCT3PG8+/v7+sMf/tDGl+172Xbq/peXl43UzX0wbAgxmEQ0ncmDKeAJ86XnbGOZ0GR1zv1zDEmMGZMkWWJsTJ6fGNbzLi4uWluwRDntNEnlm5ubpp8u90mc5fs+Sw70h86pii3jFzv8/PlzraqrdZD1iWclEsuWLjHL/ZIE4nurataJYi5TlXby85nw+d73XN+daFgUNwYQfvzxx/b/7P29vr5uyQYFIuSqsZ9dXzRgl20vuai5WJwqxWTcHE0CsqqJ/aJgGfBTUBgNiY/5ZKJhDAyekS9ZbI4vAVPVlLz4HHBE6Xa7XStTk0U6OwosUMv+s1q0nHsqZRr3kgGqqpmjIQPrl4mD56WR58ZJiRJnbixV8zd9532BiIuLi/bCQWDUfSk5R+y7LpUCRrTZbGZvLTe2TLwSVPnM+fl5O2klZZqMfyYEVdMLBzlEVwIThp8MBGcoyROUtSH5ngCYzsB92ZzWCEENGKUHdFTg0B9tvByfhNuzMLopu9VqVR8/fmxJIyJBxc9Y2ZNxJIDJ5DVfbuTzQI0154O0OVXVbK8UEM1OMnElA/5DlS5/z0mTux7tLNlnkKQzAlv2Q69WY9sI1tJ8AAntc9aZTmQlKtllF/+RYH0YxqpMJg45F/ebxt5V103MMj0BbpOx47fyBK0MTq4E5XTNs4ehZnqcbNzSR2ayDShJ0smNLWiPXbKSbNrnMNzi1263a9UPCdq4/iMYMFf3ycQ5K4Sj/KYDEwAqJMXLy3Odn79p9sPPqbqyx/RndDjlylfRERWFp6enBhAyge26brav4tgfZwmgdcnuASSYtTsej23TMx+6tMfDYdoozeaMGUDMBCP9QOqHMWgtonf09eHhob15PCvZ7gVYk2e2D/pM2ixbFMPyXjaD02+t0UiYJD7YCjlUVTvFTxxarVZ1e3tbl5eXzbYRNtZAAmQdYSW2h9zM6l6etmdtk5BJHYXLMok7Ho/1pz/9qflscVzsRljSWfb95cuXenp6muESa54kED3KijhbT8KGfojB4pl1ESOShJVQiAMJhjNJWpItXlOQMT+fm3sq6dowDLM9F/QrSU3zE0cySUzCJkk9Nuy7bGdJpiY22azWtf2aJNFdvox8s7tF1Wv5Kgdx4Vt2uZR3EgtJjuWaf8/13YlGZtHZJ55lUpk9J5QZWQJVQa2qGvMvazMpwsHOJOuaiYnPAv6ya05Hi49F6Pu+gRrOo2rqX1ORyHHn+fmr1aq1ErgH2VRVa3uqqsZccCJV0+kuQEJWRJLF5ICzvapqOppX8MsNjU6TMR8OEADBEmXwymoGxSWLDGzklyxAMsWZIZPHkrnJ4JTPTubYxviqeWUjg0yyNCoTmTxVzTeN2e+QJUGyTxCxTKByc1qy4VXV5MgZWVuydz82Yu307OaJO56f+jEMw6z1yD0BSLqYrGBVNVlgbJZsT1W1U1Xcw3cxMBx/2lYy0MMw1MPDQ72+vtb19XU7u51jzONf/bGenCBZc5rmlDbOT3D+QBjnbO4J9JN1T2YQiCNzNpBJegK6XLtMTMmMT8wAul5PPepZAWBHCeTIEwNMv9w314EuAMvLBIEcyEz1hbwSuPr82L5Ubd2raraBOPvfc77uASTk/JdJtqT9eDzUfj8/hnPZarBMiEbiYexFB9LoMJ1YJvtklnEmW2zoJOCVydcwzDces5Pb29vGOicDqSV3JKgmkE8OQLb5ZSWHHma737fYfuTXUv7Glgm0+/Ox5+fns/cvsfMEjVXVqoAIAZ9ZvuNGzOOnkuBJG8/Wo4zDmaAm28sf8FnkuNls2tguLy/bATL7/X62gZsOaeE27/Rl1iQrXlXT+yLY1evra93f3zeih8wfHh7a/yVWfs4ujcO6mvv19XXbg2E8YlauoTayTGTSviRTdAcJp9LCHuwJk2wkWQuDZezz1vdMMDNhTiLUutERpA47yPvmurDtvp9OhJKkiCNwGtxlbTNJAnrFNiQBfJbJOF1hT3T77OyskVMJyruua+8x00mRLb2uJPVS/zO2JTGVSZB7SfhUvDKBF9fYSfr6Vc0PMeDbksRhs9ZGtSTtP7F46oY4LA6Ym+Qsv59V5O+5fldFI0FCspwmaIAWitJhQ6qmsl0GbgaEDSX0zLqWoBN7LOnAPuz3+7q+vm6l8hQMhU9AlBuJBEoLkwxp1VR2Y8SUl4MHkikpkJ4sKfkB//ZraMtKx8DYc2EZtp+nEa1Wq8ZGHw6HdgpXAhnKlxv5JSCMKB2B+yxZQwA2Wc1kq3zXz8mPUZJ3GkAC5gS7yw29ZJrBe3myg+dl0M6An4bGQWUiUTVtvvNHgCOzZCwymJMf4Nt13Yw1YvzpFI3D+Bkxx8V2zJ3Tz7XPwJKJYp6WRg+WeyPck36wLdVCTL35YBitpwrearWabWxOWRlD2kkevahKWlUzW8w1TP1R8rd+6S+GYdosmolKVtiyypRJm7GQU5azyR0JsNmMbYbJlgEJeWrNMgnKxM/vjCuZabZpDlmOT2ALJGPz6EMy8/zIeI85cPV5zzSOBCfWih9M8iHXhb7yn9vttp1ohGnLmJLVWuBpfO5YDZFEXl1dNd0BQOxxsInWZv/00WIQlp7s2CF9qZqAjc8CPnrnN5tNOxko9/aoYicj+PLy3OTO1zsggJ+29g4XMc/Pnz83MJpJWBI/6Xe0Z5L52dlZa6U89n1t1psaapitb754N8m/TAKX90zSJ9tn8oSrBGl5KhDgSN88L/co0ONhGNrLayV6OR76kq1PkgSxg52Ss+8kUyzuGIfvvry8zFquc+8Pf+PvjNGpb0k2SCBsjldJyAqMRIG9IV4lKjBQErdJBtL5ZP611GYFSUwXU9wzKzP0is8UCySl9/f3reJBFlndyLimc0N1JlvjEAkw4f39fYtNfIn1YZfGbj2TWSd745HoZkXv+fm5YU3xkT/i59hJJv/0hZ7n/JCqWTHJik+ST3xoHgrD/uw9sR5Z0R6qZvHw9fW1np6eZgeYVM1Pd5M0sr/8XY4L/uGLxQ36lNjM91Muv3V9d6JhISx4PiRB8PPzc93e3s4M1hsmLy8v6+7ubpbtmYx7UQzBLIMnp87BAB7X19dtPwGWgEPLU3EIlxO2sXy9XreTHDjFZWmwalSy6+vrOhwOLSnIJMg9ctP8EkTLzCksxUrgkQ4rZQ5w+JyxSfrS6LJVLZMEz12CzDz5igz8Ltfa7ykmw7JeCfjNKRO8qumULXLhmLLyk78H+NNxZ7LCKXnut3Qqs/p07gBx9hVnBSCTTmDbvTl5xpzOxbPoOpuhh5noJGtpTMsEMpOqnJv1T5bfdxKschhL5tQzzM13XVdXV+13T09PdXt7O0tSOGrOG1CwHuQElAHvdAZYFUh9FnhjR9nDyjaM8+bmpl5fX9vbirOMDyymHPy9TMqy3K8qQC844WTsfT7fS8G2PIdf8AxykXgKMNnCkbaWCXnVVCUlk9RhdpHsmPagbMmyDnTK2Oh9Jslp/+mXc335i5QvImhsEzrWhw8vrRpuPsa5BCZT1XQCg30/ntpDP7Xz5HoD5cAaAOtZgme2GJrnKNNJNvb6ZUI1DMM32numNril7wT0yDxJK3uh+JYkZ/Lko2wFTfCQP7c+mchiTPm21XaKI0vCh39Nv3t3d9fAYOqFZIrd8wVpH9lGcnNzM9tvgp22xmxDUp66TC5JqonV9DtjrOR+vR7bPxEs5JrkBHkDrlmtS5tK3JDdF8mw05HlH7ZHLmJVVgvOz8+b/5Akk+HxeGxtdsfjsd69e9c+9/nz51n1QpUjiY0lWLbmTs5SCYGx7u/v214z2CxJRrF8SeplMs3OyJHfyQqReZFdJql0NnGXdeA3Hx8fWxUpTyrNKqu1TxshU3aUyTrdE4PS72T8TJIl55+dIEuiKCtFxp1knESOThoDotbnjkNf+93k83KfofHwU/wamzOujN1iiPlIQtO/+5178LNZKPie67sTjWRVshydGe3xOPaGL98bkacoZKDjoASMq6urtgjuzdlVjT279/f3rWJiPFXTkaHJWhP6VB6fynlKsgS93+/bC8AyqBrbxcVFe8+GAOV3QMZSGc0zWxcEcRWQDP6ppBY9M1Iy5rgSMJCVErMkLTNRBpVyMyb3lFUnQ8FZZ+uR9aXMjChBcgKhJeuR43LPZCHIg34tWajsQU9nr+o1YwKiIpTJC53hzBOALkEpOQF6nIB7mSNGtqpmxmwuDJbOcGY53vxuJpX+/fz83AJWOjKyFjjdV2KbpVJjNy7PzPaCTJIE776fXnrpMxm8MIoCsgqez05s70tL8pX/HRBgvwdn6d45bs8XvLMVDNhKoGxcy4qA+S0ZP3qaDlyQzX1d7J++klkmz+aTYCyDKV/DvsmuamqRoev8WgJXv0vfMLH001tu2cco18n2JQZpZ3kfbH2SIwkcBPUEb6+vr+3UPYAz146vSUKm7/u274etr9e/fhmaGKHKYJxZrbI26/W67alzEpFAm58fe923v5J1+ky6Q1bn5+f16dN9G0cCldGODrN9EABdJq+ZfGbSoAJyOIwvbBMHqmp2ek7GDMBLzM22uWHVNT9J3+g2kHpxcdGOdN7v9+19G0myODb28+fPLYlIkMeGAP4E8f5ms1n9OxwOrXVoqdN8gMSEHmSszUoXn872rffSvrLinn4kkxd6DdDyj97FlTEtY3fK2vr5HZt3f/rluSrF1tBcbCzXl0+H2bDqheqWcZkTAErvr6+vm1907P/hMD+l6/Lysj0XkE6yB6lJ1p6b8Z7PNzc6TGZswf9VJn2f3LSe5iEc/tze3rbxpf/NxM9zkliiU9bHvKqm6lkSebl+2VWQbVhkbF3pI3t2H/fOJKPvp5O/8nS6ruvqsJsqNUmsJulG7uZO310TQTIlCvxnkiI+m90wYmR2JGVHyz+6ftd7NCwUwWDNq6plqFglAAMz5PcmkiUrQVHvOCdCiaqmXj+C1ZeHscwNWj/++GMrq/d93zbNWQhOBuMgmC8DQCYcHB5hJ1Pi39OCDjUejTgBEQD0/PysKnrtshrkORwYh7vb7RrzA1Av274AaAyK9cp+eE4NQM1NyEqiQEyWmClivghJ4MkgzumRSdUI/Lx5dWIqp/kn25TfyRJrGn6y8ow4mUtBOoMo2XLM1rcZwWY6MtAaZ9CnM1U1k7nnJ9Ob8qbbgs6yEmAcWaJMBo0uAmP+1lqRTH0GPHNK1iWTPoEpT03JKkY66aqa6aLPYTmyZSWTuO12Ww8PDzPW1NGQT09PdXd3N2OT7+7u6vr6uj5+/NjYXifKbbfb1ppkz1YyVFXVkpZcG1VUPknizReQSdqvAJ+VhwzYEiNrQafpDjbcWmdryrJ6QY6ZNEhGBaVM3DMpciZ9tkACWplYmsft7W1jjkf5Va1WXe12h1qvx2Nmh6GvzWaqxqko4APowfn52VdgZvPkuE/B0bSHA+Z+qMvLERB9+fJa4wlNx3p9tXdgVcdj3wimrqvqutXXxN+JRtNbz8WViSxZVdWmhsHeqlGfP336VLe3t22NMsFjG+zQeiSxgNzy9wjUtm0T7H5vD0hfVciLQ63X53V+flafP38pez7YB9ujt4I033J3d9f0pe/72ZHxdBs5kj6LLmD5l8SBGHfY7WuzGvu8t9tt9eu+np4eq6uaVe/YyMXFRZMhOdrbSIfyhZld1802udNta/XmzZu21wZxx/d33dg+kxVRpJZYw0atk43ZQCKwmzLOhFwsIO8kYvhcvibHLllP4lCcZXdpy3QtW8eyhfZbJJbfb7fbevv2bavM8gfGaP6Xl5f19PTUWsSzupUgEB6hR/BDVtPFdYlcxj5xPCsZGRPyBLDECTpFMvHlS8UX2CN9FvLJM/LZmeBnZULCyp9nIpHJtBhET30mCUDrjJzICgPskCR7xptMAOge+eW+nqqq9Wpdw6qvbqgajuNLNlc1+tXDbl/dULVdb+rq4rI2X+/T76eX0NILf9N9sjG+JNj4P/HDXH0u2yUTK/IpSeQilpb7h//R1Q1pKf/g+n/+z/+3Ga2yj3dgcGxAp4kRBFC8ZFS7rmtKyTAtFuWkfAzFsxhgsslZdXFiEiYpjbzruraZCoOZ48pSGgOyccfP0llkW8fEek3MfGbKfT+eVGLvBIVhtMmsUiC9nZzKxPZNCpXz4LwAc46dogPPVRN4ur29bZk3BePIn56eGqO+TMiybzPLiuksKer5+fgyKvLkqDm7TPqyzzqBHDkzfGuWDj1ZQb/3c8aVACPBYzLOdMD3k4XLxIRDMz4G6FSMrAIK5JiZPCko1y9ZIrqeOmp96SO5m7txsaVsZ8IWuR/mxNgA/X/5l39pjm3JvuVzrRMd4Vyx2rvdrp3GYu3YUOoysO1ZEtnb29t2ik4y6VqC+r5vB0Hc3d3NKggZ0J1tz4/wYcCStciqiL8dkZnBOv9m33nSjntbM+uLjWSfmXgvg4B1ogv+OIKY3DIBTGYd8LBGAmiSE/QkE8q0GYEoAVruZSBnwG2/38+OoX15+dz2+rifBJufS/IHwzomD2dtzID22L66b89hd8b3/DwdSpL6uGSb7X+yrp8/v8wqp1l9WK0mIin9ytnZ1HKoIoCNxNomGZIERzLuQLu5JLDynSSIJCDkgpzJdp0EXsk0A0FVVf0w1P44bgpm96op6buzYpota8niJqM+vTtlYsCzslA1Jjh52lwe8ZuthORhPknS5DjED7KyvmzUmr1586YdYJEx3vzcbxkL6QUSzM8lhskI+11WV40rK+7pH96+fdtiZMazp6endpyqmPXly5dG3rJF65RHh1sDe4OsD38tlgDa1oI/yHdesOG0dWvNBsTu3BeYMoEN7a1l45kMWVdxgezFMc8G5DNe871pN3zrksDWfkaeS/+eODVJm8Rzqr1ZCebDMhnKBPVss6nd63QCmbF5dmIXGDrjuvZPvjCJvhyrOJIYKH1QxhgJo/sn8U3njsfpxZyZ4Pyv//N/qd+6vruiIcsDAixs9lwCAQDHajUegZm5TLZaZSadAHoJZhMwWGRvw85gmQJ1n6qpjy7LQhKQdITpGAiWI6+qWXZNEfSp+v6UXc6PXavq6uzMC1SOLbnIDXmMLsu3DBYAz7esC8zWIZmFZKaMlbIzdkG3qur+/n6Wofr7eJyOSvVMMiRjQNnnGX4GpMy+raOxAH739/ftnvkMVbFsXeC0AJJ0NNZnWf0hnwwcS6CWTNAymaiaTljJ0vB6vW5Bc7/ft9NI9LhmxYQM6ax5ao8DANLZZxK6ZM99PzddWqthGPcUZUUp9T9ZO+X9qqqHh4e6vb1tn8ukO5+biS75PD09zXTg3bt39fHjx/aOjD/96U+tRTETLusmeGn7SPZGa17V9BIt+iFQ/vLLLw2cZKJlA6+9HFdXVy1p1erBoSpdp7zTt/F39ERwZHdVNQMG1hUIrJpK7SqzAtOyVG0NluAfu2VO7J3OS27T3yYr5fmZYPB96UOrqoHPrNoC73n6Cl+WVR7A9PX1tbXeYUbTDwAZKjnX19etH13rHH9FFyQXkvSscFoL/hQIBvR8ng0YJ18jgTLf19fJJydQS1ae/SRJxEZU3FUk3BuQZGfac8k2yTBJt7XMam36EL5ls9nUx48f6+bmpgHhBCB09exsOkiFbFPvsqc7fTuQmXtB7NUSX5O8Wa1W7UWswG+y65kwJRGhpTIrD9bVmNm7JIm/siZ8ReobmWf1d7fbNVIvEyVzyE3ECaCTfHS/JJcyxtDxTG7Yk/iQhEzOx9qyYetXNe1H5c8lqqphdJUc6GnuA+HXjM34UtdV4JPYSVLQ9wFwskjwLw7xAQnuyRLWtL7p+1KX+eaR1Hhp5JmENbtPsguAb07yLolyviFBPH1ADGR1I3VKssXXJVh/PfZVoXeJ+7IdNkkgnyPP1WrVqoLGBitqgcvuET7bONg3/5aJUJKj7J98Ex9mvPit67sTDad7CNzLTVypnASdCsqJmxzF893cjCy7FAyBrMzWBOkMfJwSYS9LZ4KBKgtFSieUgSdbKjKIUwoKQDkt4Ai6V19ZVmcwd197gFd1OHxuyuG56fwyAGeLTAbwZKQBK/NLMOE+1sDzsjyqUpJAiNInOOFE8zn57Axyfq+NBiNF6dMxJ2inO5JVa+87WVEjp6VxWjdBzliSOZY400s/z9/RTePOZINRkm06YIcC5J8MvJmwcvzua4zpUFK3soq01Bd/kg3JjWBpJ9g+6/vw8FCXl5ctCLJvICM3sScQZheARwIwtnBzc9PGs91uZ5t6BdhMjgBE32OvVdMR2oCKcSRbhd1cr9f16dOnVr3K1swssVdV3d3dtQpU3me9Hl+U9v79+7ZGCWDJml3m+3MkS8fjuPHTRsunp6dWgWGTWTHAtiWzS3Zd180YZP4rq0xaMLIdQZCVrKdO8WNLokaiAuymbfznf/5n/dd//VetVqv613/917q7u6v1et32WHgnzijnbra/jT55lue/vLy0FhrkAICcVcwc75KVZPv2djw9Pc3Y1/QTAjwmfGwh62by8d2qX78pOP1Asu7JgmcwF7ATyA/D0F7wlrpk3iqk2+340kFg8vLysrUqL8dmjnnAgj/50tjj8Vjbs7N6/ZoEAUYqtznOTOjIjW8GJPmn7EKgm9aSPBL0IFXYVxIP1jXBIUBFTuLO4+Njq8TQ4evr67Ym+/1+tnk9wTRg9fHjx1a9zCN9vXgzk92u62bVBrGQ7SMskpjhU+GPJBrINt+TUDUB4KziGAO5Z2U2ATY/YTy5Zj6TsYAfEotgtuPx2Nrz6LqYlmw7v6HLQbUuq0bWOG2F38ok2dyTOM2KS1W1OWW8ybmLr+w0Kw2ekdgiSe+Mo74nicsT4ZKEMxZ+7lsvTx6q6my7/ZV/8Bn3SF+UlRx+wRizBTgxQfoUMnZ/yVR2EiTpagzwfhIk7pmJ429d39069X/9H/93AxiUK4GG0xOGYWgl5Mz+vWCGQVAMvxe8M+PODbsElJluOjNg9vHxsf2fgqgQ5JnQnPHbt29bewdwlwHRgmBRjCEBrKCEIRsXtGug0AKNgOmsnYHsT1ZkGCNFc/9kwquqfdc+FGNkbOlk/Dzfnk7pOfJMCv0MoE+wsywpCt5ABflQaglD1VQ6TwaRDnwLJGfFapmFkxunbY7WMYMcY82NcuSEeaEnyX5UTUePAjXp6OjccrwJtiWqSt25kS0vASj3KHEmdFnS6RlZaaC3HOiS/cnkf5mAVo2VCBUQ90lQUjWViq0Xe+C4JUCZ5D0/P9fV1VV766oxJTuapWF/qn5d2k2bMx4BgD4snX7VWKHJKmu2ntDVZMME/0wu6HLfzzfDJ9Nl8ywwIjnKyqm5JrOudz3bCTl8vhJbLdFOYGlOZJAVuXz/A53wu2z7WrYwsWPzz7aN3P9mHKoVj4+P9fe//71+/vnn+h//43+0l5UNw7w6tjxy05gm/zmBDDoHKI82NJEPAASdGF9IOCdD2ETai2cKsMfjYebrMgnqOu1Vn9s6VVWdn5/NyJhly4rPZZtjgnO6S+7skZzdG8to/fMITgl7MtgpMzpov1KCkK7r6jBML4zN6hIwmIQaXREXVqtVe6GeSq4rqwT8bOr42dlZ2/eSTHeyxOZubhINMk6S4fHxsREkSU4C0eSbJ/4gpsx5t9vNEgxxwVrk3DK5yM4Oa3Z1dTWrjCBBzQ0RsFqt2ntZ8lhtSRs/wFbSZ+W6mItEhK37TCaDCWaX4JLPyKN2HQDB39E3++esNUDP/2ULO7umm0k6JpEnPqW9pE/KNvtMHPjNrGbn2lpv5CJZZcVNDCCnxBDr9bolXmRAvnSGT6Gr5mv9hmGobhhq6KeTp2CCXNMkODPO5piNJdvWYJOshFibxKmZdPhe+vskKsktkz461vd9/c///X+r37q+u6LBuWHogDasFwNJNtPJDFnmq6rGQhFKbvBTKgeMKCVQjY3E9AhSwHIy7glCzEG2bWGBCgJfvjCOMaVCLxWYg0pje37+XPvdvg7HQ9VQ1Q99ddXVsT/U9fXVrxQrEyiKn0kPBchWo1QI80uGW1Ll80Ag+QCHmRQy4mRiOArPY+BpCC7KOA/g0xG2jFHglDWbJ7m8efOmGb31Z/yZ6GRbFTYuf+bCquU+gATUWuASNABqWXY1ZmMQwOhKBi9jzPJ+M7zNdCQicOus8mTIrEHVdCyw72E2zCPl6LlsMTexeXbeC6uKeXx6eqrD4VA3Nzd1OExHbm42mwY4PTerChiQbMtI0JSsCbk+Pj7W+fl5e9eC76Z+S37pHt3OIOM7EjKsuPFYQz/z/DwaWzuAVhL34BM4WM/y86oxYDr9JMe1rIq6D/v3eXZorVUPUqcSfCZIzbe5Y71S55bPzaTTPDJZFaxUk4zfvgjj/OWXX2bf77qu/vznP9fl5WW9f//+6xpOZXtAL+NJJq983TCMLUXGaLzixmhfQwM1/P4wVPX9sfka/jJBTspv8kOr6rr5Rsuq+krKTMfUelbaNp+f7ODyPvnMBD3GybcD+6qL1h9wBE4AuHxjdiabxpeJPVY+mejz8/N6eZ4IOD5ClUc8UIHzewkAvwkTILKQEhcXF/X09DTzrcfjdGR56pzxioOSejqIuNBqRudUIvny/H5VtZfSkTMfpzXPxbZVisQ3bVtp09aDjZBxzsOeVRioqhpgPx6nk4iMO/0cW0oWXwU32zEzOc34k3aT/tQ88sV5fC5C2O/YJj+cTDY9FzvpOxv3TAnpdAjFr1/cKcFJEm2ZeLMtc4D3MlGEx5IM9jN6lMmmGJb6LL57Tsbxy8vLdkw7WbNH38+Eis+i0y1B6la1WhBd6a+XRCJZJjkAL5tDivt0igAAK79JREFU3ov+ezGhMWWlPqu7xk8f6EISJYlPMxZm8v2Pru9ONDBaqfTLMlOWr2RcS+UiAAPNxWe8h8O0KTDLXfoBZc0CN6Og9NkuQiExYdmOVTXvUwO4CLVq2gvCeO7v79vzHA9n7IfDoT59+lQfP36qYeiqvr5s6ng81Gazraurq7q5vqmhpnJXtpxZeAFHQEpQR/k5oTTOJUhI8J4Jie/n2uQaZtARlCgXR5dOJ5WeHJdsU1Z7cp2z5YhOABnGBiTmuiRDDKglsDIP43GRKUOjTxxFrgcdSuYnS8vknPPPo52XCU0eipCgI0ud7969a7rAuWalyhr5zrIPeuls/TuZKPapDUni73MvLy/tlCetT1UjQXB1ddXu6Tz3d+/etefRS59Ztl9Yo7T5m5ubmdOjVxmIMjFIGdAHICuZ3ZeXlxmgBgSSfer7vlVbJVVY63yG9gM6DaTkPgntQe5tHSURmSxLkruu+1WPtNYQ/oGNSzSqpv0QeboVHWA7kselHpKfzfQ2ldJftpEHFWTlhs0I8n/84x/r7Oys7e05HA71448/tsT4/PxNYz0zobCWSULliSb8Cf3J9rhxvNOeqayWvb7Og2i2LAI0QLPnjQna1E6XAGG/3zX5L2Nh6msyrQmA/F+sxJwC4uzSn6y8JGBNUEAHHVIi9qqMOSzg8fGx9vt9vX37thF6CIrz8/Pa7XfNDt3butO9JK74ZElKtsVkuwvgrx0u/WwSLmJakm5YabqR5GHqMUDkj70VxgA/iDfitmew/2TqMwnn1/PAGfP//PlzPT8/N0ziHn5vbnyBqodExpGxZJuJGF0251yvJIz4V8mz8bunBJE+8Rvk/OnTp2ZTVTVLQtlcEkbZiresgGViAKxaR/GbbMhzGaf4Kf5SEkmWfLVnvX//vrX0WzN2eXZ2VvvDoYZ+TtQmGM/10g4lVkw+YUoe+fNMANLvp0/jY/gx2HSMVV/q7eXbpk98EX2jM8ad5Cg/3ce80vdkJ4/fV00HBiUuEpszeckEDEGdPpMd+Qyf+FvX7zreFvvHcXVd1zaaYtoEKq1KDEOwXB6DmVklQQlmlCtbSr58+dLADsfMECUlyTJvNptWtfD8ZFWvrq5mTJr/25CWAl6vx5cFHY9jvyLje3x8bGD97u7uaxvBeOThaCTrryzbyLat12cNUGDNjdvFgQBlwIA5M74s0WeAExjTiCmn+VPAVERsFDDC+PL+ycA4EjcThQyKmQCkkWIDqqq16CwDdFZvBBiGxMC0qwBUnHP2z2fC4RlkkYmCRCOrL0sm2F4E8qd/7EJVJcEhmSwDEZ0hj2Rokj2VEGSATvBIdxL80ZVc3wk47VuvNwCcAGC327UXXgnMXdfVu3fvZgB9tZraK9iusS3XLAGzi30rTwvExrlarVrrAZ0yPsGGf9lut61l03cF4mVFgt2lo+YDsrXNelozLXvJZkoOUt+TPT87G4/YZXfGxC+5Hx9mPIJhJm/8MHbasaSqLypCd3d3sxNaXLmeS9+RYA4ozMqN7yQx0XVd/fGPf2xgPWWUyfc4j/E43XH+5wHAvCl6Xefno6/DpO/3hzo7U4Hu6/VV1fq8qrrabjf18PDYdGm93sx8xGq1akmcQzSyspntApnYjycDepHkrrU8OhHI/X1+s5kq4P6Mc5uSpQSA3wLXEnd+jA9i/5kEZAJj7di7yiNAeXd311jYw2HcewV8d11X27Nt9eEfrDebSVJLpcX/Hx8fa7PZtL0R/OqHDx8a83k4HJr/yviW8YPOp19j2+RDtyT8iMz062SSAJ8tpg9EDhojG7cO1sjz2fHV1dXsVMQcH/33fGNjS5mwqSh4H4m5i/NwR9r7spouOZl0fzpp0/PzCNm0Tf6Oj+aXM1bQGRUiJMTz83N7ThLI9uWIfRIYsZh88jt8ufZ1CZg1yz0TCE5vESdT7Wn0axU2UVXVH4/15fW1LuJQlmw/Y8MS/hzjkvDKamTGtrdv37b2XLGFj07CscX68zfNLyzjdMYia4kYdQ8+OqtHxuN1D5I0dgHnwAsSuSQCMwmDddgE/U0yJbH7b12/K9FYClmwqqp2TrYB+BkHBZwSbDJtHG6yT8k0Ml4Gp1z1/PzclI1SJEDgLPwhWPeSKAjwHEe2aCj5maexAvzJ5KaBjoFkO3OuIzt90ebqvoySsWsr4HyAilQCcqIQwFr2dgPa/vg8p5R9nMlMUGblXXJMZpwcrGeyExTd+e5VU1UhGd9UYBuzjT83WHKy+V0BkM5lidDaW2PJqiRjqU/DMDSmJOUkycrgk/sQPN8cspSZ1QptftiCBOQZCOkYB5JlW/JMNiETcgENgEqWzfeqqtmgoJPrla0R5JLJP/23DgBT2rG1sV7GVDU/MckcyBMz6jL2BDrs7N27d803ZAKB9Mg1Y9dka30BBfJmf+Y6DEM7qYqO0yV6kkCHn+q67lfJTiYlVdPxmEvgKZgKpJko03u+LG3QKV5JDNAbMsCU5fjZgvaXTChcqWdki62UxAEX79+/b5ULx5bms8gr2UtAItcoNwm/ffu2sZqXl5f1+Pj4VacO9eVLte9XjacleWEpoM2nZXDNdkP/n0iE+QEYgJakzthfXl7aCUrb7ZhoPj09tVjEdrTDGc/9/f2MYDBGdsvf5RHU2pboAEYd0Mzk7vr6uvm2l5fxbex3d3dVNVXskrAYfda0UT2rbnlSljUBgN68eVMXFxft6HXghw1Z5zz6Mw9vIXsgi/7ZmJz2I26nTSd7nRgj1xTRqW0m24X4FXqsEsSfek4SJoB74hcYgK9Oks6cU9ZiK33zb7Z4c3PTZGCdPduJY3RjeWJlgr5Pnz7N4hP98Xn3eX5+bof7kKWDCKrGQzLE6awA5r+TcEnSAjGM8f9W5YXes3F+YL2et4OS6bJTQfJtvbRO+/3wVTaH43z/x7KKkDbE/2eyCmBPNjPt/TE32CpbPd0PgVX1dQP7VzmTX7aQZRLD74lL9Gy73TbiBDnMF2dVNP2tWJ6YMLEku1+uqXVjp6nD//REY9lnp+8yN2clELUQAoF+22z1+etf/9oMZrfbtXJvLgjAeXY2nqdu4xkFS1CdQrKHROUkwTYH9fnz5+YYEnCn8QpSFomBUs6q0bnobUxDS6DAeBIoZ2Y9DMOMKU9nx7jSOaZTTebphx9+qLOzs7q/v2+OtmraoJQgOnvpzdVnjDG/67lZTq2aHyOciWIC4tVq1V7ClGxCVrjye9oFMDfH47GBUgZkzatqZqjZJpO/59DTyMggWeZvsWHWUsDN8i/HkgkkuVnXZDuTdQXgVK6ATHbk5KVsX8sNnZIKFT9OZrsdT3dKMuBwGNsWBW17YMhdkuv41zwxLJMDcs4Ay5lm6ZWcABSBnJNnz3kEsKTIuPkQ8uz7fnaSkM9k5SFbQbL3OW3FM7BldPjl5eVX/gXzykf5WVYEjC8ZzKxSGVeyickM8UnJEqW9WvtMkpEiKiMAdFU1OVt7fjOrOe5J7+lvtpciGzL5SbbaXLQfZH95ygQoybGn7yMLNp6bhodhaBVkAPpwmBJD9vLw8NDWrWrqkU7bzWD8+Pg4e9t9Bk3xpmp+gEmuA7tmD/yU1g+fA2yylUFSqULS932rCkiuyNW+LYlPtjbRKc/TUcBmxCl6C/TR0/M359V9/Z5LRWm9XtfT01NLkpakkqSIfho3P0Tv/e1KfeVrM5GSgOaJQnQvSR5jpDv813q9bvs5JSk+K6FIAigBF19P91Lf7Zmh89fX17ON5b6T+4lyjxTdoQv0lzzsLfR8YJu/yipMtu8Z436/b1WHpQz8AUz7vq+bm5t6//59q6rALuZKLkggeMVx91VTlRThl7aRFZSqifigN3Re/BUvJKzIHGtKzzOpyKreer2u41dbJnck7G63qy7ieIJphHjVhBPMVYxeYo30O/yTVir2wNcmDjSPQ7TusQ+J/dJmkjzOWOX/fk+m5M7m/WFffJoYnvHHPZftu3xnkq7pD3/r+u5EI1t9+n4s0aTgCP/p6an929GSFxcXs82NCcYeHx/by7goDCWRaBCSf1NWDjpZw2TJBWIMDIZH8MueNXNIJ0bwvmNRjS0X1iJiJimRxXGlklCAh4eHVtaWCKUjYVz5EiwOz/OSLUlm15wEc+DAlQrVjCCAGPkK8ilr9/XcVNwEqeYryJmD+5NXbpTL0hzHg0EgW89LhsE6+TeHYs4CJsciMaJTHHsy4BwScJBA05obYzJdggLHZQ72CEjOtV9Zg0xAAN8EZFpt7JkwByXkbF1JwGatvRAKeCRPgXGz2dRf//rX+umnn2bBybPT8XHiCbJz/bIsT2aZNDkJp+/79m6LTHbZPX0kV07O32SKWQZk6HO2PNFJclFNY3+ZnCXAXq/XbV9WkhH0NBNF+pYVFjqQ7C1mNgOX7yBw0obYXzKiQIkxCvL0qaoa022MSZJkIrhMcjIxSgIkCRiyzGOX3ReQYifZ+mj9lqxuMqNJrli7EfBOOpZBmN+hJ9m6gCAil76fXmCYDCR74A/MTxUtE8n9ft/Y2KpqukxOh8NhlgBlH7yxJElgXcyrqtqmTskSooIf2G63DSylXt7c3NTLy0s9PDw0nfn48WOrMkswN2fTcaCeKwbf3d3NYpbvATZ8mHXMdc8KB/Cjkig2ZeUrwZa9Y9Y43+WStptkW77Uk62IWdaCTldVa4ljbwnm6ZwYaa3NJcGzqgEfSP/MBdnnflqPjG273dbd3d3Mv5FzVc1spqraUeTmku1NXqonDiznJgk3dn98Pm0xWfCLi4u2VukDgP0ka5MYMvc8uATuMkdJZRJyCDPEk3F5W712+qyqGAMck/aV9/fyWD9PsJzJDL3JjoqcH1vxmUyk0s+kPPb7fe2Or7XdbGaJEj3ImOU75CO2ps9L/5Z2RPb5f/fKsVhrc01Sjh/xs+U607nvuX7XZvAEzUA+p2uxDErZW6bN6Bh/1fSG3Kqq29vbWaCz2BYCsMLuUJxs+xAsCc5iKwumQwBO9NEt21sck7dkTTm1qvnL25wskVWLzGQlEmlEwIKNesYPYDj5J5OaPOUge4WNz31SBoI9WZsD5fNZIJpDT8DgZwlkkt1mpMADQ04WlxExygw61id1jO64t+CXjE+yDRxuJozpFIBrwUGyyRkKHhx+sr6MOZkogZPs0pAzCVy2xnluBkrPyt5xDtYzfCaB88ePH9uYf/nll/rpp5+qatqLkG1a1i7ZEnubyObLly+t754eY9DoWfYuV00BMeee/bYZ5LF3SR5gHLMNK9nSbIXDbnGQdEt1DBjO+dFbR+zm23HZnHJ7Vl2yZcy4MihYQzLITZy53wJATFvC1kkyrTvAi2nzDMlW+gCJpLlmwMwAkq0MSSJkSVxlOokFCXzKNvWKTPIlc9kSRi8kOQIh/fQ3maQd8ZlZPU37lBSmniR5A1TxH9mikGtYVbOTZOiiePX09NTu9cMPP5TN88ZhHhjkZHUBOHqWbTXZ9mPc4l4ehEEnrUP6V4lbsun8C8DqNDX6AuwdDodWQcl2yvSvmejZC5fEWybBGdONIxN2OpQb+hM/JHlovZLIvLm5acx7gj52s9lsWr+5fyMZk8k1P2NUHbVOeYpSVmaQFGSfxIs18VLSruuabbMpuqxDI8nHJBARTn3f19/+9rfWJqodHCb485//XB8+fGjElZgmRqROJUGQ/tLvjCkrbmyY7X2r+4IfyJMZ6Ys5mo9n060EuZ5lvOQuXljf3HdJD7Ny25Kg1bxDhJ8hg3wNg+8lqZM6g9xOzMYO0/azIpcJbiZV5P2629eqm97nkwB+iUHYOfydxFbik1wzOJRfIPfUOc/K43ozaU8/kEmN33+rSvKPru9ONDCrOXnKtV6vG1jO1qi+79tufgEU2Pc9gG+1WrVzsH02y+1VowO5vr5uxmtRMgMUWCQOyZ5SkMw29QHK/jMQV9WslSMBPSWxiQnQSOYqy1wJxjLYJhueLULJoFO8VEb3/fLlS2s5E2DIwWf0YmKtGa3Aw4HmqRIUjJEzmiWLbM4Z7DOZyg2v32JHycG9lxUPgcafBJ6Ck0ugyXYsDinLz373/5fJZ9C2DlnSXBodmS1bqPzhILMC5HtLJtvc05GmzMkLM/WHP/yhnp+f68uXL/Xjjz/O3rqdc8SWeC5wq30wgzR9SoY6A5f1Sma6qlp7ZDI8Kauu61pFQFA6HMY3wktsJBJpc3pZbXQFLuhLBnMEAVDDTgWvrEawT0yeNSevJBKscSbjQFHagJ789E/8ZyZOyIlMQAFegYueJCDmdz0/A6h7sbEkA6xxBilBFQgiB1eC9mTr2MGShZMoYMf5U76YzpBLMrvZhslHsxugOKs3w1DNPvgMczgep71lKStVeZ8FhIyZDmY7Dd98f3//q5aJyS6nag5bSP1OFtD888AFLRfZCqUyncQPP4Z9Fnv4O8lvssHDMLRNzHRDcr3f7+vy7duqL59nsgfQ0g8maeI+yIQE4OxRO022eokhFxcXrUJBxgmK/TxbYCXbXvZZNTH9Ei7VHTaeiRd9FEPENqSN9XDPm5ubljgsq27LPS7WV/Wo7/t2MIPTxbQ0sznJDdIJQ+99GikTfuLy8rKur6+bXd/d3c1egpz6WjUlqBkLHFwiru33++av+GjzMV9knLWhXxmHl4mi/+crCawrvZQc8Q3GZ935DsRmkkvLzfgNcw5DDYf5i5b5yYxLVdO7UOhO+ib6l99N4lscpF/kl1WxJRFrXS4uLqo/Tu3MbD5tnU8TC+hakl/uDyvkM4yZ7WSiAdNZ29VqNcOh1i8JQvfIeJ+x9Leu7040klXHunOInBMHnOyAgSpXYdZzQTAvXTdulnOyxadPn1rGTqkwTAm8OcBlKS+dcwaBqgmMLnvPMiHIuWR1ANi4v7+fMTuYjHS6gmH2ryfYBsQ4S+VfymJO2+22Hh4eZr10VTXrG3Uqym63az2TyQrmvBkgwzNmypPlt1Roc6Lo5scQOKhsz0gjYMx+VlWzqpL1ygTCWHMTZ7LwKh8M+g9/+ENj8jwLW59ldWwV3cjAyskAIFVTVSCdSDpZz/F77yipqsYYmz9QnJvMlNkFgQS+nm2OnotxwWznWmVivd/v6+Hhoc032xAF53Tsj4+PTb8kzgAZHfIMtpyJXAbKBCj0INtEHImaTk3Asv7AET1LRh5gTPmTc+qiimTqO9Ys155OZtvmMhml60Asf5TkBjCbBE22xmSiWTW1EtG7ZKAzCEp8BMilfQmgmbxm26IxWjMgNJM67UB6pPn2ZEKXgdta8DPZOiOJShaTD2GLyarmHJOhZQP7/fx9QyPg7WfyUn3j3zMREWTZN78txogfCb6zyuU5T0+P7fep/103nvjEFjKRWPp3MciVm2dHOaxqGOYvHlRlkTTmv61JypbPpDPAcA3TgQvpi6yXdb24uKga5i0wSIqMy+njVqtVS/wx8V03tTPTowQwfIy5+6xuAOx51fTeiARB7Jd+iqupX1l1+vDhQ6u42WCfpCOgKZHc78fT3Y7H46zl+f7+vt68edPeRO6kLSdyJfGQFfQk3TyX3nq+JJ4+kj/byngMl5EJ2+FzszKTsTYrHcv48S1/6v/po9h/3i/3Mibxl8QqG1lWBYzneDw2wlqcz6o62axWq6ogv9jEfr+voe9rG5WSxIeZfNOLJJfYZraiJemIQCFn8WYYhlYF9Jn9fl9nm2n9l2A+cQgChh1UTbhUDLHGZJeVZnJc6k8SnT4n0UvfYa3Nk1zdNxOi37p+16lTyQY8PT0155nsOGacI2HUybT4vOqGSStJA7ecsEWrmlobGBfjzcVNA3HCSwYA9+ZYBR79uNkCAaSrvDAijkEA+/z5czv6NpkB9zgcDu2ceQzo1dVVWywONhcRCODIBUOyo6DZbnB7eztjxhioz7hnspUpF8aBNTAeCsrpZLUpkwJrwbEBhZgMv+MwE1BhQJJ59EwBPpMm6+z0F4khloAj81nsybIdQzBenlq02UzHNScjUjWBhGSIs9XE/ZdvAievb51YlImZe5GDtU4GOYP0ZrOpn3/+ua6vr1sgs5500NHNkiABjd47IYSuVVVjW8k6AXImDsMwNFBB3xNsCyxZqiXjN2/e1IcPH5o8D4fD7KQsICkT1QyiCfxUFICp5eeS2eFbciO5+QEcGDY+j0NWmeB32IcXlPEPfs6vsFcAmJ1mJcDzMxmnI+n081jOZO/ZFt/B/ugRXUqyQa+6ewswSQwl+EqfnOBTIgDE0I8kWKwFUEq+SbzQNeufgQ+TejiMJz6NYGJdVauqGqpqfjwx2WiNTZ1UbeHvkBOexQYy0TP3cf23NQx9vX179dWvjMfuHo/5/qih1utj9f1Qh8O0H+N47Gu/n0Dcej2esX9xcVnjUcBDrdebGZDg27MtFcBLP5nxkz9M8oy9W58Eupj91y+vddzva911Vce+sfMfPv9StepqE4xvtg5bd/tVtAzlQRt8pHGT6fF4bO9GyITb8aH0aL/f19XVVdPL3W7X2P7EF1VVf/nLX1qyKw64v8qX3n8JsuRb/FENPDs7q7/85S91eXnZqsd8m/W4vr6uP/3pT42xp9eHw/SCxWwnT/b9/Py8vSxQMuczqZvGxQ9l8uBKEo2vpR+ZFGdsS9I1q5sIy4wB2dZMNxP7bDabOj87r8PhWMdDX6vVuroaX6q56lbVdatab1Z17Ic69kNttmd1PB5qqK72h6/vCDv2NVRXq9W6+qFqtz/U9qsNrtfr2u331X1NMMiffiUB3K2mE5v4Qr47wXJWLsgasew6Pz+fvdA1CRTPG459HV53ta6v/m3zNbE89rU7TlX7TODyZaR8+bdaheElcxEvMlFLnCvW+bn1RKa6klim6/A6PckEPmPpb13fnWhk9rxeT8euVU1gKZMJwnP+uAly8toAgEGOymclE8kge+Z6PfXDZnafTCowxeHk75IJIchsG5gCRF8PDw/NmWZiRSk4EFWerhvLpZ67Xq9bTzgHbvGr6lcsu/sn85YAjKKZE2dj0WXB9/f31fd9O9pwWZXJdaN4fuaIyGRgzDXZk67rWgUmg1uW64ydEWZ1ibPE7Fuf3Eux3W7bi8ew7JxuAqwsQQJwTrnKYzhz3owRS0/eVdWcCz3haLICkEA2dcGVJ9pw5Flh4NQSVDVHNUx9sP693LjO1nxX4l5VLVjTU6f2YHm6rmvyBHBV6QTEdMy5ydaaZuLKZjnpbOtJPyEBEPTYigSBjL0Yc70eX2LIn5gzkLDdTu/P0I7Bv+hdxlZmK1WWjZNlT5aRH8Boevb19XUDT+zD+mZgoKts+Pb2th2L6l5kSc4jS/7U2i2SmeL3jA+BkOw1OWUVMFk8smFf1th6eo71S1IgfXImOEuWNH2ZuJD9xWTPV7lPJpAJWPwubevXScn4Lo4xNn2ZVdWzasv/sPNMxrP6ba8Bf+z7q9X8FJ5cY7r05s1FA9jDMFUql0wqe0+y4fz8TXtmssRJaqXOksVqtfpVexnflq1DmXgYd7/ftfvz++Pc13X+1UafXp9mlZ/Ndlvr7QQsJfdsyxjEv6x2574Z+sBHwwUZZxMn8BXGq5LSdWMHBNJvs9nUv//7vzfb87f3XO33+3p8fGxH80qo8108yfJqrzo7O2vxnJ4iWegvv5BMNz/svQ/p78ipqmab69MvZNKcv+cLyH1JrFhLMYQt851VNSMk6JS1ySqFeJXYIAnVb/19PIwJdhIhx8Oxuq9JzSZa/0YZzNtxjV8yOfqLY0vArI/Lc9mW++6iopiY0rPYW/qXJD/SD1ZV8//0NhOAw+FQ/dek0We0i51/Be+IJsmOtTOHlEHaDltjX9kiyK8kMZy2mL5m6e/FVr/L5DiJZN+hT+mT/9H13YkGBcakbLfblkXJ7Bwrpi+PoIdhmB0VCIwnyM4WAI7Hm32BO4ahmuL0DEGQA/v48eOsdJfALo0v2UxOWQabDAQgaiETBBt7bu5LBgKD6TvfarnIQJVlT/chQ/fOTfRVE7Ofve4JFLO8mCx89pqSu/tRVs+ZAue0GTQ3QvvOZjNtitVOAIg5IUlrBkPq++nNz8mWZKl7WfJOhi/ZKwadfeFATjJIkieMFuO3GTQZmjwZKVkcYwL2XNYv2wkzCRHEyGbJDBiLQJLl4nQ4dMjzJJXYPc4MU0Z+Pi+QqJqYL10FBI1FEDR/c8J8C7bk6T7mr40sEwa2DMCQt8pTyi5bTNL5ZcKQVYRkxpcssERF8OHsU0ZOQbMG/A3Alsmm8S4BrXE6OcyesCxRp46wL+wsEJBJXq4JgJQJfvoJNm0c2Nw85Sx9RK4dUiKJnwTLnkV2AAwb9if1wP3ZvTmwFT47K8PWTRB3v6yk5BiN09jcm83bIyAm5JGsub/OWjsOFKPs3n3fN4ba/z2Ln0tbtr70BamSlXLJJHlmsjseZDCBDPq32+3aHjy2td1u2wv1XE7UMx7rXjUBNFUddna+mZJI6zPKeF39MLRN4hnrAGPjdu8ffvihuq5rR1rT67/97W+zOGHNz8/P2z6Vs7PxvRi//PLLjDGXHPz973+v8/Pzur29rbdv37bjgBEOue/GGqnAGqMkgy5JDshUgtJ1XSMbxBV6kzYHrxhnHk7Ahn0uk5V8a7xx03XfG4Zh9p6yJGmtI7vgc90fFjN+c1ThyiTXGroHPfZ/f9NfGIrPGfphrGR03czH5Dq7X+KVrE6IYxNe6Wb+THxYkn5Jwg1f7ysuwH5pS5Kr7Bigy2m/YhFign5kYnzY76sbJpyQ5Kp5J4bkP3JjPVyRGCirU5lAJEEJF6QMM17y+2mb6funpK+a/3QPvo9vTNzyj67fVdFYbhZORU1QkCcyPD09tZYMhu7EEMEzy4BAA4AogOamPe0ePpdl12T3JTv2MagSKMNquRF8zIuym6tFlZ16aZTfZ6KU7LRE7HicNjmlYwPEjYGhkl8CpGQkBd2qKdtlkFmOc0+GkiX2BLrGS1E9VzIBlACt+SKnBOfWGHjWkkFv9Ly/vLy0z3Lq5oiFJdNM4rLnO98Qag4CfwIN60SXlKzfv38/M7ol2AYW0rFINLInVSCno76zDMwJQhJ4eE5e6Sj8n50BF5ls5LqxH5/jEDIBzrXL9c+x0X+6ZS6CQbIsfT/2e1sj8qMb2UqZ7wUZhnGj6u3tbfMxyfRIms1JTzgbEhitgyDsiMfU6b6fTjCRFKX+W7NMfj2TL+MXkrVfBt9M1lNf+crUHT4u/VUy93xAkiyqnelDgJSsQrCfDBrJWhmr+3wraNELRBImK4OQ+5lvAhRzTrvKKiGdyqQyCYws7xtLluwz9qgoL1m6JF3Sb9LvrCYkg3g8jlV2B144mSnBnTUi10zAsP/mmWCRbPiv9BHsgP/1XXHz7Gzb/EPaLd+S5JkEgMweHx9nTDiwz3dVVZvrfr+vy4uLGs7OZ3HNWLfb8Y3iyI0EQ+a4Wo1Ht/NLfKz4Ro7H47E+ffrUKtvug4x89+5dVY3xTbICGPPH//Zv/9aeK0FGIBhL+i8gLjcaW/tMmK2JuMqGjT/BtljAPpJtXh6Zyq+l7bEfe0BUZ+xRTfkuCR/JLnuwvnyVikh+PqtqibWSCIIVkDi51gkyM2bN/EJ0QGQ78G63q6GbDkdIXyN+tCRhmA64GP3BpqqGhi+cIpXgW0Xftdlsqg/iiZ/Kiqd1FNOyHYkv4RvoauoODPnly5dad/NN8u6dOARZT4/ShyzJOnNIPRQnE0uYP1nmmqY+Z8KQmE8i7J5abRO7ZtXU3H/r+u5Eg+II5BxqghoO0oAJIlsFGKSSpUkl+4gdATqwC8BCMgMqB1iFqmrKw8j+/ve/z5gxrKKEA/hNdphRmZONvZSBwmF0W1nwOG3kpRCYDsZC8QBMBk/xzI3cl+DdfbL64VmUDdjKrDaTDi/2yayfoeSxmtY3y8ien4wPOfoch6ji5Toej22vQPbsYqslnwCINcAuV1U7c9x6LjN565PvZyFn6+kISXsB7MFJcDMMQwN/1kiyC0SwhSxtc1ScvXlnpYxs6RlnLik17yWzRK85wCyFJnOWAAdIYqOudBqHw6F++umnenx8nCUZXde1pCQ36wKEdCUBpbL28/Nze/cA9pDeVk37rfq+b+CI7QOOWXFIZ0l+9Jz/kHxYA7LBACYRIXAkC54VBoyNZxsnNgoDmi1UgAVZ0IMkMCRa1kxA8DtAgC7yFWnvxpPsPP3gg5ONy97v5VhTv5OdpDP837Kfl3wzoGWLSzKqfEKCFT6L/HLuCbqdrpRM436/b3uLtOClHWS7GP1O0IRcyIMN+BT+Jkke+s5HWBsAku5ltUWVNUEfmYpt/G6SG+6BnJknK7tar1czsuf8/Lzev3/f2H/Pqfp1AkUfJbabzabWw1Cb7ab93z63Vbeqi69MfX7XeA9hK/x2tj/yl3RKhUXSt9ls6unpqc7Ozn6V+N/c3LS1rKrWSml+mczyE8AQH+HeYmCeOGYMNzc3jUzr+76tU7b6ZWLPtsUYMRYp5rNkkCRqVkD5FXaUVYTcV4Qpz+4HesiHSRhdeVx3klnsM5NaeobsI99MHK1Vkhj8W7aAmot5sPH+OB2ekXH6cDxWP0yEM311LzaWmHK053lFBG7ISkruM5VknH09DIGdJDHtynEgtjJmZ0KUfpbNtPjaTe87s378EIwgmaZP5iT+WadMxlKGyyQ1cQ5cRB6e4bLWOSe2nFUs658kQ1Z7xfLfun7XZvAEPhyAB8nyMwFIUJPfyU1NJqmnVh9e1XQKhcC1Xq9bVYFhe04e+aeEyEkky/LLL7+0e8pMjSuZNM/PhabQ6RyW5czcQOMSxLDpPlc1JVnAo/8zsiyx57iSwcqMNAMN4CGICTBOxtDaJlFbMmhVUxDE5Nq/cXNz0+5tjP794cOHppScuKDLKLJFYbnZmNEm22eNMYq//PJL2/9DT7Qh6IHVl8+g6SPAKeGlgwkcOMp0CvRIkkKPOTmBTIIFtHg+I+UU6FC25qn+YV8Fm2S8Jd/JxiezQT8SNFtb4JmsJWNaHnNfC50i11xrjJ+ArF2So7q8vGw6mxvmAAO2kM7YPLQ9kKv700m2nck1AOf+dC2TOevPrswt5ZLVMcAj7SfllzqSTt+YcqxsJdlWvwdiMzgYw/E4tjoA2/TCnBEvnmN85psJTgv8/bz9CRiSsJEhv+MemeBkVcHvPDODdSYUGaD4ADaB1VbJEmw94/n5ubX+mAtyKBOK0V6OM7BIH9kRvy3x4N8Oh8PshbIS/gTtWpSWSdowDG0vGbk/Pj42gklCIA4Yg1iSCQsZqUAAv6OeHup4nOKGceU4Ly8vm/9XGUHS7ff7GTnQdV2dnU8vma2aCIBaTce7S8x2u/FEug8fP9Z6u/lVJbPrunZoQr4kEpn37t27WezTmXBzc9NaqgA4ui+5o+dkfHV11Xwbn5+br5ORX6/X7f7ZCkPefLbYkwdb0OHUY8k70o5uiTnJGNPzbCtMjJOJAPtUWcmKzBxsz98xltW6JH6TxU4SLIGy+dN3PglpmHa4JF7oWOqj7492eqjjYQL84pk5HY5Tu7p1SRvyPPqdJBPd0rWy2Wxa22Fih6+DmiWKfJCWVrg1ZZOVCDJyb7afrZzGkwA/k4dlJSCTlyQn8zuJx9J/ptyT7M6kIv22uGAd6VqSTIgra5Q6lgQwmSyJy390fXeigVlxOgxHbQEoswyc8Dg8Qcsgl8y4yVdNp5gQBGH4231TmTASHESy7JzI4XBoR83JeJ+enmZHg1pkikLQy151rRrJsFEUji7BIUDD4BJYuC8npTVoqciMX8ACxNwrmTByl0QIsMmk+Uy2XGFMliU6Cg4EAmlnZ2dtv4UexR9++KGqpnP/tRzs9/u27+bt27ezk6X6fuxP1AcrQEgwGCR5Ow2KkQjeuakrTw6SpFRVK0VzYkBcJg3W2HPp+ufPn2ebgRNUMdZkpMmOzDIpFEh8BsgnL5+l+xISDhMwxl6pJJj/5eVlffz4sc0H6KBTq9Wq/vu//7sxca+vr/X+/fsZuyURZ3vKzbkHSJUwq2fGxvZSTzk9gWy73bbn0Dn2y+llqwOdlAy5j8TAmOh8JiMICuPxfetunubIJ5kTu082mu2zQUlTrpM5JHnBD/IT1kjCiVmnA0lyqDzquyb3ZIzpHdAi2TWOqpr5IYGIrIGpvIZhaO0cbI0vShDArv0/AUTVr9neJIMygKkuqhhkEpetJdnW+y3dWfp2Ok6ePpvMYSbzWQHOMVo/SaD78dHZqsafmX8y2Nkuk6CWnWSVMXXXy2uddMa282jPvu/bQQl8fSN2Vqvq+2Ntvla8/uM//qOur69be+Eff/hDi/HmO7a+XtRxmE46fH5+bi201hvhxp7evXvX7ENSROceHh5m8StPRsxKBr1KG5MM5DHS+Xtrk+A7kxn+XYxiO8hCYDs/m4Qr3edX2KH1zEoBH5HYQDwTH9krXeP7MxGlP34vDicWy0Q4QXAC4Pw5/5Ng0liTtMh7G4vfJWnLD3c1YZwZCdFPB3J43tL2Mnlio1++fG5xM5OW9NNJAHmmNVqSfcuOAXLnh82JbHKN+b/szlmtVuOpU/1ETtEj6+pK3JC4jR6bR5KM5pTrmsnCMkHLyoj5sellJSbjSxJ5mezQlyTMfuvqhu9NSU7X6Tpdp+t0na7TdbpO1+k6XafrO6/v28lxuk7X6Tpdp+t0na7TdbpO1+k6Xb/jOiUap+t0na7TdbpO1+k6XafrdJ2uf/p1SjRO1+k6XafrdJ2u03W6TtfpOl3/9OuUaJyu03W6TtfpOl2n63SdrtN1uv7p1ynROF2n63SdrtN1uk7X6Tpdp+t0/dOvU6Jxuk7X6Tpdp+t0na7TdbpO1+n6p1+nRON0na7TdbpO1+k6XafrdJ2u0/VPv06Jxuk6XafrdJ2u03W6TtfpOl2n659+nRKN03W6TtfpOl2n63SdrtN1uk7XP/36/wD5NI2I58ZaXQAAAABJRU5ErkJggg==\n",
+ "text/plain": [
+ ""
+ ]
+ },
+ "metadata": {},
+ "output_type": "display_data"
+ }
+ ],
+ "source": [
+ "plt.figure(figsize=(10, 10))\n",
+ "plt.imshow(image)\n",
+ "show_mask(masks[0], plt.gca())\n",
+ "show_box(input_box, plt.gca())\n",
+ "show_points(input_point, input_label, plt.gca())\n",
+ "plt.axis('off')\n",
+ "plt.show()"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "45ddbca3",
+ "metadata": {},
+ "source": [
+ "## Batched prompt inputs"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "df6f18a0",
+ "metadata": {},
+ "source": [
+ "SamPredictor can take multiple input prompts for the same image, using `predict_torch` method. This method assumes input points are already torch tensors and have already been transformed to the input frame. For example, imagine we have several box outputs from an object detector."
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 26,
+ "id": "0a06681b",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "input_boxes = torch.tensor([\n",
+ " [75, 275, 1725, 850],\n",
+ " [425, 600, 700, 875],\n",
+ " [1375, 550, 1650, 800],\n",
+ " [1240, 675, 1400, 750],\n",
+ "], device=predictor.device)"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "bf957d16",
+ "metadata": {},
+ "source": [
+ "Transform the boxes to the input frame, then predict masks. `SamPredictor` stores the necessary transform as the `transform` field for easy access, though it can also be instantiated directly for use in e.g. a dataloader (see `segment_anything.utils.transforms`)."
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 27,
+ "id": "117521a3",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "transformed_boxes = predictor.transform.apply_boxes_torch(input_boxes, image.shape[:2])\n",
+ "masks, _, _ = predictor.predict_torch(\n",
+ " point_coords=None,\n",
+ " point_labels=None,\n",
+ " boxes=transformed_boxes,\n",
+ " multimask_output=False,\n",
+ ")"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 28,
+ "id": "6a8f5d49",
+ "metadata": {},
+ "outputs": [
+ {
+ "data": {
+ "text/plain": [
+ "torch.Size([4, 1, 1200, 1800])"
+ ]
+ },
+ "execution_count": 28,
+ "metadata": {},
+ "output_type": "execute_result"
+ }
+ ],
+ "source": [
+ "masks.shape # (batch_size) x (num_predicted_masks_per_input) x H x W"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 29,
+ "id": "c00c3681",
+ "metadata": {},
+ "outputs": [
+ {
+ "data": {
+ "image/png": "iVBORw0KGgoAAAANSUhEUgAAAxoAAAIYCAYAAADq/5rtAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjcuMSwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/bCgiHAAAACXBIWXMAAA9hAAAPYQGoP6dpAAEAAElEQVR4nOz9Wa8lS3agiX3LzH3vM0TEjTtn5s2RZCaZySRZTM5ksYpFVrO7utEPhW61BAgQ9Av0LkAQBEiAfoMeBDQg6UmAHlutQqO7WqqBYzLngTnnzTsPMZxpb3c3W3pYZubmtn2fiGxRECCEXcQ95+ztbsOyZWtey0RVlWftWXvWnrVn7Vl71p61Z+1Ze9aetX/A5v5/PYFn7Vl71p61Z+1Ze9aetWftWXvW/v+vPVM0nrVn7Vl71p61Z+1Ze9aetWftWfsHb88UjWftWXvWnrVn7Vl71p61Z+1Ze9b+wdszReNZe9aetWftWXvWnrVn7Vl71p61f/D2TNF41p61Z+1Ze9aetWftWXvWnrVn7R+8PVM0nrVn7Vl71p61Z+1Ze9aetWftWfsHb88UjWftWXvWnrVn7Vl71p61Z+1Ze9b+wdszReNZe9aetWftWXvWnrVn7Vl71p61f/DWPe2Df/zrv8U//k//Q57/5GtohB4PCMGBE8E701lijIQQUFU636EKqkqMkRgjAM45RIRxHAHYbreEEAB7Nn+f/xaR0kf+3TmH9x6AcRzL33n8GGPpR0QYw8QUAiEE+r4H4ObmBhFhs9kwDAMAfd/jvWeaJhs/Wp/DMDCOIyLCNE3cuXOHzWbDOI5M08SjR484Pz+n6zpCnBCJeO8ZhoHr62tEBO893jmmYSww8t6jqmw2G/bTnhe2p/zp7/0+2+dOie++z+N/+1VOxoD2sOn7AodpmnDOFbi2MOq6jhhjgV+GZb6fse97XNqzPBfn3OJnvRfOOXtehKix9O2cK/COMeKQAtvT09MFDuXx6nnUc8t7Vq/DpX91y2vqVbjZCBsVXnnto3z1v/pv2Sic3D2j7zt7BhCBPRNDp9z/+Kv82h/+Ju8/+ADf9Ui3xZ+eEjc9QQSiw0/wzje/z/tf+3vujkJA2XvFCYgqKsq0Ee79wmt88Y9+mwdXjxBRxHVEBKRDup6I49pv+MQ/+m1OT+4SgjKpsh93fPDoQ7ZOeO7Oc8j5KRIDlz/6Ke///bc4lQkEJhdRHxGNaPBcxA2v/PIX+fgvfIYoavPF4YPSB8ePvvVdpofv8Zf/x/8zdx9c8VhvCDFyGhyh8+n86cF5xAlB7fycbDdsNz2qIK7DO0cMA75zjPdO+Cf/8/+MHz14mzMVTtUTthv8dgPiiFOEMfLWT37GxcUFExHN5x0BAe8cfiP8wuc+g4gQI+A6EMMtVdApgio7p5zdu8uP/vVfcf2X3+E0RG5cYBLYug6GCbzj2iu/8Z//OeHOhq7rcJ0nAiEGphAYh4GwG7h68z1++O++zP3JQ4hMoriuQ3DsdjumKRCCEkJgmibGIZTfY7TzfP/+fU5OtogTMlpmGpNxs235u6hKrM5j/fyEsJsmXn/9dbbbLZvNppy5TdfjgN4Ld+/ewSOggRgDXmDsPS/88qd57hc/gbt7Ttdv8M7juo6N75EYCSGye/8hf/df/bfc34ETZecVnLANSiAyvXTOH/zn/wk3CFrR4kLXNSLDxLt/+Q3e/cb3UYHJCz6CD5GI4dfo4N4nP8of/sv/mHfiNRFhqx5X0agQArubG77+f//XnL53TR+UoIGhs/N6t98wjIHr/Vj4RNd1MyxZ0qeaBoYQFvOueQXOs/MTn/v938C/cE5/5w6bzRm+2yC9IFOk73vUOWSY+Jv/+r9j9+b7uADee8ZOkLunqBPCwyvisOPzf/glvvTHf8B7+0uuo/EIr4LHpxMQiVPg+uqa//q/+lc8enDFT99+h5tpZL8bmMaJj33kJU5PO37/93+LP/uzf8bV1SUhBLz3FZ1XxikSI/z0xz/hX/0//hvCOEGEje+5Nygvb895+ewu027PTiLx3il/8B/9KV/8g99DOm/4p9CrsHt4wY+++R2+/Zdf5mevv852s2UYB0h7pKo4ZMGP81xq3M3fZ7qe97im+cda7mON7+c5qCocOWP2uxQ+mt9ZO5c1P8zzzd/VfDJqXJzT9kznd+v+7TkBdYvPFvi6st6Mt/U8WtjU/dRrqXn+wTO4RR817637XMhZGK81OhVtzhVM1t7N74dKHqjnuTZubu28630JVPvRPFfvVZY9VA2+IKtwq3Eiv5/7zXJjPY81WOf9Kv07QSr608Km5rM1jukK35hx0+NkKX/ZeEqUiETFBQcIsYv80q9+js9+4bOM4rja3/Dhwwc8fO8D3vr+jxk/eMzzJ+dc7fY82l1zHUfGGNg6z3ObU877LZ757C7gZaBcxZn2vPwfvv/XB3vbtqdWNMAE+qgRjRAVFCHiEFFCQ2BUlf2wp/P9AqAt8tSbvHbI6k3Lm51/AoUYt60mBOM4Mkwju/2+COF937PZbNjtdqgq42gMTVW5f/8+AM55gsI0TUUpyExyHMcyblYisjLiO4f3JOFlous69vt9UnBs/K7rinKVBX1VY6YYXU1zcCgTzvkFIfLel/XVykaGS1aKZkSdYVkz7JZY1kpGfcjKnogUBMyfZYFIVZmGcYGEbf9P024jTgslJR2SGCLTfm8w3Q8zEczPhwAScU744O13ePToETc3N5ydebou7a9zRO9ABUEZdSIITBrBGQGWGBEURYkh8t6bb3F9cUnUgPcOjZEpanre2ZMu0jlhd3ON4hlC4GZ/xc31FT98/XW+8IUvcv/eGV4cJ2dbU2I04oAQIkqwcdWhIXB+dorDcEWEQmDHcWScTEHZ9BuiXhiEJAtcRqzqNu8rKAGi4iZH7zsQ0BhMgfIeojJe7/jpd76PvHDG4NK5jAE/TeA8MVgf/ekJ2zDhxpGYcFvEhteoTGPg4cOHPHfvPlNUJNr7iBCiwhQRhZGJ8/NzbvZ7xDs0RJJcYeceCCiTRB48fszp9nkUwSlJIYYYIE6KIkjfE50nIvafGONwsmRmrZDTKut2APLPn7/VTDLvX1wRfAr+KyCaBBnAYUKBc6A27w8++IDuoy9yen5CmAac80gMRB/x4ogxEDoh9I4YBR2nsv5JI+qFi5trHl1cEPoeSXhTn90hTHiFx+OOwZnSTVQkgERFHKZqiPD+B+/z6NFD9KxLSp8SKxiGZPTxJ1smf02nAlFAIyrGX0KiazUNKk1ZKBP1HpVHGvplgFbw8JOf/IQX/cc5ccImCq6b6ILHI6gIURQJkeiFYIiGqBKi4mLEdT04IQr8+Cc/5hd+4ws82l8Re1cUDSeZL0U0Rm5ubsygJba2EIJhUoxkAenrX/86n//8r7DdbtPaQHWa6bEKMSqPH1+QsBrnHeKESSJTB/sOONvwy1/8PL/zZ/+E05efBwQJ4MURhpGf/vDHfP0v/5Yffffv0esBorK7uZn5qzhU40KgbIXrmicfU7Bbvr72TP6+3een4Rs1D2z7q/FgoUhUQnH97FKgPaSV9XyyYnPb2mq5RoUilIYQDhSdVqZp198KeLcpcO2Mnpr/ylLuYkXAPBhrRajPRplW+WxlwDUlYJ7K4dqfpq3tdf3dGizqfW/HWsP3uckCB1rFr4VPMeSKzAJes8Zj+J8VXyem3MSoeN/hEDREMzhd3rB7dEncj/hotHgaRqZxYtzvmeJE0Mgkkeg2uI0DZWGYKTi5Atd2Xk/C/7r9XIrGzc2NCcFO0ABZh6wJRCZUZgVUAvMiskCe38nImCddP1czj7xxXdctiF29wXkT20OYNd4s8APldxHh3r17BdBd1zFNU2GC261pl13X4b0nhMAwDOX3rIBki9k0TUUZyR6FVlA3HJuRN8+l73t2496eT0Jc522+gqDRLOm5v/qw1gTzNqtI3p98GGpLVK2t19p7vae53fZ7JqTtAfx5Wmt5qltZd/qfJvhMo3mJukxg1IRVj1nluiQ4TePEsNsBhhthv7f1e88YJojO3js9YZDI5ASnikZwMSkZTstBHG5uCF5tFPGYPB9QcUSUoHuuLx7z/Iuv8uGDCx5eXrEfbxCE559/kUkVQekFrvY3qAYCSpgiAbMqERWfFCad9kgSMERnguA6j+886hynp6dM+ZxqJJPtliTkfQ0aESIiZgfrNFvhAhoVfGdwDpF4saO7d8q1jMSTE1wIiIDzWuD+3CsvsR9HwjCiCk5mq4+GYIJkgJubvTFf50jaAYqg0wSJdlw+fkyMBgmvcWFlUQcjkdEL4j0xKTFOFefMmjyOIzFGduOI225wp1uGYc8mE3YnOJetxgGY8a7+V8ZMZ/gYft7WRMzz21qrVJVQbc6hcF0p/hpNsDf7KM47phjY9D2u6wx3wkRXlHHDfRVwZye89OmP8+jvf8qZlyTFmqIxAHdfepn9YMYYZDYeFLrsHPtp5NVf/DQfvvEO7magi7Z1AoaPAkGU07t3GMeJ8XoC74m+X1j3spfo5U98jLfee4RMEx1qHkOV4rE4xsjELfekVc7WlMV6LSFG9tOIIxLCSOeEKUQ26lAgONBx4mOf/QzffPtdNmrKvaoxegUCkRFTrC+uLhnCANGjzhQNEUdU84Siiu86Nicn3NxMCRc80gn73R6S8qWqXF1dVd4Mv4BBiAbke8/do/OecYqJrwk7GbmUyC/9wif5/T/6I177hU8xdYJuOvoJ4hR486ev880vf4U3f/hjHr7zPjLOkQRZuBTncCIE++KogHibQejY2VhTBp/UROSAdi37OBRa6/6PCbql7/adI6PVuLW2lrYtPD1QPBotXWnHOAa3NeWk/TstoKzhSXOs15INc+S56fLdtb1bPF/NY8040K5tMXb9bLJlxgbOT8QVbQyRR2TL+vta6WwVjnrdNQ4VPHJihhWdIzvatbWwk0rJWFt/S8fy906SESatEQdhmgjDyHR9Qxgjj958h93lJeP1NW4M9DjCODINA14cG9fhNdI78y7HaEaotf1aUzTWzsrT8r+nVjREkiXcSTai4Z0nCJXVdHYrFSVCZ8G//l51DhvKz9cCcB5zjdnnvtYQuRaO898xmivUJ4Ug/8sKRh1udHJygoikcK4JjW5hYXDOsdlsUDUhJoc4bLfbMs9xGthsPOM4FoUmP5cZysnJycLrkEO3zMolwCy0mzCo+Gqd+WdLQPM7dShard3XikXN8GttPCtObRhTgXecXalt6MIUpsIkWyJYa+1rylDdV/nbHijrq8dMpxxQ+s0G1WhCgEamKQnNiUmZO1zYnp6Y5e5kYwJjxssYcL5DxSyad15+AblzwnQx0o0RMu46UCeMOvHSyx8lxAjevCriTEBTo3goilP44I2fcX56Ttc5zu+c8cr5y4Qw8cGHH9D1HZ0D2Q9cvP8ecRwZnZpSIxCTO96Lo3OOh++9y0sf/RhIh0Uvmo/FeY/fbhgvjMnEGM3ync8NS8K1IKRYKI14x+AdO+/ozKWCYB7MyTsmiXYuhgBbxz4EtuKQZCUOCr7rGSKc373LdH1D3/cmQMUcWANhCoh4QoiICp5M2AR14FzyUoWJd999l904mDJWECZZxYGpg/sffYXTO+fEdJaceEOLimG6riNu4ROf+yXe+ep3CbsJjSYEZgXecD2dqcpa1Qqpyu3K9pqwU2C+wlA0CbFrfVl/SZBPCKsy4/0+BPo7Z5w/d5eTO2dMTuicp+861HVIEoyjbTKf+9Kv8zM63vvuD/CTKeGDQDjpePVTH0eFIrjWtEBEEI3IyZbu1Rf41T/6Hb7z7/4GvdjZs6oWzueFHYFPfeoT7McB128WdGxhIPGeFz/+Mboh8ubffQvZV0qCQEi0sg6pbI0qa/jcfgcz7RtDQE48zz1/n/O7d5CuM2+ZE/NEppCTiDJK5P5HX+ELv/ObfPfffplOTAES74gOggjRC698/GNcXF8hW8NQTWc3xJAsjybAu87zhV/9Vf79v/trEHDeEYLRut1ux+nZHV588SWc8wzDiPcR54yOz7TYBLDnnnuOX/+N3+CrX/5KodEvvfIy/+Jf/Mf81pd+i03XmQfJgQTYPbrgG1/+Cn/7F3/FzcPHuDHQTRGnFv6sCYa1USkrxa2QW8/nmDJ4TABZOxstvrfnAw4Fn7aPVhhseePavNoxythRiyLbjlPLH62iZR7CFet8otFr7z/JWLGm1NQKdK285+ecc4R42MdijStw1ywHkOmRzvRmZQ41TWthv+blasdu92KBY7IMTT3W8noNBochVscE9xqva8NOqzAdg3/mKzGNWSsZa+dl0SeH56CMoevf5fddMhqZlVUZd3u++tdfJu4Dl1eXlh4wBVxUNl0PRM7OPCdi3n8VMww5mwQhhoVCXObPfOaOKbdPwt26/VwejYLEISYLfiDokvHWCoQqjMPAZrMpzKo+YG0cZxb884Kylpj7zM/XFm9VLWFIIrKI563zNU5OTorwXBOi7Jnw3nNycrJQPlrkzN6HaZoOciTA8h6sT2Ecp7JuFvChjJvnsd+bJ0N9ekBMMN50phBpGC1WviIqtWJQ91/Ptz00ay7C+qDmvaiJRP1OEfxdDj1pLCoAOj+7No9aqThG6FsCXudoHDAFNeukKcGOOAVUwYtZc4MqOGGIgeg7PvGpT3B6fgZdshY6D96B87jOg3r2IXDy3B0+/6Xf4Lv/+i+LshPCBOKYnNDfPee1X/gUru8sdtI7swKLQ1wH3uMwy+flB+/zzYtLPvKZz6L9lt1+x7br6V3HyfYEr8rNgw+5+fADTpxnchbOgzhc7yw8ZYKNd7z3xuv47Smf/OyvIC6J6En5D8FyEuqW8U1wizjbJdzBIwTXEe/e4e5HP8rFB+9zshf6aUJUuCbysS98jv7eHVzvONt6tPd00eG6Dro+ES9wAbb3nuPm8oIwTkQNBFWGOBFC5LVPfIztdmvn0XeIeFQMftGZN0KYCL1jFOVzX/g83/vxe0z7sQhxMSq+75Btx2c+/zm2p6fEfL6TpQkBcZ7oJkQDYz9y5xOvIY92vPOt79NhjCLnMGgS3m9jLrMF7DiRbYXbct44NJDMjHV+95CAz2piVLNCadY+th0vf+o1/Ev32Zye0G96vO/Mi+E8HQ7vHHsNTCgqkU/+6i/zxve+zynmhRhd5PO//Y/oXnqObrNhu92aR6ii1WDnbCKiZ557n/gIn/7lz/LDv/oqLhoOTSjXYeLTv/F5nv/4R5BtT7/dIs6TQ7HyerMCGk+Vj33+F7l84x0uf/qWjaMWPpiZeP1egdcThKd2/1QNb7TvePGjr3L/lZc5ef4+nGzB9Xjf4zpHH1Ju4cYTUNhPfOaXP8eHP3qT9372Fq7vEuwdQwx89FMf5/yF59icnCC9x236otShhociat6jCJ/69Kd49OiK1996m5D3O9HC7XbLF77wBTNKiS/fZR7ikifFOcc0THzxV7/I2faUL//Nl/mjP/oj/uRP/5S7d+8i5p+0vX18zU9+8EO++9Wv88Nvf5ewH9ioSwYYwXlJhhETlI3WJnjKrIC056AV4o4p3mv7sPb7be+s7e3y2Sd9f3hOW6PXgfDUvFMb3dp+yjmvxqrDUepn1+DUwm+NL9fP14bbWk7K77ZrPqZ01Z+JJFytvmvb2mcZJ9vv2pyHY/uzJhvArNy0OFbPud2zvAftfNdgW8+tlVfq947tzRo8juF5DSs4zHdZ7HH13LJZblVCMqYQ6Jygw8R4eU3YB3xQJEKHM8KuCt7RpYBvn1hGJCZDKPZzBTdqQB7jc+1ZuK09taKhySsQQiCqMowD3nd2HnVp2c5hUarBkjMr5cHWZkCurVyq5iHo+35xgNbcs1k5qIFQC975+6ykbDYbfNcV4pHHrEOpvPcljyLPxca2d/LntZIAsN/vOTk5Kc+M48hmu0V1ouu25fn8k6R8hRDYbCx5dRgGpjARJ4XtKS4R/Lx+Jw7nPSFMZZ21Bp3h1XqIMuz2VW4KLBG5VfxaJTA/X8O5VghrIlArXTWcb2MoLRHJ49WEpyUy87Omd5f99J3F94sxWVAikWEKhK3n5U98jOc//hFib96Hvt8y4SzhTUx5wjm63jOOE3dfeoGTe3fQB5c2pncEp+yJ/OpvfJHu/JSpSwlcLiUyg4W+OUfE4aJy4oWH11dMYWAIkf0wcPL8izhxnJ+dEW5ueP+nP6WbJvNaicdQTwi+RyV5OOLESed446c/4SOf/AybzR3LFxpGXH9qSk+M5PDGBSEQEBwQF3AGo0m9dDzynrNPvsYf/s/+p/z1v/pXPPzGt/AXN8gkPP+pj/OLf/TbPHj0gA2wVSFGh8djbh4LQSohfgTzsMTASy9/lAcffMD9l17k+vqa5154gWHcJ7j5haIhKQTLRc/WeaJObE9POLl7znRxkwijKZ9TDJw99zybu+cEBZdyL8BCxmJUxnFCp8AkkX2MoIHRMlKQkHJuRC08KyrgKi/njKM13poH97jV6ZilJ9OnNUayppwXemkrKkUYonWGiHD6/HO8/KmP89gFS1CeJnxI1lVvYUjqHCqKelO4Lx5/yBADJ9Gg1Z+e8MqnPsG1DwyjxfQ6vxJ7HAKKckNgHyYe7q9RL0SXCkQI+DunfPYffZHhpCOIKcFR5yIRrQFnEEU7YUyeQokRjZYYnsOnao9GEXQr5WtNYFzbE1U4f+l5PvG5X+TSWd5eH3scSpgGNDhO/AYX1IxozqA/qK03Cz+W+CpED5//9V/D3z+1ELzEY7SbrY5m4I4lzykivPqRV2camyyLCPzhH/4hr732sZTXOHuSYI4QyDDpfU/cRH7ti7/GP/3jf8prH/+4zSma5z7uR95//U1+8JVv8L1vfIvHl49xIdBH89k4J0wOohMkSZgOEt0sSEkdt9/m+/1/s7W4t/ZdNdGFXrAqON0yTpuUbZ7pdUWnnc9SrmHxzPIMHwrFa4rLmvB6oGSz5JFtAvb83Myz2/W2Y2Zc1PyfEdkSolzPRVUXuImu07waBmuyQLvOek0xhSk/SQFtv2u/vW28YwpM244px9aR/ahx6JhiN3ey/HOxH8f1ZVMSMlycQ4j03tORPMYh4pIMErGUNzC+iAoOTYqGI2KGnGNK09O02/azbU8fOuUc+93OBIkY6buNJVvGiG+IfBbUTdhdImDrBciCawihJE9P08R2uy3VoVrBt3Yd1hWT6mTtHB6VBXBjTgmhxVz9ZsWBk+2W3X6P956u60xwc44wTajGFPYkluw4RfrelIP93vI1drtdEfK7rgNRpiTw7nY7huTV6bqOmCyntbBehEMxOKsTuq5HRbiZBjqUOEacd4uDsbbxXectnKciYlnByHCqCVzt4akPSX62VvTKHshMMDO8bV+PC1Kt0tDiQz1+3YcTKQnF9Xxy0KsDvDfFbIyBDtAQic5c/4LgXcdA4PTeHWLn2A3X9F2P8z0hKuo7YgSJIESCWnjCKMKgkV6EGCZCZ14SFPrzc6IzLxc+Wy/FsiqcImJVImK0/rx3PHfnLoN4fNfjRHn++fs4VcabG4brK3QaLemr26T4VDUPRQqXUGAcdrhtn/J3DKabk60loo97eidMcUomZkW8hYIVJpKI+AENjBDFs9909K+8yD/+L/4z/u3NDTff/gEuBEYP3Dnl8oN3uKMOn6hYkDQLxZSEROVULWHVdZ5uu+HO8/dRjbx4/hJTqgCHOFTMA6Fo9ueiYUKi5bmgykjgcnfDRnTOzQkRFccYA/swIrqhw0MqVkGSFbxzaT+wqjtdZHQmPPbFM2BCaIgRX4VM5DC6bLErNK6B3Zoi3TKdtWfr5hDy0K0A4hPtISoaLazIpSyNhxePeefD9+HuGacieOxfJ5Yz5FNhgs5h+mCn3H/xRU7unBPev6Rzjuuba9754B30fEvfd3RZsHAuMTSScucsAb+zfeu2G0aNpBg9osA+BnYauNoPiPdsZYNTMZe9OBNoJXmqUYJA1EB3dkJQZSMOR0QMIrPhKgnxlvOQM1QWm1AU/YyP1VcGU4Gr/TWPLi8YtnB6xwxBEs2L4Tqj4SEGUG8M2jnw4E43BveoxCnSnZ4gXQedYwwTOik+RoIq0nnUQYh5v5XOOzSCqOPBgweM48Q0LcNeXn75JUC5ubnGN0VUVJWu7yykD+i7Da+++iovPv8ine8tIdSZD/Xygwe89aOf8oOvf4uffef7hOsdSDDjFelMJGWN9Jkdq6yoz3hYC9Fq/yuJqVK+SF6FVcw+bE8S6tYEVtI5hUMB53+ozlPzvTp5GQ7XsqZotErXTCOM3lO8o7PC1ioH7XprgfxY/7nVil+dnG7vL3lsy9tbGNgfeZ/Ln9TErg7/Wsh7a32twHqt1eufw1cjVMbN+tm1vhbKgj2weH6ttfmoWY5sFaZj8oqIFEW8/r42kq/tWxmD9fNitOu418T4jyZzmhV3QC331OVw3xkEhXeJgmRcT3xt4cJam8gtfM5gLcffb9pTKxpeHMP1zkorimFknAKu76ziToUENZAkMZX8WVt6tp549hrAeqJZvWEZUXLuQw6Vyr9n4bpYChX6rrNqH5OVvPTe0/U9iHK6PTErzzBalaIYrfqOd4zjnk46us62d5omxNmm5VCtrGTEGBFHCbGKMZa5ZOHBe1/K4k7TNCNmsnuMIhA9/uSU4e4J4eEVJ7gSg14LMSKSqly5BFPoXMr5kFx16JjFg4XSk+GV4Z8VidbaijTuvkJgdPF+7j8nytdEsV5He7iLZUnmeM/681nhEfpISZjeiyU0+xitUoxAH62STKdwdXHB3fi8ebicR6LQ+Q24HvEnSNfTqZqy4S2Z3J1uiQ+u8SoMEnlucMi24+LxJc+fPM8JnuidWfdT5SR8D111tKbAtN9x8+BD3Mkp1+PIlUZ8v+Xk9JRTmdA4Mm2gkw7NnjQRegE6IThLBOtcb1Xfxj0SN+ynkTBNnDnHcPWQ0+srpjgwaWBLb2EoTkv8rVnsl7ggqkwS6KJyEhynmxPkzhm/+Z/8R/x3P/sv2e6veHx5QRhHTp3jXDqmHsaNw2Eha3XpTEHpVAhXI3sZeO4LL/CT17/KZ3/xF/jwrXd54aUXCH1Ht+lNmXAOEfvn48TQwdR7+sncvfHEc/7yc1w/vkSngM/ilsL52SmqkW7jiS6m9ZnAFDXSeSHi2aR4WrfpOX3+HiMRVRNpFQudi5NZ01WtvOKkprBGZxXANuIrfGW1tQLCkpFLKfGan83NIbhoeKwdZt3P3kyUTlJ1PrNHFwZydnLGxjlCVDrFXOWpRGLEFMHoSTleAuLw2w1dvyX4awLK6cmGl+7f5f3pyjw9vrMqYICIT9ZutfyFENmoECKc372Hdh1xsLKLvu/onBDCyKQjfW80tZOOVCprpkRiOR8nYpXd7r38Mu9976d0o+DU4bVniBaaG1IYUBYiQobvKpfL3o68BybwmVFM2YhyfXnB9ux5nOtMefJWOhjvLa8h0RyP7YN2cP8jL/L+T99EJ6HXDZ3f0p+dczNNxN2ezeaEzjl65xDfIeKIPYj3xk/U9jiGwMuvPG9eT515lveOd955A9X73Dm/vyhC4nLoVOfpouf8zl1efPUV+pNt1mZMWNrt+dn3fsDX/v1f895PfsZwvWMME1Esv0/U1hOSfNDlnIIkLKmBb7Ysh2jejiTAmedDSljq7FlKwnMSvqJqKuu7sjsVT3mSYLoWmrEusK4L6sda/f0xD8XaGYX1cJH5+VjldmSjhNGKumzp2npqIbcWeoFFpELLN+v8glb5yn+2hot6rXXFzkVCdDKoIZQiD9lQW+/N7LE53m7b49rguphH82wdFXNMWdK08DXDz7G11wpH29a8Tcu16ALG9VyOrb2MJWK0flWpWOJz8ehaTTxTMFQhBi4vLlAcKt4KRSCgMYVQpX7F1BplmUvi85lfg0/z90IWFOHIlh5tT61oxBDsX4wWvztFuq5PRCtv9MwAJDF7tIpvTJubM95jc5jygmpPxtqhr0vi1iFNZtHvDiwG+b1clrYW/rM3JZegrS39UdUEm2TtMCXJKk+hdv/Hzc0NQIprnq3zIcx5HFnIVjWBL89nGIZFrgcoQwqrMkFBeP4jrzA8/hEn3i36X1g+ooUtZK9OXr+IoHGZ1FkTprzW+pDURKz1aJR/GScSHItSwnIv6z5bC059wNaIbW45L2SN8Ec1XEQjN9fXhBhSVRasjGWabxCzZt5/8QWGaeSs7+lcCSTCJwHIBJmEv6lk57brGUKkC8p2Aq9C6D0vfuI19teXnInAFHHe7oKw9Sam7AQRh0qkx9EpbH1PhzAOe4bdjv04sL95xHh1yUYDnXPJUuITkzJrcECYggKeYZx492dvsnn+eTZ37nD58AEn5+fobmS8umEaRvNaxJi8LJoqVK3nHwjQBaUbA+fdBlGP67e88MlP89IvfZaLi29x585dHB6ZFOkMvhItQdusMPYv9+oAN0auP/yQ7/6//orH77/P3/zoZ7z2yU/gX3qBDqFP4msOtxLU7h9w5tr1k1XbcuLY+I6bmJmnkdsxBDabE0uYj7NXoISCaMqLUIUQkSnixoiMkS6CTJYXFUJM/0J1RpYWVKmZoWrNCxZtDU9rZtwylXIeUsiQpu5jVPBSlKYDASg9F6IlSIzTxBAmxDkCEU+KyU046TB81qTMkKvxoajrCcHCzLx44jQh3op9oFr2NordmzGkULNus7H+MfxmjJx359zdnHB5fUN0I1F6ojdBuuZeAnN4oyr9yZZRI0NIHobQE2JkTHlH4j2+EoprmnBMmCh7Uu3NabdBJoV9gCnVgEzaj9cU/qiWYpH77VC2YvfV+KBWex5h0/ds+p7dNCKdFX4QFVyqOOWxUKYwxVQ1Jil7IeITrnbpDMgUeeH8HjJMxM2E9LNxSpLwfnp6ykdffY2z83OimjKvQZH9xMP3PuAbX/kq3/67r7L78DFd0KQMYLx4JZy6WDcbONYGsRafayv3k4T5Jz1zdL9WBDVDlXUBruYZcw6VW322nV9+5+BZebq5tzxs0Y/YzDXJf/Vc61CtHGq+ECqPCNX1WLfhf/3K0/TR/l6e43Yl4ra2Nq81b8GqcpeZcTX//FwbhVGM12J8oVasjtGGtXGfNN+2ZXreGsdb78iasmFewLnvOY3ALejVAczsCys9DxYhQ1YjNPEKFr7JTD8WsiNZAXm69S4UInvwKFzW2tMrGsl9bRstdN4bE0+hU75ixHbXhjFqi8FOVu60EM2IwrKUYz5oWVkADhKdVLVYetYs4S0C5X91InhG1ixY5JK1raJyc3ODz3Hvaa6zMGJjtApGjJEpjMB80dc+lVAVSXBLz+12u7LmcRzpO1eUGAUrkdr1hO2GKZjQlddZh0D5zpKCa201P5eVO1WdLyGsDmz+u35njUi3cIZDd62IfZaVv+yt0WoOa9aQDL82l6du9Tj1u9M04fuezXZrQla0C7DEjPdEhAkYQkhlXK0snO8thj1IJMiEXZkmBOyCvhADDCa4TZhA7cbI2PeMd0+RF++xv75gGy32XZOEEjHlRVI8gTorE6nJMt6fbJHY4XuPD4E47C1eMg6oRvAOJxYWpDN3wnmHkw7HhA6R7fYEh+Pm4prHHzxELq4Zd3vGy0vGmx0unauAyVI5qqk9G5noWK6u3fmBwMP9nseXF3zsS/+Ir3zne3SdR1MY2IjdieBwJaa7EEfM+jWpMk4Tj99+n+eCo7u45sFwxfSRVxmnkSkGy/FyFcGTJNw7U5CzgDsFs2wTleS0MOXBOW72e85DoKtwqnhL078olpMRo8IUStUrXLbICuNk+QmnXZeIsi7ucXBOjKY1Z6A9PzWuts+hWko21u/Z89j+axamLWxQoxruZIMNc9lHyy1RxjGwGwfG/QgIrrfKU9nCHApOJlhOE523ogcxyf/Xuz03+z1bPOHEFPauU7zMnmEV2/tRIzFMphylUsT5bqVeYdwNdimpOJyMdqlfD122zidjRUzrI9HIiJ2RDpeUjIkhjExTwHWe3kTymYkuQLsuDtV7oaiF200TDAP9FCAEyEaumAw0+R4czTl/EcaEN1jFKbwjpoTwm93ePEDe03WCF8WJwUQdxTtU8oZCsPs5JFh4ZZrffj8gCMN+pKfHu8547abjI69+hHv37uG6DYh5aGU/cf3+A775N1/me9/4Nh++9z6dCm4M5n1KVec0xmScXtLV2ww8cBhesgbXJyl5P287dnaeVmFZW8ex7+oQ7Py9CbnH19TOqYVBzZ8WMkhUkMPE4jVht+XH9Xe1nFQrK6vC7MrvbauNgHV/q2svMRf/cK1Wro4pVm1b0s2lQB9TCdinGTfLeT8PbtVz0Orz1jhaG6zX5LJ2n4tSn5WASv6tFSdTMlLfInjviNGbzJgMN3WrFfSf76zqARxbevHztKcPnVoI9snl5ZM7MHknXIq39jlePwTAWflATWJTTDG2bo59zouo4yQz4IdhOFA8clnYXKJWZPaC1Bu8hkBtHke+KTwL4XWfp2dn7IZ9mUsOk7L8D0HoChLkn3l+XSdljvW8Nv3GynrKXMEmfx+CJfI5EbOCdT1xs2HXdfj9jhOZkTQjsIhZypxfJmzn5txhjeTaYrXGRNqk1FZjF5jjdEUOSrvlELLs7ag1/DyXDJcMtzXNv8yhWVMhuAiu90w5hjvhoKJWeUEpgqQanScOI6N6cxh4mESZdKKTACqMZGEuMo0DO50YnOKcWTJvXMR/5AX2246baWKrCr5DxKTiACDJu6fmVdhMym430Y2K3012yZ0qvu8JZzCFHt95wjDiNRI1oOKJMltwFVAvTFGYRLm8vuT5O3fYKLz2yiv4aeLDGHj8/geM1zv6aTLhtdoz6+yQCU0aCc5udL64fMQ43NDducfDYc8nPv9ZutdeZnRWcWsIgV1nyd+dwKiWcI84QmKkcYpEEaKDxxePueq3jMMenHIzDlyHkRADGjyiMSkcSekVYY/F7gdMYdmFwCDKFCI+2ngaFec7Lq+uuD+MXN/s6E9O6HorURyzoocpf+rMQ7jbDzy6vmYnajutwuXlJRfX12iMbE+FKWpx3c+Mz9hs9nY4P5+1NYtoLRQUPNc5vr1lqKpY/oUqLo0XQrDKYuJtHQJjtKTv7HGVEHj84BFT59DdBOrROEHviL2iaiWEQ7pXZj8O6M2Obd9xrdE8nkG5enjF5dUF8S70/Q5xjq7v2TpBvC93smhU4jASdwMyTOYlCZHgOkLnmMLE5c0NVzc7q3biLOS0g6SczgpTUGXaDQyPrri5uCwwCqroNHEzDlzubtAY2Ww3M3MvZazXhZKaztR8IKoSHIwxsr+5IV5d06N0GtkC9Km0gYidQYxWTtPIzTgwOSVopN92SC+oduxi4Gq/JzhH9B4fha3LoWsR573lp2BGn/1ux8OLC6Y4sY8DijIR2cXA5X7PEIVzv8cHU4w/9YlP8NGPfITtZpuskA4dI8PVDd//6jf49t9+hUfvfsB4fcMmWhikTxcFqojFZTMrGS1e5s/WrMuzku1WFY36Z/vZmuh2m+W4FhhbXpBlh+Pi4JNDWFreWM/1gLfYLwfftfjWGjNruB6ucXnDdDuvek65tXy75cP1/A+NcMcVj9rA186/buXsJHqkstzzlr7VfT9pr+t2jPfXY9ymONV7mQ3AT1IgjuFvC8vbhOpszKplmHa/WiWj/m4Nb5RsdDrEy6IEi4VgOudKlUnry3iT5WLM+XWxGmcNJvVe1WkOzTUqM345WRjMnqY9fdUpQGOuJjXH8IdxRLwvl8tBEmRVLQ4eeyZGS2abSxZKuixrFpBrwlYf6lqxqK0s9T0U9WbN4UtzEnEGYi3w5mfzwa1dxcNgTEBEFjeD57/tKGsJjarfzWPl+eXwKPt9RGNcJRYCOKdM48g4Bc7OT9jce457H/0o8WdvIMO48CJkBpBD+jOS5KT2OjRqjSnXsG4/XyMYRbvmMEGqVjhqS0FeZ10lzLn5LpKs9LUhYfXYdVsc5BwSpElBc46olvvinQeXypACPkT0aseDDy7wXc+Lr76KP1PYbvFdT7wa6Hvw3YYpBIb9QLzeE272BhPTdhid8Cu/+gU2QeDxDVMSSjY+mmXUOcJ+YnPumcaRXRi5HPZcayTc2XLpI9HC3nHARjuL1d5PMExMo+A3Hu2CJTG7lAwPTNFyh7owcfHO2+wfXzAME3e2J9w72XLz7rs8ePNtwn7AZ2U2+0USnFSWe5qFu1EUlcjDt9/i5u23OD3tuOeEToQv/P7v8N2v/B37Dy+YrvbcDCPb0w0hKLrZEhG66FPVmogOE3EfOducMA0jl1dXjOPAtYwWN351wxQDLti9G/SKOFM4AoL2IEGRUYnjxDANeGfFESZN+QaSwkZ2I9Plju3JGegIQXAbsXLDzpIiXYiE3cTu8RUP3n6XRw8eMSnsVemwiwMvLq7YbFJxABwxWuhjth4Z9U80Ss0o0DKWNTytz16LzevKM1CJVZnO5DlM6ax47y0HZe/54PW3GVG2bOjPTvHbLd2m585zdzl/7i79iZUgvri4YPfhA/aPLrm5vCrrYVTef+MdHjx+yHT3hngVcJ153Tanpzz34gucnp3S+46bixs+fP89hocXyAeX+JDyyoiMClvxPHz/AY8ef8jJvTuEsxHvN3R9T9/33LlzB7/Z0PmOh48es3v4mJv3H/DgzXdgCihCTHTyanfD46tLHML5+Z1kaT7MzKjpTM304bDK1e5m4CYEwmPBScd4vac7O0HOJ7anwun5OZJuxQ4hsL++5vrigsePHqWQVk/n0x0wIXD94UMuHzwgng+wV3y3I55ObE9O6Da95YE5IU4Tu8srLh9fMDy+wU+RLvUXojLs9jy+uESYCNHxi7/0Gr/82c9x5/TM7n/CoSHCfuSdn/6Mv/rv/w3vvf4G1w8v7FZ2hT7DoCpo4EToxS+smsdo7EJR0Nvxu21LPnIoSNZjLJTvaq9aRafppOz7oTIx50zVwn9rzGrX2LZaIdVwvGz8sXW3QmottOX+14TstbYqhKbPWpxuP7d35oqZ7ThPowy0SpSuaHprwvhtvBuWRTLa9dZejdCsb02Qb9evTzH+2vyf9rlDJZMiIz4JT5bvHSpq8zvrcMwyq6qWpO58JrquT387LLuQ+d0VRbWso5ljjXP1u+VcFLnVDHjiXKErT2pPf4+GZqucuZJ9dCb09D09gobKBRcs38D7lOyG0KWYU9Rc6BZSUmuiS69AnaBch93klr/P/1ogZkWjPjD1Yahdj1lRqIGZFYghjCUUqHaJIZTE0TZZ2caeL8LLJXutQlFnybftPRyqTPn3BKjt6Rnd2SnDyZbN+Tk+XCwQrgj4cSpW/9rTMRPhQ4KQn6uJ06JkHYeHNe+/iJQExZYg5b4zLOvP6+8zbHIYXEsoW+ZQ91PmqCnHwrtFmJZ5nhJ+SCSKQ93Eg5+9zaOrx+we7fnB9B1e+dTH+eRnf4nohJvdnjtn55yenXF98Zibmx3D5RXjuw9x1wNOU4JahDuh4/J7b/Dw6z9g1zneD1d0AV58+WXuvfAC/dkpXJnn4oMP3+NxGLgJcPHxdzk5u5vKBipOHahnePCI3RsPCDdXbLoNp2f32Ny9y+ZkYwpkgvs0DEzjgB8Cvfa8tDknBkEfXjLs3uXx3/+Ax++8W25q1hT/LopVYvLLsqwzY8XMF7sRefCIr/3X/w2f+u1/hLiOdy5/wFYc8YNL3v/693nv3be4c/8O3sGd+/c4eeUFzu7cIVzu6b1nuLrh+r0PuH50xfs/fhO3Gxm6HSLw4r27vOC3XL3+Lvthz3Tn3JJot1v6zRa/PeH0/AwXLL9i/85D3n33bYYOdu8+gAjBS6q65AjjhF7v+fCNd+g/eGx5VtPE6Z0zzp+7x/0XX2C73fLonQf89Ac/5NGjRzz68AHj4ytOgoAK++SN7foe3/cMk13kN6XcrSLcVHhIOldrbY0pzTTjMLTzWMtMUzHBx6WQthCDefCiGW3Gx4Ep5Wb8+ME3wXm760EE74XTsxO2d85BhJurK4abHTpN6G7HSfQQIsPFFa9/+weEqFxO79L3PyZiiq3bbui2PduzU154/gWuHl/wwaOH6DByOsEm2HNTiHjXsfvgEd/9i79jkoDrekJM3sR05k9PTnjhhRfx3vPmm2+g42iVnPYjMgWGkGlhACfce/4+nfNst9sZxg18W6bewnUcxyKIjO98YIK4CDdvfYjb9mhnXncvHXfv3uX+/fuoKhcXF1xfX9N5x83jB5wEY+zX73yAO98Cgfcvf8jl5WMuuo67z90nquC7js6bonfnuXuM48CDDz7kg/feZxwstPMjcsIjVbzv2Z94oo5cvf2AV197mT/4vT/gY5/4JF4cvTicwrQfub645Lt/+xX+/qvf4MO330PHCYkWbqlOmFSLNT63nC0X3e1W42O4e8yy+7RCWv1uy4fhuPe8HWNNQL9NSK9/r/nQWrjw2nrWzuiTzuyxuc79H/cetO3YPNu51d8vCsXc0vcaz86f18J+68WKzfxLPxyjhk8W+J8Gj+qx6jCrY+022nDbO2s4+IS3eBIfODav4/M4/k42RAkme8YQCDGWy6Kzx8mUjup9WZ6DZqKLsYrcJWsmnfQMZmx2OcT8KdrP5dG4udmTYkOSpVQgxYGLWvyvSLbAzQnf5bK9tOgpTITJdK98ALPg2/fdzFzFxh2yFyCkcrnOzfApDDjVvVe1mFrN1ZRmG6FUgrRL3pTOd+xCMCtVjEzJCyGpLK+FrlvpwGEYUqJqut04Je7mA74fhhTLrnhnt+vaxtqcpikAQudcsRBogq3dXC441xODIuoM6ZxDO4ff9OCFEKIdeEyzVWYCmpWr2rMRYySGfDhJlllL5ixWU0mx6hrJt5u2yduQEufTTZIZXbNSVhPzcRwtn8fZxTKxVvgwYUnJIQpW2jdXCgsxWiheTLeAZSWlBEElbTptqu2VJwa7Ndeq80yMw5TmHRBxTIy88+M3ECdsw4YueC5+9A5ff/098I4wGTxEUvI+FirlQ6QLEJwnOiHs9/z3/6f/K6rK+eUeJbDbQqdw8fq7lhDfdYj3RAHdj2yi3anxV3/xA/C9WdtRdiIMvaOPA3p9QacWvoXvcBsTgBApZY2HaWQcRgQ42ZzSdxsrSztOxGHP/uba8lNCNGu+JAsSENRitdvQqdxcsPAO2U9897/7f/Ltf/+X4DvGIYDv8PuBh2pn990OYpjwm554Z8vLr7zCwwcPrIrNfmS4ukbHiBPPS+f30BDMM3O148d/9y1GQjqvQohmGRHf0ffJ8n33nGkYGN57yM04MDjlzgB9TNXEnBBjwKuwu7ji4u9/BFEsxcNZMrR4z9ndO5yfn3Px3gPGcWScRnqFTfD4YDfHBxG22xPzpoRg5yvdFeR9VxK0Yb7ZPJ+ZJzGmjOPphVnRqJ4pZ49AJKTE/RwKkuhP+jufQ58LMKjYjfHePMdOHFOIdoO3c/ghorsrrj64SKFGkT6ms9T1TJPhkqjDpQpfnXq6G6ueMykwjujNRLwY+ODdxyCwFVNcfUiWyM4jkyXYb1zHdD3SOUUZLWcgJYyLc+j1DZeP3iRG5ZTMDwzvxXWoREK0+vB3tpaPIGpVt4pjJ8HE4LMUjp2YRyTzA5+q/YxxQgE/aIIX6BDR3d4U186KL1x8eMnjH79lpbHT3g5xwntlIx0xKNPVDXHYIzFyFScEZVJ49OE1MSalSpW3RfB9RxgnywWJRre8CJ+58wLjuRK9J3aeuy8+xz/5k3/Kr/7mryFnW6tcFSJhnLi5uOZHf/89vvP1b/LW3/8AGaxmvgerlibpfo2sFJByWTQLJwKiq9Usi8CuVLS1prHrYStrlvbyXCN/rQm1Bfer746FFEnmA9Ueu8R7235rgbHOBXyS0rCYm8wFTbKXvlbG2vfWBHZYRkhAe9O6K7xbWAqGrZfnGEzqkM2Ddd6ifLdGwSftS+bbNe84pjgeSMoc4swxRamdZ93qsLM1IV4Snait+f9DFcUWzu0a6z1cCPRH3m2bwRyoQv5SL4XfZKWCvJf5jIhDU1iniDCME5uNyWVm+Da5SUs+jZKFzSyLLhdrY1SQowhX5PNTHjQ5T8RCnGPk8e76ifCEn0PRCCrcPbtr1Xg2nVU2USub51L5UrBKJTER+ZzPOVVaT/4eNBX7yBsEuZB8QBHv5hh17DKkWdsGnwR6VYsxN8abw0RM6M018adxSETMEsld5xlHE2gnHTk9PUFV2e32hGC3f4fJwqw6Z2UGp3GEaHdqEGNSDpK65RzDsC/EL4RA7ztzaQPjOEEQereh7zqiBGKw+vFWNUat9nqMiPj0bGeJq+NA5x1u45kEJiJ974njlEJDNOWwzESn9vIIChpAtbo/JBozEVuDT4w33ZmGE0oyZGvR8s4nQXm2gOTvnXMECUX5y/GS4pPnJnuwEuycn290n2KwC2VE0rqSwmoFoIsmHazYJaqki2hAo+fk5C5Cj0jAtOFcMjXBiA4fO5zaJVoi0EVFhwBM9BnPY0yHwmLSM7MdiUUBO7m8MYaQntsMJlwQrYpLHCdEAl2BjzPhb9zDZCF5KJxg1WxElDCBc5ZnEsdIvLkpMZIxhRluEbaJJ+nuhqDXZtlIypnTSKcWCz9U3kIFJicosdAZIVvKU6lUHJNasnU3KDINKENKsjZhxfILwCUrNTHS73c8/OCnpmyChVem8+E6hWi4p8GkD40RCZFN8rRNwepiITbeoMrw9odJyRdOVNmmczSpmkJh16YzZo9h0DmeVEwAkxCJDy55/OEFHsdGYxKMMQbR2b56DSBWDjCmM5/d4S56Rp0M45wHnZLAs2RkbaxzvntDJN1Qns6I80YffNoXagOBBtRbDkE0gktHYONcYhpzFbiagYWQLVhW9lUkJf/GyCQzW3GFAZlgE6dQbqYGhWCHIohaAnPhgGpVlEIsSlyhJQLRap3iO1dyTAQPcZY1i/ibvLhaeYpQTTfX2oNRpeQzdGEWLK3DRLNshPzWjJ8xomJhFyFb8KMiEQtR6h2oI4gUG4ZzSSCPgBiCiFhYY74zSlCc9NAJ6iJ9KpygouYtjVZS3Hi0Cfl5rhIiW1y6SEuJokQn+JhK6p5v+dXf/S1+90/+MWfP3cN3zs5qCMSbgct3P+Abf/Vl/v4rX2e4vLYCl0n4yPvuNOdhZOEm4wTlzJLpZYJWoQNSIYnmO0psDcmfvFAqbmvzMzPtqT8/Zum/LUevPMc8zdJfPFZENy8nmQiOxM/nz9qLgzMu3eZRWVtH2+/ynVj2J+9VKVOd5Jz8bh32nHlsq4DU47aRA+2c1z6vFY01haxWZNqV13sGWVadeXumbYu/V9oarGaZY5lv4RZKWmNcqDw5x7D0SR6Gts8Wd2uPSpnzkT6e7M2oc3lo1q6zUl3Dl6ScKliVBw+OFEqcvE1E1IESmZgvLs5hgLNSUc9Ey+V9IFacJT/RVqor8/FMqtx44YePHxysda09taIxxcjJySkalXFvCdp2gZNjSrdoi1g8eZxCSk52xWq9SBRPITtWAtcVYEtiphpDk8QsqeLLrHlJNLLpUvK25gvAoml9IZpQ0KUk4e3Wbu+2iwQdPsWaSRKqx2kohFYQ+q5PN3E7yzFJysM0WpiSSwQ6x0pv0jyG3Y4wTfTOxsg5GbYmE+g9pn2TEncA0IgXh3PmWdkPA1wrvfNMITLsBjQENn0P0UodojANQwoNOLyTwqz9zFW+Ko22HOgVy4JL1s98INqkwAX5rMKd2hCyNhG+tjQtiEN1yOu+VJVpGgzeddiadVbYplUJmvND8v4sD3xiqImImUGhJcAsCFVtycmGgWJlWBzYJITXcM3EIyoqsQiwuXJRJorZOoFaGcwaTtmKYcKhKzdD1zCuiV++EM2qWC1r1Wu17xQsyPtnSm/uV1XRlM+kOiuMihkPRGZPlJBunI9VScHKQpfbglnmZ5Lw01rmMtyzhTZf2FjgHQKkc3uwX2l93vsZ1o7F+1qejanCWCwXIiKkykgQg+2X3QQd8akqVgvLBf5y2OZz6RYCRc2wvfN0qR+7ODAnRudqfanalM4GlLLu9P0sgBmTrqEaajxJFndNCF/X91dVojadqybjhC7i/03XNLxx4pbv1esv8GLOeSmwmem6mi6azvZs7cvCspGvlFcWD1DMno0pETKFv6UFmOKbLg7MpMAq1GQl0cbMnQatzqzOl4jl3wuuJcZfw6/gYLRqb1lInkSJvWMSoN/wsc98ij/+83/OKx//KNGnMxUUPwoXH3zI9771Hb7xN3/H9YcPkSHYPSuyTAaeYdzgREXb1sJNWpqbP3vaXLm2LZ7J+1iN09Kj+r02zyH/vE1AfZr5tOs41k/NN+swx9xHG8Z0rL81mC6+L+NCjh7QCla5tXvQCrB1/3U4TKtAwJPLvD4tjFslr13z2t/tHtyWZ3HssxoP1nCnHue2vm57v32+NR7V7y1ya29Rc5+Eo8fGbs/oYl1l3Hl/FYsIGKNFdGSSJOkFM9HMfcZKFrCHk1G3zfxuWm2QcKSqjUq6p+3J7akVjX5r8eJehI2zG66jQiCmG0clhZ+Yi9A7Xzalk1ngDONkiogIpPxZSZc5ZUtvlyx4nesMlGLhNp5ZOPVJ+QjTWBSEEEbiZHdiuCQ1SAqnKVa0YEmn4zRYEg1mgQ7DZBddbXr6rmMcJ0Q8w7Cn63qcI4U+2S2y4gTne1RhmiK9c4T9nk1KCBaw0ARVNp1niCElsAbEQe98us11vrzuZLMpl6Fc39zw8OIB515gigw3N2wgrUOYxpHeW7iRCAyDldA9SBYXKYG6teXGOccQpkU+Sjm4MYdqrIdGsUJMMjLWCgTM79f5KHWYV55z62auhTON4cCdXIhQsehrEeJMM1+Wy7vNOtUK37C0sKSPyJbstqkml2fDFExQsXqsrTAdi1dsyTScc0VIrglZXkcL78VYlRDUEvQMl0yu6jGzMg9zqEANtxJK1xK+pNzkfaznkrTDxbzKnHXJII9ZgGqYZUWnZsoheeZMaTlkNPkMZBgXkTbPSSNTjEwpn6pWRaySnkAqdTqOk1m5JQsKS0EODsvP1s3OxmyDX2PknbOL7RQhqFmrJpRecgJeFpDrfpNVjCUei5Piec3j10JfEa7ThZ5CFpylhJumNy3sLXm2TNhP69BEu6HQi7WW52ZGgEMckgqmqqYszGc2Pa9alKmoFMNTHiD3E1P4gKIQYerMwych0odI9C4pO1rWYOO6ufy6ainbnJl3CNlbXmkqJKVzhb4IgqSS5NE5grdCEnuv3Hv5RX7/z/+Mz/3qr5g32hn8JSr7qxve/PYP+Lt/9xe899Y7SIg4JXlE5pvR6zNfw3I+s7NysabIt4J1SyfLO04W76z1k8eeMUYXtGJNWK9/X1vLk1pLt/KPY33cZmU+oJXoQnFr6dSTFI78TFvwpfo2kSujyWv914a7mu63sGqVofb72+bYttuUu3zAa8NjLUvkd1uvyxoPXlPwWhipUsLX29zNFqZL+KzfQXLs3Rre9ZyPGUdrgxnCwXuH8zlUrDKdu20fbmuSDOTZaNP3G3ZTTAaxWdMoZxkWFcNqPjHj+mxAWx9z/r8nAiPXE4Sn0zOeXtE4vXPHJhYiGiw5UaPV05e0ALPwu2SRotxGnDWwXPa2S3datJVC6svsOlJVFe+ZUnUOL0IU66dzHVGDhWeJMo0THkqZW8XhBfquNwakpiCcbLYpOftkQZQ3Pt0R4h0xRLb9xtZ3csIwjkyjcHK6sdt6U4zdbrdnGAemdNGfV+g780h478m2/2mccL2VMN3tdjjXMUVzT9tt5aZ42QVZFgd/fXPD1c1j/HaD7PZ2y2OIqVypYVLQiRjs3o6MQNM0lcsIVa0EqHdzsnWdWO/Vlb3p0h0pc3lftzhkUB3WLHtXikV9uNYqXmUBuo59rYnIGiOTjEcsiW8hJDEmwQIuLi8sFwWzFsWQQ2yWBKkWissYFeOOysF8siJhScgs+sxN63NQ9W1wD4u+asYfm7/LHCtQ3EZkb1tfTehs3KWiMs8xW3d1QUiNabhZCKSWJm3vAoeXY6qqlUOt8GahALEUZtbeL/ApFsYsZJtgl59wmLAsFU7m94pVilRaNsxmcNVo51rjos9a8TM5RgiTrTukZzNe5fMUYyznJ5cbrOeSfxexW8tzcvICnzXlq6Q8C+dT9aWouKg4Z9X+NFI8PfmejIxHxVuQJPe2YEPeg6w05P9iSOE1CbsXnglJY5qrbIaLzmFjee9ijbM1TlMJF2RGWDYC0czoKMxSFdtTyfRG0pxtguZRnmlT9jCXUo4qiPfcOGWvka0KXRAioVReM6VFy3ytDK035SsLKingMwYL0TVYZlzO89KDWP6o0XKWRBidciMRf++c3/3D3+O3/+gP8Ocn6f4dUyKmm4EH73/AX/3bf8fb3/4B8XLHJvUXxslKQHsLWWhpZW3IqZWN1jBTP7921pa4mteft2ldGF5vh5fBPk1be7Zey5rAZlrm7NlsvT01Laznn2lSPoN1cZma3q6N3fa55pHJ3x8oDUlxTU8AicdW9De/W1errNvaXra/5zN3W9hYC5fFvle8wA5jFc7cwLmF1xoc2nbAX5tnRNbfW8O5Mm9IZ3OFPzf4eqtSBQfrqPnKQnm5pb8WxmtyxdqaaiPBvKfGv82LkN5NY15dX7MPoxlFrONZaRBZ0OWD+YjdwVb+vkXZmNelBBfZR2WSJz8PP4ei8b/63/yvOTs/N2LsXbHedn1XLIrZI5EnnQVXyVndYqxCSZWnaqsUM+MyTdZu7L25vjFvRlZORNhst1xfX6Nq1vBpmuj7vliC+74rlq0s2Drnae+UGIY9Nzd7nBNubnbEdImYT4K3otzc3BCjcrLd2qVwMgtn4hzTOKULCucqSuK8VYcJId3+PSLJ8hvixPXNjjfffLMQAlOkDIZbb8nwY5jsboioTFc7NiFZb9XyXHIcNpXwlpG9VFlRRV1YHJK8N7kErvH8mRAWARNZMCSoDoTMloz8XiihNnb3ST4oa4S3WO116YHJY7QMsvWI5Hm6guPC6ckp/aZnuryyPAWNSDw86PXP8vZCCdD150SQQxpXvsv3d2RhvzAMADli2RJZrCl/X4hmdehrOK3Nr4ZtXca53JrqrMKVSVn1eGntzLiRL5q0PmYrUWZelgxm72ZL+G2CRz3fglscWuDWhIKipEQtl8stGKEk3UGy4rlyT0tSEEKcPXoxiZCKxbdaMt0y5lvUwqamGFCNdMm7mhOr27VlJV8bxaqChDGLap9rXDAPgRRvcUTsPpEk3KLQda6EK4lIUrQSDHNoTQpTncK0oAtLpT57FW3oXCwiJngZrc130cyV8CzUzX4XoVR7E2cJ2HXLq1O1EKslrUn3LEn2qliLjVI4w0hmJQXKTddFaU3wiRoJCJ0qQYXXH7zPj99/my985JOcdHcYNSyYsDReM+/mOSpquXoxh7Wa4j0rG1lfqjzIVYjn2Dl2Eonbnl/+zX/E7/7JH/P8qy/Z+Ul5awwTj95/wNf/+st862tfZ3+zw+9GtqTCJdEURuOt5m2KFd7VdPuYoFfjW21IqAXr+rkZW3VVaGufXRNm14SsY+2YwJVh2npkarpQC3tP09q+6v7qOdZruk3Qz/PM/dZ0p8aJWgGwPpo5yTotbMddo5N5bxfK3RFBvX6vXnNNw9vPVLXkXR7jPbXisYhYWBl7KUCvr09l+fkafh8Ycpi9ocdwqt3n284MrONL/W6maS1MaD4/xuNaWLdrXh2XmbYaXCIhTsVomXmMyx6hdl5J1g6q1OVwsxx5bK25BRft7i1Rep7OpfHUisYPf/yjIujny7WmdEDWwkIyMq0dPCPodnNt7q9cCIgxcu8cvus4Pzvj+vq6XLDX9T2np6fEEHj0+LGFTCWB2ydL/nW6fKsGb5imyrWUiLfOikot9PZ9X6zy4zgSQmCz2bDdbOg3m+KdyUh7fn7OfhgI04Tzns1mY5VYEOI0crrZcufOnVIa+NHFBSebbaoCVLkiscRFiTCEiWkCN450XZ+SaZnDRDKzSIiRrR/AwaHPwkBbRhY/r6G+LNH2rWMOK5j3zSaxjGktCmUl0GTPUhZ26z7WhNL28NdhRDn0qGY8MUb6rmOarNLZ9c0N4ziRrY0uWSXbMdYYR80EjjFIs4of6ScL4awQlPr/KwSwZlI1wZZUgjM/Xyty9fv1GlYZBBRcrshYnnaZG1DuuFkynVDAqMmoLSJ2aZzMfbUwVp3DZA7wR5fzbeG9FlesWHUiTbAplwZFq9fUsbQqLoi8JG1Es9W88mqZQTopH5T3LXSK4sGI0dY+hWCCOEumvAgnaEJWirIsjqDLO3TKjmhO1nXFUxtUixc4hyjV1QTFQYzTAc7WfWo1zxnP8t7X86ecHXHOilUcZAOS7tBZvitiShlyuJ/1/uWWrf8xRtBZgVetwrpssOrNlVAUmY+4Jmtf0GgV4qIyorxz+Zg3rx7xiTgxhIC6uSjF4RkSgluzYlu1P1WHSO3VICni85xqa+SOwGuf+0X++D/4U179hU+ZByOtwYsj7nZ8/6vf5Ot/8Td8+ObbSFC6pHxNknPNUr5Zho8NehCKlMdeo2//w5uw3LnmW5kNQceE2tvofCs4P4mm1Z/XwmE99AHerQjVx9pME5brPtYnzBcA3wb3BT3OoXdNy+8fu+Ct7WcNLguFZoXPtGOtCcJrxkH7uZx2Tc9b+GRZpCi1Dbxa2n9kseVwS4Xva/tYz7/2ONTrb9uaUlz3V4/TKl/1FFuF6FhrlZljyz+meEBl6NR0zQBKjELfd2x6n7zaUuRc51yKLNLZQJNkeIOVEpkVdSfHywYvFA2wIhjA2ebu0TXX7akVDbsd1uJbw2TEMMSwqKNrzHUOFck3epuQZJO1sJ5ZSO77flY+vF/0pQoXFxezppUsb48ePaqemS99qwEyjzsflBCm8nyx6DfIFEPkZrpJ851j/40IRMLlJScnJ5aMjc3ngw8/LGEmYAqPYEml3jturm+4ePy4VJ1xztN7T8CY7jQMSTA3AarrOnRyeFHC5TVdCJbPkUpZFoEBQ3QrWpEsopkjqSYNf/bq1EpBnaOR4VUzSVP4jCiKVAJz6l+pDng0pjuFOQHfOQtBQ+eyfhle9eV9RRDNY2Jwz+V3M82vvSf5vZCIkcaIs7JBtgbvbX6NpwCRFFp1hLHFiFbx5wkTk9CZQkMS4TTBkbIPIQl8koClKYE6UieW5h4TsTdJNoWOaAllmTd2yQhIFkaoPAg1IddU2hmh9qLkz4zRLVgo2Vk6kZLGCtVxSCFuVpkCTQmrIunm4wyrtElawdZ7fBKdDT4zA/CSbyyN9WTSOnPojuHwzDgqeMScwGZzEWASU4gkEcAp5WSpISAxGhwyXhj+2C3RJSQsrTmHCwUNKbTK9t9hXosQIuJn3Mnhht77UkI038oqUPJbDFcPBa2MFFHNWxzUSmF7BR+VvRPMhmI4I+kSSolm5fdCujzJ1huz4cX7BMOwFBTUkv8NX0nCfiwwDeNU5lwXVTCaOs3ejozHkpiZqzArzuvK75YPNIWfqSTr26xMwBxOmJWJ0meY5t8rxp2tcMm+WMLhxqjgHCEq17s919sTOp9ujS8yZSVwKOCXQkHGScG8Hzl/xVi0pFzDVOCgMwUhotx/9SX+g//4z/ncl36NIEBnNFemwMWHD/nW336Ft3/yOg/efo/p8gY/WWEQh6Rytdmr7NOqxCoCVpuYabLRgqWA1ApKNa+slYM2Fn0Bk3rPKmNJ2YMV4eugLYnpwbu3KQCtUero2Lo2wmFf7bt1q0OArfLWejKwyLKv2nvc9l0b4ubP5pymjNzFe1YZ5OpWw6pWJjIfbeFi/2T29Ob307ha7WWrWBTVOuNCziurWMOaoF/WX8+j6uuYAnRsnaysae3ZxZpjxPsq1Ld6b82AuIa/tz132zNrrcW5tefWFNTaaDXjTxbuIEckZN7cec/98ztz/1rRN3uE8kHiAxlGtSlpOYtZIZ6ps874k2XO7dMZNZ5a0fApBjmK4LtEgK0+YuWST8/6biEY+pT/kAGXK4NENUYgSfANcZnUa+/7qizrUnC2A5CIUb4zQmfNNrvy8wbEDGfvEe9RLKZak2Cu1bOZgcVUWjVirqjdzUC/3ZZSkjHGUsKyjD1Z6NJwNRCjlcQ9PT2lS+B2rg5hgM3GbnYU1+HF4/HghCGMhGFkurJEcEnzK+FD6XfvhE3XmSUhhTs4cawRca3mDSwQuiBF8gyJsEgSlySIlYovcRYGRVIYB8I0WKJ69vqAoGLwrW9LnUN6zP1nSo0JMZLujlhUaaoUkzzHKYyEMHF9+YjtxrP3ki4Pm+9aSdtrybFJGTQ4ZKUqW98hHR+U5Imhwg3Jwq4JqSW+G2aFT7I1NuU3pDDDSFwKX9HKO7uUXaxJoXFJCNN63oVuSPl/Ph/ZC5HnEdUUPOelCJ4aTbA0Y1oWLisPBsJIUs5o4r8VhKncRqr2YjkPYaZHBjs341kYQ1Jc3SJfRlFEo5X6TKVrszcoqqBqyc8xKbBF2U9zLIvFwjKdcxZ7r+kOCbW5FdqQjBZTlNkwknIiQmVhNCUzw0sITojRldwMjTHdHG5wVGYlwmWPrLM8r4xJInPssHe+eJfymcv4HJP/oDvpCVeXOI2EYEnhiidO6ZZ7IQmgAhEc6SLJkDEjbYaI3Z2S4DTDLCtzEZW4mGeGi+LJ5CAzs7LD4lOiuhbeJ7kaV8W1YtZ3i7JaspvQ7BojyxOJPid6YGRlFnCysj+TMqMTmvhBVtxzXyFV3RpEOfEnnATP1dUNl5t79JMNp5o8Bt6BmueoE4E4e3411cHOFbwkeRlUI3Z7lBUa8dE89MMQOHn+Dr/zJ3/Eb/7x73HnhedQSZ6/qAyXV/z029/j7/7Nv+fi3Q9gDAVYRTATwYsp42CVkWsheCGYaDYTzIaINk8DOPiZf88GuhIt0K2IA1pRHW2EQXfYb94y3yh/BS+KmFs9vyKk589rHtZ6tMo/ZDmvqtVe/Px9/Xfd3/yu4YHgUmSE4ewcXhiKYtcKvO34reepCI0VtKLOUFnbq7q1isvas9mTXBu9IBkjaoG1mnN+1j60fSId03xn2jFhmbyi3K9U4Wwi5XwuntdWgavCZHXGmqNGwRXly2it0Zs21Kpe51qftdKwNlY9Rv7eCYsbzJ/UZrlnPhNrCk1tcF/iTzK8OkrEjohyerJlgxnwXdpv4wQG+xBDpWfMSogK4GYjxbI5JMmrKlm2sOiB/FmrEN7Wnt6jwVyuNjNU70y4jRJT4qEmJuhKbobGOU5RxG7h3u13KZ7ZmHPJv6gIagZunRC1sDpUrrkWCVoky+9nTbFsqmPRT4xxvg8kCQ6eeY4iYmFbMbLb7cq8c0x+jocHGMehjH1zc8M4jpyenrLdbk0IqypAzQcgouKJajkb0zQSpoGemJ6fY/ChqiIV7XbsmlGsuVFrt6U4wUVXktBq929mPPndDMtSJcp1RSMuSlwF891uV25T3263s1LD8rDnPQ1ql6TlOWflJu9fXm/XzfdudEmxEjFl8frqinEYjLA58yJkpStWc4R04YwqzuXDKKQrrxYMpByqzM4rPpSFNXS2+kgl5xlcgl0Mpw7H7I0oVmAnTD7f/K04L6mSkithL61lBkjKkmNMd1OUePtoykTM9wglYmBx71ath/zPsIRiIMiCo2qlLMzryYsr1cGi3U3QWoNmwi6mmMWkfMR57IlIlFgpU1qtdfYoxUgxSmT1r5I1y3wtOdg+zMqwU7MGl5AzlBApAnTuX/O8Mq5X300KIUKIYvc7aLr4MCXQ5fNfnzFL+F5aJOuz0wp7ZSfE453jZHMC4pkiSLKub8Uh6ojBAOgcdq+HCGMJV0pKSF1usCiqM9wyLOYk64QnNcNQo0XSlA82+l7/pXO0lC5DJNJHlE2vvhJneSjZY1oXAZHUjyajgGiqSBiXMB2nYAphDKX4hnl7NXnehX0MnGzv8InXPsNGHbtRrbRsXjSz+uMUegedd8QppHPtGIfRPFUh4CTvX0ywFlQio3P4jfBLX/wif/af/ke88rFXkU2HRMvrGYeBB+99wHe+8jW++dd/h9tPSDwUdmcASYmvfppW09Ico74Wnrf2fFucoxZy6ufzzwUP4enmt+zs0JhxTJi8bf4LmrgiGGYY1JEOtQxwbKzCk+L8dz5bRfl0y+fr/o+taRZwK4+DLPto3137rqaxreA8C9uQlc66z58ntE6gFDhZe7q2ts9j/n/WFutuPl9T4Fr5JhsbWuUlP1OMc418+KT2JOWvfa5dy9pzFoo5hxQ/zVzyGrxzOE9iXsmwlWSSYkxk9n7msvcH/THLOIWhUq/BVEyUcidejV+1l+tJ7enL2/YbnEvKhMzabd9vbJqyTA7On9mEZ8LQdT2nYgKu9zMDruPU6woeGZnt1vB+0X8d6lMLxLm60X6/L7/XAsGalSRbd7KAXCs+eYw812maSsKsiBRhehiGonSIGPEeBlM49vs9+/2ek5MT+r4vfZyfn1tOR7JOT+PEzeU1U5hwOnLS+XITqsZpEQ42K1CTWcYrWOc11h6EaZqKwmQJp1qE0RaurTI3E+yccDUTsXLze/q973uur6/ZbDZF+ZLkHl54pKp+2/yRmhhkxaMOsatL4276nvvn93jD/YQYAlNQam4QQsXQxeKwTUhS82ZoraCGWVlgtrZHIIRlbGtIwrlLakoJYSNZ7iJ4NS9FZrBoTtJyBFX2GopVFk1lnNO67H49XRBPsAstcS7dTi/lTEY1id5CQ5IEnYTGGBWVWUGUBAstcJ6VKruTbcaj4uMR8g1x5jEqZqcMWygsR0i5FOBy/D9ZgQPSfs/uf1NOaoIY1QRq2xuF+hY4ZniS4K6Ay14y1G4yQpPwbcpCiFIE7xghVPGrxcqEBcZMKuVCJFVBgn2WNacsqNX0LYQKfzL8Ktp4jAEJVh5825+gkzGAXGEuBsOJwoxCoOsSHmbvVwq1yfto21vTRRtFM8jqeUgjNKoZlsrD1XO16hE1w3fG+bqPvN95LuWrKQl6wSBtF/0lw4Bo+XuBD0seyGSEi4AyhgBxwif0kAAupgpyAmebc2QMDGNglLnYiOlbMTFvZVJHJy6VMYcQBvsuRrxkj62iIeC8Xc5JJ7z2C5/kn/+n/4LPfPGX8RvD105tfR++/S7f+9a3+e7Xv8nl+x+yCYKbIurmCxYPBBmNZbFPI4RnPmUGh2n1mTW8a418t41RvE3ZM+DkoM+nEpYa0aQ1otzWVytAlnN35Jk855of1rytHnu2NmfP81JoLHKCBlr1u36uFfxz3/Vn5V4izRDRYvBr130YerX8vVU28ufOyaIoybxvrih6q7RIdVbcmuPfrrWWqW4TOJ9KsWnn8wRFtN6v+jOpPlt7vq06+TRzbRWBspe3LOuY8pjXWZ+32vD6pLnV9NxK6mdcrQ1xmjzhaS9r0l6MP7kISnNZZk1vE32PWcme0cLecy53+MT21IqGKRl5Fo6um4XFeRG26Fkwag+yWYOc63BExGlFJJe1itcOVO3eravptBp9/nd2drbQZOuNrQ9wEVg3m0WoUD23mjjld7KQlOdi8du5TJ6UPrJ7Oj/T9xYqtdvtCCFw9+5dRIRhGhn3Y1I0RjqJnDqXLnyLxZvUWmq8W16MN+/ZYe3y/FwI6QZvZpjUORAwV5TJfZhHYVYoaqWgVvgynIZhQETSeqHG+LrfGEMp2dYmma1ZJfJcs8LWdR3b7bbA36tjChNTjFk0KHCKGlNcPkAoxCmhblmPzBOd58lsGVh434J5IuZzMFd82EfILgJVYyhekxVRzQsRVdMFkjbeECa6OOdgIHOYg4igrrOSq4BotvqTQj0styUn9ipUhRFSUnPMyp25W6cQiC4WpWEmV1lBMotuRaNKHk7NsBekVcB13twCeRlpfYLggxSFNYdIlRcLQa3DJcySP8O4sQhrsuEIwGxpc05QnRbKQAym9IQYGUTLnhrdsrk4MU/hNE2MYcKp4jRZ25MVKc8t/xzHsQCoNQa0Z7E2AsRoJaqnYGGXTrVUlJs0EDXgXZfij01Q6TB89ip4cUWZdCkv44D1J6G9CPFVPsUy6VoQlcUlfgvljzkvJq9DRIrgmfetMLNM/4uymvc3wSLBNBtMCnwAopR1CLLET2f8xTugSwYhrCx3nEYLgVJl46y+mFNloxAISV+1/uKY+u88qoEpzt7UTedx3uNIgrY3Y5B0HTi48/x9/uTP/4wv/eHv0p1vib0gXtBhYtpPfO/LX+Prf/t3fPjOuzAGNlGsIl6MdhG7P7RO19bhp1Ey6u9rT3BLS9dajYu3JdvW85tfZtVKujbGgpfnfay+O6aA14pAK6i1BrX8XW3wqr2Ia0rK2hwN/im0u4muyN/n+ee+WjmkhlmrSC2rziWIJJpYr6mFQ8sX63/1/PKzMepBbiZQyjjXgnrZ29poRJJRtTrD1Xrb/eEJOFrDJL/beliW657XU8NkzUt1TOFdk/NyH+1cWqF/bb2Hc1yG860pme3v9bNr82ufreemFbxEmC+0jcucDgurzeVwk4KgczjazF8VzdUybVZl/wULM3Z20Z3RaJKxWNXGXlnXsfbUisZMVWrAy8yYXSZ2sTqgGXPzJVAzkEQ84qyf2nNwjPjUn7UHrHWHttp23UeNsCLCMFgeRd/3C+t6/VyNoHV4T30nhaoWb4jI8nCP41gExVxvP0arvT+OIx9++GG5O0FDtMpTYkIPImjMN9wuD14hFhpL6EPtGagJXVYMauJZt7XDmity1fdf5PWtEfF67zJByMrKZrsp88vzyDBF1Zh8VTkL4ORkvutkv9+XkK5WERLnePjwASFMjNNEGILF+qfQD+ecCQmpxGauo98qZiJCVJuDQvL6zMHqgTmsIL8fktDaWjcy84gCsfa6xVQsQCiKUcZX71OlMlUmlwoX5P0mK5KSiIMJbBnXwhQSg6RcdJTHizkcy1neUlGkZLBkVifsw2gnVeZzPjMjSyYWmWEyJctpETklu2hnk4jEGa/yzekiFtZEoMrhqaoNSVacjLYYjlhRhRCyMmBC5rwXeR7JUp0EYefsHgNNxes1PVxyt6IJ3AenQSPTGNPdNQEXA5Z0rfQC3rFQ7hfljCvlKAt+i1yMOnSTfJ4jU5wQB6fbjvvnZzze3eDUWeims9A+l4R4SbCV5LWRdKu4CJaxscLzrbAFhUEpsKgSVXY908n5wyUjnJ/JZyOpeKjLOWuV4SFdPOmLZyomfJTFpZrWX6OsqjAfrFrgEPCxXEIl0pU8PlOuHV0QJEYmgcmbXrKJllOUlYacx5Y90OKyIhrKvUvmmfNMKrjeEQTcScev/Pqv8if//E+5/8LzsOnwznIr4s3A2z/+KV/+i7/g7Z+8QbjaWfhktEIU0UHsXVGuMnwXAkuzd2t0qv459yGM4xwNsCZkr/Xj3FygoxVo2/1fbE/T11Kg/vnCU9o5Hft8TbhuDVhZiT8mA7T95PmWZ45qUCbLWLXIWZ5oIx4WvLkOL6q+S3aExOcP8wfqObb7fEwYXfJhFry+hWs2ctRh43Kw8qXm0cpepc+fY49vw4ljilb9dwvfNVmmfQeWURpr72b41XJbjRNrCku77mPwaeff/r7kBcv1t563Fg4ANzfXxXBmhXGcFQ1hptlUc8vnIsRUckLElAjVig9oiYxQzd7q9H+NhzzzCe3nUDRmy2LWyo3454VnRJf0bJM4s1AckoLSxBDWxLZVNGqLOSwJRh1rWm/A2iHP79ab+ejRI1588cWj7qw1LbzNC8nPZM+F9/PGZiWmCJOJKOXE0Ln8rAPn8OKJ0eJ4DcoUJMhj156XnIXZEs46hyV/duxgrr1fhMRmn3IIVHtwW5iDKVnjONL1XblALK+7lPITu9Rws9nMYyRmkV37eX9r2Jef4vBeOD09Y7q4wdKFKmE8JQbHlFScYmFALWSkZhg1blFVfPG+s3CNuolZAHIlptxCxWRFHLFKzM9KqqrSdx2xW+5xIQ7OwrFcRRzy7/Z3xmvAW+IyKM515CT3ltGY18UXgcy5uUzzWdwUpU3q9aX9ydbwci5SnL0e8UIiZnwo3pFqHpbHMJeVrv9FLEHXyhbX5x0E86rmz7KBIltxlsp3rgwm+FylybQrtFy8lhXChLupypwpeCmXJ4V/dU7oMYu0U1O8YpRyfosFNZ2BaZoYxxEROTjnNTzK+iyLj23f8ZmPf5SL6xurniTKRlyqTMYBjYrB8gWcc7OYICw8ADVO5/2ILGlBsWklb0aBfUsuUjnXmT66fAzInitFF30UxUJmI9jMF+Y677aWSqhqFY+CWoLz6woVwIhaiFKEkUjwll/jwxwGIFm5SPhoXj8rIpHh57sOVInOM7qeySkf+8VP8Xv/7I959ZOvEVyETWfK0KQ8+MkbfP8b3+Irf/PXXF9fsfEbXDDjkXPe9CbvGEVgCiXU8kAQkeXSbhPMaoNSCHHx95qAstZHK/ys8cwyt/x78/fBHj2l8FnP82nfaQWxuux4/r5WdG4T5OvnS9+J1q2tQ5Lu2+bAHBMED5SEWD9bnUk9FEhbpWq1vxV5yD6bZbDFvBYy29JoGWMsRQjaVuNUPZbB6+fb6wM+u7JemQn2qiD+JLzO/ddj1DJiLU/W0QJrONhGtpR1Z95fPVfDql5bO68lP1zKpccUq9qTZI8kPpgqwk77PaiaEVANAwQW9+4AUOhslokOcd1kTTOIROb8u2Li+/nsB0+vaMwItp4wltvaZq3FzIEgYmVgQ8ylAn1iRorI4ebU/a9pg7BUSNpyuYdzgO12y6uvvFLWZYER6WKkaKEttVJRr2cJFxbj1xYi53yBXX7UuzmvYbvJCdNpDeKI6qx85X7AYTHxpOfrOxWycOrcfGjauUmywmgpjZn1VVkefGwKJuympHDnk/Ux1fhOumRWlnLOxbGL98phDjHdzaElOSlil2FN48R887F5Cby35NcYR5xzpRTxAtYKEavO9dy95/j4Rz/KB2PEBTWLEfOehxisGpOby7YWQR0tXg+lSUaXWYC33GuTlmKGZS2MY4JUHQdqAn5DnN2JeS6SJ8Tml/pzKQxGWVh8c4ldTdaEHGpll9C5IsRpTNV4qtLMhlMCEvGdn63wSbFAsVK0kkP+mtj+JHjlOOJpmoqlOocZ1J6mDI9iLBDDaVcpfFMMwIYcE23wSrkwFTMpylcB8tLDONOWfK5cYdzO2157l5QNkUoYS3CJlQBcC+ZOiI5ynZGg9EnZcwhxqmJb1YRkl4plDPv9bAhIz9idQZWFNeNdArBzgsPCI0/6npPOM4wDAWWDQzR5ExIDzqEWsfflPMKsDFr52IqGVoxR82Jzsndad3auZ4WlXF4p9smck5F0z3SfiX2X7pXwmY6nkMV0Dm3NCuXMpPVoFeblmDfAZjDTG6Tsq6J0OpfelbJD1tPWeUvcDopXYUp75kSZ7DCkaEZ7N5fNdZhyIs48c50zfjA6x/2Pvsjv/OM/5FOf/yyy6VAviHj219c8fPs9vvvlr/H4jbd58Na76H7Pibmn8WIVBCOa+k1Ks5NScS6fMTSz8YyMmaYshU3bzkMhzYxV/oD25udbobRupcjDyphPYw2uP6tlgAOe1Ozw2lraNRaFyrlEH2c+Y56hw0sHa6HvmALT8u3y+coc8zet4WQNDmtrsa01pbbgfma4CadFDqM2asG65a+3NklnNZ+LWE4ZypJ21rgzVwypqG4jDNfrnflfxQBrGNRTWpnzoSLX9FeNU/Y8xqOwbodYe+8YPOt+67VZuCxl75PwYGeYJVyOKRlLRTHTv/wvv7+OW/N7c7+zsbBDcQwxsJ+mpDNoOWgikq4XyAr3nLNqMlfmUbPyIWC5f2ktIcsRktmWWC2RZq9va09f3raqsFQTpVpLbQ9dLZjXWmF9qGOMpZpHWaiLiMz3c9QW7LyRa8RtTdCt55N/1u5CTYRqfqcao/LK1AhUJz/nflpBO1s4SRarvt/MISuaYvNTrX/nzHqWhT8FxHm8V9gPxfOzuOiKGqmXjKl2G5MIWgipDGQhcHmNQIrnzMJkhkPn+5lJpAo9zs2ehfpffi5bmGslr3hxUj7FNI72bEjhZD55OKY6JC95GWS2PBaGk4QmgiU+jxpxnUfHgTvbTYpzr2JsJQngflYEazwoOAaMUa3CT9ors7gCKUk8M4iua8XfhOsoUWalMQpmrWYOvcsbM9/RAkGMkboOFAdBi/KIagr3AhGf+rSQs4RiZa9zkJ3IvJ9lH5yAmEJDKWGcFItCMOfzomrCZoyWY6Q5sT8piy6V7hXA+RURIo+tIEQIifCpeWpExMoe55CVaApWVvalwD4LvA5kLjXrcGiiHVZhTE19UxPqfGLkImoCnyjohMtCMZmwZlGVuQwvER8UT+VpzbHBZoqYBTBxJUQthmXoEOXMzUxQKvpTaI1mr4UiTHiNdBoSnGZlys5sQhoUn+efQZ9/DYdMQFUX97hqgm1L38h4F0OCUCpTvqCHJAVgDp/CWdqXJBzTqFYefBFGY0wwFzEozDbjYs2kyedjfrYozqTb5QuTLiwylfw1b5Ag+NSlJqVa05oKyMQlRcSnVB+PdsJehO2dO/zW7/82n/2932Rzfop0dleKV7h68Ijvfe3rvPvTn/H2z94g3OwJ4x6v0Gna/3wPAQl9Ufok9Imb77gplWG0QLO0mte1gvjMDx3eH3qt1wTEFieOCctrCkP5OzOWlXfafheKxDERvlE22t9john5szpHLuec1bQ897kmm6zJDEv4HAqxJQyLW6r4VH218omTLnleWmt8UsSExfN5He286+IuLdwOzjEw5+rVaz6igKb1zUpQOucNjtTwKML7IThWWw2XY0pGUYhq3vwUOG3rXMK9fudJSlotz5Q+oVRygoo/NPhdK4TteO26Cy1jhmVdXOdwfrMhrswpnfkowsOLS8IYkVSxsRgxUURhilp4HYD4lOcMZnRBsg27KB5U58o+T+GxUML+fg494+dJBhe6zuMqi9QsYNbCZr2ZifA7c+LMBGDuN2v4+Z08+TVBthUOc9+166t1aeb36+/zRjo335zYKhRlHF32Vbc14tX+vjYXqhyFtiKWWZ4F1ZCspiwuNsvKRm35sFK4y/yGpRKy/KzMTw4PSVEYUJzzZZxSrapiZBn24zgWITorGLVHJ1fVUlX2+33JZRnHkb7vDyr3LCxnHO5B/s57zxSzcma5D5vNhn1IuRtaEQ1v6kDLCOo9jTGVq2XOHyh7YhtU8h0y1hYhKd+dUO1hhnGXKkM4J1kLSNb99L6IXQCXFSixRGpRGNtbVqv8ApGc7DwTIOcpShqYpyJN3mxbSQg/TF6s4TArtK13Ju9x3rN807WIVEnn817VsF07w4fGgST65zNKJUOny5hYCV+kwskWV5KBGhGh8x5NBpN5Dku8MmgIzq8bNdq1tefK+fVQzpqWtbka+ZmD8EatLJEVzHKr88TKXFZCJOuzVcZLfa/NYwnfGSpt6NYMgyXMs9DiRJDkjZyF1YRtFb0t4zdGqLrV47WhercJEfmTdLQQpSgfqAmOVo1HoHMMXognHZ/79S/y2//kj7j7wn2CM/xzwO7imm9/+St868tfgWHi+uIilzCzM4GCMw+eT2e+xtU1AeqYgNIKwsd4iwmsyz3OBr6a/7V4Xj/3pLY8W7mk5lJgmuWAef4H7YhUWq+9hUGNJ0t6IWXd+bP8ThvGW/O6ti3gnOj12phPaq0c0QrP7RzL/Kop1WMe27NaTllTLm+jVSZYxgUtEBGOYlaDg7WssKbcLMas6Ndav207pgSsPdOusb5D7VZFZmXcGsfq50w3PD6ntbU/Da6s0dC2vxq2x9aT84v77Yau7yjKIYklijCQy1Ibb2/PRIyW/5cvT3XOWQhdsCJERj8yLbHLfQMmqx/f3WV7akWj63waNG/IoQYotRa8+JkJ6goTkNxPZelVSlhKfaBuZe6VpTq3/F1tYW+/V/ul/J2Jcn6+JtrHxs3IXSsMB4c7C06SbYCU6lMLBipJG51MNxexC9hCDLQhay1CiswhW4Xh3HKohDnErGZKMdp9HjUcsnBUC0gt7FsBaDFW9X0uA5wriI3Jw9Guxf5eCjFlDYmxOucQtdjq66sr4s3N4vbvlrkviEgrXAGC3bSMpL2I+WI8BRW8LC+AcrIkXu3eW3gHRakrLKc6P5mYibM7RYiKiSuHDMk5xxTDARMtsCqWCz0kBDLf/VDvYS1s1mcmwybnGKzl7fh0x0WOr88eOVQXoVui0OWE4EaIWKxR53jQ9gy1sFgIALaIeV8SA67xd5H42Agpt53d1luJLuFV40N+tzVs1M/Ufa2N1wqltzHGuZz2oTBStxbvW6GhjJf2LrdaGF47R23/7fzqPtaEn1aYamnIsfXbTe1LZlx7lldhgOGhy4qGMbGSizM5IfSOV3/p0/z2P/tjPvLpTzA5GLxLhQEiH7z1Ll/9i7/m7R/9hPHRJUyBOOytwAOCOE90pmhQnd8aL9f25jbh5OkEmfnujcV+Nud6DUe6ShE8ELRUD4xbZR2NcAxz2OihIeNJ8z/kZ/VnvqEbZdWZvnLIm+t+2nCbzOfyGMs1p+IZsjSsle+za/uWlucxGywP5Z8Z9+dQmOXncvBZ/W4bVXHs/C/pDQsFH5b8u+5hDrNcP/s13qydf5gVrGPrWJsrMhsq6vWthe7VsKIyetdzrvcit/bMFYG7irwpz1Xj3HaOjskcbWvnVY+V53Ebv6vn4Jzj/gvP87v/9B+zPT1hs9kY7BIcnfd02xNcirDJ97uBEFN1lXqMkJULVeI0sR/2qYCNN4OJd/h+g/guHYF/YEUjxrk+t2rekLkGvi283oDKZIRDJMeiHbE6LRJSHFEPQ6dsrEPLSY0cdd+tZrsm/Kuamz/HT2dCma302VXW5mm0yFGX282Ce/YCLA5rNX5ej6qWalS5Dr+qphj6+V6QmkXVd42sza8cTubbkDPsMqzyBXo18mahOu9phnEt0NQhHy08Wwt4S9DqPutn1nJLbC5zPsqiP63g4GC335e/Jd2aXLuZ1whFLaDMglZMIQ6ClWJWSBd0uXxFJilHIvGOWlDPY5UxijNTyk3DRgiYDw65H/NJ2rznZL7s0VhUNWnGofQZF90uCEHCqzrHJysHU5yrt+XPa6WkZf5FiE5dLxiqUkLwcunURShdJaTUOFPGWCHYNnbNfurCCyWA6ICRZVjmM90qBLmwxXoe2RqM5+drD03BYWXhIc2tfr7uu8XBdty1PLPW0l8/X+/FmqX6mGCw6L+B/8IL0ozVrqX9vqUTx/Cpfrb+u6Zzi+dCJFawP9iHarzl35LCzUBFiJ1j8sIkyr1XXuL3/vmf8qnP/xJse9h4RJVOHMOjS77ztW/wva99kwc/e5stjn6ysz2EiIhZFi2l3LyGdpGkO1hbW3mvxqljikj++TR78LThUy1/PIYXrYB2bPy1MVr6Lqn0Zv39bby9rGlF0M6wXJtre26fBnbz81IMQWsREibIrC5/Med2rBoHln3Pnuk1L0zdWhypeWtNT2peX8+njkCp4VjWXwvqHCoKB7BgScfqddZ91HvbwugAbqoguVT5EnZr+FXTunAkib+mYS1NaNewdgbyM2v0tIVPS/Pqz9aUnTXFou6z3tOWT3Vdxysf+wj/4n/yL4kpLy8rGZLWnYuWWn9qURJihWB8kjNiqlJV5BNRM5jYTFCt5GzF7kDSHJL15PZzJIMvE7qIcxhG8+DybxE0hnQhUxYW1ty32UV/yIiPHdqWqSyncWjVaFsR0lPVkVq4mqbpwNtRI1V+ds3K2x6oVlBuGUEer+u6Um7UOZfSAgTxrgiXtcei9CGW75AROSPkmkUwvw9YKEBFmMv6Ugxx64KvrbRrwke7zvaA1MQzj1ULEi0jiXG+rbvFgxgjEix0JyzGj4QAnuXN5u2et3gwz1GXh1WMVFpu3Zw0b0qJppj8+RwcrtsUWfF28WK1ZYbpGXdQu+m4fJa08tQW8fwi6Rbk2CicNnc5ut5DIm17UN87cVhFbA1eho+zUiDMeKOqJYyqhNNpJciWIJblPCxW+RAPjhHhhSKZxqv7yng6x3LHIpzYOTBPan3zfCv4AKV6VPlOZ4ac51H2O0Rwh8ymFSrr3+uz0yoCawLTsfDQtv9j7ZgQs/bcMYVg7f1j56wVnlo6etuZrL9bCI0N/bmNR7RzVBEro+wduw7k3gm/+Y//gF//0pfY3rtL9Fj/U2QzRV7//vf58r//S9574y3C1Y5eBURxviOEie12W11MKlZYIcXBZ49ibXhq51sLYbVBZw3Gt7X6/KpqCaethfHbhOy1/lp+VebNbIzKn9f91J6Nxd4jB8+3e31sPjWfzX3XeZC3vdPCu11nbmYsUERmz1gbypvLKrfvtmd3sRadY94PBNFG7oHZSFYLqLWA3PLU+vkiv6wIqnCLVV4p/HZNk2r3p75NvqWZRQ5p5IH8zNo5KPMRytmp19Tyu/bdFmsWNJulotDSnqPnzJj9z3Vu1lpN29f6qOWrFs71+avzg4FyR9vklEk0mTlypI4VO9GgizvYxHludjt8dGxTtIJUil2GvV3orIWvOhGiaDHUICCHdpHV9vTlbesqUDprnM419ZobjS0LiU6XglgNSADXhErl+uktQYKlJSYDT5dy2eJw1Qi2WEIWYHU579qDMsXQHHKlLh/axlqvxV7XRMEnIlALQrXgThbgBOqqKhrV4varg3Gb8NIenBlOS829JlYLT4Usk7lruNR9t6Ebea15TfmuiEyQgMIA19yUrRWmzuFp1yNOIBhj6Pu+hFPBoVJXE+wWPrMA6lDN1nXKP6zHKixpScSaAmlLvBYxwTRbWtIeNy+gGhHv8Q5Ercyx6pJ5Ffiw9ECR9ZJ5gDLWYp0rMJy/yef58G6LNdjnAbSyTvrkDRMopYyBKp8knato6JXfXDDQFTiWs8x8Ttv4YO8NDrWXIf9TXd4+vxTWmzsMFsJp2pdqnKxo1BOt98dKHa+fz2PMrD6PrbXy52FmT9tauEIV3sTtVqoavre1Y0LjGm28TZhuaVPBo6RU5z4X57GlfczbJc6UjKBK6OAXv/Rr/Naf/wl3X3kRXCo9C3RBefTWu3z3L/+OH3/n77m+ukb3I73CpuvAO4Y44XuPi7MXKFOJWOXMtQJOK3Tk+T4Jpk9qa4pgCXFslI0Mx1Ji/EhrhbXqmxUyVtGCysi14Iluyf/bvVrDTRuNQjdrup55/zF4HBP81/gYZPpnYW813yhzERY86ZgAehDKpEpddKZukcq4xTrMc59t/1mhVNUSimz0cC6jX/eR17YWAWJihxRjT1rhwfpamNRW9va7WsloeXLb52LNyYZVzzO/u+bREZHFdQn19y0cb6M3h+/PJWzXz8E8/3ZOa8+swac+I3U/9TlZC+3NvHocBhgnfJciJ7IymXhm9FIU/DG5NzYnW5NNcq0ftRLckIz+qvgKd7x3Fs4fI9551JEKoDwdHJ9a0di4fq4tr+kyDzGVpu/SYTeFOR38rGTMjCzGueqSE49zPmlNoDnhWRwuVS9JjxLCbMWPiVi5LPSJA7okaIQ03mxNUrUqMOTbbsmMZ7a+5jm2BMKI8Sbli1iJRBNaqtARmWvpZ6Spw4fqZ1SV6FwJ4YgxcnZ2VsHHbsgW5/CuQ0KEONilYULJa2hvgJWkddcHodZ8o8WykMuLalp/mILVis+CaTnAWohUrWSIzDkgNZFaCAFicYFFqINU2vPQUpxbbWlumXCGyxqDCAIuQDcZwqsKfYggMYW85ToJmvIeZitJtuJnGOWbruNK2Eteb1Ts8kSRRATtPgXvvFXXyQpDUhRLPwm/S6yjmY6MhKdkUQ2kcg5z3kcWvQ2OVdnWYvEhzSUW75sRmtkjU2RGnStjpR0uPKSrzqHhtZSQIkTIKd6qmipXZQX4UNCr1cKpsuDlnchTKBW3NMXbi1RezRnmmr5TjAA60hlVy6XJOEcWnpL3z/tcchdgzjHJqqJPgnWu9BZjIAYQ/MIqXM+jVE+qGHUp1FApJ6XkIWlP83nhcG21gFG3/F1+R6p/i9bMs513/TP/vipklIGzwKsz7PP+ViasDPNZMDi0DtY0qqypmc/s5U6DFwShKBIZDpI+jyGmcr9WDhmZvb5g50bUqk25/IFzBFW879gReP4zH+d3/oN/xid+5bMEl9bnTWkYH13x7k9+xl//63/Dh2++g4tK2O3mC/68szGyclaF32nM5b67RZ5hu7droXI13Oq/2z7W8SUL8wmulYdkUYWwarNyPwt3CKnweRKoC+JJ/aT9Xk3jYI7J4JHPx0JpqASlej1rwnX5KUWwOBA612h1/fsa32lhvQzrTX9XvNKetTW5dN6TCbA5c43hNeO3VAJ8hTPWxQzXmvfVc2sF+0J/KkWyhkt+v1UC5jWu04sgdiYtSngh0B3F19b4UOhqQ0dv25P2uRhnXl0/d5shxn5fCvOtLHFbP+1YZb7pfy7js42ywI28hvpnC6d6Pq0CVfPQY4pK5pHkcdMdGPubHTEKPnqmYaDznmEc2Ww2JlOJMCWZc5OSwsXNyoX3nckMITKFia7r0SRPFT7kOnQKXD68NIPopufO3bu3mKSW7emTwUWIOPCOqHbD8OLwK0UjygRPVcFZcsnMiJNQkFWFzIxcRo50syEUS2jnct6A0vWpBKHaJWrgQRPzrJedBDZ1njBGlIB4m2MWgDWHc5XNN8t7TO5Yl0I+THikuBXtApNglmcOCViLcHVIlZNZQakt+iJCNpQoWGnZcSROAReCMcxkgWoJbN93hOQ5yOMUpM7zSHJlFsRiFFRNeHb13tjEF+EmBaS6DM0qa8qfVQnew34/w6IhnFmpWOBXt0TF4iVp3OL1YQyi9Dg6FfZjAOc4dR2j7hnjhLC0qsFMROe+ZuZS15JebxaBXRinmCcOsoJgS52nW8U9pnHzd5mIJzWoEqpTCc4QF8wsKzD5GREpN4HWMM5lb0sFKE3rdEsGd2A5yYK6y1ZjiCwJtpNqTZps3y6FHTpX1pLX41OyoOUd6UIxqXHYAebiCAVPC8TTWkyhyFWoksKhihMtd4povQbSeFnwEqk3hqw4CLMi452Nke0/IrM7PgvdWbBXSYoSGV1mQQMS7WIe+0AYqvZ8sQ9Vy3SqZkj58xnD5nfr0uO18FT3XQv/ayFNqrkEbmJ+lWUXsaTc+gwWQaH873hrGbAmHHLl41Zwm+eQF6uF0VeFNYQU2ligYV5qTeex6xiIROfZ3jnnd/7J7/PLf/jb+LunTCJsxeMRhus9b3zvR/zgK9/gre/9iP3lNSow5AseUaTrmPIcytmYaWEIgT6H36aQu9rD2woUazhQ09x2z2ve0gpZ2UhSP9uGvx54VhJcszJR8N3+LJePaoPfLLltu9HFqJN/b8/e07QDBaHCvRr/1hTmGr55/fnzxfqrPuZ/bmk7yBZiyXDOBqRcLETKM2UuauEo5e4cIKf4KRTjjTBXS8qt5bnHFKQ6PK3+7hhsMj2rC7Us4C2YpTqHfmZjUCW85/fafajnulA6qrHXPLyra2Metx2vnXe7v+1n7VgtXrTft+cMqoIvFU2fxYT5uXzGDpUfFn/fppDUnqp6b2Os5OLCF0xOePjhA/5v/+X/hWEaOT8/59VXXy05xvfu3WOKwQzhiVdfXV1xc3PDNAUcc4RN3/eMw2BKa+ehs3DvzjnOtqeQZI8xTOzHgbv37jEOA//y136FJ7WnVjQmmQqz9yh9561UZDqAxVoogvQe1OLnVQQk3bBaAdmLIBrM0pwNJ0nIiWEqVkcRe++k6+YLo1LyZ754BMBtujKXvDFZaFQNTNNAiBNIVwmX4HyHxHQJV1JCphBNSAojfZKHxxDYbLaM6cbiqBCT0N8Sg4wcORa8FtBbRaFFPEtoSiFWMcWhJ/JUWy/qAzFNobgNa4bSxjPWwkUWWOtjUCs/XbrXI1sm6jwNmG/3zvHrAMM4st/tyhxzVa261QeqJYY1M84tVkx8lSilA+98KreYmZrOz9WEL4RADPO4fd8Xb0a7j21rhbS55O/SLX4gCKoeMHl71iw3benJYkXIeEGyoCThSZhlAw5wqJK3WBK2Gm4LGDYMuQ2Fc+JKXHLbX31b+IJoMyumLeOr8b1lVvPq5lYT8PxcG8den6V6/rWAUX+eYZ77q/E1f1bj6CrTXhEU6/a0uLTWjsEp/51bNvhknMzfH4vLr62PtaLRCjcZxmvz+nlbPfe6mQAbqW/3WGP0q7ASQUXK7bd1+GKnphRFgdALNxKJ2w2f+/Uv8nt/9iecv/wCgzfv8lY8ejPy5utv8MPv/j3f/9q3uH7/Adt8D0/y4NVnd3kZqwDLMNNQ8YUaBvXa2v18GhyqBY81nDSvhhwIn5lW18LL0wr7P89+L/fn6fu47QwUXDwS+tW+v8Zvjs1h7VlNMkY7/zVeXdPM+pl2n4GiqD1pze28boNNKwfcttY1gfdQSZNZkG3och110N4jVo+Zn1kLhYVD/vE0raUfa+8XgVyXnrbb3mnbOkyevi1yeXSpyN5WQa8e/9jnNU/Nf2fZzCk8/tnbhGnicYi8/rVv27Mx0vU97nQLWOXYru/ZbDacn51zstny4dvvJNnb8fo77/DwwYOiCE/J8I6me6hUOdlumaYJv+k5Oz3Fdx3/8n/5v3gibJ4+GVwsNosYIEa6rmfrLawlOo90HaAM494s/aIQI9MU6fquJK/OgAs4h13WlUQpu3zLcX1xwUnXcXp6it2YiykKYWLTb+hweO/YTxPjMBFVOT09JeIYx8AwDOzT7bwzUQ9MYSSEwJ07dxjH0RK/R8em2yDe0/cGjpOTHhEL9tCwZz8MdB72+2tudgNusy2Hqa3+BEuEq4l6q/Hnf/OhTrefMpe7y+54ScLzGjKuMbRWyGs1ZVVF5bCyEHAghNUx9FnZ2O12jKPBs+97O+jVoaoFmSKQV8JQVmTqcWthKbeFK5uK6NsLZb5d3zOFkDxjEIMiLJPlsnKw9Ab1xRVdw/M2hlULPoXhiVudf1YJavgt92wpcJRYTeeWaVFUrvOQk+TXQmVmQb1lWC0hrd+/zXMVZd6bhTVMcxGHdSZXr7nFp5Z5z8T00IKXyyi2Vqt2j+p+a69hu4etoLK2N62A165xjWkcU0bWmPFt79Xvr817QWsSHcpwqsds96JWKtZyBp6GobdwmR8+eHT13Xoc1+L4UwqMmXY5LJzBGQc25SN9FhBGD/tOeOHTn+R3//xP+MQv/gKhE4Z0gWOvQnx4yQ+/8R2+9ld/y4fvvw9joA+QAxdDCpXsZJm7VBsO2tr0xcjlZgvkWrjawujTeJ/WYNHykUP4Qj777ft1pavFHpMs2Q0dXhOYju3JwRwrS+9xYf7JbeGZb95Z9lvMLkdbDdP2Z/2MiCRz9eGca/pV/575WOZzmffVNKu+9C2/l8d8Gg/Gbcpo/dwxGtS2dSUNSnz/kdYq0DUO15c657EzN1qTgY4J9LJibGrXmFu9NzHmoL91HF6DxW24fYxezw8dKpDH5nxbP23+Rc2fFu9UuFEblcZh4OrhIz54771qTWmCIsa/8z4xG92sML2Vpt9uNwzDWAzHvrOKe6itcIx2hcDNfgciDDvh5tGjpz7LT61oPHj4gLt37nL/uefY9ht6Z26Vm+sd+2Gi73v2+xuub65xDq6uLtkPe/b7kdOTU+7evWvCXro9Vwl4D5dX1+zHgdOTc3Ad5+d3uXN2xumm5+TkJN3fYSW5LKQkcPH4AlB2u10ad8fjxx+CdAQ1q9I4DFxeXVZej0CIge1mw9XlBZvNhqurK05Pz9huzzg/u8PJSWLW+OTyVNQ7/GbDww8f8ODRBX2/5c5mW9z2a0iyCAupDl4RcpmrcsDsHYhq3gulK7F4QBE6s2P7wCoJBYFyCFJ9SGqhPr/vnF/cUFwTPucsvn2fSsZmIgJWgWcYBpxzxROQL+CLsrxzoFUgpiYxrW61EDsrh1Vsf2qLRHJVVMD3Hadnp1AEGI/EgKiUueZ5uhTi4/x68n+2FNR7WvahIvoHZUdXmEiMsRCjdQI371vLzIrKUP1Ned4O/1r8bT2no4S8EfLrtdU4MhO8Q2vs3NfcZytQ5TNQK5w1XGvBt+6jHaOGSxaW6osua5ivvZP7bgWXFk+zu3mNKbaf1f/qsVuB8tge5L7WFKF6zmvnZAHbal71uO3abptTu/f1sy1cW0VmsU9H1lvD6cBzWMkUt8Gqbs45KwCnglOhc8IUo122FyyEMnaOk5fu8/t/8kd89ku/gW4c6j2d2B0aw6Mr3v/Z23zv777OWz/8CbvLKzqNxClVHUqGk4zg2cvbWnZByRWKMu0osKn2pfYyt3vTCn1reLomeLR0Q5KAn+l37jP3n8dvQ7mysFQLxsc8yPXvazStzKv67EnvtuegbSJSBJ72HKYnFrrB0wiWLZwP6ODK80/DC9pnjwmsa+doAb+VMeGQ5re8ql1zO34OExWRZQXKhk7URuEWD+sxatxdC8U8Jmgfg2uZT5KEWnis0cjcTB5a4km7r7eFN7Vzb3lBHqP0pUujYkt76/5rGfDYmlo4HITCV+/V/DZqZDfuGHU6MCQQwaniZc5R1hjRMDGqEpKhc389lHf7rmfSYNAXk1+is39GYrTINS0MjrWnVjSEjt1u5CeP3sB7z6bf4DuPRkuYnqYrlEDfe3bDjgcXj3n48AEvPvc8u5srNE6cnJyw3++5uLjg5GSDeMtn6XzPbjciDvpu4kJ3XF5fMw7vMU0T4zShKcSEKTLu9lgCbGQcB7yHV155hX6j3Dk7t4TprafvYL8fODs7I4TIsB9M0YmKwxHGyF4GLq4G3vvgEWCCrLm/zVNyM16jwKbrOTs7o+tPiNOINhaujBhrLrL64Hrn0Mrikb0H5h0Zofd0Xcc4DuTYX0Mm24WaEBRPQwx4v7w9OjMmWLduiaTQA+eK8J7XnglYfQ/IOI4lDGyz2SwOQs08qZhibqpKSOWC28N4TJCaBRFZCNyLn5KZZ2SYRsZpSsXdMKUmuRbb29dz4mjLZOrx6zlmuK01+97+1Uyndh3nPTkQYmERn9taNWUxhnUmKCEosZrOkpEdembWwmJaRtISsHaNGV+zl9DmumQoC0HFLyu31GO2xH/xU2fJs2XsrVcr/12HsizgVb17jMnV/bXfHfuZ32nLW7fj1s8em89abPGTxs7viUhRruvPjsE399Pi/rF5r53PVlCr1yCN4HabgDnPOccbL9dxKywFLP7dDBExKuqFGwLxtIOTE371936H3/iD3+X8+XsWD+/Meud3I4/ffo8v/5t/zzs/ep14vWMaRlDwndit8RpLNZJcSn6h9C/WMt9XMI7jUmgWQZNiXHuN1+hODde2xO0xYbSGp312WNVo7Vxn3FVdCgq1cSGfr7pq0YE3pJn/jA+6qIzXPru6p096rqGHx5Sdlsas4W+73trQBrOSsTantfFa5bk+2zNeG11bE1xbYb7tP/eRaflRfnGEzixpVOZJy3LpM34kIbLBzzznmsav8fJagb0NlmtnoG23KSnrPNoBh5dL1v3U0RbHaMxtbY1v1OPUsFjbj6dpNd2u5bk1Oi5iCqP0qSBNSvImPeuYDZr5rNdzTL4n2ztvxtuQ7g3LK41YGGpUu6PMOYekGijqnm5NT61o/O/+t/97PvOZz3B29w6nZ6ecnp/Tbzecnpyx6c4IYaLrhBAGzu+c8Nxzd+k2G7x33Lt715JK+h7VyP3n7rHZ9uyGPYhnmgxBH19c893v/oAxTgzjzkKghoEwWTLLxcVjxus9u6trbq6vQBTn4Jc++wv8j/+L/xGnyQMyTVNSQBz37p7T9xticPT+xKyW3nN1dcW4D3z9a19l6np8tylKCCjb7ZZhHBl9Sr7VwCsvvsBvfOElvHM4IipucfiOCWtrxC0T8tmdbRqiVUOyakYiTVy/LK1atYuy7rdF9nZu9SHNSkLNRHK/Wajc7XZ470u9+LyOOqQqz+MYsVNMEGkVifqwtn0Z4ToUPsr8sTKVURXnPeId4zhBZ9ZHRQ88PPb7MpSnJVytspFeWqxrSUwOGUh5BrI8fhiyglluWBP2YgSkJCCbdyTta1XbuvxL8MihTPV4WSCeYXooENZK6gJeQsn/aZmpCV9LprkmeK9eXFkxwKUCYX22eFArTIVIVvdo1OOtMch2v+t+jgl99Vlq+11T3o6Nv9Za5aB+P3+/xmDa79bamiDW7vmxdT1pHbcx1Za+tGtdhwNFsGnP4wEdze+0c3LC5EC3Pa997pf47X/+z3n1Ex9n1EDwziqURXjw7nu8+8Mf88Nvfoc3f/hjOqtETHAWk+wUrJSZR5NHwydFKIcXHXgD1Iqd5DLeqjPNqfH6GGxqmNatFTBruBzCMCndahRlzcue+4Ql39BoXuE6pLWec91q5afur+Zl9rvQLmltjS0u5d/X2m3KU0svjsGrPgs17Vhb69OEAubW0qVjykD9TH3+68/bVsM8K4htqG+9tnY9bb8hBkSWVvWixGgsxLeFXd7jYwpcPcfa0Fl4YPXMMdqz6FPK/47Cpl1v4alH5lhg8ISSzre1JX+n5C4+CYdro8zPq3DMdPYQFsaHhZPOcyWg5MJIc4uSvJY6G2qyH9MnGUPTgmba4PDpcyfKFFMlT1WYYskVfdr29DeDj8qPf/hTXvnoR3jpI68S3cCp6wgy0IeUPKweL3ZZ0cdfeZVpfw/v5zJ7d5+7y/Z0C2qxxbt336f3HX0nnJycs9+PvPHWm4Aw7gd2ux3X19fcXN9wc3PDbrcDr5ycn/DcR17h3r173Lt7zsdefZnNySniPTe7PTc3O7abDc47XnjpJTabLQ8fXxL3A9f7azyBbtsxoOydA9+xSzkbCnRdz6AQnGMKASd2O+y4n+i7DZIE2Dge5mfUpQTz54sD2ggWWRCc8yJyaIgjToBzpVqFsLSgFGakZqHI5W/rQ5/Hz2PNhM3+F1PsnWiKsUwXy12mygTb7ZaTk5Ol9TYaPDKSQ5qf8+QyiySB16cL0RTFd10pK6pJcEa1WKsk/R4TLLquSyWFsQuwYhov0VjRSBgnJjUFbSOejfNMPhFQ5+ichTdoYsLiUqWa3NeCSR0SjHyw7TAurU7l2bQ5c9WqRBBSib5cQSNXJ8kCQek/70kwN6h3HhVfRR5r8dQgFEuuwUDKWnwaw1TlpJhKriTlmoRyMcUv70GDx4WYpedRq/gkzlfKgLlkNWkcIuAdaLS/s5KYK7BQEsrDvB8Jbhm3NJW4dRXsixqVAJKZWSsUtUJ1K0isMeD679bqHMNc4QiRhLMJTprOctpTSYwxe6jymb+NQbZzqAXLlqEcMp1DBakdT+qfagKza/D7mODaCkK51Yyy/U4ii7rkSqWAIKXaW129y6xp6+53l2hJgBIqJSlcygeHOGEUGDee89de5o///J/x8c/9IrLpGYg4BR8CNx8+4qff/yHf++a3ePDGW0y7PS4LhNYtUa30rVUscxVDXho5ui6HxNpixjGU6lKd94QYiSEV56hCauqQK4NfTXsSnpJpjS94JOTKgBkHZg7fKrgt62/Pc2tMqvlUDgur2zHloOUvh89KoaVtn+17xz5rleVsSGnXnHGo/qw2ZNQ8r1VA7Odcyhl1ZW/qsdq+898Hwj1m+MpCnIjhVilHWD3bCp5ZRmrPdat8r82n3adjNEfEwmey5xEOQ+Tyc+1Ya7Sm5ZVrc4blvtVhfGsKRIZjORMNza77aPfHBGwpckWWl+Y+lzBa83q047UK1HKe63xziV9LmK3BZ+37deXX1lZ/r6pJeTzBHBlGvxavLdad+mE+O7Y/OT9JURXUCSHLNdHOhBcrjRtjMIO8rBcMWWtPf49Gt2WcJn72+hsMU+DVj3/Mkon3I/1Jz/b0FB8jLkSYRkvIG+2ehgic3bnLyekZp2d3cM6x3Z4gbsP15QVhGrm8eMQ07nn3vXe4vLhhd7Xj+voGEeH09ITn7t3n059+ge29LbJxKI6u7/GquL5nDIHnn3+BYT9wefUW4jtOz8544823+chHP4LreuKw59WPvoJzwjvvvs/p3Tv47QlDVPCOgG2aE7OG4xweE4CnYV9qEXvJ++4QyfdqZDwwqSyX0a2tX3X8a23NLUqAmhU7xMgUMnFVQoyEqHR+eTjnMK3Dg1/HCufxWqLr3KyUFAUmMcoQAtvtdpEsnt/r/Zw3YzknUpA36vJgLSxlkksHG7IfxmtLEYqsX+Z645qF9VT+NQtOzpkALNi9I1MgilVf8Sm8IrHwFGaWppqE8DLXNAZJGFjEWku6Z6Fa14L4JqFz7sjmXW7HzjX+NQ8yK42acCcTEKu0lvCoEii09J2ZlpLjJAvRExB8ecSEIS3KbRbYa0J3EKrWNE1E2/6R3q8ekGpaxesSLSZScrEDDoTJJdHNlmEtSky+6X5BdGV+9yA0r7kZtx6jHa+2IrZrPVBuKhhk4bNmODFU1cdSGWxZYYTHYFtbAOt51ox7jYmXNTZrawW2XE57ZsTz2aGiGTUdaBWJts/bhIzcv02I+afM3xkarQsZ9RqDS6E9Kng8GiMbl/IknGPqPf7+HX7zj36XL/zel3CnW9zGvncxMjy+5O0fvc4Pvvltfvq9H6LDSBciLvUfmXMpvHN4N4eM1jltmb5nxmwWZaORwzCU8soZ3uKWl7CWW8MrWAuz8CNllAovSHQrK7b594av13uTnRo13c3nIZ+Pel7pgcW5WsPFY+O1+wUpzBcz8rR4Uj9b09Da09sKfLWw2vaRv88elFrBaMds8Xym60bPnHSZMSQlYV14Pybsl78zMUyGHiQbfo4L47dFQxxr9XOugnXdZw2jMm9Zwin/nj1ixxSHNeXnWGtz1gqe34JXyzYbBvPaao/ZmlK6Nqf83gKXVvavfr5ee42/a0p4Zumt4vCkc7PgM40cdBts1hQtEUvm1pjLW5Muza37WfKSTIOdE6LKLFuIGSTzpbsqYsUwynt5TId0KYrmKf0aP1fVqa53xCny8MGHTHHihZdf4s69uwQ5J6ij7zcm+EchqOPk/A5d73n33Xe5d+8e5+d32G63XF9fI+J54YWXeOH+fa4uH3N1fcPlzchbb75NwHH//vN89FOf5P795xaXxgVGcMoUFO86Tjc9u5tdIaR37tzhtddeA+Ds7IxxHHnn7XeIruP0dJOSg4XNZpOQJyU6J2KXKynlZD/TFg3AOTm66zoTmBuq3yJojehFcE3r6Pv+IJFrJpxZcUlMyzt0nC8tLISBZJmStZvPtXg41uaY1yEii+pcMUaGYUBESpJ3+16OiR9SzeVSdWqlicxVg0KMhwy3WncW2HIlqHotNVMqnyVBwS4ztHmfOYfZQNcPtuHyMlGzJtpx5TNIgm91AddhbP2SCIskN3fVX6tcZsbUwgPMakAVOtcy+JYJ2O+A5nyeNYawZCSLUCc9Lni3nx1jtjXOl71x7gBeyJIM1oQ6hwu2iXD17/Xc1yymLYyWwthSCTjAjScQ+7a1/azhztMw6Lym/PuxZ5+W2cMMr1poLriox1nEsXm0glC7H2vPrM29Fm5qgbjF8SExwk2APgqd2zLEgGy3jCeeT/zar/ClP/unnL18H+m8XdA3KXK959033+LbX/sGb/7oJ1w/eEwXFJ1Cqmx4SJ9rmlivLc+zDjFVtUIkIubFWNLuZXJsXkt7b9BtgnMrjC/gwuxZPQbf+vd6znXFvTUBvp3P07YDerBCS27rv8XpGp6LvlfGa99fw9m1MebPaiOXoFWO2Np818I9yzOCJdyu7OExulKfnTV6tqaAPA2NqgXzY+1wH8woRCNkr53nGt9vo3lJeDo437c324OsgB7w4pV12Xqz0Wo5h7JHi7U+eV9aHlvPIwvemX/X/d12fuu+W3it8du6aVwaBZ1LebXnZ3R9Xz5rjXDH9k6qPON6HvkZ13mcd0U+bGF6wNdvaU+taNx//j5XV9dMMXBzc81+2Bk6hEi3C2zPzthsJrwoo4PLmx0fe+VFwjTy8kuvcPH4is98+hznPX0X2GxO2DHQ+y1np6fc3Q/cDMrnP/8FtnfvIm5WLmYXt9D5DTEG+s4UGxD+36z9V69tSZImiH3mvvbeR1x9Q6bOSFlZlZVaVFZVqhKNZoM94PQLwQbBR3L4MuAQ4BP5Y4bs6QcCJAE2wGliZsBBT3dXixJZlZmVKrS8EVeee8QWa7kbH9zNl7ktX/ucqGoP3Djn7L2WC3Nzs8/Mzc232y04AkOfDo1rcHP79m1473G22QJINyRerC9w685dLJcrJLmYmEFStS6Xy6JcZIto3PLOk+AdONSgTU+ELlqASDua2aQt7zyQb3mOMQLKqy59lHHJYvPeI+a0vRZM2IPpWkiGEKobygXcb7fblPo3M65mJivQW4tLvrdjFcNAFLmkF24tAhmbTR1swRwg26NpJ2qxWABYjzssPL5TnWGJXAEO3bZuowKzDXBdhAihuh24FkgjD0zpg3GuUT+nfRItRWrnOin43P8ZPtTty3sSMhF45CmZ8zkwo9u0ZwxK3xRttXFox2JpkpRLLcTkpycHUoft9ZxOPLVoA3bdR8uzVkFoBWnB5BzAlosRdT1zykMrIivIdb/0uQALODQdbXvakVHVTTTecm7G1pxL1ZdWX1uK045zbnytZ9IHgGeCD4QupsQCW8dYH3R45lMfxff/6Ad44TOfQDhcoPeAj8Bix3j0xjt48Na7+Olf/gQXp2foL9ZYhHTWgiPAXZINOpxV36osY+66riS/sOtd5kK8wJJMQ2jekit6/DHGFF4IatJOrz/LX7pOW5jb8yZt6PVReA9TAGbnpSXb5+bP+5QWM6hEJpZnrd6w/Ck8X/WhGqfm/2Z39vZXv5/WMsolven8ggQ/jc+3dJ+mVZqviKjqbzn/Wn2Y22HVpcUj+8aov6/eZTa7dfqdHJVsvtNYQtfX0kGWT/fJl1Ypn+dwM60DLA/ZOSAC5gxFkeegtvzR9eodNo19rIEjulaKjVixxdLN8uFltLHfSz/XF2vw9euVPtlH37LDXeaj1tPp/UbWqwb+2MezulzZ0Pi9730XZ2dn+LM/+zMM5z367Rb33nkbTx49wvMf+yTW5xdYrFYAIg58YpLj42NwJsZyuUTXLTEMA3a7Ht4vsVisQHGAdx0OVh7Xr13H0dExAhz8okvnBdSkDX0PUL4QBg4cgYAIH4GuW6LrugrIPvvsswCAzXaLAyZ0ncOzd5/Do0cPAXK4e/duAomZAWWXQUB4IiwQhoCld/Be4lg9iNJWu534yhhRE1QmpqFY5HuxyCUGTs5NhJhiw9PZjfEgV9/3AFL/vKOy5S9KsMS9G2aw2aJijGXczIzFclm2BPU4gDFrg/wufdF00OMqz7h0rkAbEBZECQ2BaezoxMtKacswpmizcnGc9qZLfRaYSWiR7bcoXg2Si5ImQkBdjxWodmt3DmSW9jAudv0uUT6DsUco6r6VtsSbMwfqCNWWqsy77lOhQ2MMliZaIOv3iMa+C8/quYYBGhaI6jmrQJJ6xh5wt/Ng0yzPrTk7l8KLLcA4AcNmLoDRaTGnTOw7cyBmzjibtMe150+PraVw5Dtr5F8GImy7tu/CSxrQ2jnV87APwFJCDFhGAgeHQIR4tATduYFv//D38blvfAWrRVfud1kMwO7kDK++/AZ+/u/+HB+8+U462B3SOQ3JHJWAC0BuCv41LeU7mxIcqMGjcw4he/ssOLbFtkduDEVoKW0bVlraYACon7e8N0tT05cWn+rSkm9W7ln6zX0u/8Q7alOZ23613tfJRKbf7wdo+8Yn+iTtaDBA7edsf+33UQ7ToF6XUlr00XS1Wez0O5ftTthi16blrdYdVuR8Dr+bn0ddh8U2V+1X63dLV0072+4+PWtlTlmTSidJ/bof1hiarC0jvyeYAjVGaa3DluxsyVvt4NQ8QuSqOdP1CxYU3Wfrbc1BmsNa740OvIgcNVWFr+n5svy9r1zZ0PjWt7+FzXqNmzdv4F/8i38BT4QQBoTtFo8/eB83b9/BsNtit9vgadyBEHCwSsaEDH636/MCZAxDulPDgxGJAXJYrQ5xcHiE4FwyIFw+KA2dQjVPBnkwEtjuOoeuW+D4+Bq6zuPo6KgwRiJIgO88Pv7xj8Ej4rXXXsX5xQa0OEjhP8uDcplctbDzIdrFwsETm+w7ESBfMZxmXu9rgVMJakwXe/Kax2TIY2QU7zy2w5jpSUqVUjYDTK3sNUNp5tC3lRONjNX3PbbbLVymOWxsYy4xxnIQWVu82jCQdioBzwDT2G/NvJpG8r54Ca0ybCl8AmG1WjbA0tjnInQ5GSc6/KBeuFNhTkSwy7UOkUiDa4I7xmjMzpQ2mJNY4XnFNhG03Ox+eiYyIut4yzZYsd8DtbGg37FCRmdESWcy6kupCs1kh9KAWauEtJEhvwfl6bWeIw1i5HOdHKG1S6NBsOY3oumOUpOutj7UvDL3rubl1ny2PpO/54yL1nOt9SXPzSkhOw/aCTCniFuGxFVoVstpA8yIEFYe4dohPvWN38XXfvD7OLh1Ay5frNqFCDrf4IPX3sK9V9/AL/7qb9BfrIHdkC/LS97NwDEdgs/r0Lv6dmMtm/UOrPU0a+dNUcp7wJbmK0sTDY4/DFCbK4lf//71SNEGN9A2eDX/TftSe0lFfujdozmg0jRm3Nyh7r/7GCugWz5L8e76PK2dH91nCbOWSloAda7tFk3t2rBOlxa9WnPQqs++Y4Gz7OpYuTK3prWjR8trXXTWRAvuJ4aOfneP3NQyZ67o9ij3Yc6AsqVl5Ov2dR/1dzVQnxoS+/pr+z6ZP0bKNql5Vs3L0eEhPsi82HIItPgxScda/xa+kGZV3/XOrXx+Vdl1ZUPj7PwUF2fneOGF5/GZlz6Nl3/zMg5WRxj6HmFzgfvvrbELASmsieEowju5ATpmAohXI8D7Ab5bwDsPR+ns6Gp1gIPVAc53Wyy6DgBh2I33NzgQOteBKR+aDiF7yR2GfsBms8Ht27cAjIItncnwuH3jRiIKAev1GiFEnDx9iKHv0QdgN/RYLpdIMeKZKSPgfPYUIeUSToLSpX88FSyALMBx90EEqt2S0wtGDA1yDt45hCEAPG7LM4Z82JSKwGZOlqzDuIi0p1f6NQXgo4Eizw3DgNVqVb4TAQFMs2ZpAWhBzJwntgUs5dlKWKsy129ZDJ7SNj1zoutut0OIMcUVxtHQqIR3TudYz1VbgOt5LYe95ZBf9QzAPArvagGqzzR9Ur/qdmpPTfqnhYDdwtRzLO8HAza0wCrZdFS5LJaXaDxj01IqViALDSJzORStgeQwDPD5osd6q1avo7any7Zrx24VnTVEWkJRxtdqR2do2qewbdFGrB6fFfz2vgRbbwuISLGGfGte9BqzbcwBHXl2Tn7od21o5qxCBioD2NYP6PWVno0g9AuP57/wGXz9T36IW5/8CMh3WFAHP0T0YYeLJ0/x+l/+DL/6938FbHZYREYc0sWhSeZk2hDKPRqEUX4JfTRgsl5UO2bArGEFLKwMs7K+lmP1+m+twRbfo7G+576zpTVPc0XLd22ItWhi150OKLHOIrsGLJ9YoK1/1zS2fdo3Xt2e/q7i/WL05dj7mX5Y2ulzjjFEMNX8bR0Crf5dFbBZXWvH1qKlrTuNbbrDAci81fNjZcmcPNB9qLBQZnQrR5t8o+nspmvBjsfqgtTUuDa13h2TtUx1x5RG9V1kczpAcE0Z64ys1d/PzZ1tWz4veArCm1O+9N6DHE2cJ+Wn4ue6/RFf6PVU5JM6Z6nH0JKTl5UrGxr//J//N3j/vfexXl8gDAN22x2u37ie05du0fcRIUZcu34Nzz53B91iAeocUhhQQIp8SKnkjo4O0XUeoHQTtiOfUklSBGiAX3jAd9hut0mw+JRxxPuUUUeATOcchu0OwAKHh0e4du06lstlxSgHBwd45u4dMAH9bg1aLnHnmWdxcnKGDx6eIOx2iOB8i/mugCBH6aCfYwAxCRDPHgSC8z4JpsiAyi6UZycdEHT1YdWi2EIomWKEiSVsyYkyJErj7Dw4BJBb5SwBmbkjpzAyTulFwemgNTAKdgmjskV7mIjSZXf6cr4iLBhjP5EOuSUPXi30hfGstT4BbY4Qwxi6BJKD18nroQWyvSxQ00/qDiHAxZT1IBDQbQNWvsPg0jx05EuWKOd8qT9lYqo9s9rjGGIo+toaDY5QUsgh7yLlSzJBXqY/JRiQyCftFZ8oIAIYozCxW5RJ7IuglhixtBNlhay04cs0pMY5jbY6t2F/FsMA6l2jPMpIpD0jYFreRjTmruu6Mrcy76IE9K212jiROUrhU4kwkZM3WYzsZBSU3sORg5yK53ziReoPmb+RFRMV73cx7yZKs1Kear5aXm8PSme4tEIT+afkvBbY1gvWml9b5tacVhxSNODjPNclhTAAa2a7VFGam/yc5FWnVGH6qfsnPCS0y32JYESK8CAgZ4OLyGmmwVjAwXOiew9g3QHXPvIc/uCPf4xPfvELCIt0q7cnB+oD+vM1XvvJ3+De62/g/TffRthsEfoBIYayw6DnqMuKWNIVa/3Aip91nxko2aRI7T7L56Rop2neAsctAyLJC33BZaJF5r6UhhQoN7+L64GLAwL5Yq70RhYTSOqgBhW2bxbsy0Vec/xmweHc93bccwDagrsW2JsYu5ieZRufT/Ro1avXMSveSPIph2NyvRbJze8N6d1VXbekxhfnHUceZzOBA8CMSctKDdz0M63Q1JbBUc/xuKME4mqnixwQuI58kHYcEUIDyLb6NccLFrimyJD2+QPLG9UN6xiNPyr1JvwYaepASX1q71gX/kUlfptOKD221vqp6hcSN/Sq5UFpw/Kird8aN1WkSHq46rfULWH9E8chcwkdjYK9kJwv6fK9Qo3EGznRDxHBC9VUJISjlGp/bB9XKlc2NIY+XYJXsiURcHp6iuPjY3jnETl5xA8PDrHoFjg/v8CTk6fwSDH96YxGl0HigBB3AAI8eXRuiRAJZ2dn2O522EYG0wAQYbvbjSAROWsmCKBkHCAOCIGwyPVvNhsAKBmXvPdYrlbohy1CCNhsNrh16w6uXb+Dn/3tr7FcLHF+sUM5A5EFr8s5g/vdAHBSYAtaQRaxqJjCRDFtuY6Ke8zaJIIhxpz+M8aSqUnnM+cQMnAWpZa8wl23QreIAAaEPojpnhV9HWsvfWJOlw7Kjd7aczdavlxSL1bZqbj8D0ASmkNIh7d1TLIGhLpdMZ4q0ASaLEhJL1vgoFng2uuojYHSfmT0iIAnbM4usPA5bnsIcPm+B7HaZZeKmRExjfMtykd5Uqziy+RIACDW8z+Yy+PGOlIGKStwYoxlfm1oRfmp+iBAI51Pkr9M3yCGCcZdG6Lqaf3sHBigJNkLP0O9LyBSlIDcANyqQ9Zga2dhAiyASrlbepWfPNJv7GwyLAJCtvESQGYx3FR2uGLgFDBMRQNpemtF1goL3LcNTgntjXKLUvYkMZS08TRnSGj6aAXV4hXLdy3vc6OBEfjYPuTvZPfSab40wNyOu7kGsuGNyCBO/JivxQAoncFgR+g5ort9Dd/6/u/hC9/5OpZHx2Cku3A4RAzrNe699Q7++j/8OU7feBvY7bDL+kE7dLQ30rkUOotYG7CaNszprJSk3pbnWjHz4OTUkbNqznsMM0B8HwDXf2v6AUj36WD6OZCdW6Xf5YFZPtL90CDHglT5uQ9Eaj60INgWkduttq4CVG2bUO/pMe1rX9NXn7cp8xBTiHN9kWycINIWv7Ta8yLnOI9DvkMt23RdrTascWSf2Wf4ybzEnKjGkSs7rIWXqQ5zLTosO1RjjDXoV++2+MaWis55/HNj0u/osMVmiBiQXUbT98c13959u6y0eNIC+in9MdnB0t/b8dl29BppvWdlhegxy9uRI4ahL7rB0i6dTHCQiCiGyF5pc4w4GfvQ3rUoWOKKBoaUKxsab7/1FmJMWZxu37kD7z3u3bsHIkIfAkCEvg949OgxvAcePXiEG1/7WomHFQKVfy5juggQOsBRupdjuYQfAmIO8+i6rmRHYlYXHhFhsUC6WCQyHj55jFs3r+H2rRsAxtApAPAsl4URnF/AdQEXF1vcu/c+3n77bfQD4JZLHF4/hss7CzGm2w9Z3SLtHKVzG86lLXiqx1TiodWEaabgbCDoeDfNbJIaDzECpG5OlvrJJWONU6hTHIYCYrUClUxCFrhbC5oop0fzvlaqhom0EGwJIPuMbm9O4YiRVQQj1yFXtu92ccnvzjv0MeDgYJV2wGIs4VTiARnFfN4ZKMZ+aqPMhfFkyaKdi3OfK3phpl+nihZAdd5A01CPV/ezvLtfx6qSPX0jNpn0syXkLKhtAcryngmT0G2LJ0TXaX/Xn82BBwvIW3TRdcnvc2DoKnPYUqhW6es+62dE9lg+Tlh7WoetuwVEWyDe/q2fnTPuWmVufvcpzFb7rb7J8+lQNqULJpPgBJFDdMDWMehoic9+7cv4+g//AMd3byI6AiKhYyBut7g4OcUv/vKv8cpP/xZnDx9jyYxF50vSDqG5PbsjAFMnsdD01EaK5jObmadlJFQ3bDd4YY4m++hbnuN6LuaKrefDznPM4BKYhni1+tXiw8uKDR1tgbKW/LF91zxVn5OYAkI9X/rZETzVur0eaHsO5wymObpdlU5zHmw9dqlPj0nPhY4GSPys7mNC7TDhxudFZpDaPTZttwB8SyZpY6EKidxTrs5bKZJgX4hjC/O02rN/zzmPWn0TnGTDmW39l/G3xhaWd1p16DbEIOTIODw8mtRPJEllzM6N1rlmrHqH/T9lufoZjbMzHBwc4Ctf/Squ37iOi/UaZ5sLLLoFzp6eYbjYIA7Jy3729BwP7z9EGALcYrrIE2MnQ4O8A+DhugVefu11PD2/QCBCGCKWy2V1GC295xBDwK7fgbzDwns4T3jn3vv4xte+AuI67MZ7j81mg912l7xPQ4B3Hc7OHuGXv/wVHj8+wdOzc9x+5hlcz0YKczqz4bIw6jzBZcUSc6hRGkrbq6gXvWZCWXhawcnn3vscopRCCpIxlqxQ53M6RSRvfORYQqec8whhvPtD75LoxWMFcDrTkJS0vhW2MCnqRSXjaS0MHZbRijuX5228rhgtjDboEn7R507KAsgLRkLZnEqHPPqQRs8DkMK0Sr+UMKz6H0MlBOZKJei4zuIzFRjt1MeCJ1rAW363gjPG8ZIcq1CZefQ4KCrIL1aEzyl8LeBaArBVh1W0ROP8aj6/DGzNef60Mtf9tABffpd51fOk+aolSO08aH7TCsWCTt1X2V20a4Co3gXVc9sOA+DJ/BbloYBBa250fa0+7pt3TU+r2Gyfrgo6CQCYEt9SuumanUN0hLDwePbTH8N3/+Ef4fanPorBEzYAOhCWIPRnF3jj1y/jJ3/2H3H+4BH4fIuDyGDH2Ib6cKLupzbe5V8IITuJxudsLLamh+V9K+/s55ZOdv1anmnNoXw+ZzAkUcZV31v91XOzD7TLeOTzfUaNfsburLWMA90PS1srKy8DhHYeLouHl+8sH4/tAckZZZKWpDcn7++jRWvtTOb+it6hFr9ZMK3Hp/uhP5dEL/vklOY/IkLnHYbYTjIhz052+Br9quQjj97yD1t03wsd4/xas+vhMppZ+Wzn24L6iUymxClWHug6W3q11e+WY7iqyzgr5VnBe+v1Gs65yoE91pN26mIO50sx2zlk0qRj17Sbm2fBFVeR/VKubGg4Ity8eRMf++hHce3WTfzmlZfhlwssDg5wa7ECuac4eXQCB8JmvcG/+Vf/Bj/64Q9w++7tknaWmccYbQDglE+cvMPZ2QV++rc/x4AUb7boXPFWCTGTFz+AyIGcAxOhjwxyhF+98gruP7iPF565i91uVw42x5gyKqXbtsdMOD/5yV9jGEKJeV2ulsnD3PdwPsVZx5i2sMMQsBIgmb0BjtKBYyG2hCcVIJ7BhmYgCZ2SEuP0oFgK+SFESErbFCJE1UTnmNBcX7dYFEGmjYHdbjcBRXYhWaYsTGyUjxgxdjtRexCJxnsZxNreZyGXfjgNj6egVegn3poEKAmQg18MeJ+zZbHcsp6/QAK9tSct/bQpPi040HMk32salc+yIpHPa/Az7pLId614fE0jDVTnFrMWepqW+nvZuNZKTrerPbJzdWnDstQr31P6nxXYQnnnqKrH9ru1QyQ00/RqFUs7S6vLQLDwrv1M98PSWH8+p8gsYK14phEe2OIDGbf8beOpa1q1x7Zv3LpYR8Skz2buNd00H7c8jLI2IkeQ84hMIO8xgDB4wtGdW/jOH34Pn//mV8ByH4Zz8AGIFxvcv3cfv/npz/DqL36F/uk5aBeAIV1kGdVdOLqvdixWhrTmjZnLoe4WL9uxtuq/jO66D63+VGPgtoeWiCr90Zq3uR1mPYd2LRYaNPpi6acNo8vAo5UzVnfo9lv8remmf2+trdb3QHuHID0XwVzrszLHqdKqz9oZpWWDXgtE9d1V+jlELuu/NT691qyXfB8A1vVpw4IwXReCXxBrwFzGZsap9Z6VW3rcLWxQ+oPcZJyGK+siPGq/s2u2zCeN3+uxt2grz+1bn5pGrR30Vr/IUeET+4yVS1KflZPyng5ls/UVXRCm2CuEgEXnsd3mC0RVNAuAfN4rOXe8dwgxIuTQTAaDUGMbfba3tT7LWC6RdbZc2dBI6Wl3+J/+9f+Enhmn63McHB/CLzr4rsMz3QEcLXD6+AkQAz54/wP8+z/7d/jH/4t/XG6EFmaMMaWuJSZQPgvx81/8Ag8eP8GQhenQ77DbbtF16VC4TMDBYoUYGT0HLA+X6IcecbEEx4i/+slP8Kc/+mEl3ApoQ/KoxQis1xf41a9+jbPTc3DMd1UMAf1uB8pnFUTgO9+h65ZwWUi4fHtmCBHMU5AmC8beMF0mXzGY3XKNzGAX4fwinddQt5KTc0BO09iHAU4OnzHnNLxTxhZGsQI+xpgNPodhSCmC5RC9Zir5XS/mfQJDj8nuXmjQZGPcJe64pXSsgC/gkMY2+6EHkGJkUSlv+ZliN8dxzCwSGjMsWUEgv7e+S3Mz7xVwKtxMgwYRVFaIa3rOdLQJAIUsySjFqNgohVCphByTce0rWolU/SRUBqkt9hPhPQuk95WWorAAbe69liHfAoaXKSH7nn639V3Ly67fa4HD1ty3ANVVaKbft+tQA6cWeG4B1bm6rTKee945jyHmbFDeAYdL/PZ3vomv/P7v4fDmNYRsYBxEgLYB2yenePPXr+A3P/sZ3n/zTaAPcPleoeiAwTV2woyinwMKludHXm4fvLXjvQpYaYGJfe82gbTY8mrOmZMDSw7XWpCr/00dWPvPU8wBWalfA2vtgdV1jINA0Uk65NmOtdWP/xTlsvVeADlG95ZeLyHGKh4eGOlnw+Wu0o/UVu1A0WUfb7RAvh2j7n/5jlOIkTZi0nNq0JYmBMCsAXnGjtdGYwCj426yk2JBamPMmp/138zjBYNFTu5hkzmZRERjYoXG3F1mBFk6lmcbY7M002O24az6WUsDLTeIWidT5Dlgt6uPF4xGC6XjC0QpoZH3qc8xICj+0AZuq209HqGldoBdVq5saCwXSxweHmK93YI6j9t37uTYTkIMKcvK7du3gSHg9OQxQmD8y3/5/8Uf/PAPcfv2bTjny+HoGCOGfkDYDQA57ALjX/+bf5sOgjNjEWLyXAHq4jztlcnE7dMBmCFEcAj4+d/+Al//8pdx+/YtiLHBhSAp5MpRh//wH/8cJydPESPnW8VjBqwDEAOWyxUWzkPOaqy3ayw7j+ODZe6Ly4dua8/GkE/se++BHEIhE1ZyEDOX7TZ5R0K9fA4NA9LWZwgRMRLCbovt0GPRjYwdQ8h1pUxWeiFYwSQCVD6XG9Cl37JbpLOptJRXa7HZoheKFka6fa2QOQvEUd/XoEovRr0QxsXH6DoPBmMIAY4TIMmyNtcni52yPTCndFnshQp46cVn6Rlj1OfHZ0GnXZBEKexLFqwFAvtBzfQyqPJNTFmCJJNS4DgqUzU+3Q8rJG0/mHly7ifV1wbg5TPRajTSQvhNnm3Hgo4GoqaF5uerGAYyT63vJn29pC47xnTmfp5mVwmvkbrmwn+0bJHdPL0OWuBD12HDveQZC7btrtU+OlgZU+hRHpK1nGgEQkq5vOgQHOETX/wsvv3HP8LdT3wEu4XDxjE8OXTbiPjkDA/feBc//Y9/iXtvv42w24D6Hj6ndQzEYE8IDqAhZ9y7QmkZnJpGdmx2DlrA2oJyzW963i6j5+zvPJUZzMlpYflK8xtRfYfRnPFQ2iGUQ/CtsVlwPt7BNNUNpdDUGN0XzteiwWXPXuX9fe/moVfPlnM+DTlT31s13785A6B6Tiu8mTJnYMh3++Rf+k7OJ6L85CSwK9Bq9XxxXoqMm+mDHZ8GqhXfGHrtm9OWMaPfKw6viQerZXvU6ylyrTNaRkMF6hvruzW38kxr56wld6282Fe3/CuJdTBvY0lEjWBQ5xwW3SLRISJfEKp0So7+YIwRQ7rNJMIv17f/yQ2Nm8+9iNXBAVarVRJ24k3hdOHewAHUOdx67hkEYpyePMF7D57g//n/+n/jn/yTfwJmxo0bN7Ln3KEfBmx3OwTq8P/713+Ge49PUtqyMGC97dH5RQY3AczJ0CZKMYQMoOtSStxh1yO6lNnl/pNz/A//6t/iH/+jf4jdbg3nCCECkQjEARx6PDo7xV/9zU+xC4zV4QEu1hfgOCDsNoi7DdB1iM5hQACHCIZH5zw6eIR+yEK5w3jYuGHNQpR3zGnHQhZi2SI3i6mkt1106fJCDilVY+Ys5z1o6EFxZLqI5E0OMSYDCpS2RJF4S7ZHY0wX7MUhlJ0bZkYYhnTzIwOd88loWyyScRUivDq30QIUeuEIUB4PotVxixqg6kObYz3IXvd6y1bqaQGb9C+C4wC38FguOzgHOBLP2ZimrQbIDFCAHEgdDzEQ0qV7KaOaHbMFErXiVBOvChFVdVnPtQBV6aMd31zRoMjOCbr6sD6HmM/6UM5W1fZU2NICXROFh1rmayGdUtcmgw+MnCY6A1uiaidE09JVxl5KwMAs4IsrPmnNUUUL1e85QT4LlhrvlvXkHDgohSf9xchOcwpVUl2ShLQxikKX8Du9g7RPwelx2tICzvY7eb+1tuZAdXax5PSIrpJnlDfiPfKa9Q7RE/qVw+FHXsD3fvh9fOqLn0O36NIuBjO6yBjOz/DorXt486e/xJu/ehlPn5xATiIxGAM4pQd26XwFh8Rf9p4i3d9ZQ06DCcDc3zE/dkvrOeWrd+5t4gwbimINydJ3pLEWMCoAcIaPdf+0DNVyZZZnLjGY7dopazUJ27R+8/m3shxUnXPGjvTR9k+Hblg6SWnt5GjQptuy4HGkOcHRuHs9CaPMISfiDCwp7IGyW9MCxro9bZw6KAIpIxxAyY6nxya/N2XIzHireSVGSnwi8pRBOWc9ufGQdtUGc+mnZOImOHBIdWl+bRkEUvRzhNGI08/u42M9H3ruR/piJF7uNyBps1mla1b0yf8XsJ50M43rTc1ZS1/YtSt1suq77uuc/NR8MSdn5NnJ7n9Muly3J78vFwscrA7Q0y7tMjkCcZIb5Gvnn8sym0AYYuKRdE1FBoQxJdnRParWFSdn7lUdPcCHMDQOr1+Hdx7s0tkIJ7FdYMTYIyIPwBFu3b6NECPWF2f4i7/4K/zn//k/yYCb010V+fI+UMqx/tY77wDkUxhUSKlJpTjn8/XqCSz1ctglEHa7XZqQkCfOE95+911sdzskH3dEiACTR8cBjjxOnp5hs9mBGVgtV1gtlzi/6DPDpcxOfT8ArgOYMPC467KKPuXuJwLIIfJUcBaQQCjGRfpetmvTpGpLVc5SLLr6QLFeT0M/AK72sAF54RpQInVbD4Oue7vZIl1pn5WxWQBS/+SGb9RGhv4nC0Lf/q3p01qI6e/6Mw0cNODSbQMFoyV6IGJ5sMLu6UVJ56Yv75F3i1KlTAsBfQ2QOae8JkLStFGXemxVO0rZyHdCbyu8awNl6smeA5xFYEcuOyj6vZYim2t30g8jLFvnWSRMT+9qsYBVxSN1eN9Yf3UXDE3nyhqCmhebNG/8PffMHIi5rOwzEgvgESMz/wtZZthduzmAuM84bPV3TrHb9Wjn1L5fFLP8y4tQfx8dEDqHwRNwvMJX/+C7+NL3vouD4yPAZeAfImgY8PC9e3jn5Vfxy7/4awwn54ibbRoHjW2NsYCpX50FhbrthtGhS53Gmye0tqDUAtHaQbLfKLMyqwWaowF8zEYoZCNjbr7tpYm2H1fhWT12+3wr9j49F8HR0mCUqZYWrb7N7aBdaf0YQH/Zu5b2Wj7JOOVzK+PK85kf960PuwZbjrLyDqQPXG59bgHxlszVY9eAdHwupa9P72MCGluygUqPMMlUSOTQuTFVri5zskPTpDXXVs9Xut3wr9Wbtm8iUaM4b1DPRTnXiQZfqjWu8UtrfVc0zEd+5/pseUIXO7/WSNXzWeYcbTzEnKNxMuakTCPkd0Kc3qcmM+2dr/gOaIf+6r7Z/l+lXP2MRgYLZYHm2RTr0bl0U7ZzKUf97du34T2w3W4QY8T169fhXDrgvd1u0XmfPAV+kXY2xLOB5MFnllu9p9mTQghVWsMRWEQMQ9odOD4+BABcbLYIzEg7SgSCRxgiQh+wOV9je7FJd2bkS6TCkOLaXJeYOXrGQLHkfQ8xYAgRnZsqJL19rc8QyE/v/WgUqYmrremUirelHvRC1pmYmKgcZpRiz1NohTHG1jG6blGelXhLfQdGS/BJvTqNp10A8rtehC1BMgcUW4aF/jvt1GRjzjF2OQTOOQKieMZagI0yZsm0ZKUYwdlNMfVQSD1zHpl9ZU6BzD1X8VGj0ChLm3VUz0odAtR46oGZUxx2rib9ICqXmgGojQJMDVL5THP3ZW1VfIB2qmTdnj3TM8d3pS8zYMj2Wz6LSk7pz0vd2TvQApytsUqfO0WX1pmNv0uZG5v+bt/3ljfEAMjBnXBcZ68BEaIj7DywWxA+9bu/he/+yY9x9MxdoOtABHgmYBdw/vAx3nv9LfztT36Cp/cfAJse2PZwcBg4h/8RlV2T1ly1xicGrS42LlrLxDma2NICfi26jXdFhckzen3L73ZsKclHEUFXKvvW59+32DS/Y9+5eErngNgceAQSneyh0xZAL++iMr8m49N0tP3VbUu/YmSAx3DElkyZMxCs/GoByjlDoV3q0dm1N8d7+/hVh8NU8je9DMA1xzbfwzpt/1yx/eLshW+F+u4DrhZH6Hf+UxRrHJH5TH8312cxOjUukGcukyUtbGHrt/1t3esj+tS5dDHpth/vORNsY7FUxV+ECkzIGdp0brZNs79LubKh0XVdid/TE1AAbe5ViFwO1F47voaFT1mfdrtd+bzvexwdHiLGgB6j8eHEo8/pHIQOxfHZMBGCacJkKmC1GK2z7XaHdMdEyojQxx1iHBCGdKkXDyHdfBgCDq8do/NdCjfylH8HyBPS2ZmUUnbXbxFjyDGcVFLR2u3fGFPaMAHt8rmkxyWMoUUiUNPPFGtHzmEIQxVG4rzL90OMjF3AVBwXigYveueDKN0XIcyW6ObAPGb2Qq5DlKVlflu/1NMyFqxQ0eOdgu564ejFYAWrVVppN4MxDPmQpEuH5vV7lTJJHybMzeKdpdINymmLrdCx45v03y5g9X1roes69dg1v88rgnmgZesstHdUDK/W2HQfrloYXKUb1E4ByweV8AYA1waPc/QjoolQ1KXl1ZT5srssc8BIt9WiQ1lzKixxMqc8Py/W016PbwSXOnNbq7/WiGkZRBa8za2fVv3ybAsoMpB2frOSYgLYAdETonOIC4/bH38R3/qjH+Cjn38JceHSLjgA9AHbswu88/Lr+PVPfop7b76d7kza7tDlm9yZkqxjMfh57KP0w8oPCwjmwKaeJ8uXLWOmtas6kSeGb23GON1H59LFtdvtdtIfeSbpUjmrN87HXJkzvC0NdFuaZ/Rzc+tCy/qxPkzesUaVbkv3dxJC2uDLVt/tnAq9WPHIVdb2SDeUQ9/6Tqe5eWHmFIbqp+fu7FrTf7d22Oq+0mRsLdpJP+yup01gottpzvGHkPHl/Zw1S4eF2jmyPFZ+Gpross9xZMtcKFmRy+Zzy1dWVhb8pJ7Xz7R2Yco7zDn6eppl0OIETZ8WjaysaBVd74QGyiYomEZEJ08dI6Vvqj493lJHg78tLa5armxoaGtWJlwfIvbO5zjGceF3iw5HB4vKU87M+VbsBHz96hDLxSLdbJhjPSOnW7a1d3ez2Uzux5BFXLYP40jIdCP2Dr5bAZKhidKOC8cB3kU4DFi4AB62cOEAsd+hy894ADwMcBRGj3fnC1BNOw9t5R5CCtMSQ0nidUMISUjlG5flgLhMdpRzH5XgRAlrInAxuOqYXi4oxQo5qxRHxsopIpmrPrQUkl58luH053onRL7TzwGjolksFtUYJWyk9b5dxABy1jIG9xGBI7pFJy6GTNv6ng9pOwlaG9IVIWmFrdEzp/iqYjwHtcCSez0ayjNv884JIUuHkR5VN81Y2saYp/HSzJYR2BIimu7687lSKWQaY+h1e6Vvqm3tpbH1zwEkKa344H39s3XOtWmVaUUDjMrTvp+E+9Tgvgzg68OKNoTR0s+uR11fa+3NrW37XGv8lWLO3zmJde48IiLCwmHoCMd37+DL3/02vvTNr2F5tEIUUDJE8KbH+2++jV/8xU9w/413sD55ilW3BHYDFvm2cCYCeYeQaZivRS00EXq2+NUaCfJ3teOint1XrNdQFytTrIyUd/X5DGkzOcC2k7qkP2VcPF1vLYBkx2KBkv29BbauUqxcST+pRCHY8Kp9gMQ+P6cv7Pd2fm29Wo+1+qDbTr+HFPoyQwa9Fg01mm1oPVuHwU131OxYRYfr71rv2DnUu3dzYWhWHxARQHWWoX0yc+zn6OyRdWWfs3hDj99ikhYN5vSdpYH9Tj3UDBMax1fLVztGS9+5dsqaB1frvaVXWjLX0rwlyyxNOIMke0YUQHFgMEdgvUnvCWPTWKfFgURUzk1aXSXj07w2x2NXKVc2NEIRUIBE/wVOnn6KSIoXBOc8YpDtGyDGMLlafrPZIIR0IR+ruxYS4HMY+qHEoQuolsUnwlrf0ZAAKrDd6d2DAd536BYdhshIWxTA4dESBysPioRbNw6xpJtg1+H4xjXQcgl0Ht53wJBS3PkuZ/EA4WB1gJiNB+fHy/daExhjrHYzyuchlvfq3QzxanLzNs0YIxxNGTXGWHY6pOjv7cKUn96nHRTmaRyuDo2yC8X+vg+Q6ee0UKzipJHtNaNQWmPQCy+ECBdCOnNAwNnZeRGCepHod0pdsb70jkjASy30tXeLaGpIzZU5Aa5BChFNhKLt62WlpXDl84kSNEBLt2Oft+FHVxUwUq/1AAstdZn6n+ox6TL2Z/rsnJLcpyjs2K/SB8AAvD3ty3M2paelu+YnmgEZrWJpqdu1fW8piNa60N/ZeGFdEsQkUM7+FBYe8WiF3/rm1/D1H34fh8fHxVjwDGAXsX7wCG/86mW88vNf4sHb72FYb7DwHULYocvgJSJ5CGMOm+oaYLQly+aA0hxAB6ahaXYe9RwIIGvRcI5PWgAJqOdiH9Cw/W/9va8Pdof9MrnSMlbs59N30HR2tMYzB6T2FQ189tW5Twbo5+xP5xzA0yyGUqxz6rK51jqrtX6bMrl8Nt9/W4fsXrRCRC8rBWsYOszpdI25UvuojJRW/fLTgmVN3w+j41r1X1Zaa97qDw2gZUz6fWAMT58rjtLOq6ZHy7Gh67zqXOl+7tMx2hFfUvhfsh6KHEyfVDp6DPmcvqvn78MaHVc3NHLmJIBSxqKcNpOcS+FAOU1BiAExBnBk9P0OxITFYoEQUtrY9XqtRkElXV7f9/BI6bhGQ8MV4yNGRoyDSiHrMAz1reEBcYzpBaXQrL6H6xbw3mG72+LunVv4r/6r/xKnT56gvzjF0jscHt3ALkTce3AfN+/exXKxxLJbIg4DwAHM+bI/53B6epqMLHBOo9pWWMJ8MnnCgGlnApNn0veycxTLYUtxuhAIIQyVAVMEQq4vNT0ymQ6/kTAvDfqErvpZK2jmlHpLkWkwLp/bRTK3/dlSzuU5ZkC17/LhL3IETx5DHNIZDc5b25ExRM67FA4xBohp75xDkEPieVGKZwJAvjxQ9YNHUCxCXo9ZKL5PQbf4Yq7sU5yl7chIuRQaQFAJAS1AYkyXU+o5bnlhdFtznt0y9uRkmfRP/92m1zzQtfVohceg5nNT4MyZZaxiG5+XjFhEUzBzqSLgNPA52gltLwMBLdnBSDuYrJ8xr+t+6gxeTitTGusUTGjXqW5XXiQZX+6LnmtKQVOAIwTvMCwdXvjcp/HNP/khnv30J7B1hOA8OiK4PmJ3coZ7r72Jx+/ew29+/gs8vPcBeNtj2S0ARKDzCMzwjhCY0421VHuSRWlbA9YCGK34Qkjhsc5Pgf0ceK1ws+KdlofWzkFrHoW+Wt7ZmHm7VltzrGWx7fPcTmRLlu7b0bE2w6XyJ8vjqo5G/+bG03q2JQ/0+mFArVmtkwABS61iaTT2Y3rPk3UC6HFJiWqttMZn+bY1Fv23NaKltEB5U17sqWO+qOyJXKeLtUbBSP8kUyUFfrNWgx1k3kh9b8e4r89X5W1dHLkUEaP60CrVfKt6LV3n9JRgAlK7DBpbtfo9pwv2jUnzi0QV6TUtMmS92eD46HB8j5CcV5znkBQ9tKDLY4Byrhb9qLDQhwlxa5Wrh07FdMleGEK6NCj3kwQ4x4ghBGw2W+y2W6w3a4Rhh2fv3gTIpUsNB0Zkh65b4eTpBcARB8dHuHPzBhAGBDD6kC9/IYnpTyE2VLzVAb4okLSohyEka857HB4f5+cjEAPAaYeF0cE7RgyM06cPcf34AFs6wPriAi994qM4ODzE6Z8/xZMHHySgkDNfDTEmzzOnHZzFYoGjo6M8R2lSvPcFtImAiXH0ggtzpD5zAfcTpmTkbCvAamAMDtisCAsOOASB8/Mh72IIIIAyyhIjiJDIKfoyc7jUqFpYqbEwDGmXgRngmA7jO6oMIes90Vt4Nt5ZijCljn9tKmwG5DY5ci6l2Mv0EKHuKG3VM6d0yt45REmCGQmLxQFi12FwEcsYQOxBlA41pf6iGCuOPQh+bJuyR1kbbsXASPQjjCBoMsYYpwYKlCdW/14JC6oU576QjbpueSb3z4lAFLHe8lTXcyLzoneaKuCl+jsbWgeugPpcaSkunSyhZcTa92XckklM+H18nhHCUMI00+coPwWQtMA/cw3C54Rp+U4JcCnFo5U98q210RLUhc6RIbG2KYsKwBjrqtZEHpQ8S3mdyL1G46CUl658M7bj5JyZGosDwXGSrMEBcLnlELHwHZgdNguH7sW7+Paf/hCf/d3fhu86DIhwnuCGAdRHnN57gPdffRPvvvI63nn9DfS7FJYaly4pPU+AS/zDBOgbakWpSnY+ymfQUlipUrQyb04uZBU65zFHhh9HnfUUF4Ygob8JbWRO7xERqOvK3HCmM7nUW8p0mgvfa4HFFtiwskHAS8VzprQcCtoos+vN7uLUHVYSgyEJ+XI427TdJNOyw4enDok54+gykGKft2s0rV8NtqfvWVpWw9TgETXdm2CyBWSVMWz7LrKy8LA5TzFHm5iZc84B1QKi9rK0Vl8tDYocJQAly9VovBG5Mqfy/CjzUPCM8J7lzdaOXWvGW+ejJn1HzqRFBMop92UVp8D2JqEAcDlDp8cs+raA66zkNWgfeSxlY2BJz04jX8UYEXm81wKcsAgnN1529jDI+3yp8zQyojVPrXVuDWEd6aIxg3ME36UrJ9ghpf9Wco9ZZJwoQiXrM4aG8xgEqwqN5L0iD4wO+hDl6oZGH7AbUtgPGOmmwXyvw2a9Rt/32Gw2qc/OYblcYXl8hDu3b2O93uDiYoM7d57BcrlCCIwQIi7OT3FwdAxiwpNHT3B84yaYGIvlAiX/cz6ILYDGOz8KmAyGPUlaL8a142MwAN8tsQtbWVMY+gDnUuYTAuHx4ycA0n0Vr77xOj7+8U/g7rPP4nz9Zhov8hZY5xEHLnddSLaM5SLt7sjCsrHYwHiCX37XHq1C1+oATga7ADpKCpldWmiE0cui6wRz3v2RGqdKLSqwCLWwwKNhJAtCDozDjYq75XXTRoj9ThctaFtWsRU29nsNcidgl5KXK/FjXjKUQpII48VWBJXqljGZt6K0matx5+qK0SFGiw6JkX5Y5WHp0TbCRlBUf17XofvqXLp40nuH2nDj2TrST9kta05T9Z5+twWWigLCNORE/z67c0N1H+eMDGvY1GUKIpi5MmpjHM9w2X4me7umh93+nhtbbrBqW0qMDEYdGnlZmQNEcyF4ek6c7Zcp1PqDgC4rwqTA1XwQYeeSknGcwLwnB1p4REeIR0f4re9+HV/54fewvH0d8CnReccevB1w8fgE7776Ot769St479U3gX7AbpOyDPrOw0m4ShHiKEaTpkVLnshOj6zXQhszv3rtlHnMbWrjX76fA7jpvZrm6QuMlgvX/Snzoni/hEqGRprJmfnbB8o1aNFGhAbOH+bs0lzbLeBT9UF9Z+W0bjfGWBIc6M9aBlHLUBjXKZl60++tsBcp9QF21Z6xF1qGkf5O180zz2gAPedUs7otjarO6NQGyXXZp0OFJpqm9csjaCRSdTOX3QC7A5aTOVbjsP1sJevBHj62fa/GmeeHxTEiuh6AOFSn81UbSNOxZ0NF8LYqlh9b+lvaEQyod72IJgzV7EvN0yMWu1QOMJc7NCbzmtsIMV1MLREDyOsmMiejgWoeBusYASUz1Zh1P6p3P2S5sqEx5PsvEBkcAra7HhcX59hud3Cdx2q1wrVrx1gslogxIEaGd8D1G9cROeL6tRvl/gwigJzDervBxfkFbl6/gccPHsGhw2J5CJ/zE+tBMjK49WKVJk+uGDwEwBHjYLFADBHBdYhwWPolIkdstlscHx/DOYLzHRbLFYAA7AhPTk5wevYLxBhyGEKqX9oEUGXASv2pAzkqUGEEmA5RCZkBrGIYwXMKB6I4bldaASuldSCrgOZcvPMIYaiYehQUdeYrKQmsJV+gFcDyzwqiiWI3xfarFSctf9u6NdAuxlOMCBwQshCSS5QYAtLyNjd06Ej+p8hm+yFKZCIYUHsR7FzYOdc0as21XtRa2GoazG1X6svu5Oc4RzXNq/dQlzkgvRdgq88dXDmsq9+Td8TQnvYjCWVrYLQUawWaLgFfEq4k7+n5s2EMEtJoFZ2eq1mwxzy5j8Qa4/b9uXWxD0iMIZU0mZ+9/btSaRuCkQi9Y3QxGRkApTsxFg4f/9IX8fU//hFuf/T5tDPhCB0csBuwfvAY9998Cy//6td48O77OD95Ch8ZPITk+Vfr7O/ab2sIyO9W8dpdJPuOfdfOt8znHN3tnLUA6iyAUuUqh3Ftva11KmtEAxZrbNnv50oNEuvPq7EQVYJ0325sC2C1dMowDJN7hMq7XMs9O0ct4D9nPKR3uAJM9n27dsszDTkla9W2r/tlx1vrlrptPVeVQa2KvtjQ9rf1d+lX6kSzTmaxoKdrLdXHE16ygPnD8PKcISbYSuuRUX7sca7w1EEnc7NvHc71B8hLwLyrMdMcn6Tdh/06wK7ly8Kqbdu6j855LBaLhrxL0RxknHtgLkac1EvIBnhzH+rvV65saByvFji/uMCw26FzHh6Mw2WHm9eO4BZdzqbB2FycZu8FI3LA4eERwhBySINDCH2yTAm4fecOnHd49tlncO3wAGGzQdzswKsFdsMmUwDZkxwzUORyaZ4IJdlpODpc4trhAcAEJo9rN27DO4/zszM4vwDnTFHkPQgd4hBB3sNzPiPifTrkrQVB4y6GxAy10qyApGIw8eaUwjWoqZSiHKoXY4qRvbJUGEIYslLaPIJfexC3NKveK0xNrqpLAJgcMJedEBmbjVu1wlwX208rYG04jo2Ftopf11nonY2MEBm77a4C7wAjxHwPSwkccRKN2BY8qr0JSKExxGLiITdbozXYnQKeUn9pdn5bVY9fioSRWcE0zlO9ywagZHFjTAWcBSVlzOqZlhIR4SQ00X3QdemdPWD0UrUV3TwAzJVOlPc++tm1oo239J2fAL59YEz3WSsy2Unx3o9ngMyY5taJ/XtOYVvP9aySq5RZawyAeAU1nZNMICxDupwLDhg6h4OPPovf/5//KT72uZfQLZfoc6xNFxlxvcbjt9/He795FfdefR3vvv02HAhdTKEE5NIlp2KQXhUQFd5q8Kp+z3rSp+uvTfMWYLd/T8Bu43lydWikBTlalrTaaYKPBh5q8YNtr1Xs2vhwYGt03Oi6Eo/WO5otua3nahJSY2SsfKf1QEUbagM1yxMtg9+e7Rl/n+pw3Rf9ewF4qHcL7O3vluYtWkz6QbUOsfS0/dF9mgLLeh51u0RU3XBun89kbsrwtAuC6jMtS1uGh9THGOWalNYOYKmLHBijEVWfdQ1wVQIhY0AqntTnX1s0apWp/Kx5zspgacPyf8yYoaWrbNkb1qj7hhpb6v46R3mnZYBHxrmc5PTYN2f4KYc+y3wbXrI8rHui279KubKhce+dFGe76BbovM95ehn9Gjm96ALeOThmxO0uhTT5Djdv3sDdu3cRYwqXGk+2O6y3O4SB8fxzz+BwQYhhAw4BQ0wCLuQ7K4RJd9stQj54TuSwCUPeTmN432FYL3D31i2AHMgtAFrkXW6C9x2c60pccGSAyYntDOd9ynySlajY9rINpZWPjr2UfxbQyCSJl7XKMKMmqVJQNC5KPaldtyhtAKNy1V5v26ex/pohtJDUh8Nbnn39t/YqzAk4oQ2ACS1ayt32Scamt2CtstZtDmFA4LRzcX5xXgkVonwuQwAOdFq4toLRVLf9TvdzTL/XgsV6emKUGPt2/4W/WjSxwGVOEM0BEPluHNu8QGgpQWs42L5pACA8ZL0x+0DfBFyZz1uhFS3Q2aKT5T39Tg3OreCt57XVxyKQTV+K4gNP5mTf3FlFZGljv5vrV7uu9pwTpbHbtetzOJVzHgMIq7s38OXvfQtf+v53EK8fYPAEHwkdOfTrDU4ePsHu8Sl++Zd/jSfvvY/1yVP4CLBkUyMqfKfnyTog9Pea9sxakbYzBFkguQ982c9mD4ab+bI8ZOk8N48tGWjrFVrMGQp67LaPesf0qrs4+nM7ztZ6ae3USr+1gVXJGlsHpvyt5YvWG/J91bcMIC29WwBtbu5a/GbHPLeLNUcPO25d9Ny05k5+ElE6l4n23LXm8io7B1cBrpN5iyl0yqZmFixkdd5la21faa2pqg5DZ6C+VqFVn+2Tpv3cPNl3J31TfSDan+zmMhq01rLul57XlryoiGLa2263WCw6OOcBZnOeogS91U5S5iKf0z0p44BbsvbvU65saPwf/sv/fTY0OqwWS3S+w/HRIY6OjrHoOpydnWG5XGK5XJb7Ia7fuo2TzbYoXwmpSoMgbLcD3Mrh7p2b+L/8n/9PeObWDRAGgBw4H07xPhHu9PQUT56cYNcPWC5WGELAdrNBn28VH4YBYRjwkReeT3c0UAqdIhCc67BYeXAGhHAeqQsJQDIhXxA1LniiNjiriT5a8yKkBJAzjyFTklmrvG+EndyNMWFgl+IBZaeFYu2RHZmxrVDTM+MFSVYZxBgqY6Vifq5jAoH6kiS7MPW7AlpaxSozqRdIgl6nQrbj0b/HGNMZFhoNN+9c2aXhEkSNxE9R6C0+lsvLBLSqrcaWsLfAhTn3gsYzHZZ/5t5v9aXUaWg/BfQzh/MxAj/LC1ZQW+HS2qaPeZdR1oD17GhPf6sfrXY0r82FDdixt/hFnrM7PvV40+d2Te0DEMyJB3TdlQEeL++TrmtOOc0B1hatdF2Xbb2PdQKyPkRWAQB1HtvVAp/92pfxzX/wIxw/exvBAQsQXCC47YDtZounHzzAf/hX/xr90wusItCfbzBwxMApe57LoadO2lLgxK4T+5nuI5l11gIDmk/a68EAuwadtAGkn7EgxRrgRDQeADUgx9Zvi57/ii9mAMVVFH5rXe97/6r8qPsBZDqYUC0tEy1osuvBnoNqrdOxYVSeWdv/Of6w/FC/S5WMkWfmUpraevbNRUt3aX6xZ0qsM9O+O/f5nJzRdL9K/6Qf6czrqF+rULusy+bwgPzdrF/10zoVLY+WV9QWig0hbsmEMpeNndOrrhv5WT1PVNXZOntl5caIM+q6LX3suC/jq7kiuDPpWgDZsTle8CzOJcZ4vgWIIOR8I+l/jXWk+zt+ljDUh+nrlQ2NT3z0ORysVgnYDwMWXQcOEbvtUwxrxrDZ4vrBbZyd3MfFxQUWiwV22zUOn3kR3nfodxvEyNj1PWJgLFYrkPPwXQeAEcIW9++/haOlg+8W2IVkZUnGga7rcPPaEjF2ODw4wsHBQQY3Hs55LJdLuMUBdiHd5eE6Xy4UYhC6RVdAgs8X+FEOp0lSjMruh1h2ib7WEyMLAxlwjBOTGNHD+QiE2nOjmUtiDLXwAVKcHTyB4NIBx8jwcNj1O3SGCfYphRoE1xapDn+Ksb7QyoZWAYDvOoR8WzlBLQZOoVUEqsJGfK4nhlClGpaxz/W57/tqR0KHbOlSCVbHCENEiBGbfgf0u5SSGCkzl/cphA95vrzvADjEOECD/KpPDbAdYwSHkNJvmndG8F97V1tzYhWMtoU+TNELf6pMqeLJ8SWMQkbebdSpx9QqeoyinHQIoy6tXbb0Igr5LXDUvNjqFww/cIwIBkwJ6GkZJLquFmgd66nkriZUkR1pbGmHLMZYaJHapywryouwkz0qHhtWkohkQY01fMe1YMF6aldmODlSaMwmxOl/0hvXdehjBHuH5z79SXz5T3+Ej37xsxhWDmswDuCx2kb0T57inXfexhuvvY712Tk2D09w/vgEPjCcd9iFvvSDY5JzzvlsoLfD88rvwlO5T0nWYDIJVva1gLJ8J6BR88McsLFFg9AxbGPkZ6109wE7zXtzO36T2GymiVzYp9T36QP9uYzlwxRL5wIu81okpDTyBXCZ/sj4tVwXx5voDNv36brk5HFtAH0rbyegtAHGa/CFQmvR6y0AOCVMeo/SA5Pd8En/eWoAjMB5dJYRJWfFrGFVfiYBpZ2Bc8btPl6XcEnkHftRxI59L+JaQI8p1rhrkKnSqS3ZO5G3NCoJjZO0I7IJzHUlPBpHUtvcOprQWfqndqhbxrHtR92ncWyid9k4RaStFs/tMzzke5fn7datW7h79w7OT8+UPpE+jM5HwR0xRnBEivIR+s7wsW5TjBSRe1c1Nq5saDx9/128d3aGk5MneOWV32AYdmCOuFhfYOgHHB0d4+joCE+fPsXQD7h27Rr84Q38Z//0f4fVYQfq0hkJ363QDxu4yDjMh7Op63Dz1i0MF4+wwA5HK4c+AOuLC1w/uo7dboeLi1NcnJ1huz3DZtUhBMbT03M8enyKGAnkPJY3X8QP//gfpY2iIZ25IOeQgoS64v12visBNSFGOPYAXL4bhBA4nV8YwpAWPCIiU/6Xlp7Edo+hOAIsGICD3AidwG0Ac7oDA1yffdB3XQRwPoDJ2LoUpdj1AQxgcKiUtUy89x5xaOf8FoGqmUR+H4VeLQTkgOyqSzdtxz4d0OMQ1LNZMTIXpk4CLwA5pSQzg4cA+HxwLYYCCLXi1322YVctxahBaASwjIRdYBzcvpHA3bsfIBIB8ACn2+pBIshCUS4V7lVKSxbkZQfIbJiUDWeTegUIWvBbvldLuxWaJkVS0apJa845US00tRDrspoKyghk1QMN8nUdc6EudntbH1C0oS5VH5ESOUjdUq9WRFLHJLREeFcZTESkLhRt85PsGtqdF0B4ggovy3qulKqih6MRXHH+L4e6Zh6T/jK6zikDLDkqrNGZqs87AcX4CAWEJmeBjEkbIqmP49qWRBbJJl4w0HPA4BzYJ+9VFwmOGeCQwIrvsHWE/sZ1fONPf4Tf+va3cHC4wtAR3NLDDQF0MeC9X7yKt3/xa9x//108fPQQMSRnAjiHYMaILjtrOnJgl3exOZYzOnrtl/UDjAYQESJiATzzCrxtdOmkG8453L17FycnJ9jtdoUf9inufYBJey/NiyBOcrvodeEeQgmpLECcpiFPGsikdsbq9TMWmMjv9jNt3Oh2tVGzj66l7nE4E/Ce1REIXG6KH5/NFzCacVlaSr1z8zExPoxcbIU6zdXTMj5i7NOuWwZriUcBIg/moWq7akdkVpQd6zT+yAzKWTHTmdJ0f5NzqU5Jec+KJ5JuHY1sYnEAUHFoKAk9rhcaDa/W+C141TIVcTyn0eU0/iw3RGe/KxFATjtHMmBFGltyUhb4jsvSnFuQDgCRQ+VZKI4bkrVW83MZq5IXduyd8xBDmLOTcTQZ9hvsQp+5HS3903433QGKY/gSUqKiLNRyHVP93dSxM/2wz/f57DQkFXh6AGl3I8lnMU5Bacc5yiFXRrkXTy5KHWIEfJtWUo9OI3xZubKh8cH9d8HMODhc4Hd+97dxenqKYRiwWh3g6PAo7R6AMIR0J4MjwsVAuH79eom512CMOd8MHlOKWZDH6dkF7lxbJiYBY9tv4Tce2+0O680a799/HzFscbhaYrPdAUgXsq03awwD45MfuQ6U7byArvMyI+MCz3nu5QZzQIQIQJx2PySXtAAamVsNzmMGsC1QB8WUNvyDMsrVwLO2ZPMi9ynLscurnsFVtoXKqneEjroJKEtMMBWwBXCpLD1SZKFpANhSFPK5DhnTAsEuzCGEZMC5+oCWBQxSP1CHUrXKMAxYcAqXgpND0BL2VpabmbupN7S0613hF/3s6N2o3y9jMN7Sqk3Fe2IYFsOm9TxqoKC/K9+nD6p3xjIC5kkMdyVAR17OUqk5Zk0f/bcofudH4ar5QRdL70mP1fvyt+1HK1RNgzhLL6lDQoKsomsBHcsPI1VQgRwNFOy8yoVe1vut15A1qIB8uLahaKZhRvXvduyinGWHBUToooD5tCbYEYIHYucRFh0+8eUv4zt/+ke48dyzYO+wAOBDBF/0ePTeB3jtp3+Lt37xMrZPTxF2G8Q4ZuuKeX12XVcAl50DPX79WQE/NJ/+tVXq8U4v55L2Pvjgg73v2mJlxJxsmgPHwtjl3WxQ2zrm3tdyAWos+r4b4T29WzM1WttruLVGbPvW4GrRpzyPmperOUH9t14PrX7qNq2jI3euMvZHHDEFZbb/rTVejyklhQC3jUxdh/R1uoa1HEvrORkusTgwK89MLkV+Tb5RQ2/osdoAmZa5HWHLL26Sqr1uS8sb3d5IxyxTFKbRhWNMBhjVzxBRjjipns5tjjtA9sxjmvMZOul51/MiFFNtza3B1udz68HiFfud1d+2jhZNWk69Vh/td0+enODo4KAeez6/PDYoFZj6GtEdzrkJL7TGeNVy9fS26BFixHbTp5S2rsPJ0zXIbQGcAEipVLuuw9HREQ4OD3Dj5h0sFgv0w7YSksycb+xOnoS+j2DyeOud9/H0sINzEXBIF57gAWSrp1utQHEJIuDg6BBHR9fhn55jFx4jbnu88OILE4FHRInZKTN89lx47xFDnzL4EFVKW7Z3hcAWnBaGcG0vUpkoM0kiUCyjSJtVLKB3CEOyPnd9j8XMvDBz9rDG4jXUaT4duRKWIH0qApqmzCNGgCg3HbMq455s9avvLEMW8ECoQJ8uuv6WQaNpK+2nuzLkxuhEh4uLC0iIEKimp55HO1d6W38uPhpU97tWyBGk8jFrZaQ9F5ctTOuha/EcAPCeeiQ7GzB/u216EPVuBmrgposFCKOhUa8P4cEWsNo39laberyaFvpvDfiJqMSMW1ClwZpdy7q+CbBsgAgtiC1fJTpi9JKiXuuHh4eJRzE9gzLxiBlaW5mhgVbTaPIOPTE6dliEfGbCeew80HtC7wnPvvQJfONP/xgvfv4lUNchkoOPBPQDto9O8PYvfoM3f/0KTk9OcHF6CmLGbrcr4FnWq/yzfZeQI2tg6fG3eGQWyJv51zSytLGGzVVKCzzq+i4rLR7f18/ZtotRWM+z5ttWvfrzFrCRotfMhwmlmgMbTQCm2rdpp/Vzdg3OjVG/29p1bZUW0JvI0tKv0QOdnhl33eyzczzLQMER6dn5/rXWxGVj0J8VLDHTRsugmjOihA/EwavfUX+U1tp0n9FvVO88V/NvHp3TAxXdLUg28wrM70poo8m20dIFl5U5mrbendtNtfL9srabbRY9nHV1DmHMcX2XjsPWDyBFh1zyrNXR+8qVDY2f/PTnAKeD1bvdgDfffAeb9RZDH/D888/j9p07iPkGbebkZf/97/8YLa8yESkAnLxuy+UR3nrnA7xy9gSgAbthmxdTAjTireYhptAcEHy3ABPhwcNH6BZL/IP/7JnKs14s5xDRibPapTMQi8UC/W6bbqKOQMjp1ORQdsmy5I2FLpNMbaHZEkZA7aXXz1cgIpPK5ZuBC+gRmjmfgaRtA1V4glyOlIyQOjRGAyrK4WJWuGtGnwrkqedCntehM3YOpBc63tmC6tbv8oxOkSrKOHKKM2QCzs/PUzhO1nFO3TDUqrupyDCeO9FjTnMwPTwo42HmyuuoBSbL3krDgIhRLqNsAxBNc00PNs/UoHb6bglTy2uNaPReOe9K+ugYp3Xa/mgecc4hKP6w/LUP1IPaQncOKE2Uum0HSCFBubR2EGxbdlwt2kONq9muAbiybi2/MXO50HRufDq0ptU/C85bdZXvCGCXQj1TWKhD9A7bjrC6cxPf/cHv4wvf/jri9RW2xOgcgTc9dk8v8O5vXsH9V99EfHIOOrvA+v4jwBMGGndRhIaSu10+s04Jq8T1PIseINRG/L65mswPGrwFVPS6rNg51PVah9NVgble//J30yBUfS80a+hMW8dcvLgtGlhbnrQXj05AfwN02vaaoA2obphujbM1Nhs6q9sQB8qcXLH01Y5Nq2v17lCiDSdE4RxQHEa1vrN8bOchOanEyZDDVTRpaNQhUvSOlNSh25zSwBhrjiZ0lr5N5JIag82cJJ87YHLebaQEitEwlZdj6JTVj7poWQggh1ur3RXFw1pH6rGk3SFf9c+OW79T46upzNaySMtZ2+/W71fR2/adfaUlX8o6RwrZBU3BfVrLKeSyWstEJQmOc9PdSo1ptHwQva5Tktu5ueqYpFw9ve0HZwDnEJgQ4ReH6GKHi+0p3rv/CB88epqvi09K8ujoEM8+/xH0Q58PfwGOfF6AKaY5xpTmlpnAvkPEAn/9s18jxh0i6RjlcXudhwCXT9WHGNGHgNXhAT79mc9gsVyVS3+qiXBGQDCwWCyKQNBCRDz4RVGpRV4xmRMjYOqR2cd8wHSrbfyO4SjtIvQcSkrVsougbsTU9XXej6GOillijJVnCdBAINWtFZEUG8LSWlBzwkq3pQU+Zp7VdQs4bO0GTf4W5eGAMPR45tYtnD+9ADsH5nwrdEP5tMBHEVg8AoMWmJM5t8Auw8umwNc01n1JfeAqBELeadGm9bsF06k/rs1rag608KUMKNJ2/1S5WuGihaE0Y8Mi9LMT4dYAhbpPVd9mBLluo9BZtVH3cTqflk9b7SRBXPfTOgnmlDlMW3ZcmhZ6rvfFru8DEy2jJMUnA+w8tp1H8A5D5/Hbv/dtfP0Pv4drd28jeADOYQWANj3O33uAd371Ct597TW8/8ZbOGCHYb3FwBGRHQIYXu2KzhkE+vPWmQDpt/Z0C6i3dNX00+/PfaaBZYvf9GdzbbVoqj8T/mrxjW53vPx1OoetdV5ohSS/LM+2eK6a80bf9fvW2cU8pl0XR8llNNEGjvX4l3YJRe7tAyX2u7n5SmHKBGC6bu347T/pnx2bpS0zikxOj8SKl3SZC/GTepjH31ttaXDXkgktWsi7FX0a9LS/T+QkpsaLftYWrW/lOq9WCJz0xuqjplyVuUJ7Pdj1NeEjGnGXxQ8tHWlp1dTTs2UMubJh3HNzpH9vPWPLvjmo5EkS6bP1JUw7YlawOIZmjCKq56mF4cpFyKZ/LVm/r1zZ0NjulqljMQJIoU3sgIEB75Y43+xw8+YNdF2Hvu9x7eZdPPv8iwjDeH8EsxL2DKQDj8B2NwAHB3jxxU9gvflXcN5jN6Tbx51z6LLhMIQBK/LwRCBP2A479ENEdD2efe4FxAhEGuNXS+iIhNgQUogLJU9c2h5NB76t0C9CLqeH1f8SCKkJbL2nZL6rAN+coIQB5FAeAgWStYCy/dUKu/Qp8uQZlBja0ctjAZpVylJkPlugXQuhFqCXOvXhUNuWfQeow66ENvL3YrHA6uAAfHyEpyEAkHCq/Z7fpiKksV79XowRMdT9rEKTfDte1+4PWwNNYtz1P92upQnz6JnRn42KdWy0epfT/+Q93/m8VS5AvQ1srcKqBBHPGGyKZi1Qvz+6+GqlBSCKuT4DbFqlKYBzsd5QfealGo/mo8Z8WSCov7PKaC4sca6efYJ+SR0GR1gvgBe+8BK+/aMf4KMvfRrwDmGxQAwBbh2wfXKC9195A4/fehfvvPI6np48RrfosA0DBpedLj6d8Wl5zvVOi5UXrT5XIZHITg+MhkdLpjUBhylarlgaX6XY5+Z2j67KX0QErzzr+xwo+h3K56ws7VpAWXvFL+uLvCMXyNo1bh0GMHO4r+59NLHj1jTUgLAFsmRO89GjJi3sWpxrV+ssOx5XnHoy7Hq97xuP6jEE0lY0IyA5VNvzbmX/nLzYV5p6wnxveccWC2LtOoo0Z4ykt62cci7JjKjarfEBV+/p9+dCjQCJ+LhcHuixEjAbCmT5sRq7wYZXLbP1XeG91lzOzR8zp/tPaNSF5XuWZ9thhoQaj1WYxz77IfnRlisbGq++9g4iR3Sdw3LZYblcwHuHbnmIyA6rg0M8OTnF9evX4ZzH0dE1LJYrxMjgCHjvIJlmUqdT2IvvPDqfiPXSS5/BwfF1bNbn8IsVfARiiDg9X6fYYHI4jxFHqwMcXTtCCIwQGD4CH//4J9H3PZjGXQGhVrLy5FaN0ZvmvcMwFPcLgAweZR4J5RIbOXiqGTAlSJl61iLXlxnpRRNjLHnXLfBFjnOUDABSh/ceIMmskw5wxRwixswlNl12c6RN733yjkGHk+WsDFEA7jjHwzCMuydiHFEeqgKVxISu8yXsahQUbd4pRhRnD36IJaVfAqz1hW9zCieFxckWOsAhGY9DCNicX6DfDQgAPJLrRRtOen4SKFUhUqYt3YcRxE5vbBaB6LsO8vFoxKDMKfNUWCWQRdUuiVU2Ff149BhF5uZz6e92W4n+WbjnW33BsaSNzJsypq6pAah3CwmJV3UYgu2X5o/i2ebcvjRKIz2sCdIScFYx2bE6atPUlhZYseO3a7ulCLSHmGMsByxbdc0pclmzfd/j8PCwnvOsEGImF+vJkmcoxdRSTowQmdF3HsfPP4Pv/PEP8Zmv/jYWhwcYYoTvPPrtDhePT3D+wQO89YvfoH9yivtvvoPdeg3v0jgGjuBuDFPocmotTh9oMQk5p+RUv71zgKS85pRNKgIlxBYu1ZcOlwuAE49yoVJZ73LQveYJC1yhfmr6lt8mc6OLne8W0J/ju2ll9Z9ziloDq9RuffGpXl+Wj/aBrZYcaLUN5LucQijzlNZpIvy+uyUksUg1Zq5pNX+2rd6J0uOZkpL2ymm7LkX/idwRvWYNUSkSaUvU4rFp31ufEWGUa0l5KxYYZZvMn3aW6Pr2GRpWZhTTJutRYOT6WYNiTtfIQpsZ/xwfJV03Gr0uh0QxoxiIUoS/kEOKGe2zj1bW6rbHZBQ1ftH91n0svJXD4CkPVa9Py5d2nHq+9pWrgPHSvvob+TNqJAUp628GEyRaJvzkO48wDHAkUUPpwH27XxoHjkayfAeq1+lVx9cqVzY0Do8PS2YRIMchAui6RQIcIcD7BbbbLY6Pj/DMs89guViiH1LUoycPTw7OMQIB2z5DQiYsnYMj4O4zz+Da9Zs4vzgDhgEERt/vEIYe280aALDwHnfv3kKIA4bQA2DcuH4DH3vxo1j6JSJ5cOCkkANjsVyAhy28S6lXCOmCJUcOy+UK2+02xaPlmDSmdB5EjIsBnOIWkYVhZHBIRktEfVCvAhyYAt3qeyNcE019Pl8hACxNPhElSegIIIfOeWyzgPLOJeCuFIII92EYUj8DwDn1pHi8ORIi1f05PDxMFx+GIaW2k++BilkZSYAQEZxPRmPaRZFt/2mIF1Ha+qPI8EQlNRoDYHI5zKAB8NUZEuu965gRPTDECOrTQhy8g+9Tml1S6dmqBeIoXd6Y57sUJbWswCoxuEogpV0xMSZGgZjCS1RcMNVhIoUvaGxzX0iXNW7IuZKPWz8rBjxQe8QLvzEXKSex4JJO0YoPK1haikmMz5YQsllxmoaAWLFIqZ05K3uhQg0gZ3ag6k7X52HkOaM0KxBPCZRLQgWr3Cw/ljkwGk73j4CSgCGNTvWvjB2FDtIHMvwn7zhOACYQSl9TWGWEQ0ozTTHJj9h5bMDorh/jC9//Hr76B9/D6toRyCUZgAHYPD5B//gx3nnlVZw8eIQH797D5uQUcdsnkMsAeobHyM9ElFPWRjiqlgrAMT2bwUMyHBOg6ByBYwAJHbOjJXIERRaBhHTvyKBoy/A+rSNtRIwARKgo4FADf8uPBEHAaY6m/LzPINV1ad5ogc40lvbB+H0Ggb1PokrooXabte7QgLW1XuUd27blM7mw1nmpJ+svJKRoZbnIEnYpNl9CNZJepULxqg0DoKVOkXk2jE7TNMmSkRatsm/3XOsP+U7OciaeADinuYZLhm0IDWfNzNyVfhIBylAbcWCSc/pMjMy5BfSVHGnwo/7MkQbOXDzUAhJbcszWMQl7U59Pd7e4kqU1bVLYmRj+VVuU1jfRuKNP+RLd0etez1mLp23oX+JQVsxGVX12zkRMEI+yN4acJMjXdVe4jfdHXeg+WpnSorneWpHVMq66dv1arol80TwvGBaIAI0OWRR/wdyOVki4jQhEoq+lH6PDrDW+aV3z5cqGhgaxaYGMTJ7kUSJs36czGc8884x0sfqXmG3IixsgB3iXL4Vj4Pj4CNvtFn2/xna7Le1fu3YNfd/j1s0bcN7jYr1Od2A4h9Vqhes3rmN5sESI4wJzOr4sRjifBKF8v1wuAdQhXUI8ASpR3fQtAn48PDOmZdSH0MU7pCdET5h+TkpqEwUcUSZQjHG8+M4lj6HzDouuK32TPswpvuVyCWauDja2wjN2u12O1fVwbtpXDcS0Ahtjq6NwRFEQ9fjqzFSFzoRq4dTAenpI1Frz3ntcnJ5iwUlJyGGmlvKt6DNWjFbR/XXkysFtLQRT/1Mi4nEnaPQCiyKX36v4XiVXWkpsTjlYI0M/z5w8xEAdzjdXtxh7ehvVAnoLEsY6xv7rOltAqzUmCwD0WFvPXaZ4bTtST8he14mxABTjcQ5E6Nj1VpuWx6zingOw+pOyJiiFdNot7EApXaj0Ocnc5MUKMafZ9g6x8xiWHT75u1/Cd378Q1x/4TmQ9yBHcEzozy+weXKKe6+/iftvv4WThw+xPjvHbr3BZrtB53w+I2AMQk0zMxSq7Ln5cwR6TiwN50JU5gxK24Z8VntUp+E5+/oi63oEoNOiAb4Fxq0+XQY+WvUzcxZMUzAo31uem8hT9azWXdLn6mxXqyPSR67HoftCSn/YddUal362FSY1V8rcNerUbYpum5zPNPJMz8Ecn7bGNDfHmoe08WedFrbIs63D3voge2ss4pS6Ks330brimQ/xnl5nlg51AyjGieY7oqnBq3/uOw8n76d+TEYEbezoudbh9NIPkXdy8FnPddGNvH8ur1Im/Ud77OEKPNme74jtViVQSo3MLPBa70tbdb1XW59XLVc2NAAUC7xStAAWXQdyhO12gPdd3tU4RvFsZQMjRgHGgM9uMeZYDAaOETdv3sD5+RkWC5fqwKiIb9y4gdVyiYuLM4SYbgTebrcIHNEtl/m5dEle13W5vylunZyH97XAsecJWsaEWIplEqhWALLw5UIwIE3ePqYotDNCL93UKM1Q2UXxoPEwPDNiGFO6hhDg3RguZesNM0LdglC9ENOuynj+wCpWYLzJu6ZFfW+AfkZ7b/RP5xxiqIVq3d9RcEy8eIGTFzeDNPlcYslB9SLaB4DnShF8PBobE4AxQ9Mynua4MG55t75r/G373hLCzhFC4CbvkeFdoYn2VM0pv5ZSiI36Z2kwo+QnCiiHGOi2K2B0yZrS7Wka6fWoFauj6Za4VvganOlxzikyy6Py3T6DSICUU/0M6uxOFI8zpzAqx5RlhcfgCcEBw8Lj7ic+hm/9yY/x4hc+A1p0IHLwRAi7Hif3H2H75Cnuv/kO3nzlNbgYsD0/x3a9xvriAiBCzxGdc+XCTUu/3OMJPVtz3/Lg27V/2Xzq+bIguvVca+4t/eeAlJYvrTakPutwsSB0sk7M+twHaMc+K284poZ4a+wtmurx7DXiGrxp67OhTTHGFILZ4AXdh1Y/tY7YN0cir0MIKdB1pp9ats/xhpZtQtN5nqkdCbrd1o6KDntrvdMq+3jZOuPs9/psoF0j6SEAHJtQca+eYS5OP13/XP/n5lvr2SEEkJtmlNq3ZvfxUasf5pOJXBIekr5N1qmppzaIpsb7f4pixzvSZkxPb8e3bz6YgYv1RZY5EHAhb851YiJfx/r/7kZVq1zZ0Oi6bhZ4DMMAkMRCptsw5dI+AGAOiHmnYRh6DEMPv0zGydAPKZOUI3S+wwsvPocbN66DOe0SyLmD4+NjLJdLnJ+fYdf3GGLAZrtJhgAzVgcrADGd2fCuGBjMksc9xQFLfbXga6dwZWZlMmeGiHEiIGtGaXsiihcCKAcEpY5ReCUvYj8ERDcylqQu00J+XAC1EOz7fgQoMcIxiiFnFYc1TioF4OpFZrdS6z4IhQgh1vTQcbF28cv3XOKwqeIzq8Q0IHQub/kjhRLJbddpLDHtKijDR3ZgktAZgCsog1qBp23afYpb07cczHJ1NiFNc80fVlHpemseGd/Rv7dCKVoAQJ6vgCDlNInmuJwGjLY/QBbQxrsG1IrX7gjMAbiyjqj+zI6vRfPWOCvhqdasBWE6Pa+l7Vydum3L11Pj+3KBTZS2BebCYToGHFMKj4oEsEMPIJLDpgOOn7uDb3zvu/id734b7nCJoXMYCKBdwObpGbZPTvHea2/i4Vvv4uzhY2zOznF+cZbuEOK8c+Hl/IWVSZrW4zkJvSbl+dZ8aPrZQ+P7AEULENbrsS4toNr6nRR/6e9b/bHv6yJyTRdrZJMx2Gy9c7yUwkrrrDtaTrcMiBYtreyYkyUMNPtpx6jnQjuW5uakZXxpntFjtzLMfg8Viqo90zKeOZ7QdJuG3kyNWQCTG4/1OFrzt28ubH/0c9Z4k7HYOvV8WppagFwiG1yLhtM+aBqwGavdlRHZ3HL6aHlgZbeUlpHWkrvyvuwwtpyiLRmin7Gpm7XsEVqVOSfKoZvT9OL2bpE5mtoxt/RD6fcMiLd0997vdbAVHcEpY6Qjl87xImEje/p9bo1quo10RTVqiwPmsMVcubKhYYXMGCaSYtcRR0ODKF1Otd1tEULNcCmlrBxsSTdosqd06Dp70UMYIAfilstlORx5fn6O9WaNGAN2/Q59GOCdQ7foEMqB7YAQBzB3hUBdl84UyI6KZN2Qhal3MPTOhj6UVw5KzxC3YnpKsX+tRSK/t4BljBFD3rp35MvFbIwU29ip91wemzfeWAHqY+GyG6JLSznYrU15Ti9SEd56e7cwnaGH0DrGWFKvaV4QegvNrGJI9Y4xk1Uf8kpgZgQeEMgBbpzzxF5ToaPHb4WFLG67gMo8oVZIVhnpurQiXB6sKjqPz0XoA662Pf13xUszAiPRvL2boWk6GVeMYDd+VnnTlTKc9I9QDDaZl77vy30q2rgDauA956UVY1zatAL7MmVejUveTX9MxrGvWIV+VaF62TqbU4wgqs6XaGXqY4RngJgQQNgREFZLxIMlvvB7X8Y3f/SHuH7nNpgIAYALQNjucHb/IU7vP8Abv3oZ77/5NuJ6h+16DTBASrF674sDjIDi1dTgbBz/1AO9z3CwgMM+Z9cQ0DYuNK3sWmvRswXUWiB2DiS32myNW/orAKUCsZERMa3f8tSk/QbII6rD+DQgadUp77acDhUdqPxvLw01LaVeGH2g37U7gC26WmC2rw/6cz0uW1pgUeuVuVLP7zSUb05utPhqjp9avNMa59z6uKx+ouyowzQUaI7XKoDcqLvwExG4QQIN5Fvv2v7Zv+dkqpYpLbmi6xhpCQDt5y/TFzHUBmmVHXJy5qt2ZAFTp5LFRkWWe48QRiPHGswBPKlD9GgIQ0o2ouQMc3INSUh9xx2G3Q5yLsiOvZojwiR0asQ61ExUcxUd2CpXNjRsWk75F2M+IM0xe0RZdHq+YCRdtOa7ZIQsuyVAiXGHEFKoEDnEENB5B0nFRURYLpdpZ8Q5bDYbbDYbxMgYQkC3WKTwqRCKx37Xb+F9l0OlGCAGOU75n8PUkzDG406FhACUmCcyyjmMSwRWrqUCxnVYVV1qxZA9LhxBERj6bNyEkM+zjIeAhxDgiOA7Dwq1l7zy/BNVnrW5Ugl9tIW+zPeccCWSC8LGfogAannkq+1UFR6lQ/TSIetGfyIXweiIsFwssaCUdYFiyOFlVPohIQ993yNgqqxaCnCy8+BoMu45Wm42G3jvscjnY2wbuUYQ1cBJA4irLGqrrLUntKXI9RqWOQlRsk+NdersZbNAmYHIoeq/VmgWGOo27RhKvTwadPvASKtfdn3LGt6n1K9a5oDth61vDlCBuVj3Qifn8kFv5xA4IBIQlgvsVkvc+eyn8e1/8Md47jMvAo4xeA8EBnYB64cnePrBIzx860289fIrOH30BP16A46MgAi/WOTsUKnvPp8YFGMjDerD0WMuDKY1j3XYXtvpoT9rhcXMGQgfpkzX49WKtKtvm299z8zFaLN9nuUDoBlaremoaSmyXgOP1jst0JZewCRpxj7aij4jjknbN/rUApVz62ZOj9gyJwesETEH+q8it8eXUC7Cu4w3WnOr+1v+Rjpsb89X2L5andMCt/v6omX2ZXN5WZm0N2NIWKOg4gkzx1cB/lKnjaLQbbVALxFAzkOnc23pPflb5EpyWo7PD8NQpYAm13aOWL3dakPPCZB1Uw05K7oAtR7TdTgixEY76dhBiiQq+lX6BZ3kYV5u2jkkUCWD5uh41fKhdjRSZ0SBj95YAOAYseu3+eAl4eHDhyAiLLxPhgYlz/JytUQcegRmHK7SBXuOgEiSDYpBxFguV+i6DiEEXFxc4OLiokyY9x0IwGKxBNGAx48eY7PegNnh6NCnQ40AEAMQMziPKduJdylbCwOIYYAwpTacCtDLYPbi4qIAfMaUkYTwJRwl78yIJ10OiwMpNS0kRWs+pyKACEhMHoYAsEOIIX3vPRbLBVy/Q4jihBJvEpdUt4t8TiXboykBAaXQEeFtzv/2AQlSwYNtfgABAABJREFUqk4zZcvL1hIa2hCR9IfaUJW/5dko+RYaglK6WpSlKNTIxbr3jtBdO8K1u8/gyclTxA/uw/EYkpWZFs57BDnTkzOoSf9HoRNHD7jW+A3BoCkm3gMgnV85OzvD0dFRut/DKMay6FGDSz1mK9haoSzVnJm5sErGKuqqTzkMIobEby7TWYSb8HxLker1IEw2DEM51Gy9OhYUWMWjvUdzinKfkJvQBTPArUG7y8plwvqyQsn3UbJr5caTMZHpTJkXvfMpAx6SIUjLBbYEXHvhOXz7R9/HS1/7XeBohUgDiBmxHxDON3j81j3ce/kNnLx/H4/u3cOw3WJYb4rnimi8wdg7j2zZpQw2XHvgiVohkjUNNBho8hanNSgfpXpaM5KK3c3QP+V37UGf0HiPQZJ+n9Y3Z+Tsq6f8JJSL+YLSkVkgjMlHSl25XpH/QEUzohR+Kmtefyc7hXaNA7VzqdVXO48Vvzd4vwUsKsOAx93mOeNCz4mla0teJepQ+b82vWisuPyU1PNzxoSlqx1Ha37L54olrjq2y+SCxhj2/YoGNOUL+6wtOiwsxghWoVN67oVHc4v1MqTp2IpeBGNoGLPT9WUMJ5bdgnp3DSpcuiV77U56jQlIreO83gpbTI2dFkbRWEYwiN49kN+99ylLpUS8MBf8ZY05O29SB9E0eUTr9xhjSRyjaTj2t866WbcN9LsdvKfqPQDlHrW50up/SivK+RqC5JRqYcar6E3gQxgafd+nF7p0HwY5AMToh7543Yc+be0sFwu88vLL+NEffh++c/AEdLmTPPQ4WObdCAY6SjdO0tKDwLh/7x1cPzrEdojFAy3Zp+SgsoDs5aLDcrHCdtvjF7/4Fb79rW+BhwAeBlDnwSGAspETOXtpFx0iB8Q4YLs9A2EAMI0hlwkVZgkxhZREJehbAkGUiJ6UsshDKIYacp+opK0F2FEKiQoOkXO9jjC4ZIghZM8VZ08BkHIl53sJIicrJKbcs4hqd0giDZnFcz16e7WyyrNUxqKFuB6LvdG6/FRZv/TuBPM03r/QJwP1pqUN2RkbUxImtU5gWmCR5+mUA77wra9i+ewz+Nn//f+BQ0qKqFz0l8fkFx3Y5H4v/WW1lyNgwcyjHqsUeUvvRKxWKywWi+p5LXBaws8+2/o9f1D1ySpUy5+ASdfXEFQAo1Mxn4XHMu3ZtFfeN6Ff3vlED54CC13s2inP5LVjQYMdT0vBa0/5hG9rIlc/W2EVLXBhzw3oNkQRWi+Urj/dapPCm9hRykIcGMRApLxCmeBjXtuLBQYOCN0CODrAV/7g2/jtP/wOljevgR3BI4B2AcP5BZ7ef4T3X38Lj995H4/f+wAXT0/B2XERKWfgA6FDOlAOUEptTOMWOUCgGCF3CQgwT8MYDXI7Z3PzLDRI4XwjyWXndpyVNqDSn2ngYb/Xn1n+1EX3TWST/V47mrR803wgJfFDnse0753klKZbZEDAMAMSNizp4a3usIaBpUdrDdixtww+O845gNeSJbYdG0Z9lXWqaWff0QCSE1F0bXnnWjs0sqEGwJPLKelDBYxt+5rGOvxsjlatudf12LG12tL6LoWa7Zfvc/Nlgb1ur6kzqU6XXckh5nJ+I5GRi/4F0aROLjqR8n047fGLbrPFQb3D6SxgWsvpTKCdA/33LB9FgJwvu05gmqyX1rpt1W3XcyvUnUQdKpkpPkKbEEXan4awzxtV1fiotv2kL4Ir52gCEHb9DkfdAYAx2oMx4pMprygLDajkHpjQUT6rUfpMJeR2H7+2yofKOhVjwNnZBfp+B0aE98niS2A+MZpfLDD0PX7+s5/h3ffexa07twrocs7h/r37uHPnDkKM8D6FlTx68gTeEd59+y388pe/BAAcHBzg/Pwcm82mWpCRkydbe8qdc/jn//yf4/joCJ/73OdB+YK75WqFzXYHZsZ6s8FyuUDkiN1ui2HYYbPZwpppIqzSAkuhKFws73yOYggYhoCuS4xTpSwFUoiTulHcAj67za1DuSIDiJzuFYgppz0jhUotsqBg5jG3fWR0XR1Lr3cQ2CjoKsQqGxsWODHS4tqn0K2CLGPKhoYOdyieAUPnlnAXGtmwpil4TnMT+h3IoxyiX6/XiebJiqpoLPXqA+eTGHTRatqLdoWi+ye7JeknJuOoFm5DWbTGWwla03YNMK7uZbB9t4cli2DOAqlVr/YuF2NDYv4vabO1Pogo7eSp/lih1lISc9/ZsVi+s5+1+LtVbPjP3Bh1/QNzuViPGaCY1pljYAAjegLBYReBzqcMZ9E5PP+lz+G7/+hPcfe5uwirDtQ5EAPDeovto8d49N77eO03r+DtV14H9QFxuwMPARKGZs/KMPOEt2vQU8crzylIC0hawDf9BDTXarpIFXPz2wJSQn8rj7RsbZ0tahVrfIw0mOe3ircycCthiOIMcQ6eXNXHfWu4Mmx46qxp9VnaEXkvPGvHbuk4kS/ZuN9HH2vAMccJyNIe3BbQ0/2zcwdkILdnvlpGixQtg2xf55xiWh/WMsBNDoRfVjSd9p3LtOOw/ZHvdATAPnln+y6GAe15PoW82sscpsZOmcuZsdo+tWS5nAOQ51588UV88MEH2Gw2WCx83Q9M17W0oeV3NLqo9XvLgJHvNc4YMU/bOaH5dtSxI7/aosPlqzW9p0zlQhtvEdUt6v5454rTj1lk7uWlxWOCI67S36uWKxsa5+fnWbABq9USi2VXFvAQY7qsJo5C5NGjR/hn/+yf4X/7X/wX8F3EEHZYLhe4feduAoCRsd6twcw4PDjE2dkp/m//13+G7baH7zo8PTtLIUtZmMpZDRFu0rYs6gcPHuD/89/+S/wfv/Tb2O6ScUHOp2xUzNm7TPCuw9Bf4GK9nh1rAV4k2at8Mi76AVEJIO1F0Z4wQu3dbgk//TPIGQwat4y9IwwhGXfJmBngFQDQVi4wCk2bxk0YZgrUx4UiC0KDJgaXC4F0/boefSB8jPcf+6Y9BC36Son5ULQ2hmQnBBNwrhdFfj9GHBweoHMe3A9YUPYbG4Vn+28BphZiGrxfWrJk14u2gAMGyI07QLVRJ2ElbUFox7u3C6pOTeMPIxRk7eo4Yo4BEZTucHHTuGXtHQTGNcENU2MiqKk+J5M/nN35agEm248WmGgZGGNzbQC2TzloRXJZ0YAhUvqXW4Mnn41kxoKzAeI8QufRLzxuPvccvvWDP8DHv/IluOMVYs5EvD1fg3YBD9+7h3d//iu898ZbeHpyki7n7IeUWc+5fDHV9BxEy6jSdJwAUTNmuTdHK/LJOqp2zdo0t7KxBcxaoGyufzoc8zJjpcVHVsZYJVw5adT5Jsm+ZOtgyOVX8xfN2XGlMbiSsnyOb3UfNXBqndVo/a3HJTuQrT7Z+kZacDFitbxvzaMen9Sh1+tlcrYl++045vgFwCTcTI8txjE5zHgX1mxX9vbPyjbzVAaA+2WRpaXowqvI81Incwn3sf3KPakAvabdbIiuadauCf133cd6HfV9j81mk6NEYqG1fka/3zQQ4Sd0uQrP6b7qaBUYQD9HV/3M3PzJGtSyqMWbV1Adpc5x3NPvgBwuR+ksRsIdV6tc0MLfxXD4sO9c2dA4OjpCyRgFBiPktLb58DIn2OrcGAP869+8jL/6yV/jG9/4BpbLJZbLFYgcdv0ODMJyeYCLi3P0w4Bf/+o3ODs7x3K5wNOnp1ivN1WcnF4QevJEOIcQ8Ld/+7f4xS9+iS9+8bcwhIh+COgCo+s8Dg+Psd1usNttcXBwkA+WD2BO2lsrMD25KVyKc/YsQkqZSthsdunQOaVLtqpL+9xUgI4xhih/a2ESQ0C+5BfO0SRbif5d2unyYVFWsM6Ow9JLM3wM4w6Jbqdlqdv6AJRD7uM4CUTTg3kCAorxABOuwrWAqQSr6UcZD1I4lPfpEsPQD+icT+EpiUUrL4Wu2xocMgfk2ovHChXdV2YunZS6Kg8/TT1Ouk+s5kzeswrbth9jrIRjaStTTHbTJv00z2re2Gfc2FvbdWkBU+nfbDhcQ2CXPplnNHiy49UywXqO9BgrA5rr0AndB00DqxwskG71R9PU9pOIyg3MlEOogCQnezAO/ALMwIYI7uYxfud738ZX/vB76K4fgT2l3RAGNk/PcPbBI9x77U1cPD7B/Vdex/rpKSiWPDOpPVffh9Eak52L9HtbMQp9NP30HGqngq2/FZo29inFb1vgo+vdV4edFyunpnPVBhL6PctLLaNGr3VuPAMge+indEgyo5aNJbzOe2gnr04qommq+235Tb8j+lGvgcooN/xqxyt0sSFzti9XAcBaBuv6yzOcA3lm6tK8Yc/5ybis0WLbsPpddp8nu+mYOtGkvhYGsbpxQhPCRGbP0UrT2q4HSw/7e+EtjHrU3ruhx2FLKxQu1YsKY+ifUrSDqOh5ZuVpZ3zwwQfj2mkYL7Zty3vpw1pez2Edrde0nqjHJWGO9Zpp6U1Lu5YO0TJEj6Gm7bz8lXMYtk2g+DOr+qT/zJyOLnB6irJTKgyh0F/mSOpl5kkonB2/FZeWNpfxs5QrGxrOKUCuEvRyZHTe51hUAVfCZBF//Td/gy9+6bewXK2wGwaAgSEMGIaAMOwQI8P7Dn/2Z/8OwxDhXDoo3Q89uq7DYrGomIaZS7YpZsYu716kz4H3P3iAz30uwnfp1u9+CNhst/Cuywe6CYtFlz1N6QAsUzrA+u677+K5556rCCkeqRiTsTEMASGnru37oey0VEwX6y3i9P6YGUQzf+XxZC7xgKAxW9JysYRzPi32fE6DkA+UcmYatIWRVaKVIATKXFkhob1cLUUmn7eAiwVumgb24Kjupw4RGIVZBGG68McFl86mnD99itj3yRMY890Abupl0QtJC3AWSWoWjlVSUkcFZIkQeDo+Ma5sHWVOHFXtzSkpCyz083bh6+lvPd8am22vajM9WADJ7HNWCaYvZ5TWSA/NSzHG5lY6ML3wSbc9e/ZHyQ0bjtcC0XO0sM9Jv63ibr1frzfKuwzp+8AR1HkE77B2gOuW+OTvfBFf+dH3cevjL2LXEXbeYREZfjfg5MEj7E7O8OrPfok3fvMK4noLyqGhiQ7JEeIkyQSmvGznSwPJ1jh19rEW7wn9Z8dsgOh0nsYD5VpGyju6Hd3/qyi4dp/qz/QY9E+bZVGv+YksUHKmAjmIJQR1Mi4DNvTZreSomtLysiIGi6WN3XW09Ckx+qj11L55dW4apjk/x9PSkqtQHGsNBNuPGnhOQ0yuAoIK2DIOhsvkph4rgEv1IYCin+UzHe42azCoYuVkS1+WtUxUpUmtdC1NwbPud1Neq9+sDN5Ho7H+8e+qDaprn6tnwoNc06klF+xa1HVP+47ZbKK6v3ptybhqrDg9nzdDlMk8a4fa9PFi4gGYruFsw5asZmWrgvPunFoPNpQYM/Tm+oNZ2ly1fMisU+PfYniEHNrTapJAuHHjFpzrsN322UuQDnjHISIMEc4Rhhjwta99Ha/85jdlsvR2prQ/DAP6YSh3WojC995jsVjg7jPP4/Nf+CI2ux7Lg0P0Q8C2H5IAHgIOD1bw3qHvh0J0sSJXqxWeffZZOOcwDAMuLi7QLZYg8uj7LUJIBtCwCwATum4B5xboOj9RwnoiLCjV3wE188cYU8iDSzmTY/ZSJmOrEBW+60B5gZWsQHFGYDiAwwj8ZWE65wrgEcFXGwbTGd23iNK77fekWAEuRRuxTWPI1FH6gmQQcYx49u4zKXSvH9Jh8Qbo1uNvKUhHrhwan+t3U+lhXK92vqV/GvQWQzOiXIyox9Yar+6HfsrSS4egzSnMufMvM6oC0fRTlw8jbFp9tkpCx/O2nrWltdsxGYFRprquyzzGH6oocGjnBUiOOALgxaDtOgyeMHjg5ic/hm/9+Af4xBc+D3QegQieHfwmYDg5xdmDh7j35tt477U3cfbwMfymR1jv4EqWjanHS/O6Bo2XGX92DC1jSj8DTM/qWCNMr4/6/Wk/tJzRddizcK3+7x8bIAfdpbSMGf35vvrG32nCW0RUxflP+1eDhmrOTHvzddRzYHfuSkr1/L1NWe3yjrjE6Nv27FhNr6Bldos3WqVF53EO2s+3ZKAFTJrX5+SFjL0A8pmw3uTIS7rM8sFl/CD9Gfsnz2AC8j9M2ScDdbvpj4S9NI00EI7c3v39+5R99bXOrCR5xLOONlvm+ljpjgrTTddK6wxXbhiR55PV6L7V9dXp/OfGYWWKNqjtM44ITLVjp+gvY2do3tT1Ualv3HFt7eTMRRxctWg+v6xc2dAouxiUNFphYiSBKuQTQemdx/G16/jaN7+BPjJcCNhenGO5XGLXD9hcbODJY7PbYtF1+OwXvohnnn8BJ48eYbla4YjSuZDtdpvuPtBKhhLQ7zpfhOdytcL/7B/9I3TLJXbDgCcnJ1itVliuVgAR/GKJCIfQB4TQwzmPGEPyRgVCv+uxXC7Hm7Wzx0EyODGAPgzohx4pWwJK+60tt/HnmJpsjNedhmyI0QBWwBSUcucDoMigEFJ4GlFJs5a2xaaeYfldDiRar41uV/+rgB2mwkPXr3+WxVT+p61wTKxi3R4AeCKMl9dlzsoCUyL+0/N5xwCuGFs7Zgynp3Chx4N3304p9TiCeZqBpBLYeYHK9mGcWXwa4KednhSXnd39YKYxCwYwphOm0ZjQ9GqVlhHG6jv9GTMKeBzdF6Ox0zIuLPisnlPgp2yzjvgVslWdJ2SM7UTN63U/WU39vLK2/fPkUHKfMcAcyz0fumhw1QKl9rn59Tk9E1J4sxCVIPsDFThJxAGrXRjPgIdDJEJwjMCcUxYCXQQWnBwJg3foO4K7cwPf/sH38JlvfRX+2gF6EDwTlhHYPjnF6f2H+OC1N/HGyy/j/XfeA4UID0q3hAtwSUIBlJULkPmONNBJmY6IaoAvz4wGQw2cLUgZNR2rvznPlXVSSF31XOvf5Z1WiEpqd5xT58SDGxUoHT0wLeNO+lHWhvqUslyX238JecFCCKcM+30AkROvc5bdkNAFUElXOY5X9KgbqdQA07K2LG/Oj1HP4eiE0zLd0ljaygg40ZgyeLoCCNkHvse629+3jMkrhpZXdY98Pd0h37cLKp/Jv5ouErWReZcAQtYXhZfzroJLzlMI0CdxVUU1JAJo6gFnRo5UmOoFLa9aIN4atRVtYpIJThxxWSyIPEvqtUjvvP6nWbHsbnJkZCceyp1L+/iRs1BgtOVu5DhJVjNXqvHaNjDuNkiYoA6Rtoao7vco17jQJkODFN7KKCmU9RoS3UtU98/uyrbnbDyMX97jMTW2yOci2Shnmy2xZgqLqL9CzLoyf+Y0/xr9mGQVJ73Rpnj6f/4+Klr/XcrVQ6ck/SJGIJh+dwg5JCrPC7zv4LsO/8t/+r/CZz/3hXL4BwIQnYfzHWIEDo6OU/iRB/7p//p/g//mv/6v8ejR/QIg1us1iKiEKAnlRiGVFsKPfvgj/N7vfQ/d4qDa5QAT1usN+iHi6PAAPh+Sct7DRYcw9ImZVBxjiBGu8wj5ZtcIKiA0IoIREGKPJembqBMTloNnToSRUxhbJqod3+fy4vfOpW13l7Ij9dxjQQ6Lrks0LNiC0sV0sc7/rBcd89QIKgKYx/hdC8JGVZd7vofJJgqnAHfVNziA/ETxee+zcZVD8ICKNsJjWe2nRZwxrEdEzxHBL3CwWGAVA04+uAfvAI5U1VVlZVGG2ZxxUeggdKHM+FkKVRlXZCETCr1H70o6CzPn8dGKsIpTV9yi+5KwbboRfnxfhHTbQ6x/aroWIUsEdkmYRRLVKBIU6udohCgRUPGOBg36zIsWxC1DwK4D4U9CAj6dcwg83W+y87ZPYWka6DWr6VIBklCHSZEIOHk+B8C0vFpE6vwKON8R5ADn0XuH4fAAL33zK/jqH/0Aq2duIlCAiwEdA7TZ4ezxUzx85x7eeuVV3H/zHZw+epLSdjuXzmtkGefzXCQgYL1WKHwhBrFM2nTOKNOFJoBI03bUoXrNE4ikDm0s6GxJIx+25kdopW+/jhGlPg0cpQ8i/9Oc7/NGqt9V00GSa4hecwSSEKbICGpitVEwts1ZDrsyQjljUJwOSGfJRhkzdqAFSBKfTQ0y+V5/3jTwLQ8r2uk2qvdYQrbcOFYe04oLANXADaYvmibA9OxWawy6jM9NZYPVT7q9OUBud3daNLF6saaPrJm6W+lvAecAKMJ5MSBFximnqFpLCcvndOs55XMsdxzUdGrxsg3RapXyXhx31Thf7suyy0GoohnK8Dgb3YZf5KdT30u4HWNqbFR9N/SW31NoYnsco+6sdcP4bC3jrT6ztJtgGx4z1MmzvjgOM7bCGJIUQU2axHzPmT1fJsXqurpfMiapM/NQxnaUPywyzkY+sJgT2clD2XihUXrou461fqt0ZBEBdkeQAHIgptFQdLUxqmlxWfkQOxo1YClMb4SlxJq++OKL+PLv/A5WiwWOj46KYuz7dO9GOA7wfoGQPZb9boNPfvIT+MY3voH/8X/8H8DEOMiXnWlGCsYz773HcrnE177+dXTdAsvlMu1kLJflfIf3Hqen5wCla9rJLQAesNumXYZhCIXmwzCUy1sks4YsDGQBNISAwcTD6gl03mEIQ+m3fUbT0QpBJ4qKHYjSYe3FosvfAwAVmo8gqQZN+rAdlILQ1ngIARR50qcR0I7Czy5cveCsMrEMXW+bjp/rXRcr9Pcxb2mP04r05OAisD09x+mDR9g+PcN1Hrcg9TsFqO8pLSEl9GgJ1bn+yjN6J66lINg8X36q76ZgeuxHy0u5b0z2UCcnpJYNmP0Zn/ScJt5CMa4nisnVAtYKXAsEtKCudsgEfBHVkrPRvxbwsv23h4t121aQl/Xc8ALPCdtAQO8ICxAWgbDiZIBGAvrOYbvq8MLnX8LX/+hHuPuJjyE4AjGwiMCSPC5OTvHgnfdw77U3ce/Nt/Hw3geI2x4+96PruiJ3vPdwEC9ce60C0wOAmgfsuSIdOy7KeAy7EmN2qlTnDMkWjezn+uI3ey5Al0l8sZmPORroZ+fuAZC/rxIKMBeLPeHBxjO6WIBc64t5T7F+X68lu2b0eZM52boPGNlytTjy9vqYm5s5oN8CjLof5Xk3XfMtI2JfXVYn1Z+FMh9j3YCAXavjZ4v6WuS3vGfX5xw4nWCvS2hs+UEatzsopZ6MXXQ7RR5nB58YKYykgvkS54/QTvqgjQGuyTLBRJpG1U7CzLLQfGN50BaLT1oYba7MrRP7uWDh1pq7DOdcpdTvJ4PDe9FvORzMOMek/Q9bij7AlEevUj7UPRpWMcnvq2W6J0MAPpCyVN3/4D7uPuOwWq3gvMdi0aHzHZaHB1hjm3YMYkQIA4YwAMOQ7rpQyk0UX/GmKH+PHuzF+XmVXQFAUcwhBBwcHKLr0maic0AIhL5P7cYYsV5vAOQDmjoHckxGVgihgHY5I6KVq/7bLnrN9NYrYQ0NbWQIk/iuQxQQFsYDhpxjSYmoePvHbb1MBxqZxGbp0P2fMB/NL1Q9Vp0xRdpu0SG1O/Vmt4SJ7d8cqIsxZ5oaIlZugSfvJVDmAoM5pksO1RzkP2rp1ih2boqBQjXNxrAdN9l9kMOkli+qdrKobQlGMTQm/WAxuts0Er6142Ee88nr9xKP0NjmJcJZ00dAogCZOt9/e7t6bk51v+dAZOpq+24NSwsNNHR4lQbZ+pmW4N/HJnPCVoKsfCR0MYVg7jyw6YDjjzyPr/74B/jUV76E/sBjQymUyvcRfHqORw8e4t0338Jrv3kFj9+/j2G9TaFSjqrLH22IkfTCGkQaPMnvNgONHrs2GiWLXtWO4X87V9K/OXrtMwD0Z+NzFoq0M7LNGRlCq6sq2HFtzRsbLXCp+UzzVgSXcxpWFto+Cf2TgTKCqRYQb4WE2MPszDxJ62oNEDuu5vqb7G2PTiN9KVwL6F8FjMi6Fzm67z1LvxACHFIoog5FaQHVlgNF973lNGzJUQtmLb3mBwrItgGzfb52oMyBZNu+LfpznVygfhcFM+hS1kkDqNc/Ux0h74wgy599a8vOadlN2OM0snytx6D7NPeupYctc+FNzTBaJHpO70uj4pyTOuf4d4735nCjpUMLk8g7LreZkhyNhh/HCM6ypKV7NT6xMobZ6ESRO2TkwyUyVcqVDY3VaoXVaoWDgwN477FarVIFXYeF70qaOCHI0dFRTmmbDI/ddgsCsPAdhmHA0PfY9gN2Qw9GSs0FSqFSp6enOLp2XA6EFw88JSNDh42IMXFwcIDNeg3nF1Wmn91ul7cLfTpEjQgOsUxMP2wAEF5//XU8PX2Kz33+81islkLGZAyFfDt4YPT5cLkW2NrwSoq/FmzyU8YhuztNEMajcE+CNxliKWOWMB+gVUWIYbwB23r9HCBR7zpuMSmi6fakvCtFC+lq6xz1YpGzMjYueKx/3K6VYpm8pVD17xNBT4Q+BBATdhdrnD05gc/tDIHBmUi6P1KsMmwJpao9cIlTnCrrJIC1lxyo71lpgRM71lnwOgFzdR9tn+eKFTDVdwrUzQlzK5Bkt0/GWIdnJKNAAKs1QKX+lnFgFe04N1T1Q+hr39NzaRWtHXfLCCnC2tRn+dPSlojQMcEHl+Kjlx5nFBBvHuG3//A7+PL3vofF4SGGpQMvCBgC4nqD9ZMzvPJXP8Xbr7yKk4ePsF1vEh/HdMbK5bUtfa1AowqN1MBSyya909niNcvTmrZ12Mo0JtnOVWvHaA44pX7XAFHTU+Kg7ef6dzvvVglOvP1AvlB16jluARRmRglnMLTXvNei62UKubUemBkxDBDQ3SoWtLUAcgtsz/VBg6xq7MbQq+mNAhSt4at5rjUHtpR249QJptvV67yiG+o50XJBntOx83reWkXTzdJE03qi9xs8UeoUoxMEogiXw6JjFJfSSL/Wbqset11v+kxOS5ZpPS2v2jElQM0grudSlwSslUOKAfL7d+3sp1au67HL93os9h37rOY3vVsidJS+tUJ2pR1xHuv0+2ObaczyvnYwpkfaRtmEdupdO9YWP07mpqGLeZxMxBiw2/W1THF1OL29+NPKiHrHUtEhDyXGdDCwhW0vK1c2ND772c9WikgzOId6YQDJAHnhhRcQA2G5XIJWB+j7Hp1PZy1673Gx2cJ5j2HosVwtEbZbfOxjH0tnOjqHxWKBg4ODIjh2u125dl4rxtVqheeffx7H165jdXiUQgryd13X4ejoCEQdiBjM6QD4bhfKYokx4KMf/Sjubp/BarVKseAsqWzH2OeUrnSMwYwcq0vt9ATKz9ZE2Lhw/Z54REHJoEo3Q/TohwFLTl5jlthxIkAJE91eMbbm+sK5/2h5kUYml8WnzzjYRWS3fq/i7XTOlTs4pNhFbmlnDZPo8vkHOKwWC3S+AwEYQph3R9MIlmzfWnNV969dpQjeVrz/nACea2NfaQFd3W6rTju3LQUazdhb/W7NJXPNI5UiZyrphcUJYeuz3umW8q/6QrVaskDC0sUqHP2eBTJ2V48Mn7TmsdVfAuBch40Hdkcdnv/iF/CtP/kBbn/0BTB5wC3QMYMuemzOL/Duy6/g8Tv38MFrb+HJ/YfpTBMonRdwSPza+VlQw4n5KiBm6WbX1T7QaddBPT+jwaFBp27Php/oujQgqudo/N4q3RbAk781TVoeShvbP85QPadza7TvezCr9O2Y3rVi26zphupMyNxa1PRLn0/HXdZqI3zMygALXjQdWjwxK3+ynTHHK2J82f7bsi8kq+qHtKm7MCOTK/oo2rTlVO0Q0XwqdbR0jbyvIwXm6HhZ+Ko8K71L9Wter3Wjbrt63/BPc4fa0K3CBS4dXreOu1zjnnlM8lBM0CZ2adE+1docgxiI+ruW/LHjESq2+tnCE5ORGN5vtadqFAhVdN1Yx9yezLTf9u6YObmmQ1dlfufWpx3fMPTJeYyydAtbzenZlpEj444xn2V2DhFIDi+q67sKvgE+hKFxfHyMEAIWi7RjIDsF6exCWrxdl0KjQOmsQwgB3i0rL/4wDDg8PMQQAvq+x/LgAIvFAv1ui8VigY985KM4Pj7Grt+Vcxb1XQQoqchEaCwWi3ygfPSqh3wAKmRA65wszAHDboOTJ4/Q91u4bKEdHh7i8OgIb779Fn7161/hG9/8JspB6sh5F2aAY4wGT2SwazOMFM0oGpCJ8GqFC1Fe1C7FeJWD7S4M6d4PyzBmcWmhy7FeSEWIEcOhm/Hy1OBAPtcAR7cnceMyfruIdNHv6xhieymjzKP2zmnmJiL0iGBKl/YBadkHTrdk0ng2r1nmFJCdwwoMzFcGSSvbAlhzC5KIRu/QDL3m+jOn4FsAzc5Zqx85ycqVhIduI8aahq1i4+51G3uBzrSnFQjTRWRESzFrBbFPaFfzL5K6AeLHeUNxCsjnwXucu4hrn/wIfu8f/hgf/cJL8MsFiIGOOoQ+ANseJ++8h9d/8Uu8//ZbCLsddutt6udikZJREJWdW8L8jlda4+1Un7NUbPCENjxt2N/47H7jU38mfdChry3vcDpfFqvdmPH9cRG3xq1/b4XGtD6z3wOo5LH1AAqPk1mDc7KiAgZXVMLCt9Zwa43bvrePn+347Tq8rH5pw84ZMMpCK5NbYHPf39XnvN+zq/usdQXyGpTPW2mQtVzWc3SZXNTzYef6KkB7fAGlrxKtkL4WPmq3qdtu8d0c2Nb9sXXK363dvqvyrHOunHeyOr+SQQ1+K33eI/a1/NDvJXk3D5BbYNp+J9/rdubomlRBvYaKLHb715Jur+VEsWNt6far8Kn9nlyKYaE8AI117G6ENnDm6mQe9zYZ06MCVylXNjRu3LwDifVKC7lLE8BAP+zgQDhcHcA7h8ePHuUD1cB2t8bFxQVijLhz5w4iGN1ygfVmnU/Kh7wDkcC07xb4xCc/jT7ssFmvcX5+DuJ06PfZ557H8uAAb731VmJyTtt9u36LPvS4uewQhh7EEefn59jtety+fQtnZ2cAORwcHKDrOmzWO5ydr7FYJOIOMaR/IYCJsDo8Qh8ZHIFhu8Nuu8N2F9CHROrzdY8Y8yl/4RnKDEljqjIposDkvIjkN7cCkSNAXbLXPVFKa0sEeA+/XIK3WxApjxdROrtRCV3jOUwPT4RXjBEx9GlHJnOQ9N/e+9ASTFYA6HpbCzdN15i/XQs8aUdv7dntfyvAiAgIAKXYsGRIhgDilCWCcgpM0UNFpnMtwCfGgcsgEpyzSOW2ZJXxCDLHkr0bzHsFSpnnMh81SNX9sYdW6z7XoLkSoPKMrj7PLYFGoSmfkYQ5UTkTUo1srzBJ49ahc+UbRyl2es/unbx7FaOjUk5a6gFprK5Wqvqn5R9NM5fDHMXISlnckmxJZ6RkTIwATmvNJdp1cKCBQXDoidIh8Lu38I0f/SG+8M2vwh2vEAnw7OH7iLheY/30KV7/1a9x/uAx3nv9DZw+eYJF18F7h2WX5tU7X/U5hgDJBpX6LiEQBEmzWbyDjkYeV+O3ns+QeaSsqZh2FgrfU6IpE0Z6uEQxqGwxDAEUI9+VA7rAGIZGKVNbOUgK6Z+aUi+5XpCM9/wFUepHCcETPuYpX6G0FXOoZrqniSjtElmaWGDSCtcE0oaGrNn0jDKuiUv2uhC10dfg35m/tbGT6NdeB5eFLVgw1QLeU3qNv2R1kX5S/bzu86XAWvVBAx37ef33qFtqQ2LaRk2HWOYGxCgmMdfvWf3R6pP9nVlS0CLzW6q4ZWjaUvVfZFYRWknOJPnXDqfZN78tOui+l0h9opxNjMGBK8eWrlPCqh1quVmeJT3+vJu1x6Mv/WBmRA4lg5lEYYBlB2tmJ6QBvMvvKgOqXLdALsnyEPMdKMTlduxkFCR8JTSzDikp0zBnLlOm5UP6AON6Qb3exQFnsdAcz819ZkOt5kpkRuedShxEJRXxPh2uHUAFe2T5xggAkn5TyqfUuQ/j2HJlQ8P7Vcm8RM5hdZBeZTBo6IAhIg4R2+0GDz54iNXRIR4+fIwnZ09L9qjl+gL90x4fOzwAdR4L78vac+QRA0B+gRs372C32+D6tZvo/AOcnpxg2S1wenKCT929i5c+9Wn88je/wq7vMYQB5AmbzRoxDLj//kPEGHF0dITT01MsFx2ePHmMyBF37jwD3y0QQsTh8XUw99huLxBiwC4MCDHizrPPgLoFtrsBznmEvJPRB0YfkpLcbPucr7hOKVmAOidQJ8BZ774AKZREA+zCkH70YDoAu2GAixF9GLDsFghMoEhYkAeIMXBAAJeYY2Gc0p+syGGE6vg7ox92KU1mTjNbxlHkVDvuWSsE643TwEbGL59LaW1d275bg0B+l58eKQtCiAHOMZbOpRR8IqCydB/bHQVH03ABEpBU90ZEjqN+KIc+pK5RKWuh2FKSU5CtAaP9vE3Hsc6itaYLPoqRkSWg2tFy3kFnUivv5Tz0rR2guXFoA0WHRlWKFVNBqseQPpoK3lYYTFpTKD+zKSmdKqhI85JWmK2xiMJL/9LwBQiDkqHvclYozlqFHQBi+JD75DtsCegPlvjCN76Gr/3JD3D03N10l0uMWJFHON3g9NEJ7r3+Ot569WWcnZzi9MkTUIjoQPABIKSU2jI+R+NOhc9zI9nxUtfHM1t6boqckfEDE/omw4SEcYvTRk8/A0WuCOAsNwNwal/TthiMlNODu5wgQQwfncYzs2aQtZUUQFlWYrgI+ITweAjFSPHcBkRE+VZkGuuT3/Vt323DdwRdukQWXqVisEi8e6J3PhgNGmW48JyJn9fF9tue22sV/Z3ekWkZ1zp7mD3YX81zbRFlIDeKAwv6CmAyfbOAUIBLaOzCt+QKg+HITeZGxtg2TrgKpWEedZcYxCIPpD0LJm1I7timApGghGYRwdwjxnoHZ05GlrGRwHMuRjYjKlpPz0bY+bT1T3YkqKym0ZjPPyPzmGYZNKm7GN9mHVj5rWVx5bhSpdbXcZQrnJwHpT01VS3azQLkJNSKc0UuIHRecvClURNlavMom8Sgb2GL1lyK8W3HVun58uX4nDhEWmHNpeYZzGBpbd/Rn5fv88/lagVwvkg76xCRLS35Y89WF0ODCClludm9YM73s0wx3b5yZUND4ul1uJJzDiEGkCccXltiWG/x8P4DbHc7nK0v8MH9+4BzWF9sMoE8NusNnnv2BTBSuFLf7xBy3eebC8TIWB4cIMaAEAbcuHEL64sLxBgwcMSDhw/xu1/9Cp594Tn8d//9fw/nO4A8zi42eOvd97A+3+Lo6AhMDoGBp+fnCBE432xxsN3hgH3auQDh/sOHOD4+HNPbRmC73cJ3C2y3O8TQY9ilywL7XY9hCCA4bDYBYQiThb5YLBBCwGazKedEYozl4LwtIgBFGHvnEmP4LhkyPFr+lHcnRgDCxRvA4BweNioz7aUvQqRhELSYXAtibSRob5+EO0mxAgmYZlQQhdDadrPhCnohlUQAVjCyGGsBm/UGuHZzHMMe/td9tQe0dGkd3GrVVfoKwAoLS5OqPqAC91c5AKe/03M3zjWKkcFQ94QgYXF2OZxOeebEdNlX2lul6d4FTYvyTAaKrUOJljb1vGIyphY9bF/s9rbUYUGj7T9RrTyknUjAzgGO0yV8AgQIDAqEQ/ZYO2B9vMSdz3wS3/7jH+LZT3wMfrEAwoCOHGI/YHPyBI/fex/vvPI63nv7bZydnaDfbMH54j1XlPXUGSA/7TrVxYbqFcVJCQa0Yri1XJEi82Prq8OnAH1fhf4pcmMSBqppeomCl2da89j6W+rZp8xr0FOHEEx4yIxHCqVOTvoxAuga5Ou67Pj2tSUyVu/kzL1ny9xYgGk63jl5pH/fx3fCC9HU0wKuLcBo6y+0iDHJJ0N/DYLmaKDbaY1F00E7yOb6l2s1dXJZA1pOtWggfZoLeax20yajmRoP076N9djvGPXatuu1xVfFkDNOqEJzc1mQ6Drd0j5a2Plm0UszYNoW+WwuZEfXb/uTcNj4u7TfOktqaUTFQLy81GtkurZn+d7IpX3zpOmh1404lGJxprgRC1Abn1m6Vcb8nrb/LuXKhsZ6vcZqtSrnMpjTPRdHR0eIiNieX+D8/ByPHz/GZr1GAOPhw0d49sWPIHCP5WqFi/UWznk8PTvHZrvFwEAYAnabLRwBDx88giPCtes3AAAhDHjyaI3F8gB9P8B74MnJCU5OTvDpl17C7Tt38ODhI0QmPHnyFM4dYHV4hPuPHmN5eIS7zz6Hx48fI4AwhIghMB6fnuH99z/A6ekT3Lp1DYscPx2GiH6XDl3vdgOGIWUiCH1f0tkK6O13O2w2G+x2ByVvsUwaACyXS2w2m3LGRHuepAijayAdOSJyvpwuH9hKtyKnbVbvHCIPBfI4l+7rcM4nNIRaiDNzybClt+alEBycS8w9DEMlzK1Q1wtA5l94wSp6Gz40LpzaYCn9ICq7KhMlr4SHNYjkM+ccnE+GK3heMMwt+ppuI32qcAaipvAu9ZnPbVtN42OPkuP0x4zQoUa/5wSDEiRFwIuXhgqIQkNhXNaGKF1NI0sDu/tlgaGuV/ONBaX6ZwskgkeVp2m+T1gX80RNbDWvnL3UDHTkAUYKZ3QOF45w/LEX8LUffw+f+sqX4JYdQA4UGLQdUha0h0/w0z//Czx+7z4uTp6iH3qgS2Gg0QGI6VbjOSvPhkVo2sjftt/VWtlDs2TaTEHZXEk0TXKp1Rd93sqCbv28BWJEbVA5Po9mHVmTX4H/a6+15qvWTmuTDpQu4JMMakXmFMdQG8C3gJb9XvdFdh3Sgd3982H72TIGgDE0Qq+/ag5MX7Rh3gKH4xim7gm73lpy3uqGSmYo+TAXPiXft2jZMjg1sNROD70erJ4a+5vGOc6F/re/zAHLmvdl7LUMsPrtMj6Q58rvZq9B2moZahoTyA6BrQ/5W6FFrmRiZFzW1zYPtccxV8/cGrN3VrTmcy7sUPP+NBSt3tG4apHIgZZu2yerqvloyDcrUznPQwqPI2y3WxlV4anWurM0adF7r1yly+WTLlc2NM7Pz0FEOD8/x507d9IB7r7HwdFh9vYPePjwIbbbLTbbLa7fvIHtdof37t1H1y3gu01JIfboySn6oU9bXTEBeoSI87MzcIx47vkXEGLAdrPBnWeeRT+EdKYjBoQY8cabb+LTn/kMvv/DH+K//Zf/HWIE3n7nHj54cArXLeCdx8PHT4vwds6hW3Z48Ogpzs/X6PsBu90aZ+szHF//TLphuh+w3fbYDamNYQi4uLjA+ZMncH6JgR2GIaDnAIQe680am80KR0dHhUaixPq+x/n5eWVktASMLJAKOOT3mbIlPvSlbpKQBLnTI1+Wo4WoTH45p2GE6ChkAeIxA4XsvtjUvdIvYTphWJ1OV96x3uN6kbliWbdS+zKPuzIWJBJRtWNjAayIVtl1IxIPdC1M5rbfNUjSW8e6b+n36cVtgMDVqSCwQkLPMxGVPNwjjdSY0fYQjm20lSMjhUiBs5HpBJhls4IURGCkXY4chOSdhzUCpGg+LuPKlemD1uP8TYGnLVYBJ/7iSrBboGaFZWkzEWwyd7rvkzqBKra24kkGlpx2NIgTzw6UwrXctSN84fvfwZd+/9tY3rmOHgEuAqtACCfnePLwIX7z81/gvdffxMmDR1iSB/oeHcmt1jEd1svGgISuWTBg51fW6KUH9xqAU9NLcLqlkQbQspYkzDNTCJL0YE7xaaeKPjhp19M4nykcRa9rKSFMs7jJe3L+7DJlZ0Gb9WhaulnQSZR2kO09DVZx60srtTGj/57bOdV9LfHRBnhKuYrxoudhXFd1KGFr3HN12v5bQK9pNQew9XP6vWoHi9qGn6bxHN1adBojK6ft7lsjLXmVPkuGNpGA7qlDxrZR8VMDJCadTxPTpaVH7PcthwMgw24bgnOAEpDd7xEnSJKXsZ+ogC2F0diwckD3sQWUy9zT1EAFppksW/1t0cjiB3m2nO3iaZp++/s+gG35uYUpWvRtrY25umUce+e4okHeF8/JM3S4YowRjmsDqzVWeacVeWCxq1paVy4fakfDe19ius7Pz9F1HfrdDovFAvdPT/H06dPU2RDw0ksv4fHjxzjvH4M5Za3qug7Xjo9BtMFu2KFbdthtdzg7PcVmvcZuk+7a+OQnPoaPf+ITePXVV9F1HW7dvoMYAz54/x4WywUePXmE0/NzfOGLX8LJ0zX+5qc/x8nTc1y7sUS46NF1HZ6ePkUMAcfXruHatWtYcrIyh4TEEMnj/GKLR0+e4va1Q4SQjY2+R4iMIUTce+99vP3aa3jps59DtzxMOxuhx7JzOZY0TeDFxQUODw/BzOVil4uLC9y6davKmGUnV77Tyk/+i4zkKcvvDGHAMjMehZB2PxCrm1E1MxXFp5hkGkbClUBpKTS7iGz4QstokFJZ8ahTBlrBo5VJS3DP7gqFiAjG4FBC8CIzugY4uUyBxYZyGt/ZJxgA56dCzyou24eW8ii/pw8mbab3ACgBTzTmjgehbJ1ztmM0sAZEqbEaUjJw9fzouuf6aJWE/ukyKG/RQT/b8jJpYWvp1Prd/tSg3SrAiYDn0S9XgQ9muBhBziN2Dmti4OgQn/jSb+FrP/4Bjj/yDIJjMBOWAfCbHrvTNR6/+x5+/td/jXtvvYOw2WIJhxh28J3DECIopnAz56ic4+i6LsfQTvuhx2rH3lJE5ZnGelS1VTxU1z8azZa2wuvANIShDczal0cCOt0jAEzB+1jHHrDRkKtjB+pnxfCx61DTb9brqDCbNURkDFpWttbMnPJu0UbTufVeSz7a91s7gnOFQNVZw7l+jX1LfGLHa0HY3Fitrqr1TDvs9DIg1+ongJKlsdUf/bzm5wnPxuySIAciD8YY5jsHpC099ve53klvPSe/W53clGkzoVNXLW1dnO/BorzsGrtVf9+yTx/qndMWP+7TBfK9XEuwby226omYGgr6vZbzR3SxdTq0DLLW9/by6VbR2KYS51mWOVV/9az6XYq0p3f95su8DJorVzY0nn32WXSdx8HBYbqw72BV0twe+HSR30c+8iI269u4du0aPvGpTwJ+gWtuBUCEODDkBb1YLgFi+M7j2rVrODw8SGcPImOxXMH7Di++8CJOT5/iYLXCndu3cPPmTWy25wixx+Mnj/HCdouvf+MbuHHrLg4OjuEXK/iug/cdrl2/DgLQLfJN451DHyKWfpmI3DkAAx49eYy4uUDnPYYhguDAMYURPf/88zherXBweATyCxwdXwM4oHOMbjGmdD08PCxgDwAODg7w8Y9/HM65Kn+yVmpaaIzfJS+xI4cgYTtIWS9CSPd/MAi+67BwhN2wQyQGD7FSugKygDozlmaydB9HBtgqdlXncLaHvfXCai0YwKR/08xIdUDTdIsSE0NILwgLSK1V7vLFZqNRE6p6dJt2YZd2MLXUx2cZ4LYnmTBVCHZh6/aL0BKDwAhLSD9mgFy6z6DeYXDOpdoE4IOTl98IyDnDSV+mqI3jfYaGBWfSzxhrA1ietcKs0M8ILU2vuR0WABV4jI3v7TyXtojK+Z6cTmg690QYHMAdISw87nz6U/jaH/0QL3zus0CXstB0zMB2QFhv8OC99/Drn/0tzh4+xNN79+ECQJFAHOG9Q3AER75keiLQeMg6RsRsgGh6WO+7VRR6/lv02Vd0XfXcjcDZApu0mzHfloAvCzatEi48QgQ2h7qn81d7R6s0xsxNQ9WuG3vuQ/fdnkezQC5XWNGo5qWc8W4GhFiFPld0ncxtwKSftZ/J37JmWsC52Q9K/+QGc1vm+5+N5dg+g7DvYPvsDk9eF9LXufdbpfUsM1fnSDTPt4DUFPDlfwSk27yz15imstyC/8v6PQHV+nc1dsurdf/Q5le2pkYbTNtCQNqpaALozI8Sglj6095t0e1Y2ly1TGXTVNcA7XNqVvemz67c9N7xaAdY29BrG0Bt2dJua24c9vsiE2OEnJesNDzVOqWF54A018MwjE4vl84PtvpMJP+7ermyofHjH/1hakTiPdWg05VpAJgR8yHplEHFIYCKp1gGN4Sh9FOy+sS8Td51HZCzCDz3zC04RwjDAOfSCflh6BHikA5mOw/A4Vvf+N3ERNnjQJTAuTBmENBJCcTHyAAxhqEHEcMjA3XOOwnOYbPdAreuwX/kueTxl/CJoUcIA64dH8H7FGKwWq3KRIgXQC4atMyWQp9ivjZ+XKhOYlpAOVVnCiPxqVJg6EExgLlHJAfvOhAz4jDApyOqYI4gHg8/xSh3nKC0r3PkwwBiGyPfUvxNkJ+VW0vo6tKK4weSCCOXNDaJxyQbXQIEbR9iTHzjM50657DsFnmaHQjtrFYC7LU3n0pK0Kk3qy4j8ClbxpmvNG0sgIvlWZ6AWSv9KuHVNBCEdhKSlBQgURpD5Ho7uwUCWsB+3yE0LagExAAYw1cklXDeLSGX6UgjfBfFnepKw7bCr+WdbymxJvjK7Y9EQjEgHCf+SsYdSjYnMINzOkzPBJfz+AcwBiKcO49rzz+Lb/34B/j07/423GqJgSIcGBQDXB+xvv8I7732Bl7+5S9x7733Uoao3QAHQteldegXfkzgABR55DufjQs0i95hmgMxLeN5/H0Mychckng9Jv7R74xtRRD5IkPSGTSRIQzm+r2WId1Srnp+dR+ToSFzKeGOY9ij5l8dLhlDHI1q8RzKOqD6vRa/W4Bg5Zq8V5SyAcBjvfM7pq3npf9TEKT+YbojZz2NbaOsDTz3yWWO3LzdOa2VJEkkXbs4VEZ5Vtdrf1rZJT91PH01pmx8M+fziLJmeJQd1gBr0UK373ztkLG76i0APr6fQn7FgaPXkpVR9buJryVUR8LlRxhIRR60boDX+tjKOq1zLR1af0uxO1wtR1/BBcCUNrnnzmUnqMyfwha6n3Nrq1oP+XvBQuMr4w6bxiFzRkol/1i3K4YrQ9xvLf3R0q/MKuuWkidWvk3GVOpp82dLn7cwkZab++oQGaRlr+y0FbqhLZukXuENMTJKG6q9Odk2V68tVzY0bt++URaqFZR68JYwujMpuxMDWKgFsyh1SYwYM8E5rya2Q98nAwMELBZLdB2Xi/pagk5ijZOCGy/yA0brDVipBTumPVssFgjxCLvtNt3hoVKDxZj6sugcKO8A7HY7MHM5AK4Vohyy1rQpsdaUQPLIk6PnUPLYE2WhFBPAEa9KyLnhPRxcziQUYmbW5N4tMa9WeLSEjJ3LOSZvKW0ZUytMrLSLKWNWwjONDGJ8FbFM46Vw8k5pOx+m9eQAvvyCLt2OPCag14K1llLWiLDen2mDek4IavwbKGcmRAG12msp55ruI33GStLZBlJ902tC6rCAQ37OretCNwOK5HeXjeI0VtkZGVOmWtpouaS9r+OYp3SdA1d6PBNxR1nAChgSo5UgYchpDJHzu+nukugdegL8tWN87Xvfxpe/912srh0g+MQoB0zYna9xcvoYT95+Dw9eeQtv/eplbM4vUopWoSEBgQB4SndWQBmBWXH1fQ8iyucg0q5GS3i3lJulgwV2lIFReVx9Frg2YLR3Nj1PCCGqHYy2opEdKlFu1ps+p5A1eJbJkn7GyHBuCt41DbRREUUhSv8a77RAaYueFsxbAClt63mRZqfKf/y81f/WLs/Yh+Q00DS0IRj6c91/O047ZguYiKjIzklhZHg21sPqfAKbPs3p/jkANZWvqVE1lRgNjBEw6TnS9GgBuJb32c5lS8aOdJJnFA14P/gSs55BWTy7nOVZ6x0BhorYmPLZHGC3Y7f9Fz3T1GNAk5f0fDVlLajgDn3287L3WyC5tM/JyUyk52c6F0Adtt3irfS8/jfyiGSdsrSsaGZkVmnbjXOyD7BXdFW6rmXk7ZtX26eqXjMG59J5TLl7Z7FcYOEdzs9Ps8tmugPUwhYaRzNnx0pjqII+9uGsVrmyoSHC0Xqt9GTJwg751m/mlJlKBsk8ghnZ8pEByiT2fT+Jx2sBL2YuWz3yN9E0X7BMRuuQpdTf97uiNMsBqBw7jUx0eb/rupSuloAhG0a73W5Sv4xPLwhmLnNnFaCMTaAwkYPLlqojQh8jmFO/ogC7zMAc2wunBTQrZYQ2U7c+s3227dmwsH2C2Ap8xFi8ZC3BMdcXT4RhCGBKt7U/fXqSgQ5no6xRmIunrlXmxp6/rNq3dNF8W94tc1q/N6fk9HN7+2L6W/7GKB/mlPyUxtMQgBZYkjrswfAWOCYZe0OhaR4Uuo1rdD60oUWLOWBe/Z0vakPMa1n7FtmBvMPgCP3KY90RPv5bn8d3fvgD3HruWbADIjE6Bng3YPv0DKePn+Ddd9/CX/3bf49uFxAutmOoWFbCc0B7bi60TBIa2/lvgjP1rpXLWrnq8EidgKI1J7odHUqpn2cePX5yAakFAPscFfpni0dt2Jwdq5Yz9m/97L4dSiubNe3quqe7ffZZPf65tnSbrXHZtafHNgdyJnd+mBA72wfm8fxeeYamjpNWv1tF97El++14rQ5p0aB1lsY6ZWx2LD0+3YbeaW+tE91ua+yWN22be0vFM/WYmyF/mPKBlQ/y7j5PN5ddoLqvrbrq7jJAbUekHhKRmFKAVaR27dvSkgWaZ8vaN4aX/N7i67n65z5vvW/1mqwRCWFv6UWLt+pnRiPS8rLlx6uWyzAXAJycnMAT4H03YqA4vg+gcoDrsVdzRvM77ckImflyplzZ0NAEaS1eUV46TaoYG1p56thNq4xSaFK9AyCTLulPdRt6C7alCDXzjPSrt6916lqtOLuuS4ZGHAGAPqAjl8RoD54YKQDK2CVbUtlFSebghKbMyQyPIWJgBntfLo6Ti7NiTOluHQhe7c6QEQxWIGnaVFuujYViaWfrnYKZOkRptpjvqn5hXjHCxIDquQ45fIpz9YeHRzk0bWha42Ucajx2nLOCbM/Y7DsVSJkZX4vugDKuZ+g1t+Vdfk+VNpVVRYMZBdqK37yKgp20YwCnNrpbYG2uLeHZFsi2wrsFOED5RmoAHadcZJJRttz27Bw2nrB47jZ+/0d/gJe+8jtgTwic6d0P2F5ssHl0godvv4c3XnkFb7z2KmiIGPoBnfOIhBLfbMcnfdIxzTaO3hpv+v2W7N03HwIma7Ozpqn+3cpzvbsldLdzRZScQjKvmm/0O1ZB23myxRka2rme8+xXa07x2T6ZNAd4dT/F+A2hdrRZuWfpOlf0Orbtyffg8bZoC05a/GH7sa9d+y4RTTyUhWYkYY7z7en5bfVxjl+b4KYxjvrnfmNHjxUY9eacvGzxpP5c02yOn1v1jkZF3UcJQav62JAVwneWn+2YZ9cSA9W2LabzK0DaOkhLX5VMkDo5Oz5TGv4UdUGOipGq18WcrtNtteatjEkNpyUL9O92bvbN+dz60LpG10s0hgw2d/1MHQXfonZot9Zuy1Bo1al/t1hBsHGR20Q4OjzEk+22hJ9J1imtR217Vu9zlNDnmn5gBtP0/cvKh7gZ3E+2IeV3KfK5xHppA0ODdPlcwo705Mr7AKrdCnlGE1ZPnmUUeU8rdCGmGBJi+CwWXTm7oFO1WmDAnMIdFvmAOWj0+C2Xy9KuGBXynY1J3bcz1HUOYRfAGA88yjPO+bzLkheloYGuX/4W2o/gQ6WyhEOk/ecxdN+sUtHzavnCbuPLYrWKxefb4SU21wrgFCfuq/7rfjjvyiU1wi+SMtMaKenL2ntnF7nm8aqvzHXYkylCD61gnXOTvROrdK0SaYEoy+fST/tZwpUuHwyb3sFgaafHrOu1wnoOKNjvNIAKmXaX5TfXijeNqb2DOadsLgNfQhfivNPAABOhR0TwQICDO1ri81/7Cr7y/e9hefsGdp5A3oGGgP7iAuunp3j07vt44xe/xv0338XTx4/hnQMxp2x1MYI6n9LgqjWo+5XWPCHG6UWfdiya1i1A04pbnspCmdvp3LVAsvyuPcU2A5ydF6voxnFOPa7Sjg090p+1dp3l3Rbo02Owv1/2zD4gJO3pfrbqJRLPXtsJZ+sUXbAPXKfvU5VzckGe13Le1mN3Nlr0sGC2Bab2AR07Nr0GLT+29EurzjqMT7dd+3qsA83WTURJd+51Yk1/b8m81hq0dcm/NLdiqAH4/7P3J722LFl6IPYtM3ff3Wnvva+LF5HRZ8dgFZNtkSySVSwJggAB0kS/QwP9GQGaaKBBjQRIE4FiAUQVIVJFIklmJpMZGZERL+J1973bnv7s7e5mS4Nly2y5bd/nnpdMVgFSesR9Z2/f7tYsM1v2rdZSsoOHYNkcf6/HS8dUMUo9ljVfjyxpzu3Y2zGuT4onEoWM7nE1j3LOIZ8kKS9N360wxKGxr/m9PrN3cnWSK+uxmZtLNUg+hE3n9rS6zDks9K65UPPtdBf1LduGQ/P80FWv5cm9GFMsklUSAeoSGUdJCFTPgYyhDL/O9HE0mbO5biko45p3rQ29vpFFozZx2d/UMhANwFDgFwwQrDelEMLEjKON1/ztzjm0bTspZw7QHWKo9cCqhcGmpmMu9eqE1/7GUdzA+r6fvOucwxDGySBofdqumpnbgbHfM0AjScfnvJODwUj+kxmDS+UF0SjULhp1ubXGSBlCdsvguMdQ5i77zkMmX9sfpZ+lp52TU81BnIyBLUvd13RuWem9ceUQrd0uYLu9B5Fm2prmXM9MCATvCGN1srnO6zmGWZj34c1Ky7Djnsur3GAOvb/HKGfaoLSbtGsCXKbj8C6Lk96rXXXqPtV0mmuvfdcRpUOEHtYi6V97Lgvzfvvn2j6nfZprvxxM6cCBU1pooPfA0BDe+/EP8bf/q3+E9779sQgLzmERCXE34vbta7x6/hVefP4lPv35L3H79hJh16cTvYEARpDQXXSJJ7gEPmtBw/IhbbP9/Bg62fHWdWXPbzg0HzMdZvi2rm3bpodSK9YAolYS1dZnyw8tuJi7al5p65lryxz/mevru+ha92/+c3lnAk64aC/rd+o9wG7yNZ+zdNLg50OXuj7USrW5ts/VMTdPtNyKQnvPH6LzITc3256H6K1l1EL03Dt7YzDT30PteOwztv66/3PryLZLswLWRb6T3x/YT/WaG+85QQJAUVRif0+269YKxkQPjFl139G+5fJdl+1vfX7Y3jyt+mYVGA/hDusuemgPrMf6IT730DMP9ZM1A0BVnqXVO70TaCpAzj2rtBKLK2EYRgzDAOUfMcSstLDrvOazM72A7UCmM0hij77h9Y1dp+wml5s0s8lMwLrZzOaYrwV8XdeJi5DJ2DQH1uc2E/2s4HPO1GUnubVeEFEWePRvjJJuV8vTOtSqAWDPulLTbJ8ZcpYuDy0e75wEbOqEJFcEkeQuRJmWwCF1Se07rZeOoSP/IJCzNKu/zwkW+lnBymRyH8gTHmNESAcPWgY4GfswoxnBlEmO44ChHzI/lL8zm0L627bt7AZUMxdtExEB8dCinLZdy5L70xNo5+bkXJ112fV6q8GKEiWgMLG6jLm69F69ac29W7dlbs5MNI0zQpsto9a6FuGstGNP03IA9BCQXSXUpU4D0nMqWyJE5zB4YPXeE/ydf/T38N2/9hP45RJjylyGPmB3cYOb12/x8vkX+MXPfobtzS1uL64QB8kmxQREqRCuLcJ74z2c8xO3Sitc6FX7yL9r45sD/nNCxFw5c3Uo7et1y1yshna91Wtd7ynvmgNMc+Dn0FWAzjwo0PleC7z2s61vbu7PzZ9vAh7qthZQDMCk/J3bj+YAca2R31cI7AssFhjY7DA1Hex+PFEsvaNP+6AaexYBa306NLZz9D7kJvKQ4DkHzqY0Ogzebfla/5wSSfp5OJ5ojm9quTX/0kvaLKnydRgfWgEPuVHNla3KTvusXQPMDDjamzf1/mqvTOfKylV+LzPyob7MCQG2/noe1H3O79NMn2boYekmY3x4jwCKcvuhq15rOFDeN+Ef9XrQNTy/9vf7Vs8zve+cZoCVf01TsLcjyutX36n3AzsO9j4DE11HHiuC5mz4RtejBQ1bmTIxq1lVV6QpMJDWFMFDbMKZsFGI4Z3L2uI4joDZeOqBALBnOpxj2rW2U0G3vq8XkUiBUzDooSBVMi1S9kWMaRGDCN410Awp3pcJ7F0RxMZxkMj/XJ+40ygQt6CRHDAODI561iPgvEfwnFIIO3H9YDFcab89ueyapP2z/bfaAxVuAICJEBmIyRddffoYSG5Z88yvLqtmfkpry6hjmg9Eou2OZGRmohyYvrcIAIRM8zRPCGDnMm19hByySIxAjJYBkEsH1lkBNzFMdnkT0HHJfadk+qYyXkSSYcwGmI+jjl9icBBXOkrpFMGcsqRAwo9z3xJNmLPikhN9JyyGSlCxnav6GztKzDglU1KG4QAPl9ea9wLcNTuUXnYN1Yx5f4MwYCCNiY6dMjSnWVRSEJz2EVCQqJsXAKXLDLip21GDYfubtsmRQ5MSAOxiQHQJIDlJWetHh+gd+lWLftXgJ3/nb+Anf/tvYnN+igERHCJ8BMaLK9y/vsDNy7f45Gc/x+vXL3F9fSWKgRDgGz8BeRr74RLvQ+JxdkO1Fl6kdV9v5Lkf3hV/eY4inBOhabvEeyIij0hJ1oSOoMxTGAQiDxCLkIeyMc25xGkbVPGQNZSogsPtfIglRTRbXs/lzAKCCJk6TzIvstMbZX3nORnjpC47L9QVL+8Nph/AdC7ZfilvsvNGP9dWvPr90g6AC9FFW0llr82bvu728mL5bO7nFhMBcDJWLAdDigJKLKCqjNJ21tagGgzZNVLzUB3Dwj/kP1F5PGxfacLfGdN2zIEWfda2y9Z/iMa2fbb9Nc+z9dfzeQ541gKwLesQOHyXAsjeq5Wmtnx5BgBi4sHW2kjpN7WG6Yul7EM8ztLC9t8KHBMMRPOg/9B4yI15hU5uI5EcXqhtQOFDdi3MWU3mxqqm3UQgPtDeOVyYy2U50yaBIY2USRXIfjzn2miV4XUbJbvWlBR5r3aJJvVay+0qNM37EcnenPm86eMhRcrcd72n/yIimnTemuzJSFjRtLlam9p3u6YndWn2UwhWTHaarBSu5+dD16MFDdXyqyYfmFonLLjUDiiTLoCs3I/pLAmOMXViKj3Wfr5U3dd/cxuHtslu9mppYZ5aKBQsWwFKJ13XLRBjkMAn7+GSO5gGfXtnyZc2fJaAbW8mf60FmpvUsimTHDoH2XCYGDGMcMktg8M0AB1Ee5uS0ikLPQZA2MMDOYFAch4E2dyc+pPGfbcjuyi07XPmTzs29mKIINX6NoMFHZu5DV7HNJEWRA4IaSzyfRJrh+T1TYdAEjjIgXGRGRFWG6wmTfGtJwMAch5vngKILC6zZHKwDE7aKA2c26jywEIZaHo3dTFGGeO8wCez6fA1EVCq76rdkLrKHJDNbT/9Zc28awCR6WxA5JQhKV0VzNTxB/IWUXleP9fWilLetI3vuhiMwVMO8sYY0XhfQPiiQ+gavP87P8Rf/8f/AE8+eh+RIwIz2kgY7na4fHuBy69e4vkvf42XXzzH3fU1tv02K0msFTdvonOWhtQDC3InGw8OAB4dOBYQG2OU8zcSTUNQKy/S9wDvXQGxZlNRXoQZsGLBpPbLrjvr7matkpmvpjW/p4VLbZ8IVjWQMW3I6wpGSDCf9TnoGrSbebpfAya95sAE6jLqOfTAhsmMSSCvtr+s+bg/pu+cuwrOZP0Ir5F+6ZlSk6crMDDX9no92edrn2ou1J88O6Fjmotz82ev/BkeXq9x/c2C5Nm2zgBk+7kGS/WeYekhSsN9+lmQNgearNBTz41DXgDzwD71PxJUyaRChr4eNe027Vv06n7pMzV2saDRAmzbr30gfMCdbjKNZ/Zj+VLKY57uXYaeNd117Gvl8L43AGWazI33w+1mY4kz9xh7NJwDy/X3uZWseML2d899sGIpBMoKmHpdWe8TpdPcerD1Zfrm+gPWmzMcHR3h9uZKa0xbxHxcoO3zhIdVYwpKyh4nB3XyPot68PpGrlO1hDr3vXYDskw/RgmSbttWtHdBvotPmXS+67oJI7cT0G76uhFqHQrerYa9DlS2LlpWuIgx5pgQbYdq6Imm9dqy5hhuTbMMSlDOmrDCUm6PMjYgaWIdIlQ7GhDjdCJMgLqebvyIRW3/2v7qc87JCdsciwXIPlP3yTJ1y5zr39UaVG8Wc4u8Nndn4dT8BWQdO924Rsbd3R3GMWCR2quArx6fus5p5hzsPSd947xpaRtz35y408xBFSICMU3GpCxmlMxiMxvaoeuhvuzVTbZuyszWe/9OX/z0aQLq6mcPtbvewO1nfdzOpSk4MeDzMXQhYGwkba0LhAU8ODBc16D3hMW3nuC/+K/+Eb7z2z8CLVpwZLTeI2x73L25wpuXr/DpLz/B88++wNuXr+DUjcq0UT/XAof9WwONublONJ0DmZ4G1OjcGoYhx7nNuZnNbUA6j0MIszFcdn3qfeVrmV9W/MPWp2XXWktb/p6SYQYMzt237a9509wcreuwm3T9+dFzaeYiEiv1nAJlrh223fae3n/XZcXtufIeEjbsXLP8S89k0mdq0GnbZ4URC84eumpeY9tiwbB+VmXflC9MQZbdu+b6X6/Nui3vGqu6/fX3uv6aPg/52NeufvLefCyVvR5D60PvTeYA9i3T9tn/mPLrS8Du9LsF8nPjpc/Ve0CmO5eg+nrdPjSuh9d5UT6/i/5132oekttUKY6sq1o9Hy1uIVeEA/sMEU08bx66LE1lXYm16frqCqHvASRrzIFYoYd4yaSOLHdwxluEeazz0PVoQcNq8uuFrI21bgF2Y7WaC+syBJ6aYzOohLgMaQfnQI7NgqXtUJchuyHoJqrpZm2Qes3YNFNUcQPi3HebsenQxpE37uQ3V2sLtY215ikLVA7gkQUkeZ/075xONZbAHkvbssnvMwHtD1ERzKwlxTmXBTzblsxcmffSdR4CENZiU9Mlt4vEzaN266o3J71/SLMzp7XTXNcqGGahhPbB4NyGoUwxhIA5lwjt5xCCjAOSm0vKwkHOgXN0BGY1GXN0tsy5FtTqfk8Z3JRRPSQEADAbeulvDXZrDU8GBa5ohebmuqWR3VztOqnXgAjNUz/nut2PATalHQQfXQ7SBjHG1sGdH+En/+XfwY//xu+hXS0RiODB4DHg7uIKly9e4eKzr/D5rz/FZ599lqysqY08VUzY9LyH2jrnUmjBVaJcfm8cx7LRVuch2LVF6fnJqa1cLA62HXNzol5v2sZDYw6zadr22M221kbbNuvZSPVvD4Goh+a9rSf3b7aUfRA9N2frOt59TWk5bY+4KM6VZ4HUfhv217Y+SzRV7NRl1n2xdc3dY3DeO/RerZSztM/eCc5lq+hcnXP3HhLo7P05V766b5PfqnLmhFH9fNC6jOn8qHmUveb4cV3OIXq8C8gqzQvIpuwyWGclK3Niymdrd8DJvpjGXK+6n4f4ruxmDLG2TOfu3JjmMjHd8mz7rILE0rX26NjjFyhj/tAYvOuerWPOgl7zlneB8Hfxr4lAMcM/m6aRvdtYnHQ/tu8c6m/NF/IcTSayYRynwooAor321xjyEN1UqJgmH5q26THXowUNdZmqJ5xO4nKqd3GfYRbtlwJ7nYB5gwtTTXuMcvhdt1jAm+PQbefnwJdqZy0TLcBz32fQZsGyk0/bpwcOWuBq+1vaOx3sOVeiegJpXVr/xPwJhtdTgtNEdOQQQj+ZWNaio3WrD24NdrQ+23brNmE349x2mBS4lTBnF5S+P/es7T+zaChC3F9INeOvF7qWa4PxM6NIfv+exBK2Wq+A9Lkf+uwGcuiyDCczRFdcTibPAuBo032WuA6H4p9ux56ZxZphBMHJJkjIB71ZWtQCm7aPBIEAPD0tvQZQ+8Blum7mBMJ6LPK9GAGaPx/iIUBof99n3tPx3WdW+2Cq7oudjz65/REcQuswdA7f/qu/jb/6j/4ujj58Bg5p4woR28sb3F9e481XL/D5Lz7B81/8GrvtFpEZjfcApQDO9K9eC5bfWeuGzYhX00Cft4F6NVBSZYHtm84hX60LO44Ty1o1djUYOQjaq3Gy/bBgcA4k2rmu7bbW4bpdc6ChBsD1WpmbZ/UctxYXu3HXYzFHp7m1OQWxU5CiChwdN+fmYwvs9xpw1fVOgR8nJca+Mmd+vWB2Xk36XfGKet+17S3jG/f6UPfHljUH1Op5cGguHgKyBUiJa6tVIlp+YBWME+34DI1q+s9dDwG+d11zfMrWV5cZZ9r0LnrUAshkX+QE/Wf4a+22Nhn7GLPLUd2eQ5cVNubaUYN5O1YWH2VaPLBObJlz6/sQz0k/pr1zvh+HeIbFWfqcLRJufk3ZdtQ4UF0SLT3m1uMc7ebwESD7NHOEi5rSNiCy8VAxvFGv2sIzN9+ARDKlX7qjPPGx6+MbnQxutdGW8dqTwG0jJQjVTQCxavFcGnSrKbQbdw1WrQZtb6FWZjoLCmxmqTmNY51uV8sZhiG9Nw2qtqbfQ+2xbaqZgZaj3yfuShzBjgGfYmJ8QjosAggN4xR0pnocT5lbvXHOLQTbLsu4y1hVGiWaalTtNdc/bWOmwzsMbnVdc22vGS0TA2PM2oEwirvIXFaJhxbEhD6mb5b5SCYhSn7/SaqnIu2LsSBZnnSBprGTdLvv3rQOCQATRhAj4BUJv7tv5V2gpv8hxqLv5TXlpmbnQ0DxobZM6zo8F7Sddpwf0roAKcuc9wiNw/G338ff+2/+Id773nfglq1YJoYI3u1we3mNu8trPP/0M3zx6Wd4+/I1Qi98q22abBpmCE/1jiZzYA7caht1bdhN1G6qyosUlGpfinBPe/Ev9QZlaTC1kkxpXI+H1Z5a2tXCg22PHe+6rgkANPcP8ZspAJq2t27rHKCeBS8zfZ7jt3Wb59pl9wwrME3oZdpdC0NEDwnN5ZrWP7+GxIKV+MgM6Krpo3PEKo/ULUnb553PcS62fbYsu59nQZGm67Smjz4/N7/sVVsHDtHI9mlCjwO8cG5eafus8u7QdYifPOaae1bbX4NoZgZ4GiM3eS9pNOaEoDlgOQe299aW3Nxr7xxOyu+n/W8OD82VkW7aGie/1//m6FXzVP0XzaGVtu6aHjWt5u4XeszT6tA7j7nm3pvjO4fqPFTf3NycG4u5q21b9HEEceLjgWd5ST0uc+uInJNEPGzrK22pjQGHrkcLGrvdLptkYox7mYVsI+0GXG+4spm6PD/tMwrkhSlGjCPvWSVqgljNvd0Qi1WlaNvqGI36ssBG69Xy+77PWswQAjhOTV5ah/bRzWzAc24l4ziWQ+vUCJloMRJLalvvs/beMhilKXjKiGo3r7nFrFdus30ml79v6q7dp2oBoDaJK8AKQU4cqMd8DijUIKfWVOXFBkpZogAQEMKIGCW9qbG7CvPcG+10VYs3Yn+jEwIkqxG06KQxArL1iZLgwak9Ok1jTD0nFeCU5+UPk3lCOVA0d63QFeV9NqD8ge7Zb6X1c4yv+o1AOf4kKk0z+EgzdkK/qiYi01bOGjbaq99qmkob6/lUaCPPkEuZnsCgsyP85O/+bfzgb/wEWHUYnEOzG+H7Ef3FHS5evsbF69f47JNf482Ll8K/0mGQkQiBuQSQm3Z5zSiV6VmC6yiNJzAFakSU1mzM/fbeYxxjBqV6Oadn6JDQx4nbZYiagpp0JEAEhMCm3kyqTK8MWsB5o2GgtCUNlOXb1hqjz1thT9deDQLrU8Ezn9V5bPitBQH1plnzKKGLK5mmgOzCV6YfSVZZkvXF4EwLglibdZzMast8eQ4Y2Lrtd6L9tWH7DpS9oMxeTD7nlhHldjFPlWS5fLtWZgBGrcSySh27ZvSySrtaoJpTIORzrQhgKrxIaafrlyplHgh5TPYEKbxbA2r3Ftte+1u9X+jnGmTmvfnxssOjr0NC1RxwUx6Ybsy+p/tG+S6bRJx53o77Q6DY7q8PCSv6LGDGNTWoFhDrvV/fecxVz0erQLFzMa9F6HYzxX71fKjpU9Om9FNKzAC6ogFyrQ/3bDK+hJzCXbFOja/qd8zNaR3p60Nje2gMSoulvIwPSV2Z98Mc6vkw185Mo5Dc0DMPlDLnMPSh69GChkvR5rtdjxiDORF2n0FLn1JKWS8pWX3aeBvn4VM6xpGLMGDdn0ByAMli0eU65FLi7LsEKLHmTO8SGCmaHWSgTnnzFWCd3iFJOSgpO2XBpW0eHBljsiqAIWlrE+IjkmBU3QztINgFa8E6kbj5lEUnWaucEzjlCHBo0XgP7xpEHvaEB5ncDE5Cgbj+pFiIxovfuZMEu8ySPpJYgIhDWbR2oTAzoBltIidtPsAs6XABwJNDFKeh1GcCceq/azISjiEAzsPB5XSY03mVTs+mBGjBSZMsWmYigkeDUQPiIaADDLjAYOcAT3CIaF0jaS/TqZZJR5zckw4wjoxcEuNgAa7qq4oE+hlyQJtVjXhyOeZnDCPGEJKQmcZTU+Y2lBknO12ssilnaEuAYzNnkhIhM1ZtL7Oks80CRkqXxwq+E5BQ8GUv0rZzEYRYzKAUCA2lwGMZ1QQ0gEhiXZN5Z3KzM4Oigl7llIWuY0p564gK6HROTunmBgSCo6mwxRQkUxgr5UWhEhmAaxAD0BDBeUJoHXadw3d+50f46//g7+H4/AxjGMXy1w8I2x1ev3iF119c4Pnnz/Hm1WuMu51kKYuJZxDDw+f1i2yViogc4KkBHIyrAad2G1AIhqPEw5gRdJE4WWfeyzr0rfIZ+SfTRNogjLxsVCIkJGsvs4hXDDTeWEwcEBAQwdnSpn0SpODyuEdHYBjFQUpOKRoviclCFB4PShlQEj0YDjEUAKQBgSrtyCyUU9Gjrk3ncnpF4Q9FuSTzOOYp49I8V4WLCLWJH6RkCeAymyPHlAQizRBH4KiKAHGzEWFLhWFAbaouyyNycCdSn5glRaR1HSESXiBCi2T3c5I/egrAwJIqPO1dMfEzB4YnFp6S5j2cF5oSZJWlOnKwthE0mBmUUx4nMsy4DVnAZHn5HBi3/7QcWx4zm3hGJ3yNCNx4ACMajmg4wEcHoiVGDghO5qJDhI+SiJ1T1jObxUwFXrtHT9pn5ieM8sHin1pAPASmZf4WcGnBnwVWViFmnzkE4msAPw94KWGUxEB1z6iVAvo+K4jktEbKugLXYHj6vu3LRIFBDwtZFtxPXCEh7EO3RS2SJQ9+mUd5rIpQrO2ydLVt1XqVl9ZYaK/9M/2qx7gG5bUbom2H88khwJX9K+9/U+Ki8Ol97JDbQwpzKoFtRlhQgXwqTAtGiQkMePJyfprpt/ZHsbFVJliaUHIdZo4Yg7ip5wVUCfj1fDo0v+Q3E9uFIow6N02G9K7r0YKGAqoYI3a70mn9bcrYkqkGiTFGxi7sZMgawDlkxjonoTEznC/aksVigf/jT/8PuBgvLJZJzz62B3PSKmfB4JuVZ5jho+4/fO2NF6NkNEiLgNcDaDXXOJ5+VMZgmMVsc9j8YS6PGUZ3+DpUqKVs/Yq5MzNBtVp9rH6EDcCf1K1cgoHGewz/xfDnVmLN2z3oHV8px1moAPqQuf6Bov7c19zMru/b3ywVa4oepgDt/frYpUcz3/jBSrl6un5E2kLeo1t0cP6/A/7w/5QfZIiPewxBEgWEAH4C4Mm0IFJhIRVJD4zIQ79NW7hPJ73/0Lww0KK+OV+N/T2vjUP8qPw6T+qqUDJ94Wm5PBkbwmNWDdd3ckMsaDTPlyH5xtceaKjb8Y5CD3O2uqB0/QUtYruJ/4UU9mguJBcdGGMAcI2HaxoMw1AEvBAlRfgD8/3xHGL+qkmhctjc9wyIq/0cqOb+wSYd4pYPPTfHQf8nvh5i3Oaa505/AXPtEdccZR9DtYeW2bu47eEC7Qp/zJt/znE9xLsfanD6bUKbfO/htq7uW/zv/snvIqm/s9I6Q8AZgXTOgrH3PcWYxvS8ePMAzh12CZu7vlF62zFFtJdAaZpIWlba13+By0EiSBIzmqRRm9GwqItGjMipcMdxxMV4gTfj68c29//3rsdbqf7/+1r+z92Av7z+J73CLfDQQa8Of7l2/vL6y+sv4mrNZ1d9/8vrL6+/vP5nvQRzGwsRU/5+6HqXFU8tbNmIQ+JmXFut3nV9A9cpN7FgENHkkBFrgrTxEcOuR5/MsZvNRgiQ/YCnZqbiEuDgyMQ8WJMaHM7a8yKTTvpZ6aOM4CpCUHXzAfFyTlNSfy8alX3Zu37v0HXI+qSKxGzRGAZxb5h/ui4VWTSupOR3XnMqoUdes9p0W561nAB79Tw0MrU2Kz9lyvfeYeyHJNA+vg+8px+Zf5urm1kLPek417PwQdo/vpWP0d1UFNxT4z22VY9vAxuaofplv3PfYFSqIvWrbxo0XZsnhLq4MdtzVzhblwAkE/VcXwCQHa/pUzWFJt/LJJ7v08zvnBrzEA32XCdMOaUd0/k9x+ytW1ep3DCCRLtvqneesziW6o3t4l08ZKJYTO8l87x+5ykBJnXMlfdo3fJMHx4o+cD77+KTNP2Z321hmPDMP+/F9uMMcHinZY3M/EruTkRoFi2athN3wHRuE4eAYdcDUeeRrikUGj2yyXujbMZo7vO7rvzsOyf4n5cP2vcf+v6f+PpPYtGYszk8XMGc9eE/Zt977Kg8mn9NeNQ34XrfcCwPWTLqZx6AbPOPzrf3fjlAPa4FQ8+ko64wXe1+pvdqCwWn9/QQaiIC+eSQXrlevut6tKBhBQt1lbLpTbNZhUuwzd3tLfptj8urS2w2GwzDgOOTEwxhxNHRUT7pWq8cxGxcqkrgkDx31pzj//w7/5c931S9xnFEjBFd102C5DQjkeZ4r4WbOpCu9vOzgtZcQJLSpm3b9Pv+yce1T6kdLO99dkbnEDByBHuHJjBWdyOu/ugP8SQOJVAPRcADi5uIDaiqfXRrixOQJnHkSd5l6xtogyJr31idBzruQElr2bYthmHIQeB1IKnNuqXxDQxgLoOBFW61Hs1cpv6VnBIj/MYHH+JP/vW/RRsiWpSDaiZBZob2tVTOZqzrmB8mwpjcbi0dFBxFcPZLh2aOSaWqBqD2QwVLnMzER5aK3zfM/KiZwpyvsvjnV2DZPCt++TNp8xho09fIEpND3oGcw8gRu2bUiuCSrz0zAxFwodBYL+cdaITEfBBJbIuTwGo4J/QgyhmeAIjvtvdgeIypLiYAnhAi4/T8DL/9V34bx09PcTPucD1s5dybfsD167d4cX2D292Aq8sbxEBYLtZo2yW6bgF0LXzToO1aNG0rZ9So9NESmrZB13Xo2hbeS1pt33hQ49MZNg7b3RYxBDhPcG2DZimxVfr79fOfA6EHnMtxOIC48zmSteTIwZGXOIgkCGqQd9Q4jTSGGgSOdM+OqsSCSWxU1HmrySJ8i/Pv/C7COGLc3WLcbhG3PXwEbt5c4PLVG9xfXsFd32DYbhGHEWEYgTGkchlMjBCDMgjhD4S03iQTn3M+J4sIIcIDwBgQo6Qzj6GkFyfvkaJMMi0yzwWnJA6arKP0Dc5B40qELOIOECOD3IgYpy68SHRAbJDCPKCHbGrQtst8wxy+SAQQY+Q+ZVpJ6ylRPTIQJTBDeC1zipVIqZVT5innfU5QQN6hbbq8Xu7u7jCGAd4n3hLL2T3qg53XZPLbn/MSkFlReJld53a9q9Cd17ifPzNiDjDkzzGgdQ73nnDdOJx+/zfwj/+3/2u0xwtcXb4C311hfHmN3/8n/xz923t4ajEygYhBXM7UmmTTM+2t28wsvvl2P7aJTWpff/t+fT9nk3T7tNLLBuLv8Wbs81m9dG+ci8/gJN1ITI/uQapZngK8OdrbtoSQ4q9ovg+W7+tcyrgm7R9z7i2WbjVGUQxhs+jVtKrLCmATezgfU2E/z9Ha9kl40PT+ocxlhzTqdVtrnFcn5rFtm7bTgTCNh9DfIng2hX49T2178v5uEjHYNSKnrO8nFZgL5nbO4b/93/wb3K0HrRjOebRti91uC44SR62Lbg43zCX3mfyuNHOUEnKUeVU//9D1aEFDQaMu/FABW10YzjmM44jdbgcC4b//Z/8MX3z5Bb77/e/jb/2tv4Wb2xscn56gHwZ0fnrqrQ5EjAGO/GTyl2u6oOwz9qTj+/v7CUPQwN06kEbfVdBrJ54t0wJvYCoB2oxWJUXvPhO0AN1O9MwUuYBLRw4RlLMaOOfAodSpdKYESibM3NQ3juNEYJiAUhMwbAUM/V4vEnvV9K83BxvkD2Bi/fJeFkMORmNXJjTtp9PUcbDZKvTy3qOPI0IMGMYxCWsm00d1zQmomV4Q7V09XiGEFMx8eCPSDUFO46SsgNBqasZThJQUTJosAJSCdsmATPveXBkTBly1b8LUXQNmmDFHnnN9FEYioIrz6aWOgdOgB+FJ/5S5Bg/0rVDO+RRKnYDVCELvW1DjEQmAIwxeJMLBEULjJGVzWndd16FtW7imQdN18G0jCQkaj9Mn53j63jMMHPGGAwDCxnt47zHEgE0Y8YFvcXVzDXIOTduha1qQ8yDvgLYFNU7a6HwK0gZuf/XvQMMNiCIcjcgJipIA4E1A3fvhc6zHa2AE0AN8O50/DXqJNAYw2SWTjCZjGieKKUrzhBNtZzXNWciw458/7dlTmAjDxb9IcoGM/70/xt3mOzg7Cjj73m/jvg8I11tcvXyNq1dvQHdbhLstwm4A+hGu38HTiBBHiXHhmIJLZW6ChI7Op5S9SSh1iwYYA6jxcDGmA99Scgbv4bzHoHwvbXIRMZ9HE02QcIwRLjq4NC/z4adACtpnUNLecYg5MJxjBDHljU2VBx6ytgZIfnkQISTaKj05rgoP8ppAg+X8nLQFKS9yDcG7pHBT4dDLfHNJadS0CywXa/jGIfoLDMNO1lgYgfRvjsfKn/kA5j+PAp7NpLGKn72y6/cIGCnCD4STweH+51/i6pfPcfzDj7DcHOFmd4vmyQl+8+//dfzLf/I/oBsYHfuUeapYdCa8K7Vljp/B8Ca7B9h93SZ40XfnhI+5vhWBZnpg4SGweohn132q32FOgd2Yjqdtx0MAzbazfmxu3A4JXY+5akHEHjdQ06YOtK7L4JnyDvWv3sttndMMh/vv1vuaBeFzwN62X5+vBeAHGrvHlzNd3L6ScPJ7uiaKEIMbtc2TZ6ouv0sonTwL5GQwzjkE804tTFk61G2rhVcAOTOinq1j19Fjrm/kOjXXSI6MSHEC4lWjPQwDfvmLX+C73/se3rx+DeccjjZHuVMK0C3hrYS93W6xWCxMysWKwFysKJZIbduCk0YnmAGsGY32xx6cp/fsQqjT7lmaaNvlHc7nbgBFWLEMUr+rVWiiGXEuZXlKgDNKOkxN01fqMdJ4AgIlo5PkoNb0UGplqFO6EYkPn+Bb2mujcH2DliveUUvdlk4xBMnApEJTEqaCavEig0KA9430lRzAIUvODi5luuKsBY4sVgLNHiYZOkRzQ94h9IM2TDLgpAxjqhVmaGaG1Nacoq1e2WWtxxhSCkcJhyK4AiIJGcwxkNNvhhihSWr1jyOdJ6qhLIc0qouC9IcywFd3BCQQA8PuNNhL50VOgyicJj+nwgEgJ80P5IAEjBgJUxMQmTD6RoSpBHhjenf0Hje+gUsHaOZTn4nQrJcYVh26xQLNcommabBYiMDQLhbwC/nt7cXXiKEHNR6+bdA0LRrfiLY5gT3fNGhUWAGEoT3/dyAewHiB3euf5+xKPgHAEUjZmqSvP7z/Ci2NlZWcJdNQ+qz9lu4lxmkEfDsRskCG6c8ZOFDK28aM0nCAzEgpWNCsUekBAC5NJc61Uf6E1CakjW4qu6SJITMhr02Z6w4MzzsRYEmadjy+xsnFa3nt5t+DAVw15zg93SCuBly593E3LHB9cY/haovm7QXG3Rbb7T04eHAcobJzQ63MO0dwibd45xGcQ2xaAAxqWtH0EyHEAPYO0XmxaCSh1JGm8I4YEbOyhMilHPoEbtokHBf+1TSNzEFeiNXClYNTAU78cAs1gsseIOnICYxFDAhJ6WEto2AHDAtoErQJcAsDmvE+ZxpTsK6CogrYzomQoZazRbfCcrGB9wR0K+x2d4hxwHZ7D/T3wJhmSrLC63Rg3VMMM8qaRLYzuMxz2r87eSCEsu/MgQsLQnLfPWGLgAU16EYGxxH/5p//S/yd9/9XWLRLbI6PcXt5jfsG4KMWw+UOCyZQBBj1Cer7Crf697w8DNCplV+1gKH74SEhwO759Tv297rOuc81vWx99hmXBGwRqPT3h0GiXvUezdXzdb02KxEAo7TEHmh9jABQ07AG8XNCAnRups+2WltjXXZNt3rcHhIEa018XcahdywmsVhs7uytufLtdw4MUBGC699rxfS7+jtXjr1q7LnXRyoKf47CU9Xyqu/r3J8TSG0bIqeMoRa/EFImwfLcu+im1+MP7AtyXkPjfD5TQiqPIC/gp21cOqoccMRYLlr8+Ec/xvMvn+PHv/ljHC3XWPpWAGMkSUuYwCCRpm11aNq0uYSAOIaiKdS2GC09QdwTdAFwjIjjmKVrJXbRCupi0QlizbJ2QihBy8mvdrBkYKYSY9MkkykiQtJWWUbVJLAWI0qZqV7nCDGIW0BgBkVG5wiOR7iFx8AB5BvEEECQQ1ga8hiYAQREFqBNzqUJImb9yIDGAwkzTxyIGRwIxC6Bd+MyFiQto1esnDZ/QDZBpLHyVFyd1N8bFMGR4dKmHzii6bqU+rFFREBkAsPDdwuRh0IPxwOSZw8ihcJgATh4EBxco2dJiHneO8Zu7OE7cb8COSyowTJESceaTLo7AqLzaAOwDMDgJYFrBgtpl2ZmSTdL6cAgAEScXSmYfNbmxxDLQXaAaEcrYU3AAkNkTwajyaZ8EMGn/8EBkUg0v4ScCpMiRKvvUupMT+JOwh5wDrFpwI1DcOldT4iuBSUw5n2DNgF71zZYHq3BbYMRAb6Ve03XwrcNyMu6u3v1KVpEeC8WB+e9tCdZEERADTh581M0/DZrnlQoIkCCs+8A3Msofhhu4Hkwu04SnlQQzCM9c5EODvKaRgJheS6nv7LRTbzLc7EWqOd3k5BdwJytmHPdRR5I3/Pnut31Pftu6nJKK1sjw0KJtAnR9AECTRtohBAVXICyDjm1c7LpEyVmQDgJb3AyvgEAfBSeAwTsnixwdb7B8+98F6/fjIhvrzD2vRyM6QR4NqtjrNdLLJctlusVRmI0iyWobeA84f7FJ2gbh+7sIzz98Dto2wbUeLx98QXGm1fC+5PwDiJ015/jePcaEwk/E4OqDpT7+zhCN29Zs5NfuPxOlvDTP7h3R7g7+1Hig5wVA4gMHgaEMWAcR6ze/z5c06Lf9tgNI4YxgkMEjYyWPHgMcIHR+g1WmydoPYGv3mB7d4nQ34FuLtHf3SBs78HbLZphhNttQWMAxoDAo6SnjJK/XniuumsVTbmqTQgibLFHVlKItjVZzhn5bJNa+6r35jX/Cbg6wugjogMuXz7Hl3/wx3j6nSe46y/QNB1OFgv8g//y7+NP/vUf4vLLV1hSm1NqWkUagIn13+6P6kpWgzDLU61QoRdRwhGA7PNOLFExrzGePmv+8sxv9n4NDO1zNdi2z4rWF6quSUKGz6e9z2n9DwlJMG22dKzdkS0ukRewV1595f1+5v2aHhaYz9HOYTpmesmMnaezlqP/rOJVhX19fiLcA3tzAtifxxM6Yjr3rSBQC1NTOtLBrWmuXXkOE/KZXJFjLkJxlHismIINLtBDh7Xc2r3tUF9j4v273S6lB457Ta/HuuhNhS/GhH1j0HjpgnFkuy7uZPYA73ddjxY0Gu/R+AYjj9n/Uy0BE2meZJF77xHGgP/6f/HfyEJLm0ZIfmMhBlBgMCvIL+cBjMPU5YbMYDNzdgey/6y0nTUhRGhTrIbVhMQ4ZgZWLxzty1zaXf1dn+e0y7uUD9+e71FbMPIiYvFhz5pLIINXAbQMpLMcIgehXePRrDr0V9dJQBJLkncO5AkxyqFjzCznVTgZViaHjkUTFUJM+7ZocSMYowfGKGkKW9cUadfJFB0pQK0dTLq5QYQIZjClSQuaHCgoC4vzogpJYPMYwRRA5LBsPDofMcYAhAiiVuqgtEFCDt5jTwgkWntwSAKF9KOLHkssENkDiwbd+RPsnp1huxuwvNmiY8IdIhYffwA+WmFgQtwGbK+ucH93m8dFx0tiFYrVQxaaCGGRgL6RXPtlHiThAoSWy1wqIFjiImJysSDvU5yCgCxuGwyLTiwJjSsa/8UCfrmE7zq0i04sA6slmq7F9f010Hq4rhFhofNwXQffteBhB3z+U3hKsRSuuDkBBA+GH69wfvuJzKEA8BbAVmcj0HAvfuwRQI89rZhR1st/2N7Mi6QCxTPMOv/O5ff6vclzyBozmdtavxVJSyPNljnZ6OyzXNd94Lm975nBz+1ApjYilBNQUnvpcL8reFwVW9W9p80q91ifO0hLI6ARZXmvww7PaIdn7hJ35x6fnX6I+OwnOP/gY4AIu90d+MXP4D3gfAT4Cuc3n8D3I7gHPDG6RQ8QIdz8GfqfEfq+BwP4buvQUTrHJ52xABV8zBxTF0Lpkpk3WSGgdJh03NBhbhwx8/vcc7egyxcTgUeFWUrKDbQOw+UniPkhsRw5R7hbHeNm/e0kbEdwvIF/dor16YdYb49wdfUW2+tLhMsF2vA+xm2P/u4e95dXGK5vgX4EDyPo/gboe/AwyJkvzCBmeHaAGzOAjUkgIu8A77IVn5KSqdZKyxSYAvkpafZBpO5FajnsQPgP/+r30f6hQ99fgeHgXYOjxQl2V3fookcI4sKqmuLZGDTjtmE19/ayABQo7tpqVbUWBMUJs4LITB8PWSPm7s8JBRMwbYDqPvCq15xc1pNjTrNtPx/qz6G+Afuze66eOo7HlmNpb3GV/T3Xl/YAe3hdrodg+CX25kBtjVIFtt2Dtc5a2fuQEPXQdUggsaEA36TsuTmiyg3BQ2qdMtY1EqXvIQGvVgjs0XWmTvFw0fUW0e/GvbjXeo3nvyjzXUMkPKk7dJlNtavuY69HCxpqZq5BeL0wdaF1XQfvG9zhPh/u16nvtbwIQKQn5yQuQ8uw7lDZRGSIGiq3HGtGsu2wz1jJsA50skxFB77WINi+6jtlIoiWUvdO+7zVgEiZAMhli4btMyAWgEgsh3EFEUJGIviuywepee/EHJ8P0PFQf2KwbjIAQIhNxIiAqC5AXAQZgEEc0TSAb8TliYgBlwQWMNTSlCVuEdXzfq37v2jMSIQ4l1zPfHEv8ERy8BmJP3frgCYdLMbOgdBASEMpHoIhri6jBJomV6iARjRDRPBuCYAwckRwEe7JMxz/tb+Cex5x/fs/xXoA7luPJ3/ld9E/PcHQNNhd3+PZ5ggnx8e4v7+XoF/VnEbGOAxy7gIjxyOMw4DdbosTJ77gKuETSCwGrcQiEAhjGHHx9i3627fo2g5N26WgZBEa2q6Db8QFyXkPDj1Wb/6DBIkmtzt2AwgBhFuhpU6oXcS3+y/hd+MUZ0F5vbXc6Y+cH9DDyljvKsi0wHwygdN/7MSmUt5EXT+pywI5Nt/NZQHzIaZOVd0HgbPUVWC23WZnyn5M3bmMQ0LFTL/z89mEeKBc/e2b1G3Wn5oorTCRgbsdg7rYx9GcibF2I34rfobti18gfC09OgLBNx6to7RuRIcmshKJgAoAHMFjj7DbYb1YoPE+GVwcPNLmRpTaWxJ9gGjixmZnDNs+7gmyrurPgblmx6wWfufmGunGqqtK/jbcl3aZtpyMdzi9ejERCvmzPwA+k/eeshx2iJZxsTrH3ckGYQi4+O6H2OEIV28ucHsXQVdXGN6+wXBzC+oD4q5H3A1AiGgdARjlUEiKgNeYKiR+PAUqNViddbl44GJONjJmxFEO6sPAcFvGmpPFHBE9ruEC0FGHgUZE44VQ+8TbvdNaBmoQVN+336fC0L5b1n/MVQPqud9rvPAfU/dDwpC6i9btOSQg5TZW7bXvWWFozr3H9vlQTMZj+qENmYtxqOvfE7pcwWGH6Pyuds2B9rk18a5+HbqIqARI713Fbc62oRYg6netsKPfH1IKTGpksZeLUnZGIDT1ZasR9vlEHpO0TUjMDO2x1W9yPd51ynTYBjOHEODTQX4AMAxDnhTDMKBpPZxPcRDeiQme5fRnRHGzEoBUhA4wZw2FTy4bEy0TFz9Z51yOQ7B+irUWxTI5/W2OkczFZsxN8vLXMgA1MXLyCQbAJmMVK9NgMAfEkIQp75KlIiKEIQcWhzAA1IBdAwcHHwgUCS1Sxi8eEQPDUYSngIgIB5eSV6XAbBBGEFwjpxZH1jgIQpcOXfLew0cvLk0xCSCkOdOKm4mYpj3QeAGuSZBgiGAovnwyFuRKjIXEHbhk2QDgHULbAL4Fe050cDnrDqdJzQAoJEif6O2ZMYaAECLeth5DR0CI6GPAV3f3WH38MXxHiNcDLr56Ae6WuOpa3Acx/fvVGm/Ge1xcbGV+xADftJIx6PprsCsuUG3Tolt0aBctNiuHpuuwXC7h4oCnlz+FJ4DIid/5qG1k+NMd1ke32UrAqlUfCRjLvbTMhSYy/Fl/6hhw6l6pDNLMUwVAVN2dAm3zOWlUIpnnqlO50wKZfs/Mpb5fg2F9uK7btgsF0LF9x1Zhv1spyv6m4K6q2wLQDD6tIJA+VzJIBrH5O6NozyvgnuKJmDlTX1wlRIukzdZ7UKCQm2HbaAGEYXFk42sMcYhA0T5Y+lXmQUacRSDJ/Z7ZEPfulXmpFtbnX36FfojoFh1WywVOT46xQgfvExhIZevMBpEk++g6NE0LdWXKAsa0VZMu2jaVYa8Ei0rAnApZM+Nta+G9D9OvsbpPSo9KWMnzOGnQmVPXOPEuVeaE3BKidAowE07CKxyHVwADH49fivx+BNwfrXD/1OGL73+Et9cD7u4aXH79CuPVLbgf0Nzdwo09wCM8IhzHvLeAHNiVuMUaYBzS0APz4I3S95jWTOMcwhiw9E3qewtiEUJDZHjfoo8xKUzCnra6VkrWbQOmMZq6F9t9XIUTWy4rbWeShdj+HbJO2HbUILTWOM/R613P5Eaa6yHLy3QM5p95sC4Sd/F9Lft+3+bq1N9qetQa9UKD4upkBRldF/V1SHibfI88Of/okDXDgneL8ebafKhves0K4VywUI0ZFRfV9Ei1yBPV/Vo4rC0LwBSDqhVvT5CcaX8METr9tWyLZWsXRs1wpRhbn88CyoRoSCq0xGMPCGuHrkcLGsvlEs45bLfbCVDXTlvhQxe9+IeLm5R3Iiz4lNrR6WDHMf8mXWD4xsM37cRyoRcDk0xKTSNd0O/W/9MSQttoNSlWCOEk3Khp1qYbtGVYidNlq1RE06QAZkQwi8sRWIIfxcWZEMdRJi2pxUYCjj3alEEloknCVj9KGRqz4dsFnG/hIEC+30lwcuMaRPQC+r3JzpI2vW5ssAhtOrwFyIiGCFvuJXAzpeSlWILKyXtobIYnyagSQ5SYB085SJrI5XdiErLElarEdDCAEQ47iDVDA0lF6HEgYhCxBBw3Hr6VYMqmaRCaBj0zxmEnwKVtsHSSwea4c3CNR8uE7ctfY+ku4cI9KDT49vcZ738c4OkOrvspoiMwkwR0LmKx0CSM4sBolz1car+wifRfJnEzunfg+8RUnEsAC2LhmQEoQmoGIYKIITE9JbJAF+9kcpv3ozMASjE8AIZPOnPOBoaaKewBqrmKuLpt6p6Ct7nCLUo37xlhIPeZpgZX1sWe27XPoPeEglQ+J3BXX5n1J+FAmi3gCzbwM79gtHy2VwmsKtvhpPkBkZSjDLzWt5MI6URKnUIfTWRQqk6abX0YDBg3UILE7FhoW8DsPj/MmzAMMCKL6WcEDHvlspOQwpzmLbDoFohjwO5+h3GICMOI1nm0JGl+vRdXTKbiolbiMKS8mJQXYGQXTKWDjsVUMCrtygdQGWEt0/bB+XngmsgiZp5jv+6pQOxmFotoEH0sPQerm5GdBTqZzObNAEhNwyOUGaxwi2XrcM4/Az3x2J16vH1viV/Tb+PtdUT/6Ve4ffEKo8Z3xIjWMeI4ILj9zb/+XAsUc4By8g7EhRVJSHIgsXw7h9E5cZmNEZGAwCPYC4+Vrk210nVCkj3NLk81uocAmi1Lhqb8VmuErSBg3aeBqUeDpUENWC0dH6tdts9K36aAtW7bbFlVsYfqrseQkdIE05xLD1du5PsCz6Hvh4C7rimbleohQdJ+r8vO382Y1sLjIcH1kNA4V/7e3Kvu1X2dE3Q0hbD1mCntUA+Xw8KkvlP/duiaEzYmvzvhwdvtFoumuMJrxs+6D2o9ni03s1hSrVfmZmU+P97F7BtlnXLOYbFYgIiw2+3ypm6tCzZoqPEtiGOuhpN2TzvWLheSoaZtJ2lz+yGgHyMWi0VeDPZSQUPbUjMma32xDG1O22EZlH7XvuWNvxqMwjDjZNJlJgdktyaY+kOIcBSAMIAcoW0aUENYdA6UAqvHGHDX7zCECHDasOGwOn+G69eX4qIUGeMwIoZRaORWYCfB85I3PjlGxQgaveTuJ1cyBgFgAu4R4BcLcNMgxlAykzQOzot7hHMeREDbdZK20TssW3H7cd6nswf0XJUGu90Od7dvpRzv4V2ySHmPmE6DhwPIeTAA33k0L/4YXdiKCp8IzvVCxxTk7MI9zndfm0WRFnHPQC9CHG24ZODpgdgRqGtStqGQYiuSewcDXI4OQYGpQHAK2gxwSsDE5QBxACnNqtI6+LkFp2Bxgm4ycCVOVgt91qx3Bor1oRJISIFuvYkQku+nNnJat4YL7wO0vR1t2osJQ6mFgKrRWj7EqscQgJ7D0vYA3AxWTMVq3E+Zz6KBUaubVmcZoAJv0eiVsQMkm1uujMoYl+BwZbzJOpG+i0Kk4icoQghzSlyR2hjGYHhjTAGwDQgSd8Upw1jbtlitVqLkiEG03UTYrNfouk4sCnlsHbL2PHejCE5yP9m5nPlLAGl2rEN7WT0AjJIRiwir9QZvr+7geESkiG67xXq9RNP4pCBJ/scq2HHE1dUV1us1VuvNtPy9sWbzp3wu2kJdYwyUBCrVXMNEWLGCCO11jWfaMCewlLr3G065fIamtnZpr0tjRpQVFvltG5/DEAXGHrAUd1aQBzhi4SI+bAd85P4Yr997glfvvY/P3nyIu7d3ePOrzzBe38D1A4g8KO7AXKwAdZDrobjDhy4v/q4Iun4kxhQBUZKWsGR1awgIHBDhMqDWa05hqO2axI9E3vMpz79VwHFSBk8zFNUKwkPXoTL3ANwjQODcNeGbf74i9q458Dv7HKYWrPpZKwQC+2D+EICswSogfEavQ655dmzqNs0B1lq7PofnakHWljXX57n+H+pv+Z0KW5rbF7FvnappUVsTNAsnMPUO0jLrMmoPG31uOmaCtyiGrHACpkr5PcFdejWpz6aSLj9R3o+LzuQ/kaCxaBusFh3GccR267HsWsQQ0A+DBAWn57quw67vsdpsBBSPA1arVW44s6TajDFiuV7JwVKjBPkuF0swM27v73F9e4/GO6xWq70UWo6Arm2wXC7Q+KYCQcCEhCxZkMgMep6gSkSUOA7nHIZhyEKDxEPIGQoCxst5DotlJ8KCMvIkWIz9CD10SrWXjgjHmw0ax1g0SaOZWyxaP5kQHuMw4KYfgHS4V7/rsQ09xrMjtL7BcrnEKp1BwsxwXQekDCMaC8PM6McBfLRA9IRVskg1vkHbdegWHU6uLxFuXqUzLSS43Pk0sV1aqAQ0l5/jaPfrPOkEaqYRL+7KAICWe2xwI88NE6SX/hYQYHT7yJ5agCDsKMzSsWSwyugnjzWV0ohSALu6cUiWJmLJfsaUXIZYDyFzU7CdK2d4eVAhW+kYGViXAE0GpmD4DJTI/E3CIkqqXZv9iFGABgHZ35sgmMSbvtr/ijCRrDIKhlOdLpqx0XawMIjMprgyizLnZAL5vRqg5aKMOw6ziC8W5FVCjAoF06tiyvU7QBbSY4wYQ0gZ2RKAJ60bGdQhiwy68ek4Yk9IsJ9Z+x+FT0Qup4vrcyG5pmQwk38vm6akFNRNBRjHAWM/IETJQBdCFMUEVJiRpAdnpyfYbDZgIrSLFszA/d0dmqbBer3GerNJ1o867qOMrdxJ8TnkcgyVapWds4dduYTN7bq0lE8/UZqfANZHGwR+KbwzErZ9j904om0bAcSp7kgERElgEZlxcXmJ5WolNSkQKKNiqixzJAOFNJ+UXmD718n8T0JsnkMxVrJB4snVXJtYUkB7AkCpB1BXtMzGtF3pmQhZty7fMyk0rXRHSehW9zqmqTIjuRSDSGLSYijr2hGYA87jK5ziNb536vCrZo0/W36M7ast7l+8Au7uQTsHN45ACOCUNCQkIc2D0kGZyMIZMUo6Xx2bCnwLu6QUOyh9VaUag+Fi4n2R0XrJ1iey537cJEz5cyBflVMhaNZBnTPWXUX+a5OsMMcU1zcPRPV+fdXtm1ggqnY9FlDV5VvFxCFhYw4U5zbtS8UHy5gIbYRJ3+cyM9XKWWBf4LDXIQtCVqfNgE910z5Ev8MAf8ozQJQVTxFTq5Ut65BwUbfNAvV6zswJqrr0c7B6EkLI5Rba2qb9wbxV5lBa5nqtHOrn9H55d7FYiPv8A66EWldNxzlrHmwb+N0C1tz1aEHjpBULQowN+k6A0xhG7PoBY5LY+l2PRddi5Ry6rsVms8HdzTU8Aeu1HIZ0f38PT4zb3RZD43B/vwWRnKi9XEqGqHHowYsGbeOxWXXie2YA2cl6hcVygdYROIpqOscCCF3krAWOCICcckwtAEJASKDao9AubWJpkrmuQ9/3ABiOxPVFg+EJwKJLpweTZBxtWxE2hmFA3/dwLNqepmvQxxGRIzov4c7rxqETzpzrjQgYIVm4PHXowHAxYkh9aVyHj3/yW1g0hK716J//KVzQWBjxh9V8zuIT3IPigKdXPwf1iflssYcr3kdAE4eZ0VYBARMAuHdVANG8jbyB1yAhP6TMtxISdUUDKWc8CYzJ7dGNuwJKXARMQKwPBVQQXFbHTV6Y1F2+v0MTxaYdrA9xElisoJGEgNQnu1VqF3IoLLMhTwJaltFZ5l1viJqGE3KKNri0gVM8gWCo2nUo1aWCRgJa6nNbyJTgYd6gzIaQhDc2/cWkjjnf1WjKmzJLhrgLDsOA3W6HOIpbiTBsBdvyJ+agFhILIhK4I0IYQzpfhhPIl9LHcczvhxgQg/rBqhKBwRwxDqMIOLFopPQ5QIB0iFHSfuepXYCtHS8d3/Kt9Pnl20tRaBBhvVziydMnODs7hYPD1eUlLi8vcXx0hPXmCE1TXEyt0JeVOJSsrNAlRwl/q0WXkrtjGUM7H8tGp+NEABMWbQPHQR6NQBhHDGOQwx3ZAGoVzgAcbY7w6Wef4oP3PyhrYFKbJY78Po5D8h1Oab7HHkifLVCQHO9FsSPzQwGhzqMy/yyIjjC5+esxMnPSzvEySyn9v7hhiPVInvONz4f4qdbSe8laJ3uTS++XdcjMwjbGmPklMwHOFbdIPTU+iX4tAb+5ucYPlrf47OwUv3j/PXx13SB+fQ26uEZzc4smbBF4i94FjBjQ9qLs2nJEIEne0USJ+dk5AfbBrHHNlKMgslG3n5T2snGi/okckstsmotMmQ8Wbbmezl7AULFMlxhGBiOwKFA0xkDlIs16peVINZQA9f7pznOXzp9ak31Isz6nZa/Le4zWXOYa7ZX/mMsKo65Slh6qS+e8BcWHBLCHrAp1v+v3a5qX8Z7us3Wsq7bL9sO61WUlsG7RugZJMlhaLX9Ng1qZtKfFnwHptRVm8k5S7OnW5lzapZzsH4gmyQ4KLV1aA6JodjmgWvtjr7mY4T2BvxqnuXnnGKDk6TOOAyJSzLN5zykOYey5ex/OmAYgirJC2TzTw3O/vh4taHgCusajaRbglfiBhdDgaLNBYNFE3G/vAQDjMKJpPJbLJTbLBV68eIHrqyswi2l0vVqh7TrcbXe4vbnGYrFA14qF5PLyCv1uh9PjY4whoGsauNZOYsKT87PUquTeQ07M+CQuXd5LbAiQDmwKEiYdQoQLJT5DXRg4nf2gk1+YH1KgeZtcimRClQBHyOmuLGeLgNIhwDEmwalB4AgHxjD0CBzBTQvvFlDdsm5gFAkcxKoRHWM3DOj7EYujY3zv+98H7y5Bn/xznPTPcdbGJPwURr0HbittZQYiwMOCg73sc1ZIsAKIFSDqvxlZvKO+uZ/fVfdUBzcjzDyy7kMN0tcsEJsIXlWdUCHG1G0B3BR7l2o4WSby45wBsQYzZ607UAL8SBkRRMgAijsRUzrsUOuTsTBwqyJL+ZL5jiLV9IUSkpZ0uZQPW3PKUDPN9+m1r1EsYLZMXaF5ZBEwbm5usNvtQOlwRoJY20KUM3LGKOcWhCgabz1VXoUBsYAEsUwGAcTDMGIMI2JIAgMnywSjuGSZ4YwKYBWC6pArrZDiYypey9W9PUCQtX9CC22vA2HXD7i8ucHiqw7vvfcM7733FIuuw8XVDS6vrnF8coLNZi2Z+6Kx6DwAEIpmFOCgfRQgLZYSAWq5mXaNsczrrm3FIowIZtkU+36HEFbweobBpGKxbHNk7Ppe3p+AO+vC47C9v8fbtxcG3ALr9RretzluzhHB+UZivzQlLseUYjutlWyR0jWsQkPRwMnxFDpH03vpntBG7TgEIlmHpII/ZF2V7IVymKhj4fGJmAgai5f4sz0Q1nuHtu3kgMo2uZ7qqfXqigsHhCJccKKJgOrCf1rP+KG7wA/eI9yfjPjpyRF+cfkBxjdbDG/egm5v4XZbuMGhdyEbhDkGBBck4RcpPyiAbwI4J0s6jXUFLiO4OqfmcVcNDOeuaVsSH6JyPocFqMC8684cYLN9mKv/IWFkTgu919aqDCuQzsUx1GUU4QuZoIc03FqXuuGEGOU0e0ML224L9h+6DrVvL7YF+2OY6TXT50PlziXfST8WCxbJGrMZRA+NgRVk5oStdwmn2rf0Le3L0/k9fW2qLKzbYzcY5iII2j4c6sucQDy7bhi4u7sT/p5SXk8EGfts1ee98uq9K7//zYXmRwsakq7W50m2XC5xf3+fqmWAI7oUmL1eLvN7t7e3aNNGs9vtsNvtcHx8LG5VKdD4eLPB0dERiAirRYej1RLr9RrMjLu7O2w2mwmR18vlXjC3TxokbYNO7gCga1qMDPSDmJO917zbMgBhDClmooVzYpkYRxGK+t2AxjcgdX9hOViPIKZi5xzCKNaFMAwY+gEcI5bdEouuQz/2wAAQBzS+g6qpsrYqAgSHFi16RAwRIN/gO9/7LhYe8D//p3j//ldoeMRi0cGhyUKG9LNku5kAYHNxjZIeumbeR71Y5p7l+brzc/s3S5v1+2zdFpSwWeX/MXXPNccg3/yKETommmhKQkBqHxHUN7w0V7WqZQHL4yYwOYEcTn0ozINnSM7p/5QAH5txLRpcoGImRlCx88ZsvZBSKQswU7TM2SVojKMIO1Eyl3Vth0Xboe3aaZrEpHbPJTDvMaZcRSz9vbu9w+u3FwBE40pg9KHH7c01bm/vsNv1GMdR4pNYLA9FSEi0ZAGyRZM4nfZFfLBUockDxZoVC3XS8lFgBWEFk/nF6audcbkoK59n6pb/qjPbGBjj/Q73n3+JFy9f4YMPP8T7z54CBFy8vcDV1TVOTo6w3qzhm6a0PW/sU2cLghlTIjm5PgkaIEqa9gggCRvMk/YROLlcOuzGAJ823HEcxSKk58fMAI2TkxNcvH2L999/P2v0FCjqFUPAF19+haEfslDBzGjaFuvlGoBkMuyHEeCYXVfVwhxSMDJz8YNW1zdOc0R7I9aQdJ4QUZ7zMg3FSpKmrsRAUaIAIYM2TmuFUiIMT4SGrAVD9gnfNmibDk3TIHLJwqSnkquWyTmHtm2wWHRYLhdYLJdYtE0WTmROcdboR4qpfgfJKShWqvXS468t7vDbT+7xZx+e4pc338Pdl1fgFxeIl9eIvAWGAc3AaMGIFDG4IAeqxna6BtJVa1rnMtfMgTWuF5255gBpDaK0bn1+TnCwgFzvTSwID9Q3aesBwFYDT9vGQwBr7p26rofen3vX0lLbWifjqcuU9Ou8Rxv77qHA7UPXHDh/6Fl9TlPW21iEubofSxNm3avKe1a4nEsHWwsYdXrfes7UloVD1hMVerT+fIg15109lzGZb0jL/wBN67ZYq4+6Q+0F8ednkXgHYdht9+ZA3YdvIiyU9xJffMRc0OsbB4PbCasEbr1oZNomBSInol9eXoJciRnw3uPq6ipL6pKxJKDvtwhjh/Vmg91OiHh1dQHnHJaLJWIYUYA1pXrKsfEMyWbl0zkE2+1WGm2A2xhkcxyGIRO9bbvkm5023BgwjqINbb3ERzSdBJw3vgEDGIY+g5sxSGyJblj9rs/uGuO4g6OAo8UC55sn2O224qsY04FLRCC4pFkFwIQQCVh0ODvr0H35r/H07tdo4oAYAyhZbqohn8IKu+HXm3/+XAN8Wxw9DNpNvXlHtvcyeiyAdlqVU+RTlcXV+1ze0+L26jc/0mPqLkjPyg7ZbS4KIMmuRvmZ6fPlNuffLFOyggJPaK6aDPk9RtWQlDMA2FgiSovteKUyoIcAlXdV9y6nQVsaqKnUtk3RrqRQDqEcP1Y2AHlXfiuADGA4Rxj7EVc3twiRsVytcHx8jMVykXhE6rsrNAcqBp7vyzy6u7vHi5cvsVyuMQ4j+t2Ai4sLvH7zBtvdLiF0yv2hLFwksYGmfUbG1uUdFagC9JwYbZPQQjYxGOFBYnt0yqpAo89Yccxe+0uHssDDSaQwYcPS7izJyJ8xRNzcbXH368/w8uVLfPvjb+H09BQxBLx+/QZXVzc4PT3BZr2WtOF5I1EeESezQNolwbvROTgGogMoJsuG42mLsmQkbRKg3SOynNETkmWIucksw8Y6MTNOT0/xxRdf4P3335/wFru+hnHEdruD9x4317e4uLo0ab8pWZ10zkpAMoHFbSFPJGljcaWadjwiZUsCI6fazUSZjpPOyzIPihhoAYLw7/Ie0RR8yKYvgdGLrgNIzjdyzok1w3ksVyt0bYfb/h63t3dpH3NoGof1conlaonNeo3FQs7jkdPBAXJypgUAkHeyfwEg57FsgN89vsQP11f41dlT/Prbv4mLL9/i/vkXiFfXcEzwQ48wDuBGzu5xcGkKFoEi96zSos4Be/2e+V9m5/Ma7ENACpi6+8xZFQ4JBTZpS93mus66LbYPhywVDwkRFsjaoHRLP7ZzM102zqSmRwaSlq4zdds+HspgVI+dfVfrmqPJIdpMAG5F68k8SO2vQbG212rya0BdJwXIRwQAeZ1YOtb9dc5NUsPW7bNuaHMCmaX5XIbSVFF+z9JHntmf53Yu1vP7IdCvz9psYYcsMAAwhoCT9RG2d7eTvbcusxZO59pr6aXzMeLwejp0Pd51ylgztBESRJyi3BnZPDjGEeOux6LtAOfQLRbo+x6Xl5foug4hBDnArGnw9MmTnEGKY0TjPbrlEnEMuLu7Q+ucYfjyX/UzZibsdltxP/BeTNJeLAwhjEmy82n7kBSjwqwDyHmMoUfTtFh3q7QgGGAPmMUnWjZgSCeihxBSujBJMsqqOWBGjAGNb+BVQ9V26JL5qoFo08ZRXKucb9LbopcawojN6Rl295d4+qv/Dqt4J24AHJOU6nWXM6OyvyFOfp9ljgcmyETIODAJLKDXv7bufH+6ELXcImOYdrGWG017C0QqxVnYZEE+gKThz0KBZcql85kGuRTtw1SCmDyj7SMCEDWLtF2knEEo0m+1nEap4woyBYMLKIwmHoISBNU+64JWcTJriVK7Y+xFyxFi0XypOwEoa0TV5SqyxDSoe0mMKSZB5/UwyEntjHyiM/GUkUoShAWePn2C1XIFJsL9/RbPb57j6PgIx8cnWC5FOGez8XFNEFZKEsYQ8PbtBTabI9zfbbHd9nj95g0uLy5yYKidkgQFwgr27Lyx1VCuT5/TPmXRitNbRgDi/GT+Yu7rsFsxYbpgZrYA835lcdI3ktCkgpNuVjFG3Nzc4mc//zM8OT/Hx9/6CKcnZ9jttnj96jVuV7c4OjrCer1OfNEmMtA+lE1fg/UjUpK35PqkwRYZTJtWykYXDY1kLoUYp1SpNp/FYoEQAoZxlEP7DmyO3jusVmtctzcCuNWbkCIihznJbZ+CaUrVm7B0nREmLGlaXulBeS+CwZGyrOzMdOCar+ZpRqWPqVBHDv24M+cTJYCXsjM1jaTx7rpWXIi7DhwbXA23uLq+gSNC27U4Otpgs15juVqi61ICEjAQI0IScNwYJLbDExYN8Fv+FX60fINfnT/D5x//Li4+e4Xbr15gvL4Gb7fwxJKlRvKv7wGmGkzPCRUWrCpAzOJ/BVjnwJQqIOc00Y/JkjUFdyV165ywUddbAyv7uQZhlh5zQcQKWueAOYAUyPzu/tQAV9O81sHatYBj+xBjTFvkvpA11885EKyXdVGqhYXy7n5GpKnAsX9fy7BWACss1u2xv0Uw6viTOZe5uSMX8h5aWefm5svc57qOOaFLP88JykDZUy0d6/fr+m2Z07aUvY9ZzmRbLZdiTX79aq8tj5kT9TW37iP/J3KdktgHP/GNFHCHlKp+hGMvfmFDwDDuJLWhE6a4Xq8xDENOSUsEySp1cgSA0HjRdh9t1nBECG7A3W06wM4yHBLm78gBnnE3yjHrYRDLQuMWiGHEskupcUPArt9hF2WDaJp04Fwi3DD04AHJB9jllKxjEDerrnFZ8t7tdkDXAOl0ag5BDguEuJc0bYMYIsYwwjkS1ypwok0K9lNVK2SzHwDExuPk2Qe4/eTf4jfe/H6y+JTJ1DQq5CXwNmEsCigKXC2XvTcH9Oyj9vvcBKLsF56RMFF2fdFHSjEMRPHrFzBXwJbOG8CCerMAEnAvn20zp0JBZPtuKjP7YFvBh4pAY/qUF9FMvzMo1HMQWFOm0sRlx7YtJtcisTik6pLwphmNkIQF3XwU7IPUVzy5eziXMhwVlxAGUvzBmOhXsqENfS/+uYmB61kwQsaImA461CvkzZ33QSCJBtanQM7iLkK42d7h1dvXYAaOj47xwYcfYLPZ4PpKXJyenD/B5niT1jRNNc3VJWtwwGa9QT/0uLm5wfXVLW6urnN/yVEaNsrCNieJQTG0mYJ5LOvfyu8J9KGIKtB3YFeQMlh5i9jOlUwmOBVgpgSEAsvpHVuync9FENU6pe0KNBivXr/G5dUVPvzgfXz04Uc4Pupwv73H69dvcHt7m4U87xtTJ0+BMSPPL85BjMrENWYtNdTwidVqjZu7bQo4l3aPYURkpNO+U+HpHe33arXC7c0NTk9P9+YAs5yZ5BqPtvU4OjqSw0sJUCHUlaTMGVwXoYDK+BreM7NXlrlQjZOO25QHTcvQNT8dNxFgVCTLgEp5FumGDHBgAOrmV9rAzHD9LtUlZxU557FoW6yWS6zWayyXS8R+wPb1W7x+8xbLrsNms8Zms8FqvULTepATlzgmBwoBiDKGzjs0FPHj7gV++N5r/OrsGX7x/Z/g8vlbXH/2NXB5B9/vEPkGyouhdK4A55xG2gKfyb9MyfmrBvF6OG9tDbDPZt56gI/MCRgPaYnrPv1FX3vAl6a8Zq6P9nsWNkZVNu4D13qM7JXl3Uo4mgOcVtiYA6B1ZqL6OVG0ljHK787QvhaQiEqMwqHUxrVVoqbtRKip6DlnhZmL3Zj7PPdeXfackDA3LpNn3XRd1XNXP9cucg8JBKzqLmbc3N6mjID7DpGHhMq5OWjfmbbfwfE0mP9d16MFDTVDTaQaC4KYwWEU9x9H2GyO4JsGgYvGo+3a7Hsagmi5GvUzptRxJ2axkDp4c3MjnTNtGYYebduBCFguF2Agu01FDlivVhIoSkDjPfphB0+NHHyXUrgSUtBsdEAcIYYTEQqIGEebFbquTfhUah/HJS4uLpIw0ki+/MhYb8SXOIaI++09Otdi0TUS4T+OIE5A0svAi5WEEV2D7ugE7WoJ90f/d3x79wLjOEAO9SNwOsW7adtq8C3TqSaIPGgmkH2Gqr/TbTa/kECxPCoMQ8EFYLH6NO2wtjmXyaU9tn2cgKf+pmBnKkMYoYYUygG2vfqMbtQwC6g0KbU/9TWf3pwBV/msft1Ams8xpGBh8QHnaAAzTf2WtS2cBY0ohyax+n9HcfdItJQ5kDIYJd/tPqVVZpb1FqJaKkrAs/SUijAFZUqSRS0SCyNIwdogERAavzAMC9DkBmDAeZ9dUazgNhm0RGLvXEqI4DH0A64uLvDTn/4UH330EZ49e4ab21u8fPUKYww4PTmGb3wZY918uMw7gmSZ6hYdvvr6Be7u7tAPfTq1FGnM8iDn8Tp0TQCv6YAVBAjYY8AMBQIGyGZGndYS2feNcEF7+cwyOC29LG2Y1K0MnAF7UAQJWk3lFzQ99AO++PxLvH71Gh9//C289/57iDHg9vYW2+0W6/UaR0fHWC0XsqElabcsETZtFE2/z8oP7V+KS8jnQpBsXFDrGuc5GmNE9LI+54DU2dkZ3r59i9PTU6gGjrQdRPBOyh5DwHqzwWK5xNCP4uaEokVV2k3OQtE170qbJ6Sd+5IB2FR40H5Nx5dzxaIrkHHgqlCX5ptmRixtlH+q9WVWyyJACJL2OJoDfcYB5Bz63RY3t7fwF2/Rth1WqwVWqzVOTo4RI+PiQrKRdYsF1psNjo6PkoCZ1naMkpoipoxwzgE+4nvdV/j2k9f47PR9fPqtv4rLX73C9ZcvEG8YPOzgOIAgvC5Q6mnOGGzAk3bNgFmZ6+oJQBMwdeg6BA7r73Pa3xocz2nCH1O/Xg8BpkNpSDPHYCAdyXsYfLFx7auFjjTPakCpK3VqQS/tjTGi67rcRksXsnOVuSS+mREBrTBiT5Wv6Zr3RkOPjAGp1K3ty0qMPW5bLivE2DrmhJsMvCFgV5V6hDwIea9i831OIQjsW2kyVki8Sb4XLGTdtyjtrZpUhFxJLFHGYY/S6b7LwqMKgPYIBzvXbPvq83Hqyzspt+973N/fyxgofRLGTp/Kln5g3chcEdrpgbM5TbzBao9ZZ8A3EDQAIUZjThzMGR+EDBJomLSebdcI2HeJwULyyd+HMZ8y3jWr3Kk8gJGShmuB4+MThBCwXC7BP9eORdze3WOzkYnomzYTSoK21cevnDOx6JYgEheNtpHD5gABe+QJQ5LOvHPwBCyXHdarLrmelIBxD4/d3Q5N2+L0ZAWfzv1okyBARFguFwjjgAYyAUeWwKwAACEtZu+xDcDm9BTLzRGaf/d/w8n2BYZ+SGAuMR6wtBeAHOjHZSFJ5xQ1ls8TRpxOV9KLAYCyoKCTKBU2YUEcp5p/VtALKryDq3Ywp8wmqQ1mYpoVODOzyoafGaMBRIghb/KAaPBlDxSLlQL8qTCsaV2VHjBMVKxDAt6T4Jy0jZzc1SSDjVgXwhgQYsi/c2SMQbLfxAQgwiguIjEt7BAjxmFARimJHgwT3wQ5RI+s76wjNM6Dmialb2b4JgmtrO+L1Y2Zs0DtyKWNTAsqm2CIIfdPEiEExNAXhts0GFPsErO6EAqb0Uw9eZSIcJIywq1XS5w/eYK7u3v8+rPPMYSIDz74ADfXN3jz5i3IeZwcH+XjPpDdYAigFK+TmO32foub61vshhG+EesiB0I+U5vEolCsTEY0YEyRvk7JlAhMAX99mRmWrRK1wFD+kpmBhR5mKRjBZHLwfNqALLAo7wsJFNiXgGPxZJqC7FQFQmTc3W/xi1/+Ci9evsTHH3+M8/Nz9Lsdrq9vcH9/j+PjYxwdH6Ftm8mmR0kkAJL7FItwqumgiSiFhpsKmbFaSm52hwi1K4yBEVMSKJeFmun6Xq3XeP78OUJIftekvIXzIG3Wa7x5c4nl+gib4zO8vXiDElkh7SHdxAlQiUJo59Itymmfycx9C5Atr1IY5vIPNDkDJmd6SnXLmCbwlUakzCuNzUh8NzKQAriNhAdil9JEMggOjWsyr+G0X2jWIELAOIpSbbu9xdXlBV6/7rBeL3F8fILj4xP0w4i7V2/w5vUFjo6OcHxyhM1mjbZtUupnTtsDA0ECx1vH+JF/ju+dfI1P/7MP8ac/+F1cfPICd1++gLu8gt/eg7lHpAGRgIY8QDHxXAbYw3GbqDdm4ULI6opCAfvgXfmeuiAraLJAtg7Otc9YcFum55wAgMnvD2n+58qwQNteUw2w4hbZmx0RmALqGL8M1r0HReSYN90HSK0BVFJjT8AvprELFghaWtRaeg8RbBxrKYWHhKoetSTUAsZeH8zztVXDfp+UwfO0tW2fEw5tWfWBdflspsl6T310U1op9mAV8Aywnhw0DUqiopknCRfZd6Zjk/ikK7GSep8z3Sw80rTu05goKaIE6de0nTuwz46fba4m+mjbFv39Xd48ZPwLH3TAFKvVY0mUstIh8SPZk4X++wLKu65vLGioFKgD1TTNZKIqQayZRcmx3mzE7WMcsew6DMOQM3UoMdUMRyQHj9zf36cDSMr23nYtbu/uwCwB3k3ToG0btL7Jfnney4F+wzDi+OQ4AcEh5dRnNN6jXS7BABqKOR984x265KokA5mGyMnEblP2Lcn4guQ6ZQgP0RAjBowsAsYQI9rFMuXdD9gOEU/e/xDbt8+x/tP/B7rtBba7PrtH3dzc4OjoGESEpmlgA4YV52taU2TgrAuvyKuswC5NdgF7quVAFjIKqGcjPCTtan7eWAWsAKGFA0noUTBefi+AXwqXg9fSJpJBfQLs6WAz/R3mGfVXLYsDYnWI0QD/4r7E4ByLIAeqidViGDXORgSoMcR8sjOS77nVxhT8oUKCT+MtAN+ledf4BmhkTgDFJ1SFXrUadG0LzZyjTCDKwjGgtlgOh3HMsRdImxvy7/oZE7qpAOVM28v0KJ9Vm16DaB3OqEyyvIpXux0A4O1b4PTkCKenpzg/P8eXX36Jrlvg9PQUt7e3uHj7FstFh8WiqxiS0FbjupaLBV6+fC1n6jhgvVlhGALGwPBlNue5Jm21gfC6LiiXT9rYJMzUVwGRqTVEEyFD54Lq6bl6D+mXGuRMVyDK+pm7spLG0D0Rm4hRrIOlXwxKApScD3J1dY3r65/h/PwM3/nOt3F6eoqbmxu8fXuBu/stzs/PsFov9E0j76fvBJl36ndu/qvtBwDf+MIP03ySTGQRnVJjZtOR4OYGfT9gtXKYnoMDEBgnJ8f4/IvnYGpwenKCu+1dWfM6Pnnci3CG1B47vFQ1X5ur5WQapvmh5ShAtjyyUF0EKQayZlgnnY6OCAppTTrd+4zWN0QAEeyETiSO2unciXT2ZpTDSZlZYi8SbxN3XDkc9357h4urK3RNi83REU6OjrFerXFxeYHLq0us1yucnJzg6GiNxXIh/HOU+EQFOEwMTx7fx+f4zvFzvPidI/zRs/fx8ssTDF+/hLu9Q7PbwceA0QVBJc5lBQ9LkFM6oyZMXFnKuMwAoQof7AG3mecVaNbWBwt833XVlo+6nIe0xHU59ZV2OLARfvM8KrM1zQ3k/ls3IdWYT6wHM+0H9s86mNC9elbB4XTPLM/n1NEzQLa24hzqv4D8fQ23vutcUoARJvdr64d999A92wfbNtvWQxmiiOTQSaV7HU8DokncR65zpizbnj36yxfTbmPBBbKCca7MWsCenW9GGDx0cWT0ux1ABOdJGejMg4lvVX3QH7NTC1xORJQPTUyH5x46ELC+Hi1okJcgbwrFZBU4ink9lkbmIEbmnJLPLhw1ed3d34Mj4+hokzTTAgwbahBGs/C8y0GKeu/o+Hgi+Q3DgBACdtsdeLfLzG/X78DMWC6XkmLXORCLL2DTtiI0OQJ7l82ay64RkJ2ZT/FJBiC+xihmNAWlzjmE1Ja2bTFEObRvl4QpBmHXy+Bvjs/QtC2ePv8fsewv0ac4E+89vnz+JY6PjsAQa0Ye9CyPApPAaSruQFl01s/6LuuiMD/l9I9Ts2seq0SPPEf1vIb0Dqe+x3QmQdRNMQHeGJJlwNabNeuV5pxIDn0MI0LUgOmY4gxEgxhiyC5nALDr+3KuBErqtyIUYHLolJ2f5N1EkPRti26xyM87L++EKEBdzaIxfddKImu2M28Eq+QKFVLygMgA90mokr7d8l2mbRGK0liZQ8+QhMeJUIDKXxLFHF4zIGYkf/f0XMVQCi9MEC6DsdzFLGSAUxJUohx/AgCXV9cIIeL07BTL5RJffvkF1qsl2q5B3+/w9uIS77/3LPfISDu5LeQI2/t7xCiKi8VyieZuh6YJGMZ0VgbShp7hctm89KJCtSS8lVUzAY6WRipMMhvHJW3h1IpRYIOpzW56M0JFLh+GtvqZrWiUaJFoK2DYIep6qHuSN3gRSN68eYPLqyt866MP8K1vfQvDMOJ+K5m8nj45x9HRBkbqLFY0Ttor3eCyGwDKOQ5MWHSLnIRDJ0pMa5Z5Pz2q3SjPzs5wdXWF1ep9+4D8IULXtTjaHOHu/h4upYQdgwjh6q6o9NWNPAN9nct5/uqzKoeUcdHfVDDVLFmJIyGfheNU6FTKo8hH3hmlV/qVIEJWEhhCbrM84xK/AXPmWXb8lTdIohKGI5m5TdYgikUhCx59j3EYsd3tcHlxga7tcHx0jKPjE1xd3+Ly8grr9Qrn5zLuy9USxAGMZC1xTtLkOoJzjA8X1/jo4yv84oMP8Iur/xxv/+w5ds9fA/d3QLwBOCRBSedocpUxgL8GhocA6hzArOdNrmcGbNrnDoFvez3kR67AVC3htt5aC2/B7aQ81rULyHxx5QfLTdK8m2RPYlGUzqVYPdTemq4PAdL63Xwv7SWWbtZD5V0CnAXDWVFl3tkThjB9pi7/ofr2FDlmHObopfE+dXvVolELKURUvAVmBJ0/76VrfG4uxaS9s2l+63k/Z2nQ73Ppbe2VLWUwW+QcvYgmvGxaX8G9iukVRzGrpfTxNHq8RSMdYIfkBxpJglIjuWxKcZRcbCjlmofGGYgJvPEtmBlr70UiiuJPHplF0wMxkzeNB6P4qe+G6enVpM6oyXes8wvEGLNLlq7xMAYwWCwE3qFpG4SYLBtpoJarpQTNNY0E1IYgPrccM3MNUTT/IQb4pkFMZURm8a3vBzStWDiGYcAiLrC73wIE/Mmf/AmWyyVOjk/QNA22ux5/6+/8Dp7/23+Kp+M1Bk1ZFhk39zcYhgEuWY38ZMEqPaffs/+13p2Al7TJ6kaWNCshJnegccTQD5nJSAyBgAn9roJBjIwQxgx2Y+QUXByysDOOI8Yx5Po4A25Z3CGk9MIqFSeXI1DykFZEC4BIg9ewzxich3dOgh9JTp51rgQnkSsWNmaUE+PFOToBEIAjkuDCGKMKVhEIxZ+Wk+DEXDSWWQxQpgF9RglfMkkZ3j7VUhnoylAA/4BWjQENEJYyC+zUzzEHnhthRfF9Al11O8qhZVkiQSa8+SiuPcjKA+0/EeHu7h7dQlJxvnr1CheXF3j69BmCl9iB8fxMkjBYRscM0oxwRDl4vaO2+M6yAjfbHOtCc5BUqd3J6lEDevPXSis127RVTASV6tmHAQKlNhfa1+/bchRICwDVk105J2JQwVLppldkRhxGfPrZF7i4vMYPf/gDrNYbbLdbvHz5Gk3TYrVcFKHSzJ8Jl2EBzUxygJyKOXJAo1hciZKox8jrXTcfSw/9u95s8Ob15/jgg/ezMsBWSI5wdn6Gt5efYUE+px3f0zLnub1PPUfO8BBkmmcwnywJVtjTp9hMKEaa53akSGOX5MfpOoY5wVv+I2nbhf+pkKMKCqJiGcpKG0S4mBQZnsXCRAp+GXDpdHFuwByywmYYR4RxxDgM2O62eHtxifV6jePjY4QQcHNzi/Vmg9PTY5weH2G9Wkqa4sgSy8UAxQjvAHYOP2i/xgfPbvDJsx/g65ffw8uffwJ6+SXG7Raub+AR0XBEjIO4VRgfd6v4U559CLjVVoo58PgY0Ge18Q9dc1px/Tzxua/Ktm07JOzIXhhhT2DODEr7hXl3JNu/mo71M/a5iXa8Aqlzf20/QLLe4wzNrSA192/OKkJEJf00psKPWuD3Yhtm6F3/VtNnrs+HyqqDtrOSjyjPmWkddBA4E8yGZ8p7l8AzNxYTwZCmhxgeoo9dK7YMdfmy7aTUNtfIkRK7+7t0btI0rXFNm8MCg85LwZ2K42z63ncJx3o9WtD46Z/+FOM44r333kPTNMkc3mOxWGCxWIkLiXPY7XYYQ8ByschapKZtcfH2LX7161/j+OgIZ2dn2Gw2CMOIu7s7vHnzBuM44uzsLBOjW3RYLVeicagmDkjK1cmjWoHJwS0hR7HBOYevX7yQtnctODJub29xdXUlJ9eul8ndSUzMjkRrwzGiHyJev3qN733ve2CIcNW27cTfNHKUfqdDpF68fInGN+iHAc+/foHzszO8fnuB9957Dz/44W+iHxlnN59k39bttsft9Q2+fvE1fvDD72Oz2ZRA3jJDrOpkMhmsNg9kfNg5gll8sjmKtL/b7bDd7tD3fU7Vq+eLhDFgt9tl16bIjHEcJAMXFw2MDoVaMWqGY13h9HsWmsjBt8mikARRFaxKYJVaFESTRxpUnXPncw7SBhFGzUxWcIH4oSrIhmoSoqET8oagQoTSThZjgiqMfEBbmnpmYdoFOx0a+11HURkBAHE/AOUiVBDM78M00dQv5VL+0WrMJ0CWyqFjU63bdO7otHLq655/EaFC6aGF6MciFAlYur+/Q3tyBOc9rq4ucX5+Duc8BhXEU3a2KbyXAnOgfKKDTxoZ1TMDhqGlTlgBrqYZpQcyID7wXC6vAqBzrLPCxjCkzYKaDoutJ1F5v94D16Ru3WwUHSSBV4QNE+QHgp4Yzcy4vLrCz3/+Z/jhj36Epu0w9j3evLnAt771IYzzlGmN+UvJcmVEI048VNcpKc2Sm2GM4hIkTZ72kEgOdgSAcRzgXJVZhgQYnJ6eACAMY0DbLnB3f5/HUf6waWmhrApn+/tDcVlglYqovCt8kbPSAZkyasVN/U+ZzUTA1vVq1pztrgFlYE6nkGtMS+lL5lOkri2iwJPNO4rb1EhgjOm96lRl8oBneFUQhYAQR4QgZzvd3t2i6xY4TrFUNzc3uFitcP7kDMdHR1htltLuZMCJMQBeBJoV3eAn9O/x/WcbfLla4Bdf/whvvnyL3ZtrhNs7+KGH95AgdpqOTRn/6Rx4CMwoyNJnFATae3PvHLIwzFlU7DuHgNGcFnzu9z1wKZNvv52sggyDOYiVzLqHG7rUFgL7r26//VyneK1BtLZpL3gbUxo9JNS9S9OuwnCttc/tnClj7qqFvlrAmSvDCh913TM1ZKBsBZEYoySTqF7TuTgnZNjPds7agG4tY/47Fd5+YA7b73VM0pT2dfsA7zyWyyWu3qrFqTw3EU4f2Iy4BJhlzGHbbw9Ifcz1aEGDEfGnP/8pQIzvfu+72Gw2KcvJBo5KMHTTtej7Pg9o04kp3LUNdkOPj05P8PnzL7FaLPHhBx8gcMRqs8bNzQ2GIILHYrGAazyaTsq9326h7kGRxe2qSW5FGqPBAIYgJxeL21SPMAY4J2dU+K7Fp198jqHv0Q8DhmHAs2fPcP70CdbHRxhDQNc2onmKEZeXb3Hx9i3On7yHzdERbrf36Psey+US1HhQEH9aDeAexxFXV1e4ublB0zRYrzf48qvnODo9wS6MaNsWp+dn+MGPf4yf/av/AT8MVwgM3N3L4YKL5RKnJydYrVYizCwXWbupYAhQUGRAF5sYDUWNOhnkLsLI2G63uL66wjCMGEPA/f09Li7e4ubmBmMIGdw5Iok/UdMbEZbLlaRQDAEb36TDu0qshU+xJXJScGJEZhLqZqnMl8EYo8ZmRGAYckpY61qg1gYgvRc1awtPwKEGbmcysQIIGx9i57IAqs1mIwJYGAt+gG74ZbE7IafMP9OnDO9JAIIFqwWwHb7mtCVSP8HpCfL6pApBQLbkzPEKeyCZtLsw5VoQkp8VLid/fTvHiAwDVjDrEmMmJGkPDMZu1yOEiLb12O12En/VSkKFfhywwirTuFQjYC6mQFXJziXM2lnSUAG8BGWCBRCCxNVlIiTYjfmBMbDzqPS0CHhiRZpaJPKre3R/lxhxoAlV3fY+ocTJEHmQpkllA7YAaOS7wuXrm1t8+eVzfPvb34ZzDfperI1tK5snTWIlVPsfJWB5QgwB7CJkJC1ayopHRNl1Mju1VRux9ImwWq9xdydB6tnVkyBWBpa4ptPTE1xeCv9svMc46gFVKH/TxFexeH/slIJKo0LJzE8NIMm/6PkjiY75jJC0yYIJTGoZS3VTcbEiMmAUECs+EUr4HFeZ4vRfmaOc/hNZUt0irfOYFC4xxmRtQga36nKrrqr90MONhGEcsdtt0XVyEO7Qj7i5vcPR0RHOz09wfLzBer0EgxGIQRxTinePSAEbd43f3Nzi+991+NnTE/zxl2e4++oK48Ub8C3DRwca+1mwmtfq7G/mqWqu1JriGlzXVw3OaiBuP2t5jwGlcyD/UBv2L/uMDL73bTqnZF94slr2b6Ih1ndV4WmFjbqMGqQ7A7Yfqm8OBNsr1zW7h3GJz31kn+bOJ6m/P6yBn+8DgBILZbI85b5nDFXaXv5NY2hm+5nua5D8uwB4TDGsWmatJP8m/cIeBxSuuF6vZY9NXkPaVts/xS51f3RMJQHR4fpr68hD16MFjbMnz/Bf/+P/JU5PT8AMDGNAiMIUu67LZjLvgWXT5nMpQhqIZ++9j7979gTD0OPVqzeIAJbrFcg7HJGAnNubW5w9Ocd7738A733O5jSGkCcCM6MfRkRIWkQFMwBSOkdxxRojwzUNum6B1eYIMUacP3maQWxIVpC2bcUNDIS2W4quMIx49v6HWK6PsVltsOt7rDZHePHiBfp+SK46DjEELBYL2RRDkAw5zuPi4gLb7Rt8/eIF3r69wGq5xHe/+z08e/Y+fv+//3/hd2//QAD/OGK1XILI4fNPP8PJyUnKGmBiCOzkzujSZeAuNEkmelaQmF9ACIzrmxs5kT1E7HZyGNqbN28AME7OzrBeLeUskhAQjXtQSJrmEGVhxBDQDwE5aFstDETQ8x/U1UqD7nXMIkcgWiHBuDlM0sxaLU/xyC+XLBA1Vct46sFalDyBXMJPiQnYvNXpb4iMrltguVzh8vIyuYAohEgMNsOnIpyoV7emOFDsk/IjFz2xAVlWANThJCqtsQKKvm/BrvotUfrrVPBIfZzALQN2cjNIN9xSfp5OhsoMQtc22KzX2bVwt91hN/RG4JD2UKI1YtE4hVHWaYwj7u7vcdx0IDhxj6tG0Gp1I0dRHLAIl7LeM/xNrUtAMb1MhUBZoJ5WkuwnCixNv2ua77XtHVceQ32eJqM1fXamrnfVMZlDNLVWUZr7sgEmoA7OMQJI9CQAb9++xdn5OdbLFUKI6IcRTbuEI7X+zW/YFkzrJiztCZDAwPKqurxF75L84UoPdR0TcHx8hMurSxwfH0+IEZWfAXj65ByvX71B61domja5vhoOQIBaB3QuZF6RaAWO6XyQBOIzSFH3J3UH02GTNaUuo5zmZONacIziSpvelzWQ2mPBYvpvEfrkjiMCOZ3XEREhsbpkKU2uVRK7VcC58kXN4Cip2z1CiIhjcakqgraH9w6eOMcbhDAihIB+lFiOrpUUuWMIuLm+wvHxMc7PT3FyeoJ22Un96Wwo5wnRRYmPJIffOXmL39oQ/sPTNf7kxXdw+9UL9BeXaO4c0A9wkIMVRwTE5DbmMm2EJnrgYWRMNOq1y4iCbk3qMic02OctuGZ+ODh1znpwCCzVQHfOapI5DxFKr/Q+4DzlfdDBlfHC9FyLGtDbv4+xwCggzhyiMMpJOTK/HJjLuQ2H6qhpNWdZyH8JWcE4KQMQS04khJl35/ozp62vrSgPCaO2nbaN1grkqJxyrWvV1jcReMB79+boVM+rvPdgugcAKcPhhAScs0YW7rbvdhe4uABrlru5S/bh5OKUFLipcXuqGWO4yO3m/L1ELTLE04eBhPGiyVj67uvRgsZ7H34HfT+AnZzo3QLoVhKjcNeHfNAdmBERweTlFGznMyN2jUPnWvzV//z3cHV1gYubG3Hb6XsMMeIHv/VjnByfAM7D+Q56tkEHZKnMOY+j03OJZWg8YICo0izGiM3J0rg2cVr0ssA8EZqU8jayENAlock5DziPITKaxRECO7TdGj5GfOtbv4EYo7hbLTpZPDEFsTcd/Bhx/t4RuuUa97fX+Na3Psb3v/dDtN0CJ8en+NN/8n/F33+2BTUdQJJRahxGhNBjjAHLtWh928bA2Aw2qGgGsmZMwY1OchPOyrL4b27vcH1zgxAZt3d3ePPmNa6vb9AuOpw/OQcAbPsB2/srjMOImIKY9XC5vKkZKT83LTHa6drTwKHSPvmkWj+7vpUROCMsGKZTelMx/fKubs66mBnzVgRCWUgScBsRGHBNA98tEHgn6VN1MamgUzBOFi5Kn0xdznw3Dc8faeYzK1DV9pV39hqvAosKDIbp7FWULg2gBgORFK4rxixpQxUnO5IDLPvep8PDEnjUdlb9Vw2wjLduZB7MI4Z+FJoRSkAvkFOIZsEByfSerGIs/iZYLJrU3kJ1Hd8MMqH9ml5Km4nmcI6us/em3ISMTT0qeN2b3YU2Zu8C2y8H6isChN4o/VFhQxm8M4Ab8PAp+5QALXHDdAR4SokqxoCbq0usV3KGytAHYK30obqxRTCA9JMN1RoitF7XqSYDFpAcogoLZYSK1ULKX61XePHi63KfYWgTgRhwerxB13qEccwHRRbCFTc/XSuqTBCXCJnLkQHKCSXSMyqsMbKQofNZeYmMdmq/awQgUYdFiOJWGkdxD4ZauaSUCGtNo4mCQ5Qhci8CGGNEiCPGUOLqlB9agGHnCQdNGe/RNR7UtJI0IwRJoDGOYHBaV4D3DZwz5/vEKIlJxhF9v8PdXYv1ao1+CLi6usXJ8TXOnhzj9OxUsuE5QgwsZ2rECDhC9HIQ73/23h2+9yTg33zwLfzq10+A52/grm7Q3G9BNIAwInrJ7kc5QUzZq4hLz7K1uApsVc2uukPPWT3m0tvOudQc0oTPaf1rgHpIw7xvLRAuG9OZV3pAbdS92IkAEtjDpnqdS+06ZwGqgez0SruSUcLqvCRKSfU5nZckqcPSXrMPxlVIO2QtsEKcjsFU2Il7dM59IZoIVnq/HlsrJNq4DpvV9FA2LCt86Ptz1Mq4hdOmxpyVC3OWK3Fbld/KAbjTuAqtzwqRan2sebnsWcibPRGJ90dyjc1bOCO7hqtQpPmqRMaYWkhT14ReTSPnaCSaUQFWYIhIzLqBkiTHyfyCSmmK7/IdUtoQwC5j7cdcj8865Tx8oxIP5QnULhYYhgE3t7fYbDZpUoh21zVNjkMg54AIjHHA5eUlvn7xFYgkwPhHP/pRDuQexhGdbyeajnrhUQLpEyIbKdKaEfPESwHkek81JjFlqGpbPY8DOdaAmRE4ym8QF6FhuxWToPOgGCY5lNUScXxyimXX4vz8CYg8bm/vMP7i/4PfpS/QNh/AOYcxBUbHyHj9+hW6ts1nlMwtEs4wtmZ09ne9If0I44jbW3FFuLi4wMXFBe7vxZx+dnaKu61kLdlu78XaYLMqJYBa4IYIAvKXkoSrcRd5cKCb9j60owlOLSCd8pTeFyqmgkmsmJiMdamGMKmiop9pKhX6SD0FHBVzIWWmcKhMe98KCZZXU/U8m7UrH3kCgKZtLvrc+V9NDZa2leZIhSt71kBeUwpsU8YbkJOMcNBzA4CJ+qWiR2bQab1459Cz5P8HJ4EmhpTJKFnBSjo62WDIwXuXmW6IUc4JmfTXgDDT9v0VUcbYwNg8N+a26wlVeSpc2Lem92drNWPPk7lr3zg4R9P4WMg5hWrVUksfnBcQoxpynRkxQoLxhx5NI3xa3ylrNNWgBdrGkq432ZQoaQKJpuMuiT0i4I0lkqYj0yQXn77v8yFjlnbMEW27wMnxMV6/vZTzg8iJ0koBKhfrBieAACDzI07AIVpC6WnuVOoqQ5QEE4ciZBEli43L4LFbLDBGj7HXOc3whoJKNpf6TSRt8s5j1/fC5/X0Xw3iNMkjMvDJwjqZAWYB/g6I5OCJ4BuhZcMRY0qsEsYgZ2egAGV7wFeMAXHYpWcH3N93WC2XGIYB17dXuLy8wvn5GU5OjtF1LWJgGf8Y4ZgR04Ggx3SHf/x0h8/PnuAPPv4Bvvr0FW6/fg1/fYt212Pd94gNsKUe5CSRCrusCoNjBw8BNjZDkAW6Nj5jTotdZ+s5dKK0jMv8ieMPXXOa9zkhoHxP+0dMlt7Mdw1u0UnyDep/xJPpn3I4ntxXvi57GkHjkubqqo8okOZOBYY5KwORxjqVGBD7rtrK68sKe4eEvnpu6HvexorNvGOFs3rc8zszY1v3LXVAWM9MG+v3aoFXy6qtLzYphb43l0WKq/drJSuqpzO2UWHMrKe5fkr2qwgOxQpTLDIPx1XZtfiY6xsIGnKQnjZCQX3giG6xwN32Hl88/xKLxQInxydouxK3wcx48+YN7m7vMAw9mrbFe++9h6vrSzx98i0sFqucfappOuS0jgc6ooKCXroIlOlYqVMJXedIttoRfXexWOQJpeeD3N9v4Zs2a6vaboGw3WK720kmHZQBbNP5CC4JYGGMcK7Bp5/8e3znk/83Tn74G0mYGnKq1nEccHd7h/c/+CD1y6UJAgP4zc7JZfIV055BrpkmEbd3d1itVnj+1de4ub4RixQzjo+PsN3t8PrlKwyDgG3vPHK8tjKJCXidyB/pgDOFumZhmXaIpWJ/WSiI1Y0V1TMpOdSkT5zv7Wuwq67n8mqgpmDCpfrH5F/uncOgWgqrZdGKtV0H6t5rC+Ngv2ny2eiM9cC0mfcSpfKLVpBjm+o4Va6a92KJUJoat5FEDyjTI3XJKWOaXRdwiOpSH1Ha7pLbAzi5cHBImcdioaM980WBuHNo2y7VHzGOQSwaVGJiMtjXdqNss6UpRVxTxpnfQT1HdJOzgsWhPgJ70YLvupLwmGNmcj3TtZLH2258pXVShpFWSglTcaQAsJA1lkQSOzaMAU0jn9NuIuNgF2tuVFnobEadSM47ue+H7HqgPCiEFF+lz5MK7dI7/bzZbHB7e4tusUiLxM5pAscRT589wcvXb9A0LRrvMcQAOVMktyRTT8+0CBwMoKEi0KOsGyG9XQFI849kcTiUIwKVDyRrHUMyubRuiZCSaIBF2LAygdjfRCElZUTc3d3lvYSBDAK0XB0Pi2OyK5y58tqiMjcIhLZpwPAYXcjuUiK8p3VLqmEVgT/EEZI1ccQw9Oh2WyxXK4zjiOvrW5yeHuPJk3M57DHt93KKMRBdhG8agEd8y7/Chx9e4JPzE/ybFz/Exa9fIHx9gfbqHg0PaEiEHueAkUdEJ5muEDkDG50/dSYhm2VHpmQBtXovKwrj4dO4a9B5CDhpHYdA6SEhY++Z6vkpwKO9pXboegj47gtBhQ/U+3UqDZqmf87WP1G6VpaiuTbUYLoWFrS8jMmMn2U9DlaQtFitVhJbK8Zcuw7NJftMrbC2fZz7rb5qC9Sh92rBQO/t4dgD79XXQ3Nv7pItvZ4jmFirypqIexnDcluq9+cE9Vr4fOh6tKARUcB8NJuRLDCg6zp8/PHHCCHg6uoKdE85O1Pf91gsl3jy5AkA4O3FW1xeXOD8yVOcnZ9DNcrZjxUENQfOdcRKgJYx6W/6u76rzFezIVkBQyfAMAzo+x5AYWLSpnSCrnMplavDYrlEjBHDIAeXaRltK+l7wYyhF3eQbrHEKd3h2++dY7lcYRgDhmFECGPqn5zzsV6v4ZxDk+JbkCXXifRgPlqYlZ4zgoAeUDeEiOura/TDAIYIU0QOV5dXGMeAxhdhKR/OxjrJjORNVgBQvSJlkCqNSttfOtlc39WWkvnHCVxQ/p3r3uZ39a8GdOV7E4GE82m+9XsW3pVFVnykc7DUDJ2twGIpsidIKOGqttfP2bMaMuajBFISYre2imnd8kK0AFaH3lSiWg8zW1LzpmBXGQoDAgCo9ENMqyI0ZKrOzEmFduIdxZnRZasgkM5akKKzmEOAutEUt0iHcQiIIcD7JVQ7qPwBFe0ntLVCRkXzvbHKr9R3LZ3Mbcqttk9OBcDSDKExJeibaF4EjjRp1RrIZawJ0/lRt78IUTqOrAsjP6sCPEE3goBh6LFcrLJLpAdN1k4W0Cabofav2NSapgH6MR9EJ6RJLgXmTBwRPq0rlfy02Wzw+vUbPHmS0p+bcVVLycnJEbq2wZgOgx373nCJ6ZhoG5w5vJGZ02GLCXQozdPf7N6Ueu+IEZnE/ENCSnFZkPYzUcqABpAH2uUSYRgQhiGtE0LrKcXWWb5B6RyhMoaZPRhhntm4QBj+nSegORw1coRjN1Eg6BkAYjFy6QBSWUMhJdNgppwi1yUrfowBA8eccnx732K1WqMfBtzc3OLk5ARPnpzjeLOSzFgp3iXGAc6TuGhxwA+6C3z07Xv8h2cf4JefPsXtZy/AF5dwdwyKARQDXKLtwCMoOQBay4TOoxow2vv6nLV6AFOBwwoqOt562TlgYz9UQ26vOZCqbamfmd6T1avneFWF5jk35/5jy5xLcWvbW8rW36YAM98E5aBj6QdP1oPer7GT3jsUl1ADdwZyjKf2rzxcgqnr92qgrr9bUF+D9rk21RYMS0NbVi3QztF4//v8vLR11220QtKc0IEZoWLu+9x8q5+f7EkJE5Irwl5N45r+eiyATUgAFKxhx8O2qxZM33U9XtBIO5Mwci7pV51D4AjnxdeLwDg9O5NDiki2qDWvTTYixtOnT9F2nUi/bYdh6MEkzMyloNpJ3VWHagtFLamNySVGnx2GYcIwbBo46yOq0rjQOGkEQ8TtrWRLEdzFYBbHdec8NJOEPXFSfN0Ivm2w3hyh+/qPcf7ReTqZvEx+3fiPjo/Qtk1K+WqvGnaXe1kbZjZzmAU3jgGL5RLPf/1pMlEDRA6LRYdxHNH3vVgxJhMvVZHlBprWuo+l849levL8M1WP6kfowOfJPZq5l8oiK2TMNWBvISMflGfPK1GwN9duNjaNPVBrFuhc+w9dztI8AXMFbNMSE3ClGnYZ4asCnQUw6/oonyf6frIOWqZ/XJ63lODyMWe2yhu4E0smx6RxBnIKVAlqVepSErDk0MM2HaDZ9z3GcUyWPQICY9I0BW4KjhWgvJvUs9dctigqna96bkG+xvLsTa298uxsmYxHVfb+wpk+V1zA2Kw5Ww7lwyWJxLIVQsSQLJnKG33TlFRWkw6qoIA0j9KCT491XQe63yHb3ZJQoXFwnN7PAtgEREQsFgs5fyiGPWYjazaibTxOTo7w8tVFzoSHEGHHQ3mzoWpaBqXuDKiqTT27LehcUjKkBRSTUoqcB3nIiekqOBEAInSrJdxyIYdMjpouVCyjIErnVKRzosiC1QKEpGmaYS/xXy4uYEZclDaa6ZF3AE7+1sxJKHcgT2jJIfoGLgkUY4hQd0VyDk3a80IYJVPggHTyeI9u26Ffb7DrB9zc3OD87AznZ6fYHG0AjmCKCAA4Ai1FSYnrI/7m6nP84LdO8Ee/8Vv44pcvcfvJF4g3N2j6HdwAIAY0zIgmnZzdb+vUoPay+/wcqLQAsdaa12DVuuy8q6zpfNvnMHPChi1z77mZ9xW81m05ZH2Zpo1PFjWXzmGKmk6X4RuJHIqTvk4tlLa9dd/nlLeHBIS67+bG5LdD786B7PqZOjFADZ7n3rMHMdYxIvXnWgCdClL7Y1kLLLUwaudafeZF/dwcDeprbl6qIJS+FVppIh6ejwWya+JQiAK4uE/VfWTmnATkL9x1CiiQNlcIGcxhGNB2XT7vglSa1I5pw1MDfbPAer2WFLQxYgwRTdq4JVJ+agZ8aOLVl3WhUiIuFotMIKBYHlRgAdImSvVBQsDJySnu7u5wcXmJrpNAeNk9KB3yN+YJXdojQeWr5Qqf//JP8YP1Fs4vxU2JkQdYMjdFLJcrGYwUo5GJu4dXCtInIKdD1BtKa9lkRbN1dXWNGFMcSiOah7u7e1kARApfizXDjDWsLnHCQOyETHlcyp5YCQDmiy0CkyLKQp2REewhcdUv+/UpbfYenUBzOVTSmN0nkvykNNvmvENmoSDjFS5Cg33zEOScq2HSZrba12lvZkiUCi8adGnmYbHHau1VjLHPljfnNtipuJLwV7mf2iy8ABnUNE2XhqGIa3Kgpwi83qdkEsqcMwLkXPiE5piO90FaYvpeJtc3cofSjcTSZN8CkgEw0Z4Qos+pUDzXxmlt9t0iTNkAeJUJ2MwTrcOhCBcxSqDh0A9YLJqZYaW8zrVPCb9DrRqLxRIcr6BWbEoPaAyA5NbJDZ70S+aIuPrkOI3McAiEtDlGwpMnT/DV168kwYZvEGMv7WNp5WQ/IOsQQmAycQ6m7ZlO2iDllZR7nqatPMTRuEom65MjAnkR5tqmwWq9xnC/xd31FeIQwd6Ju1HqV+alKahTJ4QIDZLoRAUGaYB+1lPqCwjxySKhNCiKJuXhqX+J6WqMiCjVJMOhgM4EIJxHQykrTYwYw4AQ5Oyifhiw3C6xW62w3Q64vrrBk/MznD05RbdIeycHDBRBTHDs4JzHE3eBf7i+xvPfPsEfPPsRvvzlK8SXbxCuLkHjDiAnAebYB9PWurE356mcVfDQNSdc7JVHU4vHHKDW3+p36+91HySj0wE3naqd9SFstv0P9a8IJJrlKh0a61KocOb99lA1WcX63TbIKlvn+mnrrttgL4t/5gSlhwTFd131ew/R6dB4HhpXW0cNwrNieqafNeB/qL8WqL9rjL/JdagvzIzt/f2eIFULC4xptrApX53Sq3ZJ03nzFy5oMJBT1YIoZ4+JkdEtllmIADQorvjAt00jDGzXC7+NLAfDKfGRtA0hInpNjecKCI4VgdJ7GhBuzaaWsEog+Q5IUJQsPP1eNOGiAZB7pYwxRjnbgiOuri5BIKw3GzTeJRcPh6ZxWdhw+WCeiNVqjc//1f8TP3y6yLEbYxSz9jgGMImZ1XtKKf10IlYIRYZWdxH5aDJPWV9fpQd5j4vXb7PUyQwsugVilDMPkltyPjhuUh1PP8wC92nLyuciC+11YeJ2VG8CMzUUsG7cgCoNAFXPc92Iol/dezKmQxkpadmm63bfDSt/Tibyab/V+cu+w3vl1O21VxZWMmOS+zHdL0Cwrkffn7pGPTRqUwAs9NGIGn1LwQ5VLd1rd6JvTBYigp6pIq4eqlmXeUZ7Y6GH83VdY8aOoNKrChVQQWYCJKdtsnSfa7Ody1MXqbqk/V7WkoC6EtY0V7BYBA3d7Mp8KHYdZCDFUcN5Te2pLNtuDeyHAWKlbSJ6Cd8Umo+jaLbJUTqbona9MKKalT5R6gYR2k5OptY9ABAzfQzFdaU2lJDSPIG69WaDm9tbPFkscowFmCUTCxgExunpMRZdh3EIaL3DKEcVZe191bzyN0kSKgCBk4zABHCi7aR9nMC5jo+WKxYJUY55eABwHuyalBTFo+kaLBqPo/UCZ6cbvPz6BbbbLWLwaJs2xbw5eCfgnWIR3JQoRHpWUGoNi3WVQcmaQyXhhuHJmZspcdPvRDoXEqhMC8b7BiCJ3ykZytLkVZcqdhjHgDFZnEIYseu3WHZb9H2Pu7s7XF1f48nTJzg6OULbNQgIoJgCdF1EdA7kAj7yb/DR+xf4/HiF//Gz9/Dq8wVwfQu+38IPO7iUKEJ4MKdTxksmM6aShINYkIAFe7VC0GqtHwJftQa6Box1efb+RNNteFLhUMn1FQWwTUEYATx1r7HWDHsd+j4F0BJTSVQLO8lSnLCZfY+TEgduWpb+rbM8zdFgDmMVyFIBcKWReccKNA8JGrWAMOe+U39W5bFtm7oQvetSAUL/ZtyoHaloYAWTb3Kp8MyYjsuccPTOcirQZvHV/W6HSIRohF8gWWaZM67mBHxknAB1eRUe6lKCmLyD5fLFpdTP4NT56/HB4JC0sFnLkBofOcKhkbR9/QDnHRrfgKMcAtc1nZj1xoBht8M4DBi3PZxzWK6WCP0gG2dIAkaIIN+AIxAomRarg0OI5DTwHBNhiK+/A5hYNUSaB8YxwHtkacxRymYkubumQk1kNE5YytF6ga5xuL6+ws3VW5yfnaNtujyArvXZTQuQMxo+/bM/wW+1r9G1x9nUxDFmi83NzZVYSboWvqnA4QRsldupYWXHygIG53MVNLXe24sLMKvkCZDzCH2Pvh+SDpHKBjW5GBY7qUuCBlIyV0AptS9jlLwwCzPWTVA3eqtYmeC3qi2c+pebo10G51Sytat9FjZQLZBUdzTcI8YRTduavpYG1SxkykLLPZq5Vz+ZN6Xcb/2gbxMm5hwqWm/FkZza7VJhFjTJc2rRwIPXHs3Td013O3dNgH7uVGJekDUXVMuWgsrHOKJxkmEoRNWskdYkVIhRUrJ6NzlLAyC0jUe/U5cKKhmzTLsn7ct9sRYDKWu/V4foNLUKTd3PkpUpCR3ZgjWhuYxjLWRMy0cG2MprnHMIUUXVEhmR3WqqPpchqOe5rDHnfLIwC08TQU/4nyC7UAArDBhIDScdqjzBGU3TyNgkfkmJP3ECjJGL0ignezBlRmZs1hu8fPkyMZAqVgTCu7p2gdPjI7x89QaNb1OO+ZjGXye+Nqv0IgvqSZPP1XpyKAKalGT6nL4zKFuHOEZgSH7xbZMOqpTN1TuHRefREMF1C3z8Gx/j7evXePv6ArEHusahaYCua7HdbkVAg8amCHhuWo/IHkM64JbIYb1ZY9jtJNVsOpuIiPL5RMoDlLqcaEJktJPVGiZiNN6BHeTsq2S5iMxFECNG03pwDIhRYgg5KcX6oZeUuOOIq+s7PH3yBOdPTrE+6hIoleyMFBnEAYCHcx7fWd/iWz8CfvHU4V998W3cfXUDXLwB4i0aFxGHHkBE4IjAAZ4AQKw/nIVGhmNKyQbMKqrAGarfpv0vQkIdaF5r4m12o1nwp2Bap47d8yjtlRX4nWtj3d4awB/Sxk8VqDPrFwVwx8jwrihjgTLnMyg1dJkry5ZpaWFBPSrgnZ9NyhN7YJwVaObqOmRdssLbnEVFn7P9qGlv22cFPEv/vfNNgLyfWdoeEgxs/+b6xlNNxx5Na0vJHG0O/Z73OqJ8REOArB1PlASHWHYUDfDU3YO078JCQuC849X4hhPfr3nNoevRgsbz58/x7NmzCTEuLi6wWW8QfUDf7xBiQNt59L1kZGIASAzt5uYGzIzzs3N452QTpBKorQOkjFNAyH6wlj43jhLEZlPd6e+6cKYB32pxSekYOQIoFo3IARRLBoacvcMlEJXePT4+xtdff42Xr17g6dP3yyblDGAIEacnp3jzR5/gw+MFxlHSSjpyCMTY7ba4ub3FMA44OzsTjZL6AFsYSOazmRD5a9arTG/HyNhud7i7vYMGqHnfghn5oMB5ZlLAUQbvurcj3YfCrTwiBbzvrSH1Ha4EDkwXCdVlsj1To+q5MmH7cgaNxpWnoom4l3ARlNMPIQT4tjMLfY8s3/iypGOorawIDVZCKBrgfRBdb6zS1SJ1FDhaap0Ge8+B6Qm83Gv3oe7PbpNUfeSSXYoTbbtWwNuYsptlolBivOltZza7ECU5gwJeqgdzrx2FFc5p1PbWjv2dCJPDLyeV0OzY7FdvaW7mn048y6TtmBgAFEKwpIFaKQ/Dk1SEmUuTNcbJYslxwmPFusFoGk2xOi+22fmWwQg5jCEkuhjRhkgESWlQEfPqxcSMtm3EmmtvmwXDiT+/9/4zfP31K0SSwxz73W4CMPJ4p/VARuCFrrEMCCm7TRVrB+syqnrP5dkkMHKMCMMAYoDg0HgHsJyU7tsGHgznCO+9/wwnx8f4+quX2N7fI8QGTdNgvVpnoYxI9gHdL3bbHaIfsV6tMYwjPBEGaNCzxKhPTxRX2kJ7k0hbLGlFEMlvpTEUq7n3DRqI8DmOw2SsJf1umyz0AXEcxb156LHddtisj7Db3ePy+gLP3nuCs7NTrJaLVLdY9DmO8F5q977Bbz8DvndyiX/5/gd4+dUZ3nz2JYabGzATfBzhwoA2OjgS9RERgZ30m1nO5dJxPaQFtvSpvyPTcwoY5561QHQ6dYs145DQ8JBQwUnoB/YtMHWQsi3LPm/L1mle163PNE2DYRgnQgdQrMf2OuinX5Vfa/RzAHheS1MMltfjgbJsfx6inZZXx1vYsXzXVQtBc3XMta+wssPtq6+HLGvf5HpXGfXvrhLouq7LWC9yZRUnEmu0nVsmXln4fklmEdha+fbn6LuuRwsai0WLr756jqdPn+D+PiSgv4PzR9jttlAEIYcC3eDrr7/Grz/9FPfbHn/j934Pq8UKp6cnkvIyhCxoaLvDGHPwX2BJ/arasTCOk0l1v90igrEbejiSheMSkySWvOMUA5z3iUBJ+iKG15R9MaTDkFJgXEwuAaOIczoIcQgY+l5cQVI62u3uHi9evMDd3S2Ojo7RNA0Wi1UWiLpugZvrS3z77mcSJJ+AxPbuJuW1H9GPI9qmwXq9gUt5oXWjpbJ7TGULpUGeMkXDJQBUAhAdES4uLhCSb7BMPAF+ol0zENUwLDLjkbew9CefeZFvF4AiYHqO6RfQY0UiPY/DFF9+rWIHipCTQAFZJkuTd0tMQ3pf6ZkrZSCk4M30nLq0OefSSZe8V67UXRh81WIDDk3d5u9UYJC7E5obJjan8WA7UMrUdQT3MLTWOK+xZz2LoPqtfnSfsvtPUuoJJwlTAxEdOUjqvNL3MZQEDdKONH8TiHLeo20ldoBTrv+macDokUGrKW9P7s5rQ/7LZgTynqEa7jLVxC3DkHGy9CoBh2GC9yd9MXOWzJoET+ZzbgMZ7aE94Z4teC6AWvnX3BZnyZCnkk6V1HfdOMWNUtKcckxPEE1LouLvDygRKAsJ4toTUc7UkPdDOugTrL7iiRfsaegIXdtit9thuRSXW+hcIAJBNunTk2O0XYNhEPfU7EduyptYs+2HOHWTQZWhS4aHymnqyp8mZSMd1CXliYvViCFGEBiLxmEcRrTeISK5mziCW6/wne9+G29fv8XrV28Q+4C2acu5TzqHk4WibRs07ZGMMQ8pIYjQyTsRwAOlDC9qhTD8cdJvc7fMA8p/nXMleJwcuq7FbpeEz6RIQzoWrGkIzB7jOIjQQRFhJwq+xWKBEAPu7re4urzBs2dPcHxyjK5rEIOkwkUYAO90l0LXOvzDj17g1+9/hD86/yG+/NVX6F+9Bd3fwe8IDRMcRxEqdDyIwYiTOajXwZiOGaBea8J1Pz4UhF3Hf0615NM1W9dfWyfsVd8Xt2k/6c9cRiprxajnfNlHKP/NSttYzoUSWjk0rliL7HuHYl7nALaNSdXMbiIUF/ej0sYZ11sqlqXHZi6yQk5tMajp8pDAZAUl27/DFSMLZo8B1pZOBy0b7yzlcZfuobbuOctTeXYq2DHzNJ1/CCW+mjknudhrL5f581hh49GCxieffIJPP/0UwzDIYUGNx2q1xnK5BMHDecLNzTUuLy8QWXw81+sNGA673Q6N9wJ+xzGnmaXGQ82/fZ+EBmZ436S8+k4EAJTJFWPE1fUVnPfgZO3Q2BCbuUIOw5N3+r4HowSIcxSBY3u/xa7foe/7fGAgRwmeFC2g+LOCkH1lI8uJu9fXV/jkk1+IkNEt8eTJM6zXR1gul/i9v/bX8cXv/1P8CFvsQsD9dou7uzv0ux3GcRSXrLbBkyfnUrZmV5GZgH3IWiDtVC5N8kUaeIJDCD1CBC6vrgFQzg6m9BmGPuV5dxOf0iK0WAEiCV2pZmaCdznj4qSFxe1nhskmLafVEen8FCYlG5wKFocoMAfy1N1BQZNuxLaszFRBCISU8k9AVEhxRM77lN2GJqUDU1ea2f7NXFOYaO+V/isOc4YR1WxZfs+ig3o5FEA6V/cD7lOkhJlp01wfLPieLxATpqMYOysIoqaYNmb2NDCTrDxOz49JZnkGmsYXgZamc7FUPkff6X39oOOY11BkRFdbhvbBuwL9aRJkI3BVVou8Hrim7764prFS5bsemmn5+VTIIJrasaa1FzdQIVlKOsGFf4YQhLbVxpSIVOYI6cSr+1xiPMRXXDf6FMg/lazyYucE7FfrNe7u7rBcrooIRbIw5Rk5JPXs7Axff/0qpY6lTH3Ssszk00+2P2yZTGGh+yucnDIFQ+8yAAQkAVKEouHuDjcxoAHQeXGpanw6xNUxmBhP33+K45NjvPjqJe7v7hA5ptiNJm3yKZ2uZEtIPFIa4Bxl/gXId8CJkieWIPLDi1eYhPIYpUWI+Uxg4SHOp2xvDQBGvxOvBHVrI2I0bScAOKXM3UU53XwYBiy6FcZBslOdnZ/h2bMnODrawDvhUzFIXIzyV0cR33Nf4HvfBj49Zvzzzz/A1RdvEa5uQHdbQE8jj6MorojBLmVO4hnANgOC51xPrKtPts494Co0lwY1/wODkifEIf//OU27Ctm2/FrQOdSXg1r/tJ4sAJ8EKxvBStpKe+tjdr3M0FK/z8VYZEfEqgxVaM6Nx0PWpRosz9NyWo62be7gQdueOetR/Uwt6NX1ajm1UDihyYxCZDpu07k5V8+ha/r7vhDHLDHQFg/PrZ3sjkgo46RtSZh3bo78eaw1jxY0tts7vP/+M7x58wZPnz7NbXKOINYz0WTc3FxjseywXq+w2azhmw6//OWfyaJi4Pr6Gj//059hCCN++ye/i3U+TVwOjfONR9t2aNsOfd+LAOLkkDsAGMYRP/3Zz3J8xjiOWVvUpJPIc+NIYjmYxVUgpOxLMUZst1vstjs0rbyz2C7gyMF5EYz6vkfTNGjbBqvVEuwkWB0EsGMEDnCOwRwQ4oCbm2sADmen57h4/RIfXvx7XF1d4fb2BtvtFiEJL23bYrlawnmHzeYIjfPwOlnTRjbZZfYGlc1um35OAT6SPSSi70ds77fpeRE2Yojoky/wYrkEgJySUoPGxOzNeV8WdyNth4LtBOpLa8w1BVI18JsID5Pu1eDaQCeaYIQMvM0Q5zrUolFqm18QAuQcAofks16CUvcv66N/+JoTjPZLMv3We1WxtTA15U3K2JH7Oe0lTd451MK5w+PmLjvGZKhaGQZMuQxwzD71ksYUIgCPg2jY/HTj0Q1i0Xbo2jZvmCGMaJsWVvC2Lbagcq69+722zxktDU9FdytY2fmlNJ/2F/Nzw0gpKhIcPLCPGTZLkXOSLWgMwQj403bUI1cLG7UWMSR3J/X3F3cHf4A6VUcN/V1KQywKGJdnRAE5nInCxpeSlFipA5vNGl9//QLgehzI+EMz3nvvGb56/gLROVEoJTdYzlpQM6dt+5WPsnH/ynQq7cizKq1/PdvDtkn7wAw5PyRZS4b7LS7GgDhGHB2v4b2Hb6SvjfcIkdEuWnz8G9/C1eU13rx+g2EcwA3DU3IrZgY4TKoSa5BL552IexbAIMegCMl6RQk0o8Qf2lnFCZSLEVethlYoK3yyaZqUrl5ovNv1COOQQLnOSUm9rsKGuN/1GMeAXb9F3y+x2+1we3OLZ+89w5PzUyyXncy5KLFbMYp7GTsJeP+Nc+B/f3yDP3q2xr/90y3evl2ju9/B73bwroWLI4hjirlhWGOWrntVMtbCwyEteQ0C50BhXb4VTrL2/wGgVQM6qhl+Kl8tKnNpV+faYr9rW6x3l30uW2tMtY9x+XlI4HoXwJwTGh4C3XNlHXJfqoF/HWdj31dhqw7qtr8fEiS0Pnv8AVUb8pzAM/f9kFB86Pm63w+dBTN5doaHW4uRfc9ag/KYZgUOFys2dH9NgoWWKy9CFS7f5Hq0oHF0dIR+6HFycozFYjGR5ok8QhhBxFiuJJXs8fERmqYFyMFTg816k05IFZOtix6L5QJPnj6VeI4EOBrfpBS4DbquBdGxaBPv5SRbR3LCrPMOQz9IILXzSmGEMEosRJosXdeBAYQ4oHOdHJRHDZyXMyXkpFPR9rSt+KaumzVW61U6YyKmjFAe5IrJdblaYrV4JtaJRqw6q9UKp5sVNn/43+Lmq0+w3W7FshIiuq7F8fExvJdEvr5psFgsoOeG7IPT+psiy8xtkfF4uhdigCOHq6sraGaRHGMSxV2tadoZ7R8gQIQzsCmQi40Fg8xvBdyoAEBJMp7rx1QoKGXM8r8MTpA3O31uDvipRppyuQp45GOEBBQit092dZcZD4rlZ7KwD1sG9pqMMmIlUmSu3/vPz12WpoDJOmX7nap5V1l7dT8irasFrhOBY68vU7orIONRfMAV1EgMAmchxQpJzGJhFOaaNvMopxCrtQ1ctQNJUMnNmPZpflrxlFCZycr7NrBa6hDIboGcPSxvbj5PrV+ltFma27Wsz3LSAKdsTqBS3qSvc5tU1W9hDWyyDYnLzDiOAHUVHcybuXwq6yjVp+fu1BtuCCnFLfsE3KUFc61sfIOgKXedWk5L3UTiE3ya9pp+GNB4n2We7FqmG2ml/Mjl5L5ZmpSNNVOJFCChHPrJ5vfMS4rPMiJhjMDF6wtst1s8eXKK9WYp5xeQJDcAyTw+Oj3CerPC5dtLXF5eASkZCSIKv039kbNnVDsrlgaiFG+TwCNlAUOTs3BeWwyaKivMOGR7YJoHul6ZI6IDmrYFkcPQOwzJnSpnqIKD85K2PYaAMYxglsDxMYz5/JvtdofLqys8e+8JTk9O0DQ+8a6k0PIjmElcJRuHv/nRgL961uGPP7/Gv/g5o79awAUJwncMADZu08xXrg+ve/dVA7V3pXWdFUCoWA8e0no/tj01YC5CxBTk1+WLlWseZD4209Jj2mbB6iHgDzOvasHJ+vnb+3Pf61iRWYvrTBl1m+TYgZCFUL0eOpjxUJvqqffYqxa8/jxXPfaWJtkFbO+laXtjiPnAxNoSZHFgLrOojyb7c64bAHFltX7E9WhBwzcNFkTibrTbyaF8WWoiDCOh44gnT5/h4uINusUS6/UGIIcXX79At1ji+OQETdPgBz/+ES6vr3F8coaF+ukCWDQNODK6peTl1mAwtjs9AT4dbqf59pk5azd8I7/B+GACyRc7BvgU6Oach+t8ZoDkJVq/7TrxT4uSd967pnzWNIEhYrlagxBA5OHQoPMdlosjfPD5P8PVZz/Dze01Qojo2lY2mtUqbcSMEIGTzUbSF5r4jLmhK/OsLLgieBrJkiQ9IZHD1dW1fDaLPoRyyGEODNKsAzMnJMt/efpdq5oBEdN5xygihwKtNHiTEg8AQvOhiDu29PI25/9OGQdl8MLqlKV4ddIXjhIILC4MnN8VUD0VGDC5py5Vpl1caNN40VrG6iAq2++Hlqpiu8jTBwvgTfutLfhB965vzuxquEzppo0XYMj0yTIal2Bgjpry2WMIqtW0JSZwBTnszHkvWk9mhKCHTqVairxhaMBmhlXtnPRCAdl+v0oHyTgE6V8NaNT5VcfFTGfmZIpPxq0891AbMuOPcUrwmedtf2y52hdAQLOe2D6moF7nPYYxpPlT1kUOWldV96QTCrYJ6/Ua290OrmuhOxElhUzM1lAq/eF9d0RKfHY39FguFpich66CTAzoFgucnB7h5cuXIPLwzmOI4x41jCxqFqFtQz1Syb2SS9dAqRVmzFh5bKKJZHo0My2Ka9DN9S2Gvsfp2TFOTo/Rdl2KK9FWRBA8njx7gqPjDV6+eCVnTzUNJOWpgAHd1AEYH3vk/ujJznAuBfoXlxE9S0Uzs+V+sPLLKRNxScBjiNKLo54/5cBdB3IjQnAVYBOXL+cbdN4jxlGAzDggxIghjNj1PXbDDvfbLW7O7vDsyRNsNqs8JBFjcheUbETeNejWC/zejxb4zfcu8e8/eYN/8fkxlv0SbrsF9fdoguRIi5C0t6ztQMrA52Te2pSxD2nOJ0AtA+J9wG+13xmHME+yEM250Njysmad2Nyfpt2vwbSO6aH228v2Q8dKhp3Svq5iqHwtgmMB9IfK1bJyv5Q3kG1rWhMs2v+J8gcFJdh5XYSl/QB9e+lYWvrXyX9qetdjYP+qADcnJNZuUaZk1DvKXB1782SmP1WDDY1Kuc77splmnGb2jiwQ7L2dxoIE70RxV44MOJaDpUn3VoQ0j13iARrLp/0FGBHx/0vbnzTbkiTpgdin5sMZ7vymGDMrMmvoKgCFAiBosEmQPbAXoLR0SwuFK4pwxxV/FincUsgNF2STjYYARYCYUYUaMyszI2N48aY73zO4u5lyoapm6n78vnhBgp4Z7957jru5jaqfzkZvwCOIyCBQGvkFfO/1wYJGIAl2Oz09x3a7hWQGqoAASWPZiJXgCT3F3f09trsOoWqxWq1xdHyCdrlCaFrUocKPf/JTDDGhaYtlhAiibXcbL5H4Fo9B6qFZrlKw7iW2bPryBwbViEELASAknXgKNaiqEJgB0mwtkRGoVhMwgahGCHavuAjUVKMKLc5qYHH7DV6/fgMKwLOnz7BcLUEkqT7FF1eEqOVyVQQhBljjGA4ERSLggFmzgvASnyBCDKEfIh4etpK7XRYOSFL5VabMEQgab67RbhoBRz1uSmfSCNSOL7c1vWw4esZ/PhoqMnZxoH18v30nH3jv+ilBMCGERn0y4GAM2QJMfXVwyQQ1bs9Sx5pwMXWF8X2Q8RrDK808Nm5/ldttL49dezz2YR4v2VSbPtYkHQpG47eW50kBp1/mMfMosFk0qZwHlVgqfYM98Zcc/jFF1KgyKMxrzECoa4RAqOuA/b5HHBLqoxplR6hrHKQ+u+8Muz16uCtLMLiDzTO7pXzBUA1yFiZtLQBLClBepDvwYB3kJs57af7i0e+lPsv34IvRePxPIGMh+VTXoY8as0YBwyAZcEx7X3CEUw4UIom84UBo2wab7XYk6Mp+CZrC2PUn05vDTbdcr7HdbrFYtDaNE8YsfXj27BzfvfoOfRxcDM9k7kaPEfxyFD5hXztXNEf/LMurf8YL8jYuBml1cS6uSQx0+x7v3lxit9vj/PwM6/VKLQBq2SCJj6jbFp/96DPc3Nzi6vIadag0QF/eExPn+iyHw3L0KIiFX4QRy4mf3LjH850tJ3mtNU4gN6mp6oNkpmIIb6dAoCqIBYoTcqQSJ4SqASghadFaICGmHv3QYegHDN2Ah/sNnj97irPzU7RNBXPoYWhwe2Ag1AihwvHFOf7e8TE+/uge/7efn4Kv18D9LQgbVCkCHKUyOY9BJEmlkxH/nwLbuUxF3od9zjLiwWd+Dv5oHLr0TAOAiyaYwdxL2v5oFqUC8Ijmgf80XasXiMTLAqP3ANC01pUKBMXVa86N67GxTt2ORvRt0p983gxoK+9Ixmvd/VNhygsI/t1e0Hqf5WjO6nNYQLm8/7EMW1NM6feSEUj/7DQeZiq0juYb473pD+d0ve37qSJpdA8ewRAUNO+FKJhC2wL1DoDEOg7DADa3S06gBARSrwFO48BwADkY1M8hCl1PfNj/x64fVBm8qiq0bZuDbsydiHicaaCua5ycnIAZuLm5wXa7xdOnT7NPYkoJdRPQtItRmfhpSfPZDQZkqdObF+u6HqVt9Zt37vIbY6o9GBGmIeZ753wDQ6gBDjg+PsGqu8Tb168Rh4jleoHj43WBuCmB6hoxJqxXS5m/UAKgH7tKsCR0A/pvC1e3ubt5d4lhGHIeewMPfp6FwBW0NztDuseKBcURWhoTlinY8Rm+vX5jUr7o8csOGStjp9I23PtHjNf1zW6cih0Eqaqcx0wAa40BCThVkDgzIyXr1BSiHgJX1vU2zfS4H/6vA13jqA1ChrGj0R6A/hE2nPatoLLvi8uQeS3mUT8uH6MxaptQ3KFItLNW6Md86VnQru6/Orfi91BlQrdmMzJLiPWL/QbDZM7tzLu9XG59fN7sJvs+F+DTp8gylWWBI79qlhEYESYnAI+VJJzn9pEVkHfrgKdgc3yn+51NY0k5YJ1hOgYJ+ht6sWgA4mKZpdTRdvQIfPISCLhcLJaIw7uyrxKDakvF6lwV8hj9ithXjKP1Gm/evMH5+bnNXJncvF8izi/OpeCrVpa3NZCulrP8PloPlL2tEzbqYt5L+RyVtbNnZG+Uet1ktNhqGjEhRsbd7R32ux3OL85xfHyEhcYqWIxJRXIuzi4ucHx0grevX2O72SINIogMGh/RNjUY4nZCyKYRmMuTXSGIcDKmho/PgQzR7W3NSkSqkBIhlVDXFVIiRIoISWraSEG/IWcwMhcKqmqAYg4kT0kCUbtuj+12g+3mHhd353j27CmOjo9R10FreJglrEegiFDVqOoaP/30Cf7XZ4x/8vozfPOL19jf3ACbW1R9hzomtCkhgRADI+r5soSBJZsRVGgqAHOqiX4fQBwBdxcHYvM3F1Q8zRo1Bda2CAItClz8PqxS1s/fnx8fZXDKVhc3xjnhZQq67f7HXMKEFx8C5KJtL88k5XtTwD0d59Qa4O99rB7GYyDe/23zML13rjji3Dv8fUSklqD393nufX7+p3187Pq+PfCY4AUAlWZgjWDsKeEP/u7fxX7o8eb6Crc3N+j2O2wfHpD6PXgYkCIj9eqqCc4uVq7FTGr8vpCMgzWQBtQzxR3nrg8WNDabDeq6xn6/H2sHVKqJMWK73eLh4aE0XlfY7Rjr9TqDByLCcrlE1/VZo1CsGoeah7mcxP4QS90KRwh4nH3ACwjWrjehMUvlctNA2z3WjvdJHhEOAEMfUQUxUX36yWeI//wf483rN2BOOD87g0nzDGQ3phAqHB0do6oCcopIeNbhYVEBt+wFgpm9KIJGjcvLS3GRCgBI4j/6zBxsPqGFW2jUXvYU90RPgeQUwE3B6EHvuTA2afOwz/56FFDR49/TwU8BT5zZwfddakpMEVXlrGk0vwbjfj1OEAQcmDBDrpWZwbG9xRFxzO2C8WPu8YKQZlt4tJcYWTgc0vJr6vhZ/nvuJytQZAUhosHTM6TJjwux0tgHOO2wVlJuG6mZkJK4z4zWwAsobpwjzRQO96r/wzRuNm0HY9NzFoLb92x7q7x8KryMXGpsPmbWgGfaGLVH0317CNT9p6Nx6tjI3SAuhOwAYtHGBXK99lKUB/2sk6Qdb+qArutytizfv6zMYD6QYUbtATkezmKkijRpt7EKNi1Oz47x7t21un4iC/2FYhUFjF/z/G3BeIXGKWFjt6xsgoWN1xbf5kdT7+YRJ87P5L3NQLfv8PbtW+x2O5yenWK1XKKua0mSAAHYMQ0IFeGjjz/Bz//yZ5IWFsgZHfthUFeUAGQBp1DfPGdRO6+JPKZUYO4KKmSIhWhMq7NiCwrMQIiIEpyubskxisABEziIUYeAxCVgvFdMMAw9Os3s+PCwwfNnz3B+cYHlaoHASd0uEzhI4b4UanBV4fSI8F998RJ/dVHjD1/+Bh6+egm6ugU97FAPPRJJ2t8hJNRJFRxALoljGXM83znQVOd9Nub9UyD3WLzE9P45sDkF14EIiajI9Jh3ufJ/z4FbwDJK8kHfmJG1fXxwpubiKA4FiKlFZnrReGL1JwQv5LGPn3kfGPftTkH9VNCYxqBMxzG3TsCh29bcNSc0MB0KM1MB4rF3+vvm5nLO6jKnBJ+bD/10/C6I8J2Q8Ft/4/fwN/9H/zGaixPsNg/od3s83N3h22++xpuvv8Lrl69xe3WPy3eXuL291aykPfb7HZgDALN2CNarNOlQZEbVLFDN9P+x64MFjZ///Oc4OjpCSgmbzQY//vGPsVwusVqvsNltwMzY7STTUV3X6lcbUFUS9Hx3d4ejoyPJwW1+hDphPsrfT5oxIl8Fk7X9YZC8/ESlyJ4XHnyebLtveiCzhoII0D5NpeHEKTOSEELObEUUUNct0pBwdnIGThHd619iu9thuVzg+OSobAJWhsZA20oAuqRCFE1Vxh5+0Vyu/QwajBcrIyzBfaL52u87qTHCCYEr1JX48nbGGPR5Adca7kOUP9euWgeEKTuc4QWHcYdcVzOxGbc3ffYxhij3F0I1FWSmLRyCSvOs9zvGFcZToCtrL37RMSbJG4+pUDCFgh6czxwwA3lU3DscRtO/PWGYzoG9o8yXAZssXLhnObfnUd1Y+87sR+PfbTNG+fncZuZltogjjJ2BSAZuwu/yWyhofIoOhEIAJeeqQGEkARBZQgT5PWqNAVLhQzSlnPuRhYbSewcu3U+inMo4u4BNCTvGlwF1WTOdS39vTpHr1oP8fHLew+QRv875iD+P+iGjkXc7AX68IUHwRR4n58PTM5soXaMhRk1zq9YPW2iCgLQs4BDASeYhCwy6Pgy07VKzS0ncgVWTraoAjiVF7Ph02gvHY68qoeNN244WNq8hi8Lo4uICV5c3+qkVduORwDGeU9cD99qxawBPZh1Z6DWNcaGJXskjzkMWO2XrJVtdKvAygKFPuL25R7frcHp2huOTYzRtXc4DAWlIuLq6RN/HvI9Cilitlug3Qz7fCaRCsSiHKCvOZH0seyCg+9fR+dHE0IRKOkGzzLn89DSgqmuQKvMigDpIZfScBl4QLQIqoBLCY7WpuJe9J3W3IvpuwP3DFk+fPsHZmSjcbEIpiIsxI6EiQl03+M2LHk8u9vj3P/0f4+s/+jmuf/lr8P09EAdEDHrkhHYwW10AjRdgBnOJMzhQFk7+tvse0z4/BrrngPFj91qGR6MRglHmOZxvcw742x7wHheCU+iQzo0EEYd/ZjDRXNYuCuL7P69xd7jN3mXYwt8187dvzwf3zwH4qdA2Z43y75Gihf1EG3/YxvS5kdCgB3NO2e0F0LnxTPs4Hfdcnx8TWqfC8Oz+YkE0EWLN/j/9X/7P+Ef/+p/jP/tv/hf4/Eef4927V7i7vAQQ8elv/gb+4D/5ezh7/gIpRmw2G9ze3qGPA375i1/g9etLDLHCq5cvcX93j363x/3dHdgUIitx/Tcc/n3XBwsaJycnWK/XuLu7Q9M0WCwWaJoGQz/A/OBtAo6OjgAAy+USu12Hd+/e4bvvvsPx8TE++ugjPHnyRAvnlUn1bknepOcl+DKfY7Omlxani2NtTIWb0eKksflztAmSabxFih6GQdy2qoCEgKoK+NGPfoybb7/E8PrXAANPnjxxbhekoEgEgtVqld10DugQu8PpmeJICiiARsYJDIMUtXr37lIqKuuKkDKhOAyAakBSmhTJyQxzIpETJB+/BinSjLbb+jgdhr+n1IAY/5zeP/2DuXzun9UlycR5qv/1f0/fOe679a9ow4IJHwexDuXvkSyIxy9yIPVg1Rw3P9gCoJylxd5nrfh5OwBy7m/vIkVzkwuMxufnZbrOc2Oc7tsM4lncXcBcaqSllH3mctE+lWgstoM1nsgEeduLIaiFkyXJAbtiXnmsk36O5siAoxvn3Hime+RgjOR/5Jkaz6H5/ud2yt/5eSpC8OG7HZDwN9D4zjlLyWiPsetfIFCUz+IwuDPOkj64qRya1pS1s6CntGkFT8tBtecIUdefla08tn+MLq/XK2y3WxebV2qtAOaKEvH06QV+9csvs0Vm2q+5c+3PT3mvmzMhbfl7idWTm0zgClSEE79ORM491O0xRskUxhBXhN12j75/h91+h7OzU7TLhezrKuDN5Wtcvrm21copoWNMqKqAKkj2ROEfSV2XGxFkhsHtx7LRQhW05hNj7KteYtWQheAyMhlmOftwfwcCqAoOJDO4IjQUUFVR0vbGmK07VdWgCqxjEctH16uFoxcLx+Zhg83TCzx99gTrtWSqTBEYYo8BIrgOMaGuKpzRHf7W+hf44n/1X+Ev/vkf4U/+8P8FPNwDfZJ4yszO3EmwjFyPFNez60PSiPqg6BH9nxEkyn1jwWaqRA2hArN5IhgemAelQNHGlwJ/lBU9h7Ut7N2Yff9cf+dqjIxBL0apXsftzZx0W4aZeX9MOPBeKD7g+/u05nPgHhhbTT+0H/Z5EcpsMPPXY9ao8Z55v8XDtzEV8j7UYmD3BiLUgXC0PsLRySm++fLX+Cf/w/+Ajz7+CDc3V9jc3YJTRB0Cnn30Ec4//gS/8zu/g3/xL/8l1us12rbF7/2dP8Dff/4R6sUR7m/vcH97h2Hf4dW3L/H29WuEukZUJdB+v/+gvn2woPHFF19k7dKbN29yhdCmacCDTOBiscB+vwczY7mUOIT1OmKxWOD29hb7/R6/+tWvcHt7i08++RTtQuo52AKYBcJnBpirAGrP+CwT9pn9PpX+/CEy1wFAFzbMS7hgztqjvu9HAeZWb+L46BhH6zUefvbf4/7uDnVd4+joeOQvDhKNVAgS40LBNDAOiJAh8sLAtQuGIKxTed/bxzFKBo+bmxspYhiC9lu+6/pe56sMzbRe5DSDU2Zt7Jr0ZnekgEf+smFY3wUol/4erKONY/J5no6ZZzOIIzq4ZwoaZ4Gjjoz1oUHBQQiEOPj25QbKizTfd//u8RjYPe/uI1n7cSyLtJjBzKh9dvfAfVLeU4DqGAC/78qB7b6daWV2HP6Oyed+HmKMIjgE6WVKUa2CQByingVzXyqujgRIFppaCy4lKYxZso5on3UvTveNaeD97MyJYXPrBIzyHo3H/ajAyfnvEkRvzxy+hOcsIe/pz2h9Qa7vBC9ITve5vEs2r21bhhbqS0WDb0XQxGG81B4yID1SerjWxX+/BqsCQr41ZqkpTDMdK6DHK1CEfiYsVytcXV7i9PQM+TCOGLJkYzpar7Fer3F7+1CsXGo98aLXwXpzoXP+yp+Nzvd0pCVmR2JfilMRc6l3kxSIyA9xs8jzqH3qh4jb61sRNs7PsFyvsFy2WK/XeMuXOjeEpq7x7NkTnJ6d4euvvgYCodash4llDbscfydvDSGIxQGUgQa7PQDLGMVlsxhNzgKF7l07AyZA5bky4aoKErjOUlNKrD8ya5F67SdnFkUBqAkYhh4cpZ7VdpfQdx32uz2GvkcVArabFk+enOHubouX375CSh1ASeMwJRZ0uV4jfvVLHF/8Lfzm3/+7+ON//IdYxAGLXih5qHSeIvJeY8ynYx6v9hjsAofgT/a74Y1DXjJ9fu7nWAvvS3TmRTi411+HGZrUOuKyWY1x0rxQNLWITN8393eeKffsSLlrQ3jkmpuHx+6bWli+7/KClM2BzcNut5tdi7l+TMdswo5s7x8G9qfzOhVip4Lf983Lh16ipJJMbLv7B6xPjnHSLnH/5h36+3ucnZ0idT0++ewTnJ+dYd93aIjwi7/8GbqHDV598w3W6zV+/YtfoF6t8fSTz7DbbHF+coqPnj5H321RV8DZ2TE++9HnuLu/P8iq+dj1wYJGu1wixYjj01M0bYshDqibBtv9DlVdlfSylTQZQoVQ1aAhYX10hKPjY3Rdh7u7O9zc3OCXv/oVvvjiJ1JZnMbmumm+4+k1JEmlaLUyEIISPq3grcRR3C/Ez7TyrkgK8iXdZiWp81KCNFWpJkAqiMeh0/GETCBSkkMcMeCTjz/G7eU7hFd/iaHvcfHiAnUjxeAKIZfUuuv1kRBPEp91qX5aGLAx2kNUbJIFHfxubLbbi0lavhJtGAOIsUdSc/zJySmursc2tf4AAQAASURBVK7RdYMyH+E4BDU5MzvARRkU5Dlz8zcFoV4eylaMmfP5qCCAGaA+eSbDCtcn6Xv5aA4s2mU5WcY67gBW3+/R4T/ogQOaDqTMgVnfgoe+o3G7/rK7j3Kr5d0CHAy7CTEhHY8XyKYgFNN2JkLI3PrY84I/RjrQ8ThN8KTJXJMiGabsqhMCwBwQYwEhRQ0po0+c0DTBVbAV7a4U4+wKcHJ98qMbCfY6GybI/3+31w6FtrHVgvLqZ0HUCyWjteD3Cn/5fSYcmKDg598YGPz+dXNPNGonkHPhsrMdB1hdoBgZiQjELkZC33N4eIRaWZa3qgpICah0MggscThJsx+x3J/n2xjphLk2dY2uk0KsJoyOo77E9a1uGpydn+H29n7mxM2ddZvzPDWPCBvlyQTOgLxYfkRwKFES052jAJxD+VQPaxbgWdYjEWO/7XDZX+HktAedHmO9OsLp6Smu310DoUIdKuz7DgmM47MTCeDvpSDtkAYcHR1jfbQGSISOvuuw3e7AvQeS8s6g7ogMSbFtWQ2NluQTTeaQZd3PnDMrMLwlDCANACcpXJtICs4GUgtGlHgT0lhABtqW1M1qAAc518Omx26/xRB7fPTRCwwx4e72DotFg88//w1EdaGCpv7ddwP64RYvXv9jrHaM5Se3+KNvamwflmiJgMRoKEifCNjzgBgYxAHgIkwHQs4WFsEYBlHMWTyKeR6ESjBCcbETxjbdayPLhSo3c8ZBsya5jSghTCWeBJAEDkSHAg5wWFsCMCWqvdc2N4ETASzj8JjK4mqm7djlXc5ZsUBVKdZx58grckft6B6y/cNKTzzQflSAmQiCU1A+FYx8n/19vr05F6O59h+bj+ncSNICGV2MaYQVPH2erpEXmqZ9ms7DWBCd98z5PmEkKZOjxIibPW6vb8BHC9CQcLpY4/mzF0gc8frVK+x2G4RAePXqNRIDfYzY7Xs8POzxsN3hD/7O30aFgDhE/D/+u/8epycn4MhIQ0Rd1Xj+7KnEdAwD/ov/5r9+b7+AHyBoUBCinzgJMUwJ5xcXqBoJEF8slqI1m2zoqq4RWAJ4mqZBXddo2xavXr3Gy5cv8cUXX4zfQ8VsNs2KYFevmaAk2DmI+7ZqCkgPFRFy1hoRQITyF9OibVDNnqFChmnmhLEm1E2TD7JUkRYQlZjQLhqcnJxi84/+D7h5+wp1U+Hi4lTebYQArEBWguBDPhA6GI9sZie+CCJZMwVWsz8hRanlcXd7g6Ef3AE3U3zCer3E+cU5jtYSN/Lq1ZvMUD1YZveuDOjYwxrd/DAwyTZTDlS4rs8N5z3f+c8LW8Po/f45Bks1eSqmSmA6pQ5A6bxMAU3MBFlA1ogRj9rwRHAK6h8fxw+5rDjitEibn1cT4swi8r7t43uUAfF77jn8bTwTBj3KOiojJjvz9rT8Z+4TddUqk1VtMAO5jIvu6aapsWgbkAKpIQ6aNEH3uu1JGvdqbM0YCxfvG/F0jRzelr9n1ptG39FEL2ADwmRvzIk2h+/OdTyINN1qOWPkzqFvTfaCY3pU6oFYtLswNy2olxKoqkQI1NbIFsGjY5rOHmcAvVisMERGnUGI3C9pWhWwJPNLcvPANpdqXda6Kb0W5DN6k8UrEnedFBOePnmKr379NSTdecgpYe2Zwxl9/Jrl12x0rYAnG5r+Kbd5gU7nx7xkrd+MAhzYClyAQEkSiNxc3aHb7XF2fmIisSQfIKCpG8Qk4PrpsydAYrx58wahClgerbDv9ri7u9Wg8RrHJ0dgZtybdpEIpZCfuFIRARwFJJX51ZM8lv9gBLC4/pVA9PHZoAxoOUgl8zgID05k1ZlDbkeKbwakOGDgATUCujTg8vIt+mHA8xcf4eHhHutVi9V6CZCAXVKanIaE7b7H9fUd6O4K53WH//STO/zhNwvg7LcxbPfgTYeq6xAYaDVQH1EWPFHI/Y8WxA4rwSGnr9CuorwiFCF5SkemANl2u63/wa5ktYkpnSzJBx4HknOuOQWcFhcpuYJbo9LWYyldrU2gKHcTWNzClWbYc7nSuAPO9mzS56aX3Td1DXrMPWzax6m1YiqIzbkVzQH3x67H8OVozESjem7Zmpg4Z06zPs4JUx/q9uUFirk+PiaojO5VglWx8JJQBVxtN1guWyx2e+xixMAMqivsup2+k9D1ERGEdrnG28sbvLm+xb/94z+VuDsG7h62aBYrfPTRJ/KebsD1zQOYGbe3t+8dn10fLGjYprGN0jQNUkrZfSoLFhrLYIJC0EBtm8DlcpkzH7158xZff/01nj17hrquJTPHJG3c1Nphl594a9+nlntfxdDp9yEQAsJs5cjUd5kwVFUFsFRHjSnhi9/4Apdf/iXO3v4Zhr7DyekJlqulSJWmRWHRHLZNK/MUCBTCfGVF036YMAQgu1CNb8xYTjJM1bi6uoKlBB1J70Q4Oj4CUcB2v4ekDxVfbGYLkuVMIAlF4Cg0a0KcSi/GwN9hFQ8x/NNzx863xzP3jQh2ZgByWdaa4qow1vdmQMacW7IpNg1W1Aq4ucDhwVu1LUtxC3YtP3593x26zCB4AcN/WT4of9LBnLtqXbBZ9PUf/n+9Hl1vezWEbQ+AAFplqBYPRIrgk1o48j5PCZbOFpAU1WaBBJGC2iUS3+dx572Nwz1mP1MWFGeYnxvLwV6jsicAlPUmXW99iU+BPHWhspZn97kF6c+8ezrHjPn9Mz1L/Mj9eSsQcgrnYYgKgEhy7WcXN98+5/kvb9Tf9bPVeoW7+w0SNygORQoyM/r3nTGUPgFszFit1tjtdhLXJ1JTXmdiYeaJGWfnp1guF9jtOlixOYCnpGnmcsDFiValS8XyM/rezfZ0j41cjMprgNGq82j/MCgX/LOEKv3QoesGTRMfsFyucHFxAQTxV7+7u8Px8Qk+/fxzvHr1Cvf397i4OEeMA/pe4u7uHx5QVxVOT08xDB3u7x/yPIKAwARQJRYbOB9wKvQy93MEeqbLxpPx2edizQiswbF65jkBcejRRwBR6EOoCGw1OVJCgMSa7PY7vPzuJZAYtzcJJydfoa5rLJcL5WeiwNxsd7i+vZfMlsOAKg74W0+2GP76czz93f8U//If/RPcf/0S9e0Wq02Puovo6h6RksQPQazAycBh4gPNOCDWIIv9NOWMJT1InDC1ThbNNWBgX3V1WYiRXWN0xZaAECiAcIhv8rZ6BFh/r4sRF+FlDsD6drI1QIKSRs/Ze5lLgp1pELRTDYzun3vnh7oIzbkXPfb5Y216ZbW3KnxfX6b3Pibsef4yFWymRRy/b9weW/t4mSzMOQz9mBCVwwYga1lVNXgQ/JqYsdt3CFUDq4MrRZ0JdbsAMSHUrbhiBhr15fT0BA8PD6iqCsdHx9hvduA+ouv7jFu+7/pBgoZF8Xtpz/9uaWVzmkMam7GIKFs2zs7OUNcN7u/v8c033+Djjz/Oz75/UeaDvqeb4zCoppjy7dDkgisOuU7Ng1TVmdDJAZMbF+0Ci6rC+st/iO+++w4AcHFxIQSqouI4QARKCavlUvte+lGYubKtPG6e/JjCEWWLKml3u31OK5w4oa5qJE4Y+l7M3PpsHIb8WVTgZN4DHuB47fAjR1H/fxjcOvecAWkTQjwTmz7tRzrC2m69J+zOgY0Z07YSQfFdLtYe/wQrV/BF+1T+cvihmJA/QMZ4FCTaULJMqZ+7ODt5Nu8Tc45zk/bYG0eY8BAYFAFkTpyb76sfTX7KAfl8nwFonUs5K5ZXXtLilaA8KusJcZtiFg1MVdU5kcLQD/m8iPAydqzxI8hEVwXK0Z8zo52uj6w35cFQGejBZeBDpVWM4zbG7xkJFT5If64vzHkjzBVKHPUht0kFvBd0U9bFuwclKdQENm2l32H+9NheOtwfBELbNOj2HZbrBcRVwwBAyH76ox2m6zudD4CwWq1we3uL4+Nj6YeuM7QN4SsDmnaB4+MjbLe77J4lWmTn3gOU3/Nx4ZFiwYt0mc/oZE3pymhzu77brFF+nxNSbO6VPuphhk9Ra8qBtO8BBtbrI5ycHAOccHd3K9maSIJZhzhg2Pb4+NOPcXV5ieurK5ydneH+/h59P4BTQqcuDCfHKzx58gTX1zdIg/aPCFD3uEqtRtnqlBVKCmYYAFKOf0nK863ooD9Mc5SfKCDUQEiSVa6uA+qhQt91GGIPKxxW14TY91qNPCHFiEiSwWroBnz55Vdo24UkTgkV4hDR93v0w4Bd12GICYEYbSDUVOH07b/Gs8/+W/wv/3f/W/zLf/hP8OU//3eI37wD3W+AahCPBdVAMxEiCW1qRxYADyJDdj20vSY6SFaL4BhI55/yR27LnYDZKwNRnr9nCnAf+2zOLahYmMtnltVpznXH/224yGJTfF+94JIFDgtmmun/e4Whyfse0+77vz14n/bpsfYfmzvDeXP1RKaC3HQeLNva3Pz5vnuhwb/bt+Xf7bOnAsgZVf34xms4I8wlKazZdXvUbQNUAXebDX7+i1+COeH07ARHR0sJGYgAx4i7hw3uN1vsdz3adgHSdzdNg54kGcubN69xdnaGdrHA2WefYRgG3LtyFu+7PrwyuBMsbDL9Bpnm+/VB19N7bJMeHx9jtVrh7du3ePv2LX784x8/KnmPJvKRDTl34Kb9bZrmoB1j7va3T40rJnoqsRsaUPnRRx9h98t/h7Pbl7i9u8dqvcZqtURMsTAgRZIUKrTtQgCAFjTL/XP/0OhTd3AODhGrsCTzeXt3K2nG8rwga5aadlF8R2PEft/pOpRArgzfTN6ZvMvBmpm1cEIDvf87D7B963NvAk8tExMXj8k1D4kcuHf32e8ydrW+sQu4y6Kd7YsCJu3jxwr7HY5svKpueCMwTCbs5nGPwT1GhGoyr25gbM8ryJoLDn+8Qvjksv3rxjlqiRwg1k7IOeMchJlSksQRmi1n1IqXtKBucEGEjcQRQ4xYLdsyNwkAcfFuwXgtyQkZ2dWpyDT6mjKvHhgYKJ2Cb9/jQpt49EWJx0B59/R52/vu6blTNTrqE6F47rIxmTAu8Rnzdw5apAnwroZmjzh8Vd5nRWoBQFgsFppBzNNNsWYPQ6+CjDJyzr08AGFEQNs26FzmEj/vFlgtGvKIJ08u8PbtpfZVNMEmD0kXeIKHJ2KNDpJ5wkMemVejAcQ80jkXeZSKQIGy5lnYQEk9a8HkuR9cZl5qTDygCoQYB8QU0TQ1Tj/5CBQqxDjg9v4OZxfn2G/3ePv2HZ48uUDf9xKjoRlgttsdjo5qPLl4gndvL5FiUlBeAEsF9TiAJvdmLdSl69Q0Lc6OTxEo4O27d5IqPVdMKUqrTCXZWcCUP5KuI5Gkxq2qCkNfS/2VFAGSAPah62D7UoK5JcPjw8MD9rs97u8fxP2Zpchk4ohowj3EVWRR1xjurnH2r//3eHj+e/hrL1oc/09+B7/881e4+dXXGG4jaCBUDKCPCGBUADgEBCZzGBgBWWYJLpfPk2bbkrUqNOVw10gCFpeKn4UWTFlWUVRA57cI1e+zPtjeAg6zY87VH7Of3v1mmtFzCtIfw1D+p28rg2X9aqrJnwP6c989Nk4TROae90LPtJyBb38qIM1Zg6ZzMbUgTK068t14nR6zMs0JTPa3j4+ZWkCmAtV0X7zvPYkZfT9gfX6OPgTsY0St371+d4XzeKZxVYyu6xCTlHE4Oj5CYqBp6uypRJDx7nZ74eXLJRbtEgsAz198NLt+0+sHVQY35hRC0DSqyGDCm6h8XYzp4tnnVSUBiVVVYblc4vb2Fn3fl8G5SZVcvYcb3ws7pb7F+ABJgHqFSl00vMWkqiSDCYexe5bfsFP/RtkcFdrU4fPrP8a3r9+AU8Lp6Sn23R5VWylT0Sw7qrWzNorPp0U2OGRvKNw0gBmd++GLpoUhvqZEwOXlu1FdEeaSlrGpK9ES57nsHUpVcEbqFqTMZiLmYCICjK73AVbDkTS514MuoLgNBQMCmXWXh4w4E4p15PDVHh6MQSiUuTI7v1xmmJWDkyUyOICvE6A+7s/hNYWRHrwqu3LzwHncKhRMWhuB0Dwn03sUxBiQNaBrQgIbUB6/W8ZhjOVQ+BjPBI0A6WiWMxotMDFUATEOCiKqzDBSSkCt1cHZ3AmE4ElSiVCAWOJJSsXpvnR9ZZ5g2sLs/ZRZZfjD1ZmZ2Dwv/D37fNKKA7TIAsh4D7D9Pl2Q8uL3irG+x+41k7GUfic2K67VC3KgN7/TN+CRkb+F0bZtVlZ4pUkIJNnCUkLNARnFwei5EziUPlcaRyexZiHfP6KLSEgc8eTpBeq6wtCnHOw8vUZCn/7NzAf7fjSHZJ/72aPRpGaIzQVuZ0ANW0/dW8aDSOYgayRJxQ3VAAeyoF5gt9vjaC256Y/WS4S6AojEOh5q1ETYbB6waBZ4/uI5vv3mW6xWK5ydnSLGiH3XgxNht9vh/Pwptrs99tsOnBLqukKzbLFoW4ASAosPvtWOosBoFi0uzs/RNAIJ+n7AYrVAt5eMhbLU4q9e+KtUgLa6KpwPoMWIQNcZIAoafxKQ0iDzpiCrH3qEupZ1RkQfO0QeMsCxdUvGCwmoAoERkCCKjPurS7xY/RWoCvjREvitv7HG//vZj/DVz1bo3t0g3m/QcI8QIwKlHB9W9sBUEshcK1tn5fcKzMMBMJSf4pZsgnfJOmi0NeX19ta0aXHL91kc5gSBueuH3Jf/m3xnHiqGm4AiYPi/7WyPuOQMYPZ4bQr+7T8vQIklqZoVSKYCzVyW0cfGav3z/Zqmo/X3f5/VxLf/vrS8j73b3zsn1D32fttn0yuxxNl0w4CagOX6KH8WQgXe7bDdDeIGGGSvMwKCFi1eNlL7DkHDHtRdrq4J19fXePrkeXbRf/b8+XvnxK4PDwZ3IL2uazw8PKDruiwY2DUXGzHdFNJeAFGJ9zAw7jdX7mRtABAoB79I7u/TBNjmrSqZLF9gxALqUJXPR5KkvEBNvAW4PH36FOtv/gWq7Q0uLy/RLhao6xrb3RbYM+qmwaJpUVcVUmIdm+qvcrVXQ3++t+4DY8wZrRfGq7KIWCi6DpuHjQQmkRRSkjR/MQtgTa3ubJzE3G5uEyNCq766E4JTNOJzh2x6kA4+mhDQecGkMHpkYcAEJpp5KN/vCPQU3tvvE5HB3SRAwmJUYkyoammQkx32DAdnxv6eyy3b+x4v/VPhyo11Ts+aQeX4VfqdAVljcOX7udeXmAKAHzHdz79bOGN+hGjk200KQIIG8jJEQZGCaEyUy47AmS1vFSo0TYu6brDbdaJpnYLUybgfu0zYmtIFArLLiN8beMTKM075W2abeX6Nfug1t29Hff2e573wZz0qS0NuP6G4tMKDNgFRc5DdP2sHjkJA09TiZqhrKWemCIUpiaVh/ryrpTEDfxFcdrsdlsoDygFS4VX31FrT3N5c38vxNQByAAAM+EwZ8/dMpm+BkNc9GblkzvRb3P1kTpIKMlkZkoGR7L26qnKsicPK8pzrcYwD6kYUb90glmdCpWmfRZDrB0kJ++Mf/whff/0Nvv7mGxyt11iu1mjaFpyAX/7VL7HZ7MBJ5rrvE5iEV7dtm8/EarVC0zYIlYCQtm1BBNR1g67v0C5b7LYdQmAEUv4ZB0kqwJyVWSZ8AGV8DGSFG+sEUqikgniUqISkvBWcEOOAqiIQJUArkQPIbpoW+Ayd56ixkkQ1UBM23Va8CVIE6govqnv8158/4E9On+Gf/tkRupeXoNtb1N0OnEQAE/tGWQDKe9MLGmoZIEssY0XlZJ2rXF/EBFCzaBTLB+VA9HI6xdqn78kKF9unh14a07+/75rT5M9dhqWSZuogh9+mFpM5QSF7rcybUUeChFc0P2aZmY51LpDd98E+9xYW/+4PucyyMB3zPLB//JpTrvv+zMUae4+fYRiKq+Lk2cfWb45zmIskJ8F7tZZTIM0E2y6WIIhLKtWEdrFQl3rZvXVdrGFEpEpYUQJWVQVOjD4m9H0PxiHen7s+WNCwKqDmt1fXNTabDY6Pj6XKtfrnBpIB2eILCNGMJ1xiOpihmTYoFwLc7XZYLBZ6gIskW1XVaDrlKOtmgDCakIOcQ5bOLS2ZaM7K5PkMRU3ToGkabOJGyYMtPDLwExISdHEiTlfHeN69wdu3b9F1ezx79gysSQIDEfp+QOojQqiwaBcIoUYIIiyRabXggY2DB4agR9KquQGVz5Ia829ubtEPWiyJoOsQ0XWDBgRV6tIQ0fcxv4K14nm5yhs8eDfmmZlIZsBOK+wAhe+pvwyYzYFa0vcUS4WZ4+3b8o7cP5oIEjyJc3DTac/4NLhMqlnUd8cUUQUrlucqeb3nkj55IOoGZO+EWRecVOTu87NlY8+rzKx7CgfrYrvf2p0jgabdZXad8q93gcyjjuvlg14962WwFHOEm09431ECQgUKA1KMqEOlrlSaZDI3RCAkjTVKACqEINpKooA0SMEuIMFCJnNAtQNpo/kYjVuZUZbQYYmY8tjID2IE+w0QyOQKePYuUu9nOuVMzEL4fJklRs6a+ffzKJOWX4NpiyPNqLUxOmMkgmGSA1bOoTDx6kAxNNdfnUMCwAlVIFQBShVDfizoQZaijeO2rPp4sXKUMa1Wa2y2O6zWayV7abT/s9IhAGdnp7i52cj6OYGRcj8PryIAeDDn9m6ZQkfTxhYy22Vyr9O6KqBMYJeLQfaPKEmED56fnOH+4R5d1wswJT1/StQiMbqOkbjG28tLnJyeYLfdYcEogl0ISLUAtq7f40c//hzffP0Nrq9usdyIG9Ld/b101VyCVKmVIjD0Pc7Pz5FSxLPnT3F8coKqIgya9ni9Xmeed3S0wu3NPbZ3W53/pFknY8m4Y3uXbd7K/Af3M6ogUVcNjo7W6PseXSe8vR/U1TgOoKqVDJJaH0LOg25sVvCVJTUCB6m7U6sVRrJuAdyLdTQQ8Aen7/DJ71f4Z88+wsuvTjF89wbN5gHV0KNLAzpidIiomwY0JFRR3p8aGm2MkrwlwCc8TpYiXsGd6USC4RD2+6/OmEYwiFgAfWIYD3pt8+rO0+54Slc2bNLzWfhhAbpT4OutBVNBxHgi3FgA52Y9EYIy2LfZmbgv5WxWk/iQx8D49G9/z1yAthc+fLte0JrzULHfU0qqyC79t++mVpZD1yzkOZlLqeuFI+9ydWgNGr/bxjcVUqafHVy61xJJCQhmAu861CD0YFRNhbptQDFI2uxUSyHOyCKwE4OqCqGuEVTpR0TYph1CkP3S93vUTYVQBfTbPmfs/L7rB8Vo+MGuVis8PDzIBEK1YmTaeqhgAQC+AJ/8befXS25t2+Ly8hKr1Qrn5+do2zZvzByMpldTV0iJcuAhAK22Tbm9ZMJHoPwua8sySoQQskBDqkETLWzZvMkCPFnMxhdnT5BuXqPu7vD29WspSni0xjD0qNQMVSmIZRCOjk8QqMpp+pgTENSVKSM4jxRLhEBBojz5HojDAKaAq6sbDJbphSSLxcAD+mGQiuAXF9hudxiGiN12p4xctd4skF5ouR1QoHBMDy6nIMsRFwPWDnROryKglM88Y5/enJzgwJgIEZPni0A0/gwGFqCBjUr0YooOnMpVaj4EDBRdvx4/2NP5mLs/g01XFXosmB0KEQWHl1Sldt/B3B4ICWNCOAVY7sFx/+bumABde256d96v7AgtipYMOZlCPVoTa9iApBSDU+CwKa2HQFCPH/VnptF8TYdFWSjW2WQ3rzR5aDKY6R6NUd1uvMAy9+C0G+9JfVzucYIFDoUJn95WxlrWeq71/OwoNbJlttEsYDHClBmWTIJIUbwfHxU/ZKPt1oOqqrBctIBmFwqVLaRobkfZxbSjIxLn+8uSxerm9gbZOmE3B2ThKMUEVIwnT57gq69eFcGFdEfmM2VAZrzQMk77HQe/Z7rhNqdMf3G5HFlP8p4Qd7y6ItRNjaP1Gl0f8fCwAQFYtq36amrhN0g6Xyt4F9yqhqrG8fEptrstbu8kfeRiscDpyQl2XYc4DHj69EKqs4PR9R0++ewzVOE1ri9vpE5Fkn2qWwcElqK66sK1WrbgtMbD5gHHJ0cASXX4/b7DarXWMUlsxdnZGa6OrvHwsM2FAEOokKBxBVz0mSmxWjZkPSgQTk9Psdk8oN/sEWOULFTDXvekzp+uoYG+YJKLgvDC9opykIL2hQiLtsF6tQJBLEKktTQ4AhVLqt2na8Y/+I1r/OqjC/yrX/4W7n71FeLtPertDnHo0KjikwlSYZAZCUNRVkEsKASIC7ZiAaoCLLyF9XzY3Gf6nonJof89ESFm4eEQbDNLrTCM2ip0Oyt13E6fCgO+Lf+3rNl8IeR836jP4/umQc5T4WDqJuT7MLUMeOFnCran75iOxb/TMJ6fZ3OPH4bi7ubfNdd//3dRjI9d5QBPjw+f8eOcPjsnUPh+z8XU+HHO/a4fABBvg6TELPUDiKG1eBLSIEkYYhzEtT8K/t3v9+j7Hm3bSnap42Ocnp1rmMSQ+3V7e4vPP/sNgAhN22J/f3+wFnPXD4rR8BOSUsqpau1vPwFTyc5Pmv/e3JfOz8+xWCxyYBwR5fZLUGFpf85lanrAppKtH0eOz2DO1cztO38fICljAwUMKeGTTz5B+2f/V9ze3uL+4QGnpycIgZT4FWBmYz46OlKq4wBMDggXVkM8ITTMk9+lH0bKoALBdrPBw8ND9m8Wk5m4AQUK6IaI3b7Der3C27ev9dXF5G19HcEn143pd4eQc9xNY/TG4MZWm3HbPBEkgPHfnvk/Bqg88B7fwxifwRKcnK1d+Vn9NxUtg2nf33dl4P89lbhtL1h7ftzT8fh2dcfg0fn+gHePZ2fG8vKeayoAEaa/lD6yuqBlVwrbs2zuImbJKlXAzRIJIAv5MEGjcn7/lRSfjFRAqOyvGSFjbvhWdMy5HhqGnR23A6sGiPx++f45fP+cTx8NgBbOOxxNmfMxs/egYq5ND6QDESLJfEtgfqdKGBMgKhVmJvTPA2rXB5uH1WqFboioGkfzIO5vzBo8zVoKLoOp+cu0niKg+oGai50plSRjymLRYLvdZ1AL8Mjnfny+R90fnUP/+fQ+P5dZ2DB65pRUScF21VQ4OT3G0cmJWIoWDR7u7jGkhKPlETbbHfb7PWTbF4VcXitmDH3E/f09GBBhhBl9N2C367JybEgRn376scxbkDN3fnGBd2+vJGkJiltcVRGOjo6waBfYbjeQwq1rhBDwzTdf4Wi9wmq9RuSEo+NjzbUgwJ8R0PU7xJjQa6KRUFVomwbLZSPCju2rGEU4CYQ4DNjvO3HFqAhf/OQ30NYNbm6uNTlJjb7v0O079F2Hr776WvBD1PgtopFLmU3SVCAEi7VxsWjRKk4QS1EEaQwKVxVCpVmNqoBPw0u8+I9O8E+f/wRf//wN0jeXqLY7oNuDU0RkoK+ByBFVVkaRWKVDAEi8EkJ04E+FTdAYYE+vqSbfA/Cgwt28xrq4Ek+vOdeax8C878f03sfanDwoaGXi1kM05VLjeZi+b4oJp337oL685/IWAwAHVpupC5glSbBnDyw8Mxjyh/Rruicea/tDxgXM1yF57P6UIob9HrvdDu3JMbpuj8vXV+i6Dv1uj/1uj3a5QlVV6LpO4zBEJHj69CmOj49zPLY3Mjw83KOqOiwWC7Rt8z09keuDBQ2TYL2fr/j9M2qiEfCfSnBzUqk9b99ZrEfTNNgogDaBQtwWbOMmPDw8IISApmkm5qexr52P6LfP7LKxdF0327/sy5ySumUR1usVOHY427/Cr1+/BhFwdn4uhNjDXz18q+UyCzTSLmDVxfVlM1pSxwFzf70WtwgKb968Qa85ySkI4Y1RsvUkJZQvX34HImiNgko1LgWs2WuNmBHUxeixjeAovddk2xJk96Qp01fhI7+Syl8eGE1nY/qZnyWbnpGAcnB3gctjIaPsGaKgRbJEe/7Y88JQKLs+AI8D/fweoryUhIllZiJfelDP+sAU8Pv5GAdy+98x+jy38QFaduDwXaN10LWi6fflJdo367z0K6UBdbUQwEakGQB0xZjV3SahrhspkglIvEZWCAxuIxSIbW5AfrxTbbZfo5LUFcguQbMjt3vKrnpsnkf3f9+ceyavCgcRZmYb0zkfsfGDd49GwFlkcPeU4N2hj7k5L7iM317oU/6p+9EUHVVVY/+wwWK5zAeYAVAgxCFqXFt1CNz1xVOQVIVKNGo+K6BtNu1nSglt0+DoaIXNdif9NCFeVctje9eEtnyvZDq9T/ao0Y2gNZCsXxl8KOBerJZgSkAFnJydIFQVNre3iFqjR4Kmy5DyvtUZH4YBgxbds3lJxOj2llIe2G522G73WK4WwksS4+uvv0YchuzGRiR9PDo+wmqxEABRVeiHiKYihOUCKSbc3d7i/PwCiQjb7QZHx8cq9BM293f4+c//CtuHXRYAiSp0+z2aukazXGB9Iu0DLP7g3R5V3WJ1vEaKEX3X49uXL9E2NX7605/g+PgEgKSq7boewxBxeXWJzcNGtLCaepnGx9d2QlbSmLXbEsm0daOxBeqeyUldO2UsQb2dGIx6uMF/+Qnhjz7/2/j2F1f48o/+FMPbK9RdhwrAEOXZCgmUgMTiICjutCI4Z2zhFFfQhDJhdNTHm38KMnN8AjzNdmCWLPh8jFum7U8Vrv47357HQdMsVe9rP/NNt+f93s2MjMbPzY3Vfz5N2+rHMWe5mCqR7bMp1jThwf/nFeRTK4UvyTBN/wsUFyevKLexM/hgTubaeGwObB6mY/KfT6+pNeaxi5nRDwO6rgO6Pe4f7vH23TtJLT0IH9j3A9q2zfFbJphtNhtcX19nd0o/vr/82V9i6BkXTy7Qtu17+2DXDwoGN7cj/2LzRfSDA8aTPc1K5aVZm3yTpMyVyTIb2Abw6zYMA4gIwzDkGATJOsVgHrIAMjcG24i28PZ5XYv/ZN/3ue9VVSEiYdEuUKHGJx99gs2rL8Gba1xfX6NdLBCqCjHFLDSwMj8AODHtlgW3K+2TlwpMMiZOCt4fFzbyKHLxrZvrG4Cl6ipYYReb25q0GVT4srgYac5ElkLgjICPQMMcZ3ZcYIIt82d2nx+u/yy/RrlufreXfDAGWcVPnNwd43fbNZnFCaAvICETJ6hrhmmuDgedh05EAia8oOLeidLzDMpGRW3cmhre9kLWdP7yGOZ7dPj5XGEtu5cP5+uAp8++x987bt/ETQN3wc0pWDKjCa2AA4WGGGzglPsXNOAMROj7DkMv53m/j2V/Wvva+Sx2OIEiCz/IGFn6B10XKnM4vQ4TIHy4NWgqMPsiffa5gwPjm+17Gt8xYbfv7wfNu5VJm6RpQhMqqnKSC7/n7KUEEy6CQ+vl+/XRGpdXV44+yXtDCOi5nzBaQ9c8fo+NlxnL1Uo0bE2T904RVB3jrYAnTy/w7p2829aZrWAll0eFvvJo39Mhij0U+MkBLtdnCuqKqx9ZgHfQsaUUQUmACxNwfLRCW9fo1ZIBOyus1iQ3/nGHlD5ZXJf9DtF+P9zcYtk+BVXAq+9eYvdwjyq7L0O175JhcAjA6ekZ0jCg73YIJBr6uqoQqMJus8XiaIXNZoPlYoHQtIhDj1/8/Od4uL2HOW/KaUhABDgOGIYefbfDcHyE8/NzVIsGi0WD3X6HvhNt53K5kOcS4+tvvwUR4eR4jadPzlHXDQIFXFw8wf3dPQiaeQyY0CmlHbYcus8oEOqmQrtoUdU1mqaVfUslvjKmBOIAUiF00Ta4urpG2yzxNxd/hI9/coH26DfxV3/yNdLrO6S7LeqUwKkDJUIgUTwNfUQVSpxosAyXEE+GyOUcPaahnoLnMZCeUAXH46CowmvVp5aPOY8NYF7I8N/PXY9bTpzjphMkiEhih9yZ8X00fDeXPWqa1vUxQWJ6zVkCvKXFY0wTHnyb3irgg7HnrDX+nQfCj2Ms75vrOUvJ3Po9VuPEt51rl/BhSMFo7kjOXdeJS1SdEs7PztDHQTCu4sW6abFYLlHXNVarVV4nC0yfWnyEF/fY7u4RbjBKrvS+6wdZNAz8p5Q0oKsTc2q7zIKCAWv7fXq4vNAxTYlrE+kzUGXp7V1ZoMViMRJ2UkrY7XYgEgGi7/u8uQEx80/74s315sPnMyDYBmmrViQ91GjbFidv/xXevnmNoR/w9NkTsSholh0TMoiAOoQc2D7ZBjA2OEJJBYILo5s8lXkuZAM93D+g60XgAjOqpkZMCcPQ54xTYjWQwDgrfBaZ8/kgjLuQWfCMgHEAXiwIzt0uQPzg0fydf54UIRhToUMOM3rQ/2szaDzfz+jBnM0AMx9wrVEqYLYYjQpzF0FdEvhQDy7dtL01nk0R/uRNdVOD1XJiQzUN2LQy+CEcctPDLOZ88s/MMQghJiLM8OQ+G31pd27+MLrbP035X/IPsAa+TYhimWcuDU5exGA0tSRnCCTWuZhi0T5hXM9gDoTLuI3hUX7vaAzTdLTue5u36WwQje/+EKGj9IWKRvCwwTIn/vvR2MxKU8Z20D/Xpl+rQITIEp9kChYD6NmF0tY+g3uAMw9jiIZcR8EyjtVy4TSy+h2FfH4KiLAMezzT60I/Vqslrq+vcXJ6kmsxACboKCiICVwnXJyfSdyOZTtKZU4yndEzFpQee83jHIkpgmE5CzEVF0xzjwWQk4wYPbA5aesa+/0Om74Xy1xVoSLCPg4Y+j2C7UVmiJNrCXo3IJezLMnMixBj/UtS02lze4tFUyGliMtXr5Fi0grgAKqAH3/xUwxDh5fffothv8Vus4UJ7t1+j33Xic96jHj37i0+WX8mFon9Hk0IePnNN7i5ulK5rVDefHQJSBSQekLs9tjc3uLZi+c4PT9Hu1ggpYjN9gGJEtp2qUJEws31Db79+mtAXbguzs9QVxo7qXxsfAaRBbSDU0qSraxtW9RNDQoBnSol7C5OjEjq8gNGYMLx0RGurq7w7FmFT8JLfPqUcPV3Iv7Zl2v8xa+XwENCHQd0+1twiqCUEOqEOAwgTqgriXcy/hqhsaBVUL57KGh4AO6BZPZ0mAGmbqT52cfcZrxSdfoO/71PSzv9bqq19v2xd+fMllU1HtOkj0BxWTJM9z7ha/qZf6/9nmN4tL/eJWoqSHghx5Ss3hNn2h/fz+k8e/A/tVxQoBIj/IiQ4N8xN865tt8njBwIY4dQTfmMfNH3IlgsGWjaFp9++qmctSQ4mUKdM12tViv0fY8Yo2agoxHetj6cn59huVyBSKqLf8j1wYKGWTJSSui6Lv/XNA2qqimxFDiM7PcTM53QqSTnN9OcCQqgbK5h5lFdjLquc1Cv+ZWJX7IEAlmAuU2gf8/0AAKQzBVg9F2P04szpNjjeP8WX755g6qusVqtse+k2JT4xTIIYjk4OjkGWDS0+X0jIMHup30qXJ7Zf+/vFtaUmHF9czMCLVUIiDHlrCZE4o5ggC9GH6Dlm3dwxhP6g9mY9MgHjD8CuqbMu4zQNQPng0oW6jsNs5oIM/OvG88k0aNCU3m3fB2CBTPOZeGZtK0M0Y9j/B5PCEjmSSfcLHHWjO/Joy5YDvhQGdx758CAaQZYk35N735MUPEjOgSIZnFyNzgZwmup5ExbHMDMOE3y5VKN1ApkxpTQNDUslz3x4d4or2b47F5TcXAW5GK8b6Z//ZDrfU9OoYMH9vm5g/PnAfTBiSjfAa5Qnxdm5EfTNGjrWrfu+Lzra0eBr8ysxzujdjfJ0se6bkZt2H0hqIIjuwk8tq/HwkHbLjLTGtEna0MnKaaI9dEKq9USDw87EYJIkw7oRrSMelO6NCdkWNPyYvc9iVBn2kHKAosBAPk8GL4HYb/dgohxtFhgs9mg125JocQeFYQvQXkFc8pF8+TM+jmRdYwOdJgvf+w6vO077HZbTUtJSAlAAD799HM8f3aBqq5xcnyEX/78F9huHwAIH9hut3jYPKDb7/FQVajqCvvtFkerJfr9DnsA716/BseoQ1R+bYIQJFowgJE6xrDbYWgbvPymw3a7xYtPPsFiuUS7bLHdbNB1Oxytj8EayL972ODq7Tvc327w9vUbNE0tGeSIRGEXgioH7PTa/LitqOuxXC7QaIYcgPDu3Ts8ffoMVS1/M4CeJcA8JGgx0AqJge12i/WyBULAk+Ma/+D3GH/wYov/+1/0+Pl3hCEAX/z4J/jso2f4iz/+I3C/R8URgQlVrBAsGYHSdQRxsQpwe4WRA9qnmu285QiiXSY9ufagznUEZz5ugvsYYLO7n3Q/zwBSvcTiPBcLonveK2D0HhMwrA95P3ohBeO4WVOuecH/4HUHYDs4cXJMp8wi6/FkeX5mKDOCg7lIHYxvovj2czONK/bXnHVp+v3cNWeR8u+aPv+YAEKPgCGjHXVdgzpgv9/jFMB+v8PAjKHvkToRyoeYcHV1hcVigZ/+9KejObD1NMsGkXj81JVkVYspIYT/P1g0bNEsVddisQCgmmUuVcBj9MJD2ZxeUvSLNDVLTSfVAkjtsrRbUhOCdDKEuJhgYWYzM/1Yel6T2ABxbarrGsQSxGhUjBOLOTbUiGkAgXBx9gRXP/+3aC/fYrfb4cnFBcRvEyhewQQoARJ/VF30QFrXSghF3h+jfaLUZiQA0ORXQuwThj7h7u4BCUKcm6ZRAcf8EZWYaNph4ZUlE4wAE3fAx2/LwMUD6rFwQBmcTPe5+c8KYNH73U1TOM7k3GmMtYyIpKXNdM9M2vD32odpcsjJ/+aYVX53kv+oLrA8C0gOEBYPeBx2aHJl5nHQSeujzc0hdM5M9pHXmGOVn4uCzZRNZ+w15/M67he5HcBuDWnuXo8tbR5zb0gyBSVNda3KAKJa51TPNrtYCtK8+pB8/k1T5fOCJNWKwaVDgW3+HAhhnRVy4Ejvt/2eO5yFLzerB2cPEEer6exzmS2y/V6sWY49OsxQVinouvhXWY/8+SuT+/59bg8Ea4H8nEj2oOOjNbqu14QHjLbRrHdJDjFZLY2ATCOQ4V7pv40ZEOGlsoJOKcEsR4Eky5UpfHJ2qIMBlCtxsXykGBE0qYVbNB2vZPlp2xbn5xe4v38JUvrPJOlCS542Lm37NfF/cfmMiPPqlX91XCT1EsRvaAo6WBJsUIV+W2O73eD87BTDbqfumKo8SxHgHinu3L7kQmRG/bQ1NnCHvB7QNPK7zR4paUyZbt2TJ2d49ulHYDAiR1w8ucDJ3/6b+NUvfok3r16DKsL9wx0eHjZIaUDX7dBwjW+++hopSQr4ioDNwz0sDTEztOI1nJCvQf4k0o0o9Ri3l9eIfcQnn3+G5XqBk6NTpCgB7qvlGlUVsGjaXGuHU8Ju6A+wgO0/U5jNUa1AAW271CKroqC4eneFKjS4uDhHqKRYosSxCE9JDCAAxycnuLq6wvKjZ0KnNL7x84+O8b+56PHuzTv8xa+v8O+/e4O/Wvwd/NZ/9l+iIsZyWSHudtjfbQQHpQEPD/dYrVY4Ol7j5c9/ie7ttQhODFBiUJI1Zs1maftPFKSqYU8iqIYQlG9apXag0dgSs7h7IF9pa8TiEgkAFSqAgIHiSIEBTqhDBQ6VnM2o66qrWfi9YC0y5ata8ohF8ZN0FAhBrctCcysynqt9tSOkwrGdlcSQ2iPQ/aRuqoFCsWolBlHCwGYdEQWyYEJJgQ7A7RmrtxTAbCn8Czj3uNNbY7zVws6p/7ucxfH99hmR1IGxREBZiLPz+8jznhdPrTGPCWRT4eTgPgJCZYk9ZP0CgDpUwKYD9pLs4E9/9pe4ubpBxcDFyTkWTY27h3ucnp2h+2gnaZ5Jkjr0ccAeQLtcZhoDIlQoqeer8GEixA/KOtX3Peq6zgJGjpWIAyoUVyUizT8PLdqVwcbE9OSEDp/L2E/m1FxIUO0zl4rgGVQ4Sd6Cxa2dxWIxEpZ2u93h4nKREoNuUE6M1WqNft/hxZt/je9evUYgwunpCbq+y4coaxcAtE2LtpHCSEVbZeM1oGLAwKPwsnmEwGakovmtpU8Pmw36bsg5r41ASbV2QlUVP1VxOTncoIavpyDGgCW79fFa5ELoD5YrAxEjcB6YjO7j8XdTzXPmNaN7pn08vMbAbozQ5mUBB8ghsS0BzRiUu74wxiDbN+rkkZHQVvprYLx8N4e//Hin8+eFidHLmUu9DqIiHM0+N+2XNeEyLOkXtqOnIkmpEIwsJBgsJTKFQonXyGmoyRqz8w+wA5PMkimnbkSDMmhl8cViCSJW//gCfYk5v9sIfO5lFmYEZBQ5Y3wecrXmPEEHsN795/rP0vfKAoRNg892U9nVeb0niyBTUuZi+vbx/gijzxUzjYQBUzaUHQc8e3IOgDD0HQaWeLOmadF1nWqp3CqboiX3lSedsN0gALhtG8R+AC8aGJwgSApUpXpuve0QFWAtf5bxLxYL7Pcdlqtlnjm5tUxcSgLELi7O8O0334GZYZWJZA+Z4krWoogdXM66jc3xjcTiymTTIHxC3S2IUHMpTHugoCGAIyPGAd1+h8t3PY7Wa8SgdzCw7TQTUwCs5lQGJQeLzVnwyMXw2Gn5uQSWEkhAYkU4f/JEUlcOA0Kq8ObdJfa7HZarJapGFGoP9/fY73fglPD86ROsVmtcXt9gv9uAqwrNcjniCwxRGhQ5nJXecCGxJC4k3X4PooCvf/0VLp5eoK5qDMOAzWaDlw/fous67DYbEXjZXKj9+SrJvEe8xJSRboasRpVSHXBiDEPE69evcXS0xmq5LEJKknMvcQRFu317/4Cj9RoZNzChrgM++fQjPH/6FH/7YYs317/Gm3df47J5jr/6taSMl8xbC/zO7/w2nj79Cfq+w3azwcmL38fQEeK+Rxp6pD6B+x5D36PvBgxRAuA5iStj3/fYbLaohoSFWnCHQe/R+alZBHnmBI5JkgXonvKZgDhWCEqXOSUQ6jJfKYnQS5LhMrCKCwawYW57DEo610yoQ63LnRCZEaHVxFhPux1pSuCg/dSgebE0MlSE0hUmgBgcQq4VlJXRYAx2rgID7JXSCaXKOlTAtuD/Qw7lL48h/e9TxdtjvwNjnOp/D0QyFtuobCfG/hy7ZE37NbZMjQWZuXdPXb8O+gkVlixLK4lCqO873N/eojo9ArNYOsLA2O92CLRA09QYhh67bo+jRYPEEXe3t3jzzSvsdjtUTS1FqFfLfNbX6zWePX2Kpv4PnHWKiLLflq9D4c1TvtaG/F1loj03iT4YyE/81Kw0lTCnC+83kAkY37doIQRJ+9W2AoRiHH2XJU0Qzs8vcPflH+P8/iVub2+xXq8RqgqBYzb31nUFsBRFOjk5y+OnIMGUIsAYKy4MaMTMjQE7DWnpewFst7d3uXJqqCoEzdhSsni5nPjMqgyW97NlTJoIGVOQ7LPqmyku3zcjeOirRvxynA2qaPCJJs/ldZHvHks96vuY50V/pgzaKOd8nxcuDtuUnxJk30AIyPCI8OPH/Vj7o7lyP+fI4ej7R+ilwWgGH/QDKPt6JFASjfo4DThl95NgazWOPmF3g31q7huwGGGYpg4ZSWcmoGMKRFoBGOUc6EAIyOCY2SwaImjs93tISkypWMwKWotiwfrl3GTcpJtgz1QcyDJcoQKM2THN8ZwXHTdNZixo3AKYERR4lSkWF4ADwcLex34/lL3voNx47UAo6VA5n8cyIho9SZDaFh+9eIbz8zO8ef0GVufg/PwCKUpxynbRwnHI/DbDfOL55w+1MUR593K5xMNmA2aJqZMgZHHjHAZVhDCKeSxPxJiuMQugXq5W2G43WrjP3JjGJ84A2OnpCZqmQtdFSYfM0GKMCQzNepVSVnTlHaAgCxMa5ulAFkqSxhaRaPpNA20CfV5pDcpkjU0iaIFbtah7Ws5c2jnYF9Yf1lVk5H4zLGOaaItzimIF2c2iwebuDgEisL18+RL77Q6ffvoZhr5DGgbUlcSQxCGiaWr89m//Nq5vbvHrr79BXddYH62xbNrcP+MVByDJBEDoWScDPqLsCvsK3/z6awHF3i1FFhqT5tx4xp+V7eKEDKUfFvAekwaQqwb+YbPF7e2dxFWaX5s2KNYSAbhHx8e4evdWqtFHAbesAggDqJsa5xdnODs/xU9zfCoQIyFxB6DDAv8edAmtfM7YhwrDugXWtoaOrOhackrYo8Gb5Y+RILU/qihWjaiKleH8p0BoMAw9qI+IfY9uvxeBJUYMQ8SyXUr2rv0eu4cNut0OlBjDvsN+u0dIhDREDL3UTUBKSGzFNKPsW5Y9Hgx3saRqTjGBEqMiEquM7r3OuYH5RUxk0UZyXqTgKgCWOiESa1RorcxNQOKIqFXRmQKokrOXAGAo+0GsrQSrpUJUHQR/z7k2GQ7N+08/ewwbPubeNtqrfFhaYSowTNv9vssr06fKjGn/psKSvyTxT6UZ3GQ9AhHa1QKRB3C/x2pRY3svSpHt0GFAj+V6hfXZMR72G4S2wna3w+buHk2oUa+OxX4ZArqtKBKWx2tUyxbv7m5wcXHxveMDfmBlcMsdnsG5anvMkjGdPNjAJxvhYIImC+SFBtss02U3K4lZQnzsxdTPzO6dSo7mQsVO4PELHqqAFAN2d7f4rat/jm9evwaYcX5xjl4Ln4RAaJsaVV1LLvBY4Wh9NAqKJwqSscShIa8RcINCgZQoiFKL68UYkWLE3d1dnpPVYqFB4EOxGmVfP2PO8k5k5p2/yhdNfk61WhjfPmoiP6soyjRJYwauDNoA4mQPeKBd4NIE9M682y4hSsFGjOl1MNUoYC0DTnXzCFWFkAs3UqapGQiYpkwZoNe4zQlDo2cP+lQ00jzzvc9KJe9+fFx2Lz/y/dxzU3w+WvXpu7UDYkGTtyRESQMJoCJfBBNqWlXfaxMsHJNS2QalxkYEQQqMLRYL3N3fY4gRi4VoXfp9V2ZKB2pzVM1NOvnTlEUS2NFzn+QruxdyaYT0Rba3RIjw/siAVC7mkePOdO59AcSM5o1BmwRi/VGNvM1RINO2e0WMZMYxQF5V4s56dnaKZ0+foaoCXr9+jW6/Q9/v8fTJUzx/9hQPDw94+uypxFNYX90BdDLPRFsgdEiAAeHk5Ah39/fqZWMwImSFUzKAz3mhtdtjoGKTslqucHN9retg4CKvTL41MWO1WmK1XqLr7oTHdJqhMDLAg/Rxht8QUtb3GF0s3ZIxBCNTpMIGJ4BL6kvBy9ZOQIoDkAKGSjIWnp+foWlqvH13CStcK5jOhA2rMm+rX+ir7edcBFXpT3bzJKPNxqeEv6xWSxADm7t7fPfNt+i7HsvFAvc3NzlGMXFC34lCqqoq/Mmf/Alubu6QIPuq33fotmrpz2efYPF4ef+T8kcKWakg1F1+dvu9ZqPhvLkCI88DeYUbifZ8xHBQaE22/ZMJOKJIqpsaiS0+QixSx8fHuL9/hevrK5yfnyK0Daaprk3mIxL36Pu7exwdrUFc3NRE2RUQLL6OgKqpUTU17FAWQRh5BZfMmpEQygfDgYIHCDhGxNP0VzAIT7W4eXENYElIwyttQgQjNFCkJm3tqcVl/VzTASdwqsFxhc36R6DFhaTsT0DsB/Rdj74f0C5PQRTQ7XbYPtzh4fYOQ9cj9QO63Q777Q5xGBCHHjwM4CHKugwRiOLZwbG4sHPUVMQMVGhE6QqxvFQUMl0ZOCIRo6JKBAxmIKkXBgUMHDPzjykhWp0vcrQxmGujWmu5GmFED8qnmn67x7xvfJC6zfHUvWqKT6fK76n1Y87tSfpc4mmmYQEeaz5m3fCKd/s5J8zkvphVnTSlc2LEocfu4Q4tRazrgLN2ga6usN8PUgG8Cvj4xXO8+OgjVBSET3dSTbxdr9As2uxiZ8Hv/9Ff+z1cPH+Kf/yHf4hf/vrLR/vjrw8WNGzQJnAUQDGerKmk57NM+Sw0Ux81A8kAHEAvbed+6L0eyPt2pn3w77agb3O5Oj4+Rtd1aJsWFGO2hOQUuwy0bYOTL/8xeHuHy3eXaNoay0WLXbcDkQgZi1aeGxioV2s0taQIlPd6JqcjMM7OKAEIE3govLiYOxmMmAbc399jr25fdSV+jUNKOdOWw/IO0ClzHC3oHPgtQMOD5gJrPCy1T8aE1JiIwTsafzlaR0y/z+889Ms9BOhzIHrSl4NPDu8qQItyFeic4lYHQMZYcgNFwDjskwGuuR6Vbw7cxZxo5VsNZK3wZLyHb7DuhMk3h6s27VOZh4zt2L/bP6OtGDBgYbPGFs7OTrHf75BSkmwViBiGAe1iAQqkLoXjMVrtC8tL3zQ1zs5OcXV1hf1uDyLGs2dP8dU332Y4U7pAImQAsOrrI0HTQK6bn7yPueivDTxloZwIQF2Qie0FP9/6fnNrrMj8hTlnO/IpebNvcZ5zBZz6/qAWAUvgYDV46iaIMqOqs6KnbmoECqjqCsul1EqQZBdS5XWz3eLyzS2urq7Rd3s8fXqBn/7kC5yeHuPs/ARVFdDHoaA/UF5Loz1Zq07+7NvPhPV6lc+Gp9FCl4sQllMeT5h7fq8KBXVt+e/jWCCd8IEUI+o24Oz8BDfXtwAzUhwE8FsMjg/stmKnWbAYE79Mgd2+NICfVyolBY3ydx6TuRBC5rFtGqxWK2w3G8R+yKlQk8YsxaQW5yzdQCu36/sDoUg6hZ5yzmzIAoBzBqyAo5NjHJ+cgIhwdXmFigJQ14hDxObhAVVVg2NCUp7DnND3EW9ev5Z9W7eINKCDFIGVQvHFpc7mUawSpDQxqHJP9iybOw2g/vQAmIpVzHaOCnNVFbJiJ59XWwsicQPSs2t7zHgpVU6YTQmRCBxLEd6H+wd0XS+u0zkDHY/ezwys10caCCuumSLYyPvJhCAUfkCQ+Erz9iRA10HHx44+EIF5yESHJvtNftW+Kb3J+McznqlmSb9f45UGoMvGoRqgeAPcq0sSAA4ALxhYMB7CCXpU4JqBI0Z6Ki5c10c/wVAfI/YDEhhDt8ewlyr0fWpRL07xcHePfrPD5m6D7cMGFBndbid7ahiQugT0Yq1JMSLuReBGYjB6EAYEiIWFWKqrIyVQYNSUNA0xgBgRWNZ2ILFEpzQofxC6ako+K6vghQdzd5yC+ClWtMvTrDkAP1VUGNCfxhrb8x7DipF+XgCaYmaPi/33j/3+mNUDrHEiZOdO/tte3yDt91gkwnHT4uTpCwynEfu+x54HtF3E7s0lFk2Lpq5Rb/fYbzfAYoGz8xP0ccBuv0e36/H8oxf43Z/8BH0C/rO//z/Df/cP/58H8zZ3fbCgYYzP3J2yexHRyFrgr8zY6dDS4D+3330WKJ/O7DGTlD07TdHmhRvf/6mQU9c1+r7Hfr/Hom0zWLfCJSAC7l/jk/gK3719h77v8OTpEwxxAAho6kaZvDBFTozT0xP0/YCqcqYt5SIMTZOYqQ1NuBtlBmOXmbFTkorfV1dXBo1QVYWJlfRt9l51anEqcQ+8p0LAgVAw+pvGd+V+HgoTnN/8+DWtHcGFb+ZW5vr6vjYP+zw/Jna/MUQTH/RBCagrIMI/nHVrbuyYHvQZ0Yfcvz9szv33h+3Ov2fms9wIjVzSciC/A1OjOc5/OLckAGCWeWIAqmWyr4+PjrBaLbHbbbFcLLBaLbHdPgihDwGr5UoqCms7pNrCrCVPCTEOWK1XWB8dYb0+wu3dNe7v7/Hpp5/g9vYON7c3MFtUogIIs7bLRmL7iwDPYrTbeZAh18tglS8ogwGrFm9tUZkwPQacz1pVVzljWQhS2yZU8hkRoWkkjWAVpHgahQqt+r4SCFUd0NQ1zEXK6gMlnZOqkni3pMC2FKWS/vR9j+urG+z3O9zf34tCQhn+xx9/jM8//xzn5ydYr1skZuy7LmvlZQgF2IM1MJ+gABJa/T2MgM9isUDbNI7eiiUrqEUrDgO4qfNeykCPy9lhHp/upm4wDIP4/tL8qTdXqIvzM3xF3yDGAXVVoRs63a9mjRyTV1vpEueja640zX7muxkoMUT2XglmNfc1hoIItTCHQFguFri+upRzEhUYZeWFWatlLioVFutKtIsEoHcpIz14iUNEHHonGDHWqyVOjo/BRNhsNiIoKG+UeyQTYXZ/5TIvnMRVkVm01RERvcbu5PHrvGQrIkyzKhpbAX7Gu8nNZUC2ylFuToF7DXBEjH5loIG1lSoCm1GOfhN8QlVhsVjg/PxcikWGAE6MPnZiOa0qdH2P/X6H1WopiQVszON/RFiqxFVk0bbwybODadTJXBUJEs8lxfvszBgb11nIQhUTqdshYNzjUWpeGil71mGCIqO4fau7L7dFhGJHCEhGD5VGHvEDLMCfiIBavnve/xloQGmvAnhlY6jRowYv9bwy4V37CfaVCCZDN6BbfYrINXabPTb3G3APPNzeod/t0O877Pc77Ls90hARuw4UGTxEIDGG1IGR5O+YgCEiaFKWoNYcwgCEBOYBzCrooXivTK0PVXWI84CCKT1WnSqn7ZqCf6+4nj7nL7u/qioNEB9/NxWApkLEXIjA3Lumbfn7SX+aG+B6uURdS12M4d0VepZspIIHpDDlw+0WD8yoqxqNJkViArit8PrNO1R1JW6QgfD63SX+2f0eZy8+wd/7z/+n+Bu/+3v4kOsHBYNPU4tla0FVfOa8SUsWt0iVj0lkftPYvd4XDnBYHNDifMXd6TFzkl8cnzbXv6ttW2wfNthutwCEgfd9j+12i6pu8OLua/Aw4O3bNyAKODk5QZ86hCpg0YoECFKpOVRYrdcY+ghTs+p5yYSaFelQJj6jDs8MQgaddF5ub2+1DQGAMSXNvmWaMiNIlBmjASsP398HcN8Paznz/kPvcBz8jpnPpoHk/rzkNjJzKC4GUxDuu2OYdb7HpZ/uaBeGrX8lDbTL+07nMwCiaSTtl/mgWjskTltCyMZufr7fxk8cVkVZj/HoDlfp8XnO7j7TcbN/93hv+fiBPDvv2xQoazG9mqbGxfk5njy5wLfffIth6LG6uJCafCkhccJ6tcLx8ZFD+noWspZYrj4OWLYrLBctnj9/ht1ug5cvv8PJyRn++l//Pfz6y1/j3eUVUmQM/YCoUis7UJr7qRr1aVg2kXe1FC1Q09QIlRTttEBnExRCFbBYaJXySoIum1YEB6utYEIEI2RJ2rttxhhzP2KUOTFwyimh23fYbraapjqiH3qYLLvfd1moYE6IQ0Q/DCASF3hTkEgWLk2S0dR4/uwFnj17hvOLU6zXS6zXKzAS+r4r7qgM0KR2jAmCkstKT8eBEkTOyfpojd2u05oTqkwhdTtVgaIIE9aue49vlxnL1RK73Q7NSYussFDhZAQG0oCTk2O0bYP9doemrtF3udWyhSe0hUep8tzJzDSGFezCzafEIWTBxCly/CGJQw/WPdP3AwKFHEuReZ4SALN0kaZQOz8/x8nJMb759iWISC2AAbHv8yA2Dw+aAahA1qqqsd3ukMDYPGxEO6xzKkKuWpW0/gPyc6VqOyuh2O1LgpRsVXAaIQPckkWxQkWqjDNKqpmDyM74GGnBaCURMAxAFSTomXWe7KqqGuv1CpvNNvP3upGifKv1Cqv1GkfrNZpWhPQ4DNjtdyJ0MyMOEbvtDuk0qtBLKuA5iQcibx4fH+P6+gbPnj21LoLg6hrZ/OS+mwAGFWjzACHBHu5Pv/MIswVwSTZaBogwrADHE3INnfGzU3VeIhNnogZi67qZcjNblmQvs7WhiyIxGk6hhoiAvRFMAIwX/S8RegXcNQH9LyTIfgnsVyvcLj4Cx4gUgYFX6J78xxii7ONh32O32WJzf4+UWqQ04GFzh2HXYXN1i36zQ4gJw64H7zukQarIAwOAiBh7MIt7pGX6CyposgqFmRdSqb2RkrgNUiWu/AQTPGS/hOAsjH5duJyNORd8c703a4nh0uIaeOhWNefaZT+n33lBZ3odWDOsDXsuqls/BY0jq1GHCnWoQSRuh5FZYlFt/yVGxYqRmUH7ARQSmDswaQHMqsK3f/rn2Nzvwf/J38Oy+Q9cGXwYhlEWJ2/2qaiW4jgpCfMFRPuVHKpylw8mtwnyQsPU/Wo6qd59ayRtam5fqMRmtVel4FTSwG3RPUSIZjYQoWlFuDhaH2shQnF7qvs9ftL9Grc317h/eMDJ8TEoEAITlm2L9aIFBcKQxJ+xaVsBA1B5kYoLjvzuoe0YAOfLNptKldBUdylFdPsB+30EhYC6IdE+xGLSroIxd8vOgow2p6vwmDAA+5zo4PBNnzgEH481PhZIrKXye9FA5s/1+TB5zv8MlsaXyjcGFmCinDJl07zJlQDNYiRu2OZnL5qqug44PT3Cs2dPUVe1ghxk17qYGL/61S/RD1E+bxsQMYaBELcJSKLNSz5zxmjcUzcof0e5j0bfUX5u2obRofI5ZYuFzSdDGKPib2lVBSTT2uWAcELOSGQWuLpWYK0ApK5r1FWFpq2xWIgV4+uvvsJ+v9dgxRa3tzcY+oiz83M8uTjDctkgc2ljvrk/0svYM1IdcXp2hH7o8KJ7hu++e42f/ezn+OlPfwO//Ts/wW/HL9DvO1zf3OD67hZ9HMCQYnF1LTV9arVIBiK0TYW6lsQMVdD7mgZBGUgVppom6ZNYEaPbU0K7hkGsh0MvyReixkeJtZwQh4RO6/jIfokYegn0tHSsMQ4icKipPyVJ7Srb0PayMM2KQp4oCmVNwEBbV1gtFwhVhaZt0NQ1lqsVlsslVssWi0WL9dFac6ZH9L28l9X1IIGBGPNus7MiIJkQWGtj5Cy1+ouu3Xq9xmaz12B/c0/h7EqQ9JyOeKWjLcRldhMzVksp3Hd6elbovqdDWRlFWC5WOD5aa0G6AKYKBEYIGiQ8Q58yFbB/yPgZ1DIGcByy4qIKgrHUEwQMcdOy54W1S3LhFAl11WAYGEOfkJIGyuq9iUscQ9CEzmAGJ6ne3fc9hkGsf4PyILuGOEiQrrnvgLReRMB+3+Ps7AxxYPR91DWESYxqfShuzrLvBRzFFEFBaJWBKEKx6hrYJQpgLfgQSBKQ1KhhCi9yPzkrD0gDfAlmLRjiACCBogDzBEJSHw+L9WnqWuMcxaWSQkBVBXWRkWBlMFCRwJf9sMdut9cYSYlX7Ichc5UiXjlrku6rupKslcMwCGBkP3k2Fk9F7b+Q59dtLkzVV4XYPsIqlUfbufHPFuWYzLsJY4WnzLQ4B07jlN/oGLILn9KbfFz8eFU4Jg3EBiGWT93YCTX1eNrd5HETALz8RZ4XEo0c6BTYVkfYh2UG83FgDLHFq9VvYrPvsL25x+Z+D2qfYHe7web2DhgS4r7DsH1Av98j9QO4jwgxIQ1RscJWznOKiMwAy9kcCNhWUXgeBzlLFKTyCTMChnw2CQGBZX3z/tR5n3PRn6s9cYC3JljKu1yNBA9bnvy7EaUSv+EjcEdX9pnmUhwUhBBaJCSxxGoQPiC0jSxtMFmfYla2scYFU5AU0QFB9hIPiPEBqU6o14tpL2avHxSjEUJA13Uji0KMEVWYZpIoB8Em0Vfi9gtkLgDeIjJ1c5rLa+yBQfabC5Jj2Xz1hMhqWzrxklJNg5tUA9eoP+tut0VVNXh4eMDFxROs7r/FInX4+cvvQEQ4PTvNAeiLtpVc3SQVRwcAi+UK/SCarEysPOIDAC4mzQm0F0IzSU/JasINIWC72yHGhDoENG2D/X6HEGrRJjpymjLxoLzpC5gbvXHUg7HgXDRAjmzqNwXcZ1nGtDtTUDFzOTovfxvgzP9an8sNBa6TAwvk6CEXHjF9F8E9b48UB68AksxEKtSFqgIx4/PPPpMgfxVspZ5DQkLC7d0ttltxU1itlxhixOZhh/2uL9oksGP4hhV1XklAlp/bsj/FbcVnYpF6AHonaZpBQh5PrZo7IxpVVauLjgKbIAycVEC3StEGxongtJfC2HzK1hQH0Q4B4JQw9B12W03Z2A/oui67752dn2O322Gz2aBpW/zWb/4mWhXKUywMzIvZOXAOEV03YLlcSJBm+AghVHj16jX+8s9/hpt3N/jtn/wET8+f4vz0AkOKEHgecy55y0xktRxilIxiwxCRYkLfddhsNPgxDjk2BCzKEhMcjEbYuDxNMo30WGNlAI1z/QbLxGRaxQABTgRIVeSqQqgCAgF1XamfOSFUtQhHkOQEYjGRZ0XIU1ebINYLK6ok1oRKA3UBRsCg2XiGIWaazBDhotDoYnY34QsAqArqPqMrZZ+DgBBwdLTGm7eXMo+pkR3KLOb2ISLZltXzOn+my492sURvgcR+P+bzXihdCMDFxTku371FjBFN3YDTICBUtcCmoc1nzNGtXHJED18RtxylYAhY4VKl204zKxUJQQLf66rC0fECMXUABlCIqENRcNQVY9B6RoECJPoXICa8+u41+r4XKwGTBOLCzn4ChoCaWpl5zXjW1g2IAyoQMASEgbCqVjnDD/KYxQJh80lE2TVP3i+pb9MySVA0xAWlIrFoEGkcibpKhaB7rwpZ8A1q+SPbK8zyPQVETtj3Qh8GjkIH+h79fo8hRgxpwLbb435zB+aIdlmjbivUbYMUAWZCQkI3DBhYfPoZDA4Bi7ZB3ch/r96+wjD0YE7oh06tBaJ4LJS/EGTJCJlwcnyE+/t7nJ9fwNyLRsJCvjjzUcv+Ve6VfUouZuNgD3vlXf5daa09bxnyeMLPjN74voDGGzZjBy8gyZfJgf+smOOIERNRuDIGc64d8mjAjXsCq/Md9k8+62Xc1dBjTSao23oQnu3+hdDHcwI9qbDHDfARMKQar5rfwH7XY9d1uMcTbO4esHvYIm063F/fSurkbo80DJI4ZIiSfjtGECccxW1WrgwxAZWeC46IpFRBhzuwfB8QhKa855qzOjCXSupGUx+zanhXKOND2Soy3YLuT/LzCr/V9D26B+ycp8RIcAULUYowZquQXtF4HSDZ9BwGZ444vzhDvWgOBKrHrg8WNFYrSWFoGaf8gGxrTQNuCFLoyDNqAKNJnVoyPEP3maT8gGxRvVACFMHG/jbTFhmjp8JIc6VzZqQkRQD7vgdRkOqiocZnuy/x8LDBzc0N2rbBYtGCwVgu21w0UExrAUDSyuSsyWREG6ORddpzY3gmBIy85md+L76dVRVykK1V5R2GAXUdtDiaLENFwUnzcEwemW9O33YgF+RHLWlduSQjio7CpHJyrRDPHg5r2JMpWZvSC4MwWdRQQcJoptV6GDVuhHEiTMxd9m6R/aQvUb8Q0CHP1oGw2Wzx619/BRCQhh4xSeYMSVsZwSwpQkMg9N0ete6H3DviXO6N9J/pns5VhYP4CodKzLrisy1+/AQRfBqt7GyuC9m9i60GAEYMIqaSsjnH8KjbDcDY5fSfKQt1QnDK35mxeZANZAHE/otRAvWqqsL5+TmWyyUuL9+hbVv85k9/iuOTYzHVRsubr7vBa+gygBQasN/3OL+4AOEG9Pw5Vss13r15h5urW/z7+z/D8dExYozYDz1Sikg8SIYfJZicEiy7aoJWTs5AAPld01zKXiNVad9EKKvzcwL2K1j19UAao1E3CCTBuqGuJM7AzPKhZOmpQqVrWKGqRHAIQRhtbsvcmdS6YFrsoLTMAA+zulUyAyx59mW/JmhSGnHTsntsre1s5TMjp4OCCj1VhYYrBYwAWczZBP2Y+2hMUVNnMhCCzBd1Oa2xndORwDECQzK7lglLaJsCRHeuzEVOAokZT56d45e/FLePpmmx3zEocT7jcAK5tOH92gv+Syxj9BczI6kpR1wuiluJzpacyVChhmjahz4gNRWqIL7RpokOFDBQRFMZjakRqNL2AppQo2kXKiSKVWbUG6UZJniGqkLbNM59j/D82QVIFQp1qIvVHwSiOrtwEUkhR3NxQ9B0mVx4c6XWTAnLKe9mRol7sIl17WbEavsMsv92+w4Wb1iLFgUchX4MKeJ+s8W/+Xf/Grtuh/u7O2weNqI4rBrN1S9tR93L/TBg33V4/uIFmrrBdrvFThU/pHEyElhvK2X99SKY9HO5WuHm9jYXX7O97e+Zv8ZCiI3Zrxmcy/joc3/fCHRO3s2+B+YaI7/zwfOuv9N3ZHli/LlZT2f7Nzk3FktXmjBQ7B8WvFOsWvp0PmhjoOuekr9CAIZe67QQgJ3im4DP4zXqqgYdAai+Ao4Z9+EUd3SGu/gZ7quPcHd5i/0O2N5tcXd5hd39Bg+3d0jbLVabBVIcRNjlXrNkiRDGoVLnEel3IhL3dwYskZh0L4ww6mMXkWYtQzk/HgM/djFzQUITgeRDr1HMMgyDmOKw8BnhtfHRdvwYR4IRJOnFD+nbD6oMbi80gaIEJE7ygjsJz8dsGLj3wgVQJtSsHFMJcNS2/pwKJ2UixxvAUvkRihXFB5gXs1dA0yzACdh3HZZVh6d8i69fvUKMA54+PRdty6JVFxoICNVXhVBl7Z30Uw+ht8ZM+appT6aEyD4zAE0ESpTTFFYVYbvdlnnXvuQigxagm31IKQesRxuv75CnrflT9uTORqRMuZTgyUKJJ0o0BjA+ONw+JwcAxilcCxM3omYGggwI8ldc7oHbG/ldPBqeaVbMHavIRqz9EADTtit0+06yslBJQhqgYD8ATVujbVuAEpq6QUrA6fERzo5PMn6y+iq+BoJ390taHZY1pR9zVJc3ERIsRWjf9eh24t5g+eijnjsbt33utfP2Ts7jS3mS7HdGcRvztUgMxFobnlmawC74WbIgtW2DpqnRdRIAeHJygs8++wwvXryQCtIqEGSlgWeOml0trzrLud3v9jg7P5P4CM0St9tscX97j912iyFGdH2nGy6AUCPUIsBXVQH0oAhJxFOrwCCbNtQV6qYWQKPDE/CvVgV4N7ISd0ZEYn2oqww6KQTUwWLV3IZ19CCLUllblQQ4mzbJ70NdU9kjUT7LQpS3rBSi4umnuQP5k26nkAGUwn6jQw9EAVsSeJ4Q6wqJGQ0q1FBAmb1GJJh4vV7i/mGTFUrZjSa/x10mVOZ9ULoge05cUKU4bJV76OGh7FJxhT07PcFv/fZPEUCaHvcGV5eX6LtO923INNQP1ONJcxWDWp0oUP5MLOViOcpxDiT8wmJ26rpBVdUa27NAVQU8vbgAOauBpXk3+lZVVCwBqmgoY6QsFNhcEVlWNmRimedaU8UxGXCUMyB3BeeKR+UMjpSFle5BLYabGIO6UHBOMlLOJSDv4aEAEMsKJP0yvsqqGU3iypRYgpSJgaQuUEqNu77HcX0OdA8Y0oBh6JDQg3mHvgpol8scQ9X3ESEQhv0ew65D3Ta4vrrGEAc0dY22bfD06VNUVe0SGHjgrAAyVHke1us17h/ucXJy4jarcc8xfx7vpfHezsqT7PfvPsvNTnHNdJeXQ2Gws1gC52UUE/IyOci5zs2qnom5nv95kMheoBjdMhYiy2fIvLgghgFiFzMa44QLc9ci2TOMMp8MiBunNatrI5ZYmdMqDaKMiDIvS+qwxlt8DELgnyGcArcX59h90uLd8ndwd7fBzdUN9sMK1199h9urK9DDBrTdoIoD4m6HGgkDA4FZK7kDCJKF0vg4UOir8XHvNlXGpxTKzqTDu2XNxn+PvH2Mxs5hwpn3zK2iFw5MqZQzJHICRxWk3L253+7do7CE0dhEhZpSwsPDw3v7adcPKtjnXyzMtsZ+LybRRrOPeAHCMxX7fCrV2WRYhe/RBDE7rcy4L97dKj+jv5vwM5o8IIOw6WQSiv+qbCxg2QZg6PDm7TuEQFgfrQHSqoqkfqeZkBCqutGMMGES7WyUQdysjPHZeR5tJ5X6LZ2tMTQiY1Q2NlZf64imBRbtQqwxMN9keZ2dAXk7aT5kAzjwXlr5PtP4uRUa0S37LAfLZc0Ju/zv40MyAllZZzAfY5C/ccRRzr2uoa51nhu3/pk427yyZIFh1vTGdrjUIlMFwqKVTD6iRaxwfHSM07NTrJdLLJcLcRNUAdnyFw1DhyFK2r0YBwyWZ1z3YOwH1SiLmd8HxXriZDn2yeYoMbxAn13guBTgyUdnIlDb/X7mPevKl5trVsDFSoQCyllhFDcszm0py83AjVCFGkGBad9LxqgnFxd48vQJnlw8wWq1QqduE5lose9gcRUYkU1m9KlHSozFYoFnyxW6fo/NpsXx+VEG4YmNoRZw5ZNIACy+qFkri+w+FoLWt7E4DRAkoLWkmjWMkneiozOcioUHBAxpAEfK1XmZoYDYrAoFoGfrEIASp1DJ2bR3KKNKnuk7kJglep8u1Z1eAQ3q4qELV4SNMudlG8nflAgpJCSuxB9YO84gNFXIYMZO9MnJCW7v7pHcGZC9Y1q8BIRaCI6tV+lSGYf+ul6vsdvtsVqvATaliRPgtKuJJUbl9OwM+12HdrHCZ5+f4Yuf/hQpxpy1KGhwN9zWM/qgC6lCZQmYTmIKUjocJuDO1pJzELwXhJiBpmrEyqMvGfohr2mymBhWxp95koDvOMhUxSGWStCA1BhIUfuT1EKoZzgxtNSKTjODELLySbJAyfuyZUbPeOCQ+Yx1knQ+qmRU2TK0qYBUB1Ct7n4hFKGbpBZ05nM6H4lEYOk5oU8RCVHrVAQkBlaLFVbPjtENe1zdXePy9hJD2iFxRIoDuu0OcFYla/ie7nLe6EBA29b43d/9XZyenuretUUbEb7s3mqKwJOTU7x+9R1OT08xQvO2z7Pib8wd/WX7lDXRgym23JZ17dLoObZ5t406fU7vLHSoDEmaNWpvZ1UbHSkcdMxy6EbzKO2ZmokLnXEKz0Nuou1lGiyfyeusH0bzteeB86PSbFGG2r9Eqsg03FeJsEEp6X5JoGR8StI2EwEUIzgAi/QGSwBPhm8F8D8l7GiJ4Tmw3RN+vvkM31wFPFxusLu8we3lO6AnhD4icEINSBV2ikhB3IjGiraxN870Yrag+vH9/sqCwoSHmyvTtCQEgEeFGv/8Y+8BkFPf+vsf+z3zS9dPo+lEUsE+JaNP33/94KxT3goBSMaZFItJSXzZm6xh/ZCUXR70WzvTe/Pzk/v9z6lZMJuBq0pAfjqcWFKQYlwohID1+hiLN3+Kt2/fYbfb4VzzzovLlASVitY4ghEQI6NuqgLOck+hTFbdIBR4FJepTMUAf+jd8wAjUIXICcvVEoBYXJq6wsPDHdp2gePjNS4vrwTccgGq1k7RxupGQRBw7IoLGXNB7gm7HnC+ze/VfNT1M3MVkiJMDpwBIAVcebNqu4Wsuv7aM1leFSYZCGiIciYRC0q0eg9B3VAA0/YFNHWlVhzRQpcsXRJ0CRZhASrc3d/f4/7utqydgkRh4KrR0P6ZBQRgZe4pgxBJO2oEQn7PmVVUy6R8YDL66WWWH3bfkn5eXPLMJ98+y2tHcIWoWOdxSqAgQcqAxhLobsivM6Ij7ZMKbaRuQItFKzEVx2scHR1jtV7g5PgYq/WRVLPtB1ga1kIsqXQQZa78+JglFmQY+mxBODk51uxOZX3k2Kfcd4uHyG6NbH8XJYcAYr0nlWrLnAYMLO2ZYiKbym2y8q71O1y/49J3U44BXMCpMf4J/54CqHJ+1Uqlr3M8213JViznT7cq6sbsTUAysHvI6Jw7EwEh2XwlWCyB9LMWywYou6Ws1kthPlHc1wJbIoGgcTL5pYXpjuicCXQibK9WK9zf3csMO4FxBNo0UxEzcHJ8grdvvsTr796g7xMWjRR4BHsLDzTYVd6tb81nWqMVRvMyRO+KZ7uURRuf044DCabwcJKM0YIsQUmWmwKnKgBaPAzs4iryWzxUKfwqC8A6l4DWviHUKmgImSeARKioqoBgweBsfEBdOAOAitW6Iha5yuKGIOc7p/MlTbtcV6jaAGoJdSNWnaoKrv/W7XJOTBEDZo27MAuICj+q8EMIeHd9jZ//6pe4vr3CbvuAOHRZWC8kSWNCQkDbLrBarfDk/AQ//vGPcX5xLkKYbvismFJ+y0DJAKU/g7o+9n0vlmp/2TgcPfQCs7XjlV2eNpd7bO39/redTfmMjl49etbma/SNvt7T0EOams+5DD6/i3Q8YtnWva73FXrnfo74EPQscZlPUwg6UOwVGeQ/B7JFl1QJa+/MykIitE2Dpm0k2N/ot90HsYJmXMhQ4V4aMEGywgMqAtargBert+CnFW7iCr/A38TPvrrFV3/+l+ivb9Dse6Ru0ICtvIF0aIcChgfl/rvoxlmsvGNhxT9vn+VkYY73TDH3wZpi/Iz/O4QwyTDp8XIJLPfX1Kgwere2f3d3h67rD7DEY9cHCxoWBO0tFyMpGuJXawHeNkg4ac4+n8tl7POF+0Xwn9vln7ENbRkjTLAINA4onpXYMmk0kC2H+Gh9jGZ7ie9evgRBUg9WlQCqUFWaLMSZmlH87+3AMxhMRYsOZjFqZI2I+9wLG1T8r2E/VFA4Wq/Rti26/R5HRyt0XYe+7xDbBU5PpcAZqdYqkwUS47Ro6CR+wxg06WFOWWSYdCf31IFOBxpsrQKj1B2EPqzMrrIDJjtcmValoJW0CBllV566lngE66NlBLK9ZUKTgYBAlQBSDeCNMQKcRAsBxpbLATSQx1lAIIjLkFgkwJJQIO87AGBvgXNtjFcRZeScU1rmORp9b0utgVgGGmQy9aZCOI055iknA80K/HOFPa0GCicQjDqn7nPlFcjBnaRxACBJW+myMJlrhlkw67rWgnGNuEwtFmhbEcCrukLbVGiaBszAfr/HfrdXojvRXOX9lFmb7jS3943tMaPrIrA3rQyy7zmUOLMyS9vYhehKpBE7wG3AjVmCXwvLLcCctc3CzCZriMIUS3Ez7bvtNaAIGLo3pDBhmuwbAlkmNMUwmY4wRPvKyH/r4ZJ363nPs5bfS5kpeIjAOkay2iWOfhdQEdQXXjTsNlfMMDMCatWQI4nAfrReo+/7bNUAS4G63gmWo/1IGeoXgKXDqkOl1r6pVtjvXwEoiRmL5RKffvopXn33GrtNh919h24TMz0wocAAp7UVmE1kku8m+97/hGYNtEQfVkOFAqMWUyAIlOu3idVM0sqGoCkmc5tB6pLoGSUS62qlAnwQkxoqcu56ocoCQk6PbrRDhQSq2bl42RkHKiKoTTvvBXOltTmdpn7Pa2Q0Ju+RpDUCGKVMp3CRvEZ5X0GqqusZJQoITOUsKZAziyApSOxu9zh6coz6eCFJJroOiWOm2RLnFDR2rcGyXeD89ASffvpxpr9lP0+C+PUcmZDmN+XFxTmur6/w4sULaP5a3ZvjuXLEOJ89KMhF5u8eBFI+z/PXBA+4efT4yr7P9LK4FWS6Z2tUntD18ATMg1nXbv7KxpjHbY95WOrBd35IXR+QA6GtP4+NOo+JASKxWBA44xboniUXD5cy/rL+WV+TK4woG4pj1HOWUBEkaQUFUIg4qSL+gP8EL54Tvvr09/H2ivDlH/8ZHl69BmlyE8vYJYqy5Fcqj98Dc/sMqcQD5s90jXJpBhjmcnOp93vXLMOr32fRmCqPsuePCTBsVEDuS5jyYYVpM+1X5o0EgJgxdD32u/2IL77v+kGuU75gn6WY7fseVNVS4Kmu0FSt1LvVQCzvAmWT4F0bvBQ2XSwDlZZi0vfFF6lrmkaEmBgRIO5DVrjFiODQSxtBNSFBo0ATJwwcURGjCrV4IvcDTq5+jm9u77FatVgtF5JXnyqYPZY0owuzxKzYMZXNwUhBC15lgmYwarL58lWIl0gyBVhC+71cLvHs2RN8+80rxIFxcnSKzf09qhBwenKKzz77FNfX13jYbJCGBIQSXyB+3qpFMqCmkyosdGzqMxCbBRJ3oEJeG2V8uoaVBjB7EFRXVa4BYsxZgJSmUySUgFFIbYSh61FVFbquB2vgdXYl4hKHkDVkpnV0nxXQxUrnHFGeAMfiRlAIguwVjNbLFkVSJMPlxycFrHJ3cR1EFiiK2VHeL6Ben80AJC9AJgbk+lCse5a9aAyMzD2sUq0kZS2jnt9aYhckDWqTg5Etq5HElDQIFeXgZ/m+gBAr5sWGnmFuhKLBjUNC120Qk2qERwxazw7GIL5sPM7TlldsRMiMSAtTyl2ACftlrHkvOAJf9kZ5d4axGdB6QbKAA+FnnD8nS/MKBsWxlk4+dhYTP57JHnPfKOAdj9fwS76TTRjhPIbCsKl8fzB3NvMOK03okZlDbJQpSYby1PWIkXNAPYPAjbjIVBUBATg+OcbrV69R1w0o1KhrsTxyL1mASmplP+c2YWNrBSAJEWJKaKp6hKHyQ8qoTQF2dn6C1arF9c0thi1j0S6x33e4v7uT/O82x5qZkNQCaNp6WZdxIdpApdo0B31W90qJrxABgKjEcNiZzULADCDwq3/A2G3P+jsOPpvcR1SAoMOodk4LGSl7bzrnBrzLa3S3s9+vDIpwsYfWt6nnQQHnPpFT5BKnye4tNob9fo+bm3sQV6irAFrUSK1k+zOhPsfHUEBTN6g44uTkWLLhqcXZzgG5tqGCpp3zkMcqG2y5bJHiAE4Roap1jnQyyfU1+yw5q7I/52VAwGilH7toBMYzDcEU3JfJYq+m9oLVhK9ZL/L3hCKI6bfsA4JdSn7A0WdPnGxfwc4zRtmqbPtNXXkBjIoYeuKmZACAWEdIBf8QirM1oCmm9U9zXS24cdxY4aemyCguigQGYg8KAefY4az7t/jy9HM8/2//Af7ij36OX//bf4Xq+i0WlJB0bw9KiITX6qCd4GDCASkPzp45bq4JLAl7dK6Cm4NMH6korqfZqt535TgM/Tuf/dFBKN8RgBqmNCh0SjBT8tseSGK3ZWZUCThu1qhD7Qnze68fJGj4aHtvWvHSls88NZWs5iSwqcBRwMz4M//kMAxFWtMFzVVEnXRpTKgseKEW7DYls/jaVhXhaH2E4d2XePfyKzAnnF+cgQE0bZuD9sCMXiu0ppjQLiTA1Gu+C1ScTiQy6LHFLvPiDgvGfCUEcVN79uwpLi+vsd1ucXpyCuaE+9tbgBlnp2f4yRe/ge1OMnd0veXqV6KrWYyydjJrHQrwzoJhFUQTnOzAqvaGAQvuYGYhUkp4hj4B1Ln2GJvoMhshlTRqrIHpBdWNBAUKAVHrVFhbI8BxwCknGtMM1Ak+05C5EvlnRsKUAucRYDABw+3X0d9U1tDvaRNCQtZceg1myP1iHa/VeLBKwVbHogQg11phusoAqK5qVHVVtHxBM8pkIcSsJSUIz/YW6/oyWFNGlvimqIJDP8r5qcBhtNf9fBdGZ3E22W1hxAABZOWB80t2fMI2pP/X9koOarcxMMMilMegvOxT1yTGd+kc0Xg8eXwZoZmlIO/kfMILsPHCzmPv4smnrm3AsYm5p8Z9my4B6z41EHfA5H0rpGuU2/dCzVhzyVys1WmIaFNC5AYtM4AKFQLWq5XUldntVdG6VBfTEmAsIDFPahmczQEbHmSs10vsdzs0R8cjhYs9lD9iRt/3aJoG7aLFRx9/hJCQ14L5xWQGPZ1I4gduGmCH8PzbxlQ5z7QfwOFizMLLcn7k0QLgje65j0fPjN85826a7hLfLR7dnz3xeW5k77lGW3lKiKcHfMzHslWQSyBJ8WTWHoWA65t7LesSJGC+kiKYZP9z2dvKNCYs2oWkLNXVGvPVQrPzn/lZx7NJBOa7+zucnV0US8jsUvKE5BVs4enCeI2c5XO0X3j8Gzv6Mzqzbs750O//sH/jfeN5/Ny77aZDMqnjyHNxKEAcCFqEImyOj1/Zk3aj0USCxqcq7bbCHjl+SJVA+T/WqeDMC+wlhJSfHSWkUAGEktKBlLBYLrDf7bD67t/h+PpnWD/7TZz8/m/gj//NAL6/w4KjFLMjo7HiBRKIsnfOVBiYro0XNjz/fEx48M8/1ub0bx9yYD/fJ5yMlfooCoC5vjGy631KCd1uh8UHFusDfoCgYZYFC9o2s46XvmywB2Zn/dz7z/vvvelpJFy4z/NFJR4ka5vc/V6yNDcvyZQxzhxgGmAbG6ECJ6kUPrz6U7x79xZNXeP09AxNXUtWqZTAHLFYSvB1CUQtWUWEV4WR2QwGpKZaqRFyPrwMkNt8rVYtdrsWP/7x5/jFL36Ju7sHPH/2Ane317i9vcZuu8X93S2qWiw8McZSsdcF4c/9nG7soBahru9HGZCUCpSDDve7+iSPArw8E5wMvwB5wxvGCDU7SqCywUcA4VCoyG3pTwHvxp6k7aBAZ+R2oEKsWAdCYRTq7x8ULFnaTVAB9MWlAUAFNJUUghOrgNxXhZJ/3lyPKq0ebH0yQcFb8ciAABWTsWjiCzPNQeZ5DYV5x9iBh/GaSrpXOwNl7QDLclSIdPmuTPJUO1/cvdxaesambklEyJqn0ZX5rwmyDoQxu7Eig+csXHg0z9pn+1P3p+3LzMRGHaDCN/WeUXwXkduzIbPCvEe5KFr8ZfPqhdfxNZ7T8pnr8+hhGn1fXqeiAY1FgjH0m3vXYX98DESGDzlw1t4tbcaUsEmM/TCg2XdYrRZYcYu20eKNdY1uv897uNKUzGOTv+vliB56YY+wXC5xe3uPk+PTvCcQStA7OdAmxRPFChoQ1W1S2iluZ2WU8moF+dGvoRS08m4NZUKLosXmTLYt51sOQJt/fvrndIPo3xkUMUr4kn5vgqR/5jGsObYUunaIRv70o3ZHjfldb6MbIevHWdd4ysdNG22xs2uKIJZshrd39/pxUZQEqlVJ5gQlO2sMrI5Wzi100qmRsGEdK/yoMCV5/vT0DN9+8w3OL56WvZZjMmGH3I3l+y53Djm5OfdznDvr5sbPuZ87P8ns/5rZ5/LuQpUnNG7KjFUoKPvDxwbYZ66rI/js+uF/y/drLxi63pw7Xc6Z8Q6Zg5izlzkldab3fh2mc8DiTQMAXFzvs2GNIbSGBLfFGFE1LY5Pj3F3t8F5/Bn+58+PMfz+j/Fnf/oK9c1r8BBRgTTWiKTcppu/aXmG94F8j7fs3rl2jMdMEx/NPTf9Tqb8/fT/+75/tF0Qtput9G/izvXY9YMsGuZeMQaokhFgmurWCwD2vE2eD47x0pov1OefHzEqHk/QVFiZFv8DpKJzHFIOSPXfybNSYZUBbG5e4+zNH+NVt8fz589zcPvrV6+kTsDFuWjyKGDohxx3IhpVDcrMAEjb92BBNcvS30kmFb1HhlkWVXIdE5q2wXLZgM9P8MUXX+DLL3+Ft2/f4tnTC3z+2ce4fHeFy6srSSXI5SBkVyP1nzQCZIfV3Hps3i03e9QqqxbzETT7SrBsT/qPeFAp2kZh8o52lUNONhsavAoXmAm/tt69SIUD8yMGVDtKmnpUgEdlpkZtoWlqFUqFuVWhysX4LOixpJ8U4aGuA+qm0boV6oKkPtC1FU6rStX3YBVrzf3DfExHzASOZ9vZkTW2M2RxIvb3OP0oZQbAtmMysZoBArp/GDR5Jo4BCIx3yruMAXBmiFZBegpCuHTLgRkqb5IPcsagQ4bK5iA6IbqlTya0w717fK6gYLsIA/Kv95RjAB5r5p6wY1blQ2RmTKNdmZ80/+ER3+Py92g9Rp+P53xqyS3jsz4A8K4w5W0whq0zWT51QtAYWJU2RgIVHG3y47a97KbHqhYzS6XzuI/ouj32uxbr1QJHR0domgYP9w8IVY2qHjJQscBco3d5vFPQkwG8KHy6vtc9RjnI3c5C6ZyoEqJaTs1qMloflNflzxl5cOUcpQx2jDa5KR8vIAp4s2DmEYicA3GYtDHdM+wAoYds3wcO7ffpYrt7JgY7GSG5TqRpO+8ZuD7/eL/KyZkKQ5YakwCoD5t8EQh39xvs9j1CKLAkUFCBq+xpU3oQJN7p5OREhAGN9ZhdfEzGlxmYmwNmVIHQti22m02uHYYsePJ4jafrNKUyE14+Ot+jDo7nvGjgp2d4+r5x90uL4zUb97W4706VGVk56ut76VqCLF1tXr3DayxROgRjVMrV18gWaFb6zHmvCOnTkWQ+EV1/Z0OYMZrzRPlz2+eU6Yz2igFLvUsaZ8YIuLu9x7ubW/zt52tc/vXfx+t//U9Bmwe0SaqPRyQAFRJh5AY1VdjKlExiN/Sn4cYp2PeKdv/8lEdOf/ftTxWC02D0ufb9/XO8aYS5AfRdj8CAM0u+9/pgQWMYhmwh8C5OOa+269Dc5E0nwd/v22TmnAqz0aIg73O5sssEDP/5dANMJ1Ta1uqlkbFcLBEu/wpXr79FXde4uLgAAGw2W1xf3+DZs2cSc6ABkkPfY7lcYRgKQQn5sApjNdYJhjLLlNPxGYMajZFotHjGeGJKCCmpL+o9njw5Q13/BF9/8y0uLy+xub/DxZMnOD45wRClQNLQdxiSVTpOro5Jyr7ugMY4sNVRgGi/oxCe2gqV6Rk1k/XcAcqfo+Spr0KV56KsT/E/DJbnPgTxyc1aFKBSUG+aIBMORGMq8QVS00T2Q2PWBA2sFEtBBUAFEp1NiWEwNw5NcQpljhTzrGO0f2wOFLir8MIc0Q+D8x3lDFAyaJgcZre4Ofe9d3cpe9j77RoFNgaubjrZbDwGnYVZyPwxjIGNWVFZQxuTvsN+T+IkNNoE+S7l//DMtzAis8pMaylwnhudAy7jF+tKKh10b8tnyXVAPh10yGbVVJqTx1qQ5wFAGJERx4wd+PfB2PmuEaAcE3B2mbTGuNCBL3j6ZFNh8zQGdJSDmf13M8xeN2mxSJU9hRxDVARYWR/rm7bt5m3qssosxTpNRUAAdrsduv1O4qmYEVPEMPQYBhHUQYSo5yPoGRqTblW2UIkHY0hle4K4pubA/9zRcq5kjlM+kxZ8PJ6H8f70c15wXLEUHgoG5JbE7VsHXkkz240nTKfapyO29sDjokD+XQebn1yfJus+UlZNBIz86dznWUwysjL7bhq9219unmYk6rFlzr2bxHNgs9ths9mKUkzftNt3JcaP1DpNhHEePQD5nCXUVUDbtpOpMSA9GYkcXHeUxzTAYvnOzs5weXWN9foIPlOdvRtk7nZlL/j3HMwh0eTsTveWtygftmNDy/QlV3GWuS/KgBnFpaeaVKwbJhh7mkpU1rvEUpRmiCrXGT8O39bhEArvYth5z/WD8vecPSaYOaexZ3DhRY6PkJ41GxdbZkj/6rw39XE/Zuac4p+IEBKjqmocrZYY+gGbbQfavMUXzz5H/N2/gdd/8ecI97dYBsVRhCK4WF8dhvVK87nvp7h2+vssvpq592DKZwSFKfaeV3J92GU8gWPE0PdYTDO0PXJ9sKBhHfLR8OKWlEYF/L7PHDNdDGvPV/E2QGrF9kaTMaJb4wWZCi9TC4kwpfECMyfEnpBYzKbrX/w5vtntcHx8hPVqBQTCy5dfY7lc4vT0FKvVGgDQ96axIz2gRtDt0Kqka8zQJOhcuGAMQI3oHxItZAbT9xF10+D07AR3dw84pRP8ztFv4e3rN7h89w6vXr/FEAcAEohZBVmPqFoBKVAUkZjAKH6PIQCEElsjREgEAKsgSQQtKlXGW6mFCyyB4E3bZIbVqJuQ1FjQVLMaeCyxBRpnUElVZLOkWByMpGQMgMUpuIJWJf4gz5qmdKyU7xnRMaBHkIByo3dm3SJwGsTNyBF1iQFIZQ3d3pru5YxUShWzAiTLnXkP2P35VhRCLDysEHmz9xStegHkJV7GxBHWTEK61g4YFeuK68dkPOV2cznzRJtGNxkwk7SCYeY7Vv7piWzuJXQJ8j05OPtg3vxx93Nh33h/VwVucJZSBSpgnQ8qTN1wVWnN6ZLzPUUJMAUCPJnfPPIpA3YDMeHU5iSjamudWYsr+Xf5tXPP5Q2DLFhh9KwDlAZAGKVitmEsTjBrbO47W7YTtUTk25PEYZAEgbO6pT7cP+D2/g51CHj67Cms2F9KCaHS9NIHx4cwdfzyrlMAsFhI1iFL6z1/GeU1AaMAjLIUU9ct22/lM5k+3QHs589mcTqrk7YOwBZhVGn04OkAZIvCdHImPDQroebGrm1kPuM/t9/IPcvlzOJwXx+M+9F3mxvbIyDTzaG4Hkluw/uHLa6ubrHb79zYhN8QESjUen5nX1r6QgmEhPXxifIgZwF257EoXFgVAKMOll8z+JJ9N8SIfujV9fUx640Dmr4xLutgPLaMpdBxu7/QV86fZOKu+zGPKAsl1o6n6t6CTGWqwvjdvkL8FK/l7JE8mXtS2ptpqtt3U6E8b3POGflGrrDGA6pCgJkZwfg1J0TNLFWy2HEuZJotIPBr6/e+8sc8R5NTm/ls+TQQIcWItgo4Wi1RVQ3uNx1+a/fHwGd/DbfXnyP2X4L3D6goFUHoe8D6FOeW6RwLBO97/jFB47Hn/P0+w+tce49ZSOaMBeUPsWjcXN+g/cA4jQ8WNEbVC10nqroC81iK89dUMvMuSxY/4V1Y5nIOTy9fkM+09HO5hkcSpf5bpLzCoBmEum4Q+z3a7hYvPnqB9XKFdtHi9u4OFxfnOD09Q0oJ19c32G432G63ePLsI8QoVhGmHA0gP0dEA6M+5blxfxc2oc/aOPR3u6/vOqmSfHKE5bLFdrvDp599hmfPnuHhYYOHzYOkFe36HASeC8NRWQ8iCaprGqmWbFqXQEDdNBr0bocQeY3s3qoK4l6UXY4asT4Qa6aiOgPkXMODU86WVOZCXawwPrDer3/qP2/1QgowsudtpSnXcSmr75lFmXfrg7Vte7kQ0BELcVqMCXjw/jr+XfCAxoJOS68yyDaxQos+EnOuhcCZsALgQuS0y0qIoXsQyG5BB33xI8lsTIn3eO7Hd9se1X6OgLUqCNw+T27sZe7HrTEZA53OcxkX8vzk3w4Y+txl/bMUwFMAz7BzrxMwgWcORmQAWsz/bhye9h6M2bfon3IOg+ypQ2GCownQJ4hHK6rvnjB55lwkUs6PJu9QepmSKHT6oUdUC4T9N/S9poKVeY0xZv9bwRZBlQaigZYqzbJXpEq9ZPpr71ocH59kOm/V64eYUNXGOxgwwSCfJTdnuqfX6zV2+x1W69XkLE+vch5zxevRfaLxnAM7fhtJV6bAyW6T/pb1m+xXTIXz6R4g139yf9l+d9mLyLU0As3Tvjk+kXuhbdpY8nP2bp+SlnNv8mZ3+5zKpLg2yrsz7cy0ys2s0SIyCyPw5t0lbu8eJFYsK+lKhi8mKxo6nf0ZLKBn5+R4LfzM0fbRc3n+DqhHuZk9LBdAe3J8jM3DPU5Ozgp9hdEVoAD+w776z9nvbwYyD3DjyBn4bMknqYJ9W1P650SaPHHFLQYAhZwpLVsBLA06GMheF6VNAJpx0s9SEW+mNCe/jJ1S5mAfKy1RjwjmpIpEdnDH+EQAhUKbTLEdWArDWvN59Dzm7YWmjC3EjJCLIQdIbTWGpOePKaIKwMCE1bIFhYQhAZtNh9+hP8fwkx/h31ytkYYdaohOq48+wxm5eafRZ3NWBeAwVvlgTv16mOIMjpJMsbYNP3G2PIww5iMCxtz1uGJVOFJVCS9YLv4DCxo2YQbwLRC763tIjMPhgB4TPHx70+J9XvozQULSDdpoceBqNQ2WMeFjLLSw+NFrZUqzoFibq3YF7O9xWg149uMvkFLCZrPB0fEan33yKe7u7nB1dYW72ztQICyXR2gXS/R9j7pSjU0WNuRnNvkzgV18gQec0/kpwYA86l/5hTBEzYJQ1Tg5OQFY8kOfX5xqAHhC0viKlFIOBA+VZCkyLQNBLAW1WqIYItkHjXuwS4qz2S4vDLF0S8Gw1QwgZLMoyARDG5sB60xVC2PUfXAwJ34KRpe3CDnG7rLIFD24f/f0mrbhX1oOl/yS3KGftmQMZWw1oAx0y7yZ1ly5cQFAZKAIuV5LacoYnnubEWi9P+k+N6BBro9TMCRMFaM5ofE/AIBEKWu1OY/PZiWTs9FzGcBgfN7td3uZzU3GUnna3ZxlMKbz4Zg3+zGNCKm2Z2kxIX7+BhKswWQJxkfLqOdXbx2BBV27PLNOeMmAho0pl71crESp3KmKFwaQhkEr0CcMMeUEDMMwaCc0fXCU81wy7AjASClqnELM9xjojtoup5T7+Zj2ytataDzFzZBTRKAabbvIwDBUQb08GYtFK0IIJ6nmzEkyc1FATJJCvKUaUszT5rHsl7L6ZU6XqyVubm4AnCNjYdsbts+MiRvdUU17EeAn58e/zxAOGexi3Y9uf2UUpFYPpAKq1RqU/7RYJ6dRHo0r77PSDwPjftzjZ9zfeR/aeaMyBr+eDkCPDzwd/My8kQ+/H52KcmSUBhXgOr3HWij3Am/eXuHmfgOgUhdHjMEvJmMvhxr2tqJqELrQNjWWtVScz6fqoNNFATj6igjmVgoAxd1R7l2v13jz5g2Oj0/yePNxmxF6y5Nc6FSmF4cxBZ52jGs1+RksFgtwyrMwFvoovxPIXtkji8XYLSeAPM2jQk+tWRq1PyK3qsyajr6MxY/VK0dG+9X1V/pk4zA+kaT2i/MoSKY8GVk7xoo7U5IounZHQmikCRkj8M3QmjYoyVKSZBmttjvUFRCHAX9j9SWuf3OBv/h3jKfcAH3UmjkpK3D9XM9hVC9sTL1x8ppxzHvSpoWgXiG2k3XuKnAeu+5mmWaHoXI9udFSTfiw+3zaR3+/PTPEAUNM+O7Vt1h98jE+5PpBgoYXCsZB3xhNsL+/WBBKLIZd03oa9tODzeliFF40DmiZBppb25Yta27CcnHBCJydnQJ/9U9xfXWFruuQmNA2NT799GNlRoRnz59LbvmUsD460s3JIM1I5fmYHZ5M9FPKGmfTrvoNkPs23hGOWnM+5JIpJSGa1KqEwQoq5g5MQJl8HMZgkUhjTqwuAav7leuDPe0IB4/mswga2Zw5IpwmdDjOMxlqXlxOeT8ZyBYm72erMMSRlgkz+4UBy6NNlu40t8FlXOQ13p6YEuAZhWfquj4FRtAIXI6YfCqfGeZhTJYnn3vWtPEToWtm/gyulPUZC4CeKdl6e//bkkGnCECFodpPKi4UIyYrzH/UdbdDvKuYjLvs5dJFO/eAcwIr75ruv/x3KpM3xXF5frUl23sHzFzFFDJ3QMopFm1UIxBptGkEALhgwPw9kGJETFJUMjFLnMIwIMUB/RDBKWIYxLoAZi12V5QCiV0VXA9atM9RXVHGNKfEOVjfTTAzVyhmxnK5wGK5RKhFydA0rdJKUSDVdQPAfq+K+6TGbFlMk4w7oe973N3dIsaEECbFuvQahgGMhTvCYbx+ZdPmZ2vL5DfTHuWpp3IkdKyc91tevLKWuhfiIBZfO7+syRiC1meAgSGWuBMQOcuv0zibpcT2S95mnNehoLSyD02Yodw/u1d5W54N51rj9q0f12hfH+xzcnxk9LRr48OvcdN+LiYAlY22MO7uH3D/sIFYxarczTwvur+C+2hCVFC+sjkH1uvlmE94YcHtqZK9i90+IcAL/Y6uAmKVpxC0XlhxK4Y7k2ydmvKS0eabjMDRj9EAObcA/6HxZAPoOeGDtucxEAUqmRZp/N14Yt3ksm0Ps9Qc0toySaQxezac+b1XlHtl2LbPOa+3vNPv/bJFC/03fENVBQQGsxV9ZKQUs2tVYgYlLb5r66N9Jh2k8X0GQCllmm/Tky09CSBEHB8f4eHhLepmjX7o8Z9/vMXwrsXXv2IsawZihBMJZoWJKe06EEaSKiso7+5ZAUDuK2tmtX5GbRv9gN9Zjj+z0RZS0uVwwAwdeMzqURFJjEbXIw7D7D3T6wfHaEwnTiagOnBh8sKIPTuyImB+QqfVD/PzjoCZNcVbLKb9G9wEeJetscuMBZHX4BTxfHgFWq0wDBFICWdnZ1KzA9Dg4wrrIzHV1u0CMfH43dKwIxcKcCnkBWag5G0fEUA7tLY5C3jJpNAfcqUI+njZYp6osCN+mWCV/erTs2VtAI/JndHRXO1awVgBDPrmvG5uoXImLsrvzjzA81bPN/Ox8L2wcXtimXtns+wb0d/NXcJ/7tr3jHJm3crnDkRY0Ke1NQK78nfOrmPuVL5LxiTIuRNlwQWFaeaz4cZlgIHcN+TdEc1C4efWz6Mw2ASMYjgmI9a+Fy5Nk+WwOWX/XAYzZQ9bka28OlT2/+hdNu45dKFtlzB2G5YDDW53ZCamRNsUAGwFBJMpHQBmqQthANxcMlNUDWkaJN6AWT5Tq0B02fWKG5PE9iTNCpDY3JaMEYpViLzQwCgMxllkJUmCMI5QiVtmqEK2LJpbYxUCSF0afZV30YtokalhQNftcX97i26/ByAuSU9evJBCp3Wdq9h7ocvWwUCKLa3VhLF+VlVAVfe4ublBHCJQW7CjrFFQZU8/DHJ2Kq+IKIyzrGz5nSFunH3fo10s5FMuCprxufe1MGSfw/ap0tO+77Hf7tCrm9gQB8QhIqWIYUhitdGsSHVdY7FYKDkNSADatsXx0RpVXSPrRpnh02/aPibN0OfVSSOhItN9uHNTxlM4itcfe9pY9vnoYn+Pf9/kPjfP+V7PjyfCSf47/wSmxeS85c+EjsTAze2txtiF3PMCfo2eeTBWLFblm3E/CcB6tUZiLfTjeGHmje8Toow2mmCQSTpni/zR0Rp3d3c4OzsHa8weYFWi2b2qzE1ZPR5NeaFv8r4cr5WH5dfdGnY0TueI3LoYmyAqtEH+Jvj5tPbMOpf5kl/e5PZNKjzPv9uSGkzs364Zz0sKoPVbVJqy8+HpNtzfZY8ZnrHPROsPMGsxPxWIUkxIRIi67knHNOqrG8tISWrpBpLsPYQEYklMc3F+jsvrWzTLFXpO+Pu/dYL/49sOi80DqpTys9NrasEfYV1j8WzH0q86Z0wyFVDm3vEhl78r21+V9yTdF3N17gDk+R19lxihIrx99Ro/+vijD+rDDxY0bAIttgJAtgx4V6epZnmadta3Y65Y3hLxITEa076NzGwq9Fj7nhFMTVeLxQIv//xf4rdxhXRyguVylRmkpARFzoC1Wh9hGAateizM3rSG2WXMwK3rnxGMPCoiB1oN8BrjEiKV8iYkSGXvMSDLmhGTUidMx7Minz3DsQP9O72HMMudDEaicuCNYMJSCjIfHBpJHTcRDlRKyVrPpPqPCdC3dx8AYBsrEYDJnMHxRmM8o+fNQWLKfN2b86u9pQKO6Ns/nqEzMiA3IjamKyMmbWs2jTooD+j8Gq237DS5u4XZiPBp45m2Yx/ZetmH7GwHo1E6aFM+T8m5H3jBESassuuSCRPlc0uXS5nYZwqbr7Ifi0LA/5eYkfoha+ZTtJot5VwPfS8uRSmJeXeI6PsOwxCzK1IZn3WhWPKsT17wyfyObVkmM0Tl5Akds2rRmsa6CpoeWdyQ6sqSHQi9q6sKFKpcnMxcR6VuAI9/Go/wxF993KHzbACBNVtYjAOGvgMD6N69BbGAvXa51EQMLjNe5kFjBmf7V14n/fABpWJFlX2dErIVByagkNDhGBPqUWbAGTDkAUFKWK/W2O12aDW7SbH8Gl10tAW2jvobs9RyAfBwv8HbN2+webjH9fU1un2PGIcS7weM9nD5KfMSqhpn5+d4/vwZXrx4gXa5gLmzSflGSWtNGnvAKY3qfgBwNUumwx7TuOmc0Ogvz/SLllbuUyWfyyyW1xFlzscCgqNjmWzljTbTT6NDZsH3vbN+6LoECf4eomjiGZaNkPJ2KzEvBWCSwqHCj/RO5dcElsKlbQOr3WQ0NQttcySRvdLDPvLYwT+b0DYtbq5vpDBu5tHjOcu5jowu8tgSMALs+T022gQrSidb1q0L21ojzzlBhKBg80cFK2V3tOn+meCwkfBywPMnSkE4nnfg/lVo9aMX4SCDZnaVI3mTufZIV3UuRaNXaKtzKxacFYoiVhMBsCUVSqKAjok1No2z8odt/+S1L2uXAkGC6QkhJSnIFxKWywaLRYMuSiKexSLh858+x3d/usUiBCAWTDxSwL9PyNV7K6KRggmJS5p8bcPa9BleH3vHY55A3rLF9hwzEEIuOjjnWeSf9e8IFMBDj+t3lzh+++7xcbrrBwWDT12PcgdZrBWSXrQeTYgH9f7ywshUcntUEnSXfe4FCZ+5yrt6DcMgtSEm7WULDDPe/ft/gu1Pl3j29ClCqLB52GKz3aAi4PbmFgwSsKNpYBlFePKmbgMf/vcx4dHjm60TBqzs2/xkscLAgS69zVxH7G9yfvnwmw0laDr3wgHN6bsz4+LC9DMIo6nVYjrGQ6bjqOiIBI7W3YG3cfuOaE+Av9sxozaF10yIK8pnfpT+4lHrpU/GlRg8DtRlN1eww2tLz/DRkSMmkg0oOjeZ8TqA5QBvFo3U1MsKnNjy6VJpK40C0v38FMZIgCMqmtLYCLu9k2yYIQvDNtZiwtWMIJnVCiM2Id+AfYxDHprUZDHAUDTQgQAYkGbRrnT9gL7bZ5eiGBNY0zSzWg6swntizn6p/px4sOI1WIAGFRLE008DnS3DDIWAikK2IkimtP8Pe3/SbcuSpAlCn6iZ7b1Pe5vXufsL9wgPj6Yys8gkM6lkUTCrxYQfUGsxYgJ/gMUE+C9MmTGAQY2KlVSNqGIVJEV20aR7uIe/9r7bnGY3ZqYqDKRRUdt27r2vCFgMytzfPXvbNtNGVFXkE1ERUZLzIRIhpR5JXYrkwEZJrCDJEEyxqIDaIZ+CbgOLfggjdP2GkarDl8QO7AdJJBDEzacRUgCALswHKStleeb29hnu3r3zVLPDsBWxShQqbMGpz3uS83GYZDdMMurXPHXGawsDxIycdW46sBB6z7lgM9SlFfvK7T/Cd1gyAL158xq3z56FQG97JGSzoihoueEX0zjjd7/9W7x98xaP93eY5sl3mowvpcA3GdUFqoqLEePxiP3jA3KZ8emnn2K7k10WAX9FUrMCdY2YEcZRbd0NbflXS/O4Xh34CaGVLuH5sHZBix3v5rLOcKAZ+ThFGrZaV5RJ4dn6QlMHAeoWJoR53B8BzR7YTDOng8kqJWTgudF9lXw+ydq5vLyCWgQMM2vzWg7Pgeb+m9HMu8YwYA9UhcbcU8ZpwtAPahyDAtRSZbkD8mA6MhmNqhx5uxqZilq30dx4IwikGRTNqODGTFX8TeGPYyKsTecOF7RjFOprlCf7SWmKOK8iurGxbdeijZhXYIoUQvXWXxCIpF+Jkma6ItTzLmRM4u5NxDW2jsgLF0WLwR7E3uWaFbUQa4KMck5r7RYz9CA/AImRiuhIqevw4sUtvvnmFdARTvOE/94XHf6T736C+ZtvkHDCU544TykeFJ433lmxSXQhq++ZMT7KuDVMvbY70RyiDcOFYdQWSkZs/xr+TgB6JvCccX11ffb72vXRioY1xBZg13UYxxEAuQ9j7FA8uTvuMMSy3teZpzSqZVusHrsXnxf/ynr2QizP2tR1Hd59/zX+o19dYx4PKLlg6AccDgckSrjYbdEPA+YsAnqaZ2cErOVxYY3CYhc2sN+Db50pDP4jbO3wghewt9G+FlhiI2UECnYBZcncFOgLqiwmjwNGB2M2ceMzrAYrrkwvgAALnjKfdjSLbDFeDSdqGWJLC7PgBwm/EGK+xR1BTOMjbORZCtnKWJvvK+XXHRt7xn7msziFNotRWfS1Mt6mFu8r17kTG98ADSm3Kk8lNJkXZdZym/sBcIkYX8w/QJlwhls6QO76U9QSXbIE+NrnnDPAlpaa1XKUPQGBHfQoczjOyfZy1Y/rj3UcRRFKgTTk/ZG4ETcq+MGKdl5L8r5TUlCv7X18eMQ8Sdaly90lPv3sU+y2WwybAXbeSyJCv9lg6AfM84xpmqSfrijVXY06WqoUJoodrNgpdE6Ag+0UVbBF/o79woBmSAEb/0pA0na0WonSqVaaKCEVxoCEq+tb3N+9kzTX7SCENsosqZAhWmnFPSERIZFYEROAoe+x3e7wcL8HsxzQN6ugB4kFrFDCPI7gzeAHsJ3tYTLCrpH0dRh6mVML49XZXNJ1z/p7nmdwZkzjhO+//R4Pd/fYP+4x57mZS0DdTSU700fLi3pcp2N6Oh1x9+4dbm6uMWx67HY7FDDGcZL5n7Om7u7RWMnbni57Drfm+mwKRp0zoBZG3A+yMxqe8z4YsDgDnNx+XvJdjrspraHo7H1vQZ07p+mE0zShidtzuSV9cZ7rpAr8wC+hRWHbLSnY7jbKH4oG8VY6Od9uDE6hvBAv51pKeFZ4s/C0y4sLSQpzdR1GRTFEM4qBobp8DpnOmvm6APKewEB/C8OsbEKs38b/jLcpw4hyqu6m287EGj0JruxYf63piO3QuWmvLk59dJ7tk6TOdwrPxLrt0GRRMghQPiJ9jXEl8P4CCIf1ugqlqbq9IvhOh/JVkQWaLCgXzEXkmeAiVDdMRkgBXMCFwKn4XKOU8MnzG3z3ww94+dlnSO/u8Mtf/Rn+6s09ujyu4o33Xb6zrzRYy0ditIsGczOqLxMoxWuZfVV2dSuHSOayxuLqy372VFuW75St4G/igg6Em6tr3F7/HSsa8yS7AlqVCr3kCkTcflm6Kr3PDSrubLRbpXLZGQzxcl/qkFXFdiysfrtsl8MPmkN4huVgqM8uEm6mDj/cn/Dm7RsQJbz+4TVub2+x227AzBg2GxAlDMx49+4d+n5AyScty/q5cPsKgrMKbnjApzM3bpk4G7My8G39tjIBYGGJQEO75fZt+xwvQTNHAWcW4iC4KLTeBDoFUG6uPgYCF0LDpfdyfNsm1/ZIIyoTBQAOAsmatWSeAcDLM0/MPTpngHZZbo9Yam1qS9PmN2fo9VfBMdTM62ox0jkRjUaNclXHB9TGGFn2DYkZAOoZFZE+MV6AJWapFBR1Kcp59uxkkqnIXIt0jG3rmesOQqzD+uw7CXGWuexmn+fk9DA//6SpkU0xqBnnLCDXDBV2vgoHFyR5RmgkrkYG3GvsUXXK0LEtjOPpiLQZ8Or77wEmdEOPm9tbbLcbF1SduRRpG4kZPGdpI6udLgi5BpbT+VlCURlxv+XwDPl81O/hrB0RhhY/EZ1idI6fuSbYnBN3Hpkakkby5Sef4uLyCpeXl8hzBqWEjCqwqjtpdR0qXGNdxGqoIAF6ivIwgAi4ubnB/d0d5lx0fhUP1ExJ+jTNs/DjrkN101hcS77F0i4JNK/rus5BYBxHTOMocTBJ+kqQw0KHvsPV9SUudjs83N/j+x++x+l49Lluh4amMBcTEajrMNi5Pinh6mKL3cUFLi8v8cVPf4LUdTiejthud2AGOuqRc8HhcI/74z1evni54HmLiyKX0bN72jv617IEKU18k8SgQ+tuYz85S7cfnhbBbbNiQQjgG82UhYFV/2ws3oAyJez3Bw92db7YtFGgOzcrRNdBEwho5QqfGYYOnWGOAJaleI7VtIRpbrU0qXxbv2eZ730/4OHhrZ+fJXsT59Z8l6GNHGhlQ2xN3GlojV66unX9dRT4ixlOEGWcl1iL4EivpoPhdzjJozdCQTQs2rV0xWulok0v519EwQUoglVCR9Uib67hlMUYm5odjTrPiQikCRnM0EQETVJS67TDOgmmOBCSBZCnAioFOZks1XO1DGcV9kOGCxgeyEhAwoyL7YDL3QZ3b19jt73AP8D3+P0Xn2H+7T1SziBiZE06k5galzGgZn8SOmWXA7lkAf82B1LrKilDZ/Ksyn/EeeHPnUkH0+iC0mZzTXEIy7lkoCo3lyyr5dKye1RKwcVui89evsTHXD9iRyOBqEMpGcnP6qxuArY7MM9zEFjVbSqefRGBoL13DvpULC+0KgaaZ6OS0viiBW0wpQRPUgO1Iqtv5HbY4LP9b9FRwosXLzCeTthd7vDJpy8BMKgjTHnGPJ4U4AFQzdh93mCTP2ibMPBFMPBsTNi3v6IrgC52DrSpuxFWRmQclRdTc4L0giGcKRz676JuNpJr3cmnaqoTja2/9XMLySOwo8DEFpxtyfjdKseIh5rF9hstyeFUlSZLtxjFZAh7FF4OhQUFL7kyzgwDg6TZh2qtrfWdnalFOrTZq0xo1vGxQMKiQJ41bV8uFkcg27yI6Unn7Myw7j6oO5HNrFJpbQqC1CFKCTODFFxZZg47iZW4WuEl6D8pj5U1wh2cyQsIIzkMUoOWLebAAVsnMQZINV1yzAInLkcC8PpwiKNZ+bMKecECjK4fNEg7BzAuVkADaCkk4CcbHxsXIkhAL6FjwuV1Qv/6HaCHW3b9ACbJwGSpnZkJ81yQOfvatEMsxXBgQCXuPKi18exgsKryFBMPzbqsmfuEN4hiUQFXSGQRjTJkrg+mNKuCYUohiztTKXI+Rk49hqsblEQ4TrOMfaorvbpnCB8xRa4qL4TE5GEhRIyryx0++/QliAgvnl3jr//d32CcMvKckQsjc0Gvgm4uGVPJIAsIDyvP1lPNwiI8KhFh2GxwPJ1wsds6Z7D+3t/d44dXr/HyxQvcXF9hs+nR9TK/jJ6H0x4//4M/QMkF43HE6XSSw79KNY51XR9WcpVLdb1LEoBxmvHDq9eY5ozD8YjDYRS5yAVgSX1bSsFms8PV1RXOeJ3NxwgC1ehVkXzr1rM0wMm84KBRWDERfC6us3tWfwtXWjnsUkue4/BWzBrm4KUCShBwOI3aNVsrOteisAH5Z8+Gx8vmmlwHwEWMf57BkmFxlGaZ97SoTZsWfbN11LQ/NJ8JPDNSN2DOelBlElfHKEcBaJyhtb+CNWWvbV+sTt/tsCdauUmsrjAwDBVjm6BgM9DL5gNk3VQWRE2iluqGRgvlyvhTcNsia6/8bnLtzHinZLbyRG5o0pHg/WDKg+yosuMpN6DyMiZFyyMDyvI9WZkphYNY4bzZxlfqEkMRpR5UClJnccFQ45oqxgtFrzALQFf34NwlPHv2DF9/8y1Kv8VtusOf/fwF/qvvtri836PjgqkryClhlxOQayxInSfial+Q1CAiuydFzD0AOZJs6FyKnjmCkJlt5ZLUuHXPx9YaS5S7z3UmW9MMFDGOJS5hZrdKa4MoiZA7wszAdDiAxnG9MYvroxWN5ZkYHg+B6oa06rLC3Ow+RPcpEwRxN2Ttan3KarlWX/Rd67ruzEdNmE5VeKwdpRSM+z2eT69QIJPg4vISXAr6rlPXjIShr1ldxnFSDhLyGteKvL+yXlgXUAX1brk0ZSO+riARbINdJz9zcbuC1WVlOp2EWE2J9icKaAcO1mZ7pwEwunKbXemqMNWyKaBsrs9qPcbMa7O0/42QrOU1zM/S2EUGguXnKvz8TV0ctQrx/4y8pJ1t1ivNixL6IHqBBZXlZjft7D+VLgzJguF+oSYUVXksmrmI9VA0mTP6O+yzukwFujcKK5aCM/4hZ7Qy1Kqwd8lPUJfkGkVS1BWpa7vd4uL6GkM/oOs6bHqJuUIXFPZYntVhUmCx/tkZJ3wOlMLoUkLfdxj6oUmVStQhdYRSgFxmCSrWlKMAMIfdSeEdKrR0ztouRJ/I6WoKu8RYSVDvdiuZlx7u78EgCRzMoriBpsBVUxVgvibg89dOnI1dV9HQ0KGOm8yl+JKJd1HcqXmf2XZ0zWXEJ4TXV0JbpEhVwIooYV2XkCH06siUsoSedGfJ6R8zVllrF64MCD7iCeg78jN4hr7HF198jq4f8K//9V/prkZ2WvVdh1Oe1bWob3cnFKVUVw0L0Jf+7bY77A97XOx2MP5RuICQ8NXX3+DVd9/ju2+/wdB1cpDoZovtxQ6bzRaJCPf3d9jfH8EAElLIHJZd8c925pDLK1HQq2yS2JNirrCqEB+PR0mFaspz36HvEq6uLnF5eWnQrkrrILUjyKU4N/RXH2hbIBEAKM3OItsC4GzAK8J7oexoZlm/rDwO8y+6cUbwKd4HzMA0njT1pXEksz47h3JynEkxQkgOspBnRNhsNn42DOmoxh1BYG5o3cpYUwhocbBoW5e3Tw0lp/GEzWYrCmVEXqY0VAHbyNp4KHXl4VUun/edxR3OcRL5fGv1JjFIeH1Bs6lAUUe32K6RKbBRwWlpk014ghs2RqFvpFmjGoHqRaWaIAQS/O+eDiYPyM0tte0RVRgfAESOcVYyVHlDhLCDEV1RWy+GuNucdLczkbjjpiRxvfOcjaKOjwgao8FixMvI6Loez58/x9u373BxcYW/d/0O//YPPsXxL/8Wl2PCthAmmx/J+GTFzc08XIudeeIS/LuMrzx/1+RijBchZzHn42009oNZI92U3jHswb1vND7y3bt3mP6uFY0Y0xDdpaorR7urEBu+5v8Vz7tYKinGNNz/+izosS0r1m1/l/EixBLEGbNfpZSA8RFXdIJvvTL7ydNEhNPphNFBuSpYSTK3+F6bCX8iDZDNClojTzKgKR8rKLXfDO4KQzCeLmSpdgZulk7LpCqQWRMd1Zph7lxPzvOmXS3ItfEJ1Tbzd6ED+AR35Sr+uBCSjTKwfEyZSGToVr0/xFCmz2rJXaQtNfBZJKWlpCxVIOo7CFyt56UqBqyBzf6svcdCeU8PHOhjdIuWwEgDA48CUsKuGCkntPnvbkS6U0gA9bIL0GmGI9sliIHIZPf1P1MubTdtOk24e/sW7968ARjY7i7w2eefqVVfAjgbC4pPKwtwtDGqQb91XgRXNxJbpqy7jK7vQV2v64h8Z4V5Bk8SNDznGZ2u00lTVctjFtdSY1dMgRF3mBwAzGIuQnZYSupxffsMp3HC9uISmYEy1635qjnoWqqowxm3CXT7a/XpXtHqJHYRpos7rm8CiVtMqod/wp8X3mLKI3MNhLeAdDA3weHSD/b2kioNCZY+t+742t++79F3EmxuVtSu61wZMcu0KBYdNsOA3jIJZgFQz58/x9X1FR4e98jzBJSdpkPsQTRhnmaUflCgEoFm2DlFpW0BY7PZ6sF98JSVstwKHu7vcTgccSKJo9hsBozv7kSx6kS8TdOE77595fOwsgo7q8SkcQkKIHzOCZvXlNXKP22PSrIsKm072c3bbDY4HvZSvgFwL9AHxCYVjD86hw+A3Bvr/CPcD8pvmGj1r8/jc0bPoe7za6mosBb1vnfsTWnX8XTyolqlwh6k5jyf9bJiX6QrfSdSNZcCsCiKlgjF5oxgf16UwqERCrqtdA700u8W5sQMbIYNTscTutQrD7UdDHvceD8BnGDJuBnsh6dWo2I7JhWrR8DsUS2BD0j5zFW+ECHIHdspiQbMWEeUTT7Zmotj89Yu1ilVFJG4qy1BjIIR4JK3cU0WEfmoODYIrRAsICxMsl1ywJPGp2GGEc34Zi5CPsxVvtoc7ojAZMk9OqR5BkGMBtl3yYwQddxIP19dXuLx4QHTdAQl4Kc//xJ/9c0b8LtHbDTxydwROAHd4viDeEkyEnMHfXoRuHfQijfQ2fAYlqC2PEkncr4REJ9d4vCIqc/qZTHMEYvr18dcP2pHwzSlmG3JGO9S0YjKwfKo9diheNCeXawz3sqTQMyWQFZHDIyJgxo1SUnhWAVqfL/ru6pkoC5aA+7ZgnwZ1ee462CixpgAGYhHAQoFNiYrk0mARCkaPLtE5PrB+i7z3IRQZbb18cj0K4OJzzkxnYGG8yjiwo48WGnZgMYAnNtJXC0nztBL/G4C1CDWCoNTtFV/MxBh4J9Dmrp6WvI0TaIM5OLxBUXTnppyUBWL4gqCtFEDlF2J0iHmogehwQFVBDZN3yluYwa/UCJ0HoOg4Fr/irsRNe5EFodQYxN0jnrcgR0eZtvn7PW5QPHxMTgYmXwdwtKQn9H3krL54f5BfEW7JEGs2mbNpaPGNQNIyvQU3NZfyNvmZGH2LCCm/FHqMBcG8oRRG+lb5qyCkwiEhLnUQHBSsNcIbAN+C39uW7B1igs4sEPwOBfsLq/w0y8vQX2HccqtMuH0C0Ke4qa2TRA08z8lCuu3uh7Zs8SmGASFxgSIHUPezK1am6UFbaegpEiU3y0trri1yYFj0HS7CV1KGDT2pO8k3oVR6ns26RvQFI0MMnkK6i5FnmZM2n1xzyro+wEXFzu8efcW87x1nkmAp1IszEhRoAea1nNt6liSvifg0iyfDFBSr0sxDvX9gOfPn+OH1z/geDx6qaK0mnsuqUoTVoKWGZMOLFtmAF+7LjLPzlMw188s4zxNE7788mfSTuM5RGjRqXU5zmYt05T01SvKjdI8FVae9qsEVvyEgqD8NypYrStuXd/x/Sj7sPitMDBOowfYVkfcKGPkW0LbRN/JoPCsyVpVHkvJEtlh87Jk5+Gh8/6uKfb1ARt/lfNnv7dj33U9Hh722GzUfcplVpWjMsdFyTAwX0zhsHaC6hIHWxhiwwdSl0L2u8oniky42jblw0FswsPTmTWVK5q164pp8OVvliHDA6nFiCa7vDlnlHlGnifMGmflRmaVtb5Z4vxbiyW4IDKDWEod+l5kTd93kqq4l/+6rgfIcCFE/pWQeQu6llQ+EwiULIrNQDG7rCSVJQBcXsvrCZQYqe+07AxkSWQB4w5cY4QZRc8z6vDixXN88+236Lcb/JPtb/H7n32G08MR3SjGsXnQvs4Vg7jCwGbgIW+Lz7kVpWSZMSpi56VC8ZSRX2L+4N+BdcUiZm1dGvcbjyQWJfPy4kITQn34+tGuUzaxOvXLLmxAjM8atKYhLQmyppkt7y9Th9XBqn64cZdC0poJ0Sz/cN+lRuGxd3xAHLRU0ERE7gNeMUDU7mx1QuSyLjARGBXyuUJW9CRJ3V4zq5iBc1Yt2lPVNvDf2aLWLc8ZkG+umMnIHo4CwTrjQEyeZWtbBBsxqEvLovCyubD4+OrnwgWcK8AXZWDSIFE7GC078KiuRaJIzLMcpmUIuaZOtZ2KUlNU6rgFyQSjioOLFGOGIrHImZorKwxstxuZ432nwcHCZLrU1ZiElNSa2WY86pSxCiBJzuHchULb6FvKiEq6WmVs/aiYtbgKYaaaq58tZiFyK3gZ9pdZtokNvtiw5zJjs92h22zA0yh5tfteBD4lL9fFBqUWath89zVuMj0kvfX5SQFjVbc9wzmNgmrjxxIz0/TNf0MQnCpMDSz5R3EhIlVQhIbs1k5CAnJxf/5ElUYy14M1JyUbQTBqFiJmcQWDr/26M2UunzEFZcweY65LXSKkjkDqepKSCGPb5bL5a6cV22Tv+86DRU2BqePF/p+fH6KABlxQshBp5hkRpTmrWCh0Al7qM8aeODzL6ne+u9hKsgHNFlUKwJ3svBS9TxhQncWWILiOr833lHpMU5Zzi+x/XLDb7eTgVGacTic8aPrZXCYZSwKAunORiGROhSxxBsRy4IveGuMt4RLjQXIQVdloQUKH69tbvPj0U1XstW9+eFjyA1ubYuMXaiZ7U38MDF+/6u+mBJ8B9obe9mtBfLo6a4RyHZAbmGzPpbFrLiUYNVSZoLr+IxCNLSCQ5S1Y9AQwV2WT4xabBIYDfo6l+XfjB8ZbqrRssUcUHtQQ3WSDyBwF6HCO7rw7l+w0Nn7jbr/c0r3OGWrqEVBrvMXFn9Ba/e/duyGE8nhfOMq9gD1c8bJ5aI9LHwpn5MzIc8Y0TZjmSXfyZZ0xs8YreA8bvl/1idRgicrnGXkuvt98OolxIKkLFmlsX9d12AwbbLcDtrudJGToklJaXaVMOVe+KofricuZyc6ErHxdlAhSeeUimIIXwCCGNZoTiCaNiYTOMdsNUFqWgt12i6vLS9wfDhiI8E9/csB/+jcJu3lAX7IHa8erSZaEqkBWLNLi46dwcZ0r5zsXS2P/8nl75imFJJ5zB5xjeH8+A5uud0Pwx1w/6sA+23mIvmBELZuJDbbGLstZS3e7vOLBfUuiR2JF95i4uxHLN4tYlzovj1mD/agqEQ7aGRqsQ77IfIaqAAxoxuv0rXeQCPNik8bAtU3AukXq266+ACrbZYdkIZ7CHiFzOYlSCA5maxMNylbm5TSuVbmbkE92sIACYzSlYJonnI4nTKMcdrXZbETQ54xplmxGksGoKgoSjyBuSmDLbhSYn/bdgIv5d5J3KFhHdJvRgFzqjZHYbpWCEiJALbkEeHYj+dzpeQeVGLkUzNOEH354jTJLIPLzFy9xeX2FYejl9GQFF8vLrd7cKtyGFSyw14G/TiEZJnbhAWeCEpwlQFSIImW2eeiFcXY+1nVxVKZvcREECDAyIWRlJkIaBmwvLzG+m9QtUt5jHwcK+YFsLrGviZipqspqm7kBzHCOTUQxocnxrgL9MElNcanpB+vT1r76tsIakjZ6sDpZyuma7U0UqVR3kJSQvnOQpCyjZRhwALrXs2T2+n4i9l2rXl2P+r7HkFQ5UIWh7zoXOiJvqyWtKk0KSW1+LUCQB/Yb7irVym3b/TY+FdyE37G8DFi3AqnyQHbMqZPMgQ0zAznj4vISAGOeZuRJdh0xCE/PMzDPBYkUCDiPcyKGPtdx7vseo2d5EmtxzhkvXrzAt998h3kSy9qbt29BYKQkczkR1H1JCpuNUD63jPcodeMiYwOMNSMNIDE9tuO02eyw3W2w3WxxcXWF6+sbXF/fiJtuAFrs9c11bbQahNUKSXdqsTyLQ/+Ce0qTeCJ8riOpvdNxIpRwwBzX35qXYptWJkj8nYMCG36f5xmm+JsiWWXbEgSF3RvTMMj+cPOUve0ps1VexzTj3mCdrwYQI29qngxgOawMLJc8kYLF1NX3RS+SVNh9LyfNa5pwNoGu67EmOYlKtNAoQfiR1xrWfC6M5GNO/r41V/pnOxvye5Xj8VmLWQtuTyxW7DmLrK5geum+V3cOOo2D6zqJs0tJeBxIDi+2XXl5PykfNQO1qtpEmOdJD1Sd1ENB0qGPpxPG4wkPD/Ad/2HY4OJih91uh74fQJ1OaXe/1x0N5ffEkjKXlObenmQucaq0AG5gGtDpGUnABHGlcpdeGAYiMAmue/78GfbHI/Kc8SdXD/j+Zwf85V91uAGh83l3HvsAQPmeCebqftnGrcFxLjfz+7y85fWUsrF8Nyo2yx2XqKAu8TfJyGIaR1xfXb23LXZ9fHrbPHsaLgf2Xbt7YLsMcadhTalYBpYvs1FFIqwR7WmNTTPWENB3cnBg5tIQMZabUkKh6nPpGxTE6pLLzgy4mE+4+StTyMNsDFJBgGXBsGwUqHTw5wwMAW4Zdvtl0HwNaPtuC+vBbJzdpzDP2XcOChfJ+OIZenJ1HXKGpMwubI2Ci5x2rkGkKPWMhKw7ELOeqYDlDhOMmcB5E6NuVcKBdt2JSpqxTFzagJQ6PSAtuBFJxJa7EnWaEcjiEkgVC9ulcLqlzoG+I1CTP6F9vouiStTj8YjHuzuACDtlbGQKBlHQzHzWVRq4ImFA0O2XLRim2giZW2jgslsdG2uVBtVFoZhsFta+xY6a4Mzmdp7VvYA1ikH7nXPG8+cvcH11hc12h9Np1GwntZ0VNBjtYt0VRCWyIF3paGauAMOEb6BdY6SgpAKXqpIEYdZd12sRLNvXCDxA6b48uMrWDuDhLoHmBllEKJgSYwqHbTX3fTh0TxWHRFaXggR1S7LDvbokioYotx2ioYA4a6AzAxB3hEobo6iBicD/Ig2Nh+gcKD7W8OehQl5Mnr4H2iSplBOzk/MEWB3+ZFuwAeMq+KrCY78VTWnbdz0AwjSrZZQ1cFfLzzlj7nrNdGLVmpA1dxPUfoOx2Yif/LDZiAEnEeY5Y7vd4o9/9cf45uuvMU2jxPOo33BRwJRI0zsriCoMDL2AoxLcT5arm3UuJGYY8C+sbgWU8PLTz/BHv/wj9IP0l1nK6zcbcQ+08TAFUtc3u9LdAnQbVlDIrkZLQb9A/s3YRQbMzZOVxjXRAEixfTPOZwWHv4u6m2fEXcXkhPfM6oi8qWnXssygEzR3WPAGMypTWyjeyvMCsoAD8AAaK40WLkSukHLTBoLIp3GcMGxqO1MiXF9f4/LyAhcXO4zjSUC7Jpa4u3/A4ZRrvVzlj7XZRy3GF1iXVNHLzgtQx5VNhqHhC8y2A6GOVPp8sXtu+AuuT9pf2R0goDMewegGTTVuuwMy0iG+iTFNJ5QiymUi0mxtCRZHB9Q02eLKKR4B2+0WV9fXGPpeDT+COU6nEfv9I47HI6ZpxOHwiMNhDyJCPwzYXWxxdXWNzWaAeYoQJc+eSJSQOMTcmZGxmEJSeYsb1IjQUQf0mjWQZskpwDJoRidjon3f4/ryCu8eHzDNE/6DX+zwr3+9Ry4bZIgnRhfwXmdxbsy684UaJ9epO5ILfPnPpEFcO34vyOM6HxOWuNnnuzUlzmvDlj4l5ZMfJKu8y0UmqtKTS8bVZoPdxRYfc338joa0QNNsSexC3KpZKgmipdUdhQjyW/ejqjXVHYm27rUtorXfYso9dr2L3D+XdAWbYtQPAwpu8MgDLmiEsANu6hAwZacyi+JB7vuqFljLDV0kR7wEykgLLLOJgXs7MZl1URXfSVABq0DflIWi7WXbHdBsG/acp0lleDlO00UsgswVdsZUXMIaow4W5qKCOslC8MOsSN08iNzFo0ldqkyDCO5eJ0pCPUgtJXGjMNejOI5m4a2ZKlBRYvsxgKgWnMXyWPtlsQLGKIWpCh27vgcj4frmFof7B4AgAcuq4MhORlUY4CULgj07zyMI/dheEfMmlDVmImQks3bPyvzgw8LNegEAZLOWtrFNpDzFsmVxKNsYpgXx+XkchYE0YMoFuRCIZpgi4DxK145t+UIVIofset8sS4Bk7DC3JOtjjT2wMkJ5dkqslafv1/FUepoFJvQ5mYufzxvy3Yqhg1jfiNRVyc7HgCgGFiPjfbDlXXdxxV1UAGYD+JsrCHs71BDVek3hseUukHCIsizKH3GBEKvN9Y3lTof5a3PN6+3lsQOuuu5tp8faUp+3dlr53DzjArvINy6M7dDLQYd5xpwnEaxlFgMAScrdrIHSRJZAO7iZapsAdbvJjM2wwcP9I0oR0IRMmDMjg3Dz/Bmunt1Wl5pcmpWa84yvvvoKr169ErDDwB/98pd4eHjA3bt3ciAgF10vJlilhMKMrksopc5ZUMLl9TX+6Fe/kl0anw8yXxnilug0PFPYdMTieBnGtblgzI+rq0oz9kvgz3EOBOOcg53AY+JkWLmentu+OH2s2qKKypBmYmvd5kffmhvWL+PSoXQ1SlQ36orKKn+ru3cg5VDM9ZkGyWn7o6IT+7OQJV0vBxQP5loKcYPcbgY8PtwhTweRdQD2Dw9IXYeLix0Op1NtHy3WKEXXSum38TkGu7HJ1mY0FJqS5f1TwW3YwjajJIuhKhces2h4QHhkl0TWJ+X3gs1tfkkpXSL0ncVRdOiHAWB5px96nMYjSi7ode0biOci2dpOxxNykfPOpmnCeDrheDyJAQBQ19AewzBgu93i5csXcjZaIhwPBzw8PODx8RHjeMK76YT7hwcM/YCrqytcXFzIswxwBiglFDf+aF/dYMR1B4mCfNE4ji4B6OX5iUgO/iwyBqkUMCWhHzGe3d7g8bBHyYzb3RY/eX7Ew5sOhUelaZy/Oq/FGuc8WJpVHCdwDnxVF21yeVvXrsvcJ65okKrvVMOe8e34bJ3zhqfq+24KLSwusCUDiVG4jZ9+6vpRWacs45QBdaC6Ri1T3MaYiahgnHeqrcOsZXba+NqzkcBxN6Tk0ig1Z+AsXAaCry5f4EAXuCySJcMUKRGaGdM4oTBjmkaMxxHjNMtC6zqcTidP41iKWFvznPVUZAF0eZ59K9MYH5m7l7QuZC9SIaMA1K0NAXDWiyvTQVUkTFBXX2ZqAvklvlgtdUjV/5Hq5JunCeNJFK9h2OD22TP0w0ZSN/Yd+k7ciXqNU4BmfRAAmOqiATlwNDee2mbvRUTZC7AkvYp+w1XYA2E51nvBikBCNE/fa8C5riBzWZHFfHV5hR+6XujX9eJ+QQTLOBNEtLfGlDh3gQKDfSdALMrteNnY6j2qPriAKQhtv9cFYFSuHIqgCgeqpyxr/xPr3CbJQ1GIAUroE0sAOKUae6BCzzPu+JqrYNzKikLSLR8AujAOZrEyZSHuONjYEIDEcvgRswifmqkkOXgQIFUzcXV9j74Heo+TqS5l9UyQILSZVWEoMD9z5oxctL1kZKu0lsBIACEYOs61CsLb3do6+oSajSq8y2HUKM6VYJgJpfhugo23KT4RPNWnHZDoiKpSUP3xfSfS320t4fX9Nr5trX+cK9Dcbbe4fxj1VG85HLLXYPRiaYupaMIaqjTkUD8zmBKIZwx9j9M0eryJtbdL5EG1YkntQInDXAE2tMMf/epPAEr44btvwUXiOf70T/8UuRQ8PDzgeDggZ4khs534Oc8gSIDou7s7jKcTUkrYXlziV3/yJ8pj4xSwWLCVYNuwOhVlNHRmrjfEcCU0pzpD7cf6mcJn+0353fJcgGhsCqWtgn5vY+2YS5gwQ9ffDfzrTBkyGhg/XlNoVtdVfb22ZNlmo5/R3MYhUH5RXUPzhjr1j818cfubNcayrrXXP7zCeDrgeDig6xJ2lzvMc8Fmd4Ht7gKJNC13iG+jUH/19CCYQlZZuGEBdpbhysYCRzFXY6bxDoass1xykwjEDcCV6Og7wSvqjYuuI0kTPQwY+h59v1GDrZRvSv08F0zziJwZXIDT8QTmY+AzJh/Zk0H0XY/Liys/b4kAjc3MmMYRd+/uPDnJdrvBdrvD8xcv8Olnn2GaZzw8POLdu3cYxxHv3r7F3d07XFxcyq78ZhB+r/hLYh2rMmf8KyWRIcTZDZueya+rh64SqAa+Q410RChFdm5ub27w5v4dTqXDf+ePr/Gf/4uMzZSQi5y94TSnhM1mwMXFBY53j5hPo9CnsJxz0RyqF+anjdAZNlq/lvj3Q95A60aF91/uDcQcDvF+//XRikaMyYj/mUa6zERl79ggrcVjRGJE4oiSQU05y/fsfrtbIu9aW+Jpysu+TNOE169f4w/+4A9wjys8m77H48MDHh73OBz2OB5PnuXId1pUm9tsNuiT+PQRgIfHPcZpxJyFQ5QcApUD7bQxLcMjYxIOBRybGsgSvkkO5JPuLCXLKGN/e9nmZC6aoQV+FgjAvntgWWbI3JQ0gEtOfGQcDwe8+u4bgAjDdosXn7xEPwyyAJNm8HJAitovNNixatIpGZJSflpFBYHFh5oBO6QNqMqVY+06eAtBvQhFDEDR3o+zx3B3dWkQVwYGQF2Hl59+pp97TBoobOkKmzz3ZBaL6E7CXocLZ5MbbL2ooK/dy5DPLqhdwVnWAWeMriAamPca6vpkVAXLEi7X3QcWAai0N0JFdyHRhdKCpobEa6U+oqZ0aNcaFyd9LlHN/MOQcDsQe2ak7SAWMwsE9DkaQHYzOQAAM8R+xwDPRjZx3woHQhKS5sI30NS6AcqGn1mQg6JH8FPQvfAwbjp6aHzemsugTLC6nv1aCeXTJUKrJRBH/P28Wb5j6efdWz79tn6ri5cFOFFQwdWyPl+gNaNbzrmedVAKpmnGsJnR9xsBICiSGIN0zRf25AfnwjTS0zKHtSBJPN2MH1UrZeQPKfX4o1/+ClcXF/ju22/wzbff4ftXrySDoGHLkCzAQBoAP5Ty+vYZnj17js+++ELPVLB1GpYsotW9rsgIhOX5drwb+rOzyobWkcd4pWsXVze5cDP8i7PPZ0/GeR7o73djh5uqK2+Xi8K/eicYf957nSm07Hx02XZXlmHT1W5UV7HlGotCwl0OFzRlba8onOJi7DwVhL4bkGnE0A0YpxMe7x+wvbgSkKtrtmnPUiABKrO0h6VdX+ztjDinWsStvWagcmXDXZukExLemNqqtTw792uz2eDyYovNdouh7zVhS8F4GnHcP3igeNY1bv/Ns7hc27EARZV1QzUqCERcUHU37ZS/d10v598MA7bbHW5urkF6+PPxdMTh3Tu8ffsWw2aD3XaHy8tLvHj+HOM44vWbN3jU3Y7Hx0dcbLe4ubnBZrtFSQQqBaQur0ZnShojqGdqWOrdEuQekbmAySXu6cI/a7A04fbmGveHR4xlxs8/u8Q47HEx9SCeMQcZ3SXp52bY4DDfIRUzFMHT9aYuOf+R8qsRv5TiSWbqtDnHxWu7HO9TPNauDysfMrabzYBhGD5YHvAjFQ1TGKwh8bRv+06LwYrvLsuLv7UDSzUt4sq7dqWUMM9z43IVdzGWOygxlW4pBf/iX/wLfP/999i/3gAPrzA93uHduzsQSYzHZrPBcLHBsBnQqSWOWazdwmYKpmnCbrsBdQn9PIMo4TSOyJraTPzvBMR2FmegaUs9k1FvWY1kWzJ1vT6b1LJupy1bUDMFZcEAqdtJMOfsAdtF00Ky+y0XSbtnPsRKR7d6J8b24gJdP4i/M4k7FMzdJCWAusAKlWm7QlD9PWXXxqxr0mcfKBl8uGigIAqpAuwlpDRrlfzaavm8/EyE6PsoPLo4M2ZzLSpFs2FlXFzdgEE4jRlIFYRaIHq9Uev2XhjSZrMqVrAjAN9eq/sP9k5lANVXtyL/BVNx636t3XaSCB2YqwuS1CG/FbPcoAIZs4iT00vHIFA/gX2s6o6LCmDOmrI3xNJYIgcbh2a8RQ1h3X0chh790GMzDHKisz0WgC1KRoH6fS+tPHo15yHEy2hNNj/0FFYO4AJhPBD7b2VY0a1S0l4KC5cA0rWxAPK9cP3dDQ3Ltsc/9Qs3n4uPTf2Nwls6T81lsmkXjGn65zD8tRsrMVlWho1VXVOMOc+4vLjA8XjCrYMSzVyjrxZmyWlvbhylunhF0kSQR5QwTRO6vle3zgQuYYfJ15zRXNuodKDU4ac/+xKff/ET7PePckbSODZZYsQVZPC4oL7vsNlslS+L65cZhhr3TCdhBNo2qhz6ZnwjjlM736T/Iag/KlGg8CaHys9lJDefnKBPPGM3FmWtTEnj7/F7fDTysnC3KWxtN8PiHtcuYzvVPBHKPGsuN7LB//XGBp6EKCvW6pb3CoB5spgqyQBVSsHu8hI311eS6nmekHoA6h5YvJooOyrFDHTHuk05CEtS51Txz2w/aNvjvTNllICOqvupxGoUXY8Fu+0Otzc32GmShWkacTqMeJgeMZ1GTNOMcRwxjaN4dcwTypyRi8ZrMmtKeA7GO3Y71JKi5HJQMZABfU2OYWlu09Bjd3mJy4sLPLu9BQAcTyc8Ptzj8eEew2aDy8tLfP7ZZ6DPPse7d+/w5s0bHI8nHE8jNtsBt7e32Gw2ki0rqexLSc9UE9epQkAScdC4+pvLb6fxZgABea7TTfFk3yU8u7nB/f09dhvglz8FvvlroC8pnP0hE4g64PhwAEBgTR8v8YAikxyzoo5tzJS6piTEO43nyophP14fs5PRGBz1HTNSpsJqwP6466MVDaB1g7ID+5aNieccbDabM+LEjFXWeM9eFRQYUxqe2v4xFy5faMyaEaLVBO2v1WttTinhH//jfwxmxu3tLV7/5hv86vprMIBJt7X2j4/g/V5OeOWCx8c9hn7Azc0tcsk4HvbYH454/vwZPvvsU6SuV99FyKwC+e4DNCMCSCdZY9UxCwXQTh2qEzX2HXBNGQ0jq8rCbpBsUHmeHESDS7U6MKuQFuYQz/Wgrke/3WEqBz1YrYfkrJdMPdIAs45EUSNtiaxOPqcGtbmYiMwyCIxoNW5FMJqFHg1TbskxwKXCI1qArDzWfyKTlrgF2RI1l6G4M5BSjUhIqbZDcGpdAzZe7u4VaWVKBWSR2tCduRHFMs/GvSGF/2aAUQJ89XkF82bNkXaJhdgFOkk8ESrW8jkhyoIIObt6tf50fY/tpsdmkDzonipw0e4IZCP8qEJRbjBYsoRQHZ/aR4dVCzAQ10ZweQzzB1AXMsuO5YVaVp8wiZprAciNLk21Nn9bZmyBkLIWIoCOAMlLhc/Z0L5la2rdAYHYw03dFOoOK9HXVvFinJ6x78wVuH9AGBHFrGFwnjJNwGa7xXg64nA4Yndx4UYPE06ShY5qjndTBG0qG010fcySwg9zyUjoKr9St02OayCMDWwlmmwBgboe1ze3uL6pazYaphpe5ACdlE82pVbYb/zG750L8zp/l/Mh1LMy+Nz8W0e1ztD1mbV8m85vh6sqPU27l/OAqsuo/cZrczKuTVv/T0wnc/USvhjm8soc5OZD7Nty7bSSg0B+eF7ss0x17feiHudakUezGnUgc+Du8RGJoIeLMpDF0JeLyr3Uo2i8zjmOMRcmk082/xAMgVz7ZL9FfhH/BgVWwLLFxEi98zxhHEdstxu8fPEclxeXKCVjPI14+/aN7FycRpwOR4zjSTJATZKOOmdJ6gBmtAfbATXGoO4CSv8AwQtk5HZFOamyQXFWErkcQTC8bjYDNpstbm+ucXNzi9T1OB4PeKe7GbvdDldXl3j+/Bnu7u7x6ofXOB1HvBpfY7fb4frmGpthAJPwKCoal6dKjiX/qR41CdBEEkTQzFoMoHPlygw2pWTcXFziuN/jOI34e19u8Jd/M+O2G8C5GgtSSuCUsLm4xP50BHeSvSwxg1jmTgcNmg/zJK3JVJuj7+HPsYzojWTvrXkLLQ3zZvyPZ4HoNHR+ncKuz/uuH6VoxAYvG2QXs/httS5N62VFBh8VFZmsKwI+fI/bQYApF9QEodt7ppDE9pqilLoO3WbAVzd/hl89vsLj414UgsI4HA5IXYery0ucxhHzNOPnf/AL7C4uME0jfvf4gNvnz/CTn32J22fPdMted2OoC5kZap8bq7v+WxiaVYga5oZSQUR7BfpUBAthMIwkqwYdJZSux1zYBX1iSy9bwDz7zhE0w1QpBZwzLi6ukDNjs92hWFAamQWzwAJllagu6FnBFUWmaS1U4dDgAP0Y6WLMqsqZwPZVfhXNq+5iVpkxmVBAAAMUdgmIJKALZukE4POI1GIJ71/dGWCAzPUotp1cgXRMEusO/8b+akzY+tBGALLAHhWsWLkGUcw6PLlASoC7DSUQhgTYgYFtqmA7D6T9TxQXhDVWYyBkjZk7oLmc5EBXo2kEbQoKZYHpeJF3R9IJRnWktdAtySUKkSlBZtmP9Kk0q5b9AF5C2W35BtbXrkBzXm9XE6C/eCe27XyXV55d45mqHoQ6w4xoAF5ohi2ICAqDgFlnzWwLsm2j060CyGZX2tpE4pbadx1KYewfH3F9e6MHaRb0qdOitC0lefnOH03517YQAZQzhs2AeZ7R94P3qd3pW4D/JeCNvXRNy9gshWlh/MNWkVloyXWKQC0AFtRpfMhXwGIuckvP8P4ZU2xaXwOjo8sSL+af8Td/t5E9Wr/z1qXh4qnxfs8V1lF150SAtotrVZa17bY7zk6jjKm/tiyVQ0+oKh2qt8ZS67o5U35EdjZ7RlzpruLBY1XN8lwAMCU/TFLuJgW1KtPTAFardSVFkCMsY2z8IY57XY62zrmSPQoG75ICUwP1LPFI8zTj5vYGX3z2OahLOB4PeP36NU7HI45HMQiMp6PGnU4Sj1Jmzcom9ZZlfIi304LHcQ5IQ5yMjzND3CZtRHT9maKRUhJ+RyMSJRz3En919/Y1hmGD3cUlnr94geurazCAw/6Aw/6gCscV/ugPf4HXb97g3bt3vnN5c3ONi4udJ6CRlNWSUc4ON7S6xWjNNQibbGdDOpV1vEwpGABcbS/w9v4dfvHiChfPGZwv0DFhmkaNGSSMKaHfdaDbSyDP4HkCzxlUgJ6BDoQ57FwZ1jawfybXwpqw709d78Xizcy0udTymLPdFAZOpxNOp9OTdcbroxUNA+tRQWgnVfub+Jx1Ojltm4X1yHLJO21nNNjZB4IzBASZrCtgdKnVmiaNCyGYRYwFGEIzkuhBW37YHmp6t9QFS7IGTBOATD3e3d1JXAZLDnjo24kIp+MRn376KV5+8hJJTye9vr3BxdU1UkqYplngHInFmwFkBXiWiUQYZ80IYQPcuTT1h6RPXaAt0DJjL6C1i2nX5Fk9pC0xY04JJc2YM4GSjF3hDtAsWMS2Kc3gAuwub7C7vNaMEjOoS6CcqxsUoqW8MvTKFB2OKWDltv3O0PUbVduLT2pCqMN2Agw41+BW4HwhUPPe8h7O31EhWfsTAZUtOHLw4DjFBbN9rGI2nlhdd1gi7ORAhRZsuLArjcMNwKxnOHDNlpSEGfV9j66Xw+S6rpcYB/OH7TrYUVBGY6upjnxkVgTPYKbdtNzrwghnXZ/a9ODqYT0kJVI9mFABuOeUJ8RMP+x0N+VxEbS8oEN7hTKDAGZDCC4cn4qhkDLdMg4O8yPsloX+LV49Ly6UFd9egkAr0+fTQoBoC/Qpar7H1jTYS/9hV1Ha+2ftd7rF0PHQX5/ngdsUhhzoWXcCiIG5MLbbAcPQYzydkMfRE2agUzkRYryYIb7UsY2xfczILGdjHI4HbLc7uGuePlr1/LYU/7sEzj4favydrU/rvVMgEFeUqXpPWPACrj+h+C2vZgQjyK0sxf8uBT4bGI9DhKqIOhWIFgpHfT+2wuquwB6VV54pCNROqEbBa+ehKyFP0CBwyMUvfDaWy1Xnn8M6lU+p3l6uM+fBWmtTaDD0hXEm7Uff95hnSQZj86IAshNrPAPVgORziRZUMdwUlULUMeaAW6DrqvKfKj3qHLQVWzNDllJwOB7ApeD29hme3T5DyRn3d/fY7/c4HA44HvY4Hg8Yx5MEdM+zu5XD00zrujYysVcauLIZuYK7bJwiC7bJgcdUvlElhCSrkVjQTFnO3eCMnAnjOOJxv8e7t28xbAbc3tzixYsX2G53OB2POByP2O12uLm5wc3tLV6/foP7h3u8e3eH0+mE65sb9F0CJfFySawHp5YiafOjAhLc1FNUNvIsgdwsRuICwtXVJe4f7kAg/NM//xx/e/oJ8v6ABEKeRkyTZGcqHeHi+efYbi9BhZEPJ+x/eI35/h16IqR5lJ1fHV8zgLAyyjgOS9clclkT+IBicupSEzdsY6RpfHxMztZYKaJE+pwWc2ECYTwcsL+7x8dcPzrrlGt8QcEw37Azn65SPA1u16kCYrsNCoTBdtx9BZFQYGcTvDRdB6AHcDEkI4jEdkg5hWU7i0i2230LMSWdGKLcWPD0PM/46edf4GefvET/7X+Cx4dHDMMgac2Y0WusAjPw2eef4ebZbc1qA8koMeUsoF4nJrGkjhWQLFZwNobDuoWrQ5qgrh2oE0Po451dMCpdzu5+hTozqrRFhCREQE8JnHr0fcKc9VRudEDqxAc7ZU0bKUxOhkkmLutEY9vaoM4ZhQvFlPTwoiS5rG3SB6sjy4MyoRuLujW/bqV6DAHM398rgpPD5gvq++GLPlfnqSk8NedG6ybR0J3Zn4QJYDbWWsURKCgKYSyMMZiV18ZGp0A4UTNYKvSvHfg2dIRh2EjWj2FA38lhb0NHnpaVvJ+W/anECVH/LKxQVShXIe6KQUMM+Y+5yHYv226irbekLjPq/xtOkmUmBfpS6BJ4V2LVNvroONhWDmCK2hkvqGiLTQFs+lrrrmW+59L2sTP594HG0Dd9hrVNDPiBeU3xzWQLZdjaNcvTEhh7d9fByVM0aao6azve07+wZxIPngptXlq9UDRDkq7N3e4CD3fvMJ30tN2SAQywbDpLIBnh5PnOrxiJ5jmHPqICHzZgibrmFuC84Y+1c/ULG6dGc09aVS3NgXww/uzCHwiKtVUR1qP+Vhys2dyNu9lxjWi7PGtbbafw1qaiVrFo2hFhRJUNdn/VMZMReOxyfgSa1hFCHMWoYNR9ToS67ZfFXI1zMhRvtjjtan3G+qYfm1kV2x/G0h4UnhD7HdoWjX+Gc1gyBPluVfN+VVSZa2+jQ53LpOUcafou5XvWLO+ryUatm1RmEuRQUqkU+/0e4zji008/w/X1NU7HE3549Qr7xwccDgecjiNOhz3G+YQ8j2r81XhbhAMimzUqN6ofgTloxtEM3M2W5WLaOI9ueg2TxNJLFvcmUiNGZlvDgiUSFcwlI08jTocDXr96hYvLS3zyySe4vL7ROI0jLi4u8cknL/Ds+S3u7+5w/7DH3d09rq4vsd0MolSxuJpbfxIXMcxBYhOTpbPVM5G6jgAkFFITDiUxhncdLi4ukOeMP7894D//v/0l5pFkJxZJzgrpCGnbYzfM+OT5JS4vboCrvw8+AW9/+2s8fPN70JvX6PIIIKPTuJIC8cJIXN1ATUTEmZFsroQ1kFSGdYozS+ANzKxnkBB6+25zms11GpqOt67rRAkDJUzjhHF/xMdcPyoYPAaYlCKB0K3LS2n+JtvyQYicV58uUQbaFLZLq82ZIFu0J2a6iul1TfmJ78bfYhtZMyv8/Bd/hN9cfolh+Cv0vRyvXgCM04RtKdjudr5laoGB0zhClB7N6ESk4MqEHeSe5piH/gk2drh/vTN1qMCi8D38hvoMiOA6i9HLFJAFzeS0bFk+XWKUYcCsgZqlFBR1dSgpgwfAg2W5aGx2dYVJejSnCRNXEMisYtWi1PSjDl79PYAAE3mWI4esu0aeBjijKVcYf6m/u7Co4w/NGsGewUiJl6j5XpngGkisks/nloJkf67htlJvvcmacUItJ3qyatd12AwDNpsNNpseQ9+h67imWzZiuOUhgBetY8l8WrBU501t6UKKu+mkXnV8kgeMW78TKGQ7UVdBdRcserKqnRMjy614FQbMKkI0gRxAhgqYArYcwI0rWdPViqGaYfOMZhb4vxR8K5/OMNXZPDiXoK0KI5y+plE/51+1VJsjyx9qZ+IuBnP75nrBJuWXT7XEqWOw9sQ5uKx1r8wRhgMjTR+A3W6LuzcF4zjKIWZzBjbm4x4SLYSB9J0x7UP9TXepNfibzgkW5nk7PrGf7c7nkoKV5mu0XcLR5W9t3MZaDcH4sxzzs/JaAFdznK+Bfm2BAYxGVtT1Va+n+12Le9/z7WMtvwufgsJv1Dnf24juSmfdqd1YvazdagBycbnYjWuKXYJhau/pUzaSFGg69L16UwS6xjW27AKF1P7gZu5FdgUEWSJfzgtDwEUwahY9B0MwyGmc8PjwgNvbW/z0p19iHE949f13uL+7w/FwwPF0wHg8YZpk96ImiDC8oCWTtTjQySlbu1y7U3czIpxp+U90TYx9Or8nMoIVHxgfsL+ihCU1VHIRV+t8f4+Hhwdsdju8/PRTPLu9wWH/iONxj81mi8vLS+wuL/H4uMfpdEJK4lVjfEvcpDQNcWGJ2UgJ6MyQkD0hTqc0Ioa7YYMINze3ePP6NZ5dXeJ/8umvcdwfMc0F/+p1j5ITvuUX+McXB/yD59e42R4wdFsM/A0Ol8/x1//eH2P85Z/i2//r/wvjD68AfgfwAXMeAU7o0avsX3eBYhjNaMHj1ueQfV4LgfhQ2AMXieucjif8/re/e7KueP2oGA3bNrTGWIN6TYU2jqN/BkTRMHBu71hshJzaWpWDqMTY8zE1buz0mgKyplBY+wxMR8LGfrx98waX2x0O3Q2+/IMv8fjwiIuLC3z3/XcoueDq+gq7i0sUBt69ewdmwjTPogl2PbYXlx7UaDsxDjQM/QVLUzN8a4J+aZFcmTieDnLFekbxnsszZwUaJKYBSroNXE8PN9eYCELbJiQXahUIVCaoYJjORcqqrAvVGLuqTlQIluiF7zq1f1u/bCuvWrGrGhMXUATfrLRad63xkbPySIWW40SGKQH1Ki5cuy5h6Dts+h7DkMIuRe8pig18CCnVpYjcOx8Sh+DNkA8hQxeggH7VGl7nHi3uCQmeABMLgHYeV6BzgQGoAs7M4K7oeQmS4WRG9sPW6iGVdXnYJCMDYaGt7XoBWivie9Dak9156p0AMs8eWbHgo9KmVQDeDyJX24VFX5tGxDltwOX83fMS1+81bQ2A3uBNhLhtPe29Zuel4TOiaF5cXIpcmCbx+9YDSFsFkXxNyT8tBAsGONjJ035/RZ6uqghLFNPUfdZJrCoqZ9XpXHlq3TRPLUsK7z/xTtukakVmBVoVoJ3PkebN1XW7hLnnrTULMp+B3kWPnuh/nCMt8Kl1t3RdrHTG2ZEhUYGoLC7INfCiZGCVLrT4QljsdlbeIkqtlJi6Djn4pMt46O9rdOAAzKPyZ/wO66Nwxr8XMt4e6fQMCuaCu3d3SCnh5z//OUrOePXdt7i/u8Ne3aOmURWMPItBYIEd+GxBBWqQzfWq4kh36jvLHTHrnVSzJp31ezvkDe9hXYtEtW722EzzSyh63pUYD4+HA775/e/xw/cDPvn0Uzx79kzdw0ZQ1zndxtOIhIR+sAya5HKcQHoKOCOlomlvExIsgYVmeIzOAyzpgfuhB4Pw/MUzPBBjnjP+hzfm3vyIOcs5a9MsWS07LnjePeCf0n+Nv7z89/HF/+g/wut/+2u8+u5f4uHut0jjCM5SO3eyq2JG9sUwVToG/PuxV/RUWlNYrM5SChIkkxnPBXev33xU+R+taHRdJ4et9L0f2GdKhDXATq62Z6jOSL/EjapzEGKdiJ2xz63y0ZbhvoSLdiwVDiJqlJ+4o0FE4FJwGke8+v413lz/Cl+8/Vc4ze9QDgdQ6nC5u0DqBxAljNOMcbqvKRkp6eEzl0gCv2VLrQBZj7u3QKOl76xZhjl8J/sblJMF8ZrPziQCY1qWb2W2E7L643pQZEcNqC9NpgggFpAatrECcaz53r9olTXrk7VXLNZMcD9NOGNqfWaX8kHoWr/LvcDQjVHFl6R3qC0Tidb4F/suiBZrYLoSA9WqbSCrZhBJ6tbUJcLQDxj6DsMwYOgkcNz+k0LF3YA463gbYgt/Ac+Y4kLL57nEPDlYR1V+Ft2uZfn9KNAqlUxpihcbHRpxwSDNrgYXPPqxSxqr1CHNGV2nhxhlVTyKnXIPTQVpljQGxXMugtUwuqS8N9YitBlebrxiH1rheu7aVB87AxP8xP2m7kBXV3pXiqcnwArMRaF5GKzlGY1aJZzOxi/el2fNnzu4B7bd1TbXlrq/cGUNqC4x1e8aJO6rfd8DBEzThGmaq3A0I1VDsBbmcfggzZZYPru/BC32ZrRONy6bUWPRdeS8o1kD4Tl9sPIgb6z3t6XYE/PAaIfzRwK3wgoFHJM2PQsVRxB3fj01z+1dbeOqEqKNJdQB1+9PAutFCc47K+z038nGMIAb589OlJbm5xXFnelYd9jRWAGyUq9VYW5OK/12GSJ9tsPJKMiZdpd9YdlH7Jcq86zGtMA34vqu67m2OhoOxStEUi8nAsbTCXfv7vDixQvc3Nzi3ds3uLu7w+PjI46HA04nicHgMmv/LP6CIKm/0YJKRrNUArFBwX2CA78GoAlt1F02Ejz2K/yN47F8JkbniDwzHlPlcykSAcvEkEOqi58HVgrjeMz46vd/izevf8Bnn32Gm9tnmOdJzr/JGQVyMDFBjc6JHbMVkrIIQM7hvLLUQRKIGr0SiGo20dT1uLy+wf5xj6ubW/zut79D0bOEhq7D7bNb9JsBm6EHzyO4S+DcI2fgYtPjn+C/xrH/Df6fP/8z3JXPcDUcsX/7PdJhQp7Ew+bM8ycsTXOljr/XM30CnSmOYfv8qiwLcsy9V1i8ZK6vr8+eX7t+lOuUnQy+zNFr94ZhcCXELJmpP3eP6vXciJpdiJrflsSMzMrKBtrUX0stzt6b53lx1ga7QpQ0arujHtM041/+63+Lf/TZFl988QVAhNs5i59e6sKg1SXDLHmUx/0e33/3HfI0o+t7PH/xApc3N9LWVJfIGas3q0IDDDhKgJXPjm4qwDBEbPcXVugzwBZaQ6FMA7GybpaQiLRphJpV51x48eLdpZB26jHqCbH1RaNsfTJYr6sokr8pgG/5yOpKtg4NVJuBuW34jgQxLCEBoYCSnGMiDKbzNHguity9w3iplG26YZfsVGvbqSD9q31zocRCS2tvSMEqoDScpm39sPFlDplzuAIwK9f7bGPPrvhXn/qQqWlNkEeLtSrlUfoQIEpBIPaZ4CAC9R0YHbpSdxf7OWNKSVJB2mnMzNomuKtULekcMAXZ2I61DY7O5WXMQzzOrAGmVmhca/a9IsYGFPuai/WHMYvKRVS7z1rePNe2pZKhXd+LDusjCwC/MELU0PCV9R3eDJAiUicMvym361Z9O7QPgJ4OntWal9EPnfM820GtdSjtTAvQOWvgrbNMG01zbUdmhcci0DJ0J0KXlj9awUGJQwCz+pzzsYqKXf7EXRsCdBcCOg4CDpLVEOYmLcYgztGl0rp8oh2nKkuaaWsvcTu658pK/R7pZO/6O7wciPq55cBGZxvXwNfIQGqgY/NmlCXn86w+F41Fix1Pp29w09KmBvU4KIOhHlc4hf5Zz1JwUroQ4EqfILOXuzk2DsZLjcaVSla/8S9CBICS0VPod393h3Ec8cUXX6DkjG++/gr39w/Y7x8xnfY4agYpaMycZVDkplYErKWjdM7S9PcabRJ3cQ1+2Pf4vvU3cpw4t5p+O5UCddl2NNpnJXeDJZBg5EwoegAfKHkM6H6/x+9+9ztcXr3Ws0LsvAlJ+FOYcXFxgd3FVsZHvT3AjL7r9cTu5P2Ww5AlVmOz2Uqg+pzR9eLu3A8DKBFub2/xky+/xHQ8Ic8zTscD3ry7AxKwfdjjJz/9EhgGgGf0NOByK+niL4cT/hz/Ett/+j/AX/+XB9DdHh09AHzSw0rLmYHeKBMP1I4G9+WzS34dU9g+aewq9RDsXGSOl0R49smL1eeX14/KOlVKwXa7PdOIiCSlYc4Z2+0W4zjWw0NKBAat71fslCkCpqgs33FIp+9E7c3aZs/H+zF+w64mTkP5xNdff4O/94c/xW3/Vp5RBpNIgl3LXHPAayFICaDC+P1vfou7N28wnU5gZnz/1Ve4/eRT/MEf/hK07XwxmC+fB/stlYiobBhAtO+0WKq2sqMy4hIwLuGGmPKHoZg7coOlhc7aYW0zK8j7mH28w2gLtHdrH2TnJgQ5noHJKhg4gA9CKCb0g+wgOwJIc3uTon8yJkKdg2OzFBGRnw6aIi29HypuXVhxmxOe4NmfCKpodJaqz8orAVzBlQQGNLNUlF7qb8xhLQRG67s2mm7Q05xpXJEx/zqnVGiFVIOxLqOFf49g27doqyCNlmLbmbL540KD6o4akSr0iZCSxj+lhL4UzHOHMcvp0XOeka3/IFc26v5W2/o4Y1dnpWMAhh1st3yjOcsGwdXOFcFFybzwAHflJcxdDuVRFK4L0BrhGNWdTAq0XtZtLaf4XOiRg8OolIR+y2+17nUYsFi64bk6EvqdY1/qZ0u4AQB5lsPMSp41xqJzei13HSJwr5euOpac9jnPoH4IuoOBxWpR5kV/alEtcDQ+S81vsQSu9AxjsKR55OfNOkANyHTDgH6m+LdSQceQnAyETvMyVBezZnfR1ovypzMLeTMylV5RMVuOd/teS0eru2KXysNtTbYQKN5raQv/G3DCe+r28oyXKf0aJQI2YyBj6/PEcux4rp0gLwODbVrLfs939OxXIu95MweDXPVeOWYyRed8hUUKmAGwMZyasYsLXr16hYvtBp9//hke7h/wcH+Pw36Px8c9pvGEcdrLOmEb6WrDiQdB1Xln360+m+rk899nnM6/xiZjMgc161Z9tl0PSx5cx/t87gCsYiC85fjRa4Gtg6L4KrHE5xHJ2Tv3d+/wSA/6GKtMEmywf3hE2nQYek240nfoU4ftZotht8N2N2AzbNANvRodBU9YNkdrZ+aAOVLC0A94nB7Rk8RvXF5d4YfXP+Dh4QHfffc9vvz5TkmgGa0YKAPw4vKEv3z4HbqrFwD9gIQjgAMy6TlAK3NnbT6tXU8ZhaQIevLZZucjEaZSUEDY7HYfVe+P2NEQ62wp4m9ulXddwlwy+mEDphlMUvk0Terj1rlCYqA/2eEojHpgU6mMn1ICZ2UCBQurl31v/wOg6TetwTI5xd2lKjgioNUVrGQkSpjyBFDBP9x8jY46FwomsrpE6CidDzABhzfvcHp4AM0z+qQZCsYZb7/9HsfHA37xJ3+C3c21nUfcAFQKH6rvoTV+OSF48ReRG5zdXoNeFVyhsfxHEOlKh/1G4femkvNta3lcBcmZNYebzyYE6sFpXlll+wwQioqFuAVYdw9k4Xd6NoT4YEpgPtdF73RRAblyRELDcJ0D1/Su1moDRNb8pPOi79QlKonLUBMno0WbpZOJwiEa1Q3Gx9OkWXi52HhxBRv+UK4pYmNP2oM62Cdc4x7UCOdIg2r58/6Hflealvr8EjQ6qVrBmzpxi+w4oesKulzQd4RpAsY5Y/JDkQrMQ6oBe41IXpvnK1egXWPBXdA5zvS6O7AEOt4iBEhT33TJqc8FpcCofQaf1pSLxvgQb7dr1MdlrbwWDTRtASL92rVsoI2Wk9jWKFm9oTcBITLEpz2lhFwyyjxjzupaq/ObwJ4wpOTlnLSibM4JyOsSgcvSzWutP0ANx19C3AWN2Ma7WT3B6BCoYrJEy/NnwqPM7Vwj5ZX2vUIquIFDDCJyWnGbua2VfSUCWQCWyl34h9Qh2Wdsbi6vOKaxnLMHpX0K3Px3MjrG2LFKNcI6XFxWRDDAp/RRoLh8b20FmnuvrN92nvtzS14IQHaPwzvWBpwDsLiyfaxogee4yrEmS16sgyp95Cs7UK8jtITWaGgoHiPS33me8Or77/Hi+XNshy1e/yCH1u33DzgeDzgdT8jzhMITbBWfcU2OymiUbsZXqggSN+fYvypTg0g67/eiR0uOvTo7OM7N+EZsp65h2+lAlGDs815BlZz4TeJVIIcWy5qTz6aIFKDMyN2ELsQVHw4H9PsB3bDBdrPBdrvFZrPBsNlgMwxIA4nXjpzuiy71xu4xTTOev3yJaZ7x9u0bXN5cYWDGi+fP8d2rH/Du/i12ry+w2W7AuMD9/QOuLnbohg6FCJ/13+PNz/8cX//1X2LgDKYMpg7I53M1UquZnqVIelr1RKIVukdc7PgEdRx58axdHQF5GrHt/44P7Eupc9epBlTook+dpN+yLDTFhA1LCtpoqSJKErkOP8LLmQYBauElOT2WjBlUEtluRQxcsfu21VhKfBe6M6EHyYE1cl4mLXPBbtfhk2mv536lOnAmJGLyH+giSwmH/R7Q8yUEK5P48THj9PCAv/43/xo//9Uf4/blJ8gm5jyVYQsAag1PCc5at3bYwVsLSiJYWZQZBcYCqCzbYv/yShvioWSunGgFdeNaxF61LrXttoZUVysVNirb7JXOgDulmtKVFAglsSo1/ooISV4bXMFAaJ21JS4sQkvHYvnEUdklQZSZLp5jQSHdLAlNoh5mgLsJ9HfLjCrIxKFuWrTPemUUju+3IM0h1ZIhUZxNRnN1Q0SoO4KhqDy0LZPPrnxEJs8BpKPOUxOwhJCQoEPfdxj6DlOX0M8Zp2nGNM/IsyhQheu6AUXFaLk6opV1pcEUbfHxWq6Xld98ArM+U3lSVB6W9fr9APhjjvMomN9nqVqWz4tnVgX3Cm9pwdMKv/AnlyPO4T4tfot4StZhYULfD0h9j2k8+o5GNmOQgqeL3Q4PD4+uSDQ9IaCm25S2d6lD0cNFYXLE+2fzN9W0pcZPwpxpaVLpXgG7fk9pna6wwyXZrZt2Req4QuIajDA2LuH3nGXTXxUK57VEsExy+nA7nhy4EZMfAErqBmpr3RWVJ0Hg2v043uFW+K3tsdyn8PuCy67Ssabs5dWnYnn27xL8a0ErLY/lrhXfuuPY37pSorHMFBsBllyKn1EV+bAPnf5j7aittuYuadi2PM4fInOXAk7HI7795lt8/vlnQGF8//0r7Pd7VTAeMU0jSp7g6aiX/NErDIouwftW5Vy9ChASqmipFCU8uYIefRMaSdPAi7bfy2kdfkGL+uIvVHnrwnhkhRaTQQVgymr8E48HP6dE2wNV7rMFyeuCKSmLwZwOeCCT9RIiMAwDtpsNNtstNptBdj82Gw8LUIsnPvn8M1xcX+Jyt8Pz62v8xb/5N7i5vsSbu3ucjgfM84TpNCKDwIWw7QccS8ZPd4/4V3lEurnA9MDIKCiTGGRWwxdgS5yVP4bfzKOHatzzWaxHGAyXkUGueDyg1pOYQbng7fevVkbo/PpRweBR+7FGzlng8ziOZ8HYcpDd1DByc6liBYnmlV5dTLyX7qbtwMo6uhDI1i4JlpHD54iAuWRf5EnzHUtKTgkmSimBcwaKZAzgURSSBuytWDpCxZimEUPXY8YJsAAlFRgJCeV4wm//4q/w5S9nPP/iczsPue2PYReq7kFW/vIKOqfJ9Nqyp6TiCpBYK//J1/2BCpbeXw6FczAq82yYbQN5jSVWlk960FxKQN8lZ2gRtJmgcsHCoQRLZ/qhPukYG5jnqEBZyVw/UyI/IK8jUuuH7qyoyYvNHBTZrmkdvCidi//WVB3ElLeJq2PEmjths1pM9i3xot1cjGEbcGzgLALrANGpZTryYQma5VcK73q8lQK/6oJBbkXq+h5932OcJoxjwpRnsAn3ZduN1xh49+m5EOEBQZyBlNUZonQMilMEAlgp76m1Q6GdZzSqhGpaQ4vP523+cN1Ln1ymJex4ut/t5+VIs4+p7UxbcTbvbOb2vSiR40jI8ywurjkL7yVCKcA8TRVSNOgn9D40q2ZHqZafpbuVgSd4vwVkxF3aauqJa9IErYDQovKjWnilTZUSAlBaZq78jy1Jt4K3J1lwC3NlrAA0CpR2SssjTcfZ93Io52azEeMb1yQpWeOh5nmue8FBbrd0loYbYDRA2V42CE9x1JYI7S7TyuXKVyz7qZK138aDz8RPpaHLRwLCYVRPX0GmpUYmIfCnUCQq/3EsFOcQ1d5TU42946Uvus3NszbHOzWkHQ9HfPXV1/jJF19gPE24u7vD6bDH8XTA6XiUgG+W8zCIcO4QsWiTfZbsn3XNLp+NMoFXxssAfoVvtn7qm0RmgG7r9r+Ltlp57+Wp9iwDMYYjigZm5ReAxuS2vIJCg5Yu/QLIU+CdQNZGH49wwydBd+d1J2RQpWN7scNmM2DYSGbJkjNO04TdbofH/R5DSoCm/M6F8Xg4Yc4J04aBlDDtT3g5fo2Hn/wBvv3mKyT0KFkO/Yvn2QXA422vtGld70xRAuBYPQaLL5WQZbzH2nX3d31gn12xYj8WnWqwiMVLWLD1MhLe3wM8ih4AOtRD+GQ3I/tE7PoecSGuRdJHolnATAUwCyGTCD1JJirqOnDJGIZBV17DMbzaZnLrv8QAckGZZ8k5RAmJErJEt8lp2wUo04zf/7vfIHPBJz/5AlHfVAgmOasWMis+E+ut34LQU+bSPrNouXDPp6WevxLAd7zW3jPgF/9av5bPLy2P+qC5aIjFQayIKcnCMPedsDla3WnYa6p/teizQx5bIjTfI1CvTbb7csPiLbqU0PWp7mYI0vHnHBBHxkxh8WKxG4HQ7LhGDLQ5wJHfW+OZngvSrIcWYC5nT72/ZLqLMgIYcwzoSMR20VphVONhDCeyCmgFcMFiQkY2skSFtiMkAX1dIvRdh9M04TROmGbJ3lHpVHcvrG0NuNZe2fw5p459W5FyS0BOtcTlunsSRHk7Y1EtkHlqHRrIiXUshfNa3dEajyBk7HvLOZ6qefm5jllcH4uiEWAwTIkkArbbrQSnzpOAXs02mDrh6fM8B2oaCwnzPYA8UnB92O9xdXUlgCQlnQ51Tlo5NYvdskscspwth4Er72D95qk1FdSgfS+OKjGhIPAA75cZIAIBda7VW8prADDVnWDrVyJx4d0MPXbbLS52O2x3EnCf5wmnMeNwPGFmYC6zuphJrJi1qZHFzgfag/ZsprXz5MOSKdIwflqbp/TE82vX2lyt+zm88iwFheCpss2oV9d3E7NCYby1EwThSc4B1D3XrGoLc2igoq2N87b6HZ+/VYZ2XVIl44Cvv/4Gn3/2GQ77I+7v7zVl6x7j6Yh5GiEKhswvyS9yTjVa+VyVGrT9f+JtmbLnyWCMZznfNZqy9b4sSjKaRL7W8tZ48eJdL0sXRwtrbL0ybPciJcGUggn7pm1WTnXvX+wImBkuyFNZyhmUOpSSMc+Swep4JDxQkl2olND3CZvNBrvtBlcXO7nPjMvtBfaPD3i4fwCjQy6EmTvkwhg2AxjAz/JX+OrmH2DqemzQgWjWtq5z7+jlswwMt3eWRz0sMVq87y5VC7xNRY84KIy03pSz60edDG6aHhF5p3LOchI0tdsyfd9jnoUwpoHZAX/2+zRXwsnpwkUs2V0Psb7I98JxkpK3x3ZHPPCcAEpJDqPRk7qnPLuAYoIG7Kj7FAHMBePphJe3N1aBC84gb+qAITCzUuQE8VLQgdCZ1ogCJrFEFOgx9fOEr3/zNyAAn3zxBQoBmSOAEMbVsmZdfo1EjEsubFCvKQahD/X7+VNLF44nFYSFgDJqxODVphUt9oftWkTha+nhyK0NtnNhjI0XQFrL9GdKc7/pYtPsCLOStz8Cf4YFnhldJT4kkVktVNGwmBBvTLVaLi0K0HEtkaZGExuz8B5r59jejwCx+VzOfovz1X5bF7XteMsdFczGuMNbIlQpjI+5VVUACNg0qQCu7l7YDJc1lBQEkgrq4s/L+4mAoe/cUJFSBxpHTONUGWh9oaG3t8V/rhQ4Bz1caUfVfcAKCCPsa8RpG34/uxqFQk+XXdyPb8bynW6LJ6vrT6UtM2t2labZjWVOH27KplAOt/8sLmrWsI1X6wara5ArwMghm+Cw3QIQ91k5zLHmvQIIuZzz9ugDnqyxDLfiZz3NNoL0uJZqgdrvRddsZXBZ9tnWq9GLF7xjlX2e0Y5CGbQkNgmzs5gKQnLlikhckO0Vcy802Wq8MunzdkYCIDvrp6lgzsWzObqxwsG0tjQosecypfanWQ+r1xNzpuEd7dMVhC6eoPjU2kWBv9c2LykPoIL/cC+uyHZ3wV6oBg8ic0MzdlhdskkVQD9IVZ93Nz297AxYmwvLXlHTvDrOho+6TmTM6XjE1199jZcvX2D/8ICHhwecTiPG0xHjtMc8j1qPuPiSt8doZfWdtaCRw/buh64l/1SbKmqCEvbOmYuTGT3iWqrKWyw37oDXZ9t666daVTDALQ60jMqixQNn9WaxfltNlW+aMTsaa0zGVyWLiICS/TMD6hogyU26RCiZME8zjoc9Toctfv7ll7i6usbj4wOQCG/f/IDHwxGXNy9QqAcoYUdy5tYOJ1zTd9g8e4b54a3zdjv4eqlwxPsxI6tdnmkV68Z6k61Am5zJcH/cOexThwTg7u3dWTlr149SNEy5iP9JxHpqCAAAp9PJG24H/YlFqwa5FRWUzJKZhAjokXAaT+i6wVaqHFbiXVywlrA4cy7gnDFnsZL1wyAKBlhTgwlwszqLBoN3fQ8+PaqfOkJNdfE01kIH3kWOcOciApEBFKDn+j6JfwF6BvKU8fWvRdl4+flnYM1oxQCYis12qDO7111BAnC+COOWZm07GivVktm2JTwhPc/uL8VRjRlYFmj1xffb7TgDLMYYRbjWhV4XdKyVmzatxHS7gD/f7qPQonDoV0DnrBK+xvWIZb1LCX3f+fkYiep2OqPdEZFy2X6U36s6o+DGmFuV/myAQK0wpvQA1U3KlAm2/+l8sWkTn3Eace1fAypccajjU0kohAg8NliOKAB9HTvdMTRh6QpIqsDRfwNQSFa0yaaU6vy2ukGaEpjIY2CORDgeTxUsGXNvBFgQDsxnh19yaEcDTBoakM6HQEgfn/A9vLemdBiwWt16Dm0k/Wv32VsmpSzfdxceOgfLVWGN2G1tLVi77esSEVtzCMuu1fVeBZOtGRubUmQHarvdCFvMs1vTbK6TF7YED9WKHNskbh4JzNQo3bHfC2Kc3/Orco8YewUf4xW+SvG5+kz1l678zJ6n+G4fLcZ1ngPQZBYy7zw/SjbfakhsS8kaxBpdIqzJ4RDMMPpMtX/xk/Y0tGXlbgSQ/tv5HGmViwXRjJdo3Wzj7cXw6mtn3/Xm6piYfFwUebbG7KmzcTwXtwRS2gGJjadJP0uRjJMt/GX9l30cDQQ73WgJ7kUe1LoDiEwJ4zjhq99/hWe3z7B/3OOwf8RpPGEaTzidjshl9HUnbVAZ15yPUYkZ7Q7L/rezeu13hN8Xu61cZXtUsJ3KCyWjacMZb7G31tcuL+d+8+7amDIKizHUmgfFF0Qdon5Y+82A72QSCKnOM6YV+rHzowRyHlY4AQUoqaDrCKfTCQ8PD3j27Bnu7+9wfXWJcc7Y7x+AboNu2IHyjDQJxrjYbfCPrh7x2xc3ePiq0hmQlOFrPC/uZETeHH9/6nJjx0LJWNI9kRqIGLj5uz5HI1ZaSvFD+bq+x1xqetkkjnCYpsl913LOvpthsR6FGVOe0VMP267qul7BHkngtnZo5nYra55nPxnb2mXKBHUJxPLbnGcUTg2RmBnmu1RKAZOUt73/xlNa5ixETF0Hm35rMMJxGwObftD3ZDImADMATsKsUy5ITJinjK9+81sQgBdffOFA0LV/oAkWjeJ0uVibawGoLJitvhE46VOXlUEWmImmfsfkVbqdt8ZfZAcKFAWLF1SFky1S07XayhbF1560bWuaEJ5yYV8DKx30++vGoGUwCRIjkjRORLKOEeIp3BXgKR2Y9FA9+S+KXZufraWZnZFZ/0th2LZ0PTl7qVQYUyPYeR4OulwRqUOhjfMbUYjUHR0CiD2WgZRuFQ7p05GBRSUxMCcCAUmCU6mgeacyKsCylhFZBl2z/qrVkAGQCPQehLSRrWikhOPh6Ew3pZozvSoWdZTXsqXUmb0EKEuwRO1cI6GTzxpfc7R4q/3bXIt1enbZHKEW/rWAahGEqr+3oOOJuhEeOF+8/txT8LLShL1OwJRBApBk57gQ5umEYbMBAZ5xqsnXTs4dYBENhgRMqbMpTNrflAhcLB1jBE+N2G+7fQaihEcbHSrNktdrQLsCTKWL0c3uByXa5i90XhbdoXdamT98sTgreKBmdp5QQWtc784nwkGnAGkGPXOPKPq78hWjxVMiA3AX33b21u91OXH7YvPOeQU+Z3wtxmcWa7QdnPdcQUbGumnxDBZlLxGp/a5jFw1F0d/fS9OuFpKdDtYEIU25So9h2IDAmGbddVswBW+3zxOTAVKu+frPOeOr3/8eu90FDoeDuB9OR0ldOx5Ryqxdt11ik9krSGUpQ5dNB87eWq7/eG+Vt6DSkaGuNRDA7WWSJIloyl62haNZjs7qXq0X7ahXfl7rBQRTJlQ55N+bGms5zMLua9w1LdoqT5pCXpU6w1FB7pYOTAX7/R7Pnz8Xz5uS8eLFM4yv3iAlRs4TkNWwOSeMM6HkO+xuP8Nh02E6lEZRiDsyRruGjiuyN+5aPLWr0RjrQj+buBCWE9a7RVD6U9dHKxrznFEKo9cdi3nShZTU+44SmBKmLCnEMgtw6kCYGSANiInbU0Sd7TyBqAMXYBozCszKGXZJHCQCMyckTrJNzHIwmuwcTBKczgJWxB0LmOaMLvWSsaQUd9Pqul6C5koBd0bojGkcQUToufetfdup6fveBVFWC1MCY+iSHrgmDInB6Kyf2p6Z9d404/e/+RsUIjz//DN/PmzGhgBWZa5ct0VFdqxw5cUKbnx8TcTGo7TPOFD4S/Ev+yvaOth2fPy5PlO87ZZRqjGM2oK0fgjS8K3+ahVprcFrcqjGboRFF4RYBWeL9wMNm4VF4irVdR36rmaVkgIEIBSrIzBWBoASt3DhZbOdPmvtYugRGHqOC1eLCFQJLxFk6PcKPNo+moLCXEOM6u5I7HTrbrWkpMdSUHvX3AaSmYRMsaCa8Yso7HaW5NYjsdTWTGGJCEwFBWZ50QQMBjqZAVLYaUCP5aC27aBjkWccxwm2TggESiIRqlUPrpDZdLPl5JYbnTcErq4S+tC5+6DN32Bri4qJ8oRlykWDzS5e4wSJZr1oJFgDRrYe7JkVZcUAb/32FHJjtK4l70ciFWjD513TVh1X67MoyTKGm2ErimMpKHOW/0oBqNclxBWQUaVupJ/zEp8TEfg7Q/TnlqIvutq4ckA2mi0ZmNvxcj/nSF/njQTYTrmSTXYdBPRb0pNm7MxIEGn+FD932pMrZg03t/mt2URsB1R+r2vfyaVlGbGaaWbKpc7F4rRAmJs2h/2flnjNHV69HwoIz2kZzbRvV1u7K1+lGgJIbC/bRakJQ7x47ddiU8JLr+O9cCdSmUqMkB6ewbEcFgNnlSf2T+wHa/ga+S8M1gNeO3BhfPf11+CckWnG48M9pumEeT7J3zxV/uRnvkT6BEqtkKYC4kqpeGcN1DfQwr+zswq3URrvtYoW9T/l01/P3ogvSEHkNISPS2xRw8l0nUi79J2w/gtzzUCl3+UzubtbJAbDjmQIuxpo2yTfI1XkXzOW2xgVJoyjzI3NdsA0TeiHAb/4w1/g7uEotCti6J47AKcJZdoD0zWO04jEOWCA1n0PgBjkOWS/1InZkSmy7OECzFBbX2USZtREkflUWBTGxISuHzSDF4E72V3tGDg97tcHdHH9iHM0OiQq3mAiiCWxmD9jcuw1jiP6YcBpHFFOJwCQYOuUNC6D9Fj2XnYBDFCh7ogUrvdy8WSlAIvn/DxXwCWAfxKwEQLx7C8zoRSSw578dOIK3jabDRI6IMsgZ3W9SgRJbwYA2MJiS3RFqcKi7MIOXWNbCCLMSa0NIIApgTmjB4nF4je/wbAdcPX8BZg0A4QLAIpdQJSvoFZoLHlJBVShLQbe/aml4Kr0jWW0tET7rM+N9d9MMEdA3/TLQJ9m6vJn1pSMFbMMN5KSV8EXP0EjLaL+pu92FOICDJCQ7VYAliM/ggObh9Wdw36XRW1JD+p/5ABEwElx5sF2D6V9B+FZDm3nGrwmNHtK8FqzIliIHyr8aZm9pKEGCchnSzGrzEzS+spcFFIF4Ol/i+48qCuUTt1EkgShJMkGRxr8L0YSbUkQGB0RqO9AV5dg7HE6TTDfaBd2YI+pIV1TxgOESAjCq84D8gGrv7mwdOEZto8bwpKvyQqE4uqk8wr1b1QemqEyCa5zqnluRSnh8DmOq9QewLGt+zUE0tQvz7aHlNZyvY16q1AR45LOVTPobHeX6FLvrlM5Z7fi17bHMmt1tlOWOtnhKjkL/wVk/lggOANMrXLQIiPyOK+k8YRy9o70pjnQlSKItDUsC65wlX9PUE3asxhrBlfjpq77VTTXrED25xeYRu5HF0zHCovIKl1jROS08Tactby2v/5X66hP1Qi2850iap7zu4uDbisqrcqp3Dqfv8uOC0ZemecLZd1psLa6qG27Qv/FI+xdiE9azF61JpPiyCizKh3OWkBWuq5MIt3Rtfgcwps3r3B/d4fLiws8uJIxYprkjAy2ONOwHm1OOkQI3XnCbhFwM7/n2Timizvc/o12k6aS8L4pIZV6y5rqvFm0uP66IuOS0nWtr00pDOVNCONYkFKn77NX39bQmgdkmO3BWq/dj+JVxljW0qiHl+4uLrA/HHA4HPCLz3+K4+kVmBIyhIfOOSMh4eHuHp+U7/CbnLFRRTfyvEidoo2w8zCSZiwrOe6MAubKLOXY7Ne5y0ZlGTpiNQ7mgjRskMGYLWssgFfffPd+guv18a5TOml860UzTnV9r7sdBV3fgUDIs1hzulR3BMZxwjRNng50mmagSB79aZrdpSrnLEFwXT23IyrGDNldiaeB+za1gQEhE+S4eEkhJhH7Jzkwqu895mQ8HXF7tcM8dCpHGXnOrvBIXEoS5YOSt8GUCwfvpTjzlS34GjTELAuhV6134oyOCTwBv/+rX+OXfz5gc32j+dQ1w4EtWmN0zcq0Ly1zWS7SmP5VXlvYmWzGqvZrAtqFa3jPriVziBqx0CK0JtQXn/EW2IIJbk3+XlgU8WoUEH/pfcpEzbbSPBvBmv614OOuSwJq7SRWNXfLK+0p80YDA7wGSIW0CrpYLLzFhDfb8mFYelsDPLW84sp2o5Q4javAl0MxdZhciMZxgc5B/exoKvTB5tKCiHJfFJm6q0KgHIC9gTeSnTsx4gi4TnovMYNKkc8aVMxJdkGpEDgREgNyYBk5kKyYRNpMAPquw/XVFeZ8J7wGEIZZEnbbwY0eBC1P6R8F0TIVt9G3pQacjhS+rguzCleidXEJaHxMzt6MNNe/IR++KxwrNbfQpl3fMWbmiRWy2o8KDMri/srby/WgfxMRNpsNuq5DmSfn2QbY3a1CJy8v28OaJYWLH5haiqR2Lbn4mquPL9rnipqNIXmgOizXvCvx5IpHbEbsX7ViNntUBjcrFGmUROtV5Msr4LMB9dzwyXOqx7EIgDfww+UcjTykbQ953Vy7WpWMZUGRdUSFIdDLY7hciC0LgFJMV4t2Ie5On83z5eQ3Umv7GhfJ5bvvu1zO1brP5rl0yrPmFeu7yTxtBznN2nX/v+j/M7ym09NNCG1mZszPZ6QXIQ4p/F1/67+9PvpaLp3wQ1zP73105bqdOvyv/+WncAAVXnAMy3LGxfFwxPXVNd68fgNiYDqdwPOI25e3uDvOSNShTKNkkTscsKMDOPXIkDnm86IseIPb2JWnpSQ7EMpOTI6SuTtZWSZ3GwwmZ2uRYZIEjNMJNPR64KGU++71mw9QRq6PVjTGcULXS0D3ZrPBpIHdAyTwu+97zNMcDueTOI3M6lfLjGmSd+Z5Rt8NusXMHu9BJEG3DGCcJtktSEs3Bjmzw4QOUKPprWwiA1815e001e1Mu+9+5UTAp3+K8vt/BQarUtGDC7sS5JY0GIAvPugyxuwuIBKDUhk4AJCmAksEdCQK1UA98vGE3/3VX+MP//zP0O22CmhlAlnQcWTiqwKfYl1V8LgcCO80vPpJs4eBVP8xCJQg2KNZ5MyahPY5+dDU4dYUXrE7cRR89dfWr7AFRe9pQG0r6phFP0Zzl7K0tYba3T96saiL9cfbaQqBglj9vZjSoIqF71j4Z3blw87+AAOFGODsZ8l4j9Wn2gO2nQ5GDnYLm8Ehhtwjy8x2JkfD+CkIiENvFkQGZA5QnIMFpYT2kNFU1wkRkBhF4zVSSihUt6ntYKVUCCnpZzLgaWWxp38GxO+97xJurq/x7u7e6UxcMI6TK9hm9TMmv6YgNhcZtfRvu1hgMOTDl62/CoQ/9F4F2XWNRZcG+8RoRsfn9Zpi7p950Zezq/KM5Vri9p8nLYbn8S1Sf5cIm82A8XSQHY15Dtb4ANZAYR5GgMriTgBzHZWzVkzhsLlWAXRoQ3tzFbJDlQxC2PUK1FhXr+K7oYqGhdb119CIFu8j8PegKDQNf+Ja7vou22W/u3HQFI2gIMTDe2QJ63i4MrRUWlxrhVn9GXWuuS72VNupju2S61eaf4Cfv39QPvqKxdS9h1Dw4mPrbsc15gaAGWCg8tYzYQJ4TSd8T8ePb9TmY3vwd0CE//bS6++Wls5NlXeKJ4QYvveHIz59+RJgYB5nnU8Fl7sBd8cJXGY83N/h/u1r8HwEXrzE9voGx8e9nukb+ENgu3muPFKM5EDRzJkN3lIjSzI8DN3xDMURGKReOp6UZujw4rNP8PzZc/z1X/wlckkY8Hd8MnhhIKt/GTNhniV2Yp4k69Q01YBtZgH80zwjc81EJW5ShJR6cV0CXAkhEjBvgKBLg4N83yJ3OtX0ZOcHjwi4KEXKydm22LMDHQOXUo64yJTxURSHUrDd7jAMAwozrq+vMU7iDy59Y1A8pcEYDdkBgy0D4sIo5gZjoInEwso8o6MO4/4Bv/vrv8If//mfo3SdWkuwHhC6WBDnm8OVUNFCu7yiKDtTMeppe23dC6H2lNuHl7WiWBDVz6vGIwc1rVLQcn2FE4RW8XlPW+y9pWC2blKSTB8eWByVC1XicqCnKQtuPVClpFrHWRVOdgWCi+14VFcOMLvS4rsi3riEjmw6tH7ilrjAtzy1mZb21taItZ9UybWsWalL9R1I7JW5QHkaUj3zQNwU2cWwuVKtk1jaJJtARV0adA+GJFV1IrGWrOHwAAEAAElEQVS2FDZXQU0hrABH2ih9cR/5VN2jDJhthgGXlzs8Pu4d0Jl/fLUi2ZxrARNHZGh/OAKOCPRDHMF7L3k+xYpW1shaMa4Uvbd0Cs+2AXvWubOYpiUPwVP9WEdvtKaZLt6yf0wpj373pLsaBNmFmDXNrdNfae6UP2tG234b13mesVXjj6/FJxpY+dQq5eH+1RyfqQ1pgXYV2Avu5nzJlabmdzgPtROJW94b3C+eampb2hl/Xba7uvGQ09unsSrVYQD9bWuIu9ydXe399m3G2i9+Z2WewubY+eC3Ra3IDPN0qTsKcvHZej0vN47J+y5GkDPRCGB8g2p/hFeogWWx9hIDn2D3ZD0xs6fJESvzfG5+qMVr14fe+//3a21uLfv6I/r4xNxe3n4f1d9tihtxis8NnZOBt9RjGDLGcUTqxZX47v7es7H2fae6f8bD3Vsc9w/oU8F43CPTDWYmzQXPzv9j72cEtz43LLC7lYHMldhsAQv+YXIF+rplsOoHYOiB7RZ/75/9B7i9vsHvvv4WD9MP4n3wEdfHH9hHCcfjAdvtBqdxUlDW4XQ6YlbfW7tMMci5IHPxLE6lFMwkp5XmnHGxvcAwDM588lwwTiNAhK7vcH//gO12i81mA5PCsuOQndBLC7flawcQdi3k2HhzzbK2yvtSVvf610DJoqRwBYHmNy6gx3IT6x6Bjki/lQNZxuMR82lWTbYCTRC7gCQGOiQgAZP5CoKwf/sa3/7ud/jpL3+JmQuADnXjvc6F1dluQnvJjKUh4QYWn1eK48VzT9UpBPTt5KaWakYOjNwEadzJaDtWATPB9wGZ19lLECwc6ogC3Nuy0m9vG5G7S3nZXNzQR95URoYBcyBaAhuFQvtmCQeiJb3uXFS5sXTt8h0WyLwxxaLZCSmzngCsZ1Ko8rDdbsVdZbvVlLy9K+/SF3b6U/ATkYMITfmhmFxLmY8w0WmccDydcDqdcBwnlJzltFQVrgmEAoJllGID+GEszDOwlOyHMsqOljE5jdlYGAUKEyjJjkyXoAoKcLnbYjyNYuhw7T44y9gAhol8BnLC9/WpTg7AvB9hRjnoCHi1zqUKcZcByO38fEruhXke6mzeD4DmbLkaLdjqt7Ke8F9f9PucbzzxV+eK90c/l8zYbnewnWLmLMk3mL1sX2OhOuUI4V8TAYyUOnG/8v6/pwsMj69qKgt/mhpjP6jSKf59GshFyq3BFWrqp7Pf9e7CXa2O1fJ7fQao86uWHGuoNDDDxRnhiNRQsfL6CtKPinjbh/PeeSvWDEdeWjs3l38bQ9tS4bCOGa8LfN/LXSoUjUW3peeTNDcQ530I/WSWTJXK1wUHVTnxCXb4P0z/Y/9uWcn6LmE8jfiLv/gLdIkwnk7gkgU/zSOmaURKJl+4Hbu2eifKutj+OFC4FN2uAIfP77siC3iihpZHYglZlkaitm9tX9oxbdto/L/+PX9XrfmUPHFJShTKqQZkKafuogLA//affI+32+LFUTMs3LaHJTXyaTqiIOOTTz/Fu7d3+Oqbb9D3nQamS3askmckZHRdwk/6exzmLSbP0FDxJEJPJpV9UeYRpSYFuu20RRpH4jWxakmwQ9f1+Nkf/RK//Pv/HujlC9DFFf67/+F/iP/sP/1Psd8/4mOuj1Y0Hh4fMY4jTuMogd2AgyixQnbeEfOJ3m626AY5D2OaJmy2W1xdXUmcBgNgOWNjmiYMw+DKAIgwbDfqBqVA8KsOKJJS66c//WkDQnyLOBcMmw1Y6wMkCF3A18Z9hFNKkj2LCFwyUpmx+fodutKj1+B020kRpWcAAei63hUNluM30Q8Dvvj0M5weRDOluXjqOSaAzR3OBr+gWs0TIXMGFUIqBa++/go3Lz7B5fNbZJ2khahuTr13kQdh6n/XXviwkDTgUn2On6g7AuiPKrk2MLp6LN8zcb5UMpo6OH62dtTUbat1G0A0BcP+CynauLAqLnauSZVomrZAquPqKiWKhikV1j9pj3wtgOf+J28OCKK8gsJOijA14uJMd55qlpFhs8Fus8Fm6DEMA7q+F5/1Igp9MT/4acJBz7IxBuJ8SvyYAuBQAEdCmy51oEQY+gHD0CP1Ms83Vxe4vroEQ+KkxmnCoyoep3FCnkN8kQLkteFgG/9S28IkQZG2s8FEmiFEA8ghgJGU9uazTwBurq7w9u4ehl0L1ekaGWkTlxPbFYH6ipRs3JEWz1c1ilBTxfHqu8vLLU+rwDfUSAiWJvJH7Z61e7lMn3atqTPNgUkjyE2xim+cA0QB5YE/NMS2P4ydHtonyrEZggLNGpclDm2rBZk+YYLPLXPGP96z69IwjQak8YLm1uiWJsbdWJu1omb+iGtdUYk7VO2coQDo7dtTCoWBoaYbWqbF661GQDS18ZO01IVlO95cW7TozQdkQaC7g6K4xrj5u9YMLOf1k76BcYd4gayCDNJFBnyg7qalK3Kx7+SgYonr04xkK94lHl+qg/Xtt99gnidJoVsyUApKych5ho3bWt0tGdr1t+aYEJ+r5bVPWZlLUrWs7AOznrAyD9eBxHIWn7X2IyBL8zzqqozy2JUNNeDJPaVsAUoikLsBQ6dpG41VxcNTlI1eBiYdjNepPJ9HnKYTxnnE67dvcFsKrm9vMIe4MUuIMnQJmw4Ytls8zAXQQ66tDZErHzVsIWaT6pLFVkoT2A7JxrlsYLazigBKHbgQfvLll/izv//38cmXP0N3c4WHeURXGPenE/bTVGPePnB9tKLxD/+9f4B6NHv1/WRwyP4jweGWos0Cu7sk1nkD+cmCq/V/toiMkceOG0HTN0mDxxNePnveKBlRoEaGHe8xAV2XkAA/1Vna2QN5AF9+hjQP6HuZTKnrvay+sCodmo0IAJBQKKGA8d3rV7ja7VAGDX7f9JgyS32aR71PCdM4IU8T5mkSQFUIHcNPNUee8O3vfo1fPv/3wZw0tZhOEFpaXUxg6QoSBO3M336rE72+6fQ9G+WoDdet9SboMtK2rh+v2y0/C27lC6JZqJHNnYPSusRrv9kLqUssWpsaAfGeNWBBUeI6V63qtW+VS5rbm1mUjOFYgDe4iA95WLiSQSzMRx0S+5hS8mxtQj/xhxS3wwlFExJsNxtcP38muxNdQs4Zc5ZdwdN4EMtXYU+ryXlGyeL6lHPRXRVNu5yLHrQTBI0S3WJULMWizd3U9QDpwYWd7JAMw4Bhs8EwDHh+MyDd3mCaZxwPR5zGCcfjUTNTJO97Y21jY8G69ou5FUqgZSpFAsyLpSOk6mYFAAlg0sDyROj6hO1mwPE06nysZS9t/XGOuQtSEHXRGhYXS6NQILotcdM3ffPjriWjR1wRcX6HNRbqqKDj6brX4kTOYwWCEI5rvTFr1hrcl71BCJVexFUpL8wYdluZfyWjzDN4nuQsDO7q2tBG+JjYGozDQBa3Y9kAS+xV5YHLhb9ya/kDx3KMIE3/9S+fc6X3gnejCapbwpr23QIXO2w1zrnlkEUZgDUkuPhqc4BaesRu6zhbWsylc5i34mySxcfOCb1Kfp9vWjkv+xvWWgOnzq/3y7Tlw/Vp6e7yjbCLwmzE8GlF9mIoy/4lO7WXq4Xb0n/Hq0DwiGSjZBwPR/zw6hWYGVnP6CicUfKEUjI8ExKHefoBJrO0di+44FkR57MNiAYVqzTrHN7PCYc5JCFZLa1+JzCe7bIfvdxR3a/05RVoGd2Bf8y1jv/jrq7wFeMchW1tFlCB7hwZXyJ9JxLT1htWxkANigssUrx/MojzzJjHGReXF5jziMziobB/eMSQtiiU5UkSD527ESh9j8eS0TdGrna+H3Q+d0jYXVzgyy+/xGF/xN3rt5imGSklN+qDGYfTERmalj5ZZizpc6KEP/mzv4er62s8HifcHCZgesA0nvD7t7/Fv/wv/gvk/Qmcnz4AMF4fn94WUrmDeu1wtnMu9LsdtmU+hmSBpFkttJnBSTJEoQjwoa6rln+u9YlP+4qV2twvuLglmWC5/fUZa4O9om4Xakj18sEMZODyiz/FdPdfgkiCSedc9HCoSvwqlABi9a3vO9BmAO22uL69xjTJJLm4uETX99huN5inCX0/YL8/gFDw9vvvcXrc47Q/ABkY5xncybR5vHuLh7t3uHj+ssqQaDVEbYd/MgEWBeJi7D5+vdrTEbzUfsOs4UAw9pP/XbcE1RYYU6KG4TPYrWThLbJaW4AFigqHLbzkDD4KRC8uzFlrqfvSQhk4qwLhZVd3pbCfUbMv2X8AJOwKOucBhx9h6lr6QttJ0ITQkhltGpHzjKHvcXW5w3azRULCnGfM44jj4RFzzqJE5Bl5LpjmCeMoius0T5inGfM0yu8ao2SpcwFbTzYO2m+yfPLJA+GZ2VP82gFSm2GDYbPBZrvBdrMRxWcY0HUJw9Bjs91ozMQF5vkKh9MRh8MJ85yV9OR/Zb4akCS3Ktm6Aghc5L5sJSdQYnT6PDOBU4eUim9fbDdbjOPkgtAG2izk59ZiBTFR4V0ITF9GPg/rfFwzbHxQ+vu1viLJ28DNEm7BqdFrBayi5XkRMMSnIrY/K8Ceb/pO9f4q8G0/MeSQq1LERXS32yHpuUalZOQyO+/lWL7SUnhL69zjh4QCqnjqoXexZmoabW+2tHwCuXhJBFTDhb5P8Xu87JDKZe/by8qjJeFXmnJWN6/z1LjvE39dNrFx9aL3POiErvP8fbtxT5YTby+U3POZGeWY0ki/Pe2i9n5pVkt+eo1ZzU5Brr/aPeJzClsGH+FZcpvD64aPQEneVyNrUz9BUuELKwOB8PVXX6HkrOSSdOIlh92M0L73X7T6tRn2QJJW6eD6XV8oDMwZOBXCm9MVmBMeyi8g+Yguwbhy2dIaYtrLAPY3p7eQDIYF1+l3SClj153wfCPeJ5sujtnaWv6IPj/xTDu9A57R9nlGUeVRspPeLTBIeMNwz1MXV+8J42P1AE/geBzx7NkzlWdilD8dT+gvdspAO8cev71P2FxcyvYEs7tCpVC/vKKjmID9cY83797g+e1zjLstcs7Y7TboOtId4YxuTsic9eDCBOokhtL47zfff4v8zVcopeDy3/4byR5YCk77B5TxgN3N5cfxCPwIRWMq1S8sapuFJbaCkoHHrL/pNgwXdBDNzHwWE5JkzgHAelgKQH5QmQkcqSZhKRsK2JUQq8sWqYNzBqJ/JDPrqeHwtLSZxAUjjxM+/fRTfEWf4Uv+G6Suk0P7hgEl19SeUZCztn24usLtzbXn1e+2jOPhgFd3b7Hd7fDFzedyYFvfY0g7DH2PzAU3z57hb//dr0Fsx4bJNeeC199/j1+8+MQD5sF8BoJWF3VUMlYUDnvrqW+IzOIM6SyvBSMX4qz/ZmzfAUzwBfSm6zthd2q9rMCCXEmw6ql5vGk2JUR4JvNVnhUa51AXN3O87mK07lH2OwwYcKxbgSySHy1qrlqmhE/TiDnPSIlwdXWNjcZTTNOIx4cHzeKWMU0jxvGE4/GE03jCPJ6Q5xnTNDtjtOQHrIf2GH3ieTQiGSthWoNtaBu1u4Xi2tUhdQkdSTxL6jpsNhtsN1tcXF5iu91gs91iGDbYbDbYXe5wcXGFcZyw3z9KCuxIICQHzK3FyA5R4tAGiMHCeUwCkFXhUEFJCf0wgNVl0uyg71d862ShQJOzR1feJQekEcfbnAhwZ/F+63fe/hIr/BD/forBt/eX64acKmtv1xaQ4y9jOw0we5K3tDDOAiE3mw1S1yPnWd37qvvUaktMOAeSOAAkQt8PAB90JLQMUxhXBpAsxVncnQDOno1GrnM1KrRTP5qgr+6QvDpwrUe60Wdxy9q6/N4oTxGqh/vr+G4x1yKof8/1kcCheXat38udoKcu1nY23YtfzmWJIjj/el6k9fvjYOjyqkrncjSsQo0ZW1aui6XvJHNml0TmxB1EI0XS3djH+we8e/s24Bfd1c5zy7cXrXjf9TH9bkokgJFQCuNxJtyPWxzLDaZyiZl/qhht17wbVLJFrTbmscWK7/DSn70rn4uRaJ7x7fEEogO29DUu+zvcbk646GTXo23zU4bMj7la5cIMfnWKqtxDNS5aXO6TpbmRcfnLOU5zAx+LEjlNs3v/ABLPfDydsNtIfj3xKBC5m8cZ2+stLm4u0Ws205JLs1tGRLi43akreIeu74Cu4N3jW9CGcb25RNd1uEg7N47dds9UfgqP7vsenboqZzDQd+jUs2e32+Gzzz/D1eUlLq8vcXl1gevra9zcXH8U9T9a0TiOo3ZoEV2vCoUFdhrAr37vVE9OVQGTklqeFRiWeYZZNDMXcGF3bzLQEy2I45TFFz1YZ30HhRbARYe6UEEqJHWqpTeBkBJhHkccDntc5JMPgvsT5yzuIyH40KZSlzpc7C6Rul7KmTPQMVLfgxLhcf+IcZqkPBRkEiaWdhsM2y1o6ME86U558Yl+/+YNyjiCu96F7jqvWUzq9zF0fz5eVQi0yzAqBnzOlYAFE6Tzopf1WJnvEyD+N/brvODlmzYPTRnjpjdWd7BxUWWTEmehOypsuxZVuZD/szOe0OO2fVyZF/x3jSNI6vSjTGY8ncAMXFzs8OL5M2TNrX3/eMA0zZhGUSz2+0eM4wnjOGKaR+R5FsUhi5+lBZsD5wyTwVVxsJYaHmDrX+gFE+bCvuPQAF4V7B6ormu7Sx2Ieol56jtstltcXFzg4uoSV1dX2G632O52uL2+Bohwf3+P42nU4PU4kgHK2ZRj21IXpUM6l7x9zEn9m+sp5F3XeWzWGbDi+m2pGBhtlld9Ls64pyd6dTHk5h4132xWLulvdf54eNS6isb3z4ESUfI5claO84Lgpha+v6cBoe5QmSw2dF2PzdBjr4f2NWeYLIt64kvkBilJ6nTW/jRWc1U4ml1YbWPzd7UfCCA2ukgteJYt+TPG3HT8qV59xH273sdUrZ6o3q0rI8sg6+apxqDUqlQm795LsydkjvMdjvWtP3s+5z/Q72UMyYLktd9eQcME4mja97OVEvlTQKQeCKzy2uYak53xIpksZee7NEqGkKO4lRuF8d033wrGSLU1snOdUWXhWhvfSyGt66mhCzv7BOQC/HDq8f3pjzDzz/Sl1JIi1H6+Kqj+3grA88vWl7/cg9GDcYUDf4LDxPhhyujxNV5u/gY3/YTLYZ1nfvh6H3aoO0W8iO8x+ZMLozc7eGx+/aedtWzjZIZyfcaedT4NTOMIsB4WTRKgfTgcQNtJT/xO+g6ARPiP/6f/MabHR3X9F55HhfF//vX/HIf5B9zcXuN/+b/5X6Hve+wuJGsqiBznmkLjRhwyjw7xRhrUJVq8GcTDiDuhuB3b0A8DEgi5zACRunHP+JjroxWN0zg1ILO6VySUXIAM5DxiGHowA51ug2V1QQLCYX86dmZ3yBqjYAGgMcgRQGOVZWbsj0cfhHryL4do+uRpPLP6e3MCMMoE6FKSkw6V4GWa8PDuDf6If4C5m1jWoFwYfS+nkQOVXzHUolUYXeqw3W6ArZyKjsygzYzpdMLpcMDl5SXAqk8wgK5HAqHX80gkW4+oWgnAfDzh9LjH5vYZ6nRu3QSWmv3ZkloVAOvg3gRKBCycUnMI0vsre/oBW3hPKxYrrXQwBLQpD9eE+KLmCLaItA9m15MrKTJtdk5CXzkqlQEQrUIIimXLxLDyEwBKHQDGPM04HY8gIjy7vcUwDDjsD3j7+g7jSZSJ4+GI0+kof6cj8nzyIG9z3bJMU7G9xjjsi7Unrjdpa6X7uTJuVvoWnNiRB6S0lTWnu3ypoKOCmRnjlHA8HfHweI/+TY/tbofLC7F6XF5dYbe7wOXlBa6urvDw8Ijj6aQpdVOFPs4EjdmHMWUxFlCSWC2CpM4VhSoBqdSU12FcZaU8lSSAAristKyf3qNUsAIksu/1+baqp4VjoxLEl6IVeNUi/ISwVQG+jFFb9v3J7W7jzRy+84qSsQSn3IJXV1ZJ45rAGDYb4HjQAFcx4MgSb9d30+ZAoCWt6g76+dpcOFTVZj/R39V+rV42Jg1U01/YecGHLudv73+qrTMoOKYILd2q3mftjbsb9ixbWR9sy/ua+WFliRe0auY2sd+KJVF4v7274lbVNH/J1+AywLiBv63jaLxtre0+j6PhEzo/KZBP+bFlxBSWpe8HlMVsp9MDh8c97u7eSbnK8EphlDx7O8ORnR+4zvFA9QqpwxTX0X4CXp8ucZe/ROafgalryOdGHayAfKLz/Atk/zwlLUMRq4OtOIcJM36B78af4/vTHV4M/xJfXB7R+3MfN19ji+vnp2lJtqZIzkFLEA+bmK78nLef1yfToaaVbYyAgMv0eZ6RlBeUUjCeJmznDBo6xcNGEsYf/8kvJUmKnR8EwRf93/bALErAn/6DP1cX1Zr9kkP7a7yojisDplDmnDFsNqCUxICpgphLQeqSz8ashs5UCgYiUMg2+77r4xWNOUvnFXkQEebTqKcNSxA4mJH0YK5RD+ezziU95Tv60dvCtWDbKYs1MmYBsoGpF2n8RBLwUYrX0/e9+jZmSfSgW5incWoyP3Se+FiUkIHrJGBmTPMEsAazo2q+Jc9g3sCYPgGYywxKwEZjMRIR+pTAXQ8uwHg84erqWq0dCZnNT4+w3e0w7Q8V7ivuQZ5xeHjA9vaZMquFX3bDFBccenWhL4VW/c2fXIKRjxI+a5ymrTsKjGpFf7/iUK1hTQubZ8+ZBdWFBJUPbum0vgZLp5dtdWodXCpQDUw2sqe1uq2dKZEzAiLCPE04no5IlPDyxQuUIqd9vv7hBxyPRxwPB5yOJ4ynI6ZpwqwnKDNnVaLbA7XqfDSh6011xuaCyxm3YZNom6amIw5SnClafYtLi2XWc3FI0uzCXZgIc9dhHE84PD7gzZs3uLy8xM3NDa5vbrHb7XB5dY3Ly0vc3d/jdDphs91I5iwzMujZNnaqt1XMTDVjlrpegRPQFQ+86roEnnOjLvmoc+1EzCzS9u18rj01z+N8Wp6sur7NTyvfpJwoDNqCAvC2lnAYJHvnqeuDQHBxNd1elEutK44BrOXrkdswM1AY242cQlYsm44ac7o6Of1tA35POpdZKsqmXRFML5p91kc+pwvrPKEzGOttWruij/rTu7WLNxq+9qFrjZ+/h6+tzrtWCakKxxKFCl0aLuuDuXi26VL4zZXVSpnFw6GNbZs+tt+N/Fi6li0m4JnSGRTjVazrrdGCYv+JwCWL/A7zjwP9GPCEG2sjTCofEgg/fP8KPOeQJUjdYLPtnH+MDF6/mr6FLwzG40R4dXyG+/ynYNw4oz+juPLDuh6BMwI7jdao+b518J62+44HodAzvJ7/Gd7ePeIy/RV+evEOu97qXuKbcxpUKfj0ZTK+Ho6rh8YCYigJB+Ta+l1lqzbnnWZSuie4CDw8l4J5mtH1A0xGmxGm62V3vmKZglevvsNulrNYSs4SB10K8ixAf55m/PZf/TU6SphLwTSesBmE51qw+TxNcoh2KTDviy+//BK73Q7//J//cwDA5dUV8iznu/WpkxTLObppFzy7ucJPPvsE9/f3+PWvf4P/2T/+R++hrlwfrWjM6vuds2SxGYZBZPwwoEwzxnFUkCBZa7Id9pFSdflYCNCkCgiAevAehJB2oJm4anSBxaj2N46ukDRb8fq3WhZYt+vVOYtZzhjQtKKlMMZ5AhNhzxtc0AnzPAMgHRDgNJ5gQGdT6hkeRHIYX0YBDR3KPOqsZsxFMm4dxhHPybLnJJRZFI6SMy52OzxWBVMYICUkBh7vH/ACITYkiAcRBmvCZcmUz0FTI4ie4gGrwiT+Hr/TykPnTDYqGS6XvP1PV8bhuWXlLrCJQpPX2XM9a8PAnKViJZVPkW5cx1hvmcXSQHx0BJOtUk3DSnLuSimMx4dHEAHPbsU96s2b19jv9zjsDzgdj5imEdN4xDiNmpZ2BrjoroGAabeU2vwA9KwKuBXQfJwLgtw1sWDMk4E1URGfUbnSMlJ9z8otqDtzibi6RSqXFlyZQUjIqUPXzZinCY8PD9i9fYtnz5/j9nTC7vISN9fXKGC8e/sWIEmhyxAruDF296+3djI8MxWIkCmDoUkg0qLfVMebUMH6ylQKRHlqordiOCoJLlbJLJlP+RIvy67tPNMVFrsa7u4UlOBFw+t7TZVPScX3XGv4gOrNM6AanqHA543mlAgXFxcA4GculaI8vuuacmKWrCY9Z8Cy5qZSwhr9aP/tJaGbIanzfOEUsYCrNuorQIeBc1PvShveOyZP8dS1nezKh+TNNW4aFOJQznorwzjbvGzm3pOCoO2XzoW2FzJXn+LnyzUW36lrbr3uGlehd52Z1afrHD6D1IvPi79c6y65hDm3dDFEnbtYv+xAtdPphDdv3jS7YIUZeZ69r5aHJl7n8vD8irq7vX6agW8O19jPP8GEn0GgX1zT8WoxQiMbA02fVDp/LL9ZK8MhPwD0KHiGh/JP8FcPd7jt/wJ/cP1OMlfF6bfox4e+21XVojqSZu9JSWR5332g24v2Lw9brnHE4oWT54w5FwxDLy73YAAJ8zyJW72mo0ZKyKXgP/+//HN8/1//BW6GHU7HE/I8gTPj8A8fgQ1wfNzj//i/+98LVg28EgBykfM4QOQxx8ySFfWLzz/FP/tn/wxv/vq3+Nu//Vv3UkqckHJyrwjWpE8pJVxcbvGbC1EdvvvuuxWKnl8ffzJ41m2eIv6DkzKdx9OIBHGfutjtcDqOePHihViwkpxA/O7uHR4fHz29rfnVSkqxHM7eYN26AZg7tfJJfv0416cxu+LSJdkpkWBT2YGwxTCdTnq2xiAMgRnTOKOkhG63k12WUsCpQ3dxhb/Y/Ar/MP8/MNlgQHYn8jzpQTyMcZowTSMIwHYziNtGASgzEqQfWcHQsN2pZip06/oOY5lBA2GeCvqLHdIwAMcjChO4mGcecHh8BMrspzsz+Savrxg7tI4CmmTtZ8NUdeLXq2GNfi+yyOpvfn61tyNDWgqy2l7j+5H5rYnEWnb4NVp7l/VqgwSgxt90oa5YrlsruTbOmQNXweJm/QBmqGIJBim2rbELxMDxeMJ4POLm5hkAxusfXmP/+IDTUVyjxtMR8yyZokqemx07Vyoc9GrfgwJwFuhI1crSUIjNneP8Yi3UyFNstCxL3GKM23LhglDqrMqQKEkMUlevXLKfRD7nCcfjHu/evsPLF59gejZid3mBT16+xP6wx+P+EZuNMFkLCJc00tKx6sZcUGBZu2SrdyYLzlUFpW2xtk38Up+0FJ5JogiMzoGPrTWZFx8SY/WzgZ42Y9UKvDTJFJWLqAnyos6FcPv/SNz70m1BNccfI16L9QXMJlv1HXaXVwCg8z2r+90KyNG+Jh+jZeECgEthfcY4TX2+wflUG+Rgc4kn9Us1gOj3WuKCAoEfBN5L9eWPup6Gi2cdkE8U3aXeDzeji5R9X8ZsnF1BmYzGFPljMQkr7Wwmbs1KaLOnrXOF67Pdr2urfUDP2olNXe9B+C207Uw5X7QfAFM4qHCxvmWtihW4LBV+65vKgzoyy1kkV9IUuG/evsE0jeiTzNfqql20eNI+r6r0Z1ezWsjGG8jM+P6wxavT39dg7GVplVrGOV1ucp3r8dl14se58KHWfuByIXveMcYzvMv/BI/vfo8/vPorXA4cdltaFv7eOWKwwHEL1aqDXJP4Y5OObYn27mpdWoi9xUE+SjtZXKdSAiyBCxcgz/IxdTqPEubSgw8j7r/7BkeuOIdLcYN84YK3r78Vtyk1qpuRvibXrPKeKCHPwO9/+4j/09e/lwQd0wROyc+0olIVjZQS8iy0HqcHvLnLvsPxMddHKxrD5lJO1GYCkDDpjkGfejAS0kA4zTIgr968A5ix2W7ACRhPIxhA1w2YLQhbT9DMXADq/ATjnGccTiMAOdlYgEvIHgUgI+mWk+S4Sn2PPg2Y8ugxG0SE06w5ggtQiihKGQlzZmCc0Q+kB/fJ4WPTzc/Aj/+VxFlADupjqI88EbiwnyQuc0m11LCjMukBhIUL7ETw5nmdeAWMzW6Lvu/lsEMPqhEL4DgeMY8jaLvRExoBz+ltTxrICauyWpHavxSBtDEXhgOeylyweL+FGPaes8AF45Uio3uALCq3jNkVAIAJNfJV2TLCOKYM5wz6XitYqo93FC4rlsDQPoD0/46OQiOXQk/u+0Km2u6cZzzc3WO32eL5s2e4u7vD3d09TqcDxtMRp9MJ8zzqgU6yg2Gnjp4ZrAPrYm1ws9sQmFalp5WxAKBPXlFYfvyl08aGDtHn3HCXjLkI6AIgccE8S8rGPBecDkfc3b3Fi08+wc3NNS6urvD82Qvc3d8jEaMfej0MSMfdK7TGSvnggkIESgWlSFY7qTvsYiiTZ1VeCNKu2u/3C9C4xqLLBykIM6BhbW3nzLnE5PB8vdrKyYlJPs8B1PX9hBHg7P5/k92M+Fmb3/ZquY6XddcJSsxAIuwuLmBJNlgVjaVzTaSQtbv+FvgLE/pO1QxT1gLgbxrcLIUAnGP/9MtyilUXDq47StY+ez3yDW/rB3YMPmpIlh1Y8LUwH1uqy71IQ+/DovRK24VhSCqqn5eK7ocuV1LgfMubAXI5JrQ2Ba0G9cc2AhALwxkxz6nbAGIfujhX6ayOtoBAc67ru5GlQZlvATjroaL18afmQCkZP7x6JSmguVI9Zz0zI0xak23U3D3nHF6tzlkCYT8Bf7v/GY78KwCb2NRGxlVVvaqFy2fadfT/g+s9IhjoMOPn+M1+h5fDX+KL3eEJFr76MoA4DWqfl1O74gpzn2ojwz+0FLx2xyTkeDBn8bTpNBMr26G+ZXJPHQPycy6YTyNQMnKp3jpmhLZ+yGlejMwVoyZkyXCmMtpNAGUGAeipQxn1vC0AxFWpIpbYUKKEkie3a40TYyqTroWPmxQfrWi8fvcIkJzkbZ0kAo5lBlhOa81FNDM5jKwAhxOoI1cUiCRSPaWkLhHA8XjEbidR8tM04TSecDpO6Do5KZwAHA4HlI0QrpSCH97eoettp6BmuMosuahlCzKj60SBeTw8ymFjmgcYAKYyY348gnPGNjE+ef5Mdm0S4cWzZ5iLaJwdAfv9I4b+AlldxkqWeBXTEvMsfpWSinSCAY6+77HZbH3W1QwUMjhd34OSKFTjdPL7Q9/jlDPmecRmt3NFgMxFRGZhdQdqmGG86OwPheVj5WDx+Yw9cvslCrQIgtuqK1OnlUXc1OM7Btq+1bkbpFXlqsve1B2BD15c25fIBd2TuyaogkNypCffBicAh+MB+8c9bm9vMU8TvvnmaxwO4iJ1Gg8YTyfMeUbJswri4gJhncmdd+JD8v5jccBamWtwL36Pou+8jjWhr0/rNPB1N9WAx/ndhP1hj5vbZ3jx8hNcX9/g2c0NHh/3GE8jNtttjdsgA3/AMktIYZaDLVF0OQiYiX61vnNT5NTVaq0M8WBPCNP3W4KfFmbr9AlWaXr6KUQA/dS1+H0Zq/H/FVzgZn86m3AO0BEAF8mu31YDDaExdTlnd7dr27s+iRuBphY2LgzqnuglL7+sjNOStKajmESNa4PWX1sbo49x4VqHoNQ8sf77UqkJb9Gy7nNlZO36sDsVPgzSnyhzncixvfrhfS08mxLUzPXzGVDlUnv7x6zTcMfWIjSQGzijR/W/r+600rYl9CUc9nsc9ntJ80/sh6raLl812ggfi21ZUmrJtZnFiPnb+2d40BgMh5cO3mnx/rnq9N9Is/i7UkbeJ8iUAAwg43N8Pz7HVP7v+GJ3vziHY/3V8wafVx3/1p2PFYyzKHMt22lU38ztWH5TRaOXsAAzDlbPnjqyuWTkktVQI9425gW07IrtPrhxPtw/ayNXDJSI2t0JHQNphigcXSfeSGLK68/6/77r42M00CPPGcwC1stcG5VzBjDXz7oILY6h73vYNpQQZ64LkDrsxxld1t/RoduIO9SkFs1+d+GHbYIIMwjTlNF14htfNCCm5IJeFZBcGLOekAza4HiawNpGcc+qaTDzeMRpHPHy7tdIibDZ9BAVZwuUIhmlmDHNGZthkBPFuSCRDFzhoi4iyQUgw7ZZLR2wHjLFYjuww3zEJ47siMogrAvG4xGbqxvXMM1hxDivB9wFeW0uUnaqqS8Y+33x9+Mv9nbUO3Vh2+5I/VJZLvnbFEoK2nBonPHvuohaJtgYWWwnBgg8P7xnCsxTAma56M4fQMPeCWEBkroSFry9ewciwu3NNe7fvcX+8RGn4wmn4wHH0wHjdGpcpMw9y+pf7mb8mOucIYY5REaP5egv+4jm98ogF3Utno5taIY+vNHuHAFy8nlBSTM6ziicMb2esd/v8fz5Czx7/gLXN1fY0hZ3D/fYXVwiWvRF0dHAPbMusu0cWl02J+rnymDlub7rlG+FXkXEFtuMdkescQdpBsDGNdJgBTSvHix3fsVYh/Cy/XgG+j9G5fmx19nMqQt02dj3vCv+wNvNBqfj0RWNmv6TKk3DGBjfsG82OwmauaUUP42ZIvOsjVrrQdvA8Ei1A8XFqHtZS6XOXlsp9skxWFrXPwqZRf7Hzedmja4uzNqadpVXjoyV+23dAXm9j1+GnTdbHUtl2lod+13Juj57vYd83oO1q1FAzIL8BOhfqSy0NNQTDRbx+VWFOPz2xPD+8Oq109MzEVnaZ28rexEVE3xgfTPjfk742/2fYsaXYOgBsT4OfEaDdrRb2Wllyvf3VfwjrqcXR60zboG1kKM2z3n2Bm/zP8Pj49/gj6//GtsOQQ7Iyz4nwoJtZtOiapMltjsthjKWAPH3WPLWDD3ubm38mSQRACsPpBA2AGI9Hw6eZEl2EySud57lZHCra6nYLF2wmyyizI3B3+JJExTLpKTxcvobgI7tAF+JZ+17+T1zQRpHlZ8fd320ovH27Z2DavdrV2pWH+0q1E2Id4kw6S5IDYhhB5Pmp2adr7slMkBFc/vzhh1cPuzvPd6j73vPPJUgpxmzficijKeEfugx54xZt5zAqHWAUVi2gS5wglnf3ee8kxOTQYTtFmJFYwkoJ0iWG4slkbNEOqAnDCyBspMeulZ92NU3W6d613eyfepnkABcRGE67ve4fqkp1lJY+MbUg7CqOLuCxbioLZ7DLrKxMz4emNDahnxd2lXcE+KuSpQoBnzqvahkSDPXOc65kmGfQ/zGgu+1RYUfmQELqmqfaNob5+3yTIK43UmQQ5jsBO1pHPH69RtcX12hlILvvvsep+MB4/Eof8cTcp4xZ9nlwrKd4dbHKhkR7zQGjToBPixQm6vGV8i3CvFa0f4+mtcpsLbjcA72bPtYUpx2DBwPBd+PI8bxiPH0HDc3N3h+e4u7+3tsdxJILMqFttDxVx0zgPXg+g/3/8nA8FX0WAFUS5UW/J4h16drf/LO2jTwEpdrrCmgtuDv6jLBeP7Dei20/OZuajI5hmHA8bDXHS1JHV55R1QWIs9Zm0vqwMYFRH1LtI9cRz5WZyStIDxywQo86msLzvsEHdaatZwn57x2fR7ZfQN/TwPuVTpo/5oduiVb8loC713MrVUSv9dQY18tfqaW1CgZK8oXBSH1satLqlqUsWLJ4TNaB0XJBaS1s9T4DOvvGg+JM5bOaZWnCffv3qkKIDQpfkCfBqNSy1EQWnjOSeUqzPjq8Qpv5n8E0KUqzZGuOC+BQlvPGLo9/nfJUdAOHkf6oyUW4UcMOGHiP8S/u2f88c2/w7Zjd0kG2i5Eo14jS8GoymzEAHqHLNXt+9ph2EbLtjEOSgGRHjjNknlq028AEDKzptPVg0ztlHlrG3ROBxoVzW521oqAZzxOc/G373v0lLCBYBkzehMBqZOMU6nB4iQeOADmecZxHHE6nTy4/EPXRysah8cH/2zW+67v0KVOLO2JPDBlGAYkknRaWYO9DayzEoiL7HSIa5WWRx2QJG7ieDo6uMulAIMJBcbQkRxkX2bkSSwBXddpJik9pbzrQUTYbCR9WO4STmM7KJ1mPOmxgUThd+iQfGJYbIEZNAiMAsY8C3C0wHYTel0nMSV9l8DcoZvlEL9xmrDb7eq5BoU9RV7qexewNrEkJgQ4HvYwoSfXmSg/u7d6La1x0WIAXxVBrP6Iax3tvq8x4TmL8/gQP1sILK9qHWF4CJb/aelXIAAnLsin6qzPwBWMRITj4YC3b9/i5voGh/0eD/f3OJ2OHvA9jbKLwVYX2pHi5Y3Q/vrTE4DuCbxp+v9TpDwvtzLGqGKslbJKoWXdK8rHWRsWQMPdBdRv/+2bguPxhOPxiOcvnuPZs+e4f9xj6Hs9gBBVofFDPqr/rGQJMebXUBww6MjQzHJr1/lcO38izrWF8vHfUC5HqFnLOgdHqwDn7/g6A5o/6uUAxLwEsZ6ZG6lnAgxJN9bqWu6CSknybNdJ1pyWHHGdfzQkXa2bwu0Kxmqrls94H1qk2ioiT4Lf8xlVrzUlZK0P8fmPCRev9dh4f8jlq2njE6RtadW2jQ38BcDkrXBZdF6bPBc519pqYW8XoQWJbUFrawqo8Y+ENpuA3iUC57niGF6SoLZP3AY59Ktejw8PGE8nsWrrbou7TTVklRfLEnzrL5ECxwx8u7/FXf7HYAxKxvUBimtqnTZ4cmwXBZ1P1fh9ZWhWKqwEa0XSmoD8wEWY8Ef4dw/Alxe/xs2g504xWuVAP0fd62NqqXGi0SV3pT+xbO1Hk4HK+ZXsMGwGOQya9HDfot4wgg/hygVzOMQababV5eUH6uqREkz1zDv7ve979KnDVnctiMizSnVdJ946bF5Jqmh08tswdNhsO8wXPaZx+gjq/QhF4w//4Gc4nU66S3DSg/B0a4XMYi+DkVInSkYvqT67rsNmGJC6zgll2y5Zdxq6lDCoW9Iw9BinLcD1dyryZpcSfvHlF+AigOR0OumWDoBCeqp4Quoka9V2t8U0zSgomGbbGgKIhNhycmKWWIzNS9DxdzohjBOaZau6ZthE41LEBUMzcaVhIzsqmqGi7wfI1pcE3kA1RC4Mc//YDIPn1p5t2ywJiDoejv6sbafFnaMWRNfr7I4yPQ9oLIsMIssdhGb+cvgbBeXHgpAziN201HhTqzj43aYMWvirfrDeAGqleAvqL8snq3ASBIsYUG3ZG+ygpYfHR+wfH3F1eYU3b95gv3/ErKd5Hw8HZM0mZcHHDPg5EQ0UWpDGvj7F+BYYrvlsvy3fjVUs4yYid5c2nsvgJaaNCsWy7va9Ok8bVZnaMmQ6FrBmqZpYXCinSZIqzLng5cuXeHh8RN/beRtKJ6NHYVAn67I0RF1KwwBc7TkTNN4nKXzNu2l1zpGuBdbSG6C0JoljSSu/L7es1nFwaNQCsS3Ndd6eD9Udn5HnWpeDlcnhr53zkgiLWZ+5vLzAa61D3Kd0jTQzpLax7ilQ/ayPpSQGKiJxa61B+LVfq2ysRbZwcMvLB6G83/odYXYsLIbShjnpbZCWrw5jGKe29++DPsuJed5v+96uBFMklvzcaL1sXXQbsuZGGrQlLGdXc+lDXoevUV1/Bsq9gLVSWhv/ygiHXrZjaAzHLcRO8xZ1clA21mL1zGha7y3XS/u8/N7Kmjdv3oqhsYuBwbldx6HsJc8vodYEwjEDv77/FSb84WLW6NxyqskgtCO4aO462WtZT7E0H7Ml311UtSQZLf421/vWwFOPi7LxN/sv8GL4F/jJ5SM6WsifxUsfU4thsnZlLjsDtHEcEXecryUrI3lW0lAGWO+xKziAuuDrbnDh80NoO3Xd77pOMGXqUErGlCc5HLermVwJgoOmUkBFvvdgdOjU86cghTWQTMnoBwx9Qp8Iw3aDy93uIyj4IxSN203GlCBgbbepc0eZpSkd5ibUdVvfbrYAcvPNTSlh2A1awoB5nkFkikZCKRPSphMrci9WsP5bAoqAoUucsLnYYup7TFthIHnOuNDMJjYActbGhOFykPSyqUevAeZzzgpWCMgzrgYGP/8Z8PW/gFksgIVQIQnITl11c+q6DiXPctptKXowYULHJKdCTxKt3yWJbelTQuYZ1HUo04S+l2Pdh64HIXumHS4ZeRolG5WdFGnCIjBPA7HexgUYOGOXxmDPpR6eXtytY5W/rLioMiOoleZsCYbqztFpzZ61fHoFNLH+HiqJ2Cy60Uh3F1t72v8GG/l9wLIRVZcrQupEmycuuHt3h2mcsem3+P67V5imEePpgHk84HQ6akYpPVncxsx5dGD2K+j8KX78466Wk68xxvOsVLTYEq5Cjs/KeKLWswYvRVqAPATf2i4qOUXRLnIgEY9gFLx9V1A4g0vGi5cvsd8fsBm26CikmSQBK0UP8ZSdj6QHH6rPc7CgGv1NDLDtLsaOmBXqTBPkNU8872TlFetgbg2cVAoZCCthQlP92Z4nfWZZuVcRwFwzJuegrK27/vX1t/J+C0gjClruh1JTMoiwvbhwZbvkgpLVJ7k7D7CNbpxrzSYQypyrQujKgLmUnkMrAGennrd/lySKwHwJbsl/b0CMTpCKFzm02UqobqcVZNu44Zw3LT6139fn2vJsFlqx0tf5hLMrTrmze4u5EOWC9bs5D4VjCfVdrkW18+oJI1hL//DIom2yKwGXkV6mPtgoNqulnfNfZgYrtjEedkbzWruXtazp/uEOSABbRkoUca11Nzhaqb2SJM61w0z49eMfY8Yfts/av3GJuwQK7WkI94TEocVvHD9UOeHjQytr9gNVxNLce6lp+4+5CIxLvJ7++9jf/1v88ur36BP9v9n7k6fbkmw/EPot9733ab7m9tFHRkTmy5d6T3qNSvBQSWUChEmYUUZVMdGcGRMmFBgGZjAAjD+BGQOGYJgMZGVWNSiqTJQVpRKSnqTX5nvZR0RGxI3bfd1pduOLwfLlvtz3PvfeFE9YDdiZcb9zzt7be1/rt1o3bk91BWVfipLi85lEiGuTswlEiueXebrdw5ksiyXLR3clQQwxtbHSMYhC5smaMfR3cGBQiOtkIZHGxnk0UaHvYjbTfhxADeGDDz7A02++wTQMIFBMBQ8c03wxoNYJjq5n0dKhilnvPLz3WDuH826Vkji9zfXWgsaqA9adaN99ccieHjAmWZ6cX4Egfl5hEmA+jAPGYYyTtEoSl43LmGIwVNM4ONehidlERINgfdwI647gaES39nBnHTRtYtM00e9bTivO7hYT2s6LVBeDb4L3cogJAGKPtnHgMTIW5Q1KMJF/J0JMiUtxs09xfLo4GQ7DNGKYpniiYi9xJASQI4To9uU8MBwnMVEFRgMnTMlJkCOIMA0CWpNuilU2V25UEY1F8mneQSYCluVVhbz5UjC2hEcohauXjDw/MN/TZH13LUGsyPQCxnndNYN1sT2l1iEzo5QVTJkRczQnCtF+9fIKQ9yoT799KlaM4RgFjUN0x1kgWkUnTjWc3vjEKYVyes/gvjzs2p4SJlDVTlUKKOYO+q6C7tdX/Ya21XVbLBHjtRJBZyAETFE5cXUVUhKJJ0/ewdXVDdbrtSHIsW1O6Mg4jJE+Ua6wqLkaaSrvVQPyhl7XfVzef+X9chEXWub0iJ3Aev+cqPpf4SopgWGABpAUrV0CHabbmYXrvsoVMTPWqzXIyRkpYC4OZk0FFnSNq9Gyn09kl1OMWQHZ2VW/vECr5q6V+d7SbDMopoREHkOu7oMrgK6gW+n6ifbWnZzVbn+zYDjff11WqTdXG+n9zFJWlx1Hvxrfeq2ZYstfDK2Zk808P4Vrs3ne1mPMS3ZJnbxO1ByLchFj+NQeqbsac1Trx84/M/rDIWKSyN84vHZ7Z45YtuowAV/uHmHkT+Y9SCx2ibfbEhe7ujBBJaLVns7Y+OluvPEi8zcts6UHuXrhZGEOh/CX8HT/Eh+eH0A8LVH5t7qSkBGAOv3wqX7Uy23pDY7xx6KgHyMfjDxNrVHMeNwFvPAE9lH5TgQex5h4SSsmTJ3H4Bhu5eFXHYIjjD2D+wk//+VXErs8xoREcd+4WJe6YiluC8maIpd4Lsm9hgi3TYvtdoPz84u3GsO3FjTW6xKoy39OthZPcK6TdF3RhcF7wuRkIzVNg7ByGPoBTSsBJdMU4HwkvEQAGgzjiCa6WzlQCoCeplBM0nbTCKAllwQRSXY1wfl4kiHnwHIxR7mYKYjigMUBp+iqFKkRJdeMhQOK0t6kqKhidF2L3e1tPAckgKJmgsOEqe/B04jVeo0wDuKHTsJgwQHHuzvg2ANTNFNxBk4BkIPIhgHtalMYYLM2RdszJylly/PuVBgxJ0T6fZl7Z/LEM8KYsZwBZ2rZmJmgX7/VF90GKhBgXSq09tJvMjO69AbZZ2rQp0zeIHUgCRkEwssXLzAce0zjhJvrmyg8H9EPBwzHA8I0xSaWhHzJKeTtDLblqNTfXleGdd8wdGgmGFoRNLsUybOSCE1ZynL5+vyb2mGfq8ciK5MzUyaKwgUY6IHr66uYMYNw//4D3O122Gy3sVzdpxngaJ5xhsZa2ZqpYMRFHJYdAN2PJ4SNU3usBB92EE4w+qKICuzWWndb5puEj1/xypShBEu62+z3Cj2bNtknCCBOB1syM7ouupZGBibMTQrJBynWddeXrBO14hKQE1Lk229/1fNddUs+L/u117uDil/n8z0rwZAw+7wy9FSmtQ4UrbNzY3fzW6y1Rfj6misCkyW/cEr9mwsYp6/U8aJ9VDyRxyLu7vS80otyzMueLffvbSMR63cZwzCgbbvZE4nSL1jI7HjoafbO0BTGKR5RtsR+3o/AT29/LVoyLCc/Qa+qMa4zeBmCmDBI8TIV32ZtOn3ZtW8FUVv3ieYu1MGpyPmaJlCKE06lEuHF+FfR7v8J3tmUa/PNmCn/rtb+pAh7i2u+FnObdIcKf5KEQH0/RsFUaIe6OIEk26hvWrimhQuQbJfk4Hx2pGMABwJ6MH7wG7+Oz37jL2HwhGdfP8Wf/Wf/GIf9To5hCEHcr8IEBEZDJnZD28aIYQgxcN3J7xOzZJxCwO00oJmOWI/HtxqPtz+wzwPkonadIjhnIcAhiP88uUh0mAGe4B0SQPBgUEsgF6KmmOM5PBkotl5AhtNOR8uEN64NBMA78ZcMPIGZol+aLGr1aXNOpcIoPAwirAiIIslfzCoUxZzEzmEEwZO0WQZ9zlQVbAt4dTjs93j57bcpHmQaBvDhCAwD1m0HHCRIWAJ65KTxaZpw9eIFeHcEj6Mc4xAZMMXTQjkEHA8HtOcXIBswZQmz1TZHIldCmzfbLDLprQBOtU1qP95EimsBQwamEjJsC04Rw9haQ0iyUMXFa5nF5tiHzI8rJjEbt3zvf0j/KV7QYaGdgFpawhTAFww+j8TqSZb8LUD+r8w17+avhCnekouU15so979i3daPmujPJeXeuUvZ6E5yZHM9xAr/x+m/adqiZv4T3vAW6JuiORH/13vRv/6q9tqpulPFVP6t22cBcv3MGywyNdRcirtKrpqp3hrEFg+ngoX0ylgpOHbeS5a9CAbCJPnhbQrS1w2sQiomRBfVWDJbYH8C1L/uWgTPmI1fXap1wquf1JaguDsHvcsE+TXz+ysJmJZ3hYUMYsp786PWbZUW2vLacbVyQyrmVJtfU5bhP1KeuqOVNpmclWehDa+5lmYjw2CqO5A+i2v0stuMtqeO7bDuNKL4jM/En0MIRXu0dqCMx9C/3+4bfH38XTDuFXXPnY9fsweKCu3epvrm7JXTRb7OXrYkBM8aUt07WdQiXSOSDKDsnKQKVtpAG3xz/B1cdP8UGx8PxgNVo7NgnUl4pKqeBfu5+fmSRU/qHtqbumrT+3GtJw8hICnZmSFHNQQGxgBMcl5cmCYc+z41gpmx3/fgdYd3P/gI9548wYEYq/UZdj/+Gn/w+/8czBytyUJ7RZ6YJCmTJmxiIdtoCBM5uMbDrVpQ26BbrzAxY732ePTgEkSETz/9dD4IC9dbCxqeBPjqoUsumsDFlCPaqMbpyYnizwgguaDooDfxPHQ5sCnHSRCQcqI7csmPkgRxF23hSYQReU/zEnP6DiAHvcQV431KKJey0hBROpkRAC4ev4OXX5/jMV8jzTJbjScp4kgMlIgQpgnffPUVNt0KjXe4evESGPKZGToOIQRQAFyIUmKY4FjuTcQIRGkh60I87g+4hLhbLW2wlE+5IOgyjvZfpDtWt2CJg+U2FXDhZcKVSlXtIlFiBzIJ2aFdmBYlgJ4OpGGU76Q228u0s5IfGAqQdL7jfC1SAlNH/PiCDvj2lKCh12ne8v+//rVfJ5jPrzInUfgUJWMGMTXOK1JiVkJG/vR6ZpjoxOK9vEcXSyk08ycEDvs57cvTbcqsfNkd6le7MqhOsS8nSkt547VCFpq87roU/Krusopxah9nW5sWo+DXeY+hP84Ye4aKkVETXgvO7fszoGjniwFN12trKulneZ2kl+n7qbmj8mUjcJTneViauVADmzmqLWX1Wi6+phnO9ZlxsWl+bUfzVwdGMCXVvXvNuontLuc+z9IyoK3mLG1sFVQsaySzKOur2mNG2aaW0qZpiirtNKXxggJSw+fib5kORT7PmQ4tCRz2934Cvj1+imCEjEIQofrXanjqxuaGzWpP/75BWZGLqyuRscvzZYWJ2ai9VR1pLuv2C4iMSmkP1zpMoygxAIDpAj+7/Qzfu/gxWqpH+UR/UvllvwRfBDD7NzQ2r+ClgnXu0xKIWFpcSdWlSl4JgbE7HLDve0yHAXp8xDSOWaBixt3dHqEf8Mf/8o9xmBg9AT/84z/B8z/9CY7DiIknaZEjEVYcgTsPIsZqJVlaj8ce77zzBN/53vfw6MP38eHHH+PRu0+w3m5A3iEA2G46tDGZwdukkgd+BUFDC3REYI1sD3o8eZaQ1F1JjkdnAGMi3i5NVo7N0M96LgYZ5uVI83VUM8YunVKoZp8QMz05s7HLsz00axPgIT7ckmY3pGwTzAFX/h4ej1ezfmcQnr+qkaEhh8NxwO3NHSgEDMcePiAtKj2vgwhwTHBwsb8EzXCkwoUe6ofY3v1uJ0zandqcEWxUmpRTlxUZSqY6f8e6KFkANQsoK955PVNPVoBQwoc3KepKs2fe/KXCl83nOax63cZwDDyCyaAQGY0kKqB4CGMGgf9aLBnVUvvXcr0dXfj/zfW6flL9VcFXTjzxOlAPAM9xQDDrQ/2iZ9CUbNzO65r0/+XEKPA7tdgXfn8TG07k0momlzR+/1oX1UK79IOiAiI477A9O8PN9XXKJhgiYwWQNL1LNtgaeDmiKkUxFc+mX7n8pQapglHmPINKwlKsNaVjQOZpb3fZdlhByl4LqPBXsmLY6qxQJN9r0aReYDaGj2DbqDEaC3RvBroz31t2NSmFltLN1TbrX6XfpjGvr7q4cr85CaqZ1XPMchYKt6cZjVoouwgcTmCSY6miYa5dp06tqK92lynwO1kM0wvlGi76emqJpc/z2jO9zY+9fqVbodC+t4RLGGnEo+CXd+5bznn9aATt4zSi8Q2atgFGzW5KGPAJfnZzwK/f+0IfP3HxrK+l3tUtGpBPNXGxBmMZVIFUKwpBFfDRxT3ivgCHF8MxZ+ojQqBQjOgdAqa+xz/7F/8S//KHPxRdNwIw9ui2LZxfYXt2ho8//Q4+/e538fidJ7h8+ADOOVxeXsI5h6tXr/CdTz7BansGv14nwY6IMIWAvj/i9uYah8OAruuy4P2G660FDWaxHUzjJIHeAeAgi1ECpTQjA0HUjQ7gAEcNQMpMCGFiqFHQu0YGOpbFQB7YlEqO02IEpPiu68CM6DOpB4o4aGBNmszEe+PneOiKfk8WGd8kqfL2/EPg1S9yv+O/wr/jEkxYQTZL263QOgfyDbbna7x69jy+E7dPJCYu+rqNMccAhQCK2QOI1f3HyXjFPStA1+ypgiaIBadkJwtcIP18ksoufl8+Z6LytUxC2kLdRhN2gjeZds3BhS3Gdi2lF47aIFC2XJWH7BjWxzleh1l9fPOzj7DG35/+Lsg5tI3HNEz46U9+AoSAw/4oZ6fwhGEcMI09QtDsUk7ZcNGPU363p2j/qcuODMexMMYgM/umZDJsk+uxhS7h11x5LJPQFucpuSu9ATPb9jtCtfzYfJ/rwmSXuEgLKGW/cOTRNA3aboX7D+7j3ffexzCO2G7PkOV6tWwC/w79R/gWh1SqxeS23VnTqPu7HJ1S8/xmZphAXaUptAD19MtUCAu51bGsCMbLAZvriDU2ZQkgUPV7ruGEht1swLpVsWtl4Qb4JDdTCG3brDe4evUKwzhiFUIOCHd+1k5bilYia4kiz6k0/BbYkm336SuPhYG2SwiCswtYucdODcSpvpgiy67F3zSInJcPS1x66dS8vaEN2p8ysF6pe4xrs8su7se8eQ0RIAKUB7xVUyLVTOYsGGXZ6/ZYbaNH0aYaY9e9lcctnkjMblZ36poZH+d89ZzuBeWDZeKaegpDqECmCbg9tVoZwHEEbqbvV8+c4Cb1flysoH7X3Hxb5mSrcTlmlijSbGQenON6gcCTuCMbkK2CzSKOqHhcesL8HKACYhQ2qEHbyGGeYtkgHPFdfHn3Eh+e7bKREEvjuTwXyl+Swmp2MG31fPzPJkS2zVb8ZtPABxb3f4eAAGDdrbA79AjOAffP8P6772K1WuGDDz6AI4f/0P0p9hjQdC0++e3fhPMN1usNVustHj16hNV2jcvHl7h4cA8PHjzAeruFbxtMnDNJgWRde+ewenSJ23HAbn+DVRjEQhSbKxk1GRfrrXjhjBN2N7vXjoFeby1ogAhjdIcKMUWtpIYkNI7APAKIqbpCSJ/HaZgtNs1aJZMmHe66JpqBGHAODPG3y5ol2xh5TrT8IQkZ8qges56fTUIF56XqvQhAYk2RDTGOIb7+GtArHZFSGKDAWG1W2JND13Zo1ivAE3icMiQnFQeihYY4e374zCJ8JGjsAOYAz4Sp76UPjqwlVz4korYMJZJwxLntpIVEPFVoD80eL5gqW29RLv+m3cOJKQmvqbQ0hck6Ozup/22JCTLxZ2TQRM7WmZkBIbvOaXvS/JOLmbso348+9iExF7kcyWGRFIAvP/8CYQxyZsw4AGFE4AEcBgCaocGyGHvNAxNrbJieVB4dP1vD1TKrfYP/bXpGC6ietIzYjnnNhGTgC95TDFfal5laW6EnsH09Lop024BDqAbZrqxcEqWKBXiN44gA4ObmBk3T4PHjxzge9lhttrJ1uQruTuXkvWhaFOsvXTMpj5A+YQpk88zSpRug2if1fW1LYVWk8q/WnXbjkl+7bacO+Ik2mnKt51ncEsBi+WU95djoZtOvBngZBYPG9REDm/U6ZhELYJ7AHM8QMEKt0GwLBpHK1FPnCQEauG6xSVo5qTy7F3Q92TGJ7WMACGbd2V3LuR9pOMx6tqrs2XSbOTafU1dTj+346r953nNzaxSZ14e9spCbB9Eq3vJIxbGflQDAllETALsfdAwTbeH0vrbAUPzoCcCm2Vx0gYlnKWhr19rox2DWbi6q/ECmudoSRqIys31qbTo6ZZz+I42xSG0uiY1m6FMlWG3lUHomiq6A0i2cZuMsRxADX+4eIOB+XDfLu9SunYqgz7bsEgVTzlKjnwW2LG2LGUi9byIWo0zzaV5Kxi8+lROCHuwczBRQGtbSCp37VpRu6I8K6uOYLRvci6cIo8OL8Xdxf/wvcd4GU3Y5VkXZnHmG9vkUZ070PK6BxI9in4ohMXsxu0s5gHw8IZwxUovze/dwe3eNdz/5CP/23/v3cP/hfYQQcDweMU0T1v/P/wOuDjfYnp/jf/S//PdBJKd+S9yqWCGmMImQENud3a2AiYHGNxinEYEhZ86FAO+A/u4WYZrQ95I5tes6EDnc216ibVs0DKwf/AVnndIzMKy0HlgO+xgjyJsmSS0p4x2Kd3OsRPZtc87FTAwyGN77IqVWMhHZRchIZ3GkIG6Zx/S7vqufCw1DLGYYhtQWXUzjOIIpmsZ0N7GNmcgxANoW50jO5nAOHLVzzjlMUbsmgFYYe0AGPIm4UybBZFRIRJIla+h7WYjeEtvYr0Wmg/SXSIkgZ5xXxEagyNSQmqblZbRe1KOgJN+iktEQYvB6tSkrddMSESvhnN6zPruxoakM43vOaobO+kl1eSqD/GIAeUWwXdTCvHjxHK9evpSNOg4gSHzNGM9LOZ2SMEMGKn6BIZxI/MQOCZnP1ZCULDNpr5eFjRnjLZuGWePqysx3y/OsUGoFIlIEWRUgWav0XQuUFGiYzDHm1TTPCQPkeeIQBFpMQH844Pr6Gm3b4fziPLle6vkcS3E+xcBQTsNs3bJSB+u1y1ystWIS672n9MZKPEuCx5JEVLa4+LacXKHe90tAg3N7MIemJUCZ1z2f3RNtjLF6zMtjQABWK0l/zkFOQw4xXkPmzGU4YadqgbGntNP6vK4RQ4cAzPfpqe86/7OqLOA0mzUNop3D6nP6TZ8vC6/pbSFYGMXMbB3Y505cVN23QF9HynQc8xWhcJwX+qnP53fZ/gw7BWyejrvNCBGFQBlfpFkZ9bSUFtFyL6IaZy4/WQF4hhktLykqFPDlM8WQx3OvUgnFnp7vb6F/keeq8FK0p+4p8OrocRf+ctm/Argu7c5TzKSed61lmZ8Uv8WloIcqC9ZLOxaFq5wKU1oywSToQbJuEAHOyeHM4zTmYxC0m8iC4am+liuYoZqHEAIcHJq2wTgM0U1tg6/3j/Hd5hvzblmmnUJZnpyeUiuqxIPM22GtkEqXlliu6ikkQFuV5Q7Ot2AgYm3ANw2IgLbtMAH42S9+ARDh8ePH2J6fmzYzPv/llxhj2tvD4YDj8QhmxuPHj/Ho0SMMw4D1eo3z83MJACfhl957HA4H7Pd7rNfrNId93wv2JkI/DNienQEArq6vk+Bh8fzrrl8pRsPGU+h/jhwmDkkQyYtPOq8ngEv6V9lYsmnlOTW1tW2bftf0lCHmWNe/dlA176/6iBUZSEz9dfv1yid8ZoHHkcP2nU+xe/lPsIWm7VLEZWiGIVCBIYejeIcwjthut7gih4ny9nXRGpHAGWfNQRJi4r9yEFn2EwUk8Mc3uo0M2JkR/tmsJVA6V63IKwoKhEBGQhpUw5whe/HOArC03xPPrrRqReikxXRQhnOacZaAKpeRcj9DRzEXzERgqDVDfktKB0A0CObyzmE49vj8F1/ENRaDVnnCNA0mePV17cwtLYhLNVy88Bze4ntNsDJ5rUWp2YO/cuWJ+VVlla9ky1m1WpLLVM32Ceo8SVF7aUUDMg9GppEwl+xtDgHjOOJ4OODq6gqrVYdhGHFx776cHK70Ytb3uuX6s0WOtIRAoALefDYUJJsw1aX1YbRdr1/nC1cCenVfTJstsDVPlM8ustU3Vl8Po5aUS8t1W+aK+BmGNjdtK4qYuI/yflKXIVqYt7olHHlLMAIAp+r0uTTD9XSm7wa8cB4faSuqlzitgZm1oND029GZz82SsLooQM5+yvOtZSzNS/nGwjpeLPMNlRdLTZlA9VzNG03RuibKog2wtUiRqx+V91reoY8nRnO6X1x9V2JMHBbes3gh8z/mfCp42uWUVmx8TeqYnzkUwbftvhEuEkrIYMD8KnTy6eEDMLo8YonF6bt5wHUnlaXY7i1trtftufyqcw6rtk3gVwULUQRn74P5u6K158BJwacnWHsv+C2EgAYNGi8nU4/DABVWXucYOEMiEZ8Qk/BvkmRF3nsg4spd+E083b3Ce2e9GlPN2Oncz3ktK0+Kc1q3ya5PuwWyl4Lyllxm0CxYTo6OSKED0wjvCI4YIxPu3b+H7//6D3AcjhiGIcc0x+edc/j0008TlgUQD8D2CYerwr/v+5jYgNA0cuCeCI8t1OPIe4/NZoNhGNJvMgaiwNffFd+/6fqVLRrq554/y4ZV8DWlAD87tvlAkFpgseXrgCXrAmeTpS1PhQQVVjQKX1LVeozjmAJGdUKsAKICTS43b3kminnZza+6qOqNSuJ24dsGFDfIYb/XV1J7lT7bxauaotrNj1w89DEeDCMpbo84W+upuvJSEX8AzJiX6dYivJCflDlTfk8ZfQ2sEhMwoAAKLZbJQCZ9C7Vz9eQb8U69jed1pxaTfSfOuZipoOZyAgDDAPT68osvEMYx9TXwhBBGjFHQKNnDcusW+6u/V/y2ZkrlrNqpPMk+zHqhOc+YUWLz01IH6mXESizJ3DYMUfBXgnbLbCyvhGTRoXyP+YR9hqPvLQc48tH9MQBeYsLGccB+t8Orl6/w8NFDHHZ3+TC/k2Ceiz/SCMsWckzB65kvFf/av8HOnTUJ2e/2tzddleCT975936wco1U8Wfe8KzXZSJ+LVlJl0XzN3s9Vxvk3TEzT2orCqu5bBfiqKpglhk+zBybXO+aFd3jexFMA01ZdNIPL8k72m8v3Z8/Vqzw///o4oBl0LUqmpXcW10hRc/rXCiSn6Xm9hupJyfQhCYzFe/Fj5DEpbqvuSEF/bE+tGqPkQbYK/VSPczlWAl9fN+ZKpzhim6EfRFkKTm1Lb1Hub/LH53gWAleKKWtVZB0tnlkbtf2vDg59PJQv8dIkjFNqYxawT6+bxQ2O9PJrODnELbxtkrAVOGBS9/BirHJyBwJJqn5IzIZr5JgDOQwuYBwHEByaRmLvfCcHLjck7j9j3xuXnyVaNw+iT2FCcU7ClHGlY47u/w7P+0/xePNnaJzSpsplbnmw8hI+QUvr3aY8tNSsCn5jAOM4gXyDhjyYBfgTAf3xiEbOh8AXxw0+e/IB+nHE/nCQ07ijRSiR+thOsVQQjsdjUsI75zCOY4xpbrFerwVDE8E5X2DJYRgS/t7v99KHKJworm7bFk3TSLzkX/TJ4NoAvawPrjdSFIBklQAhgfxxHKO526Xy7EBomVqPCgbTNImFw0y4lqmXSsghhFSuvq9lqyCiz9lAZ8leZTWhLu/4RFDsYlcCEQSXOznp3DmH65sbyRoQKWlgTql4AYKED2vDy7/CvwlJAJBBwTD0woxrBMmIGhQLKAxoI1TvVEzc3rQfawBERp/EhsTmpi4TqFq7s7A56415+onYX3XJi2giE6Hc78C2UUYDGF07Mggq19DN9Q1ePn+RiIAesDSOA7I/JxZWwmlMOgNqRa+oenLOKmu4kBi5KTtlQqkqSoA5NUIZ9IkGmWGzRisrZOhjevBUIThZfgrR5JhoC1j3uoKMl1Nc9lsZGIzXX2CAxLeXQLi7u8V2uwbIYbNeyzxXcRemtrKC2SCYniqNo7m16JSObTmWkcq/C03I812+vASGTgtRVGgacyGnnreNjjvFWl5mUC+XNWvDTJOLSuuXg/StwkeTc+T+5b/lcGUXViC7ycqZHHSij9rWopm2RQW4yJirDirX3+egtNzfy/tw9hvbGWXzlxTFFPWULlB1F7nkAeb3eRuWqIl+NUBIf1wsA6+9/9qgdN1Wqeo4sBYk28+n9hgszC/rFnoynwBx18rumsK76n1lntf5jkVN0xg1vnP+qJZZSz+lDBLeORsnVlRe9NC2Rmu4Hs7A6Ewri4pz3aYts+sUE8odXXgs8lRy6FYdGu8Byt4szIwwidu7uCcvXBGDpdiP6O6uygbNHHc8jujjYc5d18k5adOEpuvgfIO+PyZlVFlPtY7rnyOtlERDkhLbsShvR/oQv7h9is8uXhXDMFNqLA7d6TW+hA2KESWCV3d1ZhxUcCCPEAir1RoAYTgeQABevXyBfmRsz86xOxyxPw643R3Q9z3W63VRuvXuISIMwwAACXdbBX7XdXAkAogq3jWLlCrhu65LAso4jnj16hWurq7wzjvvpGff5N2h16+QdSprpJauxbShnI8xtx3QcqzpzZpmgCxMqEVicborpqeCRm3mqS0nVrCRuiJ0CIy27fBF9x38+v5PElHJYGeZIYIY3WqF3c1dCjyO3UfmUhmYa2g167jGz1kXYMsGjocjsmBRBshT8Xhm5kvbck4Oqo1a7xI7zsyIJzKmtuTXFtBVYQWq2jqrms1HRskoKpZMJfgpGJ5lYjVDtGWqxaoCo198/nmqUgO0prGXwyHDVPLFupqF71j4XiuZT13zachZNRi5S7Iuo/m1WKPm/YIB8qJnkNRpgZKa/HOwtt7Mw2mCJGftlZPFdcm8jhwZp6MEuNIMa9vDFAUIk1mGxcoqLlSvcH5+gZuba1xc3iuj6n+lS1FIxXmYwXKqpvHD1Z1mdm0FNt7WalFaCPNvORi8HsWlUeVMs5Te2G6dnIWqzyjnXPfla+BucV8F9bxAI4hj+U3LDZHpa1wHOSr2dx6PuDYofo98JcXgVePC1fDMeRNX79UCQqYnubD8PfulK12sB8Ou6OVreb5z1ZbCvc01e/K1665WY8xbB9h+mTnQEuy4FDfe1NCy39maYufi9b0vlX5vX7e6QSl9yy+VQkZ+Qdaagrb1elPRe049KC7mtEbUgm6vwMgeHsi9tzuakTNN2R7YptOpTr+OKdUQZvkrANlfq9VaDilkpLMppikkoAwgWi1cbluFI+QnBnPAOASMw5gOiJNYXwaHESFMmKYRXbdC2zTJLWe9XuN47NPhhnMcVo5Q8haJj2hMJUGEnCnSo9vwfezHf4Jtq2RqzsHrGjTetlQ8lM/aJWb1FSBKSjvnZbwOxx4Xl/dwOI4IAWi7DswBwzigpYAhTPhR/w4eP3qEtu3g2+xqZr10CEghB0AZGtD3PYZBPDJadV1N6cURY6NDUuwrblahpG1bEBHeeecdvPvuu4VHUR3WcOp6e0EjcAq+Thl+9B5nl6jALBkEAEgUfWQmLGYiCQiKQeBhLOqwZarkrINmeYAGqEi7gv6c2tD3PbquK9qmwodaNqxLlvr6EjlJX+rayKTjstZFm1aQIZYxwInaBn7VonMr3PUjeBrjDiOEBAbjgo5ZNdRSwBAhI0ADaDW+gDAFxloDKGP1qp3XNqqoktK+pqGqvebthCp5q8GL5a81keT8avHWElONLSPbcr2l7ilzoHTyYq3HeCcTzDhmwl8i6YiKKRISA1Jzj2Vd7O7u4OHS6fLTNKaNF6cyt5Cr4VHcocMGM47mEcBiAAuoYvvSi5nZlsQ1lxWq4bLPKgTOzytQKNCjaRUnARhxvTIo7YvsUpcDvRlIGYQsZLBQgVgyeWkb6hlOz+Z/zD2KMUsQmuIkgFszahCi73QgHPYHrFZrPH/+HGfnF4B7uyC13Irq0rVi9lTWzaWHzL+U7tt7qawTNTFpfFQuo7gff50D2npl5blMgmCon6sv815ay3kPpaUdtcFl/ZQrsgyaTBlm3xAIcICDg28aHKMPdvbv1pHjqmfG+dI0Ie2xSuhLPV6gW/N+o3qmAq9GQWF98xMdMf0u2q5C1wKY42rM6zgKBfAzIci005ah2QgXafBcRT//rF2vWln2Sz4xR3pu1mtRz7wB+ZnMVJAsmwt7fpFyJtpqlGjFIxWfWtgaJbmza9bwkmL/5vYKLwhoGl+sEtsEXedFsyMi5YpQEwkNUxrKQEpMoe0kAnaTR3kCeLUzTrD2xcdN/xco1OxyzmG1XsM7H92cxuRdotZLF1OjSqyjKmSjBwAY3sle17UDCHZkFkFlMFhM9xoHxvFwwNS2WK06kHOYxhGrVYd+GDCNGhNgO17x+7rbHGNfFcN6B54CwOf4en8fnzUvXz+EdtxmitCyGaVy2Txq/ooHjQeDcLbdiqDx7CXa9VoEoXFEGAeMFLBab7C+9xAXl1uMiAmTpgmNeg2Z/k6TZnDtcDgccHNzg2Pfg4iwXq3iM1M6HRwEhCC/qfXDORfdj8V61batZPBqGmw2myT8afjEX7hFAyymMgXsjkSD6siBCeIL5zKgV5ehxjUYpkEOaGPGNAZ0nU8TYgO+bdxE0pQmt43coTEezqeSlwxYkAmKVg1mxmq1Kty1bF1W4iOaoBlFpmkAc86SFZigQkJNV6X9kmaXVh26B5fYth2GMMHvPfa7HcZxiofwIdURgvqrM6ZI3PRMDweGI48JhIkI8B7bi20irOpZSpF6qg9kolKJ0ReTB5h3Fn5FEjz0kQJFm7+cQWutjbOwK9NvLTMfLiPaVjbtRQQl1gzMhhFn9hoHEinDjelQuVIyM8xuCRznFGAOkVDGOZkm8RtmQLzsR0zTEcAUv+toGYYQK2WOvrmkv+eohMyu8+ikjBsVuFmaPu2TlpP7pmxXWJTyMg2QvOoJRzhYWKxrzOLD+82ElaeUjhaQlIoJS7DkPU9wy+nqUy11SBr0rAGPGZ2SsGQ1iSjalGaMaKHf5ZkhgTmd+J7gFgdM04i+77Hb7TGGgOura9y7/6DCjRag2auGC6Z1caCWMdp8jyWhIY2Cmdu0/MoNqMea2n1VtC5VqPuldMUg+8FYIcC6FhAVJVUcDCG31bh95D2Wqou/xwmcMRZdOIa2MCAZ7+LXeHZAiGulaTu4/QGE6IrBkWEal9GilgKrRrpAdryyVakAXyene6kPMA+bF+NGYNu/VD5BUpSamauBRfE1g+y8FN7MqNOcmPZKN2WSkxJBLbXxnlreEjgvKXS+Vy4L6DxzHnElpbH9WbmV2qMutcU+1r2ThTR5XJ+hkgcU1HW+1ooxtNuI9U2X+Vi6WfW+KLLgSMgtjf3m/FzmF2UheW4qKxbJWIQwVjPMcZ8yCFbZRWlpqtX81fGeuRv/rdZVvld94frG/PtCUVAav1qv4ZyA2WEcMY1jpAfxrIy4vhx5gISPOhIiN4WAMI6YQkBDPoJqABwwYsQ0jOJWm5KxxFHkeKYZWLJPhYD1eoWmaTCMI7q2RY94tljiGSf2j1lKHAdWD1x05BCIEZhwF34Nu+mf4qzJmvlCPkfGDWX5Khrmq7T8V+8kputAzqFbrXF2tsF7772PwzCiXW/g2w0cORyONwAC2tbj5djho+99D2O4xeE4IQRKloe+71MMSmBGP4xYuRWev3gVlfEeTdNht9sBcDgejzg7O8Mw7tF1nWQAJBEY1ut1SsikLl02xEAtImrF0DAHZsaHnyxPgb3eXtDQ8Y1Wg/pSNyeNg7CuTwCSJJTiK5jTEfH22SQ8vKEu/avxH+M4wkF80Pq+B4AUqGIFizIIXNvNcK5JWu7w5HuYPv8TyPawjk7lFcCgwNHlqsXu+hqdbwBHGKcgWdltykcATIQQCfUQgpjxUi2yWT0RnGvQrlZ49P572B2OuL85S2OiRAxJE1CMzomZ49mtAlAVN7S/1dgXVNS6jGQYfKr2GlwWfq0zSsnIddSPZEpazwrXfTTA1vCMNM/2lFfW9zXd8jRG/2+elUGmbCknl1H3BIjrNDKYeqxqvmCZelFSvOEiyhomxhCAp2EFBuPGn+FufZne6882CM1CoFY13u1xB5+sb8DmeIt74y0e0BFrzyAGumjmZQ7FgVPSNCtkWKYYmx3EoqlMpZ5PBbOn+IXCYxXdQlQyWM0SB44p/fZwvsHTb7/B5f17s26f3hvL+1sblufEtnrh8cWfOd8zPEtxll3nxcTEJs1wcb3dy2rK9qR350KGMGCzqgsME9sUGXUWIE8SkPI7ISuIovU7K40I6/UKN9einEqWa2vNK0fCrJU8eMngVM1s9sFfKGjW7lNX1Z+F9woInpZPRDVmA9TxNcVam+3x0g2vXrNSBUM1ysv0maFCQp43AKxHmtkJVctLTZthLG35b614spTYLgXtpcgcZJ6oLD01IbCL+6SmdOF37UfFj8pKuKIzVExF2X95R9NyT5N+L0h41Z56buX5cZoAV1aiiqZcl6nbLJ+RN+YuzcatxEbFRn39Gj9xnyE8cb0yQoZaEQjxUD4P5hCtFoD3LVbrDkhCQ8BqtcboRxks5xKCInJofCMKYZ7kWGfn4IwScgoT2uhmPwyDWKrXawkOj8IGWFLhvjHdtxkvpQsThXSwoFg6LvCL20/xg3s/SWtU5wHQ9WIooyErtUdBOR3VnEPma7XqcHZ+iSdPnuDy3iXWmw12z19KWllqQFPA3d0tHAFnZ2f4f3y+xX/v3/k9TNOIcQzwvo11UTzXIlc6TRNub28BSBpxtUDdv38/NkkEiO12C+899vt9smDYK3lxRKvGKlpD1AXLxoKMY+mVdOr6ldLbAlkosMHg+ruNh7DuSRqIop9tIHZdtn635SxdWrYdlHEYi6BvW08dz2H7lfKxx7qGQc35VsiwhFKe80DMiS2S3nEYMfTXkjKsa8W8NY5oSCL8vfNwbQPXePi2E99H5wDv4RqPthMLTOM8vPNoOtnAh2GIhMtqjWrCskC9EzWLTL8mauVAVCNsNpcpfx64WV81GCup+exTBFupimJjL8CN1G+ezWVmHlz0xxJrBsAxJ7rTw5e06KBrRHwkRWHJ8b283mnWK/mc+DFU289FfyPdTW0pjnVY6LGtQN0Sr0bgl3SOl9tHmJo1pqYrgE3B6RWQSwFVobKWhm6LwVR82FziJQG/mEZQmOCnAffvnuNs2uPj7hgzqdhVRglVlNYxucT/FmgqT6b5SrR7jBfviBtitCBCXajkvlgyR3gG+n7AzfUtrNdBiiM5ZfYuUGRaEGmvaSa69OTCeCaMaddwMcdmT2Hh9xofQfcbYbl988LsuFL9y9J2Qu3ypVYWQj7QoN57+mZdqGnHjNHmMtq2S3KFKnoUuuZ9VXcujgPr/hJwMndVMzuzogMLjZzdX4S3dj+l1umcKeqr6k5XEcFTtbEGikhrJ40Bs8QGxc+IwloaMQLS+R7VXBctIVN3vabSdym/VOFQ7l7Rh/zRcMb4XX/JAhGb31GMnfxug6lnVel0Vmst9cgQ0pol2LUkZMrwBbZjrnQ+/ktAPo9B+PtMeI3vlSuVooVI6P2oShzziiYrUdcpApJFOdEzBgJaU655mJB2bTEWVgqqCYFdbie2BBGhW3Vw0S1HNOaTnPJNJJmjyCEEPdpSrBdq3UpukMzxBHVtBCPForKkuA6TS+dqsOoZYiYrAqFtG3Rdi2EYcDwcsN6Ixn0YxC2ej6rErhdNpYDktHji0meAojI74seBP8bzwy/weD3mxxcJQTVer71ZWZ5JDonWgOy7/R7b83P04wjXNPAkPKzv9zjs73BxtgI3a1x+9rt497338PU3T3F9vcfl5X1sNhuc6xkaCUOLy5S6OtmQAU0lvF6vMQwDVqsVnHPpLIyXL1/i1atXOD8/z2fbmZgNVdw/fPgQu90unbehuP5trrcWNBTA28P3VBhoujaZUopzNEJ2mKkzQDEHTGFMuXtPCRe2PnvZVLb6vWka+Cjw2LbqfyqcqMBjhREBnVLPfhjww+sGv3Ehp3LLlRcsWb7PjJvra2zWGzx4+BBt48Wd7J0n4GmCc14O9COJTSFSg6kJ/nYOcNEpisS0J3xFiLXEm5QuHSng0vwmA5F+yATGasGskGJ3E2fNoxlkFDuPrF6qYka2HcV0FegM5Snj+ZnSDUApbqaONYAlWJIS2Zjtm9FGS1fyd4K4/DmK6e8iCJbYA1mXUn3NPGuGWnYb4OKg1wJKkNXMx8uZB6t3GJxOob0ZCC+5xberh7h78BDBNTMmLCXTCQJZIcyM2cwcK9CQP8G3gG8wtSs8XZ8D04Rndy/w+PgCHzRHtIS0BnNTLDCVsZAxLd0gFd7aizFrwuxS6KIAQeM0JG5sAgeHaZQWvXjxbC5oGHfJ+YgvDRsVf8sdN2dw6oNS+N2bfWmD5mcgMzVFJ+Y17YLxc0eevrQnClpQoRzTtQytFLqW8MXSm6K4gkbkZ4qYsGp4MnRm0UoqcGakOLu8gvIanS1zLScpuwywULI2o0cL41jRtTc+N1uVuZ9JTKtxdEUrct+UZlVjZmh3ep5MvTPhVl2WKhUSFSuwZgP53bJVpr8lX7BUT1tsXenSbo78w851Xsq2ReXaNiRsfhVLzfKdGj2nri8sz6Vnl5FkmjPOz0gQbROtc2aPGeWDvkQE8XKIZ2EN/TBDWRpRaFtiLRkA4TgCPX+U72vn0jt1f2j+sWbTs+Eqx65tW7RtW7jlqHBBzoFcA0ceTUtwvsE0jSAnhywHTAnQEqnl3fQwbfeAME0IzqV973wDcBABJh6jwOAInDv0fY/D4Yj1eo2mEeGj61ocjsdT01juH86UjljdliXGRBVh3x4+wsPVz6KXg9KYRZgEObR5SdGpdcdVZ/kjSUrucZD1c3N9jbZt8PjJO2ibFiEMCGHCq5fPQJhw//4l/nx4iN/4zb+M+/cfYAg7XF62ybIzjmN0fcp1bjYbEFHC1PqfnqeRsoVFXLxarcDMuH//Ptq2xfPnz1P2qa7rcHt7m+Jznjx5grZt8fDhw+I8sb9wQYM5H44HlO5O1i3KPk9EIhEbwUQlpnEc0LS+eN66TVlrhOZuThNJ2aXKprKlSE3VpMPMRaYra0HJAeyyAJh1QRHu3buPG14hhAPUF0/pTlpcDJAXqTiEgM16g7Ozs5j3GWAO+aj3uOm4ABJSl7YncycVOGLAt213TVSLDzXTiMCYYmMTMGGgXhuWMS0IF7WYbz1a7ZXAYs0MCgZKtijzqKKmjJ6y24xptxUYYl2prCXKEN9lszacy4cohpAFDQlUmxAmyd2dslJxLocSotO4CE73s17YWJ9sK8ywJWWaxYS5exgD8Gz0eOHO8PzyXUxdmcquGF97qJ0tLBVYvVo0qhqrRdpJgPe4uXiCm4sn+PJwiwe7Z/i+u0Yb4ztcbI+mMwTEDM9w0Ggap2yczVgocCmmLYOnJXhABllrmt3AgOMgOeYBXF9dzTqTgVbNicvOZ1nZIhaNjiqZUDVKpk/6jN0rnKfOwsCZtQRgu1hi/TYmobREcOpKGv0CC1VWC1bXDS48fU4LUnTi+2wxLQ1G2t9Kh5umiWtDg2LNgV9VOfpbXhHySV34ipbFwctjsIASqnKL3+2kWoXFYr8zWJyx2vhI1pNYy6muAare5WL47FrT70ub07pmlbFzp551qVJaGvN6UVslxGwNa7n2vXptcEz1zlWfTq81tjyjUIxh9k5VE5Lvfmp7/VR+tzTyUNw/RtkW6xyGMZ5PUPZXlnXmR6n9umyIME1j1TskWU4xrSoUlTYRgCkzU/Omfqr5bzWm9Qn2swVaFqu4q21bhInR9wOmKUQ+6eJZCw7kGzgnGNA3BHI+vdt4nzxDRGiYgJDBOIEkmQc5uFay94UpJKWz4qyEEacJQ99jtVqh60TYOB5F2JCA6Ul+Px6XOzXbBTIQrOMdZF2qMDDiQ+zHn+Os5US3SffrwrXkJJ6wAfIaqYd+CgHh2CNMcWzI4d69++Bpws2rF+gPezy4d4Ht2Rle4Qf4Wz/4dTx48ACuvQ8ij6dPv8Xz589xeXkpSvaCvHGhmNexrwUM7306NVzx8Wq1wkcffZRPAwdweXmJzWaTXLT6GFhuA8f/wk8GF+lJNqEGhWjK2uPQz9LVqjBgc+1m64GLB37EbDTG4mCzTdWWk1NXPpAPUKKukfJLcR9apm2nmvu0jS/OPwXRv4S6wWhmHbvHRXtD6NoOd3d3OL+4ALwXSZ08XBQ2BEhFAq+WCCI4jjSULfHQLRKrSZSJUgYny1KkKXNQkoUC8zt0gyjDkOdqFlGUqbRrVuv8mrfu1JOmshkvsHUYDaflClQxyRmTwwKAjiH9zHC+hSOHly9fgLclw0uZFGbgR2ANg4ssIqqlVj2fMquinzC8ktMyKHl2fG43Mj7nc3x7/i7GZg0+uZGjcLhkkSj6PX+vvFG9QPXE2Gelnn5zjm/WZ7ja3+D9u6/wQXPEyitcMcJkdGlQQUBPhdVtlEvNa5XTGM01tdmqBJkbPYwTkngiTDkWZByHQoiUV/T+aZCswv0crOjslwCwblvqB+d1YzWYi0qwpamYgblSuCgtEbaPgAolmV5wUcasbqorrIEqo56x6mXzVkY3Ng7Jlta0TQJocvBezArDEQibdVxipbINcyZXAWIjQNQznj5bYWQJZC/RlhnKzvcjpTaPElKwS0VTC3JVtS3RNUYu88RVr4si/itZGXL/Uklk4i+q7qQyi/4rr8p7cG4Fmq8NS6d0ZSwNgv5rXa9Kel7XNe83YPZKWtemdVy+n4ei3IRWGTmOA87Ozk7UXZek8xdjNMaxuJc0zXVpVO6y58dzAKcOQ7NPptWSf1ta6EvDBx0PcZlSEDmNkwRNx8x90ziiaTvJ2IRodQgTCIymaaOAwZjGUWIbpwlJmkrVZ88S5xx84+Vci0ayKI3DWCqkvcM0BfTDkM5sGIYBfd9j1XUyNwHwjcR8zMenGF1ZEcwxD4EoNzzLWR5MhIAOz4/nOO9ulgeqGrN8NpqpRV3wDZ9ykdkzI7mKeYhny3AccPXyCl27wt3NLW5fvcL5do1Hjx7gJ9MDvPfJJ/je974L37RgN2LoB2y3Wzx9+hSvXr3C2dlZ0VPFyVa5rhYJG55gT/NWjyB1jzo7O0vWj+PxWJx/p25f9vC+zWbz2rHS61eO0bA+YPU9AIXlQNwVIrHk0rrAyOm4iAi+EanZuXjKNyCp1ZL2TStDkkobr8KD9WEFyLnkrjRFMLLkNGHP6ND+TNMEMOHy4RPsnztsPKdj4qVipCwG6oqxWq3wzTdPcXZ+Bh/LO+53WK3XIPI6SFCtDkgJkZyQCmZz2icnsCXflOjF5+Iz861g5kPfVcRz4tmZyT0PcQkGuWR0ZrZRChb2OSoZrnmjLMOwmeKYdDMIBWOPrCoxTTaxDkGnyJBewwzi+vCRIDz95inwmWlHBD6AOfTPtM9as7SJ2doELEPQeM8wkqWHdiPji3CGby7ex9DlLGOYlZtBiwUMJy/SEupqFcnZedUxnc9OqicyJpDEc/x0c4GvDjf4+OaX+GglB+ilzRZymUQK/KL1Aqo5AsplQvHZopWpJVT9pnuKtXzmlH/XChqyFU7tBS1VrVgRgMHQMiiM5jQU1UiWn83eq1eSDACVL1RYdIY8kWfcaq6LlaGbNeEQa/nLWC19X6zMfrc72+5b4xKQF2H1bgZDhTsXYvyclhoYyUm7qrsurR4Q3zTV70qfl+bZvm4G5ITFY0nQTL/Pfst108LEqYbUtHKRNqb7RFk2Se9kOjPrTvq3EPPlN5tzVWmVJWMV7aiFlZra21UYG5t4he2f/UViEcpWljKKbbF1n7OWqaWtkShzXtvI+6AsT0khmQIWN1nmHaS8VwB12dGyl/VUKqieKiUpx5bN10MeBemDwxKXt72e68vrxpR7qfyUn2maRoK0p4BhlJgSjWFQ7fUUAlw8GV2tHU3TgiACxjgO4DAV5VqCJltEeOgUM4Q679A0Lbxv0uF9zE3CZRziQc9OlNocpD1NPPBvCCGft8G2r5ab5C2QyaLcl8xMSPT4bnoPU7iBd5ht8VTeKVZr1jJHFihFR6ziYoyud9huznB2do5utULbrXB9fY1XL17ifHuGB48u4VcbfIHv4O/87m/DNSRxPixneR2PR7zzzhMcDkfc3d3mvrBYoo7HI6Zpwna7Rdd1GGLcssSkOsjREpo9KndSj4M4HA7x/JQVNpsNQgi4vr5OvzVNI4HrlfHgTdevJGhkdyPC/fv3sd/vF6POE/hyOQ8+SE7FBkHOnuDobCG7GRztjaL19OkwF1o44de7phBmeNKYBRUKANd4qF82AxjGMQoBKDRhYvHQvqlfW8DZ/fv4yc+AD90VNqs1GteAQHISJonEzZFaNo3HOPT44z/8I5xtN7i7vcNxf8C7H36Idz/8CEOIp4ODchIr4hTYCiLjwlBvlAhwqGRiJeNZIr3Ipzsrz+HqeUZBrBJoJ/Pc0joy1LVgrIYZyBdlK1qnqW1G45WBK4hh8+4cyqU7bBhNqqPsOBnC0jRieTvs97i7vTHlshxgE4UNDgkKJeqiKRxT5q+qVYycD12ez0O4RKAYwBgYX4xrfHH5McbVxvQwA51C/jrFXNLd0/eX7hSsQHltOaUnCtGHHQ6be/hRe4Zvb57ik+klLtuANh6CWZfJyER8pkzW5bZQf2bEZbsL1ylijCGgcc6sCW2mmOOzIoRNiXUvq/2DGkDWw6H/xnWiQo8C0OrpumqKnStxbn7AKnMLNyi7NtLjp8AJQVIiWwe/ql3VCuGF+0rzktIkAbp5vVlYz3uWHcG1DZrWgydJHR3zTZtnIzxkzFqqO41ZlQ0pQXBePGyeJRiro/ym9KCE5bJ7kwU5jTnlhbr0F7lORkBJTyNYLSawjr9ITxYDn0AmEebn1BROmqlnebPEMYxNJHVsNGNcqJi0oZFgJe/VNDZxzeUbpr2ZwCW5jUr7nqX/tpk2EUfuQtpw+bsqKFK/zaxVe2nZYUb+keXBeYjyj1Aea4cwRP6WUti7eGCn9sqYqCm1XTCLI1FuUu2NsQDMRBdbjlK5c4rVWyzvebnzt09dWmLTyInnIizE5D0azE0ZdXNgBB7hnXijMAcMwxGTBB7EMrnqBKctBBCUdTJLSvl+mtA0Lbq2RRuzJMq5ZhLfy2HCMPRwfoWmbTAdJxz7HtuNZE6aJslS1Q9DsUPqnqZ7CSADwQW4eNAgEWHkxzjyT3HuxWthCvFYArvbVOmLBRxAlLJCOgK8F88dcl5wKAPvvfcu3n3vAxz7HrvbO3z77bfY3d6iazs8fHAPq1WDPz6c44Pf+AHO7z3A86sXIKIU6H15eY7j8ZjiLnTgOQRcXV3j3r17Me0ssN8fovdQm5T8euYJ4CCyZOnxo15AevI4EeHBgwcAkIQYtXz9azmwTwscxxH379/HdrsFEeHm5iYxbxsgood96HtqxkkTtHClGI9qLxZSE+czN2zMBZBP3Kz91EII8KZOmx9Yn2GWXMG2bU/v/wYuf/kf4+rlKxA8Ls4vcH6+zeNBBBeFlMvLS3zz1dd4+fy5tIkJX3/9DR48fgfwci6GarGY4jkkzgnxjgcSyoLnZL3QTVvS9UpLCUuMMmBLveD8NzFRGIKc9h+n0gp2sITFljHX/FKiXpHPglAyqhOtF4DZQpnypA5Obre60BX3iKI7GyAB+cDLly8LEyIgsTpgLrRQdo3NTKVVi2u4lpkVMj/W1hJwOwA/bN/D7b3HYHuuSwKs8Z8F2rnknjUfqxO/LzxWtN0y3MzxS3ASn9P+sG/w6v77uA5PsDru8P3dF3jUhXQmB5DP1rEE2g5pmsrlXs6uvMbFcprM48zzNcwxZkTvWZORKa2w3BXa6zePtxUA8uDYWbeAM/e/wIfpsu04VZd5zBQtZYpliEFmb2uzZjOOt14sxaX7u/yewV0Gr6kfLJZq51w8mVbSnLOiVLIllG2S4rIrK1GbnzFANbsOcUEL85rQuSlBGSlxPjXXSojt32JuXKpZS2HzbLHC7LATFfyoWPVm/WS4ZEfcjJGx8mofeelJrkc2NdT088S7xW86/0ZwiaYYLh+F0uHAZddR9Ns2xzwV3+dqbXDqM6e1Vgt7iZZybGcSNOZ7W+dKvQaUXqgmmEOQFK9pddFsqag7te4xSZE+GzqoJ/UCdUHqlult+qG2qBXM1LzM9QO2hvxZ4yumEDAMUxIyyDl438A3HUKQ3wNLAHXTiHt43x8QphEAp62rcQ92kjUmQiw5woNd5KditZCzy9okbIxyEKsUiMAB4yCnWjdtg6EfMIxDAsW+aeBGPTyu2FhVl6m8o9uEKLpVbbHjS/zu9x7jxz/+sQgjiW/Uk5ixgZRMWEWrQM4qFuRE81jPdrPF2fkFxmnEyxcv8PzZM0zThMvLM9y7dw/rrsVN8Pjm7Hv4r3/0MV69uipwc9u2ePDgAc7Pz3Fx0UT3JZ/6JCneD8k9Sl2eLC5XzLPb7XA4HEDEKSxCwhmyEv/q6grb7RbDMKTTwcdxxPF4nGHwN12/kkUjhICu63B2dpYaptmbAMw6ZX3DtAwbDV9HrauQ4OLJ4TpQNsgcQHp3mqbiMD45HKcsU4UH53whYFjrTD5ILwso3ns8+M4P8KNvf4xPjz/E/u4G337zFKv1Gh9950PJHe2cZLkC4fziApvtBnc3t7KpiPDk3XfRtB1Gc/YAQ+jExAziAHYSLEvOA2S1XVwSC44uJ+SsDi/eXbIUsLmXOUf+bhmUZY0o7xXlLS2qGhAsPUfm94rLJT4RNWKzsiycOWUuNroMMs+bw/8YUbgjmefnz5+VWYh0iCKjSATIlKvAROdwBpL1M+ezNYzSK7V8CIw/D5d4fvk+xiZnjkhtWOYJpqfz34uGvN3eT8XMAIhpTwruJsRAa2Wydm5yQcG3OGwu8YerH+CDlz/D97t9DPxVIJCJfGaipgiq7p3smmoz4xzFeMKUDaSaHCJKZwMY3FOVrn2pmLkshvKZk5dpZfH4MnAunqNqv6bbqlGO/Y7v0sLzdVxGXfW8/IXNuNwbUwgvPJ/3dzGsNaAjGJou2nqNi5rPedkeq0mUk5rzPtR1U1t9T8CO+Gxs7WwtxLrZ9s38TX2iSJrJAFz5r3BbTSC4rF+helYz2TFbWm1c9cnQVNPumka+xkFW7hsrn+6N9OZJIFHS1plpIdXBpqpYT+pb2VLbGzJtZCpnT54x7tL6I5GxxiohkY3iIqFRRZ7G2YV4zo+G0gTWGFHhkeo6RGSApSZpOTGyMEqpEELRxxAViGSIvO2dLBvGyCszAnaQMn9a5s38egZSXW0rEHAYomdKFDScb0DeRwVtm2JNxIUpoO+PImSotS2Oj+7rkp7K1+x9EOJuoeRarzRA4zF4CCmmj1iwpG8k7f9Io4DfiD+naULT+NyHU/0ullH8ogwo7tFv7j7E0xffFAKpjf8FAHIObdsldyOZFsZud1coDCQWpUXXtWjbFZq2xdXVFZ4+fYrDfo+u9bj/zkN453B+tgU29/BD/1fwt37v38Ll5aUcXmg8emRsxTIyTZIm3N4bhwm3Nzscjgc4cri4OE8pbYkkG5XzHquuw9nW4eLiAk3jjLWDorvVgHEcsd/vcXNzg2masFqtsN1usdlsUky0nhb/NtdbCxoK+o/HI7788kucn59LIHjfR5rMhcChgkDKGmU0wzYlrV42MFtABKcy6+Ap5pxKV6UtfcYKHrZOb87/SP6TcZC8z+nA7OnhZ2fnmD76axj/7Kfwfkj+ajc3lxjDFt2qBaLvpnMOjx49wmG3R7Nu8c57H+C999+XQXbOBMNx6oMwWk7WEYIcAliAHALIOOTUwaD2uZq+x9Gq2FB+yGpN8ns1GLLatiXGxuZZGE1UfRlGkebYtJAN2U5WlzxOyrAsq1WCm60X+ruOs2HJ5iTwu9s7HA975FpsbzgFGAtt4TQs2Ts5a73SsBVjlg/zqZQ76APjT/EIzx9+aO4ZpB0Z3BKhLBhMzdcLTjV71ZSPahpVmDKs37xfuDcQEhOrXUS0s/oIO48vH36G67tn+I3hKc4aXR8ZvNQ9rIFGPQr182ohUbdDDhKr4UKAb5zBxcEwCmUgS4Nj1l+SWMnMy+krgdYZg6Xys9ljHJUH9rWl/b2414t7eWLr+I0cGFuXy7O3LXRdqCq9hQqYZnE87yiC9nO+jn30zT7sD4n+Cd2tZ70E+AqCZR2V/EJv5n4jlVcKatqxbGG241X1tHjeEKxy1JSW23FI+9+8l14tfwso12NVPGD2JCE/7KBWcUlyoNY68frMZ8DknuUxsCsmLXWO40ImccOcusUlzBFvl+4k6RmKLl9mM6ePrK7OZSRIuVJORSLFEY4HqwIEDlNKoc3MmMYpBivLMEzThHGcUqptVYBSLAcAXPRh9/H0bxGGgbu7O2y32zROllZmwcbwWBJurXOkcah6OZIDe+vxtGM8MnAIH6X7lrGnncCWBhu+cJKq2m+Z1nvfJHdhOZBPwL+mtQVJ5tAQOAJrFnepaQA4un6zCGgcg0vFxQwAcZHNns3iE2WsxEsSST5CcdkZsOo6NG2LIWZAsmc6tG2bAsMlULmJ2ns5PTwPY0V7ZqQoUwh13w/MmPgxfvrLP8WDLma2i/uB0wYBCBIofTwezdlbEWP47J7vXZMEr2HoMU4jXr0MWK063L93jk08G6RpPH40XODVw9/GX/2rfwNPnryb1vI4crJSCBbucX19k3ipYlgOnM7pONtK4oJxnHBzc5sw9H5/EMwehbnVukMIjKaRTFQaUqCJnrbbbRSgdnj27Bm++UYEMD1/Y7PZYBgGG+Z68nprQWMYhmxxcA7Pnj0Tc0pcKGotqC0G+jlPRgn266sWMJZ8wLQNGvleu2RZqbLrunRCYt02fVcny7p5ERHudjvce/I+fv4nj/Ex7pJVJ0xRSxFPBQ8EcJjwznvv4vziHJvtGVabDcRj32d2yUA8TxxJwxV9PvVvdiEQ0hv15wUgnYNTc9Frvy6QbdT83ICHpcsyTcPCFnGYYWwJ6EWybF9gpH4WsKoucxm3pAoU3FRs3eTpB4gcXr16OTufhYGYZjM+B0IRKG1xKMo5MDAoPUDmc+TfeH4k/Nn5pzisz0vs+obg1cI1YQmHzV8o2jLDCgvvnpzvpbKqMmz7CkDgHG7O38Ef7lr8lcMXOGvjmCoAtQCnqFMBUl2VmdkaeQivkD3KjMn4aITAQCNg27punF5MKNq4PICLL6ViVfCwh4lJf+nEd7PWKmBX1L3Y5EwvdEBLKFOOm4C8U13Qsk5Ot3m0RK3L27N8S4V0F5ma0lPhHwGcck3n5mgddk+WtBrVMFWiUsL9JfAoWsaclANp2lMRcVzT0NQUJleuGntT7KlCkXad2QQzYTV9N78puEkVRL4bhS9Q+hk2nsNSLZ61HIDJyGbpdTVQZq2pBEHp57S2GJBUurqWImCM5adc/Ig81PBhZkY/DFFwEh5SKidlf2tmJK1XwZLOgW9beOcT1tAYTQWPhLyGs1JS+s1gOBJXocNhn+aJdVxSUpIoyBZrjxNPG6r0tnkU2fytqYAuaP1TUqzZPpttutO0SlcAgyVAmAhDTO7jnHx3RPBR4ODo2ui9ZGgahh7TOICioOnIyaF9aiEiXYeuGJPCdT4KNPqb81G4AyGECcMomaaCbyLmZHhP0XLRpOMOJO1wC++kDb7KqFSM2QlSz2bdknPgifFs/xD322/SWCa9U6JJpYUj1eMcuq6Dc0DjPBrfSGYt79E2LVbrDTbbrRxeywHdqsUVb/AHh/eAR5/ht3/wO1itNrh6JbGj4zgmnKJjt16vwUFiji1eARCzpkYrXZTwxFoB7HZ7HI9HnJ+fgRnY74+4ur4CMGGzWWO73SbjAYBCwbzZbPDhhx+mvltPIs1W9abrV47RUAFAzS2eREts3aK0oTal7HxDzwUNzjNpQEJcnPpMfE6tJGU5FM/EyP5omp4rcDTWxUmzwoWLkmeK54iDPQ4jfNvh2/V38MnwRSw/CIhhoPENmijwCMBxePjOE8OYRKujXp3SCQfHwZikXWYYzLi9vcH5+YVhDZRQbskaTjEknKQzRSDpwt30rwXrJSKGbjx9Z7kqA5pSVaYPnL+X7yg8i78QQEyZuJ+AMkv1pl8UQHDOpPHq1SuAFgzfVnu/0DS1pZS6Nts788UUGcD48XGLby4/xNht5tr01C2qXrefaP7OQn2Lz+ignwwUrlzSTk0NVd9N3cQL4xnB1d32Af6AGb81/BJnPheiWsJUjQVoKGc8wS3DGKQMjiBHAY7uEguuQ1JKWFpRuhcZgKhcJbWtXP9vumrXLfs2gXNKYkYCKvm5vEeti+NSkGtqUQSUWRpenmepO7+XPpl51WGop9s8bYaJyv4aa9XCqMSXhH5sVitcsbitTGGKgZe27Wy+y9pNFFBP9i1oVtmrVCufmjuqPmcrTf7ZuE5C18OpcmQcs+azWucF3XwdPa/X18J6q2hqHas4p89mft5UN2kQOeUtYEChWp4UcKglIUyTiXEUq8E4heSLr4o+712xV53PiV/E1aSBJ0LbdRJQHX3+M5bQ4AaO85PHoIy7NNshjg1BlEk5xXXceUlYzbZyxRDr9Rq73a4AmrUdsACyadBkf09VetsQ933e63nW00o6sYUydzhBg3RcihqXnpUV6TV97SRCnHMSy9iPB4zDiPVmk+apaTzkwLkB4BCT2Gj2OLVsWl7LSQlNEEtzAswMwDmxMCXltZRHCGJ98jEz0uQxOWmfYK8gZ3Z4hylMCCyCyhRjNcZpMqN6+lJlpyieStf8kbcIEEGzFjLsTKRzQ7TMMOHRwwdouxatc2ibFk20WIBE4Ty6FT6fznEIE748vgN//hjvfOcjfPbp99Ct1jjshyQkhDCByCVgTwTs9/t0yrdlM+L2tILGsIUwJYyrYQ5t2+HsbJvKbpo1fKMpxrMRwZ6PUe57FMoAAIX72Ouut3edanyKxJ9CkJzKgTGMI5yXDARZGa+AXladPYHbulIRIhDXQ/pU88zZamFdsnSK266NJknZsZp9gFw2mksQZCRMIIxjiJJwNK/G7ArON+ngGAApuEh8Mx1Cf0R3+Qhu34g/IcmCAktQIzMwBQYjgEJAP4zYriV70BQ4K3BL1JfSZwLZdM0sAUPW3K4bXTQwVJVjwIyWVzEze1kAEz1F03MZJNaoI7cjn2l+4rIYoWjLvDxlwEqY537FlNLRzgln+SzZ/puSLMNVbc3xcMB+t0MGMqZke0BfKiQDsTyiZP5dgDem2ADGnw3n+PrRZzlwQ1tZABNTlv5jMUBdfl1penZOYHnh0/x1I34qaLMdPIV/zLIhGDBD5e3d2UP8wR3ht4YvRdgwZdYrz1ozavHFVQBeiW1gdRtyyUUilc/Acb/D2fmZZDJhVJYGiyLM50pgKAaBUdyzbSzm1IDTJFiZ+Us9LZ5DBORV3TSfejb/zYBIEp4qWlHUpw3O76l7m50PbaTESmflCBfPUMrUFQohQeuK/eOALtLIEBjjOGEaR3GFs8JKYR3IblrMLKltY9+ywTK2f27iKC55LaQ6rDuZfUN5Req3qSP1mRS2ceqqtEstprrWLfW2Kz6vNR2xZaCkY2fBhbpJaalzhBpYeVDAFAUCDcxVS7+mkM8aVHlvGkc4BwkOBlIwtGi3JZGJpM2Uw9q6bpWCSQs+L5oBSQThyPQzWpGppNlkl0095joaCROYlW+AIVE8LDjWaQFZdh0CAJfSIdsdYloUy83ESlhCyZ9tO0PIvG5YOONBMA/F2J48u2UbZt2LH7n6eYkZLLxcjLrMv288GNlFCJADBqcpYMSU0886B3KE8ThGFysXXfY4pUi1K9aq37yXDFXZgskYhz5mlkKKx+Xg8gF6zBiHEatVB994NKGN7QyYximlt50mEUratgVBDgO0qgHbb0NZy9FhRC/D+B4RBv4Q/fRzbLyCan0aKFBUBYc0Bez52RYEjkkvZAzGZo3fD5/g2t2D27Zw3uFytcH7732A997/CP1xQn/s45j5FICvAkTXdUWG175Xq0Kee50LEZIdmsYlHL1arQDYAxhbNI2D8xMOh+zto8KguqZZA0OOaS49l97menuLBkcwSplYgMTfVgQM3ewOIbuHAsgH/Kl0pBKap+jLF1QjAWjwqbo1Jd+0qi3KKEVoCBinCT6dziUMSlK0B7TOI0AO9JIJkXL7eEiMc07S33qPtuuEOOskTgFP3v8QP//lJe7Rs9QGNbUREXwIaVL2d3tsujUceTRO8k8zuCBUuTNUABsiTb1rmE4CncWLyIUtfTZXISxUYJIAoLQYAZwDGQtxvrZyzCqC3YzLz+U+JKJpGmSJtvLoQlvLuolsl2OQL6zzVW6PAhMhaoTbqytwCPCaetm2jZCAUiKfFSCtwVcJ0TI5IwATGH82XODrh58UoIlNf3JnzTjW3Ke+KHW+/C0RxNczHoNpZysovVnkuDXlFeuxejk+kKenBFT7s4f4s6sjfoefxQDY0m/euPPOumY/MeL+Y2WZnNYCpQm0XIBxd32Fi4tzZLe9LHInkKylF43IDSxdM8vzdxRPAgS4/LsVmXRF5gmoLy4+JreKVK9d59Y6mRethUxiZQrKPxeqMtClAHyEQmC0wJ0pvTVPzZDdZrJFJu4hBhRMcxBNsWrKp3GKrrnGfakYoryiQiy/7VYSkFo8ojOo7ec0NBnI5vmybcplcFGOrLWCKMijRCbkJhira6Sz6XGO8xCVakRgycWWK03aeYgQwDlzUoodjPR4CkG0yrHeMbogAUAIkHvGAhAmAYyOYuYkMJqY9Us1zo2XLEPrjbEeEEXXJENvkQXlxILT76VFobwyiAGQlGwytjBjofwfAOVRShrxE/yODW9ULTMzI2VoTcvXBGZznh9bomIWETLlsD4RztQ9W8rh9IXS97QWQgA1DcZxwjAcS0rNggfI7MlaFJiPHVXfdOEB841dP5uQRPGMCGMuBsNH64PikVisc7JmfdOK5XEawEBcSxRddKIbvDkyQACpw2q9koBlszacY7RtiykE9IdDFGzzmo/qZ9HIB4mrJDdB3QI5iEJb0u+OGGPcBpwTHOlcnKt5vy1CSWPEciSCI2vVyIs8jbXlPfE9UCheaZ1HoBZfD+f4KZ6gxYD3w3P8lN/BcfUA67MLOOexWZ/j0+/9Gj744EMwi4fFbrfH5eUF9rsDnPNYrVYRWzOGoZeMmBBXQXEPxGy/ieVBnlMFgByYPSUrx/G4R9u2+Oabp3jy5DEu753hwYMHCZsfDodCua9/beiBTfpUJ2o6db21oKENmbs8lQTRfrZahDqlbDKXQcA4xed04VofXLE2ZLIwRP9NNe9MhthaMKACzdXVFXZ3Ozx+9KjQthwOhxRQrnVrlgmJqA/YdFuACF/c/zfQXn8B4A7TqJkWJE/yNAU0rbjlMDOOfY+z7Vk8eFBBWQyOq5mzBUSF0GHB3CkCjryPTKrGRPSzese0oYyP4VRGBR4rArbkw8+L3wRYUC4YmeQZhlK8abhXRQ6EYUcmbIG+QQ85QZcBSjDrDtHflBmvrq6Sf2jdCYtBzGjO+m0BegYwmg9drpEZPxov8PXDTwtLBqD+vGUJpJ1duhYp5EIbqu9LBSWNOtsiLbgyeGupXAbK44EX2qof1d0lri8G8OryXfzo+R1+rdvFbFQla1xmtmVVGfdomgRDd6Ba3LJxNzc3eA8ZIMqEuUKeOn2dYuZ1q7JrUiGUpqfJnOFQuW6dqJVhrblL7+Z9sBQ2KyDtdRRE992JBqTHtG6u5mtJU48SwJt26V5fr9aifIpm+b4fxAe71T2fWpfAUnb7YXSrFe7udlGpRZn51+0wfUhrkeXZmsLJ6y6/F3IBhVBllGLS2CkD7wgAwsRATImqfuYAJ22hCkH6XYoV5UeYBPioEg8QhZ73PmmSm6YB+RartkvKOAIKwJisf5RjCKxTXmpv5A8pElD3B+Xe50GJvxMl3kXgSF/j/FT0LeMFzvTDzErNw4yTXF7PKjjai+f0ImFvXX+qREj0bs6DtLlZ6YCEX/r+AN/IYsguglY5pwtKxjFMk2jrQdjtbtEfj0XrChYbm6cCq+UldT8tbxBBhRY6Pv9yip5qnEqIniEUA79XqzW404xJTTwwz2GahoT/1AWZFbdJgRlXkMN6JVmW5v2RveOdnCp9OOwBCFYTi5mPAoVY1PxqDecdgp6VZgCuWq2E9zpMkLaO4bTKasnBV+mBvXGcgJ9dE35wX4hRIRTmJVlM0T963qF78Cne+/BjGTvn8SfHj0EErNcbfPDBB/jkk0/w/kcfo4mnm2sSoaRQD8Dz5y/w1VdfRSuEzM0w9CBy2Gy2mKZxhql1varQnfeiYGfvXXSnkrX73nvv4vLeBbpOBJdxHHF9fY3dbofj8YjLy0tcXl6mFMLMjL7v0+nsbdvCOYf9fo9PvvdrC2NdXr9SjIYNAlHAKuA5/2YFEpWI9VKCk7IIJFcVYfqaKaJpO4zDqBQj7sY8o1pP3/dpwINKv/GcBG0Hs6QCu727xfnFedwkwP4okfwBjOMgAwcmCfCWKUIA49D3ABPe/+S7+Mc//Qz/Bl5hDEGxWgo+U69PsY5E/7ioaSdCTGeXAb8ZlJLWKoktwIGA9xRgz1pUuTn0ylo7qogUF1Wz+WABRE2/inLMX2X7pjMV/rR9rRpqhSoYIRUlAFCmxXVfUt+V+eXybN3MGjQo2pvdbpfHvKJFZBrPuYj5Xyp5ZWJu5vufnxIyAGMgoPzrbNBR/pZu1XNej9gSgTV3FjElLXyyTSlZNPHpOoqxwpy0Mzl8+egzuJc/xa91h0ogqHcBkgA3q9EsLWOLkD1ilB5643A4YBwGuLaJc6XraV73fNIXJsQ+YntgAHbaO0Wj9XW7SxRgzUUPMv/aEiwoZM7t5OrtBBpPChOU2siJDlDqi72ypaBsYAZ01bMJLnLerpEhNm2DzXqDu7s7BA7oh0EyCK7W8FooIa8e5tQ2BTTn5xd49eoV7t27L7zGCAOyT/IkJcsXdL04cyfyLu0fi4Y1KbtAyYoAAOM0Ypo4HbQWpillQApBgHIC/y6fGeB9A+cIbbeKgbgug3mNR0jzHefO0jUjECTBjYGsjLUrr6S7OTYnW3gtHRflEMf26KicWpEMkcLy/mFrLagFiYWPeQvq2lSmZh8z2CHNXr3Cq4uzC0m6z0DA0jiq5tv+yd+ZGbu7G6zXG0zToDIlrO1V2DnH54Gh78GQuIdvn36LYIKTGZpwRJIha7p1248lXnKS2tZYYmFUEmWsFB+6j4IKayTKONe02T9fFcsQgUQPRwXioba64yhaIqKbete20ZKRsUiyv1Lci3GYV+s1Dvt9keJaadIUE0R45zGN6SSyhPXkLJ7o7ucIPJqz2AqaXTKlGqPIFOZ+AA3+w1+c4evJ4z/66ohPtxNaF9tXra39X5fPu8lh+PRv4tNPv4uz7RZNu8bZ9gLn5+e4vHcpmaAIWK/WuLvbYbq9Tal5nz9/DmY5z+LRo0e4vDzHO+/+Nu7u7vDs2bfo+x6b7RZt02G1WuHly1dgZuz3u3RANYOT0CYujOK2NY5jdJHy8A3h4vwC27OtiUkeUxKFJ0+egJlxc3OD29tb3N7e4vz8HEBOBqWng2v2r/V6fWp1FtdbCxppWuIKUXco2dQ52LJ0k9I9zendJBR4j8kcWe8iwHfOYQwT0EjcRX/sYbOkMJAEDM1CoEIQM8BhQrfqjP+eBMI8fPwYIwe4SBtHDvBM4DCBvAgcYRLhhoMQ4in+5n0D3za499lvg37+E6xWMYdyAIg81qt12rDiuxrQjyM6lVrJgVmEqMLUr3SaMhOnpBanwqpRKOvSTrFb5gSghzAB+9iMYBOVoMJYhWZiey10zOqeIa/8UWYaVnNUC0M12UzVcCaWc6BD1QDpDTbdIfRDj6EfMquswVHkdxSZ/+zU5Qpc1qRMrz8fzkTIMEIhlCERobA+JaRRlr3EP0qIdwI4Yj4L2cUmz31lG5q9v3SPl54oJeLy9myy4m3n8dXlR3hy82Pca5BaV7Y5f8j9icF7lH3ibTsorhELKrWMYRhwOB5xlrRsuuYySJ93oGRQs7YV302n03y+bo50vZcuIam2hDiq/V+XU+9PyHuisY8MvdCGVjUtFZyE/nmrTz07v1sugiTcAUJfQdhut7i7vU3ay77vsQkToCfecr2341qJKVW71QpMwKurK2w2a3g9WAOc4gmTu5I5GFAtaRYEIgImXRbqOqvg33kvLkZEWGGdgpTT22pJ0OGeWbQyTS2AZOpaSVM5An4wp3Mksqupya1PCpDymi2FPLPnGWCEbOmoaWash9N8ZRWG3inml0JZjim3bEFslwo1bElgvdeisKHpec279ZXbZHag6ZPITUbVwZGGKi02KYBVsLKeGeM44ubmBtvNBof9TqiKukIDSbuuCk3BITK+u/0Bz+LhvcXOSLw90/MZF2cGwWTzoflK4mJ0OY3brD5LjyzNVx4f96KMPKV9SmCT4jgqj+PmmKZooWMkIVfL897lAOHUV50L+dEKso7kILpxHAQvpjqR5kJd1EW4yYKkcwSMslYcGoA4Khxqp84l+mfvlu8wOzTbh/jf/y/+53j54gWePn2KL7/8Es+ePcO3336Lm5sbSQDEjICfAZhwcXmJf/9/+j/BT376EzRNg8cP342HHYqbfhsD1Q+HA3b9AYj9bpoG9+/fT8dHAMCxPyJwQNN4fPDBBzgejxiGAdMoJ3Zvt2uEwNhsVjlJQlwVko11SBi161o0rUfXdcUBftlLKK93dZvqug4PHz5Mz+nh2yqQqLeQpht+m+utBY0yS1NOIyZWDUoSkiW+zpERAtg8HzcnIVskojlunEaAHbxr47tc7zMAOXDNe4++79F1HY7HEXKwXWQgTOiPI5IPLYmEp0E13Ih/cAgB3WolgsAUc3CTBLs7bhB4xH444qNPPsMvP38Pf/leg6ZtoYDZ+waeROpX4UnP+fDORR9A1biZk0KLflmgosCHMhUiGHNpfMYQX6pKmV2RYOQNWA5qcUjuEviwk1BYI+aQdt4IBTU1WIYpZ/liW7d93/xWMqvMgHQUNavJ3e0N9EyFmetEVaxtUwZ+ZUOX2vyiJzy9/GBmyVAOy2by66xrJ4WMpXFbgDGnYW0168XYzT4u1nBqSl9buY5pYjGJ22BsV/iD7XfwV25/hvuruiYy4yTrJjrAJQC0OPpW6KkwEbMcqHR+cW7A66kRszO/tBfKv1mxWIHLE8Kz/LY8n3PacKJPJzaMYKhKUKj3c2HJqdtwehWdvpS2LM3MvDx1gTg/P8ezb5+CmTGGCcd+wDhO8I0BmQnEIrniRfYIBmO1XsVDpnrJax8165KxSOISnHNwjX6n1IbCfVQ/LYK6BPOhkogKK0X7XtvvSOdchIlKVGqLF8nayC0zn60lOdErhuiRRENf7G/k+dCgdrkT/dwToAuxXjPmZOGs/dns5eStwOaPvpf7qexCXYctFpD+Sb8LvRZnnsQJDKXe6P/T/GSXESQFGStANgKEurFJLIVJeQ9OaZYBYBgnHI9HeOdwfXUlz6iii7Mr3DTJcwK+p1TH8dhjCpwyO+kVYtIcz5Wgap5pHGHrP8fN9ATzmVyixVT9uOggZN6ktEayUGmFEBUIswVD1wgAiYEwcUHO5z0l7n1lv5glhII5W9MypSE0bQs6OAA5Y2haM4HhGilvnCY5h0RjMGIfJP1tXr9z0vY6mmYwFVToGTFNIx48eICPP/oAjiRwnojQH3tc31zLgXZ3d/gf//J/hpfhFdq2wfnFOX7nd38Xf/Znf4Yf/fTHeP/dD3Dv/r104nkHOSDxcDxgClM6j+JwOGAYhoirR/T9IY3n2dlZPCxvAyJXpLzV8QYkWdPH3/kwvZdxtggU0zREq1zG6iooaMjA1dUV1ut1OpDbe58ECTEqZMFDz9r4C4/R0DSxtoPr9RqbzQavXl2LpjgusKaRYnOgj/yX/OqiVYMayRIwTiN4zLEZYSJ4n7VNjW8yAYIQkr7vk28ZEE07E8csJmO0eAio9E0DdoxhHKIvoFgOpmGIAyfbcpzG1FbJZOAQWAKRpsDwHHD/0SOsNz3UzDcxxxS3A6ZxAihqNsDYH/bYbs+QQKXmOT+lnnzDvTL4EzgtXmT2mE3g9vnFChbKMe3Sa6Y1PVXOa2Fq0dcTsNGUV5eTe1MywvgLKVAVhqME/ebmJt7LSQGy4LKI7wu8d6orUrfEZfy4ew9ju551qoRidb+WCrQfufytKnfp82tr4fLeqfG3a+dk961A8IY+WTcqBqFfneMP+VP81v4XuNcqICBkQdtWkQONrZyURtQIrJyGy3SU5KBGfjfPgTGkIT9Yo/rTeyztx/jIkkLEXoXLy8J9XdU2nqEW3BkRoKXh1s6a/lc9QXrHuCbMauby62tpy9JVCrPFW4z6FxARtttNzFgYLRDjgGkaEUIn4IVjWaerFIu0I7Rdg64TppjcVE1jLJiqyawIDSGPulqS7NCrxUyDjVUAiKfR5+KXqIj9nBukbnYzWJhAs67fmC0xlPdlAEyNVbzfnDbkNZ0iXozlS0EnGZRfAnxkugogZ+njalDtHjP7WGmxjiuHPO5RQEj/hZAyamkLOCktNcOlcW/TGBgAPIWiLG2XBtRngS2PiiNEYSFgfzjgLgbnrlYryawZXeA48RbC0A+4vbvD3d1dGieKQigoulMHMyd2qBDjIhYuXRP1L/U1iwIzG+9ENALsHtCBL9degJ6mrv2Raci8QL03lL+GicGO4UksGuAYSF60XZ5VIU0FwKZtAM6ZQ5FmWwYrhIAGqJRy2pa8RvV2yvQ2G7fX4BsG1PNiimeKNP4C+90Oq86j8ROmkdG0LdrW4fGje4I9jwP8Nx4IMj77/R7deo3v/6Uf4JNPe3z1y19if7hF211imERB71vCisTjRvo84t69e8nVEhBLhmRvy4dPhzACcDOrhK4vxcTTNCXrRVbG6xkzMSFEnIe2bSJGljF6/PhxcXyF1iEB5Zx+1/r2+z2GYcAH3/lkeVzN9faCBhOmkaGm/ocPHuLy4gLTMGLaBLw8vgQmSEBUkKcCT5CId/GpG0cxffXHHgEEPzXZ2mHWxDhOAIakie6HMS0SZsbu2OM4DGhBcJEYiRAh8RjTNKHxTcQXBIw94ALImfiQXgQUmSygP04JpQRm9L34BjJJdqxhmDBME9b3P4bzP5FN4SQN2XGUDaLEUInbFCYcdnuZ+Hh2kQZJF2dDcCb6JcDKcRDJF5IzYciW5bwJs8bJCBecN/sy+DgFZqqNWUp7pkQTjBlBXapzpl2FzRg72/olXMrlF3WTfTaPmVZLLPpv1W76KKTtdpYhIPk3FnVXNH0OAGzz8sNjYPwxHuHm4jGoeAaKB+JHyuOL8pm61hlZXHjmFPCb/7rMrOyzdYkzRrZQvV1RiTmeQoeE8rwNAvrNBf5F82v44PoLfLeVAHEkgGDaXfAZillosuPE6d7Fm8w47PegYLTls4nKLiN5uenaKkuPbDjTmGos4ksRVHHa+/N4Grvf671bX1TIFmBbRg06lvzr65KKglCuOJ2jcu+R+W1e65K9NDt5pCQV8WYT06GOw4Cx7+XvqHnkXbKWl/75MReRjmek2U7XCGvfUX6fYbIMOGG0rFKN0hSlzwBBsrnUoJrS82ZMTR9zkTmmUSxz0apgQFUShgo6K3XnOJ4SiOWOiYuKXYUzCqG0ON4I4OK+Chvl3pZxUGtE6hsjAn5TX3RVE1CCAuwHc08U4mMEllQIDkjPZ34fQpBMbsY/XnliSHNHKT2q0g2OvNzr2RsF4OUUI8MMjBNjHAdcXV+j7wesV2s453DcH+JBbC3YeRFIoqJ00tSfRCkbmgyogN0phNKwDZMwJE6djSrSK2MB+0v9Sd8h+2px7xQV0frr9RHChN3tAUSE9UY06LLjim7B8tzUCjZnnpHMT553sRbZrgpojeloycRWMBfjmPAFScYlK0zrfuE4mElBkEhbTY1OiV+JkMR5ZFyefYL3PngHhIBxOOBwOKAfR5yfn4sbZduiadp8lgaL65Fvmniq9gYfffQRbm9vsdlsUtrnFMPsHHw8r0Jpg4xfPDJhCmAWkH84HHA8SjD42dlZAv4yBpTGYr3uUugCALStB7PDzc0VjocD7t2/H1MVx0OuGWiaFQCJHdFsYcPQg7ykC2Ywhr5H07QYhh59P+B4PETSQxLz+hbX25+j4aRz4zDgw/fex3a1QUse3hPun53jYnuGYZpws9vh+naHMQYLMSb0/RAtDKNhNh7HcShS2BI0h6+cIBq8Nm9K/vTMjJv9UZ5nwjRMKVBvGAPGKGh0DdBEM1GYApgmNI1Oqi4+qW8cxVVKXbAkrzRj4BGIKcYcJI/0bVjhGDx8EEFlnAK8b5KAwQCYZJLCNGF3dweA0TYeXvujICAF8sSLlMAUziYFHsmsQRkeUKdgRdIcGbBgCJJlbqliQ5PU9YJiX8wdZTsZMEXGk94omKwlZZE1UIZahbMFxe9WA2ZqhmEgsE9kLJBq0paqPzYB4DChP+4RwwKTVD+rrAC09mPSLwMV+GEGvhjXeP74A8PokOfNIDI7u6cYRCnfzUJcFxr5GoEgXW9+5l+lVPs0m690qgSCETbk/tiu8PmDT8HPf4rvrfYJCCQgJgtxZlijIv5Hd4w8XsffgCWd4jiM0e1R9wmDFyY/CxZzIKC/zbId2amfCTNIALgcmfkYlS2vBQZbQm63FbtooT9s2pTB8Ym6bZuVzqQORg1iHoWKsdeLuqItul+J4NsGbdtgOO5xGI6SW/7eBUKY4Dm7YGT9Sxa01IlK4xhkXWkt2RVI3F3U8c6MLmnBdoBsthoBpGkLW2HL0uJ0jkA1q4Q0J0KiS9/zGVAzTUt2DkOfk796DGAW6589fC5zjMJFKWnvcx8Sn4qxBUjfOQsDaQ9GV6MoKKj1PysDBLCEEOJZNhDeH4x1oqg3//a/+u5XuGqmckPMt1lxFfvmBIGi+tubCBkrfc/9cLQD6EVe46mobGXM7lraR7vnc1+uO05//zf/5l3ZUEs0zdXtB/x3/xPkvVcJlYudKH4/1enMwfU5/TSNQ3T/Ao6HgxzYp4JkwhUup5DVcUssnFRujy5OGkAt+1FBbnaZc9C1nOzmKvGz+Q9Cu+TcMhW1rbWtpqcFQpmNT0mlWJQZ1XDd3t7iq6+/wCff+RghtPBNtCDAITDh1dWNZIWKLzrv8eDhwyhUyZperzfYbLZFIiUB8yYoPqgAxlFokeMh7LkVzjUYxz28R7JYtG2bEg7ppQfvAWLdaJoWjfe4d3EPL4YJ337zLe7fv4/1eo3nz55juz1D0wRcX1/j3r17OBzEZWsThcznz77FbrfDOI5o2za6psrIqQuVvvOm6+3T2w492qbFp598giePH+PFs+eYhglEhNY7UAhwrkV3/z5ubm5xc/USq+0GDEI/xCxMZrM0rQOTAyCWDnL5OHNdDiFpQIKuHzCAYaQU/zFOE46HPk12iBqT46EH2hZgIZDOAcMkOcbVihKmCc55MAjT2GOcJkzDAc67lEI3kJx+2HiP4djDU4d/dPm38Cm+wXd2PxI3LVA8YRJpQwLiU/jsxQt8sOoiQ5gK/0VZXuUHJWQG6sfbJXhIiqU4pslQqcwpEb4a1pSUPG1Y5Um2UcUXzLYugXM2qNn1hrpjmznVkYMdOU70LNCvAEAoxtqOlH7j+AgIGHpxbStMxjZpP5UttnwjDSl03Lk48+FqAH7x4NMKXJo2piqq+6k/uYKlkbSNzKNRfyr7LllEXBLia//0pGmcAgKHlFVEQcdS6XXX8ncL4fTfBX2aFkcoLRsMMDl88egz4MVP8d32LrUzW4DK5tg5sitdiuMquYGM3BQCjscD2q41JxmYdqY1QOlO8uRKgM4Ua9dSZpXLrj6mgRaH1I/W8680JfdHCU0JRm0wcAIAxdor/54CIlq09puJDJCIbSk6ZHtTjnkGcIaRM8eyZZRXqxV2t7eSZrw/xnMLRrB3ALVpJ9e0QpUE6voDbetSf2L9smZKmKFPyXO6q7MtGUAMgs3rWvoQ/8a1ZmMS4jBJiYkcK4EtxymtYdYVlMSM4j6COBk56JkayIHJjCgcxIxGGpzMIQF+BSDimhyzJrJas827RjDQaWVECwNnLhRihkhKCyM+Hg8DTAd9kQPFDFussSGO4MjjqpnwsrUB+f9Vuv5V2vV66s0EXK1f/4xeZ/bw2IIHl3wxX5Yw5ieXrkQ7gcIaS86DRz2vIZ4jxgEED0di02MYS1Da25QyrE0RlAKCxxykMjkLLTM4RoxzkmWVrEOJoMc+WOGczD4puGqyZiztbZz4rR5PQK2lDNk7q26F+/fvFx6JGpt8fn4u7vWZsEFjHWQ8pG0phiL+1Wys6rIv7kx2nhycCbB3TqwYm80mhQkc4vkjhRAfGNfXNxJv3HU4Ho+4vv4Gm80G2/UGx2OPr776Gnd3O9y/fx/TFPD8+XPsdodU3uFwSBaKw+GA1arFfr/HGN3J9vs9Li8v0fc9vv32W7x48QJN0+Df+3t/7+T46vXWgsZ3v/Md7Pc7UJjw6sVzECTwuetWmIYRgAB/17bYnm3x4tVLHI49AjUgajDpYgtC1MLIGKceCqxDkPy86TAY1mDyqDHYxOlkYH9QC4kIERqLwRiiUOFAgSU7SdwYfT9gGgeR1vtjWhSyeBh3d3cgojSoyeSHgO12g4vzCzTeo3EeXz99he/9zb+NP/rxJX7z5T+CBsNn5YNshmPfg0gEKD091QWKmMUKDipaFAgVWTDLvq1AZoMKiaxONl1ziaH6VH0j800pUQIL+jObxxfqLIQO6+5gaoxdqr3V83DEFWEtAzhNQuSVHC9S1KlaRBa3GduiwJj1QLNsBAUDFrslgGDD+QmHAPyoex/Bd2UDK6GogECneEAR4L/MJF53j+Kpn23bSIICR1CTsmrfkdaoNEQtB4jAZJomjMMo8UrhNBim6vvJttUTV8xpuYrYeXz56DNcPv8h3u2EpljNVD1fidEBBRhf2gscO73f73BxeZkAWrICUO5VsQvTz2btqwCUmHU6fjD1C7E+VpCt+9EwWko9sPsKi5+toiFr7nk+D3HfZrFncUSMVZfnt5NQYZbxMoEp/loLk8au6OFsyZZDQE5HGNB1bTyB2KNpWonTGAdw4wHvQHBwaceFPObF/KWRye2vAH9EuNF1xTrdAdmybNwyFFQbbXzqm9kzAGLApdKhPAKZBLOJN8gKjqTtRTzYNWTAD3CMU8iCQopHmPIhsPa8qWw5MG1QxQFLPGESymD6paDRCNNKU1MKXhLXJK3Px1Oj9fwO37RpXkAUNbXq7qJjEZICRK3NAOAYeBDekL1mgRC9jkKmoQfy2jO/mZvleKjG0I7lQkVZofeGRgC4XnES3C+PprBCKNBnUSkqYgOqNhQa+1odnwaLF+5l4C63I89mhvNetNnOJWFhnKqToUGAIxF44wnoGrxNQMzsloXM3HZ1/9ZWZFor5zvUJ6jHfpGlrLa/mb6legzfX+rz0lU6e6rQLuPz7Pkz3O0+goNLccfq4rVer4uTuSkKFVmpp/9R8tqRpuv5F6IsEW+aKLKT8JJpkgNMV6tVOrtiv9+nbF7DMCShIMUojyP+6T/9/Xj2BnA8HtH3PXZ3d1h1KwzDgGfPnoGZ8ejRQ9zc3AIAPvnkE2w2G/zDf/gPYypc8Vzq+yOaxieM3DQNvPd48eIFzs7O0knlm83m5Nja6+1jNPoJPCEG/gBTYPRjQMCAMAWMY4BvGwxjQLfegpoOd7s9XBdPumYPzSY4DIxxv8/gMBLgcRhlqZADyEu2JucktmMdCWJgvLq6Rdd16I/HRLQkCElTbjUI04S7YYc+DvgYJ4wAuOgONY4jhmHAMIhZ62x7ljWEkeg6R9jvjjjuenRNA0eEm+4Gf/InP8T7H3wfP/7mj/BheI6265KPKJEkcd3v92iaFn0/oGkacd0ia8QvGb1ql9K6j78CStjMZiLz2yKxY1RvmFuRGRQbkmZ1Z22ptLXY7kugjk9t9Oq2TKR5TFuZN/sctb+eolutQII+acwI+/0+dlvqnrWRY/zODMxafpDRRYQC+Gm4h2sbl1G0teJSFe4resU4yTBmvM4MFwEpO4T6gaqJusgpbpgpoGkxAasJ0iC9rmsRJtkf/dBLkoOqNyf4b9FN29dTFwEmXgkI5PGj84+xuv0Z7q8QA3sX1lo5RLP5nD8rD+73h/SV4t5JADkJ9sudqddY4cqFknkCAJMr3RALRotU94weLIH/uUgxa5PWcXrEKnSVQKW+VwLoomYL2E9dhn7Y058zbZFRchIliwBREDWt0FUJDGWMwxGhjYKGi0JF/F8wCpBqNhKgpaj9tBYE+RgSirO90Jg6PasIyFZeHcclUJ+UUSG7G4GzK80UMp2RvZWzEulBotBTwAnJRQnKB5Q9sNm5LAoBEXQZ6t8tiI0juM8ne5P528R+e+cA5+AgAo7zBKeJXgDAnEWVhadIizjI+2Q1sVLHlPon2nGx3hs7Devp5Lqm5P0HocX/6ZvfBAA0UWBRq4jyoHGcktAyTmPq6xQPnGNGSrnJrOk39aTkTNvGacrnnsSyJQDWAHAoSeHiu7ZXlRQpuNxcSk+ti/b/9m/c4WrNuDwS/tf/xVkes5hlKLnwEuF/9zf2b2X1KChNva2rp5YutTwpWNZuOC84haJSWPmGurYzGI13gGsxjEMSzITVyvP98Yj1Zp2EDw2mynbfsun90BfxHTrGQBW7AZkTZ4WlyMPsHlnm4OUvCyOCZMkmyfb03c++h+12g8PuiN1uh7ZtU0YmIoJvmlxy/KBrtmmk3aq41mRKr169SuC9bdUFaoyxD5K9TIUETWq03W7x4sWLlMn0eDzi9vYWd3d3+YDpYcA//+f/HN55XN/c4Pb2Bru7HUDA2eYsCiZ36PsBbdvg3Xffxfe//338/Oc/T2dmdF2HzWYD7z3OzrZYr1e4vLyEKuW1L8+fP5czj9oWL168OLXEiuutBQ0iD6IWN7d7kD/CNx5jCBjuDhBYTQjHCbe7HX7++ecYpoBABM+imZymKS5MzcEcAA7JFKUChRBJCVRjACEMyfwLyObeHw7oh0FOjoznaHjvU5m7uz3GYUDrvZwcGaLESZLZYIoB4W3TwVOLVStEvj+OOB6PKe1Y4AAmAZ/DNOEw7UEAGufxx3/4R7i8d4mvH/2bcD/5+3i46uGbBi6awhrnsNsdsF512B0O8Tj4Fk0jbZHzMjhjG0ZilLLu1WxooK4+rJoxQPpsAEx9sX03/QYkX68C6RYTXrgEWLBKtly8jpwt2T1iOSfRaATAWpMBKKXveSy5sKKYu0o4nYz1MZ7QmvyTee7cowKvFpncLaqWKjT/Wb/C08cfV0KGbWkEOeZ0Z1tYeiZRSEsqswCw4IQEkAgY3WqFVgWMCBYUyKRDkBJgYGNmVqYa64/vN94D1CD4AOcd2q7BOE7oj8eYpGEmLxW//epXZddgxnF1hj8K38F/rf85Vu5ktEcCaGw+Q+d1AQAwOPuUpq2l662shNP3uf9u+Wh831Snz4sQRWmgimJShUZoMJ8L8YTyL3a5ALqOzTuWhtj3llpfKRxqvDLfooz5rC+Ur+Oa2pafceasBmah22fbLfqhFwscAsahx2EvT7VNl0BvGiNGog3ZDTCPR2qqwFUwQhoXhqQwT5Zy1jMQpgLYZpBpLArqihQFBBEWYr3x7KVMVvNE5dgEpPosbSEgBmjKIYAUNbnqZiEdp2QN0ANI0yyQAqR4Onh6Rb5PzGKNmCQZSxPdOEJgrLyLllxJLy9pNgXwS5p3qVesLaIMdJ2XZCvxHaXDjmMaaopnZUXWNEaBKwkB8UDb8CgAXtLCP336LI2lCALxIEQACIxxsrF1vDBP5QLUNUFm3Nqmiec1xHlVCsxAzgBld1O1EzjvgCwH2j1AsSxb7inYy2nuSne+vM6JJoB9+TIy7ywoY5b58l6tlBC2BWpZU7fGZCHjAGazjkjWtvcaRDwhTAzfOHjnMfKYByMATJKYx/cebUcpljZbUHMTRXM+4Hjs855QwTauSRc9DELglDxA94S6EGpws43ZyFeFoWZXOb/6oW0aPHz0IGHP/X4vWSuBdGDdFGkCAIzDiN///d/HZrPBu+++i91OFJu3t7fo+z65P93e3mIcRQj++uuvczrlaMHQ8pumSZhF3KCu8erVK4zjiNvb26g4ZYzfH4FGLBq//PJrwbVti8Z3aJoRL1++BE+IQotH3+8wjhMOhx5/8Ad/hMNhh8vLy5Tqdr1ep4RJbSsKzIuLi3T/+voa3nvc3t6iaZoU7vCm660Fjdu7Hr7xmOBx3PcINOA49BiGEW2zRj+OuLq5wVdPn+I4jGi7lRCJwwjv1Rw0mixTDHDO0KSEs2kaTBzQj6J9SNH6pi3jOIhpp20QxgHjIBYDniacnW1xdnaGm6trjH0vvwcGw8FjwsADpjAhjAHBmK0cRMBZdysh0EzAFEDjNTa8xwPag3nCNzuPK95it7vBN99+jXfe+wDvN4wjBvjA8E2DmOEN+8NerBuOsCPJF711axAFOHZmwxWrHIBihJJYFAg6wlem5e2THgdHZlAFlc4Ik2mDMmn9S/l+SbDkj82gZcFJYraG+CmZm5+GZ4CEKSnLEQW8Kt+shA3N7iKfRRNzPB4zYFHtZEV7Us5wZCBQDBFlyL8fgV/e+w7YeWS0m3oX36sQ6pwfpt6mthejkMuwwI9IDivr2g7OS/YKQDR6Yww6U2HUaj7tRVRqMVULqD6mbduKZTAwHEm6vWEYcDwcE3Fc6lo5m3W/8r1ybMxExI/95gI/OlziN+h6lrllBoL1V0Y+vbaSDrT7kjFDXEImFiWCCoKzoGsFcEWfSv/gCmfMsLhqm63rXS4srhezvskUa5Bq0c9iLDmvzVq4MrDIdiA3tcIo9l79W7kr9QqoVpW5ZdqunWJNZip0bRx6eO8kBfhOwVnANA44hBHD8VhY6tRlQLRrIQoHJv5gEjfaaeJE90Biodts1sninEOzjJDGdi7knhVgLDDNgno5Rqr1BQFNDJrV7+p6oq84IrHCx1L1XA51kSXnxNoQQaH+LpkcZWfnjDeqQIj58UeJL/RelCwaj8QUg501oxdxDJN3CVDpQYXDOGEyOfslaYqcQRXuROEW4iGIUzw/KoQAhCxQqAsqB1XuSNalVOanMc04B1xf32RhEXO6LzFd2UU2zQrnZZ23fBbSape3fGp4pqwqcOr6dRFlEwGOfFr7aSlHWh+Sa6mhCLSsmDAtS201BiEAZVvl3gTA544uFrzw+2saoBSIgHSWg4trTVijzJuL5TgS4UKUpB59L/NMISpLp+hyzHmNggn7gwDhtuviWSKZ2ASWNdEPvcQHRLepJOzF9e2jVV729CgxtT5b6lkteLqvGGkMyxF403gwNLsdiBCY8PT2azx79gyPHj7A8XjEer3Gfr/Hy5cvMY4jLi8vsdvtJJsWpE/37t3DixcvcDgc0no+OzvD3d0dfvSjHwEQl6v79x/i888/BzPj5cuX+Pjjj3F7exu7zri6ukopalerFa6vr/H8+XPc3NyAiHB3JzGMamHQ90SYkPES68Q28m9CfxzQrSTRUZgm3N3tsN/v0DQO6/U6lTsMAzabDaZpxDBIe1WoAJDGom3lnLt333335Nja660FjX/5059h1a3QdnLaYT/EDE3MmPZ36Psed/s9+gmYOGo34oKyh9mIqTBKWK4BgWKQrgxA2zCcd+jaButVF4O17QYlXDx6CA6imXHk0+FMQtcC7l2e4fLyEjdXr3B3e4fhOIgbQyOLd+oPmCYJPHTdCh1acAjxtFePcTiCjjv8zuY5/srDPVYumnGDaGKu+hcCbr3HH3z1OaaHA/Zrjw1t4SggBDFND8OAqesQArCbJnRti1XXwFErLlTOgTgkz2BLKJfEB6byd0tkWX+AYYQo7yfCnawib3mlBw0yUSacbJ2c2pg01EYoqoWDDCwNQCJjbVBKzNqfhKjSu2zLIkuLjcnbCeHvhwFqHieaA++qo8UvFowIbiR8Gc7Qd9sEJE4Pph0z0+VY+uteraE4CPC+kVOQ4ymdgMQAqZWOILnA9SBKTStpKs0Amgg+Chy+bSQGyct+G4YBxz6ga1s0bSvBnyR7Tky7QwXA522vhY/yHhdjV9g1ovD//PIDXF/d4n67AGd1vhf4LINBs0ZJjQKWBrSrVVx3BDX5l8uLIZmu9JkoR2aoWGjapYpKmAfynmT9pxQahMHBAHKcXBBlVFP523yBMWBTFrACZW1j7F/dVgt60v7OhEbTyZoGxOdDGsBkCQCQUpbG1/SQtMAB/bGXuLWuwRZb7Pe7bDUjwsADbu5uMI0T9vsD9vuDxOUFk1UqtrFslogzzhHW6xWICOM0gQLBefWVjjnqY79lL1EC7cmCoFYFs41VQFeBVS0ZivslvjCeu8D2hGUdZjb/5Ww8eu/QH9H4Jp1JoL7ejCDqspTpSdVHym/1MDoJyu2jRnQKIcYlyqxki04ESVN250rB4EkhY9A1a/+0P7X7bephumc12XpHxrl+Jbu/OLuUtQ5Ckdpd93+OazsRIh014ggBw+KZFkZoJAHYOk4an6JdZwBDCDjGwPzQAOcfdrj55YB1H9A5jQHStVBRA0IWDq04b/qqFQYmgDVuhW0R6Zfc36WeV8Mby7fPC01v4LxP8a7MEl8zRbcdcoius01KRT2FAEwqWMulp3ZrDcERdtMOzSCnVHvfQJ3ohnFMcYAhsHrBxdTmkQ9QdE0iipgxC9MUMSGHSfZfDEKXPoVqJMqxeS2vJRJLwjhhz7c4HI54+vQZjocjhn5IbsS73Q6r1apInKAeOc+fv8CLFy+w3++x3x/w3e9+F9M04fpaDvlTIWHVrfD48RN89sknWK1X2KzXOB4PePXqCt989ZW4R5LD8+fPME1TivP13mG1WgmGHvoC8xERmlYwwXrdYbVeY5wGdF4seUPfo21lDomA9957F8PYw3lC23VoJg/nPIaxl7M9SBS0coCh4ImmaXB7e4vtdothGJKV503XWwsanz+/koY2DTyJGbJtW+x3ezRdi261wjRFUtj46K7kkfz7SA4jcVGr5L2Hi4vPR6JFDLRNA7BkZ2LIYgvIBIEcYXu2RRjF39bBofFNCiIHJkxjj/3uBs4Bjx89wtWLa9zd7cBgTPsX+JvbX+Kze3sEDviT2w4/utni1bjFR6tb3G9GfHB5xLurAQ4MjloiktUEhIDzRiRH54H/1uMdAMLYj9hNIun6boVh6ONCkBRx/Tji7s5jvergtw4uChopq02xEyIApRjgSsIQUzuU+CXAbMB6fM4C+PyvEQAWNaC2GSUIST7cZAMpLeCwID6hx+IiU5aArKhNgMkuEcvSdibiqKDHMBuFptqSMrhWCZOMxziMCRAkfFn1GKa8+XhkQHuYgKeX7ydtdS6sHk+ynX7jNQfnxquVCF3XYrVaiWDgHcYhChTg6F4QXRLU7xsqaHlhYZELyvTIaE1BTg3t+14OPounmOqJoRrHtFp1aNsOE41AFE4OhyNyiuBytej3U4xwZu1JnVcxBBibFr9w93Afr8oaFoY1se9klZoPOBFjChJ30nRtWndpT6W51PYGJGBu5QkAom108ZmyVzlD0tKlIB8RzJqI+6JTPHsrMRWzOhB/Txo5mD0SAT9xfja5mynQtXNj6IK6+iAB4miLCBqLkDM0iSdKdiVSDaQcoiruBQq6bQ82201ywfHrVcwZv0ff91H7PCGECbv9AYf9AQBhHKVPEneQtczq/iO+05KffrNey8nhrcTPeefh2za5Jy1NkdIhF0FNbK6hO5kyagplp1rVOG4+zoG4fIgLombYkRz6BGISjThPGAODpxGEmDZyDDj0h2gtmFKQ+DSJ24qeLi3gSsZgCgFhygKCdQtKcxT7l1xEcQqi2r07W4rQ2KZlVVVekxk2l2XZpV6Offl7oudkXqwapPyiaK+5a+X3upXZ5ax4A4AoR29B2H7Y4P57bXrnyX2Pj36w1gamhDX/4j++weFPDljZ87u07ab8pBDV/i60wY5A3ejSu4CWnztZUjlfIR5sqIlsmCMf4SG5xHRdh65tMY1jtGo0CEMfU7hy0XAbHaY1jqNYIlRhwUFil8R93CXBgGJAt3pBOO/hnY8K3gDvXd47ziGMorD2jcT8pEQu09zangYPM9RSjk7kdyGIC+Gf/fCH2Kw3uLvd4e7uDvv9PqV5HYYBznv0DwaApJ8/+9nP8erVFYgc7t9/gM3miC+//BKHg2R2uru7w83NDTgEfPD+B3jx/HlycdbMT3rQXp6X6PIYaWuAnGvhvResbK5u1aSA8d3+Dk3rsd2scH19g7b16LothrHHOPYYhiNC2OLe/Uvs93sAcvq5xpIcjwd0bZdiM9brteDYvgeRnJ9BRHj+/Pkb1x7wq5yj4Tdoz87EZ24c0XZrtE2DzcNLkI++e8xYdWfwjSwQYVKSupZIJq9pJDgcHNAS0DYeDiJ8rDvxN5+CBJa/fHmFADn5wDKAFQU0K/Edp8BwPKFtHLbbDtN0FMvIppMF8uoVNt0axAHPvv0G//bFz/GkGxMU+a2LHr9z3oP5ZQbtEYBwFH4CHEAhpRNULTkiwdW2TVPA1asrgAhD34NDwNXVK2zWa4Qw4bB32N3doPEArdfAyEAyK0bCpIA3MXzKRFsFDCVUbEBHYRkAlDAncpRAhMLX8rIiiQp9lkEoW6bZGFWlsGlHxTbsJ2ZKYMXGMCizsUAp1cFclGTrtu2MUE6EWkQt9jQWvGpJziqFlrJchZQOwKvJY+g2C29WRJeqlpL5VtRtmUZZuzKt1XqVzKmAHHop2rogAsekmmDJPAXV/kAEjHEcEaKWqmk6kI++wRFEEkSj1fc9+mOPpm2wWq0k+wgzDoceTSMmWc2F7pzDTpM6sMJ7Mn2Z9252nZLs4vXi4j3cXL3CeWtcV3SsibORgPIQL2N8VrKDMI0gcFRwII2TheN6zeMmzEyzpPicAaBT6KYoBQDrqcjq6mOf0wVq17+9xcWezmCS8/riGMQfNefZukCRXue61YKRUxxzBpNRs82Qc5R0ranbBYMTIGDWoNyA3W6P47FH4IB79y6w6jr4phFBtutiULG6DXnRavotnCOxQA5yRtF6tYZ3DY7HHuN4TAoEHRQC0ER/4m7VYdW1ks3KOUmxGa0LcC4Bwy6eSKxuPHb8NU5QgQsHhnM+0t9IX0JOBz3F3zR1rAYlk3MYR2HUKnRM0wSe5NTrfLqvZptCMRc6dwUQNlrUrEiJPMgEvhVBzajpHRsKk/9dWqlWWDArs+IXVRl2iZsl+iZYbK0+6V1ToyqmtBSdDwCJH7P5rkIKF88gWpFkHeTxy/f6iRGeNPhv/70H8M1JMSV9857wO/+dC/ynPzpinRQXLrXJ9luEYauIWB4N6eeIDNHK506dKr7UPv2lLF8tYPkcsxRzwEguZkM/oOs6wWQc0LadKLR4ikH/JFYcpwrZfP6DDmqIGcg0joJAslQ1ANxp+mMkJWnTNMK3YoIgFdz0LLIppmhOp1ZHgWXu1mv2xGvGK0WTMWPigO985yPc3Nzg+uoaQy/ZmB4+fIibmxucnUnSoIOeKxHX2G63k0xPux2OxyOurq6SYKIxFYAIeD/5yU/QNE08syLjWz1WQYWetm3RdR3u3bsX8XOTUtFeXFzkbFZxLCTGSubi+fPnWHUdxmHA3d0dVqtVSn2rMWfOOVxcXKSDAbuug7oYalYrsdYIdjg7O8PZ2RlevXoFIKftfdP11oLG5eV9ECToxa/EL9zFBRF4FBcmRwiYMI0BbdOkfMDTOAAMbFYtjscDAEbngV//5GP82q/9Gi7OzrGOEe/r1Roghz4E/Of/+f8Ln3/xJVzTwB+EWjnn8J13HuPBg4e4OLvAcXcEB8YH77+P999/jG7lEcKIu9s7/KN/9P/Gz37yOX7601/g+YsXGF/8GA9/SzNMUEyLxslsnbKKxGAxRwR4LydNRxOf8x5gkarFzCC+iqINCMn60jYe3q3EbH3YC0PjgLs7B98IAexWazm1mqwPo5JWA3FYeUjJEC26Ig7laeOmlLSJ4uPRSL/APPRdK4pEwKHWFVNtelctJ4mbmQdMc1S7lrvpMk7SB1lbYKvKLU3CTRoG82QsgrRNkeirfyfpe+n02pIoLYHUmkEGBp77c8OZzJMVY0m/L0gwJaRVXfQCJCdgvVknX3U1YQZmjP2AcRD/VuccHAiBKAoCkhlGCVHoxxQE6RugabsIPoVIT8MhMh0PkOzzcZQAsM16hfV6jb7vsd/tsV6vUg7xLRH2u10iorp2KP07Z6U1SKHk0kYJyOm4Td7j29DhjI8JENihZCwNbz03KJ6WIEhdhy66amTwpm3Ia5Pz9KZabN730lUwWwpMG4rFlYGGDTguvutnBZ8ha7IJet4BTN3RxzoKBsyAj/2yhxcmIFEItkjtV7/n0rc952xX4MwApiDuCoRIW1L7RGt7fX2DoR/ECr3d4mzbRQHAJw0mAUZDKXWu1ms0bYvjsY/+/sAwlilktXXeezRtg/PzbYwpCjG9c041KTSbo3DcAAgIQQUcSlrWtLdMNqlxGDBOIbkiaiyTaB1DtJDKerJzWsbk5EVg90MNcO3fTF7SIqwVyChkzWDcszgHyeelZywDVpAuBBAkmpmBvbmFvN+YWazxWLhMly3Q1z2V7a2mL/EfS1azdbKMiypoMtVjVvc7XwIWH+Hzp99iGEYwckYuJdPtex4f/eYaH/2gg28oj6/+BVAfHgoAviFs32nB3+YECBJnQKYlFEGgVTDE/laMRzysxGWpGCUdxNdep+/nMZF/x2FEt1rBNw2mvkcIDO8cmngmWdM2EmPBE4ZxRBeBr4JVjj6DenSBCB7q6hfnL27YFEth2pdjl9TCCjSNWOzV1V5pNkg8YThITJBzYllPh0WmPWevigMtMaRibBjf7kdMl3scj0e0bYe+73F7e4vr6+sY6ynxDJvtBrwJgBOLxp//+Z+jbVvc3t4m+rHf7xOA1772h2MSBvoYR6zB1qq86bquOAEckDOHVJBomgZ3d3f5PlESSjT4fL/fyyn3MaZCBZd79+7FE84d+uGYhCErULRdC558+k3THRMR+r6PdFaycL3N9daCxsrHQ/JckywQm9UqZoiQCV+tVnBEGGJj+8MOHCasz9fRdE3YvPsQ9+5d4PJsAxp79LdX4NZhmI745c9/gr7v8dHHH+P9jz7Gr3/2MaZ+j/3xCHeUXd54h+9+52Mcdnv83/4v/2f85Ec/QZgYjx4+wt/9u38b/9a/9d/Aat3iwcUFOu/wL/75P8NPf/ILPH/2Nf7dz0a8et7h/oOHaJouaosEiClT4ph2MSjY4BCDrgmeHJiif+sopm7nGjREYCJMMP6vEIl0HOQAKnIOU+NwPBxwG1M2uuRnz8lagbjYrfuTpjdXhqbPyOZQwmp9r3XWlFPI72qlUKqZFe7l9q8Dx5PYoYDMLH4L8IhrMgJFINqa9HQGVlpHMGWR6WeuSKq3gKyoKP2R8RMfR2YR9FLchwVpyyWcAMZy3U2EF5fv5adqq4Vp78mLlz4uNAjAZr1OlowxBmeGwJIKLwoG4ivLGPoBAQzfdJJeMAE6xoYcjoc7MAPtai1ETMeLA4bjXlwfw4g2uppwLHOaJF+25s7e7ffYbDZoWyGE2+1WDvoRh3dUDjmvvWbPFLhMVsLXF+/j4+Mv0LocxJ8eM2CHFEwZBm5HV1m+pEeJTJIYRE1a28wanxCzFcV3OYTCapiTDQjIY5I4hXRGQgji0sYK7qv0qKlhaVNKpj3O5wskMMK6Z3IaTLuArQCfhDEiDBNH4dicDwHZ3wFZlVBkJIvKIfW/FqtZdP0BYxpHHA4H9P2Ai4tz3Lt3H6q81ExOgPgrBw5ZCZP2XxSEU9sDQiCAHAJL6lFA3Jwa3yAEwPsWjZ/Q01CA5a7rsF6v4gFYARx6EcDHAOf6RDP1ROvA4vvOKcOUZGvR+VJQtEQbyoug6Wo1Paiez2HpkE6VzB2KtZrnjqLwrC/YWvSh6gNREQ+SBeJUYX7fCGYqDKm2XwXSGremvRK7w+Z3LUf6srTDtT/5eRBQnl8+v7ybpWKIAnIWNhJfBLAPwOhLzoIo/Dz+jRWaNoPatM6dA29H/O7fuYf1WaQGpRyYlIDA8tgkoRqlcKB0x6UXjBBTjxBJbOaSZ0G+GC1+iQGf1ZWcqPztLjuXBD04boJ3ojyeND1r28LH8zTU1X0YBgzjiNactRAmTmfBpAxfKmRYGqWzn6S2OA5pLKNyxPsYeEwYhpgpMtIVTQoxTSM4SBsdOfSTxAtO46ADYnqaaz99KeKQp6YgMVs3NzcYhzHFMKlwAAAXFxcYxsGAJmnj9fV1oahwToKtNc5Caa26OGn8g97vui4pMnwUotq2TWlsgYxVbZY85S/q6qTpcUMIOB4O6Tl1iRuGAU3bgCHlP378GM+ePUuKySGeaadKEz3ZXK/VaoXVapUyY73pemtBo/ODCBgt4MkhTBM2bQsSzwpM04AWEjh0f7sFEeHinffw4PIM9+5f4t69Szx69CCml5tw9fIFPBF+8uMf48Wzp2h9kxbwy2+firvE5QV+8L1P8fzFC/grl5SIK9/i7/8H/1f84//ivwRACBPj+bfP8fMf/xhPf/kV/upf+y3srr/F+/fP8Zsf38dn/At88FmHj85XCIFxc32Ns7NzdBoQShogGBddTMkGDmDj806ILjQhBrdPAQMfsWPVeE0JCKoWUhe8c4RVKyb9d995B8+fP0fXCeDzLrpKIYsLBoEXGjxLWKVFmhv+xFbi6ksqaA7F8k/mYKy0kZYAtZRXsbaFJiizKKE8mSes6kiJYPEQ277X71d9hACHxvsIQsRVRoGH9qsegrfREz0PHaZ2dQIhl58XffUXpymx76KUrutS1g4lGuM0oT8cIVlnGhE0vJODzkxlzjeSqCH6dwIBTSfp8yRLTA8lsM6JhSMEIRreN1B3GEAYye5uh9V6JRZHAHsVNroW6IHNZiPCho0VeMOYzp5IYMwEhgPo2zPc7DzeWTPGUe64Yq3ACM4R6CzNbazKEcWMOqMAva4DkDPSaAB9Dq4NMS23MhBOBFiy8QzJlN82ProT5fXlDPISrB0tqUa0tszQniuC2IZk6YyARoQqGWk5NsHnehCZeHoht0OstxxdhnKwa7J6qADlfHZHULeeuJ5evbxK++jhw0dwzkeFypTKdBG4yG+y5o79IIxT3ZU4n2KtgEdigkZM04hpErdADboco1+2/DfheDygH/oMK6z6OV5hmqLG1cfxyGDB0rykPV8Al1q0+Rat9b7QwJduO0qjkX6rLxUnrVpncb8kUkhJYNN21hnZMt/gJGQs4tCKMM09/uc8JULzbJGwAjGysKRxQLJOzf58TR9DYPQh4NAJxmAA7//mCmf3s2tGnmPg4kGD++80J8dtSajJSyOfARK4BvsnBAwyAthCuQBAPvfwFPanmBFQ2kJJSJ/zIoKnI4ZCyJzXzkB2Z357ecO8L+mGXeclHrbvU/C8CCIhCQ++aZLGu4sa7v7YQy2egQMwxQNtrQzHWdAgZIFEH1Bk4BuHpm3F5XBQa33m+qLhB4YhugC3bUqD7Cif2j3v49uNgz776niFz+49ThaIJtJ0pf8K5Ju2hSG4OEZXKlXIqeZfs7ZJWY14lwdOlgsRnnLGxxBCsnQA+WwOFbZUKKn7qK5bmjVSn3ExMRHi2Pd9n6wYvnU4HA6pXm2ntkljNdXaq+NgM169zfXWgsYnHzySTDdOMmEMfY/GN7g8P4d3jKbxWK83qUGbzRpD32PVenzywTvYH3b44md/juvrK7SNBzmP589fIUyTOaRHCM6rq5e4ON/Cu4BhDLg83+YBDYwf/tmf44c//HMQET5sbsEuasJGxtU/+w/wZPtDbNsJzdcD/t0Hd/j89hZjT9FnHzj2Ev0/TQGb7RYWZOiGOB4P6I9HcJI4Q8yYEvOpcxQiDFUS2mo1kIaIBUk3+L3vfQ/rtWQNuLm5xmrVwa06iLtBNhMzOKb0y2Vp+1I9pM9GwcgqPCLYmmtfjKhiFkpiHIlZcmrP0lY9vciUGHIh1yjjkbZRmUEktSfnmE9smoFaK1QYERJSiP9QZttEolXqe8nOIAKk5Ko3MuDitUTWGcC3m8emwYA5OjrVmZ+vxs60O4PM0jVAS/ONWAgb72N2Dtncxxib4SgmU4iuIU3TCIiaJrQxiCvEsXOO0PgW2ac7ageDnh8g/uTdei2arSjwT+OEQFM83zDgeBBCqqeBJmEjMp31ei3nVCTB9zTny08sTAIBVngOzuFbrPEEe5lfZVyG+2tKWwHGCujLueO4B8dxwPEgLnVTCBiHVmhP1CxJUP2YXQP0/aixTLFccb+oVkrcB5p4WJPcF3CvwfguWpnK4RGhQN21KAVnxh/K8TJCSA4kpfK+7jvTf/WTVtcwCUOIvtLgZI2UJEOcUk6G5LLFMTMNYb3ZwnuPi/NzjMME5lFiKqJmc5wm7Hc7DEOfxu7q6rpI4WhXAbPSTX0agNJCBazkwAgp8FwBdzxWNY6Li+smCzLONQniWJrNoLQfVHqxJHK+erNQm+IFnZVtOK9DfSP2SQXAon9pDtPqir9SzhVmaWb6zfKaso1ZO4yZkKHrRmvXthtKW9ajv5o2aGHOzo3pjWb108W4HHPB6SC/PLJA+E6Dv/R7a1w89EVcxBIVqQWBN91PY6LPp3t8ot9pScz7iOUxB4Bf+70tfvx/v8O6yZp9qgoQ3sPFu/w6RaF9eaFjC2LHG8qZlYpxGtFyC+89Jt9gGiWGNZC4KNEk/MiRi5b1AWBO1o6+75MlUsu0ylEQpUP2rMBp8UHjvVgovMMwjFEzP8SsUiQYkcSNh0NA04gCbpiiG+c0Lfb/JA8+MRYMYFoFPH78WDI9kbiEpfMlYtznixcvJPuWoVcKzg+HQ7J+rFarZMn23mceErKVQMH9ZrNJFgwNBlcFo3WjSu5mdlHH59UKYoWErpEkMlaYaNsW5+fnuHf/Er6RczEOh4O4yRFSwDlbvhHHmSB87XA4JGHoTddbCxp/52/9dZEm+x6vXr0SyW4YoxlHTDKNd9hsz3GIfmkfvv8uQAF//Kd/GINh9HCSHs43sPwaANhBMt80LT793vfQdR3u7nZ4Zk4f9I3HNB2x6lp8dj7gf/CBLPIpiDmt675G2z9G126x7w84HvbJhCmasxFAAIcRx8MdAo9YrTYx1kQm4fbmNp6BEd2llEEB8SRSdYEIUP/Ocv8rA82+3gGEm9s7/Omf/hAPHtzD5cVFzERwC0cXESgS9IAfKU7Bes5Mk1Jsst4TxircLm8q1eiKsJK/K9tS7VjRasPUdHKSp6XWGxd4mepzqe+5vWwIZAJQlnmxNTkr7CZkMmHjQ8p2l4BSx0Q++5gnsT/2iaWkqhUcLFxcfbYtC1RtmcTtC/Zsxbn81/wpny7hBznCeq1rUs4HGKcJx2MfD+sSQZ28h2vaeFglo+uQMv803mEd71FMARl0XiAzSw1B8rRzBNxj0ih75+GbFi449MecXvB4PAJEWK9WYJaDjM7OzhIhFG3LYPo3vwqGXn0vLWd5JJ9vH2Mcfm7c81wx95ahk3kvFctqAma8eP4CbdeAk7UgPZTWuQhiUyKy6kok8QXG/YcIU2A8f/4Kq9UKF5cX6FYduraJmVNEEFQGk9OYmqWcBO+42kntpwpvtTt5VeXUm/ORVmZoYyuE9EoMmTI5cRMTi0w/jDEtcjblp7iMSbKbTcHEKgDY3e7xzddPM6iIdDKdmBw7qBaqMaagLOhD7lZaY1l+5ERb1bUynXhiMK3BMEYciH8oryKb2c5mEkuuY3YM6zE1M1IKBnJpWlN9Nt/JvurFXaKk3FLaODJDU054cqAoMAECTkdOXULjCBTXbtlu+4MFIplUEQHGmy71v4ylsFnCkPhcHh1ZU1ZonlVbVi98kIEwleO1OnP4vf/+RVrdhVCA5et1kHomZJiCuPzntfXU5WgBp2JT2pUrfrdjOi/bKizmzzCAnp+YftpBNYNefFro+BvlDmlHP/RYdSs0jY+JDoLACkhIuiQdEeVVE7MTMTjGFKwwDvFA5kqI0vVe9sDsBRLFVtNIApO+jwoLHZuY+rlpxHVmHAfAieUjQOiYB6EflLYARfzcGwW43DIGcN0z2rMRXdfgeNxje7bFZr3By5evchaoELA73Ek8o5mDYRhSxjyNEVMFoRU2HCjRV+99sj5I5kef9l8gApzHarWWMYvr1jk5eNoG3INEQbE2SkByDp4InW/Q+AbjNII8IaxGDPsD/PkFrl9eScgDExp48Mi4u7sDOcKu32GKiXQIhClEYZKzC/PpLF/l9daCxi9++hMwM9577z2cb9fiIz5M2O/uUt7g7XaL9957D0+ePEHXdfjq66/w7bOnkWDloGvftIl5c2o0iUKKASbCq+trXF5e4uziHOeXF2j/RQsMMZNQTFP51x71KYsImBF4whRIghRJQJBOSAhiVtNsWIinl/ZHeZe7FdqmxW63kzS+UbJTfkl6ABPF/MUAkkMz7HPCKLVLye2KCMMw4pdf/RJPn36N9XqN7//6r2N3dycBt7SRHNuGAjMy8LH+sBpclZ+CIfYZpEOFkOLxxLnNuydAfByAzFYjTVSGtEREKb9TxITEz4WymyPBRb7BDFknFMEAxJ81taggnKWXsGxQ0X6mE3YB9HpYX2ZlRT+XrgQTkhQMXA2Ew/lFvlsIGCYYc6mwgnlyNaNlH9arFdpWsm4MvWjdj8ejnBfj4+FaIaDrPLxvIgCUE1qb6J5HUWsyjkcBj5oVKHJKIuSUn95HC0qXgsaGYQQmjq5n4n4lec0lzoggPvJhCtjvD9huNpjchPVqlcCo7dVrM08tjJe15oEYfbfFs1vCk07nRR6cZT5jTveqnxOQvb6RdH8SKCyB896pF7kIE945uBhUrL8RIfmperUQwaHvRaN/7AeM04Tt9j0436ST2pOLRMwGJgoK7ahqvKNLBZxYEOK4aVYijTVgjqlM42F1KjSoVSUFK08TOFpi1aVzii5hYLFU6GnLQMy+ZJapClGyTdTSWMZWWT5XLHJFdvq3eCb/LQGULU9ovIxGfkMSbcS1pMjV+HkrkZmtiVpoQw0iGfXWtcrjUnFYugZaEQScxw1gTABuhuyeJnyB8Y+/IexGSr1jDrgZPJ4evQi/IHy4Bc5aSglVvtoBO27Q+TXCNOHD1R6NBxow/vp7jAcroCHxL0+Z94qGo4jLySNDYKOFSj0jbW9mC2QOrZkJ8/ZdzD9H+In/5EvC16vv4P62Bdp/hmLFxUHXrExzSB2fXCAkp+rO/Sz/zt7nstxUd/V7UTeVz9qfa0FtflX8vKhZ/jZ4iQmPTr43/7lqyRsJrs6KnGU2NZO4zbaSITSdSUGEvh9jOmUgBI/tZmvOVpAgZFECT+l3VdDOx4CS9t17DzgHDkEsoIp3COmgv7btAKJ0v2lb+MYLj+JolWelZUtj+TajINdhZFw8PAPAWK1XckZVPBz0cDigbRucn1/g3XffxatXVwUWUv7CIbqjeYfdbpd4hgoeLqbt1QxSLsbCOOdw7MVa5Mglaw4x5CTymNGOWCxANd5Y+QZt20kiJgDHw1HS+vsOHBNbhCmgP0gWrK7t5NDBIGl1+76XOJxhSIJNcvtykoFP17VaZzTW5E3X258MfnsLIuCrr77CatVhuz3DxcUFVqsV7t27l04MvLi4wPPnz/Hy5QscjkeEmGJxHMeUOku1n2oyUklRr2ka8fTpU3zxxRfw3qfDQQCJAZn8hGHocXGuWU7UTCm+0VM8IVbNRPpdTgqVpR80cDWmLxTtsYsHmniMYUorUPawBJppPRpgWTKj7CfufVx4gcx9cT0YwoQQ9vjyy1+KBgEB7qH41bmYESvC7jQmQkL0xGcFTal1CUBG8URRN2wBCl7UypE2iRIctlu13KSqDcsnkc//1TISoDeEloFkhgMjms+l/fk5YTZCNEwOezW8WkAB80P8owf+pLZEht8PfckgTgkZCnLqfsc+P8MGXKRzm0GzcjROVFOze1tKE12m1O+dmUVQghw2FqLlAURouhUo+rUTEA/yk2eOxwOGmEVkyT2JATnVFSN6IJmnu9UKXSfZLw7HI6ZJgtKGaI7t2hYTI5mH266V4OBB/D57FgK93+0X6ywZsoDGGTCwCCM+GZyHtZOEwAmEgau9EiIoKsoMcXybmKmoTQelNZHhyRkkHNOuql+taiU113wU3MMY96GA9O32THx0ATnzgWQ8c9rXbFofouAWkpuW0Jop0qsxCWocz6FgqFshYFyNdAxnmtPsslPsz7RU4z5hPak7ChCFxt8yT71VwXdLXipNZkl6hKbZidb7DpQ0xNoWioSmxkk+7k8GcD0w/rOvgFeDw9/+kPHB2yU/WWh3BtL1vdeUYApwyKHOwM9vGM8OjH/2LaNn4NVE6NoGm9UaZ2drrNsW/XrE7u6AMOk6dmAPPHp0hvPzC7Rdi4ePHuDi4gKPHj3Aw0cPI8A5w3c/+z5+9vNf4B/8g3+Azz//HHd3d/jhT0acuQEtBawd4/femVLqUI2v0f3EkHX4/pnDWRPXViiFQaL/D3P/HWRZluf3YZ9z/fPvpavK8tVV3T3dPT1+dtzuzCxmdxZYB2FJiguBIISggiCBABmMIP+QI6kQ5UJBUSGKQYkRRIToBIAEsQsSZgHuwqyZ2fE70z3d09PVVV02/fPv+nv0xzH3vqzM7uoFCfFGVGXme9eee87Pfn/fn3ZAEDhOPe+ai1I5z6eM2maaSspmu0iEcPh7DyRvZUP+D//mv87m1ja/+I9+EYIGqYJxMLUeO9cpWH8Dp9/IU87Jmjxfe4rzbXHx1C/vf23HxVIdG2dDnNI1xk6QjTs57cyoPQRd75CsuHXGE5j7ME7f+tOccgGfecuyjChSLFPSq3tKgGJsFNp+sgEaRzkoWZYqUhzPtcxJdV1BXe+pnFdDf6vlaSUpdC0Det4ZSmkE+JqmuiwryqLCcV0CP1D2XVmqpnJ5Tv1mTo1V02O0N3H28wvg4eKQj3z8BvP5nHZH9UBTxdTQbrXIsow0STjKckW+MjKyVROnGHIJlDyPwhCh+86Z+gkTgGoy3ClHosR36gbUVVVRyhJPOMhcrWlHStvQsmrYqEhJnqTkSWqJY3I9rvNibmtAVIZC1Xg82d8D6toWE/gvy5JOp0O322U4GBKEgaXWHQ6H9Pt9Wq0W7Xabfr//THPrmR2NSlMZJsmK6XSiIi8NFhVVl9GyhSeO41jlbjw2m+4Bm1ICbEEM1Ia8KawxRTUGdiWlpNPpUJYV+ysY9WomFtMUyTab8QPKsq5pyG2/gZpOtNKdy1ks6Ha7VoGbvgkmNWyKxiw7VVnVEY01QbEu3owxpIwDE+lQbe4PD48IAk93Z3QY9PsqtdaQOs3onBA1L766gmheGCOeFX1e7fQ0DeunnIjmr2t6Y70g1xo2UqyJurojMNaWqAXoKSGLGoRmpsTenxloakWjajnAxOJMtqZWcGXjc+1YiLqY19G0czVjg6GhrIXDeZs1PLSwqiRMwyHrzs1pY5azhdgzSH3z9MrJcCxPf6aL8xzXQwjdn0aPg4G9uJrZQgjIs9Q2/zHKWhqL2FzLrjV1ZYFyAvMspcgz/CAkjCJaUUiaZpgGmo5haAMb4el22gRBQJKmeJ5nMZu5pzC2jXLQp4ZInvP52YpAcux0ucTEOu1KPpq6EzN3aqOlfmaFCw81e5dEQyCVNqAqJY5T6dSwggqo9ar+Lm3GtA5eKEpUqes6KvteyrLgwcNYZScbToEZd2Wzra8rM6eb2bMmvKA5gSz8xzgdes2YQWvWP1j7UKqXvbbMGu+ghpY2Met1HUNzcxzVadlmDI1cEA3TR6zfdb1um9etb9tEsCud+dlbCu7NJa6mwLVSRZ9gkgpem/hklVLa/8nbBZ/bzvjshQrfFTjUc6Eet7MMvvXfm0Gjpx2OhhOkZU4FHCRwdyZ5cwyTrCKRknYn4PJzF3np5Re4fv0ynU6bmzeus3vxAlka8/DhQxzhq3+uogLutPoMBlt0O0MbsTVFoYnOzB8eHTEeHzEYdPnVX/1naLVaLJYLslTBmQ8Oj3jw4CHfefyIk+kJSZKQZ7nuISRV3ynNAuZSEghwhOSTW4JXt6DrqeesELjGoKE5NvqFScNmZmpSdI2jBCnq4vbSQKsQ/P1H8NpyyJ//8/8CP/GZTwAuwe+3ieVMj7l46h01rri2NR2J88Tt6c9POxZPOR9nnOiDXru36ZG3BTKro9unT2jklFXN51wboOOnnBSn7sP+0dRD6yf4IE7GmjyuFJNUGAR4Go6rgh5SB6JUg2UbiReO/V1BewubdTdkEAjXrnWL0NBGsmHoBA2BMlS1lZIpnq86ihs2JeE4BIEi8CnyXDGc5hmS6pwnoyE+msLn6QUuUI14V2KC57lkWWzh+K7wqcqSVAjKqmI5X9mMxJog0WvAdR2FNCgLhF4jAqXb+72e0qkCC5fKskxT6fpUmaqBEEJY+zhDkbSYTFGuexlJKamer5E642NVYmBkeVEUeL6Ho3WyROKHIR39ftudNp7ncenSZVqtiCIv8DXr1fXr19ne3qbdbmMYPH3duBEhVE2N55GeKko/b3tmR8PRdJdlWSCsFY7Fn+V5hqsnmPFcEdJyKq9nLJTDYXiBm5XugFL4OppmvKzm+zQcwz+cBrzUz3Ugv44RZGlOUZSUlWQ6nbGKE32fNb7YGKfq2hVF4RDHsc62qJeoojJqT2P8P52WN86R+auhXq0CrwW1gVEYQzzPcyaTqYVIRFGE7/nKUNFef+1Q1IJ+DQaA0Lhs9Zf6prJFiFUlbbHsulaVp/9UT2CtgKc32dipRpVLKzAMnara5QxHQ39rjRv7pf6uqiymHamzSMaY1Eb/02SJZt7oKF5ZWke4KOoupwbCZwo3z3rC2vCr718CcSlY9ke14GpG7xp38l7bGn78lBqTqGyGofAzwqQoCtsXQ7gukWb+qCE8jmaCksSrmCJLwYyTrAla15wxvVbqokTHGhVSStJUrZd2u00UBmRC4U+NoyFlgRDKyE7TjCgKcR3FXtFutSiFIIpCFovCjs26+StOfS7XP3mq7kA9zywakCRjAqc5lc0crpWNKWhujq1yeiQ0I2zm+tZoV8dZ7PwZb1A9v/m7XvfrBc42oNx4Kh0jrn0J/Vg1Val5bU+7Zo25KptjaeZf7WQoGVqPcu2GnIYdAqLZKrP+zNSLNFayuVpDXoin9q8dJSXwzPUXmSZfsCeo180yF3znxCUr4e2piqIrunQPF4HvuvU1de2JcAR+5BA4tYP0rWnOt8Y5oSi51sq5NZBc7lT0A2EzIWAYmNe9jNp2O+0Q6XVjouyNZ9pblvzmI5epP+DqlW02Rjk3Bm2C0OGnvvgZhqMeQeAStTwlw+WYw8MTFVTjmMuXblJJh8VirpX5CskEx/FBhiBVB3PPrWi1PLJUsr01otPt0u52rV5crRRldRiGGpLskOeZ1atlWXF0dMhioTobL5cLTk7GxHHMdDrhBz94ja/tHfO7B4qFzXVV9HijJbjUkWyG8Orm+nxsZtNtnSIqQnuQCH54ouTluwvN2uP6DDe3+Rf/3J/kT/zKL1NVFUEY0opaTOMZpbRDX2czxPpram7nSdGzHIDmqpRnHMOp308f90Gv3dpwqZ6U5zJBGR1mC3vF+ZDSwK2AJdA9dbNG69LgInkWDbT+YGfVmpRFQa6z26o5nqAoS6pSQXxwlJ6VBTiisgx7hp1PuIrRr2hcsFlntI44UP+yLFMZDGksCoHnB3ier4NpBQid3XAdCg0vqmSpa25re+6Z3vg5nt0khd0rF4njmCjySbMEKmGDRQYm5HkuVVUS6AJrdUrFKpqDCpJ7lc0ClGViM+ar+YK8LEh1LQeo5zc2sYurUDZSKtSAruHwdQNDw1xVB/6M5hRsbm6yc+ECvV6XnZ0LRFHEzoUdcOv+GKBgWL7v2+SAKRQ3VLWGtSpNUzTYmihUyQAVi5MKlVOCH/73DJ2qpCk+MdkN8DwHxzFpshJJZRuolFXRMJYbRrqsvX3zz2DEalyjrA3PM6SNwoXH9EpFd2gMA6E97P2DffZtWkjaLqzmnxoqbWA5GgqlMWyu6yAQp7jnlbIR5kjTowFz3VMGQ2OTNOd1vbKNQK0kUFRMJjNWy1gzO9SNpgy0zHS3rWFmQk+2WgE203LqGBdNEqY+E2KtiFU0jmuG86SkAW06S4QJOxfUq6rHqmngnNYUzfoMy9FsBK96szbr42j4irk/G0nU99rkKG86sQrnmFEVKhoYxzFVVdZOg5l/PC3gm06X9kXs8xfSasJaK57xnpvibW0AZfOX5vG1EWeyGaYBkcrECEthayA/fhDYLE0URVBVrFYrzSNe92tQOE8VIHBd7ykjFzRtXVlRIkHvL4SCLy4XC9rtNkGomvtZ8gdXZSsrIciyFM/38H2fJE4ow0qzVSg4omnuhn3iM5wImq5Qc9i0QtVDlrZ6JCuH0D0Ltrg+3Ga+mMlVVSVVpqM/sjlHhc4+PL2t3/fT977O/FHP0acd7DN0m97FXNq4B2epyyYEpam41RytZ9yicDiM62sLey+nnkBP8JYHF9v1ee1+DePn9DvTkgeAZSE4WEl710aef/NAsCjUvK2k5CTzMc6klDVrihACL1T4bsd32Om4VgkGQcD2aINet4frOKojbbeLr7NmUbfDaHODKIooioL9/X0ePHjAeDzhzdd/xN95tI8Q0HUSQlfYNVEJFejaDkte2VD3dG8uKKXg9vBUrYYWAqELl9rq/cSl5Ov7kq8fOdx47gb/q3/pz/LSi9d4/Pghg2GHokw5GR/w4ME97t+/RysKuHnzJp4jSNOYXreD73q0o5CycvEcyXwxZTpZMBpepExLhFAsaMPhiChqQyUZDXt4rk/lejiGpVHPM8MykxeldjB8+44d1+XChS07AcuyoN1qW/l/7+49Xnvth7z77rscHR0xm82Ik5het8edO+/w1vEJv3Ogosmuhq0obL2KLge+MkAM9fXw6pAbL/fwXI8vbW7Q6/W4dOkSL7/8Mru7u6yWM8aLOQZGCJCXgodLuLwGfzMQuqehRec5CaeN/tMmpzhjv7O+P+tcz3rtT/1Sj6//tTnyoKTlVrZPlt1s8KqmKS4qaWlsm5Kj7YHHhILuU/dh/lLORuNurfI6x/GoBd9TZ1TqrUny4+IKVVdmWPhEpW20SlI5AqeqyDWJCEIFgQ1E3gQLhaNq3KTEIkrUUChjXFZSZfYAhKrJMPTseaYCRIF2POrCal3T8ZS2rcei1nPv/cbNtyfpkosbPVqtFq4LkgBZSqpUKna9KsNxDB0szGcLqhtarlQVhwcHJGmqa0JF3XtCy1MLUfJ9rZNdgiCg11PX7Ha79HsDkjhhOpviOC6DwYAbN65z5cpVq8u73a51/H7/je+SFindfo+/8K/+RYIgqMcsULUt09nUBoLDMFKF98DJyRjP91jFKzzPo9PtkGU5SRITtVqU8YrRaIM0TXA15NjxXEU5XpW02q012+u9tmd2NKBO3ZRlobHOdf+JVitqFL0YzG+NNTvtTJiXo/B3Og1kcH06Am8LUYwFp6eP53uKC780BqRxXFx80z25LLQzIGwEQXndNCIyUvexUANfViVpkihP2l5TNIxS3SxG2mncMIKf3qxJKUTDGFL3qyafMS9ASMizEng6CmyMrdMvdc2BsVayOcIksM1X69kGExE7b6I0m7M0z0vTUABLsVsbdmeKMDuWpiy4vr5yaowzJbQTYv92GhAw7WC4bo3zrA087KLOsxzXdVksl8ymMyQ1X7/JdLje08VU9k/5ND54jw5SEwSYx3lqr2bA5ryQ2BnmtNT37uli6zzPLFbfQOkcp5HtKFRvgXa7DVKTHmjGD2mygzr6axiASkoc3VekjtKC63kgKk1PqDDdDjV93mq1ot3pEIQBlYYKOY6jGDGEKnzLs4yo1cL1XNI0pdVSAsgPfJv+PV8cPYOgarynIyKGIrbreP08jRVTaxn702YXzd92XwNlqD2XJiGQ2bs5x+trrDscRh6d96R1FoJz93vawVHOhr0PJGkp+J0ngtcnnj0gqwQFrl2Arm5Y+dSC1H8LJC1XZY9bTsnHtyo+vAG+2zTV1HM/mKuC5O8cCtJSjWAuHSrh27nr+x5+ENDf6PHyrVtEkWry2O+1Gfa6bGyM8H2fODYZsxadQY/Rxsh29a4qFUQSwuHjr35Ezd3CQNhKKxfwFO+/4yiSjapSPTyyLOOH3/8Rb7z+Bu+8c5e7d99hOp2SJglxklAJyMuCg1nODybr/YK+daJkXrNfiuOoOd71BZ4nqISkdB1+8ouf5E//6T/J1mafBw/u8fDhfbZWG1y+vIuDw+c++5Ms5zFlUXK0P+Pzn/sMSMnD+/dZrTLSpaDd7nJ4fKQinyLg3tv36Xa3uHT5EkJI7t97hyCMSOKMg4MjnnvuNp3RBoPRJr7vqb41QLvdsUW1BtNuZLvj1HV9nudRaax2UZYcHR6ws7PNl770BdL0U5ycnDCfz3nhxReJwpD9/QMe3H8CqF4CnU6Hzc1NgiCkLHM6nRatdtsWDSe6MZhEyY2yrCzr2vHxAYvFlCiMODk+YbFY2GBJVQZ864cgXxZc6cqGg1y/G7PezHo8yzlorrPT6+ccP/89pU/z/Keved61XU/w2X+mT7KoeOc7MfOjwuZarR5q3NW8Lbnw8S43P6bYgvx3H0NZMs8l/8Frko9v7dGLrpx7Z085H2dGNU5tSnGf+cBq7CvSNLMNmJUt4OEIZftVUiqInBRIDZUytahQOxNGt7c0nX9Zlqp/kbbxTMDP0r66Dp4fIHSAwpDuBLruo9AwVceBPM3PkP9mbE4/VkNTNydQYyukYFmm5LnH3t4ergt5kZEnOeTCkm0Ye9R1XcqqtM6DgVI5DSiR53lcu3aNbq+H73m0Ox2iMMQNVK+Qfr/P9evXuXLlCqFmcQyjFmGrZXU5wsCUfMqyINfMgIVhrXrLg0LZD61ul0pWZKmCTGZVSbvVot3p2BKEJE3wSo8gCOh0O+RFQaut6MpzzTA1mU4RjkOr3cZgZ+IkJs9zy6ZVliWsVirQ+QzbMzsaKsouyHP1llxDT9uc9MLR/L0epqmVYnsyqVCDyUMrBmEnpZRKUUip8H6uMF2zscaKnjXWIJVo9hZZOzyepwa+zAuKqtQUZOjv66JHBcvSBrlwlFMkJUVZkpeZZUUQYItDi1yluKReqCZbgHVE1rfanjj9vYnWNPc0kY7TJpO5R/17w7gxjbxqxwntVKlf1EKu4VEGc27exfqV1U9bX2uv13BGtAG2JsfE+rOtKQieXvaC9YCLcTyEoxaU3ckKTdnQCir67KgQiXV4mp2UlSGt5ocqbmsR+AGLbKk4zKvayXz6zupBrBpjYaJ/zU02/j+NQX8qCbfuA566snrjvu/pqI96X3mhuiA7jumDUXduLcuKKIxUIVwSK4EsTerawXM9KxSrqlTjIlWWpNnx2bCXyUYtlekTY9KysqqI4xWdTkfVYiQxEmm51FXH2AI/qPA9/X2kaPzcylUMYtV5GFpxao6crb7VPuq9rdwIKVd679oBF6KuCXta1wpbdNs0ns3JpZ7XFj5mvmr472YeNrNCDZfDfi5AKV3TX7T5gEKz0MlTRoxeQ5kUrPJmVF0d+IMTwVtTwWHiaifQQQhfR8TB0Y3CQlcQouCqlawQotSZLAfXc/X7UvMsz1VxpTI6C7JS8psPS37rke5YrG/CKNZSQ4dAR+VcF89zGXS7fOill/jiF3+SGzevE0UR/X6fwWCAYWCRVFDVUALDv1+WJbP5jL39ffb2ntDXkb0oDBkMh4xnU1VnV1UkcawdbxVplUjyIicIQqpKUSovl0uqqmL7wgbPv/gLFs+8Wq04Pj7m7t27PHz0kP39febzOYvFktlsRpamar1RR9n7/T5hFJEmCVWRc+XiDp/93GcYDjv4gcPLL7/AKp4TL04IIo/RxggkHO4fsblxgUf39vj8Z74MQkESHj+ZUGQZV6+8wB98//vMlilBBCcnS1zX5cKFXXZ3u1A5FBJOxlPCoM1gOMJxFuxc9Gh12vhBC8cNkFLQ648UhtzzqKoSz1NFp6vViihQjDkP790n1gZBmqYEQaCfOePCxQvE8wVPnjxhNpsTBAGr5ZK/+p//fxkMBnzk1Y9y7+07XL58icHWFpHvs5rPcbsKsnVyuM+jR4/Y3t7m+eef52Bvz8Ix0jTj29/+FltbW9x95y6D4YDlcslivmQ4HClZ46v57TouyfEXeTL9Gl0vZxRKG8RoLqDmmn4vg/9ZP3tazz4to81nZ/jpZ56zkqous913+PCXVYom/NEcihInEAy/EKDkj5JBr9zu4AXqLPsrRWFsHvaFT3yW7711j9vViovtduPG9NVFXWva/Oz0dq7ekTpYJk7nk5Xgy9IUPwi0U2AazvlYxjtpMuGiEUSuI/cCVDNZTcaTZZmCN2sdJwEDj/d9TwW9EBRVSZGrQm8vUBTtCr5V4ghJnqU1Gc/pZwJqeLd5msbYyPq75lDtLUvmxQP29vtIWergiUtVVHiocgDPU6QO7Vab0WhEXhb8IHiLnIIgDPnz/8pfZDabcf/+ffr9PhsbG+zs7CClooxVdZQCx3VVnQZK586XK5a6JUS/P8Cbz1VfIh1M9FyXNMso8gyJqlEuctMktg5wLZcLS8okQkGh6XZNzXRZlqqjeaPGw0C0PM+ziIoLFy6QpqntTm5oe5sNBE2PjjXb/D22Z3Y0hHCUcUEd7W5epIkBq6qaUaoJq2l21D0rYmG6DRojyGQ8VBESjfOUSCSHiUMhK8UIqw0F29hEOHiesMqjGblCqkJjFXxUBpjrgis8C/2qJBSlOreKqFX25QgBNSnSuoG5ZpycOY7NgtD1xV2bXutC7PRiyiV8/xB+cKKetRtIPr1j4CTaQEdHZaVg4EtGETayZRorvZfgbT7DOjzkVBRBGnYRc/S62fjU3VsnqHGv+lDlBAiLOzXZraZ3f3qT1GNqx0u/A1VvkNrfK328iYo24XHm3poGozlnWUmWvqK8W+vCLhoq6CxP85zttNMJCjcpHEGRazhgUSpIj4Q0zagqRetXlOpzxY6WK0YMlNB3HBfPV8KasrC1TmqchOWqNALe/tNRNqmjMqXO+pieEWVRkCQJUUsVj+V5Zil2HY2hz7KcVitCaDKIIAhwSqVAjFBdV9ZnQNfOcdjNOEkkk84m8fyY0FWfqKgZoClhhVA9RFzP03TalYUB1pDNU7VJT81r9Xm9rg1FdZ3ls6v11A0LJAiJxNHRQfXcSSk5WsEPjl32VzrapwMrai5CUrpMUg+ENm6EDqq4FX7gsLXdo9Xq0Apb+G5Iq9VmOOjS7XZxPZXNdV2PbrdLEPgEoXK4o1ZEt9Ol1WoxGo0Iw4jjoyn37r3LvXfvcffuXZ48fsx4PCHLM3JZ2Wc2kD1fKMXr+SogcP36DX7iMz/BZz/zGS5duoQf+MRJXK+tSsEvSl0X57kurXbLymfHcQijkP6gz9WrV5E6M5dlGbPZjDzPebK3x3SqioWDQFEv13TDjlWiBjoUhqGCUpU5xyeH+L7PyckJURRx7foVbt2+icEfA/bYPM9J09RSUVYaimgUaZllyCLm2tXLFGXGarXgN/+73+SLX/oipSyYTVdsbl7gxvXr3HvnLlXhMjlZsr11mclshuM4vPjChwmjiO9++zs8fnLM8y9Akldcu/k8nU4PWUG326PT7iKFx2hTkZMslyva3REAvV4fN2zjeoG6z1IFEUrdkd2w3pis/vHhESdHR0zGE+bzOVmW8bGPfYw8Vb2nskQRRwz7Q7rtLlEUcXx8zLv+ffaf7POb+/8dr732Q0ajEZcvX+bBgwdsbW2pehDXYWtrkwsXLnB0cEgaJ2RZxqNHjxBC8IUvfIHRYMjh/gE3rl9nPB7TCiOm4ylFntsGaIpIUXLl8g2+97UHOF94l5e3K1quKkC2NuMZAayzwxLrhvXZOvTsz087F2dt73vtMwMRavN8wY0Xz4gAa3111IA9+r7PKy99iAsXd/mtv/UP2Qg/Sug2aPbWwhz1/2fd09nmyPs9oRpz00XaBGuEg86MY8kxDLNUs2bMjEOpM/O2zlaamigF4/Z8t8HCpKC8pUa/+LoJrWrSpwLWedag3X2Gp3zqebXN0ZTbywL2yzEfevk5Op023W6Xmzdvsru7y2Q8Ztjr02l3bPAh0FS0JZLf+oPfYZWtCMOQ0eYGrU6b/nBg64hBkRIFkapHllLieT6tdgdTFyGEYLVakaYZy+XS9uIQQjAZj4miiFjDm0BydHhoayyazx0EgS0uN0xWUgcDi8KgkNzaERTC2tiLxULBztPUyvAkSSjL0iIpZrOZPYdp1HtWacNZ2zM7GubBTSGqSRUZzJxhDWg27rI8yXozzoh5EPPAxqkwBTHNWgQzQM3ncV2XbrfDvYMjfuOhw24kebFf0nZV9Nd1HXzP1YZ2bbzKhhOw5rhIhT10PVcV1krV3dZMcOE5VFJFeJWTY0rEzbwVZn3Zz9bm/anrOgJ9hvUid9YPqcdeDRKVhO8dw2/vuSwL3zpybukxXW5w69ZtDg8PePfd+5Z5yMHBkQUboeSnL5XcHtr4e+Na0uLW7XNYx7/hlOj/KtkoLm5+f2Z8oX4egWFSrCltTb2JesRaZAqa2Qc1qM3C+ua+tTH99HhmeaEdUdXoxnV19spxnlokZ0XMAEoJq1YfawGelXZ+r+30fDi1WSYziW7Qp7MQOuqrshMJfuBTacIAKSuSNLHOgqpP8q0BUplooDAKQEfRdE2S8rfVtQr9LswA2IZMVaUL0RUcLQhK3Wcjx/U8G3hAoDi6Q4XfzrOcMAhtkCBNs/d0as8edRpjbUgHVMNEpdRq2lXPd2m3IzrdDhN3SBH1mQxugvdXgARQkUavwQBnMqqGZrGqeZvtPKh7+ak5upY51PcrT80FKZSjgXak8wq+9jjj9Sm4XgQyQrhCZZ0qVR+TpTntnsB3CzZauTaolXPg+yGt7oBf+Wf+WZWG7/To9nqAxHUdWjqzpRpnORweHjKfz/F9n7xQRkK73Va4Y124mec5Fy/t8rFPvGprmg4PDniyt8cbb7zBdD4jCEOrUDY3NnA9j1Yrot2OiKKI0XBIq93WBZJq3bXbbSvfi0Lhtn3ftxAZo1iNUQ919NNE3UwELU1TirKyhYpmnltGQ7DU6uYcYRiqcRDSKvrhcGiPPzo6Yjwes1qt2NraotvtWnx0GIb2fGZ/M39XyzlpPKfbVUW50+mYwcZ98tLn6rXnuHLtBdpRC9d16XeXCCn59Kd+iizPePToiBdefAEHl3bU5+Mf/wkW85Rbt15hZ+eCLZD1PQ1NrCSrOGZz+yKu6zGdx7z11h2yLOPTn/o0gVuSZ6ruzHUVfn61WrFYzEnSmOVyyWg4ZGdri6oo2NzY5MLOBba2tiw0zejtra0tXYiOZfy5cvUqr3z4wywXC7797W8zGAw5ODhke3uL5567iet63Lx5k2996xv0+32ee+457ty5w3g8ptPpcPPmTRzHYTqdWurL5XJJURRMp1M8z+Xx40dqfT2nHI2qkrz147fwnQv83V8/4Ohzc774sqCtYybNAJ6REE35UYfBzncuzjL85RnHnD6uuW8tCT7Ytc/aTl87KyVJCUUhwQHP9WhFIRe2t9i6NOTOZMpLGyMMmYc6SS2wztK/77mdu+up0ZAKGut6JgirnAZjo7k6u1hD06W1VZpPaWsrTe2oK0BDdCspqXRDUMcRBIFvs/tVqSHBslIR/fcxbGvCmPdwFxsflxLuzjL+2D/9GT7zmU8jhNA1GsqWLYuCxXzB1tYWURSRJImC/SU5nW7HBisdbbS3Wi0roxzNBrlYLABotXQT3krZwkmScHh4qIvPI4IgsJkE4wAY50E0andB2QwqUKLGwwRH2u22TQAkSWKPN79XVcVkMtE2hJKTcRzj+74NtBi73XEcut0uq9XKNhY0zLJG3zzr9oFqNFxXYbA7nY7NXhi8mvkdsF6UqyMr5nPjWdXNXLDKo5mqL6WmKdQDrc5R38d8Mcf3PVrtkLfzST2SkAABAABJREFUgB9ME/72/ZhrfcGvfixk6EgL/7DtiwQ4ODraaIRX7dAYyk5kpSjUcqHhK0q0OAJc36Ms1efqecGY2sa5sHLARDZk7VxIIC4VH3yw9o7WTXID78pKyCu4v4DXjuHtqUS6AQJotXyuXrvGCy+8wO3nb3Fh96KaqHry3rt3j29969sc7h+RZznTSvJf3StwKfEdyQuDiitdwe2BtJc3zqTvKBjGac/fLOAm1wEC2yXcwI3M0zShR/b8jdM5Nvoh7OlVfY5hRHpa/J92BkyE5PRo1jh80zvFHF/Xf6w3lWsoNM7bauP9/WNbjdt+H6ff1DRlmYJAFYZJQzgYDnMzLxyUI5DrVKrZTLGWRFrDy/XchkMsVMfqIMA0n1MN/Qri1Yo0y+xjKRIB4/Aop7JCpVjbnQ6+5yGrCt9zbe8HWUlboJZnuSaPqJtc2uFbGxrjIJ4zSE1tbI6xCk45rfPeZXZe/CjpzjW8QY9+1EYIGJYl3PdBJnZO1edoXr1eo3UmTP1+2m1WIqvOnhmHd21OSoFUACeysuK/+FHKxrUN/o0/99N0upJKKmaPMAxtBvf4+Jj+qE9WFEzGM6rSYdDfRFYu16/fZrjxKpevvEq8SnD9EOEKHFdQyZKiyvBcj/lyxeGh6tK9sbGh0vytln3XijJSjXToqsZwqsBTUJQpG1sjdna3+dBLL+AFqiB7sVgwnU6JogjX9UjTBM+r63cmkxPa7TZhGKpGUUFoG0CZOp3JZMLR0RF5lll5bgrBm00Gfd+3UW4TeOp0OkTagO92uwwGA2sArFYrHj9+TFkqmuU0TZnP5wyHA4LAR2oGlSRJrPNw6dIldnd3bQS1ptNU2fdOR0FdTHbEbF4Q0OldsE2tLl65yS//iavaqc4IPA/XUZBFRyiHrio8yqLkzp0HvPTSRxmNRsiq4u233uDB/T1Wy4wg6BAnKUeHx8RxQq/bV4ZCKfh7f/NvI4Tg05/+NFG7y9d//+/T6vQUe1pVMRqNOD4+5vDwkOeff147ZgqHHS+WeAh6vT4rHak0DXVXqxXb29tMJhOyLNPOmc8777yjHKV+n6IoePjwIbdu3UJKyc2bNwiCgO985zv0ej2kLPiZn/kK9++/yze++fsgJbP5jK3NLVUA67o8eviQ5XKJ53n0ej2WqxXxakVRlOR5YYMlas1U5HlKJXNG/Rt89/empMl9vvoJQctTa0rFSpq6qtYFZzkJpx2As8TKeVK7KdHP2vc8h+IPdW2pIJb3ZpLxSUWeuRCpcZmMT1guV3z+M5/mb/zab3Eh6bMZ6W7UVgc1z9vwxBrfnSN+T91XrS/PulMVYK7qHmhaUNpgjSPw3Xp/a/BbO9F5ahCVg1FouFntYIDUtbBKv1ZFqYNaZ3ZdWn8G62Ssf9MMGTW3g1VG2T/iK1/5aRtYMVlO4yR0ul1Vpxj4xInqkdTudFRASEPzhaPoX2ezGUmS2Ih/HMc2k7FcLrU8GlJVSuaNRiMGg4GlCTaGvcmoGhmlMrou0+nUFpAbCGrzuabTKYvFwgZghFAMlp2OquM67fQAawmCZmfzo6MjKzfm8zm9Xs8GaPM8t8yUz7J9AOiUUgym14TZbKOrqm6xbg1HU8hNHTFpFocbDJhxVKxTIll7oGZWRCIZjQb8z/7UrzI+GSPLim9845u8+fobHFUV/7B4kfLkIcPlissdI8S0YyM0XFw7GYpb31W4YlHSEcpIS9NUsyEoUJDKYKjpajw+U9TVxHVbwdeUMAL2Y8HrJ4IHS4cnsYPvVGyGFR/ZqNgM1SJ4spS8OWk0g5MKGpZLV0cCJP2NFpcvX+bVV1/l9u3bbG5u6iJAdZ08L4haAVeu7rJzYZMPv/oyq0XC/t4BD+4/4GR8wnK5pCxKHs1mvDNJ+M2DXE/GTDtmEq8q2ArVc5RV3dl8O6r48KawUt4Tkt1ObbiZuz+vwLwJi1OhKiVgzKDZYVtz2mQ9phiGMWm96fXPzZA/LYzW4HoCW4B26g7tDThr1zZ3VqsXU9beFGrnCfJmEOqszRGOhRuq9aEFOIJAF4n5vmKi8XxPEQfkubpdDZkyTkahu4Dbgn1H4Hs+rVYb13PW5bCjHJQwCFisliRxog1taXn8q0ri6gLyoiiQZYnne+r6QtUpVRqHX5YlvuuDgKIo8bSj44innTp1GzVhgY57Pf3mmpkrc9uO4HeOQ65+8sv8xJd+ikG/TUVGWZUURUmRF7iuyu5Qnj6hep+eZ2hTZa23OeVY679V1E0bOmChmme/U9XATVDyu09SPvXFV/ilX/wIvW5KVaVUUtdYOBVINS79Tp+sqjg8mSBEwubGFnE8pcjhYP8u05nDcLRLkTvkcUzUadPpKYcqcAOEdJAC2t0unufRHw70OLnWqc6yzL4HA0nxNCwqbEW2WPBkMmYymeB5XgMmoyKZ3W4XIVTtkzLOHR48eMjly5eJ4wzhrLh//z6bm5v6+irydXx8bOsvut2uzV6b9WVgUae7zE6mM5v5NhkKYwS4rsvu7q6dVwZWJWVFWRT2PZp1YJwXo6+MfjH6yug3k8lI01RH+yWe67FYxPZel0vVVVf9HSLLijjO8L2KS7tX+I2/87fZGG2QpAkvv/QqP/j+D9nd3WU6nfLd736XbndIlubcufMOq2WM63qsljHf+Po3uXHzJu12i5s3bnL37l3+wd//BypTcOMm77x9h6os6HTaHOztkWUZvV6Pb3z965SVMuAdx+HC9g5llnPt6lXKouDRo0cqI9Vus1wuuXDhApcvX2Y8HvP6669z8eKuHavXX3/dZqbyPOeVV17mm9/8po5udvjYxz6KlJLvf/8PeLL3hNVqieM4nJyckGjonOd5HB0fkuc5GxsbTKZj9Z6Ecsp7vS7T6XRt/bRaIY4TKLpSKXj7tRDfe5effDWn55u1tg57bB7/1LrldPju6d+bpvT7OQ+nt/POfda1T38H60GtH48rnowrfve3Wnhf8MhQgcwiS3GpaPkuH/vYc/zwuw/4xMUbdLyzHQprcsjGJ+JpOv73i409/VS6b0pV6eyGi7AyXVp9LkWjlnFtUDWEvsIiGUDJVdfz8XWW3QQ/pEEy6Ga0VVViunqdd+tP+xdPRZbW95eSCoeHyRF/4le+ShhGOI7KuBqbdLlcMtrYACDJU6aLGQLBcHOkMrK6dlefkPlcsaltbm4qatiqIoqiNVtWZRPr4IqpWTMy0WQXBoMBLV0Ubrp1g6TX61k5labp2lgYx8FAmsxavHbtGvP5nDRNbRDFZECawfZU98KSUpE5DAYDqqoiSRLrqJjstJGRZ+n1s7YP0LBPCemNjQ2klEyn0zXHwUSqmqltc9NGyJtJaJSHeaHNxn/me5PibToZoFKKruvS63UZDQYIAdevXyH++a9y795Drl2/yd/9u3+P33rnQHePlGQZevXVxqa5tu/77G5f4Oe/+kc4nj2h++jrbLmxntxQx8KV42QW03utVRMhlcA7M8FfuRtheOalkKRS8jiBhw8rmgaw57i66aA6geu5XNjc5MqVK7zyygtcu3GZTrsNAg29KJCyBEdQVnWmqNQCIc1SqrLg9u1bvPDC88RxbA1sUzg5m804OTmxmDwVtcuJ5wlzjck7Pj5R+Nss5Uf3l3ZySlkRCUUx52klL5B8ZKOg7a0zWhkhUZYlN7slg6jGGK+n4GrHwkQdzTxSHbBL+0bUnFLREnUpbZSeAW1qFoyrNKSriw3Xr2uujXm/QtT7NcJQT5u/502Gs/dqzh/HFsGb+gntKDhCOQKRalIUx4k2tspGE0J0x3AFlypNrZSep74X0O606zG2hnszNIjC+TsOSZLaG7SMcOaeK0meZ4o/XFvbwioXBfPy8e1xqsBd4Pk+mY4wnzHaNtb0vroPCUISe20+9yf/ZT70wi2oMgLXJU4L1TmWgMV0qRs9qauUGvZYZx/U/dqMxDlXe1o/CWscrGcx6v2lrDiIS745gc9+9bN86Qs3cMUMmaUqcudFIAtkUdOSpnFM5bRYzgW+O6DIA2Tlspgv6LZhsdrjW9/8R4w2rjCdZVy+dp1L4WVKCqQrCLxAMYd4HuPxmDhObKRJSqmYSjSu2dfGfKGztXGcsFwtefjwIZcvX2EwHLKzs4PjuJbfvQ4OSdIkxfN9giDEER7OtsdgsKGhWjkf+tCH7Ho19RCf+YmfsIxEpoFmFEUWwmPWuEnNm5T+9s4FpGQtK25guVDLcCM/jfwytXpFUVjlao4LgsBCC4xOM3AuUOvA0GKbprF6UVKWJcvZAj/weDw5wfddfD8gWamGW0WWMz4Z8+Mfv0Wv2+XHd94mzVK+9KUvc3x8xMHBIXfu3OH27VvcvXuHx48fkSQpr7zyKmVR0utGHB08JstzJtMpnXYbWRbsPX7E1tYWo34PqaO9rW6HVbxCINne2iTPc+IkYTTaYDlf8OYbb7Cczxn0B9y+fZtvfutbLFcr5vM5nU6H+XzOu+++y7e+9W0GA+WY/tRP/RSvvPKKzUjN5zPKquATn/w4b7/9NleuXmZv7zHj8ZiDwwNUz42C5TKh02kRx8pwabVafOhDL+pGZIk1rFarFUE3JAwjnfE060aQ5RntKMIPfVzXZ3t7h8n+Lv9Qvsa16xNCDzZCSceDSBFsIc+RrfVqXf953vent/fU7Y3v/nGujVDQzB9PJI+P4Tf/5ogrl14EHulzS1bLBb4rmE9PuHn9Ku/cfcgbJzkvbfi0vaZDcdaF3uMpxDm7SXRvjbOPNZ8URQmUa0aqWiIq+mKf3XFskBIEwqH+3a5nJTOrKteyWFlOeZbpQK+kbiSg7uL03UlzInuT769JhBDEec5nf/pj/NIv/RLT2YmC3J+qO1gsF5ZEJdeya7FasrOzw2Q8VigYaqa6TqdDq6UYxJbLpUXxmGyolIpi1mRQDazJ1EuYXm7tdpskSZjP57pY3kdKlb012XATeNEPZO3xdrtt5ZnjODx+/HgN+lTqzuDGcfA8T2VuOh2klBZ2b2ozjD43/0xNSVuzVT3L9syOhqmvODlR3QcNhss4EAZnZryqNf58URuGzWONY2K+M59HUYvN0SZHR0eN4+pzuI6ji4NVqsd1HG4+d5NXPvwRikIVJ21vb/P6a6/z8OEjXFfoRoNK8RlPz3VVNsMPHOK85F/81/5Nfvzjt/gH/9n/ncO7P+SVoQqHRq6CXmRS8GQp+Ov3I1ZpwZVWwc9cqeip2kK+fShYFvWcT0rBj6aedTKsbWfHRRerGicEie8HbG1t8eEPv8Lzt59na2uL3d1dSplyMj4kSRLiJLbj5fs+fhiQpKoYL89ysjyjLAqOT07IVgUXLuwigInGzRZFYT3tPFeY8OFwaPHUSZJQ9kv8GzcAyHWBURzHClOYxLqpoPLoU63gXdel1YmQrRa024StFpubm/T7PfwgZHtnh+985zv8R//Zf8IvfPwqnxjOWR7vaYiVzhHoiR0GAUEYEYaBNZJXccxiPlesDYnC3iuhoDqHm87waGF5OuJl4DCuI1ShGTRk0jqzlHEW6w/0h81QzbmhlfM/OC0kBaYBkHYAqmrtELNOTDNCxxHkWVHTA+p0SaUNIRXJ0HVOugDXjJ+BELImk5XDKKtKcWeXJUWpBbxbU0+rxlLKaA1DBaXJ8xxX1NBBU3xuGIXUGGmn9KnntqvgjEFk7T7N/hIohctry5CPJwmvv/Y6yWpBEi+ZTKZkWcF8tuDo6IQkSVn+/ArasCokb04qPjQUdRjRur5Pv5d1x0G/B3FKl9nj6kLyCvj1exXZoMef/rM/xXPXPBx5hKgkRe4iPJdCZjqqp45ZLBcqGFKpeTCdnFDJMa2oQ5bHHBw+ZPfyK0wmh3z+C3+E/mCXEo9KSKSocKRDmVfkeUkQtNjYUB1pJ9MZi8UcwKbZl8ulNjS7NsCjFF3K1taFmqHK8XE9jzwrcB1BqGWFEAJ6inEQlAMwHOp5p6OVJvNQF3hWpEnC1samZpbzLC2kibq5ruJmR9QZcmmy3mVJUZaEQcBK094WRYEfKFhulmomQKSF7S3mM6qqtPIsz3NaUYuljr57nkccx9bh6Ha7NuIXBAGPHz8mDEPiOGZjYwOBYDFd4HkOQegjZUGSLnn8+BGdbhcphbqPoiReLjk8fEIQXCaOlyxXCd/97nfo9/uMx2N6PRUZXC3nDLotNod9picHbIw2uXT9CvfvP+Dg5IjJbMb+k0d0Oh263R5ZsuJoNgOhsswnJ8daVqpxVjCoFqvFisViQVkULOcLfuLTn2bv8RN2LlxgPp9zdHTE3/pbf4uPfOQjvPHGG7RaLW7fvkWn0+XgYB8pYXf3ImWp2KmWqznj8Ql5nvH7v/81sizTkDxBu92iLAr6/T6+73N0dES73WY2mynufW1k5Vluacpzzdw4Gg1r2IdQ9PggSJKMIAwoigyBJB5/jN975yHdzbt86MNqPu62KnbarCMH1tbkWev07L/fRwq9p9PxXuL/vUxdCaxyyZtjydd/r2R2+AJXL20qxj6TRQeGwwGT4xNKVzKZ7bMx6nF/+oQ3x9d4cQRd7/RVTBDJhG5M5uNUVMRG4c++Uck58lkLxFpOSm14VorNzlU0nDXRiMpiOIbMxwRRpYGv14XhoMhFDLRe2Ht4T2+qDvi9v2/x1C5H2YKvfPoTjCcn5HnCdDq1KBFfZ+0d1yHVNtJyscRxFfzz6OhI2RCN2/M8j8l4Qp4XKhsyGmpD3icIfFvjIYTD8fGJtZ0VwUpug/WO49i15LqubWytmmIr+TibzRiPx/Xltew1SYDlcslwOLTyrknDa2xgqGFTJtDTrO9ot9ssFou6a7nWF1EUWRa7/wHobeseGOam1fNJZAVlIRGYfSo8N0BQM/uY1Bg4FEWllVBJWUqEqDMbQii4xfHxsX1Ykyoy18tThfctC1UEmxclrh9QUnI8PqI3aPO5L3yKT3zqI8znM/b29jgZn3Dz5g2LMzMTQ72cnKPDI/7Lv/6f8ws//8v88r/yb/EX/vxf5HfeWVJUMPRy2l7FUeqSSk9lEJyU+7HHX3qrstFy7TKoYmnXoSoVTEFI7VxJZRK7nocf+Hiui+sqLLVwBJvDAdeu7HJh5wKDQR8pJceH+8TLGXlVsIhVpHaxXGjaUdVYpdNqKQhLqdJcmU5vdqIu3VCQJTG9fp+b16/pFLZgMBjQ7nRpt9u2yNEU+jiOQ+C4qgFbqaKCsf59Npsxny9YrVaNFF+E67psbW8RdSN6vZ5ivQlCbYQKsjQni3Mmx0dcvHCRL//Jf4XpdMJf+ff/rwy7Po7rkSQxw36PL1yo2OqZPgBK2KjovCrm9jyX3BVURWWhVIDKNjlOHVERDSYrHUkxRnjgezRZhPTkeioiIk9bl+dFTAws7H2yHKcjXVKo+WKzBtI8T02BKAA0pz/oWiKb+dFF5No4U99LHCGJgkAVv+t9HWOuC0DWyWhTZA+qAeBiuazzDDbDpoz0qlSOvOs65Jk6l4lEKSpTdYypM6ldhHXVfqoX+KkRPRWdkg2YmuPw2l7KN/9ffwmqCle4lIVSTK7r0m636XS6DAbbeN49cgpaUcTBxod5sXqdqizwXM+c1iq5ZuapqZfP+t0owVK6SByEA4us5O8/zrj04iX++C+8TLeTU8ZLSpmrrq5CIouCqiyQTkVJSZoXzJYxaVqRpQWTccZqVZCkGb5f0Wp3IeggqyGvvPxx4lVF1CrwAg+Bi+sEiKrCDWoWJlOkt7GxqbHAdfGvEC6j0QZSqgyfrCTCUWyCTTYnR0ChITqVVJE6z1M0lVJARYXnubieUj6udLSjqrIBAjUfjSEZuD7JMsX3XAqR4bkuVVmQZSmga/ykJG5E6xzHYT6bU5Qly6Wiob1y5QpFURCGIamDjdotFgvrtJycnNjfFRRDzdcTqfafTE4oy5LFYmEVrqupeicnE7a3txgORzx+/EgZ7MmKVhQxGAwJAp/lYkFVlYx6Q/zLLkfHqk5ld3uXvCh4+OABXhBSVJJPfOJTzOZztre3WC6X5LmC5Iahi+sIikoymY6JVwl37tzh4sVd8rzg3fv31QyTFYNBn6JIqaocz4P5YqEL9Icsl0um06kNOCFLjg73EcJhNpvS6XT45ne+yec+93leevllPN9na2eb3/7t32a0NeJn/+jP0O10Wc7mLOZT9vb2ePz4Ma+++ipFUbC395hlPCfTkApHVHTaIavVgl6vh+c5tFtd3Z1Z0u8rWNzGcESeFqzymNHGBqulKjItItXbKvBDJpMJYmDgrwIHl83NAYjKUoEuFnOyeMFGb5si3uFrf/9NPvrpY8rKISkrrvXM6jXQ5vVo91l2tPnsvTIO52UszpLs5zks5zkoeaVobN89kfy3v1bgVrfZvTAkS1ZkOpIMkBcFP3jtTdK8IstLKlAIDX9KVm7xo3Gr4Wyccii0vLZGuFVr4pRAO+uBtExf20U/jVx/wlp2qkx6WepO5xqZYbLqsirt3uZstmjc1vhVjfOq60ia12vqioaWPf1S3tfhUGeZZAWdmxEf/vBtZvMZZVnQ7/dYrRa8++67DAYDhsORjtx3cHyHVtgCAYvZggsXLlCWub2elJL9vSN8PyQMBa4bkOeF7jlTIaUKCpSlBEparZaCs+oAThiGFq65WKjzm+yv0cGrVcJqteLixYsEgctotImzZ4KIsFqtWC6XAGxvb1MUBePx2DoIJrBvnAS1hj2bUYnjmF6vx2QysfcD2KaoJmMym82IQp2RzvKnh/iM7QNnNE7/q8qKUkOnbKFQpR69htjUxp5JMTXxsHUEFJu6kdpAbBaKm63JUKU8Qp/9/QNGG0NGG0Nm8ykSSasdMhxdYefCtvUEm1g0hcvNkRXsbO2wWiX8+q/9Gh959eN86hOf4mtf+zougqUMWFUC4QsCKW0BIFJNEAMDM8WOURSBUI1mOu02w/5AeafCwQ8CnMAjz3KFt9f3X5YF/U6bPEmoyoLJZGKbHRWFTykr2pqCcHf3kmVj8TyPTjui3WoRRRHD0Yig0V1XCKHSbVGkzufUzAUKllCtvRMDNQgch42NkfLq9fj7vq852xWW0vd8KimJVyskqlje0VEWk54zRaGIgiRN2djcJGq1eOGFF9je2eHJ3j5f/PKX6A36/Hv/3r/HbDbjHyQVvxw9YOireyurUkE1DPxHqLoGQY0RtdHnytCcGoYLE10xGQ2B7zkEno/rrEsp4WBhVwZisyZorQg8WxW9n5Nx5iYVha/rqiZFlWxeQRjEn41+SGkyfLWDVZWlyiaYwZEVUqrmXefdnxkL20BKqHtxPU87y5UtdDMRKFAFfFJK3VtG0doWRYHnm7Wv65qs04Eu8FtX7XWNyzm6wWrq9YiWAK4PfLY//RkcJJ7j0W4p9qBXXnmZW7dvs729TRSGfOa/+RJxHNPpdvnn/6V/lX/w7/4FbrRSRWctVE2LGdd1EXPaXDBBDvWnIhioHcGDuOC/2YOf/ZlP8rlPXsThkKyQ2iETVJWLEKpYvigKSgl54bBYScYTyeMnM5ZzyWya4gcRfhDR7Q3Z3rnB5z73Ba7deIU0d7UBOcfxElw/IIrayuHRTl1VVgShgkaZjKeJZpnImEDXbuh9JCBcFdHKDdOY5xLo6JbQGauyKK3C80zWQUpLz5ilKb7v2v2CIGA8UdSMZZpTZoZdSsGRHJc1+d3pdKjKgsU81QXDOU8eP0Y4giiKGJ8cg6xot9saogOr1ZLxeMxgMGC1imm1IguDiuMEUJS5Ukp6vT5JEhMEPqvlgjxL8Vy1RtIsZTFP2BgNcR2YzyZcvLBD3O9ZJpjHjx5QVRWDwYAsy5hOp8RxzNHRMZ1ej3il+nwonLaii8yygnv33mV/f5/bt5+z/PVHx0cUecpg0LOOTpqmfOc736EoSipcbaR4zOczLl3aBaF6Ukkpabdb5LmCJW1vb+kI5oJ2S9hoYxD4TCYT9vb2+N3f/R2KSlIUJVevXuGf+qd+hbd+/COePJkwPjkhi1NWq5jFYkEYhvzgB98nCHzm8xmdbqR0pHZ6lGPjqOu1Oyzmc+vcCiFYLhb4fshyoRAOjx89tnrIMN5IWZFlOeVWCS7a2Cx48uQRw9EQx1EIhOFwqOG+HvPFghsXPs7v/MYfsHXpkI98UjmSGxH0fbNq6yBG05loruizAxv1aj+972mpcJ5de1pinOdkfP+w4vXXC377t3yEHOK6YyYnh6q+UUD1MQ0jryST6YJKeFRaTis563I0/QFb0Uf50TjiRl+yEWr51QgI1ff3AZ7cZHvXdjvvmNPnVQ5NJYGqoGzsWQdw6lGqEQPvlQM67cKd9XvjHt/HyTCzY5oWzEYpf+7P/POkqQpmH6/G9HotneG7rYIxjiAMI8qy0nNL9a9ynR5CSJrkBMJx2NgcISs4OTnCcQVCdDk8PLJIn3Zb0cPP53OrK5MksegSUw8npWQ2m1n7N8syy+B3+fJlDWucr9W0qUbGCgo1HA7t56aQ28Bg+/0+ZVnaOiwDbzXkG8YuD8PQFrUDFqaVJAm9Xs8SZ5yuqztv+0DF4MajkVKyWCzszQKWm7yOHqvFkhc11Zcpvst098TTzofZyrJEoIz4Is8tw4GZLnmWIVFNlba2tjg4OKAVRZRFwYP9PVqtFttbW6xWK46Oj5VHlyocbbfXUy3aK2mjX8NOj+lsxmQy4/h4wt/4r/4dLl7cZdjps0yWSEwGxGVra5tup4MEWp3ITh5j2E4mE4aDPu1WQJaq6F0UhLTbLXzXo9Pv0RkOGAwHRGFEpLMBjnDotNoEnr/GNW8wy16gupU3mxhap6FSjaySJLE1MsbB0ANtm7IkcUxZlURRC98L7OQ2mzG8FguF5XU8t+GUFcqIReJ4HmmhjEyhm4E5uqmjUp4eWaZ4oVVxaUCn26OQFTdv32L/+Ijt3Yv807/6PyVexezu7jIYDDSfs8fXJ11+bmuqMmhFSeEUdeEmit9fFOrZGvxB65lhWXf+BdPpVy3oqBVSlO8dDlkrbGv8XI+arVMb/2E2Q1N5GuulYAcZrXa7LprXz2HK0c0xzfJ0JJbG1tyaiSKZyFad3taRJe1YmMxAnuTg2JgYNiymjxHOehflZsbR/DSMVcKMZSNbcypWdvbW+LKpJi/1fX7ul36em9evsLW5STtq4/g+SMEqXlEUBfNV0sDPlmyMRkwufAI5+3qjYV4zNlZndUwWqK5zE/b5LVWwbgp5mEp+/YnPr/zK53j5+T6VnCCFr417n6KqcPV1yqJkucyYTBJWK4fVKuTdd6ccH6W4Xogf9khyh4G/xZVrH+f551+mN7hN1N4iQpIXJX4QUFYSx/WQqGxqpcc3CJVBV1YVnnHKq8rWfRVa2fi+jyMVBCfLMsIgQAqhOSUE4+NjWq3WWi2D4ziqW29ZEccHio2k00Fq5ZOmCUWWkiQpR0dHbG9vsVgscV2HKGwR+SFxvFKOQJaozyMle0wBpKHErdP/Cxutj6KId945BiRpmiFlaRmvHj16qOEFqjjRUET2+31FcuEoiGpR5GR5rMhLZElRZqSZanAYBB7f//4fcOHCBcIwJAgCy9JidFa/32d//4ktPH/w4F1m8wWXfMVvr2BoMa4rGA4HHBwcceXKFVqtiNdf/yGOA6ONkdWf8/mULMvodvq0Wi3a7RbLZQyV0Exfgl6vx2q1otNt29qJg4MDRiNFdeq6LsPhkHa7TVlAGEa2mH82m9HtdknTlF//tV9DSlWI/ZnP/gRvv/0WaRoDqrGX7/kIIQlDX2dKxgxHg7WGX8b4MUGp6XRq9f5qtSLPc+bzOd1unywtLKWmqedU+qii0FlFK9GkpCwzfL1vDe0Q9PsDkjhme2PIarnkQ7deZD6/wvd+95DuaI/nXkyIIthuw4WWwHX+sUTxex57hmn71N9SKv6JRSaZZTBJFSwSFHXt/+c/Tpgcd1DF1Bq+V6qGliqopnYuy5JHjw8oKqlp+ddrXR/Pvs4wusU78iqLllTZHfH03Zug2/s/3SlBu/ZcZwXQzg62nSXRraSXpz9rfrtOrfL0NRtZ/1Pn+iBvfJbB98f3+Lf/jX+DW7de4Pj4kCgKabU6COHjuh5hCCcnYwWbFAKorM16dHRkWZySZNXQdxVxvGBzc4tVPLesfVDT1z969MgiSIzxb+TUZDJhOp1auNNkMrEyuCxLdnd3bT2HgqwOlV3WoFM0wW7TiyOKIhvciKLIOhSGftpAs3zft/03hBBcvHiRxWLBaDRiOp1aW9IUhHu+zyqOCYKAk729Zxr3D+RoGKjR0dERi8VC47MEzb4C5kFMhqLJMmWcCoOdNUrBZAHMoOZ5TugHuhusUj4GgiUlNn3e63Ypi4LNjQ16vR77+0+4eOGiihAlKfPZnKoo9TVD5rMFmZ+xv3dg+YMX8wWPk0esFjFZliNw6LRatKMWn/zKJ1hlK5I4JmpFbIw26A/6OMKhKAsqIdne2eHy5csEQWAZVe6/e5d4qfB+DkKxgBQFnVYbNwwoXDQmLiDLVNMk3/cJvFA1DXSExbdWOtqNI8h0/UQzgpTnOWWuCrJ931dFvdornk6ndPpKUSVJAo4g6tSerKjEWtGP4ZKvqop2K0QgVO1HrmgQXU9BTgw+HwHdXle/V00prCEciiqurQ37FpVUxx2eHJOVBct4hRf49AYDev3+Gg4Q4KjqAlOrTOPVyvJbmwWQZQWOqFQPBLQhLVRvA2kauOk5KLVh6Ac+URQStSIF4WtO8lOyzQiRRSGoHK+xj7RT3ibr39Nifq+FhZbB2mEQ9W0oo6tisVxYSmlVz1MbyqCKwdVtGU5vk7XS1LQ6tS1pFMVLMK0WjbOBYwJiwkZPTUQbUAa6lvGmNsNkYmot0DDd5VnDepYSWt/vvHdiFJHnubz4wvP0uhFJsmQyPsb1Q2XUa8HZDFw4jsPGaMQf/5P/Av/xv/09/sjFDEeCYn/SboB2UD3PJwwD28m2qkpUquuU8nPg9/YE352EjDY7fP13/4B3fuixudGmv6EiPlFLNTaTUhXqx7FkMQ84Oow5OVnqAuk2QbCBGzp4gaCSLstU8rVv/AHf+f4dup0+V6/v8gu/8HNcvnwZKYSGMSknwDS3EgKqUjn+hZa9aZqClKrAOVfN3GazGWEY4Wm5bIoALSNKWZKlKZPxmPv373Px4q7OfCg5lGapLWrc33tMUZYMBgOmkwm+52pjVFIWOUHgkSYpx/MFVBBFIccnx3S7bSaTmWU9ybKMbrdro2cmYOL7Hu1OS3cEF7TaihP+0tZFBRWUyrgfDPoIx2G1XBInsc2q7O09UWxaeaYNaUizVEHCqrpreJom9Ht9TdPr2/ljntPQsM5mMx4/fqxrGlRvEj8I1D3mBccnR7RbbdrtFt1ehzt33qEspXqOdps0TXCEYHNzRJFlVFXB8dExq2XCpUuX2d7eIUkeMp3N8PyAXk9RarZaEWEUUFWRdXJMf5Qsy9jZ2VGQ1pkqJL18+TIPHz5kY2ODJEksZ3+eZ2RZzGs/+AOCMMD3VIDJdZQuPTw8JEljXNdhMOirTGlZMRwOOTg4sBhw00W40LrVkMGEYahJCBx8r7BslCarNhwOefLkEVmesL29bY0kIQTtTsv2AUJK5cRKSZpkeJ6PS4XvCFqdDlkc021fx3Nv891/9JiTxT02d2d89OMuw65gFMIoFITu2WL59N/N0IeRA0/9bBxnfk9KFcFPS8lhrGTISvsNKrAjODmpVEDLgcWi4sdvxkjZNFAlotIZelETj0gJaapsDANfNGNltpP4jtYb15BILncUNb29SyvrTS2fMehPR/9PjcipP8/OOZzlfKyPaJ2zPuuYtVFfy26IM69mXbnzExtr5316KyvJm8cPuXZ7m7/7G3+X+/fvc3J8TL/f56WXXqEo5vR6fWXDCo/VMsV1BZ6virFbUYsHDx5qStohrVaEc7+GX+d5xsnJEVDbuwZZkue5he2btbC3t2czB6Ze+Pj4GM/zuH79unXo5/M5k8lkjdL28ePH9Pt9Ox+EDkpfuXKF4+NjOp2OhZR2u10N2VSU3SZT0Wq1SBIFxzLNUqMooixLVquVdVDMfsbZVfa4ml+D0eg95kG9fSBHA7CCY3d3V0e5S8up22SWMhF54ym12+06MqaVo/lpBLphOBkNR/Q7XV0PMKM/GuGcuFAqI+PCzg6D/oBKKqel3+vz+Mlj5rM5gW4QNp/PFcd6mpClKQ8fPuHho0c8evgI3/fZ2Njg1u1bbG5ssr2xzc72BRUdbbfxPF+91MDHcesi9uazCY2xlWCZTExWY2trA4eSw4MDup0OeZbRH/R1U5oSoTMWJtpmO946QvUzEIL5fK5eLlBq6slUj6Pq/BtYjJ3nOqRJzMHBAZcuXVIF+XqSZ6mKiEdRpBwF0O3rS5Up0O/NKBHb7d1R7y+IIlrtli5GUrjqqsgtbjqOY1zHpdPtqAJx4ZJlKb4fIKUhCkg0jMRjejImSxKVcVos1Rg7Dn67zebmJu+8845yUoXHfuqyHRTWyS1KldV4+eWXuX//Pqv4juaoVt3d1yM6tYGsMhl1Aa7rqsiX7eCmt/NE5wKfyvMaGYf6OjVF66nsR/NkZwrEej8ToVHRaXM+BQerqqYS1FF13XDPUCR4noegpChVzZLjCKsdpXaMTEbBjJHqOn6KwcNkI03HdJ25qIxSbIysUqTgBb6OopdQ1dAqs78ExdYmTyud9zcAzhkuqrLk0ePHlHlKGPh0Oz28wqHV7uC6DllSd0cFkJXk/t1HjI+nvJ2OmN15wlevCfrR+jUrXQdTF6kalSd1Fkh9tijgbzzw2Hn+Y/zkR7YQsiR0IU+WLFYpaelxdKy6Y1cypyoL5atULrIa4rrbjDY80izX0MUCnJJcFogKCl1HlWRLFqs5YdulP9wgK0refO01+t0umxsKIul5PolWEobZx8BxTITZ933ba6IsS0Ld78I8exzHdDodK8dmM1VE7roud995x6bvF4sF8+XcptiNIjUZ0DDwbWHwu+8q2M5wOCQKW5R5qecuCNFmOByws7OlHYJ9fN8nTZMGB71HXqQcHCje+PlcOd6j0Yijo33KstIQqZiLFy9QVTXcwARO+gMVZHE9xwaC0lRBqVotZSj3eh2WyyW+73Hp8kWiMCJOYqVc44QwMt11FWPLKl7w+PFDut0X6A+6TGdzxuNjer0+Fy7sUJalVuIR/X6f6XTBxsYIw5DnuIpWeefCBVwHLl68yMH+EXleMJ3ObFBosn/AaDSgKAp2draI4xV+4FkuftOEMQxDnjx5Ysk4TMH30dGRxWL/+K0fI4AoalHIktViThqrjFJRFARRxPHJEa12ZFmpEFIfn1g8t3FKlZNWWIfjNBS6LCSj0YjxeGwNKxNMfOmll1mu5trxq9eZQGW+jB1wsH9oM1NCCHzlSTNfLHF9j8Oju7ieT1bkpEWX/T2P735jzEc/LXnueZetLZfQkVxoY7Mcw1Cs9dNpmrp5BbOsNvJPJwemKSwKuWbHprmWiUKd5WCvYO+xwqzf+XHG3Ts54+OS+C9UoHoX1vp1TabVjHh11B4KWXd+PitbAZJx/I7WdFeZpJKbfRgEjZPYTPT6cZpe6qntvVVVbew/zRHYcATWnIenz7Ke0W4+cfO3U2mV05+d/tx6g6dDV+rvsoI3TlL2V/eZvhVy7949fu/3vo6UkiAMuX3rewyHA/r9AVGkmNF832Nzc5MsU/CmoiyJwpCqFNy795AwCKxuVDBkWC5joijUjn2x1vBOCMFyuSQMQx4+fEiv17MZQs9T1zK1G4UOChnmKhP8mEwmtNtt1aVcrz1QOtbIgaIoCIJAyavViul0ymAwsMyigA3yGJvdMMqanh9RFNleHgbeZbqGSynxfB8cQXKKTfK87ZkdDXMDhlkE0JzDns4y5DaLYVhHDIMR1GkdI0gM1ZbJaGRZRqfTUYZ0q81iOmNjNOLq5ctkeY54R0/MShJ4PqE+ZjGbc7C3z/7+PmEY8GCxsM2cFouF8iazHOF4fPTVj/JHv/pH+chHPsJoNCKKFM1YEIQUpYIfFWWOwa5XVaGNM1V0XJQlrqNwvUI4yNLgSxWVp3nprushcdi9eg1ZqkKnNE0Rnku33UJq/nrHUQXjIO04yrYa43anY50Qk4EwkQkjvI3jRlXSbkVW6Vy/ft2+B+kI60ws9cQxk6xIFRuLySQ0I1PSqetnqqrCDwI832e5WtpGXsohEORlwXQ2wxEOZV5aBQQ1VrzX6eEKh3YYUaYZW8MNVrM5m5ub+H5AKSu2d3YatTcOdxYe2yNVo+O4Lj+aufz2fpvoj/8cWW/Fo9f+j1z0S4qCmnHqnM3UNZjorHAcG903W9ORXN+0YDxTcp6KoJwVUDnzvnRsSdQ0snWtgBKanufjuVKx/riOhq7VvUdU7Yva321QSSPVOjEQGtU1/IzC97UmMPWz5kVhM0GCU7JbCO2kmKidtPoMVJ3AOre2isgJq8FMtKse2Q+yGRXW7w2JfJ/5fEG/t43nhkgEaZwwPlnw4MFDRdXrwGw259/63/47jCdj4jTmpIy498Ocz152+PiWpONJBErglmVFlqviVhXJFhRSUEr18+sHHg/Y5voL1wgCn8VyTpEXSNlgAyMGqSAiAtOTRHW+RTp0Oj18L1TMOqLEcUuoHFwRUunIreN5JGlCGPr8wi/9In7YYhUvuXPnDqN+j3b0EsfLhXq3vs/h0SEnxyd0uh1cx1H9RIocx3GZzxWBg5Hdvu+RrGIWi6UywHtdjo8OVS+GrMDzAmLduTvPc0YbIyuH+j0VHRsMeiRxQtQKGQ6GTEIfWZY4KFrOoijY2tygLEpWywVCuLohl8Px8RF+oKLpy+VKOzEGcywoCgWNjSIV1Vd0mlLdV7xke3ubJEmZTieW5lFKye7uRRvB72j5GUVKDi0WS118rpxJz/NptVxttLfwPQ9Pw7iyLGW5VEXXnU7HGgeTqSoWz7LMNo19/vlblBWsVjGPHj0iCHzy3EXKiCgKmU4XPHjwgKpSTo2iDlaNtbJU1UVcvXId1/XY29tnMpkyHI0YbWwym02RslIQXyqGw4GV36ZoU8HDcl3XWDPSlGVpGSId16HMcpAlQni4jsB1HGbTKVmeEWkItOe5uj6iXGuYZphlOp0OBwcHbG9vY7pAG8fW6PbpdIojXIpCyQATMQ2CgMlkYhELeZ5TjFSNxsJZ8R+M/gt7PQBaTaPVihKM4XxaRBs59CMpkXOJswDPFwRBI2Bwtq3+nrH55vmz7OmdpYQ8rx0UhvqLT+t/AN36Z/oXk/e+kNkXyTp/bX0fZhPacT+J3yYrF3SCC7w1GdH2BFe6MAgaWQ30SEqJ1MJYPGWYv8dYWIFt3ICmI7Ee4HvvrZm7OOeK8vysxNnXPhXkO3WtcSL54fEBJ/FdPN+1tiyYDtslb//4jpI/OiCnGKeU0V4WdQNc11FNLTc3N5UR/vkEPFXrWhaKkj4MW2TZgpOTE5ulNQH3+Xxu4fCG7dOQUyiyigmj0ahm8dS1t6bPkQkuu65rswxmyB48eMCFCxesU2CgdqZuy9QnV1VFGIbWPu73+wwGA548UbBQQzBhMhuqLqxNr9dTsqGqKHQQudnY9L22D+BoFHiuqxgkXJdW1CJJUhLNhGQanbTbbUtZmyQpQsMOlssV7VabPMtZLlekSWYhUIZmNQwjppMZx/uHOBLSOCFZxbzxxhsUGqpTFAVvvvGmzZYYSsM0S/E8ldoPgoDt7W0+9OKHGA6HXLp0iXanx9bmtory5xmOELZIMi1SEDpVKZWQDYJANTirBK5wEVWFF/gNCjeF5TZOQBgGWBYjZaVhZoArBFG7owowdbikkip27Xl1g8Mm3MxE5Uw/AsMWpSZPDWsxzWzQL73dbvPw0SMuX7qE47pUSM0wU9MHW/x1oSap+TtNU8bjMUmaIJEEocqabGxs4DoupSwZ9Af0ej0uXrxIWajmbVWpwu5pkhIvY4vrOzw85MGDBypKt1zhVArjuJwt+Pv/3W+yubmhSATCkLDdYjqZgMGhIriTt/j0KMaRkuPM4bfnO9BxcMMOX/6pP8J//V//Grvie3ZRnL/VUZSqKlX2wxG48mnj20TqoZbBT0eTmmJOnv7oGbaGqJTaCbIBGUf/rt6br7t5l/qdq6ihazMUNmOBqlvJ80L5D7JSdHieqyBPYj0GpUZE1JkG4yho59q188/kTZRyUqwiqgeK0dKmHkMibYbJ83xrECgq3vNS4h/c2Xh7GSIrh+UyYzZNeOP1r/P2j9/h/v37HB0eMp1NlYHzz62gq2TX/v4hkpIoDLgw2ubW8zf51E/8BP/5f/qf0s2O+NQW9DwYhBWtKgMB46Ti7bnLo+gWn/7JL/PWW2/xlV/+Cl/4/OeYnZzw+g+/z+/+zj8iyVekeYYfRqoLeVXpzAgWDiqEJJcZQkgWSUE76iomniJXDaukh5QK3lOUClbjCZfdixdxheCHr7+GQHLj2jW+/73v4QC+53IyHtNqtVnFK2bTGd1uhyRNWS6XyEqS5ZmVJabRXVVWlhgiSWIePLjP7Vu3iIKAVhSxXMR0ux0Ni1IFwCfjMb7vUUoVaavKitlsSqChllEQkKYxnU6X7e1tppMJaZaxubGh2KnKikpWeJ5Dq91C4lvIaKfTtg5BmiR4vlJL8/mUTqdtI2oGl+z7Lp32BlJj2sMwIE4SK9tMMEYIQbvV5sHDBwrWWpYgKpIkBiRJGtMf9FUtnecpVja9Hh4/eaIzNzmep1ipBoO+DsYo/PV4POH45IROt08cxyRJTL/fs1l731fNCtNUQZpGGwNOjo+oZEWRZ7RbSvmfjMd0O8qBK7SDELVagOp3FAQ+woEkCdnc3GRrc4vxeEyRF0zGE+I4ZjabISuHbrfHcDBk0O+TJCmHhwcq6+k75EXG1vamhsm59Hp9hANpntPtdplNZ8RJTBzHNvBRlkrmz+czKilpRS3u3b2nu5DnpGlWk4gUBf3BgNlsQVFWyErqbvKeNsiV4ysrqGRVy2wBaZR9QCnw3pvq9CBJYT1N8I+znVf3+mwMn6qXZ//ZL7deY6i207rIwnuzPebpEwK3y0b7NqtiyHN9h1Ek13pIPeVtWaNe/zxPGJ/xeX3k+gCfCt89dcxTf52OOjVTO6c0xPkOzllXEYwTyXf37zPN38V3XMqqZgYFQZlXCCGZz1U9RVlVeK5r2StVLY3QsrqkLDMmkwVPnhwihCD5RApdmM/n/D///f+Q527dpNNpc+XqJUajgc0Wt9ttC8tUAYlAM9EpNFCv16sbhOr6Kqj1h3HWTRDFFHc3x2UwGNg2EyY4nCYJrj6fyUgYGRlGEbPZzNp/BorV1igcQ+IwHA41wYQifEKTFKnA0LMtqmeHTkmXIpP4nmJZGvY3SJMCSofx+ITFQhX9bm5uWt7f1WqF54e24HgmFkqIFaWONrXxnRalrMiykjfuv6V6PAQ+o16Xo+IIz3NZzVfIQFkqZVVxeDyxeLJOp0On1+fScMRwNGBjY8TFCxfp9XuEQQgoo2k6nZFVBUUuLUeySm11EBpq4OturyYF7Liu6tmhJ6XjNOh9JThyneFIH6yMVTTVqJQUmoK1shHzOhptHA4DxzIRZIVwrJCUCvMp63SlYfVSC6NuXoXr0B8NefPNN7n77j1uXL/OlctXlDMUoeFauaqnqHLiNAEE+/v7xLHqfGtgXK7j4uKSrlImcqKimp6PF3o2+1G5utOuo3nxPYnfd2m1QubzOR/60Itcu3aFo6MjDvf2OX5yQJmnfOKjH+Fof4+XX3yBy5cvUwJH0wmB4ylhUChYV161mCSCYSD5jcMRnqvSh2Ve4AjBT//Rn2f/b7zOjl8ipWObkhmHzIghE0O3qUI18AojXIfaEcIFqsZR5tdGoZr1Qtb3Ek15+L5rb93or6oSzw/0+UsMZS1IbaTre9bZAddVkRNZqe+bPWgU45Tqy5HpuhdPF+tLCwUS1plR/op2OwTEGq5noI1mLZjHcl0HRzjkZY6D0P019FOJWmWpbIiiPa27v58em7NS8GdvNp0uJccnE/7Vf+1fpypK8jQnz3KKqiIvC43dr9TasRlGwR/75S8zmU751V/9Z3nuuefo9bqEYcSl3Ytkac5f/+u/xuuvv4Evc3qRT+B7VK02L3/4Vf73/+L/gsuXL1PkhZ1Dw8Flbty6SprFfOvb34L5AkOYYApdheMThL6G+SS4BMpQbYV4jgcIPF8X46U5UhMeeJoK3HU9ep0uJ4cHdDodFS12BD98/YcsZnNe+fCHCbyAiW6oWeU5ZZbjIdgcjPB91xqIeZ4z6AyZzWdkaUzY6TCbT3Edh3YrZH/viS3YzdKM4Who6bnzPKdIU5ZzZQyqrLLH9sYW9+/fV8GewAMq8jRhOVf9epJ4ydFhbmGeAA4Bjqyo8pw8SRTLnq7bi6JIFcXmOaPRiL1HjyhS3fNHeojKwXdCAi+iFYXcvnWTvCiYzef4oU9RluRZTr/VR+DoYFLOrRs3ePT4oYpIutCKfF0AKcnipSLHCLp4TkiRK+KAdrvF/v5jWtEQWZUsFlN6vT7L5VLTBWccHu6xWvVUBDPNLIQoTRJGw5EtQl8uF1zc3cFxJEHoUZQ5rhtSIej0hqyWK965e58kUbVw3V6HJIl1jVBIlimWxMAPifwVsUiYzeZ2vkkpqTJJHC9YzuaEOgPhOg6tMLKB8SzPOD4e47kuYRQpmvA8Jwg99h7vKZIVqepYXEfV+eVFzhPxBCSUpWr8WJYleVEh9fo2OrAsS6bTFSUVJQriaBgiQenCqhSg5RMLgVM5umN9uW4ENyK1tQRvRPNP/f0/6q2LcjIqYPFsh4hlHdw5f1vvyiwE5NWcvfl3CdwuSf48O50R13rQMnwvwv7XcBRUMMlkPGqH4/3DQKfv7uykUW34rzsmjeud/r0RHDx1RONssjFnmudRmmWSSr538JBxeleRFgjXZr5kaVgcJY7QwRfXRTiustOMD1RVyFKjO7QtWAG5hvnb1r0S7j/c48EjJatdp2Bzq8f29jatVosvf/nLXLhwwZI3qMyyb2Gp5l4MusRAPU2GNo5jhBAWNn9ycsLly5fhR/XIDkcjsjzH1QQNga6rNaQZpujbODzW1jOZGx14NwQPpobPQLSE61KBIhqpSlaLhaoRu3DhvaYI8AEcjeFAVcMvFgsmkyl/8AffJ9aV577v89JLL/Hcc8+xs7OD53laSKqXb2BUhsFCwabaqihRR9uklNy/f5/Dw0OKPMP3hE3/+J5P+Nr/m3m2IApDfvln/rjmy+/YynkFJVLRf3O+LM95/PgxJycnfOwTH7eNSczWhCMBFo5kvjORKZMWNuliUF0uZamTF6LO5RZFoTIWOrqLUGlq0B2whXEWKuvNmuJu13XXk5A6W2I6S1rOaVnTBZtnaKYCr127xoMHD0AIHj9+xNHhkSq+E8JmgQzuuCgK2znywoULtuDfjIPjqFbzy8WSVqtFEAT2eBXFS2wErCxLPK/O8mSZynJduXKF52/dRmhYjecqWIjl7pewtbXFV3/2Z7n3zl3uvP02rhBIx+HXHo8QngC/DdroNanFn/7yT/O/+/X/ggvuPVyd1baN7Jrj2PjfNsaTEtdZF4sqs/C0YB85OW6RUXjaETVp59MC+awsMO8jqoWqcwoClRspEAhH6AiwcjIqqehkTbOywA/sfBBCWMddVqpxnyhLpEprEK9WdLodW2RphkJQR8PMnaapcr5VxsT0INFZFp298Dwf0JSqotnTQ2VafN8nz3IL5VJzto5cfeAMhtUjen6XBXK15NFJoXqLoCJUJaV9F66nukMbHRRFEf/r/83/kni1wvfV/C3Kgtl0zCc+8VEEghdfeJ77Dx6SxAoO2u/32L4wVI5bVXK4v4+jmd1WyyWdTpc0S3n11VfZ3NzkW9/6Jg8ePlTXRRl5js5wVmWO53pkmYrohkFIVVa02y0dMasIo0B3UC7xfRcpVePSG9evE6+WeK5DnqWs4pjJZMxLL73EyckxVZEjy5IkXqmivyzjZDwmzzN6va5VYqp4N8PTfWiyLMVzXR08MZ2WVS8Eg8t1XU/XTERIWepuzi5tDXkVQhD4ipobWSEcLCzW4PNFGOq6MbXWTUDD3FOapooFTsMDlGOsAkEf/vCHyfKMB/fvs7f3hOeee07LeJeydEmSSilWz8NzfLq9nuqkWyn66jhZ6SLqgueeu6FYCI8ONDW2Wq+mhmV/ts+N67dYHi6QlWoUemn3EtPZFBAEQcTJyVh1Bl4s2Nzc5OMf/4SCO52oBpE7O9ukq5WifM9zNjc22L20S6fTZmNziOf5HB0dU1YFeV6SxCmtVosnj/coKwWfLSvVDaLdbtPr90niRDt7BY+fPOHkaGwpd+M4ZjQcsVgqJ9f3A6pS0Ygb0pCqqljFMY7r2oaaYGBSynhCKrmhoJnSRlWLstRZSWkzr6YwOc1y0qy0JAOKflXXa1aKeKKpq9DyRlYCIZSOjv5SA2MuNcGGduSbgY6zCqGt1Dr13dOw1///b+lfTFQmYwHB/6OGmpyXnbB6HWn1e/Pz99uUw7Fgb/E9kuIW8/wqL40cOoocbU0An84wSJqxt/fIcJyzPT366zpGnvcVrN/Yqd/PvI3TKXr9cJWEJ6uKHx0/ZF7eV/AeuT6+zbYKFh1ifpbV2kVUVr5S0NCGLTcYdTj2PVJKWu2IP/YLP8329raq7/AchoO+rvHIrJ1aFAUbGxv2+qBqfJXt5FlIumFxMzrU2DzGbrx8+fJaENDzPV780IeIosjKfFUWoGpvDfzTkP2YOo6yLC2DaRzHNuth5MdyuaRZ95YkidVvNsPxDNszOxqr1Yrt7W3m8zm7u7t0u112d3fxfV8ZqL6vFbm/5hU5julA6+H7ClsWhIFWwo6FCUkpeeGF57l9+xZlmet29Y6GagiCtwLIwA8Cnn/+eWvYQi3QVHqrsNd3XZfNzU0AJuMx29vbmtVBO0CeioJXGm/mCFSk2EBBVLtbCxMpq0pF+YSmLJOqbsN4fia6FLVaBFFoC3H6/b7lHZZS4miHwrBxpElCJSWhfnFmARjP1kRRjdBt/rMOiqg5kQeDAf2+ytFWeUGv27P0aabNvDkO4Pr163aiG+/VTEBjzBqnz+C8Tc+QPM8tN7Mq3svs4jANxAyG2EHBbjxPGVul1N1ANa9zNOjzz/3pP8Xf/pt/Sy2oLKOQFZluGrhYLBgMBly7dlVhqKOQj37xj/GNv/OX+PQoURVfnC0bjS9oHChDddtMykJDqemDKikJnQphCqSN0HuvFLO1q00krv7/qU2u140og12ztmkDQFYV6PdVFgVCz5M8LxBCG/OlgtYpaEJlayXKSjUsa3c6ViicpYzTNLONe5RBoK5rUsiVDh6ZAriyrCgajjISXEfXYQnqmpHGsPyhN3u7Aun6FH5EtdDdo/W53cCh1+viBx5ZlvKn//Sf4j/o/UecFGNarYjJyTHL5dIWphrGu7JUc3w8nuK5gjCAxWKK71W8/dY+m5sbTKcKirW5uUkUqYLZ46ND+v2+wtFGAUWekSWxHgMsvNGsK9cNMNTP5pplaRiOVJ8YkJgeNVJKRqMBjgNFmXN4dKCVk2Rza4OyyplMx7hSKmaidoSkYhUvabcjwnDAarXAceDChR1LNa3qDtp2bY/HY3xfkV+YNa4wvUohdToqzR7HK13b4FKUOQiVEewPuty6dYvd3YucnBxz9+5djo6O7BwLw5DlcmFlnZFRphmVuabB7k+nUxvsiFqBggptbzAY9qhkiR+4xMmKoiy0rAI3UOQXWZ4TRhFlkpMVKUWZU6GcoHi6oqpKtrd3uHPnDqb7r+nxErVaBIGP6wqm04migww8Hj9+wmq1IozatFptlsslnU6HOE4VPXgQIYsSR0o8IfA1Q8v46JDxbMnB4aGq+yhyrly5jJSC2TwGKZnN5iyWMWGrQ5blBH6AWuoOWV5SxErpl7nK0iFckrxgGaeqy3oQcXgyBqFgq6AaLTaNpUwTjhg6aputdww9tYI1OtrhNVhw4Sia5CTPKLSuNfMWCUVZAa7KXoq6D1a9XFWvGXDsp1KaqHmDzl6o4JCKDqssiNHj7ysWpOmh9I8lXd73Gqe3/yGvd9b2h72eEDBJ3maRPUFWn+BSN+BSp5l9b2YNqMfSZhZMZOi0Rf+H8D5OH9KQ6ac+OPXZGdc+V/cKshLuznLujN8iKY9tPXElK5DrwdnaEcb+/ZQzJxXNuamLaAZgw1DZtCkpURTy87/wFVqtFovFgiTO6LaV3bVYqAaXpjbD6CBDmauC8nWGxWQfjGw00CaTXbh48SKj0cgSJZhtMBhoAqW57ZlhHJbxeGwDD6c7kRv7ErBlD4bUwtiBpnO4atwpyDPVLsK2UHif7ZkdjS9+8YtEUWSjHQbPD+olZLrIxCx+4ylKmWuj1CMMfWtASSQmwF+WhXUcXNe1EeNC86Kbf/q9q2Z2GirSdCoUy5Eyus2kGAwGuK7LcrlkqYsfm0a8EsKNlGzjxUm5LmjCwLfHSiktJavneQyHQ+uBzudzikoZz8aTNec11LPmeTzXJdT3AbUhbMa4SQ9o7q/Z9+L0wjDfm3fgaz74drvNxsYGVaWKC6fTKavVvm4AuGuzHabRHrB2TfNuAGsgxHFsaTG73S6dTrum3dT7m4kahAGF9tRn8zlTzSl9584dFvM5g16fD73wAtvbW3z1535WUcEhKJUFu5bZUew0MbKq+MkvfJ6/83f+DtneXT63rWh2DYtHc6ukwqoaxXr6Xdt3ztlxFZsVsRmP90hr66/qPSyp4JmbcRQ8XXvhOi4FumCtkqxWMVJWtlitLCs838fVzfKEUAXcni5oLdGQOh2JSdOMSkqbfXQdV0cqFSVfmig2Is/3bfah0IX+JioPEs/3VFF6riOY2gGXOoXteq4eP2GDB6aO6PyBetZNK0Pl5YMocT2B66j6o9Gww//8z/4ZqrJkFS/55Cc/infHg0LBLX/81ls681Ywny+YzRS3/2q11JzosVYeEYEfIGXGxQsXicIAf3ODIi8UKQWSzY0R89mco8NDikLRdM+mU8LA12gGFaRQmT+hKW4lrhvqFHWhi+ikln0FWVYTJ4DKcvX7PSaTMQjBYrmg1YrodLqEYcDGhoLmLKYTBoM+Ukp6vR5xrDD2YRgyGPSsIs3zjI0N1elWUWYrh2c0GmHqvowcHg4Hem1nmj1Osr29paExc1WjUVV0u12ee+4my+WCR48ecvXqVZ5//nlef/11vv/979teFEmSotE8lGXJ3t6epUx0NdbX0C/2ej0ODw957rnnmC9mPH78yDIWNTOy7VYXgUPUigjbiqmlMnLVdciyBOE6OJ6DEC5lVrFczJlPF3zoQy/x9ttvs1opTvrlUlE5Xrq4y8nJMUmSsFwubdZmOp1RyTmDgWLUenDymDRJ6fa6rJZLZFkoGtjplFu3bnNyfILv+8xWCePxlLzI6XS63L33QFF/Oy4f//jHkbLi29/+Dr4fIIRLkiwJwxZFkZLnholRkY1kGtYECjJpnDa00jeRlKoRJILagKq002/ecW2gK4dAVrXAKg1xhpRUeu4aZjx1Se1EyDqUYg5Hw05M5l99VBuziqa+ETGWqljdUGRbeOsZGYp/Ukb/6eucd433u5/3+v6sTM3p6/zjPps5f14uuD/5OsvsRSbpDle70A845UAAFo7W7E2FUhTGAfnD3NOZkT9OqU/zwVkeiVj/2XR+9MdZJXi8WPHu7Jhx+kDph0ZWDFQgrIkAMcgM9fs626B9N46DaLwrBZtULReOj8aKcKStHPbxyQxvJyCKWkRBG9fxLHSq1WrZYK/jOBZh0sxKmH415p5NQMZAMo3MvHfvHk+ePOHixYvWXizLkjfffNMiUMw6sg1VtTNjHIkwDC0bVrPe2dht5jkNIZHpEh4EAY7r0u12LZzrWbZndjTa7bZ9Mabw+9KlS7YhyN7eHnEcc+3aNQ4ODlgsFmxvb9Fqt0BIyqqwU8j1VLZDWscEpKwoy1w7H4I8y8nSbM3JqGcWdkJUVaUL5hSdapom1guM49iyAzhCqGZ1uiASIUhMBsYT1gAwjoTJCJjoj0BQ5iolpZD80mYfzL0Yx2e0MQI9YcxkMopBmhoBfU+m6DbPVa8Qoa9nHKGmwXZacNm6EDMypyI8ymhVOFohhGViMc+2XMbcuXOHvb09S1m5XC4tlzMophHjoCyXSwuTMh3bDSxub29PZ6zqvilmgYzHYxUVTWL29va5fv0aV69epdVqqQY1aIN3FfP2nR+TrFZMJifISlLIiiRLLdsBYLMnZZ5z6+ZzfPEnv8Bf++uH7ERTbvcdze6zNlMwvRKkrGwRqYrenBLuNESdbKT1n1Ia0gpe60I8teYE53zx1HsrylLPBeX4msyEdCptdNRRhixLNYzNwFYEkoqyKHA95USY1Lu577IsSeJERT610miOqed5Vn4rFiUD18KmlKMoAqkw3CY6r/EOjWh9aeub8izT12nWvZynUN5va75QSRAq7GKnHbIxGrC5tcmdOz/iZ3/2Z/A8h92LWxRvFWaAcR3odTu6hsLl4oUdhBDcvXuPzc0NHj58wGw2JV4tuXz5MlkW8+67d3EcBRXKdPbGsH0YCkIjyA3Tku/5ao7JSju16v0137WnWaiKAi3UlfPsaxiSWqttTOPAosht3wbPc+l2O4Ck02mTJ6va2ZlNNQtRqqFtFVVZUjx5k0Uu8DYu43ous9lCOaRVpbjgXZVh9DyVPj88OgAgCDzanYg0zYhaIUI4dDpdLl68YOV/r9/n+OiIJ0+eWJajn/zJn+T69et87WtfYzqdsrm5YZW+4zj0eqrjdqfTYTKZkOc5URTR7Xbp9/tcvHhRNZ1zPYRnaLI9Hj54zM2bEVJWhIGSZa7nE0pUT6I8t4aw4wbIqiJexSyWcxYLRdkryopHjx6zu3uJH/7wh0ynMxaLBbu7F2i1Q5arBZsbm4xGI9544018P8DzIuIkYzKZayYvh52dHR4/fqyhVypDVuGQv3WHfr/P8XjMbLmiKEvVxPB4jKyg2+3x+c9/gel0wtd//2ssFkuQAtf1aLc7HBycWF2oik9NJkFn7KuKslyXR6chSs25ZvdZMxyhBpc2oI1PrTgVmLEpXKHzvuY/m7ltXE/KU0LUZHb1dkY6uJJy7evTgbMPAod6P0P/g57jgx73fhCu857nf8gsiRCCipyD5WvMs00W2YcJPI+tSLIRQdvTjkVz7Bq/GZihnQD/fdyqPP3HqZMKaDSrauhp42BISgnLQnIcp7x1cod5eojjGoRHncFrZjHMZ3C2Y9e0oVRmX9XKmSCrkWEq+CosE3ye5YRhjyQuCQIV9V8sFpaGNtPF1YaQw9xTHMd0u6oX2XK5VDXKupi71+tZuJWxqXzftw1FTcG4eSaTDS7L0joSoKDDpucOKFveZFSMDdfv922DQVPHYTqaGyfEMFgJINbMd8+6PbOjoZRgaRuLmBdjBv369esaA3tEHMdUVUWcJMTJylLXdrvdhpItcYTCIpdlabG7aZriu8rI8l2XUkKsDU3zoi9fusTJeMy7775Lv9+32N7t7S3yPGO1WllvbG9vT0UqgwC34bkZXLAy1CSeI0AqmMj9R49Ik4TNjQ1SHRlSGOeC+XyG6h4Z4Xm+dSBMZF91na2YL5drzpmhFNOzgiLL8QOfIlPnNxh7xxU6+umuTf6mU3F6QZhrmO+aPw0srLlQzOa6LtevXycIQ2V4aCMxLwri1cpSFzYdKhMNaxYQhWHIxsYGZVkopiPtfHiepxqXRRHTyRRXOFy+uIuLw+T4hAlqEWxubdBub7H/ZI9vfvMbCKn45TeGIzZ3tqm082mcLrMAyixDSOgP+vzorbf4/bf+gBdHiS2QX9+Eff6qUkb56TSsPPXTHOULyXBxyOHGtcYOzb1ORXpO69Vn2MqiQAaBctTKQuPoVaM313EtAYHnehbKYFgosixH6ALiqlKMQkp2S52VWFeApoDTGBhKuSuHtCwUK5ctfquU8RDoeqoiL2zhXOArNiyFy1esa2WpGq0JG0mte2jUbZnMX88wOs0Uu5CUeU4hfP7cv/Sn+N73vs1Pf+mn2NnewnM9Ip1WXq0WTCfH9pVUVcViPiNNM+J4BQiOj4+IohZHhxOW8xXT6YRVvKTVjlT/m15Pv1aHeKXW8mw6Zf9gn+FgSBiF5FlKvFqyXK4QOkMLJcJRMEwl64StdTGenOM4+J6nAwsgUdkZx1U1MGmacPXqc7TaChoUeIoEYbGY6W61kjhe4rqK7c5rZBrn85mtnVM1FTBgxUYAs17X8quHYcjBwYFdx0la6SxVgaMLwNM0Ic1Sut2u7pMR0u8PuXbtGu12m9dee51vf/tbiploMCBNleydzWa88MILfOUrX+Eb3/iG6mzdcWymNcsy1X/Hda3SzLKMo6Mjut0u4/FYyzyX8Vj10SgOTiiKgu9//3XbpA8UI8rla1dxXJeNzQ22dy7g+wqT3et3KYqcJ08ecv/+u8xnM/r9HhujERsbm/zSL922sLhWK6IqU7761Z9hMBixvbXDb/zG3+PevfscH4+ZzhQEwfd8vvjFzytayuJbtNtL8kpx2B+Nn1BVj7h8+TKe5/HjO3dJ84y8KJnMFghcWq0l/+Vf+3Vm8wlVmVOptu7qpzxSdrrTJGmo57DKOrj1OmoEQBxNJGIOUZ+bfKq6xnlmt2zWpckzSqzPObAZ5lrPPDwVv1nfzvvuGf2CZ804/Pe1nXe997vue33/Txp+pa4Jq+yI+/nv0o+ukpZX2Vv5+I5ktw1bbcWQedruN/Q2tZGvQnfrqKZGEMmcg/qjp975WkbjjJ2aOtZEwLRvuyokD+Yl4yRmkjwgKcdUMm84GeuOap25q4lTzD6Orn009lXT3hLCNMjVjS0bDoLpym2bTjoOjgN5EROEbYRw2dnZsXPHIGlMIz7Tj8ZASQ2rk7ETjRNgHBRTH2Eot6FGnJhte3vb2uiGFtcgkMxzmyCt+c7YQ0273tyvCbKbTIuFaml9bs77LNszOxrmpTR/GmiPKU4zRmkQBApzH0VUUtFdnpwc43muTbe0og6e59vBXiwWzOdzRQcWteh3e3S7HTzfJ9FdCkFlQeYLxV61tbVJEIR6AFUHxTRNLP7XcL9LKRWmrFSRxqIoSYNUp6ZyBDlhEBCGAVEY8tz1q4CkzFPGx8cqSqknRpXnzCdjWlGbvm6CskwS3n33AVeuXlOY5DgmCANrYASBmjhpmpGlGXmSUhQ589mMw4MDDg72ePmll7j1wgtUVakieVrRVFVpMzeg1rNi8REWQy9leWaUxEBv6voAabOfjqPYodrtFqtVTFWVmpGqtKlEQzmpxlBdtywrW9TezLasYoU7dhxsui/LGk6f6xCFEUkcKzaSosAPAgQqGkC7xWA04E/8yp/gcP+AJ0+esLmzhXAEUaRqesqqxHFc0iQhripmkymTkzFxmvKRVz/CnR//mHGa0HUEUjRYp6zsU8KqkpWtrRENbdmUfQKV4Jf6+T2dkasRAY7dWyLOqiF/+n3wtLw1m7kfz/UQjmsZnSrt1Lmui+d7ik4YSZKkdo2V2nFS86TRmND3dM1A3WNEmmwTSlmoAni1Roq8RKIKvYR2ViSq3iKMlNGbpKmuY9JwjEo1CTRCp0I1QCp1qKfIa2G43iv2Dxk1RPBTP/k5BoMOX/rS55EyY2/vAVQq4vL48QM831MZBp0mLoqC+/fvI2XFahVbfKoynPsKCiQrLl26RBQFdLuK4SkIQl1j4ZJlCRcu7DAen+D7ruqs7XnsXrzI/QcPNLGAQ2C6kouaUtr3HQ3bq6xDKhyBJzwdpQpwhOoVg6xo64Zvps7N3q+OUqks4YQwDPGEICtL1Uizkly/cYPy4JBWFOGHLkkcs99/HlkWDByH5XLJarVECAWBM3I18ENcR2XUWq2Q2aywTZ5AK1lHMBmPKfIcz/coipzBQEXC4lVsm42+8847OsMZsLOzw1tvvaX6QwyHJElqs6EnJ2MyTUcex7EtWPR9X0f3YDTa4vj4QMlSRylbRzgslzGe75HlOVeuX+crX/kKw42RghoVap6kWYrrOlzcucjzt15QcyFJ2dnZ4eREyfUrl2+Q5zn7+3tUVcZrr71OnjvkGbz00qscHk5I04rnB1u4nsdkPOZ3v/4N3nrrLdqtFos4Zdl4pqoqeXJ4rIqvS5XtV+9VwY3iNEdWyrl0BDqzqlnmpKqxqmHH2omwQQIluyxVdQM9Is0O66nc+nvZNAgaLr6Q2tFoOCVrGYanM7510qKZ0mjGwN9ra2aRT+95tkywgbX1u1jb5+wEgtZ5zUs9i9g563m08G46c+bexNp7kI3rnN3WzsqA8y597j2xdq332pq6b+1zIUBUTJN7zNOH9KMrtINt7s97PFlCN5DstKHnN3o6rV1QyzYahCg0dZuoB6zpcJyO3pmf8vSH9Zmahy5SBeXbX8GTxSEn8TsU1coa0o7jKjZGOyvVeWpIlNB6Dpv1VIEPY8/WxD+n7VzD0tbtdOj1+wqpE7W4fGWX/7D7gEmlqL93doaKcMN3EPi2X5mx3wy01TCxqcakStaZhqtNIh4TVAVYLpcAFmpqoZN68zSblYFcmaC2cSaMw2DsNWO7me/MuZtF6KYuBWqnJs9z2q0WnqsabZsm0O+3PbOjYQSflNLeiLm5pmAcDAb2bxVV89gYRQwGG5RFQafTt83VTP2BSUVfvHhRDYLrauGsIDWDrU0C3wcNNUiSFa1WpJsEFpRlvnZfxsEwA2XSPpXMaLW6luarKks6vS6ezDk+OuBguYSqpCxyjo8O2Rht8Pvf+BbL1Yqf/vJPs7m5SRAGDKKIxWLKZDUhbLVJc8lGr0ee5IRBl16vhR945EWBIxzSrMQRvoKGuRGdfodktSTwA9phwIO7b/PmD75LvJrz6ic/RVmkeJ6PkKaxnMbwFTrT0UgjygoqbRI3U4T2J2bxuGvpdVMTkyQxs5kqHoqiCMdR+HAjQM1PtTgUr3cpHebzOVmW2YY0CkMYQV7aa5tUmy1oL0suX71MEISYPhGKWlhBdEJUSs4NA0Y72zi6wZcrXJuVEsJhns2YTqaUVcX27iWmkylf/iM/ww9ef5MH+7/PK32JrDTNqZF3WvhVAkrNzlRV1XpYTqwr6aY83KiW7MsKKdbhanp1YHIDTwWq5NqPU2e2R0GlaHtdR9PNSYnnqXkqheqRIRyB1JHyPFMRZ1O4G8canmcdSnU+6VQ4hl1IX1q4rmJscgXCMTVDdQ8XQ+Mn9fyL2m0cxyWOtWB3HMuTX0lsI7Y0y/BcD8f1FGwKBfuph0JY3XJucfwZw9R0ot35hI2bA2bjAzqdFmEQEIQt3dfghOViqmj/ZEP16TnseT6djqIINDKq0w3oDyIbJDGCVxn5qjbB1DVVVckrr7zM4eEhO5tbTKdTNR5CEOqML2jDUAg8rTROKy4/CEDLqTzP8fT7NgQLvV6Pfq9HVZakWUqaZapnRRCoGg0/IEsyVouYKHRYLRdsbm7zyU9+Gi8IefnDH+PB/fs83n+XpEhp97pEQch8MlXF3FmusrKBD6jeK7PpHKSg2+tQlRVRFOoeCC5lqaJs0+mEMitJVkuiKCJJU1pRRCeKcFyP1X5MslJF0sdHJ1RVxZPHe6pjt+NyeDimqiqyXNUpqKyzoKzmOMJBIhTFa9TiytVrPNk/4uD4iFa7xWq+oKxKUm3Um6zmlWs3ePmVV4miDscHY3XPwmUxm3N4eMhyuWB7Z4f5bM6DBw/Ic8lkPGE4HPLuvXdZ6EL1LM95tLfH4eGhYrJyXQ27WiCBXKhVbuSalBI5nut5KhrrXMuQsgSh6kOKUloXu9CF/kKI2lAzRrSQlKZQumHYNZFNldRrXEdbm/SaZpm8f7B8PfvQXGzijBOsZUqgrqGwmfVTp3/WaP1Z1rJoSt3mrrUztA6leS+jW9jzyKasPfNIceavajep7dTTDpI49axnKI8z7+f9xufp+zqbVuO8JzeO6TqUuoYOaQiyzBmv7jKN30UIj8gbErg9DlcX6QQB2y0HR8BWZB5TR/jNedY8BambjTc+a8jg9cdrfl4/QyVVa6+TRM2paSZZ5hV5sWSWnbDMDiirlEoWeugdBdltsMiVmgreyty1bISvGB79ukA8CJScF1qv+n7AYDCg1Wpx+fJlRqM+u5e2LVPUzs6OJcxJ4hjnxwJUGyyKrML3W8iy0uQpddYkz3PbsNIwQRkUT5Zlto7WBCwM1Mmw8pk11+3WTILdbtcymiKELRo3ASqzGfu3WdRtHCoTFAZscN44OybLYaD/5lwm0+Jo2/1Ztmd2NAwjjWEmOl2b0CwcNkUnTUpWHxCRWPMYzY03F0TzvMIR+CJg6PvK8dADmue5LXi0ToTGr5kBM8VwnufZan/R6ZAkCbYzeb+vIryFIGz3OJnMaUURk/GMrIR7Dx5z6/nnmU5n/O7XvsalS5d48cUXbV+CxWLBVtgizVJKPALXJU5iqlgZGQpKlbNYzG1Rped5OG0PPI8gUKwFv/jLf5zjo0N++/d+l6jb59Lly1TVksFgAJXqnVDJ2oloFvMpga+EsE33NZwNRyi8onIS1sfZ8wK6nYAgaLO/v8+TJwdsbW2xXKruu6vVijBUC6+qKsUuUlUUlSqyb05iIQRlUeC5wk5WC9/SirlZt5EmKWma6tSgT1WVGBao/mBAr9+3TmiuHRoVVXXww4Dhxgaepwy2xeaSx4+f8Gf+zJ/h//bvHuHNfswLfUlR6hhTUwFLqeBBZUlRFuA3BeF6EZwRhxXQEg1NDtopOSX8G800no65sb7v2qaOS7MMr0EMoBwEQ2OrGFmKPFdRc80cYQSRWaNlUVlDRErFlGbqMGpFafCq9b0IYeaOUVCqSLPVauvoRUKhMfBqvek56Aj8QPUAKauKjm46pArcFfRrzSBaG6FzNjN4zciiNr7GicPtWzeRMiP0PMqiIIrU3Lh8+RLvvvsuQgj6/T7OiQNV3QDTdFVtyoaF5gJX0L/SGv/dblcZm3G8RkEdRapYXHXHHjxFUV3DGrEFzvVYa8azRsrbyMja8U+5fv06LV383JFdKlQWN8tyVY8WRhweHHPx4i5JHLNYruj1Ci5dvsLjvX1WJydcuXKF0Vaf7373OySrmEzmOK5Hmua6pqAgSTMCP8RQ6kZRm6LIKTJF3hCGHkWu4D3j8VQzkcHJ5FBlw2RFu9VmuVyQFxVJmlMUOVHUAqmaBSqcsHIijPwxvSiElielbWqoSCce7x/R6/XY2trh1q0XkVJyHBxz7+49nZFZ0Wq3CPyA7//gDR4+2iPwA+VIFDmeo6Jt8Sq2807V1eQgdbGxo4rhVVZPOQJ5JfU9lWt6SQKlOMtwg/Vf1p3iul+NXnPNFb8WoT9nDZxaJ6frMJ6G9DzD6c78/P0dgzrD3ijUxkTonz7Hs8Ain37+hmNwZoriPZyBc7bTMJq168uz9zvvHOfWXzQzFOc6GGc4Cmdd8xzj/Lxrn3ff5+135ucCJAWr/JBF+oRJcofA7fDA7dIPr3LX9XFFiOO4DIL67gahpOc3b7fhDNL87Mw7BGB/CblOtk0zSVamVEjmyUOyckWcn4DWM2ZzNVW2sSWbVLGutm0MzKlZY+t5Ib6vaqGiKGJ7e4uNjQ1GoxFRFDAYDrhx44ZlaxoOh8TxCiFUsGixWFjoP6Dpyeu1YOxgY+eZzIKpjTA1vM16NSGEhVEZGWgg+KYI28CnDMTU1Abmeb7ukmpnwwTSjVPTZGM1jFPtdhuooeRN29LAq8y1DLzLMHhJKW1zwWeFAD6zoxFFkc1eGEPVOBUmi2Aw+01cv0m9nK4haKaHzEtobsYDs/UHjeMHg4EtWDHXNFSqJt1klJalVtVRSk83MDGDG0QRwmkTtPts7uxCJbly/Sbj42OyLCVPU7YuZOxeuUav16WsJEgH1wE3bHE0nuD6IUHks4pjvEACDsL1SZMYBARB23ZoFI7HYhWrrI3v4wYhngMX2x1+bjDim9/6JmHUYnd3FxNuV1F506myHlOzkBDSRimEUIXthlaNCsqipNvt6GJST3WejSKQihHGQM3yrOLocEwYhTx5fGANsvlspWAlrTYISVEV9n01cYJpmiLL3PZMabVa9v2Z1KCByZnF57quhQgtFwu63S7HR0e4rstgMCCMIoIoUjS3mWJeaHU7ZGmKQLBcLJGy4vbtWziOy7/85/8C/5f/8/+JH033+blLCZ5T94NQJq/GoheqTmhtmawnNNYyGoGoCOMZcWeEfSnakDDH2p9nrL3zHY/G5SvVMTgIQktf6wW+ZnSTmr63sDTBigazZpFwHIckySxkqNnfRep7loAQaiSMkmmaBaYw0/M9u+azLNWCLVO1U35ge3aEYYTjuCSp6j/heT65njeZzmqcpXqaMKr30s02aiaUoT7auMho2EeIElEpykKpWZTiOObGjRtPsY2YmiIz50w0XAjVy2GxWFj2uqYhZbKhRoEYXvGdCzukK9VQzfQGMmvSsEbVUaLCCnej/Gxhb1HaqNVqtSKKIt2d1WE+X1hl0e52iOOENE2ZTGYUeclkMuFHP/ox29sjwrDNbL7gr/zlv8wnPvkpnn/hQ/zozTe4cfsGX/3qH+U3/97fI1nFqJYnKviQVylCQJysWK0SVksln0zvH1PAn+cFSZpQlSVhGJEkqZatqsi9qiRpllIUFWHUoiorjo4V05IxzIui1EF+JSuUDnF0NlqvSmPUa4W7t3fC228/pCgqPN0babVc6TlasVxmqp7k0b6aLqJRZOuImnxD1gWcSucop0LBFF1MbySJXMtWFpq1TZ98ff425pW59lnbeTrvLKPvvRyI/7FsxlAyjIgfxNA4a/snUcPQDLo1A5mwXq94+rvm9qw4dID3Lk55/+c67/u1+f0Mm9HP7zdHn76OJvwpFqTFkkWq1pfnhLhOwJG/ReSrIOPDOWvCO3R7uM7Z7dOLKiYrl+vXQpDkE+LiWN0rkOt9pDRUs+oarmtqUbFz0Bjqxng3RvZwOKTb7bKxscGlS5c4OTmh0+nw0ksvEUWqnrQoCobDIVmWEYYBaZaQxAmu55JmS4LQZTI9ot1qA461tcwxWZZphMX6uBpo02KxsBCnZr8Kg7YxWY35fG4zGVVV0Wq1LFrE9IkzuszUuBnkjoFhmfesniW0chdq2dcMghl9ZNYzYHWfOVezBteQCJkMjJlPH2ROfiDoVBMyZTw3UxEPWKVrvK8m7/DpF2KM/tMC1nhfk8nkqciXGThjxJqo+WmDovn36YEwaSeT/RDCocSlQuJ4Ia4jaAch3f5Q2zaFvW5ZVmRZajnpJ5Njti9sE7U6FCX4fkQlwXE8wGtEiYV94VJIStQ5XUeo4isUhKw/dPnc5z5Pu922sK8mvlBIGrCOpuKSawveTOCyLAncgMl8onHIB5aNKwxDFvPEwjUUHEE5Bo5wWSV1p/DZbM50+qauCQgRXm2smUmoPHCPStQT3MwPM6HNOPT7/TVPWiDJ00QlBCpJv9uj1+tZI8ULVJ+GLFWQC89zdWM+dU3F96wckc9+9if4hV/8Rf7yX/2r/LfvpvxPbgqEKLW9La3BU1bq3PUmWI+9rzsHngu7iz3eaWtH47TgbkZ1pHgPfdP0RNarFkA9o+epDJ7jOlSVodTLEZWKif//2PuzYGuW7DwM+zJr3vPeZ/zHO/XtboDdAAiAIAFQAghQNhSi6fCDImiaYdkSrUc/+sF+cNjPDskvDr8gFH6RzRAtSrJNhUbbJAFQIMwGGkCj+3b3Hf/xjHusuSrTDytXVtY++/z3b6BpORis6Nv/OWfXrsrKymF9a33rW6Um5TdoIAgD1CCAEEcRUQoDnyRt29bcraPBcQtsEMY8JRebl55EGIWmrgPV16irkpK72xZRHBuQoUw+VmSqBSsMhgmU6V/VKgvkDi1F/bC72P/QaV+H6bLVFj/9jW9gt11jNh2RGlmlEIYxGtVgs9nYOgCj0cheTgpKGt5sNgiCAJeXVL11OBzaDYQX6tVqhdFoZJ0nRVFYwMWqHHVVYZgMkGUZ0jTtiTFQYr5HTyg4P4aSfakOBQFIVhLabqkAKkWIgOPjUwjhQWuBKIqxXC6xTVPESYzbmxVevXqN+XyB9XqL8/OHWG/M/VWL7/7Jn+D3v/Vt/Nqv/ir+5V/7Nfz2P/wtPHj0CD/x9T+Hf/w7v4OLV6+RZxnlc0gKmZdlBQ2Bpm5RVTVFPkHPw3lDyni56BGlGXvdPGmaxggULAEzFuuKgQbRCBpTxV5rqjatTJ0W9mKTL4nrIbF8N+UJqaK0ewMLGLRmXW4URfDI0UKAtNHK1kNisKHb1lB2GYASWKLlVRhfLFMtDUCXFI7QWr1VDhZw2KA7tBnv/+1tNuwfl/H9tsehNrIja78994GOt/XA3/e9/WjC3ajE2/XbofMO0T72IyDdGOracz8o7CIy/TYfXgPd67vXehPYeNPxpmd0P9tnkfQvIu2cUEpZ52ara7RthbLZAnl3Dde2ASQkvG7jdPZEjQYsVtIDfYJlZ8khGAT9hGvf940DZozxeILBYGAKPifWg//hhx9iNBphPp/bQs4cZc6yDIPBAFmWQkoSjsnzHHVRIMu3xhaoEAQ+JlOqxD0cjow9wwWUpQUMTJcVQliHGr8bViRM0xTj8bhXR4yjAa6BLiUVH+boQZIkUIYtwiCCC+ex8EtqRIb4+9aRaGwC7t80Ta0tzE5IPljAx+3j29tbU1eqA0asNMr7Hv+NhX44oPD+Vz5447gEfgSgsdvtbAe5E8L9nZEmDz4ApiAVF6Iiw27/wd2H4JAQy3zxdXlCSCmtgXBoYroe9n0vBhsP7mBXWqFVgBYd4oMmviDV+jBd5AG+LyD8EH7UYjid4+TBuanqHKGuqWpuqxSk8KG1UewxtCZWlxEC8AyFwjNeNiqCQi98OhnTHueEA4UA6qYFVFdUhUFf0zTQUAgC3ypjseRmURSo0UDAQxQliKMEWgO+1yDwIxwfU/gsDEOsVisAmiQuixRFSQn4gR8YTwHRwPK8gQy83iRy65gEXhce7LyKndoDexbd0KbQGjKMEEf0vvcTlOjdAZHvQyiNKieAxLxdjqBUZQ3fD/A//Jt/A9//4Q/x27/zW/j+OseHY175aPWr6waqJcPKPdwIxr4JLAAsvAbP6xxVmPQnB1kn5nv3kwb219++T78DaHVVIoxjqiatKOGK9PGp4q7UsMpRTM9pmwZp21AdCEPbo0hVQ4pWWncSl7q7pRYaUkj4xqPP/M22bVGUJVTbwpPm3RpvTN02gJCIYiLvlmUJPwzg+T5aU2uiMhVE7zcD7gn94MCfBc3dF5cZ/uZPfojBIEKRp4iCCNoTyLMS22xrnzkz4hEc5VNa4/b21vJRh8OhVRuKosiCb97UeB1j2pTWGsvl0s7VqqqQR5Sv8tFHP8BsRgUrOfmPQ9D8Pnnta5oGRUHVsYuisJsDg/HVao04vqIiSAZE5nlO7wEanvSx2exwevoATdPg4uISaZbhmz/9TVxdXCLPS3zlgw9xfXWFYrvFv/qv/jVsdltICPzKr8T4/NNP8Xf/g7+LzXaNvMohPQlAwJM+zs7OMR4f4dNPP8Uuy63EMaCtkAUXamxbUxBSO0VETT/zzz2jxxRn5cP1EPeTlOngdUMCBoCY3Ah3bXcGiYJRZOKxI2DzGtx2UK2GzhikyAb9ZAJ79C+DKLeduGvo/aiG39tGQn4cxyGj8430mbc4XCPpR/nO237eGzIH9m699723acfbRorcZ9u/rtuWLwc63eeuA2L/b/seYfee9/He3/S8d9p8oH0u6DgE3Mjwd36X7r20pQfxws4UH2aSkFOl7TlvhCDw0LaUIyE9ieFgYFQ7fUwmE8xmU4xGI4xGpIrHRZan05n9fGKo1E3TWsU6oly7yc5clDTCbrfBaDTCeDwytCGJOCGp7DzPTF5jZvIfWlSlwm5Lke11s8ZoOCJbFhJFUVpjvygKm+PnDlgBYnQwIOA1Ls9zK1e7n8DNxj7Xt2LwwH3qjhd2kLMDnyt7w5kfHJlngMH1Pna7nbWRWD2Wr9O2re1vou4WptaSslEMpl+50XveC9+msCbwIwAN3jA5DOMiff6ZN2j+275kGBv6HDZiYOHWZmAVK6YyMK1nP8x8X6jTBTnud9wJzUDDUiMUXUe1VEVWtQ2i0NSEgHS804b/5zPdx4MMjEyoJMPJ90npp65bCE8YLXw3N4XABnHvuRq0MU4ahaIorSHOBktVVVSkDOQ9XK/XlopUVRWSQYzjYxosm80GSZLg/PwceZZDNcBquUKeFeiUpZShdFAeTJpR2z1PIow8DIZTnJ4emUq5BGB837PePuUspjypaGJQZIITmgDYdy1EV+0c6Ba9oiigmxahZwoWao3SyLg1LSVHN3VjElMDNChRFqR81EJBS20oOyGatraFrf723/7buLi6wj/6/Lv4cJJT7ECTZ59rItRV9eV0JnQwYORrPFl9jk9OvkaF4+z4YsPlAMgQzoWAvc8PbRraqDkE8H2SQa0bo/LDY1dqBEZa1nN4n5y75PmeXbyCIKDE99YtfKnNmHQ4rFzMyHhRGkOh8c04pErDAlVFvNA4pvoL/C4SZzFt6hqtaq1/70t9jvsn6e4H/nFVaJyfniEKA0gBjAYDSOGhbYDab40sb+fcoMJE3SJMhR6pyOhkMrEc1bIscXl5af/GXqPhcAitSdDi4uICHNGl5PsYUlC//+zP/gy+b4oBbrdbNI1C29CYLKsSraFHdUl32tJ1KOrHYXFA+BJto3F9dWvnSdM0SIYJ0ixFnpcAJF6+fIXNeosszbHNc+RlhXefPsFf/fV/Be8+fYr/5nd+G//eb/4mfvFXfw2/9Jf/MnzfR1G8wIvnr/DVD7+Ozz7/DJVq4PkU+dputthsC7y+WOLTz14QVUp144XXcik9VG2fbqJNpJCMe3q+zpDh/t9/vc64F/rOOi0EAC0gocwXefI4RuP+GOrZZhqOkFL/ENK2yyAi5zt9w6F3rz8lJnhbasF/m8d9FKI3GfF/FpB0/3fvArk3GfZ/2jbcZzvcd13X3jkEHrrvUfK/+z1lo3ba7Pt9oAHcpdS9KaLxJqDRO9f52z6wvS9aRB+67XcjNKTQ6DoAlVJWJY6L9sZxjMViYak/p6fHGA4H2O22mM1mOD4+xtnZmfXKc00d9zmSJMGLFy96aqacUC2EwHZLkevj42Nychnvuud5mM/n8DwP4/HY2DmVXc/LssRkMrE5CIPBwARBJTwvgOeFaFtlBDCoF+u6NLYHUe6TJLHO1cIobQK0RvAzTafTXsVstzQER1p4/Wd7jHOfea9y0xCiKLLFTfl9cfTDfad8TwYpbBdwsb7ZbGZVrlw7bL1e27HFBf3YEcwCKexMjuPYRmBcO+/Ljh+JOrWvnsKG437NBz7HBRjckUVR4OrqqofuXITNUYy2bZFm5DUcGqOAz2XExy/Pvef+5HIpOm7n8WdQtPG3LXm5ozBAHJHcpKCLQmuH58luNhjtcmNwKi+ARBdG9APPiY4oSKkhhUZT12jKHBqkgqNAFJ7tdofdLsV2s7VFB9uWisuFUYgsz1HVFeI4RhRFGCQDjMZUJXg0GlIfCYFBkhjJX4nAD9BUyiavcoJREIak8x/AGpLSk/CkRLOHulmWk7yBRh4Xni3iJqBtUcCmrnBzdYWqqjAejwlcxAmKIjcef5JCjaLItKeBlB58T2KblYYWRwnHRZFDaVNvxPNNGJG80lJI5EWOZDRAVmYmZEjgjahVAQJP4N/6N/7H+Hf+3f8d0uYlRj7ARlBVNSjLGtKr9owRrovKv/UjGoDGuV/ii7pAHSboXKD97+Mg4GDjpous8DX3D140BkPS6vY88hz4QWCSc7s8KF6AOfnMa1u0qkWe5fYcz/fh+R58+NZz292LvMqtAfREezLXdxKVO5AiEBnaHJ8/GA0ArdFUlMNRl+Vb22XiUBdwtMVBIJe3Of57f/Ev2N81BHZpCk8E8D2TmxVGNAcGAyyXS6Dt1oKXL19iMBhYju1gMCA1JAhMJxMEfoCqKCGFQBxG8KWHoqywWq5xdXWJ7W5nN1Vp8qXKioBLukuR5VS9vSxrVAW9q7ZpKRpjpFk9z4OAyamCkSkVPr0EKVErjevbW2gNUusSAmEQoFYttKBke60VojjE2fkZnr94iV2aY/n9H+Kjj76PyWiIx+fnaJsaeZ7ioy9e4j/7L/9rjIYjfPzDH+IH3/8BYJwTZVujMXQoAQIRjRP50oqleOk/rShvwYIEIWwUQWvK14GRUdYQkM4I0NBQei8a4QwQBQWY9URBQWjyrGrtQBIBp0r9nhMJfSQjhClWib3pCeHqNdhz7Q10X5e+Z3/hz36IO4p1LsDaP3nvlAO/3wFD/Zs5X+v6gz5yDUhYiW/XOLWT0N63W6145XJ9LYeNWM4Jcz3t94OHvTsbjNmBTFdRr3vMu156biUDe44c88cEGPp9oM3eJmUHjsn4Mk9snP1C0PztngfOzxyl4HPvPisb6Ic+O2y0iXs+N+00AgZ253H2GY5ISOPEg5mnrFQkPcp54DpLLgASQtgIgx/4mIzHSAaxzXvgyO9gMMBiMUcYRhACmM3mvfphTVNht9tSfbQgsAZ/EAQ4Pj7Gbrcj5oVx/k2nU1xdXSGKIgyHQ6u45BrAo9EIURRZepIQwq7pLFrEe9Z4PHYSoQdIdzmk8CFArA4usiqEB+gWQRwBxtjf7XZ23UriGG3TIDBVvj2mLTnzjO2rzWZjowFxHNv6F/x+3NxiBh1VVWG73Vq7iUEqP0fTNLY0BNm9JNRh5xuAMAiQG6pvU9ckUw8gDEJcr69RVRVm0xmBMtlnCbVGHKer9QaysRLKu6urGgICRU7UMI7euLU33nS8NdDgkAmXImew4Rb2AGA5XxxZ4EHbNMSh5vwA/h5TDFwOf5yQdKIWsA/uhhMZxboUGzey4l6TQ1J8DReI2N/bGhKg6IMmfjGDp0YRv86TlLzI4ag8zyEk0UZYTo3zJ8IwxGa7Rts2Fq0T0IpRFyXSTWqMk8wmqJp3CwgyLKGBJAkxHAwwmUyQZjvkeWqR6Wg0slQWKSVgqhAnUWwBlC8l/Fgijuk1U/+SZ6VpGvD6w3kxVdvayeJGUzjEx8iY6QaU46Dhez4VyVMase9ju1ohCUNkaYqrqjKF3yhkyQYeyyDvdjtEUQjPlxbNZ1lGuQqBj7Zpke6oCuXNzY0Fl7Qw1bi5ocRxz/dQ5AX8IEBVVhDQiJMEf+nnfg6/+wcb/PrJDsKoy7RKY5fm8IPQ3epxX0mrLqqhIQUwS69wFT69LyBBG5G+C0L2Qc2b7tW2LcoiR2QUlbSmiFsQRWiqikCaZqBAGw5FJgTqykSZggC1qs0YoyJy3YZttmDVL/ql2xaVmeNUO4M98ApaeB3IMLSsKCFpWF70irzY864dimncNQEPHXxGqwGx2eLs9BjL2xWyjOothFGIYSKx2SwRhgFm0xnqpiHZwjgG0s5jN53OsFzeIs8LzGZT3N7eoq5q5GmGtiGVJfbM5VmGLC+gtYfb21ui5dU1aqOAEsUxtllqNj9tw/nQGhoSGh5UowAQfZIkIQXZsRbpGSUmY+8oEyGpWkCpFkrR+ynrAkq3CKMQpfFYKWjcrG6RFSmyIocyEdlqtcP1+odd/726hf/H36U+bKgKvDZOA61V91qEBlRj11D6m+ze3L5R7/yt964N8JB733FfpjVX7WUc89KAHj4FezOy1d1MPDxSnK+6MN6xP002Uu+r1khW/Wvrtxijbz5EZ8WbK3e2Yt/I5cKq3afdHHV/7zkJ4HilsQe+XANd3HV83OfdltKh80ADYPBFA5VBCgMJoF8ErTeGnOa6gE6j77gETLTA2cPB17GGrxOJctYPrfteXXL+8T6vAGFALERHBdIalODbSb4L0ZfplYZKzffv+vxu3mdn3DOTgmujqB5YpX7z7tCihXCLzHUgSQgBTwbWySeM4cgOH6EF4HVFk5UBHRCGAKHNniWlFVwRAvB9iTAM4BtatJQSR0dHePjwHCenc5ydnWIymWIwSCzDxPd8hFEIz9T4KsvK2HACm80WL148x5MnT1CWGeqajH2mDLE9MR6PUZYlxuMxtluSm2ZnGNB54FmFiQ30zWZja+2w3ZOmqbUrOS+DjfOrqyuMx+OeKiAnWvu+j+12a73xVVUhGAdom5L22ZZsHCkCTCfDHkunrmuyY9IUHO227010eRecP+Lawcye4bHDdharPHGqADN4pJS2rxiQhEFkx4aUElVZO2u4QGbqEEEp6/yFEDQNtICqKclTQvaUqUajEXaFkfnOO+AmhEDohdikG0u7Ukoh9EPEYdxT1Pqy462BBlWkFZbutNvtbBVYBg1MkynL0sqRstFfVRWKosDp6SmGw6H1hrphM6UU1us1pEH9zEMLw7CH2Fnn11Ue4POBTt6WAU0X+udQZucBkVIiMGEo8ux7aPhFVxXWm40tDc/3iOPY5klwJj4PSKKr+IhiMly2261t5263Q13W0K1CNIgxnk3Md3yzkHbF2diLwh6QxWKKtjXVrM3iDpAXv6OxKePxJmpUGAaGU92i2xB8W9tAgAoZBmFgJxM0kBY76xVXSuHVq5fwgwCj4Qh1U9tkos1mg6osMRyNjMIVRSAGgwFePH+O7XaLs7Mz/OAHP8D5+RmkJ3BxSUDt+YtnEELg5uYGabozFDNgOp1iuVwiz3PqSy8wid5Vjw7EG10YBhiPx4be5VvO/WQ8QlW3+At/8Rfxe1/9Gv6Tv/Ob+KlkBaEUHgw1UBZYr4E7hgXt2L2x7/g8IQWQtHuTyzWWeM9xvvdmd+hdvyT/f1VTFXuSSvbQgIzQIAwhG6p/IFquYaMgFYHhuqot3W8wNDJ2mrzUDCA5mdtjzq1ZKJuGEn2lRwn3HM2Svo84iiE8D03Toq4bxHEEP/BJfahVRh2rvWvU3OkC19t6/8Ge6rJsMBtNcXN1BV8q7HY7TKdTaA0EgQ+tgcVsgdurW6zWaxRVibKu0Bw1gE+L+qeffoayqtA2DT755FO7QaimtQo6AOzGuN5soZSwVdi1AeiC1xut7BxUmvJclFYmwdg3VLW29/r3jTC6rrKGlzJzVCttPVnsrRSgtkgh8A//0T+2hkXdsie2Lxtu7mDXRL73fsTX/HLHeHpbys8dSuuB77oG8aHrumbw25n2B856szP43t/vGMYHvcp/ykP0n809Dhmr+17l/c/5X7fNPXDiGsQHPj90vUN/cwGAtZQ10+Rco59omKwI1M30jgrkshzoYDp19znPI2YnuCwJvo5SXUSLAAh95kmfImYmsV+A6irQ5xoareN4ZqOQIusCsh9x6XWJPPgeqH+6n91IilYKFAEx0qUH3j0LRHhm3+ZnsdeA7o8DCFMMlJ5NQyPwuBCxsn3CeXnSIIzRaGijAsfHx5jP51TNvm3w5OljaOOwHAyHaNsG8/kCZVkgTTfWluNIQtu2WKdrzOdzZFlmcyRGo5F5Ny1msxnG47Gl77iiPVpTQjLToKIosqCBn5WVzDhHVyllE6J5z2Jq0WQy6SUzMyjhaMFsNrMgwAU7lL9BkQW3sLQAUBkH8ng8xmq1sjQppqhz1GEymWC9XveUS/lgRxXnyLqJ1S9fvsR0OrWgCkAvqZptGu4vvoZVmqpqFFWJJBlACGETt/cPfmccFCCQ6Vsq2W63s+DOZRVxv/M967q2uYsuqOIEez7PnadvOt4aaLDSUZZl2G63WK1WFvVw8oirtetywLizWPYryzIbbeBzeWKdnZ1Ba41AExVJK43dZmvD9EopXFxcWNCgtcZsNrOfcdiubVus12vEcWxfHi9i7mKttUbbNPBMqIu99nVdI8szI+GoyFsAQ19QLXzPQxKHODlamASpLoOfvCqweQ2u2UkFqthzA3ieb1+wLzyisFS1KdQnoLWHPMsICJhFiBKfS0RxbMNwxMMu4HseIATyPEeek0KONt4QjkZpTeHTytQU2e22RuGLw5lbKKVwc3ODq6srADByszOUZUERkbYhJLzdoWlqQysJISFRFAWePfsCz5+/wB/8we/jZ37mZ3B5dQnflxiNRri4uMDGALgkSRDHRPVizvp8PsNsNqXEsMUxAj+woVMAFhQ1TWWpQ7Z6tk+KP7fLJfHk1xu8//67+PX/wd/C3/0P/x6ePXuOJ0OF33gCnInCKN8AdpN0KAJAt/e4wOFYpXjetlA8ydxNzB5f5rU/9Dm1oQMoRl3KLAbsNWzbFp4fQJhIAvWbMBV+BaRR5RIs8wljIEuBum5RlDlg5lYYdVK1DMhFSOLoTKMLoxh+GEKAEumblsB2ENDYpdBqdTAxjJ+yAxuGirDfuf0usGdpaDy/yfHh0SnSzQ6BB/z0N38aSilcXl7i2bNn2G63GCZjBEGEqq6gAGx2WzRTAhp1XeP73/+ECmjKrgKs++4Z1Hueh6rRgAjQqBp1Q3MfoMXeKiKJruilm09B0SVho0D0btjw6z+oMIauUlRyk5OrpZTkfeQzhfH4yYA8rACquiJjySQj8HV6o+mAh5mGVf93d/11DT/3OoeOtwUjbNDfd3yZUfymY/+7b9Om+6g7d43iN3/vy4/7z98HBa5Rex94cNv3JjBy6Of9PIw3/dyLPmjOMeB7koHO79T9Ttc+2bsujy8AFpC4EQ3Pkz0qqPsu+buqRe8abLDxHAyDToqaI+PEPmhtlKb7j5/RrLfi0JgAupWr38fSfXeCIzAAPIqokI0h7ZwnZ4FxkgaxjTwwYNmPyvQjKC18n/Y1zyOVRzZox6MBjo+PEUcR3n33XTx4+BCT8RitanG0mKNVzBiI4XkSvk91HbJsa5+xbmrESYDN9tYanp0jh7z4DFZYhpuVn5hdwBQhNko5ysB2HxunWZYhDEOriMnMkKZpMBwOUVWVaW9kn5PvIYSwzsTtdosgCGxRO3Y+szoSKw5ut/ScbB8OTR01VnWyOcBVBU9Km3DOdCc29lkFlOtauLkU7rzi8cw2JovzAMDR0ZGlgbnzgucNt4efgecSA72iLMkuNJFvBnu8p7gOdK21bavWgPS7tjE9Nk1T2y/8/njusJgKK1659K44ji0bhfM03uZ4a6DBD8ESXgwqGCGyEcvIh5GOm0DuoleX9uN6E3mwNyYqwR1jPXFKmyJQsImZg8HAolk22nkQcSSFJye/XOacV1WF0iBnKaWtwTEajTCbzeAJA5Z8z3oY+DmU8UYKkOEtJRXy09Bo2gq67dS2yChsSI7UULAoNNpFWhoIqNoUEwsC3CyX0JqSo9ar3PLhpJSoqxKb9QqhUQlSWmO1XGI2m2G92VhA4nselsulkSBtbf8cHx3h9atXyPMMnu8hiRNstxt8+ukPEZiQ38uXr/DOO0/xzW/+FF68eI7tdgffl2ibGlJoJFGA0eDYyL5tkBc53v/gq/jWt76FP/nudyAE8M7TdxDFIeomQBgGyPMU0+nYgItzE8L1kecZwjCwE2m73UBK4Pb2GlVZmdCoB6oiTuAijAIIAdzcXOPk5JSkgoVGWREPc7fbQgOo6gbvPHmI/9Hf+NfxH/3H/zE+/ewz/OZ3K3xzrqF/aZ8qoe9sL2wi8t8GvsIwvcZuem7Gpeif/CUufZfa0a+Q7aaTmy9ohcpIDfu+huDK4W0LIT2EkWcofZyALSClB+GRIVvXjeHgktQtLXxdA9umNZEsbZTWmAGj4YUhjS/Ph1IaZU2RnCQZUD5PXUO1DZq6Rl2VeLtjr3P2QcbeB9c5kF5ucat8hFLhN/6VX8e3//A7GJgw+Ne+9pP4+JNPcHVxi1/+5Z/D+cMHGAyH2GYp/h+f/La9cFm1hvJnQIY2+RGC+qCuazRtTjRAs7A3bb/QZLdOGSoZ+h5xHgudbCucd2/es+s83XN4sCqYW6sIACUpa2Ow2THCYhKw975jpDhG8yHAcd959nUcMKz3IyJv8ozb7+zFsw7d78caSfgRjh8FoPzI18abg5n39R3vlfz5vufSNajf9E7vM17fFOVwAYOl6FiZdgloJ3Ih+mOlozHbVgCAcSKZJH+qAmTkh7tzfC9AFHZ7OaCtR5aN/qYho5vrJdR1jaura0gpMByOrIgMAKzXa1D0RMHzSG1Iazbu7oJLplyxHUDP098J7LxE914t+PE6qpSUnbpibz5BIE4itE1rDeVHjx5BqRbL1Q1GI6L7nJ6eYjqZQEgJzwOOj48tY+K9994zua45dtu1STzOrXOVPO4b5MWO7DUf0KgB+GiVRl0rSE9Yp+put0Mcx0b8QiEKY4xGoy5aa+wGKSWyLLPed6b4cJI0jxcGDPP5HM+ePQMAWwB1MpnYscjGK+e9eZ6HKIqwXC4xnU4tdYjrUvA74dwAa98YW4U98C6Fn3NBuUwCO2Q5Z4MZM1FIhX/ZLh0Oh1aFkHM1hsOhdeayzctOPHcOZMYpzKCL7UyOMLjGe1VVdh5Pp1NsNhsbaeAq351jTNC+a8BNlx/BdkR/nrMs+26XQqBTN+Vxx/ke3EbuX+5TXmM4usVjgIET//3HDjTciemWQbe8LRO64wdl2hRHLdgLYaMIBqm6m7hFiLQiIA5D5EpZbjIACCnw6NEj+6BuuJXDP8wJ5NCZWyjK9R75vg/f8zA0EQ8eEF1ITEOAFo+2IQNdehKqVSiL0nInfd83HkbyElc16TLzJKNiYoXpFwFlOHcMhFgBIUtTy88bj8fIsgx1VeP6qkKel4ayQpO7bcizTMUICUx0SJsXA/L2RGGIrZE+k1JiubzF1eUFxqMhxqMhyZQCmEweWTAynU7x1a9+FS9fvsC3v/37yLMcyWCA6XQCrX0UeYHl8gZBEOD6+tqAtASff/4pBoMEX/3qh5DGS9C2jZGoGyNNd1iv18iy1CxKGlICkeHIA0Ca7uxYCcMQgR+Qt1dpJIMRqrJCksQII6ooTtcpEUUhlGpRVSWEbCE9iSzPMRgM0LYt3n/3Mf77f+038A//0W/j23/0x/j2deZsivcDDdcjLwD4QmBR3GI3OtmPo9vog/3dMS7d6+3NrjfPPWiURQ4VRvD9zquttYYWJCrg+5xgZqT1eAwLVyWMjFTfD+xfGpbpMyADUsIPAvgB1fIAuE6CqZsR0HebuoJWLRpTvOju84jeb29+/v5X2TDNG+DZRmHgSTx9+hR/+Zf+Ev6T/9vfx+XlJWazGX75l38Zf/Sd7+Pnf/7nEf75BHGc4PmrS0RxBOn7tvZO27a4vFpCK22UzKR5ZHpfdVPDkxQJ1MaYp887RwiPP7sOuk3mviM3b8+A6mgowvxP2D6h69FnyrwdvrCGcDpOH/5XAMLkXbge4q5db2c8vwmc7H9+33XfaPQK2Hmxf86fNorxp73Ofcb9nwXo3B/x6f9+l9p2+Puuwb//PTdKtf89dy98U7TjTW2+2w6OMAgIeOY9kgG/P7O17tYZcwX7r+8JQ3HiNZITrLnNLPtMhSQ5ikjXpfOkASfbbWraR5/5foDdLoWU+R3JTTLcGgscPM831zQzzjhFXVAQRj6UasyQ7fI+w9DkUugu+ssUHoDAhvTIu35+/sDQdlr8V/ElMmQYDAf4t//tfxNCSCwWcwwGQ0P1De1+yG1YrdeIowh5kZH0uKkKvd7cUEJ1USIMAxJNMW1nqnhVFbbODDNKIIBXr16irmucnJwaz3WOJE6M3QBcXFwCGpaaRA4/igp0YiCw153NZvZzBkL82dXVFSnmJYmtS1QUhQWSDNqiKLLecaKIL2yfsp1ZlqWlQLkUMZYIZ5vPrtXGFnRFisIwxNnZGcqytPWUaBzQePSktDYte/eZLk9RoMyCIQYqVVV1+72JBHDUgp+R2T5u0T7uI7Z5GYBwDokrk87nknO5QllSoT6XpsaTgSuHc2Se7HPfRiL4nXK+Cjvx2dbiYAEAJEnSo4BxxEVrbYsRcm7M2xw/UkSDgcXp6SmapsEXX3yBm5sbZFmGk5MTALDJwzwJsyyzPDfuMEZWzMNjZGdzOrShM3k+tFaIo7gLs5rrcnSCqQu88EpJCd0cMXCpW240w42iCN0VnuHOBUDqT02FMAioYJpgiTVa3Kq6QhRGKAydLAxDCElAQhlv++3tEq1qke52FNWoKjSmsMpytYLn0TXXa+JGcrJZkiT44IMPcH19bWpcCGRZjslkAjZ77QBUJeazCaSUOD45sZzypqlRVYT0JxMKJxZFgeOjOal67bZomxq3Nzt4hoIkzYS7vbmmhT8vsFotMTRcziLbIRlENgdGtQ1m07FZEHLypguBxWKGV69eYTabomkqBIHEzc2VedYViiJHVRWmDghtKkmS4OmTpxiNR/Z9SFM8jI3EpqkgPaBVNbbbHFIKxHFkCqcJ67H3TJi4LHIEPo2dsqkwGQ3w3/3v/BrOz0/xX/4//wEuTZExCm13xsF9gQk+ngYF9O3HeH70AbSQjk3YgQ17jTfae4diJwx3OOJB160qGjdBGBkjmU5vTejdC3z4AUUftNpXi+Jh4zyZMMaElPA8H9L3qVCgoA29rVvKC5DCLlLaSCRD01xpe3QpNzpE9+meYq8TDrl7dfcnpYDPNxrZJ59DCI3PPv8c3/r9P0CRkzLUxc0GP/j0OaQU+Cff+iPUVY26oTojQgqUdY323zA5Elojy8nz4uY5eZ5HCcZCoGn3KJXQEJ4HtP1ohjavSLrPuv9ojhGn3A8dAELPSMXmIEByyd2e1TuPDLLDoR8pBLjAHj/rn/X4sqjGn+X4ZxG5eBtv/Y/z/j8KqHETyn+k7zlj7tDzvSkq4bIJDt37bfqIIwnUFp7FXT0UknGVd753Hwhix53nCXtdl+UAMIA0d5LyznV4WHZRCM/aFW5dJjacCLA0iKIAGhqejYiTA4apt9Pp1FxTmeJwE0ynYys6c3R0ZO2Np0+fQpu8x+FwYPMMPN9HnESQnkTbtJjNZ9ZY++0//H8jqzP4voef+MmvYrfrHGlZvkEYjTEYBmgUUXmrqkIUS3iehtYt/CCC1gpNU9t2xEkMKAILYUi5oORFB1pTLHU6m9oCcwAwHk/QtgqeDFBVNQbJGBcXFwiCAI8fP8bjR0/x/PkX1sGntbZysNy/aZpao1UIYSlSTGFm2g5HIUajUY+VwlECV/JbKep3Bg0sjcu5c0x5KorCGthJkthcj6IorN3J1be5fbvdzuYR39zc2PHCIGU8HpN33xj9AGy+B7c5CAIsl0sLpAaDASlSOXsrj1UGKy6NCkAvcZrfB9P8OUrE9xsMBvZZmP4fRZGJJsJGaphOz9fkwoAMYNI0NaUWaptzww4MLinBCejus3Kki0GEK4frghJWnnyb4+2BhiAOsQDToQTOH5yjyHPUVWVUaEjesiypWJeUArP5zH5HSJJQdcOzo+HAGqccwtQt1bK4ubnB7/zO7+K9997vFiMAngSqIrceV9U2ZoKRdr72PErMkhJVWdDkEl2CFUUBpEFqBYYmFEaGnIZSLaIohtIttqulAUSZTWgCSHZytV5DStIhjqIYu90OJ8fHuF3eoihzVCVJlpVViSQmBElmAR2syRyGAdq6wfToCGEUIs0yTMZjXLy+QBRFePzosQVhZVUhNpGLVikMkgRpmpoqlRo315fIs5yk4eIIWbpFnu0wm8+wWq5Q1TXKMrfGYp6nyLIM89kMTVtDKgENhavL1xaNa6VRljm0ahGEAYbDGMNBYidSGARQbYsaNdq2RhjGePnyFXlKVIvXl6/h+x6iOEJRlCaBVyFNC3geqTTsdlsICLx8+RK+72E8niCKI7SqRV01qMoSrVK4ub6G7/sYjccYDBIAtBhypeeqqih86UnkWYrZfIp0t0MUhqjLCnVdotUKP/ezP43z83P8O95vAmhQtUDdCoSys4DvM9nIQSvwRKa4SW+RjY7NB4diFYeqazhSk28z93iD1bA5GZGp5cBORK6VIUw7PN+H73httI1aGAUW42W2c9G0XbUKVUuVvT0pEUeRmWckHNA2NdqmQdvUgOYYkD7U3N5PvecUe//2vk6/PNtpXL+4gs4LlL7ADz/5FIAERFcIEppAxSbjBMQWwuT6KN0JemoAdUuOAuVwztumhpYClOiqrHFjj9bI0zp9p7VbZPHwwdWrgb43et8TbzHpnYEmehsd4FIwusgAGUyU/Pl28OIQfN6/9V70AvtASnDghoB5jwt23zUP/d7vRY4i9f+Gu30jACEkOslScQe09ozT/fln7u1+hTn3LD7Qu45zIrWH1X8csO58xji+A9j3GfjirndDmHnJkVVTSFODxjaNB2WNZe041Nye6wBKF03rqq3D6Q+3wzsgTcaPARi6U4kidSSWM+rkU7kPldYOQPD2xrqixG37UhlMcOK3OwdJtKRtG2NYH46s8R4uJRWFC4IQXMjt8eMnWCzmABQ8nyjRDx8+xNHREXa7HcbjMe0LUYTRaISiLCyggNbQUMa5RqyAVlHO5yBOEPqBNVRZJbFta6S7Cn7oI4lj1FWJpqb930Yp2hX+re/8T/uADIB86YGEI5y5LZmmzcDqbr2N/rsWNi+P+waXsM5D/k53X2EdTSgB/d2O6aEzDXnVN5S1+25f8dDte93dNu2DRL5fLx+MGt57p3xN/qz3fFrbhccCbqAbn3sOLRt9AoAvnL+5h20/7XFa9/dmvXceOQ+6z5f10v6dAQaLEYVhaKuU53mOo6MjbDYb64hn5SyXgsSUtMlkYoVv+O8uWGDnufs0SZyYKL7mKUq1QgSJxBQl/TGMIsRxhLKqnICMRt3UgCBZW2jYAoW833INjbal5H/OiX6b462BRlFkFrkqpbDZbHB5eUnFvYzUGVFrphiPRnSu50Gx552TbI30W11X8Jhrbzh3blGrpq4wGg/wa7/+q1iv18YTSd+/vb5CbWpKAI42taREraJsepOybVukeQEJQuR5niOMIiRxjO1mg1QAWZbaCAtAocvAD0zys7D5Ir5PUq7r1RqbzQ4nJyeWZ5imKaqiIKUsL8RgMsDD84d2EpJHYGdoPpG9blVVGI4mSNMUYRghDmO0jcJ6vSEEn5cQQiMIKTz56ac/tFGkZjIxXlZlBgLV7CjLDG1bQesGQkjc3lzh9vaW1AcgoU1oWKkWo9EAVU2hWKafQbXwBKn6xHEC36fcnCjwEQWh5VWyYT8ajlAVFQJfoq0rzKdzLJdLXFYXgKBnCbKQolxVCU8KBD6h7u1mQ2Msp0JxQgicHJ/A93xc3lxhPJ5guVyhVS3iJEGWUe2Mk5NjAF2kihd/DkELEaIxRdaKooCGxmy+wGp9jTAUePfpQySbBDW2qLXA/+H3FY6GBDTPBsCfP5U4HfCi0jeMBABfAo/zC/xgeEQ1EeAuTM7JcL6k3R9dg6h/OmsN9b8MA9pbFFmGIAgRmOqgnuBsD6PA1rZmce82K2EkS+EsLkoDqu3yNITxDoZRSEBGK7QNgZumqdFUFVhN6aCNzK01H94BVIcM0r0LLUvg9asl2qsrik40Lem/ewICLTRXghYC+2qlsCpc/UhCq1vs10nQQO/7bdtRTtjD2QWUdK/5nE9x0PvvPKNCv3goGwIUsnchQtdZ/K54LaS9tb+RK2UST3vG4v1Ht2G7J9/zJbf9BxPDhWMn943bu/czVrcTkeHnAvbGD49L+4fDVCMIMil63n2nzT3AuNcu6aj97FOUtGrtdVyvpNY8s+45rEGjrfFm+0l3oNCVXhXwEASR9aIy9YSpIgBs5L+ua7RoDIDmCCLNayk7rOI+i2KDAwICElIEXQdD22eiPISOBqVB6k6s3NTRofrvWoDu7UYjuCYThITSMKwFHsPS7NOdwUqF0YiaHIYR6qYw15TwPIFAB1ZiWwiBtmkxGA6xWCwwSBJIz8Px8RFOjqc4OTnCw4cP4Xk+Xr58iSdPnlh51jiOsd1urVHHVN8k9jGdTkkZ0hPIsx3ZCoa6e3JyYr3bvC82xtte1ZVVzwyiALrSCI2Sked5SHeUI8FsDtPrWJoIeu/YX8Pu+9vbHIe+d1ec6E93/Liu88/jIYQt1OcW52MVTLaTONrj1thguV8GtfxdniecTzFIutINnC/SLXMamw1FIUi0pUWRl2gbhTDyEYTEICqrEq1qbJqDH5BdR2JOHooiQxDQPOU28RqVZZlVkwVojWHq3Jcdbw00eBFzC6GMx2NAa0iQXBt7XRh9tm0L4XtWmpTRbFEU2G13mBjuHnPUOAnJ9yQ8IbBarjCbzZBud6jKChBAUze4vb620mlxEqOuKoxGY2x3W9zcXOPF8+fwPB+j0RBBEOL169cQRqpztVphOp3aiuRKKYxHFMIaDAYWsUVRBM94O1gWLEkSzOdz6vSUQqHvvvsOSY82LZIktolAxLVLUVVU0Zo3EK1Jek5rbeg+0npFOCTGPEZGjaSnPIRSBEpOTk7wW7/1W5aPp5SyURoOwXFYj0NccRxjPp9bb06SJFgubzEaUXiM1RQ45DadTg3Aaw0g6aqAumFSTrqiUPIQVdugMglYaZri9OwEabqBEBLL5QrT6QRJMrCyv1EUmUhRZTmmQRDi2bPnlIzvSex2G0ymY5MHEiGKHsHzpE2GKssCgMB6vcbR0QJJMjChRc9S2obDIZ49e2aSflvkWYmyrGwybZIk+Mmf+Sa+8/2PsN5u8cOVxm+/Ung8FviNd3w8HZNxwwcDgyNZ4XLzGqvJAxMV0I5xI3rn2h8sFeGAIe7OuXs+oTIdGlVdom5MnRc/sF8i5S2KGlnvvlLQjqGt0RWcZAdCR2Wg79VNA61N7YWmQVVX6EcxGFy5mQddk3l7PVQD4NChodEq4NPrCuXFJQ7SHF1P/54R2buW7gx3jT0Kk9uXh6JQex65Q57EQ98/RFtyDTHXELzvPD72E0n3z+sZffdc88dxHKbA/Kjn6Tueyy89NAA4tQ/QgQIeF+7s6V+eDWj62YXxUnp2bdwHGmy0dxF3973dA3rs8x78K6QkABEbKkRVVdDQCALKt2KvOAH5voOMHV+ciAkISM+HZC83/cUolDlRDN3VTpBSmjpGXftpbCmz93R0qP7zMIjDnX5nEMZdrFRr+0dr0u5v2xYaNYQUNsegrhtMR2NEUYjFYmGUJ0McLRbYbLd4+PAUjx49tHQc3/dxfHKMuibD6Ob6mhx7cYyyKDAyxc3KPLW00iiKcH5+BkBb52Bl8siqqsLt7S3m87kFda9evcJoNELbNtDaRxgGiOMjq0zEnPuTkxNbiI33WabusO3g+z4VARWdYtBsNsPkZnJnneiP467A8T6w35/v+39zowJuJEBA2Nosdp/R+s657gpz3z14zOw7FVwHqmpbG2lwbUD3X+fiPSeFe3+3Te7a6fbZnWiJuKsWtx/B4fb2oiJ8t722CSnBEWz+G0Q/erO/JyyCuWWAbDYbG5HgMQjAAg52JAhB1DOu68Hj11WXZGf6aDRCVTaWuuZWCuc2uREHIQTG4zE0NAaD2K4j/C75feZ5bsECiyvVdY3AUNwAWNuSn5ujKWVZ/vhzNMq8INqTNUY6HXjV9NUYuDjffDGHKqnqcJlTRASapBlfvniGT4sK77//Pl69eoXj42NsNhsy7Jsa2XaHLM+QZxlWyyV9lwvF1TW0arHdrHF1eWELmqRpisFggOOjYyyXSzz74hnSNMU777wDKOK+nZ6e2vLtAKlTzKZjGwLaGU+EW849DEPMZjNcX19bw/0b3/gGyrLE69evbXINh32n04l5+TQ4mSokpbCItmkaXFxcIM9zfPDBB1bnmAEZc+UAYDqd4ObmGnVDBVwmkwl+8id/Eh999BGklDg7O7OASGuNOI6tlByDG/aOaa1tSCyKYgsIWbIuz3Msl0sE0rMDmqtuskY1cyZ5EnFCkx/48ABs1rdQSsPzAuRZbvMnuCqz1pnlO/p+YKVzE0MDY9UFgOq3lGWO6XRmZWyllFitVqb9ClGUQAjg9vYWUnrWM0DF44DNZov1emPyZASur68wGo1xdLQAjINQCODnf/6bePLuI7x+fYk/+PYfY5vmeL7R+M0/0ng80vjGscafP6WowG2p8Z99plApjV9+fAk9OYeFInesDmPo3GtrHQp/uJ/uLaIwDmIhAE1iCUKWlOgoyLhhQwMgM8KCIHM7IYjuYIsKwanr4FAkm6aGqmuKrziGO9DpZd152j03tTUHe7sanF2OnrBRwHdvFVY/+CFk44AiZ8P5cR9vuqZrjP5pj4Mb7d799z97E8Bwv+P+u3/PtzkORmO+pG1vOu67Rrep0yEdys3+o/b3/Huuh87IOWSI8e+H2y4ghAeu27P/XSm7/AA2xikKceBS+1feM9SkkJDSB7RAWbJgQnd93mPcd+kqSrk0CYCTvbskZmgNzw+s848NFLdf6Jc+tcWN+NDz9Z+BjTPPk/A9NwoCyMB4Qo2Me9PUSJIRBoOBTXgNwwCLoznOzs4wnkwwGY9xenqKuq6xWCygNXHjee2xVZIDUg8i51NopPR3JseuwcOHp0iSGMvlEk3TIookmqbFbruzezrnP3AtBDbIBoMBzs/P8fjxY2RZZmlRvC9yFWz2NN/e3uLs7MwaXp7nYTweYzQaYbPZoCxLHB8fYzqdAugoSmEYWt4/R9f/98m/i6urKzx+/BjX19dI0xQnJpeyU7gi8MIecVfpKUkSrFYrnJyc2L3Yfc+5ETypqsqKyIxGI5t8zcm83Eam7rAhzNdi2+P29hZCCGsvjEYjSwFj5garPwVBgOl0isvLS/u8Nzc3VhmMvfGj0YgMXzO2Xr9+bZWT2NE6Go1QliVGo5GV0XXZChxBImZIiqOjI5I2dyR/X758aVWj3HptSZLY98uVyXmNqKsKgVF7YiVVzgPhiBjbi6xg6s4vLp/A9tBwOLTziG0ttpM48X1ftIDnpFsDzlWKYofEYrGwdp4rRMBqqADlcNzc3NioCFNv+Ts8tph6yEn3zCwiupZAVVIeCOcwpWlq1yJO0H/b/eHtqVNpZtSVCO1wJ0gp0dYNtFJYrVeYjCkp2ZceqqJAo2qbhHN8fGyv9/D8HJ98+jmurq5QVRVWqxUuLy/x5MkT+IK4+oHvY7ve4MHDhxZoNE2Lm+sLnJ6eoYZC4EuMhgOKprQtAs9HHEYIPB8Pzs+x21LSDqPNtm3tpCEJtQJKNRZg8ELDg5GVAnjQsOwaGcoap6fH0Bq4vr4yg6eC5mJoHhUaatsGUgJBEKIxBcIAMqJZaYAHPU8SHhTEzYtwdnaGVjXI8wy73Q4/9/M/jziOsVqtbLtcYMBJaovFwiJRjkQxkOFIAE/opqHaGHVd4+LVK+wud3j06BGm06nx+rRGWq8LDzIYCoIArVJQLVVEbtsGn3/2BZ48fQTPo3s1TQ5PepCBZ8ZPQEXf/ACDQWKk5hI74QI/QlO3mM0WyPPM0OwiDAYDjMcTlGWFwA/RagVPeljMj1HkFTaba2SmcrPn+VRRXLUoCwJqqpVYrbZI0wztWQsYx0AchxgPEow/eA8Pzx/i9cU1fvDDT3F1vcTLrMKzL1r8p5/VJmmffPVaA3/3uxX+SvAFvMfv2vG97y0CnD+Ivd/3TPX907p4QZ9M5dJ5tAJaXZv4QQ0YYyDwfWPomWsJ493X5Imsa6IyMuWqbZse4IDjLe237W4d9btn9Z+t91d992+fb4H18wugqm3OyJtAxiEvIf+9Z0Tf+eb9x75x/WeNGNxHKdr/2W3zj3K/N7XvEAjpfr8/OsNroxtB2j/Hvfeh+3fGOsFRe1cBx/ute6BjHzyxF3+/7XQ74fx89zm6Z1HGIcmOMDKs3TiHPdd66Pk6nr0XS0TStdGtAcyLJ5ex7Vuy62n9N5iAewZc8M4dr24/uxFGNt4BGKOpMftS55WkCCbX2eFn6OqqcF9aXrcDJuhZ6L5hFGI8Gtv7AhqT8QjvvPMUAPDB+x8YsQmF2WyKuqlQlsQseO+9d+H7AZbLW8RRBD8g1Z6mJi9sEAZYLBbYbnfQSmG7WcEPSBo18AMIQevN8dEC2+0WlxevjWE1Q9s02O1StE2NZ19cYnG0wGRCydpxFKEqQzveRqORfdaTkxNbSZoNpTAMbU2I9XoNIUSvvhQn2fJ/SyMZ71ZGZudjnufWrhiPx1gsFhZknJyc4Pb2FkmSmFpVO3zxxRcYDoc4Ojrq2RHMBhCCkpfdZGauWfDkyZNeDQi3RAAra7LaEBvvzDxwhXeapsHp6an1lJPDMeo5DhmcMA2ME+yFEBZ0nZ2dWaOY2R7D4dAWWOZzeawdHx/b2gxN02CxWFhbxfd9zOdzOza32y3G47FNJucokZuQPh6PcX19jcFgYA1gZkcw2wKANdjdtZUBD80ThWg8hja2jWWzmLnSNI1VgXKT13l81HVtbUeeb6xuCsDSpdwC1oPBwEbaWHyHxymDDH4GvpdSGk3boq5qa8tx4V0+2B7zPA9PnjyBECS3y6IHnMjNCfkALADiCB+PJdUq6wRmJ0YYhlbZdD/358uOtwYan3z8MYIgRFEWUAYFxUlC1aKNZNh2u0U+z3F6eoosTfHZZ58giOhlfO+j7+Hx48c4OqKwZJpSyPHm5gZPnjzBn/zJn2Cz2eC9994jUGMG1dHREf6jv/f30A5osQ0C3yC2Kxp0O1rEhoOhrefAC832mnSJY1PhkNEpKxPQAk6bBCN1nlBxHNuBwFJp/JJ40fd9iaZtIEDt5OiB1pSAJlqNtjWJQRFNviSJUdctxuMx3n//fSyXS6P53el0TyYTO+lJlatEVZXwA2mTg5598QVOT08tAGiaxnoweJBzsUIA2Gw2Vm6Y28mDnb1A3C+B7+MrH3ylp/Wc5znCMLQ1THgRqU0ORJZlyPIcVzdLbNYpPBlgvV5jvBphPp8gCokeVRalLSIE5CiKCFIKXF21dvAWRWk3Ta01BoMEVV1TcnKSYGQiKkJI612R0rPh88FggCzLAWibSFjXFQBS7qrr1ngsYqgTBXiklvYP/8HvwJceICSk52M6O8LXP/wKpuMLbNMUu6rE1qhNcNiRogEe/sEf3+IvjhYYzcYgw0p3xofoktSEJbfTf8Kc1plj93DBjWV0yLGq+f9d411rUjgzKmkCVLDPLgyOUUnKayT24BpMbIwdvqcThRHYc0336Sr3Hdr5/2UB3KwKiO3WelrsebpPZXKP/YjBm4xuvtZ9n73t3+87Dhn2+8ebPj/klT/0nX0D1TWsXeqFC9L2AcE+934fpLn3dL3h++34sj4ShCzujGr24vJt2Bh38xj2u+q+dmCPOtXlQQBCes74EBDuc9vvCgPA99tu2ikklILTXlY8ApQwYFy49ConR+PAc3Mfe55w+qHf57y5u9QL6gMPTcORjv72Tf3HOSht79mAbn9h7yh9p4Xna3zlKx/gX/trfw3vvvsuAY0gQF03iMw9iqLAzc014jjG6ekZhASEJ3Bx8Rppmhpud4DRKAFHWwIjynJ8tMButyMxCZPb0NQViiwDDBvA8zyqzVPVWC1XCHwfVVmhzChHIgpCSM/D6TF59RtRQzcK63SN0NTSyrLM0la+8pWvWIWiPM+x2WysU49z+bhv2cnG3v2bmxsURYGzszOs12tDXR5bA5wjDSxAwhz39XqNoihQ1zU2m42l0Wit8fDhQ7x48cLQgT3c3NxY6gnbHExfZg9yGIZI0xSbzcZ5X9oCl/Pzc2tMcqRjuVxaNSM3YjEYDGz9hM1mY5Wd2AnL88stR8COV621rRLNRjMbrWmaoqoqq0TKQIn7lQ1rjrqlKUkTD4dDTCYTrFYrHB0dYbVaWbuEKewcSeF6Kre3t5ZWxwCFIzUA7H2soleW2Srh6/Ua2+3WKjqxkpLv+7bcANOXmA3Cc5KjEpPJxNpYDLJcyhvX3OBID3/uRjGE6PIsWAyInb9s//D9eawxhS8yRXN5DrsKqXxdBqBdDY7WAlJWy2LHA9+Ho2EAbB5yreoeNcs9z61Kvl/j577jrYHG7fWNDSGNRiPEYQTdtIBS2G23WK9W5DEIAuSjEdqmQRgEiCIf89kEtzdHGA0S+FLgs08+hhYewijBer3GZrPBer3G1dWVqSmR4LMf3GA+n+P73/sIv/DzfwHqj/+PpiNabNcrAGS0z2eE+Ju6ghAK49GIBq2iCuInJydIkgTn5+fYbDY29HR2dmYrnCvVWlUAAJZ3yeCD0XVq6lxwNKNVDYQgr1zbNhBSI4lja6CPxkO7qPFLLKsSw8EYdV1juVzakBUrbNze3trqi4VJLH/16hWqqsDZ+YkFUby4cXSCi/Ww4cjnMBWJF5oso8gAeVviXgXO7XaLpmmQ7nZQDXlI5vM54jjG69evcXJyYr0uTdP0PDIAJXPf3txCwMd4NoPWwMXrS0gJRFGAplEmqkMeKgJzO+s9IaRcmAWuMBNFI88q5KbQDfQSQkoDNLSVyeP+BTo9efa+AEBRlrYSdF2TxGnTtKg/aICAPIDL2xSBFIiTGGcPFnhwdorZfI66qfH66hovrm6RZhkuLyl/4LPPPrOgo1XA7/3eJ/jJn/kAp8cj9JMyusPmNuzZ6fs/3Tn26EgH/uiAFeccbaqGoyWXrTbAhz2bDqjYv5ZtohAO/jhw/gEAdCji4bbeBRllq/HZWiH/5DNAdYDT5cLa794DNg4BDb337/8vji8zvA9FB94UGfhRrtk3WgGm2NwFLOJOn+171N8E7g61/9Bn3T1crb3+wXlCZEA1xsFAykZiz1Dfj6bs38v93Y5rDl/w3w/QsWyUwmnjXSpTZyB0/cZqNW9+9kOfM62W78HjnPIdDCgy1wgjMjBobdc97+l+n9xt411Q6v4exRF+5Vf/An79138NcRJju10aWVYFKMBPyIE3mQyh2hplVWK9usXx6TG+ePEMdVXh9PQE48kEr169oqizHwBaY5CQ5zbd7rDZbgEIo2bnIfAD1B5F64WQWK3W8KSHrcwwGRJNFoGHqmwhhURRUg5nXSmoVmC7yewYjQfSOgmXpsjt8+fPbT0E3kc5AsEG9mKxsAwGNow5B5FpM+zdbpoGl5eX1gBWSuHly5dWenS1Wln6Nu+9bAxSLkpgAQ3XzeI819VqheVyaW2L9XrdqznGexjXSRgOh/A8D1dXV7ZWQ9u2ODs7sx5npj9NJhNrmDONiMGRS0VmI5X7iQ1o9n7z87HXW0qKWM1mM+M179OAmIq+3W5t1XAAtq+Z1j2ZTGxeKrMy2Mu/Xq/t++AoDx88/hlc8H3rusbZ2Zntx6qqLBjhfAIGdL3nNwX/GIxzAUDXkcWKUETbjuw84kiFu1fxu2R6EYsKcHSFQY0bvQS68hBCCEsH4/ukaWbHEuezSo4Oo4tacju5v1vVmAglrHIqryE8Prv8TLYLOuowjx2eN0ztc4UOvux4a6BxenKKKAxNUleNuqRqj0IDum1xvFggjgJAt3jx8gvbAVm2RRZlOJofoSxK6FbDE+Q1BjoExSGuFy9e4MMPPsBkPsUm3aKqK/zuP/ld6EQDgqqMDocjuxgXRYXNZoPpdArP00YxwkPTaCyXtzg9PcHt7Q3iJEFVFmhq4uMVRU7KVVEI6ZEHhxcpADZHYjhMoLUpfBeH8KREXuRQrUIU+QiC0EQEAlRlRbx4TXz2zXpDSk6GJ9q2LcIghIAi77uR3GybGnVdoVUaURwhGSRIsx3qhlDz6dkJmqZC01QWmEgjw0qVtQMsl5SzQMntYwJ9UQigpkhUUUIICd8PqB7HeALf73h6ge9jNBzi6uoKm/UGbUMTZ7Xa4Pz8DKPRGD/84SeIohBhTCHK6WxG3Hoz8PKigC98pGmOIkxRlQXKIoNWVBE9iRMox0OwvKGK5VVFIfBWteDq31oDVVmiUUCel4DoQrECgiJJHBVwDB7f8+D7AbhIk5At1TXRHSgJQprIVdM54lul8PLiFtAt/MDH84sb/NM//GOUZYmqrtAqhVpRvQW+l9bajnNIAht/+Puf4OFPvIf3HoyR+PcZaUZ088Ac7UOTAwZc76/izmfdFdzvOp5tOF537VCxxCGD0QUY3d+6+xyWVRXOv/cvQ4ROilbjuzca608+R1tVgNCOcddPALxzH8fI6iRl7zPa3V51e/B+QLRPAevBOyd6JI3XvnPP3/0WR5l67RJd5KcLfu1fiwFj9xiifwPr5eoCSV0+zWGg4VwXjjFqrkNJi7T2EC3IyD5q8tqLve8BHQ0HphlWBhUCgKkobdpKOWv8wLSme8YT3/C8hUDdttB6r93aRBruRB/c981FqLpK0DbaYKIS3F6tYRLOBSRYYtWzn8VxjCiOkGcpGqPC1vMQ6A44kNKbAR/G0WBlX/m92neiSPI7Cm2On+8HmEwnqMoKZ2enODs7RxxHmM/nePr0KVarNf74jz/Cf/Ff/FfOWtgNDUr+7kAi9ZsGUyM9KaGhIATJtz5+/BB//a//a/ipn/4q0ixFXZaIggCjQUIUJ03CJbe3N5T35ZFSYFWX2O22iMMQ49EQdV3h+vISgyRGMBlDtxrQlARelRW0Bo6PjtE0DbbbHQaDIYaDIfK8QFM3ViK/FRLD0djQbFtEcYR0lyIMjcyn1hgOBqgbKrpZGqNsNBhASIlXr15hOplgNBrB9zxsNxuqjrzdWm/zeDyGNgY/sxVub26sIcaGlPQ8wHXaeR7WJkrBnn1WEuKI/tHRESaTiQUvrMyotbb1OfI8tzkjbBBKKa3nnecpr4EcNWewwB7l2WyGNM2wXm9wfn7uRL9a5PkOZVni7OwMNze38DwPw+EQy+WKwJTvYTAcQjs5AJXZOxtjoNYm34NEY5bwTX5tElM0I4kSSKMaOkgGGAwSa7xXVWUjFwJAbjznUkryyguBNMswMEXj+J7TyaQDwMbY5kR8jobUde3k8UTWk89SsPz5drvtKY2FYWgLrraqxa7YIYojCAj4ng9IH3XNEQoJaGWdoW3bQgqPxGMEUS/LskJdVRCmxhSDQAZOdV0jSzOURYXpbGqX8zhOkO52mE5myHKqtO5Jz9RkC+FJH03bIM9YlapEHMXwfA/Q0tK3eNzs74tML2PwwM6JumpQqBKjIQkkNTWBfK11xyAhYwpSeoiiGGXRgWQu5MxAjMcwj9kvO94aaJydPUBtBnrbKFxdXeHq6hpHizk8CWw2FBmA0EjzFHEcIfADeMJDU9ELHCaEiNIyRRgn8Dwfk8nEotvlcgmAksWH0zGiJEZRFqib2ia2AgLj8azT0qclFkJQ0bEgYAN5ibquMBxSqGy32yGOI9R1hTxPEQQeYDTJsyzDsihsPgOHpDzPw2azRhgFNhzFXM0g8FHmBaA0ooAG2ciE9bQiAy42XvphMnCqXqfwJEgGtm3IW6xq1FUBDYG28dDUFUgrnaRWq7LEYBCh0A38OEYQBp3BqElRKIkSCC0gIZFnOdqmhQiAUTJElueAArZriuB88QWJSj98eA4Bqh+yXm8QBOQFaBpWERFoGoXXry+tZ2W12iDNM8RJbBLgPdxcX1NioxaoCyPD2JJS0Xw+w9HxMW5vb3F7SwtdURSI4hielEgGCR6cP8JiMUecxHj48BGGZuPI8xyN0ojioeVKVhUBy+fPn+Pbf/xH0ECndW6MFLfSqFLaeFs6H7oCeU1ZHx2gxT1tiBcpmhYoSGGJq79rGAOn52Htwtl8bWjg9UdfIGvewZ97MkLizrAeinDIR0JYa8E1HN5kKu/pPO0Z9Rx1OARE+te1bdD98+9ey7mKAEhfvwMs5kEOtFnfaQ3/5XUOvNwC20+/QLtNST3HGoD9BfRN3n7ddaRt8V3MxN5q3f/wXo+9vvMCevCkR8/pvEoHGmi+rO/cy/WM26iEE4rvQJaBpk7Ewr2GcJ6dXw/dcj8icTea0m8QNaaqGxr3Zg1gq54MW9+5BoMJQAhFAGcP+AOAVpQUzYCxaXT3XJqKswrR2kZQd1ItBhprTnTCHPINjjTqas5XUNZbp1RLM0d0qlRCkDqPJz1IAzZIqYna19QN1XXSLQKfIhtUR8NQkcz7kFIijkK0lgokMZtNMRzFxL/2iXIynowxm84wmY5wdDTHeDzCcrnEyQlFq9frtS1GlnE9pChCksS4uRnid3/3/0NFuDQZGrZ/eP0wdajIQ2qkZJUGWg1PUH2Mo5MZfu5nfxq/9Mt/CaPREHVZo63I051lGda3G+vBXK1X8ExOZlEWlsPOlBav8KyhJSCgGmUVFG9ur80zk7pkEPoIowBVXSLLUwShj9GYchKzPMN0MbW0mTAKEIQB6qbE+fkZiqLAer1G3ZJHPRQByrqERmujFlEY2gJzTU11fmpTd6qua8xnMxRFgdVy2fPAN02DFMB0OqWfjahMGIZUn8qM0dDQsNcmGZxZAkzP4uLDbq4AV8e+NkqZTEPigmhMj1GK3tlyubTF3ZjywpEEjnJMp1PjBB3ZiJDZpqwdNBqFWC5XBqDUSJIBRiMqrBuHARVEDkNIIdDUZF9FYYiNkZpv6hq+kemF1jg5OraUY6EFNuuNXaPOzk4BoY1BTgBTG2Gb2IwNW2W6aRDHMUaG4i0F1XwqyxI319ddlCpJ4BuP/nK5xHg8tuOMDV6mc/M7BGD7lpOy2faLoghJSAUUtdIIgxC61VAg+h1Hc8oyszkunvTR1K3Nm6BifLKXG0M5YNoKCrAMchwn8IemXEDVoMgpeT5vC2gtsN3urKOgtTVmjCiAkICm/C7fI4no3WpzZ1yFYdh3ajn7BtO0KPmdc0BCLJdrk8fkQSsgiuKevTQcDunebUe54nfH1z5Ez/2y462Bxoc/+XVLPdmmKf7gW9/CcrlE0daQjYIWAp5NlgpA6j8KvhdiuaSid5wQVNc10rzAkRmIw8EQ6W6HB+fnmI4n8H2P5Lhq4k0ul0u0o5bqdQkYKTpt8gc8JEkMVgspS6LYfP3rXwcACxxY0YgPt7OY98d/Z497VVXIixRjOYZSgCc9xPHAcDB3KDIKMU6nE1BtkBaeF0CpxhjUJZRqzQvixL4GRUGhK5IqI+7jer0GNDAYDKFqojp5kEgCUyHyZo3hIEbT1Agi8kKUBXE8i7JEW1VY55lJ4vHh+R5uLi9xfU1KTHmeo6xKVGWFZ8++wNXVFQaDBMcnx5iMJxZdQwNpliLwfdRNbdUlfM/kcIQhgiDC+ekDfOMb3yCViuUSdVVhuVzj93//26TQEcf45k//NB4+eoSmrvHo6bt459138ejhI0hPYjKZYDAYoqxKDOIEm80Wy+XS5u2sVitkWY7r21vcrpa4urrCar1GUzdYr1fI8xxpkRsPhSJ5PXQygRzqdA/r5RMSWqjeGOCJeudc+sB4Kjsu9R3PtDPhVNti+8ULfHfwIX7ySCL24XzeN/CMA7rfjntn4dsf92R6HDgPDhRwgUsfyOxhpL5RvWfk901bNw5AsENr4HWq8dlVhuqLF9COZvibYiBvegiXZvNli98+zeb+izpwy0m6EwLWA/9melEHJA7Jo/YAwl57mFJEv94f3XkzrYr6XNjIyeHvkZfOGfuKAIUUnERJBqrg6ESvvbJ7DtEV0bMRDgjAMxED62FT1rgioNapJfEz0mcm3iRk7zP3XbjPI01kogPv2nr4uP98kxfBkZFWKZBWnoYvYQQ8aC3xPIk4CKFUi9gj3vViscBwOMRsNrOb/dOnT3F0dISz8zO0TWsFNTxfIow8xBHl+7GnkmgTLSYTouTO53OUZYmLiws8fPjQ9s96vcJwOMBqtcTtrcJms8Xr1y/h+QJh5FtvOz8/5WU0JveDaBJRHGM0HCIJYrz77jv42tc+xDvvPkYcB1hvllitby29oyxLTKdTvH792oqSsPeeqTBHR0fwPA/X19dWYYnpGExzYS8oJ19zcjDvw7w2M6VFKYXJZAKllDWwmUKz3W7xve99D6enpz2uP++77HjiJGhW6GEOPjMlmDfPUQ2OGPCY2mw2lkqzWCx6dbM4euH7Plrzt6IosFqtrLqTqxrJfHeOXjD1h5NuWfnJlSLdbrfY7XZYLBYAYHMpXUoTqzuyLL7vh1YClSku3GZK2J/Z/M0syywlLPAEqormQ5qmvTwRTirn4re+75uxQDmRrMLF74fpYmVV2JwJUpGcQkppc0OrqsJ8Pre1GdxIhEsx4jwMha4gI0cVON/E9dhze9mByf00Go1s7innppRZ2XvnDFKYus00MT6f8zOoVEFmE8C5ryG0Yc80tlwCTLt9rxNM4jUoyzK7drMKFl/LTbJ2SxTw/SivOe0l92vXwQDR+w73FY8FzrdxBY54DebcXO5Pd59x6VEW3JiDo6pvc7w10KhUY9CyxGA8xJ//hZ/H93/wA2S7HWTTGGpKAa2oxL3v0cQq8hKXl5c2SXc8HuOdd96BFwQo6hqtahGEHuazKW5vbzEaDeAb9YSqKHF0dNShKAmTrJPaBYprYjRNDUoIrqyXwA3l8QtlbiJn5zNHjXMZePHebrcmVFlgPp9jMBhQbkocU2LMbICluoUQQJbliOMEZVkgy0gVqja1JJjf5nke2qaFHwSo68ok9dWWzzkcDrHb7iC1xMsoItRvlCg2mw1U2yAIfURhhMl0AhhaQJqmqJoKq/UK6S6lzV0Iu6g2NVBVNYq8QFVXCIIQk9EUVVFjPJlgs9phebOBBpCYyS6kQKUaRFGMJB7C8z1IIZEkMcIoxi/+0r+Ef+lX/wrWN7e4ubnG178+wGw+xycff4KHT96F1sDJyYlB3tTXV1c3+N5HH+OP/vi7uLkmIKE0FXzJswJ5XlheIb9bpTWUbqGg4CrVaE3hbUij/KIFtDDa01pRVqfgf7rEbDZ6tWKP393DNeT2jR++/53vwJh05hylFNqixPaHn+K7eA9fP5JIPPQ92o5F3jPO+6GJtzg6U962o/fp/RfrRWf2vnsIfHDcZv97LsgwvncI+2/Xyg5kKPzgo5eobm7he12ODxmAe7GZA97su89B/29B0pvOPfDZob+5izid4/UjPm809r/sHmLvbwfGlDHgaexRMjIb2FI4eQE2YHKon5xIxB7QEU7og77TjQCtYIy5LmLXnXMXGHX37KIwbg4BVYmGjYry3GO5c2iCFPY6GvBMpAGSkrF7wEge3rY44uNLaT2NPeAsBDQa+AEZewJAFEcYDIYYj4Y4Pp4hz3M8evgQcZLg9PQUUgicnZ9xAXY8ffoUWZaiaWizZgOJefJeEiCKPGjUePbsUxwdz/HJzQ2SOIbS2iaTnp2eWwPANRKfP3+OxYKSp9lTDxBomM0kfv2v/hW8fn2F1WpJtF2T4HpyeoIgEIijCEIKLOYLjEYjoroGESajMQCNLEtRlBmtjUIDaK3hrJTC8+fPARBl7Pr62uYgjMdjrNdry81v2xbT6RRBENhaRRzJWK1W1pAbjUaWa89GKBvPZVn2eOqr1cqCBe4blnLlyICrkOPWvGIDmI22wFCh+d2wwfjo0SMsjVy+EKTyyNEFzjdkDrur+MW8/tYk7S4WC3tdBpYul3+5XFpww7YPS66ygImb68Dz5ubmxkrt8nxx6VNsnFN/DHqqmCyzyknGbEje3t7avgyCAHWZ22fjnAnuy+FwiM1mY734rGSplIaAtHYTAFtsGZaqqC2A4HHL0QygUzjid+7mIDBIYbVM7YghMJ2N28oGLo8Flpxlehnn0biOwTAIIQPZS3DuohTCAmE3t4PfGY8PBrDc/2FEY5rrYzDI5HdeFJ2MLlcIZzDAIj3cJwxSOGLD1+AkcQZDPC4450M7uy5HHLi/ga7mh8sAchWjONGc+9nNCWJ6n3tvvgcDox97RANSEg9dK2gBxMMBfupnfhpFliPf7nB9eYHXr15CNTUZpXECASDdZbi5ucH5+TmOj4/tYFit15jMpthsNggXC7RNDQmN25trXF9dIi8LxGFENTOcB1KtwmazMhMgR5puLUdys+mqcXqeh8vLS6vnzAvhgwcPTAK46qkk1HXd01fmQUE8zFc9ubmiKOi/tKsHURQFrq+vMZ/PkAwILCmlrdQZv+wwJI3iVrUGhSqUZYXVckOVmFtt6xtQFXKFq8tLxFHo1DEhjyqH/VutkBU5uMoqvS4Pvu8hiUeQrUCUeBhNZoiiCPP5DN/45s+gVgphFMH3PJwcnyAyyliDwQDSp02LJ9Vut8N2u0WaF/j9P/gOfucf/1OsN5TAX+QFRuMRVqs1yrpCmmZ28dJaQ2mFum6g0VdX0dDEm1Qm7Cup9oMbSYBgc6m1NCYIASE9AiIGRPCDa43uPIdS0xVsEz2vhnvcN3EOJV7uf68/VciQqncpVj/4BN/D+wQ2fPsF8y8be3uo462OfUrTXUDAx33YxYUC/e9237nve/v37g6+Xj+SAVAxvh+uNK4+e412uYYUnbqUGxlwQd3+z28CfLZ9hspiHNfYf22Hrn/nKcQh730fGHB73HZTs/o1C/gcN+HOXfi7yEi/H+21tYAnHYrUHj5xAe4BPGN/kJ408tOmbZb+xe2g/AMCGIdriBzqs64fPPucrqQkPUu/P/g6WpHiGW2aHdCXUkKDlVT26z4Q4NHQdr3QmgpVSikxHiXQhgYwGo9xfHxs1XziJMSDhw/I8ylJxS4IApwcH6GucyhNgiKXRpgkjmNb1HS9XuP65gKTyRTSE9hsl5Aere1hFCDLSuM4SwAR4uk7j7Fer3Bycmw9i8PhQwghkMRDbLepNbbDMMTp6Sl2ux1ms5n10nueh4uLCxwdHWG322E6HeOrX/0Qvk+042fPniGKIjJgdyvMZhPrXV1vNjg6foyqLLFLVxTxMeBCqcYUp4ts8VtWV4rj2NKHGDBcX1/j6OjIUou4XgMbrL7vY7vdWuOU995Ooj20AICNY/7ZFT5hjymrPgohMJ/PcXNzg/V63aut4Ps+drudpVslSWJVntzkYY7CsBHGUrKsKMUGLddycI1Wm7NhxvRsPodvnJI8D3ZGiZCNZ7Y52A5hER2uSJ7nOa6vrzGZTOx75XM4ksTzarVaYTKZWLUgcqo2Rvmoq9vAxiE/G8vIskedDd0syzAeJj0RF86fYI/2bDZz1lDqpzwvUBZULJgNTmZ+QGi0Fd2LPfVsoPIYZgOW7SgGCxz9YQOa+xuyU7rkNcWNMjBo25r8GwY4URTZCAQb/lprSE8i8iN7Tx6X3A8cAQFgbUA2sJkSxXYhP6eQQBxHjpCDcmh8sV2z2LBniVhXyIcNfDcq43merZ/C9+Lk9KIoLPODjX0ARI80beAcFk72tnm4Vmm1y0XiKIob+eX/WLqZgT3nGvE9AFj798uOtwYaddNl6LuGeBiFSKJjLI6PEcUxXnzxBeqSvNPpdodPPv0ESZJgMpng8vLSFr+r6wrPnz2DUgqvXr3CarnE06dP8YPvf4Tjk1MkQ+I/pkbGjTfLVil88snHRvmhUyppmhZKaWQZDUZOBHITtzh6wFEPjmRw5IMTvXhQbLdbSiwziYUEMEpIKZClGQLPw26XYjKZYLE4QhwnKIocZVGhEgJFkdtB3ykgiT2Ez1W22YtJiXtSSni+hyROMJ7NURY5RmNKlorCCLPZFH4QwJMSi+MTJKbKehzHmE4mJkw6MDkKVMhIK4U4ie272+Q5bm5vUZUlfvDZ58iyHGVZ4OrqGrvtFpvtFmm6M5Gg0n5PQ9pByl5qASN1xsaTeWPWsFIaEIqAg2PQCwhowfkKTsVQ483VolOs0UoZ7jTlTmgnSsF4Q2lDnxCiO1epnrXJG9WbjkMG1duidz6EEGi2O6x/8Ak+Eu/jp05I12Y/6kDNd6/9ZuLTPrj4suClIdAcjG7cF/Hg7xz+TDvnvKmd5kytUWvgo1uF289fAuut3dztudzXQrivym7wd67tnmR+dj3f99Hi3MV0P9+hM2LZO85VpBlYOH2gDxvidI27iTnCoB6KwMF48DujG4fGlgNQgM6gtgIEeyDV88Te10XvZyGEBRdaMyDuNhYhPEr6Nc99GNzdrcrr3NGCAI6GCNEl6u8n+FObJTGrDBhViowCANBCww8kopDq7Agh4Bv5bS8IbHSc6TvHR0cYT8YYJTGKPEMyGGA0GmIyJuWd5XKJoi578oyeJ42IyAZlRR7V5y+eIwxD7HZbCAFsNmvr2S/LEqvV0ny3o3wVRWGNEaYM7XY7eJ6P4XAE1Sq0qkWeFwjDCLe3SyilbZE2ro3AdBemajDPnPcPzxdYb26xWCxwu7xC3RQYTwbYpWu0VYl0u6UCb3mOR+fnuL26wmQywc0N/ZskCeI4MYYCVQUfDpMefYKjD1zYjdf9Z8+e4dGjR9aI4cRXpkNzMVkpJY6Pjy3XPYoiK9jClCA2elyKENOz2JBkNSKWaefoEa8bWmvM53MkSWIjSrzXjkYjGwFxqSNcw4EdaJ7n4fb2FtPpFLvdrrc3uwUFGeCwgbfdbq0RNhwOsVqtbDE43l9YVpWdblxjAwC+9rWvQSmK6M/nc8tO4PnOxmSSJFYNiSlGHF1pGmUBEUdPWPXKVStiKg7lifYNSwZfbjFfa9uZaEQURRiNxoAWPRoTS8IGYYCiyHpF8jhxncEmzw+XosWRD6afcRvG4zG2htJV17UtHcDjEgDG47F9z/wZRwO4z3iPWa1WmE6nltnAKlgMeAACiwzOuGgflwzgPmQw5ErHuipcDIaIGaMRBpFdJ7iv+P2wvcnO7Pl8bkEKv2tXzYqdve6zc1/y4YIGjsYwKGBHB/c77488fng+aq17tUdsyQPzOTuPea37MjuKj7cGGloptFoDnmc9z3XTGhnbGAIa77z3PmbTKV58/jlevXiB3S7FN775TXz++WeYzWa4eP0aMIjy5vYG1zdXaJoG3/nOd5BlGVarP2dkzgTiYoTdZovVconZfIb2tgUC2uCVbrFc3QKg8NdyRck/bUPKKIy20zS1oTh+uTwot9stJpOJCeFWiKIQaZoZCTRtaFkzq75R5AU8vxsgdV3DAz3L69cXtjI4cyF5I+PIBHnsBaQQODk5tYsLV170fR+j8RgnZ+cYDIdmssQIfB9N3QAaqJsGuzSl+ggm3JrnOTZpjpv1DtvNFqvVEjfXN8Q5bWqbtFfkuQ370kLaotZdyI2MATI4iItKBWJcqoyUEq1SgNS985WmhHQpJODQkrT5Oxs2GsIWt9LGsCDjRXX30XdpIOZMCt/uTay+eaY54GHbd1+I4NAEYc/LIcP2IGXKNY7vOUdKiTbNsPzeD/Fp8AHemXrwXc+0/YoTxdmjHd1pCzoD37HRsPfj3nf6fxXO/x86421zPPajJ3c+08BtofHxZYHNx59CNG1v8wcOvYvDxqwLBOyZbvQLd8fO/jX4Z3tNz+s9qQs0hGAed/+avSJwd9rOBdm6PtRa20gC14mAAR42x0EcbjMBEW7T3Wdxn3mfDngfIOCICgMCN8LAURnXiO7fR9v7CB6r9hXclYclwwldJNJ8h0AH4KFFFPoUPQ0DPHjwEJPxGBoaX/uJr0B6ZLRScm4AIQwlVrUYjYbw/QDPnj2z6ym0RuABw+EEbdNgtbpEkVMi5S7NcHN7g4ePHmO73RrqhkRR5JBCGyoSKQh60sfJ8Sk838NkPMF2t4MQEnVVoyhKPHny2ETGKSIbhhGyNIcf+mibFrVoEEekkJTucgyHI5yePcAnH3+CJB7BT0JrILP3kjdyluhsmgbrNSVvsuH54PwUq/UKl5ev8PTpUyg1RBh6CIIEuW4R+AHapsV0MkXTtIjjBFma4enTp5be04FKiaoskWXrXmVvzjlgEMEGCNNh2cvKAOnk5AQ3NzcWYLGB3EmW15b2wkYUJ0hz/oebB8HGDBv5WZZZzzgbT5QgT/STNE2RJImtKVXXNebzOZqmwcXFBdbrNRaLha1XxXQbjqCMx2PsdpScy5EUbqdLjxOCcilK87lrVAOwURSOvLDQjVJUEsCVfOW6Hvxu2VO82Wxs1XS+pps3kmWZNf6DwLefszHPfcP1RNhjbg3QZIAw8G3NKQZBrnQsR2Y4WhBFEcqihO+HNqLCjljP81AboOMCQDbMpaS8Dqa2sV3ERfOm06ndCxjcAEBkwCYDMKYscXtcChePW8/zetEkt61aaeRVDmj0cjO4rWwXcY6HC7YYfLtRAaUU6qaG73u21hiDbwBom47uHccxdrudHVOuchMb9kVR2HWVoy081/j6bjVzjojYfVrAAnuA6qaFYWhBOrfZBUoMMnmucT+4tEFuKwMpdsJzJPBtjx8BaBB1RamGFDo8CU8CWhOy881NFydnmM6P8M4HH+Kj73+ETz/+Hpq2xkff/Q6EVsYSKvHq1Sus11s0TYvQDyCSAaqyhGpalFUJSAllFt7A84GIQ0Mau10GIQWausFmk2IyHgPwUJcF2obCnJ70MR1PUVaVNdKpWmqLHBV8L8Tz569QVzV0K6BaMjCr6sK8xNaE7+mFa7A6irCVlYUAoqirFp4kCR48eIDzhw/x5J2nUAadc4XS4XCIJErgS0KX680Gm/UGNzfXEEJgl+W4vFoi/ewFXrx4QdKqVYXVcomb5RI7w+3kha3l8JeQqFuq5iiEYQ0ZjrI0fGUhJdqmtSasJteo8bB2lYC1UqhbLtxG3mVlDCvYBCQa3krpLmnVKE1oUJFC11TlCIVWLRlNmgwuMlCUKRTnmKyO8egJCRhVDeguGtEZhN2dFHtcOW6gAas25IIAKe7yaQzHX4OMT+pL009CQ7cEhqyxxCFGsLHfGZWuscqHygs8+86nWL7zBA8XER4O7czqX8P+0tUB3zP30MGJLprTf5LDh/vNQ2f1r6q7U/pf3AMz90R5NL2PT1cNXn1xjerq2vLkOf+GHvnue4Do8i0InHaRIP4cMIav+boUnK/TN4btVQW6/gXRfGgg3u0j+/M9YEIIDwpe7zvCgGhPeIDu5/nQdbQ90/Okcy0+16AN94qCHBPKXN/SjcznvudBg/m3HMYWNtoipTSSjQI8l23EwURTpHEaKUe2lecvyUy7kFdACAMgTKeSFCTRvjxfWq84e36HwwHCMLIa/0Hg4+TkxG6yDx+cYTRISGXG73I52qbBYBRDeFR7oTJOorop4PkCbdOiKjzooMF77zzBcrlCutsh8H34SYwgCgGt4Xk+IEh6djIZo20VJAQCz8eDs3NcXV0h8AJSl2po897tdnj69CmSJMHHH3+M+XyO87MHuLi4QBwPsFgcI01zlGWNyWSG1WqFMIzg+wEC38iktgRc2lahqqkoKlM2yrJElqaWonJyfIzVamWSSMn7uby9NYIfBTwp8ejhQ3KUFSXm0xmGD8mBVoc1dpsd5fNB2shzFMUYDhOMhmPc3N5ACPqMqlzXqKrajjR2nnGxMfaQA7Tect4EG4tpmuLy8tIaTRS58SzNhekhLCTCe8urV6+w3W7x5MkTm6TLFBquwM2ebc6lnM1mljbELAU2nLuoGIGmm5sby0h49uwZ3Vdr+EGAXZoCBljVTQM/CLDebLHbpRgOSQxmvdnggSmCV5Q1EukhywvkBUUjrq6uKCpR5JjP56iqCpeXl9bLzm3ltYfpb6PRCGmaWurPdDo1YicZBoNBL2GYDTnOGSX2R2NB0GazxXA4RhyTBDWDMTYcmS5TFSXapEYYhAg8H0kSI8tyKoJYFJhOJlit1xAQGCRDWmMlrYtN3WKQDLEq12hVgUEyQBCEkNKzAI2jO+RI9UyF8RhhGCPPyD4L/ABKA0VZWcOdqF4j5EVux0qriQpOxnuLsjIStjGzL3jtIadAVdGaxuIFWVY4ktmC5rj04PshqmqDKIqRZhmKNLdiBPP53PZzXdeYzmaAoAR+zl+r69ru95xDZSOLHsno08+dUqnWBA6lUJbaBsCKCrAhD8D+boGLiQoyqOD+ArrEeDdhncGR6R3rfGZwx99hBzuDG86nYaqZpXo7z8Yg1M0h4vWAa6+9rbQt8KNQp6rKGLEajTCFXHwfEhJVUaBoani+B8+nHIThbIKf/YWfx6OnD/HRH/4R/slv/zYmwwRaaLx69Qp5nqEuyXvi+xECP8LVBelZ+4EP6VGl5yKn0JX4sDMuXjx7YTYtetDri2syXFvy8LdNa8AB0DYNIAClCGwAnapI2xrlIc2buIRnNkmNDt0OkwjjyRhhGGI4GGI0GuH07BQnZyeYTKeIIyp8N53NMBgOID0f1+sllsslttsdPn/5Gnme48WLF7h8dYlsm9uK4FVZ2XAZjLHUqtZaPE1L0QwlgEZ3XmAeRCSx6JZpY6qSAVxs6CiNVuueoS50R2GyCbmG3sAUCy4Q5XpzpXYUgrR0vPluBIEiHVKyfr6x8zTzGWHfp2uo88+WKyj6JnHfM0uAiCVBPSGdtkpLMWH071zEvaLTbn5GOsdz+IfKI6Dh0r5cY5IXXv7Zfm5AiZQSKsux+/7H+OLdp1jORng00pgETnMYuGhuI4Mv7hs2aW1P9Q7hPMN9x0FYIA7+ePCL90YwXNyjNfIG+HzV4OV3PoYuO++TBWf3RBh6USF7DoELNo75XDeJnI3ffkTDgVVSEAAVRBcRIOlULVT3VM7cEkJAOmDCTZ6mk7tfPM7DkJLqCplcCTcZkdpEoJ/rNFCEzu0LB6CYNkvpQaKjTGnnRfAzEv2ni0BIGZh5AJMTpi0dik4RCAPPbBoDu5l1ET0f8/ncesTatsV4MoEUwOnxEcbjCYSg9fPx40eABibTMYRUxDlPUwwSoi2xF3k6nRn6zMRWL+b3FoakTHh1fYPT01OUZQXP97DLqBZQnucoisJIpRIFdxAPoJoWSkisblc4WiwgQZz2k+NjPH/+wnj4AuQ56frPZjP4foDVao3JZILXry+MoWaUewyNgBUK1+s1SHwk63m7mWpwenpqqyzzmONNntchVgxikEF8d+Ke5+a6VVki4KRY8x4n4zHROEw14szQasbDERmsMYEvT0hAadRVjdihi3CEYrVaIQgCrNcbDAYDrFZr2+/kHIsxn88sTenq6grz+RwcLWfP9m63w1e/+tVeYqgQAsfHx7i+vsZ0OgUAXF1d9cCKEPROPvzwQ0tZYW49032EEJaqUpYlNpuNlSVlMLPZbGzx2OVyiZubGzx48ABCCKsmybQVMnpNoT2lEJmIBCdlk89MYTZfYDKd2UjSfL7A7ZJyIuIkwfXNja3xVVY1Ts/OsVqt8ODBAxRFYYFZlmU4Pj62ieWjEb0jLpDL9CE2EskBUFtDj2k8JycnuLq6snKsRNHaoW2VqcpcYzKZGnYGSe1zNGa9XluHIStB1RXlVHiS1CTHJmldCB+bzdaup0VBUr1SkGBN27ZYrzc22dz3aT3hdrmF/diIpchGDSlK5DmVCiiKAnlZQBrj1vd9COmhrCqUFeURNK0iYQW0Npk9TVOMJ1NDzxJUX2ZCkr5HR8eWdTAYtHbskPAMUZY4d6FpKgwGVHAyCksM44GlRnEEgc/Ny6LL/QlozHm+DymMI0YpSyHiMgc8z9tGgYSxBdpGoW1KC0543LFDSWttBYUYKLDxz+CCowgcueGIX5qmvbwSjujxwW0EYKmb7rrE44PfGc9PzungqBnnJrHDaN/mlFLavCgX7LzpeGug0RQlqJgaeQKVaiFajaYlz3wQeBiNhvBQo6wLlHmNJBnhaH6CX/ylX4EPH9/77p/A8wSEH6MogFESIQ4SE15OoQRQZBXaNkdVUBg1jEJAk54wUEErhdVy0xUPkcIUz4sgIG0xHs+j6t1ak0fe83yDzANMp1MkgwHCIMRkOoYMOqQ3HI0ozJkkWMyPkCTETZzN5/B8D2VRoCqpUvX1aonr5QqXV5/i+voa6/WaqnyuV1iZBKq2bdG0DXnMzObTNp0mfmO8FRRhkGh1aw19CPaU9pN3ePB29ITOQ8rAIIpiw/FrnMiGk1TvDH42dpgqoqnTAPQNPxeUSLN4Kd3lO2ilD1qqFjT0AEv/b/uGp+qQCDRcY82NHEhr0O1fo21a46XtRxmAe33wANALETIHsksG72gn/G/H9fZsG3tGtVKOp52M0PzTz1BNJkgfPYQfeDgdACcxELqRSPZyi67FHZjc69+u57poxD0Rizvf2o9a3Hvck83h/LFVVOX72Vbj9mqD/PkL6KZL9gZcD/7eZe4ABKfd9t26/1FkgT7rnlDYgEcfTEoR0GYgPGPwm2tIDZaxdXMJCIi7kYf+Nd2ISS96ImBzDPjvLgh1gQR/zX0GG5ExoIIikwq+T7kEfCJ5AMk5IUD5XFzbI44iRHGEKKJE5iAIMJ8vDF3BJEkPEjx95x0cLRbQWqNuGiRxTMVIVYujxQLb3dZo9dPmpZWCbrv1qjJJjrvtFlHcSZzOTfExrnAshMB6vbJ0Vt5Ql8ulrd3AGxeH8quqQjJMkGap9RIzh5nnI0t9sleXKTkXF5c2uZkNAt6c2fPO85Y/a5oGyshwlmWJxWKB5XKJs7Mzy9tneUqukty2rU2Qdmkal5eXFoQwZXe73eLk5MQaor4BJJxkybQMblsURdbgEEKYSASdy4b6wNQiODs7s7UVOOcwDENst1tr/LIBwYZvlmU2guAaIEwb4usIIfDo0SOkaWodYq4nliVe12sCMOyhHw6H1jMbBAEuLi7g+z4Wi0Wv2Bhfkw3r0Whkq1m7hXy5ZgUXq2PDi6s9397e2hwGV8YzNkYa/41ByGJxhPV6Y9WEGEAxPacoCnsfzotgoMwUp8vLS3z44YcWkLNKD6se8XMyGOXrsZHIkaTj42NLEWrbFovFAqvVCgAswAC6GhGcMMxjcDqd2pwaBppPHj/u7YlcRA6AfSc8Npm+xJEnNnKllJbOxuOWI1+j0cjOH6Yh8vvkczgxvjXz1Z1/SZJgu93a8/n7DIDZEGfqF0d62OnAKmGc88A1SdhI5rWU92U/CBAFoY0esBoo50YIKXrSx3xv3/MQBKHNJWJFKI7UuRLGLF3MEQCm1rnRKv6XHOy+fWeuTcF0w8FgYAUU+FmYWsj0Jfdgu4PXDabfuTQ/HnM8N5mKxvnJ/Iy8T3H0it+1a3se2sfvO94aaIhWoKlqKEmVk4uKNgTpSZRFAd9LUOYptlWOIJBomhJNmWE4PEYcJfjFf/mXcPrgGB9//DE0gJPTDK9fvEKapri9vQVEC0oWVlSwzpdQqkHbCKtWBdDmfXTyADBUAX7Y05NTHB0d4fToGNL3EZvB3BpDT0jSMx8Mh/CDAEorrJZLpFmGXbrBZrtBURS4ulnhe9//mPiBrUJVaVxfXVP4vWmQG45k3bbITVivtUnSZEC0bd8wJoNBmMiJMZBA3OvGeOVhKAhU40GjVgpCC+vY1qrz3roTqDO42ZvJ5wNkJwkwjcqdCLSgcDIov2UO1VG0w777PeNw35NvjX/je3fBw773372m+7MLIHhgM5hxr7FPY+HJ6UZqmIrCEY1e2++0pW++8yLstona01ni7oLMfdCBkb60p0EnvfYKCDSrNbabDaLjY7w8OcHr1MPQV3gyFhgFTpTlzlzW0G7fgf32LsToud7tGYeQhLbYsLuXvnOeE85wgYn5e9ECmwp4udModjmKq2u0600Xadh7Z2/KJeieiv7t6klwrkKnviSlIRWJ7vlshGCv36QILZDmyIHWulNvUwpSdm2x80mwJ0jY70HARrv2gbIQwnrABLfNgwXLnk8AgalerJokTA2HOI6RDBKEQWjXvMXRFHEcWgpSGAaYTKfwPR/D0dCsP0zj9DCbzRDHkaEJEBhnR0UUkVofSK8NZVFiPBoaeekCQrSYL8Yo6wzz+Rifff45zs7OaPMCsF7eIgh8RFFs802i2EfTVNYg48RaTuBlQ4QlLwHi1fMmz3KocRxbvfgsyyjhVpORyTz8Z8+e2Q13kAxwfU1F4Zh6MBgMLPff8zzLmWYvJnsJmabA0QmtNUJHv57fK3v7Li8vezQYNrafP3+Ok5MTrFYrnJ+fW4nXoiBZdPaWn5ycYL1e2yg5v1uixtRW8pSNFpZBrWsqnMdKh/xc/P3pdIrr62tcXV1Znv1isUCapnj58iWm06kFL8Ph0CZJs4eZgV7btthut9bbutls7GfbLRV65RwDrbU13tmzz/kRLkhhwMMRBymlzeNgUMrecealsxHGOQs8LtI0JSl0p64HR5eEIDVINpA4gT6KItSmTUxZA2DBrJ2vUmI0GmG73VqvLY8xN2JCETEPRZFjYiqQuzmgvA+4yliTyQRaa4xGI2uAusnLDGqEEDZKprW2fZKmGaqqxsnJiU1OZq810BWqY6oLU5TatrXJ51bBsu3k+/k6nEvjviPe/ziBmN8HjwkAFuy4XnuAwBDPf1rXOnlVtkG01taIdgUH3GRszk/giA8b4/zOmMokhLCOT+5zN1LAzoEwCJBEse0zHldFUcAzbYpj+pwNdaJAdZRVHiMALBBhlTV2UNjvya4mBb8jjiCwjcLzhdvOn3M/8PU44sXPxOusu49SBKexzg6+r/ue2P4bDoc2MZ+dOvwO3RwtBiq8RvJ9XHbI3b378PH2ORogznXbNJZ3WlUVojjCbHEECI0kDhGGPjbrJeqKFvU8XaKudqjbFo/ffYgn7z2CAMksFlmBMAzQKoU8y0workFelJAiQDwcWo7N//m//r8DxQbjyQT/i//l/5peUtMgTTMqRFfV2KzXKLIMVdvi8sUlbm9vcX19je12i/U2RZplaNvGem7oBUooIdG0LVX0dpSKqPNb9IxRNhqFRKPZSO+/cCv/KSgwwF5t5q1r3VojtDVeVM/kDXSTiRJGyTAmMCLNggbADpq2baE0S0t2EY0OkJCyCicU8QJLizwj/BZtS3kY2jRUHDA3qV3ijqHICzNFYToLjycQ/+z20b4Bei8QEf1cD0bjfPQBl3NN3clkumCIr6XugBa6v+v5ccOd+0XCDqF519i0bbpzVhfNQatRXlyiur5BcDRHGcfYVTOMIuA4Bo5iGkM92x4wIFDwY/Y+7T+RMcztiDwMOvrVBrT9a+9qPIAdzFG2wPOtxm3WolquUN/cQhVdchn2DPBDhzsmu+jcYflhyZWq+XpOPYlDY0KITjI1MAog9G5as3FxXYc+ILZODfO4SimSq9YKUvpEZwSHlsnA8H1JPGYh4ElpPUHn5w+sV/nBwzN4nsDR4ggA1XA4Pzs3SnA1smyHBw8eWOO48+r60KBKuFxjgY3SLMuRpRkV+jLGgRSkznR9dYXBYGgjsZ7noZFA21SIB6Sckxc5IFoMkgEgWoSRj/WaDP8wDHB6eoLtdmM92cPhwGzKHMHwDIgobRKpq+bDhhbPQd482eBno9zdHPncpm4gJFGrFosFhBAYj8eYzWaYDCd49eoVptOp5SELQTWHuLAbQJv7ixcvcHJyYtQBF/jss88wn8+tEcbnrQxlhw1qBi8kDELUII4C8HlM+2K6UJIktjCZlNLmZmRZhpOTE+utrYw6EUcQ2OhjYFPXtVVQWiwW1vhigMT99Pr1a+s9ZZrb9fW1NTQ5mZnpPACs4c30iiiKbP0Gz/NwdXVlwcxisbAe+jzPcXR0ZA1jVshyVYaYVsXGI9ej4gRsrqg9Ho97iaYc2eB3xwngnHDuelDZ0GQPMRvE/M44GTjPc6TmHbPnmAHHer1CUVTWKOSEbVZUkmYOl2WJ7XZrDa+rqyv4vrTrzWq1spz53W5n62jN53NcXV1hNBrZXBw3KXvfEGSD2XUk0trkIQhgDW9XsCQIAgts3Yip53nwI2mjVQwUuF9YhjhJqFjwjaGI8ZrLSkMsZexGA1lViyl5YRja6JUbiWBxBs6HYeDBxiyDB7ZjGKjx2LGMFef98rrMBjUDVc6d4M94Hef9v2kalMrkZgWBvRbT9ZRxmLtAlylVYRAAiqReA6N059ac4Eght9ONyPDe5io2uZEoBgs8R9nI5+u5krpMWeO5YVWiHI+a2x5uA48NNxmcqZ77c4o/53nAz8NRFRZzYMEBjp69zfHWQCMZT5AaZYamaeBHMQKzqGZVhSxLMZ4MEIUDDOIZXr14jmybIU1fYnZ8jPF8jqql5MSqyFHmJZarNdI0xS5NCSQUBallKIFtWlq0d3t7i0KTNyLNcvzm/+nv2IG43Wzx0fc/osWuLNDUlW0zd5yUEq31jAtwInLbmmqqQgAgQx0NgwWiiLm2Tt97rm1ugE2kdg1AUOIzqWS5xatM4EaAjHlJWvLgRGn6MmEa4RqAJsJj+oQ3Uik9NK2G1o29fuflhbku56S0tj8AmAnDnmBWyqEGeLIfaeD2u+E53txdQ2I/6tAzug8Yj9yvfWOziyQcaoNLP+Gf+Zm6c/v0st79nPt2R3fP/bBg5wW/v5L4/tEBHv3l52qN5pqKKpUvXiIbDnE7myKejrAY+jgbCvgCCHqsIt37h59B926j757SAxL7h+5/g8MdTvRCaaBSwPOtwu2uQX55hfpmCW3G5T6w4L7c19t2+8OlvlGSdjcW+4Xm3HEge5trdy3Ka3D/JsBJljQ/NBQ8T8DXlLxN+VF0nSAMKC9CUEFrz/cwHo8Brakmw9ERIAQWx0do2xbvf/A+VssVRuMRPvzwQ0BpDJIEdVWjbmqcn5/bBTkMA+Q50ViYRvHd730P89kccRJDSoowkDa9QF22GAyHKPIS0+kEnhBY3tzQODEc4/FwDF96UMZAujZqM1EUYWzoDbptkRkvvO95BBIKWl+Pj4+JslSVDjVnDCkkXr54ZakZR0cnqMoS6XZjFIcqE63gRODIFnZbrVa2vgEbC9Pp1EY22KN8fHxsFYF4PPBmzEbHbD6zm+D19TVOTk7shssGOHv8WAXHdaoIISynfrvdwvd9Uxh2ZGkITMFRSuHm5sbWN9hut9aQ+8pXvoLPPvsMn376qU2G5MTSNE1xcnICrXWP8uTWbHCNtO12S2qCLeco+rZQGgBr7LJ31qVmsLHKBgwbqQzcWPWQPcGz2cx6dTlaIaW0kSD2brrGBEcHODLBHv+zszM7ltfrtd0DLi4urNgJG8JZltnf2RBlWgsbUG4UiqMBHF0BurWYox6uk4nfCxusrBo1nU57dJt33nnHgihWKmIJ1O02tcY+U+1Yfp9pd2wQdp73GlXVWgN5s9n0AOR0OrVj+ejoCJvNxkZh+N7cR9yv7nhkw3kymfQKGrIH36XssMHtGsZCkDM0Dqm9POfqurbAmoEnc/g58sjziClIQoge6Ha99oPBoEf/YjDJY7RpqPK75/totbI5N27iOkdf3AKJACwgZmOW7Ss2anmv4P5kEMZRGqYWsgHPiljcVp5jgKlx4ZF4EI83Ho8cnRvElAvBFE63BoerOMX94NarYIDm0qM4oupGwtyq4XzdpmlsXRs3CufStN3DVYJy9112AKzXaws4+Z1ybgjPIwYqfA9ea7idbHvyWDnUjkPHWwONME7ghaH1mDUNLaYKGoHnYRREyAqFpqhQ5Tmev1jhP/9P/z5uri6QTMYIhyNkZYXdNkW63iHNcmRlje1uh6ZujARehPfffx8PHr2LvCbjNc/ogZqnCvCBplH4/MWVDeFlNeBFY6x3N2iVhNIdr14IH8ITaDR7fkkxSnhGY1oqoiTpBlLAVKKmWg3UiYB2eNpaaHiBB99MZmgaXKrtdImFEB2AsAarQ/3RGkKx0Q1IrY133dzLJqabm1rwgF4SbReCUwAkPK+LcFhaiEe660rBLCBGRlawxerB9zqd7c6wB7RqAHRhMp5IfH37PKKLcGijKuaCj/2EokMGt8tld6MPUhL/fP/c7hx9pw0W2HQpHnvGKiCFCyQ6mpILbPbBTXcuDvy9D4Dui87sgy4+eucrjXa7Q7vdoXgObJIYr05P4AU+xuME50OJyAMGAe4c4iDV6kc57kZ4WgWkNbCtgFWhUKcZNqsdquUKuqwghTCJyx1Nzfaf05f7UTB3XLCxZIGG7ue7dP3H9+DImuiNB5Y0ZmBo+1gA0+kISRIBQmM4TAChMRoNMR5M4UkPx8fHaNsW7733nvFea0xGA5RVhfPzc2xNfYLpZIr1ZoVGNca46ucWaKXhe/Sep7MpgBp5zrSEAHm+gVIKV9dkUJ2fLbBLd7h5/hpPn74DzwOGw8RsPC3S3ZqSMZXGdDpBkReI4wS+5yMMI0ADi/kRvv/972M+nyEKI3jSw3azs4XctNYYDkYmKTJCmu7ghT6m0zmiMMTNNUUe8nxDeWx+bIqIsYcXuLlewfckBoMRyrKA1oBSAoMBVeB9/fo15vNuU+WxwJsuqwgxXcQ6kAz1hg0CAFYHPxkmIBW71hqHzMnOdhmisCs25xadA0g+k89laUn2op+cnOD58+d49OiR9VKyJ+/Ro0fI8xy3t7do2xaTyQSTyQTX19fwfR/j8Rie52G1Wlmv6tHRkTVk8zy3uv1sHHNxOzbekiRB6wAILljHgCPPc4zHYyjVFXBjb+J4PLaGYZIkFtixUcBRH9bmZ2OC3wmfM5/PoTXlybCxtlgsejWm2GvOEbnb21vc3NxgPp9blUWmtDGQcusQcO6Na6zw72yUMZ2OPcJuZW+35hUAGzUBYMc1F1RjCU+mqHE/145xx21lGt3x8bGNnPBYdWtqscee6XJc06GqyBPNFDSW72Wwk2WZlRp98OCBdQ6yaldd1za6o5Syf+eIgxvp4THCINbzvF6tjMlkYo1wzglRbQvd0t67WCys0e3mCnAiO0dUXCckUxG5z3kfZ7oTRw9cEMg2l2vIa012UORH1ivvqilxToxrY7jX2263VP/CcY4yaHDpdxxFYSOa823cHEuyvbq9hx0EvNPlLNVrxiob+tIAorque84J3p8Y4AOw6wFTD/kcBnncNikl5vO5rbHCbeQ+YHohR0zZacHvkNsTBEFHkxZd7Sh+z0zvYqcPr70uYGewx2OM11BuB9+H1yCOhPGeOx6P71gRh463Bhq/9998C7u8QF0r5GWFdJthu9lgt02R15S7UFUlsl2K5c0N1qs1snQHDxpV20L6PoSgOgwSJDfIKkpklARIswbf++gTXC8LPHz6HoSQaJQwG1tnQRVliSzPISTVrYgHA0R5ju16CSk9k8hMUokSBhEbGVVPUpK19ZpoBSrt0BmfzD3WSlmvuRREJuKIAcvdSsk5GEZaVgFURJDyH6SGBQoU6uoiFWwwCQ/WKJO686zTPWHaCduH2oT6yMjS8IQPPwjtIsODQHoeYNrFURKllFHF6bjqfLAhx/QrpRqilGltWDPmX5MArhhICfIa8zNQRMgBNEJCOmCJDXu+po0ECeONdjINGFwJbhfIqKXrdwnuzIfntkJIozQkHOBopDp5UvZAj4DnBQCMrLHjxad73J0T96F5lzLG97B3Et1zcY0R4fSbewgN6KxA/ukXEFJgKyVujhYQvo/I05BxAmk8ToMAmIYsiaqxiJ0kaeeyjQKWJf1hGAgMeAUQdOKyBJpW4yrXKNIcTZqhTEvU6w2121AMOXbHScm8UFnQyQnYDtDowAQpNUlPEl1RCPg+FbPkuhZK6Tvf9X1hchl8KyvNMplhSAvg0WIBzyfD4d+PnyPFDuPxCP/b/83/ClFEi7ZGiwEbR3mXYOt5HlbrNaApwbaqiLZxeXmJmTHamrbEaDRAVZeIQh95RpuCDnzUdYPpfIqr6ysUZYGqKuEHPvIsx2w+Q7UrERkDcbPZQLWU1TSbzuH7ITzfR2a8efM5efm3uy2g6ZnLqsZgSAWqWkUJ3FJ62O62CKOQ+k50joq6rlAU0so0qqKF9CTqpqFckaZFpSsqaCc9LKYk+Xjx6gVm8znisEvoLcsSTUteSjYwmXbj8rJ5M2YDwpUrnUwmVt99MBhgu93i9PTUbmpFUfQSYZumQZql1rgeD8fWAIijTrlFm/e1Wq0sJcpV+WHwwbWOmN4EdJQBBsZt0yDwfQxN3QUhBJq6RlPXCIMA6W6HaDjEII6Nmg/RK4o8J8pcEEArhcrJp/A9D4lRqIHWSLMMgYnKnJycWLoNq8GwV5VpPlVVWTpdVVV49eqVNWzZwGLlo91uZ+kubAAppawh7kblpZR3jG3mbXMUAugqX3MitkuRY8OEQSSDRY6gMP2JIxqe50NAoqlb1FWDJKbk8diIl5SSnt/3AgwSz8qlboyEbxIPrEe/bVt7HU/6qKsGV1c3aA0dRrUaWgokycDe2/N8NA1RhYWmUrCTyYT6zPNRl6SaJH3PGqyc9L7dbnF+fm6iDD7KssZ2uzNrvo8kGUCIEoPBEFSM0bdGI0VEPDQNieoAEtPpDGEYmXeu4PshKBKvURhJ3SgKzb1oDDMIYXDBNDaORh4fH9t9TmuFNM8A2anSaeJgo6pqrDYbUp2rW9StoYgboCOltPNOSsk7NvKyQBTT3OIcnUZR7lfT1GiNTcfvXEFDGmDATgg2mHmeM4ACYOuL8NiqqsrmCjFVigE9zxemufGa07atrdvC4E1rDeF5UJry8pRWqJqurkxrQI7rFON73SyXKMuCZPHN7i2lh9CTkBC4urrCdDq1lC9WAON5x7kfPC9Go5FVsuPndj9n6V1eP3k9YMOfo0f7zkoeFxwdZaDKRS83m42NmPFc5+gwU1iZxsmRNE4i59owfC12EPAa82WH0G8Z+/if/U/+5/js2Uu08KG0Byl8CEUvDcJDXpLet9KNQYQFGeJCk+Z5TfUshHn4uqnRqC4DPo4iAiFSIoqH8ILYDhohBL79K38fdVIAGvCLiHu358A9SE5xqOYHH5WN5P2v2XP377B3Dd398Ka2/Jkcze51D0QEDrbrDlufQcuXtIT7a69vuw8PfMX5Mwd73nR82Tlvc40vu/6h0eACDT7UoCWmjgJEKu98x/k29vv0x3H0+u4NV3+7fhX3TIIftU1vHxkRvR/ugqo75+5FgQRgjTz+nQxmogWauBVtlAY0ApSvxEDWAmB0uUlaa6yaFRQUJCSOwgVFDp2MFetJIsTfRd505x3g8ULRCmWBsAsMe+DVtA1CdLlZgHFwuFFOAFrbSJClmjEAdtrAjgGmWXINEmnEHNzze9FG0992zXDmNPe1ne72Pia3yfOc3LK+JLFt616Uku+pdKeaxde2eS6qU7dh+Wvrhd0fXKZtwnG42DFknRPm/sZY8KQHS3EUndOmCxDTtaSUXZ+Z5+T3Bq2d7qcaI2477otIskMKZlyxsWDvuz+BTb+yQ0nuPad2zqNnM44gxzkB570JSc6xXu+Jbkyx04znW28cOvfe73/7zO7zmuv1FiYLcsWd73If9J+/P2e773VzunPYdp5bXsd7ioe8ttv5AMMqgO3J/Xa4a8H+4Z7rglGWpHav40zVnvKiMO1w12Q3ot17btteN7JOcth8fUsHtO3en8F3n8kdx+62yO3k811HnLueHnxvdw7DgthbD/fHu9tPd64ghL33nfHC44TnOzpnZnee2Smc981tw953uzPcftqjfDttcfuo/znsfGOnpl0L9s7fb9L+uW6/de/Adbn2etK+9dt6CQWF4/AY/+Ev/F/BkQyOILoMFAYZrpob0NG7GHQAsOCNKVWuwpUQXS6xUgq//ht/FV92vHVE42/+rb+F/8t/8PdwtdyhrICybNDWFbQQqNsGMgyp/oPwzeLWIBkOUJUFhEeNYplXYRKsFQQgPfK8ByE80GJbNg3aYtujV9j3JIAmKe9p5b84/ts+3sY+/bJz/qwm/Ju+f+9nEtDjuxXB3/7Kf/bjT9Xu3jn/bNt3+J53f/tn0gq19++P9FWFq+r6x9OO9sdzmf+/P94ux+9HOw713T/P/fnj7sN/nvvqXxz/4vgXx5/+0LCJ5UxDdJPsGbxyNJIjGkxXcx1gTG3jaDYnhjMg4QgI0DGDvux4a6DxtZ/4Kr7y1Q9x+0//BJEfw4sogdnzBMI4gtYKVUUhQOlJ3NxcQ7UtIpNLETa1yRHoekap1hakY/UHQFMSZBL2vEBhlfS8cGCPB9D3ethztP3IeuV03xNpUTK3SGscRsXd7e4AcsHequ4kvrqLnrlNh1Bz72KMYa2jyMG01qXktGXfSdS5wfZb6vbGnfP7HvP97+7/7lyn1yn967vXdtu9f6X+M9xtY/8+97hEtD5wnXsOx1ujh8pGNGTm9by+P55jf9S85dXvOe3QaHnT4XT9Pd3T76fuz53Hkr20TCkUgihTbtiXa0cICEtdunNd0XFR3fb3PWadN409fZ2Hre/RZs+sdZU57xUAlsbbIyGxCBd3vJTs6bUeRBjPlvF2u1Swtm276AMcL++ei67nrVTKfke1raWFtUyLdCMagKUi2qiC7BeA5AnFRTXZC0j0zz1vu/scXeNoo7D0SWH7g9+DK+rgetg7j7aw6yZHLPgduPky7F137+3ex+1HAL16M3ciJ05brde8Gy10bxPx4g9sJMF2m7MuOeOoN4eccWQ957312kQT+Bp7kSTb79xvvcgYbCQAzr/K9LNyog52XJvGauu5pztzG/i+NtrmUOcovw22hoFw+s2+h73+OPSv7Zpe+2iftu9n/zzuL9fT7NyPx1CvPZrb5cz//bHmeL3pKu5Oz2NUuDfq/u70J4uzcESQd1i7J+xFjNz+c+/Bv+8rG/af3/mdv8fRhAPX7Le7P1zua1vvOc16wPfT6Gpy7a+P7j2676ObA3A+BNtHd59r/9h/b4cigO77YC8+eu1w+sM5Zz/Sdfdnd+R2P7v70d32d+f17MHec99d6zv7Th/+m2tP7Uc3hNMObWzOA/3Qu65w+mbv4Rfh3ObzMCAQoiu6yaCBWUJu3RMuPMj7eRiG0JqS9LnuDvcbRzf4Xq7U8puOt1edij38xNc/xD/99kdoGgCeB+EBSrdIsxwQhJCauoFqGwSm2E8cUmGdJIot94+k0AokSQQuK9+2CmFISY9JAnha9h7+F/7or9sX2KpOP9lNfhYghNY2NSA02rZG3ZQ0b+oKytEtZtTWNA08QYs580tZx5iuqUgz30F8Xfid+OlM6yD1mm6xdfl+UlJRLb4OIU7PJjr6vgcIiVZp+H6XHGvlbmk8WjDG96Z2dEX03JL2SimEPg0E5jK6WtRAl4DNoTRaNFsre7sf8udncikQ7t9chNslies717hj9Nnf+Wlh2+ce+9/j7+4v9K6RuH8N91j+m6+gxi1k5mHx7z2E1n3JOLe9h6h3bru17n6/b0Po0U50V0fBvdahhdlKCEuBtm0gvX6/dTkSHrQitSRtxhKNtwBSgqpNC4kwCm0yYxzHOFocYTabwvcDnJ+fIQojvP/B+xBCIEkiJEmMIAjhBz6aujb1GApEQQDPKPkIkMOgKEv4vsRgPLDjjhNh4zhGHEVY3pD09IMHD6xKSNu2SJIYu90WSTJAHEeWJ0+8+wHaljioLM3IfeXq0bPX5l//vb+B2+YWc3+Gv/Oz/77tQy4Ux2Fkfk8spclFxTyPalKs12v7DFzETGtN9X/MM3seJZRLkzeWZZlNbGTN8tlsZqsscy6BECTfenFxgZkpdMf8V9/3sVqtbCIpc5brurZ1KrTWNieBi4ZpTdV1p9OpLZrHUpXT6RTz+RzX19cYDqlyN8uxHh8fWw4wa+mzAhJznXmN4YJZ3E+cx8EHq/TkeW6/41bJ5mRbXpM4QZU3vqurKzx48MAmzroSsMw11lpbFSpOwGXlKe73jvKibOItr3fr9dqqbvHc5DWsaRpkWYbNZmPPobmQ2HHEGzfnRHDBNi7WlqaplT2dzWZ2LmdZBgCWY8735c2fxwsnDnMeDOcK8HtylZp4rPJ3uNAcqzq5CdU8RtlLyfkgbJRsNht73/F4bIuqsceUP+Pv87zmOcjJym5dAlYAKvISnufb98fJ7FzFnBPLeV64SlEArKEjhOgV13PnML97ISVa3S90y5W8ozCE0LC1HDgJO89zlFWFxTFJULNnl9f/pmmskhjTVKjeRdpLvHc9wPx+XI+z1trmEfCYc41Bd/yy0hHXOWFP9Gq1smshq16xshQrVeV5jtFoZHOleOyzjcP2WFEU5IgQtI/P5/OejCyJ6MjeGGAlQa21zavQWtucLLd2Dvc/P4/WGkdHR7YmDXvfOX/Dc0Azv3eeEywuwQpvvNdzvhKvX7xmczIz7w18/66Y6BqeRzVy+D27QjZCdAVB+f01TYMwCOCJrtAlJ26zbDSvQzwfue85id21xXgd5HfCY4BFE3it5/7n/uRndPOu2G7mpHk+z60fwvsIr3OcJ8Nzjdc6HoO8H3BCuJtD8jbHWwMNTzR4751HOD06wuvrFFpRRKIsc/heRMZN6KE02vSBF6CsSmjPxyAeQEjSRfd8etGekBCaEulqVEgSAiKUC015HTxwyrLs5LQEF5UDqrq24IHAACWU+qbYnwZ5EcsyB+oKnpDWUOAXUtc1st2mx2vjl88eKCEEWrOoc0hKGwgqpW+Sp5VJUjX5I1AWCDHqC4IAlUGDQnQvnhOZpOejdCTclFIIIlqMtGoQx4FNhlS1gmoV0dXQTWDefHiCtnVXwMdV/nG9hjyAuoktzCRzPE26U7Kif1nat6tZIATg+3frGfT6E53h3zfcGQzsG+Z362+47e5+7nsqhBlHwF5y9pccwngCbfs0eROENJ6ovf7reS5cT4Tot5E8xLL7jjldoDvHfUc8Rt13SgtVCJJk7pQieJOnDUbi4cMH8D0fURzh5OQEjx8/xmg0QhRRAudoPMZ8NqNCaVJgNBxhYuQp87wwRlOCqqyQZhk2mzW0ahH4Em1To21qbIqcFkIt0ZQ1qHK1ZyUAq7pBUJPhxAnA/CxaAbPZAnXd4uL1JXw/wGQ6gZQ+pPTh+yF8P8B6vUXbaoRhgChKTGIabXyvXr2ClCTfOJvNbDIeJ7iZTrfvnw1iXihZQnI0GuHZs2c4Pj7GeDzGzc2NVTjihEvWq3cT5VhFyPM8TKdTZFlmi5oxMGA1IzaKuJBc0zRYrVaI49iqxjx8+NAWaeJn4EV/MBhYgwVAT9Y1CALMZjM7/3mTY8DBgIATKnkt5SqvXGyO28UGLD8/JyO2bWsThDkRl/9lRRMppZWHzbLMSp7ymOaidKPRCMvl0o5dBnBAl7B9fHxs5wVXxa7rGpeXlzg6OrLvZrPZ9DZFAFbBiQ1YALZyNq/F3Fer1apXzAqAVazh8cEgjj15rhyr7/tW3Yn3Je4XBg0kB0wF9z7//HN89atftQYyV8Ner9c95ZyqqnB0dGSNSTZWuXjfaDTCxcWFVUXi5HAu1seGhbvP8XrEcq1slLMxw4YuPx/Q1SXgfmNAx+sVG30MEhmks1HIibgMgMIgsupRPC+5f7gtaZpaY4+VlNgpwm1io5GNf05K5edsmoaccL5nE2nd7x4fn2C7Xttxzn0exzF8oxzEqldsVLEymvs3vp4QwvYpPxsLI/A9uL/Y+GfAxOsDywbzGGQjktdNXufZZuA5w5LGNzc3iOPYOhfcCta8fzPAYyDKSdvj8Rh1VSHwunnA76aqKownE7S6A9WstOf2iZtozO+L3zGvK0II24Ysy3rjjPuH3wPQOULdg8eKm4hsAZHqqoi7TgaXJsSSxbwvs/OBxypf381xYJDANlBZloCiCBDfjx0wWmtbp4bHrwtgOILgPhe323V8uXYbt4/fPz8L262sxsUAhoE5v0dXXp7BgavOxVEM3mbcnWkAAQAASURBVONcWXIGpW6yPPf9jz2iAVXieDHBz/zUn8P/67e+BdEoLNcZfF8g9EMAGtkugzbysFAkJ6bMwFGtsslbaZqiqWuopoYGEPg+tOnsMCAd+7qu4PsBdruteSlkcGghECcDCCExDnyLXJumhSdDSOlDSAXPA7Jsi6rOsVwaBGgmOw8yNwGRO5q9P/yygog2/bqqIaQpymLDWBJBwItfC60U/ICjHzRBmpZePrQpNNO2kCZR0A275nkO6QdoTIiaZdWKskRdVVBthcwDml6Eg+kRBAhcnWmeRFJ6tsYB0Kn+MFLng392pSltMhr9wfGeC6vGwdEdYQZujxojusrObkRAeh6NBwuILAmjC81z09SeslXv2t0EltLbex6HPiEE+hK3DsBxcA29k34omZ7XAAT5pohGF2HhRWM/csOhaSGEqcGyF6rVHWDlhWM0GtmCZev1CvP5Au+99wRn56eYzaa4vV3i8ePHiOPY6L+nGAwT+24mkwmpA4UhwijE5cUFRuMxyrLAcBQb74rA7e0VsnQD32xAm01hC2JOJxPqXwjsNlStOYpIWlVK0pJnb+xkMkFVVZjOplgbz6gUHgaDIeIoxnqzgVAldtsMUThAsKBFvq5aCKEhUKKqGiiVo65b+/zkzUuQ50u7QPJn6/XaKpIsl8uuLoPoonZssD9//tx6o5fLpQUHr1+/xnQ6xWw2w+3trZXmzLLMFqVi71ueU2VgNtbrusZ0OsV4PMann36K+XxuFUt4wefIkVJd5eCmaWyxLA5Ps9HDY3c6ndqo0P+Xuj/rtWRb0/Owd0Q3m9WvzN2dpjpSAkwYJimzMSmJpCBZv8Sw4X9gwP4h9o18ZV1Zl76RbZoUi63YFQtqYLHIUlWdc/bZmbn62UU3fDHiGfHG3IfcWUAZhieQyMy15owZMcbXvN/7NcOZVDIcAD/A2W630+3tbWZKYRqZTQ+LCrO3WqXTxgkIj8djzvaQeQFASJoPipqcKUwuMn59fZ2dF7W9Pucf9hTmms8C0DjD4PLyUi8vL7q6usqyxWQwQCZr+vb2ppeXF7179y5/5+FwyNOtGBHLaNCmafLewRTC/HkwCfPI+vJzWFVnrXkWgMj5YWIhpMlAv/mbv6kYY57ist/vMwjmJHFsEWcgME8fdpE95QTsGGN+L1mY29vbzIJLys9Ppqlt2+zr2BPOUuDFM/q0IMAz4INAjM8dDocsp6wBbPswDNpebHU6znP9kRsmW/F/5EPSQo94Bs4MAUASCAMC+e7dcT6TgaCgrms9PT1q7BOD7BmfcRy1rSq1xuo6uGa8KxlaRt9yX56BKMsyB518L0EVwQGyMY7pwMB0b08ZQLK2BI1pDPUhZ5l8bC2yAHmRKz3CfCgiWTfkkeComjAY647+gE9eXl40as7C+HQx95+e5fBpb+wtJIpndVgD7AQjiGHcsWVkBghc2YN3797l90DU8N2sCUGdj5jebreZjCDIIJjjGTzoAmxDJI39kMkYgj8/c+U8i8s9IyvYm/PqCwIG9pbzSyB0sAPoBtlFMpVzdUORgyD0mcAN8op1w89xD27nwDJ13SidI9Nm/+GY69/2+uxA49AdVVSX+nf/nV/Tf/Xb/0Dt/qA6FBq6Xi9vHzQMM8jdDb0Uo06ng566o5icQCd93w8pTVckgH88vKiukhFv+6PaNm3QYQIURVGk6VXdoBhLNZtLXd7caHN1JdWl6u1aQ4wqx0JVKHU8HvT8/KSx2qqq17pvrhRPb3p++KjT4ZhGwcaoIaZRtEMIKqp0CucopTFmsVDV1KqrSuvVSlVZ5Uo+SoqGcVDfprMjBsZ+xmS8TseTglJgctwnJmyYnA5HQ8CGl9XkpI6nXC9alIUUpWEcVJWVxqLUcegVY5q8gzAFBRVBCnFUrlo1cDtEKZR1qgOe9qEo0+ScopiAbzGfdArcH4cE1MYxjbGtmmYKckZVYdSpXx7kUld1yi4pleYkMJ0+W5bpALRh6GYAHnppiDlACaVD7jkjE+pSpWpFRY3DOAcdRZHGv8bv105KUoxBRajy9w3jkLITRZA0fi8DImlSnlIctIiiZoMdp2k8FiCm3485wE6Zi5AOKoJRHEfVVaV6Kg28urrS9mKrd/e3Kkppu9lqtV4pjlG//hu/nseFXlwkcL5ar3R7e6sPHz5oHEddXV/peDpm5304HCfJTGNbC6VgXEoZrXWdjO2njw8qinT+wunY6vrqVp/aTxoG6e4+jcYsVWi3P+p0Oury8kpVnUpMrq6vdWpPWm8TIF41jRTmU1AdDGy3W72+vKo9nnRqW61XK8Uh6vkppaiLslDTVOqHVnWVyh822wRaj6fEjl5dXeUgCTaJ05YJNMgMbDYb9cOgru8VikI7K6lCD7bbrY7Ho25vbzPwfHx8zEE+Rvfp6SkbbhwWjh3QgRM4HA75PALAF2cmDEM66K6qqgwCMd4EC6TWkT13dKSqx3HMpxK7zBVFkQ/TKopCX3zxRT4rgLQ7AUkIaSY9jmoYhgxuWUtJOUAhmOA0aC/ncHDAv3HmdV3nUjdADSMZcdIw/JyiDNAnU0BJF5knDjNjLbbbreq6zpmzrut0O2XnfOY/+0VJFo4Zpv94PC4OsGJPADg4fFhR9gug6IDdD1NDNtJhfZdSLNRsGj09PWrVbNTUaQTs0M+TXpwdT4FJr6qqdXWZDp87tScd9qfJz0S1p27Su5XGIU7AOh3QeDgcdHlxrdOx02F/1MXFpYKkrh10eXedgqN+lOKooR8nX9to1azVd6nPErls217DEFMlwrpWXTWKUWrqOo+Vffj0mMoh19vpOo12u52urq4n/zaoadbavb3p8upKQz8/J1kd5AhZQy4BjrC3yBUyDIs8SirrWrvDXtuLC623G+0PB526Tve3t2k9Q6FmvZkC8XSa/H446tCeNCit4Xq1TmPzg1QVpYZxUF3Vuru+kaYg+ttvv833R/CHbCBzZK8AiWQfySAw2pnSL0qAYPPJhpA1RfeLosj6BYAk0HIwSeDg7D1+cLPZ6OPHj4uRsgRn6/U6TQ8tSw0TATgo5vVEL96/f59PRPeyL74T+Yc0oWxO0vd8J6VsVVVlm4QtRp9d/8gsYv+HYcjlkjw/gRIZCTJ16DP7gq8ikPRAxLMhBNxFUWi322WbNyionAI87IqkPOqZPfXyMGwy60DZJ3tJmRR4zEvJGAEOKUXZntsvgjrkIwVllLMXudJjGKK6rs8EbXr+6fDaCYXGmM7L44y2FEStpalNoOuGTLT/0OuzA40hSrE/abUqVRWj2tNebT9ojKNOx5TSJxLiAQ/7nfp2n8EBUTZK07e9+i7Vl3XtPCdaCmrbBPZOx30GDSEUauq1Xl8KjWFUuVmlMbj9oFCVKqt0zkSoKl1c3+ji+maqTX7TaeikotKpH1TGqCLG6bC+qD6Ok2KlDAINUUUR1PfdBFxGcSAYjEAxNcRmcB+C4mnqU5gOyeuOpwnwpD/Nek2LlKqyyk42rXFUOiAw5rXY1I1CkMr2mEd6jjEBFjJE6RiOub5/zFkCTQGFVJVpDHF6T/p/+t6lUhVFMTWUpV6FdLJnAvd1XWkcBoU4xWIhNQUHpbGSqtJpy/MozqhVXU1OPqqYAqhxjCpCVFXXU2ProK5vc6mLHyxYFXUS+yiFMs3zZsyjxtQnI6UsS1KOmGUwfe/EfoYqy2g6KX3uhZGUg8KcTYlzCVMIqW+lLqfUYVnm7yuKoLqu9P79O93f3ymdkNzo/Rdf6O31Vb/2az/V9VTakBivQZtNmkd9d3+rrjulnosJHAGCcGTJ2Yz69luMVdDT04Oa1Up9303g7jGnqvsYVVeVmjqBwt1+l8t4hjGlRp8enyf246Cf/vTX0oFmY5RCodV6k8szYoxq21eNVvqAkTxMzhQju92mefiwlC8vL7q5ucllJ8fjUZfT6csc0LYqmmwPhmHQl19+ocfHR717906HwyGDVNaG7yqKdMjZH/3RH+ndu3c5wLm4vNTv//7vq+97/ak/9adysArnhsF/fHzUr/3ar2U7hYMnXc6Mdk6LpowFthYQjDzxPHd3d5nxu7+/z+dM0I9BnT4st6QM8skGfPr0KTPd6/VaNzc3uXYXRwar3Latbm5udDgccjnG7e1tXiv6MgjcxnHUd999l4EAgAUQwDM9Pj5mpwXrxrr7/Hb27vHxMTOjIQS9vLxkB04ZBJkfnPkwDLq9vc0OEQfrzYmeoV2tVvr06VP+HI6b/aHEg6CI0hHY7d1ul9l3mEbK7QCssPw+lYW9Qk4414Kf397eZqDMz1nX3dtOm812AioAjUJd16uZbAHyAChMPjTqeDgqjungMHo+uq7TdrIdlBil8rcv9enTJ+12qTTu+vo6HyjYNMsD+p6fn3PZTfreWsVUxjuOo+7u7nNZzGa9mZ57zDI0DL2enzlhejNnsaO0Xq2ntZjBjhTUtZ3qutHuLd3vfr/Phyf6YW8w8146AikAM4zckSHY7XYq6gRwOd+BPWe9h2lPhr7XzfW1+m4CwnFUUzY5oMm17sOgpqrzmQGAy8eHh3SSetfmewCI4kMpa+Pch/NeGu7/+vo62zbGjfLi3sk+OHA+D4rPsZWvHXKFfp2DavSAwAdbuZtYceSEfgvWnzMgsFEQORwqh11MfrnIASR9Rh5UvLy8ZJ28vb3NZVXoENeTlHvTeEZs4evrq0IIC3udMeiUaeO6kEjPz8+ZHMP+5fM2pqCG7+H+nFgpikLNppbGOXOTce3kH7Cxp9Np0ScE8eLBhqR8Hg3EGgGoNGfysEmU+nmQul7PfdDgn3GcsSSZW6ma/j0/F4EMwSFZuCRnnM4eF59LQd2fcKDxi5//XONYa/fW66c//Vr/8l/9a0UloFiUpdopguXGk2PsvncoGQqRfpfmg8cYExCWtNluNQ6j+j6x5MM4TP0go4ahV9sfNOxbHYe9Tur09U9+XZvNWiqqBEZxnpQiTIK916DT8agYSu1fXjT0vThV+7zMZX4VGqainqpZ5ybvohyyoNdNk+bDT8+QJxUMUzmPEthPGx/TmS/TXHbvB5FSl8IQl43NAOe6qlXEubG6C50Upa7vFDQm0KxUWlWW5TRvf1ScKkiKslRdzWA7FIX6rlTUdHBajAph1DiVDpV1OhRwjFEaUpN7nuU+BchBURqDilBKscgz/kMYFWIC7n3XZ4dTFo3Gqa5x3awUgqaMR6EinNRP/SShjLkfoixKhZCmMnjpVhyjxjCPbEtnuKTpK2NRKIQUyJFlmPtFpqAv+FkMUlEGvf/iXuv1ShcXCWzc37/T3d2tyqLU9c21LqdToL/68stcHlLVtcqy0N3djYaBg7GSIXh8etKqrnV5sZnSz6+p3KFp9Pr2pufnh2zEcRjsD01/ND0Dfuq6lkJQN4FFSmqurq7SacZ9r8upLv/x8VHSPIIOY4PThj3EADlDji4rpDpNnJSXQwDueGGkvBSIk4Bh/NyoYsy32222Dbe3t7n8Y7vd6ubmJhtm+h/6vtfj42NmmDebjfZTkHZ/f5+BWdahKWtR17W++uornU6nzCjCCAICNptNZhqHYdDXX3+dmTWAmjdxkk2AgeIaZDS85OicaAFASMoO/fr6OjcnAjLYL9LyzlLyfYfDQW9vb7mpngCh67p8OB1AHFC72Wz0+vqql5cXXV9fL8owyFpgG+mHALys1+v8/YBsSYvSgtPppHfv3un19TU3rJPBeHx8zPsZQsjBHWVBOE7vifMGfvzMZrPRt99+m8E3ssZ7kLlvvvkmn/jNCdgAQQDOz372s1wy54zg4+NjDrqQcb6b76DEjFJCSA4dDvnQsWEYclBa11VmEgEdrPfT46Pev/9iUf/P+2jexMdSdsSaI7tXV1d53ZBvTtDG5/iJ4zzv8/NzPu33l7/8ZQ52Hx8fM9tOEEeGiZIWaQah3pALACKYAJyyjuAD9AqdBDDyGfwimbVsO8pS/TCz25Jyedxut1M3BaLYkcvLS+0PB5VVmYEu3922bfaTTnDw/76fS7jQQ9dJfA2BBlk3v2cCLH/+0WwUZSkASoAwQJ6AnO/GpmOD6bsAPEopW0lZIPtBcIV8goE4+R02nnIqJwoIEMm4/PznP8+BEKQG9o5SKOQun8gd4/cwEGAfm8g68IweZNGPgi0iGCegwJZ4QJjIs/Z7zc8zPpizy7D4XuoVY8wyUVeV2q5dyCnX9iEG7AUyg33Gf7BWHHgJiYHOoPveo8E9e4BJiRVyR1at7+fro+/YD88W4hfYF7e96KVneZHrz3l9dqBxc3Wjtou6u7vS3/jrf1V/57f/nl53r+r6UV3b503iJnJ9Z5NGLBIlUUNWFAkw1XU9MU/tzBKXUat12sS+70Sz9SgpjL3a00HF0Gp1sVV/Oml110hlM5Ua9YrGUg3jqD6Oqjdb3X/xtd59EfX88KCPv/xWRZDqsszZgGFIzbYYuqIo1I99HtUYikJlkVj1yje5CDkVPo8rpKma9FOR2ZI4DBOInxZ36q/ohiH1oKzXKZtzShM6ooJikMap7yAqaqzqlMbq2tQgPwllUTcaQmrkDlFTxJnuI4ZCZVkoDtOpj9tUGiMpTRWqUvYglQkpZYgKqarKVNM6DmoPe719/KD91HCYlSWmBv7pcaa1i9l41HWjUNWKQ1J8hdTXkjIIQXW5Ul2u8prC4oZprZOSJ+fNd1bllI1RCoDKUKgISUFCEXV5eTEFDPe6uLjQ/f39dNrpWlVd6bd+8zf1v/29/7UehgddXV3p//C//9+paSpdXl5Oyj/kE12LIuj17UVvr6969/69ihD09PSkccogPD1/mso/GlV10NvuWSGMenz8oPa01evry2QkB/V9o7IMue4WNpq1ur6+zs5mv99nliyvySTbdV3r7u4ug4Avv/xSp2l6COwy/Qpvb28ZnF5dXWm32+n5+Vmr1WoBbjHoDw8PijHq6vJSL8ejmKKzWq1yvwIMEiCGeyEgot54HEd9/fXX2TEAonOQNz3n/f29/vAP/zD3RGDYnbWhRKWqKr1//15lWeoXv/iFqgno0ITnrBelgQB7Tp/d7/e52e3HP/6xhmHIzk1KJyIDriTlqT4EZtSEJ9sx5Gemf4T6bE+LozMxxlwycHV1pWYqOTlP2VN2QDrdgTlsm5dpMEFEUr5XACWO43lqguU5YpynVOVSwwkUhxAyQCVz8fz8nPeP57q4uMiMHECGwJTJWZRolGWpd+/e5cZuyjC4by8TQ16+nIJ71s0Dt4uLixyI0bOBDN7c3KhpGn38+FHv37+XpAweWGMasWGLYYppqr6/v88ADtvDfjurCBCjtGs1MfwE3jxL27aKGlXXM5NNoBFjzIEyGTZ0hP/DmALOX15ecpBBEzMgFj8IqJSUm3DJKgC+AIW73S73gABAXTaQLYCOl/kAsiinxJbGGHMAA1FBMEn2DIa5MqAPIOd78/pNdoEM/ziOen19zQFzrjsvq2zvkMG3tzcNQ69je8oBMc95fX2dbE3bZXmivGW1WmnoBx0tg7bdbrMtIXBFZ8E8EA8EqdhN1p37csKpqtKUut1ul/UIvXLWnT12YO/DZ/g3pZ0Ax7qudXl5mYMZdBRZRJ+wzU6+eDaRHhWuhXwR2AFS0QOyUNhoGHwvbUKfsDG3t7e5/BEimetecHzCBHi5xjl558/N+8hQePkmQQD+k0w9wR33ACgnu+59JMgKOkgmgnWkPAvbic5iW5jU50E5e+MBCs+QM/cxLt6TnjvhWy9rI2jC5hLU409c16iuwP9gM1kbvueHXp8daHSnXqEo1Z4Our7a6C/+hT+r//L//rfVD2EqX5lr2XmIMI16LYois4IAqDFG9cOofmy1P55yVC+l+dbjOHfiMx98HEcpFBr7qBBKHfZH/eJnv9Dl9Z1ubjYq6koxrHLUVjUpdb652ErjqO7U6nTYS6FUWTU67vdqqkpxTGd5YORSA3Q6D6Qq6zSXegpGVJQa+yGB+bJWnEbMhrLUOE0nGqOkYpprXxRSOWhUUNmsFIZBY98lYD4O2cEd2qmpsCoVQ6GooKrZqCiCqqpOlTxlmioEM19ydsE03rZZNVo1K1WTAzvsD4pjpc16m+uixxhTfb2k9cVqmrmdMgYoxjhEdV1QVdYKRRrxWx07ScnIHB4/aLOeHL3mur5VU6Xxw8OgspybqosiKGhK3dXltD+dUrN5p75L5UjJqWJMwvT/QWWRysC228t5is52q6Yutdms9NVXX+vHP/6RYpS2241+4zd+Q69vLxM7XeXP1FWt/WGfnX6YmuI1SE/9k/43/+//VZ5BnrNw4kyTOPWszH0ZkjSOKSPDibHpmVB4TT9Ps29zVi/G/DtN1y2K1JPDKcSyz0iS/jD9LEj5ZGhe3GuMMQXCZnhCKBYn6ErzdCs3Wp5tdIfj71FMwwfy5zVVc4awuGZmKblGUUj/g/Jajik9lQLStGgpkP/d+bTmfJ2R+f2BRFQeTsAaIWgxLs9+eGgfJnsS9JOf/CSzf/QifPHFFxmY4ohxeN4si92ibIe+DdhFHBgBMuMkfQoJQaWXhACaYPjO650BLsfjUa+vrxnIMullGAY9PDzkRncc0uFwyCwkwcfNzU129g5u7+7u9N133y3YZAcyPt3GwRXZBS81A1jhBAFxZJEkZQY0xqivv/46Z34I8KhXBjzRdO9MNxkWGDyv/+Y7yUzQIA3wBIAwmQtnT4AhadFkjE4AjKjTZxABDGOetjYx+ZvNZpqw1OUMGtmMpDshl+KxZjzHZr1V1/U5W+CAFHDuvVHb7TaTBZR2UFYFW09wmoiWTa73ZsQxvUGAR6Z5eQaHF6AYP+sg0Nlh2GuemYAWWSeDSraL65DZYk/ZI0Cjg8WyqrR7e9VqvdaXX36ZgfPr62sKUqp5sILL1dXVtYZxVLNKgQxrMY6jRitXQaf5XF2ngTSwwNwvU6S8NM9Lf8i+UhpIYEppEwEqASElN3MFSJ8Jp8OUJdtsNrlEB9uBvhKIE6hSfgbOonwI2ebzBIrYGp8YhRzwTOh/Hic82R9sE3YRXaX/KfvWSY8pW4Qk8p4UAnwnXZAD1p+9QV8Oh4NOp1Puh/GAm2oBGsHJ7JBN4BmQTeQNws97iNarlcJkswDi/B4ybr1eL2wafgNA78EIfpN7YR88a4UfIdBhH7w0jHVONmzIeyQp98Sgg8gXMojM8jcBEaW+yDv+wTP5/7bXZwcap2Or65sr9WPU1dVGf+bP/Lv6W3/7t9XuWhWTMrPpCGgc46T4c8qLhxn6XlLQGJVKb0JUOY1Krasml9s0TSrPGodRh8Nem83VNMmpUVmvNIZCn777qKZeaXV5qVCVyRDUqYG4ilOzZ1GrHyWVjcp6rVjuFYtK3SiVMTHWzWpysgqq6pSVCEVUGWgySg2+ZTOdTdF1E0Cf+hBCCpLoa2hgWYt5JGI/9KlUaMpwXF9dpybhmJqN29NxEqR6UqYpsuw6jUrTqEJRqCrnRrBuagw+Hg+qpoj5sN+rDLXedm+Kbaf+eMgGqby4UD/0evr0Cx0Ou7wnIaQxvilDVU/nIhQ67t90PLyqCNLYtypH6guTsA1l1KpZpebvsVdZrlWWc+1pXTdK56xM4yPrZipRutSpPakqa72+7qYm4Uab9WaKmDe6uNjo3ft73d7e6osvvtAX779QKIJ2bzvVVTrCp+97rTeUbyTQe339ZQZph/3rZNQ6SUHt6aD1eqWXaYKSxOnRHz5XHZav/388sdeJiPP7/5wTnP84pzz//3h9QlHou+++049+9KMMOmBFU0nbSwZCIcy1xzgsbJrk55XMp6ael0jAqOO0meCCU8Hpks4mU+TMHk6WcglK5LbbbT4/hAB6GAY9Pj5mEOn3SRkHYPv29lb39/d6fHzMWRGaO8kY3N3dZZacUiCcG6AVsJF6a77MjolyBWr6pZlNBVTUdZ0DI9YjZ8CtlIL15bXf7xelW7zYR+6rqtLIWUofeC7WFNDnpQT0EVGmtt/vdXd3l4GxB0I//vGPczDiTt8Z1nEctd6std1e5OEABDbpc0FFGfJ1Hqb6/6Zpck/Ud999l0v5eH7WGTl2GXHQBiMLgGNNvbSM9aapGfAD0HfCARbTS/o8AGLNKLWR5qbY19fXxVoBpAmkLy4ucqAGoAJ0kSEAPAPe2O/2dFJV1YteDwC3jHDxzGPf9xoPBw1x1MvrSy6/RK8oneIZKX/puk7rzUZNUyxYd2me+MgzeqnR+TkkBKPId/5e6y8CxCG3gFTsDYEx6+LTq5BzgDVrjz1CTgjgGT9OSSqZMe9TcLKENUXuPWOKbSOQIgONnPCMrqvYWr8GwTQg10dIY6fRS2QfGWLv6INB/t/e3vKzV1WV+38gJAiOXAa7rsvnlyADkEBBIR/XwHqjkwSC2HOyQwB7aQ7+CCrJ5EnKPZIEzue2EN9BtsGDArD4jCPnfhyC5u12u+hJYU+9DBKdl7Qgc1jzTEB+xuuzA42qrPT29iYVQaEa9JMffa37u1u9vv4iNQiH8x6MXlJUVU4z9etap7ZVWVaqy1Lvbu8VrJHEo9MYE9sbx9SMzIOnMpmgsqikENSPo4Yojd2g737xC9WXl2outtmJSak3YRgnQxPGFDjUK11d36quGo19ryKO6nL0uJ4cfiUFqYtTSrwqNMSYTzpXlJp11Ga9VlEWWq/S38kYV2rbLgU6VZ0nTqxWK/VDr83FJke5Ly8vOjCloD2pUGq0PbUnDf181HsYpe7UiubnxIIlJm1o2zROOHAw1TBHnmpVVSELTREKfVJivoOmZqSyVFHXWjUpGi6vNqqbRkWQvv7qC3WnvVZNqZvrxMJWq60UglZTneT79+/VrFa6vr5K2aCYypbGcZwmPRWqq1KhnI0fjGuaGFGprhp1Hcaa0rOotjspnTgf9e7+Vv1wUBELPT9/0M31paqy0Kk9SiH1JhyPR602iRkqQqGLTSpf2O33uYemCFHt8aCgUXfVbc4gzH8vT2yPMTKIYZbTKSuX8wRZWacekjifMO9Zg2EYcm8IE8ZoVybQwyl6ZgD23nMZOCHe4ydB5zSzGRFK2sQEuOlVTFkWfu4n8fJQwRyMpiTCaMyUyEha2nUcxnw9PoTT4t7omuFuPPPC/51NzffAe6fnyu/h2SzTcV1cZ9DpE0Bgfi8vLzOAAnS6I4WthCmiJyHGaE3z7QJQA4ZgIQkseJ80lzZ52p8RrzSSAzIAH4+Pj7q+vtbpdMqHQgHWAFvudCTp6upKq9UqBxcOUAhAvLTVe3WwPzh4MjxM0mGdcMKUudIjwNkxPD/snDT3DgHusQ0ADh+JO2cS51pt/k35UNqPk9L5TqecuUrTtlYahj7bZy9BoWyR6V5vb2+pBKfrU6P0MLOIgHEO92K9KQXabDbpc2Whvuv19PRpcVYD5WUXl9vspBMxcp1lmlrs6+vrRbYxTXda58MasZ9t2+YR01dXVxk4AYa9GZesC3qEnSD7xeQ0xu9yhgf7RL+KH8SGnvCdRZEGBByPx1yuxnPBVKOHgHh8AplAn1qE/DhAJ5BKmeoy94bw/q7rUsn2NCrca+Qzu62gq6urrF9MtRuHQVcXlzkIZOJdsk3JJtMn42UmPCPBDhOCKI3xDDG6hMzwjFyDUht6g9B/iA/PPCN/BCCsJ/dGEM8YXvaSl4855kwWHy9LgOBBqgdaEAW+t5QfEmQx1ILvdjBLbxpyyPrA4EMUeEYBez4MQ84K+iQpz9AA1imhI9jyEixpzpRxHwQCvDwwCckB5gCRAJ/1wU56RstlPfvN6VnQWc9q4/8ZcsN1POuN3+L+kavZxqZJpRBZ+C5sLS/3ScgUwaz3vrjMU4r3Oa8Qz734v+H1X/+jf5Cis2FUUdTa7zr95/+X/0L/5J/+rvox9RuMY1QMhYpyYqZCUFEHDcOospwdUVWlVE4R4jThaNTQpylHfd9rvdqoKqe55v2oqmoURykq6HQ6anOx1tAPedSoJG0uLnTSqHq71Y9+9CPVdaU94/Ki1B56rZuNPn36oPZ0VNPUqutKL68vGovUOH1xeaHNZq1+mABAXatSkRmO09QodmpPafLSkATg9eVFzSpNG3p6fNJ+t1NJ03cIqqpS+8NO49hrHKI0ZXrGYdTxdMxroLFXMwUFZVWqCNOUlyJoVRUqizTZA2ex3qx1sd0qjoNW6ybPhm7bVleX6bCw1brQzfWlNpMxubm5UVkU2my3aup5gkWM6aROFC0qTmeaBO3e3sQErsurK728vmm9To2kZVEoTIxWEkKpa9sU4Bn7kpiVaeJK01jknMasDUOasgT7BbBJACb1eGw2Gz08PKiuK8WYlOhw2E/3PzV3F4mh3e+PiTUMxXQAU639/pBKKHY7rXLjZLqnYUrDU2+ewNulXl9f1LWdLi5nY3ZqW727v9epbVUEGh8bnU6t1ut5fnoCY3PaFCMK6GuaJtfv+iSe9Xqtl9dXvU3sIE64mwwk5UowfdI8UQnwDPNAaUld11o389kn7cRwkMpfbzb67rvvsozg8LbbrV6enlRVVa4d9WZQ/o2j5dTt+/t71atVTjmvp5RuDdMY54kb1Ae/vb1JmtkTQBnZAD+vA0DkUzMczOCodrvdFOhWufmZEhucLqdN48BxENSXEyBixAE97CkOyg9qI/NAoADLhCFn7QHT3DfPzr8hJHAKOGY/DNBZKN4DaQOzButNaQwMJtNsYMcoMeKQPFh62HRGzgIkcEaHw1FlUaqcDors2umAxKHXZr3Wfn/IJYchME47arVq9Pr2moMnD2ScQfXm/nEc1Z6mps/1Op/RtF6tNQy9Li+vUhBWleraOTBcr1cahlQus3vbZWBU15X66UyFOas0jyEOYT61uCiCTqdWXTcHA7vdXtvtRqdTK03kEoyus+EOyGOMmbigbJd+Pu97cXC+3W7zeFOfagMwozdEms8P8OZNbLTXwgMEkXnKSlhv1yn0wIk/gO/z83MO2I/HYw5uAJfIIEMGCBgoB0MH+r7P4N8DJW+wRRbpZRnHqMMhgfphHLRqEqE3DmlIStueMlgGLBFwRKXewhCC+mFIvn4iMNBdSblper1Jo/TpP+GZvFeH9faaeOwG6wfQIzDwcivKDJ1pdj89jmP2UZCVEBvoy9vbW15jbGRRFNnfIM/gJ3wyQBb5KMsykzHYWfQSW+TEBbKVyMbLfACqpHx4Jxkt7HAah3yVQTYZNa6HTfNA06tnpLl8iGCD4Ar/SADrZWWS8vADJ8ixwfhXL89iHxKJq3wI9OFw0KdPn/LwksvLKzXNSm170vF4WgQxUqoGgTDxLFfTrK0vME6kSK8YpbouF31MTEJM+jufwdE09YS553vm38gge++YBPuLzPFzr0ZyW4C8/Pt/46/+G+MGXp8daPzRH/2BRUuFFBv969/7I/0f/0//Zz3veg2jpizDoM12o6KsUn31OGp/mKJ/hQTSlUAr/Q2eImpPJw0aFepSRSjVNCuVZaVxTOVbVVOqWdWJZQqFVuu1joeD7u/f6eruvZr1VpcXlwoFzFCqUyvKWlFh2rRB6/VKx9M0Nq9OzTpt16bgoJD6vlPftWp3qcmtazt1fZenPYx9r/6wU5zAgyttHAZp6FTX1VQmFVSW0wngVaGx73R7c6Mf//jHmc0ry1L39zeSBm23KeC5u73TzeTwh67V+7t7tV2bx1/e3tyqm6ZgrNaNurZb1B5vNms9PHxU26Vmt5///Of64osvFmlv6kufn59zzTQCRKmAN5d2XfqOL7/8Mk/48BpWziro+16//OUv9dVXX+X0McbXT0XFYGEk27bVw8ODvvrqKw1DatTku3ivKwKN1JQnUE5CtA0LSNmFs7fsWV3X+SAkvx/m9wPYmATBvdPwhoPBgErKB9e9vb3liU7eUI2TDSHol7/85aIm9OLiYqofXuW06nq91qdPnzJIZB+4Bk4YALher/Xw8JCbG7uu03a91tPTk77++mv9wR/8gdbT/zfbrX7rT/0pPT8/5zKIp6cnvby86JtvvlE/NZrnANcaHfk/ZSeU1gzjmM626OaTUQ+HQ+o1aFtFY2gJuqqq0ocPH/KZEBhGABqgGeDFSdeAKNaB04mZMETdM41/4zjmvgxsj+8XwQPfT/0289rJeCDzOGeMPr+HTaOnY7Va5TGQXhoUQsiBCTXF7oxxqDS0eikFQwIAI16igM74gVnsB1NZCLy8rMiDKoJXAhX2glp0/n3YH9S2fXbap9MpB4Loq5evAJZT/mlclFxQrsU9AhLQmfS+OI1NrReAG0AIg+/MKWUFPCvPS+lF27aLQ/+wF5Q2Af4pOQHE8YxeGw37DKuLXcFBk8Vw/fWaawgjwAjPCXPvtfFeosLnmcoTYzqIMZd7GEAA+LD2LiswtOgZWZ/9fp+fkaABZp79k+bJeZRkvb295cZhSnO8jARdgFjgGuiAwxSGH8wTeubA2q+bAsF0336WCvLIdyHvgPWqqhajWkMIubynrCoV1Xx+BHsMI8+1kTH/PnTXy3+8b2G32+WMqjT3lBA0UH5H8/put9N2u9Xj42OWbXw/n6c80rOP3A/+CxYe2XGCEJuPPPkzuz2OMWab6t9PcIvtJNjDpp3bb/advUU+yXJdXFxkO+D6zHpzb8iopOzXsalkD8gyoO8xplG12NQQwqLsMcsAmbGiUFPVWf8JupOsX2mz2Wbs4NmlNJa+WvQ+IHNSkZvHwWn4kM1mzkoglzMhW+UsO9eDLPC9xXb5dCu+x4NSSdnus85k2fh+MN1f+4//Q/3Q67MDjYeHTxoGTjktFcdKv/j5J/1n/9l/rv/+X/1S/ZjGoYYyqB96rbcrjf2gKgadjumsAG6sLEsN46jDlH5FSGBwhjCoXKfasru7u2nUaXIw6+1a2+16MorTeESmPoWV3l5TIyRKwaFffZD6cVDXtToeD9rv37Tfv6V03JAavA/HvcZx0DB0kqKGvlcVpHGY00jH4zE1p8dBddGqqivd39/ryy++UAjplMpV06gqg64uL/WTn/54mlgl/ehHX+uwe9M4pJSyMwA3tzepFrpKQObx6VHjMDcqbVcX6ts0reqwT4Dt6vo6jVhrOzXNSn0/lwwkpmpQCKPKamYvrq6u9PHjxwwgnKGQ5pODz6dhPDw8ZJCB03dD6mngGNMYUJ9U4pNIUGiaS2G/drud3r17lx0UJznT4IRhwCBTLsLPSXEDdm9ubjLY+vDhg+7v77XdbvWzn/1sYiITU3Nzc6OPHz+qLMtcl00JCY4Oo0eam6yBs72AuBBCbpYFZFIXDnDAADRNk2vgAcnPz89qphKJ9+/fiwY3AOj9/X0G3qTXAbE0gVLuAHPfd53aKb0OqCD4Wa/Xup4mnFCLCtMZY9TL01MGFQQHzCHnuZABDNCHjx+lyajjnDi1+ng46GoK4lgPZz6dXSIAJljw2noMqR/8RskHQPbl5SUHjIBimNNxTCU+nz59yrqBoUV2TqdTPhPj+vpadZ0mtLjDJvPBGQUOOHzS1nlTLSDYSyIIkr1UAVBMmRUBDA4MkA2Iu7+/14cPHzI4IYj2Ej6u5WAaMMwfD2o8lc5n+JMAWlTXLmusnc0lmMOpE0iO46C6mUuhWA+cIXJPqRAB0OnYTtnxKtsjbByACt1k3eupf4375uW109gT7gXQjWytVqsMRNbrtb777jt1Xaf7+/v8XAARCBYvBwMgsf/oGg2v7C0ADSAiKesKDKqXMXCPyAMsO8BWUm4yBVh7zxA2Fz3mc6yvl3kBFGlu9+CCa7K+BA0ebHlQ4XuKbHoghdy6XQAUzt8XFraXe0lrNk/K4TvJ9hAcSXNJrAe76PCiHKkoFINyIMp+Izsw6gR2fN/xeFyU1mAPsEWUNbFvlO0A9rzxH38NSOf+2DMvFcP3EMjynfgyGuAJRiDlfJQ49hT/QOBPaZjvH3JLJgAgTyYFmcKWICP4Sn6GnydggOxkEhcZZ9aJzAhT8QhiyMy+vr7q6upqoS+sE8/vASr4hBc6jC2KMaoMKVOOjnoZ0zim8ybOM2jJHnZZzwn4IS6en1+03c7TDF3OVqvkL3xIxKyXy4lTrvc8MzLM79zu8YzIittBz5iiE8hAWZb6j/7Tv6Efen12j0bfJ5A+joOqqlBZBSkMUjHocDrp6flFm4tNGkk79FIhxTim8ptQqG5qbW6vtN1eqKpKHU8nfXNzIykd8JN6HcrpBOVGY48DPirGJIyn9iRp1H6/0/HQaRySEr2+vqaJQs+vin069Xl/OKjvelVVOr9it3tV17Xqh05FCOqHNE63LII2q1oX241+dH+pGEvd3LzXu3d3atuTNk0akXh3e6e7+zutVyutNxuVZVBVzCnpoghar9ZpJKwkxXFar1F1k04rr6teQzXq5v4L0UAe4qi+Pen54SFNXipKHfYHDd2g/W6v29sbdX2vw3GvMhTavaZnvrm9UlFIdVMoxmoqL6q1Xl8pncCt1PMQRrXToYgYbgwgDZtXV1eZ9WK6DYEIBz8hqAD4h4eH7Gxh/3E4OF7SnBioYUg14LDjzO/HUAIuMX4fP37MCkhzZl3XOUh7fHzMzDXZGGaAF0WhT58+5fsj+Hx9fc3nChyPR3355Zc5M3Bzc5NLD0gbck/uMEnvM+aTYJYRn5IWa83a4GAIElBUd6IY2+PkIJ6envJhWy8vL9lwYnw9cAE4xxj11VdfqW3TgW65NGJi7Pu+X0ws6bou17gzjYbg4HA46NImd7y+vub3YKjYX4xSzgZZer2qKn311VcJqF1cTCOg5zKdrusye3R9fT2VyNV69+5dzrQAXodhnnRzeXmZzwuRpC+++CLXQ7+8vGQ2y0s/2BdYfy9NAsgQPFLSQ4bvu+++ywfmUcMNq+3gCBYI5wojxr3f3NxkZ0KZHWvl4AEWz0fYstf8IbvAC1KA7Aj7zXscLMBAZgA/MVisGT/nekyqIQApimkMbCi02aSsjwNCHJo7TMr1jsejmlWdQRmkAM7Ry6Vgb3HYVbUs3ZOWtd+wfZTdeXDBs1EWQLaJdcd+eFZHUh6ByroR9NPnImkx6ha9xk4CDD3oiTFm4EAmFftBAEB2gSDDSQBsAWSLgyZKUnhmaXkomWeHHVA7WEEPPPPgGRav+XbwAqgqiiL3lPB5gj0H6NwD9tHtKADOP4MMpjWYWVi3semexlzW5dfj86wfzcae8UYXkLmiSIe5dpbBJ9Bu23l6HO8lKIONJ8hgrehDIRh2QM11PABDbslkQbZdXl7mrIcDV54REgrC6uXlJffygAvy2RB1nct/0FsvoyNDRSBDhoASKvaEHp6qms9UQu4B2B4Io2tkWAmKnYzFthLkQGRwbYIBrvnFF19kfbq9vc1yjZ7GmHptyJqTRUUnn5+fs++FLEWGV6uVQlyeTYRuJ5lIlTgEBPQupefs8po6kMcvgT+w3QSg6TwxzqjrLQDtVFV1JjAgPd2OeEbZs+VOLqFn2H+u5bqGHV+tVvnP57w+O6PxL//l70kaJ3DbqO9GvTzv9X/9L/5v+p3/7g/V91FXtzfabi/U9b26oVe9Wqlc1SrKIvcPvL29STFqs91IpfT2+pYBzDCmICEeo16+e9YYU1Dx9vY6OYvkOB6fHuf0FeULRaHQn1QVSZi327kpfNU0+vL2VjeXF1qtV9ps1rq42KosC33zo691ebvWqEHbbSrDqpoylTyFoM3kgMqinBSe8x+C+n7MjMTt7a1SE3ir4+Gguqp0PB50eXmhfujU99R01zod5/q5GNMpsOM4qihLHdrUDKoY9fzyonEYtL24UFlEDcN8YBJRZwIMg+qqUVVXqspSbZfGXZ6OJ728Pud0P84MQXamI8Z0Wil18CjOhw8fdDqd9OMf/zgrsDs1WIuyLHO2xEfKucH48OFDNmCw09LcZIVhQuCZhgEzyFx3DAGz25umySUFPiGCEp/n5+cMSjCsAAEMKQ7aS8A4dZRzLXAK7sxwHtR6ejbg7u5u4QAwjPybz6PA7vheXl/1fioh8j4OZvpjKCgtwUgBOmECV1OfxH6/13q1SueNmCPOTcunk0or+cAhD8OgZgLN/gz7/T4HhIfDIY8KvLu7S7XTfa/BmHKATVVVuUdDUg4Szp0Lht/ZVxwbe/bp06ccyCGTmDOyZQSIAFyu7YGFpIWR9ZpZrtn3ve7u7rKzwenhtACblG1lA2ulKmTQxnHUu3fvsmP+9OlTDiopRSA48OADhpJaZ5wke++snDSXNAKEcNYesHj6vCzLHCyTWeHnPDOBE/fDIWVN3aiqmlxagz2gdNDJCtYl3U+V+ismORzHMa89YBeyggxA3/fabi50PJ4yY+zZV0o6PXNIJgrbwP5zX7wcxJIdZG2xabChgATGjXq5FZlD9t3LnMiMeakJ6+r2wAMAAhYvweD72Bd0GnCHb8J2Ybew/6wn8oqs85zee8RkKB8OAOglkACMoUvYT/aclwNX1oV7IhPMM2KbnaF1ZjWtjRbgCNCanrHM8ow/QlYAd5RNIhfsN76RjOl6vVY/9HqbCBGXFWzSdrvNbD7yVpZlBvKssfdvONHGcxNE9P08wQ27DAHBv52BZn3xEWQTkDeCaPbX99PZfe4N28seYIPQOfSKMkAvYWIf0CEP3MkAS8pncHiQXpbl4t6w2ciAH0rI37woQUW3fHKglzzyXuzk+/fvM4jHVrG/rMsi89X3ao9z3xHflwiC7ULuwBuQ5yEoyz12JJX9pZH06BcymHDPfAI4Pg0cwfES2FqINO7Xy6w8u+K2gH1DlghSvKQR0suzp3/5P/hL+qHXH6N0Kh3YVlZS09SKY1DXRf3Lf/kH+jt//5/p5XWv3eGk9jSoG6S6XulnP/+59qd5qstut9Pb29vkOKMUOvVdr+PppHEYdEQJBmld1EpnFYy6vk7svUI6QOxqmoywWjX6tV/7dX355ZfJmVRRZZGMzhdffKGvvvoqgcPdThfNajou/qAxpgP04nQ+xhAH9UOni+1Gp/aouqnVda3Wq7XiMJ8Qul6v1HW9UklSqVM3C19ZpsP6+klJZsdeSRqnXoqo1Wqj/e6UwVc3nZw99L2ayUAV0/kY4zBqs50OA6oqnU4JUEZJlxcXartO69VKx9Mx125iCGDvj8ejvvnmmwxacMIAfsb63dzc5J8D2gFcMBxN02Sn6SwPfSv8H+V04F6WpS4vL/W7v/u7evfuXQZuHHZE2QqlRHy2KAo9PDzkkh2M4ziOenh4yClIDAoO+vb2NgMALwNjvzDA1ORj/AkcuB5BjTOkfu4CToYyCrIuziZiDAD2fpgRigyrgsKHotDFxJx7HSnsBPvE+jooYA3X63XOVnVdp+sps0LNNcYthKBT2+amfmQXNilYVof0NEEi4BCjCXCJSllFnxcOcO3aVhvrc/BSG9auqqp8KCDA5f7+PpeZ8HscDJkqgL2zXe7cYA2Zsw+Dxd6w5ziXYUhDCh4fH3P5lDvpYRhyIzlBMMQJZVrIwBdffLFgiAHBjMMdxzGXRqCvbuSbJo0Kpazh6elpATL4g2778yLnXppAg673LHk5F3vDPHpYSmQKRjStV6mqnPt2cHB8h7OyZDMS0A06HPcZiNHj4YAVmYR9q8pKdb3KcofO41hfXl5ysyy9IvQC0bvBegN6vQyFoIH3YC/4G1mnx8VBPPeYHayBLMCl/44/Xr7K53ke9oM9RD64hjQfQsh9sn/IMDIBOAYo8ntgAL/nj5c2erkg9p+MITI0DEOeMARZwGfQA4JpMoEQJvQTUKYDWOK+2Sv0jlIzeAvWRlK2O/h5DwwAhoBKSm1h4skCoKvY1M1mk0YPD3MzNCQYGZ7b29u8d+gUe4pfRudYez6LzAGCPYBhvdhjRrfyO2yZZ8XwG5AN+DT2iEzPeQkPe0Bg5HaFZ0OnWWd6OT0gJPvhJBXZ75whkrIdP2f/WS/8DPeIbGGzyUpDUvEcyJyfk+FZYLJt3A8kDVO3Xl9fMzY5L2s8Ho8aul51NfclIp9p/dMQCWwJ9jatbzrvy8tZ+Wzfz1kZL/NKGGMeooO8zro7Ezie/XJy2GXLiQb3kzMunXtcnFRgn/hM27Z/ss3gv/z2OylEnU579UOvoEJDL603l/rX/+Mf6vd//4/0Rz/7pT5+fNbHj8/68PFRb6+viv00M3sCb7vdTnXTqKkLrVYJ6H7z9de6urrSh48f9aNvvtG7d7e62DZab9ba71/1G7/x64oxTVa6vrzU6XhSHOdOeQBoPnxOaWQmgKepa/V9WsRTm9jBpi718vqSnFa1VlXWent7VVWVKgolAyWpiPV06ncqTwqhUFVP6cRqZt4vLy+zAHR9Cp5ubq6nqVJRZVXosN9rvVlrHAelKSfzKLHj8aivv/xSw9ApKGT25HQ8pZ4QVeq6uDAWs2LUOrWnDNKkeY7029ub3r17l41mVVX6xS9+kfsb3PkBBhFOQBAGzCdbOEDHyLnBRalDSH0r33777aIeFFDjI+soMaG8hKwFIGK32+XD3ihHwlATyRMI3dzc5F4O2N/3798vSoeo4XZmsCjSvrfTGqOMrCmKSvqZYIHvo56f7Aa9BYBKnhdDIc3gHANaVVU66Z10Z4yq6jrvBTW80lzqg+HGKDAykD2sJyfWTKAHhhIgsbOzHvq+X4zxaybAgBHi3imXIni9u7vT4XDIjEdl4Hi9Wunjp08qJnmI43yiOIEFhyjhFB04FkWhL774Qk9PT5mJ5ODFdsoCAsjJSMGY4gxZZ4IaQMZ6vdHz01PWawLwn//853r//n12COjIMAzTWTBJR3NJQZO+p+3SRJpvv/1WIQRdbC9U1el5KFHkPppmpf1+N2VsKvV9l7MUx8NRZVXq9vZOfd/l0a3pxOkxl17AdqZTYOdD8aqq0jikHi1AQwJIaXw3GRbGGScnWOh0mk/AZSwsL5+SNQeqU+1vmCfNUZNO86bvTVmWGsZBcYxarVPZKXs6uaW8XwmM9ZNcDgoh7cHry24BQtFfnCCZGYJ4L7HA9pBhcCYYG+lgW0oMKqc0M7IVVvb6+jrrIXpF0OmOHlvkfRze9OrB53nGxbNDnpX2LBbAAt/g5S0SQQnfMzdVs2YA+5klnQMZ7lVSXh90yAGJrzONowAczzRwr9vtNmfRyZBhv7h3Sg6RB4J5/h7HVD6FvldVZT0N85Qr9pi/3XYC/GeAGtR1bRpw0/daTb5hGEd1kz4AiglSyWpzMCIlb/Q94MccgLPnPpGL12a9yZPJVquV4hiTnnaJ/e/6LtvBOMacGVytVuq7Xv0wl09hS0NI/azIz2q9yvcwkwaznSymQEqSKiMhvEcgyU+hqpqz/BIAf6UYx0WQRHl0VVX69ClNkSSYY6+c/BuGUTHO5XghFDkjQIkTvXtcH93wZv2yKLNfkJTONCvS5DH2Er2MY1Q/9DMRNwWHTh41VTprDHsKHuEefSzt/Cyp9SBhg1arVZPteLrn9DkPiNircRy02azz2nhQOAwxBwOQq+gHJKtn+D1w8xd2CDvi5Ac6wufATf/eX/7z37vO9677uYHGP//H/0S7/V6pW77W6XRU3/W6vbtTjEkILy+vdDq2+jA1Gw/9oMeHh5xODCHo06dPGuOo+7s7lVNEPMYxgxsOpWrb4yR4SdmLabOpBYRhQAlgt66vrxeMGEa7bduZdS8LrVer6awKFi5NwqrKSq9vr5nhb09djqyTgR11Ok11eTWp8kHFdNjgfrfTZrPVGOOkQHOpDTWAF5cXKYAogg7Ho4pJcXzyEBtZlWlM8DCMqspKYXJcT09pjG7bMVmgzCy114f7BANGn3oKHEH6+PFjDpYILGDuAFeUDr17927R3Mf6Y3RYa5QfQcfh4hxxVPmgqqkMAQCx3+/TCerDkCcweWnQ1eWlTpM8wHh60zG1w3zf/f19NkIAlOPxqJubm8yAPk4sD2AlM6tdp7KYTwzFIZPhQDlxLI+Pjzm1SRaDjATPRrmBl+94ORVrxGnuTGhrJ9a9H4Z0yntI4xgdzCQwl0oKD4eDTm2rYSpn4B7ZL1gtelX6Po3QZSwtwQrpaJwCRpzAar1e6+LiIpdRrddrrdZrPT89zQ55AvFvU3DCMwLW9vu93t7e9NVXX+Xf81zPz8/ZGVIOyD5UVeovwkkRcHs/BfXh7F/XdVqvNqrrRkVZ6PkplRluL7Y67A96273pYnuRwSeOpCgKvbw8q+8HNavGsjPVoh7bM3ucq6AgbTfb6V6rCYCvVFVpNOzxdNR2s81ZwmFII48hM5KD6fT6+qa2PWm93ujy6lJFoNa2V1VNTHCZTqAuimDp+GkUdOENgYPqej5AcIzpEMP1xBazRyGEiZXrVBSluo4zQUJeU+9DYN1CERSKUnVdpeC5KDSOMRE9RZGmBIb5EEAfs1iW5URsabLRvap6CqAmm+blHQANrxfnntgXQI+XM0nLxl8H2jzHp0+fsmPnkDf3K/Q9ndfqs3aABwfnMPl8v8saP+Na2C10gOt7Fs7BHGWXCeSkQLZtT9PwkGYqVdrqcNhnGwrYI9gg4HG2mHp/J2nImpxnc7gvLyPxDI4HXhAxAPDr6+tcHkhACEhHf1MgMk8+enp6zOcq1HWjGLXINBZFodfXF8sENznAxN4fjgeNmrO1dV1rnDJ12+1WCnHhw8gyJgzSKcZ03fTcR4VQaL1OB9cypGWczr2KMTUVrya967v5tO0QgppVk8bfj2Me3Xs8pVHSBIan00nDmIBgVVaKSkH75cVl9nHjOC7KBtmPuq7Vdq3qfEBwkre2S72s5VSS1rWtQpF6SI+no6pyKqetUqn2MMkmk/CQiZTluVFd13p4eMz6eHl5mf0ge+9yAYnEvoJj8FfD0Ot0mjOneehJ3y/8rI/mHdpugUWaVZPtyBjHfFDwMAzq+i6NPS6CNutNDoCqKtnoOB3TgF0lcERnvVwLOfd7TYFAynwQFORqgDjLlxMfknRxsVXbztnJJLvJptPPBxEE0eCZDc9Qup0jePAAw7Mj+E3uzatX/vxf+nP6oddnBxr/4p/+Mz0/P2fB9vQTBvPcWHPp3W6X65uLosg185IyC0TTK8wKoJSGVIwNjAH/pomVmlnKYShnYTICLAnlCX6svfcBhJCaA29vb3N0ytkOOBcOfcExA2woq6DunECI9/GdPtaTAIbJMGwuxhZmMISQR9kRUAD8KQH45ptvsrEPIR1GBEODg4VBBsChvDgO6jkBo3wHAN4PhGIPmeoAyGNKVIxRHz9+zML9+PiYp0oBHvf7va6vr3NfBwA7j8ObALZP96BfYxwGnY7zCbgAXth2lIX/8/k5vZkU7ObmJsvXMIEWFJPa1nEYVFlGA2XF0cBGnSvs8XjM41oZmQjjS9DCHnBv3lSOA/czUgAm6CHlKASQOOwYY04NsycEkThwvgMD/Pb2lgO0cRzzuR5eNz8MQx6dy2QngFNZlnk6z7t37/RHf/RH2bgC0Jqm0YcPH3R3d5dPtEaeYU7c8TAOOcaYy+VwVLCd7DOyu9lsFmNzsUkwgMjM0M+j/JhWImkxdcUZv91ulxvO+35uyCMYP6+9JjhmShBOFhuGjPoZBAAzB7VeEkMw37ZtvhZnCngKHyCBozp/HncYXgZznpZHlllHru21vgTVyCO+YL1eK4YEXCghwin3fa9C6Wwg7IGTEX0/n+Lr8i4pZzEJ/pxl936PvdXTcw1Ydu6HwMbrwJHru7s7dV06mfjTp0/ZRgIAPPuAH3EiQ1Imx5AXz1oA/LArZNu8jI5r4RN4v5eAYXfwM+gLPkAq5jWH4MsZ8TkLCAjlOQCzrA+yQraY3yPLPoJ5Zlvn3hFsE0EHe44sck9OEACKPftAySlr6VkYSM10/6tF2Qy2k3v3bBi2/nA4aNA8CpbAJX0mjazf7/d5otPhcJh6PW5UValHiEweY9XBNeAStxFNVWtlzDk2A7lCH720Cj3Hhns/Fc9Ej4dPwuI6Ly8v2cfjc9Ln5tJc5DHhj2IK3OYDaLleKAod2+Sv6JnCz7FGXtaVA7bpvglYqVJgnSDw2GPWARIB/ffhG6wJOs/nmrrRMAXQBMrYGnQHnIUPwMYgN15aCpEK8elrQvWIl3pJ8yQ07ylDrtBlJyWwf25bsF2n0ykHaeANb8xmnzxYcF8/Z6ybRYDkmUTWzitXwDjYqLIs/2QDjX/2X//jRToUoMKGY0BgebzZt+tS4+bd3V2uj769vc3gHxbb078IKMal7/ucImMRAbMoo9frs7meRvX0naRcZsN9tm2rq6ur3GRM3ffDw0MuRSJL4OUZNDMTZFByQlDBZtMLgUF2JodSFYIRnhtlRMgAqF2XpkZ5YIFzZdqCz/4nnesTkkjnUv7lNYgYWWqQQ0h1szc3N7nHwNNwABjKnfgMRhG2nKlQ7969y8ABZhGQ8Pj4qPfv36cxdsOQT43+5S9/qZubG3399dep3GySwWEYFgcYwXSzB4Bs1ohno/4cMNt2nQ7T/6m7l5Kx3e92qqZr4wyRP0pr2EtAP0bMg2pA2zAMGUjg4AiskVcHiN6DwXcCXmDTzhnGcUwN6R8/fswlTD/96U9zWvzjx4+5j4T9Qh48cGCKEe/d7XY6HA6ZQLi/v9fr66u+++67bHy5N3QXMoHRvJSeQVgAliEZ6KEgA/Pp0yd9+eWXenl5yY361M4CvjHe1Pt/9913ebqTDxtAVk+nkzbriww+cRYEKA6weeEICGQJjnFOgCJqsQGE0mzICY68tAUwsN/v8z07aPUmdLImXjOLbUCHkUfu02uMCWohIJBBL0vBXiE32GV/bkoQcdou34u0fVXlchPWKdvhMWXoWCPPRgBCWU/+73XKgDPsjIMY6vwJdOkvcpDBukDoUEe9Xq9z4AXgxs6iLwBsZI4AFsd+XmKCHLF2nsE8Z/95H06etaN/Dr/r8geB4QEk8tp1QwZ7ADnA03a7zrKGXLntJmtJJpEg1IGtpAW481KNh4eHrDM8M2uID+C66LbvLUDVz4Ig+0U21DMfgKrTqc1nGaAT6BBkEvuOLckYQfMzAdbTfhQ6Hg8Z70hWTjmd+UWWnP4kD2qRGfrPxnFUIaks5nvkfbw8qEYv2V/3ZdwvsuAlu29vbwsQze/ocajretqfWQ7wZ5RUVtU8PADZK8tSh+NRZV0t7DDBCr4dO48+Oj5wueR73S9L88AN/DHXw9ehN9gO8BnZkXEcNbTzwYEE/8gy/pJngjiBdEAuqJhx8gIb4H2A6CXY1jML6A5lWPh69BcZhdwDh3BvyCS6ncutz7CvEykEt9wz9gm7A1biXtAt7CAy6DgTOf1zf/HP6odenx1o/M4/+affY3CI3LkhSloAqh5VIcxEuTTlebMhhg/GFUPGHH1vhkPgUGo36mwK5RqeciXgAJhynwgJAs4G8V2Mp+y6Ls9kJlUFOCHYcTZ4v9/r9fU1HxxGCcj79+/1B3/wB/rJT36SnwklxvmRmeH7AUwwvCjXnAau898I07kiH4/pQL0PHz7kdbq/v9fT01N23t9++62GYdCPfvSjXBqE4HqdH8bEWS8PAlEETot21hhHiQzEGHNQx1g5yn8eHh/zIYCUIUnSZqqprOs0+QLgxZ7xPWRsqHEm+Pv06VNu4FutVmq7TuUkDwReOLsYoy6NYaTMbxzHfN6FBx1kH2Ag+r7PJ59jSGB3MIwxxgzq+PxqtcpBobOCnM7M5zHiZFEwzDh39M4DCEl5epSkxehjDA3Gjf3EoKHXgAoYTphgDmqkjASgx3oAhu7u7nKGE+N+dXWlp6enfBAjmcunpyd98cUXGWwQlGBQAZI4GxpRsRGPj4+LSSYXFxca+jlDxn6VZWrmJn1P8MTnnD33lDhO3EGWZz49re2O0oMkJ1sw/h7o4BhgzWClfBoafUA4N+/PICMGKYDT8EwEoAZ5Q46Qa2fe3PngGH1PYkw9c/04M+LYjqqqUknK8ZQzqThJ3sc1caCQNJ6VRB4deHt20bMA2DCcLBmKc4aPZ/dgAHCGfeV9EE/nskB2ERDDe87ZVD7Hyxl+nsezH2TlWGcacX1NeG7kZb3eZoDKs4cQJh2Jur6+WrD96KmkTIphY9zWM8zDM2A+rhufWpZlLhMbx3ExXY3pgo4bkHUHSE6E8FkCU++9Ys1SwBa02WyzXrGulNdgzwDHdV1rGAf14zy6lslE6b6ibm9vFGPUp0+fcqWDlMbJD0NafzKU3CP6jcyAk4qiUBwGFaFY+Arkiz0mGMaXu8yw78gqAJ69BvNgI1hrPsueN00tTWVX2Cj2M31HAtUQrsipiqDRyC+u7X2hC+KhnHsDfE/BbM/Pz9m+o2+eucQX8aw8A/gAX4ce1nWdDlY+tdkGoX+8sDv8jR/m/qigQU7wqf4Zt5/YJJ7BcRJkMnJIcIJMEhjwHictwDTsDd/Jz86rIwimwYoEDFzX5c3tDdfkez1rjE0DU/6JZjT+8T/4h5m5x4BgXNjMspzn/gPOqL3mxn00FtdZrVb5XAY2AyfNnH0M6uvra2aw3717p3/1r/6Vvvnmm2xsYFovLy8XkwVYJH5HQFFVVXYUzj6wGQiFNzLiVD1oeX1NfR1+7gHOxa9VVVUGt/wfpRmGVI/NdBRSVzTLAuweHx8z+CO7gcF3wIIBl5QVBQDhDo79q+s0ghZhAlwBoDGoKAX3BvDGCBCtU9b28vKSxwMCemAviqLIU6gQfK7dTcC/nAQb8JLT5uYIAYswfh5wYcQoVzmdTvrmm2/y/jCHfLvd6nV6Hg+UyTyM/TxtxDNVDw8Purq6WjASAHayYzGmQ+BogD7XHVjMqqryxCL2mz1mH93oAMTYq7Is8wFx2RFIGZhgwCXlUj0YGrJzp9MplyyyFpwhwFpi1AE5nsHwcwkAFQQjHqAg87yfwB5dI7gGtJNRY29gstEhnMuvyhjwGb4zxpSR2u+OC2fWtmmEMM8O88X3YNhhFllLggLPRvkfL7OA/YZZhfFzVpvgwgkEaQbezq7z/OgdMgJDDGCrqioHY2Rp3YkDYriu22dk3R0Re8M+sVb4Bmx+KAqpmPeAzw7DoDiMGodhcW0H3ThNHDblR9mBTetO+YHrOyCNIAv7guOlD8/lX5pLtHgWgie/LjYKe3tezuNsKTYDH4nushbeTwKxwXXRQ6avOZvPoAlvYgVEwSZjF0KYR5JzrwSbbTv32zl4wVfwO7cldV1nO4XvJJBlrbHXlLTic/GhlBBz38gL34tesu9O5L2+vuYMFGANwtKrBNq203o9ZxaQGQ+WKTukjLcoCvVxPkcJAmQYBl1eXojhBefTo1artapqlgMnaAC1BBoQn0VRaOz6PF3JMRD7iO1BByFs2EOIAdbVASw67GDSs10A1ES8bHNzsmO1tJeNum7WAS8v7oY+9w/yzJ41JYAA73jQxT25r2L9wDfcnwcWrD0y4/aOclKfzDYMg7rjKZObBNWeIXafhB1h3bl38BTfyd46yYDOsY68FxlAzzxQxOZD6johxzUA/NglAguCZ2wLGMj1ib3xe2XvkUv2Aj/s5Wpuv5zMb5pGf/Yv/M/0Q6/PDjT+9v/zb+r6+jqXE5H+w1HBwqKAOHecKayHp5ZYsKIocokOoJnSA4xL3/cZ1ErKDdpvb2+5dGO1SgfTPDw85IUAmDjgI1VKhsEFndIuDsLBUGA4mXWPMsAeeoM1m4qBKstycbaEHzCHEOEAyOScp/X49ziO+f5cyACHzuqzJwilT4qisZf9Kooi7+8wDLkGkFFvMOzONHi/AsaAg3EAvMMw6P7+Xs1qlUf/SvPZGTgmABQ1uTxDVddp0pTmQJVn/Pjdd5nxx9mxn27gOCCNelCyKzCL7MHpdNIwKfd5tiCEoL5L44S/++47xRj1/v37HIiihMgtjM/FxUVmxb3+0U8dRy/QGfaAQ6Q8pUmfzXa71S9+8YsF+3h7e5tL1zhYj6C3qlIzK86TUa18PwEwpTCexfJ6bv7tcnd9fZ3X1ktPCOqHYchlijwjqX4AOzP3V6vVIqDlBHYcFUYS1hSZ7/teP/vZz3LvBu/zYIC1p89rs9lovzsuspuUiGDsvVfinJAgAJXm2mRn53BqOF0cpRtqSRkwnTPSrA9O4ZzNAgT6tBqCXc/seaByDlpYF4IT7DPf7faM+/egn2f1Q+ecHUaH19vN4vM5Az0FGn4tZMSBkn/WGV32lPtDXvw97Jv3xPizeckXcsd9wOShzxAnAEP2GdtU13XOzp8z1OwfssLf55kXDzp9LZz8cBaVz7DX2G/sWLIfnVZTLwy+S9JUmnjM8gPgQR4gM9yengMUlwc+Q6DAunHwJaW8m80mZxlZP/YRQuLy8lLPz8+LCWKsDcEm+8Y6OkEGOHZfxecAl5vNJpeE0s8WiqDThEOwObzqulJRhBxYo8OJhd7o8vIqlymxlp6BcT+eg4UhDe3g/6yhA36uhb1nPTwwxF8hk67nLluUo7JfYJ/0Z3liOvtbFKX6fvje8IK2bVWUpdq+y8E5GQVG7pPZw4d5Izqy7UEya4ReEBh7JhhShNIm9MubsMEBua/g1GY5477OA2tkCYLGbRlr5MNQCFSRA4glMA0YGHyETnhm18E7euWkE88CUYBdxHZhJ/CvrKFfi597sAD28zXg55CIBCbgLvYIPRzHUX/tP/4P9UOvP1ag8f79e3369Em3t7fZwT89PWUFuLm5WdQo932vjx8/5sYojBslUjhXyq8cLCOIXl4Ca0XQgcEEeGGYQgg5rcmi+vxqACClNAiTNNcCngPicxa1rmtdXFzk0ZuH41EX2206qKxf1i7zPC8vL/ryyy/1+vqWGf9hmNN9aUzfPMEkOcZSRTFHyszOv7m5WbCDMBmUfZDm5nc0kWP0KSsh1UlaFmPtDoZxmmnqVXLc9KIA0DEqrC/Gg94M1grHB9PozVYEW2ShQkjnO6w3G11eXKSSiSl7slqt9Db1UaD0Nzc3att0Qiuyxb99HxwsUtvbNI2GcVQ/DCpCSIcn2sjXEII0zqN5i2LZmwRwBxzjHL1MwcuOyJoxDcmdKAacYLLrugzkyzKVEnZdt6jbh80ex3HRe4MzpWQGEOSlKjgOQAhGBUCP0WR2O8/BugOeftWz8m9mpcOESloAMRqeKS8ax1HtqU3jocNyrj7MVZLLVM6AoRzHMes2/VbUYRPEFMVcL/v2moIxL2+gTI1nRAYwwpTu0AvAGhdFOtsCUgEZAWjixCBM0DVk3UsSvTyHnznggXFytpnrI2N8huzbeRDjToy9IgOFE3cmNoHzICZbxTifMeHrg4POzZVloaIodWpPeURnCEHjMKo9ndTkrMM8ijXZoOU8fH53DnJ5v2e1eS4APeuPrT9n8txJc+/ngAtQgF77Gp6TTB7IsK48hwc12AL0ZWbJ0wha7r/reklzthddZV/oB3Cwid9Lz5L6CxjzznrFyBCGPpcfLeUjTUyKUVPv3TJYRkdY3/OACEBOVpOM77kd4fuQcQ9Yzks6vSQ64YfLKeM0B94vL68TwK0X+0Gmkix2KNLBvMj68XjU4XhQM5UKSsp9Aul+2gzwqirJwG63V5rAVmsYlixzCOmw32EcFCQVZanT8aSqKhWndSg1g2LwE3sEGQdgvrq6yiW4AEfsI3IAcZGZfkUVIdlopr45AA9FoWayN1GTXgzzWRUKQVWZxswqSEFBwziqrir1Q6/j8aR6NY9dRhbwtegKJDL2G98AmMUOOcGKzWcQkZMqfI6sD/6Yn2Nnc4B/alVZ8FwUhfphyPanrCqtJlv/8vqqoggK06htqiU22zRKGFsCFgR7IRvoBjLg5AeYCVnmuSHd3Vawhk5uE4xjs9w+uw1zYopgAV97nplwMhPZJajB1/AsTvbGGPUX/+pf0A+9PjvQ+Pt/57dz+pOTbN0Js4AeCcL8oKgwe87InW8SToLNItjAeAJcCTrckHtttgMOHL6/YKz5XoC/N/awmAgxDaq//OUvdX9/LxXzqZxeYrBqGr1MAc/Ly4uur6/z5o5jVFHVOhz2KooyX3O32+lis1VdVer6zsbNhWkN0lxszpkgWPJUNBH68XhclE1xDZwP9eIIMILPs1RVpZfnt2zwMHqPj49SkMpyTqEzVQMAScRPmRQN6zDj7D/lCe5k397e8nQyToWmCfDHP/mJHj59kpQcEoFE0zR6fn7O7CCyg9EDbPnYXJgB1oe1AbChcN5MyuQRAAXv3W63WTYw9tLcsOZ1/wAYMizsO5NhuEcags/ZFQJxym4AecgxzDz3zfOj4s4a+ZQvancxfjyXGy2/Fs8ISMCQ+vpi6LknHMl52RygnolzUlARSrVdq6GfR2Zut9vMVicZLbVazdOFyLix36+vr1JIs+ghRMZx1M3NTdZJ1gWAxXN1XbcoV+PZncXB1hAknPcu4GCRJexMOQWwbuixRTSKY6+QYZhLaXYo6Dx7isw7k+ope2exPKvAfrnTwUkBFpCD5Mi+f3pw31OKuRxRO7PjKTBBTjwbg21HJ7FpCbCWSqPDZ+eLreb+fF2cIHHmEpuBjnsZnfsW1pyfu6x7iQzrxPdhe1ljLzPynj1IGN9H1gGZS449ndvU930m7+bM9lz2x33Dzp5OaTIgBBA+EltA1hidmgmf+X34I7eJDv5gbNOI1rkJl3OEYPkJVvEx2BV0mfIO72XiOsg8+0aG1IM/yJQUTDSLIBKmmT0iK83+tG2rMY6K03s2m00eZIHeIhf4mdkORtGHIc1DDYaJoCpDkcFhUaRzN2KMKizYREexNfhnCJ85qNeiYZhA4zzI9Cx+13VqVqucYViv1/kw4PZ0SmeDFXNvF8AT+8r9sH6UxnrwiO1HzryG/zwgR8awFd7/xf+xOcjCOUkDxiE4Rb/AXdh99gM59+wB7x36QUU5H1QJBgA8u59DDpwwK6fgRErnsxWaG++d7PL7ZO08o8reeZDuz7rdbnMvsNsc/nhWRJrJZmSK4I69RP89+wHZ6n7Nfb1nV1nPsiwXvcNVVemv/vW/oh96fXag8d/8zr/Q29ubnp6e9O7du/wQ3BDC5IEBD4yjhbGBPafmGpBPBA3jAPshzTVxu90ug2yMJoaeXgAMENdCMWKc096e6o8x5jpNBJ7o+1el9E6nky6vrnLvAGy+96f0VteJAbu+vtb+cFTXD4umU2lq9i4Khajc78HGStKHD7+cDu+6zaDXyyVgRnEQ7AETOSiDopwLJaR2m4PQVquVhn7Q6TQfXuUjel9eXrTZpnKlT58+ZWXykhnqBAlmEMq2bfM6UyeObHhJFsbDAZU7fRwrCrjf7xeMeV3XuQyMZyVY9DIa5G0YBn355Zc6HA65BI7yIQ/m2rbNY4+5Hj0X7DWlTTyvs3k4uWEY8uFzMIiU3xHAA9xxPu4AYCMBrPwePSRY91pfZA1wxO/oufKAHefKdWHZAG6U0s2AcE7pA3CoLSdgp7G673u9e/cuBxwPDw/Zaa3Xa708v+r29i7rJWVAAIi6rjN7iyPCMRHYMMLZhzWM45gzfRh+QJL3PHD/BMWUYrAPZDcBdjwHjt9T2VwL2+UGHQdcFMWi3hm7irP0wMCzFA6wAZ7YWK6JLElL4EaAAUDiXtEVB+HOkqX7mJ8N2UiykjJL51mNJGvpUD/XRQArAAL94WfpntO5HzzvOTjjfawDa+f13NwL60V5E2uMzfOa+PPShpnBrhYglr4lXgAtz9B5ltIBFYTFwv7ntUgTjLDV6FVahzmIQfY9iOS+0VXINsqMyRjOvQ+pLAZ5w255+Qnf1fd9ngiV7jM9h4/cdNYVu4/8QYp4fxv3CtCib4PhMcfjMZdbka3zXsO0voXKslqAz/PsCnaT/a3rWmOY5YbmbfoKsfdOerru8W9sRz9VMjRVvWDrPYBHTnkO9Mz7mrh31t9ZawfQ6CuBEev79PQkhaCyKrWZAgECDmfKfe0BwU5OnJMS6KX7AuTACVvuDx+EToHnwEr4DB+y4XtEZsqxhwcy2DLWEBlzmXMbBAnkusx9O9nAWuCTuY4Hh9j7pqpVmOxiT/Ct4DLHasgAP2cteQbPrLvt5Xm9B8qDq6qaz4oCdyPDnuGQtPCd+CPIX69c4F4h0iCHz9f3b/wv/7p+6PXZgcY//Lt/L5cKPDw8ZJYAY4RR84knHqF5VMdNEnhQcwfwIVhhEy4uLvLEGBh0DDMsOqU5t7e3ueQFo38ebLDInsoDhD8/P2cQxaaiJDRb47w3U1kVJU2wUtfX1zpOB499+eWXOai6vr5W1/eqm/XCaWFY6qqSprQcgUEIYaobH7Rar/JhdBweRfCFYALs3KgChghGmDzFz7799ltJyix627bavR3yWtLsG2NMh9XEIY8OpRmUgAuw+6//9b9eNO7isI7Ho96/f59LtzxS5p5RLNYthLAo/6DngfIiJn4xpajrunT6dJybmABGKBdO3VO7lJBhcGEVMEaMJybLANDyskDGNvd9n8t2WB8yQM4S5LIszUyTl5FhfJmC5Z8JIeRzAnI9fDUfUAnr6YwIU1T4PwYJh4TDwfigr4AJjCPBBIa1qird3t7mHgeCINbXU8i+lhizmSUfVJXzIATMk9c5Y4i5FzfEfI+vhRtlt1ew3X5v2AZYVhyX12r/qn4M1pLvYt9wZugP6+6sJbJPsMZ3IbPnjg4QhdH3QEOaHY875AyuxuWEKa/n9WDTA3v+n07mnstbnO1LdetzWRLfmUByqRj/zaVPzqAC4AheQtBiD8+fybOXno1g/5EF/Alr6n0bc2Azs7KeSXR987UBEDmwGMe5dBEZ9YCR58TW+ToTXDfNSqdTmwMSz16MY78Illx/ALDuX7GbHjzxvKzrfn9QOm05LO4ZogkC0ScRhSD1fbcg7eivG4YhB2GetQI0ssaeWZK0OKNKUp6G58DzXI+//fZbXVxcZTmiaR4M4OQI9pL17MYZmGKzXG78vA/Wgz10cJixzCEdcOqy6fuKrAJg/XfoAgEh6wGA575YL+zunDXssjxVVaUxzPYdDEZpoWdCWQtApNtqJ5ucPXddkbSYeHdOXvg6UWLtPthLhrgez4xNAwD7HngAga2kksKfj/XiPtynYCsds/r7nLjxgDsTVQoqizmD73YWPwo2cB8EDj4PAN0fu01Gv/kcZBnPjC9B18CTHJeAvvHdTiYl/d/n9UBOIP5ZZwYd4Y/8/f/Rf/o39EOvP9bJ4BgA0uIAWiIpZwG85hWnizDzAJR4eFR3nuYk+v3222/19ddfZ3aGGjWUw5ueuR9YK0q8EGppGR2+f/9e3377bRYuehDqus7pQRT4+fk5sy6nrtPT05N+9KMfZcdDarAMczqUQCop6Kho6dXT6aQPHz7o48eP+tE336g9nrKRBgglhmylru8WTtINCACbIMhZbZTRgXtdpwlTlLZcXV2pbVt98cUX+vDhg5o6zQQHLLFeV1dXOp72GfgCNgH6NNNTW8pBhOzl+/fvJc2Na33f51O8URDvJ0EBr66uMiMnaTG9DIYf2UuNeet8zzyjl+WhnBgw5AaZxmkTnHgzlLPnzrLnZsIwT4GgHAbQcjgcdDqlc0QwTLz33BiQESGgw4HPDZ7twkkDsrgGqg1IILPmZ+EAHhjdhwEEsGT2ZsoGYXjRNUAx6+w2AMeJA/J0rgNyMh7pc4W6dm4KdqByft0Y44KJRVc88MPgAz7OS4xcj7BNubcgzGVIZFa4DwI2Mms4eWTES6V4ZnTTZd3BgNdce4+Gg1X21mu53UmzJsiUByqszzlTxsvr5iUtnGuyO2uV5XL9eObUr6GF/MJYDsOoophrfpErAnW+y8F8+u65RMtLXz0g83IkHLEzkgAi1oE9xl4AHADLXI9nQG+REaYkATa4D2d6eTb/PnymByA8Jz4UcJzOfpj3E7+Y1j3pNfaRfXDGFLl2Bph9BTTzXYfDUWU5Z/h4v+s68o0MpXvq85hXAhrKP1kbdAEy0EfyIkNkdKqqyvYUOXf9cKCFvDNA5v7+nVJ/4zxemWD7eDzmPYSoKYpCCkFFNQdVPkjEiShKvNAFr9Bwva2qSmUoBATjXtk/7JEP00CWeb8DWrfjvyrIdhxAlQDTqIZhUAxBxXSwINjj7e0tl8id2wXfR+TdMza/6p4AoWTtIZfop8BP0W+KHPskPPdRHswQTLk8e2mT2y8PkPE/+HF0BDvG8zh24Nm5NnsAPnHCgrWvqkqb9VpjP4/59WfhGc73l99hY/j3nP2dqzp8LRwjQIA5huZ3bu/4mZfQg4/ApJ8+fZrl1xIG2A8/X8iDLyfz/spf+1/oh16fHWj8k3/4jxbMoQcMAMG2bTPgZUSkR/MwGgASgJmnwHGiAFGMNO9hw6qqytHg8/NzTvfwPq/TdQeNQ8ER4mRwzmQTALQYZlKcf/iHf6jf/M3fTGVdxZxex3jng56me8ABYLjarlNUodvbW/3e7/2ebm5u8hSIIgR1p3YBpBDWsix0ao/5vmB4yAp52RrCQCDghp8AYb1e69OnTwtQBLjdbDY6HtpsKJjKQalTKGKua+eEUYzZxcWFHh4edHt7m0ErkTVG6euvv84HtsH+MT2MWt27u7uFIvFdyAITQbyJ3VlflIvg0jMPDiYwzFyXdD0vWAdXbAInJlkBIsdxzOcvMNXMMzoO0nkBbP2+UGBPy7vxcafpBpzPY3DcqXl2EVl2IzoMQ2b0pMRS0acBwHYG2VkWT7Vz38gon/WsEYSFg/BZT4OGflw8KzoPcPFaU9bQ74E1c5bIgzKyRayTOzRnkzwYcpbMnY03G2MLAKzYmuPxmA8nRCYpmeOzyMm5I/HyCP5gE85ZsHNAwv1ihzwbRkDigRRZF4D9eRYkyckMAtG5NGjjqLIsvqdfSd6jKJ3yayJr7uxh5pPulKqqeTwx6zsHPonZgwVnjckUnwMqAhN/TkmZKOC93AfEAHtOBh+wRK+BZ8CRP9+rx8dHrddrXV9fZ9/EMzvYm31dNWWB4kKX0/On3hUHFABat//8HxlgDzmTBpY/7VGVa7axm5xfQzmny3ja/0J3d7dZnxib7BkzgisHrbzfp7t5JhxbjF3Cnjs77uuWSKVtXleffOm6jS15fX1N5V9FobKusu9wpp/143v5m/3x6/E8McbUaBznkh7kEKLKgz96L5ADQDFTvbgHJ2ipujj/fmmekMe6q5x7AVwWPOh2IsKxHPuELLstdP/B3+cnVBMMYm8JpCHD5pK3kDN2nh3lnrH52DTWku/1IMmxHrLhGelfhSOd2HA/g965nfDsK5+tq0p1Oesxf7NGTlj49/nanMNvz8K530WP8GV81r+T9UeHfM/OA2jWjgoiCH/sieOP80ypB9Hb7Vb/3l/+8/qhV/WD75heGFyAGQwbYIXNoDyEGkuEyR+SBeHgFwycj/yDdTpnath8NzoYYZpondHGYAGiYHIovcKxUwrhs72d2cZRkVI/nU46ThvOs1M61nddHtmI0MLonNpW5eQofvSjH2W2pygKaZwZsqIo9PHjx0W5TFXP9+tpQQITWG6yHKTV3EnT/M0haUTDKAfne7CmGAdY8KIotN402cAQBPB9kvTjH/84AyyYJaY/1fU8ChiDy1rT7+Bgiv3E2LIPXZfOL2FML1OwUCImiiGnbvTW63U+4I9AwU+HRw4xaDDYBHPesOYBWtM0+VR2nIUDO5cVGHbGPuLgMS7e7E3PB87Ty3rckBZFkcfJYrgxIOw/RoSgnHvDwQDmvQ4aHXBGlzV1RpX3YBSlVPvM89Z1Gg/t5QDOYqX9LTUOM9OLbANgPM3O+vN9OA3e4yl/B1vOkjqwrOs6y6mvCe9jT3hmHKRnNTwDBGi5vr7OdefScvjArwooKLXjvf63g2Bkxm0qgatPG8Muc4/nTDjBgvdFnWeEZnsbFiUM9K/0facQZlCBTqWsQeo5cLbQ199LZflZyuLNWSTui+dhnXF43KsHSugm6+LZHPwG64V/82C2LMtcYkqQiG2mjNjBszSzqx6M+vhtL7FCfjwATbI0DwlwZtL12G2a954xGrvv+5x1xXZIyuQSa5rucy4zJGB6fHzM9hr756CrqtKhocgNMnd9fZ3lJ8a4GFeOTrDHbs95f13XedIj9+ey4oHq3KNGWd9c0uSljWT6kTVsQixClhlsITYJwIaO1XWdy1R5AdC9v0HjXPJCXTvTA1kjt8NOGGCjznseIOv4buw6eyjN52/wHuwmcohtYU0JsBxM89wEScg4++Y2H18PycM+kVUCHPu9eXbWswtgQAJ27A0Mu5NUlB5z39yXA22AOv7Rg3HKvMA32CL0ytfLfQXPiK6XZam6qjWeZTPcTjiucn11ot6DCffbHthgN9ibl5eXTMSCqX2t3b5iY8jaca8ut8jQOenMHnE97Irfy+e+Pjuj8bv/7J/r5eVFNzc3C+OeNqKanGutoKDdfjelZtbqulabzTYv2n7PWRippncc46TMUVVVq5tYobKaU5Oz8I5qmjqX5TR1o8urywnodWnqQ1VNTi9ovVqrbmqNw6ioqL7rNcaoIKmsEqDp+l5vr6+6vLrS8XDQGGOaGvX6olUzlTuNHI6SFnu9WqusKn334UMSpqpU36VGua7vpCgd9jtttxdq2zkVXIRCp7ZVKMpcYtR1vX7ykx/rbbfT9dWVjvu5+RcgkgzUUdfXVxrjmNb7dNJ6s1ZdM88ZR5vYJgdwvP94OmmzWWu32ytGyhOCmqaeRwEWhV5eX3U8pPGhjHXbbrf69OmT6rrSat3k+yJt6+zVxTSKFvYsKV7KulxdMSqw0OGw1+VFmkHd9Z3GMSn15eWFvv3Ft2qaRrd3aZTy7e2tnp+fF4cSevkCjglgjCKQOvaA1RljsiOeykRhu65bGE4AL4qNU8NQHQ6J5UzBhdRPBxytN+u81n2f9kjCuRUah0HdBMw9Q4JBCCGtFzqS2cEYdTgeFBRU1ZVSU2Spvp+DpNNpLi1KhmxmBDGK7vAlZTYVfR7jKClonGqau7ZT3dTm2EcV6SbFqNmXl1fVVaWqrnQ8nrRerTROLLoHRyHMDGDbdmrqRql5eGa2cLhuEPkdjhOg6ADGAw8MJ9ciA+kGGLCFbI1Z7+deD4AuxluaWShnn9AFnhdb5lkhzzgAAjwbxHv5bpwv12UNkT8ckgNvRhk76YAthgAAlAHIJeUSCrcjErW9czCX9mKYAHjImRoHCmmc8OyoWRvvcUAO2pbTbzmbp5uIo82kw/PkPJ7DZZh7AkxBeCU7OJdv4fwZXsE1PbvCtR2QDwON5oUuLrba7w+iNwXZ8Ol3BCaASwgWABcZA8o70+9iHnnOsyEfXddm+z4MaX2aZjXJTqWyrHQ8HnKGive8vr7p8vIilxwl21KraWqN49zIjp2EcIHZBDQjl2U5D3tJRNBRFxeX03NV6vtBXdcuyvPY6xhTZibpwDgFGmkyWZriV0/BaSMmmc0sNZMr02SuZOdWmQxhrZ0cIZuAfmWCcehVT/pQlmnc7DiOKkIhBeXSyPPMU2a067nxuSgKlUWpAIjrmS42KI5xkU1WWPYkjcOQRj5PdlxRCkXI2Gg/6Sj2DFkYhkFllfxK0q0oRenUtiqqcgEUPUgDhEtzCc8ya7Y8kBM7yRAOJ4A8GJt9zNyjhV5RfcB1IQp5HmSPvgx8Ljrh/pZ75zsgFufJnvPhc6wz5Cxr4BlF9sUzG7zPgbkHHsMwKI6jwoRjFWe71nZdnjLGPbhfKspSQ98rFEFAjiApFKn0rigKtV2nMNlwhTTJlOds2zYTIDwThJFjGGwkWG0mMuYqo/PPeHbP15B1dR+D3/kTHW/73/zOv8iKxyanP6X6bsgbSeSKEUJYeQAEGqYkze+ezzjg84+PD6qqOk+NYaQnQQbMN87bU1EezRIdejrOFcknGJFqR0CIfpOgpP4KWA0YBt9oP82x69KkBUqVYAtJX0tJ+V9eXr4HonzUWj41uT3pYnsxOeTZ0GCsKJ/6N0Wx3CfMPS/miRMgeLrPWda6ThOCrq+vdTztc8AJo+mlR0TL3N84KeRuN0/skZKRu7y8zCed13W9+F3Xdbq8ulAaczkuZooDBlarVR67zPrxnfzpui4HE15/jiF25WP9APzsE6lX5JZr5DRyPzs3Z0jJMiCbyCGK7AaZ9/hECGQsBOWAHb1CvgHaztRK8wheAGRU+j99OmRS0rOWKYCoa9Pt5fkY584g1wSPg4LCgtFnj+7v7zO7gw4AOD0r6qlwfg8Q9fT5eW0ra0bZBAFkUcyzyjH0zqqhox6MONuZwYdlTDxjw3Uw5B6cOIjgOq6vgFsPZtL8/ToHv9wD4DoFqLPDY08dcJPxkuYyEi8hQ1YACuiKs3bosZePuC2iNMVZRS+JckeNvIRQqGnmk+uRhWQ/GtX1nFhHL9LeV5kBxrbOpR6zjHrgHEKRy4/c/ks0yc8yjWx5thRb4Po3jgmUHw6HRVDC+njGh3Xpe4iN5ThhZMwdugfBaX/npkyCRc98sX5e0kAmDF/g/SbIKOvHNRjNjY1fr9f68OFDtuk+YIDPDsOQy5TZc74TMFzXdS4X49lYW/Y9YYVKmuyGAzJsM5jAg3Jnxx08AqY2m02uP4d1J9gniHIZ5f/Y5aZpdGpbjVoG3s72Im+su2dRYaT9WQjyN5uNyqLUGMfFgY6sLz6GPSmKNIVyPGOpWfMxzBlHdNLXx20ReuL7KSkTDV4Fgpw5+PagHuKO67Jf7JXjD0q7sdGeqa6qanFWFWNTIeucEHDMJilXSzgBiP0jWzPr4kwaOC5lv/jDzz1gxV+5v4AcclLonPBojyeNRjq5fahX6cwu7p97cZn0dcdOjd2MXyAj3WbyPZ6Zxq64L/MAC71xHcA+IDvYddcb7EtZln+ygcb/8N/993nTnQ09Ho9ar7YLsISRQPicFXNjjHI4CCFAcCOAQ6U7nkWDQUKQEC7AOspNKQMCD6jmXrnP84Y3TwHCbAzDkKc8cX8oftM0eWKEl07womGrrmvd3t5m8Ixir9frPHkDYSdt7Y30p9MpN+860OQZLy8vc6kY7D5MG+ARg397e5trnCkZ8ZpJQBRGom1bHY47DUMq6fGSEO6Je+26zk7AltpTlyc5UYKGsHoJx3q91sPDw8SkbXQ8HRblHu4UMOQecTs7yCE1NE9WVZXHIAP4uK6DIEpA2FtnNnwaSQpID+raeTrF8/PzIpjEAPB7HOT59BhXfowsBscnkACg2XevjZbmqUMe/EtS2x2znCH3mWUO8whiruuMHjrJc1ESQUkOcsl70RmcGIYa53OeEfJ18MCQe0JOztkp9gFnxHe44fYadt9L1hZ9Z01ZEz4jaeFUCDQ9S4a94t8e2PjPsTu85tKAdIaIBzDcm7Sc0sQes0bu5NA/D4bZE9YGAHse1HjwjTx6oML13NYCIN121nWdhyAku1FpHH/1+tLbgQx4ej8xtXMpnq+rlFhtZ5rngHCZAXLbHkLMZ5+cjzqOMVomYFiMc6zrVZYvPsOwBibNsb/8Lk1lmkvGQgjZppzvA2uczni5UeprSeuPLUd3jsdjLjuWlLNI9LGhP5BYMcbcB8F9sE+uMwSrPDPrwr57PxF22INrZ80dbPv7+AM+IFvugJ19Y095nftnxw7cs5e3AtCwPbC6HkA405xlpAi5/5KSKUpuPeBxnXdgxv17L4STDugSQZ+XQBKs8RzBSrH4XvBANy6bms/JA+znnEla9tNBlGX/MPWxOZmBzWE/WU/PIKJf+BYmFvnwGfYM/WXtIKHImrFu2B0GtOC/+V6Cad5f1/VigpMHVjwv/+fZIOWcgOTZXf7dt6EDyK+vISXNq9VKfdspjnNzttu8IY4KxTxIA0yGTPFzZCL7uH4mkcgwnfsFsh5gOA8QPNhAtnkhn04Y4RdYJyeBPOD+nGbwz+7R4OUGBQCP4sCkEqHh5Pm/M2UsDJuFYAJoPSsyjqOenp6yE2Xzn5+fs5EBoDL9BqFwkISTA4hyD9yfR5AeHXLPKBYGx+/77e0tOxrui3pVDJwk3d/f53G4GBPAL5uIM+H9KCOH9cBy8dy/6m/YrfMI3lOPKBDsWY7Gp2f+Vc63qqqcQaCfhAPnkAfW0cFs3/U6HE55XQH9OAw/kA2Z6Ptep/aU18hZOWQOeUAuq2o+TwQleffunZ6fn7NRIOBi/1FmaT5ZmsANhQTcemDC+vHdPDdg0g0a3wPbzwsGyJuDuU9kkz1wtt7ZfhwABog+DYKtPEZ5nGvbz43TGMe8X+eMtQfTT09PeX0Ierh37huDRJbNWTv2y0GFpDyAAVbN9Rzjz/5jCHE86Iqzgsg3ewWz5muIk+f/AFk3zg4UPAjALjlg4ZkBkCkz+5jH+EpaEBHYhfQ8hTab+QAsDk5L9zibaX926ui5B+6LYRusFbXh3KfbZZ7L98WZfT6DrUPXHDwDZLzmF4Invb6fAUFe0s9m9s7BW12vMnDAHvGc47gcZAD4SLXeF79Sv9PP5gMjPYDiEEfsGM+c7k96e9vl+wBYUSKKLXt8fMx7K2nqc5qf1ddWUt5/ZD6EME0cLDSOXX4u/BlrRwCPHMCMj+OYR7HHmAa0sD8EpdgbB0+sk/tG+tg8IEevPVjwbDDyyf/RV5cT1gHdYiS5rze6jD1zneSzvAdQxtpASGAb3Mf63pDt4juxr33fqwilirJc4JEY55HdDsp4uW86B7PnQYb7R8+COObAlhRKTcfuR3y9vDkdcgebSMbZz2riu7gn1oX1QzYo+SNzxPsc+LIGXN9frBs4hBLB86AUnw255TI6DMsDJ5k0ir3xSXHci8uo+8lzgsMJWjLh9H4ubdCyyoVnRwfYE9Y8B0cTmeD9Hnn0bj8HyPgL9t6JDy9tCiG1BeCLE8G5X2RmnHjm3050uw7jz70SxP3gedDGftFPxXs9WPm3vT470HAW1dPRSTG1WBCEhcWkzMjZOIQdhrAsy3xmAYYCpQN8I5AIxGazydOHmqbJjc4YOib/+IJ4io/FRzG8DpFNwQlwTzwHZV48M2uDk+XzpL1hbhgpSikY2QSaiDHsjIHlmtxrURS5YRXj6IKCE/WMSghzI7s0l+dIyxFslMXgmGh6d+YrhKDtxbwmvB8FwQlfXl4uWITNZqvNZlhkSTytTyaG+3AF7roxG0YP+HxqDkaF5wsh5EPgvDba2RW+B4ONwXIj68rmin88HnP6uywLFZNTgmU4HA65v4VrY4w8gHFmh/uCxfEUJvvMC9ae9ZxL/ELO/gFmeWaCVIAw91lXtapqdiKwGsgiTg5Hu9vtJCmnqGEw+bcz6+yFg3fWs5yceYwxDxTgObKBqqqFgWTfYd88/Yv8E5iznoBvQOR5Kpj/Eyhzb9gdvu88wEMnKRvBdnn6O/U1zYcW4swhCsgGbLfrvPfYobIss3yF6TyJ7XabGcPzU2PZV0/HA0TJdm63Wz0/Py/YK4AqZYQEVKyDgxzAAUEW6+b7fH4P4xiz0z0v3wpBeeofoJDvph/Dy32SLdmo7+fDJF12EokwO2sH0ewXIM31D7AJKEX+KdfEL1xeXuZpTHVd57OCqqrS9fV1zpKQESyK748YZx0JApFXnpHAj/vinhkjigxiBwFY/Azb4AGoy7vXYGPfYow5OHQGGzuGHSVgZ1oQ9sW/w4NCL0OBMGBdsUkeLJxnCzyjBgDF1yGnHqS4Hjt4x6djO2OMWe6wCQRPp3aufGBdkSHuxe0x1x3HuW8LO+Wkkq8Bdpqg23sw6M+JMao7zgTBwgcWhfp2ebAi34kdh+hkTcEL6CIgnawD9p4/7k+dKHDQHWPMJCnZfO7J7Se669lm7Bly7wEAtnEYhtxnRokVmA6gDrmH7nz69CkfasxesCbo29XVleq6zmXfyI4HrDy740fHen74IMAffzYOo4aoXHWBTUzr0mtvww7QZ2wvttgD+PTZeRw+e8M1WTPubRznah58IM/jNs8JL89++0GJ/hn33f6dP/T6YzWDo7DcONHxqtlkI/P8/Kz7+/tFZO+g3qPIskwncQI2UTwWkwgRReSBfUPcoSIQKAkKhrF0cAJA85FxfkBeVVULRgCDgILg1GC+nWWBEeKQPhhElA9jAzNFI1OMMc8SP18/Tz+zXueCyPcRZKDUHqVjuJkoMY5jdprO5uEwCRZxdEVRqFnN045wRs56cj/SPL41hEJDPy4U2GfUs/Z8nga0sioU41wqxT3jUCjB8hSvZzh8zBvyc57Sxgj6tc+DEuST/ZfmPo+yKDUMyzp3T4HynA70PSPiPQjcIyyRM084CNYMg4RD9NSop3WRI4UxryvrnI2sykWAx55Ky7ngAGUnBLgndyLnwA5H6k4ZfeV+0XOAizOfngHx3/FZ9oj78CCWffBGRq7pgJjSTO6TZ3Fgx3f6H9YB2XDGElLFATTPBGubshKpSZb1RB6TjdlLitnROmOMXp5nzzxDh+wMw3zIIsE58uWMGjqFzfUgnBf74evvQS9rCiAIYc4EOLs4joNWq5nFZl+TbszN4rtdKtecT6RP8sL1IISSfK8yeFwydkHr9SoH+w6uWBsAHoEjr7adm5r5HbbGM8CsTQqeV2rb08LWoCv4IqayuZyEkA7R8zItXzO3y2S//dwhBwhuH9Bl7KbvI/rMfTm7zjoQQLE+rKvbQrdZHrA7WOff57LE7x1EkTX3LAH65b7GgxhkhlH7MMDcj5NV5wSpJBVloX6cp4h5eZuzuU7EYDPoz4Mld9IBQsOxgoM68IoHU4WCThOLHELIWCTGqGN7kiZCze0Wz+PZN/xt36eycQD79fV1PvyX4MfJWnRqHMfvgXcCQkDy6+vrIsMGEGWd0BtshWfpkXP3DxC04CI/f8NxIyXaBMOOQdmn//a//W9VlqW+/vrrrAPoEXb1/IBOx62M6GcYDWQT++H+rus6KUZVxTxWFjs5jqNGxRxoOB5AB7m+y9owDKrLSt1k11hDt8msm39WmjEf12cNkYfzc07wA/5cjnuw88jL5/RofHZGwx0OCsnfCBORJWwIzsmVS5r7F1gAF0AHz6R+PahgM/2BWQCcDT0A7pABFNJ8aA4paUD5eabm9vY2g0EAK+d+nANfTvRk8QFX3IO/H6CHoAAgY0wpRge73J/XETpYZl2olwcw8ax8DgEmuOL7MAw4ZjeafL8zEigutbxe+3kOeBcKqJnl4bM4Q/olYI0xSiEENXWlt91bBux8F2CTUhQHuJ7qRfEcEHF/yBLr7wEH9+HvRQ9cmSWp7Vqdjt0CvHl5EilgDCuBqAckvJ899TNoCLopb8MIs4c+bAEj4XvGWoVirrX0FHYKluaaTBy1G32uxZ77c3BfyD0Bujt/Zz1xKs5eeb+DZ5LYUwfnOFEPrDDmbtDdOPI+z4qdB6c4Hv+OX5UNQ4chWgjAnRUiGwHYcwAIywRpkpi1o5i2xR7Qa1HbvH/AoAdOAArWARae/ijvKXEA4kEI9wPQxAm6rDsYYI3Rgbquc9mNA84kY/PnAcXLjMeyrpoSw9Uq9f+8vb1l0EBPW7pemSfb+cjsYVg2EntwKSlPu2FvpBkoF0XKmJONlKgjn6e9EbwAENBBmH7s7jD02u932m63+d6QUfbNfRkTsjabiwVTzb7gPwDezuZjOx0wu0/lxbq7b0T3PMhDn86zvD5uHV3GjmFDyTJxLQIibAfrAJlH/wj6w7M6IYj+ASr9Gfi5kzYE7BA2PnnQdd/JEeSkKErVkx9AB+iVdL339UWH1ut1XiMCx3EccwacLK4TYZ4dJTDinsoQFs/kOOZ6vVLbzYdsuk91OcCmYJdWq9ViGiN6y/Oc22xAsK8dWDD7jzKVSUG8sq9kS7Dp/I7sKesuzaOxKacjaws54pkgsB74gUENZGgdexRFoT/9p/90vh4Am2CB56UKw3Uc/aBcDXvpky3xr0541VWlOMwT7rBz6CgZQXy4k0R8BhJpvV6r7zqFqW+LbKfLoWMT1smzsmRDsSvnWU/3S6wHa+e2g/V3+/M5r88ONI7HkwqU45iakdvYqjTG0AHJ6XTKZ0TAknk9PfWP7gxdeFgQToM+D1Z4D4HF5eWlHh4eFj/3KSyAJDdknz59UtM0urq6WqTnM8idAiIcNOAJpuX19TWXhWFkuBdnWQCRHlEOw5APsfGaSYwD30MEzfN7DR4Kj3P2cyT4XhwaQtH3/eKwJKJ7XnzWsymzAZ7S9BPzWhaFjkcMTqGmKRXHNO54GAZVZaXTaTopft3osD9kh4iTphmL9UZ5uI+3t5PGOI0mHkdFScOQZvZ3Xa84pjRyVdWK46gxRsU4ZVSiFKPEjHUpTFM/ooa+lzTVS8c0VUYxqpoO4BnGNAmoKEoxanHoCYKD9vvDZLQOomGVewf0wc6V0zrEKKURvoX6flDbdlKQdvu9UvOnsnLHDA6C+p5JGpVCGFXXacxjCGnkJu8DqKYxuHP2KwPLOChIOhwPGYiV5VTGOM5sNPriThwZ2G63iyAMoINuwJgR8HkG0rOJBBFe0uDNmg6yyrJcZMJYI8oeyLg5g+jkAvqBDrhuutEFpHv5IWsCeeFO8zzTBJDyMk0cg2eWkA0vSUz3AvNZqSiCLi62GoZRZTn3Vbid8r3hPpyBhh3lBbMrzWVYOFFOjWcfPBgk2OKZcKxFUSyGFLCefvgdz0WgQCCQrttaYOinyKfPPD4+5gDLmxGxU5TxEBAC7Jpm7qED1MwT9WbGPU56/+HDh2k/Kt3f36soSr2+vul0OoqR0cgHAQ2y4hkNDgzMDaF9P/XYndS23VT3PGe6APB9P0wk1kZtm0bFDsNM4kjKpBV77gEGextCyOcd4Y+8Nwed9YyeZ/mRC88ueBbFgxkHowBRdN3LZVwHkf8Y54w6P/NSJK4BaIPRdpabz0pS23Uqq1LVWKsoCzFuf73ZaJjuxQk0sIgDcn6X/t8pGlEIKASYeWCMTDsZ2vd99tu73S4H11RHQKw4M43O+J4XRRqZG8dZXp1lj5oDKHzN+bQw5MPLgTjt+TxTgw6fkw/uS7zci31nfZF79u35+VmScsmmlHrU0EnIN6o50FOI2/OyH4Ii75Wh/I0yKPdJjufIVhBseimnly6hl743TrJxr9hXx6QuX13bpjHFSmNrFYIUpH7oVZTzMAW/V+7PnxmdxPd5IIEP4V4I/hxfFUU6E4tzN9ArgnDPoEMg4pd5/vPvYi3+OK/PLp36nX/8zzOrQboH8An4wPg6U4pRJvhwJpUb5v8sJMqEoJNehtnhlolsqREkuMBoeeYFIIJw812kOFlsd4hufGlWhaEGHLlSl+U8AYk1wqigvDynbyafhZVA+V3gWHf+jTF2J8F+OIhyhpDvYV19VjvfdXV1paZp9PDwkPeLvXUldfYXw8L9OBvCHngQgeK6MrEOlI2xvp6qlWZ2xlkcd3593+dSOdaR/QcwcM3zLAaAlWfFaJPJ8lIYACpOizUG9PE9ic1d1kPznf04aLVe57NI1uu1Pn78mJxb3QiuAHlzveHF98yM88zQe9oVltLZCt8/DL0DaGf+uQ/PlkhzuaGzML6nLps4Um+WhnGkyQxmxUv3PDhhHZ2ddAbdzVnf99l2uF7xXvTEgYODIdbXHQ6OiJ9BsnjGiXXj+XEALvfOMnI/XAddByhyLWeXXMdoynUHTNATY1xMdgEUuP7HODdr8nJ2m73lbx88AZvvDbVu//waTqhgd6R0Dgv2CbsIaEevnImjgZwejvPD5MqyXvTDUSICKHOg7+UZ3Dt9df6erusyyHB5bNtWNzc3i745/J6DB0mZnfVr7ff7DAJZ17quMxlE7TnX8VILCDp00m0DgIVxr23bLso+eA4fnQugcFkn+CdgZRwqvUIQcIBqshOsKf4fmbu+vs4y6ISD2xl0gXVizzgvCeyRbf44qKzmccYLdrbrF03dnu1EJ8Zxrm7gc7vjYVFpgXywrthHgqlfVWWAPoAlvAnf/Rtrz7M7+10ofM8PYNvKZu4rcf/DNT0IYU/HcdTz83PGQh8/ftTNzU3GCRAKZKpZe89GcS9US/igAeSmLMssw/wO/+UyyL/BctjzGOOizJd15vk8UOR+sHuOK3kW92+73S7jJO7Be4QcIzju4v9O/LI+6DvPxfezP9hUJ8z5PKVb6BpYlSAO3MJgAPqbWCsP9KV5chYkuOufr480Tz0kQHHb77p5Lp/Ynr7v9df/k7+mH3p9dqDxL/7J7+QHJKoFDPimIoAsDs6CBmmyGvkGwlxKweeLYq4LxJGg4C4MLACCB/OAs3bjJWmRVfGUcWVGykE4DonfESiQCnU2jWfh5f0RLjhstjQ7Ay9TwQgBPvk53+NAyFllHLmnOd24eCR8LuwOBtypYbhgeDGgGMuyLPN4U/YdJ8Kzc31PYZ8HWzwfe899YTycLfZAg+t7wxW/5xr83wcInBt39sfT9G4gfcgAe8c6YcxxNMjWHHilw+5cUXn+qq6lYjkJgv2vijKxIWFOp9MU547Zg4h0j4kdRkf94DWAg6SFMWWtMYjOgnng5Uw9zycpG1NvdGV9HUzDlqELTG9z5srJAdaZlxtCvgNDD/jyICuEkI04n6GsC1IC4O+g6lwvHLh7ZsLJhNxTZIErsuv6gAzzPi8HdFDvQTCsHzbDR6o6W4s+EKSQXfDGYt8bb+KGLfTsC88AI+jZDc8CQe5QLlIURQa1yCYZa2dIE6PeaRjGPKEMVhMn6kC6aRq9vLzom2++0el0VNMkQE75VJpwk7KYRZEy3QCT1Wq16APzoJTMOuvOXmNjzjPbBDzoATLvNgj74EG5B/1uMynTQl498HWfwve47eO69NTwb/wA98szsYcEFy8vL1nvOR+DtYdVZpw7MgrTjzwDKmE9ncxysoGgFxuA7OHveZ/3bXHv7se8JxLCRgbAecYQglbVvI/gkb7v83h5mG5f76qq9PT6km0K944usq7S3C/jzDg+hXX097st9CCGPfDgaxgGaUwHCLOvgMK+71XU1fy+6eU2hvVh3aX5XC5khPvFthFcvb29Zdz1+vqabSY+sWkavb6+5r7Q0+k0ZQPn50fOyTg4KTEMQ85ecK/8n7Jh3xf8WdM0ecKnN/yjiyGEPEGOe0CfkE387eFwyFPaeGHPuBffK2QLP4jt/VUYbBzHnN1Bd06n00I3CeAcyCNTLh9lmbBAVZaqytlHeFDrWMYxnssNvUDcF/iL+4NQ9ayKB4noJXrIfvzl/+Av6Yden1069fDwkA0EoJ76MTaal0ef/NtTMN4MDqBz8OnKec5CsPEYdo8aQwg5QPHo2hm1y8vLzBhhCJqmycyOsyU+JvP29jYvuoN5Z5Ko7cNoOEuGknn2A0FwsIwRcQXF4J/PMsZxcd3z4AHHh4J5eYGzYG7c2AterL2kvE6AD4yTKwvK7wYEBU3AYo7QPR2LAXGWwh0k9+aK69kFvg8HirKg+DB7KIyvvaRszHh5rSzGyTMj/O118m5o5r+HbOQc3DdNoyGOC8BAMFfXtU5dpyIsJ2r5eiNDHrQ3TaP9ftl4Cdhnr7kHZM57bMhgwTifs9PspTRPzXGQ70AMfT7/N6AddtYBnDsp9t11BeOLnnBN9JY9cH33DCjgHTDN+9Bj751yXeJ+sQvIrNsvz1Z6gOYZQ6/bBlhitLEdzq6x35Q1xRgzU8+aMeWFQA+wcHV1ld/Hd+LA2Su3n5xvQ+ADM00viOuhZ8eQQQIg7teBtusRDD5+43g85bGyXZcaObGVOD0vL729vZ2InaS/jP+mBDfdb7vIisFoY899/Dn6dZ5p9aDfM7OAJ3TAGWVAn5NvHpC7/qFX5wTHOevo2UX3k/v9XuOYDn/1TKzbMkCdDyyBFEP/b29vs93xsal8J/0lDmbdFmM7fI/x8Q6CnIXGhzsTTMmhg1n3K4Bi9MCzHIOWkx8J/uq61tDORATrcXl5ma/pQRElzkU5T6nzbAR670QP9+r7y73gu7lf9tzXEtl0UOsBWFXOpU2sLWszTtmE8zIXl01/Bs8uOcFA9sQBJPgHWcIWeW8Hk6C8d1BS1kX+D35BtrBnHoCGEHIvFvfP9/Jyf4+NAEija+ALgkjIZ9c5D8TQe56V/UHnWW/8FP1b3pvotsEz8uiI9/ChU9gM5AbQD3mJf2UfUsF2WOAFJ6w8w+O+Eblwv8j6oFOUkfk9sp/83gNXruVlfj/0+uyMxt/9W7+9EFRfXB5gtVrlE0E9xc4m43TcYbORLDCHDBFgeA+BBzAIozs8vkNaHlLjBh+l9cDG2RIWn2vxnQBTT3/hSFl0r3nkOZ3F4vvcAJ/fgzslZ/hZa+6D53dgzr9RYE+1Yngwtl5G4Awmn3Gj5iVbDi6c2aXe2xWMz3rGCnbpPEAbxzmlKS3nsV9fX2scx8xQSsuzL5xl9vVxZZOWGR4AE+vPzzAebmjdCHtwwjUAXjg0wFoClulkYZdJrn88HVVO5Vc4+Qxii0K717dsmB38AoKcYZhlKI0MBTSfOzAPTr0UxOv30T1fSxw4jrTv+8W0L3TBmRSuxc+433Mm/TzIwPkD6jxL4PaC/eBeyJoCWlkjz0pIWvQjnGfRePF7Bw4Y2POMDiDCnTrXZS0ou6SGHqfna+blkJ46J5BDfzlj4/7+PgdNlJDS2Mn6AnQcVACcWDvPTL28vOjdu3fZ0QGkHWzzXOwNPye4ocSFPcP5oRcxRt3c3Oj5+Vl9P6jv596f/X6fD4WkrIlgx51oOp9ibiR1+RjHqGFYjuNkBr8DMuQROUPHkUEPsCFQ/Ln5jE9KcyeNDQFY/qqSU/QCWfAg30tZJGViD1BB1t1BE3tGgIVdYc+Q3bZtc+bodDrljBzrAchygoRAGZsBOTcMQ84IIU8OurGju91OVVVlktEzW9gfegdYA6Yyut67z2uaRqd+nuTo2KIs0snagGJnYZEZ1p3nzaRGmFl5xwWeNXQby7rQj+CsteMGJ2R8vz34d1sTh1FFWFY1DMOgfhhUNcvDXj1gcEKDEkkynfzegS52CB0B+/Bzyv4ck7k/435ZP66Djvh6eGDigQV+Dblx4hU5c4LQswvomGcBkAXHiOdkkPtP1gL58qw6awJ5AZb1e2OcLM+JDWQMLq+yLPM+8J2UVPq0SWSOPdAY8yGAYDC3rV6SzO88+DiXEyd7nczDVvnL7R17g77/iR7Yh3OEyWPaT464DORS4uFsOILA+xyEY8Tzgur70zEwRjgWNu682Ynvc4fNy43VeQCAktFo5geoSUuQ7+kyz244QCKKdTbVBcDLGQCqfBYjjCECEKAQrgDcA2s3jmNuZCUS92DG67ml5Tg01o71dwaefeHfAHZJi0wBCgwoJdPkDtjvm2CHdfLghWvs9/t8H+7Efc2dUWGdCFY8UHLn4c4eg+SG0ZkYZy2RM78exhWZats2MypluXxOjG3UnJ3j5/n5z8qJcEIeEFAG5rXxRRFUFPOYYA+OPCND87Zf04Eh8oYe+6FgZA1ZM+TuHPyjG+zdOeMGywaIxHgCrs/30wNymHvuh3XwoJlyGa9D9T33IIN9czmLcR6ryHpybwB3r211+8arqqpcWgDThy1Arm5vb/X8/Jx/xx9K9ghCXl5eFGM6gBJ7WdfzmRuwaS6vvv/eUEyWAsDatm0+EJRrY0cAN+wPewPgoPwAYEyAB9NIOYbbXvY8hJAPHeReCYLP2VNkknsYhpkkiTH1I6Sm/Y1iNLA2/Q7ZdoLnXCbcphCMwTj7tCDkO4Pa8vs9Z/xB37uu0+PjY5YDgJqDEO7Tg0Pu0zNK+Cpnp2GA8T1u8wAV7B0g0kElMu6+3IMT1o/n4mdUOdR1vciseT8Ha4v/dD2DkXVyi+u+vLzkYNNtVYwx6/to/olgHd8R+7kciBKZ83HjRVHkchJJippH5OIP6PvzfXJSztl81tyBJOuGzUGOWRMPSLBFh8NBq7rJk6XcXq1XK42K2Yc4OOc5yXoxySnGmEuiwEsAVHwxuAeymADNSyrdjuPLnYhz+47+OZns60BlDKVKLs/YJ4Jt+n/xRa5vXvHhPgZddUIEXfLsEmvufs1xmf+c9cC+8LfrWwip/N1/ThB/Huwg69wH94ie5QB4GFUZEerZHTLE3IvjGO4H/8C6uvw69vGeEg98eZ0Tr5/z+mONt/VTAR0UFcVcB+bgHiMKM3UO8tg0L+Eh0jsHdyg+jAnfjYCeg29paRT5Hc+Cs/LNxHH7dXCo0hzUOKjl52ySgyFXQITIwRz/9nIUBJL1PA/GPIp3JgVD4UCC73DG3T/DdzvL74JPoOJsi2eYuBfkAcfo38Wee+3zOTPsQaUHOL6vfr8OwN2YuxE8Zz3cSLvB8OCTPXCQ4HvEfvga3t7eLgCUKzPffTp1iyka/HscRjVWLwlYKYpCoap0sdnmIIPfc78ABQAsowVdTnnmqqpyfTpribH27IDrpgeBOCSuKc39EsikGzb2BAPN/QAq+a7zQI1r4/wd1OFAWSPYFAfbfJ8bQuTGa8OdjYR1chbXwQBjFl1nYoz55w7AuXd0gnXEucPaEZRTH+965CM6Qwj5tNzHx8fsAFiTGOdDSZFbQAT3x6jR5+fnfMouQQH6AZD10dqsM3b74uIi9wB4uQhTX9zeug2X0qQZwKI32DZNo+02TazD0XF/ZMsABW7nkj2LksrMGBJoOkABRHvgB3BBBgnq8Df83HWIF7aF/WMSmZfNuS9xWcCO3d/fZ3kHFNP/AnhHtvk8uv/y8qKbm5tF8AX4OidPeCavIEBGnW1mv9x+opvoEn4FOcHuwtQijwSGyDNgDjINeYxxLs2DCHKdcTtXFEUudfKsGs8WQpCKNIHp3Pf2fa8izuW/XBd7wnojz6zd/nDQEMc8JYq9wh56gOJ+zr9jGIZc7YAvAGjz/3MgjA31UunudFJVziWsPLsk9cM8ihxZ5SwLMkfYJMrn/IgCJ2+RHWwAe9adBTmUMxIc+1hpJ3XAEOwpWSO+zzN3yCb3DY5ABxjs4tkHJ3ocKEvzRCn0GDlGNpyEBpdwP3Vd58oKvnuz2eRJWQ7OyVKfTqc8afQc13pwz3O6rGFvnEQ4z85gt/g812fdnXx1EgR5gvjmQNLzgJ7rObnHvTiGPb8XD/R+6PXZpVP/8Lf/wcJ5+r8xwn5zbPg4jotgwRca4SQl7E7AhYFzLKQZ4PBdzgLgVJjDfHd3l0H3OSt7Dqh+lePxPx7VYqS9NEVaNnhhWN3ZOUPrRt/BsgdFCB2bilEGBAC0+D4HtzxjN4zS0Gtb1Ro0qo29xlFaVY3COKobRw2MVU3UkAbFqfFoWUJzc3MjSXkmOIyEy0BuZjYgmcBYNRneUqdTuzB2c+9JVNvOJVHpoD6prlmH2UnMhmUuZUA+kE3ki/11RWEPzksZ2G9YPu4TmQUYsnc4gCQb89SzGMfpd73admZ63SCv1mu1Xau6bqQYFTWnLotQSPZ9XgZEIMqzJMC2nZ5pLpM7L61yQ+QMqQNFB1kzozGDlFnXU5M7uiLNgyDSfYQFIwwwOJdVDBxOmWcCjEBwoHNcwx2TM4NkBrx8k2f02efs+8vL3OiYnGmSq4uLS3Vdm40x1/Xxhk1DhkAKgUlx48L+EZQgP6m0ae7pcFBycXExObmg19e3bBvRKdju0+moGDVlMuYMAAEXp1JfXKRD3DjMrW1Pkz7V2RESHPd9r5eXl+QwxzHNZYwxPeOYRkWvViuVVZlGN2pm4apq6tWp52Zj9AbdOhwOeU/KMo2jTmvU5GARO933fR45jj8BJMyB5KBxBGg1U0P3Jo+RdsCDzXQb4Oc8ONDzIM6JKTJo6IeTLxBpgD58Hp9lDZzoYN95PzZJUg4SnUzhs+78Hej7HyeJ/PsIXJ2Nd0bTGV73Ociz93mwZ/hN1sqzD+iol5N69gI/d+5j8ZtO3LFv3I8DryHOdedlMU97ijGqMBDFe/wAQJ4bezcMU1lSPa3zMCaZ7/qcMTocDwtCknvyUjB8NX6KshonTJEJ9tJLuHKA2nbqp2CN87HymlXz+UrsLXiAYTJkOj0T7P4BzONEngNZiApkGXvuQNYzMtgobDPgnD33DOn58AL3I+yH91nghwHLjgXAbfgN9Jp15nm9MR2f5CQ1+wdedGIFwE7lwnq9VjcFE1VV6Xg4SkFar6fJppqb/NkjSQt/eE7MOSZ1nxtjVFPXKosiZ7HGwaoIjERkL51wZ1896CEg80ADe8nrPNuBn2WfyrLUX/gr/3P90OuzMxrO4qLgDni95gyQRk09D+LAwFllBO7csPEg1HSSOfDIlI1BmGiu+uqrrzSOKcUFK4fDcCbCwb/XSLNZAFc2kUV3ZsudyHkQhoCzaYAxv2dPS+OkWFff1HP2xKNb7s2ZaoWgvhjVjKMuNajUKK1qxRikQWoH6WUcdCqiQgwqQyWpUJzAajUJGcJJTW4IIZ/Q6w6B9QBQuyEoyxQ09H0CqExjKstK4xjV98MElGpL/xYT8IsKAcdQKIS55tWZRNaJtWEfMaY8C/fc930+URRmEVkgQCGY8wYtSjRCCNmBHo/ztK3j8ZRPEmVwAuABZ9W2rYa+V4hSD8iO6TRRwBh7zjPwcmfA88yleqOqag5+cOjOILG+fugSeusZntmhJ2DI7xOo1uS05kB7Ob66yv/3QM71HPkFLMEAIftkP2CNYU3pBwIwecqcPgGCKa9LRj95jhijrq6upz2UpKBxlJpmrb6fSz3HcczlSW3bqm07FUWptu0Xz5WcaAqmHeTiZBLLnXp2xjHqdDpmmYhRenx80sePH/XTn/5UNze3E2t2maeszLK5zcCmLGc5oCQScLbb7aefUSpST/JYqm07ce5K16Xg4ObmNulRUaqq0/5VTZOdRAhBXT8olBP4n2QHxwRJsNnUkzMtVBRlXue0/jNBgywQCLHPXufsPoY9S3+kEEpxRk1iyucMGzpPIIAc4cA9qPWAAhDqhBn3gD857z/xfjPkF/05D/r5DADcJ9c4UwhQB5yh9wA3gBRy4DYC8oHvcb9NH9M5seLMuPtKdMYZWL8nZ5qlmXwhICEY4Tu8dIR9deLO2XmuyX14aYtXEGw2G3XtRGbWQWWRSJr1BJTRQ8+cYOMcOAJgu91Ox33KFF1eXur19TU9e99rH6NUzNlrQKrfNz8DSyB3EAe8z8F613V5PLBn88durkJgz5FJxbnc1rEC5CxED3uLj0SOkSXPvHgAgj8/t81OGDGRisDGg3q+5zwY4T79PZ7RYg1pNAf3IP+8J8ao3W6XG/fRA8cf3DsBDrLnIN7lDDnwwQVOpOJrYpzO4hqjQpTa6Zy5YRgUh0FNU6ubnteJOw9IvX81xu8PEeH78/7wnbLqmCDFoEWpvtstSbn07Jw4Rz49I3++Puga8u122ImJH3p9dqCBMUEpcfbeMIdAcPMIHIDCG/64prNebK4zOF03TzNxhhzQ6ECMtHuMUd9++20GNDguWPjzSHUGiMeF4eX7PDDy6PDcQOLMfPHZ9HPmzB0DglsURTaMCH2M81g2BB2G+5yRl2ZgxD2tTr3ipyd9EVa6LhsVVVS52er0utfvdSddvrtWP5y0Wq1VxkKnYVCzqrSuKsVhrrPku1lLslAEfwBf3293xmk/v98o7BkcFM8NE8/kQdWcIZudEN/hskBWCYfN9/pwgbZtc8mRGzC/F4KNoihy06Q7P8bhHQ6HPGqTNaEsgYDg3MDxM0pFnMn8VQrv+sGaUcuf7nke68r7AeRu1JBL5A2DzH05aAlheQbIeXaBtWFNq6qaam/3C8DkssrzYAcgJi4vL/Oz4LRwZh7sUuu72WzyaFN08vLyMrNxntb3YMOB3jAMOQvKftPrAhvnU/JWq7U4KJFrscZSrbY9ZXYSe5ievVroKWVEu90up97v7+/zOpPqxtm7nWGf6nqegOZkS7K9c/8UAIepewDREIIeHh50fX0928GuXfRVOENG8IeNJ1PRtZ3KYp4G8/b2loMfL19yBh1nh71bBi3zuRoE/JR+UNbB5xxYS/OJ3QBL/Ap6DojCaTqIw2ZwrzyrO1fsMX8cxJ87XoJUnoWfOehw34KP9f2ByHt6esrXcWCI7fPsNwyyXwMb6vrq+4IeOtjw6TistYMlZATdR+Z58Uzn3zWOc0mlZ5KQKyc7WHvvMQLwsgbsL74Re4PNQ85cd7gmdoazUNA3AD/fRbDQ9rNccb8EdNyrZ3UAZMgC9sgJIu4HXcnfNYxaN8vzedyHsBceLLEXyAk2niENToYiz+eZf7cp/Bv5Zn+6rltkndETx3PsOWvugTQy4Jky/uY+sFWODb3U3ktPISl4btYTm04PGTKHrLtNddvstsDlFFxTVZVUpGv4NM5hGFSvGo0WKLDm/p18F38cqzg54OVmfMb1Dr/AuvO3Z4nc7vJ/H0Tidsn3neuARxuTRdb4c16fXTr1j/7uP/xeEIHy+s16WpAF9nMIliz3fDYECoSh8oV1I+zGBSMxjuNCYYlcHVih6F4T6GDHGRf/v2+0Z2zceSIg5+k/7hFBl5ZN6iGE7Di9bpa1ZRIBs68RQk/9eTTughRjmlBQHd70e3/zt/XpH/yO3o1Bq7rRxe2Nbr78SuOf/Z9o/e/8mt7Ua73eKg5R+/ak1fWVtk2tt6n5FMfF/iKUHlwg+Kw564ohS/c8R9OenmN/XXCRA/aPvfFAQ5obQ7k39hRDwX1hCJ3JcrnDUcFiYUi5H/bY62RnB1uprmdjyTO63Dowx5HgMAi8Ly4usuHFeDpg5n48OPbxiABPdyTO4HkZBo6JgBUDiQyz5mkPloESsuC6hgFfZjGGhXM6b/JGJ1gHmC1kzO+9KFKvg/+O66BDyJuDLn7O3iMP87zwkMsDSKvPDnPOHJKVmksELvL/XedSKVNan3Ry/HER4KxWG729veWeB+qBuQaAJslVuQDZVZVO2725udEwDLq6ulIIMR/ABYlTluUkL7OtRnbHcdTNzU3WAWQCx1/Xtfo4gzF0kO93JtYbgMdh0NDNZxh4WQ337+DcbSJADNvmIBiQ4baCtXTG0bPAgHX0hWsANLCj3tiP4wWYASZgJAlUz0fAoj+UhXlQxn4Q+Hj5hxNNDgqdOfYAx30b13d772UYLj+uZ3zOwQN2BeDm/pH3eEYYsOf+HpvmRBrfybO7LCEfqdwt9Za9vr6qrutsA5ETyqD6vs818Q6QAFlkpPFVjOXl57kUybJkr6+vWTcpC/YeBSd6MgsfU0bDM+TIMOvnLDH239fNwfg5kPUAaxxHFQpq6nkCowcCMaTTpiGq2DPslZNVHtw5/sIvhRDyVDDu3zNIkLjshQdGBFmssdtDsBNr5Gc4gH+QU+yPg1rPMBDsoNP7/X7hL5yg7vt56hNrR2BLYMX13S964A72kZTLphxkr5pGIc4HNfPMXdepamqdJjnFNyJXvr/4D3w8cgP+cNnj+uxxvpey1DgMClpOlHIc4vbFG+fP5RD5Y51c1z2wcV3/S//+X9QPvf5YpVMIgI8gY1Gyk+qXTdkeVbLAXA9h9hTk+QPjlFAygETTNNrtdvlaCJFviGcAXAndSPsIXhzGuWHAOXjkjFPD0FKb7yAQBhxn5VGkrxNOj41jjdlsV3iibATVnSdpYJ7tcDxqVzX6dHGp7rd+Xd8djwrrRr/1P/0zuvjTf1p9KHTqOw1l1KltVcSgIhQ6HY/qjweFM+bZa9lh0tkPX1fPBgCAxnE2Li4bzng0TaPf+q3f0s9+9jM9PDwsonaXG5Q1TVcq8+QK5AjQjAHEWfoUr2zIJ+DsTcrnQwEwOv5ZQEZS/PlafB4jhpxz7258uR4lI87Ub7db3d3dabvd6uHhIZ+X4NkY9sYBl68xDo3nZx29BM/T69wrgRAMTYxzU6k7WDKA3Ds14x4Ingd/AFZnslgXP6maMyCcBSSoQv75OcHLXMZ2XJTJuF3BRmHDsB0OqAAfx+M+6xulb9TiH49L5pF97bp0AjPnE6ALdV1rt9vrdOoWowh5fggZWFXXDcY747CqKjWxJ4De5YmATtacM8DOOvvIVX6GzVUIimFZL4yd5oVOIXOn00kapxris2ABMOnEUNu2OXslyXq0ZtvtBBHBFzrjayZpUQvvQAMbzTW8rAcH72SCBwtODlCSFkJYjKr0AN2zInyetUDmCCo9K8j7yJQ6MPXn59/OSLKerIHbJ/bMe7kATug79hEddl80juOCUPDgxDMOThSyJ+f7ADBcr9eLg/2Q4aZp8nkQBK+sL+WSyKkD2nFM45gZh8yEq9PppOfn52xz8EleGk0JK2uD/J1ns/gZvrZuahVGYGFjvOwUOcPG+bqe4yMnKlwXsn6ZjCKb+Lt+aljf7XYZP3A6PX1bjp/cprge4G882OT7yaZ536p/zv09dgTgHGNcTM7D5jnG871wwhrZc8LQCUwnMfhe3wOXZx+24Hs8k3NzubcHZLzP8amv4zik6ZAe8IMd+mH4ns44DnAiAzzL83mmD/L130SOp2eIimNUKOYA7zxgQlexG9gIxzWsD/d9blPcJvlefM7rszMaf/v/8bcWhs6ZMgSGjQEI8HMMCwYXNgNDgmDz+dVqlVk6j8jdIEgzi+BOxkG9f457JXvg6WMv3+JeAC88H8rl4A02hkjXnYAz2XwHyuGChhLxXNwrwklNracAHfhyzy4wlDX1/aAh1KpOgy6GQV1/0qGK0nqlEIOqtlVsSp1KKfZRw/6k1Xqj+nKroW0Vx9lhsN+ekaBPw52MZzmQg5mlX2Z2XHYAWr/+67+uqir1+7//P2ag5gDBZaBpZseOw8UpO/PDHpw7ajcC7J8HSR7s4ri9LpH9SM5hBvEeaMLmUvLj2UCeCUfijBBr13XdgtHFIPE9BOqsSV0vJ0EQDLKOrhvnhsvrcdHLdGrxEqzgGGD0YYydIUsp7GEhv4DO7Xar3W6Xg3BnJj1IAmDgPFkPwB0ZAYKezDpaANk06YAuwDX6MY6jrq+v1bb94rPujGP8/nkd/G4Y5pGpOKYkp4XSqdXp5Fz2KAHWtdq2y+vw8vIiSbmfh4ZR7hd7hW4QSLlzDUHq+y6vGaUD6XtnNvk8sAB0OVHw+vqqq+trDXHM389YWQ9qvaQQGVaU1k2zkEvuB1sN8PYeGVgzz3RjF733AT11/eKFC+O6lCt65swzVc768ztpLuGDnSQwRg6d4HHQ5QEQpZPIBetNacVy8MB8L/QeuY1lHekLISC4urpakGHu43xNnM3k3w6geLHG2EjPqDhY8efhe32/nVV3IMrfALanpyddXl7mtXXAh36y9uwp2UwfYMAZG57VACCdZ6V8f7G3/AGboAuwy964nK8TpLKem2jd5/FeCAFsIy9+DzHD8ANsJDLD9cqyVKEgxbkP9fn5ea4QKObyoZnQm0uLnFzAnrtfZF3QLS+DdyKGNcJGAfA9KKeZ3c/pYC/4vMv1ufyynuhp36chFugOmMx1kCCa9UQed7vdguBBjp2kdB9PUI2MOsiuqioTEKxXHidfFOmck+L7JewKQW3//Syg40qXRyeAPGDzQAEZZG0hJcdxlMYonWEJ9skDO9cDx6bYN7cV55jb78dx8eecDP7HOrCPFwuKYCCUPIQbUhdmD1IwLs684VzcQLIJMMQ8nGc7AFIO8BAWBA2Bvr6+Xvyf+4K5GscxOwVfUP6w4BgMBNgNK/foht8DJDbRm0Q92EJpeD6YbqbJ+MsZC9hCSTPbFRqFrtfYHTRWUVpXKlSp7qUxDuqbUn1VqBqk1VCoLCsd+k5j32m9ntkEL1k7b/J14XUQvGQeg2JU3l93ZHweBeFZWG/vN3D2OYQ0mcoBM0wGrArrjkywp36QFcqPs8PQ+fN56ZTLBY28qaF9TiFj6JB/QC8GAKfq2UHkmDVjnZDNEIL2+30uBSDY87KnYei12azzBBLPWHC982dBBt0x8cxJ/ubMgwNOJwE808DeQNQB/GAr27bNz+0HhaEblIu5/qCjOIfX19f8u2EY8unQgDlv4Of+AA8wfonlThNVGM05DEMOzvb7t8UzorN9n6aohRByADkH16WGoc97S2C5Wq20Wq11OMwT2yhzAjg4QAeI4ByRa8gVAovj8aBhmGUVuUyB4EFNs8qZHwfGZBj2+33OmGQZKJfZag8wWAfWFd1cNY2607Lsx8ET8ueZCV4AD2TPsxi+9thtruUZS+TA7Qj19i632BPsqteDI+P4AcCP64w0O2a3i97/wfXOMwQO+ABlvNx/OLOLzePzHtR4AIbce9kwvgAAge7w/7ZtF+PhWW/faweT2EfuD4LhHDB5lsgDOfeVZOHQH2TX9Y1AFbaeIAQwjzy4/vB71umcyWaN8I8wyNzj6+urbm9vc3bRCa4QplKlaj5Nnj2iooGgwYGYZ7o8uHYdOWfVCfC7U6ty+i4yg9LkRwsf2BGybeX5HXSSeeV+ISbZj3OSC713UoN/cz1sE/7leDzmsmMH9y6n6ADXIuD3IMDX2ysSuHf+hux1YjfGuV+Ez+IPXIexO6w998RIYMcu5xmhvG9j1DjZFLJHWf8lqZgzVm7jnNRizVkL13Pu37Ega4Wf5PplCOq7eSAA1/GsPraFa3lpHd95XiIvaYF5/Puxp3/iB/ahPJ6iwom6cUHouSk3jA6KUeL9fv+9TTyPnDCa7nhYEFhevh8DiLNIihLUtp0Oh+NUAnGcwBALdsiK4JNbqmpm2X6V0GOAXYBQVi/DmZnQZebGS30A9R5sebRPBM/P3cmyD3y273tVda0+RHUapLpSqAq1Q6dyGnG7Xq2lMmjoB3Vtr0JpnTSOqptGjGZlTXnmtDfS8TgfssQI2iSYy7nlMc5MmRsgN0Rc29PEM7CbG/wA3WntBzGNiglWx+NpClbmSWLOhKY1G9U0q7zHfT9k9qxtYapKFcVsIJP8zNM5lqzqnEbkOhhuAgT2eLvd5rIggOp6vdZ2u81rnIK5o5XKlDqdEgufDvy6yJkMHNTMFs0BC2ABI0dWDVDJPSbHMKqqAGWUx/ULoOQlSjgFJn6wFpTxpSBiP4Gw9CybDc/eq6rShKa6ng/4wgGj1xjAtAbVJItBp1ObA7sUhM/z7mF/KaN4e3vTw8ODbm9vM8Cfgf9Kb2/7XPYFO5gCyFpFcZmfm9IpAoTVau7nwkGx5rB6T0/Purq6UprGVOvx6UkhFKnOO0Zd39zo1J603V5ov9tl5gxGl+CCwFJSrkvmXqOkqmnU1I3KqlSY5DQqqqxrbaead55vHEeFslAcR/VjalocxlFtN5WehmXzMEGPAyUH2ASPmY0rylQ2oKhCQcM4lZxWU7mLooqqTOceKI0f5Z7PS6jQXWzaOduHc0S/HOCfkxJ8Jsn1Uj88SHPCCnmCbfTvdJ+UnX059584YHKbwbXQSSes8BHSPLmR63Fiuj8DZSUevCE/XguO7PLy93O+imcB3BctyaK57IRMBKD/vDx6JmHiwtZjAwGC+DVIAvSPMkWy2YB6P6wNHfCAEPvDup/ak05TUFcWSZaKslRRlqpDUDmOqleN+snWXV1fq6hKhaLQ5iLpdFPVWY5DCBr7QaGUCgWFIqgsSmmMKqu58dyzs9heJliBT/KejFHt8ZSmEIagoiq0e3tT3/UpgO/mMzs8YByGeXwq/pPMA/Lje8LnnKBFZ5Bl+mDYHyf5CCaQIfTEBw9gkx0fIj+QTegi68S1vbrlPOjEj+Efx3HM9tLxJmsAYYiO++G77AvPhaxiW8Cz2R8Pg4pQaIwTlp1ICsWoMAV3rvNlOU2DilI/RoUyKEgqi0JDP2iIsx3jns9Jafb63CfyfuwOdnoc5zJLz8iw1tgWx1bIhH8nuuskmdtDJ/o9ePqh1x+7R8OZH0k5nY8z4r3cFEaABwZ4sSBsEp87L1uBlfUGN3ceRNQe+bkj4drp32mMatt2C+NUFBiDBLjSWMagGJfNUzhqz37wXCgEAuFMvzM+zsI4mw3gJkjh87yfdfbv4X0cwIVzcCEri0JBhcZR6ve96jDN8Vav/WEC70WhUUUCIEVQEQuNw6jTqc1KGqOyU0tAsVLTzEzHfn/Ia8E6xyiVpdT3g/b7fQZgrAny4kqA7PAsyBwK50EJwYU0lyEwehWnk9asVFHA4DDlqsrvT+VGQWl07hwoJ0PYTPuX/iCvyHsyLsveIk6QpbwIw+dGwxubu67Lh3FxnbJMo2pTkHXMRuTq6lKr1SbLSdd1ury81PPzs5qmyScPU1J0fX29YBI96+PMZYyz3CWAhgGZ67CpMUcmWV+CYWc50/XTOg/DoMPhqOPxlMFD3zPhKo16DWGeSuaOGaeX9B/ZD7q4uLRm5qimqXKtMj0OlHYxUckzqRjQu7u7SX73C91KujjPPL+4uMhB5Gaz1Xo9T7vCoWKjXl/fJsAxqChK3d1dJ+a2rlWUpdbbTXYQ2/pCY4y6uLxU0Cx7b29vWe4JwLlHQFhZlooKWq1THXTu7whJlq+mvV9t1opB01jOBPLLulKUNIyjDiezLeUMtr38yXXUwaRnm/th0KhUK9xaduN4OqmY5EEhqOut6XgCbnwXz4xtIBMIsHCwAZHDZ51FdjvqmQgPLpBb73Vw9p17IbAi2EAez7MLOHj/PLpCwMpz1WcAxcE89w8hICmPD8XnMcHR/YZngbzWH5/Ld1Hm5NmT0+mU7Qg9Dw5QzjO06H7f93p9fc3BvdsW+jGQEfw46wGrTUZtJkvmfXRgyrU888Qao8PoriRVdSWFoGa10hijTsf50Lrd02O+p6Io1A29iqpUvWoWo81DCJNMF6qbRkHS2M8ZNA2Syqi6qhSKQqUFtcgXxCwBn8tcCEEhSnEcFcdRZVVpu05n4ZRhZtOleegBeldV8zlP2G38JoEm++/MNvcOlvOMiA+vmP35vF/IPEDey3oJFr0XiWv4QBt8nPesEFw4sQT+Q9chXdBfbCP9INwXL9d/vhMbjxxC9OK7wHZZN8ZR/TgHdMMwSGNU380BFRUnTq4TmKwm2xXHydeWUm/4GHn1AUNufz0IQQdZc9YkhCDFWU7Yp5lknxu4kR3HpY67fN9nv7usOHGi2wOkf9vrswMNhAJA7xuHEvnvpWVqiL89/YYAeSbABd9ZV655Xgbgf7MwBATOtGLIcRbnYF5SPszIMxFdd1qweDwvZVl8rzs0BMf7C0hNIxw8r7M1GBF3Us7OOeONE8LYuyPx66ZsQ1pr2ArAdwhzGZw/iwdnrDt764wF7/OULAJLvbmfvMw+nbMJBF78nrWB8XDmz+utuS9epOOdEYBBRLl4XlduAiC+y9fe06rX11cqy1JPT0+5vjZNr6gVQrkoH0J+Sami9DwLa3N1daXr62s9PDyIM1+Ssy50c3Otl5eX70206ftOX375lR4fH7P8YnCZ8nR3d6e6rvPsdpdFDGrXdd87EOk8+PNGPYwXTdvOnpLBQ/+KYnl4E4CVDCQTTvg5ekf2xh0ZBrwsi5yRlGbHlu43ydzl5WUOMqh5R1bJvvCZtm11fb39HpkxG+h57B9OLjHA22y7cJA8bwgh140T4ACSy7pSVc+nJfO74/GoUCTADQBlbZAlZ0e5p67rdHV1paiox8fH9O8YF6wk9mZmvpb9BciBA2w+h42BbGDt+B3rzz0hezHOJ5S7rSNzBFjAVsZhzPfO5+eAO+nv1dVVtkEeBFEbznr4idP4HXQZv1CW5fcO7HPniU11X4RevL29ZXl1xtT7jZxU4D3YTg/usVnnwa/7LdaRvavrOttUPkM2CP3i2ZEz1pQmYgdlrBufI1DwYARbd3FxkTMg4AFnwnle/maffF357qqa6+c9yGKdCaZ4Vvybs/CAROyOA8+qqhTHqG5c9ufwO2yaP7dXIXgQnbKy02j81SrX5XvPW3rNZcNub5E1aS4TRFamj+XnPBwOi4AQtp015bDXokikYNYhI2iqqsp9Xuwna8Zz+9liPIeXKqK3NOhD3EnzuQysP3rlPVXIMrrh/p0JY6z3efkw9sEDePCTk2Xsk5f8OQlMxtVlGTnzDJ0HEYkUO8y4UlPmKsylWZS1sY/4LoJKAknsj9vrpmk09p2Gce5x8qEByD964wQ/mIf7d7tVFUvb4X7cCYxzMpefcY/8n/3Ht7ncum/5/0pGgxtwcFuWZWYS2DAXfISJhz5nLgB/vqgslAsGn3FmBaMjzXVkGIgQ5nKVeTGLX+n4Qkij3fKmVXO/RFF8f7oITvmcReP+MPgALQy/z6pGsTC0KKcbS5RDUgaMAMNzJoy/uT+uxz04OE/PqZzJcfDgzoK1h3lhz3BQgPC3t7fFXu2mMpDVapWnYjhT5aATBTjPXPC952lQZylyNK+5fIH1Zi1c3jzrxfrDRLA2XrOM8UoGYdTz83O+znLST2JrfSqSM9Fvb28LcAdD7kCZzMPt7e3Uo3DM4AD5mIFDYgv3+31my66urvTLX/5STZMauHnOb7/9Nu8Z+8VnMqMWgna7fXZSGGt3PKwje8fLgzUHZtSsux5joNA1Sbnxkr4NMjm8n/KLNJVmPjPEg9K0r1rok2dYXca4/3Sv6cRvn/rl+1QUadSxg9C7uzulk7CHXJ7l5QSwYawHJ1xzL/TOVFW1OPht7Ic8xhLn/fLykuX9nBjBMe0Pe202G93e3ub1d31Dz5zhckAJWMDGO9PPcwC+nN10W8HvAajoznq9zr4BWfA9IXhrqvkwqHP/ADCCtTwv6aFki4CYRk3uj89QTgIBIC2zkOi/kxLYOH7HNR3I4AP8wDLsN4G+N+cis7wvxrgAXv7cyLiz4PhZfzb2+eLiIn/W2WH2HADnftltuwMuf99qtVpkRpFDCAoCS98LJ4rcznhwRpaH9zp4ISByUMs9IgPeu8Lf2BvAYD3t8eFw0M3NzSKwcEKUfeA53ZZ4oN+2rcqwZMUzZhhHRc2ZBa9t53v5buQsred8CKJnUpyFdmCZffDZdDg+jzxwDy6r+Nnz83CQPQ9Gsf0zCbQ898sDrRhjLvEkc+HBi5PByAT6y/Vub2+zznEPPC8+Gd/rhOR5Mz3y6eQwdo33sbY8N2vE56Sp77QoFeLc48OeeUBKEMSaYBOwAw7c03t7hWIm6wl2nFTi3nhGrxaaqxDmDEZZzQORXCYYqOO9LE5+IP98jwclvHifE1+enf2c12c3g/+//su/uTB8bmSdpfAbcuYGhfQUM2CY3587Oo+WEAhXNjYZQUSoUWoYgmQMw8KJsBEOjvw+eZVloaZZgnSe0QXUAco5Y+FshrNx1Or7PbGxzpT69T3L4Y6J63iE/qs+9/r6ahHyrACAbgw6a+nX4M/FxUVulIPJYK/PGSNfSwcoGEYMA8qEALuycH8eqOBQuJ4HnxgW7pFnxAjwPawLn8MowIojr6Qq+77NQNDTtMmoJhB1dXWVp2R4WtnTrF6GgUGmCQ3wuV6vJMUsyzHGnHqv60b7/WFxwFRRFFNjZamyXB5Id3Nzk/cF2fHyumSQllO7eG6u7xkiHBI66vLrzBZg05mST58+5ZIF3z9YpNQbETLAcbsgFQsD7A5yHAd13ZzhA+jTbNq2aZoTzjWtqcQp81wPOU36MY+ORhewKSEsG+3YW87k8GdGN7q+zw2C6CJ74k2fnCXAs7tj9XS7JK23G63sZHuCHsgR2EKYfwJ5bJWzt7BzXItSJQd4lHQBMD0j4JkT5JoAks87eKD+vSqXfQ3IoNtRz6Szx+5onaDZbDa5tMwDTwJsfAJgl8CcXkEyYVxb0jShLD0L9o57dT9IdteJK57Ny62QK3yYAwwIFmyGD0zY7/c5o8A+kCEFDHqmA//jGTJkwRlSB9YA0be3N63X60U2yzPJbg8ctDtBhT4hGw6QCCIcGCPbfi/uh2bScCY0HcS6vwghSEWaSnE+Fc/9v/sU/s3f7EMOghUUh2HxHMhzVFRr8u+2kWu6PGCH6zLV+3N/Hmg4JmAf2YN61Qjw5sG5B7T4Qr7Tr4/dw1aiH+632DfkyklT9s0JNMeFyAjfi05zX7zfs0fn9ukcQ6HL/nOvUuD7+IPO8d2O8/heJy48GAshqCorDd08EQv5QiacgGEteTn57UHIfuq35Jl9v9zGc03ulX1mjZAxSSq1nCLG3rl88jOCOZcbvud8L9EDn3DlwUhRFPpzf/HP6odenx1o/P3/6u9lxcA58gBMcjmPiLhpNtIVGKXxlLa0TC36wrE4OBmM0HlGg8X0Mg5AyrnB8s1FqN0IJgauy8Dt3ABxT97w7c/va0DdOM8IAwjbw/2j7G6cMNiwpZyAKs1RNuU1zpYQ/BHVetSe7mWeusB9sTdd12XWw/eAQMDLjM4ZIA84fS0wPh50IuAAY9ZTmjNk7tjZT2eJpWX5FqUNyILvu9dRIsP7/T6DIe/JYU+SgQna7d4WrD8OOO17leUBBtVBGcAZgMD7MDKwvQRrm81aXTenVN2YhVBov5/HXXLP6dTnSjGOuUeD50BWeO7T6aTdbpcZqBDm8ZPIjY9ARY+RJwIgL2VkP9hrT1ezd4Cmpkkjfy8vL/N3pMAiZSeQL9Y7GchU8sfPvBlwGGZm1sstaLZHdlkH+lDSYIB0L5x/wTqs182CcUMnHh4eVddz8yDgFqdCYOcMUIxRx9NJ9Wp50jKyuKprvb2+ZfYJ487f5z0bEANDHNX1qT6dU7/P9ZJ1dBaQNcTGnDN+Xr7jthLZ8RGy56CCUh7XfXeMDnzjmEYzOhB1Igi9PAeX/Js9xo6d18NzPa7lpAz6TingHGDO64FseqbJAa3rHz+DFWavuCbMq5cDui3iOgCYqkrld5TiORjuuk4XFxeLMhPkkL11m81ewPJ6Vuzp6Wnho6U5i+26zZ4iC+i3gyA+z755JgISwlnvc3IO/4Ct5ProgWcZzglDiKJEWKTvPrSzL4Qg4XuQC/bKfR0yzp5TIlqEQtGy6zx713Xq+l4xKO/zeRDJHvNvfPW6aVSV87lMAFrkwveaZw0haAyz/BCYePbMM/6sG/vkuouPdZLIAx1kkn06DwbwZZBnHjTzHmQS+4DPdpvgRCxkpvvjDP6r749t9SzmOSHpzL2XC7nOeuDDmo/jqLr6/7D2bz+SJVt+JrZsX9zjHplVdaoPQBBNPpAvBERKM5ohMRIFAfq750EtYDjAcARwBPCtQeCA4EF3VWXcI9x9X/Rg/pl92zLZlQegA1lR4eG+t9mydfmt31pme4h1rg9wdGLq5MUYgzWxv/IY53WN6XwyoQlU5oR/sv7ja/Ab2G9Zh6luBKeShJ55nYl/jA29cBxwEvKtWNLq0X/3r/8v8Xuv726dchkWQ+ZmOFGCPu1DLKo3dMGORlS2qF0oggHXRmA8tdMZoBkyroFwEGp2KttnJKCEXgjnXHUTTFVw+lLpv6OVxQvDmHBCLB7XHIah7GcBDDshQo7Mg2vTqkOPcEQUh20DcDaLQVhpzXpFdBslcuLFCwfQBi6XHQmoLr2zfv6dUruTRGf8VBUchD0+jKFlCBgHfzPo8wOrcIbIB0dHIEHPHDwIyqdTDn48QRaHBwu8rlk/fvvtt8IGus0N1p45kBi53I0sc0KZ4njMsnh4eIiIvCH04+Mjrq9vSgWEuXCPp6en6LoKFklOWYeIKGCfk4gyCKsgxw+xdECxYwR0RESZJ9cuILJhGyOigHAnZOhJvsYaPFkb5gzWh0MI0GvWNuvRErvdWJhs1u7u7q5cG6ePDWWbyt/nmODa1vQWh8P7xpb7Prf65ER+KMz3NOWN609PT4Vx9vwBFJeXlzHsti0x6MLh4yN+/PHH0juN7yJJcELH/p5xHGOasw+9vr7eVHQhI7xpd1mWMjYCsIEaSTptVSRptHsxX/wkwB1G3QCqDbj4Mt87A6NTjMOwCV6c8oWNO/F3tdd+Hp+Bf0NOZnOJEZeXl7Hf70vbHPGGazJOYkA7brPEEbW6zf4lkxjIFb9nZtnMrxl9AHFK9aRBt8LgN2hVQr+Ji9in2zjxPawFYNox0ZUpnySFjEni8BmeE76YsXMNn0rmCobvFRElMXQigA+mxRRfb+KkJSlZI8bqygj2u9vtil+mkorciPGcAsgYb29vs3wjxTTP5VALrsv3U19tCTk5+UEmgLbLy8voU0640Rd0wHGGmM9n5nmO1Pexxtc+1rEZzIU92CejwyaRjM9sDyQOJmOpBriyzfpghwbmyHdd10KmEFOII6yhx+CuD/S39V/EN/TJuND4jDm5mmcf4USI76Rv3JexMXbIOHcu2B6R3eFwiNTX5MYxtiVhvA+MF7J3i1YeZ02U+L7nUHHw9pk4XlP7LD5rDG7MxmfxT7/3+u5E43A4RUoI5/w0wpVNe7UFxzviszIPkVI+ISF/L5/sRIBGiV2usuLiNBwA7KBtmIALMxg18HWxrizmEn0/xDStcTodw3sVisOQYHGSOFcYULMVBtWMh6BNz6F7VSPymd2AYgNcFNLsEsqA427bjN7e3kpFA/mQCAFqAZaWFydLndU4hoHqRv59HLdHQOa1ra0/NmIbF04UGWKkzMX7ZwBbyB1dgjlxtcJlTpzaOOZTetAn1sVlb5I5WlOWZYnn5+fiZACK+TjSYzw8PMRPP/20OU1inqe4vb2Ly8vLeHp6jre31zgeT9kWUn6GRer7OE6nuLm7jevb2zgdj5FiC4DsCAjSJGL0/C9rbovp+j5u7+/i+fk5nl9f4+HhS6xrivv7++J8Hx4eir4OwxjjyDn97M/ZVWA6TWd9X2O/v4zr6/4MhC6KU/4WC4MNmrUk+JhttbM0cHKAM3t8fX1dAhT2c3HBk3bz0cPT9BG73ViqCBwlO45jeSheZpZPsdux36CeZpX9yUfs9xfRden8fIldfHwcvwJR1lXAUvZBp5jnj+i6eo48wPfy8jIeHx/j+vr6q9NHOCr76uoq3t7f4uN4KA6afTrYLT6F5AjbN/tMtZI2sGWtT6Em6D8/P2+erwLIcZB1u4EBwbIs+cFPh2M+DWeeYzeM8f72Fuu8xDDu4vI6V6Hm0xRHsc1vb28RwxpzRJyintyVUoq0rnE6HmMchhj7vKfp/fUtnp6eYpWNcxY/uo2uuCISERsgQsWLgxSwKdYJ3SUutVUIPk/C/Pr6Wton0V+3ghKE3ebEGuKX2koD4Bi7IZ74ORL4Te5hIsA2xz2o3K7SAeyT6+HnAWRuF2nHRHwzEOEnSabb4JBNm/TRmua4hR9u21dJeLAbAxl3MDhxNAhflnxqWqznjfWxRhd9idvoDTIFGLW+CgDMe97T406Bi/1FDF23IUBKXBzHWFMGgU9PTxsSEj9JjDI+WeYlTtMp+qGPLvKpcJFSLOsa85KTG8C7E46IbSsS1wR7GFMsy7LRA/QSeTqRczJD0mhbxE87gTD5y/ysW+gm64xcfT1ijclHA19XHAzy8Q/ukPC4XF2gcsB8XUltE6w8jiUGETH+G+PEnvAvh8Mh8hGCXcSyRD/0saY4H+09xBprDKr0s1aOG24/9py4L7+DcZZ1jnmFxFjyUbpLxZPumECOTjKsp9gG87JPQpYmgb7n9Rc8Gfz/XSZqIJ+dfAZZ67oWJwNwPJ22/WZMKDvoeiY5n8GxEgxwtu2mJhYdp9WWqRGOHRPfp0eV61xeXpcEx4AjsxvHjXPHcTOOu7s7VT+68jmMB+dNAsZTXUmgHEyswLS1MHZfi/l5s64ZcbJuQJmdQER2hC8vL+U0EVpZUDTWiiBmBi+PM7ewsI60IQCgAKv83QDBxsoLPXLJ2FUOxu9g6EqFQQPJh8+BhmmE7W4TUdjmL1++FKafa8/zXNaI8Vkmx+MxpnmO1NcKGXPuui6fn52682bmwyZRJngSgCJqG87xdCznbT8+PsbDw0P8/PPP+ZjVYRfz+UhQHAPtNbCM3IO5eu+K22JgGW0nfAZ7hGF2P6mBkfvHkY83h8Nk+fP8vxlM7KhN3p3EI3McISfFYb/oHKeusIZm5N3aAyAhGfjll1/ip59+KsCC+dopI3dsmb59tzyZFWLOa0QcTrU1srZwzeXJrp43ZMH7+3vZR+AW0XEcoxuGmJesC3/+85/j8+fPG/1DvmySxifi5/zsjmnKz7u4OrcE4mMchOznXNXiurTsuXXM/iMi4uHhociVZ8j8+uuvpeLpOcIAmwGFwHGSwH4QkxjMF3Bh20XOTsBth4Al7k0iiE/mXvg+QE1ElDXFXri2q8zoiMEV4/JzEK6ursrJPz6gwQwlezbwJ9yDdYG95x7EAIC4kzgDV3SktceI7ak4fBd9pfoOscb7JvOwKdYHsqmwvunrhwHzWZJj5nla6kP3uC5+3nqO36A6SPWCF9dtTygirnZdF+uyRq8qAXNaliX6cYhOVQJ8lj+LHzEodgzkOyShXaToz/ZjoBkRMa9LzEt9cC6+2smDfWLb4gT4R7YeMySmWW0Sd/w1Y8K/Ij/iBd/j8ybaWHPL0MmHx2X/we9cw3iIdXKigi5bd52EONFgHZlrRGxOnWK9kHVphZprqzFj6YchDqevyQzrt+dpTIIOMy6vBToAucc8PGbsuFRU1u0+D/SP65s0cPud8Sf3xfZt9//6//4/xu+9vruiwWIxYBY4K1IFAxwviOPvumFzTnF1dGOs61LAiRXaoJ6AZkETcJk8VQacuo2bxbXSI0QYf7MbzIlFgGmjD9jAg8DqgMF3WXCzSwR85sU8vJGba1u5CB4OmswNRaE0zmcJbLQ9uKTIZ9wvi7KzPhFREq/dbrfZgDgMu9jt9hvHZ8dDUPG+B2SAXFJKxeBYo5eXl+IQCfRuw+En96otNXVTLic8EewM5HnglRkN5AcjbdaYkxpaJgAnXcDJeQw4btb16uoqupTiYldPNbLe4ugAzQDS0+kUl1eXMS/1GLmbm5tyApIdFC1Ax+OxJFJ23uiNnQbOwuXelFJ5LoSZLdYR3XEiiHNkjdw6x30d9AhCtgUf1YlfwXmiM2zqZy3wERxhyxinaYr7+/vouq60WzA+TuQxK2pwii4B6FmT19fXAjQhP2wv7NvAR7pyAIB9f3+Pp6enmJY5nl9e4ocffihJfAXlqSQaDmJUL+jTRiYE83ldI1JOAn766aeIiNLPbX1k/bETfroNBTDFWfrodJvcsL60oUREIUZYO7OI3A/bpr1oGPLm8uvr6/j5559LMuv7cHwpPhi9RPcJ3CRU6JJbPRkvYyF5Qae5L6RGjk+V2X9/fy+yMGHGNZmzgR7kDUw0r1ZG+C+ICPw283FlwfELHWd8Zp+daEVsjwpnfgb+xGtexA0fhADwcZuV96wYRHpfU9uuwRogNyc+ACQTe46hXNcVoOPxGN04lCQFOyUpc4WW67LnhfVgPPgrE0r4fpLD6XSKtEbxN8SXvu9j/viIi6vLjRyZd9ulgQ7w00lGhB4C2eWTj/ibk4NljRi0Pqyr8Q8xkGuaOXeyY4wCHsLfGcy2ibsPKiAmghuc+CEDxy8nscRoJxj4OFcIHd/AZsyZ6zpW4xv4G1jJa0wsRA6W8fFwjD7VrQL4MvTKpIfJqNNU2zzZ6wPW8zzRESfQvgf64PV0gt4ecOQqlmXp/8eXgK2NzWzXxrRtIobv/N7Xd1c0/uZ//v9smAsUJQthC5LMYq5rnaDbZvK1aosLEzWLPQxDKVFyigfOhgDJQvkasN04fZS/PdGoLlq/WTQCYZ5jbMBhEZwWD2XGwA3CaHWyIwUcOpCwqJaVjRkHO025X5tNfyiGA5eTG5QS4MW6uUrAGhC0YD9Rdm/KnqY5xrEeMcg9cLwANtbGDhQlN+uAPkXUJJXxwzjhUMySmVmkDQV54DzMDNFKwmfcM4ze4ZgI1jjkiIg//elPm1YqPt91XUzzHP243ZODruzGXSQFLAJy2/dtNmld1xh2QxzPm8EBxIDY48cxPt4/CnuNrpmNtCMn4KJ/ZjjRK76H0yVwYSPYi8EDcmsdoAEI8gCUUmlgTOiMga3Z0ZZFJ1C2bYhuKWR+fAcdIon8+PiIP/7xj/H6+hp/+tOf4vPnz6UnnnkSRNiw7mfs4JuQJz7LfbOsIzq8LPkJxKep7vFiTK+vrxHLEkNfWWoHS8ZNpRh/8Pr6Gte3t3F1nStwbtdgLWjJY24R25P18NNO6GPeltX5Dv4T8Hw4HEoS5H52fLD1jhcnapnhBAAhe4NzxmBShgSNOa3rWiq3jIUASkspMQJAgf8kOcT2zdbyPgk8rUrYif0plRyTBgZP6IpbU9D5dV3Ldd1GgS8yQYNMWrs0I4rdsr6M3ckW+oQduaJIkoV/NLA0UOa+3vhu0MbLcqaqQKUIOzXzi29BRyKiVKmdhJSks0vR9Xl/4263KxUzxkXibbDMGnpDLXIyKekxrWt+kn2ftoe0lFbY81hMirImJsqcLJkIYszM+Xg8xq4fynq0+Gvtso9gbugdemkcERGbhMBkURsvwCgm+MAdBuROHtd1LWPHPzI3MEGbzDoGgjFa22dc3Nd40VjHsvS8mDs2hNxZM9aHexi0j+N4fjjfaRMnSdq5LnrKGNZ1jW7oY5a9cy9Xk/AJ2CRrhHwYP+to2aKrJGDGFNhskeGy3cPjuMlc24dUWl+xNdbPMaHv+/g3//Zfx++9vjvR+Hd/879+xXzU4J8K8wTY5qjFZaknlXgTdXbCx8LCOLBa6Z1N43gRJKDGTBkVA4Kn2TkzHhhaDj5VQed5Lgxlfm0VARYFWeAscdqtI/ZY+T7AmWyYTVAYMGCCYGBWCQVomTQUlE2Up9Mp7u7uikEBwDDedoxOUux4nTSxTh8fxwIcWTNK5s7UvUcFg0dpWSfGjcN3NQjZwSLjYNzexgswZwB8PB5LlcJrYSbfzJkBsbN+M6gYs0uXfd/Hkr4+kec8kBj7obBoBuYOYMieQL272MWy1ifIAygOh0OcDqdY5roxGLmyzpRxsVGDNQMTQB1rBXCMqBU8s1LM1yyKr4n+2lZYYz9528kPrPT19XUBhehBu+ENvULmsJywuWbeHSQZH+NoGU7YSuyfKoMBMCSHZUwFxaQHtkJCy/un0ymWdY1hV48tdSKxLkukNQrQnKb8fBr2DGEnZvkfHh4i9V388OOP0fd9/PLLL2WdSKwBIcgMXSc5N8DBn/RRCQqDPYA6emygYSKGebEObkVBn8zoelN/GwMc9Ekc0Hf8KAEUYGmAj923Y8eXci3bVzsX/k4Sw/rgm9BTwJD9nRMtfAq+5/r6uuwxMoghkeKaTtyd1PPsCuYDqMG/208iK/bSMC/A4X8N6PMTPWHNuTZy9TydkPh6XMMAC7s0wGG93YKGLfJd3ye6fHQ04+d72AmsuAE/8Qx94d7YLv6AdSs6cDyWh6OhvxwD3A19HJqOAleprAO2KwC8KzhUlcau37D4vs60zOXoXj/4keQRnebztifWgTVA5/ChrogawBIb8GF83qSmSSHu5Xhg2TFmCE3bPbbN3G3TLejlmuiSKxaWgX2L9QF99d8iIvqujy7q3mNkYuyETfD3dV1jTflxr64AY8PGk76//RR/Q05uWTM+M06yvzJxH/O2vbElmxmTr2e82toOthiR90X9y//+/xS/9/ru1ikmCKj2gg1DXUhncDk45AHf3NxsQCAPqfFCme0laOB4yYxh7HhY2TRN5YFH7ucHqNze3hZgxCY2HHU2yinGsdvc08FwXefNU26tLAZzLAgBkIU0OOUfbCCg0uDJzN7V1VW5Hs4DAyeBskOgTLeua/zwww+bqoiPJCU4wiy5lYH9G54XBpSdx7bPmyf2ui0JQ7eBcx2MiKSnZWH8WcCdn39gZt3JAgmr98vc3NxsADxryrVh7Qi2ZtQNTkkOX15eNi00BuzduaJBewtgZ57niL4+zM8JooGLZZJSisuLy1iiJlK0VlxeXsbx4xjLnAMqx8MyZta5rlcNdhGVMXEVjg24yNsnNNkZ4awILsuS9zt9+vRpcyKc92M46HAt1ozqJHpp4OJ5HI/HEohbhteJixNyO1z0Bvk54OAXIA+cwHZdV/wNgQbgx99c3XGS1CZENzc3+WmwfX0PNnKapoglP4XWCd0PP/xQ/JLnMU31uM1hn+34l19+KeCP9cE/0gZjtmwcx0JmOGHvuy7SGmXOMP+AAOwGkod7Mm5sn3W1P3OAe3t72xzZiT646rzf78vY8VkRuSqCDbN+gDt0m88iY+sDycQwDF9Vyrk+ugx5xnryXQM3Yhi+tPWbjKPranV1XfMD4nhhM8RabHVd8349kgUTFYyZayMndBF/yPeWZSkEAvaIvNF3k1f4B5J4/Cx2zLNWzFp7/MjI+/+4NyQJBzsAdFsf4k3irS+f5znWqGDNrDV+G+LO/hB5Oz614yWO8KpH4K5xnI4bEgP8sUbd1Mx4SPBcYed3x6MWyJWKbddtklmD4PyjVjpYm0rkTmWdzbgzP/su4h9thE6+7ROxN/TFMiyxsOs2yU77d8uImOm9RS2QdgLoa0dsN5FzfTCkSZtSdTq/0FUwG3uLmU/5TkoRi/boKCY6afJ4IqK0tLKu3At7I1agF56nfWxK9fjuuu41ueKn28fb8UFktZ1D/7UqGN/xZ41f0QNizPe8vjvR8DGANpJpOkXXbc8CRtgkGrCWTCx/P4IHkvFy4mG2E9BCRcSZLU4OBWZh9/v9huWE3QBQAKayE8+BgKfrep9DRD0vnAX2kygxXACGEyMWCKPH0XoDU0R1dOyDcPCOiPj1119LoHRQIIi8vr5uGPbT6bRpXQD4UhWih/Lq6mpz1C7fs/HbkfC9i4scKEmEmDvVIMaB3ADnXdfF4+NjCSJmdZxoAsABaG61iviaKfcJIAAk2tPcuhVRn/wLeCK58OZgHBVyRqdubm5KpYw1X9c1lnWJZfr6xAozYWy6dZWEe6aUitzYEDstU0SqLSvo28fHRyzTErFWIGLWF5BEXzlVLWRmZoj9RTDFyMigHdnxub6vrYXI4PHxseg3slvXdWMnDqLo4+mUNzo/Pj7Gzc1NqWqYMSH5MNizk8ZvYBvIFlkzHoIwegpQ7/u+AAXAhF+cTIb9QHagwwCliNoD3R41CuA+TaeY19oa6urYfDpF39XElaT28fExLi8v4+LiIq6vr+O3337b3O/m7i4Ox0NZd3TA46HCBQhhfQAv2GkBF1GfHuv2JmzS7LpZMuwH/+rnExA30CmIJ2wRhh6ZmNxhrbEhdMl2jc/G17BW1kfLrX1yO9f+FonRsrXMl/d4bSvhtXpqIIH+Mu+bm5tC7nyLsUeOlrWBPGPi79wDQOMWM4PVfAx2V+In1zSgi6in6DgJZ1xObEwEGNAzT+6LrdlOW1DD74zbBA1+x35vjtpKxlrzd7f6cF/iKz6IdST5cUKATRE7qDzi00+nU/zVX/1Vjvl9F9e7antt2w4+ibVgb531xWAw68H2obro+rIs+cngy7aC664Pg0PIJsaMnMFAYBt8omM6vxMrsSmvMXpjYI+NGA+SuCJjxoDdo8foAuNCF+2X0A23hCF7E1pOeJhLuya+L7IbhiHmaY5Z3RJ81vHUGLWA/xQxKc6YdOLz1n0nQVwXfSVxRpdNsHEtE+jco1SK+qFUUCHxiPGsJXjbem85teNsfd/vvb470Wh7HFEkFv3x8THGcdgo9zTVXj4zKFlBDtF1feRjZwEePJX6GBG1fAcgpOzLezBeBH5nYgTQ2lqSW6SWZY2+z88NOB5Psd/vYhgoucJ49jEMXYxjLcEzbhg4Eh2cFQvvTJzP8X0D6BYAo2DI1IwOymZnYjCLIzFzhcPJc9zH9fXVWR5TXFxcxrou0XV9fPr0OW5ubs9ziMKgvb6+xX5/cQYWy3lt83GjrLmDOwxYlvWwOQbRrLjHawNy1QdZENBcnjUrA6BBthgPYBA9cOLK2rjVDxACMIZFQMbuXXYi4bXru3yW9TrPsUxz7p9d84kV0zRtno/g9XaAhMk7HA6xv6gPPJvnOcZhjLSmSGuKdak96gQKHB2VFxwlJ1GxLuiv+/KRk/dNRGwDFY6Hc+et8zhoxhMRJWkFIJi5sZ0yDoAnds0921YwtykZWBn84he4L7rqPm/0Auft1sKI7ZGJVO3wZQAnV34gRdAx7OJ0OsXLy0veZH9mmPe7XURao4sUa6QYui6WrovjfB7DssTF1WWsKcXuYh/Xl/nkoaenp2IHMP081JGed3xKSinymWcpdvt99P0QfaQY+/Oan3UrH187REpdTMcMFk/TtgWItgbkwbNE2gQW1tltSthnRA5O+GPkxHrxnAJYePSKzeJdV/eq4d84gtbXIla5umn7xQ/RUgMJ5UoUNomfsN+AySdZQcdccWCOzMFyA6yw34MjjWmDMrFgVh1bQ/eti4wTG0cHsCP0me8Qh9xqzPfMWGJTrioxX8aEnTKmFuwbDELWADLNuDJmz9+Ak3swHoPJSZXu01yfaj1HinmtXRgG2OijwSHXsw0xp9KO0nWR0nnNY83PskjnQ+OmqZw6xXfN3OPjW5txtXATU/rc5386TTHGGjHnGDPNc6Tzs5JIEgH1rFubvLF/xfgJ+VOFd0UfH+cY4WoFccmVJpPNJo39FHHjwW+Rh+Ap7NJ7M6wr4CMnDCaKjI34zLd+2n6dIDPPE3t2ljnSukSkFNdX9VlES0SsXYrjNEVKEdN0fpZZM14TfNY9t3sybpJf5OEKkjEmCatJbWOUZcnH3IK3uIY/i8+1X2ENLXPGgx/5S1/fvUfj3/+7/30DDgEdOGmffEE2b0eBkgLwzHyZRcjs6mukb7C5CBQHDavy+vq6Yes4DhKAnku8l9GdGcPD4VB697NRpBIEzCBxT7LndpM5QQcG0u0JOCg/aIsTbAggfJbrWImQIZUFlI2WKebmsdmp8aTglKrywJbA+gOUCNwppXh+ft4AdeaCoyXws28CJ23gYadhJsxAhBeBifuQIPJ9l5zbwAMYskEACpwI2SnC9nJvOz3Lr+vyca3u1cVgSRxxrugda+qz8Z1kMz87QBwr4wfsXl5eliejmm0HaHIvAxKc+el0ir/7u7/bJHo8pIyTvQCOJFcEFgfeiO1Rdsjec8EO/B5944yRz+AT+N3MS3uSE+sAiEZv+D7XwCkDaqkI2t9E1L1LzNNjNiPF/igz6siBuTs58+9UR8wgU1kj0SW58rNhpmmKaZljOq8T7TnlWOW+j3WpOh8R5Xkrp6XuocJ/sl6X+4s4aVMncsU2WG+Pl3ugtyZQ0Gsne+gccjaQI8HHV7ftAga4bqnEl1i2+HGSEFp2WEfWwm1T6CMAilPk8HF+2BR+iCoo7StuCSJBMTji5dZd1tlteu7V5jMXFxfloVwtoEK+rCcvfBtj9vv+risxvi52SZz2tS2vaZrKMfDIuQVD9mtmj2G/sVd0wu2nvl7rj5mPkx37EPs61sE+0YcNUO3wddGVdt4mDtsXscVyRH4QazyHhes5TnA/iDzGbRDpWOQqvhPEFmiaGGL86JxtB1lBeDnuRtQEFT+Hn2XO+Ehs2xVirztyaQlXZOokFbxg3+52QP6hA1TSHau8Hqwt8+Jz7h5BT+wDGQdjxZZdpbP/dEXS+76chKMXVJDwAegha2lc45Yqt7MbUzkGtEQPMnCsSinFkLbHEZuEsb8Hb1vXmD8x2D4AvPTf/5v/7it7aV/fXdFwKQVQi7MiA8VRuGUBcGnlwECYANUSsre+H2K/z1kex1+ajfVpJz4lgsDOqUxUQXKf9S66ri/vuX3ocHgvjo2s22wuwQ9mk0UAjCMHM382JByyExJYBIARcmFsBNOu6wpzZyaLxI570YfKewT+aTrF1dV1yZ5REAcJWkvWdY37+/vNvZyRM9fD4RB3d3cbRsMndZkJcqB237T1BCV3sHDAhLXxZww0AZiAN4zWwAoD894U72XAgZEs28j5vlsucG7MAf324QO0CWC87vN0QDA4wSk9PT0VPXBwtOM2k4t8np+fCyDjCFXkgYNgTA5mDgBcz0kyzsf6w++8sBeuiTN2YDR7iT754VgkKW6BQQcAh8iLuQM6Hx8fK9O01GOx0U+AgIMFc1/XNb58+RIXFxdxd3dXKqXMh/u9vb3F3d3dJlGxk4edAvwyBgI1iSp2VJPdISLVpzKjc+M4xnIu3yOLq6urAtiKIx/q8xhIZtIa+ThOkRetf3ALgnXTfdD8zcwZ86VyCijHx6Nby1KfVwCoBmhyPapPrmZ4fwiJF/8Yc0RskmZslwDuQwu6rivHJPs66AJ6hO3ii9E3+yQz4NgHgXtd19LKiez8WdaME8yclFtvWCeADNcw6cGLa6BX2ACfIQ6bqEE2yNLVlDapNmDD95r5xtcblLldxDaP/+R9Yq79DPrb+gtiiMdKUgQxAKAqydy5ku9WVye86HDrI7Ft1sr7zhznXLVDX7Ev6yi60CZt7f7A1ieik5Yfuu7WQOIB92TtPB/8AP6fuPr09FSwlzEausMc+D4Y0HrIuoFP2lhnn4+vIulGl/DFxED7Jz7jzg4TXS0u4Pt8ryX8/EKH20oaPg+7xQ8Zd3Ff7tH6Fnyf1wW9R1Z83/7DBECbVBk7mIx1PC6VqEjRNddoE3MnUdgxuM0tleiO7eB7X9+daLAQ3BSmlcCIocBkoJQ4fjaLulUBltXMYA4wF3F7e1NOquF7BN55njendVjAOEocUD1HeY11zc765uYmXl9fy/2maQ5atbyYLBjXJ2gYJGC0ZHw8ndaVAoI65WpAP3M2U2v5GUAiI8D7p0+fivPkDHscMAEkj2MI7GoYhtJHjHNvS/bzPMfnz5/j119/3bQzcX0UG6aShAtDcxsUQYU1Z01IbOzQcKIYFgGWCpDZOmSBPOxIASlugzDz6MoR48FpO4C2lRSzpy4hMwecjAM81QLWj6T6dDptHgpomaFHEdUB4lAZi4MkL2R0dXVVADPXcOmf1gXsybrOPHCsnNZCsMFuCWhOcq2b3sOALOycARdd122ezo6OoiMEHycPtM8cj8e4v7/fjMdMoI/QBUh4b0lxgEq6OebWh0c8PT2VRAZAg+zYRE/wQmfRKZ+aQ7uNq2en06mc6X5xdVnYSSoZ5UnX0xzL2T5s420VioSbOaaIr3wPOgEh40oIJwXC/LPmTtgAVvR1I290wLrZMsNOeBz4nYiayPr7v//7Eh/6vt+0wxHE8bH4JmRixttBEZ/HcbTM3SALO0dH+Yfe4e9deSAZ8T4W9Np+3fI2MOF+ACtXlLFzg0B8HrFpXeseMicjBn/Yka/XJiTYLL4I2RP/XIXnO66sGDhiv2ZsXW0yAEdvTNTZV5BQkjSgK8jLyXtElH50z8sAz8AWOTFukzvELWIH11rXteiQfTW25mQOeZGIoAfYAPGVQwKw+6urq82+TT+jjOSCuIXOuD0HsoT5oEusOWvgvU8mQ6xz+EpXZtxqxd/xRQbr6AB/c5yx3fN7m8hyDbPt+GcnxIzNRC/jQDZgVds0MsH+mB/rxloTY1k/25CTIcdl3mcN2wTQ1UnrhBMLSC7k5rY3fADjtL9gjPuhHgfMvewXTUbaLpyYu1Jjsse2/w+9vjvRQGkBmiiWDQlnCkiwkpF0cNY7CQibUO3gjsdjOZHD7NWyLPH3f//3BSwjKCscRoODrCX2fgNWCJ4REVdX26c2A06Z5+FwKDv/UVgUzCzPPNdzkklyzCbBduKAAAYGZNyb35EpiuUStVlXb4qC6clOf4yIqiwYLC0aXj8Mxm1kLhfSIjHPczkJxfciCDkJMAPUnp7BfGAi53ne7AUCcFinMDizT6yHnWnbymEm1o6CcbF+6JwDJg7JFRjmh74RHHxyFHNvAQTsE/M3S/CthKp1HCQ58zwX8DXPc9zc3ETf9/GP//E/LmN6eHiI+/v7YgvjOMbLy0sJhC6/tm0DrJGTbCcO6BqBDJBgwOJ5sYYQCMgZW7MTRgfNpGEbyBngYjDngM/c0B/IDTM6OGDW2E/Q9lHZEbXdBIDBPe2YATqMsWXY3MaAP9jtdpH6LoaznVMVQxYpbR94h16v6xp9l2K3vyjzNjM8DGPMU91bgs4SWF9eXkrVivFbPvgVJ599X/cE4YPd0ocMsUO3XuAbve4ArYhahWSjMnZL2xvvOemhoul2V/Su67pyuAC66uoLoBVwRmWgZcrxJT5K1uAUfTOoQDbeb4KNmahw+w1jJCnFVzlJQs5utWJ9n56eik6bUTaA42WdtV/lb7zXssX4Sft1gyD7W2INY/deDeZkXTOzzwv5cVgG68+YXOnmc8hzXdeIvot+qHse3Q5jEgg5ujWLdbL+M9Z5nuPu7q6AYewZ/wlwdWLG5m+SZ1cKnRhfXV1F3/ebB3QauN/d3RXdIOlFxlwL/TFwdrWVzxN3Gbt1DN/YPindY3dsdbKCXnh9+T5+AF3quq6QpS3B8fz8XOKWK7i8HNdtI8ZIrI3JKOs9fplreP8i64vO8bMF9czVmAHd5DNOsAzuHSPRUXTGNo6M8X+OYdZlk28pItLydful/QZ4q9V7rkVy7Hsxn+99fXeiAWD3Ark3DUdt0MeAj8d8DCrKxIQwbCtBdlTdJhC5lP9P/+k/jYeHh011xYtOoPBC5XGkTUbMdzOLsH1Cs1lNHOf19XV5j3+wAeM4xm+//VYcHEAqoh5pZqVCbnbUGDqsXAtyndWzoQuQ+60Wiir/FMtSS84AJwAuLRh+LgZAAceHMyDBQ/mur6834AVQ7MDbMkTOjH1tGFwHITsX9M6AnzGZVUG3DEhsWDYYrkUCjSMxq8k4CIAGSb6GE1SDCzvudlOXE3Xvs8D40WkHGnQMIIG86S0noPLdn376qTA5yAId43NOrFhbAqvBoeceUauH3rtF0HUPuFtU2oTUiRW2Anh38hkR5andbu14eHgogJ5rYhsEdkAulRaqadjVbrcr1TlkzXo72NsOAJ/4inbvQN/n/Rpm5B1MeJktjlRbiQBW8zzHPM2x320fariu55P0dmO8n+XjChjyTLF9Rg4yoHUO/8u6Mya3cgBAAOXIg3YV9BL/zRzN/hro2rfbf0TkOMOR5AaxZmB9qhd64Kr6utZ9fK+vr5sT5fABVHRMljD3vu/LHhjLrgVQAG4qTeitGT/sFPs1mEVG2CLrzU8AkT/f+h/eN5tvPTcIw7+YCXV8IS4YVPmodjPFtl3G57jWJlQmztAR3yulVNpMuq62vbHGzKWNH4BnX4fxppTieE7m+r4vxFxEfLWhH/tEVsiFOeMjDLq4Jj7V+sOYTRICzpkjfhE/iVzw4SayvPcVPXM1/urqqowPueDP7W95j/miB9yf9fLJdR4n9obOeMwtwdzK1KSm8aN1k/FDCvhgEEg11rhNXp0c4SuZv8lCxtBW4vg+fow1BQe1OMP6yfsQ1i2mNYlmWfCy7mIn+Av+3iYnXNffbVsE80XOx5Y3yYgTGCfJ2Jd9Q+sD0IX/5hUNJo0TwVGwacYPYEOB3CYVUbPx0+lUkhIMHSXKrNptpFQ3HJHdRtQTRQgOVni+b2Hf3NzEy8tLHI+1Xx8jZLGnqZasDIgRvPtZuR9js+JeX1/H5eXl5nQRnlhrlqvr6pGSOBmYVFpnGI8dNmtgpWiBtJ17/ls9MpbECNaNHtBpmuLu7q6ss4O4s3/WFJCBzGHxa1JX2Qv0AuCKoqIPyGocx/K8DBt039eHPXIt7nt1dVWCvIM71zUbhL7ye9tmYSMzYxcRBawSwHEaBmg4W8ZsUAKoY62o5nEfA3EcnMEoc8YGuBaJAN9hXDgSdHOe5/jll19Ku5b3GFF54/pUnEhMXdo1sHGLCMwRAXIcx82Rifv9/iumnHF5bw8B2vqFfLzR+/r6ugRCV/hYI9bfe1V4v9pFfeAg9rff78tmcHwBQRl/gP2YNSLYY1f2Wayd90C4woVMsg738fr2WkAzepPWLZhEvw6HQ8xrbUGyLxzHMbqUYlpr/zxJm1s7nSyzJu/v78XW0fN5nsvJdqxxW431E5gd1NBTV+ewF/w1QAxQBZPZ931p8eK6PsTCe9rQhWmaiv1fX19vdBfwga/FDrmmq2SABbeHAfR4j2eRGOygFwAc2uO4P/PHVwAanSB6rPazEbHRcWwdsgo7wd7MpuKr7AdZeyd76JdJD/tMV0I4Uc33YsxOdoZhiM+fP28IE+zV8ZH1MGllPfQhJj5cAb2gRRu23770/v5+A5ZMelr2tLjiL0z0kIQbeDN3rssas07ovgkm9ANsdHNzU4iRvu9LazfJF3gDXUBPU6rEoG3Za2TQCUjkwAv7APtb7ydpQTrxxgQVvyOnnYgRZGs/iu0gF0hWA1ySoLad04kp7yFPyxmdRved5LXJv5Nk1hJ8yTWQla/DCz/kll+uzZi5JzqDv7U/MMlpX8lnnbxxzZTy0wGRqQnaFPnky67vI9ZtNdS4iDEbS3Jv9Az980/jlH/o9d2nTv3N//w3MY7Vkeebd9F13CgFZz5n0LSc/5ZiXWEPyeJyOZzAzWJyGlTX9THP1YgJjBgUAMXADDaLsWGQfd+fTw+6iNOplrwtIICC23G4/vv7a3Ec9Fi2TDQG4QUG1OFAvXnVzs5OgYVFGQjqBAKAhqs4GaT2MQz0+H/EMIzR9xhDZQQBGcjFLK+BCiDWLAqO3POwI8bpkuwYiBZjiNgEtK7LJdP7+/sC9EgazALYkfO7WWaCQ5VHZaMYO87CDsBsB2MniYM5NUPWsv7oAfK1obKerBUOyOws44+oDIcTMa5tuaLvDiBOQtEfggDOmM3lgKsff/yxVLEAMBywAIBzpQr9Y80ACcjJrKvngS4x5re3t1iWvKH58fExbm9vN3sLCEytc+fpu6ypn9HBy8G7bdHgd3SQ/2d8TjZbZpbvwF7bT1g/SSBc/XKwx4e5BQNZRco+9HQ8xm6/j3maInX5OUXLmt3rbrfLwaKrLaZpXeN4PMXQ95E6WjDy81NedcKYbdCJqQMySSf7ouzrmYtb7dA3J5y2AxMmvj9BzfaGbFx9cEKNj2UdsD/7cP6RMJoZNkCwrTBegKxJLVdkWqKHOdhWDFIYP3tq2mog98YXuKLpDb9mIC1v+zBsnrlib9ZlTgyzDyWZNtjwhmKzrtZVdIC4Yf9qP/atNXZ84//NQLsljESGqiKHqHD/kryOQ6Su4wl25zh4Tuxj3cTXdV03D6XDrzmOmbk3WQUBQ4zxPh3v4zJQ5Bpcx1XtiChzbpMQv6wD6BUyp/0Rsoc4bfmgl64iQKbgw7PfnKNL3cZOKqOdYlmXr+zBNkIsdnXUhAn6VWLcGnE4HM/3PsUwcIri8Zw414Nk8gEZ+bh+J8ldnzc85wcX9jHNUz4KnrXoUixzTaJMIGb9izOO7WJZZlQoUneubs/aQN2l6NI5IR2HmE7ngyr62s0wTdP5M3VPcMQaKXWRUpT3TtMpxoHuivyfPM4l0vmUqNSl8/G0fVmTYehjXSNjaq1D3/WRUkTek3uuoiy0yM2Rosa6aZ7PickSY19P/uKFrmDD3jeVdXf7oMt/82//x/i913dXNHa7uoG39sPmCNgaVn6tkTdg1531b2+vxbkCWpgYjsjsyv39fal0EDQwDmeIXKMqz5bJyY4qfSUg7tsy3xU81ieTAswBQS7TEwQZ28fHR2lJggHD2A1ESKK4pwO+nVTL1jNPAtQ41jPmK1CuT39GJrDUZkcILGxyRS6sE20WMOQeVws6zC6bKQOQEwTtOJERDoo5AXA815rEzpv1Ymw4Vzt21igbSE0ozJa5hx/ACWPrPT/oG+uGfgGEuD9Bg/sxV4Mfs5RcH9uxHF0l4TMGr8gHAOBkMiKzeCRzjH+apnIgwp///OdY1zX++q//+lz5y08bp80AeyewwjyhA6wROkIwRDZsHMaGLDufyOR2Jj+rA1a07Z8nQWZfCvMymMPOkJ1lyZ4aZOx2COzbLJ+rBdzP/s6JLXZOUg6IsV6wFoUJjbqGHEkb6xpd6mIYhzie6oM8w/6mH2I8r/vV1VUs8xK7cYy38wlLTtgYO3aH3/a4bm9vy2fXdS1MIvdjbajculXMoMrMJPaPPzCB1AIx7s3GdWRKBRiAdHt7u7FhQDd64fUxGYD/Zf7YJQnBPM+bh8q5Eomtc0QoPtmVPObtPVhOPsxm2h5pucXv8ELnImrvuJMk4ij+3YSPEyn352N3bZWbdXSFxq1KgHT2ECBTCIR5nktSEBFfgRTWiBfv4e9YEwhF9O9bLc+scU4mItaltsWt65pBYV+rxJYzv/vEtNafEsv53QQVa4/cqTqY5WfMBmgkU36QrWMEPssx3qSLiQ10163SJLbFT5xfbs9zEuBkIiIiRQbT+FDuWZL6tD0dycmZ4x3jc3zwRmvWMBOkJL91PwykKf4KWR+PdT8ca3X4qCfLpdRFl+o+hpRSxFyfSo7s+N1ElfWyJNhrQ/bNa8RZrPNUKzn+7JLogqgYIn+ui2VR0ppq901e80rYQ2g5jjFmEpV1TbGcE4aUUvRjfXSDk/yUUixrPYBiEnnRpZq8suYm6VlH66hjiX3Z773+gudo/G95YdU7GxGbTd0w/lY2nDABwGXsiO2TZF9fX0tvNY6bjdsOJCxWRAVZRRnWev67webpVB2Fs/CIKEkBYMgOZ5pO50x3e2QnYIGky6dLGYg4IcBZ8YyP3W4Xr6+v8f7+Hp8/fy5Ga+WOiPKcECdR/Mzgsp4ANk1TecIyzhs5G3S0rDGMLO8zB0CdmRGzO8yL65CYeKxue4iom8lwjN9i1QhQyNyBEj0g4NgI3NLh410Nqpw4IG/PCSDRbuZrgYuDPhUVB3h0hnV1UuETbRxk+eeN2mbkDKBsZwa83oSMvbZBD/A4TVP8h//wH6Lruri/v4/D4RD39/cxDEP8/PPPBehbTwgeyI25k4RExKYtL6L2+jIfghTAx9/13Pzwwb7vN8+3aF2XgyNr6ZYdB2cDH9s2bL5B8ul0isfHxwJ6HLAcZLEXfmfd/GA0A1yviW2Sv0EaTMsS427cOP9SZRoqa06bkE+iwQ94ztgTLHerb+xrcGJi+eIfSDqoKDJXgFbXdQWYsq7tOnF9Ek1sguTBBA06hmxN0PB8GPxYRGxO2UJXTDLgC7z+2AfH65oNjtgevW0/TXWYtUUfWh8J4PH9ubf9TQVdQzmq3ZWfeZ7LKUXWeQMmqjSMifd8HXSljad+oXcmQnykLv6I/+f7PiWJOO8DQWhrdEeA8QBrawKJdcU/r+saachrQ7INSWIfw6sk9mcbNb4wmUisoWLLHPHVyOTt7a34THS8TebROxMhlhMydrw2oeSknMTY+MCJnGM0uo+82BiNr22xUiY36jO9THBO0xTLWtcfPUZnSGDYR8d3vgVSwWvHw/agG0AvRAOya6v2kDhOIADj7hxw0uzkhLVBdsYF9uW2/XbdWjv5r4FwfBpjNwayXPis8Z1xlZM2xx50mrXiPXdKzPNUHvBo/NelLhb5dggJzxMyo20tJ+Hp+/6/bUUDYMRNETIbeCPq8W8eOJNDMexs3ZeHIHkK7DRNZXOTFQAniZI4c0fBYURQ4hx4Uux2dV+Fgbs3EragLH/u28eYcU8EzvvMxQkJhsieDYJyy67h2ACIsLptcD0ej4VZ+vg4bsAXa9KOww7FVQY7rYgamJdlKUdtAihwpCg6cvsWaEdGjB99YP5OEp2ksQ4ALydrgA4rPrrnz/g0De+PYc34aRDGdRgjABHHjs44cLVME2PmfnYeOFK3+bH/wMACORrQAshZe7dVIBPux3GfbGBk035ErjzQhoS+/It/8S+KnaxrPsrv8fExXl9fzw99TOfSdWU3CSrWcWzBThE75NkCHGSAngCk+r4+YwYZQFAA+kxcICN8iD+PvF5fX8teMPeRk6QawKKjgENAuIO7yQJX4pyAkhwYSJuhBdxxP8aCb0W+BPvT6RRLrDHG+FVAjKgnIQGqvUbus+Yf9uZrEFAjoowJ+UbUk++wOXwF88Z+3CrDHOw3WTeOYbX/ZTyARMsEf2W7dEwhueJz+E8/n8nAAN3jd+IBNkR8Y96F4YzY6CKy7Lpuc1gK409p+7wB5A5D61gWERtwhR/2HAwkXRFD7yBIXAVhDlQ78THoMJ+BGDCAtIwMTDkREpvnb23M8bHDjNdxiMoK4+Ce7hm3HnMNklpk1a9dHM9rxkNOveeDOUPwpFSP5IYcNdERsT0GHTu0rtqGuAb3QmcAxLDaPogCPTRpwHzwPQa8PtoZW4JoQ4fcfYCtFR+y1EoEMQO/DWkwTXOkyOvJ4TcViKcYh31JetBF9uOR1LoLA/mg506I+r6Py8s+Uqp7jYwZ2r1MxE6TA8Q4V8uth218tB9mPZ2MMi7WhvtiD7Yr+0ePzQmAfRbx0FiLuaETPnwHWUHCMG8nUtYjYiHkN/ozTafo+q9bq/Ocp9JuaFv5ls0Q97Lfqiea2X/9Q6/vTjRgFimtwN7AwrTZF4boflFnjxGVHSJQIFAvbssKGDCxYCyC2VUDwPyZbb80C2pjK5m72IBxzOWqlplsFQV2iTlTkqYiABjAOGEOWXROOEkpxcPDw4ZBAfAQWHBEzP3iYh/nJu8Ns49j4nkITpD8VHcHC+ZZWIfjccOAuNeXRMdJqB2uS7CsvRNLg1MbqufL39EL9InvMhe+x0O5OA0MEAEQMTPUJq/WJwI0jBugEl3z+jDHiNgkQL4HeugKTnvaFWsHMGudr5km5sGLBzxh+DhTj8UJr0+o4Tu7XX4Gxt3dXQE4X758Kc9sAUAhL4N8r6ttFTl9fHyUDeNuUxuGoawfcgBMEtSQgwMS+kiiYpk5eHz69KkAMOzH10EeJK8GiugUum1iw4mFgfd+v9/07DMOdLJlx9A3EgZ8GEFwGIaYz3vceJggsozIZ6S7wgdosv3R0uHNz/ydOba+j+9FREkoCegOPPxuUEpyDphpgQkB1UAKnfz4+CgPs2NNTHSYSHE7BmCfeXCwAffEbwEm8BPYBj/RIfQdORnYt0fpmpWEQOA9dJQklTE5yeEzAErbuBNh24PbxbxuABEz6p4Da4vsvKcppVQYYGzY/oOfTqpMUHB91sv+AP/qeMDYLVvLxc8Uclua57Oua6zn3Ix7Mv4KtuqD/PBX2CanT/E9V1awW/tK2471wgCTQxOIsVTGzNibbbetE+8i6j4lJ3usnW0LzIFfdNKELIyp2j1kjGvoh9LywxHofM4AGR/Nez70Al1FLvgYA1Xkty55X4Urna3P9DoxDmM2VyexC++1w5Z8QIP1E9kZE5o4xg6MbR3P0QPbqkkNdJDrmLC1j3U8cFLt95yMWIdb38295nmOZV1jkT/y/VJKsb+oJI/1rr2Hic0si3Wj87/3+ouOtzVby2Q4/YXslwWjFQlAxaKUHspU2XUvKBO1I+G7BqcGsTA/ADhnmBGUkGu7Cvcw82xwi4Hl8dcSIE7p5uamMKUc+epgwTUxfBx513UlubBhcH3ADEdbAspSqg885Fx3nGdOaC7j4+NQDMhKSZJBtmuDJ9i6L88ZrAGcQYcTSZwlbW/WDx42BJgFUBoUYfwRdc8MzO7Ly0tW0nNA9EY85n97e7s5tYZkkBOH0Ac2mqI3DqYOfhgbZX9n9tY7J0mU29mfw+981skFsvfGZioVflAS68c1rFfYE0ks7CtgCkBIP/v7+3sJLga06MDpdIrb29tiGxH1iMz//J//c/zhD38owYS1BFAxHwNKnHpr36wlv6NT7F3hd/ZF8R56xH1oPWR9Xl5eNlUgkpeI2rK1ruvm+TucasTfcfQkq4DWL1++bI7PdUsPQQs9Yh2ctLJ+JkaclDIng1oqUJwe9H74KOP+7bffNglmWs69ymd/tCxLqQqx1i2Qw/YMnPgdOTIe/Be/o5+Mj99pA726uirgx7Yasd1Xhg0iA2TvTf5tRaYAoqGecIMdog98tmW0XcUCHOHv8bEmQ1gffCetOMgKPcYncC90wi0MBlCOEW31d57nciBDCzBYA5MJBmNlj47mgGx8RDX+hmSe5yFN01QYd67Lq2WauRYJsqvpJEvoIHrjPVZO6FwhMAC0XRAfGZ9tjp/8PzHUFfv2/3mYX0qpHIOMnmD3V1dXm0o8a41OcD3W3lVV5EKV0c+dgahp54C8XLng+vgP7+9jXfCTdGU4oUSPsRdXTcAexJmUUkzztl8/Vx0u6x6W2D44GX9gchE7tm6ynsYz+bvblifHPuwEXQOLsA4G4/gYE8foFzZOjGHd8RGWpbGIr9+Ox/NCpxmDkyrkw3oQqx0fjFPtL6wb4DzLpuLTivec3DCHPvVxPB021yzYPM4nUom4M+5mbdrqWh5v3b/zPa/vTjQ+f/5clIcBGES07I8/i4IQsB2srVwAHxY+/y2XeAzO1zViWdbgQXRWkloeHmO3G89nsh83zhbhcV+MBWDmDLTv2eORd/zzHRQ+b3jf9rcuSwUZrQK1BorRnk6n0k/NGJizEx3uA+Ajo4b9oW3g/v6+tJ2YtcRBppQKoOeaOBw7UkCHDcusaURsnprpHk0HRSebbhsxg7gstVWLQNhuUvc6koDZ+aIHyBcjoXXGDoRggBM0sIBJojKFLNg4SgUK5tNs4DRN5cn1EdXRk3BwbX53ks7v9C/juMyOYgeMj+sge4IkTp/3zAzZZr0HqmVbIyJ+++23GMcxPn36VHSnTZSc3KJbDkC8Z1DEHLgvsj4ej5uE6PHxsZS+fUoKY8XxY9tu52SufoZMRJQWRiePPDsBBpxWzuPxuGllwj+hawRt5urWCfwRdsp8Weu29SFi++RuZJG67dHdJeB2XawCl3yea7ldxj7FoHxZlri5uSnydiJr/wQJAGHEWiD/u7u7DQvpKqoBt4Grx2MCJaI+IwH5OWh7vc04Inezhg6YbUWafy1RxJi8Ti2Di09izdiLQpD2/Mws830+w3NTkKdBkwkeAxgDSnz129tbuafJNuKCgQug1okkcYa47jXDX1lerBMxB/lhm7Rosl74FD7HuCEW6JpY1zUWJYfrusbb+3v0XVeIM8Cj7bEF8/gp/uaEBP2MiM1ePrP8+Ed8RUv6tPtpbm5uylyRn22da7sCcTydyjNySHT4HmuMzEl4WXf8IddkrfEzyMKVDg7oScTT45Z46vtt6y7+OlJE31fi1tjN/s9VG2I7OkebUyEBorL7WWY+/WnbXcD/O7nAN3A/j8ex10khuAK9w55YI+NW+wjHGtbU3zPIdwXIWG6VHXAvE0FOUuyb8u9ZYmWeKWLcjRFrxOl0jGVeYjzr86x74Newc2y7JPZrbNaAF59lzcA3NQmtycz3vL470bBiuQ8QRcCZIih6/Gg9gZ1kAvlzXczzGl1Xe+T3+0sF368f2ORNPNlh9rEscwzDGBFd7HYX0fdUTpZ4fX2LlLrgdCySCcAA4wOAWYnyONeYZ3qAU6wrbVic2JCTmuz81+j7Mbquj74fI6U+OPI3K/oa65qTp3x8QVeY99OpHp8Z0cXpxNOx2UBfWRMMBJB5czMUgEDgx1nxnYgKHJmfnVlEfciPARmODfkbLNPby5r4hC6YLesPQfnu7m5TPbLzXdfaGjEMw1dPu3WCZOaF+X58fMTt7W1EVGM22DUgRIYEP4I/1+E9Xr/88kv8+OOP8eXLl7i7uysn7+Ds/SDFu7u7uL6+jsfHx1LpwInh8AAMtJ6YxSLBRJY8BBK9J6mIiFIBYywRWVeQM7JCpk50SJKQE3bK7//qX/2rWNc1/uN//I/x8fERd3d3hTCAueS5C6yNdceAym0ZrSP13iUDS/QSoMzYADacksRBE2bSpmkq/cMppXIsHaOeAADIPklEQVQsr3WR9aB65KDZMkv2F/gxZAeQAJDiUzwWJ9XooAkb2ytEwul0iv24i2meoltzBSMta6zrHKnr4uLqOqbTqZAQZrMcmJ2o2icMQ97T4L0ErJXZcFhTdNXspNk8/BAJg+eNjpgccu8yNk5wZswQK+iw7Ze1BLjhS8y4u6LjNSAOoTfEuDYpsv9An81WYmM+mtuJrNc6IkolmWu4sobNW2+YJ0DOcdgtN6w7RAUxmTnBDJtMYD25Hv9vYomWZv6GfntdrXeuFjM25kXMwtdDwLy/v8e0zDGcxzv2OYFOQx9D18W0Zn+13+3i6jZ3FCwpIg35BLnj8Vie02EyhjhngEpCdjqeYprmzVqcjlP0Q7+xbccM1sYxwzGijUv4K/TjcDxGd9aJiQpbxMb/G3B26XzgxscxYk0Ra4rjoXYJtK3Add0in0C3G6MfhliXvPkafU0ctRpd9H0XS6rMOjZIbMyJSYplXuN0miLWs88b+khnjHY6TjGMQ4zDGIfDMdYlVyyWObdHRUqxLpHncdaT6NZY1iW6PpPJ/bCLZc3tPrHmZ4Dt9mMhecZhjGVZI63pK5tsQT/+HV11MmJMYEzK342B7It4QfKYyDS26vs+TtMUa6yxLnMs07l9flkjUpw3Zq953tMcXZ91YVmXiMT5uhHzMkff9flY4ciJSteniJTn+vH+HtM8x7rkJGNZ5qxb65lIX5f8t37IJ1TNS0SkOJ4+ypwh/MAPliP/71bXiFrVz7L5vj0a333q1P/v//t/bIK/HQ9sJJs93cvrzJPBRcQZGGTlplzJiyDmDNJViG8pmUEkRohz4wXbQo82gQLnzLUROo7aTKKVrVVgZ8UkRQ4A81wfhgWg4bs4aDLulPKzD1Dk3a4+GwOlrmzqFIez84G5wMHB1vs7zMfMBEESdpoXbVGADMYKiITZR3HdumMw60wa9spl7cKcRH2QH39DrhgFINf6yPo6GXUlxMzE8/NzuTZ6O89zOXHIuoD83WqBbk1TbonjQWXoqfXTZVb/zjyRPYAPgOCeUnSRagpzskONqEz458+fN8ySdYZgu655v83d3d3mPTPOrOvxeIxff/21zJWnkEdUNsQbeFkj9LHv8wZSAy70lGswXlc83W6EzLEbKg1OqL1Xh3E4sAzDUFrr8Beu2jkx8J4Ug96I7UMyIypAIwFC11qZus/cwNEJTjtuPke1x60mLUPLT+sZSQBgFhmb7UbfXCJ3gMEPICO3MBCIGSstHk5oSVKoFJVg3PgpbAJw7WAHcYFOtUm5fQXgENm0rRy2GRhWA2szyVzbbUXI2omtfRs6gox5MR7sHRBOkjyOYyHnGAd7fuwXiLf4BBNkrAm/U4Wy/vE+8RB7hcxAB4inlhd66rYez63v+w3ZwPedHPpafGZd1zjNU4QIJV8f320f7ETHyaVZY5Iur1PZbJ1q9Y374PPG3VDGYcbXlUEDMpMJ3BvyrFTWzjGD/YMvLy8xDEPsxu3pixG1bfB0rIkneKqQJcO2woC/nKYpplM9MQv/7LU0VkFfnTjbR1E5ItaDT7wfFj9IC6UrAK6OsGb5nlNEquMn7nM/x1+3vefkqC8xAtzgOMa4jPGMFZ0g205bxp/30T1ICvtm/Lj94DTP5blGvn7+fMTQb08X9GFJxswRtbJseW4wRdfFfvyvxyrbELbiChN/M8HCPUy6WX/Qz77v4//x//q38Xuv765oENxYDBaS9wCX9D9yYpRP1GGBcxCo3/fmISslE+fegC9AjkE6i0Sgc3YLKxNRTwuAAUDoLUOJQZkV530rBt9BBm2Q4p6M273/fjDU9fV1vLy8lPPI+Xtl6uqDa1iPCFqS6kNd/M+Bku8gf4Nlt10h12EYNv3Ch8MhXl9f48cff9zMl6qGy+E4NSd2yN19tryHHhB4zaiYXWj7JyNqkosB0laDIQHSrWNc35saYatZQ6oDBkU4PgAPCRSOwAHJf7MTx0GwrgZrPG9imqbN/hhObHLi/K0gjMP97bffNkfpRkQBqVSZxnEsSSVjfXl52Rxb6YD+ww8/lIRqWZb405/+FMuyxB/+8IevAAM/Ae7oGLrh/n/Lg7ZJ5E1LCRUH/gbw83cj6sY7gBd672S1LcOzLmaUAWQEEO6BT7LOOuBQYSFYkAzzHe4dUfe0OQluqyWufLS6SqDn3ugasiVQMleXvfFlXh+u7RY/s+WQJN5H5qoFgZEAhH9Ct/Ef2GzXdWXTNzK0zJEn7z09PRWdZgwOwN4sbf9vn2ESIKJWMwEXXB8fBfPOWuAbnVQge3TJ8cpkht/3Pg4DAx5i64Mr3HJlcgv52BYMFNFBEhGAMAkGY2WtDdhpH2RNkZ3lhx9iLd2uZnvhutgRZAmx2iBmSEPM8mPcx4md4zffd2WH+4ADIqLYFfZLaylrhPxZx4uLixjG6jNIXFhDJ9m042FrJlS9tvgB9JvrnU6niLW2kbuduO/7iDVt/A7vZ7a9gmPmnm2nKzEOXbBtI28TwcgX/UkpFRugKsyYWQMSY+btZATdd/XUeGwYhvg4fMRuVw/7YN2Qr4krku+u62KZlzgctpV3V/CMESw7/JRJFq8POs04TZib8PDeHezDSUm57rK9dvEVaXuULokgPqlNNIwreSHDoi/JiUxNnE1s2x4tG+TIPVwh89/RPftlbOP3Xt+daLiv1IyBWSAE7s25ZogMuvjH4JmcBeps21mknS4Cb6siGJV78J1IwCpFfP1AF+7r4ORNi4zdrGIbsL0I/izOnmuZ+ae3mu/j9HN//Rpn3SnfI+BF1KBHcKRE7v00BDiCyDAMmwctMX+CK2sC0OH0GT4DqDfIIdA7I46oTIErKsgVRpj1YzN3+33WiQDMGkfkdgTamdo2GgBZ61QdbPq+j99++22TxXMNmCFvZPNmP5y2E7uU0uZp57YVgpSDsnUDB2HWwQAORt86dzrlDd3tXgF6/ZErc39+ft6wJ7RzGGS/vLzEzc3NhqWlh/ju7i7+5m/+Jv7ZP/tn8cc//rEcg4suIO82gGJvp9OpVJBcebKzN2uJTzCzx7pxH9bWgct+yIwz32XOyNebBgFDTswZB2tslszO2sAd0MO48IEOqiQmHPVrEG3dNzDsum7zMEP0CJnbbuyz0BmTFgaRMOjYiM/tB+hjn4wPgObKGdUHEhqTNlwL+/P7EVFsbJ7zoRS0QzqZMfvoBA2f5BjCejM2ryVry3jcisg92yTPQJ7vcvAFPiGiHh3L95xgcGqf93ZBbpE04x9ZS7fnQS4wfggfdNNryj2Ox+Nmv4d9edv6h+ztO5AHFUl8IjI30eCuBJIMxwJATMEQ6xJJCZtZZL7HWNED9iEawHvfE2vANU0eDX0dH+uw2+3KcaDoAxUQ74vkPt6E7Xnj44lNp9Mpt76cbcUVDJ7wzHoie7dIg4EAoJeXl7FGfY4P+pjtZ4ll3e6NQ+/5idw55c1AmphERcbtxbZd5ug1N8jlmugZcisxPW0rLLYzXvhStxDGWisd2C9+yMlrSwTxfeM935e50EJkcoG5o/fopsfa7utYo86fe9T/3566h974sBX7beujk+8SL2PbPcF6eZ6u3nvPIviF9TaObglrroW/+m+eaBjkczMM3U4V4BcRm78xeDuNda0ZsgNrq9jcHweMQGEq2v5dlIFFoFUCAzMLh6Awbs+VRTDLYCOjxIeioCA4EjtZA2yDTJe9cSCF6YiqvHkPSj3OkMpIvnY99YBkA/lFVAfjHmuUESfqpzTz+dZwMUQ+hzP8Sun77QZw1sUMdUQNcjyJF3BL0EI23hTdVrMwHDN/DnIGQgQog5EWaBOoqXigm7AbrDtrgwMlwQEYkNABMGtSuD2PG12wTKiaoCMEJcblfRXtw+64Btcx4GAuOG3Ig6enp7i6uiqbWZmnq4C+/uFwiLe3t/jDH/5QZM2Rq5eXl6U9iYQQEOhnYeAn7FOcULithPkgD8uOuZnJQve4r9tqaBFkTSEd2sQYvQZ4pZRK6x494dzPCRvraCBhQBYR5aQbkg4zdySSJDhmuM3MsZ6WmVlPZGIfhP3weYMKAAyfQ8/xGdbdlr02W4sf5/9Jlk0imYjge1zbJJTBs7+zLEtZH8ZsHXVSYL9g1t/+x8GSQOvqkO0S/+Jk1vqJ7tqn26dwD38XObPRmVOQGCugALDvBNHtOn7InUkRkkcTSAZFliv6wDpyD7oTiLOuEG97trcJnhNbP6OobdEdhiFimWMWIYT9mVQkucYm0Q8fNgIh5rXzes1z7n1PaXuEb2kPnlJcXO7LaVHoEeuH7RMz3TqJbNGHoqMCtC0G6bvaVoTuluRwGDfVb9ZtnufSq28wW3Q7UgxjrfB4LbDdtqPAvswJNd9FJ732Tr5tU23F4FuJ/TRPMS61dS9ie6oZtmgyYr/fR4qafBj4m9CxzXsM6Cl/43vEAf7eki/oI/rA/Iz9nCB3fR/zUokU5p2/35UqluVqotoYxuQN2MHdACkldouX2I6egklNnjIHfuIv7C+5NvHCcsQ+8RXf8/ruPRr/+//678uC9n1fAA6DQskciAC/x+OxsMwYYA4eUzlZiLK6DQaFQWguB5rJtIO0AjlhgJlljGRwLADg09UVC5oF88ZdjMNMeRFsqtWdtkrj76HgEbX9jFYTVwFOp2OcTvWJtzjubAB5szsKbwYNAzMrFlETGFg0g1uSGAy5ZRk8PwIhTgHWOyJKqw5rScsRoAPnAVAGNFCpcEBGht4fwPgNSNELQL7ZLVe4WhbdRmwmhPU3EGSuJHR1jSo772ScjdtUOHxaCp9x+4nZmHVdy5nsMB7I3wGCv/M3X8O65j5sEgIC5PX1dVkfbM5AlSDCEb7jOMbj42PRuY+Pj/jrv/7rDcMKI4qdtWwSQRrHZSbS5WP2fpl8IEgAdtw6YT+CnmAT+AnbLv7HciO4O5FtWTmqMtYfM5OAP+s2ftHJJ/bGMZe+j5Oli4uLeHh42JwshvyxC4KvwTd+DXmRdDJPP1MHf8ic0Hlka9bLlUMnCW7XsT9Fh22zZsItYz7f9/XZFa4GsL5uZbAtcl0DVdbYAdw+zpUHs+3cy6QDPozntJC4eq15n2QNsAM7bT1EnvxuoO99GvbtJvIcb1lTgwwnRAaoJtvwuSQ7EBzYF9e6urraPBjWyaLbl7Ahrm+AjW9DD9eUwTHzA6i7PcdJNO/ZP7GexE+ug9ytb31XP2f5XV5eRNdvW2OQKQQAiZJBLuveJuwREdP8dadGAbFi9U1mTtMUKWpixfd4nbtlynW3n0kRaz1EAF12m4z9JDLHP7jKxzVbUFlAdVertG6rMfEA8bv9bB+7/fZp12biTWobi6xLrYAQh73287w9ettY0ZjRzwtDjowNPXFyYgIWWzBesG/Nm763T/8u8T3yCV7YJuNjvswB3838iBduZSot0muNFe18nFyRVOCDx3EsGI01QLdNFqBj2IF14X/4n/6v8Xuv765o5JMaUnRdbT3KIK+LYajO3U479+wd4ng+Qo1F7Lp8XCzv+cx7AqdBRkSU53VUZxORUgWGLIJZNjP5OD1XBAgo7XcQuh/6hMMjyeK+zBvFfXp6it1uVwCt74lCedEwBCdHgBEMBQVCuRw45nmJrstGa8bOiotSkZg46GJsVlzGhLwjqsPyaTPMuwUefvoxRsLncOx2jjhcl6C5Jn9z0oFMcGwRFZTa2QOOzEpYRx3MzXLikM2EsNcI1oP3Ye1dKWAOrHkrWz+c0YHOjIg30fPPzBDry/3QH9sDv6NLADQSG3pvATHruhaAgQM0kwPDQiK62+3ip59+Kvp9f38f+/0+fv311/j06VPM81xK814DJxiuFDEH9ALCIqKerMXmTmzdrUSQBwYeyCIiikNlbgSF3W63aVUzaHJSwuddqcEP8j7AiWoY/8zaoV/MEz2hRandcO2x8LmWMSZooeMABOzIJ4pgI8jfYMEMJ9XGvs9tJT7GGL1zcmV7IvGxT6cixNqRpGGjBmL4Qftj9JcXIMOgjrUyyOCniQdXLwFDPuYZ+6Day5i9Zwj7dTJD3PMeLRMJxAls7XSaYhxhJ9fo+7ofxOA5J7ZpI/+aHFV/4ASCe7Zkke3MpJnZVBhlj2Hc8cDOKT7OJEuttubDStCFcQR0zef4NBSw3XVddH2XTzJa6yEZqe8jded9UfNSTn/yQSy5ApBP9Tkdj9H1NZnMFZMUER/naw4RUZ8gbyDYdfVgACoT1XeskbrKRLck0HD2CfidrMP1pMB5nqPr++Ahuu9n2zOJQYvcsiyxnMHnmhc1OgH4rtsehmP9XpeIaWJvwq7EqayXx03VFttYlnyU9Wma4kP+8DSdfeK6xLxs2X3WB9vERziGgg3sF5Cdbc2gte+7Uvk2KYBtO85CyOX7Zt1x8r7bjRGxPX6caw3jEMt8jumxxn7MZM6yLtGvfSE7revEAlc8OXU0ogLuiHyKFLLgZz/k08Roh4dYIMkw4ew9GH6mljEgn+PlpDHLqc7ZRJEfYso1WgzqBAPfazJwGOrR8qwhiZXH9w+9vjvRWNdUFD879jU+PugJ3T7pmDaUbNz7SIkS6zH6foiUIsax9j4DZOoxejWrPZ2OxdHTj4ozSynO967g0nsyfPoUjCvJA4uVnc+UnUvyAo4xDPmoWjNasKrTNH11yo3P+TdjmVIq4ABnZOaP+bTlRRtaXtAuDodTRGBElXE1+EIhDQIKQyImjGQLQ7q8vNwEbq5LBWVWoIiIzdjp23a/p58iHhGbsTnZwZGj6BHbkr4ZCTNoXI9xDcNQTupifTFm5M09YaBwMG4pcVCxkzPr7uqBmT1AqAE+9+Xe3pPhShNOn8/g+NizggNxbz+yZUx83g9rI3Eg8Nzc3JS2AHTGoNaVSuTHxnrGjk2+vr7GH//4x/I0+y9fvsTl5WXZWI6zbgEttsr/A9T5O/oKqENHSDawqfZBYABRgp7bafAvp9PpKz1JKZWKTsuIASip4jgZxVZY2+1Z49uTn/jpqg16hnxIMtznbX1nT5UDgfWWucBaWd+t/7ZLgJbb8Az2nQAAqJENOuIKELbollYnbLywLTPPXdfFH/7wh3h6eip/M9PH57w+XMstLLY7qnhO0uxbImJzapzBdq6816N98aEO9BADrAcsIXbs63DtPCY2Vq4xz5XcmOelJHkmYfb7XWQ4Wp/LkO0FkiyKb2C+TirRZbfOkFBwH+bS9328vL5G6vJpVPv9Po6npwxQPz5if9zFej7QZYkl1jTHaZ7PVfcUx2ne6OZujej7Ifq+i9R30SvBW5f6dO91XmOZM3A6HadY+to6U1tpItZljWmao18j5ljilKbou9pWvSzL+TNTLPMau90+H5cb+WFjfVcr2RxyQAVymvKpTRFzzMsZNK8Ru90+IlJMU17HjwPHfqZ4Px86kmXcxTRV8qfrtm1I47g7a20q+KKMe84nFkWskbo+pvOY0rzEEmtEV6t6Q9dHpC7mZY04+8qLMz5bl0rmVLx0tof3t3zcbIo4Tqdz0pc163SqD4kdhkqMno450bXNY2sGtyaRSOjRQycrWW/r89WMc1rC0O2zNZmKOE3n42f7vB+CRHddI4axL4nsPJ+rEl0fac2VoGHs4+NjCg7Z6YdapUgpP8gufzjqkbO80hrLOseJPVH9EMMu+++hxwdnPdvvxhiHLIMUX+/PBPc5GWS+xgh8Hl/QdtC42kJMN1mP3bcEV5tEEx9ZL9au9ZvE6XYc/7XXdycanjgCyVl5zWgjtk+7zQxNBUQGAW5JMUCmwnF1dRk8uIWWnoh6MkIdl3sK674PBMyYAGLcg0XJzqv2rbIY1YEvYi2mUpZ9fX0tv/MiqBIQARU3NzdFERxsrUDImOQHdtZJyH6/L3sBUJzdLh8p/Pr6Gp8+fYq3t7d4eXkp7CEGCkAFIHMNACgK/PDwUE6WAig6aDJP5mcHA0tjFt4sAZsQfRIU37MhcF02ohL4nJQyDvp++74+CZsXgc7OivXhmuiJq0HMjTm4TzylutcE0OsyfkTE/f19PD4+lt/NeFpPnFy47xhGlCSG/mrkw1idNAIcvL+JsZsdr6CltsoQFEgy2SdDsul9RTD2p1N+wCT6YeD25cuXkoRfXV3F58+fCwnBeFwFQ58MWiPqczfMSrelZieEJPtunQA40XJHYu79J9wXP0Qixd+RGTqG/6EigO4ChnHC9ieurjnoY1feMO1rGgA6SFBJ6bquPGyP+9LWgg/h6b7I0WQBBA7zgaghCHJPPm9/jV67+sf8CWK8j85YB3xkNGPC3pER+/4gjNpKW0TdqGwiCjkTnJkf4MjJoYGMWzDxybZVdIKkmOSFsZkYIb5EbB8El79fkyL/RMYQAVRus/7MkR8aWzf+e6/QskRpoeSadY9f7bVuq0iszzRNhYHN70duZ5LvQzYAKeaKze73lUEdx3GzbySlFIfjMS4u9kVOrnrN8xLjMG78MjK13rNOANplWcpJPsQyPo8MneyRDNZEYPuMkGEYSsyDREvnTo5pnuK9OSTAwNqHM7SElHUdWSfJd7sm+fjXwqiniHEYt7Gj72PX1b0CKVX/x5pAsLhyN83bdloTJjxs2HabUoqhH8IdJPhc6zdA1BVlyA4TE8YkVLCYE2tiMOv9bZYhlXKuW0msJc5TLG2LvmetRG+Jbq5l/eG6yAuf73lg01sCqlZ+8BXICdxoYI9PoqrBXKu91XgPFmCM8zTF5f6iHCscsT2oibiEf+dejMeVEWNak4ImgvD/Pvzi917fnWggGFj7bU9iXRQrwm43FsVHADhGDA0GnAfXASzoy6QEbSYNwfjvWTnrw/MQjp/NYKNACTIIuIhpOn0F4iJqwOK7BjqMg++dTqdNT7pL8wYXgFm+w/sGtCQGTjJglGFu3Z5BEmfHhgwd/J2pEvwJqsdjfgYDDB5rBKAhaLStUhgRrVEOtGYaDaZSSkVWu90uXl5eNgkoQcg6QfsDbDY6gHEbfCBf1onkxgy014L5AVZJeNGViNoD62TV7xMwHx4eipH7FCMzxW63MrPBe+xvMcvDPR0AkDWOwPeBQWUtnMyYRUM/YW2vrq7i+vp6w25GRElO+EcCzSZWAAXjvr6+jqenp3h+fo6bm5sNi4ouW45O9JiPr4u+skYOAGaFDPbQI+TrChLXt1w9jmEYysO9rAeukpj1wY/59B8HLduN74NvdAIMiUCFpLK59QGIbr/gnvg8/IeDmYMFYyKpMhh3goA9GUC0euhgzBqjX6yBE3t8SEsM8Dn3AWPbgBru5wSf9caXeX+b/S5zoVILm81aRERJyio7XTdkew0Yg9fIYMBVWAMNdDWveQU3+FLmjF/H51Y/18c0nYKW5ZRqBTCv5UVpk/M92/GZhCGZw2d4P0h31nXexz6xASdKtiVO1CIpKBuoL7aVbyd1vRJ47AWfuixL2UdlIovk35Vwg0r0x3EaOzPxRJsv/sG6XpPDMU7T9tABg1h+Rz9Ye/RxGIbNQSLoQkRs8AVjx8awWSeVBpLcC/tOKcUsphp9KoSAAChrmH/PT/FzNRUZTdOcn/AXNbYa8KLvgOZWPltcdZbvukTMtb3Krdiev58uz/2c1GM7XNfrYfs3XsBXIFvGbh9lQow1ccsUFTD8E/e3vaKj+CXuB6GMb0EG3Dciil56DPZVhURJtfUJveIz4AHjNvsnEnESXeIG2IH78LK8HN9+7/XdiYbZunbRu64eNejexcPhEB8fh/jxxx9jmqayaQ5HaGBKkHx/f4+Li1wagz3FybsnDIds4XXKjiPqZlazqeu6lh5zPhOxxulUN77a4ff99uQDjBZ2F6dLWxaK0Pd9aefwvgRAgReeBIVxPz8/F2YRVmCa6qk9sMg8iZoxwOaQdJilsYIwT75HkkNAwnjGMT9UCPYePeC6LajDqaGQdvboDyfukD27zaztJ4VJ54UTMHDCiZjJsmNZ17Uw7/z96uqq6KArKOyv4bq0kuEQnp+fY5qmuLm5KeMxc4gMSMa9ORQjRpeOx2Np6djtdqUX/ubmppRPuQeVBRg95Ow5Uf5n/nakrDW24eSPHk7kie7biRCokxwadnJzc1PGxHj/0T/6R/H29lZ0n6e7+zhgs5ZO5Jz8OcAQRPmMj8YlgUVfKgGybk7B47tOdryXyiDSSTZ6b5bauodcAf4R2xP3+BxzMevOfa+urgqwxH58epyZJJIQ1gNfxJwNVsyq4W8Zi9vZAHW2W8ZusIAf4bqMg++yfiYU0CmALHPBlxkEuwU0orbxYTMETvyoiSb0Bbs20ETPWBP7MX4Ckqj4+XkdMNUGMCYHsOOIKP7T7DX2vAVctZ3P16aiyXNGDFpPp1NcX9+eq0FTaV/u+/pAV0gCEzfEIGKOk0Mfo8rnU8oPmMNWvT/HPtlMOfIiLjFXdzkge1pBSZLmeY6hH+J08l6Jui61P78+0K/tq7c+WqdccTaTjL762lzr4eEhLi8vSxKOD+xSilFttySaZuXtp6x3AD6foMZ1ndwjD/syd0tEbI/wRQYm3GJZNzqOzz+c52pfRmzOiUQFoehBji27WOZta3atpGzX2K09loNB6bIsuVcrVcLCSYIJV+YOdkC3uTex1f7Udu336uMCtq3XrBP3Mwlsf2HSAZvg+iZ3WpIJXQUX4NeoiPI7a2XyjDhOVR4dwVeCYdzy5ITCcc8JIffBdz4+Phb7IPEzKU/MwBdiz9/z+u5Ew+1HNuLsXKai+AQityS8vLwUY9ntduWhVhFRWn9Q9jzR3CuIIAC6PlnFrDzKdjpNsd/X1g7ACopJW8E0TYX1y4rTxbrWvkMSka7rSxvS6+truZYVDcXDQbOZthyVp+zzcDjE58+fCwhrmRcSMR8jaGXFqSNnlBIwwN9QWgNCAwhATMTXrCzBPyLOSd9FCSDuQyZDx2AZC0ZqNsBMAp/hHrRKfP78eQPmnVR4jiRdjAEHh5MlaJj54MX8eDBWRMTLy0vc3t6Wdo3Hx8fCxrnNjXXBSbXtB1QuMqu434yLlzd48R2vkx2Sq4DIzS8zI8fjMe7u7jbJGc7HzBW2iA3YptoEFF2EGDBAwqEaeGLvntfT01P89NNPm2TGG+xcofRae72ofPA5PzWWINmyTWa3DazQ0RbMorOAuUoy9AWAA6QIdOhARJRxEZycFFgXfT9Ake0Z5pT72pGTrOD4SSrMdFEhQCYEF+biQyH6vi/tOa60GNTwHuNwdQ07JjA5wUCXAO4kOCY+zCwD9rxWXNN+aZ7rcx2cQLAGToxdhYuIQjZBcjiGWcZOai075orvZ274fB5myTVo2aAyHFE3YtbWq7qfADkyLuRpYsB6ksH3Kdb1nHCNu/j4mCKl7VH03JuE2vvmkKeZV69Riu2JVvg2dy0wL2IK7zMPAGFpz4itDvDKletdxFqxBjqOjprBj4gNHgADMB5AknXVLS+M0/sY+DzkhStfJI+H4zHWM5ZgnV1RciJs/cE/uRUQAoCx81mPEeKvjSf4abAOPn1Zljgdj3E61mc/mezquy52+90mESjJ85xb85AHILeQBlEr9JYnftfriU9uSUHsMutCrmJxLft/g3zsHf0CB5h4sU45ScLP1opfjuE+ftxkBzaG3B3znGgzX5Nj+Ad3Vvjz7lBpqzi0lRNniDvEKifLjrvFh61V7siPv7fVeOTixI/Y7Ioeca+tXGDTJhx+7/XdiQYtEV5AFmUcM7B5eXnZVDNyxlwZWbKwlHJbjysLCDQv6lYhzTrjjH3kHcaaTwTJ1yNzRUEJNDYMnm67LNsHALK5F0UiiULhAGZtywhZ58fHR+nRJ0i8vLwUJ02VgAySOaCwBh8oPyCWcXHkKcqFIrQGw1gxHmfybeB3AuHghjxwWga+BErWzuuEXGhH4H2DNJzFf/kv/6U89O3q6qr0GhOUuR99iDYe1tqBFVkwJ5yw2VkDST53d3e3SVIfHx9LMmK2GrkyjxYsUO1C77EhJ+utrZhNIZFFPrTOEVzXtW62hyE0W2dwgP2hN3aQrAGMK/P7VrD1IQpOEpAvOsDcSc5/+eWX+OMf/1h0ArnhDGmNM0hDju0RndYz1tjMkn0GL4DK6XTanC4F8EIGzA9bq/5t247JWrNGgD/f0wmAgwKB0MHEjJ5PwKn+sAJOB751XUuy4GpWRD0q25W+l5eXAjgjaqWKuTloorNOQPk8a8EBAQ60yA45Yvv4YOYRUVulWqKDdkmzidyvgKKzLXvPGbbgllK+w9p7TfiJzRFnWFtk4zWEgcQe8W9ml+d53uxf8rUNttqqA38nwJO4oJtPT09xPJzyxuZ1jXmeYhjHvFF3TXGaavUOmZmkYQxOPP1wMkAu63Q8vsf7GTgBBLFds+7MGb0DK+A7sKuUUszTXE6KYlyM9fDxESlt2/qsG9g1/svgC322j+DFXNvEBcLRMsM2OA4f0F/wRqyxrDX+MA4Sa2yOsTJuJ1smF00stay8KyHIG6LSBzcASJF/vka9D9fgnkts9yUuSz2E4vJiX3wHep914RQp0sYPs1cRneZ+Jgl5Od5WNr+e7mkSJSI2vo4Xsru9vd2M25UI1ts2MM9zOWLeVQ7k4hf+zYkE10T3iOltZdpkHPpoXEWVnLhiGVvPSUgZ7zRNhaxr8dYwDLEua/TdtkqHP+a66CD+yEQPa8c6mEThn+Ou2wVN5P5Dr7/g1KklXl8/zix+iv3+IvLRcYc4naIwgQ6mEalkeKfTqRjvly9finE48wN0sAkKJYE9RkHyMyMqe+gMkqzVLLwZRRTGAC8izlk6Yxgi4nzO89lJOquj1SmiMilmML0QLi2z0Ou6xuHwUa758fEeKeWH8hlwssARUYIW7zsZuru7i3WtJwMQTEiaMCpnoHZ8lKad7BgU4Dz8vA+zThgYxuRTwpCJgUubePBsCa73+vq6UXjWld8J8uuay6lun7ADMvjEofMdWHrmbJBnwE6A9aYn6yXzZ4x2UMURiIUz04VOon++lhlX9i/hEJw0WibYiMEm92aN0S1XA+Z5ewyt19FOpgaxajsAWcuezeQ//fRTdF0Xnz59il9//bXYIs6NYI9MABfIFXm5VaK1Xz7jYMd6t+1LrKeBE3PDN7CuZqH4PrZIwggAYd1hsHHqTnicnLHOBr4EEmwUsG1dYe0gPggkvI9MuYcTfu7PPQFY/oyrWPhjWswAjv4bto0/gHhx+d0+Bz8CefD29naed0Q+4nWNaTqVWIIt4YvMoLt1xD7NlZqI2CRi+bSf9UwgPJX32yOKy9n0XR9935194y7yRuztsbG8TOJUkNRF19Fil1uMs2/I8ZRnH7ltykm3fST+LqWUjyLt6lOM2Qi9LEsM4xiDKh8XZzLt8PFxPte/PiwXwq7r8tGwa0RcXlzk0666vFGXtUSfPA7WEj/Hz/aEM+S1rmukLsWihIs17fs+lnnZ2OS3TkpznEd/qSjCeHvvAP4JH0W7JHHUPtc+CCLgcDjEvNSKfIoUu4vansXn3cbadV30XZc7gwCh8xb42y45znYchrg8k6PYYt93mz1A729vMZxj8dD3MYePLM06h83gJx2bhiEf8epkP1cr4rzhvFaInOhx6tRwPrY1nf8fX7qs5xi4LLEsX1fm+j4fDsSJpF2f9/C2vtqJNuuBTvG7q6kQAiaqAeyMn2u5pRR9Qn8dd00ccSCNY4HX3ckG48F3G5PwGR4mCc5z54EPKvhWZbNL+UF/XCud16Hruxi6erw768/amWA1bnBlipcxDAm0W6zQG+vW97z+okRjtxtiGFBcjhStJ6XY2V5fX8fxSHm3MlXen8EE/TMDnF3kB9RVNoRJf3wcIqXurHiH6Lo1UuKM8npKkwVHuc/AC5YjK9QuxrE6jlw+XGOaao8tykwg4h4oris9OGSUHuCdg2MXXZfbP25vb89JSJyDW2WGIqIwFyw+13dLDAy1WQQSCLMuZvcZt9ktZ+yc0mOQhqG2Z/hjyMz75uZmA2xoIXNlhWchIEeD34jYtMe4b5i/RdSnlgOiSWqQPW0uyIfz77uu27SMuERowOoAghxwSq+vr5skFYDiEi4yd0IGMHVVDHtxos3RsNfX1zGOY0lqYcLb/Rjuf6f6RVC+vr7e9MwaFDjosUcIAOz1RXdgiCMqa4QO+Zq8XOn48ccf4+HhYWPn3NtJKGAUeThpA4wbWOP4zDwZoHHd1klG1M10sDLMxeSB/5+xm0SwLbgE76QAOyygY6nlf/7mpJw1hGUk0DIebAsZMTbG7vm6dcYEiMftjbHosQGzqytUxVryAD1l7ZCVyRmSV6/NxcVlHI+HOB7ZHAtoyEeXQ5YYyLFWZjFr+10fHBnK9XJb7Cz/4COR58gnQK3Rdfn7WQ/W899yixMJF8BnXSMOh+PGt5Jssobtng78Ai9XBVsCwb7azOK4S4VYMZs4DEO8fZxtuu8j1oiLqzP5kLq4vM6HMexGVViXJVI/lKcKx7rGvEZ8HM/Ar+tj6LbtNV47j524QdwZhqEQQswJv4quHqfqG2PNR73ahiDpIFHQKwgQ9DyiPiOHNTAGMID1ITYmytyufDqdYokl3g+5qr5OAuZDH/OZaOi7lPXmbK/oe17LJQPBlGIc+jitS6RYI9Z8OlQK9nzWilVExLrkfSBXlxfneLFEdClOx+ncQp6Tj3E8Pyl7N8aybFt5+qGPoa8PNwW/LMsS+4t8zG/EWsbTpT7vwVBlyms1TVNOEM9J8jzNcXmVycJpPm2ImS510fUpujXFPOenfxODUkqxv8i6G2vd/+VqtisA+DbiH77KsZT4h06aeHGV3v7f+9HM/Lu6hp7c3d1t8A1YyUkq+gS4d1WHytPLy8umwupx4kPAuMaWjjnLWe+6NW+nSSnFdJbfq3ASY3WMYx0hmBzbIcLtv713BR/EtYifjou/9/ruROPz588bUIExV4deg0g5YWK/j2X5+gmOBCoHOJwJk6c3G2eKQlxdXZfkBXAEQEZhzYraYABUMFhupfLJK+taN1sxZ4K6g7SDB/fE2dBq489kBT/Fsszx008/lQW+u7tTdaGel+yqCXOznM1wGyB0XW2lYa0Mdg0GrNQYJ0yOGeJlWcpDEwkmDgbX19ebM/7NRJmFskPxsZr8JMFx+Y4A7NJ43/elDMirDWhXV1ebU8si6pGphYlZ6oOcnPQQONsqAjJ1wMTAAbkw98iiPf0JPeQ0FsYCu3F1dbUpexp4R1QGC7sB1PhwAsub8XGahPUSYGpbM5jA9vg+iRYg2XtVSFBcQeRvj4+P8ac//Sm6rov7+/uIqH2ky7KUJz07WTEDhTM2gMPHeC1IOr0/yHphEM79aym/+gqvM4kAuseae22s41zbpAQBkYomn8XXocd831UL9BPbQT5OLrm+9Yx9aPgmxu+KC/NGf9Fb7OFwOGyeE0M1kFYoAwL8LYH8+fk5rq+vo+/7uL+/L2P0qVi020LEkExH1CrfMAxl/wk25v5hM5CHQ03OKuibN+wd+uP2TWSWZVWPmoQQwx8RL77lA80G8tMg2b7KPotr+TAD1gX782mPzJ2T3Lg343DLjpMg1pD/5/p8F900UeXkwuDI1Ryf7IitkQzwvskbru+DBNBxxsNeLr7f+hRiIzqMHFhvYrvxBeMAIDlRZ426Lj9szevgRA//iBwZLz6Z+Xt98VOAY7d8YS/oNXpiu4rIrVz87pOPGIcJCEgF7MC46nQ8xWmq2A1bpfOBDcfI6e3trczNa+59Jujbuq4xLbVSMo5jDPNQ7u0kep7nSFMqvpXYhQ54P4PjJPPl3m5jQh6Wo7tmsH/W2mCan04m+IcviKinW5UqQ1cPcnCF2njUpKbtwXHCemt8bQJ/HIZzxajqtYkOroUfN27Z7XabU9tM0BgzMH4nEU4I+Zz3+H7P6y96jgZODkVqgzI3Z//AblcZa06iYN9E3/eFnab9AOe/240liUDBfa64Ty4hyWkTA4MLFNTH7PkkKoNtFh1njvKbBeXvODOznChzu4GL62RgtG2dwAHtdpWpoT0AGaMsgDTes4OpFZk6X7ehEIiQuZ0n8nQJEwMjAWjniTFP0xQvLy9lXLAOODjvUwA40h9Mxefh4aGsMwZDRcsVIRufHYED1jiOcXV1FY+Pj5vSKb2OzJefTnxoHzLYpmWNJI97et8PugGThzH7JJqIyuweDoei95Rmv/VEaDM8Bt5m88yqYFsR1VkgGz6LLjAOO2L3DPMeYNqOjO8iR1hn9JH1wjfc3d3Fv/yX/zKWZYnffvutONvr6+sydnT44uJic6ysE8W3t7dSnUIu2CrjpXXSDBZ+yOQCwcz3sG67MoJeONFnv5CrFfZLthEDf/wnwRqf5MDlJJm/49vYw4Q/AVxaV7zRnKCfUj0IAZtGPuyZcTIPAHAbJf4FPbBcqVbid29ubso6WA85qScHyiW6btzI0G1d+G8YayfIVFEgR5A3T9d226dPcUP3+YkuoW8mKxhP25qBbiFn1o974COQh8EFvzMGk0hmIPEftkH3WDvJXdc1pnkuTyO2vpg5hchATwzCLQPiabu3kgo1BA3r2LaDMCZ0xdVEx2b8HfgBEG4yD0DG9/HJ9oHIHBtzokSiiayQvxMGJ4yRvq52WmeSfrffMJPs+OK1Z+3GcSzt0JBEvPCHzN+twSYp7PvdwnY8niLW7XNlLAvuT9XUOCefFPpRdAvf4XvzO/8PziARxvcT+3wP64r3DTpxYb35vtvfiYPGLk4qDZAB4iY9ae9sx4mcTaZDWrX4xVUIftJqR8KBDoLl2rVzNQb/6zjOa0O2rtsYboxmf2FSjperFhWHVrIBfea9FgObAMR+nRj+3uu7Ew3aNR4eHspmOAYBQGDzH8Ds7e01Imr2dHl5uWGHKOVTtiQT9xMo/d2IiOPxVAIHyocTNPABGPC7ezgd1C4vL8uTjB3UMUyYAZSNOXNdB1JApo+otNPODic/ETOlFHd3d+eHE16dFYx/S0kyaFVCEXjhoGmlQZ6eA2NFRmbceJm1idgyCRizFattVaFtiPHYIXIEKePH6NtAy3p1XRePj4/FCXFNb3p30oBjZZ4GoIADyrYwpcwPB4JDwdEwNwwQZwDjwhzaPRURlYGkOkFw8akXXg8HED5HwGQ90CP0Fnto19b7ldqKCtcwI4n8kDGfsxzQAewLXQUkcF1+kmTzN5K+ZVmKPb69vcWPP/4YHx8f8dtvv8Xd3V1EbBkSADK/My77CgCUwVkrb+TC90jyaK1jzFdXVxuwif4hU+TuyoV9E+ColTnzoKrhU+j4XkqpJJp9X/dJcH1+mtjBHlzZZGwkMJYnYNqB0YAPf8Gx2K5UpJTKQQtmWQn43M9so793OBxKNYIkHdtbliV+/PGnogOvr6+lPYm9A8tSW1YNXvHhsHSsW1672gbj8WBnfB9bR+cBHsjaTGxhYRsSwgdn8Fn7BK+L/aorVQahjJN7MCbWhXUwS13YzdgCeRN1vE/1zAloBHsU5wJCiEltHIDwww/U/QH10AB0Fjsy4PtWXOG72Ctr44TG/qglFgyguTbyQZ9MtPA76+xnWyCPJb7e9FtiTdS2Mbdj2y/jdyxHX8NEpQlAx3r04HQ6FR9losdVFaqOzDHWeuKmyQ6SDHwbeoyPQt6ufENAeA+a9dtJEWPjQIY2STB4NYi3jBgrmOVblQj7SHyS7YwE2sCZOeLH0E/wJGO2HTIGdLGVqYE+Y2aNTTwxDmyWn9hd3/ebE/WYt/FcSnUvJPK0P3YMwl5clfCzsfB9/M02aX+K7GyTbaL+Pa+/qKJxPB5LKdzZGYbDQqWU9ICuusMdEGTBU6HYZqOVnSUoIPR8r+rwSQh8fxhtC40jZQG/ZmhTSnF/f1/2DnBPgie/G9AwNmeczIvrHA6Hr5IrNkDZMQOc1zWCJ8bixFBEt7Ww4C5tr2st3+IsSL4sJ5TEoBYmHTnRJnJ9fb3ZFOdkhbXjXi0AdEuNAyfrSlLoBzpuN26O5aSIruvi6empVFWoBDkZYxw4+Gmq58mzfjgLNoCie94TYmbL+mNW0cHMRu42vzaB43Mko177vu83SVkBDms9WQWwCDvUtn1gk2b6kLMDtZNVvkOggBEBOJEIsa7Yg20zYusYCQrICZBp0I2N3tzcbNhobI3rmwEDMCzLEj/88ENpuen7eg45FUuCddd1pU2TqmfXdeXZHwQO9MgB04GEQAPDj34g59fX1wLG3T5pcGsQBjDCfhyU+DtzYX1Jim2rTtT9u5NxVwedHHEvdJVAjhywdfQPXSHouTLKd1xVYKwAW9aQ9UWfI/IG0ff39zgej/H09FT0YF3rJl2IKGzbiTwb1StjXGVvEGDWjnnzvhNAdN7rZYLGyUI7H4NPA050hvWxf+De+B8ABCDVcmb9mDuEX95XEJu1tP1YN/B/TjoZbxv70EUn5K7Y1rWqJyY6ofZpV4wbHbLumwT7Vqzjuy15Ylxg/8110FsDQsATc/U+wogzSz/V9qS20pdi+4Rqy5F5oa/2I8Qo2g+xb+setgSwx39ZZyGKWAtXjUrylyqoNRGyrmss61x8pvdMkUi6FQ995/usjckJ7MLJgp8t4tjK50wO8xOi0M9PcuuT/ZF99TznyuHNzc1GH409kD22yd/xlawPf0O/HIuxe+wdvIldeQ+ciYW2MugkGb8J+WU83Saw67I9hRA9JnHI5H59VATkFnrg59vYXto14t7eF4gM8Q3IhvX4vddf9MA+Lo6DMxBjIQC7BJhlicImAj6diTMRAn4WQu1X41oYFYy/WRpnqQicoEOg5axzJ0nzPBd20IAThcFRMHeM1r2gZlMIxMgipRTPz89Na8MSFxe54vH29lae4ZANtraboLg4g2EYyh4IXswP52uWwqwP7LnLvQaQbYsGgQjjcHDE0aATvG+mjCqQwTVOn/WEmTGzcDgcNoYBiAS4eh8K/cSn0+kr8OeedtYENv3j4yN++umncjRsSqlUhGzYEVH0BplY59AhwC734N6AWhybGVl0hjVEtxi/e3Aj6pG+ZhwAyowJveZ7nPyEnttGfW0zFeiOK1ReE+TlZCBieyITlUN06ePjI+7u7jbjJ5E9nU7xt3/7t/Hzzz+Xk9O8V8Ogl3uSNJFcVbtaNw4Um7q4uChHS2MLTghdceN3nDFsHAGDuVr2vEeS2wIcJxN+GZwbXEEAGFByf3SMvzsIICMADH44orYWGJybETT4Qw/NZnrN8W/uqccv0pbQdfWhVrREeJ1ckfzll18ipW5TGajtq6eSmNsfYf+MkfHji/ChBg6OO8QuvuNq9eXlZYkD+MzX19cCgAxizFAC9pA3RIrbCQ2sGbv3ITgxNaOKvzDDjx6iF33fRycQYXlYV93zbVvzBllXe5GZ2+sAh469rmRwTebRkk7YIXN30s7nTMIArtvk0T7NFTiDMD7j5IO18ljsmw+HQ/RjtTt0Z5qmuLy4iP1ZP1qihrWH0PR4SBzwiciPeILOnE6nkohgz/guEzzWPYN44urxUJNa7BDZRqrVIsgT/Lf3CSErbPDl5aW0GgGw3XqLz+RvJp1YY9bdD9e0HG1XjIkEBH3z/pPb29uCR/kJXkTX0Q+qxcgJfbKPQOeRq9uq7DsZ/7fIN2zIscN4EZ0yOYMfxf9yP/RlHMdIy3YfnG2XWOG1hKyAtPL8WFfsG/9nfO+47mSZz+HLvuf13YmGmQScAoLJFYY4O+x8MlROFvIJC09PT3F3d7cxCjMvBh8oI8HAoCZPao2IYaOYLSPF4hlgkX2igBggQrTRWNERPEqFwrishFGaeWCBWbTj8VhaCfK4u/jhhx9jWeZYljV++eXX6Lrc14zBEijIUjEAbzBlfgQWnIuZRT5jgOyMP6KW2XCUft6Ckx8CCuvv0jvycdCAyeR6ERmYsd4RdU/Puq7l2SbMxTqDbmAgFxcXheU0eDUrDMhxHzz6aPBmdow1TCmVp4CbFUMnkQc65GCL/rjv2CVvlyStyw6ufL9lWx1YcThUMpCvP4eN+MQJ673ZPoNqenWxF/SctbL9LUvtHzfAoRyMDFKqBzIsS65O3N/fl+/t9/v48uVLXF9fx5cvX0rLFX+nyscc8R2WGQysNzJb1m6jcKWvTap5n3v52RcEe3SSJ7tbjiQxnz9/Lom4WU5XHFgHXuiIn6XSgicHBAIsawK5g15j26wndhFRj37Gx5nldnA1cEafnRw7geAFSDHwRU61wjjGuo5n2fMAwSXWtZ5G4wdltqSP7ar6O6rPXXQdlfQlLi9vi08BnAAcsBnL43A4lOO3OY3weDzENM1n312fT2AbByi4tSafFLSUigDf8SZSbIRkynq7rvmEo3VNcTgcI3VdnE75VKk1UkTatpNwD3R8mvL+lQqsI1LKD6vFr9mHVbKwjhn21O3ABiEAOCrljpXMwT6iTQKdMLTkiuMX77kyP45DrBHnk4/ykbKcMBYR503e+Xj8Ek+XOu6awC/RpSHWc2xH94jf+LOu6zYP8CRemiTwgSeMk/Fj+waAVFt9YAK+EllaZ41BaE1cliXWWKPruzieOBltinG8jNSluLzM8fbl5WVDGHAP798ksXh+fo6I2iruZMeEIt9FbyA98Bv4VfsNZGXiEr2gM8b45+IbiR6+B9LBrZDImzVy9Ra95372wSZ8/AJbtFggIr6SqRNv7odNopdgRxNg3BebmKYp0rrGONSN48aw3AsddPU2IsqeZyenfKclEY3NHRvtmxzrvuf13YmGXwwep9J1ZIFrRMxxPJKRDZuyEQDSLB0BDIEzWcrhZt3zpLdPhTUbh2EC0MxYIiQHYY8noj5Rlu/wUD1YBgNSWAYWzv11zjJRRhyZmcRlyTIbhjH2+4u4vb3dGB/Pk0BJYffNYBvoGZwzHxsB7Bxy2AQwBRqX+azQGBAbdSPiq/XhxfWpFF1dXcXLy0tJJlx54PsG6axPRDZeZE9V5/r6uugAVQeP04wnGb1ZwjY4oBMw01wbQMN8uJ73bLCJnKoK680cfPJMCxTNRrEOrAnVGl44dp8Xz/dJprAn9v/YoQCmWAezMeiIwSVzR48iooCPYRhKFQKG29dEjugP6+uqE20E+/0+np6e4vHxMb58+RKfPn0qCZqJCQgIQL0TW/Te5V6DH9aZRMckgp8f4eDZsuUp1erX7e3tJtlyFQ2dRpavr6+bFhI+x/19lDQB1IDEhICdvjf+of8w/8iE9wl4BF+f1sVnOaDBiQ3+Eb/nZId1tA26wgYD7tYT+4eWRcvzTHE8Hsr18dGODQajjMenHFV2llPlxshH5dbNkLC5JqVqRb1WRohTfd/FNPnksrpBfxiqf8AGs35FTBNMLoeO5GcorWuNFY5fTvJaxj2lFKdpjZfX57i8vIh1jljXTtWMWhECqAIKp6kyztjnx8cp5nmKdeUI4Pr8DuyftlhaV7exuG7WB3Qzfto0XMEBUKHTrCt24vjohJR15//NArPOa9RW7GWdYzm3V19eXWwSx15V6UhdDKnfzLvru+j6sfjZi3MlG90d+u2R2sR1kirALjJATpYZa0KMMFHp9t6I7VPO2TvBvdkzh51jfxloj/HxkW3y45Bj4eH4cU6Y6nHprjZ5TQ1GfciP1ztiu0eDteczsPp9n/cfPD8/b5JIE9esK/4Pu2AM2IqT3bZDhta+lhwyRrSdEV9cSYDcwU9jh3zeyTK+gfEzzjZu8z5+r40pjLWNwSbGrq6uIpalPDOH77XJLTrpCpATIusWn8fOGadJQccIPk/s5DPf8/qLEg0H8CqEOXjwEEGKf9fX12VzuNnViNrOw+Tcg9z3XVxe3myYShTv/f0jrq6uvzqhAmVzz5zHglB8pK6DHMkDoGQYhnh8fCwPmGEObPaGQTdTgfKQLGBgDig2RgwRx48yotCujOCsKU0ajKAcKKVPOmmrIzhNQDOAA0fpTbDILKVU+q29hmaXkTsOk/Xkp9liVzxsCDgRByVkwn4L2FEzQTgYH4lMMnI8HuPl5aWcbuTEFsDuow9dJYAZASAyb/SWcbj6w7W5XssIOxlwoDVoMygEZHAdgnlETXK9QRt5oSOMhfVHN2gFg7FDrgAUxuOAYxbDTAqOET2AicLpMiczUyml+Ku/+qv49ddfIyLi9vY2Li4u4j/9p/9U+vR/+OGHiMhHa2Mf6Arjj8hsjZNfggqJ1evrayEC8Cdu5XNLjNeKgAOgx0/xOb4/z3N5CrpZNABSy8iua66qub2Cl4/tJFA4yJl99P4dAp73aUVsGUiXyvm7g7wDHN9hHm6xeH5+1gEWS3niOOtCdQtbMRDBF5EEz/McLy8vxS8xXxMSBEP8CiQCc3FFqCWPuK8P6DARYzu2DiCHrFe5ig4YxSayr6yA3FXkbEu1PdMJcx5fF4fDXIgd9IJx8rvHGxGxrDxMbnsC5DD0Mc9LaRfErxA/DGi4fgZqp0hpLeuWx5afE3J5eRU8ZBCf7DlAumDPZugtR9YUH2UmFBuxTwRfOFHhfmZ4idXTlJ/z4O8gO/4fu0CPGBMxCzvyXHwdt2/yHQClN+lDSj4+PhZZkSDA+Hs/Y0SU/V3s0wMHYd/EhZRSea4DcZJxIyM/oDeitmmhJ9M0xW+//baJvdgFPhx9NhB2yw2Ei5MG3wPCwnt28YnEUmMF5szacA2wC/8Pjms37xt4u1Jgfef6xkbImHU3KQ0+NbnEPdAr5GSfzCl4jr0mr/ksf4MAJFbyfe5h0jPWiHmpnUXovu2I31lT+33WD/vn/thSm7xExCaetP75L3l9d6JhtgbBRcSZfapMMgtL9uunWfMANQTjwIlDoh3m4+NtU/XAocFGEkDdMsIY3fNpMAawx0G01QcCJO9jeIzVp3H4xQK4Lxpn4Ky5ZWlIWNZ1LRuZ2mdD0HNt4O+ExGXMtlXG13cS5KyUn8jfc0fRMRZkxfqzJswXQ/IJGThpAwIzJmZuh2EolaMffvihPBjPrQZOsLw2EZVNRb6wQzyIxnpGEoRuknCQqOFE0A2DGuYE20cAJsnxQ6qQCS1hdsrM2/fH4bh1BXA2jmPRJ7essZfAp27ZYbi6cnl5Gbe3t0Xebh0zILEOnk6n+Pz5c7mPnS9A3f7BiZkdeJuIYYcu8/6Tf/JPyv6Zv/3bvy0bvxkjwR4AwNwYL7ru/RW8b31xUlfYyvPcAAJmviLqpuSI2jfsJNC9tU7+ISesE7e3t8UezNASEAHSBl1m0yLqSTM4f2Rp8M+TaJEZbKAD/jzPZTP2MAybxBk7MkDk7+j+Dz/8EPM8F5m8v7+XvnADTgK3qzQQAMibQEh8YT4kC7Cl+CPLxP4Xn8O6ZNueN9e2X8cvoofEotvb23OMSZsxGrBGxEau+AODOAPaPJeL4r9NcpjV5374y77vY40lhrE+NBMbPhymiFjiy5cvsa653ZaYl08T2z6tGV+f/dMcw0DP9xrrGjFNcwxDPn7YrDE+s30ZzDt2OrHhd9ubCRwzs8wP/2lSEl9WQFTUwwaIHxAJBowtS41fcoUCnYRwczWuBZaM7fn5uRANBuF8nqPbAXSAXD7z9vZW9rZBbNzc3JTvGOg5fpuM82eQNQksuMxxgRjiqgE26tZlVyfNlAPaIXP45/tj/6wbY3QMZG8uds6YkC864SSNNeRvBvbYt+MUssCGvN5O0rBHcANHttuOjXeMyYjX/n90FDmYCOQ6jNvAn5dx89XVVcynerKkYypjdNIFVkLnHHvtn7ouV3lJhv03qjvG6E7Kbd+/9/ruRIOAyCKTdWXgX4O3mXUzhAzWpzuwAGTwKEjXVWVFIa0kfT9sgr4zXpwcDsQ/vaAoM8lAmxkT2GEYMThnemYobcDMmwXBAJ3d4pgBiDgOwAP3QkZ8hmvawUzTVNhfA9aHh4fo+9wnzBO7mbf3L7y+vhbACAMMwGqZMLecRVTQQdC6vb0tToxEB6bGp0VxrbZnnTX6+PiIp6enUmWy3NAHg8TKMFYQ0cq9ZRYdyJA1yauDBvPhWsjd62wHSnUAp8P7rtpYV81qwqQDPKiiUV3BGZutIICSkPA39J61Qd/NNDoZQocJthcXF/Hly5eY57kkvMzdjJfZabP/ZlD4O3rNKXAkpq4MMf9//s//eZEB46ftp+vy3i8ejIkfgKVya5uDJ2TDOI6bk+iwPxI727b1zOAEGyaI+fAIdMWg3UduYz/ssTC7xL0cuA1sCQic+NIm++iQ29c8h2VZNi2UADPa2Zi3T7jC97OW0zRtWiGGYYinp6ciIyfe7cZifkeX/RyB1kZ5z+0UrhIQyPEfzAvb5oXOQ44AnNAN7uXkgaNzMyisPoC/55iwfY4OPfXcy5s6OT4YHbGOwWaiex6/dS91o/b51Sr5xQVkTCoVGt/ncJhLwkX8y75nH/M8xTwv53+QNmPM8xLjuK0+OM6ic+3fiTmsj4kE+3+DH/tQbN6xk/mie07CGQd+zr6ea6LbrsoYRCFr1giQ6b55QN7z83Np+ySxBqyZTITMIokg+TPuYYM11cIWkKN/t7e3RWaOXVyHxBh7sw74OGn8783NTZkjsid5QKZgHv+/CUjrJteIiNKqzDoiJ2KmScuIWimnewQbah9HsK5rPD4+Ft3Cdrk3tgB2MZlqufn/wUBtRZhrQqi2e0w9JhM2XDeixqM2YWIdnTjyHolBW5n9eH+PLtUknWvix4xb8anYDvHdJKsTfuaJzrqtCxIPuSArV1W+5/XdiYZLTgYawzDG09PzhtE048g/s+0AOTsJs8CHwzGW8xMmcYiwyH0/xrLUrArj5nQGg32Mz8rs0wAiogASGxiL7r42Pv/y8rLZINw6w9fX101psOu68lRPHG9EdmSA6IjtaTgYA4CCNpHX19dNuR8nERElqbCRmQ3c9g7XnwBZPosyOcM2Y0Fp1uOmesJas6YETVcI0Atkw3F6XdeVFifGjKNk45pLuyQGT09PJYiQuHE9j5NxuSKBEZmF4FrIhiTHCbYdlp9YjIE6IXILCuvLGjMuMyYEUYKxAR7jZqzIFodutsttFXaAtLTwlHecFZ/FYb6+vpYWJu+xiqhAE2COfTjpbhP3iNicVEci6vuu61qC5TRN8fnz5+j7evwyCQhjub+/L/7BLCnj4j68Uqqbfklo0HN0xs+fQD7MFyfLqTAkGiRmZjPRB68pesb1WnYYZ24GDDm2iSwn6GFbAG3bNqeVeV2YO/7Bx43DLjL+tr0Cm3GQAtDw4LE2iBkcOn6YqUcGZveYK3KEYXTyxd/ohWc9zZg64cn3/foBZgRUbN3rzibydd0+9RkwlfU2SlKJDmZQUQks/B9/j0jR93XN3AaEb7cvLes4R0SqLUbMJfuyKYahLwkUa5t/9l/5tNpmQqvxHHnPxhp910ekNVKqTLr75w3WiamsDUwo88ZnOh4R/40R8Jncx3rhllz7oGmaYhhrtc2HDtj/mszyOPGtjNfkE+/zN/wycyWJR5do86Eii7/Gl9/e3hZ9jajPGaKbgeeTYXdm4Q1S0YmUUmm1wUbs17FdkiDmj445ifjWGn5rX4N9rf2iY45JG3/PgBpAa1s1Sc0attUA26hBLuuDX3E1xf7HPpjrggOcBFjGkLTok30gc0CH7Uc4NMXELOviZJTvt/4WmeCnxr6Pvqt70rzHx/GPuaBDkG9OEJ18IR9wvWO37QV5uar0vYlGWpHq77z+3d/8L4WR44SRCqjqXgcCLmABA0fRlmWJm5ubYoAsPgqSF+YUfV9LQShSDhQVBFvBUFjex/AJPjhYskWXeVFaM0gskIEtRmPmwsr88PBQKhI8hArH4QDrBeSFPADtOANXFswmYTjIG2CAgfvUK7feTFPdfAqQaXsKAbCu9DBugA16gNJ/q0z4+vpalNLnvZuVury8jKenpyIbkjjmTZAyaHWyxOdIEDw+gwkcP9+z7sECMWccGi+34xm4I0OcBoGQe5AcMs6WGXAC43XlOtgXemKmBZty5YyxEyD8d5xPm5B4YxjkgXtSOZ+cAGVGJGLb2mJZm02M2DI4kA7Yj5Njt9c4sWSOgBSDb8bEWrrkj20hc4NFxhVRq6ve/0MQYp8Zsrq+vi5jQhYOjC5XIwfG5kSen9g5+oi9eYN5G8SRRbt3g+qh23TMwLlyxTzM0KNXPteedTOoxKfyd/Ta1YGIKAdcUP1wImPWzOSA78masca0xWFj6M/FxUXZD4f80fsSqMcxUuo2+wrsx+3LAR2wfSlFObiAqklNUmoC3gK1caz2wVzmObdO4VvcHsM9OZ4ZXSi+IuWTq2xTWT5z5LanZQOK0Af2mDgOI+tlrtUI+4ZIS1xc1MSY7yFLPsvasIboku2DeMHacS/bItfjfgaorWxh6Xe73TkhqjHV7aysKXJm7FQbkLtjHPdizTg5iiTHm5zxty0bThsXuknyYV1nDe1TDdK5n8kxPnc8Hku3BXPFxv1QRbPwxDHiAvJxUg8B0toQOuGefa7B/SFFIR68zqyvfTpYirhif21f7Xv5Ok7GIKLwISSB+Cbk54TOLenMz0QV67Tb7crhBozDsZt7QFa3uJJ19XzAXibo+QwHy3AvKmbLNMe61L0c3Buy021urD8x3MmHZYhN2O7RZXy82wWxM+LuPM/xf/t//k/xe6+/YDN4io+Pw+YI2OMxO+CuG8rkMWizBQzQ4MVsPJMjm8oK4aewdpHSKdY1IqWIZakCQTERCsHGDo6AxWdhRmHg3E4EMHbgN+j7+PgorUaMmVYMenrt9Ay8ImoJ38DQyuskLaK2VkTUJ8OiCIAdlNlMTkSUtiyzQy6zretaDIj54aS5pjN4s++879arj4+PktTc3d0Vhs99nMif8VClMVMF4LQjwAG45QvgbuVHLwB9JLZmDRy4CABmmJkrsgV4tC0W/GRNkRdzoHrAvACqbVBH3pwqBhDypnN/jvG43TAiSp89OkuC5z5cs0PWX1clWKuI7XMc2lK6v0PLwfPz81egDbmQoLsi43thnwZlBiwkAXzO4MzgKaL2T6PzdqKeE7aITuL8n5+fN+zv1dXVV4kPpAD2ALMOQ2nbcTJJoOGACScSJiTwS13XxXKe38fhI4a+z6fsDENMcz0NKiIidX10/Rrz4XAutXdxfX11rgrBENPylluCshzzwR6nk+65LJGZd1j+/K8STNWnR6TgqO4cE/KDVef5IfLG5Tnm+Viuc3V1HZeX+Rkn9dpVx9FfJ5aspXXTAbyymD4fP84s/VLGdjrVzY+sizf5G/ymVE8pMxO9lIdn9TEMFWQAgPPpbPmBhNjw8Uil7Szr4zl5X9cYhz6W5UyidH30wy6maY1pWqLrIqbpfHhJF8HxrKfjMbq+j5S6GMch1vUU01RbjPBZ2VYjIvIxp8NAG9ohy2pdY12Ws6zOlYd1ib6rLVYGSSYQXAl0R0FK+XkNyzIXgDuMQ1xeXcbry2sMw/nAgbM9r8sa0zzFbhxjmuZIXYpdv8tjXpYYhzF2uzHezweSDEMfXXeeQ/o6xhhQ4XvRI2It9o7/wKZvb2/j+fm5+Cls3lU5dLT1N4BxfPfl5WWpxuPLuAb+iDjGNfDL+/2+VPPxUdiEEzDAKsQdMYT3uJerjiYo0BEDTGRJXMUP2mYMtLuuKyfx0XL49PRUHoS8SZbX2l5kv+nkDXsygLducR38AiQA8iXOWG9ZTxIJfreMiD/4GZNOTkSNK9sYZj/uiiykMLgkIjbjQgZOqEgi9vt9rOMSp+Ox+H4Sykh13zT38p5At0KBYUq8SFvCFoIbm7BMnDwhA67ze6/vTjQIUuvKpumPAmRh8c3YYXyUSAmkTM497BHbFo+cIe7PRnCMYehimurDi2j1MbjEEElUDBT5HBvNzXy7isEpJyjo4XAoCx0Rxfgx9JY1ddndoNOMDgrEd71J2OUzZEFShFwA6jY4AyeyYZImM/cuZVrJXJZ2+1tK+SF3bgnCMTIGDA3gxAkaEdn5832YalpjcPAwp60Bz/Nc+lnZaMd9GTvGbYYEdsEGQ39sRN0wjsFRtXGCbHaOObplyYwF62IdwIm4aoWsLYu3t7cNm4TBA1js7M16shYei08ysYPDccGuWT+RDXqKXDx25AwwY+24Fg+ZQkbMjTmj79i4nbVP/bAMuY8ZJOwC/fTYzLbwu5N9M0r8Hbk4YPj8+Pv7+w07RNKA73FpmesABGi/wqGzhsxnXde4v7+Py8vL+Lu/+7vip/BjTp4jIqZljkXjP5zH1KU11kix29cn2z8+PWUdXCO6LsUyz/H2Vp/HUEkHWl+y7dFmBYCOyC2sWRe682feNrqC74iI2O8r4ZFjRdaPj48pOJmJOeIzqPbVNcugPf9/F8PQx+XlRQWqYn1bHXWFbFnW6Lp+Y4/zvMbFBXtpho2M8c2sF7aKHVbQmp+jMc95XSApIureQ1eccgyErcwkGfo7nSKWJUVKQ8zTKboUMQxn5rBLMaQz4OupgEXs97s4HI7Rd7RpDrEuOZnq+i7mtbYKumUr62KtCo7jZUTkpKvvc7KEzeX16WNYu8hH8/YbmeBb7ItMHMzzHONujI/D+4YBj7QGic7V9WUhJLr+fL2hK8nJMPZntvtcgT/rwPF0jGHILV37i33xOfOcTy6DZETHTEqZuOFZB7DceZ1q0oFte78PvpF47Cq2n1njdhYD5pTyw3sBxPM8l/2LrmITe6dpKq03Tq5Zh0wUvG+6CZgvOkYM8RyMWVqATbxkHAaYdEa4M4EEhArB+/t7sWliNbZqIO7E1VUNVykcP2hVNVHpDgx08vn5uWAM483aIlhbkfnH3FyF5trgEu7DuD0X4xX8OOtNhwS2wf1YE/sn9oGAo9Ar5LWua0zzHB9nPzOvSxzPR2d3ip3IBuwHOQ5Zgu4wPlevHVNdQTexZpxlXfq911906pQXh7IuC2JwxGci6iburusK2HE2S3A/Ho+FCcyJTGb7vJEJQQEcqTSQROB4UFbAiRXzdDoVcMQCMgYUnPe9p8BA5PPnzzEM+VkfLvmjjBiomVkDVUqv8zxvghUGfjweS8sBMsSoOUXGSsMYYd28QdUtIN5w5k35p9OpnMd9PB6Loj89PRX5DcMQnz59Kk86j4jCwOPoSAZotWFdcCgcj4si4/hIrA6HQ3mKtBMe9AtwQCmb8Tsj59o46HVdy1Oy7cTREZwC+sI8mBeOw0DH7Hy7DoAib4qGlUGHzcLP8xw3NzdF95ATtsW1+BvOgHG5ZcjJMkm+k0EnADhcM1LIr2UvmCNjQtfQT1pw/FA1V18qANw+CdXVtf1+v6mW8h0SWq7VViW8oZBA2bJz3IMyMbaMDjBXXk5YYC0BVMtSj+z1vi6TKU4weIYGn0F+T09Pm+TWJ54BUGolZPt0d17Zl9YxmaUfxzHSukZ/1nHGbL/3LYZrw0hH3TfUrpffx2dhgwZtfBZdYQ1c6eHa2Dhz7br6IE4THQ7uZmZZp3nOvnu/Oz/3YTwzt/OcKwQpRYrz+FNEihTzssQyz3FcT7kGsa4xjEOu9Jzm4hteX95iPNvj6XiMY6rP91iXiC71scxL8HC8XNWI4meQ8W7MD4/L65GfD3U6HaPvu1jXzFLG+aFr8zxHP/RxOB5imqcY0hAprdEP3ZnhjPLguQzmt4c7mAHHl+S1q7rUPvwt+7m+xCgn6PjQrusKqPNeNfSiJnkZTL6+vpa2JZNfbJh2QmmAil64Eos9sv7s3+E7tl1IAnwrrduOoz6UwUkn1XZAIzIy2Eb/sC3m5VPXIEGPx2OpjnozM2tFDHE7DAQgPgXdZwyuauO7kVtb6Tcxw1hNuDiekVwZh7iVmWsiy/YgAydn1n3Wn4QQ3Igc+Czjb0k21ta+Ah/qTeTouokfJ8XEUP5dX1+Xqo99dYtr7YONi01UgFuNc7zG2BExAGzG/OkO4pquqKFTrqgxF5JeTv6jy+Hm5maDVy13PxsL3W31BFm4C8H6+3uv7040DF4AgRgMiuCeYpyAs0WMmEUgOMLEA0QBnXyeXkQrIPeAIXYrloMbBk9Qgul3BcaMwbrWlhdnbw6MrTLjTJkXY7BjcO8f48ORtGwFSuQ9IjhqTsgxyAQ4PT4+bkAYlQjKpe4f5/qcLoSjpD2Fe7CelG8jorAXZoUwnG8lnAS5tueT91lzg0bkj1z85G+zBOhIRAVRTv4iYrPXxAmpP0MgcCsd+kZAYs0MWgG7yJs19zyslwBbnA5jcGJF8HZJ20wI12b+Bt9+Gi/BAGCAHjEHV3JcCSTYYMMGLg5OEbGxOycl9Iab+eOfqz4kGYAgdIDxo1fIYVv1rImR7Z3fkT/JPPL++PgoB1KYxcROmafZbIMwVx/NeLUVCQIQ8yQg27n7mG0nsHwvA9g5+ug3+sbnU0qRop7uw1xSSuc2lGmja8jOJIvnhg/k86wriRyghzUuLPY4bmRlFgz7AmShW+g48iRhQe8j6uETXMekzvF4jNfX16I3AMLTaY550h6EZdtm8XGsJ/Kgk2YpMwPfxTwtAlrsxUj5PPt5LtWXLONcySnscT/k9qC5JofIOFeccr913luRE41xzA95211sk+ucbExnefaxrkukLkVE/tmldG6dWouM/bA4kzmMwf6Y9hXWFLma5DCYsn2aBS/kWqqMOToPOWQ9J3bgA4jF+CF0Hd/YtlzjR7iebeb19TWur69L7I+oeyvQOf65pZP7UpUgnjw/P5fN3MQI1tq+gP1t4ziWijzriPwhVEwYcQ3sE5+InjLGi4uLcuy7Ew7WlxaxiBz3qOQTe8Ap2BMnTOI/vP/JvtfJBD6dagZ2HBGlQ4P3kSPrzlzxzSa5jKdcDbAOc2Tzuq7F9pG7yUASTBIhs/FgTvR6mqZyYA9VMcaBXzGJROUaH8kcfDAHcYS/t6QMSQIdKLSdI1MfjkTsJjmF1ImobdV9StGlrpwOCT7s+z7u7u5KnLL+c/CO26ftp3h57CT9+MyWpPuvvb470cCpANQAIAyKs+4RBovCpiCcG4pPlYEy5uFw2GxKRoEwdBQf5o9g6AdcGdACJCl/UQall3Mcx/IgLzMoGAMOgeDswOu2FcA8SYYzbJfSMWwDNAKowYsTIZwT/0hwqGoAhgguVIwIGii0kxucG0cpMm8Yzzaz5X2cJk6G8+/JonFWvMz0IhsybKokdsAR9QGALXMOsPJeBYOjy8vLkiR9KytnzugPTqcCmtiUqdFd1qoFiKyjda7rulIG5wQ05MNYAMesjRlC65kfLmeQ3tqjf7J2OHKcBk4Xm3B5Hpmjg8zfzIlZO5dKnWwA4txG5yBsNopx+v2WUTN77WP6uDafQT94mTwgOAD+0R2eKO9jcfkOpISrIwYE2D3y9Zw8Dt7n+ugY+kbgZF24B2tJECDIjN0u1qhtZZ53Ovfre77IYR6G3Osa2yPAW0bOjCN+El3x/EyM4JO4b5sw2ZdERAGJDvJeS7ecODluCSzWE/t0G+LpdMo+/eIm3j8O5Zq5TYjjM/HDy8Yf7nbDWSdT8MC6/N0UKfXheLquEfn0wyX6foiug1TL+wiXJf+bpimmeY503rMCiTPPc04e+yH6HgCQk5mbm6uIrovj6RgXF3kviNer66hK5j0K67qck5xjRNT2G+IcNo7ueROsWzewc59Chn3iLx2LTaK5ilESkqjr6kqE7dNED/6FNg50gHWm6u6WSrd9YkdsgKaKjI7i3/H7AE7v7aB64+c2MQ50CUIJWeIzjkpejXdIDvAl9n2AYfsIyJOUUjw9PZU4z/ff3t7K91nn4/FYjs6NqBvfnchAKuB/iD/Mse2SYI+lj9snVtmPEM8d45gPcYW1Yc74MOTF/BjjbrcrR567Mr4sSyGN7BPw2WBDwDA6Z5kyPnwH6+cY3xKe6Fe2v67Ek4htlwFx3/cgzroy75YsZLwsSznCmMoeSRv+3q1sEPbMO9aIZa1koKtRJnT53YmQiW6IMpO8zNPrFLF9KPDvvb470WBhUDaUE0XwHgUrO4ASxXeJqOtyLzQg2ke7+fhXFJZy0tPT06a9BTDskpwTDu7LPTk9hWuTUSI8gIABE+MCKBqIYixmCg0ADYBQLrMilKZ9TebV933ZxOZsEkMdx7G0FrliEVGfpo1iRkS5Bs4xIjbGj3I6uPA9g8P21Wb46AzfRfEdxEhQnTTgRJgj90dXDD4NODBgVysIZhyPyjr6IYgu9fpaZsnMBpmld6tKRAWC7OVBlmZLYbJZR0rfTkjMHCJTMw42eO/B4f7IDn0kAfKDydBTb7rnHt9K8Lmf14o1YM5OGqxHBvFci6TY4Lp1ahAQBlrcm4DNuBzgec8MDD7J1zSz6SDqdgOzwVzDQZSxe3zMF1tAVn4f/8TYkQktoRumtO8jdZXhRm7rupaWGWyccfV9H+tS21ZIBA0gsSvr2LcSWqrPEfWYc9aTOWCT+GB8rIMyOsWacG/sCGAIkXU41AesEuzN9LV+lu+epinWNeJ4PMWy1Krf5eXVRm9LsnbW18vLq8ibl31kOXbVxW5HFSR3No3jLpZly4BH5JYnEo4UtT8d8uHi4iLGYXeWDZuQ86buZVlif3kR3SHFPC9xeXkR67qcWyF2kY/ajWCPxfX11Xk8KZal+jjsG/3CnlgfnnmCfRrM7Xa7uL6+Lj3v+GSTDgC5dp+AfZR9JP4ZH+qEc57n8gyFb1VCT6dTXF9fb47MRYewkRY8Yf8GlxFRbAtCi3iJD3ByjU/F53F92pAhRn1/6zOyxJ9YHswXXTcTjR0hJ+IZuMhJHnqMbMAAPkjFgLetbpkANVHn9lfGQwx3osL6YUu07n4LE4IpTDi1sYO4jT9gUzsEkcfsThfG6+PJTX6iM23VxqSGZcE8nYQyBx8a446WT58+beI5/pX5UPnZ7/fx/Pxc1p29FST61mGP6/n5OS4uLsrJnMNQH3Acc41RjAlC19gTO7ZO+H7ouom8tppvnGrb+odef9EeDTODBCUU1gDj119/LUCdtib3TxO0cDYAHgKYFfXXX38tGydR+M+fP2+ACddFec1UOYPDwby/v8fb21t5QjJsuEuIVnzvA7FBcj+cIYoLyGK/BEESZ0bGSjJBpchAndYOB3rO9HZPo8EDjpoyXN/38fDwECmlr06EiMhgjIfioUSUnW9uboqzWpalsCUGkSigy5aMCSVG2WENABh8HgbKDqlNVpwAOTlA58y4zPO8aQVD9ugD/6yvERWkAPgZj3vPHTSYFy9K5AR4gjT/7DgcCHFYbZJu4G92wY4RZt1B5erqqiQUbAIz88A6YLvea8VPPu+EBt1gDHa2DsLoMGMjCPjlNaiAbnuSjf+GvuAz0BHkicwN8nnhLPf7fdzc3GyOhMSvoWtmPJm/50Q1jL9h++glgd/PkyAgO7iypoAcEyP2Mdxn3O8iiQ3m+SHH4zGOhxqkGFtJnM62gNx4cBifgyFD3rQpYU/IiLbFNrjw02tBMmdSwdXAeZ43B2DYFzmuEJRJYszIoY/2Qaxd1/URK+2WgI5cPci+gAdj5qpAJUjyRu/TqR7GkNe7j2nKiUZKgPcl+p5jrGF38wb6qk9zpLREdz6m3RWyZVni7b0ee31xcRFdnyIf687zKyJSWmOe2WQ8xDxPcTxW3aonfdGCN2yACX4BP0c8iqgPE8O/8TkSXMbr1/X1ddzd3W2qAqwVm5yLTKIm0H3fF+Y7pVp1cBLEPxJtYiz3eHt7KycU2i9xf+aLr2cdzJrbX9oGWBPifESUQ2NsT+i7Yzn2b/KB8eFPvbeICgFr9vHxURJyugY62Tq2d3l5WToZXHUi2eI7AG10xBV46wTywK6RieVF7G+TC1h05Gmi0rEce7Z/Rxd9bz7Ly4kZ+/544esZG/jIhBlVOxNZ+A2TIsjOlShXtbieSSuqONgYfqKQQufECUKd9bMsjFuQl+XsKjeV7Xme4+7uriT12FppR4+p4CyTwyZTWkIIG+en4xGft+wtQ+vU97y++zka/9v/8u9LpsYCAChQJBzD+/t7fPr0qWxockDCSPx5s45mll06QiFQMgvCgQ9Di4jCjLegFcGizPxkXn6YkJkeMlBnh29vb2XRcEwGLCRIKNo8z6V/FllSmaDS4Ew2pcwOPj09bZTAvavIlWz76ekpTqdTfP78uWwKMnh35oxyM677+/vy/jAMZeNcyz44EDw+PhajwInZ4ZoZwDm0TAFJCEDQpV1Xpni5EsH4Wwag7/tiqGwItxPnnhFR1grdBMgxdsCnA4wdhtuNAN68x8sOFKbDp5iZLXCyja7wfa7JgQn7/b70YZKQIlM7cjt61sFtU6wL/+/g6kDqqgttcfwdvaf027LOrAtriMy4JvPEGXqM2JwZO8ZhwImtoev4HtbcVQS+zxyt57Z/VwEcPK0HAGP3tvse6IPZ5jbJQm94HQ6H6M9zmeYpbm9uSwUW/rzvhzMYzqcb5T7+NWJlM23eP7Db5edIVEb5VEgPJ5tsMGeMbSLF/Pu+LwQGusCa8vRk1tq6i461P62r1Qexn6fGkMvLi0KYDMMYHNeb2dw5xvEi1jVinuqJZblaUPf8dF0+MjjWNdY4n9I01efELOsaXaon2xGET6fT+bjVWuVDP80Gn1c+hrEmpdZPrzvtWsi/67s4naZY1iWGvo+IFPf39/H6+hovLy9lLXIcyG1ergCSpDlx6Prtk9Ihr7Ld5r/tz0npsuSN8ZEyiURLx/vbe3R9V0HyObYwNwiz0zRF16USp5i/gSm6hK7jh51kO+HAn5kw9Mk61iWvC50V9Xkida+GfQWfBaB7rdwlYHIVnwAmwAe5WuCWXnyKq+VO8Jij4yaxiNiPLNs46jEYYOJvTVA57tPV4Yo/Ng7R6c4UrseYnzjl7qwTrDF65LjodTY5ypqC8+xnzLpDRrsKjk/gM9iQCSZXh1kTZGy7bEmyFqhj/3wf3SDeOo70fV9O4EK+xpXEZlfhHAMjYoM/5nmOZZ5jv6udEtM8xdCf9VVyMKHqiosTYfTKJB2+j7mYaLON8Y/1+D//D/8qfu/1F20GN4BhUoA3BoYRkTGaXXQZ0iytBQBopuTz8fERt7e3m95EBMEim8noum5zzCpgDadFew1lf7dfWAlcNsRgSGJQOEpXgGIDTQwXh+5WqMpIVeDkhIzfAQRmZKyQ31ICDJ4gb3aRzWGw81Z0xoIhoqjuybXjNXhyghFRgaRLeIAxxt46y3Ecy1NNDbT8HBAcDwDbwQUnApgkYJGsWrZmoZAZQMlACh0y69EmSE5c/Dc7Q4Ih82WjoHU5ogJvO2MCIN+1A5im/HTs6+vrr5IxAyDLzlUCjwmZIxfrs4FBxLZ9yECCJNlgGueFHjFnfrb+ZF3XspGQBAw/gX/hffQGXUKOsE7MhXH778jFlVSDYVc8kJWZMtaWcdufkWChoyTLvNcCEsuK9bXDN5g6Hg4xT1PEupbgsi7zGZCeAf0cGx2sDONyTubr8Y/YDP6xjrm2FeDzDLBYQ06mc1vO29tbaQ/ls8gTu8T3cB1XQLy+x+NpUz2b5zleX99inmtLB/aSnwvSRd9nHf045AMr1lhins8+dMmyXJdzxayQH4dY1oW93uc1mWONczLQp1jWUwxjil0HKQQ7nGKe1+i6NeZliv0FbaJ1Txbyg+DJ4L6SF8tSfUSazievdTVJeXt9iRQR11eXG1tx3JumrAckANM0xZGNx5vkZCxtetM0xfGUycGX15dNtQF7Hscz0J+OsZ7YDJ7iNJ1iWXUK1DjENE8xTafCzlOZJ1bjC9gfafIM/4a/MqCDQIFgw+8QA6n2r+sav/76a7EFJ2Am6WCESY5dKTHhYjtGTx1jOEmL74CRXB103z73Js44mccGiBG02RL/bIf7/b60HUPuXl5ext3dXYzjWE5P4vP2NcRV/LxjRUSU/ZfYG1isjbXjOJbTjJATNm6Aji3P81xOKES/wIr4XvTdyTlEtJMu75EA6wDm8TGOe9gL/2+C1UCfqq87FBwzWAPGRxxAf6wvrkxYVyGPjReREWNnjIXcmOfcHtX1uTlzWSKtmX4Zm3vzMkZ3Aor8+buJEuMzE6wkX8YFLZH6D72+O9HwAvEsBL8QIkbYKg2fRxFqT2s9w9o9yyQDBECDG75P8oESck3vzOd+lCx5UVKM2D5h1Qq23+9jt9vFy8tLYWgJjmT4OA7YVzOTJBnOuJ3QuLzLhq7Ly8ui7DhOHmrlErOTGCpHBFzub8O3spMUWKYtgwDARzYkgCgqDpWN2JYtxuE+VCu45e7kCMDrQwF8Kg4Os+/ryVasPTrK/0fUB95guAQul20xJAzMSaPBETJzxQ2dN2Pn4Oie24hthc1MAzbAT3QYmbuqwTqX4K4WAJfdncAZyGJT6DWgEOAH8DaY8Tp57tyHz1u/zVBZZoBSNmii12ZpsSPkYBCKY+OegH8SfwdsO2/7KHSfYGeGnjUw28P7nCjDWnIft5QZOPA9grJZJSceAH3Ghy7zPduuA4n11yxYG7xMlnBt1g59OhwOZ5+4PeTAn3fgNePXdd3GvwJkAQ/MEb3hcyQcTiZN8LR6h67Yd358fJSqMnbA55GdWxCpNHm9hqHGp1q1S3E81sTe32PtLi7yJsx5WWPouxjGMfqVzfiHktClVCvtzMtVVfsrxoD9m2CCxLNdMg/HHmyI9o2+7yPJHpdliV9//bWsx/FUN01b929ubkqc5FAX1p71dqLKWvJMFuIXG5XnuR5x7gNPDDQBjX3fl6qYN3g7VqOX19fXJWHwvjJ+95HfTpgB8u5waG2TWOeDSEwYQnw5pu73+7I/8ubmpmAKs/skgoyDmBZRT2jDDtD1lvl2JeL6+jp2u108PDxs4jkAnMoz7VroGWvrh2Kiq7SxucJsXW2rlMQb9NhdD8Q87oHemxAx+WQCBp3kM3SPsHYkdcRXP4cCHMVJVQB82xX3YDysD7GSv+O/jfXsp7BLfB0YyWS2X54fuoAcffBOIYSX7X5J9BC/7us4cTRBb78ONrBs/XJyaTIO3WFdv+f13YnGtzadYshmSVE8lMGbaDFygxUMBcEheJIIHCuBy3s9bHAo9cvLS3EgPJVznufNTn8qHLAkjOd4PMbnz5+LYpOgOAP1Zq67u7sNQDfAcCAASH8LnFn5UExntARVsluMy+w39+TYWeZnA0CRSAy4H47TAd2yIlDhvN1C4/HxO86f79shYSROgFhfAyRk07ZLEUi7rtsczcb1ARPoGKwY1/QD2bx/w5v6WEOSVYM7Z/p2EgDNFqA7keS9NulypYLP2K6QixNDV46maYqnp6cif3TRjBmfNRDmMIT7+/uSFDEvM/UGv9igk1gHQQNJdAm7cdJm0GvnDcAALOLMXWUzQIyI0kKDbZCceAyABeSML7Jjt+16A6bnz/x8gkhEbPZXOcEDQOCkfSyiCQ0nvn6PuVP+B9SYZXPFhbkzfnybr0/lAV/MHPCZzM/399xbe2wrSSYMSoBU3GCtPF5igNeRMeDf0IdWp02eAEb5HNdAz7iW50SiaeDnAM/nHYTRmXme82kvy/lI6KU+TyFWTslbvtKfrH/beaAzTtTbJJ+2FtpdAFW1Aj5tKkvEwNR1cTrHTgND1vBbxBNrd3FxUfrk8RPEdPvvFtS4pQQ9MTC132ZPmTdoIy8TCU4Kuq4rz36CiKMf3hVMCEv+HxDqliZewzAUQIqMvSZtwk/8IV4wN+s/MdIkCC9iFTb78vJSbIJ1WJa6P5LDEgCiJnaQMXs0rU/rusbd3V2Z6/X1dSEokSVdDu1mc+MIJ0rooUli/ga4Z8M8Pg3SDF9PUglJ5pPSkBO+zOQzz9p6fX3dEFzrmvdGvry8lGdi2MaobKF7rvIzN9vqxcVFScJs/2by0Sv03OQUvoc1If5gzyZo8X/4MWKFMQa+xL7BBFNbecPfkBQzRuz47u6uxL2W1HE8Qh7EBFdz/psnGgzEbUM4gYiaTTmTRNHcb48xkABgjGRIBEcEYMfkANz3+TQmjoB7fHwsp1pQiSCIUMZflqU4I/o0WQSzc96/4JOwUBRAA4bgygbBAEcNWG0ZQYKuFc0VBZIjt4YYEKF8XI9rMr62hMZ8np+fNyy7qwA4NLOsNgYHbk5LMJvK+HgPpXXFwICOebgc7VaIiMocm6kiACFn1h0DbcvSrTHjGLkuQYAA7NY/xmsmibWyw0HPDUxwJgQSvkOwxiGQ7BBE5nkuJ6s5KQVw2ok5oWtbnrgn+mRWkM8bwPM5v5C1EzPWuT2YAMeETAHrOHkzXD5Lnvs6SUF/8CnMkUSdzd0ABj7DmprZdhsG64vtkWR++vSptM69vr5ujif+8ccfy/vsleKe6Bljt01ZZwwSvFbIx76N9TDLhXwAILycPFnfub4rM4yF9kl8GjZR/VRNMgh0nkvbbubqLeNhfdEL+xvWHf2GBeaz9h+8jy83oLXOQXjY9vgsILDdD+UAi727L9pA2XpHop7nl2IYdudE7fwk9ykfORvr15vc8UPYPTLwqYgt2wqwA+Taj2KTrJfXnP1u729v8f7xEUlJFte4uLiIZfX+nGyrVCWIh/z/29tbAa34UJ/7j26bwOHQFSco1ldAEmtHks7ffEKiDyVBJ/FPEVH8AWDdrR/ES5NB+/1+0xkBKDT55ARst9uVVtWU8l4k/AtydXXSBKkxDFU4Jylur8PXT9O0+Szx0j6Dz2MTrb2jB+icWex5njfH4oKX2g3zrIv9O3bQ4gQ+764HiFzrGfrtCgVjBNiSXBD3vYcTwoe4QOxoO09McnvTO77N92UdWRfGar/Oe8RG7u8kw3tmip2dvw8BReKLTBiz8Z1J/aGveNj4jgSZeO94bJk7CaZi6HvanzqJ5f8dr01+fM/rL2qdAsDDuKJQZpTJTiNi46Bs9Byt58nxO44NBcegYAZOp1PZVIOQSTouLi5KfzTKhcMA4HDaBmyINxhRooUtd2KAUwL4uCRqEMFPMngbMoHKWfIwDKX0ZxbXDG0bqPnJPFF8kh3kd3l5GY+PjxsW5FugCGNxTyvrCGjw/Jwtt61HBobcy6wtL2f3rLufTuuHCrVZN/9vxtXAxE9Ad0DGsbgiwL3dxkFgb43Q4Jf3WY+IHAS9yQ/94J4YvRMpxub9LJeXl/Hbb7/Fuq6bwIoOo/ffGgPyA0z7NA4zIMyF+fJ5dLOtUnCPvu/LAQPLshRZw7TjpLA7y5R1tyPz+pg1clLDPBk/3wGMGFSyPgRGZG+7dCWOe3CWuefL/f7u7/6uzJ/gasYtYvuMjOPxWJ5ADGvpa2P3fNZ2wvxcmSOYw+Dhs0zSONi5pcsVZLO1rlCjd9U3bCsY2EibeNvO3T5ikOyKn9fEBAAydK87n3GV1G0vToCsJ/gqJ9Mkn7Y5Psu8WU8nTOwtcDLJtescU8wTJwQdIm+C7r7S7bZKNY6XkU+SqtUXxubKipNsdB1QbJ2v1an6LCs/1G2NiM/nA1p48GsGdBGHYx7T7e1t0Qfk1nVd0btxHOOnn34qewCsByZhUsqb19/f3+Pp6WmT3PA57ImEzYw/YJ3reXO4n5hMcnNzc1PW7+bmZoMPGF/bcsh6ukWFefMPe2F8+D5iO/ba7rPEt3Bfn/yE71iWJR4fH8vpjowVeflIe8d65uMOCWyD6gNrDoB3nz/xgFhJwu8YYb11lwk6yVwiojxmgISQWGLymGtCTHESHljMlQ38CfcAC1mHGCs6TuKDLfn++BWTjKw1/oG9LKyd2XvinPUyoiZT+AauS8sVL/Ch45hjuUlO+2LihX3ifrffxBL7B3SYdTHu8PVMbrmKY2KpxWX2Se4EII5+z+u7Ew1ALD1xGJgBg6sGBIe+7wsAw+HP81z6nTlyEqVDSDASFxcXpaQYEQVIAzRQ1B9++CGOx/yMjePxGJ8+fSrXsrK2IN8B2osHS+NzmR3Qvnz5UlhOnCYLBYAhAeKanHyBouH8cBooufeq8NNlfxKWZVnKxncMFYfH2ADw0zQVg2ZtUDivMcHFDhPZYRgeA+uKoRgEodS8zHg7kTLD66oRa2PW/VvOHAN2pcKB2WDCcsZRMUfGh267TYXxOzkxqEIu3IfxcS0AeUQFQ65WeQzrupZqFuuCfnljIfNEbmaeDdgYt9tKsA2ua3tFbqwlJWgnbBFR7DgiBw0S1r7v489//nM8Pz/Hzz//XMCC18eOkGsR1K2b6Bp/t90Alt0C4fUhmBp0wI4iE+yICh1sGJ8lCHEPB4KI2DBSsFawaGx4dVXKCTLBF1aSOWM/Zi0hWJyQOcABhPBXZrZp/+RlcgB52y4Aq14fkomWOOD/iQG0bOFruUcF2ONG753QRUSZJ3pPMoBtAJSwK1fY8HHcD1CA7ZKYec8TgI6YZZaR8TkZ5D4V9HXRpXriWNcNkVIX+TkXa6wxB0/1ti17HbCjruvKGfvohe3NoBc7hvjJY8nP90CfkHPf93F1Tg5cPcY/E2/M+lpPDYax5ZeXl82JPvgOP5G867ryNG3bK/+wZSfL6DH+se/7+Omnn8p3XVVytc7ti8NQnwxuYgIW3GDVG6ZTSqUNq/UlJMs8wwB/hi5QoXYMm+e5VECXZYnn5+fiM9BT7IUOEGKqfTMvdIKTFIlPPt2P5InkAZ2PiM3GbRI2/JCJRvSReANYZt14ejYgs+3lN26BnCVhxf7BVq0fQG9ahp9kwpjBhLf1h7V18oi+s9asV0QU+XFvJ6LcE/9El4vJOT5LDCX2OsY6nuID/Df8G9djrZ1wz8u2SuukiLGxtlTR7FuN7YilrLvX0LLwujBHxul5/t7ruxMNNguaRcZw3eKBYrBIEZU9ZVIMjioEwkSx7byYOArEY+cJgjc3N3F9fV0y6r7v44cffiiBhH4+FtWgeV3XcjY39+d399RZaUhSAEEoNIJHAbmWsz4cJycOWdlZWDaCI5N1XTcbom18XINAwee4J4HLIJTABINGguKsmrkgq7YSQomZ6xocub+WYGDwbf1wQOLvzJk+0tbhci3mwr34f85rN8vm+Zupc7kbAyIheHh4KHNFPwiILZjFEZiBRcfMAhnA42zM7DJWxkUQdCLnYO0EBMDAmtLXjO0RfFhHxokeE2RwxIwdWQEIzKAgB1dJsIHr6+tyP9sRukJAh7ywk0XG6DLzQTYE/T//+c9xPB7j9vZ205bgMeKbCDaAZSd1gCNIAZMTXpv2CEl01mDVDGxEJiQcyOz03fLSOnJ+tow2v/vFWtqevGbWzeyDhrNtnsQeA2qjrAM25mOfCaYt+4Uecn8TKsin63juwxoRAJPuvHn2Kh4eHuPiYl/Wi0TQ7Bvryr2cULH/jPWleoxOYFfoYEQFSejH6+tLSXaOx0PMc933kwEM7X20CkcM/RzzvMQ4DrEsdVP5ss6RUm0l3e3GUu3C9/MkdrOu6JurZGag8alOBLNe5ns9Pz9H1+WH+72+5uNwH56eMtAhdqU+Xt9eYxyGGObtKXv4WogrfDqJrG3jW+SPE15vALaNsx6+JzHPusM4fB9AfksCcR10jqN+b25uNkm7bQgfDtgiLpr4hLX/9OlTvLy8xJcvX8p8v0XWdF0Xz8/PG1/L2oENIqKcsuj9n+xrxfaI6TwyALvDLtmTend3V/ZnErO83xQ/g707/jnxd4JrQhA9tN65qkvSAvh2soHtYkMkSCZMnODgy3mx7ia0iWfuaHHSDRFBzCAmEcPQX8bGGBhzxPap3654gGWRka+HLrTA3USq21QZ/7qu5ZkcJHfEZZLoWKqvZa6uEHtMJORtIu+YbuIEXR3HfDKp18X39Pz+ktdftEfD/akI4c9//nN5oB7OKiI2T2NGqQELwzDEp0+f4vr6uvTc8WA5nwbVdV28vLxESikeHx+LkWEUHx8fcX9/X0q5ZHM4DxxUu3cBgICS0SNKqwPGY/DGHLyBygpEkL+6uirsnwEEc8MQUaC2ZIlyIytnkN4sd3t7u+n7Q5mmadpUTlg7xkLCBvvHXEg4+OxutytHFAKaUWq+YyDEnPi+QTdOhrXDMfgkEwcAjIEyqxlUHJidfMvGRdQEyiwY30WPvffAjoAkEwbZ8/WeG1cMXC1hLa1fMNY4PwN97ovOIgPWFmcUUXvcHTRhfjkp7PHxsciD71sXYZYJQC2TRcXSAIhx25ldXFzE29vbptXRySYOCT1ZliV+++23WJalVDHpL/706VM8Pz+XMVmfAPAOviml+Ku/+qtiP6fTqfQy28FDjrgKRQJMwPeJK2aAkAEEg8mK4/G4Sdz88E/8D6DSlVAnjegrPtP3dysd+s51XHnyWnD9b9kpOlf7qVOxiRzwxjJ+j5cxIU9XQngPPbSeoMMREc/PT5vEBZ23Hk/TKeZ5imnCdk7RdX1hT9EFtxIeDoe4ubn5qpLIGvHMiXEcC4FkG2KNKgnGHrEhjsfDBuwcj4dNslPZ8/xAv3wsboplPZMOMUc+KDdvFo9Y4/19C3JYn4goSSxjAyw46fLmV3wqtk5lOSLi9va2+BTWa7fP/jfWJbpuiGVd4v39LcbzA/j8eRMqrJEJCVeRWB9s0vsl7Bv5Pr4R/eEzTo5hfvHld3d38fb2Vio9BmzEcyqRyIaEP6X8FHT0wEQAzDrfY75mwvHRx+MxHh4eit8GlC/LUk7uI2ZRSSHRJW6zt4VqAmvpNmF8s8mS06k+Ewtbxo9ztDw+mHU4HA6bFnCTO9zv8fExfvzxxzI+t++57ZTrX11dFVLX+2CwIYhBE9HojA+mAE8wX/Qc22gTGlfnuL7HYGKMMZEkkxgzJu5vDMv9Li8vS1swibLt1KTy3d1d0U9eXMc4i+/zWeSA/qBzVMXa+IUdvr+/RxcpepH1xrMkEm1LFzGL65kEwvdGxKYThbnUKm318074+N73vL470WBRuDAA4eeffy6/u/f39va2JBsoEEKOyP3s9EUD7Nz24kX1YuFUUUyMG0djQBZR2S8UzAHfgoLRIPFhPk40GAMGj5G3LDaOz4ApoiYvfA5whNIdj8dSpkYWdnYoMIGa7N/VonbuVkobd8sARcTG0SAD1s+JA/ezkXvjJIkSzpyxRGyf9O3rAiIuLy/LAwcBo1wXJccR811eVAowomEYNk8tZ2xOvAyq+Mx+vy8nrVimZvydEETUBw7iEHkZmGD4ZiBwhiR5BGXakPgeAdDOgOtic7RGENQAo+gBOkrgoD+a8eL4SLi5F4yuZdd1XXz58qUkjRAJVPwYK/bEOAxgnLz64UZ8HlDDmuODaHOKiM1eKUA0duLEFRngP6jS+e84aeROj7ZL9g6S6AyBzf3QXZfbRmAtmQ9AgvY51hmdcCXK7DIv/IfB+rrmqowTB8+F69Wxp0ipMsvoCeDWjB1+yydoOTjxMihH17j3usZGj83GtT7SyTZAiSQduWELtMe2rCQ2zedguIlfx+OxVD9I0PL6ZzDAXLmOE2dXCLP86oEJACpIire319jvL4r94OeoumKP9mfosOWKr0JHqCi8vLwUgOAENqW02VcxL/MmAWRd3D0ACcbazfNcNj3jQ1t7nKa6URqbY8wARCcY9gPWD8ZAaxF6h74+PT2VJ4+7ks21ANbI0+2DfMY2iy0Sw3wtNoOj37RGQ8KY+MBWkENElFP8iENd18X9/X1cXV0V24awYQ1IgFhHsBK2B7np6p5P22NtTchYR8FlTuLmeY4//vGPxWcTx4ndEJboLPb98fERLy8vG1zCmpsEQo9cEcfWTdigH8Rg4hnrQowwCUtCQRwwGHaS1JItPKbAMd/39Z5KdG1d182eC/TLpCbzI444STRhY1IPG+a72E5LphqbDF0f4zlJQnfxZcjX3S1UvdpHORAXvmWXrbxNLJgc85p/z+u7Ew1n0e4Td5mUzB4n5IzMQJWgFhGF+SdrY1IIB3bGrKsTEz4L8Ce7xunQ4sMiLMtSQA3OI6L2r1GR8Lh9fn7XdaWVgGsgm4gobU8RUZgLnEhEPd0FkOCKiFlMHLDbqyLq0bwEP29o5DQZ5oMDBIDAEjl4uZqB4iILBzbkZxbATLEzZOTRMjcOTr63mWM2xkdsKxsOMmZpqEw4eYrYbhpjv4NLgsjeIKJNoLw5zWx4RBQ54oxYW2TP9bAR1o6eXZ+4w/2tH+u6blqPuCYAEl00KxgRRRYwNi3bExHlVBWuwXdhYHD8ti0z0Ou6xtPTUxwOh7i9vS1nt+MYffwr/1hPnCCyxmkyJ9s4fgLnDwjDOTN3A32z7mYGAXHIHBtwkm5A57VzYorM8IkOoH1fe9RdAcCODOSQJwww+sV1vQ7oAmC5TRCQAzKj+oK8DFz5fG5firLuEbHZQOz+d8+XawASPP82ySZpn+cpTqftMZxtq0GbEGXiIfeiA9LQYXSiTfaRmeOMW2zQSYCXk6913W48xk7u7+8L62wGkpbcTFBVkI8cANnMz5Uc9NDtft9i+yG/WvkzNifQXB8fu9/vN89fws4NGiOiVAEhBPhM+4wbYh5+ygSPbdytR47DTlDN9uIP8FnIcRiGMrarq6tygMzpdNps4EaHaOFm3vZlrIkrXhH1eRHY1eFwiMfHx0L0IPOnp6fyO4kV72OXjIN1Ze63t7dlDwbjIWZ5DWkjcyJj+yKZQncg4ai0YA/sCSPZMFkLBnPs46nvTjCdMJsIZd3QEUgd7MDX9bpg28tST4QiSSGOgNPAXaytkyRAL7ENkgB85mQcXcGe0O3dblfIKYPylFJ5jhmdFG7p5WVSz/rv2GZiykkQ1yLho+LlBJ64hp3Y13exPcQA32YSB5tlbaiW2P6Nxa0bxGHiAHMjOfP3XUX+ntdfVNEwSDDLyQQZIAuF0sGGRNSynQM3BgQbitCddbWgE/aYpAP24XQ6xe3tbSmVWzAovAGRNxIRKFkYM6QRteyGEaO8OHhAMkoKSDdLivwA/+zXoC3LjgFj98Ji2LxvI+q6rrDR0zSVU7gMZFA+b+QnAcGI7Ai4TssaAmDNapqt4ru8j/wwSuRtAzBgNthtN/QiUwfv9mQH7ueg7YBvQ8NBOZGIqJvv+EeAQ2ZmLBzMkR/AN6W0YY0wfjtFxsH4MWIcF7bD3HH6XnsHFieKPi0NPWj3RnBN9APboloIU898YBhZTyp4XddtNjZbVozBduKjF6mSRsTGFr2G1h9K/qyf/cW61s2iTlRcYXOVyUkbY0FOLmcjd0iAYchthmbLAAk+taZNgpz48TfGZWYa22QOLscb2AKSYfPQBzPz+JF8jS1w5fPck3EYnLBW+EGTD14X9BX/OY5jOdEIps0xxdVawFO+b66GkETe3NwU3QGAsMeBTbRs9rePJgbB0iM77BB9iajAhs8CfOidH4ahnAzkvT1Usc0Ivr29Frnj6zkgAD/N2nO4CPN8f38vYNRJmIkf+x3aM5H5brcrrZTzssTQD7HGullfP3jX5J+TwPaaJn3cPuMTrgzSfCoQwBF9437eo4Aer+taHl5LoufxoC9ufSJJIHZgp8iZ75gpJu4wDr779va2abn23h/8DT8do61vJhtIINgcTyXBFRgSBewN4pVEBQxk4tZkIDpv5p+WWleQiOnEFK7pygx6hc8kFpCUPj4+looHsnB1w3GNzg2qM26Ng0gAEz4+PpbYhC9hfbBLxs56mllH9oyHRNcVvdfX14I1iY/4I/wcduLkH31Bzz0/SFVXTFzxMfmED/WhMNgfe09YD1e014hNPDwcDvHy8rI5wCRie7obSSP25795XOAffDFxA30yNuP7lsvvvb470WAhWHDfxCD49fU17u/vNwbLEyavrq7i06dPm2yPyXAtFINg5uCJU8fBADxub2/LfgJYAhyaT8VBuDhhNpb3fV9OcsAptqXBiKxkt7e3MU1TSQqcBHENb5pvQTSZOQqLYhl42GFZ5gAOPsfYSPpsdG5Vc5LAfVuQ6ZOvkAF/81rzdxQTw2K9DPiZkxO8iHrKFnLBMbny478D+O24nazglLjvt3TKWb2dO4DYfcWuADjpBGxzbZw8xmznwr3QdWwGPXSiY9aSMbUJpJMqz431N8vPdwxWcRgtc8o9mBvf5XVzc1P+9vLyEvf395skBUeN8wYosB7ICVAGeEdnAKsEUj4LeMOO3MOKbTDOu7u7OBwO5WnFLuMDFi0HfrZJmcv9VAXQC5ywGXs+7+dSYFvcB7/APZALiScBxi0ctjUn5BG1SopMrMPYhdkx2oPcksU6oFOMDb13kmz7t1/2+uIvLF+IoNwmNMdvv72VajjzYZwtMKlV0woGlyWf2oN+0s7j9QaUA9YAsNyL4OkWQ+aZZVplw14/J1Trun6jvae2wbW+E6CHzE1asRcK32JyxicfuRXU4MHvsz5OZGFM8W3dWONIS/jgX+13P336VMCg9YJkCrvHF9g+3EZyd3e32W8CO80aYxsk5dZl5GJSjViNfjvGktz3fW7/hGBBriYnkDfA1dU625Rxg7svzLCjI+0/bA+5EKtcLdjv98V/kCQjw3meS5vdPM/x+fPn8rn39/dN9YIqh4mNFiyz5pycRSUEjPX4+Fj2moHNTDISy1tSz8k0doYc8TuuEDEvZOckFZ017mId8JvPz8+liuSTSl1lZe1tI8gUO3Kyju4Rg+x3HD9Nsnj+7gRpiSJXihi3yTgSOXSSMUDU8rl5XeJ0rD7P+wwZD34Kv4bNMS7HbmII8yEJtX/nb1wDP+tCwfe8vjvRMKvicrQz2nnOveHtcyN8ioIDHQ6KgHFzc1MWgWvj7CJyz+7j42OpmDCeiHpkqFlrhF7L47WcR0kWQZ9Op/IAMAdVxnZ5eVmes0GA4m+AjFYZmadbFwjiVEAc/K2kLLozUmSM4zJgQFaUmEnSnIliUJYbY+KaZNVmKHDWbj1ifVFmjMgg2UCoZT08Lq5pFgJ5oF8tC+UedDt7ql4bJkAVIScv6AzO3AC0BaXICaCHE+BazBFGNiI2xsxcMFh0Bmfm8fq7Tir5/9fX1xKw7MiQNYGT65LYulTK2BkX93R7gZMkgvey1Ide8hkHLxhFAjIVPD5b2d63kuRT/ueAAPZ74Cy5tsfN/QnebgUDbBkoM662IsD8WsYPPbUDJ8h6Xxf2j74iMyfPzMdgzMEUX4N9I7uI2iKDruPXDFz5m31DZenrU26xjyzXavskBrYzXwe23uSIgQNB3eDtcDiUU/cAnF47fI0JmWVZyr4fbL3vv34YGjGCKgPjdLWKten7vuyp4yQiAq0/n3vdx69kbZ+J7iCr/X4fDw+PZRwGKtmOps0+CACdk1cnn04aqIBMU35gG3EgIjan5zhmALyIuW6bW7tU/CT6hm4DUi8vL8uRzqfTqTxvwyQLx8a+v7+XJMIgDxsC8BvE8xObdfVvmqbSOtTqND6AxAQ9cKx1pQufju2z3q19ueJuP+LkBb0G0OIfeRaXY5pjt2XN+vE3bJ7ro1/cl0oxa8hc2FhOXz46jA1TvaC6xbiYEwAUvb+9vS1+kWP/p2l7StfV1VW5L0DaZA+kJrLmvo73+Hzmhg4jM2yB36lM8n3kRuupD+Hg3/39fRmf/a8TP+5jYgmdYn2YV0StnpnI8/q5q8BtWMiYdUUfsWeuw7WdZCxLPfnLp9OllGI61kqNiVWTbsiduaPvvCpBUhMF/KdJET7rbhhipDuS3NHyD73+oudosFAIBtY8IkqGCqsEwIAZ4u9MxCUrgiK94zgRlCii9vohWPryYCy9Qevnn38uZfVlWcqmORYCJwPjQDBvA4ATDhwewjZTwv/XBV0jH41YgQgAdL/fRajXztUg7oMDw+Eej8fC/ACo27YvADQMCuvlfnicGgDVm5ApiQJiXGJGEf0gJAKPgzhOD5lEZODHk1crU1nnb7bJ33GJ1YZvVh4jNnNJkHYQRbY4Zta3GMFQjwxkjR300ZmI2Mic+5vptbzRbYJOWwlgHC5RmkFDFwFj/KS1wky9Ax5zMuvipI/A5FNTXMWwk46IjS7yOVgOt6w4iRvHMZ6enjasKUdDvry8xKdPnzZs8qdPn+L29ja+fPlS2F5OlBvHsbQmsWfLDFVElKTFa0MVFZ9E4o0vQCa2XwK8Kw8O2CRGrAU6je7AhrPWbk1pqxfI0UkDyShByYm7kyLOpHcLJEDLiSXzuL+/L8xxll9E16U4Hqfo+3zM7LouMQy1GkdFAT4APdjvd2dgxubJvE+Bo2mnCeZ+jaurDIg+Pg6RT2ia43Bg70AX87wUgimliJS6c+LPiUb1qefElUqWdBExxLqytyrr88PDQ9zf35c1coKHbWCHrIeJBcgtfmagNpZNsKcTe0CWiIC8mKLv97Hf7+L9/SPY84F9YHvoLUEa3/Lp06eiL8uybI6MR7chR+yz0AVY/pY4IMZNx1MMXe7zHscxln6Jl5fnSBGb6h02cnl5WWSIHNnbiA75gZkppc0md3Sbtbq4uCh7bSDu8P0p5fYZV0QhtYg12CjrxMZsQCJg1zJ2Qk4sQN4mYvC5+BqPnWTdxCFxFruzLaNrbh1zC+23SCz+Po5jXF9fl8os/oAxMv+rq6t4efn/t3cnO3IkSZqAxXwLxsogk1lZ1ehG9zvMHKYv8/SDAWZ5g7pUn7oWJslYGQxfbA4en9pvRk4mE8ijKUCQjHA300WWX34RVb1vJeKZ3UoQCI+QI/ghs+n8ukAufR8/npmM9Al5AljiBJUiGfiypfwL7JE2C/nkHfnuDPAzMyFgZc8zkMhgmg8ipz6TBKB1Rk5khgF2SJI9/U0GAGTP/OW+nqqq5WJZ/eJQXV/V74+XbC7qaFd3z9vq+qr1clUXp2e1ennOYTtcQksu/E32zY3+JcHG/vEfxupzWS6ZWJFNSSIXsTTdP/xLretTU36h/Z//+X+b0kr7uAODYQM6DcxEAMVTRrXruiaUFNNiEU7CR1G8iwImm5xZFycmYZJSybuua5upMJjZr0ylUSAbd/wsjUWWdQys18DMZ6R8OBxPKrF3gsBQ2mRWCZDaTkZlYPsGgcpxMF6AOcNO0IHnqgE8vX79ukXeBIwhv7+/b4z6NCDLus1MK6axJKgnJ8fLqMwnQ83YZdCXddYJ5MwzxbdmadCTFfR7P6dcCTASPCbjTAZ8P1m4DEwYNP2jgE7FyCwgR46ZyZOCcv2SJSLrKaPWlzyad2PXL7qU5UzYIs/DnOgboP9P//RPzbBN2bd8r3UiI4wrVvv5+bmdxmLt6FDKMrDtXQLZ169ft1N0kklXEnQ4HNpBENfX16MMQjp0Z9uzI2wYsGQtMivib0dkprPOv+l3nrTj2dbM+mIj6WcG3lMnYJ3Igj+OIDZvGQAmsw54WCMONMkJcpIBZeoMR5QALfcymGfAbbvdjo6hfXz83Pb6eJ4Am51L8gfDegweNq3PgPaxfHXb3kPv9O/hYTiUJOVxyjbb/2RdP39+HGVOM/uwWAxEUtqVzWYoOZQRwEZibZMMSYIjGXeg3VgSWPlOEkQCEPOCnMlynQReyTQDQVVVh76v7f64KZjey6ak7c6MaZasJYubjPpwd8rAgGdmoeoY4ORpc3nEb5YSmg/jSZIm+8F/mCvrS0et2atXr9oBFunjjc/zpr6QXCDB/FxgmIyw32V2Vb8y45724fz8vPnI9Gf39/ftOFU+6+npqZG3dNE65dHh1sDeIOvDXvMlgLa1YA/yzgs6nLpurekA3537AnNOYEN7a+l4BkPWlV8w9/yYdwPy6a/Z3tQbtnVKYCs/M59T+544NUmbxHOyvZkJZsMyGMoAdbNa1fOX4QQyffPuxC4wdPp15Z9sYRJ92Vd+JDFQ2qD0MQJGz0/im8zt98PFnBng/Nd//y/1a+27MxqiPCDAwmbNJRAAcCwWxyMwM5bJUquMpBNAT8FsAgaL7DbsdJY5oZ5TNdTRZVpIAJKGMA2DiWXIq2oUXRMEdaq+P0SX42PXqrrabFygsm/BRW7Io3SZvqWwAHjess4xW4dkFpKZ0lfCTtk53aqqm5ubUYTq7/1+OCrVO82hOQaUfZ7ip0PK6Ns66gvgd3Nz056Z75AVy9IFRgsgSUNjfabZH/OTjmMK1JIJmgYTVcMJK5kaXi6XzWlut9t2Goka18yYmEMya5zK4wCANPYZhE7Zc9/PTZfWqu+Pe4oyo5Tyn6yd9H5V1e3tbb1+/bp9LoPufG8Guubn/v5+JANv3rypjx8/tjsy/vjHP7YSxQy4rBvnpewj2RuleVXDJVrkg6N8//59AycZaNnAay/HxcVFC1qVejCoUtc532nb2DtywjnSu6oaAQPrCgRWDal2mVmOaZqqtgZT8I/dMib6TuYFt2lvk5Xy/gww2L60oVXVwGdmbYH3PH2FLcssD2D65cuXVnqHGU07AGTI5FxeXrZ6dKVz7BVZEFwI0jPDaS3YUyAY0PN5OqCfbI0Ayni/fBlscgK1ZOXpT5JEdETGXUbCswFJeqY819wmGSbotpaZrU0bwrasVqv6+PFjXV1dNSCcAISsbjbDQSrmNuUua7rTtgOZuRfEXi3+NcmbxWLRLmIFfpNdz4ApiQgllZl5sK76TN8FSeyVNWErUt7MeWZ/n5+fG6mXgZIx5CbiBNBJPnpekkvpY8h4Bjf0iX9IQibHY23psPWrGvajsucCVdkwsmoeyGnuA2HX9E3/UtZl4JPYSVLQ9wFwc5Hgnx9iAxLcm0tY0/qm7UtZZpuPpMZjI88ErFl9klUAbHOSd0mUsw0J4skDYiCzGylTgi22LsH6l/2hKuQucV+WwyYJ5HPmc7FYtKygvsGKSuCyeoTN1g/6zb5lIJTkKP03v4kP01/8WvvuQMPpHhz3dBNXCqeJTgFlxA2O4PlubkYWXXKGQFZGa5x0Oj5GyWRPU2ecgSwLQUojlI4nSyrSiRMKAkA4LeARdC9eWFZnMHcvNcCL2u0+N+Hw3jR+6YCzRCYdeDLSgJXxJZjwHGvgfZkelSlJIEToE5wwovmefHc6Ob9XRoORIvRpmBO0kx3BqrX3ncyomaepclo3Tk5fkjkWOJNLP8/fkU39zmCDUprbNMAOBcg/6XgzYGX4PVcf06CkbGUWaSov/iQbkhvBUk+wfdb39va2zs7OmhOk30BGbmJPIEwvAI8EYHTh6uqq9We9Xo829XKwGRwBiL5HX6uGI7QBFf1Itgq7uVwu69OnTy17laWZmWKvqrq+vm4ZqHzOcnm8KO3du3dtjRLAmmt6mffnCJb2++PGTxst7+/vWwaGTmbGANuWzK6567puxCCzX5llUoKR5QicrGA9ZYodmxI1AhVgN3XjL3/5S/3Hf/xHLRaL+ud//ue6vr6u5XLZ9li4E+c4z91ofxt58i7vf3x8bCU0yAEAObOY2d8pK0n37e24v78fsa9pJzh4TPixhKwbzY/vVn19U3DagWTdkwVPZ85hJ5Dv+75d8JayZNwypOv18dJBYPLs7KyVKk/7Zox5wII/eWnsfr+v9WZTX16CIMBI5jb7mQGdeWObAUn2KasQyKa1NB8JepAq9CuJB+ua4BCgMk/8zt3dXcvEkOHLy8u2JtvtdrR5PcE0YPXx48eWvcwjfV28mcFu13WjbANfSPcRFknMsKnwRxIN5jbvSagaAHBmcfTBvGdmNgE2O6E/uWY+k76AHeKLYLb9ft/K88g6n5ZsO7uhykG2LrNG1jh1hd3KINnYkzjNjEtVtTGlv8mx86/0NDMN3pHYIknv9KO+J4jLE+GShNMXdu5blyf3VbVZr7+yDz7jGWmLMpPDLuhjlgAnJkibYo49XzCVlQRJuuoDvJ8EiWdm4Phr7btLp/7X//jfDWAQrgQaTk/o+76lkDP6d8EMhSAYfs95Z8SdG3ZNUEa6acyA2bu7u/Z/AiJDkGdCM8bn5+etvAO4S4doQbAo+pAAllPCkB0XtGug0AIdAdOmnYHsT2ZkKCNB8/xkwquqfdc+FH2kbGlk/DxvTyf0DHkGhX4G0CfYmaYUOW+gwvwQagFD1ZA6TwaRDHwLJGfGahqFmzdG2xitYzo5ypob5cwT5oWcJPtRNRw9CtSkoSNz0/4m2BaoSnXnRrZsHFDuUWJMyLKg0zsy00BuGdAp+5PB/zQArTpmImRAPCdBSdWQKrZe9IHhFgBlkPfw8FAXFxft1lV9SnY0U8P+VH2d2k2d0x8OgDxMjX7VMUOTWdYsPSGryYZx/hlckOXDYbwZPpkum2eBEcFRZk6NNZl1tetZTsjgs5XYaoF2AktjMgeZkcv7H8iE32XZ17SEiR4bf5Zt5P43/ZCtuLu7q59//rn++te/1r/927+1y8r6fpwdmx65qU+D/RxABpkDlI86NJAPAASZOF5IOCZD6ETqi3dysPv9bmTrMgjqOuVVn9s6VVWdnGxGZMy0ZMXnsswxwTnZNe/00Tx7NpbR+ucRnAL2ZLBzzsig/UoJQrquq10/XBib2SVgMAk1ssIvLBaLdqGeTK6WWQJ2NmV8s9m0fS/JdCdLbOzGJtAwx0ky3N3dNYIkyUkg2vzmiT+IKWN+fn4eBRj8grXIsWVwkZUd1uzi4mKUGUGCGhsiYLFYtHtZ8lhtQRs7QFfSZuW6GItAhK77TAaDCWan4JLNyKN2HQDB3pE3++esNUDP/mUJO70mm0k6JpHHP6W+pE3KMvsMHNjNzGbn2lpv5KK5yowbH2CeEkMsl8sWeJkD80tm2BSyarzWr+/76vq++sNw8hRMkGuaBGf62eyzvmTZGmySmRBrkzg1gw7fS3ufRKV5y6CPjB0Oh/r3//7f6tfad2c0GDcMHdCG9aIgyWY6mSHTfFXVWCiTkhv8pMoBI0IJVGMjMT2cFLCcjHuCEGMQbVtYoMKETy+Mo0wp0FMBZqBS2R4ePtf2eVu7/a6qrzr0h+qqq/1hV5eXF18JVgZQBD+DHgKQpUYpEMaXDLegyueBQPMDHGZQSImTiWEovI+CpyJohHHswIcjbCkjxylqNk7z8urVq6b01p/yZ6CTZVXYuPyZhlXLfQAJqJXAJWgA1DLtqs/6wIGRlXRe+pjp/aZ4q+FIRODWWeXJkFmDquFYYN/DbBhHzqP30sXcxObd+SysKubx/v6+drtdXV1d1W43HLm5Wq0a4PTezCpgQLIsI0FTsibm9e7urk5OTtpdC76b8i34JXtkO52M7wjIsOL6Yw39zPvzaGzlAEpJPINNYGC9y8+rjg7T6SfZr2lW1HPov8/TQ2ste5AyleAzQWre5o71SpmbvjeDTuPIYJWzkk3Sf/si9PP9+/ej73ddV3/605/q7Oys3r1797KGQ9oe0Et/ksErW9f3x5IifdRffuOoX30DNex+31cdDvtma9jLBDk5f4MdWlTXjTdaVtULKTMcU+tdqdtsfrKD0+fkOxP06CfbDuzLLlp/wBE4AeDyxuwMNvUvA3usfDLRJycn9fgwEHBshCwPfyAD5/cCAHYTJkBkISVOT0/r/v5+ZFv3++HI8pQ5/eUHBfVkEHGh1IzMyUSy5fn9qmqX0plnNk5pnka3ZYr4N2VbqdPWg46Y4xyHPaswUFU1wL7fDycR6XfaObqULL4MbpZjZnCa/if1Ju2pceTFeWwuQtjv6CY7nEw2Oec7yTsd904B6XAIxdcXdwpwkkSbBt50yxjgvQwU4bEkg/2MHGWwyYelPPPv3pN+/OzsrB3Tbq7po+9nQMVmkekWIHWLWkyIrrTXUyLRXCY5AC8bQz6L/LuYUJ8yU5/ZXf0nD2QhiZLEp+kLM/j+pfbdgQZGK4V+mmbK9JWIaypcJkBHc/Ep7243bArMdJd6QFEzx00pCH2WixBITFiWY1WN69QALpNaNewFoTw3NzftfY6H0/fdblefPn2qjx8/Vd93VS+XTe33u1qt1nVxcVFXl1fV15DuypIzC8/hcEgJ6gg/I5TKOQUJCd4zIPH9XJtcw3Q6nBLhYujS6KTQm8cp25TZnlznLDkiE0CGvgGJuS7JEANqCayMQ380c0rRyBNDketBhpL5ydSyec7x59HO04AmD0VI0JGpzjdv3jRZYFwzU2WNfGdaBz01tv6dTBT9VIYk8Pe5x8fHdsqT0qeqI0FwcXHRnuk89zdv3rT3kUufmZZfWKPU+aurq5HRI1fpiDIwyDkgD0BWMruPj48jQA0IJPt0OBxatlVQhbXOdyg/INNASu6TUB7k2dZREJHBsiC567qvaqSVhrAPdFygUTXsh8jTrcgA3RE8TuXQ/NlMb1Mp+aUbeVBBZm7oDCf/448/1mazaXt7drtd/eEPf2iB8cnJq8Z6ZkBhLZOEyhNN2BPyk+Vxx/4Oe6YyW/bly9iJZskiQAM0e98xQBvK6RIgbLfPbf6nvjDlNZnWBED+z1diTgFxeulPZl4SsCYoIIMOKeF7ZcYcFnB3d1fb7bbOz88boYegODk5qeftc9NDz7buZC+JKzZZkJJlMVnuAvgrh0s7m4QLn5akG1aabCR5mHIMEPljb4U+wA/8Db/tHfQ/mfoMwtn1PHDG+D9//lwPDw8Nk3iG3xsbWyDrIZBxZKy5zUCMLBtzrlcSRuyr4Fn/PVOASJ7YDfP86dOnplNVNQpC6VwSRlmKN82AZWAArFpH/tvcmM+pn2Kn2EtBpLlkq73r3bt3raTfmtHLzWZT292u+sOYqE0wnuulHIqvGGzCEDyy5xkApN1Pm8bGsGOw6dFXPdX52XmTJ7aIvJEZ/U5ylJ0+xLjS9mQlj99XDQcGJS7imzN4yQAMQZ02kx75DJv4a+03HW+L/WO4uq5rG00xbRyVUiWKwVlOj8HMqNJEcWaEK0tKnp6eGthhmCmioCRZ5tVq1bIW3p+s6sXFxYhJ838b0nKCl8vjZUH7/bFekfLd3d01sH59ff1SRnA88vCoJMsXlu3Iti2XmwYosOb6rTEgQBkwYMyUL1P06eA4xlRiwmn8BDAFERsFjFC+fH4yMI7EzUAhnWIGAKmk2ICqaiU6Uwed2RsOhiJRMOUqABXjnPXzGXB4h7nIQEGgkdmXKRNsL4L5J3/0QlYlwaE5mToiMmM+kqFJ9lRAkA46wSPZSfBHVnJ9B+C0bbXeAHACgOfn53bhFcfcdV29efNmBNAXi6G8gu7q23TNEjBr9Ft6miPWz8Vi0UoPyJT+cTbsy3q9biWbvssRTzMS9C4NNRuQpW3W05op2Us2U3CQ8p7s+WZzPGKX3ukTu+R5bJj+cIYZvLHD2GnHksq+yAhdX1+PTmjRcj2ntiPBHFCYmRvfSWKi67r68ccfG1jPOcrg+ziO43G6x/GfBABzU/SyTk6Otg6Tvt3uarORgT7Uly+y1idV1dV6varb27smS8vlamQjFotFC+IcopGZzSwXyMD+eDKgiySfW8mjE4E83+dXqyED7s9xbEOwlADwW+Ba4M6OsUH0P4OADGCsHX2XeQQor6+vGwu72x33XgHfXdfVerOuQ9gH601nktSSafH/u7u7Wq1WbW8Eu/rhw4fGfO52u2a/0r+l/yDzadfotvkhWwJ+RGbadXOSAJ8upg1EDuojHbcO1sj76fHFxcXoVMTsH/n3fn2jSxmwySi4j8TY+Xm4I/V9mk0XnAyyP5y06f15hGzqJnvHRrPL6SvIjAwREuLh4aG9Jwlk+3L4PgEMX2x+8jtsufJ1AZg1yz0TCE63iJtT5WnkaxE6UVV12O/r6cuXOo1DWbL8jA4L+LOPU8Irs5Hp287Pz1t5Lt/CRifh2Hz9yatmF6Z+On2RtUSMegYbndkj/XHdgyCNXsA58IJALonADMJgHTpBfpNMSez+a+03BRrTSeasqqqdk60DfsZAAacmNpk2BjfZp2QaKS+Fk656eHhowkYoEiAwFv6YWM8SKHDwDEeWaEj5Gae+AvzJ5KaCHh3JemRcj+z0aRur51JKyq6sgPEBKlIIzBOBANaythvQ9sfnGaWs40xmgjBL75rHZMbNg/VMdoKgO9+9asgqJOObAmxjtv7nBktGNr/LAZK5TBFae2ssWBVkTOWp7/vGlOQ8CbLS+eQ+BO83hkxlZrZCmR+2IAF5OkIyxoBk2tZ8JpuQATmHBkAly+Z7VdV0kNPJ9crSCPOSwT/5tw4AU+qxtbFe+lQ1PjHJGMwnZlTT9wQ69OzNmzfNNmQAgfTINaPX5tb6Agrmm/4Za9/37aQqMk6WyEkCHXaq67qvgp0MSqqG4zGnwJMz5UgzUCb3bFnqoFO8khggN+YAU5b9pwvKXzKg0FLOzC22UhAHXLx7965lLhxbmu8yX8leAhK5RrlJ+Pz8vLGaZ2dndXd39yJTu3p6qvb9quNpSS4sBbTZtHSuWW7o/wOJMD4AA9AS1On74+NjO0FpvT4Gmvf3980X0R3lcPpzc3MzIhj0kd6yd3kEtbIlMoBRBzQzuLu8vGy27fHxeBv79fV1VQ0ZuyQsjjZr2KieWbc8KcuaAECvXr2q09PTdvQ68EOHrHMe/ZmHt5h7IIv82Zic+sNvp04ne50YI9cU0alsJsuF2BVyLBPEnnpPEiaAe+IXGICtTpLOmHOu+Vby5t908erqqs2BdfZuJ46RjemJlQn6Pn36NPJP5MfnPefh4aEd7mMuHURQdTwkg5/ODGD+OwmXJC0Qwxj/b2VeyD0dZweWy3E5qDmdVioIvq2X0mm/71/mZrcf7/+YZhFSh9j/DFYB7EFnhr0/xgZbZamn5yGwql42sL/Ms/nLErIMYtg9fomcrdfrRpwgh9nizIqmveXLExMmlqT30zW1bvQ0Zfh3DzSmdXbqLnNzVgJRC8ERqLfNUp+///3vTWGen59bujcXBODcbI7nqdt4RsASVOck2UMic5Jgm4H6/PlzMwwJuFN5OSmLREEJZ9XRuKhtTEVLoEB5EihnZN33/YgpT2NHudI4plFN5unt27e12Wzq5uamGdqqYYNSguispTdWn9HH/K73Zjq1anyMcAaKCYgXi0W7hCnZhMxw5feUC2Bu9vt9A6UUyJpX1UhRs0wmf8+gp5KZg2SZv8WGWUsON9O/DEsGkObNuibbmawrACdzBWTSIycvZflabugUVMj4MTLr9fF0pyQDdrtj2SKnbQ+MeRfkOv41TwzL4MA8p4NlTDP1ap4AFI6ckafPeQSwoEi/2RDzeTgcRicJ+UxmHrIUJGufU1e8A1tGhh8fH7+yL5hXNsrPMiOgf8lgZpZKv5JNTGaITUqWKPXV2meQjBSRGQGgq6rNs7VnNzOb45nknvxmeSmyIYOfZKuNRflB1pfnnAAl2fe0feaCjuem4b7vWwYZgN7thsCQvtze3rZ1qxpqpFN30xnf3d2NbrtPp8nfVI0PMMl1oNf0gZ1S+uFzgE2WMggqZUgOh0PLCgiuzKt9WwKfLG0iU96nooDO8FPkFugjpyevTqp7+Z4mo7RcLuv+/r4FSVNSSVBEPvWbHSL3/tZSXtnaDKQEoHmiENlLkkcfyQ77tVwu235OQYrPCiiSAErAxdaTvZR3e2bI/OXl5Whjue/kfqLcI0V2yAL5NR/2Fno/sM1eZRYmy/f0cbvdtqzDdA78AUwPh0NdXV3Vu3fvWlYFdjFW84IEglccd181ZEkRfqkbmUGpGogPckPm+V/+QsCKzLGm5DyDiszqLZfL2r/osnlHwj4/P1cXfjzBNEK8asAJxspHT7FG2h32SSkVfWBrEwcaxy5K9+iHwH6qM0kep6/yf783p+adzvtDv9g0Pjz9j2dOy3fZziRd0x7+WvvuQCNLfQ6HY4omJ87k39/ft387WvL09HS0uTHB2N3dXbuMi8AQEoGGSfJvwspAJ2uYLDlHjIHB8HB+WbNmDGnETLzvWFR9y4W1iJhJQmRxtBQSAnB7e9vS2gKhNCSUKy/BYvC8L9mSZHaNiTMHDrQUqKYEAcTMLyefc+253puCmyDVeDk5Y/B885Ub5TI1x/BgEMyt9yXDYJ38m0ExZg6TYREYkSmGPRlwBgk4SKBpzfUxmS5OgeEyBnsEBOfKr6xBBiCAbwIypTb2TBiDFHKWriRgs9YuhAIezSfHuFqt6u9//3v99NNPI+fk3Wn4GPEE2bl+mZY3Zxk0OQnncDi0uy0y2KX35NG8MnL+NqeYZUCGPGfJE5k0L7Jp9C+DswTYy+Wy7ctKMoKcZqBI3jLDQgaSvcXMpuPyHQRO6hD9S0YUKNFHTp48VVVjuvUxSZIMBKdBTgZGSYAkAWMu89hlzwWk6EmWPlq/KaubzGiSK9buCHgHGUsnzO6QkyxdQBCZl8NhuMAwGUj6wB4YnyxaBpLb7baxsVXVZNk87Xa7UQCUdfD6kiSBdTGuqmqbOgVLiAp2YL1eN7CUcnl1dVWPj491e3vbZObjx48tyyzAXG2G40C9lw++vr4e+SzfA2zYMOuY654ZDuBHJpFvysxXgi17x6xx3uWSuptkW17qSVf4LGtBpquqlcTRtwTzZI6PtNbGkuBZ1oANJH/GguzzPKVH+rZer+v6+npk38xzVY10pqraUeTGkuVNLtXjB6ZjE4Truz8+n7qYLPjp6Wlbq7QBwH6StUkMGXseXAJ3GaOgMgk5hBniSb/cVq+cPrMq+gDHpH7l810e6+cJljOYITdZUZHjoys+k4FU2pmcj+12W8/7L7VerUaBEjlIn+U75odvTZuX9i31yNzn/z0r+2KtjTVJOXbEz6brTOa+p/2mzeAJmoF8Rtdi6ZS0t0ib0lH+quGG3Kqq169fjxydxbYQgBV2h+Bk2QdnaeIstrRgGgTgRB3dtLzFMXlT1pRRqxpf3uZkicxaZCQrkEglAhZs1NN/AMPJPxnU5CkHWSusf56Tc8DZm2tjIHw+C0Qz6AkY/CyBTLLblBR4oMjJ4lIiSplOx/qkjJEdz+b8kvFJtoHBzYAxjQJwzTkINhlDzoPBT9aXMicTxXGau1TkDAKnpXHem47Su7J2nIH1Dp9J4Pzx48fW5/fv39dPP/1UVcNehCzTsnbJltjbZG6enp5a3T05xqCRs6xdrhocYo49623TyWPvkjzAOGYZVrKlWQqH3WIgyZbsGDCc4yO3jtjN23HpnHR7Zl2yZEy/0ilYQ3OQmzhzvwWAmLqErRNkWneAF9PmHYKttAECSWNNh5kOJEsZkkTIlLjMdBILAvic25Qrc5KXzGVJGLkQ5HCE5NPf5iT1iM3M7Gnqp6Aw5STJG6CK/cgShVzDqhqdJEMW+av7+/v2rLdv35bN8/phHBjkZHUBOHKWZTVZ9qPf/F4ehEEmrUPaV4FbsunsC8DqNDXyAuztdruWQclyyrSvGejZC5fEWwbB6dP1IwN2MpQb+hM/JHlovZLIvLq6asx7gj56s1qtWr25fyMZk8k1Pn2UHbVOeYpSZmaQFOY+iRdr4lLSruuabtMpsqxCI8nHJBARTofDof7xj3+0MlHl4DDBn/70p/rw4UMjrvg0PiJlKgmCtJd+p0+ZcaPDdO9b1RfsQJ7MSF6M0Xi8m2wlyPUu/TXv/IX1zX2X5DAzty0IWowrRNgZc5DXMPhekjopM8jtxGz0MHU/M3IZ4GZQZb6/PG9r0Q33+SSAn2IQeg5/J7GV+CTXDA5lF8x7ypx35XG9GbSnHcigxu+/lSX5pfbdgQZmNQdPuJbLZQPLWRp1OBzabn4OFNj3PYBvsVi0c7B9NtPtVUcDcnl52ZTXomQEyLEIHJI9JSAZbaoDFP2nI66qUSlHAnpCYhMToJHMVaa5Eoyls002PEuEkkEneCmMnvv09NRKzjgY8+AzajGx1pSW42FA81QJAkbJKc2URTbmdPYZTOWG12+xo+bBs6cZD47GnwSenJPG0WQ5FoOU6We/+/9F8um0rUOmNKdKZ86mJVT+MJCZAfK9KZNt7GlIc87NF2bqhx9+qIeHh3p6eqo//OEPo1u3c4zYEu8FbpUPppMmT8lQp+OyXslMV1Urj0yGJ+eq67qWEeCUdrvjjfACG4FE6pxaVhtdgQvyks4cQQDU0FPOK7MR9BOTZ83NVxIJ1jiDcaAodUBNfton9jMDJ+REBqAAL8dFThIQs7venw7Us+hYkgHWOJ0UpwoEmQctQXuydfRgysIJFLDj7ClbTGbMSzK7WYbJRtMboDizN31fTT/YDGPY74e9ZTlXsvI+CwjpMxnMchq2+ebm5quSiUEvh2wOXUj5ThbQ+PPABSUXWQolM53EDzuGfeZ72DvBb7LBfd+3TcxkQ3C93W7r7Py86unzaO4BtLSDSZp4DjIhATh9VE6TpV58yOnpactQmOMExX6eJbCCbZd9Vg1Mv4BLdoeOZ+BFHvkQvg1pYz088+rqqgUO06zbdI+L9ZU9OhwO7WAGp4spaaZzghukE4befRo5J+zE2dlZXV5eNr2+vr4eXYKc8lo1BKjpCxxcwq9tt9tmr9ho4zFeZJy1IV/ph6eBov/nlQTWlVwKjtgG/bPubAdiM8ml6Wb8hjn7vvrd+KJldjL9UtVwFwrZSdtE/vK7SXzzg+TL/GVWbErEWpfT09M67IdyZjqfus6m8QVkLckvz4cV8h36THcy0IDprO1isRjhUOuXBKFnpL9PX/pr7bsDjWTVse4MIuPEACc7oKPSVZj1XBDMS9cdN8s52eLTp08tYidUGKYE3gzgNJWXxjmdQNUARqe1ZxkQ5FgyOwBs3NzcjJgdTEYaXc4w69cTbANijKX0L2ExpvV6Xbe3t6Nauqoa1Y06FeX5+bnVTCYrmOOmgBRPnwlPpt9SoI2JoBsfRWCgsjwjlYAy+1lVjbJK1isDCH3NTZzJwst8UOgffvihMXneha3PtDq2imykY2VkAJCqISuQRiSNrPf4vTtKqqoxxsYPFOcmM2l2TiCBr3cbo/diXDDbuVYZWG+327q9vW3jzTJEzjkN+93dXZMvgTNARoa8gy5nIJeOMgEKOcgyEUeiplHjsKw/cETOkpEHGHP+zXPKooxkyjvWLNeeTGbZ5jQYJetALHuU5AYwmwRNlsZkoFk1lBKRu2Sg0wkKfDjIqX5xoBm8ZtmiPlozIDSDOuVAaqTZ9mRCp47bWrAzWTojiEoWkw2hi8mq5hiToaUD2+34vqEj4D2M5kv2jX3PQISTpd/sNh/DfyT4ziyX99zf37Xfp/x33fHEJ7qQgcTUvvNBWm6ePc7Dovp+fPGgLIugMf9tTXJu2UwyAwxXPxy4kLbIelnX09PTqn5cAoOkSL+cNm6xWLTAHxPfdUM5MzlKAMPGGLvPqgbAnlcN90YkCKK/5JNfTfnKrNOHDx9axs0G+yQdAU2B5HZ7PN1tv9+PSp5vbm7q1atX7SZyJ205kSuJh8ygJ+nmveTW+wXx5NH80630x3CZOaE7bG5mZtLXZqZj6j++ZU/9P20U/c/n5V7GJP6SWKUj06yA/uz3+0ZY8/OZVTc3i8WiKsgvOrHdbqs/HGodmZLEhxl8k4skl+hmlqIl6YhAMc/8Td/3LQvoM9vttjarYf2nYD5xCAKGHlQNuJQPscbmLjPN5nEqP0l0+pxAL22HtTZO8+q5GRD9WvtNp04lG3B/f9+MZ7LjmHGGhFIn0+LzshsGLSUN3DLCFq1qKG2gXJQ3FzcVxAkv6QA8m2HleNTjZgkEkC7zQokYBg7s8+fP7ejbZAY8Y7fbtXPmMaAXFxdtsRjYXEQggCHnDM0dAc1yg9evX4+YMQrqM56ZbGXOC+XAGugPAWV0MtuUQYG1YNiAQkyG3zGYCagwIMk8eicHn0GTdXb6i8AQS8CQ+Sz2ZFqOwRlPTy1arYbjmpMRqRpAQjLEWWri+dObwM3Xt04sysDMs8yDtU4GOZ30arWqv/71r3V5edkcmfUkg45uFgRxaOTeCSFkraoa22quEyBn4ND3fQMV5D3BNseSqVpz/OrVq/rw4UObz91uNzopC0jKQDWdaAI/GQVgavq5ZHbYltxIbnwAB4aNzWOQZSbYHfrhgjL2wc/ZFfoKANPTzAR4fwbjZCSNfh7Lmew93WI76B85IktJNqhV92wOJomhBF9pkxN8CgSAGPKRBIu1AErNbxIvZM36p+PDpO52xxOfjmBiWVWLquqranw8sblRGpsyKdvC3iEnvIsOZKBn7Mf1X1ffH+r8/OLFrhyP3d3v8/6ovpbLfR0Ofe12w36M/f5Q2+0A4pbL4xn7p6dndTwKuK/lcjUCEmx7lqUCeGkn03+yh0me0Xfrk0AXs//l6Uvtt9tadl3V/tDY+Q+f31ctuloF45ulw9bdfhUlQ3nQBhup3+Z0v9+3uxEy4HZ8KDnabrd1cXHR5PL5+bmx/Ykvqqr+9re/tWCXH/B8mS+1/wJkwTf/Ixu42Wzqb3/7W52dnbXsMdtmPS4vL+uPf/xjY+zJ9W43XLCY5eTJvp+cnLTLAgVzPpOyqV/sUAYPWpJobC35yKA4fVuSrpndRFimD8iyZrKZ2Ge1WtXJ5qR2u33td4daLJbV1fFSzUW3qK5b1HK1qP2hr/2hr9V6U/v9rvrqart7uSNsf6i+uloslnXoq563u1q/6OByuazn7ba6lwDD/JOvJIC7xXBiE1vIdidYzsyFuUYsaycnJ6MLXZNA8b5+f6jdl+da1ot9W70ElvtDPe+HrH0GcHkZKVv+rVJheMlY+IsM1BLn8nV+bj2RqVoSy2QdXicnGcCnL/219t2BRkbPy+Vw7FrVAJYymDB5zh83QEZeGQAwyFD5rGAiGWTvXC6HetiM7pNJBaYYnPxdMiEmMssGBgdxqNvb22ZMM7AiFAyILE/XHdOl3rtcLltNOANu8avqK5bd85N5SwBG0IyJsbHoouCbm5s6HA7taMNpVibXjeD5mSMik4Ex1mRPuq5rGZh0bpmu03dKmNklxhKzb31yL8V6vW4Xj2HZGd0EWJmCBOCccpXHcOa4KSOW3nxXVTMu5IShyQxAAtmUBS1PtGHIM8PAqCWoaoaqH+pg/Xu6cZ2u+a7AvaqasyanTu3B8nRd1+YTwJWl4xDTMOcmW2uagSudZaSzrCfthACA06MrAgRz7GLM5fJ4iSF7YsxAwno93J+hHIN9UbuMrcxSqkwbJ8ueLCM7gNH07svLywae6If1TcdAVunw69ev27GonmUuzfORJb9v5RbJTLF7+odASPbaPGUWMFk8c0O/rLH19B7rl6RA2uQMcKYsadoyfiHri809W+U5GUAmYPG71K2vg5LjXRxH3/Q0yqpn1pb9oecZjGf2214D9tj3F4vxKTy5xmTp1avTBrD7fshUTplU+p5kw8nJq/bOZImT1EqZNReLxeKr8jK2LUuHMvDQ78P2uT2f3T+OfVknLzp6/+V+lPlZrde1XA/AUnBPt/SB/8tsd+6bIQ9sNFyQfjZxAluhvzIpXXesgED6rVar+td//deme/52z9V2u627u7t2NK+AOu/iSZZXedVms2n+nJwiWcgvu5BMNzvs3oe0d+apqkab69MuZNCcv2cLzPuUWLGWfAhdZjurakRIkClrk1kK/iqxQRKq3/p7vzsG2EmE7Hf76l6CmlWU/h3nYFyOq/+CyaO92LcAzPpo3ku3PPc5MoqJKb2LvqV9SfIj7WBVNftPbjMA2O12dXgJGn1GudjJC3hHNAl2rJ0x5Byk7tA1+pUlguxKEsOpi2lrpvaeb/W7DI6TSPYd8pQ2+ZfadwcaBBiTsl6vWxQlsnOsmLo8E933/eioQGA8QXaWADA8bvYF7iiGbIrTMzhBBuzjx4+j1F0Cu1S+ZDMZZRFsMhCAqIVMEKzvubkvGQgMpu98q+QiHVWmPT3HHHp2bqKvGpj9rHVPoJjpxWThs9bUvHseYfWewXEOm0FzI7TvrFbDpljlBICYE5KUZlCkw2G4+TnZkkx1T1PeyfAle0Whsy4cyEkGSfCE0aL8NoMmQ5MnIyWLo0/Anmb9spwwgxBOzNxMmQF94UgyXZwGhwx5n6ASu8eYYcrMn89zJLImxktWAUF94QSN35gw35yt+fQc41dGlgEDXQZgzLfMU85dlpik8cuAIbMIyYxPWWCBCufD2OccOQXNGrA3AFsGm/o7BbT66eQwe8IyRZ0yQr+ws0BABnm5JgBSBvhpJ+i0fmBz85SztBG5dkiJJH4SLHuXuQNg6LA/KQeeT++Nga6w2ZkZtm6cuOdlJiX7qJ/65tl03h4BPiGPZM39ddbacaAYZc8+HA6NofZ/72LnUpetL3lBqmSmXDBpPjPYPR5kMIAM8vf8/Nz24NGt9XrdLtTTnKinP9a9agBosjr07GQ1BJHW5zjHyzr0fdsknr4OMNZvz3779m11XdeOtCbX//jHP0Z+wpqfnJy0fSqbzfFejPfv348Yc8HBzz//XCcnJ/X69es6Pz9vxwEjHHLfjTWSgdVHQQZZEhyYUwFK13WNbOBXyE3qHLyin3k4AR32uQxW8tZ4/Sbrvtf3/eiesiRprSO9YHM9HxbTf2OU4cog1xp6Bjn2f3+TXxiKzekP/TGT0XUjG5Pr7HmJVzI7wY8NeKUb2TP+YUr6JQnXvzyXX4D9UpcEV1kxQJZTf/kixAT5yMB4t91W1w84IclV404MyX7kxnq4IjFQZqcygEiCEi7IOUx/ye6nbqbtH4K+avbTM9g+tjFxyy+135TRmG4WTkFNUJAnMtzf37eSDIruxBDOM9OAQAOAyIHmpj3lHj6Xaddk9wU79jHIEkjDKrnhfIyLsBurRRWdujTK7zNQSnZaILbfD5uc0rAB4vpAUc1fAqRkJDndqiHapZCZjvNMipIp9gS6+ktQvVcwAZQArXmRU4Jzaww8K8kgN2reHx8f22cZdWPEwprTDOKy5jtvCDUGjj+BhnUiS1LW7969GyndFGwDC2lYBBpZk8qRk1HfmTrmBCEJPLwnWxoK/6dnwEUGG7lu9MfnGIQMgHPtcv2zb+SfbBkLZ5Asy+FwrPe2RuaPbGQpZd4L0vfHjaqvX79uNiaZHkGzMakJp0Mco3XghB3xmDJ9OAwnmAiKUv6tWQa/3smWsQvJ2k+dbwbrKa9sZcoOG5f2Kpl7NiBJFtnOtCFASmYh6E86jWSt9NVzvuW0yAUiCZOVTsjzjDcBijGnXmWWkExlUJkERqb39SVT9ul7ZJSnLF2SLmk3yXdmE5JB3O+PWXYHXjiZKcGdNTKvGYBh/40zwaK5Yb/SRtAD9td3+c3NZt3sQ+ot25LkmQDAnN3d3Y2YcGCf7aqqNtbtdltnp6fVb05Gfk1f1+vjjeLIjQRDxrhYHI9uZ5fYWP7NPO73+/r06VPLbHsOMvLNmzdVdfRvghXAmD3+l3/5l/ZeATICQV/SfgFxudHY2mfAbE34VTqs/wm2+QL6kWzz9MhUdi11j/7YAyI7Y49qzu+U8BHs0gfry1bJiOTnM6uWWCuJIFgBiZNrnSAzfdbILkQFRJYDPz8/V98NhyOkreE/WpDQDwdcHO3Bqqr6hi+cIpXgW0ZfW61WdQjiiZ3KjKd15NOyHIktYRvIasoODPn09FTLbrxJ3rMThyDryVHakClZZwwph/xkYgnjN5e5pinPGTAk5hMIe6ZS28SumTU19l9r3x1oEByOnEFNUMNA6rCJyFIBCillaVDJPmJHgA7sArCQzIDMAVahqprwULKff/55xIxhFQUcwG+yw5TKmGzsJQwEDqPb0oL7YSMvgcB0UBaCB2BSeIJnbOZ9Ct49J7Mf3kXYgK2MajPocLFPRv0UJY/VtL6ZRvb+ZHzMo88xiDJe2n6/b3sFsmYXWy34BECsAXa5qtqZ49ZzGslbn7yfxTxbT0dI2gtgD06Cm77vG/izRoJdIIIuZGqboWLsjTszZeaWnDHmglLjnjJL5JoBzFRoMmcJcIAkOqql0djtdvXTTz/V3d3dKMjouq4FJblZFyAkKwkopbUfHh7a3QPYQ3JbNey3OhwODRzRfcAxMw5pLM0fOWc/BB/WwNxgAJOI4DiSBc8MA8bGu/UTG4UBzRIqwMJckIMkMARa1oxD8DtAgCyyFanv+pPsPPlgg5ONy9rvaV9TvpOdJDPs37Se1/ymQ8sSl2RU2YQEK2yW+cuxJ+h2ulIyjdvttu0tUoKXepDlYuQ7QRNyIQ82YFPYmyR5yDsbYW0ASLKX2RZZ1gR95pRvY3eT3PAM5Mw4WHmu5XIxIntOTk7q3bt3jf33nqqvAyjyKLBdrVa17PtarVft//a5LbpFnb4w9fld/d2FrrDbWf7IXpIpGRZB32q1qvv7+9psNl8F/ldXV20tq6qVUhpfBrPsBDDERng2H5gnjunD1dVVI9MOh0Nbpyz1y8CebvMxfCxSzGfNQZKomQFlV+hRZhFyXxGmPKsfyCEbJmDU8rjuJLPoZwa15AzZZ34zcLRWSWKwb1kCaizGQccP++HwjPTTu/2+Dv1AOJNXz6JjiSmP+jzOiMANmUnJfaaCjM3LYQj0JIlpLfuB2EqfnQFR2lk60/xrN9x3Zv3YIRhBME2ejIn/s04ZjOUcToPUxDlwkfnwDs1a55jocmaxrH+SDJnt5ct/rf2mzeAJfBgALxLlZwCQoCa/k5uaDFJNrTq8quEUCo5ruVy2rALF9p488k8KkZFIluX9+/ftmSJT/UomzftzoQl0GodpOjM30GicGDbd56qGIAt49H9Klin27FcyWBmRpqMBPDgxDsbJGErbBGpTBq1qcIKYXPs3rq6u2rP10b8/fPjQhJIR53QpRZYoTDcbU9pk+6wxRvH9+/dt/w85UYagBlZdPoUmjwCngJcMJnBgKNMokCNBCjlm5DgyARbQ4v2UlFEgQ1maJ/uHfeVskvEWfCcbn8wG+UjQbG2BZ3MtGFPymPtayJR5zbXG+HHIyiUZqrOzsyazuWEOMKALaYyNQ9mDefV8Mkm3M7gG4DyfrGUwZ/3plbHlvGR2DPBI/cn5SxlJo69P2Ve6kmyr3wOx6Rz0Yb8/ljoA2+TCmBEv3qN/xpsBTnP8h3H5EzAkYDOH7I5nZICTWQW/88501hlQpINiA+gEVlsmi7P1joeHh1b6YyzIoQwojvqyH4FF8kiP2G2BB/u22+1GF8oK+BO0K1GaBml937e9ZOb97u6uEUwCAn5AH/iSDFjMkQwE8HuU013t94Pf0K/s59nZWbP/MiNIuu12OyIHuq6rzclwyWzVQADUYjjeXWD2/Hw8ke7Dx4+1XK++ymR2XdcOTchLIpF5b968Gfk+lQlXV1etpAqAI/uCO3Juji8uLpptY/Nz83Uy8svlsj0/S2HMN5vN9+TBFmQ45VjwjrQjW3xOMsbkPMsKE+NkIEA/ZVYyIzMG2+M7xjJbl8RvsthJgiVQNn7yziYhDVMPp8QLGUt59P2jnu5qvxsAP39mTLv9UK5uXVKHvI98J8lEtlStrFarVnaY2OGlU6NAkQ1S0gq35txkJsIceTbdz1JO/UmAn8HDNBOQwUuSk/mdxGNpP3Pek+zOoCLtNr9gHclakkyIK2uUMpYEsDmZEpe/1L470MCsOB2GobYAhFkEbvIYPE5LJ6fMuMFXDaeYmAiT4W/PTWHCSDAQybIzIrvdrh01J+K9v78fHQ1qkQmKiZ7WqivVSIaNoDB0CQ4BGgqXwMJzGSmlQVNBpvwcFiDmWcmEmXdBBAebTJrPZMkVxmSaoiPgQCCQttls2n4LNYpv376tquHcfyUH2+227bs5Pz8fnSx1OBzrE9XBchACDAppvp0GRUk479zUlScHCVKqqqWiGTEgLoMGa+y9ZP3z58+jzcAJqihrMtLmzpxlUMiR+AyQb758luwLSBhMwBh7JZNg/GdnZ/Xx48c2HqCDTC0Wi/rP//zPxsR9+fKl3r17N2K3BOJ0T7o59wDJEmb2TN/oXsopo8eRrdfr9h4yR38ZvSx1IJOCIc8RGOgTmc9gBEGhP75v3Y3TGNkkY6L3yUbTfTooaMp1MoYkL9hBdsIaCTgx62QgSQ6ZR3XX5j0ZY3IHtAh29aOqRnaIIzLXwFS2vu9bOQddY4sSBNBr/08AUfU125tkUDow2UUZgwzisrQky3q/JTtT207GzafPJnOYwXxmgLOP1k8Q6HlsdJaqsWfGnwx2lsskqKUnmWVM2XV5rZPO6HYe7Xk4HNpBCWx9I3YWizoc9rV6yXj9+c9/rsvLy1Ze+OPbH5qPN95j6etp7fvhpMOHh4dWQmu9EW706c2bN00/BEVk7vb2duS/8mTEzGSQq9QxwUAeI52/tzYJvjOYYd/5KLqDLAS287NJuJJ9doUeWs/MFLARiQ34M/6RvpI1tj8DUfLj9/xwYrEMhBMEJwDOn7M/CSb1NUmLfLa++F2StuxwVwPGGZEQh+FADu+b6l4GT3T06elz85sZtKSdTgLIO63RlOybVgyYd3bYmMxNrjH7l9U5i8XieOrUYSCnyJF11RI3JG4jx8aRJKMx5bpmsDAN0DIzYnx0epqJSf+SRF4GO+QlCbNfa13/vSHJ3OY2t7nNbW5zm9vc5ja3uX1n+76dHHOb29zmNre5zW1uc5vb3Ob2G9ocaMxtbnOb29zmNre5zW1uc/vd2xxozG1uc5vb3OY2t7nNbW5z+93bHGjMbW5zm9vc5ja3uc1tbnP73dscaMxtbnOb29zmNre5zW1uc/vd2xxozG1uc5vb3OY2t7nNbW5z+93bHGjMbW5zm9vc5ja3uc1tbnP73dscaMxtbnOb29zmNre5zW1uc/vd2xxozG1uc5vb3OY2t7nNbW5z+93b/wO5WhXrU4eZ4QAAAABJRU5ErkJggg==\n",
+ "text/plain": [
+ ""
+ ]
+ },
+ "metadata": {},
+ "output_type": "display_data"
+ }
+ ],
+ "source": [
+ "plt.figure(figsize=(10, 10))\n",
+ "plt.imshow(image)\n",
+ "for mask in masks:\n",
+ " show_mask(mask.cpu().numpy(), plt.gca(), random_color=True)\n",
+ "for box in input_boxes:\n",
+ " show_box(box.cpu().numpy(), plt.gca())\n",
+ "plt.axis('off')\n",
+ "plt.show()"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "8bea70c0",
+ "metadata": {},
+ "source": [
+ "## End-to-end batched inference"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "89c3ba52",
+ "metadata": {},
+ "source": [
+ "If all prompts are available in advance, it is possible to run SAM directly in an end-to-end fashion. This also allows batching over images."
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 30,
+ "id": "45c01ae4",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "image1 = image # truck.jpg from above\n",
+ "image1_boxes = torch.tensor([\n",
+ " [75, 275, 1725, 850],\n",
+ " [425, 600, 700, 875],\n",
+ " [1375, 550, 1650, 800],\n",
+ " [1240, 675, 1400, 750],\n",
+ "], device=sam.device)\n",
+ "\n",
+ "image2 = cv2.imread('images/groceries.jpg')\n",
+ "image2 = cv2.cvtColor(image2, cv2.COLOR_BGR2RGB)\n",
+ "image2_boxes = torch.tensor([\n",
+ " [450, 170, 520, 350],\n",
+ " [350, 190, 450, 350],\n",
+ " [500, 170, 580, 350],\n",
+ " [580, 170, 640, 350],\n",
+ "], device=sam.device)"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "ce56c57d",
+ "metadata": {},
+ "source": [
+ "Both images and prompts are input as PyTorch tensors that are already transformed to the correct frame. Inputs are packaged as a list over images, which each element is a dict that takes the following keys:\n",
+ "* `image`: The input image as a PyTorch tensor in CHW format.\n",
+ "* `original_size`: The size of the image before transforming for input to SAM, in (H, W) format.\n",
+ "* `point_coords`: Batched coordinates of point prompts.\n",
+ "* `point_labels`: Batched labels of point prompts.\n",
+ "* `boxes`: Batched input boxes.\n",
+ "* `mask_inputs`: Batched input masks.\n",
+ "\n",
+ "If a prompt is not present, the key can be excluded."
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 31,
+ "id": "79f908ca",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "from segment_anything.utils.transforms import ResizeLongestSide\n",
+ "resize_transform = ResizeLongestSide(sam.image_encoder.img_size)\n",
+ "\n",
+ "def prepare_image(image, transform, device):\n",
+ " image = transform.apply_image(image)\n",
+ " image = torch.as_tensor(image, device=device.device) \n",
+ " return image.permute(2, 0, 1).contiguous()"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 32,
+ "id": "23f63723",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "batched_input = [\n",
+ " {\n",
+ " 'image': prepare_image(image1, resize_transform, sam),\n",
+ " 'boxes': resize_transform.apply_boxes_torch(image1_boxes, image1.shape[:2]),\n",
+ " 'original_size': image1.shape[:2]\n",
+ " },\n",
+ " {\n",
+ " 'image': prepare_image(image2, resize_transform, sam),\n",
+ " 'boxes': resize_transform.apply_boxes_torch(image2_boxes, image2.shape[:2]),\n",
+ " 'original_size': image2.shape[:2]\n",
+ " }\n",
+ "]"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "6fbeb831",
+ "metadata": {},
+ "source": [
+ "Run the model."
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 33,
+ "id": "f3b311b1",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "batched_output = sam(batched_input, multimask_output=False)"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "27bb50fd",
+ "metadata": {},
+ "source": [
+ "The output is a list over results for each input image, where list elements are dictionaries with the following keys:\n",
+ "* `masks`: A batched torch tensor of predicted binary masks, the size of the original image.\n",
+ "* `iou_predictions`: The model's prediction of the quality for each mask.\n",
+ "* `low_res_logits`: Low res logits for each mask, which can be passed back to the model as mask input on a later iteration."
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 34,
+ "id": "eb3dba0f",
+ "metadata": {},
+ "outputs": [
+ {
+ "data": {
+ "text/plain": [
+ "dict_keys(['masks', 'iou_predictions', 'low_res_logits'])"
+ ]
+ },
+ "execution_count": 34,
+ "metadata": {},
+ "output_type": "execute_result"
+ }
+ ],
+ "source": [
+ "batched_output[0].keys()"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 35,
+ "id": "e1108f48",
+ "metadata": {},
+ "outputs": [
+ {
+ "data": {
+ "image/png": "iVBORw0KGgoAAAANSUhEUgAAB8YAAAKgCAYAAADpkhewAAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjcuMSwgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/bCgiHAAAACXBIWXMAAA9hAAAPYQGoP6dpAAEAAElEQVR4nOz9aZN0SXbfif2Ou997IyIzn7X2tbuBRi9AswECJEESI4JDcTZSJjPJxuaFjGb6AvoqeimTvsKMFo6NTJQww21IAUOgAbCxsZfqru6uqq6qp541l4i497r70YvjfuNGZD5V1QA5MoPFscrKfCLu4uvxc/5nE1VVjnSkIx3pSEc60pGOdKQjHelIRzrSkY50pCMd6UhHOtKRjnSkIx3pSEf6S0ru/98NONKRjnSkIx3pSEc60pGOdKQjHelIRzrSkY50pCMd6UhHOtKRjnSkIx3pPyQdDeNHOtKRjnSkIx3pSEc60pGOdKQjHelIRzrSkY50pCMd6UhHOtKRjnSkv9R0NIwf6UhHOtKRjnSkIx3pSEc60pGOdKQjHelIRzrSkY50pCMd6UhHOtKR/lLT0TB+pCMd6UhHOtKRjnSkIx3pSEc60pGOdKQjHelIRzrSkY50pCMd6UhH+ktNR8P4kY50pCMd6UhHOtKRjnSkIx3pSEc60pGOdKQjHelIRzrSkY50pCMd6S81HQ3jRzrSkY50pCMd6UhHOtKRjnSkIx3pSEc60pGOdKQjHelIRzrSkY50pL/UdDSMH+lIRzrSkY50pCMd6UhHOtKRjnSkIx3pSEc60pGOdKQjHelIRzrSkf5S09EwfqQjHelIRzrSkY50pCMd6UhHOtKRjnSkIx3pSEc60pGOdKQjHelIR/pLTUfD+JGOdKQjHelIRzrSkY50pCMd6UhHOtKRjnSkIx3pSEc60pGOdKQjHekvNYXPe+Hf+Su/ymtf+Tn++t//TQaApDR4RIQEqBOcKt57nHPEGHHOMY4jOWeapkGzAoKqklKye8tv5xwi9t04jogIXdehqsQY8d6Tc8Y5s+WLCACqOv07pQSAc256rvce7/30znEcWSwWAOScyTlP185/APo4oqrknBERQgjEGNlut1P7APq+xzlHCAHvPQDjOFq7CKjau4ZhYBgGQghTH09OTmjblmEYEBE2mw2Xl5ecnp4SQkBEGMYt3gtt2zKOI33fs91u8d5PY+cQxmGY+pJzpm1bYox0XUfKifXmil968wt886tfw582nLUtH/7OH8CPPqJTyAGaJkxjnXMmxgiA954YI6qKc24aF1WdxrnOQb2mtkNVp3kKIRDCbtnV+Q4hTNfVMcw5T/M5XyP1d8oJnV1X31d/NCsCNE3DZrMhxshisZjmt1JdU7U98zVVn1nbM/9sfp2frZubKKigTtg2sFLPaz//BX7/v/8X+AfP0JOO1aKzcXGCB4KAAIMkejKDz3z1V7/Jm195i4ePH5KzEpoF6jx+uYS2JQIqgiYhZNDzDb//T/4Zd6KjGyGJMjjITnGAqAJKboS1RH7x7/4GL7/1Mk/WF+Rkew7nUQUVj/iAuEBSWIvn7pe/xksvv4qqJyfIKEkT51cXXG4uuL1Y0vmW5tYZIxnXD5z/+D0e/+D7LGWEHMF7omSyTzgyTh0xClfa4u6+yDf+xq/jRMkCWYSM4HHImGnV8/4P3uXJgw+5+uE7fO8f/xa3E1xoT6+RLgkNjugdWTOU+apzvDeHzhFVcM4TgmO5aHHeoxmc84jzOFHiONCEQN8ob/+Nb/L2r3+TH33yPks8p1FIzqGLltA0IA7NiqYMMfPww0948NHH0HiS5mlf1XUzrW2nvPrWy7zwwgtcXl7iQws4VAQRhwqggsYMKZMc9E5pFx3xwyf84X/z/+KV3qNkepcZsf3YiSf3Ay4E1kTu/PybfPk/+Ztc9VvjNd4Z79RMKnwxpkQaRnI/Mj4550/+xe9we3Qs1BFTIorigid4403DME48NWdIKdlzxvpZnngfwMnJCaenp/jgcQduWnKwp+pcHV4z/z6X3zftRVUlizAqPHn6lMePH7NYLGjbduIB3nsaH/AioJmubTk9WSEo5FTWTsaLktsWvb3k537tl0knLW65wPlAKGegCy2N8ziFMY5IVs4/eMAf/Q//irvRE2ImBZs7nNBlxWdYS8S/eo/f+N/+F6xVGWLCOUfOeY9P5pzJKKRM83jNt/7b36IdMlEgeuMfTQJyImO8MKKMHt74xV/gb/znf48PNs8YAvgkNOqmcat7o55bP/7T7/Lwd/6Y277Dx0zWxOAhO/OuO2s70phYj7Zm6nlW5YF6tmd0mp85L61/1zUyPz9yztM5XmYdnGPrI299/ed59Stf4Nm4ZXl2RggdzjX4NpA147LShABFBmDd89v/z99Cn16R+0QbGlQgBsGdrRjJBIT45AJNkbPX7/Nf/u//EZep59H2kl7tzPEIXgUnvvTJ+EuKkWEY+a1/8lusL3s+efiEDx4+RIJnu96Ss6I58fZbr+Fc5s03X+Uf/aP/HTlHNpvNNDZ1nnfzIIzRzuMP3vuA3/qt/x5NmdjHac2uton7zYJ7qzNWEojDyCjKFRF354T/xX/xn/KLf/3XUC9QxtYjBLX5P//kIR/+4Ef8yb/5fX7yk5+Y3FDmw87TjKqdG4cy23y+Dvfq/LpD/ju/5vPS/IzerQmmdXutDTM+chMPsTF3e3LP/Fq54f657HPIg+b9rN+rKlkzefZZXffz+6psVen68wF1gOw9e/63Air7bTy8Zt7em8blpjbMr53LXIey4D7vlcJ5Pn08n99fRRC8c6ScUcq7BBBB7RV7Z/nhs6Z3zeZtvibn94UQro3b4bjc1I95m2POiJO9sZm3aerX7O8qN09jXMdu9q7Dc+1539X3Vb3n8L7Ds7H2dy537z1bTD467M9h/+frYL7HRQRxZa4O5mVv7eAQ2dcbah9Kj8mSISsuC5JNSFYP3dmSv/Wbf4tm0ZK8p48jF5eXPH32jPXTZ3z87ntsPnnCWdPRhY6LzZqroWejkSGZXrPwDadNxzK0tOL35qeumWnsp8HcXxvzMb5prfyfv/+7/Hnp23/0fyQnkycdmRCUGEe+8+4nvPvhwIcPMw+fJC6fDYiCiIOs5JTt3FGlH1NpbKbOyJgTOZme1C0WrE5Op3M7ZWWMkb7fstls2GyvGLcbhqFn7LcM256h34IkMg5wdi66E/7+f/Yb/MO/81Vevd2xaCGcOZJbcNLepwt3WbS36dpTmqYh6kCMAzFHNuOGR1eP6NfnnDTKSdfQOJPF+2FgPW6IOjKkzBAjMQ5s11cgmeVyyXJ5wmpxyunpPW7duo1zwc6uoi8qicv+gqeXj3m2fsZFf0Efey43Gy4vr4gxk7OgKihKEzyC3R/jyJCEzXZgvRkQ51l0C85OVpy2DS/dPuHFe3dYNh4dB9bbnmHMxAzP1msen5/z8Nk5fYz4NvDyyYK7pytOTpasFh3eB9R7tmPkctNzvt4wqnC2OMM7k0tdFkQ93nlCExBn+s122/Pe44+4PH9GcI5lF1h2LV6sz1ltT0UVNmp87t7du7xw+x73T29z9+QWnW+JQySmjLiRrnOchDP+6f/lv+Gj3/oW90bHqQ9A5mqzoR8jH4fET8g8zJmTDH+vvUV68yX+ycNP+PZPH/Dk4TO6uwHCipPkyALSBk5v3+J8eMavvPeU/8PyTX55ecojueT/9tGH/Gs551EHzjWoCg+HDSnDrRTYirKRTAROBF7xHR7P45x5oJHHkkAzbcqTzlj34OE+reQkkzJo0QFPTm8T2hZyhnKCqZpcO8neEy4Qr8k2zjekGGmahqZp8AXLmZ8p4j3OBzxq+I4PNp/iUSBlk4ty8KhY21AH4vG+JYSW4Fu8D3gfcAEEwTZ/xdoSOZsOllMi5UQeNsQ4Mo6ROI7T56arRdNXcwYKLsZOftFsv2UaN2fvLH2PKU16NkBWJeWESMZJATV0/xx2IlRGqnL9fJrmTkHryeiun7vXzn/b7Hvf1/7I7ExLeXde3SzDlGd7P/XV2lJ19mDyBNY/EeOd3rvyDmfnn9h7EYcPnhAaKP1yIraffaBpW5w4QFHvULc736tuKWXcXNGLTk9voQoxRVJM18aPMq5Ovb1SgdpnYBx7NtsNQz8Q44g4a9NOhN6NySTPzOWrsidSiuScyCkTR/tbs6JF7yMrWSOaTRa2Nlj78hjL0Ope+/beX/QOO9MykFGtmF+EXCWnvcVj60YPFgSKaa/7spHahO/wIkBE99ff3sAe3Hs49DM9ZLoHN2uL7L6qG6T8X9Gd/pJ34zI9T3w5x2fjVNZ1laXA9Oqma6f2lt2zk4NnA+Z9MxvzgrmWvrki1zoRHCZjuhBouxbvPIoyjtHwKZSYRrJmgvc0bTvhXXs6oCpZ5/vK+uJKX5zscAmp8v9sHnLRu9MkR4IveElOeTr3VHXiX1r0cC3rM6VIrt/nyt+LrqcDkKexFCfUAat9SDmj43aP901/zXUMAXRfV7lZnyg/e2tjnxRKf2afHcig9XdOqTxrpwtNe/KA5u8z9uSsX9N+dyBh+tv5Bh8amnbBarmkXa1omhYnAdSRNZV3FRlM87QfU0oMmwuG7Zqx781epAlxu/6oKiGEctbo1PpxjKhmUqp71ebHB7fXX3HO2hNafGg4OT3j9OSMxnUM44anTx5ycfmMYdiSc9rxx9k43iQ77OnEogRxnLnA225JGAc+kp4tGS+ehbT0ObLOI6fASWgI3jOOPV/O8L/R2yxlwZ/4xD9ur/iO33C66RjQgosrUYQYhbtvv8R/+rWv842to/s33+OD7Tl37t4iMfLFe3f5+ptv8uqX3+Tq6QXf++73+eHTCy7jyKILhC/e5/GvvMLvPvopT7dbJAk+J9QnUoRc5AUlkrNhS13b0jYtbduyXC5JUte0sVvVXM4+mfaYjYsDTUBCcyx7LeIcePGA4pzgXLHTNZ7QOEKw89E3DYtFQ9O0hMaxWrbcPl3x0v3b3FouaZ0nhBbvW5y0iG9wLhBTpB+3rPs1V5tLVCPL0OCdGG7nHMlH0uggBlA71504ksai5/Ss+4HNMLAdR7ZxxAdP1yxYLpacLJZ0iyUSAk1o6JqOk8UJJ4sTWt/RhsZ4nSt8QBNx6Elq/CjlTN9v6IctSkRzJI49m/U5j9fw7DxxfqloCpytznj57hl3VwvunNxmtTiFpuNRGvjOD/6Mn378kGdPeq6eRtbnA8N2S98PKCZfNk1D13U0TUsbGlAhpUzfDzx8+JCf/vRDLh7/lM36gmHo0ZgMtamymNh5Jc6hr7zGz3/xC7z92uu8/tKrvPziayxP76CuMeydIntKc40PMfHwOiblgrilv7pis95w+fgTLh68x+aTdwhcIJ3gGk8S2Iw95/0VWx3BCQ6bT6cQ1KFeSDmTY0ZjRtR0RtViCw4enPL//Wc/uJmhzuhzG8bnIE2MEVEDhwUhF2FvDmRXg2qlcRxx4szIVISb5wF0FVA/BH7mhtI5zY3lc8C0Pqc+txqvD99X/56Du9UwtN1uydkUbhEzhuec2Ww2AJOxugr6q9WKdiYAxFFJyYxBKaWp3yJC3/csFgsbzzImlYZi5J4LEpvNZjI6Oefo+74s+IY4jHjv94C9+pNSmhSO+n7nzLAFptygGT8bm8MxqfdWQ9chIHboXHCTkjF//yE4fA3cnbXh8Jrp37YsbzSgO+fQnBmHcc+g/zww82ehuq7mAOpNNB8D1XqcC3EcGdZrFosFQ35qCkLpS7nThLKsqCQQxTn46Y9/wotvv8Tl5RWLxcIMZU1rey5G1HvEuSpRgYNIJiEYJFTmBzXjhipZlJwUvPKT736PF19/Aa3zq6A5E7OaLUockMgqqHMs2pZh2xMTqDrEO56eP+XW3Vt8753v8MQ3vPTCi9w7WeLbgG88y2WHOhjGiHeKqwq3WFs0JYQGzYnT1YrgHFlj0ZjruBoEF8dh2nt1X8+F5t08FOXmhrmZ1pRmA8IUSIrETMDGUrMBAeLNeEK279797vd585e/Sh4Sg1MGCQbU5oQmh+GSavdn5XJ9RbPocMFPxuEqSFTlspg1ePjJQ+7du4eIJ44RcR6cK4KqFtxCEYUUM6Mk7r/8Mh998AjvA5lsbVEtHVdyTiBC1IwExyePH/HmZjAgXxQnmFKrFQpyZgzOgDhSBnyAJORk1zjn7R6pBrRUZGiHKa07EGkysN2wZ4R9BeHPS4eC6yEvVOdQdmfP4Too2+9Akd7tndraOl9Xl1dcXF6AP2HRNpjorkh2kDLZBzxi6yBlIhkNjpjBB4eSTeBAyarEFHHLhk8ePeTi4oKxaSbFR1X3ztWcM1HNYNlv12zyiJ3T2JypyaWiuhPQbGD4wQ9+wC88/hVk6dGcSVFx+L0zaA/8KyBNrnKSwWUTsKIKqYBg1Zg6P39nE7R3DtxkSJ3P5Xye5p9LUYC/9/3v075wRu8hh0DTgpNIoAVVc3BwApoZxpFWYTMOtE7AO1JOOO/NcJASBFPEK5jy6NEj3n/vJ8jpksthgzbmcZARkoJ3gQzTgOeU2G43nJ+fIzQ45xjGEV92ds4ZVxS4nDMf/vSnfOc73+Htt99mHBNgRtoKtqrmooAoqqagPnz40M5bZTLAUeSwPkf8omWMmdEp0cM3/uqv8mt/9zc4ffE+WRWXASdIVoJzbM4v+eAH7/JH3/oDPnjnXfJmQIDN1RrnbTwcgoozvjIzytZ9Nqc98FfkM/fzIWD8s9Dc6FhpLmN8nidK0cLnMszz1mP9PVeU54bC+tlcVpmul5ufN293/f2zjMehkVphcnI6dEw8lMvqO+f9mD/rJuD5Jvn9efSzz+hznqPGjyeD88/w5B0otT8BdWyqE8qeE8is7/MxuElGPdRHpmPkQH/5WWlfftyXiZ/Xx8P5mjsd1fXwae+bP2P+ruqsNNcLblr7h8+a9DgF5z/D+WVmFLmJZ2iZf1wBDHFTuwDjq5rx2aNDZHu1Jm57Yj9CVgNuk5KlgKHjSMqRpAkUYoKER0JbQMd9veJw7HWHYd84fodz8edZA3NyziPqjYeT8T7hg7A66egWGR9Gk9OdGcQrz3GuyARFDihIvxmOSv90z6Cwf+aK7OuBBpCyt66UBGpmo6o7bPuBIWZUBOdNxo6xp5cNworgBxpNmGOtAXKoOcI437BcnLDwSiOOgIBTaB29jgzDwJhGhjgS44g6R/AtIi05e2LEDEQKkhNkM6CgmcRIyiORyKgj27Hnqr/kfDty1Q/EMZOzybehGC8FISdljMqYUhkUQRyIU5xTYGQcN6w3DskLvHpiVIaU2Y6JMSoiDctuhbgB5z1BGhweL2HSw0WFxsGybQAhqedkdULjzfjgcKAekhanXVv/bbPgBe3pGmdO8nnksl8jKD4U41VSC2RolOXZKbdPbvHSyV3ur+5w2p4gbUtqM7EfaLuMSOThB494/w/f4WRUBDN+NuJ56+VXOXOOP374Eet+i0e5T+DkfEN3ueX1VcuPbnU8eBLpRo8ngcCI8dhuHJFVx9Ui8DRnHmw2vJ8vedcNfCgjK5aE7BliIkfFiaP3EItcHhBOnIHyF3HkIke2ORWbUy64lOyMmTfQhDEotn6dw4cC9DctXgQD3yN9Hw/28oFMOudZmmlbA0edr8YNJY4jMSfjRdF0wCZ40igkHwnRDN3igxm9pEHdzmm5GsLtd2Pzj0MVvAykFIkxTr/H2BcMZCy6WUa3V8b3ohnE1Ra79UeryURQdnv+mr409TuX23afC/P/qRm4JkuH/Qqhmc70+pkZ3A4nqDatALXFqpdVdt9NtOO7ItUIvQNjzUiyM+5MzrbOm75bdOXqFMTMKKWqENrJUFf54U4vrDzR0YTO/i44lHPm1D4Z88SZXO28YTBlDM2Q46axMn3VzhmtToE4A3uzzZAkxXvFbTfklBjGkXEwrDHrLkBEC7bghurMkUjFuJw1k2IkxnEybIuOHJ7B9bjbnWM6nQXozOhYDH/ZPE1286ZadMZc9uVu3qGaqGdy8rSebN5cWY+GPWiRA+ZinZvONNktwt1cia031bnMIjDjD3Wt7X7Vv6vcVM88uXaNjesOy5ubAfafVXt7QAaczNqjU+dsr+zW/I4HRbLs8Aq7zpwmzChQZFRVtO+nPXcgyVib6l4Xmfphe9LmOOeZPicgWvaSd8azSltzlT0QkiYyuTiK+D19cLaKLCqr9nsmV8wxZURQ2ckp1eFkT/4ucFfjmjKXYuYTt3vvJLaVPaGTzF/HYtc+AZKOgE59mAez5LwLuMvD1W4O2Mnfc9lPpAaP1XfNfiYHEgxPULMLTHtiuta66gQSGdLOEea5OnnV8+afMTsby1js60j1XXm6xkTiVH6mh+OcZ9heMWwa2ssFoWnwTYMLHW3b0C1WOBeAYI4H5bx13rDbbrGk3264vDhn229wBj6jmskpMWrGE4qOYDyl6l7mGFP7VrDc8r3ZqSCmhCPStB0V70WgbTsWyyXbfmNOYuw7BX8aHeIAiUxP4oLIPedZ4IhZLfDCKTErvkxA1AxZwDkea+JChffo+VMZ+ZiRNgoRJYmaI7BmcsFfXnv5Re7g0ItLnm4veawbZO05c+AGW1u6bOmfJVKOrFzGeaFJwr0Pt3z9KyvOl7f4E4Wn24GzdkWva1sDKRu/VnO6CiHQNIEQ/A5PqCeZMSKmnaJywH+LzF2waDvWZPadBXyAQyQj2RX5VEEy4hMpBZxLtJ0nNPZj7EcJvqELS9rmhLY5wbkF4pQxDnjXourQLKQ8IFJsYUUG9r5j0S3wXQta9NqcGVPPMEacj+YEVPoSvDmydW1D17QE3yAqaFKSJEaJ9ONA4xukIHxZ00w3NcatGVI2HHccTQarckPwDYvuhBfE06I0LtGPjsY3du6LIF7wASRkyAPjuKbv18TR7BfONTiXcC6RVPb4bd3DdW9P+3pv3z9/zQsmG3nnJ4x0suMhU9CTyXwH9z5HlqhrqMrHdS/ZoFlQxRAjQ0r0sTjOuDzpPWLCYNHXFU2Fj2ZbI7DjvTmlSc/9LPoZDOPKdrs1o2xh1hZBJGQHkk1hmYScGThZDw4nHu/3mUkVHOu/K/B/CM7MjZ6HB80cAKpA/PxAnX8/Bx8PQff6zpQSY4wMcZyuBXMIaJoGEZkM5bUtNbLOGEnDMAx0XVdAt7gTkEsf670ppSkSvUZTt207RZDEFAnB0TR+alu9pxrXxnHEFy/SOVCUUpq8RcYUCU0wTyrZgZvTfSnhckbdfjT03OngEFibj/E80m8+R/ODeu6UMN+wFZi8CZSez/VOGSnPcG4HBM3WwiQolY0zj8yat/3fBz3vOYcgmCllHu8NTBmHko2geF9P4wbF4bse80JwxkbOHz1m6PvJ0J9yQothWJwjF8Vb1CNZIUWyF8YxE8qzQHFZ7XvR6ZALIfDkyWPG7UAaIhLEHL7EACEVUHGImkEoZxi2a05v3yFkx3rdc7lZ8/jJYx48+pg4RD548gl37t7DBU/OkUYoIIFFgDsxgSVhHoUiGR2N6aUx4wWsV2UMK/8uOkKNvssoy+XSBNaxrEFAcvUAzUwn9oz2I1kBks2Fgk9K40yZypXBonhnBl+njuFizfmHj2ga81Ta+ITHWUSPmNdV1afGceCtn/8SD376MdvNmjSMZjAXKQ4HZc0kEyJijPRb8+pXzCuKbAKDVpYfk/XRCZmEB7brq2L4DqSxn/Qv4zWKlxLZ7xzqHcM4kMv7yMZX7FXKGEfGYTBAahxoV0s0eIYhGVA5Uyxlpvhc37/s8d5D48L82k8Dxj8PHd5/aNRI7O/NagjZf99N/KeCRhShJ5MSJA8Xl5ec3T4hixJzLAqjAWwuJ1TMmBrJLG6dkbvGDNrbEe+k6OuZWIy0A5nudMV2HBjiiNSIhFmf9kB3L9A1NLdOGJ+uLXsF4LMpBRX0KXo1KtC0DTEltlc9uQt4NaF7bhgCigA3cuvObR6tOrbrkaVzpheVYdKypial7oY2ziZhv+2zuXge7z80CqlWj/CRJjQ8fvKEcOcEl0Zy9IgL+NEEo6YCct48CseYeOGNV/nwuz9gKRZJFnBmbCgCmoo5EmWBPkWuNhtC4xjGHtSUs4R5zDupCnUu4IGNX9O1bK9GQhOmvjUhTGCkZWAZiDHxzjs/4MUXX9zLnjMfG/ttRnzUsrqI2LoJ3mQGQYgCW6c8jVtWoeW1t7/I3/g7/xGvfvEt0iKQg6dRIceEQ0ij8tP3fsSPvvt9vvtHf8qzh4+QmCcBOBdtU9mdqQ53ACztz/cekMH+Xr++FD57rz9vrcw/+8wz+HPwkjk/utEIdiAr3vTdXKac93v6266+9t75eB1G436aIXP+jPnvw+8OZd/D/XTYhpuecTiP889uitbeDQ7lbP9sB4m92w5kxEM+cTCMn08OuwHwqLJr1R32+cz1tXXTuF2jG9bPTf34VNpr9s6Z6NAJYv7MQ9451wWqrnHY/5uedbh3b4r2PnzXTX/vzd/hhM2unZ5X8ZUb9uF0rRZAtoKFzuSQ4BxpHAleQEeGiyvi5QbZjjQZGuzszzEyxEy/3ZoBQdOUTSg7JYeMqBnxK2A6dwR+zhQ9t1839eHPS7aPHM4LTjLizVFguepYLDNNB85nLKvQjEfLzpBdg51kFiImCM6ZAb0K2PV6mfVjD6hmn9erlncUWCirsu57hpRQMWE/ayJpIupIygMxj6Q0kEoEoIHDedLtmqaldSbHODV9pQkOHx1ZlKQjMffEnMB5mnZJaDqcWJRxTokUq4HH5Ddrw0hMsUSGmS4To+LUDNU2duac7MTjNZRxM6NVdpngHMF1OO9pm0AXGpxExjhyeXlJHBMhdBZxMiTW25F+iIwjNLIAF2h9yyJ42tAQfIMTGyONGXA0ziHtElVPEwKN93jXEHzA+w6nbtIvVCGElrtyiyY4LtYXXK4v2KwHYkqEVHQiHC54Fq3j/l2LEj9bnLIKK1q/QHxbHCAHumVmc/6En377+wzvPeZu0zJKZogjXc68desWX1yd8OjpOeebSEiJUxXi0HNydcXdOw13Tlv8KpB7pSORG8ODk2Zi39OertguO9696nHrDU/zFU9bR8yeRgJEJUZz1nVOWHvLGCEKjThWElDxXNBzSWQg49Sbc6+r+smn71MoqpU4vGtomg7nA65E8NZowWEYZvLxDlSc86sdn8gWEQzmeFrW9VgiG7PLEx7ppQMpmq4D8cHWVmgIbYc2LS6YQaYJDVIinxCxLAbJjN+kDeMwMIwD4zAyjiPj2DOOZjCvRjEZe6rxsjJdR8VRtKh0ztqUd5nW5nLU1OfyTC3jIJNeWG8pQHjJ2mCfuaJnKimmvc+lAqR1apxMwKk9y9olVL4qJYrVTe9ybhdVbVpAcfP2foo+nfAv7wntYndmixnt/czYNq0SH3ZRrHPsoFplxIIH2tDOgh3snEo5T7wNqp6Q0IKbGe/bndtaDdqSp7Gt85dnfyMl0rxxO2eIEqk91+Wm60fDb/cc1dHiZDs1F8nDLlJXdry9yrCC4UPidDJ6OwFfAhicA7wU/MoVoFxwojuHATHsQ4oBoil6zGQHnK2h6lwhTiaT3E5O2Z1t1Yg7/97mqgQVqE5Roc55Wx+6W7I1s8rhOp/rPFJw02lt6E7vnfjC7OzcXTP/OTCMq07X7faO/dT5n8K6y1RWuSVVvb7KeGo3V9nF5H83RUdPspgNCGna47YvoiZy0oKvTZeR0kGk84RDKTmWoJI6FmW+K8KYsGx1czmvPgMBzWFnKIEpwGePe8sssn2SaarzSVkflHVGsDmtsorbX0P7Azyb80m+cbvvrUGWNdJ5nAs47yY9xORDB8ECHCadpxhpp8Ct8v6cdNpH8zVh41uy++REjkN5vUzXzoMVRATx2SJ+Kz+e9QFm+FaN56xtK3Mgunu2eT64g3VYx2X3q+Id87WbUyangThAv74yx5/Q4LuOrluwSiNduyjOXI1lOCm4i0hAu46mW1rU79UFOQ0EB03wBG82ju06WsCg5mkvWz9lcvjU0mepunjFb4uMKE5IObLtt0j2tK3Hh2Dt8gEpzmNz6f7zyO1ObW0OZJ4xcuo6QvYEzQxZic6y2FSDmyZFsSwqPfDQCT+SgR+6gXPJLEfHiFpyODX5JGumaQNfOrvN/auR9ukloySCCE/HDcEFHm4uaR59xPod2KzX9GROm8CCjA5w/1z52iP44NU7fELmaT6ndS05XaG+Ogha773ztCFY9HMIOCd2rhx2vpz/0+ac9m1G58ZxzDHXTbfZejRHmurgUfaDKDiH9xmRZAZtNZvHduhZBMeyXRFCS9eu6JpbeLdAs+GlyUEOiiw9Y9oyDFvbU8Xe0rkVy+7UDOjJMm+lPBbnTYciJRreZAIfgukjTUsbWoIrZ1X5UUymHVPE+2i4bvbTnjSZw1Mzj+RU9AsXCF4Qp0BD4xsWokUXiFxuMykLSZSomSH39NEhOrDtL9j2l4xjT1ZzorRtv58F5WbaP+fm+t5OB9z1r1LwvvAxmX5L4cs6iUH78l+d68PP7IsqB9fMQSWzYra1rwpjTAxpYMxxhiW56WyteiNaHlcdwqgOh9Zfc8i5IZvODfQzGMaZDHJZzfveBEOKkuyQokDMoxSqABpCsAWR8y5N2yxCB+y7Ggk7H8xPA2Pm3mLVuHhTBE/9e57ye35fff8E8pWDZp5ecA4M1HbOjeHOOZqmmdKoT8LowXtrGxeLhaUZLuM6H695dHldODmbp3zTNHvGnCpkxjFO6dc3m830LOccm4s13bJlu93inC99s/SUTUllMal6B4reHAy8CVytRvw6TodzVv+eX1evqVHxwF4a9sPUrJ8GrD4XqNSdN191uDiMoPnz0CHIeNNzDsFXwVK/57Qbv2EYzHO89DPGuFMG1AQpp2qMPo10bct2vd55bkUDeRTFxYiGYOumHG7iHcvbtxiHc5pS6iDnXbRllbVzzowxc+v+fbbrNZkEqUbku4n5mAKYyBgjfPrJJ7z86hvElNls1qg4Ft2Cu/df4XR1QnjrbTN8p8iiC7Rj4tH5M8ahJ6CMOeMSZpCDSVBzKjiU2G+QbClxzDuSmVAtNG1Ds+jImmmLJ+AOhMz1QjvQ51L3TfOkGefLETcpg/MDvhrhzVs9xmheeBn8oGwYyStHyDb+QkQIZS9nXNty2Q8szk45f/LEjGSppGUu81kV3jRmFmenbLdbYkwlpbuizoBRncAHRVMiRWXQgYeffGKpUEqmgKoCySTNmjfwSOJyHHj15bcscr8NRTCGOCbEm8CaS+mLOEbGolDdffklnv3gfbqSSimnBG63xysIOd+TrjjefJpR6Sb6WQwp9Xo/c8qZt2H+rvl5MDcg7EB8JiUPigNGVtwsN18IgVEzy5MVoW3oVgvGbOs4eBPAY844hSx2OqsT3KLhK7/yDd75vW+zaj0uZYtULopx9LBOI6++/gX6oUe6xbTf6/qetxURYk40q463f/Gr/PAP/4S86QlZZqkEd2OcnEXsvPTSSwzjiHolbQdcaM3zfKZ8TSCNKidnZ7z8xTf5+Ds/xI2JpmrnZY1pGacKyDxvXp2U6PiZwW9uBJnP0cRzDq8rz3fe4dqGhNI2DUksEsJSumVEzUN3TJGUYUgRFzNv/PyXePTRA7YPL1iIN9DKgQ/esmtoJmHeut3pCtcGLq8uyYajWGpDStSKVABdJ37hgufevft8uH1QANdyRoiQ8wZRc5RRzYTguH37Nuv1mpy1eOb6a+OXSho9AV544UVunZ3x9MlTQtmHmpVRYCtw+vJL/Mbf+lv8wi9+nW7RkZyQapRlzAQVPvrx+/zxH/whP/zO99ieX5K2PW60lHcRc7DSnHHV0ZBSoibnPcX78Iyfy1lTtoEbHNPm+3L+nMPvD+97nsHxL0Jz2eZwzd103SEI7m7gOfO/p3/fcP7U7w7X+Xyff5ZiPp+L2Yc7QObAmbQ++7AN8/vn/z7sJ+xH6s9B1sMMEeUEuvb8T6Nr4zyDSae/bnjUjcbLG0Cv+Tvm/z6UeT9Pe2+6TiogePC8n40KiHVw3+HauInq+6o8PZ/H5+3Dw724/7dMPHuuKx3ygDkdrjlXATeuj/Xu3L0O/O1d5yw1n+mgAqX0xzgMrPKCi6fPiMuOPCiffPQhzy7O2W578jCS1j2tCzixSDknjuViQSuWStyJEMTR+WAATIqT8Xfe3t3ssAfw1n7N232o6/xFeVXKI5LNcRSnJI2ksZ8c3bpFpu0SW68lqpaiO5rhGxw+uyJr62Qc9wi7tMm1vTNM+ECXn4wZs89ytjTqrtxLhE0/MKREdg4JgopFsCD2k3VgTAM1uxDUdLwJLdEWXkBK6lOcIt6iz1USSUaSjCgQfEvTdgTfTdhESol+2KChRnhZNEqM0SIsssfLgs5HRu+4tfD0bmAYI+OQGIYRRVhoQxCPeDNULRI03YJusaBtgzk6j1vSsAUGrrYj6/EK2i39NtIPiaurnrHPSBZa39Jpy5k/42zlWK08bRdwIROHgZgyWR1Kg5OA8y3EZNFHxRC16hq6dkVKuUR+qkXfN7dwIoxpZNNvSAqbcSRuIo3zrJZLztqWu6slr969w+3VLVq3QF0gE2g0kAWWJ7dQWXPx4Ck//ed/wEtbR1h2bNzIOvXkYc3p1WNOvAGCi6i0Q+KckY/8AOsLlqe3eHHRcefubZ69/4zOJXIAhydkQbc9bTrl8nTBt7ZrLnLkhQTReU61w2dhHSPrnPAhkL2wdZEOaNWxFMfSNaxz5lwTV6IkEUIBB7WeHTfIDPMzxsghUlJZN23Bc8JUgsh7x6Lr2Kwv2RnJ9s/uHT8s0XxxRJk7JuVSksvKk4WS5tLKSLX4pqXtVjTtkqZd4BtL/erCwoy6HtDMMGwYxw0pDYzjlmHY0G+3DFebKVo8legY1ap37fhBEUqtz26XJnnydc1176dr/dvjY1r2ZB3XwhRFdvxRxM6q7ALi7V7vHcFV+dBSGE/g8UzG2HtnNW45i050TTvx5BrFWXFFH6yclUWCu8kp4TCwot7fNN1OXlImo9cUbV1lj2wA/WSoLpFfKe0yPTnnENUp42QqaepjTFO6ZntcAh0mDMAy+JX1lCzDha3bYlCYra/5chYxg7+mnTHHeHJ1GLDz2zvL7iaitt6qE4KIlWjwUgxEnuC8lVdyZUz9zrAssjNmOyeGmYjhkwLTevJiEYdVb5ivnWmeRPYM2RY4U1eTHm7bcp1ACPZ93umbsIv0t+tmkfgHZ2+dd5NR7Jn1+zQZZ3bXzvf7XBa+ieafH661nU6r3BQxfk1mwPTKfdmquJ5NshETHqdaMv6VqLiKLadkWZHGYWtPcLVk4O6crBHTu3U/S3UPln0zxp2jhY14kdlsjKYU5EmtPEvOuBp9nXPBP2f3z/obdZbivGZJKw5IO0cQ07nr3suap5T6c41NUcaDyMCKYe7hIdUTZOqPja9NtJuMPBUHnZxqikONr0F95RnSLqnrV0SmbGtMhnn7t29mJRmYbpn1ywzj87VY16Gd9UWuR2iCENwuYO5w3dXABmSXvhyMV2vW3RxoNYqX1IJSM+wouJp1aJaNU3eNl7qHtbZ1JEVIaWDo12xUePr4EcvlKauTM5YnpyyXp/hmYUFQSRFpWZwsWJ2ccbZZ02+uWC1a7t25xQv377DdXPGDH7zHgwefsN2uQWqGr2hjWwx2qWDoImKBXWVdAXhnpT63/RbpB3KTUV1YuUzv8d4CFG2M6hh+tmM6QIOnJCDniY6cusBJ9gQigybGlGnquVqwRZcy3jtchh+GxI9c5hMP2Xk0QUDJwVkZQIScRu7dP+ErLHjtoyfcerDBNbdZ+cifDU/ZkPnp5TmPfviMB9/7AS++9Ronr7xAu+7pn6653A4sVg2r957w9ddf4d1bygcMxMuR1mWyd6iKRSerEryjbRraECYcKOc8OavN99WUccpZdsGKSVkq9VxsgxVnmSQGanaGlMzRNaViKxRBXCa64qjQe8SUAZJGmuA4Xak5q5UU+ZIDZAtsa+x/dN2Cq+GScYhF7/H44Fl2t1gubqEqRAaICi4XmcHKocXJqcTkv8Y3NL6l8eacak7ZpRxOCfpMOZJyJKsn48x+o0DJNqtiTnJSbG4hdIRQjMKa0RCJwwW5a9kmy44Vh8Q2DzzbbhnTmquSiegibdlsL8kknNTsQQqFR9ZzYvdT+cw8i6rpWhS+Js6VMjpS/jNeWDYQXuzHFUP2ZBOpawFX2OqnY3uUHaZq2EAIJmco5vwwpmivTUrMmaRaHCWayelOVdGUydEcDEU9s8I+ZgTXIpeI4dOHmcyfRz9TKvW2sRThLhdvqKwEbwJv1v36iHPj9q7OdznWb4jarrRnEOa6IXYvdd5MCKlC0RyUr886BPgOn3UI8Fgaop3gXJ9djc5zA8W8v1PUarmn7/uSnvh6HfPqrVoNt/P7au3yaiAf40jbhWlSa/r2tm2nKOwKgtWol7lxeRiGnXB/DcyycfBYqgHvwiQcVZoD3HOa0sXPBKZDIOkQKJ47LxwCoPXvOaA7H+Nat36nmOVJaKjtO4xWr8/bpcfi2jhUOmxz/azSoTBc5wsoqYuuO2RMSsGsJg2qnJye2vrEDDy1nYpOAltNCRNjRAOsVkuu1mt8G3aCvUjxpMpTzR8p4Jf3npfeep0fP3zCsukgWlpsqYKghTySvWPII195+036occvWvMazRa9TBHu5kCgF2H95Annn3yM71Ysuob1GHnxpRdZLpbkmLi4vKTpOtomkMeRtN1y9fghxBH1QsyRRn15tDnZWO0RaLzn/PEjri7PWZ3eJmU1cC3bmCbNNC7g23ZS2lLaCdHiHCQThA95zE4p2u0JwQQ/37REhbHx4ITGe8ZhQ+eClR5wBtD0ZM7u3DFP/ZAJbSAWgadxFcS36PpEEaZb8/hv2tYiTppmL9NCLDwipoT3TVE0FAS8lzIHJrhX4U+cQ2MEhadPn7LZbulTJNHYVKmiJcWNaiaKoMERFkteeesNJARq+rapjmh9tlj6siSZZtGSh8hrX3qbsI1c/PhDFlLLVOyUq5R2fP9wj89/zw2983n5NAD5pgP20MBxeO38B3bmlXlGk2uGAzXlyk3/NiCpepIqVu9EVktObt9ieXqCKx6V3rlSB86j4vA4QhEekhNwjle++BYr3/Cd3/mW7cWkBBFGVbaaOHnpLi+89koBfHe1tedn6dRmFIJDGnjx595ktVzyp7/9e3A12NyLpVRLmqELDDqS28Crb7/BZtgiq45Qzoysu8jSOY92zqFN4LWv/BytC3z4J9/DlZRLBXmwMgjCTjme8eK9+eL6XpzP3eHZMOe507OcWF3YINy6c4c7d++iXYsLAfGNhSuIzYXHm2OMgHMBJLFaLPm13/ib/PG//Ddsn5zT+sZqK6kiIVjaVSfErLz91hv0cTQv5TLuU7Y8JwXEtjEQFIp3/i/+0i+xXv8BT5+9b+CVc6RYzzVhvd5w+86Kk1XHvXt3rS4b9czY1ded1nFWxHmGfuD09IRf+2t/jW/97u9x/vS8jLfSrZb85m/+Jn/3N3+T22e3bE7BylJmxQPj1YZ3/t13+da/+V0effQAhojPSpOKEJzzBLbNs/lMoFY5cw7n7qZz8iaD8eH+vDa387Vyw303CtgHe//QMeOme26im4xZh0a8571/ApSeI3tOfMrtr/W6v2q7D41qh9+JFOV1JgfPx6AagGrE0iHfrfv7eTx2ft3hnN7Ey+d9nu/56T1cs0tcG+Pn0bzvblJ39p9xmM56TtecNNkHxOdtPmzX89p7OBY33if7Z9l8bdzEEw/7OpezD+XTm9p1eM1839bP5tfMnUNv0oHqPVN7Z+upgm+HOtpnZjaQT5/3CaTW62fCrCNUQNDeKdNYo8qzR0/4d++/h8+Obd+XrC6ppCLEIteC4Jxy0jRksejVrFqACUWyybY57Tt3H473pyy7613/FJnmZ6GsA2Op/9o0QuMdwzByfrlhvbYI6LYLiM+4YlixFII7Y4n3fpd6sxpGquPKzIBRBrzADDuZoEZnuSozlmu9C0i2DE9SgJe+j2xTJNngg1h0a9Q1UZeEvCDnAdWSYlUpoTEJNFq6SReo0IulD7bavbUWoojSLRq8tOQMWTLB+ZK+M5DSwNomwXTFbCCc5sDCndEszjhrX2JcDchmzdAObIeBrR9Yy5bt0CNxjgE03OvusFqtuH33DquTFaH1jGkk5i1j3HB1dcn59gnnwyMiVsP+anvFsOkhKYvQ4hfmUKkuEMUjJMs45EYzZEcQGprgaH2LFwMZU7L57NuRts3lnPaFx9oYbjcjwbU4aYDAdjtY2bXQ4H3LSVRaych2y/Is0HZmgK86ngLhbMX777zPn/5Pf8QHf/odXj65zdUYWXUdL54s6JYDDz54n//Td/+I1i/QKAyjMnjl9nKBS8qbTyIpBM7bW/yP+RG9mEHOpwgZcmiJ48im8/xwBaep4f6wZKOPaKWhBwYnqDpacWzHkU6VBcLSCctgacSfxS1XZKI4c5xQQRxWC3OWEvjT5IAq2/jQ0DYdbbsAICVLQ46aAbNpLGPWXiQulX8bJqbZ0qraDrJ58T6wWJ6YU+PdO9y6dYvF4oSchUePHnFxtaXpOpp2gfONZYkK3oDAnIlxpN9sWa/PuTh/wnZ7Tow9KQ7kNJBj2jlJFoyhaIwzOSyXqPTW2lZU+rRr6G48FMvYNjtL5v2t2Idli9qN4SG/rP9edid03YK2bXHOygCqKl3b0pR6nKolSe+Bc9ThPFW9Yy5/qFqa1JSSlTrA5I6U8hR4AjssrmJW9mHc69vU18k4bQPpdecEUK+Z99MwPYd312WDaihrikzvRAk+I43hNE1T0u5PUa/gPDTO9Mc5DlnP6/nfnp1cN8+aWdemc5a+XZ3J9lLsf4f6pHVV8Lov98/7Mu/bXJbYGzudlcmSnQGlXiYCbn80rd7qp8hgpqNqyQQB5Lkj1a5Upq3XXXTYNLcF9JrLWtPcPEcGfJ5eMr/vUKa+6Z75Oq0BBzd9t39/RjRd+7zOce1rNS7t5qBkykzJysWkBNGcxc3YYZk2pTgReBHcbL6JgpNmf00cyi/ClNbcuV0a9QoT1nlxuWQ7ZJ8fXBtL/+n6SKWqJ9dnVIPwIS8Y2c19/Xx+rf1Yqt55CaX6Yw4t5lgxpGx6fs6kmMl5JKUtecwztin02/XkhDNve57zkTI/e/8+0BXsIwc3OAntTYEI2rbQhL2gs/lzKs+IKeK87Y+a7SDVkgtlD3txDAftr7k0TTzOk8OVYxZIWCIzD/uD7pxKiMrm4gmbi6cgQmgX3L17j7v37rI8ewFxZtMYY2S5vE3bLmztS8O9+y/zq7/yK/yLf/mvePfdH/L4yWO26ysury5IadzTm0sY1XWdExj6nqxiNatDw0Y3aKln7lxxDBo9MUeYORF8HprSSGdITnlK5IyOpTQkEUaJeGCwFI6lDLHDq5XH+Fa+5ElwXHiPes9VM3IyQI4jyTvwFpX+9tuvcqvfcvHsE4bLS2772/hly3J9iaK0Ktxbdrz2ym3+wd/9O3Q/9wbv/NGf8c63v8/2kw0/Xl/wwR/+iPsv/VV+7muvcP7SG/ybR/+We3c97irTBimOR8XGQLFrVEyo7NNU91XeGcWBUrbRdISYTG4SUbxj0h1swIpuIjIFmqVogSJ2fgkinhgz46hcxjXrITIme34UTwyeQRNu3JJywGmmxeTh1i0IrScS6ceIYHJd07YsFguW4RTUMQ6JlATEE1xL0kjMmSEmxphQxHBD582Jwe3KN1jmCI/63dkx5oRPY7GPZsvm4gLFSoQXT+NbtJEJY/OlhJJqMufU5UjMgRZHo5nzuObBg4cw9Nxadtw+WbA6WRJDg/PQtg3EhjwERGb6+YFhHPYx8WmPqxYgZcZfagqGPaxvnj3asGxLBTPHoZgy4NZr6+85DlHlOFEPeSxOUabTpVJWy/iPoOKgYLdOxMru5mRG8epEaCum6JE7voWkSa91Klyv1XMzfW7DuC/WfKuxayHtbQikZIsI73aeOrMBr2mywdJH55z3anBPB+iB8D0fxLkABvtR51XAvSkq5hAAmkcxicgkIFeBqrYlZ0txUQ3dNwG9c+8s7z2r1WrvkJnTvC81jXooEaPzf9d6yQBN00z3xsRkPK+G79reKcpJ94UAEUs/sjtYhWEY8We7iJ6claZprX5xGpGyweeCxjyK6hCIO/z3IXhcx/3w3jlIWOez0ty79NrmZT9ynwJQ3aS4Ha6f53l43gRwHvbvcEPXdk735QwHYPPzFDtVM2J7XwEeRVLGyqfswN+cMz54+qHHrTq0gVfeeoOwXCKh1KEqY+AKg3LeDHHqHGMc8cHz2pe+QHp6ycPv/YhFNi+fmrJHnCc7YdDEK2+9wfLsFFpvka7lHerquyyVkDpnggcCY8/3//SPac/ucPfl1wnL1YzhCcEFmrYFzXROuHj8iO35OZ0zo3POipeSnig4480xQ3a0wbPZrPmzP/wDvvbLf43F2S1StjpzWdXKAkRlHIcpLeJ8qHdroa6lfeXjcN2JWGq+pDA4Tzg7IYWWbRxYdp5hsyZgKfq2OTMsPD/3zV8iB/O87RpP03qcCh6HC8EEDLH6KQ7zDHROeeHll3n25LE5upQ6x4pFs/T9lhdfepFbt24DjsWiKc9wdkBgc52d4nLGkXFOSGIei6+9+QbxjU9Yv/M+CzVDZBVcsireB3od+cJXvsry1hkslsa3nRgfKEdK9SqOEgnasNVE9olGWn7hl36JP/z4Mdpb3hIlTVG8O/63L1Qe7p+6j+fKjJsdWs8Dkg/Pl0OFIh98fqOiLdd51v475zzBfmrTqgyRg+OVN14jny1oV0vaRWcexN4TKJ53ztMgePFEMkNJVZ4EXnjzde7++Cc8efd9rJIkFvl865Rv/I1fY+syoWnsrAztbIz2+aNXxYuZm7P33H3zVX7+61/lO7/z++Y9GVpLC+6gjwNDgG/81V+mu3OGNsFqQU3rdB8cqOdMdRSTJbz99V/g4qcPWH/4gAaTCVTN4zsVn8Gb+Od8QPd1qOeDCfX7Qz6cVKHx3H3lBRa3b3F29zZ5EaBpQYJ5cDYBBzTJMjLQeHIoWWqGxO0X7/P1b36D3/sX/7qksC8GPUC8p08jd1+8z2tfeIvN0HN65zYJxTWW8k3F9ojPJVWjgGApxXxJyflrf/2v8eCTxxMwlTAZJMUR7x1xjPzCl3+J1erEzmF2a9n5ne+jlBqxoWlYLhbEMfHG629w++/d4p/9D/+Mq8s13/jGN/gH//Af8NprrxNTZKSU6FBBozJerfnJBx/wo+98jz/61u9DzMTNloVvLd1+NUg5hyeXNV8jAIvQrHZGZdnNzXyODg27N52fh3P7af/+NJDq0wxNh0L489bW7vqb3/dpz/+s729SBCbX1edcX9vw6X1jBzxwczR+sZFcA6HmbT98z+HYVvn4Zv54/TmVL9V/T7JU8Tyev+dQvr9pPPbeV3FE2Zfx5t89D8Ccnw/Pm99DcPfTrr2p//Pf9uU8bWe+9v3h+XQ4ZuUh15bKoXx6+Lyb2n54Pt5Ez9tnn2ed1+tvWk+H/75pTPdksJkif/iO8hSq32hhuOZE6JxlXRkjOoxotpIRKRvAr4U3o0oWsTptlAxKM+XfmvfZfKs09rnjcUjzdfAXIecsisLSIydC4/CyJGcYxpFYUnCHEApgYOCTuHnUp3128OBSRkSpJYd268bhdGZcqfJHNZBXHa4OiBow4ZyjzyProWczrNlGIboLxjyw7gM5lhTRtDixKNrp7BOHZNA0MIZdxCQwOZuiFlWTByWKgs80Dfgm0LSdyU0ugERwrqSiNPkEHEE8QTyWwloYiCSvpFGKYT+Sk0Np7RrxON8QmgX3mnu0TYfbOMvotPCsVmcsb72EOmV7e8sw9gyxp+83bPotT8+fcHn1jM32ipQGRBJ54bnartn0Ed8IrvNoqVWoKmbsB1QTq8UK7xoU68tms0awuod+bkxzga7puHNyGy+OtqQHvfLrEg1quuHF9or7/ZZ48RTnG3xruMKYRu7ce4FH54/50e98m5/80z9kHCIfLK7YbBOvcMqXXn6VX335VT756BO++70/4DxFAsKiCdwKnlfaUzoVVkODjI4nfsUfvHgCzyI6KskDIrRZ4aJndX/FuEr8IPVc6CVePKKRmCKimRbTuVyGe7Ro41kEx4nz9Kqcx0QSy6KAKilHRILVgHzOuXD9cy1rp8F5X/CWkkkvR/p+pN+s98Dy/Wc4prq8ztk+kMBi0XH33n26xQLxni9+4Uv8lV/5ZdbrLR9//IiPHjwi+yXtacdyuSKUUn05JWIcWG+vuHr6EZurC7bbLUPf27msFlWIZgRH48K0r/cMMjA7X6oMF6e9NPfwmfPfqWd1TxYnt71/i4BrEdcUp5tA24RJj6gPFhEysWB+kHM0wD8lRDNxHBAxh/BqgMp5FrGqu6hUrQpZjjfO7Zw8CVcyYUy6mQgBWDjBBeOVwc3SgzpHUyLk6r8n3C1WpzNf8BuPc7sxseuF4As+VPVgZYoynXTcwopEKEZOP70TKPxYiCkSZ0avOQ+uc2zzfHDGq5YMXnmnc6lOwRHWBCXLaM7y5RNLaVoNjvMxNnmkvrvWkZYaEWuLw96pu8hXwIwpsts6NSufc+xSXCMMo+E4uwv35cpJBy71bk3BKYawYrxJJXK5RAXM5E+3k5tNOJul5Ya5iXOODxSL/tQXmT2jnoP13xW3u0bV7lD7JHU86pzKhDPsjBQ6OZ/Z1OkuihtKOYqyLkppgYoB1ywN6iyYRBDLVjc5wCs5RitBwkyGL5kAggFAtj5m+O3kJFNkbgm7AKqcdwtaZJfxTMrc1mfNP5uPs8Z94/BNmIHqDl+omQac80goJUTreIpw5v2kT+/mtcx79f6av2ual9reHaU0TmnrqXXuZ0b0CZdAZlHvO8x83ynCsnM+zxhfr8mqjLlkWc3zqPlZqmHNJO2J/VDmoDwnX4/4n4zf1Z6huucc5MX4Wr6mL6pFUxf8tynZ7HJK4P2uZARz+4O1TzADk5mpquxlv2J/yaMHV1w8+4imu8vp7Re4e+8+y25BVmjckmHY8vjJFd/6/T/hvZ98zLpf45qO1998m3v37nDrdMWDjz/iBz94h8uLc4Z+QNOaiMlMTGygZjFR4rCd+Iu6RNaRxodr+1b2/rhZ753/Hr3pGiErURJbtTW2clYmZciZJFamyaeSOUAcZznTB88TjWzV45NnkZSonvUiQhYkg6jgm8A32lvc++AhTzfnPHVrHurIcOW5RWBEGYHHWbnYXMDvf4v+d36b/vySYRMZ24Bm5f7qjJP31/zKG0tefu1NfvzaA376wQ84bSzbEsXBD1UzyGM/llNYpsyM89IKVXcaxzjprZY1vDgeFGccKGVgnO2zmLI5e1asSzw5Q4yZzDDZCUcUP8KYHdk1jFm4WG9J0dMHZdFC5yP4U9sj2TLnDGlg6Ec6v8Q3gdC0BGlBA+OQMRZokcgJZb0d2IyjlYBSQVww3hlacAGVnZ2zaezMxpk9JKk54Y0FK8s5E1wgu2ILdVqysARaJ8hYbGEI3rVTHXfJC4bNhtxfsunXPHr0kE8ePOCl27dYLpb4pmHbRy4vBzQ7uraDsSEGMX2n8tXi8HGzXmrR4rYn8062ws4WNy1+44lZrCwnThDv9srJ7O0NJ3amcz0A4BBzt0Sqxp/ma8nKVpWAz6RETUSNZDIqmex3fGZPHhdzZBARfHCEUHTTAogp0DWfjmlU+tyG8WEYZh5X5iE0Zks3F4Kl39KDKJnD6IIqTM49FOeRBzWC+rDWZj1EqpH9EGw6jHio1xymKJ9fOz+Iajqk+ts5S8fkgr+2qKwffooIH8dxMh5UQ8JYvPTqQTQM415Eu3NuihSvbZ7XJO/7fjKAe+/pXItqmmqQV2N+3/f0fW8NS3ka7xpFHkJgu90WYSgTZ/Oj5bAIIUCwKAJL6cDU9jpG87GeCzzzudhTlmAag8PIzLngc+i4UJ9z0+FTx7aSSPVkej5AOY++eR6oO+/L/P07gW8/eqf2ZV6PsgptN/Vl7+AowjpYdH7XLRidI9V7y9eqmaiZvh+hDWw18aVf+ArLu7egsw3eNA3Ol+hmAaufYgq5c55FGyavx5/72ld59O77SIQ0ximFftLEmJTm9glf/qWvMXqQzoAAXxxdzGOnKAB+ByQ5VbrgWcfI5uqSVb/h0fk5/Rh564030Zjo2o6z0zMacayfPObBj3+Cj5HOOUagCQ1BCxNsQqnhlyAqY0qsusDF+TPe+e53+eo3volbmKf7Zrsl4Fg1C3wTLJ4kp116MK0S0ZxmCMBsvqZvVfHqGF3DJni+/rd/nTd+7kv863/yT7h88pST3KLbbApI1/Crf/8/Qk8s6igI+GKcNmOSQ4qXmRZF06JdFLLSLhfkZ+Ba28+bZwNnt045P7/gbLXgtTffoB9tXzvnEedNQSpAHgLZK2SrLyTO0UomihI08/pbb/Luex+TN0NZo5Rn2bz7RcNrb79J79gDBaREhzH9X8qoCThHcqZ8nnQtoVswbi5op7RehwDwHJDfN1LddGB+Fghf7608Zu4lfnjNZxmXptppB++f2lhXi5YoC7V5l51mz9mL93np7dfZNo5w69SUEQxcciiSbT6yWoRaJkPJrNKX8gCXQ8+YE606A7GD49W33+TshXswbq2m9CQwyrV2lg6Tx8jo1ASzlMmNRxpvkXNxNAlVhEGUL37tK7z2c1/gikSzaAhNa3unOMAcGq7quTWS2abIyekSbQPivdUHLDWcUk6Tt/ThHO/9/Rxjz3zunjf3lZ8mUe68cI+X33wdTjtUzNvXNY2J3WptE+8JRQFRMS9ic/bJZIRmubB6mkWJy9lSPmmGLMJXfvHrLE5PyCjdYmH1g0JAvfHECrgUjj6BeFKe9/LLp7zx5ht8/913rwEF4zjy67/+a/zCL3zFHPBcc934MJ9vsVIc6j1dK6SkrJZLvvlXvslXv/pVfumXvoELYXJ+8T6Qh5F+vaV/esF3vv3H/PD73+fJ40cwJEJWHB5fM3BIEYgdSC7OTRXA0OmYrcufw1k63G/z/f559va/bzp0lPyfg+bn/WHmg2uAM9flkJvo0Eh5+LzDyPSb2jSXuT5rjx3ec/hdpcNsAJVXzClnS893w2G899zntX3uZFVfX91q6ho0wOPmsax6xg7k3B/LSs/79zWA7ga6SV6NKU1dPoxEet4z558d9vnz0qedsc+jmwzY85raFYieX1v78Lw99rPsuZ+JN4jVwtUiI2tVvhVyTLgMEi1jB6kApeLsDIedQxMlEqJCoFVGF/bqylXHpL8ID9nXAf5ivKhtF6COFIV+3DLEkabtcR58qLqHgRmKAb2uGAtVTf7Msp8tyWh2BnPAA2bg8vTblfqws2i5mGwszQnUdMuYI5txzXpYcDIIGtZQajzGtGV0PWMaaNJopUxkB8doKR2StNTHLFi2i0JODicdi+YWrU+ggcZ3LBdnLBcr2rYxkEks4nysuEW23kkGshkaNCk5C5oyEUcSR1JPUkdCsDwrBvEKAe9bzm6fsTo5gazEmNER4jrS5x5pAw5Llb5wt9CF4lbw2u2RftzQj1vG3JMloS6TNueM4xX9uOFquOR8/YT11oD44CPLBQwu4tQRgjk+xAzOR7xvrGm+6h0lktB7TpYLutZz62TBSef58JOP2A5bfBCapmZJgNz3DOsLO6tCR+uXSOr5yR98m49+/0/JHzzh9TsvM0rmXK8Y4hXvPvyAcXNJWifOZElqEl6VBbD0du49jZFNHBjFc6+Bl5eB9y8iTco03lJd65jZXm3wd1Zo23G+TGzilpeHTJPVUseLWA16zQbIZdNTWh9YSeCnaWTNLPujMHmx6qGwWdf4Aa+1NVwy5WkmphGH1WzPORHjWOo4RtK4nx3PnrHLmNE0DV3XsVycsFiesFgsuP/Ci/imYb3ZsOkjH/z0AR9//DHPnq3ZDgkXGm6fLglNIMWBod+wXl9y+ewx50+fkNOaFAertZ50ktXrGaFao7b36yfWKPZDic0XR/o5ZrOr3c1kMBLx0zvsWrtud5wWg3UczaCSEtvRjDSTMSdXfXJkMj9WvE8cOlYDsn3ufTXSyAS+VgecyZiG4N3OUDev+z3HFoMooUSq7WfZoqQyDaVmZnVsvUH2EZmen3Od773VZP+u+A1gtWNn9YYPz0cohuPd9SlZFNQkOKidwYlq4C4auQqS3YQXmSEslbHZ1xUBVKoOW9NcR8uiJVLKYVDmuMpV2Rzwg2DweP3cBkiLLlJrZkz3U3QGNSMOKsY5RaZMrIcCjUjVM8yY2bp2wtOmeSoTozq7f5qj+txa7mleYszGdV+Old04FRmijrfOx2A+l6U9u7NwPtfCbNKNJxziEUW+0HrNZBzcvXs3INNwzx7KVLaEeQpcQKbyXW56/twAqurw2ZO1rEedZbGYjaFO+t1sDmdjVNP/e7/LKFhWMTk7pujCaU4PskZJzda0w4ZsTEpfcpFLZo4AeWaokTL1OWf8xCt2YyRqa3kaWoXtMOz012lJHBjoKf2e5Nrn6CpSpccqA+2yNdS8B5U/1gHdycWzdUrlBW63znU3mnWdVMwulTWluRrCZ3s55XJWQZxlI9W8i3bPJaAB1ZJpRid+EWO1d8RSjiUVHMd4jRn4a0TwyKh1xKy1RUQ2bLBOidTsAdUxQpFSY11ngYRz3tVvB+L4mKFfc3X+kLO7L3DvhZdomgXOrRh9II0DDx8/ZTtuQKBZdNy9d49vfP1rvPvDd3j/vZ9wkYozQDaDJmUd7+bNnD6yijn89DW40HQFG5tElZ6pZ4LUTDD7TmbX9bjZulRhzMolkfvScqKBMXsupKRTx3z4pMi2MXhUW5wEJGVyGmm0I7sRnzOSBOcbTs9O+Ct9y9d6z+L2G+S7Vmrmh0+e8BGZIQ6sU+ZqG3EJfvjTx7zSnfDlL/4cJ7fPeHY18P4f/ZBAR//eE07uPeDFO2f82ttf5b/70ftoyIW3OWpK7lAC+Gzvlz2sNkauBOTUDTqO2cqFFPzLi6BYFLgUQ/g80EKk8kAtZ3owXlZKlEj20DqaUM4rFJKVathuR1rX43OD71qCGwgS2Oja6oWnSE7RcMmkBN9ZVqTsSaOQgxQHN0/WRMw9/XagHwdSxjL2NKYQOu8Qb5jnJGcET2iKjRCPquCzGXCTJiRV/ll+RPCE4p8lODwicUrjH7zVLvehIY0DIkpKV8QhkcfI6eKEV198jRfu3MahrDdr4tUlVq61yDZlz1VDN3pDMOjsbNst2MrNi9PQjXjNBGjsIsVFps8dMmWGIevUz/1XHz5XpjUlO2sTihnKRx3JXorObmtS6/lU9mJhmGgpU1RLvFgWHm+8T0vgMOzSG30GfW7DeE2BVJlu9Rxyzjzyc0r4A6GyRnRPQulM0T4EceYAyzy6W1UnI2sFbVR1qul9CMZVmntizUHBeVra+lMN6HPDsi+bYM4Ia5T2oaCbc6bve1ar1fTZBDCxM5DPI9MPjTrb7XZ6TzW8T8Z1VzZeiWpLKTEMw/Q85xzDZruXTr2OzXq9tn5KTe9pXrumQIeSZieVqDFblPMI+cO64HXM5iB+rRN+uPDnIPF8zg/HcG5kPqT5fQb87FZ2Kk4Gc6Cnfu+cm+rPPO958zbW7+bPmJ5zAHAfHo6+eODN+3DNm4YKHFm9pypcVYY2/S5Xm7bgzLu+C3zhq1/mwdNHzFd7yslqLboSeZ7NezznxKBmKBNxZC+MmukqkOhKmo0guAZOXnyB05df4sEnH0JSS7dVhDNLlKMW8ezsIKtCnNOML2DMiy+9wB0CKSt3zm5x+eycvu59hWcPHxE3axrF6oYX5iVqynLOiooBVT6b8h5zhJwY+p5gbtiMKdE0DZJMYcDtDLO59DflZMx7b97LuM7mdz4/XhwLF9hkJa2W9KdL7v/iV/g7d8747f/6/8rw8ScsO2G9joTTU778q3+FP/vxO+gw0CamWiIqmSzFgzl58MEisbOaLpSVx08f45rAOIy8+cUvcvGnf8LbX/wi//bb/5Yvvf02Gcss0bYtKeUpvbz1zzqTRQ0NyharE4JnO2wJmOf91WbDmdjYV4VL1WpPSmiIovRxRIdh8lS3LO0y1VEbYySPVq18kEyfIiFHHl9seHZ5zqkYfydnmvYwPdku1eYccKh77nAfVmPAp9Gcj9d/z/n7nD88D4SWCRC4fvhPvEN8laonZUOL8mdKnrLNIyxanjx7zNnZAue7khYdwBlYWda+lMgtMoTGE8fEVb+ZQKSq8KWcGDQhnXkzjkNvNXTSbr3upde2RU9wQhSDxUbJfPzoE2JOBvI6O89itlpHd15+kdW922w3l2zHEVdqcjPmvfmpVJWpUZStzzxd9/RxZMyJjgKYVHW/CEq17lt1ZJqfGRNI8CnzekiHhoWMsrp7mxdfe5V3H7yP+JGgI+0i4yVAFtQLvpQkqUrk6NTS8GkmZuXh40cM44D3rQn2MbL0S4Yx4tvAa2+8Drc7rjZrtv3WnNa2W8uO46VEc9Ufy9xgCoEjJQX1fPjhRwCT57eqKZ1t2/G1r32Nl19+gc12Q60LNE/zWIEF53bpjEPJ0iPiuXv3Lv/lf/VfEQoA6lyYZJg0JtJ25OmHD/jDf/0/8cmPP+DiyROiM4XZ+WBAeolsUVGyzEGhmorzEIhgSgd+aEg9XDs3ffYfmn4WA+SO9sGLw+f8eaju1c96z03vusnQuPtuphTAtEauyV7M+Jc+34h52ObDdx7ygpvumRvG53vVlUjNw+vn8tqhYbZeM5eRpyOsdN5kmLIyZXdPfd5cBrypvXN+czjm9Z6fZd4PjZ9ullrtZ4kUPlwHhy34rH0012nqfMzrjD+vT4fPnWf5Anag98E+P3QaPRzbz6Jr7XmOIWvW0PKrGMXRUlvQPPFPVqtSyzLa8a067QMR04mrN7wUgEoKlmDyj4BYxM2fd99fb/J1fvjnJe9bfAg0bUAJjGlD1oQLWqLypICaJg+b/GVy4lyHus5nZnN1uF/h2tzPdfi5Yc2qE8p0T9LMmEaGODBmwcmI860ZorBI9joBE+Sacyn35PCuxXklZ0wLUdAsQKANK4LrrC0u4KWhCR0hWAQ6Jm4Zph0LoJatg6pKiomU7HmaIMVsUT1qTnG2vizFoeQCmIsJWdvcc9qc0YYWTYomA7tFLX/3FDGrpjcFCXShY+mWJFMWcI0zo9fpmnHcsB7XXGyfEZpPCP4xY9wCCS8BzYYPeB9JKsSk+NDQNAt8cIi0Vr/ZmWG3CZ7gGrRxrDpH8HfZ9uc8ftaTsQx1XtqSVWBk2FzSa0JWJ7hFy+WTR7z3rW/z+Ic/IW5HYuhoMnzh1h2CJmI/8JNHD3maYJ0jSSiZi2Ap4BXGbHUaF87xpjZ8zS94P4zklIllX0anVrd5a6XicghsHWSNNAo9gjrTWVJS6x/C0gdWrqFBWGukL86MU21D76GUhtEDa9OhLDnnW1XWyVq5i9WMHOM4Kxd3U6kLKfKf4THL5Yqzszu07YJ79+9z7/4LxJzZ9iPnF1e8//6HnF9ckJIQQkvTWTmjfrPh6uqczeUz1lfP2Fw8ZbO+3DvHXNFDzIhahAEB1Z0zE2L82hVjNxUU1B0vrHpz2dwojkm7L3i1kzlOI7gsiJudJQVpdFKjW3VnuPI7PmGyKcXYINM4+eqUXY3bIrSuBp6UWuLFGF+NcjtssRrq3IwXzTJYlAxyfk+G3o2BPaPWCK6rRK/xv31muC8fWX3OqvbkyYCnuuNXwGQ33Hu+w1JRi63xasAqT7czmwoV7wyYRhlVmbKf2jwWPlr16OLAIBg/c2r7R3yY5mrO13OtpV5vUjGHuGmuy5lexrMKojVLgdSFiNTEDdM6nJzPZnvM7GkzXUOkmhivjfmenFehc71hD9eUrmUiUh2wer6zi2avBvIKyFdHDinvnK0IpoeKnasVjN+9zF6SZ/LkHtepAqzMejfrZn3ndR3EfuoeqM/SaX3UxYdlx8CCz2C35mx52/5SnaV7n713753lm50B/wCznzpW9lyuzgC78RAx20jNPjDxpVIGcNe/ahjPRfc0JxgFpGTInUc8poxF9+6lDa+GdJlvHwZmcvSe7ELxolJL+8zc6RYm54M6AdM4zSdlJxPVAdGs+Lw7R+YG+CkQo4yd866k+9VpHK/L5zteXtf6jn/sjNf2XdmfpX2Tw8H0gzn7F5k95lr2ME14w1gyCMTioDMviWflKHYOEqo6ZbGIKZdMH8UYT9rvhwguBLxATvXsrd2zsymnkZxGhmFNTCOaM6e377JYrOgWHck7hr5HxUrobLZbnj47p1sseOONN1gtl7bfxxGHkGDPKF7XGpnJpmMRxQqE4shT9cpd010RZGsU6qHOuodfKmU9gVMr9XkhiTsCK3WcaWDtoqWgL0EaGdg4ZS2J6Fo0W+BMLA49vhzxCjTO88rpbV46j1xdXbBYrVg1C1DDe9cosZwVUQ3b/fjynC8u7/HivXvcfvE27aNL3pPEhXjGyzXjux+wuHfCL375l/jtu69xdfVjsijOhWmSXFmzFoS4xw2nzBe2NxVNkVxsaYU72blf+I93Hj/D66ss4H0JdKrbq+pkZQpFHE0QghMLTkpKHDNxzOQGK10TI6P29HlrpYNLVh1BLBuVaxB1SLZAM1UlBMvOM6ZMHCPbviemWLLvhpJ62zohVR7xDheqYdxbluVcAhLF+EdWq2XPFNBsWbd2MubuvLJz2CHizalEPaodIgOOBi+BRbPgpDnh3q0XuHVyimjG0fBsqwxZiYPJOylb0PKU+auy3Rm/Fpn/fcB3dNa2+RovP1JkNTtUdhkA9uTBiWfOz/kdL2DalntM13T6yWabSpnhjHqTQZyYzCEOslimWig2C+9tj7rqxOEJXnAlEE3UHFEynx3oUOlzG8ZzyqyvrkhjtBz/Y2QVOlBLgVM95W5SPKpx3BcAd964w1Td84mqzLsaxisTDyHQNA2T8Vlu7vDhcw5Bo7kxfJ6m3Hs/Taawk0jzFOUt+GC1wJumYbNec7I6KdHcI6gZ9nLODGNP23aEYtRGLNWXedEE+m3PMIzMjTq17SJC27ZkjcRohvBhsHphOWe6rtvdJzsjbh2PGgEP4IMVpsc5ckmbgjhGJww6cgbkMUNJ5zCPFJ8DiJMw7WRXc6EKnTVFt+zqsR96V8+Bunk6/fl8Ha6f+Wfz9swN7rXv+9fu10uZR+/cZEyvzzlcQzcBxPO1Ks7BQXT6YaRQEb8tzbI3thFzYhAzaGtMZZOX9LUl9UhSM9iMKTLkiPSxHDDmfaRKiYZ0RfAtkQOm2RqjCY7oLJWaU4iaSWSa5Ema2V5d2eGSMs6CV0llr+byU5mrIuZZqOZdNow9oetIw8CYe3CeJ48/Ydl2LFen5BiLp38EzYxpsOe5YO+hVBDMFsXpRIiYRBBTQnPi1unptP8QYYwjy7ZjGLZs1xdWLy9bTcIsRYEvQniuYzStnZnCOlM2cwHx3KKz9C4Ii7u3ee32GX/9P/v7/O7//b+lf7whNIFH6ys+OX9KnyOMI0FtTi3i0lKf7w4PRXOkpscSgbPVGe+9/x5N1zIMW156/TUePH3MCy+/xGa7ZbVcmDE6RrwPaM6WTrmCvDgo9TiiS6aIZkvPH8lcpa2ljk5F0SlKaIojvmvpY2QcB6TtkMbtakvaw6ncz3khO2/OEWKGfieBxW3Pyb07bD58xFloSXmcDk9EyjqqopF1PaFTTc/JOzvv5mWnB8jevjnci88zaNQ99pmkpb7P7FzORTmbPvAyA6BmIAQCar26vLzikwcP6Em83C3QYJFFjXhazKlq3AONhSZ4Epm2bfAu8NYXv8gPHzwlkQhiDmafPPiYV58+YT2saduW0LYWGVQWbCiOTarFOzwrLluqdHEer56XXnmFh9/9EUOyc3eMCZzHt8K77/2Yuz//Bo8vntIuFqyaZanJOIscYVL3bC5zBmdGdxeEOy+9wEcfPjTjf3FscXgqZlCj5ylG1woY5AK4HJrGqyBc5aU9naYoJ9NHCuKFDz58n3B7wVoHXn71BQjO0sJLIPgA5TzPKU9en8Ht5lEEXnrrNdy/7ZCyMNOQaXxHFk9yjscX5+RkjjaLbsEwjuBcARwNhpl84J0UGdoRh4hznk2/oWktNRSpKA/TmksgyuOnjyxbTLNExFnKx8kb3ZyfxFlZihgjGpXVyRkvvfIyJ6uVCdfFCQw1B7dxveWj9z7ggx/+iJ987x2efvQJadODZlxWmtCgJQUxFLxCJ1F2PvAHQm2JXFGogJXuCbk6KejVYWIOJBxsw89Fn8dAfZNx9VAOnQCkG/jG4aP/fRjFDg1QO6Dzehuf9++bP1OsaEFR+pzABMLWfWLayPMMlHOj9w5ovl4P/rl8djYncznqJlmpKsGHYzOnucxa2zInJ1V2nr27/r+CLMoERtVr5uWODvvzWfRZ623XN70mK8MOANwB9ddLuTxvTCdg7oZ2PE/Xmb9fDtb64fNvev/znuXcLjJxnm3q8JmHzhnX+iYlQtA+2IEfM+X9JiPyNTBq0vZBRHdp/sR0ZSelFFB5julGZS6KLleN5tOLpzbu4P3Dsbo+QPWi6+O29++8k7/+wmxFA84Ji66jCQuG2NCP53g30nhXDFl5Sgs7jZYYn8i5GMscezq39bueTCYjT52THVhC1f3K7wksETelw0WZSm1kLSAsQwEXzRjuRQnO4YP91FSduxYIjV/QBAjeIj8yyebKNQQNLFuDLrxYOnEtzmiarc6fFGBIHGhUUrQqTapK0sg4JlKswLygWUst0QKyi7MIHpJFKRenjTQkHj17RLPsuHt2m67rzHFVd/KPqqWOVrWIkDgmk3vUxr9pGjq/sHO3vW26h47cy1vu3nnCs4uHbLeXjOOGnCJx7IlpQ45KjMnkuiyMcWAYQgEpFXxDzonWO1Sqs7njbLnkztkJV+tz1sOWFJXAqdVQzJmh31qZmC6w8soH7/yQD//gz1g/fIwE4eH2irMsfO3F13l1ueTRs2d869lPeGfsGdKIy8UBwzsaPI0IXcnBeeICCxq+qUv+VbOh15FRs0W9B8cieobNwLKxSPfsGvq0tfvF0uTHEi3rxYMXznzDyjWMObJOiVh0Olf2mHiLAptE9gPe8vxzdn62VPnXIsZjNP21XrP/jLJqxYy1NbNf0zS88OKLdMsVFxdX9EPkatMT9Rlt17FYLQm+QTWxubrk8eOHnD97xObynLG/QrQnOEfGlTTHpszGNJJzLOWvjP9lzYjrKNvZMgh4V87O/f5N8ZJut+uFqlsVXlAA3lpPU4oe6TBA3HtXamZD46uR2dPUoIwCIgcXSgSPGYS89wYqT9lcDMwMrtyncUp7Xo28k3oosj/eJQptHl0Ks6AYhXmdzSqbViNTzglyqjO6e/Jz5EnvDjKflQh9qWFMVXfB1fydTIZ7tzMGSAWLXTVey5SNrGKE0xmkxnsMY9un3Zg4djU1y69Z+70a9qOogchaefwMwzqUFVN1NNjXN63ZFRTX3WqSakxmkvm1euWrzt51vX27y65nZ9zpGlW2VXKq9W3z7BzeZRSwJmRS3NWjFnG7qPmcEUraWleuvcGBcF8emcmkOnNkqONHbWqVyXezJDCljHfV6cMLMdqZpkUvvqYjFZlWK3+dOlv2hJQ2zI0QUs5gzRQTqU0nMul79eFa5SDHnlymdcqokI4Up6RqRC7j5DzmYSjT56bnSDGMq2XCmwlLc+NM5Zk4wZERyZPMouRSl1jKPrd1F7yQZzrHYar96T0lzXd9lVCeIzN9hWz4hVZjspRMDiVSuqxoLRkQ6vrbGf5soKbMqnV/s9MLVHd8qk6Td34vzbnUNep2JVFEarr4nS5R9/u0F1QJUnCNslbMucDtG+OBXdqGXQCMYphqKsZys7HM+l/OjRgT4xhLumPQnNkWG8R2HNhse/vpB5P3Ui5GcsC5Uu4lAKXMQVlnrpZhIJbvIuuLx6zXa26vL7n3wkvcuX2XpmsBoaGlH3rW65733vuADz78mLdef4VbZ7dwzjOOdnaMqaaIrl2Xqd01q6gqpGQ4TdJUjONmVJRigN/xnOt0eEa42TqvyNAFiTWZUwncEs9jMecziq4SUc4DXOZEDIaxJsmMwZ61HDKDF9Q52qbh57szzh6v+d7lJ5zFjpN+hdLyybDlyjW0ElggJIkMMnA5Woag9bBBnynr80uyJJ56ofPK9sFD7n53yZf/l7/OV7/0S/zetz8gDgMhYFlip2CNSCpyRVAF52f7lHo4oLkGf9ioJc00YnY/y85i0c22u/O0pz27M9vWnOXdrGtZRAje0zrBl6MWBYcrZYSEHDObYcvF2DMMgwUMiafxgTY44yVFT/XOZHXnHBnLLL3te1vTCiIecWYLoWQoEgehYIqWkdGb7CU1G4bJN4EwlYNJxVlRgvGxqkvZkOWyX8sZiydnsfIYuaGRBV1YsexOOTuJnPiWk/aE1i1ovKdzSza5YQAut2viOJJjAjIzlrG/D6hOOzusZi6PVGN9la3mNOl7zkrfiptl+pmYrLKzyev+mQmz/bQ7e3Y2OMMWTd4uNcadliwUu6hxdaUHspNBnAjiA1nMMSx4jw9i61F1N+xZJ934s+hzG8adSKn7lfFNg3lElloTqqbguusRfXPwbG6ort/NjdbXPBjKM2oEdAVq9tIiHfyeg3vzVNqLxcI6XAy2hykoq1F83maUvcj1NEbGfqBtW6hRfjFxujpBxNKha2ESWZXWB5LLhCCs15csFgtCcORsCtSw2VoaPO9IyaLOq8G/aZqdEOfs33Pjflei4XYCgkfEPMFqivbqkEBZF60LRM1EJ4ia4ezs5Rd5/yfvsdhGTsQT3S5afJ72fQJQS1qNyfBLJjTO6pmTSm3UXbr62o9D0K6ug/nczWm+Dubrpc7H/LvPApTna6d+d3j//PvrqQbZu3e+bkTEDJeza+ZtmDZ+OWh8UhIZUSXmxMYrp2pe9tFl89hSj1Nn9aqzpanbXF0hZBaLxSR8CQ7xrR1UrkW8OUp4C01GKGlAGkHahnwVadVZVKrAaoB20bFRx7PLS1btAs0RDYGUgVp3BtAQwAUDHYrAaen4hM35BXm9xuEYkqXn6QHXLmialuZ0QaOZMfW4TsrB443RFcbcFIFNVSdjbHBKi2dzcQ4pgXfEnLm4uqIRh4w9/fqcNg7Ei3NGl+hVaSSgWYiijJoPImb8JOzPo4uzmrnBqdJFZZEdrWvY5p4v/o2/xo++810++d0/pouWKmW72dD5gJfIiQ+koGxbrAa7WkoPwo7HTR6FCW61J3z47vu8/oW3uHPnBT744I+5ffsWq8WSYb2hOT2h946mba0uVBHqq/In4vA5E73QNxaN3qQSMdwId19/mXclE70jxYTD0ZTDTjVzdnJqwnMwoClhQqBzO59tzZZEUsvBE3LR9Z3g2obosdpOqaZ3NGlTXCDHwZSzZNEpqYxtwg667ARNGQv4L3tTZsr9c+gmo80eGM/+OXATLzDvMbEI/gqUODOEm9DkJrBdxKFpXuvLrs+auXV6i1XX0W/XSEqoK+m8azquIn1ngdGbtzM54SkAqXO0bUdWU/RSSXn38198i1XruIqW3sd0slnUJEwAhOAs+kqVUDCKnBJNt0BCg2omxwzZ0gZKGrh/5y4pjogzHlGV3Knd7H5R1oSK4EXpsoBGbt2/z3sh0EbB52KYKNkikpYUYAgxK64AG8YEq+Jwnd9TV57sgKvp2gp2YNHiKSXurpbkcSB0wdag92X+zXVHxNvYhWLwqwo+auPpoLu1stIR64xEaFygkZYUPGG5JHlHimOpJ+5s7VfeVYzjVrPWeGJOCYcQugbNma5tOTtbIeJBrb6TF+OnIXgefPwh9++fcXKyKsCg32V7KVGbU21CFVbtitv37nH73l18Y6JbHg388d7DELl4+Jg/+/1/y7v/7ntcfPIYHc0bPGlGXan5lXMpm2D1ogybkGnf75RpduNWwQ/RKT3mtFSUmfI/l8eKE4Swd2Yj5iwxDxC96Qyf8+ifxVi9Z7g7kCXr5/vPO+Ajs+8/zXh4+Ey4bmA+NGQeGhWf1/Z5O64bnBULDLF5ONwrlgJ1F/l8+K7njeVhZpzan5vGZN6uufx+aPw9fN/ckPxpYzJvd02TqLOlSZnasiSnNF6HcuMhPfcdz5nvm8aqjtM8Qr5eKyKTYXD+vLlMeRgxf/h+LaDZvL7k/JpP2wtVd6mOxDdFzd/0zPnn83Ye9ntOh2v9cO7n66HyfIEdSOXcBCIWZG9vv86fMb1vwv8tqtMDaRgZgIuLC3JRmFPWCbSQEiEmFON4ach0/h+02zt3oyRyKGscHmN7/a1nqvt8ivjnIYuASwTfEsIS5z15jJx55XYHz5aZx11CfTIgigbyiErGeYqU53EJVLREO1THxLL3szmjQo36muEfUnUkmf0YObUU6cklixaNZonObkDcJV6BAUS2ZrT10Wr8NguasES0ZFlxhi8smzMaJyAZHyIm3Rp46lJC4lgiJ6rRWkATY4qWOj0nMrZmhlJGzECXzDiUiKiJDVXAvKEfMsPgSKNlVGlC1cEd6hyjKsPTS66ufsjq5JTV6Smrk1NOTk7puo5Fs6ANDa1b4Cq+MVbDqq2FRGLdX9i4FaOnE2ElS86Wp7y+eIOcKiBtQQE9D9gOGzbDhnW/ZnQJCUrfXzEMl7St5+zWKa2cGihYUi5rgnEzcLtdsr11i/i4Z7vuiR6G2w3rXlkuWxpa3FZYXin//P/9Lxl/+JBlbnBnC/JwziebLY+HDa8uA8uQaTthfRkZpOO2U5rgoQmsG08clLviGchc5shTMndy4DXv+Ei8yag5W0rn1HKVodHIqvU0d+7QP0vgM1cM5GRp1bMKQT1L77ivnh7HO95xNZpxIwfL4pMEXDR+EohTCQXY58WHvMy0ci2pYzNOHWRh6EeGfiTGhDj7PjQmm2nWEgVX35LIsWd7dU4cM9/85jd58603+PFPPuCjBx+z7ntWp2csT27RLZaIJPrtFY8ePuDhxx/afX1vRm+B0CztLI/jtC9zAfqC62rDAQgiRExGRcw5RbCzSBQ0p5JeNOPE4xtHwOOd8buuMWeTJjQE562+ejC5sm3DFDjivSv1G8NUs746c96E31XKN8gA++lpLQooF4O1lvrWky6gO73AdKG54WenyyG7CFv76jCdNkXNqEY+qNUS9oxR9dK9ds/kFi1CBwcgM0x6zk06KuzO0TATZsTt+KnOUqCq1X2YmUSZM+TdAuDgHNNZ+6WC0YocpPB5nrxmQYPFCVPLZ342DjpvRj3bZ3HWe327HjQ1f+cueGa/DSbD7PSGlBJDPzBursvJc3lm2pvRnumclSvMBZdlhjvY2OwyizrnS/T4flCNEAr2sr+O5+01rMMwT2oqalXbS87Rti0nJytOzk7oVgsuHj5kHMc9PHEucwlSMjDcnAVvko2cmwwZz5dplfFaavnynFyvu1k3AnOsmJcmMnw9lvmLB/NZMM9YXUf2x+hQ1lbVyZFx3vZJvpw5N1Zsu15T187caUNEEM2MW4seree3zAK5LGuFp22biVdMP1q3T8l6lYtefAPN5d4c99d0zhWrLpiNGM9Jqe4Pw4hM9FXjeSWtt1Dk0JRv1IGrY/Tc8cbJdT482TK823vGIY8LoaFtO3Mou4GPz+dFRCCWCHFVYor048jVZs16s+H8/JxnF+ecX2257CNDiqDgQyAEM6rmbICiBVEI1IxDoqBbnj14j/WzRzy7/QKvv/kl7t57ifXlGkJDZGDbj/zLf/k7/Md/9z9ieesOi9NT8pPHCObAlIoFWpxHGiuZMWzX5BQpUA4pe1RMXq16QNYSvKOOIUHNBHJdB98flySKV6aIdRcdfVA+ZkvrO97yLaG/NDtMkVdHcfTasdFMl2BIIwm14ES/odtmcm4YV4GzU89v5sxbm4E/k8AH60vS1SUNLa9xyt3mhIDDxxFNPedpybPG8d3NE/74Wx/CMHImgS+/9gqy2XK2uM/9ZyOvPNjw+rfe5X/1D/42v/enf0S/+TGwJjUdXh05CdkNjGJR0bc2a+LyFlAyQ84dS5xYxqVq5Cax6Fq6dkEXup1jjihOEmNWNEc779X0NbSULEmGq01p+ZNhZ13T0vjAqm05XbS0ziZvyMqmHzjvx4ITWIR5Kna8gJUOCqI4EtF5tmnLpl9zeXXJ1eaKmDPQGTalBdPIELxDstKJYxEa2iYU51poQskOi6VHb5oGJ5bl2omn8y3LpsOLMKax2Hcg5YExr/FuhXcLRJbk7El5SyOBW3LGZulY324YtOX2eous1ww4Vsvb3F/epTm9x3tD4vEHa3SthEHpENbIlPVUJCPOeND8ZAEpUfwlm4gXxIGvGHe5rDrmZSB5j0dpgBahYZeJJ2EBsV6shEqVp+Z7ZE4mKWVwY5FZPYojZXP8FGf6aS6yoU2zlmRGnlpeK2eTnXzw0ETLOuwcvu2Iw5bq6DLGzJgyTtob+fghff6I8WyeFSlGJJkAraMZDdrGmyVf5kJO8ZSjempJxfGuDVgFmG4yclZDeDXSVgMxXBcCDkGdeihYvvlm79Cfp0w8BLn2DGbF0ByjGXmaxqL3ap3vSpvNBmBKKz6nmhbZvrf7xnEozzQDSYyR7XZL27Z0XbdnkDZFwsYfuJbSXVXRWbrdee30qgSmnGnAvGJSwolnjD2rszNO7txm/PATUolYywcg19wrz8ZGp3bU7+Zp3DXvIsOrArXzCNoXiicQaSY8z2vM159DQ6a1xQy/c6ByPq9V9b0WgTQD9OYCwKdu5BsEzvl37gZhb5+01H/1jClydXU1lSXQCp6pTlG0WZUklmKoWy1ZnZ3y5NGFpQabv08shZ0rCmLVFQ2UUSQpXoWFD2gacCnTOGhDwKmyjZF7r75COFnRP+7pxLJBeN8UYLbUnzXJwZxjpERx5WzX50SrgjqPd2YQi+NITBsYRy62lzx58DESRxqxiJGdsOiKomoInIpaRHsq9bZ84Mknj3n00cfIcsnq7l18Ui6fPOVW26L9iA6R7dUaTeaRKMXbcwLLi+A5X2/XlAwElzI+JTqERWjQDO1ihW63fP1v/m3+xZ/+AEkbQuO4ffseT3/yhFYxb+8iUXnMyQFhV0Zqpic6tYMxrreMTy5459/8AR+/9xMuTlc8evyIb37zm0i2OQtaK2s4WxdFcheFkG3SRzVvRRfNqB+a4p0nztLN68xLDGGMiWW3AOcN+NQKFssOwy2CRVUUtIypJIWYkaS4pNa/aEbhKtDPy1fAzNhi0uVuv5UDdZqPz+HJtaeoyn7E42fdt7e3Kw8qr7SzRSYwW2b33GTsUUo0oli60D6OSNg5CkXNhOyn9V0jiSfeWWrwCEpOEdXiPCCm5I4xGhAXsPNWzRBrTkfm1VzbrkD0MIoJJ5rz5FBR06MHBBkzIonXX3oFhghjQiWiPpmwFsIOmKigyt4glnMxZ9pFhzphSCM+Wl+aVFIIZQOhFZDqmDZT2ud7sdJnzeE1ZSQnTrolLgFDsrydvvCm0vDiNlQ8wKfEqPXLEmUotDhLVZ912itOhK7pWDQt6zgYTy21uE1xNo9W6jsUUkymVDoPWmqhZYWcp3I89Y6k4GLm5Xv3yXGLDhHt9s/EcRxN1hlHBLh77wXu3X2BdmGCu1eBlGnUQR/ZXF7x/rs/5s++/Uf85Ls/QDfD5LRQGZDM5vZwgqu8Nt+T14x1XDfq3XRW3jRn/6Hpue/T/dV2s6EYDlb7HhjxaXLB/nNujqad7vucvGr+3pvkk+s31V+VL+ieYjKXnSYArxhN5xmb5tffxPdq+w7H8FP378F+/7Q1czgGh3/fRPvQ8P+86+4w0n33bjlcTnvy+rUyOzPgdw7wKXJNZv4sXjnXb+Yy7l+MTLebP28urx+un+e9c+7gOo+k333uJueG+bPn8nvlT/X76pyp7OuPk1f6Xi+mQSqY5K7t87H7fCMChyvt2l75HDLNz0Lee0tbGSPiG9p2RXfHE9wznqzPWS09p6cN5xdbUvRIgiJoTy0RkQI47GfymjsoPo+uAa7iZjzDIrzUm8OYqiNFRxoWMJ7iNRAkIJrxcoelv88i3Kb1i8k47BtI4mmcw/uWNA70Q09MPZaquiahMSDB5I2EJnPSzZihMmZljMpQIn37ZIbwnXxa9uOebdTSHZIzQRwuNOagm3clHepPs1ix6bc8efKUTx49BnF0bcfZyRln1UDeLVgtlywWCxaLBctSis5N+nwpeRLjFGGlOZHH3rKHzfaabxy3/NucLizSBqe4VhAPm+0Vfb8h5Wi1mZuRRI+mhOpIVFCXaBvhZKXcHgSn56zX5+izE7jXojGxWracNif85Lf/mIf/459wKgvaxuGTcjvcYnF6ysc//invZGXtHGvvuLdoadTzQuO57zxLgY0MbOIWOc9EcWRngs+pwpeXS36ar1hHJaDgIktnMmXcClk80rb0pw1yfmmRREWW61SIXri/vIV3gU0auNiuGTRNug1QGQRQwT2ZHBQqzeWbac+LOQ2nNNrYZ/A5AkpoGhAl55HT01NUbe3nnNhue8ZhQEr6fjAn9SYsGSP86Z99j6fn50RVXnjpJZrQ4b1ns7ngycOPefL4Aev1Jf3VBRSHdctgbfr1EIdpf1rq0p2QXjPiTftYi84sdZ8LS7/g5NaCxeI2bdvSNIGubWg7T1uiuJrgLcI9hFIXGnMenaUpn1JdVoNhSYuex7J+Z1lT5gEc0493187Em2QIL7vghD15SepcHhjg98r6FPxDdjXJ5eD5N70/FsPz3KhU8c5xHCfnFNiXkSq2WHGner85P1+XA+Fm58PnjcmkN8+/ty9uvPZQtrrJsHX4941UdORPu7aO9/xdz7u28t6bn7H7W+Sm8bH5iDHS9z3r9Yb1eSrRw1au7DBrUWnRpJvVAKG261guWpjJvxW6qZku5/jhfI5zHq7JsbCPM88zfVVd3zlh2S0IwTIlNE2DOOHxY4uM3R+nm+XJT9M/DnnZ82Tz52Gdh/2ZywR7Z/1sfZc7SCneOJdzqiX15s+76f2N8zfcW64pCrSIlAiD3ffXgpFKeZZxHPd4foyRHHfypBnGrSyZYdSOqVYvTJGvOeVr439TP0QEQt5jWZmb5yGpTA4qe/t272+Ks2Caoter/DJ9pkou5RwOPTkP23fofHHIs6Y+JZ1K4FXZfL6mq9xHlZsLX+66jm654KUQSNmC/NabnqcXax4+fMTDR4/YDpGYI0rJ0Nu0SJWFtEZ25pLiHMZhy5PHH3Nx+YyXX32Tt9/6ebpFYBgcfa+cX17yT//Zv2R98aSUv2uJw2DRzd5xsjqlaTsyMI4RtxCGYVucrnZZZnPOxZZRPkvV0Hd9rT4XdxRKCZ4C9GSgBMENZAYHL4QFn+iWnAp+JI6RTPSQnFhwUVaaCGnM9Hgiwl234Gv+Nn89nvBXfuFl2h+d8GS9ZhstkvtxHHkyjnzYRZ4tE5d5YL1e47YNr12ueKFp+Nprb/AbX/9l7vzqz/Pb/93/h3d++gHPxgs+epb49n/9j/lr//DX+V//2n/CP/+9/wcPHv+QO/dX6BjQeElOFvilrdIHjxT7jAUZ6WTYlqxTOWUfPE1oSwnmUPZSWXulJI5g6zjnXPSOADMdcL7PvPNWdqbpaLqOtulK6SSzU6TR1lEa+snm5ERJY28p5hcLCIEsjjEm0jiy3q4ZYs8YBytDqzUAdqDfbEg507YtEgQfLFo5ZcsgFEKwIBkF5wOWCt2w9yYIi85Sx7e+YRE6JBs/0Lo4RFk0K5wscTRUdLBpVgRaFm3LpvVcEbnanMN6a5miVAmNZ3myJDZWAEfL8yyy3RhBFgiuZOMq2Xj21jH7vN2XYB+R65lp5ot8fs7Nz7sbr36O/DG1wFlWrhjHmYNFFeEt65v4YA6pZHIeSxaKEgjkpOiTtt588Ca6ZGW93tLYAwq/FJw0xPj83s3pcxvGgekwmXt/Ome1ssYx0npLXQDz6AKdopBU9w3d1dg8RZTDZJStg1kHvzIw7/1kGK4boNYIn0+Aebq2k3G4fj6PFN8XYti7f258rz9N05hhcxxL2vRdqp75IrEDNxlzCt7qws0ivmOMbDab6TqEyehfBe05U4gxoRr3IsHn/cg5W/H50pbtdju1p6afd05QJ/T91gxdYunioirNyQl6siaP0RjbrE/1EJiMz85NAuxN3no2dnn29y5qRXW/xvvzhOnDDXUoIO6Ametgzb7wslOy5uDjXEi8KXrnsB11rudA8qcxhOc9J6VkUYfO04SmjMWurqxWi2o1tmBRIpqLN7vYIeS9GbFy8aExv0xLSq7FuyerCXfV67ZpWzJXKBCSMm7XLFa3WLuBr//Cl1jnSIyRxvtd6pkKstfNq/Vf5ok+SEYbT4oJWTT4doHkjI8BF0dkTGjxdieNpGGDNE2JTjQBFsF8H4vSr2LRyZbRQ1ERmhBYLVd8+Ogxruk4f/iEq2fPePn2LeK2h5jYXK0nI1BNo5ZLykgzCMkkXB7Ok4glEAlimRs80DUtEgLrGNkOIyevvsLJ66+zufoBFAYcx0iphFH9N60+umJGeQs62A2hNQNxQtwOnH/0kMU2sryKXD75mKQjYz9Ye7NlFXDMweAiMO9gTgQzCErWUn8lTzW0pESqU9qXVcmijCkSUyQlZ4IJRdDLriggNt3ibD4qAK05IymjY7aoa3FTLT6pnmOFr9fIop1XIXvCv3NSajPWyeAaCPC8vfVpwMKnKXz2+2ZwYo9/yC6dbf1sb91QI6OFcYyMY7TUXc4VIcmyH4TSIa0zIDLNpaV7leLMYVH0eEdMmc12YBwTwZmTUcayhjgnu/Ox2F6ywIilOU85o8kqDVEEVbI5ycQhElaBPERkTOQxk5ylrTFsyUoeWMrG6kxRvZln4+scwzgSNZtDTr1WzSieNDPmaHsBX1LgMIF6cpNF4XPQfPxzieIfx9Giz2IqRni1yDhhclYRzPFj7vBQnY/cmM0onhJiRRFtnzorwRBzZiwR2WMbaTCw0UmNgnSThcSVKPQKwiqU9Oa6p9iLCTnmSDJauj9tMgMDbScz5y4hxcitW7d48cUXOTm9hbhQopnA5wxR6S8u+ekPf8w73/0e737/Hdbnl7iYkGjR61LPrHJSPG/sD/fNoVL4vDPts8C9513z75M+C+g7lDWut+d6++YA2U3v2APVCx067s3vs/Xy2Qt/Lh/NDYOHfGj+7rl8BTcb5OaG0kN5dy4PPQ+Mm4Mq9fNDg+KNwN1NBsrn8OjDfx/267NoLtMf8ux/XzQHReZzM2+nHhxmN/XveUrjbp7ZKYuzOfo0Opy/P0//b2pX7U8d3+ty9v53z8vidKic13fMwezngZCH6xad6ZWYMrxYLHDiiBpLu2fy3/5bmc/Pn2esnnf1nC/Yu//98b6+7y11oBh416fIomlYdaesukjXKU0o2cYqUFJKLIGWlOBVdtg5Ptb2WmTVDJCaGcn35tnvA6oALkDOJWWvAgm0d2jf0XKPW91tTk5PQCLiT+m6u7TNGcG3Fn1UDJwJLIsUGSSjksiayDmSynyPw0A/lnR7JaIqTkCxTA56tTZ0jGk2vzL9/2AlIkDwYnXttKR8LHLFJH+XmTdjRyg1Ni2Ffd9vLBOSq3XuAk1xdO+alrZtaNt2cn4PIdB0nclx2aLhc86ToTGnaEBcjuQ+mPgvWio0OUIXOGlucRJObA6ckEJvWW7UgKQx9jT9FdthQ9QFeejQ2PLk6iFPLy+JznP7jsfnjHt6xXf+2e8SH224WAkpeESUu77hP//qL/Do/Y/51x98zEfbLc+8kuJI0zqIEB2sgjkmnKTw/2Ptz55lSfL7Tuzzc/eIyMxzzl3q1tJVve+NHQRIgiREioSMEm3MRhJl8ygzPWr+BElv+gf0JDPJJJNszPSgh3mW2VAUiSGHIEGAAAFiaaC6u7prv/s9a2ZGhC96+LlHREZmnnsKoJfdyjyRER6+//bvj9XqlCACvuVe6PnNd77KO0Q+DD/hg+0NyYM7sYjxVL3gjdC6irp2hAdL5PIKE3KKBMBisK7iYXNCHzvO+56rfktPVOOYnZz7wzQfj/Ca/y1ZXk6iOQ7bsEFCN0RJi1TEaLBVjc3yuxHDyUng+fMXg24jJOhC4rRZ8epyjbieZGqaZcNiuYLkuXjxnKdPHnNz9Yq+vdYotoypJYjKqhlqUyfWqiOxEUiq69FkXyoTWGupq4qzZUWT19ZisWDRqIK1rmpNW2DL+ZsdgRllXwgE3+OjGikigo/Kh0qRxVOa8RaRIa/zdEyzsUQFyRIQJMO5c/xIVIPB1AmgoMiVI3s8W8dY1CTjrpbCw8soa+btrc+mkT8afttx8Bk/yz7WvWWYq3zmZ/3I/7FT19DOGU8yR86Z36dy3hhJnZJGTB3SYcyfP1b2kBIO3Lt/Nh6v8xBLss9DHv/t2LOTKypCZf3oYpHo1u0Q7DPQ+D1+PA2yslioFhWL1YLFooEEXd8zIguYQcVV8ptmNQCuMiwWC0Iygww/f9dgLIQhcrvw+9YYjTg0AqK5Z2MfuLm52XMmnJfXySBT2eIYf7jDixyQWaZ1TeWNY3VMP4/VNb08dYo4NG6l2Dk1Lu8S2dn30zqmTxT9oYhyNjIZK5WBx2tFxhaRnXSjIpJRMOxOSrOyt8vemQe+ledi5hEEyRDAk3HMejjJaRZSUeyRz8TEmE6h9C0ZquQmj6esZwmTCPYCEz7JOV5krjQ6i051nyE7OVlR+ObygpgUxSWKpkXt+46u69XoZDXSu5yJIprCokS0F12ZtWqI8kFTurz3xht86Y0HXN+8x6uLS15eXHB+dc1629L3W0xVYazJ+YUTKUA2IQ38Xb/tePL5T+naLV/+8le5d/8Bq9WS8/ML1uuWujnl5PQB7bZjY9bY1BIjNMsl9+7fp2mWXFxccHV1BQh912mahZRyhK/S2zhxTL5Nv3FQ5wFD4BKiujNJ4EPkhsC1TbxVnfBy2wJCFEMwQk8iVpaYeVsDGqBharY2QbI8tBVfj5ZHL66IpyuWfc8HvuVZakl4XpqW1hlS62mM4AVu8nppr7fIsuL66oo//uhHpO1jPvvJB2xSy+qkQZqK9cUG+f/8W/7xf/E/4eMnP+Xl9SXr6wsqe6YMGA4bErHt6QlI3WGd3T37UwmUzMFpYqhdxbJZUtk6o3BqhLKrHH5A4iwyhfLcIa9bUtrZw9Y4rK0wBcbcqlOTOuckdAtHTlZNTmtohn1lrRBiZNO1kMjrs6frOzW2Rk9MY6rmsjbEQLSJPvW6T2JSOMzsFCi14OqK2i0xptL9UdqHYI2jsorAQ8h60AzjHlNH7zdAgzULjDQIhigeUoVxFbZ3A4KN1A5bCaZWWQuJhL4jdq3qb50FB8lPeYoxBc9URs8B7rtyu9EUIEmyc8ckn/xw/gpDCh0zOUNFZOd25Didmdwy8LrDBhq3z3BBI9qLwdyqHry2mro2xZxXXWl8iEltY8ZA39P3rRrVU8oycI6kv0P5AhHjaTgYQxYCbCIfjGkgJMXwCJkwpJFpLJ5IxSBeDNyFaVXPhdEIPo0mGCPudg+mYiw+pNw4RMjKwV6I4eDlae0Au1J+L5HbA0GZeMKW+uu61pwGuRSjf4kQt5Xj+uZm6GsIgbqudyN2ouzkON9utzsQ7r3vcE52GKUQAl3XISKDsO2zZ2sx3Pd9PxB/ZxXCNfgchQ7EJPQxEZxjq5o4yMb+ucJ0GHsjlEVbxqo4J0w9r6YKspTSzrqYzsmcoZt7sU3HfT6vJVp82sYdJbgwoAWUawMTcyRK5JBCrgi9RxnHybM7iAk7TKAZorwPCVSpEIOoQl0RgkI2csUYkWyIQzTnRpRENBH1wTNYLAGTReYcQRo8aesJBvqkGcMd4OoF1wTWjYG3HnB9+YrGaX5GEYNHoyyjpImnU0IkDcyq6TVyMeaobWOKt6MSBdc4Ym2pYksyKPQ2gYBBwdIzIKYUgTYfgFZy/qJE6JMSNBHeePRIESqc4+SNRziyEmnbcvniJf22ow5Gvdgke2aCeu/JXKjfLQnwJpGcMjVduyb6Hl8ZPnjyOV9750t8/W/+Kv/xk49ppcsw4I7O99jsDV/giRUmWDJs+OjMmVBD5jb0YOD61Tlv1kvSukWipw9bNl3LNnq2fU8yRuHWZIQsyUOfGSuF8JFMzJIYuhCRGOmBRQLJTga63xPGVaw3bc4Z5OiHXGgo0SmaBaP98UajizyZJ4jQ9p4+6vzZbPyPGfZxs9W6Xa2w/pqfPu/N/C/GiHUViQkE11yQYNeAPd+fhydRFaLz+3fPmNE7t5xjw17P74zWoOi92SloohAty4kYVEG7afHbDmsdmLxTrCqxUmE0RB0GBCFlhS1ekUUqY8B7Iorw4ENku27ZbLdUfWS10L2b0Pw+VaWTJcOkafs0OFmjb1LniT5goxoPPEJwhs4r5JXte7q2U6bLdBhjsQg2WZxTg7aOl+6jlHNDpd7T3WzoWo2iDini8lnTe0/btbS+01zcKK0oZ6+U3E4Hp2336uuYKowhmAK7E1lvO1zlCC7gjeCMGYwm2kcDJqPSZOUHISLea06sFIfcq70VUmUhWHrRHFogmL4nGsGK5iuyCUQSfdCIeFXkqWNJyA4Pvvd4oM9KPM07GvQcrhw3mw0iAWk7HA3giUGFivtnZ7z77rs8fPhQhdbMkFvU4SVuPU8++oT3/9Of8uH7P2ZzdaNpGESoxOFTGNBflISM3t/HjDXHjKEwovoUOl9+nxvK5nN622+37eVDxtpj9xxr86F7DxlM57mQpmWuSJz3Ybee41HW+oXsdHY3xWWpb5rK5hD/MVeQJUw++Mez7ZCjZ3nftO4d/ulInw/1867GxcPjv8+D3XVeD9V929y8rr0HlR6zNhxTFA7vPpCfa9qn+fjNaZTyhCFDWe8rYu8yDtN3zudtWtcxheremMzaPG1Xkftg15lhXu+03+UsmkdYzVXyt63VoiissqIuhLBj9BgpPkhWFs7Hfi7fHBrLadunJR5Yx3treSLk38Ev5tYSU4KQDagkjKmpFg2ugrqqqewWawsvHTVHthhiMupkaYREnEQXSWYhxnWxo3gufSlMZ/lNRL31J/enEX80K1K0v5aG2pzSmHtYFtTOgG1wpsmoU56YEWaSWHyG19z2ahDyoceHbDDOyqvttsv5sUPm+QLej4aQmEVZzZUJMQ7upUOfTOkTRRGjkZ7TRaPKZOUlQvA5/2YgxixXZuWgEAkBRCJIyP4EqoxLXUfXddxIgW912TCuMvuiWeCyM6XJkRAm152SG3jm1OVzIcu1oLk81QygeydFISWbjYsCFirncXZFU7dU9owT94Cz5Ruc3txj4aFyNSerB4Rt4vH7H3L+5x9xtjzBNw2tRELo2GxveHX1ik4C0VmNuslpY0xKtDHxMnVcxY4mdpzGJV2ENnokes4aw/0v3+d7n1zxtrF87IR1SpgIRjyCy06IEd8HZLWgW9RUN0GRekSVm6e2YWEcL/o1r0JHlwJRcr5ryQ4ZZf+XtZuO04Wdc10Gdlr51ITKKsUYXWRwHIvlSqOrjULdrlZbtm0LGFxVsTw5Y3V6H1svwVjq5UKVwT7w8vkTXj17zPrqkthvMNFDCkRyhGLKAlvmW6XIwiRSUAcRSYnlsmG1XLBcNCwXC5qm5rRxQ35zZxW9TSgBBAnJeVMVLj6jwJW9yi7ao76fvGeg4Avv8o5mN9fkuP2Hs6V8lnP59XRsNG6X7ViM4yK7+1PnMA4v1TNEz/1UEiVP6VAa9/V0/vVi0TWNLZlG/ZYUbIfWz87aSrt0YUo3dtffbC1OaMRgxJrND7BjGH8dv3Ubf/M63vuu5TY+cfLWvfcf+jul3ShN3XNpiOSsqkoNC/dUt1kCfEpu5gGZdFhDWodzjsViMSCpxRiwaNSrMZrbOrcAi1CLHdqjzkVB4colGw0AsgMWaapVSjvvF8ALbLt9R/zCx8/5iqm++diYlefndPr2sf3ijpWvL4fumbchHn33jk6X3bMlpRz4Mx+38n26T/Kz5byBnB1BZECNnNYzwvOPfPfUzmBzBGWxaYy8hOoQNbJ87K9IhiS24ziKCOLMPgKPSD6fJnMsTNbN6GqkiJNTNNK8R2J20hiujb8VGlgM5RJVr7TTiqQHS/a/h5R1vClmHV82OqVASBnevcDwJ8EnjXaWtGsTsVkOUBScgBWDq4TFoqF5eJ9798548803eHV5xZPnL3j6/LnaI4zLKW4ruq4lxjCshLLj+nbN+YsnGEl0fcujN97m4cM3uDg/p3KGe/cfYa3j1asXnJ8/BUFp8XLFyckpRjSCebNes75Zs91uCEGDkIptpjgmlvWksvTxs3BHv5+dIRBy+kAlmZ7EDYFLPO/JKavk8CkRjKZQTEZh/jUNX1nbCQ1wS1S18F4QfmEN7ziHeVCxfPeMkxeJp9cdr/yGr7z9Fl/70nukmLi52fL81RWfvDrnhSiPGEV42W24fPwxD67v8eXvfpN2e42/6ggXHmrh2X//73nnt/4eP/j2r/DZ5oofv/8veHDmCbGmTwEhYENQ+mgDxhYinSZ7p6B36Ig452iqRnWjOUhF95UlxuxoIcXRIqfJCsWJQ9d/DEF/y+szpkCIHh86em81nZI4RBxNbXF1M+wDSap3NOJAEp3vNJWS7/Ghz4FGER88ve/wwdN1HduuJSRF6+37Lds2UVeW1WKZA1/MBN1N8h5Vh2VnK2pXIWKxYnFG+cSyX42xIEKMQgjK+1a2wZgFIPgENrnMhAYkBiRF1S2LIUTPtt9wszXc+BYTehZ1hW9U3zjqvzNyl4wOkKO8DikecHoemOB8Fo9i33h2yZj6aWpwH2W/17uCl7MOgDiVPYtoWeyhMedyV1uYFYtYsFWFOM3HXlJ4iYCkbG8OIdPuQF05jLX4kAhd+M+fY7yqnE6kFLgJjTpz1mXP6QyzjgxJ7gvxN0mVFr7rca6iypHScVD4ZS+rgdkdGb9pyH5ZjEXZPoUWL/enlIao7qmButxb1/XgMVYUjkUgKHDrpY6pYaYYfwuDVg6DqaK4GNSNMYNROkx+K4bxqTHfGIOxFd7rpix9LbDq3vsM66J1V1U1OBaMzGMkikZqVlU11F9+K8rVyhiWiwaDqABqLbZZkKoKXzm2bUcVJ57EZn/zkBgiBqYKrun9U0ajEI8SHT+H9CwOD4cUT4cUejJZW4UBLW0o4z8o0JIq8pfL5XCtROUXJf+0/rLeyvzCvlG+tGuH6UQ9W6ZMVql3+BRwlXqztH1Ps1yizInFZti0ytmhwli+JBSON0J7vaY6PcE5Q0gGLwzx4rYYsEIk5HzBpT2brqVPEW+gqqzGl8dEZwXun7B8cI8XFy/prq5xdU1yjpgiVZM92ZwhJPUyD1lwlxhxPkEMOJ+osNgue1pFhYSjsvQiOFcr42MEHzwidjjok2RPR2SIbgwx5xoThTmLRJ48+YzlvQcY77m/XFEZg/E9z1Lk5uKC9eU1EiIxqDCFzUqrrKdOmcE8piDpU6CXBE7Y+pZXr14oYRLhjTff4MXVBV/7hR/wJ7/zPxAvX2pUflQC3mU4R+PRvCioA4Ay5EWYV2W3QSNuInCz2XB5cQEp0fqOZNWZYdN3hJwfPQYPZMi2SjOApBiUaEvEi3oZhpToY6A3EUNS+B7vFY4wQYo5w6RAu9niux7fGry5YbFc4iolxtEIPjMWJhaGGax1BB/YtDf46xuuu5ZKFFrPGUvX96zXazbbLTElVvnsC0WZpxthWJMp78eyX0MouPPHhfdDwuD0t3J/OQ/mBgd9blTih2Kkz8/4lKitU+aFpGgNKdF5r+gkZoR/JyQunr/i5uqSuOmpXECSJ3nAJaKDUCn2Z/Ei98Hr2evVwLxgjCI1IqQY6Lc925eXrDc3LE9O2C43GFdlD8msJHBuENRjiCSvUeLd9Zpq6zF90Gj1bIwPOdeOJ7DpOtINbPqWyhjEeqwVzceYEhhDZELnk0ZD9W1HvNkS11tuLi4HVIKEKoJ8VEbyerPRKOgcwUfJPa2TNOSbOwYpODWCwG4aj/LZp4BHhbibzZa6bdkSqEKPWzS4EJBGFYCF1icfBqNkSnpu9dsMT+QMbR9YnSzwVlj7FlPXbHvPttMcSFI5IgISaRbgkmj+PyM4Z/FZmEtJI827tuX66oq277KQmSA7GQVJrLuOTfD4fstKhEZa6DpOT0751je+xrtvv6NOZhRjhAoOoe25ubjiz37/D/nwL3/E5bOXhK7Hbzsap9BOKYRBIC8ONUaykjWN4zw3hBzaQ+XeQ3TwLmX6zI4iEQ7rVSblmPf23LA19HNyfVCGH6h3rnw71ub52MyfnfJgU15r/uzAR03qmj47H6d5W6c8xaF+7F0vppJJW/aiyifn4vzd07Q4h8oUSWh+xs738lwJdJvCbT7e8/k/dCYMdc/ee3C+Zm0pvOdd1vUhA+mcxkyVd8f6e4j/mK/r237/Im2crp27KToPF5FdrIPp3M/beMjh9NC7D+2ronSejsF0rRX+fioDpJTwISis6myNF96iOC2ZoR2jUnR6/16fZ9fLWtlxTJl0bW/NGTPwT9q/L35+TkuzWOG3XeZxydFoNYJQu5rKWqwonUkkNRTktB8lN3HKczm2Zfc8m3ZI9cyjoWq4Jyugp2dgJGWlSJYfiZAi1lY4u8RIje+gcRUpK4Vi2uq4eoWATuLoQ2LbBzZ9m8ds4lydVPmz3XaZXwxIPidCTEN0mmaamZy/MoZnjTqe0t58dIimnMlLY6AdghBNjvRKiRSSQrtjMz+b21GUSfQoVCKIWBK6BgcH1E4wW4UBrqqKpl7gMnpYVbkMd13hrMkGX6v8XjYw2LyedL3lcUsq+6WYSD4rGSuN7HBSga1wLKiWK07cPe4t3+D+vTdg22KMsFydcPXRYz75ox/RP73k9N4DTOWoJGBtYmHgg6eP2UTh2kTEGSofWdZLGvGcGKFGaMRyRsOb1Qnry4jvPLUVmkWDLCzLbsPXMHzgHNdoLvhKAKdpnXof6NuOxbKhP10g2x7xSdNTOcsj15ASvPId577TNVfQC4Y9PSr1imJ7fqbO93ZB1Cl6wcGxHwb48BIV56qa5eIEY9WAEU3EVTV0AVfVnJyece/+Q05O71EtFpjKYStH33dcXrzi2ZPH3Jw/x2SsMc07G7Nrgzo3IxrZolHwAklhPoVEVTmWTc0bb9zn/tkZJ8slTZ3Xj90hgxpx53Ne5ZgVj0YYclgXBb6RHNGa5ZWMGmWnKd4YHxlPh9GIPi0H+fkUd+bl2P0DbHDRfUA2bqmxoNxZDOJp3AyZp5zUnbSO2+TJPFKTPbVPE8bndx7f4zfLAMlM5pzfq3XutnXOJw+0JOtFp7zFbTzCXcsh+rZTx4E+3KXsy9u7NOX2toyOWuNv4z0mGyzNWTXodwuNGvmFCV9uVAZsmkYhcTMULiniqpxqUAKmGMZFqFxFXVeA0qht2+L7FkENF4rmMMpI8zUwlw8gZT6keFyMOsxjPNRdxn3O4075z+k9x/Sq8/fehcfcvWfGKxzh9wpk9euKSbN7ZDditNSrbS91l39pQn/H877wrWXPDOMx9KHoX3Z1tsZo3wzKO8SJrDFf3+WZwp8OxqSsjy5IJtN7bYFBmfBRJTJ0QFVKShcKvH95ZRn6oS8q6OXZGOU1DaTKQUIxwxLr4Tv8XvifpCyj6g5SGtB7MDIisWSOsaBSxpwiMGb6qA/kQIyuzzYJwZCwtaGqG1YnJ5yenXB274zlcok1wqtXl3Q+QdKo4bpu6Lsu75dhkJAU6dprnj+P9N5jxPDOO1/h7N49fNeydJa6qRFjuLm+oO3anCpH86efnp5S1zXX9QJra4yxbNaXeSxGXlh2BjoN126Tz8mtzOQGo+RWdW8kNilynhRd9L7UXKZeA40ySqQkVEkrDE5gqotL3LfC96PlV6oF9771Fry1YtEn3uwiL7stL/0V7zSnfOvBI3COV68uMdvE+nLLRlpehparYPFtxHUbHpol3/kHP8f68WOe/uwJL84vqKqGJ3/5Pqsf/QXf/P4v8oPv/joffPAHxHSNiTWeHg33AJNsXptZnpjxUTpWZdwdVaX2tuhD5rVNjuYuEbwGKxqkqfx7dhBEkYejD2rADtkY3hu6Xuh6Q+cEKwljE85ZXKP8tAZhkfkF0QDQnIp463vatqWLnspZYujpu1YdMlKg7Tq2bat6TUl0sYMQWS0amqpCI5MKokJPVXusKGKotdofZxRVyEj+B8SSq36YZINgx0h4oymaY/AYUT2/IWIl4kzMDioC3rDp1pgU2IaeWmC1qNn0Hr8JKudlW8ohsjus79lvMr0ms+/5s/DGQ4T5Ds2ZnPl5/9xGxkat8EQ/jD5jjVBVjqqK2MoBMW8PUVj7yjGQixQhOwpV4vB9wBMwVlEGVqsGcY6u84TYKv2/Q/lCUOpxoqAQ0YNMRPAhKJR6htzQcRmNhOW7czr5JTJ7avA22euPNBqlpwRIIaHDwd92o5XNjgJtGnU+JexT5Upp5zzad3p9ChNY2lPqK+MxGFwyJAOAWDW0Xl9fD968pQ0hqLEqxDAYdovxvXyvqopt21Mgfso7uq4b+qt1jUbeuSJVRLI3pRrn+r7L7TcsTk+pTs948N579J8/Jl3f4HJ/pgzUCD+TBuFmqjyfGsrBMM1/Vcr0+xRifT6f0/GelymzVyCg5/fZybqcRodPFWtTRVupt3j0T3O4T5ng6bPztXSoj6Xe4XpMGlmhFWZoM43i92IQk5VZWVEjgI0QW4/Z9nz+wUc8fPiIR2+/jVtEUuWgVniR6D2YRFXX1M7gQ6DrekLbQdsjGWIjSlLYfTF4SXzrB99ntVhR9xC3keA7FfZtBW2vxCpDPNfRUNUVbd/iiVy3a6JxtI3QLjTafApc6USoUoVLHgkQth5JkUBHcoKpVHghe52nqIbeAoWYUsKESE1k8/Il3dUNFxdXLJslp4uas+WS9sULLh4/ZXt5laFwRsjkiDIpOvRpYDqmSlcm9warBFiM8OKjj9g+fYJ9eI83Fwt+8vGnnHzne/zi3/6b/M5v/zaVh/Xzc6rK4q3QLCscQm8Srm7wPuKcHfN2xwSdKir6beJsdcLTxy9o+452vcE7uPYbuvWWsO3Ybm9ITaCuG4x1gND3W1ylOVWSoBb/EKFPmCDgI63fsgiJpl7Aeo3PSkMRwWI06sVH/LojGUPlGhI9BEGchZiywdQOnnu+9/Rdy+b6mosXr+gvb/B9GBSIZEXtZrPlZr3BuQrvy9mgUOEh5OjwqSJhooxQD69xb98mHM7PiqEO8r55jYCp5+HU2y0NAs24h8d9HKMyQTHTtkjC+sTF05dcX17wfPkpy3tnNCcn2LomCZycnrI6W7E8PUGiYKsaT+D64hJ/eU2/XtM+vxgM88EHNdBebVhf33C9viaddNSx0vQD1mArR9vUnN67x+m9M71mLCEmnr96SXd1pdBJF2uMV0eDKOBTwEfBVBbfedrzLdfra5b3ekyXiLbCW2Vio21ZLJcsl0tCH1nWNTfrG8LVhvbVOduLay6ePCO2PWAGj+wQPJu25Xqzpms7Kms5CSdH5+3Y9bnwWf6e0nBB2Kxb2ui53m5o6iWLsxO6LhIbj1lFQm9YLU9oXJ0jZCIpO82s1xturq+IN9cEr3syYdW4AuADxsD24pKbl+fElKiSJVZBUSHaQF17FcSsJQWPNYIzFt/39Dcbbq6uCL0nrnvqpMZyIxZPpI/QbVuur29o2xt67zmNju9857t8+5vf4nS5Uica0eivFNRrtN9s+egnH/Af/s2/4/L5S9qrG/y2w2XeqcCrJZTvGMYXzac+6DO+wHyM+2Gyd2aC4nGF426d070d077v5nwdHGrHIWP5rUKrahX32jblb2RHKhh/K2vuELz5oXU6L/vjstvnY/zNoWtTXnVa/5zHhlERNN0zc6Pd68qhM3RqcDw251O+SZ81r53X+V6/bRym9ewqJRmm8NB6HRRBd+x/KdP1Nh3TaZk6kKhiabcP87k4VPYV8jJRhh1XVv7nKMf413K9wPyVa4f25aF+HVX2Hx2H0Qhw275SlLGEKbIa4+611hJN3Jnv22Z8vo4mnb/lqdyu2blR6hmQwODW9fxFy6M33uHm4lIRfzpNk2Mw1FXNom7UO94AOc9c9ggdIsR3FcMjh7Or1J6NeZZFJgtg8r0oei0+RMQ4NfYRSHhIPjvJO1IybDZbjFO4dEw7jnFMiHGEZGk9rLc9FzdrUgo59ZAZlDDea9o25e0DdpJcMyUGZejYXMtueuOsEB/6nFTuIkf6DPatUTFqjOo6cnIgNmGDn0QBqvHN4IPgg46ftTVVtRwjeKucYicpHfDRE/vAZtMhqBG8qt2AwFYM54tmQVU5FoslYq3CUWa6VpwGSueTRKTPSHsh98uoEzRRsKnCSUWzOOHk9E2M76hWjvXlBZ999EM+/sMfYZJwmTqqlHizsry3OOXtkzN+9/0f8ZPeE5zmXDzD8uD0HnX3kl9wDV+pGt6qK+7VDS+T44/ax9Qxcb+q+Eq9Ql6sWbfn/Lp3fG5qnhnPdeu5j8E7HesYPG0Lq7Qk3juhv9zgfMABpql4xy15EXqe+5bL5MGW3IhlXHfPrjBd5LO1PuVFBsSLCOrvIIjoovE+O4yKULmG1ckpi+VK4epjABG6PhAx3H/4Jg/eeMTp6T2qaokxhsXJkuvrK54/f8qTzz+h396QYk9VO2KIdD7RZV7dOofk6KkC/xtCILYdlRWWywX37p3xzttv8vabb+Qgh0Tfd7Rti4+evWK1LwMkJwIyhDZqNLmRwfE2Sem/Rpjr0jpEf8ZAljkPdpB228m1tHsupsl+lMLvF3ludv9waefcnhjTd1rI3vwf5lv3U7Yc0+PcVsozVdZnjPKkNma0g+/8sVP/bbLvnI871MZ5Pbfdf7R/IhMnsv3+HXvuNt5uTicP1SNGGBdVpi0lrHVCo+uFxdXVpL9pdILLUYsI6qwsQlWBmJCdWyKYkkc5C69JBoV/3Wg6AtXnarRaa9QpY3TcK30tJGy3j+O+ULogkpivMcl7cK5/PDancz7lNv5oPvavlZHYXTul7POku8+UPu1e271PHz2uIx2uRwYDiepxwBzor0yeO8RTDjLihDfcu4d9x3wr05Sa+kx/INXBnFecftfMaWOde84PAkmEepDNlcefBpZN9d7CaCOZ/jZNt1rasDt/uzpqay0pZGTeiU/UQB5Fx95YNeiWa9apYX+6Rsfx0ftKVH/RPUQf6LOuLxmDlUgXenyrOlbnKlaLBd/++td46+Eb/OSDD/j48XMub7aEPnB6doYxFdvtWlPRobpBa4UgCd+vefXiCdv1FmMcX/vaNzk/vyCEHmcXvPX2e9zcXPL4s8/YrLfcXK9ZNCvquuHkpMHahqZZslgsOH8F2/WG7bZTepf3cszOWWVOSt+PoUrBeJwLCRODOuWg/1oi57HjHM8js6RNiRuJ9JJIYpAAEjRyPIngSQgBavheMvyd+oRf+8q78I++T3rxjOpn57yB40vVKS9ly9WTK36v+yFhUfOq73m83fL5sqMPnmdpy+nG845v+Oq9Mx7cu8/Dew9Iz84JSbjODneJLeaf/0u++s2f49e++Yv88bu/wmef/jMeNicYE0gmqNOerTAmTNaadlxtJwqYnjI/XFWVwvAbO6SqKfJFokRQG1LKQVQ5hUXZ5TFGvFd5yoeergPbRqou0PYQF+rIZ52jWQir0wWOKsNll6jsSNsrpq5IIqSebdiyDRFaT9+39J2mHwJFvlxvN6SU8NHT+haHUGW4fyEHMZFo+w7ZWmIFjUvU9QIraJS4dQjq9KA2xJTV9ao7icPeztHh2RHQDKxBxDlY1sKyEs5jS+wiSRK1FZzoWJ02FW0w+C2sTatIYmJJJlEAIW4TgGWQ5ybCz2SvM6xrbVjJQ26yA+dRfUY+FwqJnVQ1iJSCkAVW/T2po6irNGC3dj22qojJo6jkomlsDYq0kNeZFcUftqKBYs5BVdWcLDWINBmh6iwYiFfb44MxKV8YSj2hwoI1BlKOWLOGuqqUIZzA26SYiVRUeFlnLD4ETILKjfDWCVUqG2vwKUNLTAzQUwPWlBBNGYkpISo5x6dG8WJsHiZuQvTLoTeNQI8xDpHFpf6pErI8OzXieu9pmmaIFo8x0rbtEKWekjJwBeZ88KRLu1HPpW9Tw7Pmsu2H3+u6HpkAwFhHSmmAdZ9Gw0gWpNtWo9cGJlQMDx69yZOPPiY6y+LeGaw3OwS3PD/kFYkj1Pp0THajNY4rg0Zl25izZSqgTu+ZjvMxJXRp23Q9DHM0EdyOraH5+6eOFUO0YX5mn0E4rPg7WIpwF6Ouc9/vjEXve4yxWQmkDEwiM84x8erTx1x9+pT0vOXzH37E/bce8eVvfpOzNx+Cgc12gxjL6qwC6dlst/TtFul6zj/5HP/yCrv1VGIhCT4GQox8/Z2vYjeJ8OkLNj/9HE4ansc1Ngn3T884vX+f5ekJS+tINz0NFaaNvNpcsfYbtjGBa3I+7ALdoRG3LsAyOVwIVDeB+HJDJFJVNVVT4XxCFgayp6NPYVBCKKq/wkHH1nMvCQuxPDq9r0bETQ9Xa7affMbVZ4/pNltchvcZxOTMwBHJMOeHGfQydzFC8J5aLFcffsznf/YXvPWD71IvljzaerYff8Z7732VUyo2nzyn/ewlrGqWJwv89ZZqUePuneJsUmNVp846EhOx87TXG3zbsznfIDctcdOxrTcIGnH/zv2HPHALwssrYrshLSIsAsbVRNtRN0tcVA86VzvWbY8xcIIj3NzQXp5ja8v2/Jrao+NohCg5nwtG0y+Yiu5qTb/d4jqQynHle+qmYXl2qnlTlgslfN5wdbnh6skTLi4uuHh1zsWzF/irtaIEoOgYPucVSqJKRB8DVjQqO2SnHlVUlPNIN8VUuTjdi4fKMeFqes4ldpVet9UzZe1GoUkjk0wWaiMZ1jaoI0t5a/uiGwTvT3/4Y5Kxmi/JOYUFM1DVjrN79zh7eB+bacqrly/Z3qzxbYf0PXG7xdma6AM+JD75yc9YZ2SWc/+Ypz/+WKHDY9AUJnVFtWiomoZHbz7inbff5vLlKz767FM26w1p23GaLKbV8e6JxGgwRp2AfvZn79NJj08BU9WAoc+KuZLrqa4b3n77LR48eAAi/PSDD7i+vMKFgEXobjaktqcHze2JGvY3vsXVdXbOcdRNfeAcnMSqHWOqDpz1O1DQMXH99AWd98QUeb7+GbapsXUNzoA11FWDILz55ps8euPRQN+fv3hOu91SVxXd5grnI8arEtJfrhXqSTwmJS5/9jk3V+fqoHbTsVicgLH46prOVdRNw8nZKYuTFSklNpsNL5+/4OXz52y3W0iw2AQeRMOm88qkSYXBIpue9YtLbtaXfOWX3uPXfuPv8u6X3h0Y78o5JCR83yEx8erxMz56/8f88e//ITfn59BHCEEN3vqQOi7qYh58rcun5LGbZK48ujdep3y5uzLstmuldYfn/ba6DylxbuvH6+47dn1uBB3pxK5x/nVKp/F5mPZ57rx4qK5pHfN75sqh8T52ztO7OhPsKFJu+f0Q31PqnPJP+tBeNXtlymPNeb3pPdP378HJT9pS7jmkKH5dOcYbTstr17fs/3ZMkfdF23OXZ+bPl/G66544UAvTTs3rue0cn/99F2Xt9Pf5PcNaKUqW4oiR76/rmn6beevJGA9y/kRJWf4+uIcOtH3+DzlsdB/ugYHnLOlU/jrFsGS5AmO3dF1H1wW6TvnO5bLm/tkJD+611M97ttKXnmg0RvlLhJw1hBJRMVyfz2NWmkxl6+n8DdFMRiOTk4ccwoS4QNte8+LFS168fMQbS4utDdftlj6pErnIgDF4SIZNl9i2gW0faIcGJ6w1WCmwpCpfVFWFyarZ0k8RsFVuJ6OifbZ7yywx8J8pQYoEcuqVYrhKDBpPY1GI89pSLzXtWt9qrkqFWfUa0R5D7tcNKV7kKMdK84wvFtRNkxWGWSatsgKNIuf3bDabcc6zTGorS2WdGsvrZshR7pzDWEWDMTZDnE4CA4wx2BgJHXjfE0PEJ9gAK2tZLe7z2e/+Jz78/T/n+vELTu+f0uK5vLlhkU6oTu7x9dNHfHh2yfvPPqVrr5AQIQjnRKQS/oQtVyGybuHt3vJyu2Zla6pVRRt7fnr5kgcS+cav/QIPf/gZl88/5sNty48w1KhDtdPwM9q+I2w9ZrHCL5eIT1RETuoFjXU83V5zk3oSmnfcZQUdB5A/zHR1TNbtVDdSnF6rDPlpjKrEYox0XufSVTXL1YqzszOWixO8j6rMDdnJ8mbNW++8x7vvfZWqWQ4GtHv3z/j0s4948vhTri7P6bsNlkhVWdp2S9d7QtSWVotGo+isZttNOUJKiLz19iMePXzAG2885NEbD3HO0LVbuvV1duSGRVMTpBro4Hw/74yNhKywHBQkajDM9yUBMzNGjkfCwE0y599uK0W3tqOfmdWr8qGe6SHFvVQV03N6Pwo1G8ZnZHgPynhS1/h9RCubtmdeXkd6tQ8pnxkTminKl5d0mjK08y588m4xsu8IeddyFz4mpbTTqr86zzCt//B7d/qQl1SEvWU1qO2LbjEbzMZ1CBBzfEUxpuk1ENp2u5PqxSJ0vepJY8r+MNYiErnZjGibpa3GaMqP3T4d6G/Re1LmWts45+GnwzlHZTomex2SA8b6DvPqt/G+x+QqOCyXzD/1vr3XHn3u2G87v++ymQdl0XmagkN1DunTSrVTuWDW351xTgkz+XuaPnPsc9yvM3+vnSLOxpQy0t7ueTfoMlDepBiV94KwcksN8eA4ljUz1VlP+bOpob0Ez1XGDU5k83Ebo9KFlMbgu/n47TxXpkskoyIqzTC1UdTMrIftUiD2HdBDRhy1vicGx8my5ue+923uPXzIR59+zqefPubi4oJ79+7D4iTnAu/VSSoIxpZx7Wnba/7yh3+KGPjKl79GCJGbmxtCiHz7O79AiJaXz57w9PFTvI+8+eabiCh66WK5oqpqlk3Nq/OXXFxc0HUt3muUuiA5ipedPTFHpZuWmFJOLaPHf0GJRAEqaIl8wob3qvs4PN50bCWnQfVRA1mcjH6sKcAG/merB/ytX/oOy1/9Nn2IxP/wMU8/esrn655nwRBizf+3/5wXn685Ywm2oa8agq05lYpHdUVE6Juarlrw/tNPef//+v+krmtMs0ROlizOLGf3vob53R/z4Df+hF/7x7/Fzf/yv+b/+H/6Nzw4CayaipSsylxWI7xtQWQVXVNVVVFVFcXIKQiVq7Mdo9DDjO6EJyaPstnKZ0gsclWho2XcS1Cs4L3QdbBpofWWxArrDHXjqGtD4wyWSvdDNgurbhP6oFHvRiJiVM64PD+nazeQA09iVLth53t6X/JXe6rFEsHi+0jfeiyWutY92EePSz1JHMYqDVJ0pzDYIDQIRFFeRdQRABKSI8M12DTv+hgAD6mntoFVA6cry/nLni72LI3LTrfqgPfGyYqN77iqApIDk60omuZ0f0/PuXIujefJ4XQ4s+N457wpzsoM59PufkiM/E7hy8Z7ss5yQr9TFrcURt2AzQ5MPmAqwVRO891bSFYIRmH1JYoG/qXIdnODiFBXFatFQ1UJ19cXGGepFysePrxP1x9wHj1Q7mwYN8bQ+R7f95jlQj0giuEppZwnIRbtHxKHURk+vfdD1PcUylxQZtjHSJCk0a+MBL3Aj5dJ8dnIUqKBi3d+23UDYZsq0gZCYUcYiFJ/MbxPmc3StkMRN0A+YHOem5TGXOnAdrsdDoqUEpcvrxARmrqm934waBfGPoSgUX8qIQ31dF2HtZbtdjswUiXavPRL4dd7VQhMDvDpJihwwZIiJ4sq53eIBJ/zo/ueIGDrevgnE6N1qWeITM+RztNo/HkkdWnvXBE4ndN5mSt7D/1Wvg+MROGpZ3WLlEj/MIyT5jCRnXYfUvDu9yUNY18g1qeMzCE4pYN9lEwsRfODhxCHXDciQgyB7TYTCwXxQawl4JEe/vwP/5h4taV9ldi2nqvPXvHy4+cszk4IZIeImAbh+ubmhs73OOswIUHbk7pALzYbUhRe8Q//u3+B/+1/Rf/sJc3La3p6Lhsl1FaEullQL5csz85IxtCsVlxeXXF5fq5ebrYmuZrf/sOPMFWjHu85N1mLEJylkcD2+RO6q3Mk9BDB1Q3N8oSzNx8iGWLeZE/r3vdcXl1xfXOtDGTnefXlTzhbnakHVh9pb27YXF/x6vlTtus1/aalysqxJNnrT2muMvCiEUR7jI1IsdHiMLiUYNNDvOJf/Df/L+o3HtCcnrG+XtP5yOnpGU9/+iH/6uk5V+ev8ClQLSuC76mcw71xxoN33+GrX/sqT588BRIuCdevLnj15Bk3l9ekTpmoN1anxLanaWokQeXh2Y8+ZOO3nF9dZAVaBaK562LSvDn37j3gwcMHLB7eQyrHZx9/zpMf/ZQX15f0C0e1DZytA1YS3uoRrF60EYPQbTt+/MO/pEsR47XvfVT4JLuoWZ2e8NY77/DmW29y/fKCn/7lj7m6vtK56XtMhKVxuJiIoVfQeBFOT89YLjVKOMWET4Hgg9IKU3LPxOxdmnaMN2Uf30VxPj8rhn0/iaq8TZgflGJzpbgIxYGl5L0faII1Sj9yqZxVSKeBEbT4bcA4jfxIKWLbjvbqGZtPnypsZF0Tuh4jwkKEPnmMy+kKUGjU0EVqY6jEkgJUNwFnNV1CSInU9bAJJLPh8ZOXPP7T96msI6DPJZ8wMVIZQ0jZwy9AHQ1OEv3LKz1TLCAdiKFOajgfz68tT55e8HyScmJZOY2SIVFFEOt0b4qmPRBjOGkcy7MzQBVBlbF7So6pYHqoSP6tQFcOgmqM+AkE/vblNdYYls7Rb7b04QbvrHo8G2GdmcHzH3/Cj9kVJmPUvEKIZ2EcVTQEH1g/e0V3syaahAmBThIxqkPa5rOXWGfp+5wCoNCFpmGxWhK8p2tb2s2WmJ3fJMHSWr7z8B26oB63YiviW18i2UTVJ/4X/8V/ybd//gfY5VLnKm+N6APJK8LAxx9+xB//23/Pi599gsMQ2hYrOUeezVBvAlFkEEiHsczwk8M43kGhOd+Dd92Lx+qZ3rfzOdWJzH4/FJl7qL5j90xp8Jx3u1VpPPn7IGQ3u/DOh95xrBT+o/TvdVHE03qPtXFa5/AbR9LgcJgnm1+/rf3l3kP1TdszKJBu6dNt757X+bqSKMLIYfrwVy1Th8pjczXnI/Xlu79P5/GLKrRv22NfpLxurd32HLP5vut+P/TuY3OSUokjOFym7zbGwBAlpo5jXd8P9Fvh9DLqkGQBXKbt2o/COvLW3fuZ339onaockTItSimRQm7fX6NEaoJvMWI1R3UVwXvWV5dsb9ZICpysFpycnLCuLpGgPJYxBikRb5PxS0my1/0t60JUyTVVuErmjRBFfBKRIW8xqMNC5Qxdijx5+pwPPz5lQeL+ozOqRUMQoY8KgR/7nhg9oQ9su0DrIyFJNvpanKDQxERMhmN21lCRNPeyGBIx268L3StUrsiw+xp85ajKuZGVMghj6iPZ2cMyueZokNrhjCN4Twge7wPR92qotRlhzAe8b1mvL7m8ysrDuqHOhm2FUl/mHOMGax3WWaqqRrITADERQqTvNnQFsnSYQ430tdZiKot1lrPlPZzLRnRTUduaqnIYJ9BbTV/nI2bjOTlZcv6XP+Xxv/4D2h9+yNtugbWOL53c5+r6mtgF3n/8gs+fXnDtO2qXCM4itsFKzfm2I6aGjXd8uLkh3byk6XpOo/Dtk7cgeK63F/TdNW8tFrz77Xd5a2H5xT/f8Dc+WvOz5LkUR4oeF8dckjfrG06qB6TlStPChMAbVcMLtnzcX7IOCcFRCTij0SIpo6+pnJOnLo40YcrDlACEwtsWuZ8kpChD2i/nHK6uWS5POFmdslqt2HQ9Fs3T2LY9l5fXvPXmO3zr298jGodYzR1f1/DJpz/jyWcfs74+J/VbKgKh92x8wHuN+LHOsTo7o2kavPf07Qaip6ktX3n7IV9570u88eA+ldPABx961pseCJhGcFLl/UmGSUfXMBr9R1bMxjQ6x9mSwnJCqkQkO8uUc0xGWNdBx1Fkp6mBqBgi0/Bb+Xv6fRpdqs/N5fB8zpiZUWbcfEP7ZXAjGTdnGlTp4343cgtayJSnNXZUU76GFtxGPoe2zXnSQfl7O7rgsTp3m5AUpWpGh9OsbWPV8+dv519KKakBh37N2jE+s8/XzJ97XTel6GCEId3d+KKJDF4Ch6JCk6dU1qsaHEQmwS+k4QwVyRDruV9TZwkjhkSmX6VCSjpQGc4kZw/zK5DRCCf60invnVKapDUqtPNwAFDZZ/OAr51xOrCGDslnc11KvKV9cwSoKQrobbyBMbdsht3WHL467Zsp63jHXMLAt5V3DsdDmsz99FqiRDbO33PIqH5INizXR3qhuo6UFIWlyK7DPTJb80mh4QsqmrVmp86UrVYmW4usNYORfOwJkzU1pomB3bze0zJeG3nWgV+b8HnFcWCIQDeq21LUXh3Ustecs8NsDOsJMhz8+K7CD+r5lPnDJNikRrS+77m6uaaplD766CFtefDwAb/65Z/nW9/5Bj/60Qf8yZ/9kKurS5rlkqpWpMS+S6QUIKQBrj70a3y34U/+5D8SvOfLX/46j954i6fPnhMJfOc73+PjquHZ86c8f/4S5xyr1YreB93vgGsWnN1/hKsXbLcbuq4j9B2KcpmyvivATE44tB+iKdG+BlLUgKQiMyb15fnUdFxIz6YWWqCTRMopAySvARJUSaiSA/E8vLdkdVITrtZc/95PefLJS+TkhE1/xXm/4VXyvLVc8lvVe/zFzSU/MZGnkqDvuVg63oyOF77jSbfm2nn+5r0HfNLdwL0FDY6zrqMG1klwfeDH//Jf8fD+Cb/8T/8pv/qr/5RPfvbbnKRALYJIhXU10fjscKFr11pLXdf5mtsZH+89vu+HNQ8gUYOPUk4lo3Y9jZIvqPaDJJX5ihgghEQfEn0XWG961suOVROyLUVtILVrFB1BDCIWmzRy2gpYA9YkrERFN71ZE7sOch7v6HtNkYry3CklrHNUxmECtOsWG9XW1iwWiFO+IaQen6DzwrpTva1zCtdf0EtiCvS+Q5LJfI7OuxHBpp5imzbSY8WRUgtpg5OOporUS02fW1mwVuHjm8rx1tkpV92al26rZ2HmNgyS+2tmcttsL+dr4315G8tEEp/wDOU+M6kvyeSATlPtI3v7ZfyuQWhFRhfRXVlygxM9TgLW1FQLh6mzI5FoILaVREgGE1RPGkKkqhtN7W0tISQ2lzdstxtFbR36fjeadWfDeIjqtSMhK98rR58Uy92I5jMSdBGUqOiUFFbQGBlgr43Lxq/gB4MlorA3KWle4ZijakEZJeMUWgzUMGtcVkw6AwH64Akloi8zMzGloY4QE9YYfPYIKYx1yT0WvBokY44A7NoWSBhrsUYZrhijhvIPSkfN91TgPmIIGt01RI+rEuR0tdJrqIfHzXpNXVXUzuH7DFVtUs5NDM5UKmyXMciL3bla35Gh1vvek6ImpEdQY2CG/IlJ26OSjuaxTlFI4ohBSEGoTYUT9cRv6or2+ppAJBKwRuiDRqZ6H3BiBg+4qWL3kLIvqdSkOY3F4EoUdwoD0wkM3jQjFFpSBYcoDLvkCIHpO+YM3Y5wM2lHMYJEowgGIQYIKugmCuPMwHAVxtZkIdugG9jn3EDGaPKuYT6sgQxXV/4zNhvjB3+/lAX0kTEhpRzZDyIVIo6ULMZACjmqd8I4a+N0nbbnLSf2FBOFetWoMbILhFdXJKBKKqR2121e41ADKfUQEy63IWaiT0pUVrj+8DOiEaoYISScsZx6HTdjDLQJ3665eLXGp4jNzhkrMbgAKXWIjfQXH2VIdDMoqTsj9M6wJZL6FpNCXg8Q1huuX2148dHnY35CPdl17m12ZsnKvM+f/5BPs9KDkDITknJagKiwSwLB5r1QBCfIcB1F8Nk918paSyIQJK+5iPhEulizvd7SVy+y44rhIj3jnhhunj5Dkub8iz6QYqQ3nm7TcfnJMx7/8ftKqKua0Pea6zEl6qx4s5kIYRQqOQXo+sDm4kYFMUCkx6eOEDy90cgQbyw3Hz/jI+/1rAQqhIU4mhhxbYfESIpCGzUvSTmT+qDODiIGf7XFGYVOB1hZpyt5EwjtFU9f3fDkLz6AEKnF8tAt6foOcQt9Jqih3ToHoud8JRXQ44MnoXlYVJgwmKTOSz72iFFPuVgQAmblkEFu2O/7N+94B5viyVhUJ/n8NEbPsOA9UYIadEUmyiNwBa4ljV51x1I6eB8zA1OEIYXjIkRi7BAgTpTGlbHQR0wq+zBHVyK0weupWN6JIcWgqCzZgabsKZOxy8WIIiQYGeBDY4yZHiT6GCnOOMYqw2GNYKTCMeYCSgVmtUQZlQicvM9SgsZURK+55GNQZhaLKhOE4uyIKzBKRZGOKNOf6WbITKrZFXsn86tj2cdIyHPvjOCS4IwjJSEYZUwrRghNJ8oMlbPH5PMjFpqSmcXB4J50PqxzOGMVgjQJZ02FOEOIGdYqRlJSpr+MiTNpYHYBYhJk2+FyqomzagVWx8UHD0lYVgtiI3gjxMphljV/+x/8Jn/77/0d9TytLB2Km5FCIHaB/nrNk48+4Y9//w94/MmnhHWLiyApUlmX5yozpSTN+Z6RIcratTK2sygYhZSNJAzC8nRTlTM4ZnqlMyejk9FEOJwbC+9iwNvZ2weUaoeUP/PndxAijmjd9n4r37NioAjxtyknjxm9R4XfvrA8P7OmfxfHnXmddxm3Y4rHQ33N2VG1n4lh7eukq9MYZv+5Q/089P65gDUdi+mYFGXgroFpf86Kg0C5Poeunwt15ZnhPaVeGZVJc2Hs6FyW/s3aM39uOg7z9TlVPBajYeEz53UUBe/enOV7dpwKZntt3v5jyr3p9+kaLN/nEUHHFPY7QvRr9vT82cP3qQw3lt21t+PcwGTZTNsnOZ9wSjlftjqQRu/xMeGjepKnIkSDOluTdtBrNUKhvOlAm4eoP+WXRaAcpzLJSXqolHpFLCFBtMJV3/Pk8uXRsblLcXZJsBt82NL7jhgCDSC5rSkp1N9i0SjNDaq8TslgkkX9hLMzDhndaXb2T0diWF+5q7uK8pGm6tkSs3OdgQzBLMYRgmGzjVzfdJimo6YmWYuPiRAM0RtIynNHHMZqzdYknBWsZDqVlOe3xipUZRdJzqrcLLvtADWkDwbyzFyVPcnQq9l+GdaD5Pnbd6AqNNAYi60WJKv8mTc9Ij199BrJgEdczIpChWgM0RM2nrbd0HYNi8WCrt3mQAGLs5XmZHeVfjdO32PB2BUpqbPHkI8yRdptSx822TkVXjQvaVxN7WrqqmJRNSyaZc71qA7ItrEsmxruVfzon/0xn73/Y7qLC+4tFipDtltq5+gTXPY9H2VlcZ8MWyyBCuMsng1IYN22SAwsmoaHbsUyRc79NVWMnDUNb56ccnoZef7DD3jju2/x8xdf4jefrvn/vfqcZ43nVBRa3hqLE8O67TjrI66uCYsG0/WcmZon/oaX/RYfBCcKKW9FlfmhRNcVuh53aXM558rZN0TSVVWOkLOkmM9na6mbBuMcVb3EuYqU4OLyCrGOxWrFZnND13Usl0u+/OWvaBoiU1E1KzDw/MVnPH36mJvrc2K/QZJHUAQghWoVRVaqGyTBdn1DXTneffsRD++fcf90ydmy4exkiSeRpOR9TViXjTXZAb30q+BCFPqj6h8NYFFxKAeheOXJhcLTxWHvBz86DYc0RtWXtT/Q+BwDIxIHIeIQ/zBe0+jdQ8rZcY4Y9QCTksabhrNLUgEKzWhXMj3JixNsdnbhcCl2vanbzCH+ZGzvcRq8048D77orj3vI2LXznry+h3eVtT1z/jnGS6Z48PLeuw/xCPtR+uzdM3+/ZPmkUPMpz7Iz/5T526FApWU7bVQ1zq5sU1zqZJjvEnAShzM0lXPBgLNWEU0pRvSUIXLz+OajRIZcfGMbGXgVbaJurZI6JQ40tbTDIGNOVA7RlN35LAFfRedR9kXRXU9HpgyNwRwd/zJ38zUIDAFg5RMmSCND+sx9R9vb+LxpKc4JZd7G62Usdjsy2007X7X9Zdyys8OO/DG2T2R3PBIT5/AD4zSg10zeOuV1im7mGE+u98XMK+makbxmhnWa8yiPDgVlrSpvGoetnXnVjF6i6Ehpx6clxjiivzLugWFdlprzGidN+d3SqN1x0DHze9Hnc0cJY9QwVfq9E7Vu1V5ijGgquKTyTGUrYopqq2mjBplI4oF7A2MCD+4v+cEPvk29WPBHf/znbDad6mecI6WKvguqf0oaNY4kjLME3/LJJx8Blvfe+xrvfuldHj/+nMo6vvSl93DO8tnnn/L08WPeefddqrrJ+mAhJDW2GuNommUOdnT0fUfyPSSrafZi2JHvDhajXGdC+c2Y4WpUB6Y0psVznjwbBz2Cj1Cc2lK2KUhI2ATWNXyDhr+8fsy7f9LS/8V9Nk87/lv/GcsOTnpLk4S3neF7b77Ld7/1XW7+7E95ennO4xh40STOSDypIx7LNkSu2gu+2zeEkwXPg8cQeNMIb1NTx4abR2d89rOPufcf/pDv/o9+nX/6j/7X/N//mz+hdi9wJpKiI1kZ0AesM0PKn6rWoEsxdtAh+hQIbau2sJR5q+zICnFI22Kz3lAjnbPsNqTvyueUT5igjjG9j2zWLZtlR7vwLKqIM4HeeCpS1gFr4EgIXo2sRjCSiLFnu1mzvr4h9ZrDnOAhqH1KjBB9IASfI/cdsdJAlZCEUFWkHGwSY8h2LkEkI5JgEWeoY8S5KuudEz54utBmtCHNo72oKgyGmNYaBe4cdWOIfU8ILcFvSaHForbGvopYp+gMYtQw7k4bVuuAq+xwLhBUj22laD536cv8O7CbWnS4yEi6i4w1M7SPMyQ7kvQhnctO/UltlaRyjqYs3wRS8KQYcLVltTrBrQzJKapyH1UmnxBj3VxRsCavQQyg9ujV6pSqquk6z2az5vrq5vD+nZU7G8Z9RHMnGUdfhOqck5aEetFaM0R6FQqWVIs/6XyaCM4yDHgRZEw+tKZelzvRy2XgjRouRTQXBlIiqkdCqZHNdiB6kOGxrSUnA8OI0EePtVbhS0UGKPTgPeIczhk1gmfYrRJVXNc1rq5yRHun7UfnrHg+phiHnDXbvof8d4yRLkfAKWMSFYoiphwtrgQmeE/f9UilwpmRzNDlfKkmQ1k4W9GHXo1NMROPWIT4otgajeQxJGrr2Fxf0262LLJ3lm0aQtcRUqRqFsQUNcdx1IVbHBTmMOhTBgWyB2VWSJHHZPitEIOUIBNYY01mdIqHXdnUY5lGcxciXMp+G4qiRyMLrLN66IWi1GJH0FMuOCtprc3jNbmeNEftwCDm64VhVe/AlL22Z95/KeVDKvfBGJarU4xUmQcvzKMeFNMDxYhBolHDUEiZecpEOkQk7AtTYfpnGhVCg6pPE34gUahTIvYaTd2XM6cjQ4+Pa1mNwAbxJToXUnF6iAr9nMJuO2wA25MjevKazR6XKTN/dTFg7jC1kjtxWEgsHpMxt2nIxZbiXl65hDIpaXZ9Wp+RzFImdbwRUaOjTYINCUKvxuaUsCNMgcKFO5fhclRZUEWoxCI+4NBzxlHGKfc7G++LwFD6TQSJkMLYL5NAQgEFjCTxGKCOU2IDSMBFzbtJSgSU8Egs3qLKmPcZpcCKgMTcDigpEvQ8NiA5nwoCEpAYcQlKqgys1X8CkqIqmosMMREYBoE12Zw7fqaEL9oZRkZ7rgyYGkAOCmSlPqNjlgBjR0EyFUE30waTIVmiJHwCExPOqzG2skIy5YzaN/6Na0fVUEVwSnnsSnsjiRgmSy7uRx+SsoBTltRwbxxyDZk8vkP9Kc9xhETAYAikwWAZh7EYGpqV4zlGKumuTvP0WfmxEMcztjS+1J1CHJRp5Ywzea2kRDbOFoV57rSMkNTlPN+Zw+HMjkPkfMrGtJCyEjj/U09LAWvUIJ3v04dkEjFTPBHDyNfl+4ezOiUIykAno0yu0YRAA4yuLnfJuUcngvtEQWFJGoGVsjd7Gs+Rqq7ogx8omTjDD37p5/i7v/UPeOsr7+lvdYWPkUoMoe8Jm47tq0s++fEH/MHv/C7rlxekzg8emmXMpp9mkIVzqxI7tLOc/TsCP8dLimmsZ6YEGZngQ3R/Oq37b9i95/B+PwSzeVs5pOw5ZPycqgPyTXd+T7nvdQbTuTCwPzbjLBxq854SdNqHyf1zxc6hfmiUZRrWyDS/5aG5L8LOPPfeFNloPh7T98/HaDyzxzP4tv5NDbfzNXFoXvcUyOzXPeUXD5VByT9pW2J/HR1rw7GxL7wJ7BoT95TBsj8uw55gPGMOrfFj7z+4Fg70Z3r/sbVc2h/SLoLUXMC+a9H2ZtZ5QheGduX/Kd1muDbfzQMvl1RQjwjJGE2tQRoUjHFan4xtIKadCK8pzzJcyjS30PIhlIHSoAMtKx0Y6lCeL9qKLZEX7d3ymx0rUhy5Q0fXrTUdkzE4BDGZVyBhjBpkk4zpg2xSRy91UDd5jHIfZmt6+JcHR6b/N2byb7xX05mXerISPkUESzI1UdS5Lnq9PuQPFUHE5s80KBdJmopHhzTt8BQlsiZlxzORHAVc2jOqKJnOlAzfiwwy6fPB8Z5fLQxeWcMGk3M4iwgYQbwhBE9AlBczCSMOY32OntEI826bSDHgXTXkDLXWYXN+Quccla2wzuXIk2YYg+wLT0qKPhazQimEiF/3JOvppWVrLDeuorLXVIsGqSzOGBZ1w9nZPbavbvjkj/4cXp6zAs3tJwkncJ3gSuCVwIVEjO8JvaeragICIZKMoh75ELgnkS9Vjl9qzmgDfHr5kqu+R2zFPXH8p/aS7//FZ1S2pj/3NGJ5RwznBUEqJqJEgkHHp9uyrCqoKmxMbK3hybpl6z2RDAtrjcK4pjTIOMq2FhqWF5BkhR4FtTBirPLFVVWxXK5IyWZ+UqPnXFVjnEXEDjISAs7Certms2kxpuLBg/ssTu5jXE1TLwgpcnN9xcXLJ2yvLwhtm5EOEiH0xBiIyWCrBa6qMGKIfcfp6YIvv/s2777zJvfPTqgrIQWPNULwcTjLVEdis04HSFFTNAiDYWRH/krFoF14RFSZm3m48rvk+0tkYowRP4kGzyIaBYshFQhUGaSfvGfGfZLyOTk994c9OaMfImWzm0EmGEo5n4Zr2bGzzO3AU+3eJpP9Ot3CMv0DkGl0FDvHYW6/XisGrdfxjVPj2liNzP48wANxiKpog+bXDo7f60pi0E/tv2KXtzr0vkOy8LCmGBs/wAgPfZGddaH1Dd/Q9bTzwM6BvS/LpJ15TFneGVbHwO9M3iGiNF2KXFf0CZOXiuyMfyqVpDQh/2no7846ymtbdhfYQEN3bhu0Igf4jrlcIOOqOOjiIaXv+3zzbfUe4rHn/OSUJz9Uz2285ti8CerWxAuvjNPAyxXifKwMPOGsH5OZF2R4xzCHM94mf9nZ5MPrZX8NjXcU2jLO4eQ4ylWO8jfIoFec1qM6DMY9M2lAWX0FtWZozYG9bQq/MZn3wvFMpX3dG0WfNe6zlHaRTkufUyr5o4fdlfmbsk6ynn4iv5uMwlBQFTWvtFHjaUYirFylc5MYjPUhetq+ZRkW1JXl9GTJN7/xVW6ub/joo09Zb7Y5haEl1Q2EQAphGHul+56rq3M+f/IJOMO3Tr/L/QcPubm6pFmsePjwEX3f8eknH3H+6iXL5RJXV2o8xRHDVI+hbfZSUGXVyZHByS6ffVLmaeQvh/UMmk5yQlvIdo0QIx+nHo/QIwiGGBJV0gCdACAavPRQDG8m4f3uhup5y9Zf8U5c8MpuOe8iKxxvSs3DtGSxjTx4eMK33nrE037N0/UFr6oVNzEgydEYRx8j513k843nS2envKTjJnochmupedsK3F/gn51z+ZMPOf/d3+M3/uf/Nf/8vV/g6c2/x6drtbNZ9J9RW4dxGmBS8npbo7ysGAGfx2ZiMiFHiY/ZS0Z9obFGnV6z7sKUUUyoI56H1Cd8B51NbLrAuuupux5rK2zoibYnZqDKQKCnx5tE2/XcbNdcXd1wdbmmX6+RHG0cvRpiS8BSCYiMoJHgvaftTYYcB5FICB2hz/qgZDUpkLF03JBST0xLXKwQM+q9N90WHxJkvh1KoFCgogZbY5IG24Ze855Hr0E7Td3ge03x6QQaY1mYmtDU1AuHzXA/Me93yXJf0RvqZ6bN2dG7nLkjCRwvJlSnOeggBPUkzP5oRmRAS40ikydBETtew49IYRYyylDOIZAy0rPB4GpL1RiME0VksDpuptKU27HviV4Zy2LnLKe/EYO1FUki2y6w7TrW6y19mCu+D5c7G8b74FksFzkKqqLftriqwsqYIatvuyGXuCA5p1UYFneBok0xbypjNHISycJdHJiTQuoGJYnkhO8xDMJ9iEEFixxJmrLRRz09ikFQ/1c7p8az/M/lA1tQGIEYNMLUVY4gfsiZkFKi7z0xBs0VbgpkT8nbKyOEfBpzlDhXac7xuiHFSJdh1xdNg++zVxYKC+eD5icxWTionVMvk65VuPaYoHJ6r9eocZIqd0zOSZXXbCYWRSukGy+FqAQqgTGWkKFkL6+veXD/jNpawnaLi3Bzfc2yrtV4HwKLZqFQ714hZbuuIxVPtcm/cb2rEFpykutU7DJbRakwvZbSCGN+LB9igb0v/+ZsWRHoBmWNUUj8xWIxQC5Oo5HmuZqKsm6aT2TuJTuFeB28MGGI5D/EnI4MGVgx+Jjo224QJFLKDhVmX4m7o7I5wBfvK0Z3+cvC3CdGZlbPwDSrO00OyDwnmXgdNFTGCEZ2FOHTsS9MZizjnO+b52kvn1MYqWl9h4Sx23IglbZO4ajmn/MywMNN3KnnTGNRDkz7GKNCWerBrFGm3ntlCmfrbLcP+8LQISX59Pehz5NHD92fJk5Au6z/yNgWQXRXOaL/rLVEmcAYy2hQLDUV4XQwhsjowZoG0lQQO5Tyxjg606hDUxrzeGbFyXyOpmuhKFEPlZ1zqAi3k309nYMS7asKxWKoV6Y0wYBsgsioaGJO6ItoNP4pIspY5bGJKY0KtVyKQ8fQjsm4HxJMyzjunXODIkGFqAPoeDv7KcJOZNjBMSw9KgLbQaF38t7ykB4s5cswLsM+FAbvT2uswrvvyoo7a7+cU5KAkAgZ8pSUo/4wkPYdEVIqqV3yuVbeIWN7ZDKeafLc9HzYMexNX8L4rmmxUQ3TQ/RJSngiLCq6FJBlTRcDj770Dv/on/xP+dp3v01yQhd6UtLc7FYEWXe0V9d8+JMP+MN/93ucP3sOW4+NKUPiz2gJu6fIIdX+XLFR6Nq8zA1l8zPlkEH4dWfqobbs/r1/xk3LdO/P6/kixri7tOV198z357H3z8d7Pq4UQ9Tk3jmdukvfpnNwtC/jqzJrWs70GX8x2Xtzo/h0vuftmu+ZQwo1yPM4a+/r+njXNbX7EMM5PD9TD/Gh02vz8Ty29qbPvU4hvTf3s3ce6uv8PLqt/mPldc/eRmtK2UNm+oLvve2e2+47pMw9OAdF1ZfliMK3JFS+8ZFs4CnvJdOZsY4445L3kGtG1OpME++wL2d/mxAH3smKYO9Qx23Fh17/+S19v6bzLRjDwtakFLOSBULqwFpFrMktN8HgJBAkIqKyYEzKwxNGnqQ4BE77o/Jl5uUyRKGRIoepUdwYoU/qCWiys5kErxEzVYPUDZWBSuIQyRpEnRgQi2ApsZuFLxvXS+YzSSOPLmgkzyR3bGWdGphLP8rAZZlo2H+oIkV5g5Gv1WrHfb2/9iTrC8oTmV8xKteJqbKTrsF7QwhW5R1JWFsRbKC3PV2nOW+77ZZUKbpetJZoPSHLtn1v6AaDucW6xRhBLjkaRCxVbbBVrU7BISKtUT9Cnwh42i4Q/TWmcrQuUgEnixWthZd//hEv//wD3uo1BZc3wrJSRerzdsuzGHiVe528Z+07qroC0VRsWMc6tAiO+ybxvQr+VrXkJy28jI4X3Zrr4LkwgQ/tJauPwL4QPnYdP0s3fKVxPMNzGSM2qsGgTwEhcd3ecH/xEFdVEBJPJPG07YjJKFKgs+AcKaMqkXlDjRUp8oJBiBk1yYA1+KCG/NRpFJMxDcvlCjEapY+Y7JOtPGYX1BG5qixNXZFCz/OXFzjb8ODhWzx66z0SlrpeUlWWV69e8vLZp6zPnxLbFnxO1Zc0HWASEONw9VLPo9jTWMu3vvoeP/jeN3j44BQksV5fcXXd44OAsQPMuZZiWRkN1odSus3TvqVEBlQYoXin5+S0FLl9b/0XGOi8qfZ5hMxlT5QJIz2Z0qbxU4r8YGAILZnSyhkNL3uOmR5J1WcjrU3l3J4fu3s6lvmlfV5nbOdxulR6mAYh6hb+4OBVMizpjD84QBcP8RKvLXJYTth51+T7Mf1e+Sz0ceJitNOxqQyYr+xcH+adMmZ5/aSd2/d4qbkEJDv9GscrxrS3bsjt9jFMfsuPxt2xLHqO+djMx2K6ro0cMl/HQQc+NJjDssSeHqjso/w5b4bOz6E27ZdDPOk0D/Vc3zbVxc6fO1bmv5syN1Lml0Gfnx/ItDhxYOD26i65g4c+gU75BAUtsavLm7et6HfIdEKN1WZ0iE9jWwZtQX7EpLGucd3l9RZkeEZyw4QJ35sKytuM15fck731kF9myOkHJ/0w5PzM5b75v7GN07qma167Oz/r5jnvS1tzfySxb1saeTCTU5Cort1gnepC+9gP140YrGgA4vrmhtXyBEF5pQf3TvnlX/gB1iQ++uQzXp1fK72sGvrUqt45jfohIRD6lpevntKmnvp0wS9865do2y19m1iuznjvy46r62tePX9Mu7mmWdRUdY2xC0QszjmFUfde7Uu+HwyTTNaCJlJXo28iIRMjLjnqOQpgBVtMQiJg87h7z0f0rKIdVnEMAROL5TgRTKIi8Q6RKkU+TGqorWLL3zbCu8lyScWV9CQ897zw02cv+Pr1Od98501ebM75fP2CqwSfxMi9uKA2kSiGJjZ8vPb8YFFzr9Yc59ch8dhG3raJVeO4v1yyfvqSx//df8/f/6/+t/ytX/n7/LM/+CFX6wtWTcA5QVzmKWxCbE5RjNJbay1V5TJvo4iPUk10+ox6bJmcAZA01irIsG5dhugSjCJlBoidjlGoDZs+ctV22GqLqyyucvRhQ7I9IQX62NGFHh+Fy/WW5+eXvHp5zdXFhtS2etZm5OoQNDBsTCuhce0+JKxtcQ6aRQ0mEQls2zXR9xmVb4ERwRtDCj19gBAbrK0RscQIiGPbeeVSxSIRNn2PJA3KDaYmxgrfV5g+Efs22/oSIULlauoqYIFKDMuqojEV20YwLmLIQUTkiPIYSPnstqIy0eSwzP8YdMkpSl68MuiORAagITwoqkE+B20yA8JxEpMDuHQNY0a5bc4/DDSvvMZoIG+KoraL4DPChKOqNW97mQ3nLHVjMXXFtt3Shx6IOY99zLrlpFH72Ta77SI37ZZNu6XvPc7ezeR9Z8O4a+oMLW5B7OCpq0ZhHa0ScZ1SIvR9jjY0gxF6UDhNPccSGVM+DrDJIyPKhAPWGdLcr+pJohDX+UDOz9oMmSui14rR3XfdQFwE8L0K1TZD6gwHYIajNSikAkg2LCu8dAqRqlaYeEKky5uqdhUpC+ZAhrUV+mwEr6xGnHvv8aHHuYoqG2eaqsJVjq7tcCKYqqJtW/0tQ1c7yQb4GFRQswrBbCUbcIJC+Dgx+EIEM0x5DIG6qnADI5ro+p719ZoU9PA3Ca6vrqisRqmXMfXe5+k2NHVNsIa+7/aU5TuK0IkCfs5sFcOUz/eUTVOM3iNjmAng9DkmTIa+fGeNTpmNqWFeRPtRrk1hhQ4xhKU95drUyFk+p7Ay08iXuRJ0aL8IkolcQr2jitKsMEcmQyNP33WXsiPQDCv88O9FGJkKlNP2ljpSUjPUdJzmY8Ck/XPlsohkI+HunE0NlMPYz5i2vT7N3jFfC4eUwdM1OZ9bbUdhIGXHYFTu6ft+b95Lf8t9pY8y1KSMgbC7fvbm4BbhVEQyPPY+KsP8vlG5EWfzkssEsglGoV29TDNRjLtjN21vMWoUY++Ujx6Oy/z+PuRcfTkqaTqWpBItr85RMUc52IkcPN87pV9DV7IjzLFdMexrGcfr0LjpvQZr3FBZzPVGlMUfIKhljD3alZnLesrjUcayaGA5vod3+iajYqoolUQKDdRx2/NAH2giwz3s7OUxUj5Pcrl8a5k6SMiB9ks+n6aK5FFomhrGdp9VeEq9HlJimvdxqAjGcy+Oa01iIkqGILcJiWCjzkiSEsk+URYM7c9jN9dbyLTd2XgSlQPMoz+eG5muTpUze/OZyNBXCTGGIJCc0l9PZEvg5OSEv/MP/wG/8jf/BsumIRShylhMTMTe49uez9//gD/6gz/g8aef47cdDhXCY4hUVp3ZYB9melrma3561h4zSk3PxrlidUrnpmdtceD6IjRqfn9hjofvk+vHDHdz2nooD/ldyh4s2oE65vTnLlCC8/7N2zY/3w49c5cyf/6Qs8Nu+8Y9MocDnY/1Hm1+TT/L39N1t9uP/bm9SznWvteV6b3T9THnYabOajttP9C/Y++ZtnOn7ez29RD0/6E1MOetpm37Iv3/Iu0+Nv9T3gKzD6U59HUy1tPfDrXj2Bl0rJ2H+q3HRpmr7ARXELecY5Og9RkWszybxjO+7PU40OoJLdhtLaNRpdDRQ22XA9+0WBQesPc9Ho2w/euUTX9O199kZDAQdI9u+w1tC32n6E/Re4XxLN3P/4m1GXFMxjVGGlLRHEIFKFf25k1Gejn8YxLJSZGjPDF4UopoTsJdB0Z1m8+O7dlxSKFns4kzCSHEEeo0+YFnNXZ0UI0hkEJU6E1rcTm/37Bu0+78Wmsz3zfyzzbPd+FrDhXdH26PX53Cz5a2eu/puk4Nokmd5o01WKtK4b7vVR+QZdOqqmiaRvnoDG1b0OuqOmkkubFUxhJEVAFkTY5IUif7sHDUqDIupURFpHcqD1sPXUysW0/94oL3//m/wq7XSOMwTcXCCCtX86LtuPA9W98jIbLCsCYSKzUuO2ORKGyS6iJW0vNLdsFvVise1MJP/DkxeuoQeBlaHvsbTsTwynjev/wpH9qOF05425zyTmV4ZTdUIbIMglhhXSuk9yYG6soSg2G9uWaNothVOYp+TAc/nrXTVBS6RizWmiHIwXuvqep8TzsxHC9XJ8QqDjD2PqNKLOqKRCT6jptNx7Onz8DWfP3r7/HmW+9QNwuMcZydnfDpJx/x/PkTLi+fs765IXQBBLqogRVRlHc7vXef4BOhXXOyqvjVX/kFvv/db1I5PZN87+m7SAxG+UQjKEqcRtNo/5TvVoeIkNdLKEt9h1+by4hDKqMiZxwQDg7pPQb5ZOf+uQEq7XwWOenurOK+nDv9foi+jNfmfbi9vv17x/JX5ctGTUARIW+XBYf36U13ek+pb5cOD7Xc2uaU4sHXTOk+MKQTfF0b9tuxrwPTs/c4H/NF5AhIuyssMf1r8r7dS9P37LVv8vttfX5dO6f8xW3zndJhg/t8fPbruG387tb2uS6s7PNjzqCHxmhYIzO546C8ZibarvxlnpN9UKAd1e6U+rLtZmeuD/dx/9l9Xdwh3nf3WUEo0M+jcbv8kkoDBtmqsJrHdU8jf3S8j+O22Zep9vuW9viVY3LDXLafluPn4mHacJjP13oLz6IqqDQ491VVpUg4VTW0res6Njc3sFAdbLdZ88ajB/zqr/4K9x884P0f/5RPPvkcYyvqxYJ2kyAEjLWEvkOs6lOi77m5eMWP/uLP+PIbX+Wtt9/m4vwVm/U1xjT84Ps/x3+4umC7XbPZbge+3tW1Girz4GsqmQ0QdT6HvmVHUKd9IUEKgRB7jTiW0Z5xSFcroug0fVI9ViQQkicm1F6TFHW5EsMyJUgtF0lYd4lHqeHbnNIlz2U0PKfiPPX8hC1/IoHfSg1f+7MP+YVf+z7fePQOnzw55+ryiid1xbbpacXTWOHLzSmvtpd8vnlFFYUTA1dEPumv+Z5dUntL0zScX57z9E/+nKe//zv843/0j/iTH/02H24uqeqO5cJhXIPvwuAcWzmnxuvsZOOcGsZjCDrXUemOBsiNe8AYMyJFowG2VkxG/sz2m6R2NGvUmBz6QJKIWzj6bWRtWxyG2jiWzYrL7Q10msaw7VvWXctm23N+vubyfM3NTUvXeoX2DwqZ7r3y4nOdgA8FgTbQOEvXBTbbHhDqymJySq1oLFE0vbGYiDNCXfc5HZLKXE2z5GSxQh0ohBjJkO36Tu89Xa/2wzpASp7gW1q/Zdtv8DHgGktlBNMYkk1gQg5WXeNDn/eawUt2CoyvZymO0oyJamzqiqY2RbVTlZSEAw9eToE78Ut66KeYBj4zBLWlphhV1hENEJYEzliaZY1taja+1fQSZES7Xh2wQ8joDkS6EFlv1vQpEURtxZUzd3ZOv7thvKo0XD0LwCIKJSxxhBjaiUhKCZeFkTmD7eyYVzrqqT5cL1HlU4XswNRnYd6IJcSAcxUlP0qBE7VIznmaqAqUejHwGpMVX+Qk7hmKTCLGVPigm906hZ3zwU8MvU690XwgiM990HynPgvuVV1rztKUBmgGstCuEx9AhNpVkBI252FHDLH3VMYQQqTvOkLXUzuHc5au7/Xduc5FU+N7XUCVc/jgid7rPOTo9wIfTtIsq5WrqIbxTLTtlqvrK2ondNstdeeRoDlwY4yZHUhDXmrJ86BQ7drfwlDtMBqAtU7hiPMzJRK83APQz6InpxHdo8C2S4SnuXdS3jCDyDZh7Ms7QeH1Y8ww9ewqf6aK/6kRYR4FPTeazp8tz+1FhE7aX9avsYa+i5y/Oh8EWa2QwVBZ2jNlYucKyGOM18BjTvbbvN0xH/ZTBegeUyuFgI17cKoEQ7LBdMZ47dQ1uWfa/ilDXTw7d4SGA//m90xLUULN79sdt11v2/HeokjQ62XdTB1cRgV7yRFkxr6Xd+V6QwxK5A86EkyYAhnbuaeQnDgc7Eebj32ez9uc4fcx56XL+zJlgbEoK6bRMYcU0XNGujyfsjNDjHEwhCuU/TiQ5b4BgYHsRZjPKHJ+8ZjX/aikHt8fsuPSIcPetL1zRr3sn1LffP1LLLFVCsmdYiIY6EmYbLjVc1Agw3taU1QeheGXnX12SNAwsr8/d9ZDAgokeNJI6Pz0QOso62EqAeb8OSpLmt0UBvlRYyymnCPMGKC0U9t47dB6GvYcgwNZkWGHNZr7UcZF68rPofnPdE5KtHhBCMjrdVDMq2OFyeMsCMkI3goBg4RI4xOWnJJhMp46H6PCQQ0HMhjzUwKJZV9lATRq1NpUEC1KhmmZR84M9CJ3QXLUvifSCbQGUmP4lV/7Df7eb/2PWb75gAT0UY3cJgFe4SxfvXjFf/y3v8vz9z/k4tUrTIIq5khDH5TWdz1WzOBwMi+Hzrvpb/O9cejZYb5nZXpeT8+w+TO3KZmO0qGJQ9n0mXLtrgqOY/dNlQMHlRTlet5q0zIfq+kZ+DqD/LT9u+fUuNaPRWgcOufmY3eszBUpusWyAHJgXZSUAnPnh3m+wTkfVN51qEydDuf0+9g8TNt0l34O/Svrin2e5xhdmNO0Q2t02vdDPMehtT67cJQ2THm7g8+OlVAW5evv3W3L9L658vLQ2jz2e3l+CEyZvOOu83RbOw+dV68rSkPG8TDCwMTVda2RsSF7oZdWD+/IRho5bs7R75l+TRZWSsfGfzq3humwSE5/0wbPRgL+dbAtrysuECWRsBizwFULli6R+i1tFxQqNkRMVLnUiIFsCBmMiNYMDqvaZhkUDLDrAFh+2z87dnlGLQYyCpBOiSooer+l9xsiHdY2Gl1tU+ZrkkJoU3iLki6ofNf5KsZ0EY2EjkkNgSYKJc8oCCEoXHUngjMmK2IrnHUDr1tKjJGwY7ybLvJxvcxLOQtvKxoVJThjsTkwoKQjiDESjKW2NaEOtJ0q5YIP+L7VXJo5skpEBqUybME6xDrIhv8kHmIZG92n3kVItSqUYsKkiHURZyInqYaH94nGsv7LD7j8nT/gEQInBu9gGYXew4dtx9PYE4k0JDZxCyTeXZ2BqdimxBXKpy298E0PP1iu+NrJfZ7bQLjxfNhf8Uo6rLG8G1Y8cEue2Z42Gs6T51nw1KHhq9WSz9DIni1Jo1tiQ9v3nG83nCyXmEXF+fqKUFc01mJzrgRfdrHsOrhP129lNQ2etQbvo+Yp1ZhyYvS0rcf7jouLc+q6pqoaKlfj6hpQPcV2s6Vtt7omTcUv/NzPce/Bm1T1CuMq3nzrLT762Y949vwzri9e0W2uM68ZhrMmYkkY7p2dQYhst1d87ctv8fPf+ybf+uY3qJ1ls73RfgRNQeBsg1hHSBti6ge9RhzW0qiL2Zd9df2Wc3aqpymbvOwpXecH1jqH+a3doofkIToyvVaQynbOx+kZkpnpyD7fVfbUFy9/PRr11ylT+fouZV/q+KLlDk/f4ZZBnzV/dDb3x/jzv/KLyXqALzJnEwSm2155SKcx/w6H5ae9aqfy5uz7vPWH9FaFzhyQwG9t2+vac9szh+SlY3LbbfLSvL67tEtlpX3Zb3/s79b3Y3zjXNY45ix8N751dh4Wvcx8vR1s5u1zMKzyW+Tl8vf08+jaPMqXHi53kav/6mU+PlkjkxJt2w76vL7vWSwWALRty/PnT1k2S85Oz6iqmkTi3skZP//97/L2W2/xF+//mD/+T39K3zvqxYroPe1mo7admCCFDLMe2dpL/u3v/g6/8Ru/wer0BGOFi/NXnN2/z/d/8HN8/uknbNY39L6l627wPipe9sGxUnndWIexFpPT3ug4JaIVUjdgGh6gefsOxzYZLAGfiuyvAT8+BiqBBcIZQmUCm6A0cyPwxHiehC3/F7nhq6liYwM3NrIwHX8jLbh88pztpw957+SEv/md7/DiL/4Us3yDf7t5wpeqFWduwdp4Kgn49Zqv9ic0C8NN5XkZPR/2W36Q7mGtZdVUtFdr/of/2/+Z/9X/+7/ln/zd/4p/96cLPnr5+zx8tKC7EXX0TWoPDDEM/HZdVcqnZ0SOpqmooqH3nt73g37dZJ2m6l9Vh1b4CJuNr6C8k5sg5qQAoYf2xnOVtplvDoQusm1bXK3R/9u2Zb1t2bYd7Taw3WRnwzjyIm23Ydu29F0/0XmYCa+k+DW+9axvWkiW7aanaRyrVcPpaYN1hvZmS7zaEFPA2MRiUbNcbGmqmsbWrOoGU1UsGoeIIyYhJuj7QAo9IUa6rqPrOiCxqAQjER9aNv2Wq3bDJqnTL8lgugixp3cd/cIRU4+RhLVCjkHOsoM6kB7S/+zsWin7toSIMdh4d46zPZlvulkmt5XPI+R8Z4+Y0X6m8qbOvzM5yFgMlbO4yiAJ+s2Gq+tzUko4a7FNg6SEs05lLB8IfU+3bfF9Aqeo5BBJ0Y+plF9T7mwY/+o3vs6DRw8Hoc8ao1HScQKBPFW2ZK+gMmgpxeyxXhh3k/UZiVSp94YxmqOCpAbCmIV6QXJQuiq5rXVIVeF7T1PVdCVjQ45GTjZSN80Qgdt3PVI3g2ARvMdUFYIodLr3iBgWtVDV6tWUYqJpGqpK4dFcVQ0eLjEGQoy57+PkhhBIUT2mqqoa4OKD97RtR0xRhfScG8TnzbjZbLm8vMR7z7bvWTU1y7oeDuG0WGArN3iZp5TYxEC1WlJXNZvths73NPWCm/XNEJ1ujc1w7jW+61isVoMRUaxhu93Stg2x84RtS5UNLqJaoNFAp+7nGpkRR+Ov934wkJeN51NiUdWDoXgK6TslEsWDe25chkK8C3zfqEyce/SkycY7pAAtz5Q6pwrtOcE6pEAshvhSDimx579N2zB9j57qJRK5pqqqXH8gkSOPQ9zNzzRhjg5Fb83bA8UAvMsAzw3ghTE7xhwnGI1cs7YM9ZKNTwcY3rli/BBEa1HAk8/eYwgE8/7O/54qqqZtmSuv8pLWOqZ9kXEs4qztQ5TKjnE6z2uMw9pLekhlY5meVYfgZadtnI/HjiGXEgt1mGGez+8hwYesAFblxiHFSXFgYm/OpvshTIzgxTiSGM/7EDKTN53/PP5q8M5QO7ro8DHQR82ZXCIeVLGlBLy8o6zZcj4MaRYmYzWfcxEZDE/FUWJq9IHsYRZSjjrSM9gaRUCJSVVmqngf89uMEz0qhRVPoaQAScOYT5mJOQzZ1JlB+7B7ToQwU9SiyBoyGMhzU6ZrO8U9BUxKaB5FoybmlJLm6y6/T9bKuAjKvk6aj7usk8m86hyVAxdl8LLRuXj26fklTJs0dZiww7qOw5gN8GSQc6sLJiT1CpbEVfLcdFtOpMLhkOzJOYWQNzBEVZd3KaydZEW9ro0UUQjWRPYy3HU82T+H9unOjiLEOU2NIRHvDFuJfOMH3+Pv/ePf4ktf/TIhRXwM6mmMIfmAjfD88RM+/ehj/vgP/iPnT56x2ARsUs9ZyalLRBS1xlmnBpG0b5Sd06MpDZ2fpYdoXOnzbcrPuVPUgCAxPW8m9R06p6e/z99/yPHsWJn3/ZiRetqGQ0qSHcci2d1Bc5p6rE+HlBswOvBN04YcOqOnAsHr3jOlSXN+ZT4PO06lmrgMUzCxsvquKOamdU7rm/NsxyKGy29H59zoebgTsXbgXdN6D62XuXPUwbWWRmeZQ3NTaMh8nKbjMH/v6/iQ6fcd2jrhS6f863RujgmZauQ5jARz6P55nw4Z7o6dBcfmbYe3mO25Q88dih7ab/vh8Tp079TBYtpu5d8YeIEi9Avw/MUL1us1fegZcHwGupbfidKY3fQjo9NkIvMGYvY83w8shd2S/O49JhJtJIihi2GKKftXKsZW1NUJEhqi8SAB4YaCfmRMwhpNxeVsIlggjo4txWmuINaWPMWDIkPUWL1zxrJ7HhaFif7bVYKYNNYn2WvZ+x4fOkLswVaAp8B1jo5siQyATZ4woGD16Lox1pCM6h163xFElYnBR9VHlLyGuZPTiGuXI4ytNWN0XAIp6DSp9GE3Pdc4DHP+28/kgXRwbYgIdV1RVZa+D/gcoTLWk6izw3ZKie12y2azGehCia6q65rKGaJ1ROdw1pGcnRjNs9ERlDeKnV5LiRR7JASu1td4OWPl7+Evr/n4X/8HVps1q/tnJBEqsdS15UUXeSlCZwyLCEsifYI+wdI4toWupcQyGt4IFd9wFcSKD1rPE9Oyuok866751Boq17CWxH9MT/h78Ywv1/d4HuFZvOQ8bTntax4KvLBCa4Rgodalw6btqeoFi6qhXp3Smg0SEkRdK8pr53iW2VlS5PeqclRVcTQIGLOkqiq6vhvS1IXsoK6QmoFt2mCcJYYJPUGDQ778te/w6NFbGNdQL5asTk958eI5z5895ubyJX17TYodVgzBQut7YkgYU7NYnmJNzfX1M77zza/wC9//Ft/46ruICOvNNX3faSR8UkQLV1lCCvi+w/su05CyX3blbZjyUeWsSjvn6LgwDx9kKc3X+a5suUt7DtOh+fdxnximxq8p7Ruek0hKcvCdd+ENUxrH5thzh+g5HB6PeTk+Fjt37fGSh2T06Zvv9vbb2zToJQ7wCzs0t8Dwl/fP2jPIBNM2znisL1qmkud02IaaZH7htrIf1XvwLjk211+sHKtjOr67/NYkNVIhuLM+J1Qev21N38bvTcv++w/fM/2cr5F5mfPzh/b1/Pnbxnp+TpV6dmUh2KWzh/oBcNgxbV7/MZn21r04MEeH+rDfrmP9P7Snhvks+3RyTqU0PSfutm5fd88ez3yHOl635m6Tsws/CDKRBRJI2rMFlACy4gDoBULfE3zHcrUiRM35vFid8PZbD6nrHxBiz5+//4k6RFrHYnVCV5zVMhqRMRH6luv1NR99+hHf+No3WCyXtF3H5cUlj958GyOOFDzGRHxcc319zWatMMs+R/A2Ta22jaA6TDGCdZqXPKU02H6MOKyJeOOPjtdcbnXOkHyvbabIIyqTRFFdaIXgUyIZwyomPkwb2tjzt2n4LZZcopHmX/VLfj3dQ+h5v76m++mHfPvNd7m3WFJJw3vbnq9XS9oY6XzHl9ySnzt5j7rb8CjVgPDKGZ6mGz7u17zJggcL4eHpGY1Z8ukf/Cc++Ze/za//4i/TyyvWf/SUKE9x1pICmuc525OiTGl6IgZPCP2wRkIIWRbo0ejySarRkPd0JEfvT+WNjP6b1IFWgOihbxMtEUmBFFp879lsN9RLQ99pCqGuD/Q+0neRvg3EoPvPSCIlNZ527TYbSw2SjAahokZlVZEHQki02x6hJ3jo+4SPiUDEOEg+210EXCWaRsppKoHGOYwVRUcNAYqzrLVYVC/e+dEwH0mK1ESi67bcbDZcrNesvcc5x8IaWmPpXEVcRUy9BAJGIpL16eqMKYNzrOyrv/bWqcjkc6Ifmp7JUgRHik5Adn5Pw+0a/V/kxULzpmeI6rQNVhxRelJ2HxWze3ZZ61SPG3Sdtb7DJaFqGsSqw3HoevoY2LZeEQVCAhzOGboU6FpFsKhtzenZ6vbByOXOhvH/3f/hf0/V1Dn/l+a2TqLKZeMUJkPYJ4JzBeU89/RUoaIG6YK1wLBBSn1D9GAe6hAT11dXpATWjrmnQWiamuvrm0EZVlVugDVvGj0UYtSI62LUKtG6IuoFY3P0txqA1dspxEi73bLZbBFRZfz19Q3kg36xXCAIzWKB9z0X5xeqELOW1WqpOcdTwlUK5WuMoW4WpGy4KO0VUUW+tk/w2TgdYqDvPaA5zhXKWKMvLy4u+PjjTxCjRmtgMNL3XY+zBpvUGcCHwGK1JKZIZSx+28G2oxHJB1A+1EOEOMaqFecAXbR2h9CVOW1ju6fQmhrIi9A6Xxvl+WI0mipvDykSxZScB7t5yQshLu/pum5QNMwZqPK+acT4XCE8ff9cKNJnhBT3I9b3FUzZMJfHom4aUsow8sXQkMZ2TcttTM4OE8T+/tuPSN4th4S1AlVX6to3GAEzBnr63rnSc74OpgNTlA/jeB6AzT/Q5ukciciOMXTqFKGKsByRO5zeZaBL9Cok4l47d6P6DCIT6PzZmJV/cbJWhvdP7puO/3RdF0MKiZxLaVehfWjt7jKmE2eElMDIjsGaydyXv4eo4kNtLe88sA4UPSIOhFC9/9LgODMdmRBTxsBKhKRxOiFGLFkOyRrWudBSzpaSZqGglsikzTuCmj54J6FBcoqOYi+OSQ2pQTR/Y8wKcpOhwEJhkkWy4Xh/jSvTJQqFn9s+nZvy977Txr5yK6W8d1PMjlQmOxOwK50Jk/yDu8qQECI254U5lHNrpw1M8ndm2iIiQ3RKSmkPhqbMebkHGPPG52JmxoCi15My7+RUKpM1FCXH10RoJfLDj3/K44uXfO/dr7G69xY2MaIhlGHYE9r0XDaT/SVZsVgibRyGKOP5Uc61lKbnJTtzY60daKsxhlYiwSaCE+69/Qb/5J/8Y771c99HnNZduxorEHpFZNmeX/His8f87r/+HT77+GMq60jbjpQy7yKiQldZBzDkQ53nr5sKXsPZwb4ybJivGb2do5zM6eswZzPnsCO6qIPvOkQzb7v/LuUQnZnXM6XF83v2lbK743qsTfO/76qQGmkxTPfoMQXNnL+Ynr2HxqkYXAdHyh1acXjcY3bC24dLPV7mPMicFh2+b2J4uk0hNevvoevzZ3b4nGzkO1TnsTrK/tlxgDtg4D2mWCxlz/Fwdv+xvh5rX9ljhc+e8p+vK4d4ptvacdf2JF6vbDv2nrIO5z/P+dTyOUXr2Z+zyfP6QIb0I0cIWxKBlHZ5uMLriCgPeHSMUoKY0EzHu/vwLmfY9A51tIuKuBUjC+zRZ+9S+lawcsKyMUgDYgIERxc7rNuCeBKBqnI4o9HlGIEcWV2OH8njpd9VeVL6aLLcOXUakUn/ixO4SFaO7JylMCLHaN0+9vRB5WedC4/kUIIiq2jE+O7ZZgZHsCltUjlfpCJaiw2e4MMwxwMdy41JKSlqUd9jTMAEdbx3E+hY1bWPBtD5fB5at0zuVf5gvD49K2S4ZjRKPpeY0gijHmJWyCZiVD6zyI7OhQwjn6C2JBdRR72AD3reVzmKqfTHkPCSEe7yPFiFZcKeLPA3W65++ilXP/yAs1WDrS1WLBWGHnjqW66IxBBpEjwwjhUV69RzZYU2ejyRCuEkwT0MJ8Zy0yl04af9JatNyy/KGUjiWQo8jtdcscHHU17YjqsYCBECgeg7FjYMuQQJhmRynsAQSZ0H41jWC9ZtS0g+O8QUGS7LDjN5rcj7Y9QMIIa6cYrs11d0fT8GOIQ4rGXJEKHRwOrkhLpuhjrefOtdUjI4V1PVFTEGnj99zGZzQ9euCb6DGAhx4kzsKuqqwVnHdrPhy++9w8//4Nu8987bVK6ibbdZwdyD+GENRRJd19L37cCzTmXRYc8eoFmHvs/X6PwZkcTUOH4s7295XLLsd4jH2Ocnd/fRPg/Gjnx6WzuP/XasvJ63OezY8lcrmVYqwTz67ul5U+6Y3jtFhzrW0926J/thZ/7H95HYUzwfq/MuMnSZr2O0dK+OhNJUmfdpX645Vm5b2zu6gCPt/yLr5i5l5z2ppPfaeSOltwM//Jo2Hq1/WusdeOm/Sr2vq/PYGL/uvXMedn+djTq542sTYJ+/PdbWY/2Y66Z3fxcOIRFM23tc1jncjvm7DjmVp7T/jjJeO7LFjGcuvNmxcTgkDxwqdzlX57LQfp93+XMoPJjyQKLJgIkp0XVexzl1NJUaPm/Wajwto4RAs1hydrbiB9//Djet8OTJU7Zti7WOZrGk3W7GdJAxEfuOWG959vQx98/OeOutd7h//wHbTUtMgcVyRQyeqjLcu/82282Wm5t1TnvT07YdKcFms8l8WUdMAclOiCEmCIEoQR1sk8UGp6l8Dshp8/UeJaljX4rYLGOkCFiGtJyNsZyGBS9TRyXClshnyfOxOP439Zf5C3PBz/or3pOKv7O4x1rgjzef8XTT0j97hq8MFwZMu+FdY3maPGfJ8vPmhLeS4S/75/R9T2OWvOkcP3HCq9TxPLWsaDi1FYvaUV0IH/zLf8mvff/n+OqXvsXX3/15fvLkhaIsm6zvTap76mMYHAuNEUiREH2WrwM+eNWhJgYHVeXdi3E9oM5zuw74RtREaUQ0AClqvnQTIPhEt/WQAuCwona7oAACJA+pF2KXIIDJebEtOcVT5v0KqgUo2rKqdUT1nSlCSPRdj5E+i4eqx+59h5iElHorSxJL2/dUvcM7p4FWAimFvKRTRosFbAlYSKQUsj494aPKNdvNlpv1hpv1hsu+x4jltKmJVYVFWMQe6Qxd1+H7noJAXOxiMUZMWVzcfiaM/JhQ8o9P93H5V/SGRT9cZC2Gc4Esa5uxvoMlnzfFVSjNfstnscFkeHTdV5V1LBqHqRwhRkKnyJuScoR8siRRHbKJkRB7KmOpq4rT1YqH9+8fac9uubNh/N/93r8fhGVn7cD0xZQht2UfIrBcg12j+NywUQ4PazVJfDHKisiOIR3IebpURb9arViuVlxeXKiyWkRzaTtH0zScnZ3x9OlTttut5rYtcL9AXdcIcH1zMyi6SylGjCmkZIwZyiCXYtjt+37oW4oRm72g6rrWAyPnLkhRodabusY6R13XQ7Q1jPkY7t27p23KeTpc7o9xKvy2bYsRw3K1ZLVaKdRD8KQk+N7z6I03hnp3I17VgELQjexTJHURQfOn13VDSKqMGxx7Y8pGoaDzkhmTWPJkZ4XgCH+e8vpwQ56RModz5aPY3ci2qdFaN5+lADoVgXcnwof55t1lvkqbuq4bxmMamZbSaNCfRw4dUsJOFfzzNS5icK7SsZlEBhXDQwhBEQdAlTTW4b1nfXOjeyEofKCx0wNGdvpUrh0XanO7Ent92WNgsiA4ZbrmwnWMcTCIzsflGDM43dMpqQAwh3rbO5Dt7pxMlRvH5uNQ/+fMalmXw1kzqqkYBMh5e2S3rn3mNA6GvgQDJKWIkMy+oH9XAfRQxGRh9m6LiNyJMp8pGiQlOu/VecmMuetjITopx0TLLCffRCmaUhpp4hAJnA28+awo/S8M+tTYNhgMUIagZJMXyVGnogbywZg+W6/l+3BOimTj8P7aKErdQpfmaA/DFCeQJDkevLRD819bI+q5GSnkWvNxDroGFeCNHaGCpuv24LsOCDa781iMseT5LkdAGg01SWHIj0FpF/pbxmGKGgHZeUHm7z0uLE3Hvdwbo3rmTg/dqUNU8ZRP8zbOPLDLmpKiKEsZHlfUkBBTIljNkWlItBJ5fnPFhe/orLDpemrr9sbikJAWYzYAMD87BRGF4SrDUsYcyFE5IBOY9fJs3/c0TaOoKyJc9y2rNx/wD3/rH/Lzf+NXqO+f4YPHuuzlKqI5yEPi8c8+4U9/7w/4+Ec/YXt5w8pYog9YsRnWNQ001pYzQbeqItXIrhF/vr6PnRW3lb/K/XtzfKBMaeqhiOK7tOMQ8/46enjoPa9f63e/f9qOu5RdhcP+yN2mUCnPFePtMfp/bOwGRc+RPkzvvcvaeZ1yqNQ75ZXirMOHxu6Qkvwov3Cor0f6d4inmf89HdcSETAtU8eBQ4qPeRvL/ij81bxft+2FHToRDyjB7rBXS7+P3T+nrfPvh+5JaTzG5/15XVvueu/0vcfWVqHKabiuipJCn4uMVjub0X8yn++hONCKyMC7jLVqRHIpui7YN4wfQJ6YdWBnLUbAae0sxLCq/3qG8dhbGrugrpscIe2JfUDCDU0bcY3HVGS+N5SRGmSURBjXuUhGnilKobw2UcXKztqFfYM408jxKV1VuomoyiMUpVhWBsYUBpobYeAPd3bxoJfOc5zPsak8Wf55ozm6C5Ia7O59yfMSU4IQEO/x1qrR1JgJgt1xBU5hg9m36Ny6z3bOS1TpVW6NMeF9oO19lhELr1UAgRIp+WwsTwiV/pYyMk7md+tKnfs1lyFUQHDFSK7tTT5RN0ua1Yrrnz3n4i8/ID15QfPOAnGGWgxE4TpFnvuOPglNTDRROEmGN6Tmgav4xATOpSdJokY4SYIzESOJdee5WXc8vbngby5P+NLqHYK/RvwVNybxNbcktsLHYcNzOnVATUKSyNIajGjueJuM5usUi8RE7HqSOJqmxonFp25YC3us5mTMy/rQ1HyFb7fUTaMBB8FT+zDoPEjqYGOtVeeaBNZW3H/wkKqqiRF8CCxP7pFQvQwkri/Pubh4QdeuVamfNJq+zKm1lqpZ4GyFxEhdCT///e/w9a+8x6Kq6NuOtuuGfPRiBet0//V9S9dvZ3x22c8HHLLuyJOUclhPkIZ1PnAsaV+unX4eq/fQ2XDoHv0cz9s5bzLlKQ61fVIr8ybdZUzScNb85yk6ZsfeNaFtt/xe2Ca0LwABAABJREFUTkUZ2ne87NPv3dboXjlOW/f4lwNr6bU6pQN1zK/rb3DL8OyVL7Km73LvF+VFJk+WX+783Hwd7/z+BcSuY3LQFy1fVGZ5/W9zPvjgEzvPvU7e+WLvv/s9adLA4fue4Pf6+vbo+rRfeZ8dXDmT6yUAYXz29XUfOucHvuhIG2+TWe5aDu3rou/bO2wnfUVG2SFmGqL52nXzxxDpUWOplRpI4L0GEBiDIgqqE+Dy5IwvvfMW3/9eIkXPk6fP6PtAVdX0vdXxnCAQ4jsuL17x8sVzTlYnvPnobc7O7nFx/krTvGZ98Gp1j/v3H3Fzc0PvPV3bsdls2W47jK1ptx1tt6YPW+0PAjlQxoqQTE6S0rshXe6UXh0qirAYMYlBlxkSpJyGyAFLhBUN52mrPGoSNiTel54f1Cd8uTL8m9jjU2Rbed6SFWfXNVQVH6+veR62bCtHHRNv+ppo4JSKN5JlLT1PU8d19LzbG047y1vO8Sp1vGDLo2hZisUYy9nijCe//x+4+i8/5OHX3uU7X/9lPnryRxjbQ2WIdITodew6PwRZOWcxkohEbDL44Ad0ZBAkI0/GCDEoH+x9wFij45p5MpGUEXRUR1scSlLWYUcf8ORgQ2cJVSIFT8ISo0AxjvukRnFj1WCbEn0sdh/1EFa01zxHMRCCINgB5Ct4T0dH0ZV0HjabCCbijKNyFc2qxtaGvtfgVV9lZ0by0ZJFJ3UMHul8Sp6YAikpgm6McYCD37Yd27Zn3ebgmSi4ZGhsZNP1RB9Z32zpW08MGR9T2EEenu7fY6XwlFLU/AMDKEzP+TJmUgzfg4J0otMdZO1RBtvTIaR8MeaAMpOdro06C0gQld9j0Q+r3OeMpaoNUTTwK4WYHeOFZV2RHAQfNdV076mspXaG1XLBvdNT7p2dHh2DabmzYbxuGgp8bsresMZaTEoE32tE8zDAo+J2GmlaDumpwh3AuYqUsqd0PjCKIbOHwcsbwAM2KJT5ZrvFnp9rO/IEXbftIDA8efKEBFhjSF5zcsekht12u0VlZYUo8N6rwJlSNkZo29QgQPZ4CYPAlbJwqrj/A3Af260eZtvNZiRMuQ02BLbbLQlYNA2I0GQDuXOOtuv47LPPSGmMmjBtOyjsnHN5McLV1SV1VWsO7UwQBKHOObU1EX0kej+MpfceKyYTh4AYgxNDCmtqa1mHnB/ZOYUCC2E4vEd+boxCLWUHlhTU4zs7C/T9CKcxXRs+j2VKY4TvDhGeKEIOFeGwMq98Th0bRCRD4pvBYF/WZCklF/k8EnUeiVcEx11oTCgKHBGhzvnJyh5IKeGD5uGw1tKHQAjq4eP7nkoYINTm3NlxJeFkLGaCSJx8L+M7ZZKKUVLnLuUDcXecQzaqHhJKSyuLkXUuSO0wgoUBTaOgVz6H7soBJnPa33LjTBgun+Payb/HpIrANIk4oQjeE+Z4GNdMoEQhSFLezzHXOeSKTiUaXB8qij2Fiy05UcpeyWqFxIAQIABGHUdUga7tCNPzMI+3ohCM0EOl6bvKtl1BNfg5pM84Hkkmc5KLOsaNV+b7MKWksDAyRtXtKMszhLqPo8ORdn00NBSnIJ8072fIeUwimr8lhkifz1472+qlPVMHhzmM8NTgICJDLsf5et5Zw8KwlkJKmEx3LFZzA1KYuzyu0/okG9VTHOZpmBcpxmJ9hTV250wZ25LHP+pICLv7b1iPMWaGe4xQl8J5TG72vh89+SZGNHVSyApZw279s/086k7KPhqNO2XQQlR40/kpNKXp8xJm14etMZmX4YcsRAXljAki9DESjdCmwLrvWKeWVW0IcsxNYGTERA4bUYdzMZVI8pSdKhj2yCD8ZS9MK5aEnqU3mw22ctSN4+/95m/y6//w77M8W5Eqhydim4oUIlYMfr3l/R/+BedPnvPJT37Kq8+fQutpMBAiKajnMVbweU1ZY1BwJwZBDHbz/qV8Dk0jpPbX2b4y8RAfVsblWETy3HGsrBM5uBrG9h36frTkNX/055T22n/IoWgaQV/2wCGD6G7bDiv6Ditf2XnnbX2btnUqKFDOz7iLPDI/B0r9hxA9Ds3zHKWmVDzRiw7FZK/iaf23GVIPvXvOy8/5EKVRo+PBuNdHWn5s3qdKmEN7eGhH5nvnebDnbT9U9s5Abq9jDos3v2enfwfqmT97TJlVFAiHkHPm835bPa+779Bn+b6z31UL9trxnL9nvx3798/nt/DtU5o/1p35IwpLqO00knmRFFktlpwulzt7qvBKAyVTAnug/Zk2lrzXU8P4oQ7Mynx8BsfJDGstzV8lT+5YartkUS+oTK08GQZMQ7M45SQmzgKcdAm5WGc+KEPsZd7BYsAYSBZM5v/KHhrGetfgXcZtem3w8s/XC31QVmjk2Y0xxIBGRYcsL6WgSivR95e0HCNjIJkGK89rzHh+jJDxo4F86shZIlaK/Dvnicr8FEO6y3oFmw3lR2c304iyBNMsed5cFi6fsTiQJoXOTakYxH1GKhJV4viYUXcEzXHI8Jz3I0KcD1BVCWsV5t+I4EOickH7YlSZ51MkiieJwYrFt5Gz+w9oxPLZTz/mxZ/+BaeSSAvVu1gMbUw873texoA1jlMsjQ/E4FnbxDv1KQm4whOI1MAJ0FuP5GjzdfKE4Pnuwze4Z8748PmWOtV8dXWfX16t+H88e85H/YYrG3HWUsWK6qTijcbx6dZD57FJiNFjkoUk+Lanx7JcLllUFW27Zgb0PIzVlNYWGHoRyXKsoho2y6U6zSZNx6NpASuaxZK6wNZXjr4P3Lv3gLpqWK833NysSRiCGE5PT6nqivXNFU8ef0roNvTbdUZLUpQlHyJ9iJyd3FP9Vg5h+t53vsGv/vLPY1JHu9myaVu2bctme0Pbb1ksa418Sj3/f/b+7FmWJD3sxH7uHkvmWe5aa3dVV3X1im4ADRIkQYADiRxxJM6MzTzpRTL9aZLMZDLTg2Qmk8xGZqORODNGDQmQBIluNIDe0N3VVV3rXc+WS4S7f3r43CM8IiPPvdXg6El+7dxzMjLCw5fPv33Zbi6T3FgNuGfk/0cjcOZhNKPQiHtV4bhAjmZpnKd/jyCf632LyJBG85hO5kWG6+xQfgyF6hSEMhJ+6R3j/S/mO1++vdwzS7RyPq7c35KMNdyf3ngYXaxfZrn+ZYe3xJOUY1vCT0t9HBrYR7o8p+lzeWqpj6UxvZB3esH9Jc/wonfN229qUB7H96IxvhxMHhvBbefnRXLG0t/5uWN7+rdpeT3Gvm9zlpAXnt2XPc8vs396fub3jjrscQdkhhynyHI+5qW1nPwszHF5P0YnuPLeUrbOn0sZcnkv5aCf+Rhg+dzPee+XGfugOxcmPGC6IzPmA2/Owhkt5dUQAjsiTVPR1DU+9jx79kSjYL1XHbOznJ6d84333sLEnsoKv/rgI3pvqOqGLkY1ChponMX3e4J1PHvymPXqhJOTM+4/fMD19TWCpLrUnqurDV/60peJ0WB2O0SUp45iNRV13NCHTtOGh4CJEWdrdRy1amA1gLf9IEvftpbOOXoETC7Zo7onUaGDBuFcLHeDBoU0GPZE1mqV4afS88/tp/xv6jf41J7wb/ZP+b9d/Yp/6u/yltylq1ueG+Eq7HgQAm17F+MD67rBi+GX/XOumoBZr9n5yBWBle/4HU7453LDo7jh1b7iVGrWtuZkdcbmVx/y4Z/9K9559T/ju1//Pf7yr/8ll/ufU1da2qjzns1enQmaWtcmxiQPOEuIvep3i2yuIkb5o2xA9oG+D1RDcnkGUQCUTkar8pixBmcsEgJBAsZYJNYQU5R4zCVARd+xV167qmqqFHQrIYIoj9jUDSJa31skZ58KeK+6TlfXKo/ESC97RAIhVGAELwFrVc/btgHjLHXtcFbwzhPqqJn+sYhNda5NVI2vqF45hJ4Qe0LokZQdVPl+P6b3F5WjOt+zdxWdrdhZdTbofeT60tN3giHJzICxFpcMxi/TTIkTMxc5C2rKtHfQBy6qO0anzZJmZseDsUtDdnwBBhlMSx81VCk633uPNeCswRqHtcrr+r4n9Lq3dV3jKoe1ldoTOs827hEPq1XN+nTNet2ybuuXpv8vbRhPs02RpIJ1lRo6BiWOmyBuFbSV0R2F6lHBOkZllYaWrIgZo9LVS9/QZ4ODgb5IZYoxBO/JNfnquiamFLgYm4T1dLhkTKunxiqdl48Rn427gKSa45puQQHFpHeRlAU+P58BKnmGYOzQVwbSmAz5tq6pnePy4oJnz5/zyiuvYJ3DuYrOJ6VmkmRCJpIxYKNGqnY79YrXFGGaX1+CB9F6rKXwocssKcW8SSl1G1rXKiDGQIwB53u2l9eYqw0tZlQaZWWJCDYZ31OX1NapsS7EIbINzBBpUNZyLA1aQ3S8qHNFeV825gxZBQBjMzwJzhl8Cv3IBqmo2qtkwJC0DaOhyQi4ZNSzGIhCWzcDCnDODt57WZmSkXepZNbUFzIoYW3mCkQQCeQMB7mNyk0mkepB1DDonEVCx/lJyxNLMlyaifFyIjwVBsF4YKgfU6nGBJNDPGy6FkOuvZsOw0yBK5KjEhIznozEOUUFRlNa5AzDxmqEdJ/GWgDc2ERwktKXjCClMBHNoIU0OUrFlMzTaFzWZ/Q8VU7vHZWlOnYjJtuvxrR5GZdIrh3uc5bHYawDkjQgxrAXkzzTdPzGjegxwyMSsloCjDJMFkXa+bxP5CczF4QU9+R6zKa4OQvEFqiMEAlEk43qOfQ1z0k9qiAZ0FPf49pYxlqOeUsSLjM2RQAJQXy6v1iTMpW0OKIxRCwh1+NLm5lAc5p21KAp3AWCoOM0mh5RUg25mCLNfRDUryjtfbH2VVUNDkoZxjIO1po8aa0Soc74aRLtXsx7MOAgms7Iga0toetxNHqPjxoxXlm6qDCZ8UjGKYjBBPVAVO/G9L6iznjS3yNpj4TsbFGucZ5XsfnDx2SUJhmjkzJaEvNfBq4ps1ghpPUOQn6TCgtpTQu5SPdNX5gNwpKilPIhySkVs2J6oIPp0I1phxP+ToxOWqiEGxcUNsYmJdtUuJZUK904i/cxwU4kGDhxK9r+krDt2N+BGxGIU6E/M2yZ5riE7zEWl/D5eNSSJ6J16kTj7ATPRAnKgIvFBjs8FnwgVAZfO97+1nv8T//T/4S33nuXuqnoo0boWWPAR6o+8quf/IR//6f/hucff4bfdWoIjYKEOMCrS1loxOTMO+BsXncZYFZ5n6ycz85PknAIxOgPBLMlRUvZSgVXPiPZEaykW4uKlWElzQDzA+0tSjgcawaYm4nmd8vsWqbNSwL7pG8zZowphfnclgy8k7kN/OpxhdP8/aUzTmnMq6pqLKmAwUiRBSfxWsN7rTrllK8qFRq3jWHRYG4tzmZHyXx9hI0SLw4Kj9m8y5bhxBZ83lzZMX/WJDxWKniQAu8Ua79kBM84Xm8aRDalMdlolnDOPB1zOa/M2y+14frs/MxbGV0+P2sTvnfo7hCuyjNXOrXMU//rfVPD+MsqM+dK69uUoSV/ntv8bzFMnC1fZhxLuD8bK8t75veWcDzH6ZJwprFKr/SZlAIZrWu3Oj1lZWp1ho6j/DGh4RRwlD7ls6iLovg4pXyZ8OTFyqEp6nJ/+pcae5MsWSA4u6A4/k1a5Yym5ZZICFo/T8RhXE21clRrM8i5mnZQEr9ghlFnejIyHYkXL87owTka5K7MO46fbVLCYFM5FsmYWzNGRC94r4Zdl2QmVf0x8kxQvFOG/TEcwlqOqM7jd66mqpSH6/t++NH0jBESPbXWkql5jJE+RoL3g2xau2ZiaC8mn/gZCiCYOgXls5t/stI36zZC0PThujdpbs7RNC3GaNR78B3WqN4jisptWsYtstlu0XJCFVVTUzUNbSphV6e645Vz7E2tkUcuIsYhpqV3K05O7vP8hz/l4gc/ov/o15zePSWgirwolssu8LkPeCznIXAaBWcMGxd5Kj3Ormi95V5vNd159NSdx9ITXMXO7/Gx4/WTEy5i4F8+/Tk/uXnEt+6+yv/6ne8SLPz00/e5RqjEUQdDJz1nZsVrtuauqbg0kU6EJgqh6wlWiCaAhTaecnJ2yrbbEnaaetxkGl/AzrCXda0l5JLOoKkbTs7OsE51Fz4mlYGzVJVjfXYnpUzXvV+1lrsPX+X50+dcbzp6b7l79z6xWXFydofN9XMuL56xvb5kd/Oc2ho6L8q7RkGsoXUnnLSn7Lc31LXlnXe+zP/in/4RFmFztWWzvWGz37LZbth1e6q2xtSVRoJttvR9z2q1Iooly8PLKCRrCxgzIGFSFNpIZ4dHE989V+BPYd5gpMgARz5zU55ozmPO+8nfK12bO9vOzvw0fdMB37nE1+b35j6m7RBr/4/RJmNb+G7eskOSMFuLhWcGkXJhzovy1bzPBd79tnkc+3v+vpKPOdbHi957bOxzvuk/VPsiPNRhe5nnDMfKD7yo3TbXl923F81t3s+xzy8j92Rd0v8v2xeCX0bdgn63+AAMxtwRh877W+JTy88Djjty3+L4ZmdpuJ7ZJ4QyaOXQmZtBljq268fGcay9SF+wdO+L7isd05dkO4CuV6Okc5ZV27Db7bi5udKysSHQpzIn56vA17/yJucnK+qm4Yd/9VPOzu8RJEIwIIEueKzpCbsNl8+fUVUN7eqEr3/9Lvfu3ePy4hkNGkzy2edPODu/y2rVYoOH4HF1RXvSEiyY/R7jHTZWyL5Tuk6gwiV+0oBztO2KEPsiDfy0lXjSBIEUZOFF9T1CxPrIPWv4sljejPAze0ld1YTg2ScQPRP4P15/xt/1LW/1LSbe5afxOb9kT2V6zjcdb9ua751/hW9+5cv8+0dPeP/yCVsCH8Vrfhqe8U4442s8JJiIly3bsOfvyCv8vN3w0X7LE+O5XwknVjCxp9kF3v9v/3vO3n2Xr/2n/xl/9J1/xr/4yf+eLgpxt2W733OzuaEPgqkctQQkqLwlUcta9ftuWAcbhW6/IwTl1SVIMh6Tygb1SdebIsRTAUcjcSgdhDN03Q4fBOtqiA4Jwn7T01iHcaMsjU1OklWjxu1eo9udsTSugRqNPBfoul7lIAnJ8C4EcQMXYRAkevo+jnXRgboRzfrYeUJXgVO7iTpEO/oIXQT8nkoixqjecdd3KqsET4jK5xMgEui7Ld53aqMjy7FC1/VsJSL9Hm80y/J+50BSLW7pVEdPwJlRy3ZM/3e8jSnYde5qeC6N4mLQCqnpDuUpST9FIAhjUIGBwgw16gmdEdq6Zr1qiauGKvH4sQ+aeTOVt6gqwEeMU57eVtBHo6WZvDoHVM6yai22XilM1jVN1dDWDfVL+qa/tGE8pwg3xiTvB1XgmmgmAmHpDVR6dJfRFs5V1PUofI61CZJBEsCklOkJqahirzDE5d/p+7oqomIRcojcoOtI/Q1MNwzCbvbsz5uUhQC9P06JQNrMMhoeRiJURjWOCs9C0DaG07MzjDFDWq8Qw0BAyvrEeSQhRvbdmC4uxkjTNKzXa00Jb8yEKOc2TyWpBYZQXZI1SR+iZi0rGklvUWMyMNmToVa7s0NK+bImcnnwSiVfue/D/TPF3Zxw5ujuvA7eh8laFxM6FAJkVGblsex2Oz0cKb192bemGJxGmJX7ba3F953Cw/CcGQTwPP4cGZ+fybXNRYS6rgEGJUff7Xm82SASsU4NbyFFDpapukthONeaGwVUxjSAyfqqPk7aVPiapqlWPkrXR0yOGEv3y/AUqtDSE1HGh2Rm2ET1YKusQ71+shdkhvE0JqPCeWDq8WiSscpYM0RSDHA7Z9YNyRPTEHL/dnSwiERNL5hxC1Ov+ZzxYfBUMur8IVAYlLOazQ1GTDDjcog6LthhhZMAhKG2SpzwgnVJiTxJW70gPHpVAqhdsTDC5H1C6EnrQnaYGB1xRIQo2bvOqFEyzuuhy+FaDvvJaLCwLhkUwEhIaUnGWscigpFkAI8Qo66vKVKAa/mUqTAv5d9RlzKIIYpJfwsmRLyJajwftscMODoEzWqRU6RrupVp6v3SwJAdbyj6KuFu+DHaj60csu9TVHVCj9ZiI+oNalINmET3RwY3OTwJ4ONA5PM5zABlRCZ7NlGeDHQnlgMejUBDs5SFuY2IWsAn8xzfSWInTYJRkyB2sj95Y4p7zMDg5BsSY+qTy4OxKUuKPhuFoTap7rG+lbwORsj/ipEqXEmZxjjTqWScDWEweIUY2cfI+ck5q4tLNps9m1VPTaVpOJNQKyQHiQL9N85iUOOBw4BxgCqlrUkwGIIaq8UmkqHCqEjEREOV+jQYvIWA8OC1V/jH//k/41vf+w7SOnCJTqLz6Hd7uqsN3//Tf8v7P/oJu6sb2Pd6eNLgBsGW/M7kEZkY0Uy3XVLijrCT9yzv1GFEZUlP5way0og3wk7mr8ZarUP5j6qalI8pdnGCWqR0ssif7SHeO+ynVArK5HO+Nm8vUu7M5ze/NldmSAaYBfXCktJ3nn57SVlYvmc6FjMYRUZeVZtNeK5IvHWrcmVJ+Xk4pljwqeV+DAC0CBPH2pJi6JiyOvcZEyMzVy5NsnqYJfNXMb6y60zLcz957gvPLRmw8/uOvOxWJdN8zuW7blP+Lj0zX7slZeRyj2MrZY3bov7nYz02jmPrddyl4PY2hVFd9nKcB/LJwvjminLlPfQ7zaqTnScs1lnatskcDibxg7l0SrqKiBqvyuYmOy8pWnIYxML+DpzUcCWarIawWle8IKfGHDNqvXw7WVms80jskyO4oapanDsl+kDVbzEuatYik8eTeJCkcQ0xTJSvJqGCko+KocgANpzRAlcw8qylgVxEUh3AjM9TGRhJaROzf66MHMmwJDKOSXkd0rMDZzjwXsMOyNhfhqm61prbTdNoDW/v6X034MFsxDcmO92OkUvB+GRkV7o3z9ggiZ/TOoZh6LP8fulzSHgqr7teT2OPunbZ2T3LkrkE2+BQHk3SA/R0IVBHQdYtXoSuD1S2p6os16ah7nqaBmrjqEwgnq7pO/j1v/lL+g8/5qwyhFNLbWpaI1yHnqfe88yrsXktHWsMvYMeQxsr3mfDtd9xz7S8Wq9oDViz4dvuHn9185x13fL1kwd8uz7j+xe/5ufXO141p7wtK55cXvB/uHyf9+OGu9WaU6lYRTDSE7ZbTnvHG9RsgMcEnER89IgzBKM1Kt1uw/mDOzRNRegsXoTemKEkQD6fOfIk719brXBVTdO2rNdrdr5nv9fa4tY52qbh7M4djK2T/GdxznLnzl0Ew7OLa7ou0NYrMBXn91+h91sunj/j4vlT9psrJHRjjXMxhJR16s7de2xvdqzbFV9770v8g7//26zXjqefP2Z7vWPTbdj2GpVmKqgqi/c9wXuCj6zXJ0OqSQr+fNSFJIyWedfsJCSZRzRJxp8ZNie05kBMHNo0Q0opRE/P8eBAlKSNiUyTTnocZJZlWqiDUWeO23ibcdxLNCu9rcAZsKQ3mvPAy/M/RkuXjNIT+mDGa/P7IPHJMjp0vIjeL/Wx9O45LzZ/Zmndl+5Zev4YnzfnOco+57zw/B3ltRc5q5b9RQ7HvdTMLbe8rNzwxVuW05Z5xfT2gzO3tD6D4qHoU++dPzt1bj3s52/fDuEt6Zhe1PKezeBigI04Oom/rCyy9Nb5WZtnd1o8PzKXG5bOmBnWd97PvP84G8PSu0tcvHRP5meZ4dGl8S/N4TeR547hifnYRv5v+dzrlzJZRil0EaXcXOrvjNXSePt9R103rFYrQoz44Lm6umTXd1jnOHWGdnXK6689xFQNF1c7Pv7sEc2qxXlHt98hRCR0gMV3ezbX1zx/+oyrqysevvoKfb9nuxHNcgk8fvaUd955m0YaOt+x3Xf46On7PVVTsZIVGHVqzGVZ1RRlIEWxVm1DHTQd/FRfMy19ByB9xFrwybHVpSCCWuCBaXjTNLwdDTt2PPbCxlhqVH65ICAW/tv9E85CwwkNb/Eaj+h4LBcEWfGV1Slfahz/w0d/w7+8/IQrqajqmljDm9UZ+23Pj+0V79hT3rSnvGag3e34bnvCR3HD8+2WS2l47axi7SLX2579zz7kV9//c1bf/SZ/73f+IX/+8f+Fz58+4/r6muvrazrvsVVNCIF919PUFZXTDMUiKos4azHGQRT2vkPjq5Ie1mSZHkIKkLHJqzgg1CmFtnGGaNRwbYxKWYhmZlK7jkNoVNYzUU2Aoo6xgUBE8AaiNdTGpXKITqPJq56u64ryyQrHvWi2Ji3fLBDHwE6osKZSOQe1Ufb7DqkdLmp5oq7zXF9v2PeBO2uonZ4H30e2u21y3IR83kWErtuy3W7ZbXfs+0AfSM4GAYmGvg/gLX1KC++9I3pNIa5nzGrw5oH+9cVtEMHyQU9/DOfW1Unn4DQYsND5qu2ACV04joeUZ3TOaWCyD2jq/KzPEBCPrSo0yE8N39YKroK2abF1TcBwdbNX/EuvMGUsdeNoqoZ91CxWIWpW7of377/UOry0YVxymF6ORjXq1eEcA2BGKzjrUmrh0aPQWlcoQcaIRU39BL73dN2erusGATE/Wxo75kRHgaibKFlyhE6pNFpS+JRGzYywyxS0JYGZG27z99nwXwrIPqUuz+MuEWR+J6hwc3NzM/RR1sTN7yzTePd9N4zbWjsc4rZtaduWuq6H+ZSIeK4gVKYsDungVXmgab2NZMOEnSD0knCGGDDGHXy/lPYxt/zdoAw18zq402iSvH9ZKZ/7zOuXiY+zFcLhwZsz5yLCfr8f/h6cCaKmrojFvs6NCvpzyIxmpF/CS65VX6Zlz4oaX2Q5EDTTQr/fE0NeT5MiTRYEBxkZaUlp9jAGG1UQ1sQv2ZkCrBk96cMQ5j2iSTEF0zUo70aDirWaynfQieVobh0KhoiNgk1Gs+xXNBhe0x6LUUe+YBjS/VvnBoO2TRHa+f2SlEYTZC6gRi0zGGAGgZ9sqAWxGv2f034OhgyTmdaE7wudQka4mcEEUsYEJSqmgGmTFQ0pgj5rFK1xQ9aBHA1oSiFnYpDQKzHBF2KGWiBSCHsBwZPOiox20bz+JONyXqAYxzmaUum3ILjkyFzVoZgkPGZ8bFOKc00jHpIhx6TazzGNRbcyOxfIMKbxHQwMkYjaBL2kiOZoUrS7GiqDGAQLtgLCAc7ODitaU3MayZPPX8adS4JoeY6BVGPG4KzhdHXKxU2vjK4xeKPG98Y6zZAgQvC6+NZqRFTer2AKWFzc50E8Jt9JOpNkGDcwyXEOBKbN5PVEEsM3x3fZcD2+VIbrI2wtpu0bbo5lkoBh3aCIkkz4iTjiIr1HBlwuyQihYJsNAdPx9rGIoopqmFbFcA1Go9xdXvsAfYTT07u885UWJwA1fUBTUpHXX8/JgBrR9K2VtTjr2AdN2aP0A7r9PpVAURhyKZ29SByPtoHeJPza1FSrmr//H/1D/uif/hPO75yqXNQ2mK6jMuq4dHP5nMeffsaPvv9DfvHXPyFudpytTjQdUuE0uKwwyd6Wo1Ba3l86bM33aDwHdtiLuSLxWCvpXeYtQgiDE9fEgDmHnoIXK3kBkUMj92/SMtzP57KkfPvN+r9daCjp4bykykBfZvxW2Q74MOwQJl8+mz/7EDFWKLs6piS+rY3vzX3ffu+8/6Xvys9znFp+d6BEMWOEZL4+379R8f9yTfFdOvkveO4/BJy8TCvPdB5f+f6lNj8zsy8H/HTsPJffZXhaMja/qC3t58s8Mx/Ly7TbFHEv28b1sFinEdo2OW5NItKzyGpGugCoMuYF74gSkIG2SHp+Yf3z38UPjFGWMlz527cTq1HgXfD4KIitsPUaY06oTcO9deSNOzd89OCKjz69ob+BOmrmnWjVgdVGl7zvkxyQeFsRBn7NZJ458eiZizBpIs5ZYsp2ZGTUBRivPArJQbQXT0yGPh8CHbASO9Q4F1TBlBXjmQdWLcNSPfbZ+pucoQYQlWjU2TM57VuHrcD2ybE4aKRHMEn+tQMyTjKJ0PseGz2mt0mXkbIWSVZ8R2L0yguH7HiUjDUxO5OOQDHIHlmGK/8GyEn7k6OsM4IJMpR1MsbhXI3UDpuVhtbStC2rtk2ZZZLuQTzWd2x2keBrthJALF97+Bo3P36fmx//hG57yfpOQ+uS/BhOeN5d8zjs2VR77knFGx20puLaBLyoY/PeR/Ye9pVmAOt3Ha8Yx512zVsx0sXIzvQ8kY4nMfC119/gZO+5CYH/56MP+f72ERbLGoO1EW/AeYONFWfG8A3vCHieWI8PJnnSKnssRpXmd7zQ1i272oP0Q/kjKWiqMYa60rSsArimpW4amrpm33V0+z0xRFxVUzcrqmpNkAYnik+qqqZtG87Pzvn4o0/YbffUTcvq5ARTOTCey4un7DaX+P0Nvt8Ro+BjcgA3EVuBqU/Z9T3G7PnWt9/hO9/6Kg/vnbG96dnt+mQQ34GJVJXKXZVNpY+i6tFEdP45jXnGInMcL0nuI8lrmZwKGS8XNJ7DTD0l5sr3mgXimh3US5yniTXMgDeY4cx8HoL4AuZH408ef/5bxaESWxZ8wgLPcfh5fMc0C90hr7Ok31rKaHKMPs15nvx3qU/I95X3zGWxCT08IBRZ2JpdK/vPpRcmacHyr3JsWXs7dmnmdyVlg5gR3iZ3DGuRZdlD2j+XCxbXZz7LBblofu/wvcnwJQvrNdJ6W8iGwzdWn4smpIwKFSbpIjCRaYdmMHqYkDzkixzSIZVvIcnyxhqG+JAlfiivy8JaHVu/8vsStpnsox1o83whDKaA43L7DtfOpvNdqgIOz+zh+4+14XzkJ8pzVJwta6ac1VxfX+rd9WwdrtnAb2W+ORb3HRtqgSeZ48lhD7LuX2eSu8z4SwoePc4M6Ev7eHAmBESWdUfHni9/6/6ayZPjPpf7VNIAmcw3v3re92SpSvxrzBj1yXQ/Stksn8LcxgAIXVfvsxFZeay99WANd89PqWqlhSKB0O25ePqUlas4lYpmteaVB/f4/d/7Dlf/4l+y6zuMddTrE/a7PbLfINLjw5Z9d83l9TM+e/SIu/cfcnJ6TvQ9vt+zWq24urji7tldXnnnHULoefrsCVdX1zx+esHl1ZbNpqVyNcRrJF4TYwCJKdhn1FXWVUsMEOIeHwJNU6vznVG9qjE2ZW4Vcv44h8H4cb3uRstrUvEQy3Vc8ZQ9kvSjWaPya+BZNNwRIdDzIR6DoTIVFsNVjHzYeX7e73gaIudVpUFjERrU6bMPnguzYVWtqEzN5uqSr1Sv8WX3jKfB86Hf8fq+5tW6wrkV9WXPzV//lEc/+DO+8d3f47cf/Gf8nz/433HRbQE4wbERwTihSdHwO3pa4zg9OePs5A6uavAhcrPdYcwVsdurbJAcY1SPrk7P1loqZ3GVw1VQ1RbrTOLTNduPBhG2ajh1DYYaQ51g1abShxYJRjOBOjPQBGug8x11XeNjpPeB3b7He4Hokk5c5ZusA6oqdYIIMRD96NRgKoNES/CC7yKdMezrQNdF2j4SqoCXPRI8NzHSNg0Y2O07bjYbzXpESp2e1sNGz9VmS99HDSYzFeJ7ZNsRKyHWLdQ1tYEoqs+OeOU9rdqThuDXgTbEpNfXgEib5jdiaP0ZMIYZz33GGcZZqgyJxmpGKpRiGGMTLkhBlzMus6QFZJ1ejrNKcroBKgyVsWxjwNpAYxstd5QGFhEq4/T9UUtUhRjpYtCU685AZTVrgBF2mx2I1l/vfcPl5uIAty21l68xXjcHae4Gg6V11PWIPLNxY2lh8vOl0S8bQJ2rcJX2kRWRZW2wMjK9jEouI6tKo/ZccTk30Ob7gcFDO6fh0vFM03GW487vKcckMtYBLyM55u/O/eRI+fw5ezpnI2uuh132td/vh/F0XTf8tG07jCcbmVer1dCfGhp6tn3H9maLMbDbbzmvbPKuTunWZTQ+l+s0pEEPnmimaUNLhnauTJ87G+iehFEMM6MDRP47PzOkIDVjStJyD3J637zXec/K9wKsViv6vme321FV1XR+GlMxwnKx5/O9y9fL7zMMicgQNZ7nmr3Wy4h7ay11VXF+dsLz7jGQImOjIGKGlPgaETKRrnReosghK6RIxn1LMgxHIZvXjLGEwsAqKYo4RDPUyVNGR1cx19R25IjzkWkafMETQ20FXM6BMp5sIO819KKRzxMYibr/ea9MTKypMNmHsUdDSCmtQ0jpls04MBEVVlSRJxhy6vF0XpPiDeMSk8EgFNhkTI9CihAu4AmBwoiny1QykgkneD/Ct5aDZqAqw9ZNGc1scLcDDBewhe5vsKkeStR6dSMDX5KwtEaZuc6R3mSjjrDoNl0w5QNzHE3y9jIMeenTZHW6GpkeyygeSfA4B4NhkVRpFwGfntPoGe1PokbiRjPWlsm4YK7wL/Eaw/xGWnRMsT8VLJUVCF6j1NerE4J/jDGOWI9MfAwBNzcIxoBzCveYJICZQkAphc7pCAahyiQNRjYai8SJ88KigShmuDPJU1Um9yyJqENa9EHwExYrcmehLjMqE5iKo0QrAj4pFMqIv5RtQ89YBLGD38hU9hqVKQGbhCrBS8QH0dpN4sd0O9Fg83kwml2gcS02CNELOx8wiVMq19wyKvodgjSWIILPdCOoF7LEiA2RpqpAIhHFV+qklJz7jCBGcCct3/l73+Of/LN/yitvvakR4hJpqxp8wNqK7vKKzz75lB/9xQ/54Gc/Z3txTSNQ2Qbb+eRkkvZrCU6NrncuA5HXd244nbf59wN8FUqFl21zo+fRsR4ZQx4vLGSq+Y3bVJmQ/54rGb5ImytSS+NW2ZZ4mIPnZvzgHNfM7x0P1PKYcnaTLzYjJvs9gZd0tiWl75o/Uzpj3dbvsc/l2I/1Y3OK5YKXKnlqdRSE5V043uZ3LylgYSHF/BeElxe1cv4jDMyUXEfgdAmmj12/7fl5lMLfZh7zdbzt3i/WlA6WuGGKu14uumly9kCF5RhxLqWEd64Q80cFo0z6YFIPMo+hbBEZmOCSxk9vGiF3TDdviuxEmvVEIKW5+2IwPm9WvKb/Dl4z7qSMQ0JDZVecNCvun6157ZU1J3duuH7miTuwEXL5PpuUGZQcgUlOWaK8tQxK8MwXJP4ycyIFvzXyxMpsqFihDq/KfwckeGIMamin4KNFud3h9EuhmMlrPuGJZnx0+pwNc8objRG2OQuLrSHaQLAa1RFjIIZQlKVKPJodM3oc8JRFhpqYjHwhxpSpKSvIc9T9yJeNdGKcUxYoJuBkkiHHGlzlqEQN495HMJa6qjEmp3yvWLUtTVODEUL0+OCJUVMy+t6rHGga2rahtQ0f/+Cv6J89wZqIaxswBmcc2yg894Hr6LFGuCtw19QEYxAT8Sjv4r2nsjVeDDc+QOgxRD6OWltyu9/y6X7D1gQuTeT0pEWM5fl2w6/2Hc+lpqkMlVIdAkobWnHcpeLMWi4kcsf2XPqgfG8c4S/6QOg8la2oqhofBLxnqdlSh1PXuCTz52ACay1N3bBarVmfnLFan3K6XrNerzk5OeHkZI1EePL4KRhL07TUbUPVNPhuz25zzX630VqmXp0kVFEYUwSUxdUr/O6a977yGt/4+lf40huvYhC22w37fq8R8WaUSRpX4azB9+r8Mso+I6xIcf4GjJaPROKzjRmNMwP8kXFXKshV0JQlulOetkWZKkPujNaV6E2EYfwikoyI+f4jzmBoFNh4vcBBM160pFfz3yYJICbhtdvmOI77b0c/px0uv2s+37lO9GjLMtjCvaXi+lg/L0VXD+6TiXw7zmnSMXkvv+j7yrHPn53rWg++L96xyB9lPUqur5rVIMZoGpWkPxIiiCMTbAmjzDzqL9JYo5Zk0A/5RZFJRoIIUtRPyTz4i9qx9ZrP8XbJYEF3AFMdT1YejS8Yn046wownlsfyxWWtvF9z5mkisxx5Nt+3dO6PvjP9lyv+zQ080z5nOHQ2tkO4nl7Ln2+D/7m8eniNyUDnZ3suZx72fbgrib0YltwYs7DtmZaUTnq3t8WxFZ/ze8rzk983OhikzCpJn6c6gywTakjQqq1o25pcxk8kst9veH5xiZiKM1uxXte8/eXX+eo7b/HzX33E3kdsVVO1ltB3Wss5erpuw83NBc+eP2G729I0DW3b0nc7ogg3l9f0+54H9x5wetJy784ZF1fXnJ4949mzay6vr7i6vqSpG4yBrtsj0TM6xBh1YquTY3vwkOSQnP2XROMTKZ/uWeI7G+OoROmzw3KmLn9Jd2cAS2ssTyTymQl82daciMFJ1ECSpLXfiPLZZ66lMhViVdaxAi4YmqZh1XmCBK6j8nD7/TUPwkPebU65jjuexT2fh4Z79Ql10xKko//4c65/+BOeP/mEb7z7+zTf/78Sw2cI0FQtwUBbtTSmIVZC1cD95oxX7r3GnbP7RLFsdx3OXiPRsOeKaAw+BF23GFNGSpNqYzuctVSV2qW0rG6SUURLpjpXYa0jOwVmmWWAy4R+YxjtAjHx7CFG8J79fs9+39F3ajw1YkDG+thZrtcgOs2mFVIGY2uMBuYFA71mGnLODIb2etthgNA4qqA5yYLXevT7vqfzHQRLH9I4+o4YhdoIu96nrLBawrTvPLEPiKnV6zeOOc707GRP0uzAnOahRHy4t5Di0ndZ3srfj+d5bAMiSWWF7fCTmIRpJ0wDiyc4ZOBi8wbp76GcZQrWDVF1vMn9TaXEZN+yxiK+JyB0IbIPgYihcsnWSZJdYgA8xkSEwN7vkO2yzDBvL20YNylq06QFyNFFI8GcIvAYC2NqHI1LcyKfkbtzahQWwohkZaoQLY2UZe25chNytHZW1JbGy9yGlO3Fs03TDFHX+X25z9LYPk+jmQ2targbDbf5ufI9+XoeX37PSCBGQ3NOAzcKBUzGVaZyy6nX8r273Q6A+/fvD+8NQet1xM5zfXWNjx7vO6p1w0k1GodjVGV/Hudc+a41y+1A2ErjVV6ncm9G+BnvE5FBKMwtr0neq7x25d5lQ3lec2SsKV06HJRrnCP4c1/e+yEzwcCUFQzInIHSfYkThJHnWlUV+/1+GNec8cl9WWtpmmbozwD3793j8SefjTBlHb7XA26Swi0mxlq9cZLBNGgUtEGGyGT1KJ85kBTIcBSss6CcGKWZMBmKlM2+dF6gkL8HQBzE7IF5GRiyJGhEA14K5xRr1Gsudahp+w+5shhlIJIYi1bvVQO2NWoszrV1R+Y0RWpkDzRrU6r0rLTSd0bJhnlDlYxrMRFK4zKPOhozJf8vae7GDYZ9k/fOaJ26oSb1sM4LQhsaDZOZvvFcT9fAigVh8KqcOEmk9cg1PGIMaPoU7VPPQsRV02wZSxGgEguSWTi8jLixxNNTpxDQaK1+iNQf55KZlNRzWmdNIaTpq9UIFEJe4/Gd5bkpx21nY5jj9CXjyNyxCvSdUUBC1PTbMUK0qrwJkV60nIQaSE2Cm4hDcMnrziqYKDzllO82GybzipYylyQhRIa0ixoIMt3XuZBjyEzIaHictjHCtDiag0CanTCWSm2U+5oZ9rQT416Iwn+Gv9JZSqPqij6FxPaMyhqTOh4YHCOI+m/gKvXU9yEMtUkNhhD6zAmBCLVTozYhYjUFBEHKFFW65j7hgMo5Tce+H/FymeWlbls1VnuvSj6ntLtuG3rf4WrFOe9+7av8J//lP+O93/oW3gm9i5pRwDik72Hv+fUvf8WPf/hXfPCLX7K5uKISaMXQYBGJ+L5H6sPotwPGsSjZksdb/r5N2TRGeU8dx0r+qKThS+Mo4aGk5fPnXqRMzYKgZKnkBe86pgA59lzJXxybz22KiiUFyYivpnxK5hEyn3Osv6Xvyr0bvitww9KeagmLssb0yDeOY5XFvSyvTZUuYwmOdKeS1aLf+brM57I0x5Lfum2t8+d5FqZJX0znuhiFn/u1hzBUvm9JqTp8HpHcrW1JEVfi36U1m87t8N1zfrDMQFDu7dDfbDxzODg25mNnrOxjfn9JTxfhyxz2uwSDx/4u8fTcsa0cw/y5cv0m95ms1CvXZuQhYoxaYzyNXawZaHW5/1L8l/vIPB+YwXRc8sGTh0UNPtnwFiXTYjPynen25YwtX6z1QQ3jPnoimlkF8YCmzqttxUm74rUHd7n7oOPJZ9fEfURCUbbHWa0dHJMh1miWHKuDVHpYrKtNPKax88who5Eul94ZZKm0VhYLMaphPHhEPERP9j81oiW8Mq0o/F2ncHpk6Qw2GfMzDme4d+RdBWMjYrX2nCqZhK7bDyW60qwRWyVehdRZMV9jlA/DDM9IHM+2CJoqfcjYIpoisoQ5KRRP5DPhEsc01u4zjUNsQGwgWo8PQuMqalfT1A1t07JuW6oq1XAMmi5+33XsjGDQqOR2fcLZ2X389obPvv8XED3NekXlaqIN4Cqe7vY8l45e4MRU3BGt176NPTtj2BtHFSPeR9r1mrAPdN7jJXLZbyA0vFuvuNwEHm22fG576srwJHTUNtCtHeHkHpXc4eT5Z9jdXvnfBF+n0XBPKryzPMDwmnguZaPetlEwLsGpaNa3tqm0znrWZ8Q4cWbIuoOceZBKy315r1lwqqqibVvW61NOzu5wfvc+d+/d496du5ydnXPnzh3WqzV//aMfc3FxzSuvvkrTrrCuZtWuuby5pN9v6fc7+k5rQIoBYx0mZt2FRm+52vB73/su77z9Nqu64uL5M3a7K3q/BaMKdZNgrW0afO/pE1yWOhBrsvI34zx7eCYEzWJkbeLDSxqosKxOahCTXmlyluY0nhHfDrSCAV0W+gCF5bnuo5QTFTfGsuejZPg2GrfEryzRvZLezb+fP3+Mx5m/t+x7iVYt8WLH3rnUlvhWKGnUjHVJ6GnC67Fw3+xaYcpaHIfc0m8xorGPBR5Qn3sxvTt2z4uefRHfCSDG0BvVdJmEuxGTar+awcCSkHbqQ2dnrRl0WFmPEcQXhoj8FjNm/IvJRG6mMHFsLrfx28euLWXvGvk7jtLJ4Z23wEXJA31RJ9XfpN12Fr7Ifct8aCqzI0cCAsomWfdxXK6Yb8tt+7SEB499P/S9MMSBl5rJBod4Ius3D/HP5Nm53Dt77TEctQRvx9uIW8b+QCROSrWNsuNY5kttRAHZdNysaqrqnKqqEz+v915dXVDVNVXtqCrH6ek53/3ud3lycc2jpxdIjKzalptdhYkBI4HQd2w3V1xePuPZ8yc8vHuftl3R7/d49Wjj008/5a0vv0HbPqRuak5O19yPkco1rNYt61WLs4YQPLvdFu/7wRHRCCmw01CFgAs9UcIQ3DNfOwHleVPAlljdiTNb04lwIYFtsDQYtCiUZqKxCOfi2BD5le34irTcj443xbIHnkskEtjTcepWfOf0Hu/3z7kQLR1YCdBH4tpxTxw3fkvve57Hjufs+Nn+Ge+t7vOZET6Oe34tO15jRbtu2fge9+yG/kcf8OH3v8/v/Mf/BV+9+x2ePP6YC9limjVnGJrqlNqCa2F1uuKN+2/y5itv0FYnbHcdtd0ikjKsRo93FuN7TO+TPcujwYFaatU6i3H6mVSaymJxFjAazJl1sWofCIBNTriq0w9BS2XmMkZDJuYobDc3bLdbul03ZH/K8sQI96KZQETLUGkwq0/7mbM66z57Zwi1xYfIbtdhDPShZ7WuadsVCHRGc11GNNPUvt+x2e3YdXt670FSdHQy+EcxdPtAt+9VSkilZnQNU0nPpBMdZJ/hz0EYysfykN8pvstPTEOkBkxATqGebYCHOhpGJrHQGYw4aMorKu5SBxNrNPCx6/bs9ztyVusYA70YEHUId1bnG2JH7z29j2AcTbtKZWHV1tn16RzWVqPyndDFPb7rj+CuafsChvGMbPUnhJwzJk8wL/ioDAxhGi06Z2xzao0p4lcDUzZ+zhVLWbGSFSBz5rdUwM3bUsR5+dycaM37LtOzz+c1R4RzxnxY8KRsLcdTRpaXa5SNu7nudNnXfr+fjHlumI4xcnV1Rdd1w5w2uy14wXd9YhgC3ifmTiKYso72oUJqrnydr9tc4Znnn5GRSKozvrAuWTFXtjJNvTFaPy7P03uvAtqMAZlHJg2KsuSkUTocVFU1MLalM8VcsIlB60fnGu9t2+rh6zQdRx5XmQHgoI+CIYgxcnF5qc4K3mM6VW75qEqc+VomvRNBNOJWeam0B6URKim1ypo4eW3LFo2mZ5m30ogYZtxavj4oNgXEjZG+eW9z6vhyPfKaZmeaYZ3DWCqhVCBlYyOAsRWhGE2pVB6dXgAzhc+Y9kqypJdqdofCM63PuCIx0H0y9GU1wFxAkAgxdMTCgSAGVZLlc+2cSzXEkoAxdjj2YxKxnRm7B8U5hgQGY8mHMBr5lVjbiUJocMCxaiA3xhByHcMlBi0RUmuroY8SZsczFAcHAzLsRWUSDFoj3ps4reQmI3yKqBeeC4L3PX0q2+CMxYrWlLOow0PpbDXgCqa4tMwUslSComTAl5Qs3vtUbcbijFAZdQKxYqmwSaBKgqZN8yBHRA8LiIkp5Y8xmlbUKMToGi3tu1GFtP45RE2X90jqe9JiwAy1A6fGbn0oHuKsdJaMUeUzSfEtMY6KDGMGpVzGvaMyWUcz4HXAmXSK7LSeKMUzqmMo+QLGsgJJvy1Ga6DmtawrA2W5FFRgqK3FiaaY7KzQYzGV0ASdi5extru1o1OVnkGb+L2RJuQ1UiEmaFRPZTC2AiPEWplwV9fcffiAf/Q/+Y/4gz/+R1SrBts4ameIEtSRYr9nc3nDo19/wp//yb/m8cefEfYdLjlaONFaSIIKPqXh77hCb6rYK/mB6X1M7pvyKnIAPuWzt9Hp+ZhKunqYunNZ4TN9zxR7HlX8zZQHtwnm87HetjZLOK+cV4kz5gg679Mx/md+39I8lsbwonEbsuPW+HxZ4z3DxXws8/0d32vSeVCnJH2uoHDFPPM+HxvzfE3KtjTfieKH6XvKMecSK+V3JY4f1rh4bRboMv9TGgHK98zfiUwVRC/T5jA3hZvZmPLvW/Z/qR2TV170Xel0exAZn1rJX5Vjn+9VafSfR/VnvrIc0xKsz2FyCR7m75zjmqX5l/0O9SizHIioEsWoE+x2uyVKquucje/FniTmpCDlxTxN4bw7wQsJxg780vSs2oFLGK8LDNmI/kM1HyNeYnJIi4gYxHS4lEZRosXFmnsnLaf3TrDrHeG6g15w3hCd8p45ZapI4mGycl/AFmV6XHK21BmNihADkxnrvqXI73SeEat126MQfE/we4Lv2GwNTRCMc4m/SusrhiFLDUIglycCJrRRPxujJmVr3HDdFHhkBCWDZ7weIwQxBDH4KPS9H+t5VzkVY+EUKtPoeX13oTZRpkZhqLD9KcccB2WQKfqdOAlFi8NRZcdw1GlTy8BYMIIjYGxF1TQ07YrV6oS2aYdAAus76JyWKuoNjfXE2LE6ucOrr77O8x/8Fd0Hv+TBa/ep1yuc0eijPfCJ33BtAnVVc1ccsuu4qAwX0bM1BoylshZjHdQV/bZTR1Bx+GCpz+6xD5Hgeiq3onEV9yvHftthVyvM6/dov/Iqr949Y/9f/T+o9j0+Kg9oLNw3FWuxXBlLY2vuy4rGdexDTMbxqFkHREvPNfU9qqqmboQ+aAa9vu/IOpi2bbVUWnKM8X2HoDUuT09W3Llzh7t373F+5y537tzjzr2HvPLaq9w7u8PZ6RlNu+Jms+WTTz6hrhuaZpWM7Ja6rtjdXLK9vmK/3xBCjzFQVw0+gX1d1zhr6DYbvvd77/E73/k6rau5vrzi+vKa3f4a4wKOejhHtWuoq5qnT57y/PkFfe+p64a2bnVelSqJs+7J2XqKExOey04sgkbWmHSGMfmemGS+Ka045EVH0D7gtw54uyl/NspekTKj3yG9PJ5Rcvw8Ov2W431Rm9Om27JXHj57/HPGLy87ltt4pfk4jvYny3xV/m7p2WPvVS3IuLZHx5zo42I/xd95+HM4OkbLy3uOjfPomCafx9GMLN0cdiWVtgBDTMmIFRdrGjKbaEuHMXEIBlLuWOlZlBSYY8Abm3iO0glLMJJq5+bzET0T2fnIfPOf87GXc7vtuXnd69tgOreJuWN+e866Yl7OLL4kEy3BwfyZ+fXfBB6OzXUcE2SZw8gtxvEMPEkkOv760fi8xPcunb/5vcdlpNvXJOvA5zx5OYWld+d+Rvlp6hJT8qrHYG2+x8fXfVyj+fw182nWe4fZc2Yi34IDk8ryJqN11mvo2fTc3FyQI2PXpye8/fZb/Na3L4g/+imffv6Y9fqU7uSU7voKKxYThH6/49nlYz76/Necn55y0p5g1sJmv+O1117jJz/7Ke//6hecnZ9wdrYil8ppmhMQQ9d7drvdkIXGx2aiX4wI1u5Vj0QkRNXn13WTsiUV+kgEmwK/oojWIRXhxDh2BB5Jz0PgDRwPqHhqPbuUuedeqHjXw2e2569lwynC37Vr9jGwrS1ehL7f4nzFt77yHn9hn1F/eonxhr0VnjpP121ZS4NvKwhC5eFBfc7/8PxXfL0+5616zZUN/HJ/xRv2hO+cnfF8s6fZeZr3H/Hhf/ff87v/7D/nj777H/PJ419xeXMJteEknFBX5xjXcbpquH/nAa8/+BKnzTkWLVsUKghrsE5TXt9sLtlvNwP4VZXKd9YZTKV2D3VyVP4zH9XyxyCp/JzaAVR2035ypt7e9ykKecxSIAG22y2hD6pbF9WxI0XgZRIBokQ636X+opbusjbpMT1Eg/iI84YmVPg+sGFH5z1NV3ES1pyKI/RhkKcisOt6rq6u2HddygCm+uwuGfc1+1Ok6zzRC2erU1xVEaPQhw5jKgRLDAJRLTr6k7ITSEoVZoBUy37+M3wnBS4pea70L8stlXPk0tg5Q23Zsqx0WxvwiFHbo7WGznu22xs22w1dt6dO8lwIgf2+JxhPMJHKVOwDySjeIwLr1Zqqqeg7z363Z9/t1SFh1XB2ekrdNgiR3nd0qST1i9pLG8ZHdKq/FXGNxLlMozlXQJbEalycjEAzAldltqZMmBoXs7ImL+r8J7d5yut5tGDuMwsYcwJyMOMZQZgLI9fX19R1zWq1mhhES0Z8no69FI6zwTgbd+YRG6Wyak5U8nj6vh/mY8xoIMvG2uvra7zXNLXRCE4MVaVKCe9HST7mSE6YjPWQEMehZlpec5Ex6n1J+VmusSRmZOnolOtUGrPzHA/3cnz3fN3nBL6sVZ+j7I3RtHX5nc65IR16OWZkmtY9119tmoamaYa9g2lU+zzTQI5cr5uGzWajtfe8pwa6viNiiT5O4MQ5p9GSZESWmJzkRSemYHcHQSVgnUveOZr6oxRQI/YggiWnYR/OzDwyK786GekENTLnGslZaO57r6lGRI3bEweSlEVC91eNw740ZKbUeRh0fgjGhCFef1CIxzGrwqDI5dCpY4BDTKpFqdHVGfiCz3CjBuXoU4TpbE0H2AWMNbishSPVlRM1HIIa5COjwJO92sp1tFmJl1x4o8gkiqIsjikhp53P0eBp7zM+yDiUMVZXo8f13ixYS7p3hBOT1mDMNFGCkbGWmAXoAVbG/kx2QJFIBTPDuAyaSmVC1BCOs1hTIUPyH0trHVWir0N0c4wT3JjPuHUOU5mDe8r9vk3JHkJQ46ZTh4a75ye88coDnl5egjVosng37E+eoxqwVRlrRfQ+H1INSkNlUp0skzd+WYDQIclYu36mTlfhYvqsGnnt6GlnsoCbn8yFD8wAc1nBnM+LSRPKHroi2i+Dwl/7zRHypROPSc+b1H+M2eCUjPWTuRqKTI5JuTLFZ5iotUFTK2lxFhwiFhfBeVElamUIKUNEHdSJIhqGGk6uclo3MjlW6FCys0D2UpbBkSLTDm8sGItpnDrFOPj2936HP/rHf8zrb75O13uN3hKhSlFbYbvnw1+8z7/70z/lg1/+EhcMLoCNgpUxCk+sIVpLSDUTxwix4/zGIbwsKxby3yWdzusfY5iUHFjyXL6tZTo6wa0zXmzOGywqB2bTO6a8yfQyw8FkLHLIJ3wRxWRuE/iajV9fxHheimdKJ7vynccUP/M2j4o1LOOlspVKy5LnHfowU+NseW1xbreNzYzzPKb0Kfta4gnn7z5Yl0T3y/WfpNPO45l9l9+jGXay49HtZ+Y23J/H8kXaksJrCYbn7xwkpVvuneOAl4Hnci8O+fLlvZ/v6THl5G3nWQql1/zZY+Oej63k18t3lvNaWq/Fs1uMa4A9S3LKSrxLStkYkjNYURp0mE8W4vMUBqdPNDPTqJjLazabIwzptyM5KtJkNmnku74Y2B1tPb3qOYwq7X1Qhz5X1dhEN020uNhTr2pMU4GLWCI1hp6Q+Pokp4odDLY6leyEXci5CReVypF8jqJoOZQYxyj29FCq424hCr737Ls9Xb/nxlTs6bGucOZzNr03y0sjzynFruVxGaNjiCJEmabGmygs0999SDXEB32AAdtg6wqL1piNXUe/l+H7UabO9tk48BGR5Fht1Rhp07pYk+auq6m8RRpvGWExAYfGEg1acipESOk0xRiMBjwTg9DUjtP1mpPVCeu2pa1V9gzi2e1VJgq+xwJ7HK+8/g6vPXiD5nrHz/7r/4azdUXTNFTG0kY4E8cnds9Tv8XgaMVgfOBpt8Mh3KDG79ZUmlnLGa62l9gQcQJ1NDy4+wrvPPwS3fuf0O4N5xaM33HSnEFVc7k+4+aN19l98x1evbris22HjYJPsmJrIg+qhiuJfCAdnzqQqmHFCf3Nja6370EEW1f4rmefnNFN4lVLZ+vspF7S67bRVOrWJj7OaKpzCZHNzTXXN9c8evQZDZbeB262O54+veCjTx/x1tvvUDUr2tWKuq65uHhGt71mv73B73fE4BNfDSFA264GJeU7b73Cf/Gf/s9ZtfD0yWMuLy7owxbjLLWpCUl+d9awXq/ZbTsuLy/UsSfJ4dHnrFz9QKutrYaSe5WrtfzgwPemE1jgqWM6kbIdw70jJ1JcS+dTS0olHQSjLJM5eJWZRlGzGko4lOM4dM6fjiMdqC/YjtHF+bXx80RkVdl8YanyPV+0fRFe9Yv2s8SjHH0+/SxO7kgfcz5hfl9Jz5d48yVd4N+mTfmQJAdnR/byezFUOMAnQ7c/4CFNcpqK2FRzde4YqvIq1hADmGhG2JBRF6I19NL6xlFP+OI2X8/yxJV0b/n+6bMvhrHACMCHvLQcvm7Wls7QEu64jU/+DwUHX6TZrOeYXVfnnJwxZirf5r/193+YcSzuUeZHDlqCR2QsWVfMQhJnJCaO127BBQNUmTGjz8uM9zbefH5v/plHh2f8WwbuGaM6WaVP+TqIBIzRTJnG9BP9Q1VVdN0WIWKcY7065e7Dlt/97reQKHS7PU+fP+Pk4SuEzRYbvfLFMbC5ueDR48949f4rNA9e5+T8jNP+hpvrDSfrM7a7a2KMPHjwgOvr5/R9YLe7BizO1dy9c4ZzhqurG0wcFJb45KASkqEwGsN+t0NEWDUNPVrC1iddM8Kg28Zo+UEEdiHgCDyJwgcEvsoZdzGcRrgGtgQ2BN7hjL2NfB49v4hb3pKId5Z9HzgBXqtPeHN9AivPP37na/zzx3/FqrNE42hdT+wj+35PXDsaHF+pTvkHd9/i/x5/zF9ePuWt+/f5hj3hyeaKD/tL3r2/TlldDfvrG/o/+Xf89F/9CX/nD36fn332xzx68pzPL/+C0zt32O03tGeOVXvCvdVdTtbniIcuZdWtrOVsvaY+cXTsuOmukv486/5Qc4JLumPAocZdzciqsOhDSEE+IEZUXS4qP3RF9t4Ytbxt13X0fZ/sNqL1pnd90j0tZZvKAX/K32iA32hLLLOeqRxlMFHwXcfOJUeWyuIqS91W7H2kD4bWxiFTQDbc9yESopYoDX3Eh46+12AtrQ+uUdq1bdQhEjecf5jiKWu0PnfPSI/yfIwZSxUfwxPK+5gD3Z1+OeoG9fwmeWawOhzHH2MXpd5aRxhjxFhSNoYdXddpFLzRDFGRiK8iUoF1FUhF14E3DqmU741iub7esN3tNRDYRNq2oVlXeFGYj0R86P/HMoznSWok4agkLzeJ4Xc2dmdBfK54zIuT+xcRNQSZEdHnxS2FnXlaxvm1JWasvCcr86ZKj0Pj9VwBOFdGZ+Xxer0e5lT2O1dglu/Jfw9KiUIxPI92hqmBHRhqbmehqDQKljV68/udcxqpGtWwFyWCCWog6TJWUAGb2VqWDgaG6djLucwjF/P4y1SkehCS9MF0f+brktc3P5v7Gcczffd8//Iz5fUyCn2IZi6Ex+xQMGfuy2jo0pkhR43ndR9StBdIZB6pY4zW+lifnNDUNZaIiRASIjRJmrRWHUbGNOXJKJwcGMhpoQbFlk126gLesDRVPZ4jpwmh4wIyy0JvjDLUUM4tpveKMBqSGZVkkqiLL8oCSKW15DK7LyJD/bSIwoEYjajMabLnyDvDxXi+hVzHKaRUzNbmWiOHMDuc1cGxpBqMg4MXfrrnJDYF/BTK+yx06dIO4xPRaKWhlkyCEySf59zPlEE1VtdwiPjO15PgJsYkRQ70fVe8jwHuIzr+mKK33RBBPuJTmyJb5ms4GD5Jjgp57zNehCHy3Bqt1TjCR5pHVAPvYPgsz3L2hkzvzSmDNOWgMsAuRVvTe07aBqInBgszR5tyvDGlrslZH7KzScZ32anlqHEASbU2I0KkcS1feu0V7t45o0/9i4HGWGzyoDYmn6upwiaGwqligLsMK6OgXjYd1wBJY1RR0SZMS0rrYxNOmBssxo6T+jifneR0MjDiA/yOz+ZsLfm858GPrEuhxM34KNMjkwxrMwmrND4UEyJryAxg3e1RIGIMvUTqaKmjjqVDiFbPRhVV8ajZg4rSHajC0xiTHE10QOoAoMxkTs8kUcA6OlsTjWEXO77x7W/zB//kj3nlzdcwrWMb9jRnK2KExlTEmz0f//SX/Oqnf8Nf/uD7PH/+TGmvazR1UVBHgexJKk6N+SEKLjCk5ltS0sGwRNNtXQKi4rmSZ1GcV+De4vvc1xcRcJd4p/l+lX1+EQVd2W5T3B7rYYl/uq3NxzznQ2Xh3pIO5fkvrc3Seya8TsmPzCSOpX5UcbHMzx7bm6X+rLUTg/SUfx//nI95Djfzvsv7XgQjpVyQn53PuTS6jnA8OiQMDnNLB2RhfEtR0cM7XwJW5m1Jlig/L66X4WDv5vcu0acXtbkcMeC+4vky2n5+/idC6mx95jLHFG9MacdRHFa0Zfg53JNjv+f9DPKEZC0GA82yRrOTOeuo6woMo+yQeSaRpPwmZWvhYH1CmMqEsXQwWxhbhskoGgE77G1i6LJD3W3K5i/SNvtHmrbdBIJ4YggEaTFNR+0cwh6sGoqNVV7fWUdVWerKUjubDPnhIFuRPmNTaZnpUctc5aLCRBcirbHeqCnR9ewHEbwPdJ1nv/es1orf+r4bZAqsGQx8zlmcNbihVniJS9I7knNuEM2iNTlTmd+UUUEb/Mg753uQdG4kaqagutHMRyGOjqpRMyHFkJS8kn/3WleyshhnccbhUup0U81ML1k2I7+3WCuA0b818bkMcwgxamYmCzF4jEQqI9TG0DjLWdvSB4d4T2/BO8eD8zU73/Llt9+j3fY8+/d/Dh9+yOrhHbw4ahGsiVxHw7O4R8RivTpP34RAWzmquoYgGiVuLL3vqE2k3/Ws0Ix+4oTX3nqdbdhycXWB83vqCjbAlROkErqzmv7+Oeb8nP7HP4LdVktWYWix3AsVjYPP45YP6XnsLFtXD7AWSWWKEGxlEBz7/X6Qs9tWI6o3m+w8rI6qrq5o1yuqutZoa6u011pHU680i0EIWK9p0H23p0oy/NXVNR9/8il37j7ENa2mbq3U+XS/37G7uaLbbQb4NbZi1/WcnJzR1g1hv+fOacs/+oPf45V7D/js8w/Ybq/xYYexgdq1hNhjjUayZ5q53W0wBs7OTpLzuNbY1PJmDSJj2vi+7/C+x7l+kH+0FKFLPKlJfG4CscKpv9RHLB7lzNPNrkvxnd5HIY9mGJ7j9oIOLhLvQ75kSsf1zC/xlkt8WIm7j+HseT/l7/H68v1lRqZjNHuJPz52/8vwzC/z/Mv0na+9iNe4bcy3PVvux238+dJ9L9Om95a649y/Ka6BQbQuuNFr6s5ePuGSvCtUIhrx51IGkvRM1r2F4GmwEAdNlsrXOUIxBRUhkeCal5zRqDM4tg7TpZvP8+Xa5HzmF3L7uZiO4fbzc4wPPHY+XwYGl97/sjCenjp450SzYUZYGQ3iyzobIBlsp++9Da5fPL6SF9FxzOX0/PfBzPK1xF8OfHGB05dkDop1nOLGZTlv6QwvyZpqB9IBjc6Do+51sE+4UVc2x9P6k3lGPaE5mC/f471mYnDOIdGzubnk+UXL+vSU1ck57737Nn3f8a/+9N8QY2R9ekZ/c03oOyIBQs/N9QVPnzzmvD2nvnOPk5MTdruOul3hxXPn7j2++t57nJ61PHn0mM1mz9XVDdfXG3rvOV2vca5iu9vR+4AYi0Uz8VpnqdqaRhradkXwyh/EkHADERHNUhGSg4NJRlkHPI89DZrF5zM8n6MGvBY4MYp69hGemw6LJRg4Pb/Htx++xeb5Uz5+/gRcxcmdc+6+/gqvPrjPSXTUbc117LEG7gdHVbV8aiNdH+iNsGkCvYO/8/Bt/vnj97nve16tV3x39ZCfdBd82l9xt6rwPnKxuebOJz0f/nf/b97+ne/y7W/+Lp9/9jH/w5/9El97ovfUckIfIpuuo7685KRuIQgQqWstKRv6jq7b0vV75aHEIpLkTptKvyUmMASL9xFJjk0Dr5/lF2PwiVfuvFdnXHLK9Ejf+2TYlpRBRCBGjRSPucxL5ifcEDAEaD1xGQNSs0HYmvEek+RPgwZb9bsuGcYdrnL4IMS4o+s8jc3nXMBamrpFjMMHHaNPGbaDaVL/GinvbIVzarfofI8z6uzjnJB1m2pEJ9nnUonj5DQwnNmi9veIINKaTiR8Chl2ihvyXZm3K1DptNsZPhyfNQsMVq7fHjSoMgRMbTk9XbM+XVOtG1zjMNayCz0X2xt2ouWcJAT2XY/f7ujw1E3F6ckpZ+enGCNsNtdaetg5TdFfvxx9fmnD+Hyik6gPMxqn8735/mNKlBxlO/0uL/ZYywuR9DlHguVTM7YSyR4i/vG9c4avNCYvzemYoRfUMP3gwQP9XoSqqgEhmLG+ddnH0t9LBGw+Hr03pNT14ziyIiunNSARyTpFKnddT+UqKlcRYkiLqwoTZ60aJn2qxSc7TS3rLDEcGpUP120UXso9L9fKmlFBN4wbkwxT6ZCUz0AiFDLwNTkVf1VVyajiJuNCRgNQNnTPswEsKejy/fmnyk4HUaibGt/3ajgWUl2JMERThpCjVMc0ld2+SwY/O6k5XzaLehWZFI132qx4952v0D27pL/ZYIOgmTwynCvLlj2LQHDGFfPIqzYyUdY6jZwhHjgE5OacSxHj4/N5j21OVyLkgOUEnBqdmaOtjTGYZPTJuyfFOPKoIkJM75f0HoM+myPWQxJAMo+WCRXZYJcEkbz3OVrcOlcomTR1iMAQSZ8VkorALUIYamP4lGLFGjP0S9T60flsWWMGQWKAoXR+8r7oeVbvxryOIdVQ1/PkDuAAwLip8b902EnLrZGyMcKqHuB0+FL1PCliP40n45PiPCksZY84KRwt8l5ANqoaa4d56fk1w29n9TcmRR2HXMdd19gOilQzMHwYUgYAwFqiS1GBJg0xCrWzmKamdhXiw5DKZpinMBhF6qoGEfpOa4tkw3SQqSFFMiCkPkq4tKjhPZqYooUiJ01L407ovceneoENmsp+TNs6Gv6FhKurahCySoGvZPTn9N+aZLQdmBGFzYlElvFWWk8z/M9o8NUJDTA34oB02WV8MBqayrFOlf8ypvYv5pDhYjgDaFrGmNIxqtKfmZwulLljjcn/xWHOzqhjRJ7TiMdGGlhXFTaCS7WBEHWwsWjEPiSHGzviFpPfEyTdkxwaQkYFCm/WWMRqOYlgAvffeI0/+ON/xNvf/jqurfESNN1sZdlvd9AHfv7Tn/PBj36Kv7jm0a8/odttObWVGlIkeXZmvDAgHRK+sJp5YFiUvLtmYEiVDk7Xofw9rueUr7mNp5nj/ckuLQi4ZX9zujFXRJb35esTA3eCmaWxz99dGpznClsp7ntZpdxcsTBGlNrD8ZON1/bgHeUaHFNaLI1pwgMVgr0Z6Mmh4mLOAwuH+1ret8TfHOxjBDADbY1x/k4GGjzHYUv9LsHiMTidNhlwYcaLyssOuzukJiv5axEZlCOuchO8kml+epzSObD8vSRjLOHacaTT9qI9Pt6mAuG83aYcHNd9dIY61ubOf+W1/FM61C7iE2OGSGc1BI+8HAO8pXw0L5j3HK6nazCD8eH78bfkA1IwnpmlGfqQET7yb4lReRFjwVb0Qb38R5hRniDzJdmBakgfmmY8ZHtyVaLz+l1ZsiYvixhDMMJQ067gvYZZZQv85OJv3vbhKSbaFCWUFPGxwRLwtgLp2fcbtvue0AcqDKZyVLVomRCbUhUaO2QrmvMOmo1Fhnqkw56bEpb1ZpNkLZuUn1Hz96lRItE5EfARugA7L6z3W+W545ihCmMQ1xOd0x+rGVdsAdclLy5pPwNWZabkpJ95oZGeJN5ocBBiiNgYFELpukGwRNSTIpctUtiKg7yZ5Dgi1og6LIpL8JUisUR5J8GQHXiB8Z0ZCPIvSXCSVFoYlc36GOmjpwseMeCCxfk9pq8I1uARTW0eAtf9nuu+o4s9jW154+GbnNQN2/d/zfO//CErCRhbQ91gbMBL4InApe9VTkEQExArrKuWNZYtJiWuinjfUzk4Q6OMjAXX1Hz54QN2v/6Er9QtvnbcrC3+9ISzds1JLTRvvMnFaw+56iJX73+MjVHVvcbR4jgXR+89T+m5tpGtF3Yi7IIWO5KM/5JTgiHie60ZWVeq23CJFjrnqOuaptUI7yalVK9qN6CNtllzdnJG3dSs1yes12vqtqFtG1558JDHj59zebNDjKU9OSWnQwXY77dsN1dsN9d4r0ZtMTbhJ8tq1SJ9x907J3ztnTf59rffY7e94eb6Gu/3GBMwDiQaVXamFOfGOEJK23x6fjqkqgTVd8SgETW5nmXwqo/QCCa93vtIH3rqUA+11YeoHqb6kMmZ5kW0u8DER+6b8w352pxWKFaf6uemNOCQ9831J5f0KfmepXfNrx17dv7Mbd/rtYNLC01l5BfxRy97ben6Ep392/R3W99L/OXYpvxxeT3j1ePvWO7vOJFM98v4ZKbnE6fJPE4RMF7z9hp18Mk8Y9Z9GTFYopZ0A40Itwp34xBFaS5Z9zbKalHGeGNSdpGhnMERnmu6Bod/D7NdOFfl9MaHld68TCtLwQxOe4d3DZdfJO8snb/b7n/RGb5NxnjZNuKWhfcm2MmZbQoMMZFRDvHNCJdL5zpfm6dsn69ffmbyfC4hU6zFsTmVbZC9D+Yti78n5fcOxrbc97E56D0j/VnSBxiD2hqc06w6bo6TS3oRh2dKnKKBL2UWUI0e1oC0PTfXl1xfX1LVDffvnfHeu2/z4Ycf8P7nF5y3a6TvU+nMHmLE77ZcXj7n4s4Fq/Va+YWmUUfAvWWz3fLoyWNee/1bPHvyjOfPnvP554949vyC7W5H07S06xME1X1K4pcrZ8FURANVVdOu1+xu/BClLKJBYCEE1SsmOBkyDBnDjkhvLD2GK4T3peMUp3yD1Sh6C/TRY6M6hV4a4dmq4XtvfZVzH3l/d8PT7TXt8ye8efGQO6++yjuvvs5ffPYxl7st566hEWirBi8dwcAzev66e0prHdvKcRk9D8XwXnuPv+qf8/n+mvP1Q1wtRB+wnWf313/Nkw8+4M1XX+W3v/Xb/OJn3+fXu7/h7vkJ1mlJn13vafsOC9TGKc9fGTye7X6LDz1NZbFNS4ia7WrvPSGO6dAxSQ/rzVBybcD/A/io/lKSjrEabFMyGMdVJ2gQzbFO8CmzF1k/lHgGaweYzs0aNzjsJvGCOe3K0m2U1LfTYEsJQiCwi1v2O0NbK0+X5aYQLZiQggnzea70rMoYyT7gBavG7pjpXZJbVAZKBGsY2nG8OUbEH/I0SeRV+dBM5ddcSmTWG0kDkz6ZW958OI5cF3yw36R5tO2Ku/fucn73nPXpmqZt1Sml62gunvJ0e81Nt2PX7Qhea8Ov12tOT1ecnqxZtQ37bocbgrPV+SL428eU2xeIGJ8q5HJkbRnVJzIax+dKwfL50pBRpsHW+6pCqB2jZrNixBBTHebl2pdzBVm+Xl6bE9xSkVxez4bP8rnyHqsSSzFHM0Sh6lgso53TTJRU8wjwpVSYoyHdpjqR0/robbsa1z8Z+sSqd1WpiqqTt8moZBBAvScqS/KiGRUIZRR0uTbZa6uMpp2OMzlIJEYjhphqHxiMpEjjIo23wosZFJsD+5GEzcqpEUtTjxR+olERVjm2EkZLpnJKrKfCkrUpRXFIClSg33d5YkPUqkt1mH2fGZiEfIMM6c2sG+FkKZ2fE5Be0/V2MXDeODZXV7jgaZuaGIPW4pg4TChi8skAVDmXDFxjFGtMDhOqnFKvWB8F7wslM6SIYlWmGSPYAvFJjjhNVMeYwQ1lgJdITMhSr0UBa2UwSmWYUN6mcCIxpOjnSIgR5ypsZTUiIEYIaJqUQTE7euHmFDvRqNEeEXzwZEY2r5FESxiUkKWCdWzWGqxNlM1aYmXIQoBJij6RJGhlY7EZjcpZsIccNZLifUPExhS9bLQeitanFKwd4WrSBq3jMINEWrJQFYc03iCIRYmiSCIiOaUjmKEe9kjosrFNCmVmCGOWgXGf09jSmQVJBm+N2lGRL6p3Wlr/PnmsiQhDOoDBAFMokTFFpryAKxSSJr87OXyEvhuSmUkYcaLFDp/FCOJlUFgOyu20nLl2C9ZMzv88+pBo1MEk4SMnITHpARM9IhqJr2dA4SVnSM3rpSkQi7SfZJyaoETmip/UYt7rLBRlODCTc0PGWyRmZDgryVEsG+oz0zRE9DPAraZpyp9lOAO69voTo9Ze0/7DoLRV3zMzvEdMGk8Iqc65GQzpU8X/iD8muHAEE82JIdM6mwPdTnBlJaXCTftpoxlqlRurqe9izMZ6xXk2M3EmlS/A4GxF8F6d1pwhGBBXse87Tu6e8w//+A/4zu//Hs16hTdCb8FSDU4YH/7i53z405/x+LPPuXj0lP3VNf1+jxPBRqjQrA6qM8mGuEzTBBMV75OExIzX1Bknw8EokOe2pGxYUhpMo5gV96jSNAz8xosUhEttbnidC90lH5dbyZfEFAVY9lc+P+fDjinfsonumILlNmVN2aIktZaZZQoq+YPiPflamfptPo9yj8p1MWYsuzJ3FD0UKqbrE2NIZzMZW14w53JsJf9orUOiHd5Z7pNJZz3EEW8ce085Nxgz9pTf5/GXBu0DJTPZOJ4MWAfK7tvHkRWfMUUb5l4znzIvCzPfv/LzbW3E5uMYyhrdR+H04PN0THPDxHx+y21ZYVgq7g7Webb2c2Xc3EnAGBViB/uxtUkhYSffz3HBsfnPx1mOK8+HTFMLHndQpJn8julzUCgji1Slw9us8lzRWJ4+v8CHqNi1wJEjT67RuyONTl0Yq1ltROgTbTFGHXxzNLiBMVLBQjBGaWsyZGVH7kTIEDEDjkdkdqK/eNuHCyRHrRml5xWBzqtCTWLPrttzuRW6jceJwTiHqwRxifdKDjO6yDGtQ0nHR95/5CXAJhqVa8LZlH2F6AhJBhIbBvmCQWGlHGSIli4Yrm6uUx1mO+JcgRAMOE1H6YzRqIhs3BtY+1l5NLHpJ0XmZF6sWG9jwEjCOVF5uZgNH0lWGGEr14FUnCVorfOQFWVpLTJvGw3kdNIZxZriv2zAF5GBfykkOyAl+s0GdKs1sm1d41BHZOt7Lf9TN8iqxdcVvdMolUqEnsjeGPrKEWzDulrzxsPX2D9/xs2v3mf7wfuctRUxWupKsynsguexeDY+UIsbeX3rWDtH00VaDL0wRM5b62iNxQXBVTXn5+c8bFdcX+145/Scpw3E84b2y2/wlWpFU0XaN14jrlZcPXnG7uPHqjxE+XpnKhqxXMWep3g6cfgAm9Cxk6hrO6yXZsOxjmQc9lTOpZ9qMIrXTUPd1GNE+arVyOkEE1Vdg9EIpL73tK2WQ3vw4AFf+tKXubrZgXU07ZpmtR6iTELo2O027PfXbHc3GmiQZIEgJpVNgyCe11+9yze/8Q4PX3nARx99xK7bEiXoucHgYypZ5CqVOUkK88pxfvdM68qTS8nZQYbWNdA0oJo1K+KTkVwjosJBFi3NwjDlE8lnmhGfl3j7QGYp4HXK6s+M4SVUl+Rh0t3UAXTsS78bZO3hJ847OKCbJT2a64OW6FK+fjutOr4OL9OWnv3bXFv6bj7O36T/F83xRfeO+pGlZ5evF3dM+il6vXVM5R1LMDD0bmKKFNNME+CU1iVnKSMM9Vhz6TmMOggxrKm+zSQ9b3oS5UcUlyn5UmchxQnhJdY1/z7kW/N8ZDIGyPzTdE9IrIA5XLaB31jqa8pnHbRB0Socv2k8t6T3THmcJXnnmAx0CGdLsl2+Ph3DEfxw0HPx3QwnKe45Ps+Ms0reez5O/T3NtHSMt5/s4Yy/PZbN46hOwJijJ+a28zvs2sBzT2WFY22Ob+aZqYaxJj4xByPl63N8nj/nOuJadmY+FhnGmYORjBH2uy3Xl89Zr9ec37nPq6/c4xtff4f3P/33Gh3atrgYCPugWQa7jpvrSy6uLzg9v8PDsxPatsVVyjNc32x5//0PeOP113j06Am/+PkvePz4CTfbLb3vqeuGO/fusVqvcVWlQTkhUllDMBaLw9UN7WrF/uaavvNJr5ZgKMkEEckVjTRTqjH0RjMj9gm/fGB63pMqPaj6pFOgIWKjZY/wqd/yp9vnfO9LD3j3zn2e9T2fbDd89Ogx31zfY1WteOe1N/jRxSMub54TDKyI6vwYK/ZG6Ih86K+5X60QV3NFpCPypltxYgzPuh37U8NZVWGdOkm2H3zM4x/9mK/+o4e89+5Xee/t3+X9n/yM9pUGZ2rEGDqJ7HyPxMi6aagrhfH9fsdmt6VyjvPTM4KDvQ0Y69j5Hu93ICnwTJKBO/EGhWCITdkkcz3xHKgWnC7sQH+EFEVuQbS2eEz2o9ylJjAedQxZl2Wt8pd1XVPVlUaQ+5jKc5EM2JKCEWW03URADBKVJ/S9JLW7o2rAoYZ+rRNuR9xT6rRNDooqmkmGcYlEUYdWQ1qn8mSZ8oQfa1OaO4jaBQ82R185EGnAh2SRKOPcBTo0eUsZxKQPG+sGXa5GyGtAYduuODk74+TklJOTNavVmlXdEiJgK7xx9EHYyp4ghlXTcHLScnpywqqtcQYaW2FXJwQMAehDpPPL+HXeXtownusa5chcVRpNkZ4iLJsY2kMFTiYe2eA1GCcnDK0CtrUjsRqvzxY6EaWyjmapyCrvy+02wluOaQSO6TjLVCEYDlKkloRySANZKCCXCNxcwVy22whl2Ww6pGWt79KwPyhvjUGSUinfW80IfYxxUmN0ygiMEdvld6VSOHs8z8c6Rr1KUuyoY0ROPy5p/HkuIqPStWRIlvaoVBDnd+ZrWVFdOiNkeAbGyKQiBX0WNNfrtQrjIRzMZ9yDQ6GuVMiOexm0zk+KmD5Zrzg/OyNsd/S9pFo4s1RnxtDY8ZhaMxX+NPVHYnBiqv8ec2qncc8RKU6QDOkC8zrlCOkskM6dHwYl2TAukke/nnnNRJC88/N7B6+QJFBYnWEeizNGo6dFCGGEN5vul0TdlEgozOQIgWIqQxTr/JyWN5kEd/kd9UI0d5Tpvuq9BlC4KFN4lwyhc466aRRWZXQWGM5EaZhIY540GdO5DMrrbI1N34+/dS42E84CFmIco/OEtFZkg8JoTBYpcN2Ap/W5KhuFBxhXg7dNjEOOQh6MG+S10vEWNG8CPyJaDzpnVogxTtZBVajTM1OecREZIpuzwW+u6Cnb3KgwMQ5hhrTsJU7KhJ5ifnn8DGo9KOEpf6/CgB3mKnHBQFfiJiWW03fMBFF9R4KDQkAYqaQkxu5QGTRfi9zf/Cd/kRmcQ6NHZmgYxpvHamf3jvhjRleH/6b78iIheCLUZjhLf2Xc7ozVCHGBXJ/TYFQJbgTX1HijzkimrbGN47t/8Ad87w/+ASev3MUbITpDWzeaymjf8dlHn/HXP/gLbp4+Z3PxnEeffY6JgvQ+QUGi/WnhRlzsCqc4k5jMQ/pdCqLl/szvmf89p4GHz3BwJsqsLktnZknRkPm7JeF+SfGY3zOcJcPBOOd0ej7Hl2lL98+VvvN1K89/yauU905wzAIfmec1FfCnraQ5S2Ox2QsYDuB/+E1xLm/Zn2PrNq718ncHypEJbzKF0xKO50qTOezO9/XYO8r7J3Ao5mjfkGnD8nzGzC3LCvES5x5dnDzWW8b+Ilid8PRHvp+f42P95LWY1kXmYG0m2ZiO9Dd3Wi3/zk5L2Ykl49j5mZq3Jf722PvLZ+Yy2dJ75rBxG+zl+eWzGhOPVhmbgrUL/tGO+TAjhpj5s9R3IPM6pqCvKVV3jGP0sYWclcolR6cYCr7MOeWlRSOlg4wKnNtg72Xafr/B95BT/lW1wzkIRmUL3/dsdh3PbgK7q4DpocJinBBsQEJyCDAGNejqb13gyZ+6BvNsC+maHX4c2DAY4bS+ifLxmGR8thZsjZgGHyseX19ycgJt01BZLeMTRRWM0fvMcKhD9aAbgMxAZN5Tx6lKpTkuFf1jgLGIslGS90KBnjzbfM0Ykk9ITrqvfGKswsSgnaOvhsiNtGjDyAZeKkUFZ6XTOI1hXXfO4lGn2NrVnNx7yP1792hWLdYZfOjpvcdhqG1FYy2V5raiqVt89FSnZ6yDJxrhjZMHvLK+xy9+8AM2f/Mz3PaG2K4Q0dKNAbgW4VK03iIxOdVZR4X6+PX9VlOLx4j3UdML4zAi9L1nfbLi1ddehestr22FB2+ecXl3TfXwDt9872t8V2o+CZ7n90/wV8+5/ugDwtVVcpSwSZ0HHZFPTeCxFbxzBBO48ns6LM46YvRILvoVeuW1iHR9T13XrFcaGLBarVSer1VO7vueIJG6aVKqfTUubzZbPv/0MdvtFmsN6/WKh6++wne+81s41/CzX/ySTx89ojk5oW3XuLomRI/vd4R+R9/t6LqtQp5xhAQjq9Wabrfl7knFV995g2987W1C8Gy3V0T6BFi1KmBDoKoNUBNNdthAI2KqlH0ihuRoobW8YwyIGK1bWRsa2kF/432g7zU6rbvuBz5My70Fmka0NmXBD/6HaAPOFknlKsajkOUISRez/mAuzha9DWc4BCnOc5Z5DnnQjPPz59vozxJ9mdOtL0LrX9SG8mIlT7Ak37zktWP3zGnnF+lviUeFQz5xvna39XHs/XNeZf6+F7XJmLLcVXx3jB+3rlIcHFPZOtEMX1YCjRUqKwRXIVbLD0DPUF5SLDFC8GmMPgzGGnWuUofNaFIppkyHiJP1OAYDZQaneZuv1XJ/JkWAJ2p90F35rBlp5oLcccA3F8kJ8/k75tan8sx4d3k9/z/y8dP7yusmB63k52+Bu4MxFPNQXJP1JUd48eGZUc8zB93pmi9nb1qSqaa6w6n+KreJjoCEOwu8tMR7H5PHB8aFw7MwOccpM08pN437Pp33Ubgo1iTGUR8+vZfBKD6OJ4+j5OtziUmjvGK+znT8MWWDsima13uPc05TcgfP1eUzTs/OaJuGZrXmW998jz/7y1/QdR7XtNSA9z3iO0zv2W42PL+84PT8Lq+cn2o505stq/Up2+0Vn376mL/4wV/yyYe/5qc//hlBIqfnp5ydnXF9fc2TJ4+4e+8eTduw7zpurjc8fPgKpq4xdaX6Yt8jIctuuiYSlRaGlJVICprpU4bTGyINltZYPjOeByESoub9XAGvAjWWPYZra/j17ob/00d/w7u253/14Et8pfN0l5Znux0/+5sPaR894+Ef/H1eO73Lx0+f8NxvuWMaGutYWX1PxFKZmr0zOBxXRrgQz1d8z9tS85nsuPSeE1uzqhsu9zu+/Oiai3/779l942vcffMr/M7v/AP+/Cf/AkdF4yqsc3iEm/2OvYBHqAlEiWz3W3ofuHt6h7qq6XeRTdNTNdd0EgibQEgBSjEZlzXQzKU1EyRoeSYhlTdK5zjGiDdT2bEy6gypsJTgXrR0E6JZtDLshhCIxMEW1DQt63Y9lKkJXuhtT9/3iAhNo6VXsRBE7UV930M0SNBr2VnGOYuYGhENUst4x7laA3dS9qEQ1RHXmeTUmHgpDQiSoWSHQdBKqTkLaURw2baNWDM516PBO+Os4owLh7hH8roMGqkkT+USwUmmTvJyiWiP0eNSx5+uEkVlcf1oca7GtS2r1Vp57Ch0fa92iarmzuoML3DjO276LTddRYwVdeOoXYUJkdgpz31+ckLdtHiBvQ9sdj2+uzwY21J7acO4evRI8kCtEqEY02qXCrIQkgJiSIU8ImybkGZuU4Va3ixdNGYMUCZgx5Rg5b3TsZuhNvQoNLgDZd6SIrD8rlTOqKKTgQCXhGsSPbXAHL0sM5j7uk0RWv6U0cZjOq3pXNQwntMwp/GkNB8lQzZ/5/idReLoFTkf38sqSMs5zFuODNKo5Okc6roeDNUHqVdFDuaQ1yE/U17PhnFr7ZD2ZLVa0feK/PL3I1yP7zyWJrucV5nW3TqDpSKYVDcO2O92+BAm52FpTUqmqVyL+RkAZYG1VuBoaJXi73Iv0slM2QNnBsLqiIdiauphmxRDJtUfztkf8vlwo6JK7NQDKu+cs6NTS6m0Lc9Pua+HC02qhT3Wij08Y6pQyXho7uwxCl1F5M/sd+kMUta1LmEMGJ0NTFJASonFxv0smxRGJa1/fDjNY/ht/vcELqwZIpyOMdZD+tDknFL2kwlguaaDErpYk3J8S+dfn6sO5jD/bJi+f0mgsIUz1vxMzOF1CXcu4fby823KhhK3lBk4lgSS30TpsTjWgW4ur+sSLTyGl44xLOW+ljiuPCclPXrRO26jxXYBBsv1eqmoTgGipiswgkaxF1GO1lioLNGAt9AZQZqa1999m3/0P/snvP6VtyAZxBE18Id9x26z44Of/Ix/96/+NduLS0wU/H6HSdkgsE6jcySZ6qziQTuDqTmuXaIVc+Fzidc4xoss0WcYcWVex/Ic5bZk9F6iN7fRtjkTneFn5DHsmOFiAaaXri+eF5ggz5flmyZ9Zca9GLf3fkafp4bz+TgP6MTsPSNvOz0vJf5RYWN0CoURn5T3vHiGh+f+kN4dUWKV/GuhS5vzFfPsT3NYPPbul1W63wYTi7RtYTpDF1Jeu/2MLMHYZN3kUP23xK+/sJ+FdkDrjtChUs5ZooFlK3Hl3DngReMY+h1kreWxluOafzeB2xe892XPbtnf/J230a8s09VNQ3OyGpyWgLEsTro/IHhQ5QiS0hJrVKyufxwM6aMMS+LnVNNlMdjk+JzHO+djozF4Mzqc/m3b82cbkFojxStLXRtiYzlttSadYAkInezY73bI3mBCiqZ3YK2WKBGB5KJL6eU/pFcXGbINyXAmRrl3+DEmKa1SBIaJia9Pyj8ErMNUNVQtpl7zxld/m9P1CW3KyhK8p9vt2ftesyzYtG8LzuT5/eO1JIIs8F4ZfxljMPUqzdQAdrJPeS7Ka5UKI5sMwtN+jVFFoq4Xw94e0JwZvpykhZ/wlCGlm6xZuYa7zQn31qec1i1tVVFbjZ7f1ClbkICNVh0eUMeLaDU6Upzlzv0H/MW/+P/w8Z/9GRc//gm1iexxPLxzB+KOq9BzHSLGw8qoLO3DHkSoLWyrSGc8bdWqo4OrqFbK92y6PfsQObl7yuqdN/jxX/yQ363h/bfWXH7py9w7f4Wv0/IkPuW/MRWXYUV33XH++QXPt1e42lJLgxhHL3BBz5Mm8thaame4iZEn0iF2hakcYd8r3AHBezAOZ2t81+Nrj1nr/q1WK9brNav1Gls5drsd11dXGGNYnZ5Q1w0xCE+ePOLp0+e0dYMgPL+84INff8iT50+5c/c+z55fg2m4/+Ahu77jfNWi+CGw3W149uwJvd/TNiv6XpWMTdPSrtY8ffSEP/z9v89vf/cb3Lt/xgcffsxmf4G1gSBO61sC7Ur0bIQEPClSLhLo9x0+9BhEs+VlnG4zDMaUiSRi0PSkjXPUTU2MK2hhv+/Y7/eDkrbve+qqHVKs/22aKkBzqbPj/Ep5Xoc5DKa18QyUvMbIO5hZH4dyzcvwpyUf9iJee35tPpdj7zjy9sn8bqPzf5t2m5z6/2+oYWof0PxiUGNoKli3hntnDa/cc5yf1jQVNLVltapwdeDsbJ3qk1q2m56nTy7Z7wLbnWPfBXadZ7/3dF4wdoUX2HWBzWbHzc2Wx2FMN3scdl5yDsd4z5lgNKQZXurjiCxw2ztf5hoczwR27Lml74fzkfTRS2u2dI6W5MgJj83huVvUOwyOcsoNLY372Pxf5szN9Sb5Wqk/ynr429qcp7ntfblNMnlpJ8M95ef5s8fw7DQT6pgVrcTVmJyZMOPuxGUaFvtMHNQo7xBwKX210qyxfxHNPuqcOlRKFLbbDY8ff461ltdWK770+ut87zvf5U/+7N9Rtw1Vu8Zsdsi+oxLDfrfl+fVzVlfnvHHnjLPz+5ycnGCtoa4sl5dP+df/+t+yubhiv91TrWoianeo65qLiwt2my0Ygw+efrfl4vlTvvTe1zg/v4urBL/b0nUdYIasLyEE1YmQYVPnbNPeVq5iEwOrGHmdmuvK8xF7XsXyJpYGw31qHtFhsLRYGiyXEX7xwa+w/8X3+OY33qP78fs8/fFP+XOuqS+u+H12vPXlL/Mkdvy7D3/Gw/qED+MN96VhFStaqTglEn1P7Wo6G7ghErznd+0d/sQZnu82rI2B6Hh+veXVaNl//8948ve+xxtvvs3f+fu/x4///B/zF8/+Fe0dIQbPzXbPxnS89sqruFWDjxEvgm1a7p+eaAa/3lO1apx2Tc0+enrx7LoNIfTpTDiscUPQGhEIKrMNQWpErdsuEUNM4kPKmFOprBNTrm5nKnVMLLJ6lmerdSvqVssRV66mqVaq545mgEXV51lOT09ZrVZgoQ+ezWbD1dWFnpOgGT4lGdpP2hVUVst1isfgaJoVxlhCTDydUdsqeCAQgkaIOwfWNip+GvQ/wyDfHlbsUqwfB93kkmOTykLDmRyek8m983PrbFGmxxSOLKkPbsFNCvkqP5f4rq5alR+zfFWvaJtVsrVU1FVOZR+RGLBEzSpWOarWQS4fve+QvsesGu7fvcu7X3mXpmm43vTsfGDnA2enm1vGN7YvFDEODAqIceEWFFmplUh8ft9I4G5nFOaGURGSdxkFwnwxwdA04NqWjOJlK42f87FPlFUqFR+MJcY41pq20+ul0qck7CWTMY/yOKowZErEJP0ujb7Dd5IVooYwqwtijcFLSosvsihATfarGG82rJUpizniDVnekz188jjLdSlTEuaIkGyYLiN2y/XKbQ4H5bqXMFyuS/n8ZrMhxkhd13rYum4yh8MMB+MaG8OE4SnXOMSoNcYrCyZSNzX91Q03Nzc0evPAIM0ZzWMOC8eYJSOaIllMShuZ6oG7pGzqYxk9PH1f+c6l74sJJ91VUhTOjAIZrgYmDLRuoLVpLXROPsVLlPOZrG2MqQbmcYE404iRwc1MVtniEK1czmuiKJ6ta/mTz1WZwaCc67BHqFLNoKUEZOE8HRgQJEW+5kiUIwx/uQ9DtNewHQUeyPiiuGE+b1Mg3vKMlN6sks7gfCxl/frREUoOxleOq/zOOXdotBYO92MBNvPZXzqDJe6cC03ZWWlOj+beu6XhsBz30vrn+c9h8hgdyu/K45nv23zdRG9cZDaOKV0Wz8dL0I45HZ33OT+bS9F+xzykyxYlpvT/ZkLzlpQA8/eXTasnGlyKPjIiqqQ3IBZllCvHjsC9N1/n9//JH/P173wTaWp2RIyzWDE0dY30nmefP+FnP/wrfvaXPyJu91SdRrDJvsdWjpzqq7KOaMcoxNGWMKXvL7NXt7UlpcJt62owmiHCyuAENt/LOd5Zwqfl3s7HXo6tzJpRZmtZOpdlP+WzL6OofRklxRItnuCwAmcfeuvL4jNLEdQD3j0Cq0s0o1wvRCMPyj2Z4sCEbxEO5JgXrMmUXzzUk5VjybilHMM8+vgY7znpY4avJ8qeW8Z+wFPMcPLBfBgzk+Sm9E/pzrGzVeKYF+3b0rUlvHPbvMo5zL+b04v5WT7ge5h/nuKA/OzUULiAJxPfXN47MaLPYKGkbXOeYmm+L7s+ZT9zJeFt75nIFRyBH7S0l3OO17/8Jr//x39I07a0bavlh0paZi2urqlWK6zT0kU+GZByJHAImnoxv8cWa1s6AxICfdelCIKIK2Qu5xxV3WgK7LxOX2CtlpqtHJcX1yAVVd3SrE4IWJypWdmKxhta31NLz732jJuqozceJ4EWSy+G3jI4wVpntQQXDDy2TRHTYgEJKeVgVnpYgnFEaxMdrAgmYKuaygjRBKTS1Ok+eNayB3vGhX+X181v87tf+ia/+70VVd0SjdYH72NWagkimsbWGKhsNTmvw+9sXrO5dpxAKs1CylYnojHJWvIkElytirLkBBARghmd+hXdClWRTtUwbtf8SJsgQ+S8iKQMXYfnXxCCBo3TRIsRQzCGvQGIuL5HrCNogCInrsYGITbahxOoqPAOVi5ivYCxxKpCQkq1HTraqNHkdtWyf/KEH/+3/y+2v/qIZm9x5pR63RDaPbIRrr3lSbRcOsNr3ad8rb7Dj4PluQgGy2kQaNY4sUSj5bns9Z4udjy6ecbX3vsq777xOneed+x+ec0nX/8S56+9yzfv3ePtyhB3F/yANY+jxXV7/ONPuPjFT7EE3uzPuHGwE0+QyLau+ZgdZ2bFFsMGS29aTXxsVDGpacKTnkDMoMfZ73dc3RjOz8/Z7G60XmhdU9U1tWv46JOP+eXPf8W9+69wfn4Ha+Hpk6e8+vA+p2enWGPZ7fd8/ugRH/7iVzRnT3nlwevcuXNOax1ia2zl2O+2bDY3bC4vCTcbbF3RVitM7InW4dYtm82Wr711nz/4O1/n4YO7PLu44Xp7CaYFU2NiwFqNmAqoOjJa6Dthc9Px7NlTzZgWAzFoVqK6ctRVhasqbG1SdgirqaElEqNP0dVqMHC2wrSwqmvqtVXD+L6j63okBvo+0vcGI4a6yY4gCukjnaVQis6BXuVFKeTGdHT0mayrHbIpjI5Xxmg5JBlkvKj4NcaFurzJITtHSk1HgWZhKMzsR/iNkX6PCuBjKLiM3i27E2HgMXSNzeG6FPcu/a10fPEJZkt5S3+HMuj83iVctXzdFN8pvzl/ZjpHM/uufOZ2Xq9sLysjz3kAm15ZqOCHeem9jDg/Peu9Z9d5NrtA47a89cYJb95d89rZmldP17x20vDGXcf9M8t5c8ppU7M69dRtRf2d/wnmS99Bmopw9RH9X/4rbn75c/Y7w6Y3XO0jz7eBLghRLJ04nm56Pnh8zQ8vLnn2rKNpWk2/WyX8Wa5loaM6XNdi1oZBJ1LuWYZFmOpPlnQh04WlqDE+5+fHZ5SkenK2Ewa8cJgtK8a5fDDnWc3B3hxrGZ4KcWAytkGvZ6af87PZwU+EAUDm67EsP2vkcsZL87OmOMxMdmfpnnnfGTbJZzBHv0qW7QxGchajEesOmTthyDQ51/9ObCIDTE3XZDoOSVs5zudQT34cj5a6jbHfHDUKOWhyzDIq6fsxm6nFjL6Okpw5BhlGjY5aFkUNYXXt1DlSBCRgMFin0bISLcY1WlLXCpvtNc8vnlE3a1x9wu9+58v8zd/8jCdXO6LA+s4ZV7trgqmwQTA31/TPn/D87hucngl3VhXOW0zV4td3MfYxe/8ULxv8JrDfXXD1tCZEwfd94ofzAY3015dsnj3lpK6wVcWjR5/Tx0BtU7bQKBpYkUrr9VHSohj6GKFSPXglEHHc4DgJjr211NFw3xrOLZz7SEvDJZE+ehwBwfAhht41fHDza77f/YofmsecRIun4w9//SnfevttbHyLZ7/+NffcCXfF80R27KNnJQ3res1FU9GGDdv9nuruCe999R3W++f87M9/znWz48k60NmGE1/xyWbLu59ccPnv/j3tG6/y1h/8Mf/g9/+Iv/i3P4DaYxBWLvLKvfu88coraI6jGue01M223/Ps8gm922Mk0CK4ZoU3J8CG4GskGmI0dKFXg3oAEwMSPdFrevwYDDFYzeIhUeUTEara4uoqObBmWJcczafnsJ/akXIKb2ctla1o6hpnnJbZFc1uix3TfLdVS11r6vgYIjFYmgrqdc9mcwUhYA24ymJrR7Qg+17Le1iLSYE72BQkaAy5pEcQS+UcNuNlK/T0aE4nDToxKSta6DWbkOLdxGsZq/KI6LmOCU9kZ2c99ypvqR4lJm0qqNOlQcTiAjgTkuNthbcnel/WLyW6DKRYdTsgb80LpXt2TCcIEDCIz9luA7aOCSM7jDmhqc84XVWsVw7rKi7DhuuwAxdoK2it7mewgj3Vvbl/fpcvv/Iar53do991VEaQpkVWlmvbLOK5eXtpw7hISMyIEKNPE7XpeiZ8eZOWmNZRiZWJXyb0eUOXWxw2fhDaF5iC6VhHo02p3CsVS0vR4uWzS/3CNLU3TIlUjHEQ3LquS9+NY1xKI1oyDLnv3H9d18P92WCTr80VY0N9NJEh5X3uO6cNH1KCJ8Eir0P2wrI2KAJP/Wel2kRpJ4eRRHkeg0OBdROkA0yMirmfUgmX+xwUh4yCVBmBn9OeG2Mm9enz39monceWx1+uR74vX8sRfcfGUirDyv3Kz4aU/mxpTYZ9SusXvMdY2G13ivhEyCmwo4x7X8JUqZSfK67L8RljNEqYiJa3z8Jv1LOT6g47Y1IqKBQhw+BUkccdZvt3MDcyXCdYCNkz3JD1+hMGkjTX/Dnm9Dl2Yvgu5zp6m99ioCfDyDS1z0EzIyyNz4zr6Zyj99MU6SV8zA3/5TjK81GObY5/jhkP5gYiZ63WwWaZMR1gPk6FjvIMWmuHcuLTdSrg3h6WWpgKPkpSrTUH6yIylrAo13Gu9C7/Lu+beLOmd5fvyJH5JR7JxpAS/ssx3Gb8KI0C+Z05Wqg0HMwj58u1WFqjOX7K/cyNhmUrYSJ/nq/VcP71hsmYl+59USR3+e7y99L9x8ZyG80tr83XYfL+VGO4NFCW577cj9yW+jHO4hJbZkAVdpXVtLLW0IlwcueEP/yjf8hv/b2/Q322IjqDqSuIWnfcdJ7rp8/58Q//kl//zfs8/vBjZNfRWofpPI2z9CKE/Z5mfaLrXCXHnpxJAY2QzobevBd5bpkWz+HnNnyW5zxf19uUC4pvxzWaw1j5/Jx+wDJ832bonPMz5ZgFGTOQHGn57M3xRbkuiuPCZJxzA1l+bo57yu9iMefyuzltLccxv3eOE+Y4YL42S+Mrs+ov0Qtj8pm4demO4o2lcZRrNYEpzAjDBV08FiVeKn/msPkyTgflfcCUdhQ4vbxnsp8wjFd5gqwgPL7+GUaP8fxL9HsuB5R4vXymbEswYhfO6tKZLN814Q+MWTS2leMo13s+ztzmjppzmFtq8/0tYbmcbzm2A2e/2XrMcU/5TAk78z5LmlfuzZznyI6sX//WN/mn/8v/MnnmzyIGIUWCm1RqdKrUDCGoIcqYoQbpqNyd7YNRhYUMms9iHmRHGKMst8iguP1bNevBRXy/06hZ01NVLazu4pzDdz377Yb99Z6mOqdtHHG3g95rELe6ayY5QPImkeXyQT2bximiGhCT9ZN5L1ElkRqHkwzkwHgGRbC1DhcigcDpWcsrr97lwYNTTs2KytaItcQqlQswpGDtmJyqDTKUiCrgVZKTTFbwCJotJqUHjAZslR2XBSNChWGXlES5TjpGoykolsBYi5eQJi+DvHKQcQnIqTBNui7WgS3UpUMdeo34sDCUXMMYrNP7qlipSsoaTO1YN2oU7q3KMyZoeS3rLKSMBiIg3lNbR5SAk5Qhxzo6E/nRD37A1Y9+gVxeUzmLW7U4p3Ufb4xwHQPbzhNjzz989Uvc5YQPHz/m+WaHEPFOqFxDCJGYFGfR9BAja2N57dVXub8+h08vuN56urdf4eTsFMQifaQ3FVdBaNctzfUl9tFzVs9vWNFQ07IishfLlsCVCK2tqV3NExPYEMZ1YuQR9LyLwm6SBX0IdF038F259JvB0Hd7bq43dLs9F8+fsd1uMAY2mxuaCna7DSEEdvs915sNlas4vfcK65Mz2naFMQZXVcQY6Po9292G3XaHxEB7ssZ3PcYY6rqhqituthu++c1vcv/BfaJErm+u8b7XfQOEoKWVUBqvOiLh+mrLo8+f8fTpY8VhzmGMGmCrJHNWzlG1lrpxVLWmjKwqC1YzNmQn6uB7hqxJNtU9R7NiRC/EkAxZcSyVgzWq6ExO8pqq8xC3D3j3Rfgp38+URojkFNQjri0dyRl4IeVhM46Zl2oaO2SCo47RM5FhSJN53NbKW0SmzvWT7CEHzx3r+7gz68uPaSqz3d7HlB8cv8u0eKmfQ35k8u2El8kwMV3b+f3zzy+SMw+uyzgqM/vOGDvRyZUwFUJgv99rBPfVjvWDhjfu3+WdN+7z+p0zHq5W3K0t99bC+YnhzmrFWWNY1Tvsq+9i3vpD/NlXEFdRuy+x/sqOk+dP2O8N13uo9hEaT4/q0G76yIYNroYgPVeXV6xPgkYSSqMBUrM1MIN717DiB3uQb5hv1TGedwk2JvxU8fWSPH84EpP4I5OcV44bt4+dQd0X7XVJFp02M3tmAf/M323GtRyy3eRJLLQ5Hzu/Pn/PBL6Ke489e/BdLt8yuYfDTdWOBj3ssVbKReP6lWne4yLOnMuIh3LIeKZfAsvrW21hcEw84oQ9HtidUoeW12iUAVXnprWcB0eSLH/EcTTGWFxlkJj1wRF1ojKE6Nlsbnj+/Dnr9TmvPHzAu++8xc3P3uf6Zk/bNrh2RYwBiQHfd+z3O643N3h/n7ZpaVYRL4YmRM7P73Bz+QTiHt/HocynOqGZge81CDFCjJ7tzQ0Xz55ROcd+u0ONjkW5nsTbTnBZ/j8zk2hAR2/gFanYSKBGs792MbCxhp1AL6oHbbCcYfipC/xXf/JvudP3+O6Gt07P+L3T1/nZ9in/9a9/yd+9f4c7zQnfvvsmH15dENuKk87inMVVNVsiwQfW5g5dd4WVhtXDezx89Q2+/sMP+StS9Lt1+HaF319xfb2h+/kvaX7yc17/rb/L13/nm3zjF1/l8cWvsK3h7t37fOnBm5yv71CZlrY5oW1WuKpm5/cYHDebS2LVYfD0cc8Zp+ogYSuMWPZ7z5PLCy5urgh9RwweEa97b5X3l8TTqIwWsVWZ1WqM8gaV+xDlybtdHHRUzjlc1vtKxDmjUcpW64r3fY9xhqZpsLbCGtXPW1PhrFNdvRj2vseJo6kbcB5rNIW6a7RUhzFO9ZTWYqsKW6scNGoxFR4qW6eAmxHvlicz80yYKV2hwLUikgzrpZAzlceh5O2kPGwDLpJMEZR5JWeDGIdQ4vT8DMOMpnRv2qJERHqMFSqX0rQjEANRPNYKrjEEK9z0e7bXl2y6jlhZOvGElCkgkhwW6obV6oSmPgGp2G16xAuVrbFVjbGOUL8cfntpw/iSkczaEdGOypS5AuV2QrSkAD5sU6asbHNFyzzyZTqW6ftvY9ZuUx5NFD5MlXBlSloRGTxoJ8LAjEEoo7vztczkwSgglt+VcxgE9qKVTFEWHq3VemvGGqxYYkjE0Khy31oVwPOz2cg/NVhNlVpzhZ5LURhzRqNUgokIWDOJ4J4zFTGqB1AZmZ7nOzcQT5RfR5i3rIhdirApx1qub065eoypy8q0GCPWTWHsoG8BE0RTqQM+eGqJEyFSZmdliSGcj6VUKoporT4t35KUdsl7z+gL0kMMWQNHdGwGwTUwwm053/KdIqIR6XaMoC9bfl+hbps8l70h9TUm/X0YhRpl6oixeHalUPQdGTMLYyxxTwhxULjl/stU+nMYWXrXcA7nwkyqd4ygnvJp4Qdl6YKQKUzhrJz//PvhmWJdlJmffj84xqS5R4mDQ0PpBDLMxYwEe254NsYM5wOmxpEydfTIzI9Mfdd1BzCcFWIl85/xxuDUkmqM5+/z/XPD4/y85PlM4Co9MzcczFv+bsnAXX5/W1vCSXOjQXn9VoXBwjvn+37MGH9s3Mdgu1zP28Z17D2LNHamqJr3u+RYcUzozsyhGENwmlZ2Ez123fLt3/1d/t4f/kPuf/lNutBhGi3/YoEVjrjrefTBR/z0r37EJ7/6kGeffg6dp1ZiSFPX9L4fSweEgE0pvHLpBmOMRpUzOpHBIU4s93++PnNadmy+5ZoswWn6cjjLuc3Ths/X8Bgf9KI2PzMTuHmBMjDT2Jz9BQ4zA5m0t/n+Ei/f1ve8lfQ1tzLrka7/i9PTzWn70L8sz3V+j87TTjDyfL+NmSl4FvoaxzzFGdMxTHmPxTUzw3+T7+b4f3B2XMjyMacHeZ5zJ5c53zVvUSISD8t5jAt4yBstGRmX8OL8TJbzXYpGnvd1m4xQPjPHYbmneYR4Oab83Jx/nfd92/zyO8r5zO994fme4aeXge8XtdzHksG87HvOh5d4sITdJcfA8v7BOc1AZyP7ZNQzzPY1Jo/3OCoYjAHjLFGE3e6GGCOn6xM1PJUwPjsvEeVlMyzGGMdMTEZwqC17NAJ9cTxbtiAW62pN4Z5eG0Kv+KytcO2atllj4h6JanzTFOdAjBgrOEMyAIMxbuRZhz1JPPvBno/4ONMZjdq2Q/S2sQYTDZZU19tEQtyxXgUePLDce+C0ZqsVqGIKfpBMxlUmMRZE7eN5zTPrnI3uxmYHXF2FDCMWDQqxTscmorow4wMSVO6CiM3GV4GcltBIemk6uVkxNaBjkcGcITYZC2Rg3xVGUEN25rxN1I7EjA6OkuaTlVbWmCGTlnUWl4zpITD0pzKFOgtIjBgfsJUjxJgM5xW+Mjzbbnj/hz/EffYM6XpMbaGtcK4mBriWwEbUKH6n3/Hbr36L59dq5A0IGEtEtL/YaT3sqMqn4Hse3rvH/fv3AcOjJ0+xr97j9I3XcHXDVYh8Ej3BGjYx0qwqml9fEj9/xunOg21posOJYYXFYXlqe9qqxVYVu9izJwzRlRN9goxGr3zuQwiTkmc5m5y1js1mw263A2OIosbtGAJ9v+fi4jlVVWlEtfcEAXdacXp6xnqV0q6LKlT76Om7Pbvtlv1+i7GGulqx317hnKZ/JETOTmu+9a1v0DQtN9stu93NRJYcYKrgZ/o+cH294dnTS66udoDQOC2T4KzBWXXSqCpH1WnEeF1XNG1Fu6qp6kplIRkAEEm1So1RudpUmvIzGiE6rd8doyQFs6jhwcQiOjuXJJueqwGHyvhbD9ftNGvyd5zK7wNW0YUq+ihwbYGbxmdkwtPdzgcty84v2+LC/V+cFo77P+/nRX3N6eLLvPvo+s/6+E1o+m3jvO3aSDkNh7ea4f+Ba8pjy0Nc4GmO7XPWcYS+R/yedb3m/vkdHty7x93zM9Z1jSXSWWFjDK2pWJlIpMI2a6jWYFqMqbFujVmdUTUN171jbyI78WwN9ChO30TPdR+46Xp2oaf3HbWvkVgDmWZkKlHMoTwDma4srMoAA5Prt6/FcJ8x0/cUPP9yH+neHOwyaO8y35O6TM/MjbBL+io4hN9Slpu3pbkchdlxaEtHbLHPl8UPc12b3PL8AV7LKDIe+14Onl1qSzLv4b0qVw5rvdDH0hqUstr8+xFEl/XembaZRGuy0nO818x+UvmNZMAk66SNBqI4q0ZIa7IcI4m8SLoXohMqq9mLlA7lsp2OKJG+77i5ueLq6oK79+/y5S+/wa8/fcRu12GxrNZnbK8usJXDh57ddsvVzTXb/Z7m9ARXN1RBaHzg7Oyc1WqN328INmBSZDYpi4LyvGZYBySw3265QvkV3/fF+qm+N+a5MIKt0jjlMTOP6IHORNamYhs9LY5aIhDYEtiiuMdhOcFwguVzLP/8k0/4kgCVcP/shK/efchpveZ/++nf8KWrS37rwZd49+13+bMf/glOTrBRs8r2tqeP0PYNdd1iemHf91zT86Xf+i2+9uAev3y+4cZ79nVk3a6Q7pqbfU/89BGbX3zAxa8/4Y3f/i2+/fDr/OX+Ek7g4YNXeXD6Kk3VsqpPWK/OaBrN0rWOPb4P1Kai8zf0bIh9oI4N1jqaqsVRse8CvRi6ENjGSMQjQTAVVNZivK6pNwJBsWg2hGf4GWU3PR0y4KPk2Gs0JberlNOO2Q6gvqZquBaLrRJ/7izWVNSuoTK12k0COCM0tsY3LcZGYtxjEVxlcbWFyinsWIOpKmxVg6sIJrNS49kxCW8bw8CbqUwUBxwu0STH7JHKZLZsbNkZ83bd1oDfF2/IX0/tbS/SKcy/P36/YI2kkpRKC41EYuzpwo5tZ9lF8LFns9viY8StW3Z+x9539CEQkzOBtQ1GKkKA/a5n7zxtpZnkjFPc8bLlhF7aMA5TBYfIWGtIFy4eMJIH3ksmgydImUQpS8YLiH1C/ZIQOyFaBfIuo5DmjGT598saOY4R7oFAzFQdxkwjxErFYun9PO8/3zc37swjIOeEdC4clGnNS+V8qewc3p1ZtozcU/0Lm4TR7XY7GLgmh8Ew1EReUmKlzlVpUCi95imKy31aiqyVrDiYRWIaM6ZTK5Wd+b4yCq00nmUBuxzP3PEgr/l8XnNjerkXEwah2Nc8r/meGqvebpWrgC6do6jKuqKTJYPdMpMywo7OxUCqH0ge45jhQpuMdZByH3msIYRFDHkgmCUB2ZgUKWHmSDnfN94vSMoSVXqDT5nzcl7WWk0lXUT1zaNJtYdDgetAibwwtFJ5G6NgrEtKhTFjQB5Xud/HmjFmSMG5tA75eVXYmqFetiofir1feE8Jn0ttUaBgPDdzvDP8zCKp8/3l2fU+HDwHI75xzhHCNOp/7uSQs4jkOWQCNQofugYTJ48Cdw59yQjzeQwlnlwUEguYmp+lJYFjqa9j+16u0xdtc0GxxDXlmizNpeyjxEMv25YEptvo3RIOepm+y7VX+jHu4fyZlzlj4wMMtXWCgVg7bgh86be+xh/+03/Cl995hxgjexswdY2PkRqHbDquHj/jFz/+Cf/mT/6Ufrcn7npaV1HjBrzUSwTnaFw7oRUGgwMkpOwFovs0j25cwtVLPMhthqPfpA14k6lD23wsuR07D7e1Ep8s37+kADt83xw+5v29aGwvUg7pSJbnPFUKqHH8WFt67+3zfzllzOHcGXis8t7bnl8eh8ACLzPpg2W4mPNhS1kDluhhdnRYOtdzvmn+HmOsKuxnxs+xk6xEADK+zfM80ubjn0cdL92rvNLxiPlj7zmGy/K6lPzV3Jlgfv/w9y10LLclOHjR+F7mfL/onpfpbykDwxIcl/Az73sOk1N+e2q0zkazrtsnWV4wOYq3fLeJKfXe1ABDDJjK4Uyt+N2CD2F0zMwwQuKrRJAQoHBksdZqPrMYUmYUQ2KLDmSE36QJK1zVYFOUjjpuOrwXnFuxbk6x1Jxf7Pn46RbvDZJq9BEFE1NaeKbn3iSzhH6WoW54uqBnrlDsGzOVcQSrxu7EOxtRJ9tIT/AbnL1mvd5yfi/QbUEimJj6TXI/iZYaSeNRD26y/VvxlQ5HYtphY0jdIBacAxyIE7AWMZZONOxIYMiC5ciJA80gj8QYcDKFZ4NJxn6lEXn/cVYj1fM6ZfgEYl4vEUzUWni4JB8ZwRBxko3jBlM5qBzGWTCiijgDNqVZNRhMFMRoNhysynPYgPhUEqtxdDHw6aef8/gv/5qTmz29BV8bpDa4uqbb91x5z4ZAYyPv1Y63X33Io+uP2AaPNxGaFuP9QAutoCmwo2O/73nva9/g9PSM62cXfLS74Ld+57d47eEr7DrDs9DxTLSe9sYaaheRR4+wjx6xDoHu/8vbfzVbkuSJndjPRYhzzhWZN0Vlqe7q7pqe6REEMABmFoPFAAOxWJLvMJrt6/KBn4BfYY1m/CRrNNqSfKBemu1yANAGomemdXV36cpKddVREeGCD+4e4REnzs2sxpBelnXvjRPH5d//WhQLyqgArFBYpWhLR1FWWKlpDHTRESCl4R4ifwYHqyS7J+fitm0pS03bhtrazjk2m01vMC+rCikErXdIKdhsNgPdB6QuKYqSk9VZUNxKRchQCM52mLah2W9p2oay0EihcUCpNMKD7Vq+9f59vvfhB7hmx3a7pu12sSai7bVdJAW/Cxn81ust65stt7d7TAtKK6z3wWk+OovgPUo5VCvQ2qK1pSgNXWup65iqWcmgxJUyJsGkpx1CBH2A0AGGkjhtRKjRmeQp5zMHMRHvhfdEREm/WZEujQIf5NSx5hDHJ31OjscTLunxS08L5YB3kiLJ5zR6mJ7odQ6JX+mvY48x8zm9jmebNs8UH8yv8c1agoOhTXmr1/GZc+8ek5Xu4of7j44sI+76m8l6zLyT82sEZ+T+vYMxczyadZH9Plq7H/Qawx4MsJBok9KSstYsFhXVokKVJU4pdl6wN561hcJDYy1t5zlZKE53a8qrj/EohC6wzQvs7TM2rePpRvJq67jcGa72La0P/MFm3/DiesOL9Z5t54IhRMdoTCnIy3WkeQLI/HxEXON0GyNMj/mXGXlphkft9yuHodedZ6STCNnD/oga9gs4BCCBYA6gDmB6/OHB3I/JTQd440j//ThHZKMclvI+78RbgoP359+N+MknVHmor0/nfKyf0fomc53fC0WOW+7K8pa33pF0NI80T2LfwydTvrxHzxlfO/D5uQBLrx9J9GSQx8I/7wllQfrxLfTyabIBWKqFDg6PkR8jGqgVIYvfvtlxe3vNer3j8eMHPHx4j5vbDW3rWC5P2N6+QhYhE8x2u+Vmfcv1Zs2irhFao0tPYQ0nJydU1ZKNuEYqHfc47HWimaO1O0XXtjgbIvZdcuDLIsTDPU0JkZIjGsl0Cd7hCEbxRjgqUSCdpECzjAC1pqHBYlFoIVggOfWaa6/4kWz4pTcsnOM7neJrb/hdfZ/zQqHallVZcvrht1n/7H/kVAsKNB6HFZbCSe45iZYdO23wfsurzSv8t5/wwYfvcv8/vOCm2XAtJEu1wErJrrPUr25oP/6c5z/7iEd/5wf8zlu/zeX+GW3dcf/sASf6HoUsWFQnLOoVhS5BCEoc3bJDO81tJ7k1Lc4IQMZU5hVaFSgluIegcxYw7PYW28Vyv0ik9AjhEAasDLxVrtMJyZEjry9EtFt5nA2G8eSIH/Tw4aSSw2rg3QRIha40qlBhv5xDaCjLilJVmNYEx2ShWNZLpIPNPjghCuFQWoTvqiCvSKVQhUZGB0zrTH8nRLxULssupGTSiUeYd8H5URJlHCfxfpDoctks/d7j7iMtfCQyDDD/TsL/477n3p0f71DHFJwPBIR1EbJACOGx3rBu1jQ3W4xwdM5inUWVGtVZts2efdsE52ClUaLAe0FnTHB2EZLz1QnLqgAfnMGttTjfHd2HvL2xYXwgtOGHj+mf03MpZVAUjL50uHmDgmqcOq9njA/GPawLOxepklqukMr7zhXGcy03PI0J1Ijt7//ul+XHiuI0TjIq+z7HvoyCyaHyb6r4GaWQ9L5PE5bmOTX8qhjJ1mWeSrkxN6UWh5TSe4jokVExkJRxiTjl38lbXjMmzWGqeBQ9YZ1XGjp/qHA9NASP04fn/Scj9/Tck/HCe9/XeM8NaCndYopUS+vIDaCJYUjC+FRpmY+Xnquo1MjXmMOSEMEQ7ISLKcQdRVli2A2CZjzbJEDk8DDtN+3XFNalTGl1MkR2gBQDs+78fL+BYPsDNnfKmA4KXICUDv7wvMPHSXHkkaRzDEonhOzTwc0peqUMdUP6NQqRhpyMMhZgpwJb/52cZ8sJUir/QKb4O2AcD9sUN6Xx889FdmeFEPjUr/c4YwKhU6pPjRc409czt9OW7v2wl4EBSKLkFGc654IXZsa4p8wSg3Hb9XOZwn+6Y0l4S8/nsnYIMU6Nmt7tx3a+rz2d9zHKKMIYDyRDQ26gP7Yvg2LlkObk702Fy/y703bs+Tdt+d5NBaF5cXPc0rznnK+mY9w1h6kwma/9TYStObp2V//pZ06jw8upw0xJk/0MFzxEpTnv6fBUq5p/+T/7L/jwD/8AW0r2wqNKHRTV3lMITbfe8qv/+CN+9Zc/5vbFK9g0LKWiMS3aO8pSg5QY7+i8C1E5PSM9RM+oWP7BexBqnIp7jqbPKSymTmH/6W2sfMx5nvQsd0jpv+XHePtN5/JNYX/6fn7mo6wQ+Z5JcQA3d/X7pmsIjjw225/Xz3+ONk1/Tu9I7gwY6GpQEebvj3k9lzBttr7D9YycpOKlyOmdj/T7Lu9Y7+l5vTm6nteoBw540vQzrSEZLvIxp/RmyuMOeCUYpo4JVEP75jQxzWNOHpjjnxJjPzq3bL6zs5rAXXpr+n4+7pzTXXon8Ep3ryN/9y4HiLl5jD4jpSk+xNH/KW3Kt05hHcYOb6+jMUKIkTNdvl95hoKubRHGopwLEdtSxExI0eEQ8FLgYzagtNPOh9TnSqvAi0iBECp6r4fPpFLEjsCHGtD5QYVU3b53EpRKggqKDvzIFfw3amV1D+E7vHJI6SkKiWRFoWu0qqnKikJqPni/4fPrX+PkHuNKlNMxIpoYkRp57kna5EDfRpT26Fkc/Iu+tiFiHoyxeCTe7Vjffs7lq1+wbc54VDxBqRDl7KXECRHpuEPIEMWCiBKIyO5SGHgw2ER8qnyQq7SQFLG8Sp/9TGoa06EROKUwSmGsQ1mPQuBVMKx7wBmLLIsx3U7wEctSiWgwlRGGhjsMjqEkVOKHRRmjUFRMeW1jukcZlVm6QBUapUQsgQXWG5JYJaRI7gpgBcYZ8BaNpessyim89Fjv2d2uefHv/5r2p79ihcUWAqcFhZBIrWjXLbfe0NmOx7rgT5+8Cw+XfPxXL7juNpi4sMIr2qaj7VqsFRin2DvDTWd4+3vfo21abrZrVu9e8E/+6O8hbMuPFLySgp1XbD2U50vq61tefv4Zty+eYbDIzrHFoAnzoS5oTqAsaprWYglOBUIGGS+nnSNnUT8YxoWUbLdbtD7DGMtms8F72Gw2CCFYLBZUdUyNLoNcs21vkVIHZZouKKqK+/cfsDo5xyMxziG1wmGxXUO729Lud1hrKBZLutahtEYXOjh4YPlbv/89Tk+XfPbyGbv9BqUdShY0TdLbuP5OWWspi5rrq1teXV6z3exC2nNR4JwhlQTrdR3GITtNJz1Ke3RjaPYt+7qgrDRlGaPIqyrgm1i72/oseyICfND7KCUQQiPloFfy3oJXMWvaWMbLf8+zePX4Nwar5O/PfY94l5JDQxgnOgCITJ+WDAUMuHnKoPV3Mwr1AU56LDGZv8+6yIxX4zenD0bj5DM77D9+9gby0V1jHRv/WDumF7pzPvGVmFBwePew8+CXdMcYgZ8dqb2y/sTo5+tar+vp/77zbcKZD/rnnHcQogjpeAtFsyphWXHddejrWy63eyQKYyyO4FByVmju1ZqzU8mTm095tPu/UDx6C7TCrtdc//pTPv5qw7MbuN513DQN1/uWxli6ztC2Hbt9y826o3UL7p8VlGVJWZZDBqSkfHK+B+/pPZuXj8IuJhjvd1fkWoHsvszAwFT+vHtXMzo7kgtzuTw50vmxcZ9DJ36fvAEmbfQk9mFnZLgpb/iN1jPhJ499x7k77n6SD7Lf5/rp5zmTOn38DgRD8bwsNe0/n/9cNs3YA0GmTL/T7+ld8kD+bz7r59x60znkXNlYXhrgk0CH3FhXreTAn3kfgm4CvzzWQSR8ns5Ryo7FqkAXCiGTYV/gsRSqQApw3rLZXrPZbDg9P+HJo3u8fHHJZ5+94PTsHF3XICzOgTcdt7dXXF1fcrI6YbVYUlQlpTWUZUVd1ShV4nBI7ZFSo3WBd36wH+DC3H0MkPAdNu6FQmFjynMPZAHBCOgzAXmIwRUScBgBO+HoJBQoOhQrFOcovqTjihgf7D17IbDa8y2vaZzhl8pyDfz1fs1PPvr/8L+V3+F/9d3fpn7rPst7DnkC/4vvf58P6wdUEnwhcVKgOofzihtl+Xx/DV3L2c0avOPkT/+AD3/1OVdPt3zebDk1EqxBbA33djX2+Ste/uRHvLr5Uz78/u/xyr7i2f4pSmjOVhcooVGyRPoCXHAALYSnlDWVtuzcGtvBdtOwb1oWeolQBZIarRX3TiuM83SuwQlHKx3e2ID1HEhH4CkleC+w3uO9I6XtF0LEqOuoA7MOZzyS4OTocTiXHKBjxLkEYzo8DlXVlEWBQNK2HQKHFBpdFGhZ4FoXePhCIUuF23q23ZZClcFwrzwu1uXSRRFKdSkFUtLZWOfcgxAuljYVYELWX611LK8jIq8WnCe8ExjvcTZk50rZVg9l7tnrP8Ijgxwdhk7BRul+9/gs8uFSDA4tiXHLWa8km+XzON4iT+xDUIWPd1oJhZOOTbOla/cYGRyIi1KjHLS3W9q2xSM4Wa0oqhpnPR5D41uwlhKFKR1GGTbbLfvdjrbtcNw1n6G9sWG8lLpPf+xFFNp8EmKDQFxo0SP/gVkmMuXEDC3hUsu4gT5TiEoR0hSACEJm3HFn3UhppUfKtzzNdiB0zjsYCa5BKPBeolRcsjeRzgf0lAhLyE4VjT1eIKLhaKwuiICVPHsJANDXbiJj9oSGZNwXMc119I6AFOE81DGeU3RNI7/yMXoFo/d9JDUEQlqWZS9YGmtIMBuehRoJ2ACQwgWlROpTa03XdQcMhhCDEThnVOYiQIc0pYxqsqa0oiHtRYgWkioHRU+qt5n6TvNIKT2TUDcyyGcKzCHCL9RsDsJxNFB6j5IhjUYyfk6ZrlxpmjMHc6lniEhojiFKzRKQi2rDnbHOY3xQphXG4TXQR675Hs5I/YlYK1UOzgI+EgEI+6JU+G6qbTJiarMmBf0+BCZ4LMAqKVNyhsjwDQJzMExHBimmcvM+EBYtdaLyEQIi4pQCET0Gg7d5ZOe9IJOrAwvhfUIUESfECM34b6hJHoVWH27lSPk+xs0E3db4YX9CPkUqK6xL9znV0kg60IG5iWwozruQ+iN5zIvwHBGm5OLcB4FtSHeSIlfCPYx3PMOlJOOJi4KFH/YiMcFz9CYwAYCUuKg8kiIqQF1MUyhyQw2IVNNNBmcFpQajeJh7VOL5sXEhDDMwtwk2rLVxn3xMsTmcjYDR3ynyIAl63icm3+Nj/EMSIsJaEhEO+E4QmO/UL37sdT0SNgOQ9zB9oOSI9yHjX4MyOY15uNkzuDFn7MXk9fF7UxyfKwAPFf+Dcl3KQQgKZ5gIa/I9zfcyriSjUfncpgL5MeXKAC/TNZEpqLJf4l7H6xDuRCohkD4j3kER7vRAi2OwmBfEILRQd9PGbBhSYq1DaUWLw60qfu+P/pA/+rM/pbx3StM1aIJCQksVor32Hdtnz/n4xz/n3/35v8ZsGyqlEZ2ldR1aq3ixE94TqCB9hT2Jy3IuMqYqCj86eRLPG37ys3ydMJ8rAPI+5947+n03VvqlO5wMl/Ne4sP3e4e7VAy7Z5J9z/sEPqZHu/2ZjXs8VD4erCdjwH0PRwnT9q8cvR93talCYgrjefRubvydznf697TfY++mlqdrdy7UpZdx/4RI/HNPySI9E/1d6HvNabHP6hh7hyM6ImYCiUgEsK8hDn2d5H6+kxObgdEcHqeG8fRvnK1Gjs4pz9gz4lUneM/MpBbP91gIgRVJQRKE3x6xMN6bY/Of8nDpPF/nZDundH4t/LnBBDrFtXPrO1SgRVp15L05OSDfu/y9KS2am/uI5uX9ZQaK6bdGfM3MXI8pOPN3k/NpPve5Oea8ncz5IZLR2yGUxFvHbtegigopamzThFIxwH7fUlUVRVEg4r3sug5jTKwDGu6MVhonk+yWCKfEmg5nQ5SKrqro0JgZfaLM5JwD63n16hVFVaKKgpOTE8qq6mva/abt4uKCbm/xpsPZlq7bU2jJ+b0TFssCicWYlkVheftJzZcvW17uO7rOU6rgALTvouOv8ExzLyXcPo/NYpPiABaAXmlincMnOVgUaNFx/fILfv4z+IuLhj/6n/wxiiXeLrCixAmNFQqwCGFDvTkhqDIZJvAJwRDe4yMIDqYEpbqxhlWx4LSoQ2Ry5/CBQ6Cxlr037HG01lF6jfTQOYuRLtQmxyO6LckxNjE3NhRnjs/D5hhvcKkcuUhlVULog/XEFOcOZR1OKpyJMrMzCG8RQrJrPeiaC1dzVpXUquzxsjWGpu1ojaUxltZ07LylEx0ei8SC85S2wNUlfuO5/fhzvv63f4G4WXMpPaoKNfdKpWiM5ZVtWYuWBw5++2TFb/3ud8AaXt7eUjo4E5JlZ7lPwcaB8oJWhrT2sjF8+1vf4ez8Pp99+gmrk1P+5G//ISe+5N+0T3nhllg0yhfcQ7FYnnP5Vz9l8/xr1s0WJTWlA4/hbXHGpiz5einYL+CEimftmi7RQikC353BFdDXEe+d1QEhHfv9vtdVhPtsez2I1iWlroPOp4QTHCf1KciQYjzUz4UHD9+jKCqsDzKcjFndzH7P7fUrrGlY1AVFWdDcGnRZ4fFUleLxw0f8we/+Fq8un9G0DUoptCpoTcJ3NtKZ8HehK66u1nz15XOur2+wzgRYNB6f5KgkezqH8SHySEqFNEEBrBW0raEoFGWpqRcVdgFlXfTypM9QTcjGEm+7l/EehfqXfdpal94dO16llvBvXtJurk154DmaldOOQebN29C362kRmaDxhryYhzx6MRM9Js2PkN6gw3rzdtee/P+yTenw3e8yClo52t8RGvD/r/Ud6lDHsrOAUNYqey/J01opKAp0VaJ8hQE+f3rJ85c3aKUQQuGcwEiN9eCFQglPzZ7KeU7qzyjFHiUc1mlu2hUvugLXXNOZjr2x7I0JWUu8QzpilhPJSXWGX2TOsP2kg4ybWmLX8zUdk71zKMxY/Lju8DM4u8w7b0a1yEg0nxvngNdMPFdaQNb8wZPjfPvrYHJYy+F9nlvPm/Q3x/fO9THX1RyvPXVonPLX/XuW2ef0hus06Ly+5RhOg/E5zeFYn/Wbvz/XRrJ+dJbPyx8O7+XwNgWc9E7SDSc5IMl+YE0e1Jd09SpkWrGZgTnLqjTMP8od2V4WteTi/jlVWQQTCh5v6bPs4B1du+fe6QmPnzzi+vqWZ1+/4qsvn+OcpVrUNM22N0rvt7dsNhvW+x3VYkGlC8qqoqoqzs7vc319Tbfu6LqGQiuEFjhPNOabYaIyZhBisAOkAw82s+zyiUB/054OFC3cOQc0eKwQXIgVr4TlXQTf8jUbv+epbtkjaKyn9QZhDGvV8C41C3nKM9dwaXdcAR8vDH+G5dOf/YL1V5/x+Pd/wL/8k3/Mj/+P/0+2pkVKgSwUlCWPHz/hRJc8Oa8p9obl2iP+hx9S/ou/z9/5y8/Y/5uGzfMvuD21nO9LcC3bzuOvr1Af/YRf/7sf8vhP/hEP772D3Aj8wnHv4iEy1WWPhlQXbV+6KKjrmtItUL5CUfHg5JyH9x6iRIE1nrbrcMphTjzb/Q3edihc4NmNxQpL72wnBXiRjRd0BVpGuPZRpygUQkPKYe6sxXqDi7XFq7IY9CMWhLNYK7G2xVmoyoK6LtE6nHm9qPAIvAQrLJ3rsNigdydkhSrKkmJZIlB4PNY7uraltQ7rfJ85VgjRl5SrCk2hdeDnvMP7aB9ExLvjsEFTihZJcs+bm8dvR7gan93pAMQiWT36DwKoJ1vmCA0E2jSxsby2RboppUSWBapSGCuwFoz0WAlGSNDBgWPftXTbDdYaVqsVJycnLFcrvHOs1xuMUgiC84VR8GxzzdOrl+w2W7rOBEdW+TecSl3LEJVMNFBbZ3sBOBCwaDTxgQnoDZtpDzxB0UzGWCeqHYUGL+mNN+lQRVSGe4LiNxRoT32nCK6h5pcUBEFIJiWoQoZiAQQjD+G96DHYz83HtGRS0XUd1hiE1mBdX8MqXJfMaOHB40LauIQMoxEj1C7QMV1CxPxpHBkQbKit6McC/8T4lDMXU8/p9EwGd5kD43Qe9RMUsoMHk4x1PbAWbyzeGvAOpUIUaCJaSdHZE6dC46wY1QU/NIqni5aMqDJ4yaS5Aw7Rl3QTUcHRt0xpmfrNCWQi5vnf+TzSM+ccVVH0xvS2afo9TYY0IozmzFTqJ8F27lGXKwL7M4oEMT+rqSHAEYzapRN4Jek6Q4ejkJpaGFosxhlCnEuAk1yhLKVE66QUdNHBQ2BMuHtBAExG/uOZEeKECaUP+uRrASpEMnhHx5B0kgnfxXX76PBAQpDJiJXuU36avXIxUxCT7b9zff8iEs6UpjDhDyGD4SzhmYFXG/aaOK/0d48/MiSeUwox814yxsosUlFIeiWYh+iRFr32oP8Z0I/vFWQ9V5kxsml0VYR7hw/RHj0qFMM7LkUdyaEurRCyx2uIcQ20XChJBvkAERH2vO8dXwQhgmKAVz+sO5D5wGcknB7HkAn203Ymo0ImPgk8KtXfIRlrMwVnfxQTQzngxAALfR3I1HcGgyOB2Y8dEKb7MTVMBJowvh/5mtJ3jgmM2Uv95zkuTkbI3EA0e0aTSN70/YN5iWCQTmzKYPgeYFsdzLXfNhKPly/wmLFnuu6poHZQGoXxGaX5BcEgU2j4AZZSWj2Xo4UEG7nAmv2zzlEUBY01wfO2ULRC8Oi73+Hv/U//KW99+AEdFltIqmKJsg4hNd2u5fbZS77+5Sf89C/+I+vLa/xuj4pMVr82QBQaG516vPdROet7fOPj+SRDSsqWYK3ta9HmZ5gL5omOjAW/qRB6XKidGpvmzsZ7HyMiD2lQ7nCXO2RMjVfDSfYTGT3zaS0ZbepVJ6M53x0rMhg7ojc+BINLVCIwgM0IZ79Jm1NakK013dF0JoG2zjPLU9wxVT7NKY7z8fN9zvFcTq/ys/Txf71CIj/nXvjxkdYn3iPNJauhPaElwYg+jCHF4AyXt6nCJed9pmvO4Sk9n8N3+Z5M4S70c4j3ps0L8DLChcocVuLFzPmy/CzyeUzv1DhiPbtTE1yan/ecwm9WASXG8J/Tnun38z7G86d3Js3XNO1jThl5199zCsMcrydHs7iM9NuBQJ1gI/WZ07M5/DTlnQ+3bB6n5d9L4wiIcuYwf4nAdB3Pv3rK//l/99/Rdh1XV5e89957PHr0qDeC13Ud6g9DL+PUdd33v9/vubm5oSxrFvWCJAsJITCxNm9RFEil8FqhoxyipWRZL3DWopWma1qQgpvNmqIIUWTeO/7J7/7WwdrftLlmRS0LioXCexOUfLKk1veRYkFIRWegs5QV1CtJUXu6duDP8DLI7mLCFDDwE1Imn0yRmLrAIYrsvXROCVf7IFMiQz1vJavoLKvAWG4ub/jpz3+FX2h0dYKXCywFxmuMFyH0QziEcEgRUiWGsWR08BG93BjWEmQpjQCl6azg7Yu3+Pajd7i/PKEQImRQU7Dzlue7Dc82N7y6vqHsPNI5bs2evW8xGJRzdN5kd0wMfHRad3y2EB4hQqCAtW6guyT8LnFYOjrwGmMB5REYpHcIL7luHX55zn/29gd87+IxChnrHIIzjrY1XG63PLu54urqihfXLzDCILVAFxLlJX4P999+C73fsfvJR9z85Cf4SmOdZVFUlLrECdh1HS99h7Ed79dn/ODRI4q3zvF//QXVzvNYL/FSs8JzpkuU8bRFwHum7dhtWn7rz36XZtfgyorFvfssHjzhx5dX/EoFdZ8gnPWqrHHbDU8/+gXXl5fsTYfymgZ4B8371SlfLBSmNijlWdiS1jnaqAxW0jP12EgZ+JKSPeGDkGVE9SnUk/E5p1nNvgU6EOF5VS5ASIwNTo5VteD+vYfB8VSIoL/BITDstmu2t2sEgsXyJMKhQZc17XbL2argww/e4dHFOV98/SVehIijkN4y4EfT5boaRVUt+dnPPubF80u6pqPUOkbwxjspohN9LC0iEAhvSRnZADoJnRHowtJ2FmMcpnMsY9ajZFjvCWS6q728EZT6wo/vf6DlyfE6BZO4oW6zHeh9MMbJg77zNkeP5/ihaZvyJonLFPFeJlo0bwjM6OwkQ08+p/Ru6p+Zd/zkvTdtIVbhOD8fnzLV04SotulbSU4efXMszyF6HMTsjoqRHPja9QhQDGc3wNLQfNQZ5DzKQTcJb/o327+5/Z7ducn8E++Z8zolkkJocJbdrWFLSwqA8ELgZEEI9rQIb1HOY0SB0JbCBHrgvWEnHXupKew68p2BFikBwitUTHerhEBoQYuOOmJG+qmk70oO4nk2wv7/k8X2Rh8Giao/ey8iDU/Rp/G+Hpy/6PsJWQCmexl7zei48ERjcLw/8QPvB6dpwSSb34xsO8cL9mubPJPDB/0zJYZgEnp5M42e7dIMyE9xiBCD3uQuPJU/G55DpvXK+kg8efhkTlZIn43G9GM5azqPfvzJ57n+6nCcMJ8pBhhwXPjnfJAFrQvZS0XKHgQUImlnEnM9s7GRH5zlBSOusNZjjY0G5OQoQqTPFitiHWc/0LgD4BcDzAfdhuP66pa6rtGFDny3c8GGEVcdxvE8f/EVFw9PePzwPu++/Zhf/eoz1k1DUS7CHCLfb5stu+0NTbOnNQatFFoJylJzdnbGyckZu/2aZrPFOwMER17TddGh1yN1koFsL4MnJ/RemPeBFvkYsAkBJ3oI0cQwxJOJcO8b4G19wmfc8sw5njiokWBccNwVkhrFyiu0czS+QXSW74uCJ+qCh6rkI7/jWy9uuN05Pr3d8Bd8xP/yT38Pf1vzYt9ww56ddJiiYHnZUkiFU44Vgm+pmt/5i4/o/s5vcfIH7/He86d8+fIlP2kaTvSC1sCmdejGsNytufzRz7j9e3+fannOqdvjiobFYhGWHxGPd562iwbmqkIpSSfOMNJwtrzg/OScZX2C2VuafcO+bWhFy64NmT6kUCES2xu86MCG+t9WRpj2DtvZaFMLWb6Ikf5K6gBPscyTQLJrd7iUMopwVM56ykJTVyW6KJBF+F7rPFILyqJAFwUeh7FdmI/weOGx3qK1pC4rBJZCK+q6YrlagpbcbtYhCMAHPl8RdN5ChOJOIX2VR6kh0FFGg39yLDDGYV2H8zbYQeP0fXYvB/7qEN/3uKVXKx2hzfn1FwM/KWWyE4x1KoPjsDjQfxxtSSdXSFQlUEsJXuCMowOcFiAKjDd0bYcxHQLBcrGgXlToQuDcHucd9RI6obDOhswRZkdz09I2hq5pCdf1kOc61t7YMG5ciB5O3SoZosSD0TEj/HhSnvhcb+6cw8tJDdWkABJpY8HaFiKBlyLVjY7G5aS0itHWgWEUOOEpdDLOglCBefAR0wjCMwEx9cWghE0ReN7nnrVh/sY0FEVB23W9h6IfpYyMKdlEMBQrrWiaFucsShc40wFBaeKdD4JTjN4mMUeOPuohKRvz/YEB0JMxeOq1K4Q4iLzIlUnpX6E11of601prurYJiN4YikyxOaeU6gnsTOTQVImYiPc0witX1IdI8UE5macwnyqiE3HNU6hPI33Su8n7zTnX1x3LheqiKIa1+Izdmaxlugc5853OIG/p3dxgPxpHhlIDQsrojUmfUiYX0ASHSCt58znnAiL0nrYNhp087XU+j7vadG15rfUBboY5TJWrYa7D9Z4KJaklI0ref4KNBC/RE6b/Th4VTJojgxF4CktBmT2/vrycwFRwn+5Rvh95kyJoChO+EAS4S84yM5t7cAdHTUz2LOsjfzc3pM3NKxdm8u/YSX+z+5XtQR61dYibJ8JLtp/JKJLvc3pnzvt0usbc6JLf5Xy+cwLVXX1OmfRj703bdNx8v4+tw8a7nNaSp6lO+zo3ztQ4OZ37FG8fW9+03zdZ/11tbr6j8X0QAsTM5zmNmOLQmcmGH6SrIJATOVExvOMliLJkbVrEsqBxlrNHF/zDf/ynfPi3fh9bazrpkEUBSHxrkLpke3XNV59+zl/+27/g+Sef47YNBYEpttaGyCTBAU4f09U05WF/c/pkjAmZGWb2fYpPpnfnrpboW07v3uRs54Xl0HJD/hx9+k3bN7mn+TwDa/ZmCrN8rDfu/w5cn54dixY/1mf+3TfBJdPvT4c6RifmaNMUnqa81phGHCpV5pQ+02fftAkh+ijZOTjN1zLF78PnkGcHyt/N3iI5fNwF+zkPBofleaapu4GeV+znN+lz+vubwsvcHtx1h3M4kFFZNbfG/N25Np3zN0lXfnwBg5Jq9uOMhs/B6nReqc05vua0czrfIGOO8VvCaYmfMLuGv/jv/wfquubRo0d8evUzPnY/6bNfPXr8iOXJCagoY0pFUxTc3NzEusSK5WLJ7Yvn/NWvfo1UkqqskFKy3qxDumbnEUrSmC4AsA/R61VZolWI1JVC0nQtqtAslksePnzIy5cv+Sf/9X/1zfc/NmXvU5dLqqJECY/RLUIWlOoMiQbfIYWlLk4pyzVF1aIKRxvTJksvkFJjScqLGX5LRLrYn1/4JwR9LeP+bNM/gBiFKkWInhBRsS68DBlcjOTmquXrz7+irFegSoyXdA6MA090rveuzwaUxa4G5Y+PBvvIY2oX6nV7VeLUgtpVvH3yCMooF9mQ7lJY6PaG9fWGF89eUGw7dDSM7/we41swBkzXO1AMjqkRR8c9UEJyWhdU1SKUcekMXWcw1sUUvaCVBuXxwiB9Qdv5oADzBuktAsmlkeiHb3N78pDm5B6msjGVYKzR7qExHS/WN3z5/Gu2X36Jw6BKSVWW1LJEiApRr/AvXmB/+Qni8iWND87WUhZ4KTFYNt6y9YZ7SN4/P+Pdx/dBKLZfX6ONZFUUeCWpfYiO9zbkqHRdB6bjZFlz/vgBX768Rq1WqLNzXjnHrbcsxBKnFdYJnIRmIdk9f8r1F1/Rbfd4LzAIaqW4kCGSc1/DrrSsVAVOsfcOE/U5KjN85rA5lk2D42JI/S17xxUYDBFJrg3G3KBfkVIilyFqrTMWIRUnp6fooqDpDEJLECElq+0aNutbbNdRVQVaF3TWoLQHH+Dv3tkJ77/3GJwN+CU69vqodwp8XHBkS9Fytzdrnj19wW7XBWCWwdjUZ/T1OT6MpSC8B2yvARUOnJPRABEiFa0TCB2uY1HESKNcARfvUUBXrp+fj4rrlAY4ebp4fG8Qb9v2oJxfoLOM8PAcvZxGoOe6lDSzkQ4GDs4/tT53WLwf3jE4E2aYIvUjGDseTtvwfPq5GP3qPclcNKaCU5KY1fqMlvyZUQ9lifyznDx776NpMntjSg9jywuOzbWArw+/N98GnUp+n0Zv+Lv5kNF3vLiTf0jNZfe955numuWMzN7DKEk3HCbrXbzbxGAIYRFeoLwN9MZrkI7OObzQKOER3iL9nkqWSB9TyBLT1yIQXibKFIARH/Cujwbt/KzS/5OuO3ckDIs4XJuf5x2Hru7SD2WvJrk89Dz9NBs6wkj/bpp5unMO6WRvYJcxU91oUvka0m1+AzlzdE/TuWb3w0WHzeQYN/CA435ef9cP/57TtYyeIQ7ez9+56+9YuGD0fM4d6JjMOG1TXcvwXpprOsLpepJ9I+l2oyNfjE6z1iGlQwk14NJDlWPYDZFgxucfDHvgsjKHfTBjojtD3yLN1w999a4PYuC7PB7nYb/vWK+3FIXmdFUHPWPM/hJ4s7DdXz/7nOWy4P79t3j04B4PHpzz6pNn1KsLbOdwvkH4DtMZNus12+2W/X5HqSSVEmitqBYLFicnlLcLdrs14Z5Iqqqg0AXWBkOd9SHAKdEtn+1DToHTPnkheqM4EO+GR/oEKcEv8JU3/HZRY+yWa2dYA9+RS750e154TysCbSgRnHrNUzpuRccTWfADUfNdt+K/7b7il2ZNaQTXbcevXzTcSMfF++/x6cc3vNq37AgZP9fGUhUVnRRUApQyfPerl6ifP0W9dc7F997mnV9/xsfPnmG1x3QetW9ZbHa4mw3dr3/N5bMXLFYrFv6UpnN9UGrXmbATIujNnXTIGLG9KJcgJVIqlvUC6TXGOUo6St2wsbd4C6WqWZYrjJJYI3G2pdCerg1lhdrO4Ewb4FKIgI9FcIQqi5JCVwFfBQNKgE1vYoYvYgZYGc6+qlnUddCZJdwabYZKhWxb0dqPVIKqDOn9WyvoXEmpT6i0ZlHVLBYLirJgvduxZYeLkeQKiZUgrO/5mORkJhnkr5RZWykRg2yDTbH3NYtZe5O9NS1/uKOHdoJpm/LOY64sUS4RM8DmQaJxnLu7n9UzhmcOLxxSeWQNaiXQUiI6hbfBecHhcCY4izohKIuKoqpBCjrbYXEUhWC1KjFe0EZ5zDqH9QqnPFY7jItlHcyb6bne2DCODlF8ShGQqQ8Ir9IK72RIxStyIwfhQGOEuXcO411Mc5yM0clAIGN/MnhRxMsaEKKPNZxDBPZ+twOCIVzKIEaF/PzBwOOj16vWmqIssNYFYbdr+vpORaFDZK5gEF6coyg0RVFjuo59E4SpzuypqwoZ6w4Ez2MRDjPSIyGgUEEqkRRIWQEhVZ9WoJSnaTqs86iiBqFoTYf3MZ2mGyusp0CVhIipkitXDCXlkNZ69N2eYRJERZDEeUHOTHbGoHxKRzQopHIlbGompl5PzftBiZ+MbNMoo6lSzjkfHBXE+F8y8OY1g1P/aT9zw3caNxkp2rbFe98ra7uuw0WhOaWWT/MZMZxibKyYRkLdpbSOuzBa95zBy2f/rAue3Wbro4dLBCI/CBzT8fp0uAxzT5GL03m9TsmdMx+zn/vglMIdQuUbjeMHBHuggCMxD4KxSU70/FYozZFlXGCI+MthNAmto15m1jZncJgi7ZyBnZ5nH/U6cd4Y9emG708NYOndIdWfHtJvMjYWz9X9ERmcHpo+hv2ZN0CIg5/5vcvHmjo6TOeQG/ny9wLjoEZlIdK/qRJ8uu8jpdfkDh1rczA1/Xx8fsfhfro/ufCRrzk1N/Pd/N05r945B4A8gjU/3yn+vcuI93r89M3aLOwEwjBrOJrC6RRmRkJl2meiMmfQwfRNBZUWToBVYBTspEDUmr/1x/+AP/pHf0J5/wwrwCZlvfNo66C1fPKTn/Bv//zP2V7fsHl1A/uWUqienxAqc3QRYxzr/eDUFc5yHCVcFAVt2/bnNnffpvsyVRq+aUvwkOaU+j4Gx/l9GykfM1hLf08j2L/pvH6TNroP4lBZ9jcBuzDmk4JQoUZ7k8aaY9hfN5ccJ7zuO7MKk6l+a4ZXmMNF0zs+B3M9rMHRce5a17S9CcxOcd7ceqbvjp5BL2QenUvSMPh5mg0c3JMp/pnejekaX4db/1Nh8xhfePRdf0jh53DJtJ/pGLnB+m+yzeH8uc9fR3fnHPPSGU1riguRDKTjPvOxC6n41sO3ePH8BV/8/Jc0TdO/I6Xi4x/9DKEV6JD2WxDSsmod6vTWdVCgnC1PWSKpVIU3nsvLF7x48SLw+UrhvQs1sp0N8/SenYkpxCP/7AFdhAjez5Xu5Y/ftC30AxbFilIVKAFeW4TUeK/BQYhmqyjUGUVxiSpahOrwwsQIg8xhUdAbxvtHIl4yMWBmEeV4D1kEtRzK5KT3ZMhNJAQxy1KYm/AOhUb5CtsWbF9scUuHLHSQ86Px0rtQMs3bqFT1LkY3hSg95z3Oeqzz6LIIUfs+yPtWVojFffaPPsAaD07EEkwSYzuUlSgjoPPYvUGsm2hUbym8QXiDb1tod7imxbYtLqbOT1nd8NFwKyXqpEKd3gs6j85g246uMzT7htbayNcLdCFQVKgOPBbvuhCt6yXWF+jFA0xnMVFmsC4olRUh61xjDFe7Lc+ur1hudoDBNwKnO5CO1cNz6sbSfPmc7tMvoNtgREFVaLxUWAENjlvb0lrLh+WSdx/c4+ziDG5arl5eB5hxwSpqRUzd7gTGdbS7PcJLzt5+jFhUvNhteHJxgVotednssMJzJkr2UrDHYZRnXzg2T79m/+oSugRziqXQ3CtLNqXnZeHYajhRFcYKds7io2JYInATupdwQY4rgt7ERVldZDQ/RGsNDk/BMB76c3SmRQqNsZZSKc7OTvsMOElSd87SNDs263XES6H2o3UOrUPUznJR8/DRBW+/9YDt7Sbw7TEjXwQXUvkjAClC1sKnT7/i5csrvAsp+FO8R2BHI4/ts4wNHhzJai3wXkY6GNbdGzqEotg1Mf1mMBYwoiCiHyf99L3BhhA5BX0ae+9CBFYKLkiGcRVx5RAAIEaGmLzN8Vs5nxBfGvMxSaE2R676eadtTYadjNeawM1dsvCxv+fboQJ4TiUs8v+JpPE51OnM6Q7mRx2zclPekJnPYF4mnM5h7t1+VOEO3puONav/mOFTJ4VLj7aB5mR6wZn35viJA94ZCI5aEoSir0kuwTkbs80JhA9u2NJrtLS00oKUKA/KgvQWpyxWFCEVL4JkFwmlPDwulhIMNLaYhbuUoGWgv2/OT76OZ78LJvKWMgPddR8S/zJ5I96pEKGo4vxzx7q55gnyfsIPr5MN5tY38G4xqCYz7/scVfjkDPNGoDYad05flz9POGf62VSmPPwZZjp9/iYzPKZnOewrtV5ACvswedczBACGfZOZboPoZGb7CGgRcdj4mFw/VlrbnL4s6BfGRvhhzmPcLETM9nvodtQvK5IZjPWs11uqUrFalmhVBoNdSscswUvHenvNZ59+SlWuOFkteOedx/z8k6/wXiNEiZIWKQ1WOLbrW3abDbvdjkVVUOtg6ylKTb1cUtU1hS5BQKELFoslIWiyZb/fsdtvcSbBoR+qX6bzGUhAOCEhE8COdYiA8GEvHJ7nokPqUJu7kQYjJL9VnnO534NruMKTchmuUHRIbjE0MedsZcF4eMaO+2g8HX7reXbzkg++/y72659iGgNCUihCho3KgywRwI6WzWbL/R9/jn/rdzh994J3P3jCxdOX3FYOIyRlYzHrPd3VBv/Vl7z49HPe/8HvUiwWtM0tbWM4O1vibODdhRBIHRyHrO9wwlDrJWWxCPW3kXSNRwnQRYnWBaYzFKpgVa3Q0mNtgTEF3nd4rzAm2NY2uz1iu6GliSVpgp2uKCq0Dn3pFDWOCGWoyjKUPLWq14dVVRG/U6GjnlAKgSiCDKJjQKyP2YqUElSFRmlQVmB9iVY1J8sTTuolZVlhrKPbWgpVhDNPPKkPUeJeREN3sssxpn15mvVIRGIZ4FjGKQbHD9cn4YvhHh9cq5HMd6RFeVCQ0WSZ0/034F9ew6dIFWq7awGFVVitMZ3Cdg7fysiGKKRwoCRltUAWBRaD95ZCOIpaU59I8I629TStozUOj0CWAlTYY7M388GMM+2NDePWG4QHLUu6pkFJhdSaQkqstzEiXPYCjLEBcegYyW2twflghC3LMjDXUtJ1XY9QhSDkzVeyr7/YC+F4wLHf7yiER4pg4PYRWIUItR+UkhRag08E3IfUWALAo6VDyVDHq+2Cp2/TNLFGVYtzwbAqpQARPEqebtbcv3+/JwaBSENZlCE6QAZhQYiQSkvHqOTFogLXstttURrwgu1uzXbb4IWkXq4QiCj8HyqQpgQkfZYUXiOGhiytOmOjXgLilOI9GWD76MXYV3BiCPWJ89SwuTJRIIZblc01V0zmz9I7IwbEhzETrEzXPKQ4lVnqrgRHdvR+EtryiPD0udY6ejceRhElIS09y+efooGTs0Ie2ZqfS7+2bK1zBqzwju/xiHWWqqzYmOBJFTzV45oZM49pHmk9WkqSQ0cSUJNTxFTYmcJR+j2HozlGVUoZvTWH8zgUggZGZi6VfVLQ+0nfubK2R/4Zj9d7i0eGzQmH9ePo6eneTrnhOaXt3P3K35umZUu/5zBi/ZC1whjTR0fn76fyANM23YO0r7kxIb0zfXYAb2lvZwSc9N0Eu8cU0/nv+bnlios5mPJ+nC3hmIAzMMiH6aVG65hRYEwV+XcZAo61b2IIeBMhbdpyB42pUWjOEJGejbIlMF7r9K5N7+yxNhU6p3+/Af8yu9+je9JLKIfvp3fuEuCm8xGeqGggCHNCROYQXEwRZAQ0Ejol+M7v/T5//C/+KQ/eegSFpIsClkKirEd3nvbyhp/98K/56K9/zO2rS0zbUVhPqGs1CKXGBOWHRoxgfbr3gacw/fxzmpoUrznszp172oPXneGBIiWjUTms3Nnu+DjHZ1Mam4+fUOkxXiRfzzHcMjfX18Hy3L2e27e5+RzrJ60pjyib4tU4EnOX5K655rhrTjGS47Wch5oqPKYOkVN8PzdeTidGfFWCkxlhKHfUyWH8GM49tpdzn+V4PjnqHTufg70kiF5Tmn3AI3AcvKdj5TxiDqdTHi3n++Z4hnxfDvmf36wduwfTeXrPQZrS6f2bngmMMwnMfTcfe+7ZXPM+OhQduaPHxkmfH9u3KZ2bwvMcD8KR9RZFULhsthuuX7zg8tWrwekw8kvOhZIc3a7pYUlKiUPQecdeCG7inn4ZSwM6Z6mqqndMhRBRqrWmMx1SCGzM3pQci8uixFqDkArTBWdd7yzNbnt0j9+knZ1csCgWwRhsQs005wOvFyr4BCOz6QqUWiDlPqjZvI1yW9wvMZYrE7roYSrjp3On05wu9ufW9xEd/PB9aRGldYjEdhKcBl9hthYrPcoblLDgDYUL6QWxAmc8nbXsnME7GxyHbYho6owNBvO6QtUr8AbjDDvfUZYneK0xQtIJQaEkyALbNQgnKFTBolqyqk+oWsnSwUousNLghcHud2zbopclu66j7Vp22y3b3S7ut8MKwV4YVnVNUVWUSiAKjZICbwyma3GdwyGRWlEXGqGLIMe4aHA3jtJpqmUdUjUqGWrbx3GtFzRNw7bZc73bcLXb8PhshZA+lrBzIBRvfet91NUlz58+5dkXn2FUh/IlShdYKTDC03jPdbtDdJbfvv82bz1+hDitsT9/zte3t+zxbLo9Bk9ReioDjahwxtDsDdXyjPu//zs0rWNrHcVqiVqUbLdram8QCBauwCBpJEjTIj55imsa8FAKTe0LLqzgrCr5ddnypbZslOJ+UfO8a9njER6KzFExx4VJzprKuiFTnwm6mkyfYa2jrBb9fSwKjdaqV56HFOxQVgXn52e07Z5QeDLInz7qmbbbNVoppJAxNayjLjSb24a3H7/Fe+++zcMH9/ji009wwiK0CNFgLswr0BuJjGtqWsMvf/lr1usti/oklkDKeJBoRBBCoOInzjkcluTIEmppCWyUjZ1PuNPSNhZTW4rCR81eLowOVHSoAxvojI96rfB7CF+yzmGsYb9v2O120dFFRD2X6EsLJgf6Hl8Mv45a4oOOZZeboz8TsT5rvZbg8JM34E2n85rSlH7w+Ev6usj/L2ZfnnQRdRNiPpNODuvTscJaBBJ/0LsQ6d1hH6cZAvLa6mm8aYR6GmuAgeGZEPJgd6f8whxPNOo/rf/AwAbjPUs6n2EcIURvyD08v8SbMTq7POBDRMWSUALibQpT8UjhQslNoKMIgULOUssKjaPzHXiPRFKwwpkdKBVonSM65ASy5pXCEkrsOe+p/bC2hJdy8SKtzZHu3kwQzZz8PQOmCQ761ftsryK+CH35gVbHD1Nf4RzTGUWYZHofY3RxBqf9/md95fcxzWXQew7G1PQz78tFHScTGMtlgGBkjwbe+F8/j0QzYs9DiZdsHSN5b7rGuWf0ffboOY0xwTOHuEyM1jm8k/V/HMFN+rqbPw88mh8tLwXxhHHDWy6TgZRU/f4lHtoYQ6H05J5nR9LD4eBMeYhjew0C407mssfK/p4meEllvvLvph6lVGy3W8pCcO/eKVW5DJGlibaoEFR5elZzc33N82dfc+/iMR9+7zv8m3//E3bbHYVUgdYLSakVt9sNu+2a/W5Lt1ziqyoaHUOZlWW9oqlrjHEUSrNaLtBKYUyLkgLTtVhh4lSjLC9DoKfvlcERH5CKE0Rc5X144HxfbkIA1sNLabGFZuFLBBalSv7g/F3spcPsXiF8w61wGAHCWzbKYS1cecPPxZZXvuNdVhj2NFhOkHyvk/zqR3/Fd//JP6X49zUnl5LSSWq94rRa4Zc7pKxRaAq2PN8bzv/qU+yHj1hdrHjvD77Nez/8NX8p9lhZII2Hbcfuak396jlf/eQjHn/4vZBq3Etur295ePEQSvqMXUqpEOhmHIUq0LpEKo1Uim7fYp1BCInSGolkIRbcv/8AL1raRmPdAmO3KCUoyxq8Yt8artdrrq+uub6+Ahei+IUINcbz0qha6uCQaLtoKxJoGyKMhRCU0Z7nnMfiUSH1CIUqQIoYjCvoTEehQkkZKT0KKCUsipLzk1Pun19QFxXeeTabLRUldbXEd3sa0+FNE9O+u5D1IKRUCFmElQqOxhk+DDgwGvu1jndHoymQNtTmJrt1PV5KNJHEP6a7mus503cjjvL9F4Y7LcYp1O/Uh0zw2lQ3nN9/qSVOSAorqYWGUmNaTbuzOCHxRlBqgfIa58KdRHicsBSVZrGSLE8VqoJKGBYVdFbTGEdrPM5JdOERyuOwePk3bBh/9uw5Wivef+99aqlYLZcoIVBCYjvDerOjaSKwCcv11TXOW4pC0bR7tps1Hsl6veXs9JTVyQlKSUxnesTsvEPJEFW+Xm9o2payrKKQA4vlikVdcbIIyGuxXA7CfnTVkVLiTBgfPG3bYa1hsViwb/aRhACioLO293xtmobNZoMxJipCLNvtmrIqKbTm6vIKpRVSCG5ub6mqCpzgwcUjtNbUdU1d1xjn0JGdtS6MpcoSCTx7+jW36y1SaZbL05Da3I4N0DBWJk0Z/DllUoJFa0xvRE3R1UNzwUFAKjwKeqX+OMW1dQPDm0duQ1S8RoYrCay5IT43xhVF0SuT0sVIEd5KKRCDgj43OORCMAyGibQnyfBtjOlrBUopqes6pLPPBGj84GmYGwH6HYkRI3ZivJtTAE+NCPl5pDlMBYc0nzAHhyMYgIqypF4uAvLrkbZESI8SscZ9FoFeFMWgzGWcOjWd2xRu7vKM8dka0tynivMkzORrzaNb8Zl4mjGw6e80zlQimhqgE7Lux+73XfaIWskhtehcRO3cmcwJblOYzfdsTujLx4MQLULcg5SaeGT0iAJq8mKfrjm/u7mBNFcaTA1W08jrfo0Zxzqd+9TzNR9jTkCf62OOET9m1J0SveQ0kN7Jf05brgTL352LaJ06aNyl8MjXkisFplH8OW7IjZBTuDk4t4kglMNUvqapk8Pc3Kd3LPWZz30OvlOb+07+Ts4sTb+bryH1NT3n0IcfeZzP7f2xvvt5y7GSXRJS5xjnkEqyNx1CqRBxoySu1Fy8+xZ//M/+Me//4PuhBqgKDjuFlGgh8J1l//Ka519+zc9/+Ne8/Pwr9ustwnRoEQRunA+OPmHyfQr8of7V2HEr0RgArQ8NNTktY7LnuWNKwsHT/ZreNRginHL4y2vVT/d1ip+SEjjIZUN5jTTnKezl68jxf6ohl89v6iQ3N4/+jO+gP2OYHmqVz+3RsX2awvixNseMT3HM8HNOcXfo2DfXpvg1rX3Ka0znmt/FuXVP6XP+PL+Xc3Qrl0umvMyUVs/Nccpvzu1JmtcU/8/9Pgcz4/eGZ8mJYYonPeO056nf6T/gwFkt7y8/r3yMfl8mfPjcvkz3/WAfBynjsP8jZzA9b+/H5WNyepjznLlDz5SHO5YVYo5G5OubGi/mQP8YbR6+M6ZPaa55qaF8Lvn4eZ82RuAmnj4X7vP9HOAipK1GQ+Pa8TwVtK4Lal4fI6B9MrIBKToYsC4quJRg3zU9rpIyGDFbZ6Ly1YMMETku8ssNJqZDCcakJJ96cXcJjdc108Be7FDa4nWHaQzKLVBO0tmQYc14zQ2eL55qdrcSjEH6WGNNAcqA8QgnkUr0+9krcAlK5fFT2RvPw1lqpDC9wglACoeS0FlJ5wtKDbbbY4TD0eLY0riKvStpbveobVSyxriZZF+z1mM8WBnTc6NoTEPTWJqmpWlbYM/ZmacoBNJ7hJHIVYVxwTkCvw/mTSHxvqbTlgbPzlo2wnBKA0tJ6QuE1Xjj2YiCZVlhiyBDd6Zj3+6wVrHrQpr0zoU07wtXcXO7p9xblFTxLoFSBVIaus7iW/Bbz7a+5ux0xbJcUegCpwyd21E5j22bUF8dReEcjRBIUdCxY+/2rPe3vFq/wt9+TlOfUhfnFLrEFdCWNefyjBd/9W9pf/VL/PqWtjvjvFxQ4HDCsbVwtQfJgrfcJX/7vce8vajxz28wH33BPVnTlDdsrUWgKU3Njd/DtuVaCawseHJyzpN3P+Avv/6Cb337O+iiZt9YWlfQICmsptAhOl14x259w8uf/RjZtShfIGWJLhXnlePDU8HP6yXrUtAVElmUyE2LIERbh/sjg2KTAcckelqWZX823nm0DkmNrTF0NuJAIUKdP2+oypLlyQUnp+ecrJaAYb1e8+z5M8p6xb2LCxCKtjPoskDpAi8t7a5he7PGdYZ6uaAoNEYIDJ4NJ2jxgu8+OeXbj07xXcvGbrFSUlHHOXikF2jpQx3KomS7afnk46d89eUrFvVp4DdEigTP5N7+3vmgNCWk3RzIiSeV3ZNKhUya3kedQUGsBBj3b5DRVeSbrQWfosMZ3jPe9n9YZzHWs9/D9eUW8BRlQaEUhQp1lbtmjxcSqYugxJYyGCE9pLTSMBhQlEr8UKJp46xbqSno1+c9SGQ/0ZRC3aX+o9445x8S3Bzj10I/4/dGdDj7mR6L/sHYjpWTluHdaQa8ANMHtF54IGRKGBTQaV7ZezH16zFeYZhh/t1BfzN9f7ot+fje52t6jYwthp0alO/hQLwPCnnRP5vr/3AeSk53bmbY0e+5eTQ/Ox//n550sbRvvyF4IFYNDs8lNHTDOoilIbwBdH/wHvBKIKRH4sEbJFD4mNhYTvZajCct+iwC6V9gM8b7LA7OKXGVfb/DKFk/Mzx9fD/s/XDYw1ZPZI90btlj75NTQT5muI/TNnft/OSAZq+m1AcGZ0SKcvaje4fInEhJ5zWsc8RfZl/LM0+Sfhdi8lY2jBgm3M9AgIiRnb1OckauzPsc88OizwaSRj6Uj9IejZ/n/Hn/blx3Kv2SNtk5P5JfBRZJMOz1rzkRygH4wGt31gItVVWgUL0cIyPf15e7IfiJWEuUO0KGkjx7R8rWIg8M4rKfZ1q28BKZXbAczBLcKQRCKKzzbG5bvvjsBb/9O+fRT8xg8Qih0arEoNCF4+rqGaXWPLp4hx+8/w7//q9/Rn3/EVZoOlvhRYH0l+xuvqY7Paepz7lRgdbt2iuWiwX3Lh7QtFu+/OITtrtrEB1VWeMdNPuOZt8BAqEVSoTsEybWMB8tRApEWSBMigmPMBXJrlPDuWE9eqf57J2v+db6lK9vPf/RwBe15I/PL/gVe3Z7QeVaGlqeEQI+vyskbzlB6RyN8Bi/pwOEEpwheavz3PzwP9D+2T/kj7/9e+z3C9ztc87fWqH1fcrFGVIsuTGCjzclv+guefLylpMffYL4z7/D+R99l//558/4xZ//iptqQ+sFe6URhaDe3sAv/orrT3+f0/feozh/yObZF9iuDfK4VH0te6xFLWooQwCqDB4NdLs2ZOSQElloyqpEWM/z64IlGu0LEIrl6QUPVhcsyiUCTWcst/s1z1bPuTp/xXa/pzMG4xydNTTtBi09i6qg1MFRsSzvcb25BWlQ3oX7Y1zIAt1lCEsIINhp6rrs7Vxd1yG1wPgde1sgLNjOoCm5t3jAWXUP7z2NaZC+4HRxgjOSrdqzabc441l3awShprh3gQcrdI2QCwxgpUNqT6GgEIJFVaLUKQIFoqBWCwqvWN+2vLjcsN83dDgkCm8dXka876PD8ggfRZ2eAFwwGuM90kWnjhjFHoKUFN5LlPQokdkfBYFnR+EAhY80ZsDxd/ItUuFUhfcO40J5aa00UleIGlQB1ju8s3jrQzkUr3BYqmrJYiGoKouze3wHqrJUqxKEYt+07LYtSmnaUlIVDlUY1o3hTdobG8Y//N73hwVqgYu+Lx6BKCtWuuZEFTESe8/jd5YUhebq6hXr3ZZX19eURcHZyQldu2dzG5S+q9WKtgtGaaUkRSkxzkdPYIW1nt224f7FA87O71NVJXWlsMayaw3ORQ9iGep1u67DW0dZLikKRVmGnPzGtDT7htXJgufPn3Pv/gXLuqIsA7AbU7FalDRNy2JRs9lseXD/PNYQ64LSoTXUqxVYz/vvvEfnQm2ntjOYfcPl7Tqky9vuaJsGBDRdSLdR6BLvPbpaIDx0XYvtWoj1anIjIzAyjM4x+XnEolJqiLzzh0aldBGs65BVjZAiOgxY9Ej5ltjZQZnYGwCISlEfvS1TzXV/qDgfK6oG5degcAsIJ+y76ZGNMab3SE79pHFE9n4yHAPUdT0aKzcU+MQpxfXMKeWsMSGdRrbXr4u6mSoBhWD0dz5+6i+kQA9ebUaEFILGhnrvQoXkwd55OteNGJo8NX5Q3N5tEJgaDnLHhGEdUwFvbBxKCuLxmU0ZzsBk58ab/J3EzA5C7iFTB4mpHRjMJLLn3kvWu4P5Ttecnk8V0FND51SJPj7HsaB8qDQW/R1L/1LGi55YTGB+7kyQh0L83J3Jz2aaKWEU1jPZk+le5/PLDXe5AX5OQZ73e0yJnr83NUBM350+m+KHqeL/2Hen4971PMeHd/X1unemd2M69tSIlpToqU33eTrWVNE/Hfuutc4ZIkbrOjB0zBsWp/s++tz7gxpwiT7M4cr5FozjgdUUSB/SU3oBO9shak0nJZ0XVGcn/N3//E/4vb//h5TLCotDao2QAiUEsjHY7Y5f/fjn/OpHP+H2xSXNzZpu36CQaC2wgBcSSzAaCBmibdKqgs7pcE3D+icZI7IMIvmepc9yA/Mhzp2H6Sm9nzM2Tu/UMQMUUdg+XMchjkt/51lbQn+QDCDOuVHEfPp57G7k78zh6IR/Eq/hJjzPXXQtb3fB7czLUXkwNkrm48KgMErPp/h2Dt9Nea2pw9DBHrzBWo7d/bscew73bzznOXia7sMcbOR4IjfC5u11DgDp2ZQmj3CQn9+zYe/p37mr5bzX3FxyHJ47AN3V7/T85949tua5uR3j52dxxQwOOEbnp86Rx3DPm7Tp/KQcshTlfd61J/nc7sIdcy2fb+6sJmU00GZdpLNM32lNh5MC433vCBWkmqxPfB+RSezPx/fwgQ+1EUeNvExiuIdNtWO9HyKTCE6v1nu888HoLILSMfB74P3rFf937ssOun2LL0FphUYGPGo7nLAY39GYln2nMZ2m2UK392AFhdKhdrIzqELHyNaw5nC+AiF8z4MHvj2qnWfoz5ReBhwxznCSnnsfHNS3uy24HUWholGe3jAenLojH+w9xsSsCYhQH85G+tuBVKDRFCLU3iuLJYuyimcXvie9iGXbJF6E+s/GW26bDcX6ksJpFAUKjUZBIfDdcNZB9oqpMyU0VYUxHc5atFZ4JWhshzdtOFtCpLv1LuhHrGffNuw2ezbNmlW5pK5qqlKjSgnCY7yhNR3GtDhrwsLS2Kqg1BXeOF48e0VZbDg53aGKBWW94ve/8wPaq6/4+KMfcf3sKcZYrOh4eaJ5uyzpMOyNYe8abrob/vF771K9vcSZDearS15eXfPctQgfUrc3zvKyW7M2e7wWPL+94b3H7/Ho+x8gqoLOdZzeX7GVBmE7pIcOy66EhRXUyyXK7PjkJ7/gxVdPqZ1AqVCb+7wq+MOLByyenPNyd42TkntFRa00l3aH8a6/UzrWW8zpU64DSE7i1hqsMzjpcCZkglgsFhRFwXa/60soVKWmrjRFKVGy5osvPmOz3XBydp/z83MgKLJ1Ad5avLM4Y9huNuA9ZVUhtAZnKbSmdS0X98958vYTlqsVV9fXmK5Dr1ZBV4JAKYlSgs12T7koscbz6tUVn37yGfgAs4ghSizhktFdz+j0GPcP6eRDhJqMeMWRShlknWbdu34IqQI+kohY/jDRDPAOrPHsdw3XNxv2bcuiChkei0JTaI0uJF0nCDoli+uCXkK6kFo0THZYR8IdU8fsoJOd6AV8HiEdCH8yNUdqg0CMMkD1PATDP5l4HA7bFH/Jg88O6e5ojpP385/h99fLqkIIEGMHvrk+p/TuOC3/zfiSufHn2hzf0R+yH7+TZKL8u0meGp7l4+d/z8sXPRzhs7MfzWJmzqOT7cc4jKaffC8a85MsdDCYp5crkgaLGTi4k2eM38z1eT1/CqhkUBxrvqaiSnwn6MvmecRhjXL6xf6qisOH6a834B2nax4Hv0z3Y16e8tnscj49/3v4fYCpEGgZ+xTDfuUOo9PxBCBisM2baC3y76VupnM7Jmsdyme5o+n48+E7jL4/msMUvrwYvZvWPZWBkhOjF/R+S85lWSUZz18IYpD3GP+lEh3WRtvF6FIzwgVCEHnIcXr2OPsMXqcweLjW9LFSGo9lt9tzeXnF48ePgnNEWl98uSprnPNstmvK8pr33n/CTz76NZ1pESqky3aiozUhCv329obF4oyyrgItkxKDpao0JydLtFa0ux0vXzxDqxBp3BmLxwV6L8IdnDpd14tF7FOy3m4O15id5fiuCaxRnJzd52t7za9ffc1/+9lP+F+fv88HDdw6WAvYixBg8ntdhUbh8GxwXMoG4UB4z4qCVirW0uGt4sWXN7zz7e9webPmF68+pX1+y0rvuVeU2GrHTkq2naHF8RO7ZfXjT1ju99RP7uP2Fe+drdisSprrXeA7bw3l2yW3z5/z8Uc/5Vv3Tnn4+DH22VOePn3Bt7/3QXC8MCbskTWUugBd4AkOK84bqkVJWYKUGgQYOux2T+E8VVGhZeCd6qqkrhcs9AqBpFAh4FNqhdRQ77bsmj37bo+xgpPVPc6WS5aLmrLQCA9XN1uE1Kz3a5quw2Jw3iBSlL/wSC3QReB7fJThrLMgPHVZsqhqiiIUf7Y2RHvfv3efxbLCuJau7UJ5Xxzn904pxYKvXj7jctOy3+8DX6tDIGfImCkj3HUUQqGkQgtBheSiPuXxvbdYLc6oyhohNY31bC5vMc01SrcgOxwm6NUiX6PEmIcZ7tlER8BYngMGOusPeaaeP51Cs2eEv+bu8oCTHc6ZIPYocMLjJIhSUmkdHJ69QRgP1mMddJ3l9GRFWSnwDU3XoIso78mSzkucdxg8hlReWSKkC5HjMbvb69obG8b/m//mf8ODBw+4f3Gf5y9ecH5+TrVY9IZlKTR4jcBTlhqlBU2z4+RkyepkwRdPv+bh/fsIB6vVCikFWoWU1bvdjq7rKMtlj9DrehHTxMFu1/KLX/yS3a4NXqnC0ez3NE1D27a0bRsitJzFGgvGsbm+ZbvdAg4pYd/sEMLzr/7Vv+LhwwcsFjVFTHnetk2oae4t1rYIKh4/fsh6vcd7hZIFdb1gu9vSNi1SFPwf/rv/E7vOoqpFHz3qnAtp5LynLAqsc2zNnqKuUELgrOXi/B4/+O3fDikYJoLPXcrKOeXiiPhlzMi0Np+1FudtAETrkMS0gD4x6LFPH1K0DcQ0GKKTQSClykuCaxpjahhPjHF+0XIjnZuseRpJkiuYk1DcNA37/T6muZf92cFhVHnOmOX7NhU0k9FIzUTqpu9OozGPMTK5ASVX/A79iRi1GPbe2JAerWlbtOkwOnqRuXGd5jR2P94ksnVOATqd4xSeppKA9/4gZXBi0NO+TZX+YS5j49gU7npB9S7BKwnCPngFJmVmem7xWVmFTGAcrZURP39MgTu3T9Pn+VoPFLQ+ODRM4WAEJxwyw/keBeXuvLA97S9ncg9gIVfYTtZ1bH35szlYzuc7fX+u37yPYwL3MTjM+5s6+SSD3Fwk9Ddt+ZzvOvf8nSnMTL83s/XD2c4Ip3k/0z2ZE6Sm/ebPj+3z9Pl4nDkJ/3D9+XcPxggfHIWBNz0bkcZLYWlKYpxF1gV74ekU/ODv/l3+4T//59QnS6wSWCVw1qGFCnmmjOH6q6/54tef8JN//0PWLy/xnUUJgS5LupjGUioZ6onjQMjgze8lKioC0WOcnd/jFIFNdNDJy3XkjmJD3dUJUznBJa/b7+k+5rB0zNCX3ss66vHkMUPZdE5TuBJRwMvXOjenKYzcFdU8nXtSEIgJc34nnZiZ6113oh8rvDDaizyytqcfc9+dwR35XHJY6LruTkfG+K27ruHRdownnOLwufOZ8glTHHRsrjk8pH7zDAT/KS2fo7GhVlf+2cE5R613Di/H8Gtqd9G+ub/n4HoO1+X3/CidHSmAxp+/DsanLb97c9/9TWji69oBrZys503aFH8l+vhNWtrrPPNGrlid3gcRZSyBQwmQSmGtCWhxYqwIBuCgWBQi8LLeR1gTHukTrcppvcc7A5YhAs1HHlckI0/4530o/yUcUZn/G139UevEBmPawD+aMF7nLLt2T2c79s2OzW7H7U3L85stu02H7wTCKUDiXBdXkeKscjjuY7dJKw7gdhQ5BpyQ8KmcZCnxgX5KERzWjbHs9y3eOopCYb3F2K53THYxZboQIeZS2Gn5CQFRPtBFyaJaslwWFFpSiBpZFXhvwbqQDQCJ9R5B1AJLMN5wvbnh5uvPWZwULKoVdbGgUiWyUEgbM3tF2UUCZVEgxYJCKYzpYor8EAEbMgHE+ug+RJN75YOSX4bSZNIZjLFs9g2dc3S+ZFGUCFUMjh5xealOu/cghaIsKpaLE+pyyXa7Q+g1C6U5qVY8OX/EZ3/+/+DmxVfs2xaERiqQOtyFJjqQl8bx2Ev+/uoRZ1bSvbzh5ssrnneGlxIKV3AhQ9ykFY4HosB7OMPy3sN3ePyt99k6Q7VcstQaJRWIkN678y6m2K7pFGw3G9a/+hTrDAYF3iGlY6Ulj73i143hs26PWay4Vy6ppOCGJkSAa4EWmsJJWoZsM1O+KBhoC5y3dF3Q/ZA5nPj4jrWW/X7P1eVLumZPvagx1nD16hVlteBkdUJZ1jRdG8InQ2QB1hraZs9ms6EoNKrQIW258xSqoN3tefLeOzx+9ICyrri6ukRKhURGOPDgQwS8lEF3dHVzxfNnl1xe3lCWFVpLnI/6Fy8P8W1sh/gyONuMDU8B3yRcKZWITjmDgjIZ+XrRMaoAXIzATlfc2ZApo20N+6hby/kI6zzSeZRLzgoKa13QG9ng5Oqc6vlmhEAqidaDY8NAO3t2tdcTiGxFI7rWz3tY0AEuFYl3GAzifsqPp4GJ2ULi/cuHCnOEQzofssFNR57S3/T9N2oiP8NjfU7Mlnd2PsXVw44OuHzu+2/Gk4hI84YpHPLOiRa/icPk+DtDn3n/acxjczzebx4xPjwb1tEPcce8Dp8dk3WP6Q2OvR90j/MOxDKDvaNHOv4WMO88mc/pwDD+mnaXLmPu+VR/8jr902iODDBwl47K2yzaNvGCmRNB/ObBeDDWT3ufjOoBT6Wfw/dSjz2GPej/UJ6AlNXC54g1rHJYqz/U3R62Nw02GO7gVPc8xrkBTzsX99UN+ytEdMSQ46wDQebrN2PQ3QAhC0Zy5IfkRJnubBg38FOJ3hziyvie9xmOF0d/eh+dN2Pg5NXlNQ8fPkRq1WdqEIBEgRJYZ2iahvX2hkcP7nFx/5T1HpzQwSHMhmjmdt+wWV+zOTnj5N4ZwoSMts4ZlFLUdU1RlbS7wBt2JsCe94Ky0oT6Ch6f9EiZjKJUsFVIpRDRMN5TsTtwohfwYtvBsuKiPmVT3PLD9pqrzvKeXtF4gXLwMYZrYVkiWCDZ43iF4UvXcuGD8+ynbscOuMLQeMsXf/Vv+S/+0b/k9vGSH/1a8tX6FQ8Ky6pcIG2J0hqNRCvBjRSYqyv8X18jfiYRXcsDNA9PVlyeK653LZu25ev1mmp9jX/1AnN7g3v4iNXqnMvLa57sW3ShkQJMdDAUffaXJNcbxIh38dAaTNNSCMmiWuB8CJoMqcRD0KyIWQpKWXC6PGPXbIJBWSvKTmKdoSoLlosFdVmFUgFItFzhUIgbBds1jduD9CgZ6LzUIc23KjRIgbVd4PEBrVQwmCuNFqHso5IhTXu9rAP/aSzJ9qhUMK6vuz27dsd2v6GzLbosAu6JkNvDuoq15q1DUrAoFjw+fcz7999jVZ1QFjUIxcv9FiM7CrWPKelbnDR4bIRJMeo30OUxj9LjmAko+hz/xHuqlEIqGeqaT/mghLN7HuFu/czwvYEOeimCc7TzYB3GBAZRChl5L4dehKzdXdvifbARCF+CFaybDmkdqGBT3JkG27RIqXEx4r3Ub6aDeGPD+E9+/DNOTk54/9vfZrFccHWzoTaOoupQWnOyPKUuK9pmT9u0+L1BKdi1LY9P3+K7H37ISVWivefk5DRGhEvKqkKpoGzTStFZw74Niwk5VQWPHp5zc7Pl+vqG1hp2+w1d16G1pu3aUB+87djv91xfX4OxOGNZ397SmZa6rrh374yz01MWJyvq5ZKqqoJirjMh3aoPCO2dt9+JACFZVEt8Cev1LbvtnqqsaPcdbdNhLBTVAq9LjPehtjCS1jrKssRJTdPtcarECo2xFi0U692Oqq6RMdJdJcLCAKQpesz7sdF4ynAkJcSgPLgb2abIbI+MQosKKfUmnrypHyFEL2RCFIbweGd7w1WuDMmZ4mkEZU7gUuqWfL25YSl9lpweUq1AIQaP8ZSuxPtUY16MaokCveAzVRKPDA7OwWT+eZrZXJE+F4k/7FVgAtL5JGNmPrbHYWyIk1NaUZQlSoZ63lIJSqmwHEYe5kIa078nLV/bdK53GbBy2AppYALyGwvh43W7I1F1/b7E+d7VXEwXlxsVUsqjxFwmz0VBJrSmuUzOAQjKqggruWI1h9f8HuV7PHfP8jYXuTcW4geGODfETOue5rA1NWLB+E7krb9HAy950IQIClvrxtkC5oxVc4LcdN3T99Jcp/3O4ZFjsHNsjK7r+r6m49wFv3e1qaPKnHFlqryfO/sDA+VkLjmchTPwBxERx+7hVKic+2zaemPAxAlpzmlmCutE4S2pHOYUc4NwHiPugrPwUcNYWnPfQ6b8yiZCynbgCB7MlJodlrc//A7/2T/7pzz84IPewJ3COQqloLNcPn/BJ7/4BS8/+5KvP/+CzauroKgTEoOniylu42pCCisG425ShEmC8j4XdKd4NUTS+N45LO2PtZa2bcM5T2hznulljBfyXw894BNchgwc8uic8pbDdRJwE1Oa3+X8bHPa5Jwble0ICkV/QGOORSuPzp3xfZrCcN5HjoPT995MCTCMd0zp8jq6OMUnQz/D51OaO5cWPv8sj2ibnpf3B2hidt55n3NrzXFPzp/Mf3eMY+dgYG78OZwMY17iGI6a9nWs/ylMisk7I/4tjRORyJRm5y3B813zm/JU+Vymz6b7MF3DHL98V5vC+hTfTsfIS3VMzy7nfebg45u2156Z9TH69m7ece7739QYPtdyfs35ubsbYLQoCpRULMuKNVd4awfl5wj/EqOL4l+e5JI54GYfawMnZwxBUCY6DzgQImRs7p05A9+pAzMborHdYGr+m2iXu1e0bYdxFuOCU0njDJtmQ9uF6IRm17C97bhsHO2uC0b8lFMv7mVYiCBELIpkyu9/HrSenorRvR3ujcz+jWWV1H8QtXxQzJJogcDYALvW+BBR4kMkrfKJrsrI88ss801wSCqLkqrQaEq8DCm4vXPxeESvrBGEyAkpRHAk2K7p0EG9EE+9kJpKLELkiZLgJTiFcxZrC7qiwHTBMG6FR+kgx5JwmgvG6KKzOB9KzCkhqVniO4O3IdV0oRW6UNSiQhVVlKmDPCNk3GgnkEJSqpKT+oQHZw/R5YaylpyenfPowVvIxvDVT39Mc3uDsR6EopSSwviYkUzgrERaSeU1u6bji6eX3Ly84eX1LS98xwspaL1ECR0VyoZSCGxreWd5n0cP36I4P+P5fsvi/B4lmhqNlB4rDUaGg91Xmm23Z/vyOeazL0mBZrUS3CsUDyqNsx0/bQWv8FS64LRcYIRjJx2d7XCxtqnwh7clx7nJKT4p4Jum6e9XcuZDCqqqYrvdst2saZs91aak6Tqa/Z6LR084OTlFSslu16LLOkbUgTOG/XZH17YsVwuEkLjoaFnoAuUtT548ZHWywONCGnZdkCwoznm8DZkZirLCdJ5XL2+4fHWNNY7VskJKH6P2jvN2d7W0DyLWrhbRoKF0MEIrFe7MGCUPVCN3EvJ+4EEBrLG0bdRxpYCDqKQ1wkRZPURuiaiwxAVFrvcu6mBCXyGDRIDuUIt8uo5hXklPMzzz/WdzrMbAj4w/D7QoX2/+/qAQHvNrjJyE0jPScxGwmJw5qwHXDX3MpbT2/f8Ons70Of/G63hbOEbLx/s0ff+bwOCUt4VvxgsN0xutLK75cO6zPPFBsvojYzGcyTEinB4f01vM8Wmz/XzD58eyD3wTh4LRewORHm5UvEYDiH4zXDMn173u/WN6jLt46tHd9D5ET/a0O+oI/BCokz4ZzONi7Fjjwc3IzXfJ0tDHNYc+MoNzGDMF4Hhc1F/0603jZms9vIc5Pns9nPsMYczd776PKB7lQTRpnSNdlvehmGovg4V96+svS9kbqAL+igbzYBkP78lhDn1K9tHKI66MfQRbuehhUDDg3/D2IXxN5cz8eYITKT3Oh7K82+2Ok7OTUV+p/IaXwTC6b7Y8eHDK/fun7J6t8Qik1HQEo2Xb7dnt1ux2t7TtHqlD9iFrLQhJWdUsFks218Fm4mxYr1Iy2EdcGxzEoqMkDPDbZxpkgNPxOY/PuJfncDzf7miE4KJe0ixO+aJ5xWftnm8/fsCH+xXF+hq3c/yMDa3wnHvJEg1IPqFhT0in3XjPzsEGy9o7/vyzX/J+d8vy4Rntu+/w+U+/xIgOISSVcNS+pNIFC6HZCEVrOrjZUpqWUwlvXdyjlAJfaFoTygzdbBoe7daoq0u4vsE1htXJOS8vL7m6vuHevVOkCo7LpS6xnSNV7UuyBFIE5wJvIx+yx3UdpdSIqsY4FcotK4WUCm+Cw7ESwVCtFZyvTtFKUGhB00k8lqLQlLqkVCWlrtCqpFIOj0xus3jnMaSa4sHm4HAY1+GNx5iQNVoriU5yTpq7lEipKHWJ947OBAdg8IEfKxTOG242N6y3tzRdE21Awa5F5Fd8z7uE6HMtNXW54Hx5n4dnb/Fg9TCkT9cVTkgaK9mXO1YLQ1W3qKIF0cKdJbum+qlBRhrRh7FaDCGio6+Q0XFr4NIIW5aTnNe2hMcFMWOA81jraTuHaTtcZ8BKlJaIWKIAgg3SG4P3weHhZHXCoi7wtuNlc43rLEIGx93drkMYg1Ye7xU2Rp6/SXtjw3ilarqd4fNPvuDRk7e4eFyxb7rg+awlt7st22ZHVVVIKVGyRDiDcPDw5JRGB2ZdKYX1jn3X8uDBgyDoVKF21GKx5PpmzfXN19y/twppy5YFRVXTdXuePnuK0gWuMX1N8N12S2fC303ThNTGJdSrmscfvMe9+w+oqoKqKJDeUtYLqroO6dqN4/r6Fq01VVWhlaBarEKtcOu4vFnjug4nHSH1WUd1UmOuBZ1SCKn7lNhlWdB1NtTBEiFNiSwLfNdiu5B43uGw3qCEAuFRIggytg2FoWSMWnBuILUupXbIgDZXvPfKvBmCn9KSp3TX4HuvF6Ukre0CMhIxMleIXpE0jZ7OU11NDYvAgVIyjwBPc8iVl9hAREK98WggjMoLpcO+7na7/hJXVTVO6U5gZHSsVe5dSMajkkc1MVohMlRBOxMUXCo+t8YiYhoUGS9qUMz4vv94ID0rngQ4F/dURUN95Mb6FIVa6IBoXEA4GhkEZmPopKDtOiqpKDyUQtLIAI9KRKVKqsmRMYhCRK/seIZ5S4gqlxK9n0lflq2T7Gf/WRxTQq/YS7WfwnwcxBSMocAZfdTI0F9EsULgiFEVUeh1DJGWSmu8kMF7j3CG/XmlzQ5mreFPT4/chBB96jqfmFfnESoZJgOToqRApCo23oeawwmmEwPkPciBQZlLjd0r6QkwInxE1LHfVFNn+A6IGJ2jVVLyh3ultMJHtaqISYXHwmFSEqTawSlrw2DcEgSPfKBPiwlBMDfe9jCTR2Sn1Pxpfek+JlhJZzit05rD1JzAkwuQudFLRiWxixkSkgAnhRzgKRFrP3g1C0JmCRUVKsO7Y6b5dQa1JKgdMyTdJRBPDSX5s6kAO8K/mbCkxAC73g/KFdfD0qEQML2T+bhT4+T0/KbrTPuPiHTD50LVcIfTnRwkF9/XhwqlJgTWDmNPzxkI9T69jSnMiXcynDU2nK0ORaHwStJKT1dI6kf3+ef/5T/jW7/9IWpRYb0HFaKRCi+RxrN+8YpPPvoVTz//gk9+/hGy6/DGUkiJ9xbrwx0WAnABJ+lY01yIqKyKGqKAg2w6FEDEqJbkPBNOrOsMbRNS7+T3psedzo3qJOZ4IhlLpZRYM3FIIVccDBESA3zHOj9x8uFqJD4g62eqiBABD+RKh3SPpy0vgZFgT8qAI5P39dSQOafwmGtzyra7FE139XdAuya8Sd5fvh/Te3sMb8WeZ+ear3/qHDftOze6Sql7niSqhfthPIf3O6c1+XqOPo8qIR/PvJ93KAYXozXH+HiKQ9LfeeahY7g8d8CYznna97EzTN+Z9pOUMtPx8/NKCrF8vOlZ5v1OxwBm93KKc33W13TvplkGpuNMVtzPNd/vpCSZU9DlfQ77lPBAhq8jDpvb47va3HjTfZrSl/5cgRl71WivEpzk53NAIyf3aoq/pndhjkeVSvZ84vS8nXO0bUulJNZ5lIwySO89H9cVjeEjjaZP6/XRYSpGH8ZvBL7FxzssQCq6yT0LkcLBWBTKUtlAyzw9DP2ntM9efEW7b2n2HfuuozUW4x2bZhN4Tw84QddYNjuD7STCRV7chZIlUkqcsXhEiJInKOHyc8mvsYj75SN/ls4mKSkRAb8JxjJp2Na4yT4Z0XRMfb4ICpHCYEuD98Ewvm8auljiS/TcrBjBv3WWznZYH4x2qRAZkZfGpWsyVpQWQlPrkqpc0BVVzNYm+uhwJUIkilQhg5iUwbDuXJTZuoauazHGYnDBCBmN9mlfOuvpjMU5j5I61BTXFo3AdaF2s8OisDRW0ZZLCqn7OwYpOkIiUCipWVUrHt9/i5UOUcj3Lx7zzqN3efXZ57z46Ff43R4bRLLAK7WOTlqQGomk854Gxb9+8RR5qXnZdLxqW1ph2ElN6TUV0dndtRQWutsNH3zru+gHF9wWmi9ernn3/fdxXoIVaC/QXlNIwBpEWbC7eoX5/AuKr54hhaRWmid1xburJe8uF1y3LT9ziq4ouFeG6J1L19AqT2u7EK0fjQ9z9CSnw4G3AueL/owhZG3puo6iKlkuQ/bBbdQR7Xc7XFDUkugAAQAASURBVJS9Li4uWK6WOO9pO0NRy5BdSILpOrbrNXjHYrkIvGI2j2UpePftx2gtaLtQLq/QBa0L+Np5g7EG4wxVveT5s0ueP3vF7dWaqigptMbaJkij8Q4dk2XmnnvvesNrYNejwlJJikKFuutS9p8Nms28Txdxm400L+I0wNqAQ7uu6zP7hUxpLt4rD8JT+hKhQciQ8lM4h3UmZuhIPK3scauKvKWPuLe/3UmZ6nMalSFnz6hqmIgy8oBK5wzhOc8Y/hbDH3HMiLuE6NNW90ZwIRByehZZHdyZM8p/P4bnD/mju2k2QL60YzT+TWTh47zKfPsm775+PgMcDrKOP3if2arzB70zTpF+vMl8P3Kalq/tjr2d8oKz3z/y3Tf9/Jh8NeXF8/cP+ueQn+z/Fv3/vnGb8ulzuqDpnKa89RzPnH6O7s7QwcCLxw+SHOwT75ve6elm4s0HJ8a8trX3Ebtl9zLJ7iOZMWMTc9lvrOMYZK6R7D2zF3P7NXdXp3LIIU4JCNBFA1LC7SLyZKme+LHzcc4h/BBpn8ZQaggUktEw3q9T0JdMlVKgtYxZlaIjox1qaedzDLiT8E9k+ryoahJM1xZ/l4fP536GuQdnwqZpuL66oV4uKEsZ70HgeZESr3Xga2yDEIaL+6c8fX6D8D7oTUUwjAshaJs92+0t+/2aolLgPNYHx1qlK1an57z4+iu0KrART2mtUUph7OCYEBwVBhmm6wyO3aBneQO8GvhBw6v9jo3veFid8NbylJ9eSX5qtnzvg+/x3saweFridh1f+j2X2vDA1jz0NefAL2RDYw1r6ZBOUjjJQwokjl+tr/nixXO+/+RbvPv93+HHP/sJ3kka5xDWIZXFe4XywZ5RFRVnCB7pgvcXJU/OVnTOs3WOvRcIWfFyu0fs94jLl9jLV7hdw+rsHF2UvHz5iqrSLFcV3lmkgM4G51wfJRAhwUdDtOk6TNvR7vfgbLDdIaAjpMJHoKRGRDuJVjGzj3DcOz1DKU+hoTUSLxxCeKTXlKqiKhbUxRJXeqTSoYyPC7rGRniEDDY66y2mMzRtkoldGEcWPY5wzuGjTjXdx+1uE0o56wKtFUWh0YXg+mbNy8sXbLa3WNf1Oo+gIwhw4USwBuAtla5YVgvOl+c8PHvMxdljltU5hShRosALyVkpsKeWvZO83LUU5Q7EpsdPQc49pCVT3NPjx6wd5CpKfGbSh0Spzw0vMEjLd9PI/j4DeIlpLV3raPaW3bal2e+wDWhZUlUFQg88oJTgjaEuNBercx4/eMDJomZzc82zrWHbbbB0GGfotoZKhtJnzhra1tHaN+ExvoFhvCiC8Xqz3tB8+hnGOR48foQuDE1nQsqIugCtkR6ksWAtZr9n37RoodjttyxPT8PARcVydYr3jqIocc5xenpKUS7pWgs+9Lnf7djuGoSEy6tXbDZ7mk1Ds9+z3zc9QNaLmrfeepuLiwvK0xJRCnzIDRKMV9aitabpDB64d+8+TdNyeXWN8yCVpq5rPvv8Cx4+fMi9iwuEUph2x+PHjyhKzfX1NevNnuXpKbquaY2LEWkS40IdaeMsRUyjLhD9vgF0bYiut8YgB9IfvLXcEG2c8GeA30Dwc8DKGe+csZozWA/KTRuIgQuRvsYNta89oY6zsY5STaKc/VCPMfw9ZpTyS5eiPdNc8qhYl61P62LwVIsKLec9IjN8p9SkKep3LpWkkgoVo3EDUYoGz0wgnH5HinHadKXCFcijwnxS7oUOBq+YCQOjVEjr4LKIu17JJjPGJRZ1EQQlsNLBw8hbjzcuKF9U8ETUGUrKjfXeuSjIHc6FBCbDjz4l9TSC0Xs/qq0zpzgOfw9wlSvOe+N1BnPTfe7FHBegazRV70OUfK48S4xv/C/jknuDYvxqv9ieGRUiEqZDxX6aV46Ifd6fHZjZOcX3tJ/RXvvx8+HzpPDIhcDBOQDAi2h4jkqGgfsf2tzY4WcywEcnGjtTl9yF1NN5LfM8JXLebx4tOjU2zc0lfW+KZ+Y+H80pJ8pxyYGAjqNR8++mOYfvpOih1ysB3qTNGSemguCb9NE3P5x7ml/qJ92/FIEBAyzOCZLHInSnxp279mCOEZnOMTwjaZIjczO8mp/JsdTY+Tyc8Lj+HgoUEukdwkGpCjpjcAIoNUYL5OmC3/u7f4u//Sd/RHF+gldBGhMmOpJ1hs3NhhdffMVnv/w1H//sF2xv11RCBYVsuvcM9FJGwEpZRnq49r43SuX4K9uE6IRGL/S1bduntcujZnNjWbozKcND6ndwRkunfXebE5qHv+PvM93k5xAyxY/p6lTpkmeuSEbzWaY1m8vhfh2fx7G/c1jthXg1jjA8Jtjnn48cE7K15eMe62fu9znlRv7eXYqO6bgDbKV7nNjrwI8EWng33pryeXNryZVGGSEPn88ob/O1pt/zrAFp3Dl8ctezHC/k55CvYXpec/ud0+Xc6SHdXZH4DnFo8D4Gm1PYOQa7Uzo7FRrnYOt1tGEKn7nTxFy/+XemY+fPc+NzoonTvbir5fOf8m7HFGsi8WWTrnPnirl9mdujKd8wlWPepCX+M42RcFrCyQG/pbq5yYlwwoNO5yeGvQm4VjJSFYh036ICw3vwoa6diZm/+jP1MSo60cDIhwNHbuabt5/+/Ge4touG7SCzogVdt2NVaU6XFYu6ZscZm69e0e4a8AIpUhR0Mj1EOWvGEBH2JZ13iqe4qyVaOH/2Dh8M8kpRlQtKJZG+CAojrSh0QVUWlGUZ5GgTIi52ZoMxHdtmz263i8a6lq5p6Kyh6VqMcTgpEMJRaElZ6sFR1IMXMuglvKKSBatiyaN7D3n43neRfo+xgaeUKEpRIISkKmvqMsxPyhAt3HUtbdPQtW3gC6IuQcAQlR4N/87npSYkooBKFChVhtr1rsN3O262Hbc2nUl0dnK2NzQqYxFeIJ2g1iUny4q6WvLw3iNOVcH/+1//j+hNx35no6OGxqPptKHwgiUajeDGC67x/L+un7LsSjblgm2hKZUAE5Rw3hka37F1DaZr2e5uUb/1D2ifnGExvDSWUw9bBWzWLJ3gflljjOXWt7ytBQ+vN/gvX7LvOgyS71fnfO/hfd6/d8p5VfKRbfjcQy0rFkVFJzxft1t2XRfSzhOiioWSMLDJB7DpnIt8dMjko7WOqfpNfwfbtmWxWHBxcYEUks16jTGGerGkKGsWixUIRRcd4xGgtMCajma/Zbtes6xqqqpi17RIpSmEpm1a3nt0yvtvP8K5ln2zQWlNKALmorNvkJ2DbqHk6dPnvHh+SdMYFosl1nZ4H2RgIp55E7w9dlgCiHKFBKmC4aKqgmE81DAfcJAQY5rjEcQUhz3zLAQhSYL3WBuUxUTH0nDPHEYIpA041lURrlGDs0KMus+dv7z3AV/FAIikPg2fDWuSvTNm+ixMLjmP51sUeN152TysUfZG7kRi5vjTng4SszaEC30HfT9eFul1fMbrPjvWUk6rO/slZwPfbIw30nHEznNjVs9h+rvHm/LD03fnv5fzdHlfaX4c8M9zd+cufmiOz71rz+Z4wimv87r7e9fnr5vLVAaYW9td+opj85x7/669CSgnHcRYzpiTg6Z9zs37Ltkil9NHfTNxmvXgmOGVez7O97hQ9t8JeorgBJnN7Y555c8VR0nU0e/1vPSR/Z2uOzwfnNqNcX3muiS7a61hhp/u9TEjJ34bjEtCxHIkKmRYyvSCDo/tosOhFDFgsKSqKopSoWUIUbLWcru97TO0CDHopcGPdPtTOJmD1WPP8p+HfSiMMbx8ecnpvXOKohx4smDxBmljdLej2W14/OCMn/AJ1ghUUVOWGm/AFR2taVivr7i9ecVyedqP27YWaz2nJ/fQ1RIhYFEWCETMHNjRmiHrqfc9k40QQednbOBNdFke6t8mLYeHzhmu/Jb3FisWfol5rvmPYsu/OC0oSsnidsGHnPOX3PIJN6zY84CK+5Q8pOQj9qxNCHJbotGiBO+o0Xz8w7/kg8U9vv3+t7lYXfBq/RQla6zwdMJyojyPpaaye+4L+FZV8N3lKW+/ex/vPdevrnnYWDBQNoJ1ayiMY//0Kesvv2T53UtWZ/e4uHjIs+dfcnVdofQ5RaFDiWNHH0BgnUXI4Hwa+GyD7QzOdlRVhbOC/baN5V32FEVwcl2UKwpZUCiN1CFj76Ks6GyBp0AXDqlBeInwiqpYURehfJLwAlVodl3Dbr9jv9/gXRscG7uWznQhG3Ub0u1XdYEqJLpUYSwBxnZBLx0rezddw369Z1kvuHfvHquTAC/7/Y4Xl1+z2V3jMEglsdGJu4xZg320AXghWFUVq3rJslyxqk44Xd1jVd9D6xNKXSNECMZ7tDhhWS0xuuDr2zVaXva2NClyXe48zh1lMc1hMP1fJP1McB5MzjMHwZYD8I7pBIe0IW/egbOeprPstobtZs96vaXZbpCuQNUFFs++axEi6ITbjePJg4c8vn+fi9MzzqsVC1mibEct7nO57bjZrGlNgzeWpRJgO5z1OBtl5jdob2wY994ilaBAY53l1csXtKbl5PyU1eqE1ekJxig2mx26CMCqfNiozjjqZUUdN/XVq1c8fPgQIQT37z/Ae892u8VZz2Kx5IMPvkPb7Li9ucKYK4qi4ubmli++/IrttkEKxWKx4NE7T7i4uODk5GSE5Fu3xwsf638J6qpEFR5hQro5a0L6q7KsePfdd7E2GLOLosA5x1dffUXbdby6vuXRowuss5hduKTbfRuizfAUhaa1ro/MTsr0siwHYUYGASABXteFFFWLKtRmD97xgwFojkDmSiwYR6L0kTuRWE6FqKRc9HhMErZVrA+igkFeJiHNGVCDIJYr9pJAKgXBuBsVPjkiz4l2Pn6ac2oim2syKOSMtLW2T5WfDBz5d/v+XHg3T207m8Z2piWDuyeknM4VvHl6VDhMJZojhn5/jzB56V9IYO97707vHbvdNiBWIYLh+wj/PGIExVhMeR2Dnr47MuBEBmn6zogZmexhDpf9erN3pob10GeM3M8QcA4fwTFj7AF8jGGfrmn0e9QRzxkzBmZ0/FlaR27QyhnjnImd6ze1HDbyvcznnd8hoGfG8+iqUd+TM877Hd+nsaErd4xRSoW6l5lzSn6v09zfRPA7xrRO2zEBQMDsfuZ3ftpPWuMoyjuryfVawT57Nie45WfzJkr5u4TtY+8nuM8NzG+iuMhhIuG0fF+n8D/dx3yMKROT9z+3vmPvHBPE8/GNhE6AcqCdQFlQPtFGR71YspOOrXB863d/i3/wL/85Z08e4mSIKHHOoYyHzrO7uuL21RU//uFf8fWnn3P17AUaQeGiMnfmjk3/pfX3dDZ7N2U0mf4zsTZnDoOJJuRnmvZnmrpsek5z5z2HV6bKg9fdsfkzC2nPpkLlWJEw4J65yJY56J7CwW8S+Ti9/877kInlNX3NwemUR0pzmvItI9xw59yGvo+NPYX/u+aW46tAm+5WvOXjzhmqp+PNOXFN33sdnsn5pDmjaD6HufXmOGcKb9M+8u/OvhMdV469K4QAOb7nOT09tub8fubfvWs+Oey8Ca6eb8kYe9xwfAx27ho3p+NCiL7kzLSPu3BPem/62Rz/1sOgOP69KT6685yPPDvgf+5ohw6cQzS+956yLAfefoLD8znPzeMY7phbg3ceqUNduVwOm6NHxxzdvml7duNR1iOcAReiGlpvKbVlWVWhwmB3w812BW1DITUohYgO4jgVsnRFg5clKXrneSGR+GYRsxeIHAZkL7cCfYhRxEqENM85vpDosqSQqo/slUJSKEVblqwWsFgsWVQ1q5MT7lUPIDqBGmOioqoJegLnuHfvHgtVoGyI9nC+pTNBoWVccDIWMWAVD9JC4RULXaOrUwpXhjSQPsasNBakw1uLs6Fmer98EbJbIUKGsNLF6AkfZRwPEJS1KQrdWIexFt9ZjOsQWiMKhVYFeEcpoHAC39k+o0yKyBLeoQQUUlAoSSEVzd7w/ltPOJEFL3/2M1784q95WC7Y32xRSqCVQglQJVwYT9k1WOM5955KSER5TlMotNdUToEsEK0JtcjjeJUosNZx/8n7PPnO99HVCfvdnovHb2GECLZUpfASrLTsZQd1xWKzhU+/pPn0cy4Lx/e7E/60esT5g1OK84LOCl41jst9y7dOTrl3fspOCj79+pKXX79EeoFCEZwEgpNLnxY9u3fp+S5Gf3sfeDLnQ6rLPJp8s9nQNA26KLn38BFCSNrWcHp2j6JaYDpLZz1lVSGlQBWK/W7NfrPBth3nZycYl8qehWCPzXrNh9/+Dqtlwe1mg/EWXQTDvFYFzppQTkFpFvWCZ19f8snHn9M0HWVZhitoXKjTHm7JG9PsnD4EfoeYQj0ZMSRVXaILGe9N2rsZ/hOwXhAyE+b42od0uVHHo5M8CT2/FpxGbe90Hww06Z9GqxKtYtoGAAedtVi/RynVG3SEEEOWtxkeZuDYDnkQIZjoQMJwSY8gRPo31ptN6Xr6vY8YP9j/sd4g5+Pyd+f47bvaXbz9tH3TutDfdMyjbSD7HJxIULlEJ4e76XyiAW8mY6cskwGv9lPxA4/u/QAzx/qck2+Hvub1BnfxNVP+5i45Ydr33HtT/cddv8/195vqZ97kuYyX6VADNb5znpCu/K5+4TA9+aiXXO6Jn8/JzvlZTCPBrfdIf/ge3r1WN+e9jzQ8GcjDwnp8R4BxS36+AQ9IP2CHN+Vd7+KN83emeCTxSykAbKQT6rdyLEMmvSYE/ldrhVSBj0l69TwrpLWmN2IrpaiqisWiZrlcUi9KFmXV21i89yx3S168eMF2uz0oNSYEaB2Zr4w3nlv7HK/9OjqY1ljoku12z/XVNXVdUdclzju0io4LQoWkJc6wvr3mvSfv8+7bX/Pxl69Yb65ZLRZ0NgR9dqah2W+5vr7iwcP3KYsqpE33ButgsTzn9PwB18+fUZ4sUErRdTu89ywWC5zpcDaU8nF5KmsfAMXLcI7FkWwX+bmHzLlgnecXX37Co3cLvn32iO+dPuHf3XzO7ceXnCnF7W7PR2y4xtEazy/EFo/kA5bct4pzKh4iqQj3xkqJtoJSOLaf/ZoX3/su3/rgff7un/wJ//3//X/P9+Q5F0Zw3wve0iUf3DtDVp66kJxXNecnS3h0Ai+27F5ecVrUmErztN3yye0lH/i3qbcG/+I5N08/5/E73+bi/B6Xr57z6uUlUsD733qPzWZDqTTWNwHmZHCG3a9v6TqLFCrUAtcab1vW7Yam2dI2Da1p2TUbnHNcnHisKtl7gTcWWUC33bDfrzG2xQuHUiWFKijUglIt0bIEQAsVE4B5Ci1Z1hUCw77ZYJxCOtFnwhUahArR5154hBKoUuEc7LoWgcJ3oQyNwNO4lp3Z4fYWv3Pc3FxxfXuFVJ6qUjjh6dqYdUDo8P2I+3RVcu/knG7v6IzDF4pFecbZ6QWVXKCkDrjSe3Cg1ZAivtRFKEeNCQGfwnEMM4V7N8DeXQqyxEsJIdCZ/iGnETnPNcdzzsM8OAMYsDtDd9Ni1y20Npy/MjTNDitCxm4tFWeLJeerM1Z6QXO15YsvXrJUBe88fot3H6y4ut3x7OY5t5stCkPjPMKH71ZlTbFYvtHc3tgwXlZlMIx6gXeCzXpN0zaURcHp6oTN7QZVGurlCiGh3e/RAgrhud3sOD875cH5OVdXlwgkm82Ohw8Vi3qJsUE4VErTRSFxtVyxWi559Ogxl9drLu5fsKgXvP3ut7h4+JC6qkmUzLng4RpSXwiEVkFwwOOlQgoZQvKV4vLyinffeou2bfHe9wZxpYIH1WKxYLlcBgN3VbHf7SiVQmnJer1msVig1S2mM6hS90rZRHSLoujrb9d1TdO1FEVB1+yRUtLstiMGPXh4zCtk5pRlI+VyFhHnM8VMrjQcR26r3pvJRWNw3786RNjOuZGBOKR4O2QY83fniGB6TykVCbZDCD1Saqc97GKtPOdc9MYelFbTiFbnLd4OEXqpr1Gk6aRNGa9Q/2NQrM8psGYVtTBSiOUwEBgNe3CWwXnBY4WIzH4U3JyLuGResduvYzL3Y4pKlwkVWuvRvEKfHqQY7fuh0m5gYueUftHaedB3vo8Qa81kn6ezTHP1HpB3K3GPnWHsZOhnuoKcCWZA/vnzPOX/3FrnYH1uflMmfk6IGt4dCM2sgJdLgjMtnZcQQyaHdMcT7EkpkVodOKnk2RLguOH0Tc5jOv8pLPTvCjHCT1MmPu8rV2ZMBRnB2HDxm7bXfTdPCZuf0zdt0/1IY/fj+/mIy6lT0tzzfM/zOY7v34Bj/GSsY/syhef0ew5jx/Y/MUvCg3IC7UMN7s573EJzIwxn7z7hz/7Fn/H+D36LTgu2mKAo9EHp3222uG3Dj//jD/n6y6/4/NcfUwiFMg7tRajdI+hr3s4pvtKzXgHnfY8HR5lBJrQ0X3sRS2R0kU/IDen5vk/Pb45GRHeoA9jIf6Z3j52PEGKUymy++dk55uPkMDVVGrxJ+5u4d0qpkKZ2hpeY63+KX/LnU7w7t3aE6BW1+fmM8dRY8fy6dUzfycfuS+L0aZuyVOoz35uuIY0xnevwDvPrnNmj17W76NoBHs/6n+KZ/Pm0n3ye+Z1JzRpzoGCaw/Nz8Jrjt7m15fzl9C7MLPogivk3gXcR4S3nc6bjztKD2AZe8rDv18Fo2t9jdHLEE03gbTrH/L27+JGDd7kbT+R89hz/8SbjwDxfOuW7p461qU3XOXXynZPtR+8wnMVdzj05X/ab8BB5++zzF6xKjxYtznbsmo6dhdNlxcliwb2TGq3g+tklu0ag1CkIiVcKJyRCgW+7lBF+yO4i4orS754ULNBH4HgIRjOb07o0M8GA4/woSijhVWsd1jiK85pyWaJTyvJYi1tIhfUWb9pQE91phACtNFpoiqpmtTjl/NQDjrPzc2qpkNbSNjt2pcbYDusCfZdSYomRr1pS1gWLtmJZV6iiYKVKhNK4+J42HUKGKPGUVWxYQUjZ2J8joTCTFAIlgmOvECLUKXTBeFP4WP5HGAor0WoBWuClQ9q4X7pGKx12ONZQD0ZHA8JTFopVXWPKUGv8fLFk//wZX/z4r6i7DdttG/an1BSVBgld4zjVFSssDk+F5xZBKRQvS4FoDbLtQsSL8zH6zaGcpTAGebPj+//wj3i4uM92u0Ntdpy+9RALyM5SCAU4GtNihefB6Snbj7/kq88/59NnX/PSGDpqRFmhK4UsJU0r+IVz2L3h9J0lxaLgxX7Hq9sN3b5hUZdIHVK2SjukuE0tl2kgOHdbF2pZh/uuYhRcQVVVlHUo57der7FI6qKmqmv2+xvO792nKCtaE8rvVLGMnvc2pF3fbZHCUxTR8V/Fkk/Ws6qXfPD+O5huj7NdvCiBLxPxvFOKTOfg88+/4vZ2gxCSQiuECDUnpVSYzg0yDQzpwvN1J6NsLBNHj3t8b5KUQlJozaKuKcuQiQ/hQ/mkfv+Y4C2F96F+KiL4tFiGyD+lQ1Y7b8dlWIT3vcGp6wyms+hC9YaWsrRoFfRtKXrcex/2JndAj/y4UCILFIi0mhRlOOxNiPyM4nu/P7nRa8xzC6H6vZVRryJEBlOCflwhYny5SNFO+chD3x6Pk0npO6bNI/o1HNM8vhfpBU/eyYHRMPU10Vkcdpd0YfPOjd+k9fQ7J3+eCT7P+BnS+RzyGAMtPeR/5vjG1JKcOScDpz6tO66TeVNe4pvwHHM8zV0y9F286PTdtL48C1l695icd0w+fN07+fjH5u/J0l8ffccP9+WO91KHPR4Il2u2iQn8T+WGvrmMH/UpClyGzAoR13g80g150Yf7OMBjOCcx/O1cn0q95/PilMSBbBjhgeF+Dv0fd9p4k/s5vRspSCzpt6fORfn+JoN4rjNO79eVRmmFUAOsucgrpf2UQrBYhUwpdT38XFQho08ypgsp0JXuU6nv9/tRxpY0Lk6AOpQrpjqbY/tw97OQCt5Ywc3tmtXJiuVyQVkVqMjbQOAr8Q7TtlSl5J0nj3hxveV6c4VfLQNvp4soJxg26xt2ux1lsUQKDQRbBALu37/H7dXLULbPOpzv6NoGyziDCRGH9n5UglBiSSm8PQxGGr4WdUqErFPgebm+5qrb8eFiwe88+Tb/18tP+A+fPKVWCy67HX/BLR+JBuMFBngmWpQXLBCUeDwWJ0PqbSM8F2hK33JNx9XTz/j6s3f5/d/6Hdr/2wUXlDzWFQ+riocnCy5OK8SpRCwlsir4/xL3X7+6JNmBL/YLk5mf2+a4OlXVVW1YTdOG5JAz5NCM5R3NjK4AvehVAq5GetIfoH9DDwIEAXoWBOhFuhAE3IvRdSBnOEPP9l3dXV1dVaeOP9t9LjPD6CEiMiPzy2+f082RbhR2nb3TREasWLFi+eXKAoNDN571ekfxoMLNJLvW8un1nmfPLrgnFf7ZM5rPP2P3a2tWJ0vunJ/z6vIFF5dXzJczvLPsvcGaNpRfcS37/R5btyg0Uit0tOFsmy3beh/5+mDbqNs9Zt1gbY0SKvBC0lHMC7QNzrHOu96mFcvSGtvinUCLAu8MzlmUDIGzS7MAb7CuxnqNdQqnFB6HUMFxZFcbjHMhyFFrhBNYZzD7OuK8ZjGbo8uSXbtnvb+hNSHKXVUxu3ADrXMUTiKEjmV9A4+jlaLUBfW2xRrP6emce+f3eevuWyznJygTHBpDFksfSzuFUlSzsuBkMWdezTC+jgiVMSMTe2iMgh09c3TJKgQ9j5ZkIyH6foUnZs2mC4DreajXN+9BeAHGwL5G1Q3SGLSX2K2j9XUoEYjEIZDzE0ztuarXuLpGNIbFnYo7d+8wv76k9AbtLNpL8AopQrnlQmkKWSH8f+KI8dOzE6RSPH3yFCECg9zs93z+2ae8fP6MB2+/S7lcsd83lLPgUVNIqJ1ls9tRVBXWOZbLFefnd3j+/DlVOUNKRSEktQwCw3IZjNJahMOyFZLz8zu8/fY7fOMb38TJ4M3dWMNsNgsEyFk0OhKWkEXDOYMXMW230pjW0mx3eA+zajaINDDGUFUVQgju3buHUoqLy0uk1AhvETLUswBYLldUsyt0obF+mPYxCWZJCV/XNW30ZHbOU2hFWZaZx2NMeW1g6I3fHyS5UWN8f6x4cyOlUM5khRoe8XCP95NRvmuiN66k+9777tCTUmLaZpDeaWxEmlJQjyOSQpR3PfA6LssyClyxxpxSB0rKscIvKBNCv4lRmILhlDJ6zHTmEWfHImk7xjxjUtLfuXJuzNSFeYQ6y9ILrDHUdR0cJmSogSdGdRDzMXSMOYctZ9iC0mY45lyZ0M2T/tBO14dw7XEkV44P1pWhAHhMsXpMud4Psr92LLXm1DocjCcTXqaEkykF/WCPEZxFxkLQbUro1I4p03MF8Hgs+dhTRGs+/mN9DX8/NLwnOKba50noui2qaWyIHkc6j9fu2E969phzwdRajPvP4Xl4v1e2jNuBADXqK5/zeBx5Hzkc87U4RndvozdjuEzha7o3hdNT9PQ2AXgKF8Zjnnp3vB/yNRz/fWwcCJDWUyHAeKRUWA9WQl0o3GrG7/7zf8zX//5voUpFWwgaBUqVIXW6BXuz5cO//jYvP3/CT3/0Y0qtUa1DeE/lgwOR8EFw8JkjV+6QNXZomIrAzeE5fi/H/5T6for+5Y4lU2s0eN6Lji6/ThCcop8Qla5uuJbH8Hfq2jFcHo83qQTH+Jn3NzWHY3t+/M30rxRBMB/Tuimhcep6vpZ5Hwd7J9w4WP/hfOTgLJtqh7T38F64H0OuSOskCJJG/MBr5IVjPEwOA+eGdCRXrB2D45h/vM2Bcfzd8XNT8z4Oj+l3BuMLRP0ADqlJIUIJhmwuuTE834P5+2O8zc/p1zkJ5WM9tjenngUYRwKm7+XnxVQ0S/57D5pDej92lhy3qTlNndXp+phejc/MpBzP91qeiSaf31S/4++PxzVeq/z5NI7u98S/Zv3kqdRvbm44mc87nEhOymMYT7UBHIhCe3Zt4IAR+07jH59Bt63FL9rOTxrun5XMygoo2OwsLy8tTb3HtlskguVszqJccbPZ4ZHgY7pmknIu1MoN+oyISwA+ne9AigWMhSJF0npk8xEdORPd//tJh58Ar6B8ttbRGgvKc3KyZDFfUBQFWkm0KtBS09UpRwEhe5sgGH1EjIwl2PJYzpfMCoX0jrYuCJW/fW8gEqIzODpvQLoQWa0VRVmwUApRaJxUWAmlNXiiEZSgR0ilrAIcOqkZj8VYh5IgRIjURoSIkqQk0kKCUHgh0SYos5wSeBlgqAuBVkG5G2pTB34+NSnCfJUKkennp3cwdc2rJ5/z8rOPWUrPy901ZXEWlD5C4LThxR6EFMytQNoAgHlRYLyjQLAEKqAVghvlEIRMZt4FXZh3noe/8hWcDms/LwtmUrCzIQWk9ALlJdoppPeUSvPkxTM+u3rBq3aPRfMEz4/Z8vXacVbPaGTFJ5ViJUvmi4oGy+X6hpvtDiVUV/7GJYNGhmv9mTcuyQHpjE112ZVSqOgMnHQJoNChVh6qLFmdnuF9mGcyGpRlQWv27HYhKinVT7SEEgCmtXgHpyenPHzrPm1bY2xQvlpnKVSJbYISR0qJ9Z7tds+zZy9wzgXcFiEKDBFK7EmhMk1kXPoxqehuTckZDiFCpiUd9UpaBz4mYZGIG3dA9zx4H2uQS9F9RHqPc7aLPtdahfUYncP4SA+dxzuHtQ7v2yhfWsoUjahlcHQgOA44GXjg3HCj0TF74eiMi14CiRsN93sHxrD4yTFHDH7v6FLUp8mOXo3PUYbPpusRSH3fdPQkZc3wPiimhy3jk+Qhj9h/N+PBBlHRh8+L5CTgX89rpfN56t74++neFI8X5JXJTx32z+GjOf85Jb+m7435QO89zvYZIK2z4MMZorTqlPII8Jlz89T5musLJucikqsX/bLlz4nRDQ+eieCQya6nr4/lFRnxODnVSARKhpInzrlQIg+6gII0niE/Hq4nB+Pb+Mmuh0RnjvJCyeUmBe9MP4OHFPx6G66TOZHcJhekvXtMvuzm0gtq4bm07zuiF+4FHmxa55HOk0RPOt0GQzmhWzMHyNzJMTw9dKDJxnhEVh3/fWy9chzLz70Q+R3oaxf85nv6kPYO0AX6hUwlEincYL18FoyntKLQoU7zvJp3RvGyDEGDVdF/swumEj6kWC+KzjaS5IFkcA9pl0OmGW+Tbjr8JD6eeJaM5z71d043pFSARytNvQ+ZhJqmYb6YgW1IZW3Ss0JKdrsds3nFbF6hi1jOVGmEC1le6nbPfrdlt9tzsgr8r9QKaQ3WGRaLGbqQtG2NFYQIYm+wRvSZXDvy2R/oQoQMQ9Vsxn6zOcCXadxQ4Cxrb3la73je7Ll7dk6hlny32fIuHuNarvC89IH3FQgusQjR8JYo8Q62GFrvsZEPOEMipadyjt2TZzz/+FN+89d+iw8evsf1q8/Yu5a1dVS1oLxoOVdz1GKGqDR+XiIRrC+esnz3AbOvvI1zluL6ksY7Xq43+HqOvHzJ7Olj1jdXzOcV52fnrLdrrteX/Oxnn3D37hmt2WNtQ9PuaZo9zliW5QJdFEgvAw8gQrYZJ3zAUa8xKKSTOG/Z1ptYTjGkTC9VSRUDHZFBJpNKgZS0TTBqa2HxhafwwSYjOwc+Fxz0bUjZHYLOBFoEXPcEfaB1Lp5NAkVI3W/iOV54T20USguMaSOf2KALiS413oM0sdxwdKYIDoPR+UspsB7jLWWx4Oz0DnfP77KYLYKToldh38bTyAGtafHOUihFVZSUSuKsDVlw5KEeJPFFPR3IzsHuseimF1FY0PeTsrbmR6RI/+/eP76HD/BdBOnUNw2+acC0SGsRtDhahDI4J8NedoJm17Df1Tgk2sN8NmN1dsreNDx7/Ck3Fy8QtmU1q7BWoHxw2dZSBznhDeXxNzaM/8Ef/gEnJyf8yZ/8CT/60Y9QIhhi271lu14jhOLOA1C6YL/bx7reLYUSmLbh9OQEKTxtEwzFX/7yVzg/P8daF72OaqpKIBUIQr0AqSRKBg+SoqhoG4MoCnSpkVqjiyIA3gZibYwJymyXajilgy8w8cF4qoDwfDJkX11dUZYlDx8+xFobPIbKks2+YbGoePvBfa6vr2iaBgE8ePAgCASiNyCmSPGUKj03RDoXPIUheMAbYxBVRSKeUsog/GcH4lgplCtoxsp+731XC3V8vftxUZiKqd6sS0dU8N5tjKVgGOmcDuJ08Dnn8M52NaKTQW9K2TeluO4VmtAJZJlRcL/fA1BFJ4pxHzlDo1RIAChkXx85/9aUEi5XcKUxh2yn/fjHESf58+N+JxV3qV85jDoIfRs0BV2kr+g9FpOAf6uy1LneCw0OYB1+ZxKPhoAY/jmGW3oozTXHvb5PP/jWuL/4Gy5jepITRD723nN7GvcHwx4pB7qfNKkJ2OTK3alxjhUuY5iM13hqbGNl8e3C2nDdxrW/pwxt48wNsZeD8R+b+3h/TAmmUzRj3NcxWAAH+2a8Vnk/Y5o2BaOp+3k9qPT8aw22ozlOjWc8/zGMxn3BYXmF1ykcJscjJYrDOrz5/Kau531PCVRj2CWB6bbovByWeb/jMdyG6wqBMA4vNI1z6NWCplS8/41f4R/+qz9ifve8ixSWUiKNQVlPfb3h+tkrvvMf/oIXn37O1ctXKCHZUyNMH3EXvMGj85Lt55sbcnIY5E5OuaFkPK9Er8ew884Fwc33ytnxN6bgONzPCvywjzGMx+uX3++/BYmITe0/IYKCZArH3wQnu345XOtj8xvvm2Njn5zviFaP6RFA0zRAX/bkgKYzxMM32XfHaM6xfXasn1vu4n00vArZGY6ixubgGDpGM6eudfijhkbwcVTqFE04RqvStdcZao+Nb2oeA2iM1mSKFispgqCXGY/z+YrI6/Eaxdl4/ONI8vEcb+tjmieaXvtxxLDzgW4coxMJjmN4DvdpnHB2z44UwlNK6fE+OlaKaDyW9N6Uc6IfKTdzejk+N6Zwa+rbU2dbDo9xZpv82+l3mfH+3VkghmWejp3hU7h+7OydGpcf9ZeXXxrzEmOY/aLtm19ZcO/unFkVDAS7Gp69aHny9CnzqkGpgnI+48HDOdf7hn1LF0nl8Ugv8UKBCIlLQ7rzbsZhvt73Or3sXpgHGV6L+HvA1Y4HT0pzkZcVCbybI6TYXK0WnKyWMcJVonRJpWdB1pcSiUa4MhrRLMZFB4RosPLeU6qSQiuU8AgclalxxmGcwySjmgjyRYjxcCjpKaTES4EVHpyJKiYRFTQEWHnfGSUcSeHssD7Iv44Wbx1C+FAPXEbjtnO4OHcpNVJphAInJM43GBfKdknbhjrpQOsslphFzXl8Z5YNa+Sw7GxLuVhw8+wxV49+RnvxitILjG0ptIuKcYfFsHGCK2d4KASnUlFKxSMJe9dQOUfhwUjBXkoaEeakfNIFSFbn59z7wjvU2xaUYLZaILAIZ5DFDB95mULEVPC14dHTxzy5uWIDCAqeScOH/oYvbGBWlFychDHcW51QLuZcbm94dnXJdrehLCukSA6Erjshp3iCRM/atsG6/JxLeBzWar/fB91U26CkxpqQinaxWDKbzanrFkQw/qpCowrF9rpmv91g2iZEK0kZsUhi2wbpPW89OOHkdMnzV88jDegNDCH1s4/BA5bLV9dcvryMWRFE5+gQ7X3RKJ3vsWEb0qJ+DwZcdfHvUF+8KBRVVQQlcNgg0fAXlY4yc3b3HuGi0wt9CmPpPUJYlJIUhcZYRyh0FtMKZ/pThESI5DzksbaPVvTWBX2XD/XOhVTxeRFh1QdbSAlCapJjooi0w2cfG7rcJLrT6w3wYvDc2CkpObf0ONXD1/uwDs77WDYi0Te6dOH9d30X1d+x4omnGq7c0UUdnjmH9yfPnwDk1/Kl/Vk9vn7wZLjmfQ/nNOQEex9mdcCtHvyZ+oh4OZITc1k576Pb5XFe1jm8c7StDRkzbF/aUClF4VPJgGDIyA1pMMUPpojm6fO/P6/S3+IA9oyMzd3cum3r02YYrLZjzGNO8NTe9wbeSLuUFCGLilI4IWjjWeJcctRK4wjzCuuVZArfyanDL9LBeQSeKXVYnI4n5BGJfWV4Pp7RlMyW4NfxS77/vo8gG/Cu3eY8Lk/nj3Vqvm6++R4U2ZpJpBxOXYjEx7pYvim808n+guDwE/kg333bh+hnIWMQ5ohvHeGZYAj34by6u28ka+LDmATBcUIpjVYhAtY52/FrQXayaBXsGrNZxWy+oCyKwGvstlEmDYuQ0kRrrSir8Hw1mzGfLTuDt9YSpURIa0xaz5D5pzaW1rhwToymEaBPMMRrgXWiQ5rkdNGtbWIZJ0BxKKv0RncZz0+pFK2p2e227HY77tw5684DCXghojOoYr25oSoKThYVi6oI0cOFxrYGoTSilZi6Zru+wd2z8d1QU9q2LWU5Zz5fcnN9SdO2cQwBV4I/31g+DjRUCklZlCzmC/brzUjOG9KHTk5HAZZGwNPdms9uLnjrwT3uLu7w4W7Ne05w6kCGAko0AgrAinBuL4SnxvECG2xLPji87DB8UVasvGZzdcPjJ4+4lC1v/9rXePQfPuJVu+EFNc9dw50bwRf8glN1QiEE0kuch8sXl9z7va+x+PUvw9UNb330iDlws2vQTc3y5orls6fsXzzG3LvPvJpzulixvr7k0WePaOwWa2paW1PXW0zbUOmSxb05SvaZpGKhVYqiAp84FYfzhtbU0agcTMQCsI1DEUrfFEVBOZtRlDO8FSG1ujUY6XAShCpo2FPbPft6y65es6s31E2NF2FNhRQhQzZgfAxIsG1wWnKhjJaUsstw1AeaOpwLzhQAugwZkUysV++sizwaIbVQXBuswxuL1YKqmrFanrCcL1FeYvctVhHGBoFfkeCxqYpVwLakS06Zuw5sShlpSXjYb8P4v3j2ZTxnwNU+uw5SZGdYPA874jzkgQbn0mB/BJ4fZ3GtxbcGjEPEUpkOj5CBX3U2ONhcr9dcbdasyhnLskTPSkwBP378CR//7CdcXV8icSxmc1orcY0J9EiqEGybZdC9rb2xYfw3fvM3EMByuWS5XPBXf/VXVGURa2RrdusbBIKT8zuUvsIiMG3NxtS0zZ6q1FhjuXPnbpeCw5g+itHHQ6ppWpwxQVlmk/Et1BSvqhlqVtE4E6KynUPromccI7J5T0xFIeIBGvL/Kx+I1GK55PR0hfee5XLJyckJEDxCkmfUvq5ZLFd8+YvvIb3j1auXPH/+nNbC6uwu+/2O+eo0HEqZ4DZWMnlBPFwkWIszpjvlnfMBoSOnljMaucEnwSavCXKQppGeIUn3c2W/s5bgZOUJHsMypK2yQdjcmJYq4nOugEtREVOK7xRt/zqFTx5ZnaKoOkIS57Hf79ntduiYPt153yFxrvzOFVSd100cx1hJRgaTpJgaK9WjLHbgmZfeSdfzKKXUR5eyWsrB2idFWT7uZNTzziNkMP43PjD6uCjQZTiQr+0Q5kNGeUrBOm4HyukRW5xgk8YePBGn05P2nfb9vI7By8c6OPyj8JLPY/xO/vcxJfJtrd9TljGxztdr/M0peOZ4MFbcHFsDIfp07V0WAEQviGd9d2uQjXvK8B36HTP9hw4GIjpn5M4rU4b3PCNE+iaEfTtWTB8zDKTvjNOedWOZgMsUfG9tEyg+ZcjI2zFj72T3E0xq/u9URFj6xliRnmCVZ2w4+K4/NJQNbx/ezZXsU4akfC5jBf24jzf51vj312UTcFJAVVJLx/JLb/OP/8U/4+1f/gCLhUIjvENYh7KeYme4fvqCl58/4Vt/9hdsL66ptzuE9SBGEa7dHiMFt3URPwm+aTw5HUtwTzQ5n1NOn8cp1r2PdbBHe37c8r0yDcdwfue04hdpx6n7z/fM36XlZ914PmO6MkUHxqPN8TaPQE24nRvEx/up62WE+wfnBiAy57upd/5Ttp5f61VmHVzwcBBpNGzj8ef4JaKgbvMsP9l3X2f4zWlY+vu258dnz22ONbe1Ywq0rkX9whS+hDFbEJm38hFadqjcHGaEmOIjx8OQ47N6xCe8Ec5M9D+tfL2djxnzn/keGfc3fu/40Hq+dur5aV5DDIjL+Py5DSZTmUryfqZ43PE5OoBVEvDg4DkAqSSz+WxgqL5tDEfHFpEypz/53IljyffIuK5jmv8b481r2j//rffRhcRgaJ3FePjKFyVPXgg22w260LQzxztfueGiEXz+xNLUgHcUXqKsBDRWmKBQ8X3aVB+d0XstSVJeJ1WmoPVRs50it0WMCCU6ZiOCdplgDAzprqOJTkn0suJkdsKqmjHXAnxDXbe0W0lRLjmZn1DqEqk8svRRIVsE2Lle6RNqOXpca3E4Wusp9pKtM9RtS+ttiPDyDpX+kx4tYYbnqbVsmhpcQ4GnEoJaeGZiHmYsiFEiHuNsSM3ofMQ7j7Ahi5yPDhLJCJn4DQAhNaqoKMqCmdR4HA2O1nl8HSLOXymH393lfnuCF3MKq6mp0L4EX2Nty67Z88QYviQa1j/7Ie6zj7lv4cnaMCtXIfsYDS2ShhZhKz52a76+Oud9sWRfC751fY0oCmZmQwvYOPYTBGsE3qlQD9EKfvU3f4OHsxMeP/kc5gvUYsGuvUbh0BZaKTHC4YTnTlmxf7nm+cefcXV5QyMKhFfsy5anqua6OUO2M34kZzy7ueB333sHMTvhxcuXfHrxgnV9xWxeIVtPCM8GpyQ+8mw5f5v4i8VyjnUtxrYYE3lqERSmrWmomz1N03Rl28rS4Jsde+f48pe+Sgi6EChVoMsKXZY4AfvrG5rtGu9aquUpsqpo2y3SSNq9ZVU5vvrlOU65eP7K+J/q5B5jTNBHtJYnn75kc71muVz2speQMauBRaqwV7wXBzRmTNc6PU7ENJJTkvToQjKbFcxnKtTk9FHZ6C3C+ZDVINalDKUTBN6GsoXey2C88IHfllKG/ijCHq+DQ61wrksBm5wvJQLrfaez8D6UjvG+DZFZNtQdT2UKpRUIFXgxIaL8iotjzQmvTDdjNFh3I5N3Q8T9wZkaA14SDEOpA9lFdIVno6OOi3sZifVmoHuRoi/BlAYrhESM6LgQQx0G0Ujp/JDXnOJpun4OxYVM/veDGuO3y2jJcSnvcshjiMG1Xn+Q65MS/Q+Oiq87sxLd88BhUMf43AtTEljvgj0gyljGWowxNE3IFokLmC5VNDpIGWPzwn4ZrnnMxDCCSViboY40b1O6njGfN9Tr9AEhw/eGfTsfsi6EzIz9ewM4CIH10dgvguFOK0kRMzV4L3HWEE7pcVnGYPJL3+75o0Pe8mDuIuL8Ef5ZxH3nvO1LqUzBiYD7famoIVyH8mEvr6f7MtszvQbkUD7uvi2yuYgwj24kLr4qUh+JdipAZeOI+jTvA8313UYbypgi4HOARQY7DwhHqFudnfN0RWTSl/FCgnddnfLb2uR8Y2dhSoLgZxvWXYmoJ3Ym/MR5OGMpSsnJcsHJyYqT0xMWyxXWOZ6/eMl+L2KZWo/SkmpWUVUFZampqpJZNWOxmFHNTqPDIghSlHlyDvQ0Tct2V7PeWV69fMlut8VZE53bLApBoYpoh/GIwmKtwNmQvSjolfuIYLAIcbtc2ctyCdoO61qKQuOMBefYb3esr6+xDx6gyhm+MbEecnTOKGBTrzk7fYuHp3MuyoIn65bzuxV74/GyDNGp7ZarV09o3vkispAILZFG0lhJNVtw5+47NPuaTbPrgx8JgY2dPjxtkEjvtCpYLFbMq/kbzVMgkE7QCpAKrtZXPH75FPXeL/PFhw/4+Kcv+UsEX5SahQ1H9Y2EyobyhV4Its5yg+OnCr7o4Z7TGEo+Zcfv2jkPveC77Pho84Tv/OSH/M//4R9y+e3/nudXz7DGUrQO0Nx/+oqvrE84PzmjmC2wzZ755Za3v/4V5O9/k7Onl3zjb37Kez/7MfXGIxrLO7st7716gv/4+9hf/W02mz33V+e4ky0//emPudg/ZVlUbJprnLVUquL+vQfBkF0VFDGA1TpYViukKNh6gfAChUKj2fkNRjYxFbuhNS2ts5wuS2azBYvlKbPZElBsbrYIYXHaUdOytXtMVfLi6iXPr15wcXnB9c0NdV1Tm6azQSV6KBDgLEoIfNztTdPQEMos+mhw1UpTeUVrW4pSUxSasixBK1oHm23LftdGA76gUIGfC9kgHRiLdwKrBarSgUc0FrdrsFKxlS2qKtAq0ivpkQoKLbC2Zrtfs6n3iFITChKZyLtAcoT0GW8SdnZixsJPwEAb6KrUHY9KPFOVi5m0pMBGG7PyvW427lSE6E3Lw/M6w3fvkdEoHmy9suPNPBbjfeTXw7NGOJ6tL1CXBW/fuYuultxYx4vHF3z3xz/k5maHVqGsUKVKlJfs/C5k8VIaURTIsji6//L2xobx2bzi5uqahw8f8I/+0R/y6NFnvHz+gsVsRtsGwdHWe7ZXl1xfepq2wZgGa2qcaZlXBSbWqEiKipzxMsaw2+2oZssQSSf7BTXOs1ysmM3nGO87DyYlFd7aQBwheHF7KLSOXLVCqmCQzxVv2+2WQkuWy2X3/SRI1XWN98Gj9b379zHGUOoglF1fX6PLOS9fvsB7qPd7LCIKYCVwqBARMqb/cb2SXURmCA4VZFPM5Vg5mq7lETFCiMFBPKV4C8JCSFnvXfTU7BivPvXMWBmaouFTNL4jpsKK6ctz40MS5KaUW/39oUI8wWs+n+N9HE+m/MsZt/G88qjAMUObr8O45TDpjS5D42Ae9T2OAB+v0ZgBy+EX6q3EObUJdorddjeovWytA9cLylPRcLkpbbCuSVjmUNYaGJicyxjJ17cxzLMbMQ1JvzZj+KTHD75P5nyQ1cHI1zvHl/z99G/CsTwN0rgN1ySKKdn+GsM3eeLepnDOjQNjIeCYsno8dpH1MU5j3o0pF/AnHE9EhH9u9Baid57J53+b4WBKMZ3PcWxIOQabPJ3vgTKZvtb8sTa+N8VAyokxpWenFBD5s+NIgnz+U7CYVLpn85ui1eMxjXFjamzprdvSvY7xZzy+/G/v+xIPY2efvL0JvMdzHSvvBuMBnJY0SlDeXfGP/sU/58u/9U2KqsR5TyUrhCUq9Ty7l5d8+t0P+dHffAfqFr/eoGobIqFEim4JfdtIo4NXZPBUFGJ4ZubnYg6vMS7ntHUMizF+B+er2/H+2N4anC+uT6U9Nc7b+utwdcKgeqDUuNXN4u/e0rgHPMfIOePYHKZafn1qb43p7LE+xnv1gKa5PmvA+Lu30aTbnrl9Tr0SLTH6nUPbiJSPadlhZpAhT2mNCcELIxx/k7Hdxge9yfNvQjOO9XfbHpq6N8UDjL87vn7bWI7RrXEbO5zm4xvj5dR3wviO3xuf8/mcht+EPhoxfDcJ7B28vB9+jB5u42j5qTFMzWXynKJ39pia17H9+SZ7a/y9nJ7kdLrra8RvD+UK2Smki6LonFPH+/5N5pzzFPk3+m/32ZByZ5401kHpolvo18/T5mdnlDONMQ37es9uXzObzzk/P49p+2paU3O9vaEqHWUlaY3EWI9xBiUV0xJCP+fDcQ6dGnucOQazIKP4Dr8jrknJYjHn/S++zZ3TOVp7WmvY7Rsu1xsuL15y+fwVSgQFkywKZmXFfF515cn6dQQUtMZirKH1IYqjaQ1N03TluBAEZ5rWg3Wk0CYH7PchWkVYQwG0WlDam3A/zsHFfdqapnN6EEClilEWMYfzoRZo27a9vCFCCsWlLikKjdcqZJlrHI0xrDWcbfdY4/AiRCg7fCgb4QUYaPct9955B//JYy6/9wP8k8ecasXFZY2rJOezGY0U3EhPI2dID3f3nvvfeI+zt99GbFrk/+dPqdctRiukKJBegNvTYLHOIVF4D0YIvvr1X6O2DhYValYEw6oBL0MZtUpVWAmNEqxXms8+/gnPLp9zs99ioq3hYVlReMVjHJ+ZDd9eNxjbcnL3Dq/2G15cX3K1DopIrRRzVQaa6F0XDTreb845yrJksZh3vN/l5WXH6zZN09G9RCcBdtstrXGcnc85u3OOdwF3pQpGYKnAmpb1+oa2aUK5AV3QGItwAtM0zGcFD9864Z13HrJe3wz4SLIdVVUVTdNwfb3m+fNnHd7mdKE7y0eO2uN9lJ4P38kE9rjHhFSUWlBVBdWsQJcSY224B8E4AzgvsY2jMT6iv6AqqpD+1ROMLVohNShlUMagpEEpQ1UFfVjC65AJMTr+AyiJjqUD8nUyMdODtYEmpvS/SkoUsotKVzqL1qTXF3RGoSMtyb5DWA0pVXedIT4lg2zHD1jb6WC8Jxrx2qwf2TsidGselMSJBiRDX3cvZ8cmSOXkWeAFndDTH3XYEa3OXx3247v7x9ytkwapd2Y45I8Gw5k4Zw97TNccPktnmPNbEOCaSgA5fBcUZa2ljYZxY2wnc0khKKLOwDuPEw4xZp4Z6u/G12/j29PeGvMb4/em+M4pmAmRIuwTz5/VqZ6ALyIGb7ng/JBSXyd6oZQCYYbOVqQyTe4oz38rr+Fdp9+akoG8T5gTs3pOyG9CJD0a0fhyCNcBTFKAWvatMf0M16d1q2E+oYuOc+nohI+RsCSbf/ryrfpAKWK0o+9lw24skj4oL90jk8HwiExHm2ctcj6UJvG3OpQcl+MH+xEf0jrHlNCJl7U26BJSFkAhQhnRk9MV9+/e4c7ZaYj4LguElKy3e7RWMfq77KLJF4sF83lFWQXjXVkWVFVJqYIdw3mP9eCdx1jPZtdws96wvtlwvV5zeXHNdrfGOcdsVrBcVCyqMsKwD0IIMAqZTTIWPootgt6t4E1ayjgqcc5gjUOp4DhpWsf11Zbrqxvuv30XF202iYcDUKpACFiuZpydLfjZixe07V2E0EjpEVKDVGw2V2zXFyzP7yKlCrxbFfb0YrHk5PwcpR223bHf7rB2nEnQdUutdEFZVZRlOXDOh1vk9O4MkTjj2HvDdbvnwtW89f77fPz5T3m03YNX3BOSBxSsfUvIf+SQXqCZ8R4l/9Ffgxc8RLOi5IVY80Nxw1ysuOsF9fUNH/3Hf8/mf/8v+eLDX6bcC3b7PUpUyNmCQs942tZ8+vhzTGs4USX/2w++Dh8+ggcL1L0l5//8a/zrv/kB/6ftE96vV3zBFHyhlnzyw4+5+cfPWDJH3jnl/N49vvrWe3znw79EfEkjXcjkJCvF6nzF6d1zSlEivIx8mmRWaJwSWDcLGZwcaAUnC40Xhtrs2Dd7hJVUVclqecr5+T3K2QIhFPXesFzMWPiWbb1j22zZ1Tf89OUTnj9/znq9Zrvdst/vqesaWahQohkwxgfjrBBopXGyD3Ixmd2mUApdlFRVhRIh25NCooVCemj2Lbvdhv2+AWR0PAmp1Y2NWSkB6xytrWnWgvNTz772rHeWmd1jtKSYz5jLEqQipPC/pm02XF+95OryFdvNpqeJFpAa3+kBDs/xY/IwYhi4l+hcCpTrSmyNmBsRmc8prJ7SNcQ7hPMmZNb2LmZYKEs0Ai8jD+Q8GIOxLY9fPOHm+pJFUVAWitYbnq8vOKkWlKVGakFrG6yz6LJAFwVCyZgF6s3aGxvG//2///dcvHyFlJKLiwukCHW3Z7MZVVnSNg3eNly92lAbG2uBeeazAiE8zhmcC7XGiqLsohRt9ERVSlNVVfRUCmkMOtbWO3ShYhozj4pG6LYNSdNSWiuEiCnLgzBhvaOt65DqTEaPK6VoG9PV0UgHXtu2KKXQWrNYBK+rolCAo2kMZVWBkCilubleY02LR9Iax76paaoWHaNNlNYdU6EKHQvUe6S3HROnpIpCTFyspOiCwYEbUGdosB0be3uGhuww6lPHJljjLEqnKIo+ork1Bq1LMHVvcIdOueHSIQxIrTrlVDKa50b6/JAf/54znUlggiDUJuUSjJTkASAIEVJs5PMVfhhJAwwMhd2zRxjnjrmhj/pPgk5yMhgz+ON3x/fG73QRP96hpYxKFyilRiOoIdSqTzUhIp/wpkaCA6ZKCLx3g3fziNZewRj/l88hCaRCROIYsS83anY4OVTCHhMqEgzSmh8y2ZGYJrmfyBh0u/+QgOd9BIY0eBhnPcc+6NaxF1wP3+/WSySQjA27YRydEB+9zREhA0D6VjosPK8RykbrmOOu975TAiaFw4Eil7QUQwX7AR4SjclSRqai/14wMGZCSqZWSHug65+gIEjrMv6Oc7HOn5IDOIQxJO/t40LzsXaA6y4gaKo11uF4Nyd6RMr6SDh67NtHGQSG+2uM5+M+pvqZEgLz/nKF0jEYHOz/RPPonQW6MyTrP6UCP5jv8ANppn06UUQnuIhICzo8dEHBXIjo3Qd4JWi9Q58u+ebv/gN+/Q9+l+r8hEYJjIRSFKjWI41lfXPFzeUlP/3W93n84UfsXl7h6oayqrBN08lJ3vsY6RHqlUud1VF2cbzeD7IUJFqbRzN2CoT4uzUm8gm6228dDkV4jHE1/RxzUEnrDIcOCOma9zHF8gBvfNwrSVjMvt1Lj2lF0ip1f6Xfc+3bFL0Yj3dMd96kTZ2jU2ds+hk7Hkw5ZlhnB0arcTR6/mz+nal7+e/jeZkjmV3ydptC6bZ7+ZjSknX7OVtTrQP9HCstx2OdisoeOHd4j3d28G7OU8nIK01JJ/n6vQntvY0eTvVxDK7DDshPmogrI6ewjGYnoS4vIXMMx6cUfmO6Px7j+PkxjzKFbwfn8ZgXzMc6fsYPaUp+NuXjmzpfDvh+Dpf52Nk6tW5jOSN/dnBNHuLC62jIWAY41m6D9RQOjrH2WFaDqSwuXZ9dR0mVPTWuw7n19Dsfe0/Lg6NokOucTWn1jvMWP28T5QJVlBQVzOaWRRNq3UklcFWDdTWN2eOE5+zccLVVWOfZe4uvwfvkAH2IX3AI/0AzA/8fzkUmgZV4hG7vEjNkZf0KIZjP59y9s+T8bEFV6ihnQd0Krq731PuWoI0N/wiR6gQKEA7j+vrEAZ4SLyUChZfB4GLjHvbOgQoKFSVD5KhEhnTz1TwkLC8rhLNoguJW1btg/DOG1hoa0wT50vsuva93ngYb5HeZIsNcrLdsu3mH2BKLwUJrKF2B9CVChWwDrTNdmlljYe8cMy3wWDr7h5Cocs795YLNX/wJ86tr3H7Pftsg9zXvrk55e7bglXfsnOHCtcjdFb/z5S9x7ytvYecV4vkFv+NL/sv2hgtfBgdtB15a1qbFOUm93+N1yf333+OdX/oKP/z8EbKaUUkHpkF4QaMVZRvTwBvPRjvwBZ9859tcXF/SOIMQBaKsKLRCOsGPabhA8jPveOv+A+TJkscfPeLJi+fcbDc93ZMhijmdl2NaneiyUkFpKaWkbVvW6zXW2mB0HTkEp+vWQVXNOb9zl/nyhM02GL+1LiiLAi0l1+trrq4uAE81m1FUFcZ6BJqm3nB6vuQL797nrYf3uLi46s6VgY7Gg1Ka7faKZ8+ec3FxGRSl6jCyWUoZI7CHdOH1NLPnArWUIdpvVoZ09FIhlO8cM6RQFLOKtoFnL15xfbOlNR5dVNw5DdkXy0KjtQAZKpRKKWMa3ZLSGozZUyhojcTZktYa2mjA7LI2SRF+lEbKkPGx2e8xxtK2IcpQa0dROLQLYy6KYCjQRaiZmVJph7VLNOaQ2ARjeJJNxrCDA9ta5LmTcSQ3ig9k/hS47rOU8N4HWi5FNNoPsyCFn3BNieF1qRg9d1z2PSZrTNHncR9T15Ic6I8cN11J+9fQfuSQ37iN50vnybi/YNxI83LRQTTQcWuDkc9YS2sMbduXn1RSUig95GtlED2n+cnj/Ork3I60Kd5piqecap3OKHPEEFNMeLgJUgVNke8Nr1oHI2XbpWmOjgNti3dDXEr/vj4zVzZGeYhzUzy7x4dSAiP+sz/fw1PJMD7FD/ed9bJpjkMHY/auk799tr+7MfihjmPwPTI+e2QUH69dp9+QArzv6lDDUHZ30mFaQnaa2H8Ww3OwFmm9A08doej76zleHIxfiAM8w/dra4yNhnAT5ctgz5jP55RlMHQvl0vu3jmjqkJEZN3UtK1hs9/RtHtWywVloePzs5iBt4h0WKNU5PUEtI2lMYa6Nex2Ndc3e65u1txs1ux2e+qmDiVHtGY5L1ktF8zmJRLLfrMllK0J/Jb3fTkna2wnI/emJzFF6o+08KAQfQlWpQqUDHtms97z4vkV9x6ehQBMG881FdK5SwnGNMznBffvn7L8/BXCS2Z6TusFOAPesNuteXX5mGI+pyorEApVCtp9zWK5ZLU/xZma2jnmc0Fd946TQJcZJi2kMYbNZkPTNJ1eZLyPB80HXl0VQbddW8Pz7Q3f/vwTfvcrv8bizj0uxQV+X6ON4T4lW294JqH2nhtveaEMv+JWPFCaC9vyiW/5ZRQPveKZcDzCsERQ1JYPP/kRH718zN//nX/It7dXPPn0IxZVQSEcQmlOTxbMvaBsQBnPp4Xh/g8fU80F6ne+TPkPPuDv/+Hv8sG//X9zdX3D8zt3eccX3H9+w+WPvo/86m9RNy2FKvnlL36VRx/9BKkVy9UcLxWL1Snnd+6hixJvoiZfpA0X9kWhZ7gSpNTAgrJSeN+G9OftHuMt88WMs+o+UhXgNEIq5pUC09KamlZ4pGswe8/j5894/vw5zoRU816CroouS2Eqhzzclz2iqoCEKKWoioqqmjGfz1Ai1KAH8M7Ttoa2bdjvG5SQnfMTQtE0Bi8c1hMdCR1ta9jRcnVzzdXpNWfzU07KGUtdQekwIjjSmnrL9foZNxcXXF1fUtfBKK5VEbI3OFAqZDMYb64p3iTZLJItw3elfob6mNwZUAmRToCsPw7287jMMwzPgJBFKTi+FUVFqTVVWVIbR+sajDXUtqGxLV6I4FTsLE0bykoY5ZmdnLAoSoooBxjbYp2lKOegJcZ72ram3jRvQmje3DD+l3/5F/z4wx+x3+975YO1tKbh7PQU5y3GhRpFysJ8Puf+/XssVjNmiwWyLBF1i/eW3W5PWZY4Z6ICwrNczghGDwsiRIcpofBeYBG0tkZpQGpaH41IBGHEuRCxHkL8Y8SN8AjvmM80zlrq7TYYcsuS+/cfsFqdolSvwNUxDZUQgqqqeOftt8G31E3DfLZguTrh4dvv4hA8fvYCrMPaFrzAGUvta2xRgBCoOJZCabwNhk9rDMp7TNPgfeKNVBS8Ben0Dcy57Qy+UkpklhIwV97lyh9jTMdgJSRORoOEiAoRInR9EDK01GANSs9wogDhEKo3hnsfBC0lgleM67zWQu2Etm0HhD19MxfukkCbwznUYBMd0xcUx3qwaXynWI4b2fvwE5Uu3rpOYEkKlCnGdpLxSwdYhI11NqbtigY9HwQIbx0qGgTzd3JBPRdm86iRNKf4QZQX+MbgCo1zFnOzYSE1jZI4JLQGJQpcZ3gUSJmMN0HZHQzUPbFOY0pzD9cPFZsJ/glfVGc4ygxrHewiXZPhlxC1lAEvYw6nFGlpXMmbUYre2JErLzoiO+jDpU1A8rqTCPI6GVNCowRkJ0yHQ9UnBlkkBfIhI5LgJvoJZUgSvu2Jaf1Fr9ROzHWo/UN3CHjrSHm9xuPM92FK1TQQ0CN8xgac5GzT4VWYRHfu5GlfcpqRRx4mfEpvhT0UDasdvoVnlJQIHxS7Qog+lVuCgQiebcJn70Ylcyyw2AFQEI3YGTzG0Vu58JvglM83f0+NDdPOd84ygriOIsJnBPcpg0MnzN6igBgLP7cJxlPzmsK3nDbC4R4cDSIze/b4lxwXkhNPqOkUBbvOmSETCmFwrRtf/J+JClmf0VkhZKwNKki+IKUs0ZEeOiHYKdgVgi/++tf4gz/6I+48fIgTAoNDOkEhNL4xeOu5eP6SH/zpn7F5/oKLly8DfS0lFsneNTjZ1/RMTUqJFEkpFWh1MvinNZlKuZkO2Q7nIt0TWTRRqj+YzhFEcJJK7yX+bqx8yNcpNwBPCTkdTnqPiI4dY+cSAZ1yLfXv0/dEbzj3cU0CKQqeoWl/JWLnfZ/pZIyTR8c3avm7eV9TSrxjSqNxv4e4nUVPZc5+4/2Wvp873+Vwys/bSQWNEOiMNgohDjy3c8VN6mO8rlOOf4eZakJtrMRHeHLnF5d/agDDqfFPwTWd3YnPG69DLuQkYSVv+fk7lY1m/PswKnKoLBw7nuTne75OXSqsWJMUkc8HPDG97AiWiX/KcSQ/06YciW5T0B37PY23w0Gmjavj+d/63Uz5LLtnIi+UVidGgdx2puTfy9f42DtvMs4pfuRAwTeaT58k8DUKHabhPB5TzvPksE7jGuPBeEw5DuR0P2XmkKqP4M7lgm6+vo9TCT5WvpPFfJQ3kGntPJ6Q+thDn76Z1Ec8JRJf6F2nwBXed5Gb/ylapWcILxE+ZFTTM4mz0Jq6izwrlGRRNcznDbM5bHeWtgFrkjwVeOyOFzzg/w/5NBGZfiHy9e/XojunRFKgiBBRKkAQnRij40BRamZVRaEDHbNOIITGLUsqbfv6e0JiEx4QIrK9DY7xxrZxrYMF2WGxxmKVjs4IEb+7MSqESGeaCjBEoUSBEBJFUPIoZfFeYlxITWqtoDURBxz4mNbURPaCmAXORyU4BENaqpOoZJCjpBN4L0O0rXW4pmWzr7lRlrptQ2phH/SAUniEdSGKUghO755Tf/aIi598yGkd6oRerbcoAe9RsPSSaxsi53ey5R9IwS996S2WWiOfXlN+9JK3yhlSFPiYVh8RosMbGXQU9fWO07O7fOXXfhWqgu1ux3IxxxGMV14qLIJSS4TxOAleSdz1FvPJI3wdImGEKFCFZqkrWguXSvJCSjZC8aUHD9gLx7OrC15dX9E0bVASqiIYL1P2BSEwuQNvRu/GDkRlWbLb7Q7OZICyLFmtVnhRsDg54/zuPXxM4yxEin5R4Bzr6yvq/ZayKCirGULIWKZPI7CsVhX37p2gVK9TGZfOCbXPDVeX17x6dYH3fpiSMxv3YF9lLczDZ7/HM9L3lCYoimNN4iJEsxWFCnvM+c6ZnSgXXK7XfP7kGZfXO5xTzKsF2/WG1WrBYlFRlQVlqSgLRaELhFRI4RAiKFm1lhirQ+SgCzVlU1pd71zkzUNElZSKqjLUZUFTN5i27SLMjWkh1v11Luh6lJJYR6YDCNy4EIKBFSqDnRBDqPX0a/h4d864mIXBTfOnQvRK4OTk3kna3uNt2t9Dfld09NDihBwojRMPcSxry+vO+5wXmjpnc1qdxjLmh7w7Yhw/Es16MCbfwyP+2V8n00OM6i333x/K9mlvJkejgENu8O9YHk79hnc9cCiHdLqXEQ98bH5TPNGxd/J3b9MTDMaaWwTC5j3ysCVRACGSPjacRSbDaWc91gT6ODiTu2eCg8ZtU+hw1sePke+DbvC94VkyMIyPZZEkZbyJYVzcEhE82E/9xU5TNXYiTu9MfTNd68eX6z4O+0nzE/gYaBGN5WS0Q/SuzH0fPY0OfxGzEAe45npGqcC7wyCr2+DQ/Q2kDAkpNX8wngWHuvk8RH3PZhVVVVLNQkTyZtPEDB8m6EqEZD6fs4gBjCm9c1GU8d/g0OSco6lbtnXNftewb1p2+4b1es/1esNuv6M1LeApS81yNWc+r1iezJnNSrRWONtgraHd10jVO0lqrbC2xVoI+uQ+eCut1LGdNTw70/sBNlLqqEtNv8PV1Q273Y75fJXR6sTJO1rTogvF6dmCk2XBZrtnNj8JdiSlUUqDt9xcv+TevfeoyhKlQjSrUoqykFTlDCkL6saGfSyGspX3QS9pCU6TxrbIdjrj7HTzWCwC1RnZr+uaDz//hG+8+2XO7tzjyjZcOsPGWs5kyR1bs/dwLTwtnpduzzOvmHnJWgieCEvpGywFlYMrCc+F5blr+KS2fOvf/Qe++Bt/wOffvcP3H1vgGiVaWidRW8McwcwrPJLV42csKPly/ZSvNju+srpL9S//Pr/5Z/+RH202fHK14fx6y/uyYPXp56hf/U1M3aKkYnn3Hm89fI+fXvwQFpLFcsZitmJWzsGFSHHpI29lLS45n2lJiUZrSaEkZVVinaUsF1hn8MKjqwJt5/jI3wuhkPHskISMWRKJt4HG+QjnTpcRebq6rqMNzga62An0PU6G810jdeCbKlVQxJrjuKDvsT46NhmLlJqqiA6cQmBdwA3rI69vguOIcRaD4Wb7iqubBVczzWklWC3Auh27bbAhNtsNm/UV68srHIJZVbJczCjULsizkqg0dB3/eGxf9XPrJkjamJ3cH3neXL8VHullv9SvgK7u+nF+baRD9TEDuNIoGZkMF+hn0ucKiNm7BYrgQGW8xViPFiUippYXIpSwFkrhhaOxDc6FzKOJxr+uvbFhXACLxYI7d+50aQcCAjkuLi85OzujUIrddt8pJpqmoTIF65s1l5dXrK/XzKoZQgjqOqRXKoqQCiMoKxNb6tBCo6QGFMbDixevaIwJk4zpM4QQMY17ZJiyeqNSSTzBm6dtG5QQNG3DZr1mvlxgTEtdm+75JMgk5Zsg1BcDz83NDQjF+fldhNK8evnnlGVJ07hg2I0HuQgSC846lA5CumtciMTLlD290jJJPofwzomstRbhfefNMk7Zlw5SZ23nkZLez2uwhnrcwWvL4XAiKiFkqLlVFA58O4hITN/pftxQsQU9Y14UweMmeUb16xpaEhysNfEgC4SjKIpBfwnjgqKpR0AbU+an1DID/BwJnwfKvZECPVe4idHGHit8x+uS9533O46c7/ojCH9CBE8koSTb9bZjyKx3BINGJ3IMYNatge2Z0XwuuaKajvntn3md8j29nyu5THR+OCpoQGfgzb+T4NApmVUvICb45G1AKEfMeDJojUsZjdcvOVGkcWUPxovTzHTuEX3ItPrO0HhMKJq6nuoOHuBAPgbvMMZQFMVAeM73c3Iyycc9ZiDH3x8KTMN9msN/LFz0qYbUwb0puI0Pt4P72b0DgX0kZHZK5iNKhMH8JwTmfCxBoT1kUNP9PJPE65QVOezG4xoqRg73xtjLfjzmv0s7pizJ6fSxdpvw7zOyIzwILzqhXUYGRAmBkJLGWYwSWDy1cNx7/wv8y3/9n/Hur34QyoqEj1HpEmcsZrPD7Go+/Pb3+MG3v4243tBcXw/Ohhw3cy/NfL3GNaLzcgRjOhbOKXeA98ecLlJzEUdS7fKg0DO3Cv7T8Dx03smvTeFFXkcu7f9OyI8w8BN9Te2nMU3Ov5P/e2wuY+eVqflN/X3bWfMmbep8Gv+Madp4vq975ucZSw7bfM7GmMP5Jw2J6MdxIAiPhnBs7MdoejoTp5553TzGz70pTt9GK1/3XRF5234N+vu58hcxNEbn37TWBsOR4KhRIt/3Y0eoN9mr3VhuffL4++O9mzsg9A8evjdem5wPGxuIx3OZOsduO6dv433Ss8fOKhcsqkf34W2wyX/P6VquLD/WzxQPI6SahEOflcjSNu1g3oPnO0N2wrk0x3jWdyzjIY0b84v5+/n3ssHxGvT7uZpA9ClDhUQIHZxlhcP6mHRXeApdURQGpWxQFMgMF+idOY+dTwdrMZhSL7uKKL4GvivWDpbZ2ew8KXmFx4c0oB60KiiistE6j7fgvYqOl9FwHx2AnAtzS+P13mKdj1FUJiqsHb71WIoYqZ/Rp0iDgvI0pGkXIkQ0hwrRkgKB8wIhDEpJtAv1Xq0VWNvEUMUI+JhOUcqUli+6z4q4/pHPUFKitQQlKGw4F0JtWYezFtM49jTsmobW2c6BKBnGjXc4rZjP56x/9gjz6imYBt86bG04nc24JzU3znHjLGvT4P2Wr52fc/72feqLHVcfP+fy+SvWWmCSwUUFxX7jwUgRlE9KcXJ+h7ffe5/r3Q6lNUrGXHY+KJ6Vh7lQGGFBC6SW7D99hn/5CqxDxtSRM6k4USV713CtNRtdgCg4PznhutnzanPDerfDWEtRhox93iaH6E5UO8qXJGf6RHNzeTLhbYosr6oKUcw5OTljuTqlidmCQrCBRApw1rC9vsY7i9LzUHrPR3oXnQHunC24e/ckRHJGPMr3g/dBd7TZrLm6uuHmZt3JdlMOaD0dZOJcCJtTjPZc/3vYz1pLyiLUsVSxLJ83wZknZIsPSt/a1GzbHdv9DttKmsay3yv2dctiVzGbaapSh3S48zllVYTsCoLOUVvpwAtrH5TM1qboXx+M6IT9JQRorbq00G3T0jYhBbv3ySDquiyR3g/pDj4ZhMiE3X7ucgInuvMz6tIG51LEp7HMLLoPhH+cAyd8F10emDg6XVfXJ4c6JBEEpr5/GYJP8rN8arzH2pgG38Z/vcm9gyeOfP+gr2xtJp8/9r4nnDDZ+/lZ7wc45DoYjx1j4VCug4myQXFKx/ihn5dPmfr7dTxkfram98O1TLCe/nKHR3ndbdHfHsJqwM+kp1x3Dh/j83teM3Z6ZG79+75bv2P6EjqT8SEsjsmDt63BJIh9D9M3ld/SPJPj39CgHX/L6E2KZhQyptr1Y/2Aw3NYqjPN/9BwPppTp5x5/dgH8BG9bi6ccwLvg/5eEIzlRaT/UkmsNWy3JpSvjU4mQkrK2ZzFYsGiqijLorO5SKkCXUfQtI6mqdntdrxab9lsduz3Dfu6Yb+t2Tc1UnqKImQUWSznzFcrZvOK+WpGUWiE8FjT4pzh6nmLjbRSxawbKRo9yFlB3x0MmGLAJ98u1/rB3pJSxahx2elr9vua9XrbGcYzl17wIkSRFprFouD8tOLyYsdieY4WIVBTtjVCCna7G9p6h18skDo4VgbaI6jKOVW5wCMxraVzNk3zSzxMdK5KwYRySi6cakLEc8nFwDBB4wzPrl9xs9lwenKOWF+x2W5Yt5aV91Qoznw4x9YiZBB6wo7Wh6jeVgi2XiKQFFi2OC685QmOxsJf//Wf8fu/90e0773Lzed3ePLiU2ZK4K3GNw1zIaikopaCBxgumz0/+eya51Ixu/MF3vlXv803vvYBj771A55ud3z/5opTLVi+vMA2e1DRuF0UPHz3PX74N3+N0DPkUlPpGcprfAtYQeca40CoGPwhLEK6EKRZlFTFHOs9ZbEI+gMVZDdbx4hzGVJ+C28RyuFjiFfgUUKqbqlk/F7c556Y6cbE9QxrKrMsW9DTCyUVAhn5JRF1pwEvQ2pwg3MmZr9SIIOTg49yT8pSbF1wbDUp45Ty1M0N15uXXMwUy8KjVY2oQyZq17aYXc3+pqZt9hTLE+ZzSVU1QAis1SGykymjeNhnI5lvuFNIRnGB75J+CJl4nvh3sl9m+qkO87NbB5TbB4ck19HS+FGRdL0OScyGJiRKCLQUFEhQCiFC1i3vw9i0AEUIeDGEgGMPiELhXNDhuigDCvVmjupvbBh/9NkjmqbBGINSipPTE95evM2TJ08oy5K6Cak1UqRTvW9pmguUEjz+/HOUVNy9c4cqGsYTEJPwkBTiShM9LgTCSxAKBSitKcoSZy3IEJntnOvqOuVKdiFDtEnwHg9I66xBS8Xzly+5vrlhXhWcniy7saSo2m5swiOsQElNVSqULrD2mrptubq64urqKniUW4/QCoGiaVsKWXbEEATWQ6qv6/FRsEqe9bJb3NsUoHlK3FzpOmainQsGtxR9LUQwxPYGybQJXEd4k5DSKTjSJicwa8aY4LnjHM46pBIxPUO/EZJn9PjbOUOcDBNpF6R0aEDMHuAGc5nig3KcOYj2pXdwGLcp4TnB6zYBHKKxMG7i8VhyRnWsiD1Q6jlHEdfAOctiueDV0+cY01Kkw9THSMjwFvlh26+dP5hPriQIzzC4n8abjy2/NlbgH2NBD2E7NB6kcXVRXn4o7OQR5VPjGY+rFwDegKscjUtEiUkwRZmH8zkmAOaG6SmjRbo36IshkzxWzIaHhnMaCzRTY5kW8qZxdyyUjxWgY5wdC5v5uI/tjzya7k1ajmf5/srvp/Hl8xzPIY9GPIjWFYfYMh7jbULwkP4MD/vbGfZhBGYe5Tj+1psoRvI2hsuY5k299yZC5KBfiMbwqJjyiamnUxB6IWi9Rc4Ktt6yuHeHf/TP/jG/9ju/BRJsIfEWSqGCwrqx+Mbw8vOnfPfP/oLPP/6E+mZDCVRFwW63QwhB0zQURdE5O+VGr1yxAj3dFxm+jvdmB/OOjvY4EBR0h4L2eF2SY0/+bg7jN1GU5GN63bqPadRQmXG4rlN7ZWout9GrfK6D8WbUK4dBPv+p+ebz/kXbWIE8vvcm++egJfzO5jCmdwFvju+7RGvGcEi4ms4p746XWoi9TvI1+ffGfGD+vddd+3naWHk27jO18XdyGpTTOu/9AB6dcobDqPP0XrdXY1rDdK+vZRX5Ew8y4uU4o0q+Pvn+n5rfFAzye4MxvWEbn5Nvhp9vsnZD56zu6mv6H/c33jfHzvMc58Z0K5T56RV1x76Tj+82XBrzH8fo1CRsMv423c/LaXjnWZ2cdPOa+mbQYx2hZcTVGfHROa7ncJiaYzf2UR9/19Y2NWVVRKUCMSpQ46XCSRVlFIsUGiU8QoQaft0oomK8P+n9IRzS3/k6Bg1JnFOCZTy3EEPYiiA3hiikXunhnAv1v40FFFIEZarBYY2nbVys6xnHaV00+IUcut4FxabwEnxMwWxCmj2EQ1qJ031UonUOrXKcDOmeS12ETG5ItFdoERUuQtD4FiUUpdYIocEr8AqXFGXQO31G+WKwwrlem6C70LKkiEo6J0FYC1IiqXG2Ztc2NMYgvQyKIAATnqHQyN2G7fd/SNXuoPW0tQUreHuxZFYofmwaHvmGK9+wavf8ypffR8xWfPzhT/jwp4/4WX3NTgqud4ZdUeGUA29xracVUO9rquWKuw8fcnbvHj979YrVcoWWMqSYFyGqd+48S6G5wYGSSOl58dOPaTdrhPMoIamk4ExqFrLgmbLsihKvK+ZqRlXM+OjyKVe7DbUJcr8SmZNLpAXOug7XxjyvECEQItW99r5P05o/VxQhRawxhtm8YLZYMp/N2exbpCqC4V+FsEhb12xuboLThNYgwFiDlCXWGFbzkgf3TrlzvgrpMFXQbyRlahq/UprNesPV1Q37XR2M8mJafgnyesz8M+I7pvn7aDRL0eJKUBaKstSURSgzhPBgfTRCeLzyiEIwPylYnS+ojWOzbqibHcZU1K1ls9tTloqqUsxnJafLluVqHqLIC02hY4pnUYRIex/0FKFSYDobfKfvclFPpVQwwpiqpGka6n2NaUMFVCF6PZXUhxmfuhmL8fzT9cNzKtGYjsxNyMlCjM4AAl8R5PVU79oNHGG9952Dbd/PWO8TxupFxD9/Ox/w88qAv0g/3fVI7/3w5mv7nvrGbTJn/y8QjUFjHmIYNZ6u+e73wXz8cP19xLup4SZSPB7TbXLEsbnedm/8/lh+7B84/r0OTnHgQongOCYzHlIk+Zs45wgz74KhSMoY+R36lD5qnPyhfHpMjnwdPLxzua/Hwfuhz34Mt8HuWBvz7+PxCGCKwxo8y7RmUIh8D/juWv5t7wMfJCKvEs4Dic2M4omPyHG2Xw/f/Yzx94CXRYx34dE5dfDwuf4UlJL00dK9rtd5j7EGW7fY1oB3saZ4sJfMFwuWqxWlCqn6tQoBiR5BaxytMdR1zWazYb1e83y9Y7PeRltPyNJTFIrlqmK1mnNysmB1umR2coauNNWsiuU/Pd5ZtILdek2923cBijKOP9QZDzzTIBgHDuj7FHzGMrjMoj+DMTLIAtdXa+7dexDkUesy2T5hjKcsFPfurPjooyukAiVLvLc09Q6lC5p6z363Zrk6QelFhDlY55nNFqxWp8yqBVfba6RMOpQe5QJ+JfwMNpfcoS5f73ye3fxlLGHrIUW8723Nq5sLvnT/XYpqzo0uuCodd/d7BIJTQnYCIzw74CUtGyEp8Sy8QqHZ4Tgj4FHrHRY49YIffPw9nm4uufPF97n3/Mt8+OSnlJVn4STaV1SIUC/bWs7Oznl+ueE7zQ2Xn3zK6X/7l/yr3/llPviDb/LOoyd892bD9zcXvFXAL19eIK4uUGcFRhfUpuWtd9+h+kuNbaDwmkqWwbHV2pChNxJAKRVCC1rT0Jg91hq0CvWita6QXiClQsZAFmMtxgfnRy9SQKINjsN78ATjelGpUEZH65DVJj5rbSijlHiA5OSXsrb63Dje13wMi+x8LI8Ts5WJwAuEjHhRf2piKQSCk0vCjBSImmhJoQTONWx317y6EmjX0OyvUFVBqQu0kEgDpg184HwxZy8NWilCpLsJ8roYZ0YcYF6Hf+l8zRCxM47n18h0MklnmfPv+aOiu5TR98iPEEtP4V2WdSSmkzcGCFmqpSzQErxVQCiRjQjrbV2Qa70ApRUSgTOG1jmEtUilYjYqj4vZCmMc6hu1NzaMB0Ow5YMPPuAb3/wmzlmq2Yw//pM/pqpmNHXDer1BSkXbhkhrrSWb9RbbOubVHOdcZzhNAsI4HbVSkpCqRCKFwouQquDp8xfUraH1jv227ryC67rGez8wZBY6eI7XTY1UEoejUJq2qWldSA17dn6GjoR1rBgKOBEE8WDUDp57q9WK3csLvvWt7/Dy5SvqxrBvWh5+4R3eff+9IKRZiyTUBdEyCPbpoEtnY5dSyNkoXB1GQQyi28TQUJ637rrr06u3bdsJjJ1Cx8dUyPTzlEikDClvXbwnEgxEjNaxNrjUklJym04RNU6FWpblsNbGSIHZG8hFZ6TQWgchKVOwimyc47kmoSoZxscOAmOl25Rnea5Qy2Gd48AgYlxkR9yY6cneTzDPW/68tRZVFjhnmc1mUXEc94JLkZL91Ce/JXqlctgvanCguiM4IiZwaKwUTt9M/eZjOJxXP6bjTPHQczqH7xjfpxj3/puHhowBE+r9kIZDZgwJB9fUCMeM+ZixzXGpi4KfWJOpfsfzHDrdgJJ9eYE0hrHBJk+9PW7TAsFhVEL3fHZ9PObx3usUnJkjwxRc8r6P/Z07S+RKh2P0LL0/3o8dLcy+P071KxADB5bxfp5av/E383nCYVrpnLbkLT/DpoTh24TTqbGM1yjfR7e9l7718wqqoYNw5oHo8MtHr0CvBFYXNFry63/4e6GO+N1T6sgBeWuZyRJhHDSG61eXfPev/pbPfvJTtq+u8LuawjqEEmybUIPHWktVVd3ZPXYoGO+Jbj9Y20WlTSmRZIw28xyua66EGwu047MjXRvvnSn6ObUOOT7kziRTLdGYNP783cCUH35jTLsSjUp9TeHB1J4bPON543RDU3PO+xyP73U4OYZ/7nwz5YgzRdOmBE03WrdjZ9l4LMfmNk2XDx0AD1O2931P0ZopGjGme+NMNq+D6TGa86b0aPyd8XiPtY5mipjueGS8GOy5jDaPI8ellKGOlHNdZMB4/DkfNHbGfN1Yj51BP2/7ueitDwJxDtOcTkzt7Tcd43gc43U7yLwxOlvzd7rzUkaD5M8xzyk8EUIMeO7U/9gBMadb47mPlWhjvGnaFhPLM+VZYob9A6JXajrvexkrzZvsQxzuozEe59eyib8R3XvTdrNecyIXFKUGDK3xeEJ6QyGTolDhjYyR26EsWYg0ily0dwivDirPdaWqEqwgGqSjAWw0lrRvpZQcULnEd6fmA0z3+5q6sbStY6ZVNFIHI2tra4xJmcoESii0llg8bdsgTYshRGkooTBS0wqFsQYnLdoXSD0LkSMuRGVTaIjO6Eo5tAqRIlVVItsWZyXKgXIxktsFY761HmsBG+pkInUsIxZg1OGF7w3j4zM0KM1DZJQWEq1VqEMtBLKYsZivWFqBldBYE6Km5wV+vwfvqeYLyt2Oi+//iP2H3+f9qqLe7zCtQ+mCt6oVn7Hje+z5yNegHL9/cof3v/YNnn73Cf+PD3/CX16/wBYF928U69ax9I6NaqlFy7lVOATPXl7w27/1Ae9/8AHFcs7VoxvefusdpHdo7xA+RDut9IyV1exFMKzvb6756fe+y8bvCEkuJSuleGu5wNYtu7MlO6kpygUP7t4HKfnxpx9zcX2N91CVZdCPpLNNBpxxti/ddbD3vadpmi5AYywj5Lqk9XqNMYYvnD5gPl+iihK7byl1iGbWRQHest1s2a5vWM5nKFWCUCA9RaG4eXnJW++ecO/eiuWy4uqqDspaAdb1GdW01ljjuLi4YLPe4J1AlQrv7UBPkfN3kJR1r3dcSltJ+BBkEYzZJVVZoHVIo27xYV+4BqE9s0XF+dt3ead8h7OHd3n06BnPnrzi5fNr1q9gu9uy3QWDflkUzGaG6+uG+WzDfD5jMS9ZzAvm8zmz2Sw6pCa64MnNVok3U4keeoEQqSxYiGxs6hZnDYhgvDfOQnP8TOtkUTqN1QF8hrAanhfH+JTQZ+BJ8DHVbYwSa5qQ/l1JhVQi7G+XRZBaOiNm4vNEVl+8v3Z0Wre222TTY3/nvML4s/1zvtNJA71zz0Rfr5Npxi2cod1nDmSf/CfsgfE9N+AN07vJmOV90r9NtzTvKT56vO7H+KhjPNPP36LRpDMYHPY7/r4UIYWslDLWAI88V56O16eMRg7pe6c7oHNY6Z0J0tzDI9mj5GfylFwmRJD7U4nA0ei7sQc/1iNKtV+gpfGO4S4B94YfGcN2sPYk/Ai6t8RjJ9h35waBtKVAvdaGdOTWus6BKfGGNtIO3+H/Ib4nGL2OJo1hER44xNNAXwrKWBvcOUtd1yDAmUBbF1UZ6ofP55TVjLIsg3GvLIPxWAga46nbmt1uz3q7Y7PZsV5v2Gw2XG5DlKtSkrLSrM6XnJ0vOTtfcLqasVzNWCwXzE7OkVqgtA5lNwEtJecnK/abDU8/f0qzq5HegZcILVBOhbIW1mO8jeUvdaLGb9Ry2TqX8YQg8r+Ci4s17+4blqslupA0TRudIFQoCWKCY9o7b91juXyMMzV6tkDHFPPzasXNzQVXl8+p5gt0NYvOBJ62bljO5wjusr655uriWdxjma2FTGcogv0oZbl5XUs4I7xDSU1IsuTBBxfXj1884t233uX05JT1fstz+4L3N5aS4DwufSg75KRg5mElJXc9lMJzRaj//sucAZ4ZIHAIJWmt5cd/8Sd885u/wVe+9BX+8k//Bx4AD4sKicS4lp2rwVnsbsPfl0t+uiz4vN3yf/v4b7j3f/T8w//df85vffBl9t/9Md9/ecmPzlaYp4/4ypMnLE7v0yqBu17z7jv3+fqXv8Hjq2fMfYVGUW/2WOWYVyeUpaSoFEWl2DZrLtbPub55iRCC5eKE5fIUXVZ4pwAZyr9IhcZSzB2tbYN8LSVKaNp9Azic9DjpQ3rtusEZG/ipQmEltO3QppIy35RlGdalMZjkaOEdXiRn7GjUFgIZM2A7G4y0jbXUxuC8p3GGIjqsqKIEa5HOoZxDI0DYoCO3YdwAdbPn1aVlu75iuVpx5+yck/kiZG4oZpwul6hqyc3z62AsjqUUPUH2+8VodKI9GQ2VqfxQ1Lkf6VeM3JU6OpfzHgffCoZyZ0IpLa0FVVmCLGldi/Ma5y0lUb4l1CXHhwwClRLgHFJFuVcpdFHEjBihXJf1Fos7cEQ91t7YME5UYNy5c4d79+9RzirqpmF1eopxltX8lKKacfHqEkxIrdU2llo3fO873+PRp484PQvpqFKEsJSySznVKYRsNBQTanKhBS9fvuRb3/0Om6ZFxeeVUux2u075kaKWvffUdYOWMgj1kpgey1HNFxjn+Pb3vsd77/zT4KFgLfP5vOtHKYUxhs1mi3GGqqqC5xQOpQr++q//Gmsts/mC1qwpy5KT1UlQ9Fgb6hV5jzWmM8JLJZDeUyiJigdpYAYDojk/VLQk429yJJiK0EzwOyZUpf7yusXCWZRUGJcr4hTeB2FACNC6oNnvA4HQmqYJqeTGSuuxAi8pLHMBMN3PDc/p8KjrYBxJxvTUeqY2baOhIntswE2/A4ONOxRCDxn7sVE/NwQfMNQwqJWd30t9dAdh7tBAr0SXUkbFUxCubHQGEFLibfL2EQz8JAUQvUGTt11IuTdM9T4cL1h7aIg+YNhGOJLjzTg6Pp/r4O9R/cSx8DFWSObPuRFOjZ/JW97flLKk5yEPDbZjMpyPKzeUHjMUTDG1U2Pr++6/mPedj2vsDDSlvE3jy8c8+JYfGssSTiSHo7zv1HJDcupzKu1rL+AfN+K9ybrlMMj3SKJdOb17neAwpjdjhX8HHzGca+6ok8N43NI+Hdd9zeGaf++2lo9xal5TMJtimseOErc5Ooy/dQz3jsLCR7rkPFKH2k0OgdeS1ju8Vrz3qx/wO3/0T3jw5feoC0GDDR6bHkqlkK2j2ez45Mcf8f2/+RbPPv0c0Rj8vkE5jyJ4ZKfzLM/SMp5PDu8xLgbh3R3gQU53ve+dxcZzh8Pzc7wuY/zKYTmFp/n7U0bpY+92OOs5mMvgzE3zzvbLuN/83EvwnZrPeFyDeU7A4LboyPRcDsupDBSHLxME+tE5ndOCccTnVJvieabGOMaP/H0xUB4xeL5/5nYaFx49NDLmfUkpOoetRGvG6zdFt8eG+BzeCWbpb6VC5Oj4bBj3mfc1jtgaO3C8juaNaXyOn35CSBpHHY8dlvI9L2VIkSYzuMF0dHe+TjnNyB1EpwzP6ZvJCTWf/zE6nn9zvB9zmOTj7XD8yB4c8mlDffAUnigh4AjOTLVxxEU+nzHfOjhXGZ4zr/vOeO+O4TWms2ktp+A+ho+YmGu+P5QUbDabjrcZ02Pvg9JXCtmtgxICE5WhPioyU8q1MYxSf1M0buw4N3bk+7u2lhM2jQ4GS5FSfMZoalw0XHmwEqUESgfHZwBLEPa9D2n8woFz6Aw8XjMXFcDj0adoq35egb7ljpDI4CBPiiKM1KBpW/ZS4TRIWQJRdlNhTYIBWoCCmdLMSgXM49gcxoYMcW1jaNqG2tZop1GqYlZW6JRVRoXUkcKEUmQCYi1xhStVjPII9ckbaxEqRI00tqU1JtQujHBKPwM6hYh0P9T0S3tcShlq8RFkpFCaRSMleBw4R6MVpVBoJfEEZ3YfDyJZVbjWsvn0c57/8X+gqq9p7YxX6xtqY1gsljw2hm/tX/LZrMAbwy/NKv71B78Kzxv+D3/+p/yg2bCsFnxQnjA3liczw65tOG0lghLrLe2uRgnJO1/6EncePmSzqxG64Kbdc0qoxyidQOHx0lN7STFbIveX3Hz6GbvHjxGqojQFS11wZ15wMi/YrbfU56fstaBcVSzfvs+L7YbPHj/lZrNFCMm8KBECGtPGMzHKTaPDOKeJbdtinekyzemon0iO9Qn32jak7z49PeXu/fusTk4xLtTMFkKhiqCMr+uay8tXeNtSlXdQugQtQQQvEu8c77/3FufnS6xrwauOKIcorliLW2suX1zx4kUIlihjivi8xEZOL4Lisi//BUPe5YCW+xARrmId4korFvOKstRRLxDKKBgEVglmq4rTd85571ffZXay4OQLK976pTtcX225vtjw+Y9f8eTxc169vGF/07KrW3Z1TaUr1kVNVe4pK0U1VywXC05PlszmM2ZFQVEoVDSQB7rtA0yVwssQRGFtrM2JC9F4WqGljoakEMEFSU9xO33Mr95KQ31K0d3XqhYpsit/zYtIY4LurzEt+9bSNC2mCfV5lQjRlWrkIGq9Q3o5oHGBbuoB7f9PQOp/7hbqtPexqUNdwfQ7Y57r520DLtP323asM8l5mvROlxlkYkxjXvd/rPbz8MDTbfqdYL6LuBKdR4b8oenwc6yPCLzMUF4SyRwRecZAQodyzRiMt9KbOEohpuS4NPqwv/9/3Xru4g2eHcnXx64lWCsp0UJ2WW47uuVDGdUko/U8cWfGGeBp6H9k7hnw/0N99uta2isqe0eIYOPQWlHNSsqyAHyIcBciRjEvWczKYDPQKmTZ1RUyGoh2TUPTtOx3NZvtLv7s2e9rmrrFWEelFOV8QTUvmK9mnN1Zcuf+KWfnS05OVyyWc6pYUzyVuBJShjrLZYW+pzonwhdPntPumsBjSx1Lpgq8Nzg71Pe8STuUCfo088QoaK0V+63n5ctryrJkNi9RSkQeWeK9xLQGIR0nyyX37pZ89vQZSx5SFCWqKKj8inrXcHP9ivnylOXpXWarBUKF4jtCKMpixt2793nx/IS6uUT53vZgM3xJe8g5R+441M9hgrb4QEw1AicFPgZQGjw/fPYJv/SlrzJfLjhp7/Do5gJHxQK4pqXFhSxMHmZecK/VKAm1sKAc51ZRa4m0jhM07wvBroDStnz/v/vv+PK7H/D+F77G7//6P2Pzt3/K26VkW2heeYNxgrerU35fL7i3mPGedPy1WfOt7Qv+z9/6D/zKv/saX/2VX+alsTz+8Cdc6Bn+xSvuP3nC7P1fQs9XiKZlX6/50q/+Pa7/9s+xraU1NUorClmgK4+qPEbWXG5u+Nmjn/D05eesynPunN5jPj9lNj9F6YrISgfxAksiggFPQuT5tt6z3ayxGCyGzX7Do6ePubm+xLQNLu5zfLAjCCkoymBj1FJSqOBEbAfLE2VQ57tME53eTIBxlk29Y1vX7JqWxhk8UEFIDU8IcPQRL6RQaCnwwtNaj2ktZSXQBPokReTuhEUrT6kF80ozL2csq4K9NbR2T2trfBBEghOf9zCqCX473ckc3SLtyfUmA2fAznUq07m8hvc5OGFEsGs5b7HOICWoUjErJaUuaL3v9lLIthDlb8Ai8CLIuTKVqm49otDoQnU2xu1+H7MIEMtIvJnJ+80N48BiPufevXucrE5QVcHLywv2bcNsuUAimS0092TB86cvMHWDUopmt+fCWf7tf/1v+V/9F/9LTKwRlWph90Dq66y46C2niwqH5C/+6q/wUiK0BimpYpRxUgSWZcl6ve6ij7VUGC/QpaZuGlSpgwLBOpx2fOf73+f3/8Hf487pCUL06VwTIxIUZFBVFXXdIKXGOsdmfcMPf/BhMNh7EWqmARDStCIltrVBONc6GPkjM9gplgibL2BQZBbdMKosGUlSTXFjDF70xv9cedwpNbN1Givm04EviRE4EoI3okUIQroYaygi4dZah3z9cZ2SB76PhvqQor4fR67YGit4oVc69unuh4ao6YPx9mi3sRJt/FyuDM2VVOM0nQMGU/SGjQFjnglIU4q78fhyuAwYJBdSbSQ4pvXtO08HpOj+nxQvOVnJlZSHjGCIwJiCWf7eeNx5kyLUEB7PdyzojJnBY8re/HqOI0l5+SZCxxQDNX7P++DhnbzFBvfCAwfjHI9/LCxOzSOvg3w49nA45rg1Hnv6barvQZaHI/Pu5nOk3cZsTl2f7P8WWE0xd8f24rExjQWLqT7HY8yfHRvUUku0KX9vck8fGdd4DFPOBMfa1PzytR0bS9I7Y7o5FRWa9zGl0Mhp2pTB6Nbxeo/xDikKUNAKcFpipcAowdlbb/M7/+gP+eA3voaYlzSxdk0pNcoLhLHU12tePHvBJz/8kI9/9GM2l9dQt0gH3ho8Ahuj9IIsJw7GchTXxzSO4/jf7ckJmjJexym8e50yZHy2/kIKpfE8D+SiQzztohg5vj/y62P6MYV7U32J7JmxY84YB8cKrOTokN69dU1H40z8wZgOjr87XsM3pWdTrX9uyNDn9CV/dowvg/lk+z39DXRZMtK+FFIe7OuxM9/raOHYIXL8nvd+YHw9flYNx/8msHwdnR+PP3i7v6FCILufPxPqQx2nwVNzG++hnI6P90LOsx3r97axTrXcMWvcl5Ky46+Ot+Rs0be8r/jL4O83oUW3nc9T9zs+U/TPTX3n4ByO8sDYWJzfT/3nBuzbxiCEwBs7kLAPaYPoDGdjPOrpSxpL5Kuz/emS7JDKGo1oUP7d3LFlijbifbfff5FzYtwePWlYLj2LpWI2V1SFDhYGG1TVwd5kQ8Y2H421aXwIElfv41ki5CG+j3E+RYznsA5/jNZFiI7n9j7iqRTBAJL4YeGxUZ3u8cGL3zY0xtMYG9fA4rxDomK6eEGhQ/rP8K/E+wpnDft9y3anEKFgNoVS43gFvPNID9LTyd5CChpn2bd7vGnxxrHDIaLh1WJwwuJkjL7BgfRdGTHjsvJo8WOphqaMWS20VFHpDstixqya4wS0tsXg0XXAZedMZ9HY1zWlLmGmufz0MU9/+BH2kyeczxSbreWq3uOcRckZP/J7nmpFaz1fUHO+MTthheD/8lf/DT/zNTNd8ZYquIvjUu5ppaUwhgqNEgW1UFhn+NJ7X+Ttd95FlSUvr66ZnSzxhQZDVNgpnDC8NGv2Hmb6BFM3XH/+mGrX0DqPAuaFYl4o2nYPVUlTFohKw7xiV3oeP3qB9zHbm5Ch4mOMuAsOcsmAcNy40bYtGNfRlsQj5FkI87P27t27nJ6copRmVzfossQT8NR6S13vWMd64IUugp4Hj/UOTMNsXvL222+xmJc0+x3eK5KRQ4qgoHMu6KCur6+5ubkJ89M6VJ73ciCnSCk7XZP3vYEln2N6djB/KSNu+a4+ZlmVobar6jMTOCS6KpmtZizO5szPZpQrxYmYUSwVp9sl2/UJd1YlX/jSGS+frXn+5IaXz264fLmmqfe0FlpboFuJ2gtutltu1mtWyzmLxYzFrGJWFVSFDvRnkEsiGPCDM1tQNIc9EvgeFR1FEgVIQQAdHyNCwsyxClWIw2s5bkB04MkCSgK9CWUBhw4IwYCSatU3bcO+NjRNS9s2mKZBilALtdCalK7Xxz3qR5GcKbghRI4H/FMH0Z69rq/zcCXoavpxhYxnZPrC7t1R6bUOFkk35KPOIxnFs2e7fgY82bQs+ibNj/r5+SLSkno+Oon6YMCQ0g8dSUbnuxjx5/m9Y8b1147kiDw9vv/zyXkCIXK4HkqqU/JLdN8YjN+YQ6N4Sr8LozF73znc9uPIl7x3tBzLOQdjgkAjEQf3ujEjDtY9lzEGPBlD+B2TH3zC5VHLeU98kCVyejCUo+MehcnMgQkgSQespUJJebAfvO+zTg3wI+5dfzBOP/q31+t0IxVpHEH/MYbdYYtf8b1OKNg6iizYSlCWFVoXzKqS2SxEiGstkUojVbAX7Pc1dduw2+/ZbPsa4nVtaIwN9gwESpfMJCznM5anc07vrLj39jl3Ht5hvppRzmeoQgfjobBU5Sw4HwqJEMGRbqZmvPP2O9xcXFNval5snoUAPyXQWuBcDN7Jytrd1ob7RQ5khA7fus0jUErQWsHlxRVnZ0uKUoU9KWSkNwohg1NxqQvu3Dnh488vcd5GWqTxwlKVC+rmkn29Y7fbsZhXFFJRzSpsYxFScXpyxtnZGU+fXcaU8cFAWkT8ahpzIA+k9b5NngVQXuC9AxVqUwvv8MJz41ue7a64rwuEkBgvWa8K7q2DUXTuNXe94Ma3gGfhBYUtKbE4tuyE50d2z8xrHA7jDaL2nLDg2f6CT55/zFfurviN3/wGP/jbP+VUG679nh17bOm4uzjhgV5y7W84lXO+pFc8KVrWK83/9d/9Of+LX/5V3tEnfP2dL/NnO0Mxq3j57Cknl9fMlncAx9X6ivmDd1jefcCLq0c8f/mEtx68g9YFe7Nl72HTbHj66nM++uxDROF5cOc97tx5wPn5PapqjjUhNb3U0SkIi/MGfO+c0JiWfQyerY3h6mbNy8sLXl1esl2vQ3k2F/knQpCmsKGsQq6T8d5jcockH/oPKdADzXF4GtPSektjLLu6YVfX7NuW1lm8EhS6wFiLr0OZAmMMbZPknkAXrLEIZ7GtxpgC50NEvC40unAIafE0tK2nafds1oq9UVxebdjtdsFW6ATeh+DiziAuhnsmx71ElwZ0LdcxjPRUQYKOj4i+n7xPP4Hr/ek1PFeDLdeFlOhOI0RL09TUNjhfeQFOCCwhQjykUU9OlSEFe6yahbOWeu8w+z2bZofQgtlyFvhlHTNFvUF7Y8O4inn8v//97/Hjj35CbQ2b/Y7lySoUQC9LhJVUxRwpNK+ev6TZ7VCywBjLX/75X/Cf/8/+Nef37nZCjve+M0gnACoRhE8vAmHZNg3f+e732NcNjfdoIRDesN/vu6ioVHcqHWaqmrPf7Sj9jG29Y6mX7PY7ZmUVFm2/52//9m/5J3/4B907xphurt77EFltLFJqnPUUZcW3v/09Li4v2aw3GBuMm40xAcnbFqEUKBmRM9ZpkYpCa5QGgcdZGxihxNA7h/OHh3yuaE2KTuhrVAEDxklk7w1TjCTBwUMUHoTS4C3WWZz3MXoiePZ63/bfTIqt2I9Q4mAD5Aiexpancc8VkykCXgg6JXpKi55Hrob3mPxOgtmYsR8zXGn+4zS9aW5jRXaeMWAc3ZoEmKnDLI1trNyeVN4CzgaCHWChgvJMxEOwX/30Vogy8KlmH0zwjoMmhUBofcDwTzHBQ6a7vx+I/xEmNXvnQIDPGOOED4hh32O4vZ456tdhPOac4Ir88aSIjxzpUEgYMsE/n+BzOO4pJUYntx5RNk99KR/HL2p8mzrwppiuN+1n6t0p2OXf+0/xjfx+3qa+MaVEy58dC2vHvjWFo7eN701a+u6UwDiFe2MaNo7cfN14Bkz46PrU3LJOKXRJbS0egVQSoyRiUfHbf/B7/Obv/S7laoGRHi+gUFVQNrcOs6tp11sef/RTPvrBD3n+6DPWl9dUSoN1HQPlVVQk+myvTsBpaswHe14M/R+PwW8KV8ZrMF6LKVgPheY+mnWKvr4O18bPd/264d4dP5t4gIPo+Vv2/FQ2iNeOTQyjcW+bTw6/KceMKWXJuI2dx6Zg+z9Ge1M6MxZ6x+905yDJO3iahxj0xeG63jaW9Ez//vRYxn+/DhdeR3tuOx+6+56DOY0FJ16HX2MpbGI+UzgzpntpHfLsRmOYT+2tMU0dz/u26OF0nh/SsMkpT44//zvHGZ9du41XeN3ZnMNucu9l/PixfXkMb6euT539UxlqEuzyORzYCA4HErJc0fOMSR7p0y8GhWi0Q4SWsmtEPtyLfny5U+3UnI7ytInnH2Vk+EXbxWXFrpbM94L5QrBYCBYzRSEdCouMBieFQnqBElGvpgDpcV70BnEPyVxOcuakV/p2403rjoOoaJFDlUtQ3qKiXBvP+5h3WcqwJt57msZTN4oipSAUEoRGyhatHMYD0qG8RwmHkpKy1FRFFQxVSsVamyFVofee1ipaU9KIFoHtlOfeg3A2fCNGjYb1cVgZ5N6QPrnGmJjm2fjOwNb92N7x3HuPFYEeOZ9laiDIaGHtBc4F45wXEqTC6JCustQaZSW71uKVQjmJbAOOt7FMtCgEO2e5ePQp1x9+l+XNU+yi4qLe0LSg0TRIPre74LjoGk7VnKUr+NaTl/zZ5TVWSL6mFB9ozbku+Aktm8ayExLlJSsvuSug2Tf88q/9Gov7d9kJz6besjhbYnFIQvpBL3yI5DeCRjuEb3FXa2afvUKzxzCjINS9Fsqj9jtu5qfUUrFcnrCczanrHY+eP6eu646Mu4FRNGFSkt17B7uElUIIbEzFHeAejMH4UKtcK9k5Zjih8F5xdv6QslyCCJHezjuKQqOloNnVbDdr6npPWVUU5QLjDd55lNTsN1vevTvj7nlFWWja1sSxBVldyOA4gHe0TcvLl68wrQ3GWCkR+JCGXwwdnJSSUQUZdTYHZ2qadb8bRdxHUgmEBlUpdCkRGXsnfKj3rbREz0pkVbF3nt1mT2NAFiWzZTCWtNYxOz3h5P45Z+9cc/7sFS8+l7x6fMXVZYttbfC3iSUFXL2n2Tt2G8Nu3jKflyznFYtF1dXh7BwxCeks8X2EnPcgUmrybLW97yNew3RF9GDxjMunCRFoDiJ7L9JaGwM3jLFDJ2M8Dov0Mtb+7vestY7GWPZNiBivG4tpLdhAe5xyEe+GTsoJ94IRRSBVcFgQ0iOEj6Rmii/KsDyd1bjBUeYDUabTXQiyBIIjc5ynczpkZCgV/SODsTs/DKC5lcfuPOHy7+S9g+iM8nTnSboTWL+w50Tc9CLVYSc4LTgRxhPAFs+DnH1Nfca+wvoFXBdyulxWD1viHusOtr7jn1M+g+DMmK770f3huZ4zKEf4WtKelp1DVe4M0RqLiUaXECQ2HHbOF+X62fTdIU3NRibkQV8ivDB8Lv4v70eIsEbZS4O5T60B0DmSDEYjemzucTUwY9OyTlzDRAOOtR5AR3ktIQVKSpTS4d/IAxrrs3Pfk3x3fIJ/WvfkKNjxGT1d6cd7OK4E57gT0zA7XiViRZyCiLxjwmXfOaEkPPFeBIOZLqiKkqoso+NgT4uNMTRty2a3Z7MLhvF9/GmNwbQuVMXIy71qh14WzO+uWL11h9WDc2anC8q5ppxppApnWik1ugwZWGISb3BB/7xYLnjw4AGb6zWbmxuaTYNQHoRFSY/WAmMUEo1yga9ETskw/Z4PtDgHaea0GuEVMRUpgzPAbtewXDrKSuMg1HiW0b7kwz57+OAuJ7MXSBdKxiAFFBpVVtB46v2WzfqG1ekKMVMUzlKUCrzGIzk9e8DLZ58GTjplCpJyIPPl+yI4AIp+H8qeLnf004OXIbui8NFpRggsQX/26NljToo5cyWpyjlPlOCLm4YTX8eSNBJhDQLPEkGJY4vnCk3roVFtDFbxGDyFF1xjsb7l1cc/4+G9d/nyl7/Cs/IeO2dwUqEosdbwar/huyhkYbBWUAvFHT1HzBV/c3PF6uOP+NXFKQ91wZ2m5dIa7r26pr64wN57gKhK6n3D6k7Jw7sP2dy85PGLR7hScmKuqdYltTFc7655cf0MUzfcWd5jWa4o1QzpFc54QvF11e2JAFaFlwpvW5yz4FqkaHF2y253yXZ3zX6/wdkGiwhlGqREE5xllQrZX4K8K6O9LudDRTjzRDpPQ8351jq8dKE0gA2G8aa1WBfG5RBY42lE2MnGW2htsAWK6DAYiA1CgC4lzhnq/Z4NHmwJWqG943J/zabdhDE3kllR0VrFdtvi2ppCiJj504bzNqYeD6Qm4F1OohIpD85nAR7Oxx3d3wxlJxhswI5HzeXGXpwc6RwieZGITL8o8C44kyBaBAZ8yDbRQEhN70M0OM7jjMMJG2lF4O5M6zGEMllCKILzraN2htq3LOah9FhZBtqo9ZvJ4G9sGJdCsFqtAjJYi1SSt995G+uD4GStQ0VmdrlcgfW8ePoU29ZIHE+fPOW/+q/+a/6L/83/ujNo55ECyTC939cER5kCXc34sz/7M56/eAFVRUtgiKxpu0icpOxIdQCCAtmhdUG9b0CGunMhFB/qpkFozXe/9z1++zd/g+Vy2dU6T8b6wFhLvLfdwbzdbvnrv/pr2sbEb3pUoaEN9QyMtfhYQzpsMIkSIc1C0zQ40zIrC4oooAXcipXefH8Y5OmQk2FaqmBAHaeqHNTm7vC1T4+c13AXInhIdYeJlAgnMG1QMNR1jTaGquyN9p2SOynfECRvunE66KQAzhWCuaIo9wjN76U1HBuyphjPPCJtSoE3pbQaGwfGkWhJMX/MSNXjQyYQjBRh4/emIz7jGsX1sWkNrUEnQfmAmfORkCXm2JN8qo+1nGmfSo04hk+aW+5wMcXcHa7HobI1X7805xSBM4Zb3u9tCsMkSo9x4uCZKG0k3LbOJkrcAeb1BoXbWw7X1xl8pvDmde2Yc8WbjC21qfSdP6+hKd/Px+6nNt5zbzrf1xk2bhvzgQJ64v7Ud46ldx2PP8eJ3LFmbIR4nbFhjFtDejBNO9Lfvwj+JIF5nLYxvy86AYKwJyLz0xiDLkta77Ba8pWv/xq/80f/lLvvvk1bCGoJVggKIaH1sG1o11tefPaY7/3Nt3j86SNcW9PWOyovkSZ6VAqBFYAMEePChAiu8Rq+yV6acsQ5BvMxbMfrkGA15Xww1eexc+fYHnmT1o0nUzxNnTNpPmrCKD6m9fn5MwWD143Xe0JE4W3KhXh9bEBPPMub7hE4rHk8ns/r6NYUHfn/Vxvg78T9nE/KHezydcoz7YyF6GNrMEUrh3jBMZ3cLzy/qb011V63Hm9yDk2l1B68Fec3ptdv0qbws1+fQ3ryJm2Kjo9peL4vg5Pr6/D69u90853gtcfv5Gs2hTuvaz6F/b7m+SlaPvV8eu5YSvL8mfR7R6v97ajt8TRtcxA9CMFALoh6jagMQESeKa1RNNo677t6snk5lmO0/zYYp/Z3pU1NPcd5aIxjV3v2DbhzyaoChA2Rd4CWBVrqULpLueBci8cS5HjZiZ1TdNqT6px2OBWVT4JQl1MkRQppb0YzoEiG8RS7KFHCxTPF07TBkF3KEIkslMbLgkI45lj2FvASRYhC1lozm1XMylnw9o+KR+cc1kha19BYRduU1KYFYQjO39EBz7ugeRQx4laAEA4rgvLbtJZ93bBvtsh9jRnXv3XBkT1t1U4pLYg1YMO5LQQoKWK69PAtDVgk6ALrQva7uQguBUiFVxqNRlnwNqTJ1AhEqbh+dcHlJz9l/+mPWNkbtu6Uy3qPcBJkQY3g2jbMpEbGwV3sWz6+vuI5mlPheV8r3lMCvKPyiqVR1Crgx8xbzhw89/CVr36AXCxYmxbrHTNE0GUgaX2IZldCoLxGVJqm2WFfvKL8/AUaQyE0MyGDU72UqH3D/n5JKyT3ZgvmumC92fL04lUscRAMvKlkAXSUJW1KvA9pygeGAojpFlMGuB7+Ekmpy65et/WgdMXJ6f2QHh0QSmHxlIVGCU9b79ltNhjTMj9ZInUBJsxXek2zrXnn6/dZLguUkDQujEWIRJtThkPJfrvj4uJicN77lOaVIY+kdG70pzNqTZ8I4WNC+pDGVQtkIVCVRGroUvt7H+uPS3RRIIsKKzU3m5Z9u0cSSxYKAUohVzOWM8nqPpy8PefOFyreeqj57Kzg04/XbF5YzM5hEw+PpW1q6r1jt22ZzTX1Ysa+MSxmBVWKXhe9gcJHxXPQR6Rr+dmVjFApUESl4LgBRnSHPVF/Gvt0UclrbaDziff0o3DMZGwOND9GZVlHayxNa9jXLY3xsQ+HQqCEDDgvJVpF5buLpTdk3OsyBPEoEZ0WJAgZlMkp/nfqzBieDb2xe2D2FlHnIcCPHCvSHz77PV33jM6YBPT0j4CBZ5lISqkI4/zPDPqZeDLouhtq0l/53njgs4/3/FtvRE8/A7nMBXx3wncRed30Rv9mOvvJ0n9E3RmiH1EAU3JI6X9P59iUvuVAZh7J9Adnega7bMY9HBLvQ87bRkcf5/CIEGjlHNYn/V/36Wn+O2yMDDD9d/Mn834Gr+cPiAw/yL+XdnV6jqPtcIy+owsDZMpoe//tCbk14mdvAH0NDyoOn0iwDynUFVoplIyY4ft3c2eEDvbd77lRPIfR8NKB7ibbszlliyufwSN/QhC8bAL/5LzDOhCWYNxVIaW3lKEEjZYqZinxWBtqIdetYbvbc7PZsdm21E2wmxgToomddxBT7kshgi9TKZHLkuJsSXX3lPJ8hZxJZCGQ2qN0MN6VSqMLTdBHS7xLDqCOsiy4/9Y9drs1Fxcveb5+Cc4jpENJj9KBVxImlHcNc+x1FmGtEpxEd+YGmPbP9Hu250UhOIIaY0KK+MYwm1U4YeKZHMrsOBt07/fu3OHOyYrrbTjjRCHwMtROF0LS1ns2m2tq84BSznDOUOoicGtWcHL2gFkxp3UmjENKIGQTPsjwldY+/d1tKz/A6XC+ESuouH6bRGel5y9f8MH9tzlf3uHOyRlPLxu8qnhgLCc4KikprcIKx9wLSiwtHofC4FkJixItey9okFRoXlKjgZtPf8bmnS9Rff3XufvOl3j8+Q/wakXhNcbsWbd7HpcV2loKDbKoeKucsUfwM7vnj589pVnVfP3sLg+14IfOsL64ZHvxinq3oVrN8TXYpuX+nXu8en7Op08/4dMnn3J+PqMymm3Tsm62bM2Gk2rFaXFOqWZgoa0bvPFopVFegZdRPpF4HzN+eYf3Bu8bvNtRN9dsthfsdle0zQa86cpFSpXO8wB5KRQxnCfyaT7AXUaX4Cg85me7iY55Iga3tDYYxVNGlGRgNzbIIyLKQzhPoQV0tkaHlAJVhowQ+12NaS27uqX2jgaH0j5kDhKSRVsxq2ZAQdMGXNExszsyZBjwQoX+EYmjJj+XE7kXBLqCEtFvJ9B6J+L0Y8YfIejk4p5Vi/RZJD2BOCrXdzKjj3B10ZFSOIJjsw1yl4plapyNWUc9rrUY16KqkCkJZ4Pzrnc4JymKwGdY70LZG60pqgKpVRxzdF58g/bGhvHl6R2K+ZxqPqMoSkShQt0IpWjaBq00tg01xbw1zFcL7ouHvHj+DNvW7K3jv/0f/pg//Cf/hLPzMwodiqOfn53jvI+I5Nlt9yAEThge/+wz/uQ//jlSl+yaFusc9a6mVEVnRDImKVZ9Z3D3DpTWGDyl1iE9gRC0jQnprK3jyYua/+a//2P+p//6XyF8qDeVDJbJYQwXDeC65D/++z/nyfMXOKCsKi4vr/D7XRB02gZndNxQHmbhoGhtGz3LCUZy67He4EwQBlJapymGLCf8UgbCH+YnUSoYMVOaJxEF9fw9733nbJAOaSfCYYyzYZ4pJUFM04Jpw8SliLzMMALY+ZBy3TsfBSYCQ+6DJzTpWRcIvU8KJwQuHhShtrYKEfUIlFQ0TYPFoKPh3sc0hmOY5PPL5zWlGEyG3tywNZUWecrokv/eHbyj/qf6GY8zH6+UUdkmgnBeljrzlpZd7UQ4jGpMvzvn6KhRt8ETMxV+0jpNGVjGfebX8vn1SlcmW4JJDv8chv214TfG3xvDevJb9ILPlFCQmCifkX2iUksEehsM5VNqhwyXphT4x5S6uePDoQLUd3v60GAR+0wMaTbH9EM/i4N3B+PGH1yL2zYKyNDjxnSbGtukUDiB91NC/20th+fYgND120vl8blRH87hRe/4M7VmPmhEM6GETkyPs75FUTG8lgs4x56ZgklqueEwh8FRoXrU71QU3dR3OlWUEF1qv3B92KToI7289/igxcEKgZ+XXJqWt957l9//n/wLvvjVX0JqidUhriGqdFF1g1vvWT95yc++/yGf/PgjXjx7HvBXgIhng49ppZLDT1ob6Y+np5+iU5P7cyxopmeye2N4jtd0eu/y2jVNbarkwdR8kmFlPJ6h4Jz2bC80iZjiLc2v+zfDjykY5TR4fI7cdk75DKa3wSXvO792kHZ9QNf9IfUVhzQkH2c+pzw64jCby+G5NQnj0XzT9zrhAPFavBjPewB7CA6Mo2/lzjhC9OuZUhw7H1JBdZ8Uh/thzAeM1zwZDbsxJZh208giZ/rBDc6oqf14jE5NnQH5eHJYJaHed6lyEzakn+PnUNdnOtCSABfZ7JCOl56ejcY7hl8ycOZOFwd8iOgVaOM5H+Nhpn4f49F4/QZKwfw78ZYUiaWf5i/CxOUh7zDFb0zA5xhdO8Zz3AaLcf/5u1N0KH8mj/wbt/HzIi08h/Snn2tIWTebzYKALRwyGjq6dzoy25+bHS3xYa847/AuGPGUVGGPprG6kMYyL4swhlf3rbgfhegdjn/RNq8KpA5GN9NYts4hnUesYFZJfOEpJEitQnrookApgxCxnrGXkQYlQ8GhnCCIwRg5bYj/5Ss0oJUdzRIDGpcUSEEBGwweSoLWkqpQiLLAK42wjrKQVF4HePlg2VZKUVUhYrdQOih/41q1wjOTFU56vG2o3ZadNUG+9l0hKAQqRq1lZxUhktQ5Q9PWbDYb7PUNTd1HnCbcDBEjvuMj85ImdDge6Eepi87hPxjWBChNUZQ4CyerFWVRBqWNVKGOvY7Gw9YjKh9ST/7kJ6w//inu6gqjKtrdjna3pdSKRgv2rkV6AV5xIla8aC0v20uemw2rk1OWZk1dzPjUtVxtLrkUJV5rZqalkC1WKNY7z91793n41ttcGINrW04WS4RxqNZhCsL4LOzqlkooisWK+rPP2X/+OZsXj6nQVEowUzPKYo7SilaBuXsn8pbByL7ZbLnehlTjs1koM6eU6oIb+hZwZuzc2zmPjfAucfWy0ChdoAuFF9C0lpOz+8wXK/AxkEMGBVwoBdeyr/fsdju8D1kLjW2Dsj7We5cKvvCFdymKihgbEKLiOx4rRrB5wc31hs1mG8aSnJtT5gmGZ2J6ppNV8tlPnAnpLJJSopWkKhWlLgZ7MMFKFXPK2RwlZ7R7qF9s2Td1SL9emZA5AovUnsVMoQvFqSi4f3dOc+eUt956h9M7r/jou0958eiS/abF+0BvnBNY29I0gu1esNmUzNcVJ6s5i3lFVVUUhaYsy6ALglhHOtWJTFF00QDoTHBc8g4lBUXhgyFaR0OL93RnnY+71stoSArrYIzpaswHXUrMaSFSdFPPTweFOZgYKd7UDaZpccaBaVHeooRHS0GlFWVRhP2sVTB6C4GzUYaKOjipQg1QRfgJbhByits90iSJRg7W3Y9+H5yNPb85MLpm7IrP/i9Eb5ROxrbBWZvx4cNhp7d8N7TBWdf9T3TyS+JX0nMu4bgg6ngtzvZlFa11GOtpozGyNi5kPvACj0HJkBJa6WGc8DHefnA/GmPz58fvJ/gc43kG8s147oNvHXJyt8qPcZ+H/RA69C4GV7loGDcBPuPsmJP9iv5s9n7I/464tIgDIo6558RzbjdEnYqOb+lgAEgf4RrnHcZEL1+k+UB3XSA7oIUx9adz5lp4CCYhMthOr/WkDgXwR2Td7nxWKvBw3tF20eKQyrj6CYflg7W8ZZuP9Ty9XBBtAUR+Ao+XQwcQ0TH0/fVEO1NN5P4MCeNsncXXnqYNkdH7pmEbI8W32y1tG6JbUxkLKYONwvskQ4co+qKaU86WVLM5ZVWiCoXUJP/CkCUDoqNWWiOBMx5nAo+8WiyYze9i3Z4XL57y4skrPCJSSY8SxKhxG3JmeALffSCDDvUAqURP+nusJ0j6k/Csi9HxNavVIju3k1wOeE9ZVpyennC5vqRuDTO9oG1dyO6jNMa07Lc3tPUeJc+RwmFsKEGrC8nJ2Snndx7w4uJZ1PNkPEvk/7tgR+dQMZtrWm0f14JMXk/4IpXEW5cknmCfMoa6qWmdZTWf80sPCj579DFUC77kHcq2vLCGz8QMqzzGZDKxhNoZfscseCH2rEVL4z3naJ6xYyFgf/EZ289/xH79e5z94W/w0//7XyP8Eghn6ntU/L2Hb/OXjz/mwXzB3cWCay/5zn7DzJVsPfzNTc1Vu+bvvfuAR8rx9PIld1+94Gy34VQ/pNwqrndXPDw74f7Dh5w/O+fHP/sJbXuKanzQNpaK+WIZHBtdwumQJbooCmblHKEkRbQFeu/Y1zvatqYoJI6GvVlzefOcy/ULrrcXXG+v2Ow3tLYOhl6VMmj0MnWQd2SnR0l7I3i8KTwWLDHTsu94QWujY0SXXTjDURdobQoSTJl0RbJh2uDYZ70PHnY+ZF9ojGW7bTDOcnEhmC0rZgvNcjnjZLlkVi5Y72oKpfAUICTGpmzEGu9ahsdEr0fsZDUR9V+ZnIcY0tSk21JKxfI0stNfJe1DOAvSb4l+va55EB6lBForrJQIpULN8KxchM94hta0WGECXZJRByQlSgqkljFrg0CJEl8otA7lk4y3CB8yjr9Je2PD+Mn9t9Cx1ldgfAV4gbcCLaqASDLkeEcJvJQU84qzu3d59eolddPw6vKa/+d/+f/i3/ybf8NuX6OUZD43WGdRMgDCi+DZ0FjHn/3N33K53aOKIjDDHqQDS4i+CWd0TF3uU0SxZ++a7hDEebwJxKyrZ+wFWxw/+PFP+f3rG1bzGdtNqFGOkMGT3TsKGQ7K3X7Phz/6MY1zGOeYL5Y457i+vkQKj2sbvC2RKkQktHUTvUIgRfiWpY7e7oamDnPvlIR+aETJlcwQES7VMEtRJ3GDBWUfXX32dC8dGHVdY62lqqrunaCsiHUo4wE5YNaiBwz0QiXQeXGqEIIQvpmU1QTjtwCsNaFOdVQqhG84lJCY1iBlSGWVDgglZUhZJ4NB3DsfvUjC/Lu1pP87vTs87GTnDJDgmaLMx8aBXCk3dcDm/R+oJicYnoRbYyVx9298x8Z0xQjPbFGFg9IYBIog/NnJMXTXokKLnBHtITP47ni8U4xiuj5Q/HPYDvrMYAV9Tcnhd4ZwmlJcH1O+jtuhs0L2rxSMI+lF/LwAhAuREp0LTTbX1M/Y6DIlhIz/njLqp2iwsTAzwC/Xw6Zb2yhZCsIZTGY8TGMbGA0Yn1+9kg7AOwtCjc+4AxhO4caUsS+9M7Ve4/mN330TBXuo2Td0phD5vwmOWbT+2MgBo5Rnad2IfGdWTyateb7/xylPx0Lzm7bb9tuUEJ7voTEc82cPBYfQkqewj8yXigxQqvFHElyt7xgyL4Jw45TACI8/W/CP//k/5Zu//feCl+CsoLUGiadAIK2n3e+5ePyUpz/5GY9++BNeff4U15rgaJUALcDLqBjMaavzFIRvy9Ea5r8fo9FTMMsF94HCOjzwWjpzG96O4Z/6yLOwjNd4bBi5LRp9SDeDp2rkVMMZmL45eu8YDR+PM/93fO11bUqon3pmKqq7g8uEenBKYZj6n8p0keZ7G/3Ix3HIN03Q3gzu/XinjeJTNHJ8PnTX5OE4pgywIvuvkyZ8olG9Mi+HwdgZYPz9fNwdPc0kk87RKruWIDWF78d+H5/hY/rrvR/sDYh44JOisusIkmGhU80NcW78XZnSQEdhKc2ng6/vcTJ/Lx/r1NxyHBEiRGLkte7H6zfe77fhZt7G6yT6pR4+R1CcuaQ2Gwi2SfEZ5J4p6VNOjDPfI+neFN3I3xvQYzXkc8Z0+TbYppbj7RQ/NT53x+Pv6JhL+HIIU++DIsq6lJEsRPzJ7jz03U5IKuHu2xF2KSW2FDHlcTJejfgSEe/fdp6nPd2h/Yg+/bxtXmmEKkDooOIWgLPU+xrhm+D0XVikvcJYcE4ivCKZtYWQKKGC3O4tnr58WD8PgZRD2SjBL+y/7FkxXMOQhrxXe3c8aVSBCwQ4hxYhnaYKVnKEdIiywMmSkB7bdrAqtURriY5RHUKAsOAcaCGo0P9f2v7sV5bsTOzFfmuIITP3eKaqYpFskk2yB81SqzVZat+WZMGyDVwDfjbuu/8hv/nZgAHDMGAY8DXsa1/pwrKGVre6RZEssgbWcOY95RARa/DDt1bkytiR+xx2t1fh1N47M2KN3/rmAbfwmD7iNx0Oh0916STNaUg8n8ioVksGNqWl7mVjLUNd01nL0OVU7PIvZZzftyh3c0oD8v0yKDGUpXTaxhp0XWGrWrLLaYlGySntg4et6+m9x2Bp25bb6y3P/82/pf/pT2jWN/RmRVzfQNdTLU/YVpoXsaePoIZAZVtexIG18phmxdlW86xq6deRLmpWZsWV2/D57ZpVq4jRoHYD7k3P9//lP+D8W8+4/eIb6m1PdbrkethQG4moi0YRNEjKn0DUlv7zrwhffsEpHU/UBZ0faCpDFRUhKNb1gpeN4WyxYLWsWe92fP7V1+x8NkLbUZ7JhvH9/c3GiH0d2BAMSjmGoRc9hd7jgwjJUdaiK4s2RiRjq/jgo49olyuGVNZO26T4rw2bmzWbuzu2mzVKKWxd4YcOUSyKsfXZ4yXf//63IUq9X61MkjMz3QGiInjPixcv2G47qqpGK5Pu/KHsluGlvGtKqzE17x6338fL1ooSt6oMi3ZBVSUHkQL3aVOhF0tMe0LAsl1DN3S4GKmbyNAP6CqgTEC3A82Zpa7TuK2GZkFzatlGy9urntubnt26I4YoTuW5ZriLxC6y3fXcbXbc3K5pmpq2bVi0DctlS1PV4hRCGLMPyb+9niAEqQlqDLRtRWM17cLK2jCJxqToTV/yNulSBoXrerpUQxRSRhBrR+xDhCi2ClxMRljv6Ac5474fCM5TkZwrjKGxFdYYrLWFHAxaaSqjRv2nGZFRMpYnhbFSShTc3OfFp+c6KuAVex7pAN8kec2oycf3aVIM2ci+571jpLhb+cnjxr7DZ+/zfVPeYB+dl/a6eC5ECZyZZpTyfi/XSVSl6GZDCAxJQaOVwhqN94CxLFQlqVJRZGXlMZmkXEe+r3Ntfyb36fe07xhFL/2QLqB8Y+Tlp89kHqcYdi9/SCaDGETP6p3Hu+RIkOF/Rl9JDERznJ87+FnIZqMMcmT+x1qROyi9FIVnmurCYuZR77f8aTnO/ln1jhmU78zwv6XuavK9TgFgVXLMQimcB+97wQduECOV2wdUHbu7aZB3ygAPydujDqOEZ62I+czyR6OeX/Chc24sHdv3PXorGUEUol+W0rI9266nHyR6UmGgcBD0IdAPEvinVKCuDc1py2r1hHZxRtUuMVWNsQa0RHWT7C7GGHSlpbQqwk1jIyYKj92cKNqmQdVPWA/f5fk3L7n9ZgNKnEwrA854vFTbo5RkHtqzWZhmHg4A1us1t7cNZ2crqloM3aMzioIYPMYonn1wydcv37LuOmAJAUxlpbzK+pZufcXd1VueXD5F0ndHlI5YDVo1nD36kJdXb3BeUrVbY1E6UlXJNgXEBPU20afR2S8kpPcutYxKcAD0YeDq7gZ10fOby0f837XmG3p+UJ3xkY68CDtqf8tbH9ni8MAdgV3s2UTHPzn7Hl/EO/4794rPhg2/6U94rjd03rOqKpZXt/g/+gmP/8U/5Dv/p/8zX29uOI+Gbz9+wv/qn/4+5vPXfOfpiiff/4jt7R1/9N//e/5mp/nl+ZJ1teTt7ZZw/Ya/cX7KR23FT/tb3rx9xbObN1z2H2OCwg0bnFly/vgR3/34e/z8V/8F7ZWUZbYGXVWgK3TVUutK7GauR2lNrcVBWGvw0eEGT9d3XF+/ZYi3QGAYdqy3t1zdvub67hU3N2/Z7DY4P6Arhd84fHBSQimKU15ldXJqNULbUtnjFLMvmRgGcegjxiRTMdrSQEpXZQdMtGRllhrZcsQuBnBhxIFDckrN99toQ9eJPcj5SO8C/eDYdnC7HWiWFSddZHA11VmgVhW7nePubuD6JjIM+9IlRulRD3T/zjDeOqWydCb8zCivJlScA2fH7NMj7dgb2hWI84w6jr/N5PMDvUsqOa11jdaRAXGcdYM7sN/Bng/MuMhWBquVOFprjc9yaWWo6xpto2S7qEC9X4nx9zeMV1U1Ej/vAzopHLLSPYQUkZGMO1mwXq6WhBC4vr4i+o5f/OIXaK05Pz9ns9mgtWa32xFtTrftMLbGWsPNzQ1t27JLKUBiDBh9mMJ7TtFZKt6HYWAYhtFDOcaIdwO1NWy3O66urlm24vGqlKSpI9c8j0EEIgXrzQ6jLBovvqFKS00pbfAoQXxKyz5ET2NrlIYhSBR9FyLRS02TIXmXQKrvzbySKCNRklBRGl9L5ZSkAjw0CJUG9PxTZwb7CN8RQqB3PbYwJpd95lSGJQOfv8vKxHLvp6mLY4xJGPaMdU3YE/4yeqRMs/iQcWGq5CvHnEb25jmVcyzXmZ+djpH3a8o4l3s8vbgHStpYKlFk9/p+oGqapAgSUSZ7aj7U9uqmLExl9HRfAf0upqz8+eu2zPxP7+FDrdyXOUXzX2Q+0zZVBHNkvHJux+b7Lgb3oKmRXIx9zKW3Lo2wpYE2vxOVuofTprA6neuxNbyrlessx3rf98s+HhJY/+JnOy/8vdebeX1RjLZT/Pj/jzZV7j/0zINC94zAXt65Eh9rpaTWTXa4KgTgSBSjtdU4DR0Bmorv/+5v83v/4p+xenSRaogbVAjUxhJ9QLnAm2+e8+Krr/jiZ7/gi5/+HOsi9E6c1XLdxLjXJJeCcsbro2PaZN0lDS9hcW4f8ztlX+/av7KfKS2Ywv60v+nYmX7k7+bSPpcp2ucMTlPFun5AgXOsZf7gmJLr2Lr/MtoxnDieYwzEoA72dVbZ9J70o4SPdz03d4ZM8P8U9rJzQkmz5/DCHEyU68t8UMl/zc13Dvb33x3e5/Kd6X6WaynLcDyUonrf317BmOE493OslXQh38H8+zRjwHStc9+Nz8zg9bm7/dAtySmMH4L194X/cj33z2cPJ/m85/Zsyju/z5gHf8M9ZUmeV4xxNBxNx7nHRxSfWWtHGWgONx1rOdX4X6RsxHSdczLK3L3JMDbyUUkIP8ZnhBj2pZlIvNW4R7KvYiidMwjsIVErNUYdTZ0Stdapn3mcNqUHf1lN0vrm1OASnawIDD2SilgrrIl43+P6rUREeqHJxsSUJjhFRQXhU0sZSilxGFAT3F3ub8ZOKkfM6wk+mpEN0+4CUdIU64ra1Bhbo6p6zCITdC3OIMGTVfBWa5TSkoJTJRlJa1CGvocQBiIDTnV0YUPnNgy+H6NUM0uiyBH7hi709LHHVHB6uuBktcCfXbK9XY/RpyNe9AlWkqUpxpg8V2VJqljroZJIo22KeKwb2uWSumpQQD8M9L2jG3pi37NzA4MO2FXNV//637P+6U/QV2/QKHYxsOsGlLFcx4E7P+BU5ElzQrftuY5bQhTnRa9hEx1PouLH7YplVAyx569fnvOTeMufbW6I2mCpqNqGb//e3+C226K8o0ZBMlrRWEyI6N5RRUXdtOyqmtu317z55Of0X33NUtWsYk1P4JFVtAG6aPjF4zPeDh0//NZ3WS0WvL665ouvn3N9fc1isRiV0xkPlXJNhpUoFxBltESNWk3VVPsoPoAkR6uo0dYQgW4YcCFg6obTy0tcovtKi3JSGyBENne3bDZrvPcsFguUknrqKiqCC5jo+Y3vfouTZcv27m7MEEEUZ+OQeccQ2Wx2vH79dlQckjIElvdq6jy2xxExpX9nfGfalJJIdVvpVCMxp/eO4giDKN2rqsEslzilcX0kDJEQK2qrMRGiH3A6okxkaS1NC1YPqKhQyqAWlpuwo9cdwShMVWFNjXM9IUq9ypGdQjF4cCHS9R163VFVW9q6YrloaFPUuNagUypwOdvMx8keVBZWJ5XUgGwttknKUZVLB0a8i3jEgIOCGOUsh0FS5e52PTFGMYpHjVFilADEETqIk8zOeQbvGJxnGDwheDFwqwZr5HxF1yfwuO1dYcSXtJyr2tIqULYZHa/2eFJ2JsYIKXtiIYYlHdCIPUvb6KysHUIoHMUP6fmU5u/f2+/1XleQ+0iOCcnZbnwvxtHBYtpPOadyrLHvvKYozhMxRbdnOjCWO+BwTmGcYxyN494HXNBidEr0xYWArSsqo8V4lrIlxiJoptR35d3NAfeKeV70gD7fu3HzbU5uSMc6/h9I+tF3NLXfJ8b9kXsx+MDgJKvB4D0uyL8DfriwXkhq8JwHrhwizVHt6fyod8ufFU5GivxcTPhOH4yTHeJG3jz1I7hM5Imsacj0NiQYURT85vvIA5nXyns1/f4BviqOa7kvr011DSFGBufouoFt1zMkA1VZOqfkUUs+B9jrPLgPH1NY268rb6kaa0sbpQkqEgjkbIe5ZE1+zxh1cCdzpox8ppmOhhAZBs8wOHrnCVFJ9qB6n22n73t2vWSzJUo0aFSa5XJJXZ+iTIsLhs4H+jBQKUBL2mlrtQT5GbB1shOEiFKR2kSJxDY9Hk9zovj4e0/53m99zJ9cfYLbecneZDRWO0Kl6HYPlbDK3MDeaUKpw3Ms+VSB7cSXRtGxr9eSzeWyvkCNTkEJZ0VPt9tyebni/Kxh2/WEvscYS+8GTNVg7Jph2HF79YZuvcEuV+hao43cFT9Ezi4/oK5/Sd93EuSgLUoFjFGHNESLA0OMceQz87og3oOZmAWWjGdTdmQPvLh6w+vVa378rcd8/+Pv8PVnn1D/4Ec8O12y2N6w/smn/LLv2aC5wXMS4cNY8QmOP7Ebfrtv+X234swN3LHmHM1TdcKZg/WXL/hZ///in//X/wt2f+Pvcv2T/wE/wMnlKbSO/8svf8I//Ht/He8Cr17fcNsP/OOn3+F2+5ohRH7Q1ny0bPlic8N3F4/4tNJcXV/z5vUbvtN5tlia3nF7fcOibvnOx9/jR89+wM/f/BR9WqFVlCCxPoJVeA/eOWhCgr+auqnwXhxEdv2O7W7Dzc01g7rh7fUrNts7+mFHUI7N7o7tsMNFyZTsvDiOhOhQKWONtoq6rmkaCfLtB8+QiImGlJ1mGGXLpqlT0KUnqL0zSxQiS4zhAD414FP9bJG/4r70weBGRxxjAiYK7xQBrQ3WwkCg9wO7my236x2vX9/yqr3m8dkjGDR9Z3Cuxtoli9bQbXdobQ5sLcdE0ZJWzHyZa1DJ3Sr4HelP/jb52bGPslzQXgOtdM4sLf9ElJLU9+i4d4oLSdcUFSrvgRuITmQy5dLUTCYpmsEPKCwYi0lOJN57MClYTKuRN3xXe/8a4/Zwk9NyRi4gZuJn1N5LAUXvHMulpLK4u33DbrcDROGxWCxGpLHZbCT1m06eAkqQf9d1qHTA3uc0BGokYFlRXSKfjHC89/e8kkWZkABXpY2LsFgsiDHgQodPZzoMURyEkNQGQzfgB89uu2N9cyt10pKiIqAgRJwbsLYieGHSghbhxymPASpr6VJd8uClpkDpWTdHxJXWIxNSMkhZsJT08YVyZ6LMUEqJ525pqJ5RLKHuMxOlMT6nrNh7OU+J/v1otbJNIzKrqjogHFnZOldzPEfqTVs+86lydk7YyM9MDdpzysT8fLm+6ZpKRf1cdNg4ZjJ+a2PQOhJVpO87qWlG8raMkiY/hPtRkgdHVDDzwljn6JestNp7IJfnMu3jmCL7123H9uuh58szeC9l63vgsmOK0vTLwX5Mvz+mvJ4VhObuTdG00gcEJq93bm73lY6H700Z8YcMDtP5QlYCv/t8RuI9o8A5Nrfy3bk9fdd6y88yQzv3zsF4+r6gM51XeZ9LOC8Fw7IG3Nz9+MtqD+3T9Pv8zFyb4tVyzlmAVEo88hSMkeIxioIhK/mxmqAVvY50KvLhD7/HP/rnf8iH3/8NOkDXony02qAj+G3H5uqGqxev+C9/+md88/nnuPWOOmgpu5Fwj/dB6iElxmiqVJ/DseXapkLONBJ57n4e6+PY3pb7+9B3D91JKCOZ5utwl8qj0ng2neeh4K3GqIBftx3DXdO1HSg1/oLtWPTnCJ8hStagCa/y0PyPwUfmO+Zw3xQ/wmG6daG96dnJmNOsGFOYnbbSma4ct/wX4lzWlPk2vcd7ZdA8fTq47zP4tvz5vgbMh+Y4deyYG2+OThzDaeWz5d4LPlYHNPrYmO9aS4gP34U5vHTQR/HZMeeCaR/HjOJzsPm+65F3Hl7H3Pzn+Jm5s3nXvTwUphU+HpYD+fPikGNywbtwbvmOUfezVEzfy4ricc352UKxmO/ZHJ06tr4DvBLCvCJhMu+/zKaVFQfsCEpl438kRoP3mmEQ43hjHqFUD9GJYkd7+Rc9mT3VCogz8M0hfI9K5mzMUdkItFdAR1UoTQoV/f7OMxpBjK4wykoddFOjTC1pwZUoFEXH4UG5vRYhdSimtSjZOUw2dCuiDvjYs3MbmmFHl+plqxSx4UdjkPTjomfndmjXI1lME80wRpwoFMkIm3B6ennE826abaTk80UW04kfilpjTC8Gu6WkfowxRZkEICoCAac93sHrP/ljeP0C5QaC1vgwcL3ZsqstnfLsvCdoWABnytKYwFs/0HnHBS1/dbHiZHfHygwY57l1Gz48PeEPHv2A1z/5Od9c3xBMzbMf/IDVh095+/wVxIhpDL0KVAFIziXLAGdKUwXHm2pJ/6tv2L1+QdhuOVE1ixhZ2AXfXlWcVjVvm4Y/W2qM95wYQ3Ri/O+9Z9h11MsTsgK4pFMHNARGPj/L/HXVUNcVw+DYbjejcVxpyYAgUdqaru/xMXJxtqRplgxelI8qOU1VtiJ4x2Z9R7fboZSibVtCENiyWtJka2v48NllynqUjHUJjrPGTGtNP/Tc3t5xd7eWwBGVjeLybNaXlO0Qx+xhe/oM7J0mtZGo8ao2klZaCZRJHgQw1tAsF7CoCEpqpwYiSknqS5UyKIh1K1CpCq2gsgaLAa8ZBsftdseb61s2m47gwFpRPlPcnQz3kh5ZJuIJBN8RUpTrUEtwRb6jKiMKJCMHSUdR2RprK6rKYis9GuqywVlUdL6IOpfxQwx0vafrHMPg0jt7HjKnKg5pvS4GgvM4N0j63pSetjIWbWTcCAyp7mzfDfRJv5h1U8Ya+sawdI5FCDSxoa6qpH/ck4LsRDNHgw/4pagSbsoGY8a7IfhEIj3LfZ/jOR8aY+770bEkf4/w6+O8D2Bw/OPwnfR3eSYxRomKi3taesgLlw4SkK3XQjr22YOEj5OxlHMMg8f5iDExJakXuCbRowxPY2dFC/uKjAf7mGE4fy53tnyu6HOmjc+ne1g+mtz6iv6mOoBsPI6Uus8QwpgyuO/Fcarv/ZhWvYQPKPnPiFf+gBfZ03BGugyM9HLPwxYyt9rP+cBgPvIBxfOJX88vqLHf/ToP3is+y9yBUilSOM9bTXiv3P8Mn7e/a9z7LsPqnASUYTdnFfVBHBC6YW8Un+qLSpmlvE/7czvU783pEaY872jmVWSOhoSlC7eZKS98n7cvdRAyF9K/ODoVaK2om4rTRSvpikNgfafZdUMCfrV3IIoRMLgh0nUD1U7ROcVSVyiTygpV4qSlFOL4Fxjxl053OdAzJJ6uPbF8/P0P+PKzF7z66grnJbCwSnp+yLx4HB0N7ssAqUymmsBW8bPkV0HsKiFA1w3c3W24vLwc78KevkpE98liyeOLE27udtysO5YnK7ZbKQ9s6xrnB9Z313TbDcvlkoBOwZGyJyfnF1xcPmIYdnRdT4ykQEypaa51lnvMwfnle7M/30ImieBKGTQ7GWnJrnu9vuPN5obBBn778Uf8x0/+jFcLxebDExpn+fanLwm+4it/xw0OReQRhm9py39YP6f3LRcefpuWF6pHh8gzFFVU7OLAK/eSm69/xeO//XtsP/sjrm9foV58w7/7Vxturzr+7D/8nI1VvNzteKksm9sbVF3zVFe0SrH1jq9ub/jRo6d82LS8vL3hmxff8Nu3a5qzD6jiVhzUGs3i5JTvPPmYL1/8ErNcoa1EbVvdUOlWYt41Y6YWpVSqIb9js12z7TZ0ww4feu66W9abNbt+S4gebURqMKbGR6n/3fXibGS0pqoslTXUlaWpaqy1yf7kD+QYueMhlVGxVJWEHmcYRulky4uj3JBpqvhx7WUIkjOXYu9kJKUT0/nrdBsyz6YT66a12Bh9wLmOMGj8oGjNKVYt0aYCkrE+eAnh1SVeyrLNVL9Q/H2E7OW7J/yO2CyncnvmJw4+z++WY5VgT5zg3f2YWhtMVaGJBCe2FU+UzCkxZUVUBrTCqwgGdCU8fNQpRb1zmORsWWnJ+vM+7b0N4zn1yJ6hIgmR8lk2VJeXXUWk9rj3NE1N8Evquma3242EJofnO+eo65p2seBuu8UaO0Z7KxNHRiLGkBh2f4BkstF0GAZZWE6plJBhfl6i2j2LpsYNLkVdiReVUuJdpQOJUEaMVvT9gDWVEBDnsErh+4GmqagWC6y2ECH4SNu0gMKHgDUiyKCjZCJRAR8cXbdFm2ycFU+sPaN5qCwtCXLTNKOxP38/MlWRMe+/CAqChPu+F2A2+7TrEY0Lbs+kZkBUOtUmuF/ji3J+6fly/8d06wkG8twlZdJhakpxcGBkRqZCcnZ2mCrEjymF87PZAHGMeTimuJ2OU7aMuMqzKVOmlhGE0zneY47Iqackk0GdUkGQHDzEA2lfd21WmTlhFoWRKuc6mXv57uTzrOi7F91WrPmhfS/3ujQclHObvpP3rYTt6d7fVyjeT+19TIFa/j4aQrUa6509tC9le0hB+lCbeyfjppKBLvd8qugNmVimNU6NcHMpjHNfZf+R+4LF9LnSCWMqSE8dNKbn/r7rf+hulfBTfn7svs7drXKcqXF/5qHkGLWHjxJvHGvH4PTYPI+9N/f33Pqmn80LDHLHfAiYNIcswIaY9FZa4ZSk8lGVpVeR5ZNL/kd/8I/40d/+G+KRWYkhwYcg0SW9w+16vvn0Cz7/2Sd88ckvWV/foJ0jDo4QFSo7YiVloihF4oPwVtKBcm1Tx5G585saMOboxrtaeX/KMadwPx2vbM65e85i0/tTVRVN07Ber+/R8HyOJR4UYd8czOcYfis/Lz3bj8HmQTTWXxK+K+lgOcaeOT5M6fwQ3n4ItjPvkJXO5Ttzfc39reJeiZfb/Ywx83h4bt3539QJL4QIcT4F9xR2p2ssYU/S/N6n/9N5jOubzLvEgXNzL3ZnFELK/Z+eZ9nKaPgszMxmOzly3iUeONgjvZcr5vbooSbrz5GEh3TzGC06in8nNO8YDogxcr8+7v1nHhr7ofPJd2iuz2O0u+QVyv5U8Wzuv+Rfy3eZPDvOSd3n3x6iaQ+te249x74v3y/HOIavy/mJYqzYn7I/KIy8exnnHq6ejD91uHnIAWV6Hn8ZTaks04LSEaW8KCmQEl7eG/pBUasVMSyJYUNOBKiVOOcqJQHXIjKOOyF7l8aJB5/mfUolWwpNRxyfLaC1UHrI2ezvtuBIjUrGTK0NSlt0Ujp5klN9UWcgK49ilHqceT5ZAZMzRQQcfejpXEdfRIyT5hcL654n4kKP9j3KRYJXdFuJsnLO4b0b67v6wSF1PRnxw97YmfBvmqMP4mSfYUQrie6xZmDRLKhtjap0QS+AIBFbpjJs395y/V9+gt3eSWCAAu96brc7WK0YQsAhPJ4JgaWC1tYMsScGz4fK8nux4ZV1VChchD5qXm03XC4eU0eD7gL1ScXHP/4xsarY3t5y0izRVcUu7ZGKkTpCqzW1UhAGogr0X/8K7m6ofWSlWp5Y0X9857xmWS/wuuJGOc6qFQtjeblec313R+8d+HBPToaZsnH5Z8FjWGup6wZQ7HZq3HeUTpkLk3wVJSLl5PQcW9X03u3vuVZU1tJv12w2a5wbkmK0SvJWKr2mAifLimdPH+H6IfEGac7xUE7uu4Hr6xu6rqdtF6mechzhFhCtaLHEQ/1A8dzBug91DWKQEMO4NaIlzTWztTHUbUuzWhKbit6LwSP4kOQAjVJB8IUFU2kaa9EY2qqi1pboFMOw4W7ruL7Z0a2dKCKNlsj9seZ1HBFDZZNDAlIe0Kc6mc5BTyTYgAnJgDBG+Kpx3Tatp2mSYdyYZFhRyZlXj/iYEUcnPOAjg/cMyWg4BhTETOP03vlHa0xUaDWkO5mju5IxNnoGr3A+MDhP1zt2u4FhxAGemIIW3KAZgqcPnoV3NE2NNRaj1RjNnBBFwlmFETpvX9xHbBPEGHbfMJ70ehzyUvLdvg+Y8AwHfRTnlW5V5JA/SFMr+hE8H4t39mNn1VM8uBMZfLPcmUuiR5KCOs8/ZkN2npciRAhK3NRF5a3wITvzQ/CSWcIHT4w6dbyPnC3ndtj2xq/p5/vv93SEcU0Py0AHPM94F0qF2/6jcdn3uksXqKCRIQQpUxmjRPr2A10/MDiHcwHnxOEqw41SkIOpQorW3c9R1lfyVOO8VTZSy/tq/Ls0OjKJJFf3+lTjQOqe3m/KzymVafrh+yqdOwefxfGYYmH8369rvwbUfl7jM8Wf5fvl3EZZMEZciBKZPwwjPVaJtxnXmd+7dw/jSMf3fOG8bJo/H4+h2NPMS+U1Z/5if9cfloXKNWa3AzNGkQeU0axWCy7PTmnqWjKqKMPtes3gsmwc8G6g7zuiD/jBM3SKvlO4oQJVS6XKXD0iw4dOgXlxf34hOKLyUo9eK+rG8OF3HvOt7z3h9uaO7nbABS81vJ3HGrksIQYpXaPU/hwO1nkoR9yD7fy72tseQOGdZ7PZ4pyX1O9KJTgT414MnrpSnJ8vOHnTcHV9h8nys9bYqsEOPf1uw3Z7y2m4REcj+E0LHQzGcn5xye3tNbtdLw6g1hCGQZzyUIk+SVkWCqeYEV4OrYV7WCtge3RIAXZu4LrbcOO2fHt1zv83wqebW35DXfDt05ZHpyt2nWHtd3yN4KtKwfeoedlv+ePY8bu0fE83OAtfDTuaCBWaHtj2a775k3/HX/n9P6RaXNDqa06tRvuGD0yLe7vjc3/H8+gIpmbYdZh6xUJZuuB443redB27wfGBPeXlZsPb16+4u7ri4vxjKWEwBIbBY4zlw6ff4qw+w7QrdCuGTBMsxtQom7LlmCLrQdfT7Tp2ux1dv2PwHYpAN3Qp2HVfAsoiZ+S80BGXss9Ya6jritoaKrtPFQ4cOPSNzi9KYZKdRjIGhfGZDJ/jqRU8ntZZHtAjbycXL31usmedGvmlGEV3JZcil9iNUsLFB3wQ/LXrHVUtpZqNNng/F9RwqOPI5VQOoEwdQmD5UyklfGDizQ5x/B4mD+5rcScP5Ui1X3+CyzK6Pm+d4Es59+j3JRystaLLNgrSP2U0yoBpLMYalBYZzxIxlWXZVjSNpar0Aa18qL23YTzXks5IR3FIICI5GjtzRvK50RqSEnu5XLJYtNS1pCHo+x5gTHVeVxXODeOmVZUYwN0w0LTNyByPxmD2XsV93x8IE9lAnpXgGei992Ma+CzQ73Y7tEKMyMaibYXWhhADu/UaY6X2WWU1XgPBUVtFDJ7oPUPfYWqDNpYw9HKI2hKcI+JRVohPP4gXiFZSm8oonQzn+sDYTbG3AEPfUzU1wMG6994tBcOWGa2J95tP9b9DiOKREgUonXMonb2d877GMXI7p/w4iIgu4WKGEcoXs0T8h8/u15GRzDR9TX6/fK9s5eWfKsqmRvry3akBvpxbhqvsDTT2OUmzmvspFXtTRd3UYGOtxQ+9jKGz40aqVZHgMuJHWM1rLKPbyzH3cxOv9nGdBZ6am9dUCX5UISmy40E7PMu90HOfidkza6XSbO5c3z2nfUTG3BhzazumhL03t8nzxxT6U6b/2J5AITAdeWaaZWB+bA6MOXPpnKZzzJ8f1EbicJ/Lu1ri0Nxf2f8U3mfXeuT8y709vsbJOiKzsHHQbwhjiu48RulgcGxv8vP7SJMZganAIe+z1odgrfx8Lrr2XWOULeOCMvXk9B2ttTByXlLRkCJVvIZQKbzW6LrGGcXv/J2/xe//V/+E9nyFI4DV4pmqDMoF3K7j+vkrfvrH/4lvPv2Ct89fYqKiUhrtAtGDNZqogqSaNRL1II5ZUncq782cY8VDsDtdV3kuUzoz8iFq7/hW9ls+dyCATAWpmTFLw/cxXFJmLynvjFJqdOgrv5vDIftxsrB8HA+Vcynv1tzapvM+dpen72UeoDyKKb2Zw4vTPZB1MZYsKO/1tE3XPDfvEldN79wUdjIfdbim+/s/d99LWJp7bzqvvLZhGAjeHfCZ+d25Oztd/4EhugC3h+jr3BlP1zKd/yFMJ0NVMc40QuIYrSvPOf8E7vF7x+ZTnk15rnOlFqZnM4XFKIys/NQPGL05hPly3PL3THen/NvBMw/ciWmbm++xaPzpHk/34qFxps9Pz7T8PO9z5innIl7m4GbKj8zt9TRzUnnWGUdPx5r2MQcruYXJOOWzOf1n3TSIr0V6P8ZD4V3dx7cljlRKhPlsaCm/G2lOPHS4yc+Ue1W+N0f/f92mtEWi64L8RJScxti0Dwo3wKBqQqiBCnCoxAdmXjzjmaySm7phxKy3oVSQzCnt9mvdc/oKMV4UaSKVPJtTuE+7ynOXGtJJvoykM0vnG3JslcgeArNZ2SRR4y4MdL6n95JSm2RMCKm2popS6TGqKGb46Ig+MPRRjGG9GMe9d2KoCIHBicFPSf7fdOZSuFgpPaYZzHPM85O6wznWyUtWHR+JJqUejbJPKioaW7OsGq5//gXrn/+MpR8I2uAC9Nst292Os5MznAKPotHiTN1reGIW3HpL1I6PVM1HHbj6lME5dkHjtOWTr64Y1orN3RbrFOeLc77749/m+W6D8z2Vkox+6+AZoqeh4txYrFLsVMB5h3Mb+i8+p9psWKmKR6rle8sFi/MVH19WhOaEz53iTfeKj549orYVr6+veP72Jdt+i1W5ZvPegDC949kooIoSHfd56XSnFJI5QGm0toTgpH5p2/Lo0WO0NpKSMwa0AmMt1lputht2m60oxOsaYy3ei/6p3+xobeTy/IIPnlwmnVJIET8KpSwen/QVkfVmy9XVleBRpfH48fwPYFXtZYADmp3hPN/JfKviIY9hrMLWRuqkWg2kDHtaY+uGxckpi7MzvK2IvTho+OAJOFxyCDcqYqymbjXLuqLC0tYrFlVDdJH11rPdRNa3jn7jiUMgqpj0CRmHiQOLUYq2rqjrChQ4N9B3PSF4dDaeHFxzle6GBERorWlqw3LZ0LaVKHWNEQNpNrSRZeD9+KSU6j79cyFIuvyUjWJwHqOF/7PZoK4VFdDUlZQ2VBqv/Wj07oeB7RDpBi9RuoOj633hHBZQMTkZBPBIiuthGKj7iqqqJMOWzsYuxui+ORo+fpb+Bbj33CizTDDzSD9igpMCfsKIb7NR/D6M5bdinHyYn8vndnh44xNKjU+OhpyZXgoDeIL5wjAfY7kX2flV45xGO+idwxHxAWJUDD7hzpj7n+cNHpLX4Ig+IUZKPfm76PP4fdnX9J347n4glTzLvAECyyEEun5g1/f0KYp5cNmYNtVDlXqSfFvu63rKz4JCIu3S+/JM3rO98xuG0Qg3fkb5mRrhRWsz4vNxXK1H8Bl5IJX5qkODe/57TAav2NfYnvwskUqGxUMZqNxffQjihWgVUoYEqdcdcEPSPSuFQoMOqLCHDcUhH5/vZ2mLkHXu1zyVjQ/nlvZ1DABLBicYoxxd8Awh4R8OZbGStzw456CSw6QR7KClVvbZ2YpnTy5ZLBa4IPz/67dv8V4yrBADwQ1suw2+d5hB4Qdwvca5lMFBRiYiNFobgyKmtOiWHC07OIFlpVKEuTY8/fCM7/7Wh3z91Qte7a5xnWfRtFg9UFcSWb0vuxDvnfuczD/lDcrf83Szc+x2u2W77VieLAoZMst7gt9PT1pOVy0q3uHdgFKREBXa1NiqYbe+5u7uivPhQ3RVYRPvaSvY9oGz8wuWb054e3VN7zzLukqOa+K4qVTADQOSnzuMMHS4Ts1+ARGUTr/GMejRR6HJTkVu+i1fX7/hbz15hK1W/OTFS3749JTvfvwBy4tTTq8Dp31FGw0w0BP4Vqi51fA5HefG8z2r+Q2z4mfuDqKiVRIoutts+eZf/7/5vf/5/5KPHn2Xuvf88MkJ3/7oh7xc/we2tuKTuzU4x3nV4gZLExRBDVz7gSsnPOyLu1t+8Pic1a5jd33F61cv+NF3fodXzhOVlFFWdcPTD7/Fk7NnOKuoVi3GVMQeCWproa6sZGiOCjcI3+6Ggei98PVKYNOHIDW+U7SpigGMFUfBOEBQROTOWWuprBhTc1T//i6LwVpFiN4TiBItrk3KSCbHZLRONu5SngwjHCslGWxsYXTPtMr7OOI/Y+yIzzK9FJu4EjzkAyJuiBuZUlEyGpiKylYYbdFoyZSlJLI9y0Z7oJrKegWOKv5/jxkQZCX6lYIuZLox9qT297DUeM3T5MT/RHE8VHmcmO2QyaEALTZUoKorlmaJiwNRe7RVKKvQlcZWhmpRQ3LGUzFQVZbVyYrlqqGqBCe6pJd9V3tvw7gY7uQgQ7qoIIxNNp7aXKAdiT7L3h2Z6GhE+TUMA4vFAmCMvMieoTExhFVdjfn+x+fYK6kycbDWjobwTGimUcrZSLxHRhETAwtrMKk+FUBd19iqJiqD8w5jDaumwfmIwjP0W4gD1kg9DR8DjVEsrEYHMbhbo7DGgpfxbEo9TohYbTBKvE5Qso8R0DOKr6mCKu/zYWT+JPqtINyloXlUiOn8+7ySOsSICiHVhzpUus8x+WU7YOgLpVipvMrzlL4PFZ9l9FFJMErFUvmMSXXQyz7mGOW5fZ0K5aXSbvYSq5J4HZ7Lsf2YKj9z+vkQwz5trtH4ICn2y3Gzs8fUGzOEIPWVDic2OYhDpUOe8/Qs5r477Of+WR/8Lj6B9/o72MO5zya/zwkzh9/fZ4Knc8p/Tw1a+QxMSr1VEqtpX+U9OiZc/UVaeSY5m0U59sGa4YCAzZ3PHMxNlbsxqvvgESfG8wf6nbs/eb5zhoXpM/eVWoff38MnBSzMC5f3ccMU9o6tJz+f0+2WzjPvalNGfHpn5uCmPNup0D6HR4/BXInrpwLC4c6k89QalSI9BgKqMewUfP93fsQ//Kf/FY+ePQUtnvpGV3jnabQldI7122t+9qf/mV998kuuvnmB3/ZUHuqqYug6LMIAhigOXui9YkQUMPEeTs57PZdR4th9m97Pcp/LZ8u/p3tZ3rcpvp/Dg3PnM20lDSqdlqbPZ9r0PgqSce9m+pni6PKzcvzyjh3b02N0/KFsKeW70zs2R1P3f9/XF831+T6f/7q4eO75Y7Rn/9n7zXd6bw/WrDV6ktnkGFxnnDnHc8QQRSF9ZP5z5ziHf8szKfmcPHamLw/B6PvAb3mPpvfz2PPl/JVSo9Nt6RQ4dxem6zi413qvtCsjnn+dFuPURHifl3pXm/KJZT/TZ941lzkHwsN53B8j71HpTFf+nPv9KE3JnysOzjfXyZs6p5Z9T+F0bv/eFwcc4KsJz5vhZpQLlCgYs1w43sUja5vyJxkGDozIcHB3Rt5jahaYPDOd/1+Ur4wphV1EHN9UDCld4z6KQRHoB08ImhgNCkOSvIHkhJwiWxXvhmsVEUOPEcVKuaZ4IGskJUn+CYw5AAFiKm0WuiTHS125EAYUDqTCZjJeZ4cGEDN5St0JGJ14/BCIQROCOH376HA4Bt/Tu2GfES2KkoggDgV5UcpAVWsqa6GpWDSafjeMuoxRX+D86JSYmzZAGT2symjIzPum7UAMt5fnF5wuVlhjJQVktxM9gVY0ytJsI9/8m/8P6s1z9EmN1gbfD9xe76iMZeEVa98TLHzLnrDyhl9yQxgUNiqexBa/c/zv+YbL3SndMKCNYlFZ7Cby6eY5d0OHPjvn5Nvf5tFHH/LJ85/RLlsWxhC9R/uBXfR8GBWPsFy5gdfKw3JJfPOC4fPPsXc7ToPmkYVvn59w9uEKXXt+QeCnEW694u8++Qhsy/O7W758+4KbzRWny0XC7XtjQum4XkbKKQ7v/DAMqcajBFJYK/sm+CBnfYpUdcPFxSWPHz3Gu4AxFYQBrUmO/gNXV1cM/Q5rDG3bjgrniKHrdpzUNd/64DFnJyuev+whOaFINEEDccDYiu12zc3NDTc3d7TNXuE+8peFkvEYTcgK8P3ncseygtwYI+UFq4itDLYyKCPZoDyy3tXZKRdPHtOenDEkA1pQkaBTViUtpQMUokht6oqzRU1jLJaK2jRoo1k0A32nubt29HcDfudwcZDanoIuRFeFpMG9OF1ycrpCsi12bLdbhkEi7I2xyVlXF7ytRMppo2hqw9lJy9lJy6KtaCqTdIf39T0hJCeUdIeJEjG+x9MSeey8R/UDMQaaUBOsFT2WEV3RSdsQQiWR4T7Qu4HNbst217PZdGx2A93gGVymF5Lt0WgjUVxErJXVODfQITRj6AYZR6kx4n2PH4/ryRJozPIb43NAjOH+Q4ygNTZjkiI77l2YRriL+2fDbJLpok+V9CRHHjvgpRElfq7rPJfAOnEFSS8ljHZefYgRn/CA9w7TpWjo5MwVlTg8OBf2pSJlc2bnI1/dlwNn9VvFGt63xZiVUfHomcTIvR7n5Lisz5K55bKfnq7r6LqeYZA08oMPuBmHwnJNQi+lz709I49VzEbLfVEJThNlTc/CiIv8YbBB6nk04uQPBEYOM1ze1xWpMcpwfGbSl1JF+dUZmQmlDrJoTfdh7vPpvpdnMf4jRYPmzA7yBO/TMm9xqCM/hLny2ZI+aJTg8+SsVVtLVVmM0gyuG2uA3+76/ZrSaR0GtEjZCWvEgKQROhjF+wFlFHVbcXJScXFxwsnqBJ+yf3z15XPW217WqwQ/d92OoRPnueA03kHfefre01SKIXiMj5gQafWJ8NnaSMaPVGrXOEU3QFQRozV1ZdB15KPvX/DBLx+xWffcPd/ivE+OVYEYBG8Xi01wMgMLxbnP0lWVMpQgThsxRobec3Nzc2AYV5D08Jpdt2bRVlxenLJarbm7vUO3UeqMa4WuGpSGN2+fc/7Bt7H1gsYaCRKpwIee1WrF6ek5bfuGzd0toW1Hnjwvo6oqVIjIdb5fs/4AZqZwGOPe2VIJ/X+zvuOnX37BX3n2PX7ju7/JL7/4hF89f4s/ucCeN8TWcLppuYwdr9XAjeq4jj3RWp7ohmfVgkd2yYVTfBRrLmn4nj2j1fDG33L16eds7q74g3/2Tzn96hPM1a/4+fUr/uj1p5jFCc9OFvzW6TOenJxx8+KOawX/LlzhgUvdclM7fvbVl/ywrvjO44Y3fc/Lt18R44YQoYoRNQx4a6kun/Ds6bf48upT2pMzFifnuDqidcSuIhWSsdk7KROjk8zTtjXWR3oXuN1sk2wQic6jg6epDatmme7WwCbhoqyDFz5UroFVKhmYhQ8xep+NI5+lSf+yDGitgRDwE/1QKT/qmI3fSXfqM3+TSl1hJjBsxqwFSntQiQOJcq+tqRItiizaBZWpku7Vg5KIaTE4R6yaGqkZjdgcXJv7tgJG3Jv4oAKWp218X+3/Lr87oMvCuAneDTmI14P3xOAgBKLaB+sqwKZo8UrVdKFjCD3RSGAXTYVpaqhkLKulDv3JasHJycmojx2GgdC/Xwa39zaMB2KqdZ0UCbI24igLy+KdcyNg6Qjeu1FBEfxeGZiJRY5M3u12NE2D0oqmaUdAE89YQXA5HXjXD6MRzDk3GsVj3BuEcwR5jv7NgKyUGKb7vsfVlbB2IYg3ndr7NgbvcX6QaH1bcXK65ObG4pXn/HTBwlzinMe2S5rVAqwhaiOeGojgrq3BWLBWo1KV+LwvBPHEkjRQEyNqnEQzT7xZMqCVCphQKFlLI8Q0rWaMEe7VGBi/TClN9v3ncxp/j/MKrRK5H4vu0gVCCWG/zhwxXvYV4z4qb0oQy7mNezTD/Mwpog6UqQWBnRLbsqkJ0zZH0I4x3qNHYQiSGiOCMpqrqysubXMw/6nDwrH5j7MqGIjsjR+JhfewtGnUyjyjPhmnGCufUxnRlbiXQ2IQJynVZyS/8lyOndH9Nb/zkQfevb8fZXtoD0ol/a+rIC/bNHXpX4ai9BhsTIWCkpIdVdAc6fuhSMeyldGzh2M/PN+DZwuB7uj9zTLp7Drnx7l319lHZPw6Zzkn6LzP81NYv4eLuY9Xpt+Xd+teizHtW/JMTfVWBg2xqTn54DH/7J//U37jd36bqBQ+0WoNKO+poqa7uuPVl1/zq08+5evPv+DVl9/gtjvCICVQOreVlJNehOCAKAiyQJkj1oEUqbWnQ8eMdtM9vb+sQ8/hubVP92ruTPO5l8ay0qh87N05GDxGJ47RoblznYW5BNel49h0TsfGO7ZWn8pzHHvmOAzPO9M81O59f0yRV9yFufF/HbxxrM3h8ykM3leePTDpd7S8DnG6OYShucjaufkdOs/A9ACmuG7680E6XvBv74vPjzUpO3R/zJIuvi9OneK06ZlM5zqHR0Y+ELJN4eAOHKNL03s+F+U8vbvHnHB+nfbr0Zv7CqDcxxxff//90gli3+acad7VstNy7nPKr+dnfl2+7n3alAZmJfwxfizGyN3dHefnZ3s8d6TfB3FqnFfSHoz7AJ78i8LKXHNBPOe1TrWVqSAGnAOlItZCZS21VrSupaprtO5E+R0VUoTNomJERU/EvXPMbKwk3ncagT3WHGFVa6mXp1KpM0VK+xxwweN8T4gOHz3Bi0I0ajE+uijzMUphTJXQYMKvSqfo4MxTBLyPDMO+RugwdHSIYtl5T7YIheDQUY2ps5UxBBVHxa6tGqq6Zmn3Tv75jJ1z+GGYwFog19JFZaO4OFdLOu+9ocFHUXLGKM9aY1g0DZWp0EpRNZY4BK4+f8U3//bfcNZohgiucwzrHeu7LRcnp7xSAxbF0htWg+IudDyql3zldlhVcWEalDOsUHTWsQs93zWW32sa7MWSs9/5AW+/ecXVyVPCb/4WfWPhxQ3nH11gYqSPYozSBC4HDW4HMVK1Laye0v/HP8K8ekXbBxa6pmk0YaHRjzzsDJ9udvxJHzDNGYtmxTc3V7xY33DXb4iuQzfL8dymeHbvJBYx1qJSoMMwDAe0QBSTFTEqDAZjFd6Js4wfHG21YLVcSTm+dY+2K5Q2aBPRWrHb7bi6fksIgeViwWKxELKhFP3OYY3h8vKMjz/+AO88WlmUjRA7yfDHgmhED7Xb7bi9vaXrOk5PzsYAj9FwUVyWKS3Z45V4T7ZVam9gEcWrxVQBbVMt7FS7Uimo24bTszMuLh8RtIHoGGzABoeNFm0VGBhCYBgceogoGlqtaOsFKlqiT7V2O8fLF9dcvbrF9JpKCxzuL7ngEDGi11ycn/Do4pzB92y2Ep2/2yVHK/RIM3IARKUlF6+1ikVrWZ20LJY1VSXRW1oVytdkKPQhEEKSRZUElYSkqPYh5jLVRMTAGp0jRj/qqELcp3KvMFRVTVsrfAz0vkKryOAd686he4kSzBHtVWVpKjHaV0ZhtUIZSzZoZIOiViOaIbNuGaYEfx5zIhUHoKx3LOFkj1sjYGZh6V5LEafls3pO1JiRkY7JL+McjpKwKf1NTNhcU2IsiBQGXZVYXQURRWXAaYWXbLHJcBlEb5z0pSrudZfv4jEyz3uMBguMHJ3xcd1CEZwyfUarMjDh+D577wk+GXuSznoYcm3xAed8chjYRyRPdSMjL1JGaOd5pm062KKQRc2YIotFlldh/57wnYcZhEa+j4msXMxlLjOgUgofFLHgZfUElkddE/tzmO6d8BT3ZYKSH51rc3roUm+slCJzh/f4zImcozgcT2uN8n++MjnKiuGmaWqauqataxaLhtpWuL6j6zrutluc2rDdboU2qvswH1OQVUBq50r0fj74KEY0HTA2Yqyiqi2VMqxWK5q2PphTjJHddovbbgmriuAM3jmGLjtoGKogxiwfhfc3KRDSaINJrg3GGGpVExB9d3ABb7bUK3j28SPePt+yvRroth0niwVqcAeyznvv4ZFnlXw5PiNXIXJ7e8uHfHB4rloMjm7YsDw548mTS54+7nn18y+5OFuy3TpCMCgqmkXLenPDZrPh9CwSArhuoLEVi0WNrjSXl5dcX12xuZMSek2zSEZ6gad20eD7YXT0k399Cjrdw3/MUBnTBc76oSxzGEkvfdtt+OL6FTe7O3746Fv891//gj9++Zy/GeHH9VLSTDc1prPEAF101Nri+p7WWn68OOPvLp/x2m/5a7cbWuv43rNzniwWvF7D//Hrr/n0//rf8aP/yT/i1VvL1//tf+aTr1+wDY9otgO/873fYHm64Ivnv+JpGLhtapyv2boB5zu6ztHUNU8tnKuKn247fvrNL3gdr9HqFNP3hKhw1rDut/zmj3+L1//Dr7ADWG2JxuL7NSZ6bIqAjlHkA42h0mAMKB3p3Zbt3Zr15hYbFSeLBcumYlXX+OjQW4PDy7/o2e02+BgZnINo0JWU5TEmZa4KyQaYMhBmWK9sJVHmydgakl3HxYB3RbADjD7CwUsadO8yPk/6BKQUjjhw7PUZRjdoLbZTUsaInB06Q7nSGtNURDzBe3GOQiU0keww8V1BL4Ir9ndPHXyT74jWUooZoyXLdZLDRJtedpedFfelFKd3U7HP+qaSDSkEKWXtdzu03wpfkLII4SUTlFKIoxwBtETY61pTtRWLVUuzqOlDT11plouas5Mly0WLHwa6XUfwUGnLycXpA/uxb+8fMR7CmOoI9qlds1IelTz3lU7CqDA0GQC8dzg3MAyWpmlS+nTxmLq9vdsfjtICQIlY912HbdqR6XSDw/l9OnEQhV0ZEZ4ZjTKaHNjXEIganQ5Rm1SnCvG4GIaeqm6x1qKiYdftaBea/+a/+V9DiFy/eU3ot7SVRWtLuzzj+u6WtzfXnD96RF03VLaS2uqDCJtKi+dj8IGoNXfrNZvtVi6BNWOq7qlCTmAtjmstifKQhPW98mvvpVwyUlPjhPSXGQaB1JiZ+fR+FvJypP1BJO4Ml1wSm4wwyvXkc9orQfdRp/ndMgVp+V3JEE7HPGBwjiiLp4q/Y0ry0qB7D5nMCC9T5eq0lVEspL211qK9pJrxzuGjljSISSEkQuTeyC1nXkxD7Y3n+XP5e59aEBhrO5VK3XJ/Hlzrkf29t1Z1X6C49/xU1xjjAYy/n9JQUh4dEx7Lz0pGuFyb3I/7SvzRo+/IXMo9K+Hx120lzM3t5f1+370vx+Z7cBcmRq65aN5yTlMBee78cz+lAPGQ0fKhMz74LiYM9BBsxL0z1dF+Ztphn8JlzkXjPdTm1jMKdUeE7xKPzWUkeGiP4fB+hXiYMYP9Ndyng1OKaDROBeqzE/7mP/p7/NW//3s0F+esU7pIozWV0sR+IOwG3nzzirffvOD6xUs++dP/zM3rt7hdh0WzWrQM3qV0k5LZAi0GceFeDkuq5HVkuvMu/DwX8Q/7WsYlPZlG4R2DuYfwc55HmSp7LuvI3JzGM5ngmulcSueXKT1/Xxibm890DnPwMncO032fGt2n/ZSCZdnnu+Z+QFezMDeZ85+n3VPUvQfNmM45Z4mYnsevQ4fm+JApLtA6eexPxsrfZ9ibflbOI8RDQ97cGZbKsfzMtE2dsOCQh1S8P96c/n3gkDlRPr0fTZ/ez0PH0LlsC3Nnd8DXFArch+Yyh5Pm5jT3+fuuba69C9fPvHGUr8lziVPFJzO4Qe2Verkd45OOtSk8l7Xmy+/H+zYTST63d+97t8u7HJOhfw7XgSjudl3HebG+6SbFKM8dxaN5LkqcTmNMKv2CZoUg9RuPzvPPySs+1Ey1jzjSCrSWUmXWWuqqorISPdSqAa1O2GzX3G02XG0dfdez6BXGRbxKUUVHwDkrarz3KJMMOBGUAXzSzWlRkKioUjSpx0fJI6WUwhLxOkjNWNkQQrflehfxGoyyGFXhFfiwo3MbdvQoKirV0tpW5Ghbo8lpASX6PSD1d3WKVtupwOBX6FARQo8LAz4YdLQEAgZPVJGoIzXwxJ6w1mfs3B3bbkD5a5HNuwo3DGMa9RglbbJ3/ch/SaQ6o1EuZ80Ckc0EVoTvzsa03kNUFWgjDgFDh1Ge4AaeLT/gIhi2n/4nbn/+pzxaVRhbced2bNwOR0dbndNvBtqq4kJrTr3jjY2ixwiWDkenA2f1ir9tHtHXhutY0fQRv4M3feTrb77it7//Ozz51g/YXjwlvPyMP2gr7rpbllULuuIGxafGcB3WfEvVnBhDbyLrzVte/+mf4AaPoyYqS6U0p7ZiUIYNml8ReGUDH5+eY1vL51+85M3VNW47SB1rkw0rsmuiFNNjtIjOaRpjJEcXG2MkVWRVU9cNMaXZ98lBROo9ghs8nXOcL085f/SMkI3CKoCupG/v2d7est1uwFqitTg5PbQXo/nlScO3PnzEh08v2dzdoYxOSRytRA8hPLR3nrdvr7i7XVPZWlJiqqS9VgFUwBqbAi72fFGWN0e6lcSRiEQ5aTKqikQ82kSqWsnd1pqcCNM5g2ksl0/PePLRKScXGlTFZqPRzmGcpRoc250jeEugkoj7zkldzmaBajwmQu816y7wy9cDb78eMDeIITI6Qt9B9GidM5xJBGizaDk5XdEsKugiuuvTmUoJQcGDalSECm0WnGWNpm1q2sZSVQpbKazRGKNQWvJahBDRUROj3uumtE4K14AOZsxW5ZI6SydjXzcEdq7DOk9tDbW1+AHa2lIRxPhuFK2xKLUEHdAxsrCazWaHc466aqkqUYBXNkeOi+EpM2dlNGPmmVX+IxunSvw66mtKTBvJaZJjzOcuTZK3xn2K6ZHPyb+qAgclwJmT5ws6Jh/KvVAxSiB3poNJSU2qgRrIRtKc3jeO+G2fWlsjxYclcGq+ZdwISuX1JQN5SCtUYuDwBExQmKjRQVLN5rT0RNE9aqWJBd3NtEUe2c8x72cu+VfuxT6yPX32AE+4396Em/J75Z4qgQelQBlJm6tBPBPSHoc0tlZmxHUxRrxLcw+Rroustx27fqD3UkO21GvPymqk1OAqmSnSEoW3OZRVjAoy76Q/iOhEr/fzJ5Vq2a8v7lOKF+/KqaoR7ITficWs8v7LZzGlbI/3vk864hgOdIoHa41R0oSrVNOXrFtOc9Ch7DLhidljPJDvR94ww07Ihp3Mx8ax9jvFO/k9bTRWFfrVmNafS0+kQzIpaMEo4dXauqFtGxZtQ9PUtG1NW1e0TUuMCyntai3boPCup2NITtcGUqSsd1uMFgOiOGNIRKqU1Uk0JUYslipU+GiIymKtZOI9vThFffMSctBQAO0i6+GKql9R7Sr0tkX3hr7fEVgRldTWJkJQjiGCCQohcWY0lMWopNRFDPgIZleBX3B+ec7lRzdcXd1w9fU1DY04JlqhdyF4Qkh4ZSzjUch9ZLx7XO4dZzLKA3K2m/WOzXrLyWqRDGwOpQPeabRe4DzUJvLB45rPPw1UaklXSQcmBOpqyW63Zn31nO78CW27QjcV3sLSt9z6HXZxwsmjC/jqEwItbfWIwW3xYYuxkba5xJmegDhkhRjRWsogOedEJmEvrmjUCETZyKoAHYRyuABXfccnL77gR6tn9NbwycbzH78e+LEx7FSHWlhqb2kHTaUj3ncsWfF52PGn8Y4f6xOeUfPf8oaPwwL19oqLmw1f9RteKHj5//x/cP77fwWzPMdefMRvvVzTfXDKZ6+v+OUXX6CN4rbf8tJr7poNr23HKxRozTPlIVT85PWW7yxO+XBQ3Ly54fnr53z/ySOGTkoWaDx3ds2TD57ywbPv8HpzTf/mmouPnhA2gRhrQg9aiYNj1ApTGTCK3nUM/Zbt7oYhbjDBsVwsWbVLllVDYyze90m34nBux/rOsw4Rok+ZGzRtVWFNsrtEj4+BqMDWFdEHyfJgDFYLL6AUVJUV5y0/SFYTLWncVTAQfHIIjjgCPga0NmiM0FhN4m0EJ6qIlG8wml4FDJraGGIqBxCI9Lqjd/2YRccpRW00ziuMrTBIKR3TSzmiXQpcMlFLHRiT074f8hFKSTBVJKJjEB5MR0lDT3Ju1ooGS0RLCc2S/1EqGdKLGt4jc5J5GxJNyToDT4gyraAcOjh0NCizQleCS4yPhEpSzBMDUQ1YHalrS7NqqJcVzULKC2lrqO0qyYwVRlnoo5QMWtRYrdO/95PJ39swXgr63jni6BmRKKOX1Ol4ASjnxJPBO0fX92y3W8KwQz25JAJVVdP3LtVQiSyWS/ohsF2vaRcLNPDsyWMBMNcTlcIFQwhR6ncHEeCzEVEp+ZtUp9na5P2RhCyllHhgIIdstcY2NcaK173SkRhcSvXeJWGgEo+UqLi7vgYCJycLdltPt9txer7ko29/xMndCS/+6DlvXj4npguUU74Nzkm9J+8zx4L3nsVySV3XkkJI7w3P2TMlK2DEECIp8qaKqQNCHfd1hrJBYaqYVQSClltReyH/XsPOgguOxcgcy5m65A0Tk3OD1LM+rG2a9z/Bfbp/+kD5qlVmsRAmJwvByJnEKDWhvPfCdKUa8Kh9pFNWSmVYzPuQHQVK5nHO+Dg1YuX52+T9M93PUrjQRSSY+H3sU/+kRY1Crs7171J9GGGGlaQ2jl7O0geqpkXZmkGndCEhEKIGlRiM5F0v8wiM6WFCVhCJYKFj3v0cbcaI+fbK4rhnKlI6xsx0TBWMkBSnKqefO4zk3+/tXvE5VVSPKfLS9pRK0qnDw8E+T853fxYiXEjThRdeErbicUYpZmEmyzAT2JhT4pZtqjyepgDP694rYY/PY26/55TDMcbRy7bcj/L9Y0zh4RmGUe7LAkUscERuIYiCURyM4ihYZaAelTUZ1skCaCmP31/bVHE+N9fx84TDyvWVhpAYJWNJCUf5PMq9e2hPsnCb3cTHOUbw0e/TtBbCP2nJo8iX4HqUOWNSMnO4PkVMNDLdvSgKZvaYcHzDaFH8hhjGPcjzNSGOT8c8vt7XvhFWy+CUZlsphmXFD/767/L7f/gHXDx7IpEyvsfWFfiACUDf4283vPzsS1796it+9mc/oVtv6HY7VAxYqyFGej+gjdRINNrsa3+xz+QR2Z+ZVoIXYxRhWsW854zPqSjpFLMeRbxAhWfI8JXhiSj7ZlAydozj/sfRWUae11lgJivqD46PGFM9oAjKygchpjo+aYJ5/jqNH5g3Cpf3/6Eo3HFfCpoz51kfo8BI6fDxUL8Z5+Tfxz4md2ZunPcy7oXDZ7KeD/IdmJ9TiXuUPnSaKMed4r1ynnPGwzm8Od3b3Kb4MSRlxf757HwnjPx0vD3Ptcf7U34g/5zSkrl1HZv3sWeyY+lcm6OVZWrnKX2Y/ixxZ876MDfng2xFExw8R8fepx2je5nWkWhMiIzGz5JHyJE45b5P6Xa5vsyjTuc/Lelw73yO7Pv0rKcwcUjfwt4renQU9glPKWEiE357kGbF46nO53mV8ds0x0NnVEh15WMYFVxyn5NTrRJaX6Y1llqCILV6M61O3u5KUsOZ5CTlw2F00/SeTs/jWGapuXUe8DWT+zPueggYragqi7YGL0h9jArLhiXBCMnkEFUiyYXzIhKVQKZfWiVjaeZ90pxi4qmhwI97fibeZwv+Qu10uRj5aq3EkFQlw3hV2SR3QqU0RgVOFksWi5aq3aA2vdQ3jEKYS/5SpjvB+eV36b/iy6QUTxc38ecZ5jLdHrmmDAsh0PUO5wfJTJZ3TEV8dPR+B3EQo3c0KGXQOvH/ZPiOSM30IDIxomRCWQyiZJT5ZD46WebTVI1StLahtku8cXgVCaETR+UhMgxuD/9IGlvn3b6/GEfDuMDtvqRUlolQyXEh/W6sTo6EiaczFh9BW8vjdsHqbsPdz36G6XbUpwt2yuJ6z7DrqJSmV5Gd6jkxlpXRLDFsjeZ6kMh1pTWeyK3vsHbBeljz9PIE6wzd0LMOA/VXV9x81FGtFsSzJfrrLzlpIkOABTVGWbR2rNC4qDnREGqL0oru5XOuv/gS5yNLkoLJpnuzc7zqFG+HgWArHq9O6f3AV69ecHVzg3NeouMLJ8g4QhWJxwoF8hIcVVVJwaUtVdVwfn4mmflVZLfbSYSJ87Rti3Mdpqpol0sWyxUoja00zkdQosjzcWCzvqPvdtRtC1qMQlLiDJzrOTt9xONH5ywWDev1HQFD1DE5ZQjvaoxlfbdls9kyOFc49O9lXV0A7JT+wN5hVtIDZwOhGGjzlUJJms6qttS1wqT99iHglOfR+SmPnp3w6NmK5UmD9xZTKarBUDtL09cYrVjfeUndqTRhiAzbyKbxqCZSE+jiwNu7jq++ueHmzZawCwQvzq/TcncKMNbQLhaCV+qKwe3T4esUFb7H2ZBpoUayWTRNRdvWVHU18mCiVJE9dCEZqGLOEJFLDqpRT1PZQNNYhqGSyFontcejG/A+0Duwg8FZg68qfCU6vhCM7CkGW1vatkaZE7QyMrfKMvSOuqqxVmBWygqK06N6QKmqstUiwfBc28P+/u+xDmjckzUhScn5J+5lzagymcqy4OEMKHk6CmfVkt8KSV+S66AGPT4jM4/7fkvYTcvKT8n/92se15XlqWJW+z/FdBbH+wHErG/QKB32+5xlu4L6hESLD3jHsK9PXBqRS77uPs+9l7MkVX26d+zlyYOdPfgu653U+LkaaYHCYMmlNHR6LafrJiaDX9rHEAIuBEzi89zgGFLglx+j5GNy7E17Ne4jxd7n82DMljCvbyn1o4ooHNI433xWKjkgFQq8cR/JsgQUjk6l7DPHR8zLdIe/Hy+rNv05/V2M5pP1qvt9jWuguBvj3/uzHQ3jRJGTEnKPsbjDif8qy2ep4v5lbnPPD0ja86oyNHXNcrlguWhp24a6rsSJp6oEDpzD2IraWsGpUWorS/1dBG+amhgGkkqeiEIZjansqCuGHOlajXO21tK2LavVirqp8MGLLgVJ+dwNOwk+7B2u87gevLeJju7XOoxRzsnYZpKePBkBvRfYdkgEroqW07MzHj+55O3jW25e3zI4R6PFTuOjQo4kHsDTwXmP/NXkqO89Kw4xkGQURCe93WxZLlpG8VZl3CaGaWPg4nzJallLhpVkT1JRUdkahWJzd8N2c8fy5Bxb17gYWFYVqh+o6gWrkzMWJyf0Xcfp0uC9oveewXXcqhu0QjIapZTgxuTMyj7ZV/KeZqTPyBMc4mChB513/OLtc36zvuDMNNzGNf9le8eVWlJVgW5VsapqzkPNKijWSrHCYGLk5bDhp7srNKecUeFD4KbfYvAQNB+yYvfmOZuXLzk/ueTyR79F9fMv+anr+Y0PHxGqmptdj9t0WGVoY8T3PVpVLKhobGTtHV/0W+puQ7s1nN0Z3r54ybc/+G28AhNBhcjQDziluHz6IXff9GxTZL3XHrfzLI1FW4sxkag8Q+zAe3q3pXcbBr8j0EuWl7oRGl5VaGUgBmpb0dT5TgkfZRIvbo1NDiVJPlZyV7QWXsFFl0rISHmW/XlEQYJSA4q9HC38XLpyonc0Rnj+RAIIMTmPJDk9waqOCkPcy9gojDZ4Aj4oWltTV5blcsXy/DFn9SW7jWK3i/SdOD2jFNGFPR4v6eARHUdB0UcAy/LyKLckPm3k1VW+k4f3aa7nfbeR8hGlFUqLXKaMRRtQlUVHhQ6ewRiCCuPcq7ZmeWpZnFiqVmMreb9patomn7fgkuAVTVWJY6nRGJXl0ne39zaMD6ngPUD0gWzaFKItE3fOjxFe19fX9H1XpDSvWSwWnJ1fMDjP3d0V1lqaZkHdLABD1w3c3a3R2rBYnVDbim63o0YRtSF4qZOUvf1FwEiCFRRMi0ZriDErBbUwUCMDJMzo6emZpIcMffLCSoZz70kVzTBa+gwhsrm7oasMbuhwbkDZCl0Znn74AT/4zR/wySefCAPnh70RJynYQ1Ie+FwHKmRP6fvpYcrUYfkzxV7BWQqZx1LVTr8L3kskcWL8TKp74LTCGTE8aLKHVarNrPVoDAnj5WKPqWW0cYzMJOW9HpXWMY6K8oxwgt8zHKVyd1SsJQ/hUgl5YICkVPrNM17zysP9/jnnDgzr417nNYdwb39DnGHC4qEhI+99HksrqXU1hEB0GRGKN3RQkh4sBA/RjHsr09GUjLpsvaZUqGaFcXEA476Vn5XMRe6zhKeyJn1+rky/OlXQKjUncEyRYoE0J3tb7tVUiTpliIjHauHmtUXK+lb3DBoxJq/ayduF0vYh5WzZ13Fl+NjpPcJTri/v90P9zBKu4r7Pwfu9fkphRj5IZ1Y+u8+wkd/dp48PB88cU8TvP79vFC/fmd6juTs0lUjLs8nZK6ZtGhn50DnOjT1m66C49xO4nvZ7Dz6PtvvRn2UTw4JEaKCZ3eOgkxMLmSdRUg9SGXTyQPZYdjpw+p2P+Af/8p/z7d/5IY6IT0ql2lYoZQjOEXY7bl6+5ouf/ZLnn32BGjzbm1uC99RW0qxGa/Z7nRQRopoSpuhgFQewmITg4iy1Skx+vpMw0rLJVmU9yX6/yn1L90rl/T94Ko7nd6gAOlSMxFEVzz4yV6nxwo1MZD7nyD5d4wyumxoQS7pxjPZM28P4834r6dqUxpU09Jjh8ijeOtZmGcnjyouYaP2IbCbPPGRQLXHsNCp5aoicW8uscadwgrm/rGOKs/t3uywBdLwdGmofMnqWhpY8ntZ6dMY4WENqpTNQSbuOnXM51v11xXv81RR25mj1MfiZo0n582M4+lCBvr96sUAEJQzM8Qij00k8HGOuTZ0i7813ituOtLl9OIDPw6cP95ZIDJ7Suajs46FWzr/kzd4117KpUvItfo2JVuXHVXKgHVNpU2TcKvnAyS/Tu3OMJ5+DyYd49vSSlJUadZqHjhrjApUoukYlf8E/E5M85+87Eh3MK9OV5PSmlcLHmBRV844h07W/nwj+/u1suRx5FfFFUFikXuU+raU8a2Nk2S5YLpa07YbKdqCGcU7H4HyKL2Qde1ltfDft8yE8xPR0sTcq76V871yP8z0+DKhQEbPxG4hRHMgVBq9j8s8qZhoTLsejVCAqUV2rNIZRYkzPZxfwjCHuOYJVSZauumoIzUIi2qPCoZHM8inyOxn0lHNJl1Cc5iQ9rERKFCUKVFKEK4UHYlWzWLQ0dS3jassQrjm5eMTjylJ/8w1vf/pz6rpCa0MXIt1uIG49jam5Cw5nBhbasFKCOWpS9HkU+AwR1s6xsZFbv+VMn6NtxUZ1KGt48hbutgPoSGU1i13P+hwGZxlCTVSSajLGyEJZGh0xtehEuq+/ZvfmCh0kxXZrDU1rcQqqu4FvhsDbYQBdsapbbtZ3fPPmBZvtBhDdD0kHU8qmGU7ieLZqZB+bpsHaKtUBFUO5sXI2fdeNNYerqiawo10sWK1WtG2LUkkeD340snnv2azvCG7A6gUmOfQLLtEY5bm8POXi4jSlLIfI3uirkmZaKc3d3R273S7hYAlikJSbiQZoTSzwSyn7TR165TvRA8i9Eh2VTjUVbWWxVURp8FFqi2IHLp8tePxsyeXjlEayg6rS1IOmHyqaQWGNpdtt8BvJVBgHGDawrh22hq2Hvut5+fqOF19dsb7u8EMURe/EKB6jOLTWdc1qtaRdLKgqgzFSxtBaS/CQndRlvYmexCgRULVlsWhoFy11UyWlaCq9gKRdH4aIClGiK3UyhgeJPFRKo4wlVpHlosb7geAdPUgAyuAZ3CB4Rmuit2MJO6OA4IlBAxXaaKrWsqpatJZAlspY+i5l1kqRl1nmUvq+wXSKN8v9mmsjrBf7o7McsfcOTNG/UrdUhTgaxstyjzmV+9j3ARuTDYaFITTRwRA8wTsJ3FCMapNxxiPazlg7wX0kGWz26VwzD7kfeP9JoRU4qHGeZdlyD2TOJf3c05RcqjMkZ66o93JF5oVyuvHy35TvjHF/fmLw2s8vy48HnxWEMu9DSdfG54t5a62plSJoLQp6pcedkNfE6QQk2jjrXgKB4L0YgnyOnPWStjqlkKcYV5wLSOVR8lGUTM48DKoxCjetpuCtD3jJifxxDJ7DEfnrmHw5K5+Vc0NRRrnnxe1h5JCXnP4rn5Hyo4zntxf3xNFgepljYJS99obxRAfS/mcWKLCXKUsdtC72FNQ+0h7JtGGMFgecVgzjJ6sFTdMIbTPiqhmGgZgN4CjJrEMj8B8zTwPGVAwu0QMdErwJPrWVHfVmWmspT5L2yBhL2ypOTk5YLFtJ2+/duElSwqTHDT1Db+n7iuAt4n2Y7pwPdIM4IRFk76IFY2SzQ5QyNyHGsZSOUpqT1QmPHj/i8ZM7Xn7xGnczELWkaTZBgvZGw+Qch5rPtsAPs3BwIIsI3QjBs91uce6MqhI5RsW945UPHqstJydLTk+XfH21QS8a8sYYW2NUxW67YbO+5aTb0i4qvI+YRkpvtKHhZHnKxeVTvv7sU8CnAEHN0Dtu3BWVtpKVKDkDKmvB7++RooDXB5pKvJKLgc+uXtNddDwxC17pNT8fbvkqrvhWUGxWsKxqLnzL2c6y1opFhCcYdsPAn26uGLTjx/aMGAds8AQ856riTD/iU/eam88+4+yvPWL549+k+7/9K17yJYmSAAEAAElEQVTcvuLvfPyMYdGye7shvLzjvF5Q1xG9u0H7QGukNMp6GLiOPV9tb7m4haZt6N9c0yuf5HzQMYLz7PqekyePOb27wm3esl2v2agOd7dDLTXa6uRMZxiiI/qB3m/o/Q4fe1CRpl5Q2QajLWMAoFYoa9DOiKN3CkQ1RhdGcU0UD0IUBmMS7ojCZ2sjvIg2++zY+cC0kSwnPtUOj0FSp5skF8Qo8k0IjuyAgkrlNMYAn8QPRqkLLobxRIWV4ILWNJwsljy6uODp4yc8efQtls05L99u+NWLN7x8c8vAjqgV3rmU9vx9eZMJzJVAmPDKgXw79pvk5Hs6wRmYlZEO/o18NamcjlFoa9FRSzogFcU+ZiLKGupVxeKsol2axBcHjFEsVw1tW0FUeBdwTsoPNU1FU0vEuEb4qfdp720Y1yklDJHRcz5HDAx9jxsG1psNXddJOqK6ZrlccnJyOip0DJ7Hjx/RdR3b7Y7z8/Mxujtvm60qXr56yXeXJyyaBS9fvOTs4hGr1Zl4eTQmRbSpcZECiEoMDCQQS95HCiWAZvYR2MYYgutRUTyJpLZRxeB2WC21IdabHcFHFm1LjGLwN7bCe5fqVgVev33Lv/8P/4HLy0s2m40ohCfMQqkUKxVaB0zE5KzKdKejgjjulYNZQZUvp9Qg4R5wHhjGYwbG/ZwyEyKMf3o37Uk2GE/7YUZxO2f0KpVWpfFNJQHwUDCMB7/LmeT0S/eVyDLNw3kcSw8+VXjl1PBl/fJj6dXL96fM15T5y8bl8u9x70NIaSNyuQGVHDL2yt4QA0rb8Rwksi3vjbonVGVYLtcQs3JB75+brism5WI2/pWZBQ6eV2Kws9aOa5jbkznF/JRJndvTY8rTOJ2XUjCTGeAQFg6Gvz+uykqxw+ceYtTLueTvHjJ05H9jHZhJP+Wacz/lHTvoj8PJlvM4ln667DcT4vdiror5l3ckjzWnKC3nIc/uvajL994VETZ37nPtYF0TQehdwthc/9NxpwLOsfmWa3nXeO/TZMwHDDVa0WmAiAnJuzJCZSuZq1J0RqPOVvy9P/hH/O7f/zvEWiLlrJWqT3Hw2BBx1zdcvXrNm+cv+dl/+s+sr67ZXt1KXT4vXsNxdIp4OBL6121z51zisDn8W8JmeXZzBpV3jVn2+z7v7hW389/NOdK8z3x+nT190EBU/H0sAwfMR5vOZVV5V5uuc25fDnAJ2f//8PvSiHUMf805QM05xOT352qpl33fM/IcmcMc7p/7eU8Bo7IDmSIcll1+J+2Y4rFMm5nBxeWYJa9xDBdO78w9eGWfPSSPU9KY8rNje3iM95tb56/b7vEksdijYn/KOZfpPDMPMe2zVJi+77weoktTuJaOuXeu03s6h+MmvY/flTx0/my6tmPzm+KGY2uZrjNH5+Way3NzLt/JhqrpOHN3rcT9s7zn0ZbWoecdgvN4ee5iHBPv/Rjj3ls85sjMOMpNknkofRb3Tlj35qWSIuAviQf4ddpJ0474NbPGNjmBa5OydGlFpIIqsmhalu2CRbvAVhtc7KkUKCUuYrGgH7K0+/QFGI0kBzprledQwDlJwTKjfFAR8AHHgI89g98RnSJGizXJKVeJ8c2g0dpiTYU1tUQTJIOA8JpBjFwxpaqOoDyiTElK5cyXSgrsSpwakMhvjcFWNU2zBCzRtHjX42s/lojLd9b7YfwsN425ZxjPTH+WWbQSRU/nHXaxYLVYsWpXNKZmt+vZusgPfvNHPFKe7qtPufrkZzw5beiV4tV2x+22JzpoF0u+7re0eC5DpPWeLnj6tgZjiYOjGxyN1jyyK5YDBNvQXW3YDp673Y5n7YrvLp/y9bOP2bVLvO/pQs8r3eI8OOXABzbB0SlYVYGtCqxVoOt2DJ9/Tt33wAkLbThtK05OW8kMeDPwS+153nc4LJWPfPHqOc9vXuGVp20amqplG+T+TenSPVqd9nOxkJrku90Gv91S1YaqsvR9x83NNUppTk8v0EoCKs4fnXN6dk7bLumdT8ETEW0Fdp0b2NzdYIgsKokcQhmCkaCHk2XNB88uOb84oR86opLUtxLdGhJuEF717dtrdrsdMYakgN3fk4wfUn7Zg2x00+xk+7XvI1aVQgKojTi8iNOLSzYdcbSoVpEPv3vK448WnJxqtPZo42mbQD0ohsHSD4a2Vtzdea6uNkQHPiiGCHfW0TQKNSjWN44XX2149eUt/W2QCGIfUiRumaJYglKWy5bz8zNWqxVKReyuo6oq6rpBYYgx4xQpRSDXUNKP1k1Fu2hYLlrqusJYUk15yQTZ9QPXtx5LZFHDstbUqQa5BwIarxLdMBKdSIwY3aG6FFww5HI1kRCSrJxSUksGgQBKHA10BW3b0rYSbKCVoqv6hGNTvV6VkBqROZ3qPToY4z08WtLh8hmlJQpLdB0p8yUSmelCQMdA9IVB90DJnXBi+jvl2ElyRjlOzrCXsgC4DhcDksEmkn3HBAqzmTipkOL4P/JvZbR1mBrGZUP2T49fZnlqP14s5i60WqJvpZa0pM3NeixxUyrGK3jj/C87zuefMcZR55nPX3ZIp/rajHuSqN9kIXny6vCz6YLVXrYzUaGVk9SuURfZHGXKohvykhkCg1fglGRScc6z6zpx8Eh1aH2KKA/JueNAxsuspqLIXrk33o5/Z7gAybiRViR9zMiN6t28WNYv3UuxPt2ayecPyVvy7Oxok3fiyHccyJyTv2MsHNWK8csAC7XfmTSS7FaIKVKcQzmI8a3DNYzyZyFPxXz2iafUWlFXlkXbcrJccnZ6wmq1pK6rZP9AMuj6js55hpRxt7ULoq0Y/IDXDgjE4AnRoHRDZNjf5TQXySBUjZlnbWEYt9ZgbcXF+TmXZ+ds1ztcL/yNI+B2O4Zux9D3Qke2Ct+LI2lMMDlEx0DAKIuzAVdJ9GuuvSzR5ZKmJ9c8JkbadsGjx4+4+2jH15895+XNSyLp7huDcnLLx4xzE73DCLeTc5/CQBkxL5koFCF47u7u6LoLjGnJjoyjnO0DysBqUfHo0QmfPX/LomlGCDS2pq4XbLZrtutrdts7Tk5PcH0kLgNNXaFQhOU5Hz37mK8/+xQfBrQxVFWL873UFu86sheTMklPmmElwXccUxwdb6KHkZwPX91e82a35VGz4nn1lp9t3/ITtvzQnxKdp6ksZ37B2W7BF2GNpue7ZsGV6/gTd81/sjf8b05/ix8MlufdHXfBszCW77aP+M83z/nVv/u3rD78mNWPfoefP16w/qzny+2a3WbNq7drbl3H7zx6xqUBG1+xdj0qbjlXNYsuUFvF65sbBu/4vl2xuBuIeAYiMXqU82AU267n9OKci8sndP2W529e83rV4e7u0MoQDXg9UBlNiI7IwBA6PDvQAVsbbFxS26ZwmE80X0KyheYak1KjW+HfEt9CUOSMtFYb8BE/ZF2BSfXAUyZJFcWho9IoVaGclJvs+x4I1CmLl9YG5zxsPb1yaGWwWFAKr0CyXpkRL4eYnOHY47sYhPe6OH/Eb3z4Md/96Ft8+4OPeXLyDFTNVxc3KP0Fm/5XXN9uCYQUhc2Y5W2KB6c4Xh38rvZsLNJHzgJNwtMl1hzLrdzrad/fsRYi+MHjBo/1Iv+pJO85oB8GXOVRVlEvLfVpjaohGg8GbAVNpWhqaBoDEZwReZhoUiY1LWWXtGS7ep/23obxfrfDWINBDNDBezbDwHazoe86fIy0iwVnZ6copWmaWtKpB4/3blSCnJycMAwDJycnNE0rm5OMlSCH1nU9u27Ho8ePGHY9N2+uqFSF0laYxiGzb2njU3rokNJ7GJM99eKIGJVKKauUlxS0KnCyaKmMIQSPCxFtKoyt0cbSdR2VqRNSlMh1baxcrpTa2gfF7e0tXd+J4VfrQ+IIY/R0JspZkXugIJvsdf48K0CnDEO5X3ulFZQKm6niUmstqbet1GkjpRAbFXbcV6zmvo9Fax5TDEk6+uGgvwPldQL8vA85crv08Bz3s5jPVKjMTgYPGfDm2jSib6oonRViJkze3Bhz4++NQAEXfOFbs4fNvZKQFPkUJ/2OssAIXuU+3FNWcoj87imS4+FaZ6PhkmL5wLnigSileaXafS/r6R6W0eoPMdgjTKj7yt3E4z8wpxkB7s/RHoKrvXJkfqwpTOWfc4J0qVifiz59SMF9cE/fcQ/gvkPJ1HA2B/9lhPmcwFAqvv8ircRfUEQfT8aZznfapkaUsv/y7uzx7fzdftc4v66ifFR4FI4EB7hjjylGQVRpzRAjsa3oVOSv/r2/y9/6H/9jVo8vpFRDUyXlr0K7wLDpuHrxmjdff8PPfvpfuHt7w83bt4TBCS0f3MiU5TOLM3f/z9uO7f3UYAT785iWtijfmdv/qVKqhOfpePdw5QRHTnH43D2cG2/OCF22Xxc23qfN0TA47jxT3qf3nc8cXp9iuCktyri/bMei6Mu1TM/g2FyPPTPnYDGLX4vv59ocni4/y39Py2pMhYI5GHz3vqtEz+ZhcQprc3B3j95P1huT4ifC7PwOFUz37205l2k7hhfL8z14Xl6ane/Yf9wrfcv+7j0708/cGf5FHFSO4aVyfXnaJR89Pc8pL3t/3MM9mN6vh3iAgz15YN5QKmTmYeUga9Usj5eeDykCYoZvmL4zXdMcHZ9ve63vQ3uglEQ2KqXwwR+8R4yURt3D8eJemTx2mzUEJV77y8fl79MWlc1Zh2VmGZ4RR1qVNLFeFkdlKpq6pa4btNXjfZd9k2cfgiGlxHCjp/s0c05BNDnZejN+HtN+xhAkJbnZEs2GaBqiigSspI4NkqXNJIO4SYZ+ibhREJHouRCl5Frfs9luudtt2G634AK1rQnayrPJSd6HnHZd1lLpikpXWF0xhI6+9wybHd1uA96J8vKecdyP/yTtqB4jNPewDBkulNYS8au11IrVb7k8P4WzJ8T2lF3nQVm+//G3CP/2X3H3yU9Qwx2mvuROKW63A8MQAYPzHg+cGIWOGq+NZHlThlZZfDR4t+PEVvz+2TO+01pe3kSulOLD737It5895vm//vd80Z5gf/gjolZ0z79CnbacqgXXquM1HTpobNCo1rBVih2K296xe/2Gzc9/zkK3hGg5MZrTRtM2hrjpeOMd/5mel86zsIB3fP78G663d1TG0thazjFAJBzCxRzsRbC2xpqaznXEENjuNtx8ekVlrSibtWT7q6qK3dDT9QMXl49ZnZ5K2YMY8VHgSamAdz3b9TW3dze0hSEixECMhuvbW773rRM++uCC1bJmt7sDqtEhZI8KDNvNhrdv39L3LhlPFTlwIpIzv93njw5hpaCFBU0wGjFeaUkFL0rXiPODRPQHKbf05FvnfPT9R5xdVmg14IeethFHe2sVg1V0VqJWH1+e8ubNhtvbNb4POKd467dY3bEziqs3G55/fcvbb9b4rdT8dK7HDwMSPZUBPVI3Faenp5xfXtIsF7i+w1hLVde0IWCN6InEmcqniEJxOmqaisWyol1U2CZHBqVgkwC7ruftmzteX3sqAmfLlriKVCeS/lwruXPegIkGW2u0ilit2TWW7dZSV5aqCICpbUVb11Iv3Gi0QUosWi0OE0rmRsjptMtgg3QuZIW1KIj/MvQI0j+jrJPL+SVMTkTKOfkgTiuHMr0e8e9UVlQzesWDwAfnMHiCHySTReaN7s1N3f9wppXlxpJ7/HhfynJWpTjg94SYEV+m+ZmoMFFh0VhlCOkMdIwS/R7yfdnfozJCfNpyRGLUioiU0YoIicq9RI6t9Z5WdnzjcBDZCaL0PwxSXsEog7KJR096Vp8DuXREIfCW1zAMA51LEeMq6bR9dvLKyr8oJTpghF0JnjlSbmfUiyWDr0cMMWqvc5gGBMg+3udVj7XMd88ZPzLdnuPTSqcOYGIMemCs8afMs5Q1y7lqfd9x2BdR+TKHlHFT7/v1JevHoafzfm764LtSvlFx71ySW2UMbV2zXCw4O11xdn7C6emStm1Ho3XvBrbdjuubO+7WG7bbHd6Jc1FUA0o5jJKgqiEoAg4Sr5PXJvaWgErONtk4bq0VJ8j0sLUVF2fnPHn6mFdv3rLZbLMgBr2j77c43xF9ix9gd+fptgNNbUcahY+4OOBDlEwmEVoUjTapdKpJ+CFINL6PxNBTVYZHjy/4+DsfcvviitgFcYJEE7xOfNv9QLg5WJjKxfOykeigtVbsdh3b7UZS19cNKipC6Eb7UAiBoDwfPL2k/eRLlI9EI0Z7MCxX52y3a9brt9zdvOby/JLQNmz6jmW7gqgY6pbHjz+kXZ5wd3vFollijaVtTojxWozgygg9MYaqbhiikgzEWsoKimPAu2UM0QlKGcJPNm/4K+1TVs2SK2P447DlX8Qzhs2GcNlStRVnty0VO97oHY9RnFHRo/gkbPjp5hv+vvmY5xGex57X0WE7GNB888ufcv7FL3nyu79L/z/9+7z+3/6Mb37yKzSe1ijO64bXN1cEa/kn9QXP1Y5XQ8+OwKKuCP1Aa2sWvYa7nu3Ll9zu7jhzK6LzbNVApRVxO7BtPIvTM85uTnnxzVeYGmxTE5Ri1/eE4LAWKqvQOkDK6mN1xaqx4Cuyc08gIKWOPPKX/AfQVg2VrlAYCALUSlmUASm/Jc63KgasEUcTbY3IjkQqW1O1FmstfYh4OqzVRK+p2ppF01JVEsC02Wygg7ZZSJp3U6OiZrPuuNqs6QZxhMqZLFTiNbIeyHuPMZbz1RlPTp5w2Vyy8A3hjSPGgVNt+ej0ktvLjpurDVfrHhXVWGrTHpjeZniHUp+lNT5wiM/Td1pr0Stnw7n6i0nCstxkK0BwsdFa3ASUQtvksNgY7FJTtwZ0oBu2mMqwrFrOTluWlWT3qZVGaUtjNNQGlUtEpYIXRmmaFFT2rvbehvGz1YKhH7i7uxsXYVWkrQyr9oymbcEoui4JM5s1MRlwXarFFPCcnJyw3WxZLU8IwWNMmxg/ITS2rnny7CmgODs95fL8nN22Y7e+E+S6XDD4bkynLjqMvXEvE4qMXHKEOCSDDtDUNW1bsaxrjDLs3EDdWE7Ol5JSfRDPDlPVhAgGhTIGk9JFBR9AScF3E6SOuLU2AfYkeinV78iAN02lVbYS0R9EpcVDBX1+ZgrgpeA1F0EdgockzCklf4thNkexC0MmjrjxntI1z6Wcw1QBOaeMK38fFbvog+j5OeXpeGnSWrKxZqogzPtyjJCW/ZWGr2kq9rl9zPtQrveAEZrsz9x8VFJUKZQgrBCkvkpdi7OC1hCEYQ1evMN1UYcdEGcG9umLpvs0zmNGCL+vdN57380aXvVe+JoqS/OZ5RQhDzlMzOk9jjHac/tZIuw8z7nSA3mPpndjnHuC2QCzY5djHc7/UPFerj+PN01rO7o9zCh85+7qNDtDOZ9j8yzn89AYcfLclJmcu7PT9c7dqdKBRXCEOfDSLI3rc0LR/Drv4xGl1IjXxywZ8b7xK/98SKg6NofpPZnDP9O9neLV+bH2BpLjc8p12g8jf0c4M4YKMdZbY0FBMJo75fjgB9/mX/7X/zMeffgMZS274IlW0sXoGFG9Z/v2hjdfP+ftr77m9a++5JtPP8MPDqNTOp8QqY1FgZR5mMDDFF6n2SGmsKjUhKFK7VjU65yBaQrX03lMx5z+/tA5Tsebg80pfmdy1sdwQ/nZsT7nxhvXFu8/PzfOdE/yPpbZSu71/cB+vU+b7ltWtEwF09HBKdGuY2cwFyk6vYdTvDo/jz1Nn2bh2f9+uP4pHjzW5/Rul+/nZw5TNR6Hzelnc3CS5xSSh3A513Jt97OlvH/06sG46jgtnnNIeGifjtGJ6ZizvG/cu1nM9Z+bntnHg/GUOsA9c3d+SpPu3UU4mMuUJk95pRKOSwNyzpeQny35hfzPGnswl+l6VVpPOfdyPnPzf1ebXfMEjvY0/b6yaW7vxr8nmH/ab7m+h+7eO/kF9vLUdG35p9Gauq4ZhkGUDFmCn+KwGIHjigKVBPScYWlurDlaeTjGn++s5pptkriuJqpXpfYpPJWk2VROolkrI7XHlU41lUedcpxdx/u0/GTM/eXP9UN4SIyGm91bOvcIRy3GMdNglcZEQxUtmgqDkYhBlQwf7A0E3otRfNsPrHdr7rbXdNtbonc0GnaIIXtwKb8njPE3WulRyWWUxgdP13dstms2mzXDdiMO3ckAnvcmO4aHlPpQK3PPML6/Hxo1RmoZjGqIxFRWbsdOVWz7yA+/812Wdxte/cmfsv38MxZthVt33DUGXCSi2SnY+A7TVpyoGq1boqlEMRU8124NJmB1JMSOT2+/ZuNWPH/1kisdeRoGgnO8uLrh8R/+If3Tp1y/fU633nJy+ZQPg2djDL2xnCjNExSb6Pm801yeL1DbDerVK7Zff0MMjjMUF3XD0lh8PxB3mk8a+OV6i18suTg7pYuOT59/jR86Fq1FG41H0sjGMPDQLch0KShFn6LYqqqmbYWvqKsKY1pOT0+p6oa+79n1nmax5PziEls3DCFQNXVKgW8I0bPd3PHmzWt2mzWnT58m+Zbxfu92Gz58+pSzk4aq0gyd6DkG57Aq1QvWBq0t19drtltJ5a6NqP5LZ3Wl1KzD2cH9KXhKeTa9q0HpiLFKUqhbjTJgdM2QUirXC8v3f/M7XDw6oa5TsANaoqhCMvwauW/dELCtZnVWs91t2PU9/cbTOaj1Fh163ry65eXzK9Zvbgn9QAiOEDsiwx7FqIA2mnbRcnp2wsnJCXXdilOt0mNUImhCKhXohixvS6DKYlmxWDY0raWqFNqITBcidLuBm5sNL1695foGKq3wvUOFSKU1ZrWUaCAtCk4dvGS8aNqUQctSV/VYvzxGgTejRMmqlCIluySiiFERosa5QN+75DyTs0kWNBhGA68ioIrgnf3Zyl4f0vH79OCA5qk9BlUqRbDpbMCWucWUbjWixHBfjLunV2p0nh5haEZWnVyyRK9J6bgLGq5SR8QE1Hvdijx/qItKuymwnPeq3JsEQBkOMo8QEYMuZPqRiZISvauOWBMJQZTjRotzFgGii5ItINOvCV8yOpknA1MamGy6z/sody+b8t+Ddx7/r2eelrg/OQ9w3qOTc5VSMp7zeT6aqCLKSw4ErwW3+SAGLmU0Omh8NmZPzj5T/j3NPuTlRzgrjIsh9Z8N6nrcq0kwRFqNH/n/fDZHdkTN6+xgZj73YPc+jlRHLC1qP5lDmXby+dgv+1IDOVtC5muHwaeyF6VsqMeMU3lvDxz2tdTtNvp+pibZt3z/pdMQxYEhxsIo3jaslgtWqwUXpyesFktMJZGjznu22443b2+5urllt+vwLhnkWs+jpxc471hvttzcrnEOrFV4P0iAW5DMTs5pQmjImcDynpQ6AuddKoex4tHlJaenp2w2O4Z+kFK5Cvp+y9DtcP0K38NuExh2oM4tlVVYowlaSS3yGMB7lBJaYIzBIHRJ3K/30ezOiTF/dbbgw28/5fNPPuPuxY3ceaOxlcH7iPdQpifKa9hnKLjPd821nIVD7ooEQG7WO9p2IeVdCrKstSVGcH7g2bMznj464erWg6owdU3oA1XVYKuGbrvm7uY1280HLNsFO+dpE+6pqorl4pQPP/yYX33+C0KzoLIVUWm02aHjIOVAlMZWDWfnF3R9z5sXqTzMtN7n7LrUeF9VUHit+MXVS3740RMuFifctGf8u/UdX/MU3XvsAJW2tM0CE+6oo2PjdyjVstQ1v+kdv3X2lJ/7O34xdFzHyOPg+TfDl7ypKtauo/v0V7Q//YK//Q/+MZ/87/4P1J1DtTW2trRKcbXt2OjAQlnO7IIuGpxyrGyNcwMacRp6vr6m+dUXtC+/ZvX4hyhdibNKP7DqA7t+YFHXLJanXFZLLtqW5bcvCc4SfYToUXis9mgNQTtq3eKNOEBv+w7nBwKSUQoV0ARxgvQRgkR4L2qpLV4biSi2WmOsAo1kZ3Ae7yPKaKwVR1eXghaVgsoajJYM0n3X4/uBxlacLpfUxiYSKrJIhcYslizriraqqUyNVpa1kTO/clt2fkhlPYXH8d6P2Wej1ihTUVcLjKmJQdPvJIuoVZGmMVy0LY9PVpwtlrwNV1K/vto7/eSLM96Xd+DZ8h2tNMYKf6KN2Ka0EiP5lNed9DZLPUq9jHdZZ5h4acRJOqoAWsm9NA4fHF03EBSsVoqmqVkuGlZ1Q2s1lTWouESrCqUsYDGmxupavLZDQBElWv892nsbxt++ek7XdXS7HaerE4KS6Oi6qtmsb/HDlj6lUI8x0tTizauUxRCkdgaRi4sLHj1+lIycWfFpRk8nFwJWS8Tx+dkpTx9d8OrVKxa1pu97Qr/G+16Mumrv6ZMZzK7vRiFaa0Pv3biGbBQdqortWnF5cU7f99TNAqVrlEkpalGp7lGqaQQYY+m6nXyv1OjFp4xCR3NosElIq1SYTv+Vhr5pPdTS4FYaBaXrvYG4jLSVWmv6YIwy/XQM4jUfYhwZ1kzIY0zpeWMcGcqS4JSKPQVjBPz9iCnSc/PG2/H3lNaojFQux3TOjZcuf5/POf8rFYVT5rHss9zPvJZSuTdVApd7nz+fGn/zmZTE+dhcSoW2T16jMUa63Q7VDykKISu7pV7FQerKXGd89Hw7ZBjKnwK7h99NlXKqgM1jLYspZerOcl9LoaSEg+nvMXf2wHzy2ZYM5z2mZ+b5g/ke+XuvtI0J1ufXO92fOWXu9Pe5+cx5+k0V2jDvFHPQd0wK4FIImKxxikdmFdeTd+YMHlMYmt7pub2YGgSkxqK6N8ZDezcbtafuv38gYCkOUrYe7WfSynU8pJSfU9xP/57u1xycjIt5UA14/0zLiPWqqnDOoQIsqoagoFOB1dNL/vk/+yf8xt/564SFpVMRGyKmqohEwuAIvef26obnv/yCF198xasvvmT99i2xG6TWnk/rKg0voyPO/T09gO/J3TrYhxI3zOzbnFBc4vT87DG8M53P9EzftdcHd6Podwq7U5ifE+qnc3kXXB2DtdTL7Hyn75bzmDp1ZceRe0L95B6+a0/n5lDSvylen+srSnjN+PcB/3DkrN51t6Zndgw33T+fvZPXdLw5fD53n6f4ckrrM1z4cP/5KewcG/Oh/Z++M8eb5c+n8FrCzgGNUIz0YeqU89BeT/f82Jpym3MiO7a2ubOUscGHeQcymCoKpZX34aG7cDD3Aocdw+9zuGMKHwc3e/Jd/lu8wM3RPZ2Sj9LwPocf59rc/GbxUDx8tqTzGTeXkWdlP0rNG41L3DEtrTLLk07u+nGYegeuj+KovNvtxvq0ojsu6Va4N34IZdakyGixyrzj2P/9fXxfGvQXbmoCq5NpCYurUtyhKpTDKZ2kSrLfkT0+CvchpjC1NKwq+lVqn9kr73KBZxSMPgkxRG63W+42t5wuapSJWOPFGG4sEjdkscogXXpClJqbIQSc93SuZ+vu2PkdXbjDhQ0hblEqUhmPUx5whCByv1aWfRLeiESPp9Sm1hKaBvwSbRW9FuVt8EUWtRBHGW2M6EAVBp1DY5QxyYBnxDBexxZXGxarmkW7xOoKGyM/+OgDhp/9hO6b57hdh1pYdhGu+57r7ZY7t2NjBna14tp3RKXprKVBoWLEOc9G95xXFU/DkidO4Vzks5sta2voiXz56orXz68YNp4//M7HbLYDsddouwI0r1zHXVL2aRXxMeK8p1cGv1zhXr9m+OY5vu/xGJbWcNJUVFrTdZ4mGn6K56r3nJ6J4fN1d8Pzqys8mspWWGPZ+UCccdybbVHSlq5Oz4jRs9muCYjirLKWylRoU6O1xRjNenvL2fkFy5NTtK3wQYwSPkpd6egc/W7DZn2H0hKhFZXUlFRKomraxvLRs8c0lU2KOjHQKeUP8LGPgdvbNW7wCbYkxaQnJBk+3QJlKIvJHKX5iK4JnWAz1RcXOFJooyQYVVlCGEB7zi8XfPvjZ7R1DSoQVQQrUT7GWqICHUDpgPMD3dChK03dVLidY9g5cTzY9LghcnNzx93tGrcTQ3SMIaXBjSgkmIUYqGzNYtGyOllR13UyJKVVqhxRFEFrUGIUIaWzt6aSWo+Npa4txurxn3MK5yN97+m7QL/zBANrBVYbrLFoY1G2ojZKyiqIEoragKqzoxQoFTHaJNStMUpBFH1S5waCixiXav1WGkm1LrL2QWbFmM2l6YQUpNoJM7Raznx/xmpEzVPansB7r3+J2XAj30gf8ndMEch5fOmnpLPyXRh5FqQ2uSpTqUM2kmW5Kg6DGGHTWAdzHWe4n+0+6fSexhDDuI5UeUTgplygIjkh7B1AYoIVipFG3UyCpagVGIWKKXuIlowBRutxH7IMEpUSWFNKMnkqPdJ7gh73wftwcGb55xxdL5Z7+N34cNKrqCQ/Z14hSnaEqMSBJUe+ZuIXcq1whJ5mWqxC5seVOFTZCIMjjunuwz14HF1JM0yixvnFuJe9IikteNaZIvgk5JMNklEjy+7yfhhLBhyTqfI+iM75UB8wbuEDPNFUFwA5Kn5vnD8qD2UeZPp5OWbi9+TvrJvKDgLCATDScrlfuR52lp+lRrbgdGOE/41G6njrg/HSrCdyFjE7NSuq2tC0NYuFGMeXiwVNUxO1Fno7OO7WYvReb/rk1Acoz+MnF3z88RP6oePq7S3KaF6/vBbDl5GzDHGvG5fMNveDHIR/cqJfitBUNSerE05WS66aiqHrxv10/Y6h2zL0HW63ZNhFhiGgokqOhYY+DlI/PETAjbyPC172ZxwfQKONResURAOcXZxwdnHC+s0tpOBBow3GZl3QHs5HWBj5ycPzPibjaH14NwB2XUfX9SwWXmiE1ckOheBRFWmXlovzJde314RoAYMLHbXWNO2C7W5Nv1mzubvm0eVTBi/nYGtDS01wjvOLx3z55WdCj42htg0eR7e9TfdLgTaYuuV8dcrN9RXDdgOEkZ9+d1OolCHl7faOje9oqobF8oRfrt/yC3b8hlKE3hFaS3u2or5+TeUEF90px22UWOrfevQR32y+4ev+lp0LfIclX9Bz5Sr66Hn7+We8/aM/5q/+/t/kb/61v0Hz6ae8VT3XMdJtA1HD22HLL4JnFyW7k8IxBMcA1CiC0ijvOHl5jfr0G8LJdzBtm2p8G4Lz6CFAbamXK87PHtEPjo8ef5u+j7jBEYOH4CTSX6zP+OBxXmwpAwHf5XIU4vRm0h1RsabSK5a1ONZZJVmdjFaS6EoHAp6QSi5FBB5U4vFCCl60VqO1IYbkADgEiUauaxaLBdEHuq7DD3LfrFJUiwVtVFiv0Kn0sQ3QmorGDDgdCN4J3sh6joxTo9jdrK2o6kayWtsKVIXVkXrZsNGRtk72y4TAQ8J52SZR3pN8hzIdvMehqv3z2uix/LA+uHPpwfzKeAcf1uns/5MnfQxjpuQYU2YLBSiPw7HbbQn9QN0YqraR8jtKE3xkGBw2WppUdkurCjD4oAgO4SUST66Vwuq/ZMP45cUJMSypbSURD1pSdLi+50c/+O7eP0AJEm6aBufcqMRpmgbTLPjoo4+o65rgS0XTXsHmXOBmc8vJYsnl5Rk//vH3+fDpBW7oqIzCGEtMhuF+GMY6Gn3Xs9luWK/XUi9CyUH2fb9Pg4Ywzt45qsrwG9/+WBgpibMjBAVa4+NAZWt0OoCc3koANVNm8fyLCJALY5oietkzfXOtVP7sGdS9smGatrUEqlzz+aBWyhEm5OAiTAhHTPxd8B7bNlSVTWcwP9/x9wfWk1tpXJ8KEpKuJEDcG6jnng1xXyMy9z2nwD1Q9s4oeuYUuw/t01ybjl9+VioR5/ZiXHcM+BhQ2kCUyIfLR4+5ahqi69EqRdwVzKZWKjsLE6PC+zB6ef46rYQBrTXZm/TY+o8pO0tFaYyg9P5MpwJgevMePL1r7seUuMeUsrLf4t08VcKXTWv1Toa/hJPy73IOWTE997lElewZupytYqqgt9YeOHjc34TD+cy1WQX35J1SSVnC8EE2igf6neKOOeX1lPCV/cwpBubGKX+fRkeWZ5oFl+n9f6jN4YA5IW7aps9N11firrn9ykL8u1q5RzHuPd6HYcBYC6bi1g20l2f8nX/yD/mdv/u3aB+d02vxqDNAg0YjeOVXn33G17/8nDrA9YvXfP3ZFygnZSm0Fdqnc32lJNRnhcUcrSjnWOKBWfh5gHbMMUj57+k+HTjXxMPIzWPwNneX51rpPZ3xIexx+0Hk5wOwNYWhh2CxLBcx78iRtUnz839ffD/lFcp+yp/Hzrlsx/b5oXEPcZDwgtPMNQ/d3akRrcQD0/k+hKcOF3L4+ZQXmZZhyc9MYfCAv5k4yqUOmdYty7+/ay+n9Kz8/RjunH43t4ZyX8r9Bw6UwQ/N631pULnGcl7HjKHvagd83ahUfPhePISrp84is7zgzPdTujr9buqYFmNEzVzx/EwuExH84f4fRpzv51Ku4dfdw+lezL1b4rlyz8s2vSP3+O8Hxp32N7eGh3iZX3eNSmvcICmxZdxEi1Oqzv28GH/mc8x0W/pEZEO9F+D/vO3XwaUPdzT/cRzVHCopw1PEFPvIKUbcRBbTj+Ljg89imveRuR/cU62SYWx+ojFEtjvHdrej6zfYSuoGomsiTcLVJimrIzF4XOwJKStb53Zshw3b4ZbedfRhQ1AbTNXT1lClU6qqCErqTBtlZDox7VSUtH1GQ2U1sbEoarQN2BhGnUX0kl45+Ljn9wvYDXkjJ0paMYxLmmhrDXawqJTWVCWF2qpuOTear3/yZ/S3tzitwWiismw3A3fbLRvfM1iIlWF7u6G2DZbAoAIqBAgulYUztMGy9JZdVPRDZLAVITjcumO3dSy/9R305SXu9g7de6p6gQO+joE7Ik2M7ELERPnXtApHYPP6FZuvvyZG0KripLG01qAiDH1gbeDnQ4cLsLBSM/qr9Ruud1tMVWG17H0AmfMUHmb4BqU1ddPy+Nkzut0G5x27bkelGqwxVLZNb2uMtTjvOTs/p2oatLGSbj8KfVNaE9zAsNvSdx113WCqhpBcR4iRYdhycbbg2eNHWK1xwyB3XxmMhhgd2XGodwPruzUxQja4CK+Q5PSYDDIaYrhPD2fljEJLJNdUDOLaKMnmR8QFhSdS1fDsg1OePjrHKvBRIvC11vTOo6wYMn0EFzz9MLDutvRhEAWhMeIw4hW+D2y3Heu7DdvNljB4VJAU9HEC2wB1XbFcLlktV9iqApWDLCDX7tQ6O4zs74pSUlu3ri11bagqLWUSrDiPRBdxIeJ8JERNCAMeRTc41ttOFLJVha3r0dlEK43BiLOOqQhVMuhHD6iUVS8l8g0RP0S6YWAYJKpMMopYFk1FiAqjQgpOyWdSGGAS8tAZjid0cArPhx9lo/b+79FLSCly+u1sCNpDRCBEiaYf70eMhU6m4K/SuPkjBWNkd9yb4RPPEfDDQIg5HjnrAdXYR4wx6Q328x6DGKPQlpjTvmb5Mc9RFbv3/+PtT5pkybL8Tux37qBqg49vihcZETlUFTJRVUBhKMxENxpogGwuuSCFveBH6QW55ZLfgsIVRXpBUiBCEqQ0AIINAt1VharKKeZ4s09mpsMduDhX1dTUzV+8rAapmR7P3Uz16h3OPfeM/yOTc3Oq3uQ91ecyFcO/UTLJKCoaZCxa69V65aEYU+6dyDSz/bY/2EvptaxnyX1dXgrSQ57M/WSZHpBZxr08BBXkgUTy+G51wGqAjcgga+dS0EP5ziB/m5INr84QwZRAhjRZ92EnToY2DlXkiFgw6ctwkxjROSq80WSdaynzpvDXJTFqyOZ/gM6HScoa+gD7lR6vcc4ZaEpGuWOUNyf3a3L/fT3tsE3hIJN4/8V9uTXv7enTa7BdTgk8DZgyQ0xFqaWdSjBcKiNFBJOklCwYpnZIXRqm/rB/zip60aKuWS0WrBZLFosa7z19jIQ+sNs23N5uuNvu6LqodCJCMomLx4949PQRoe9w3hNi4vbmjqYJpR8DfTNxjIcD/0DOxf4cEzGq0886w2q14vTkhEVdc8fd2OkQOvquoW9bQhcJLfTt4MvRusmSehhKAWRKEEHe25JGPmBK5qfapxRsIrNcL7h8dMGbb96QdiidGw1aCjLoajO73UgDx/WUvZyt9t6hH8PiGGPoe83w7fu+BHhBSro3ctbazELi/HxF9d0NTVIZMOdIykJVLejahtB1bO+u6boW72r1Vzh1snat5fT0gqpejHb/uqqp5ZTYt7Rdr6gCKROT8OTyEW/fvOa274ndUC70iI1hcuVhj4uBmGhi4F235dnyjFW94g74M3Z8KjVt39N5oV7VnGG5yZmAIWTYSWJrEndEvFvQGthIIGGo0PPRiOf29opvv/4lv/fuHT/8g79C//IFu67nLmZMLhDkqUeysMSytI6VSRDhVd/iklBjWRmLXN3QffeC9mct9WqJkVKLO0VsCERvMYua5cUl26uX1LLALxzRR2II5BQIoYJSJivliISWnDuM1bIBoexhS0kuFIc1lto7ThcV1vbYArGt+kYiSyCnrtyvzCqTSzCRwp1rYJ5BRKNSchJcQTxYVgsW1YJm1yhDS1rS0jlLXVXYPpF7DfCVksi6cJpFHoJmtKeUsBisd4rskTIhJRbO452WRrDO4+qaql7jco+tHHEXaPuGXbMl5qxIRynqunCctw7BQwe8VLfnqE/KkB1u9iWLp/aC4Twf5Y+RPx+XefeyVeG1JUM85aAo4IVniEAg0qWONrZkCRhfl2egC5Fd22FywlRQuwpnB56RiEGDh7PLOGuxRv3EmMNz6qHrgx3j/5v/9X9Fu9uRYmK5WFBXFYKwqGuc1fpGq9WK25sbrq6v+fj5c4y1xBDp+44nT5/iT87493/8HyDvMyYU3qRHo4os1jis9fjK46zwv/if/8/44SfPqb3BSHHIuXoUuIYU/9D3dH3P3e0dGWG9PtVIj17rHYU+jEYshR2JJBQCSiNtjQrJCGTB1xVZ9oJYHg95AIOYjOQ40NF43f/9uDFqz9jvG9jnxuHBkTkQ2fj55DOQe8Q/FQyUiAtRD8aO4kx0TrP3xRhMPnz33IHxgG1m/873UtF9I9FgkJo7vcmJlA6DBeB4Ruv0Goxc03sPDV8P9/Ahw5Vz7uC7Y3WIH8paH39Qg2lKanDpQ89mu2G323FiLX3XKTSbGZSliIgtMq7FmEFxe/+Beey6N2dH7rmvONw3Ah/OtwY3DM8edRYceceHQIbP+5LhgPYfuveecXn2HqX473cIT/8+pvxO997ciJsn8zZHJzjW9nGa2yuzh3t8dpfcD6Q56Ku+7IDuDwyZR/bP/L57CqHsgwD2DgEmCv5948H7xjDlK+9bl+mcDuv8ffDRw98PBbS8b16nvx8bw/cZub/n66H1A344pfG6rulCYGMiP/ybv8/f/6f/mEc/+oReEo1JmAzLaFS43jXc3N6yub6lv9vwxX/4OW+//Y6npxfU2bBpt/RF8NBzbD/fYy0bGPfZQ0rp/OfIcDBiDnjt/Pf5/B0zjh4olzNamtPvnE7n7T/U13nG9b2zcvhX7htJ5u3m2R576BrOoSniwv674888zCM+/DpqgH7POk+f+02u4ZxJJXvEPOAoHt7zPp4wtPdQANE8aO4hOqAo7WPfJtmv3ycLzPs9l10OL7n3/dD/gWcNEH7z9xw7R97Xvzk/P3Yezenz/jh03x8LOpg+8yE0MJ3b7+vz0XPqe85eMTICWA70MASIHjwj9/v9EKrR8Pe9z7jvCJ7yrXn28/xc1N8PxzfNutZ3HtLv/LwZ7pnzwen3v8k1fce99ZnJAXM6P8bnhnYOZfbj75w+O3/P/Dr2rg8Z631+dmjITjEig56VVbUeDLcqu6R7/lzl/VIy0WRvqJ5+P+vD/c/3AXLfdzZ8yLUHsN23P/6bh35oBL5HDrLGxchYZ1JyHu//kHNg/xlMoR4PZAFT3lYM/dqXMiflmZQzXQNNF+hDR4gNEgRMR85aCkaAJI6clsVJF+hDT9Pv2PV33HXXNOGGkHs1jNlI5XrNFHWCzYa6FoxNxBxxWQPYyUmd4tpVnBGsA+syNmSsy/jKkUnknIhJSmZlHHW2gX4H9C8d38BLJ3zAGoy3uOSIu0zfCuIV8tqtljx9dEH39jVXf/TvadsdsfJqFFpU5KuG2HVYSXjrScbyro+cOEc9QEOjjutl0NqUmz5xlRKtrzm3RnPiY88Sy+XJOZd/42/SrSp233wLIvhFTWMSb4wQk9G6qjkTcuIcy+3Kcre54uabL7j9+isShoWpWS88RjIpZEIU3rnEL5ottV2w9p6YO764esEuJ06qBbaUS0tkKinF8u4dz4f6qIhwcnrGDz77lBfffM3V9RU5gyK/OEXwi4y6Z0qJ8/NLNdYbizVyUJ4q9h3dbkdoe5bLEzC+oLZBTpHt7o7f+eEnPL48Rwi0fU/OxRYklpj64stMbHedlhKcBIZOz5k4GPbGzTLbvxN7xHQGhj08wvUOTjKj+6HrI9jE+szx2WePODtZ0sWWGHX+ktFs/5RDyaKBXRvYdg3X2ztudoEUBTXTWkx25D7TbDs2m4bdtiGHBElhlBXSdeiVbpi6XrBer1mdrLHOohmteez/kK08OK6GVbXGUNcVvnI4r9niInt5O+aeECMhZcCW/WkIMbNpeyI7xDmqWgMjjEhxjmsiBxZciiRrCdbgXCqAWGpU1myyQNd3bJqOFBJWFIpT4dUNlc0jwJGI3APmyKW9OfEOS5wnvPT4eTVb72GaxKBIxHFMgBDRLMeQUnF6l9nM6lzNMx480pNMz7zpd9PftRxEZkBRmT4PQzCr+gjlYMjDSqesqIdxcBpO6XlCs0Md0owgA449+SBgZKiBrc9negPFZQClVrF1Dls5xNtRVjlma5rLR5otfhjcOpWt9jbQ/fxM27onM09WUmRv3J9md4roPsg5K485WPVMxpBNhpS0fnox0ou1pY6xICWBa3A07rOTB9o8dv7O9Mciu5ihn6IOeUVCGa1LGkCS8v6ZrGcfYg/7/qDuIxyj9vG76RwXWhq4w/222N83vfbsccJbJ79P5gLZf6o0cKhn37MNlY04IMFoglyh2XJvUkIh5oQZzpysaCTTzk7XYJhzQOtLVxWrxZL1csVquWRR1yCGrutpm5bb2w03N3fsdi0JhxiLsYKtDacXFywWJ1AHRCx9F/jm629pdgGy8ksKHH9GfRt93yvyTUqj7wDUphxCJMWI9xXLxZLT01NWqxVi3u7vi4m+68pPInSJrulp244+WHzly8gzSGJcjcK7TaG3EkuAiCUnQWwmo87neul58uwJ355+x6bbkmMsKDAWkaCBEhMbaM65BALIuNbz9R/Xd2Dghdj3dh1DDImmbWmalrpWlEWyJjxKFsiRvm24vDhhufC0GwhBIblTClR+gSuBh5vNNdtmy8miVp+AsThv8LXj9OQRq/UZt5trutCxWnsq4+irW5pes/rpI7uu5+LRI548fUa/3XDXtQ/uqaM6hBFIhkDim90N62rFulpSUfHfyZa/i2UboAsGLzVPrOfbwmMthgXCW5P5b66+4m9VT1iK49ZoJviCJWt6nK1p6Pnl5jv+8p//Mad/9Wd8/s//r1y1PV2G2ni8c9iUeO4rVlKxNJ7aGTYpsHv7goVYTmzFqXXcbq5pXr9gHbZccMaiaDYNkbrrCF4dw/bROZsX37B913D69DHOQpdbkjgES4xBd2hWtJtEIGMJ2RCSkJI6dRGPkQWVFXKVIfdIe1sqUiX14+VIoCNRkoiMRXJp36osIabwalMSZhM44zBGURQW9QInjiblgq4wlFTSWuSx74gpQ0xa99o7alex8FFprMhfTjzLIu+QMyFFFssTnHElG1ywVUV9doI0tzSx5c3tO168e8XV5oZU+KPLgs2HusmE+Y3sS81Bx/YUo79kRN6YnCmDfrt/YC7XHp5dwy2D11TRSSIxx32wnqD6GhBJ9CmQJCPWIFZLjDR9IBOIwZJ6j4mG2iWc6xGjZ2/XJ9o2EqqayldUzoFxyAf6zz7YMf762684OzuFGNndNVw1Dd47rDE0u0bx9INGK52enPJNv+Xrb76mbVqWy6VGb6wv+fhHv60F67vinE6JvtQqqqxCXcXNHVKie25urvhXX/0CS2BVW6x1dEHoQxyhctq2o64rjcpLCmvlvGe5WGpGeanhY61GjSyWS3ALnKs0K4+i2KSElZK5JBasIxcYA2sdUqZVY+uK4DU6tqX8fkgb+/xxRie7GsoGQ2LBqBuJyJCLw33MZssZJlmqU8fsIDAPhHjv8B8ERRGMc2ANkgXJmRh6hSiKWaOyc4I4gXifGbPm7e6F0MPas/vNVISLuTMTKVBDes2N3IMgGmPEGqNZ/KU+/CCIHhib8j6aVuRQMVaoM2VsWfKBUjtcU4NuzvtM9en3fd+PbQ6/D8rdQ4alwXiY9JRXISUqbESfVZk1Rghthx/pbxC0p/1RWoPjDugDI+I9gW0/1hGC09xngtO2QBWgYa6POl7L89P5fND4eqT9D72GPfN+J8rMEDe/N1Pqd+jOHQ6BhwzyQxsPzfXw/dzoO6WJqXF9ul8H+nzIcTF9/zHj8vT7h4zU47057yX2Gb0/tK/n++O+0fn4+k6Vz2HS9waDmeJ2+ODhuI0aJoZyDApxqsaQUUc6aG9Y/z0dHLRXDmVjJnx6wmfm45mOVyZ7aU7jA6zO9PNBwR/+NcU8lIvCvI/EUwFBg11KNkKm1LHJZGu5DT0f/egz/pN/+p/x4z/4PZI3NF6IGFyCOlvsNtBd3fDq1Qt++fNfsN1s6HYN4WaDS8LbV6/xogbjLig8W+UrfZmGaI+wPSN/PbLO4zxN1nlcuyIoKb3tI4enz33INaWdqTN96Nv8mu7NDw3KGe49NJIUA14J0ju8f++gOrpHmeb77MdwLPhn+PxhpIiHeea0/++7pv2cr939/flh10OGvv3ePtwfOWeNmRqE4axGNHVMTYNp7ssXU4PUnOcM/HXvXDwcz9xQPe/rlOdN+fFD2egPOT6nvHa4d7zHcBC3NrRz3CB+eN/YBqMNcU8Sg1FxtiZzGp6Pd76fDvu6DwJRNicjBNfQj/RAf+dGqYeuhwyPx/6ef3dAx+N4zIGhA+6v9cNt389kn++H9xkkBvoDRvSp6f7Pxeo3KIzT1kRkRLZSSMvDPTm97/iaUmSYNBpembzloT090OqxfTHyh4nxacp3j52Nw5zN5eODTk7aH4OuihPloXP3WNb9fF4euu7RVUpcXDzhZz/7Kf/6X/9rjhlRj7Ur2tgIPTpAxh17R/nwKOThAf+atJ75zXnv/cYnv4x0Nny+l4MyKkc5o6hpGi1vSXpQ35v/aeDx/bHoGsooBx0/qVS+Kk7xA5rJKLSyyuDbbaRrMn3MCtMsPSlpBk1OCkFtxZJFQQ1jDrT9jl17y117xU33hibdkKRj6RYsfI11gq1EDVdicB6sV0h1g9ezyGimniRF3ULUoNaHjqbZsW02xCax2+1o25bQ9cSQil1jgMrOI/2HkpG1p41JUJ0RxGud6PN8QZMzvW1plh2uWnH5+JJv/8V/y+bzX9PVNeIdtoukWjjdCdGt8E7rRrdNz/nyMcuTNTtJmCws8HSSOcnCO4lc0/EmNJz1gZ/VgSqeYUT4ZL3i98+f0338jF80bwlVg5WMlx6bFiy80O5q7rIQJHAmid+yJ7wyhtdf/jGbL39Fc31FwrG2FculUwNkhIjhRe540bX8+PIjzhY1t82GX776miRwslhhYqRLiSRgBUIusjBMMvGYcNCM944f/vhHfPyDj/ni81+x2e3oY6JyHowjl6QFI5m+a/G+5smzp8qTVIAlBpVl+65le3fLdnNLCB0Xjx+BsWX/aM3zvm355AdPWdYVbR8QBOM8XRcQq7RvrEKV393dsds1eO+1v4MTueyhIev4vqp83CajIqYZfzdWcM7gvNZbtVZG3WG5qnj6bM1PfvIRdWXptyUDOEVF4MPShpbcKyrDZtez7VrudlveXu2wocYGB+LwroKYadue7a6h2bWkEJCsmXNFWht5ihFhsViwXq9YLheqw4ZIH8IYIDLI/6PcLoqC4J1juVyyWFRUldachz1EdOgTXRvomp6+D3gtYklMiabtdR2MYb2oWHhLZQVfjNPq+EylBrXBiSEaIZeAAZUVRLOmjCOlhrbvi34J3nuctbhas9eHLPMBCe/gPBu47RHTyaCP5kxBtjEDA91z5bwPAVHZQQOJUk5al100+1ZhTy0xRxS0Yi4rFBuj7G0j+u49/OvAq/fP7OV1c0Q+GUZqjJRan/ua12onKeMDQvlOgxki/eQsMWIwGYyow07KYWGiTpBmmk955l72TAi9UWj4NMimxoC3SKXOwgzkGA/k1Pm+GvWGvD8RD3WJ8t1Is7mcieNCjWfreJpmELtfUzmQTaf2kf3hOAQNDEVG8gidnsgFWcFQkEW8w1hLykJu23G+BYoDdjK2SYmq4bssZtRTB4IUYwrKqTp3c4bUx4Mx65RMdPm9J/PgjJ/zrwftbB94/1zvG5bl3sYa5p9DXftQN8kH/4y/5/m6M+rgo/4w2UN7+UbKNAhYg82zwNGBLvKEVAAY0A0Hfq7vqqqKxWLJcrVguV6yWq1YVDVtCPRdYLvZcXN7x83dhr5L2MpgjCJsnD+qWa5OMXaJc2rnr2pLTC3WGsBrcIUM85TpY6ALAR966hKgruesQvPHgohTibBaLjk/P+fk5ATvPG3sJuSQiSER+kjfK7rIdiusdorII36vxw9zaozBiWCF8TtFNfSaJW0VqpqUqCvP8+fP+PLynO6mo+uCBobZofxracMMsvRkb486+X16G74XGWRPxuBWtSUFulYDEsz5mj4GjPGkpEhF5ETTbnl0ecHZ6ZLbpqMLCecyMQScVFjjCH3HZnuniW0XT2m6jroH5xQy/+LRY84vH7O5uyZ2mslsrKOul2zbjhh7Uow0bcfloyfErufq7Svubq9JMbIvmSqzMRaulEGDOiIYR3SGX23e8mRxyu8snvCROeWPecubaFhS44MnEzk9XfGsueXbnLHZsIwWnxz/5u4Fl1XNUzyVXfCm7XgngTobPkpLviHy/7n6jvzP/4/8r/6r/y3/4fwxt2/e4tst5xWc1E842SUWEmjlhtcx0vSe02pBJ5GOHsktvhMqyTSfv6R5c0U8eYwVz2bX0q0tpu8xDbhVTb44IVQ1r75+y8VHH2EqS98HpQ2rJ2jMSs9R1OHaRwiRoot4vKuozBInC0IJthJ6+hgpKd9opGXQ/PEQaWM7obVSTsSUc7e461JxbnvjtUa5s3i7d6d67/Uzr/DmIQSaFLQEgjMaTOBrYoh4F1hWCW80E712a+rK4cr7M2DrBV3Tcn19zcqvOFmfs2sbcrPj5btv+fkXv+CL776ljZHlakXeNHhxqkvxMK/e7xuVDcwxBe+IzHN4TfXRQeZRfjQtsyrj/CVU+ld+YK2hXixYiMFWkLwGKHmpWBCobEU2iSSBu7ahzZlFbeijh5SpTMWij9BtECPEkNg1PV2bSGZNtgtSdPRZkPhhOvgHO8ZPrHD78gXb7YYXL77lT//0T6lrjZwRgXfvrgBReI7TU3LOvH2jUUir1YqT0zPi4hH/5e//dbquB6tQ7H3M1MsVu12jQqURVusTVYKs4+zyEVYCCxPI/Zaz0zV9yDRNi/ee5XJJ07Z0bUvXddze3tH3W2xy9KniZtdwd7fj7dUt1nq6PhCTsHr8Gf/oP/+fEBG8CKlvR6OrsUIXc4nqVOHHWAvGkkMPojVkcgKHY4y+Q4XrwWgSSn3zfQSggFitc5LBWK+OCeYZkHJgzNVDYSAwoarqAu8W9gYt9plRg3PLOad1akXJNJKQVKKQTaY3iSoLrk90ORO8wYSZcas4gkfDXkykHCYHzaGTPue9AfdBo3OBvp5+NyiLAwSMiChkV9a6uUOGUC4OdSNCDPt+MHm3HqR6yOWUcEYVkJwyOUSyyTivUW99DGPU69zYPfRpalwcnO5zo9nUuX/oXCv3CUiCVTZsYsSeLTn76DHf/nHGZ1GjlTgEzU7Ppa6fkp86B0X28zS9DucfjJsYvSfjeIg5Tg34IjKiOSCHgQ/3HUp7gXdeg3K+7tN3zfs8vYa5PoDgPfLcrFWm3Hzo89QZYgvTH2H+R1iQwSSj1zwbYG7cP+bEGZ4D7vX1mANmarA+Nh4pSsJAU3M42gO6mgjh871Yfil2071SMRUwQzys3TpXxAdDoIiMvGSaIaj3KN+yg6bGlD7uK+JDv4bLDvQ1Nc4OEfAFJmqMcpe9g01jZqaO070jcw+ZPXdClpqKBwEt6WA8wzqNT6R9lmXWkP2yL4d7zXQ4KuBnwaRETyKIkK2iP5gMNgk2QwwB6zXysHKeLsNWhLSu+cN/8j/mr/6Dv8dyvSISyZXHOIPEyAJDvLrj9a++4ttf/IrXr77jzZvX7HY75ZdRs6M0qDFCEnzpo0m6nnGyxl3XHdDA3Jk3nIu2BBVkssLUTZwqU7qf0tI9pQWO0u70O1tkA2stz54948svv5yQzSEfGp55iCdOn5lfwxk5Bi/N+1aUYDuKeXlPxlmDmrTG1+G5MUUsmTsdpnxtyuum/Gs0Lk6enTuojgV4zffudK/Oz7djc/++NTvgg5M5nN5/sHfyPhvBFqNGPpCw8z3H65R+pm1NHXHvg/+ejm96zXnbPEDhIUPO/Jq+e3pGaD8hJYVhVfgpUfnQDQZchZOLMdyj/2kfzJDlQt472WX/j2YNaVs6zQOE6GBIEEwpCzRtf+BtgxyVYhjpu3RmNOJRzsnyxTh+DeQtz+TBWHV83cZnjsztvXNz5pQzxpZ7ZG+RlYyYwXg3+X3876CI6e+DLDQNqtH5OIT2P+jr0Mqkf9P9rOuiQY7DO0XUcTLAoe4DjY6jY4DSxzCtD+1hI4KdBI+kVJQG8vhuXY4PU/SmMsJD38PDQUbTdZujXoxBGFM75zBHKe+tiB/goH6/nMfR+w5lNGjbFmsM3jraplFdfOifQB6MnUU2GAydCAWZoBj1Zm3bIjPFlIgP8Ihj48o5lfPiQ2sHPjDmPYWWn6JHiTBkEQoGDwTpwWYqoMZirCeiGYpjbcp0uA/v0alIgVUVIGFLxJMccA5BxBUjlZ6Zzjp66yBlsvSQY6HVxImFXfOYfnOKqZcsqgV4p5kynRo/smzBeBKZLgeasKWJG/p8h5Wei1pwvmLha2q3QMRg64rQtSzFIi5TOwhyqhCIWR2lWSAZwGTEtBjXslgETFboxbZP1JXDG0OqFsSU6dt+3DOF/WEmuvlksRnKtxljyN6SK6+Z3tlQLSpOTp9wefEMu9tw83//P7GttbyNMZaWzKurN/y8eUE2Fau84LQXzrF8QuI6O04lE2NLChs+dp5nqxofLItqhUR41+4IVIR8zaIX+sUJX5w/oX72nO6LL1l8fEkWSxfU9VmjUK917ljbHbVr+SZ7Xpmn3PzyLc3rWw3EZMGTRWBVeW5ue062PQux/ItF4qbtuKgdnfN8GXe8CBGTAmssnbUQe+oQCEZwGJKgWSBFDhdQh1kCW1WcPX7Cz/7GHxBiz5s3r2i3W7xxGFuBOHpgtV4S+47b2ytOzs5Zr85ogzrskYwVgyHR9S13d9c0ux3e1XhjSbnBuorQBWIbuFzW/N5PLtmFVh2RKPy6d4PzxJGzp2tbrt69Q5LKNWpTMSpfo8RlxRZUJsbazwdOuOlOlsHBFotx0CMWjFZPwjo9a0IEsQ3Pnp7zsx99xCcXZ+SuI2ahjaJrmTMX9YJdu+FmE7jbJq63kZfXHZubiOmF0HV0oQeEJJmuidze9oQtmGAIQIg76HdFZzSoAhGpvOfx5QVnp2tqZ/AO2qajjx2QcNZgs6cLPTlEiBGIiEm4OuPXlnqZqFzCmQoxJ9zFDdf9O25u4XaTaFpDHzot3dAH1X+NZoZvbhre2g21rXAodHG9NAVq3uEzgEGyIcYd2cQC857AWLyrWS8NJhk60ypyj1GEhJ1J1EEgqUxhrFFBZ9A/iw4KYFEjdxLIRk/gPg3ZmpSgtYlRVZRfp5y1Dv1QsdsIWSIiudQyziN/Uad+IOeCchI123Iw0A+1vGWiUues/D5LSdfJ4CZ6t7CHFs5WChy6ym5JIAoEl8nOkpwii5Cg76LKm2lgnpC7MvYMCaMZcCJaCsI6dSAYRa2IKiTiLJicyFZ5Zsz6uSJ7C5KV1hoXyxEtDMEFzmbOKsepERYpYSUhcSZTDXtLEzuxSfZOeEEzAqPWp1U0hHJeDr4RIBoVVUJMODH4In+FEBAjdINMLhlJah+zg3yNKFqF1VIAiBQqlbLmmnGs2bXK63J2nC1XKo87Q7DQpMjGJIJLGEk4yVoC4cDeMxX5is4gaSSInCEZAW/I3pGcJdpiX2yD0nlMWl4tJFyKI6XoL3tbxlEZrMhAezn78Kv7948Nz/o90wuGwR1vYFzv0UI+eXz+2JBblFI8kHEAJMkkwBoiBXY4g6UEjojROUyQS2NGlE5DSprNLcP8lIAWhp2WUHsSiGSq2rA+WXB2dsrF6RmnqzWVt2x2d2z6Lde7O97d3LHbJHy1JEmPq+HkoubJs49AaoJ4ejq2RHoRPnv+Q371i69ItlXZByCX8pcJYp8IXST2AWq1B6UuEm2iy5G70FCxRnzm/OKUZ0+e8Prla168eIUVRW1oQ8A0d5y0V5idJ+4ec3tdUdVC7SO15thhBKxJeN/jvcH7mso7TFZklj51pNzShx30e3sZ2bK6XHH5k0e829yxC7ekPrC0S3INm+2WkCKCJSEsbOFosl/f0RQjZVMMR3ae7hPlKIPsrTq4OvqbLuFcVdpqFR3AGIgVlVh+8KTm5nbD3buO1WpNExLJOMQb6DPddsfNm9c8fXJJa09pG2HlDOfLBbd37/j4kx9zc3XN3e0Nu/aW9ePnLN0P2LSQ+nfE0NDcvODLV2/44U//OuuXb3j75i2uuSawPztELCKDfyGVnBbBJqFKws6D7xK3Yce72JBWwu/94Cn/+2+/4c/4jL9CZBk6NtvMx4+f8fmrazI7sB21GD4OlpvG8X9ofsnfrh/zMWtesuG/dtd8Epf8rWRo6QnbHV/8/D/wqLvir/3Dv82f7F5y9eu3bKXm+u1r3sbILgde0fKWHmM8K6lZxYyTyE3saWPNZ4/XLL/4kvBH/57d6QnVZ7+NjYbHu0CzjnjjqbNAdPzuZz/hq8//lLe3n3Jxfsq6MtxKoGuBmEmSyaJIKDFmck5UxmngSAJJHjFLbLVUiPKYNFDOPib0O2LaqX6dM23sSX1fzjxDTpacC/y2UYU2xESMLb2xVNaTncV6AZdoU0OMAesii2WFNR4QNk3D27dX6kgXT+VqltWSGCPb5oa225EyeL9guVjz8dkTFr6CpOWid6HH+IqqWlJnQ77b0ZjX5H7Lpmn56tvX3F0HfFhwYg3bNoAXOkk4SSoL5BlzHnk8KvcQgJ4kmqFtsyIKJBGyEcQ5rGhddmOsBtEVXXqaETLoSFP5pGzSws0n5WVThBBY2sjixLEQw8I5qsqTK/ji7g0xWGzMmAhdEpXRa4P0FrMw2GwwPhJ2W+qoNjHJWVFZCNC2BDze2xKQ8B+5xvi/+H/83xCg7VpO1itOz9a8e/dWDX1GOD0/o64WTOtznJ6fMUT6NF3Ls48vZ8azYoBgUDTUeLBYLpHiwFqvT3j36huqSnDWk1OmrmvevHlDvdAaDl3XAXB9c813333HojZsbhWeqO36AlFi2Wx3GgEVMh//9h9gS730wVgppR7ZaKw0phgeS30B6wgHKz5kPqWJgVE/z2lwbh4e7FMjtTpu4hgFeMyoOBpJjzx74ICbGef3BvfSraxxYyYnFX4EjPfEdodxFd57Yt5ii2F1ePdg3J++z3t/YFieGtuGw2sq+EwdAQC2RAXPjdxzI7HAGJE8GOPm8zNtezp/Q124qYMzz+YICszlxME7PDtt/9g75+3ODXTHDJ4x9LhoVHGvPOvTE3UwpYyptKaUsKc50n7ulAndz/aY/m6MeW900L6tvVNr6ng5cMIcMWgfrpeM9SvGdZ05x7VeUb7XzvuMnt/n2D34bjauuaPjYB/ExP23FsPFTNH4kH4e67OIjNGJ99Z+VtP4GF1NenUwrulYpuswnYthrw7XMSPsnHcMRvwpLc+do3On0vz3Y07J6XcHdDrty6SdNNnj075MHXe5SLpD5s7w3dRZf6zEwTHH3rHAlum9D13DPpzvvWmfx/EAvhwVJktxEBQFkRIx7hxREtFAlEjwjh/93u/xd/7ZP+Hy0x+AK9CCOEIfcVkIXeTdt9/x7Z//ki//5OfcvnlD6lv6vrvfh1yCGrTzB2Oej+EY4sC0rWHNBkPAfWPfw9fB/oCD+XqoDS13Enj58uXR/T7999h1bCwPPfdefsREvhtZ0sQoIxzd08fo66F35cxhUAiMtH3s/B2y2+cyxXz8x36f9+NYn6d/H3VUvedd0/4PfTzGi6YQjMfO3Wm7x+hl3teHykkcGmQOz7npvB6TLebjOyY/3B/b3lg0oAEpb8sMcu5D7zhYk8xB4MkejYSSITLQtCr7ercGAmqdp/tZvQfreeBUfuiewzsO5nfgx/feMpuNmdw1vGN+hs35835t9vtMn52S37w/h+3dl8fsg7Lk/LmBr09pZTLsg2tKr/MM7ekZuEeKOQykOnbd24uT0Q7rkvn+fTj97CGn9/edewfy5Wwt3/f8fRmqyI0zOeYYj3toPPPP578LcH11xa9//WtigZMc10OFDhgDKGbjPDKnR8fEfo8+4Ou/17/3yUkffg0vU515/zP9rlCKMJijSyaAwgOOyGMy1QeO923Yf6SEKYbkvX436ZWUbAqGG46d9fp1jBkjHmeXmLwg9x5na2rraUNDjD0xd3TpipQSfQ7E1JPp8FaofI2vLN5CZRd4WyPicFQE4+hS1ozDFImxxzh1/MynsbiyMEaoa88pJ1RGDcoppFJXEvoujLruoM8cc4znsi5jYLpTOMhlqlg5Q9sGnn32hB89eor5+Z9x8/kXrOoljQFxwtouuH23Idw1LJ0huYa3kvk6tpwvF1r/OWaGuoVvYuLLpueigcdiWImliY7sloQQubnZEGrL6bMnnPkl/aomhB5sBGOJ4rhNljPJmhiQK95FT1gsSG++IXz5K9L1DQZL5RyrxQp6g+002PStE160DWvvWS3XXIee17fXpC5wtl6roywMAbOWaIAwBHHp7A8Q9aBZbavlkucff8xnP/yM//Zf/jdst1tyTljnscawOj2h7TqsMYSsdamfPH1GzuUdWaGzY0xYJ3RtS9vsiDHgSn3GUPTq0PeYHHn29BEX56ca7DKxGYz0a60aMLfbB2DUj8uSQ33jUsh4JouWWthpCPa1hRYLhHo5IwSh61ounix4/vwRH330GGeEXRuwxuKM06DZGOjbgIgj9C2bbcPVTcObdxuu77aENkNQx7Erzvu219rtXdcRU2IPxS2lz4VvGcN6vR4hd6cZUAeHmMAeSrM4Y60dM6dUUHEYZ7FOqHFsNj3XdxuubxLtVrPtUujVxCqMzCbEyHbbcHt3R+XAe0u1zAe1L82k5vugW+akTivrDG5h8dmBy5hg1eZiDDkEusJOLerwyiLEKKVefS5rBNF2KoOJlmwQVK/TQImB8ypyxiAHJrJmAqvbbc88k6gzLgN5fz5N+ejgaBNJpFLiIY1y15AVmUr7pQQfEAQaKc5eJ1q3u9SQ2Dl9VktqqQMwiSGUe7IpMl0Sch0V5mH4SRmsV10lJiQmTMks1x9DNuoty2VC1DGdGCoxZ1Mms9xfUkIBi9jipc57FM1gMrtSc7RPGS+RR7En9GG0BVD29HAUqv05E7O2HVL5CRTnSS4+akGSOjIp6AxDFmZHpENIVmuf13FC3pLJMZIG+4gYJKtTRiZOX5UnbAkCMgW5QDAWKi/gLV3lSVVFsIY2RlppSH3GhoTJmTgLXJ7bH4b3iFAmu+gdZR9I1uHpVCsii8kgFiSLgoePMoqujch92fj4dShHHZcD7+s7H2JXe0hWmuReFP1ofGAiueWxtMMxPWAqy5OEwIhIPSlXY8glmET3WIYcMdFo8GRxput6qI0nM0URVDv5YrFgtRxqiy+oqgpyIqTMdrvj7m5H07SA+mQxio5Y1ZX6QQxkyXSxJ2U4PTnn/LfPSb3hy5dfEUIsNZqNyi05lxrjisgbY8S4wVCrdBtDJKaIc47lYsn6ZM3JyYqXL/erlWIk9AqnHvqezXaHvQnUS8/JqsKv/DivppT/cM7qj9FMVZvVpxj7nmgtOSVFSRCDEcfCGz559pTbJzeEu5bdux2JhLNujwwn+0SYPKX9IzLd8K+Z0u+wQDPaCjHSNA2np6cTvWyQ79WncXJywsnJDnfd0zU9KRmilLPXOZq25/b2HV3XITbQ9Y6ujyxrRVi5ODvn/Pyc3W7D3e015x99gjs9Y7G5IfQ7UupIIfL21Ut+5y//AU+ffcTti8e8++p61O339oM4DnK0/yjFqc3ZWFIK3HY7rpoNjxcLXITP2fA7ZsFpEtKuxdWejy+f8vrmG65DQ28SS7fEJcc74BfpFiOJJ37BDwL8AM8TPAtj+dh43qbIv/g//z/5wc/+gCePf0z69Tty2/O4PuORjVzt7vhxdcayrqm6no/qJZuY+Waz4Y7AyrXUyyWrXUZev8bfvQNp6bsNO2eJ2bDtOiIKTc7jx+x+abl+8ZZVXbE8X2G2LV2MmCiklOljpAmJHASRqtCA+tW8rXF+iXM1IhZjtVSESqE9BEtMokEwE7vHGP6bDX0/BPYWE27OdLmntx3LulYnvAgp9sTUayJmkaNiSrRtqzXt3YIM9CFw09/RdT1NCVasfMVqccqTy2c8Ob3E5rIHU2ARI20s8PsCkUgbWlIntF0HZCqvDmXb9DqOmBTxaGb/urdfmOvoHOiO6gsq0PIyLUG4l7WONvvgBt3/bq1luajpWkNKjtOF53ylqEQ76XHtO1IfialDiKV8SyC2AjmSU1QUjBRodq0mS+SEkUzlLMvaYBZaktsI6nfzD6HdHV4f7Bj/y7//0wLxUBTsomzvdg1VVRUjh4wRWsNkL5dLnHO0bYc7fcYAS61G+wF+qmRaxaRRj1aZfN9nKuu5ud3SmcD5ugY6XKZEMViFCREU3tpZTs/PqJzh9GRFCInbuw0/+OSU71685ubmjpPTFU3T8+TxkwNH39QBlHPJbxoO1fKv846umWSbFJiDqdIzzbodrrkxaZrVfQxada6cHdr/7humhvmeCwGHRj1Tohe1XWcsfepLbRvo+p7lrI2p8Wq6pnMD9X1B537fpkZGlf0Ps6XmxuohM3tqxJyu0xwe9JhRbf7sdF6GwzCmWKKyHoZFP2aMP2aYn38+NbQOhoCui8jCU9c1X335FSEE1s7SxV4VFfbzMDVYDeM55uA5XIvD2T9mlM4Th/Whkr8f29RQed84rAr092fAHDLlOW1NhdT5dXDv97xFt+ihE+EgWEPkXsAUE6F6b1o8nO9jwvlDQv24D2YC+UDLY5RUPiw9MDXEf8j1kPF+ThfvMyofCABzJWtG49OxfJ+z774jYkKns2fmKATTZ+aOk2NjH/4e6KfrOi3ZEeODDraH2pvvpzmfe8hRd5z36ZWAXkAwmtEQNOo4icLGRSMkk+gFkvesnz3hH/7T/5yf/rU/AGc1K9QaTEw4wCfh7rvXfPHnv+TVV9/w1a8/p7vbYnImh/4ePP90HeYZ2fM1mK/V/Pf9fA9QfA/P6fddH0rnoI6kIejtfbz3oet9fTzOF98/pmN7A7nPn6b08iHnyf699xW4+d/z82V+3/zMmLcxp4VjZ9tf5Hqor8fO5nLHg3tvziOnYxv+/b49On/Pb7LO8+shvvrQWgzn0X6v6I/I/Tmfyg1TWebYfh35vN2bb6ZGrOG9cEQtme3lD1nv7zvrMnyvI/F915yfz9sf7zvyjmP0Nr/rGOT3X5Bt7dejIIZMr8GhAodBMg/R//0W5jLcPAv6uIygdpPj+2C4HoY9/4td8333UKDfQ/LTtJ05bf8m11wOGv8t34VJ6aPywG/U/vveCYWPDk6EI99Pr4d54G96SfkpDoSj23N6Jqj8rVk9Q/3XIcPx4f1/7AzJKYHd85u5XD/0T4Z/pzy6/DeTCSFjbc3Cn1DZGomQOqtlvnLU+pixQ3KnjuhSQxAJiAk4A5W1VF5hDK1UiHFUUquGGyN91gBKcsBiCGP0qxqKhgDiEBVaVKJCO6eUCCEQ+0iKGsyUguqKihKgDheT86i3Z6brvt8Lxhmst8AJxgmdWIxYbLvl+o/+O2KzJZ5W+/nG0HeJVbJcGIdYTyORPhuCddg82BoMJMMmZ+5Cx12AdwSWYnAp43uwbSBaT31+wu7ZGTe7Lbul12zLrNnMuxyx0XIqQpcyPZbAAvFLqq9+RXz7gr7ZgBgW1lD7mtRm6i7T58xLE3nRtTxenmDripvumje3N9BHlicLgpQsyZRL6S6lgjTU3s1oENdAh0ZYn57y8SefUFcV337zjSIqFQhSzcj01LWM62SM5fGTJ1rb29hxd2ieQWZze0PbNECmriswhhyLiy5GjMBHHz1msai43TRHdXgjhja0bLdbml27RwTIh/qr7qkj8soRGWHkVwhZDNaKZu0Y1JhZnG2DzeBk7Xl0seL0ZFFqyCZsXVGZSj2r2WAxOCw2WWKX2W477u52bHc9sVeEqsqUWsYZQqc1Y0Pfj0GZc1mEnBAjLJdLVusVi8UC6xwpK6qfjm34KdLAhCdbK1SVxzmDsV51H0k4n1jXNb1d4F5vyERiMtRuQfSKZjMi1pTpa9qOu82WurIslhWrolNPbWlihiD4yRqg82od2LrAdEfIsRjDQ2ZnIq1JSNT6opGSGZaGGtooDdseJwZnLZWxeNSxaopepOqAOnNTygWtgjHxIg9zpVOlsyZDjqkwAIxC1gzf4pHPuTi9RTNWs9nrHVnQfhZbZBL9LFgITojeqHPcCtkaek+hL0s2+pOMJYkdy32RM9InJGZyl8hdKhi1CZzOaU5qHzWJ8d0UJw1Dqb6hnzLIKgBp/72I0rkIZAM+QDJDWAXqSU50+kbalKlC4jJnRf3IBlOE61h4MSKkFDTwIe9tLoRM7pMa2vtIDllLSqKICwM+WCUGciJHtSt7b3VVBjIv51gWyMaCRR0jRofgigwyBreI6HsMGK91Uo0TzNLS1BqI1Nc1nbG0fU/XVFQLjzQtZLlnBzzgLYWnDCfbQBMmo/0nlZJtMkK3i8bAlB+lLym8S/lyQbP4IHXwYf3gwSeO6DXHnnuf7vc+/Xb8rrCkOV82JchimKyYFVkgUOYnl3JFZT6LtDUGGUhSRAGbdL2zCFhFJNUghD2Pd85SVzXLesFysWBRazZ1s2vp+8h207DZ7Gi7XtFjRUv+ee/wlS8BJokuNLShISdYrs549uQJMcDrzQvubhrIGuCn49cAmhhVlpomncTiFA9R65AvnKeqPOv1ipPTU5yzxBLMRkqkEOiLbanf9TTbzHYD261lGRyQMUPMkzWlbI+WL7VisAgma5an+BrJWgpGx6mlbZ8/ecTVR2/ZXt/Q3G7KmV9p0mKMpSSBoqrk/GHuqgM6kmE4h2WiYoy0bcvZ2ZnSRUmCTElLc/R9z3K55GS9pK7u2HU91i6IqccYh3U1ptM6481uh1+cEnOmj4mQNXlzuVpydnbG9bs3XN3cIimwunjM8u6Udner8hWJ1y++o9ltODs/5/zxU9588wWkUMayp+tjdrk0DLXIIbftjlfbW55ffMS5r/kiNFxLxeMs0Acd8+kJZ5uabejYpUQo+91gWDjPwjpWyfL38yNOzYoqav66y8IuBL74l/+Wn/2tv8fFZ59x/cWXNK9/zcXakSXhYuZ84Xm0WrGTlqe141UUrlsNcHUOQk74YMlXN+TrG1LXYZylA4iZLBFLINORzypWiyXN62u2Z2vWpwtyUJj/PkRSH+hDoo9ZSzFJVc4aLUvr/ALna6xV+Y+UcRhMaDHWkZKFPJw5OplWFC0k4dQ3FBV9AqP0pHxHz43gNKs75kiKAVC/VUiRnCOhDxo4Uc6FmDXoNsVM3weigLWeRbVgvVxztj7HFkgWEaMBnXUFXcdmsyOkni52NKEhNhqk6iuHr5yW3ilw1MaYgpJ7H1lSud9DfHhfUmbUl6ZnmQyB1sMdhT5nbYlMVW6ZnRR5vMe6IiPaBaermtP1mrquiDHjvKGqLLmUZknJkJIGtwHEkGianq74k8UkjIB3wnrhIXucZKwRnNFz18p/5IzxP//ln0NxfIde64KThaura+7uNlR1RVXVY4SCMRotWtcVdVVjnefv/qc/GbOgci5QbhNjnkIcDZAmRiP3+kDXR7759isWFiBgvC1RURqhpU6BQYBISEp8/fV3WOtZn5zShy2r9Rl9Nnz55VfEBI+fPBnfOzhQBwfWCK0qGpUjZdG9c+OKD0qPyHGHyRhRnvcH+PwgH95zzHk7tKe/3M9Ku+eE4lBQmDtEYDjc8yi47fukiuZg6EozJjzMTc4Za+zY52ld1um7rbH3+jK2PWSRyR6OebimY5w6NqfPjWPJh47v6dxP758b3MYDJe1hbN2sbunc0D5VGOdrNTCLaXDD1OA9QMMnySVCxrFNPTfXNzy/vCjGokA2WaM6OW5Ee8iwNu3f9zn29+MfqOG+sQ+Kglyik6afz9uaChvHheH7wQrz+Z1Dex5VBL5HiE6ltttU6Jnec7RvxbCYJ7/P+/ngsxzZfzOhfj7WYz/zdt53HYN7nhvfj2VcH+vz+O9kD8wdZseenTv0P1SR+b5rPk/z/Td999Df4fMQwmggqaqKtm1HXjWn2/m6Hh7k953dD63NwJ/m7R8obwJBEi6pciApa6YLCpvWW+iNwZ+u+cP/9B/ys3/wd6jPTtjEvkBRGY3Ij4nNu2vefPktX/3pz7l5/Zab62vCdku1qIkhKERiziM/nq7ncefQfr+HEMbf50FaU143CETHIMd/k2vOJ4+1YYpi4r0/CJCar8H7rmN8Z/7MMVjh97U7b1P/VcPXMVo6Nrbp84fjvx8gND1fp2fPPJBu3t7w95ye58/Oaf4hJ9df5JrOwVHDDjOjct6XbHgfXPrQt+GeYzxxfg3OiynveB+U+r3nj6z7vD/H7hlKxuyViv33x/jMsXW5xxvLmHWuBn58GLz40GjedzY8dB3j8eNYHzgn5s8fW/9j904/P5A/MepkeeCevP/wwFF139m6X4uHzvfpuojsSy1835xN5f7pOTmd83H/Zs0gemg883499F6Zjv2Be4/Jkb/p/p7P57E9M5/ro/rJe9r/Ta9j53nOeTTAhxhJWfdJLg6PfW3S9/Xm+987nIWjMf57rr/oWXmkpcN/Z3LrKNOPDlo1imtGz55/yOTh7+/Tfb11NJoc0MEw97OASNB9WfTgEDOCxbsFtVtoreiQSGLI0dL3mbbvyAVM0tiMSEJyRHJQ4ypSjNh5NF5DcSgWaOOUojr8BK2drN3YnzvFbtB3PSn0dH2gbTJt0yrMdlAneI57BLzhX8NeHk/j3tgH2ooI4gRbWbCOvEssnz6HFNm9/JZ3f/zvEGNp0WDGkHq6EIi7jk/cmifVCucdLZm34mik0veIUIthhSFbw227xXoN7m5ixyILdQ+mDdSXFyw/fkJ8vOLt7RXhkcOkAFkNk02OLHFEY2hiViu/r1hai/nuNe3dNX3ocXbJyikEZNz1mD6zNfC1SbyOPX9p9ZRshat2x7vNHSZB5T09k3rCuThsmDoqiqMftdlY5zm/uODjH3xCs93x3bffkbOWIjHOYa3CUi4WC9rdhq7rqBdLzi8uSFnzcQc7jTNCjj13N9d0ndZjXSwqpdBsVB7PiaoSnj59hDFyj7eN5y+ZtlXHeN8HFr4uNDfdeGXtp1bCYa+8b+8XPmKtUXofnONGjbQpq8Pj7KTi7LRiUVtNKkkWky2VCNYbjIlIFPqUWUjA00AUQpfp+0zstU2xRucziSIndp3KwCMNx8POo+9frRYsl0uqqlKdoZ8G4hpE9nwwDwGPBs18rBTG0jhHNonsEn6ZOblY4roTXr294+Yq0WyNOhvIpD6T+klZK2PoY2Cza1gsPet2SQhh7M+xrPGRJwnFOa5OHIOQjCUb0Xd0mW2KlJwwUs70CCElYlaulkWDoGzu8MZSk6hzZiGipbEQpb/y2t4ojLg6dSDnEpifNTCa4vjO7H9GJ3zhZYNjfMhAz9mSEaJJY0b94M5MJhFMNzrFsxWiFWINqTYkb8neKPaxz4hVvoSxZOP0d/GMXvqYkC4gSaAN5DYqDHcfR7ql6CwJRR8szHU4dIqDXPlsAU4qeyYVB4OUD5WGchJy1WsfBqe4pjUTytwojG2iMz0xlHJlIgVVTec0lWxuUsLmQX70pBAwnYPWQNMRe80yN9kqopvR+uguC7HtiX0gA1Xt8VbLD4wzLkUGsAbnPc56rHVgDFbBH0rgXNFnclZneGW1lr23sPK0YmiXK9qqohWhbQ2EJb5piLudBh48oNc8KBMWg1Ye9nIe0sWL6z9nKMgj5AGxY86b7gkW96732cfmst/7+vyQ3va+v98nvx/0YRTz9vqKUSPrcNcYAKNlYAr6wRBqYCwieXSuSplKYsYaPXNGekdRCIbXiaDQvVVFXatTvK5qnHPE1ND3ge2uZbdrCX2kqmp9h5FSRs5p4F6ObJodIXV461muTnn+/DOMEf7oV/+WzWZHjnlMcIO9E3xA3XPJj/L74BxXxy9471itlpydnVJVFdt+V+ZN91EIekakLtE3kXYb2DWRpos4m/SsHeXMIncyxMQIRhzWJnxVo+l5A5tQdJRH56d89NEl79685e3LN/S3Pc7WigAzBB+moQzFRBfeC37v1WeEffDq9GxIxTG+p1XlOzlrpnEIgbquWa8WrBaezXZLVRv6ThF3rK2wtqFtNmzvNqzPIzEnupgIMavvq/KcnZ2yXq+5endFv9uy+MEJq5MzNjdXYK4xOXLz5hXX796yWp1w8fgZpl6RdjelP7o/ZTgPJls1g8LI56zBUgluux2vd7fI0094tjzly03Dq9zzSfZIzmxubqkuH3PmlrzrGja5pY0lox94Vq157lf4LvBZWJCs5TY3hNizzYG3dHzzyz9lEVvOPvuY+kfPuXrzZ7Qu4EIkG2glcZ0i70hsQsuraLnOQo+jixm6QB0N6c1bulev4XbLan1O1/SYqKWMJSWk6wDHk4tzXr++4u71FcvLlQad9YkmROgTKUDOVs/F7At9ZYyxGFtjjAfjdP1NxkjRG4wpzvIBuUT9jtZYrMnEgYaTVodJMZJlQotGz+2m65AAkHDO4MikFHSftT0hRg10yWYfcJsKiosYrPNU1YJltaR2FbHpCy9Q1B3jLSb0hNDRA62zuOggaL+t1zIeA10bSnb0sE+m++E9/FhGnc4wUWbGvTrsn3JyMzBYKef4/fbLPRO9CKZnh45xsahYseR0WbOsK5y3OAPLhePULcjGICYoMEwIdG3JHgdSzDRdT9O1GKtO8WVtqRz0PfROWFRO58QYTP4wNJQPd4z/4tdFHhKs9bRNz+eff0nXdnRdQMTw/Plznjx5wlDbQxVqNQ6enJ7yj9cn46F2LBPZOUciFmjzAq+HsFqf86tf/0scGpHRp268ZyCIwSEmIuRelWeKA95YR0yRd+9U2fut3/4py9VqH/VdFqqu9XDq+55pJo4auiJiLJX3tG0YobtE9v1PKdE0DYvFYg/LdUTAmBoYB9iPuTFwLjBM3zF1XAzGuDTLGDxmDB8cr8YO8EWD81w30R6u83621jTzYnBWDPcNdSvVSWVGgWvcSLJ3HI8OuHxcYZw6babGxmFM86jmucNuOpfTIIf5/WO/8qGDfXr/1Kk0HctD6ymyd5gdW4fQB/qUwZb3xDRhRgNDOmz7oazO+VxN+zINbDh2STkAjhkDhoCHmA/7Nt+zU2HjocCOwXA0nfv5/E/7fdTYeWSu7zsk1Tk+FZjvORsYop0MOe0z5o1RhXEIYDgW+DC/pn2c0p5z7h58/P3D4D7d3zdml3IHc4PkkWfn98znefr3lG+MMIaztR3WZZ7JP1+r+d/vm6uxjdnnc6fP+64YYzmkD/fAFL5/s9kctDWnp+EaHEtTWpy2OV3bqVNk+v1DwSLjZ9o5fX/JLuuzIXlDa4BlxU9/7y/zt/7JP+Lyk49oXaY1GbGeFBM2JLq7HV9//gVf/+JXpJst+a5hETI32xYJkb5piBwGpww/dhLsM/w+h4qcZpkf4/tTA+G4d47s0Yf23fTzaXvzs+4YTQx9GXj4sfbmzz+0FvP+HENzeSgy/1gbc0fZ/Jx6iDaOCaV63uSh4sr+PE/34Z7ft++ne33a13n/53M5P+uOje/e+3NGJrLHcE3P+Om8HF0zGYw4h20/xL+PzeWclub3TzP6pm08tKen8zZ3ms//Hu4ZzsvpeEXmdGUGVvugLHNsrY6N2YqowTbnUVkZ29GbykD3yETza7ru8zk4hg5zjIeOfZvQ0rExHOO9wzW841jpmnvryn0Z4t4lh9L2/TPlPmT3PMjk+/iH6iSHZQwGGpjS+/t4Tc7DfpcDOpn3e66fzOWoEa508tlDgSLvO2cfmoO5DPG+9T12Bkzbe4irTp+Z9296RoGeqVZkjE6f8+C9/qLtOOtogxq/BoOcymb7vXNs/MMeNgVGeRoEN7wj5lIeYcK357Lj+/bOX+yaGvFmnw3MNGdyUf41eU9hLo0VnGFvRJNJc5NxD/3er8WRvs9kjWmf9kaToTt7p3jOEFMoQdhgbUXtLLnvafuOmDIhRNq2ow1bnDMsa4/3GWeLQYtA6BPETHQJYzPGeLoUibmjiYmQK5wLE3TdQd8caFV5MhlCSvSdGklDbwghEkIihqhZd2VPpZxLFnph5OVncFzo0svIg8QJxlukcty9veW3f/hjVmQ2v/hTrn75J9Rnp2xNBBfZ9jturjcsrzb83dPnXCxrfHGu3dgT/jy3tFmxfB+L5Xf8kr9y+ojvrl8S1xXXXcfNdkfX9ixPz3i37Tn/wacsP/uUuKz5+t0rVu4jfG/UuJczSwurSrPFh4pvYgOLLvHFL7/gtu8JxrG0npOFxyShbwLEzK3N/Jqeqxh4cnLKNvS8bbbc9S3eegShLZDvQwB+zFlhcCVr0HXR18gQYmZ9suTx02d89PHHvPjmW968ekNtLVKyxRerJTEnzlcnXL97Reh7Hj17znK5pu0nZ4roHt3udtze3BBjoFrWVItK4TfFQ854J5ye1Dx9cqE1HtOhjDjQdegD2+2WzWarfN4VfsjeYJ2zGvjUIaKB54njZ8nwvdKMGi4FCyZhbCoZeEqvMSaWq5onj1ecnnqsS8SQcKaGbKiMQwScF3KXoXOE2rNZwtUi8sI1OKJmSYmlMp7aVYRO6TuFiJR1SkkheHPOe5ZiMs5bVmuFt/Re13bQlYfxTE/dnHRurBV85ahqj/NG5UWbqVaGy49qHj8+4aaNvLpecnWd2N4ljDicWxCyZoPlgi7gvAaGtH1g23bs2o6u61gsFjjnRp4/nMMmFsS4oWRcCpgITiAZMyKDdygk/21MtEnhhUNSCO1sUD5pLViLWIPUouUcjFDbjMcgFAeZyXuvTxbNbsq61upym/BJEUJOdCVALqP2i6HalsrHmUwgJXWMD9D65KzQ7RNjs7HQmKBOEiPgAW9gaaF2UHv9t3JgIVtfCgQXJ6HRTLt9+noiZas1KBqvTvHBMZ4ococGDJBt2QA6NikZ41qmTcccRWUVNfklnSuRwnSGNDxBTADRsCcjtsCbCyZlJEZMjJgQuX2cSSEWmnbUJfMVgT525BBIIWCTpkeLCt640OO7nm6njnHN9HdY47DG4kMmbhq2Vzd0u5acoD47ZXl+QnL7zH/18GlGn3Ue57wGnBhLbyMidq8fDWvqjRKgNRhrcZVX2vSOYAWXM9J7jAfXt/SbOwgJEwdecd8mO6z/uF/Z6x5SIP41UxwGjkVhwUOk2Ggdmxzcx2TEh65jcuH77h3aPypPTn+T6edTeWUyDhm/Hc9dvSXvxzT8yaAPyZ4H50wwiRyCOsgPoCbMeEYNaP8CEIUs6hh3MZOHjOkBpp7SthF1ji4qlosFdV1TeY8xlpACuzaw3fV0fQRs0R/i6GpKMbNrWipXsW3e4SpLfbpgtT7l7OKSagVnj054+/qKto04cThnKXkOY8Z4CJNSMIM+ESMhFtReYxX2++Kck9MVm+1unOucEl2vjvEcMqmD0EK7S2w3LYulxVgZz0PJmRgyUSJukI2yYMTiK49hkMMzpEzKgXXtePr0nLcfX/DdNwte397hiVgr2KhZoYrcqxnj4x6Q/fpCQTIc+NLgrDtyjTJ/znRdR9/3s+QR7eGg25+sas5PF7x5s6Fylj4obdmS+Nk0W26vrzl70lLXFV1wtDFzvqxw1nJ2dsH5xSUvXr7k3euXfPYzz+npBbert9y6CmMizXbL62+/5bd/9jMun33M4uIp22ZTaHmayHCYIAUluTRlhnNlU2SxJkd+dPqMf9X8gs/7hs8ynGTD7Zu3nD19yulizTo0vOt7utTRZsNN6nlcLflRfcbbdM3/K35FG4XHyWGBO0m8sfAn+TuaX/2C849/zMlv/4Q//tf/gtubaxZNxa04XnYd725bTA6QAn3ynOaaBYZ0E1jWnp3A7osvuPjFx3z6079M/dEzYqN+N1Og9AEkJj755FPuXt5w+/od+czy9NkTUpcIWRAMIo4Kw86BBIojvOh41pPRTGOGoJEU93q17HmNIFjjcEZ1pCSGkI2GGadE33ekrAGMrnKQha7ryIHxfbWxmKRydgyRHFR3rOoFsRe6tidFRU2xVoMVrPVYp7whdr3KZEZw3mO9JRLZbbc0zQ6zEEKqSaKoBH0Ipb56YAjqcNYgEaULeeDMmG0PQZ3sMthQhprgomf64I8dEgv2+2+Q/+Y8mzHwddiLyrlVK1OeKVgL9XrBqYksreBdkROt4fLyhIVkurwlphZSJnSRvlIdrU+ZLiT6FrXJSMY4q471UoZUjMKqV97jrTuaDHXs+mDH+Hcvr4uSqOn7OWWMq1nXa8L1LTEEXr5+x/XtVichaxSTiDKR33/2A9anZ3TF0BBjLM5cOyrO+uBQh0rIWWi7yNOnH/Pi1Tvurt4QYwd2b3BKSR0mZK0BnnPWiK7C3GJKhBjZNQ3L1Yqmbfl7/6N/pJ+nPdzePaNrYTQ5JTBmXF7nHV03WfYpMYhGex0YlDg0kNwz+JlRNDmY76mhK08MMMfumb5/+Pchw7ExGhETi6huzN5APjLdmZFq2pYeCIf9GO5TR1Iuov6hgWhujJ4KK3MD0vD7YJB6yMCu6z9x1s4Mk/M5mBvb54a1aX+mz0/7NBjA5obEY4bs+eUrT94pCsLp2WOqWqPPjTEa6XqERqbOhvl6HxMuVRG771SYPoPZZ39OM5wO25sKoPfbGaKE5nQy9FkRF0o0/JFxHW3zmICd1QlzzFmzb3OAR3pPWw/MRcp5LJkw8KHpWh5b2zldv49W5nQ7n4tjxpi9geW+I+h9f0/79pAB/KHvj7U1fH7MYD1/7r30P8zLrO/z4Khje3xK8w/RzLH9fqzvInuBd579/ptc8/4c7XcqNW+sp88ZsY4+ZxpJfPw7P+Hv/JN/zA9/60eY1ZI29YixeClwXn3P7tU73nz5La+//pov/vTPMW3AhkTYNhpJbLSGWiJjZX96zBE0js3XMXo+5oQdztjRGTBxEBw4LN4zf9N7pnv4mPNgvi/mbXzfuN63H+ZjO9b2+86H6f0HPEzQ7H7ZOymPZbcfG8PQvi0ZQsf6dczZMh/LnF/N52P6/TQoaf7s1EE0dZjP3zm9Z+jjPMt76uycO+tKK6iAfL/vx8Z57J5j15w366vuI0fM+3NsLqZzP88Cfh/dDOPLmYN5UTF17+yc09cwVw/Nd/njiCi4l0f3XPb+80NgzHQO3ifLHGvn3rkxu+cYfT703TFZ4BjNDoaOzMM0IqIK3DH6n95/bA3nczLlUfffNzUxHp+/7wtoAUa9YD4X83Nx+t09J/uReXuIt00/O7iHQ4fuQ07yY3zwobYfop+Hrof29PysEJF7BHevr6L/WmsPghWAg4DFaX+PjoPDwIRpOyIC75FdHlqD33Re7l/zvhaDxAQxAikZalLgKousb4cAbNGgWKW/4/D1c5nqfjfy2Jf9nFCyre7vp/1j+lzbbbm9veasNlRnp/iFJ263xWGugfRkRwiJJjf6Og/eq5OriT059VjXY2xLzIa+tfShpcuAS5ysnhKAPgNWfTFj3xIIFmtrKhcxlSNli8fgfU0KacRPHdZfM8O1zrjGfR+utc6DBtkaY/DGUHsP3nPhzvnpxz+E//Bvuf4P/45T09GYmvMqEKynaXdstluuu8AvK2i6t4TQYXBUywu+EEjOsKGlTi3fhJbdRnjT3LFyp6yCxcclDZZgEu9S5OTJJdX5BbnPrM5XnLXqgEqiZXyiMWylpwo7PjYOKs+NT1y9ecWf/fEfcdsnFq5m4SvWVUXotJb1ViwvCPwqN7i64uL8gv/+5g1vdhsiwkm90FMopzHYPpXJ1Ky8wleLQzYUW9Djp0/55IefcXZxwb/9N/9WM7Z8BQVKvao1S1i3XmKxXPLRRx8TEZbrE9pWM/8BiIm7m2v6rsFZh3cVEa0/vqiWbO+uWVaGj56c8/jxGU17g4hDBu82+8D63XbHZrNRuNS54WO2Z5jum+ELIxP9cq+v5kJPkMh5MDyqQ8AYIUYIseH508d89Pyc05OKRKTP6tAjRK2dbSwOC8Zy6RbU60gOFW0jXF0H2o1jR483lpX11OKI9MQuksMgl6E8JKvDdZ8xqfXFLy/PWa9XeO8Q0ugYF9G+ZqP2N+WXAZGMs4aqctS1RTPyA9Yn1hee55+uOF975BounljW31n8y4zpQKwr51FJWogRazQbVx1KPZtdQ9u2B7YRY4xm4054Vio/krQusMWAJHpJ3ObAXY70ktkBvRgtbW1FHcuVh8qAt1A5srdkIq0RWoHbsRZ8JlkK1LbqAz4W+6VS0pRd6ryKQLaQSkAlQwnKPLGpZDJGy70ngRHe1DLG+UjW/hqwvYBkshX1VTugBmoLi+IcX1bgl8VBKwrNWbLncA6LHeGgA1mZZwemy9An6NVG4pzDOk2NTjHuHZNyGFCvvDFpfe7RVpqhlMuc3psyVDFTGUNlLc5avLc4Z/AimBSRGJAYaNOKylXUpqYSpelKLClolqxmmSd2XRzPOCNA1oCqHAIE3bPGZjBJHcltYvv2Gn+1ot01xJQwtWf55Am+9vtgGLu3x4kxWKsZviIGw2pfNk906UzlwQsBheO1VnA58el6QWd6dqkn5oTBkJYLbrcd797dsdkG+q4/CFo+Lq8UOW4iH5myrOXUV+d4GrSEssPn6thfQD75Hy7TlCsP+kvpxv7PA31nWM/hsz0Gzsi1KKbJ/TOlTZE8ljxAIFvBJ8PoFo2xEIryM0zh2eWFKutT0vOKiFB4oLf7zySrU3y5XHByesJ6vWK5WOK9IwUN2NvuGtoukNAgCWNKck7I7HYdxu8IxpL6wLa54vzJOX654OTyHLeuMMZRnS1xC0+36TEWLaMRC7rNJGM8xqhBTTMdI+WIMZ7lYsHZ2RmPHj3i5Zu3SCrBbCmw227Y7XYsVmfQQ9/C3SZS3Wl2bK6HNvVcDrknWQdW0XwNBmMUVYPMGCIkotmeToTLyzOef/yUb5+/5NW3N7S5wzuPjRYjgSSJkCJ2QGAj72vNT65BGj52TW2toPa5pmnYbDacn5+PZ/Nw9gzrsV5VPHt8ytdfvSamgnac9LxWPmi4efeaR5uPWS6XdD5xt9tytl5hrLBcrTh/9Jizy0u+++ZLJEcuHz3m9vodb1+9IO06kJ4X337Np7/1E5an51w8fc72u18ztY+QC9pJkX/EKNWaHMv5Bs54Yg5sYs+31+/48fqc3Qv4ed7xGZa/Igu6/oacIuuLM1Zxh29v6NHgpY3AH7dX/Hix4q89/oz/3d0vWGD5q3lJjeXaZE4RbLrm1//1v+CH/+VTPv3t3+bdT/4abz//Iy7sBT9cOJ5L5lYCv1Vnbu4iz1ZnXCxW7PqOX9+8YblY8ulJhVwH3Mt3LL/4iovf+ynbLtEHCCGzqyHUHtNZmosL/PkZt2++5foXDU+fPSNIxiVLdoLYCCHjE0QH1g5yloYyRQBJyvdMUrSg2o66EpIVBcRooJOJCekj5KRO7wixT6Quqb3VC04cVjRYKoYBEVigy/QhjHDjxlmVX3QzkEiEFMhJcNaqL8aDqwTnBUwmEcA6bK0Bee2uoW9anj16ytNnzzk7P6euanIfub6+JsWEEdU3VnVF2zSEPmDckLBxbK+UQKKpTWSyewZLh1Cy6MuZJmUvGREsMoYSSWHaE7Z9uBcHGRPlBd5q8FtlKlyqqGmoDNS1xS8cxkK/uqAhsO2g7dX+Ea0j2EAfoA+ZNiScrThZZLLtWC4s64VlvTCsq8zJquJkfUJd1SQyu+3mAQ5xeH2wY3y5ejKDutQJbduWza6jj5kkjnc3G+q65vz8XCNyup669nz08aclIqIrh9Rh9oMaIsvkZoUr6NqeGCJPLi9I2fD6zQ3GZiKREDWiVAWUpLAIuSWliM26aKZELoYYSVjq5YqQ4dnzj0dGPjcKDUaVro8YMxCMHrsi4J0f50AKh58aNJ1zRYHbK4DHjP/HiHGkoWNGKDk0utmSzTB8/5BB6sC4lFFFTWQPK5gV2lEd4jODZOnjYXTwvt3hs2G8Q1CAKqiHjo8DY1/ej2tucJpmaT5kyJzOy/T7Y1lEU0fR0ahLud/O1Bkw/XfqWDjWj+HZ4e9DR1AiZ23HO8/pyQmruj6wdanR/NBYPDeyTQ2Xx+4ZxjTt8779sp5Bg0nmQQUHbU2GeCwLaSCn6TV3dKZC/9PPHspgOzamcc4nnx03QM6NdMcNeoOQK6KZd1MgTDWG3j9BHjL0HzOiq8By2NcH+zGht3uG1P9Iysa83eHvA+fpB/brfdcxJ8JBP7Txe+3O12veX5nQqGbqPTzGOW0M15zGjzkuHrrm6BTzMb/vsqJ1lkKMRG8IHvzJKf/gP/kH/LW///fwdUU0QshRYdwCSAiE7Y63X37Lu69f8M2vPuf6zWv63ZYcExITMQUVpqzF2eKsfg/fn49j2n9jzMFZNZ3P+f05573A8wAvPebImNLG3OlybD7n38+dEr/pNR/DsP7H+j58N4Xb/r73GjElolwO5IkPuUYeYYScHnIg78fx4P76wH06tDM/E+ftTOlmijwwfvfQufPA+36Tvk3vnzqJH1qvh/blSKP619Hxzdud/j6dl7mMODVUHeubfjc5J2djeJ+8Nu/fQ98f8r1hjJnB6jPt0lQ+fehMmH82799R+Yv7MsCx/fvQ+Kbn0XQ95/0aRZJJH+7RA4yy9kPvHVBljvVv6EOcyTDzMalB6Th6wJRnzOdu3h8jhmz29DB1eg/PHvtsOg+DI/J910P7ZtLYe+n4Q65jZ8ZfpK2HaOVABjjyrsP9ABQ53PmSeTDwkVEmKzlUR/jB2DZ7fWs6pkNZZ2oGOOzzX3Qu33el3DKgHsho8j4wGx/cP8Com4JsOw5T7u/cY7LXno6P8aMPuWf+BKTQAImm3/DuNtH0t9i6ZhcCXWrUyIPBe0+OPTkGulahzfu+wCxah+Do2kBIG/pkaLfQtDvaqI6IkLZ0MZGwSEyQBMmCKaDbORtiQg0sXaZrM7ltx/riWTGQD3XR8j+FQ9x/Pvwe2TuHnNHyPnd9w9/+3X+AvXnL6z/+97z58z9msazZpUQdIt6sOU2Zp73jTYj8YvOKVnrlMcbjk2cbBSSQ+8CNwCsX+be330LT45oN62hYBtGsyj5x+vFnLJ5/TKqXmG2LPV/hNr3WwLWQjbDLgrQtP5LAuRWua/jOCy9//Tlde03MHuctC+9wYuiaBpczbyr42mXe5cyn6zOk8ny7veFqu4GYqJYVFkuOPSkrzLGloGykOOpYg9Gt73uqxYrPfvgjnj77iLvtjl/+/BdUzmOdK1kzFUng9OKc66s3pBg4O7/g0ZOnxJCo6pLAoDZOUgrcXF9DDFSrJc5VxKCIf84bQt+wOlvz0dMzVgvPdTM9M/RH95hlN8DdhjTLLDsiHxujvGaasZaPaZXD88X8mME7i3MZMao3hxRBIo+eVCzWjmQSbWhpA4Swoa4MK2MxpsJKjfdLvBVsCuz6zOV6x5PTNZvTROvAisUbg5HMZtdrbXFKpp0xhHtne0Ykc3q65vz8nMWixlpD6MNYfmk/dkbkvZy1pqOvHHWt9cWtUxuT88Ly1HPxqOJisaDLjotHNevTDrGBvutIyRKCJoPkWAJRjDpEYsx0Xc+uaem6buYYt1hj7/FnEVNqamcCiU0OXEniisxGMqmGHNTZjBPwFlk6pLLkCrIzGG+x3o3w39nkgvidyc6W2o+FdkTozWTFEwW2OjMWqh745QDrGfKB9XpAEwfUIR0TZE0UElMCB4yQTSKJlouIaYF60bP2xQM2I95gK4urPa52rFdO6607MDZrQryBymsJAisGyYKNBrpI6jISBAlCThoEbMve9FmoonZ4vxcGmVdhz1POOONUxwGFos2DM738p8hdxhhq56ispSrZZN5rBp9JCUkRSerMM1KRkyEGtMZsn7jrNYhKRIPiWNhStiaNyfGSMrm3pF7nSktuFP6BOp8WvqLKVs8AZzm1FbhqDD8zdlJKJWVyhJADOSUqCpoMhUYc1CdLbHYYSeDUhrxeVTw6XbBenCISSamn73q6bLn9Uc8vrt8Sbu/o7mKZqH1gwf6sHoIsCt0wNR0NVmu9LOqkn9p4R3ob9/GhLPy+6yEb6PvuGd931FYzlcXKeKdtjeN7KBd4eOdw9/yz6Vv0Mkahd+vKQq/BIElknDUNpBSSEQ04MZZkDCKZ3greCdkpPVg3vFeRaIwtzvFqwbKqqb3HGUufFVp5s93QtVo6wLkKjCWHjhAim01DnzJ9go2AqRPnGC2b4TN9bnl1/RqcxS8qvB9QqwRj4hjQqVnj4UA3GZISc9CMVltppvlyseTy8gLjHKnR8hoGhZkP3Y4UAzl6Qpdom0DXWiRP0GZRxIvxHEAdk1piwiDZoMFXJfjMQColKiq34PzxJR998gN++YsX7N51VM7hnJCclnbtYsTb+2WqjtHbQCGjrWJmyx5oLMVM0zRjnXER5QOhoBH3faRynsuzNSfrirebDa5ekkV5h7WGynm2myt2d9eE8wsyK3ZtS9s11FVFv1iwXK85P7/guy9+RbO5ZvXkOcv1CfXqhG27wTnPq5ff8frVS559/Ak//Mlv880f/78hasLMkCw6ahtTuylCyhHBoqFKQhN7fnn1kt/++IJHtuJF7PgFHT8R9TfsXr6j/uQ55/05Z7dXbOIdFfATU/Nqe8O/zBl3kvlfuh/hOkNbZzYEHmfhD80lT08/5ruvPufim1/y5Gc/5W/+/b/Fv/vFv+PysXBawUe9Bng8rStebjuenNZQJdptB0QuW8fZ0nOxeEzXGtpv30DbsV6fcNtsaEMg2ETvhXobuV0a1s8fs7t+w83XL7h+9Zb68WPyu44udvQC1EK1y/TGo/7DqAnTkrAuU/t9uZWcDXXMbHaRTENMilo0zqkoUvU0brh2XtuwWhfbOINYdZSHHImlREhKQekHhe62RoNVuhwIPSXRVpfQOUO90PIKYjN9bmiTwdcVxkOTW0ITaXY7njx6yg+e/4Dl6gTnawRDs9tQ2QWLKrJaRpZNwPlWZWwjBQnm/fbID7E1KW8peucksUZkOGNkznL39v5hLw7toSzAicXhERswwbB2FetaEYbEQ5caFkZwOFb1CSkvSUlLp3ZtYLdT5KCmiyxDJovBVUtWC896WbFeOhZOcCVI4m7X03Y9t/+xHeOff/GS0CvOvRqGMt476rqi7bQOeFV7fC30IdD1CYzDeXVIf/bDH9N1A5MusCbWFuKbCFY5odHGEKMqI32I/PRnv8fL715gjNaRaduWtuvAGLxVSKm+D4ozLwZLxnmN8gtNQ9+3vHj5hsVywcnZOQOE6TRjdjDAaF3BHnNgLNAfjbwy5ByGmIsDw8k0Q0h/Dp289wQOAcnHGfzBy7mfgXpghDdmNObMr9EQa/TQTmPooEweN1rPLR46uR6CcpxnMg+H7gCrPh/rATQn+6jpqZF47hCfwxw/NLbvg3sc7jmWjUU+dCIN751nwA1tPGTUHv6e9uUArhTZ17wTuL275dFqpZFpfU+gwEjl4+84lr0yNRpOhrP/PR9mvo3tZM3mnrYzRBgOmTbY+/Q0NxTPp/K+IykfGKOPGdePremUvo9lOd93ZtzPWr9/7z76U4w6owaF7N5AZn2ZtzWl7YHeh3dOjfjTZ6Z/H6PV6d/fc1Z98DVd34Gup5/N7z3W7w+9Dg0S93nYPKDj2Jw+1P/heb6n38cUrukhPg1UGbInhyyQYw6jY/v8g+ejiKq5EnYm87t/9w/5G//pP+TxR0/pYqQ1GVtXqnyHSGo63n39Ha8+/5KbF6/Zvr3i6ruX7HYb6vWCXrIqCeJG4crAmJVzzAEyd/Aec0iJHAbzHIxhtqZG7p8983NtvgYP0fu0n9P3zT/7i15zZwZwsP7zPk3f+T4H9ZEX3duv38fj5mej/n0frnu+f4e/h7mfyxofSquHvOY42sUQNDHNgD/Wr2PjA8aI67G8zf/ANZ3u87mc8BCvHYwo6YFXz3nPlIdM+zz9fLrXputwPCjPlv23d6ANbT0UdPF9e2Taxr0pnSgqeTau6c9ctjr2nvmzR/nzvU/uXx+y9vN33fsu59GIelQGYJArD9f0voy2b/ND98u98cte2Zvzvakc+9B4HrrmcuPw2XSPz9Ejvu86xluP3TPdLx9iFP3/53Vvfw8/PLRXEipm70t/MOxpM2SEKi28V+YRDR5+SHfII00e7/P/L66UQxmT1l6VwRB7+PaJADlE/KsR2AwQ6sCQtpPJlP+PzkoK3xyChqcDFZFRhznkK5QsBLkvpylbIgN917Pb7di1C+5cpA0G6TzZeQ36SxlLcWZZp/CcWdFr+hAJOWOdZhHbLJAsORtIQo6Btu2Q2NMu+rFUVU4RsinB7QrtSbbEaOj7TNNEtpuOsNsR+0AqiHg5KS2NDl2hzNcsqL+UT0p5r2saqxkp2y5w+fgR3Ve/pP3uc/rdBuoKCLQp8XLzirrp+a1K+M9+/GPc2rHtWrYhsM2wsZatV7r+4fopC1vxLvZ8/uYVv/X0hzR9x7bZIjHxpD7hTz9/yQ9/66c8OnuExdLHhmXWes9qpS6BPRE8woUsSFbYpcjuZsubn/8cmzJeLEtfsawqNRZ3PU4yr03gOwK7lPnJYslV2/B6d0fTd1g0azelhCmHboayZ2fB7nnPM8/Pz/nBp5+wOjnhxcsXvH39RgMLUNnUe4WaXCyXfPvlLUaE9WrNcrkmAX0XiDGNvKFrW3abOyQnnPFaSk+SwlLGgDNweb7m8eU5KQbAFD112Ba6p/q+Z7vd0nXdSPuDTjyXf0UZyqhXD/dnDs+ZQ56szmdBHbvG5mKf0Xbq2nB24dUhHTQbLyQhRosv9itBcLamcqf4mOnDVg323rCqPaerBZUxGhCSMyH0pD6RYsYaQ3aOEPdy8SDLiLPUC8/5+Rnr9WpfjikNpQ4P9XxyqVEuiqpYeY+vPN47jAGSpao9q/WC07Mlj1bntHHDcnmDdTpnoYuEqFmyMcR9bdmkJQdjFkJItG1PX+qcQ0FBtHYMah3mXu13GXGWzghbIrckbrOwzZaYjUKlF3sI3mJqjyw92avTCyckbxHvSG4gkFxgyzO4oogx0I8hWT8wVKWJAnerjw76gtn/JF13KfRr0OwzKwaTIqQIEVw01Di8cTgpWeU5kIlc0492WWeERe2ovAZFWSuaeV05Hi8yzqlD0DvBWR1CZRPWGsYqi0ERz1Iv5CDkZEpwkS2OaYMVhx1NyDLSrtpVMzFpgJE3TktbCvcd44UPxBJwWjuDNyWIw4D16ogcZsshiKvY7gJ3Tc8mRLoQ2LSBbdfRFrpQntyXsz9jrMJom6Qw7KEPGnjRZc0eB4VubhKpVTtoZSuWixMu1o/B1ePaiygKRIhBg6Riog+Btm3Zdjfcbe/oQq9ZiJVlebaiPqvBC652RGrqxQkm15zXK9bVCpMS22bLbcgsnp3y6umSt99ZeDnwjEMd4mDvDfJoCTvKkvdn+eT0NlAQcvPsG/1I2JvCPsRO933fv++ZqR4uRW+Zfj7IHcN3yhL3ssix/k0/e5/cvX8HOJtZVBZnNBtXd5+Wqwo5kRFaa4hWSvkBS5ZE8EL0llQZstduGecQ0XPIWYdzDu+cQu1bfUefoQ8tu6ahj5GMIvvAUH5DSH2mlYAxO5x1LH2FsQ6xkKSjy1u23Qa7qFmsVsQ608c4yniKAqvjHDLGcwnimGaT932Pcx4RqCrHxdk5i9WKpttADKVPmRBKeYI+EoPQB8jBY8QrYMVgXylzFlOgTyU5pJx/GSb13ZV/ppKBb4ywXK159PQxF48vaW5ekgkYIzhn6WImx3hPBp9eow5zhD6O2YJUTrO0bU/XdVRVpeef3jiehd5ZlrXn8nLNi6s31MtTQurIkjBZqPyCu+aWu5t3nF5cslyvsVVNCD3r5YIuZurlCadnF9SLJVdvXnB6fkldLzg5uyBsrgk50e52XL95w6Mnz/jBJ59yfvmI69evBood5Q4ZvKrqOAIR5XWAFNSRPme+bW/ZxZ6Pq1PehHd8k3reSWCFY3t9Rf3RU06XKy7PLnj1boOkxCk1PYkvtnf8X/qv+evyCImZb2zDNvcsIqxxfBsbXnc3nH/5S54+fc7ZZz/iK1nw9fVrxHqN40oRs03cdon6TUOgZ9f3bHvDq9sdv06BCytIDvArz+XXX/Ds098ldpCcIM4gkvApYruG5cUp3cU57euXvP38K5794GNClbBdT0JITvBO2Ugssjg5IyaXQLCMs2CNqLwVLTE5+mDpo1GaFkrJD4sYj3UqIxsnSHalbJPKbVkiiUgiYY3WZw850MWhjLSiVVvJ6tNJmZgFV8omWDEsao+vNWAk0rELiRgDi2pBDoYQFblqYWuePn7CxckFKRlSBzEnXPZ4m1hUgUUdqKu2ONmNoo+gQcb2IV4ok/0x4bP7SwMJhsDDYzYjMz1Dju2zg/8W+5RR9B4RizMGi2W9rFktK4w3BOmITaBysPQOY6qx3ZATbdezW3Tsmo627YkDAliVWS0qlnWl8o8RQurZdhqosu0SzYchqX+4Y/zlq7daN8h7qrrCWYN1lpi1VthyVdGHhPc1ISTuNhtWq1WpAS48fvJY8fgLPJAqqKYc4hpdoQISWvfFOrzLVN4Tup7f/d3f41//q3/FZnOLlPouWi84c725oWvb0TGbQ2BZVVxcXJCyCi05ZZx3fPbpZzw6f6SR4QlCClhjlWnnUrMWzSjVmmZDJGERbIsQ3nV6Th4Y1HMqCrSMhhOViUuNsqlBtMg6Up4TZlAfU8W7OFSV9sohNHGIpqR1OGRiXDt2af3voW8ydmAYl0gi5DT5W98VgkKIkFGintXuHvqVc6aqKkLX7g+x8sygOKohQeduft3PYC7OfNBDYBjbuIml1HQZsn1n2buyFxDmh+o4z8WQrPQHeYCYL9BVCc32FmOYOsbvG6uHfiu8//Qe7a7SRrJCILHGEEOii5FKBG8cA5rWtH9zeij6xyhsTBVxfeD9RtDRKD4z9o1wZOWn6GqH85WHwQyGsEPD8RBRv3dAGbzb0+QxQ+SHCDCZ41llx645PR7M3cD4VXvYK63MBjtr71jfh38HB9A4x0wF+8M+za85PY4/s1Sw6dwPUax5QuvHxn9sbo8Z8QeeMV1Lpt+/Z56nBqF5P3JxZD90TdfyofXc7+ES4DHL2Jg1OL7vniEq750mQz8Hp98AMTWdN4toKUSG6OECAzmiATAa4eyg1JQxGO9o+57sHFtn+eSnv8V/8V/8M57+6FOw0IsAlqqq6ZuGdrPl5vU7mndXfPnnvyRvGnbvrrl6+QZSUr4Ukyo2RTG3zmKyKh5D0sEw5ImOiZHSL/aoC8PBU0zYOLvPkFYyG+hdDW/Kv015fnDaDMpXnrQ59GHqKD78fPr+ycKVdg4dzCLz5/XfyTJ/0HWsBMWxvfmbOinHvTqMaNL+hxgR5g6f4ZH3OmtmfZvuweNnkty7/1ib877LWCPQHMAP5+G/ZRGOOdGk8Cg953PZQWZsQYaCbQ/w/rkMMF2fY1l6D0HNH+Nf32csmd4zP7MOxjd799Dv6XmvJB2LJWo6pvs8+/vOtOllynmo26MIkIM5YKijOyktMrQ7RwY4Zlh66PP579O5Pbg/FzFt+KP0cd7m+86th2h5vumnbcjwvRxv+/Ad+4BVMONn6VD40uZE5cGJ+A0zOht+f2jfzj8frpjieC4dfCP7usW6zeSerD863o0pZ1Lh5nkIOt3LD/Ps9nvrKeOQfqPr+3jcPVrOx98zngpTPWFyTYNOBj3nWPuH/N0QUyzQumrcEwZZ4r5x7dhYcgqklDFjFqI6HYogxmSKD9o42tYDff5NL81psmW3DwR6bB3k4FcRCoSo3L9tSoB5/+egWwx/HMin4xxMeYCM7zq4t9w/NBX7yPXVFXcXnrpakYyDUGg2RiymZH52I22nACFC10XamLDOYSvL2lZURg2cxltSEDbtHSkIsS8ONfaZcjpkdYyLWNQhakhJSFFKpngajciDrpAnRvtBXxzWc5TXyZqRPjjnRAOjPrp8wvn6hOtf/hnpzUsqY0jZsbSwy4brZst613GSK/7qxSOiy7zBsTWJTc5cp8AdkQ7Lx67iqV+Rc+Kpu+W36iWt97wzCkn+1C/J1YpPP34O3rPLic6Di5HgrOruCUzK+JjIlSEEx9Y4NqGjf/2KzZdfkLKwdI51pTXgQxfoQ0cthncm81YSEeGpr3nb7rjudsScqaxCXseoqH15kBFTgQxnsk/IY+DJ2fk5T54+xVWeFy9fstvtWNYVxli8q6jqBcY6Uk5st1sena44OVkjJTO/bXrlDWRSDLS7hnbXaECIWASLmIxxQmg76spxcX7C+dmavmtH+WTQWYf6813XsdvtRlSl6Rn1kLz4Phlsf8/0bxjqNo72mzIvy6VnfepAoO17UshgNJA3Zc1sS0lrVPpqiQ0JUgOAkUzlhIW35KiBICklUt8pneeCfuiE3McDHU6MpfIVq/WSs7NTFouFyvsplRr1aS9f7FnHGFygaB3qFLfO6mfG4n1FVVVUlWO9WnPWnlIPDomU6bsINqljPEaF9S58Q/mXUSdkyVqf2jPMxD4zzVKSnBEvpMrRimErmZ1kghgwBusc0SYNGrEWFh7qilwZ/cwJOEfyFnwq0Bsq6IjR7DHLgIygzmzrTPFyFbtcqQluC6UNvZOsPMjuDYVISpisDpnKOa09nTISwEbDIju8WHU45UTKgUTgJjuFRhaorOVkVbGoLIYIoolGzhrO6h5vhdobai/UluIcF6zVOtlGDEQUxSoIMRp1jGelowECXsRhZEiEKf79BLE4xgfnhNURKs0MjvGJPpqywtFaz+gUt6JZ/pSpNGKwxuCsI2Pom4YcWrpdw+am5e3Vlru7hr7r1ekdImQtraC1TE1xikAKiRh6ckhIK5iotOMwEDKmzzixLO2C8/qME3eCuEWxiQ72mEQyESzEEGlTx126o9ncsn19w3a3pU8BvFCd1izOauzS4RcVq9MlzvTkxYIqwolUVJVlKRbpeuxpz9nlgsW6Oiq33bNvTK488NlBd0bG33UvyURukcl/Kef8pK33yDL/sa9JL++97xgP1X/1yfG/E/uDzHTTqZ6+p0V9b20stbPlA0PCEHOmTWUunaGzhmQN2RgwCZyQvQUvGIuiAUSn2cRZkWO9d3jvFQ3E7m3HXd/RdR0hRTIaQJeH4JyklbhzFGKIOKkQHMY4xArZRJL0JJOolksWyyWdb+ljKLb5QaZR3jg4xlNMZKfzkVJSmPW+J9UJEQ0+Oz09ZbU+ob/ZkQaTZoauawl9RwwVJgopqeNN/SZpuI2cNYAxxECImYDFm1T4AJrBOrnSYD/JBu8qzs7OOb+84OVXryFov/bOuEP77/v05ffRzHCZYu/vu56u7XDOFZSY/f4YdEPnDOcXJ5BfI+JBunIGCt5VkAO7zS3b7YazvmdRLQh9jz1Z43zFYrnm9OySk9NTrl6/5KNPfkxV15yeXnD3+jtS30Dfc3N1xW674emTx1w+fsLNm9eq/wykPdkg01zKwYc2SO9JErexZdO3PPVrXpobXseed7njL+G47hrSpmWxrDg7P2d5/YKYEh4hGMNd7tm0t5y5Bad43sWekHv6mPklN6QYuZWGrz//gucf/RaP/uAzwvNP6V78nC5HbFVhneO2b8EabrsWEzq8s1xenLDbBWKTcCeWqu0xr1+z/eY7+PHv4bNg9NTScjHWIU3AXS5ZX5yxPTnh2y+/4fHfCmQn2KQBfz0q37lkNJg2JQ1CMwqtLiaNOr0RsBkqJ/jK4HtDUxBNYlZ5zBin55E1uKRuZlsCGTOJWHSlhEGs0eM+FOSoIu9KVuvXEPAGhiQGW4LXnBUkR5Lod1EybYqENtC0HSnBslpyfnnGerXCZFPQTXSpnanwFmqfWFSRyjcqI6WEJp4y+orm9pNC4XvdbdTP9zYJodgB7VS2ekCPlck/E/veqKuSi69usE9pYKYTlZ+cs1qexZWyVZKovKGufAnq1BMiSMZb5a2LuqLvFJZesBgHi8pTe6fZ+iK0KWCDonpqdN2HnV8f7Bi/uDwbozIPM5uU+IwRXBZiDHhf0bYtfd9jbc1qteTi4hJQoi9qtU6UqEEkGqHrlaE6ZyFlvFFoKgGeP3+OsYrVH2OniybKtAWtbRRCTy7C4cn5CeKE2AZSCqUoveWzTz9jUdc45zFZSl0PjVZMIbGoFqrYCTgJqgjnyAAZAlDXNbvdjpQ1ciPnvIc1FCGUWlcpq5gyQutQlOsyJv3XHTilppnBcKhszQ3FcJg1NocenRrPBxgJMYYUczHyUJRA2W8eY0bD9xAJQwiaGZs1OhK45xwf3t91HTmkUfnKOY/RolCc2CmVumN7o2KMkUePHrHb7dhut0rIJTBhdAAYKdDcwxgTWUyBzBCM1Q2Y0qQGVhHc5xlaB0JTZh/RS8kUoTiLgWzsPYjs6RoMdUOHa78mcVSCJesBFy2EGOk3O+wlJCNELCb0+t5ZVM7cEZPQ/aI6RzGMv89oPFPWB6PNPHtSRCZ1aKQIyfsMYzMo75Oxm6IkDLQwZOGO9x0YzvY0+tB1zLg8tDM1CM/n5JgxYi5EjfcM8zZkZck+M+iYaH7MMTB31hyMbbAATp6Z0swQef8QysEBfU2VGIE9FNuA0DZ3rh0qT9OMs/k1rsvAj2Zruyfc+4rZvK/Dc0M+VioKBfnYXnnYsP0+up9naAzXAYz4kbanv5uyf+AQLuxe33KJhBOt4T3yl7H+VMIZR44Rhqj4qiIYYRsjyXtWz5/y9/+n/4y/9Fd/Xw2zrqw7hpQTdy/fYtqWzatXfPf5F3TbhtsXL9nd3NJvFW5U+Zs68YtqUAK2TOmLihuDoWEca9mXuTgSlJXmA2NWTlpOQb9Leyg5kRKopWufstbkISu97dfhkPfnvA+Mmc7lZHGO0tB+eaZrcd/JMPKliVF+vsbHePOx66E9/ZAz9ZiTa3znrD/H+NH8OkbLInveMO//PEP8QzJSj/HEh4KLDt5lzWhYMW6AUZ+0O/w8gEIwti9MahyV9xUDYjlelL/N9v2Unu7Lmvv3DLT2PqfTlMc9dM/w/hEGdAaTPm1r+r7BuDCfU7130A3SYGtB5ZJBfrl/zfna9JrSyzAeM271qaG9qDSZAyfjlK6nZ8KxMX7ffM7/HYzQg2yrfWKU/Zje+8DemNPxvfIX7NEqptnUkwYYMmTmrR+u2z5ATj9OB7St8oqORueP4iDToCwRrf06OAqHaxocd2ycU3ref5eHo3zSP333MIv7I/i4jCMU2TXnwt+L8yClvUxq9/LkfO6GPTnqJe9Z++n14Ln5nudEHtJJhwDP+2s3b1NlwTzeONWZ9jLTfm9WlSPEXiEGc9r7gGVQce73f5yr4ggX0QAKYwb9ak+TYA/W+0Pn7y965dyTKAYeZJQH752TOSvMrz6l9xv9GXj79P6U88HcT/nFVCqeytDjEGU6Xu3P+Ox07QqnSAnevH3L9aMFJ2tPvaoQ58oelmJjYNTHUlY4zz4kmi7RhYzPHuwS5xesfY1YR6wsFs+ugTZWRadTnUsblCLyD7CjDmt8+bfCuYBdBHJwIyw3ufB2VK/ReUoMWTtTiSQKpFwC6o1AinhT8bt/6a+zTpmv/uxPSFfvWNdLdtFzYitSSEjvaHctV23H5iLxttnxddPQiyOLpYmGTerZIPwibGjrzA/qJU+qBdvNNb6qOHOOkIRwu+O3Hj3i4vKEd6ljA3BiCX2g8w6XoEoJl6FKkCrL28awsyu2m5b49Xd0r7+lBZ5UNauqwhpTIOt7eut4R+RWEkYc537BL5oN216DGCrvESNa39CYAkub97rE9JwcbAPGcfn4MeeXF6ScefniJTlFzbBzDl/XVIslYi2b21u6tuHs0+ecnp2RUqSuajZhV/Z0pO87ttsNfd9S+cGwbrAFgnrbbXi0rrm8OOV0vaRrG/IA7zrZEzkLbdvS7BotVzQYBidn2sGe2/+hgRLDR2aiS6F2sqFc2sDAB3lBsKQCmWqscHK6YLXWgIBdGwkp4SrB+4JSELU+ubMV3tYk6cmtzgMkdXiWmuV5qBsbo8JWo0Z98ULo1NA/yCbWWhbLBRcX5zy6vGSxqEGEGBUeOw9ek7z/mfI/dYxrfWhTnImIOqGd9Yg4vK9YLdZ4V6udKWf6EDFZs6ZS6eMQVGOtwQTVnWJI9KHYeNjDwQ8B/wNPGnQesQK1J/pEZyEYAy6Dd3hnyXXx9VpDrhRG3VYejCDOaEq1t3gX9qgbRrPPFs6wEMEjeDFURli7BptQw3xOmKx6m8Xsx5RAgsL1W9FAbGKCKJgk1JVnUVe4aDBRkGiQCC5rNnpOkZQDfbZawiF6yBlroPaO9XrJojKk3JNSIOWASEI8VM6w9IaFE2pv8VZwJStMjMOIVTQOhBQtMQkpWXJ2kC05mIK0Nz1DpTjGDSlRHHMT7i/CWDpA3QhFRh6yWDPiSmCUqG04kQlE+pRBMs4K3lm6viOEHd12w/bNHVffXvPdV2+5vbold7HAz2coNYmtHQKWypmUSm30lKiCxWer6KXOU9cLvKtY1jVrs+TMn1LlCjFLjHHqZDdG19DpuZZCpKXFNIauv+HNdaJ/u2Xb7Mg2sa0tfmWxK49ferbnCyTv+PH6krzqsH7F0ntO1jV9uyN1O07PalaragwOI6MZ6KOVci/TDLoAogEYqfCh8cqDfCxF5tzLSiOjkv19U2lgLnfqn/f18z0fPNTf9/TB7N7h+UIXM1lYivOEcR9Pe1skOTGTsR/KiSJy4DwcJJmpTD3YwK043YNSgkJECFnPyiyQrSLABGdoS2yIQiobnBWsyTgC9OogE8B5S+UdVYEqHxLLYkq0fU/bd8WWru/TuTCa4SpKj1Ycla2xYgsss8qh1gv1smZ5ckK9WuAqQ96pzWqEOy5jjVERcFLZr0OG5yAjp5RGJ/76ZM3pyRm39i2pH1ecrmvo2xbf17hoi9xpyxoVCX5A2MnQp4iN4CUQJSqMehoosKyDZEJG1yCpHLBarTm/PMd5S+ojJpdMVRFFqD/Qs4/L2gP1TQMYj136nKLiNU1HvVgU5ETGZDyVpZW0Li5Oca4E9RcayWhZVGMNbbOl2d7RdS15fULbdaSUcdayXC45Oz/n4vIR3754RbvbsTp7xPr0DFfVtFsd3+3tNVfv3vHpZ5/y9Plzvvj5n5FD0H0vw9yVeSh7RhkDo9FBytkXJHPVbnnuaoz13PYNb1LP3+QE6OmvbrHVI07OTjn3K67aG3oyvTWIOGyI/Pfhmp+YM1IIOLTMwFe54RmnNGbHn3/xJSfPfs0f/uHf4Ud//a/T/fMvCNlzdnrO6mTFy03Dygpt33MaExenK1YfXfInn7/CAZ+dexYRUheRb17xJGVMsmxiZNdlRclcGPpdwK8D1ekJ6yeP2PybP2f35jX+/BInDtNnYuoV3hyLxIxERX1QWUCDVTSwmvEMMCbjHTg/lEKII1qPcaUcEnqMDAFr5FgoS5OSlIwsfYrQaSBKGmytw/oUOsoZQoqIZLxIkVcDYgXrHdZoGY5t03F9fUPlKxb1gvV6hRGhazqMrRXxyhi8WA2QyRVV1Rc/TKbvOkVCLT6boR9aCmamK05sHuM1kBYDIqkdA8RNocODvTUo1fO2x+80QWaQF1Rck7EEgzBMkc5/JCHO4L2WVSGqkz+JYEngLMYKta/ISyAPhQTAWS2pQ1YO4E2iri1BHEEc/f+Xtz9rtmXL7vuw35hNZq5mN6e/XXWoukAVOgEgAZIibUCGRdmmJIcjHOHwgx78YH4B63PwzZ9Clh8ctqkX0mFJJsSgAIJEAQVUX7e/p93dWiszZ+eHOTNXrtxrn3MugNC8se/Ze61sZjvmmP8xxn/I25m839owPqXGHKiLDo0ylMmXe1VrzW63w1rL6ekpdV0RUz6cDiBRVo5yR+W8RYcCT5t8SPXesVqtMEaXOmTamiHP0ABoWmvpuo7T01MWiwXb7Rbn/T5/TdNwfn4+UjyFKBMwfwoeSok+16OgGQwRSimqqhoBxluGt8mkEAZaoRmdevlsb+zbg9ZhQhky1EcrRUiHRsF5iRNwbDjETZ+T821mxSnXrSgPMZKSGiMKBsBNDxMMRqPJQIs9pbAavKmHyA7vPRoZKYoHY+m0b45Rktd1zcuXL8fn6nKgmvbbGM08AU6nc3HovxFUD3HM4zj03Zw2eA5szQ0lwAgyz8d5agw4ODwP4z8D3rKhS9BGZ4q27bbUc5LndxDgszq+ydhyV5mCokO/7AGz/ZjPDRADvc9wz9xgMCieU8B9GjldeuhAIT7WhruA8v0TDqOkjl5TnnFAXX9kvO56r8jeAP2m6+8yKs3H+q73HBvLueFtrNOk/sfaMp+3x+6/6/nH3j03pKSUD5B31f0Y+D8dpzmoPcyPuVFrfu1d9ZsDz18FgN7L3uy8MMiBY44DjliAtkNj1x4TE5zLJwfRmqg1TkFLoH5wym/9/d/jN/7e72LPTkHJSLevReg3LX7XcvP8Ja8+/4znn33GzdU1u5sNvutxfU/veipTFJvJMVWGA3KM2dv2yHi83jhxdx/ftV6mc+IYlc78OV/l8+k7pnN4cLQ5du/UgDS9d16v6X76pjLM2zfJ3GPvOTaH36a9w3Wp6EzzQ9yxtfW263f6/Dkt89C/wNG5nwDeclnN63Pwrll9XqcnHZNT0/YMe+tXKa8bi2MyZdpX81yi0+fNn32XPDxaJw6OH+P181Q+r1tjx8Zw31evv28oxx0zjutB8zLV3eaOMUdLEZrH5unhZUf05+G69HqHuuOv3fctHKe7P7qe4aB987POXXWffn7McWU+p9+m3CXf584Y0311ugaVUgRuz/W9jjeAcvHWejmmX33Vcvy+2+toev3rQNl8912xRYfPCcFjtC2AZGSyifKG24EcobZ33p3qn4dOlv9Tli5doFNNosaoGk1FKka2JAPAESHdEKkJqEIP6Ahyg9cdUQImqYP9JsEBM4guZ/kBsJiWQIIRlMsAJKqkjQiDwSPkNZMKq01x8tOiiAhdgJud4/qmo7Y1Dx+eorUl2ZTpgyUSgrB1N3QEnPJ4HQgGLA1PTt7lbPGAlW6otcVYg48O2ze0tmarI5VRuHhNSKclZDyCCigClUQMFZGaqGqUDVQ6kqgQQzE6xczUkxKgSx8V+RADsaqQrsOmiGhFa2raoDApgNoSWo+OK775rQ+5+R/+H2x/8WN8v0OtVrgQgYpabnivE55fOf7k8oqPW89zem4kYRZLzGKBU4LpE/SBjd8R1AuaCt5vlnz2fItOwn00lYu83Lb8+h/+p3z7/JRnl89JyXC2fsRnOFQvCAFlEpVRnIrlpuvwKqDF4y6v6X72DPEJoxXNosFYQ/QRd51opOJCeT5Ojittub+8h6we8vOnf0bnPElrqLKeG3QCAlKwnkDEIPTe49kzyREixlb80q//Knq55Pmnn/H05x/niCMt1FWNNgu0WbBqLD/58Q+oVKI5f4Rd3Se6gDeeoECrBMHj/Zar65cgmnp9RlUZtFFEU4MsuLn+jF/+4AmP7i1Y2IbtNuB1iyn06XkVZHm/3e7oug7SRCeQwSh1W56mAVFUwshQEfZ7Sr4PKFTHsfxtK48RIXiDE03UkboKPHpyzrqyKCV0LWzbAOw4O9csqwVNtWZh72HSChOFloiPLSHsIHisaagXFW3oSR5SAAJcu461LOmk50Ycjp4QekxS9ET0wnD6YMXXvv6YD99/H71I7EK2NcYYUPTEZBGxSEqk2GccKTiERFXnXO5iVD4fpUA0IacxXN6n0Y/pQmTTJzQrGmOpK8+1ZIBah2IMSYORL0d8GS14n3ONb312llExUZvsmNJnc2Xufw2ppEwzmDy+pxW+UfhKw0JBY2m15EhxY1BGU+nEqgqslaFSBq0FbEQtIo+kwZKoFNQiLASWWmi0UBs15ug2uuI8Frp7cUTx2bEu6mw4koQPELdSgmfKthQSKURUhFW9oDY1xD57EyVFJQ0SLa4PIxbrgqNzQrQ5oKg2VflZYLUhJk9ILSHtQDpUiQ43Jb+4NYrG5ohUJbqA4AYtNjsARYqhG0KJZu09+CATg3k2lGU5qXPObedIweUc81qNKb+GjSMbwx0xBTILmpB66AsTQGatygFPCk9KOTdsTELbw03X8vLpSz7782d8/GdPefHRJV7y/LPR5Oh9k9dglENMbtTplMKrBCZRVQpVASlgV5pFvWC9PGNZramlRuwJaogqVQpUDvLS5HOVtR0hWq63N9hmQXQJd92hgcZq/ItAqiJed3T1Bvey5dv33+PVqmbZaE7QnC/WbBvoHFQrS7XW2AW4a41YBdojSaOjwSShSzcEqyGQ0wYUw8MtUH80XBwrszNZWW/5o0F3zE6aCcb5kEh7trqUCn6c9YUB8wYOxvxWtWT/bw70KY6Hkmn0M1KZjVpKKHi8Gs0yKhVZO4ztRBbPz0OjLi37vwcWhemcmGIc65Sx5BPVsDOK6zpxtRZao7AR6gR1SpjYY1IOeuiLxi022y+GyMUQIl2I7LznunW8urqm6z3GZOeZWJxFjFYYralMxaKqQWvqKrG0noaIDgajl5yenXFvfcbFqSWtIjwTFtqw1TtiSriQUwNICsSSa9zabHjyPjNuBO9wfZdTGNSW5bLiwbrhCyP4YXBiwm23OH9J8JbUNahtTfAa1yskKHSIhQE24jToGNBRo0v6mlhwxOQ9iAaVdfg+BRKZzQIlmKXl3junVEvLduvRKKyyWOXQ0gN1dvKJEMIeox7mBCkbz8ixfiDDHJufLbOz8zAZdrsdq9UKa2y5YTg7ZkOmEuHJ+SkP1orL3RV2cUIwhu32BY1NNItzXLeju37F7uYV29M1xCWr1nG6rLFY+tpy8uh9vvjyBdvra5rlKYvVmur0Pje7S7R4bq5e8vzLL7i6+ZB3v/2byB/9K5TvSCkHzwVt0dGhU8iyUISIovKC0wFlNCpEVMgBd3++fcY3Tn+J013FVaf4PEHFGqUcl6+es24UJw/v88H5Y774ckugxQSLJjNSfvPknMdbxxfS0aMwquYbocFKz6tQ89+nS15d/YLfuXjGf/4/+wd8/C/+e1aPLevzB9T6hCQXvMRjUDQPLWpt2CbYecM3Fpaz1RmV1uig4c9/DH/wGWn5CO8du5RIVc3We5qqJW4qWKxw7zzmvL2i/cEf8+D3/zFOC04iK21RqSN5wXtFX1ijYuoIyaNVyPT9IhlXdRVKPMa2VPUW63dI12VsVYFU2RCeYiD5RPQTx2oSipij0LUQSIQ+sktdpjhXg6NvZpESssNM3zlSDPQq4ZMQ+5rKaiosOqWc5iM4roKjJ3HarFjVa0Kf6F2kWtTEqNDWUjUVuurxN4Hgdry6ecmXF8+43F5RmwpJxbYp2dg+nuNEBkE5rhFSdh4VyQ5ppngpRSJJC6o4OWpkdLAeD4dlfWX5OrCzQd6FInu2xMG2KBgVC9NEJOJpLDnti454An30RAU+RFrfoZXZp4GOAAqjLKINYrMzn6BQhdlPF6daUqIPPUqZvI34QNW8HY741oZx2OfTnYNYA+CkCx/9rt0U8EZo2x3L5ZKqqmi7HNGdo4BVEU55I6V4wldV6YThAAWE4KisoWlqXrx8DilHMI/0F7I37p2cnHB2ekLXtoQYRgPGoEiuVqtibAukMnkG4CsffmLZ3APa1GMdhxJjvAWcTg3f0/4ZDEtjFPiohEyvzQrBNN/r8ExgNGjnCOy7DVwDADkdl1vgVmIElaagc5xsHKpE6aeUvZJTAUgyHUvA6MMI7GHsp7mdUjwOAg6fzY1s089HA/PgvTj5blBeBhqtaT8dBavltoFhyHk6lLmBbA5G5u+Kh9ZsbPeg8CEAOwCqB/Slkb0nS8qeZjmXWRZa+UBCPngfAZu/CqA6L7fyV4548+HzDwwZR957y1A0/f2oAWJ+1e3yxnZNwIfpXJi+V2RYR3sHirsMfNP7Dp0BsnEqTt43RHBOjXTH3z+Ze0eaMFW2j7V3uibG59xhtNnPz9sI77FowNcaLbgdOT01dsjQsbM5OZW5A+Dzun6G28bwN83tqQFgYCOYXvtVDWWwj2RXs/6e91lQTGigBxxYGBAMEU1JuUZUQG0IxvCd/+DX+K3/6Pd58M5jUsqU54NyHruedrPDb1pefPYFP/vhj9hd31Abhd+2hN7RtR2u64gkXIrocvgeZMa0zoftvz1/pmUqi6ZjeGw8jhli5uMy/f2YMXb+/VzWz8t0vs/l79u+59gzh+/exrAzfe6xvek1d77x2W9+N7fE5LTOc6el6efza6f3z2XIXdcdr9Dr6nt7T5jPG7g9Z4+9cw4w35Kns+fPjYKDjJ7LpsP75aBNr3vP8Pddusvw+/CeqYx64zybrYX5s+9yPJnva287p+fPGNo+feexeTG/9th3x+bVVK4M9w+MSnfV+a523Npn38aaObv/dX007fPpO6bRx7fn9N1rbX7PXXP8rmfc7ut8vJyv4+l1U7lw15gdW8nT+orkvW0+57/q/DpWDuoyAKt3lKw7HTpS3vHQW4apwwflNl1f3+CbCmMMoe++ct3nZ4/5vjcYtf6nLCFdEpMmxpqgarRq0FhIhpSKjEsllbTKUbKZHjdHsaZiqGTq6DtpU0rp1nzZ65rHy3Rfnv8cPIfcpzomjFiMNBhpqFTDolqiK0sKoUT35dRjoetxfYf3hSJYJRaLUx6ePeJ89YBabGH0SiinWS4Dy3JPJBvQBhB20KFiSNlGTk7fhmSD7U3bEdsWYo7Ezef2MLY/5xDP/aVF8DobvsTnCFynBCGzBrnUUVcrHjx6AP6KT/6//woXusw81CYWtuGT7TO0eL5Xwe+++4DV19/h7PSETbej23b4CFvgi9DxQ3PDN5ePeawFwbELjnO1onrnHqpShJi4udzytHvOb/7qd/nMetx5hRchxB1Rada6JulAij0+dHwZb1hFg12s8d2Gq6ef8cUnP+cSz/31PVbLBTok/LYjSpbhFypxEz3GLHh4dkYXez599YJIjtS4a29L5RwokudhiIHgcy7G95+8w3e+8yF93/PZp5/x4sWLzFymDKayVNaiRbHb7Xh1ecE7777D2ckZy6ZBImPQA2R8p21brq+vMcawWCwQoHM9u+0OXXmqSvPw4QOaRTM69Q8UqkzO8d57rq6uC6XsZE7H+Fo5tp/3e/k6yPFBBxnPRMqQ2eczmB8L4K2NZn2y4OGDJ5yu72WWiNRD6Om6ltA6zFrTVA3NYoGxNYFEHy9x8YZIBypgtMLqRG01nkjoIylmmmkRqCqL9hpSCWAAVIkc/OC9J/zWd7/Dh++/x44dH7+4od0NFObj4FIkYdFFE6LAGEVV2ZIbPqcoqOyCxWLFojnBmBXOObpeiCHnkLS2QmtHVRVmFufvdIaLMY45xof1OZU7SimUFlLMhrRkQK3g7FwRVoZ7jUAlLGvDsmlY6kClNdZYaiOc2cR927BSNZXSaBUQ69EiGBGs6DE6vFaWWlms1iWYQyEWliE7NXsJdBLwKaJ7yYCuMYQUadctne9GuuMQAilErCga26BFEbwiBTBiqPQaS413AR/yTx9cZuesMi5ptcZog0qmYIdCJGbnBBIBjzUKo7I/gFUZDB+w25w7XBWD4UDBnwOadCjGcZUj5wSFT4KPOXd9iGVulNwVisk+LQMKX1aHUggKmTrSG8EYO+p6kYB4hUqKmBQxQNt33LzsefbxFT/6/i/4+AdfcPnpBhMqqsaQksv508Vkims1o9mXPY6otUbpTH1vVA6squu65BtWJRdzT9M0SHA5SljsngWBbDwTydHDttJYq7GVzbnRC/kmJtPb61qDFoIOvHxxwae/+JQH5w1utSbFhEJT6RpiYtlYVicN9bJmd+mwoguQkBkxfUolV+sQxfe3o7MdQnbT8xH4ODuvle9DIsuCvZ2ElISRzvc11ZLJ0Syx36tHLu8UM3tryQ8vkiOcRzn7Boxi+vdcVxlZt0RK1LTNKWInzr8AcRE5XcPDkwp/UuV8421Edg5pe5SPGRvqIkYyJXtVabTJcz6EHJ3tfMj72KvLnDaCbGUaGJ4GfdMYQ11X1HVFEIPWESE7rFSmZrlc4lXH6ekJJ2dnLE8u2C1SyRwgGKWLPSrjZs45Fovb53bvfUnHkYMAq6ri/PyMk5MVrnej7QSg6xx17/Eu4HpP2+9wwWJ0w7KuWFQKYwzeaGoxrLTJTotaETV0kA2VseRgJhEl21oym4smNYqHDx9w7+E57qonddlhQFuD9tlJbxivu5nd3oQ4T8+W+V/nsgy11mArQwzFoSbm9CxDWrknTx5z9bOXWfapzDAAiqpu6Notm82Gy4sL1g8eQ72g61o6TXbWqWoePnzIZ6uGl8+fYhdrTu895P69h7RXzzLtuPPsrl7x/ItP+eXv/RpPPvgGzz/9Ga7vkYEZkuGcFEkxsyoMTilZzoKobLO46XZc9S1nUtGZih+5LR+xwybhhsDN9oZmV7N4/zHLp5/jUkcbe7YKpKn5D07f5e+894D/6pN/x4vNBhUin6qOH5vAn8mGUxf57ufP4N/8Ceqf/p/4F+89xD37Id3TT+mowVQoIt55dpeKGxzbdsuTeMI3qnNi2nKyrjmta2hvsD/9EV//nUc5urfzGAemrrHJYV2AE0E/POfrv/zb/PTff597f+cZi/V9arGQAruQENUCHpJHiQMVMZJtL1oPeKpA1SFxh8QWlEPrhK2EkIb0zlnmRbLDb3Dg+j6vUS2oEvjpg+dqu2Wz6+hDAK2IhZadQS7GSIgBL5EoIQe5BkVNohIBVbSoGOi84+b6hlrXWFNhtAUUzjl627NcrmiaGm01m/aGy4sLnj57wbNnL7i8vKR3jgO5PV0Nw7yXEgnOYN/OslrGFFMufzbDzQ5KadvAwnpwHp/OxeH5SInWL38XhhqtGlTMLCmiFFEyI9DF5oYYW85Wa5pFQiuBElgt6MxqIwpF1nVSEoyqscZgdHb296nLrOOVQqmKqkq4+HZYwFeKGJ/+PgiXg6hknXvCWosv9NtTUE9rQwgl0k72URmDITGRSCKFkiMV17REVWVl5fHjx6xXK7TeC4JpRPJisWC1WtF1Lb137LoOYw1d19F1HcoaTF2NVBlTMH7wFstgqyreacVTrtRzGpExHASmzxk+H/4ecm2O3+9RiImSlmm7pnWZA/MxHgc1X/f3/FkpZU7/ge84G4iG6GFB6extJCLFcSD3fXF3Hsd+GCsROcjzpLUejc5TKvNjIPMckE0p0ff97BmRIbz9LuPKcP1AaTpVfIZ6xrCPFJq+cxr5NJ1DUwP/oERPDWdzg9JQJufeg3kwRrmnlGnIJFNTDP0bY85HE9ouH5BlAtTOAFERGbXMt1WCh/YNbUtFoUYOo2VvGZ5iHGndh/l/cI1wMOf+uuVYJPjrFNtjYP4g2Kd9dReYPC9zwJPZPXeN+bG1d5fBY/h9OhbTa4Z5cmw8pnP+oK75ogP5MozTsbYdqxPs5ykcoewt75j3+zAX9ukKjo/J9O95qoFjYzw3Styac+zHY94/b5qHY11mbbhVRFCJA69klQZgOeWTsNI5KqbSeCU8/NoH/P1//Id88MvfJmjBlwORRkjOE/uOi6fP2b68ZPPiFdfPX7F7cYHrWq53W/q+J8RI27b5wF7ZnCOn9G0+eR43SEI6OkeOGWamMm16z/y+u+bNdK7M5fe8Xsfk9XHQ9NDpY5T9pUwjnffPfHMk5oFj2WxdzMvUqWnaB8O6fN3aViJjWou7+mQox/pkOKAdE+fH3nnsmmP9f+zfoT1vu3e8bX3mYx5jzNE6d9R1Kkvm9T/WpukYzveCu2jl9+9gTIMyfD7I4PkeMezVx+bTsfoeY/k5Vo7Va3jmdDymRv+77h115cl4vk05JheOte9190zHd6jv9P7pc8a/i6XydetiXo46KarjBrexrgOoNrlvuqfO+/ZQnuzbMHX4nMqF6Zyd33esTsNnhxH9d+/nt/p+8v9jz53P2+n8m/bT/Pq5Q+vw2mmbXsfO87bl6Hzibh1t3AuOOPsdPuM28HUwHgIx5PNIVVW0bVvQsgSj4f3N7ZnLhmHt7ef14bX/U5VEJOIKTS9kaj9NSjq78SWISSHSISEQg8uhzjKdCyXvY/5jfPY4zsOxb/L5XA7JxBi118dmhvGDeZP7PqVEbWuWzZJFvaQyDUZVOdoqdnl+6gDG0fuervPEEi25qCvOl4+4tz5nZZfozGWbjX4JjK2pqgYbhaRMYUNLRYfNgJgWhSZhlMHobEATDTErfaMBfOogC4WuNg3nPI0W0MYgolExYVTOsa3FcuMtDx5/jQ9/+bv4T39C95OfUDcZUFfRsrAVtYYXL7fUYc37y3s8vHeOtuCTYZcqNjFynSK6N7ggaHa815zyRC/RPmJ6hX5wRogO1zrC2Qr18JdQZsGLT79AHjVsl4Y2ONZoEp5lcQogwVIlPgg1/bLi6cef8/zTj3j28kuU1KxO76OMIuxa2HWEIlmfaeEmZBxhXVe87DZcdg6tLZWxt3S1Q/yjpNpiv06VUjx69x3uP7jPj3/6U54+fUqmdrVoY2kWK5plAyJcX2xxfeD+w8dUdZ3HRGtcKGBx8Liupd/tSN6xXC5JMbHrW0KIiNKQPKtlw/3796mqmq6wFEoaZGWeI4lE2/bc3Nwc6IDTckxf3suL0kCk0B9P5N1kPYz5zIs3SwoJiDS25v7pGQ/OH7OwazrXUyuPVI6KlsrC0i6obYPRFUmBjx7HDS5t8HQkyUyA3ntiodMNwRO8R6eEsRqnIkkizvd5bESjrebe+Qnf/OAdfuvDb/D+gyd8sX3Bpy+vcd7jfCSWtklJMZBiKLhexFiNNqo4uAx7cqKuaxaLE5r6FCVrgusJbouWFZVdUFcVRntqW6FE8KL2+XFjbssgTzJdqMv40yS13ii8GMYMQBFMwCwDD+4LD84b9FJRV4q10awWC051xCqDqEyLW5vAUlsqMeiR1LtFqUXWCwrdd6ZHzykaRw6OlNDeZcxOJKdYIOGjR0WhUpqahDIGb9a0vaFTHZ1r8SlT41utqXQOUIkioBVGLLXW6KQJKgP4Hp3zI4vCmYjSUgx7GpIaqaRzzmSTc14nP+Y3zbnFsxF8COwVlUAiIfrcLlEo0TllYcFdoTipF9fxFCNd8DgXC4NJlv9GiqzUeo9rjXtMZm5LstfbkgSSZKNOCJ4QPD64zNSRMibluoDbRtxVYPu8xV17dMw5opURkESlDFaZHNWtckpIUYUVU6nxM6WyE8qg6w3BViOrZIyEYiC0Rmd7SzFKRaUARUq6VK7oTpT80pVBW0XwkSABCpuAMgJaY7zl8sUFfbvFu44QPCRNY5dIgkVjOTlZsjxZ8OLTHZD3yJyeIhelFH7cj//2yhDzl/fDTI+dUzBM9NfJG1OZ91khybqWJFAqlT3z9fqRHPySN9osK3MKAvQQpa8ZAtWm6sX8jJ4DqybnwuHsUN6UKfXV0ESUUtmhwWTHEl2cXFQxDJl7keqepTpv4NSCVviNp7vu2F137DaatmsRyUYzEUiScMHhXIdzOfWrc552u2O7aYkxjcYdESkRFgGtDFZXVLaiqi0uZsO4NgZj7GgLWUTLclGzOlmxOFujF1ucy9GVFSAq4osRzoWJHC1n8wE3zzLWk5LFGMPZ2RknJ2tubja43o3j0fUO5wLexWwcd56UInVlOFlUnNSZ/j1og1GaJpusGDRJkRxZ60IgFF1c6ZwT3YUAMRAksjhpuPfolIvPXtL3nlDS4Iraz/s5FlVOmbzNKtjrssNcyDpL3/c4X2ML603+PGV9O0Vi8jx5/JCf/uIFMfTk9EqGGLIuqZWm6zquri55uNvC+pTOeXxM1NawXC65f37KcrXgendD2264px5xsj6hqdf0dkMMLbvtDU8//4QPv/ebPHjyHhdPP6NvO8Dl9aVKZK7kVufULnu2myRSzlmem67juduyQFNJxS9ky89TxzsJOvG43QYuK/STe5ycnvPl1RdEybpu7Dp++PxT/sOTd6iS4if0/Ezv6DVcm8QDKv5BXPLbV4nrv/xzHl5c4v7e3+Xpv/gY465prGGz2/A0ab5jK3Tv6JPnWlUghqeuY7nJ6662FU3ocb/4lPjhNbpeZH3NZ4YjpQ0pBqRrqWrF6nu/zk/+/E/ZfvwRqw+X2OUJ3WZHhc8MIBIQ5VHJA45Ai4p53adi8xLZ4cIlvb/G+y0x9WgdqWspQZBlb0MRY8DpQJJs4I7kKOy2c2x2HTe7HX0I2cnKaoYUDSTJKQRKUGsyhUEoQZREIBFLKuBhk/Mxp+cUBV3XcbPZUEnDyi6xdgdtZNtd0zvHdrfh5uKS65sbnHNI0UWiSiSfRrbk8Qwz4qYTeXxENMtogyrBH6Oeysg4fev+2dLLevF+vQ14xiC3RUCSInkQrTOjxqZn61su+w3X3Q5MANWzDYw54ittqW0DBEj9eP5VaJJJRLG4CM53pORBJVJyGIF1XRGxb5QR8BUN41PQawpSDuBFCOGgg4ZDw+CBl2JP3vQCIezpyZ3LtOi2qlDWoMomEkMoOWQDbbfl4aP7aKNzTtSURsU5e1hlT6rB+8f77PXQdR27tkXIgM9isSh5NGMxwiaKj31pR/bI0zovCMjew1OjLeQBd26gf78DTJoAapAB2nyQOIyCnJZjQHeaRflOwYcRLJW98WruISmD8inZU6QLfrKJ7KO0x0OejNM4KydKHVAqTylH+74/iBqPMeeGOlBSJiDYsSiXfX+6g/6dA9pDP0+jT49GrI+HVQFu03DPy7w/h3oNBvMkjHmoB5aCqUPHHDibGx9SKpFtMfezT/kAHEKeZ2l0fNgf/oY2DEr68ONdOOjDY+V1iuhYz0mfvg7YvQsAGPLVzw0VbzIOzIHQNwL2s+/mv4vsPVOnMmoOvM7rMozbODcGBToezrlhnI8ZSqa/T+f74DE1B9qndRsU1WM0rVPjw1DmBr4pHDCt2/S66bPndT425lPZMlwzV0KPzYc7jcwcnxfzd7xu3szfO3x27PO7yi2Ae9bOueODSmk0hkug5AxUuBSJUcAqdkaxfnDG3/1H/4hf/Tu/TbVaZoo8RfZ8cw7f9Wwvr+ivt1w9fcGXH33Cy8+/xLcd/a7N+YgGtpCUqKzNYMYgQ8h11Uodbe8g49IsKnMqI+8y7E7bO/192OeG5x8zws3rMt+L5vNluH8a3XtXOcZ4MH1H/uxQzk/X8fy+Y7J//tlUJmVg1hz02bG9bGzbBPAfnaBmMmMu5+Z9FWOCdDtieNrvg8wY6jHde47pDNP7h9/n7BB37SFzmTtnHDnGQDBtc/5s70R3zJA6H7/5eBybJ9P1Oq/PtN3TZyvFuNdN5dX8uVMnzlv9ceTzu9bCXDYdfh7LIeO4zJozAEzHdqrbzcf1VpnsP/M6TNs8n9fHyrG5NP1uPn7DvB6ZfyaAxvS9x9b39Jq76nKs3SIFYJ3cNjfaH1sLxxzepql25vPtdXvVfF0bY8b1OsyteV2mz7vdZjnI+Tpv/11zfl5ktuYH/XWUUyke0GhP2zvv47nDwlymDOWY7DsGWs2vUSUf75Qafj6OMeXz0Hy+DHsLJR98jir005eN4HX+97bOdFA39s4DU2PfdM/zgVvzZKjnvJ1v2vfepkhcDptf1g1iJMYux+ZJBupHtDcGCAHvN4SwIwWfz5ERKGfBaW3GOUKRl+koZrKfZ3L4Wf55cxtSzPpMXdU0VUNlM+CfYiR4T0wOoiclR9f3eBcQMRhd09g1p4szVvUKK9nBPUkh8I0RbUI2jkeIhRYz60K5ZXkeppKzU5CMtaMrTbOsIalchxAgDNSJZd1OZKoSS9KZ9r0glIhEltbgo0FoePDgMfdWDTf/6k+R7ZZY25I3VEjRca41F53ipzdXsEt8LYKPLdvQ0kqiR3BR6IPiShTtbkOfhMe64mHULDq4lkTnO8KmZVGf8vXf+E36KqK3jtovkahofY+JOS+iJudBXmL4ICUemZqfh46rzz/l6otPcb7jbH1OvV4RNh3S9YgPRAK9sjw14NAslcYq+OzmAifC0tocSECO4KZMMSZzfjhzpjDoh0LVNLz/ta9jtObV8xdcvrooFMcaUzVUzQJbVbi+5/rqgqquOTu/V6JK93o2KTPzdV1H2+2AnJrN+4B3AaU1zWJJjIH7pyecnp5grCW4TJk/6hBFLMQY2e12GY8Y0jEMK0OyJDu2h+3XxyBuZG/rKV4V0/zK5e6CzeTUDSLQVIbz0zVnJ2doaVBJYyVgqgimoVkqVs0pla5LnwdCcrThii5s8LHPubgD2ZjhQzbQlb635AhXHwPBO3zviBFQQlVZ7t875YN3HvLN9x7xYHXKTm0RifjgC3axD0whDYbriFI5UnIwjotiNBDXdUNtl2i1IIaG5DTEFVqtsGaBMTbn1x3YGIv+GENgNIaV/N4pJXzJMR4H+uUEKWXgOpWgCpFsEI3asVwmTs4tqwc1y6VlWWlW2lBVlkYCOXtlVfQIjxWVc/0mlXPkYkd5IJKjoYfRi0XfLUm26QBVGCk94GKkdz0ro6hFqLWg0FgxRFVlCvDB+bpInBBjBsgpuThlOlv2slpElb0voBLolLBluoaUHc2kdFDODR/LM7OBf5DZKZV43ZiIKiIpEdGIZPPW4MSR53wi05onJA7MagPLxsRZSu0Z00aREIc8romQQum7gYotjTJ6YJ1UScpebIhJ4ZPPrgptIGw94hKV1hilM/uCtliV/xa1N3rPI8aHv6f02cP8Ein+7yrP8xgDkuL4k2IY5Y8I+/1XKZRklhatDaI1yWfDsip7iKicJz0lg+tc3pdTyLpeUlTVEqsti6pitaxpVvXoXMOw7WZC1SKsjuv0f5MS2csvCgacHenS/rxLIkUZc1anqak8DdcVmTnVt4SZLpjGdUWaYNW5V9HFccMUNoRBtiKDkWWvpw2Ib4bgDgOcjmFOw8+QNlQrVVgXsnOEKQbyZg2r84rV/SXmzGJqQ9glbpYtF3bLCxSdc4gacHUZZZEPHh8CWmVDdN9np5khXlPKfBvbMjA3KI02GueyYdBYi60qbFWVPsmMF6v1kuXpCrVQtFeeCotR2dHPSx5LH/epF2KM2SBV9r191HiWvctlDi4cUqHmDlP43uF7X34CzmX3qMpomsqwqHJfRZWjqE0SJEZSCpnqWIqDUIqZ5aUwUww6QyQSJKKM4uR8Rb2q6DeO4B1KNSiti7PX/tyfU0AdMWHJ8TPk4ZlhcjHZxuOdI6V6Mk8GnDXbhM5P1yyXhk3vSMFgTY3vWiAzXbiU6Nodu+0NwXuCykZPUYaqFiprOD0/5bp7SdftcK5juViwWKxpN1c45/F9x+WrZ9xsd5w/foJZrGB7A9GXnSGNe8SgksQYCzMS+bsyoTofeOlb3vUGFYVrEh/pnifB4FVCQkfYbZBNy9n9ezzbfFkwCkFH+Gl3wV9dPeOEil+uzjg3CV0ZlsGz9DW/IjUfJsXppiP+5GM++N6v8PSPTjndeb61PsEvK/6bpzesqppfqZfcpJ5/t7khdrnqJyI81IqHVrEG1OU19y4ucQ8Mrbb0IXPmxyTZYcv1oCrskyes1udc/ORnnL77DtXpipA8lYr4UOS3JKIKpNgSwhUJzxDXlEVSz7a7ZNff0PusL43nzaKcZfxVEWLOG24F8Lm/exe4anfcbFta70kCVgRUQpHy3pEojgzFCURAi0GTqLSi0tnWGUMiEUgRgo9jbnPfO1rV0tqWXdeijND7Fh88vetwLgeUep/tVKJKgKuKhNF5bT/3ZdBdby+XUV+fymUZ7iv5wKXMq6n8TqP8loP37dfYWIP9GXHCvpxixEVPio7W79i6js73KJXTztzctITsQoAxipMlpKXBq5xyhpjPYbWtUWJpfcYPnO+x1lBXlphicZIzWP23TKU+B+2mxrmDCL6yURujcS4PzsnJCX3f4bwjhD0IMgASxpjs2RojWiQbxJXKntwhU5XpAcgpxuwBPKnrmrquMcbgnKNtW7q+yweDGOhcnwWo1kQSVVPTO0ejK1LaR/tMDauD9+CQa3wO3u3B/zgR0vO84YxU5EP9ByqGOXh6FwA8vSaUzQ32uQQPvLNjLAqsHNRhLAm8D6Pr+5hDukzWQRmXEA6eM0QG5IPjbUpna+0BcCsFgHqdQeZYmYPJ6dbyvQ3ODo4KQ12n9diDc7dB2xFE49DYMbRzOkZZ4OwX0zi20+iRFEuf3o5OHEGkVA4dREIxhMQ0pBTwByDcUKdp3cb2TObG/HA+b8O8b4+VqbI4Xg+HEm7S9rGvgWbRHLxjDpLHFEdammMGn2OA8HR+jaDoHYjbFFgeWBXma/UWQDv5eyrTjoG70zlyV32n78x/7HPXTB2GshOEHv+dHtSGZ8zn8+vKAAjcZfg4Vse3WYvzqMzp/XcZLL5Kmdd1umbf5r63KV/lWdO1Px6UYkSnHC2eyP7xXQxI09BJItaGX/0Hv8Pf+8M/YHlygi57iihNJYrQB9Ku5/rZC9qra7746BM++tFPcbuW1Du6XZcpaIqjTIzZez4bwyf1hNEJ+1jd92O6B6UHY8Xr+mb+c6wvpgeQ+fodrp3KprnhZ7hm2D//Jof2uQyc7tXTdh3rozc9d/73vO/mDoC3ZHtkjHKc6xHz/jxmxN3XQw4cEqbfTeXC9NnT64+tq2N72nx/uzVXjvTdtM2vM6KOa6gYRG/vxYfr/y7nn2n/TvWbqe45fD/vq2OfT583HeNj75q2eQ6gHKvz68pUH9jrUMfn3V1lPk8O9Kw77+GW/jRd08fefey7W9G6R945XdfTOTXqMxz28XDPVF973TNf9+6D/VsODePTMp3vU8P3rfGf/P7Gff6OMpchx+Ts/HnHdKeUbutJr9NX5nWAvHfFIjvm+svo5Cv7o/JdfT7UzRhz57jN7522SakcT+d9GA0fU6fgw7Yfnovm58wY/K1xm/6bDZ/5+sUi0xlGkRGcTdyWj0fH+xaAO2O9AUTsuDdP9fZ5H/519715kXQKKYP0SCQSCNHl56tcaZFMESqpgugJcUMILTG4Ar7DYACcr4N9H8pwya22jD/Hazj+m+cWE5AplyF/t1KKyuRIYyHrQiE6YuoziIXH+4AkQYnBSE2tG2qzwOgq0+eJgMpHWqUjSnuMrTEJ4iQl2eCAn6nkBS265MkLIB6lA1WdIwK9EqJXJdE6kLIRc4AkISHJgh5mUjYIawK21rhOcXb6gHvrU+z2ios//VNECc5HrMmAXfAtS5WgV3xyfYPf9Tigb2+4bAJ9lRkAiJqQLBc60fWRz90156bm66pBWsen1xdUKSFtz8n9GvfoHpXaYmvDGZo2CFcx0eOQkOiUQqNZJcPXoyCV4ubiKRcf/YLds6dYI6zPz5GqIjy/RHU9KmYC5q2xfKkCyeaI95QiH99ckApWolVh/Cu6rHC4Nqe/xxBBDM36hG9861u0u5YXz56zub7G2myIts2CqlmgtWbneq4uX3FydsZqfYa1OdBiCDSIMRBDpOta2t0OpbKs6ltXHEs1dVXT7q549OBhpolXGhddYUaTQTxAOYdtt1uAA5xqmlXvmNw4PEuU9TDq5cPy2C9AGWSMDHhRwiihqTVnJwvWyxVCBlKVymCrNYn1yrCs12hlswERh0tbdv0VvdsQgidGIUWIPqcPiCERfW6DZWAZCXg3ocxVQtVYHtw/471HD3jn/jnrasmzvkJUIhQnKl0i67ORMBs/8r4PtjIYmymqh/UnRtM0K4xZkGJF3xkIipSWKFmgdVPSNGZQHq3HoBiB8Wyfja17x9NhL8o/2fCfI1sDShfnAwXKRs5ODO+dNZyfNpwsK1bW0pgKNITY4b3gvOCDwqOKs1g2eqtUjHyqQ8Ykm6UPyI7UOQF7pkJvU03yPSkmQsmF7kIH55aFGGplUSqRcnJdQoz4GHPEOHnP89GjUBjJ7YiSCjtyzAbvFAljZmKyI09KIJk5ROnhs0AgEFLuF5FA9vIp+37RM/KUjNl4SyrOSqFEcev8meQghBgzXaySWPCOwTiehWw25w979vRckogp4GMkscdPU8HBlCoOByIYpQojSO5rJZZAdjTQJiAuQOfRIedWN0rQWrA2Ox8ppdHajnrDPFBo1DkmOk5MGasNhfEyuxWkzLhQHC6yfMvyYOgPRBCtUTpH+xpd5byoJWBjjHgHRHKKk1pr8LmnsnELYhSsaaiqhqZqqBc11dKMLJ/57MCevqSIk2w4/+tjM7d1lKkz69A/g91k+u6c+zslkJEZg9F4LoVbIt82MbRMZOIoM8u9FLkZY8aoK6uprCkpAiAwyFjKnBmiGqUw4yTUfIy5faaeYqwDrX7+MWhjqEZqdcPJSjg9aTg9W1Gfa5p1TegVV02LFk3fey6vLrPTM8OZj8zSEWOZRbl6YTgficouKoPDifIQ08QAlYPYEhGlFcYabGUx1qBLGoRlU3N2uub0/AS7VHgcNtls2CwONRHJ8qXM4ZgimoxZZwdmX5yMAsZULJqa1Sqnvi25EACFdz6zdPQe3ztcD4Mzv1EKqxRG2GcVLuwXJDXOzFRWVCShVZkLZSqFlGVeJLJcr2hWNTd6k+Wgzue2qNIYVDjYX26N7WTPnZ9fpmWYe7APVJraoPbrQsa9ZbmsOTtdsHt+jQtQ1Utc6kgqYazFu5zGZ7u5wbueYMzoGGa0QYnw4MF9nr+6ou93bLfXPHrwDqvVKTeXr9B6R+93bK9f8fLVS84fPKJanSCXL0m9G9daYr8EhUEvPQAJEWUIEnjlO+67hApZtv9C9/xWGJzPAqFvkedX3Hv8gOaLmt7tEMAqzYvY8W9efcKjVPFb9pzaWBpreS91bKIhJMdKJxZo1F/9jF/+T/6Av3rwDs1NyxOreXL2mP/fix2tBL52dkqlllyGnh+1kUopViLcF3hHwVpFVm2Lurrh5vQEbxSdyueFEBNKRwiZDSyeNJy/+z4//cWfcf9Xn7J4ch/RAinuHWNUguSJaYfz17iwQymPKnzeMXp23TWta/ExkVBokx3WBjaJbBg3+OBJCNoolE8kF9l5Rx96+uCIko3SSaXsvDHKGEEi4z6vVGaasSLUxrCqKjRSHMrIumjM36mYnYUzq4Oj7VuSimhJxJhZHpRaFvmlRptCxh4mmO1cDk6N2pM5BFP5P1lNw/0j6wbj3r5/3gw3GObgfnsdz9N72Z/KgSzgQo/3HW3X0fuekBKmqfB4rjc37HpHBJraoCUiukdSIHpHCgFjNUtWiIfe9fjiLLtarUAvSAlU0mj2QQZvKl/ZMD4tU6BSkKIkZ9En48E7ThQTgFi8oXIPxRCpagvkhZsVpjB66ebOzMrP/lDB+ExrLVVVjfmluq5jMDKllDKdXlGgQwjUdV0EayhUHvn5A4VQptohU6xNQMPh30GIZmBn77WW58LhJBzA7iFnSSy5Rgbq4TeV8eA1gEJxH3klImPEvIjcmtbHjB9aq/FsFmPMHptlUQ650IfJPyjLPnhMeZ81dh9FPQE550pHlit7EPdtyjzi73V9MvwMUUnz/MXDc5Qo4uxxg9PDtC/nwOTQ1wcGB/Zg/hT8nG6ed4KpkYmfV6ZyEvLcNUajS+6cEGJRotOtORUH5WbW53NQaw5CHAVR5fa8fVMRyRH904jBY2DowdzgthFr+q6pseNty3Te7f+Wg3Gcg8DzeTE3CqVy0My55Pfvmrd1DoQcBbuLIjQ/gM0dSobfh5/hs2NGv2PvmwL5x74f3jntg7sA7fk103Jsrr3NfHlTeds591XLXfPpYJ0cGcMR1E4pM4qkiIsx06YbS9CKrjY8+qVv8Q//kz/k0XfeIyaPF02UBFqhEuwurgit48uPPsZdXPLpRx/x8sun+F1Ht2uxWtN7T1XX2ZhTQDkpBxkZxvVAaXn7Mp1PQ/8d27un6/EWMH7kvvm8nX42n3fzekzl61cxLB57d/nkzmv/JkaI+Vy/a90OfwMl+oE719BdRrbD56RRSZ3eO4/Knq/DIRJ1LkeP1RNuR3IeXe/5poPPjo37XW0Z2A+yLnfYH3f14fw9x/pw2ifT+TmdW0fl8az+0z3idf0wj27/KnvlXSU/53Y07pvuma/Pebm9v+/H4nX3TZ9/tO/uWNdvU+ex3mkA1Y7X4avoiHe+Y1bHablr7h4z8E7n/lReHdMf3lS36XuPybzXOZjkugxplm6vn2N6zbTO076Js3oM7dmzd8SDqPLps6a/H9PjbvXfTN+ZMkjcJbIP1rkcysuh3w5YdUq+7GP7iUiOYMpgn6eq8nlFKFEUTA7tX3HKDX0wjkVp0/Qxf5v60bFSqfvFEN6TYkdMO3x0OY908sRCem2VoqpXmcpWtSjlEIpBBDXq/8e6II3/P9SRhpP34DQ93yOAUeYPRUTGtE0iJRIST9ftCqNbwlqNqBJtSKYrpACAlbEYVWfjoFgkKWIkRwFbRqdFRJFUNkxoW6FjxhJ8Oef7kA2CKQopKZISlAqEuMO5a/r+Gte3xB76LtNOE1Ohqi/7Q/4jA2/Rg444ciSdJMEY6FBc3wR+9f1f5p4G/7O/4tUP/hKzXuJiQoWA1dmxYdP1vLy54bt1xXdOTnlybwU7zc4mHAnXR3Yx8lICQTSn1QlGeh7XDQ+rE/51fM6LzRV/5/Q+6+YE//Ahn98zvLt9wTvvPeSBqqgJuFp4kVqs03gUKlQso2GZhC/F8cUPf8jLn/6McHnN6WrF8tEDXNuhbzpi56E4k7y0wme+42xxxrpZ4Ih8tL1EkIxvFPxniDyZp5fJ0b2FYS+BqTTnDx/yrQ8/5LPPPuPZl0/ZbjYs6gatLfVyja0aUujYba+5vHjFd7/3q9TNiroqEWQpswYSAzH6Eq21YUwQpxWRhHOO7WZDu7vg8ePvUBmdz3plbzLa5rNe2Zu9D9zc3KCUye1KlPWQRvkx1SOOycIBG9ovo5merBhBTVGFVjOCtsKiMZye1ixqi+81lW6QQjvb1IrV0mKrBajMMBXp6d01u/aattvhHKRokGRK/taEj4kYhBR1NrUrcMHRuQ7vSqSjFpbrmsePz3jn8T3urc+wylA3ttBUD+tbj4DoYDSIMaAVVJXBmAws+5hNt6tmxaI+QUtN1wnXN4mKiuAXxFgjYnNfSwa2tQhB9lHSoyyRIbfsYZDO0LcxFuNG8jkqsuhB2ioena/42umK84VlaS1NXWPrhs57rmKXg2q2gb5VGdyOiRhdlhkhEVJPQ8yUnUkTkxC8kALQJ3CB2HuCC/TeE8Iusy24bBgPqqf68IRTs8QbjTH5PSF5et/Thz7nmAeIkRQ8lSn02ezlZ0zZWBZLm4fkIzHlKG+fUqGR1nhJ+OjKHuHwBBrJK5pUjEzj1pwxKFE5mlVrnQ1ZKUDyoz6S50Ae9xR9tuim4kAiiShlXSUKpb4e6ylATIEQB/rmLFOz8Vww5Fzf2eHJoNVgNBWIhp6EUxFtb8B3KO8xKd+vbY7ENtoyUGXPo8Vv7VdlzgTJzvBKQYyZIjqV/WxwxBCdqZV1rBCTUIZM76oilLhpozXLekll6hwxTt6vimUYSVlOqiQQFSpFiIrgyRTVPlJVFctmTddtMoNqo1B6rDCDQ9BQf4U+cJ5/HT71Oh18WrTI3uGCQffJYzRx+SSlbETc6z2DWlCiJBlk4uE6nv4+6nVkh4NxNibJOd8rS2UNRmV3vR7o+x5gdIBSKqc1mDoHTt8zD0KhyBYpjjaDMdyYbHg21ox2BasNq4XhdLngbL1mcaKxpxUpZkaC3ntubq5ZVAm3yxHtZVoTo5Cj4DUojZiI2OywoZRGkoxpW6PLfTo4Yik1sNdGtAFbaapaU9WCqJijj09XdOGc65sr1meWL8i5mLO+nNdfSmq0V+QgwOkcyHJ7HxyYAw1PTtY0ywZlNNEFIOQ52nf4viX0Df2NwjsIniz/Q95vkZipo4vtRomAUozxzFLWq9YYk2VritmhLiRPH3oWywWL1RJtr9ilHolDAEAanS4GVrL5PJpMrjec2/OiGQLlQgj0LqfnsFVdbAuUvV4gRawWHj084+XFNf3O5RQNmJw+obKo4PGu5+bygr7bUVc1vcuMAY3JVPWPHj7hk0+/5Gq74eLlCz5472ucnN7jxbOnaGUgRvrthudffM67v/ornN57yM2r53T9DpUSAUY7mZRdOJBlECk7oguCUYagPa9CyyYmDJEzUfww7dixpEo6X+8C/ulLzr/+NR6cnOMuHM55aq2JRvHvtk/5JXvKb8QzvhlqFh5+Sdf8SHn+1L0iSIRY8Ws//BHf/t/9Rzz89V/js8vn/PkXn/DLj36H7ywr/uTmS37pzPDdkzO+c36fP7t4SYpC23u61uGqlp1quddtIXYo3yIhsyYE8egAiUBUNUFpqtDz8MNf4d/+1b/m6SefsHrvMef33uPmcpPzf2ePQLxr6d2GPtwQ4jUpdUAoKYQTXb/LUemiUNpitBSHpiF/vQaxOK+ogsInQ+8dunO44FnUOjv6xUCU7OyBJIyo4thVtCQDRkxOh2IsjTE01tLk3Em43pU0NQGtHF7nKHmjDcZokiR2rsWnHiURLWBNlYOCtSGI5tpD1QZE+hJotT8Pq3FJTM7uZT2OOvrh4hnl8GDHGwzqUs6OMjwnZW0wlTU3/DOmCJo4cA3bwIg7xJDZwcpPSImUVHYmcCnLlk6IfUnlogx9l/BxR++2ON8RU8BWNYveEXyH7zuQyHLRkDx02zbrIkrTVDXKnPI25Ssbxg8BqazMl9aO3jqDsJXi7XhxcTE+R+uc10UPQAuKuq6AfCAJxDEKWRWmsuAz5XRRyVCiqKpqjJx2zrHdbg9yXk+BjAFA9t7z8uVLvvGNb7DdbqmbBmvMAWU3KRvJUsxR5sOmOgBKg6dtFvKUA9btn2E2DH9fX19jdTHIviaiL1dhb6wZJtHw9/D9HDDTMyD3GOVmSuBDIITs6RklFnoljai8SVttif52VEZKqUzcNEa9TnOuTwFqLYe5xt4GTJy2ZVhwd103HLSnAOHUOH5onLn9Du/9+J7RsWBS1+l75v09Bz2H748ZT6f3S0GIVTngaG04PT8nkAGcSmfvUuE22DsY6l3vsgFuovBP3zlXit8EiE//fVMZ6OW6rmO9XtMsFkfnyMF7J8r664wpx9r7NuUYqD/vj/nYze85XCd7oFVNxjCWw9/b9FUsmvGxa733xTN+HzE1pVk9Nrem7Zq3fdreY+D960D06XOnbAWHa+c4APq3VabrY3jnvLyuz4+2afLR6OQwe8/8+dM5F2IGPEULSWcwsddw+v5j/uH/4vf5xm/8Gmrd0KWcu7SxFa7tUSGxeXXN9ulLvvzFp9iY+MWPfsjNxQWu7ZCQsMWbWLTCE8d9Z5zvw76V9mD03KAwH2c5YnQa5uyxSOH5M+afHVsnb3KEed2YzA0lw2dfpdxyUkpxVF7n7/2bGCWGth8zyMxlxnytzo2Q871kvg8e67d5pOlQ5kwkc0D2WD9M1/70vvkav3U/qVBH7ssxGTLv5+Hvoa4+HeqL0zrd1Qd3tX3ahrvk4F3tGfXyO/aquWFtXufpu+96711l6kS3X0uvl8fH3jOfg6/bT489+649cHj+68Zh/q7XvXd67WhQLkDZvF7H5ubryl1yZdTj0t4IfKztMEv5NPt+//xDvWjaX3exZ9z1zmOy45ieNmWSeF3b5zrpXe8d51sBwMOR+bsfW4XSe3392BjNdaZjfTBv87H95i79ZhyDib44v27/rNv9Mm1P3qvy+XE8Rx7UNVt30pFnvGlc53I4z4fs8P22OuvfpFizQsWeGDUpCZFA9Dta19O6S7p+g/cOq2vqZkmDYrvr6bpuny5LZShtHmRy0JcU48nhBflHZARFjvZXOd8MDrzMr02w2+3o+5aYQqY0R+ido+sDqMw2p7WlqWqsNigxiFi01IjApt/hEmhrEcn5B0PKecaHl2SDeJ9pfwiEkPAu4SL0BhwdojqU7tCqJcmOaw9d3xH6bEhXKZ/Jsu6fGLwpdPQZEDQ6s38hiKro+4C1Fd98cI93by559f0/wdpIZzRNs0C5FkmOxWrJnzx/yeXuFb/3tQ/5u++/C+cruGmJm5Zt2/NKeZ6ngDGBB9vAj/stf/D1M37lwQMufM1/9dGP+U+//Q7/4cMnLO59wNXD9/l0WfG1Hz3n3m88QPqO7/jE7ynD8wJUvdKarVKkSvihSby6+Jyrf/19Ni9eEirD+vQcZTThiwuSC/TkqF2tLV9UwtVNz+O1RmvFy77jVQyYQod6lKWuzKuQsiEvhICm0NMulnzwza9z/8kj/uhf/SuuXl1AiBkbqiyrs3OqZsHN5YZ2u8GoxKPHj3E+0Uima+36dnxH127pdxtSdCyWyz3YbwzBB7abDWerhq+//xhSNkJBprhM+4lDjIm27djtdvncnRLCsM5HZO/ItL/DIJUV9HH5wD4KXSuNUYqgYjFQCotFxcmqYllHnLui72sabairOqcfWNTYwiggmGLIdER/QehzvuLoFMkBUVNZoXdCGzL9rXeCEYMjsyk677NRFVBa8+DBKR+8e4/HD88x9QpJccwZjhTZN9Fh4iSCz2hBaQNSgjZiIAic3atZLNYINd1OSM6zrCpar3G9JsVswDeztGJzvWPEm9KQ0nCEfPMxVWIxbGYJlCQRVcLoxMnC8qCuODEVlamwZoGYmr7b4LeGm2c9F59v2TzrwOWorD5EfEgF44vYdFLap0loUhQkgriA9I7U90TXIztHkhaDkLzCJwiLlv6JJqQ1yQQwESOBLuyI/ZbkC0OB6GxkioIEjVI1SgwqZlry5EKeryUMWXQGcZNRJJUdi/rkM/tFDLgQSqRodkqxVo/pVAboe5y/ai+jgRyPnnw+E0iOBZVkslOHlPlbmDVCBK2FELLALPHteS+fGMSIoCU7ySTIuKPROUiEWNheyloTCq6sSKIKK0jC0dH1PcnHsidFlC16WiyQfwk0mcuiuU4S2euNVu0jiUUpRBvqakGzWKCrClvVmKrKdW0W2GZBXTdUVY3RhpSEzcWrnLs3BKwSqhIAlkIkhYAEjbGCrgyEnuurHa+WN9RcUsuaE04gGnynSEkwjWAqQXwC1OASMs58rS3EfUrPv60ymDWUIud9F01QaR9hrQQ9nS9pSPMlB7ifmuj+x/TB6c/kRgAqa6mtzUZxgRAcPkzO3DrvRYpsVxicshCBCWXuNOXjcG8RGKQkWW8IiSR+zIPdOY/pc2rPVizXW8fqZY89BakVLiR2256byx0Xz2/orxLicq7ckLItZLfreXV5Q11d0tQ5ErIvwXHDHFOaMX+uKprTXo/VgEMZMBUYm9A6IPRURjg/XWNMIvQbPnvvlJ/8INBedTQpOzJpLXifctuG81gatLO9LhtKDnKlFIvKcro+4eTkhKZp2LpN6bWIdx3BdaTgCdsl3Sax3Xl2S8XCUIIXIaisKonkdTvgVMZUZHeJhDXFrpIc3re4EnkLUC9WrE/OWK5v6LcRTaZVjkpBYcoc5lGMHqXsOHfedhXMz9UxRvq+o+s6lnVTPiMHrkg21vV9y6MHZ3z62ZdstzuCCygxQJf3TxGid1xdvGCzuWa5WLPrOiprWdQ152enuL5jvT7hZvuc3fYK73vqxQLbrDDtAu02OL/ly49+yne/8y1O7z3iYvU57cVLfKHHRnSm6+ZQbktuDClFVNIoY3gVHDcoHinD+3rNn/hLngPvx4qgPDvlqdyW+PKCRw+f0HUt1/0Fyges1iix/EW64hN/yb+Pig/NiuXJt2nE8D4nvHAbfvHiBd8Oieonf8Gvfu83eP75Z/zgo5/z9z97yf/xvceoT7Zcv7ripYMPT8740NS88h1n0bB1lou24awO3Ny0LG2FVRXrpLEoXoQdTd2QguBdhM6h2XDya7/M6b/+Gs/+6iOaZsWT/9W32VxqAjf0oWXb3nC9uWTXXZKkK+6dkp2+lAJxhLi3QWrJ9qxKW6xZopXJjCXKkHCE1NH5ls71LKuO2lYsqprNtmPb97hJmuUhNYNKgoqCoLNBnJrGVlTaYJXGYkgRnHX03tN7T+d6tAt0XY8SDRJp/RYfeqw2VErT1DV1nf8Vm4iiWbqI3WaHoRgjiuyceChfZ/N/Di4f0blEdKnHkdQU0/UmMq7AqRF9uGIwvefzVHbIib4n9C1NownK0AeH80JKFqMUxixYnz8kEvDJ40JL1265eHXNpt/Qxyyvk+pw/oLkekQFmkZzduq47nYYCTSVZtlURLWgju6t5MNbG8bHnIEyoSeTVBZiBsBiyrme+r7D9a7QcxiePXuG63ts8WSC4uFFjgSvraHdbpEYqCuL1iZTYolgK4tUhuAdKXQYRc63YffRy23b0vf9aOTMByI90q/XVZMPACHw05/8jN/9u38vUzWllOsUIpWt6Luepq5RQB8CSbIhs7Y2q3oxoDXsdh1CYH4OnINso/JVgK84RBVPrpuDj8dBtQJYT0C6QZgfgE4FCJMCTgw5B5L3kxwUeZMEAZXHTIwiaIWyBrw7eO7UaANppIYZcubswSyFKnMjwZhbIU+NDNKN0dsyPG9f5kaBYVFNDQbHwNS5gXja95H9wW24dtp/g8F5MKrPAcDxmZN33WXgkGn9BhB17Ld8RfCRSkeSgrSypPef8Kv/2f+aZ3/2F9z86CeoQrE+CDSQfR8rQbQmxL1Twl1AZhg434QDT55j5U6AXvYGib0CNfHQm43VcHA96P+9O/LBnJ4aduZgyrx/5/WcG3f2zXt9dOd87QzPHFMlpGn+kRwZMDqbjPToaRzO182D4hqdPy8Aowg5mjwOXtV72XAXIDs3zkyvDSEUB4vD/KPTvj1m0JjWezQqlHGdjtF439D/k9+nYz8ZgINyzJAx//5Yu+eg+EHU2RuepUTGA10UhvSP46atUm5JlEQKCZXAqEzVppWh956kDBlKhWAVsl7w2//oH/Crv/s7LO6fk7TCJcdCGfCesL1Bu8DN81c8/cWnvPjkC65fvOLyxUuC6wCIfqAazPNp2DpVAYVHsimZREmkLKeHPGfDmWbqJCXFO/+Y4XQ63sfKbSPZ3hkppcG4MRifB2qzw2fNoy7nhopjsuWuOTndb+aG3LvKsf1z/uzbhq/D+t+1jgfaxvz88py4z/0+7HGSUo4ejJN9YFAZY2LwlZ7X+1h/zfvkTX037ZtB9r6OovpYuT12d6/luXyZfjd32pv+fpeh69iYHXvX/LPDPXyIXtrXvizz8Zn7PHj5/ymNqmv+TgZM5W6j811tGNo+7CXH9q/x77RfM6+TZ29TpvP6NuV5oQI7Ms+GciyafFr3qdy9LSvuLvNrju3j0/amlHKqmskYHCyYCch27F1jvfeX3jlfhjKslWNrf2DsyaCgkMhUZ9qYorZmPfiuefymsd1/n/MmDpFUDPmhD9bhcUP4dA5No6GGz6ZOJFEO5+ncmTLT1RbaxWF/HAz1ad+3o04704OnMmg+V+ZOh4McPbZf5BbLLfFz+2z0Zpah4D1dDGy3uzKWg9P23X16bH4dW8Nje1IesZH9K6USlb5n+Zoa0P9WimQAXIkGVWe625QwyqFSNnaHuCt0rz2hj1xvW65vOtqtJ/mc63GvYtzRj4MesHcfmLR7cs9UVk4fPK/2wRhajGmwpkaJJhS5GVFQqOmVtqysxbmOlGKOelCCNkJUgS72pGSoybSiETINcUoonQ0/MWW6xBy5YxHyuWjX9Vztdly3FyTVsVoK62qBXlmeKthsdrg2ED3opBHZR+QVk0vWI5UGqzJAmUApw6sQ+I1vfod3RQg/+zHP/t0fU5+uM2N78CgSUYRXIfLs2Y5/eH6fJ+dLtIZ0teXy4povtju2AruYaFOCoLjxjpcI217x6cuWH1xd8/La8537D1m4hk6ds6vv0+w85w/P6dyO6+iwCOfR8DgltloTQqJVkYsm8arStD/+CP30BSoKab1Cr1ZwcYO93EGUokNHgm34TCVWyrKsLI7Al5sdIWnWTe7bIXd4pm+dyaA45EBURBdQynJ6fo9vfedDLjdbPv74M4L3VFWmSF8uV5ye3UeI7LZbtpsb7t8/5/zeAyKCcx4RcvoiEVKKXF9e0HUt1liWyyVdH0gpy/rgI8E53n/vPVbLBt/2BJ/KmT3ndRSd69r3PZvNhhAytWyarl3Zy+e5zJ/P99tybsDJhvvz74lCLx0EYxtOTtacnTYs6kjXvcL3pyyWSyrb0Cwr6roiaYGYUwmk5EnsiOkalQImu8ugy6us0oh4nM+gv/Meg8KFnk27o+27AqTCYlHz3rsPeffxPU5PTvBqgU2epA3K6lF+5/qryd6c9xVjBKVVzqXrenauQ5Ti/fc/KMwPFSRDjJoQLc5B7xMJVSJ91airHds39/Mpjo4P437DPgd2NsKWSGFtEBVQJgd/oDVoQ9SZDUB8xG0Cm6dbXv74Fdc/vaHuYmadSNlIa02FrS1+lUUUWhCd14cmYmJEoofoSNEhShGk6P5KgS/MFjoQTUdQbUbQooEQEMCgRwOtxiBYTKoQLCIWiZoYhRinToeFwUCDRpFUIipPjB7nHX7Av1I2aqsBS6L8UqKPRRmUHlgkU45YTwGRiJIhnYUixgqlF4BFG5sN/1Bo9rPhLiUIYcp8l+m28/Yw1DkWVoFBT5Bi29HEkvc8pUTwOf+2tVXeTyWRtJCqmnYXScEiFNaEort57/DJk0p0/zBnpj9T2ZRgTPejSQe4WkwpR64bi8RMaS26zDNrc+5nY7C2wtocqJV6z3Z7jWtvsDohtWFgaTFKMCJYlQOQnG/p20TfQd9D2zts2+IDhGDQpmZ5uqReVKTLnMJgoKJGJVIAjc4UvincKYdeV25hcuW/RHEoLDhgkIDEhK0MdVVRVTW2qke9GOLkpDvogIzPo8zFUBxmhoCysQ6DMIay7nI0+BApHkPAp2m0eHbMyA4aJcBkTCcgSGEByeOd65fSoIvtcbwCto71HfHKiSoaPhKUFqpaoW0imszcEEPODxx8IPWeyuSUBTFlmba97thdtjx7+oqqznO49452s0UpsmEcIAYGEvKcb94X2v78flspbJUwVUDpnA5B64TRNYaAu3fCBx88YnXScHPhiTHnuldawIGK+wjrIU3AMP9DiHgfxqBCYypOTk44Oz1luVqyvR4M4wkfepxrib4n7tZcvWp5dWE5WSaaukZbRUgRNwBvKSAp02CL5HQrytg8P1TMDBlpEmSYEq73XFxccHW1oe9KOgkFXnKw4r7ue0x0sEe9DY6610UHjGt/dg4h0rUtYbUu1wxnUQ0Iru9ZLQz3z0+42QRuti22bmjdNYoSRElit91wfXnF2elDrPV0zhN8YFk3kAz37z2k7Xs2u45nz5+yXD3k5PwendvQuw0+dly//JKLV684v/+QywePuHj+Bam7oZw6IIbMYlS24TztM/opCSTmM6ZTjhsduJcM97xBRfipBN5NFZZImzLbyPbzLzj54F0WZsm13rIlYAptxFnQ/PryjL93/zFf+9oTvv+DT2hCx5Pf+BZP1iuef/yUP/rkh/zmn/xbvv77/4S/+81f5uN3fs7F0895d/WI//0v/QrupKLvO64+e8690PFURa57z323xuglD04r5Gpb7H6KhakxfeC6c8QalFSoAHHX4pNBPX7AN777W/zo3/y3PP3BT3nx2z9nuXzAF88v2Wx7brZddgruA8pEjAFRmSY9+oQPhUmKhBT5KQTQisosMkuPykFrWjckKiplWOgOZyvWdc1549itO7a9p/UBH0PBCHU2TMfMKKOTzvLSZ8O7kZzzXUUQNGI0SCCJJybFUhJGVcW5MNJ2LQKcLc+wdcNydcLJ+pTlakW72dL3fc417vyorw6ycTyL58k/4mFqIvfuKuPeXJyhRPToZDT+FDkyRI0P+sURRG6vB8ecTinFhEaDMrheEVKV9fdmxclqTVVXKGW5cRsutxdcXL9ie3HJZtexdY7W93Tes3OObdtlpiAVsRaWS8X9ewvee+cey1VxYCs247cpb20YHwSnCFhrcu6dkifCe5dpnhPICKBQcnRovvj8c54/fcb5+Sl1k72+peTTUUqz225YLhr6vsNUNZvNhrqqgEgMHmsNxMRHv/gZp+sVbR/oug5r7TgplFIjMFnXdVZ4igHYGENV6DH+7b/9U/6z/+w/Z7VckkKka3c0TYP3LhvrB9CjDLounpXO9xij6PuO3XbDQOcExyPXhk0npj3l90BXPgW2pkJ6rsDBQFMPTADL/aRVB+My1oFyiJdiLC96cAb7ci6fkYopZd/OKFl5z5Rne0q0UrFcz1QMBgOYnPbGzcQelA8Thedg3RWlZQDJpv11a4EmYNqm2XVTY/lg3JsD8jF6SHkhT/OyD/kY3qaIyAG99jFFU0p9pSh3UgCkASDL/aQh5ahRkcRV9Oxqy+Nf+x5PP/6YXfSsSjv2VDr7CGREMNaAPwTppqDTCMCNU+qWT9BblVG9nc1Fa22hwDEHwPut/hrn9WH97gJEp98dtGP/5dFr98+ZKfd3XD8HNw+oMcvaV5Mxi2HwglVjW4Y1ddeBY26YGtaAknxwFZG9gwx3E45aFAABAABJREFUG2Om38/pXHOd9MH6mL5vbmyfrtPpZ8ciVI8pkfnAdGivOCjlgDmdK8fePy/zMX/TIW7+nLlBIKV9lwxiVZQqWnQ+8EdJhOG8l7IxWJEPOFpbUow4LfQC3/kPfo3f/cPf5/SDd/AS8RLRCDUC2xa/67h5dcEXH33K5ZfP2L664ur5S9qbzQimhhBGSrahLjn/k9qvznR8nQxrKKXp+Ozn1F4GqFt9Oe+zY313HHySW79P3/e6MTzc025Heh8bw9d99qb58Kb7hzrMQZH59Xe9a6DUkwIOpOFniIZGGBK+MHnmXG7K4JQ2ecfhXnUom+B4BOJdfT1d29NnzMfjWLtv0wxOQYPb/Xms3NWX8zpO5+HbgDbHnnHrnanoOgf2mplaPqnP+BnDFln291m9XzdHj7HkzPt5fu+x3+9q713lFog1+3t/HeOhZyqPj9VrPvePzZmhzGX0oINO63Z8Hb1hfQ84ytH9Q2Z/3y5pqAuHust8zszp8W8V2YN404oZMxyoyvlgduveafi4TJ2PVXaQGN4giCqRcBOZfiylyl179PQ98zYm0q1rb5WU9vr+KOTKPEpposMeX+dzffr4fJ8p9JMytuHI14PMHp+VjrdjfAYFcCwOZYNel68pv04+u6tfRtkwWwvT/USLRsEBU8Hrlvfr5vDblHG9JSElTYqaFB3EExSCUZZkGpS01HWNFo91Ca2ykSOXSKYt5XiHD+1gKjsHPSRNVsYEHBl+GPST423OJhFN3SypmiY7+vpIMBprF4iuUEZjjaaWiHeBdneNjw5RGmMbbOWxlULVDZpAimrcnyNpjEDUMeG94/LygtOTFUoqUsq0k1u3Y9ve0Psd0GOVx4inXixyuiifcYxsGDdIEgYjZkrZwIQ2xKIPGjIVbt86vv74XdKXL7n56Of0Fy+J63ucKs3OB0TAK81L51n1Ff/o9JyHTUMSCLuOi+2Gl73D1VWmjE3ZaPvCtdzXQth0PL9yXF/3/MH9+7yLR9UV3aohGLj3/AU8ucdus8kUsUaTtMK3Hc+7lqtmzc7UJFOjek//6XOS91QYomkwtia9uIYU0cUy4FTCk3gRHCd2wbppcEq47Dsk6RwlNhjrYkSMgTRxrOJwn4kxsGhWPHjwgK994+s8f/Gczz//HOc8tgQ8LBZLFqsVu80N1zfX3Nxc8c7D+yyXS1qvRx1sWI8xRtq2JYYwRh1776nqBXbRYExHFzY8fHAfoxNBZeMpCVIMKNEjfuGco23bcc4qpW+de950jj3QWcjyIV+bRrkynM1TijnFXso5FBeLBYtlja2EFHu0jlgr2CrTb0cFSRToAbqLxNCRQgvJoyWilaBUQquINoKIz5F5yRUZKrRdz7Ztc+RtyHN6sah5+OAeD+6dslouQGdHBWUM2uhsaKGcm5XKabVjNnhN9aC27dnsNmx2O7Q1+BgBg1IWrSq0rtHKkulf8/pV+nD/LMe3sZ+nY51/DtOciOwdv0bZpDLdsTIGMYagFK7siSp5bAAdAym0+H6Db29Iuw0mGLI9OxFEE7WCSiNaMl2w0URtQBVDZQplSxEiChM8PTCk4A4x5y+PUcAl6AKJiFeCDwKSaeRzJJWgkkWrBpIlJo1PwmCyTOTxT6M5N5T9JzIYobORuER6IzkStagtzmeaea0ADZL0uE5j2jNKqmJIV4MjBwqlHEYntFoiYsv6EFQAo8AaQ4oZXxRRmEKlTqlfKpFikOfoFB/zrkdMlfemci5vnSMmBzr3T5CES5FPPnvGZ5+/YLeLkDJ1eu8zDbJC8CnnUlYc4khHdV0Z9rP89zT4Q6khFUOPjp4UZNxnUDkaFkr0fNGBNIaYXMatFZg6RwUmUZhCN08KpOQQFE294uTknNOzc1brNbbW1GnBsjlltTpluW4wlcEljxFd9tdypj/w2bl9pjp25p/r78dkl0gxrk0WYSqLzGqVI2AXDc3yFGstygwpOhND7vhRF2BIUZcNcN4HvHNlnuVUnlkypr3ikIpqonTGqWMgxEgfsnze59PN+7JSGi3ZGWW4v+26iXxIYxvSwPA6nhkn+knRv4eVFUeDbY5yVtcRU+RMQpMGI6UkjBZwvsyNbEj3IXLVbeh7jy6OORFIAarKIsoUQ1OmPScWRxXJbx/2UKMV2iq0FYyV7ICkFCIaiYZVU/Hg/gmrVcMV1yXyeo9/WHTOdx5CNkjN8JDM8JvTD1lTs1gsWC6XNE29pw5IELzLubO9J3bC5qrl6spwfaZYN3nPcTGV1DUJokbIe3JdLTCmyvKTsnenSJKIVuBiomtbLi6u+OlPP+JnP/2I7fMbpIdF3eCix7k9VjJgHnmM9/NXiYz2h2NluseklA5Yb0lpTE+bmT0H3gs1pmhqzIKTkzWLRcfl1ZZmZYhdQApVuvEa13Vstjf0vaOuA8472r6jMpZFteT+2T2ubi652W158fI5p/feZX1yxuXlM0QblNL01xdcvnrJw8fvsj7N7Dltt2FI2yCkglmoHIQYYnbYoqzxQf8S4UY5dlF4HGtO0XymevpQU0eFlswM0m2uEf8Ys1yg+4Zwc4WIsEmex2J5//ETPvyt3+Dk977J1+uGX/ybP6J6vODxr3+Xk1/7Nn/xf/0L0p//jOUf7vje3/k277v/kPa//r/zp89u+PVvLDg5W7BjycUmwhcbTlCEGLnpOzb9NUEZ1OVLNi+fYT94FytLVEycqIYrn2iUQhMRFfBekJstT77zIZ//xfe5fvopn3//z/na3/9Dus7QdRrnDCFURGym5E4BwZFSHt/oc95qlf3ksvONjhBBokK0RUuVg0slM/pUKqKhODdBrRXLWrMK0PpMxe+cyzIhCtFnGZLzW2dWZ600RjRFS0GJISlDwKMiJOXRUai0FEeQ7ABhjWW5WrJcrLG2IUZhs9ngdi0hZvwhp4GwKDWJipbJnJ/8OxjHp4FYgzwc9wXJ2KdSeqJbTddQ1gen1+/x4/1ZcBDBg2MxRf6KKKytScmhdE3d1FR6wbo54Wx5SqUtoInB0krCpp5KrVk3+eExJvrgEB+plYJ6iTKgVJ4nSlXU1QqjG6Amek3/dnbxtzeMD50RguPqaov3ffFEzFTlWmtE60KFwxjV6vqeFy9e8Md//Mf8x//4f8mriwtWq9W4uTnv+eyzz3j33XfzwSQkmqah73suL17hXM+77zzhX/7L/w+ff/4FoUSh103DxcVFmYh7sDLGTFWSYPQq1VrT9z1aaz777DP+2T/7Z/zT//M/5fzsjLU5Ydd2NI1gjaHtOpTW3Nzkw6W1uYvadofSQtft6Pv+Fug0lMMoibQXYylPsimI3fc5n8M06nOqmI0GrglgNo8cHd6Z7z+kG52DSsF7tOiczyNGoho2z+xdHYoCMoBkA9A2REVk71IZo0eGeh5E+ZE9uOdGngNwkOFYeNjmaUmkcRFO2zSdi+O1s41wD15lgTcFFKfK4dQAPa/jsUPv1OB0y3h9y4B1qJBK8boJJU94iglrDH3X4XuX+zse0lrP65G9ss3BuM4NKGmQSH/TcgQAr6pqnBPD/JxHnk37SCZCdt6vb2toAW6tstuA/+Gh520MLvMynRPD37cAbRmMKK9/ztwYNDxDa112irevz7H1PpTBGeQuQH4o8zGYltcZdaZRg/O23HXAeq0B4w3jMp3TXwVEHuoYUqY8HA75KT80y5GUZXFIGeizevDAT1gtoBQ+BBywevKQ//h/+0/44JtfR9UGT8JYm43dMeF3Ld2rS65fvuL551/yVz/4AdtXV+gI+EDwPkekclvOvMkhZzqPpzlm5zJr3pdzOTuXj8fG6HUydP6sfO0g546P4/y5R2XTkfoOf8/3q6ms+euUY8acY/U8JjcyZaOMzCdDma+5gUr3GMgwvvc19dvLy8Pc2fMyBzWGzwbdYeoY9lUiFI8ZI18nS+b1OSYP8qF3UH73183HdD4fpnN9qu8M98zr8zq5Nq/r/B0H3+cvj8rsY3rHXeDTVLc7Nr9Jx9fnX6fcVcf8AQe66bF3Tet16DW/dwab7jvH9Jq7nnn4e5Ybb7r/2LhMv5vriG+SC3fN4WFOzcfyGICYUmK9XnN+fs4nn3xSjC0V8+ic6XPmMudYvUQdRuXPn/OmuTeXV9N1Mm//XTr0tF/mn0910DdRvE/nz1x+v6kc1/Ner+eL3Hb2POzzVJjCJmOU4NZNb64czNb2m8b27kf9LejjsHfaHByxMAgNRiKVNghLrOpQbHN+usoTqpqTyrLUVyTZEQgZ5psZxWX+xwQ3TlnBzj8TFqgBGtnvg+MnB+OR0h6IVuLRtqauF1TWIiRELFXdUEvO02qUQgeP04GbuGHTOnxsEeNYLDSn5oQqqRxBEiNaZyOB0gqTFFXKNLREuN712SihIwFN63N+7753mf/XZ8A44xk5minFgHP5LKxUPAB18jlYIcGTmWMSfYp0vWNpzrhfL+k+/h+5+fhnpJTzDkrKeTe10USBi/aGpcD7LGliRd8l+k2PIbFeGF4l8EAHbJLnwge+oTRNZbGq4j1T85tGWF227L52SrdegYms3RVx+ZDu5oZFU2OtpfOBrSioLVYlaqNJETbPX7D74iWb4GFpMZVFQiBcb6nKOUcjBNG8tIoL1/NBc8LCWLYELkMORjCUVFAymSsM6yWnahuMEZScxtVywb2HD3n08BHf/4u/YHtznYFDYzFVg12fYrSi21yxu74mhsjp+X2SCFVdIbFQXKfsauHbHa7dISnr6SFmo8R6saBeLJEIarHl4YM1hIiUiMRYgjN0of913tN2/YgBJeayMx0Ya+flAFson0VRJYZ7wIPyTIox0qaOJIlEIETDjpZtu2XbNez6RF1VrKywqAzWaERBIud9V5KNDiF6YmwJoUNiXtsKwUii1pGF1ZAivhhFhjm8c46ubUl9n4NZtKVa1jw6P+N8uWRhK0Q00USMVtRGj9TJKglOckRyGBwiGKhkE13n2Fy1XG9uUNbQ7xwx+mwsQWNUhaDRyqKULakSBkfvoV+LzJBsUIspoQadMA30/J6SdbXobyCSBmowcuR4wiqVI56T5DUdSwh3SmTrtYcUslN0hCBCkEBQQjQClUWqGmUtyRjQ2eEkjYxykJLN40rOi7lxCucSrov4kA3qLmiCi8Q+4JVDtBBiKsZDXRaQkFdejjJOMTO5iMBo95sYvoYKTPdFkX1X5vy9iSwgc1RkkOIYVWR5KtTtIRbDZTFYKpVQsg+A0jEQoxSKXRhyQqe0nwNa7xllUNnokmVqprkPPhu7ReUcqiI5L3NmDXEFfNdZVoRAkMg2OHZtx+WrHV98+oKf/I8/5+LLK3zvCt5YML+QirE6Ftwv5+E92K+me3HpqFFTLVtcNoao4tAsJXWkGrbFcS/Mhv68soOXHFikLKJKlLwu/aOy5FBKkJiIzhNCB1Y4PTvjyYP3eO/he5wuV6gmolVFbGF3suHR+X2ak4rumQNy4JcShSI7C0TxxUh2SxzdPjPKHned/z7M4/GYL+X34ZLSjYPDla1qmuWKuq5RWu37hYEts2A5gw5XxsgHj3MO5XwxkOfAroEiPrF/P0jOSZ/KfT7LENGFHbD0BQg+RlzIkbkhRrbO7fHHoVGRPFenOuYRw/io9zD0Qe7fbMhVxJBXetblU4na3QeQSDE4pQSJbDBTMWTGCiVYsdS1zYESRYdQaKJYtAZRnpQc0Wtc6oh6jTGayhisgaQjoLG6QmlPUzec3ztjfb4iqStSyutbSXZSIZRo67Ku8zjvme+GcfHBU+saYzSLRc1i0eSNzBeVMEZ8cDjXEwO0147ri46LU0vdGLqYaehDiIVBz2AUNFWFUhGtUl5HogjDICtNUJ7OO64vN3z8o8/56b//mC9/8ZKwdWg0W5sIUZFCwCiFNZqBvTDGYbyGcWZv7CsycS8X9w6cw5xIZLvGUJ0QIs47qromRl9kbtn7VXZyWS9rTpYVX6ZrhMKsA4jSWGPpti276yv6vsXHJS4E2r5n1RhO1muc37FsGoxS3NxcIyJUTYOtG4ypcSqzSbx6/pzH735Ac3JKfXJKe/miyLXAQGmQCq45yPusTydSKtG+SWhjZiCSFDlF81Q81xJZJdBJ2KmE9R1+s8NUhmrZkK4v8Bq6GNkQ8CrXsXrnAe//+nf42b/9H2hfXUNK3P/uN7h/co/+i+csnz/l/MNf4eR73+blasUnr1q8C8TWYxrLyf0TTpdrbrY7vERa3/LZ5gJpF9zfgHn5gthnpk0TBGNBfCCZQDKQJO9T+mrL6uFDHrzzHruLL/j0T/+SR7/7j0AqtFTZ8U5pkkv0wRODQ6LPaQB8dgRJAtoqbMg2LVGFBSKTNyCq6BNjWsDMxEBJKWFMoIqBKgiLkHDW0bk+szC4iEsRHyMx5MBiqyzZwUxRaVsYv4QYIqrgdzFkdgWlFSZqkJw6etEsWCxW2GpgnvCZqn1gtLEBawymOAll2bdPY3CgH5S1MMyb6SqRosTk64e0IoWZeVw3kzKeiyf7aJmMozufDMGElHNrwoigjMGqGp88ShK2sjTVgkW9xtpltlUmsKphYZas6hNc6DG+5GrINWRZ1SCCXVVoq0BHkjiWS4M1NUSN69PohPM25a0N433f45zD+0xlYoxmUS+oquw5GFNWgTSDx8phntN//s//Oe+9/x7f/d536fo+H9xtvvfevfsobXCuxfcdm80WpYSqqtFa89/9t/89/6//5/87Ty5r8VF49erVaBQfSl3Xe3BSJF/rPQCLxWIEon74wx/yL/7Fv+S/+C/+C7bbHcvlokRKZ5r27Mlgi8FTRmF+fX2do5Dz8Bct6nh/DQqMqOx1rCQWr6yAc/lwA3sq5OGegcpnaiDPetghBecARnnvRyqRY4e1A0Nl8fhAsld9ioMDQXEqCLFsnDPgrdy/n/h7kG5uIM/3qFvPODhgyhCZs6/jXWDxHDicgs/TMqUT3jsn5IPBFOydg/JTAHh67519eAQozsqT7PO4HLu2zJUQAkkpFk1D33U01YJ+12JFo1UaGHnHsZ62923A6SyE/uYlFU1hCggO+bEHRVfUYSTgbSPLYfThHOR8m/a8TSkY5t/4eXPQfAr4jvP9CBh8DMCeGy4G4046MneP1eOwfcfWxX7OH1sXXwXEPWa8gtuGzbueNwePj7XnTUD5VPa9bd3n1ybAlw1z0GdF9gcVpcCOBxGVadm0ItQVO9fTnK35nd/7Xb73+/+AxfkarC7jnfBdDy4QesezTz7Dvbzk05//gudfPqXf7mi0wbkeVxywiIPX9e2IUni9zNuP6TQG8vg1UyPG1Og4XDP995hxZfr9sTGZfq+1jOv5rnuOGT2H+s3vm66TY4wBdxmu3qYce9Z0j3rdew+p6Q+de27vBfuImel7puvprvpNPZ6VHBoo32a9TPt6eO/AmvM2hqnpe76K4We678+dZ4a5NWXFmL9nuO9YPYbfpz/HDGTDs26bye5u37SPDksex7ncPvasY+tmXl/glsNCBmhgahz/65b5/fPxno/8m+bDdEzmaWnmjm9vOz/GfyfPft298713Xr+3Zfi5q13TOTt8Nlwz9s/s3SEEHjx4wGazoe/7fJ5wLkd3TN5xrH/nOtFcFxBRR+f268pRXXr2vnkfToHh18mieZ+97vr5tVMZcGz/3tf39e0bgefZO6Zy91hPTfsjxkgsddnvhV9dIx7OSdO2HOv31z5j1pd/Uz03xVTkXT5LKCVYXYNVaGmodQlRjC1RAkZ7TH1CaBa8rCI/V5e0KmFjXXLQDfEwe/6zsd4ytFOKEaA4GhcrjaQ9CJzvUSMQedj+grSU63XcESWDbIu6pjag7QJTn1CplI3iSYCAryLadvS7npt+i+96zkxiKRUuZA51I9mAIiSsVZlWNw6xkpY2Gtx1m8FmZWmB684TvGCiJQWD63q2faBrdwQfcb2n2/VEnzBWT3SEDBahLSp2iK7pJNGHjp3f8tu/9Css2p5XP/r3bD//GapeobWwCY4gCqNqIonNbsvC9uycoK+FDk+36Xl0UrM+M1w/2xASdCSexY42au4rw713H/Dg0QO+nRSLz54Tf/gZm+8+wC1XmMphz4HOkxpD9WAFIXH9fEu3WPDk/pLw8ooL3/F0e80Xf/mXXD57zkV0pJMVdaOI2w1ys6XSDTuJLJMmoPis1lzvOu6d3seIsAuey+jQVmOjpacb0LbinJrXrC9OBynm8dcx4ZSiOTvj7MkjVsslH//4J0iMiLWIrdDNGn16Dilw/ewL/OaGRbXg3qN32TrH+cmK0CecS/iUsAT6m0tit83ROLbGBSEgrNZLhIqgd9RreHR/ge8zywBINjQnSJIQo+l2bYmi9mhtCSFHtlICQO4qc/mvAC05ODgoTSgpEHQx2MWU2PWerd/ikqNWDSYqLt1TxN6gGke1aLj/rXd4eK4wdY1oU9agh1j0RYnE1BHihs61iAuoZFFJ0ERW2pPqmk9DIniIIaFSJmPeuo7QdohzaBLeWpqThnfurTlrllTKoAS8BColLKzC6uxQY6KwZUuXIj55wKNVzPmxXaTbBHZXPZvrjqR2bF7dZIrY4EhRUFgkCkZXGFWjVF1Ct7KxESlAKinnCU8ZjQijvlzS5OFJ4khSkEcRRGWqYTAgIVMga40OKsuFGCBEDBGxiU6ViMOk8dRsUoRoSH6LqTVaakSWRDkj2qaky8iWkAEojkh2gNCaYCwxCled4aZ13LSBPgqLWvh2UPQu4qJHxx5FgGLYlKRGeSrkdARaSpBKHDCdVORojg6HjMGAkNQ+ijwbThXESAj7qFBrFZKKjCQ7ZPjgc650FClBCIngI72PIBGls+OR0SrL2ihItBgFiCUio9EyBEFEo5RBJKeODD6nnEwpEGM2UMTkyj6SU5kppQkBdq7LuV2JqJT3GJ8iF5c3fPrpBT//0Zf85PsfcfUnnzNgakly/5higIZUjKWMjgRvwstg2OsOWXqGfwfcayjzvXyq7w7n9ulZYtTbECRC7AORiMGyWix5fP6E9+5/g1W1ROrIlX6B6QQJju7hlvPHf8mLX1yX1Goa0KhYI3hacag0YZ870rZJzUePnQP9rMzjcYqN59k5diGgNGIMylpMVVMtFqXt0/7JlOCkzDigii4hMWVHc4afNBqjR/mairmyPDD6vJ+7kOm+lSqRl5QfpYkx0fqcd75zPb3zeB8Lzb0dDaUj1fpo1J4Yjco1g8H1AMcbsU5zgNfPWaJGOu+iP4lRZT2oA+x5oCbej4qQRJOqYf45UoLoFF5t6MMJKUmmRzYQcIgssuzUibpec3rvHvcenoP+nFhSchptsRZSaknJZEeTUIyqSEnFkYphPMsCyCnzmkXDar3K822gJoiJ4B2db4kp0W8il897mqUjGke98MTQj0EoWkUqq0FVNDGzMiKppCMASsT8zu14dbPhi4+f8Zd/9BM++f5TXBfzXFGR3vf4boGtPcuFYYXBGCmOLAXnL9IzpUNn3vmZXoa5L2T2yODH6HDIwYFt37M+VdlAWlJdJYlYs8w5wmvLvZWlVpntRSpD5xKVZGcFA+wuL2nbDcuwpg81u96R0Jydn7BtL1k2Tc5RfbklhswoUDcLqmZJu7sBvePFl1/Sfc9RnZ2yeviIy09+jianFAADSYGUdVZk376RRUfw0GPZJYWXwBmKjwk8xXOOYESzNYnzPuEurjBP1jRNhRbohZznOzl+8eIFn/zoYz78pXdYf/CE+uQ+Vz/4lFeLH/HkySPe+8Y3ufzhL1j++58iJ49hfcK9h4/5JfcFtRi6pzeopebRvSXvnp1zuWuxVrFNjk93jp9ceH45nvArz15htx0+KmIUgt1hd0K0HV5y+hidIrLtUY8Mj7/5LS4//4i/+rN/y7cvn9IslqjgCHFH6xPR9/R9y045VEgoJ9nhJLrM+OTAWKEKWb9f1jldbYou23OKUwRSXLxEAVV28pC8dgzQAEFHvOnZdR1t7CGGzHYRAp33NHZFTlOpMFWF0RrXB4g5/Unoe0LfoxoNKTPVVVJhtGG9OqG22QDsC6PzQi9Y1RW68lz7iNHbMb0XKTtPqhK4U0hvM5sxmedakffIorrnf1MaDe7DmY4iKylMIGmwtShGp5S5VUMU5YyYT2KppAFJCbQIlVYYDUonxK+JvsKairpaYOsF0WRGIkhYa1ilJaiAquBiG0EnbFVxtl6jACOKxUKhagELXgf61KFE4fqALzJ/sFe/qXwlKnVrLctlUwRPVk1HwCuVaJPhcDzZKJ1zXF9f83/7r/9r/i//5X+J1oYQE7H3NE3NyekZfd9jbEVM+T1tm3n11+sT/uIHP8C5QF3XtG3HzTZHbQ/A8rABTg06A33VHDAeQNE/+/6f8ez5cx48eEDb9ezajuVyyXq9AhLL1YquG96RF401FV0/UHfEkoN0H9UJHOQ5H4CVQXiHkJ+VqQnygds5d1DPgRJ++ky4bUg8ZsAbrhuumYLv2cUzHdDvDOpaGn3HigJTvh8jOA9vyJt+ef4A/E6NplJW2jFjzTBX5u26BYZOwOo5IDgHqAalY260EMneRcaYg+dPDQrDeE3LHPhKZSznxo+DaycGoznYKQUwyDlWctSAtZb3vvZ12qtN9synKG6zNk7rdEzBvwVqymGf/rUMSxNAe9re1wHWU/BycsUtg8kxEPkYwHvw/fyps+cNkOrtA8rd43qsLdNrDpkfBkpsKRL/eF2HuX5gGJiUsX8mr56/d3qYeh1InT2xDp97zKljXqZtOrruZnN8uramDibTa+fPnhuQ5s8+1t7pmL6p/seeMcr8ydgAo1exQAZQk9Ck7C3rRdNpYaciH/7eb/N7f/A/5+zRA1Kl6VREpfIcH+iuN+wur6HzvPr0S37yJ/+O9maD8w6jDTvvx3bEGLM3/KSucwPivP6vK/M5cWyuHDOaHHPoGX6fR4OmeQTZkbkdi9fOINfn4zm//k2GmLkcnbZv2pe3++d4f73u/a+TOdM2Hx6iilp8h+ydP2+45pYTwJF2HozX5LO7GAHGa2dlbtifGzan82MuF+/am+dy/NZed+T3+XuOzY85UPS6fpzXbc6kkq/NIMy8b+7aJ4/tMylNPMbvuHd+/V3Pfp0+AllmJw7781gf3fUOuD0W07E7kC2zvnjdM4/VZT6H33Y+TuuS2wyI3DmnExzIybv65o2GddhHfEz65ta+OZErt+pTQLlpX3788ceI7JkZjtVvOrfn75z3f0qpABm3dfZ5ne7UH7g9dseeJVIOtG9Yc/N7j831abtS2ufinJ9T5u0+mJ/cHotjY3Ws3eMaG/zb79h7hjppvWdpSQfXZ+NLSm/QqY/sf4c/HOjId5X5fvY3LfP5PZxtxvNvyrTFUQLiO1yCqulZLFYs1ye4riV15bQ30ZXuWitTo/B4YpyAyQf7VZrFYo1rYsgbCyEJvQuQNE214nxhkcUJ0qwwUiL9oidKD16hTcOiuYcyp4ixLNcrrDGAK/hfBsZ1Uc2VpAz6pIQ2glIW35cIjtixjZHOOWLSGKlBRYLkvJ5Cpjg02lJVAqbkLiVOzs2ZOQuWSMqGtz41qO6U3/qN3yL85fe5+OwTdruWannC1gfQgk7kdvmAdZ7TK8f3Ty/QFxdYlTjVmnU65+lG8yoIW+/xrkftNtw3K04f3mf93cc033xC6BIXf/VTqiuobIPXHlmBfe9Dwn/z3/HOr39I0o6bT57Rff8jHv4f/hB1FjBfvED/1VNufvGMn3z6Me3mFV4pKl0RXWDz6oYzwIcc0emAGyIXbodyPZUydES2MVPGasB5lymZZ7ponjOHazKGhK5rnrz7Du+99x4vX7zgFz/9GSml3Oe2YbFYcro+gRh4+eolXd9zcnLKyckpGAMIPuZ8jhDp+56b7SavBZtpSJ0L2CobMbpdh1aJh/cfsl6t8J3L+EpKIBnDiTGi0XjvcL2bpDObrdc79sDbciSViDiQGDAi47kehN5HLi5u+OLFC252Ox7fO8NEQ+83XF5Fnn7xjOefXXFu1nzrg29Q2QUhVbiUDZ2iIIon0ONiR9+3tH1Hcl2RdTo7sVrBSk4HqKMgIdN7ur6n7zvCEMWdsvy4f3/N/funLJYrjG3QWpETiAiVNVRWo40UgFWQWBxxJI6G1a7r2W527HY9fe8JKfDRR5/wje+84uTsMUkiIUUqa1Eu5/y01lLXNYgixITRGpJkGnKfMatQ8oHm/MMaVQwDOcKrROOiy3c54lqJYLVQVRqjE5meOBG9wqdc310b2UbLdWx45R1fXPeYXlGbBYtYUUuN1ZY6qex4oEyR+zmyOUflaZLXGXD3ipdRs6Gh1YquzjHttgpsY6SPiiANSjdYlYhB6Eue3QFpi4CkbJJRaUDCEpLCKLRFsqHMmLyfefFEiYMZJ+cT9nFC45/nnlLZgYCi8oYQcTGQkpBiNgblvMPgQwcqYo3CGkNl9Jgr3WoPkvAhM192LkHSiAaRvL8GnxkFMi6co8oQRUqm/G4g5TQGSkmeW10PUZOUZZsqfvHZJX/xxz/mR3/6U774yVPaC8+DVTbG6pI2QUSKbj09U2Xcbq4fH1u/x8p8v34b/Wn6vLv0WIBAwqmA+YuOP733Jzn3+AJ+8xu/y9Leo0kV9syAKK53O7717a/z43/zKYLNThMp4GOf9zyRA/aXu/Cc8e83XSMyyw5a9GXY4yFl/uTQwtLnaqLn7qN7CnPfED1NNgBLzAb2MWoykVkb5EDEppQQXXCbEj04lEjCxUDfebquZ9e29MEXGv2E1VXu60LVTpqOTZbtSglKHzeiDroNjE08MG4Pfx/eMzGOKzn4fmocnz8rQcHnmTw3Mxacbw3dZxs+e3BBde+U+tE5H1QVtVf4CEo0lamp7ZKHDx6yXi/wN8V+kOLEeFzW4sS5iBBJDEwRfgyyM8awXCw4WZ+wXq/Z9NdFjuTrXNsTnCN4zc1li/oi0bmOZpX1rxwlXtPUgk6e4DKWppQms0GA0tkY7bodm5cdH/3lZ/zxf/enfPyXz6mloVkKIXl6n3N0k67pWlBErAi1NWRYXhXHonhwrnozXgOg0JNAiaGfuq7De48UNgIp+m8IDqUE01SsT1acna15setYLBt2XUfMWTYw1tK1LdfXVyxPzqiqht4Yut5zdqKwxnKyPuH87IwXF1suX71kfXJGXdVUVVPSf2iuXr3i5vIVZw/u88HXvsmXP/hzUnddHE1e27yDubRNngtRbETz0Gs+9o4v6XiC4QFCFfOSv765QN+vWeqac7PiE7/jHWou0o4fXz7ln/+gR9ot3/17v8ZvfOPruI+fof/8Z+w+f8Wj0xX115+w+aM/ZbteU/3D32b9G9/jOwtB3nvA00++ZPP8An3RUq81SOTXl49RtfAzteVf9q9IpubB51+yePUc+/77dIsVS68IBvoYUc4jMcv52Cj6zZazr73Dw2ff5od/8Wd8/N/+Mb/2T/43xN0WE6CKGl3VhF7Tt57kA8qDeNh0/3/a/qzZlu2678R+s8lmNbs/3e0B3IuOICCBhEiRKjZqIsqSrHC4Ihz1Kfwl/An87Ac/VYTDL45w2BGOcpUkS5YoFklRBEkAFxe4fXPa3a8mM2fnhzkzV65cufY5AOV5Y9999lqZs59jjvEfnQEpUHlAZySjG0NjGpqsRuDRXkdDLaXoMpcKGe832lQQNu5rFRX2TgSk9UgN2kfexCqBspK6iVFChJCEpkKkdDCrqma5XrO2NWQZUkqMcZHeSolWGjw0laEoNEUxochLpvmEiVbIuqFYVWitkoPNRifSp22IpDdgm47Hs7KN+9O+3d4x6XvZPZnoSr/+9q10BbSK97CpPkYcoaW/0YgvzzRaxQhXeZb3jJmSLKclMpe4taUOFTNxQFFqAg4hY8qX4DxaekQG5AKnPWuzxNolAlBKorRGZf+VFePz+RyIYbej0jcKPq3Qs5ngzURJKQmiVVA6njx9yt/+5Cd85zvfYTadMZ1ON4CTlDSNQess5c2Gpq55+uQJ77//80jYnccY2+WBaMM79y362sXq+sVGcd3/+fjjT/mP//FP+Bf/4l+gdYZUCp3lbEKaSvK8pKrW1HWF9575/IDVs+jN7gPJAioyaK1neruxWoWr7Swm449PlikhREu4um5orZza/M1j4PIOmM7GG2mfx0bfUyZ6qLD1fvw33QnYAvFCLx/rwAuxD0K17bbPtoDZGCC0OXAhhfUaZxy3nuuBbn0vethWBI4BzO3nY0qB9rvWS2qfp2N6csc7bwvoDdAGA9rHiMe/I32QSrJcLvn4gw948/W3yLTGhg3BGQKG7e92nw2/6yuqxFCY75UxALXPAG7Xu9/zvGXmpNgFD7friXM3bHscRBnU39bFrnftXUDjPq+zsbClY2u1r40OB01jH+t3v+7teRjUmSbnLrB07Dxvz8u2Iqb/zth42uf69KLfxrDt4Xnv7/kx4e+usg+AHr47bHc4tr6X39gekFLik8wm2ORPCQScj2DVrCjAeJxSGOE5fed1fvRP/pi3vvtNfJFhMgUEpPNIIWhWaxYvrqhvbvniw094/uVjhHFQG5RPQI3z5FLhgsfRCjbx0m/nbyxSxXDs/TnYnO0EKIysT5/u9uscrn//jA/nuVXgDddod0/s0tX+s2P7aHiHDcc5pEFjdHo8asEuEzd2XvopH8b26HCPDfsnxYZ/GRtLCCExytv0YufcD/Zpf64ij0QHvLd7ZXjXDfu3j/70z8jY88PPR2l/r8nhHhv2afh++71A7KzP2N4Zzkn/bA/7P3wvKsU3TPvw+X1z1val8xwP+9evXY+7+ttvb2zP9c+0pOdVn0CIIW83xofsu/PGaGF3V/XKqKJ+5K7bt87D78bul9G6xeZ8byIk9NY3bISrPo3ct36je2fTqa3P+8r94XtjvGNsd/sM9fsbf7Oz7mNROtr3+3R688U279yf0/5e6adHGN7t/feGe22rjIxhWMboft+7pTUTH9LY/hjH6uuPewhYja/j+B2y1c4Iq7FFT0WkBt77GBJZRs+DSJNCSgMVduoZnns3YoTQp5ntZ21UsbZrsZ44mv5avoxH+ruUrahjgCDDSUeQmuAgyyyT6QGT8pZraXA+yndCjsspwxLaets1EHG8o2vP8PM+lAKgaazDWA9BkKkMITO0ylDKYqzBBIOlxgQPomAymTLVeQJNJEpGL9YyUxQ6S+tl8b4hWIMIjkzHsJZS5UgpsSaA8WTWIUWB93lUPAmFzjWFz8E3ESx2Di1DBHCHpD8IcgE2n5L5FZU1CApef/AGb80P+fzf/1vc5QU6z6PnpDU475gUMy6c4Xlzi1zVvBFKbqTnhIiJX0vP/2e94E9fXAOet6Zz7uUTDpxDGc93v/0OJ0UBXzzHfHaBub5l9k//CPnmaxyFa+Tj55iPPdkHH8Jvfg3x2VPyn37O5LPHFHKN+OgZ/mefcvm3n/D08Tk5glsC+vQAnWX4dYO9rRBoHCYCcXnOTaG4ZMkxGeVkyhd1xVera9ZVxaSYQyY63qVPH1wKkdvJKwFsCBzM5rzz9td54/U3+ezzz/nyyy85mM0p8oJiUnJweMC80Kwvr3nx/DlKKs7u3SfPJ6CyFPbe0uYqbuqKm5urGJo5yxFS0diKybREiEBdLZiXijdef408y1kvViB0ktc9SuoYet161uuKuq56i71flr6ziDZguojhO4Ml+hULhMpY3a756uk5z14sqGpDc7PmzYf3OD48wctAs4CPfnHFv5Z/xdffPeTth/dRCoIXuCDQOQQsLjTUZs2iWnK7WKKMReiYu1tqgQoSLWI+aYFAeIGwkqa2VKslzjTJ2FVTFjlvPDzjwdkJk2KCENGbL3iBQlMWBXkRQVtn2zvN0YFbwgMSYzzrdU1dG6wJGBf48ounfPnVl5zcf435wRlOuQj2OhF5XwG0BjZuoxjqMzGtYbr30Uilrh228QQnkSH+tKmuvI9he6WMmF6RxzkJ1hOUwiuBRyNkgW0c6xrWFlYucGE9wgTmucTlEldKillAzw2miKGOO7kyeIRvQ7ULFBklmmO54ljPEGKCEAolJXnR8PAtyexQkBeQZZKcDCPWKGIO0jZEemOjV7kUHiUCSmikUBQiBxFQSLRWZFqhFfhg0x2fQrP2+MvARgkUQpxS10VS9xjrqI2laSzGRY9w7wXWBhobla9FUVCWcT6sCHhvyUM0CgghOnVE9FmCkPggsc5jbQxvjdzIBEpqoA1TrnAt/64g1AopCyoXuDhf8tOffMKf/esfc/GL58gK5rLkdJ5jqdFa7+W72uJH7qd9z3ZHd887++Scl727oX+b320Y8FxJvvrTD/ifnj/jg88/5qs/vuJ/881/yb2Dd8jzQ2RWsqoqzu4fIfKAMDqmAFBAFiDomBagu6HH+9V9fke/h2PYlm8EGrDe04qHQogUKh7aD+MvEefdyxQ4dIOR4qPjglAxcoFEdY4M0qtWqt84NwRwNnpPWmNjMmBnoyehdTQmhmWvqgZjDb6jI2qzL1z09OzkL7lRSrfr0B9399OG0x+RYYfG5O1nnSJctjzS9uf999pUsomR2lWyS0BYiuKUyhi+eP8x11fXXD5/gfjt7/PeG+8ircDVDhc0KhQ8uPeIg8MDrlaXuODQArJMUTcxTYhKyu9WAR75xtApJ2I6A0eWK2azKceHhxwfHHJzft3tIO8cTVNjmhrhDqhXjsWFJTiBPcopSnAKMhQohbABXzuCkwSncKhOhjImsLiu+OIXT/jkb7/i4tMlJ/kpx9M562ZJZSqyTHN4qBEIHj+9pa4dhDpF4pVkhU8Ka5Ay25F7953n9rtNxFgQyQO4qiqMMdFYy7c4gyMEhxABpTLmB1Pu3T/k8QdfMZsfgWwibZaSyWzC8uKSy/MXzA6PmUym2Dxn1VgWqxXlZMLp6Rmruubzr55y/uIZ9x885PjkiLpacHN9QV2vsItrzh9/wcnZPV5/4+u8f/qI5eNbJOBENBSTg/EM6Y2UEhccK+G5FIpvWQ04PpZrHoQJZ6Fg4hQGQ4Ulr2rUbMLh/TPkV1+SkXEkFGtq/mL5nE9/dsn/YWk4/UffQxydsfrwCy4/+JSDr79F/sNvUP77z3FfXuOv1oQ//G2qL36Jt4JrJ/jitubx+QtQDZ6MZ/UF7xZH/M70hDqU/Of1ktsXLxBfvSB//ZbqbAZNPPbBO1QI5F7jlKbxDq4vmD885fS993jzrff49P/1H/jaH/0+UkGpNVZqVnmJEwphowxgjEc0AesKAp7GBITyaG1wrkKrBY0zFJkiV5pSR4WtSAZoQniEjLxjm8YlBJ3oViAIh8PivMElA+xoFCJYrmuq2iLFCnzSSSBprKNxDg+U05zaW3zwFLqgLCbMJ3O0zJBBMS8Pmc0OmE3n6ExTLxasVytWqyV1VeN8cl5L/2vPSZRRYySZIEP0vpay0+21hkJbCFHoycktTX6FO1Uk4h1fT462YvOd0ppMRQNIpTKUine51lmMioEgeI8SMfKSxyCI+cjLcorMATFDSlAyGQ5aR2NqvPR4FbDKxnRYzpLlGp0pkILK2GHXR8srK8bHgbr+JwKlJaLNJzXCexhjeP/nP+edr30dnWVom+MSeNEKPI2NuS6EgHIy4ad/8ieslmuUTLH/Q2SSnXNd6PR+n0IIXQ7t1vM6EmGzBerkuUJIGXMkWUuhogd33Ri8j3kytNKAj1aiiJQj2iFlhrOhAwlub2/58ssvefPNN7sLrn02hE2/vG+FxhiCw7l4cKx1aE2PSA8UU30DBLaZtC0wJxkLCCGSBczGc8k7DzJ5OiTkVAqBVAoVIC9LVFV3wkjf477P3PT7MwZgdoDR2DgGgHefSRgCpkPvkjHgfHhIdw/tuOJgCJS2AGhb+iByCNGjzLmY274f7rnfTuiNdxwIS+NWEmMs1WrNpCgp8xxvLDgf82CJcXC//bs/r2OeOgMeeevd/jwO56Q/Fy0zPNxvbYk5l9QOqDv8aRnEfX1p2+uXocd1rGd7v+8S5pCEvv1WvmNA7pCJeGlJhJ7eHhwrQxD71yl+sJ+GoPTY3hhTrozN9V3M4rC0e65v7To2prG+vayN4fz3Ad6xMjyzoyB/iNtfiiRYeYcXIPMMgmclPRSS4uiQ3//D3+ebP/ohel7ick0THCIEMh/IHCyurlhdXhMqw6c/+TmffPBLQmPBOjBmc+EHoldQskRuhaKW/Az3w9j57tO04ZjbNBqwqzwaBQR6ip0xQX2MJreh+fbNeUjMXXvHhBB2lLd3gRT/tcq+uocGAm1/WuFnSDvGzu/OfIpdetHf2yGkkOG9PuzMxUhf+/dyCJFxFD0aO1Ru7+vv2BzsMwzqC+b9Pg7P6lh/9+2zvfe9EBs+cE/5VfZI/+y8Cs0ee2a4N7fvzjHe9leb+7F+7uybkPivXp+Gd/jY+oWwUc4P74Xxedjch0NeaV8UibvK2Blof4a8wZBORZZ999xs7anB/rprv/1dy537ZvD9GJ8oxlmal+7n7Tvg7v4NaciOMcFg3Yf3ytZ4RmjJWN/a38NIIt77Tnju7+8hrdu3Xvva7e+f/r4c1rVzpuJTd4wh3f9SotUGICVEuUWIlP+R7TUb3pmClyuMX6W8Ki/069TZr3dTf4TLhIxeOV7lKF0gdRFzJBLD9Ka0yltl7D4EtkyPWvqO2DyzoTFyK71Sv4UQokTngovytTf40BCCJrgKbxWCgHENjY1KmsaClCVlVqB0gco0Mji0MBRaUSYPAykl1imaxqXwgW3exQgEKakJ0uOVJEMijaauobYO5T3CCxojWN6sqCuHqT3OhOT5luilTDmAfSDHUmuD8DWrpmF2cI9vf+0byM8/5fyDn+B9jSpKQKODTjl9A7Vr8NbyNlPmecB6mOYZQsFzZ/mxW/FCeL6Tl5zIHBEE11JyNlNMbhao92sEMPGC7Owe/Oi7rGpD+cVjsmdfYqUkO3udm//8C6ijx8nsvdcQv3jK+Z/8mCdfnPP50tKUU06V4On6imJS4moLq5osAFJGEJLAWgouZeDaVrw9O6SYTbla3HLRrGMO4tbQJHjYOrO9CA8dLQ8EITm7f5+z+/dQWvHZJ58SQiDPY37NcjJjOjtAh8D582c0TcP9szNOz+7hQyDXWYriF5XiwTlME6MHTooMRIzMhiBFF6zAN8ynR9w7iVEJoXe+077UOmOxWlKta6zzydFiQ3uF2Ox7EXbvsR15EghSpX+4mI8+8WbWwYvzay6vljS1QSNQMlDmOZNiQlZOQGa4IPjlh4/587/6gIN/+IDTkxypdPSGFuCxNKZmsVxyfnHNsxe3lFKRlSB1MsATnjoYmmDxnVdydC6pq1UMc51wrcmk4OHZIccHU7Qq8EFFRW1ISrxMkWlJVB4kAzJrY2jy4InehA5rAta66C3sohfyctHw7NkTbm4uOT19jbJw8Sh5T9MYFssVt4tbjDPkQW94+R4fJ3r/DsEjQ5rfTshqKVWU/ZRK+YdDzAsanNj8ILE+xLC5lcGGgNegDiTTRwmAPsyYHeVMD3MmB4rDY01RtEawEfR21uCdRStJnkkypdBKIqUhLwRS6WjwIzOUyDk8cBzMCmZFTi5jGgeFRsucIDzC+RhVwtvOcEgJi5KaQuWQaXKZkamYc15rhRABY12k6yGuTTT8in0Vvnc2PcSj42OIegLGBla1Yb02NMZjPTgHxsS8xJnWKZ97is4pHUYaskygVQxb7jwgNFJqAirRhGgI04bI9y1mSFTyCyExAYQDETxKS6Q+5nZZ8/mnT/jF337IL/78A1afXTL1GflEo5QkBIfMss5bvD1wfR4z7p1xPOFV+LT9cvi4kffWc7LbjEDoDIQ77Cg1XwgFc0ez9Nx8tuCX6/cxNzXqXxX8t7/1zznMDjgpH3A1P+f47JjT+4fUn8ecx1KDUxZbCzIZjSGCFIP7vN/Psc+GfMM2D9VGkNv6Pni6zNSh93z7QMp7LISM1yVx67X8omezP9vjLVLYe9WyCyIpa6LpRkzzYqNXphQKF2w0unCJnlqL9Y6gJEpETF8qGdNzEDrldnQ828jAslvn7TXv/wzlZdj1Gm+/7xTdsKUYv6tuhOh4663oByIq8JUSyLxgGiaYek395YpPFh+xWlTc/Lbhm29+nXlWUoYDplnF0eSIsshA0ekWtFLUMqaRaJXifYPbuEZJv+BifnalM8q8YD6bMZ9Ne3sqEILDNjW2WRH8DOF0DPleS4LRqFwihUd6jfQKFRTBQdM4MunwKm6wQGBdGdarhuqmwq08mSiZljGfujBAgExn3Lt/j/sPjpkfXvPFF09YrpYsl0002HEOIWKEKITGt2duz95uxzs4GAjatIVRb1TXNXkeecsQLS6IsR6iQVieKU5PD1DKE6xH65S6Ak9WFCitWa4WrJYL6sMjJpMJVd1Q1TWzaUHRlBRZzmwy5ermGoJnUpTMDw6YHxyxrhcEveL82WMeXr7Dwzff4bW3v87PH/8SFRLIKURak3FHwE4+d446BC6FR1AwRXAtPBcE1kGQBckNAaEk1XKBUpDN52ipufGWidBMRMEqSN4PFf/+/Cv+4PIdDoNGTQ4p8iPq85rwvGKlFe7FNbz/GP+P/gF/89MX4D/l+GDKveMDirLkwy8+5YWAp7WlXgh+C8k/Ojjic7Hm8e0Fb5yfM79ZUdyLEYpUiugXQoiGeCrDGEMuoapqssMj3v3tH/Hxf/4Tnn3wIY/eeZNiOqFp1kzslGl+CJUn+CbmG5cOGUJMueAMLjiCMFSNx3tYz3KKQlHkmmmek+UZCE8IFkTUo4FDqBCjqagyyhgBGhOjVxjjI/8T0vkW0VCoahzO1DgT0yUEEXkRG2IKsEoECqFihJaiYDqdczg/YpJPkWjKbMp0MiUvSmywVFXDalVhmjYNQvRoj3shGrWHVjYTG0muo21deJBIgIf0ri8Pb8l+vctmC9vuzlXLYffOnEj8mRQoJcgzQZHLyDcIkFIjo9dABO9l1EM6IIiAyhQzOSX3EIie4lIKFIqQeVzh8MLjVORRnHMIL1BZTDNTNQ1XixWvUl5ZMb4BQlphOV2AMgGyPfBvX1FSc3J8BkSrVSkqpFKEkKyYnCe4qEBXWrJervjBD/4e//E//Adub24QIrajlEImpXe7eC1Q316WJllF9Z+RMoZtklJxfHLGD3/42yyWKw4PDglBUNcG7+u4GMYghaSclGgdL5amMUipOoLjQ6z/8PBw62Ks65r1ek1RlmilMY3DGJescyXWmqTkF2idkWU65THfeHdsM3DjTMw2E7cbhnV4+XnnUDJDColNuQ9IzEqW6c6yLhC9HRkwllKIjrnpAz798DAhEe1+H4bguRQbJRvsMrDxIEoC2yDu8AIYU6L2/y2GJ3jQRv9At/0fC9m5z2NsODf974ZKlGTXgnfx8wcPHpAphakNSkRGMHgfrW57pa+gvwvw79pJTMdYGe6roVC/BYiy3UZXd++53XDMQ8CbrTrG5m3Yl2E9Ufa9W5jpk51+HftKf83H5nRvO0SBb8h0Desem9NftQzrGI4pXju74PhWf/f83Z3DkX39q/YNtj3Rt/b8SJ+G9fwqwPFQubJTX1qbLneKAKE1VoATYCSIecnXf/Cb/O4f/SGH9+7hhMciCM6TBYkwnrBYcX19ze3lFRePn/H4sy+4Pb9kJjS36yVKqmQdLzqljggbAw4hBMGHDni767yOjW97rBvhsn/u2jL0PB/OU/v38JmXnZNRQQLxyvu+7VsbSeWu8ioKiO1+xnt0X3/7zw8BgJedye01IAIxIwLyFjM4cua3+jtob3j39GncGChzF83sj20YMcAn48Cx58YUralWxu7M4ZiGZ3GMvg9pwb7+7ytD2jy2Bne9O+xjn/61EX3G9sfYGIalP8dDa/+x89jNM2rr/VcpY3Pbb2tnT7cgHLvrM/z7Vymvck53+BFaEGycJonEUw7r//9HGb0zRs5m+zM0ImgjgSB21/dlZZs+jH8/3Iv9z++KltLN4zAyRoiKq1e5i/vj2OlLL9XA2N4Zq3f8rt4Gb8fmvv/+KO8zQp529vSIkVe/j5FO7oam3+JHYsU79fw6Zeze/nXrefkejnKGIAIOUmY9q/wUjlRs5PgxuWLnbIvuf92fA0h86xvRgc2Dr0MgeIP1DcZXWGqC0gihsU5hQwzrG380QcioDFcZUkVaImVUkOZKo6RKQ4meM3mWEyPaEcMIu5CMI5KyTIQYtlZpfNBYA8IGhPc0taNaNzRVDLvuXYgebiGl2lJRURWnzdBQY7wHPeXw4IS3Tg64/Xf/mmpxBdMMIRXWOBpvUbmmsgZpPfdCzrsyY5mtyIVACc2awAssF9bxMCt4N5uiPZw3Ddfe8rXJDH+75sVyiZwUHD46Jn/3AU+PJtQ//Yzs+hIlAxwUVMua5fufkT88onjrAfL+KYu//pS//elnPFs71lJCVlAU4LRAaY25XUNlU0qvAMkTaS3hOnjWTc3hvMRJyY0zrJyN4blFz2gnLvDWnupjGT4EUIqHr7/B/PCQ5XLFF59/TqYztNYURUkxmZKXE6R3PH3yFVIK5geHzA4OiZH8FNYmfkZA8I5qvQYimB9IRttaU5Qly8UNpQocHpQcHEwxTYMQycAh7el4fwuqqqExhpBS3W22bP9MhI6CvUwWiSfQI5JC0VuHsZar2zUvzq8gwPHRnINZyWwC0+mEPM8pihKtS2wQPLu45LMvLrleXHNwdBT3MtDm8G1Mw6qqub6tubpx5EpSOE9WBLSOZHBhairbYIMlYAnE9H113eBS1D6lFbNpwdnJnNmkROscupyQEbvQOnqht3klQxDR9dj7qLRO94+xLiqufEjO5AJrPDe31yyWC4xpECJG5DDGUlU1Nzc3XFxesq4qDspp4ok3dDik+iM/kVhlkby2giMET8y36rs9CAFEDNEthYyRaXz8cVgIHhEEnuj1nmvB4WHGm29PmUxLDg8101nGZKYpZ4LZgWKeJZ45CFwA50XKqx091FXygiq1IisipqdUhhIZwkOmA3mWk8sJMmTRAxeJSmGFBQ7n41kKbXhzouGBlxJkyveto2JcKYkPjv7V2GKSLb/SyqFp1XAuqXdS7nbrPI3xrBtH1Tis8fEZFyWsEELykIsek5mSeO2xODIv0TIaGkgRs5ZGw6vkra1iCjMnHDbNPTIqx0GmMP4hKjydYFnDpx8955d//Qmf/PgTbj+5JgsSWWqkSl75XmDVNn4Y+gpo0j0rSMqu7XO8c0738DxjMsur8Mzbj2zX0+dhNAGLQpYlGIu5qPn0rz/i3z7415yenPKD1/4eM11weHDG0dEJ+USzDiYm+xAQsAhRoCS0AXDu6t++sYzhESJ5+7XK45BCnCsf1xMfCN7hXYr8maKmteMPYZMSsqP/zuGsxTu39bPhtyLmK0SIeicJQkh8Z2gH0ZgmAK4zyPLeg4wmcELKdNY7TgQhRJdWp81PLoTcKMZ7OdeHP2NhuYd7o31uS2EeAcKterbq7nlqbjw2N97mbV1KtQaeGZkAaxXNsuHz9x8jvMQ2jndfe4fT2TGHs3ucHJxQllkXft57F8euZBfd3vtBOPX+585hnUPpnExrJmXBwTwqqq1LJs7e453FugrvLHhNcBJnBN4GRFBoobooHniJd9DUFiUsWhEdzYLH1A5cGz0grp1UEh+TukejGqnQWca9e2eU5T2MsXz5lY0hr03UYSghILiExdHxn/v2fR9z6adS7VOIqqqYTqfRyCKdAYRIinGP0pqjoymH85xlY1DJM9u6QJZH/qNpaqrVgmq9ws4OqIylMYaZKFFKUWYFx4dHXNw8ZrW6pSgnFMWEyWSOzgpkkbO8vub64pyzh2/w2ltf5xd/WYCpYafHu6VzaArxvr31jkrAIYorLBcEzgWcBUEQAh2gqmtsnTE7OGAynVItVuQBdJAUaI4pCQbsR8+5FHBzc8u1XUCjWH7ymOeLBVljOPr4jPk/O+D6jTd5+v5fcE9aHoo5B1ryxukpmRLc1oEbF/hsteS75YS3pwW/WDzj2dUFR8slM6lYe5fEOU0gKpADkZ7IIPHrBpUX3P/We8znRzz9yQecvfYAnWeQZeQuZ5Yf4LMGY2MCJo8gBBMjmliPdQ4XPNZEHNc2lqLMKAtNXdjkuGvwwYL0CAVSebJcxue0QAtH8J66aajrJvIjQYOPWLC3HqVyvE5yuo1zHgATHLV1WO+RzqImUzQpVRmAkBR5iSJDIfHWY4XByUhbtVLkRZ6iZ8eY7yGEjsZt0aOeLnEjL2/OzBAr2KVfrRTfykI9TKj7s9d291E6c0Ikxbgk04pcZzEyUfquw4p677ZRBxUqRgDzHu9dpxjXIqqxQwh4GfDKYYi55YOzOGeprWO5NiwWzZ1npi2/gsd4Clsp2r83RLUVgvAbBeHQfg2gmEz4zb/3A7IiR2UZXoBzFq2jUnZd1+QqRwiJtR6pM+6fHPOtb3+Hv/yLPwdE9BJX8WJpw0obYzoleAgBmxTk0T0/evn2LbK0zviDP/xDdB4FgMo0uBDQmSbLMzIpsUpFCzQRwwrFdmqyLMOYJnqEm0hUm6bpPGittZ23uDUW59tpihad1lqapumU0m1OknbztYR6m2EDGbZDP/bDwrdCW7sWXYhQ+l5kUdm95X0iRAwVQrRudYCzjtDl2NqEvwS6uHJjQFtfGNZy41Xdf6Zdk6hgjJ/3PRAHO26vgnd3bBvgsC+QR8Zo12p0DAwfjmNrnAKk1l2kgjGF4sYrMfV9MB5BwFkbBUhguVximwas4dmTxxz1AMBdEK/vlZHWPvitUM3bipjx+Ro+GwgpXOAm103wKfwWJEZzM0d9ZYJzbhNKaVD3RgDYBcd2FEY9JmVr/js6Am7LS6617BvWuS2ADEH8MdBvCAj2dsGe+dsoHDps5Q7Di53x0r6/oY5jyobhuzveTGnexuYh9I2U9vRp7AK8awzD/owxm/3PRr0S443Xfth9P6qcDz1ApFcUm4veixQybvCiDhtr0ZCYIK8lRgveePddfvCP/4CH33mXIGEVokVyJhTaCerliuX5FauLSy6fPeejX/ySi6fPkD6gkbhAzPkWAl4kgVyCRCWmvL+fAq019GYuSIz7hl4Py1C52d0eYmNVPHrWtlsihrlrQbRxJcNQwfKyEsImzHdfcGz71z4T11+k6+KuurfnQYjWm3L/+aPVjPSqFURaRaKLwY8oCzeNbPYhu7R/tF0f8PjufLF1BkViLIfj7zcpt0a0u3ahty/GadSvUvq8waYPvbvjDgXNcP4F2ykUhgY5/Xke7qu9ipadNjfPvWy8w/MR9g9lpz/tv4fngRABiX39H6t3jAb2FQHtWRm8SQzHldY5JQvbnEGRtmfifXrt9MHOlnfaGCBu08FkkrNFbocRFV42z/vozF13Qp+WbO7xbtI2d/pwbkfo2BgoNda3uCd7O7ZjXu4c3ngJGx4Vdo1G4p3iOy/sYZ9Gq+yt4WZudrvXn+O+oVkfXNvHw+y/B1L78aX2g0i/2F6n/pz2jT3aUOpuDz3dlkF252KMNsQvIm0Zttc3kmh5gC0eYi+/1fud1tH25KBASMZy6e7w233bCo+ewNadNRq22X6+06XYz/79+uvQ8Vcp43OdxitU9LSSrfwbeWchSLkn0yjChlawEesHn/XlhtTeWH/a//bxFcFhbMXa3FK5W6yIKcScT/luQ8AGhQ85qJC8IgUxhqxDSUGeZeikFG/DOQsh0CqGTzcq5rT1LqYQk4So5ZEeC2gZlfEuKIITSAvWRCUgJEWaguglkgwehSQkZU6QCqkEQU44PX3A26+9wRkNn/3Vn+GFRyqFD8QcqMEz1wUXqxWZFZy6gjOvuJGeQ5XReHiB50nwuBB4L5vxSGW8MGuumjWN95zKgnrR8PS6IdSG5njK6btvcxs8+ZOvkNUCdVAgpiXXq6dwcYv62n30g2PCdMLTn/01f/P8CiNyprMJM60w0hG0hhDwjQVj090efeS9kqyF4DY4gnFMi4KFt9wYgwmBPNO0KeXY4sO3leKbO9Gjiimvv/UWRTnl4vKSx48fU6RUeEVZUk6mZFlOMBUvHj+mKArmBweUkylKZVHV7JMyJXiCM6yWywiyZVlUVjpHXhTkmebFcsHxvQOOD6dMypxqsUaKPHmVp3OZcKu6qnE25nDuR4zrdrqIvLRgmw7vyPl9QpSUxt57GmtZrSqePT9nsVhxeHjEgwcnnJ3OUdLhVi46SWiJzgQiaLJ8wvWtY1UtMa5C5RMSWxCV0M5SNZZV5alqxcpD4TyFg6IUCDy3tWFtGoy3eKKyJIbCtdF7GIHOJQcHJWfHB5R5jlIZSEUKQoxEoDOJ0lGR5BGR6LUyXYi8jPeexhiMjU4gnblEIKUkXGNTntbowBI98xaLBTfXN9RVhZ4m/qab4zjvkW619fkEbkcPvlYTJoToUsm1iiAhImwlSfm6Q+LnvUNIg5ABSaDMBKdHGcdzzb2zGYfzjLLUlIWkKKCYeGYqg8gBYIPH+QzrIvYYebV4d+c6RxdtHs0seqz7OGdSZISQ40Lsf0u3ZFpY5URylLAdAhaIBFuImN5LK5lCjsbw1s61qRTZeIzT8mSSNow/IWBdwHqP7ynGY9j0QNO4qGyyINDR9tt5pHFI4ZDSIUSG9II23XnrjdYqxQPxs9DxvhHcdy3mFwIqyeZxiWNEj8Y5njy74IO/+ZBPf/wR1x+do60iP9D4vOWHBVpmeLFroNLePUAXEWb8Bh/w7ZuD2+Nh07sd37YlMt5ZhlfekH8k8evRMEOnML0Z3lrWL9b87M//kv/v2Snqh4r3Hr5HWcy5f/aIooiKoXhFRRqUKYWQoc1qeqecNXYfD/nSzfcRL1at53aITFUIGwceby22MfFcJScB0dFJh9ziL2ME1qh4tTjrYiQ/15NFhUy8isTLiJ1EMh+jUcR58yk6SeRHfYoOEvd462UeOv665V+7fOJJcd5XQm/I9a5hxNi8ia19IkY/G3qM73iY9xTjfT5bSkmbm1xJFY0ZRTK40QU6lGjruLq+4KO//RiLh0ZSvDPlcHrMvZP7zOYlUoOvY5TYIHzSMdDh7i7doZHH3tzXzrkUijmglaQsomK8LAuW6zWJDBOcxdo1zjaEUBA8eBdw1qOEQMuYR5iUlsHZmPoCDFqHxDd4vAkUuqQsJmRZzBlsvUF4iRMChwAfqI2lLEvOTs54cX7B5fUNq4smpuuwLkZNaA1vugXdlZPGzscQa2v3cNM0WGvRKvI5zid64AXOB7QWzGYFJ8cTrr9ckk9zAjLeByFGrGmWK6rVkvVqiTEmRUKyeB9QUjOZTDg5OiJ7nKKp5Dl5UVKWM7KsxBc5q9sVt5cXrJcLHrz2GsXsgOa6SVT15biKENE8yAVY+8BCBo6D5io4zvF8JRwHQaIRMaqAd/imoTCW6cGc2+UipXkNKBSviQmP8gPUsxuuaPiqvuW8uWUmS24eX/OFr8gXK8LjM4694fD3/j4//eSvWFQ1dQh8XUveOTvj/lzx4tJxcXnLZ/WaN5sFXz+e8tG15fL2msvFDfMkp1jvQMZoAAYf88kTEF7A2qLyKdlr93n43jf59GcfsvzR95k9vAd5TlZpSjVhLUskMc2SR+FcFfe78TgXU21661iGgDeBsoSmDKy1JQB1s8Z6h5ABpQW6EEwmmslUYrOGTLQRLAzO+Xg/i2hQ4a3H2YDOVJJH4to4F+93bwyNNdTGgBEcTiZ476lNQ1XV1HlDmAkIRKda6yIfVUSj0nJSUjpDnkUD4rj9+zRKbOizFIjQM9ARrV93uvd68mqfLm08zDu1eHvMtrCX7vN0Z7R4YcvLtIY/SsWIblrplFYlRbxp77geSCLS0YuSnEQLTUhOClIKVGvsCtHgT0b6lquCRhSYxlFXlvXKYMydR6Yrr6wYF7IHwImNUOB9BBUyrfDWEfxG6Rrzo8ZLYDqf87/77/97zu7d5/r6hiL3ncKrLAtsyhnSVBZjowWH1opVU/NP/1f/nPOLSz7/9FOCj4KnEFEhXdf1FoiklEpe4TGufuvl0YYSUErxu7/7D/njP/4nMdScj9ZMzgZyD87G8TRNQ16UaCTBe6wxRIYhWng6Z5Ai5hDHx9BtjoCQAusc+aSMm96HSODTBvQiRNd+4ZFK4IOjSOHg+qHQW0+vEEJSAEUGIYQ2j3crLNCBrS2403pg90GvuFljaJm2rwhJUBnee1ZVDR5KuQmA0NWXcriHxIRLJbs2vI8WyP3QsO04WsOFNlR6nyEJiVHSWm8p/vq/7yL8QwVE/4LrMylbQLSIAnoMf9vmkEn5rNgAZMCW8scmhXbWsyRvgb1OWEtiYL/rG+ZDxHwJStBYR8zkJhBNQ31ziV0tcCKk/m3nrOwD2i5ZNsnEsAZ6goHc7LGxudzaBzJag4sQYt6uTvjcFCnTOrX7iBAZYKKiur/+W8JJj2EMYntddgD2PqDS63tnbdp9tR3uY1iG9Q/B2DgeubU3d0BRAsg28kRfgdFrT9KtcWQ0k61IQpNEz7OqPxdbIEvYVmMMmbV9c9n/3vsoIKvWMCJ+EQVdH1K+so2OYGy++melD8iPlbHn+9EphmFV+3MbkjAs0tgREaToDsoGJ+9d0qHDXLo+BMiIUWycEqAigNfmnZMSpINCZAB4IamVYK0Fk9fu86M//m/4+t//HqLMMFjwgUIqtAOaimZRcXt+weXT53z2/i94+sVX1NU6CRcisaEiAaJyKxRp9FpIongnRPf3UEur2rxsG8B+M2fx397b7mw5F7o7qw2B1Q9nH9ehpfWbedv8DSQr7BBEEjzb9fb0jYbkQDHYlm1lTNii1TtKjeQl0tbrfejyx0TP8f5u3N5Tm77vghet0NLbKVuPBCLzvEVfEj3soqCIFjTyXTXC756OLXpJwtxkUggLMC6CnZEpiwpvF0ICEcfPLGITonioANvx8hzpT//8tUZvnTFTb83GlDB9kLfdS8O6N3O8mdCoEGjB45Z1JhqCjCj6h5F5AmGrrTHBdIwG9fsyBty09HR7zsbvhNFINB29kL21CCihOh6sP2/tePrGhrAx/umfx37f+mNrjSbjneG3vHjpKF5bNjmdI+IlkoEaxLxWEVgI2OjV2L7ZAWMbECQCRpv5iePWibbuux02czVci3YcQ36tX4brGHyyHpaqA18IIY1ncze2xpSIDt7qwiACUZkx0k53PsImd7Qngt+h5dEGNPOuPvfvQK31Fp0LSVgb3tH75mw4ny1f732M3DT8vn23r1TqC6Vj0aT6Z2e7jaQslL0ceiGKqi2EKGkVYdvnrT8XrfwxHGdLi8bO7xhdaemIT+souzy8xDnFd3QG2hxpG2g7AEHJ3kkfNw4LHmQKmdkY09FnkYTo9mj1xzGcP+/9NshG7/bpjk08a1LKTU5MUgqq3nzu23O/TunXtY9u9uWetg8qgc5at6GAHd6nkPIhEN1Ae0Bbx4iTaIWnjdDSyjPtgDft9XiOAb3u7wctJat6wcXtcy4WGadHnmmuMN5jDVgkXiiUyNBZ3LTeW4JzCJLHZRF3rg8WUohoJRQhxHCXUhK9KX3kfZSSXRShDEeuY4hjKTVeaKRwaJUxKefkyicC0so9Nu6JEBWCPggcnkLnTLIjfvNbv8n3HpzhPvwxX/74L9AnE8hygo90WOcZGZplCBx6gW48Ty+vEBPPg+kBH5qK9/2aj6Thfjbh7XLCrVvxpVtyGRrO1JSHK8FCGlYOLr8654uvnvLd7/w+M6e5f3mLtmscYF+sWDx5yqMHp2RHJ4hGsb684cMnT3ku4SQIjnJFUQg+WawQRUFV13hTo7xFoiiUpg4BU2bcKsnKBWZCM52WfFovWZiGEASFzpBSRPC7t9/6+7RPx8BzcHzMW2+/g5CCr76KOVPvH5+Q64zZdM5kOkNKRXN1w/X5C975xjeYzWZkWUY5nVOb6B3rgsc7g63XLG5vmWQ5WukYntIHyrwAArZpODqYcnI8R6vNnoysekAogQgSax1VXXcKxj4f1UUJaWWSkTuzz590vF2iw8J7rHGs1zUXN0u+evoCrXO++d67vPPOAw7mmvMX5zxbX6LzLObTxOK8I1cKJXJ8cHhv0wFTKQx2ShfoAz4ohJyyWjdUPlAKmAiJlJ6blWFd25gyMMTc73WzwjYe71NIyyLj+HTOveMjisSvR51E5D+UkBSZJs8UUoEJ0SBRhBB56ABKSDyeuq4j+E9Li5KsHCzOx9Drgnhsvfc463HG4YxNjibtXEcP5aR1iR6qRIW29w5rI24htUJlGVpnaJcjVIzWEGiNgGKdSmqUKGIo+hBpirWJv1KBYgK5VpSF5vX7JUeznEmeUWSKIoM8t2gVwwr7EBXjxhrquo4GWL7lvRQWSSZ1dOBJudLjGRG4EKM1igg3IDWIICI4L0BLyDQYn1JHJpqZ6UjDJIEIA0cwv0mRCEIW2485xiMNVkAQMoWUj3PatIrxHl5gbcDZ6CXubcQ/lAypvhYzcwQ8SumYx15meKFxxPD+CEV7EYZ4AIj5xh3eyyRIhag8Ch7hJKBRKiPonMXyhl/+5d/w4Z//DYsvb8nJmZ0d0ogKrT1YIEic0mi2+aBdBXjib2Tv/m7vMgb3eo8XGMMw+vjevrM+Rgv2/Y1IXqfEKAzCeoxWuCxDu4D75RV/9j/9B5bLhn/4/d/nt975Ad94+5ucnhzxVF13zgBSCDKl8K6hxdjH+PEh3/ayv1v5W4ioUOvG63RnkBu8xzaGerkg2CLignIzTzEKbmt07DvP7k75mrzFW89lgNA6okkVz41LWKNpMKbGORM3aM9BT9DeO5FP2KB1svNK3Aqf3lMWbaI/bc/TvjlsP+9HW9uua1sR1f98J6KY2P1eKRXl7fRvJTU5OUI6LDEEudYFczVhXh7x+PIjfv5XH+CuPWKp+O3v/RavP3ids9NjVK7xy5iXV7bAW6LnLkWK7Xj3VswkyR6RsKOVYpLnHBzMmc5nrKqqOwPBB5p6hbE1uZ/i27QW3qGVTCk3JN7HaCFBeGgMNoDOHCo5MSghmU/mnBydMJtPcRiq5hYfJlTGUhtLCJ7FckEIgsPZhLOTI+YHM55dXLKqamxTgs6iF63y6J7I/1I5bee7SL+VjFGLjTEUWYbSKhkbCUB1cmaeS+6dHfLhxxfoWQlK40yMupGpDEmgXi1YL26wTRMNx1yMZpxnGUeHhywWCyZlxs31FSen9ynLKeVkRllMWVca4RyLqwuuzp/x+ttvcHj/ES8WV2BTrPme880QN+loZARXMV5wkVlec4rMCi6F5RNR8wYFD4NigQUBjXPcrtfkB1Ma4aJDUOS40QgeHJ+Q55q8DKi1ov6i4nx1zcnBjGOdc1s3XNw+5lu//Bm/8cc/4G/+n0fcPr3h8bpByopvHJ3xzr05H7uK9bLhsrI8ZsU3ilN+c3rKzari6vycB1XFRGbcepcwDfB4ZDAIoTB11NkJ46hlzrf+mz/gr/9P/0defPo56mBKPpnibtZIKxBCI6QGFM4a6sZhTFRi44nGXh6MCwRjcY2iWSd52jqqJuKvQoLKBPlEUc+hqQRWewplUVojRB4DHaAgSIIjnbUYtSZXEplpTNNQ25pA1DVW1ZrKNsiku7TOsbJrsIJCFRzOanLpcCYaB2eyIPeKsswxoUAulzjvkp4ShFAkCr65HcXGeIgeHRrDz9Jx6BTZW3di+ung2vbZrup+nQN8S4TYf6W6CEha6Q7Hdz6mhem2drquE4JFaxyNiIbRQsYQRs67iP14G41QXA02IIMiWIEzAuckWpXjYx2UV1eMDwCh+FnPa6wnsPcF9BZg/J3f+R1+7/d+n7oxnJ2ebnlwhxBomiaG+kZTCoHONEpHBfRsMuF/+9/9d/xf/of/gWdPn8TcN1lGlmXUKUd5URRorZMgtmF+2sX0PuaOunfvHv/qX/0rjo6OEFJ3l5LWuhuLtZbFYoGqDJMyJ8tiqCOlJEHIeD+zYcz6oDeBDQMRNoqK1ouz/XHeJYtNS+b1DsPVAk/e+wTyb4PLw/DF+0DK4eUQj0Z7WNJvEXONexHDmqsszVvPyCFJkzuAV9uXrX77XqgWtkHkEGIYDPz2Punvm31l1xNP7Mzb8Lt+3X6gCIl2xyAHhGErBFwLArMNPI3NQ7/v/QgGcQ4D3kTrI6k0wgeOZzOunjwhWEurdRjr95jCamu8+6ese28LQOsAyXEgV2wo0fbzvWf9YI1bEGG74U3f+mNp+z5kUNq2+8MJYUNn2vUYMvSwvW/GlCxt3cNz0/U/jbPFPIfevltz09UbEhjXvtMzJLhjL8uU+2OMGd/37nCNxkBhKSWy268Cu8edcl+/9rX7KgqFsf61bQkRDWFaUDUakYwr/bf6OfjDikS5RAQTdGjpoozWg0CNBy0xUsBswvd/73f4zd/7HSZnxzgtMd6QSxkDGjcOWzXcPDtncXHF408/59lXj6mub3FNE+kfdBFARIzdglAKGfzWGdzsh925FGKjVGr38/B895/dKOQ2Spm+sdNgFXBuTLHR1rc5Q9vvbpTx++jM2Pr07/Shh2zrKd4vQ8+h/ed0bGz9Irb+ufPkyP5r7/ZO0fEKZdjHrZB93kehjt7d0xOs77q72rrH2mjfHz439u62Qne7rn13RZ/mbZS0r5BKoQcE90RH+ntn2G56rVOADUt/H/bPwT6gaTgH/fF6Hz24hnR02Maw/v5c9j2wh/Ssr/Tuz/td9H24d9p9vwFT+nfIroJ5+7ON8rxjwbZNEsZmiY3dyOYC3vQ7ntGWXg3ndzgPY+N62T4f1rGPrrT3QPC+MywhhC7H4OZu3t7XQ8O2eK9EPs7TepdslK8xnOivdv777W3xgUlYvGvMY/u7b0Ck5Cac/th8td/1jQ/vKmNnqv95SwNh1/gtkjCxszZb4/HROKydi3104679A2m9e+vW0s/hbIruf4N9N2hrTGZqH7LOdQa8tnfPeUjW7ONl79035BdDPFshhB4oTAKo5dae7fr/CufmVcpddDKEgBSeNpRGe84VSbaTInpcBAHsRtPaqS8pUQQ945B2jgbyYKJU0NLkwTwLJIWSNE3N+e0FT24kB4eGQ+GR8hQVJjgyglBI2dt7Lo5HqEDAYF0MXSxE9BiTQhGw1NbGaHEEhBZoAVI5HKoL8mtTlCBgEwrWR8WjMw5jbIyi5gPOJ/BRxqjRwUeDS5tPeZgdcvLgdd69d497TcUnf/KfaMyCaXFEbT3OeGQIHOicxbpCoKit4+lqRb065w/ufZ3DIudLv+Azs0ZYwzfnB4QQ+PliybJpeKg1Pzg+5iib8ZyaetFws9Y813OO7t/jW5fPabTnyZNLPv/5x3xy8YzfffQ2X5o1V//uLxBKcTib8869Yy6vK1xQTCaKmoYnyxXyZMrF1SVZbZghUGgyC+sAFzLw1DasjeFRecD0cMrji6dUIXo7qURrQ884ayhXdfeNiIbo3/rOd7n/8BFfPn7MJ598Ej29lebg4JD54SHldIYP8NlHHyKl5OzsjNnBAUJllMWEql4QfDTMNlXNarHAm4ZicgDOIXwgkwotFbfXNxwfHvDo0T0ODkqaahXzPBJzMLYnSGnFclnTNC2guPFkbXM19vn6Vy5e4K3DN5Z1ZbhZ1Fxer7heNnz/u+/w/e99h+OjGbeLK9arhsYH1qZBZBlaRRwp+IajkzkHh8eU5Rwp85jiUoG1Fc4bbHDRUDefIFYSYwWioVP63147VsuAbRS+AVtZVusbXOMhaJSWTOcFDx4c8+D0hExmCEQKox4dXSSKQmcUuUZnKuYs9yHFcI7KWGsjqNlYw8ZRQwAxn3iWKTKlorFbokWTYsrhwQEP7z/g+rU3sIs4pug1GbNVSRnfjTnDAS0QQpIV0avdWMe6apAysKwsjQFjFMoL6ioglENlhvMDi6kaiiyDALVxrF3NyjUsVIMlKvl11bA0hlmRMylKyqJIIdVhmlXkuUZn0aAg5FEW1C56cjljcNYh5AG1cQivO9wuba4UGtUjUKiQR75OhJhjXHiUhCKPoK9JMnOrbIo4ccpzGwLGxeiTJniwG0/QCCpHJU+eZKUQPE1jaYynaVzMGR48LsQ0EsGBEpqgJBBTWgoNRa4pi4yyKCiLCXmRobNp/DJICBKlk5ERLS8WknwQzRNwEukVXsXzZKzH+gYhCggBs6756U8/5oN//TeYiyXTvCAvCqxoUAQm5Diig1GQOilGxM59PMYDdXdPjxdry5CHuKuMPfcqPPGYDC2FjF7z2lMpTeYleXBY6RHze8iv4Mf/5j9x8YtnXP7gnD/6l7/L9779bX7x549ZrQ3CKwqVgXFYYnqQ4ZjH56CD/Eaf7x4ipSDoTChF5BuEwPg26sQa7xymykBuGyEAKaLLNpbd4tmtUnZjpB7X1bUKmDatKEQDKNPgbI2zTZcJOu6xDV1WpEgLIinN1Ub/0Cmgu7jpgdboeGyN9u2foYJ7qDDa7D+26u4/2y7AVr+Spzi9/sbvNFZ6UBqNRPpIJybHB7w9/w7Pnn7B008v+E/Lv6SwM37wm1/ja197m5988EturldEI+oNfxw9WqPiyKZUs21PhQ/g4vcigFaSSVlwenzMyckRFxcXKcJIHOdyvaJa1+RTh7Qe5+M9IESKbuvABE/jPdrB2ljyPCfPdDSyUorZZMLR4SGvPXyd5w+e88v5L3j8xTnTSZumwhGCIZiK5e2C9ewGhEPpaJhvvaduaia5QmkP1iMygVLjGMuw9NdyeA5CiNFMJkUGWdJvCEDomFnKe5ytePjgkNkkSylYNFkmsE1Dngm0FJhqxXJxxaq6ZepP8C5gjWMyyZmWU/I8Yz6dcLlaY0zDdH7M8dk9bq/PWS+eI/KM28Ulj7/4iLe+9Q3efu/bXH35Oc7eRD5+a4g9wD0V7z1CJWdID1/Kmre8Yi4UV8FzHixLFIdkLLDoEPB1w831DScHU4QS1MKTB40Iil+qNT9zC+6dvMPrb9zjwFsmxRF/+pO/5B+5OQd5zgtZ8eTqMWf/43/gN/7h/57f+vq3+Wrxt9SLW/J8zsWLJZfLNf/lxRW3jaDUGV8ax2tXht8+esTHtWPx9CnXz1/w2sPXyJyNhnSAkyCcxWmFaQJKePx6jbmp+fo/+Ie8/n9/yPOf/JLy4JDXv/dtVkWGWAJKpxQBBicEK68QQaPSfYqkCzOjjEKgwEWDL0XOVExxOhqIeWNprEU0glB7yCQu5cvOynSWZTTIttZjkwCaCRl50OAQ1hGMxQSP9zbyOVrH1J/OoULEyY1rWNUrbpc35FKhhIwh04VGCo9UURlcN+sYsr9ukkGMjJ7hoeV5EyUX23Qpnv8WT9k+BzI5AbdpovdhnK3RcQLmR89a9JLvfd2ji1opAiRnXRXnTviEA/ieYj/RVymSo3bkh3yIkcCCb6hNRd1U1KbC2SY5LWuE17hGsGq2HVz2lV8hlPo2AzK8EIZMSQvseO+ZTCb8/u//Pk1VMZnNO8Cn9chomoayLJnNZsigkEpHq9PgWK8j8X7nna/xne9+l8uL804YK8ty6/LtfhIY1u9f60X+xhtvcHR8FEFuHRXqWRZDEmRZ9OJoc204F0OGaa2QRC/t1mo1hEBjGvp5bNp8qp2AyEZJ3nnLtAya99HyNykY+mBT31NJSomQAmPNDrC9A0gPANsxMFGIGFLKIxB+s+m01jQkobAHiHXMZNhsyn4fYVsx3oJd/fVon+kD9H3F+Ng+Y6OmfGkZgnljSoH+31tthgji9/vfByL74xwDPNvPx8ax9X2aY+ED1oOrGy6fveDpZ1+QIVGpHT8Cym79+xWwtSFwNgQsQwKfx57fnOtdxrDfn6EH3ZhiY7h6QzoRz+ruc3cpSe5ieMbGPUavxr6PNEN0+SzG6htrZ0e4ChvDkCFI3f0W2/WMjecupq7P6I7Vcdf87atvbGzDMba/h2dqOAdDJZIPASXl3veH7Y4JoQEwySg9C4LMg0ph04OIVvJWCepME8qct7/3LX7rH/8RR48egpZYZ5FOUfhAHiTBGJaX17x48pSrp8958vlXXD1/weLqJgIkPcvgvoVwR5MHR3FMkOr/e3hPjdGs9rnWM3wsykH/3+05FWKb0dkHyN+1J8aAg2EZetS293t/vfa9Pnx2OPYhjRrrf/fOHWPs9xU2dOpVzkTbjzHFz/79KvYqyob1Dvu6fXZfvkZ31Tn8bHg398Orb6/X+Lj6+/VVBMyN4UfYYsDH+rZvrYf92UeLNsaYtI6Md45pWNq+tvUJIXYUWWP0rb9u+2j2Pr6s37f+egz32j5eYp9Q8ipFJKBGyk10nBhpIuzsmX28JWyn9OiPqz/+/ufDeodtbJ5JUNe+tgWoZPQ6tj9DCF2+SiFEivDQM1AdUVL2+9tvp++l3q7T9p31q/EEw74CnZXzy8qQx3yVMrZXxu7bl5Ut/mUP7zTWxqvQi1+3jN2bbRk/j7JDg4NPBhPtc2Hz3vDuG6Mhd513xPa+T2zgf/W5GDuTO30hELUayUteREUFgFbRSy1IYl7gv2t/2D6P2z/b0UJCkislGVJGz1MbLItmgbnNmU8OmBUHKDUhkBGCJQSwNkVBF9Grva7XeGfJC5Hk8pjnF0i8YASPY3MZqEAm4nnzPqCDIyfmBqzWGtOAcwbb1FRVhTE2hni1HmsbEA4UBC8JQSKygvL4gNcfvc03vvY1DmXg6uMPefLXP6M4PEQjMC2dEIEcyaVwlE5hlmvMuuLw4JC3Dk/5RfOYW9vwQE94pzzl+5M5H6yW3BrN1/IzfjCb8l455bn3HBc5508vcWrCydd/k9nhEQd//mdcX695ellzvvRMHzzg5lbgH8zJj0/Q3iFszTcODvj8dk1zfMyNrHiyumVlLIdFwbqpCD5wIApKqZGuISC4Fp5bb/EBjvMJHni2uKW2NiogQlx/Qi/NTBgaHPstmvqtb3+byXTK5eUlT58+pcwnaK2ZTmdMJjMm5YTaWj77+GMODw85ODqkLMvoQeOTMbbzOG9pmpp6tY65zpWiaUzMk5lFnObm6pp33nqNe2fHTMuMer0mE1lSFkgc0WtRChG9fjtPm+RlI9p8tpvdLqRAeLEXl9iSeVxUNlrrqRvDqq5Z1g0euHf/hOOjOZnMMGtBtXasqzrKntKhpcQ0HutqXn/tlIP5AVIVWKciJpVLvG8VodFgV2pNnnlsE6MfWhOVpctFQ72yuEria7BrT1Wt8T6GsM5yRTkrOT094vjwiFznCKU6Q6io+I5OIVrHtAzem6i06GFsxhhcsEnei5iKJxBcBG+j80n04BSQogRMOTw84tGjR1TLJcvzS1gbch0dUSAgdTy7eZEjQoqa56MZXbWu+erLp1xktwihqV2kJ2tTIWWWDKME8kv47NMXEAJKxnCmLgTWzlAHi3Q+RgxKNMZ6E9MOSo3IJFkB+aFjNpuRF5LJRDGbKg6PC958eMyjB4dMyylaBKQwVKEiBEWhVDLWi8bL3vloyIBFCIUUCZfDJyPsmEO8kDoaWNlIi2J4YoEMIUWr8tHMJ6SoAcHjjcUF1zNITam3EvX3yUu9qT2NjfvG47HeY1IkBilEchAKeOWZTXMO5yXTaUlRFOR5iVRThCyBDCEytMzJi7yLamadjdEN8AgZCEFC7RAiEJTCeY81NY2N0cWapuH8Ysl/+rMfo596imyOziRaBpSIyvDGmaigUCBdg5O74H4rJ78Kn96WV+Wp75Ltf73PAk0waD8h9wGhIkbijU7KlYzJouTqgxf8z8//DZerFzhjmcw1TQjpbDqUCOS5jkqcnhFa/x7uFyVCrw/jShKA0Kb3bN2ouu91jCjgfYzOYRucVQTZGkK0MqegyIoUMl/ifTy30UMznt8YkSfuOSll3MNeRDzd0stR7lL4YEPMcx9V423EqU7+6zq/mYM2hWqXT3xoyCfFzlyN/Xv4s2/u9j239Y4YCU888j5KUGsoVIk0JqYuUQovoyLt6PCUTBQ8v3nGcrHm5z/9Be+8ecr9hw84PDrkqb6M+ohco7WOUSXCtkNTp5NIbVtraazBeUehc4osZzafc3h4mPDiGO1DBHBW4H1cW5/CmLcspfexPuc9tbWIxqAyifMeQo6WApXnlGXJtCx47bXXMb9hWFxfsbj6j1xdLLA2oHPBwWHJvbNTMI6qWmFtQ0xpQnKcjNFGvPZIHXAOUKG/I3Ywkd5pTJGFtqMgRnkSTBP3XggKkSJRKqFBCUIweNdwfHLA2ckJzy5uQWi0UhgXUJmmyDPWdU2zXrNeLlmvl1SFYr1eU2pNoRSH0zlnJ6dcrx5ze3tLXhwwLWccHh7x/HxKMakwqxU3z59yeXHBw9ffJCtn2GoJ3m9xIn3xpj92GaIxmZWBZ6GmoWQiNFUyEnVIJuRoaSm8YOIDwVgUcO/4iNurazCOAzIehoK/uH5OXlle//gLNJrae5AH/GV9w2tVxkkoKIXgo7/5MQ+eXvCtP/onPL56yic/f4YXGR+u19wuaqS3CAHaVVxfNczVAd8pjjmyDr9YcH3+goPXXkOs410ghUB6CKKh0ZpcTbAhQFOjK4V+MOf7P/z7/Olf/RfOP/qcs6+/hZEgiBGSrYhOpqXOKUuNZEVwJspLeBQyRQ5UZLpAq4xMSaTQ0QjPOeq6ihF3vKfQBbOsZJbPKHSGEB5XW4IKkMmo7FYBKaPRxNF8CiHQ6AYBTKYTHDFpihGkNFIO7QWlyslkRq4Kcp1T1RVGCHKtCNKjnKQIZYweIzZRJ7TOUNIiUF0UkY7mif00f6zEZwY07KViY8IyhehsjwSd+nB7s0JHo51vI4GELgR9CJHeJGE6HWmPDzEdR3SoiO4V0QLIIlSMyJ2hkEIhyRAqGiWL2wW314uXDQD4FRTjm/FswI+WGQG63B1SxrzeraK5BTKvrq6YzQ9xPlDkBSEE8qIgyzRaKsqiiBenDVTGxDw+NtZ9e3vDrJxQFiXOOZRUWOwOkLaxgNoWXvoK2eVyGevQ2c5F1va9aRqcdczmh4R0eKVIYSQdKUS4T32Jin2ZvAr7XkI+0HmqtXPVggRRSb4dhrgvWPbnu59Luv2s/7sP3PWZwX1hrkUKjBF5i/is1hqTMB7XKsxDOkipXpk2fQuItGu7FVomnYQxhfImHGW0Jm4tCIdjic/sV5wNP+vvg/6Yd71jdgnBy4Cm4Xy27/Qv030Epv++Dw7pY8g/5T2TvCTUhstnL+I97uIRb3MzDb2xf1Vgczi+rbqgU17098wWSLinrj6wP2QSR96gBbzH+sRIO31wYfPZbr7PYRnb6/06h56WY0xuvAVeDYS+C7DuC2ltZIxNx4jYZe8Mtf0b9rtf+mvVtjE8X8O5k4P53dfXYT3DPgwVw8N9s++9rb/DXftkt3+jQmVShEsv0F5ErxUR8yHW0mMzxfE7b/Gjf/yHvPHd9zC5ZC0i4JAJiXQeWVvsas3l8+dcPH/Bpx9+xMXT51TLFRiLcvGC1il9RLvX22gk7XhlTyE9puAa0ox2Hvs0byjE9+e4f7e2HuvD+mN/GN0H+2hdf6/dNf/7vr9rDeP7u3sgAmu7Hu+753x/+8Pz/LIy1s6r7L/hs33auLedVyDNY+13a844ve2X4Z3e7ruteoTYOqtjUT36d+OrMMf9aAWvMsauncGIhrRijA6/av2dMC+3wY5XrafPKwgRo+UM+wS7iuC2DO+SYd39d9vn+9/fFeWn76Xe/h7yIf15fPXS7ut4RkUPyNp7Pw9r6J2FV21/OPY+79R+JsT4XhyCTMP+bfchtKNMXi49HlSMz9lwDfr88BjA9bK0By/b269Cg8bqa+vaHfPu88Nz1sojw3219Q4bY5GWb+n3Vwqxhbj0+b/h3nzZWPp1v8p7Qxo3ys/2+df0Xp5Hbzzv3EY5EMLGjLnHj7zqGm1/3tsfg3PpXQJ9fw2DhFcp+85fNydJwgOBSDnGMyFiyDqlAA3B7zlHwzlO8h8BFwApYv7IlgeS0a1TChGt9kOgi0Xe8ibpDMZQnoFpCEhRItQR6FPK/Iypuk8uZzgELmy8mZT0KEEEl0jhlX0gOIEXPrkiRGVm6NYngTNBdDyjlwKvJQJN5m0E1kWSRUWGyqaoPOBlhbQWIQOFynDB0SiPQaLLOYdH93jj0T1enx5w9vAE+elHLH/+N9gnnyHvTQmIOE9CooXHVQYnJb6x3K4WKFPxteMHPK1rPlnWnCjB1/Ipb+Zzqtpx6WruK82DrECi+eB2yaJx3FjLk+sbsrcf8OYPv8O8XqAeP+H6doVRgrPDKa+fzrmt1pTHRxwdTyiCheUSW8NFveTo9B2atWdxE8i0pFkvsTFXDCoIMh/DnuYy51LCUhiUCMzzGV/WDasuwlr07lDJkLg7S0l2sq7pUg7E4ASK+eERb3zjTa6vzrl4/ARzs2RSTlDTCa5QlPOSMtOsr665vLng0ZtvM50eUkwO0fmU2jkabxDSR4+huqJeLAhKYbSgTU+hswxkTlWvuXdcMCuy6NSATLJ1VNaLICP4HQK3q0XHrbTbdZsOJAVfopVdDsSQ9logDbb3d3Kv6zz0jMGbhlwLsqxI+dANla8wvsY1FSYE1iHiAMZYzh5Oee2NkqzI8SFhCFITrCH4JSJUaAIFGVMJq9yRB5BIMILGKJqlQtUSXMD4moVb01QQqJBEZefhwZzX782ZK4nQJUKotHbJyERAKQsKlSNUoKZBWPDe4JMyHCTGBozZeISKIJBCpciDCdgGCB6ZSQpZclyeUB0uuT05pzgQ2MahtGaSafJCYJ0m+BCjNgaip573uBBzz54bixIVMWx3zLvugqNV4sQlCdycL/E+JcZOxYUQ17JzvIu0znsPgeTdDUKB0B6tVigdUNqTFYLpLOPBo2Pe+84D3vnGCfcelkxmAu1L8DHXlxcOHwzWWdbGY7zHYZFIMkLCSF1n/CNEDCmdS4mSEi9AIFFCx0gnQmFc9PY21uKw+GAxweCSIUtARyW/VJFue0dtDStrMTaGugeBR8ZQ6l6gZJY8atPNIRxHBzMOD6ZMJyVFUZLpHERGIEeQIWWGktFxSAhJkDnOK3zQBG8JwhF8jEtibUzDuA7gg8IFSdXA9YsFX/70M/T756g8IDOSM3qko6ELBx1puu9ymbR3bjyKsB1JCDbHcevvjvfdFMHgg7HSYUSb497+3WKeYtOZrsU+n91vUaFiWoEuz7VEqZgmwjpPkRdIJTCra378p3+GpEGgKHQbeU8TdDSQ0UJ0Y9jiWXtNC8HGY7ob0jheI7pBDt5XAR0iP9iGdA94RDKQSRxH9DR0yYtcpvQtuHQnhI6fiLxb5M0UgJAgIr8maHkpFyNv+Phsuw5JHdJF+2zpdlS0J+VzV9NGThSyx9vLVvbor3FvLcXInLa/2zRj7R5o5RjatYh/0yLtok3HRxd1bjOxvZSeQoHUkQ4QI/sIpfEyeq8KFZWvQgqm8xmH/oCbW8fzq+d88uVjlJxxND1kWmgqU+HIUSpDyXj+CD7ldg9pTkM7cZEWuhBzwGcBoSVZrjiczymyDNvYzfOuwdQrXHMAZY70CuEynNEEqWL493QnOhHTz3k8XkSnrEzlTPSUkimTQvD2a2/i/v6PuHyx5M/+7MfM8pyzs2NOz444mE1Y2hXzZoqxTTw3Is6jcVD7gPQW6RsKURNCti3X9davjz23MnF3WrfkrRjiumkKwjTukRj4OUXlEJ5oGFRwdqp5fmljpCOtcHEaUVojTYM1Dcvra87OGlzdUGUr1qVC53OOTx9w//Kazx9/xWpxyWx+yMnpfaZlwaQ8wq0rLBVmteTZJx/zvd/6R0zPHmLWt9i1ic6LShCCpD1eordPA2zOHdGzfxUEU6G4FJ7bEJAy5zBkGCDIQBE8WYjRUw6mx9zcrGmI63YqJY/XK/4fVc3vy2O+qw44UZopOcYvmekJB2Ssvedje8PTH/+Mt7/3Pd568BbLD7/gs+D5oqnwGHLtONUFj+SUNyYZJ+WcyguE80zWFeH2iqUzqAC58JGvAQKKzENQJt4HPqCNwi1W3P/e7zH925+xfPo5zz7/BbO33sbqwIHTOJWz0gGbSSbeogNYU8c5DDHKhVYZSiq0jul5tIiRpBOHg8jiPgh45sWUg3JOofN0ph1COYSMqT2FijRQKs2knDIpYxhvax31xGCNQ6iYPiIIcM7TmIbLakVT1yAEFseyWXC7vo77UkvK6YRjcUJZTEDEzNs6xHW2rSzsU2ihPr3r3XQtH69k1AXKtG8Cm4igTgqQKs5HkqcQrZyV6mzvgZZfFhBEkgFF6O7DgEjpXaPzlOjodLwbAg5EMl4PnkA0gN1cRAohfBcpx/qYQit2UaCkT/yTBhEQ0uNl5KW9dzShoTEG7V4Nf/kVQqnHClvPa601ZVroVhFeZHkMl5HnWx5vIQRub2+Tlj+GTRciKkZtlpHnOTWwXq8xTWTEK9M+Y/A+YK3h4vIi5mSYT5BSkmUZTdN0YL8xJiowiJahfWCi7bMQgsViiZSGYuKw1lIUBUIIsixDKUVVVVTVGp3lZClphXEWQgwXJUTMI95O8fvvv890NmV+cBBDtLeEOPRzbLWAVbTetNYie+Fe+kDcjrKp20gbcGsILLVAVauIG3rnReDLdftMpM/kRk2aiOrGkxcftr2r2HhX99e2Bd5CosqC7fyefXArtIxRD5gagsxjSpD+vAwvs349LXjZtj8G3G2BzUDrRTUEQ18G3I2BlUPlQ7dOMlo6hgQo2aqmWa5ZXl1TAFpIjDP4Xv2jYPjI2vf73u/D8Pu29B0c+2s5LPuA2b6V4cvmo9/3nX61+2xQ17Cel4GL+5QUw+/7e2H3ne32+/vuLgXITp/Z3rN9Ya29nNrcp63F5lhdd4HiY+s72t9WWBmcD9jem/16xyIsDOdyWLYMYwZr3b034m3YPj+mgNpRMkiJcoFM6Wg5LyVOCmoVWKlAfu+Y3/mn/5jvfP/7qGlJo8HnMbd1ISTUFrdsePzRJ5x/8RUXz5/z5MvH1Kt1ZCJcBM0zoWIMv97YhiGVI2vG1roOvff3rU1Ln4frOxS+2mf6SvIh3U1vd4LdkO4M2+7/DMPz3hXqfMzoqr+X2n93wt3I+vXbG+7jrbuutzf63pr99/rztlmT/fRiSHu6OyvO3s4dMbyHh+dia917KuB9NKg/hn6/N95VEUDuj+Oue6dfz9h91Z/zsfQjd9HK4d4d7tf+Hd+Wdiz9tlzwO3uurb//u7/W/TnaR3P7dEMIEYH3O+ZruNfGxtqNabDu/fDX7R5o+db+3h/jTYbzPLZ3hvxc/2z2x9Seg7F9OKw31rfh01q+TsoYjjSEdmzQQYWD/dj2oR8FYGwsbRlGtujP7XCM/efHzn5/TrfaC/vPvxCi88Lun8WOB5bbBl2/Shlbt00ru8/198kdtQLbZ2p4jtvfwzPdH/ddfR4aV7WGXsPnIri5naJmuKdbkbktLzMQ2Ko/bKLEjN0BY+Ppn4Gxu2w4R+1vIZLgnuQuYyxSKYLZfBc99LYjNozR9vF1H+7NAb+dABTvXWdsMxzP36UM52j4nRDJIFy0ccxkBE6kQIuYbx4h6fLvsnumhqWFUzxRUSREBL5DMjgUQiZgt+1PewhbpQARhEx981FbhGCKVKfkxUPm01OmMobMhmh0HjksB8EhRcx5K+VG2SaRMe9wCHRevlLShvKJewoI0WPei4AVAUd6RLTAt0AQUSyts6jMESBEjHJkfMDnAp2XzI5OeXjvEW+dHXCk5pRSsH78FYsPfwluRVYc4U2byg2EFlRNDCFrmpraWSYinsWfVTd8VFe8dTDjYVYyDxmfmJrGGw6VZI3lcwtXdYOtLC/qhsrBWyfHPHr7IdmLpzx99pirdQUCpkWGclBLj1qtaXKP0BG4f7auqIUkTAua+obaWIo8Z7VeRlAtZl6Oc6UEOsu4DQ1N8MyVpCimfGEa6jSXIu0F5aE1sw4kr0cfvW9a5UoIIKTi9MFD7j+8z0c//SWXz1/gG0M2OyCbTMmnM6bzGcoHFpfnVPWao6MjimJKlpVInVE3JkbNCxbnGlxTYZsGkSu8jGBc3G8Cax1KCU6PJ2RaprtOpv0bevta0jSGdV0NzlRgm8ZHHjteQ+14aU9Y9xnd/1NaD+8xJnnRupgnWxIN+6q6Rkqw3iSlkcU06W8hyAvNm2/d5+GDQ6TW0aPGp9CZzuF9g/cJGA8C4aMnaZ5FQwDnBcZ4bCORNmFtzrCya5rGAxYpc8oy5+jwgPsnB0y0QsgsjqK9m4UjCJG8lzRKCQwW7VPe6dCmLhE4B84lbCcpg2QAgsAFlzzcE94iovHStJySqwwRPEoHRCbRWcs3qI2SXSTZOdFRlxxTGufSbtzQwfa+8iGkjBLxTPoQNphDaMlSzOXt04chhITntso7urkwoSZgQTiQAaUl51/UXD5f8eLZDV//1invvHvK2ekk3QWemBM93sONcaybBhui8i+XgQKHIIK6Wkav6ESRQIIiKstj+o84LpeMA6xPXrTe4rzBJ6OKDS8RKa71BuMMxpuU8zulRiF6d0opyTOdvOPifZhpOD6cMZ/NKIuSPMvJVE5AE8iQIovyXsrn7ANIJQlKEoLCe0nA4B0EIVDCYQKYAAiJF4r1uuLi2Q3PP35CflFDoUCFGPWjozQbDCOE0HOM3si/fT62/R3StbNVEp+/9cXI9TfKu23lKw99uGhTpxA9ytCvb6Q6VOLR2wgVApm8V52LOaWzXCK85fbikqaxeBdQosWYou2FCJv82W3fOx5VbLf9q8iUu7xGpImyVbR0irhANEDrVipG1ZDtxLRzluTR0N4TvpvHds9KfKIPSQ5K94nvvJElQm5H8hC9PkopOg/0NkrJ2Ii35NLeunbz066lEDvPd8+J7cmN33fhyzYK8q6rYu/PVv1pP0CMEBF8IChFEDGNqxRRUYUI6EIzmUwxTdRXfPnkKfODgkk+ZVoWrG4XhERbpIx0LoQUzST0zw+JP4PgQ4yWGzxaSXSmOJjPKYuCqqqxIXkpe0fTVFhjYppEJ/Apl28oBK1jmxJRobUZo0Sg0MkbVgRFpiQnR8fId7/F9fWa21WNMYbZbMJsNoHgMGbNuq5w1kDwCJE81YWKxj0u0trgDZDtrOnY3t+SEQf7A9ooBw5jPEWRxb3YD18uJN4FTk+mFIWisXEepdYYH6N/CCFw1rBa3mKbGtsYmkbQ2AJHYDadMZsdMMkz1k2FbdZkmWI6m1KWc9bqGik13tacf/Ul8h/knDx4xPr8S8z6poc3b2hSu7QiMS2h3YcxzA+3InBKTOfQ4FgEnwyq4nbQCHSAZrlmenaG1gXexJQdRRBcWc/nwvBIrHhExjtyRiY0JhlK5im/dQiO53/+15z+zg947Y234N5n+POvINMYJxHKcKRKXsvnvHMwxWvBU1szCYK8qpnfXBKaJdYFZPBoGaM8BKLyHGXTsATOeqqbW07e+iYn9x/yYvkFLz75iNnbbxIyTWkySpXTqIBVgkyBygVGyBj5JkCmNFpqlNJopWPKIBGjt4SQdB5EuUAKwbycMS8OUq7sADiyXCCkA+mRKqaELoqS+eyQLCsgCKzzWOuwNkbiUTL2wVpDU9cEcq7MFS7E1CzWGZqmojEGIwJZPaEJgTdm9/GtXB3iPERWV4ALnSzYp0Bxg3RiUjqTdFho6J0XJ0Q0epaqM7SOlcQKWp6k5TTaEmUyn3i/xC+3d3rY3J+tYrzjI1uDaiJPF6W1lvdL2JslGhf6yCHEACIenCUQjSMjj+OwpsEGS2XrGAVICqb5ZIcOjJVXVow/fPiQsiwpy5IsyzrgrAM7ehPdesa1AKJSikePHvHWW28RQrzArI1Af55l5Ekx7Z1PceJNtG4nhlcpJyVmXXHv7IyqrhBaMp1OsNZuKUBbrz7CBuxpSwvavfbaa5wcH+NRFOUUrXWnyO+HVNc6oyinCHxi/h3R2krjrMHYBu9jKJuqqri4vOA3v//9BJAk8DSEjinugAsfcC4ytmPhrMeAmT6zOwaO9EHJoRJjDNjsc4PtdzblK7LW9toahGr2MRyUVNsg4xDYY9B2fzzdxex8Z6gwBGdCaL3ZN0xJPzRuW28/rPzwpx8GediPLdA19bdfWvC7fX84xiFA16+zf9n22/EErDMEGxBCE6xDELCNoUzAwja3vbvG3aT0Ph8qE8bmcl/ZWbdBu2OKlSGI/7I27urbWNkFIhn8/Wr19Pd/f3z9f28rfRPzvefZsT4O2+u3O/QU7/qcAJYh0z0sr6YAGRPC0jy1/9sjGI2t3fDMtn+PhdAd63ef1gzP/b653Af2DvshgByF8pLGO5jlLHxDVUi+/Q9+yO/8sz9menYCTmBEgkqsJ3PQLG8Rq5rFswu+/PBjPvrp+zRVRa4zvLFoGdNViABIEXPyKLVDS7fW5Q6Pq9H12EO3h3RlbG7H7obNc23fxo0S9vVt7Nn2zO9rr2VS+nVsn7Hdu2tsDGM0dEw4Gc7D8Bz0z9DLaBn00pmQPKZ7+EZ/LsYiAAxL93xf9mX7XI/1YfhZf53uolX9dRpGlxhb67H91l/zoaJ+rJ39g9+AGfuebb1M+6HcX3bWf537oSVyL6OPw728r63hGRzr55jx3bC9fXXv+3uM79u3h+7aJ6nm7ldICqqxe7y/c/ed62H7L7tDxvuzS2+212vDM43Rnhb73HeHpBY2V3eLA9xBC4YltiuikHXHuAK7tOquMnY2X8ZX7OPj9q3L2Pvt777R6j5+pP93/3x1999Id4djGHp2t7JIS2/HeOahQdM+/qP/cxddDaENwxZBBmOaaMkfxp8dXd8RvqXf7uZ3ayCQ+AWZwraHVlG7Ozd/17Kvb8OxbZdIh4VoPf8jb9TCr3cVITbvtrJ9W2eCpzZ9azGTIRo/KFJ6vM8IHJKpM2b5feaTOblQMf93CGRCIdAEV2OsT8qomPdUK9l5jvgQZWzZen4RAWORQrvGVGUOqbLoaeocpon5kaOhkMaKCCxZa1F4mgAeiRSOECweiS4OODg54f7JGa+dHHOST8nnh3BxyeIXH3P9+ReIgwmZUNTORiNQLfBKscgc9qambipypZgXGWtr+LG/4dw3vC5P8SHn0hhug6MIgrXwfOSW1Aac0xgXWOGZHJ4xOX3AvaLg6he/5MOrp0xCzkyXGO/569sLMgGLz77g4plGTgtcnvH8pmJ+cB+nFKumojEVk8mcq5tLSieYhKgYNwhyBKEoWLgVIJhkJXJScGuuMDZ6ukbb0OjnsZUqzqfw5BHt6vhTnWnefucdDqeHPH38hOvry249y2LK2ck9jg6PuH5xzrNnXyIEHB4dkeXZRu43BtM0OGtoqoqmafA4tMwQHryPoKC1lqYyHB3MODk56mhQnweMezqqtKNXmNnhkYbn4FV4k80LIGQ0yq1NExXCtPMUqKoVy9WCMtfI4FAihnRd1w1NbSkmBQ9Pj/mN777L/dMHcQw+evvhIyhpnac2lrUxVM6wMjG0ZJYXyKAJJmBMg3NR2RS9kSxNHTEeAiglmE1LTo5jGPUsL6Jyk0DEvLYdIbRWaBU9533YRLAKEMNa+jYcZvRU7kmiNNZijCVY0CKLThdTjV96blc3XFy8QBpPXpZbxph9gyoR6BS6IvVLJa/ori8hQNg2VhViozhse9xfzjYMcLfGIzJUyx84FyJ8GwTewtV5zfPnl3z+6RO+/PQ1mmXGwe8pprMCgcQYDSYQXCBYR71uMCY6/zS5x0mPTuvv8WjhkSRaraKCXCKTB1iMeBBcipYZXDSI8NGASAiPlDHHLjJ6j3siHSPYqICXGkT0OA8plK7OJLOJINcSJWNfyqLk6GDKpJiQqQylcpQqkTJ5jMss8RfJ2SbEjR8952RMCUhMDZg7EUF0HXNpK20IxrG8WXD15JybZ1cI0aZZfnXeqltvxnjl2J99ctDWsyP1jvZjwAv0n93wxuPK2P6zIWz4q/aOHY4p8haKPM/JtOb8/BLvbOQv2Bgnaq2Rnk4h34rhafgdf31Xf3bHMCYzbj8vRVLCJOMon+hTCNHYIgiJJuHd3mOMwSSdQJtqsJ3LIEHgNhFfWj43GYH47jz3Zb5N2YQl3w1NvrtOgwnYEt6350EgtqKS7ZPJus/F7upv8VDd+/ux3s12CLQ5u/v96z8rpSTPC8pyirWWFy8uCOGALMspikmctxA9NzeygR+NWhjCJg98zD/ugKgLmc6mTGcTbhdLrPVdR2JofIuzFu8s1qqUTlZ1NFwIFZVXMqBljoqJQ2MkI6UwziCFJisyzh7c44c/+i1kUfDhLz/k+uqSpl7jXVRqrddLjG1ARI9cYwxykicP+MgDmCags5fv9/7S78OU2jHWdcNkMsU5u11PiN+fnJxwOL/i8rbB+xjtYV0tYhoPKbHOUa2XrJcL6nJKZgTGOJz1kEOmFQfzGeZ2ibOGYA0HhycUk6eoPI8h4+uKq8sLqmrFo0ePuPxsxuIyDiJ230MXsQDo351KEKRAOoH3gcvMc+wFBRLp4TO/5jmaPAhqICDQQXKzWHBy7wHzvKBpLJVpkFahRMZEwLWoeIrmoShACZzLuPaeUnqU0Dinef6X/4Xjxb/k3ffeYv74XcJ/fMLJ7Jjn6zVGrjmRBVOVIVXgi+aWSw8PRMbDesXR5QVufUPlJgQV8DqgUAgR8I0FIZFaEkTk+26XS1578z6P3n2X65+cc/XREx7+1oosnxAqhxIWJRxSeoJUqCx6iBOiklfJZJwmdXSsFQohWl4kGftIkF6hpKQoS/I877yuhVAUpY757vEorciLkul0xnR6QKbimXQuRgUJ0VIzyiamQYYaMsFh4bGNoaqXND4aokgEVVWzbBrk2qApMGcOpWLO+mivITp6KhNX1OEnvT09vHKGd9DmPPRpa+8+oN1zGwxh59br81OJlsWbIjELvSMqfKRTIf2OhrUeGTXrUaYXbKJcuNhovB+i4YBza0SIsq0NHtM0rG+vMMFSp/5MipL8cDZOGAbllRXj9+/f7yZGiI1H8Jb3h9vOYTnMIS6Aqqooy5I8y6JntnMoFRkAKeLBNdaSFXmyqrBMy4LaO9555x2CDywXC4SI3kyTyQTvfRSUkvDbxqxv+9oKV1mWcXx8HD3N7bZXRT/vhhDReg96II6IOTiqak1d1x3TXtc1P/zhD+OzAm5vbyEpjn2bT6XHWLT5yTtQ5SVCVwgbAGIMXBoCN8NndryBE8ckiKF1lJBkAWRwyGQ91wFWXftx3X0SmELYAN3tT6uwds51Qsg+MDDWv98jMD67ubjbwzkO7u7+LcTGI7KvSG+/22JuRniU4VyOKbrvYuCHQlUctCBoSUhWojrPmM8P0tgdjbMvYakBBowS+8O9/l1KvGc3jOtdgO3dZXsef2WAgY2AMwrqjvV9BODdB5Bv0S5IeSg39fw6QtoYsN/fCxLZAc0tHd3Xzj5P2VctiXfb6t/dz497Ng33wL7+ju2PTgE3UCS/ytxunTdEtCNTAjctuZaOs2++wz/7Z3/M6+99Ha8ElWnIVUmW5VCvESFgq5onv/yY88+/oFksqW+WmLoh0xmmMV0OKkQ6fWITWnlMSTw25jGFxNhY7hLSd+nj7jtje/uueRsD9IdKiX7dYwqIvjDXH9YwL1P8NwyH3v++T0/az8csdtvSGt69yn4ZOytDmjEUfFoBou1HW8/Ye/252ALM2oGPPH9X2b6P6Dyf73r+rvUc26ctjdvnDfoqZey5kJQiY3RiX7/73w/nsf/sq5YIgG4Y9J11ecW5FCJ5DbzCfmzrHEYi6u+fV+p3Kn0Fe9v/fbSj/b1v3sYAGzoxeXtPRDq/nZphrJ1XSRfTH9OYMcnYeIZnVAmZQJxx5efLwMax0vKsY/ff3vVlV6k5fL61jx5+3z9b+8fRNbS3/q3H9vGsg+/bZ/bJB6/Cd/XbGqZO2B3xbtnXxsuiQPQ/6xu/tv0eU6y/SolRxiw6L7p76WXzPBzPPgOku4qUUXHUeiL1jUtfNSXFq5a79lgbBhgRQWwlNp5UTuyu5/Y93uMfZFJD3zF/sald+tNa+YvuM4jZnTMCR0hxj1yckhHw0kZj+QBaxBzkLjisaBCYOA4lUTqPdXlB6xkkhAY0nY7GOwLJ0IZk0J72gzFNym8bQfzAxoPNrpYs6+iZHJxFGYssDpjnh9w/fsjrJ4fcL3JUrcjfnGH/019z+5O/Zfn0GbPXjnAhYGz06tMIgoHVzZLMeKhq7oeMe6rEBXhsVrwp5hxaza1b89QsKacl75UnWASf1gueNAu+rCxzechsYXjvB3+f17/9G1Tra376b/8danrIo8khwjpeLNdcNp6HR4oHkzNugafW8uWq4vJmyR/81m/wxWrBzc0tpjHMZgJTNxwFzSGSTEgaAUXIuNKCy2pNieYgn1LlgqdX1zRNzSyfkEmN0Al66/iW7bvLOIdLCpJyPuMHP/gB69uazz75hOXyltlsQlHkHM6OePjgdU4Pj3nxxZd88fknnNx7wINHr5NnOSF4rDXUTYUgnqVqXbFer3DeMi0KnPEQZFT6hcB6ecPb7z3k9PQQ6cBZh9K9dCkhgoXOeVarFdZasizborP7MJUh3sIeGuy8jdEOg035tuN/DqjrivVygQwFEk8uowGATZ4ws1nJN957xG//6NtM9QGNS2kghEcGR+MMV6sFz2+vuFjccLWuuVlbEDnl7ABBRmMMq2VD01hcEFgXaBrLujY0TQOA1JLDwxmP7p9w7/gEKXOk0DhBUpxGIFMGQSYVhY7RHREJ7+nOeTw/prEJb4lnq+8sE7EjiQgKRc50fsBKLPjFp+/z05//NV98+imFKCimRTfnQ3yprQ8iXdVSMbzztt7tMlBuaNAYDW89KVueUgzabyM+OgxaBwQSgsJZRRFK1nXO5eMFf/n8Mz778JzKvscf/uGPKEoZPZlsTD8R3AIlMhrnMTYqC3ESrQWZFgStEFojtURqTSYlBInw0WsLFMLH8NnCB2SIRkLCkcK2RqMVIeNOa6NBainxStPINh+0RAYL0pMpmEw0BzOVPMZBS5iVGbNpTp4VEDQkL3Epc3xQJMqZfgTRazjeFfHuFOCjZ7iXLir1pcTg0SrgsSyvrrl5fE7z4pZ5obvc1uO87F1ll28L3efj2E+7F8QYqD/WZtzIo613cgQAcue73ee330ud2NrrxhiypLiRWcZ8PqWuKqp1lfLOK7RUKdRB72CINPpOzh4f19gcD2nflhwMIFRSR6TZdaFTpNqEocdoKQJV153jUovLtzQjsC0TCr8dwa5rN/EpLQ81JmH1FTddLvGhnL/nbzFY+WiQshvhsat/YEy+88NuO8NnNzzlRvbfXoc42y1OvHluu/52goq8hFnkbW6uF+gM8ixnNptuHMdojQdJCmSPt62St6VzkV+y1mKt7fjuPM85PJxzcDDn4uKKumpoc080dRW9oI3BmCIq/GyD1jOmZR4jIHQRWiRaakpZkMsCJTSVabBKxCg9KqBVjtCSt95+mydPnvHi+QuqVc3R0Tzm6HYrqvUK7y1FobAmKkQ1Gu9CUg7+aumL9svOsUSdT5UwMw1s9B4AwTrun55xenzB7eIFy6piMj1gsUyGBXmGbxpW6yWXF8+YH56gTcaqaijWFVpWFGXOowcPWddfUC1vubh4xptvf51yOqMoJ/iypGqWVNdXPH/8Ja+/8RqfHp8SnnyJsE0HvKXMQDvjM+kOVEIQvOCZDLzpFVMEhfS879d8xoQjBHWI+a6VhNCsyZ3nZD7n3DYsTc1UZjz0BRmed09PeFPPcLeGzFhWWDwTPBkBQW0lX9qPeeuXn8EPfgO7fsHz//n/xvvmAs0xShie+DVPbl6gXwj0bM78wQFPVIOpr9DPnvPopqEWOauJAEXECkgRYIyFIAleggo0NNSu5u3v/ZCrJ8/5xc/+C9dfPeHeN77J6tagpafQAqMEs1mMdh1cdPYMIXqCZzoj6yJfpghgyUFXuQAyw/vWgCyGzpci3ntKQVnmKB3PVaZzynLKdHZInpcoCoIXMcJRtsE3m2pN7SReCnKlOJsVTLKcVbOkMksqs2K5XrNeV7gg0OWMaTmPUZuE7KIvZFmJynJC1UT5s38t9On+yPHY0KjNZ1pEb/Y+je3Lc/Fcp302PFeD7zefRV4qpHMk2js4BNpc7yFlXpciIBQQHMHFH1xUoLee4S4YjF3SmNuoW5ECh8eYhtpUaSAarXOmkwKhM16lvLJifDqddsSyDTneKoitjUq9kO6Nfrh1IQSr1aqzFGvzpYYQyPO8YwRaANfaGD4gLwVaZzgXczRNJ1Pu3bvH8fEx14vryBhr3V00eZ539SI2oQP7QHfrFY7YhAhtwYpWoQ6tJZRDSpuEaoe3hqpacntzjfc2hkBQkqaxXf11U/Nv/u2/4Y033+Lb3/l2ZGCkwgTTWaVbGwWlpm4QIuvGvRNyuS+U9XbXGBCutd5R7I8xNxtmIDJi8btWIZBCyTtLMGYXPL6DKQS6MbTW4kMl0VZIzfivrWd2ATzRPdNXwvfnZwyMa/fcMCfvsL+bD0Yf2/F0Gyowt5jGsDveLaA8AXPG+84q1gdPXdf4ELDek3djeTkEPLYH+nvnlRQWdzeA87t1D4H7lwHNYzT4ZULOEIRI/3ql9/YpYV7p+RFjjlctW2sfdkHp3fFsyljY1TGA8tcq6RLb935L//pnbJ8g2X9uf3P7DRi6fRlaBcQIENs+G7bH3gqPrtDcOkN5fMAf/PN/xju/+S2y+RQXYo6UaV7ivMRWNdrCzdPnfPL+B5w/fky9XrJer6KlYapT51lnQBWFKpl6IToPiKFAtBlPNHIZjv1V1moIro3SabHrrT+kk5t/j7fRX4Phfhwqvay1ifmXO+/Gv+P89I0Fxune9riGe2Cs7qHxVn98L/PcHhtvX8k9VFxuhYf2oTsfY/Ri7Bx3PEbbLtvKt5fRqThHfm80jrbf+8Y37NvL2u3P4VD5v08h9NIyOMM7IHIS1PpjGt5RY2VogLavf1tjD2Lnu2G7w7JjLNi7c/fNzRi9gpH98Arz97K1/HUMonae7fC2ds7bOtu/tzD9nX60a9q/J/cZ09x1RsfmbGedetMxauAChIFA9iqlFeLaml5Gixj0Zezuftma7DuXQz46Oqbv59naul72zHC8Q9q8j+Zu2ti9j4fj2McT3FX6Z/muvvf30CgtecX2hn3rnk/3upQbE5EWCBnO0XDuhnLZ7hi2723fzdfmHuob2vzafNzfoUTeJhpAayIf1/wKB0nESrpbLoSQon2KbVFFiOjyJ0WiMTE/LincXgjt+B0mxFC+QkQ+q1qtCZOAD4LMy5S3rgEaMtUQMEgZPWKioisDmUUgVWRJSSVxIWC9w9o2YptAyJDgLTqvfucsjTFYG+VyKaIMbZVGiRjK2glFyHPmpw954+GbvHn/PmelInc1CzyntuHFf/5T1k8/RRWCUhU8b26RtWBSKECwMp4GODCCUpbIUnAlGtbriv92+pBvH7zGxDVcsqYuC9Z1xf3ZGbry5NZT2MBMW3I94RvzY773/R9w8vA+Nx/9BHNTI6aHfHT1PHptecFRUXJaZghRsFjWXDtBJQvwK7I3j2g+eY53AUTGcnFLHmCKpgQUAYNgKQIfNLdU1nA2mTKbTDj3NefNEpH2kRBxN9jgCSmlXOTt2/DVGyVjMZnw8NHrvPvet/jlzz7g+ZNn1HXFwcEBxaTk5PgeD08fgVlz+eIp58+f8I13v8lkOqeczREyo7ERO/HW4GxNU60xpgEJuZbcLCryLEdnJSKAEo43Ht0jUzJ5sIXEr2/onHOOpmlYrdY799eYDDPOizAqSAcfFQSB1gnCYZ3DBo/WEIKjrtfIYHBNw6SYMp/PMUFQGUcxyZnONIcHGU3laIRASA8y4IRjWa94cv6cr14852q1oDKexgsmBLQkeuf6QF3XVI1HeoFxntqYDrMDSTHJOD2e8ujsiMPZFCcUmjbnbvQoFvHgIIUk05o8Uyjhsc4m/iHuBYdIc2qxLobSlyKGPhYy3ndSaHQxJZ/OccLzX/7qz/lf/pd/z/mTJyjgcHa4RTf7dDjOa9giOWNGjFuOAiKmVgghtJF99xh+b/ihEOgUDD4pHZOtE0pk3byEEMP1e1czm0gm5ZTaVLz48oL/6//5L3n2Gfzwt9/l0euHlLMcFxxCF9i6xiCoiXTSe4V2kEuBDQJLiLnHvacKLt1ZEiU8mZQINC7E1BBBQJBRCVFKjRAeklLcpygFnWmkkCihkLKmLAQCjVZQ5JqDg4J5kaNSJgopJIXOmags5ogXGkSGkDKC0a7C+RBzicoYFjzeMw4RUtj30ILfFuldSh8aJ1LLEMM/36zxt45JyBG6Au5OQbOfj3g1GbHbF79G6fjoFidigxv1VaxhjCDc0ZctjEtuojRuFJQxTenZ2Rl1VVNXFcYYiqKnpJUDZYWIIWo3Q/3Vx7yP93NBJI/HeNabxmCMwfqNA5IXm/cEdGcv9kvg2fAOG57Mbilx2h/PJipJy8wP8Y/hO0Nee+zvfTjHUEbdJ4uPtTNMIzX+bL+Ou+e+HfSYvBj1FTHyTZ6XTMo5IQRME0M0C6HI8wxrLXlGjErSErJeHd57ZPAIL0FCwGPdhjfSOmM6nXJ4eESWPd3qR9NUmKaKIYuNxbqcAJR5xuH8gLzICRJc41AqKq8zlZHrHO/h8uaSybTAGMn5Rc2LF5d89cUzjo/vM5/PmU1n3Fxecn5+gRJgAedkoiMSrZPRvwoELI2pkUqSldmWHPF3KdY7KtOwXK+ZT6eEILHW7Oy/46MZz55fsFjWSHlIpnOsMzEcvVI0TcXV1TkPmjWFLagax6pqmE8tR0cH3N4eoqXi9uaG82df8e3v/ZCj41MW1+eY5RWojOANH//yZ7z3jbd58NrbXD1/wdWTz5DpnoP2pyfbd4J+AA8axcJ6rr3jCMkhGZ/Kil/g+H2vmYhotOScY4JkfXFJeTRDZRk1HiscmgyrFjw6PeON6RGX4jmPqwvOHVi74pm2nOkJ35w/4P3qOR/8v/9H7j16wDtf/w5/+E//1zR/9m/4s9UlBQqpJCsFHzZr/MLyo4MpD44yMgTPr65heYu8dwJ5QCmBTbJHcCE679l4aUtAKMWzZ19x+vrbvP3NH3D15WOe/MVPefi174CaUk4LitJxMHFY18QIyY0hyGh0l6Xo0Vq0eFmgsS62A0kh76MDnUz6oOBiDm6lUFqilCbTEp3lFPmESTEl1zMkOSp51gspECpGVWhMhTMWJS2ZCtFjXQPKYUOFdZJpnnMwnXI4m1PZgFcZk3KOzgpmkykqg9oJ5uuaLLsm0CCEjEbNXUqJHq2SGzyoozJ+wyN1nyXZeVee7oMk6TNeXb5tcZl+ChwpJE5avDM4bwhYgkyRnnzkJYQMMW261ymNlk9YfiDL43x6EaNf6Txjkkc6sGwcdmlxxiHMqzmwvLJifD4/2gEtfJR80To2Zq2NHshZRp5nSCFZLhZU6xqfTNgba1gtVzRNw/xgzsF8TtXUTGZT1lVFY00MgeZcJHJZhq1rJrM569Wa+w8fcXB8hJRR4W6aBkS0cM2znDe/9gZ10/DV4ydYZ7cupahkj9YUucrAt+HMA+cvXlDkOfODOdY61usVk+msy1lCCFxf37BerSiTNVTTNCAF1thoMescQmlUplPOBhHDfxmHMZbGuGit7mDdxPwILWAQ+pd/b9+FiELvXOJ9L3ghold+P2R7t+E6UNzFkA8pZLAkHpAQNgdV5zmhqpIk0woEvuvXvrCx7SUbHxMbi8Ie8NQHolqLNb3lKZUYOREFy5Z3GgJ0/TC3+y6/to227jEFRL/v7RjHwqb3BbTtd3bHONYPiIfeh0BwHqkyhAAlBd4atEzjFzGPRTdf7ZwPWO1hu50xAj2hUPaUZQmkC7SMcqp788FGIBSbz4UI3d78dUJBjgGcowxteLkoMQQqRkEK2vt/I7D0d2voBt0+HQFSIdhZu/5+fVXmaggq9w1tti+SGKpsCPoOx7QZZwvQ7jLHY+127e3UN8AyQ5yGPgM/5lk6tBYbK/HShdbCtd0z8XcEMyQCmcKptJZsngQmCwjJQCiTMgrRPoJZDnBCYERAHk75we/+iO//o9+hOD4gaEljDVNdoAKwtgjbsL694fNffoy5XXLx5Vc8+fwLrKnJ8gytdGRWU3tK624euv1qY/QMKXWiDe1aiM2ahG1jAtGiK2lyfdhE2ujvJ3qf+ZbusQF8QojG9SIMzr7YLFvrkRHa9aJljNs+hGRVt1H4xHtE0IUd7dHGjXKqpd29cyuIYRyJxlOth1XcF4IOKuiNPbDZV76l5UJ2j7xUwSNFtACmB1h19eyeVWDLEGp434zdQW0/eqcw5SBMNDQBFSRa7NO6W9fLe9P7uYtWjAm2W0oZEmCwh84O637Z/A1Bjdb4bp839F313UX/hu305/lXbWf43K+rROq3vw/cGSpfg+9liheCVvEfv6S7Q/vvbO3vXrv9Z/b1rwXpgRhC0/XWWOzO6fCuGJadddh6rqULMXSX9+NGW1vzsYffGbujhnMx6jW+6XzKBe5ThIQ4723+z+Ee7+oNMTTbkH7u5QNSWzLdaYjdOvcV72P+z6i4698LG+BhbF+N0ZvNsLdBsjgnsS7RXsrtWMSG5m2qCBt+uAd+bI2718bYOo0pf7pxhe2zO1zvFvYNob27+4xErML5bc/ufXtn35lsv+vz3WP7acjvDM95S6t1Ah5kb15kmth9+6xf+l7r/Z9+H3ywCGSnGKBHv8fO7a9L016lbNXd3+9JQaWlQosYAjDm+PXbD3fGEfHfbZ/p5D+xdV9u5uTlfWvlTY8geIlzNc7f4sM1UGCtQdoCqTQxn53HB4PAImUCRFI+uoBFCI1UAkn0ZAxCEZXmka7E0K3JaMlZhDZ4FTuqhAJM8mBLeeyFQEqFyAom3mOVwiEhm3P/9Xd46+E97s0mZMHhnKQ8nSM/+YJnH/yMdXVFNs+RHoINKKnJlGLtLRdVhbWBA5VTWkOpoChyJidTzvIjbusbCq05lRlL5/nrasGfhai8doArFachxzcO943X0Y8OCcsbbv/mA5aznKVY87qCB9kh/z/i/qPJkiXL88R+SszsEr/Ogj6amS+zklZWVRdrOtU9TaYXMwJAZiACESyxwQLfCPsRiADYQAQboNEyg25M8+7KIlmZ+ZI9GhEvmJPLjCjBQlXt6rVr1yOy0ILRJ/7C3Yia0qPn/A8TouJZu+HJpuX9QnGi4cI5us5y72sfcFs5njx7Sr3eoJVis1lSiRLlQUHIZ4pnWWo+s0sqIVmUE0RR8FW9YuscVVEEmuqDB03IQwp4ATblCEw8n8ILx3Q+49E776Cril/94hfU9TaC1xNOzi44P79kNpny6a8/5cXzZygFl/ce9qn2rAv52b01AbRvWrqmCWHDi5J4qKF1ReDPO06mmncf34vK28i3u11Y8JAbNGBBXdf2ThR7a3aw14+u7ZEzNAB2gX5ZZ0MI8y6G8I95hNuuQ1qDadrQVymYTEq8DI4Tt6sltzcrqtM5BofwDghg4M1myYvlLS/Wt6zrLd4rpNBIHMIb8Arvd7l5vQfTWZqmpWkarHcIqahmBRcXMx5dLlhMZghZ4YWI57HFe0vIbx1CtGolKbUKYTrjWRAgyyTzeoz1GBPGWStwUqLwVLJkPluwOD2jnFX84tc/59//u3/FzfOvqIRgOj/B2/0ojweGnORYTJRHBvOTpiOycT0vNCaL7TCUCDyl+Y7jthdRzns6JxE+pHYIXpgeSVBgejyF9kgxoV1q/vU//zkvntzw0Xce8ME373H6YMqyhau1xQkZaJg1SBPylUoH0gmEBe8tRgVvqkIWKAGFDDlhVconHxkFKQWqLDE+RNUQMnhNCacxLhgveDxSOXQBhRExT7Gk0JJppTmpKiZFEdJUiPCjqRCocN7LYGCEdDgbPLSsMyAlShQoGfONe9OvNwjhT33M92mtiGeqR0tJc1PTvN7g1i2VKujcGqlCfvue3eplUZHxRAk5OO5I0vMDg/UxJjvmSts37e09vid7b4zXGytjNCXn2xBiL0paOL+Dg1lVVcxmEzbTCd77kELAB4wkrO3hGOwa+Saedyi/7V3rMYVA79uuDT+toWktpuswNoTtT+95GXk9kbywo4wr2IVL79u5z7fs8WYRk5D9nu07tjfux+Yu0ZHhs0N+7lh9Y3z7MZ7w2LOxk9nY7uSK2GXG+Pmx4kl0NhkhhPQKIjr8laYCLE1n6UxIm2ASRkVIJ+GEx/vovW8tvk8uvTMvsdZirME6QyHC2js7O2U2m7JcrjEmYi3WYKNS3BpLZywWR1mWLKYLJpMSi6WVJuBRRLoc6QHCh/DQXUO7rdnUWzbNlu7FVyipmcwmIWVuW9PWW15fb2itp2tD1Npk7OpdiE7jnMB51WOvYzLub1q8g641bLYbThYn+M7s3ZdKUDcbzk+nnJ/OuFmu8dYyO5mzXl4RBd0QcbjZsN1umM1O6DpD1wbjg2oa0ofMpzPa1uBdx2a55HSx4Gp2wmYyR5dTVNnx4umXLG+uObu4x71H73D97PMYTYYIlBHUN7F9gS6HewIPSiGM4UZaToRkgaJS8Lk3tE6j+rQ6lgLFzfKK6bxCa4UqC7ZtSwfUtuFpfcO7sxnze5dsn3+B0hVPbcONMzTWUwrHN8SCq1/8lC+ePWXy3YcsvvtD/vjP/5KzhxN+9vwrbrY1Ukh+++w+v7y54Wrbcv/slFM55f6mpr56hnv3W5S+RlobbN2UBClQUa4QiBC5qDNIr5FKc++DD3j/29/j+X/6H6lfLqnmpzjT4k1HIT2bjcMKG2iV1GgpKbSikDGykPN4YcO551Ie7Cj/RG/xQmkKqVFSoqSi1FFBriRVWTGdTplUc5ScIEUVQ7PHNRmt0IQghlwv0UU4j7y2CBPMeaWUVGrCYnHCxSIYTrbWI0RJUUyYFFMKJZhNDZPpClWUWL8GQiQ+ISMNzFJCJH3iHq1NeESk9z4CEDLRcELkmZyGeS/2jsPAow34MdJa9D1f0H8vO6NCXnCDcwbrDdZ1ON8FnYHfx+QkIRW1d7aPfCiTczAeZIj6KpzCxJQFXWvoGovo3o7WvrVivCingbGXAXzo2painAWmK1qsbJstWIfpLJUq2W63fPX0OV1naOqOV69f8/r6mmoScopv6prpyZymaTj1jtq0eClCCC3ChHgkWpcEMwfF5f1HWNvStg1VNeXq9Sts1wWrIWO5vb7ma1/7Ot46njx9Qtc2WBcsXItCs96u6LqGSVVwfXUVBaOCtqmpN2vwlslkwheff8bFxTnT2QlVNaEqK7SeMJ1LhHA0bYuxBqkUdVTOq6LgD//m32Sz2bJpWiCEUzdtS2csxgmsV3gExsG2MeAFfZCYCDoFYcMFi8y4iKSUvbcb7Dze8/yBOYg0zPlHrFcKgfAhd5FzwQDBeodxHiclXmmEA+GCtaqUEustzoMNF/a8w9Mh3X87O/SHINYOLApWHp1pESJ4qvtolRP6m0JajzNRCTgDRvufFADDMRgFmwfh7NN7Y6DWEPj3/lBpfAC6J+HLg/Yh7IZxhokqKKWg9EEB19FCUpBlAGE/DEkyyIjaGADrCcynF1EZJgIz75zrFZjJi4MoxPTggU/fCf/uMXA5ET0ibAzBzxBWaX/+huA20DO+w7FOjH8SgI8C4x5wIV9WUjGKARibwven9de3nx1YKuV+mPMxkDvv82ibnN9jxg+YsyNA7PB7Ybpd394k6Oy+lyza99/f/1YCR+kB4jQGIo1dNr8JjEjtyEN/5qD13v6OdckooCU0QmYCbVpbUpDUqAE8CubpOAWIEMrGGYdGoYTCCEErwU9Kvvbb3+P3/vHf5+LDd0FA07aUKDQC2XjMekt9c8v186948tlnXL18zWa5pNlu8cagkSgD3hpKHUKCpQ0ghQyKV6ISsZdnotdEttaGkSBIew7fMx8BXHH5MttbKzsaQfCwyubBOotzGcAjZTj85S5LXsBuHBmcQ9rq/VpIzu+poXH+cuUvkBk7BcAzrN9IV+O+y73FiOH6yKrv//UEhi/1RyQQ1QXrXh/CjKb9eIzW2rhYfD++HuOTF4rolWi51fdYhJAkRKazMn/G+2iMlO0h19PBwLBqGfIZee8DmCgEUh8au6RzYNimvE/9+GV/74XqdYee88O+HKPFw7Np+M183eUGY8N6IZL+zAhHJJrQX9h9d9i/nH7EGwf9ODY2QxBy7Pkx+r/71HGgJN+7+zQ262fat4lZ9363t8iNK+3eWB8TvIfepvvtCYJ9IO2qP2fD+W0Yi0Qx/D3vV34vzZXoW58MPVLWqaQojpb3WV1DvmJsnIbf3osENFh7QH+e5rQi5L70ASQTgRcV/vAsTTxmimaR9/dQAR9poOwXaORhxNF3ht9zzkUiFgXEyHwd2ZIHfc2vjY1b2ntKKYSMa70XRrP+B7k/6lkDDxV4JHojjmDguvPEHaMbQ3oyTl8OlZvDSCn53thxEfkc+71IHHu8WfbtsdD8uUyT7o2to/x+/u8BD0wYIycEZVlSlRWr5W3kben7kQDosXkSQvTKsvxeeiedI1IFsd97g7XpWRE9G32QX4XqB+0YrXjbMjauQ74Z2BmbBoYLEdePlDLkEJbZLGbbJf7GvtyVQRuR39vdSTxeVIKwM/HbnReiryU4e0ic3VI3r6nrVzRtRaklhSl2bQzNDsblMXd4epd+ZFVUtIdvWh8MbIKs7+iMxbnAq7RdB05gEyeT9lEyMPRhzXfOgbUhooDUFNWMs7MzLk9mVEpiO0OH4nRe0vzLn7J69QznWqrpCZ2zSAdaB6DaWGiMxRlPTJvH/WrO49kJshI83SzpFLz2jlXn+NK2vJQK13YoJ9BFANlKJ2ltzcl3f4v5Yob91a94/oufc+0bHk0mTIoJxmhum45f1Uush3dminvzCcIZtsbz+Pd+wJfNLctNUGhJJelcx0RUqL2TwrPWihvbsShK5lWFUZKX2zXGOWZZ1LSe9xQi6sMPjakQgpPFgkePH1N3LU+++DxEA5xOmM5OmJ+cMp/PEcLz/NlTrl69Yjadcn55nxDGUmCNjWnyDDhPVzeYtkMgKMoSZ2xIFaB02Je25Wwx5fJsgbdtv1ytDWGflQo9ttbRdSYYR48oxvO9dWzv5XsjPb+LBpRCC4N1vv9JbTFdRxc92tuuA0IERaELikKy3RpeX624WDwAoaKI67B4lvWGm+2addtQmy4onpViUggUIe+itwZnQ95xa2X4Xttiui72RzGZVSxOp5yfTpnoEilLghxgYw5xh8y8cVUEjwNP7KKiJp4/LoSB9/EnOF3Ec0lAVUyZTedIJbm+fc1Pf/qXvHz6jALBpKwodUHn2yA7Znzq3vhDULD0+M7hWSPlyHmd8brD+czPkyQrj/GtAFpqnOtIwlWQHWK0CetwPgDk2gk2Ny2ffPyc7WbL9c2Sdz56BzWbsmwlXnuUspTSghNoK4KhiRUYFUKy6oLo7RXIuBUBM8PZYDSceB2hUEjquL5DBNgQfcP5YEzgUt5O6ajKsg+XXmjBpAghuZVQAeRXOgD4PoQcDQZvHVI48B2drWnNCucNCoWyE4I2XwZa7Dy9rk3K3kjJWDAunBPSStqrmu62wTUhWijZ+Rknjfwcyuc0GJbmfx8arR0rB/xzhkkce273d66g7++MPv82bTiUQXbndGhfguKCM8VsPmOyWlE3dQy1nuNMWZ/6/g2X8t3K5LH29XucQC/rtqFpGtrW0JlE7zw+yjD5UCZFzE622YNE0sj18OZQLkYkg0yyeneG98d4Nwb3x64N37nr2rCusXrHxvCY3DQeYcunB/pJG2LISUbanTMepYJxtdYFQihUxKACtyX78coagIt5xvexUA8+pNhKechtNCzTWjGfz5lOp+hCxygs4ewzXYvtTJ83GeEpC818MmU2mWLp6JShbjqsigqtmOKiqkq22zXNeoPrgqMcPqSjfXDvAfP5jJOTOfUWtBK8frni5nbLpg3fD1Eew1kUlOK7tr+JDgzn7RjOEPh9R9O0A7kk9F8ApjOczCtOF1MmlWbb1kwXp2w3GoEB4VAynMHb7YquO8d0IdpC29bI0xnT6Zzz03OatmPTNFy9fsnJfMZsNqeazNlWM2S9oV3e8OrFc+ZnF5xd3EMWBc50uyUkdrxZaG/Mf51wP6lQTrJUlkZoLhBcOMUzDLc4ZpHbDgHzPVvToNoGJRWTyYSmvUEKz8wLXixv+VTP+PrknPfVnFcImpjPyDpLR8epnPF8/ZyXn33GxYffRnz/27xqDPe05lvzc67FhrXtMCi2qmSOpPDBAKz0Fru8pnSezhqc8gglETrKpd7HVR7mznqP6DzNtqE8O+XhR99g9h//Dcsvv+LRDx/QSRHWKJZAdyRa6RAxSim0Ejv9iwyzq5zEiIBBJmwsvKcodDAwk0IEmV3JiLMnQ97ksR3ylgvVC4KhvhjVRWmFlEUICY+n9Q1KF0wmM3ShKbViWpbYLhhIaulBFChVBiM3ISh1QVVM0EWZiGmSznb0Kv2eUpZkaz1hHVKElKXpvhDhmhTDPZItuKyeWM3emRql5Gzn7aFB+MRzOrdL4SOS85mNIHXASPKIPc4ajOkwrgFjgk5TSpwQQb7rWpz1GGPxnsDL+kOaPFbeWjHufbQkMr4n7lVV9MTDOEtZVkyKElu3mLZluVyy3W7Ztg1Pnz5lMptyu1pStROSIFA3NU3Tcnl5yXQ6w0VG3BoTBdbABNZNi9IFWmu2mzUgWZyeUhSa58+eYZ0Niu/1mpvbG775rW9yfnHOj/78z2jbtlcStm2HsZbVes3LVy+RSnF+fo5UivVmxeW9S756/hwvBMaD0gXGOurlCqEUhZ5Q1yuch856hDMRcAkh2CfTKSDpOrsLG+8c1tgQbsSEA6czBuNsNDbYKQn6xRQZpJRvRkUPCGPMXgj59N4Q9MpBqPROUpTJXsjYhawKyoaQy6jtagqR5WzxDuOC56SQAmzuEeoOGIW0MXJPtbCGdorx9G7q4xBYS8+PMRg5KJvqSUq8PAwX7Dw/8jFJ74b3CYCfGHhQZqVf48b03xmCkXl/8jqGAHMSmpu2Dd7+hEgLhRDQh3I+Xo6BrXuhgY68s2tzIO5jY9o/nwOJR56762/v/WhPDgSYyAgeB0P3w0nn4H3fn35N943erbkjY9Bfj8B0Iuh5yZU1efvvYrpypj1979ic5WtubHwO523IsB8yz307Rtp4MLYj3RgDDN5U/JHv9feFx6QwbfEnGG+IHluSFgoXQnWZQmKUYCvh8oP3+Fv/5d/na9//Lq7UCELOwFIotPV0m4Z2U7O+uuFXP/2YJ59/gu06TNOyvLml0kUvYXqXGB7f08IhQ5zSeggh3shgj9GJ7A8Ymbf9dyLAMbi+vxf26xjbC3B8HeWed/l6HuZPHQJR+f7ajdPb0KYhUDWu7M3X7duUPOVJfl68KYzzcD3vbrKHtggRAK60BoZ1/CZtHVtX+e/5eeB9yHG0Z29xZM/dud5GSqo/9368ez0efuuuth9rV2L88eNregg4pDkcjnt+lqbnhu1yLoRpy8+EYXuH371rvNKPMbll+E4Bn4Pf+bn7m84NEBWOqS/p7N6BFceAlWE5UE6PfLo3CkhKLvYfO3bWvE3J3xnOQeaLv3d/yCONlf0IOOPn227eD7udzvmc3ufvDH8/1rf03I4e799/23Ea40NTSXzwkFaPtWOvf363JoftzvdW/t09QOitWn5Yxta7H/D1B3zaG8oY3z82Vm+ij+m9REN8BLD8QIjPZY67vjE8M++ec99/6e1Oi7cvbzuOeUsgypKImC9ORaOzQyB4rF/Dz/VjHP+Xnj7G6ydwJTwugqGVadmurlguX7LaTKkmc3QxD2HyolEIKKT3WBy9X4iXeCHBa7xXwcAmhnA1NoCuxhmM7bDO4JzGE2VQTwRMoPeN6vdOOCMb2+KaDmc9qpKcTCaczqfMC4W0ltYLnNRMXcerv/hzTL2m0AIlBXVr0E6iCoHxns4Emd952HSGxlvelZpKVdR0fLx+wbuL+1y1HV92DZ/YhltVUbSSghAqNHlLnIiSd7/7A0ofFMhPv3pCc1rxcDZHGcfz25rPtxu+aGoKqSmkYKEkXaVZlBM+/Bs/5Ef//P9ObTskBokM3ltexLx8kfcVnqWCtnO8P50xqSo2ynPVxby2UkQnCNkrcZLXWU7PPQEYLaop5xeXPH7nXa5vbnj5/BnOeYpqSjVdhHDpk4q22fDVsyfc3lyzOFlwcnKKLksQEuu6GFLYYI2hqbc42yGkCN4xbYOWwXusbTqkNzy4vMfJdMJy3UUePObMxoX1TwDLui5gTHJkrw/X8fD+XTQoeMjmHtsiKAujkNmZjqauoSgiphZCs2odIloVpcS0kpevN3zwXovQMwTByLR1hmW9YdU21NZGXMYipWdWFZRKRIOM4MXnrcN1nq4NMpGNinEpFdP5lNPTKYt5Rak0QpVxrIKyARHOT+kDqKrUTjHueuO9lEM4KsaDAJzR8rB/J9MTirKirje8enXNr37xUzCG6XRCqYodaBsP8vy8JSkkCVEh6BU/47z2bh1mStoRfnY4h+EM2z07vK+VpOvCt4NxRRe8q6O3UvJeKosOZzXbpeHJp9esNy2rteb88QM66fClRRWWsjAUpUZpKEqB1gKtBFpLqkkVcpbSUXhQWBQOhQ6pOCF4rhUSpGPdtsGYISrQvXA4DCgHwpFM8IpiihagpafQglILgmo9en8LTYgoEqM1eAs+GgNIT9Nt6cwGhEVQhDHGInxwUwyGIMRw7zIaoEg6J+kIhmLdxtG83GKWLc44hAhy+YAjJR/+/T15aMyX3xvO6dEnE841dn2k3hx3OeSc7joJx78hst9TkTGvay/T+4TNwnQ6paxKkNCaBqVLdqaLedsgD1O78/Z4q6bt820EemBdSP3Y1C1N29J1FrvzIgl9ELsGCEGW83vXLh/7EhDI/fuJV0jX4qYPeaqT/DUYr30c5O2ujV0feybnnYf3xusZH8t+Gvwhtj2Uw/K/hxhM4q93NG7H4xdliNoglUQXFUoVIZ+xBWMdwYk/SkPRuLM3ohb5utnlhDfGRGxdMp/PmM5mlEVBva379lrTxRzzPnqSewqtmVYTTiYznDd02iDY0DpDZ7rg4aygLAtublqctZS6RFVlH0788YPHnC5OaC/OuJWe8uyEm9cbnr9asd3WFJOiXx8QsD1nPc7t6wCOndXH+NWRi3g8pgvjIdnhECEyTFDCTSeK05OK2bTgerVhLs8pijLksPZBMd62hvX6lrZpMJUJhibNFo/n9PSM8/MNN6slr2+uuXr1nK999FtMZ3Oq2Rw9mSFXGr9d8/KrZ5ycXXByespkNmdzc9PLOKLP6b5bZ0Gp6Qn5uxQSwUZYttJyz2seec2vMLwWjolXaBQCicHR4ambBjWZMCsnXHGDEI5zUXG7rvm5f4U/EXxjckbRNmwFWG+RXuCloKLCOMfNz3/F1UfPmP3dv8Xn8zn3l2sey4qHpxUr3/DpzS3nUnAiQJqWrZGsVIlcLbloW26soSsEoggG9dYD3iG9RHmPFAovPMI46tWaycmUs/ff48H9d7j69Esef/+7aKmxQmNsF/aKkAgdFMtayTBGPeYAIPEKuhR5WgrwEiVCyl7dK8JFP/aBZQnh1r1zYa1HjFdEi9+0Lk30gFJagRcIr/A4TGeoqilS67CfpEQ6y7ZrUMIidOB9dTEJZ7UHLQuqsqIsQ+Qt4fJTIZPBIp1KaaX28J4BLRIxuphIkUFFxLSTfJsw1IymJV0oBL0hIkrDPmFbSWj0kT+LYeq9C7nc2TlNJD7UR95CELzEEfHHh8jTbdfiRcekrMAHw9Cu63BdBwSZTyKD4cMRI9hheWvFeNu24YVBDueksNVoOisplKJSmlXXcXt7i3OO7WbLV199xde+8RFFMaFtUm4vjTU1UkrqumW12jCZzWIuG4+NhNk7z6ZeITyU1YT5SQjh0nUtQijKqorhjEA4x4uXL3nnvXf5/T/8A7yAf/Wv/zVFVSGlouks603DyxfPKKsp27rh1AuEKlBFyWdfPKEsSybTGcvlGl1MmE3n1G1HoTV1s+XFi+dcXJ4FDzPnSLlX267DWI/3IlgBdx22aYPQYEOeqRwYbLfbyEyXe4et937Pyy0B28l7Jo15XoaHaA4o+X6BhcWmpeg37X4Jh4jWCuGIVtq7sOZSyuBhns19Dqj0mywTNoegKewAkiAM6oP2HmNc0t9DAH3M6zAvYyD+sefHwaHdATvMWZvfT8xGKsM8NlIEzwbvoW0bbm9vKauKZtPgOvNWmZKGAPawP4EmHfZ/HyA9BDbzOQwv7YNi+XfyNoyVHUB/yGgceG2FF/bfG6kvJ+wH3xYB6POJ+IpDsDt5AbuhLJSE4RGe6Fhb0vW3yQU8ppAZKlT6NATZ/hdifO8M67kLLD0E9e/uY96u1L83g/6CnZPePnjcfwMwkflWESDKD20PKC/QSKgUGwXV40v+5t/6I37wR7+PLwu6QlIgcF1HqTWu7di+vqZbb/n041/w8stnvHrxAiHh9uYa7wIzam1I79GDX9nauGtNDwWg4TiNgf45oB9A10PPz736emZhf93knoXe7+/NfO0NBbp0b0gP83D4uede/t2ctg3X1E543V8Lh9EyRH8W5u+OKQ/HvnOs5MYKqT9v2of5nIx+Q4Bglyc+n7u+fhc8MPK2j9Gf4bq/a6+NjkEmDr/NPh0ro8LfQDDMlW5H68l+z40lxtfEeCQPcce8DscxXRue8Xf1c39u715LQ5r2prQgb7Mex9qX80FvXfcI8CfiHsq/M3ZW5/cP5uENCFiiT8fa+KY1vFfPW7xzrA13jXXeJyFETyfzdqT15qLRZj6gPrU17q8hn3oAUB3Z3/m+dlGQTV7px9bbsf4M2z7sz5veueucSkreYUqJNxbx5vUyVobt3QvVNmjz3rmYvTuk0fk5MeT3jjZ/pM501ifjluCFJejNTjMEYEw2yH8/dtb/z1HGeMFDurnbKbuTJYTV0wl0HyIgd5RQfVwh+Vyk+RzhLd80QtLC5mbF1cvXvDpfML1UzMoOWZjeM0FR4pVCeBWj3BDy1wqJQ2JcWO/Od8FbyTiMN3Q2GJxb5xEEOVmlucuMJfbmnehl61sa7xGyZFKdcHl2zuVUo72jdQ6vSyqtkV884dVf/TkzpalKjfCC2rQh0hGeVduxahqsM1gled00PHdbvlp9xY+3r5HK8WW34Vw2vBKKp9byoutYtJrzsqJRHmkss87zkZzxNxaPuffNb/Plj/4Nv/j1L3gmHR/Oz3m/vM+vNi/45WbFq67mndkDZGk5PTtjVW/YTmcsfuubnH7tA57+6pc0tgbjCEnmg6+NRmCxRL9Qrr1BdZaLyymq0CydZeMtAhmMWmMkIRcQ6GA82jmsD5HnEt313rM4PeXd997jnXfe4WeffMrt8opiMqfQE3QxRZZTiknBq1fPefbsSzbbDe+98xipFLOTBUqXtG3wprbW0Gw31JsNwnuU0ngUpjXoosJ7h/Udk1LwwXsPY8Q7STLNEkIg0CHUvg9e6G3bvtX+Pr7nD88k5xwu4j1BISUjjBgMCqSAelvz6vVrJtU0hOQUIfqT7QyTsqTUE5ytePliy7rdMtczRIws2NmWZb1hbVo674IHrvMUwGJWMdWKrrbBOLht8dbRdY62qem6GucCyKtVweJ0zvn5nMU8RA4ARYpSFozJLNZJpPcoBEUMF9qHUidEbAjKz5BrGEBIFYDlqPBUSjA7PcM6y/NnX/LFZ0+4ffmcs8UCISSms3jToRXRSCOAzFJG+GknuoUw4Vm++CEOM+QbUjoVz2EqobHofgIBcv9cCp7pnpAvwYUIBVqjRMDjjA9ArpQ65PWko7WGspygvGLz2vNJ/ZyTr7bImWSyqFBTQatblBJ46VBaoBQIJSgKzXQ2RSqNtgJpBcIHmhhCqwea6HFI7RFaom2zi7qYFOOio6gE1VQxnWom0wlSVkgRAnsVUlJqSSmj7CY1IEN0SAydMxgbaEOI3uVjBM4WpSS44JXemQ7pg9GV8wJjoTWBZrbG4UyBFRIjJcZrrl9sWD9bYzfBu7D1IaLbb1KO7cmeHxiRq4/yZke+McajvYkfGePNx+pTyYB8ILtLKVFe9bQkGc1IrSgnJUVVorTG++CIJYXaz9kdeYCdImNHpUL0u7ujXe3zmWGfmYhtb+uapu0wJhia+WhkJCDDB9LfQ6X4zrhekvDkeD9OQqon8QAegrLLB/w650FyLCUf37uu3XV9OBZDfCV/Jy85ZpBQrfyaEKL3ph/iwWGc2c0V43xdv9azJb/DeIJ3allVIeKIdMymJ1TVFGs9m00NXlOqGBXRh/npHdZG9pFzwViri2HypdDM53NOTmZUVZm1EbouRCExnaU1FocPoaR1xayYgjC0LnIYncerYCwoNTRNzXZdc+/0lPPFGd5JPi2+4Pnz53z4wdc4Pzuj1CH1zsP7l2hKrpdrtt0W50yIXOgj3fIC0wmaraOs7KiD295YvkG+3cOa8BhjqOua2WwWeFFCash0pmjpWMxLzk7nfPbsiqZpkFLhnUKIkAe9sQ3r5U1I0zs9wVhD0zW0bcv52QWrVY3Wz6jrLcvr1yghmM5mTOYLysk8eAPjePnVEx6+9yFlWXFxeZ/NzW3ka/tOkNIl7u1/QupQLyStMKyEwSJ5z1f8qWx4KQ2PfMEUhYj03yrFut4yV5qqKECW1Gy5V8152W75+Po1ny1v+d89/g4PNoIXzrB0lg5opWLqCyZMWP35j7l+5wPe/0d/jw//6f+KX//3/0dOleaj9x/xzuU5P2lueN4sKVrFak1YN2rK/OaKx9s1MyEwQuKswHpBIwSO6GUsQ5oRqSTSCmy7xVIwOT/no9/+If/Dv/p/cf30GfN7D5BS0jmDUkHpLIjyIYAPTq4pTWTiQ1pj4nMgZEjDWeoCJVUIayWT0YqLSmCHdSZEqXYGVNjrSsaItJ6guFYy8l0Bh/TOgjVUxQytJpDSXgK2bsCtkbYDJSmqCWU1Q7QdOEuhC6bTKbPZLOhojY209ZBeSY7Tw71nSTR6gIH7jGeKiqI93lkQcZdEXsbO6pCux6boxaTUqg7rgzzRRxXMjDwcIby9VuC1CNGQnMJ5x7yaBW9302F7gzuJwYe87YVCiWJ03w/LWyvG67qmKIoeWM9DaBdFwWQ6obMd29Ua03a8fPmS9XodEtxbw2q1YlPXSF1gnacoSnRZsVotWSxO2dQNTduB7tBKY4ylrVu88zRNzc31DZPJhPnJgq4L3uNKK66utkgZ8gpY71G6YFvXvHz1ivsPH/LNb32L//ijHwWmXWra1rBcrpnOT6jKCa9eX+GfP+drX/s60/kJ11dXCClZrVc0xiBVwbpuePHyNa9evqQzNffuX9B0Fh1zoSbrqnA4GKwD74MC13RdEMYy70Nng/fxdrulbVvKTh14wKVnlQohLDabDc45ZrNZ/9wBOCUOlQ9Jqe5c9Kp1Lpnk94ej9SF8r3c7AMtagxY7Jb21QThVSiK8HvEC333Tu8Dw9WAiI0yp323G3Bs7D6049IQaAme5UJSvySFwlIddz8coXN8pfVJ7h4qDxNSktg3B9bwfOQB/ALSJQESklEg8Z+fnFEURwJiML3ob0PQYcBcYzH2jiTQ2fYhv9knVnmD4Ft/O740B3MeAu9H6/G6tHCtDUPWYYmAMNE7A7/C9xHgnJt4LDgxFxr6TezCOFSlkb9mZ1s1wnLxzMYep2FvXef3Ddhwy1Ice/2PA7tuUYT9/k5LA1zwk9ajBAD54HgQ+IuR6TEybB6EVNeBOpnz7D37ID//h32N2cRoZbRWwirZDGc/25hrXtDz95HN+9O/+A77t2NyuEN7TYdBahfMg5VBKZ6sf72Oag1xpnM9fPkb5Ozvg5DAka+RJD9bc/tjt13dshPP2HCoZYl7c7FpuvJOvm1xpkt8btm1s3QfSdeiVmD8Hh0zU4XgLUnj6vF93lSGNG9snY0DEm+rOPZXTeCmldt6b3kfGdbf3RwXWwZgcC9k8HJMdLZEoLUn5n4+VYX/yv8focP4d2BmyDa/v1ck+UDT2zTeVJJCNXh9+b+S8zs/nnIYeO5vzfgwNFPKxH+6JYTmqNPf04aeG4ehz79ixuTi2D3qhte9/IFAJ7Hjbkrejpw0Zb3gM3HEHFmL77R6epXvDcWS+xsZVsK/UztuRz2Ve54HHMfs0b1jXXSXxREMe51i/hnUOI3RwxzfvGrN0P/HcY4atQoi9iERvmgMh1R5vk3tJDPub76O8rYn/fVOf3lRyejyM9DA2d6nusX7mntzHeO1jJYxLeKaua05mc7xPQjU9ECiE6GWjFNkrr2MsRUDexr3vjazLu3ji/3+VMd4j533fruxLC977w0MCiIHS93ie/Hvp+50zlFSYrWd927G8qelObEgrJUGp4NWrXBU+IzzWWxBRIRYpCk7ifI31TfQ6sIQQnV34XYAQJaqQzPSU1nTUXYt1FqVACo0QKnxLa5wrmGiJqxZUs0sePnjENz58l8t5gWta6g7kyZxJVVL/5U959vkvefToklJoWuNxxuLLiqmCl1vD2rR4b3gs5ny6veU/mdd8qE+Y6/t8d3rJWhSs1YSJqrgvCloEi/mchdC8bpdUznHuNJU3iH/wXfxM8OzPfsztx19wNr3EruHfv3iFayxTo3hHlJy7gkfC8eL2GjM54ewP/pD3/5t/zI//7M+4efJr5KzE2ALTQsrTq9C03mAkGC1ZdjXCtUyqgtq1vKrXNM5SSoVG4olOCymdgJR4JfA2pJvJ99G9e/d4/M47TE/m/PjHP8Z2NSdnF1TTOdVkwWy+oCgKfvWzX/P65QumZcmHH34NpQoWizOWy2UM2xsiECYnAa2CEs50KRqdw9gWIWF+Oue99x5Tb9d4r0DEyHeRJhhj6NqWuq5pmzauSwm8OfzqkA6MybbeRw9PomODczE6YMj5WmrJarWmXt1QFMEBY3FS4JqO9abh4buPubz/EO8rrq5b1tsV0/IcoVVQ6FvDpt1Smw4DqGjsMtUlE60oVEya4hzeRtoZFddt28X5kZRlxen5GRcXZ5yezELOYqHAu7SLQ38THZfBs0npXWS+1GfnQv0p5YlQ4exWMoYF1xpRTHjx8iWvzSuunr1gqgNuaG2oVyuNsh0tAY/K6ccxvnZ4lh8860VvlCCkCDIn+7xAeK9/gYFUBoRc4t57kI5qorDGYW2LlB5VQddtA+CtJQ6FaxRKebxtQVQUfgI1PP/8czoM3gcjCSWC4Yb1BqFciNAeEXilFA5C6GHrI2qsmKhJNPi2GNvhMHhloRAxn6hCqJBj3tAwW2juPzzjnffv8+57Dzk/KykLoJKUU4EoFSFBazBwMN4GUF90WGfDOvO2p+vOuZjWogz5ignpKFwMuy8IhrGdMWybhk3bIZgilMZKz7L1PP3iitXzFaINZ/3Wd+iEor8tT/eGEs64/5xn7uiht//EHe3aO3+juuLY8z0/IgROCFAypBdTkgcPHzCfz7l6fcuvfvUpm23NRBdoqfYM4PtviYy/ix6N+Zl8jIYFXjekcLA2GBJ1XaAfXgAqhbOPeyj2KdQfeCfVa7t3/VcZRpB/WWbt2aXw2fm9jxn0H8iTR/q0Pw7jfGj+e248foyHHRvDMaW4SGfPiEF64KWOm6WOycvpvfRjbVAQa10wm81o2g2TyYSqmmAsXF91eLeFSdF7t8rMsLdPfQGIrH02hil2ziKVZjabszhZMJ1NQwSvaLBkjemNolST0q4FGlHqgrKoqLsGXSmum1sqKqQKhpovvnpJqTXvPHrMo3sPMcbx6sVrfvpXP+P66jWzScnFxQVaC5rtikeP7/GD3/4W5azgV599GRz3PHStReoKVUxQsnojjvK2Jced2rZltdwwm82is2ZIzJM86q1pmE4KLi/O0OoZy+US8AhnUBHDVFLRNmu26yX1dMF0UtG1Ldc3Vyxm5xRVyenZGffv3+fm1QuWy5sQUnt2wnR+ijk5Zf36Kc+efsHis0+5d++SBw8e8OUnv9qtkzinSN+vKyccAosQgUO2WoBzbETLBviam2JLyfOm4Vu+Yoqkw2IApxRt2zLRLTNdMj89YXm95H6jmPsJt2i+cFv++dWv+C/Ld8FZ1hhWeFwj+U5VcqbPed6+5PmXf4X5+S+Y/G//Oxb/5/8LmCVfPH3Bye2a/+aD72LbP+ezteHyZMaJmOPrltX1Da9aeFyVYGHTOLbaoKsCrwuEC/xWZw1CKgqvsd7SNDVMp3zzj/+If/U//D95/slnvFvNmSwWoAQYYmSOSBH8zpCuKFSkNx7vbDzvRIwWIEJUn6JASYlwHu9tMA40Dl0EJaz3BrwFEfhT5w2ddWGPRZqejMEk4H3Il+1RKOdQRRnOcRHa4aRFlQsa14EW6FKj0Vi3QhlJpQqms47pdBr5Lxf4CyEYQ7WO0rOMGqVQ8KMGPQTaFS7mPBVjJLbHcZL8mMv3UiuEAm8cnbW0tsO4Di9sFCujwaI34DqEd8EYqNRoPaeaVijtmVDQ4dHOUpUTcB7jLN1yAz6kKFTyUDcxVt5aMb7ZbJjP59R1jbWW09NTJpPJzqNZSupNjXOWuq65vr4OXtFti3eOk5MTXr++RpYVk8kEieT11S3b7ZbVpuH6doX3HmMNughexMKHPJ+b1Zq6qfHO8fDRI5y3bDYblJJc3ruPNSHMi7Umncx8+eQJjx4/5tvf/S6/+3u/x3/4j3+KtSH3zk9++jHWSoqq4uzsjC+fvqCJQlbTNEFgUiG/z3L1CzabmvV6E6yWmw11W/Ptb3+TzlgUhBzqbRdzSEnapgkEyIZ2SqFCqLcU7945ttstTduy3W5BOBaLk/1F1B98ISxAslbyfpf791jevhzY2RkwhFBY3vlghRjXrxAC21kQqvdIt9ZSKAkROLLOBoLrD0GjvM07BfQO9E1gYHovtNEjxE7AykPJG2NGmZ78kBoaBRRF0bchN9jIlZKp5PUkpURi3Ib38u9773vlfWrrGEife/fnQGEqSqmYG8OHcGpkrOUd7TwG6OZMWB5CZjg/++Dj4beOKQzya7nCYnhvzEs07MXdu3eBiGN93/2uRvuUf1vEsCZhDPxOORCFenKrWugVsiE3Ylzb+GAFxn4I/uG3hyGW8nvJIncUjIyCXwoNO/xGLqjn+ywfo/R8rozNDT/223Jc8AFCO0bGcvjt4dwMSwjhdFhHf99DmVLbGocWOgj+QtBai9CKjRY8+PY3+ON/8g+59433MKXE4lEOShRi2+Dajnq55ulnX/DVl0/49c9+jq0bKlUgTQBTikLirccL24dsT4PqCSHedLSmTNFPxhQKw3kbzvmxvdVfH9CPfF7253m/jqFglYyFEl3LaV2sda+OvG35ehgaFQ3TV7ypP8ECNVg2Jtp2KOg5jNlXdKQ1nr4rpUAK3a+TY8qxvOTPpN9z+prvhbz/YzQ0Xc/Pivzafl3hmzkInI9LvieHY/imMnzP3TEHY2V4PqXf8/2b7+Hh/eF6y+vM687P53wOhmMw9OI/1t6xKBTD9TZ29uaM9N67fU618ZJ4pLs8xdN3xhSHY+Ocv9cz94O9kP4eKgjT+RsqoG974q3C/jpsy9iYHaPLufHj0T4zrhwb1puP/ZjBUx7tZKz4YdtGxjPnJ/I1uDvrPIhdaH2gjzS0R+t8MDr1EaEL1v6BLh1r33AfDPtzMBbO7fIpHun3mCda//4dPNRdY5RfT99IYdRyvu+Qvz3c33t9T2gm+3t0yNvn/OfYHh8+PxyHMd4vtWHI2+ZrLd/zd0UG2fVnn2YorZEquiFmRma5kVw6B4bjlEfYyNvR812Ds61vQ2pP2tsHrf7rlaZtYs66UHPKb+clBM/Y8NX0/+DPtQt7XHpBJUoEIQy5dXaPTg151jAWAna+9oDEiSRmixCGMKgBsbFdeNHzV1Z2WV2hPkVQWFlR4PWcWXWO1hM8CmkKtCwQ0UANl74Vcnd7wFiLcV1QQgmNFy2eLcbcYl2HALQsQ1vdGudlCEeoCrZS4pVBaw/a0YmOxjXYpmHbaOpCMD875fL8Hu/qAunXbNQCqxQzbzl99gVP/8X/jcXslKqYY72hNS3KOU6EYeOCh91ElVTTgi+uNny+3fC31ZQ/eXCP33vwAOEr/uzTjtelpTFrNnikLlkvW1TR8d35Al147NrRNhNWf/tPEJ/+gtcvP6cxa8pyxvXGsLy+ZXJ5gvAnaN9itePTdcMnmxd8/0/+Cb/929/Hzmb87N/+SwpXIMUprdhiWDNHUYoQHl55hRGKWy35pHvFt04fo8ozvmyW/Gq9RG0NVTnBVhKPwbsQntPFHMvWGwwe7wTKeZQw+KLk4de/hV7c42c//zVf/eJnLKpTqnJKMZ2hZycgp8yLgs9+/he03Yr56X3k7AGqmISwvW1L19Y40yC8Zbu5xfqQVg5nMXVDpxx6smCzWnGxELx7b8LipGR1s8UX0WsE8ISwsqrQ1LcdTdPivEMWiqQUHzun8iKEAO/QQkb5MeMd8XgszndBIdoajG9ofENnLcLA1CvO5xNaZ3j5akk1NZzcU3z7++/jjef5ixdYYFmvMVKw3Shk972AKzlP6wSrLWxqjfcVAgN0eOEQFRSyxboJmwZWa0Hdaqw3bMyauttijUF1IYekPoF3zk94MDml4gQjZ0jlca4G3yGcR3iBFzVWa0yt0KJgXmrKiWBjWmZe0XlHazs2bce2NQgkFQKJDfmwDUwu5uitoLneBuWMlmgmKCf6cJsIaJ2I3q8xp4J3CBfotvc+5uDancNCqEjud57dAVuivw5ZOHURZCWR/bubxp2cGGvc/R3YD3ACj0SpYKSTollKMUGwS0noFDgEUgQ51MsWKRVTOUW2Hev1NqYE8Ds+LOHMPoYXTeOSr0cPS2779RbGIkZEcEmeF4TIkAaP55VwvJgteXJ+zRePb/n23/2AR+9/gDmb0wmoaTibg/Ye13V0PoRPNyYow4XUIQ2FdeCDQbsPahaU8ljhME5EQ6Ng9Nx1BtM0mLrDd+DYossKraYUG83y+QucV3jfouyGCR6vypCmIfV3cGru+ORj8sVuvoVITg87yaD/LXs948R3+/tIGToijD8zzo8f8JD4sL5V5HHw0TswLNxEZ5zTuG6C6ATeeNyk5OE3NPceV5TlnD//yzUf/3KNfy2gjvyOCue1sZa2NpjWI7yi0CXetwQdqASvcCbKRBKIqROkkqjOwGSO7UKOeIuhEUtwUPkZW99haFGE7ZHmTcS+Jt/pwFv06Gav/M4Gpuc5VB8lK8p0MvLIfcaGQCRElm5S+J38J0SoPzTCBwOREX4mPC1jm/dljVyZ7X3ADaVSkTwN8BlE/1+cxNgg+jYIEfrBwFhBygyjgN6ghGhUInyg90JKsA6Xvi0lQc2l8NZhuy54oerIVxUaGkFRTpnOzphOT2m7a5ptSJ2gdVSKu11KOutsxB5CHwsE3jq8DnSoM4bpZEZZKE7PFsxP5wgtkE2INCNcS2dXmG5GuZlwvYaV8EjlmRSaYjaDumRRGBbTCcYH4yHvO768/pTf/foP+cb7HyAlfPrkS+q65o//+I+ZVlO6umF9s6FQBa3QbJcv+MaH73F6cR89OeNPf/SXnM4rvDdYX2NxeAXOlX301tzQ2KXx7w+IGAEsi1ZxuF528kjbNdiUC10VhHzH4bm6g6IseHjP8d69ks+f1shqhsXihMchKMsp7XrNdnXNdn7CZD5hVZecO8G6XnJ6OuG9dx+z3W55/fyv+OrLT7h49C6nJxXb+YR1OUFPLuiaDcsXXzItC8rLr6FOf4q9fYW3wSDPCwnKY1yHFlOkbXECOlVQUWDpwAmuBHwuPV+vCr5j4HOveSI8U2FZAIUrqFsAi2m3tFIxK6eseInx53RCYOgwNDhxj69Vc/6q/oKJrelcwYu248qsuScmLBCopy95+S/+Ld/5r/4h/+7v/AH+3/8LTrYNZjOh/OSGf/T4fa6d4afrjuVqxfTsFP1yy/PtS9T0MVPh8F2D7SqYLFgIQes8tXcYL1hgMZQ4JKpuwQvkg3t853u/x+effkrz6AJ5WuDlFEUdjOac7WkfKoRWF0KD9YH/kMETX4lk7CfRqkCKAkEJwgZDXA/OSayJxmkIRDRICDnNIfkVSSX6vOhJKnXoYJiogzNOikoX5FQQSlLKilJM+nPCWPDVHE+LMo5SluiqwhYhHZOLVCV5xMsYaceJIC3m8nK/R7xHIDEmnPdWBJ7MWYv0DudVSJmD7z3lSbqVSP4CL+N2hk0BhEF6KAQI4TDRhLmKvJh1HrxCUqDw2IjPOixCmJDDXQrwBd50WapwgRaBRlsX+jhViqmuaGxHt1lSCMFUh2Q03u36e1d5a8W4iZZBCVDWWrPdbjHGsFgsqMqS6XTK9XrL1evXvVK8bVvu3b8HwNXVNctNi/eO6XRKURQURcnJyQlX21u29QbnHdW0YrPesFmvscbSNU3vzfzuO4949Ogxn332GXXbMZvNubx/j7YLluObzQapJNt6w1cvnvM7v/d7/K2//XdpWsdPfvIzVqsN601NNTlhvanpjGez2fDsqxdYYyjKkvl8xmw+Q2vFersKinIZcxH4Cettw+urGx7ev8DUdQxJAm3T0lqH1pq2bri9veGnf/ljHj14yMn5BQhNCo8Dgqqq+sO4KIre6KAoij1BbbPZcHt72z+fKxxgBy6NAVt7B0NcnCmufwCMwvw65/BdRyVlCEvt2OUgF/H5eKgOmdPUnnQQ+bgR+qU72Hzpz/zgGgvvOwbO5QB5Aq1yZfSYx+0xgTcBTGOA+66t+6B/Cs94DMg7ChCndpM8kz1N0wRQ0wYDi/Cd/dztY33Ir+XPOuf68P75Nw+UEZGIHWsjgNTq8IHBM/kYpL/fpFA4AHvZF04OvxeEv7E6e6AyWUCGm/vfikJS+Ej2nPcHHx6CvmNr8hiQ3b8n9schL/31wX49BLQPlYFD79/823ndY4qdY8B4ENIOr6f1MqbEGo6BEALcvhg7HEfhfQztIiiLCuOhA5xWmEJx+fgRf/j3/hbf+P3fRlQaKg2uo/AC1TmkbWHbcfP0KT/58Y/57Je/pllv0F6gPVgT8gxa74KwJ0RvmZendAhK5hzkHY/skI/X2L0xkPwokPaWZah4yCM85HRv+E5aL8f227EyVNyl+vJ6hdh5MIZ3oqcp49/znoO1ltPkUNeO+IyN2zEr/1zxc0zpkxREYx6L6XtjNOtY34Ge7xhGFHgTPcjLXTRjN6/j7RrWc2ytDb87XKNj62eUNvv9GbiLfo+dz/24c7fHxgGNuIPOHF/byUthnw9K79w1VsO23DWPAZTc34N3raHh+4dGA54QPoteWgp1RGXnIOxnniM+1XssksVdfdz//TDqSGrHWB+BA55kLFLGyJcZNnGMng3nau/b2TmVruceaxAEKylCODUb6YCI/BQ+5Wl8U1vHy96YZO07Nu9j38jHbkzxPIzAlGjvXXskyR3De3edBQfnFuxSUGbrbYyPyNsxrFtlkXKO8zWHc3BsH+Wep28qh21jJ48kgwnnkAkIdeO0fliGZ0v+7NCQafhOoKUEfvQ3oEV3Fetcz1/KvfoG/GcO1sY2hHdkBKfZm6v8Z8jzRdIHIqOH+B4S7uHhWG/6nRTKcbC2hJDxTIVCaybllKqoYn9imqf0DjLoxzwgZLiRAJg8xDIeISxCtEgZ8+ESwhx653YgtQj6COGCl62MPfBO4Ay0raM8nXI5m3M5n6KLEt91tF1HeTqj3G7pPv2El7/+FdV8jigUpgth+ypdoouS15sVy85QILhQCismtJT843cf871Hl5Sl5i+fvWbjBGcxvZqzoL2kc55WKSqpka3DyYryvfe5980PeP5/+pfcvHhOa1rmaoJ2lm5TYy+mKAGFtZxvO35mNtzOT7APH+AnU+qvXvH0F79CouiaDmdtWCMelA9+9gqJRbD0ho1pOZvO6bRiW7tguOp3hs6+P9+zM9/n+UoFxjouHj/g/PIexjqefPE5y+srTqoFuppQVhMm0ykn8znr1Yovv/wcrTTn5xdMZnOm01l0CGix1oTwitbQNA14Yhhn4pkcfd8FnC7m3Ls8D4oHguGHkhH4jtsjORocM5Qb26d78kD8Vkp7u6MJif+0eJ/yS7reY9xaSyk1i5MTGttxvaw5OZ3w/ocP+Rt/8ANOpguePnvK50+veP5iyXazojOzCGwG2toZS900mC5sEmc9zlo6EcFOIdg0LatNy3oTnvPO0XYtbddiOoP3IQz4yWLKxemCxWxOqSuETGHUbc/vBIZ+Z3AjRQCGVW9w5qPHoAn5ZYWgLAomhQo5P73BOMOkmlIoHehwf7bpoNTK6agQ/R6PJyVC5mdj3PP9PIj+enp9WML8sPd+/u/4ImCPdu/aRq/I3n0r0lOffyS8H8hvzDErFFpqKCS28uAEXdtBvzZThb73uhzry9g17z0qnUsQ0yWGXNSdaWlWhlfbG7a3Dabo2N4K3vnwMef3TrBzhWlaJhMbPO1MiHrpMQgpKYqQU957j3AOLwVKhDPUJosBH/rZuEAHwnp3IZqm8WipUV4DGm/ANDZ64yU+lz76zW7Ossns5+swQsCxsRH9vxlWMZBJctkhr+8Y//Qm3lFkGNPbPD+se/jjhcOLDvwUax1lCY8eT/noOxWXFwWX9wUfffuW1U1L2xiMCflYu07QNZ7txtLWgNUoCkoTjJms8XStDcZBOKQSQFACFVpyUkpWBm5eddxetWxXDZ11SFTYi8L1NHCnMCZcSKrnPWUwvQw9HJc9z+r4cIjusSeFQuQ5IgHYm9+9ccuV1dm4js6H2Mcixu/vz+no3PVMzsGNWPzBTTGou+ebiOs8ERCRYSL9Gs8cOdjJmOEnpLGYVJPgSAeRPidPcY8QO6wk8bE+0aAwWYG2O9vLAlqHyLXTyYSiKDCN6ZtkrcGaDh+j/LYmnNlCBLlgOpvgMVR+yrQosLbjxYuXnM1nXF7eD2l019e8fvUcU99yXhWUsua2uWZ9/ZrGddTtlnp5zWw+59H9C77//e/w2edfcnt9y6wELUSIF2Q6ikIfGAvnqymiLfRavJxn5nCdpL/btqFrW9RkEo0b8nzjnkIqZpOKB/cv+fzJ58F4MBorIQKm7msbUsJsN3RtS9dZ1qst9bxmPp8znU6YTicgPKvViofvKWbTGbPpnEk1Q6qgstuslmzWKyanjzhZnHKzfEUfckSA9yEyjPcu8gaxL96jfDBsst5Re8cWx2MqPhaGG2EBzT1f8hJHiWMLdK6j7mqmumCjJF/6Fi8FBofy8OvmFS/f/ZB3J+9gl0terrYoOj7raqwXnPsC/bph9ac/ga9uuPdf/QM+/uTnPP/0l7xqX1M7w9kaFvMT3puWvLYe0ywpt4b6+ik3lw9ohQ6GfV1I42GkwIkQxch7hbKOTnl8pINOBcOFR9/6iE+e/Jzm6obpo4csFhe0tw5nuhCRJYgBYU6tw0kbjjXnIzwTogVLQe9BHTadQHqNVCG/ufc+KJSFQymBUh1KtUBHoWw04snIQcZDyJwm9skmfD9niIjTRjrpib4PWuOtxbtMt5AoSvw7nXNSygMSJYU4pMEZptCH5I+b3cc971O7Ik0J9MP3PBLC9+0g+63/RXh8NCTKZWkpJQqNFgZnEvYcUz54GY2hdCTNKUK02EW7jnKKkBKNoyoqxFxhCjCdxJi3O5N/I4/xruu4uLgIuSzEzlJ+vV5TtzWz+YzNZsPV9XUffkVrzXe+8x2stdwul9SdjznEtyjVIlXNJoZpd85RTgqapg0CowvKw67rMF0HzvP66pqLy3M++PADPvn1Jxjn0Lrg3r0HaKVYrdcoJems58WLFzz76jmPHr/LH/7RH9N2NlhmbxqM03TGsq1bpJRst8F7t5xM8UjqpkUYGRTEUmFsFAJMB8Lz/NVrCiWZFiHs+2azpTMOlKSum+h93rJeb1jP1sxPz0Hk4b7DCkkAUG/BFT35nAsKdq01ZTQ6SIdfrqzIQSzggAlI87R7Lno7RGLunENHgafZC/dug0IrO1SSADgGsu+1ITzcv3MIjBFCz2UAWp5rPA+hOvQcSYBhGiPY9+wYMjhDUDpnukUEY/zA4ysHJI8x4nmf87bl3xsqMz3Bqtnj8WJf6TQGUg2BxGPA2hBovqvN4YVDMHEMrD32nbFnxpSonv0x+uuA+KnuvC9C7IfPRYgY1itZMiVleCLoIx/JQLv0TLKoSvXmvx9jrg+AlDsEtyGY/qZ9NDYGw/HPD5SxuRkqOvaecelg2+9P/u+wL8Pr/f3RVu+KUhKhNLUz+KKgEYLJ5YLf/Vt/k+/90R9SLuZYGQ9L4ym8xDcNorNcffWSm5cvefbZFzz//EuKKNwFligwxCiJcALlEw2IEQQAY00/9kodrtOxUDHDPZiPa372jY3JW5de3hkHznfnxGF0kN2zohc872pD7tU6pFv5GIyBguGa75mksXHZjcPhesvrdlFRNbaOgkB4KGTm9DQ/E/L383YN9+1xxUcCyQ7nNz2QcuykMdzv67Dvb1/22yYOaNRd9Ptt1ttvQlv2Kx+hryN15/fGwKWEOYzR0DvPpsF3csONw7ncGYUM+Z30/tvOy7GzrV97dp9fGfb32Hjn63L3fPgRBIVuuhb+EXt9Gq7h/N8hb/Wm/g3LAY5zx1kx/O7YGhijHwk0HX4n/94b12Xch/m+T4ZDqa3Ja8XaoDyUkW+VQsa8pePfOLYmx/r+tmWsrpxmHqNfw3Yd0MbhNbdvdDA6/kf62/9LULgO9/DY3/maPDwnQm3H9t7bjuGQjt9Fv1MZztUeL757qgcJesVF1tacbx9+Lze46ts3iKQx2sbEYg74hb9uMcZADJmK2CnHx+Y8ABd9M3bykYyN8vtRNHLj2jHP/LSPvfcJ/9iTC0Pfkje7gN7oJl8D4S/nLAJBoTXTsqJUBSHscfiGi3xdqC+NX2xGfhZEXysf2VitYl5iCdZKfCcRPvl2haaEkMqS9J/wEu+DwZ8UmvPZGQ/mM86nBVYrRFPQdZYTpZCrWza//JjNcsXp4zOc8HQuRKErS42XBa9bw63tuKc0l6qkw3Pj4d1F8JZ+0dT87HqJ0wXeWKT3TKWioKAWYApovce1HlNMmX/vm0wqyfVf/YT2ehm9/yYUjys23qAXc0rVcGY875bw68mcs3cumH/9Q5xWXH/2BdfPn6OLkk0XAmRKCdLJwGPjQWha4VlikF5wUs144VpWpt3bS/34+x1FD+sv8HRpjjovuLz3kOl0ynaz5skXX9C1DeLkMuZGnIS0ePMpL1895fXVNZeX9zg9C6nFqklF02xD/lJrovF4cMwQ2QZOa8BbQ6GCYvz89AxjktNA4id3PEnbtTFEbGZZwW9G4332/34MyJQNLoYsdR5jHaYzOGfRVcl8PkealslkydnZnMfvXvK1b7zLvbP7nF+e4NSnLDctt7crhPBIEbzzjfOYGDmw7dqYws8FZQSeznhaJKu6ZbnZstnWwUjYOrrooNJZgxOeQitO5jPOFyfMplOULhAihH33LuOhs3/xO5wgd2YwnaXrEm4lmE1LZlWBFB5rW+oWJpNZhhnuMBwhPbiorvRj/B0HystwUZIUZ0NZbG+eRq6PXzuc47F6h4+F9h7KhALwPggXzkXMJ/IouiiYxA+GCHeeFGEjtcV7TwjBmtp2yHcOf5fRRs7Fb0opESooGY3psM6wWm354mfPEUZjN5b2/QecP1zQnHq2tsMJE/LRdwZEi9KKiS+Dh5ugd4rxUiAzh3YRz33jTfAwtjE1Y6TiWlZoWeF9gW1bTLvDOoPTgw+euUdCIPffuWOPvmn/3iVHHZPlfvPzWjD2yhtluBFeSwiBFwYnarw4x1rQ2nN6UvHo/jnvPDhlVmoe3r9m1bY0bUfbWYyBtgXTKJra0zYC1ym8EZSdxjsfIpw2LZvNFoulKARSeaSCstScLzRPr1d88eslrWu4WVmsFQhCiH4iTUprPSk6klSz68O4vJL3tXfCSGMn2XlLhhHKNt6b578Xr+54Lud9uUO++k3LWB9TF/I2jcvL4uCVMdnAx4b3l+LwJJoqVdhz1aRiPj9BSuiMxVoVZCMEQqQ96npDN0jnWKRfcR/vHN4kk0nFdDqlqkq6lYk8NDjjsMZgnaHdNsFIIxrKSQSqkjRWUcopRSHZbq+4ff0V86qkMx31dsVqeUWzvkU0a2iDYZDa3FI2NzRtA90W2TW4esnJ/JSvf/AO7733mNevrjFWBN7PeWR/Bu+MB9JcH5WMIm/7JvpijKFtW6qqAmSMWrJvoKq15t7lBVp/gYqOJDGQSTBMkNA2NU29pW0aTNex3tRs64bZfE5ZFsxmEyazKXW9DY6iRcl8dsJ0ekJRlLRSUG83rFdLTruOxcmC22g8FycS5zxKgfcuKG1FlAecjylxgvNjh+NWWB6IKX8pbriJsSDOfcmSjgookHTO0dmOqbVIPeVl11ECTli88HyuDT851Xx08h1mreF8s2FNy+snX9At19ACdc36ya+4+cnPePC3f8gv/9k3uXrxFdvlS6RXXC3hvpHIas5UCVa+YbIVzG+vcB62QiOcQtqA9RpACIn2Eus8zimscqgYYc5ZT1e3XH7jQ6p/M8HcrPDLFScPH7PclnTeY50JxrNxlThrsN4H5bTf4YNSqkCb4pM7o4voSOqDkau1jiIG7JNSIWWDEC1KWCQDQ3dktAMc0g2VPbPjHXzPd/tg2KoEwquoHDe79/tvHBpbiXg/P1P3vj18Potk0m+WWIfv137kffzeE4Pnd3QqseQ7M7W4T6N8FiQzjVIm8hYhYnUKZR/yrns8MjhqOUPPQyQDXgL2U5UVha6whcB0grY5usX3ylsrxr///e+FSS80Smm8d8zns5jEHpy3FFWBfPSQ0+kMrMNYw+JkwYPHj8LAFjNsDItsjQ2hrKLHr/cxNFwhsbZjOp3gT0/jJg8EXAlJVZYIKakmE9577z26rsUZA97RNO/x4YdfozVbksXCar3msut47733+ZO//w8wxqF0CUJRFGWc/F3IbaVkH87bK0nXmsCII3DO4pzB+Q4wvH79mnlV9gusqipa0wWQTgkePXzIvT/5E7x3Icm80DyoJtRNTVUqtCAKDCGH+2QyiWsuWZ8Eq6zpdMrZ2VkUDMcVb/niHgOUVAwNHxRGyaPO9WH2pAzheoMgIkHsFPOdbemM2THtB6DYzlsbxnN15l6DiZHOPWHfdCgNQcF8nPJQ4kMF4R5T4Q9DNIoE5rwFYz0WqvoQ9D5s945gESltEIrKsgxzHAmWzYjbsbk8BCT3rw/bNAqUJu4qG5eD+oavjNQ5Bpbuj6Xv83bf2Z47x34frMy/0+d8j63tc4QPx3BQx7CvxOFI6zLdGxvbN63THjgcjMueByuHa7Jfj9k6Gyot83fSv3eB1emZfE3sfS9r6/D5Hgju0d2B0JbPZ8pRtP/hTJ4RdLiQN6TQMCn51t/4HX737/0dTt55Bys8VgmEJVgzNi14R7tc8+qrr/irP/sLNqtb7HJLc7uiQIZwnC5wIFJrTAyFI93u0Pc+hsOSu3DKAcDZGVoM6UW6PuZJnv89DBP71yk+A4TG5umYMJnPgfceaw/bcCBoZXOfhzcf9mVYcm/VfA2PjduQFgohDgy30vkx1r7+38G9obfeEIhKJe/HUCAf798+sDV8PplPHqOxwz15VDB+Y9kpePdaN5j34RgMSz4vQ4XysP3HyzjNe9s13q/dt1D+5WvorvqPt/sQfBm+87blWDv6v/3+d4ZrYehNnb9/ePbskJIDOhK9MYZr+dg63v0+FFwYEOTdrb7csQyO8VD5vbxNx9bUUCl+7Bt3lbtWa7+G/O5ZF2lIr+QTv/l6+E3K2/KOyQh2bK0cHb/f4Hx5m+eG8+o5DFE+5JPfxIMmg8/hvTe9NyzDtZTOnLehX/1z8V6gfwkQy8ZQiJ7XG+O1D3nYUFeSvYqi2EUPYX8fHNBvREjlMnLe/XWKMQYvQpQtrRReRjAs2+tCiN0+TwCE2Cm04nbAe0bHNh/LPXqaKWfCGPmeJobndsrx3fl9qGB3BK9aKaBQmrIo0EIFA3QkNgtSSj+uIiMCu+hg0sec1yKEdBdCB+WQ01hZYH2oW8UxETFXnU7KcRGU4taBRTGbn/Lo/D6PFyecVZIOj7QFTnZoY3DPn7L82Y9RUqFLEQz2vcfLEPq59Z5XXcfKdtxXmjOhedZtWbs1L9s162vLk03Ns6ZhenFKY2q0LljoCRdqwtI4Xsqam66j7QTq8oz7f/R96mdPuP3lz5l0gunJA04ePWL2g/dZC4n1HSdXt7xzr+br8wWfP3zM2cMLLr/zHdq64atffsx6u+T84gHd7Q3WdZQSCqmorKQBvJRspOUaw4mqmFVTXjSvuG7WvQHS3llNWkPx3PMeEQM3ei9AFlzcf4AQguvXr/jqyZdBlihLyumMcjqhmpRMpwW//ItPaZuO+ckpJycLAHRRcHt7Tds0WGMC5uJsiKwmU+5HF6ExiW0bpqXgfHHCYnHS5w4vpCKlm0jAd8hZ3vVr/K9zLPR7biCH9TKGsyE/tHF0ncXYgOOUVclsNsPWMJlWLM5nXNybMz+tmMw1Z/aExemMalIgpKeqdspk5zxtF5RZIVKjDbmuu2CUsG0sawM325bbTUPddCGllHGYJleMg1CC08WEs9MF08k0gL5C4JwJXkA+GphHZb9McqgI+0ZHzM9GINiamPtdSubzCYtZhcDRtWHNzOdzqkmJlGBMotNhJEO+2iARy0zh7v0+eLtXJGHvj/Dj+3T4zQZJ4T57/PfQcG0n/4zx+wP5jUQXZYxYQZQ7Qy5NJSVljAiJdwFfJD5PkulCmPh+bUWEPnmlh2fC+LFbhmEME7YjQ7sKXaCVwkWsb/2q4fPuS+qbmuXVig++8wHnH84RGFA2KsQ8Fot2ApSniPnQpU/hk0MYV9HTfxnDM4d+umgsJFVJUUgqNaNQU4zTmLqmrVts50LamxgyXsT0i7ns3pd4Xg+vv0kWGls7b8t3vQnnedsyxtMc1nOonA17xOFo8SicC4o4rTRTfcJM3+f+rKRUJ3gfsOK2MUGBZTzeF9hOYgy4TtLUBm/C2WpdcFpbbzdAR1FJilKgS8VkUjBdaCZPntF5wc11g3+ywjqNQhLClPs9JRGEvSqF6D0QgwKDvf4kpUbe/14x3ss4gAzGc8Hj1SYuKx/VyMaNKLUzWWk4ngeyed+m8Xf6utj/1tjPsIX9yEQmdK/1gzUwvp4C/U3v9s/0mz3cS5QaovGjEAipmE6mnJ2dojW0jY/7cj/9YlJ654rk/ss+ONMZY2LkJcV0OuHkZMZsOuWWFUlxaK3DtB3WGtpNw3bb0ToXDRyDEZPSM+bTS5zZ0KxX3Lx6zuXlY148f0apPLbZIE2Lbmua9RXONRTWcCYtnTaorkVog12/xs0XXDy+z9c/fJ8f//hjWmuh8yADpp73KY9KOxxdceSvvbljt04709E0DbPZDKUkzvvId+7GVAjBxcU502mJFQLjZYhI5EKUZa0kxrQ09YZmu6VrO2rVsa3boF/TmrPFnIt7l7x4fU293XKyOGexOGM6WzCZLthubmiaDavlFZvlLdNqhhQaSxdV3oQo8RrwIZQ7QkTjqZBK0nmB9dA4xwvV8i15hna3vKbjxmnmzKiwTHBMUeH8sRZvLWflgq+6W4I7tcMoyfrxA/7T5YIffO13+GhxwUdK8RQBf/4fePLxf0K9eEmzWeLbJ3z1H/4Nj/7p/4GHP/wB9aefsby54oVv0HXBs9srHpxaZqcT9ESi1y2PbtZsrKAuNB0S6QSFD1FzJoD1js45tqrAe0shFBKBtY5mueXsg/e4fPCQ6+UV7cvXzL4n6aop1lmEU6QIfc4TPI9xkXbl+zQJTpHHIyjCwzEfcpx3XYPwjkkV6J9UCqlKtO6gCmtsn77IGMVhnw74Ia0DvNx31oLAA0k0OIc1fmdQlOjokP4mmubcgfzb/7C7JqOMJKRkSH4Od1Pe4t1zPr0kDndYesv7oMNJKfCEkEgU0iskEu+DIhxA4WPa1uTUFZzfvBCoIuoBfdIFhXzwQiu8Vlglw7p5i/LWivE/+IPf64WhlJu1Fyxip613qDgBzlqc3YEVWhfUnQGpY3izsAil2g8NnkII9eHuMuKmtY5/W/Dw4PIsKLI7AyKEZtNK0dkQgss6F62HJc7D17/2Xlj4MoT7zkMGQwgzI2Roez9xMXSCj56+QkDXtYHYC5C4aPUZ4uIHQFiEkO5SIvycqiwQUmFtyBHbtiGcPDgmVYkqdmB28pxOzHYC99RAaOgXVDrsYoNFZMp7b4JoXSKE7McWEQCbBCACeBNyQnljET7kcBNSokQkislroj8EwsEtCEp1iLmcvN8LC5HanHskpG/misA8t2Pe91QSWJeD/rlndw5qpefyDZ/qP1Q+jHuM5t9NskbKLZkUqD5WkISgXZ37eYvj68HiBbDWIySUugihHiHmj1GM5cPMCWJqS/6t3VpN43YE3N/vef7E3j5O/x+G3Ux17b6ZWfz0/wU4rAfLRtpxAKzfIeCE67mn7FDY9dn/D7/1JkFo76AZAMS5wDv2/pgCKoW9C0xroF8hZ5KIUcc83lni8UHqfupbYtSHEQjy7w1D66Z2DhVnQ8Fx2JfkVZfPkshWgIjghPAiWJ/Hxtq0L1O9MvyufMyd4jxSxNxkwtMBG6XwZcGjj77O3/6n/4j7H36Aw+Okw1iLFg7hHcp65HrD6sUrnn3+BZ998glfPXmC8w7tBd5ajPDoQuFtoGNSSYQLhlY+nispPIsSmjCt4wLIXQqxRHNy+tSPXWa8cEyZts/g7IAEZPQKjcLP2PtpTq3No2n4ncVcXDfhut175xAg2rW3N/ryh9/N+z3sSzrrvSdbV0kxFXsrDscxp9HhHA3qhKRU8CKOYaZkyBVZY4LjHl09cr+vKxvPIY0Xca2M7Z/w76GRwl3KmWEbhvs3v77H5CZZVwxD0I0b1uzmwx/M1xi9G/ZhjEb0Zxa7yADDkq65yOgGozqRoinFFC0+Ata7d4Z0dHQMsvr3aNRgPHK+QAjR033vXRTCRQRVYp+8H5xCYzzA4X7J2+CiAc5w7Mb2/rG1mLc/XMuB1J1AA4drN/17SCfy/Sh29Jjwp8jq9XFMSGvgDiAgn5fh/jq2H4Zny66t+33a42VG+IFj42lHIgfsjXUYiMBHReHVE2nL3mOHczy2LsfWYt8bH6z/pZA7ITQ7N22W+mWMLg/7Nz7HYrcu+rlNCsMw8YmfPzYPY/Si58HzcZT714Zzk87B4Zrs++IJCo4jNPnYGhnOw7CdY/fykvbgkM6mv7uuzTRETfoAAQAASURBVOSmwHPL2N68vjedhxBy2ic5zHvfp6PKn9vrc2pz+MBBvX+dUtd1UHTEuVJSotEkBfjuizlv7Ps9H/S3mdf4kb7unXOjcO9hCVb8mZHxkT5bHAUgpUZJjSSA913nkFUIl+5DNMJe3t5NWLomEEKhvQnACSWeCT7mCnRC4tAYXRBk4dAPLyRShkhohdZAAgfBFSWX5xe8f3mPeyczSi3YmpZ665k8uqC8uWL7i59y9YsfM7k8R9qGdmNinvSCzjlu65pndctEhsyCr5otn189pZl4fnT1gqbzbIxnOp2w0I5OzploxVxqKg/rtkPheFJvQV7y4L33ufjj3+H1f/9/ZbY2vPu7f4j4rW+xefce+gcf8lDPmFy/5v7tDefS4D485yP5LstGok4qPv/z/8iP/tO/ZYvF2palNxQ4Zg4m3qGACYKtgGtvuLEdH57dR01Lnr9YclNvQgjwshw1BO3puDURHxA4NKcXDzm9uGS1vOXF0yesrq+pyilWFUzmC+azObNJxaQQ/PSvfkxVzTg5OWMymSOVousCAG2twVmDMx1NswXvKMoiGCQYg/UWJUq6esN7D+5z//KU+WzKdrVCSd3Lsz5b23Xd9ikBpVTYkT2/v66PGwXu3fMeXEiLFpTjULeOum5CGGRdMptN0bLAGENZac7OZpyezfC0bOsVDgMy8Pgqhq5FCJwxGOto24b1ds16vaa1dVBAGkFrDLebhq9uNlzftqw2HcZ4hBfYLhj12BiBMWiVBeenM85PplRFifcSKwLG03NUvmcnIj8XlACFUugi0NTeMzgkx0YrwXxasjiZgHdsBDSt4+zsgiIqLOLAsfMWIgnAgdKMpI1JY53/nY//8KzZv75vdDycv3Ae7jCG/N7e3+xH7UpXhdg/70QcizzUvouRXbx1IB1SCwoUziqs7QiQWNpTwYO65yd6BWTOd+4mJ8kxiTERBAzBsZ/2T0mNFoJqpqCFF5+9YHV7w7q54hvVR5zpMyazCiEbhG+xvgzpaWwwWJBahbZ7HTBAFN4HxU/wngRvg/GA9wovBIWqmJQVJ+oUpSo2jaHbtLR1hzM25nGNR4W4Yx/6nO7fzT+Mze9/njJQaqSm7a3Pcd71GC/ZXxOH70gpcV4iXDQaE9C0HduNod4qXHtJpS45mzV4V2NNQ1e0dN5graGzAfs2JvxbFA7W82gE47BTw/nJBKk81RTKSlFONNWkZN04Fqc1k9kWpW7BaFxn6QTEYzNn60N7I+YsZUxXkvaF3N8j+7/vxjRXjKewxPtltyfG/hwdVw6/dexn7N387zE+6ODdY3UOsIX998fXhfceL4KOIGg4x0qQt1P0VyFElFOhqirOz8+YTKpgYOaC1/8OQ09Y4r5S3DkHOuD54Xy3GNtRKcWkrFicLFicnvKM57tWGBPCgluDXnes1g3rrqXDI5TEmo7F2RnTasbnn37GJ7/+Ja6Dk3JKvX1NU6+pV7fcXl0h6i1n8xNkqxC2xZqWxhv0ZEalNtxs15jbFzTTBQ8uFpSlomksTiiE1Fm/dt7u3vuIr+8N8G79HJnfvCTev2kb2rbtnWvydWpMMCKcz6fcu1zw1csNWmqEKOmaLc4ZtJZ01tHWW9brJfPFGfPJnKa1bOuG+azi7PyUR48f8ezFS16/esVsdsr5+SUvpy84WSxY3RQ442lWS149/5Lz0wlCT8CG+RKJb3YBaZNJDPCCDosmpa0QNDieiBYlK95Xc5ZuzWcYtgimKCpazlDMkMHD2jRUsxNmUqKsQ3hJWZ7yzb/5D2kefoNX977NopiicJxj+e/+2/8NP/rkh/z4X/xLXv7Vj5isX3Lybz/m8bbggx/8Hpu/+Bntz3+KLxwlU0BgO4+ttyjveXVb896vP0P+8AZZVniga7aoTqAmion0WAcbLLW3FFaDigavncOaNYt3z/j6D36bv/w3/xOrL57Besn9y8eYlx0Oh209xjb41qAIui0vLELKcO61EUdICbO9QzhPLRqc0hgf0ocYYyi0TNwSCB3kDykRWkQPch1lMLUXrXWH4QiS7iDBCgLRG47t4WVe4nCgFFKYnv4EAnyEn0k4woDHGuVxRZDrE20eiwp8rIgM1tqh4cGwznoRcoiT+AeBS+31iQdy/ZhoJWPEmsAbhesu6B1QKJXalmP0O5xNQm/QqaqRaGgj5a0V46eL2d4AKqWOAgqB8O4rJ7XWqCIR5vCujSFuA8AX8xa5dKDthOwgaDjwNiIbu5BtzjuKoorKV0sXPdSU0igFZQFFEUJFpfDb/SLMALt80m30UIeUlyM8G4iuxfe5wfdBxAQg6aKgmVWBMXUxt6rYLbBOh74HhX9oV8p9lcCeuq57MCaNwRiAlwNavaJLZKBljynE8Ok4bAR1fNwgksC0C+eRuMik+njoxtBXUiJ95snkDH2IqLTW/PHclznDcBeQPyxD5fgYgzEU1NN3xnI0HoB63N0u73cCnGe8vYmAHVNepLEBotVlGOJCa4qyyO6PM0/9+kqqtGxo86eHe3FMmBx9kQTu7n83FzCHe13EtdYrgMNFICpOBgBt3p7Bh+4c+9izrMH7YFkvV/jD98a+exfQcZcQPnwm/zvf+7mTjBBk+xGSkJ5CnR22bTg0u8NrGMZ5R8MOBbVjAPSwzkBD2V8LIv0jeqG1N3TJ+54mHx9ppcfHHCD4AAwaAUIXdHhO3nnIH/2Tf8RHP/guSI8vFNYYtPdMHHgsq+U13c2K7vWSX/7FX/Hi8ycsb27wAlRR7NYKIb+Z0LJXsgohQqi3mLvER8bXmK7vs5QKIcY99vIypOlj62AffBkPsz2wTwmRSeLvzg9CWI3QzgTegSCFaExnzlBQz98ZhkVN51u6NwybPvbtvC85rUzLIOCAh2fSGGiwd15l9fe0dUS4HKtj2Kbh3OTP5vxJHgo3H28lRZ97aUjb8jI2JsP7+XiOhajN3z34lhC9EnOs7iEYfez6XfR2bExzQ7yej5A7YOZ4n/2O5gfIiiEhGUaNGbZ3CFzk7Rp+9y4+M9FWn46I+NO/5/zBN8Yi2uRtHGuTSiGajvRhbB7G+rc/TwkoTtcOlZpj59VwP4ZY4envdNak9hDpuMr4QdHP3bDOsb4N+3WMdg777n30CLsD83zbs3bIi+TPBPoV5YFodPumaAT5+n4Tn5LWS38fgvGVyL2Uk6FD2gqHUUfGPNHuKonO5vt1jx/0x+dibFzHaaXrZa7hM2NjMVZ33+83fHMsRPeQdg7rH6Nbw7YM94pUsvd0vXfvHq9evcBE2apvpz9Ci0fKmOGs6Gne3cWNtPmvW7quS45Ce6mk9kvGK4vAx+UtENHQT8nkCTBuiLBHwwj1CPFmee2w5EQ58waP4cutEcGbzXuKyqNLiUJhrEB6T24UK6WM+VCDyaGSAoUiYAcF+AXOW6zfmegKEULwCUnIZ4zD+5BD17qGutuw7jZIJbm4uOB0okHCxhjq1YqXNw3f/Ogx/MXP2X78V2xXN5y+/wFaGLy0/XowDr7crFg1NV87u2TuBF++uuL1puby0SO2NpyU75zM+IP3P+SFveGXqwbnLddty8vOsiGEEdyuPKfffp8H3/se77SC5//qzzn5X/4vOPk7f4B4eA+6lqZtsLVhoSfMTwQtnl80JTdmgyjPaV695uknv+bZ559Qzics1yu0M1R4Jkjm0TN/TsUraXlNx9Za3pte8rJrWJvgfQg7rGeXBm6wv+MB7J3HS8/J+SVCaK5evuT1yxchElo1ZXZ2znR2wmK+YF6VbJZXfPLrX/DOo0fMT86YTGfMZvOQPs+YaEjuMV3LerWk6xqmkzICi2GpK1nStisePzjn4myGEhIlS0Ke8RBiMdFQa21UuAdniSS//OYlnrGDcdhFpXJ01rKtOzbrNhgXTDSL+QwhBG3bMpmUzOZzimrCtmkRTNgaQ92Z4AEnBGVZURUTPJ7OtNTNhtV2xWa7onMNEJSL1kq2jeGrlyuWV4b1xtF24Kykaxq6usF0NuA9SqKrgof3FlyezpmWVeANIGI6LnoXx7MBh7IhTrcg4ECl1oCjtQbjbE9Td0qx4K3lvaOaTjm/uAciGFSHvNRp0PZT3R3jyw5GP565Y2fH2LNJFtp7f++Z40ZrY3Xt7u3O4L3rfXOi+sGnNgZ6q7UKihXngoGHdTEn+24thTQguxCv6TrsjI339qJLspVPtg8hZK7P3negtKZSFV1X06wbPv/F5zCXfLP4LYqHcyZTRVFMkHISHHicxPsCKTSFFMhkPOEFzie5RQQeFAUiGKg7G0KbTso5i+ocKUq6bkNdW0xrYoSQ8XEelhz9+Z+rvN25d0hP3v69XUl8knIFymu8MyhVsm0ML6/WfHV1w/0HS0pd0HqLw2KVw0qBEwWdkTRNR9NB5wSeEEGlLE9i3twQBrsoJkymiqoSFJWgKCVKCmRrmcgTfCMxW4NvOzQOi8MKies5glC02CnDE6+0+2Hw9+4nx8BkZoztyZyYfNpPSc4LazyZOw/lyHwvHlPk9M/dOSX5/bvlnvHXD58d5/nHZcV9vtfGM+zQiLannd6j2NElXWhmJyfM53OWt03Yb35fFktRY/flpHiWs8NOsA60oygks9mEs8UcoSCJr846TNdhbANtyWrVsKy3rEzNmffMygWnVcXz55/y5Iufs9nc8lvf+h5mueLFL/+M1VefYduGYrrg3uU7LE7P2a5v8N0WbWp8oaivb5ho6CpBZzdsr7/ibHbBxdkpL19d4Z2gMyC9oSp2mMaOX//rlzBvwTi2azvatqUsi5DLfBB9UQgoteDxo0uePH1NOT1joqdsvcCYNVIXOGOp6y3r5Q3t+T2sd2zqmvV2w3RScDKfM51WFIVivbzGdS3zezMW5xeU0xPK6Qxj1xjTsrp5zensMdVsgbMdPjrwSHbpE5ULvJ6X0AnoxC6trhOCK9HxpTJ85Ob8GS2f4XmC411KvmCNQjKJXuNXtkMLOJuWbLcOYzzOOD775Rfcmz7i17MlZ87yobJcTjukKygef5uL3+lYdi1P/v0/58s//Wd84z/8ex5991ss/87vs/71X/D0F39Jh+GcOR0SIzXTasL2XPHky8+ZXn+Fvn+Onla0Nyv8tsWUJRSKUgvmDpqNwZeeWsjIiygKrdlerXj03e/w2ccf8/zZpzz/+Jf8/j/4Dqv1Na1pwxxDcNBSmYxOwGktuZ4t3LPRIKV1ls4Gw8UgZKgQQSpLJeVj9JegHxC7n36m6I+NHa62x0bs4LUkuyIQSLAikEixeyelU0h82SEfs389GZMk7CTHosZ+3n7jHF4IaasM1nqMEZgiYBo26nK9T3out2unTO2OtFHu2pwwJqUUnWl7XCT/eJBRAt+kZPlWTX9rxfgwBPUYkJEYUCGyMMeR+TPGZJ7Pvl9giQlMh1j+XKrPWot0u/zcqf5cWHMuKJbzNuVCf1mWewfJcJLT78nKKPfSBqISeOe9HqxHw7dTuBHvg0d4IpaJufV+34taa0VVlX1dxuxy4Kb+pHHIwZtjOe1C/QEEGAOQ8zkUyfBAChQyAscSIYJhQVhTcXF6T9u2iPyQyTwnh0BfPpZ5GJMDkHUw5rlyfzgfxzxn0727ANV8LO4SnvJvDgnAKBAw/F64sfet/LDsgTQI4Tuix8br169xLuZ/lypEUJB3E57h19/UtiMdfeMjQ8Zr9+rdFvSwbyAwJKTD9ooErAzqGY7lXd8XYl8kuYsZPlZH+jvRorwfx9qff+s3PjTuqHPYh0RH0zcCXRpXmCTP5qEH1dg4vlWJIASeYPEuQPVgZyjKx0NaCJwUuELSCTBa4QrFH/3Jf8H3/vAPKBdzmq5BVCVYSykkynqa1YbrmytM1/Cn/+bf0Vzd0lwtadabEDoRH0Ogq56OjgHaoZ+78PP52A7XZn7mjI1FPn5jgM0xAWVX36GQnOfFzc+nvJ6c/uRnQmrD0NtveB7n50Te1/TOsbV9l4Jg2Nb8+rF9Pqx3uP7y7x16YuyeObYHj+3xfM5yATwH3noBcDBHw37mn8jP4LtKPoZvGpP0XPhX7o1V3p9j9YzNU96GtykHRiJvhULtDKmGZ11fzci5OzyPh7RzuAZy3mdsDeX15vOyv97Z24ZDXmL4vWFb76Kbb+INjp19eb/G+I38mbcp3udrOn5X7Pch8bLH9nlqS5qDHLAetmv4zlgfd/8ea/P4+jj2XEqJcZT3iH1PisgUVvAY3RzSirvKcB/m8zfG4w4F0rH187ZzO3z+Ln72Lr4sb8/Q2NT5/WhMw9CDY3Ocj1/wbtoP0zhGw/469Gmsj2P8YGr3/r6SfPHFF5jOhFRSRM8kxC5farY/0jmU15/zCHlakPCMP5T9B+WQC/j/rfRtzkC/cGP/myL7umBH95SMUYmkJHgzaCBXSg0NJ312JOzzNyIBNexoznjZtUgRwNnOWFpjqZ2nReCNB+uRXqK8xHrXR/0RJMP1OPYRP5Ai7bsQrtKLAN4jLXiHlx6hitjGELZQa0clFGfTCdvFHFzHdKIpyoqHZ3NmlcYKj/GOQkvOH54yW69Y/fSv2Dz9gmI2RaO4aWtq6dBCo6Vi6xzXpuGy1HxQzrjvNa8ri1QbOquYzQuqUjGvpjjn6ZyiqhSmdTSdZ+s8VkvqZYOTU85/8G0efP8byL/4JS+fPkP/r/9rtos5i87wYOuotp4bvWEiPbdS8MoqPl9qSm+QF4rXz1+wev6EYrtmUkhKC/eZUxIUGTquFyEFK+mogamaMC0rfrl+zaZtIdsXae3l67DHBISAaDgvpAIky9trbl69YLu8CfVUM07PzinLKaeLU6Zlwae//An15pYH93/IZDJHSI3Uim4blNfWmeBRazpslkYuYQsOBw5OT2Y8vL+gKiVd2+zWm9gpAryHpun6lAhpRR47Z4/Rqv76brdAGosQwxHvg2K86yxtZ5BCUJWaySSCct4xO5lwdn7KfH5K2wGuYdu2tJ0J3rZVidYFUoB3hrbbst6sWK+X2LbFe0NQmHikF0ivaBrBduOot462DfSqaVuapsV2wUlDaEVRFdy/WLCYTqiKAikVRoRUbtqFELhJyeqcQ7qQ4zHQT7lLn2hN8ETMHC3a1rDd1tjo5X5yesZ0Po153YOhQspb2TsJeb+H7d11Puzz54e/D6/l7x07h8O9Hc9zl2yc7g3lw/y68tFozsuACznAhvDQzgk0Eq0kvixj9EgbDY/25b4k43tPMj8lRYtJK1CIeE97cKKPyAUhQkgQh+Nq9wIvNK3r0IVCMKFbG26+qNm8s2FWKSo9ZzJdUBaSNp4NhSpC2gulwFhk9JgLobODMiBAyT7es1gsShRoWVAWE4QoENQ0TYPpTIxgFMdeBo/zfNT35vHIHOTrZIwvfRPG8Tby0xgPd6yO4do7xv8drG8xvlYF4IzFmholpxgWbJuS1RrqzmHEllW9xTUGZ0KEVC8F1gm61tN1AmsU3km6xrJtNoRoWg4lLKVOuXBjJBwZoh1Zs2a9XfHy5StuXl9j6pqiDEbk3kI4xSVKBBV5bnwf5jPyGD7xBeNK8f1roS0eet4sjEUYoPDnDt/Jp2OvnmwfDe8dPn84l/nYj83zGB97DBMYnhWp7NOYQ7z+YK31+31EZiKTj7O2Sxl0DPP5HHhNiIqRqts5WuzL1xZB0RtN557XiUeeVhNOTuYU05J23RLoCnhn6doG381ZrWquNyuWzZrGdJzpS7yxvHr5OW1zw6zSaAc/+dGPePLJn3I+FZwuTpmdLTi5OKecndC6lpYG4xyikOhKYTuF8Ja23tC2L5ncP+XRgwtubpbUdeBXimnRtzvxCd5nivE0tuKQM7+LXngfooRZ52jbFmMmVFXZ56fuZULnsKbjwf1zyirKIy44hloLSpRItnjb0bUbmnpF09VsW03TdhjrUFIzraYsZjOatmGzuqFt7nF+ccFkfsrs5Iy2WdHUa7r6lu3mlLKaUG8U4agOOp2QapKAsQPOC5BgiDxblJodnk/9lu+LggJYC8vnouXrbobA02HQaCZIKuuRt1ukcmipQHmcafniJ/8JeXGPm/ML7KliWhXITvHF1RVX1RnVh+/yQPwRDTU///f/gov/xz/j0f/+G5z+9reZ/vB3Wf7iZ9Ra0pgG0VjmquThtGJeLWi8xL96weTdd9GXD2mRsGlpS4XQgmpSYvFc3W6hAGM9KqX2wdLcrjh7fJ/7H3yd25vXfP7jn/MHf7dmMZ2w3CzZE118iLaCIKYVcb1+TkYwKeAtDuODN76NxoQiKrmdJeQ8RyJUSD0tUDnSCNEwdbeP+90c2x2f3Ck14t8+PuxjozP5L/4qkxNHTsWi0aoSO1mMft/naV6z/ZBoqQwh1ffw8iT/euCQWsb/78vHCWswziOsQ1pHY9jpM1JHRDS08kHOS2lghA/OTMRVGw4KCw5CpJq03wnGgTqk4kgCrBAyRJJ6i/LWinFjTA8AJQBhCBbBvkIiB2KapqEoCrTWox5tvQJ84OGWvpmU63k78m9qrftvpZJ7WPRTNnJIp/am+7kwmN9LoYlSW0OIKtO3M28rxPB77BjdHHwqYp4h70PghZTPo+s6lFJ9LrsUNjn3eBuCQC56bA4948ZKINQ+cCH9IZrm1EdhM4U+3weGghXHYUi14YGSr42878NxHgonY2XMizL//pAJ7g8ovwN7jglLeblTiOr/d7ytYwDycO0lAVCi8DiWyyVt24bxEqIPf3+sXfhDKG4oTOXtO9rnnDgO2j/sy9gYpzqHbRlaZefv5u04Bjqka0MQe1jGr40/c2y9jZX8+pixxti7dwvbx9f0cHyOMd574Ofe/UOlaKp7+N7YXjvWtmH/PCEcegwiEaJGREYiPSmdQCiJU5JWQK0Eaywffu/b/Bf/9J+wuDxHConxBj2tgpLbC1xds7xeYrc1yxcv+NUvf86LTz6nXW6ohEKL6GEtQv3H5jDv05A+jYF6wzqGioB8/Ibn3NhYDefIR0FmuMxSXfn5tS+Y7CuxhRB7hlqpjrwP+e/DM3HMsyCdJcNvjq3ruwCqNG6pP8BBuPnhOA/HcThmb6LRw3rvupbvseE5EM6jnYVifjYfa8dwju9q29hZMja+/Vw4Tx5KcGyNj51vxzww83fG2pxfz3kwoGfM7+5j+N+bzu3cEOHYGZDuj9U1VLCNlXT/WMSDMa3UGP3L2zDGP9iRMylfE2O0duy7Y+sr/3tszt9cDt85dhYP+zzWxnQvB3zzvTN2to/V630S3vbvDccsvz5G46Nc05fcwGg3Ar4X5HqjgEG/8vEda8NYeZvzfzj3gv11MBy7t/puePFgjFNdQ/nkWH3pm2MGWaGtEvyb99lwzY/1ZSyqzRgNuot+vanctc8SLQsCskVrSdM0vXxDPud+v19jMumx7/bjLd9EKellrP9cxfO2Z1ECD2IbRMr9mQMcqZ/7IPGw70KkPbjPZxxKEVk703hlQHX6z3lBZx2NcbTGYQk5AY0TKAt4h2CXIkzGPS29wPvQ1lCnQgoFMXSvlwksCZ5QUjqELHBRKS68oCwLpNcUhaYUnvP5lK3pKKqKh+WMqa6wwgfgvyw4XyxQv/g1609+RXNzQzWdobxk1RqsElRKIbxg1XW0XcPXygnnzuONpXaSk8mUstAIJTGF4FZZvmg2GK2YaM2yaWmspzbgu5ab1YaTdz7k/Le+wdnDc9p/9//hlew4rQp811JZS+Ekl0qj/IaZ0zz3gtfA2guUACcdy+dPaV48Z2otU6k4RfMuFQJB4x0dwVOmA258R6clZ5MZaM1X6wBoAyglY9hQv/ezA6EcxgMxDZQqgrf2erkMHlHNNqy5ckpRTphP5yxmc6Rz/PoXH1MqxWJxRlFOQ4o7AcbZ3qGi6zq6rsUaQ6HVztEi5su21vPew0suzxdUWmKNAV/gIk/lPfHHR0Db9GvS83Z87l07DIhemFleU+sw1tC0Bmehqgomk4qyLAKeIyXz+Yz5/ISimGCMA9vRGRPysqoQSl0oj3MtWE/dbFlvV2zrNdZ1OGsCAotASI3wCmckpgNjwriE8OstremCQswHZeZ0OuX8bMGk1CghwcsQZcHbPmWgD9qOMM8xvHdvkJLxWta7GKEh7M26bhFxXeiy4OzsDFVoTN0eyvVyl4Iu5II/5FmGcqv3KVpH4lcjfeqnsEeSd8pkxmja3bzW8Pt4fwgysLs0PKPTORSHMfJTQTHuUcHAQGt0UWCMx/tEh/POJIjc78Dd1C8xjjlFS4pdA2OaM1yawYDxCanRSEwnaK8Mm1db6vMps4VgSslES0oZPCK1UpRSUyqNCEnTIfoNh5zGGo/slQNCKpT2aFGhRYFUGu8lFk/btRhrd7IXwdjCZlvwQEYUu7NnOEdj5W3kw7F7b3rvLt5t99zufDr2/uG9wbna8zZxvlyM9iAmmK6g3iraRoO3NBtoW4PpuuB0o4JCxLvwr4hyrfWGZV3jvUXK4NWqUCEyRH9GS0JO4par5YqXV2tW6xaJRMqYHkvKnVGR3+cvhRC70LvEaKvxWt6/HONP12XPSw3GNjEfvXL87nkLv74tbrjje0bXR6r/6PuhvEkOYqSdx8oxvnNX1z4+tYdZZHMopKAoCmazGSQDGxdp0V6+Ykjn+di6TopxAWi1U7ZPppOdYhzwzmFMizeO1XrL7WbNutlinUFKTWNqVusrumaF2W747NUVTz/9OVOhmC/OWVw+YHb6CFkusE4iVYjZH1LyhjDRFoFxjqZuWZuOcrHlweU5n5RPqesmnL0+GSDZGJXXRmMQFefB9zLim+ZkKL+lEvRQHd5P9oxpA2l0dKbl7HTG2ekJN0tCqt8QCxpPgVQK6zzGNGyjYnxiJyHKQ9Nip8F48OJ0wbOvXrC8vWK1vGFx8ZCTxSmr+Snr5RVts8V2W7bbTVC+xsjE3nukCyku8L0UEK7HVB9egnCBJ3ZW8Ew0fCQVE6FoheMzGjomlEjAYHBYBNp7OtMRJUdKD6WzvLNquF+W+PmMV6XiV8JiCsnEl7xnFKvJguKDjzCd5cVPPub2f/pzHvy3r5jdf8D5D36H0//x/427fUkpCMrfztFsWuazCbVvKV8+R91eoc4vUB5U62DbwdSFFCE6RAAyRKNPRzCUdQ7fOpxXXL7zHq+efsHLj/+Ml8+eML93TlUq1Fb0dKPnGwW9Q9b+/t6thaAQDzyQC2pwUlJIKQu0qiiKSTBwlJogVcRIRX63l4Ho8R3mJv3Wr8Mweft0IPu950PZGUHHQzNKXIMSmeKeBrhchZ79FuXmFOl6WEfiJ/K90rckrrNeb9ZfB+cjf28NrTEUMeQ8ka8LfUhRED3eGWxUjMvIOwmRIlULvPDgbDx39wYt8K6OkAZGeNRbQg5vrRjPy5iyIA1y7imeACytdZ/bFOhzlI8BJOlanh8nCfO510vuud22bV9val/6XnovVy4cAwiPgZpJQZ23IXkwwr7HQVJkF0UR7rv98LVpoyUlgvOZQJUpLFJfUl9TmPXcayH107mQ+3sMBN71dbcJvPchD4OSexZPQhAtnuPGicp2ImDkrBuEit5nFNM8pTEYG9vEDL+JSTgGwibwagiw7gFWWfveBBrmjEZqU57DeQfuioPvjK2XY4J22KAerRSOcLi+//77XD97TlmWuK5jDCc8aH9GUPeZ6EG/sveH11I1x8pdYOYeYc6I4hhgfOz7x5i//O8x4PXo++GhvbbcBXgM5xsOQ68eMzB5m7aPPbf3/mB+hp7LB0I5d4/nWJ+OecENvzPWh3RNRG9tfNj2Ooi9CB8AM+NcsNuKuYadFGyFZ/rgkr/59/8u3/zdH+JLRYsPDFYMBe7alnbb0N6suPnqBc8++5LPP/2Em5srlBeUCITzeBlzBMsYoy8Ds8fmMAl3eX8SnU3PjYHeQy+xfK2/yZsw/3b+bvj9uJL0mCf00KhoON9j7w09wpum6c+jvB9D5fqQyXobmvw2zw3rHPMIP7bmUjl2Fh9bs0MBMm/rmFGBEAJn9+l4frakfZqzlXedJcOxzM/EN/UhkvT+3tgYj51lb6K5o+fQwFt0yIcN909e715bjnwzf2Y473cJ/W9aV8fo2pjwutcvfB9OffjtsT0//HtvHYrdHh2evfk8v+ncyvf0cD7eVMb2xfC1MbqR1z30Bs/feZMh0fBsHXvuLn5g2L50L48wlLchPHecVuxoKkAA/pPHW/Iez73Nh/tobMzH+pvThTFatjemoxjbrs6xM3jYL4TYE16PtfXYd4b1jdGNNLY5uDN2Ph7rR05XA004NMYb8vD5mfo2/XnTc6kdOwOyFLVM0nUdJycnLJeWtm3AR9nDB7qe0+gxujh2pvd0yPuDaT6gv+Lt+/ibFp+1S8b0TD1MImII3XiwCILxc9pbO4U4R9fhm0pPErPz9fCZeIbmdXvwCIyDzjha67FCUSiJdYK2tVjpAIOSCiVE8PYXAicd0ktC6omY09wLUojiHlzyAucCTCW8xsXzSkpBITUTIVkIwaIsaO0pxjtUWVA2Lc5WGOcppEeWmouLU65//hM2T59g2pb5+RnOOhrjUWUIu952htftFtF2fPf8PifO86KueVl3LGYaNQvj3glYeovvtpzqU5wP+aFrY9hagWg66s7y+Bvf4PyDd5lIz+rjj7m9qBA3LylVSz2dsqnmFJOSMwelVRgcS28xssOVE0TXUH/5BPPVcyqgsJ5TCk6FovMBPOwIoFkjPNeuo5Oah9MTWgmv2i2tNQghUTqEr/eBqpJ7rAaPZYdxMY+flBRlgVaSzXrFdrPGmY5Cz1BVyK99enLKpKjY3Lzks1//kvOzBdPpjGoyDWFGvQuKMxfCs7ZtS9u2WNNRzUIeeWNCCG9ZKGznePTwAWeLGYWWNLUDJM51COkg5jD0PijGrbW910ig1cfPrHwdH5xncX/1NM0GfMS7AMa2pqNpO7yDsqyYTicUhaKpQyTAxWLGdDpDCo2xKZynR6gQClMpAdLhXIdxlrresN2uadptUJQZA1ERKSOI6DqwHbioMzcmeIwnjycAISUnJyecnc4pdTBI8cTUTtED34vgNZ4iBcqY01p4kOR4XVwVwuNFyNW93TS4rgtREadTzi8uEHI8GlAkB0BKMxgVrkd44P78xvehSPvlmKBXT5xTv8c2HJMnwriIvWeO8fnj8sjh+tjnF+PMeo9zxDXiEVqgC4UuCmSb8r8HWsbe931vJDQ8g1L7Q90haqSHSAeDTO49eOvjUeBxvkMqH2iolxRC4jaG5YsVJw/mzO9bLJ5KaVSpYt7ckFu+lBqhfYwcZ3vsUEkd0oVH7XZQ+iu0mKBEUAhYiPsiRBnwfZ6xqCxNgzXgk9Ic5/1+09wM5YC/TjnG/x5bR+G5cZzrGI6TrxMGz4bv7NphbeBprIGm9rRbgXYldluw7Wo6GwxYlJcIGULzSy2RXoQIv62lNQ3eW7QS6OjFiPdIH6L+SS9wFlph+Or1ipdXDdtaovQEqEEEnFn43ZrcM7TL8on3OcPlDu/Kca6hx3hSjDufG1NDn3N3bw34Pf5jTxbLxu3YPO3uhV0xnJ99me9Q9j2sZzeNx+4N6x9t08iz3vtd55Mqyh/+7N4JtkaC4KU8m836LnjvcR6k3znRhfdhRz/TmER9hbP9+aF6L/Qpk+mEJbdJFYf3HmM7fOdZr2tWmy11W4fIEFKyaVasNks2qxs2r17y4pNPqW+f89E3P+L0vQ84uXzMdH6P1aZjvbpGOIlw4I3FdiH1QuegtZa6qdlsHeem5tH9e0yrkpUM54L1/kAp7pNhV7/P0tyIvXnboznicF14H7BIa23PS+jMqSaMvceajtliysXFGcvlLU1nKcoQYVgqgVYF3of86dvtii4aCzVNy3bT0E47Ls7OuTw/56tnz1jdXnN7e8Wj97/G/PSU6XxBOZlRb24xzZa63jJfnCGkCpGgXOhbSERjsWI3v9oFPtkl7yYnEc7xWjasioq51Fjv+My3rOiYSc2tsxg8dQxv3XgLToVM2t4zA+4zY3HvHaqLx7woNdftirWW/J6Y81Ftue48Uz1h9vgDTt77Lc4//RL5yWfMfud3+OB736f+5rfp/vKWSTUJ3ski5OOeaQGmY3HzmvntNaprkT7wtKrtEKZDiAJVhNTJNVC6oLR3MhhxeQTttmNx7wH3Hr/LL//iT/n1zz/m9x//HcpCB14rWwPEPZQMi5Jsn2MIztM7S4SUJ9HkLJ5hShUURUVZTNCqQIgQSQn+v+z917ItSZqgh30uImKJrY5InVmyu6paT/c0MTMtgCEUzWg04yXN+AK85QUfhA/BW5JG8oZmgMEIwMCBIKYb0z0tSqc6efLILdcK4e4/L9w9lq9YsfY5WV0Abtqrdp69Q3i4+P3XYgd3o35qJ7xRYpFZ7CXlP3L8SVVcl0N4lgKPqAS8U7w04natR93X3jCO6DpKnkqk+FZaqxACPnh0cLjQokKFSZmm4jhjTfEQUsC0eIJ4UmguVqlYUis9J6QSTzrOQwKIig6Ag3MQFEFrVOUwhMMBz7S3NoxnY3aZwrxcyIOUnOwiuZVSNE0D7ATprMiYKmNEZJK6YF9xkSPOc98iOyNyfr6MKMnPzkWAT5sUBCOPNf8+TdMOpPTsuwj40vg/pldU82kph2GI6TWcj9GWY5S2Gmuil1EM5fjmlFPILj3wnCInjiMCvxvcCNQ+xNQD+Z3sRGCrCiVJEZ0VMCYKYdMIvLJ2u1I5bciuHllpaM7vZa/t8r25/ZhT6JbvlTA1NRpNn51bmwNlVvFvdoKY1qGdMs0xCpw9p4m8RnsKcx0ZRZ/gpHRyyGk6MlN3VEgvUq0fG/tUsTw35qkAOMfwzcFtflY4HN8xRnDaxr1Tas+oPR1bucdzUdblO6OScEbpXwrac++VfZcwfGztyjZlpqbPlIIAcFAOYm5cx5QIZcRxFran4ynX6z7mfLpusy0xgqJitI5WSYBViiFEhisoCMbglcKuFvzWH/wuf/Bn/4LVw3M6HRkwrTTKC8ENbG/v6G/vuHnxmi9++nNef/WMZ0++wvdDVIBKQLzgQoys0ClKxASNNno0ck2jnHfX/LinU9xybK2me1muW+5n2tccfJXnROT+db5vj6cws+tTDmhlPid5nJkuloacKf6d1iedrk/peJTfK6+V/ZX0qVzD6XpOccjcHsyNY67N4a+5/qbj2e874toyw0BuxxT9JcxN8WV5LfMkh96m831GJnD/+nQdp3MscXwJsyXNm+tn2leJ6yPDH/aUU8fWYkpnS9icOq7lNuVd8vync5vOa/9cHa5/6RgyvYcwpnmeG/8cHOVr5e9RvDp01CvfKXmNY/tXwu7c/I+18rxl/DKqlUchaBTx78X75bmezuXYWpS8Vckjz42x7C/re+/DmyV/P3dWgSicpTbFiyNuEzkUFQtcOv3G3LynOLt8tzwPU9llSsOnPGbJSxyjI3ldtd6vETZ9rvzG9ExM4XnuPB2cBb45HO5d0yqrGO8d45QWH6MJc206nzmHEqUUEoS6qkan4biWO/jIe+aHw+wmmbea4rM5+qW1PuCBp7AkySo9h7P+Ia1cUxFJ5yutv8pKFkEketMrFXkwkxy79ZiOLquGc8cUZ3VPA3MwT6XULlUqI8lI4yueLd7J/RkTFS1OhN4HnChEG5wPONehUrS3NRZrLZWYqOZTELREZYgIMYWvSfsQ8xXHz0QVjBdQOVgoXTPKYBEqFKu6RlQd5TutqAy82FQ0BlCBDUK/ueHlX/x39FevY0SOMWw3PVo3WAXbvuNq2/J0e8cZhj+8eI/LYcMXd694drPlo7OB5mSFdLG2r7GWKgS8E77uNtzd3XI3CBsaauDk/BEf/sHvcbE6hc+ecvXpL1C/9T4v/u7fcP7++6h33+GzR4/54OwBy/UC8Qu2txvu7rZ4d4ecfIx9fYV8+gR5/goQhhCVdr32tGLYhrgfC11zY+HaDTgMy6rh2vdcuw4XHLVtipJ2Ja6Zwl+M9o1wprDG0LYb+q4FEZrFgqpeYquai/MLfD/w1Zdf8vWTJ/zO7/42dV2zXK2oFgt8inIWianUh6Gj67YMQ4cxa4bB45PjS1U3hEF49PAhTVUl85uK0TniEj+TlHPCmJ3NmgyjGfrvx0n7+CmeK1Xc2xkZotFTUgrztu0RoFlULJcLrLXcDj1aa05O1yyWDUrpqGRVgtYGbQyxRGVAa0FwdH3Httuy7bcMboAQjZJKoiOYEcCD6wPBRQOs98LQe9q+i4ZIiQpQoxSn56ecn66pUlSeyFSPkOKe4lYXis2o9N3JIAVPQkwfuu0HQoC1WVA3DadnZ0nHtI8D494U9FpFx4oQ9vvkGO5M45o2VUQx7T0+Q/d2f0fD3BzPWjycP3p4edJfIjWQvZLGe8l5DEl1MS11XdN3Q8waIAqU3jtnY6T3DL+5T/fznYAPqTQjKpVo1mRFuWaLNrGMoyLQVAoJPS++esny/RWrD1ecs6LWSxZNg7MhObQrjDKQYuKi0jrLCKTsBAOxXIWltrHEhE7wHfJ5dkN0Aih5FMzRfRvXdOba3Bn9VWjsm2S0/a8feWJvb97mmX2HWyb3xo7SvnnfY1WLeM3Q3dFvOhYskR7CoAhi0NpQ64rsFGEwKBX33ivPshrwYcDoSP+0CNZrbNAYH0th9L3jctvzyy8vefbK0fYLzqyl8x2SaK8SD+LRphqHrXQarlJpOlNjdWkE3zeQA6MhPSc72G3tjqPfO1dvsSez9qLMhszwo0c7mNya8vkjPL7FqA7l0PzmYX9z08jfGHHERAYQMm8ExlgWy2Vat32anc9uzgaSmw8eq+zo0CCJj5bktFxXVXRkWy6LkQkigcENiA9sNx2btqUfhsjLWcPN5R0vX7/i5VdfcfPVF7z6/Cd8+913+eC9T3j0G/8OZx98l7pa8Muf/oLXX1/GyOEBcIBXKCr6sKHtBtptx9ALy0XFtx9/wGq1QL+OgQ5R976TWfd1EWoCOW+3bzt65AvDeHTaq1arAhcrjI7OScYoLi7OePLVBtn2KKXohwFNto8M9H3H3eYG5/ro/NZ1bO42tMslH3z8EQ/OLzAK2nbDZntLVVesT05pFisWzQlt1eA6wXU96ixmmQlGx5IaPgcJDUiyS6ggVBKXlERftIAOms45bhaeU1exJfA5La9wXOiKS/HciGerPJWB1glWAiIeFCy05TfCCer0fezZJ/RaceVectne0Q2XvDdc8c7tHe9s7ui7G+SPP8TKK57+/K9pvvUh3/nOJ/zun/xzzOVz7HsnWNOgsDituK167m4vscpR9R3G+ZhKHUNLj1ItojXB1NTW80oCJ75GGcGb6EiijGZ7fcvZ+SmP3/+Ix+fv8Hf/5i/54z/751itko9dlpMUqrJkz0edHNWyvDnqsESQEB3SlJGd2MUuW6cxFq0NiMY7j6mrvXO+f/ILfkYYabdC7VPFHIldPp+AuuRJC4wyhebI3+VXE34eo8ITrsg4PDopxMnt8UYSnSFFdvyOymC197ndWEunnphS3aPDELMYZL0+Jjn27TK/iTiiBo4Iczo6PmilkHTeQogZDTRC0CCiUlbvjhAU1qgos9lfs2G8VPjNKbcyMp8ziE5Tp+QoPmvtnjE3t1x3u4waLxmfnLY8R5hUVZX2aqeAKQ1DpcJy+vdU+TFV4uTId9h5UOyQ7b7BpDTQ57Hldcjzyb/ntPLGGLwcKuym63zf35npztfLNctj1lrjQkqPpjU+ET2tNVpiig3vA54IcFprxO8UdVrrsa5d2abrldcsjyH/lGsYa7AfGnDfxNSWBpm8ttNWKgDzGMo9mzpKSBDURCd4oGifYdlLAdpoHQ2G7IziIjvjSAiBKo03e8MLgbu7O6pcWiBkBmVe2ZZ/NyZGwsw5e0yVoHOthJVjrXx3ahQcFcM+xFSSBXM5tx9z45gqV2Xm+fLfPSabmajZ0vkgMzGT81IaFKdrOvfMMdiaixabG+v0mXI8Zerue4Vx9uGsHF9IDi3H5nQMBqawnfstz+AenoFdLbFksA4IqrIMSnAahkrz4fe/xx//+Z/x7icfY5qaoMEqhUlBJn6zYXN1zd3VDV/+4pd8/cWXvPzqGcNmiw5QZScUUgobBK1krIEVBa5IuEv8vr9GO2eUPL/pvpdrc2yNyudyGw0WE/px7Pn8zhQey3fK8U/v5fNdOs9M93naMnxO4bCku2XfU3o3pdlzqdEz/JfZW8r53ufoVI7zvmtT+jFHc6bC6Vx7Ez2ZthKvaK1Hiak8o1MD0jGnq/L6dIxze1+mYpnyAbmPzPPMpZI+9o259SvbnKAe09Dqe9d/+u7099JxcsrfHRtzyUfM4cVjuHXqlLm3fszDyvRslr/POmTILprhPhpxbG7H2nQ+cwbiaV+7Z5LRIkoM5VDfqKGZm8OUD57uwxzMzcHHAQ2ZkRnyHMqMHiW/PEdLpzzvveurVFK0h70+59Zgrk1h/Fgk9fwYdhzjnEwyB1/l95TKSqn9NSuN8mXfc+N9mxbPB2+lY/ymbXqOSzx2P2+6//eUr31TE4mRodmg9/r1a0Ti3meloQ87mMv7UdKzN8IWjI4L02+XD8w98w9rmhyhs2sBFTSY+DVFdviK3vVCrB/sjKJxA2sRgjUMWqFCwKikLBx1LFlZmNY9GTZEojEnMI+LQKWIFRPfwSBYPMkwEqKyXklFPbQoFIEK5yzbO2GrHZXvaLqKKmjCsqeqHN2gqKxi0dSYaoGpGrQmyWwpY1HOGK8rYgStoq6gsunc2RIO4570qQbh+L+gcOGU5nRL53qUqni0eMjdf/qfsvk3/wZnBLNc0QXPpepQC41pNS8HzXOnaUT4A6t49OEp603Nq7stXy1eQbWmbhtMVYOxuBC43NxytX3OM1q6waGlpkYxbDcs/vBPePQf/cfYzz9n85/9t8hixff+d/97vv5v/ku6Z7/k5Nnn/Nbqgs9N4IuLU1Yffp/X1QpRay5W5zw6u+DL//r/x+bpZ3SbWzyGrYKPaAhe6GgZlGelDQ+84S9sT18vOV2ccWIW/JfD1ygFCyyVqmLEp0+AHFRSBmaFVVzTRQiI0oiukKbBWKG7vCGIxtYrmsUZF+tTqtUZq9NTrl9+wedf/j3O91xcfAtMQ91orBbcxuG7lu72GhMGpNvit3csK4vvY6rRYfAoXWPDinc+DHz0UZWU4govgg930Vbvo0E/BI9zA4NLwQgiydEqwfZo8Dwui8XrMmJ2UfEsBuUJMuCHLYSYva93gW4Y2HYbbGVZr5YsmwUQlePLszWrsxW61gzeY5zBVIKSmoVasDI1vdU0dkEnHXeu5bq94mb7gq6/xNoVtTlBgsfoWB4gqgT7GJHs49kOwx2uuyb0HQTQytBUivcvet5ZPcaYFcEolBmQXoNU9PSAR0t0AIAKR4+TDhd6lAir2rKoFRuJ+hMjikY1hK7nZgknnxh++IP3+MG3fpMgD3h1eYcKCmti+nCdIvaNDgiO4D0SPFrHupxkDJQinePW7EdUZs1MxrG7HxmVydEoLHu80ZSWRJ4j8737OqP83AgTyWl0xJEJJrQueSfSWiv6rDDWatRnK1HRecEFjIGmsQxDBe0wOjWo0Uw8gIrGzTfpCZTK01RoZccVEhFECaLjJHVoQCq88tHJyFrowV17Nk9u8I9PsY8dstxg6gWGWJNcxBHsAOLpXUBcPGuBgOsdITliaB2N3M4A2kPVcmJbutBzKZdc3Qys+oret3glBGMQpUFqtO6ZS+ms0tp9Ex7nGP98yGPMOQQeZkH5prJkYaaYHdt9upmcjVQbjVeBTdezRKEcSGdwnaX1A6vwgIZbHBXaC8EPGOtTWQRNIDrCaKUwSvPgTHBBp30TWqJOum89V0OHENh2Az/5UvH1X99RXwWQjkFuMVazkGbHLyqdTqpKxvJ4OeuOSz3DgQ5PT/7eLUysgSyRriulCSqksx/PdQxSmjoJy8x3Ync7g32CI0Cb+Sw3B+Mkn0U1f286B9lteylTorPjiiQdVclr5q9HhyptTCodo1Id6LSm8QVCECobJyUQcU0QNAGCQ5Gd/hWVrTg7XaNRDEEwErCj8+BAGBxh8AQnkLIbqpiQJ2Z/UNFR1EmgDx5Fg7U168WKd05O+MIADjQeLQ7vAxsNzeuBm+uOy37Ljd5S1Zarp1/y7N/+jOsvf06tO37zt3+Lj370zzl7/0Ps2fv0LuDcV7z7ruHqqWV729OHAR9RA717hVWWKlhUD24YWD9acP7hd3j8zmOePb/i9nYTsw45TV3r6EDmuug4Uhm0XuzOpCRKkdd/chyncmbcq+gMGyTQD57NpuX05ITgYv6dIDHTirUN27uOjx4vuXzUgPdsvcEpi/gtomzilSuGTUd/cwmrFdQVvfdctz3v+J716Snvf/Qtnj9/yfbqmquvPuODh6fcPHzE1c0d5u4OfXdJ31/jties6iVd6Ghdy5jjU/XgI++ttWZIjL5NOgPRglOgRPi0F/6JUpwbxc+C4sfAf+yEK12x1YotjsYpzoCXOkWfE3ile34aXvPtv/9vqD4ItG7g1Wef8/r5l3x6fceT2vJ9Ed5v1py88wnrf/q/4emXDxn+8jO+9/EvePQffJvnf/SH6P/sv8V//gtunOdODFtdodcLbruezc1zHj18wfsfbtCPHjK8VHS3PdW5otYLqvUZD/RPedmd4ZTDacFhMKZh0fZUSuFcRfPoPX7jT/5Dnvxf/s988fOfIxfvUC8estgqTrjjtlHoYcEiUXmnBN1YQkrnLcHj/QB9rGm/XtSY2oylPittWC6XMbAuwNAHai1onbiTQh+wA7Z9byBRO6N4yW/sw+mOr/Gk7HhBsCHizs4IjSJlE4s/4zeLzB4ASseSGkMI9BJtUSqd/1guTKODAmMRiQ6Q2Rk+y9RRnosDjNlf4lglJ5dX0QGzdyDao6XDhBYnHYiiqmV0Nhefo8TThFUcgwRN78G1PVVN4rsE76MtpFYpu7XShETX1TLyQ4YaTR3n9RbtrQ3jc0rEfL1sWdEwNaZlQpRTf0/ruubnpkrOrEzKxvBSsTkXAZINCXuRujNjLaObphF1ua9yTGUkXumFZK0Zx1MaF/JcJQgh1SPPhvFsEM/1xKcGiGnLa5rHNGdYK5n1ct3Ld/Oh0tqMSl6tFN55tLbs1XmZEIaoWJpnDsuDPhdtOKdgzcfobdsUmUwFnAPF4uS5OUPPsTYdr/MuGggnzFcpXOXo+rlxiCTENVEoXb6+HA3nVineptZj/t7U4FKOJ8NrbqVCMivScwTAm9agFBLz96LCbH+Ox5j9Y32P32CfJynXbMqMHvuGJKmwhPtjyuepMnn6vfLZt2nTtT3WjkXVHnu33M85nCuyY/Sn/c7N776W+y6NFOM6SWSax01SUThRlaELPevHD/njP/8TfvjH/xSrNWItvffYYLCA2/b0d3dcvXzOl599xqtnL9hc3/Di62coF7BKjzVHlEmp4HTCNTorUmK0E2rfIH3IvO6yYpTC0jEjTQnjZZtmLCnfzf+WhvL71rV8fronU7w5ZhmZvFM+O51PeT7ncBPsOyCVz5T088DZ5J45lbSlbFOae8wgOsczzPUze9a/gXLkm7bDtTvEF/m56ZjnxjVnFM9/7+EiOZxPaVif7s3cHpf9Tp+Z0uN/aBOJCssprpk6NEzfuQ/HzeHeuTlOn5uDnbkzMh3HHO0q12xKP7TZ38tjisqDvT3Sju3D9HxNcVc5h9065XO3M5rNRd9Mx1l+s5xzef6O7cXc2Z6ek8xz5r7LNZ+Lxp32M97PMzpC1+Lf+/PLCvP06jiOOVjYe28GJst1mZMvDmF4Hkbu45WmfUjYeXWX45q+N83S8DbtYN3/R8Clc98E9tbuvrNdXruPN5vye0pBzKAX5bTFYsEwdPRdF28W+LY87/u81aFTyBwuune+7BSbv842nodxKDsFbtJ1kY3ycU4KiKkJc8S4SSkXy30/Nr/MV2U6VTal5vdsrsW1hsF4aiU4FK0o7hCc7VlqQ9UoFsualW6omjVVHbPNVUZT15ZFU1PXNUZHnKe1RkmMVhxGR/oY2aitKRzPXbFWhzgn4ydTWxpTY+saVIXqB67+8n/gym1p6hUKuO17+qC53rbUzrARqLXmA7PmR4/OsR8+ZPvTJ3jnWNUGXRu08axNYKkEJXBrFO9UFb9DQ9MYGmWpvCJITf1Pfp/VuuPk6nPWm5d864cfcXJ+zvDv/Ck8vYTXd9zd3PCXl0/4i0+fUH/2ktNqxePzh7z3/e/x+Dsf8uMnX7O5u2SgRynDAqiSqU0rQ6M0S69QyvIsXLNY1Cybhmvludncsd1sWJhdtPg+Pdwp+HILRENzVVWsl0uGvme7aZEAurFUzZLlasnjhw9YNpZPXz7n+dOnvPvue5yen2GrGpXSQHuJiscQAt12y912Q+8cy0UdlY1tF7MQopAw8PDBI05PTgl9j/cR+I2NZ2Ho3Einur4fU1/uyw8RJpTaSaLHz/mOvsaV2HeE9N7HuonDEKPFfWC5XrBolhhrEYlewstlTbOw8Tw4h0aiYdhYvA9opamrGqUMbee52XbctQP9EJCUJlVrE9N1WktT13iv8e4G7wTvBDcEhsHT9y7pXSOerOqai4uLpLytgCJdpReUz67JIUYFixTOENFYXuJEY+LPgKeXgXc+vODf+5e/zz/5rR/wYPUOf/23l/SbW5bLCmMsRlt0zsoRZNQplSue8ZZSyUAkM0bxhMunO7WPz+OeRnx5GDAxJwfezxPkTC5z8uOO9msd98lowY96rn25LhuvIo7KRimVar6rZIBRe+++uZXalBl8rmIGei9hzOoagk/pzmFzt+X26o72piU8WiA+RbYn+updcjDpAkMXjUBoQauYGt37gBFwfkC7GCWutIUQcP1Au90ydA7xMdVxXjuT5P0wo7RWas8s8NYy6tu0w+cyD3B4f6pzuO9bIpk27vosn3+TziD/GK0IodCrplqwGsYSAhK9PxCJqdTFq+Q4FgMLrIGqsiwXa7btQO8HhlTbNe7pwLaNNZxdEO62A189eUW76UGSbkFBPqEq6WWy5i7zAKVuFHZGC8bnCplrRv7SObXzlK9RyUikMv8RcfUxmJhb2WP7+OvXIezO317fEzw1/Xa5Dvn+Xo/3jDPiEz8GEe7JASN+Ae92Ot/4U/JB95+pSNtiRhQAYy3r9RpV21hWIcHiMHi6ocP0De2mpWuj8dC3iq9+/ilf/vKv6O8u+db3f8Q/+1//H3j/+/8um2e/wAXYuJbe1ZytLmgevOL69ktEDVgrbDcOfMzIGxLuUhpevnxN86jDGEvTGLat0PcDrrHxLIiJ/nyZTks2hkdHA8/urM7pV47JI0pF/FwGb8alibWPo25QWK2WnJ2teXk1cHcz8ODhY/rLq9GWYFKt8e12S9t2LBYO5zxBhLZtubi44NHDR7x4+ZqXL1/yxRdf8Lt/8E84PT3l5PSUu/UJ3dUC397S9y11lYpdaht1tCqQfat31El2gEVBw4Arv+WqNtS24rS3/L275d/nHB08MRuPYLWNzhk+x20rjNes1ILqJ19we7Xhum/pN7d8cNrQNhf85dUV1+9/wD/54Af8wSe/w+cnj/jv/vwTFv/Ff4X6+c9Y/NbvcPmj7/HFH/4Wf/n//O/pb7egG8QuuGgXXNQNl3fX3Nx8jd885+EHj3il7tCy4ZFa4q2GBurTJcutjyV0gsYOglEesYZ+8OhNx7JZ8OG3PqZ+8Ji//dd/wSd/9mdUTR1ti7qmsRqlTeJLBBsExBIC6BBiBtS0d5XRrBYLmqaKdsBEq7Q2VLZGGxsDyrRC5fuTMz5Pz0o6fp8uR4P4UU+gc01wUwT4TXSYKBVruJdfO0JTRcWfJEzuyYuyP8TUSv2H3ns2nzMUKVuOprKaymiEsAv2VBqjbeQJpMh8SbR5eO8JvqdtB1ABlZx3rK0xJpEQFW2kjdHUYlHKgFjEG97W7PjWhvG8eDlaaaoEz8jeWktVVQfG5qmhvBS4SmVlqXDLxvCcEm9avzwrhOaiQecUprmV0dxThW45n7EOeBHdUs7VFMrSMorLOTcavMXvG4rzd7uuo2maMWq+nHsZGTKOKXskJQa1TKmdFQRTBXg51lHIQKLxKOXvt0Ynpa8miKCNIeQ090mY8s6lVAuMSqVjCtupY0O+XsJBZe1Y6zzPNytgjskAU0J1TJlawtY0wrPc2xFu9GGfU+X2fYRS0okvo+n3vql2ClWd1lMRU6EJEiWVzBBGLqhQak0QkAgSAlVVjTA3jqlQ/o6IUO0UQeUc8l5O51u2cb20SnX89lN9arVTrE3P3lw7JlAcYz6mf6tk8MxrhMwj8x1jfpj2+EDhPhGW3wTHczAwx2AnUSC/RalIUkrNRnzOKXunuKlU0BujJozubszl3KatfEah0BL3uCSco/IVSI5uUamkDaIVXgWk0vzuP/3n/N6f/QuWjx/Qq0AXBBVczI7QOe4ub7l7ecnt5SUvn3/N0ydPuHz5CnxA+yjoeB8i/tHRwznXdEFSzb687nmcxfnN8L/vKMQoKGT6MV3fvb/vYX6nypO8fqPShgyGeX93kp0qhOK8F6Wx7Rgc7X9nH1bnvJzLueTnskKzxHXlGShLPcAuw8nbZEyYwubBuqZFma5f2cexvvNYcptzfJs+X97/h7ZyreOagTKHuGP6Th5rGYmf1ykzfOO4U19ljVqld16hx3AU7HivsszDm+aT+xz7mSprZvDyMRjc+31Ci0teY2rMnxqZpzi3PG/5vTkD93RO5XiP0uaJADh9p7w+5yA5N+454+jct6ffuw/ucyud2ubw+D6/lJ0iS0HkQBLe/z1/R+YzXpQ/5T6W45/iiSn93P99n/6VNC1/ezrX2WgtPX8Od/0y8qd5qns4IlsLJ22OZk5hvaTXc/jsAD/NrA3sy05zTpp7a5GMEOU4ps4F0/Weczieju+A7xj/s7sSJnN8E5zPXNz1qziA14y/ZjMzzLRjZ2c6hszTQJQd69rSdR0hOERCUlroqFyT/fNeOvTmb07bwXjVZOnStQxne3reX0Pbx1vJskGsGZ60x5OhRH5JyU62NjmKS+s9w/0uQmHkYArDzAyNnxnX7JjL+wqCDARi5FpQNdVyzfvvPeDdiyUsoNINjalpjMaYNFYyz6sxo/N2ggtAaT86BYwlUrLhJ9OAYnh5LUo52zmHlxhxZWxNcEL/5HNe/c1f4SysqhgJ70TTOk9baRbGUvtALYELZXj3wSP02SmtD2zaHucUS2fYisOJoTOKCkWvDIMVJKgYYe8D4uD08Yc8+r3fIbx8TfjqKZ14qt//Ef7VHW1VYc7O6eySl+dnLD55h+/dbuievcJsN5j2lvbpZ+jtb3L35RcM21u8CmhtOPE6OqkmrVAtmhMsvVW8CB1re0Jta64Y6PuU6rgyqDGNejjg9crzTOLBq6qiqWv6TYvrB2zVUFUNi8WS5cmaxxfnhKHlxddPefHiBe88fkTdLKgXS1AW50KqiT0gBNqui+nPRTAp0tv5aEA2xtLUhocPL6jqiraL6UqNNsRU4BH6BIXzga6LNUG1MrPwO4XsOT4jAkuCahUVjCIxe5qI4IPgXKAfHG0bnTRWiyWrxZLKVvgQ0EZYLCuqSgEB71xMo65S5xJlIFNVoDRtO7DZ9Gy7gX7w+JDSw6uAsio5u1R4D97F9NbBR6V933cM/TA6DCitqGvLxekpTV1HA7VKeiUfIxaREBWikgwiIUZJ5f0PyWFrPD8a0IJRgljDww8bfvv3vs33v/tdhtuGzfAU7x2VXVPV1eiUIyI4R4wqlp2OYae7USmnQ3LSm8BbljGOyblzdPk4L7mP74/K+MlgXd6PtC3T38jTe21QKub3KPmQbPwreQ1jdDJeucS0RFweRKEwZIJS8ijTOczTxkM5RUTQJubZ0CrKHHmtQdNvOm4vN9xebQnDeUz/amPmLAnC4ALOp1T9IWU/FI9SbqRBCk/wCu8VSgVC0AyDo+06tttt4nt0DL4nbqXWsb9MMQ/3c/76m+S++/j43Zrsrk/59bk+5vo8LjOrPZJ8DMaE/T5GvSVJnvQCIcS0x9H0lWp9R9iLh1UIwTEMjqq2VJWlriyVjUYbhcKJxvfCEDwoF8s1mEj3nVN0beD6auDF1zcMbUgBg2qXeUFRGMR3esrpTw5OmMpmo9yQNn7/mXm+Iv4yIeATXn5/r+b36z5YuU+GfBNuyX8De+WejrWp3PuNW9prRjZf9mSUnH7Y6Jg5p6oqTIrszvyRZLqVeP25IKmoJtjXtUX5Q1Mlw3jdVHRdlyzMEUe4occNPZubLdu7LT4MDNs7nj99wmZ7g5IWH+64vv6K8+6W+uwx1nsq8azMOyybJWe3d7x48W8JnQM/IE5ADEoFXBBcyKUcNGdnZ5yeniSdeNJvuYD3aW5pfiHImH5ZFY5Nb2oqw35BnzIujTS2p6kr8EmPo5PdSMWSTienS1bLDa+utyyaNYO+Tqy6QkvMILPZbBiGgaGP/FfX9Wy3Wx48eMDZ6SnLpuFVcFxfXcUa7ycrVsslzWJJs1zTtbf0/RZr1mNtbq96tA5xb9KGvklntg09L8VxoSwXpuaX5pYrJ1hggWYLdOJYUNEAgwKnFEE0l3jWz5/ir19xFxyqqfjovR8yfPxd/v75E5YX73F29h7vLh7zslUsv/Uh6IbNly+4/flnLP79P2f4/d/nxX/2Lnd3T8EJNjha0xNqw3U7EC6vOHn1ioffN5iqptp02K3BtAYbLIYVjenYMOBF0F7wgyDLBToEZBigrrEPz/ngB7/NVz//CQ9+5zmLB+9QNTUhgCGmh3dJT2ayjlylA5eipWtrWC0bVssli7rCmkjzM8wZbbEml8aJgYxTR+k3yZv5mUOYnNKvpDdJRuWp/mSWLjEdy8EjEUfnX4UDBD3iMiJdGOnYqINJNr38t8QMJkqRMsGqVN8961xBpTJbKkW4a5X7z2WRAj5I4jt8cgKLAwx5MMQyQ0YxRo4L6Rl1uJ5z7a0N4+N6qZ1huzRMZEa5NF6Xixc3MSRGKEqtSmUCEScsCbkiMT21SRs8ptl1bhT+56JaSiCYRi5PFUf53mz9a7WLnsyMylwUavaiit7ru2i/6ImbvOZyPVfnIqBEu0r0ejYaL1F4LcektSEETwgSlQNpTJW2DMNA8J5KR+PoaExVhwfhIJpVa4bkja1UOvRKpXGAV8R0DMbihzjeEKKQ6fM7So+nKH+rjHYslQ5zTg9K5dpSmhATwESGWkXPkYTB4zpkvmiOCSkE9gx3pYKrNIqVhqCpYjEkmCSvhdbJ20olj9hDjq2E/bEfUhUEoyEE/DhOjeiADzHy3AaNEYWXGHnrEEQrVB/it4kMVlT6SPTIy0YTJNZs8iQlgGVMs0VaayYMmopIXalsXI41F70PiYEF5zxKxVQx+eygQkZ1I6+Z4TR3rNDj2kVlbl7fCCKS8itJVpSSRZyMd/fPXLm+434DQe0Y9Kjs2od5FDFaWSThkVxzOe9BXIMSF5Tnuzwr5RgOiEoSJrPiOE5dj/PJT4YgUYGXlTQS31GqNIDl6ObDuvewX/phOsbM2E7Pe5lRYwrn039VYhCNj7/3wePEY4zGOR894ESwYvBtQFYN28Zwqz2f/PAH/PN/+ec8+vB9tDEMErDKIt6hguBur2kvbxiu77h89oKf/+Sn3NxeEUJg2LbJMSbOz1qbGMqoAA0hEESobYWqouInnsWoHMlnPK/HFP+EsIv2ngpFpZFlxOcJh2qlx7pKxlbjPnjvQVze7ORYlGFpF62XdGUJNaY09+xH/s5F/06jETMtHZ2yCvozwldB10IIY12jLMj4Ce0l49wCF1PAlVIKYw9ZgYyHlE44P+N7kRHe85j2BL3U/+Dcbg/0TsE1bTIZWwn7UyNk+Wz53WkE55xibP8dxrNbvpfhY0+ZXvZfMrAie/xIxNlpH0g0U8eUm6NhbjyrCXa9H3HyffObnuc5GJp7Zjr3kOlqBtZEZEPykS342lknhUhr7Y43kHkBX03gaw7XTzMilGek/F555o8JEFNcma/lTC330ZjcSmfJA1hk3/A/N++5PTv2vXllZqFw5hAWpn2N9A/Zl2xUUqqKRBoe2HMAhIjvsjfxsfU4BlfltTlj7JQvUuyXvZlGm5frOV3/zAfBoQJx75vj/GRMQR73jfHd+0Si+xyoprA8hbGS1qSXEn9yqGyb0uqj+E3vFI8hSEqvmHuJdKt8J9PScoylHHZs7CXfkq6i8zjyMwUuLHmRUtYacUUGxQR7mX4opfDBjzg9j6U8t9O1LtdsXsDfvw8R5wYEE2JatRghDUPCsMH5EdfO8XzjCs/AfslfHfKGpCpoO149r+wsL/krNJPSbKrslJpd+iX+Pe7T+JmEt9K/WqnRMK5VTovOjqYpig5UcUntKUphZJvGtZiu325dJkrz5JQQMGi75GR1yvsPz/nw8SlSgegY3V6LQel9R3mVx5MUJBkrqCT/RQNgjjCIsl3kM3eDzZFSxuQIjh1uGBgwPkZqDu2W7c9+zM1Xv6Ra1DGtrUQlIGjQFiOaWjxWPGfGcHZxjlotcUA/BPpBqHq4UQ5RmtpAlYxCtwo8Du0dunc03vKdj7/N2Q9/A/Pjv+H62Sva2rL+/rdY32y5Wxm0VQyrms2yxq4aPrhzdHaN2t5ghy1GHJdPP+fmyZe47TZXA2aBRiMMBIIolijWquIzE7glcGFrlDG89luc84jS6En2ovxvCcc7fsmgbawHb5Rm07YQwJiaulnQLJcsVysuTlbcXr3i9cvntNuWs/MHKG1oFkuUtri+o3cD3g2ICP3QJx4q4pCuH3DeU1cVdW05WTc8fHCR4EFQKhpdhzHDm4lOGN7TD0OMuLRqgu+y3FsAdDm3Aq6nMlpk9cPoFB+SsXAYPP0QDePLRUNTN2htcN6hjFA1ClTA+4FhyIaumEVvdKY3UZHaDQObrqPtewYf2KUw9kRbVaQFISici1G73geci3VQh8GTSYDRmqapOTtZR7lL7eozRmchP+LtLC/44BEfHfm991HnFXa8Wj5AChCjePBuxSffesjFxTlf3QzcbjcYoKoq6qoe4cqnMn0hp/jUepQJ4/om3YLK/FchY0ihT5jQ5v2dzfurRj3EPmrayeLjc/f1O+Hv0sXxa1onGpaEP5V/h8jj5yAItTtLxsRAImOjXk58vK8STERaejiWY3zhbo7H+OTID2aJQxFlIY1m6AY2Ny13l1tcJ7AE0QEkjJkvvUv4W6L+0weXeKCsi8qioows6TAMdKOTSxjpb5Y3otf7Tg930L4B2bwPHt72/bnf72vTvdjRu7frc55sKjQxAMUFn/gWGVOVa6UjVs/EK6X5dYPD2IAxNVUVU0obDeI9tlJoJyjtQXsMYI1BvKbvFV3nub5y3L4eCI4RPmQ0eqSxpSh1paeyXfmTZeaZVOrpPO5fh3Kj99dJsR/qd7iex2TQ+/5+2/ZN3pvKSnPvHrs+95yeyBUqcyv5oKXr0V6w04EGifi+qipG1jy/lroLST4IsisNO65t8dkQPD45R2mtqKpoGG8WNf1NX4wPvOtxvWNzu2Wz7eglsL19zcuvn+C9sDAG+mu+/um/wtYPefz+91gsTlgsTzCrU6xdcfrOh1SrJd1VdPYwKsJRzsbSDw4virPzR7zz+DFnpyfUVTWyrd4HXEgGtJDloJKHjDzuFE/Mw1LWdcXOx/2VSA+7vmfR1BRqcpQSRDwQWC0bTtY1RgtKNFnfq5LuPQRP224Z+p7BRcP4dtuybVvesZblcsHJes2yadikbD6r5ZLVKvJUd8sTuH4RaynXC0CjdQWqh+RaNtVxlbJX2bwKvA6ORlvOTM1nRvjaed5Ds8Jyg6OVnhNqGhRBCU4pEMsdHvotD3Tkc4faYk5PMY8f8lg6TlcLjA5s5A4JlscnF2yWDwlXW7pffsoZ/5Lme99h/d3vs73bEC4vaXygcYEFgnee5c0dzavXrLoeZRVWoNoOyKbD+CVS16xMz8Y5godsMOhFqFQsW2PdQL1e8MmPfo+f/e2/5vrpV9TLFcvVOZutog594h2j3KQBEyTWr04OZCDU1rBerVmtltQ6ZuNSpLTmPpYUMaZKeulsIyh0Gr8GeTDqRtjBpd63QybwnX2vJDqjDmnySuyzcIKaGYMU/0YUniXfTDVgH19nniPxHXqGfuRTqvTICyWWajxDUV8v0Siuo61uCJHn0MSgApv8xUnvB1Ec1E0+0t7aMJ5TRkSGen9Ry+iHUnECuyjTrIzeU3jJzms/eyUZtcPis8wfRANi0W8ZGZwNC1kplBVPmVCX0R/5+fJeyVhN+8r9AYngaET2CWFZS7uua0QE5wa8Usl7JH63rutxfaw1B3ONxvadIUIrlWrH7JRRo2KpWPdyffecExLiNsmzBSERzOjprK3GVpbQ5zol4fA7WhcKhv19nkbAlO+V+zNVfJbR8gQ1zrdUzuR5zQk25f7NwV7ekxIOyiYolE5wXcBFnqMU85gjpNP5AGNq7ziXXeS1pPmJj3BU1zXaZk+kKPQKabzFHPfIdBCCKqO9dqm6ovFYOOYUkwXA7EhQ7mO+V67tvcybxG/urVUhlIUUES9q4l3JMZGtHOe+whGlkOKlrHA9hJJ0V6I33445359bnl/+1pSZLed/oAQqz9sMIzXCyrgmjDgK2IvGKrqYbXPRetM5lDB97O9jTZTCpTRuokCLIvSO2lhiuQ6NVwpzumajPKv3HvMn/8s/4zu/9QN0lTJ5hIDVGjV4urstd1c3bF9fcfXsJV9/9iXXr16xub1j228jPkx4JdORUuk5ZswgOULMKKfyGk+Np7tn9vdvb+/S3VLYyHgy4/qQz6GA926MkFBqZ9Q25nBdQ2mMGRVtO1y9t+4zgvQ0InHEi5M5T5tKdCXfP7ZmuY8SJ+exBTmMJDxYtyPwV96be76kUXNtzghS7u3cN44Jlm+C9/3zzF7N6CmzuluP41H+9x7e3UOw7zURccgEt2THs/z3nJD2JmF66ow4956IxChCdrizxKFzqzdd72xQnVvr48rHfdiY7m0J38f6zjXWy3vTaNS9eR6BhfLefcqLvWdExkinub2ZO59zsH0MrnOby140bXP7XD4W+ZbJuxNas3Pmmc8wcgAzBV2c47vz88f4rHK8czS2vHaAw5IyZw7878NBlOPItPjgCKuDvZtbh7kxzvFI8Zl4quZ5o/uVE9PvpzcKYTWhkciEjHQnt2M4YH98k+/NPKfSh9TkWp6LK5yeimEe9JH7CcnAVY4j9zd1Utzn2+Zb/vbU+Tb26QkSqJTl0aNH3FxfsqGAH7VzUMzfnePtp2OdO7OKAqby+iRjbZz7/TTpmzRj9Gjg3sPGEnk3VN6CEg9lh6ddxLgtHDkyvOZzlgmCpPmMU0t/796Rg/3ePRmVfuOejHcUVVAYEbALFotTHq0ueGe15HS5RBkYlI/y6KjIlB3MyzgSIEZHTZ17SgfCnPozL39I6X7H7DjGjIofHzyOAbzGDY725Svu/s2/oWtf8ej8Q0RrhiEaIFe2ZmAA7zC+Z4nj4XJB/fAE6hgpYojGv40fuBKHVAbto6otoHjJwGsZ6HrH0Dqa5oz2Rz/k4Sfv8+A/+c95drXhyYM1i8ePWN49xXVR6WYQKlGobkD7wOnDh6yax9Ti4fVrfvG3f8XV0ye4rouOGsGzSFxkh0dhsBiWquIJG6SusE1NR+BFdxd1INaMBswd7ArR4XMXcDCuu7HYqqKyFXhH13VoXVE3S5rVmma9ZrFcsl5WfPqTz7m6ek1dN5yeXOCC0CxXCOBDh3cON/TJEOtQWlGZClHQdm08iyia2vLgfMXjh+e4fohnIDv5pXFZY3B9T59+RiWIFLimgKj7TunsmRdSpOYumnpwnmGIKVGNhuVikdKiRwOXskLVQAgDw7BFMaDQaFWjqPDBIeJjjXQVcN6zHVo61+MJmEpTaQ0upBTsPd7V9B10rWMYPIMLDINj6D3OZfkl4o/louFsvcZqk85QUuYGj5IQcWdyLhYBFwJ4T3DR2O4Gh/O77EiQSrN5YUB4+Kji4YMGEeHV5Za7zYaTDB91nZzrFeDwPqe6jxnCZA+HZzm6UMzew9/P8c673WLkdebfjQ/M0eOSf2CGJmSAmvIsmU/a0RONNju8KOwcyuo6KtCdClG3k8zWSpmo75ny3yL3zDcNU/YzzuVxCX7vuZwxThGjvLvbgduXd3RbD2eAjzocEUk8VFQ6I9EhQwJjBKRSSc5BgeyU9M71DH2fnMzzJHa7E4OLZE8u2t/nGd7uSLsPPt70/n0899u0w/d2+33suQwLc30ppdBBI+LwLq6dJgYn5chQJPEEgJKAcz3WCYhD66jrVghBWowVjAXjFVVKk14rS9cqvIftFq6vHf0GVEj6wYTzk9Uj/5P2qqDx488+/1b+vYMRxr3eXSfqhmRexhfYMb4qr+3b7ddURnmbe286Y/e1KS85/d6x+3NywkF/koN/du7C8XzmVOf7GQKrqkKPWe8Ydabl97JxPKS0zJLgLO9RSHWVM7621rBaxajlO70hFDgluB4/DGxuW262A3fA5aunvPzyC3SwrJaGqt/y+m//FXLncD/8Ix5/+ENOH38bu1iiTcPy5IK6WZKNyFVlkT5m2e36js45VL3m29/9Pg8eXrBsGiptMAn/uOBHB7Hgs7NYkkvJMtThmZyDhVFTovefjY5Bnr7vowFVRd07pGwnIrh+YLWsODtbUDeavu1R2uB9j5bsoAp9u6HvWoa+p+87tm3LZtvhQqBuai4uzri+Pufl5RVPvviCh+++z+nJCev1CTfLU1RVI+0WPzi0NWidbVMuYYZ5PcQBTGrFrXhaEd6vGoJT/BLHRyw4VcJrJdwEjyAsUfiMjzD04nlsKn7r4Ttsl5Yv1xWvlzU1jvdWSxbS8WrzFX9953DrD3jsHvDq8Ufoz3+J//xTlpdXnD4+5wd//Husn3/BcP2ahygeqopHyjJoz7Lrefz6Ne/cXDIsLEYHVHtLf6tpOgNrzYlR3HYBJR6lTAzUagdsVWMkELoet+34+Ie/g1EV17/4nIvzR5x//322XYiZb8QlXU90Vox6A72Hy+u6YrVcs1g0GInluyJqEtAx6NXYKgWRpGA5s3+uj7a3wDUl7osBWslZqsysd08/U7o04vXxXWIK+LE2+b7MnOXO/FrigsbeQnZGLswvmT3QSlAqoHV0tImZt4tvqORknrMzjfdiQEe01Qloj6iIewbvgIB4QaOptIBRKCUElZl1/VZZPeAbRoyXyowD5RXsKcyyobl8bqrEyNcgGWyJUeUShGEYxr6z4aKqqj3FaKk8KY3d+d9sAMxGbaXUGJWXnynrupbfG6Oq07PZMWBqiC2fKZVSu5roMZ1QHt/0e6Ohmn1lW/59ZGzVvkIyz3n6/VJo3T88ETjKsSPJa0NFRB58SAz59ODtlIdRSTyPXPOYymfLetj5uTy+Mgp/Gv0d6w3tI5CSqXiTkvnYGpTfj78fvle+XzIZ07FMvzV1JjgwVOVxpPPRtm30ovUxuiWmLZ9X1E3HV46jjFjyIXl+z7yzWzM9Rr3OReIppXb1Je5ppQF+us5jyspSaJoZ/5uacLjWb9vGSFuRNOd9p5c31ZyfZYaVOoCrY+8cw5Hltamyvey7fHaqKBbZx8e/SgsKnE0J24Kikuj1hgugNbo2bLRCnVT84b/4M370T/+A5uKMIB4/OJq6QZzD32y5u7xmc3vHq2fPefbkK77+4glXL19RaYs1O+eZqSFrCr/H4H26LhlX5P4iXt8xgVOjzZ4ibAYn5KwSOZrKJWeacm/mhXb2vpfHIhO8kfsu93t65krcPOKOGeGsNBzne3lNRqXvEZw1jfI9JjCW85zDRcf26VcVJst3yvem0aXftM+jTaWo2Qnu3ntE7ZTq5RjLcUzX6G3GOXfumcxxKpi/qc8p3Tp2bY5mlr/Pwfb0+Vgb8pu1OXgr4bHka/L9zCs55w7GNd23fHbyvfJ6SeOP4eu5ue/dgzc6dOVnp++W/d3HP09/n8L+9JnjNHVeyN8bZ1Q57417bm3m8G/+e44OTvFk9huewuIcDEzn/03asXNYTCbr046+P8U/JUxO75fjLfGtyGEq8jkaPeUDjtHx6XpN55R5mmM4/E28U0lzpjhpHFfRdUmf7oPnAxzEziEtX5vSwx0dN+Pav4m3meMttdLRqU2EZ8+eQXaAIuMINRUtZuf9pjY+UzwaEsxnPuNXZM1mm9ZRPjM6/mgTYiUmLSidv1oOMBA1EyFGbWqFNRpro4E8V972SEy3fq8HSvG77JQiUzyjVH69OBd7/RkQMKs1pxfnvHdxxolWbLoNS7tAW4Ukh+2o5E2YV/LYSofenSJGa0tV6ZFnmuOPIkxFGHMSEO/AJ95NK2pdoZuG/nrD5he/5MVf/Gv0wlArw1YCvfc4L1xUDY0LXMmWSjseGM0nZydw0dD7lgfG8mFT87QOfF1tGJRwUtXJ+OTxoqlNTaM17XbArs44/97vcvoHf8Tq+Svkpz/DaMPy3Q85eeqpbQO9Zes6NIGFsQQ0tzJQOU0bYDCKvlnw9Jc/pmuvCTpglKUOlpVYtjicgkqiAq3Xir8Ptzx68BC9WnEzbHl5c0XbdZjVYsw+EfFUGLewXMtxn42NKdGrir7taNuWKkWBrdZnrE9OWSwWKO/5yd/9Lbc31zx48Ij1yUVMJa/1WL/YuY6ha+n6Lf3QY62lrqIOp+/7mI7bKBaN4eGDFe88umB7+xoRhQ+CEGJ6RqURT0xP2g2x/nFKHS4ylXnfrqQDBWzFvwPBOyRl4XMhMPhA5xz94FktatbLhspUEKJy1NYaW0HwHX0X8F4TnEbCAhHNMGzxoQftEANBQx86HAPGwqqpWDdLlEtp2H1g8FvaTthue/ouMPSeYegZhj6d05R5sbacnq14eH6WMibkDBuBEFwqRBtTLQsBheCcBxcILtYr7/qBwTl8ouwhCMErJBgcPe+9s+bBquH6Zc/Try5pNwPndpFSOldR76DABR8Ne8onDBTrs+7hk4SLVMJh98kWx/UlqR6y2s+4tv9OxjdzW54RXfzPFDNG/mWfLpb6uZEX1QqFSRFSsc/s1GYrg7WGXjvwuxzjmV+JcsihM91RvqDA4XvyduLFsvJcSbqfIguNsgwbx+XzG65f3/L48SO0iQp9ZTUoCyiGYSAmxdRoXSedXTXyEsbYGC2HBp+U9skpIISQ+Pk8zx29KPnEg/n8A9sxPuLXIU/O6S4iDO9/+5t+S6mUSSI5jqiQMjpIhGfbLLD9iiF0UaeYYFEkMAw9XQviNcYqjIppa6u6QmmN9zUiARkCwxDoe2hbYXMH0lcYZaMz8GjRyOdAQOm9M7njgTP9362HLqIY99ZpvJfOioqGxaMwwDwYHOPV3oYffpv2jd6Z8NBz4yznNiez7P8eCEAIZv8cS4xIFlEIeu+7ADl7KCiqKjv/kf24xu/kQL8yQ9tUDsjNuagPszZgrWa9WrE+WfHKvErUM8LDMPTUztHdddxuel50Hfz0BXdPX3JyZljbioWuebg8xd50vPrrf8Xds8958PEPeffb/4SHHy558cUT7q7vkKAxpmZwA6I9RitsZTg9P+Xk0cd8/PG3+elPfsLrl8/RCOvVmpt2G2ni4HC1xnmN8QaTIryt3mUrPsTm+y3OX8a1g32duEfo+5jVxliL+OSQrhUag3eB5WLJg4s1F6cLnjzfoIxl6FqMFqyNNq2+77i5vWaxPKVpVnjvGbxju91itGa9XrFcNtx9cc0vP/0FH33n25ydn7Jcn2AXK5rFKW27YXAdVjWgDWIsOL+jo29AokopjA84JfQGlLY8ZMHfm54/9ktqgTplN+5C4BQD4ulStz2C7gbOrOXs0UPUgzXPqwb17IaVMlwPW9rXt7x+dcOFqngQFtS/8RuYq9foXz6h/ruf8r3vfMJv/t7v0v/tLwgvPXUQTk/P0WvFdrvFSs3y1mOvNsjqIbpZ8cp1tC+vqX8ZUI8fYJRmqTQaQ9AGpwRuOmQtSLIfurbj9L0PefeTb3P76Wds3/ka8/0fUtdNcl4VVDCIKJwWlLJJhjRADFJdLGqWyyV1Xcesq5Ky4ykirdcGGctdAWRZ8C2DXo7gnJI/imTARLlQx8j0/J1RdzyDh96WoKrRKTGel5SxPOKbZMDeyfcFX5Ik0TktoVIKpQVrYkmGukrZUkOIvKQIkrJoJom9SOOe7LUYUB4vDh88wzAkXBjxnlUarGC1RRsVswkT8aI6FjU6ad+oxridpFudS4WZEW6p8JwuTNm8jxNrmia+H+5P/xeZzH1DypyyLf9kBY61di86vVQIld9SalcHvFTYlnU955SaOSp5xxzu0kuW70+Z8/j+IRNVKp90Ma89z7vJ/pS/l/sVveM1IcQISCQhbxWJWQZgpTJwHRqk9hRgR5RK4/5wmIY1j73c9+l45+Bl+o28f9PvHsBIMYby26UiVqmoYAqyf61kEqbjPqZsnI59ejbG8WfEImF0tkBFrzwV1IhHjzFj9yFT72PKmwM1udpXVAoeq/YFuZIhVSMjfA8SUaCCml2LvfGp+Xv3tb15qQyX36yfPaE0vgns4G5qPJxTTJeG0czMR3pzvzK6LCeRv1PC5DSqa4qH4nk5hO1fF7O/awqdvOpUiKUVALxRqGVDV2k++tFv8Ef/3r/Lg3cfE7QikFKUonCblu3NDcPlLXeX13zx2Wf89Mc/oWu7VK8uEkdfrEmZteNQqToP2yUe3hfE1N71ufUoYUBEEt6bd0go13+qIC/p21yN+LnxljSm/H3OaF/+ZIFlineORdFNDUt7+Kb4u1yz0mGsdBabzmG6/sfmO137bwKX0/XPZ2T6/Tla/6s2BWME8Fyk7zfBV3NKq7d5pzwPZQaP0qg7h5fua1OccUCTVDzD5VqWDiZlH2Wf5bPCvEPVN23T7x07/6WT5fS8zsHcHD84dz6OvZ+f2zMCvsV87hV0Jt8+ttbTMz/Xjs1t/E68cdDHdE3Lvub4yWN4pMTB+dk5fifyGjsBqcRD02+Uf/+q5/tN52SOL5r+PsUFU15zioNnM20kA2O5bvfxSXPznXvmbdqvsm5vw2fk6/neMSeUEk5KR15j9MH6T7P6TOWbb4L3di0r/6OT3/X1NctFTRmlFMe9P69S8Tg1+t/bEosrlFljMp39FYZ/TzMWbBL0o1Khoq5i2mvSGKL+QGNG01Zi5VPaOavBqlhBI/PV90FMlgtG9ccII3HyB/xbwddMfwBEG1ovLMyAXfaszgPNWU0HtClKQEHiRUs5QBUZB5KyJkeNp5+c/pkCz0zhSSmFsoaKgv8JMdLAWEV92uB++guu/uqveP7kcx49fkQfhL53BB9iNLiSGCnjAg+C5sPlCQ8/eo/w0UPMi46zrfCBXvK988co3YJyBGvpUDgTlXYNGuUCog3nH3/M9//0T3n0o+8j/9//ms9efEH/Bz/g5Pd/QNMO8bmhZRECg4Eb5ZGNY2kXnCxrmrbDt3dcyx3h+jrCsIelNjxUC5ZYXrHFKViiUMrwohY+8y3fWp6wtYrL3sXo4gC1trE8T4gRxCMsSOnsndc4lo6rbI3Rmm1/h/OeRd3QnJyyOjvn9PSck/WaVy9f8OmnP6NvOx4/fh9bLzl78BDQuKGjb7f021sQR7e5I/SOqrEYY6IDeQjUdU1VGU5WNe8+PsMaQZzHqDqWOg0eTHLed0Lb9bRDT4DkODtPM9+2ZWV6ruWa18N7z9A72ranbaMh/nS1ZL1aYnVKh6zALDS20aACgQGCxjmDax2DHgiS6v6amAa+dR5S+lqhpqoqTlcNWjxDD20nDBthO/T0nccN0Zg9DAOD64t5ClVlODtbcbFeY4wmSMxCOASH9wPaOXLZL58cR1ysAYcfBrq+p+26UW8x0m+lUdqgwx0fnZ+xMjVPr7e8fPYa33nswmJthSmy8llrCSFggwGJCme8ItDvzquSEUchBT5WirdDrjuDEG+gwW/T14iSJI4nEzSlk7OFRKcsZKfzIqcDHenmDodFl5NIL2LkVEocOCrRFbsU4/v8LRzh/cb1muHjifXk0ZZckFOp6EyCjpFWrvXcvL7j1YsrvvUdT72IhlWrY2S7swbnFQQf69qHGGhhTUWMwtyV1FQCRkFVKapKY4zCy7Cng4nrIRD2efrp0v86jOP/Y7Q3yS7/kD5RxJqresdPORezUUhQ2KpmsT7F+TsGv6NzTdNgbHR48Kn2cVUbDJpKVyhjo4kneJzqsTqk0qUGEYvvktNYcCgJ0dEQiyiHQtA6s1Olvj0ey6mOZk7PM8sjMIosY5vKLpKM9Ert86K7Mez0jcfaN5Ut5s7X2/Y/1VuU78/pV/a+Q+LbcrCgFOXEQkAFRfABr2JkbFy8QBCXnt/hWWsMKpXeECGmmdY7eh5pWDnXQ74w8kkOkQpjKuq65vx0yVdGM7DDORJ6tASkF7avtnz14y/58q++wKw1J2tYVgGjAywq7Nkp1va011/x5d9f8vyrL/jeb12jxbM0FU7XDOixHO2jBw9QusIuz/noe7/H5etb/l//9/8bz5++oDaG09WKjdvSd+B8dPgYbMB6wbtdWnUZ4e1t4SCvRkb4aiwv2CVaq5ukT4qJNIiFEKJ9YbEwXFw0PHm2oVqsUNstg+sJwVNVhmFwbG9vaU/u6NeneO9otz13d1uWTcNi0VAlvnNze4NWmtVyxcnJCc1qzXJ5Tnv1Au86tDZotcCaBcPQMtbmuKeN8OmgZ+BWOzZa892TR3z66ku+pudjLA8wXIlC4dFUVGgcQk+sqf4/cM3rzVe8oxua1ZJXL39BoEZRo1XggQ+890Jhuo7wW8LqO99l8+icZz/+Kef/6i85/6Mf4jaPePgvfg89dNz+V39BL4GhhQ7ob1uC/4rqyRc0jy8gGG5CTbgV2l/0+MtLWFm8aAbx9NITsKjg6HpPpzxa1VjAXV/x23/y5/zr/8f/lRefP2H52ac8/PYPuH55S22I9FHApIy+RmSsf220ZtFUVFUVywcZFctLQMTVOjlpyk73YYzJQtfcBrwlHE5ey7CY4Lm04Yw4ZfK3iMxnFA6k0i+FHGlUKmM0P77xW+wgbO53EZLzYOTB68rSNNA0iqpK9ljRCVZ3/KpWqXxZiIOKQQCR5/A+direJz5D44jyig+BwSuMDTQqyjIxvXpAKEo/3NPe2jCegSAj06zMOIiKVbvo4rx4U+NU6Y2sVGGILjyX5qK6+z4yzdNaeqXgO1Xelwrn8rmytngZIT6nICkV9aVxIbc5RetuHWSvjxDCmEZ4p4BJyHSiZJgyDtPr5TdLr6+5tYmEIBnCRSLiVuB9MV7SHjBleiYGnIkSdFSYy85oVMJHqXQsswmUY83rUc7H6H2l2Rwhmyp2SwZkzng1FSpEAHXoLHHse/t7O+8EUI5tMtiILEMg+MByuWRzfUMIfgdjev+7c79P55qNBqNBzxw6X+wZMiTWQgOQjKwzY6RIiFBGmIx97SuMszfRMQPF2NcR4e1AoTYzx1HIK/o9EPaOEJVyj1RiGsv0OXNK4GMK/nFM7IhPCQfH+ps+M70+/c7cHPL9Q+b50DAyPafTczGNDNOAdhJTc2kVa+A1FVsdePit9/jT/+Bf8v73vgNa04fIYNmgCMOAb3u217fcvr7k6599yuvnL3n69Clt28ZalkpHL8qC2Y7C/85APndu8zmYXp8+U85jH2b2lexTh6XSS1RN4EqpXP905+E8hdWS/pXfLceptR5x6BxegkMDTNn28Lba1bSfrsU0+rt0upiDnfxsWSu1dOKa0vEp7j1G5/LfbxP5X6axn1PwTDN0zOHlss2t8TFhdnp9ulaHPEDkju/DMXNjmJ7TKaxmfDwnOJdrM923uTlMz02J8+ZwjA8eo/adII7Np/w7Z/AREQLzYy37OLYXx67NtfKcTT3mc5szJB/g5yOfm+7JsWvx33neo5zzFPcfM7JO1/e+sR27V57Pcu+VmtDz1OYcH47BUjn+OX63/HYJv/Nj3n9vOofp+EvY3dvzRHynODv3W6733LmK/MgOl5bfLsc/t0bTZ8rxTddOJEbiC/t93ccDzOHs6Ryn70S43kXuTnHz3Pmb28fy+9O5zM1t2lf+mXP4LeE0r8mx7xzj6+bGModrd/sRxXpBGJyjKp2cx+9HmWturaY0/Rhe37uu8v3oeDQaPyY4/B/amiYqrytjsFZTpejvyPJkmCOWxVHJiTNkNUc0k6uUxi5HZ46OuON/ZTxnJQyXLX8nhhDsOyqqGTy515RClMffvWJz8yVX2y/xZs3anOJIaYPjUT3Ea0Q5xI91and4rh+G0XgKia+xOV2ljtEISVnlKZz4JRk13YAKhu7lJc9/8hNe/ewneC3Y6oS7rqUdenwAjOLObblz0eiwalacnz/AvvcOigX951/z8ssXXF3f0mjDe66mrmpeB2iVAm1Z6AYfFJUf+M7FRzz66Ed8/Mn3eGw1i59+GtOInq5RlRA214jTbPWAFkGUAaVZGkNtagYLWju0b6lvL7n8+ildGNAEmqA5p0IT06hbMTQYMJovTU+nFGHwvNrcctluUMT047Wu9vdbSoP4DtYzL1nbCo1icANd12IqG+s2rk9YrU5ZLdecr0/5/Kd/TbvZsFqtOTs7p7ILLi4e4JXBD46ha3H9Fi0B13Up5aJCArRtCyHKKstmwcX5OY8fntN32wxWEebRBHFA3leXdBw5dXjS+0RARqnk0DIB2zmcTYK6gIpOAz7K8d57nIv1T9u+pxsG0LA+WbBc1Ik2CUrF8noZTcWSrtnBQ6PFYnWNtQsCnsEpNpse7wWtDXUVnQJMUs5SW5wIqosKeh9iSR7nBoahjXVHR9pCNIyfrlk2dTKSRgO489Hgpv0AovDE0gLBDTgvhH7AtT3ttmPb9vR95AUDed0Er2Jk8ePVikYMoevxfc/KVJhapyiqdBZFQGX5L2WvC0LQMVKLzHcnnJafy7oAISBqPsvM/jVhguAO2lwf+fohr5F1InrsM74vY/apuDBZKX5YFif+FPQTwViDrQxmMNGQSSHfKpUM7/NOg1PaHPmPfZZ373mtUSFbNgVRHpGATb4J4qFvHa+vblOWBUXdaHS0pGK0p074N0hUeIuoCI/EM6bIEcURn1RGY41CK4mOKyqtYSJWsY72ffQxzmj+TB554x7eev+53P+b338bOfCbjOu+b0TaHB1oUDETzV5NaAW2qnGhwtYV1lXYUMU0zdrEPVAxIEopjQ8JjzvBD4rgFVpBZRoaG6hNLPLh+oC4IQJCMngpbVBBIbg4JInnMabD1WgdjRYlXzxnFB/51wTTe88j+DCvO5uc5Nn9uu/OsTN+TB4pZYf78MJ9+ziPP+afmTvXMw+P72S+RYXknOUd2kSnl9GWkZ7VJvGjKnHGY+mPZI844I3z9/Z57xBc1DMT+6yqivV6TVVbWt3npEwENxDr3Ss2r+54/uPPMS++xDQdLnjQDbZWOLVBGo+qG1ahwYvQt8/4xd/8F5w/eA+No6prxC0R7ajNAm0Ny2VDs15jTcW//eu/4dnXT2jsAldXbNqBpq7o2m6khXE9ioyKIuhChstres/CgyT8Xm6PUkDUL277nqrSEb+lvdLKEh2kPJWF8/MlTXUF2mCqJkbqe4euLMbAMLR03Za+39D1S243lru7O05WjzhZrzi/OOXBxQXXt7dcvnpNszrhwaNHnLx8zu3ylI1tGNwGHwaQGqVrUAatctr9eTgu4VxMhI+teF4Gzw9OT/nFpeFZCHyA4l1d88IPBBx1cl11OG5pUcryLASuXr3k3a9q3jWehYmp9YfBYXWgFc8rF9h+/ZLFh485HT7k8mLJi0cL+r/9t/zxzQY3WNyj96g+eh+1XqCNsDhpOMGz7Rx3wy36q08x3/+EwdfUqe63dcLQdvhKo5RBK7ASo7+NAkLKfsNACJrt9pb3vvebvPO93+Bq85rLp1/z8DvfT8l1VKSTGEy2kCqJ5YV0zMxhjE2yRXQ03eFtUjadnBEljUfrWGL3G9CVY/dGfEaG4eRItwfH8/qy400OflORqR5lPLX3tOw9OwYDjJ9X0aAdigh2VKQfGrSJKdS1imuKyaXWYrrzGHqnU8p0lWhOdqBMaxoqbCoTYYyl9S39EOvR976PPKgYmrrB6Botlpgf983trQ3jZbR4VkJNlYiShMzMjJfKrngvepqWBDMr5b33BKXww+6ZrHDJnnK5LnM2Lk8jLUtF/rSVY5xGBGfiXEaFl33ld3Jk1wFCkX2jQBbQowH8UIGTn4/v6D3FVMkYjYq3BJRTYlv2N1UQHUYlxnvWGsTJLuVfUmZE42paw8I4kVNO76I89R7DPx371MhSrlW+lo0xUyPIdD1LZkspNRqAp/2W6zDHiM1FtOT3fNivC18+l8d3qHzb36sS/kr4mjLyIYRUByLWc18ulygF1lhqremGQ2+Wt2G29xQXBXzkb0+NvRLCHvLLXwgJuSGCqFgfvRT4yrMQkfIO+U4ZjVHppuYZ0D1GeWYuea2jMKz3lHRTRD8nmEzHNKr+3oII5X9L/LITVOcjzaf/lvem330TI52u7OGVufulGHCMCJbvlHCptcakNF0SwBvNUFdU5yf88Z/9M77/h7+LOVnSe4920aNYeei3d9y+vsK3HV9/+RVff/4FT37+KToI23ZLVdV76569zcraJ9MIsTy2vO+l49PUISn3Ub6fcXNkQNT+eZiuM/vwMzWmQOQFUPvwXML51AiQxzKFzyl9msJHeT33sY+zI/tRrudUUVz2W85parSZOvGUuG36/nSM98HUFO9On5k7F8fmPEeX58Yw9525s3fsrGd6OBVM92vVx2bMPK4qccSxdYrP5XuH4zi2xsfW6Rjc7M/rOB7ItH6u77JNDeuZro+wUk5sppVG/7n+p+PKY3nTvs+9+yamP57XXQaPORibfm/uHE+dAebafWcmj+VN9HyOlt7XT/n8+OxbrPuvujdz70/p5AEunNDV+/BX5guPrcvcHEo+5xhPcWz35vb72JpPcdAcPxnne8iLHBvzdI3n7k1x6PjzFpEAUx77vvkfg7ksJ+R75bjm8OIcbh/7VPsy0HSec9+fzmnuO8UTo4O11VF5oI2JKY9FkmPWjByQnOeOjWNuTPc5t809dyzjy9u2qkrReDqmRdU6GbqJ/LqKzELiccJIc1QKY1EKtI4RX3oKE0pFvn90YMjKlx2nOfJOxVJEVmln7LmvKZUqHioFd9dsXn7J1y9+weXNIx4tlwwVIAoCOAloHWsfl+c3BMfgHCrXWS0yX02dw/EpYk6ZnSGdgo8qx6UN1A2vvnrO81/+kuuvn2Dqim3n6bzDheyE4mmdY9MHvAg3BF51LfUXTwnPbun+7Re8fvactuvxTcOJwGq54Cw4XFBoUdSACsJ3B8PJx5+w+Pjb1A/OaDbX+OdPuHh0gV2uMIPDhS2X6hQlFYqAF4UT4i4NPaqyBBtoQ8vzp094/fUzvAi1sqyk4jTGxhMUKBFqHVMUfhW2YDR9P3DZt9z0WySA1oYqp4CcwU1kx5OCJ4/RojFt+TAM2HpJvVxSL5Y0iwVNs+BkteKzzz7DB89qtWJ9cgraYKuKMAhuGBj6nuAHSIZmpSKcBh8Y+n48v8vFkvPTE05PlvR9m/CcRKfyVC8ZIZZDcn4PZ4mUMu9OmbenDGRe17KvGcx4OIz4xnnPMHhcKuu0XDbU1o4OGUprTJXgz6f02koQo1HKopXF6AprKpxonAPvHL1ziMS9MdpGnKajk4DxAjpm5Yp6mqgrG9ywV4JGaxXrYq4XVDamSc6pK30IBO9RIabn9RLrtAYfa5S7wdF3Pdu2o2tbhqHf8Xgh1iQPolgu4OF6hQng+p4w9CysJdkI4vMqrkU0yOxBVDT2RPeduPZJDoOMnrJD0w42p3tVXss7O/Z15Nlj7ZC+qMk4djCzo88QS1gUTe2eG+ml2vVvjMZUJukWU0bHcd760Gh1z1inbW9sRP1Fpn+KaGBFRUW1+Eg7vPNcX9/Q9T3QxPIblUJEoVVIymWV9gy8j05XOu1NPn9KxVTOVYJXVAAJaKXwkJygosPIdKx7c7pnbnNzfxs69KvcPyaDHmvx8X1+afZddSj7x+cY4TzkjCiZGmuDMhalDMZaqrrGS40f2p0+RCtMqqbinI+4pBPcoEFiCYvaaqyW5LQAQ+8ir0Dcqzi8qOsj0/nEJWi9o/tZDtifx+G8VETqh9fTVNW4PpM9Rc2egsN92D+b+/vxZqP2MfzwNvLSPoEodYYq8V/z/Za86JSXnsrs+Z2s44nGXo/ITj7PhvGdnjbuWDZ2T3+CSOL9Ch1C4SAJWabf6Z6aqma1SqmkdTJ6w+gwJi6wvdny6ulL3u+3VLRoUSi9RtsVqCWKGo2irmoCAXEbLl//ktUy1o+2VYWvapQ2NNWCwTsqawjB8/Trp/zdz76ittGRr2+jAbSpa6DfM4aPNdnTPCP/cj8cFKuddjbjzpJXiCWbhsHhxaGUheyQonIZ3Zh6/vR0RV0Z2gBVVcfyKy7iQgXRmc11DEOPcz3OObZtyzAMGGM4PTnhwcUFT1/8gpevXvDx6Rnn52esT09Z1GusrXAu7bkElKmTQ0s4WhJ1KssFFXnzTjzP2w2/cbqm0pbXBHqEEzGssTyjY4lljaZXwkZHp7weQ9cPcHNLuFny7umSejB0SuiDo/U9r13LbXfDo/4G73q2D09oP37IL//tp/z2sxcYs8SdnlN96wOWf/gbmOcvYJnKzwyB3lu67TXKdbBcxSwXSjNoSzhRqMUSYyq0UlilUFajvEesRlmDmAplK9BQn5zx4Y9+hPriZ7TbLXfbWyprkCEgOjohGy3RcKsEbe24X+O6Efm6SMMSbGVHS4nZSffk3CNwdlye3e3V/rPT5wq374LXPaYPPNb3zMiK30auObHOcvBY2dM8LpUkhWU9iUl0IuTBAzo53EUblEn13SGW2VbEVOwYCxKd/LSyeNXjvcapmGLdDZ7kIkRtoVJvL4N/oxrj2TBZKknjXHaGS+fcgUER9qOxMlOda4ZnBj7X5NZqFwkDjHWqtdZj+tNMAHbMpXkr4CrfnRpC8xzK/kpF6tQ5oDTel/3nfpSKhujpO+W8psbeUtE5zicRrzmF03Qs5fU9BwJA8FFJbGJ9KgG00ak2hmCNQcu+YrtcxxACJVgdKL2KPcvvTw3J07HPRbnv+tmPzpxdm0kr1yT/ZGVrqXgclagHPTA+U/47Hd90ruW1nCLy4D2lCsyhdqnUgWEUYt9OaCvHeZ9icwozIQRCLGRO5j9LxVf8N6G8PNwsVFH8neDkmNCSpnh4abL/s68V84iqum+2JvNtf23fhlBM11NEYirutO9lSvDpWXk7Rvrwu28vtMPItBXjzL9PjbL5Wn4uhEAgesGF2tDqwG/+0R/w+3/6z1k9OENqEyNrRKgchKFjc3vHsG3ZXl7z7KunfPnp51y9ek1ITjVVVcezJtl4lj6sotdqqSAujfTTiLmMF0uclte5NAxPf0KYTxuU12HENYWiIrd8r0wpvgeHE9w69405nFTux7SVuKqEl725FtfKyPfp+Ms+587Y/jrtr+EcrpvO7dj3pk5A02dK+gk79Df91n3fmIPvY61c73Kuh8/tGL25M6MSzKqJcH8/E7k/ht2/mWkuBM80l/FMFPQw083ynMzxWyGEEV6nkbY7oVBGXiamJdqd//yd7Mw4xV8lXGReLQ12D++XazN1wsrrWv59rJU84tuud7meea65rzzv6b5M4X3uGyWuUmp/vm/b3hZe3tTHsX7LPcxthJE39YvaF2y+4VjK9X6T8HUMN5b9lPhqmhEkMydTHFl+d4rvprjiUNUW29z5yn/nf6eyQv53Cu/5esjC3wwPON3P8lr5zJv4hymveGzsczzJ27Q9vlcfrm05r3Lt79vrb9Le9P436b+ua/zQo9nBV/BhjzbMza/c97m1HHFmnv9UA1XAbUm3f9VmbYzyMprR0CC4OKuCYQ8SIwHzNaUCogPGCFaDUQGlo8JMhYw/sjlcEn8vSRWt8v/H/0jx+26uavxnVKBkPpDds1qIWaraDe3VSy5ffsXN6685Hxa4ZY0yFciu3E4IjpAMMCLgQ0wlq7SJNeSUHZ0utU5pi1HEjMbRsK6QIsIjRir6pDyOOgWFqgwsl1x/8RXXn31Of/2a86bmru0IStDKgIagSFHmgUELr9yAeX3J5ctL+quB8OKWDoeuDEsHK1tzqjQPlUGLworGBEFax9rXLN/7iOGjD7le1XTPn3B985KH3/kRZ8s1i60jeI9RQggWQsBJoFOeXhwMoFnhLNy4LV988UuuX71Ci1CrmjUVJ2K4UwGlNbU3GGXYKuGpb1nais57tq6jHzpC8BitsUrnTJLjPmblclb+QZQBtTZYbRAfUr1Nz7KpaRYrFosVi2bJsqmpjeWLz36JUorVyRmr1Sna5Hq3HX3XMvQdwXuCi6m9jY11p51zDEOP0TVGWU5XC85PVywWDbc3LVZVUbGeyYXSgGZwUWEfJJ/TCcxS8A+TszbFYSNuPliTXI4oMLgUoR6E2hqWiyVax7SPQpQdjY1GLh8CeE3QCiRmARAhRiRpiwoK5wKDc2yHHtGeuo5GMG006IBBYayKZzmkaFDncUNS1rucmlKhjaZpLOvFgiqlvZYQ8OKJKeEFXMALDJICXJxjcJ6+H9h2HZu2Zdt2DP2Q0uxLNJ57h0ezXGgu1ov4Xhf30hoDOqedT5nthOiolFPRFz+F6pUp1d7tyf5eZp1FfjTrKFS6Vu7tN6VNI84f+5nnJCL+z4+qg+ujQr00+hNxmjIxAk1lXUJ+jqj3jdXLDjMQ7dGkNKw8jNGQKFIMOfc6CsDx71QDOhtoCcLt6w03m1sescKYmMpX8MkwHmcZSCEyA2h2Tlp5BbRW1BZMAG0ErT2okKr0hVRTWlCS5Nsgu70c51hOuFizvWO825O4HoUDxdTAuvfi28vy30SPMx1wOd7p98s/D/RcSccTIDmxRAcn0TrVlI0rpbXBWksVGgZfEbzgJDorDALBS6Sb/UA/QAgxW6g2Bp1CIp0f6AZP3ztU0g8WU4j8izJpjxkN2VpneW0mhbpW4zEt71HA2g5+U69zy6wU5Owhv9I+zOsOpjL1uO9p3jux73j09977SVd5wFMW/PhIQzK/dGQ8ZHyh9k5s8UumP3rco+yAJSJFGZSQ+CMVaVXa2l0O38T1STKQZ/o+kS/G/tMZrSrLarmOdZnNBpwfp+q9xw0D7abj7uaWpuqpZMDoBmtqlFli9Ak2WIwXjK0wRnC0BHdH8BusjaUbwlADjqqq6d2AVpqb21uevHrFp798yrsfvkvoDUo5NJpFVUdnOgkpajxlhJHoxFUwr2Mr5a+pLLO3Fxmn5nckEoVhGPC+JgXmx7NAdKaXAKYynK5XrNeW20uXDOOOIUS9qVEa5yOP0w9drKkuQttt2bYbKq1ZL2OWHe96Xr54xiff+g6nJyecnJxQNStss4T+DgmCeIc2FqMtKL8Hf1Pd1D6sxjPcB8dlt+G23XKqK14rz23w1FhOsHyRnNs0GlGaGwW9OBoMTuBy6PGbW8yy4sQJfr0GqfCd0IU7Nv2A8Q7tHZysMO895OX/8Hdc//jnPPzt38Uv1wwffkT9p39E9zc/pmtvkZOKFsNdDzdeWBnF6mxNMBYHeGWRM0vdLFC2SiUzQenoXIgxKGPAWJStMZUiaMO7v/mbdAw8efoZN1eXvHP+gHbo40aalA3DxNzqJtNJZLRRotQoH4tE3m6kRXqH76TEB29ox/RUue32MQuYkM9tlr92lDQ7Ssv4bz6n4/WS/xVQEuUckjNUGlWUCVR8OYu6mSfafa2U/dROXKD4ADkjUDwrkX7seLUgIKND9HioRv4RFZJuNkaVZ/hOCcxQ5OwZDucUTjssDjEmysVv0d7aMN73/Z5hPNY62Rn2yki0krGYi7y+7++SOch91XU9PpNTIZbGxzI17H2tJM5TRUX2ssvKjsMUboepYo8pVaqq2kvVnt/bdwCQvRTYcwq3PUZ4QsSnY58qn/NccnR26mIEMq30aCCNUcyypxQp576/t4drOReRXf5d/l6uZ/mT12hcN8pDLAdGyLn9nhN6pob6skVvOygJ5X1Kyrl5Tb87NfLt9WMEvIzGCZc8wUOK6NBa83bH9njLAs4UNg8Uv4XSaxRFMh6TKMQLaoz4lcSYQ0T40fl337t52qbrPYXbufemxqmcNrEUln4VIWWOuMw9U+75gXJd7Z+xEt6ncDnHiN83tqly/20Uw1MYfJMSPJ+zvMYOxZ0JPP7kQ/78P/yXPP72h/RKcFYjg6MShe483fUd29s7ursNz79+xue/+JTXr17F1IWDK5ydIskr8STslAGlwas8y7mVsHFMiTyFobwO1trRKSs7UpX3x/UpBNT8Uzrf6BRRk8d8YCBjHv7mcEsJH3P4Zy6ifGr8DgVsTb+b170cp1Jqb/5z2Svm5jE3p+n+zDHWJe2aCpp5jOW96VfmDNdvguspnZkqMKZC7LEzVYqm07llBniOxr9N21+nQ0Z3b11DQNQhfM2t5xS/zO3PnJNcZn7Ld6aOMlN6Xc7lGC8yne90HHBIE9+0Zm/Dy+V2zLFuB58Csl+2JX9jur5zNH2afeG+down+Ye2aR8H8FPsdcg0+Q1DVkljNT07x+DrGH6Ynv9pK4WuY2sx9/7et5NS5z7ecpqtZ9oXTOSzI+OY0vDcpjx6eb2ka/GaP+jvGP97bP7Tsc+PlYO+cvsm/Mex/se+4GBNpus/d/6/yTme6+fYmObw1X0tyz/aRIM4xVymuGqOf5vCxfT+7t6+MlHkeBaDX6Vp42P5G0XUXuiA0jG6S0nkW6KBqMMrjyXV6tYKb4TKCws9YLhD6BCtaDpQFloNgeyYpBAvWAchFySHmJZdQSpRGUtdSTSkKqWTUU+PdYTj2hliCrwUcSgVG9NijWCwrF3D8u6GK/c36M0D1GKFshVa9Jjq2ccZEoJiEAPKotCYlKJQqZha2lpLiMXyEJXka5fOXlKUaSXUumLb9qlmoIppaTX0StH97d9gn37NWdCslg03dqDuFyxWNUELrQxoPN7dolUFInzd9nx6fcfty9esjWXdLFjZCjEV6+UJwXlWtaEyMUZqGSpePN9gzt6j+/Axm/cecIPhxU9+zBcCv/nh++j1EukcC7fgQ3OLoWERwBKNjHcMXOk1P7eKPijazZbrzz9l8BuCqqnQrEVR4/ncdqwGyzssQVmeKc8z8Xw4nPLixFKZhsp13LmO5ckpViu6PTwY0y1nI7AkmBIMxi5QCvp+oO8dWLCNZdmcs2rOOF2tOTtZcHt9ybMvfsKDRx+yXj3ALs5Yn1+ANrTtDV13g+t7/GDoOoeEjmVzihdPN9wy+C3np+9RmyXvPljx6LzBKItWdSxbZImmOgFCNC5v+w2D6wji0UlZHUEzwnFO55x5vR3MzhvF4rGLqkYXPC7EdXGuZxh6Nm3HdggEDKfNgouTs6Scj/CorcJaRe8cxtYYMWgsaM2AZ+tbfAzbR4kwDLAdPJebDdo6Ts2S02aNrU2MrNcqlh0goLzDDIrQC653+GEY6y+KEqpKs2oqLhYLlvaUoDQu9PQuRvnjPe3g4nmT6FDiBk8/eLZbx8124Grbc7vtGbYO5VN652DwYWBgoFELmqWm22zotw6oUDrQu7gPWke9kwRPcB1+GPBuSAYLjwSXtwaVYY8cBSd7BLxU2whZ0SvsCRhS3MyX3vD7rIww/e7B82qfufBJXswwoxRGmzg3iVnalNIYa+K4RaGMjgp4rQkur0HkfbI+56h8LwlFZx2xAOgxM2AeIgLGx1+yXkdho4EjlVQ01oBowteep5dPeF+doGTBggW6btjKFjf0wJDWVmNrgyZl0oRxEFZJnIRtMJWnqnvEeGTQiPew0GAN4lMadnFpPXY/xS7sOz+kf3dnV43Pzslecy2u6aEe4k1tjp7P0/d9XmD6icyDj3BCmkoQCILCo8QhSnAuEHyHlyVem+g8464IfkC0RG85ZVGuJgwe29QE0WzbQDsM9M6hgyEYwZhAbXsWukKxoA9wtdny6rql7QcgpsZWYlG4xBeAUXaEyV3mnUjf93U7GRaS/lCp0emDgg/e47vGszujr0zfVMaOkPA27FQpv0159vh9Peo0x/GzG0b8vCSHyt35m8oCox5Hl3C3G0PGASoyhClVcHKGPyL7lNf2HG0TYlBpgNlUq0QjLvJj+IBoienvw5BSFisGAeeEwSiqkILlxvTrAh6CDGgVS71qSToqFCFEB4tsfNc6cL58wHJ1gq6uCL0fz2YfWqp2i3Q9VQDfXKFvLSdmRaM1RjvqhdA0WxRrdPDRSZMVtvG0ruPh+jzVKh9ohxYhYKoFd3c9z5+/4Bc//5yuc9TmE+6UwqeyAUtpaCpN23s6H0s/1kGxcAMyKNRigcIkAfn+Mx/xgk74U491pPPuioC1Ne22p1usMKuYIUNCwDOABY/CiuVk0fCt9yq+fHHNorkgVAv63uGCZ7FYsNls6DZ33N1tWJ54/CAM/Za2u6NanrFcnNAslpyuG158/QXD9vd4sD7nfH1Gta4wpw9R7ZbQ3cJwS6V6Kttw2xugQ+F28KjUwb8AFTYG6CkhVIrLq1s+0mueqpc8oyZIxUM8axp+om7xYrgOgdug2RrD0gdulUP3cHtn6U4uWKotH1UPWC/XLIYlqxdbTrYDVhRD79DKYYNgzZrn/8l/wcff/ZCBBZuTjwhnH/Cz08c8+etfIOcrnFH0g6cl8K1mzeMHJ4S6woXoqNromuWioq5rlIo4RevoCAS78g7GgDKeWhz1w/epP2gJ257bF6/54PEjsCmQRKlkFI+7rpVOeE9Gu5pkQEiZg4Qi62T+0QrZ4zWPw9u0HadLguAR0cnLJaC1x2iFQqcyPfGpOCqhyv1JdKqZ9kYQVBAM0bmflJ0o8yDOMGZOlBETx5b11OXhMMmTON4TlIGARwjJSTiWXI38iyE7MpflT63WOydn4jVjDCQeNUiImY7wBBdQgZTqXkeHPh15bBGFCwFHd3T9y/bWhnHvo6f2MAzkNG1lujbIDAOUxC0r6UP2Dk3eFqPxGLDaHBCDkjBmo/XUMGqtLaK4M8Kej04qo7SnAFgqbkcil5Um8cbo8Tl9J32a3awZvx+Z43igSHh4GKLXk1JqnNNeP4nPGxW3IaasMceU3bIzok+Jdcl45PXJTIY2sSaGz95FilgPYGLkzk4Q43xEENkdAKUVBFLKg12U/RixJ5Hoqt0oCuZ23zherh061p7KHniZgclr432eb/zJKtRdy0xHZMq0MKbq0ibe8y5Wgyhhbi7ibRybYmT2lIqR4SYhyCAyelHvGMCIM7OwMHZjNUZsdPhIimyf1yXPqRD67m1Fv1nJE0JycpDdmchnVemIqALRU3ecU4ar9N2QUrCMXtzpDGSYlLSWeZmVSumyRZBC0FBTYaDcI2FSt6WYxwgX4MY9ObYaE7yTvnNIU0pkldauuKVQEZmneY0Ru2mSohhTzENcS9GyE8pFkje0FN87FM6CSp6v+TznJ3WxH5IcisY4p8nwE9HLe5AdFCQRvRAEpU1URhKfFQ0YQzCKres5f/cxf/Qn/4zv/95v4wz0kqJ0+oHKBYa7luFmy/WLKy5fveLpk6949fwlvh+QwTMk2FBaYZRBTJx7VgqMw5aIH8ZsGYqoIKFYS7WrzRnrAGaHmywERQVT3Aq1g2e1E4DHNIoqfm+Hv5Py20RnD8mCWfLmCyGmih9xZdIkRJ4mMgmZ3kWYVUTl626OehSKRvDZ7VWmKWHHVmQgjOOPYQEhCN65kWYqFEZDWbpiXJeMyyfRyGUb8VmCSQkeSbhfAaP7MBHf5r5GeE+C14ify/mqwns2zdF5H1N25ouQvslIT43JEbhRiR9xRRYgM3aIqTFJsFVsyciQ6bTIJWOvC2tg9oTexw0ljcnrvy8clBldMr8Slyr5YGa6lzZbkdPzjh8mF9LZPbO7JWQHtNSL2l0f55uGPqbOG+nCbl/zWOcyL+R7pcInOoHtFGLTqOyp4q1UXjjn6Lpuxx+puN+xv0hbotpZMGRHB4s2NqbpFDeeCYXEqEEVd1GK7+3WKNGdGQXUlE/IyosouOyezQ4uWUIo+YxyXcrI4+n8S/4KfTyCZM5wVq7h3Njva1Oj21xU8v63IcNyXo05g3Y574LVPJj7dCzTOU7nNTfH3bd25246r/LdOYPkdMwjwoc9x1NgjADO7+w5HeVhzLRfxYA7neuxsb/N+5mvLv8uYbPsvzT6R34/eXTv8Rs73Fcs13hvbPeM88DZZGbOc7hiDv7Ldxh5/4jpR+4r8aXl2Zzbk+nZHcc3s+75XGTyJgEwauRrsxxR9j3dx+nPMeXl+KPU3rJm+H/bjBlvaqv6PPGLcVIZn4Ir5CpB65gNSLAotcDYhqrW1Npycdbz4PyS51cDt1dbggoxMa5SUR4Ya5ITDS0ZjibrdGyPjrW8hlGREY1DSFQ8altjrQZjxv2K9WqFGBUASIpYEJV4MMETDX/agEl6AJEcYTyk9JZJUaRBdIyYFh2VhH0/jHWStbX83d/8gmfbnubjj1l9+A7BBjSGhV6gfQBx1G5AvdjwqLKxxnRwaIFaG9qrG0I7UBvDwg8shi1+WSdeXhADISjkDt77wWPCxx/x7JNPGE7fYUHF6x9/zt3piierhqeA6j2r0NBXNaswsNKwUooTXfMwNNx54cQbOidcdi0vb18jGAYDC29ZqgqlDM0wYFGcYLnxnkE7lusli4uHvNxc8rrd0A0DRlWxrqdWxILqGY8UdJDMc2sqW9M0DSA41+P9QN0sWa8esFqtaeqa05MTzk7W/Pf/7X9D7x3vvfceFxcX1FXF6ekpXddxfX1F226SAVvRtrfj+er7ga4dqOyCxaJmtVpwcrqmbmr6fq70WBxb7wb6rh/lX13wY1LIffdh64Mzn+QL8QHxHp+isgXwEmus+6HHACenJ6meuCbXCVZaoayC5NzgvEcNA7lknNh8hAUfPIOP6dC71uNVh/MOIXB+tqKqo6Hibuu4uetoHQyDww1uDFrJ2Q8hZs1Yr9esT9YIAe8Heu9o+46+75Hg8f3AEDwuBHyIqZe9g23fs+072q6naweG3h/wJJKUs3d3G5Z6Sz/0RFxk6bZbltWAlqjk9D5Gr8ao9IHR4SJkveI+zGWdQ6ZzpZN8PvPfBBd9k+ejLnD/vQO9EIUORuL4snJ3J/OU/cUIfzwY09BUNcF7umpA6wHPLotUIpckIDugd6NcVkxnavjYa5Nnj61D2w5cvdzSbjqGRUcwsaanimgaEYsWSVTIoJRGUzijjzXDA8ZAVcUfZQKDF1C5BIFCgo6GpJKHPbY/e/zObr6/avumPNs/pM3xTnNtpyeJJQ4G71jaZcJjUc7SSkAGvNvihhY39PihT8EqCj8IgViG4a5t2XYtwQuq0dSNZdlUGAN3w5avL3ueX99ytdnQDfuhOZnfmEvHXOqb808pV2Z9xTTj0PT9so9ynYCkO1YzeHrf0fS+dkxuyzxTqbOen9+hLFf2/Sb56T5ZKdOkaX9A0v3vgh+iU2TUOeZrPgRwDq1jvWpJmTkQwXudcFDWl+XzWshTb0CDUggRuYa5SLS9LBaLVGe8hru78Z1hGFKGF8PF6RlN/YzbzS0nzRKSfkmrirbtWa3WBJ0j2YVmsUBrHQMxh5iZxChi5l2t2Xz9ksvXr2i3HSFo7m63bAbNMPRAoKkrmqqiG1xy7oo0MdRmXNPIg6o3Oo9P92vuXt6rMvNvbmXmPqUUDx48oLGXxHrVOqaKH2LUuHMO6Trq7QbXtgy9p2072m3PegG2qVkuYur6y6srnj37imZ1yoMHDzk5OWG9PqG9XtAOLSH0jDaIGOx8gPNnz6OX0ZFFfOCp2fJdX1EF2BK4VsK7suQD6fg77nhByzXCBjBS4ZKuq3LC0loe/cG3kCdfsr18Sh0uqJsG8+Ad7m4d1z//CQjoi/eo9CnLb3/Ms//qv6f/X/0v2LzzAa9MQ9tUPPyP/pS/WWturi6x2lDVFZttxy/8Dc2ppWmWeBdwbc9mu8UuFYvFAm1imvvttsX7gaZZjvs/DI5qYbm5ueFktaZuGk5Oznjx6kvcEDAm8s1RvM57fJhdOqbjT44TewcprX2BMxRvh6vu25/yvohgCkecbFOEnX0mm+mmuq+Sp9/7Kfn9vSmVTkp7SoXdmNjnpSWyN7FkD/FHH6ggdoG1Ocg6OjPsoshLpyavdMpKPqTSaDEjRjkcow2VViMvUqGSA7W5V+cxbW9tGNda0zQxH3xMHbEfkbyvTNkpJpSKERTOuVGh6kOggtGIpEz0bFdEEd9PUtyV9d8gegoYY2KqjYMI9GhUmRrRM1CUEWrT6NW8UbE+i8ZKrP8sIihr9vvLxCoZekYlCJEZIBl1o1JGUgqSZEBKhkslaqwzMdZyDslzM+XVF30YbZLXJM+xrOs9Hhqz72wQvfkBH9MQ+BBrGyEGnbzvq3qBbG7HtSmReplSNK9jQGJ6CRNrhGljUom4eMBGr8Jsb8pjiVeBQ6eHUdEp2XiWxXM9wpMQlfPZSyWqPrKhLe2tUlGZ4hPDow2EeOAzs6CMxcjOsWC6nruozQDFISYEjFFJoWKS4V3QlWXwLtVcSg4Ryc6hUVht8CpEL9nB07cdNnkSiTWpNoUaD/BbMX1KFfCXFivtUzbARHvibiyikpF37CQaD4yOda6ausYjDEMUzKPBWI3IUqNiGiyzU8QTaQQ7I4TCSDoPxfnaI9CQ6ppkBjyr+/aN6yL5/f30yHtK+r17in2xHdJWHAjVO6Svoqf3WD+LFPmShXGI3mABY/WIa8jbJdnklec79o5SO7IhShG0HjMVxLNfCLI6eoBl2I/pbfYdkGJXjugHFhUGGVKic4KOwoy2eBdTl2ltCFYzGOhrzXf/+Pf4g3/2x5w9vIjvB0/tAd/j+57t3YZXL1/y6tkVX3/xgqvLS7q2jcI5giSv92gQFiRV89DGjMx+Fuy9hFSvPhM+gy2dSdKua3b4IZbUiPBrrQFRDMFHBpqQYCF6fBujcc7HFIN5eRQjTtBSnOMMzSmCRCW4j96ASYGRhXqRUdEmCXfk9Did7woeIUY0RTjMexHhKZ6HBD8mKUglOqdotXtGKwsqoK0eFcFaK4Iaxtpt4xhQo007wrwfDfPIvqFFp/NhALRJiu6ctYSEO+IhlISv8zfy2RMirrVp/CM9yvCW1jwaN8Ko3Is34h5JooO+gFUSnGT75Xh6RGc+dPz2ONh0MY8xnbZD41L+nxQOVIrxrHkJcc1HeMmeiOzwlTH4VMMGtXOoEKIjU1zXsOMIg04KhKSMH78riAqJYc04O9O6dH7LbBRKjYaiPO7slEEeW0Iwe7W/J/zN/jJHwXqkmRMaM/dv/t0WRgdrbVRsSqw7pRLNsyqg3UAVArUyBF+BNvgQ8FpHZzQJkU4miugzf5LhoIAblWitZqe4mKOHWutRECDTlwwuo8LyfoOsTNZk+kwWMsvsEXNGwFJQPm6su18TUSo0594v/iIDXuaBIlHXmVIfjG3HI6daTVqPzjFjBFFmuIp1OPb72/AnOmWeeVObKp0PMk0kXCchKhVGHokysnyyn+O90olPHez9dH7lvovshLO51PWjDLA358PMMtO1y8/NKbDL/Zqm+y5/z7g3OYcD0aEoVzqYhbVMHCk2uiiQND0LGd+FQjieG++05bll40zJ++XHNRnOM09ZpHgsxjHKG4VjwHSc49oK6KBQyuCDA2JK4oBi8CHRovjcMfidnuNjZ3Z8f1yXCUwFQSn71hkn3tRqs058VqwjKHiCDCBupxBNyE+URuklyqzRZhn5KD1wsjrh0dkF69MO/6Jn2PpdCkji+R+dWTP/m+WSmabL52fanOyqARwxKsYJPmiMrkHVBGURMQhVihaXEVKVSg7iI23N672L4nLexdTOqbwPJnHu3if+w486Cz06Uka88vKLr7lTGvPe+/iFZVABsQ13HYSuiykqlWDftTHdosRIdYiRvXdX11SiCErTycCVxKj8B6pGu2h8tAHOfc13Pvg+7QfvEtYP0G7A91s2V694/BufsOg1nfIMEqNAWgedt/QBnmvHje5YGUUbAo8XF7SbllevX9J//QqvLE6gw3EjAxCoUNRYHlUrrsOWG3pWzQrz4IzXN19zkyKyFlWFsTYaUEY6ujsHo45HxajAHJjgBofzPV48C3vOavWQxXLJYrlgsVig0Pzt3/wFVbXg/OFDFssVSitsZdhc39C1W/qujRHjbsD5PpZu8UK36Wk3A1VdY7Xi/GzBo4enrJYx4iq3DIIq8YJdt6Hvh6T7SA4rBZyONID962/TxOW04FGuERSD97Rtj3MeWzWcnp5S13Uy9jqUFkyVs/cNeB/QKsosWQcS6wDH4JO+72m3W9phE6MBg6Lb9rwOA0PfsjpZEARubjyvr3o2W0ZjrHOxNnjcN0BBVVUsFwsWzQJPwAdHO3Rs2i1d16NEcP0QU7pKNNr7weMctG3H5m7L3WbLtt3S9z3DkAJdJET1gSjEBK6ub2nkjqFP2Sx0Rb919F2LSnyYc9EwHsQhqQb8lP7v9GySjH0FnZbI14+8zOTdcZ/uuXYfbzPeT3Ridlx714p+JFJTF/yk3/jjnEv6oszDRLmjsg2VHTCmZ1AhpRdPkVu5f61G/WCG4fFcKvau5bbH06YzsKN7Sd5Lcyl1psENXD1v2d60DKdbXGPQIafSHuJ+Jw+zMQ2qispvFcFhRzKUw9jAYqGwDfQMWKMJ4mN0qxJE9RCqcTzTsR+jwXN88n386Rw8zMkW036P8T7Ta1M56k1jnuureBJUHF/EGzqdcQdhQEKHCm3MWOFcdCZXBqMUqJQxIDkeIDY6uimFU4ZeabYi3G22PLvZ8Pp2y7YbUOx0+aNOPKeFLgl9wUuXuvNpQJZShzLllG+brM7IN0a+L2vU9NhX1j1M13RPBzqz3iU/H/VMWT5X0cE7OwUmeY+R748wPj0jU1lCyc7Z85gMNx0XECPJJ7Cm0jymmQchugwqky2eClGB4BxBD9FBzTmUjXonN0ycqifrnI3dZTbYBCilumXEuT5FdFZ1zWJRc3qyoqmr/Xn5mOHDELDisUpzenKCrWIErjE1SEVlNQEXs01ojTWGs+UqOki6gDgHSeeqdODq9Q0319cEN7Be1gxbRdcPrE4vcCGWHTHaRIe0zTYGmnjP4AZ6Z1kmhy8dAspEmMp7dazNnecpXhDZ6crramdSK7OYKaV4+PAhJydP2W57CJF37JyjSXxUCI6ha+m6SGPd0NB3jr4fWC0rTk/XvP/++9z87Oc8+fJz1icXvPvxdzg/f8DL5YrF6gTXb3Hbnj54rPFos6M9b2oWhdMaJOCd54V1GFNz4Rq6IHzNwI/knAfUaL1lwDOkvr0EuhS047sed7nFf3HNIlSc1p5qc0W/0ThrMWcN3+suWf7y75B3A9v3vs/ljz7i0//8/8Pzr75k8egRylZsX7zmO7/xbR4+eoftzR0aqFQFwwbrYRksctcj7UAVhDO7JHhhs9libNRNN01DCNW4V0oprLHRGBscg3MsFwsePnzIi5dPuL6+4fT0NOosijWL+xzxRXkeRaLue0Q9U1yX9M1vgrP74O8or4JAKPiwpIff2TiibLRPUQpgKIGi4GHGq3tziC0bu3evRJynRAglfh/tHZPPiCSHOIkxoVLo0lTSt+9mn9Y4lgXJQWrBuyjbJ8O5NlEuVA60BFSIgTohRP7SI8nJ6O2N49/IMF5VEcByGvOp4mYuhWupxBCyUi7QtV30BkqGFJ2IdjZ4lIzGHiFNjH42XnofU1H8n/7+/8jr4XVez0PCOf7n7VtW2oydTnqc0LO3Qj4zozra//z18v6bN3kKB+VBGaPf0rVQO3QV7lmnyUGa8HC7jt8wNCl6Kg6i2v/PW7Q3r8F0iMcHkl/IBtqDy/ENmVybDEEelF+aGVsGGonGqbD0hE88h6zer9YODb9HxnHkc6NnU7GX2Zj2TduvZ0ZzvcpbnZy5scy9N92t+2aqiv8egag3treBWJnC1vT3ma8dh/W0ZglvVnWDMf8p8lfTF7LAT6z1F2ItPHkk8Gi+86jvLs7RjNCyP4rpGr6p3bc7anJ/HvoPx6HKP8YuShJz8Pny+bnrB00O/rofFxUCUfkxNZm/TNfjcNYq4Zc3w/F0LPPrcvDUEZr36zjvU0Zu9plv8LFjFOLg+luizWNtb7neQJb2IPZXYUzu63gPPt/uPMy16Sme60lXFmsr+qFHJNZg0joaGfzgxp6Oz+++e796myNVSh1eL6/NwfQB75TfY1ze+0Zx5PpbQfev+O7/TO2tceKuzWP1Xz8svCWbvPf4XJtSmm/az5t4lF/5JOwB4q+wEb8OmHoDr/8NGKtDerJ3/c3zWm4r/rf/798mKzBiau99ZWoe0jFHmPLa3hBnhGqVjBsiMjrrRkVUzNBhFDv591fgocsmPkRjggSiUjSGggjFuuXLOjr+KlUhqgIJKAwLu+R0ecJycY3U13glozNC9Gst+Kg5pJnnDSnzxy5TR/5vXtvsUJSXbVSgJw8I54RuCAxB4yXW4E5pjRBMzCiLjAoaozVGWXJGFq2i8WiMuBWhMhVax7TqWalCzgKFxFR7WmNsShOYUvldXl/RvniFsgZXN7SLGq8Vohta3wImZkTR0OvoPOuCj6n5QzQOqpOTaBTvB7wSpDZUohk6j9ExCthog19d8M5HP+Sy8yxWC3zf8vKrz7jt73jwnU+wzuBxiAZPhwG8PWHw4EUj3hBSFrraGK5vbrh88Zy7Idbb1gjXeL6mpRPDqdJYNOt6QXAdWyWsq4aNeLbi8CFg0FRJqety6ZGUeepg78d1j7qewfUEicEKVbWkrmK09MnJCmsN19eXPP3qM04vLqjqBbaqMMbgB0fbbvAuGsQH1+OHjhAci0VDcDGFMEFR2YYQBs5OG07WC+rKsunbkT8uax4K0HVdUkizU9QVZ3E8U2+C8wljEJJxIOu1QhCcg64bRkP9oqlYrxaAxgdHUAFtoWpSTV+Va23vapNr5TDaF8btWHM0ZuORqFqVgB88bQvGaoIY+jbQtYG+9XgvuPTu6BiSmq0sVV1hbQxM6Z1j23VsuzYZxsH3nsF7huCiYdx53BDYbFo2m5Z229F1A8PgEB/Gb2ilMUphK6EdBnxwyfEBnIvBF94N+JTSN3iPH/rRKEPWEcrOASsbmXN09YETWxG9OHUG3Xtu5tp9BvTSqWlnhH+zYby8rzPeKuBnF3yhUFrQiTYEFwtTGGPGGqZKqTH7VUkDlVJj5sly7BH3pRujcBTXKP89OksekLB0YVcgN/1juXs9sLnt6YYOJzU2NCgtiDjwdTpTyflUPCgVleOoaCwn4t8QNEZrFnVNszR0bLFEp0wJEDRQlQ7Q83syzneyp+U6l+f1mDNt2dd0Haf3jxndy+9ODd33GUXvM7Dnd3bwvFuD6LQdM00E76JTie8JocW7geCi45cxkY7GtzRKGWzVsNCWADgdotO10gQsXei5a3u27YDrYyRtPpO7SSaqrkdT8igfHuOJ9p0v5p/bf373MQl573ZGE5mcpx1fOONkUJzHubJ7034URDzDbsyCShGO+/M4VhpHqZQNh304KJ1XcmDVzmmgYG6TXriEeaVUdApKPCZaE1RhKE/fJBnGnHP0fYfzAybVjh+GRAtItozRp3jneJRxUyw7pg7Z7GJsElKQC5q6qliuGqraxuVJjOSY6ZEAIWYvWS1XaFMhQsw87Dxr25CyLaO0jmPWOjrmwRisIiI4N3B7e4d3A7W1nCwN122PsZaPP/mI5y9esW1bhtazaGpMCsD0Pv94go+GcpMyAU2dG6btPieX6RnPNDeIjNl995dQWC6XXJyu2Ny9AjFUVYxMDhId13oXcENP124YhoEQFgyDp+8H6tqzWq959Ogxn37+Ba9fv+Ty8iXf/v6PYiT6Ys1yfUq3vaXvNjjvQQ8R5rQiOjLN45v8+5jlMFGLXgWubeBU1TgZeEaHxtKgWGNZIwzJdbUjyhHZ2dlvWppfvGDxwQlrEX704IIqGH726jVf3r3mVCzf9YaV9NyuAn+7qHm1anjysyd873u/zfnJkq27o3/2iofNiivb0LUtzrXQBU7fOyV4ic6EwWO0RVlD222i40YVA2ebphn5KREBHYPflKgxqlwbw/r0lPX6jOurO9brk3RGD0vpyWT9RIpskiLIKGsm2aJwFPqmhvGpA9ws3xKiXOGTXZWMN1QMUirxUTmB0gCefw8iKWGYxDM5ynBpPHsfJ+KE4n0lhYt95lNGy3h2LNjxdtlxRUT2ypnngKbct5Lo7D8G4YkvdiLJvypmfZUQs6mEAOI9rnco2QVPhrfUd7y1YRxipHjXdWOqsux5PU6u2MDsXbXn0Qlj2trs8ZnTqUMiYmqfaEyJXtqC0TgfPW0Cr4fXvHIvv8l0/rFNW+Z6/rH9T9eSUPCP7R/b/2TN3/FWxew1ZTDZP7Z/bP/Y/rEVrYv86ZSLNOnnH9s/tn9s/9j+Z2nZcBXYc/bMBpc3tDcpxPeejS+MSlaVsiRkGffX13JkeEhKj6S8yNnJiOlXNQqPjrUidco8pkApTW0XrOoTmnqFtjaptaJCNDsPRH2wJOfMQ5eNrBjfUw4mo8puQRj7K03mMbogGsaDh97BgMYHFXlSszNuelG7kk9ao1U0LKrRgMRooM0GBQCrLNkJ33tHJkbReSEkxVEy6GmDc57L15e0169RWjGkclN4hQrg0GArFIJTAVSMlg4SxsjaEALL5Qoxlv7ujkGBXi6ozYLN9R2mMgziqZrm/8/afzXZkmT5vdjPRYi9d6ojSnZX6xGNEQChDBe4dgmSZjTAyCe+8avxhXwiL834CNJoFDADee8lDBczYxhgZlpWV5c++mTmFiFc8GG5R/iO3HnqVM9E2anM3DvCw8Xy5Uv+F+H979BdPmb3m2e0D2rU7jXuk89ZRYN9cAXPBkl0N4YQB4xSjEbeYUJgHRU6GmqrCd6xff2K18+fMRCwUVz4OwI1jorIBRUbZUEreqNwxrCpW7467HBeELaM0hMyjMOnMIC7TsC8jiV6l3MC5W+rmqpZU1Vrqrrm7PwMrSLPn3zNzc1Lfvijn6JNhbEC2S72JMkUD8ERvGS8heix1rLvemIAayvqqkHryPlFS13PwkVZJzZTpg+SdT3T4DcYNe6S+F1nS74lOWUz0koIgcF5ul6yxY0xrNqWVdsk459kTutKU9eCyBYyelsEn+bPaEMVwlSTXBzkI+iQqZfs7PSjZzg4QoDhEHAHjzu4lCmeDPS+yABUiqqqqJsKrRXOe7pxoOt7Dl3PMEgGcBiDOMYz6oKTOuNdN3DoBEp9GEacSzDYPiR/jcYaRdMEvAJtNHUDVaM47MFqKxmNCV0vpqzXI+S35MzK+U5RLM7THB/TYCT4u5nmb3KOv83PqS9pukuH+7dxjIOaAzViICPay3kkjnEVJVN66IcpQahMLNIpc28mvGQgp4gzKx19KZttyggrnHoled9xMEKyuar5DFMKoy2H65H9bUfX97jQEoMgPqkY0nlhEEj0vDfSZCRneUbYi9FilKapauq1ZmBkHZuESiFoayGqlLF7/xqVY77Dk97g4Pqm623P6PuC275t0Ft5bi4dofl3QQGYETvNhNaWYxgCzvWMrsc5QXAlMkHqzg54gzUabapUrtGBlvKlxtSgB0IAPwbCEMCV9JPoJPlL8xE/neaFjX75723nYf438+p5P51wBMWY4piOmXbJG7IT8L51KX0JMzIjRw5gRUJfyiW50nMlGlTZ/wlFTAZSrGVGKZQMfinJJfMXY0Z9UrJ/J+e8mmSp7BiPSqFDJEyIhDn0QX4GI6iKw9Anx5HIJ4euY0hw3VOzanbqZVqb5+nuuUdJlyk4QymNtYZV29DUFcaoKSiUGJByiFJGYRhGVsqitJ3a0mmdURC1xtgKUzV4L+3bhPIyI8bFhLKiqKyhshBDT920fP9H30c3FV8/fcr+9pqmqrBGHOMhnachiNMvI71wxEnvD9y47/NyfrTW+ISKHELApqTNvHcz3RpjuLrY8PXXz0SGrEQW8mHEGotKAYJ9d6Afeka3YRwDwyjtrtYt6/WGtmk5HLZst9coIg+uHtCu1jTtGVWzRtsb/HhAaYe2FepkrMPx/lAqoZMkWoyJ/r9SPY+wgON1dOxUYBUtl7HihkBPZMBziBEUglaBQoVAe32LftSgzcCHZy2Pqg0mBGI98MHmnA8ffsj5uxds245Pd3v8puLZl1/z0a7jSovMevvkKe995zGvNme86MX/WNuKtl2x7w6STGs0wRoO0TOOLu1Rm/bY7HydaDgFqE6BKkZT1y2XV4948eIJ4+CpGz0hYAqvy+sZyYFsef9MzmEFGYFq4g0TEvI3oxP8LtcU1JJKyYV4Ikjw6IyZ/py/JzujmeUH7vLzLBdNokXMz80NhphQAtMZomKc2i4OFTIk1YQGnr6adA7mxGqVXxo1k1M8BcQKcrXE5NQIWkpM/uWAlHsMXig7AO4tz+m3doyXh3n5r4TCBo6c5Pn3ifEqhR9HMHZSXOq6nghoqmec3ney9p6a64nl92Z8ehD43Cv7YDJS5Ove+SjP10nilP/FaR2PvjjZ5pLej5+Nd96/JNC5/aWWpqb753aPmfp916k9mKawlJunSA8/jug3Ek68+2vxjtz2vGm+7ZUe+lszj7Sxi7+Ovy46OjEGufJ65edPjSGv3ak1PP1MPPpBeofWWrJAMtxk8f9vc0XiZHQqe3JfS+XaH/X9vnk/JVy+Zd/+bo+B43cXYs2JT7899b3pXXPLb5zVN3xf3PkG7MlvhRxwkjjLzyNRKWxlsVU1KdZkpSMyGXBDgqwTe4T8fmo0sm2Wn5aoD4VxtJiSt4HTPTmWE+M86sMk8S9vVffsz8yY596W3PR3oZo7z+bz44gJxnlujjr1u2f15neVHOwoG+a4Q3N/JyZdfnd3fUqheT6aCuGmfMmp+acY3amj7XgY9/Ti211/q92/FN7e9p3FWfJt3lu+7u+KX5047O5t+e6ZcfqespVpVRVEpWhWrcC6qaREZOOW94yD1Aib4LlLupto4XeQEo63/OnvyzGo5XfH8tNpWaz4bnr4rXr3Njd9w3WXvx5//ne1W/6Ort9h050e0TfT4mmsmOVn97ez/ObNd9/Xjze38DbtnZLy/3Y863flfH8LGvomUai8703duqMvzOOZR/XmcR3akZiD+JTIMN4HRpzwCnVMPaUhmuIz4F7j7inHCzA5QcQwEVMJJcVygv62TnKlhmQkiBCSRKGlFFYu10GMWAxex2QkDyjtBcpZKayuaOyaulolJ9186WwAouB72diT+wATwpj06Rg6T6X7TxnNRQ6U+pcqQfGOEUaktFeMAYwnak1IlXZ9mN8blWRIWJ3bPW5/mYnloycqj0oZ41HFXI2dcRxTrVyBiv7y86/Y7V/Rnm3EODsOqKCwyqMbK9lZydFuY8T5gKkstalwUXHYH/BaHLoohXIO3fXUF2sGJU6foEC3FWePH+B2PWx3xA9a6m7H489foFeP2MaIwlFFqILBxwqnNTFusT7QRgPUXMdArS27/ZZnz77m1fNnU5k2ozReSbElHaGK8NiuuPE9WxPQ65ZNs+b5y8+IPmBI2fipLEsAqR9cOCeOnFB6zhif6gMqTVWvaNsNVdVQ1Q3nF2eEseezz37L2HU8evQO2lbU9Yq2WTMMA0Pf0fd7cr1A74ZUEkDhxhEF1FVDW7e0LTx4sEGrY9RCqTMozocQc43TMdGcms6N+/ZfBCkrcsIRd9e5IhtDRXEOex/ox5FD7/A+0qwqzjYrVk2dso4DxiqqxlC3VsrNeSl3EmIk+ohWARfS3wivE8hah7FgVZwNjESiCww7L4gL28C4d/hOklXGYcQ7D8mWFtOmrJuatmkwxuC8p+969oeO/WFgTI5x7wPOSza5947gPM4Hun6U+uL9MGUghiDObJ1KWRkU7TpiK8uqbVhvAu264+VLh9WGGHxCvCDNm5/LbKRFmM2hJBSGbDuca4+T1tHnDLBivd70805N9MKmuHR6q8idz77JMZ6/U4BSmpAGtbxXay1rEyQb9HA44EdH1TQYa4tyfgrv32APWNDokk6XtH7KSXjEm1M5rekzo+huHbev9hwOG0bviSZggpQf08qilUERwMzlqabyaNET8KAC1kSMsjS2oV1rRjPi/QpN2gcBnCc53I/7f2pMoZjPY3337uen7vs2V2nzvkMnRZtZByyz1I/17ON1OvX8NL6pbMzsGM9G2qoy1G2FtoreDfTDgcE5ghenVExBN+IyFacBWgnP9gGjrEAMG0vbtLR1wJgbiEogsEc/rYFWggBQyl4qj4OF0+TE/JbZhvdd5fMluk/e60odlwkVn0MKDijWZMrk1qqobz+vX/mzLA+63BPL+8t1y/6O5Zjz5+JDT2dOdqhL6iVRxRQUJGgSc3u5H6BSeYWISn4fyewXc3Uq1+cD4kA3CH9JpTiNxRMY+56qkmBI5z3Xt1sO3Sj8WpNK602jPckr7/KzeX6yEw6UOMbXLat1TV1bej8So4IQJKhLBeraMFwH+qBo2xpdVdja0tQ1bvTYSqNMjW02tKsVw25HHKQEUranGGPQtsZaS2UNVjuIUi6kXa34/k9+hDPw81/8gm7o2KwuqKxlGH0KNAtT+do48ae3s0iW+/8++lVKEVNmvMCpV3eejUkfeXi1oakNo8/BajXdrsM24sj1bqTb7+i6PcNwRj8I3Hck0DQN1lasVyv2hx373S2H/S2PHz5ksz5j266omxW2WjH0XbLhzgG099F6/n1E2IxB4QDGyMf1LX/CFQbDjp4v6Hisah4x8Co6rvGTnS8kVCpBcgJrR7rhlkPdM4Q9l5tL/vGDH/Fh+xMeffAO7cN3MPtb9JdfMPzqU8Lac/v6GYfXL7kaBtZ1w9Onz/iDP/4JTx895Ga359B1nF1cEBXc7m5pNhvqusIbxXa3Z5WQrauESjQOI8M4TH8DkmGewg0FASiilObx43d59uwpXTdgKyOoA34uUxmCJ4RUclGdQCRRauaPSkvJlFzWWefSBzPd3Edv913LM618JgQ/oQWF4EQ+UBkta74v21mWckyMxf6IAZDgY52QuebM82Ob4PzMjDgWktwrumLisbrQ6Yv9lINUpqC4FBqZz858hCjyuS/BCSrK2oUo/Ej5SFU1aKWptMEYJehePuCUw3m514W3yQj8llDqrhBGM1TZUimd6jBz9+AIzrHf7ohA13VTHaYQAs47USoLx3r5bBaicw3wEEKqH3AMdXBVPeB/94f/+6nGdnkYLiNHgOn5so5mvje4sh7ZsdJdElSOeihrSuTvpCbnvBiloFZGEpVBBHn+chRpNgAsBf0Y50L1y01azokxRhQyolgaQsRFj1epxnHvuNI1T//yL3k8HlAhTIplOb8ZBr/c0rkPxpiJPnLN+XJujoxO+dCL8SiQIj+T57KEn3gTUy/pLytcxphp7qdI+BTRlcdmisiucs6dc1KnZKoxLnUty8wE59xEF3ncmfl2XXdUY1Fqpcpcj95TtTWKyHsPH3P99Clff/wpDQqbhKDl3lmOu+xHOWcTXTIznzz3ZR16b9RUIzdfR0oSEHVRj8fLukvddlJNnITaGOa6q3cO35AgcTItJuVXJ+ERwKe2lkLocsynrml893yXaUurBN84NVgI2skgEkPAMguNPglSSmuJSIsRrwLOLIyn+bCZ+L5EP3Mk/Ba1aZ1P78kCs+ikGd5R9ijYWKxFSJbILLQqUFhSLJXMZcpy8akON0Te//Ad/vSf/mPWj6844NiNPW4YiaNDu0Dfjzzf7Xl9fcvudsf19ZZ+L3WmFEYyNbTGaqlRrkUbmdY692+IbhL8SzqQ+uEQlKLTGd4ldbfglQCqMujKpBpEsq+mQzkJGjFH16YxG60l6lJrqW2uNMpWiXcknp1oK0dSo0HriLEWm/hi5jXGSEaDTmdHQYCijBR0E4IYknJtITHUyEE/DANDtyf0O4Ibcf1AHB2xdygf8MMI3qPHkdgfEmqKmvZYDGL40dYQtWTAhEwDxKPzNcZI8NnoIvOUDZwSfCYqlIoSgGOT8WXa22lvaZPoKSbDu8rCYKJdJfvepyC0qpJ59m42cHmrcNZM9bFl7+kpilHelaOJRXkra1vld6tYTfW+lMrZNbPwZGOkDrL3vPfoZOEueZjXHhe9nFdKamKW/QohEtHkzCeKszciCmSOKs0TILQhMdohhgn+kHR/CFFqQzmHsdL20piS56rk2yEEgaUtZIqZ9BK/yTxmcZ06F8t/ZUmbbDgIMc5G8IXBcMl77/wN6OAJRrGvDdvG8g//F/9Tzt97zIff/w5dt2N3/YrWD6jdwJ//v/87Xv/2KU2waCwOxaDAGI2OblJST70rQ/SWslo5RoAYODr7M12X9x0L4m/+bDmveY/MGUB3DZK5b0f9incV6pPrupDrslxSyofL9Zj7K3wuJvi7vHXlvrvPlX1eysH59yxLSqZbNrJxdM+yvbLdUsbOewl9fG85rlPy9Kl5KuXC/EwpB90nY09tI5CdIcajtpZj+yZZo+xLvkpDGxzDwZb0UfZp+fupvi95x/K+kubKPbBs91SdwnndJBP3PtpUSiCjKcb/Rrnxnj4v5y7zwnz2xpgdQ/c/t4TMLd//3/6v/5z9ekz3ApEkQ6hJD/AxpIyG43k83lN3nQzLvuTfc+3PQJyyZo/HKdLKSdn4d7i6fpscGBalLEZbjBE4xlx+LI/BGjBGoVVMZq4ICSLbmAprRFcpezT9rpKTPBlny5iLU+acYxo4TRuzXhHRPkIE5wMH5zjEwBjBJiYWYsDHERIUISSYvzGgwkiMPsFQipG85NXAHX6Q4ZEiUlfQR5HbaltD1Lx+fcuXX31NpwaINSYYxKejMHqgtpJtF4zGVC02RF69esV6vebs7JxVvcYPA7e3t3jvWW/W+P2Bw+vXvDSKddOy325xleLCGh42DS9/9hs2F2vM4SXnL5/w/jDw4e99j796/hlXXsNoGL1lUIYbImvzih9WZ5yZhls0Px9HPrp6hy+3n7J98hU3z55QB5lzg6INigs0D7FcYvlec8W/7Z7wchWpmnNoK17eXuPHEYOeZOFASHrKMYR1Occ6wZ5mfu+9p65b2nrDenVO1TaS2dTWPL9+yicf/xyrNWeXj7DNCl1Jvdtut8f1HYfDDisqjAQemFRffOgIISZZU/Ho4TnvvntBZSwh1U4tdV2UIvpI3w+4UfjgbMS7x7BY0rZ6c6Yh5OIFIsNm9IbBB7peavw2tuJs1VJXAhurtKZqIvXKYFtDUBC1gTjrCz6kc0hZlJIMfu89w3igMQada7vGEZSYcLrB0Xew23r2Nw7fB9wg8Oc+1e2edqOONE1D27ZoremGwDgEtvuBfTfiRgcJclZqtfpJpwlB0Y1O3jeMMrdOHBciHziRCTG060i7abm4OuPB6Fifbzn0W1ZxnIJtsnwhGePFvk2ZlDbJ+kEhAeQqn0VJD45MtqM7a1n8PekxkQlidHkmTVDsszcWplcsaD/fwrFcnR8r361UxBU6TykfZJkoEhOseuCwP2AqKzpHoXsu6XCi3+yqjPNnpd21pOHjNjJFHLc52zbFmadSoBV95PrFge3tQN8HvI7U1qBVLdC1USdI2qQDBald72NgjBLQkGtkExW1rrl4WKHWA+7a02iLSXXTgzfo6KfJvE/mOZ7n+21kSxntvnvL7+/b8/ksP/HU9K98dKlT5fbLM/Lu2ha6RqYvFSFqtBYo6SpomlXF5nyFrS2Hw4597xnHVGtaKwmiATApGCxKxqzSos9aLeUUmtrSmobGjhiVIsRCEBj2PHe5zydQY446fs8VKZIBvuGS8RuMyQ6s3I84/Z7nVmuIzJneR/J8iKKrL3j9KT2stG2f0uvyOpT2rpzhXd5XyjdL3TN/dmSj94FYlCIpZVudozuVSsmCSXYpbG8TfRf9zjZokUktCvGxvHj+gr6beWhejmkvFfK2jCFnyAtcpEqONbnPE4ITp3cUx+563bBaN9R1xWE3Ti8IQRx0SoOqN1ytH2FUj7YKbcCHATeAXjfU7QWb8yvqtub60CeRzydHZMTWLU27ZkgOYikVLLKfbVoev/8O237H+YML+nHk6kzT1g37bkww2gFX1FLP/0wBa7fkF+X1pu9mnqwSlP3AerU6yU/6vue9x1dcna95eTswugFjKpyXfWKNxnnP0O84HLZ03QXDek3fD/QJoXm9OuPq6gE3N6+4vX7F57/9mD/5B/+Iy8tLXr58hrUNlW0YcqBf8Ec0+iYdxKtIHTUacEZjnOc69HSN4VI1DIPjP8ZX/G/VYx7Fis/pZa1RWBRdDAwpWKMb4LPrl+gLjXGB3/7mcy5fHvjR937Ej3/4U/bXN4RPfsXNV7/lk09/zs8//YoHP/oe3/v0Fv+rX3D7+B2a7/8E9+wrXm+vqZqaZtWit1sqYzlcX/Ped7/LZrVBKU2376hdYHN1DiiGQXw9bduwWq0me2XWOysjwQvGZFRrOL94yPn5FbvdgbaxWF3Ru0FKwxTnhwkGbRQ+phK4cfZpAVPg6OQcL+zQf9eXMYboFaMSx70bHW4cMfhCBiqd35yUhY7lHaaxap2c4+T+iz6YZZipjZgCqpNXIkiIFipLKzEQAslpPr0gtSnyVYiCX3Zs7BRflU998wXPVlGjgkcnX4kEaSpUsuOHymCRchLD6MA73FsuwbeCUi8diMAdI3vucM7gDkGcBHVdczgc6PcHQgh8+dVXvPfee1xfX+OcY7VZE2Pk4vJSbGhHtSpOCzrLWuaF5EoI32wgPWnEK57J7yj/5asU0EqhN89FaWgpD50SWr5sLyvxOdgg98taWzg057konz0WbI/Hd7wus7ATVZwMNkZrtI1EH1NdC4HuWo5pGqcxhBSZUo4JmBziUyTwog/TenI3WmtpjMufnRJoltcpY9mSZsp2Txme81juwFkBY6qHVQpIpVM9vyfDmOWrNFz6GBJkVKDre6xWdH03KbGBKLFdhZK1NNyWY1t+VvxRRC0dC2sibEMWzE/NYx6L97MhV/jhsZIhTPYuYz3uC1NkKSRGGqLAn5R9V/Pv9/VrOd6j8am7zvE8f9Ne1SZBxJTMP06OZa0NWjh7ekeKnNJS3kFlR7dODlLmoBaVY+aCGP2sF+aulTiiiOIk00qDsRgsCk0gJijLxNQT3KE3kZFThnvZg9ZWOBQuOUszlIitLC4Eqqbm9//w93n/O++z9QNfv3hJ5wY6P071f3fXNzx/8YpdDPig2O/2BA/rh5c01UpgEasK1TbEyqJshakqTGWoEspHpolNYzDWUKdIvbquqeoaawQuqLIWY5OTOxmrnzx/yjAOGKXlILNa/mVHpRKYwT/7s/9OBHGZ0MJBlaOGJYJdzlKFGpYCyEJpzhCh3HNLzKruTLMTrcXMh2fYofmxiDGWf/JP/6Xwce8IbiQ6R+wH3nvwmH675+Wz57x69pzt9Q3hZgv7PXEYCIPDj25yZldtLU7oKLZwIU5EwCj2mkTCMkUlaq3T+BTGSrCADhF8SLGjZhJQMryPTjQe05BUDgJKY8tZG8mcQ4yBES02K23E0CduZupxRiXI5wWF4qe0p7QbhLB0UAJBTyiCR7w29yFKkIrIpJqYgxnmJRQ+GJRk0eVzD2ZooyhQrRmMLMYo56JJxKVSIEc2ZCTHOHoO1rBWamxrJUEjw9ATXcDURgKplGRRq4WBbHI8lor1tMfvV+Tf9Nl9Z2D5d/plioS97zrFg+fPpM1KaeohsAme//Hf/L/4n/w3/5zvvfMeZ+0GdR7oty9RreEf/ct/wZ/92/+el589w4SINTXKi8IW4mywPPXeZc3BN40vX0sZtDyzj+nsfgfcqf7kM2b53vLeNymdy3eUhpdTMsqy7eUYsywVQkBNxgzuPFv+fcpYVH6W52o+Nxc8bjHuPIZy7Jm+cz99vGskPDWm8vNT87h837JPpwxcixakDnCR6XjKgLl856k+LL+7Y9A8EQiwHOOS3pYy633vXs51+f1Sz7kT0f4WYzk1fpXO7TetzamfyzZOyeRl38v5WbZVOsW/USeYaELmoUp6anDJwa9Vylie257GeeLdp658LomynuukZZkoG5KP1+Fvaxi5vb3G2JbKtlhrxKmgi7oVWgzJcfRC51GjvcxH1J4wjoxDxzDsiH6giiJDGqMIKtmU8/SpeRSw5C6n52MaY3HW3L0RrFE4IoNzbPue/TgyNk1arySjkYLNp3lLcnghD+Qrr1PWm0s6k7Mu6eoxTE6wLPPs9x0vnj/nsD1QNeeYaKltjW1EF8cHttsbfARb1bSrFRjF5cNH7A8HXt3cSgDpZsMYFa+3W5S1NO2K6oHhRT9QX7aEVeTq4RUfvvc+q1Bz2HVs/uC7bH/55xx+/UvquKX70RUfqZHvvnsOHva7kVf7njMMH1w84Kpacxjh1e2BIXgOjyq+/PRLXr74ir7bYitovEITWaHYoNlgubQrhlrz20PHTrcoY/m833KrIt5H6toKrL5WRBfkNMkZzPHumWhSkGyM4oRWSlHXa1brS9rNiqa1PHj4gK7b89WXn/L115/znQ++S7tas9mco7XlcOjZ7Xb0fU8MUidy7Dvc2LNab+i6IdkYjMAIq8i7711xcbYm9KJPZ3hfEvqA0uJYPxwk2DQ7SLKZ/xS3f/OJPdN2SWOSNSdZ1c57xsHTjQ6tFetVy2a1xhjNOMiZWtVQ1wI3PgRQGEJ0yRCoUT4HM6c+hSD1xVVEacMwHnC+x+OQzO4GNxj6Q6DbwXiI4G0RKJ8C2VN7tqpYtQ11ZfEh0HWBvevZ7jr6QYIIQq4ZrmB0AssenBgz+25k6MUpPoyjfBdSdm9MQabBU7eG9fmKy6sz9qHn4srS+wNmOOBR9H3OojIpcUHklix3+BgKpIK79h+jEry/1pOtbCnLHf0d45365EueoZQEkog9Y7IIzGdBSEbdI2vHm+W9cRwZvDvmiekK074SY68PA69eX2NsRSQlsRTn4/L8PHpvwaDL93yzzex++V7OernDBs325sDNbc9+77gwjk27RscafG7DEJ1CGTFUE7P2bIiIjD+6AxqxD3zn+1c8/MByuBmwXs4eyWwz85qdWK+jNXvj2DhJP/fJVct5Xs7H3GZ5rB3LTXfsXvf06ViGO75fjk35bEoWSjSnUTg3gKlZn7WcXWzAanb9SDd6CQ5WYgga8CgldVYdoid7FbFGY+uKylgqo7FKo0LEDSPD0DOOA86PBJKeHuW9IdNwjJNcGzOt5br02S6jUjb0G+bx/kujddapbaEfpQCfaXkEYUBpcb2UayHBvLk2+DzvR3r2CZl5+flyH4XgJ1lytleoac3mwMd5j5ay99JHoLUElITIFKxfBk+elBWT7uKL9mOMGCO2STf2khmNQ+kG5x2vX1/z9MnT1H4uO5PtuWLfLPWW+/ZdOb+5XrNzDm2hXTWcbTasViuuX+3JTMl7R9/v2PdbPnjwLn/89/4rnn75S7ruCYPrqXTH5uKS8/MHnF0+xjRrOndgd9hjgsOavAaaiGbXB15d36DDgDC9gPeR1fk5zdmK80eXXL3zgGhk16zblt2hw6dM7pzAEnw+uzU62qM5/7bXMc8Um8rQ91PA75KveO+4PF/z+NEVN7tn3NxssfVqykC21iClNxy7/Q3D+Jh+GDh0B/b7mt6NPH78Lu8+f8WTr7/i9vo1n3z8K/7xP/6nvPPoHZ49ecp+dc2w2jDsGkLoUF726FK3Wa6tUrNtVQWFiSnDOSieVJ51ZWliw1+ML/ifxTUrFBdY1ljQggpoYybVyI7IrwHz+oanDxtexp4n1yP/8teBn3y+Zf34itjfcti9ogeetIpH3Z6fuAbz608Jj97HfPQR7+s148dPuPrRh/RaMQTPs+fPUcrw0e/9iNVmhVIaW1lqa+m7kcNhB0Sapubi4pyqtkc+qaqq0EjAEUr2RQiK4COPH7/P0yef0XU9WgdC9PQhUmmbfEOC5pJMgUyBOwh6zkQP0z9mOfXv6JrXUd6dbbUxSADlZM8k2c/K/Y2a7JFL2akgCCDbzgr7GccqXX6qNPGUskm2A+e+hlDyGSYfpJRcUSkoi0lHk70QZrmAZO/XZk4uJK8BmJDs5SF5RKKUDAnaozQEfzcR6L7rrR3jJVPMjD47R0tGIB1VU9au1pqu66Ys3f/2//h/Yn/Yc3Zxwb/+1/+a/X4PWrE+2zC4kVrbo0yh5cLJwObMlmycKJdrXojZmZz7HOOcxZsXfBiG6XDK7cUQJYp6Ma7pLUW/lg7V8rAp37NsK9+XhfxT98/OMXVkzC6d4XDs7M1tlH3Kjt2ohGJVMhCFEFBBMvu0MRKxlig9Z1sv50snxaR0iJeC59IQdGRgSxss+GMCXQowp4xt9x3a9zH80hGR/87v0XpGHpjpSsZSVZUc/MngaReZFeX859+zIb4c/3H/8jyJAuhjxHknSDtGc6QZv+Fazst9B/rRob1Yl/vqv5ZtlwakNzH1uwrEseEzJidiNrAorabMX7hrJC378abxLH8/NY68zjFGceBNUV2z8D5lYytN7+cM1QxrNykAgA2wcem9iTErXzr+YajA14gBVhVIGkoOzxChN5ZoDVobgiY54JAsfSUQiJ0Wx6ZO/bHGYitLZSuikf3XVBW2sgJlbCTqfnNxzvsffgBK8TJIFpNWmjOteGCryXneDT2/37SMGPaHA6qqMNZSmUqcjCnijcoQcyZ1guQiRcBFIv/h3/87Dt0WHKh+nheIE0lrSLXJZsPD06efMfSHI8vrZJRIq6N0MkwocTCSneNxfkgrlRxs87smOiALJEcWhDlD4J5LqRlWcWpHFX8Uvwh/men4//pv/g8TXWWnutWGDz78sRh2QuBP/vgf84Gt2T1/gdr3fP3FF+yvb9Gjwx8GwjDiBgfeo/oeEyR61geXhAuhYcm0yOw6GY61ZJGG4OcAGWPQrSU6h04ZzipKhn+IAQ94pVFWMqB9DIxllmFItWsUxDqdqcnhnYUfqckJJqTzSCeUkux0SHOYBbjpnA6B7KDPQtwU6JBnOinIOdgkaiQbXMS8Cfkk35uv8jzNQl6+J3ovczAFtYQpGMgYnRzbc4CAzGMKcDGGqJFABFtTV43AXA0dQVeE6BLPlSx97aU2bHnGLYPbuIefT3+/3fHwxiuvVam4v41RaNmG10LbJkDbR+qq4Tf/4T/zp3/8p+y6A+fvXrK9eS4yyVrzh//VP+LfPvu/U3tFt9+zto2giejjgKb7nFz3KXPyubrD7/O4ysDH/H3+vGznrZTiJLeUcs7SsHIUiHWPrJL7cWrOv+kMXPY5xlJByiSUFf277zz1+7LdN8lZp/pVtlWiAx3LAN/uOjU/JQJUOf+5T988d6KkHgUVvWGcy2vpPC37WvZH7jvdz7J/S7opHb/L/r1J7i37903oDyevrECf/Cr1vdBDlnLnqT6eUj7vy/Y+mp8T3c3vKYNB3mZccsvM95VS0yG+PFuWxsj79sApo2U576K05+DLWWb4NnT2pquuW4ytqWyNNTVaV+SMnqBShnpK9lOKVFstpgwbcQ0Ow4F9f8swHETvi3k+hY9kOR0zG3+neStlouWYTqzJqVUKatbJvff040ifMqiSaoqPktmtVSRqMOoYBSj3V7j/cZCyrM8cLBkjBObaezJH+VzX9H3Py5ev2O/3XDZnMAaMMxht0Y2laSpuXr1GjRHlFON+pK5rLs8v0U6z3x8IzlPXFtOes3+9Yzw46rOa1fmay2cj4XpL1dY8Xp/xSNf0Xz5hXVtW6wp/7XHXilt9ztPVQ37/62c4biTzdtOwbi1+3VBr0K/37G92vOxHmrPHmKjYfv4Vw8tXWDfSAL3SrIPBqAxUHLFNwxfhwE0V0U1N1JrPd68Ya03YS2k6U1mCEuOtQomvKsSjmoXT+Zr0t5z4YIymbdesV+e0rdQAv7y4ZL9/xYvnz+gPWz743p+gbUW7XmOsTfWwR9w4CJKaGxiGPmXoGbpuC0SqStagMprz8zMgEAQpHEzmIWqy2Xgv9cUD2VCZaDupeVHNZ1JMn5+i6eV5cvx3mGqKjuMgtbfHkcpY2rZl1a5mfVeJoxENUQemeg8TL8lyqdgIcv+HvscFjzaWMWXh+hAZRs9hfyCMkbGDbu/puoB3orOI4T+XLpQx13WdYFjFZtP1jsM4cuhG+lFqiUcnwQlKKcbgRRZOdV2d95JF7iX7tDzrZnUoUlWaZtWy2TRcjIqz8xq0x/mBwYkMr7Wmqmo26zNsgpzNvFlFDcm+eOe8uIeFlveW2YBCD2FCmVqub3m9ycYUpTDtNNbZSFsG2Gezgnw2DLJ2tqqm5KHcfggS2JzpyA0D2+2W9XqNreaykpPtMp1jk/pZ0GKply5lrjv3foO96O53SrKtOk/feYZBgiVUVOmbiEKLThshuJgCl0GcnHmfCvSzNoq2bXj3wysevLtm/7OBcQyYqFA6Es1K4PPfsBanrlPy/anv7puPU3OwlGHT0+lMvzvH5c+3krnu9BsyP81XCCmgGsQGEyO2MqzWDatNizKabhgZfBQ0xOQNDt4Ro0d5jY+RMQSC0lSmImrQtZGEBUAlZ2tUGVJY+Ez0fqG3S+LG5Dgr5vmUDe6OHWcxZ/dd2Y6e94zYVEtHu5rkqljYkk61Xcp15VouHZbLcZT353t0YQ6aP591z3x/Tgxb9mWZWJc/k0NMbDilnSJfJfqTUirBlQQpyTLpuXJmx5iCwZXAKvsxcHt7y+vrG2IEo6VOfflcmqiF7vJmPhmSnWQcR+q6om1a1us1bdumFRJH1zgMbLe3vHz1kiv7AGM2VO2GfrSo2HN2tqJqKjmvoiIG6HqxodvaQpDAsUBItcnFBhmjQMQfDh3d4NhcXFE1Ne26Yb0R2SI6T2WF96pBbIjjOPuuyvG9rf6/vG9J02KrlLOyRMJa2iCMVpxv1lTW4L1jVdVUVUMMkhCjlZQAGsZeYMCHgX6s6MeeYRi4WD9itVoL0rL33L5+hdFwcXHOZrNhtVrTtSuMsbgxEnUkozPeZyuf9bCEJojCqITsN0a+Yse7nLExNc9D5LfhwPfiOQ9pudABGHApX1inRBOvIia4VDqlpguR6xB4voLf+4c/hR+8g//VX9P+4jWPe83F+or/cv2SJ5ff48Mw0rx6TXj9gvOLFb98/pKH3/+Qx5cP4P2B4XYLxuCGgb7rROY4W3PYd/S9ZLFba2kaOU/HcTza7zFGrLZYa3B+THZTQ98PbNaSgT66EeegasX/pStFXVmssRhjj3xrImcVfASdgofSl8VclzTzTdfyHD91JmW7eYyzPjTbbeNkU53OqRMyb4xivxVtceaqmWamn3IapAHP7YT83qlN4V1GKThKRkx8M2aaVNPcZVkqpqCXIxak5lNg4qVx7qNRQrdyLszBkHkOtTGotPe7oXuruX9rx3g2TJUO2dKxCEzO8KlDWvD+vfesVyv+05//BTevr/nTf/D3UUbzs7/5G/75f/1fUzX1JHRKnQJ99B44Ntop5uzcpmkS0aRFIR9i8c6zpdCcnbnZEVp+nye8fDYvSnmVGTansntLR3h5nfosKy35uwzhssxCL+c7t780GM0Q7McHd2mkVEm6CCFgVCY4NemReezLNQgxklvRCf4qvyMHP1hrJ+H/aA0Q48qRwprHorLCfTznR6asxXldCkZLATnPVfn+LGiUQpLcF4t7AuDSvMY7c68Uk3Mp9/MItj/Eqb/5vhAi2mR6lOxk74YjY5LSWmouFXxrWq84s1cFR3ObhcR57MV8JaYZfJgiHidrUWm2Kpcir5Mu11w+z6yv7N9yj03GE6WO1i7v7dJxkT9XSYMXmuREDe5sQBZDQg6OYWpHlVNZ0EBi7lrjUFM72bAWiomLKIK2CR5uNpyEPKlKMSrNbUxKPPnAmBEzbFUxrCyutlTWUtX1tBebpqG2Fls30Eo2dt02dN7hVURbS1VXVE2NqWrqukkKggGtUTFS1ZKNbbTBqOQM1IqnL57yX372l6AVrznw5fPfyHiUQhGxma6C5AwHrQha4UPAjyOff/KziVaywJ//Sjadad0ng1K5tkXdDjUTYSbWaf5mQ0KcabF48GjVc390SXGgUgRxSfhlhPDEKiYh4kgKgBhTLc03KMgq3nGeLxUjneg2lvCsMStL2YkvQqKLkc8+/+UkPHz+xS/FrKAN3/vBT+FCM1QNFRt+9M73ePH1M/avbvD7PdXtFp0McMPYoYJGWz3xImLEVtXsxFVKlAMv8EZKa7zSOCvnsMpZ5ClzMmbjubVELXWs4hF/kawrNII4QI4uTcpyMpxqFBhDSBBFLswRyVnhNdoSoyH4ee1DiGSgBqEPT2SQWBSlJjj+/FMhcT3Gjcn5n0pbhDDxA4XCxAYd5oCtO7zKO/Sww0wWU6k9JFGMiVfAVF8nZ4wrLZH3ppLI9rpa0dQrCVo57PBKEYKTTIlxIIxpLP6YR04KVRYyS6myYGbT+bMQaO+QLG/8Orcm9VNDuCM7fJsrNpZDP7BSNdYrfO8Z/YH/8O/+e/7of/7P6PqeD77zHV6/eMH+ZstWecbWMtwcOKsrNJE4etAifpZGiDvjOrFPj41m8Whv5u/zOVQarpZBcKUhZLkup4xqp36W8lrZ1rL/5d9H8tgJJf1NCtRyb8pnFLxHOPQpQ9FybPe1/ybDyKk2Mx2V8tZkDA4FbX+LazmX5bzk9y7l3lJHyHznbd7xpu/L95V0Us5BGXBZ3v827d737PJdp9pcBqAuafGbxv+mq5z7GLxAS+ez70S7+fOlnnKK7sp5OKK3e3SlN+2nco8vnkxih8J5gZnU5fyUhoyChu9bu1O0uLx/ro8JM1+av38TSsfbXKvmgQQvm0qc4sqScrzTWGXvB6uK83Qk4pCw0EBUnug6GPcw9hJoiEFP1bdJ65BPFD3NZf4+TveU81caUhQoyR5UKZgy31PFiqikBl70Add79j6idQWmQmkrtVIVKCVoTCEGQhhRBIwWWScSk5NGTXpoiDGVspN+St5ApI8pqDA6Ih6jDD5ogoebmx3XL19ifE8MNbaqWG/W1G2Di4F+HDB1K3VdjdQa73ZbzjrP2eUV7dk5Y9fjDx2hrXnvo+8y3OwJvSNahd00jFtPu15xfrZhbQyHZzdUzQq7u+Xi5hVjFXjx+AG7wfHVCO/sAisGdBPQMaDUSOcqnm5HvhoV17ohNBW3bsf22ROG7S0xKiKVIN4EWbUKTYulwfJnwzVuVbFqKg7Ak76n7was1dhUIzr6IEgKISOcFfyUZMzSBq1nGPUQRprmkqpeU7UttmmwVc35esOzr37NqxdPiCGw2lwRUVR1TWUM3o0E5+gOHUYpeu/xbiDGgHeB0Q2T488YzcV5y+MHF2LkDJpsQogJ3FyrVCN7FMfyjN6QxP5Ezkvdodzf910lDwp4ohd+GDwMLnJwI8F7VqsV67alqSrwioBHWYc3mqAUOuS6ixHJdsyoFrkPgpLlEvwrIWCtoCuEYHDO0B0i29uI7z1+jIx9YBwku9ulbLgYJfM7acnUVlNbkb+d1+y9Z3fo6fqRMWXRCdy47HGfg2+jGBmnutE+EH0ORCAlWUgtYyrF+mpDW21AXdCsO84f1dQPe8KrmhAOjG4UOdt5mrqdde1kG/DeS6kpL3DwkxNDNjcwGz3HZOjMNshpfaaMpNkgqLTwiSNHGul8VKASD+XorphsHmIbyDwnImt0x8FCPhP8HdvXsTwmMPzJyEIMcNgPdIeeFp3NGqAS7CizDUzosLRPFu0XJp2lfaug8pKqj+QGrWcblnwXMRZip3A7oTOHx4UwIWdl/ux9cqhOAUgZmUOjlRWdXSnqSvFufc6HP17z5C8OuOeGflBo6zDK4bN1Id6VQ98kT02juyOfzWfwfE9pM1vYwRDnUH5fnuPlq5e6wqnrTd+Vuov8Le+ZSDbTckLUalSNbzXt1Yarhw+42lxAVOxx+CCw1kSFU5ExelxwBB/xU+kUQ+U0ukl7NiPLhUjUgegj0cWEEDHKXlcSbJftckkdTz/vBiAcDzdyLBPMny9mgtLeBMIP68pSV4bgXUpQUWl+kq4cpx0qtDtPoiS5luswbahEFzHXbL9vjfIizH0K6GIccaKLSR5MCAsqRDKSStl2mGwhx3YkYOK7dzPGdTGHwpVKqSzTeogeFQOMijBGTGukLnwFZqNZP2jYdQNGSe5M/qkn3svkQFN5HuP8c7LPFmvto8fjiNFgtaFtGlbJMS6p7ZHowXeOcXvAn1te3TxFaUVdNwJ/bFt01LjQ0+2foocG7yKVrlk1Fa67SchBEiBidc2mqRk6T+c93RhQBKrGgIpUTcX6fEXTaAbnqaoGa1Op0+BxAYJXUmokBAyBGDzG2pT3dLQ45CQKVdCzVgUFqzmpIj0ieyYExtGJsxs5GzOKglEaNzouLxsuLxqev9K40Sdf1IhCSsxEPG7cMw473HiGGwPDENjvD5ytB6rWcnn5kO12x373mmdPvuLdh4+4OLvg9fqMqj1DNytivxWb7xQcfLzXymvaR4n0daLJGDxPQ8dr3fKeXtGqhl/g+AjDSjk2RNZEDjEyYsSZDpgYcSPUEWrvUdayVYovXU9YRfRao9Zn1OdXXF0e+MnO8cut48mlZjMeOHvxHPXpE85+/BOG118Tdz32Ys1qs+Hi4QN2t1v2+z22aajqGnyg2+0Z3UBdC3KpQnHYH7BWyhFrI+d8DAEfYUzBXFImF2xlCC5S1y0xjHivaZWUIG7qitrqFFxisaZFKwMkNNO0ObPfRB0xPtn/ObM5xljQz3RHuRryXVx8emQLiDM6Rwo4rKuKpm1ET8n6UIgonfZ3FDttaSM5uhIvCDESjSBxCqlLf0KWU/O5WmyZsq+ZT+ZzLSS5MiDJMNoYsnieqfHIl5XPZpVoMOshQWQ1Hc0sryYEWKUUQZkkH4WENBZFJg5BktciNLa5Q/unrrd2jHvnpwhMrdRR5jhRao8aa1AkeA9FOoREsYkh8uDqAQC//PkvaFcr/vm/+Oe0Vc3VxRWH7oDvHXqVuzQ7sGYjmBL4pUkpE0z9ElotHx4U0azSlZRFnTOoi7+z8J2zOoVwlwd/4fCYDBGLjARmJ2upe2m9PICzcWnOBgeJ6MpXFlQlU0LGWl5l4IBkdYepjSV0ucoOjKTwBGKqnwZWa4EgMJHej8RIcrKYSUmuTIWOUusWcubibFwfx36KIjfKEJWRd6WJyLQes6IRI8oLkZvkvNEpeyykiCsVI8YwRb1rpfEcz0FMTkkVJVIJJNoqb+R8qMn6BhGSojgHdKpNHKNNfdMI6qAiomnqRhYxSF07FTxz8n4kqiDGgzSvGoMKYsSpUzRRjJGAJihhij56YZDW4F1mXGAdtFGhjCLqJJgYw+i9MAcUVRSIoEELADfkYBVhHFmpzXJgpscYE+xwgg6JEXQU+LA7xnklB0eIkaCM9I+kPGYBLebI2YhRhTMgS87J0RMBqww2padnJ7MyEk2VeCbKJcdmqkGNQhhwFl7RUgtGqSmjWphgalOBR+O1nqB3pTk1C85aMzYVobLClK0h1ww2lcVYC1pjUga2rSpxgFUVxmqJErMVoaqIqwZb1zRNTWXlAAb42S//msENAgWlVYp8NRNvcFoqPaqU0qNVBN3zycc/Y7d9PcnhWXSZxRQmoXipxE0yfIK/CjFMSkCWbZVSEGLB56QZH6M43WOY+EPZtjQTZwMITAxtFq2SMjPxRDWtQY4Cy89NfUkEqjJviGE+B9Xc8vQhWTGAo3iJiSfPfULJ/lOL/oqMMQemcKRAHyvHeQyq+HtpEM9rMXUnkqmbI3E6v6Mog8F0LkRcCPz6478kYzJopfji+a+IIXJ1/g7t1Rnv2A/YPX3J4faWOI4MfScOYSP7zIeIss0kCGit8HWFMgZb1yhjsZWhalupi20rmrqibdeprqQIVNEa+lxKw8oe0FrgwLXRjM7x84//euIDoijoaRaU0pCEqUmAS3Omi/tnkWMWGoslhVRgQBXrdvwPEfBCkaEQZjjb/M87eO/hhzx+8A7OB7zLMPVpXUJAjQeiG1Pmjxcahgl6S2otJicbChUiVht8MgwZWxOrDao9p24b1NARNpeEsSPGka7b0e33xH5PdCNqHDCjQzsnZ1aUAAsfFVHpVEdS9kQ2Ggo/DtNcpZ1A1uUm/puSkaR0Q5KXkqCeDU2gJllkGXBXXqWDs3S25dVyvcfamuiVQPVFgdJ68ukn/PDJj+HWcGt7lIbGWMbK8k//2T/h13/5M26+eo6OitqaI+H8PkeoUsKnp2wSNasTmR4y75k/uxsMsdzH+Zo+V7OMIhGpYd7jiunZpXN26bBdBi6Wz5xy7i6dhvfNQ/79eL2ykSapSEnenhAYimtpNDxlFFp+VqI93tfvU9cxGsIpNfy4zfL9S6Wt7O+pvt8HF35K8RPjhDpS6ErlFGYYr7JPub0781PMyTLgb/l86cTPRvUysHbZ3nKcSzopx3jKULmcn1NtTZMS7z63HOepdu44tRUTXHWWD2RPhYmYtFZFQGI8EmlmmeDu+JdzU16n6DYms1Qk4sYxOcVn2ehNV5Y3FrMw64WTeJHm/96alrMWch+dfpurba7k/VrQYUgBbiVBhxjwJlK5SMATcOLBixEbvMieYUCNHYwdQSlCnFGhJKFVzpA5QFXGEnO2t5rnCbJRt5CvyjqVCcVGnFNgY82oHEoFCB4/eHYuorBS7khbjDLJCQ0xelzwAjutHEZFKlUR0SmDPaCjFhhR5xMyUaZF8Bp6Fwh+JAZHjA4dU/3ug+f69Q23r69ptdgwVpdrNg8vaVYttze3bF++ZrPesL44p1lviApuPr6m2+15/P67VKuG/fUNX/7sl+i14Qe///t89Vcfs3/9CnRAX25gGFhfnLParDAj9Dcd1XfeRT19ytXNc8Z15PoHD+kOW54ojx81qvdAQprZel51Db/C8Mw0+LqhaSqeb59z/fwJ/X6HR+FoMErqUBsUDZY1NTjNX/nXmMuH2LpiwPNqdIz7gbP1Bqs1KmT4bc3oxwJ2vsgMVskuoQ0KTfA9SnmqaiW1w+sGWze0zZrGGF4+/ZLXL55S1RW2OQNyNqCSUiquZ+h7GgvByViNUZJNHgaknFXEaHh4teHR1QVuPKCiSc45CTbRCLqPCx6XMlt1gicVsWc+49MmzVv6SM/INL3kMeXfHkd0AZwies3goXOSkbRpWzZNS60lMDVoh6pGgrGiT4eIik58O0on42DaWwla1wepo+iDZOG6SuOVwnvLOBj6reJw3TP0Xsoj+SBOZO9xzqfswRQAmPpcWy02CWXx0XBwI9uuox/Go/IDM3KJ2EGyQ0dFsZ/EkOTMoIlBEVGSFRzBrhUP3r2gsWc4f45tai7fWbN+33Pz8zO0GdE4GZsLktiSsqe9dxP8eJXqHQc3O8fJGUDZhuW9ZLp7SY6ZdGaVnIsqcd4pIKdIUMnsW80lAaTW7KwLZi6GSk7RwkyX++29L84xJTRGQqRRkCM3YrKnaHJgbRpHrkuKYRgcXTdibS10TRQHSYzZGJKyJWOS7fK5m8/EPP5jvnzqEluCTnJ0PrdKyFSmoBJtArFXuD2MnZwrQxipFBLUqvQ05qnM1YQyITqMQYk9LoIOkUfxgh/9/kN+8f4rXl0rDrdQx4BV49HJfEoGXO7Fb7rUJLcfGQ7Izu/sYJjkgrLtwkYxB0sfn+/3ye/3ydjz50kKKWU5kpxEDgQLKVAb1tqArbl89xHvvfMuD8+u6PyBTgkaWYjgiTgVcRr66BjcQIiStbfSlsErVNLVQOxbQXkCI3EMxCGCixAlaE2QAbPtdYYnz1LNvJHKK5ajObLnLPnq7PTNa5LzDiN1ZWnqinEYk+lEaDQkFL5cvzYjEUJMKDlpTWKxLsz7AiXzpPRy/dQkvxTi3TQaRUIfSQiGsRgXSk1x7WlrJ7o7XvMYBQkni5BHMv9i34pOEFFKHHrKZBdsLOY/yZQ6Ci/2Gj+AXVvsusZuNI/PAu9/9Zib7ZZwEHnYKLEFqkTfMZ374hynyDKdZyDb08XGmErSKCmTYLSmrVvappVYyOynCApGUJ1HDTe8vPmaq82GuhZkCLRFB83gDxxubzG2wVSXVKqhthuiOaREvUhwDqMM56ua22EkBM0YoNagrMeHEV1rVhctqzPL/rnjst1Q22rK2h4D+KAZXcB4jwme7BPI0v6k4+lZbldpzos4OyaSLJ5L+VLECEM/smpJYnTi52nhh37g/Lzm6mrF+mnFzXbAWMPoBFlSAegRP+4Z+z1uGHBjYBwCu/2ewe1pVhWPHr/Lzc0tX331Mb/51S/4b/7l/4oHlw949uIFpl1h1hu4fUEIg8hLGbaGObCqPPehTIASu4JGZKrXOF4rz6AUD9SKX8eef6EUFZGzGLhUcAP0KHoVaaKgCY5OUUdF5Ty6qemN4sVw4PDV57TWYUeLfu8Dzjc1f/+3PX/9wvC89tjDLQ9ePOHyky+5+Okf0iiFv9mh6wq7arh45xHbm1tBnr68gBgZ9j39/oCuLVXy7XjnccPAxcWZ2Cpjpu2IDw5UmOREpaBpLF1wtO2avjvgvcyBUZq2MmgDWuUgiQqjNIEubReFUuYOTxRWIfxNmyJoeuKLeavF2c4fNWWpjaju2h9E84nY9JHVhrauadsWow1j2s+KKOiMEq8iEkmMybFc8OPchyjlXYNWRDOXnVQI74z5vEzzKM7q40tIXe7LUx5UslJp8UNpLYEtYQpUk/vFbzMnNeZJEhsEEA0aQy7pKXsvYqzCqdLnI2eZ91JKgQiNaVhVZ7zN9daO8Xw42JRpHfwCpjQdajGGqbZujAkawo0cDge++93v8K/+1b/i888/56OPPuKPfvpHbLe3NLaaMiuJEpFZLNcUhQXz4WG0RlB6UrZYsSjjMEz3llDGRzAqydjjxvHISJwdSKVAlQ945/zC6Lc8Quff8/NzhOd86N01MKnJ0Zyfnft6V9gqn52ylbWZDVwklJYp0k3hxSYyfR+JmAhWCfyOXrVUqxp3uwPAJWOKHzzW2Gm+stMzqskcKw7LNMcoUD4kx8XMiMrNk8wZk8HNaIXL0OoRca7ELARlY8xCIFYUUbwpEkXNQQ+z0TCvQ6lIhBRoEFM0i07jEveWNRXKJqEfGY8qHIeRmAItJApJG6mzBDqtl071o5KJUCkqlYwPuc60DShToeoGs1oRh/mQjkQcMDYVg1aoAK1XWC+RPCGmbL+0X1Ac0bXOhqwkxBiTlUShB68lmxglynhITqUJqhAxrKjABBmS53My8CLOXa2kVrbAOichMNFnQDOSnGUpSzlq8JHJkR6SlJHhwKMWetLWoK1FaUNQyWnd1Ki6QtcCK27qCltXoAza1DR1TdO2KZOzlqzOqkZXFt3UqLrmy6df8vL6lTgWtQKTgkCSEKYVvH71kk9/89dZO54U7eVVCs7j2MteP5aK8waf1kd+Fk7ofH+hYJUO3KN7yt8jx++YNn+c+qQLg1BMGbVZpxEHQToco5/vLQaXFcNQtHt0pb5EmJTk3JOl+flIMZrk7uIwjOVBXc6s/CyjM09duT2V6LqcldKhVOqqkwEjzvOe9QGl5vEtnVWLSWCe8dkYNdc/LJXB42Gpaf5EsRM4G2nh+e3XKOCZqfnud36fwws4txtWWtM0NVFFtDUoa6nXZ5xtNqzXDc2qomkafv35J/TOSRAIcob+zd/8Gf1uh9aaj773B7z3/ncIUWIeXXB8/OXPub15OcGoicKYxxgZ+v3R8izXeVLf3kQrRxPM0ZJOgmFJ79MUFs7P6V3zdKo7MoLi+f5z7NeWSfJNjU335SMn/f3dj36Pd975cDJMiMFBEZzAyz28eMS7j94hjI7QO3w3oNWa9eoCozX9fou9fsn1y6e44UCsDaquUH7DeDgQ+h5GhxpHdNcTxkGEVrxklicYKpSaoPhjJqZCgcvzF2JAZ6OeyjOY/q/kHFJpfGWGS+mcW16ls/w+g5RVRjLgAazQra0t1y+e81f/w7/nh7//I17efMm+26ONpalWPL56zE++/0N+9mrP4fWWqOwcMFEE+ZUOsBhjykyR2mp5rY82MSWdHNPe0mhVBvMd3acLIZt4FFxznxvtlEx2ynl66lo6N099f2r+7zpBS36ZNRQ5x4jH++GUEW/5zmXWuyoCNZfPlW3dNXidnoNT4172pUR1Kud3qcR/07uW6zHN2AJm66h/FIrqop/leJcoC6XcLmfI3Xcs13OJBnVqjko6fZNxeLkGb4I9v5tFtgy2OHWpI13vlJI+ydKL+Zlc5FkPwhSBPtNAp5+53fJ9S+SnN41dJmBexOADfd/LeaE0wbs8pDvt3NHLKD4rnMfizPGTPpUdDEezqrLMMs/t3yaDHwTyOik+Sd7SBX/K85CQlXTARJ3OO9F3hmFgSLDP2aEkz3k5W1RJeySN/s08Y/nd/XtSzijnI0F7QadRDhdHDqPjMHqiDVTKp8B6MRKGGMWJ6sWorKNkyBllgSAByiHinDjMJE1W+u1ixGuwwaK9InpDjNDtenSj2F2/5vb6FePYs242hN6zWbc0m1aCl72HYcBWLStdcXZ2hm4rnn5R07tA29ZU6xVdd+AQHO82K5rLNUFLnWbtFY2yqMuGy4sLqgDDbYePis3jDdV//Gv0YYe7OOf24iHPh46fmD1G1aizDfpBgyIQv7rhy2HgZV2z0wZtFGebFV/+7K94/vVX7HY7CYHQI43zGCwNmhaDwfA0Dnzte77jNVuteIKbICezMwCO9WbRHf2kGxqb7QxMdp7BjVIvuqrRVgKB23bN1eUVN7ev+OzT33L9+obLy4ecna1pNxuMMfjRyZwddhgDwzjQdR0hRlarFcMo8Je1FchmreH8bEPbNHShJ4QlTcoeE8hvgSR92yvLt9905Xd574k+FJndDjcMaA3tqqZpa7QxOLGqCky9selcSRCRWgL5M48wpkIrKbMmY1Ep82xkGEaUVXgX6fuR/SGw23UM3UhRMEAyRFOyyISolsaXYWWFd4NL9VbLbOvyjM12hHLcS7ksZ2uP40Ag0q4r3v1gg7UVUQla2sXZYx5cXvLKOlarDS0zxHyMsLvdst3vOBwOUznDddtydnZG9IG+kzr0fnRH54K819+RaSdbZNYBkw635EnH92qqHMCO6IdGCy0bI+WgJtskQN/TO0efA22VOTqrxBGTz0GxLWqjxRmlvfiEdJ2COgLayvPDMND3YtfI61FVtWTzhrtn3h36FCX2aD7u3FeYDsRGK+UklE4lFlMwrtIKaypiHOhHJ3Xlo0cZsUxFpAwC0WISrLpGpTI1EiSbnW/Be0xVQ3QE52jbh/zR937Kf/mD59x8cc3hhaMyisMYUDrbQO+eIeU5fzSqQpUsxz3ZUMg65+KhdPkw22jLNsq5BLBHsnB26i5pKxn5JwNHIbep47/VQkYDUMmWG5yTMotedDhXKy5XK374wff5zuPvcN6es7/ZooaAjRV9GFPtaSSJSStiHFLyA1ApvA34oUfbCqMiCscwHvChFx4fJNBGhxl5TrL1OLaBMJuRSnlthms+llWP9mRhw5l1puM1UUoSveq6xtoBfExQ20r6icCrxxScnl19pySrpew9acdhthFEjvurtTryFYhjKI0x5vWKyegg3FcnThxDgmopUXxQiUZFJ8ttHAWaRqGZqGa5OoRkt5XiuEyTa471P0lAS7IVA5WpePThI9756BGegecvn/Hpr39L1yedUM80m5EvfEpGOyUDZ/lw8tPFmEps+LRWlZQPWUkJlb7LhoFIxBPViHKa1arF1Be4OIA/YK3DxEqSPRiotaWxhn6MODekspGWoYv0fY9zDmN1SkgbCcqjLUTlOIxbvBqoNoazq5bdsx0mZbI3dcNhGBmHkdE7QpQygyV6U6lnTvNMXrsF713Q10xjfqKHcRzx3lHZWhAJk307eAnyrJqG9XpF29Zc3w5YWzGMQp1GC4Lx6AbGcaQfeoZBYNTHcQAUVw8esN/2IisNjp///Of8L//V/4bHjx/x1dOvsNrSNit2xhBGlUrllmt7z3lS6DCJytFBEA+uzchzNXJhV3w+7ngRR67QPKDmIo5oRklcjAoPCL4TROeI3qADtNayjoYn/+Nfs/n1lzz6ez+l/uPf4+zRn/IP/z8Vv/r8CZ90O/7jMHAVAv/o5Zf8Xj/yHXvFy1dbmqtzHr7/DqOCJ598Bt7T1JKgtt9vsdayOT8HJMg1Bk9dWc7Ozggh0A/dBHOPkvKk2qRghGTvq6ylqS1DDzE6lInUdQQzJp6tAA/0aCXoVc77FAxm8CHJEiF5RHNZJwXBm6P5zra+mZ7Eykf0lBxNbIGZf6ls8ESj0DGhVRtBNJi8Vrm858S3s/9ulvOX8v5S/jslG8dpb0cWWnyxRyICyD//JfpEJIQyuQy8c0jMkZrO/hjnAA7ZgnKeag1GV9iENDn1ImeJawhBSV14N+AS34jB0tiWarVivT6/p9fH17eCUjfGTEw0G7Cy4ywrWKeMZ1Ulju/dds9P/uD3+JN/8Kd0Xcf2sGN1vgGTMkBjKGpxzownC/t50UqYcOfcfFjlyU5Me2nEOWXALAXJPMYY5zrk+Z7S4LOESC/bKOtKvK2RNKZoyySPLeC1YvpurmGSr2NHf4rOP0XMxPRdiqZHHFEB2eJoYWKrsw3D7XVyCEjBegBHMlZYS/CRGASyQGJPVZIDJJIuoGh0JAaJrM3jKefRK4+zsk4+eowOAmePZIxPdYkAJmHBH1GrAoFDyZuZ5FSaw54ANdVIyxQy1YqSBcMoj46OXHlYK01jKqoUEUd0GG1QKtWyTzWWtZYsBQkgUIRKICtCiISY6mSp3KaCYGl9I6asYAhGc/7Ou+w3ew5Dx8EH1PPXPDAt3ThyMIrHv/9j+nUtDvAxMO56DtfX7LZbERQSrWZaAIExqaIuHEeSIW+MxmiJaBpNxBupFaMUGLNK9DvPXaMrifKdFOa8n1PEFAbQGCuwetoaMQBoJbV4tUY1NTS1QNpYKzDO1mDrinrVYlthVqauqKoaU1ts29C0kpX92Vefcxh6qNKcGyMZ58mhrVL20X/5j/8DcRxnFqByRuS8A0yCE++6Pf1wmAS9knMojs6pydAoc6OO9uK9duRCiVCpjamWrpp/pgmdBa/MQ4rfue/eSTNh/i6veHlPcQCJsTi/i6P27jOMT59nnebuYOd2FcVPUZTmObzb5vJnqQyfMn7nIZV8voTCn54q/7quAAEAAElEQVRlVr9UElSXAv/0WNGu0ur473JO8jweaeDHbSw/P7p/uZ7lu5ftzaMmoujdwG8+/ytAcVOtePed7/PdH39fhAKt2e23/Of/8h8wWqKetZYn9/sdzo9J0IqYDPGFBMN8/PFf8stf/gV9J4pxVdUSbJJ4Siy6NO2PDGGalEx9p9MS5Tz9dQ99venv+2mxpItTxHiXpsQZ4OeyEAWaS4hxqo+X7//tp3/DJ7/967kf6T6UIAFUVUtdr+QIiGoSWN//4If86Ic/Ja4CVBXrq8fiCN82hO7A1fqKvusY9h2H2y3bV68J3YAOUbJiDnvMYUd0Dj86iWqLUSAIQ3KIKy9BQ/ksixGvIkGHyUARPRL9HWcH4n1OwN/1WqqJ05b3gU3V8OzTL3ny2aeSuSanHzHCp6oGr/DdyEY3opwmKDNgkiXLq5TXSsOsWu7DePxMeX+WAbNMdl/Jm1yXM8tvy/t+l/m7L8u25HP387pjXlj+vK9ET2rh5KflM/c5QU8ZI5dGruV3933/pjZPOdTK75ZrfYo3lPOwnMdT4zw14uX7s+u2ZC/lOEUXCUfrWn6e360WbSzvLT87NR/3re1y/Kd45fLZ3Lf7aP9trqVOcZ9uc9/aLte1DIQ51d+yjftotWz7VIe1UqgoDtXVas0h7Oi6DqWkbNV98zYbiYDIkb5V9imEMJdkyfLCt3DI/U5X5o8p+yOf7UHqdMjvUWDjxAaS4fvEyemdYxwGMRrd4aNZyLvD4ZM8d7z+9/OQgrZZ0r6WQCoVIThCcIzeMziFiy2RFUrZFKiUAvqUpbENlQ4E70VfcXZqT4YtWa0mpiDXHKQZPZFAjcF7hQsQPahgqaPi1dOvefb1F+xub1lfPqZeW7rdlsN+L8jNIXB5eUmMkWdPvuTZky+prOWhtvgPH/Db33wswXFG894Pv4sfR37x//tzVlXLg/cesz9s2T674eH3P+Ldx1dU1z3ddYeu11DBoy+/JtrIq4sNz/SK85tX/MBsWelz1ODgYOFMnFe32tJZzZgMYFXbcPvrX9Ndv8R7B1rh4oF1rFljOcOwQWqN/0Lt2a0b6mbDb/3IfxlepdrgRkozGTvJDVO5EZUhYFNAEgrBaU+BPyHgXaRt1zTrc5rVCltLeZl33nmH69ef8+rFM4yyfPTdH7Nat6zPNgzDQHfYs9/v6PoegtRkjiFgjaGyllfXr/HjSNWuWDU155sV77z7KAXJFLSZ5FmVtPdhHOhTUsQRQb6Rh2Sd9htuI53nMeJCxPnI6CTYpOs6msqy2Wyo6govLgEUCmu0BLCa8pzUU6kAayx11aB1jVaWnC3kfcClzOqmEvhH70b6bqDvR9zosdpgTa5R7nBuOFmuoWka6loc9j4EBn9cb3Va4xSEFBJMZZ7j0t5H2tNkZMIAxgSaTeCDD89oqhqPRcWWxj7g4cNzfn3xiouzB4z9wG63Y7ffcXtzw+3t7eQUH0eHHz0PH14QnThruq7jcOgnXiNlgOIkk2d6PVU3dtbd75fbZr6E8Mlka6q02AGrhJxlrdC1MRXjOLLb7dhutwzDgK3baX5KG+LROwBjZb6MIkG9Cg8jShDN4dBLTdwiIWa5DmWbd3Xo+bt8/52EhliOW/jKVPoy/ZfLXokt04KKeB+FFsdAqASFwyvFGEecPzBJTnGebR0FPRJr8AoMFktFiIrvbj7kj/7Jh7z8/MDHLzv2twanR2qd7FRpDo/LaepJB4xHSSppbmIeXj7XEkLkYr2XczmbAo7pZymXOF8ivhyvRbb7Zh6SE4TIdoXivuWV17AsxymBHyMoi21a9q3jD3/8Hf74p3/Cu4/fZWDPTX+gaRpwYIPGqihQwVrq1kOgaSqaFKzTu4EqenSUzHyHp/dbDl1H329xw0D0kYyXOyGOHtlNju0YSzlOqWy7Pra1eC9IdnpyGsOb9mZVSRCac4Hd/oAfPN5nO+8UzS5IEhm1snBiLuXouZ93Zh812czzuub0pOzEBlSYnGfzzWq2oymmAG6yYyrdE2OuE17wmeQgP2E+gZjC4dOYVOHrUETJlVQpNjKhrjkXGIYdurFcfHDO4x885uq9K17fvibWEVVLApcKM5qsyK1q2j93/pHKpsa78yZngqCkVJWlaRraVUvT1PTdYZ5dHVHGobqe3fY1P/57/4Jh94RXX/8l2+4Fl/WHVJVG2RV13QrarYmEOIAXxAOtI8ZE/NgzOse+27PvDgzOoysIJvDi9gVOjzjd0VxWklTnR1a2Zl013LLDeUGOCqFKqCx3kwWyLB+KhTFaH43/PhHBkJKriPRjx+A76pTVKkgxkegFhaeylovNhgcXG14872iahv1BJTu9BIZ03Z6uO9D3HUMvyDr7/YGu67i6lDrjq9WKpmn46qsvuHn9gscPH/DB++/z4uUztrcvqJsNgxunfVwmWy7XU6kElR1j8rsIfWsgBngaez5Wln+iL3htA5+4A3+flsc0PGagxqXSOwGnIGpNRWTsI26FoMTWGm8NqjOMnz8j/OAjnNaEy4fYf/ATfvD//Xf85sUNvj2nay3Pd09xz5+hjWV8fY29PkO//5CmbanahmHXyz/b07uR995/jxA91zfXKTDB0LYN2+1Wsr11QpwGqqqZ+XHi2UaLfbPSBkKQkgHRcH5Wo7TDIOiwApPT43IdbTWglEOClauUjV4jxYwqMJ4YNcQ+bQyVkASYEGFK2tIp+XRyChfrlBpIeRA2+bckYCgyQhwgCEqYlCKQYJgYRSaNUWyEpex36nd5yxwAdtQHtTxZ717pSEbl0KUoNkI/RqL3eC9ObJvg7Y2k4wvfCZ6ppAmIHJESO3PQkUi5Ur7Fh5EQRKf1weHCgPcDITqsamibDSt7xro553z94Bt6LtdbO8ZLQfqUILqEmsmbMDvwjDFszs44HA7su04iglpDVdeS7ZzcrFlJyfWEY5wFcq3UFMFcCoVLJ1ipuJeCS2kcLA0wpcFo2f+ynWWd9fyeZVuzYf5uTEVpKFgajGYFTUgqCxul0JsNXeXPGGMq5atYGkCVUglmHTxhqh2WBTYXPEZrRkA3NSRn8jSWBIEXQ0ibMTldxd4ikLJ6zlxQSuF1xOOlxrHSqdaVCASQM83FaGONoqptCojIAQJxUihyP05CEZbKQJx1YKUSzK8SoSz/FwhYY+f5SWUBlE4OfiWwwZaUSZ+HqMQJHJOUIMKURhmBExfHd49VYjzITqswtSARuKqq0DEwEAlK0WtL+9F3qFuDqgw3f/Y37LqAaxtcU9H+6AfEsxVuVeMGz3iz56N33uHBgwcpwjpgjE1zliC2fMD1gwQYJMLJSAw5Mt+7HqPzmkSqqpqcAVkJVMaSq/p659jv93z9/CnGaOqqRlc1Tb0Ww0pdUVcVdVOjrJVoaytwJhjNf/rP/55hPEw1eiNADwwKdaPyIjKTlVDTzfUz3NBPCs685xMyAFIrUpj1MV1MhspEI7q8JQmwMf0+7bmY6aegK+4a3u8a4cts5BOOvbg0ZOeDp9jbudxCjGL4zF/clWI4eS2UloJpTEbTo++L75YKT56EeOKze/tzZ06Ox3yfIf/OvBT7fjmOO5HdRZbwLETc5e/5PaeukheUiu/J+++Zp+m75fws12DZxvKZsi0ShWqpMahiZD/u+OUn/4m//tWfYatKslJSbXGjU50co2fhpXBkHw0jiMGt6/pkpFnN9Acpk4Cp/Mg0KzEZIgt+u5jNI6KWrSHjK3/P51w5ZnXfd8WaTvdxihaLdoqf5ZzOtJjRRuSxmPlOXNaJVpT1SvthTz8e0txkhqK4/vglv/j4z4WG0run3RPh/OodtLYEH6BW/PS//qd02wOvX7xgd7Nn4yPx9TP67Y54OKB8hMERB0cYBdrOKo3RCVUgSA04ZfIY4jSOpRFjybvK+fld6ovnNhWiQKooRvLgPMYa6hBQ2lDFVG8xGUC0UgQfqaiwGEaQ4KZin5bZS+U4SkPVsq50dkKWctqxQW2WyUp56Xg8c5v3Of1+l+vOviv6eJ9zqXx/+fvfVZ/edC3fERZrkfu0fOZNjjI5Vk+PM/9cBnGckseXxq782ZIeyj79LnN235q8ib7u6hsc8bWSppfruTwXT9FnOa5T71v+fWo8fxv6ycbD+/pFUriXfTv1950nT8gDub95z77p+fvGlXmUUpJ9GoLUkiPG07pE0dcY4wRfd4p/TutfjFl4sjqWQ/+OrzgZk4tM7vnLSYbNUrRSmT6kNrRKmVh1VVNZK8HOHNNlzAcJGjEI55Ps7pou+VOWhd906QrJ3o4Cx+wdOD+S875UtJhoCVrjnCfrTygjqFJRcsYgZbdRoZUSeF+C1MtWSrKvXI/reg5GYVqNbjW4iO1rhmHgcJCz/OLsnJj0I5CAOYPMWZMMv/jA2Pf4rqdJsOtDDPjDIOLIZkVlNP2z14QHl9jNivPqivEQee/9d9nYmv3NS/bXW1ZnV6ivn9J98jH+gwfcViu43vIPvOIHP35MXV9Cpwi9Q90cGF7e0KhzzjCYqkI3DePuhtuPPyH0AybapLsOGBdZozjD0GJwET4Z95w/foxen/Hs8JTPb28I3kvCQkIUKh2MPttQCKJjJYOUmfhASLKnomnXWFtTVQ1N01BVDWebNX/5579ke3tDZWs260uc81S2ou97ukNH33cCnx7FSZvh+IdhYL/fopQ49du64vJizeOHFwzDQPA5SFXoKZdwC84zOsfoRqJShU1iEiZPnl2ZvmZR/LSekucoevnpgmfwjn4ccIPn6uJCYOmtJUTJapRimzCh7EWm/RYRvqp1jbWNZB+lAHyFTskHYEwFUWRHN0LfOcYhlW7DSCZljIyjT4kI5bkg/a4qQVbTRs9oSCf46qkzxSP15nPZuPzsnGUo/CIQqBqpIWtMhdINbbXi8mHDVl/zq49fsL/Z03Ud4ziw34vRX2wwQoPD6Hn54iV9N4AiQZYHtE4JOSEyQYyqWQYN5GzlQuYNubxMIVvEWRKZdUwSvHRxviMqeLYZmlTW0NoaBRIM0Y8MY0D7Pr0v89yZn2b0PTmHIsZYjFVUg6euDHUlNpsQPX3f07YNdROpdIXzjujT3lvI9Ev74UzLx9ddGlZJr1dzhrg2yRkf09/yT1kleohSBBcJIyhVY6sziAdCMER6MC4pULM+pJK8X6esexcDJtbY2DCajsv6gj/9vR/x2U+f8eVvn/PVU8/5qiWoIAHHi3PX+wjM9OpLFM4kXx7NTdIJliCT5Rk2zc+k+x3Lkkt5LYYwc5Pi8ynzPumOFWLv1BMcc9kGs01KZ7NMnHXfZINQ2gjyQtDgHbEK/PhHH/LB1QWN1nSjQ1vFwwcX9CaifA84vIr0OA5KCDhqsZHF4GiSXDr6ARMjjTVU64aoD7KvM3y7c5i0BzRM6I8lzeW5u2vfuZvtfyyHL+Xf+XedULuyzNI0DW3bstsfGN0ggUC2EZ6YaEya0hPNTVQ+qf6Lvkz+6tzf5KY/YgrpPAgxZXvKZ/mWjHIWi8dywJSyuZzj3Ohki04oITHZckKMqKDmvV3KTXI4THNtrC3KQqhUFgjCKMgCznlGAg8fXrF+eM4+Dtw+/ZovvviCJ8+ukbIHc6KfU5IZq+bXE+OcZJjtr+ktiVinDyb+L3K0pqoq2qYVOYmD3CfkTFSKs7bi1YvPuXrwkOrhBu2f89UnXxIrjyagVEVE4YKnWa3QKuIGNSUIhugYhgMhKlAWMBBHTNVQrxtuD7f0aqCPntXlBlNd4xICX2MNlRFY7cE5RuepTmTMHvPPyAT5mPU50kfpDLnDbxNyaoiBMXh2hz1tU2OUEXk0IrDdiOzUNBUPrs6oqxdyzliLGweiE1tPjNAd9ox9xzhK1nh/qLm93bNenaMMbM7PePed9/jssy/5m5/9Fb/3B3/MO48f8eDyiqdfSrlE3+3ESZjQ8nLgf3kd7eMk7+sofgMXHPjIjRv5WnccOKOpGj73Pd+LhocYLqhYK+FBKQ43oYyGdE42xN7jrWOvLXq94YNdTf/zL/HtBU3U6NUFP3z/+/z769/S2gbVO1789rd88fGvOf9nf0r9xYGw3dHf3mIuWj74zoe8/voFQ9fRNzWrzYa6qXn56gV1XaF1neY9sj9sOTvb0DQNWivcOIIPOOIUCKaVBJxitAQS2pp+dOz3ngcPVsQ4SO11QKkAqifGHhcMXvUERvGNqQpjPEQPRuD6CQGlDEEN0/kxzTuGuewKxKiwuTzWRI3x+IhFo6JOfMQTYofP/0IHjHJeqUjI5XFzku+pLHEWenr+ueCfeQ8sz9F8ldZEaUKXrFDaUh6VkHmt0djKFs+Io1v4XJFwXaCAhWS7Fj+mBAX4MDK6QeDzg8OFkTFISal6VWFNg1Y1cTT4/f22hPL6Vo7xJfRSeViGFPFbCmO5pqe1NtXmcdSNOOGys1xpUIaUvTpX1lVEIa4YIeZNrcAzKQBKqSkbvVy/Mps290ciPs1kbCkVgzIDPV+lYz/GeCcK9D5jTWZAMcaJAX2TcTPLRfmeMjNdrix4k6WpyVmcnRc5SlGy7guBREkwgUIOGB+81IrTWiDoRkdrK6I2GF2Bl/qtMYIlRcAqTT92xBAwJjskZW10lBrQuTajQmopD8mpo7VOdbjz/lfYqGh8TPDpijogcDkZ+i/PVZ6TqKUWwTT8FBCR6tABWGOSEz9MWeGgMLoW+owBlTMGdRashNOFEJPnVIHRBFsRTJ2cSiHBPyRFOxvskuLts8DsI4Yqzbl0PTBHWvfGsm0t3gW8d/RB8eRmy3sfvMvZR98l1Aa1c2w//hynNHG9YlvV7LXB6wqzXmGqFU/3W55ub3DOMaToeJPgwG+3N7goDB+VUR4sdVMLrEzTYM4sVje052dsNqLI/81f/wX9sGeOGJ7hxbUSpdMrxyv/FHwkDjMpTqYFPSvieZ6YIMCSsDnJx7MjWQemGtUws9xSVtWx3D8KFVPGatRMTpHl1iqNmcxBDpPAmYWdwnk+vyMWTcRpTafWlns/PTLxRZ20nrSxTyqoU/uz0iDP6DvQafnmex0Upww+St2pIzKPT039u88RMzUNSdG8X/Eujf/yWbxzT0z9jIvPp99jTIpLJqosiSfaySUViuM3G3/KrsXMJ/I9cuPReiwmZFqBe41iSt0hr9xFtZiHoifzb2G5BsUv37CO02hzsJDRvHz+Cucjw+Com4amqVmvVqzbJtuByKpWno15X8nv/TiKI7NtJKJ1MQdLeisn9U2Oijvzm8Y51a5ajG+SnGZtdt5L5GWL01fyYb7n/m5M67igx6mbxOL5fNBk3jWPRSUHQ0zPaDlhEgpEnte0l3Si1Th3TmnN65un0/s0mn//F/+3CZ7NmoZ48RhvLd/9wz/h+ddPUIeR/nbHuN3jugHlA8YNxCEFjeExCnQ+6xKEW7lP74XIPFqq+yfwPp5Q0kmeL532hxtGmqoieoHx1VFPWbgueJSW0hijDykSPpc0OX5fVuBOKa5HzhiyzDOPYwn5vJRVS+NXfi4UQTE5c/1NzsnSOPSm78s+n5zLe+TBU/O/lLffdO+p6w6/PfH+pdFrOiNPjGe5Jvn7u22GI6P1qTPsrnPtrox9ag5zP5aBD/n5IwdojHeM58v3ZaPHqbm7zyi9nHP5jIlf5+tNa32Knt50/5uu+9b5Pto/db1p7k+9R5yn39zefTS8bD/vX6XUUQ3c+8Z7iq/lciA26Y0Z+UgXa75cw9JY5uMxPG45hsxbJjQlyv1S7gl1JB/8ba8jEeY+8lARlbIDIxEfJeBYJTnWJFhfo3Wq55bGX+z3QjhGjpRSJj59lhx1QZ3mBRCJwaOCQkepMYkfCf4GzwtidBDWxNCArlFKgg1CFKNRUJEYA6N3DGMviFZI8K3VdaopmegrSLk35wOv3TYZpUZwgcv2Ma+f33Dz6oaxH6grCyGySjqPZAkZ0Z2HgbqqqesabxSditAPxO2eR48e4VbnHK5v2T57xdmjKy4eXdG7gDsMVKsVF4+vWJ+t0d2A2vWYEGkuW+ynv2HY7titv8+hWdN0O7670mwerNFmJZYZNeK7kdtDz2pzxSpKfVDdWF48+4pnX31OP3o84kw10aOBNYY61eHbE3geR86qFTcqsg2B0cfJTqE4tofkf+VnxoibJDv6cj1rZSzGtpiqwlgpW9W2LRrPJ7/5BeMwcHnxEGtrQlQYbVGxx7uRYejxwaEVBDeS60eP3hH8SGVsgsLUXJytOD9b48YBpTRSJiTTmgi8AqMuKHX5s8mg/8ar1Bbu543TnDif6Epg28dxJEZYr1as2hZjU2A8IQE7SJBGiCQEtrKWc87c02htZ7SDPL4gNpkQDN5F3BgZBi+ZZbaa+jo5qb2f5V0VJ7FaYImrhMTAke1rOcbyukMX0y6e54OoiQGcg/1hSLY5jwmRSmk2ZxW3/hWvPr2m33XpTGZGeozgoyeEyDA6YtToLsOWJhRAHxN6QZbDwQc36Q8hleGa+COz9pP1+4VWOv2QcSmmTNaYUBRDdrlHSFmp1vo5qz7J2qOTjNC6rmnqBmMN2+2WcUw1TJWakA9tiPig8TrinGIcEjyo1VOd9XEYJbtfGfwJsNIlT51Ko8RjUl+ecfJ7MsLlczih8In9cymLgbWGqJMNMJ0ZKgZMZVCqoiJBkSdeq0KCoVYGqw2VseIYMqBjLUFMNTRVw48f/YA//qMXPPmi49Vvv0btPKYS2HmlpY9CZ7k2c5zOo6Ucc0p+UMUyn6Lt6TM10/Ob5NFT35X3TDKWI52zZna6nAj0RB/LYyJjzKWeqromDh7lR84vNvzBj77Lg02DspoKw3q1wprIxjYotwccTnm27sAh7hmj2MR1QpTQwBhG/AjRakKlcUExOBAzddKl1Gz7LmmtTLgqA6pLWW2yLZGDB8VZnuvXL2lzOX9lNrnWmrquJkQx5z2SlSnZgjpIpXGjAgYzIXSkkaTAKPlLeEK2L8Spn0pN0tpkn8rvV1FNtchDjLPrPcb5xFCzvC+fmcm2nPmO7LOY9obY1rUOaJ8QAkpbUKbDPAYj5TSMNXK+WgtUKfNeHNnjOOJjoDlbsbk4ow+eZy+vOfiBJ0+vGUZNZTeMaodHZOmsB020XdBlzDYQInOd4GwTgnyQ5bPBmoq6rlmtWlarNfB6mmeURumWzSrw8vYpz599wcOLM9p6ha0aohI+rr1BWaiMwdSWfuhSfI4sUPCe9abl+rrB2gZjOmBAG4utWnb9SMfAAKyurrDtc8IQhAdVlrqq6FLgnHMSSJAR4u7whVj+kjJYZ2oV3jkT77RWQrPyvdaRwzDQ9T1n7UrgtoMX65HRjIOjtoar8zWr1jA4R13VBD8SXSCoiDWWcRwYhkP61zIMDYd9xzCM1HXD1dUl11cP+OUvfsVvfvMr/vDv/REXZxvONmes1+fs65bOSgZzTjB9o14ZZf0JSKBHpYlGoSQ3gy4EXuDYqIrndDyjpsXQYjmLGqsjPs7O0Iig3nQ+shsGmlZzbRo+GXZ87+od2Fj8q9cc/tPfELXHBYu6eoTWDau9573+wOHplzyo/oSN1Qz9gL/Z0l5tuLq6or/e40bHMIw0mw0vXr5gv9/z7ruPAOgOB7rDgdW6waaSJd6njGQXsFUlKLRKkTP7a2tpW0E/GF2P6yGGhBqgRmJ0iU24hEAg6Mo5SU+rCmMbKttiQ53K5FRIgugw8ZiYNluW+9AZ5VfhnEk8SfZa5jci34gTXSco9UDA0+HigdEfcK4TObCApJjktvLdmddM/5hkqEzb+og3J76dhKxY8MqjbaMgxvQcx7YwrcEYJUGBjaKqhDdCSvjx4p8M5LM9jRWFikkmiEHmO/rCMS58zY8OHx0ueFwMyQ8julyeL/WWuvhbO8abppkgyrORpYScFAH6OFs6G63yTyHObFw4NpDkrDeKGoAkpUxnp1uMEnWjuH+Tx/ngLvthM+RzYTAtYeBPXfm5UpEoDXFwLJzlf9bayaCTr/uMiHJwpkNHxSSQanKNkQmWvVDgjEkxc7nNEI6ye7KyFBEGq7KyFAMq1cLwzk3E7HzAR6iqmm4I1FUFSOT82I0ErdHBYIwmxhFrIkHLBrBGozR4l2sCaEywGK9SRoII/ZlZAglWxKGD1NOwWuYr1yiS+UkCpRIHn1ZxMliHKFnOQ542pVJ2uiKaIEJ6EvxzwIVBTc9Oy60UXmlcFty0JmiF14YuRjxBDocwt5dhsWOi2ZylZ2xDVzCVyYGQ6HhQkYOJWDQ2gh8GfFuz9Z7YVNimRb3/mKevvkoR3pYvb75m3Gm8UlK3SSlsrbBVUmZW6SVa4MV3L78g+JHEawhKan30SrEtjXYqq3x3FSpIUZE+zLw103piihMrjNlZCXgmn9WklCg11WsV41zRFoWwWeyRaX8Uf3s9R6LKXoiT8KnIfTrN8ErD+BTtpE7cE+MRnDZQ/J0mojgMyizDeVjHTrH8s3SUq0TP6njgi/7MTZQG2ekLNQeJTEbLOIn3qX1RSOLU/7lLczbrzNNKXjLzKhlTCCEZ0DyTolHMUywbn36Uyur8zGSITnxYlY9GCZRRWqXINqbAGukJYmhaCPbTe9L9FEacaX3IWRrlnM4K63Ltj2qxqpn7lis1bQ+t03aYQZhOHSl3zoBTNJtpURXKVUGblTFoFDevr0FbvI8M/UD0gUorNBVGz4pp6ejN8046T+q6vmM8WJ6F81nM0brLHC72rJr3RTlJ0xZcjPd4/ed9kyHb87l3RGtF1q8qFJN5PeO8J5j7dTQW0qsWZ3i5TjGdEzqFamZ+FHKJD4o9EwNzSF/pcCfBr+VIeMgRYmlXMPoDL15/hlKK6y9foIDH73+XceM5r9/D7zr211vC9S1mZ/HjSHQjYRzlTEBJIJwLYPWU6ViOu5R5Spns1Lws5ZlTNYWz/FUi+SjAKi1OfK0JSqfs9gTvO/FrT7BC+7qYw1I2u8+Bl/tT9gPAu1kuLWWg8vfy8t4nI0Nu8zjjKMu5uQ9LObXsYzl/S2jvpbHtbeHZT31+aq3ufSbe3Wf55xsV46KtvLfepn9vanPix/f0CZgCSJdrX953bECbr2XAan7mpCE0hMkZcR+ak+zl+/nCqT4t9xuKk30t9+MRDyvWJ+sly7OtpKtTfSvpsuxn+XtJf2V7qujvMrhADHXCrUq4z+X+KgNZ7oNsL/WoU6UTTo0XOCqD8Db0q1Wqb5fGtz8c0FGcMW3TzJkxpTxSjGU6ixbzoJSaYdjjjFg0zcmkj8jjpez1Nv3+5isHXcj5dix3ZR1PdKgYU2YPjhADJgZ0TM6lrGOrYs/lVI+JT7+5v9P5XNC5SnLeHQG7fC4ECArtDdpD9D0+vCaoF6kE1QHvVvi4SqhVGhejGDuCZAl0Y8/usMWHUfqtDKv6jLP2Ak+LRUp+9ePI4DzXbsdueI1zt1QhcvbBA25ubtnf7hi7gWYthqjGZthri1KpVqAP+HEgqkhlNGZV0wepubk+28BK6mbvvtgzdj2bsw2H6y1hcNStYv34AU1bE54/Rx9Gaq2xrYLPvmJQil17hrctZ37L+dUae7ZBdQqshirALcQB7LkgmSlj0JXi5ZPPefHiGb0LBGXQaExQWBQNGo1mUNDpSKc156ri6Xhg6xw61YE0OiUPFDaXvK5ZVwYSgpASA14Uw6IPDm03aFMLOpitqKuG87MNQ7/lyVdfYLTm7Oycqm6wTYM1FmLEuRE3DiILRY/34yQjSk3AgG0sGsWqrbk4X9M0lt12j8pZKIneQM7uYRRY/lDyn8URcGoPzvz0+Ng8JXtIxrjIPc57xtExjg4FrNuWqrJorcSRlxzjKhn3Yy7VJhGMwksnmPXsQDNJ3k1iImLY817hRhjHyDikzL+ky8ZFJvfy0hqapp76BseZcuX4js6c/F8ad5aPIsy/xyhML2jcELl+NTB6B9GhwoiJjrY19Oy5vrkmdFLqSSlxZhtjpJyfF6hkWzWcn58TgsO5UQyeGYYz66JRJbmy1EXvyrwx5vnhaEzLdZefOWurdLJmm4c8qZQ4cUyuNa2Snupk3tp2xeXlJW0r58vWbSXhQsXJvpfPDbHPBYJ3KAWtbvA+JHoaUz14i4hOdx22S9lGqTmAermmp35X6Z9UpNNpTLP+RYxS1tioqeRUXdWsmgZjFFXK8gpO452lP3R03YAhOcONGLM1A7mGuRjFoQqGUcE7zfv84Q//gM9/euBX/+GGm5/fYFoLCQFBJ6N4KCCP32SnvTMnMxGcnLNi8go7WB6/Kr5LH3GXJ9xtSsEioM7obMcs+wu5xjyU8OMi30wlPccBg+f87DHf+fA9qtZw8CP7vmO36yE6KqtoEFSItmpQjaF3vdiOs51JSQ15F5w4GJzC9zAMgW4fcQNEn6xxJ0S36Ywv5aE8KYt1yHaBGO/y21N0e0pfy3NRVTVNU4uuFgdG55HtF5JNNOJjxBZGlyyDRKn6IW2h0u+Z9ud+qWwfichmj7NsNfFTpZgSE47sGcc/TYhTZvfcvpr7kehC0GjEuYWayS3PUbZ7aJOS8myyk1cVzgsvtlZn6ydKa9q2ARQ32wNaBTo3sts6YqiwqkGpAxLyEyd/ASFONvd81s8y67GOczRfMWeMe5SVs6VtG1arFeVVVS2bs4fUzS1h95KXTz+h9u+iXaBt1wkIWROCQoe85paud0UAq9DGet1gtcVomxBGFAqL0hVd79nhGKKm2Vxim4ow9CitqBJKkuo6nBdUleADwZ9GG0uDnBbliGKXZ2Sm57SutrKo2tAYGLuBGNWUECiA0rLxvXNU1nJ+1nK2rvn61YBtKsxocM4TA9S2oh/clC2ey430/cgwjLRtw8XFBZvNGcTIV19+jnM9q1XL5fklm/U5r6sWY2qUknKJp2wix2s7/6KC2GeiUWgnROpQPFee97zhFsczHJfUVBjOUVSJh2YraEzn7+AjW+8w0dFoz6/GHT999AGb77+LsZZws2X8+glxN1Ctr/AejO54Rxl49hVhf2BlDH5w9K9vWH/vfVzb0KxaKXGRaGS7vcVaS1034mT1HudG6uocpfSEei18QE12K4ipdJLMT13XNE1D1x1wo6BVVHUgxF4gyqMnxBHnDnKOi4tWeICqsL7GhwZra4wXXQJyaZRSZzdoU6XgJTPxfxUrcvZ0doxLH5Wcp0on3mHwSuEYGfyOftzS93t8CjRFzzXNJ74Ss464tFFN3oPZrr3c+xPfz+fkTDTlPjnSAbN9IYHRSKkAqKzCGpGLgZT5nhzjQRJ3VZCzxGCm81Ts2UlfzXNU2HwVktRpImJhjHrqk1YSlPQ217eqMQ7H0WTZkCKQ2/OhXhpIlFKT4aupa0iRGaWRZTaoC8N33kNwyQE8G/e11mSzdH5P2Q5pPUTwnBlBNtpkyK7sEJ8UwHuc7Euj7TLStmQyZU3yHDTwNoKctJ0/F0IxxkiWbhBCIZIERWFYSkEIEpTgnUTOWpNgBxPEq0ltW50jih2VkYPHEfCDbDhj7BSRu16f4VYbjDWMvUSiKVvjQsqQU1rgjkwkIsY7r2W9Qgps8C7QeE0Tq0lpsMpOm0gphSdyTU+1qol1xYgwqpDr10dx7OkCalUBuq5l7KPjECNjZaTWlck0UGxinSChfDLEleus5ijHMSqGDGmjxfltKzF+KS0RbDGMaCN1tLUxVLaiWbfUTU1VNyhjOWh49voFz59/LUKMtUKbWUg2motKnFomws2Xv+Xr609Rn32eaivIVT2uAXD+IM5zZOp0lLpOu84nGKbE4JjlOgBt1JQBKk5qER6PYKViqk/IMS2XezEmhS4bTrMhbRaY5t9zU5FjIU/FVK8kM0fUUfasImWBZOUkC6mZHsgGADUx8/zW/P7smo/Fc+mTPFiyWzNn+JRXVhIjkdKnp5aWkkIIkjEUCviCJ2SlYHpXyGNI92RH+dT23BuFEviqSVCVz/N7VHp/PggmPjKNIreXjKBlPa4TSl3Ji0rj2B3CWtw7OSwVR89P486KkeKo7WmOXA74YZrL7JueDLMKiewkB0LkPoTJcCf1Uo6znJfnz+QkjmKoUimSNH0sdO6Ps0ZDQac6wSQt53FSesLibyXKWS4vUj4377OsPN5ZkuN35HkM847dbDZ8+dUztNF4N2ArjTWGvqklQ86m0iR5LfRcHiM770MMSXEW3lcGk5XrdEQXS0ODUlNmXpwJbx4cCqVm41QsB1zs5ZJvRyIqhiMjllZzhlC+JxZKq9BiSO86PalTFPfi0+Wfy/vmM3w+h6Y9nniUKvd2sWnKs+to6xUBRRkK1Ke9pICnrz+HENn717zz3vf43u//AG4O7D77mudfPcH3B+KhQ/UjjYLKRMI44uIc7PYmI9p9zrW3vSRTT+HT1CS3JjplKYUQGFOmVM5ckoPA4yNELXC3y4SYU87mY+Gdu9/7Y4PKfdfy+aN3hWPKKJ1739ah9TbzeWpNvs3z97U3z5OWGnRvoIHldceIdWev3G1n6RibnGzlPflcVscBTffNa8m/S5nkba5TzuRjxe6uY/juIAsVcaE8HjkB895e9C3z/uw8WDpzY/H5fP+pNr55b5Z9KPf0KYPkqf7eUXrvyDFJf0IdlWk4eX3DusLdTKQsj79pnbNOmefsbfaHsVb4cBB+6EZHbS1VJbL1UjdcjjlGkQWX44kxTihopfFselbuKvoYj+b+dy1dMXcgIHWeRVbOEp+KQeS85GiMwRESalhI5seQIP2Cy5kOAmkHCU1LBEySuHli9y/4yUIunGW9e3TeaV4UeAVBiZPR9/h4S9TXoAM+HPBhRe821M2KqCzdONKPIy54gors+j0322s6v2WMAxHDWfuAR/F9xvoMG2uiUwzO4Xxk3w+8uHnFYf+cjTWEdx3ddkcYBpQbwVmUrjEamqpCKzG+mkqMVtvtDeN2z1nbcr5Zo0OEszWDd9RVy/rBJVdu5NnXX8OqwVvJTrDKsHp0SVtZxpc3cJDscxM6xt98Sn++4VCtQVnOa416UIFtYLeTOfIRvfWsfMNgI95YlK1AB55/+Qmvt9cQKtDC76sAKww1mqBgpz3XNlKtWhSaz/Yvuek7bNQ4pbBTYMrMOwTYR9y4kRw0o9EYrDL4OIjxKgYqU6FMTVVV1LZh1Zzx6OqK61dfc3v9mkeP3uHi6oqqbTm7vJJA+3Fg6Hucd2gNQzfgxpGmqVFRoHxjlOSCuqq4OD/nwYNzjBbHr9GVyBUxTvvPB0839DgnIPsl0l6mx1O8peSHpfx6in/m/RuSY8J7gWbthxFrFOuV1EhVSdiT+bFJt886jIg81kiQQWUtVWWwNtkwkp4XfUyofwo3BnzUuOQUH8ecaZ1d7bLvl0bOfFlraFdNghfVwgtOOMaXslcpR8coGcE+ZcqHML8nIvVah73m6dcdvZc6l8ob8D220igra9I0FdoohrFjHJL9KkRGH9Da8vDxu3z03e/z9ddf8vLVM7qhA0q+L7aNnOwwqxIn9E+Ov7vvmp4NeTyTi5kjXhYRtIDgxdk52ZzEBrlaiWP87OyM3W5L3x8YRy/OZ5MSG4yhTkkNMQaGcSSGSBUEPXEcx5QN2MozpR0gEWn582gNp/U/Ne75HEtJjQkqW6FimGyL2UkWkTKqWsMYJYux0pZ1u5b9Fwe2ux23O8ftjePFi+e8fnlDUzWsmlaSiXxkHEaU0jRocTasWjbrcy6vLD9+9APeWX2P731wzcNHP+f5+ALVh6Oa3NlLezez+u65XF6TBrYsvVbIGcd7XB2VEjuiiyxXaXPn+2kfFutQwhRPc74IFIwx4tJcw5wklr8zxkrwQfDUjQZr0asVr4YDX798zW+ffMmnzz5j7A809YaHZy0PLs+4vDpnc77i0cUj1kPLYejo3cDovdS0VTVRGUav6W8jt7cD25eO4Tbiu0D0HqXdSTklZtpjlm1VyJxmltdLxNR5rsPRXCznv0yeK7+v65r1ak3XDRwOPYeDo7Jz2U4JONcMOidOqHReKYzKjuhjZ/s01wpMyj5XKjmptZqh1fNeiJHJQK8USvlpD2baQclRJLW/C0SQE3SmU9nOUmfNnOdI/szzkubTWouxFpOc0JvNmrppsHWNTnWpr69v2B+giZcEpfCjBp9B8dPaZf9Bol3vvfD06QzxhHBXzlYqDVVBVHFyjIOc1U3bsl6vjqpArtZnvPPuR0T9K2ob6V59zjYONMazateMncdWFxIAlSA9S0j9bA/VWlNZqfs880DJtg3R0PWejsAYDLY9w65qDtsOlCAFN3U9jd1n9JHCl7Nci7x22ZqzlAtKHpyfs9ZQr1qasw3N2QZGT9jtUz1loW2vEsKvD9has1k1XF6s+ezJC+rNGcYaKVnhwVYVQ+9T1vgggWIpeKrve9brNZvNhrZdcX5+zssXz7i9vebqwXs8fvyY8/NLqpSZb8Y9kul8rI+UZ2WMEowUjeh6gYgJQXwiShyyPiqeGc9Hg+IV8Fw7HuL4IFZcRMMqgiNmnBWckrNlDJF9DOjoscHxGw//WR34R7/3IVfrM/j8Gea3nxKf7Tn74ILRDRxASi1//RW7L59zdvYO+3FkePGaeozcAtV6RaM0pqqTXBK4vLwkRkFyIULTtBhTJblJiMwYKeEcFClxRXwdWlsCTKUB9rai3+3o9geMHYEdPvR4P+DjQD9s8X4kpFGTZH7rLS5YjLOTzUFkKDPxKa01xlr0hHIloWRKK4ypU2lhP8ngYu8WWVzKDFk8a7yuGAkc+j23+9fs9rcMY4+OQYKgogQQlfJhKM6sMuAxX5NdXuVAo/lsWsoVcMeMV8jSya+roiBcmohOSULZRzHlBOMhOmLIKMvSlg+SDGaxhORzVCqidRSZLdneJZlAgmYNkYqIjwi6cIigHdqM6Hrgba63doznSwRcKVyfa7eBOGqz0SALMLmewZStTYSoySmtEaYsDpOikY0xtG1LVVVT7eO8IC7ViJBsaFiv14zjOClEeVGUUhO8VF0LDFqOwisP4fsMrvlfDgY4dd/y3iz8uATXARxlpB8HARw7xsvM+6yAHTHt0qGY5PVjwVDqSmfI+craFKWpqGuD1tX0njF49l2P8oEYFcqK8K2jol6tiZs1+2GUyHUU4yD1qgHatiWqiFNzhHIJQ++jHDouGjQGnWCYtDGzA0zBqGAIjtg0hASzH7w4QY0x4lS2CfbPmsnBbIyhbpICagyhtuIYT1GZQjOZ1kT5jCj+5ld/I5tcZwjBDNlksFqzyXMpJ2Kqgy1GqNv9az751S/STGfjz7wGk3lKgfdOsuNjLGpGM0nqisx08vtSVJb3KK0JShFUxESSBiMPCXMR2q6iJoxZcFhCNEWCigLzrvJn0s7spJG36+lAXBhYUzS618n4ptX0/nyVCtt06Sw0FMbXpLfLdGXnVkm3pW2xMDJmJ1Su8RPC9P1R23lOjwxy8U5rwoCPhYHM+PM4sv/m1P6cf5fWJtSA0slfGg2Z5zqm/47GFuZ6VffzluUHd4aYfj1W4MqfIvseo12Ujr/pQFyMdfpMqamPmQAzAgCZbsr1npqS9qaI2DA/VxqZ8v0TmkBMfUrBPVJXzk8ZLSEIrFKmDZjbsdYm2P+Q5jcF02g5T3Km2OBG0HJ2KRTnF+e0TZuCruZswTjRUQrQyPs8xmn+o4pHa5HnUKcQ0RBKIVv6kvcUcf6ZHryz6MfOpIhoHbDebEBriZZMylM/DnQpklTiaSMkIwdBTcbuLJM8e/aMhw8fcn5+Pu2HU46RIxIs/swGwLzecXHjRPuhoC2AUunOhgqO90AU4ppoMCtxxYNFf5KBQeWAkdRGMnTNbc7vK5Xao3Gqu07xIYRU06tw1CXazxBr+VyYxljuN6WISD2gtG3KiUr3BRTmiASiEojJr599wvNXX6CV5Qd/+PfYPDpj5TVPf/0b2O5xhwPKJbr1kZw7suRj+TNZgr+dg0ahMCkTyk9BDIoY9SQHuOjJfnEz0UOYhl06KfN1KoL7lFPxaAbj/Rmq5T3lVWbBK6UIzE6yUv465Ux8m/eUCuh9/T41vt/1utvG377N+65T9PSmvoiB/S4/KeeknKtTzso39eHUu08ZyIEj4+e98774eNnP5ftO9SUknWaZxV3eu8zMhmOUkiX9vLHPxVU64st3l88vjXXLM+xOoPDENuMb+3JqD5VX1gNL/ettrpNQpMU77+uL0oJAljPiYowMwzjpdvc9l+X3U20vnfnHz2Z5JstOasrEOdX3b3vJ854yEEteGMSTET0x+KRei45gUoqmiRoVHNZY6sqmGuN21kXIInXZx3neZhXp9H58E23mOYkxEq0GHyTbOw4MzjN6g9Ib0CugRiFZyBkKW0WFSZnCWkXO6hVmA3unGXxPDIa2WlPrCh31lFAg5bUiTd9yXp1zdqa4WK3pX3ccXl7zYN1gNlJuyocKrwcsEe0cwYutYf3oinV1id9uiX4k7A40VcO1ge71NSZuMcbga4MLEXontbbPWtbnV6xXDSsfuH51Q/SBVaWpvvwKnr+k+/vf5/WZwVtH7UG96GB4QbzeARBcZH878sXDC740nrC5wjQN/e4lLz/5jQQ24tGMGBStVlzFGh0VI5EdA0+U5+Lsiq6OPN1teT3scKOntil4OxYVr1jwdz2LTLkW+ZQppjRV3VDVK6rKsGpWXJ0/4J1Hj/h//Mf/J86NrFYb2tUaZTWbyweM48huu021pQUFruv2xBgwae84J1m0VldcXV3y3vvv8PDRFcN4SGd1JsQUMInsya7rGZ1jSkl+i612H/8+LftmnibBusM40Pcd4zjSti1n5+epxmHAxUDUCmVUchTEJP/NSRnWWqraUlVaAgoT7Gjf9/TDiHcRMAyDY/SR/aHjcOhwLkxJGiEFw4QQEqR74RhP3W+ahtV6hamrFCA7w+DeB6k+j9dP9iyXYOPl38A4jvTDSO9HBhcZry2//WTLTX9N9AfJ5hx37PY9u+3Aptlw3pxhrGZ32HJ9+5puHBgdEDWbzZof/uRHfPeDH3Hoel5dXzOMW4iBqkp9DKRMv3jHGHv/Gn/zPZHxWLc5+m5BTiFBvxcoZkYriJ6hP7BXkao2rNoarfr0vcYo4Ud1Kv0YSck90U0oJD4FH+TEGgKFLhkmPahcv3mcSQ9ZOHFAjMiQ0BaRvatSsHS2k5ItFSnISinDYd+z7TraS8v5ww3nFw9ozYonz7/gN599yVdf3/DsyZ7nz57x6tUr6jo5xo0RJ/9hRGnFShusNZjKsq4aHj885zvvfQTW8uXzZ9w8u2V1uUr9zDrlvAp3HMsJgTKfwyXka/lvKUeekoOO7KxvIa+X35UBJpk3LOWfcq3K+12h0pZqaV5SY0AZhXUNv/zVV/yf/y//hqEb+ezLJ3zx1TNev77GAFVtePT/5+2/mm1JsvxO7Oci1BZH3Zs6q7qqWqMHGJAAzEij8ZEP/Aj8TvwWfKRRmI3RxgakkTRiaBgMobrRjRYlsjIr89688oitQrjgg7tHeMTZ52Y2ADLSbp69Y0e49uVr/Ze6uOTm5oqPPr3h9//wS37xR1+wulwjixI1tJyGU2izq2hbR3c0nPYDD2873n5z5OH7Pft3O9rjEWtPuC6kkpnRhzQ2aQyiUiLgypCUpvlYzvGLicfNld/ps5I6hAyPBifpX1mWbDZrhsFg3X3AgByjcY6bUYJUb4iuKdLaEU/TgVxXIaUco8Gl+c3XS47knVs3Aj9TxIMYnSPSGEgpSCYWM742Yh7j+C54qsTPShUiPGy3W66vr9luN+ii4P7+wMv7t9TPr7iuGoTWDMeB/nTE23CmDF1IqZrs4cKZG3jhrus4dS1bsXk0RoEfntZowmcnJ7aoTKxrpAyh+YWUlFVDvbrg9n2PMFCebnHa0WqBqDy6UFxe/RRjjhjbYazldDrRdR3GW5z1FEXJdrtlt9thXY+zA8JblBYIXWCNwxvHIASOAlmsqC9XHN4/YLxBSEXd1GgdoscaY7CDxRk7ehDP5MWE35EcnDi/eOL6Snol6y390CNtzdXmgj/6xR/y7nff8uI3X3E6PFCti1F5KoUE71DS89Hza8Sv3gdP9qhUVl6gpUJpgTE9Q3/CRK/xtm05HI5stxuUUmy3l/zsZz/jb//2r/n1L/+O/+ofXfD5Z59zc/OM79cbjruGYTjgXNLVPU3XNGB9cFZzCqSxqEIEnsqBMY43hcEKRalKDh4evOFzr7lBcxVT9wwEZwnrLQ0lrrOoSiCPFuNOGL3h775+wZ/+9h3Xf3KJ+OmnVL/9CP3VLc8edmjpeKg83+iKn/z2Lce//BUX//SaClDHFnu3Q91sKNdrCqGw1rI/HmmaBufgu+++A++pq4pVU3F/fw/AdruhbuoRpwtpCCxKBTojVOCriqKkWa9YtSfa/Y7+YNhsNdY7+uFE2x04ti2n9h7vOzwG8CghkCro3Moy0jIBPqYw8LYI6yY65yqrEZmeVkqJLDSlFjgXwoI7b/ExJW9QdGik0MEznS1O1rRecHjoePew535/jxl6Cq+CY6sH5edRDsezKKM1+T9G2kaE/Z/GQJ7iw0IUiuAJnpw0tBQxdLqNUY78SIukAl0SRE4TDDEBdCGDzhGDjNGDcNGgx8SUTiKk1A5bNRg4CKmD07wgeImrAac8gzDnG7y4frRivCw0uq4D428MWkqM1oG5MhZjTXSXlyOx1VpzatuQe0kpvBnQYlKs54OsVFjgddOgImMV8iY5irIcleRt34PoGMyAFILtdhMm/MVsWkKZUlIWBVVZhhDs3k+hWKPyZFSuhdmMi8BNAAfTQjoHwOaHVwJb+r5fHLiT5VoIDRTyRAWASFDVJYUO1ukjoxXzsA+DwQ0pr0E8MGObhQ8hvJSUFKqhUJkyKlL1VJYUiqJQlD54g+8Hg48h13DBunPX95xKjVcCJSR1XaP8mqYs6NoOJyWiKEKoOe+RcZ7LshyFtaKucOsSI6Cuq0BwhIghLkKICqVLfvfqe07tibIsxkNGipA3PITL9yDdmDt9v9/xV3/1r2cKk3H5CGYKrUn5F549nXZM8qJPr6QJDAqkHAeUMXzzKBX5rPx83iPY7z1aCLwL2d6AyaMRxpzYpBDBItWRtCDBg9NH8MdFBsvh8SmcFpFeeR+sP2NPRoVvAvsRqEwZndocxiQoJFL4idT9SUHjx/e0T8xcDuxN+0sIESzMcuBPQDB/8empMBtCZOOWtU0EpUmuPEtj7fGjsjqMXSw1vu8ChxYYxtjnfO6nv+Gl5GUgyOY+td250NYF8Busp3PFTHw27cW8jFGomnvFjxO8+OpTz3KBfEYTHwtvZy/vU/SnSQCzbgpJQn6YTestm4i0QAJ989MABTrpyW/mStQ0y875sU/WBkV2Ct0zKjUjujAJ9D7kj/JMDJtLcxpoiQDsaCUawrt5Fwyk+r4f6WgCb1IuzdT2RFequubm+prVKoRvIoaxGozh7dt3KKVYr9es12u0UnHdTHsMHw76uGRDr52fxtBP7YaQ15MYQmkUzqZJHqM3hNezQsVCuZut8ZExEQJVFNRNw8O+HUN9d8YEoMkalA4hGCdSGY0kYMwlKqXk/e0tm6gYH1dHEhJm6yZbKiODNO/+uLbGfXAmVHF8dlrhcf2LrDwhJqQ20btlQaPQmNYdGborxj050T0/VyYs9/TivWmth/0/pikZX0qpChbe7Mn4Y6YE9uCCxe0oxEciNCphfAD8AyOX6HTon8czmAHHwF//9t8FsMxVPP/ZZ1SHgf3LVwz7I3JQiAGEC8oRHxEEGdvv43gnw6jUJ9I4ujkvk5GBx4p0H9suweJCRBIZLY2dD/XH56R3QVFBDKUUAbkQCXPOT43Rh84AVOfAqiTQpuhBT0X+SX3J+5SMEZOFuhfzNDtLZe2PUUo+JTwsf0/XUvH5n3o9FlwWNOSJdnxQ6Xymu+fG/0NtAUajteWcnpvPJWCZP/NDxg9PGVPMPvO477M2jKAIj9bAEqh6qu3553NK1CWPsQRw87KX7/3QGswByXTl+2nJS0x9g5xHyQHB8Rz9gbrT3hpp2pl3grwjx3FZGien3/PrKbnrHDCZLmvsxOeJoBxyJoD/iV4sy5iBY0+UC4ze62fbk4XjFRka+2TIxr/nFbzCY7nZ+eCdISnFRUQDvJlkBhHPGiklZVWyWq1p6iNaH4KBsE30Yi7j+HPn81P9WI7XEzTNMCClRcoQRnlwglO3ph+e44sblK6D/FdIvBUopSl1McpOASga4rnqgmctGiEKtFAhlycBEDHC0g4tg1VcaE2hLRfNhhd//ZLXv/0dl2tHtQqRg8ryklopnPV4pYLhtfecdnuePbtEVyX98cB+t0cbx0orrj/7lPt3O3Zv7xA4Li4v6Xcn6q2iuVmz/fQ5nDoOb99hrUdsGxyO4S9/zQ2S93/8+/QYDv2BqvM0L/fw0Y7+sy3Kecxh4E3p+L82nqaQXKxW2MHy/Tff8u5Xv6L2UBKUatIPVB7WRK9gCTsMr8yJa3HD/UphTxpzCGHpV2UIUeuNHRVx49+4hmVMk+acD56ipHx+wchF64Kyalg1K1bNhqpa4b3jX/+bf4lWms16Q13XQbEnCg7798FpwIF3DhOVuSo6UFhj8M5TVRVSStarNZfbLau6pDvukbIebaSlCOnRDMFgNqVHEFER8php/M+/vA95DPsh5A9t+x7jPNuqYrveIKXCYEY6FvAeG3AML6JSI+UfFgjhcM4EvtB7TOs5no50bYeN+I81jn7wdO1A3wVQryjK0EVrCNBkKAfPiHyEPRkUFmVZRZrnA1YXc9PmdDo/h4QQIfe01mil0CK0u64a2jYA9IfDkbJqaNsDfW/xsuBwgPv9Drs9UdQlpRAcjwOvX92xPpY0okLJAq0kq9UKewz72dogMxnn6AdHUTY0qw1td6JrDxjj0DI6SqiQii6B2Km9S5okory5zCk5yu45jzIazJ3hSZhYISnUo7NIac16s6Wqa6y1PDzcI6Xn8moLbjNG+lJKUMQImALwQuKFwmNRSgTDJohje6DUBUrpiCk+5puW/Glan+fO+LzNIyvvA58+ZMohRkwiyPHSSrCaX//tS7759jv+3//i36PZ8PbdO+4OPbSWqgcpNdJXDN5jZTc6n+ALPHAvOwYExkmUfcVXYsu/kL+iNorCa0xVsLrRVMhoBD8/PvL+SDl5wJ27xnUgpnNvPv/zdyWTV9ykAGVsQLofPOvO15WXN4YRPsOvjXiy91g3Ra45xxMKIZBopJfY71v+m//df8Mw9Fgrkb5ipTfRAL7jpXzLd8U7VPMb/sd/++f87E8/4x//sz/lD//4Zzx/dk3Tlfz2q9/wF3/7Da++v2d/39PvHW5vOb7pOLzv8YMhmFN1CKoReyDro5u1j3BO5/0jraHH87bE0vMxDLL1ML6fDIe01iCDHuHiYouUknd3ByCFM/bJiXjEotKn1HQh7MgHZtOaKg/70JvZD2mPTvvrHA0JZeYypfSZc3n8X1oCUkyOWSrGWCOdVUzrJe1fF6OYpRDQAbMJeoRhcBTFW66ubvn888+5vLpkfzzw5t0bLpWi3OxQdYUdOsoCCm3ZbBpMacF7tAoRLkodlLpVVbFer9lsNshCL1LMhjF1bmonwiGsnnA8pajKkqZpQrrcqGzUhaasa4r1Bf27O3ZvXqDsCb2p6QbHR88/Y7X5BGvu6fp7WjOMupO6qlFViTcV/dDy5s0bhHBAOPO0FMgi6ImULfFaIlWB1o7N5QXv5CuGwQZP7rpCFwVt39H1PVWhGYZi5BnOT+70dcnuirh2lFKjA6f3ntYYhsORGw//9f/kn/Jye8Pu7S3Hw8PsbSUFzgw477i+vKAqy5j/fMA5g/RFXHeCoe/ou3Dmdl1He+o5nU607Ymmqrm+vuLm5oq+b/n1r37FFz/5BT//xcdcXl6zXm+5K8qZ8+LUr7nsE9Zv9CCWBKO+1lEpTZd0BtbSOoMpSxpXY7ue1oX5WFGwjuarAYVVQMCBTm3HZiXRPkQeOm1qvKlx37zHHST+sub0s4/Z/P5P+J//9g28ueO3p4Fb67gTv+MfvnqL61qq9Ya197z99iWrj/8UWegQPUYKNqsVdVkwWBcMtOqK9WqFGQaOx2OImDNGIHa07QlVBP4m8GmOvu/H/aB0UF57pzkdHJgaT4jc050sh71hf7SgBmwn8TY4bxalYrUu8bWmLBVaR2Wwswhi5GQHzoqQtjfmfxdCogtJ5SWdPWLtED3TQ2ohkyJtiwIpNUoqSnmkFw3HQXLY9ez2LW3XktA+RzTI9B7LhMWfM6x7dH0Aw8oNhc4BRd5PuKx3LqY1SzxmwCSUCN7jgX8NWKqSInjxe4u1PQiFlgUQjAKdCedHMG4xGBPw/1KVlKqIzpkR+/aBc5Peg3cY23FyJ7rB8vnTvR6vH60Y3xaSsgyP9z0Y3SClwBrLYAbargsWAs7Rti1YS13okODee9ZVhV417B8eqAtF0zTROlhwOp4otOTQtewfepr1ir7voxewQsqQJylsYEd3OrHZNIBgXYf7Mk6WFAKNoyo1VV1RFiVaepzpg3VTkKqC8k+pmMDdx3xbKcRIDEcdPVZDnuwUFklDUqIlxitjHpQM7xgTck/hLWVRhVAP1k358gTRQk6hpQBnEFJTFcG7O3nfG+8otA65m2Sw9BzsEKxPlaJQgkpLKi1QcaGltgWdicMKB86gnQKpqZVE4+mswSmNc5Zdu2fbNHzyP/0zfvLFl+hC8/3r75EiePOLhGyLCWiDCQwTQvCb3/wt37/6NX4X8RuSUnTiJNKb+90dw9DF22LaiONnP36eqyvSYTX37huv5V7Nv2fAziREuEd729mQhz1t/9DdBHhNPZkUyUkvE9aCj2hSzmiPckfy8vZMCvOkBE0KnLiWPIRwekLODrKc+QtK41T1pJRdYgOjGnPs7xwUPQsOzpRJ03OJ/3ShQeOvM4OE2JPx+VR/3Fcpd1gsdRyTicHNLpHP/aJ/PiiUJl1aGEObDBuyINgj4+7j5+zv+GTW/3COzD0wl80TiQP3c3Axm53HVyorjTdBETsLez6KWJkNqw/M8UinRPhsjcUMA0PMzydIgHJCNBlpmSdjwrMxFQiccKNQ7OMBmgx4koenMUGIEFECsM4G45qkgEthouPYOecwgxlD3aTQ58aaUYEfQhn7EZhLz4b1POW3c/m85F73+aRk6yOtTSF2vHr7PjD8QlBXFTc3N1xcXlBXDd47dnf33L1/z8XFBav1OoBPUiCiQYYXk1BLFAxHcw+RhLOw5sYV4EWwzLcpR7sbc0sJEfcCgBcz5jsnhakOGcPE4IM1dKk1xByb3gVmwBiDdclT3QfPsQWtJtZ3eXnJb3/7Ne6LYPEbKdZIWfK8k/m6TWlQ0ppI68THuU8l+MjIEfuZ1plLwEec88dKvWxfp39uGueR4croJJ64HjPGPwnZufI1Bx1ip+W4RpISKJ1pcvQa9H4yeoOobMJGRi9avcsp7J8fQZTUHgUpnGZasGIy+BAxB9y4kBbnFTGSgY9egMgTb0/fUBZrbv7BLzjeHxgOHf7NHXJ/pLIOTic0BucHej8wFOCMYWU11kt64Ri8BylRQqMAaT1OOIbpiMIyGV2l0H8i8p9CCLQPTC5xTgNtUKgobITYoXIM1RbOvLQu54BmAG9FpB1LyjlSq7j+Im2OBmSJp3P5/l++GufHuqSpj7ygnytD03o4d50TKP++Cszzykk/+30Jen7oygGVeOdRfT9WKTedDY/Pr6QU/DGKvnwvLxXc6XzJy0hATF7+j/EqzgG3Jbi/VLA/yv+3GPsJuJzqT2XnXt+5AnfpkZ34nbSNhZi4Xk/kMTyIMRQrY3nLMUljkfNm6X76niua83fz3/LrkQIBgVATHxhs4/zEaxBTlUj56F0fz61ATxOf4kNIYLJ1l4jeApw5176cB31qH/yQAjsoRgN9CV4VFxwOe/b7YNA9GpFm8kWILhUPl0eGjfN6xnl4ZDAUEn0JoUissz/Tvv/0y5/56oFgVe+ln/gPGULWCO/BhVzj1nUY01ECq1LTNAUeSeDg4p72AhFz24Xcu1O93ovI6U283bh/rRsV0kJ4vBQR/g1G1oXUOKkph4HBlzhlEGrA+YJ7nmG6Fb7UDLpEqnIyr7VqBLQE4JB4F0AqLywoh0RRiBCNwERDLeM91iiGrkL7FnSNVh7RO/p3L7isLHVZoKQGL6C9xxcVrlDYQuOURjqBbA13r2+ptyt0UVJsNrT7Fn9/Qj6D1lmOfYs2A9WzS4bWIqs1qtmi64ZSSPbv79EWyqqk7k6Uv3uJbEoemi0P/RHvLI3tkPaEvb5Eb7fI1nA47vneG1auoHAaXWr64479+xeY2/cB7FIasMGr3kNNTJUmBmwh0c0FR13yYnfEmDB/Ck+pFQIXDdssFhvxDI9LEfgsCCRaShAO4waMNXgh0UVNWTRUxYpSNlxdX7O9XvPq3Te8/f4Fnz77CVVzjSjX6KpBuo7T0NIPHYMJ4SixBm9CmjJjg7HrYB1KNTjbcXNdc3UVQsa2/TFQFRn6igcvQsS6w37H0PdhrUlFoAB25GtzGQ8ey5LhphxPvCTDSCJdtC6E0R6Cp6qzns44OhP4mefbLbqQIcqaDdENrLKARlg9yREeZKFwygajQhvYQCE8lVQ4LN4MYAekB+EUrpcMxmE8iEKzvqq5uX6GHRz7uztOhx1DZ1AIrO9JPjxp22qlRkzK43DCYxCUq21UvGqULtCyQOsaYDKk9B4zDHSbExdDj4me4kPfcTwdgpd+f2Toe4wF7SS/+QvHjXzP9XXL/eHA3d91/F7xCfIjQkQHJdFlQ1kWrOoaY4K7aVmWuOM9h90LVqXhs482XKyhazdgbYxwMcnCUqrJazvR1yTPE/n3cAhN8yyyZ+JfH2WydEYF+SRTuGc86rkw0MmIIHmGOidjZLCAE4rsuZELGGUY8D4YLKS/IDD9gBsM6fwK9TJiTknuTX3yzj/KUzzyaKkV8feUd3qEMjL+KLRjel9JFSI3esWwc7x92GHtA947aqnQRYkq1AxrmslXcf8oUVHFlkhxA16ircSrIMMXhQhGGDFCSB7VIJ/bhHGR7ducd5vzBIy8yYhLRXk4RPwLcz1iVPnf8IX8ElG+mKSQnFcT4wBI5rxzasPyCvK/JkV+SNiiTHlhY4c9ApzGeaiLGlFKpAgKnbCrVaSLAm/h9GrgV4eXyG6NaNf4P2koVwX/9j/8kv/h//g3tIcBb0E4EW1qRDSKTv+K0XFgudbHdRfHVD3F14hsXMS0LvL5+iGeKClApAyyb1koLjYrtFSjDJccI5JRV0olmuRvH2XFkOc98qTRoUHGFGa5Qnpqblo/0bs9yelT5xaSUZz7OIaJl45QUfgthUsWgkKJ6ZlY7xj9xIZ+pWh0oxSVYRcgKMoiOBxKMRpRPbu4YaMq1q2jcJbGFlTFBRef/hx/5cYUjCF6Q4ESweggGE+FyLrFqhzTfwqZYyB+wnQAVWg8HuuCUbnSkrLSUZ8SzhqEQ0vJRfOMt/aX7O0DFSu25SWrzSX66kucMFjhcVIjlGfoWup6RVNpnOlpTct+d89w2iNkkC68CzvMVCd8L1GmphI6RE7UB8pnH6HWL3DvD9AONEXJRV1xOnUMPqTucMYjnMcaEw0BbYQEgnc0XiBk4JGEc5H3lcGL25vgGdwUVOsLpC7x/Y7u6BGyZHNRsLm65POf/R4Xf3PNm/ffYfqBuipDZHunMVYAls1WcH3j+f5tj3Q1HsFgD5QEhf7x1NH3LW17oOlXAc8Zeo5tT1k3bG+uWG+u2TRrXn//Lbfv3/KLP1Rc3lyw3a5ZFRe0xZ5+6EJYd+/QWgWns9nZ6BmiQ6h0wXlnkIFXlAQvcu89yhh+uxZ8dg+lDWeGwKOl42OneIHhFNe89jGqZ1FytI7G9Fzpkk25YVNd090duHv1DqFg9Se/QPyv/ohtpfj4eOLtqedFU9JvNuy/fwG37yiqAo3EvNmh2gEnLXZwCCcQKlDD3e6BqqooqwatK97fPuCFQhVViOg0DKFNHpqiCo6qPuScl0JgjaPrB7wM419Vijfv7lhfFTTrGuELhHNo60JO+K6kMx7jPEpbJB4hdIhKjEJ6ifIOpSVeVBibMO6E5akoJzoG1+OGAemOo/GiMSZg5ZE2S6mQArTSWF0hvEYaESJeEeQ9bXsGHNoHHlb4IJGnNCnpmvBVG3N8R6M452L+9ZGBRngZzg0h8uM30rCpvLxsvI/yb4xEYDxKSJR2eC3wKimwA80zzjK4gd4N9HYANFYICjTSi+Ah7kNkBeM9Jp4BRphgYBr964KMKmmqVaCppmewHVZ26OK/cCh1jaeUwWV9VRZTiCUp2DQVw6rBE0J9JOX4arVit9tFcGKLwFMqye3tLXVZ0rdt8PaxBi0r6qpEFgWnrmO/34d6teb6+hohYL/f03cdq6okhfGuCz3L5y2koKlKqrqZ8jzLEHpbCDGGvvA+5YsLIbgTYJfCoGtdYF0oM4QbUnERxXAYUuDFlLs1LZKkkAoHb7AESR6OqS2p/LIsonIkMIBVbAeEA3oYBqwZcF5EJUvMH2t88AwQjr7rafQmfGdSTKQD2eHDojEOJJjB0Z6OCAR2MDh6ttsNP//5z/FY7u/e8d/9i/+WQivev3sxLnBE9GbMw/+eu6IAcA5AfvJKHESqK79PLgSICLzHv4v7wBjSe/wuFr/H30T+NysnzIdIvEgGPmUMc2ynmN2L72cCwdiEyPSIaO069mNW99g4UrLlien2jMlbMkAvb/d8TuZs2yyndXo29TWB0T5j/GZl5ELg00C1EPOwkbBop4jjLWCmAI4SfC6ojeMw/gllzfOgTV7e5If8ohyfPvskaEwK+an42FeRhOYo2OSMA0nICpBdEr5UBFRlFLjk2OdMfJ3kpmxMUvuSoDw30JiWXrY3EEGpA3gvMMbQti1t24YIE9FSO9HCFHZ8rGMxd0lRHdoVoch4MCY6ByJaMwbltomRPJK1ZbLamjzFo7I7E1hHj/KkLUjrL83XSKv4IG2ZH+s/4srW0mAdMCARHI8t9w97qrLg+uaajz56TrNaBwOh/Z77hwc2my3rzTpGw0hCUyaoEFjCcZ7EVF+iAXg/0ZNEImywyJQxuYogGUeIcf9lr0eBLq1DMTK0dVVGeuAiUBjCzwxDT1UWwZM80hEfhbmxTXhWTYM1htPpxHq1mtYJGcM0UoAkVAJecDicaNs25CqNa1lKOabdSCCLEOFsTfQv/JYGKwFNcgyfluhLSueQ1l8SxAUTaOcRY3neO4zp45zEfZ7TkUSClnnkksI+PpCHu0sKrgTwOOdCnq+olJUyetXI2P4YISeEb42hkpRECgXSjcOPCKTcGQ8ieVCGkHBJWJ8iJ+QGE2P8jTA0Eow/8ur+VyAKTCW4+Olz9N5gbncIpaBrYRAB4PeBr7EurL+0/5wzMf+chKggm/O9cwMGIaZ38zNUiBjhJN93ca5suj8CTxPANL+WCt7HAEpaP9NynpSHea4/FuUkGuphDF2ZjIBSPct6z511T7Xtx/I7P4YfOqfsO1f/uXYknkFkY/n3UWTnylovzj9zrt505V7Ao5FIfPcpJWeuCD3Xt6WS9Nx1DnhblpdSdCz7k4O5ebjLXAF+7lq2OacdMyU5U/vTWbBs3xygPt/+XM45F7J88lKcQOXzoOw0VjlvMKubdFYz0uR8bSTalNiTfDyXYzSScub79e8ztsv5zz8/snxPioJosHN/f4+1JtR3hi6M7fOLe2faNLuWY+snmh3WPNPZ/wN7/u99jcdbmgdByrEWzs+oTBm9nUIYau88wgXjOq1EvJ/YsIl2QAQ1mHi1xIOQrZkwDImXWQxJYn/TWUY4i0CDCIof7zWGFbgCgcILhRUC7y2ImDdOCEJaGBdz0EVDzHiOKRF4BwAvA/9pcAzW0Q0DAYzWSG9p93t2t++oiuDtI7UO/JH3dM7irMArj1RBWaMazenhASFbWJXoqkS2loddR3f/gPeesq7o7zq0cdQXF9TrDUVVBT7AWtztntIrSg9F1yJ3B7rnW3aDQQ+Wtfc8KyU8W4EOwLSzjpOxvHceqTVaaIR39KcD+7dvGNoeSUiZJb1AI6hRaATEMaTQqLrCaM3dcUfXdnjngxewjhH0xlQo2aKKey2BeyIKwtZZPCFFmdYlWpcURUVR1my3W+qm4uuv/4aua1mtt1T1irJeUTcNOBPCgpqgXHfOxhzzFq0lg3WBNyFGCSgcl5dr6rog8JJz78RIVcE5hr4Pey0zZHx05fv77I8LZUfiMxLvE2mqdZbBWrpo7KuUZNOsUErRe8sYjU2mNQ8CiUh5LJUM3lgIjAvOEjLmvu26nn7opjzF0Xi07weMdRRVxeXVM9brLbv7ParQgMQMBjsMuIx384BQgnrVUNYNZbWiqDZIJbkoFUoVyOiRHFLdBYOCkEfcBOcAZxHSonQRPPS1oigLTFWgS81qNeDtJc46jPH0puPbX3dI/ztWG03b9bz5bc/nFz9BlkPoj5//y43gdFFghgNlCddXG7abmmHowVq0VGNYeg+jcdMkH0/nLD4abvswhin63zk+YzQgX5xPM4VZvlKye+fOKO/nEVry954678/9SwooF8/8nE/Ky0x9GJ10FmWPFD31fcH/PHUuzQyBrcBZGcIWO4/WKkS4lMmQ9XGbZjzQDEMKOKqQYFVMiyZFML5JjrRCpEPjPI+Q9TP1Kx+b3Aghk6qz8yjyx3I+H8s+PK53mkfBfG4TfcnuRr7Cj0YT+fNKgJce7wXOiWwf5HMVz2enUKgJy87WoBAhTH+YB8AKfCt4/fV7/qP8NbfvHlhfV3z1d6/4/te3SC8odEilMuHhkSbFsX5cx2O+SwgRFfOP78/eEWImd5+TA2Z8RLxyuhDuKwqtqcpqtkdzmT03Sk+fZZTFUzS/R/z5WO9k5Jn/S1EUR/F9NKJ5fCUDlrxPqfy8PqWyMyqrc3QASW7wqRwhRsPU1KbkUR/yjBfU1KzXa4qqpEahrEcjkdUKUa2RmRGIUjoqEuWoD5EJtyjU1N7M6H9mXIIfDapk5M+KomC1alg1DQ/mhHM+GFAd91wDhS5xCIwXIEuq+hKvGzozhMgnwqOlQquQT9wTUpMO/cDQ9wg8UpaQ+ADvcV5j+oHDuxd0SAYHXhwZxIBqNBQK3wdHES0r8JLB+PjPYUx0ynEE/VAyfhGTbkfggnFGtB4OkfZAqpBKpixKvCoY+pKi0FSbDRcXHzOYjqurT7l59ikv11+xv3uDc8WIseCD0ZGu4Pqq5tXrDukLvLAYPMYZtC7BBwORoe+xZggpTaJnvbUuRuVt2Gw2nE5H7u5uOZ1OXN9csdmsWTVrdscaqQoQLd5bvA9y0JQJMjpTiYgxBYAtRABcyF3eOt64nk8IqWidh9ZbKg8boakZ0IAXPpYfxszE8NfeWrq2py08rfe0fYc2A/bdHryluFlx9fyCy5Phd92Jtil4f3jPcX/Hxj5HFw3u/ojuDLJMmHDA4vphCEp/ITHDwMlH+qhLrPMh+rKXFIWmrld4L6bUt0KQ0jMMgwnRjeuasiroB8PpZCgqgbcS4WTA1JzCGR08uzGoKCuJJE15haKgEKCkDxFi3ID1Hm/t6DzqhcNZg7eWfnAIecB7gRlCRJfBmsDnK4mSjmAfKFBSolFRYnOjvCS9xPjkjR2F9Cjre8TEIyb+iZRrPOE1uUH7RMPitltcc12Tz+jWiPv4cBKHtgQdhvMupGF0IWqQ8VG5HXloIcK+tdYhvEX6SB9FSN84OItxJsokjnaQIFQ0/I2E1RfR8KHDiw4pTzi6s7R7ef1oxXg6lBPDVJYlXdfhvacoiqBIJoXHc3Rth0CwWa3xPlgKSCVQqxX7/Z7b21ucc8FS1LkQkqIs6QbD6XDA9D3r9SaG/Ciww8DQdfRtx9XlJavVisPhgPeepmmmzes92/WWOt4L+bDiYSDEjLlQUSAJQCmIogR89LwLzLW1CcQJAmFSCHlPDH89HerJA8LHvBtKacqyivUXgRB7T1kWVFWN9w6pBcIZzBA8KIsYXlhJifHBMkQSwoYYZ7FmwMbwGqKq0EIg5eg/Ny3kSBREJMI2esF7oZBa0+5OlHXDH//pn1KUmn/z//nv+fabv8bZPhy6RTHfBZGBfRwmenF5PymnyTcK4zhNjFBqrDi34x7/tvyb1ykmAjBjXJZl59/PfM5f9T5n1p6oe1l+YmRE3mlGJcKjMp5q3xPljn08d43vLAhaFPJHkDKWF7qWIiMk5XS6n+W/Geub5i3cy8KmJ+LrJyAtb+f8PiTrpaAMi+HJfUZk4x5LarBciJuG0Y2tStXlzNv0nH80j7MhFNkvnmmcFvyvQIx1CkBIGDCj16j0MljYjfGUkne8z96fOOIwNdP6G/cFTFZYsT8ifhYEhfix7djv9rRdS13VJCHQ+RCFw8MUNq/vRw/tELnCzgBx61K+DjMy5cMwYJwlYk/jfI0M+zg8mdKUaY4+pKgY5yONb7RVGOcuE2DzK5MlHl9JyFncXgr+Lo6THQaMtRxfvuTtu3c8e3bNxx9/EhXkjt1uz8Nux3a7Yb3eUFblGCYLPwfOx76JfCExhrj3+BDSJikWXAiJmjCDsJNi17OFJ+S03mb99FA3daxz6qN1NubisiEsjfNjqoUlTZFKcXF5wfv372ma5pEgN67YbN6c87x+9ZpTG/I9aq1HwOFiu+bq8gbvwtqxmcKGJOwVhLCJERB03uNtAP7G0D7eR+MPP3qVhzbJkWlzyds8KrryM30Ulm0wg0/55/K+JaZPqElRIkiOgjKGbAxKcOnDfBkbwr8iRDiDrUdaONk+RpOZGOsE0OqoLBdKUpbBKltrRVFodBFym4bINNFrJMQcmgnX45oQRMv12PY4HgF0GNAF3PffoTdrLm+eUxyvGN7dwW4Pxw5OJ6S0dEUf+uwc0k+mHVYYehG8saRPfoFZOxa0/Kzi0c/3/4cUmTkt+bHXEthcgnAT//Xhcs/9nivXPhS6edme5eecxj31fP73HCi0HLsfAu3OlsF8bH7sNQNbn6gn/36u3WkPhvmYDA/O9SGft6dC4Z9r41PP5QrhR+0deYN5WSOQTKC5Skyh+VMZy7Df+RiksPzJEHd5PXovWysJvDtX/rk1NNHiubHDEujLQ6g/VUY+BueusbxY1sxowk8gYyjv8bp/igd4ylDjqX17DgDPy5q/N4F6+fk1jvGZ9bFcK+fWzn/SJcQEKH6gf3+PAmM5OQ8+VoX3wXBzytUyeRqCB+mRog/PeKbnonwwKsaFCN7Y8ZrOcf6z++J9rNtLcAp89K6UGiFiyEc8IcSwRggJXgSlnw/hcIJ8HRUHUuKjQt1ZG519PM4bBtdi7IAoVmPY8GT4eFEGkNVHYFcUktZ4vHEoDNJJqDRiUyNPR1zXY6QHVVHoAlN7uocdZdmwqlcM+shw6rn+/CPWqw1lUYC3yL5D3neo9QVq6NH3DygzcPryGcfTgUsz8ImGTzYNNCukM9B1mOOJru3pUKA1WmmcNZzu73l4/QbjPAUFwnkUnspL1gSsYCU0B0HwRtEKKwXHvuN0OuGtm9Gpp2h6jpVAjLRiPVIqlC5QqojG/SV1U7ParJDS87uvvwEEdRM8vauqirkfHdaaMUe5j94e4ZzQI/1VSqK0Yr2puby4QGuFNUMIt+7jWvaMxqcu5kgeo/bMyKwYZabEK4snl+0kZyYWPE/lleidMYZ+CMC0szaArAl/8invd8o1G8oVkQ9NvGghQ4hp66KBgJe0znM6tJzajj5iQR6DUjqGWLVUdc1Hz58Dgtt37wnGI8Go0jqLUCVa+xjGVlGtSj76/FMubz5iffGMZrNFyZgKT4jMKD2cYcPQ0/chV7szA27osNbgjBnnyse/AhvyIMsSoTWuANFp3r0+cH/3EiGDTD8YyfOrT9C2C2XYYEiNiEbl0QsxrbtjH6IhKlWOMi8uRk+LwO0ULS3HBKa/uYztfZAT0ryn+UkSdYiANcmi+dn2IX5neQ4/9U5+LXm6c9FcRhzFzfvzIb4Solz7gfN0/LzgPXIjtZyHSPxIiu4zynsiepyqYCDsMjxwWf/E18zrS88mpwIWY5q//xQfnI/XWR4ovPFB3jk5SC352LPXDFJ8zB8kWoPPeVMfZbXH/TvHo/pxXSYlrZxF6lmmxUl/k6IEH+ZI1SXmOPDr//gVv/nVVzTbilfv7jCDoyp0lEGLCdPXcqbwHQ0TUrcX4ytI+OZ5mebRXzkfg/H9xZifm4Mlry+FyvC0NG7TFxG/58Yt53jh6YzL5mak0XJUkkKMAhAYqTFVR25okeoNBkZLeYiRD8zA13iP6S+MoerHK5NLlkYRo9I6j2yXRb5IqdyqsgpGEIm7E0GJOJsfMUW8S17t03/BuF9JNdaTxnQ0jvGCsii5urzi008+wbnXdF3P0Hfc373hpjxQV2uUqhC+BFegVY210HuL8hYRI7wUSoRIJcYEJ5wYUURpjVI1UobUqx6PZAUYXnz/t9yfWpyQrLYdpq8oNx128HASeONRRqNLiTcW64K3qbVDDNHsUFpPxlYy/HPGIUQ6q6bIlVKowPsUNYUM4bw7oyjLiuvrG662X3LYHbi6/oSbq4/Zbi+5e/8txq+D97WzKBnwHykdV1eXaLkLRgNeIaSKUQAS3mUxZsBaQ9+nsOo9fd+zaiqqquTy8pLDq1e8f/+e29u3PP/oo2CsuGoodyU6zpWzJp7fMqO7j7bd7FrKW/uuxesNOM1gHTtr2HpNrRSll2gcBh+iWPkQgcgbgTWSvrMYeeRu1XJYb7lkRdG3dIcD9bevkbXi8nLD1e0R9f4NKMeDPbK7v6M2A8X2Cvn6AXlsUTooPlPkzeSMa52j7VrkMLBerxhMT9edcE5SiRJZKeq64XA4xKgUUzo+COlMyrIMkXSqEiEVbdvTdDbsCa8J6lcd+TeHlCbghQnIdSAI0Ri1jFE9xIDEIbEIb4Ks4sB6g7EDgxuwbkCqDikLnANjA2YaNm/gg6SYztMUgVSOdCRz2PR+xrsmWjLSu8Uc57+PdGak+Y/XRHjw8frJy3beB2Non3Cega4b0NpC9HD3zobYVZG/k0KFaN5e4r0IeDEEYx4BdnAMdqAzHdYYejy96ylkSREjcBdS0tsgE1rXg+gRokOa/8KK8aIoZrknvA+5oEZlSpDM8THU6noVwiVJWY0byxjDw8M9RVGwXq8ZhoGHh4fRq6zve3SM+19oTV2XbDfr4IVuPU1Ts16tWK9WCCFYr1ccj0e0msAoIQSrVR3LBGvz30BFbz2tFWWhSUq5PK95VRZYLzAOhDBAsvoLoLXWMaT8EHKdSBlymWut6UX0MMejpeR0OOK9pyyryOALnHEY0ccF5Si1oIpe8EPfAQIzDLTtKRAW62iqhqau8MKj8VQy+K42VVDmIyfQL1n8hIUn0F6DdPTeYxwYDz/7xS/YXl/z53/+P/L1r/8DxgQjBx3Duyf0ReQLPQp8PwiKPPpdPAJyzj4vFrss/54Yhg/VnZ7Pn1mW/dRvs/oi18d50HleXvrssvtJ4Mnb/ATj/ZiqfLhvyzHJ++Tniv14c1b3KPiPPQyfZgx6lj85EMw87Hl6Pp/PyIyN4ZGnZ1IZSYHn45iNitm8meOY562fQmjn7U+9crOxmPqb2zElZnk+KpNSKP0mU1LoBM4thb7UducZrAk58VJIyWhgUxUxJFFRMCrSI1Od1HzJq3wsPQEoLK5scKLeGWMt9/f33N7doXVJVVYM/YDSir5r2e12HA4HTqcTdrDBOsvahTd/LHOc52nNx6ka2zrNx7QnzgmrI+OfLHPzsc0mQEShy2frcox2HW+dEyTHOs4P0LjHHu+ex/vOI0AqjHMID7brOb18xZt3t3z22Wc8f37DerPBWsvd3QP7/YH1ZsN6vaKqyigcZfvQn1cUPmpptOxPeUJDBIlYlHzcztQnMdvz4flCa9IGSuTeR6vMFJ5tTMEg4riMcxWefXbzjG+++YbPP/tsUa2fhL9svx0OB97f3gbv8GHADMEL2XnPm9fvaJoGJcOZ2g9DiMjifQjHj5/ySMIsRH76nOibi8+PYdHSXs1oiM/WYhj7RLJCaxPYls9TWFeZgCrmZab9Pwp/EIznouCoZIiIg2dUhBVFyNVZ1w1Kh/esC/0cBgt0YwSFxDsUhQ40oixC2KeyoCqLEB4vC408HnmRPiQQKfTDkayblVLgPLoqQAy8H76jWm+5uPkced9hXt/h3z9gTye80PjBIF1P4WPYPuExIoTP9R6Emyv3cuBoCqM/rdelElEI8QgwnMb/x1/n9tM5hdYMOFkA/ufKeAosyxVoH8y/9J9xPUXblu37UWDd07XM+v9jxj/9NgKXcp7aI2/zU56+S7A3F6yeUiw/Ffr8h65zwGTaC+dA53NXvpaSUOjcBKY99ey5emfA3xkQLq8nARPnFLQ/1N/zYCqPylr+vmzvuXVxri1CBKBq2cccLHmqTY/acWb9PKWASH/z9QHzsPbpmfm4RRqZ8QIB0IfuFJ5fAuI/dHbn9X+oj4/egdE47v8fVwJvQ3jVdEUjPBdk36Io41mTjIgsE/83gSBCyBh/LPIYaU54gss6A57MwZXpnrMgvQKncPFf8HbwgEUhqcUKQYm3MsojCik0QtiQkxkZPTQkWmgY1BjqT3gZYvcNCunCuaYU2N5yeniga3uoGrrBBsWYLigKjVEegcR1lv50RHUGX2vqyy1mv+N4POFOJ7bNJb/3X/8DXvzyd/THEwLJ9uqa/f0D5WZF1TRUSlH0A/QnnAW7reH2DcW3L1j1ltMffIl/6PhCWb68aXj2k+f4qsa8uUO/uaV7t8OdLJ+ubtBDgb5oOJoT+zevuPvmOwxQI7Deoz00KDZoCqHY+IKjNQwuZIw9CcvBBX5My3mEPLvwuJvTzaAkCClOgldL4IOKIHtUFU1Tc3l5yaqpOB4e+A//4c/RuuDi6jp4sylNWZR0x0OMMjgE4xTP6K0DIWoO3qOVRgnPzc0Vz55dU2odw6ST7dewEr2Hrjd0g1mkyciUZWnNJvlQJHFkSbcmZUJ6D0H0KHNYZ7AuRM7q+o42OoWsmob1Zh3WbpIPA4M9tpnR0FDgrQcdPFu0BCcMfWdxg+Ow7zjsO47HHjsYhLBUMoSplcaCNyglsMZzOu45tUesN5RVwXbTYIVgtV5xdXXBzbNrPv74OV9+8VM+/vhz1qstShU462iHI6Yb6IeWYegY+g4znOi6EObe26AA9y55eceUWi6GKmYKNY+XiUFFCrAG2l3wMPaAUtA0AqE03kmslegz/GOah7VW4z3wgZLF8NLCR3DeB4lgBvimc3WUARLrL0Yjc2K0jLAe4lmU1sAoyj0+i3K+5xy/mD+XP/9jzojQzmztesI6WrBYy3NyycO6R/JQ/J6LyDOZfjLKS/zOPBd5jJCQpTVLOXWFmNqi1OPUOMuz2Y8R+ObtHnlCEk80je3yvF0a0z3Fi01fmJ2753itmXIwu56cN3Fe5piX88M8XLiSZy54nyIB5Ur+x6GsZ4rR2To0UR4tAEFT1KA1L1694vs3rzmejhRlSaGDt2TC8YPXcVB45pEElHhakbz8/KN/T+OyeGacz2x8z/HB8/sLpc2yzNkcnK9v+nm+V8+lSxgV4/JxfYtOjn0VQmRp88Tsd5+1Ka3TxIHlIcwleSSBubyQ5mu0gVQyhNOH8YzF+6AE92DHFBsC6Xg87k4QUhykdGmT3Ka0C7aLKrQt1wGkfVtVBV9++QX/9J/+E371m6949eoVRQl3d6/YryyfbOqQqsNrnAHvJM46ykIiBosbOow1DGagKDVaR8/4QiN1iIwilaIsg1MBQrJdb9lerLj73Te8vH0B2nADNFpx8ZMC+UmJ7wrMUcOto9WKbhdSQ/gCROHxYqDrD8jCI5TEeIM3Dl02qKIKIaR9OPuFAFSIPix1SVkEI0nbnfBqT735lGfPvuSjZx/TnyQ7/ZbNtuLq6pKvfhNS50IIWy0jkGeM49nVNVX5EnqwQqFdjTEdReGjw4Wl7zvsYOjbEK3xeDhwaGrqquDy6oLnH33CN999x4vvfseL777hv/qzf8DNzQ11XVNXNXVRMeiC1oaINFrJEX8MAWrmdDWXt2bngne0dsBUGmclJ9/zzhp+Ss3KeRqpKJyj8w4nJocfN1j6E5wKQ1HBUGvumoKPK0U9FJy0Z//vf8XqckXtC9Z9h3j/htoaLpHsXn7P9hd/wOXv/R4rrelfvgV9he09xgLO4szAWumgXJaCsgxj891333E6nWiamqYJZ1jbtnRdF9e5xLmQfUopNUWrVgJZhqhSx2NLXUFdKApqCtmDGjA+7FwZvbVJ3vgibc4QZUkI8MIipEFKGwwHnWMwhnbo6PqQZshYQ9NolA7npvUhjH+IPlmEepAEZxoZ9gXRQCYjMyNPIwgptpgwDs6db36uRA/n/XT+cEZODrqZx0VBTNkyYtqJSAm6ziA44L3BVBDZvcCPSQHoMf0PWuF9SLPkiBGvvWVwltb2nPojbXvCDME5qdYrmqqgLktWVQnCgAl8rPcD0CPEf+FQ6jnjlA+Q1pphGBBAocMESSlQskJKEaxDved0OrHbH0bvNO89q9UqCBpRyAhCs0VKGIaOrj3RFjqECCk0sgXvLPtdCGGGgNVqhXc2A79B6xCSI7R58kRLwrtW0yHTdyYKh8FKx1mLU5KhH3AyKMuHYRjbnELPBCA9zLnE48xAF58VIniLSQHr1SocAGU5Mk7GGKyxwRraBsuk9K4uCrx3DMOAMyaGDY+hYltDWRRcbtZICd3phJKSEA6VIIwlxkAInI2L3AMoBmfxUvLJF1/yd7/+G371//w/hTzfmVAhY86DNFY/BLSNg/4DQO/Z90dhwM//pvLyZ5flx2emV1Ib5gzY+G7iAM60eczLPWNs55y192Rh5MVY3gj4ibwN41szxe/o5fdIcDj/d+qjfzRGHoIr76IvqVy/HMvst1TA2Lrxz6S4TspMnz3rF+M1jVN8209/xzbk0zC2IQ9nHtuX+pqXnOhMBCikFAGwd5MBwGgJmZhXwWxOSEM3MqB+fC81avRUZZ5bOxdUbAzbPDK9cXzCXtdYM9B2R+67O3ShWa3WbDZrirIcc+eKBLTgZvULEQHIbMn5JCBnCkHnPPf397x7947txRXOObq2RwrB9y+/5/b2jq5rx+l2fhqfdCAud2kCPlPFo5DtxYQOieyR2dqV4/y6bA5CCCIAGQx28tkf30938r2ZM2fnhcxxtfnHCohH0vCsn9MzQoScx8lC1Nmwj6zr+O3X3/D6zWs+/+wzrq+uuL6+4Xg8cHt7y/EQFOQX283odTOmIMjXW9b6OSPB+KMDRFLCwJjXJY2ReLQYGPeI8z7krCGECZQJJMKPQCc+WusJMVXKRKM8sN6ssdaOFpJ5HeOen0aN3W4/fut7w93d3agct85FhcMEnuV0QIjgUZ08SFO/fNam0XhjeeY8mt2Jrvh8wGevjTMw0qXHwEX+YtifIo1BvC9S+4DRmjp+D8Zy4V5VlpNn5ShQapQMjHhdNxRFwTAMHA4n9vsjwdJUUtclZVFQ1zVaK9arNVVdBuMHAThiqPUQASZ5zKtovW5MAobDd1koenfk7fEbqmbN9R99zmr/GXffvsA8vIfjMXiO4fEGnB0CAKnVtPbyc5X5Oj4HiuQg4fK39P5sL2RhrT+koDpX7xKcnKXSWfw9p3TM68kBp2X46fzvEuw819an+r1s71O/PxI8/BK8n5e9HJ/Zvafux/efAp/GZ86U/4g/4fFayOd5nNMz7c5/z0HPJX907npqDJdjtRynD4HY6fkUYeocjwYTmJuXn6JoLfue9yU3DMjvpf4/lWs7XUmRlfcVJsA4pZbK+7fs71Pr5lwI+Fm/F/NxfownXjz/bXpWjCDLU/RjeeVrLPdc/dD6CzVNbXTe0/chXZT3c6X8uX3wY+jd8rklqBp/mCkh/n9/5eeYYLSOdh7vg0W+wiLkALLD0mFsH3nxp3iteF8s6cBjep6DJx/6lxQ+3jm8DeEsB2uix4BA2MDbO1UClm44Yv0QvN2jLaBFIUVBKSSFB+8sfWfo7MCAofMdp+FI3x8ptMa2HWYoMPsjd2/fBUVbWY9tNlJw6nrq1RWrumaIqc/cYDm9uWf16XPkxRZ/7+jvdtzZEk0I0d89nCh0xeb6ki9/72fUlxfB2FF6ChzD+1t8U+OuGvjqHf6339CVgrZYsTEtn6wtV5cFXK7h/oDsjrTvdtjDQKVKPqoKOidg3fDu+++5+/5bdq9eBcUgHoGjEJLaS1YEz5E1JVIrTCnpS8W9N5joTK2URqtiNG5MYbuT3LOk3WnvJQVZoUsKXVEWDZv1Fq0VH3/6EVI63rz8HS9++xWff/4Fq4sLVBG9u1xICze0LUPXAi5E2xqGmSGTiMqdwbR8/NENF5dbtPK0pxafsKfpMME5z/F4pO86dFURkJgkWf0995xI630UTPA+AMHW2Vn6qLYfsIOlkAVX2wuapgmKY+/xwoMMigvnDDgfoEupguGlV5je4hz0xtAbC1awqa+pb65Y18/p2j46jdyx291HD7GWYRjYP7zn+bOP+elPPqPrbiikZLtacXN9zfZmy8X2is3mkvX6glUT+PvDccf9w3v6vqXvW7pTNFKwA84OOGvAhVCW+MifeyKcFEfTBVpCFubXAcgBRygn7O+CoigDL+kJYSxdj3fFRJvI6HN27imlUIWM6Qz9TM5Pcx5Q9rD6063gteyRMWOcyOjV7H0Vva3cvMisS0/yfB86n/LPaS2n69yZuSxjyXPNGz2VM3t2yV9kfNbsvfDy9DmraHn+5WlkpsiYk7Foknm9T8ryyUlqyZekNhtjwlz5ycD6bCN9xBMW47b8DI+NX8+dz+H+vJ9Lnmkpr3xorkZ8Bh7Nw6LW6V44Xmb83rKuZdvmZc6xtKf4J6QKoZ9xMdpnUJqUaPSgGXYwCM/zmyDjG2PAQ6GDZ17CIxCxje582z7Ic53px4f692itjON1XjaZFMPzcX/8bOR7xEIWFSmS27LdoeJ5++ZrB+TZcZi3PQrqGSuVY6ZCCNJ/seT5+6nlqe549qQrOB9mWMg4hpNCLOgioNJlemtcNyqrN1+Pyes85bZXRCOJxRxZZwJ/lu4rcN6gpYo0V9LUDf/gT/+Qn/38Sw6nI8e7dwxvX9C399hGUFKC7XH9CeyRptzy/OaS9y/fcNrfh7FSEil0wK2iE6OUIWVM393ifBtlfmi28MVnn/Dz3Z9QbAda95L1GlRlEcoiRIvwUBtojppnvy/p94r2aBBW8cnmS7wpeXjXBoMtV1HIGi9MMNwcHEJqpFRY11OtCoRWWCtAKlRVstqu8QfHzq1pttd89PwjPrm8oe073t4eKFc/5eqjO5r1XwWPxKjP9ATe1ww9V5dbri/XvLs94g3UdcP+0GGMCdGJjKXrOo6nA816zdB2HI9H6kPDdrPh+fPnPHv+EXW94v7+jhfffY3Wgo8//pjN5QWrhw2n0462PdJ2x7BOcQgUuTtWODc5e42yug1h5d9LizIO4SwlFoug8nBhoQEOEf8DUDLwgF3r2KmBzYXj1nf8xbuXXH70Gb/42R+wWgmO3/2O9j98w+7Qsjs+4A73bNZr/lH9nMO7A8Prd/Q/P7J9fsHp1Vue/+JTDpuSQ2/puoFivaKqK/b7/Zi+2HvP/f0tm82GplmhVEHXhpQ1zaoZPcWttZGOwuF0ZLCG9XrN5vIZzfodp/17uqNHlsHbu2uPGHvC2I7WDFhnkSeHMZqi1JSNQUlPJzosklJoBtthnMVg6aXh1LfsD3v27YluGAImLQTGOZRKDEkgZU2TFOHhhhAKLQvmKYYy7C45KYrMEdJHg5oF/jH9m55LtEXmZ3L4MfDeuW5rcc3PTznWZ4xD+AHBgFLBILsoE48XnZu8QaIpiholNVIpmrLGA4MznEyPVoHXtNbSti2n0xEzDBxpKYuCstRUheJqVbOtKqRzOGdCyPuYUvKHrh+tGE+5KHKGLB3UKWejJDCeggQEOZSAwViED0CuEFMY9rSApZQcj8fgRW4HVk2DFCFvRcqHEoQyjSCEGe+6DjMYtIwWzWIi/DoegEJERjj+l4Q78FEREE6goe/ovR89wQUhx9hgbDycgtXsZC0V+r1er0YhLIFbyZMvHCiTYq/v2/GeNSYqJALRcMTwYrHutKmFlCihKLSirBSlLqi0pohtKJSMh6/DGjcC8l6EUKlCaowJVvGDMWyePaPZXvB/+W//99zfvQ35xyOI6vEUughWItm8Lxnds8x5+DI+s7we844ioSvzH7P74aeFdWbc1BMFTyCeG8NpjOX5HFzMy/HjbzMgKbumLkwch0hCWQSKUjtG8GjMXS2m9onJuCC0M3YvkZSYCzGskTQPUUB3yZp+GapyfoDl4cQF8705I11pqOPLc+X2Y2ve1JaRSMaxHYWg2E+xaMOop4prcfJUzj3V5aiScvlYCzGGCUn3RPorfcxHEaTYlDcsKQGJh1syzHHOL0DUafwmQS58tzHfnScoSdOexcNgzEi4w7iF+UtKTF1oyrJgtV6hV4p+MBzbE/f39+x2O7YXW7YXFzGscgGRYRDjGkoMNPNrPj0IJKfjnvfv33N5eRVAof0RD7z6/nv2h8OovJ+96plyXqdheCzLLQ45kUvp0//THk9rIZul/PAV5EL6Qhz2sz9nGpPfm7fKzxoqzjBx/nxxy6fyPSMEiJRv0WOd57A/8pvffMXFxQVffvF5ZKoa9vs9d7e3nI4nNps16/U6eKNlgno4cwJ4EJo50cVx+DOgYjYlIoSdw7lJsBNxX+MXobRDSKYQvivRkOitbN2j/MDj15HGhNBfddOw2+959uxZJCpn2J2MTqf0IF3Xczgcx/QgqY0IN4bEmc3iWOxiYWetS4JgtpoW7+YdeootO9vrSJeys8Q/csoY6dn4FyYhMbVsmS8unh+D6Ue6K4QYaUagnTKOWxnDqYfPVVUipcQYR9fuebjfobSkruvRk3y1WtHUNboMKVbGANcx546I4GXQg4TfpJI4Ec6W3p94ffqapt5y9Q9/RvXuOXffvsAdjrj9Ad8KsCH6jLcOLybP+WlY5jzA8h7MQZ+lV+c5QCo/388pXM9dqe6kABxzcT7x3FNlnVN6CTF5G+cKyPy5JVi3HJcl7/MUcPrUM+favazTe/9IEXsOkFwSx2Wfz7Unn4cUBSVXmCzfWY7Jsp8+8hlBSeDO1rMsJ1eA/tB1TkGal7Ps8zI8/HJdQk575vOQG03k6/vcnJ2bv6VnvMPP9siyjvzKgaxlfXkblnN1Dow8t06fAoRHg4Uz/Xs87o9Bx9lY+MzISogn5/fcnj0HjC/HbVlG4uGkEKw3a549e8btu7djFJIP7YH09ymw98dc3gfZymXt+08pZ34lbx5ieVNdQuTrGYSwICxeDHgMFoujp7MPHLr3dMMOfLTqt6mPwftzHA8RxzWXxc60Kh+n5ZhN/08K++DBHfgEg7E9rWnpbIuxJcJqnPC0bmDwAw/tHQ+nW/bdjlN/oB+gqC7Zrp/xyfqG63KLd5K269gPe3bDHffte+5P7xjske16xXP3Cy70BXZ/4rA/IsuS1nmE1qAUDuidwez2WOfRVUmxXqEcdO/vef39G8pVRVFUrK5KaLZ0xw5ZlHjRYaxFKM3Np5+x71tUGXIwl9ZwfH1LXW9ZGcNmd0C7gcMffsJta2iUwl812FqjDj3m/QH9uztE6ylUzVCWnDDBq8m03L55yd3rl/SnA06E819JKJygQlGiQ6hC6XBNhdiUuFry7nBP251GfGDMx35GVs/nVEqFlOGs6fse5wRaVlTVhtXqgtVqg5SS5x89pzvd8erFNwjg2fPPQRVUdUNdVTF8qAseyqZDegfRILOpy6iECzIOgFaOj55dUUgQBIVGpKKhbZls2vUD1kMRFQSTiP7Dhmvn+I6RF4+8cMq7mHvQHrsW6y2rOuRWl1phTQsxtZ7DU0iBIXqf+aAUL1SJROFMMHIuZEOzqqmKFVebG4QLHkEgGLqe337zFb/79rc0G0JkAKW4vL7i5vqCm+sLlJRUZcl2vaZpmjFik3XQnw6cdg903YnjcY+xXQgdaweCB7gdNcIyntPSQkrx5DwhnaCIPKZPMmp2jjiwTuKdJng1iTjuBkHwlvROgC1ifnBHYuYT7UqRGMMYG6yNRpZCBC9I5gZsOZ+WwNylwjE38FjSRi9EMF7Inv/7KEifur88gz/0+7Je730OhGR9m0dMyddr/i/Q1Sfat/jsEkATr5wHystMvyXv4jzdC6Qxn3iA/Nlz4xDkoGA0bGOUvXPn4pKn/NCZueRBzvX/nHHgkkfN632q7oQ3nWtjXq/IpUofeN8kr0zj8Lj9aU0/0dH5uRr/hZyzMhgNxdtSa6QWwSNyaOltH4yqCQpxHT3xpMrLiyoXGcJsu+jBvgzd/tR4f+h7/vmcN3Y2WEyK49FEabwvEz0R53nkc22cP5PSocoz6/zx8/NyJno14+1FRCgSSJHTmXg/KbuW4xmbNP49KwemMch+T7z40lFxmUYsPK+wWFAS5Rk7ETALNXqz539dzO+7/Jcib4//FBg3oFRsiwBjB6SWNKuK9aahqzUHe8K9fMexHShWJcYfaVvJwztJI0D2ntPhAWsHhJQUWqP1RPfJ+mPsnr4f6FuP6QVSapyHLz77M/QW3h8Ex9MLpKqwymBEwDOEBqUMVSPQF8AeTCswckflnyHvC6wtGPoCXSjKqg7KNG/xBoRU1NWG7XqNFZ5uGJBa4aXAaYmoa7Q0bK4uubl6zrrasju8hqbm7vgd7/tf4dWAa1tkvQ5nIT6GzldsmprnN1vu7vZYY6hiapZhGKjLCu8sxvacTgecsxgbUib23cDQDyFtSlVzfXXD7cMdr1+94OWLr/noo4+4fn7N7fs1u4fgaBGiEASFqR+dloLBifc/jt7iPG9cR20FtXcc8dwpR2MFzym4xfKABRl4CO9C2GyPou+Dk+zRHHnvJb8ejtz0B/74o0+ofvEFOEHz1UuqbsDYE69PPcUnf0i185jX79m/fsv2D36f7pe/Q+6PtBiOFqQFtWowMT94WRZoHRx1Li4u0FqPxl4qpThEYo2LER3TeSRRqoDolV1WDboMhqRaarwztG3Hw8MtrWs5njqOvWWwFikcximKGmRhsaKgIEZosJK274MhsDH0Q8+xPbE7Hmi7Dus9UgXDUHvsUSqc/UpJykJjhoCwykKgCh3C+FcVGMkgUrq6uFe9H53i5Aydn66c/s1YhLTvIs3ygvEf3mM/gLtGjjktqYyGiZjjfUArQVFUFIVFa4uUhuCx74I+zHmcCPypkg7hJcIFTF3KEhQMoqSipJc1tjAoJ6AwmCFE1N3vDtz3PW1TUX70nKYoQo5yIzHmx8ngP1oxfg4cS99HAo0PITxEyAkhUPR9z/GwR2nN5eUFnhhyuKo4HA6hEfG7lBJs8Pi+vLjAeRe9s8NAlWVBqYsQ6sV7dl2P8DB03YyANlU9WsBppRiAh4eH8XAbhp6hD+GO+6HHO4vWxXhAhpxO0RtUh3AF2KiAdh5jw6LVTiESmC/CQVWUUbAZgrWKsxYEFJE5MmaAmJ9pGAYG65DCR6FVYcyAVJL1ZhU8wiIYr5WkKgpqrXHDEIiNDUo7RwhFG/JaBQsuLxW9dTgEVgo+//lP+Xd/9e/5u7/9C9ruEMNRxbn1DpWYsziGuUdXfn1IKDjHIE0gi5h24JJxnxCes+Um4WbUCbiccRhF2fHvXDCYNmvezgg1xjpFBO4WIC/BCjMo0hdmxqPgnJQ3OYOdjClmzYjl+PFGIkKBAWA+3tOZNXt2VEDFe2KmxJzvy9SHACJMIKwcEYTU3qm/qXuOEc7KBGE/vh+6n4+ZYDTF9h5rozmKmxtfuBiabVpfc0EvMbBCiMyQZS60BGWcy8bOj3OUvCmllOM9Y2zMbxeVdlFpPgzDZJ0emVhrLCaG+BMIBjOEJUrY41M7IiMvQ8iR9Tp4iK/WGy4uttR1zaltefv2LYf9ge3FBRcXFyEckcjnSY5rZ9wL499pXTvnOB6PXF5eo7Xi++9fg4Pb21tOp3YCl8QENAQP0rA+0gH1+EqQk4jb4OmD76nradux5bWof/nasnkL7e651j8Sip8odLrvF/fTMgyrPTAVHu8td7d37HY7Pvv0Ez755BOuLq/o+57DYc/t7R3H43FUmhdFMbUhMSZnuxtqdD5E8shDqE+0QYBMBili9EpPjIf3Hh2NmFLu90ATEsAUwvQED+AzYxOFJGcdNzc3vH//jmc3NzMaPY6Lnyis0gqEp6xKthcXQPDIC1akgpTzMNGlafpyGjUJeBPzFGiU9HI8g5fTmH8VnD+bnnzh8ddI235MEZN4DpkSZgEuyThHeUj4NH8gYOhpu9MEEEWDvqIsqMqKVdOwalboQtEby+F4i3eOZtXEcFgVdV2xXq/G1DOjgYcPeSalF1NoyAgmCxWMiI79Hf2wY9Vs+Pgf/zHtm3vuX36P2x2whxNyMGjnca4DYUeaf86bd0kjljzhUzzCDJj6cfzp2evHhjnP63yqXT/U/v98ZdaHryVQ81SY8gR8LHMqP9W+H6Ljy99zXmvGo/xAOflcpDYmAMha+2jf/Zi2PxU28ykQc+kFnNc1GmMoibfzuV3yrY/TjczLfAowT4DwU/sjvbME7j7kuXSunUvF+NLYIAe3YVK0n+vPjEcUjxX+555/6ns+Rst+TA9EOr9o/1KGzMvL6/lQnUJM1DzV4ZxDKkaAqeu6cS0ujSbOXUsAfdnHc2syfZ9kHmKqlA8r6X7s5Z2JZ6Mk94iSyVMpPIVHxPBxXYgm5k1MreIw3tC7DusHhAqhcL2NgLWfypj+nw/K7M90ewSP0wPZ2C1KCmHQPVI4PBbrBtrhRG8GrNWUPtQQ+G0Q0uOEpbcth+7IqXNsRMNq5THG0tMF7x48KI8dLMYOGBuivEmlKYsKZSVDbxk6gyprekEwULTB87GuV3Sd5dh2lM4HozWt0ds1x/t7hBdQlaiqQlUVd6/e4xHUmzWFKqiaFUYItJCgAh8ljga3H6ieFRSv36He3eGl4PiTT7jvB7aFw54M/tUOZI8fDAwCryTvteRNpbgtNW/FAXEU7N68Cl5Y3uAQIAUaKOI/JQXCeR6w7LWkKzSDFNx3LX3bxn0WnAhGxdTI786VRNOeElEhbFCqiKH4a5p6RVnWUeZpePXy13z77VdI4WmaDShNtaopqwpnGb2j8AETcSZ4KktZx3R8gWdWHq4uN1xfXYbcg97GdelHGSWBAdYHg38Zkl1H/jVfoYFzTfJW2o/5uh1p9nzpj0XkdDXJjKcYgrOuKtZNE3LaOxtzJXqcBBeFaC9iVIQhAIDWepRQVEVNs7pm1VzTVA2VbhBeolWBc5a931MozXZ7Rb1q0FrFULIVdV2MRpZFTAOgtWRoDb0L3lB93wUPGTNELCrK3C4kSBAO8DIzqFQgYkgGIZDCEdIIAiKm3crG1uNxNpi4e6njWWTxzgAWhMBHft4YUHp+pk0Ky1halNV1os3js0ueLBkF+4m6jLQ4PL88B9NcAyFShffjPCfM4Rz/c/b9J3iAH8tvnRsDYnuWZ/5TZ27OL45nfZIDl+fSolmj0Xrqt4NpHBnnONHzXAE38Qd+NG71fvI8zdNs5vxFSrEXvsuQmiALv74M4576m/MleV/PRYhajnOSwVK7z53hy3N5SQOX7fmhz6neqcj5OOTP52Gyl9dcVorK1Gw8AiYn0UqjdYFXU/jeItKJFOnC+XDiCmlBhHziWodQtTP+WYiIz9nZ2OdzsZyXJ8fgzPUUfzjj7+I6TFjH9PL0fP552YZlO5f1fqidy7Nv/mw4B2c8Yf7buMmelqkm3ghSGiVgDMy45C09fuatOetPPK9sLFeR1klGu0h4jwiOG25u6BmwwaBfCA4nInBmo3wen5MxlZzKPkuB1JLBGBAhJ7aM568UKuh+hEDrEl02dKrCaImoV4iywkvo2yPqeM/JKoR0FEWJEyBS2gxBMNrMDKfwAm8lzkmEKFivnjNYS9NccaN/iih3OP+WQRpU6XHCYz3BmclLLAJfgKod1vXct2/ZCgGVxNoeLzVGCCyaQpboMoRSFxAjlSqUElSFRJUa4jl/+exjlLlke/ERuljjhadZf8Kb/hv+6rf/d77+7Z9z6gYui9+n8yaMeeRJlJIo4HJbo1XAHZMHf9+2iLIKe8O54AxqQgpPYyxDP9C2Mfz2es3V1RV3u1vevf2eb77+ij/7s3/CxdUVzWoVeOAYKSiwfRPeHol9dubO1+xyr3njeHCGXhQ4oekkvMPwczRXaLYoKgYMYkzHFHzUwTmBMwMIh16tuBs6vnn9ij++uaG4WtNtGopNw0234ffqjvv9jr9zOy58SXk6IHYP6EojsKi2Q66KENpeBnq6P+1jdObATzg3cH19Rdf1IVXMYKmqkvW6wTkXeE8/N3JPodZ3DzsEEmtNGB9Z4NFYK7Eu7M9CaupSUhJSQRVaYqzj1A1YHKoPuII1js4MDPFfbwb6oaPre4wN4dalS/ihYjAupr6SaBXOTSEUSpVoHXSXUhcxKrQl18TYpBsRJA1RRpTInkw0yk/YckZvhJxojWdyyjnLFzGVO9NrBa4d78GYEBZeRMcxY0L+b6U0oztu5O2ds2FPCoumQEmN0gqNQHrQQrEqKzRgigLT9wzK0PWGk4XB9QztwHAaqBEoIVFocv/6D10/WjHetm1Q/EYFQGKSJmYp5DBzPiaoT2GYRAj7WpYarTXWT5ZjSilWqxV1XdP3PeBDvnAvqetqZhGlyhDGRwDeumhp6hiGQCxyYADhRxBMRY86FYFoIYL1c7onAK00VVkGhZjz9H2HQ9BF7Ubqdypv3FDWogWBkIl4xER+rCyKoOxWYcMVRYG1hq4DIUqC13mDs25ULIRngtJPqSBs9H0flBxKInzI/SS8Q/rodyvDwSaixYWzFickFui9p95sWNUr/s1f/jv+41/+D8F73NoxZLqPjHA6zAQ5MBkBh+UmeEJwOAdcjvfPCQ6J2P4IkCrfwIz1y9kmD0rGvF2R8I+fFwxQthlzJcOj/vmJdEzVp81P9mxOgqLggc/am933jqTkzhnp5eX95ME38oVjs5dA3WNmMBD9uYeAdW70nElUa8zJy2Qdm8YiBwaW9YkIRkxKcDcKQlMZE6A/A7V9VMDLCYBJQlNQToe2DX1MZxCHKHnDO+swZsA4R1IQjkJUUshnDGbyGJOR4RMRrCXiKSkihFBT4KGqKtBKgxDBUMUngVFkYHgo++3tLcOrV9RVzSeffsrV9TVXl9fcP9zTvX1H1/dcX19Tlnqco0feTmmFjGsurBJrLUVRUVYlL1+8wBrL7mFP23Uhl3MGGiV7Wx8F3Hxl+fGXUPIUmtCnH5crcL6sZ6WlNp8RevJnvMjujuYXj/r96BIf/Mq4/p6uOd7K9qZPIHK+t+OcIqJ3fRhL6ywY+Pbb73j/7j2ff/4Zz5494+rqmrZrOR4P9H1PVVVstlvqqkIXBQLimsujORDpTKY4jntmCi/qIzOSmu3HPe/HeQjv6aIIntsp/2L857wPOVkS2JLqeiRthq8X2y0vXrxgGAaKophCw8MUaSA+XdUVsRuUZUGzanD7A8T9MbFWGYNFPvfp+3kBNe2l/PczzR7b8KErjXNezhwIEY/qmhbDrKaxBTPAIz0+GsbFZ6PXkA+TQVoDAYESMeJMoiGStms5iD0POkbHKQuaumEVw0I5D/cPOx78A6XW1E1Ns1qxWjXUTR3mLMDkwTMXgieQS1PixjCLFsu+f2Df37O5uOH5l39G/27P7pvv6d/coTqHGA44v58BbzMAeSEkTfMx8QYTqDOdR0ul3o9RFJ1ThAkhRk/xFKloCSKeK3upUD73e1IK5krOJc/zoevHAETL65yQ8dRz58bjqbY9CRg+8f3cvWA0Fq5zCvscWFuukakdjJv1KfDpQ23JwdElj5n+LUNrngM4vUv59ua5dNP7P8aDOV8TOWi89AR5CnCd7Yksd+S5Pi/H8ql9l7+bjBLOtWc5zueA3zy0++y5BT//mO/8YXq8NOAEnhz3OYA3H6NzSu1za13E88g6x+7hgULrkHbqR+yjp9bjh8bUe/+obVIEME4s3vlPvbyzEcQiqjcSKOGyoU18dY9xp+Ah6kKUIqUUViqsUHgZvM2kFLjxiBPZv8fjNAPSmNb1cl2J/PnIw/j0X+RLRIRanDMMtseM+1GjRUmhFIUogiwPSBSFaGiVYb16xnV9w1pXlEIhpQ5p3HwI74m1aB+AqsvqkrXawt7QnlratkM1NUaIYNRuPUp46rKkaAratmPoB4TzUDrKzQqxPzL0DosNUdiFZPf2DgRsLrZsNpeU9QoTw2ajJMI6xKEHJHpTIr96Dfc7bFlwenbFfm8ptME/dAjXgm6Rl2tY1/Rty2sl+a5U2KLi3hwo9p7D69e097fxvNchT7VPivEQbUsheZCWvYaTEvR4DibkrC6qOiqRg/F/4JEm2rHc42Kc42DMoLUOMkjZUFUNhS549uwGJzxv3rzi1YvfUSqFLipUoanqKqTa6wb6fsCYkHLPehfrD+vWGBO9dsLKef7shsuLDc6FvNpLvizQqGgYMQzR+ydKNNPyHEWa9E4qY7Y+n7gSGJ3LwM45ur6n6wekVNR1RV3VUQkVjVGjAgHholzBiOM465BSU+mKzarmYn3N5cXHVEWFMw5nLN452tOJ+/tbuvbEZrXi8vqSsiyRSo6RysqyQBcaIcAMfZCDj2E/GdNjbIdzQxR1PNKHMPMpqK6QPoy3T4PkMx4ewMYgdml/O5JP57T3bSw/8WVuHPhpv0cPNRPKnmh6PtYpE6mczoTxzEnnQSYHPJITpjMo0OHEL0w8exo3JwXRnSpiXZPQe44/PcfTjOtpsY7OKeM+dI3PLdIKpS4lGSY/W5ZtHPctsKTFT9Q60uSzAmGUTPMDPZ3RqfwlK3jOo3zeFp/VGQ00MlqTykje1h9Sbi7H77ESc/wx4DwLHmJ5hi/ryPnC/N1zfM85viOlH5jk/PN89zljpFk58axNRghCSkSK5iKTPBsNCqL8LUWI+imUoh8svRkwLjhmeRxSqjHya5or51zEfpmiGMX85+fGfsmb/dD1lAx3jrdIPNvj54EkU4/r9um6523P5fyJ7qS/T+3t+b3H9bns2ZwPS0Q/VJmtnYy3Sv05V3S+L1MdMjrkICbjgcRHSakQEuS4XuL4plJEOo+SnCZHJbYYN3I8N6WM2KgYFeDjXCe5QsqosE6pFRRKqpG+SqURUgX8FQW6QVRbRANq9RxVKESSv2wPNkTYQVXBuU+laKKZQs654GDodUybGyKNqKKm7Q74ek1Rrmj8BWWjcb5HlxEMsdFITQmcFSGdRiGQpePU7lBW4pXCE9IReBl5Tb+mFlcUskJHNVnXdRRliMgg8eANUig+ev4F10JQ6SuOnePFu7d0WH754i/5d3/5r3jzu1/xTHyMum4Qdh/qYdr3bhjYrmvqWiP2HdY5tFT0OQ0VYExP3/cMUTneD0OIDNH3rDcXXF3fUL78HbuHW373zVf8s3/2v+Ti8oL1ehP5tRIlFYaJr0vp95anRjpzlvtCiHB+hhziEqRgcJb3DPwhFRscWyQ1gqMP/LAjGMhbHz3IhwFhDQjP6dRye+gYLl4j2SKUpNw2fCSv+FNX8uY7+LvDW770V9wMLeXpRIGnqjSiGyicpyw0Xnm8DYaLzaoBPH0/4JyhbuqogI7h3aOx0TAMM8P5ZHBUliX7/Z6u61BKorUMUYF8MMjQxZr16hKnHWXtMcQc2IAXDuSAMR7nBxCeYXC0vaF3A4MJvNpgh2i07HExlZWzjBiws0ExDo6iFPgYdVKpAqWKYEASI2iEeglRAPBjxE4yvc9Mtk3fH2EUIwEa8dI5bfKPIpEuKOdUzqP1FGBJaz3DYBFiwJgOITqKwlKo5OwTFmNw3LUoEeQ4OVbmwFu0BIqCUgqMVvReYESIsC2FRHmBtgbXG6yUqCLI/7mx0YeuH60YT9c5gDER6WRR4GJeMwj8VdM0QSkejtyxnKRkBmhWTcxVHjzKQxgmPzHKkUEOCuMpXPR+vw+KobFJAeDp+hZEsBSQSlA3VXwPalUTvL8NTVMHRbcNdRdVEcKieii1wsU26Pg5AUiq0BAV1cHIKYV3dhQqhEAtCj2OQVpgzq24u7un6/owLlJjpWPoe4Qo2GzW4/i0bRus+2I4BS0lbjDRID3OQ9xIPiq8nfN4pTF4nn3yGZ11/Hf//P/AYXePtTbkso1WWT4qFFXsX+hFZFIQ0ctgziAtQZDxwM43Wep0xuDNrijAJCu28xspMePZPabNHPb1IrwRi9CqfrYsQnumCoLQlX7LyxzrnYCcZd/z76PwlFUVrGKm0GGBaLjINC3UR3EM876kDggRlf/JyotEZDIL4XQ/KoyTZ7dnUnjPhKgkxE8DE+YwM3SZ/RbrSQKrGoW00A5rTAAGYl+cDeFCrLWjB6O1IU9bOozS+A7R0zkJEqmuUTAY2zFfRVLKAHSLFO4jhB0p4r10qCsZLRjjeKTRFyKGZor1aa2Dd3gCFkfv99kwjPfGEZIy5BHXis3lJf2p5e72ll//5jfc3Nzw5ZdfcnV1zd39PbvdHmMtz5/dUJbFNM/ZuhwNJsS4CPGIqBjXdKeW/f7A0A9YZ7LlIxjPugnbnNZ4NoD5aPqEHjwlT5+TOZ8USrJ1mz8jCEJv1hDBos5xI87py+yBfP/mr/xQ64TIDA1kEGCYqkrCzbhTpRyZRgcID4fjkV//+itev37DT37yJZdXl5RVyfFw5HA40vU9dVWzXq9Dig2ZlKCRvU88Roo6ENua9gwExiZ4mTCCDxmeN35IBhoT3+pHA4ew11LkhDjSfh4rYKzTe8qqoiwKTu0JHY3epvp8HLtQVtPU+Lhnq6pms91yOJ0QyNEAR04dJa2DcW9PQ5HP8gRkjtM8j4Txo2CmRwJ8AiVSbY+Fbjfj+9JZlorK1mgEWXIcbprD0Kkk/LoocIwCrvfgQ07JwGfM114KSdgPZqRbO7VH3+nRS/ziIuSxxHn2hyO7/YGqLqmrmrppWG/WVFWFV6nNgZGcbW0JSImTgeY9tLfsTrdcbj7i43/0R5jXOx6+fUN79xbfuuC9Zg2FBO8sPoo3XoT9MK43kpFN7JMDMRqsnQEVPWPKB6mett9cAijnFHNLz5GlALB8P79yYCt5r+QKxWU5P+b6IfD0XDnL8Nnz8ZpA5HAcJeB4ngf7XPlj5IKsLdMuGCdvAnHOPJODsedC46d25h7iiS9P7Rmjy6QVsVgLZ8+XbC7zfuZ9zD3T82fTc/l8Tga8T50t+bg/0agz74xjHccmN6w49+xsjXpmfZldftGCxR5Yfk7fUx3LMZMxzLDNxzQ8PNafr8NHoKiYlGTjWmHBEvmkrFj2dx7aPR+jfPx+7JWXM/dun3heSF5QEVATfvQYT++OAnJ2xvgz9eTAeD7OEPgEouyVgKbAXyd5wOH9XFnwn3MF71kRz/08fLBDyHxfWZzvse6IsT3GerzX1GoDqkEUa2TRo9SAlALrA71Q49oXRIFjXCM/1Pb85zldYrbmvZdjWOYEeFrnoqdSgRIVpWooCw1SspYXXNbP6DYtXX+i7wZKtWFVbdDCIXEIoVFC0fsVjaq40JcMdY/0ilWxosNw277m7vaeh/2BuiqRUgfjfWeDgbvSFJcX4Qxve0zbYwaDWDWU2wtO93tsO6CExm083e6IqgtWFxfcfPopOIk3wetZS4lsDRwGxHqF3lbIl69wXUt303CsV5we9lw6g9gFrIErjXq2gq3n4XvLGw9vVcGaEms89rTj+OY13f09XgiK6CWvnadGUBNDDkrJQwk7DUc8J2PovUV5F8OUBiVKMnpKtH1pLDSud+fH0LplGbzFq6qmKhuk1Hz66afs93tevvyW9+/esmk2KFVSlOGflIKu6zidTvR9h5RgfDB8VkpF42YTjd0kUkk+/vg56/WK/vQQ5dTA16SIHiLyMElJ3TQNOf/ufUzplzCXD6zb2Volht1mOgvT+CT59XRqGYxh3dTUdUNVloGvSw4LqkCWBVKFiAzBi88xDI6+H5Be4Sp4dq1ZVSs29RaF4DQc6doTu4d73r1/x5s3rzi2Rz766Dl1UVKVVUhzJxJND55XxhqGwWC9w3Y2MgoBdxCRfwhqZzmO43huRl4x4R5eJRqWlJdhHOwoMU0yuvMO601w1CDgHUIQ8nSSMAYfjQZARUQ1KVyW5/vy7M4/j+ekn7CMRP2W5yCQreVIy7wnxa7J8UsZeX6X+nym7iXedW7tnOMVlzT/Ef3MZO4l7+a9R4bFN/FqZ67l+XSWRo/wTmrXh/mI6bmJp3ncfjEb36d49ZEnYcIncv4o4cWjslaoD473cr0seeC8nalOKWXAoSK/kfMd5yINPaUYT0vpKR5w7LvLv5/DtABPiDDxA7wcBMMS731QJiblZBRSE7+t4t5zgNIS4RWnU8fp1Icc7wq8n5SbqYwR0/MBQ5aIoETMxuTcGD91/9wlPlDefL+kEN5R+pjNdRoLBz5EZJ2NeZI1orNLiDg5hfpPazRrFcm7eon3wlyuDO2e/goxgTPTmk/8coqcG7/n70BMPeFAPd7Xs3HJ2jPyu+mXJ/gsG2nibH3HtgolAw6qUmqUOUaaGiuVQovoICfkOPbe+2A8me1146EqgtOQEpMaWykNQobUPULjyxVq9Ry9rVHbj1BSoIYTwj6glaSpJZQaJyQCPzpJpTPIWhsi+FpDCMUSIpkIZTicbrnbfY/SHzPoHVbsUKUPIdq1gD4MpPEeqTzoYIgXUodAvyZEA0JgCNoDKwh48lBR+R1rvWGt1hR2FbzTbUVRego0WgsKCj6++YKiqbm9PfLt99/x17+94yRe85d/+8/51V9/hWh7Lj619H5AeBVDmCd6IejaE9tNzcW24d3DibbvKIuCNuq+hAiYn3Uh1/gQleNDP9CeOo6nExeXV9zcPGO1ari9+57fffMVQgguLi+52G5ZNSuqsgoRlGV+tkYdgz/PJS3PFSll9FKOxmtCMgC3tkOzpUGyQrJCcOc9DomQFufB+IAdYgy+O3IwgroHP8Dub35J8X7D+vkzZFNQNZesq2e87wX/j1/9LVwUSFquTi3FqWe73dB2HaX11EJyxIINRj5SK6w1DNYiBBgXjIQcIdJmUVa0bUvf99G4IxmTB7pYVRVKKbqupT0duLzaYIaWbgBRlKzWz7i41Hjh8KLEuA7rgl7j1Lcch3t6tw9Ou9bQD5a2t7TOMhgb0xu7EOY8Yrlhzwu89UjtMINDyjA3pQ1ykxQqeP0LDQisC3xdnsrTZY456awnO4NGAjPSGT8+l38m0d5sLQSSlDHWiXCMD6SOMAKE6TQWEcMaBsPp2NJ3B5RqKfSALyuo5nI9hAilwdArmHR6qTEuyLZg0TLQXuEEVoBUoFRBXVbYeo09nfB2wHU9HlBVkUkJH77+XorxdGDkloEjIyFFTJMTFKqJMQFBUZYRMLCRKQ5ee8YOdH0bFdQNUgq0LEfFm5Dh8NdSB6HFCZRWCCUoS7i8vEYIQV3X8HWaG8/hcORwPLLebAj8vUAqjS4kfd9PAx7br5VCq8kjvNDlWJbBUmiFVgp0UB4aY0BKpNacoseelDKEI9eSpq6pKhXWjw8H9AjkIPDGcdwdKVVJ0zTUlcLVNUDMUR7KK6OXuhsGVAy3PsQ8yt477ABucJRlgRUSpyWddRjr+eL3fkrbGf5v//z/zHG3w1lP23ZUZRV4ZWtGCKTQCkGc12y+A/O0WARZ6GcfGTQ/A6jIDu85yDv+nDZhpAgTkMQMBJzKOcdACiYMU8zfY7JaEVLMhCGf+jUqLXLikRiBWScCoxObk8C+dA+IDH2+5hlTCoxK6ixXGUwhiHOBzMf82bMx8j6GAbehnyn8jffTvaylfqRM+ViHcXU+RCdI4eFdnIPgpZ2F5Y1rdRgGrLEjIOG9C97bJoZ0FHJhVe9H4UEwMbuIZDEZx0vKmB9JUdT1OGYyWiGm+UmgrowMXajDRu8vGe9FJWAm/KW/NhqKuN7ECBMhJcEwmHG8pVRYa2nqmq7tpvEizs/IwHhsFiJfRARFIHj+/Bn7hyNFUVAWBc8//pjdbsebt+/oe8PPfv4zLi4uubu757A/xneeh/B4I+MxSlTB/yc7lAK/HQyG3rx5R98HAwMk6FLjT54QPWHaLyL9J9LajUBH2jvjkhHzJRQPxVRO2hMfvMa98aGHlkfsot4Z5J6eyoSO2Nb5K0mIeqJRs37GfSw8IY8mICYGQiQ6QqIHaQ6C6i+tl4fdnr/5m7/j6vqSLz7/nM12S9OseHh44Hg80HUtfd+x3qyDwYQSkb5NAzXSjlHgC010zgXhlTiDYvobGjnRXSUFTV3Tth0SjxQTDbMu5EofhepHebEn5sc5x8XlJbe391xsL0dGeKQjIzPlKbSmLAq6rkcIzdX1M16/u8X5EKbNx/N/pKE+ChlpOmT6Qcz4gyR8pbGfFEueSEaz+fEj/5Xfi02crQ2fp8qIa2e2Cp0bxyanH8CMloSzcVobPi6a2JrxDErnl/BizCMPIJF4r0egkEQvE413gWv0AnzIkMIwSLr2yG6nuL+/o6oqmlXD1dU1TRUi7Ly/fUDc7VitVqyaFevNivW6QemQN3VEaQihMwWO5LnuZZiFh/0bdrs3XF5+wuqTn6PefsTxdy8xdzvU8Yg6tUg/YBnw0mKERbsC6UGIcJY4F0BtvEISUtJYhtFjY1SUIhd0aD7W+ffEZ+bhw0fQS8znIleQ5te5EIr5GXwO4BlB04X3Z17+DwFCT5WZl3sOCBv3XtojArwTgX+Nlv4+CT4ZeLTsd1AKTmOXQHCRNlIO+PnRTCgqC5MCewHWZOOW93HG0yw9jYngczoznR/3fYqsBBHG949Dt+We4GkdLeWP5bN53Y8A2myscuBtHDchxohWqT95+ROYkJ8T8zlM45HnU8xB1/Edl81heDHsl3Rmi2g0IqYyw7MZPysfG1QkEDjVLyNvLJPCIl8okTCfG+vH8ziNiyBPtZOKenwIC5H6HPgs5yf6nsYDpj2Rr6nlnOX9y+9ltc0+ht+DJ4AEqqrC9CEfNH5S4s/40jgkPjX+zBxPsgtjrkCUwBqLj4pJoZPBZTo75v39T768gyhr5DIRgLOp5Q7rBqDD+x7jegYT+AGhBdAg1RalTgj5MLbLueh9lJ+zibF7YhyW98ffs2eWSicvNN4PeBvy3TrvQcjgaaQapGoQUuPlgHVgXQFeU9CgVcmmthRICg9WaYwilOUtxhmkh0YXNKpAWwWDZNcf2T/sOR5PaF2CVDgpKaRE4RDOcjocUE3FzXqNKGu6Uxvylr+54/KLzzCDQXaGy3JFcX1DeXPPxc0V1fUlvRa4k0X3Hq890jpM33M8tfSlxmPR7+/xWnJ6fsmd8PSD4bqzbKxHr2rss0t4XuFf3vLt0LNTW4Rc0+K53n7C2/e/5vT2lv5hhxBQUyBcj8axEpqGEu8t1nsOVcmplLTC0xlD7wxJTZDktHNn2VLhJJUKYFY/AEGBVZYVTb2mblYIIfjoo4/45Te/5O27twjh+fzTjyl0iVRleN/7kE7veOR0OrFpqnDmODvmfUxyrFKasii52G7QhWJoGWmYEQLn8vVu6dqWYRjYbDbRGyidm4kmxh19XkCYX2KiBTlVyZXixhjatsX6EAGwKiu0VLSmx1mLxFNqTdlUiFJFft1hXPAod84x9B22h+PxxO5hj+vf4Yzh4eGW169f8Pr19zw83GGd5dPPPuPm2RVl0QT8CR9TZjm6vg1grwchFc5ZVGWDHG8lOIV1AmeyiEXe4XFEnxWst4SQlRaHiR6jJtApB9JGekxuLB/koIQPFKqg0EWUZQuIihWLxWERwoAY0EwGRIlWTbzbdFYkI4zZ+Mc+uHGeINkBTRFAJhlgPC+J9NlNtGpGg5Po4N1ZOrZ0Alrybfn9scgo/OQ0cPlOeiY/Mmf0NP3mfTCQz87EJ/nZhYw3FZy1+8y5vuQhJ5zscT9T+ieY+CKl5hByzruP/HlqCCCEmhlm+PhOMhD2C9oU6pgU5h9Km5P/hQW8wOTZnuZVnTHMncl9WfnWP3a6SZWItCg9ozyZ+gc+OmBkcscjvJJHnyE4mE3pBKd5THTKGINxFtUPY0TUkwuRR3ES7yTWCKz16EIF/juOtZJq5KmHoUM6OYbK9rEfucIoX6zn5KYPXUte7dweSnL98p0lLy/OvH/u+zkZL+ENOe/k/GRAZCMem64Rh4jGRulMxCcjUsa/+bXk89IZktZdVWQ556P39civj8YLQQbQWof1P66nab9oHYwHPYDzQflNNLrAg1IUVQlKIlURQhaPcomayYJCCJRUVKKKodNTqPWEkWW0UAhQOqR08wTnQxEc09IzSoG3gq7sUesbyotnFNtPqCSoboc7CazvKbRn8B7jQ5pL4Zi8dFVwCkxzJQV4TiBPIC2//vpfwU8tP/loTc+33LV/jfEnlJdIIyjxIYqxBIvDFUHXgfRo4TAejg8g1Qo7GFpvGJRFlAIre479W+5Pb6ltw/PVlzyrVnT9kfZ0RGrBqu/Zbr6g3Vvubn/L33z9r/j3v/yX/M03v+HN7Y6Vgj/6meD3v7zm84vndK880ouAD8mARQrvGKxlu73g+vqSF2/33O4OrC6aGBEvGr+okA+7bVsGM+CS13jfsz/s+OT5Z1xeXnJxseXlS8HL715wd3dHs2lYb7asmnU0rlNzzEAIHrkBn7lm+1EQUgsTUgs7ZznEqFUCQSkkK1FQe89uPLcAPAYXjCOc5XC4Z2UlBs3xdGK4fUUhFNq2yEqgN5dcXG+4GDz2+YqH0nP75i33X33L6rPnHPcPyP6Gai3ZYxCDoVo1tO0Jaw1aS66urkaDkJC3W4GH/eGIlJMS3PuQA7ttW1arFdvNBd5a9vs7fvEHP+Pu7p7bt3dcNAVX20ueXV3RtnuEXCN8MNzoreGod6hOcugdfrABB1OSpi7ojiHl8yhneoewfoTppBBIoRk6i3U+5EiPWHHQwciYazso8J0NQNrIIzCZRCJ8jPHjgyHI4ux4ao5zXClEmsiej1DqEy8v+BM5RilNcqDEMQwGbIuQJ7RqqQuDtw4zWIwLeo0QARfKpmS1WtGrjlIVqELj8PR9MGqwxgTd1WBwroehR6oCXazQTY0REvfwHpxACSi1pl2e409cf2/FeGImkiXedABNeWJyUDMNeP5M+l4URfAkt8ESpqpCqNYcMMk3cs4UlWU5vleW5egBIAgJ2IWUIRxC36FjWPLVasVms6EoCkw/xHDKYrQcKcuSvu+p63pcHGmS4uyPB5VzDi8FRVmEUCLx0Cp08FyVIxEJjEbOKKYQoGVZjv2rqmoGCuUMJs4hcIEgCsZ8yaosEM7hZci70Q4dRbXi408/4+uvv+Iv/vxfsXu4pW97rHMhL4GSnE5H6rqJXqhqnNMZsSTJDFMIy/HvOBxPCwlBnfTYiysVnDZgIpgk4DMrR8S2TO8lpYgfPy/rfcSsRaLjUvudi4Rjan9gBiMYlHkVzS2PQzsTs5rXOwrrGZCaPqdn0+cQZjx4FCb5KPUtMVrTexMTl0K12RhCbmqjxwwD/RAFWsK7gxnG/ZkMKZKn9ozJSWCAmLzMEuM0RguQQQBS0Uu7innqdFHMQL8kKJVlEUKfxz5NoGvy2poDGN67yJQmpfz0jMVB7G8SNgHoF/2Ih4cfAedwcwJSprmx1uZTiveeO+5IiaETNug94+cRI5zhr4FZ/e67F2P/V6uGq6tL1usN3sP797d8/fXX/OIXv89ms+Z0atkfDpRlxfX15Wg1nUDq/Ap7KNDNoizou4H7u3v6rgPhkUpQVTW73QExQl/go7esIFqjifGXuRBxRriZCxmTkPehK7XzQ89O58S87LyUab2LR8+chbZmbZ2v56dP8NTnvL7YC//Y6y09k+baRUbw3bv33N3d8+mnn/Dxxx9zfX1N257Y7Xbc398HEPDigu12HZWqo4kFkAxzUhWCRy3yjpBXxk/rcFwjYZ0WupiN90SHJq9xIQlKWrHwn87O4cuLC7766rdTGHURMb1F2VLAdrvlm999h3VQFBXr9Zpu6EgWvkn9nJis0QhpGv0RSBBpry3nPZ8D/+jDCHgtmbyZwioT6h6vjfydJEj7EeSYlAMpBGOmxIZptYtMmRDpaoqmljd5fF4KZGZxKRM99H4cv+RJ4KyN6Wgs/dBzPJ3Y7UNu+6Zp2G62rFZryqLkeDyy3+9p9hXr9YbVqmGzWVGUIVJGipSDj8bu3kf7EBnCngF3D99zt3vNdv2M+vefY++2tC/f0t8/II5HlJNIO1B5hRMCJ+1k3U3mrSUDwRF+CnmezsPZPGUA1FPXeQBlOX/ZnGd/P1TuOe+RH1NPDqqdq+OHgLpzvJD44DhEO3wX8qWJzPjl6e6lyCF+9u8cbz7ymXn9iyHPheinxnQJfJ0bhwRwLsck8YKJ3w35Zt1MUZvzxOeA5iWItmzTaGCR8QtLPju1USzOyHPzcw60y5/J11X+23L+l2UsvbaXIeLTle5bP1cs52OUyiqUnvGrwIxuntth53iCZRumY3weEWQJZKb2BWt8HvGLS9liWde5PZbP7XkaMX8nRd9K7yqtR2XJuUsIETx7nri8DwqLZOgk0tm6mE/vmXLa8vejN2cvB4gQgnAMVyxM5IMt4PHC4kTLyb6mMz3WroALEBcgVhjf0/aS3qzw5ceYm7eI0wPagxcGqxTCaQQlpR8IpQbDnKBsiqfvYp4CWBPWU2CjFUiBEzJ4DgmLFT1WdAHU9RUDMNgD9/fvOagLtJOUZkBLh0PhhKM3J6y3CB/5WVlgippeCDQW5U0wBDQu5KQLmSRRSrFu1hxu7/HHlsNux74/oS9W1GWBksHTVyiJqAukcwyvd+yvoFo1qM0aJSVvvn9NebHlcrNGVJa+Hei+fcPlz38awUpQDycaWdIVlqH2XA+G6nDC9EfWq4+Qv/wbVocX8NlnnD7+HPf9gT8rWv7ok5qNvUA4hXLA1ydu7wylU1xVUOqBrvcYIWm//kvu9nccfAgxX/rQU6lKtBfUztIgGFYb+rrAAae+422/h5PFSkUhBBIXFKAwyoe58VnCI6SUOAzGW6ywFKqkLBo2zZbtasOqrtGrBrUuefGbP+fu9XeoYsXm2eeUTR3Cg3vJyQy07RFzbNFS0596+lOLMz11rTmdDE5UKAWrWnNzXfLx8zWndo8Tgbewka4oAUIpnPcc247dIRgjm2ioLSKTLGUM6x0BRJXTqKcuGz2eSYY8UQ4fTADeBotpDfteUCK4XtdsakXfHmlbg0WgV45NY7m4hnLVcDy2nE4D3lq8FUhf0axWXF48pyqvOLYn7ne/4f7ujlcvv+PFy+9oTy3rZs2XX/yE3/vp73FRb4PSwNlRwTKYkKdUqzo4mqT+DQZvTDBmd1MktoQlyBQaN+5bHVMqaKHxPjqDZN5sjOcyI58qCee4sYbj4UhdryirKhiVRe8+7yxKEjGVAueCUi6dS/nfkbS5EdINRmP5+ZHYZ5bnVeI8p5lNlF/JEL3JecbgGiJ6zc5olwDceUNGrfXsnrfnz4QlT+eCn9zYmHPnJ+Kx4ebs7HCOhEml35fPpWeTUjlvQ/7OU+3Ny3vcxsc835JXeqqex2U9HttwV46RuEZJMMoGs7Mlkxd+CAfIedlzfOuSH4tfsqZOn92s3My5w2f9WMII2bjlptjCi2AgvVip83GcdyukgZZBAR6VAM45lA+OTMnbEBnlRy9wznB7v+Pu/j1df0QIh4IQ0NgHRYtzYGIEEQBrI8LhASxKqmi8EsLXze0HgnyRDLzPrce0JsMZMhnV5Dxv/k7AfRNvlLBRgZdBDk4D7D0IO5zdCx4f0rGIMOZKFihpGeLzQhZ4oZFC4WyHkhZwCK25/ugnrK8+Zxgs1nYM/YHj7iEYJfuKwT1gzBE7WCqvMe1AqVUMKx481L1wSFMgVABPvHBIJTgde6QsqFYbytUaWRZo2aJUCaKgLFc09QrvPe/fvQXh0To4xTV6jRMdQlQMpsPjkVLj0VSNxVmB9QrnQ85epQVFkYidBKmRoqCptwhXRFnLIXScH6EZYvS2RCSdDsak3kUaBAwxx7KUAimCkYCTYa0IHfL5+ojdV7oMnrBImqqkvNjQ9z2bzQrbvaUtVpSra4rrjxlu/4LOhXKSO4i1DmcNha4JBhkKITRK11ghUKKg8iWq7zmdPJ194HT4O7y5ZbXXrIDVAMoVGOPpnOUkDeKmYGgI3rrKU0jJtWsQ6xP7/ghKoIzHdeCtp24EtrD0Dh6GPYP/JdXFPZ/rfwQPFf2+5fhuz5v6O/5ff/m/5a/e/RXv39/T7SyFhv/1P2343/yT/wV/8tOPGfSBv/z+t/z391/TtD9HCwdiwIqBHommQQvJ9abgcqV4aSyi0EhdYIcBrSRKCnA9ZjjQtS1t3VMMHUOvORwst6cToqn4+Iufcvew49e//Dv+4t//a/7kH/5jbp5d8uqipn5Tsa0u6I4dPUNIvSc8CAfj2bbYl2fovQziBy9ki5QFf+Br3mI4WsEGyadoDn7grW9xwD7sNDyCTsDDMOA6hdwoMAY1eD5ff8nDi2+5391y8dE1daNR7Yn/2aef8m+bNe3DLceHjjt9or/5hM2f/in+199R1G8YhOYoaioF2oXIPNYZlJJ03cD793eUZUlTl3jrOB7uMcbx7NkzvLecTh3D0AMCreUYwWQwltvbA/fvj1RKUcrAg/XDCl1/hharMXqnswZhe3TZoMoKfaop+ntas+c07Dmc7ikj/9oLi7XQmQG8pBAqpLqxAmtC9CFZaHCSoYfD0aAKS1EOoE8YHJVtKHWNkwKpQEuDkgqvFEiN8kMwTPSeFCFCCQk2RgvOZOjI2gUHK+8ZJFgl0C5EplJC44NVygcvkX+KaXrEFKsnnDlesq7XrEqN1h1edRG/cEhjUU6EPS8FjaiofIF2wZjBeYcVQRFu+h7vPVoo6nKNkzVFHQx/vBBBZiwF7brCSDhpTz8cMafjhzsRrx+tGE/gZr5Zcrd370Oui2Qh/whITDzC4vRXWuOJymwhOJ1OKKkoo5c5TJ7qo3IxTqpUKlgtzRgbWK/XVCkkMZOi8nA48O72PV3X0VT1mM+4qiq2FxeoQqOZFNfWWqQPHuKCoECVWo3CI1JQuAg6eU9dFgQDsMgCjQxiYt8Dc1CUJevNJuSjjWCJyfqoYh6wwZgshGuw+vJYTD9EpaSi6zqMDay4R/PJZ1/w7fcv+Vf/8p/jHZjB4CNQoJTi5cuXwdq5qoOHvnp6CTxSiqf7gXMZ+z3eC5/G7/nzPuZRIAqouWVoeMaNgFNiPEVWbuI/yWuZVzmttQi2pvH2WZ1k9yYvnNCNJHwGgdIFxtj5MffOJABl4xAZtpDXKgeiJ2EjKLLjOohKYGMGjLHZdxNyA495uoJVfAo7m0KXOB+UOBKRMe4LZlMEqzul1Gi1r1RBpdTIxIuo1FFSZh6lQejVKd98JjCJCIwl73XrAtOcz33oawjRZ8wwm9d0jYogFnMR5w2Cp7bzySDBj55G41wxCVKPBJRszeWWvGlcRkWdj58zAVlE4j9bW2c+TypOP4L5QoS1vd/tGfqeZ8+fsV6vsdZyf3/Pmzev+eSTT1BK4q3j/uGOZlWzauoxbN200j34FJou9FRrTXvqaNtTyMUjBUURIk6UZYnzwWtoUlKH/TYqYAWEXHB5Vx4LzpPAOA3oefA5v6YBfurZH1Kuz8v5+1ypnSL7Dpzp27n2TGschMjrj8IYSQCDRJxCHyXDMPDixUvevn3LF198wbNnz7i5ueFwONB2Pd27d/R9z/X1JVqrUWj3PpwlyadhbAuB5hKBjrCkPEvm1BNoXVEW8/sjXYpevN6PBmM5HUWIMaKFAOomRG3o/r/M/WeTLUma54f9XIQ4MtUVVdUlu3t2dlYAxAq+WSzNaDSj8XPiA/Dlkq84AIzALgzDFcCo7W1VXfLqzDwqIlzxhbtHxIk8J++tnqEZ/VrezBPHw7V45P9p2giX/uBMT+0mcHl1wTfffI/pOpQqmM/muFzfKG7h0dk+GlHR32dicoUMY5D3WLz2RgKJPB9RGnA0n3EvRuH8cHaM1vuR8GJ4lvsVocflSOEzbgsJ/rUf4L4omfZnNJiI3jXxDhqLQDJRGfq7Ld6hMocBQhGV5DKM4auH+yjSWo6u6zgcogFGWRTMZwvW6zVVVdF1ht3uJUVRsl6vmM0qVusVdZWEns6P0D+iotV7H0NSICB47ravolCvhPWfPmfWfsz9H37AvrtHHjqUsQQZYamQiaLOXughTWaIHurHirHzZ0M/5CcELKdgXqfplABs/PmBUm/0/MPOpYEGHd+Lp9p/ijbOaTwOx3frKQ/YVGYseFTv+Kwb5xrOwUz3jNs6VrLmO/pD+z7u3/TzWAj6vrk5JUAdOvkwTQXo47E9Vd77khSDEuGUwDfKaI77Mx7Had/P9flkH0d/n1qPp757LF/MQB8HcOpJNd1LYy/2PyY9tkZTJT1PMJ6n/DlC6mYvM3W0bsZ1jNt8rh3j+R/zo+cbT+9BKESC9+/vntP1SCFPrss8BskkIV+oAzR7X/BgITXe43+XlH0CIr3sCDh8MAQsISQFOQ5LS2cNxgFBIWWJUnU0grIgRYHWM3QRCFLTx8eAqJTyHpQ8SR8+bNPQx/dmIhpqZANWZEA6i9wdaHYbulqAkihdIISm0IoQope/IEKUK6XxMAi8KdAy3rsiSKT0UIBSAq8EnQpsd1v2+z2dMShVpLPc9W2SSjKfz7kzGzZ39zRNQzWbUVYlT54+5e2r18zrOZeXl9x8/BGtFcxmM1SIcaEjORLlAZpAEUA4MEFQXdYU//uPVJ1jP6vYr0rCds9XZcFKK9TVEtqAe3nLm69f4UXF5foapyvapuP+9Vv0xze8e/mStjkggkcl3qVAMBOKGZpKKMog2CuJqAqC1nSmYd8cMF1HWRQUWke40JGx9vT8nirofPDRKyzFxi7LCqWjkfTl5QVd2/L73/2W27e3aF1TlBV1XbNcLoGAMR3OGaztMjcyEKqpLdZYUIJC11xerlmtYnzx3lAztoYMVWutTeUO6BjvXYOnluVYOTMcX31ZkSd3WOcwxtKZjraNIZPKqgQR4dy71uCVo1QFZV1S1xWqVFROYLqAkwYpNFW14GL9hFm9AgTGRDhU7z1VVfP8+ccUumC1XPP0yVMWyzXGhRgCI93vUmrKUvdnfi/j8BEpMMiIDBGCOkIOGaeMUjb+GaPyxJ9j78lsSCSIyAHSSjodhZPO2riubJfkFX70E5UdItGFQ6ihY563JwVG6/F9d+exTOY4b5YpjI0hxnmP8rtj2vIUTRNCQJxZXtPyxkrec7RRpsnO3fHhxH1xan0Pz47pynF5p8offz59Nx23+5wifEoTPHZvn6dxBx4vMJmbEQ098E2jtpyo91x7TrbtA+m3no18hOYd04pTQ+BpO6a8wak292s4fc7vZPSKwbt4QGC01rHf72nbJp7z/XBlpxBP8Kbn0XtHt2EDRrRyHNJJvPKn+YUR7zJeQw9QlhjFvOX4jpnKFzNvfCpfP77y4T3Vt62XLUDnLYWGaD4miOYq0aBI4mhdgyor1qtrnn3yJ3z1y/8K5+DNmx95+/p7qvouwtdT4OwC0+1p9g1dc0CXBca2eNsCUZEd8OggCDbEWL8iIkxqPePJ80+4vHnK4uKCqp4hnaDpOopiRl3PUUrw9Te/YrZcElwM/1gUBaIoEaEAdDSCUgqlSgIKpRxBenSwRItJGY0LQo4DnsMVeNquI3Af+XI0ihIpAsY1eExUrKWwr223R6KxXYR81loSpGW5nuGCjfdkkNy9sWntiMTzRxpBIRAhwf0Hi/AdlbB05sBhd4dSDfMFXFU3lGWFdY7gIKR41c45lI7OhHkt6KTnCUISlIyG+d6jDMy6DeVdwHf3iP2GooBW+uRRCsEHNCDe2kimhRDjjodApxvqKipuuy7Q2oBXkRw2XSCk8A6FgtZ3fLt/w/VXjuef/gPsBn747jf8/vYvKNRLvpwd+Je/vODJ5ac8v/lTvnr2EV9WF+zNt/x4/3t+OHyLX3+KuM/rMZ952ZDPMZ/PubxYsZhvQSiKqkqIL3FRSxFpH5fC/+SfpjnQHA7Udc3F5SWr1QrnAr/57a/5r//5v2S1XDKfzdBaURTJGdPaKCfr0SzHp9zjMpLIJ3s6AZ3UBCTBwWsMFZoCSS0UM6HZ+RiiWCLwRD6w7ToOXUc9n9EKeCEcvxENX/3iC9xaY1qDP+wxruVO7LGFRB0MayyXM0djNhx0x2xRIzpH2DX4ywqt5OCwGzxKyR6RSIjoSCSLyH/u9w0hRC/xaIwf5yHrHUMIvdxus9niOpNo6IjIaaxnfXGDc9HjOSS0G+8NyhQILRB7gds7Du0BgaZQAWsNruto2waPpywj/2Wdw3aOYH0/XhExK54lZaeYdRVF6dAq4HL4ZhH5wpB4quA9JJ2klOIobM00ifFdk2iwTC/F8GtyJHsd7ud4p5ymG6I8dXgj+huF1KeIqq2FpBCaUgRCUGgRFeGhCvhi0MkVukBLHQ1tkrNN5yzKWgof21jpkmU9p9QlIUR0JmttdNbSDqM6XDAE6xDe0XTtg3E4lT5YMS51tBJ1wcW4UIm58glCwYZ4kQqR+UTZw6tHwfMgsBsmg/4CFUKwPxyip5RSCK1iPE4BzkcrNojKy8EbG2yy+h6TpQjQCTYEIiGhc3wtIoHRtV0P2d51Hdvtlru7u9hXKVmv10eER1YY5jKEEAitEAyQNDHueCRGepjqiTA8ED3lr6+vTxJRY4taY0yEdi80TdvgrMXaaDEstMY6y6FrE4yJ5Onzj2mN5S/+1/+R4ANt26UNH6HjD82e7XbHz372Md57ypFiHjLhkS3OknBrxJz2RKoQMP77FMGeGDnvfU+cDYyMABei7XoYyp0aXoTETAUEYwVrZgSzwjRbUo+ZvN4Kvh9XxwAhNyLGiIrYsXfblMAL0F9GUZk9EKr54HV9H1yCH/d5gUfCMoSjQ2U8thHCKFkz58syoSuoYlCoSakShHiKK5H6IJXqPTq894yhk08J6DNTikj8rgt9TG3nj723+8MyMbjZYGAwiBnqkEIeEcFZwfVeCMmeKI//5QO7X4+jNdbPZ09A5xfDZBmKXheVXxejdQkJRqkXkA5lj8mAwOS5gN56Y3RpiFFBbdfx6tVrbm5umM/nbLdbXrz4keVyQV3PCG28kG9v76jKMh9ZvTIwbpFkcBFiDMXI1Di6LsLn6aKgLMsoqJASb0ew78PgDw0Pufzh4jqV8lhF/nPcx/Opn74Pyn9ulKefp3lO5wtpkod18NPTlEmb1p+JBtnXET3KBJHRbFvDb377O96+e8fnn3/GcrViu93SGcP9/T3OWW5ubigL3TP2/d7PMcd74jMMHt7Bg5DDug2DkgEilHpGdWBEpPi0V+NelCBGAsY+34DooaRisVhwf39PXVcP9iGj30VRcHl1yZu3dyAVZVUi9vlMSyzoiJgOfT/F8fQIBsG7CP36zDQBgR7pYGxEM34/r4eeSe7v3bT702KO20k8WB5hNLf99h1/yRih8FjYNdxZw9hKlSDI8n2f758wzF/eLL1n6tg7RoJA9Z4x0isCPt1Ptr9jAgHfeozpOOwP3N6+o65rFssV6/Ua6ywvXrygKEsudnuWyxj3fjarU7z42BYvIpqIDxZEil0vZCS2tWDjXtHNVnz1r/4Fr3/9B7bfvCLsDtDdIxL8e7xTZWx17l9IrPpjsIchxLGapKmw45T37TT/IFw59rKdeiWdKmcs3HksTc+Is0K+9whXx/XmNo6Fj1Ov0kFAEAXK8RBI63nIRT6XILHc6espslNOU2OFLKj90DGY9jf/fU4w+r4xy+0bI0SdG+tz5ZwSJI/XQT5fpsK3MW0e6dTj708Jl0/9PtW+KYx2rvucR/x4HLPwc5r6uRTH45pphDGMux/19ZQw91w6N5bn9sv0Zs5C/7y+M3JRT/tOxiOvv1OhBt7XtvclrSLf1h5MRCizbrg3z6UTXx/xH0CGGD4lpM28RQj0wuf30sHvSSJ7ieOSYtzig8GHLirIfYQvtliclwSvEaJGiAqpitQpiZQlWjuUNoCMrFxCEomXVfQ+i/6YHz7W45zn1pj0Inp2JeGNcg65P3DY3LJZwqyyBGWRxQwta5DRyEqms1ECzhmCMxghsVIiBXhh8MIRHd0USElrDV5GPtpbh0T0MQVTK4fzVUqq5Qx3v8NZi2lbVKGYLea8efWauqipZ3Ounj7l/v4Qj+H0E4KnS0KZ0gZC00FrUUFRlIL7b76j8I6ukHgNK+m50ZIiunrgmg7bNIR9x2y+BFHwzni6tsGaFm1a3rx4Sdc0SKIHoEBSIpkHQRkEOggUgp3wOK0wStB1jtZE5DBdlkilkxFj9Bg5tc+OlMU+Iekg0CKGmCvKMspBioJnT5+y3Wx4++Yt1jkWixkkfnQ2n9EZS9e2GGNiCDspsc4OHFg646JRpaIsFevVIsIntm2PQCREPlNj+4w1dCYqlB9Ag3L+fjh3D6elwPgOzU4Tzg8w6m3b0XUdi4uIOhiAtmtoTAfBsy4qdJGgb4NIspsKQYWUJbN6SV3NiALZFm8t3jqqoubm+ik3xJAPs9mM+WyOVBrjHULqXuYlxMDBxfnzPa0fQ9oM4ySVQCt1LBwND81dxvTF4FwQf3o5xujeynIPm+bAOwtEI4hxWdH5IdKuoi/y1Lob8e6j707N09EZfKKsY/ni9Pm4rkk94SHtNqU55KlLYVrnifdO/X3q2Sna8dQ9fPrzQ+O6U8rsD0UteSzfufGePhu3I4TTNPZ0rB+dz35ej9OYT+2fPXK/H5X3AbRQynxyXs/RpafGfpxvjOIzfWdMj077NZbnRYjg5ADjJV76PtxDZ7qYb8T2qhSOwbkowx+jSAERPn3S1kzfPKD7Tpy303kPIct4z9Nzfd6J09KUlzs1hufGd5BdMDi7hEAILt7ZWuCdR4mC2eoJn37+J1w/+ZS7+3sCb3FBo4oZ3jRJwVahqoJSLznoHV3X0h4EOEnwUbGmi4SQm8Lr2BCwXvDkyUc8+9mXLFZrdFnGGMihxIkD89mKoqgwCRUnEHBeIShwXgEtQkq879BlERXGOKxpAY3QELwFZ0BovBdJERV9K4oC6jrgQsdyoXAmcNg7dnuPNYayDlSzgCpCcmrI8Y0ljbe4EFBlRTXz1GuHNV30uHaKqpyz3+2J/hXZq9TjgmAxW1AUGms9zX5PMC3FHkrl8d7SdgcOhy0VEckTKeg9BBhB2MeZjsa/MsZRdyHGAfdSUMhAZbdUh4bQ7VGHDm1gL6BtfLLXF1HPYzyuAQTREKAErx3zmaSaCbaNxziwyXlauqhYjDsGmgDbu45v77/l5uozrpfXVOUl7273fPTZM/7syQ2fXn/Mk8tPWS8/R3HA379l277itn3Lji2ufENQhkARFYUhqYtFdGCc1TUX6yXzWYGxDq1LOtn295iUCmcN3nY42+JsjbWOtm1om4b55SqG1Vss0WXBH77+GmsMs1nNYr6gUJpC6xH0PUmckOVwR9v6bAoSCB6LwEiwQiKc4EdanqBQSCokCxSvMMgQPcajyC56/O5NR+VnNAFeeMdfdVt+/tVXlDPgfoPfGWgDd7tbhBBUKC51yZWWNK9fYF7/yPJ6gRNwMB0zCU54ukSDKKlQSvcI0PP5PMomE/psXcdwhG3bABzFGu9SeOSyLCmLkt1my6zUaF3gg6NtLdYFZvMlXdeSxTLBO6wzoCQuOIzt2Lc7QhBIoSAYBAGFQBNlbaUsCEFghMOLaLqDi7yK8gGPQrjoJNs5S+k82geUDxhvcEgwDmeTLI5MaEEMGSoe3o8TOU4vb83ntIhrf7oP+1/iPA8+3NHHZ7IkoPBoQKPQInp7K0QMfSBjiGxyBLkQeT4R8rpJ94AVaFujiGGMalWz0HPqssZ4Q2cNwnc4AYWKXvbWCrzrYritD9QRfLBiPEiPlgpZKAgx3qizjiCiFYsSuhfYZ4GMgF7R6hMR4onxgb33VHUFIlpsyxRv15ocv1ggdYQsV8mD1RP6eOUCMEAQcGiPrQACRE9ZQvKGinWrZK0uHMwX83SBSGo/iwJE65AqQrDvmwOr5RKtYsD3zhoOTUNRFnjvo0W0g7KueosUl+CgZAjEWE6RaVFaY6xBCon10WIox0/PBFBkMgJN21DXddygbYsQktIVHHZ7lFK8u73lr//qr3j+0XMuLmL8BGsNuqj5J//15/z5//jn7Hf3ma+JmwDBZrOh7VqKQuOsR9YjS2sYCKJTTMl4E43y5HwnyN3oMBF8ypqhxYnWxd7jTIwnMMB/D1bEQooeprCHA0cki5ykuCWkwyaJipyPsDsiEncuM2/OJYYxMvrRsjpCfvXKFB89uGOc7ZDOlYDLnt75Ekl9z/S0GHmVyCQMi7FDBEoMRKuoZ5l6j8ptKRLB4/t42fGgyrAWg1I+VjnAC4kEESa9J8M6B7oU5zy2MpsDPCBSQxJ6ZQOB1M98Q/bWqRPGcZjy6efRpRrfoPfS7pM4ynX6QD3WSkXWWky0VVOmJI9NrnmShix9W8PkS5GEISErG1LZPaspRt6q/aRzrKxDIOTAxMR36C13o1Jqwf39HXd3d9R1HQ0hlGK/32OspSg0eXfltvQjk+JTZai6QDTkEBRpPeQ4IAMyxikFYGz6aDzPCH7zWA3W7NPMAyM+tPEDmcufIGQ9bui59wQZavynlTm8f1TaRFFCvzdiykxH3vu5XuvivfH27Tu22x2ff/4ZT58+RcgoFNxu9wihePb0Sawj3435XI2Sv3gOHzGD8sHwDyMiemSRdF32AkSIaBNxz/sj5Xl/MYh4rmSBynq95uWrVzx//iwpV04JxeO4XF5e8vLVG6yJ8D1SxliUGV6tzz1hmPPZELfsYMzQK8197uF4p+adMYpbN80TxvM0ICYcnV+TuYxn+njtJEOE9Dci6wpGFpBj4aTMRl8jAdAob2TAVEIOGRRUg/AgCQwytLmXvZdUzJgVSRIp4x0RhY3x/HbB4VxIBlEuQlseGm7f3bFYzFksl3jnefXyNbe3t6zXa+azGRfrJbNZncpLipY0TzY4lEzoIELgRMC2d/zm7X/mo19+zvUXn/P699/RvfiO7vZtjKvZGQiOUkiEi7GWhBAYlcZ4sjnHxPhUUH1OqDjOOyjZHnrJjgUzp8of580C4HNetKcEXycNzCafTwm8Tr2Tf5/ydovC56xUlL2AWcpkoX/qgGfc39HVeUKoNFX45rGceuWfGoNpGisyz9V1qp/HQkQZw3+cWC/j9o7/Hgv13ic0ewwCP7fDex+NOVQMLTBeH9N2nGMKe2X0ROn7UGn6UEl9btzGnnzT5/HuH/owFWbHu2ZQzI6fD/T8QK+d6td4L51bB5nmOTWufdgCIXrjr7ERqhADH9T3a1LXuP0hhCNFc+8VOWpPvu9CUupILSmKgvZw6CFJZULKGvdvvL/Pzd2RsJ9x+LDhvbxvI/0vzu6Nn5wk4FOcYOGIwYIdIRhCMPhg8cHhpCdQIsQMJRYoUUcIUSAEGWFGlU1rXeL7eyuQfeFDiAZSGQFmnAZZyR/Rr4TIEDm4gLYOud2xuX3Dq5UFapamolzVKF9jrEAGTSFLKkqsjxCE1hkaEbDCoWSD9DuCV3hXIdwM7eoIYe1bvI0eckpKqiSczlOdw840bUe1mCMDdE2HdY5D07KcR+HYbLZgvlxSLhboxtKaBp35R8B5i8MxR+K3B3zTUSpJ4Tu++fa7CFEtAt4abhTMJOAlft/htjvsvqEuZ8zrJY3QtLalc5ZiXhK2W969eknXNkmwFhFuSiGYe0GZWQYhuA2WBmhEoMHTOZv2TIQYjPCwoZ+7c+dtnN7IxwskSuqoGC/iT1VVPH3+hK//8Hv2uz1FUbFcrYmKcRkN8fcH2sOBtm3pTEdVydieKE3HuejZJVEUWjKblaxXC6qqotkfjhZbpvi0SELCpPgpy/JB+8fnds/PJR4pZGaofz5i7fplLPr7N+/nqBhvE8JgjdIFLnha03LoDlHApyVSy2iYajwhRAVCXZZoVVMUNQRB27VYY8CDlpr5okyxLjVKqxj/V0pcCMgioiSMFVYipLjgPsoxnDEYa4/C/gkhItqdAILoYZgz2lzmDbKcxTuP8y7li6MdUekGRXmUW8X4t20T0csyEiHEkG5ZsIrPHuPgvU3C4yRbGfNXjHj40XenaKtjecT59XvqvjzKm+Qe7xPuDg+ybONY3jFOp4ww3ys8PkOPPFbG9N3h+cM8H3Jv5/xTmunBEEzG/lz7puVlPvan3BGn5nr8258Z158khcj7/5F01OZc5/jsONOGqcTkFH16iic5OR9nxm1KY+a/vY9hYyKdk3jhVER0LjsOnZFpKIjObDEM6LEx8imealTsZABOeHJ/wO/xcJziP6Z0xmPrSYjMb4z4tRAdDqSQCR1OUFZz1lfPuX72Ebu25dWbt7y5vWW7PyClpW0brHfM1JxKzyhLiZAVfneH9R4dCrzrOGxjKBrnbYKPj7DuQZTcPP8ZN88+iYZ6XUt7aFHK9xdOZzt2+y1Cgg0WpMSLgA2W4BqUqvChJQiPCwbnDJ05YH2FVAJvO7w1BBFdna23IDt07VnMBMsLjQ0Hrp9cYxrwb1ru9zs2zY6b1YJ6XSGVi57iQlCUSw4HkN4hg2R5pVhdaKRuoWlxnSFYxcXNNZ3bY01yzop6PrRUrG8WzGYzTLfj9s09++0d+z3MrxfJULtjc3fLvO6Yq4BUOnq4K5mcKuId4wdWOsq5kwNXRFuWlDqg7Y7SBLAW4TzBClwLzT7eQ7oUyFJHA4ZdAA1FLZAFlIAqBfNVYGMEBwLexIVdKEGho0e1I6IAta3i/u0fcB9/wtNrxT+8WWMPn/CLL/6Ez64+43J2SannWKN5e/t7Npvfsbcv6djhlcPxGi87CDoZtktkCo9mrKGqIv2zmJe8uO1YzucgJcFHY0KlJJ0xONNiuwbb1Rhbo41JuqI1ZVkxXyxZrtb88P33vH3zChECdV1HA2GlKKSijSr5tI/FSFZz/lTsZZVKgHVYoBNgZAzH8j0Nv6SmDoIZiiXZNz6HQYkyuOA9e2NY2+jEd0fgb7ot/+e6pL6oI63nPKJ1mP0tMymZK81qXlGVktvvv8X95d+y+Cd/hvWBzlvWBF47hzAGRaSZhJC0TcP62ZrZbEbbthjXYqxlMV+y2Wzoui4qwMuyR/nNoZXrumaxmHN/+466WCOlxnQ2ooF2jqKoIx7FKHRg6FoKPGW5QBczpCzSPMuEsgtKKGodw88UqiYGkrD4IHC+w9qoy/JE+aB00FlLaw2FMZF3kw5Jh5ca0Xmc9b2CPo95ptsY3Z9SiKPPp2gqEEl2+bhs7PjMHdMwiV4agqkj8GgRKIWkFAWFVJRSUFAiiO5APb2C6A2OM5ouEOHRDZQh0pyFLqhUSREqtC8JoSBg8EJSiABFXNdNp+iMwIUAqjq7vsfpgxXjv/3tbwG4uLigKIp+gLJX814eqMr6CL5pt9shhGA+n8cLI3iMtX1c8W+++QaIl1hVVVxeXqKVoms7jDHsdjs2mw3z+byP+x1ChDovUnzjBxYNxBhyWameGSORGKosWMnectn7Ned1xjGbzfjhhx9wzvX9nc/neO85HA6x7d9+y6GNkGtFWeCMpW0PVGWBkpLFvEYKiTGe+/sN+/2eL7/8kqZpjgU6IyIgC4W6ruvH1dqWzWYTrbSF4OWrV3TWsjs0vH7zWz755BMOh4Z/9X/65+way9d/+M8EolW1kJL20NC1Hb/73e9YLOd89dVXFIUGBu/wB4qTyYLPREkIoRdu9RsP+meZ4aXfj9n7Onq6dl2X+mbjxvdJMZPG3lpD23WDp3LySHPO0nUZmjsKiU0yJMhMi+thx4+tT11viCAfEK0yEYFCEAUAKZa2TMx97n+Emcle6/RrNirg3SjG2eAl0x8+JCYswVx7P8CJiaQIzRBxRwR/fx6k9RlyXwcPnMiDir5Mwchbs5+TYV+EvkFjxmlU5RHtnz/Qt3N6Zz44NJOA7RTk2IjtOn5+hskZtylavI9LmZRxSnkqj/OcYQ2H/oVMUEcmfxiLweIqCkPza6MLhdG+GYaN5tAwm9Vpv8F2u+Hq+ipB2Cu6LipOi6LIG6pfn/2YExmWuD9sz5hH4Y/ohRLTQctrJ6v2J2z02RF5/Lu++HP8Gufm6H3pmPEZCbF4zBt8Klj44+qepozGENdmMvYazUdeirnaqBiO33Wd4Xe/+xoQXN/c9N6Hm802QhrNk5EMCaZytHbGvYhZIpUTEs6jyGskBIIICSliRExk2HQfEvKDQ6usXB8EjKdGcbFYYL//HuvsYE06Gs2Q5iGEwGq1RCmNsZayqiiKEnPYHZc5Jr5yGRPmNg9kosV64VPcYMM6jGWM/NeOpjmMVrhgPIrhwSfoRVt5j6T9f7zsQ/IwPxYC9Mx8gncXxNhe/Xk/PjdTOX4ADunnp+9T/+PBRxg20Ssnjw1TpFQQVIrhTfQO9NFLyDiPTJBY3kcma7vbUVUVi+UC5RWv37yl0JrdbsdqtWS5WFDPqsFQO9l4+WQMJnQMu+FFYH/Y8Pvv/opZtaR4Mmd18Tndjyl+68Fgdwe8s0gPWomoHA9DP8epn/9HtuiHKEjH9NJY2TgWGJ0SCp4TrjwmnBw/P6VE+5Dyp+VM+/qYADO9lb4/fT7H+2EIWySTJ910fKZtONqnE4HmuXRqDnLKRqKPwXZPx9GPDAHfJ8TNf0/7Mq1v2pfee+ZMnqhEPv489agZt338eQqbOe5HTzcf0VwP19qp56fWyfjzuE+nBKXe+we02IP1Jk7Q+CfWxlSQ+QAKdFT+qfr4CXvx1BhP+zad23OrNQBFGfm33eaejGCV2z8WDJ+q+0E/xmUPKIeJJsp9zGUco0/9XVMg9GBFee4kRFrXje52IdBiCVwgxQIhqtg+FxBIpEyG5i7BKSYJhshxyhNx40LojfjyGBy3J/f9mFp4XGitEFoShEMEi7QGd3/Hm7cv+EO94fZWUBYO1gZjAD/ncvGEy+UTLmaXSB/Dh7XWcOsObN07nPkW6X/kor6mlp8y159Q6xtce8C7O9rDrvdmFUJQFmVEoyM6rltv2Ww2VMs5y/WKVrdstzvubzf4zvPZ519SL+Z4IXj15i0CSbc/UFRRyY6QHIg0wEoUsO8IzqBmmu7+Lfb1Pd1nN+zbA/b+HZ9cXGCDRWwM8rYlbHa0+45ydsGbuuRtWbB3HlHOuazXfPcf/jd29/dYZ9EixXgkUITADIEGvACjBa9sx8EZNs6zDx6fjLeFEMmzON4f4/Pi1BnUPw9ExbUseqV4WdXMFnNWywX/5Vd/Q9u0rJYXPHnyjGo2pyxqurZlt9ux2+1o20OKbB5oD4lWkBJrDG3bslhcslzVXF2suFov+/3StwXI5FgQRPhLE+F9c1iGqTKlX6NT/jbv18mz4as0Bvk+9EQFvjUc2i46UtQVqOjk0JqOQ3ugVhqZjGCatsN7KIuSeb2kKlcoWeIc0UGhbShLTV3Pqaso2yoKFQX+faMFhZJJVpagOpPnehSMG7quwZgOa6K8KHupZ09SR3QeGc9n8L5XjI/PpinqHiJ6HfZzQeKC0hpp2wNt2/Q8qBACn+RrkaY/RqoLzp+sczxn8fvT8zjM4ek74OSZE0b0/yN3yKn6pvfvY+mYln9YzmPvTOmE9+U717bxfTNOY/QY4AgW+zwdEuNOn2rLqT491u5Im6kH358r+31lAj1y1jRNV8Bjszfu76n6HqfFz8/rg/PzA8o6RS/2z0f15Xzj8BHjdzKyRS8bHfHL8fx3UYEpZIxjXZbHdF2qbGyoCMdGH1P6dty/U/SdGLPkj6SQWV0e8kfj8qU6TUP2Mk+RFPxC4UhxxIniBBlAaM2uMchCsr684NnHH/Hm9hV/+de/4nA4EFwLwYC1NF2LLmqq+RwlFG3bYAi0HgyCsqjQukDsW16/fs28KggixtJ1CIr6gqKsQRWEAM5CezgQ9JZPPvoSZxyHZodxWxaLBUG1LJY6yssPHn8oCLYA0bFr9ljXgehYrATv3tyyb+8IXhJCdN6bzWuabotjRzm3XImC6moJsuXt5h4tZsxWNZ9UNW/eWmZzKOoQHcW8Zb1aI2SN1JpqJpCq4OpyyeWF5rsffkdjWrwI6Foh1Z4n85rOwOFgsaalKAWrRYmeH9Azz0IWXF9/xre07F80cX5kwJmW9n7PKhxYlyWFUsjkHBTXOSSipZ/npmlQpCiDCtACUYC1LSGA0vHZ7qA5vIGmNQQZ9WDlIqBmGrk2UIKoJKJQBAnGOXQNl9dQzqE9gPZwNQ/MdED4SBzoUjAvr7iZe35ef8PP55KfP/8F68W/Rrmn7BvHt/ffY+wrUIoSTRBFvIODoXUWj8TJHd4VEKJOQQpB8NFZsFaSxaxktSj55uUWfXkZQ/8k/ZRSCtdEOH9TNXR1S2sshTF0bUPTHBBCsF5f8LNPPuVv//Zv+U///i/42fOPex5JS0WhNdqqnvdGJKjznpc5ffbmvSYTsq0PHkPACFiqih/tLVsccwoWQbFCUoroUGQJI0mqoLHRu3c2n1Poilf3t3zzzXf8fPEFs4slnsB2swPj+Hw+J1iHLxzvqpbm5S3N//3PUUXJ8pOPULOCjej4tg3UgCo1SEHXdtzdbbi+uabrOpqm4ZD0b5W1WGtTWOGq10l6P+iQ5rMZT2+ueffmNZvNhuVilkIxWd7dbUAWFGWMC+6swxGNv4OQ+GxwPBpKKwImGR5qCubljLqag5a01qLlAWfuQQesjyjEwQYwDnUgheMs8E7hjULOCmRZopDEGg2S4a6NvO3k8E3n5Fk5T/o41k/m/Sh4/E59sGb6F6LstlKKZaVY1oJ5Jai0RoXyuB2BIaqXj3SvTDy1D5ZCKKoCyrJKOmCFCOCNoigrpHQoOaNQC7zoaNwB1VSIpsSxjfv5A9IHK8YRgX//7/89CME//kf/iI8//pj1es12t0NJGWNlyILxZbxcLWmalrZr2e8PzBYzyqqmrCr2+x2/+vWvKQrNl19+SRDw7vYWQYS+e/P2TfTc3u25vLxkFTzNoUmMSR1jaNZzIHC/2fQKCO8D99sNIinb84VpEjyCSh6WNl3+UiqCIHmLRy/zu809ZV3x+u0b9k2M1bLb7VBK8uLFC2azGavViucffwxS0DQN8+WC65tLCJ79bs/3P/7I7du3rNfXBKDrOl68ivE/jekoijIqSUJU9FtjUFrRNdGLujnETbzb7XDOsVgsePv2HW/fvkFqxe39PVVVYYPnT//Rn3F984z/+d/9z2w3tzjvUarg3bt3eOcpi2gR8+zpM8qyxFnbx1LIHj9ZGfRgcU830EiA1j8fv5c+JkdwmibOfdd10TAhWSjv9zu22y2HQ4PpOqyLBLvPnuMTJj1DiMtEaSmlogGEkAmCPLZBqwxlFj3LhRwUEonf7YlW1cPe9qs2Kgd6CLB4OLm269sRegpODFC5SbkjBL1SKj+bCiAETKDIB7XulFE7dUFlxbeUEdr/WCaVDq/s2ponpGdrU1tHAofRy2PpZrrGGB2Go+/PpbwmxgTyqJJT/EFcS9M804xZKZh6MyXA03+Zoc8MfJ6bQepx4j2yIHMsIJZ9fX3vU3nxd+glLkIm6ybyuhgo/GzgkmFamrbFdBEu0csAQtJ1hvl8aCa9+m88KPGjtTbNTYZ7zfE6GRZ3HsQEh9kzJiNJUEi/TzNsU0bx4Vycvx7PP58u5ffDrkdDlPcxlUe1hNNrbFrue6/3EPONBd3Z++x4XAZPuWywAtGD/A/ffEtRVcxmc1xiUne7A7P5LOXzD9dlnsNcJ8NnQV7fQ70RJjHFgukJmJilh1w71dWjMYoLryhKdFHQHBoWi0VU2ud1lN6Ja85RFBVXV5e8ePkGpSOk/+Fw6M+Mo9Kn62x8NE1PoMBo306nJJ2xDIRa3t9DSISsJKcfs7jeQz8WPQM97n6ixI6U4aMsMpeXmXDSDEjwMSBbf4733To6rwYhQejPb5FLTkLPZHQlfJ/PpTjxo8Mh1isCSIWWCu+zAWBSMNo4b847jDU0bUNZlBHhJsCrV2+5u9uwXq9YLOdcXKypq4g+kZFZgvAIl484gVQBLyWHdsuBLVvnmD+7pLz+jMOLDbLew+GA3d5jWxdRfZx5fJuFY2FPHsMPSbmtOf8Ygjl/Py7vgUJnIpA8V8e0jHFbT0FNvq/9p4RlUyHQh6Vpf3I5SZkrjus65UmcFYLjfGeZpcdaMhLWnVKsnhJaZ7pzPAd/zBoYv3tq7MaC+MdSvw6Tt8eHCjSnbZnO72NtmtLQp8Zouj8etunYK3u8J4YxPvamfrDeQgwT9Fg6twd+ivKAQB+uZ1z/dO8+Vv/j34/u5ckV72wMpWWtS8Zig/DgUYXD+JoIE+VHHocHc3xsbPoTyJf3phAsPlhCcITkLQ7ggkj3kECgU7OXaHkBoiIilrQgoNAKJUDYBswGGbroSU602xfCI4OIkH6cQgM717bzczRWqFkXaIPDBQfO4kOgafbcH7bsvWYmCoLr2Lx7w6EJVMUVRbFmZh2NcxSAVwlRzDs607K5u0e6W/R6hp45ZBGVisZY7m/f0u73yAClKpJSWaZ4hBoKgS89zsP923sWqyVBCmRRMC8qvvr8C/7xP/tnvHz7ls1mi/eeoiwIdY1S0TMFEaFZsQ7lHebQYqXHLQTNX/1nFvcbfLvg9tVb9kgWswt+dIbF7SvmRUk5m6M//phbr/lfZIepZ3hbItC4wvPqxQ84P3BkMgWm00CVhKtGS5pZwUFAh+C2a7lrDhhrUEqjZeSJe9jHE2f9eF9nozsIaFFQqpJSV5Hem5XM5hWbu7f8xb/7n9htd1xfPWG2XFIv5ixWSw67PbZtCdZgrQHhUwg+gxLxTmrbKOsoCs1qPuP6csX11YqmaYZQDGQUriEsXtM2GGd7B41x+/PdNqy991L7sc8+1QWIED1wvIvKps5Y9m3Hvm0olU6wnJKua9m3B4zrUD5iLURhqELJirpaUVUrlCgJIcpXyqKOUOnziqqsKVQ1nOGT86Q1HfvDFtsmhbiNCgjTdnSmxdkuIkOluN4iagcSbzXc7Q+MIFI4uCNFOMdn3FH+SZIBTNvSHRq0VlBEQxtro/FJvnHGCDRnQ91Nyg/h/Ilzbq2Of0/vR+8/8H76e07nzsM/hsb6sDTQQ6fkSKcU4ePPD437jts7Tqf68HAehzzn5uCxss+lkOUXj+Q9teeneR+jNz+U7ju5NyYhck6Vd2rcztGxpxClpvRg3ssx1F6HcwERsrueI7868J4xHvl4reT3nRIoqY/OgscQkE7146i9p0ikkyk5Hzyypk4pxidFJL5fIDwEKXDeoqVESYEMnkJp3txvefLxR6BKdrsd33z3LW9u36ILhfCR/qnKml/84hdcXT/j9vYl3//wDd//+AOzesbz58+5u3tHs98hvOPy6c/Y7jp+fPUthfIoLRBKsd+3ONPhrKVrO/abO7w1fPanXxGMZt/c8/LVN3z77dfc3+348pcXfPW5RBWWt68afv+Xjtt3BxaXmqY54INhvpDcrJ/gblvKmcLYKPu4ubhCVxKh5/H8lw5ZgOSCFz9+S/3RU9aXV6yWFyyXK6wPHA7RKScE6Iylrmva1rBrDtxtt1Fv03Z8MnvOk8vAvt0SVKCsC5q9Y1HNKas5d3c73r27w3QNF89uIBh+ePU79rd79EFyUdVUZcV+f6AoC5QqKAtFayy7nUEVJYXSeALOW7ouyua9t2RkPWttDCsZPFJ4VAFqprHe0nbgjeB+I3m9gcPBxTA1wdN10UDQCSgvNIWOa6o7WF7feroGljV8caG5vJKsSs9CeNZVTREUy7piOS+Zz0u++Oj/QClXHHa3NG3D9sff8X3T8WbzI4tyhvUOg0DPnrJSmkrs2GrDxmjuuoq9EszUHdovwEWFnigDITi00AQPVaF4/mTNr765p1SauqrY2Qhhnw3ejO0iNLSzdF2HtZbDfsv2PoZhuXnyjE8+/ZS//su/5H/6H/6cf/pP/iuqosI5ixKSqqg4mAbjTdRhCAFKpriqD9P0rpAh/tgAxnu2wvGknPPC3XJvHTco5khuRMGaxFND8owOMcxvlzyjTYwpv1itqO73hO9eEp5douqS+c0FT/Y7vry+5OvXL7gVHU3QyCfX7P7D99z9P/5fmOsL2l98jvxv/yXhl/8U9rtorJpQced1zbyac7+9Z7/fI6VkuVxy+/YW5xxXVxeUZdmjAnkfdWNKKaqypC5LVqsf2G83EWJfKaSE5tCx3R2o6pIkYQQ8qHiWtuZAZ1scPuoVHbQEdtZC51jIknV9TV3O8CFQKosuK2St2chb2i56tgfn8UbgLXgjwSqkK1HMKOWKurqkKDXKHdgUt2i6FDc+6jbFxDBuOq9T+ciYVjh7zv8EptbhUQQKrbhez/j4asZ6XlCVKtKODPLTKMga6ukdm5PjUTSujY4XWY8bQpTbKhF1LFoECu0ovMVhEG6P8xLrNNYVOFecb+wofbBivOlarm+u+eKLL7i+vkaluNdaK6qqoq4qvD/2UDHGMJvLFJf0iiCiJ3MAqrrmX/zLf0FRFBRFwb/9t/+W7XbLv/5X/y1lUfBUPeWjjz6iM4bbd+/i5m8OrNdryrrqlaHOe+pZTR7REAJt11LP5ggpMcYkoj0xUolIj1CzIBKBvtvtMMYyn88oypKyqiirisPhgA+e1TrGjf3s88+5uLhACEE9m4EUFFVFXZbxQgpREb1aLzl89BFVNY8Q7t7z7t07Xr9+TVEULFerXjnftC1N0zCbzQYiRIB1FqUVs/kcgM50zObzHv4BAfVsxpdffcXt3R3/5Vf/KVm9BDrToZRmtZzRHhqkEJRlNhTIwuRIQoqskEnpiLjJ341+TwnTkR6ACNUt8c6z2x/YbjYYYwkhHhibzYa3b9+y2+8IwVNVFVVdsyxXse5k0SSVTHDzcVMUZRHhKFyEYI/e7gLnbDrUInPoQ4iWy3lzWQ/JEyKPrZTRACKY0EMOh7Qp/SjOVtyUcU77QyRDkec+hwRRPmi5hjRhLB/+JYbPYSTsHefKQrj0LFp7x5gY69Uaay273f5oPrLAs69jpKTJ34dc7YiAzb/GcsZxaN7xtRmVQxPlgBiXldr8AYfoURbRvzk8kqpfn/2YjFJISjHG49ePmRh1avRO35/R80wAhNQokQ0eRP9S6GsIHL0usm/2cTzTrjPR0ktGQ4rtbkdVL4C4B00yze69kcMY/iopZBkuMaUkbTtY+OfvclsGxf3xPI/7PXT37wHec5L65fR3LvahB/mD/XW0Mt/ncTlNjwhg+vJivqQKow9SEIb383hmuN7chLbrePnyJZ999jlaaYKP53yOSR1DLpzoU38Wi6OvRB6CkJE+Ihx/VIDkvCPhSEKZyArl2NiQGNUIyz3s8WjRd3Fxwe3tbR9m5Hgyk/hcSJzz3Fxf8/LV22j9qAuUVlhzWgEVktg9/z7ejmlHJbSJkDTncQjid9GznnT3hH54xou7Byvpz480hz3MrhgMkiaCoqNTN38Hw49Ip52AHLMnr48YOUP17+bwGLkfQggGrJK8rX0KmZGFD0TYOylR2fhLgMpe4elOH49XlnBnyCPCEHrEJWvTLJDsuo5Dc6CuZ9TVDCElr16/YbPZxnAPiznr1ZK6rggSbIihOqSIsxYvxghhJqTEacXGbRBhQ/FsjlhcIO5rVKkJ+3u6Zg8hCvD7Wc4emkMP+vvzwb49IxsbE/FjoU4WsmbG8UOEjnn+x2XkOvL30/yPnZcfUucppWhO05jfx5VzdkziuwLvZToLVAq34o48784pV08ZFHxof04pp3MfPkQZneufGvF+qND4VHunAsmjvx9phxBDfMUw6sM5BnHchvHamL53Cgp9+vlU+Y8ZC+QyMrLHo3Mcwtml03tNh8f7eaotD5Tj7717HxrH5XLGMP7T76Z1nto3Kff4TcYbRkrJarWKApAU6qFv1Yn9OO7P9IYe1lmuZ1rWkNcnAcXfVwrsCD19GWkRnwwgQce7CIETiuDnCMp41+PweLRQhOAIvkH4HaXfUsgWJ7PSNd7P+dyP9MNoX4zOv8wznlVO5PNg+oVMBqbpfkREOEavNYt6yZPLNau6xhe/xHlJXa1Yzi6p9YyCAg0IHbDOsDBLrqoVh+ISEf4RdbmiLNdU5QopC7yGXdtFg3ohqMuCEDxt26KKAkRAK4XWJZeXBW9evObWbyirivl8wbObZ1w/fcLBdJDjXDYdBBlDyTkT724V7+0QwO0O+BAoyoqZrDG//Rqxf8NmV+CvFhS6oukct99/z/r1K+Qvv4Crp/jVBW9vG94FgVOSZV1TCs/d7hXf/eY3SdmRlqUUaC+YoVFIXIC9d7zzHerJFUVVc9ge2B0O2KZFK0mlCzqXDOgmgrDxfOU0eA3GNRynKhriVnVFWZd8883vePP6Oxb1grKocdZjXaCsZ+w22+jh3Bmaw4FAoDNNihUfjV5zCDxvDVoLFvOK5aKm7boUImZop0xYrbv9nkPX4bzvPR4fu5fFZO1Oz5JhPaednmmyFJrNWU9nDE3X0TnHfDZnVs2w1nA4tOx3DZ1tKGcFzgaE11RqQVWvY3zxoEAotNLIQrFYLNBaU1YaLSWCDNsehf/G2ojk4B2dNzSHBmdMDEFnXVKOJ0eCHpku9kmJyJEHN9z9RwrpJGTM3ttHco7R/ZlPmwy9PtZF5fPQ2A7vHc4HhIvKcNsdx33vy/MROSl+Tj9JjjxyK4p32QfSDYwcOU7LWE68M1kTp777u6apYcZjCuNz74yfj+fnLH34nnqm9Mmp9AAB5gPp3Kk84VReIR6iU5xLp75/cDdnZ4TJGJ57/9Tzx2irU+8+NnbjPB9yto6/n/ZhasQ6RWQa583Px4YmPWqmzPdv3F8yKQ5ivTl8pD1GzBEplKMc2jc1thzX/SH7KHjfh3Y8149TZZxbK5kNPvle4psFIG0gKIUJHi+jEZnwlhaD8bC4vGG+vMJ2sN0cUKpECsHF5QVPrp/x5MlHzGaXFPUKIwPPC8H1J59w2B1QSL64ecr2/p77t2/ZbzZcPvsZu2aLOdzSNS3gEdJSlRprbNQjeM/zZ0/wzvDDD6/YbN6w3bxFBc3Pv/wz/uE/foJXf+B2+4qd27H+csHyU8XNk0t8WOFcS8CwXCn+9OmnPH/+Me2ho2s6Li5WtHaP957ZbI6QCutgPluxmD/h+c0TLi4WlKWgaTfRw1paXAAlC+bzmiAVq6LG4QnKx1jrCNq25fmT5xhuMCRF6rLir/7qb7i8VNT1mqdXc968esXF7IbriyXalHxz+3ve3L5ArFbMWPXyFyEswgooFEU58EluJOuMoQBsv/6irNTivIVg0XgKrSmC5nDv2d0F3t06tp2jnkGpIagYT5xSYLWgsyIi4oVA6eFnwNOPFnxyWfLRRc31qmI9r6KM1RgOnUFLTa1LJIHXL/+arklS3uBpjOXN23vKeWA1/zNEoWlEi5UNwSjqWUVd1qigaF1HY6HhllI8QckZIigCNsqKZIzJLpXk6nrFvCwwXZcQYDTORkSY7NmckSGUsVjbYbqGrutYrpaU1ZL5YsViMeP27SvevH7F5cU1hS7Yh+GckUIhROQPXZKxve8cJQQkIRpnOk+H4x6LrJZIpdk4yyFo1miWQbICdpCwG8CmsRPWRx1XsFgLqqp5Uq1o//ADtz9+h1rNWa8uWczmVMFwMAe2+44gLMuLT/GfXOHaPfu//g7z4/dQFRy+/Ac8Xa8QPuCNRStFtVjQNA1dEw1Ey7pCV1VPO0bDkITGKiICkdZRLWpspLtmi2WvRxQp7jzCc9jv474JUd5ivcHZjtbsacyeznVY77DOc79ruN3t8cYxkxXz2QWlXoKVKCQzGSiqGQUlXhhU0FjlEBLKqmBe16xmay7nT1jOL1jML7icX1HWFygrodhS60Aht8TY4tHJZcyHCZEP+NP39DiNkWbiD738tdctnKG74zEccCHyEUpCWWou1nOeXFwwn5XoQiKUQowMtB7w9mF8DyS5MC7dAUk3EwKQDL16x6Z4txnfUtg5Ss+p6kuW3YGm3Z9e15P0wYrxzz77OV988Qu01sxmcwIx1q2xht2hQaqauq6x1vUXrC6rYfBS54siKrW9c3z8yad479jv9vzjf/xPefXqFevLS5rDnmpWI5Vie9hzv91weXnJV7/4Odc3T+KAIhLEckhC5SicFlJgfaDpLJ4WIUSMqVmMYGMCaFX0F7+UgWoGF1dV72UBUek+W6x6Yv8ZAwGkUizCeFg7EFn55UBJqqqmNQGpCqTSeG+4vnmKLir2ux27fdNvTF3WXC1WVFW2XHGoogQZLcXevHmDlpLdbsfvfvt7iqJgNp/x0fOP+flXf8K/+Tf/T968/YHD/hZjTLSm1gXlYoH3ntdvXnN5dYku4qGqlOoVzz1jJcQRlZsfD0q3RBz2XtL0GywERoKkCMG32e64u7vvF/ahOfD2zVvu7zcRPm215OrqMkLRMFgseu9pu46QPBVDgvsIW5KQ71j5MMQCy3G4M0EXht9pM58i8lJHElR5rxI7XvyTvNO/4plxLJDvPdCF7AVLIj3v1S5Zn8WxILPnPkeEbRjPQeqXKjT1bI5xEap+rKQ9pUMcP5L9gzB8Oe7QROj3gOUMWTg2qmL6yiPKx5MpDL7SfRNIB/D7ihXiCDY0zkUWejxkmMdznNny5KNLANarJfP5ol+HEsHb23eYzpL3y9FU9eMp0sVEL9zxPhpjSBHDJOSY94IYC/pU146ENql1UkZrXkIT14BzSTHnR70Rffs+JP10wUAY/T59KY56wbCOztWT98nDb4Zn2UBhvECPFuuJ9ozrmz5/fGyOupCeZCYzexf3ys/cmjAomfLnzf2G3XbLcrlEKYm1UcGpMkTvuJosaOZ4DeT4qWG830IUjGchGIBE0uvHUy+tTYIrKVJcrVzuRAgTFzjL5ZJvv/kDo4OURI0koij7lgWWywWlkhjToouSQhe4Hkox7ofAMeEkGNAVcggL59J4irSZAgP8ZeZ38xGVshAG757jhZPvoNC/07dGKQope6YihEi8DWrugU7pxymX2G8nkY5W0U+6FOIobEMUSgA5rngAH7JwMrUuDJ0b4NVzbfEukiISe0oqgtJROW5dH4aD0VqIgyOiVbzM8anjWrPOIqVKQpMYf67YlyxSeJtXL19zV5bsLi5YrVYsVguqeUUOYyIIBJ8IZRnb6VNbpZA4sSfMA0Yrbp59xrvvv4dtjd7skJ1B2BaV1pwNFi8DQUePPxXEMP5ZoJHmBcAFeg/eU4KQTLS76Rk6EYCfUoSN0zkhzAOB3OT9KS0xLXsqTDsnXDvVnjwm0c46QFJwTTLGrSslQuY4oT4aJIz6farP03aeMwR4f4qnWBjTipmKEgJEaj8P+9grlcfoOeLxmODj988pO6b9GpQfD+NTPij7xFg8pnjJZ3T+O6ceseNE/mn7Tn037c/RePU0efzPpzM+M8KZMMm08DhNBa/5jB578J8yPhm3cSqsH33Zv/fgfREFCn1p+VLLDHzfmnS+nph7wUAH5m6KPs9wF+dPmXZu25bD4XDUj/E6iLSVJLi+wFiaTFCHgUQHhoSGFPOFxDOMy0m3XHxfhN447Vxc1J+SXNj2UNhxf2WjL5nmPuJMKmqCiCDb0Y/VRag9ofDBI4WhVC0L3TJTlk54fIKMHJkyxVJPnhM/oS8Ptle85FX6KghJqKLX9EW15mp2yeV8hSxnCKlRuqTUNVpoZBBoCUKBUQopNFUo6JjH8VAFuixRSoA3hOAwjUEEqIoSVURoy84Na9P5GLNdFyV1Oaf1lqqouby65tnTJwQBb2/fogtNoRUtEd5PFBLnkpAvJIVGALNv8AQKIVCNwf/4I4VveffuHnd1QLuWsr2j+uEH5O0d8uc/Q2hiW4NjWdQ4VVFqjbMHNm9ecv/9Nzhn0Ug0cU0WCGZCI0OEtWxD4LVtkHVFUdWYTaB1FkJAS5XixsYY0sGf9wI8NniJShmZaI2816RSIOH3X/8WZ1pWNx8xny8QSsXvREToa5sI79m2DaoQtPs2bfto2JDDxSmlWC3mrJZzqlLRtsfrZrzmYig728tgjtfliGbu5RHx/6kg7wFN0dPOgxeNs9EIv+tMDP8WArOqQgTomjbGUG9bjDOUZUlVzqjKOVW5pCyXkX5TGq1LCl32yGEQjQOcdzjXRbmH9XSdiZ7hzuKcwdgI/4mxyUDSp3dsRChgmLvMewy0UOjv5EzL9UYRY8X4SD4yGGfH/3KIkyknJURESPDeIVyKYy5kUu5HqKHodCH6MHmDGGlwQhjTDPneep9gvr9Teh5mnG9yV+XboJ/nMMmVz/HY38fojf6Nk/Kjh23MeR5TwL6vrCld8z7F7LTc8XeD3Oh0WI9TStpzdUw6cvL7D6ljWs9j43H8bKBxTqVT/fhQOcdPVYy/b8ym371PmfyYgeD48zHdOeyljLggEOOpmaBDZT53fNan9SNBJPS7c/zP+Pd0rZ/i1cZOH2fHYIIUcXa9j8p/MLeJdhMBJEMYM5eUQdJ7jHGUizWry6cU9YJ902BdYHV5ydNnH/GzTz7j6c1zpCp4+fodrW1QsyXPL9ZcrNYcdge+++YbbNehdE05X+KDpJwvuGw/492LwGHzmmBbdKE5HHaoeo9QkvlyRTWb8d0P3/L61Ru8t9RVzeXFFWU94+r6mk61WNHgpOLiZo0UJVW5wDmDkBVFJZnVMY51vVgyX8QY1ODRHu43dyAduiwohELpwCc/e45wHc7v6SzsDneUlcL5PTZIZNCoUOCcoJytIRi0DhE5wFoOu1vmhaLpLC/evOXVu1v+4S/+BNPt2W4EpYZ5WWGXNSo4fNsxL0ou1xd0hwN3d3eEfcFiOYt8rPe4zuHrgE5hfcYGe/m+D+S7IvSGcQJQBLQKaOnpTGDTSrYbz34f8EqgZwKLx0nwBVDF9a9soPCBMsBKCn62rPjq4zUfXZdc1AXzsqYsZhgUXbuh6xpsaFFFx2J+Qdtt8B48CuMs++5AUA6hKnzYUciaWaFwskR7RfCOpttxMHusC0ijOLg7Zr6hYI0QMbywkIpAdAKUUrBc1KyWc3a7A4UuKLTGmOh5rYqCrrV0JsWbNibqTqzFmA7nIi1bzWpubm54/cO37PZ76nqBLoueD5EkqGwkQeRwKefPr3GSIeBF5MZsCGy9xQBS8SYvWQABAABJREFUaLYEDnjWQI1gheY1JnMoZBwLZX0K7QMWz21zwF6U1KZgu7/DGEct5wgnaDZbClEQvGFnW8oQCMLhRUFRKArTUH/7PfXthuJna5quIbiosyuLgru7O4RSCUFacn+/wVnLfD4/MjIoioLFYobWOunh4nqczRe8e/eWoqqoSo1zHfeb2xga9WodOxTymnVEZC+XfsB4aLuAsDDTM9b1mvXimqpYIp2k0AVCCRwWKRSNP1CKGOZKKElVFVR1xaK8YFHcsCguWRYXLMtLhFgQvKcEatVQ6xlKaGxyEhUj/nuaxvz++GyOOoUk6xQj7tz7IaTRiXN+XKYI0cEmhIjyUVWa+aymqgp0oZG6QChFL7QOyfB3VE6u1/d3QUBkuTeZXk+rKtOPxC+V1AinUaqmLBcYbzDO0Jn2g9b4ByvG56tLuq6LGzgkF30Nla7R5RxjHe7QxU4LlcSnEucdSsmejhXIGA8tyBSTWlPPl3w0W3J184S7zR1t10bmyVjevH3DJ59/xscffUxZlfgAUpVIqXDORtpWDZMkpeLm2Ue9d7HzHqTuBzwKLOgXSnbNn1f1wCw7Fz1vlMLjotJdxvaqFHvT+awgL+JhGSB4gRCaIAKdDVSzFc5YtCwoqqg4WK2vWCwvCD4aFRRliUsT36aNiNQIXaKrwJOLK3RRYrvobXhz8yxCeQnJen3Bf/8//Dl/+9f/C0+fP48Hq1LUqsJaS+siVMahbXh+8YxCR4gcrYt+aQ3ETJ7pEbR1lj6l1BNVPVMiRgK4TMzAbnfg7n5DURbsdvuoFH/7lubQYKzh6UfPeu/4znQcDg1d20Zmy7leGR4Zs7FVc5yx8d+pZeNmTr57qHgYf+qJxPT3aBiG75Nl91GaEqvT78YNSoKFo1pFhswepUHmdfTuWOAcCU0x/JYCoTRSjYLZ5oMsERVT8vK4CjH8/rB78cFrj6XeECDle8AYMeJvxgcto9kIoYf1Pcpw9Ghax/jQftjQU2zSwD57ttttRF1IBjdKRRQERmXlQ3gy+ZHQ8dmbO+aR6Zmz0WJfKhVfS9R7LrGfrdF6ycJrH6IAHPIWFOhCoRKyghAyIXRLBK4X1B617j2M2TTveUVO4HhPjetJ7U59GAtUj/dpvgRhshIm5YZBED4sifTuVDAiTpTB5Nnj6SyDK0QSMIJPMSWz4YQYvZsFP9Y4drsNi3ndrxVrXIoVE0ZdHJ8Xg+kMRGIkIibEfFmIBRGeptDRUk6I4VrLaygKfacHyjAk+QwS6Typ6wofovWknsBUxnM+3xWeQhdcXV3w8uUbvHMooSJxmJbFWCEyHvW8r6OQZqRcyct+uHz6N46E8+k8yyqB42pG+dKAe5IySEoC0VhP6QLTmWR97CPMaGae5TDOIqkVBPEWOTqdQvTwzgZGvSBCqt5rO8fzG1qWaY7Qfzo+nQdGMCrH43qTUlJIRShSLCMf78iIkjJ6O20QpWJ4ETmCq/T5JwlWTddSlSVVVUOQvHjxhru7HZeXa+aLmouLFVUVFeRCxtAzEokIHryLxo1CYokGdmrmuRNvmf/iY/av9sg3G/zdBqU6VNMinEWKGFvWyGjYgSMaE44mMhs15JHq12kYzpFpDNKxUHgK6T0VQJ4SAJ5SDE+FQueE6u8TWE7P0Gk84/Hf5xSpvblYiIgUQh174gcRlXYiWhVEwwX/0PPkVL2PPfsQgexATYyVtoNQTvQYAUNA5qzQiOIrzuz/oQ1jhfD07/xOhuQ+5QU3VpJMjYJOKXFPCSJzPeM803WYk1KqV4yP40Hm98ce5bm8cZ5T6+zcndSfO/muDQP9G+1nhvdPrfNo7HW8h84JOMflnBobkenoCTE+JtHyd1l5HLJHVJoXOXSmN8Lt90yI1FB/1ovcz9HaZjT3aTCqukrwzMmQ5shLKrbDhzAY4QBeJs/WNM9ZwU2/rkNvJDcZ0J5eSx8gSAR/9zjjrb1L97BGigIpNAhF8NmYWyLQKOYEURO9xS0Ih5DRyEni0cpTa8eidNSF5174PiRIP1chJAHJ0dO0Nn5Kqyd8RYjCGpU8Rr2CUBbMZktW5YKlXjBXM5Seo4oKoTRKaJSQEcJRQhABJxSF8EhdoClBlHgEqpAILMbsCV2Hb6OMQCoZw2xJiRfJsExEGsl5i1IFs/kC7Syr+ZLlckW1XLDd7Wi2GxbzRRTw1BXOxPXuiH2RXoII6CAwbdeze353ILx5gyw1+7sD9uVb5qsFTxaey/Ye7R3etLDZYDct+/uW8uo55azCCbg/7Lj/7nvM/Tt8cBRINBIRoslDjUIhQCiccNwFQ5E8jDwhegEJEUMHjOgtzpzpp/d7RCQRhD6MWdxDlq+//h0hOBbzBfVsnsLxRON+0xlsZ7DG4JxBlwXOdCgZvfazEXxZ1BFKfb1kuZj1QrnxWZ/bIwQ0bYwRmT0i4SHayvHZGk72b9zH/nOi67LnpbWW1nS9YjwEmFUVzkZP7rZpscZiffQkXy5WzGcrqnKB1nX0DC8KlC6iAUDiJa11dK3DugZr22jA2lmMsUnp7aJi3HSYrkU4HxF7whheMhO+A5+cofJzPyIbkhXgvvcYF36AMz+n/BrfVePxEyIiIOXwPwJiHHsZ15dzHhEc4UxolePyB57upyszwwfl6ekLxtfSZN4f2ROPKvNO1Tjpx6nxHX//vnJP3cWP5Z+O9TR9qGL8g9Ok/dP6P8QAYNqO9z8X/ZzFT+f39YeM7/vqn/IR+b1TvMRj6X203Lj+9+XJ9Gf8HBWLuSlZNtjfveJ4D0xRbIZ+BKJTx/E8nvr7nAHGg7Y+0sejZ4+EPBjyh9TE9xjQZBouWnTHcyx5xHbGcrlYsbi4QpYl2+0eoRUXV0/49LNf8vHHnzKfLbi933C733DwB8pyzmpxw8X1U1bLjmbvePnj93gUupyxKmsCDhMAPIWGw90rmtaw2WxZP9Gs1pcUhaLp9rz88QX73R2r5SWL2YKirDh077DuKbpeMltco6qCxfwmhqf1FdvdLUJaFsuKWbVgvzcQCmQBIRj2hwNlIUF4XOjAZuMnzWp1wfb+HYdOopzCuJZSVNhwgCAJFPjgsUbgiwbvO1xGHLMdQUmca9lvG/7w++/4q1/9mvW8ZrmqAI8PLUJEdFpJ4P72Htc56mrGYrXi9Y8/UneWuc+8YkhG/pBp5OzgNvApY74t83c6OQxEZbxUgYMNtEaxM9CEgCokXSUwweMUUBAND12gFoG1UCyU4LrUfHG95GeXcy4WikprtNIgNKYLNAdLszdoYalE9K7GSwqt8EhsSDIaFaVDLhwogkRRI0OgVALjW3Zuw97scAGwin23ZREaaukjelLwyXEh0ucxLHHJxWrJ3bu7aNCZQia6BPPtvKGzjtJYihQr2xiD6dqo4K0qqioqxt/+8C273Z7ZvKFWupfaphizcfjzJfyhScR45EFExfg+OFo8Skj2wrNPvFRBVIwXuJGUIMnTsiFgpXFS8K7d8045Pl3OUc0O0zqabYt2jv1hixQa52DXtsydxbgOR02YVygF1e0d5dt3mKfPkpx+OBfatmV1cYHWBda7yAsmxfngKBPXmE46MuccCEGhNdWswocYQqme1Zguxi/f77ZY00Wv5/QvBIexLV3X0nYdrTEYBz5o5sWcRb3kannF1eIJMzlHeklRlAgJNnQEIWldSyVdlF0qSVlGVO2ZvmCuL5nrK+b6gkLM8b4mOI8WnkrNqYt5dJ6jG831keSyP5NP3jFi/Fwc/Yryk4lM5dSdmm/kEPMppWIs97KI+0VIhNQIpYcwlrmGEbsY8n+5/uDow4ZmSbJIqEsIwMWnIclO0SgZ4tiIyA8Z+/esGEfI5Pns8UTYptAfDppKF7Rty/1my2q16hdYFDwIlFYPLlbSoDnnaNuWb7/7nkOzQ2tF27Z88cUXfPLpp9R1HfN0hrqeEchEQTxApzFsRNr0SmvoIcHy4A6X/FgYNYaUETIJlieTr7Tu25sVthl2Ic+ete5IaOaScEdEDhMlBKaJzF1kmDTWdH27h7aKfqNeXl5j2j3L5Soq7IXCOc+bNy/567/6d6xWS7z3aF3gvY/MY2KC7u7vE4x6jIWgVLamFpEZGAYm/U6e+L1HZBZUJTH+qH2QmbCBeDfGcH9/z3wx5+72ju12w2a7xZpoDf306VPKuuJwaNhsN+x3+x7OPHFysSYRGb2TS3FCYPaxlPvv+7845Z09KezEs7Mfzjx5mPpxzcLCPOZH5UxKel/Bggg5HAZr7sgkxL3gg+/j4cZfx0qHs/X+/yylvdYr847rH2xJH6ajNorxgTwumX5p/jSm7pjJiuXG/RA9auI+bA7N8B2JqeDhPB61O5WTPWbz2aSkorMRIs86R6lU9BpwLvUpwlvnyyC/fyTsYYgpnlESJnLLhz0dMxU8FIw/2o/T3zAev+Pyx+/+lPk4lf8UE/vwu+m0j/f+0a363jSca+cEEeN8gwV22n9hEKrnfCEE9rs93WVHWVRISQwvMiv7vTzuxEljmVynGKzEs2AsQ2gLIjpBv+/7scnQ4TnuMCfXS65TKUVd12x3Oy4vLx70Os91RCrQ3Nxc8+OLl+BljLcpJdYPniyZSBmPbi8JY2Dw8z2UBXoP1sOIbg+TKR33NXrXin6sQn5x5C7vvEdJSVGWKDQmwXL2cRFhhHAf9/FwdIvkHB4zRA9tFeEtnaNLkJe9ADHTF1OmP4zOvjCsp3Hy3kfmRfroFZbgTLXWaCIjJaXB9d4/juwtkJuf6Zi8DoL3yZPcEWQ8PzpjaNu2V4I3zZ7ZvGa/P7BczlmtllR1BQi8S0opERDeIRWEZPHpg8e7Bud+pLye8+yLf8Cr3/1A8+YtYrNHNQ3aakprKIwjKDjQ9UIO53xcoyIMETnCYIgSPancQKONhOI9JPQZReU5JV/+e6y8nH4/TmOB+zmIw2l6TOD4vnYev9/PKj4pLx8IHUd8zE85fcd1/RFvcXygnCtjuH+kzLzA6fMu93mqGBl/d+qdqWHBsaBFYP0wbmPF9ZFyfNKHcf3j9TUWMI/XwlRpPH2elS6DccD5d6YK9fcJJk+VdWqcjvbC6Pl0jKdrbNrGqYD2XFvyvTht7YcoQHJbTnnlP/bOuI5pSIHxWhm3YTyfgSj8GQvAHwj4T9D0uczp+j0HF/9T0r55hxQKJUuUKlFUECq8j7eXEDLFlCuRUuOFJxumyOQJJqWnKgLzSrAoBZUGITw+ASSG9EYP232mf8NYH9N7YvRzKgUXlcnCB4ILeBUIWlLP5szUjCIUCAfBGWRZpDs2ei3LxPtY73E+iUakRxeCkJAptNJ4a3Btg9sdEK0jOB+9MZRGKU2hBF5KQpA4H6JnsOioF0uuiop6UaOUYntoIqysDxx2O+rFjPXVBbevt3hnSGZ3ab0EVAgE55ClhuCw97eIt3eYizX3P9yj//Ajy2D5cu0oZgGrF7T3d/imo9sL3mwaDl95Li6esu869q/fcPv7b8BHIZcWWTEeSZoqKcqD0ggtaESEtwwhQeOLuCa00n2YFX9Eaw3z2a/VRI/F56CkQCd0n3xPBqBtGr755msgUJYldV2nUC01XddFSHDvIPE01kbIUCUlzg37r9AF9azk4mLFfD7r77ZpGIu8Z7suykrG97UQmbkf89rpHpwI8uD4fMg0WKZVcyg15xzG2ijc7Npk5CioqoKuaTjs97Rti/cghOLi8pqLy2uWizW6qJC6oq5rqrIASfSSS6h4bdvRth3WNXgXyzatjYaO3hO8IziLcQbhfYohPr73xkhHKfSBEAR3DFmdx2ysBA8+KbNHBmT9RoYj5LwQQi80FmIw0mR0f8ax9b3sKvjQK1Ue0jLTv8fnab4nH9Jnx2WEE3no36Wf+SH/+xR4U1ju6d8nlYAf8qkf2mykMDT2wd03lWtMO3ci7/EzMalvIl3x4/zHBuqnnn8oLRg4pkUeo1NO0RHHz8XJto1ry6Rwv37CKXnWILmc1jNtw9So5hzv33+f77kwOU9GBM45g4ijcsWpdh+3d0yvnKKHh+9IP2Ew4kvPe/wakcsbRmZKM4uUJxtHPuj7mXk8N1bp0/F3Y9q6zz9e5mHy7fn3Tlee8uQzXUh6VCIRIZ1XF1fMlxeoosD7LcvVkusnz1hfPsE4wYu3t7x++5K79pY3dy+5uvicsjQosUELwfXNc+7f3XE4HChryeXlKkImh4LL9Zz9zQU//P5X/OY3v2W7b7i8uuajT35GZzv+9q/+I/e3O7S2XKyjR/ib16/Y2m958XrO0i/Rs4L1/Ipl/VE0IpRLutZg7BZvBE5I2kPD4kJhzIbN4RVt23K5XrNYRTlT2+zY7TbUlQKxxbgN0muUmlEUFWU5w4dblBIopZGihKBwLqK1dl1HZ1qCa7l5doMQDms7bt/d85tf/4GPP7rkX//rf4UzFmscxhlW8zVKlrx4+wZsdB6Usoj0pFIRHSgM+yWCl0QI9eAjgoqQMrVJkt1Toww1omVKIdFKUCrwpWBvPThBKyS2DPgZNErgCwFFpHuVC6jGsa7gs+Wc61pzOS+5uVkjpGLbQRegICBDy6FpafdbaCxqNkMVa0IokJTo5DAphcS2hm5/T5AGNRcID741BAy6XLD3LTt7YBc6nATrYN8cWIoD88JSJsRjJARLRKiSAl2UXF+u+Pr3NqKE5tjixvU0jbNRoeuTYrczXaIrWqrZnPl8wdXFFcF77jd31LMFs8tLGJ0heb/kM7wXEp7bWmFwcgtSQBB4EWiD4+AtKih2dOyFxwIqSJayoAwWNdLlSCTCB5q2oa0LilKzMR2/Odxxs1wiywphGvabA1WAw3ZPo2c0B8OhbWhMC97SGIcqFFp62O+R795wd3dLXc9QiUZp2xZdFJG2JEQlstKIYJOeMaIWVVWVZGARYUwIQVEW6KpEdwVKa4SIck5RFlSFpj3s6doGXVTR6NQH2q5hs91yt7nnbrdl17QYEyjKBetixcVizcXymqv5NaWYI0IsM+AxtgOhIv0sLUFEdCalNVoparWkVmtqvaaUS4KRIDTSB7SsKPWMspglHaE4Mh4dOxmemuOjMzvxDcd8XH9an18iQuQbvDfQHCvGo640rhuQCJFh1OmZRkHo6bGswyTDuiN7e45jmiHyrQl7fVhlUiREr2gYrELAfSBd88GKcSGiojkkL6jcMJm8V7z3VHWNsYbvvv+eWV2zXq+p6zrCEjiLSIS1FFGBemgabt+9Y7vbEnxgtVpR1SVv3rzi6dOnXF1dp7qix6VSOhGYx8KSsZApf86X/tSDaNz2U+/KBLc6FZpNiYGp5WVWkIcQeuU5gOlMP35RcCEoihLrbGKsfIS4mAh182HoXLwsirKmJMetU/yH//i/8m//3/+G1XLO82fPkFpjjOnhep2LlkSvX73i+uYGpRXeOcqySO05P9fHRPXwexDQDp9DoI916H2M1V5VFaYz3N/f0bQtpuvojGG5WlIUmuZw4PWbt7RtS95oMjHl2VosGiUozqfBU2a61MfMcSYOHylm1O8Hj/rxGH8RTuTJz4cMYvzKH52O151IhxaQFKPZmi4E0zfsMcYyNu/9sCmnBNZ/zDvTdpxX/p0v68jjnGOmOufIdRwL8/J+Hwv5wuTzkDMKGWT/XmZEsoeROFH3WeYmEw5pXysVFd/xAh2ECmOm58xApLMullmWZf9e9gCRUtFzvmfTT1uJ55mfKXP7/jznd8y0zofPjq2bHzLOD+sfX5g/tc+5vtPKgOO8I0Y1pFiffiwMiPnarsMaE+FypMIY09OfU7nzdF/ksvu9Qxa4R89bIWIoDpcKy0IrkWNO+yHWYD6TAvSKx97jbXRwXVxccH93x+XFxckTQCLwQuCcZbmYU1UlnXEUZfSQ8c6NhOt53o/nzDvXQ/9mAdpwt4iHyye/32/rQQpxdEslJkMECJKEWZMHOUAS8Frv030jKaqqj+EoQkCFTBAmExgxXknx4JDZalFA8IHdbo8PPkFnqn599GuBcNTeY0Oh2LGoCB/Ok7FXvRDRczEz9yEIpCR6aOmQYJ/MkcEefTkjxW8IOJ9iVfpsJRs9yLuupU0CbkS0sr2/r7m8umS1XMS7OxsBekcQAY9H9C71Kb43gS4c+MPtr5h9fMX6459z/91LmlfvKHYNehsoTOyHVR4XorLbS4/HR29AGRepdupo/cOxsnN6duZ+TqG48zyMaasQQk/nnRKYjdNUSPTBQsMTQsJpmir8zpV9SnmajS8e9POPOPv++BQYvMHz+nxsfMZjcr6N0zmeClqnY5nv03FsrFN00PhZr+hJz3x/KPPgvemzx4Tt4+/zep3G7Mqf8/yPFQnnaIKpkvexdE6pfapPgePzauoleKqvPf8n5RG/M34+hu8MsZNn2/K+/vyUNAiW43nvfYxHrHVx9kzIbe4ZchEmd9PxWLxPgD5dpx96ZjyWvPYgDIQGbxXOztB6SZAKE+YEZogwo5ICx5YQLEIqJAXKV2haFAeU3OOlYCkuWEqDky0iSISXSTgeoc7boCME+2i88r7NkNDJJpcIu+2jLVey4hdBDlc2ma8sAYsREXIbrzD7O6zfo5VEao0oSgo1p9Q1CJm8+aOARCHQBoQL4CuCmEHhsIBxBUpqPJbONry+e0FrDavZDOPBOot3imK+ROo6KuY7i8NA51h8fs3l+oLgHM4YpLPMZjNa1eAEGBE5Ui8URehYVJrgK1yQeHFAHu7wraC6uaLYv4Hf/g33v/+Wzc+f0wn49Nmcn98UFL/9GnsAPxO03/yBg7PsZEDudvzu21/TzAX7zvHid7/j7ocXHHAoFCpECPUaQSElpY8IflaWtGWNqSTzg+Mvm++4s9tIhYUIf7hTAq81mKigDmSPuogjEITEZ/ouBDwCHwQiRGF6CAGjPNVqjVSad6+/5+33v2Uu5shqjihnFEXNol4Quoj8duhaWtsh8DjrKVSBkJKm27NrdjgLkprri4rrS0VVStpDXGNZnpLtLKVQbA47rBcIUUSeJwn+fOJnRYbv7vn1yRocPU8XVaSTQ1YyxbPCeMfBdnTG0rWWw76lawzr+QqlS+7v79kd9uyaFh/g0y8/5k/+9M+4uHpCNaspdEFVVInmcpjOYWz0AO+6Ngo+jcEbQ0gGfz4hF2QDxpC8ntJpmuYs0+sDwl9/R9rh/O1RgkbK8NzX7Dme80ZhNz09GpzvlWsIjsLUeBGNNLXWIOO4x9inoae5fEgoVeH4fB0Qno7v85ymR+lUXncuf/xO9PN3VAbD+9N0dDZP18ckZdp8nPdUeaPW9fVntiZzcP1dGyIix9ARhjpGvEGWdY7vlcwj+LHjyCNjNbQlZAak78lpuej5e63v4Ujmd4o3ft/85TKO/x7277m5CASCO37/VHicYQaG8Z6WKBhgWoc9MDgzxGNitEZGl1m/thiNqQiokXPTEe2Tcmcjsj4s2InU84B9zNSU/EOaJdYT70jnDdab6FTkRfLCzWPSQaiH+1rQI5r1dE8ynJ7yFMd1HdM/p+i3h3TRmPkfrWU5cOdjtj/06/N0G6Qc5MJTWlQkHrrrZTMOKTyEaJSEVHzy2c+5uvqM2fKC62vP1dU1Utds7nfIokOVmouba5aXK2bfL9gfdrx6+Vtev47yHIihNJ48v+GzTz7lZx//jP/9P/0l7358ycXVpzy5+pzFxS8w1X/i4vojjLH8/ve/49Du0bVm+/aWX/7JFzjfcLt/zcZs+Sf/zf8R5zq+/fr3zFaCi+sFbv6CV69vub55zsFGz9TWBb759Y/AOxb1itbccdi/QCpQ8pJaL0A2aBFQaITqMI1FqQXBCzpjcWHDor7mZnmDZAG+wDpHKN8BT1kvFizqhkOz5fVrw/c/3DNf3lPokl/8/Dne/HO6vWL37h3X6wu60OGNZ3WxYr93bDZvqHSJpEaGJU+ef0mtLyhcSWgbbNfhREsIJTtvwTmKUqFVgbEWqaJnrw8CIVSkARHgHRiHcA5ZCowW7HaguxbnI2y6qRVCGroSKiFZeLhygdoFPnbw80XNbFURSmjNAQ4SbRROaVphIUi8DWAds1JRF4ICizN7iqKIcbkR1FIg5ktUCgpUyIqyUCgtEU5SUuILOBhD01lCAzSB1lXc+jfM9A0LdUXh1ni7R8gDUniEqxDMeXrtY8gWUxCkRpeGptmAs5RSIXxHsAe879jv91T1jGrm6TqHBJ7cXPP95SVydc1hv+Wwe4e8ucArQQegFCoU6BAiymhC4XkflxLPuxAV445oxCoFWwHPqfleNlz7wBehQAjLtVdcEdjhaInGnA3QCYFsDa0xqFKjrOa/+83/xsfrX/AkeJxpeeW2OFGwtnPeNQe6Duowp9juebfd8pKaX6oVqu34/t1Lntp3/MXLFzxdLXi6WrGaLdjuHfemY+YbNAGMQ7eBajWjaQ7s93uKQlNVBUrFUKdN01DXdaTfvKOqKj755BM2mw3GGepSc3F1TWccu+0eUbYgA8F3/OH7P/Dd6+/YNQes87hQYVrBoiq4Xl9Sao30BZ0pEDJQSkUhSwiC4DVu1+JdgRQFWqtEQwqEVZTzeQxFLQLGtVixZK4DVrRYHF5qymJBUZWEwiNDQFIkWSIRUTqdqlFmOBg9KhQiRBrPikAoK6QoIr+VzlYndE+b9Hfm+MwPIdHVoLxACofDgiiQsiAwS8p8hbA+Lp4USjnf0+P44UmoHeXIidYJbnRP9P87QBBsluNEfrRfsWFwSMjw+O9LH6wYD5lISJcqcuI5I4hK37JkNp8B8OPLF8nj+RIpJV3XIURUim82G6y1LJdLLq+uOBwOGBfjOH362RdcX1/jfGSQeis2RrTJBwiHxkLH7ME+FphmIfZU2PSAEB09n0JQGWP6Mcjf5XeUUjjvMc6jhcSFEK3ehUDpgiKA99FbPivCs1AqW1lk4ZnD07YdWpUoXWBtgxCBT372SSRyjIkb0UXmSkhJ18XYV/PZLAntZWqXJiTwgQcCxETo5f5ES+BsbjpejPTj4xOj1jSR4ZsvVvzw4+96b7SQ+jObzTDW8u7dO7q2673BpJpAocWC80T3NfaKpIE/7IngcyR9JuCH/6Yc2FCu6CsYjcaISRnfGg+I7NyO/uQ4L+z7KUL4Ey/3TI5Lcb6U0pHwFVNC/Hz6sFx/D++cYUqHdOztfypPoD9vx1zjUcuG9/I8BsbZM7EtTs7zuIi4RgZhebQ2Hbw+3yPATUxTXsMhRNQIGLy8rXOUIsZXFiLGhdWjeHlDPWlxZmGkiIpQxGDZH1ElFGBONObh2H6IgDaEqYHBqHNH+c6X8SFy7mOF6B+XTrXhfXUfn3nH6+T9aThtxsRBBnfpBW6p7BA8Tdsymy2ilWmKb524XE6tp+HMmhiwiPHcxDSbz9ls94M3R04hQRt6RwiagHgQVOJBt4DFYsGLFy/iuhfJIz0JnUQSmsp03yuluL664rsfXqCcS/fLdCxjbWNBVrRklIPAIows/HuL9lErHwhsjk+iIIbxDz5Edyof+ux5CwWiF3YvQCXCoeuqRCqFadveojAjb4hRGdMfJWPceOfcKH7k8R0awrFAM2ShynBQkWGBCEnYlcfcx7mWCaop30d5OHLbpIxwTEq53itpLOQa73klFbJMxn/O4V2aVxljIhljaNqW+WyG94H9/sBiOefy8pLlcsliMafQyQ/BBpAp9q4M8R4nCS6EYt/esg9vWX/5MfrjZzTfvsS9vCPsGkLXogkEG1BIlFBYHwgCXFSDxLU0gljrDQVHG2AMVz2FC5/Se9O7daqYHKfp3T02tsxjnsv50HSuHeP2PqY8PycIfEzReS6NadpBkfh+gejDPgz79GE5eb1DjiEYxzAyMtno6ZRBUN/XiYHDuTE6pYA8Usymc2fah3E9GbpsXNe0vjwXWWEwNbw94okmYzam8cd5c/1TY4D3rbFTSuufrGAW0Uth7AE4HZtpPVN+aCokHff7oXD4Yfsfm9PpmLy3OwxjGYhIIN57mqbBWnN0hpza/5HBH8Zhut9zvzgpoA5Hv3O7P8T45kOSpOpjTCMVIlQQaggzlFiAXCDEDIICdBJ4RQUWwUJC55AhRauWIqGKHJ9BPsUjf5+xZT5nhvUwSLdDOL0OvQioYGmDjd62COrdnv39d9zaGy5UzbxaUs4KZCEwLtLLQgiUUPG00R1Kg8PiQjT28hQp9uOBttvH0FzG4ztJqBVSC2SIPYpeyY7gU9gJKShnNRerCOfdHRr2bUtzaJFSsJzPcAR0WaAFuPaALMG7aEBhg8d2hme+ZqcPzEpP9fVLDn/x13SF4p1rubwqeH5VcTkvCfceJUoOpmOzu8d7qOoZQSvu2j23//H/Q9s6dm/fcHf3GhR9TGlJ9OAuhSaaCcDBGbYuwgzKsmC32bPf7XEmQqtrraOHkekewEyO0/QMVUqjVTQmUUqhdcViucB5ww/ffYf38PHPPkYXRZx2KSkKzW7fYBLvb51DK401DW3bUhTgjUUEKApNoSVXl5es12uqssR2tqdzfYoFL6UkCMF+v8cYE8NQyYf770PTEe14dP9Gw+UMTdo0TZRLGYMg8V5Ksm8O7JoWhOTJ00v+2T/7Zzx58oz5co5Kwkwv6MPpmDYaxxprsKZLDgw2htvyg4d6Txc+clacu4+HPoSHZ87k80M66Viulnky78OD8oEjGZh3Hi98T3NOPf2na+rcOTi+Q07VeW4sYlfOKYNP0xZHNIEYPO3HeR7UH9JZcaYd40rF8MU0Y/9MjPI/lv1UXdN75rE1cfJz35Q0QuF47cDjcqheCD75/tTvD73zBrrwPflgxBaen4/AsRxgwKwZOOqjc2CSL/KMQwEP5Cj5eRiVk3m7UdtOtjBwcm6HyhJNPREPDOfDhH7Pfc58Ienc7Omn+ND7gbeM5ypHbZ0adf99pOn+64c0yzjy81OTkceAYdZ8VnBzTB8erdejciOEbkbVvLi64eLiOn3r0Drw+69/xe7Qsbq84vL6CavLS0oRHfqMcRy2++jYpyRNs+e7777j808/5ZOPP+aLL77ENh3BW9brFfv9Pd57lhcz/i//1/8b19fXvHn7gsNhx2xW8/nnn/Hrqwt27YFSVtSLJdcfPeX66orff/MrXt++45IFuphz927Dr3/9Dc+eBw7tHauLkk8/ecqsLhByAQgW82eU1SXW7rhcfcXrt/8lzqPQ6FJyuX6GNYLf/PA33G/f0bYd3gVudxIf7liUT1ktrlkuapyLCjLj3gGOoihYry55/fZblJ5RLOY8fXrNcjWncZZDu6WzM4IUOGl5tfkWLeGTT5/gDpqXL2751W9+zW9+9zf8k1/+N/z86ReUhaJto1fuQQaaSlIoEz3Fk46msxatiCEHQ0mhNd4HZCHQRYHsSkLoCMEgBHQWbACrIUiH1pLQeEo8a6l5ogtWF4IrHXUone8IBdSlotVQlwWFiiGAhVAoWVDXc8pSoVRcW8YYRACto+drz2OHGGpGCY9zB6xzFFRQajo2WCw+gLPQGc9hZyjlHV31Fi8uqcoSYxSSikCL9RYZDqzXK5arBa2J72cjkuBJTlYBk+KKF0UZ17nzmK6jbVrms5rlcsnTJ0948X3Dbr/nbntPUcSwLvkM79ElxE/jTwbj+0j/bnzH8xDlg4fg2AXLJTEe+xxNhWOfTgMJGDx1AO0dletQCL7ebvnvw4/8g1ByRQGq4od2i10uOEiwWuGk5k52vGLPU9lxUI7aWMx+R3G34+IXS4RMcnshWCzm2C6GE1KAKCShlL28TmsV6dCi6Omasiyj7o3I589mM+xqxW63o2kOuA6qqgSiI6gwGuMt+/2Gu/s9+62htVnJC4UsmZVLfFDsD4atbRBiy6KsWcznVKbEW8f+0HB7d4vwEuc9bYgyfSkUZa1oDh4tW7xRVKWg1nccdhZdlEgkuI797o79fo/zCZlPHDuXHvHkPW2TefQTa2BEG8RD+sNobk80kJZJf9iahn23Z6lnKAVBBZSMXFuvLxnfFuNqwkM5uej/H8vHs85kMHLNt3B01woP7vFz6cMV42lwjDF9DD0AIQe4y0x0XlxcxIUlJZv7+2SVUURvpJTv6dOn1HWM6+29Z7/f8/r1awJERbpSffw5lxiHCBMnAX8k9JoKNadEdhZGZQHqOPbnuN3GxIU4Jvx1gk+fEtRZIKZUhH03xvSfM3NgraUoS7quoywjHKlztheyFEVJjPlpeuuNLIAVIsGfJ8LHe09ZVDgfWK/XfPft77i5uYlxE6yNkHAut5sI6SYldV2zWCziZPdxrrLC5eEmGI9HHEt/9N2p1/KYWWup65rNZkNzOERDiLRw6ypaUGcIsowcEBgT4SLrB4aFn2UtYfg9TBz9ljruwriRI81GT1E/7PapcIFjRcz7DoRwYkc/vGfef/G873ISQiSTmMh4Zyi1vu6sJHqMoTz5aXLwpIvzDOtx8p0zLe7z90QsY5jwzKwce5JPlZcP5n5SNieUwI+35+Gcxr0tEuxkUpwd5TkxRpM0fifCgOSll88rksIrtrcXSGfFOPEeyBDUed1HD/S+p711vs9nEUmAfDSGYwb4w9MfK3CalMIp1nNa9rGl8Sh3mK6xMdP+OGMZ0mIZC9VP1Xe6nY/P8YOxTOeKYCBYh3Uto9W2ix4jdVX00NcyB/AczWkWuB+3YtgfWVkaktI6Q4wmTji+l+5FKWWCZYzwkGqEviHF8dqODtgxLlA2RLPGUlblIDRhBCvetytwfX3Fd9//gHMWrSLUVQzpII52WUgT0/cj3Wu5vT1znxTa8Q5Md3d/AYwNlYZ+D17WQ9OOlNE+KcQRsSwRkrfRoOyQhaaSEms6nI2xaqSPCoKoLBt5FYxQBTLxNR6jXH9eKzLTDqlxY2XC+Izt12uqZ6A5PMeKhvxGbn+MPa2UTvRH6A3k3EToF2JFaCUIKR568D4ZUARcMtQxXYcuCpaLBfvdgaZpWcw3XFxcsF4tWCzmSJk8BqWMEJpEj8EQQAcZIcKAze4FWpXMv7hm+fSGd19/j9juENtoKChFAE80rpAqwtKNYPEz/ZaF5KfOp/H3cBqG+tR5MPaWyPnhIZLQKXjB8Xv5O5ug9PtQQhwLY4/mYrQOHgh3zggoIxNLTzdP+5TPnvHaPgX1PX5nOnbTtk6V1IMwKn8fzzMpHxoYZHpECEmGxHvfmTqtf6qU9N5HJcWoTdOxOpe01r2HXh7DcT9zHNfx+I7b+Nic9ufaibHObc39mbZ1qgSfrovMT4zbcXruj8cxlzHml6ZjdUr5e2rOx32c1vFYX071a9qHafqQuRz3f6DTHqIoFEXBYrFge39/xP/lOZ4ig4kUx9AzGELnMA6DMGEwygHOCmvH58Tfla4SLiCURgiNlBqCJrLw0VM8hKig9M6l+01FYQAegUEIS4Q9jgJAKUQPVT5cL6ORlBIRjpVouY/9mE+61MtPpm1P/xlh0TiEBLQAL2C758WP3/L1s2vqak6hFyg9RwZPZw3Gt4RgQRiCbyAcKAqBp8T5Ah80Wi0S79xhuz3tbottHUpWFLMaLwTSg0NGGkxED/Si1Oi6ZrlcoQR0bUNz2HPY72gOBxBwdXOFT8ie3lmqWuGDi143qgAvME3ANh51NUPdv8L95le0v/s9anXJtrN09ztuC8mPxuObgD/skIVlSYEuZ9xrzX+5vedNJxAvX0SDjsM95rCj9dFTXRJ/FwEqn7yp0OyD5957pF6g5jXdrcUnBBytdTT6M12kB4lC0DHJK8Tpe0aGTFt5VFFSz2tms5Lt7p7vv/+OAKwvryJ0uIr1BEge0R1d2xCcpdCSrvUpTqZLtAYUukRpwXq1YFbX8f1go+fSSAgXoDduyQh7vXD3j0zjszDuz0Dw0avGGEPXdRzahkMTFeMyoXW1nWF/aLDOsbpY88WXX/LzX/yS5XqF1CrRrvQQp23b4kyHPYofHuH9QzKUHuRNycPfT87zyT1z7pyfopD19MlIKT69s8bn2dF7YYhpnvONz/7ey925GNaJ6LzibYzNmRVzQaYz/pHxh6nM6XT/hs+kcfsw3jbzVb1Cd3RInZJwnLurzldw/OEo72gOc8oqwTBGvprMSeYpxPiIDYORfS/OCiREO8HRKI/7N0wxIRyP/fjv6Vyf7e577v/pPIZRW/N497zUUZI8uFD+yJT39IlvJvOaWLpMy4Zxnwa6QmW+rp/O0+vByeHcGqeMqZQHI3KUo4mJj+kVTolHD+4UDXVctiDv7949vC+vz3OCVsxoZFOafRrWa9rfnyJPCpyYZjGc66NCT5bfr+mJbOjc+uzvLqGOYkB75zHGcrNaI5Xi7bt32Lev8b6hM4b15RVtt+H2ztOaA/VswXZ7wLSW1WKNdV1UjG0PrGYLPnn+EZerFd52vHr5I+/evma32bI/bCirkvXigqcffYpSInpwCkuhNbvNnqIQvH71htXVJc9Xz7i6uma7v8cLRz2bY43g3dsD3ikuLmbM54pqtgAcr17eo6Tm6bM5RR1hz03Xstm+pa5X3G3uENJEhF1Z0JoWEUqsCczqBbN6wf7eo+QCa+5obYs2O7QNKLHCuzs8Fu8NIcBsUfLZ4ucoHe/fpolGArOZQ6LwwrFrLIdDR1FalrMVzy4+4bZ5jTF7nG0wtmHX3HN3/5aZkOBMWgMCbwNd24EQFCFEI0hrICiEVv3+jGFgHCFRQdKL6D1OhCh3SkAhCNqzN57SQuWj4tV6j60EYak5hGgwiQSrJFWtCJXDKtUbAupZgTWOw2FPoSVVVfb6rK7rIv8govJNyxi+yDtD8DaFLxJ0akcnDzgC1mh294Hbdw7bwUF07No9TX2gmtUELyN9CSA8CM96ueL6csX3r2Ic+DKFAXIhUBQFnYnt8ClkjTEdpmvYH/bsdjWr5Zz5fM7l1RVvX/5I0zTcvrtlXs+TgXY0ipVS4jyDP0q/RR/yeXnPuRDIuIoRWcjzzrUEZgQkezwbLDdoCqFYUTALli0WT+RYbIjyNOkc0hq0VMzmS752LUsf92xhwHaGH8Utvoh0+yG0OOVpVeB1t+MQVpRCIJyD13dIa+g87PZ7tBNU1YLL9ZLgLIeuBQdVFfWQzlmUGhyKskFk1rt575FK9DSaszHcjSyi02rXWVwAbz2b3YFXr9+xOVgOHfigozwwQBCCpoHORjrQO4sSAmcFnQMpDxgbDTH3hz21jOpilxA/QVDhaIXnEAwLb1iIOR0KFQI1gU1jeHn7lhevX9M2XXSmycajYkIXTOhDnzZZyIf1SL4jekLj4Tk+XhNH9GFIBsiJf266jvv9ntd3d5TC4Ys5WipUkHS42J5MN00qic0JPc3Ud2GaiYTaOnqYDTuP+jqVT51JH6wY9yRPLyWT5eRA8AaRXO1DggNNeUzbUNYV9Xx25PVSVGVkBERU7gHMlws+qStevXqF1AVKFyPFqkAojZKSKH17/GIeD8QpRmBMJGQCP7ctP7PWHlnQjaECx4KPLDDN8cCngispFW/ubimrWTxcxwxIrDRORBLYhXDsKRIticE6T1GUFFJhnefVq+/46ssvUiwvH+NTJaIrBNd7cS+Wy2jRnbzIB4o6C2qSFUViGh4oVXvaLZ2c04WbN0Ia66os+foP32JHgiIpJGVVEXzg0DQQRJzLzBfkhS4eVMtIrXIiTaUy+dGY4DwnpZn27/9f0rglZ5iENF/ePRRowjFhf1zOQ0L87PiGUyzje9p1KufoYB23bWjjoDR6r5xDnPkwYrimdec1Ph2DkNbGMYEtxllGzz6UKR7XnS4Mn+HuRc+ExPjwg2DWWkuZPMH7yynV3TOSIlpLVmVFNo6w1uGsoyxKAvujWMZZyJ8VET+FmXk8TdZSX98032CddVz1I6sqzdXD/OJBnizjGM/vKWXO40KWoWxxtBceCu8f9O7UcyFGwuLh7umM6fdqSLEelc4K4SNqdGijSD7QSaE7kvunOyJCpVV1DZvdEGcwROMqEWI8ld5QarSfcw+zQnw8UUII5vMZu/0+wvYLkQzUIpzjWAkdgmO9GuDUhYhQ4lnxEFKZIU/WeKjiLDLeg70iYTTGmbjpef00T7k4Md77D5ZmNEqI5ovROxyVx5jBqCC1QxaaRVViOkNz2Pf3Gmm8k8VM2qOuB5kVec4Cg+XtqLsxVk7c2MN3ac3mlo6ULITQE6siMWB5DMKobyEcE3l5HONZUxBCjCkbIfWzEj8gwmCQprXs16T3LhlSgJcS66IHeVmVzOdzQoBD27LdLri+vGCxmDNfzHvCNsLkpXAv0Mc498FjbMvW/0Dx5Gc8f/aPuPv6B7rvXtLd3hGcjQpyKRDBJ0h7UvzyY2XjOZSfU2msqBwr4KYC4ky/jZWsp4Sj489j+nL83ZS2PFXG+9KjbRAPy3t4tg/vTb+bKmfHDM24vlPvjhWD+Xe+1/LP1CNayEyfiJHx4bAH+yejPo3rHp8NYy/tMc0+zX/y7BfiiE44pcQek4tTBWcu71Tbzo11Tg+E3j1vMND554SR43czfzBVJp9TyI/nylp7BiLzNJ03Fpafq/PUXjjVPxjdqGfu5Q9Jp+a1H6NHtphJ0MVCcGQUfSwkPl5PzvveQ/B9Qtjc11PC4zGCx99VMR4h40oivGSEmAxeQShBZsi8GE4jq0mEcAgskhaERQpHENHAXCSluBAZjjr0vAUwvukf9Hugu06n+L1g7EUOIp4HKf5cSLQpTnC3a3m379g1hqY17HWDkBIbDNa3WN/g/B7r7hFhR1kCYgWskWJO0AElAwJHcB22bbE2oItZhOuTAuFj3aazBGPQZYHUJWVVsVgvovCsaWgPDaZrMV3LbgtX1xdoqXDBY72jmmnMzuNlMpoLMbydkyBqQfjr3xN+8xvc5p7i089YX86xs5rbwx7//QasYOUlHy0Ey7Jg5wLf7Df8wXUYUzAPILEY02C2W3yAUkhUEFExjqAKmR6R7INlkwRoodTRbjopK5WUR2eeCMeeIeN9/GB/icEgUylNVc/wwbPZ3PH69UsEiqKso1yiKGMoHe8xpsPaDudsolEk3ll0CvfmnIcgKHVBVSqWixolVTT6HK+fUXusdRhjkUomj3H5gOkYltnxeT1OfnKmjs+s4H2MN29sittpaLsuCUg1WmuatqXpDGVd8eyjZ3z5i6+4uLpC6xIvBghzb22M09q1UXhtLc7HeOFYF8PRZONmP1JsnThDGJ1Tp+RZ0748yDvu46lzN4SBR+jfoX+vf59sRBN5AohIBgGPnRgYRq/5rABMtOCIPg8P7p1EP59p4wM+Dj/yFh9P+1SINDJETXf8gzE8IXOZHm8hcDQ359o1ffZQ3nE+Hc1d/jxiR4e54PhYDiHF9DwqrZ/TcRqv/1NtO7tGzrX14TdMvwgnMp4aTnHaO+VE5X9s2yDzjnmpnBIlB8b3X0w5XzjVGUZuRqO7bpzLp/Xdlz6iNwdjgcEPc9jz4371DTw6+kReF6cGedSRRAKP6Jb8/Jj+f5/y4LE1P6VFA9PReigLFFkOcaLsMc0tsnwF+t95LkP6kEcSIfHWHMmHpC5YXVwhlKJLCB4Im4zHoil/8BbvOoKLIdbWqxXzWUXbNQTracqan3/5Bf/gF79kMZuxvb/j7ZtXmK6haXZstndUdsb66iYiuzqDSKgtUghM24AIdMZSlhWL5YrZbM677Y+4YKnqBd55msYS/IGnH69ZLZe4INjcb7h9d8dyuUDJmrvNK7rO0XaWpmkQ4ocU1ztOtLdg/T2SFdeLn4Ho6MwOio4nF5/RuYJ6tkapghAsRXFBqTzWNRi7w7kOrUuqck3T3OHZxpAxBWi9YF48pSiWtN0Gs33L9n6LNYrrZREhi4VnPitYX8yRGmxocWiEiHSU8wFnwOhoDIdIccmdi4pDJ3rnjkiTR6NwKQTCC+hiqBXjIRQStKTzgf0hMJeCOki0CXSt52ChKSVSRDw6IcHriHgSjMOVmkIHghZoZbDeJ09vjxUWiUTqxMMmOsV7j3c+xrN2mXaOZ0VnOkzZ0dnAfie4fxPYbkB7aJ1ld2jZ1y0XMx3PPeGT7Cieg2VZcnm55MWbHS5E/VChqygrUZJgwHuLcwaCT4jBNnqMty3WeRaLBRfrC+rZjMNhz3a7ZTlfJqdEiZLxxwnRn3njPXwqJakk2Y0rAI7ANhgQC4RQtALug0OiUQgWaGYJ1NsQjYw6EZ0qQrrPPKCDwDqHqgpKXaOc4JPZFRt5wBKw3tA6i/CO+WJGd3B0zsb2SEH36g1uv0csKqyVNL4BL1jcXOICGDq8CAgd+xqdVIv+nMl0WEYwHl2w/1/e/uvJsiTP78Q+Lo64Km6IzCzRXd1dozAYYAAuAQoY+bJG2zW+8JWv/Adp5AOXNFuCXBqxhDAbDBbArGEwoqd1VaWIzIi46ggXfHD3o+65kVk9Q7pVVtx7rh/X4ie/P6QMOizwaC3RWU5dVyAVddPy4XHPN6/v8ZmkaiNvFU87Zz1ta/CKGNZGBOQpb9jXBpPC7ESnnFwF9F/rXAwp4FHVEXXYUZY7Vus9q/WKPM8olCKTGQ9PB37z+p7X9+8wxqBlhvBjg8QhLZe+d/9GMtTkgBJDc4r+p0+8oUeyZmsdx1PDe7lHesu+bULIASHCxD9Dm3rve/+fnizt7zvf1zWOH+67tRXy9XX84R9+vP3fy2N8TjCSLiQTGYEE1RCsbM9jdM95dzvnUEoFBjV6NydrVKVUFwMqxU6dpqlQaXjRJ4HQULA2bP/QWyZtjARjPhqoQQzxYbudcxRFcSYUTSnTObe3t+x2O5bLZVdXN5ZeonVGmsg5KCrvPVpnWGu5u33JP/+//zesV4sOnj4IIIPBgPMJ4iooyouokE6egB8TaAxGsdsQ3keF+ZDMEaIj0mUc2yzLOJ5OHA57nHXBe1AEiF0lVTi427aDXE1b7WJrBkTmRzKEb4MNfP5rX9TfVjz1/7s0bfGAKxqkJKzoYkRI0R0CKQdEonFuvgfE4jD/eUuGHNjfftTmL9vhEXqpjtHxPvn7sdX8sT6E52Pvl7TWL49P//aU7B/X4we/QLCidwNBqfce0xpYTPdYDJYMRA43QPboYO1nbRhPay15kY/PWfGcUcPH0jnTd8ZhfVJ6dhcOGLu5tTh8R1x4JzHS5+vh0+TP83XM7oXnBAV+OMOiI45l8nqJZ3Gy/ktndl6Uo26nSz60X5CkHz5FyvbjcfGROV6UZXf+i+HYiUT8WQIFKrsYQkNGctgHEb3Mr69vePfuHTc3N3g38JTtlkEiMoLX0s3NDb/+zXfkmYwWmKJTjnZCynSfJWHPgMXtmfQwfgkpplsRgwlNRE7IONl/g/Z1nfQ+eId1QiaJl/Fuc8FrTMjwXEqJA5brNcvlkuN+T3M6oaMnlMCjhY79Jwg3fWxVJ2wYG7P0xKgbLBVPB+3n+0XQKXjishYiCLaVCnMb1uFwDUy9H/zouRAKKRXOqSiwNn2ViK4VQki0EjgpOwV6a0zn/R/ebVmUC4qywBrH8Xhie3XF1WbF9vqKLA9CcaGiUtibGLc2GFOGdiruP/wGpd6weLllff07+F+/xT48YXc7zPGItC1CBv84MejLtK+XYKan36dC/0v5Up6hZ+2ld4djPG3H0AN9qlidKtIvteO558mLfjguc7mmaeoNPqUvZxXFM2M5pK3TevSkEABxnoP0AAjet+GdrmdA//1T5mGa75IiePr5PPVeMs+loZJ/Lgb8pwiO58rrWvGJ788pgqcK++fKmsszpwibQsROoXan63hu/Ka/jYSZiU/8O07D8uf4wpScC9CNXUzLyVycGdn4CDHIeNwutSGlS7E5h+vpb5OUGNypInhreKEQIsBAhgPT4kl70YNvEaIBaoQw4W7u1rYYeN4GunEofO6q+q1pfzEiswSghASvghcr4b6zKqdyS6xfgSsQFtqmCh7awmF9g3ENTVvRmiNSHLHWoVWBkiCVxgkV7hrvwFmsMTgvkVmBE7IL/xbQ7WwQiHqCACtTqEwHj6jjMcoJAgpLXZ2CMDKLhozeoQuFPEmayMdL71DeIzR4c4C//mv4+S8ReNRmxWd/8HtUzZe0P/sV7371htxZ7tC8tAJpFb+uT/zF6T3fZp4CzUJnAbWmaTDHE4IAny49aAQ5kjxKi6wUHJ1l7y3KQyU8tqOvQn8DDehRIik1p2fQudFYWgfBgEIipCYvFhyPB97fv+Xp4QGtCpCKLM8pFwvyosDa6L1kGpKRhrMhFnWW58Hr2wSkM51lrJY5q/UChMfYMZJfoKGDR2zw1LIoraM3zOU4uNO9esYBD+6v4T1mI2x/ayzWBgTBtm3xgM6CYnx3PNBay+3LO7760Vd8/fXXwSMQItJQgIRuTfCaN20b+L3ogOFNDGHjQtjADso0GmDOCS0FRLptXsE9dzfN5Rkqr0bvxTE5S+FiH52Pzoc15ayLhpA9/PxQnjZFyJg7R/yIlo1/L9BI02eOmXvYJ96pP8cTbT4984fvuk8450PG8zE6b2tsyEfyDeVr03Z5JnPjxuM0lvX0z6b1zo7boI7pnPtnfpstV8z1dNDDAd/YF3eZDk99mKOVpjTec3SzjzyVF5fv27BOhvWL1NRRK7t1OfhtLDoI85hMxqfy7S7S6YgGA9+FLxkURZRpdHtY9Gt6Jm9KcrRu+ueDFRTLGJ7xAYVMzNAkyVltbLQ/yeQ5nwMhOqTDbr5EULrNnT3DZyKtuygHGRoLpLUm/IDuRXRG8cP12vFHhLPEJY97qcjzBZvr2/A5y8jygiwT6DyjMS1SBX47zzTLRYk1nuvtFWVZcDoqqsUBt93yP/njf8SPf/wVjw8fuH/7hv3uCSUFxtSBXkBQNw1VE1BTvfPgoixHGByecrHgartluVoHJBUbILMXxRIlM6xraMw9t3drNssttQk00SNHPAbnJPt9w6k6YK1H6xWno6FY5KwWG/CSU1XhRUWWbfjRzR9SV0/cP36DzY/84MXvcTQblqsNzjl2hx2LYst6uaauD7T2iHMVgWdSNO0TQmqKRR6QaPUX3Cz+iGJR4Pyvedgd+XD/mtOxZlve0VRHhITVuuT6doMuBF45vAz3Rm1bjMlojUC2LsRojvtIWY0VIbawjWi4QTEeeEuhYkjaWmCcx0Q6zgtJVcPpCCrXaCfxjeNUOawDnTmUcEgBWgpc7jHG4VqLtxDiW0o8FQhBXmRIAd6CqQ3CBnpZqiAXscZimjbS5DlCKfASjKRVhgbLqXXs947dg6NtBaUKkOrHpubQVHgvUVJjZR3Wsg/7XgDb6zVav8YZUFJT5AuOh8dORhy8mINivG2bDqUmhGqxLBdLrq6uWK3XPD1+4Hg64b3v+Nr0Lym7p/fkXOqQpXxiQwKNdhIWKwXKKSrveBAO78McLlAsUBQYKjwKhYuKX48CnQdDilPNdV5yV+ZcZTmtdXy12vLG7Xm/P9BIT6sExnqulyv8qca0wUEl05rHN28R1Ql1FUI5t20D1iO8JxOSTGdYH4wimHgPDw2jkwwzsJVhTBLqmNYBhUtpHQ2MFXV74mG355u39yyutrRWoGRQ1ksRPMqbpsVHhM/Ainh8VdPUFafTISjFXUDFluHYxHmHcS6EgiB8z/KccrmgXC7RRUGZBfSEx4cd79/v+PB4CvxVvJH6U390dJ/JBOjyBZpfStl5nCd9E5PS5mRq3fkugkxXEmTKTWP54I40dUP2eIxrPciQ/YTXTm1JTUxBpJKsGD9UeKc+iQjKfmnh9rfh//ZSnkH6ZMW4kDLG83LoyGAlyi5MWlgsInoamajsDpd9ZOQHkHRCCGyErNJaB9iTyCgYGxgg55PVhEMl6G3rBtDRIQ3hQr3v4d4heBhNvYyGec/6KcaK6yGjoZSOTHPPnKTDxfsYC1SMCVfnYblaY73ncbfD2aBIL8oi4O87G4QZPjEUPZPRe9kH+PjVasXT0xN/8m/+n7x8eXcG9ehcgERNijfnLEWZ4/GdcrqX/YytBs8J4Ui4DIiU8c/RuokYS8taMp1x//4+evm5CG0XIeHxtE2yFvcdIXlpISfo2O8nkkmLPwl6PqGECazchUyTv5deuFTXRysYvP9c3qjKiLLnc48037VhuG7nL7tpXXOH3LQPw3cEw/q+fxowr4M1Od/WTx2/S8lP/gp66+R0hvnfuifjNBFmex/jHsfvQnRoCilWrI1GLFIJhCV62EamgP4sSQzhUMCaztOu6m6KkqJ9/pybT9M5/v79Ph/rtD7nBAh9vi7e7GzVw9/GnrOi2+PjtTynVOjb8izfP1v3pXXedyMyb4NJCPx5mO9kRJWgXDs4fXpF6rRjQSgmxkPbEaMOQUApCSEV0tiEMkQUfId7wONxOD8+c0cKC9+f8ovFIlidmiBI96MxiOelSEpVuLu74Te/+RZjDUqGcB3OmQ6yPUHaDcQdF5juQPQk5td5RvfVIAtn62lYlo8MepoP74JAOB31KkTn9JEhF0hEhB7KsgBHrkTGarmgOR65v3+Haxxey86IT0XmPHjqJyWeA9crX5KSfHw+p6USJtP7fu2HvsvgFRXfSR59YS2M90giwcZCpzkUDBFpIIGNSvIUy7wvLMQyktLjvew8HZ0NdITzGmMMx+rEolyyKBa0TcNhv+d4PHK1vWJ9tYpXrsdJAQQmWDqJUgrrHEKp6EH+Fi01+osVxdUruF/QvH+POx0RLsTfFMYgcHTCobhGEz0pRRBGT1NcnqO9MxWsJSXWUNEbxns+5vhZHTOMxfD7lDa7pFCdu/OmyuC58i8pO8N74uwIn3rEDts2VWp+ivJXRIHgVPY4hSbvx3fsfRzOpdjHCYLmHO097edzwtNLZ/+wv3Px6qf9m47Fp9+j5ym9m+6BoaHqc8KIYd0JkepTBBjTtkMfDuAMYWjKlH6CEHqaZ1jnJcX5xxQeHxuLYV3nc3L5PSFDfGIfYeMSDZX4VilEp2ibMulDOmWkMKYXKk/X59n+icKQOSH090mZLgENXuK8xHoNZChRIMiA4HUS6vE41yIwQIukDcJH8hjPMe9i6SmlMB3CTRjKJLhIgv/n0sf2RSfEAKRxIDIUHu8sXlhOWY5bfMXV8mtuF5+xLZfo0tFaCyrHkmFshkJTyBKlWrT0aLFCySukusL4Inht1wZTG3CSvChprcWZcO9opcnz4HFvjUdnOtIqjsNpT3sKyAJFllPmBXmmQ9gvJdEyhVNzCClQRYnTQZjrpEWLlnV7Yv/Ln5P/za/g6YBYL2mkpSgkr/7ZP8X8kz+i/eYN+dt7XvzsO/w3H3jXnvjF4YGf7x94WJZ8tbnitD9Q1weOh1MUCAUBo8KjgRJFSWh3pSw74agkrJDcH3dUbYP3oGQ0ojU23Kc+ygnOkGbO95UQQQGavEa8EGid8fbtt3z3+te0bcXd9g6lc7K8ZLlcs1ysqJoQVq6pa1S8ftumwTQt5AWtaQLPIjRaaK63a663a4SIYUiIgloLQoko+/BBMe4shcriXr28Lof3QC/eiHRlvJeH54ePa9R6R2tNhMwMAmZrHFIq8qxAKcV+v0dI+PyLz/n6J1/z2eefUzcNxjbUbUNS7pkmKNWdMVERboPXeNt28OMegqB5oBSf/uvocn9OR1y6m87ojcl9Pxynj+/dsWI83ZvpWaARU3ioFC5l7GwS5uHj9QBjRMWZfqY0VYx3gttRtp6+vXT3BFryeY63e3eGJJy/G+fpk+ndOH3VeX/WdzEpY8i/prjJl/aBG9L3MdnIA83RESFrWhPurH0wXmOBLo+g4OPrbtTmxOfMpUs02qVnl+//yTNxuc5LaUTTMKYonOjHbfTOYPGk82WY5riIOLxndZ/LWZOsY0Jf0c9EeCcYwYV+050Vw/kSQoS7ip6+8d7j7HMGtoMxn/l5diwGn4fvTUNOjdZ4Jx86n8uOn+0OQTpl3tydFZrgMW3bhTCzziFQrJZbyvU11glubm8oF2vwitY2/OqbXyJVg7WexWLN7c01Esn+8YHjTtGaAF19tdnw+WcveXV7g28byjxDK0FZ5iA86/WW1WbLcrHi8emepjmhhcZUBmFb9CrEqP78s+sQmqOu8QdLlhWs5JI8W/D1T36XFy/veP/+V+xOP+dqc4MxK1bFCz5/WfG4/zWL8orPbv8Jp/pA3exZli/JsyV/+bN/ze0X/wghMn51+AsQkpcv/pjPPvsxu8c9TbtF+Edurr/i/ue/4bR/INdrlsXn5ChsUyB9zt3ma8pyxane8Ytf/Sn4BVfL2yCjFJ5X17/LzfKfoIqK2rRI+TNOpxO75uccH77j1fUXKKlxwnGsD0iZs1TBpE94g/ENjgV12+KED2gr8QwXTdDXWCFwpqWxJobTTfKUoDNpTp7agssAAcY4doegBPVNzv5kOVaOxoBcwNPJstCwzBRlLql0y2olkD4anTqH04amCQZyxTJns1qSRxTB9nQiyzKyIqB7hsDmMYScDqb8zoNwYDFUvqayQUktPVxtcwrfgnY4tacW7zH2gPZFuPg6Rlhg6ort1YJFqTGngOeU50uOh8dAP8TzrY00R9s2ncymaRpOpxOb5S3L9YrN1RXv70ueHh7jXEWlJ2Lge/X9EK1kvCvSfrPeUSnQQtOIlvdYDCBwFATadIHkSPDwRghaYxHZgvzqBY3fYZvv+PHtCz6zFnl4x3214yv5e5S0PB4PnKRE5hmnw46rcoVBUNcNRmmyXGPfvWcjFa4s8MbRnGo8hro6xUPJkWWKPFNUx6AjTA6vSa+ntBzo9Fw09GxBioh4pGLoYtBZHlAMPDTWcv+0J7MSCwhv0BK0kl2IHms9PhpJGtPSNDWn04FTdQx0sbcIJaDR3Vmeroog0gm8h5ASoSQyl+AN2ouI3CPJ1ILVokQQFfMzyEr4c3qq0xWQeL5eKd7JnIXkYyuku4OFBQIP4UVAezieHMdjCz6GAfA+hks4lwGM6BJSHy7VHo2ExbicuMxG733qGv9kxXiqXgqBEkkgHLwfk0d3lpVR+d3irUdEZVDwcGxxHjIdINHbyDBgHc4brJAcTidca9DRM1xLhRIS602wMDfBgxwvImOUgJrGyTlPlvVE+TDu93Rw5gSEifj3XsRYJS4S+WEUAtPosT5MvnNRIOLCwS0jEx3q9FhTs1oUZCoIaPb7R6qTYrPZBAgxL1AyQ2uF1+B82DjBoS0aERjHZr3ln//z/xYhHFmmcS5Ygqf4By5a70opqesGorIv06qDKjkTJA2Gz08e9AL5nmjzkUAR8UBMxaRYsA8PT3gfjAgAtM6CRb+1NG0bY+TKETMykD31dU/n1fdNTj/56X4f5Lvo5TCgsfpxmK6hS5vHfyTHgLAbKJPSchNTBmE6BVEqNWz7mFjuDwdPFDS7EF8KEcYjvfn8ATAkQFP+8e/n748ZqOmBMyp71OSpkHXCOMVyxGhtzjBHIfD2M33qCexx+y69MyTG+zENf+ffiWTboE1zuaLRR+LTuz6mPeIwtsURhbQIjA0xkBNjGpoeLyjfK8eD0k6gM0VdB4bJGMNiGTwuArOaOKPU5olA4MJo9OM2s9HO5nlyqYr+2fl6mipxYh/FmJm+7MnXtye9c17HOUN5iSlORkzeW5JCc1jtb6v8EIN9G2I/+k5w4Z1AIHHOImWGMZbg+xPyjJhi0fc4MXpB+eR64kAQCA4fhLtJSN97WosgGICglAcSuGpvknSeEtOtdVAON3XDcrkKkEMqEIpeJMY6/JPA1WbNclFyOtVIFYTNluA9Q/IcD9NCb5Diz44KUp87RndI4KR1FM6BYdiAwdB1a/isj94Hz3E8wquQUUkQqh/TaEyQaUmmJErA4mbDal3y5s0bDvs9FkWmM7zUwXpUCDKtqJu6O3fCDuwFSymsSYqf3vntex9CKMTzVklFUqIM54QzIceoW/T7I3xOQpH+rg71qShodjLQLAli3Xf3isc7EEJGZArXxSr3PiC9YCz7fUvb1CwWAVr1VFXsDye2hy2bqw2r1TLEYBUR31EEBTlCIPERwldhXIvjEV94zK1ElLfIpzViX+FPNZk7Itoa6UHYYKRhvcWJQARb79FKAI4Qliooy4WLApTEZDLxTvgE4nguX/o+jcmchMLpt07xFmmzIWx5N6eTehJ9mqZzOOMdpDNESNLeeHPOuzeECOg96obe14E2U33eiWf2tE1zhgI98wIC1zFOQ8XgsL+BTunPXmvHqEgIRsqa9JtS6gw+/PsoTtP4pzFxMDsXXbnxrpaDsZsiOE0NJuYEfc/BogshztCnxmM6VqwOv0/7P5ynaXvS56QMH/I3UyHIc+gLl/bAMM9z8bOnCpphPXNlzT0fpjmDlV4gmmi3AO+Lp2PKnRfhtlJZQHDxPoRzUirKqMM5mBRlRNqs4zVIRkpxP+ADbebTfR150tCi7h2U7ryoPi262eWUiTUIjUXhyBFugeAGKddxbE24W6QG3wRBChaBRwpNOBELEBapMrIsI88LtArCrLSnR+P6TPIw2kdnvOXcC9bhtUKi0FGQdxQKWd6xKu7IyHG1o/Ga4IKtsMZEuFCJcxl5vsQBLQIpHCrzyNxjZMv+acdxd0L4jLsX13z37hGpNB6BtY7atTjnMM7jWo/2DofFY2kONVJKlAhGE15IVpt1d17iPCLG+47OS4hcgW/h8S0f/q//b7L3e8R37xBFSbbesny55uf/8r9DyA9sf/AFV68Klssrbl+WlPofUvzqG9Y//Tl3f2O5qipOD4+IdXAaMMbQEFBqMm/IERRIcqFQ8X57lJZKK7JFydXVNX95/y270wHvPIXOgpeMbRHehXUfOI9zin5w3qW5l0IhkUFYl2VY5/ju29/w7s23KCV5cfcZi+UGleXovEDnOfZ0pDU1VXWM3vyCpjEI4WmdjV7hAiU0EsHt3Yar7RJvXTBgiDyPczYiG4Q9WTV1tzeDMUswaHxunYbn8a4enIGjc1QKsP1d4azrlOJ1FQz5y7Igzwva1vL4eOBHP/kBf+/v/QFf/uCLCL0bPcsjMpS1Ft8aMBZrgnK8C6kQ/3bj7vxo7Ec0ghvfy1Nl8XTuvm/q3pt5f6gQH9aZDLtSf2yECaU10dgLAn8nEG6AquMtl46T0T3IfEibkVPLgN/sC+m78bHxGN+vXYGzbbo0zs/Vceleu5RndIYOpA9hDQz5XdHxRKEPAH1Yrbk2ngnApTg7t5/LP/w693kQ/Wn027ic+fX1t0lz7X/uOcyPuYNu+sPZM3972ZjvY+3WF+6+VE+iM6eirOdooTN5dfoHEfVs8PtM3WnNJIOWUKYkiNnPw4lOFc5z6dJv5zL2eQOF8/fnqaNpec8pUVIfAg+VoYVDS2ibFi/BCcFis0WpjLY1LJaS7faWuq142Ta8fv0db1+/x3vF3/97f58f//Ar/uzP/oyWgFqileLVizvWiyXV6URdVUHu7hxv374FIXn5+Wdsr29ZLJYcTveYpgEyHt9/4HR4YrfOSBTk8bDHuJZFW7Lc5kifx9CLhs36mh989vf5zz/9f7Aq1ui1wjmLMTUvX92QZy/4nR/+b1gUG6w9cTw9kBdXGAPWnmjNnkyv+ZtffMvdtuX/8+ZPWa++YLH8nKpu+Nnrn/JU3SPNirurW66XN/zm9b/l/vgzluVn3F3/iKvNHY4G53aYpubx2FLmazZXV+xPv+Gb1/8uoKO0mu3iiq+//GN++tcFb16/plDvWS5yjqcT7x8+sNvXtIeWm3LBKsvQhaZxdSAJraNpQCgdwuueTlhrgld3jL1cVVXg6zE4TKDljlA58FkwkK8MnHbgcjidLHZvsa2nFhJRSd61hoWERWZZFpb1Gj4TKhhUNpZGW8rSUS5KnIX6aNC+RpoeteXUnGiqJoRzURIlM4qsRHqDN0HulEnJyZ/YuwNq5bh5JTGtYF9ZlPEUt1DoE4W8x/r3aPM5tpV4FfhUhaOpaq7WJdfbBaf6QFM3EZlY0tqWJLus6yNtU6GUxrQhdEtVZTw+PnJztaEsFlxtrlgulzw8PLDb7Si0IiC5DfbRVJlyIfWSYR+U80KEw9E7HlzLjZccgHfCsMOz8qCFZOUlGyQHBDWBdm7aFidyrrZf8Nnnv8M396953zYsr2+5WW54eG/4zp7Y3mxRqyLokrTG7x/ASnZmz0larMrIMg0PT/DwQPHjLyArcUYi2oZTfaSUJdmyRGUCfFCKF0XRhX50zqG06gyFk1w4zzO89xRFQaZzsmwfEJG9IMsKnnZ7VK642qzI84L7xz3lahl4BOsxpg0oRFbhWxNQBtqGtq6o6xNt3dDaYCxpXZDV5s5gTTyPpQQZECsDkKKIaIwCLUucs4g8I89LdJahdRHuIAkuIvdJ5hXa52dwT0SJqcfD90g+yXZ9kPuEVZPCf4FAkam4CDBn75/ddzJJw5430vbIkYZumvf7GH58OpR69HJI8M1EIkrrYFWtdE4waxAhwLy3WBuUOW3TkGUa4YPQXQC5zqiPAWoE53HGopWiWJfB+sG14IPll7cOmWWhThcGKAx69MKLHuEpJUFPiieXZdmZ0GlKeCQCvouP6ukU6sGSGXSWBeGkUh2xMRJik+CmfNc+IT1KBqFzpiWb9ZKyyHj//j3Hw47t9hqBjoSLD8IMAVmWRygvg0CwXK7Y7Xb82b//F1xvrztGIc2H9z5YeCvP09MTbdtyd3fXw0JEC5ghwTJHsA4VED7GjMfTK1XEgPCNn40xCCnZPe1pWkM6PpUKgv5AfDmauiUt2OECnmvH9NFwTSfh8Xk2kf6bTX6u3Gnhl96LH7qck2afK1PFYKwm2cW4LT0EfC8o7gsevjlQc4q4B7xDiGj44KYVDVp3YTznuz59+AkHytzgfsp7o7ZMLVdDZ0TqlB8rEC+uHeKYP1v9nBDvecGeH+UZtvJMzNSV4T3RWIUOmsQ4OxIiWhugBfFJoeDOihOSDvYyxWz1Lggl1krHWDEu7sm4CeI+7kfJz4xYauv8pTPPYA7/DkqfZaLn5ud5pnXyyzPlTPPNz99UCRAQRubW+FwdlxfRSNkA/RwyYNiiMMnaXrBjWjva10ngJ4YHjA+Ep5jUk/aykKHsBJWZYv4J4rz4uJ9IcI1jEwk5qCeWGoihWNdquaKuG8pyAchJ/Pq0LoIAM9MF26sNp8MJZy1aq8DoILrdm07I8Wqk618oN94bWmMTkzsjjBKpA+n8hD6WYaQRgq4kWUF2FYV+eI91gug3DkKiJKBC66QUZJlExfbkMuOHP/ySD+8/cH//PkDhZ6F+nQVYNhcFoq47ePo+aaVQUSFX1TVugJpTlkWkcwyZ1gQrVTcS2A16PVx9g78irgs/s+/GAoUQx1sE5bRLwpLkRSaiAUQYq87AzwePM2dtpziv64q2bajLkkW5wD45nnZ7bm9u2G6v2GwXEYoszIFzHiFjXCcvY/kSh0BqRb6CRuxRyxuKw5bm/gn2wQJbC4FoG5wx4SAMhyp09Ex/R3gfVpocLnbf02bzipzxGTGkEaeK3uHf55SGcwrMOcHjWZ40n3PCas5XwbDN3d+01meEhFMl6ZxifS7vXPufZVIm4+yJseEEeC/PxnhES01o80+BoE5l9dDQ/bNOcRsOhe5ZRzcPleWTdZAMB4bKjNS2uXQuGJxPZ17bg3GdE1JeWndJUTHNn8qca88olFP4cbS25xQwc4Lbadkf6/P0hp3uqelYfB9G9hItngyVkQLTBvSxeLzFO7JfD32d6d/gjxAg+zUiJRjTKzIEAy+KUbPG4/m3Sd5InLIEoG+P8xols4joYcEbgq+KwbsdgieUsmQytEv6nNYF74gA9dwG/qGDVIx0JS7aZQqIIUDOafM0T74zig5hOKZ50qdg9S+V4mQajDUIa5FAbg3Sn3AcOTWeJyvwcoEuNE7UHOsjx+pIXZ/w3pHrDJng/nSGzBy60FwjORz3nE411kiWqzWte8dSlb3RmVBonSME0UAx3EvKw2azoWmaEF8+etasVpvAX8VzSCmFlwKrDDlgc4UwlvV339L+d/8vNnefk1UtDYqTVByVoLl/Q/sn/5Hj//g3IBSFc1Svrji8/ALfGhZKs1nkbNojn/3wC27/6R/y87/8Sz58+22E52zJvaBAkaMCjCiCDMVOGhotyYqC5WrJw+tjEPLFGJJSCohhlwIks+/OwG5dz6TkTZNnOUWRsVgueTocuf/wjsPhCa0ky+UapCTLS5CKxhjquqaqa1rTInWQOeAsZVEEBACCV04WDTOutyu0FpgZD0qS3KBpqaoaqRVC6niOR14/fu7Olin7OOHOOnmPFJGWCeU4H9H6rKXt4oM3CCnQmUZKwX6/Z7XK+eN/+Ef85Cc/Yr1aUleBDsKFkEXOGlzb4prgdZ48xDvlkwvGmeHMGdMYwztp6Mk1/Dt9Nrcnz55/wtmT3knttNYG2Zsbl+Oi8NS0Lc7YACkbPauscz38phAdHxQQkMZtn6sfGMQdHfd3bBDlR8dskLH4QOeN6CAR+aRJXfguf6Bvx4Zlo/r98D4ZVjq+Z8Z9OTcUG9E6sdFdWyf5XKLfICgsBhmeu9/Pxtan3vaVTNEipm38Pr95GEHrzrxFIkc/5Safr37uzTHNmt4bypG6tz9Gk8R1kM6Q2OyzpMR0T83Pv+8MFM5bOyRz050626ZR+8e0cCeroT8zEj831baHfTEoF87OmkQ/TlEhwvvnZ87H2jv9/il0z9w59qm033xdwTu+MTVSQOs8elGQlyuub16gswXOE6DPmx06z/jBl1+yWCy4v7/HtY5f/PyX/IO/9/f5/NULPuz31E1LphQvXrxACMGbN2+DsfzhQJZlLJYrrrc3bDbroExzljIaHJq6wrY11hjaRiGF4vXr77h79ZJ8mYFwaJVTP7b86OsvyHPJ09Mb6pPlavElp9MHfHXPsbrneGr4na/+GU+nHf/+z/9PvNh+xWpxxfuHX/LixU+4vlnw53/9p9x/eIM1C/b7D/zLf/N/I88/56uvHC9f7nHi1/zlT7+hzCWvtv8AnSk+HP6GX77+F9zvX3Nz/Tnv9/8DiAZrDavyc7wvqJodT1XF/dGTZwWmeeT26idsNz/kZrOmyBSi+YeYL37Mqfob9odHmtax3KxxTmKEoRUtViky6agPB2yeIVzkB53Dy8SXBkO6ZCDofTCCD0ZW4Rp1FtoWfKOoracyDtWCyxzYOoRwsQIjBKJRaMArsEpQeU/zZBDK4LZwtQxYNbJ22PaIxbNcLTCNpXIBfSDTGoSirS1NWwVjPRyb7Zb1QiK1RqkMrRytNJxaj8wFm2uJqTzHtxY86AVIFWDQ66pmrQpa5zDe432kI3AsVjlX12vefag4nlrW603Qt5kqQnqDaVqq6shisQpK2Ih20zQNbWtZLFZcba/YbMK7j4+PfPbiLtKGAU1ZOYX39qMS1rTHhFB4HC6h7gHeeO7FiTtX4r1kLyyPGJZR7pghI5x60HFJ77HAqWo4VZYXX33O7/zxP8W4mv3VS24o+PLuC06FxG9XvPRw9CGO9M2LFzzt9nz73Y6DdTR4lnmGvX9kRTCA8Uqh8gydSx6eHigpuC1eUuoSb1ucUgOnAEcKI5WM8V2k05RKERclUmqkUjgHVXWgKAqa1vLyes1Xr17y4y+/5N2f/wzhAoKHwCFcMGz1WkWURgdeIXwOEcVJGLAJicc7Mm3QmYiXa6BPnA0IoVKE+OR4kBH1KsuyYKiBCIbH0d8nqINEL/sYnLVTmirwxAGdCpEg30NIQ5LC2V+ieCZrhHDnJWOLQIYn2UrgKZOcWg70Dn0dAxmTB+GCIQcMLtAZumCIYh5yTPI8c+dO0ycrxn/961/z5ZdfBthz5zqriv1+z+Fw4O7uRbQeCgxFucgBT9PUZJnGmBapsi7eVV1V7HY7VqsV6+UqLFIXICySdVsSdHnfw4sr5VEqCAMgCpFGfQ3Q3dBf+undVGaXcyJ4S/nT897CLhHnNlXReZel50lZJcQYakoOJmMIp3t7e8svfvELnHNstzd4D85alO6V/IkRd86z3W755S9/TlkEJs2YAL8uRfS+Fp7j8cDheKRpgnVRuViEeN4yefcMhXEzxD7nCtQxwXLueRL5JIQUvH//Hu8d1vkQl9V7Mp3RDqDJhjV/ss6LCdE8rH+YxHmRYvzz+PklwvSZdkyWGmL+S1eREIPNOBC8ChgoxPu8Z/UNPGtHRK4InkLOO6SXgzmBziNxIEpPCoRP6NX3Sv14TyUSvqv/XDDff55NfbNDnsRsiLk6hv2a+z7O7wdcYj8mYpBn7r3vm8aC4nBuDGK8xjMrePr251JifLyPHg4xn4vMX4J3CfAooSzTGpwbxCyfLtDJaJ21VAyZIM9cf4V4roTpmF8YkVjGlNn6tIvqnNlM3/vX/ST/ucBgeAekM70vd3gyfMr1P9PKSIgwGK8AoeM6gYSQoo83rvt8Same2tlvenp6wEeY1LSGACEHXqrJQMwT42aLsbAtcubDvqf6evV1KG97fc3bN2+5vt4ihOwIxW5nd6+He/azz17y7bevMcaS53m0xGwHgqbhSMU+i7GAQCRqibRPApHUh07pFYdp73aE+aQ/XRlddaLbc2mynLHBqdm3veJDpTsueE0rwnx553jx4o7NZsPr795w2B2DoaAT5DqjLMrYLrq/wSq/X99ta/D2RJ7nFEVB27bxLndRgRMgQoGoYEj/+nWe1mo/bn2ecyFRUkQKztEWBEKpsGZ8MJ5oTRssPLtM4Y8SQRkgXe9BDiGGqz0eaKqavCjYrNe8ffeW3e6Jm9M12+0V6/WKLNNYH+DEQpmBZlIiKGWccyipyJcl0lfUyvPy1Y+ovr3n8O6e+njCOY8SEuEswhmUdSgvo8dKRGiIe8+78C2ulE74PT175tZMNzbPCHtSaJ5LgqOp8nn4+yVv4l4xO65vTrA0hSWcKy+dD8N+DsscCr/mhK2XhO9DQayIc/ncGCR+IRkGOefj57Q/5LyAcXhmXRiHaf5h+xNd39FJHR3P2Xj0gvznT/6p9/hcny+lBCs7/D6nAPg+aS5m/TRdEtD3Geg6PbdOPipY/kRG87dJ33c8hmm4z9K4F0XBKcbZG47d2TqYKkegU/gk9A8hJF7Y/l4TKTTO35Z2vJya6oRVBoPE+BbnNVItwNd43xDQGzwtDms/IMUDmXIYJclEgRUlmdQ421LVB06nE03TdvRjCisVBDg9fzfdFaM1S78OvfOD/TWkpQf7RXisNzjhgkex8fjDjuPjbzhVP6ZZ3WJ0QTi5FafmxP50oG5qrA2w1q0JghUrLdYFj1xZO3S2xDiD9xKJRmc5yGCwIAke/dZZlI7zR0Cik1KSKUWWF914qEHsbOs9wsV7GahcgElUxtF6g2sqNu8+oN8/IDZbVOuwecZT5vmw20PrMU9H9vuWGoFWmrreo375nq1ckLcVKgPrK25fXKHXBQZLU1cIZ5BYlMjIvERHCkYgyJSmpqFOAighqWwwHpNRkORijGiSQEz0NNM0nZ/1EilUVJLn7HY7Doc9pm1YZhlFUYBQFOUCpWQnkA2hguKZbwMyYJ5nnI4nvLMoESD8y7JgvVoypGESzaqUwvpgxNG0LW3TxjjfKkKukpjrPiwKYz7Uk1Bj+n3eCwkFSRgazgoT7wkbDUeCl7dSKsST9HA4Hbl7cctXX/2Q1XKJj/Iuaw3GtJ2C2FkbFOTWhNjiNoW3iyhhkW/3EdlmZJDk3OiO+tQ7cO6+/nSlVPg89AY3xnRharozETpnlN5j3Hbz3sUsnZynIaTiuE2X+jWnGE9tGyVx/s5Znwf8RGrPpTYM81wcQ6n6uzL8eD6eqUEdfRSzpTLT8/RsUP2Qtu/qnt7JLqEwJV4m/j50Ghj3KORJ9O+QB0o/dx9F/3f2gOjHKLZ0fNsN5r3vk0dxPgfzSTCteC6/UgP+bjjdYsJL+n76e6XyTJUkHjg1eqZP8vy38NWfPevb1hvq4pnM9WXaqjunRvTElO4W3XnV1MG4OZxnqU7Rr7lYHwMUq0Cby85Dckj7zO7Lj7R37jPQnWcy8mBpuIbZvPO4NE4IptWkfRG/nbVtWLeUEqk0QhYo32LamsoYdLlmfbUNChspWZdLlJY0Zs/hZHn56gtevnzBZrOmbQ2ZzjHGsFyu2dc1xoU7rChznp4eeXh4CGFXipKr7TVK52hZoLTHtCdOhyPCCU6HE011wLmKPFdkusB5w+lwYL/LWaxLiuwK4RVKZmyvrtheLZHa8Lj7NcK31M0jUh9x/oR1T7x5/xe83/8a6w1180sW2ZYPj2/57t2vePP2NX/2n/6Uw/HI9c0rimWBd4qvX93y2TZjlVesVI49OFr7gOWeQ1uxf/qGX735GToD604Io3GuxXkDywrbONarNZ6CU/Wedw9/xR/88L/ks+s/wpqKp8O3tPYNXhmkt1hjqasAl31ze8duf6I+VRy8pVBwtbmlFFA3e5wKjotStQidQt/6ePfH0CtSgY8hSFxE5/Vh3Vgnaa3DWcEiU6xeOtYyoPtUJ09jQUY0JZNYbCFYKI2xjrpxtDlYHZSgwoNxlvrUoDyoPMSdxlkCEmCAxcYHNKr6VIf44zpHK4HKJK0UNEZgM4eQlqKAcgltm2Gcp2k87bGlOJ24uwl6LY/vQ8B5T54rVssFOlM41wSlu9ZU7eBO8CHMjIfgSNk0mCIi3tQ1UgqWyyXr9Zo8z9k97vt9IgOdqITEivP741kZRNzHPsoOvfMcnQl0shDUwrN3LZYcBCgvyVHkHZqX7+SI1nlanXN990Mqf+BnqgCfcy2XHHzFTnmUy1h4hRUeh2K5VshFwelgqJxjXRS4pqZ5eKRwLoR1zgKs/sm0YINuTkkJXmIHdEpw4BwjpykVwhBJmUIkC7RWFGXJctVibdApNq2hOR7BGjaLRQz1LNHCI30wMPZCBLQp4RDChfjiEpSWKBPQpxACpES6hE6SYPWjUjp6jbsIHCqFwGqHzwQeg/ICjeqceaTrjRO7+aSntPv7aUjQ9PMuYujqXjYyRpr5WPIIpBeIIFAMT2RYG0PjvCCzS4RSuCM78WO6sgcopV1vhBzTMQAiYSum/SFH8o3Ut09Jn6wY11rx9u0bttst3iusDVY8VXViuVwE5XcbOqxUgPjNc433gsPhQF1X/NVP/wa84Mc/+jHeWbTSFHkevMuNCRaoApTUgYATyeMtLLa0VoxtSdC7HkdrhgpvT9MG5sxEwl029SD+0RASL8Qfcd7RQeT5GOZdis7zTOnk0Z2sfsNkBaazh6dJwq/OAyXOibWm88xK8Lqn04miLPj5L37Gj3/kuLq6RmkZDAhiW5NQL8tCPLg//ZN/EQ+zULaM8dGOxyOnwxHrAhNp2pbr7TV5lnX9CgTJZcjDlHwcCx+FI8OVlTxZh3RKGLtgff/09ATdFhqQMs6FWCrPWKuepW5XDDbukOhl5DQYnnfKnX4DTTeP6P7H+OVR1efv+KjISWMiJhnmvYbp1nFfzlmOcdsmY9exP93a6VMn3BMBhteKBN87rMlPCMvUx3HvPl2IN+3FXPJdvssH6TN1DjiUpCvwZ6+MCeVeGXHugTQs69PS9x2T4asRW2HARA6hd11kFJLgURBiADrvUYl57cath0WGEJZAiMDM4MP8W2c7BcM5HNXH+zA8N8NSOn9nbv0MUzAQ6s+Hy2fMfBkdD/g93hm8/Ql5+jZNPZrO6/n+c57Ohz4lmKLBeSQEdiBANtagVIAe7M6tTpAyJADOWzUcX600ZVl2d5DSGqIQX0ZBvrGW3CdFE/1ZOh30AfO7XCyo6wrrXCQQBb1MJpzNgWiSWGfZbK4oy4LDoQ5e5Jnu4vbMze2lZyL2n6SASB4TIoxkN9aD/TV3xvjJl8DQCBKtBMTgPQ7vDW30JNdS4J3GOo9yHiki4Swl3lnyIuNHP/ohHz488Ob1W3wM2qeVCuFD4l7xXoSYrq6/j6QUrDfr6J0HTdz/SkpMijkvklLdkeI1zo3hvKGTIHkYjPdsX6730bhCiA563wOZCqgjxqSYkQMMRwKsqg+wFxHSzUQiPxhquJPFWkNZloDn229fs9sduLu9YXO1YbksETrQjURFvcPjnQ2CDEGEmpdQwE7f8/k//Anrt5/x7c9+AYc9zeMThbPIViCcRxKNRAKwMWlZdFcgjAFXRmP3fPqYcjgZbCaBkR2gAMwJVpNAaqiwu6SA/Jhi8uPMSdgw6b7pYNpju6bC6+eU+kPl4TDv/Pobt3/kmZzIuBFDFsMcTe6t/qx2F8fgYs8Hgr8hXR4a1AsLZ8t8pp7hnP82aVjnkCYYlv9903Su5sqYOx/H85uuAn821ynvx9ow15//f6ZpG6ftT3OXjDRSnmGfh/syCNzGZdrB3g0Cit5Ius86vU/P6/nbpMrsaW1L46C2R1rXIFQDQiNisBSEp3UV1j0geUJLSxYV41qWZCpHeMexavlwNBz2NbYxqSsdnR3i05p4pg7X1Zi29fG7da7zgO0V6sM1GWiGznggCoK8cIimpvru13z3q5+ybQ/Umw0UGaLyHKojx9MpQnAH6EpvJXhBKxwNIYakaiuus58g6mCwle4U5cOdFcLbgPcmCOaiPEZohdYZwVNConQGTqKzqPDVmqZpcOn8I4TzUEIGz3Hn8VVF9v4DKwetBuE8BjhpeNjvyFxAg2tMg/ECW2Y0DweumopsJciERXoHMhgN7L79jv2HB4xtAUNGoOU0ggyBFoEXdEqxE47GCzLrqEwb0ahAKBlgF6OCWvqxEi5NQT8/vVGDiHdH8DpXSJmjpGR3+EBTHZBCUJZLZJYjVEZZlgghaeoTbVPTNsFTzzsXvYoDakMIDyfQSpJrxWZdsL1a462P4YZET+9KgXAhBF/TNhhrKZdlCCUS800VOV3Xzu6o4d0qETIYOvRwoqHvzjtsdM6wNqxnlWUBZcoZrG358sufcHt3EyDi24a2bTrnC+cC7eQ6D/HgRe0iopNLinEfUT484fDwouMLfHw25csupbnz/TmOqJOpRXqX2J4E6Z76YowJ6D4yrAFPOBP639veAST+c5Fv6ZCuYn29XGNIm07aHnmSlHeAnRPkG2pANwF+EC7JD5SWiQ9L78URJClGO3JkwO6lkDtDXivRz8OhFSp5TqVS55OP0uuRmCnN6eB5EJoP8gzb1X33475MDbo6GmD4UvzflB6ItP+wvK6cQZoK1IHR2TE0Lh7OkRi0qavD++h9Nimvu1XEYMHO0y9DXjXQc4ORHSyfru1TPnrAi4+63jc+lEu899KzlF8mD7qzxg0X87h/HZ07mP/hGHqH9QFNQSQ+xre4KMuR8RxIceflBNrWe98ZbB+oaNtgmOPcDC9EMAoD0cmghZBopVgsFhRFjlK6U5Z1AqrBhkj3wrj/gz8DGWc3H/E+SXTQeE4G+8P7wOV2Y8loL3d98Qkstz/hksLEI5BKk+kMnZVIvUCrwNvXpkXkC25u7wICqzRsrnK0FpyqirqpaOqK9eaaq80G7z1t04B3rMqSsgg6Cq0VdV3x7r7meDzirUVnGSuVhftQFDT1nkN7CuFknaU+nWiaCvDkWU6mNU5qtFDYNkAmC5mHezFXlGXOolA4Gk7NPXX1iFYKLTygEdLz9v1fU7u3FOWS3cHw0CgeHp54evop3735Jd9++x1aZ9zelby8/Rwl1vzw84LVogbRonJ4eXPD/cMJ7w+cmgMfdr/m8bDn8xcvumVtfQgzJxR4GpRcotUKnOFd03C1+l3y7Ib3x7/iYf9LLI+UK8/x0dHWjrry1KahXCw4+JZjW4FryVvBXXZNQUl7NAgXlY82IAHl8S501mGNx1ofEH8Q0QgqnBmW8Nk2YD2gBctbwd0rwW3jsQ1kHmTrkTGUh02Ac14gfAxDKIZe6D44rPhAs1njsNIiCPIfj+lka0pqjLGYxtB4jTIOJy1N62hKT+PDPSsBnUGZg1VgrKTeW47vDfrwyNdbB8ojY+i54HGs8c6yWmQsC42KXgUqKxCnPeGODOMQ7uKITmMM1pgAqV5XLFcLimLJYrmhLEo+mPc4Z0hGj+Gf7OVunPP63ZmT5Ao+KXPDHSYJYcpO3uKViDiMnnfe8veAEw4pIPOBfg2+zeFl7yy2baido8iWWATfOUOOJy9KTlXD0bbcOE8mkpOMoi00uiip9ztOxqKEpnEN6uE93gYE40xrMiWR3sR5Jv7VdKFKRaAJlYzOAhKEl4HWsR7pBaq7T4PB5mKxoDpV4A1aqmAA6Q2rMieL6NAijg0Q5VQC4UOoP594DxF1kVLEcUy8ZQr3mU7IFGO718l5AU76wIMEig6BJ5MghEOg6DHAhnM45vXjATwIkSk6WaUQ0aAJif8ItPrZWhGxLhFouZ4LDGGQ0jnuvcKnI10kcth3tMTQCE9AkG1P7qFexNTfeOGHxOR8f977kxXj2+0Vf/qnfxrjHIiRkOH29pZvv/0WCEob5wxVdaJtG96/v+dv/uZv2O136Kzg9uaW3/vd32G52LAoy+AlHpXB3od4KcfTobNiS9YbgZlVWGc6aIOkNJ8KZdpItGd5hva699aIAygjRHpH/DqP96Yrs4nMTidAijEAkqeQsR5bWdq2HdWdLGlTu4MlbSRaIhSj9542woNUVcV+t+P+3VuUUmRZwXa75ebmjuVyRZYFC6Hbm1v+6q/+gqfH79BaYU2IR1BVFcfjMUDiRYbF2hAr4erqKhJUIZ5nB7UdVgy95GLwsRPiuO63nkkY50nEpIuM+GF/oGnafr68J4vjbK2NMc/7MlIFYd/JrpJpXQy2VJdBiDE9PUnC90zLnJKb4XuCyTabT91mFMPvPjlZDAqJrToTUorhr4PPfpylg58YMvcpXkRq++BzZHCV1tDGGINDrm/c24+kYb5p+3tCeU7gcD4bn34YzV3I3TobLtNzzuRCPfN1nwt7L717xjlN2prGYcg+9S1Kv/lI3Lu4HnuvMd/tm+7ZYE91UOjEM93TKbFSP8QkrlSnGD/jsP3g/33+PttQsH42YhfGaDgW55fifN7xuKR+jJratWEeUv9SG9I7PbqCmPwuunp7JcDw4v00o4lZJaz30YNleE71ayQJwTpPWx+eGWMpcg2Ds2q8nQbnxUSgMm5T8gxyZHke+jsdXxc8kpPABiG6uKdpjAIxl8JtBAZZZxl1VbNcruI4hjWWxtg7cFhUjLd9c3PDfv9NdwcO13vq0tTCfnbtDH/vmOPh3k1nLN1R2wnJfN+foWAsjaUYlB9BvvE20BGtd1QEyK5MKbxUGG9QSqK1xhOgldrWcH17zXq95vV3b9jv9lhnyfFopUmQ9Gk7ehGEIlIIhFIBSl2pzqs3KVz6sy+GPxEO50RcQ1Plyvl92Y9pP3beJ9j81Ps0/mFUnA0QWlmWkWc5QhiccsFYx9nOE6Vrq5BBmCMCwo91NljJSomtXIBXzwuWixXHw4nj8cj1dsvNzTWbqxVFUYQxcUA01LNE40Kl8JFnqcyRX7z7z0ivMS8UtchZFi+wj49hKTiHEiIwQUIifB831cskhBzv+ZRkhK3qz4axEnxubU4V13PKuOnnSwrySwrIXjAkuv3z3Nl6+bex98cUGnGq4B4q+Kd9+WjdA/ppTsBqbaCTgzFEHx890c3OObw8N2Ybzsus4ctM3uFvQ4OA9ExwPh6p35eU8MN2TUM0PTc2l8ZwqPSfKnam63CuLdM0VejOfZ6WMRqvyTiODRfm371U/qX90v0+26L5Nv5dJu89dV2Pyp+uj6EHf1KM+2lbBnSpj/d+uo7m1SRBuDdsx98mPTVPnIzh0BoOreVkBVaU6PwKIZcIApKaad+BbxCuQhI8jqUQ5Koky0q0zDmeMt59gPu3J1zVIIlhwrpY7A5Fi/NJtDKl9eM4EOgZG2Go+zifcX1LGemGaFQFSKHx3uCEwGWSXAjMz7/jPzV/wv3nr7h6dY24KzqvlyHSm/d+wEsr6hZ2h4bt8Yl/dL0FV2LJyMqMxrYIo/AqgzzE9tTWo7NADxaqQKsMJXOOxxNeGcrVMvDNUlKWi77e1HMhKITEGpB5Ge7GY4X/cI/ROWWZYR4bauexSnA87Vhai3EiKBqdIM8Vjc3Yfn5HLhewf4LGsFgs+c1vfsPjnx942D+SKKccCQQBZo5ggcfQsleCt3hqL8kdPDR7vDXgLErlCCUD9HWMXeijslk5n0iA2KfwJYTmCjSMlhm50uQyQ4kVQniqw3e45kCuM9ZXL7AiRxclWR7CwTR1TVNX1NWRLJP4NijFhZd4B8Y1oTdCU+SCu7uCF3dbTN1AUox7D4qAMCMznHU0jcELGcL1IUaGn9P9e343T85QBaKLipEcIlyvFHe2My4w1gfkQ+8xtqUoBF9//SOKMsPYEOauiSh4zoBzIgryHdYZjDUYFxG9XA9XHPjaAW0wfB7XeKTOkB7GsRP7dXjpvBaRvh9ygOks895HhUJsQ1RApDttqBh3LiD6eOg86RM8fDIIkAQ5j4wojUnBNmyL1hrnbYe6Efo4vIPCPIU5PTcYSwZ2c/fl9N4fPU99nOQb0TkieDbhx+/PJak+foYn2uPSb9PU0QPntYU/yYBhUMZ0vgOtm5BM5mnZVNeQ17iUwtj1+Ryci4MGbZujU0bhaWbSlL65RH8P0TyBgeI2sTHndHX6zTK+r0f96ysJSonY3tbZMzpHax124GQMOmXLiP8fnz2Oc8MdgScThspqVJ4jvQZnsXZHKzOUFmRt2L9WgLGGTOXhLIjry+MxLij7cq2pqppDVXE8GlxUpIQYwLFVTkbVSaCDc61ZliXr1YJlWSKVhkifh1ZfoPeGc9b1h7N10I95MGR6bg7C5x5V72w+hegMBHSkPULb4skmPRaBlAVFsaJYXCHUCqEd13dXeCVBaoryCrynampOpqVQGUrlrFcFDw9P5HnJsizJs5zaOwotyLOSQ70CggLy9evXKJUMKSRKaoq8xFlBkRXUp12ID+zBugbjDEoVYY3FkG1ZATebW8gVnozaSKRyqNyDdggs2hmEcrx7/DWvXvwOrc2iIVLF8fgtt3c3bFYveXw48v7+nvu3j3z3+jXGHfnBl0tevtry5RdbXt3eoFmjirfsTBuMBITmxd1XmCZDIajqJ9q6pihKNutbwHFqd9RtC15z5a9B1jw+/oZSr1iWV6yzL9ntj9zv/g0fdn9D3Xzg1YtXbLeeX58OuNpQnyoqjrArMAeBsYqDbJDuiW27YOVv8dYHozNtMV5A61nmIeSI9wKHwqPQAoTM4u7xeAmtALzCHBxWe9QaVj9p2VzD3RtoozJ6lQUF+UmFkC3We3Ae27aoEkqdkwkXEfHCngr3WIZzwVkgeA2DkD46AgVFp20cSnicViFEnPUY46jamlPwUSFX0BaQKYHQLZlRVAfP8V3Dt/dvaH6nRmTByTNIaBRCLKkOR66Wkpsrzf29oGlbsnID+0dEdNqUOhgctk0d0YVNQISqThyrI6vtmixfsyi2LJcbPA1NewIypMjjudYghY/Y2/P3wnCvSw9GBapEe4ESktZ5jt7R5oLMgTKenwn4r7zgwRukFxQIFJYCwQmFx+CrE83TE7Y9IlqHdJ6jcHxQhltZB6x8qbDKoqUjk4rSZTwJR1bknPCcGktWS2rd8MXTe3amRgALoShygTQOrxwGg7EgKXDUASESF0IFCoeKIXMcgsP+QF21CB88x7NMkxeassiiNzm41nK9WVOuLcZJrq5WXK1KKtdiAzPVQ5JLhYrQ6SCCPkcEhMpE+woBSIE2WZC/EelAEfgfme6pKMNzArwNEP5hNhyOCIkfFms4KzseNYXgOufvrQxjEPRZwRhGxvWIEDgZvgeE6nm5TM8rBXrEdnL5cFdKT1wvKqw3BE7ogJ40vF/jMlRCRRlmvF/DAPWGjInG9f0dErzEh0r8ebn5x9InK8b/+//+X+Cc5+3bN9R13VkJZ5nm3bt3HdyAEJK2rXl4eODp6ZHlcsFqveRHP/4hVd3iHPzlX/5lZ61m2jYKDzwSwWKzRufZQKEaBBrGmKg8zuO/bCTcCBblQSn+s5//vBfARcGv1jrCWfnOc09AZ+XaDJTcdVVF4WR/gRsTvKHqOliLJQZCKcVqteqs7RKslLMh3lKWRSgypTtlliDACSgdFNZv3wbFeFkuePv2DZvNa9brK+qq4Sc/+Zof/uBH/Mf/8K8xMeb48XikrqsOtizFg9JKs1wtWZQLsjzBk/QGBlOS5kwYSd++oaBHJAEQvRVkgpE3xqCk4uHhMfY/eVKEhZyYqTBPARpeKRl19P1xmzzpg+LEg5A9PzAhePs2ztHr4d30zvm2SM9jG2dKOWcoOMuTWjGfZp77mZ+E6BTr6T7qPf6GRGbfjo7nij8bY1BaDxiGYZ98997c83HDLrU/vTNH+PdjNzdG/TBOPeLO86bvU+LZD+uAgXI8sftDRpfRu+NBH5Y7rH8oPhBneadpyuTMCUTFMK8nMuiRyfQRTtaFmCGQ4GVtZxU/Zv58ugMQki7WjSAJ80OeAAdjBuMmxgzkR/vTj//Qa3w4jpdkAlOBwmWhvu/QMOaFBH07+teH7bvEZDNo87lwI51Z/fOkRB8zsSHvvNf7JUGCh6hkjsIVegXMMJNzPbPpPd1dRLxjBP24TVfteD35ziMjEShFEWC/iq49Ib+UPRETB6kfW59O0LSGe4MnCO1dLpdUVcVyuUSIyfx351a4y7x3vHz5gm++eT1ATUkjlNbPPITnGfPt4/neKTvDSMTh6k/wwbj35316lMocVhSsQMPVJLsyESAdgKU5ntgbg3ABhknrYHfpXRD6eRxaa6x1ZLnmh1/9gN3Tnndv34V73zm0zsiyHAYwpt08dKMuuvUz9gboDRS6uUJ0tmMJ8WA4V+l8HfY1EaNdqb73KgmClfPxl0qiUYBCFgVN29LUNXg3shgN4RxUhH6SfXxJHKBo6pq2tWRZxmq54MOHD+x2O25ur7m5uWa1WlHkWWgLxLENxnRtCnvjPVpmOGHQa4fXnkLcUucK/7jH6SOmasm1AmvxzsRzNilkROeJLAb/T/2fCpbnlJPT8RmO5VSA97HzYirEneYZKmDE5J1L7bks7GOw15MB4xgGfKgUnJ7bl4SU52l8rqSyhpCsvRdKnJ6BsLPr6aTojwmoLzJkM3M5TMlgZzjvIyH+TPlzHsapj+n5VNE+TBeF7AMB9XD8k+Bz+GwYgmmYppD6qT/PKa3n1vywjOH8z62zaf5LSvSpkmJ4Bz0nlP8+aXYfXMgzNExOaYrw0AmdI8PtI80iIlM+Ul7Fcznd2z4UPuqvS33+O0r/l3/xQONaKtNQmZbKWBwSrXOUypEocAJbt+BDnEWcAW+ReAQKKTRC6BhiS2KNAK9I/FZaFwIVb24304cxLXam1BueHz0TB3iU8LQEQ6tkNJDnOdIL3r55x7t370AGqENrbGeknuarKxcgGhi2jeEffHnLOs/ZV46syNjebjkc9lSZQDmHqSo8jixTAfCNAFLYti21s4EOkyIqCF0YI3m+zkPoKpA6xBusqx3Nh/dc7/bIIqc+nhDW4oUgs5LibY11gnemoakqxLHm9GEfhN6HJygLXgvLr3zNwVv8wz27XcXJ1jjhENEwIRcK4YLoywtNhqZWgrq1qKxA64zH6jA6O/BJCNbPk/Mdvspo/rqZjTIcFaEKpRTkhUZrye7xiaZpWC3XlGWJtZbVaoUQUNcNVVV1YdPyQtN2ZyyBNjIWrQqyTFMuCu5eXJPnOW1VB4Q8qVBChn4LgfUO48O+1VrH9tHtNT7xHLl0Xw7PITv0lDaW0+mEEH3MSessV5srbm9v8d7HGJ4BldB7j7fhjLHR09r5IJfxJkKpD1BMhuupI5Gne4fkNd3zwHP38VRR2u/fZ87vxH/5YAyR7mrnHG3bdnTs8OxMMK1tdH4QIsxJCps0HFetNVrrKEAOe3bo6JKSlHqGJjrn4+eUuXN3yNn8pueTPKPxEDE8/AzNM2oXiXI/P+em359DT5k7J1Mbx7dYvI8HvM2lcsL79uL6gMt0yDDPMDnbf54J0x7KVGLkjDUMT5Lu27nynxWqX6ChhoaLc2v/bP6ECIqPC7Rh1zfGvDeyX4Bpv2p9vk6n7QP6vTxogxfn+RACKyQFLbujR4sdmTAIoajqdxTOcdALvNBIEfjBxjadvDnth8YasjxnsVgG4yQpqaoGZxxy4AFu4hlkjUMrTZ4pyqKgLEsk4Wz2rgky2QgffLGPEx4ijOF4Dhl8937s4TevPB8bnZzxRQOZiIEgNwuXAEI4pBagNGCjct2jC4HINE5oVqst66s7rm9egdLsTkdae8QcPJnIuL6+oa4funjhJi847PcsFgU//IPfx2UZzTff8O23H8izZNwbFKMCwelUoVWOqSvu372mqnZIGe4GlWmu1utgNNbUoB1SluR5RiMajH+kJeOq/IKnpwzbbLha/D1WiyVH+2fc37+jyG6xdk/T7Gnbe262P6R6hP37BmPAmRVtW4HL+V/9s3/Kj3/8gqJwVM2e9XLF6WDx4sTh8IF39+942h+Qv9+i8wVPTwcenj6wrw58/ZPfZ5nBd2++43H/xLE6YVpHXbd89eVnyNzydPyG1/f/mWyZ89Nf/XtO1VtW65yXL37CzeYr/tW/+j+zzJfocsFinWPbgvf37ymyazQZlpq2MRx2R379WHHrNSLT6HR2iJ5Pcy6i1yiJEwKoQdiwmizkHpR3NDVQOsprwXKj0Y3DGUnjJZXwtCKYhJQKViUsVKBJDih8Y3GHBoWg8ILcKRSStoV9fSLLBGYhaYsGpQVSFAhhEMoilEHnHk+Os8dwV4s8ePMCdeNB03uMl3AsJc1B4Kynrh1P+z2PpwN36w0ihlwx1uCsY7GC9XrNdnvFcnlkdzyRL/KgMIyOnHleUFd1oF1aQ12fOoTDw+HAtmnItGZzteH69oaiKDgeK4oiKvqF6OVPn0hPeXxA+SEiPaRjzUPrHVm8s9/IhkdbxlBGEo1Hi6DYVd6Dh6ZteDztuKoObPWSpm7JbYA+98KjckGuQtMC+mWczwKcNFS+pUIhlOK2XPHwq2/IGkNRLpBacjh9AFmCz9kfK1rr2ZRLlBad0S2EMJRSSloLT0973r2753jYoxRcXV2x3W4QMse7Fu8M1lYgoCg1WgTHmZe3OS9urvnFu/dkizygLXlLa+sgGRMGpAVvEYl3JxoOCxV5TIejBTWWR3gsloTQLJAIlA8GkNK5TlnspMepOCddGOXpvPozmmj4ING9Q4NEpvln0lDP2Ns3Dhw0RDgvZVwDHoel7njpwIQlGa6KBpwgpEXIxH8FpIjgaR94o/6Oj/Li6ISRME7mpc7Pp+/lMa6U4uFBslwuuLu7m1jdB+gJ8BSFpqqOPD66qKP0HA4HdJazWBQ8Pn4gz3Pev39HnmW8ef2Gv/7rv2b/tOPzH/2A3/393+8I4izLuonRWiNlUCA7F+C527btmBcIl/W3r7/Fu8Bwp3dDPE/ZEfHJ431IbAkxjG0uQQTIWyklKlPsj3uqqsIYE4j/PBBMxhm87YVsbfQw10LjjSOXAfLW+bFHubWWxjRIBXmuOJ0OrFabzqPm6mrL7/3e7/Mf/sOfcv/m1zw9BcZ0v9+H901QOksl2Ww2UXDvWa6WHYPSM0eMCUDOGYkp4TnMMxqn+FuIcw7WOna7XfgtMTGx0mH8qSwLwvDE2HrvOwivtIbwQfEz3Kjpo+h2Taphllyfee4Hv809/1iavJeEDaL/zXcPBq2d3Y+T9g0YuDRJ3vdt6xTkHWEay4iPrY1CneGcDt7vqxkKqObSc2PR962XR3zKYfN9hIKhjqmC53KZw3HsJmPmt/C7PxuTIfzY+Pl8GZ+Ypk0hCF2g3z/BM4PO8tQRhDJZpoOx00A4ktaD8w4lNUpr8iIflRuYN9VdA8817WON//S5vVDChcnrhQbPKcWnzNHH1uyw/Pl888xa5JtlL/jq9+9s6fGd7z8u3sfYfVEInEJPtG2L92Xot/cDSL2+HenTVCDkB79JKSkXBU9P+77CSAwFPrdXVHkXjLX8VNjSjfX4XrjabHj79h03t7edEC3kD++keEjBqs9ydbWJhPcxCFeVDgZiQiKEj0Y95wKos88+Wkp2W9F31YYjckjY+a7fw5nur5CB0iLdLwSr+GQgm/aNt+FBU9U8WYdtDev1kuVqGcqU/dqUqoepXm/XLFYl799/4PHhCWNbvA9CiK6FURmdvMm7sfRpNiEZh6U6OuZQ9AZpxBhX/XgN//rR934v++i5NRgg+r74OEoyzlm4xwWlLFBS0jZtYNYS/Gc06BFCIKL3eIL1sy6EjNEa6ipAbhZ5TlEW2LeG4+HE7d0tVxFePaCzK6wNIWqkTBbhHnxPROuFprYP2JeS96ZCeM0yz7GnA9I7tMwgerhHH5ew9gdjktZXENYHWtAYMzpzLimjPyV9TLjaCYEGsf6GdYrY3ufK+G1SojUTwwPzZ9lzxgGpnGEfxndonyeV8SkxsH+bNJ2jocLhUtuFEB1KxlT4OhbEMboGPsYEXno+5Sum6Tk0gPRbupeGgvY55UCqYy5+/TSdeaqL8Wn626Rz5cZlT//nUnonKVHSs2meYR39s3Taz7dvyOQPxzTxWmfMf3cfxxtkMo/hmnJRDt63I/E9g0zfawyeS3/5p48IHaz5iZbxUnga3yBc3QX+czrQh4GjUgivgjJMxPsHj9cGcijLkkzrIJihn0vngrJvusd7umxqUDAwKpjMfX93AT562Igwrs55bGvIV0vKxaIzALNNgCxvfRboGCk6r5203p30NLLB2yP/83/wj1mWC37x658j5AMLrWlPDYvFimJRkmUapYN3sLWG1WpNpnOs8VSnBmMsWaHjOanJ8hypVbg/RPC06NaP8aiipGkM7WEPuyey45FsUVCojLrwiGWOXy/JFguOTzuauqWxAeVk4wW/c/sF3z285q+aHb+SLR+0R5VLMiFBHJHSo4RCoMBYcufRhDBqSIG0invbcLKGu8WS1eaKXx7vgzxAiI4P7+eh9zRMS7OHJO6yIBDoGKM8jLlEKUlVnXh6esI7R1Es2WxuKBchdqV3lro6cjqFkHmubZBl1q0HpVRQmrcWnQWAuCxTXK1XeG8RUkXPaLDehXNaSpqmoakDjLqOshylBzTVJ+ytS2dvSkNFdTLiNzag+SXEvqqucN7z4tVLttstdd32KIDpnnMOZ4nQ9SEWKbZXOA/vwrFCr5fLTM+zABz2HF8y7uclhezFszS2y1mLMzaMt2l7mkgKjAu/GROE9YIQdqeInlM6GuUP7yCdZTG0UK/Ek9kgjjH93XdJUTaXLsml5voWH4Y/8evsHCSmYoZGnNalLsjGpp8/phifa2tCKOnLinK0Sdvm6I5Ar3/CeEzembZp9I7v90iCRT0r14f2Tcd02M60Lj42z4kmn9KMw/s63dNWDsrwHYc3GhvhQbhxexK9k76HC1J2d7j3kTf8CH05N85D2nk4PrEX47ETHqdbfG0pZAa2wphHvK2RZcnOvkBJh/ctjTVgXZRlB69l54OMVEhJVVWIaDSZ5wWLxZLT0z4a+Di8tZFPB5xH55oiLyiLAkUyBEtsaOx3dk5HjmjGyTrouNbRueZH5Q7nPY3ncAylYpQ6Q5pQeV9/Wk8xXJ2QHts6TN2wXGUsFiUvXt7i9AorHEpnHKsGy47F5o6f/Ph3WTx94HDakynJerHEmDB+x+ORoigo8pztdsvhcODN6zcYETxGi1xHWZskU4q6bmnqFikVq4Xk9dtvqOs9WosoBwnIt9vbW+rqyNPTB2rbUK4KKlOxfXXNq6/uuPvBDcKUPJ0Ef/3zP+F6rfjD3/kn/ODVf8Gvfv0zMqXA56wXP+b26vfxVvPXb/8ti5WkdTWt36OzmqtNxpevrnlxu6I1e/a7AybTlIsF7z+0ZLrkiy+/5IUx7I/vuF6/YrECK3KcWvD27Ts2xYrt1StaK9jtK+rG8O7+A8vyli9efsX27orjYs+f/fX/kZc3X5JnPyAXLxHmJbgV2WKBlIovf/gViw8tf/Hz/0xVHVksrmmPDU5YVJ6xWWyRTwEDva4aPBKyEqE0dTJoiXHvhntKSo2QGoXlKpNUzrETEnUnWL70WAzXH2BTOQohWBSCVoFw0EqPlpBpwbKQfFZqWueR0uGUZy+DwjxzDi0l6/UCMDjTULUKITJ0Fkjl4Iwrcd5QLiqElXjjsb7FiEBPegFeBGBxIQLdqzIRaHHjaRv4cPD8/PU3XN/8XlRuSoQKUPvONmRKUZYFRa747u0TP7j9iiwrqI413nvKMudoLcY0eF92cdkzY9jtdux3e1bFiuV6xc3NDVle8rB74mW2CLyASLyPREYf5UskR/I9cgSvcZzHJgddK8B6jq7lWilKmfEzv+cNjg0ShScHlmhWGGoENdDUNYfdE9X+iS/utghfcOMkL7znxkoa7SgB0za0SIwAJWFhar4qM3aZxreOfdPwebbgfWVpTjXGWoxQnA41Xmhq32CrE8tFS5EXiLZBq5zlcg1Imtby8P7A/nBEIMmzJcVNyWIh2W6voiLWk2lFrhfc3mzAg5bw8P4Np8MBvOZms+YXb95i2rB+pVURJt+ibHTAceCtRzmBNaCMDLJHK4IhrG87emtoXB1CeshubjwKQQgLILVCaI1QGQiJ9SBsi0SHAZumKY0zkJMlOi7FoP/eyQ+MpdJi8iLuh0Djd1llL3/wXnSqK5m67aJnvICOJhIC4RKqZrxbHJ2DmhCT+9h//z58smK8KAqyLGO/37FcLoMSRwwJGdF9d86wXC7JiwzwbDbrEHPUBe+osgwWU9urDdY6bpqWoihYvAoxpNbrNYvForscjTHB+1pnnUdRXuQdrDuAPAUrMiFE8HBDojMdYMet7axYE6Pmve8s8EKsXodSkiwP0FnBCy7AsRsTYhSUizJ4i7kAq66kpG1bhBDoLItMqUTpcMsHj/WguJYyWG9IJcOCdyFeQVEWvHx5R55neBcg57wXLBYLPnv1Gb/8xU/5k3/13/Ltt7+hrutg3RfbLqVkc7UJG52w/pxzbDabThDUL45zRmSYzgljBgt28NcThGm+9+Lf7fZR0RO93QAlU5yGsAl0psdld7uwV0xAIk7Ts5ihf23w+TnCf6oknfuc+j3z9kcVYGKmqPP2frRNPpXVCy86mVqX8zJjLISIMaZj3CUR1VS/lSzukqI5Ko269ZPGbBz76u8yJeFXqP2ysvJyGv72vLL4/L1+LX5KmkMk8L4fFiFEMP4gnH0+Ksi8c6B6w5WeQRnG40hKx8hgRkV6iLfju/MOT4fYkZ7Pt3Xc0/kcfpJLDN78dGZ7+rzfU5fyzJc1jnn+Wy3ss5QUht4TFY8hbjIkuPC5er7/vuq3hu/uCR/rM8l78VKfBmPmJ5/DPg95PB4ldSi/a3mvkEmw0c4FIisC8USCJxEofvIXBJKiKCL6iY3jMs7mB/93zqJ1wfX1NYfDEe9diLk9WFLd8oztTnunE2zQQ709P9W90VE3J6K3/A9zJXqmKo5ZJ6QZvBfq7kMQeBGsMa037B531HWDdY7lsqQQWUB9EWkfCkjEqxK8eHnHer3mw/0HjocjCNAqGwu3fDCSkF0HgBjfJwiHhp776ftQ6CMHBgbpX1obAjHSfovRp/FRnQRXgeAmEqIuwqkKJ9BKkeU5QkhEKzt49TMhrhBopfEyCJedtbRtE+isNgheW2Mo8hxrHVVds9vt2N5s2W6vKIuia6O3aSI81rX4aLzihIzxYOH2R9fcv37Hm0fLloxVhKV3tSOTMl6nroeiGo6D6D2okzAu9eP7KMXn8lwSml16dyosTIMwFCheSr+NkU6q55JSfGoYMBcH+0zQiB3lSb8nxupjwu7fNg3bNq1jVkgJgTY9a3/fr8Bk+sk7Hx/nqdA0tWlU9qSc4dhMx3WYJ63V5zyev0+aCjcT3/B3lf62c/0pAvTpmH5sDIZjO4Iz5jyOffeXoAx97h4aY3Al3sX395inP+f/DlK2DHR+p6jwPsStkwqtEsSc50QT7n6R4peKjq9KCn+pNEpnCDTOgRBm4EEvOmSSRPuPx6enkWaVKs8l73HWQLTuD7rZgOQSJOzR4EZ6hHN0cKkjwXw0FiO4Rihr+OFnr9BlSVbkQaFvGoSLsa2doT6eqOqK4+HA/rAj0zkvXrzi5vqO1WKNsSfqtiXLdECkywMUOUKisozeGE0gdYaT0ALKOnTTsKgrhJIsAF/kZMucLBO40wmtAg2iVUa2KinyEr0uUG6BaT01UCvHUqlgkEBUVnaY34ICKIUKAlMHTire2AongzwlK3IeH09455BZgI0P9G0fymZI3fVzmabFd7+k+OJSqo6veNo9YmxLnuWUeYnSGav1hrwsohKmxbQtTVV3Ci5rDd47hFSBPnUepQSLMme9XrBarYLRvJAEFNJg9CcjT2NshDWXkGc5RDlKWvuX0iVDneFvU5QPH89YGz2vjDHk2QIIym4hBVfbLUppqqYJdE4UWtoYQzyVE2J2j6HTRzRBB48d6K+L9MKIRmU+z6R/o1cjrSsY19HddRGpzNgeJj3xoUkple42pRSZ1ighyZQOazpWlAy4krFhqi/dWVJKbOR/0rk0gruc8DZz/RwaMAz7PDce3TM/XvdTb33vk/HBmIufO9MEyRB9XMecovC5s3BY7pxxXKLJu3PXDyQxk3me+/xs3ZxfZ11fB3mGgu0uz1zfvO+jM8KIyQh3zTkf97Gxgcv3eW9YEfn0xOt0PCDju1dN7vRJuUOaP31vnT17HtaNGMi+zo+f/vkc/Rj3fOKVhadCkbHA2x3a7GmzLQ8//F9w+sH/mquf/Tfkr/8Twh5xWRbCZFYG2XOreB/u8KzMOTV1iBWsVEAykSqs1TQf3tM2LeUy7z0BY1uTsbxEklzFkxHtuA8MxmI8fqNBGKzvZIjgkxBAiEiARL62e48uhMKID2PI3casIsiUfZR7ZnlEILUGBGRZQE2luOVw2mFsS20qWu84tUdUpsiyks/WW7QEa6qozNZdu5VSXF9fs3v8wPuH93iV4W1A0Dsej1ytr0L4idahZIg9vts9cTruyTKJ1oogw1+yXK7JywXWW/LFAu0USI/OcvJ8QZ4vyVRJVTXkpUMXDU/HX/LNm4JW3NCaBw7Hls3qjjLb4pzgm7d/jtAPKHUD0iOUo1zmbFd32LamrRq0zrha3dA0HistRV7ipcX4mmO1o25qEBuyXCJOhlN15HRqKKSmfao47o8oqfnyizsac+L125/R1oKvf/g/5Q9+959xe/2PeffhPXm2xHvNqa74m1/8Fa9efcH18pr9h4zffPee+/v7yPNXVFVFUUCpSwpd4pXANFUILZcM77FYI/CdU18vd3NW4cgQokXJmlwF+tDnFr0RFFcCJ8CdPHULrfVY6UNoAh3itBfeUShPrhy5aFkWAkQK1Rsd+7ynbRzW1pQ6QK0rtcA6h/Nt2IBO4tE0xiKx5Nkyrl+LRWAttI7o+AdIKEtJ3gSFsDNgWrDG8363wyOQQiGUROkiIna0KCFZLko2myXe3ZNC/LT1EbwleckaYzoZTgp717Yt1enEMgt6q6IMNFdwYnTRgzfsW6UyrG/oWB4/vm96UWaUOUKMbR3OeSkEwjkOznKlNKXUtMJzLzxXPijGMwRrr1jj2AcwczwWbIM/Vai6oXSetdBcA1sET1gKB0bnHK2n9YIsy9j4lpvFFT+XD5imYn88cV0saE9HHnd7mqbCFprgNxiQCBtXI4XHO8P29pr97sDj0xN1ZThVTfS8tyyXC/I8i3yAQOkMnQWj3LLIKIsM4Syn44Gn3ZHHxyfq5oRSBWUhsbbBtwovs2BAgKX2NW0dwjZaa2mNxbSWprUYExAXfaT9jfdYL9JxGng4AcRY8P09U5OJHK0kXim8DAbHVgQsWjmYtzF9E+/nIY3j6S4xEWU3nfEY/f34qbKCwD+nokO/Ai0qEDIgOARGNtJAwjOWJdmoMwVFGIPAj/Re4km6B6IzVAlX3uS+j1Ds30c28cmKcaXDwsiLwAidTqegIM+z6JUWCL22NbStZbFYsF6vMdaQ5znr9RqpNW3d8u0337DerNl88SVKSrRS3L24C0psJdhsr0YXbpGVQICfLcoiEt+ygxUYTlhQUgfrYq11OOiM6BTgUgWIOOtCPHOpFc4EbymdZd3FLL0HEZQKOove5c6jshhLgrCWZFSCIyAvQoxXbH/BZ0UeYNedRUePT4TFm8C0L5YLJHmMFR1g8TJd4KzgdNrz53/2L/nVr3/J6XQMjFtkNtbrNevVCkQkZJBYG+KUJeWZFOfK8TExEwmWCykRmdPPSbNgrSVXOY+PT3hPZ1yQFDIp5lyAEY5wnlJ2QqQzBYiPhXuPjwqxMfHfe9QF4chvKXQa1ClmJYPPb6AzYpDzkZwqbuYU3GEuiJfR5AJKzYiCo15c5wfvimB44OmVTD1vOcg/bp0/6/+QKZn2dvhcDAS6l62ix+mS5/ywDc94ic8u0W7Qep7oTCF0Pt6XK0hpjnVk8Oy8vDkDjWCckAR5MPS09S4wbSnunI/Q4mlfD41YECD8YCF53zM2MUxEUnh2l5gYMmeTeX92Xc9doX3fx/zwM8KI52roFsIzZ47gwlqYGedu73660rpnvEI9rosplob4fB900/HcchosuXSMdQ9FMO7y0J2BIeREOhXiQk6E6qVBmD6PDVosFh2R08Hwp+UvUnyueIb7bsSmzR6UG4SPWZaRZRlVXbNcLLr2+mH5hAIcwRr3xYtbXn/3XUewa6VpvemQAi4O4fCYEuPPo7sndbsTuvhOUCqE6DziR8MUx0QM6hFCdN4io3ZFei1qnzmdTpi2ZbVZsN1uKBdFB7sUzkPAhzPYOUdR5nz5wy/ZPe149/YddVNRZHmA9RvAoHdjmNauD8gr47uZ8WcRiErJ8AwW52u2m5t+EPs13AskYve7+zq1SSkVYk863xn6CQFGSqxTIwV5FHN0NJhSGqUk3geCPxDIHte4jiEoS0vTthyqI6eq4vrqis1mjY4Gi93BLh1OCLx1CK86oarKMz774Zecbo68/+YbHj60vMi2rPUK3zQIZ/CuRdigXPGid0fwomcchQioB8ixcOzSWfbc8+EYDmNoD9NQ0DYUvKUynHMdPTnaz4M6huUMn4+FuGMDCSF6T/HpO3OC3Y+Nw6WU+pTo1F7JPljLA5Kv3/Lfrx5gdF+OjYYiLZTOUvr65ECYPhJKjw72cVvmjAOmaagYv2RYMZof0aN4XCo3lZXmbYhsMCwz0QNTQ49Labru3MxamEvP/T5Vujyb5ohPwjrovLrnyhrxAYO90JUz/j4gobpz38UzbchnJB1vMlgct22sfBnRBIATUTTkh2s47L1OmOe+/9q+lERh+3M9XMSk+GsDX+AYG0520HUeQQidQoxtR+994Hv6NPRzcH92Ian6+Z1bA3564TJZ7/S0WlKcpXLTZz9BI/HC4ITHidCzsKfp/wrwXiK9YJ3nfHZ3R75YsNysEU6wXC4QueTtwwFf1ZxOB/b7HQ+PDzw8PIDz7A9H2tby2StFY1qEI3iKqxDb7lRVnVdsz2cI0JraGVrhoa3JDnv0fh/uztayWG8oNwuUsMjqiPU1i2zJIivIVYZUgloY1kXGmpLSC5Rs0UJhpQl7AR/jRHsyUVB4RSEVihhmRCs++AaVaZTKaL3jqToCA4MZnxR8YV344SoVwZGh4xdG+yUqMKUKnijCczzuwTmKrAhhYrwgywtUlkXjSYO3hrapoxNEijcfCjbG4CM9sVgUbK/WrDdLbGsQZFFXHKDihRcBTj8qn4WU6DyPZ9VgTX4i/z89e9P5O7rzo2LcGEMbw+pJ2d9lmdKUZRl5hnOjrKQIDnzdOKb4WWzx5MnakbCXz4g4daM78mNn7NnvgzYOn7noDe6i80gK+yMifymkCDymdx2CgBKJ9k1nwbiuOTpKRB4kveNEMGwJ6AeDsGH+b9HHyfM01tMWzr+Xzr1Pq/9jyunv094LuQdL4kI/u9M+/v9CO6b0nZ9py+yzYXkTCm2Ud4ZPnuYLS913eWfpowvPXeStEL0Xm554zg33h+j4wt4o7ZKhzHB9dkZzph3BwI9p7VDZ+bP+KJrrQ0+dxO9eoI1EuhOGE/Xqc053/wUPP/nfUX32P+Oq+hnF7meIqsIUq+AZh8eZNhjyR/TNvFyiMo2pQ+hO6zzOV1jraKPBdjqBXQyZMJzIIb3c8SbpXJq560d7azpPiQaG3kBGiICRPuJR5xEP5ED21p0Xk/kTQiAVmNZiaoO1Dmtddx61bcPhsOfp6ZHt5y9ZlAWn2nJqbEBxE6CyDJ3lrFZXFJnAtBnOwfFY9bxbHIO8KGjbmqataG1wyNNKsVquOB6OZDrraJu3Tw84Z8myAikFpm3Js5Lrm1t0DGvq8ThXY9sa7yTWuigXkRhzoqr33H12S1kuMa6lNo84f6BqLOvlFudDuBJjT6zXJd7Z4D27KFgUOVdlgWlPHHaCchGisVf1ESEzpFacqj1Phw887R5YlIug5BVZQHNVJddXn7EqNIfjDqXWbJZb7q6/4GH3De+Pv+Fp/4b7h2+5u/1drtY/5nG/w9FS1Qf2hw887X7GdluzzCR1W2FthVaKRnqcM+hMIYXDtpbqWLOQGdadSASn9z7KNPuN7Z3v5JwggkI6OgbkhWKlC5b6RLYBXQiI0PpOBaMn6UA2HmUdQgdY7kJDkUOmJVIGX2mirkQqiVASKR0ei0wyB2HxwsS9rBEEnktah3AK0xqCwtghCQpv62TsS4gPrbVHB19RrAn/kMGpEqCpG1pjkNqAF3jq2BZYLgvyTKKkoihK9kJ0YVyUlF242kB39DRG27ZYb5FKUJQFm6str797jbUmQMMrgWjpdEVTGd2lW0t4ujCwXvRn7cG3GDKWMiCYPoRgT2g8BbAEStoQY7ojbiw0Lc3xhMPipASVoaVEI9BIrAre4taG90oh2N694mn9yMPeYIxlsVmRn07Yd/dUT4/Ya41talwLMs9ZlgXrRYGUcDo1PO321JUJIXGMAyHIckmWC8qlRquAZHh//8D2ekOmFUYpWmmxTc3T0579bkdjQkiL5XLJ7d2acgFeWbSSKCEAixAWSiL9B7kVOCswRmKswDq6MEcuonyleyPJP21CKEvPhWBRFGiV47zCWhlCK1gXeCOhzjy+h/TqNA15g4tG95NzeZauEYGz6+gGAUIEQy2hPEq6gBTpg97Yex/im4uwsBJZqKVCKUEmNToqxaUKIb+SMYHzyWgt7N0k203tS4ZYqZmfSod9smI80wXee5aLVYRK1RTFIgqYQMjQ8SIrsEfLOr/izlm++eYb6taStZZS5ZTLNa+++DJYCmc5mc6oW8sf/aN/TN00NK1BqTx4IEWmQkVYptSxVCeR+ZLx8k2zkpTgU9jAVMZUeDS1FuuZmOAV7r1HChU8mHwPLRcmPV7pQgYBrAh5U9uFC5ZAEOP2eIGSOcQ2KlUidZxYJBKFRLFdX/GrX/yPPLx/z/27+yDIkJLNZk1ZlMFCQhIs/oQHgsJluVpFBYHsJd+DJAZCpLBgZgi5CTE92gAyvGdsWJDGwn5/jFbDYVvjZWcUnYgzrVIcu1COFHJsbTpQfoSlfL7pxozY9PO0D+nTiKQPzFLqXxLAfxp/PS5nJs3z6X0bvZi+N+nfoCFJANSR/DF2zujS8kFALEUSGsVDpiN0e6HIJ8oQxq3r5j+0CHyIwWNMDJvwfBKdYO5T8l5qxFnOuYcXXurHXpyN/TTvtAFTsXr6/PGBjOqq7oLAR8vvOCdKhsuLPApfEbTW4vDIaFksheq9N3teLyJfKKQA6z3WeqwJXsNhjbgoNOz7kWZg3j/5Up/S87FXw6cYowwVzcPvw7p6RvKjxfX9EEzOhLkzIpU7nbe+LZ3yjek51zO/c2XOtmrIJKc9GJdoYrYBjLMY02J9jpaa1lisdQHlJo2P78sYKQ2SsmAozKNnuBdlgTNtJE49vTdGFDL7ENM+xJbsz4ZAfCeBiaBbaLH71nnysuQU44yPlEQDwyVPIHKMMVxtV+SF4niqUD4QMsKcz4vo1kE4I9zgLkoCetL5HNsdiHbRMVKplOH55CPBLiNN5MMlFNsc29AJkmT3Xp/F9/kiEWuM4elxT1u3bK+vWK6W6CwogAXBCE14gSQwJdYZlusFP1p9xbu3b9ntjmRZILQDYkAUJAgR4Ny7GU3w2pKxYnO4ImWATfSAC+dar2QbK/hJffF05aWhSyeCp1eMuRg7XAqBkxPYZSmRKsQaFxKcC4Y51tpuMfp+8SJRaGwnIHfRK946Q2vqDhrwXXvPaV9x2tZcX28py7yDeA2McjjPpA/w7kJqrA8IGeV6xZe/9zWP7x+4f/OAEy9Z10v88YhuTuSAx2KcxwiPk+ClwHiP9AGIqoNsGnjnThXSiZZL6zX9nQpF57ya5mgp1RkAnHsN+X5BdAzKkJEZehEP01DhKyKNloQNKXRHUKCG/HMw7lOGaUonn98BPloXi1G7hgry6BdKUlaTxi3OsXU2znFfxrQdHxtDIDBMw8b2B0M3DthJ+2N7IJ4VUXEzHM+pMcJc+4Y8w/D39E5SXA/HZk44mNbQkClNAo/hfAzrTwqZ8bz0aQ6edDRMQ6HjwKBjaMSRUmrbc/M0Ndp4Lgnvo+CAeAcO5nlGQOPp4WxHXMyEJhBSB5QTH5CrwllJgBYVwRBbOhH5laCMw4NzwVvSeYdQOp6mvXfVUMnthcfLuN/TMhPgkyAf8CIahQgRFL+/DRE+HANheg4p8nFepLhr8Rz2Hi3CzSii0jwc/WIU7xQfFGNS9Ea3SQmR7gghNONz5OPGEXNKiNTWtG/D+rEdXRo8bH1Pg0CEMPcd6oeIbe6WC8GjOEPw8nrD3e01jXPovKDQOavtBuUzzOOe6njkcNizj/+edk+Ypo1CGYn3kizLyfOcq6sgTLLWcTweyfOsMzwUggD7rRR1U1N7iT+dkA8PyP0e7wpoW8rtivJqgW6eKNqKozbohWSd5RRCcXINVXPgM5XzQgleW8cjlkIoqlygpQx3U+xpLjWFleRCIvFYHDZXPFSGLFvhgUNTsz8NFOMT2rbnwXzYa4OxHizY4CkuRHceyHi2nY4H8J6iKMmzEu8lQmqEVlEpHpTCpq0pSk1b190e9j7Erk5X26Is2F5vWK1K2tMBIXSKAjDYa8GT2eGjF5UOhm5C4KPhx3CpDc/Dixzd4IwZ3rsJkaNTjJu2K6Fpg3d4IXOyLBuEXQrrMSmUO1jyiWJ8BKPu/cQ48vxIGCsdfS989jO/fyR1YzHYv8NxCv3u4d4TfS27uQ+QnImMnDpaKBWDf4p4fyRo9bjnBXRKdumTv6vo72bZ39nDMZ07Y6b375TWmhvDns+J6z/xZzCQr/TjMy1vPBeiM6y7dH8/+/6F7/3+HH/v6x2UN+FLO95tuJAm69+P8p8b+l1q4/D8mCrGp+lSv0byw9SAuX5cWNOdDDWuNaUUWmmyQfzTbl+dv9zRFNP5umS84b3HS9GFSfjYXM89c9349fIEMdnoCshqg+WB/fIFhy//lxx+8F9z+PyfIZfXFF/+MZvdf0Tucoy+YbEoUMLT1EGJqLVmsVqS5SVta7HNibqpOR5P6FOD0jmtb/EmonsJcAiMNT0/5n2Eou2dvFL7h3TVsP+fNI4yxNvNshBqQcgg953jn1Ky1qIG15FP7ZjseSEEeaExxnGSFdXpFEOkBvl9XZ14//4drfNQbrnZbqDIqFuDlwEhx8vQJq0Ui0WBXuUIJI+POxCic46r6jqsOacwzYmmbXHWkeuMPM85HY8UeUamFXVTcTzuWRcFRVZibMPxeKIoFqzWV0H2HTeAsRmHgI6PsTXWNIH2sTWHwxNX67/P9eZLFnlJZSpWqw04SdMeaOoDTV2zXq0Q8o7Hxw8oBetiRa4U21VJc3zgcNzRGoVQgro+orICLTIOhx0fPrynqk+sl5ugDHQgyFkurrlZXaGcwvm3SGnQasXV4jNMIznkDziOvP3wV7R/6fjBZ39IZb/jdGyoqpbT6cDxtOd0OGGOGbYNiuXr7YbWHpEKlosF3lY0VcNhd6TwW7wL+yHJIoKxgOz2dbqbA28L3tlomC9YbFbcLe44qG+xGxMgzpXFXinc0SEzEA3o1qMah/eCQnoWSrDMFblKCMQKJWPoD6XIck2eOawzSO+Q3mJdhXcGpRZIoeO6NGhh0V7RmBPBn90jyIM3uFUhNrpwaCxSeXQWzgJrffBmloK721uEEBxPJw7HI8jgHeuxtKbFekWeScpS4R0UeYBBNwM0ZGvMOGxL5AkTCoxWIdTC9fVtQJg0LUr2cNSBYuz3c2dgNDnqvPcRYbDnwfoTQ3BwhsZ7roREC8EHbxEodJQELBHkkSFL95OLdNHxcKK1LYtM8ZTn7IsFJhrredm3sK5r6tywunvF6uqK0/s9Qkj0YgFv3lK/eUPz+AG/WSO8pW5artcrrm/WrFYFUnjevXvPfr9HCo1SmuUy0HdCuuAVvihw1nN/f+LnP/85X3/9Y9brFc46mlrS1iceH3c0VUWWa5brBdfbKz4zR168KmlFMITIVDBy9ZmK8b4D7YqXASbcSVoH1gksNoooFJlSQTEcHXCcszTGYHwKySjIZM6qKBFojifP087x+OA4PEbFuFfBiebstmJE80yToKeVx1g6n5Y8ovP9Dm31QSGuHFnmyLRHy4heahMPHeKIBzChgCxVZI4sUywyRaEiKrIMMqO2NfEcCLItIQUyjzHVYy8C+TdGmPpU8vmTFeNJAFOWIYbE8XikbQ1ZlnVY9I1pUCjyPMQ4Wy6X3edwgQUFdl03rFYrhJBY7ykWC4RSFGWJVFknaEoKlQDnJSeXNHTx0ob0K5x5xwwFTkMF+5RoGhLdY4tiut+H/6wLsPHhew8dKUTP+AQocT8g5Hr43gC54rFYlNaY2qBzjUJz9+KOP/t33/Ldd6+p4yX94uULNpt1JwS3xtKp4bxHRatmIeg8t0fK1hHDMe5zOgh9UlDMLKDEaDjnMa1B64zD8URV1RFuLMDEyxjTwJjA3OKDN1zwTJDd2IwmbiTb6j0nn2ME+3mZK2RQHON5HNf5/bf+5QNlrqR4/M/8NJ6fJBYYNW5Ywtk3IWL8Yhc91kSIrprWX8ozV8rldKkPYfzatiGttxFzOZN8XE+/jTywW6vnHM+gTdMfw7Pz6RmOxbQx5wxtej42Inm2q2cpzWbizZ33nVVdsuhLjEnyTBDpMB+0J4oU4/4OEOoJ6sTHvhpjKIpiMhrz833+9NL6C8+mw3JJODp9Fuja4RnTlzk0cBnw86O/c2lc9wWrtzEPOmzh5YKHuc4MKJ5/byoQDqM4FmZ0AjIfzs5koOC8RwtFkh37JD0YMoUzdXSt8h4vBGroIRRLD/tzuOZCG6TovXtHc+Z7MjdWBsBms+HD+/fc3txMxikhtYjgXS3Ae0dR5FxtN+x2e4wIAmekQDrB0JamEwcN1kU4TsRgEcT9HPs62vtdUyd31VSuJKL4ffSqGGU/u4aGbYqveufY7w+0bcu6qtlcrcNdK+nHX0qkdwgVrJqdt3z+xRdstidef/eapm3JddbDo9PD1iWlV6Al+r3YCVdEPz/dGpMiQNAOGz9/vF1IURCa6kZM9mpfm5ACJTTCOqwL+yTEXRJdaJjRWepBKoWQAcnGWtuF/fA4fO0wrWG5DMxGXVXUdcV2e8VqtaAo8xA3SMruDCWOqYjSYhGhz25e3LFarzl9qNDmjqxcYp4eqY4HpGsROKSz4F20HRLdWFnhO4ZrqPxJit3AkM9DcE/TUPgzB5M5916CLu0z9fNwcdYm7Zz7PYSGAO+SsnoYxO9cOPUpbR3mS3Urle7c8XncC7rD4TZkTi4ZrM4Jhof0+fTuGbV/dOYyYvy68WJICyalXGwT/qz8ab/n2jakn6cKfH+hv3PCwbkzftT2yfOp0HDu3Wm5c/elEGGPDZU4l5T3w/49tz4v5RGT388oro9wrcO7cFj+tCXOu6iMSR5QAicFalFArkEpWuMAhbMWY8NZZiKUs840zvoYsiYglQ3XLxAUVmmJDxooBuKi8C0IRe3fgef4wiwiLemCIVe6BmU8HJN/mIkGW51kS/RHXuSpnXA4WrzKGBrQ9ftB4G0TzAL8dB0OxmFA90xTUoqL7jsYE84ipcNZaU0Yc4sNvLSNc2o9wniETfRQMmPr6ZOqqpC54gc/+iHL6zX/9n/4jxjj+OLlS6yzWKe43V7zm90HlAxe5OCp6xpXhJjK3/zmNzw+7Li+vuHHP/4arQvyvMRag6DqhKDOBQMVISVKLXHGcbKWYreneNpRtg178hBmbVOgVppF1bAqJcXLFxyahoPZY30QWMu64esXP+SeE788nBBNy2p5zeJqyft3B05tg3TB6FlYQ0YWIAU9OCFptOTeN9zKa1pjeTQ1bYKuHp5x6V+cg+E6npILYW0EWYskeMcpKWlNy+m4x3tHWZYsliuyrAjOAPgAeW5aTNNg2oblIqOxbecM3JqGpq1QIpiq5UXGclWSF4r2lO67MKdSKCSCxrnoEQJIFYSv0YhUxbts1KvAcAyQB55XkA/PkQ5OfACjnmRQddNgnQ0yDSl6zywfjE2NNWHfeY/3SVA3hlInjfnZJklykMnTRBymeZsgrswmP0Pr9h0e7cMxk3WuxEzx6V0bxiQIw4OiPNOaXGdkeVCCi6iwTP+m91yiLYNdUH/3OecwphmN58fQTrqxmfk7ny94po9pA9/97RXL/Rk3rWf43X1SnZfLeU7BOr4PB3SdDwZcz9UX+jP+232e5ZE/ds+OaaxAbs/TYJ9a5lya9n84/9N7XqkgV860RvrxvTOMw5pSCOM4hgSf0q6dMnzwPDlVJeSInj6do53G9F74zOiziObofgATq6yl3D+yv13y7vf/D1Q//i9x68+Rx1+ylj+lePEVpfivWO9fs/KOzXZFU+1ROK42a8oyhDj79tvXQblTKlRekpdrFutrtrdH3r3/wOPjI8fjEWNaPILGBOVKZhWtkYhMo3tWKFALiaaYjP8c/5P4nTReEJ3MsgytdRg3qeLRPEOPj86K8VrueSjCeZreUZJ1sUBJjfOe+rGmahuyLIQhOZ6O7E5Hvn3/hn/8R/+Iz7/4ipvNNVYv0ark4XHHcffEepGR6wWLxYKnxz1lWVIul51C3xiDcZamrbAmarKdZ7Fc4aIjSr7MsMawe/zAsiy52mwp8ozjw4G3b95QNTVlueTly5eBNLOS5mRp2wqpPXkJOnPgGqw9UJYRUUeCkIIi2/JP/+H/nv3uPf/pL/4Vp+qBl3ev+PLV1/z0l/8aqTwZCq1KVsuCsshRApxpORxr6rahKNcsF1u8F9zdXHG9/YqmralODabO8S7Dth7vFM4UCDZcXy1omwbvMsrsJa9uC/b7t8jsRNPs+Nkv/jVv3v8HPv/897HNCq0W3Gw/4/bqSz68+4Zf/fIvyVSG95Iiz1guC6zw0FgUklxqNBnVsSKnN4501jJEF/NpYcb1JpXF+RpjGiyaq1dfcfX5jzg1FY/iAy0tSsPrF5abBaxcxsoIlrUl23toBBvj2GjBEom0Gis0aInQGqnCfYYTaC9YFQVCeFrXUDc7jD8ivcOLKtCjMih328Zgcx+QUDxIV+GMpm08xktyBVJDpmGxkshMRSNCRy41P/riC6TwnSMU3tE0FmsN1ekAUtLUBiGCsWZZLijLBU1zwpiGPC9paotpW0xm0JnFuoB60zRNWIdFTlbkXF/fUhQlVVWhhGBRliilghxKyui9OTjjhvMwSFYQ+xqkJykkyclbqiD8oZCa72hoCc5fiuDpHaKuOySKFkcTHRYO1rF72nOShibLaIsFWVPjraMoCsgKrJTsqwMfipZldsXeG2ymyIqCSgge3r3BfHik8LC43VIKzWHfsNxcsV4VSOk4VEeOVY3Kcm5ublgtl+Q6AyzGNmgtWSxKnp4OfPfta/7tv/t35GXJj776EinBGKLRtebm5g5jK6xxVMeKZan5g9//jJPYozLHIoNMZchMkOGQ+ABzLkHS4LzBuIzWtRjbYr1BoNFSB4/zGMrI42lbQ+NMgCiXAq81hc5wreDpyfP23oLy1I3HHwXOSaSTMSB8v6dGfMEF2cIQSl0MZKaJpph7Z3gP2hB4PsqgHVo6ityxWjjy3JEpixIeJWToj4ihDJRHRcV4nivKPKOUoEVy+PPRITChbfio8xLILCEXTJCyY5tD6z4t3vgnK8aBjvgtiiLAS8ULMClpkKEhCYoqETubzQatNXXdcjh8YLfbcX19jda6K7cTKkpJnuddGUKIkcBxmp4TZKUJnvPomKapJ84l4VAqO/2dI4ZTmzpveiaLbfJuqCdAk1nj2FytqOsTVVXx+PiIQKC1YrNZExRksvcskQq8xxjLer0Ogh2d99ROL6OZEWyEz2f9HOQf5uuIGQnGtCwWKz58eB+EsD7CnI3mZAgjZkfldCdtJ1yaMA2DMZ0jQMPz1LbuydlcjdMc8T5z6v8dpecElt83desRBtOXIDktSsWwAZOYnzNiAebHoWv1zDvJul10cL+hSx8bu0uiib9FSu64QRKA6NowI2H4LdrV7w9xlt+PWMZLJXeqyVFzhmu+V1z0TG9gLPxoeoYzlRjnLMv7fUiwojLGBkWST0Y5nzYKZ20/u/D6Flw6Cy+VM03Tc6/fu8+XH9bdUEE/npvpeZYEInNrOD07PzeGecbt+tQ1PBy7dOaHyQhMem/NGWKZ44PhUKbSIT2zL0V/PjNgSIe9CfdBIJ6sC6FCUnuSQCvda2nceyV6ghoMpY16GNfboix53TQzPe7P7xS713lPJgW3tzd8+813BOjaEMsooWN1xjRz1PZAAHMmbhd0XHt3u6Rno1EZvDKsYlq/iArgtLC6MUnFpD0PuGglCzRNw4cPH2jahqvNhsWyREbjPyEkQgX4SS88MjLYy+WCr7/+mndv3vIYYVzxwUNPOBcEr7F9zkcoUTEwzOn6MByb8Cns/7SHxiPw/IqNa0v2SuFufQli7FqZNuBYiGEjLLEPNIjXwVDO2ChE7dZGJEWlindVhD9y4KTHSc9uH+KdFUVJXdfs90/c3t5ydbVhsVygiF71IpwDQoIQEf1ACCQaIUP8rPxlgbSw9D9g/22O2ZW0xz2qPiK9QHmHip6JTjqs8FgRzvUuDq9PdF+CFA6fldKdgOYSFHqYgzGtkvbh0Ns35ZvSgOn3Yd5pXXOKwbky+rnsBUzp3u7v777tn6LsTHVM+x2EBH18wiHT1dN747qmZU7p6GlbnoMdD++d05DDOi+lpISYG4PnlN3T34dpTsA/LHtu/cyVl+Z/OmZDpm/4zsf4lSkP0r3D/BxMy5xb78PnzzHbf5dpyMfNrgXno7FSQNVBQP3/pe7Pfm1L8vw+7BPDGvZ4pjvkzbkya65md1ezKZmySJkyCdogNQCCHg0bsGHA8IMB2/CfwGe/+0mQ3wwD1oMNWhSlJimSbVY3eyxWd2dVzpl3PMOe1xCDHyJirbX32efem1VtQ4qqm2fvvdaKFeMvfr/vb3KWH3zv23z3t36d5WbNs8tLVsslxrTsNlvaeodCYY0J6RtqH1I4CBGiTBjD/qsE+1nckhF0GjMQQiFV1kXVyGLIxF+2GFRMi9J7yomg/Q8e7EnZowUST4uDlLuTQMsgKL2VVOhDTy5B6FN3JtjgJX9Lzu35sQ7APpyDo3tOIIXGiwZjHW1rcM4gpSaBPy5YlNG5ELvBmZcOgvACbNuQz6Z853vfQmaSj3/xKQ8uHsAZrFdbvnj2Naf33+LexQXL1YLrm2s2mxVtXSGEoq4b1u2O6+slX375Fc+eLrl8sWA2m5LlmixTvP32I8qypGkEbdsEj+Cqxa13NEpzYhz3EJyOMlYbaHIw8ww9znnnpuTkwZuY+zP+5PEXbJqKygmmImd+cUbxxgXq+XNcZal3W2Rr8CgaY6mdxQpPoTRTAxki8CFCoqTkyrbc2Ja3VI4Xgq21CKFA2Nv7cU8NeLukdSFgLyJEki/rtqaqd0gpGI1KppMp4/Gc8XjKrqqod1u2mzV1vUOpsDaNMcEA0FmqqsJay+n5jJP5mJP5hOm4BO+i99GgLXikzHCmDh7jsQ/BsSLQVRWYgH4tILqv+xF0CJDsEVKUxibda9ugFLfG4NoYOcIFT/fOFDG2o7Xpuo24Bl24V+9DeMeUriXt02ODn9jMjp/dw2DSuQQpbsKriqc3yb3VZdEb43bnSsx/enjOOGNx1tI2LUWeMxmPGY1G5EVBVuRReRTXTIygkCJBwP4a6ug0cu/sMbalbVvW63UwVPGRBz42Ti/hH14ul95R4d6YDYfoVY4Yx42xX3XPXef33vWjrTouzB9rw8s86I/9fhef4ONaFQO56nD1Dd91Fy93OGfp2svaMqw3fR6m5An4k+2MKZxzMdR/rzw/5FcO+eRuT0c+W3V0Iz4fZba6rmnbNmLTKRz4/ngdw3K7YetkSxeh+D7HKlJTP/wuf/HjfwDv/hChVsj6Cdo0aK35aeV55N/hR2dnfGtaU9dbpPfkCipjuXr2nOfPnrFYLCiLEUoarDM0xuFRTE/OmczPqOua7XbLcrlkvV7i2xUyUxjv8U2NsS2qExMkCb+9yz5lj88khrkHbBuMCIBOydYb/IZxG0baSPxv8iwfrpl0j445ptu2pTUtJq6DspLMZ2fYNmDerTUxcmyYO7zEO8euXvB7v/tPePjwPc4evsv9d79NUeYY04D3jIqQnvXm5obFYsFkMmE0mQDQNg11VREMnlxMp5IhpSLPC+q6ZjKZgLes65qqqrj/4ILZaMbl5XNevHjG02dfs9vtkMD9+2+QZ3nczgavdigF1bpmvVgxmuQUec475w9APmW1WdI2E7y6j/TvcDZ7wPtv1TTtFXkJX3z9U9bbJ9w7+RZlcYIQirataKuKojhDlpLCWsbWce/ePYQQXF59hVYwHhXBWME6Hn/5FdYG5elqvebZZ58ghCDPoWm2OGuZT864uDhHOEepRsxPxjw4H3Ey/h9xenpGiMjW0LY125VlNnF89eUf0YgNRTamLAtYeYypaRqLso5xMWY+mWPqCm/rsN8aEE1Dlpd7fLKUkizT1EBdtzgT8kRnxQg5veDS3bDY7ahkgxYOXUi2taaWDUxadAmjDEYaJmScrz0b65h6y3klQ3qanUO1hsyDlpK28exayArF6f33mZ29g0BzdfUFVzd/RmOegW9RoqTklLKYsaalrW+o62WICKFBqoDzts6hBHitEFgcYLxHq5xHD9/k3YdvYO0WITyzk1lIP+hc4HOcQWjJpjZs6oxPPltTFEVcj5KmCYpx7z2tachtAS7wKXW9Q2vJblegJORZzng8ZTSZcHO1oTWaEWV3dksvjp6Bh3CdJ+Sy1gSdq3dgACElrXA0Ebu6n0/4vFnwpaix3jFHMCHnFIXEY/A0gHQeZxyiCKrjpQdrQjSFtxpJ1bQUosJrQEnOZI7dOX732c94+vgpo53hVCumO0GL52w8Q8/PUNMZ9XKHGpesqh2r1QKtIBuXjEdTdtUm8G/CIXUwdtFe0baW9aphu20Zz8Zc3DujHOXMT2eMygJ88Co/O50yKkfYpmKzXHJz+ZydW/Dm/VO20qHzlkmuyIXGe0XZ6hAVWviYKsnhfINxbfjnTXD88DKYKse0q5IQjcdoj/EO632IVpbX4FuchgKBJKM1ltWqom4t1pvOa7yn4WH+9s6sI2f4kH/bR2OP4LZ3FScQWLQKBgKnE8HpTFIWlkwZhLTdeWlJOBLRs16QK0+WCXKRoXwf1dMnOVUIvBCIqAhXg/MpnLRDndnxvt5VXlsx3jQNZVmy3W6PK3hFH1KwaRqcc+x2u73GZJlms9kwmUzQWnfKXedcp2y3Md9uOjiHjNFhuMbE9OzlfIp/D8EfGfMwHDJN1to+Hwr7YNPh4kkh13ulg0B3YTXE3t/OQ28whkMv9GF7jXUI0Ybc5U7w9ttv8wf/6p+FMPR1jZCC+ck8Mi+u63dY5QEs0DpjPBrHMWJ/7R5dx/tCwx7TKo5vlvSbMQapFNYabm5uulCO3vsu3NYwH/pwg90K5fQSweX1lHHHNurhM/tzcxf4+pdZXncDvo7A25dO5br3zbkQZiatCd/hR/sRFtIbf9myv+9C/cda2H0W4hv275sWf/D3VeVQUPa3fuv7dliv4LUPBUHvURT3aIqWkGqyCYgYCIB7bUn0J7XDg3eOLAuh6nSmoarxzmOtwbmQvEa8Ggu4s9Gvux2O0YZvWnxChUhD9DJAgsF9w+d6YCzeeeT7sG3p+8vae2wAX9W/2+ui60/kKl0UDN3A1csYg891t1hSBJS7WnWshck4IindQ7QOceu5FFkitUGKbmX1fdgDKEO7tdZIpajqiiIqgFP/hrvHA8KHtXh6ekpRFlRVgzGiz9t1uNcYmpqI9P84yQfjcNdXEengS9ZPd454QjoLH/ekAETfApfePcSjEjjp0pkbPq9Xa5qmYVZPmU4nFEUewpBHYzWZwlereF4KyRuP3sAZy4sXl2gZ/PmUCvlCvXM0piXPMqJevOvnwUmdOhVHMBB7Edt1OEavIgdywDiGcNQRGAscdH+WdMs5KImFcBE3COOlM93xBMNINrF5aKlxUgbl+CCfpcdTVTGEaZZjbMuuCoDO2dk5k+mEshysO+cRxHNIhFx0XjqcVCgtccqwsI9xDxX69AFiMYKrS8SuQVQNsrVILzBCYITHShcEQr9Pg/xgP4bPLyeqh0rDBLy96plj4bHTtSHveZfCfcgHH1W0Rs/1xHaJwfK5C6g8fM9efQM+V0pi2PvjgHHiJQ/rPJQdhuN011nyap7t9vuHY3MXfej7c/ydw/emf8dA6Jcp0A9lDtiPanWszcfacKx9Q376LoX8Yd17v8lwHqZx6qNe9fcOw7sP192r2vsyvuCoQvvguZeB7C9TNKhItD2EczZwyTx85y3+9t/7n8K4xCjYrdbU1Q5bNzz5+muePHnMl598zHKx4PLxFc44VqsVVbVDCr2XezQop9Uev5tC8QspIHm76iyEafS+88T8ZYvRO3DJoEvsKS8CCBDDvjsNuJjHL4WcDp5rMXs1wguEDwpMJXOkCnJskicgKPmEZw9USEr/w33huXuuh0UohSB6JStJimRhfTCs0jEKifcG7wxeBpndJaF2kP4l95Z7Wc679y64Nz3hO+99Jxjuao0Y5fhpySdPvkK4mtVqydXlJU8eP2E2nfL97/8QZ6FtHW0TsIr59AF5PmK93mJMw2hU8vbbj5hMJozHJda2NHXL4vmS6yfPaM7PUY0hq1uwLTKfkZ+MKN59RDsuMKs15mZJUwgqU5NpxVyWlELRCI+raxrV4meKsZ6iPVzd3FDbNnjse4kzloKMTGgiBARCsGprajzjcozNc0y1wxuDSoDRAKcIR/o+3xVUKGHlEGcv7SOFiJGF6LzBwVGWBVlWoFVGlmXMpjOWzZK6CdFemqbpcB0boxMNFVGj0ZjTkxNOT08Zj8dRgdJiGhfOcizO1giv2DY1q80G4wVCZyjnghLFB2+UEK1GHgB4t2lHUkil9Xv4N+E0KeSoiSFJQ4qy8LsXdDl6hzTXD+oN2FIfxjR5jFtrA490hEbuSaK3aHzkgV3MO3mEF7iNwaluvtN8HiqdUvsC1hZkBjdoqxvIpcJ7RmXJ6ckJeZ4jtUboENZe6xSRUAZa6HynvLIi1dHTbqWzSP+CLNzhZHhaY6jqCikEk7K8Yzz2yx7md3Bv990HxZYTx89R78PY4gc82NDL/6Akx6u7zvi7gOY9zFAMvej7PthbzyasYGjucLy/EA0ejrTlsBzylUfHztOB6QlY7tKFvEbde7QHunNYdF/SA/G3XrDvS7IUTsZc3mOcRXgX0+9YWmNCPlWCcbjUqje0GcxVUnoP94AxJqSli+Gwu7zYgzDtyXsYQOrIrw2a2e0/oqGY9905KnzfCCVSRMfQ1bp4yGfv/2/xDz9Emif4tsK4Fpt5xJVBuobyrEBlNa3ZIDKwlWWxW2HaCtPUqNwxPy0xrUVKTaYKSqkw1rOr6xDRM8s5OSs5u7iHluCaBQKHswZnmhhdw95KYwLHIxyFKUuT1o9BUownfLAoit4LVewbK0Bv7JCiAKTrQ2e60WjUKf7qpsFYg1IhnVdZjHA5aJ0xmYxROuJrIvBACInzBmEsTbtjcfMUPR3zRvUBD8dvczqds1k3rBYrjN0CkrIsyfMcay0NUNU108mo40+UCiGXTRvaWBQ51W5L09RoHaJn7OqK5eqGutkyHhecnU8pixCKXeHRWRb4Qz2myOZMxiNGxQglNM5o6o1lubhipO5TqBGL7UfcLP8MzSOwOUoJmnbLevclQhpm04eU2ZjGrKmrmsZtWa+eUzc72rbCecP1ZsRmvUTIGq1zdD4iy0Y4I1htlmF/ScVoDP5yw/XNDbkeY9rgqKOlYFprPvjW98i1om42LJZXfH31j3mxyTDNGGslznpM0/L06y/JcsX9s3dRIufq5gXb7YrKQKEmwZlShfzJLp4xtmlwtkVkBVIFpbgxBkTgoa21IUJxI/A27COpJZXwfH71ES82a/TYMs4F9UZQVy05oGXwZDatZ53DaqRYjj2F8pTaMhUrpkimVjNpNFMjmRgom4J5k1OoEVbAtoWz+UMePfyQe+e/RWO+YLH8Bc+ef8S6vuH+w7f4wbf/fZY3z3j8ye+zff5zvG9RMjqeOLBG0LqMPLMIAdYCPuP+yRm+rmldg4lnsfAGor5K4silYlQWzOdz2vYa5yDPC7Iso66rjs4lvqVLDRP3pAvhWmIaTs14PGa5UIEL9EmmuY1f7kXKG5A+7wHpEQ5UlPFbSZ+CT4AQijNV8sdc86WokTgyr7nnS87JyICWoBzHeVzdoieKXOS0GlphWLWGXI7wZU5uDK32kCtOKDkRY65VxeqkonLXPFvd8P7sXXQxoa2j8ap1tNaxsx6dlSih8M5QNY7pOKXnCJjUerNhs9zQtBZ8CFkvFJyczvjww28hY1QuGSNEjkc59dby4vIZtq5o1hs2iyVOGU7vnzDKIcstI62QbYYWU/x4h4xe1AKQNqQbMBicd1hC9GgZFeIiYXE+yOnGewyBnxEICivxfov1LbkIEYxu1jU6b6hkjXUCJfIQYekbYPQiYqLh73G9wJAPPVakV3jvUMKTCRhlktlIcTHzTErQKpw5TeQVbTSclFLGSG0hP7vWCi10r9xPGGxclUPepPB5lwpvTzfQsd/+FptxV3ltxfhHH33EgwcPegtP5/j2t7/dHYQez67eIYRgs9l0QkaWZZ0yvK5b8jxnNBphjGG324UQCbEjxhiE1NE6fx9EOhR4hqH/jgFCyQs9gRnJ233InA5DwRwKWOldh0DYXrtkDAoxaMMQPBEieI8N8/wlhX96b2AQstgXOD89YzqZsbi55vmLFwRvcc18PuuIWNemgG7irGM6nZCME471JT3Xl31QNYAdA6+cqHRNf3smN3iHZVqzXG1omjYKwaFuqQI4Y5yL+bmSR0LI9ecOhMQ+RMMQPIR9L9FBq/3LAbdbAKmno/mvErZ+ufJ6CsV9lXZqzyG9So09fp8QdIq1cFfKjWiBrCMK+/Wl8RoCibflkP4ecfS+o2MehbE9pcBL1TDDR2+Dp+G3u8bzZR4P/ec0Tq+a6v56UioMBd6w/g6Zhdvfb5d9v9uhsNt767kEPITTB0H06E3wohCdkkuk/4owAiH3jI8hVnqGSMoAZjm/b3jSt7sXUm+vsL2RiXe8vof4y8rLlC/dG1/zNYfzfOygS78fn6ukxBnma3V79/brklu/9+vy+Lq4BVp5OqWt864PGxjXnEuGQ127XAdEhN8H60f0K8v7CLJH4VuIINgFgyVNSP3Xt7E767zfpzl+f6/c2mHxfCiLIubMKmMdh2PRnxPOO0ajkslkTNO06TUIJJ33WsdsH+6VPiJGqj8xNP1tBzDRAPQa8kJdnTGUc78u6EHJQd3DfZHmUaT3i/5eQWD4vIe6anBmSVM3zGZTytGYPM8S2hMAfheU4856ttsdi+UKvMBGL3RjLaOixJoQCstFr/+uHYP+hHy1MR+zEDhHXEvRgzvOgxAM5uP2ediN7QAMkVL06/BgyNNvw7NaSBE8LGNu27DeHFIERZAzJpz9IinIE98VlCLWmmAcZB1SgDEBXDbWMDIBrNntas5Oz5ifzJhMRjE9DHgRFNUyCb4uhGHyMayX1gqpLGJc8d63f8T1n33K5slzHBssFViH9YaQrTXsU+kjyBv7noB9ERfBkPd6mYFd4v/2ciCmZXkAaKf79mjj4BxK7zis59CLeBiGP10fVHDQ1uTZdTw85+3zeL/d+20TB7Rgf3yCJ2nwRHkZWHz4nmPX0u9D47zhM8lr9fCZPcOBo/xkr0A9vP+ucmw+hoD3oULi8NlhH9O9hxEFDj8Pnzs0sB2+79gaO5zTvTbdMSapHAtvevj92HwcXk/r/Jjy4K42H66NY2He+3r6vyIeap6geLF4lM74p//in/MXX33GX//bf4v3f/BdRvMxRnuKWck704JHH7zD3/hb/y6utai8pGkN11dXrFarzrvxxeUL/ugP/4jlYoXSYwQh1LRrTaC51tG2DVopmqZFFwFwbZo6phL7VYpHOU+XN02GQK04EYyqIz33BO/LDkzwQKRllmAQ1unUpcALg/UhlU/AYoJS1qNBmH5svQ8xkRN/mObKe5JSLuwnAQNZxAu6aHL4MB/ChzabSD+ECWeVjdHHrGloaoMxMbw/LlTpPVLEMJ3CcTrSTCfnOFkynY8oZMbF6RmjckxjrkP4wWrJar1gu9uCEBSjMfcevkGRj4AQgtW0BiUzsizHWYO1od/Wmc57TBC9laXD5qOQO3RxjXnyhGqrGCsPKkeYlnZjuVxu+chUyI0m9zkCwc45Fm3N9W7DRIz4dLflet1gG8fyflAeWmGwhPcH04uQpVHShrNSaJ56h495Um+8ZVVtEd4jtez4PetjipuesQlTTqTRkfeVHYcW0vLEyNL4mFuzrtcIYD69h5AlLRKvBUp52uWWtm46b3oVjd+SEsh7hzMGJQUOiZAe7xrq3YbllWG3q7DOR17FRllWsa1rqrrGi5gSwQWvbCkkSslgnBfbLpXo9GgAKIlI55KXHc8qI/M7VHB34c6dx7YWU4cQp9Y48A2mDUC2by2Y4OkcZAbfYSZDg1PvomdLF/UgGSccOQvwA9wj/ae/CsSIPi4qZT3DULOHxnpBKTR8+naRUoLQgT5Ij1QeqYPSVwmJSOPhPVpIRuMpeTmOzxF4LC9RInisuUhfktzpRYicYWzA/3yi2TEs9eGxamIeZLygjSHt+/t6eS3J0B0vLPblgH2ZIHKq8WDvxYEgLw1vlhKEHVSgDudJdDK5TOlphu/teOnBE643gO+uxbUnE38U90bHsw3XSXqvEAM+MtTUS7b9WAohMNFAdSjDpGt7PFkvVd4avI7vF+Bl95a+IwNhZI+kRJkipbu8JSenSFeDufd7NaU//frt7vNBppGqN4Lx1pOMULo3id5jvOMn8FHukJ3C3DnXRbaSUpLrELJWSBnmJhpxH4b391IFT784rsZL8kx1eb+l0jiZRRragnNYIzCtxPua08Kw9hO+8A/4XH2XzcWPOMk2rN0NwjhwAqsNxikeFR4hNJ+2c541GR+KZ7xdKFYigzIDMQ90sm2iMRFIoYK3a2uo2gYvdTjzpUBLgRIO6S4gyujORhpoTTwP6GReFNHIT3R8czjXfbfeBTGlhew9wq1pccZEgyWN7fhb2a2PTmYRYU6V0mkl7c175/0fI5Ol/WGdiTKMijmSgywzxMNDVQ5MS9O0GDTl/JRSKJQjGKG3BmvqgFeUBePRiDwv2FU7vLVRvozpTmOUP2cN3jpO5jOctWw3G6pdhVbhnrZpkFIwm51QliNGkxFlMQoYQPBcwhqDko6y0CgRFL1tC8ZtyUWDMkGzKKRiVJ7RNjV1e4VtBaU4YaLPOJ1/i8Y+QSpL6za0ZgNqR7W9oW4tVbOjqlfU7QbjpnirkEJSFmNG2ZTWOLTQZJlmu93hvUSrEffm97G1xVrQmaIsMx7eu+DsbMp0olitVjR1zXg0pRydIkSGKGZIWeCcY716zk32NZmOob3Nmm21ZjKeohuL8AJNCFveeIfDgSVinRZT7xBlQdvm6Dwj6AB8OE9cMHhA5Tjladlxef0RW7MMoe5baCqPluFclJnCGYfZeUQW85j7llYFPrPxUGeOjSi5LhqKwjKRLSd5w8yNOLXv07gxqmnR9gtcsyX354zKGSPxNkLPcf4+Wn2M8Ybs4kfcv/gryGLGp2rJdvwlmZQo5zACGjzCeIosC0pl6cilYKIFy8ePaQWEmNGS1vvOQ1YoGXEdw+lEM5IO2zYgNVIXeL/EOdflGU+4cgqN7nzgbV1rUeWIohwxn5/w4sVjrLM0pkWrDCUlykmcCNiTi7msgzwxkNUAvAuyjgAjACxaSLy1KA8VsMwkF/kYtRB8Ss0IyT0yBIpSZuRO4ITvUpi1TQ0KcgmNACeC4ea0zLnICzbVBm8qhPMU85L74znbWlJsRhi1wbQtQjm0ELBaYJc37LY7msrS1GucqDE2GOAKGaJSvbi8DLrJ6YRMBz2l9wKtMvI8pyhyylLz/rvvcX19zfX1kmpXk2cZpnW0dcVmVUG7RXnDbD5FaEEuYZR7VGGDEYgqkAmHjHidCIcRHofygb5ELhiPCexCdyiH57RI18N8KCcRrqC1NVbVTMyOrHR46RFG4GWI1Gl9iD7QwZhRfgvnazKAjgZ48ez3MWqYFCJ6uQeDas9tPOCYTN8ZtUiJUI5cOyaZYKIVYx1SZnthyfygR1IGGS/ScZHOCJGjkqq6M5gb4ESxVVJoREpNGrnrmHWx55XvhnX2ymsrxjebDcvlMuY4CCD8er3GWst8Picv8g74z7Kss8jL85ybmxt2u11k7gRXV1cURcHZ2RnT6ZTxeBzzOmmcvw30DUGkoeL5eAlMzVARDvverncBb4cg1bHQPkOluk+C/OCe4SJJbT60bh0CPAHQC15YzlreevMtXjx/zqcf/5TNeoNSivl8PsjD2Lv+JOWZ956yLHtP/sR1dsjF7VE6BpbdAnLpx79n4EOosEzK4C0egYwkjIgEzgTUfk9Z67zjMF/S8B2DKdxr58sVdIedG34//tzLFeuvU9Lg3q0UHwoz4b+327IHKCOOtnZfRjv+MusGeezZw0BiHS9/97AVx+8T3eeXTkX33tsg6e16h/PeM+avXV56qxiABsONcOy3YZte3r+7XrnnNRSFscEPCBEVT1FISIrS8E5JH6LX4qWK1sb761iQDHh6wCQBBt3+V7IDaY7tm1dM3SvL687Pq/fsr15eXr244+/w+cMK/MGe4WANdWTulWUIWEDvrdydXUm4jiEZB1AIPUcU35k++QMjlG6Ow1rQWofQhzFE2B6eEc8gl1CMBA69bJ6ECOsSyXQ65Wax4PzsrGuDj+1M291DFKAdUmnOz8+5vrohOcF3OOygTYdnjR+AVvutOhz0wbx09CaAhglgFPS55zpqnRoTBWc/WB8d9T2i2EmGCeGx5C0U6mmaFmssbWOYTBum8yl5XiBVZCyjQFxVW5bXS1pjurq8syAEpm27UOLFIK1Mz7+EyVS650s6IDLSkmRs0YFNSdHdzfs+nbpdjp8/+6Pee/gnplV00Qp640ARjXSkNJ1Xku/eH9qtdRb4J2O66BlCuAASGENj2vC3rtlsN5ydnXJ6ekJRZCSvQe/peCCDIVMh1HCItCqxtDxff8Zv/92/xeKTx/zJP/9ddpdXqLYBJ0MI+xS2Ko2zj8YEBzzUS5WLsQwVlncpfId/D+vzft+r9Bi9vUtpexieOykiA08KPQ1LhlT9O44p8A8VtAkkHCoxe1J07Cw97pl0THn7MkV0B6QNeO6UA3b/3WGPHFOuDunVkM/am8fE3x7w6sMxfVlfDz8fUxQf+z6s93DNDBXKyYtmsVj0vPgRo+BjhhvH3t9d8/35803bfKz9L3v/XTLX4T2Hz96leL+rhOOzn3sV6ZFWit/7ye/x+Ysn/Ma/82/xg+99n9VqwZ/84R8iEkCMZ35ywrd/8EOmp6c8fPsNto8t29UalU/5te9+i3/v7/1ddnWLFzmLmyUff/Rzrq4u2a63PHvyhKdPnlA1Lfl0hi4KHJ5cljRHU5K8fnEWVHCkAcDqmOvPOvDBKyB4twYDc9+dj4GD9DKAJE6KhLfEkMguKrcjYBK90h0qaMwSuhDBnJSTHAKI4qJqNQAnQ6EmMiGCPf7eRcAirL0oNdpwXisEUkt8npPnOdpJnDUgggdv8OjM2G0azicFF2dTVD7iq+dXtLbhZDRmOh4zLichfKnf0bYt1oSQ2DrLEVKx3dWMRnNGozFaZ93ZFNZL8Giy1qC16sByFb0KrfCI8SR4sG2W2MUNjcvQwiOkorm8YdE0PH56yReuoTQ1b+gRxlhu6i3PdhsmTvOH8opPqi032x3GW9pvleQInAyeI6FIBDIaPgSvklrCpffkKiPLNU21ZlOHUJxSKaQKZ5v3/hat6xRl8bfEW0oh4r8+RKHD4a1ht1sjEMymZ+hshJcKLwXWtbRVRdumXNGWTGdYG5SgnuSRHMbOuqCMVcIhnKXeNTgDXjmS4YGUCidUDEAsiQsaLxymdV2+XxeXpZQS5YMHeVp6SZknfOQqU2hzn/ZRiFBj2jaETnfhbVpItNYUeR7GQkrKIkMIyLXCW0vbNoHvYIAhuRCWPIQnj+9K3tJ+yEYckXPjRxnBwGHpxIAk58W52ttfqXjPMLXDQEzYp7ne46XD6uDcYLIcG5XYNvYjtVZLxWQ2IyuKWEcyyuwjPeDTzu9fKkT34rjmYu5SAf7gLFVCUGQ5SkiMNWSZHmBw/cg55ztsCYYmBXT3HI6v6M72Xrb3e/cTwFgnunmKje/HMf4mhEAMFeNpcgZAbirKq06+Gs7ooZI6pEvqKutxAT84/1VKM7F/PicD2NS2ff6vl2UD7tArrA/lqu63rlMibqxu6FLj+7GIf71L89Lz/EMFc99PtzcOqa/DMQvGAmrwuR//9L377G7TsttjHDrVt4HhMonjJzq6x95zcWxSf4XASBm8fuPYGq/RStDu1oBHZTk1Gb6tyLIgV9hWsqs8zl4zzSQ/b99k6b7DC/ltXFFSqmdsTIO3gkxKTnPPm2PNw+mET9cNX2wcvsk4y5f8ejkmL8BJjVDBgEq0FUo7aiPACzQerMF4hxMyGBWJgIUZW5Mnz0EhQ0QS56KxUQhDq2SMSKIDb6mEDEd/ckITYOIekEKSSR0i1EkVZbkW09RYa1CqwEd5O+3JIT+evAOllDHq2L7slPjwoczhnKONhnJJt5DnGcZET9u4x5MiXfqQGqNpPaKYUEhFu93haBAEgy3nLGUR1oZLyn3bDrATiVRpDDx5pplOxlxdXVHXqa+StmkxpiHLMqbTOd5BXpacnMxp2pg/2BraVqBsQ1lm4cxyIX25oWaiBYUu0TJDqoxxNqViR+se04odxgucHzMqz8hsS2uXWBPkZUdL0+wQjNCyxPstdVVRlxknszcptWQ6maNVwbJZcXL6BkV2wlPzJVVVg9NMRzMW+YK6bpASRkVOnutgANeu2e1usNYzn10wmbyNbQvaJhi74x3e1FycXeBcRbVpWG827KoNRVYgvMVaj/RB39E6E8bYiRAtI0YxwIQUGyqeA8mgUqoMSTB+8AqsqFmuH2N9MLZzLbQ7CUqQz0DnYGw4dlyksdI6XB6MEazwGAeNkghhUcozLqGeNVSZQaic0p0i12vk+hlL+4zCFczUQ0byIWo8ZSLfIxuNqasv2bZwOr/P/bd+zNp8zWo64f64JWuXrM2a2lYYYwOvoiHTkkxJNJLFs2dYJRk/mKOzEkugNYF9DykSBY7ZSDPS0NYVSInSOSJG5dEqj+e3i7xrwFxsNPq0Jhi+FuWI6WyGznLq3ZrGNORlgRKyU4DK6H3cydN2QELjYSF84BFD8EWPFlEB6z2196wlvJWXFFJxIywVEofEeoGWktyR3BDAO0zbYLNAnqSAQgjOhGYsBKWWkGuE14GnzAQiD+dOoTVWZQgdnCOkALVc0lxfs71ZslvtaOsFymU0PvDumbZoNLvtNhoSSMbjcE6WZdFFshiVBeMip8gzvv76a9wVzCZTppNJiLLhLHVjUN52ecmFyDDtmlKVqCzgOV5kwVPcye58EQKQwWxbRP1NkqAsDb0Cuj+TJUmBHiLhIDzSFjgrybHk2iOVweGRRkAuiCacg3M/0tjuOOw/dUeflIFPi+ekJKXZ6Nt0F5bVH7UhZUAIAy/JMkepBSOlKZQOBojCoR3RUNsHG1YCYx++R0M5oRGdqjrKLh3mm/K2J/4hOOD6eBjs4UP7vXxpeW3F+Lvvvst4PKaqKrbbLet1yHUwnU73QtMA7HbBc1wpxXg8ZjweM5lMsDbkPri6umKxWLBcLpFS8t5773F+fk6WhVAw6QBNCu5+vuQtj+xj3uLJ4xz6iTsMBzg8qIce6YfPDMuhYt0NGNX03LEFk9qTgO5hKJkgiGvwgnJccnFxj9/95/+EJ0+e4D1kOuP8/IKhdSnE9SIl1ljyPGzmxOyJzvtrv+2HJYHBnbI6MuR7YNkANJPxfTIq95bLRcyrFxnLGCorCZ7DRTnM+5XqCwz/cOF2kssrQfq9Z15zsffP/Krl9VqX2vYy4Pebl0QW+rWXwjQrdXeoxuOv/6ZtGkoXt8s+kfzL7vc3actQq+GP3Hv43DddQ9+kBE+ClIMpCQkBSPGIQU5Aax25PvAqigTe+Wg5Hb2Osiwj4Z5dGPbYjV9uyI+NyWs8deRg/O96SUJz/PbK+79JH3tDjyRs050TxkTAMIIwgXn1A1odhG6RJLxUT6+d6+hw9y4hkUJRlmXwRo5giXchh7MkKpWsJXm3dEfmS5QPQ0C1LEuqp08Jnr5tH26XfU/QEJopnCcX9y74+ONPB8pCET2o72ao+sbA4bHw+kV0wKgkhAZP49lBLSIp0feNl9LrhjR2qKwPClnXbbAARYY66qqmNYambZjOZhRlgZSCrMgRwNXVJTfXy86zTwpwvvceadsWpXXHEwy9mVI4e601xg69VnzHN8s451KqGKI2ggQIvEvrLM0pKV37oM/hQsLHbhn4pFvi7wNzgwAsRYAjAcaB19II54OlrrHd/SIKfALIsgDiW9MGZp/Qh7oKuS5NUWKtY7fdsV1vOTs/5eRkhsqClb73gl1VBQZZgtbBIDLLQlglZ9f85E9+h7/zt/4THn7wDv/y//WPePzzn5MbEMYhrI0OLcf4pcTX0e3Dl63bQ6Xg8Pw7dhYOecFOCfqatPsu5fIe/9kBrCA6j066v8cUusNy6OU77F9f77DOvg39OPUg7TFl57F+DK9D7yF/qJi/S4l6l3L8dejIq8bkWBlGovplz8O7lPB78kaUhw7fcfjcsbqH99669kswDIdre2gUcqwPx949/O1QYX5Xe79JCXsKkJIiL/j2+x9wdXOD9vDVx59y/eQpdb0L8o8LIUbLsmQ6m/LVk8fc8458VPC7P/n/4J3n4cOHPH32hO9+93vMTk6ZnE4o51NO7p8FzzMhqdbbICOv1+g8Z1dVFEXehYP8VUrbCmhDTj7vQ5hrL31M2xHytTkhwBvQAXBMCuignFLhHwTSJgNw5pSKnjbpXLM40QQ+Ag8dbpPOhB5SwUX+Ux4aqnSTMOCFBGIQ0jbRjeB5Gn4blQWzkwn5RUZZTqNBjCXkzg5ztN20fP7ZV9w/OeXNd9/G4vnJ7/8ezgsyJzm/94DRaMwbD+7z4vmCTGWMizF2ZKm2NfWu4ad/9Ke888673L//kPlsHsLRlhEH0J5MZ4xGY8oiY7eraOoKLSVZnrFzDpnnaFORuRatQUwLjINxoVk8fsGz62uefPklDQYpDadlyW6543rdsq0qLmaP+OMXL7g0NTtjUGXGbDTGNi1eCJKfvsWjUCg8jXfUCK6lZWlrTlWJd57KtNS2Rfj9iHHHSsefSjpPwHTSBWO28KyMc9/EyH4A5aiMYxLyUqbc4W3b0jRNwAbKAtsGZUiXD5gQRhZnKMuc+XzKyckMZwIH5VWIBhCMCCXGSpBLnCd4wkoFEQB2zuOcQWAQounOzaHiT6R1N+D9UqQm7zzW2C7lS2tabNuilGc6LZBqzmSS0TZtiOhjQiSI0XgMGOpdtc/zDrAgn4wQXdR2xE2ScBmk6IzXQxMlSWl5DMfq6XpMc+APr4W6e169ufX8sSJtn6M5tXno1BEeDmM45Ec7QyOlQIRw+SQ+AzoPU6+CR7nTqsPXJPvYz37/Er/iezohehC5b1IwEkGkcK2JWxckEH+PR8DHyAUxNYAYML1pboTACQ1CxS4PzjAxUMYO+axwQwB+ZU/bUmqmbCgXxTkazkdao3ed9/Hm2J/bZ3syEBCDuhXJaD7xqeFNh+8wR4KWiHQY9E0mO8r773/qFOMD/vUwv3worpPjDo3w9hsyUIwfa2NX3f76OcazBfZ9IFuLQ6GSKCOJFDhjTw4fzr0QAiMDDZZRRnIio60r1GiMkuCFYlEFwyWZ5+QiQ2SOTG3xZHxt3+EPmu/zGW/jshkiv6RRBt8opITzieQ3Lwr+g/fO+ESd8oufXbFa3lC6his1QhTnnKDYYmiFJNc5ulRo49HjEus80rSMcgHSsVwuUECeZSAlq8qRySIo1FVQINR1hdIh4mQKYRsihgRvTa1CLmrbtvi0vlzThe0XeHIpA11DIKRGKhHoaVYgpUb4qJ2Mo++i4i7Qe1DB1Y9kbBdkVo+I9EL4fu6l8GS57iIkKlwwaPSuf4cPCqsGRyZ8iAwmQEkHvuX6+hkyy9FKhQghxqGzDLFYIKSgjYpZ73sD3EIrhAx55qfTGd576roGIMtz2qZmt6sQ0iIjH2isDWldhKIsJHXt8daSZxnOCUZlgVCKPMtQQmJFRlFmjEdTimIUU5J4PFuk8BSFwPsbVtsF2BB9ZlM/BzdC+BGN9XinmM7m0Z7MsFo/p65bZm/OeHT/DGcUq0WNaeCNix9Fhb/k+YsnVJWnbmvqdovF46xntWlovl5zWo04nc0QIuT7drSQX2PtmCdXj7Fmh1aA15yfvYH3FS/sEzbbEAGvqhoEKkaSC1FCjLEUSuKjVzPedvyCaVucL1GRDyHTAYOyDcJVCNEis7h3TeAdfC2wToJSjE4NUlqUiHtdSEwrgqGcFggcXlhk63Fs8BtPnkEmoS499bimmrZ4UWInNc1JTbt7Rm7WFG1B1pwwUW9wfvoepxdvk92cc/3V7yPW73F2/jbvfefvkU1/nal/yvPtX/Bi+3Oer79iZQ1OQFEoylzSyIzWZNyslzjZoE9ATxRKlbjWIaXGe4uzDhUNo/MiY73ZoUcjsjzkGnfOITMw1ndRklPqYG0NbUx1YK2jLEdMJhPyvKDabWhbgy9uu+3dxTt0v3vfRyJKJFWEaKitjZ7oY4XONJmzTKymQFJjUV5QAIWPOncH7c7QBJtHtBecypz3VEZeNyzdjjOVMdcFOzyL7Y7HTUMrHSPlUaUia8B7iZMSu9pint9QP79iudxh3Y6sbfHoQHBKj5aee2cnFEXBaDQKCvHpmNPTU5wL61MpSVFkuNry4sVT5qdnzKYhrZLzwQi0qSRalagseEdbY1lXW/R5jtIBz2mNo8gzaG3ADwOli7ybjKSvN9wM1DfwOt35JgSeNhrORUcT4VBSB2MLIQI+Gee/w3iOzuLd85zOvHCGH0aASVN/G084xANwAQtWQpApSZFllLmmyAoyHQyuvfCgQnQAn6IHRK94h+vXpBedfJjauN+OIDf4uC5BdOf0sGdpPF+nvLZi/I033kBrTV3XnJ+fI6WkqiqyLOSbKsuSXR0EqPPzc3a7Xcd8h7AEBdY6jAmbtiyDBX1VVXz88cdcXV3x5ptvMp7MbjGLQ6Eh5S6B22BaGoDDMJbHwJkhk38olByb+KEHzrDO4Ln5EuAHulzpTdN0jGOq07keVHrnvXdYrZb82U9/Eo0GRJdrRYhDuw/ZWcaNypIuXFBqG76Pt89xEBKCEqMDM4dKgNT4SP06sN4GcG61XtNE5kCqQX98UPg1MSysT++HTki8TYbjxY4wdOLtS4HGftzvvOX/hyWdCi97eX9y/HJK4mPCAwMJWfQKNh+8BY62Quw9fMfno08etOHloG+/5xIxfXV/e+XUK+/8Bm15/Xv7sfnlAO3XKQEkcmjtO0Mfl7wYZG+g4wZpB5IAnoDrpFBMwq+KjPp+SgmFsEHwcINDZF+gvXtOEkb+30dl9y9XBoIw/fq9xSzckdbhdhmO722A2BobvWcDU+Tc7Uo9MfyL6C3j+iU6oCVSdkC1x1GOSq6ursP7BwAT9LmCnHV3Tv+e/0VHVwNdV0ohhaBtk1K8v3bYe+9CDrjJeMR0MmGxXIWwqdEDZH9XpjX6l0HAkwdFrNnfXsd75/rwgx+eSR2MNWC0hm0WpPTZEU0JezOGsVut1tRNw/xkTlEWIAWZVpydnbG8WfcqBSHRSnNyMuPNt95ks9nyxeef44mKNvozw1qL9SEEYA/YhLZ0QDjhx3Tm+6jAUFqCHRj5JW2Gpyd+e8zvPo3YN9ygX1t990FIlAcvfcwBHulVtD7WIlh/O2ujp7uIoHwYdyk9Msswpo3RT0RgkBuHbQ11XTMqR2ilGY1HbLZrHj64TzkqePzVC54/v8TaBudjCNfoJSOlJC9KylHBJ599ynvvfI8f/g//Kutmy/LzL8mMoCDlVN73ft9fNylVzKHSd78Mec5jStJD2tJ5TAwUnxwBQg/fcVjXIUDYt/EYaNjTp6Ey9lif7gSwYwlG5fvhLL33HV0TiEjHbvOfQ0Xyy5TiQz79ELzfq+9gjA/Hqauv6/3xcqydLyvH5upXOT8P53BoHLDdbveMg4cA9MsVYbffMTRk+FXbehja/VX13jXvf1llaLAsPOA81WbDZ7/4mFk5QhnYXt/QrNc8fPiAzWbFar3hx3/1xwjg5uYadM5CZ1w+fcasHPPJJx+zW6+RQvDVp59TtS3zh29wdnbO8mbBg4t7fPDe+6xuFlw+f85us2MynfCd73+Puq7ZrFad4fgvW5pJSyYUuZRILK1vabEoGQwlZZYhdYYWE6p6S2s26AyKXFGWmiJEPiXXGuk9beu4WeRcXWmqRiOER0mLlDG4XZRPcT54X7r93ZPm0EXQOoz5Pj1K54QUogvP6wgyo/cuhIH1ntoGnuHhW2/zwQfv8vYH95mOZyGErgZEUGbWzY7NuuLTTz/jvekZ37n/CK8kT58/wxpPqQvOlism2y25znhw7x5ffXqDRDIpJ7g5WA9ffvGEzz75nMlkxv37DyjLkvP757z15pvMZjPyPAC1J7M51S54CQulKIoRIyeoJxn6cs3INMyk4ORsRiU82VtnbOs1y6sG61seTWawczzZvqCtLc7BhZxSWahq8FqRZYJcF8zzCc9untHE8JsA0ktypcmdpPWCFY6vfMPXZsP3xhc479iYlm0bPLCOYRmH+ESYl+iNkXJMCtF5eSZgLOQHb2hsSy4LvFCgNFlRMp5MaK2haWqapvcYF6J3QmibMIZKBcPN0bjg/r0L7t07ZzabsFpuECha+pzcIPEOdosbdut1VIwHb5VAZ3yHQ8QDqFuTh2dz4oH2qH1grG7Rn5EWjE4mXJxM9u8lRboLBqX14ubO/dnxiyIpenqgMe0FMaR1ziN8ctg4wJUiGJoA0aEh/GCj7cl2hxz5UTxKCHIVNFJ3naUQYB/H7bQtwyIz3fsQxfaIg7q69XQEzzlUZPeTud/ujpdJ/IwYIBe3MK1B+0Tybk+b6Vi9t8fnru+d91V6rrvmQUTUygPe9rL7sbYlxaKUt/mQYZuE6EOsv7LIPSDsZbLPPm9xG38JItTtVDvDdXBs7Ry+K/19WZqY/Tq7tx9973HZ/Pa7X4bH3mrHHgd7u45UnDDBw9F5WufwugTbor2laSrq1jI+e8Rv/uZf5y/+9E948tlPMZuvOJspvvzBf8w/m/09WqcYy5qz0RWXruX66TOKcc5vP5rxt9455X/89gXfe2vGP/g3S1rfgKlomoaflSW/e7XkUX2Fpaa1DlmDvBhD7RFFjpIKjUAKR9VuWVxfIb0jU2HPZGXBZmWYjEfBaFsp6rrm6uqK3W5HFj2wg0I2RLywMUqKlkEeRYDSms12y2azoqpW/OS3/oC2MF0kQ49H5HHc08AOCdMhkTqW0clDzB3B3npIH1Mdls6btX8Q/PAdWfgnpURdZRG3iKhYlE3kdTTCOVxb0N3T89ie6/oyhAG//er95euBpxxb0r3mZRf/ATw56KaQnBZnQIq0KkhR71pTRVk/7a2gLAshj0P0SWsNfu2Rl/+KLAtRLHykPdln/7eIS5oY1SUYOrl8YGAQeWd9o1CrYHCOJxiyR2MKZ4fpjQCv0DrD0OBODe7Ex409xBBAyk+6aASJ1gghkOLrUF/0FhWhSnzh8PcDfuDC4FDpXjmrGg/CgDBR/k/RODwI28Eah1Mh4njQgrgJ/6QCKX4fwR8E5V2yDPUANbAEvgD/EwQy4q6EGOLPRDhnhIovC0arzsWlvgabW8xvW9xvXPNU/IS0iLX+5BaGHyk0SZav/6Og4E7eLSEdo2cTMeOVeM4TKeOaDTidEIKRHfOfLv6XzGYzTk5OmE4mrFcL2raNCklImOExY6NDeu+TPNDtexBKYo1jZ1pW9Y5tWzPSClG1TL1m7DNaHLkQnFEwo6YW0HqBWe4YC01jobYGoRUzlZH7Cr/bMh9NKbOcBfDl+pLGG8pcUipBVma0S89mXYVIQsYwUYrR2SknFw/DxNTgbBhJlVsmo3HA5JbLYAjjDMWoAG/JtKLIs4jPCJyzjEYjxuMRs9mE07M51lrKvODi7IQiV3jbsLi55BdffELtV8zvv0ExVnjpQkSJtkWT+EI/0IL1vGKfDDEPV2LawVAcggLRET2LJBhtyvQ/T4x+4yPXe1zTdlh6PCCsgRQZKynHD+nisXVxGysJMqMUgW7oTJMXBXlekmc5PkYi895jRcAjLTaqxG00fnVdHw4yMA+wLBFThoXUXAm7TbwoRJ5MRA7S38atj5XXltSzPMd7T14UaK145913adsGCKEemu0WnWdA9H5SGjBxcYUJDli+iYtsTNO2NHXNarVivdnw81/8gm9960Pm8znQK6OTVw3s5xs/nIhhSeE5jU1CjUDE/LyOJNTLDlQLVUVQLVq/p9wrxOuuC3kwaFsU6BIQm4hxWmimbTphIY0F8buLjp7I0Jb79+/zxSef8dUXn1DXIU/d+cU5XQ4VhoIROBsUbeWoRIi+TR1hi4dG5zXHcSJ3tIjbwGjwCAu51Rc3i25s1eC9zvl42BoQUGQ5WmdsdzuEFF3O8ePCT8fa3EIuj22845/FHZ+H9/7yYODd9R4r+50QiEEI7WNKuEMyJkj5mXxSeA3uTIybS2FPUtMOGZG4EF42fqJ7+Fg79uvp701tS4JrXE93PH6XwNLvsdTu/fnsj979dhze21ebPOKG7z7Sm+764Tv7eobj+LKVs2+0kr733HLPbEQFqQ5EX8nIBDqHtTG8cwqTvNdYCEYsEqViGGMRLMTSu7JMh0N+0NhA24aH8LGepnm5o3O/ZPlVQPf++ddVSn+jmu/4fve63885v78ShgYh+8UPcnKx5wXcMyMp/OiAwRjUJO5am10d4bNWuqPHPb0fKDV9sO73zoeES0Lugx/dUh0ceHETSSnJ85zNZsN8Pr+lOAy3R/rvQzhUpTQnp6csl+uu8tS2wageG+y98Ts2psfKkH75eOYdA2L239qbaaXRSgIzJIZqX5kvEgPZ7a8EAsQ966CpW66vbhhPxkyth1HBeDTm3v17PPnqaSdoa6Wom4bVesV4MmE8nXShr3X0tjHWUpQl85M5SmuEgKZuqOuaqq6CYmHQr+AVRYwaE5QPHWvtXFyPrzfu+6cN3bGc3iP2DAri+MSQikg6jyShAv/npIoCezDkEjJkPEzrIothPW2K+JNC9DUGa1rqpsI6w/n5GV8/fsqDBw94/uKSosh59OidIOD7EBkhGfnVTY1xjuV6yb/5s9/n57/4Kc16S+23nMqCe2gENoy3dWgRvBcRYHG0OKzyCC8jU532Y9hbXVpPH0KJWRvnTwUvt0T7U17SXonrBysv/JHqCFDKUHAZAObpewJXB8C0HzzTh1JPU5meD0ZWdymj03pJ1w7bk8qebkIInPXhHT6tSnl0uR0qsI/1eai0d/GfEL2Htve+E3jSfj/0Kh++yw0WcLeFO/5/n1bcpRQ//P2W4v0Vh9VdBgHHgOwkM+yfF/vzdQgaf9MztwOhutf7GLoPeqbyNeo40pe7xuXYGA3H4y7F/TGvymPFD5k/H2l241hcXeMLzXg+wVlPVuacn11wenLCRz//C37+0UeMxiWjUcnqasni5jrkuPbh3FzerNBZxovLK/7dv/k3KWYzpFKsb1b8k9/5p/z++PfJtGazXHU0/vpmyfX1dZcu7N//D/+D1+rDsfLjX3ufi1IzLwS5cgF8FFAWM7Qeg8owUrJpW5bba1qzoCgs47FgMpEUyjLSilGRoZBUW8+nXxj+zZ9Znj6zNJXBWYsihKo21qHlEYUb7M1r+G4RndflAS85SGreGRkJ3/3zzmGzjNH5GY/eeZ9vvfkt7mUjSlkitSLPFUoHY6m2bTAzx5uTR5yNc87GBdIp/tpv/9t8/vkX3HvwgGI8Yrla8kc//TMW64rPP/kFUsK9e/f5K7/xm0ipef+9G24WC+qmxVvPdrfji8++pG1axuNRFw0v1xlXV1c0TQiTul5XLK7XVKcz3rhZMFutGW92UEE20zgNZhe8Xh6UJe/ef4c/31zziy+/QtSOQuSUOuM9lyNHE37qNiydRUmNqxvW1wusCee0FAJtBdpBhmciNAs8WzwL23Ba5DTCsfMOQ4rqLAYeI7fpStirg3mkp9Pd7yJEpmpcQ2NaQDKbzwN9xyO0Ii8Ldrs+TL0UHqGTMr0lz3VkIQVZlpNlBbkWzCYlWomgTG9bdKZDZJdoKCzxaOe4ef6EzbYCqTpDwaCwsX2ffAIUB1EEDzfNECA7co6m0M/EEK8BnA9nSEqTpwm4kTcOKezd9Gvw3Q0MR/ckwT2aCLhDo7akiB7cv5cE+6CTUdjzgER1fMGx9kVRAeePG9Dv1Z/q9b6jZem7jYZQWimM78N/+4GslrCJ7v3H9EjDm7vnLSA7uWZYZ3gwybDJ0NPv1XcoY/T97z/4vppQrN0DCPbG7wBziaPS8QyRFRv6N3WRGI7JL/2+DGkGDq8NixAi2LD6/lria/eew2O4zTvuK5zDZ2kjbz9o4/59gbO16iBlpe/f3f/dtxHu5sz34wNRx3nQbDGY8/TuTtk4XDdpPfueW5a3TiTf9Wd4b2B1e76kG4XhOGOBx3oAAQAASURBVIt9g+3u+VhHv75MxxM5ITEoNCHilHOOYnrCX/ubf5cP6rd5uvkpXz1b83ydc1X8DTbj/xnaThHtV9RmSVvteHO04t/67il/8ztv8YPTEQ8nGl0q/vBpzf/9yxue1QahNGRjduWUj0zOi88/Q1UvEGaHqgXtcop2ngmGB/fOeONb7/PO+x/gdMGf//xTLhc3GNOQS3jx+Sdsdi1ffv2Msiy4/+A+777/Ll8+ecauMVC31Nc3vHj+Ah1DCltj8bZ30ChGQQ5t2pbNZsNms6LJW8zI8N+PUh//+Zhy/puWY3zyy3jnl1xLa9F5y4vqxa/QqPgeb+Awi4+5I3rRERa7xoFtD4wQ6L8PDziAtBxej11/dRGxrj1t1f55aMs7rg3rOFaOiWvJjfm1FsYgOsze868oOZC7GHA6lObWJB0po+MvSTyQv6MBooGqqphOp4wmM2Ynp1zfXLJu6r2odXuQ+EGJ4vaAr4yCtIzGRZH5b6xhVe14sV5y6iUr52h80Kcp4dEe7lEwo2XjLa1tac0OMGSTjHzXIAzsJIzznG0r2WlNrjTKRf5UaFzr0XkBObRqTVVV5EjWbYWQLdk0Zza5QNZrrAGLijhCHfLPWw9CBUMIKWlaC6LpnNeMaWnqCi8k77z9Xgjvj2KzqdBa4jOo65abF5e4eocUlgenp2wqCTvwpSefBO9oa2TI3T04bw9QFYjGDTLhOD7JVWn8e54i6CgD1+ed6IzBUwogkQ7cPV4mVdqvlGNFqJSCI62Jb47jCxzCR12Gl0gvECjwGrxO8UEijhhCyoeY1yG2ukLgsP3JnM5yD4dOWWk0BY7jXuFi0N2X4zOpvLZiXKgQjlXIEBSpMS3GWu7fv995flvrGI3Czg2hg3vr47CPJDKCWlprsuhJrrOMoiy5vr7ms88+48MPP+wAeCH6ME5DoeZW6KehAktITLRkitr4mA9BRMHAI5XurKLdAaCWapWqt7JKzBeknOFBgLLE8KVSdQupV6B7sizrgF4p1QA41VjrEUrSNDXf/fb32Kw2/MFP/gnPnz0DPJPZmHKUB09wn5jZxEyGVhZF3rUFDkDMl6yBTqmSllVcdHvMbzeuYdwD0C1AqaDw8Ok5H4VLunu9d5yenHB+cc58fsJnn37O1dVNaJYDISKwnhjq/dbdau8xsG1fmTt4+o5+/6qKur6e7tMr7jsQiggKrGGO2OG1W/Lu3jt6ISutwySRWOs6cEGI/Wnv25AAkX0haL8c7ic/+H0fbI6Tv98uekVcl5Zw0KlXjX8vxAz73K9DAQOBdtivfm/2+/SblME7xP73b1SLH3jODOpLYRHD9xg6KCpLnLNoGQ7coGQQ3bim/w6FYoFHZ5IiD/llkvAWwnTHVote3ReURK9bhnP+mk/8Je2pUFe/Lvt5GBonHQEOwpVeqE/L8u637D17qKB41XOH43NoWTksSTAPW913+Ra9c8hMhWghvlvZgQkQwcutV1gcV04xoINSwng8Igj4YU2IYI4bwWrRRTbxPoa/k/746k5rc7CXnfdMpzNWq3VntHZsvMITMihrBZyfnfHFF192eXxC+E5JsKJ9yVB3w72H4B674Uj7+5Z066kb43RD78Xa19Rtnr4aIZApn3VXf69Mx/sOEBOJHsd8hcZZNmaLrS12NmI8GVNkeXc4SSXotroQbHZbkPDuO++wvFmwXq1QWuPxzE5meOFZrZcYY8iznCzPGE9GNE3DZrON6VoC0xi6IIM1dhp3Am3yvYF2BwIlJnxo9d8NeNp7wyFOzwxpOwf7IK59l8LnC9cJTogY2r87ArvY/l1ORWsNxkWLWClCfs9dzZOnDVVd8+DhQy6vliyW11xcnHH/4XlvICbi+o9tNcax2zVsdjWb9YatqbGq5bndsGnHPBqdBI/FLMfVLcpHZayIfdUS1wqUi/FniUpLIYDguRb2i0YKEc/hAWvt42AJYo7NRJsjXzngwQ5X9TElbFBQdD/2fHGs2UV+LLw2vrfjY0U/DUcUkIcKymFJ/Piel5eXJPC6Nw4a0GyI59zQs2A/TdJdSuH0LufjvCaP0wOQ+Bi9T3kIu+hSyTN/yB53wpaPaQhuC1XDtt01LseUuseMCo4rqcL9Sel713k65H9vGcAOnjtUJh+rZ/iMjErxPYW2H9SXcs4Onhm2G/ZD7h8q59O1w36nthwq7142/kNv+Zed1VIIrIxhqH0A5lOe4cY76s2akZyhbcjFualr8nGJsYbWtridBRzWBEOXqm1Zb2vq1lE3htpY/uBPf4Z1jrIsAMH1YoUXiocPHzEvgtepN45PPvsKZx1VbXn27PmdbX6d8s79NznJLWPdoESF8Z4sH3MyfRMpJhifsbOOabPkwXiMk2dobcgzT5kLSqkoZUahM6z3LF3NycmC6cUl11WFcQ7XCPAagUFJgxjkLWbwydOvpWj+QzLNH66f/adigEAhQh5U71IGbcgy8umUfDKlGM05GZ8xHo/IyghcqcDDOG+p24b5+BzlNnhX01hLpjLee/s93njrTcrJhPW2Au/ZrFY4PK1xVK1B5TnvvP0O4+mce1WF80EuN9ZSb7aMxmXIHR6NAUMISkuWZQgh2G63XD57jswy7NdPcE+eYm8W1IyQpUc3jjfklFF5xmWx42a94PFqxbZxjJxCIlGm4QfnJaU2/OJmxZU3ARdpDO12h3BBNpZAiaL0EodlLDImQqCEQQJZpti4htqZXpFDb4B5V/EeRH/k0is+k2I4hc8Ooca9gHI8Ji8KirIkywPmUFUVpmm7SEJCyEEKNRHCyboQBlQIwWRUMJ+PUUrQtnU4531MTeNjvl8E66ri8y+fsKtqhArYivMxEpaNYJmXuJTaZnAuhrNtX2byg467DhgcLmYPJEV+T9OSgUH6HhRubf9IwjriD/07BSEcZvx9f/T7+yJOsj83++d9d2IPmr1fV3omKWl93y5/eG+QNxxZNzaJXx72KRXhD43jRF9PDKHtZc8Hpt/p+IBBbYO2HI7HYZ/2ePvD8fN7f45euDW9r/HWwx+Oni4HeW58eslhJ70/eLnn4I7YzuGgHHljx2T7O/udDBZur7ODlsaLh24pB83rnxAHbR7wWftrNFQ2HIa0ju56xzH2pMc1b3HAe31/Fdqwt4ZfJiL2rdlre2+2uj8lUqT9LyAa+DY4pHeUkzkn995nfu9D/vUf/zO2WUHz63+fHQ9ZiQ9wNxa/+wS/vUYXLY8eZvynP/4Wf/etB6iJRduMBoXF87gynDLlRm5pSlBZTusUs/d/jXt+By9+ill+hd1UXF9d8fZsxv3CcaFqJm7B3C958+G3mWTf4+PnV7xYrvCm4fKrZzi/xKNoWsfNYoX66jHOOe7du4f3sKsqEBpTVSxuFiHveMTJQ0QQT9talM4YT+ZIVaDULzCYsLDWYT1mWQjvbI15yZr8/39RSlEUJVLpDl/oFECHkbriYpNJno501jrHwl71sserVuRdlw+J1N6leOYgOC9n+1EjfDBEkkIN7g/8bVqfPvG7MRqsUrqT+WDAR4vgHQopUhoY14a880rFqJS+iwADQR4I7ZEhxVsMgy+ERAlJa2qsa2K6VSLm5WP+6/4s1UqBC0aR3jsESXaQHV7V0ZW4GZ0NPKMXQTG41W1HeFQdeBoRmjPAQu8YahENCeO9YTwTXjpM/dDPlYz3DumCGHw4LpL0CmePx7SepgJvwgwrGc9N69FKojMdcB9/mxoKITDG0rQm4Dpx3q11vZwliJhJmFczaojsA1VdUzctWmdMpzOKYsTKL6jrirIYIUzkoYQIupkjUUNu9y6WBLxGvKdxhmWz41zkXArBwju2WGZegHXM0YwRBHsGR+srNteX6Bq8deyE4FNaDIKtEzxuWyonUV6QC0GpM6q6xVhF7SQ7H7Jaj4qSZbXF3lzhVzeQz3HrCussziusd7SmIkPT2Bustex2FbvdFucc4/GYuq4Zj8eMiiLkr1aaLCuQWlPXhqq6oqkrTuZTVosFvm0Y54rzkylnZ2dMzAQnG7wNkTccLaJTyvfOtf2J7fsDVKSVMuBcvQfvOoxR7C26GHLdy/A5yg1D3O4uY8Ehz9rfTUy3kYxOB2hgbOOQv+6rGtbl9+hNwLXjvgKIGHWgocE7WIiQnkdEmhzkgd5bfqiXPMRUwrUQbarP+5X0myK2p9NM3R6HI+W1FeNJCPbed+BEyrOR5zl5nlNVFVoHYDOBUqkTSZGdZdkeEJRlgUlPoNSTJ8948eIFWZZ1YV0CcVcdkDbMM36s9Mpp9upIYb3ueua4Uvn2ghIDqtvl5BqAanu5GZ3vxiRMiu28plUMZ1UWJW+/9TZ/8Lv/ks8/+Rm7aodSkrPTsy7k3NBil05gEUwmMfSX6Nt2DBgbzl/6PrzW9a2H/eO1XjCyLozfer1hu90G78AY4lLHefU+zM/J/ITJdELTtLx48YKiCHnQ20jU8T6ES/2VOKf9pT48SPbklf+OFO89Siuw4O3rtS6RycQlhPmJymDC96EX6nHQ9rBGuCUoJllC9G89/nfvqaN13VWOgpl71b7OrN0SDV9yra/z9pY47Nux52/3ecgIHx42Qtw9HimtAATmMtFRD2RZAYTcd94TFS79/PYHJAgl0EqjtEKKFEY/MFJZnsNmFxn9dGi8Tklj8Je3Y3p69frPeL//XD9nd4nE3/T3u9r5zZ8/plDf++3I/c4mj/FAu50P4atUSvh8cOCHcysJBwcKqwE9d86TZ3kMMWmjQVcYQO9858XbA6ZqwESH9+7tzQQeDt49mYy5vLzszrWj4+aD4smYECnm5GROURQxrUpSJqbc2nfQg9cuQ3Hn2Po93Jupif3eeu01wvCZARCa6oh9SWOZnnHOBa8qU9PEHE/hljSPUBQlRV7QOoOQksViycXFOePxmCdPn4aQlt6TZ1nIwdW2Xe4zKSVZloXUNdWO3XYT85KBiEZSqQchF2JQtFtiGgfRj5qIfdobLAJAn0aqExLjcyIi7N2RcWTckve4IqTAcdYFZbmSeOtDeHgXBOJuTFUvvAcFuifaU2CMYbPZ8MUXX3JxcQ/rHC9eXLFYrIMAr2QIgxUkTmyMxNE0ht2uYrlc01Q1vjVIa6ncFadnb/BXfvhrfPnRx9jVBlU1qNaRWUduLLQe612fB4kByOzj/pIKbDQAOTiS0joJNCBYAPf8YKT3nWB9e090RomJpzy6/8Qdnwe/DpQfv0y5m7c84CH3+Oj9NZ/uu0spnn7rlG5SBqN834MzQ4XFoaJ2SIuH9/k0fuL2u1I9hzzUnrJ4cP11x2r4+WUGB4eK5peVY2fN4fUkd93lYX147ZjxxXA8O3n94D2Hc3o4Fy9XzvXPHL536MEwVMwkufFQoX5rHHqJvCNaSip0lmEkbKoKWRaUrmS5XlPXFXlRYm3beYg7G3gQ4xyj8ZQHj97mjUdv84/+8X9Du6u4WSwYj8esVmu89xRFQV03OOeYn5yglMJEbwIpJZvNlqq6w2PpNcvZ+RkzWZPLLcI7auvI8pJRMUWKGa3LEMZRKtDagp4gZYuWnlwpCpmTi5JMZDS2pRYrigyKyRadV6B6gzXREaR06tHTnSjX7vGlgylI9O2QU078bGe0E6dIeoETCpmXoDKkyMh1iLJSjjKSUVUIr+lRYofWiu26ZrF4weXzBbJVzMYB7CtGIxrnGRVFyBM4Ktntdqy3G75+/JiLe/fRuWaWz9FZTpbn4YzYbMkyjVISIWUEjYPMFnAKHyIySVBFjtiuYbPF1oZWe7ImRDupW0XThtRpN5VlsVjTtI6RLNBSk1nL+ajgxq/RwoV3ZRrrLL5tkT541WReMEZRorAYFCUSifOWEonDsai2VE0dw1rKbv+kPdXNwIBf7LdHNIA8kA9FBLXb1oRc2wKKcoTOcopiRKbjeNU11rQY06KkQGuJadtu3xpjQr5LEUCqyThnNCqRMpzjQiqMc9F7JOAhwkueXq/55MunVE3bhXd3LkQa8M4hReDj7MDIMvHJ3X8SnRxKad53RlXDEsZkEIXE0xmSdgZdHZ93fGz3fxMQvcwPj/OhMjr8bxi1aX8jdedgzP98pOX975Gf7/nT9J8hjY7yWGdQzUEbh+2PdfmhLCY6muoSbRi292Bcfllx8mVHrD9s4kvuj8MRz6/jclmq4JaC6whmItz+T70R++BFAES8TgzW4eFZlfi/V535gsOWHTQ98ed+v65j/Ljow6bvneliGDcr0uThg4dNHPCuftgdYhMOfjt8/tjv+28/UgS3ru4t2yPjNHzt/vl0hEE/pB/sr2UVvfnC/1RQzlmDs56T2ZyHj96hnJ1zc/lHXD34PlfTH7H2b+IWIJdf482KhxN4/+GIX//ghH/77Qfcn2jWwtGiaWWGlJbL2qI2DVlbIZRD6RzXOjbkjN/9HmWxw+qaxj/BWcGjieLhSDHNDWV9SfvU0IqGmTohbxZUq2tWm4bTe4+o2jbu2xDV48Xz552hvvchH/mbb76JrWu8dZho8KSVJssylA4GU5nWFGXGZHbaR0DdCGb/lxnvfesD/s7f+bv86R/+Hn/8h/+a9XoVDYWDDDqUe4az1Bse7c9RkneSDNvxl3HenOvpWn+2CWzCkDx4guPQaDLjb/9P/j7f+bXfxggNQlHmBZPJhMlkzHgyosgDz+BMoPNlUaKkwjQt2+2axfKa/9Nn/ysW7poJM/4X2/8dRZFj2pZtXdPUTYik6+Hh/YdcnJ2gRFAQ+5jqy9kV9fUNCihPJuQXcy7bJUo0fOeDR/zv//Qf8KK65ryc85//nf8Dq+0NdV3RNDuapsa7jEzMghEawYh8tX7BZlMhxQkqy/E0NDbwpo8efcjFZEJZSJT2WN/w9ePPULrk3sVbjMoZxngWNxVfXf2Mzz//itOTc9548AZKSb748lOcbbGtBS/I8ykX9/86bzz4NkK2SJExLs54cPYWX379X/KLL/4rpJuwXVseP37Kzc2Sm8WauvE4B5NizAeP3sFer9m9uMHVl0haiixnPpmSFSNm81kI+Q+0u4p6s2H97ClPlwuafMz4jW/xn/3oX3fr5Tv/WDM9VUwvQJ5DMQaVOdAOr0KKMqkUjbN44UOq6cxTZJLzM8+D+Yfkcsp2d8my/iw4VzqB8YSoCVZwNptSjjzGV8GA1nm0z8iUB+1xBmwr8Boyq9HqBJ9PgyFNU/H1k8f83j9q+eQnkqyeclqOKPIGV8HyasW9+3M+/N57fP/Xvk9bORrXBt2RD2dNURQ8fn7FP/9XP8OKKVLlNM2aJ4+/ZjoZB7kJQV6UzE/PUTrnF3//D2nLGnxwVm2aFikVo/GEshwhpKRua0ajcc+3d3vsyF4cktwBHU93CxEiOxnnWNqGR3ICEhZYls7yCA14RigKIciARnicb6mur8h9iROKtZJ8Tk1mJBPjuXIVRjmmQpMJQSYUO+FpnGBrPBtnsQrGoxFyW9FeXtM+v8KM7rG5WWDbJvoweIxvKYoJ6+2Otm1Yr9asNxukFIzHEzabDffv30PMT8iEQOeSLCvI8oCxNnVFVdUUeU7bWpwxKC1wUmK8xUtJa0AYj/YepMNGB4IecTuggHtjm/jCcK8YyGHBoac7uBFIpAgGt8KnCKL79Q3IbP/V3+bX0qMy8S4H5XXYuY7PibhsCMgSCbFw3V9/VPYgPRX/l5TzSd81GL+OkeklSR8Ns8P4RDwlfpZChjP7Lq/Zg/KNFePDz5PJhKZpujBxRVHseQjcAsuEQB+AHemvjHHt67pluQyeUefn58xms702HAOYDq0e/ABEG4JAQzBlmBfvWA4cuM1o3QIGhehCu9+lcDdN7/UOKRR8tJOXEmMs73zwPtv1mo8/+gOePHkM3lOORsxP5zF85MCqMQmBQqB1FpXufV9fB2Q7BBGH3nNDS9FjVsKZllxfX0EE/qVUQbAQIuYXdzG3Z46zjrzQnUUT+C6v+i9f/MHnw5Cvvxzo+5dR9gXj25YtEIxJvgkwPRRgO9lU9D31gs4DXcWoBb27dnr3fo2v9/puxQ2+v85937DsVdv16u633pK7BwdyJ3wO23W7zv2Kvlnbb9n/7wHUB++JX4UgeM0SaE3rXDexw9QQxkbPD5Ee8iQLqQRiSRmsCruDh96oKM/z0GN3V59f0bdfZVseLb/M2hjsZj/8/pfVuJfRiLvae3sf9PjG8dC6h4PpvQ/A50BhEGiww3sZpzu0rWvdHU313ncekKnoLAD/nhhy+BApENEa1ifPzf73DpAYtlv070oGbdaGMNgp0sr+uRlpXsegQF7knJ7OqapdPJP1rf3zy5SuiQfbrl8vYr8rkR4cGoAdgnq3A4P3dffjFBrgu6Vye5J6PiWMSNO22OWyi+xRFAXee8pyxMOHD3DeoWWwvjbGcHOzoByPeP9b7/PV119zfXXFozcfcXZ6ynK5wlrT5ZhvmqbjwS4uzlksljRNM2h870WFD0YJw9Dq6bbEnyVgGAbHSKccP+bTkRTxx37txzrRLiWTJbkDDZkLucXbtgkAigw5RgWOTGdYIXHWdLnLnYvRMaTk+YvntHWNc5aPP/6MLNPkedGNLwS6a0zLrq5Zb7ZsqxpvLMI7tHcI7/h6/QX/0V//n/Mbf/Nv8C/+8e/w4rMvcNdrxKZh5CTaWFrtMNJ1Ib2dSBGIBE4Gm1YlYo63gRJiT2lIiLYUhmbAS6dQ1h29P1yE+3TGe9HxfMO918OZh15ow3oSCPXqeG/H+JRjxkCHytp9erjf/mNyxCsVwt3+7sfyWHuGRrTHQpAnJe+xZ4c8+l3K+tdVXh9T9h77Prz/deoeKpoT/X2dOTrsR7rn0Is//X7byOE4z3NoQLC/Rl+Pzh8qwA8V/sP5S+09rHv/e5T3ougiBQjrOmMxIRRSCqTSWOcJETUUtgWl85BHuG6QSqJ0hkTQGMvjJ0/46OefsF6tujQ2SYFvrWU+n7PZbFmv15yfXwQPYwfjcTBc3u120dP2ly/lpCSXkAuLdwbTepA5XuZ4cqTU5Bnk2RSpTMxRl4Uc5DIjkyXaT1CiwLEjk45MtWi9BVnj2GC9DWCOIEQ/ET0tF6S5ToaeHrp9FsYy3XfI1nsIwAR9TrhwLIuY51HgpMKjAqCNI9eCMpcDH4AIeEjNqMypVp6b6xt+8YuPuSjPMTPD6cMHFLMpk+mUsigYjQoaM8EYS7Xb8fEnv6AoS2bzE2bTOTrPkELQWkueacqyjEb5gYbs6ipGtsvx3mGsZXZ2gjw/IRMeaR3WQW0EGIsVni82S57fXLJe3GB0QbOqMEKAVsgYftpnEtdYpIw5/XKFxSKsQ+PJgRGSaVSH2xg2v/VQGcsUTWNartsmePp5QghEOfTa3qfT/X4d7JYo46fzKd3jnKNpw7mspaYoSrTOur/BSC+kOLGtQeUhJLqPdCkpxYMzQvDGnk5KyiJDCof1NvCDJkZNiueSd5Ivn13z+bMrmsbs0QdBOOFkYGiiYnx/fR7Kvt3v/VJMHd8bn+Sc4tMAJfbw0JKqix19jDXvL4Q0Np677iS19aC9nUI1tc17xF7M2mO9SuXQECqlMelpuACkP/AgEvsfEr/m09rYa3Paw5HhPjbWQ/o9+DscjmOelkIczuXtHnb8xLCrA1Fn7zwc8FkvU4yn0KXD673Cue+PSLhl/K2PtDB4YWCGB+djVNp1/Ro+c3s/Dl4X7hb++FR79sdxuGaOjG/XnkOMU/SRIxOgLAD1SgA5RnvcX7wvWZUHAtkR/uBluNgxvgn2eY/DuTjkY9Le6uQhgEGKI4ZzDv28+RQJMGZA9SCkBlNTV3DvbMbDhw8QRUl2NuPZ9G1eyIfUVYlunlC458xnGX/tgxP++odn/OY7p4yzksfrK1SmKMYanRfsXM0nK8/yconabslyhS4VTdXy9fUN33nvAWe8z8jcYOsbznLLw5nm3khQ5BbMgvrZc57efEVx7x3EVcXu8YKvrxp+67f+Bq3dcXN9RdtUCGeo6x1lmdPUIdprnhecnZwwyjVawPX1NW3ThqguSuFwaK3COTkaM5qc7I35g/v3+P73v8d7773LJ3/xp5zORuSyhS4FoBzMk+iIgvcxWtmtc+n2/ItI+wcLoPOoHs63ER7nYjoMH6L1GbNlcf0EQUNeFAiRBScTFaLqSS/ItaYoCnBBthbe0zYh5Wvd1KRUF6lkSgTFtw8KLOFDKjmpJJmWaCmwtsU5G67LkGar8eBsi2tbhAse4NY6rB2GpRfgRuSZi3KvRamM+fwNLl9c0TQ7sqwgRGoJhnjTScZ0OkdqS9VI1ps1zjqKsSbPBNY1tPUG7y1tXbNZLxAIinzCfJ5h5AXL6xukd+y2G8pRwXaz5uryKc7Byckp5xcPmM5ynKuwZhdSOBrL1c2Wxr6gLD3bxYZqa7CtwbaWMh+RFxl11YAXNI3BtzbkDo5exoFncGRRTutEWwI/YnwNziJag1uuhlsdvdZkMiOXmgJN0QhUbiFr8ZnBaY/MAu+pCo8uCLTVKYxrWTc7tAi521srUBKksGQShBLkQpFnEu9iJGQkHotxLUUJ3ioECplJHIoyP2OU32fnPavdlqvLik9/0fLlz8BsFLNSMxop2sriXYYqFLumZbmsqTaGPMuQ3kQiFPlw7ygKTZZJbBv2jdYaFfkxpSTWOlrT4JxB+aG8EYw667qmKDLK0YhyNELrjKauDvZYOis4WgbHaniuPzQREUty3rOyLUp6ciVZ4rjBgRMxW7akQKIhcBve0m42ZJnCaUmtPEvXcm7g1Al21rCxoJQny2SkSRqcpPWw8x4jQBcFarFAXN5gn71gc/YmLy6vcPUOEQMMiFzAWUbbNCxXS9ardYehhZDqAT9TWqFFiIwwmYyRWgfHIwHWGspiRJFpqrpCayBXbOoVrQXrDb6ADBDS0noRMlh24zaM5LpPu2yntwiRFDo8pxv4wAkLIRBSoZxCRcU4nuh4F961x9odzOceLpKwEUFnjHp07jvM8yUlynODpkadhgNh8cLiRKgntPG20nsPh0y6XJLHfZ8qKoCFobPRpz6820WZJ8Ykc1E+fc1sbN9MMZ6Uv8l7JSmzE0hzCEQlr/Ghh/fQ6yNtwFRPnhfcv3+f2WzGarXi6dOneO+ZzWb7XtjcDTIBwfMy1jtUwicQIwFKqa1DJXkqh8B5Es72vFViboVh2w69NMKhm4C73gsmeSQorXhwcZ//5v/9X3D5/AmLxQoQnJ6eRs+7ATMHXagK72E0GuGcI8/04L23gaPe6zQx6gfA0nChHwCZqbjo7WasYblYhlCYMaRQCv1hraFtGnSKAqCS15cPYJOUXd6uKD8c3bAvL/0DaZOmX44KU2J/Mx/Oc39tvyH7Su34nlvPDp8Tg8+3wYhj737d0jPx/uhwhTCRHlRc50fu2b//dd467NuhQO4PPh+KlcN39eP+Ov2/Daj+cmN2G8y9fcft5hzrx37//CFXwMH+OagticPJk5PINHh8p+xJ6yiBjd3e29uWvg9FJFIYI4kxYT+H1BW32/O6YP7LNuKhMuPo07cGM/TpVc/1z6d39d9f3ey71sbrrbPjbX798jpruoNjIsPSbyd//JWRo0nGEMfaNAQ4kqAoXfCmscaitNy7NykkjQkCVqfUTmd1aulA8SKGyu/4rizLujBDtxUa0QM5fk/PnpzMefrkWTxjjwuxR8vLycpLynGw6TYNe433Hrs90VdP159wNgSFbx/dJT7oPUgwJljlF0XJfD4n0wpjDavVivVmzWQ2Ae+DgUOu2e22NG3DO+++y/Pnz/jqq694+PAh09mU1WoVFL4Dxcx6tcKMCi7unbO4WbLbVgnfDXyK68PyHxoK+iFQmjjqAZ/lfWBIvfcB+NYhek8KdZT8KI7PxYAWRZ5KisEalgEU0VrRNA3WmLj+1YDn9J0Ff0pHAEE4SeH9nj59htaashyT51kIv+ocbdNgrMFYQ90Gwdvjg92yEmipuNls+Kf/7L/kf/2/+T/yn3zwAb//3/4L/vx3f5/mq+eYmx1+V+GUCUKDS6HnA0DmpMTGvaPiQjnkAYd8YaL3w9zfQvT0X8jwecjfpn2WwtUeIxmvWw5B2X0+57hX81179ZAfh33lLfSy3KHyNUWv0JF3PN5GunPwUJF7KA8c4+eHfbHOHV2hh8r2W+0/uH547bBfh/04Np7ALdnksM7hu4+NzcvOnbTWhn0Z1jlUMA+jeqXxHHrz9+kJ7n7fYZuPyVPDsRrO1fC+tMbT2KS2pLVyCILfxdt477sUTUF2DgY3dV3j8pIsL3B4qrbhL37+c1rTkmWas7MTRqMCqXOatkU4AwjWmy2rzZamaYPnsFLoaIQqpaQsS9rGMB6PWSyW7Ha7GLJT8cYbb+Cco65rLi8v7xzD1ymuWWFVi88sUmXkKGCGFDnKO5QwZBnIaY63ButapGxRClAeKxTWt8HDQFnGQpBtChCnWLfF2gbvLEKGXM/e5/SJgCJgAV3Eo6CEiTwpAkRUrtxFj3yHk4RoaU7iTQg3aJyjNhYTkxUKHIig4A0exwJnAS/QAgop0EQjL++pNzuerSvy+QQ1Kjg9Pw/e3UBZ5PjplEpn7HY7/vk/+Wfcf/iADz74Nvfu3afIC6qq4s2HD+mNBzVFkWO9oSgyiiJHaUU5LhH5iObeKZNJiZCCXWVY2oaHo4x2POJnn33Bx8+/Rq7X/PDkBI8n1zlCwtLVPDNLPt9ueV7mGKUQ3mKFxTqDkpAjUUIzRTH3igxHLTxb6bn0LVeu4kSXNK7harNg2wQASGvdr/8jtDkVgUB4iSdGGgua5m49CxEM9JxpkQJGRUFZll2EGiUVTRu8403ThjXjFSLSE601m81ugPGEFHrnp3OKTCKlG9CxlJ4kGo45x7PnLzB2kHql8xxxCCVQUiGFiAHBhzTxELcJ+QoFIuAmHUYTjdoY0vfB+h7QmaHhMsTz/4DvH9JkEUEI748Zah+eg8fPPREfSvcpFXnsA7nu8NyQouj6kOo4rFcIknnerbYN7w08n+9AyfTbnnwiBkT2SJuG9ckDpvouZ5SQkHq/XeGefUPgNHYvVabSG3vs2TekMYrPZiR6t89PHPZhmJ7nsL9D/bWXrz6jh5jUne0XYd0ex532ixNqwE/e5t3S3pbmdhSXfToRcSz5ahnapRCnw/amPTjsh4fD2g6V1nf1K11P6+HwzD/KA5J4xrvr2Pv9oB2H7Qx7oUHrcL0xTTBirg3NOOPi/inz8zNalfPl2V/lurlHs3qC2lZMheDdD97j730P/p13TzibllTec727QTaGSZ7x9lhRS8E//LLhP//oivWN4bR2lDOFGCtaV3N9s+FPz6cUxRk/fPAt7ok1z5/9jFK2lOOM6SinzEoKZZC+YjpekWcZGQW77Y4dLT/+q7/FLz76c54/fUxbbzk7mzKfjpFI2tZSVQ3XL54xf/dt/tpv/xaPHz/myePHXF9eBUM/rULq0zyjGI2ZzubdGCsp+MH33ufDD9/h937/X/KHf/ATpoXk4cUJekBD07pPfF4/5vuphPZpav/ZYTsRdX+eQr0dniFFwDuEREmBaVsWyyVffPoxD9//hDfe+y7z+YRSl9FYO0QJMo1BxbDgyVPXC0frW3b1js1u0603KQR5rsFaMi3JWkHjLFpJ5tMpp/MZSgrqusVb26VZlMKhJDgLSkqKvGCWaRarHVVdMYzSOtY/BHONzBom2ZhC32M21VS7/zrwJfm4S30ynTTMZ29SjicgGrZVRmtblstrPtldk+WW8URx/95pSH1rFPO5w5mabVUxnZyhXEa7c1S7FdtVQ1HmrK7XVDsLUqKzkvF0xCdf/A5V1XL/3n3m01PKfIR0sFx9zNMnj9HMgIJcF8A6hOQXmo3ZsdtVLPIVeWuSlVuQz7yPRic95uQHe762ERswht3VMzpyBUx8wfcezMi1YsQYXStEmxhOhxMOqT1SO5becvqWZi1ayAQ0N2zcDVY4jPdYX1DqEVKv0dKjEXjb0rTXgT8QICTkKvK8BurG4bIJurzHrHibUoy5vvkFl4uvuVlsWFzC9aeK6oVFAVK2eCsQVuKFxWeSxdZxeVWzXlS88WiKcW08X8MYeeuYTkZMJiOqa481Bp0p8jzHmYYs011UwWRI2I8jXcrjsswZjcZMpzNGoxG73WZPZhYi0cWDc0f0dXUYBYN7PVEbE1LkLExLLQ0nomCrHM8wVC5HCUHmJYVQ5F4iXcAl5XzMVM8wTiK8RZgW6WGe58yFJqXbyZXG4skzReYUNlOsCsXWe+55AW2NWa+orq9ZrpZcX18jTENuFUWeM5pOuTg9CREwjaHMM+bTCbPZjOl0itaak5MTTuYzJmWOdUHXtlgtaU2NlPDw4X3KImNcFnENO4SrWS8alk9uqK3B54qilShRI5SOc7HPwwyV0t05Rhp70UHFXf5s39PEEEkoyVvxCR8jDCVjyu7eW7N5lI9JdG2oI91/0HPHMT24g8D/JoZT+LDGMTjRYgWdEjtkQ/ddvUG+dAjvo/IcROThvSdGGxMxYroN/yKf7+RgvHyqVyJQyBhqHn/cgfmwvLZiPCliYB/kSMriodL8EGjpQKx47xDs22dS6EKol2XJixcv+Prrr/nud78L9AroY8BLX/aBlruEmHT9rnuFFNgIxqbw70qpTjHuvUfJEBZiyJwN+9cBeK73mA57I42f48H9hzx78pjr51/w4vkL2ralLIuYYz1YVIU8p7IjWD6OVVmWe2MdxsfdBma7zZjeGz4fDlsgdImxFOkREEEhLgTstuHwTgYG1jl0N6ZB6aeiB1SaY2ODNZu1dk+I6jn58J9OsOgIyD7DHPp6xKPqlcDw4AQ9em34Vxyp8Pbz3h/ee6wR++vuuDLu5aW7P3GDgzAaPZESXbgiJRUGe6SOVxO0vqT+Dvt9WygctqP/fKsH3fU0wx7/irE4NgfDS7ev7wtLh4xz9N4cPHIICKT77lonad/cbrI48mlQm0jqTd8BtAnsdzHH+B5onPqSxsfH/euD8sk5R5bnCBmAsKYJ1n4p97CIgunQhOLY2ns9ZfkvX8JY+e7zsbJ/TuyP7es1byDI04Net6/vvfWgnf7g2uuPy6GSAfaZjAAc9+/0PljFdjlyfQglncdjeB9YS4Dl/vt6+i86xlcKgQGKosAYQ+Yz4pLpQb69MyGGpR2uh1v7KTDWfnDWTiYT1usNo9EIIcSeUiVWQtpozhm8l5ydnaAzRVOH80OKYL13uP4SmBFfzl37MI1T/8L+rBr+fvf66WlbGp9uvl7n9XGhhtM8APiBngWr+HBLmqd4nnZeRkEAXK83jMoCj2XRNjRNRVXvAMH5+Tkqy0AIjDVcXr3g7DyEVv/6q685PTvl/Pycm5sbWmMQRKthpbDGsFqtubi44IW7oq5qvA9Gbelsl1pGoSmwpC4aLbpEMbzrhihZcSspyfOCLNfsthWtNb1XJoneDHmHdFa5xLNHgMHTrTSRGPo+t/OolDF8axMs7EUQOJRUCEWnNLfWRgO7kHPW+xCyPtDDlhDOPHglBqMxi/UxHHpsjyeE1XJaUzjFJz//Gf/X/+z/zLd/8NcYnY9468ffZXvvHlc//4z6ZoXZWTAhL7bwgDFdCFgBIVQbqjMMOVyviRZI2Ssvev4zCaNhToTYP2eH50PwrFADQUp0a28Ixu+/n25B+7iGBYnm7gNPL1M6HtK2QwVM4neHfHUy7Ayfe4VnUjp0OcCP1L03fgdyxWGbDt9963v8La3ZofKjb+s+WP8y2WEIJh/y4IeyzaGCOv2uVDD+GMoMSb5ISq5j4z9UDh9rz13K4m4sD3i4w/pSKoxOfrnjTLxrnIZ1DvOCD0vq+3AfHCrFh++4Kwf7sXWaFCkxTWFn5OVcCEfY5jlWSRprES7s6bo1PHl2ydn5KXmeUzcWIYJCOxgHCMrRCCkUrbNIGeTCJPcKgtdOlmVcX19zfn5OnuVkRRnOPZ0xPz07Oo6vWz5fPIN6jSa0WeVj5vMTfC7JhEEIi/CW0aogyyS5zJHWI51D+qCctD70G+NoG0/TGIzf4mSF1w2oBuFTn2zPud9xnr4WHyl62U4QZW3fbUVUPBe3VciBaJynVQKnJTsXUk8EDwBFJjMQmnVdU5QF773zLqPRnNUXNzgnWS3X/MVffIRXiv/6H/5XjM5O+fUf/QjmJ2y3O+rWMCqusNbx9KuvuXr2Aghr/vGXX3Lv3j0uLi44PT3FecPzFy9AOHQmwTqqqsbWNcp49LqivV7jVhViek5zs6F9uuCs0lww4dJu+ePNJa7MyLXCeYMRAjW/x59tt3xqKnZSoFWGlxKkjKeyReMZkVEKTe6h1rDG8sK3XPmGd/ITdAaNdRgXjNCzl6SnOLZHB1e7vZf2fdsavAetNOVoRJZlZFlBkYc9UFcb2qrGtm0MOQ82pgqSUodQ6SKk1NNak+c5JyfzqGg2IAKwK0TAUKy1NN7TVA0vHn+Bcp5REYwTUjhRnGEynlBoTYiqn+hqwhEOwT/6dTYIjR4P207WCriJ7PjkTlES5bUge0XAUNk7aW8/miBvsQFi71wPJEp23jmHiqNhUZGXGTK1R88l1TsdcHAu921I8tLx0oOznY76pf318Xw/dr4Mz1gtVdemw3N3yH9YBte6OTrW3ttGZcP2eR/mPg2l9z3QGrimEJo5GP7e5mmGfEVX7zDv9pDnObjPHRn7u3iXY21P14QI0oW7NY+3SyYH2AH9PHQScuIdhDtYr/16GMpBNgWTesk7w1K6m/6nsdRaHh2H22vg7tQve/e6fblzyCMM33M7imeSrwfzICX74Qdu9zncW8b1a6P3r8U1NeXsHidv/4jije/xaTXjp22JrL7m3ZOC73445cfvzvit93Pu52PKbByUypliXJxSskWUORvh+NmLBf+PP1+y+XQHrNn4DY0ZIRuPk1NYeX5+ueM733qT8f0TzvMFrvmYMWecnCuy3GMby3VtefTOA8oRvDE+481HI/R8xX/x5z/jt3/4HX7849/kqy9O+fLzTzmbT3j/3Xd48fySxc2SXGvmsxlNvUFn8OEH73D/4oSnj5/w/PlzilHJ/PQ0YOMeWhsiwUFIp/r973+IlJbnz77iN37jB4yFAaHxMt/ji9MY7/HKzt/6fW+eUslUJ7OKeF7dkkV8CGFshcLYkNJD4CnKklXl8E6z3RqUqnBZwMvP5ifgPdVux26zQRDwjjzLaJyhamqWqxWb9TKsoSg7TcoS24b12NaGbDpjPB5zenqKEILdboNt2mDwLIKDjJCeXGchIkvTsN1usVNNlqmQe7srkrzMMMLiah8NGiVPrz5lsf6U+eyEyWRGrucopdludxTFDFAY22Bdiobgub6CoqxDdBZf8POPvuCdN7/FfPQGozJntbqk1I+YjT3b5U95+uSG1lh0ppjOR7z16D6L1ZLtxvHs6Yq33vxNxqMzxkVJkU2Yjs65OL3HT//s/8ny6hLf5oBGqWDIYIzFeY9pbfSMtzSNwe0qtDOIiEkopYKxNFEOIcj91jqMGtP4oOC1NP0wCfjw3RHCCSQ5TgSvW5kUakbiLAilkVpzJgV8KjiRAqkcUj3E0YJwoMDLhrMP3mE6K9llDWsWtP45iBfUbosRBkeIDoQF53PevPgfkI8+xIiS9fojPn3xO1xf1TQ7zWaRc/m54+m/tjRLGI2gbQxb6ymFpvU3WJmxbQXXq2uurz/n3ffeZNcMHbGCHDU9nTKfz3hxtaRpDTrPyLKMXbPrnU6dHTisJCIGVdtQNYGvy7Lea5w41oJ9+f+IiuhWCWfMwKAeOoMSi2ftDTORs3JbrlzNEs2UjBxBIRRSZF3++fn0hHM952pbQWuYKMWZVrwjJ0xKzaJpeVHVtC3U9YY8zxjJnLEwKOlZbCqsDkbPfpSRnU+59+ghM5+hShHykxcFs7M5J5Mxb75xj93u3c4gW2vNaDTqUhUGh1N49uQJWufUbYuUgjIvEDLkei8Lias96+WCy2dfsFm84PzsEWfn98nGLbpdolXAKC3++CB2E7VnZoZ3if757mRUhPNKSAlSgQ80xVkfnKejkUyaP8GBo0biC+46tof4zwC7SYvodcS9we24mH7QuSCnGK+RvveXF14OfOeDs5aQacUDUncwb+AGYxpSGfC7gFcGnj5EgCNijRDyr0dHLe/Ay9dOYfzainFr7V74vgTiQA94pX9D5ngIECVQf3jYHXqBJIWrUorZbMZ6vWa73TKdTrv7DxkeY5JVO2kEbzE3CXDKulzYx71jupDnMUT48LchA+a9D/m/D4DQWwyg83vPQVC4p3Bjb731Fv/id/4hdVXx/PkLpBCcnJwAUTEihuOUCJGgLMp+nEXf/WN5BY+BR4elu54WVhJuosLCOYdWmqvrK4zpjQNSGCprXWAcXQhbmGUZQkicCwJyyIeSMPN9IS++9lirjnwXR757erK8X6ff+/3w+W9S9p8Vgs6Dt1d+De+5DZy+TMi4643Jy88PX3WkZx3gLMXe9WFbhkV0bR5eHz53+Peu60NB++Xjm5Qn4f3H7xsK8cebLjgWLu/Wu45c718pugPn+D2H4/Ly0sEx3fAkaRyGDjQduBI5a2MsZRmFABG9CGN9txSVg89D5lnGz9ZailIhBvvhG51hRwCL9Ps3LftjyCtaMgQb7qrr6Fv25jBgXYe075vv9Ze9767y6jEKB7jzvWVsCHcec2SJMOP9UPiuIWIgzA9emO5CiORpp5hMJqzWG0bTUWRw6JhWJUP4LmuCYC/VwBPkji72zQmrcTKZ8PTpU+BeuP0l54oHnLeMJ2PGoxFtsyIp8u5SvPVlD8E6fu0V5XDMvO/pzxCEHIJBqfq9/XfQhm6PxDmTQg684F3XvyCgx/NTEL2rRRQSDZutZTIuo5eYJCvymNtUEDyjgteYtYblcsF0MuG9997j008/Zblc8uD+A05OTmIYqDq2C5y1LBYLLi4u+OLzL2malrYNwIBSirzIgzc1Fiki7XAhN7dzHpKxDlCWBfcf3mc8Hge+yXmePX/GzfVNHBo/HJiBzZbsJiGacfTAxfDc8v3e8S60X2uFIKdt28hfyqgM9tg4rtbZkNdUaRDBc8XYFucdcuCl1s27d12Ujo43FIG3ks7inGCzWrFZrvjpH/23CBks+fNizOzX3mX59Quax2BWS5T1+KohV3nwlBOgRKDzwqY9eQj4DRbX4Lch+BPWYrD0Pabc7IGfuLj9vgfu/vtC7tXhWuzq88EEQg6EtEPFaFIK3JWjetieb1JuKbtf8vyhYvQuZU/ixZMskhSuQ55dJgVEVIq8CpwelmOK++GzHYA9iJQxbO8xWpfaNDQSGK6J4bzeVm7sj9EtpcxLzu/hu+5Snh+fk9vvHsp5qT/HyrC+YVSxYRmm3xr24XB939W+/d9u86uuo28hb6aajpBZgYvt1irkA66qiu22pqpabDQ0bWPOZHyI8iWUp4ghpUX0hAptlAjhGI3KGLKwocgLpArGMmVZ8vbbbx8do9ctuXds8ayNxxnNSJyQtycsNjtKZSm1oMw1KmvQ2iMxCG+RhNQROEGwstdYoPUSpKV1a1q7Q1qHcDJ4zigPRqL8kKMEkwAcEei9EGB8CH8pYujmzgDWRwaY8JtEUAtQBAW9jGBRmzuyagvbNdvdikW9YlvnLJY6eOkpHxQ60qIVnJYF9XpJVdfsmhYB3H//EToreXp9TeOgNY4GwcgJysmU+fQE58IcT09OCd7JwfCraWpcBd4pTAvVrmWT7fBe8OzJJQJJsw0n2Wa9wTeOefkV8osvGFUt0+kEcaYRpw94aluu2dJkllE5pm0b7o9HKB2MF1shGPuMT6j4wjRINCc6Q2c5UmnazRYcaAQ5kAlBA5RtxvPCsdQtwnvOfcZftBWVACF9oOdO46MHhfd9jsLbsqgHaRgaWSevbg9YadmZLcY2ZCpjfnKBpUQWE5z0eFfRmi1tu6UxFlFkGBxNU9NUluk4w9gd1rVoOaLQY8a5Yl5avDFYJI4CrzzOVggHmcpojePp5YIvn1zjvedsOmM2HqFVCBsvlaTMFHmmBvJ3NCpL9GdAIw7pSlIUHhYhen8akfiDWzKYiHWmyvYvyT3Zo5dzGd6eaLmUPWRwq0Vyj3ndx0qGssDgnvRXHfIaka/Ya7K/5Qx8TMkYzolXe9d44ffGKXLYA77a450P+sdAHOBwdMRwDo7wM0M2M/43oW5SiH486XMOB15qoKBGHBgHh/eGNTJolxhejnx+lKVcmteBfJs+drxAd539z8OKB8LGMb6iv9YNQj/HYtim8LsQAhfXiU/4Q2yLkN3K7vpx1x6Qg7pBdJhjt8f20vf0e+WQ1zk8r8UgN3Sf9rHvZ8od7ZzYa484mJMhBpZwyU6e6G7a71Pof19Xdz7F252PuUeVR3lDGfeM9QIT14xwliZGqVAOROvJvKHF0haPWJfv8qU74xfC8J3Jih++e85feTDjw4spD09HzEc5Yz3GS0GLpbENOnOMlCaTmi9WNX/4dMvvfXmF1zOyxROKac790xEnc8Wf3FRY5ckrwXI14nGWMb/3HdrtNcpuEGOH1x5ROE7PM0bnI7LxGCsbRqMrfuv7ght1xs8//inf+ta3+dFv/Cbf/+Gv8fTxYxabBT7LGZ3MKaYWJSS6yNhUNUuzYjwZ873f+g0erSs++ewz5hcPGBUF0hna3TKmRQGlMyYnb9G2Oz788F3G5QicBheMcNMc97lzZUczTUwxlooUAhXlajGQU5xzkDwvRU+he145nAkhqlgNXmEbgfEKspLx2Rk/evCIs4t7PHjwkExl1LuKtrE0u5oMgRAWJ0Lo87YS+MYGpeG2pRDgCgkV3VqzTiKw4AxlEQwlsyLHeouxlp1pcMYghUdLgVYCrMV4h1VBVPbO43YtQqoOWw/r3bHZfc5q9zVVW2GtRPgCbxtyPWKcnzPWFyg5ZidW5KVFZY663bLeXnK9+JrF1RVv3HufYj7j6vpLnj3/mnzyFCsLHj18j+lkhNAeTMHWX7JerMELVJZRO8fVasHV+gpdfsCucayurvny8Qs+fPaC+dv3aGXFdDLh0fk7qPyvorOCyckI1wjWS9g1huVmw/XlllE+xyPReUEjDRPt0UbinMB4gZdgnA/GkcaFiAda44xnU7VUmwoQ6HJMLjMQL7o144XACo+XLon2kUqkMxeENJFnTXRMItAQFeqIGGqdKZuPPJVu8Hicn6LEBMebaBrKkwlnb+QYalTuaU2NcR+wbBsW649Zrv4cVINdeNpVS30lqR4rVpUPodlNixWexnssDufzEFreeKqm4clNzQ/bCkEeIiQIR7AMDfqU+SynzD2t8SiVURQjdrsV4FFKYC3sdlsm45MBQfQIHG2zpW2nKKGYjCbMpidk8gltW0fHqkCjlfCYqGjUSuO8x0Kn7xIDIu4JZ2Pw5iV4UHuBE55Pgb8iYKM8Kw+XTnDPQwtMrWCK4zmGRgra55fcnClaAWMJ96zgBzJHFIaZsYx1QTHL+aq+4Z4c4VzJzns8mrdEydhtuJI1tbeIbUVZNRQfvIHSM6TfsvMGoXNG4xOKPKNtW3a01NU2pE0QgrNzxddffYX3Hp1lSCX54z/+Y7797e+SZTnWBsOC8/MzlFIslg3bzZrNakm723J+Omcy//8S91+9lmx5Yif2WybcNseku5nXlu3u6mb3DI3YIimIAxBjOAIkCJgHPeib6E0fQl9BDwIGI4iABpp50Igih0Mjdje7WOyuulXX5b1pj9k2zDJ6WGtFxI69z8m81S0oEnnO2Tsilv2vvzc5y0WJk4Ku1uRliZcOHSP/E91KtNp7EdcwfFY2rGf4PgTFIkRIlz7iM4TTaKCTCi+CkVzYDiscTuUUSqLlqHBVIpFixPoDwntk1Ed7KbAqpH3Pver79KSX3q3zEULgfAjYkD5Ef3sfTNTeg7cdQgS4NvFwCrLEYUd6reKoRVwyj/MhECjYJ8NQnHchTbp3IELkuO9bGvhAPIS43Pv1Pen6XhHjyfANxHrgDV3X9cZmGAtfh4qMXhk5UW5MDYdZlvUpFlO/SfGUDObvUmb1fY2useHnPqXQOHpBxTam6RWTZ7XSGqxhqtQZz2eawDF5LFtrefr0KT//s3/Nq+9+zdXVNU1do5SiqipWmw15qZEqKG60UHEcAucs1Sx4tmRZ1jPAY0Vz+u60wWuiTBuLKT2zKUjegCGiRfZp1P0oraFUckgN7YPjQVifcIiUUrRtFz2SBnHiWERNgpw/+Hy4R8djHwSppAA4BRvvOszvd+Dvf80f/B7D2Sll4PfrJB2dpNg/kJUZO6nomHp2fPUCxdEQpuuVPh8rF9Pap7Ue2rxv3Y6VundFH73/FccofD/y76mfJ8zjHe2fXIt7rrvaSwSHCAfx6xRdEdIcB2/JlFo9tDfgUDEaRzhzIZWxinUzk2EutS1jrZnvC9Z/HUbx0dvvfmIkYIfP73pjPKG7Hr4LB7zP9W5YHs7joRB/l+EmHdiEupwNEa54ENE56m5QDAqOpHg/wtsiRuqKAE9VVXK7Wh3QgeHvgDv6lNjpe3HqxKd2R4jGe8qyDBHvkxTAB/P3Ho8LqWy8QOuMyweXrNZbjLFolaLj797v6dn8q2KM1OZQ9zHRmZERanio36vwy4faPWI03/52UhgRI9ru7L3/nyKCB6OYJMsVjx895urmejDiRdumkBnWWNbrDVVV8aMf/Yhvnn/DV199ydnZOYvlgvl8FuuKBu/4qppzc33Lar2JnqQholjrYMwoiwKdZXSxlpInCOcIEWquyuCFvFgucNaxWt8glaZpGvI862EyrZuUQbmU0nd5YhRshKODsxH5ix6neXo4c6k2EgFuQkSxwVlDz6UIETMPxTrrBKHReYvwwVs6KTRTf8l/zYvYrydE6CUGXMK+adjVOxa5IjkGWrumERt4mLGYfUb98ob2+gZJjW8bhAfpHR5Lqs94CHMTQBaCw6iYFBkx4hlwvcIRhiiY4czF6LGQ/LNXAECAv6Dc9JEuJ4P7aGxiyOYjODSUnkpVPp3H9zeGD+P7PtcB/8Tp9PTv7vswiuR9rqn8MuXn4VgeOBqvHxwLTjlBTJ0VxntwqmTUXfM95RQxXafgNDz0MR7HX+Uat3dKxpj2M4bng30ZzWV8f7pu913vmku/LgK6zjDXGlmVoRQFIGXQUGrrcUicA+MhyzTFLMeajiSmSyHQWqJ18NgfFPPJ2cFT1w273RbTWebVGV6AsZ6sqN5vce+4uqbFOoUQJZmeU+SLmPLThvTkItS7zKRFYZF0CNEhCJE3IYtLBl6hEGjRUbAmlzUKE6K2rMBLiZMuRC+P+P4RSzFRSCdaMPBeYzluvINiZPfrlRtSBMWMCwZd6yxdV7OvFQjY25pdt6OxNVUh+dGjx7Dd8ur1FVc3K2zruDx/yKMnlzx+UrFrO95e3/Dw0RPq/Y4vv/yKZ0+f8ejRYz549gHnDy6p64auMxhjaJqG/X7PxeKSsgyZUQJJCviwbVuub65om47NdofKSuoXHZffveRyu0dJRV7myAeXiBy8Ncw8zPOKtffoQpLlOV4IjIOmc2yFxfmQtlWLEKXcmbanmxqJJkSQWxwZkr0ztNJR6FBP86a5xdiQlFCqZFyy/frfhzsGSWwwWKUz4nxwNLPOorVC6yzUMkyl8ZylbevooGYoyjxEtzhDyJxg+owvqYzPYjajLEOdducjHRRhv6UI0Z27uuXt9TX7uiGTgsWsYjmfoaSkNQqkpMgVRaZiJr4JXpvgoilffhePPuZzD3jayXNE6B4/cwoPAn2polHn/ekYajh6ghPDwYjoFfcifU70OjLr8UyJ/o10tg5LKN017yENeXxbDKf0LsP4FA/3tLBPpz2M6JRxNBjGDu9N2+u/T+MZjSvOZODNY1iRHPM247nGvqSYjumw78C7hhf69ejHNFofEQUDMTa09k+SDLnBGDvaB9I7h1dAfcN7/dql58VBC/0zh7AQPxMSrY7Xe0rv76Kn77o/Xrv7dKdpLU/tvZ+0M+1neP7wu1OwMuaRTs1jivNOtXO8BsHhxVpDisbzXoILZQeEb2hEhcKjXIdzHVoJVm3Oq+6SVz5nZw0/u6j4weUDfnQx44OFZjlTSAk3taFRHVUedNutbTHSsagyLJ7vtpbf3Bh2e48sDfbtlgu55Em1oKwKfPeKv/87H7OsNNLe8N1KcfHgAbPFR1yo7/C5wGmBUI6smOEkGFtgvadQ8Oy84G//cMY//4sd25trzooZZ4sl11qxtZZ5VeKqMspfEu8sznUgNULnzM/O+env/xGPP3jK7ds3uKbBOQPS0ju+JfyL5/LigizLI69B4AtEyoTlRs6mCqV0DyPexZJdLuhHlBD04g4gvQcvkUpG6fEw+4Fz0THGOtoWlCwoF3PKasni/AGPn37MB88+ojMupFQucopLSds6Xr98Td3s6IzBCxdonZLs2w5rG1o6RKZYVJewEr0ca10sd+oUeSbI8hypFd5ZTNfguwZ84KWEFyHzrwy16lvTYRuQdY0XGeipbOEp8we0rcDaFVpCpubkskS4kjyTOL/HtHvq5pbG1MxVTp4VzKuz4HRmJWU+p/aSpjOs1jVFDdLN+O71NQaPUp79ribTNd998xV13bBZ71itt5R5zsXynIUoOFsW3HjJ2+trFJrl/BO2tkY4gW3nSL/g0cNP+PL5v8K2HaZzOGPQUnBxtsQZTd22dK2h7eBRtcBlHfu9x1iHlzJEQStDVQaew3lomo6mNUidkxWeiwuJEOpQbyXiQRYpQCE5yg2czqD3DfTK9w6EgS70t5wk14Zoyhv0Dl7hKGmuc65XGV5k5EXG9c013739M3b7NcbuQHTk+QX7bYM1Emk0DxtN8dhhzkOqfa0CD5OCE5q24eqmDc4AwrGv9wiZExRLwxy8h6rMybRCMsh2LtVUjvTHmI7BfSzOOOofu7YlU4IiL5lVc3SW0bZtDGYUfbrqMa6WAlw0bh7w82M+Y/w9AhysMDipUULihWeFQRAyApRSU3qF9obOe7a3K6SssLkmkwqkJnOCq3qP0gXnmeA8z7n1GuM9xhkcoIUk1yVetiihKFE0qxq+e4ta79jXNfX+Bi89eV7RmZxrteXt27dcX1+z3+97veanneH2dsVqtUJpxdnFBZ2xbLZbqsqHMs3e0zQdVaXxSFbrDavrGzLpmS0eYp2nrlu8NJAFbr6zHZnIR3xlciwfVk/h8H5MzRNgy6QqG/iQ0WoH3l0hpYo4U/QatvfRe/ih8f6/FHKUCSf8fx+VQZrTIP0NfFg6okFWDHo7z9hJlJEMmXQ/w9kNeqvh4aTHFtFJO+DOIbN2f54ZeLbj4LnT1/eqMT5OcZfqhwdlaX6SET9OZTPcv4vxGd/PsozZbHYyxeHBJLRmLCaIkfQ9MOYp3Zc92Ub6bpziT0zeSeNSEanpTIM8jBaZMn4plfogNAUhTKkQ4fen/9Of46zj1avXOO+4PL/EE7ze6jrUtdRKUeicLM9x1qJURp5l0Tt2pGgWd6/RsXF2AnwHVAYgRagngPNsNhv2dR0is8SgyEvzbyJyzbQOTgMEj/z0P5XYPXnChH+vg3f6Gh/D+6533R+3dfe7vewlBsX/sLbDQk4FhPdR8qUR+KNvBiQzSlrbt58Q9pFX9NEc/D2fT33/2ytQp28eCCsHM3jPq1++CQn+LWDnfqPc95t7Iiy94qL3rOoBJQS5JwGAROCCN731LtS9I91PGsjEDEVfsniAtAopl7IsVtlzh7VC+1fF3Ts8nUF459AocN/1vrB83/uHfXxfWDz1/KnP33ec77dicAqnTscRmQpPv68p80pUiwRFZq8IGeBlaOnQ+DW+Pxi8g8NYWZajchViYBpcUEzJEcyhBmaZGJEbRnx4Lsc4RiB6h7iyLONQjvcxGRZd4Na5vLzgm6+/xYlk3EtKED/QrgN6NOn8t9rHU1cSjIaDMeYPRIwq9H1KnhOQIMY3fD9fKVM2HNfT5bQ+ac2TEwOx/bZrKYsC8CFqzVnarkV5jVQKISRCekQW2MimaTDG8Mknn/DyxQvevHnLdruhKAryPEScSyl58eIlN1e3hNTacU99qHOO6OhUqBUnRUFDQ6E1VVmRFzkIj1QiOORpRZ7lQEi9dXt7S9cZsix4cZNgJ87R2aHefFiLwWHubrziI27sl6Vft6SYlYJQl8iqmEI9podXrj9ifXImn5xQhjPoUnZ4EVBzMKcLpFQIkSG1AiVo2oaZm/d1nJRSWO9Q0uDnO9TTOaXOceoG1ht0KxC2DfP1HjOC3yRMk/72Y1hKswzfDPxtjJwQvo9MC5GoY14iLEgy8I+PRXB0CUKsnyh6e4HAxzxV3h2+d+Lv6TV97v14moE2v+87R/d9LxEdXYnnHpdZgsO06N77kKlD9OqPu0c7khVO1SpPbZ9K9z1+pjccxOfGBuupE8J4vuMI+O+9Thzv37he+F3G6Pvev6/v8ZmeGouAgzWatj1OH++979O3jx2f71LiT787dAY4fkYpFdLRejCmo+068oirhJQx8luSlyWC4GSqhEBqhY48lowplZUIRkjvQ+SllLEGesxIFsqMhLrjSmZYa+m6rndQ+KtcnXF4cjI9J8+WzPKSTHkyBaXWFJkk16CFRfmWYBQP/72zIToOhRAaiSenpZRrZrohl5bae5yTBOYgpLseeIlk5DiEo/53//f9/FPQsxxxuhAVRr1E6i2ma2lsx9V+xdXuhtV+xawI6RXnxnF7dcWLF2/AKbraszx/ysXjJ+i25Xaz59Gjx7x+/YJXL18GHlpAXmSURYUQoRRZKgXXti2Xy4vwTKbJ8yIoxs7m1HVN07ZY12Bdh1MV+3qLrxu8CeXOrHUUukBKg7CemYPHKkMWGTcZ6FySo8isx3WGZaaZu4YmOqQppWiNCVGpIkSH6F79H/DW3lush5nMsLlie1sHmqt0kPvEoX5jet4P9iDRBaYGtJBBJmXYk1IiVUiHnulo2Glb2pjRxVqDEDmIUDYjy3SvZAy0K9Ch5dmcsqoGvsDTO/MLIZBK0XYdV9c3OOfIS81iMWM5nyHxtEZiHFTzkiLXKKmCEjHh0GFKkVyMPtxz9TgoBiwkGXtMb6YG2zHeHqfRHhsCA/82GhSDk1q/3inX98EYk8MeIQoY+mjLnnoJMaQ5HzY0OsWN+zzFnxPS+o7n1fMKjI6uiHLJCK8npji96wN0epHO/bg9Qc/h+yFidNzG0FPsX4ihPveYf+nHNjbBy543Cqjdj2fd93lQgiPBybhvIaMN5fS4xvMV/rRht78/4g+m99I1GO5FjF6821Hg1Hd3PT92uJwahcftTfWDd83nrrlN+bepM8i4vXTPTeHvjjlMDePT30M/x0r6ob1El9LfIgbpjNsevYdHCo9CULucToaSodLFEiQ4rNBIXyKsRTpQwrJB8/nujOd+DnnG44XgP3oy58OLBZe5IlMWZwyN9Gw6TynhIQKFxbaGnXcstcCg+Xrd8uVNB1ZxeWG5fVGTuzkzFMtC89FS8Z//7lOWsubXb6+4aTsafcnjhx+z0C2tgE4QDNWywdDRoVAOtNDMdcEPHs34i28s9fqGt0rjnYvynUIIHxyRdYHUJc52bFa3WC+wKDyaR48eo4XkF6s3rFYr2mZP6w3jpBLWNljborJQEiuVUQpnNND0IKP0b+BsoH9uLI9EnKKV7nmFQC/AO8ugTfGR7oRMsy4+pLKMKl+SlRXV/Izl4ozFbMm8LClEMMRcv3nLCsflvETJHF/v6TYbOtPghUMXOWjPvrEY2YRoxSzj/PwS9Vyl8E48FqkzrIFMa7IiR+DpuhbXNnjbIj0orYJx0FosgT52XYeTgoogX+/MHu8OTTJFdoYSHUp2kTeZo3yG1jlKG4zfUDcNu/0VddtSlueU+QKtJFJYyrzEmxnr3ZrWGpwTiE5TyBnffvuatzdXZMIjjaCaWb766gW3t1v2m5bcZfz0wx/w8ZOHnC9mgOU2m3OpZywvP2BRPoHOYsyOZg/73YZqltM2AlN7nIFCSzIlyKqc7drQNnuMa7FLSVZqGh2yBlkbZKKmNWTaUkR84LygNS5EARcZv/8Tw9/4HRBY/k/rMacZ8Zo/IcOMadoYAfhkRBeDfJxg6yDjTsT9gERSigZci5SS3Dka27DoVmizD2dJzZBe0mUlIhNIqVFS4x6D8YZMa2TPGwW5ojUln3+xo6kdpbLs93vmi7JPjpool3M+6HuyDCktziVHocT3yD4bsXOHMkewKwW40zInywqqakaW5+zWdVyaE3wPg5w1LYs11e0cvOOgwdDi0SiEsNzS4agATyECT6y9RPmQzWm22+NEhS0krRTUBq5NR+0kIrc8kbBUmhddR0sb5qsEUhV0TlGg6dB06z3NN29ov3vDm6s9+901szJHlYKm2bKn5pvn34SShF3IOO2s4/Hjx6Fmu3eYJsz10aNHKCXJslCyMNjgwmetFUWRMZtXVHnGbL5ke3tF02zIS0mZafCWkC9KgE87mUzAqSgj9MEOsaRe7zSZ9CdRj4cIQUdJsSREcLBQUiGV6rN4+PHL91297nfY597JLXT3nhrx0ZXGFjXKQsC0dGeYi+rXZcrEe+GHqJb43UDmw8EYdMdJVB2fltCeEBIZM5T8tRvGk4CfIrittRRF0SvJldZhQ2Ugus7HFDpSpZVASRkVm6EWtrXJkCx7xtkY2xueZ7MZm82G7XZ7FMEyPbQDSw4qMk4+YotgxA1AJkViXAev3XCg42fv+3qbqU+l1EG0vPehBmBZlCF9WNvFMSXEEAXaKPR6IUDIvoh8Zw2XFxe4ztK1O9arFevVLUIKZvMZzg5MBQKscdS2DTU5nOfx4yXGenRSIo3XIwmckRlJho5jxfQQnXpooPQkE11iRkN6e8X1zS02GvKUVD1Qeh/gw3SWTIca8VpF73LrsDYYbIWN9VhHfae1Gvc/fJ/2t//rHYq7iaZ4BB/D3E8JANM2j4Wew/eHMY73ezyGY13usXB05Lxwakrx3UR0PNE7ZvSwkKOIca3j3gcle1KWHzEHJ3ochInp2Lnzu2GeJ9adAeWPvwm9TJXKSQCatH8w3PGkD9t71zWGod8Czb+XwthHI8+oVyAIcn1dJIISCBHOjJIDg+QTo5YiBkjnl6g/ScwaIELanKQmsCZEdwjh8dahZMrkMCgZTs9gMFzcxRSdUvyPvz8WhkcrINL9JKRKUl316Tq9zzW8ljyQT8Hl+JxP8clw73hPxeT3qXtpHFP4PTHGnkiHgQovgtHVBbo0GGIdXqY5xWdPEfCE570P6d/iuAQBNvJMxagdQn2lsUJPBAWBtXao7wI9Y56Wpj+XwNh4lp6tqor9vmY2m51kklMLKZLDOcfZ2SJGKHd9+lqP6ZVrqf0RVh3RpLhf0y3xx3tydPvUl2GxDmmeiIyaG4ShoOAc6GNa456Z9QO8pwicsijIspzNdovtS4eM6G2cpIt8SGc8xnTkecaLl6949PgRzb4hKzx5HhnUCAdWh3FbZ9nu1jx99hSpJK9evqZrDUVhkUKw3W1pm67HJ2FPk+He4yyYLqz9fD7H2I7HTx6xWCwQIkRJ1m2Nd47FchEZ87Baj588Yrfd0zWG25tVQFMRZ/lY76dneBMcHTC2ASYSg5wU795FWuUc1nZ4D7NZRVVVdK2hrnchZb31mCakL/fOQnQoIvJ6g6PIAACBB4rCRz+uSEBlEKqyTJHHaA7vbDhbcW+VVkFI8i2iaOFJRnHxBPdqTvf2mqyu0U2NwtE4g5VQW4PXIih2jEO5UHPUiRDZkeTtFEWQznEQDgK/nBRF3seQCeERKkUy+sGoEN9N8DocqUFxDKFshxAiRo36PhsSDPj7KB124qMnNHs4M+LgGIZzP7w3nKNDnv2ovNJIuZoMudOo7AM4SmMeCXSkZZ0I5+nZwDvdTcvS/McRzeO/p+OcyiDpmWQ0P2mQEKcj8cfPjdOrT43Z6btxG6eM3amNlHVrqriepnAfyzZj5fYw7kN8OjUEHazxaMzTdPypTNaxMfvYifqU8nzqqHCah/DRL3Goy2YFGOeCH35nkZ1FS0nnLCKWsRBSIDoR6h57QaaDQ5A1DiF1kONwiJgRCwFZVgw1iF2Dc548D8bw7XbDgwePUDoY/Iw1HELD978EGUrM0eqcQs0pZEaGpdKKeZFTZkEhr9giRQe+Azo8Lc6ZWINNIVUWUty5PZXcsSw6qtyxk9AiwWdBVpOG5PSZ1nvs9DTeFxLfF51Up7A/nM3wKUXjJP4z8EaJ5RAoKRDeYY1h33bc7ne8Wd+g15Yfnp8xK+YI57Cdodk31FvL5eMViwcfIIQGIZkvFyj9Aa9fv+bt2zdsNmtevPiOjz76mPliTlnO0DojzzOWywUXyzOMaSnLkqIoIvw+wjnHdrtnu92x3TV02ZxSr3mwXJDlBY3Z0FytmH3wkLYk8N84cuXItGSrOrAd2kNuBaWHR8sl667j5abBC8iLktq3/ToF94SoU4grtsNhBMzJ2SvYdSFiRvY1BwW2O+TJDvagP/MhwsRa2/OGA58eoopMzNKidUGWhf95URCy0nSYruvxSOAzHEJ6yqqgrrd9GRQif/TgYsF8Pmezr3Epy54fzHlCSpqm5erqGoCqqrg4X3I+r8BZ6rph3xkWiwVVEWrWWn+IJ04aE/2AGe4z/p1y7jnAQQK8EHFPJrRTHPI0nkFuvdOAKpJk5yfPBR5JBE3i8XzGep7R54N+hDi4d6KRvqfDv/sfJGp/qt1e4Ir8VqAPx8bgng1La3tqfyZrYvv3ietw+LxP8/bHzm+M2hoboMf9TASNID31tTRPrfewBop3P3N8byI3ph+CPi//3duUYGoY66GuZeAB1Lg01j08TirhNX62p9uxsyPeBmI61EOHvqkMPM0kNr53JGmfaOOUYfz4c6BBd90/pcNw7i5nApA+1CNu8RgRIlTpOrxt8b6l0xl75uQ+pNzWzrCUns9Xjv/bm5ynT8/4u08X/P1nFQ+qGderFdeNC9HDVY7Us5ABxbdYUaClB+VZbzuWRoJQfH674/OrPQrJT55m/PI5bNs9bb3lg7zkP/vdT/lPfvQBsnvFg2rOd1vIioxHD3+E6WpyW6NMi2larNEwAz+Hugu14oWVVKXjkw/O+PybK757+Zzr3Z5PP/2M2ux4+/IFVTXncn7O2eVj5osZv/j5v2fXGqxXtEbwzfNX+HbDfnPD9vY1TbvHVxXotO6glaVxDfUemrYjz4NNACGQMjh2B71+hVKaruu4vbkl6eKzLCPLglN4iKoN/IC1NhqjQlkaP9IDK6XIlMJ1DkkoxTWfn/P4g59RLGdY4RDeUq82/OKXf8G8rPj0B5/xy1/9iptXL6mM48H5A3JdoAi6KedD9LLXBUJktAsPZU5VLTmfXQa+2sSssgqKTNEYi87zEDBoDNZ02K4FG2RxhUSLoDtv2xpvupBttyyYz2fk8yW3b64mco7As2HfPae1azyepn1Dvd8gxY6ZvMA5hXENnWnY11u6rqYoKsAhJSwXc/abLNQ6Nx2ZLijVnFKe83J1w6sX3yGcZVEsefjwnKu3lpff3bCsSn7vJz/gv/iH/ws+OJtTCMF3z19ym2/54SPBVSXY1Nc0TtLUb2l3G77Kr7hYPMVZh7Mh69vZueSbF5bt6prdyrDb7EB5lFrS0bGnxQqB9UFH2naWzkLTOqzvkAg6ofiv/lcdeItPKQSm/KWHIbRI9HzNmH+NS9rjP8egbxW9MO0j0zCWq/yI5hFSEwAIiZYabIPyAk1I8y+swnYenI4Zc0LJBKFCyvgiz6NTfujS2hA9+5MflDz/rqYzDXVdc3YuMb1+TIAPBu9ZWTArMzLV4qxHqxwhFN4TM4lCvdtjTDdaoICfQ+mglrLMyfIQeFqWFZv1zYFMOKzrYB9LsttpnedAR4QQCB/qYbdYauEpw+niNR0doPFkXpD7kEQ7VBiwaMArhdeKnRSsLNwIwZv9nnmW8bTUVC4EedS+Q2lNloXsXU3tyclQSMy2ZvfyDebbV7zY1GhpWJQlGknXddS0NF1HZy0q033W69lywfn5OcWsYr/fc3Z2xuPHj2nbluVy2dtByypklnLO8eFHT8nVRygvwLc8v9kiqHnw6IzzfI41W/JZjm9HNMgHmAuyT4LZwSInIszJlJMnPZP0ydGBMtkIRORBlQzFAMIeHme2O7VvPe2P14FhfMQXTfUMd7XXX/E8yX6O42twNMGnstVxTkk/6wGfMhKlMxAYuJAhLWSO8FEPacRIR+UFod66QhKckoKt5d3lgeB7GMbHgkKafFVVtG0bjOMptZEcFJ6Jwe+jJnqhLHgIjVavx3PTfpRS7Ha7UBtsseDs7Azg4JD2DC9pLVMdchEjE5Ih0QeD7oiJGvPPQgiElCGt2whBjKOi0/cqRm2a6IGGDx4nY6TinAMZPLCFk71i2BnPJx9+wr/8H/97rPG8efOGzoRaZVmmqRvTe4CHPiNDqkJExXyxPBR8xoq2qSBxQh0zVbSlhROCASiBFP3mPXTGsl5v+3vWObTOeoGi7QzOWup9jTt3rNebkBbfQlM3/TAPDKGJEI3uDfuREMH91yAonJjnief9iMbd0SKD5HLXvdRWghPueD6NcXrv9HiPx+z78Y4zGUyfDGfMhpS5SvYEN27ooTB7eoQneh+vg5+8LkjGoDvw4+i50acT63SfsuLw8kejOxzfdA7iAM7Hzx6O5a4J3HfvXdd4LIfeS+lKTjtEYVMpz6EXQNzXZJyM5yHhRCUFWitUqg0c7kYv+VBPow9ISNb6k2B9uCYHdG2MX98143c+M4oivmNtT+/JeN+O35vC5XD/kL4cfvc+1wDf7wujp58bnB5AxBpYQ95tn/j2uPjDLAfnoZ5eMeDPw0gVB0JRlUWIaIvDFwyMVvJEdN6MUvaPz4gMtYz65ZuucxjVfD7n+vqaBw8uD+4FB5z4jov+js4jtCDLM86WS/bbt/1cfZxyL4+kNYh9C9JxEIz0h/et/uTvEy+MeIT0OzFgBwoc0e9++CBCyRAhJEWeY6yj64KhQUofIqidQ2ea84szrLM0TYsxJqZGnWLW4NigpWa+mKMzzfXNDZvdHtN16L1mNptRVTO2dY21hrOzJVJLcIGf2uy2PHj4ECk03337Hc2+jd7AoexJYmdThm/nzVH06Hwxp2721M2eywfnvQIu0xnXV1fM5vOedgTYg9l8xuUDF0qq+GHv+311IwM1IFQ0HEWGVvQwF2iDFBKZKbquDXXCY0aF9bpjt9v2hicZ+csgP8ToYGtRQo83s1fuHX7n0k73+s+UKkxrTZ7nFHmoH2VdSE0b0tn7oABRsodtkXla2fHgZ8/Yfl3Cm1vEZoPb7ciMwNkOLTVOjozGiZUTHk8wvA/4xfV4X3iBiiVzvBPB+I2MBi1B8hhOHrhhyUfCaIJrH9ZoUAwOdFCIZLicHI0TArEdGadPK7aPcWwq65HamF4njRcnlKxHhrUpPpq0dYoPOTDckPb+EKeODd93jWna//T5sULhvjmfMvaeGjMMTrnjSPhkUO4jZEb7MzZ+31Wz+9S4TmXjmiqXpzLEXXs4HsspJcvUGD4e55i/Hc/llJPB9O8xvgExOJ+HjzgfymsDCOfxnUUhsFJhnEXEFNDB2hLSejs34IukTBJCUBRBtiyKAiEk52fnNE2Dta5fe2M6bm6u+eDJMzwhWkh0EtONFFW/xZXpBZ4LcnnOXJcscrioLJdVTpVppHDgTbDzxEiv4KQO1kaFYsqSIR1eQ5m3LGYN5axG5g4vUz3DgGcOaGPE81NnjD4zwFi2u+fqDYMiRZMFPBjwb9ANWGup5mcs5ueUZ0uK5Qx9XXB79RolSx4+eMJiecnZwyf8+ldfsd/Di5ev+erFK7xWiExwvXqDxHF+cY7pDPv9nm+/fc6rV6/QOuPi8oLl8ozF4oyLiwu0kGw2ay4uztE6KDXzPI9jllTVjMcyg+ocsf2KcykxnWG3a8mMxDeGK9+wMy3eNXjRsZKeG2vJgyoQ5SXnouCz6pxf25s+FWs1r9huOxweRzSsAzouUItipyReCkqveFGvMMKjCI63KNHD+HR/xlfKyhDO1iEeDY63KuLwkG52NpuT5wV5WaC0pu2amE7d9GX0hPdYE6wwWaXYbFqscWgdsivoDM7Pqz4bRIIhYVOGM0FTt1zfrnj59i1IgcoUZVFQ5lkIDBAu1DzXmrwskFId4vzIKx7IuhPcPzw/XRvR12E8oHORXozx2JRu+PTdKMIGGJxPJ++Nz4BIupYRLQ8MzmF6yQO66ydf3UVTTtLrw8uP5YrR36Eb0fPBU+P44d8x8GOkXB3Y9r6BXrV5MMR+OuLonvd3cvEkp4rg2HGwscP98Rj6YR/m2kume+FlYhxHU+sXuB+b4fCZocPh+yPD7B3nUCBC6YpTcxs/18OVGHVzihbaE99NO03SIH2t2OmY7+PdpnjliBsc8UVHNPq+cTFi2e8c+ri341JeY11t+jyNYD85NkdYF63wtkW0W5Aer8BKiW06XHeD8J7C7HjRwn/TPuRfq9/jP/3Dh/yXP674aCnoWsOL1zesFFTC8Gx+xsOHl1xenFPvG7wVFHmGkoK8yNj5lhz49282fP7tDW/fbNCy4AfVgic//Sn/09fX1MryqHCcLxVff/sLlOjQDh4rwWr7DT/ftHz5zW/4qBA8XpScz3POpeKDrOPxpWNvJdtmxsosOMuX/OTxnvp2y/OrlnbXoVyBpgSrqLc1r80rrlYbfvTjH/DBs6fMNmfk5ZyLB4/pnOTzX33JV18/R3RrlA4ZvJQMKeeLPOcf/y//Ibt6z+3Nnq7rkBhylaFVhhCwXoc6yOfnZ+R5wdvXb/nov/+/h31TEqV0MF6M9tD7wWE9fHb85h/8Qy4eXiKEiNlqJftdi/chMKis5iwffIbH8ef//k/47vmXXL1+werqiq3SVFzzuNQsLyTrV29488XX1DdrSqkRTuCMw0SHyCyfYc8vkcszyvNz1Mb0fKzWGU8efsB+tSbLJaKah4xExtIah42ZxJAxHCzRDGtwpqOta9quQxYlHy7PWFQz6v1+dAg8+33DYvaUrHuAtQolKp6cZ+x232CbPXleMX+Yc3H+hNfXX7K6fcvrV9/RdFuc3/LgwSXNds5us4bO4DvLt7dvWRYZT/KHbBpPTUhVPS9nNG3JyxdrPv6jj/nbf/i3+MnHn/L6y8+xDrRR+L3g1du3vJ6tKJ49QooHPHn4lMtFxjK/pFAXdOaf0TQhS1HTdbTW0XYG07S41oKCdtfwxeY7br+7puwchZAUWQ4iQ2UluqjIsjX/6O/e4rzHGBBSRdx1Cje5Xm8USN8YX0TFRlIQJP3OgcyT6P/hK8n5W4z7EfQymfEOZMiyl+Uq3gNnOnSmoj7WB75aSFznMc4hXMikEVKbd7QmOBpeXsBm19Lu65GMHzgUKRSu65jPSs7PK65ua252LctFRVHkpMyiUkqsMzTN/mANQtlGRRcz+iitKMqCajbDozDGHDkoQ+DvlTx2Zh7W/tAoHsYcSxELw43wfOg02juuRMMtgqdeol0wQGqIQRGW2hloW4yAWhl+4yxFlvNUWQpjebvZ8m27oxUCGovF441Adh1rv6NuKrbO0mUSMcuxWeDNHpw94OLBJWU5o+vgSbmkqipub2/xPjiRd13X8/yXl5cx+5foA4DD/5q63mNtR1UV5Lnm/HyOcJ7XL17z9Vdfcnv1msuLS4pyweWDZ+zNC5ruFYo8cpqRFPvgIJycCkXkudIv52N9ee97mBfxXwqY6YE5lieS/nQ5nVN7dpeuYmoYTzz7+N37Lj9+rtdpR8O9CBkNETLyBOns9S/FP5LOLsmVMRPiSDcgpMALhfMmlEWLRu9kchdCoYRGCRUStjvRn5F3Xe9tGE+DgWHxvA81pYOgJRBS9Wm0tNYHyo5pWr2x0gMOvQ3HSpqzszOyLGO73dI0Ddvtlvl8fqAAOmRGh7rkY+P5tK/gTTDMbaoYug+o0r22bemisiMZy48iXZISWIaNcdYxn88RAnbbG+p6z5s3b1BScX5+HhQ1cgwpab1DhHZZVuiYGvDUOA+j7Y4/H4/txBrQx4zjXEgbsblds9/vRykeQ9o0EHQueo8D+/2eoiw5KwpevXzFbrenbTtggIFT0ZCHyq27riFKdPr9u677D3MSwd6l0El9v9/z94zmJHydQFN9P8H4fXyoA3KhX38Ixgaf0iCK8ZNjqv/uMb772cFA/tuux33w+X7XdJz3jWGqSTm1Jun791Py3X8N+MZFHJSiqHxkjGxM6Zllod+RTB+ceXpBOBprIiwET7lw/tzImKOU6iNCQ7qVsbB/ajfvE1bfvS/HDOj03rCWQiQm6hDPn1JUHe/HXWMd7+Op/R0rs945ncn7kGr1/nZwIJLuqF+G5LXpnEMRGG2RBjdSrKXP4c9RxMVEcSFjPRkIKfaV1sEgLaMQMIo6kUpCF5l67xFT2omIeIN+LD3TG8dUVRUvX748YIYHuhEic/txu1CPUquMy8sL3ry5xtrBSe6AdnsGTHCPQumvcg0wl5SaEwNhlKp6pistoQzG/bIqOT8/wwOr1Ybb1RqJRypFWVU45/nuu5d9ZKRM/IAf4E8Q9sRahzEhowoiZGBZ3a5jfxJjHLtd3WfL2W53PP3wg/6Mh7RjLReXl2Q65ze//iI4PIiUBtrGTBUhZV5RVVRFxXa/I2WeOD9bslrdcHN1TZ5llGWJVJLdfo+O5XECb+v71F/Oe+bzBXlR0jYtgZZJlJLkRRHxVpioialWVYx8d87RtV2EjWCwOV8u+PTTT9jvt1y9vWK1WrGv97G/AQcIATpTNE2AY2MiMyxlD6dx4v129ls7Rqp+UFhKIYKiPc+iASTR2ECVJMFZxAOocP6SofD15msuPn6EWz6meaUxbz3FRpHbHG9avHU4EeqpWgVOi+CU4lNkZRC6Q28pxVOkhvFMJSFqeoXsR8d1FsdwDoPwk2jO2NgqGXDNXfzuNEL3VD+nDLBjIXl6/5hfP3znFI9z1/wOrymuP/zcfz9+Y9TfeLyn5IapgnXcz7ie+Kmoqd/mSu9PUyMn45IxZtjLkfE8PQOHMlUa23Rdpp/Ha/F9xpneu88gf8r4fZIPvufe+P5dnycjRIiQrQXAGEvTtpTWkhU5zna0bct2twPn6JqWpq5BBJzuve/lHiklWoeamIvFgo8//jhkykqlomKa6YSflQ7Gdq0VVVWy3W7uGee7LyVmaDWjzEvmRcF5CQ/mjkUWaqF6Z3Degsjx0uN9HtJiR/5TCoVUOUJkoARSGjL7lqLU6JnB5yuM7EJGVtEFB4GoqblrzQ/Oufc9qzN68IiUSzFOQS3xPkTpOxfUkEop8mxOlc/RKtSWNnlHl++ReU3Xwos3K6xt8d7z6Q8+oyjO+W/+yf+DxnnOH57z8MlDZmWJMTuqYob3IUNK27ZonVPXNbvtjs1mS55fB0ixgpubG+q6ZberQ8rwtmFWLbAuKqeUxp8LHr5+SXa9RhkwRYXJMl7ZjjftPpzHqmSt4LprsA6UyjFKsbOgnMV2ntV+H/C/kiGSrK6xBEe6HEmJCnUh8dTa0yiBVwpQfLe7iamYQ/pEEAcRQtOzmPCCUgqt9YAbiKkMR++0bYP3wfE9y0uk0uRZgXfQdSZmyWup6x3zaoaSAuNCJLm1HU3TgJBonVEWBctZxaxS1E0XyrkQnEXxoeyP0prVds/rN9e8ev0WvKfrQskD4zKsg13dstnseOwcUoZ5dNZOge2Ahw5H3p8QGw6ZPiE8EpU+jrI6HkfO9rJq5BX7e2J0732vU+htYIdPP/ZXIysn2xg7Eh04FaXvTtCDscJ0mirbR1mlV/TecaWsV37U9v1FMdINGdLMp34TDzge64GFA1La/aHlFHQgjsYfX+jn2fMDE97kXbTrXXR0ev8UHUslOt7Vn5sYLe4ycMujAItjGg4c8QonDcsT/HLvHN/BJwT+5Hj8p66UmXM6vqk+eMq/nTKMR79b7N5TKIXIYO88rVU4p6m8oezecn3j+BWXfLv8jPwnf8j/8Wc/4Q/ka7bba16/MdROMy9KHlUKJTyX1ZyzvOJMl1SzjLYN+FdLyUxDnu3RN5Z/+ps3/ObKg6/wDn7x5S1/58NPeOqX0N3w5fOvKdWK6nd/RLNtELqklZpX9Zq//OqXCC1oRMamhscCvq63/Ld//i/52YcZf/zj3+dnH/4uZXbJtzffsFMbFk9mPF08YNct2Ww6dH5JPt+w2d6w2W3QtuHP/vSWy/MHZMWMm6trXr++5g/+6A/5o7/1d7h58y2vX9TQdFws54HXdODblsU/+SfMgYdeIBGBrjMEBgSZr88JwUOgevCAIPn3uclPQdGgD/GOH//Jv8FJMZx56ylHZ9t7z9q1dE3Dh97zaaR5cqEAif/uSxQKhMMWHfuFoRWeL3/yYwqVs9vs2W/3NG0XytdYw/bmBd9++5d8/pf/hvZvh7TTWik++/Sn/Omf/Fvms4qsLGnXLa01dM7R2pCtQGcZzkPbdnRNje32WNNiu5Y8m4eMu0rRtZY8C3MIPyOOdRsQe6w31HvPbifIcwPC0hlN3TrWm1s22z1FlrF4dEbTlNxuWraba4RVeCPIRE4H7NbX/PDR7/L3/sbfw9mat7cveXXziqrIyHOF1jmrmz1ffvGaj86fcPXtCm86ivmcjet4s1mzrnN++Ad/hzfrDa41dHWJLp5ws/qC1e4LvJEU4pLMV9T7lr1x3O6DU12eafZ1i+oc7dZwvljw9PEZ/9v/NJSndeYWIVbkmQ21x6PAPFKFHsHJsGIRYtyQOap/Jeq9+pptKbWyDzq0xI8SdR4i1ismgF0vs4tozwmBJhLrY8m3JANaD2iUCI4wUoWMyN57EKHMQDKKh+CJwKMTdVLWOVa3tzhjSWVCA8oKHvZFnrGclxS5pLnZcqEWFEVFvV8jbMgOKJCBDxtOENZYlIylcNqOPNMU5Yyz5TlSKLqoNx4bRXubjZOh5IRS71kWymMJa/3GtTwTObnO2Yiab2zHUyvJkVRkVDi2skMJz8Y35DZDWo3PFC8yyw+t5D9+dEm2q/nmu2temg2XHz1jIzNqY5HeMsscQrasTYecVxTnc1gWyEXJs/KcizwnrwpErsgzjSTY4bpYEig5jCZ5uygK2qbl9uaaWxdK2wkXnNG1VBQ6YzGrghNC19HUDbumpq4bjPU4IWg6w3rdIGMmjMAkHvKTgsEOGX6HrH5CEBwhvAxaIukRfqSLGOmDg0ozRoozBP46/BAUl/qc0N7RjZFO+VTWuMDLvY9NgGQ9jLptFUt9ailRsXa5F8H5NtDnqHMZFiFeSUaJDi+xHnmfCTEup3ESSYsUGSmgTEZX18RRek+IWn9PFv171RhPByUxJcaYwQBOUHYmA/HUSHxKGXYqrWB6J7XhvacsS7Is66PTk3LogOEZ8WpJOTE15Kff0xSw42usTJp6z6TP4zqASTmVIjh6gSF+b3xENlHxaTrLRx99xO3tNZvNFVdXV3RdF2uOL6ibmgNFxPjQCDg7O8NGZTdR8Dhg+JJgFZXZx8LaIVU5NkyG+4EgD5ETb99exbToob64lOF+mLcdHSbB8+ffUpUl19c3vfffcKBS/2KYXG88Sx5bfnRveqWop+l87hdARp9OPHv//SkDHr57d7/HbQxr+37PD30GmL1DEQ69owSENKvCDQJf4imP30rtvWseh0Jm+i4ZTvpOxo++5/VXM4qP53As3Akx/Tyd8/j36TmOR3r83ZgVG24H48bQVyByw2cpZfAG670PA7J3zkT8k7ypkjAQ93EUARfSgshYnsIhpOgdklppwSTXllE6oZN7c4gPvo9S+viZwzkn5cPweXy+B+XBIXzeqRLqFRnpufB5OrHjvxPtmhpq3u/qxa+jOd6FJ2BC70Y41rrADI/PZo8bEhMf8ejRufXHCgEfh+YJ9KbI8+D5qVX4joFGpiwuKbtESuXXOyX17cWxHU4OEH0kVdt15LH+ar+PUY0+rE00FCm4uDhHKYmxNjY1UmxN+ztFsg7GcuqhUw9OXhsp6b0fYR4Rzl+ipTLyDjYJBSqkKZ0v5iEyy3nmZwu8kmzXazpj0Tk9s+p9MMCEtVFx78MZDGghCFXW+T4Li5Dhs0BgnWO72/eCsXMO62rW6w2XDx5gnUUpjZcBnm5ubwNdDpJbH2nvPWR5xnxWUZYlAiiMomlCGvKqqpjPZly9fctms+H8/BwhJUUVorusCzxEKskhhKCta7795gXbzTZElo2MglprijwPtXq1ohQhWrLrOrqmocozyrzAmCBI7Oua1WbFL/7DL3jw4JKPP/2YxWLBZr1hPp/jsXRdE4SNzrDdbPj3P/8FbljRKMBywNgfw8r0q8g8S9kbxVV0phTELB1OYn0wvHvvsZ5Y8y7wh/umBvmWrMr44D/+Kdvnb6l/85J2tcHXQVGk4n447zGEPMHaW1wUxMMEREg9HmHPWofwQ03qsWOKEINgc59xcboOA549xE8i/b4D19/lIT5te/rO2Fh2Whl5mAq8H889+PldPJOPOHAqZ4zHMqhIOHpm+nkabT4ewymj8l0G5r/uK/GCU6X6NM3dNBL81J6k76f79O61Pl6T8VqdMsqlMU2fOzXGU/A67T/JV+9rwA94OUQld9HgmWdByXO9uuX69jZEvnaGrmmxHvKi6GW7JE8mmdQ5R13Xff+hbJTtZUtjDF999RVaFQghuLy85Oxs+X5jveNSsgwOTJmg1J5CgsaBsyHhXswbbYUOymqvsB6s9zgvQeZIUeCFDpRaBCdsKfdk+R5ZNKANLtbFFAiIDpz9uRjXAp3stzhxvg4/iqjUUISSERYweG8RKJLDlpKSXBXERHsUQnCWFdjlOctMUWUF37x6y/r2Cms7zs8e8ezDR/zBH/4BX3/3Ha0LtEJJz8PLJcvFJVIFh8EQFaJiXfEuOGoJQVmU0dkE2qZjdbvm5vaWtml4+DBkYqnrmroz5B+0iK+/4Pb1S2RT08kQzbPzlk4KGh8igpTKkdKRO8B5at9hrAXT8V23Y+UdTiuQgrZrMV2HJ8gK2sugnIklsbZK4JQKfAKClQtj9TGSR0TdwljOGO8RDNkkAl/me33BWE5y0cDtfTBYZ3kRjekZxhq6ro3rFjLiZFrhnAm8KaE0TGfD2ASCMs+5OF+wXBZ0XRezFQW8kZTDRTlnX29Ybbbs6w68oG06btfb4NfpHJt9y3bf0BkTy+EJ6AI8DnyyGECup2/D/IZ5HuLyxG8fwm16KfwY86ZCHtPMU3Tkvr/735M2SJle7sBrB7QmjudUu/deJ2j+0ft+Qr+SxbxfO5FEhoPakUQeapD10kiPcfmh4Tz2P3lMJMZnckmVfCB9v/ehlyT3ykOYEIPIMf1+OrSp3JPqz79LNk73kmxx53MneIRT+9G3dQcsjd+f8mqn6O+07Wmb4+fG+tu7DMsH8D7u4z34h+m8T63V3fyTOzn+6d+nxnncUsCBUjqMFxgTYvg0oRTJvnW83pW8efApiw8+4X/+6BkfLx7xabvipr7BCCjLOWdZhRCQiYDj17sG2JJnM8qyZG9ukV5QFhlVpqgax8/Xe/70jeGlL7BLhaPj17cbZk8M1ayi3K0wruUPPvkh59UT/sdf/lsMoMqSBqiKikePLkJ9aJlRkLHVmn/6zY5/9vVb/vI65z/5nZK/8bTl0aXlkbtEeIFWClkXUC2ZLc+RswL54itur17SbXb4rOD25hq4oWkNDslXv6l48viSjz/+hMvljH29xesMYeP+OUu+3xFwZYQTF+vqpgxmgj44JPHqNtWYTTk2RixEckTpj2tkPbK26b/3BCdwGPQb3jsy12JNyBarJSgvYyKc6CQpPDiL95ZMgCtzuu0NRuWcA76StJmk7Qw0G5xymEqybWv+61i72TmHFoLZYoHKFQoDtsWZDuMdnQ/ZKDwSZw22qam3G5zZge0wdYNxcH11w/LJE8pZRdPthjJaOIzdIJTHW49EUxYVZZ6zq1/RNR3IDcZB0+xx1jFbLFnMHtIUC7p2x9vb55RKolRF060wneNHj5/yN3/6e3z00ce0zYaq0syLjJev3nL18ordek9TdzRNR9N5OhRZmdF4hSiXXDx5yjdf/px/9j/+16ilw9qWTEieXFxizIoHZz+hVBfsb/Z8/fXn3FzdIosFxXLBbr1nt29Qbzd8evmAP/67Cx49KHn6WPH0SSjJ1nVBN+qSM+J4s4GDyO4IM9981/Djz/KoT4tfRpnw4Or1VIkXTQa01KDoYbj/1oH3Qb8SnP6DkiWUcTM41410dkFfk8rbDH2AMS2ma0NWvDhQ5xy4qPGN9GlWCFbbt9T1jnyegRNY42IJPoHEUuSSPIup/51B65A51GJDpoMsi7WzhzVy0ckgZcDKtCbLcxbLJVIprDU4pyZptBO+DnrpMZ25jx56ETPJONgai8kFWioykfO8q/kjFFooShSlB2KJN6cVSmehFK+Q1LSc+5zct4impthbnpZzzqsF1/WGjbWUOB7mGWo5w0jBvKyweHa3K+ztig9++AcstUbmARdJIzGuBecpspzGNXRtR9e1qKpCSxUjtR1dtDmenS2DjktJ0BIhw34qpUBJlFbMZjO0zimqEp2F7AHOglBZkG8CokygGbTCgui0fciD+n59R7zeOKDUJ8cPEASDc/gf0ob3HKtPcvUJOjiW/Uc88ri+ePrO96/cTVN7vRRJx5YyVEm0VGipJ3yKD+tB0gcNa+MFDKVjg0k82B1VPH49kQip0lVOhh50e8TI+riEUx7mXdd7G8YTkzT+HSKbTF97PEVInVJqnFLGjO8dH0Tfe+gDo/Rfjv0+pIhI0cspeiK9u9/v+/a0DkhivCHTdDvjmnunIr7TvaSQGiumvPe9c8BY8ZTaDL8FUgUlc5ZpHj58yP/w3/9f6dqW169fg4CLy4v+eTHyhkveScT08KEGeeQexCGTe/B3NMYMgtQxQIgxxKcOPQgpRzUuPXXdcnV1FQ+Zw/oQsQpBME0KoeRJtF6tWa/WoVbMSIgKQpMfhKwRFyRGJ/P4zI0HOR7scOiPnxm/KsYfpqswGsexMDEIzfcrOY8RxYR4v0cbwxhHQhsJQUzHEf4W8cE+GnksWB8IR2N5ZVAGBGeOU+OYrtlpGBoav/Nuz6gcC3VD+4ORfRrFOpCGsUPE+N3w/vEe3j+H6V6M7901k3uQ6qTr8fIP2xD2RUlJZ0yoqegd1iQBVB6M9XAL/aDMIhi88jzrz3dVliFiWKl+sw+C+U8P88Q6vN91TGAitjqlaUhPHCjdJ6PoFS53ndHpO+Nn096dFq4Hhchp48vdBpljw/4hrrgL1ibjGH0cnImig9mJ+R5C4giPiEFBN9AaQnSz80EAlZK2a8nLYmAyDowfvhdMh8HFT0mqGBDPSYVfnuc0dU2e5XGNEi4eBp7GFoy6htm8Ii8ymrYFP0SbpPmmhR6Pqt/h3w5E77z8qK+wfoOB5XD3BqbReYfOdTASqEDP5ssZWgo2qw3ODYaaA4fAOLdeWebBi4FHcDHq2UWv1V5Z7RKERSOpF6xuV6GUTKT7Sirevn3L1du3YeTRGzV4ZAbnm7LMKcscGfsMDjVhbHkWysFIKal3e3bbLWcXlxhnubm5itl6JFiHkJJ6X/OrX37OerWOaYl8Pz4pZG90UnVNMa9YLBcBJ0lBVRZY27Hdb0Pq2EVFNa+CIr4z1G3DLz//nCePHvHJJ58Evk84dBa8yE1nqGYlsy9n7Lb7GNHvSM5F+LRa/gBuemNoAs4kTMjg+JgXBVmeB+VuD5PROO4FgqAUVYT1FDGlfl4UXN1c8/jRI16vvuT3/vYfI378O/z5v/hXmKtbzPWK3BqUEAjvcbZDSYV0NtTO9QIpVEjtHBWvQtA7lybc4P2It5ApO8j7wfgpnnoQXhJPMVwHOF2IPqvD9NyMn58an8eOs2N8fzeOPR7rqb6mn+8S0N9lVL1rvuN375JhUl9TGeGuuuT3jT99N577qf1K0Z3J4Jpox7Sv8bvjDAHT+uGp7fF+jA3M4wj6fpzpFE3GdmTkGcHCuI371vLU2tw3lnE/qa+kED19jZxo/ZCxpWs7vGow3nJ1dcW+aXAmlBnBOmSW0TQNRVGQx9qRIX36INtdX18HnDpyoE5jU0rx6tUr6rpjPpuxWq/e69zed0mRozTkmaPILLmWQRVgO7wwIAVCKfAh0sA7hUeBCLVMETlCFgTDNOANijnaL9DZEpVtQO1xPij6nE2lEY73aooXEn2LXwzrEXlCEdcmRCgntUUyogHC47zBOROcrVxQeFsFiBBJdSFLLpYVWmhWV7ds9h31bkvXaarFmk9/8APIcm7Wt7Rdy36zYiN3ZHJGXoLSmqqaoZQGT5+xRUrB2fIMiepTKQoR6pXik3NEUJDt2w5bN3Q3t2y3K+hqjFMUnaVpG6yG1hkwHYVXSCUphaIIU8R5xxbD13ZDo0RfMs1Y26+b8EFRqhhSg26kCxG2QtJ4T5OsBMnh3wfagTqNe8bpEYMOI5Vo6n/0uC2k3ASlNFmWo3SGVBprLJ0xdKbDGgN4tJLUTXDallJgrOlxlfehzMzZ2YL5vArZghJTimeYgmKz3bJeBz4KQo3a65tVcBQDblY7tvs6ZJ/zPsaO0JduGeMnd4AXxjz83SfwSBpMOHJyN/BzYzlgYJcHrc1xX3fhygO+hOG8pEangQvpLCVecoxU3lvxd+K54/GBd+Lo/rAOaXzx2X5sg27hQIcykelPtdnP6Wi8Q39DpxIhk1PEgEf6WueRn2I0r7tlv8PupvJOWo9xOyfXpJchhj0cP5GUtv187oHLA17oju8Pnj/57Qk+6p427qKzY95kyjuMHj45xlPPnuIFTo1pTGvuWuv75nAXzzmGS2dD8QolVCjh4UAKhzU1dduy8XPE5c94+MmPeXh5wdN5xQdaINoa46GqZszLCq00bzcbOtfReoczltbAfLYkywvW+w1WWOauQKkFy1zzi92e77YNtS8QhUC4hk3r+Lze80OlmBeSM1nx8fljvnlb83pd43xL2bSovGKRzyn0DC0V0gta59h1nttG8Hpd037+Dd/tLL//8Av+wU8f8sPZD8iMoPSwlJDNK/R8QVl+yqzMua4qrl99x229pW32vRFPCMmbb3+Dr6+5mM9YPn7Mvjnnqjb4dVxr74NeWkQJLOK29C8YEYl6ZT8iASHFdJKRYTjrSQcthED4hAfFKOI3/HJ48A5n/QgMA60M+F+EV6I86IjZ8rzH2fAsUvDRdhMML9FYap3B2UDnhA4g3kgB1oCCrtnz5b/472h2e2Y/+Ql0FmHqUJrHB5lZRJ7Tdw2m3tHVG7xtwBpM2wKSrmnZbXeIOaMI6TCuPDvHuBaJxwmHFDlSlEiR49kADqU1s3kFokSgUKKg0IKqPMO+fc5m3yB8AU6Tq4qffPIDfvrJD7k4O+fqumaWF2QXD2k2htu3t2ihWc6XLBYLOufIipL9bseuaZF5xYNHH/K0fsmff/snmHWNlFDqDG9eMiuXfPbR72P2sGp37DY72rpF+BrfKqR1lFLz5OySH35wwT/6Y8ti6UEEXD7YLFIEdTzrEWASuzI91nUTvnO9HmCEE9OHkY4Hfz8/EPoRsc9AVYQIOdxc0rvFdrwNRuueV5CRw421yp13eOtCBoK2Hcnww0RGYItWggcXnt1+T7HIDvGY9zhnyDNJWWYoJelM169RmL4gy3K6zoxoh8e6wX7Vth1l6ci0ZjZfkBcFza4dZLU4oOQYnHjDu+qMn5ThZIi+N87Teg9KkKN542t2lJyhKRDMBCjvsd6SycHIC1BIeJzlZAR+7izP0EWGRqK8RwoPsQ63lIoqL6lKSeMM3K5xqzXz5ZwSgRcWbyzOdFgX+G0pBNYYdtttyCalNKbr+v/BWcDGbGBN5CuhqQnlnedBx+WlDIEmiwVZ7rG+DfKAg1yVWCdwIfF7VOz1uQcifZOMlv0e/cVYno3BYT4agZFDivW4Lokfmsrihzxzz5EBQyr1gU+8Wy9z+vsIiJHtk4iDEp8+1U0n2p76MQ1I3cfnwvkbxiLjeKIlMcJ76EOL4dwH/sohGPEOglie8N3XexvGx0qVcVpyY0xMDX63QmpaJy8dzlPMjhoZ11MEZGKMkgJirCRKv6e9jpUqqXZCMrQHIAxezeOU79P3U3RcGvc0RWFak/G4UnSBi4Zs04W+y7zEO8/Fo0uM6dhubrm9XbHdbhFCsFgsaLp2WOf0MwIOwHw2DwcqAZwYlNwDomXENIwZ+GNm/2DO4ZQcMCgm7tHN7Q3WhEi/TGch9YSQPaFJkWMiCSMEgT/ViwmG/IQQxgLfMNN3KzSPhdHjR+8QGsR99/3omYTwB8ZkEARSf76f56AwuqvdsYBw9/iGURx+CkKfP3pCJseFtGf44XzpkJ3AO9Mj3VO9jdPZh37uYhSOkWJ67HDuCVn5U6/eO+uh3wF59/t9MKZD4/hd7Y3Hm87K4TsHoubou7v2kju/74XdodP+UdHvzfB3guKQXj0xg4fjCo+Kvn16ZcNYGRzraUQDUd001FGRuxa7ALMnBdjUzeFZGsP6fdeh0HvXugxrOpzrtDyHeEic1IQcrkdqM+yj5x1DnIw3vfs9XjrAleH9Q/gY/z7q8c620q2QeSPUx/ORWe09VMWw74MSZmCK+1bTXonk3BLO82I+D9FvIhj3lFCjdlIJk7Ex2w19JHi5Q0ECAW7n8wX7/Z7lctnfDzRxwJtp5klxqbXi4uKczWY7KFsQSVodPACdP1jCu1b5CAjuA6N7HhwbVnwUgsLxGAQE5zxZpuJaxfkCSgiqqiRTiqZpcTYIGo3fk+p892c29jAcjZFh0rvANPYe8qJHykHgcQgPtu2od3tmsxK8Z7/b8PrFC7A2Rou7eEbCuiotsc5S7/csFyFlm7OG3S6kN8cT0pwDy/mC9e2K84sLBALTBSEuU1FR4Bxf/uYLbq+vITLhxHlhLU5YsAIvJd5b7MbQNTXL5ZLl+TJktrCSPMvY7/fs9juqqiLLNVme9Tip6Vr+4i//kvl8znI54/x8QZ7lKBl4qouLC9arNZnO6GJdrn6v0njS/vXbPaah4ZxJAUrLUSkgFXFqdET0Me2aj4JwjNwTeJAOHZ0BVrcrzs/O+Q+//FcsLx7z4I8+4+br1/BNhtjUmM0OLSSFL/C2RgiP9Z6qKELEqQ+e1MRU8yo6giYaKGOt8mkpounfU2XktM709PP7XFMD5Km+DpTfk3GdUkafUq5OFfqnjG9HSnTvJ++NXH0mStyk0ECMnHFGvOa4nXEt71PXqRSj0/WZrsl0LtPnxm0lWWK6Rkmm6EuxnKDV03JR03JV07W8y7ngeKwc4OT7FNXTdUhGuWmK+en8TsHnFKbGCvpEc1L7B7L9weAHGueJhr+2xTqHdI7l2RkXl5fMug7TtuGMO4+M0bJ5niOj0iPVm057YYwhi1lTxs4IaXxta2jbNUJ4OjOU3fptL61ytPJobci0IFMCRSzRILqAp4VAkIMPplXIkDJDCIWUGimyoUyFsGifoXxFphZIWeKFxvomKKLd4Z4EPuUYB/VGcZ/U4IcEPNHMsJ/RiSGlFBQJ5mI0f4yqwYQyHGiHUBalYC5zynyGlBkvl0t0XmFWNTerHeXrK3708ClPn33I4vyc9WbDi8awvt4AmqIsKcqSxXKJisoRrUPq0DzPWSyWlHlB08wQIijlpQLvQo3BsN8F6AxRlOTe0pmW1nR0xuORdO0eX1UgQtrKtm1gpigQLKSkEpo9gq1u+dqtsblEuRhZ4i1KStIKSxglOYeVN/Fbyd7bvqKwVLEsRsw2E6Lnhmt8BgcdTgwESP8mZzboZohBBQVaZyBDRLo18b+zoVQAREN6SBnadbGsWqwhqLVmsZwznxVsbmMEIT5Gjid5yHNze8tqtU6jpjOeq5sVdRPger3d0JmWummD44SIaxNl8F72TLKGAESC1tP87H3GtSA/HaOT3gR7wFeMJUDRw/T0GuMuIBp7RoZwwYHirx8rI2lNDMrUg2N2gmad1PNArOt+PLZ+jKlh9W6ZKSgaR8ZT5NH69nqhA7n4fvp4YoCHexEdCw91EhMeQfQ3jnkFP6LfbihDF/jtqcw8EJeD/btjj/1onof0dPye6Mt7HPRxgne4i9YezPWO9TvivU4+dcxPjenzKd7rrnGk78drNHUkPD3+YQmmcHuKv73rOqXHHY9pyp8ZZ4ICXjqcEXgHBsO+aVm3lnZ+wWc/+Z/x7KMLFs5Q2hYtO5qlYi7mXJQVWiv2XcvN+hrpFT5X0eG5Zd/UWDdjW+/YNnvqbk6ZlTw9W/Kr/Q5jWxa5oixBmZatLtgYSyc6Zrnk0ewMEPzlF9/RoZHS4p1FWo/KMm43LbmUNN5x2+1Z76+DgUAo/vLqLb++fcv/C/jNyx/yv/lJibRBDpN6yeLiA7CGxfkDzhcLHp1f8qKa8+/+8t9hTYOiI9MeJSxu+5aV2XD50ccslwtynXPrDiNS4+5EGuZQSRbtb/u0gQfnLGKQEQ8noiw3/i5gxaT2HKsGBSHLGtiIQyUSiRMe76JKwSW48QRn6uhUaoNB3TmL7eE9yMbOmpBUT8s+8lEqyGMWvKxt+P2/+H+z1xl/eaZpncA5FV3/iM7dFmNq/H6L3a2x9SbQXxMM40ppcJ71ekOuMsD16EcgmBWP2exvwG+wpqE1a5p9g9IOKS1Ch5rcValxbovtQhYcIUDLHNfBZtWQyQqMplALPnr6Qx5cPMZ1ls31NabbsZwvePZIoRw8e/SEzz7+hMePn2CcJS/nfPfdG25We6qF54PFAz776Kd8/vYveLmpmc0KZoszZsWMD5/8jKpY8t2br1lvbxAxcrbd1eQmZykyHpzN+OlHH/O//883aDJa2/V1r6VK9IPROhyC2RhXDOc+6pocTEjjlCMd6VZCeylooO+h51nTe8d0O2DwmHbdDfrckM2G4IuKx3mLs56uDVHaKXhQyrGRL5gwe0MpQbbY7bZc+GUsrRt5HA/WGIoiYzGvKIoMY9o4PkmysWRZzn5fH9AyG9fY2uDgaK0lz3OqakZZVjT7dc/fj/mPgMPDITplGD9JI9I5loCD1lk6r8ikYoVlh2WBJxeCOYLcC6yzyICKEc6hkFwozRNZIJxHq4yzucNlgl3TMhPQ6hAUVLcG7SXn5QylDWpXI7d72OzxElpjka7Dth3NvqXzvrf7tW3LZrPBGENVVdR1Tdd1oSQpkGdZWDvb9Xy0NYb9LpyblAY8zzOWZ0vqxnJ984p9vcMYS54t2XYCS3DCSvxj2u8AUxG/cXwlOBU9PQwNiMj7hpeCbDA4CCZJ4rhFT3pvzDvF3yJGZSd4T7zbietO5wgfJ0QqIxkOiY9BII5QZtALF+cUSgMOfG8aUKLViV7Ql4sUMatuekeKUUDMAIFxHL6XBcYZz+67vlfEeDK+jT1Iuq5jv9/jnEfprI+cHqdEHysxTileUo7/KROV+kpMvxCCsiwPlHXOueDJfxXXgVAfAOjHOI6a6LquX2xrByXYOGqiqqo+AnrKBJ9CCiliPSmhrLV9nXPlFGVZUWQFXdPx5MkT/vIXP2e9fsPLVy9x3rOYz1GZptlFBCcHhJmYCG8ty7MlnTHkeZF67xn89HlMEt6HgZ0ax8fMs7chSvUmpkQPRY+D8i6kbg5CtE3IXghcZIy0jHXnk2dv2tZDCnXir/9/X+PjNdEIHn0ef//X2//ANx4e91NdJyQWHER8qCWcxnry9aRAuRvpHXTA4FU9FkDDGQwIp8iCw0Sf+ia+mgx8IN4Jj8f9Qm/g6Pu+6xomOozxLiP6EG3bs+z+fcf17mtYq2G+KTKyyItoeAkPBiXPIOAHPOJ7IsXo+0H5E5hurbOo2IqlHKJTThD2xzB8eg0mo/5rmftxW/e1O703/Zz29L4z8I7zMYLVO0fhD9fq+NEp4zfu8zTM9E4ZCdYYsp4EuDw+F6GnGA3TK8BGBoUkMB4oedIwREgNVBbYq+DhqKaKIx8NEKOIyJ4GiJMTPzizAS4F1azi5ua6fyZ9f7QuPgihzjm8clxenvP8+XcxCs2PHh+xhBHue4ZPDOe+H91pfu+d19hY4+OaiBRt2O9VZCp9TCFLYDe989S7XV+2IEQZB8/WPM+iscVGYcoj0x4jkGJk1JwqKfuJpT0f9vogjaQX4CWbmxuUuCDTmhfPn9PVNVjfO8oYa9F5zrOPnrFar9hs1nilcDcdTVGErD7WhVpnxlDXNd6HcjVvr67YrNbMzxZY07G+vWVWFuA9b9685e3rVyTXaI8b1gzfR385J3BWoKzEWMNN27Dfrnnw8AFVdKDMixxjLZvNGimD4WGow+7xNHzz7XO6pqbMcxaLBVVZUs1mVLGOeVSlBKNXD6cToEi4s1/nSBMijGVZRp7rWLZH93hayIEHct4dCDC44KQgpOB8ueTVq9fMqhnOw9ur5ygkpmxon0j07AxVzem2Nb7r0HlG24YaS7Vz+LxE+ujg6W1QvEwjjpMQH2uU9bWY4AgPnDKcTxWjvQHyHeenx7ziMIp63FZqf2qsPMXjj98bG3lPKT/v4rXH1ymh7DBScGizN9zFayzLTNNjp3mMFQDjvk4Zeae4eBrJncZyiEsP65LfZ6gZ95Po+zhyPN27Cx5ORY+Pn79LLuvnI0SPEw9g6Htep+jWdH1O3b9rbAf37mJ3RFBg+eiA5ZyjaRpM16GrAucdH334IcYFZxfhoWtaHKCzvM9YlmTKcX29JAcn5+okL6YxzecztM4CjhKSsiy/95qNr1lVkWU1WtmgWJOhPp0S4JQAHeiZdqHMhnAapAahAR33zqOUQ8rgGGClRLoc6UsEOd5JrAkOVpa+Qlu/R2P6fOAU2sO3j0rN8UaMYO1A8RHPmpA4PMa0tG1N14aIKoTBKEdWQKYlmVRoHzLCtV2L8wqlK4SU7BvD55//motHD3n06AmffPQpHz95xurNFTe7a3b7PZv1BtNZyqrqHaFCNgBF27XMqoLZvMQ5izFdX2ajLEMtwdlshpGS3cMnnP2qQnkR6J5UiCKnyTNm8xl5e8nOhChnax0Kz2VxxtNsTuMd1zT8hd+QFXOUkUgV5DCtZIzx8CgEGTpEYTvL2jmUKBFesLUh5bqQEpmFtPlEfGLd3Xh3anASQh6dt4RTUvp0nWmEHhz/B4feAPdB7jBoFSK/922NsQapY6knramqnExHx52E+31YFx1L5L1+8zY4dMpQKdE7y2qzZVe3ICT7pkHhaZtghNcypIx0WA6M+ySZM9Q2DOUFThszx9+NHcWBkH1hBKM9q+pG/LcYPzPw+mltGZ2dNMY+EgdAqcD3pnFAdBCd4MDR+TlJI8aiyHhMJyHh+OrbHPGfadSn1mraea9MF8EwHnhXfzCspIoYjr4Y3R3B7HT+6fm+ASJfF9ZNHqw5vdF/nHlnvB7J6DJeKz/a+0H/dnyF2uljuhPnP6LBU8PCyXYSnTuxl6ck4PHY3nVN6f8peE/37qKpdz1/6rn72hjzUke8Y1r7Ed04OIMRhk63fVzOY/z3mMfpeSSR9mSQqaWQONHivaXtNNpJdrtbVlZg5o+oPvkxn/3gD/nRJx+g9i9RIqOcVSwXBaXsWOFYt4ZXqw23uw213fOBXDJbLpCZJM8ERe6QwiDRNBuBbBStyrGZY7fu+HCh+ezJQ37wYIHqbvlaLvnmtcO3z5HSk4mCf/P2Nzz3ax49foSQhs4b9k6wv77hdbvjzeoLVLfnXOUY2fGiu8a4HQoNNuNt6/g//5sv+G9/+QWPdc5jVfLJ/CF/vN/ygx/9bdZ1y3x5Rnn5mA/LnC9efMPtqy0PL89ZFAqJJVMa6SUXhSKzHbWRGPLRxoQ984T4TSHA+RGOdC7IqCLJEsExXEoxvB9LI+DH+CTcSzzeIIslns/TW0OJ0YV4AvcSysUJJXv9tQC0UJjeYh7act6BDXp8iQjpro1BK4GXGV5lYYhmkDM9Ht+tWFjN3/xX/wNGV/wPz36IvnxEJhQ6q7CmYb/Z0W3X+O0a2j2dB+8sbdOAA7VaYauKy+U5xjY9fHpg13xLbV6x3r/i5vaG1e0G0+158uSMs9kjlKhwJqeuW7arNVUxw9qauql58+YlNze3zMsPsTXUtzWNa9g08Pp2y5d/+uc8f/4rFpdzfvcP/gYPLp/yD//+32G+OOPTjz/j4fljuv0OyHCdot233K6e8+LVK2Qx49H532K2UCwvMj784AE/+egP+Nnv/m3+L//k/8B3rz9H6pwPPv2Qv/zqc5ZZxU8efcZnjzT/5T/YIvUq6FS6Fus8NmYSkKgocxMz54qRDrRHDcgJfj0uLxXphfNRhzzIgWNOIQDVULPYeYdwoo92dohY7Uz0keLIxAO4UA7GdSgRCv+IBKs2GMW98xhj6doOZ4NDRjB0x8ClCMfeEy3qAZydNWy3G4zpUFke+FU01oG3jnlVcH4+p6oKdttdkGOlJGXQy7IMl5xIRmvknO1lFWMM3gUedzafs7oRsXzuKeOhP5J77788VnhQIJygtoZGKhZKY5RiH/XcyntKBDOpWHkPTYcTodyRLAUPnWbmLa+v98x9y0JZ8AK/a3lQZhjpWTeWppN8ePYBS51zXW9o9nsoS6TpeHN7g9hsKaVASUFtPXbfsVgswDlM29E1bdCpS4XtDMJDkecsl0uUUuz3e5SSFEVOnmc0Tc16fUuWKeazBXle4L2nmld05hatg/OxtR4lY4p/MeijAoT2YW8RDoebh1yRP7pPomUQYdD3hudkWzjektM6yPEV6PVhnXkO8O07dn0iFw42YzFklRYeJ11MV2+jbXAoOxCi3mNWMSn6s+79gLKVlKOyUQkeY3CWjzRhvHre4ZzFv88k+B6G8TTJxGwAB+mzZYx6OVXrZqqkO8VknVK+TRmqpBgcR0IkBdNY2M5jndUk4I0ZpKQc0jogm2TYTvNIwl/qZxwlniLIUzsQjB0pUnwc4Z7Gl+fhUDR1w2K+RGvNb371p2w3W1a3twgBFxcXtE07rDEjBjsi2qIoybIca2LKtTjnHm4nyOqwHTEg7NBqfGaIUOt9qyOcJUVjGyNRIRAH6xxZphGENW2bJiqTk9HHomSsMe89PtaUnZ7FRBAYwfYUbUzfuPt6XxHwfd4f958UPeLEc3e18/0Vhne1I8T7tDcI1kHBPmQwCC3d7SUMQYC/X8k5NiKH8UyVXmOieTS2E+0NfQ8Ib5jviRYOGJ67IoaP+xoPc3jHH9wX4hg2//quMaUL+yCVwnvRM0fOe7RKeIzDaYwEhOFzOKtZpkM0UzKmOI+xQWGa8KSdRI8cjmlMUP5/e93PR41hfNjju+8fn8/3n8dduCXcux8Opv0cns1jQzW9skwIgdIq0qLYWkSKRwoKD6kElheJwThmaHwC3hiRHYx1kvmswo2EBDlKnY0IynTjuj5qvFdijGcpjo0lY+VPWRSB5jl3WF/woKVhXbwPDNv5+VlgKusOoiBhrLnjzen1/szZfddJBU/vwCIPBtGbQ52nLHIeXFyy223ZbDfsmyY8ISRK6b5+VNt0SBEE34C3ostsX0NtUAQxYtPCsMTRfiTFrIzfOtvhTUfbddxeXQUeR6iQli2mZv3kk6d88OFTnronfPnFl7x++ZLGOpr9PjDR3tOZjt1uF1JINQ2vXr5ESsn19TV5WXB5cYEUEtO2ZCrjmy+/xLbtcOQ4vRVp3CbCj8o0bV2z22558vQp5xfn6Dwny3OqWcFms2W727JcnoWocGvReo61jlfffcfbN1e8ff0WrRWLxYIizwMkuBBl752LytDDM3Qw0EgD00+8RwooipwsCp2JX9lstywWi5FiOLxlfVD4SB/rfLngjLBcLnn9+i1Pnz1FWo8XlqwoyB7DJl9zIyxeKApbkXuL6zLwjirXtLsNzlmEtXhn8N4hI98mY7YdL4h4XZFnmq7rGI7zsbHDT2kGHJzz/j2f2EZx9Hy63Imzcpfhcowzxv3edY3fm7Y7ntNYNhhfY7484FAO8NVJQzGHazOtpTZ2jr1PcXyXcfe+Z08pcO80dNzR9qmIwLFBebqX4zU7NZdTYzo9CCKb+VfjF+5bu3c5B7xPW3c8GXRcnt4T3nkfaZekbVvyqhzgzA7Zwbqu6x2HtNaUZUnbBjltXD4ryYopuhySog6yrOsdvNO7v+2l9YZcKTIpkRisrTG6RSmL8ALpMiQO5w2Zzumjs8UYG1o8EuczHBUmkwj1CmVXCHsDdoMyDoGkzTqkDTgvGIwgVkPERXlATg2KMPDrPqx1chUzDqzweOmDMTimahdOIIRHXV2xevEbvrwsePBY8ExkXMgnYCwKg8oks+IDrt/s2N22rDcNjXVcnp1z+fgxZVlSFgWZlGglmC8r5suPeCw+oNvtqNeBdhslKIoMu63xu5rG1Ehl2e9q8ixDiKBYUQKqRYHwnouzRZi7VmwuF8y7mv2+wUpYVpoPS8G/QGBYkTnBMpuhzyTXpqLeXtEUHVdmw9p0rMye2VxSG0HVNqEkjS7ZUWMkId2uFzhacII31QKTe0oneesbvmGLBHIylBUY73A+OFel1JdhGwY8M3bCsdbgvQGpcD7UoBeAlJ62rRFCUFULimKBUhVCZOhcYbctrm2hMSgTAhK8BG98rFsvaYzFeksuC2aF5myuOZsVdK3CSYXwHiU8UnpMZ9FSc3O74c3rt6xvV6G0iACUwuDobEfQ9QYktNlu2DYtusgxtqMxTVQK61CaJIB7iPZT4BMjnrCBOIysHuimPUkzwIe0u4nGqUNngl4qSHi+74cDdlXIwJuRlOLxnMCxc8J4rGOaduc1UU/4NOW78KMjygLH6xAW8P2N6lMcIEQwJPTZyuIaJP51cKQ5aiWOY5hKMIyd4E9EwCP9xxhI0i+AEAiVOjmcV9942ndAaXWoAZKHfQ40VjG+wrQP1yqN2482X8pD+Duazz2XTArjaCQ6xU+M+YA0iOm6Jf2Nmy58mvMJ3ez0PBzpccX94thdcHsX7Z7yAtMxJCW94FhnNYwtRdxKnFd4scZRo1SJJAencdaSR0Oppcb4mq7p2O4NXH7ER48/48nHP+HR009p65bd9UueLSuWizm6KDDCc7U33LTw5s0V2+0WgEeXj1g8zDlXSwTB4anIFcp4HlRnrIoWJztuzA3/+rXl9y41/9Wnn7EsBEUhyNQn/NMvbvju9b/j7338mA/PH9LYmi++WHO9e8FvXv6Cfb1mt7thtXrN/uYllAIvFVoX5NWS6vIhn5x/xL7WbK+v2Nsd7sESl+dcdTuu1it+JTf82X7Hf/i3/0/+/hdf8bOf/AGPP/qEi4ePOZst+KM//I+Zm9+hNBZv9rTtLZ17g7MZWXmByM7IOkfevD7cvz7uVfYZzHyEuMA/xDPqCTwCwVEunC0fM6qP8MMIhwV0GjiJkG0vZUyN0az4GIgFwfgeZELhPVgb6IDSg64xgo/zoc54QFTBqGQ9fcZXoSUpj5xzoZTWeMZSlhjv8N4g2y3/8Kuf478WvFQZ13/wU1oveePWvKlv2e5rtNL4HcjS4GWDUIpMKZbVnEVecr22PQ6UCGhvyH3HXGe0SrF1Dc4ZfJtjdY6UHUIZhPQIlfPy6hVltkeSIal4eP4R9W6Lb2fYFrarmj/9l3/C/tUNt2/fUFYzivkDNlvD6+ZrfufHv4PvLLl1mPU6pEj3jmdPP6acLXj99i0vr6956XP+i3/0v+PZJz9G6QqtFJdnOa9e/YLCfsbM1xTW8SR7wLM//sf8vd//gnkpwVmcVaGsivcYm5xUBIiw1jbqKIJMl2TA6HAdo0jdxAHQAp3zGG/JfCiV02sInUfEUrY4F33wUz16PyiCGdHyRKNHsNI/4YlOUqGUsI30lDhm54J84b0fbEP4kGJdjGngGNdGoI+GfCHg+vVbPvn4EzKtUdLhRYvz0HaKssioCsmisty+bbh48Awz99T7FdbUVEVGpkJ2unS1bcvcD3XG67pGa4XKCh49esqrF1/RmAaLJdMZSoVyUkEvFQY5zlh2r8zmPco7HBlWG17LlrnUfKArlIZ9K+kQlOQ8BC5cjfWCvbWUyjIvBGWe83Zv+Xl9zdvVlk8M/L4OPKXPGs7yklvj2EhJNp/xYG2Y+T0bD74Ds22pmo7trOBy17KYaTKtme88K3ZUswKlBbNdyb4uQ4Ct9Oz2G+bzOfNFHOu+Dtmfou0hyIYW11jaueFsmVOUFd53OK/pmgW3N1u2m47V6opPPnmINI+x+VcgPMJnCKEjDgzOPIlv9X2dbR9xp8cT8FNAczFboxBY2WG9QrmOzu/oxB4nBRWSawzehbJaY1jrOaWR7tlGmHD4UK5JF0ivkbGYkxVB3ku6r4C+T+tG4pEBA+RA4fAx85Zw4JVD0CJch7UdLV2k7TLYDUVGcOKWgAYvkULFDNUACiF1dCD1gEOIgMPTeR1Hy4fyXMFJKjTxfnzXexvGTUp1ISMysDakG+g96JPR2fYKCOBIoXWKoRk/m8XI03H0Rnpu7BE4VgZ5f5gqIxmkkwE91dNyzqP7tCiarjM9Aey6rheaUjowoK9PnqLjQ/0xcVDzPI1lnELdex/eVYKm7TBdSAMqkFhjefPmDW3bUlUV1axit9vFVRzXVgF8ij6IadRjFLbsmcWYWkCMBAMgGbuTcXVY9vR5pBTjeE/S/FfrTR8JYeOeaK1DfTZno4EFfFQoZVkWBBMRvYb9Af5nIFd956lT7r7SvO5lww/mPxwSDpR6p5n1w3ePhVHfC2kp/fVADIb5JOHjvuvAu3iixD5cmck6TfuaPCtIKcH8EDGFP0QEB9NM63EqlH+Al0GePB6PiMyAAIw1vXDL0ZMHK8DxGt2jQCcJmtNvj98fb9mBHC1OrSVH7wxjm/6+a9xHQ+gNMEfMQmK+0oFIuMxaUFl0LpGkaIfDV4c0IZ4hfWgQBEQviHvnqGbzXjlx/4SPFRQJ3xxjhPuu6brc9eapAY0UFwd/TZ8VB89Of4p37c07x8HxOrzroQm+OH4nMsrCo3VGphUqlUCYNJmcmBJR73U5PgoE71CsBLAKDFWW5X1piwQTXqhgGBAi1CTqJgZ5kcBiovi4w5iS6GvXtjEKbmTs7XVTKTIj1tL2nqLMmc/ntM1NeFQG70QXPbkHPiB55vYD69elx5nTqI7JWE9BccJlPb8Qz9DYCY2oyO/xng9KfJzj9cuXeDyPHj4IRuXdLjgHti3eO6zpKHPNtm3o2jZuLqR0Pr7Hq364Nx5c6jfNQCTYCnhVColtHbdtQ2dC3bGwLo6UuWNxNufR40c4F7LW/M7v/JSHl5d88etfU+/2oZ1oKdqsVzRNHXgkF2qdd21DU++p9/tgfJaSTGnq/a6PwukVfZ4JHA3URiQlQ+cQNigeX3z7HdvdjqfPnlHNKrzwnJ0taYuC9XrDYj5HZxnewdn5Gbv1hnbf0LUdbdNx1VwNAoQLtWGdHaWfH4ChB8V+iSP+TTyRVIo8L/rMPs57lFR88/w5H370IWVZBkV2nJuNsKBcUP9IIVDOUlQVN6s1u+2WeZUjpMT6sJbzizOKueH67Q2vXt3SrFvabc3vfPYTfvL7P8PUe37+Z3+C7xq0zNBCIK0Ck86tCLBjLcY5DA60RDkRU8mKngbjBxgT/R4TFQnD+Uhoo3+fEX31hydGEmsDSjWcSRJ/GPuJdfyEG85Vf/YTyRvvjA8KJjyxlm5K00bEQyNHWg75pfFZGfP/IuK1oJSw/fNCBqUyI5iJmo8eDySjZYLdlKHqlFEiUZkEF+HeSMnb8wCn8WdyxA0y0mFUe79moz0apnsoA02zcSVDWD9vcagoH5etmhrXxxH+dymyvQtyx31C8an5nprD973SuN7pTDBmxw/kIMKJEB6lQiktbzv2my3zsyXCCDarNavtlq4OkeRVXiCVpq5rrq6vyYuc3/vZz0IWHu9DeSg3GNCnKewBOtMFY13kTrTSyOK3W4N0OeOCQdoHTltFA64kyYUgcChhkbKLipTglS+EBQbDIb4O5ZbclipbU+R7hOzonAlR1TLiOVSoXQcIBzZY1eJxDUaxTOkYaRIzSPXM57G8kJTXI4oIQpApTWcMq6trvvrqc/LsitrM+fThMz44K8lVSSmXSHvObrfl6vYGDyyXS87Ozqiqqpe7u67FOct2uw4Z4hT4rsM2LdZ6ZJaR6RwvDdZ0IaKnMyxnecB33tEZw2a3xVrL2XJJNZuTZRlCa1zt6N5e4ztHVVScL885V4pznVHXa6xLdNlg7Q4qyZXd441ioXL+wYNn/Im/5U9NixWxkp51CBMijLR3aEQog+M9LR6V59jW0XaWznYBz0nNKG9zpGPHaYunOMHFzG/ex9Sl8W9rXShP4oPRuyhKsjzvI8PTOgX9z1CqwfmIQ53p03pmOmMxn3N+tmQ2L+k6E7JqOj8Y4pUiKypuvnnJeruj7SwOgR4TjUDMYmp/xyZm7QGPtV2I6HMBp3oRMjNIKcjyDJN0SByXjRjz0b0OabRWp9aQ0ZDG/EZvwBWEaPeegR+MN0PnnJDB/QkZdxjrqWs6Rh+bOxrrKVwpD52opusx/n2ko5i0PTWkhmFEzisimyTf3Im7OdyLU/OcGsaP2xn45OEKWObufuNyTLhHd2Idg8w9UZeOnhljvF4vch8cicM+j+bYzyoFwJw2Ut+v1zoBJ3csw9RJ7uS6T/uJeoZTvMNd6z1d0/F3p+6dup9qRx+eyV5g67/xgLWXZDqUzgSQMiOTOV1b40VDs1eYfYaVBR/88DOe/fD38bJECIXb75lrzePHD6iy6Di727JvatbbHZvtFm8Mi9mMqqw4Oztju36FFR1C6OAU7AvqZkNRlDy8WHC9avj621ucVWj9gJ9vDR+bgqeugNzxfP1rPntkOc933NYb/uLqJf/8L/45b178Gq87vKtxdY3Z1XityfcZclHgZEbbdrj1hlZLnpwt2Hd72u0a37aQSRblglaW5FnGWTVjLxX/3atfciUcf6drqDpD9+gRn378Cb5t2F+9plt1OCswTUaroG5uyJxFiJx5IRFNTQrS9j7J/8NpSLvho04CEWQXR8zONjkniS8fHyiR5CAI5cbS+RcTsT/qGxIMCOhNS+msJjkHgjzQl0VN43XBKXBwTE5Bdx6EHCcriLIOfR1xN4LnR97T/btf8OrHn3E+zzFtyW5zy5df/Jqqqpj5grOLhzx48gkXTz7lu5sdXG95+OQB8rUAB8YZOjK8eERWnDFbnHHpHlGVZ8xnBW+vn2N2W6q8oGCBMBbajtlsxuXlY4pK8fVzyb/4Z/+BWfEh5eKMoig5f/AEWZTMzi/Isgzj4e3NirptuV2tccawXglWRcmjywfMqorOtUgtyAqFMTv+w5/9U378zGO3P0Bqz36/Zr9Z0643qMbzo4dP6XY7fufpNzHCGbztQlRrXD9r7UiPEx0vky5MDLJp+m4kxp68xlDnYumztB+9DBxp9QGl8v6I/p/UK/qBZ00tJD6Wg77H+DDOZSwHT85I/7mXv0Pry0WQP55VJUrpkJxIhoja4IibMZ9VWPeWJgYouqgLSPan/VirGmVFpaPcGzM3aF2wXC4pijLW1I5G2BGOTXLfONPZO/mM9KLzGOEwAoRWFEqzjxW3c6lQQuMsWAnFPOgTm90OZw0Xs3PO50s6KVHbmto4Cq3YdC15pxHGU7QgreOF2aGURj9+iFIaaz3sWx5UFcKtqZuG1nSYThzY+NLY27YNes2u67M+Z1mGMYaiCPbExWLBYrFgPp+z220xxrDdbvHe9euaZRmz2azf42AT1LReRlmsX7S+lnrAn44EYSG6OUY4x5IQIQGGCrRFKoRwSCfwXmA8dN7TOdvzICLqBqfXeKcO4LSH1Tsc1/qfxzqZI7tumDjOgbPgrcRaT6+C8QJBkG8GT06Jl9EIL1P0uIpIdhxNnnQgwfHKRceBhCMSveidXkb6mL/2GuMJcSQli/chGnuxWPSe8EqFRfM+GEyT97LWOk7ksBD8qfSMyQibFA53jWUc3XGgGIo/Q001FQX1UNtKSmLazBDlPTbCJ6E6RaIkR4DUfnquaRrOz8/7vrRUeBEi32RMaextOBxKSLy1aCHJspzz5SU///M/Y3X7ljdv3iKFYLlcBCE3buQgwKV1CQrmxeIM6zxaxfpwEaEeeoaONWvJaz8RgzDiOxVgYthj78GYkPf/5maFd6J/N9TUE3FvXRSyU1RiPFAi7fOIERkJM94PgtywqenIDQLDHeq3Ycj9nCcE7N73D5nn9OQhgjg+9N4nL5T03XQCv/01CManRnwsAIa9lQSPTGKKIBGyCTgGhmC0LD0zEPGQP9Hm0JfgsPbzVMDrRz6aROrw8Ks0v3Hb3+c6FgDH/ad+DiFmeGfc33iOfnIvft9r8+k5sNRXMmidFBTFZP2E6F9M76Wo7qRkFgTjRFLkJ4ONS+3F5oT30ft+GGLi/7M8Q2kFTYLRgI8koofPwGQeMm7jFGWp3QQb/RozvnHXNT5/77qm+3D8t48jDnVYgodxqlFNmocYvZn2Jv4MpHW4xkLQ4VCm8D40PxWs+rd7qwWMsO6IgU43B0cT4UEpzcX5OW3bYEyHFCHdUVXGlNCJMfAChEIwqoeKSwllhl68J6H1tGn9LATkeU6mg1e8SAbnuOcyeaz6YFAMOM1F4VOOtiLB7hQHDIxxURTs93WfYjaMWR7siyA4wIY5B+PAwwcPuH57G8bfR2YkPiDVeO4xR/iXhGdBwEueozR7vXNBD2ZjuuAHxnPEKGkpECFsLbThTMDB3o920WMah8sUWMFut8O3LUJEHiEagKWUuLbGZRn4LvxPdJjkvHfowDf+4MZwcwCDkd1LMGFDVGMSzoQMyinroFxUfPzDz3DCh/S6LjDhT54+5ux8ya9/9TlvXr8JZVC843Z1Q9PUeCzGtHhncM7w/JvnUUEQ9sxZE+vjhjFZF+Eyeegn/hOXlrIXcj0gnKVrW3SWUW+2vPjqG55+9CGz5Ry8YFbOqfIZN9fXiEJQFCWtDfWHvI0p8XxSPATHtGD3DcW8Bu9x0ePBMcyOUX1wIAsCRooW75lwpdjv9rx59ZZnHz4j08Ezt8/mQVqCsJNOBoPCxfkFV9c3VNXTQIslYf0UZLnkybMHnF80XF9d8/rFlj/95l/x5e13/NHf+Lv8rX/8vybPFPN5Ttc2dNua/WYb99qy3W9YrVY8efKYs7Mznn/xBavffINrOpQQ4MJZkPE30fCR0tGliVtreqFZIBDWoZikDB/j8cjG+XTmCUYHkU6liv36iFNEcAhIvJJCIyQYHFa4fh+EJ0blBtjCQ2dcX45KSoUXIZLUiwRDHjFOAS4FxlhEcMFHRPwiACGCl7PzIVWdhSiEBcW2j+NP5zbVZYbQp1JZj0+8j046UiKV7L9Lp1OKmD1gZChP0QnW214gllLFlMNDKvyxEl/1bSccIKPc4kZj8b18kkpPjR1y0/0kP6Tv4bScNf77LgV1X28dAh3uPa5TfbzhTPS0+A4F+VSBf1f0+1010ceG/akSf3qpFNXp0/3If0UZJBcK3TpUB0JLXl9f8x9++Stca1AelrMFy/kc8NhtQ9d57K7F6yLw1j6cJyE8ddehtSYvSzwhUoQIEw4XUipaS1VVtPb96pvddSU5P1DaRP7dAINAqAPokNIjXSxt5B0IjxBBDg7YyyBEgxQbSrUhlzX4PZ2tqa1FeI/DYL3uM5wCWG8i3QlKCyfDWRZOBhwkoXeQHfEBIioHhT/k1j0CJxwZEgWYpmWzuubV9ZoHlwse5XtsPkMVl+SoYJw3QRkkpOwj+fv0kDbUJu/TfKcsblLjpUOKgDckKoxfWIRQaBWcF7uuwxlD1zTU2x3SezKt8QiUavFC0ErNfL2PcC+xQlBDwEtthzchTbiQkp2raUTHtdV478hVxo/LJbfO8Qtu8J0PEX9ZjnaCXEoqK9HpnCFpBSAlLZbG2+Do70EqHfgC54LRYSTHjpW9Yxw/6FQCHewNDASjQNClCIq8IC8KdFaQ5XlcS4N1JjjzEnBR3TWkMi4pg6AkOO5XVcFiOaOqSrquJSVA9QS86glzuLq+ZV+3OERsK2oB4zgT/ADcrtesN1vOl3NmVcF2u4/w5EO9WCxoHUujSJIzxrREyV2G8LsMjoMBZwTUHOKmdEZElP/uMi6KMe97os/7jIqnjKMQI3nE8TOn2sAfK7WnBqq+3RGePqksHdGP/rv4U0Q6fpex+67vTt0/WKOJ6DZ6qr/h/aGD+Sk6MezboeZlrLcYj+VkrWzRA8K9fZ2Y0JGcJU7ATEiNG/YsqhJGUx85U/j+x2E39wvwB8MJ+CN9Pg0Th4bxOIaxTlEccN3hndFZGbczNcCPz9r4+WN4TvcPBjIMK8pKQebK6TqHsS1gkbKmlZrWNLRmC64gLx9y+fgZxflHoJdkSqOEQONQwuG6lp0NmZu6mK3LtB3CQ1VWZHlOHnFk21i86vDeoIxGSEmxzFEi0JFdW/PFVYOXl9gzz19c/QWvq4IPy4Km2/HLr/8d/+AP/haPyiVf3j7n69Wvefnmc5r2Bo3HtzVu3+A7C53Fdg2utngZMnJw7ulmGfnFQxZnS2pv2O335NUcRcZM55RZTqVniELzXb3m//PmC6RwYBp+zzScnc9pjGPbtrSmQ3qJEAukctQ+OEIJ4dCuQY4NL54oNCTHMD/8TaixG7J6JD3xKXiNG9vzCb1w2fPYPZyfhPlkIDl0qBwgMjHwUfdB5LNFkuqinmGU2tePzqqNTr1Db5GmjsfiPco6nhnBN7/+Ev/hU548PGNeZgjb8vnzr+n8HKdzxO0NnaoQ2Yw8yynLQfZ31qKzBaZbkOuM84VnlncoDV37CmFb8BYtZszLM15aT1FkzGZztC5omz27ektnLJ0yrNZrunrPoweX5GXF5nZF3exoGkdZeYx3vH31HVVeUBUFqsjINWQq1JmflRp/vsCYh/yx+ZjL7je4568RWpAbC01N2XlyWaBbzflFzceP93jrMCaWznJBfncjnDvW2/Q8i5DEIsoh2jrifSEGHHV45gMaSPYL73yfurqHHQY90iDF9VAR5OdEP3s4jOMbiMLwf4L7Ag91DHd9+0S+YIwbR+Mbz0VKyXIh2Nf7YEPL8iFYNPaVac35co5WCmO6aNS2ECOAg63m8GwYY9B5yGZoTEfXdZRlyWw2i/W195OMHRycpbFh/KDlCc5Ofwt8cPLwng6PFYJCKrZYLD6UIpSa3Cs6ZymkxFvHbl/TrVfIZcft+QVLITmrCpSAtsrZdTUbZ9i0HW3nwWle7Fa4Dj7+vR8zPzsnv1nRrrYsOoeTMXOLFKAV0g7ZoPM8p4hZMJONM40/ydRlWQY5LwbcCiH6MltxhRicTumDR0OtcotSGd4mXtsRchxESS5+1xvGfcj65XzU8wnAC6TQSKHRKkTzIz3KgFUdziiMh9YFh4MehuPe9I4cE16n36fAZB/yIAd0dYSv72BvDvhRVNDi+6AVltGoHfCqjjKkQjvVj0H2xm+NJGWASkHWopcrPbGUNxYfs5IgHETdT5IsiWsnxJ1DvvP6XqnUU33ucUrxBEjeh0OXIqnHioxBSSP6FK7jSOvEcB557Xh/INSlayzk3cfwjgF8HKExjqBI343rjKe65XCoVDLGsN/vewWVcz4GtflAv5MCJj7fG9aN49HDC5q65Ze/+FfcXF1R7/dIpTg/P2NX7w8Bsk8NFTa3LCvyLKdt28j0cTD2sB6uB6CkqBL9vfFhGAiviEaa1A7QKwy9h7pu2O9rGO1RqJElcc7SNG1M3Tw6dD3jMhyuwCRBP4rx39O9O/nt9O6Y2TnxxsFj0/tpbONxDmsyFg7eZ0TDe+8ngBy0PBYGRlFTd7c/XdfDUY7re48N7cHgd5c0OZ77qT6nz04+3dUkDBLRwVrfN47JKPzpcdzl2NH/eVIpcB9qPCQAifE4/dRh27LHVXFmicEjMtoiMVBJyA0tyFhnPOEx5QdEnnrpmY04nmRgI74vpaDIc/a7oKRLTkgBJ8R6NwwDGs7hsCRi1MMhgxr3yot3bNep8zX+fswgCvo6IJMzl/BWYhyDx25Uj0XNrJ/swP0nzo/gb3pr0n/PVY/eG+PZ/vnQa38CRboXBKnA8IxrAHvOz5bM5zPapgYG78H5bEEXy30cpDufMiOj6RyC9bBmQsXxu4CfizzHGoN1NtSpTIwPRGZDRtQownjFKCVSr30XHNLdQ4eqxWLB9fU1Dx5cDvR75PQx1EYPhkthHV57Li7OkVJg7RBF0huNE53yrp+6SMNMAkZ8Vh7QFXrBJ9j5h3/p7KTz56yLUVUC50xwLCHRrsM1HhQ3KcpVYI1hs1lTFDlFXgRHPhmNalLQ1DUuljRItNrHaNv7MNDgC5DUCIdXwqBpnkFY96TUtkIKHj58GAxnJgjveZ5T7/e8vL0FD1VVkWXBacI7y3q9putavHMUec752TlSazbbHY1p+npFWabjXoyxhe/5hPHepKsv34YgpEjzWOto6waJ4NtvnnP+8JKz5RmpvI3pLG9eP+9rn7e7fVTCB4XE2GXO+95lIALKOPJfjMYj+jM6QjGoKOQMz/m+vtb19TXnZ+cszxY9no1L38MYggDDQqC0xnnHZrsJkYsiKPedjR6q3lOUGc+ePeXRg4dsd3tWN2t+8at/xi+//Nc8evQRTWvp2gYtFYv5nLIs+OSTT/nZf/Q3o8GhY71Zc/7ZMz767FNWN7cI53CdxXUGbx2+M9hYFig5dtqojJCRzjRtS1PX5F4gpEYohR1FTvQKSzyZCDQsJRBNGZYSdRTOh9qBUfqwBjKd9QJiEFpEL9wIRCj9YE2UsQJcSNGj3L5GaDL+kaIIRL8BCCdQIsCkt9ERQAS1lvQJUiN8HKBTG5QlaQ4yOln0sBNgdUzIfRSmvRjBXsI9AeVG2IwHQ3qSl3YSvEOa3nggIkLrjc5yqFn+Tu43vjfOpjX9POWNxkb1UwaV1O74+VP9wuBwOSgoh2scLXNqHKfGMzWOj58ZG2vG4x7LdHf1lYwnaW2kVhH/B7lNAU1Ts7q9oVQXdNG4DcG4a62laWrKqkBlCu8tTVsz8zOUDvvVmpZXz1+wWa2x3pHlGTrLKMuKrAxKlpRx4/LyAcYa8rw4Od/3v9L6xxqMkQ6qGEGS+CMpQ6rqpPjFD5kcYgNIOiQNUtQUsiGnQdHhhcFJD8qRKUdwcqevAem8RcXU1V4Q0og6j3I5ODlKeTfai9gnEH0bE3EX0Ts07I1EIqzDdR1N19G1Etfd4rsGbIbyDusyujbMPDg3ZVRV1RsmOhsUSkluT2m2vRI4lRxKRF96RimN0poyL8m0pmsarOmwxoS03yEfN6YzIVraeTqtqHY11js6Qs1vOs8OhREC6y3KWZwTbGhprGGmMjrv0M7gheBMlSHaQ0pEptF5jugsGYJZcCuKPJ+ii3vb4mh90keIUHoknouQYWQ4BwdKqpHu4/CMjM99SgFqAR0M9VmOyjRKZzFlqI1legbc1ZkOpRUhY07MKiiCO2dRZsxmIb19vatJtTx75TECoRS36w2tMYkA4J2NvvVT2Re2u5q31zc8uDzj8eUZ9T5GSlmDMbZ3zFMqOykHTnHheD2OjeCHaznFn9PSG+mZni8Z6V2OjN4jlHWXUXjc9l2G7t/mGsYSh3Io3vTnM9E4+tvHOH2Mevt0t+MG/bDXw1fTKNFJZpY7aMfoBaaPDE4L43VKMvXx2h3u72G/04jxYR/sREYYaFDP607mN/7+LgeBqWF8SvPuG/up5+57l/eAoyQC3tXGKV3sfTDqxPBs/93IySDN91Tmm+M98ByE7d4xpiQFSjroCCWoMCAtnTO01mC94+L8EedPfsCjDz+jERVtZ8iVJBOAc3Rd+O9lqM/bl+KUCl1W6CxHxCCu7W5H14CaKQQS5wRtaxEqx7YG2yl2RvC6MVy3V3S3L/n51b/j5sGS18tzul3NZn3Fs/kZTuW8rdc8f/0FzfYKqUG0FlcbvAVZVCijyXTGLK/QUmOF4MY4zHqHKZdUuuSiWtBu9lROIA3kUpE7hfASdI7QGS+aNf/+6jnSW5RpmT88Q6mKtt7RWhNpQAnCgmnxIpQHxWwmu3B49oZsAiHQwUW5KWWUTXoI733gr6MsOTi9+/5XeM4NPE2SQnsVTuI7RjA2BmSRpJYxNYlw0+usR69HWoSQCFyvj7PGHmBB70YOrCM5ONkE/uam5Z9v1zz74BEfPX3C+aLian/DelVz9faKbW1YtoaPf/p7FGWO1sOQQ9Soi7wXeBGi2JtmQ1vfInwbefKA95TKuDi/YD5fAoLb2xWvX76mbVoK2VHvdzTbDbZrKfP/L3H/9WtbkiZ2Yr+IWGa7465NX1lZprvasC2bTc5oBmxAGspCA0HASNBAz/Omv0HPeteT9CJgJL0QIDHAaEDRDEWw2d1k+66u6qqurKysNNcfs91aK4wevohYsfbZ5+atHmoUiZtn77XXihXmi8+bFq0Uw+BwSuSxShtaPCdtTaUVOuzod5f4XtPtdihtaJTj/smMi299xN/5pR/RNrvIX4jTvmSO3UYDeJTNvI/rRM5m6OM5nWCXtAVaxWyJxeYfgteBrFRuNUlOD+EQJEfQSXufaEaS+TKOGgMSyrGV+gYSL5P+hZiOuqD7CbQUUcYt6OD0pumsjNY47xlsH/VJWuRmFTPkOI/RhtPVklnbMDgnToteAgq8D9HxvFzhiGPjoJyz9L1ERzdNw2y2QJtrnB/L+socR/x6DPcftkwL0nI6MYz3QbIf1cpwHfbYWJquRbHQFcF2mc9w3rHZ7XhK4Hmt+bpZcHK6Yr6a8XLo6G8GMbaHIKUPQqBzlmc3He/dv8dMG5q6Zb3do/Z9gRtE5iij3uu6zmWyUsZoEAfrMiPYWJZZHENTtkFjUr1rSLYwiVh30fnAoo0BrwlaCZ8eHEi4gWgTgssytHz2o2E8RMOyrqhME//VMo8q4H1PUIYhwBAN4yJXFTxVCWdH2IJ8LEq6q6bHRyVgONjrw+/CI0nAgVaKSmsqU1HpWnRjSqGVKXSY6egJTVBaozDRUG7SyOK5EqcCHx0JJFpcAmcORjLq66KDTclPfFV7Y8N46SGh1BjZDdyqvZ2AzlqbU6+nqIZkGE/9HGP+D5mmctGPMUoTBYtKUQXjM8BkfKXCpTSIH4u2OFTEhBDY7/csl0uUIjsFZANXdAwYPfgFO9x/8JDv/ukfs12/4umzpwQCq9WSlBZdoFAUGEaLYCm1wODs7AxrB4wRYBuFlEPiMEbCHtv+9PuhsuJwn5NH+s3NTa5bLcYqUQI7J6lXnU+CwpRJmRyWTFfkgN9lEH+Tpo58erM2rtU499uCb+5dHa7r7ZGUwtHfpGWin5pOfU0JWUE9D/4eDik6qJAMTqJgOAYnt0ddCMLcBT0/ezu+Rnf1fXycqZ8SZ0z3SxXIVU0Y4YNevmIMI4Ie33soYB55Th0wOnecrUSXy7ObHYNKgqWm40zyQnIwGfl2iZxrmoYQpL64804UtJWhH1x8mTCWQaW/h05G+U0Z3NLnkm/MP46cIbc6Ccegs1yPcPB5ZFwVZTxJinROiUh9XoMRNg/PStH15M3qrp/H3yaaIbmugppMeWRoi/kEVSxxvEslmqQ4O13x7rtv8+zZM0yl6Xsf8f4KlNRBbJqKqjLlqzNDKm+OtEzF9x0BwRRUgJKsKG3bsl6vaecziCuYGDepdahyGjFjdJrdBNHdpZxKZ6Jt25y+KbUkIGUBkXGXfBAD3Wq1ZDZr2GykdmtOz1vue4LVJGQU/5IE5CgNeePOps/hcKvS77EeWWLCIDFNYx/Zs1dFiFOKZOTTSl4y9ANNVYvxOKat9uU4KfeRsd9xdHe3Qvs23Ye4Lgf7FELAVBXdfs/6+oblckmoKr78/HNePH9BVVW8/fbbYiyNEWHee7p9lw3PH330Ee+/9x4/+fSnfPnkKUopZm3D/Yt7dN2+2MzbRrHb4xxnnIzKqQ641NodUMbw4ulznj95yjBYnLMyt8JISxhhKTsFRbykbkFZXqEjw1AHH9VozE0RhVFYtIPFec/Lly+ZL6TuVIrayWgujIa9NNbz83NevnzB22/PAJcdRJQLmfeFQNVUnLdnkaez4pgQ9mjTo3VHCJ7r7XPWe03nnvDZ0z8rsmZIFOLq7CF6HvlLH3JdMjF0VIRgCL7OiqFKV/zct38l8+J931O7QOVhsJa+6+i6jtViBQG6/R47DND12FhnuU+p2rzHRiNE8DGy1DuctQwx6k8pogE81mRH53NLAON9jhgUpUnkW5JABeh0lvwYXS6RGXKf1mpMIKLBEhgKo1HCKxkgVMAphyYaxxHztqD1hH1GIEkQU5VGfSXZTFwcb6Kn6PiueF+wPgYEKmBahy1gs3EuyQmHtcBHPr4EYblQ1g8OB2fxLgNAKTMdPnOsJdgunzumxJ+858j7XocnkrxU9nPMCfrYXLIBo3AImL6DKJAb4XeUjvRH6gxqE6gXLR6HHTpmbc2sbbAMhMHR9x0+WDovWS6apuF6t6HtFsy0Yt91bNZrXG+pMCKrdRZvPfuNGEyrqkZXmnox40wjsOntsWm9cVPaAElBLwrkytRU2kTY1EB0AnCyRskLX0GMiJG7tHxEBai9pw6ettIs5i3qBFZ1w0w7ekxUPkWldAjMqgatNNZ5Nrs9+7BnFupct+4QCkPedzE026TEVpEfUZLtSgHGK2rV0FRzZtWCtprFuVV4Flg752YtURh1XbNarTg5PaWuxTAe+oKXSPAes7glhWXwPqcl1LU4Eq7aBXVd02lFHzOirJYr7t+/T9XMYokM6WuvHcN2TecGKhXoh44vd1tePKpgMcNue/aDpe8sGzzKa7pQcx069m7P+/sNawO7jWM2b6gWC3Rd06+3GB+Yo6kTr6A1rpao/S2efZQCshM/MVrcB7w+dIBgoteYnv0iijrjQPnNaIPRtRgwtCgHd91enC1jlhwd9Qhd37Nq56IEdEOM0J+hlWbWVMxnFXWt2aNSxt0MEyk94na3lywiSJScRiKJPC7yGylLjGGwjs+fPOPsZMnjexfM5lKGrtt1DHbIEpI2dQwwCJOMCqXup8QdSbd1TAGcninx8m2cc2BMdz5nPdGpRnSBu1JZmnCkr7Idw6V34VXJuDJ1grhlsFfirC1jmT4/CpvlO0eJ9di7cxCRur0GeVxBTJSHurtjhuK7skRObyQ7qh3TCZJrUI944Nj7UktOqa8zjJdjOzxfhzToGI28/W5BgIf0+5hhvNzLu9bw36dhHKLvIMfPQ9m+iv/IxiKS+DzK3CXsJ4MPhJH/OkLbAVSS/TjEaeN4JOWwwvYbal2hvAY8lo6b/ppdD+cX7/P4g1/knfe/jTI1/c0NM6NYNBo79KzXGzrrWJ6eoyLvbbTGBOHj27bFo9h3Pdvdjuv1DWEfWK3mzNqWEBz90DF4xXBt2Q2KwWu2pufffvFv+PL7v4v3L+m//XW273+TE3Wf9+9/Db+z/Mi+4C8+/2t+/OMfw97RzGr6qzX4QD1f0Dx4zLI54/zBY96/f8H5bM6+7/jdv/wTXv3kpzyzT3nr4h4X1Yp1vWG26XG1RimHdYGt0iwXMx6aFZsq8Nzt+cNXn/L08hnNyYJvv/s1jN1hTMDPWny1ZNhZZrVGe0O3u2LYvJgKXHHfRCUWs7qUOhMfYpwoGANaV1IpKsoFeQ/j/0ppWcSHmDUs06v4/zI9btInROc4bQzKCJ3x6T2lrK9CzrYCQTJQ6Zi5JBvG0yOBfugZB5tok4yktG0Q+VvvPLv1GhU8jx7e471332Grev71/+ff8dkXL7i63hCUoTVBSuIkPBlEZ3K1/ZygW3rbs91tWF9f0232XKxatO5Rak43ePb7F5wszzm/t6A2Kzbrjm7T8eKLS4bNDszASdtyYgzLuqF2gdP5gsE0GGOYNxXaVPzcB19jtVwS3Kf8rW/9ddRZpDI543nUOmDdIilcZHuVYwhDdKiX9fRBZOpMXkKsv42UUtGEyJul7ZO1T2WLopSW9+BOySXKlyO+ils9sjsZtnKMWCDqdxJaCnk+avLY6Ait8nhUBGkxYPo41yyrR73USP+ODPnwQklvADdImT5n3QRtJ32vUoqT5ZzVcsHldZ+dEUJ07q3qqSNuykyWeBHvQ3aiFwfTBVVVM/RDHLfYD8b8iSONvkuOnPAAsQykQurG77xj6xzzYLjG0hFQ3tMCK20wUbljqgo1mzGvNJ3y3LiOQdfMH55x+t4jPv/RJ/hXgWU7w1WGXfAoGzibrRiuLaxO0SdLTFCiGhn2eBUIgwWrJEF5CDllOog+M/FOKQC4rmuM0VxdXbHb7WL6eimlnIzpIYwGcpIzhzIxG7WkpXfOok2FokLhUCRZCrzSqJAyKUjKLc+YQTpx5ZU21FVLU82odINRFUErlPFoU+HR2KDoncc6cTQSPJwA7W6ZP8MrY6BfCZOlPej1moNpU4hBv9I1TdWMsqquJJwnBNlzBA8n+Eo4XBi9MVWjJ2ZAixHiyUgeYoapMnNkYmXJOqFirm/Q3tgwXkY4pAkkpc6h4qWsWwej8Vhl76ZxkK9TnhxjDktlyFEPgEB+lxh5i3RqB0xcqYhJQmJSVpUG8bxY8QBcXl5ydnaW6xSUYzs0snfDwGK54ubqih//9Z9yc33F9fUNRmsuLs7p+47EICsNlTEyVlKaZc1yecLQ9RK5FUIk2KPyT0VuRGXSUQg0R5h0IeR3G6mtswTg+uqq8O4OYoSLxH7oh0xEcgrIiNCP8uPRsPSzGMfLnU2zet09f5P2JgfldYLrm78HSiFNGIUDIXLKZR78nd55rKWUPkorSf0ZGZA3xmYHTMRX3TxdOoG9v9lavZblObjvuJAZprcc+3ILng77mNKDI4LskakJHo/xq6J9HBVwRGNvjBardZ0jCMWBRtg975NlczRgTsYFmTnxkbGsFNSVoW0l6tE7iaj03tPOWvphSxYqKBn2OJdC6VHKLvFE5/MaVQvFGoTpM+XBVAUJPRR0Jt/UwdeR9U14KQRQSV7JpHkcx8iwlitVvO3YUTq8J10J07OnVTEmVaTgSjCO3D/6Y00VZ03b8ODhA9556xHPnj0j+FSH2lHXDY8fPhKDpJIamWNEqme6+6UzROLkx5q5mWHPYwiEIOU5rq6vMjwYTIbnVKMoGbkk5XMW/eJrBT6OGSnSteQ9meryHFOKlS2EGC1fVZycnrDbdTjvqCqFDkrq0ESFfwhDFnKOKcqiSFL2nrdHZ26whNtIn0OQ/QzJAS3VO5Pnx6QaYZw/cr6ddejKiHeoNty/d4+r6yussxhJchdTxo8KZh98Qe/GsSQhcTL8MNLIxKSWN4zOKiM9V2mvlKKdzXCD5ebqmn6352a95ubqmrquOFkusV3P1atLnBPnPRfTpnonRoDgPT/96Wf86OOPAWjqmspU7LuO/XY7rvFkT4uxFLCSxpZrPCdEoqLDVgg4a8WxIjLlhFHoUqrcUhXPmsBsSGeNpNAYo1hH/qfcdfKYSLhaiUdvEjBDCNHwGmjalqurK9abNbvdTryGK5NxxMTIWSgN03m4WUutdJ2cehS5JrVOdZpDAK1o2oqqruJxm2d4i2+K8wN0Ug9IGvvL9fMR5YbC6SVdY2oADSHwB3/2zwlxn0OQFOiqmANKcRHeoq5bgg6oNqAborA3Q4c2Bm8HauCXf+E3qSpNlwwmg6Xf7/HWczZbsN/uuLm6ZugGXO/YbbfstluGfsC7FHkY8NbhnXjFu1hjN0RnTE0U1NKKRAOXCvGsOU9w4ynXQZQTmRNOWY4SExREQe+DH8tMFDKEDwEbo1ry+Yr0TRGdeJQIe1lBF68lx58pdSvkjah9z9GQ3mT89qbGjxKWk0w1ccJNcF60r1JcH2vlOT6U0cr65mUrM2XdibcP5LZjGb+OGXSO9XPY5+R3iGUFiP8iFxPkTPngMCowDB26r8VBTSEG8cElB3NQFauTJQ8fP2I2m+Odpdtt2Ww32P3AbD5n3s6F147KJp1KcXnH4mTJt3/hO/yb3/89UPDuu+++fuG/qmmDdT3DYOlNwDYarVsINd4iEUXGgI/1CKmlDjVqVDTGKAQfFMoprNM421C5Gffm9+genWDPG07rhlUDoZ4RKg1GUTU1M1PRmJqh77m8vubzJ095cnmJdvGUhkC4le4ypQkcWyiUyFJewMexQW1mnLXv0OoW5+Fq16GbmlDPwbds91tmNSxWCxarJYMdePnqFZvNhlnTslwuWS7noIKUefPgtZRSUMrgBkn3bXSFVOMwBCc4xShFv9uz2Wxo25qh69l1A+1yTtW0NEaz6zqqYaCrazwKpzxbrahPllQzT69v2PmeG9fT6kCrjER9GIOrAp/4LT/tOzbK885bb7O6uM/1bmB7dSMOChgaDBoY8AxKE7RmrwN7NToHJWNoRGRkLrY4O2VkzKjQjOdES/SLipk7vLOAZrlY0dQzlK5kfgT6YaDvOoahA++pTIXz4mTl65a+79jtd3jnmS/nzOcNJycLFvMm4r5Sp6IxRuOVlGp7+uypROsghttsSM6hphLNbipD7x1Pnr6kqQxnqxVf++A9nHfs93ucdfTDwHq95ewClJFyYwpywAKMgRyHGSsSrrvLwCc4Lsphd2TpOHbNKQ9+mh3k0EBfvudw747h8Ltwucfdeu6wz7J9FX49tg53/pY7OHavz1LbV73jK5uiKN1xd3+HNOSutU7K2VJuzzzAHXrG1xm9v+r7uC639+LYGA9p8J26z6PvOLh+8P3Yehzr63V62sN2e74ARQBAeV/iMSbPlVLteD3vlxk3P0uuCVWkMo4x+0VdKQyiVHfBSURdqHnw1of86q//DvcevkvTzvB2j/IVN+s1L15t6Z3HBWjaFjvsUdrTNDWzZsaibamNpDa+vLlhs1mz2WxQLlAbg3JA8Gjt0PXA85fPWIUzvDFc7Z/zo89/n598/I9he4N6uWFYrdAXH/D4g7f5sH6LL4c1/68//G/4/vf/CJ68AGWwL3rq1QMu3nqLi8dvcXJxH9s0XMyWPH54zsmsZdjveH97ib1cc/3sFZUzLE6WmMWSzW6LG26ovMbsDdV2RxsUpm04rZYoHeiM5y/o+Phf/BP+17/+q/zG2x9y3i7otoF1vUPPzzmZ38Ntd3S7F+zXL7kNUYewoKOTaMCrMYsPKJTyqBQ9Hnn0EEq4Kv8WnwNi+KE807fxpNaGylQYZUgGzYCUcso8oYrQFnkPcRhUWa4Wo5HHeykTst/tRriWN1GZCuv6yDOmVPLgnYz15uqKp19+icPzH/3mX/Of/seOpf57/It/9vv8+fc+5i++vGS9H/g7f/8/4OT8IvccgufZ0zXvvf8Ryxksmj0Ls0ctG5Zzx2ef/zucG5jXPZUJnJ2dw86x272kQvPNh+/x+Lf/x2w3e074U77xbqCpWrR6grefYd8Ro2iSX5umQZP0yNEJ2h5z5lTRH1uyhYlKKjrA6JhJTYNk5glR5k82oOiQN57u8qRLhh9T5frX6YzHTeXO4BAOa3tHOIr3jtmusioiO1So4j8SX0WIae+KIabnUKNDZ7QvHTN6jEbxpL8pcW0azG2cmFk6DcPQM9g+Zh3MSC7umWY5q1m2FS/cJvM44nA/0M4WB2sRctYLrUUOHoaBrutp64rlckVdNWzDRgIVchrD0sFltPF9le0kZBlM4KXznmtvOaXiEs8eS49F+UDwEqU9dHvqpmU+m3G2usDpwMMA923DonOEV2uG55fodcfF4hRvYLfbstl23KsWVCtH0BX+7JymbWnXomPSswb2Un6i1oYQDdvDMJBKQ+73e7bbbVyTDmsdbVujtWaxWPDgwX1OTk6o6zrzcX3fU9cGUxmcDXgHdog1r2PmLu8DddWi+zmeAaUsKIcKZoStVEEIKSEQIn6SqG+DMTVN1dKYGQojDFAsd0zQUa8hJRVThomSmpa817Hmi4ChUmb4Ki7tmI4YYsmJqFusjKY2FW1VUymZcwanACkLSC4RnWCHQMAWegiJDg9YwQ1KSoSN9CGenCI7cmn7SDz8m7Q3NoyXde1SXa+knIHo/VMoR7KyqRAEkiHoLkZrXJApE1/2NRogDhQsB32oggin9x0a98v7D/tO7bCmnY51zfq+z57IaW1STYfMwFUVWMfFxX3+6Pf+JfvNFc+ePiU4x2wxo51JZB8o0OKp3TR1HIfCKiP107TGaYEmqYmZNv2QaUzOB1NV/Ai8r4/8KA38fTew3W2zAtAoqck5WKkzZp2LhKpUgpRECZIymds//8wtK3HjiRq/f9XRva3I/vdh6J68IUzfc6yNhKX8fuuu1ONXvDEe/oKhFAYvjUeIprMq1qg+OmB5Pv7NZyoNLiGTAqkekPAjc/ibrevh2hy/55iwVYwq/15IzBFBRvw7HX+Jf24pVoszkQwxoTxR03u1VjlqNyiyElLGILhGvMtiSibE4ywRAmdtZISK83kwNAH9GLkalfpVbZjN51RVzW4nTjrDMHDv4pzNZoePNQS9dUw5vDiXEL1tJ4sTiv8nylWuVbE+R8FUTe5XGZaKSAZ1sOQJN43saVbgKUS5NT4w3cnSGCZb7nM6XnE2Eo/f5E2WgoTz4oYA+nBnXSFwhZgifEx3noxsJuLh5El4crLi4uIiGrs1z589p+97NpsNu/2Otm352gcfcHp2wosXL3n06MFY20ZPz95o+lcjzQ8wnsv4f5XZ6Dhnz3K1KNY+OhsU51tSYNriTI2cShIEYbrt0l9ZF9fQtm02jI9GZJWAVd7rU7RtckCDi4sznjx5ShIqN/sB72xOSQWO0i/3Fp5R436FJDjlc+KLcRf4FpWzCyVmKTiJOxeD16iACkGcI5IRzUchLfq0UFWG1cmK6+srQiDWz4xpqvKRGZmxsRpBoj9xidLWKkQYHxc6bm1cN6aGhhJHJH6sbRqqusZow9XlFbvdVvgTpen3Pc+3z1jMZuy2GxLOCbkWteKHP/whzjoG5zB1LRHAQYyBN+v15KznMg0F+Z3S1lFwlO8JbhKRUvTdkB25QpB02iqAUSN/mEBekXJGxPcleYsQce8hoMo9peBbLq02UZBJSpoABIvzksXn5uaG7WbLbrdjPp8Jv6iSQ0PiYX2GL6nlrjg9PeP5ixcs5gskfbaUg7A2GgScz0p/fMDmPR5htBANcpS9LkreVMYUaQfzzQWeHb+nMz/htYt9CuV9wHr3CnbjtbSux4yX/+z3/ivh/SJ9KGneO299Q1J9tQHValANOjQsOQMfaJoZv/TtvxXTvjv6/Yb9bsduu8X2AzqA3fesr6/ZbjYiqPZ7bD+A81JfMQSCFccOvCdYH6MOE08aciR9YgV0kMhKHb38dV43WUhNICjBi0abaQRsCBhk74ZY/0upMVOEDMML/Vcmng/ZTR0Rx6SmYXRWKmWZcn3vMpak1G7JyJIMPKVMVco5dxnbD/f0mMxzTEZLstOhQT/Vjjzkse96T+r/MNPYXRGPh+tSzu/WOJNMEqIcFJTIUEnBOfRsXr6kXcyYty1zrXjr7JxLF9ht92ilcVpKUTy6d5/z5QkAbazzN3glka0KqqZmvlyIo5GXEiDWOVaLJb/2a7/OOx+8R13X/Lf/6l/yJ3/6p7fW82dp++ChHyAM1JXC+RbnaobQ4IMGbVDUaF0RvMJjckS7rInHh4HgbD7f+15zva9QfsX5oo24pmVZzThpWxZti641TgWCFiNDFTRd17NggR4qgm/YXl1FWU+890Pg6N5YL9EvOmVZcfEcak0wCt1W1LOWWTOnMTVKg0PThwU7WoKzdMM1RvUYLf2Xyt2R95OsEnVdo1yIET0GXSnsZketFVVdo7QobRQedGC5XNLt9ygVWC4WnJ2dcb3ZorU4G/RDh3vynKV3mMf3cduOrhvQXjFzgVcvrmDfsWgM9XzG/V6xWpxz/t67XFQas1nzxZMvebWq+I3f/C3OZyestz2bF1f0bmCla3QIuazM3lt6IOiKjQpskcw1VYJ/5UYlbSSMx4yrt6N8xnPog2T/sNaileb09Jz5fEHbzqlrcYa31jK4Hu8tWgfqxuTSTcoorHeS/QRRAp4ul5yfrZjNKwbbITzAGLWvtMZUFV9+9iU3V1fgBmaNBjSDS3gy8kaIzAQKbRTOB7549oI/+JM/pZ7PeOvhI0DR9x3bqyus85xd3JMo8JjVhMjvgUQoBq3xanRm6fs+w2jCMYf6J8FTboKD0vXy2RKfl7qmMlshJIc2NeGPvffZWVDHaP3EBN9F0+82vN4+g4djKJ8/xM3lfA77Tb/dwr0K7iy/9Zr2OrpxS69S8J0qfh/lgGJeIZH2MM0wk29RWb4vBjLWf79j7q9b76PjPdKm638wuUJ7p4p9P9yTu97zOoPFVxkzjo61GFl5LfGQh7T6UD+bjdVhdJi7a/yvW+dDnfJhP9M+PUoHQqiwQB86ButQpuWjb/0qv/abv8Pi5D5KObzd0/mBYei43u3YDGCqhsV8xsnMsKxA1S2zmUSCG6VZr7c8f/mS3W7PYB1trDO+Hdb0YUNjG4wJ1L6nbU+o5w3/+i//kH/xgz/gj598l+b9rzHM95izgefPr7j6l/+Szz/8FP8bv8OTF0/56Sc/pH/+FL2+wtcz5o8+4K2Pvs3y4j5NO8N4j7q+4tUnP+GHv3fFzdU1++tLhstLfut3fofv/Iff4M++/z3+7EffZxc6Qq1oFxXBGNzO4td7+qCZvfuQTbdHWc+8bXnrwUNeVor/+x/9Pn/95Cm/8f43+blHHzJXmlfPX7E5B/yGJz/9Hl/7d38CvzTuj6THjtWE0n4mfYaSaHutPS7y5c65WEKwKOFJiGq7JOMmmjZCXglXScIjctdZHjIVdbwnZ0lUKvcrqakd1tmYmTVQ1Q26Ev4p65UUeG+x0Vjm3XALZpU2KK9jVsY4Xh9AabQK3GzXXK4/5bff/wLnF9i+42//4l/z8x8suVl/xI9+avmLT+/zcGW4aOpsxK10w1ucc38f8MEy9J5lp+l3PXXfc9Ev2G/3BPbomaXd/tcQYGnEFtFWLe+cNHASqOsh8lwO20upGO98DL4DHxx9LPMi0fZRwo5nuYwYTyKTJEQ3MdV2XHtVEZCyK/gwwQX5bCfBHiRbWEgX1QQZhsm+56sZDiZXE7+fHgjlrYX2JYTiVQWM5VtHnYFn3M90DTXFvVKWLuT5jzok0a1kvfGExISsw5jQK1U6e4AJGmct/b7D2iHztiikTJOC+axmMW8IzlPXNdbVDMPAYMvyXCGP1XtyynCtFA7H0IthfLU6ZT5bcHNzzeB6al2h9aivAjWmxv9KGiM2CY2UeEApBqVYK0czW0BX0VnFNoBR4OLZ907kQBPAr3fYoeed1UO+rha0X1xz89MnnO0Hrtdb+vMttdK0leLKDTzrtnzYd7DvaVYrTh8/ZP/0JV3XMTs5xe529LstdljTrFYMw8But8vODV3XMQwD8/k81l2fc3p6wm63Y7vd4Jzj+vo6y62LxUJ4ZiN7VVUVxlSR5zNUxoAK7HY7FosFzkU6rhxaW1AtSbuVcI2gQeFLBE0qkhuJ6L5CPldoMOiY4UlTaZMDNIJ3uejE8U2a0uuQ3zE1jB9j5L6aD0yHz6N1TWUMdRWzrZh6ZA+DcGBDGJCI71QvvDi8KmXqif+CxzLgvSUFR2ld2IpRJG9hrSRgwTDaQ9+ULX1jw3jJkKcU6UqpSSR2WdfrUIkx/n6cCT7GVAG5Hnj6dxipcGucJIP42GeZAj5t/F2HOytli7GXSpyqqjg5OZH0E1Wdx5PqVSavncS81U3LD77/XZ5/+SM2mw2vXrxCKTg9PcEONhumKiNG8bqSnPrWOrRSXJyd42xUdGWrTjQgqRQ1fgiU3Bp7ud6Ha0/sEWCwAwrF1dVVTIEi61Q3NalWSErJmhjjJMSOQ1CkyNK/CSN+V7uLUX6jZxnH+ro+bisPbq/d7XYcjn6WsR7cTSkcfeVzYUzxJkrKmAoo9HcjRlWYFEPhzX1LCB2JevlLUnCUY/4ZtuON2uvWTIh1AesHY5MPBwL0YQevfTmTTblTCOU2/kpnxkQ8UFWGs7NTbm6uxYs51jVMXqjeCx6tqzriqkDyZsi8pNY5Ai4paJqmoa4rFsuFeM1ttgxDz6PHj3j67AXDditKATWmzRPBI+3paBQppV8VGbmSj711FgKMC5Q6j3gzG6vGaGcVa4qklClThDF1RUhXylqG3gdQfjSUJvzlXT4pOhmXI9MwMh2qqN2UHLSITK4wiDpG8GulqRtDXVeR0THZ8Fg3zUj3TMV8McvKq6qqsHaQSNPtmt1uz83NhstXl3SdlN545913efjoPvN5y/vvv01V1/RDP6mnOAG7yCyO6EDl60pR4N9x5ZSSuvPG6IkyVGq1SB/aaEIfBVOj0fnN6VUHgkzxhgxHITCfL9hut5IaPvUQSkeaMOKZKCj44Dg9O8EYje0lclSUltFQP4JmGkkWjsdhCCNXwrQuIOjg6I5jCSFxngLfEGtzjtH+ycM903w1pvLSSlG1DYuFpBCT1KIDphKHuEQf09rpWFt7IszFyWmNpPYtHCLKMSSHpGQwGmnXeFaCkprOZ+dnzOZzFIrNZk3X7Vktl+x3e4KTaN3ZrOXm+iYKZSFGDkuXzju2m62MMKYxc0jUrvc79rt9PF/RQBsZ5iSnyVol8BRHoVRjSKELXKvywocQ68RHOM5GyIL3C1GIVUpHB6/k4BON5pl3lvuNMVhnM/4qmyrSXWtjIvwkRb3H+1TKQcpT7Pd71us15+fnEUeW/FLC9VPjoNJihNrudsxmM8CCK4XtQx4sfU8wIAb4LIneQZL1weQUEo2T1j85wkwRe4E+ApJaTI3QFOXe+Nr4rNHjxTT2xFOrKa+ehQ4fuFw/i2VckLOV1y3idODTZz/MsJjTYMXvDx9+wPmjB8zvt8x5CAoxohfR5rNqzruP3mF9s2a/2WB3A5ubNTfXN/hhABfodrucDSG4QOgDuAj73uPifSbSVuctlZb6XiDpnUHqSWoV+yGgKwPOR6cSwElmiBrh/Qc8aIX3yYCejOGRh1c6npcpPz41wPgJ/cswVsgwx+SnvE/F/cfaMSN2+lwanEul1l3R7SoKoIdI91CmO7x+OI7DOR7ig7uuHZ1j7LPMIKKQs6MCDDdrVN/TKUPTzlhVNWf3H+IuJPXjZugICvx6y7obqKuaUNfCK+w7qq5nbwdW9x9w0tZ0w8BmuyMEGPY7Pnz3bd5//IjN5TVff+997G//Xf7V7/7ro3vxpm0/DISho1IS9QY11lYEXYOqQVUoX+G8hiAygAomwlwgKE/fO/rO0XUDXd+x2Q1crmu8X7KsA7VWhFDT6IbVfMlp21LVBm8UXkNjDMYF9l1HpSt653m129Hd3GBj6aZjSpK8T1rnGn9GC+/hnShRnRHjuGoMdQ11ragNzJoZbT1HUdMNPWioqxl1JQ55XSwFYYxhMZ+zWq1YLGY5otkNnYCmVtRVRVAavMekGtpKS/rI/V6ccpzFORdTfopRHR3HHhSNGwj7LfWsoUVTBc16K7LySTOjOVH4fmA77Hm631I1hvnc8G4zYx7glW7YDg69tfRqoBss1nksjhox3Ho8HsWAYkg02vXsYjr+ylTx3AW096jgJQX0wfkC4UvKIIZkVEi8BUEME8576qrJNdvrpkZXFYP1OGdjRg+PlFQz7Ieeuq0JkU8J3kfqo5m1M1bLOU1tsEOPosp6EcH1Uu/W9j2zumLR1gyDwzqP05rgLTrRwshTuMTHakdvPc9erfnjP/1Lfu1vKS7OTrj34AEBePHyJVdXl5ycnNLUY6R42VL0+piSnlt45i78mXRBqR3io9QmOBoYHU4Tj5h/yddh5F9DiDx6NaaTvE3PVT5fhzSlbHeN8RAvv6lO5RjeLQ0Ngel65uj/8v6C91BjJ2+kM1KHH7IoWtCP+D39XjqeJ1njqJ5SHV/H1+rPDvb92BzuWv+vXvO7962klWU75AkOn/+qNrmzZBwPriee9pDW/1/q/5K12r7x+950THdBxuHMhJ8NEZ6AGnSjxSn2skb/sygPJ1nSx4jT+LyOOFLAJMpdBUxlB5aD5vEYpTNs+4grnPdsux2DtoR3YhTtCiyAlzrSn6k/4R9+/l+JQe1rFj4IELNr7NQXfMzvyTgG0YPrpSYsAu7tiNujo++/q/9LvqtmuG87wtcHqlhmr0fq/KY5rJNTZeTrk8hgVhX+wvFJCPzD5xrz0lDrKhq2xehih57mFwZeGnEoeqFjkY94zoRkxhI2yB6YKMsZHXJac++TM2vh0B5l/4Qek9wm+2LiLYpkqCSUGCSM8JpKKvgYAILoelQlvLwLHhuzvipj0EbSiWstNo3gnZTU2e8Y+g43TFNaJzjzIM8FKSmVhGGlAs4Htrsdva1pmxalV1gL87ZjOdM8erDkrceKh28ZTPsj6qtP0EFovMHTffrP+eyzUYcSvNDiqjboEGh6i/WOsIPzDyRrpFYelIPQgRUn9f3O5T3OZzXVR1dKYND7rLsrDWWBFB0+Oh0mtjoVSkjFDcQuEXJCv9F2o0UOis9nXWHRRjQT9XwkmZ1bB18dwQQ54CHLKon+FvqAUuYNUQZOQQlZ3k4OU9P3iryn83hCCJlHFP1WaRQfdVZJ+k/3TeerxuEVehIBV81qaXl1+ZKLBw9o5nOGYShwXcDgOTtdoc1TtBH7lDaS4c65aYkuVIrej+OI+5nSss9mC9rZHFPV2L6Ptq20kVJe4y7SfFv+lN1L+mCFwnrPjbNgFNpUWBvolRO8ECA5jptor9tc3bC7umL2+AT1+JyhrnFe8fC0ZTtYFgqqStPXNdd1zbbbcz5vmAE7NL6uhZfcDaiTSGdVIGgvda+1ojaGpoq1w+3AfuuojcYNA7vthqrSsdxdyMGvKcK8nTWSKSTqS2S9FHaQ9N4+6hu7rqeuZygqnAflHSgvZd28QemUElx4XFnrkPnkoJBSSbFckknnzGhxe3Yi12qknrdRhhCiYfwrWKmJIwnT0tLyj8wnlbjjWJueZ0mjb+K/Sunkoo0o51WWSZVLUuKYIr1M3y+0QX7zweLDIM68SecVTNQdkeUFCVoYbVzpDJaWhte1n6nGeGlQLg3gyfB8qDg5rlyfMoOHKffGDVG3vpdKojKVYFLMpfceMrvHFColI/e69IBpjCUDnKI2+r7LxqyUdiSnJNEa5zzz5ZLv/cn3GYaBly9eYIdBIs5WK/bdHmUUGjlodS0AUxo3F4sVu92OujZ502Ug43xRjEZzNQLDXYb/Yy2yh1grkVOvXl3G10hvVV1FBOFxzmdmkkTCcrnWQDa+5YF+taDzN2nZaEJCAIfEtiQhbzqGcrxf/cxXy3DSX2ImfrY2FYRvCdHCYUyIvdQWqTMiSM/IGVGR0YzPxXSvyXxZCu8ZhRQ8RTnXY8aH/77bZK8nY0ssGnkJj4nl5cO3tjEzNSOMHZtu8KLAGmFfooaUkjSFWhvOTk8zbgkhcHp2yr7bE4ap9/RiuYg41mWBM4NAQvpRSRaCYTZr0Fpxfn7O+uaG3W7LbrdHKfjwax/w/b/6Ac47SW2U93j0BPMkI1fB1BSzVGr6fUQ6txcrdRMigUqsUfothBi5oUYXlUQcy1OaXjwStITfIpxH4UrFtMRKCe1JxmkTCXsqe1GZKtZdFyN3Sj8vnn1iDK+blsqIscI5R8DFMQec9XnpjalQJNoj2Tucs2y3O4mwteKBuF6vublZ0+0HtFacnJzy3vvvxmjyJbNZLcKGd9mAlKae6VKxfiM9G4l/VqplziUx9J6qrpjP55lGpsjP5ARQmQpUjHCmnm6lOs46lOeAuAbL5YLr6yuU0lJHp3QvjX8n2DQKYsvVgtmsZd1LyqbKGGwfY4ICRQqnUdi5BXGTS5KqaRz4KAylM5R8BoOK9OlAITgyVbJOJVwmoTRdmM9avHOidBegyTeW53zEy+NYtJZ07Ok+caiwDIOdKLOSu4LRYiR3wzAKo+mYGM3JyQmLxUISDFnL1eWVKNG3OxQSkVdXFbvdTry+C1xVbHnmpcQAKE4MRmv2uz2EILCvAt6PXsu3+bvkHBUZU+L6F4qKcUEpYC3ihZwfU/6nVIzcVSo7MIy4Oj4ZlR4hyFq6mIp94pyR1izuz6xtOT09o67FmVFpSZXv7KgsDyGw3W4l9VgwGHXcIfMQNk/Pzri8vOLhowayoi3uabkm2ds1GUmj4qA86yTaUKwRKtOHcgMn9DhrH6Y0crJfWo8rmRRj6b74/6D85MyrnCbwULgvcH2iL3G9A2SDTT4NWuODG88bGlOPPPrL6y95efUFKftRXOjCcCARwF/efCIOsInfbOH06/d4/91v4AY5n0PXsawXnMxXdNuB/WbPzfU12/WG/XaLi8b2YB3OObphj/KSTpshZlVwMV+BDzg/QDJ0R6/8YB3ax0gXFCr4zJMrFVN+4ZCaa9Hh5YiMk+BJ8IRC6kWHCV4o9xLGrFilbHQYdX3Yjhk0Dut1JznnLjmulAFLg8ibvO/Y72U/ZTt0ADg2lsPndDoLIa2tKLMc4kh0WmlmjZHIildX9OE6wm2sx60UQSs6axleXoMP0dvdUEVDolKKYOBys+M68huBQDcMNG3Dj/7oj+F6y+riIR988yN+6ds/z5dfPnntOnxV663F24FFHWtf6mQEr9BVi6KWyPHIvQcMLlauhID3sO8cm03H9XrL9XrLprMMvSGEBfMa5jVSLgDDbFaxaBvqpsIbhVOBpq7RToyjvbfM+xl1W8UsGIn0JyWKn8g8SgnNSvJ2ymgSgjg3uuBxAAbamY7v15zMW5bNAkONs4M4IOkKVE0yHoYQct2/FPHh/IAxht46LAFvolOEIteyTuUtfDdIxgkj/GPOgEcyVIeI+6RWfHAWccgLmAAoTagUc90y7yTi2zjDF03D4t49um5Hv+2Y7R3omm4z8OrjJ5y8F3BNS9M0eJRktYiRZ0JKDc5LyY/OWYboCKp15DOcZMrQmd+YsudJv3EYZZlqxGcDb6S5VVVR15E/jnziMPRYZyMt9KDEUchaKw7z0XAuOKSCIJH6bdtgKoV1A1BFRZUGUpSYpME0CiqjCA6CGznfpJQXXjvWeIdMaTrr+fSLp8zahg/ff4fVouXk5IQQArtuoO87gpfIneTAelcEd4gAepjufGpUF4KmtY4OkOmqGnmOrBIZcdZd7U3wc9anpDdlobb8Dq9DsYf486uMvuX3N8Hdt9/DgbRwpBX8egmzh/q5r3yYKCOky3eM6U3Gn68Vv0345PKeMB1FrrxFlH++UjE0mfUoPx+smsD/MfnnuLNZaRg6plsNh9/vgsHintTvIQ659Uxxba223Kj10b7/e2/lUF389/+PphkrPzF+LpsjZq6o0n3u6HCH3EnRj0l9dOyHm1vvPGwpDu/2GG5/3gWma6eBpuwr8qlJxMuO0SVsjvKMaB79BOYnEBW4BasoHc9doTNK8siIQCLdHGlHkknjDWitGKKjl496CxMNikpHPbuX4JO+29PtdnKf0lTVgb4ElemE0sL35/kqOTOb7Z6un+NDU9AFH7PVaC5ODL/xcxscNxAC1aUHD1Xl+dY7T3Ka6TRfH6R2ujHVRD4RGVU+ByeZYACwouvLeg4KXBDVE6lGtvaJ0sj/Ez5LNpYR38m3RJFVlE+z/i/Jk1mkj/dlWYF4H+P32HwU1pUWnUAICTmOOG4CLWrkOdPaCgpWBKKRuaQNBTyUsktpMM88/gFeDmGEvYwToz4lTDIUx2cmMvkEbLLMrvT0gKZ1VkpxcaZ5te5xMRg1DjqSD09wntOTk5xJTmst+j1PjPI/PEeyPmlAiX/2Xvjnummoqpquv52JLPM14TaPctiUbKTgJCWfrXNs+g5biX3LqoD1kjGqAmqklJGpBJE5Z3FDj94NDCHQ1bCrKlbNCe/wNsPMSUlfHWjaBmdb2n6g9rAPknfSB9BDLDMK2BhxbLSK0f4OU0kQlFZyrW1bFAE7DOz3e4CsP4bR0dRHR2AfDbcSrR2dcSKDkCLRtTaRN046DYFRcQzyUecZcSiMgb1JjxKIjvmR/04OTQrwHuUdOoRoINcjjN/B/9zaMRVxsz6UxUcAPsYqHIeDyKGrEVRzkxSdgjEKXjafFZXWZnQ4GWuyO5wf8CGmUs/vjftM0qWlHm87oxyW9LqrvbFh/JiHrFIqR3Qn5HlXXSR5XmVgKFvZ3+EhSwJNqSA6ZApLg7bKz8jUUpqEQ+VLyfCldx6ri1fOu/QEbZqGvuslvUoEfvG6meVUFdY6Fkqz21zhnef5ixf44DldnmK0zkS0qivquhLP4IhsnZO0blmYkdFSUBqJINU6e9uUROcYY8uxa5nRGK+lWgsJEWpEEPQ+5PVMRFG8gqIiTrigqISOzI56AxnhSHutOJMIoCrndOypkSH7m7VbaobJ6A4RwS3Kl5+R30Mo703jLsdc9ndsBcY+D8yL+aekJErGQ6mTMr5fPAqnkYwlClSZix5h4vYCpt9uj/HNHRD+5q10UkltuopqMqc7eqHci+muZClXfgslA3jQMiMcjZUx+leIjOHexQWPHj7kpz/9VIyAVc18PhelTfAMg2exOKFpJBJ1PO8F/AQysx4lDfqhZ24WkqLdG+aLJYPtefLkCaenpzx48JBvffOb/OjjHzFgSbxQZjqTAjilLclCliIbIRLzVu5pMRyI6cVT52pU1EzWNl5MyjxjFFVVo42WOs9aR29HQ1UZEVKigXs+n9O2bY5s0dHxaGJM8MkQIW90LgkBIb5XCOYw9AzDgPNeUno5z243YK+u0FrGFKKHX6IXiUFxbjReAljr2e120YPX0Q+9MHIxDaTWhsV8wfnFOe+99y51XbFczpnPJaU+wYthNRkkyIua4WyMSB0jh4UvLaPqEvcxqqK01pydnXF1dY11jspXI0OgUmS8igKE1KnJdHG62+MZmxxruauqKomsckVa9sSZRBwU8AlkSYyf1pqTkxWbm23OqCDphseU+fl1x5RCx3CPmn4uGTtt0ho6sdLFs5wxQPxQxVSswozJWmsldZ2DF0bZRG9RO0TFuBoFY2NMzgKjo4Ygiqkkg2HiTWazNtc1GgZL3TScrE5QSqK+UwkAlGa3205rfcVBm2hk3263uODZ7/YMVsYV/EAyCvV2kLROBBHCVFq/BC9mPE8qMbXCi9gh7a0c/My3FPAh/FU66xJVoHTCYanPiG8Q2Et4MvEemaFNiuDC+SUg50+FsqyCz8KnOBGEaXkflcai897UbS2RbCcr5osFdcQj3lpQsO+6og6qYhgG+n6QEjnmgJFRaqwBDnmt66ZhGCx2sOIwOnLqEX2rDG8i08QVuKXojPeEEefLMwXdTsqNEApckZgjMl9eHJzxmhsd4EYyP/JyEL3ji/GjyixLMkBPKkFUXB2PGCgVk/+OoOuzF2Wxdi6lD4v0SfIrx7MYz0+x9s4H8Haq+FKK55unvPirpzltqkJRV43UTldC/+qTll/+7d/CDpZ+u2O/39F3A48fvA1W0kQP+45uu8P3lu16zX67o9vv6botw7AXI5rzuH1HGBzKeamXPlgaJ0KhcxYfHDp6hIuXc4KvUZ44VDKPip+pTJVSRo97pSZ9HMpQxyLXynuPGdVhzNJ1lxNy+jzlw0qpg8m8SiN++X3cztdy+7fa6xT6h/0lxV4gZvzQBuUlqmvRtILng6IyNSrWjrfO4bXG6jpnE9Co6PEuCl0VIFhLjcNjCUgtu9YYus11NI7/KXp1zuNHj1D3Llg27c80z8M22B68Ay0157Su8V74TG0aUj1xQogKXoktcAHAY71n11uuNlueX655frVlt4dat8zqilmlqIxCardB1YBpFVUtkdzgiLZSdA2mVuhG4auQM0PklQ+lPFTwNWqMLiaEfEadkpquLniUhvlCc7KsOF0azpcnNO0J1othXCLRZO4JX1fGRMVeTV0LH1kpRVUZ6Hopn2AETnujscGhVFKdeKzrMcwBha4q6Ss6V0JUgGovRvLgUF6c1eikTidGoavouDRY1K5HDR7Ol5w8esTzn3zMs+sdzmpM3aJ2a16+ekJz75R6MaeZ1Rlvih+H0EyUwQYxlwxeeFYteQ9kHZ043OTzdoDvD2taCz0UxZpyIfI74/N1SiUb67ETJIvcYS1N4bMdTdvSuz7iCI82wl+0bRUdUA1DZzOtE15X5+dvrm+kFB0SWWI1BCvv0VrwfAjEKESfHeGED1Zsdh1/+f2/Zn19zbvvPObh/QtOTs/R2x19P0hEoB3QWhxnU9BCiGuS1yfS77QO3otjoJ/gppjxw0vtyBxoFnUko8CIRN6FQzyXjyejgn3Ep4ctv3pkhid8V9bdlDx65qHSMSx0Dbc6LkDlAJ8eygHlPYf05pZyNPJwBRm73Vk5mzB+12EafVy+j6xDmXDvox4r9VOuZ7EWMvWRJt1FR4I+NOjFznPq5iNrQ8GP3WF4Te87NNznLGql9iROL07t9jijbD7y7Ez0o2UZyXK+RwY12Ws1/YmsZwqJNxvHPQ5TjfsT76WO/GpQrMLi6JrdGkox9X9fTfhiQ1WPzvDJ2WR63yhvKzUdi46lcRL8pRTJae7pHAI5O5+LEehEHctuv5HarwmWUvmnWCIznRHRGwmGz6VllKQ/JqRI9ox4pOyLj9mLQkAbQ1u3NHWd4U3kwYD1km3JxQhy55OuQmfnYuH9AlVVR2M3KGWYNTMqBS7yIME75t7zvB7iYokMEhz46GANySkxGoFCiOWLRtjywWWal9ZhAu8Zx2iRicPUQSPjmUM4T2c7jLJ3iY6kjJMlEI1eVRP1U3E/YzT5frdlGDqMFhhqmqlhPMk+GZtHeQefDF+Om91AN4zZyWQQXhzTnEabJN6lutrj7GJym4OzYfBBDL5KKwyGEMil4nxc64BkUZTYi7QGoegnb8QYWBCKNcyrpRjdLeNI/NjfiILEPpD4ujiDeL7G/dFa50yBt1pB0/I/Cjx95BGl4HQ1fvcRHnRxc/6k4vxkUFn+VeVNaQwcaD8FuUVeVwDVO4kMzlmKEz1KL8uPHjiUp/fqpEM9Mq8YvZ8CJ5IONM3B+4ALntXJgroxdFbk96qqomPEWO6NNF89ZjZM8rCNZ0FrE7OQ1vnMjEct7YcM4PWOa2mpZI3knHusc2zxdF74wYGAw1MFaNC0GCyBoER/Wrc1frVgA1zt9lwpx1VraWYnfO3dt3nWvWD/cs/WDaiqpl4s2e5eMPchZd2WrIxBnNadDwzO5TKSfd/nGuOpDcPAYrEcg1+7PjsbJGfQoe+jjW8V9Z8BrR20YIzO+AoEn+73exmHqqMOS2W8IWF1SccRISUkWs4IgyFItjwlNdTRklVKnGZ70WE5jw4Jv6bTqib7Mdo7R94m8aLpvOkCf08ZTpibAAEAAElEQVTA5w0o86gL0NF5RpyKXZAMHZJZbsTPAZfugPw56UuiXosAIUaL+yFmboh4J5doLYcr9wv/NJYmQinwt/nsY+2NDeOHde28Tx4SKm9inepjJ2GDqOBMqWUKRrRMkT4u6HElyWE0Q/nu1DIqUmOkwzFDOPk+Hb2fo0CUmToy05nTAyrxMvNJWHMuenQZ+n6Pc4rlckHaFmMMXdfTzmZ88oM/J3jP1dUl280GpQ1n52diSAeaumbWtpLijcKDOcBysaTvh5E5zQxo4fkZQh4/YUz9SiEkH1OO5QMYObIQ1xWl2Kw3DNaJB50SY5SNKdxsrOsohoNETcdNCOUi5sUuNuhnascfzPQrlDLebbb6llGnFNKOyAjyDAc/HpPsyg5Ggp/WVBDT9P5xC5LZNhH6kA+0LJ26c2zlmCSocTx7ifQ679BaYYwYFZr5LDL3KiM7YxLTKmmVu64r0q6IwUzrVE8kiGdlyGJomtHRcZUrJERx3KRyWplwMhpTJz0e7pkqL6R7Yt/Tg5u9SuX2Y4s5ngs1AdMjMIQINvnUHYJ2ob1I6W+q2nC6OuH+/Xu0bctPP/2Uoe+x1nKyOsnGVEnHBavVktVqgTFShy8z5+V8C+ZbvBPBWsvp6Qnb7TPefectrN2zXm/45JNPqOuGt95+yPn5CU+ePKXb7Rn6ge1ux27fFQJJIoDjHpW1pLUShVUydCX8aoyhqiVCW4zbirpuYuaLqOSLira6TnVXhKE0RlPXJjN3qZ4RGowWA57zXlI3JoNPgBAU1nq2622G3bSO2QGKWIeX0bNvGIa8l9Y5+q6Lhs0YcedcNjwm5x9RLhx6mxUQmgW/EQbqqmUxr2nahtVyxfnFGU3T0DQVy9WCRTSKO+9jPcbx2QziEW+HLNwlsE57X2CeQmEkTdJHBe9ZLBe8enUpzFRWfBKZYxGEkxCV8McE2xbKlulhHM9HgoNhGGjbNj83CjGFi0qiFUHmfO/ePZ5++RRnPTrW+vTOx3rf6dnYH9OmAhzoHCfnMDGW43cx1ia86L2OcCwwmei80HVfHG+J7Ezp0V1Mu2x0xXq/Ba8ISmWhKPESzgqzHN9Ows3CKEpWma997UOauuG7f/ndfPzWm3Xmc3LtL28Z+iE6DjAKUdGRo+97fOS9jKkiTCWnu3FfbexPq5RhJxqp9bSmcPAOjEYrza7fY4Md36kSui0J1qjISUoMrTRaVTlCOsNO3CPhpW7T9qyoVMkhUYDTR8V5no0K8ryCXE9IK2bzWRRUJOW6NrH2Ui0K8XbW0jQtTVPT1I0Y+QWQ2e92dPuOqqpjytgQHWl6fJjdPvu3eCoRARRSJufy8pIHDx7Ga2m9890Zv2c6GJl4dbBvRPjLL0nnI30vxhTi75lOF/zReByiQJEVFYwkJ4h3bhqojmnyRoaLiAJGcSsL/Gng8XdJx5fQpCrmqQiMzgchJMeIkpmTFITi853eF+/L+FYGU5gKJqnhEy8M0Nke1W1jBLy85l/87j/OiSmSouSLywvqej6um5c9dXNHaDxvPf6Q+xeP2G7X9F1Hv+vYXt+wWa+ZVzNmumK32bK7vGHYddihxw4DBAfOxrSNUoZIxwiAnH44JCDy0fDjCyGwWIW4zC4EnPY4M2JlFcQrPvikDJQ9zOtDclUR41QmLkyzY2UoLZTsaZ3S36Q4yPgq3KaVoyxzm1c8vJ5o/MgXj/0UnWb5J0EfJa+XZ1rQBxVTHPoQU3jL3JOzr9ZKlMhBi9d5gKquCCgG71GT/fEZpjRi+FLDEEvSRhPrYJkrRdj31Kai261RwaGMlOH479K8fcHSGFb1ikW1oKFFBahqg6kVTovyp8WhMISgIKQ06hB0oFeBde94NXQ891v6S2jDhnXrqZsZs2rOvKqpajDzmh7QwaO94OMheu4PTpRprnfCUxFwHmoVMAgu06io6ELSl8c91MaIUo6o3EEck5y3KDyNcZw0Wx6dGu4vNcvFu9hwj3W3oAuXKNOjlIegCTFVfFPX1JWiqgI+DPSDRH5stld01sVSB4q6qXEnS6ztYxk4MTpcbtec6BpXwbDbQT9gY5aQRhmqaOjQRjELAbYQNo7eBgZTUbeKE+X57OUav17T9zv22rOaPaBzA8orhmAI1Hxo5rw3h80Hjzh7+z7WwO7ZJVWwBAzaR8cTKnbes5sNXFbCKxsP3gS88WjvqYPCKoU1IZaIKKQG0bwJvCoVHenSv5q2qRicpe92eO8wKJqqwjmFbk4wppG0j8OAH3qIaTC9UQIHADbgO0dwsq9V06K05/79ltWyptK11Aw3wpc4ZyUFpDZY67h8dQVBYUwlSthgUUgJCucUxMhDF/kXkyJr4jy1VnQu8MOfPuPTp684O13yzuNHvPfOW9y7f0botwy7Lfv9npt1x2y2YLFcooxBqSD6DO/RVYPW4vAaouI2pc0slfqhquhtn6PP028myhw5k5W/w2hMyfMn3iWmNLVW8JNK96pRn6YS/5T4SnJfEwN14iuOKa6VymmTy3GU45sYMJjy3mJsmeLsQyNvvvdIlsVyDcp3lX9Lvd4x+pN1gOH2+Mu+INE54eu11igzVYpKVsfbVuxjBv80p9tGbZXHWdK8Y+tTjk+uH2RJUYm+j/2oXMB3umZxglkmD3oMDkpG8aMBSAcybbp+CzbDcet+3isSrzXOtdxH34o8v3Az/vMn/2nmT8v1OYS3Uh6+vVbpmge9R7sGEzOGeBy+qhh6TaXAhAHrtmyHLWf3PuS3/oP/GQ/f+pBq1uKVo6k0dAETKjrlcNqPhpDdDu+lXu98NmO1WtA0DbPBsR4GrgfHTeeYDVc8GXac7uaEAEPreLxa8d3POv7550/BOB7M59w3C/7fn/w3/Nvv/j8xYQm+we8Hqutrhusd9Apqg6oU4GhPz/jP/pP/Lb/87V/jRXfFv/3Rn/CTjz9me3XFTGn212vmVcN3vvktPnj8Lo2pWLYXOO+52d1wfX3Nb3z4m3z00dfpfMdNv6ULniEY7tslPuy52l/xdP2C55fXfPzpj/juZ9+jNx6jK/z1wGc/+WPufeMjZqenPD7/iO+8/Wv8vV/8Rb773X/IT3/yF5xUivm253/67AX/i9/8gzHq3Fkx8+iAqoTeiI1KR3gqDDNK+NRJeYkI1D46QyVHhqiUEtgOIwYcjUmJB4wQqRRoQ1ADo+xNzDSjGfoNQ78DAnW7jFHgChWNzZIqfs9mfUnf7cUgPpvTNPMk0JRHMOKV5KhdGKCDZHN5vq/Y9IrgAnXwDAqcl368En0rIel6pkF+3jnIEaD5FMj/nZhvUxZX5Q/OMkQ/8tH5fBTkC17dC/dalvIKJL2sOnirXAs6S68k206Sm3Jml3Q5nXtGJwfJohVlmjCVUUTsj7Ks1mBdlis1qoCBsSW9RAjiKIIySNxg1P+YAufEaelECwPRQK0k7b6JWaeSfAhZp+KT80yEU2sdw5AyP0bYiGQ6kevsuEVybJH+VJJlQwqgGDc+KCOGcSc1xjc3Nzx48EBkUpX0J4paKRarnvlKsXnucU7qOHv6PM80b9sPNPMK21tCxM9Ka5yLma6amsXqlMVyxeXVS0md7kQXmc5iH9P8+6I0j6z/bTqnTMweFCq8kswXVgWeq4HTIPXFHY4ZMKOlBp51axbdnJP5CfOzUy4fnPKvhwXf2V7z8vOXfLHb8OTRmtNvfsSr9RUvb7bcdAFHTe8a/shV/JJXzJ2iGcR51bQBbxzWBcJgWDjRVUopSTMpmSkGbwNo7OCww1YCgILFGQl0UAGMUrR1S7/v2Q8D1oGp9rRtjdJgdIXG4Fygtz0YR8sJvX2GC1DPWvZegfFoE4HDabRyqKDRuhkPXRAn+05JMJ0PPToYvFW4zYbL/Su6fkvwHqMMtnZUOKoQHXuVnvCF5b+0dykDjtdS1rVSmhDLD6ooF9sE1wf7fLjvgh9qFB7nofOWNT1nVSUJBIIFpUTyG3YSMKAcSknpukCQc0jiQT0hWAiOZEUAcVjTukIrceIVR7QAQRyQvPOS5cr7zJv7OzI/HrY3Nox3XZfT0yajc8m4VlUtit8AdnCSmiDWXMxpN4rNOEyRl4wRJWN8THmSi6wnQpmY5nyT/BkjZ6c1+rKyRsW6tYIhozFfkFpi0gJjH6jooR1iSq8QaKuKujYCkEYixHe7Pbtdx2q1ot/vuXr2E5T3PH3yBBcCy8Wcum3o9juqStM2NbOmit7RCq9EYSMK3Zqus6MXClMGdlQ83xaCQhij2cZr/uBuUZKK0TPk1M/rzU4UKmh0BXVVYZ2LXtCyyGIoM6PHtU+OBXJ6SgP/keEdbQp161o4ci1dUrcv5ftL5mBUlh5/77HL4zofu0vmOKZvKYlayL9PnyiEiKKP6UvjPWV3xSRlKQthJ3WR1kMpSWmsiJG3io8++ppE2dY1hMAwDMxmbSbISms+/vHHXF5eCiNhNMvlgqAcTd1wfb0hBSuGiKRk7oWyf9S6HwiGh2tfslYHk2O6nxND+IGTwfQxWRVhOohMXVlXu8QfU0Su9VQALr8nQ3BV1/H8xVrU0SBV13WMnhRFiDEGU4khRishZFfXN3z6yScMVtI0DoNluViw2+/o+w47OB49fsT9excsFrMc8Sz/G73TR11GUkyIgdiYwKxtWK5mbDeBt99+i88++4Ltdsf3v/d93v/au7z7ztv8/Le/gUEiIG9u1txs1wzORUIiCh6Zj8whZRRQKCojNa6Sk0zydAwh1maN40p1u4MX54ysGAmxDk+QUhMKRd87djthDlO0inPC3Hvn8o4lr16XxuqVrKONkdkRV0u6eDFmBedIhv3UV6pjJV7RkQNQYzSqKpW2WlNXzehgFOFCaJk8p1Q0RNYGo6UeedNIVHtVxdTtRlPXFbPZjNm8RWuDdQ5rB2xMxZ6Y9HSGkvfteKYFx2dhLzB67qoCo8So/+xwoxSzdhYVv4Hkhax1FEJUdHayNskFY/rZfKxu47tDlBWCROlut1tms3ney/G8lfQnGg5coNKKexfnVEbjrET411XL3kl6MaNj3aP43C3TuCIb9vLwiqEl41FWKHnxkE/rnNctiAetJmGQaLwumAmFyYK4Vjqm31Z0+y4zmkWHMraYAkwxCshkRVfcJR/49KefMQxOstskb+O8j9LEsAaqqK2GSllxapyTPT1dnbHZbNmaXT5XOuUQi2MUvDbWmpcoZTGCS4C4nFWNkch6p6iUeA9rnTBSsdhKRFUQdiFHaCuNjvWWSXCaBcKRUudxaR3Ta8v8fZB/g+1BBSqtCdrHNNaSDksbiS5MQWxKwWq5pI+1ZkMQATzBwmAtfieCbAgLqkqM46AY7EDXD4QQWN+scy1V7xTW2Yjv/ARPpHmVLcoELJdLLi8vsVZS+ZbG2lsOZQW9FPqZyKJ0lgyj2SEtSIR8QR0zzRgN8AUMhfKIJHgY6Ul+U+TryvPrDriv0Rll7D/fHULSjeTMJkkZQqmgTYuU+kl6hEgrklIpzSsUbxkNoUSieMjPMuEpvBojtEpFb5YdyrkR6F49y+ekXLOIirn65DnqJ6ODoYoygWpgmJ3glmcMp8D9OWGneXT+ESezUzZXa9aX18x0C9Yx7Hb0u7Wkch8GXDegbIo69xJt4nuqSvh+Z6MxnchnB0mZFrTDKicp9II4vyjEcQcSrKSISFBB0q+pIIKwQWi9U1MjxmEq9qQ0LrMplP8myu3XKEvSesEo/4UD+FcF/5s+51/DtM+EC281NTrTJSjSKvKHIRDQONPg430egY+QNj1GGlRx4xPf6L2k+tZK4ZRCKVPImRA1IiP/EizQM9BBq1HNG4vbR9tJU3Mym3GymLGYVdQVosRTvUSxYhCjfwUMKGx0sBMKp0KgVoFZFTBhj91e0duaoDTKOrS37HTPrm5ZecO8m6PaFUQaGEKQs5xkQFTmUpOzSpg46xYtHPDeSUGaNtALFwLiiDmrNKtZzcliRlXP8baGoLC9Y7/twELoepyCpm6YLZe0bct8Pmc+n1PXdT4/67Bl6MUpJWVDs7ZnNptRVzWNqZg3LdYOogBfLtGNo43GvBQI0A8D/dAxHzpebq7obUewATxoVfHo/B43veKzFy/Yux5jZqw/e8azjz/j9GTO4BS9bnnr4oxvP/gWu9WKy6stL64u2Xz+jACS3cJC5RUOxU4F6lBH5U7iNQpZMspht1mkQ9lmPG8+OoQoJU6kVmt8lG9mswV12wDCxyvIxmPnXELW2H7IikV5oaYyNfO2ZT5rWK0WVLXoNVIUeTb2RTywXq/Z7tZRXghZr1QZjZXXcFT+l4lnupH824bB8uz5FS9fXPPpp59y/+KcD955zP1759w/v4d1jhcvXvD81SXGSFrcVAaw0ZoQYrRMNZ7TXIc9vrOMwC8zaYx6EKErtwI3DpSRsicGKcfkcqCIj+WGki4slee7y8ieYOBYpsa7WnZSgTv7zIJB+krikcstuI3vS0Px4bVj4z5sh8/fOQdur216PusIIWY6lBIJZd8lHB4zYB+OsTTQH8731tiKsdw5/oRDy7VJ+ovJ/Ecu6NjYxjGoLFOWYzi2jsfWd/o9jLrC194XeewCtrNO+JE870Pg6vr6jdY4ZU+7q2V+RGu64RJtAkYZNFVUuwUGP7Dvd/hqzsnb3+E//Af/K5Zn77AeLFhH1UKH5fR8SWNmzJQEOnVdx/X1NXYYWC6XnJ6csFqtUCpwc3PDlVO4wdENPcPQsaVBmxWb5obTmeJstuCTJ47/wz/95/yHH77N/+4Xfp5ffnjG915+zP/5n/4xbn+O2TuMdtDU2EcPmS0d3asr9G5AdVIrev/Fp/zuW7/PWnuaqkFdDyx9y+MH73P/7JR7qxPee+sdfvnnf4FaVXjnOD2bYWxg2Dj86RKrA37d45xCMQPbYfZbPtUdru9RBM4v3uJbH/0S/8nf/R3+/Ht/wp//6Pv8+Iuf8rx/SVWdsv3yCqxiW11zs39Jt3/Ji+uXOGNoVEMV9TUHGyTRtMFjB4tXDlKGslCmTQ8i74YoVwFZrxkSXZPsYPIOJXK6iSU8cumyGH0cRD+kE69Tnv8RVKOILu8xxoDRVFUTA8LkNmsHhr5nt10z9D3zudRcNlWdI3gPYVLF8ieK6GSOmdRQT1kKAyNflGwM0kn+Xznio7QvsbWlhJJ0Umk8CXWHON/Em439hlwKJONnVJbH03sO3lzgjRADaiYrkd8x8oKyv6LXUgUPGPIjB65Wk/5KfJbGneZ9G6uNeHocj1yfzCXL7SpPMuldJElZ6XwlfSRjtqx7+i1miux7fMqanAUVhTgj6MyzZWdlBLazLrUU5PMQizErhQuebi/ZAI0xclKUyHDee5p5w3K+4KW+gViKxjmHrtSkY2sHGub4qC9NWZXBZz6nbVtmsxmVqbIOVwJCZQ9T4MCbtKQv8CplxpPccX0IBGXYq4BXNQvVUDtPz5bnl5fUVztCNUO3Dc9mFTezE/7+40d8a3Wfn1w1fNGv+b/9we8x97A4P6NvKl7urjhr5nx284T7m1c8dj26OqUKCvYdDOJs2TtL1+05BbbbLW3bZtq+3W7RWrNaLdHaMAySCens7Iz9fi8ZPiOvttvv0FrT9z191FEP7YyT5ZLVaoXtOzbe0e33VLXOWTm8kyj5kGtOjCUOStgAxPkkkBUVzlv2nUXHTE5dP2AGyxB6vApTuNGiw0u4YIIvuM2LltmPXkeD32jf4xn33uK8YfAa6y0eh4vKJ+dEPnZhEzPpSZR4cuIRSdZEo3cNNOgQKG2yorsUJwaZXUprP2bnE5YtypmH0VSvaW8sqScBSCkxsDRNk5l5F40RWo016Y4uWPG5ZOpKT8wkbJXCxrFa3+X35K2bXnLI/JbG+PScMdM+y5SCGWgmqbpVFobK8da1pFTf7XZUVUMIsY7lbMZuc4N3js16w+XlJUZrTk9PxECkFXVM2VauRYoZrZv2qKdsWscpCWEMyEtK2yMKq1uCU+xzjB6St2+3Uo9UBySlThDDgtFVjj4U5awvhLnUJ4zGcaIiaqrsf9MWXvMtvexwHY4LVMefvfv3o9q2117L8JavHcy4UGCEpJnOtDTc8Ya73lkyIePwkyCIikZehJl89PAhohzU7Pc7Tk9Ps4LVVJqu2+fopaBgPptJdFVQ6PUuKgbTu5JxnCw8ka8nxipM5jWdyrguKZouwcctoTiuj4rpvfNakwRgIfyZyWCMYi0F5DK6WcdoBVMZSect3OGEqIQIs2kc3kmUb+TUhDjagSFGOocwpqNxzuJjvb0hGh6dle9nZ2dorXl1+YqhH5gv5nz44YfRYy2m9/PjDh9yTVnZGzd9iCUbLs7PsIPl9PQMrSs+/+wzdvs9P/rBj7h6fslHX/uQRw8eMmsWNBcz7l08wAaPBI0NOf13YkRT/ZSkBx16h8vpEkccmJRl1tpcZyVtkxjCXVwPP8HLKSVsqWwolamhFBQCse5JTGcWkmtAhIuUulmpmI7L5KhY6tGRa6ydQlSKjenatTbUscYUECOLZU/SuZW60BVVFRVeWuW071J/VDxKdXQ0kHcFnAsMg8O6XlK0RmN9PsFpfDCB/UwTkGgHEyMeAkQNf0EH4ofkwKUgG+v3sdRHwtsoMbantN/Oe6kynhijYlwqH/rJ8cswGUJgtVpxeXkF3KYvaV4lJAsK9MznM+aLmTiI2EHWcoip45zHhJj6Oyr1J2SLA9EoC9wjvvQc54NCkCg1acIwiUNKGY2YhDWP0g6tEee3qma5atDa43yH0R5HoTiNwmXQRUq0IFHao9ypCA4+/clP2e33kckVJjDNI7kCOGfBi/dmgrn0W12JR6rQ/Zp+57B7y9y0ZINR3L70XUFWVGQqFdMm5fpIHjTiROVxgh+90A5JwS9GdAERxZgRiOjUIF75GB0V4jFbiU7nVBcGe0CFfO4C0A+DGLGDxyJpdfEB23Vi3AiewQ1Y79nstvTDDnDoyjBbzNBXCmUMPmVqU+AQBYv1PidqCmLNiCUdDMvlkqvLK66vruJ5Cdnh5igZPsJnqMh/aW1YLBbsdjtWq1VxphMs3342882qoKskEDrkhIqzVhDnWwqG8vd0eUSrxTxSJFmi5/LMWHLlcM4lrR8nH1JfaW8Z+bGSzk/rQ43roojZG4r+Mk9we8FuraFSU8VVdiaIfPzhuqvIO/gC/6bsSyqtQ76XeIbiWAuFuULR9S+4uXk58hza8OXVX/PkMj7bKBYP3kczI/QKhpqPHv4K/WbP1auXaAfdzZbtzQ1912P3e7ST2r2uG8B7bD8QnCd5g7T0tLbPsrN1YiRXBpIx1KnkVKGyYsep0Qilua3su73Ur/8duCWrvImBozRKyP0FvPwMwrkq8Vnxf9QBmKS+o/NOGt9h1KBSyfkh0ovDzDGxr8y7HMxlvC8wX8y5d/8epVL0b9oerJaczGecLhtmraauA5VSaOMJ9BHZa/AVPlhcjBwHA8GgvEOxoarWNGaHdnteXb7ixYtXDHbHbLHi/PwBbz1+zHyxwLsO7xdRcRNl5KBzsaVSsUqknaXy9K6mOIQTJRE3Wn6tjGa1rFm2FavZEhsanBOHSjs4bO/AOalHaEwsw1PFCB4rimjncG5gGIYYOaQwpqaqhdZsNjfgESVf5HO36zXLStwKtPPgLGa7ResqptpWGK1pnGOYaWhnhN7DPmCCREDf7Ha4Vuin8wrOT7m4OKFxjqp3WF3x6nxGN6u5Xq+52vfsr3ao9QBovLdi6EEzKMOV8uhQs7dbbI4cjo4rPqVnPcBreT+kJYfNqREtxFSsgu+89wRTUTUNTdNKCnqEd+26DjcMooRtqhhpa6V2uPJYNxC8Q2lFUzcsFi0np0sqbRB/JD0Zi9aGvh/YbNZYa2nqBoWktwyAVQpUdE6L4WHHJHSlFNaPZzrJTDYErtYd291znjy75HS14OGDCx4/fsjZxQO5p+/Y73dsNxucs5K1r2lomoaqbdGmmuCFpOfySCQ5TOWZQ963LO+XWmlMT7xTKdslOZC4H3VdT/o/7KvUa6VzdAxtHuIdT7iFq1Kfk/UtpXh1mw4cM8RP6KJSt66V95VjyMYIpkrbjIsP6EmZjeiYwVvSzgaRAfTUcaC8L937urmksR9GvZe//+zKZFnhrG9M+odbazUaqY+9b1zbaeT6LVoURpr/1Ybxu8ZxZBqRNzvc25xZRSmWq1WWDw71kmXKew7md6i/zOvmWhamBy0lTbTX1Erh/IbdYDl9+A6P3v0GH33n7/Dg3luEULFattSNpmkg0EvGiv2enXV0g9AMAyzPzqIxtIplrgastfR+oFcKZ2DuK5oOLrdr3r43I1SGP3+64f/0z/6CX3nnIf/7n/8l3jlZ8hfPPucf/dk/4/L6S4JvCPsNttsTTI354APqxUD/6hXKWvTgmemWX/+7f5svt3v++I//Le/ce4tvPfqQ3/zoF/nOt7/JvYsLlBM+0A0D66sbZu2MjV1Ta4MxLX7o0b4X/h1FqxStqXleV8x7z+AUSlcYa3j25BnPu453Tx5y8Z0F95dL/tF/+1+jLKjg2Dy9ZFG9Ynv/hp88/Zx1t6Pfd1gdMH0Xo5kLUCBx/5LxTIytpbNDKUuMuvxR3y7Piy0hELwb6ZuX4DUpb1KA6CSARkUHUCQjooqueyrJzZHOBYqzHGE3iDwoPEPHYAfqRjKMeUQmS8Fzhyfde5GVEzx7QMX5Ox/oraRNL/lIlWWxYvyEqdIiJI49yW/xzKd1S3pTRIbKaYMzFyxGzVIETLLAiP/K88cEbxzHE7EXL7JQNpAHJlmjMq714/vK/U5jSXpo2asSHsj9JCcJJjiG4y0EYsFhsvQsCCrqysLBuqfVj7qzmKFmXJPbL8rGcZ9o8wH+VwEYsyQTYpblUEbNF++IvaZ5pWCFRKeds2y2W7p9x2y+oLdDIe8rmqrl7GzFF1/eYAckM0KsN1/OcxiG3F8qfQMpMEnOctu0zGfzWBJun0sXOOViv8ed7w7xfyCDFEGHzMcRFNfecqLgGkvvazQVGxyfVh0XTrMKgZ3d8WVY44YZ37t6wf9mrvnOvbd4Z3XBD19e8Rf+kkoZVsuVZCNyjmA9rq3YYRm0p6kqqqCofUBbT1s3cHYKdkYqf5yyAqV51XXNfL5A7Jw96/Was7MzZrMZm80my3xleecUONf3PbZt85LLXkup47S+yXFSyuwU+FMp0FIhPARHSreOQiL7fSAER/BSvk54Bg8mYILGu+S8EaTck/P4oGNl1JjLMEDwilTiJ1P2hDOUyg6E2R4S5YWvaiXvEeIZCFoRlIzT43DB5fTvPgScsng9Ok2opCtEo3RFhUSDEypGGUJHPrdwcInNso0OVyGeq+T8k3RAR/RId7Q3Nowvl8sYGV5RIsxk2E5NJWG1yNufmtFjbalDJq6sZ1e2ssZ4Uj6k1EiH0eOHz5VjO6y3Vxq+gNx/upeEoIoo0mSsT++zzlEpibYcouB4cnJKCFCZik9+9GcAfPnkS6ltWBlWq6UQ3boWIcxU4okmM4kIz9E27TSyMJAVjjoCRSIv0yi3uB5HmMpjCE0UfiKMaa0Jg5U0v7FeWNu2XF6+RCmJ5Atx/pkoaznISTwXReFIUALEjAE/W7ulDJ7yBvmuNPG0n7dg4c6TkJ49yu0f3PO68Y+ETeho+nvXrVFplDV5h+//qqMbGZgoBIeiq6CIKXijwAW8eP4co1Q23Fo78OLZC7wH6wRmt7stSkkNw6ZpWG9uaNs2KpRKRbBEyad5HDID5ZRHJ4EM2XJNj3XcTDyjKbIwpeNOtX6TMaWqKipjJGo5Kd6JZ7xUuCcY9JL9QMV5p7QvPiRjrsV3Y/rt4POTBaMcSIrVEGu1CI8zFdyFYR7rTiUc4qzLMKm15vzinHsX93j69CnWDsznc77+4ddZLpcZ5414VBV/wxF4Gj0wh2FANS0PHjzg+fMXrFZLPvrGR3zxxZdsr7dsbnb81fd+yPOLlzR1LWkv7SBVPZxFDOMuM9Vp7cZ6ORoflNSxOsDzirhWyVCbBHLUxPMSKJSpURGhxZimCyeG5JEbkPrJSkm0ScKRKtaf1DHtTWI2IUSjXJWFclXA1tSoTQzsEpgzUWmYTl6iN3mO0Yis9fRce5nwBDd777G2IwShDYRYByieyVFwKQSyxOAewc2JDhkdCIYo+MXotGikROv8bGmE0kazWM7ZbrdjWr00fkU2Wo7jT5HTk0M82e/SUJXunM1mdN2T0TBw8HyCkYg9Mlhrrbj34B5XV5eEIBlnjDEiSBfZEgQFTxV+X4mR4zj9kZsCkTNVKRo/8RDj2iUBEaQ+ufCNAW8D3d5DqPFOU9cLYaCURDskY4sKHm0kPRoKKiW1X0fjicYPilpJJgFUQB/SgRDwJhmc04wjb6UkJWxV1XKGtMZ5R3O6Qp+fZpiW7BXF+VISTZjwJggcSJqswnitR/yilBj5dDzXRmuCIQvEybCeaF+u35mYetI5SmuuRrKbPsbPQQW6fsA6m+lOJaHs4ogXs0RY5xi848effMKPP/mRGNKd54c/+AHeB0xVx2isKiv+ZU0dWNkrawe6YeDevXssFwvc1rLf7dh3+8jDyryaps4p1+8SCssmPKLj9OyML7/4IvKDU6/9ES9myj3Z93hTxg+3YTjyOqPKZIoDymfCkb7TK5WcycQvJjVLNnDfmmvJ0494o+y7NM+HYq5pXEk5kOYhgmDCDwVuTM53E8VRWpoxqrz8baLviLS6bJPM/iGMmSUYowNG54ADeSGvayxBosa9SzTee6lPLYKhjYoY8tnYfflDtJYsIwrP1WdPSIfh7Xc/4kSd0OzPef/xh6xf3nD57CXb6w2269muN9i+x3UD3W6P7Trm+x2Vq3NKaoWN3ujyXk8gGENyWEs8DkpSOHot+TDUQeBPihAv+ZmvaqW89zqDy2Q/bsH2lId/k/P2Ve1Q0Zf+JmVWKVdOjTBTZ75j7ZZi99j7EUNaStv+36VdLBbMmoq2MjGltKRoNybxrEBQONWh6ABLQEOoCdTIab9B6StQW5zvuVy/4pPPfsJ2fc1yccqDR3t0ZZi3DzmtFzhv8aHJOSrSewS2VeRP9Guzl43XE25LeW/i/+MZicw7ikBTQasVrWmxQ4W10A0O74LwVcHJ2LykwW2ahroxGDM6Q1rrM58lGYZCzIzic4mZxGemmtJGx2rRUS6w1jJbNFLaIcoF2nuqZctsuaLfDuxfbtneDKz7gb0HNVvQVjNMqDD3FswvVlSbHXUTCFXF9aJmo4GmYqEMtuu5aTReQ+O9OMdrhdWKTmsGI5njXMLRKSNS4idHtmqCcxOBPdTJBB9w1qIrnaNPQAwmVdWKs1glwQbJ8VXKaTlM1UotcBvdy7zHuUGiy7XCVJrZrGI5n6Hi8wQxHJRnO4RAF7O7zOYzlOpRSrK2OBWNDTmLzhFoClO+Mle9IxknAvvB0g2WfT+w3ne8vF5z//yM+/fOWC7mLFenwr/u9/Tdnm6/x1lL8J7ZYpnlgjRepUenkDJaPDsdpFVXU9mnnLMreAmtTVY2J2eOlOlnklEjy1JTPCbdqswQj9FG5btLGg2JCz9mGD9sybh5XJmR+g2TI3+sz7vec2gcT+/KytU4k0OjNhAdpY/TmXR/Og9pnyb0JPKht3RGmS896JtYtzzT0eMtyb5f1QTvRYNR5I2P0727aMsoE5X82qGB4tDIlb+Xczvof9TrhaO/T587eDbNIcG51qxWUgD4UCc8MYxTwvUhnJffFdDi1Uxq0SLZcvADvQuc3zvl8Xvf4u33v8X9h+8y2EBbG5qqxqiAH1LWqUDwFZU2mFlFaNvsaJR0RokuOOfRQWEQB/OeQOV7PrxfM+gZ/+6nl/yTv/opp8sl/8VvfZvHSrPtez673vDx02e43RZlKoKyBCzBKczVDq+9ZD3pe87m5/ytn/sV/sE/+J/ww89+wo3f8d6jd/nlD3+Be+fnnJ+dsljMUQG63Y4XL17grcdXjjWeudGcKkXfDey2W2b1kkoplHZ4NzCrGwa/xyZdju2wdkvf7Thdzjk9Pefdt9/l/fff56d//T16bVg19zlvTphXLd/7ycd8/vkXvG0CulH4qDs8gIgIP5mkCJ+dax1HeMmMeigeC6Osnz6HUjcn9G5IqayjkzhJ56Sno0hQmWuyq9RfzN6W9IXZQO8JLkhGPyuly6Q8nBjk0SG/69aME5wWuhgfF8CHsd58MlOqQu441GQcPWklLYnfU0R6ie+z2lKNd+dyp4oJ7hM6OT4nl3WWCQnJkF/oJEcRNuKSWGInBmHdHnzI9X3H9eYIXkl7X/LSI10Rea+Un48sUdHN7TUMEzIV8o0hr0XSVVHeU1wb5ae83KN8VOJZmFb9HA/CCDvhYIyBAgx0Aa9yZbkIXF2/Yr/fsViuCphTmd87Wc6pDfQatKmo6ubWYgzDkNc8yXfpn+jCA6aqaNoZddWw32+o9OhQ4qzNdOGWIfwIjRCHFkeIesxULuDG9uy8yMCfMWDY8VPVceo1X2fJgOUJPddYGDq2fuC7z17wtfqUb9w/48N2wct5j28b2kWDc5ZdUKzXPbWuYnmyIME2SqE84rhJiI6Hhq7r2O/3zGazbNesYqDqGNikGYaB9XrN/fv3SbZH7z2m0jnAyxPieUlZLxI+SBktPPv9HhNLDBKE51baE9CM7i0RphAgGs+UyjxJ0AluQasgkdUelBLjctL1ipymCtAaAUruHGE4/1XRkSjZP1OkdcEH3jJXHWuBXAc88XM+1Xd38v5YWEPOdcqGGeeolcYgDhNalI2MuidJm87BaYWADgW/nvhepeLajDaeN2k/U43xxMAnQas8XFKTeGqEPsa4+kTI4m+lkTw9mw7aXcbyaW3zcIvhSgirFAbLw5sYnkNDT5kuUCeDbxj7TgaTPG/vCdE7p6oUKQLNDj0K8G5gv+948fwFClidrAjxcDZ1NNTomEU/AygQxBhorUentIgEUr24LAlxh9BxoNBLHjwcIq8QRIFNck6Q1KHJUzspDfa7PbP5XOYeRLmQGQ6Sl0jJFKWjKPf4om7l64SKu34bGeJwMAWVqVBS2ORxJAZ9ImJlf7n8xvGvOoDZCbWavPcu4U9ggkjgj8+QiAZT+uPJOCKTMzI3B0JH2U00UI8phUOO/lFKDE9NVXP56pLrq6usDJS6PtE446OhUStOz05ivWBJMSiGPVEENLVEYwAobagrEwmIRGskQ0tJWLIhnWRs1FmhMyri09qGfGbFUO1jjWmJHOz2e7Y5ilkW+PD8lvufifTkeyiU36VhexyHz44oPtGe8fkwGr+T8ewQXDOUBnL68UVM7ei844svv8AYw2K54L133+PBgwfZkCT1tCMhIRwA0BQW5ZLc56yj8x1tK8bxy8sruv2e999/n916z9XlFdv1mucvX0QDWoxkj7Cg1RQ/Cr40Ix5WDq2QFOuRYchCNqIIM1WVHRmI62cio6GTATyul9IpMqL0vheFdF0L/KRzoBiN4MmoHYsmZUO6FmDPOEgceFLWAPGiVUnxQCKS8bwcMHnJo9fnVMBRMZgdKyKu8yFGNshm+yT8FfAmUVDjyS0dL8ZzfptQZzytJEW8UsQI5BAVuTLmymjxlAzpnKnJs0opVssVz549xzsnis1KHMpk36NSxhd1hBP/U4xK5T0qzllxR3IWS/S20NaMk8q4OCpz47weP3rI86dPUQoW8znL5ZL1zY3UQIpGUOnmCB48RMFhZKzSO8MBnlZq3GOU4DIxBI+p19LaCchojGkEx8VzspjPMbrm9OQCZy2mFoO+c1I+BiV1C9OMtdY0lcnlUKp4Vqoq1ivSosysTBlVnT6b0QAd99fEmmuKGOUdo7CVUmDIKeV0jOQmENMNIYyzKnih+P60r0mJWtLytJVJCW20llTP8fl8Z8IJSpxBcHJUQ3aw8YkNLvB9yLyU8x7nHUOMGJeOPVVyRgxgB0vcOElltnNUvsUHjQqebjtEQ0EPSORh3TaYmJUHxINfjIIOOwyoEHCDZb1ec3Nzg/OOuqrw3jGbt5yenBJggifvamldjTEYxCC23W6Yz+fcJhjpu5r+lhS6BS9yi5VIZEyFLKgks3besGI8h2PMXYS0dQVdpDRe3PHiA55qsi4FbJHnIXyx8CajAJj4t6ki/C4hu4hm98XnUI4lrUTCA9N+tFfjfMO43vm9JQd6kHo9G2HS2qYMOfHZTBsi/vXe5espo1ZytNVaYyojNQHj85989v14ZuHZ9ac5Xf573/k5jKpZNicwBF48ecrzJ0/ptjv09Yaw3opT7tDD0KG9RZR8DoIVBV1Qwidm3BdyhhrBm1OYtrF2TpLzsgLorqbG9SgV8IcK7luPHVHcl7+9aSvhJ8TxHP4+eYeKPHaIgjhSogWlCBEfe3c7W9fh+BLtOyaDpnvGqPLAer154zkda2ezOdoo6shT+ZiaEKVRuYYncWId0COaFEtiRpTqUewJ9PTest5veXV5xfbykt1sAGoWJyecn865vzjFeo8LfnRuTvxvPA9SuzrSLUZacayVZzx9GpWKCoInOOH78S6qRhrwUvfa+Shf+VifPM6pjjQ4lW8jRl0ko4aPmRcEh8RsLtHwmuikOEWQcWCiZyLvKuGhvMc7C96im5qTexdszZ792rF2e9bOMWiDbudUraKmwrQtlYVWNeha0Wl4sd3yyjvqQbZm6PesXYdVnqWqMRi8gl4HbKUZ2or9zmF9dCWKdN37IBEZBfDfNq6N39NvPqa6rdqKhMOlnFJDVbWZ7xCFqRiJfDQopL0m0gkfywN557ODxKytmc0lHbv3ifNN9D/1K2lI67pm1pJTXpsqUCEZ/QRvFoBzAE2jnKyyISIo4dtSrUEPdNbTXW+5utnw6tUVN5v7PLx3wfnZCYtZw/LkFFMZhr7He8++71GV1BiepESPBomUHhcQh4xoGE+yTh5hQYfz2hfp+U1UYFd1lRWwiVbUdZ2de1VOpR7neIAr0zu0Hh16y+vHWgknd7U770mogPIsH9JhxusJLic/qZFfjzyP/E/fmttduLU0rB5bjxJvjzqJOG5FTPt8G7juWpO73nXXfa9rtwzjTNd7VFRP6dexlnV8R2hoyQOGkPR9h7t2jEfUI39f0NeDN+dnD9esnMtsNo+fD+9TBVzfruF+l6EcA96LcjyVQ+s6SzW/x6P3vsm7X/t5Lu6/DUrRb3raps06FoLD1AaFwdQN2ii0kXXruo71zQ0BaFLgUlUJP+RSISlxQ1zOoV00/NknO373R6/48cst//Nf+oDfevs+P/jpZ+yClCtsTQ19h6o7wdVGoyyE55e4pYZ+oDKGxw8f8/d+7bf5pW//Mm/ff5uN33Lv4j4fPHqftq7Yd3u69Ya6roT/9ZEQhiA8i64kytT27PaW2lSoGrR26BA4CTPWrscq8IPF9j3Bd3jj2Lgeo2acnT3gF7/9y3z2l3/Ofhh4cP9t3jp7SI3mz3/812yePefdt84xweL9cAsegw9iJFVJFqfQZaV7k+OmXCuNhZMPimzETso4qRnro+yso+yA8D9xd7K7bObvdeZXSO8tPibdjVJStmwYerwXWb6qa2w0JqpwHM4zv5CnMeoxE37zkT6N63WIXyZUg1ttJHRE4V/GU+CIUn7MvUZ8On6PZ1+NznVMpZ4sGKZ1SbqwW3Q4CB+BkoThUWGS5yK4aOw/yVfceteR5SjGn6JDKZycI/dxe5kyrN3qidvrOtotRrNk+qmgbKq4drBNZaDLrYHfenvEc+mdI2tG0r8lXVDS9SQacP9ME4Jlt9uN+pr4TwKcPKvljLqKpkylqeqGYegm4xjs6MySZLpD3bvRhqaWzDk+nmdIQVsuZyu7q912HBHjr9B/CXbY2IEtCgf8mIHnDHyhOr7ha96j5TM8Nu2ADyyp+KPrGx62L1lWK050xaJSsKgxs4qul8yzetAsgqYaPMYHjBLbk/eCA43WhMqADrjO3hp7yjY7zWIa2G63PHz4kKZpsFZSsQ+Dy5l8Ug3r0tEghJH+eufZ73bMq3nM8miys42KhvF0rkMJFyMqzDwL8aylbJ4qgaWikL8F3nK/BeAmuJnoQChyCyTknTUTI94p6ffreaApTpT+Ay54bEhjVfHkpYwVRHlSo4jlUahRQY/DieWd5ZmU2SGeghDQiJ5PoyME6Qh/Xuj2QanP17U3NownxW9pQElANJvNcEkwKiL1Dg3e2bBUKBUODdYlM1cqHErlTBkNXiqt8rYUjOIxRgtGPJuEtNRvek/y9igVPeUYpYkwIkaBGgJ0+07qDfQdfbfj5cuXdF2HNorT0xOGWNtM6m+Z4jCoDNTaVIJ/4sEWL5ME0gKgglzjmJLVKc0z/j2sMR4pTfF1jPRKDGrUn4lyyHuGvmewlplMV/bNjfs4KtHkxaP4O96PL6Jhy+FQCEuBKYEu1SgRIdyG6VE4zrqVksHK2KSYc3zPoTiXRYQwRpOM18olVLffWzyfvPD8xEvyUCYc+1Ulhcx//cgQlO9VFHAgKMIXexzw2RjRNDX69ITddkPTtIKG4j5XuopRghptpF9tNHWsdS+Ga4ENMWJWEyOGpIOOXmZODBreCXFwzjL0DutSpPboeZgNjpnJGaMCyAg9TJnkkJjNqdCXCZD32SvxEDympRdG+Dk4BiTIS3Rn3OfbbWIUL/6mdMmSStvI+kfl0s3NjTgq1DVn52c8fvSYs/OzbDCfMJlKZSeEyQhvndv44vh533U0Tcv9+xfs9z3r9QatNfPlDO8f0O87qYcySHpJybGiUMGg8thjPXFdpgP3oERBlQzaKfVtajoa6CT1buKRZf0Exsb67IlGhECuyy7pmfXkPJVzzKcop64fcYWP+54MvJlZtKK4CgXTMsLIbW/4BEcjY0GUyUaDd3ygONElrfIZl8IU72aGPSs8yEx5cZM8R4rW9ePTQeN8oPKaYDQxfBxR+8kYTEpvrVU+F+2spm2aLOSEINGy4jA2RkoVwJ2FyFv4MTJhaex577WJUeMdy9WKJHDER4o1GXGrDwEDnJ2f8p1f/AUqY5g1LcZUrG9uuL6+ottLqksTs0eMisdx3mm8WZiI/IBWYzaZMrNMVo6FSDOVRNYrBEZLXiUZoFPphfz+KIi+/95bMiclgsgknTqJX4m0RE+geFzutC4uQEyl7t3oEJQEJO8cLsGpCqPTkPc544Lg3yJlFUT+IMEo4EFFR78kCGkl0eb5rIWAOjRgprlQOEK4USgUA6BE4aVpSqq1gn4lr3JVRAwn5r6gYfkMEnAEbHBxTiE78gQU1nmUWnCxesR2t6V3Pb3rcX7AB5v/DUHqNmdHn7juOn7eb3a8fPEy8mxDhF/xCH7//fdYLBeRvkzHefj5MJV0CIGzszNevXrFcrkseNJ0qsYzUsJNZizyeTkQ2sdDlS8lPFIaau9qmZctFVIFbzs1plCMtxxs4dSjjiiLY58jjvXFno9nNyREWzBuGabKdysVeVI5uxO6kIaWBMbYV8KuiQ9VSKRMuT7SjcCjRFzLWZ7S2gKHBcglYzIvPvKDIUQ+IITMD6jEx3sX8ZZBAcMgMJkdxhidL4acOlfxg5/8kaTEbGZUVSNn8Z7l/Z//iGHrePnsOZsXL1mEGn2zxm63+H2H3e2k1nQY8MOACVBpLanxQsBZj1Mhp5ktZbVD4feWAjSECZxrpVFmlNlK+e2wj9T3pD5x/D3j99uM/tF3j3s0hfhDY/uhzFkqs1Tc5HI+txwuy/fcOivT95UGGJQfHcidYxj6O+f1Jm3ezglIRCkRHF0A4xViyIgRVkYTlCj/JW2eRqkKY8CYGkWFR2OVwgZQaKpgUBaGbc/6esN6t6PzYGPkNDFjzaRF2pf4iYzCDgcez7hKg4Z8XpJVyMTfrHX0/UC37amUwfia4Gsg8p4h4K0jGCmDMZvNcp1AKd0zRvoNwyCRGsEQQjSyYgrHTB/HLzLOdr+GXSUp2r2nUgoTI0FsPzAEKSlEVJbXTYOpJGH9Bs8ahTU1BjnzDqi2Pf7ZlsXpGZ1RvFiv+e6Tz+mcQw0Ove247rY8GzZUwKI+ZeYNvfd09Axtw9AqOmul/JGKkbxxHX0An0ojBHGUONR5uDBGkYQgzrQ2lnsiyl+VqZjPFtTNLDvLey+locoSGypuXgiSdjI4L30FT4Xw8vN5y6wxKIKUvNQGpYYYkakIQYzpfS8l+byDvu8ls5PTWUbQWqPj/EYHd3F2lSw7EQiJclOkF6OeSAz/AmceHyzXmz3rjz/js8++4HQ15+3Hj/jgg/e5uP8wKz13ux2b7RZnLfP5gtmsFQN4XWO9Y71ex6x6YkAzhXNiiXMOS0Wk/RhlI0VlFMv5jObinLZtuLmRdJ113aArwR2Z7zzoZ3IUD3DT4bXDew8/3zb4pBvS2R1J9bSz4v7i3lJOuAtn3xpD2qs72gSukfUrU6qPMlVybD2gEWntyGjnVv9vojg9tq536Qvu/m0qP5b3hTDyLilLQUlLy3a4tsfuK/fYpnd+1VgnfChx8w/4gBKfv4brVNrkJxL/nXi+bHiL63F0LMX3QMDpHdobdBBHlSE4Nj7wzuNv8rVv/QbLk3O8CgzdlqrRKLXHOU+lxfl+uZxT1y0uaLyXDFT73Y6rqyu2G3FkraKjdggSadn1HqsblDKcVXveOTvjn3zS8X/93R+ys47/wTff5j/79il/8uMf8so63jpt+cb9U379/Q/4g99zeL/BOA2+JvQWv34JrgXnuf/gLb757Z/j29/6Ob789CnvPHzAW7OHoAPry1d0dc1gO/b9Lpdx6Potzlt0BedtzaxqUBj8pkcFx1BpaCTL56qtmW0bMD1KS/R7P/SAh7Zm4wbUfqCtFvzKR7/K2f9y4LPPvqSulnhd8+zqJR9//Fec6r3U7HXiTHwIZ95LEIWUb8kQUug5ohwXBKjG7JMAKSCkLG0UjeijeID3Fq+jnKoijEb8ixphSGmF9lPHkyQVKBWifS9QIpxh6CWTitbM2haF0NfJLG8BeRjHSBj1ocFjdCX6AZ1kh2PPlx0fP9/xA0n3mJyJxhFEuVYrVFlKKgVNTHCfOAAKjxTy2Z7oSSFmxizHQR5fPukhlqULCqNSkIoqbKejzBsOJ1/0nc++ym/P9yb5K9OecDfuyv3l+SYcG2nLZPxJTxaiLqiYaMSPerLGxbwR2HSFw2CIcmqSJ9JDySEwDT/Jxdl+o5IAGB29lM46vDzlIA6Km80mG6rTTnkCQz+wms9oG+Gz8IGqqen7bbnIWCdlIbQenZ0TryROpGI8rpuatp3lPUi8VZKfy4Qox+xsJZ1NVhDZBDlvW2fZ6JreaLbKEbxlUIFfpGavAjfBMwQ4txWGirnW/GHYM7z8kqHz/MZb73A5bDilxVQNHoNrDWcnc/SLS5rOUtmACcJXqqGj0ZpZVUFdo4KjN5KhZxadH0vdX9/HrJ92yDJjVVUsl0sArLNstxux41VVPCvT0qIZKSCy7nazpVlWAr8+Rps3DjHBxsABlRZ3xJ8lfvHpbATIAV4qra0GbUCbiHdC5LULuqoKOOfgHIUgfH/SByTDs0qSm474NoHr63mlpGNTuY/4GqViRLqKzj2CPxRI5ro4BhCbgUpO/UUgaTzV4xqppNdrCKqC4ET/5wdcsKJJzGvxZu2NDeMprVSpYJgqCXxOcZ4ApFRKxxsnDGvZ1yETnRi8UnlyaKjWhQB12Mqo9UMGq1T+JQRR3ivpSlPE+OvQsGzgOD155/37D7h8+RRQPHnyBIC2bambCmcHKlMaost5y1rUbSNISCWBq0RA8d4S2soRHQjF+W+iMFCClMBhodRP73DOR2WeeEwmZfh8PmO33VFVdfaaTofHF/VkEuDKPsUI/+zhXjDvmWgeW9vxMBxvaX4jES2JqtDmkH9Lr7xLhslE+EAImN6fEGjhoVsIEUlRrGNnKdVdjtoLxQFX0z5Tk3QfYnxMWQ/y2OIzSXkgjKZ4JxotSp97FxfM5nP6ruNktWK1XMr5TPsYIy+8d/RDj7WDENm1z3VVVYiOJ3F08kw0PoaRgU2IOl1PxiBZlvFcl0rHlNY5FM9OmbOD3yYatzBZsRCZ6Ds3tdjz8pbELE0IerpfgTo8XHl/iz61mpzFxIxprWPdbokMa5qG1WrJvXsXrE5OmM8XnMd649ZJevusTElI/m4OOs857UNAlE17t8PZmrquuX//HBcc292evuto5vVo/CVEryrJMjAyZWpSMyhNWyJBxgVUII4VRseU5MnweKi8SeselVlxzGUtcgDrbXaWmKSqTzgvPeeTAWL8vYzUC4RoOw8T+Mh7K6PM39I5D4WwNpqrj9GMuMd57FNYTNfSk+IckxYSklFlnPsUrrNQEPPAhCjypCjg8q2y57LulTY5bbiK66VirfPVyZLLyyucr7Ih9ZahwHtJyU6x3uWU7lKeIWd8sViy3W5ZrZbjc/mZNOLk0FWccyV1fF69WHN6ckYIMJ/NePudd2OU1li3fspHHOD2NOJCKCyTtSYc7bJyWBTIPjA6TngfUyvH+jzO4ZzUw8nbF/chn9WUTSAKgM654v7oSeoDYvRWcS7JACfsZvBO6o85ESCljEFyskjTCtkrNQtWmT+IsOw92jEmoU/4NKR6i7JXxDN+KLimc6ujR6aCIpJe5XsVigqNDpoSH4heQsdoWA1VwFSGqjIZT2hTRFQVwqt0o3KpC+/86GHqfcxe4pEpp8wIAhPnnOKDZ9Nt+OzLz9j3sr86iKHIOxufS+m8Qp57SDCtBReaaKhsmopvfOMbvP/BByOcRSnkqAAYwoSHSmu1XC55/vz5Aa+c7rmrjcb7xClM2Y8Q05klGlq89qDdxbuWZ+fY/SUPnu9P7y6UIvLbaGxONHtcr/F9ocCLoTyrKj5Z7gkpVeA4HhQZTtO1Kb8w+V/qOvlSkfDyGBceD1fmMRKf4ybvSIbv1F9IeFmNz480QVZDq4iHo5KDENMohnhWIt8UXIhRa4k8+JEnUUhdLC/nY9gNlAbgjz//Mzl0jaJ+HEArZvachXqXsOnYPL/k5vIl/fpaDIrW43sxkJsQRd24PjY6tPzsyv2xTZ0Qp7B3l/Hl2P2HBvVSaVH+/rpxHXr8l/Ik3HYYTvxj+huAY5EgrzNGpe/lPSkDV9/11O7NUtK/tukW7y1aVWJs0JI8X4VY6kIFgvZIMu4VxLgLqNCqBqUxBrTpwQRc1UlqbIzAABIt1WhDTcVgHda6HJl9OHcd/40yyi3O4RAVMC3HEPsCUcp4MXoPe0e/h1rN6PfQ94BpWKxmXL+Kcr2RMicAzlq2g6WqdcwslEro1NR1wO77nKVGlC2erhMH0br2wispQ1vVVNqgk06oGLjSWnwDgoH1BoY9auih77HdQOc8azfQDw5jHctZy3w1Z9iuMZVmXre8uL7i4y8+5y+/+IS2atnbHW+hOaViyYyfsufjYcuvqQtqNL12PDWW7uaGvbdRySgUWqWawvo2/3nYQgh0Qy+1VyNvYVSF95ahE/lj1iyZzVa0zZyqaqQsl3N4O0bWGJMcSyQD0axpJMNLdPioqgajK05WM5pK+DcVRlomWQVEKdj3HcMgEeP7XT/ClFFoB7VROKNxIYgk7EotgSIZyMWx2pEjSCIMKmLaXGVI6SGVqqOMZ9kPnv3LDc9ffsx3v/8x777zkPfee5fHjx7x7nuP6PueVy9f8OrqmnpjWC7mnJycYBpDP3RYN0iGtLYCAs4NmfYFygyAx3VQWmu6bk8IsF6vee+993j44AF13bLZbBicpdI6G8LS+nxVe50RejRIFsvI62XN4rY7Xji9a/L/gi5OnCTjf+nWyW8HL7sL5yY3s0y7JzRh7Kg8wyGEMcXmwTE5Ltu8ns68bpzlc8f6ucvIDUxgZ6LDe03/Jb0qZayJ/qX4/a75ZKeSYieL6nmTZVOFnK3uGB+QS0X6QpZSpCAa6VRsUwU/daQlOd33s+gE7RjswIDhgw/+Fr/4K/+A+eIEa3doBs5PHtO2mllTUVcKJTnXJVvFsKXve5yv6Hsvzi59z7179zg5OcklQ/e7DoVmtlAsUcyqGe3sjH/03R/zf/zHn+CM5j//1Xf4L371Hv/m4z/khhPeqi5QbqCd1/z6L/wafrWifbnG7yB0DoYOr3r2z26gqvnNX/hV/v7f/Y/QyxmXf/0lJ+cnVEHqbJsKdKUwtWZZLwgxLW/X7aR0SKVZ1g3Vasneefb/+g/h93+P8//R/xD/S99hd+8+r3aBxi0xsyW17aHbMlMt1TDjcnfD3vVYvUXT47o977z1LX71m7/Ctnf88ff/gt/703+F/fQHnHz0PsorDDU+VJI9ZQI7jhTCKHlQEz8wAtChMTrDiFLRbhayTJF1MdmgodDG4Lzgd63FsV38TVV85yjfZBk7QAhu1FfGGuY+FiRXKPpuj7UWoyspU1Y3DP0gPHyEcgmY01OEGIozo2JGy8j0RHGTEKJzWqr3IRM+wEF3n59D/CHHo3AIIuRrWo911MnXRzlbxb+jg6iavkcx6uDSJOJ6Tihwdgab6gbLrU3yStJhlXOc9q1GvH8M58aMY4RjAW0Ha1XMZdTPQwmKGQGRYCzqFdU4pCQLjB37yfdUXzzpYUo99K0xJuQZ602HSA9VXjf5m4ziZUuvdM5zs15nGEzLGZQEqC0XDaerOZdXPdu9ZdbMxGmhmE/wgb7vmc+iPSA6J4u+WvROla5o6pblchFtYMQ9Dkd4+XGfbtFpkIhtFdAu4GMgCh6ch7UOtI3UkZ65mrc8/Fg7fhSu6Jw4UDbRQLzxO65qw5/5LWH7BWq/4J3TC/qguHz+CuscJ6Zicb8iPFWYXU9lHW1d0ba1BGzEDBvBe/CW/X5Psi+m8WutJVjNeXa7HTc3N+z3e05PTxFHEp/LCiX7Zh3Lk1on2Q63262sq04OKHLWdrsdc12DVSgMwzBQNQk4lBiMM6FVI9jklICJHktgUCDalOK5T04VxhgwAkcpW9PYV7E7URctmU/VqMXRBhVLkh7+EwP2FA8cgwVIftTpWXHM1rqOAQNSpikolzOdSXR3PLM+EEzUGJlSXox8P6BUKt0ZsbNSBG3xXgzhHhvrmvdxtZiW0vuK9saG8WTUSkInjMZnARCNd6OCMC1KXdc5F/+x2julkj4pl/MyJIRzoFg5yrAWXetCyV/eMxEWDpm8QphI4wlMo9RvEaiygyAK57pumM8X/MWnP+Dy1Stubm5QWnHv3gV2GFgsJFrcpA0P4nUlugdRCBodib9SRf3xAi8X64UKOX12oRM/XJLjzAgjrdCxg6qqaNuWzXpP3w8sV3OJprIDWhtOT8/YbXf0fZ8V/SGeumRUj9LOuI4hAIagBfBtjojhOKadHufi0x0HMhO09EGQjVKlQDY6FQiyL5clRIKm0Lq8Hrsv0tWNz4XYZzImqlEuT8hBH0Tj6jFtH8T6ZLXUzyYiXkLIKQElmljqfhAkGrsfhujlJn2G6IQSYupP5yxPnzwVY5oWw8uTOKFQTCylrhsR5lQhORoiy4jsMKnbmerciHBT9p8gqyCYwteMvyhV3JUX+mDhGQlCWtzIbSYGb1z3CUsz7o2KRiCVDIal92RK8RP7LDyKEtKddAmRgI0OPimlt0JlZtEYSTXfNA1tW3NyesJ8NqOuK+aLOavVCq10jt4+jGK6m+wU4yASycL46r2j6z2DHWJNds2sqVnMZ5HJOUwlEvLeT3BkuQ/R00rF9UqMvixZjLaLDhM+yklJACgFAZfqnIaEU0dj9Hhuy4WO8FOuRmIGkwClEvwVY0qPJkY+da+SASJG1aRVO2D4CUlgL5XBI9wJqlC3wPQW7ObRkMcRis9TFvz2c+NZFI+5kM+oJoSUMrECl95vSI7JI93ULFdLXrx4Kc5q3mFCRQheUq9Fx4yMByDjpoRP7zJ2pO9KKZarJU++/HKCo9Xhfsb+UuociVyvuLi4x4vnL3ny5Anr9U6ce0xNXcca8hEHTWi/KiJL45C0krSeojDRCaXLTse9EaefKHR7cQvxYUoXIGQFjjCWYz2bvGMJ/vKOhjw7oBA404bUEY+FvLYjuU5rWkQpFnuYVy7jP5VxU8KnGU9GACgF4OzwosSkLUYAeXuINGhME47I20bWcMwaoSZOMFppqZeUU8yHrKQwxlDVBtqATobxXDPzgIc7xteFQgDzkQZFXig53iUnG5mjIShFPwyYpeHp82ds9xu63QbnVN5HIo81yqEyHol2Nazmc9q24exkxbvvvsPDRw/juVBjCuq8hwdQfUswHGnMyckJL1++5PHjxzma8bjCteTGxivHWhb277jpUHA5VHynCO5EQ0ZcO31HfirzPgf4AOJ5TvCvJ0a020b06agSjpsaKkucP653CIleE2nL4T4Us4yPJdYu9XdQcCnDXxnRDmWEA3ltJh9L/H/AxOQRFzye0Y3gLJ8iNxXpvE+cD6KwqtLBTjhfKQR4Uw3ZiINicXCjNTbsUEZx7dcsH13w0Xd+jcsnL/n0Bz9g++IVft9RaYWyTuonBxWNBGECQ6UR+VDeKnmEQ6Nz6RR722n6bhmuvJ739iDd36FsdthCCLdgt/yb7wlTo9HIKaZtnfJ/x9qEfyzmdawFYOh6rm+uuffg/hul2H1d23uFtxU2VNRU1JVkeHLBSGQu8fQEobPBj5QmubgGHMZYmsaxWux4676le3dNXQdAc3p2wr3TE87mc+qDOr7JoSTTOxWzs9yBqUYeZtwHjzj26CwHQQmCznn6wbHvNc4aNp1lT8DV4LWn77YxKiopNOUcz9oWHWut7/d7vPdZ+VXH9K6EgI9RIHUsr2FMlcvTDH2PGmqCVgTn2Nse1wpNs4OjIxC6Dbx8ht5vaN3A3g4Y26Nsz6KpGOaKzctXDGHAt4qN36Nbxc54nt9c8/TlJV41rG1Pj2JAcapmPNJLcNf8FRuqsMZT8bkPfD54WqfpfQnjMeuLGnlYFcSAHAspYFCTc5qzfXmPRuROgkTUiDOzRpsapQ2mFh4xRRiJ0tRSVzUhEOuNSxTNer3G+YG6qnNU9fnpCmU8wYozW9CBoCSCTilwnaXrJINVVVVoI0b3VJJG5CqFMZoqRBn0gL0OIaFEnSOaQiBHEmZ5xdvIM2mkNn0qkyXymgcG7/nx58/5/OkrlosZD+6f842vf8jbjx9CCHT7HbvNmi+/+Jz2ZMGLZ+LsdnpyQhWDIYIb8ZRWmuoWTzC2dJ8xVVbCfvHFF7z1zjtUlaGqa/qY9vQYvjmGp0p8elTfVeKpA5wVEp88GWSUde7kQo7Mq7j3UHZOPIuKMnzGnYEpz/AGOPiWtHRknUf9XEHH7pjKVxm9X0d7/n/13FfRltv3p/NRyB4FY1I6hZFuO9ZX5n1uZ00Z+893TyL2ocgMWbRj9PmQR01Rwqi7IS5xpFWYM9gdgwZtGh6c3ee3f+Nv87Wvv8319ZqmORXDpjcYo+jdjqtdJ4EA2hCCpus9TX2K0pa6HlitlsCKpmkA6PsBZy3WigHEtHPOjObzVzf8P37vr/inP/2SB2dnPLz4/7L3X7+2LGliJ/aLiMxcZttj7r3lq7pZ7di0w+ZYjsTBQAMQkgYQBOhBgF719+hBgP4FCZAAvUijEUcaDcfQNYfsZhdZfbu7zPXHn22Wy8yITw8RX0RkrrXPPbe6qXlRVt2z18qVGfaLz5tzvnW9YjcENnLJj84vWF0+ojWOrmlYXF7zl37tr/P5T/8zZPSExhIsmMMBbnt+/Lv/Fj94+n1WzZK7zR3dheNuf8PF+oyubWMEoHMx+9tiwf3dLXf9Hf1h4Lvf+S7r9TkmGKRdgtmw++SnvP7P/i+0/+T3Wf+Nv8nyP/h3uPi7/z77b39AZ/Y09wd2d8KAww3ntNs9w+EObwZ64/AmcLgfuUPY7UdevXjJsy++APGsafng+ho39NzN0jTHfQ1IMIiJJUZRI3He7cyk1N8S76XlLwIxZW6KJMx67pL6OwSJZdCcw7kUcZn4ciUMKr8YhbcK3KIMGCMgtXRjPwxYE/V2jWuSU34aatLvhhCwMydB1XkbQ0kzXfGfPukktH590QGYwt+/46zPcZsGKxVxpfB4ZX6J+qWhRL6zGMtFIp8lqK5A+6paqURdg0llu6a8unMNmj1SIOtqilyQdlnlMZnqmCf7kfZW53KaDhRNy/wyc6BKE4rlbiP9Vwciq/3XuFB1DzWZTH3rz/PxlAhqW4zQpuK7KniPbhtxIZytMmURYX8StV6NILYTee7NZhOjkQ05e2MMXhCWi5ZHjy548WrP3XbPeCLrqLWGvt+zXp2lyHFLCE2y0QSCF2igbTsuzq9o2xY/9iWLLERnEvEVXNXLPdVrmADewEKEEYPHRCJshRsZWYZIP1oLq1H4DS64ZeDepEx/GL4wO0QCT8a4Fl8y8LM3r/ndJ9/mRnpuXt/BrufJ9WMW155NsjeO44gBFq5lM4yI9wlnGGiajOeNMfl5iKVxNOtv0zhWq6ivd85xc3PD69ev2W63uMbS9zH7s7EWKyWLdnRmTDrwMeDFc3d3x9p20FicbRl9tOH4MaTzEWJ2aGnynsb7avxOuBGJuFAgBIt4zcKUHJGMZrU0BbSp8KCCOhL3Ygbwynsf46NsKTna63rPs3PfGGhsxBmWWG7akOqrB5tgusFIC3hifsio6xBjiabpFkudPj3hTuVxjeqT09k2krJsW4LErGmSZI5sp3tPnuobpVI3xuS6sZriKRu9cz3X2PHd3V1MSdOULubITiQaAes0X5p6Tj325nVn6nbq9JXHvxejbJ0yohhry2ftC6bKjqkgNlPuVIrd8gw0TcuiW7Lf3vHVV1/hfWC5XHB+fo73A92iS0piWyIgUaIRFdIhHTKMiR4uzia8bXJK0ikSYiqAzJhLRe7MgdkYSESbpsn14s7PL3j96iZGs3qPc5btdkvbdPSHA48ePeLVq1dHiqd8MGplih6USUTJhOom5Wwhe9UAp5/eCdPFI650kTUHmWlSI6ZOv/AXpqxb+muspnUryqDG1an44rOxPnKbGSGFWfVG8r6krdVo4nHo476HwBBS/bqcgyauz6Qmdl7PyIBWK1xF2UYPeo0Kjcydz2srKrQkJiCk/nPb9XJmeE+MbRpDVmDWe/jwlkTEZaL3VJ4aVHvwABI2FNjIPZppmhlTjES53QeUCCb/XvdR/Uf0wNK2rCpTTOm95j9NdnQwNG1Lkwhi03V0XRRi2rbBNZbGORbLjkXX4RpHCMLh0Kdo/eQxZepoYuFIjX/ETFYRehEh5Oe894zDGKuXJKarNnIpA2wMuc5aXlOSYbiK6AtSDOKKR4qBVxFYfFvTXKsQkN/TDa3ezWxwdUzjH93fCUQQjQaaPl0S7yH1kclnaiJs1I0bgNoQAnUEe20oqPGRUXdSOd6LU2Ovj0Z9vrJwlCetg5q+MN3bmDJVxBNsEbJEhDY4CDENNyllvWR4EJbLZVQC6xpKgq1Qpbk6gq3jOn+KF/McpZy1Rdelsgoe6xwgZb+OUhMn5y9i313X8b3vfZ8vvviKi4uW+7sN2+0BwwGMifVGld5S+StWaB4peQAMlWFagSstZMb1qGd5wMzOmY5XhUlra/xTjpo16gxDTpWejddpTBpxXSGzhGdSinfFO7Ywo7EkgeKe6r6xKW17/KzMuypijY1RBVhyFJ+pnIE07aTBJicZSftjqu8k557Ih2mmr5hGqfBVKsTFsZS9UBgWhe98JgvMZ2cCBW+TDN5Mr7ifLtUuVi9pNZj5vO/GxNRtuzDglobrD685G8/pDz1j3+fashGfmWyk1/+apqFrOlbLJVeXl3zrW0+zoTY6joScor9mQk4ZuI+ceIDr6ys+/fSz7GGsz+bHchsF3+rncl5n1ymhhFn/1f0ypJpfm96ruqVs6JS/O/W5OCvI5Pn5+hxPofCChc2RCS1THKk0KiT8byb7oI9Xsyts0wSuCs3SnjWLA2BSJP5MsSv1fuQ5mXoBJ/AfEgWNW23QbD5aMzyXITElU5a+rhlcst1cl0GjQo3kNTJGojO1CN5DUG9xY7jdveH2s7c0zZrv/Y3fYukdn//xn3Lz+VeE/QHGkeBHfOIN6z05rbgqe1mXttIzctrRo7xXG+jqvurnTNnI/F1lt/q5d9Y6f6DfIwNTldVIyb2p/tXMIfVVf6t5y7x/ZipvFj4Z7u/ueTyby69yBdsSbMxEZIPDhgZjWwKuyH1GiObRFrQWGwISiJ70DsyKtj3j/OyCJ48E+bUfcvXRGSEYzhZnPL2+4qJdcNbENNFiIjiGkJQ4TFM7Kx2I6ynHB+/E/tS/i75DPO9hDGx3nu1uYG0CoY2O4vvDjs3mLu+NH0vkR1h5FouOpuloWzeBWT9UNdaT/BCjlnuaRrC2SVElkpzbG0zjGJ1htVqxXC4Z3IAEj+8NbruBccdhc8u47+kIfHh9yeV6yf5+Q+iiQcZI4JFpaJqG1y9e8uXbF7zuNxhxnNOxMVEZ5xEIwve45NPO8scEdsQ6jGG03Dc+s9jTZbVgSomyzN+cOIP6OZYrSGc4ZQ/Lv2X+wOCl1GfXDIDLRZt1CXoG+l6jxRu6tovOv8kRF3zeXzGaNpKUsrxnGMYcsWSrrANFHtOyOILJXgBlfsZGnBrPVaUKTMxFZt0MmXeIPEDiFhP/izV4AvthZLjbsjsM3N1u+PKDaz54+oTL8zPWZ2ecn62563cMKZV+rZualFBgisOOYD+PJL63WCw4HA7stlswiX82JQBlfk11VKcj0h82qp7gEo4BawJP+sgR/ZzNd37NDbxf9zwcz+3U81Lhl1Prm99XWNCxnOzxdD9zY9VJfu+B8T101TpGON6z1BDM16CWKyi0d/bi5K/ySMaU/vQ9NdAcd616QiabX3OQ+d9qLgZy0JM1hZ+bvDbbr5p2ANk5u0hap64IhZY7XAdjKgMxhh37+1+yfdPT0NHfdxyCxdrAYOAwjnhiHW6xHcY0rG1DIz1iLd40iMAwRHriksG1aVratkNEeHm34f/15R3/7Is7fnkD/9vf+12+eGP5gxd3fLHf8cvtwNKtefzk26wvz7GDZ9yP7PYD/5u/9ff43/+rn3Dzs58jd3eRj+s93/nwh/yv/t7/kh/9+m+wWC7Zj3uaRwusH7Ah1jX3wGEYWC4XBC/stgd22wNWLMtmQWdbegv9Yc/w6gWPb/e8OBz47PlnXP2jLU+/+oyLrz7j6d/9T9n+8qe8+PIzNqsl3Q9/jeZ7P+Y+xFJVy1HojAHv8OHAwfd07Rm//v0f8x/823+H3/9Jiw0G1w8c+nv24+4EfpqeO6mNyJmnZ3Ivy4pSyaKEFM1tEl1wSZY2iHhsZIYpdbKV95iWSsJoaa7EZ7skT6gXVcKzg9o2UnnJSI4Tn53S+hbj+gk8dwSjaRUkpDJl9XNJ/6bkTOJ6vUNUmuK+mb5WA3OoznQ8xyp8C/XHopdLOEEl8mr9dFxmhkt0EqaSozEm65/rgy7Vuj90WVM5Ulfo69iRW5Jeh1oEP16nar0yn6LzqXUUD6HO/EQV0R0HMGFpNdBA523SmGuev6aVtd4kp25PMqSIZoM8pnm6b4rDD/0hGnwrnVQArAiNNZyv19FB1ByiY2EzjbY1KTJciA6LIY/fZB4vhOgoulgsaJqGcTiQaZUxsXyFL1nVHqR7Khc5g/X12kRj5mH0UVPsLAsMwbT8sL3m4vqK12bk5XbDzZu3tBhecwcSGA14Aq+2N9y8eU53fc16tWI/wt1uz+qyYTBg/MhhHBj9yDD07DdbHIZF1yHWMPoeY6LNptbJaBDvbhfL6ez3ByBmE7m6ukr39ox+ZLU+R0RYr9e0XccwjjhjcqCichvR3gM3Nzdcdmu6lYU2ZVOawWvkeR1ZZkvriGa1RG1cRFlPGpwLOFqcb2maFqe2KVvDrjohmiKfZfqtKdpTmyeMx0r1a7p/BKsnvjvraJuOrm1pmxZnW2LJLZd4bwvisASCFdTwb4wB2yCmQbBZvxO9QXw1vGhHzYrKsERriovxYKKeMNv23oU8Ztd7G8aBbOjTw6BGcYiGc9u4jOSXq2VM9ebjRNTzq168U4x/zRDWjKQazOvnVLmpqZn1EiEjbk0DrmkjtE66CSV6xxgw2n5CRIgnjD73lQWVTGQiqA5hiMnNjEUCrFYrXj1/xt3NW968eoMxwvXVBcbAer1OAlvJ35/RsDWMQ4g1t0KgaZtp5IQxyUBbANVUY6vXLq3QZD2qhZso48iH0kCqt3Z9fcXzZy849D2HXc+jqyc8f/GM/nDAGjg7v+DDDz/g5ctXjH4szEYCaiVEgjD6MRGRkL1Ctb+J8QcoimDDNBz/tGBTI5a6/quke3Ut3ZKS3mbnjuLdRmTA0gFSw1NkOmxSIPg4R6N1oGP42TD0INDv96jxOcOuKcRP8vyUaIZMmJSRDDkSIm6aptAt0orWvKkRW4KIah1tNkaVZEa1gFgLOErQRVSRkBoJU8Et18nNzELsr442zN6DuS8Lmoa7FsaEIwM3lLqvsb9keEpDn5zBevQK+9V7WuczVMyJdQZjo6HOORej+ZPRSQ1L6rCiRm6tgR1T8UWnINe4nMa+aRu6tikwliJhonEwKilNOuM+KaH6XWRuRh/wfszGsxKJH51jJGU7KPAxg32FL0Sd0/L6mrgxMetEEMQHMFUmDj1nRlOokNf/KCVqvbiQiWzGzUGhqB5iLRykT6m+TCayWREq5c8Mf2kdlbLDkvBXVXqjDCzDs8JoZtVNIdomKQYkp6hJvVVp8SWLC+V3jU7XsVGeQA0saRhF2JfZvhXklIvvGMyUV9dxateic5YUFSOpDMKY0gQX1xEBGhM9U+N5jXTz7GzNbrfHh4DxEb6Mjd7zyvRHwdTmucT2irI/rkvIY1OYUHhwzjKMI0vX5GXLKblNJQyKRGV7iPDfdR3Xj65ou5bnz5+zXHVIn86cITOjPjsNpb20lSnDSBJWSHMg0g81gk6UMJGOKv3VDB4qYCoN0Ahn62IpEKsG64rO5PvOTvop808gDvkdY1OSOVMbvU1+wSReACEpBKrf0jrWkna9tsEESDxCRDuheidXezrmDRM+1s8iU6G1FlQL3pbJOSkKWm3TlLOV9qgYb6sWhYznc/8Q5yExElUAfPSUlqD4IjUeBsRYnr96jRcwpqFpHOBo2g6UUQ5F8RLXPtL7rmtprMVhePz4GtK8JxF2GTdMFy0f53Qn0i+9o3vcslx07LYbLi4vS6kRnXtFj6tFzue+4IH8Ql6nae+maqZgpoJxZ9ccj0+YxAJfUHjkWoFT9rnCrSfaq+nFKd5+gkcNSA2nGc+roic9r5H7xkycBydLqLxXvsEEz0Z+MuRlkySAHl2TcRenr4nBqWwQMTY3jrHsc6rFZ6rZalSviqWprYAqYUzSBBkSYKc5R7wqIvggaL1AIGUOIqaXNIbXLz5lc/eCtj3j3/uf/z3unr3hn/x//gG7l89xh8AieOQwglgCcS19chbSyDJr47LURt+5EchaO+EDytrVnEENt/F+5DcSj2RqHFIcU77OAHH0HUpqR4loKITC+0g2BNq8P1INT8foEl+rMG+ZP5OUWhIxgRHlLco5sB6aEBXY4+CrWqu/2uVsrOVuxAIOUe/7CUE2IJqpKhrZssyBARqMaVk0a64W1/SrgLnsuTxvEQyd67hcrGnaJjp3pD0fg0d8xPvelXNk9SwYwEiMFtNocAnRyJp4h/qImkR/i2I88VFB6EfP3dDHaF7fxnb9gN97Dn7EE9Mz+mGklz1+HHFEp+7gQ4xQVkKGMA5jVOYhSONwbZtXw4hA8HmuJtFMZyzYeN+m9I8heKzf0xzu2e569ocDh2HAGc/3VmcsaHgWRq7OV6yWHc2qY7g3uG3gZy9e8Wxzz8YEWmlYmjZG0Ri4MTFNe+NaFm7BczmwMUJPVBztx1jrO8IWQIymMSZll8goRQGaxB9VSDqtuTFJPkyeyiYIxkRDkG0c4qKnXxijo2MQj4T4OUYQRQcBQzyv6rjoXEvrOpaNYb2MuhBJfLYhxBT0ybFn9CPDOACS+Clb0vJbEyN7jCeJj9ggWBNK6mUyhSXXP6dEICcIy3xXGmx+b3pVSkNiJN12d+CwP7DZbXhzu+Hx9RXX1xecn5/TOI1oietuJOqRPDbCfaa3U5lIh6H4LRsCrcFIzJQ4DANNk8YqRaEpubXq7PwFXqdaO+rCqJxTYKlchd/QzzLhT2TS3rvG/y78Xsv6R/zM7NnibFONsc6VWz1/mgd693VMk4riddqOyWshFWzOxzuZB9MVff9ruvbGFKX/RKaveJoH5zQZ0GxOmedK/9TnruKFyqjebfir+zR1+9NGSMwmo/jIGxsQP9Dv3vL6i495/fF/T+MWHAaD99BYMC5mlMI0YKNcAJamaWO2FSw+lQ0chpFf+53foVmvsU0bHabSXHY3G+5evKLZ9PyNx4/5O9+75uP2jt1mwyWBYVzz5GzJatHRGgECowzYcOBvfO8H/J2/9e/wJwFeffEZu/2Gpmv4d//tf5ff+xt/i4tHT+n9yGHYMdqR2+evGeyANQ3OOkIvDKajH0f22z3j3QYIhNZgupYxeMbdhub+hlWADy4+4Gf3t2xfvWQ89Kz3Pd+TNZs/+WN2X/2C3dkSfuu3Mf9+oFldI+OCxkcMExixMmJZslot+eH3f8jq6oyrx4/ZfvIxMt5y++ot17seu1hM90/PgYDWEz65jxm4Kt6wkmmxNvt71ea0nEI6n6kM8UzOVwW8GfaM6ripJNeiO6nLwUxKQCY6Gb+Git6UvpS81N0bSIFlAZN0HiWzqHnwrJ06JnN9nFRrVbjuIisBMfU1JvEEiQeUWtYoC6j66Wl/RsW/9FmiPsWoLr3MQ9ssKOCY36s7MJlKVgs4WYvpi0q5xdR6guOVktLApD2Tf5y+YxJNM7nXEhU/h1FDlB3qaNq5o1Oe/0TvV9pT3WCtI8pk6QSit8SSIQDLheXmfkfoB5pFl9UrNvEh4g2rZcdiER0JnWlobDeZszMu2cM8GC1Fo5k8oz3PhwZnLE3bsViu2O82cYuM2mxsdlSvYUDnPflu4j8jqscRTNK7BhHGlBHXGMtLM/Bze+AvrRqurp5wiWX76I7PXn/B4q1wz4E9gTYYXPCYzY7u+pIGOPiRzw8H5LDkjkA77Nj5AS+CGQZkv2cYR0zw0UF9NByGAYNhDAGHitrR/rXd7qLMIAHj4ND38fvgYYw61DAMbHf3BEaatsUYl20/zjkIIdXHJpel3Q87XNtgbcA0HdZe4EyTjMVxq2yVoVJxm5ik+1QY0TMpDqzggot0zhqwI9AQCDitsyTkPasPSDGYQ9ASGMbgEi9euK3SvUcy4M5PoKpltFa6aaIOrmkWtK7D2TXYBoxLgQJajlFwhqyTj9Oz0eG7Wof4W0yJn1YgntfYIYY2sfEBY+pCO/GAvT939ysYxqEYxHVho1fEmA1bPvjiuUAmWwUXn1Ck1QijNpg/ZEyf1zk/YsWkpA/T9Ow65qjkVMVmHJ3R/1LatXEMOZuQGtCQQqhTLwx+oG06GsA4y9XlFX/6x3/Esy+/ZOgH2s5xdX2JHz3Neh3TkRLTkdVRX0L0hjPWljq5FaJRAKlYCQpaN8dgaipmo9yMiKjeg9m6ucbRLVo++PApn37yOdvNjuvrK87PztltNypu8uj6mt/8zR9ze3vLy5ev2O33SDWqbJhVg7SzJYLVmOj1ZwozZdUAoLCg9WOMyVE82bMmSZkaPTQXiEIofSvFKR5/Qggjo5dYdy7tLyPVczLxisrIRYlQWruu69jtd8lwPkYCo949lVODGjcl7avCTsWbJBicwnJmTBJBnUuE5Z4pxEsRmgqRpoLZqbRTdOxSzlVtQNJ9nDscZCNPYlYzvtb3KgNTPeBMSCuWdI4DFHnXRiNVmqjhmTSnmN7XxZR7TYrYTk4PLhmnldl1zmCcoWnalN5XDYgmGcmT0pEybpES8VobB3RfsxFVIuHHBwb16BTybxJk8lnRugAkQ2VG/EYjKEvbJ/j9GZ8XD0Lhl2M/yoBOBNPEIOuVU2zmszdFG+V+8TjX5+tnTykwavwVNEI5r59OQHLkd8Fq2nmBFcnYpZr/iUsoOEHkxJP1mc7vmPJiLRToCCcLkv6ZoAapkXJlrDnB7VZ9T2pY1mOg4oNMZXxE8YnP6feDD4h3SJeiukRomqjYj4KEcHa25ubtLda4bBhoUoYQMNmpKSKCgodz5Gyi6+bkekZ4W69X9IcDq+UqK/4UgZX1S8rcNEE1jhtjOT9fsT77QTSCH4S2ifVobm/vJ9EEcW/ViE3+a52raEFZYKU/QFLA2nzmlRlUx6m8OWkfMv6td+mBLc17aKbwojix4BNT4ZMTjSW8Uei+FBqgdD7DnhTaAMkTPn3OyxD3tdCYMq4JXAfyuokIHn9ifIa6jnseco1cSPtjCo4xpoKx2Vzrj3mUoeyf1tIG9eJPMKsHxBgO+4HNZo9gsabBGMF2NnrrR84KpER1WWNpkgOHtRZHiGy6i46USDlzmSc1aZSKIxKcFR4hwRJ5t/PvT54+5quvvuLi8iIb2a2pYSXRgox7lAZVaEVR02QJy1lVWvHgAld7oc/P78/fV1zPqd/SgKa04nS0V0aHJ5QZpb2iSKn507wuWTBP66ow8ECbdYSgnmnlX+Jr9XuS98JUh15Zq0KD0sxTVieTdzo1nnF42gt1pDVlbdTRUZhmjDo+GnnR8t/iQFOiLILomCL8ZgdUY7g4PwcRXr5+xn/+//4/8/0f/mX+5n/yH/Ozf/GHfPmTP8RsDyxd8rgWNWKlOZmC6yLMHtP1bKhI48qKNxSn6mzKWZnIe9Wqln2TSR+xf3v0+9H36o8f/eSZ+bhP3T9uT8+zQdnso/ExIfs5C4ue3+hsYbg+v5j096terY1JspGo3I88Q0iwoTyEBYlpsp1LTkFJ0RuTbccacgu75sJds1/swC0Q16S63Q7XtDGSLinORu+jg+sYYXe0Ls/ZiUSjsgOxITEJIVXC9ikKmcQjx4wIsWpYVHRGf4roIGKJst7BD9xLj3WGcexgDOAPhK1nMDE1Jt4gY8DLgB9GDq6JmWuGgZEEiz5ma/AhMA4DJgSMdJiuwzQO513MTBICtokz8uOAtG2ssycwjHv82LIdR0bZsTrcYscN95uebggcJNBa+F7XsB+iDP/4+orryzU0hhfjQHh5z7O3b3kzHBid4zxYsC0rH91obmzD3hna1tN46MRysNA7Sy+W/XbHGMYk7xgMISYeNAFTZRlLbjuZBmlktOo/ikLbgjOEQTACzsboyKZroY18ox9ixHhMAxv5zWgYP0CIezWOY4x8sRZrW1rbsmphvQLvSw1XCFhpERkRNHVldBSJ5yXCskvp062Lij6bUKi1gcaeylyVqWXBIsof6F/leY7OXqQdhV6jzGWEeYG39z1v75/z+fPXnJ2vefLkEb/+7SccRqFJ7buUfarXCEdDLH0kNvHumm3GZPJg6++x8HukDd5jmibGC6keAin1nk1xDD9FS+dG6zm+Kb9z9PtpVrTwIQ/yjUo7KcyJ8uBSt/sw6X9wvA/dI9GWU7TgyOg0CyZRfvkhXPwgX/7QWADNoPHQc3OF9ENXrcsspPOhPTyxD3mRZfLsu8d+ahwPw9fUoGem9yv5fvLepO3T47CJhzAPwInyeiIw0tJ4H41/YWDcbXjzxUD4Z19iJZKLkPbZJX2QrqiQ0SWGglNUf/J2ueHs/BxjHUFg9NERcHPv+d7tLT9wju9cDYzPB9Zv3vLX/EvMwcKbCxarNXdf3ke66QXvA94PCCP/yW/8Ft/a3/PJ1Yqbt29ZdCv+vd/761h6Fo1wfXmNMVfc3r/hdnhGcAfMwtE5R+sDo4lOX+PdLePLZ4wMDOP36Q8Nu+0WuX/N4tUzhvsNP/ro1/jl8Ce86nu22x3tv/4zfj38P7l/9pbh9gsGBsyf/Zxw2HP5n/4v6BdLzBhipLg9YCSwNgvOVwvas3M+/PZ3+O0f/ia//KO/z8f/4r/g7G7Df0QJiqn31pD2MC90gam4/qpX1N0wWabKOqC0d0LKSBXT5dGYBjGpjByZ866kgho2478ioSoVYWbwFb9M+MsihcYWJiKGIGHKW2biofKFRM4siGEYB/pRMD4axiOfk/7OsjVlfcORnHXsVKJfc2Y5ip4wO2cnx9xYZiTkEiJK93LrFT2tZR/dG9VpgGZvif/pesf0+bVxXHK7ZXmKLrOWw4oSsZqVqfezWmOlmZAcUOeIItFLfVZmtCf1XdtvsumvAGfGC/PVzrJbcm6NOk2fZcZaPy+TuSQ6nyYUo7gV3k0MYDEzZ4m0GWX8wtV5w9ka5HDALVqCZhETSY51sFgsWCwcjfNYcViWkxWy1nEYB7wfaZoOQcuwCmAZxh4fOmzjcK5ltTrj7duXCY4geb8e6bBO0dPI9YHxgR5ixh+SeCIxo5qIYEJgQPi0Hfgv/As+P7T8bnfBD598xA++/wPsny5YbzyfD6+5kwML4JHpuPaOcRiwY88w9jw/9PjdASHQ9lu24wFvhIX3uP2BXT8w9gda19B4x6EfYokkX0p8Golp5IdhxGsmbOcYveew78EnXizAYX/Aj57tfsO6u8DiGIm4pukaQh8dPyUIFsdytWYIPWH0NC7gWGPd9zHDSGN6gjF4aVI2DDKvqBgp53JI9g99IDQB03cgCzwOjwdavAQ6ASu2wrmh4umS0R5i8JwBrGAsNNkBRnlok+G3nPsHCLXCuhFM0+CajsauaMwSa84ItgXamPEMwAw1hJZTLXUxl9iwSfdjKVCT6Uy2JxmXl8ak8UUN4OnMS++63tswblMahjzuigkVKbXFj1OWn2bSTjF4c4WLvq+HNxq43JEiw1bGOYyOdZo+T9/TOcwNgdpHTpE9U/KdYsJDIkCJIuVULL/403/Bs2fPMBjOztYsugU+RagbY2lbB12LHz2jHyPg+xAFQkypuVgx1EWYme5LVuBOb0aBrBJsdE4TJaeo2liwErCmoesanDU8ffqYN2/ecn93z2a74YMPPuDlyxfc398jQXiLMA4Dj5884fr6ms1mQ9/3DOOYBOp4oEtN7bSOVUR15ik0UjoBfajgINTpFQzk1JdK7NL0cmS10rhMhGdOEenZ4NWjJKXaz7XHSPeUEU+HLjMQRSlrbUyTrul3aoYg8xP17uR7SSloZ5tpZh9VyVY/UgH6xFieiHBkOKq3jCr2CitRvN7Kc8ZOCZxRBoP6TBZjkao1lZmKaxDhKxumq71QfGCdpbExErvrFsXgbW2qWRON4o1raLsmeXKqoTzCUtu2JQrUWpCknEljruugZxZQCv8lFCFLGTsffKz3gab919rqBXfVxttCtqoO0nooS5n3Jr9RgGPCeqUSCqpgnxKe5JxgT3k8SWEuQ1HQayrQyKCHTEwydEsNpzYzWNWfGY6dj790XZjBwuweG1GoCH2BKTV6ZfFGpkqsvA5Gzx65hZOanHmfp1asSMXTh/NepQ9K2yh0oKzBsbBSc+HK85ezmQ/C0RgnynlbhqXnLxsGM/632UDtq6jWIYSYsqZrUKUbxLO+Xq0JIdAPMe2lSSmwNANMSOm+MqOtsDhZM6XV9fgLDj87W/P27S1XV9f52doorE4RtnICCRJTmrZtF/GtgfVqBctSu255/li5sSn8FeqRv2k0c8HRlL3QeRdgxeZzVh4SxcsKbxO8XtJGnzIkznFDfb/G25MUczCFL80Xls+czkGOnz11zqo2C40tNCsrs+ZjnNPOo2uGzGZ0qa77Lepllp880ecxKs1nVgVtzWeRlW6Kt+qzby23t7fJGUX5jSgMWGfz3A2Jhmga4Gog4+h5dH2RhYfJDMs/FMeEJGhksm4mPjDK9yidWXQLRCRFhLUT5bZmDDEi2cP6fXjl+vtpWDx9PfRcLejG75DP7SxTU+ZN8/mOz8LpGpMRdKrDWI079jVLX46UPc7EZ2p0neyTmcJmXi/dr/lwTJlf3UY5Z5IfzLOr6rIr8cv95IwCiTqkvTQpYpaMC4tyCEpq7VN7+C6ltiiOrkoQ1GO3KfuV1u0NEnjx4hl393d8cfExq3bB2fe/w/0nXxD2O1YSvemNxHiqSAbTPqXTG4LW/i0OyaeM2A+NWRVLX6esV5mv/u9IcTS7lEf4uuubGAcUV9av1Pv1rjaz/ArsDweGfmD1Dc7og1eIUQ7WuFQuI/6nGD6EmDrdNoZx7PGjpEwmFmMcgw8MYyB4g4jFOsNyvcBfrDnsdgx+xIdhwn9576OM4yKsTeWKiGM71yQDeGTyTFyk3IaiiyxH5/M5Y+P02AEGoe/3LIzBdS3jvefN27fsNzvatqVrF5imIQDj4Nlut3Rdx2KxAATvY6r0xaLFNRZLixVoUrT4OI5RsRaiI8VohMPhQDgYuuUqKnUkKg5HPDFqPeD7kSEI98OB9XZPJx0Xq0uuLq7Z+cDj80vOzs+QYWD7/DXd3cgbPK9sNCJf4Ohcx50feYKjFUc7GtzoGQ8HDCNNa8DBgcAbGdi4EYNJKX61PJcv+GdGI+YG1Fr+Uh7Oj0Uxr5n0XBvTHWrpuRB8Sq8pqdxcybzinGMYhqRPiXjHOcPZ2YrVapUC64ozk8SC4HFfhjFG8FSyonOW0ZDbds7FSHEbjQreGBqj/utKR45AZ3YV/PR1V63LSuCd5Huh70f6N7fc3d7y+Z/9km7d8eHja67WK5qmg+DpmiaOLfic+tI2GkVUnBSCxOwhzml2RUnihpmMxcwnN+PNTuHXdxln58/OPx/TmHf3l39LtP29jdrvMaavv07IXyfam8hWX/PsnPY+tJbvM855v19HG+f9znl85Sne95q+X9r5uv7rd07pO4/ljTnsPjDGB8WJWgiYyxenL2OgtU2iMZ5gLSbElKtgivNQYuMMkFBPHos6D0b+KTpP6bp/+n/7b7OIqOMyGBob8Q8YvsLw6TjSLjpaIl9zJ8JtOuuj92RdnDGMw0DTOP5yY/nLy6fwrSdY1zL+w3/CH/9X/5CL3/st/vrv/VtcXJ7zRHq4vqexB2j2YFacN2vkAAvj2b/8OV/85J/x9uVLfvO84eVXt9x+8ilm3OEPd/z3/4//K//rv/0/5tf6j9i/+JyXmztGs8K9eMtyP9KzIIwj/ZdfMf6f/u88+d532P+N3wV3jtk2NJsFbRe4PFuyXrYIsf7uo7MlfOspP5ORIB6XsqVNt7TMORtbdYfzmhbTc4XUsixxBAES9QRBIi3CtdMscMp1S5EzY3I/5TPib+qjVeudEZnoCid4xZhsXJEEM/WQ8xtThUg+O1HfMjCMIxJC1Hna4qiVZcZyQFNmgzkeVlkn6XEnjv6mVl3MJfKEN0gO85T1SPMjrbhAMjbbvI4mwfoEV5jSsqgD/qQ/7af0r11lvj4FRtRqLSn/5L2awEGNJqpb00udXCqcW/GxUa+jGQynzeXmjS6TpNrGM1xpTNEVe5/KYCbcUemMat1vldwMY6JeWzPBGn16LhsYhWWhLGmUR2Kabv1JsnN1CIFF13G2XrFYtByGfUqbXg9fM2MMMRshlmCLbU35PiGWEuq6bkILjDG5rno93knm5qqvh66pPlWjkIVPxy3PPvtT/unnv+D7jz/k3/2tv8Lf/e3fQJ6/5PB2oB2FVno+sC3fMxf88c09j67XrM8WXH75Cnt3iDJL8DDsGfoda+sw91taDKtuQdN1IJbL8RLnHMu2y2viUsDc5u6et2/fEoJntV4ydB3PbMPucGCPENqO7vICg7D1C84MdHZkHIeYBaoRDv6evWyRNmDoePrBjxhvv8QORG/PHtrQMXiXMhE4rFnEPWEAMSUbOkTcIcnmqEEsIsjgkcHjx4bgOyS0YLrowFGfgffiH7JVpwTAZB3I8fvvlMdDtD80tqF1LY1Z4OgwtIDL8B2knY2g8L9zvaHN0T4xaFn1eIrJTHLcKLJn1Gdow/Oyme+6vrFhXIUWPQR6mOranLUSRBdvnjZdfyvK+emhmhvH9eDV9eJUsJpv0JwprsecU8POlHNaC12N5z54nG0nyp96fnkBm1jLLYTA6mzFzc0bnj37ku12g7WW6+tHjKPn7PwsGgtFkrd09M6XcQQMox9ZLlb4EHCuzfRFlPHMwlLNpFfrWc9/utCoJnCuUIw/R4VfiNIyBlgsWsDw/e9/j5/97OfsdztA+O53v8fLF894++Y1/WHPYb9ns9lEQ2bT5ugC1f3Na4zUysi58XJS2zFRL41UVAE8EgE1WErOaqMEQj8XohHTLtQsd1GKVkSZYwWqHjalQkaKgbk2EDWNS5+VcXl4j+L3IgjMf8vjMiaPU5khrXVbM0VZ6cr0GRVW6r5K1E+eOVCi6IoyJfVho+HfOUfTNjGCMxuwY6pGp8yVtUfR2tnxxMZobudcjtZEyCmJZxOv0mAqAx2jodQooucwEEAMMqZ6b6KeX3PCrbhIYylKfyWyN/6jcalF4J8hfzMV3go8p3VI6bbjvFL94szfVH2l9us9zuM+gsSkWJlWi0hypc7jODrTAKP4ohgjSgaKT7LYUp9PHUF9PtK86wi8GgYlv8WkrbyH1d6CpBpSE+DmqDZUet5ItRZlOzMjP7nMvM2HGYHMwE/w4vwhqQhsJUwp0qiFmvqdiq7kvUUZy2P2IhqB6u8U2qQTrtO4VwKnIHgR/CgMo6cfRrrBMS46louYGaFtYo3LrutiPcjq7EWGzBYla4bdMoYytgoudKnz0ptYh3N4lYZYzzIacaAYZU1qRJXm4zjGSCHUFJqi3JDKw1t3IHk+VsJGXG9iqldDUt6W2jN5vKFK71XtlR7j+NzslKmQIhWky3TPZhs6P1aTS8cywQfVjmb8o2uuY32ou+pVHV+Bn5R9olr/qQE7A2g94xkG+nrj63TdpnzVqbnnLicAVVYgn5csyBc8M1VSWsQ4bu836dyoUbzAWqQ5xWiDKUsuovW94OL8HMmDO6EYVeGwEnq/zlCtvIB1hsePHvP27Rs++tZ3Yj3bai51v3Njx7sUtvX9+p3pmn+NQXH2bPUrWluvBvZQK5Ly/jDBuUdrkmrA5tT+lewAZKVC3TNSovnyaCq8WIY6XQ9jinJtjtcn06t4o3rMp+QJbUufLsq1NN9KiFTjtG5pQLMNFMe0+PeYX9GxHynvqlmW/SyKuqjIKUo3rWcfkjf8+cUFXgzb7Z7X4TWX6zO6M8fqB7/G7vMv8JvXMUVcCJE+V5HsAXNEa+cpzk8p9E9dp5Tr8zWet1Eb4k/tzUNnYv6Mtv++10OGnvdRMMyf2W63XLXdyWwb3+RauAPIgKRU6RGvW6AhRonHVLFewBOjcsVDCIYglsELm92Bzf2O+92W/eEQy3Y1DaFrkRG8CLjodNEfehrXYpLDt824Lyr14n5FmaB1Ke2r8blcjQGM1vOs+akKb+Q9r8+pBdsZRgkY71muG5CBw3aPwSHGs93fY5uWtluyWi/o2iWr1YrFYoFzUXk8DAPGGO7u7xl2e0wQuq7j7PE1bdsi/QASeaD1aoFcDJiFpWtjXTwfAoe+JzSCaxtMsLhh5HC3YWwaXLvA9JbBe+78gVeve169fs3mS1g4WGF4evaEn/z0zzjstlxIi6Xj1nsaHEtWPFmdcbFas1h2bOl5c/+cL8cbvpQDd0OA0dCMBqkcl78ONmsdxXuAK9a6lEkr1hAvhnFNtRloGluyByA0jWW73eLDECOMbHT4v7q+5Pz8nPu7XTaOK3NibHRi6A99VESmIATXlJql8b84h8YaQuLxrIkVy60IPiHETHIq3qFcf76zFtdOJn0kVQ27+56u3bHbDzjbYqxj9GB9Sg2KROUm4GzivPK+xeifcRzSvOyxuGKmjg18A7z1ddf7GMW/0fUuXvh/wOubzul9cfuf9/pzrfX/j64aHcsEZ88uqe6/Y15VxdTJu1EOrMDnPfYg/uojD2kMggMTkBBLx1mRVOrAYIw6U0pivyreMPVnKZnGorEyZf9TGpb0VQETK+0k4SGIYRiq9hN984wYl8rOSDSwmcYxSiCoo5q1BN+DByeB/b/4mN//oz/DOIuzmmk1OdFIwIwQbCwV8uFf/S5/5+/8FrdvP8D657B7yXf9cw73d3z+9i37y5Z/8OxjzkKgMYFA4AvZsn/xOb/Dkhv23FthdIbF8Jr9/+7/QPM3/yqX/9HfZfFX/jr7p5dwN9Itl2CEQ79l1/d0nPP8qy+4u3lDFwKu6Y4ixsvCSvVfxH8TBJ23uMId6liX2lC5I6tzchtxnbONxFTN1LSxytyofelo6prYWa6kxsFV0BaQM+6IEPyxvFF0A6lFiUELwxDLuBoRmlRurch4p87Tu2HfTOhCVn6no5cMz2l+QcuEVrJzvR+aKnnmhw9GS73O1sRUq5jOktL1/FeqXlS2qYQXpYGxzakDuuqCTL2vZcio3j3LIrOlsgi//4c3/Id/+2leYw2XjMtdySimlizTA6mky1wHlPGfTjl9CSFUwY7FkUDhTHFHECkpoq1B9VNZn2DywubFyAZBKc7BEOXfw+HAWQFMVC/uvWe1WnJ1ec7F2Zrdyx22cZO9VYfp2sFXU6tba5Ij5EgIsbTOxcUV1tmEh6D4wRyfgbK334yGWmuxAn7wSAN2veIuBH5y85wv/sl/xdn3XvHr1nFPw04c3hju5MDHr5/xox98hw//ym/RfXDJ5otXvP6Dz7m/ec64OsMZCMOOve2RzRYzjoy7A2HfEwLcvnkNxCh7PZfOORaLBctVx3pYYYCry2uuH1+x3e0wRnBWwHuG2xsO9zvErdh/65xh6RiCx4UGexDCZqTf9PRjz8WjNbvDS7h/y8E6QioVuTQdbdciviXqKrsEAKlERRUMF0JAjCSHkgpvScBIg5U25l2ye6xZEGhiWTSJNFGdgib/JVwVghqabUzrLlMZwCjum8U8vFNPYmJpqKZZ0LgljV1g6TCmQfE6kkoVS4rprpuTqc5Fj6zizuw4kv8zkJ1Zahkz0ahZGZ2vu75xKnU1INdMtSIGjZ5V4Wocx5PP5rmfQECnrvq9usadEgrtJzbExABep1vXfuox1pHuU2O9JfhjJUz9DhisjWnr/Ohpmoaf/OT3+eLLzwkhsF6tuLy4YBgHrLG8ePGS4D1X11ecrdfVnA3j6HHrhvEw0LRmQrzrdNUFCGpD53zB8j868MR0htlDVTRGiHXLnLOcX5yx37/m4uKMH/7wB3z6yadst1ueP3vBtz76kO9959t89dVX3NzcsNtsMM7hmiYT4RBkZsQuDIP2Xep7VyCe1r5tGlzbIMA4jPRDH70F0zxqpXemzVRElZT+0Vq0zi1GDchq8EmMQbUctWGuVkzbySKXTrJSbq7YqYRgKqE4PlrDrj5X2lcnjrLXirCSsiMpmaMiwR0J1daSIoWalDLcZaWDcjtN+i0qQ6LSy6SIbDWkGZfmUdXenmIuU1IxV8ylAqSITFOIS6qfqZH6vkRM6fN5EysGKUY/J0Iepk4OukJqwFMGaA4PkhBkZgJnCt2cLSCVUcgIeMpZJ2VxwmXpGMaM0RV3aSjMmwkTmKsZvzwOIaX9m/WlK5oEBF8RwzKnGd6sYWH+l8q4lWDdVoRXEiOrcKsGw+KRG2FHDapx7qH6Xap5kBjRNCjtwJSx1BuZmeV6v5LgW8+1ns9RKaDMMFdPm4mpPT8j1fcaHvSdglPqs06BC6iemcKUtkk13Tn20HYmdEm7lgLPSvQjjkEBkLgiBW+SjIH9GL0WD4c9w3LBcrlAFh1dF//bbDaAoRlHBmtpXIR5P1ZMj+JjnUe1YjrG+Voh0HaxntE4jhF/JPpa8OB0G+KUIk4JCbd7k5yhklextXbiBTy5DBiNrq2EzYrC5H9rBDkx2qnhzxjqGtxSbe7EIDsBQylAMZ1dGSC1M8EDfA/1eBJdnHzXBmbLOBPgykPVkHJDYXJ7+obyATa/MjGEmxLtLwqLMp+D4gllYsvnycrI9G+upZ2+h6p9MKVOqsKiMagCRQwYa7m727Lf9zjXpO1I+2UreiWVAidM19z7wNlqRdtG+I1z13dlsh5znDo3AOvfuTJRgnBxecHLn7/iyTBgnTt6v27nXQbEYqg+DdOnn3+/69joWDsrFuJyyigqsyji4zbL80djqmhS7dSg71WYrvDeCRmVY1WeUZ6qKB1O4w/loes5qZJUH5o6hBXDd9VIBR9TnKAlfQJMzn+SQgs9qs9bmkd22iPhpppvNcW5QPGr1v7S7EVG4nnCj7RNy3q9AmPZbXe8fPOG68trHn3rkqZZsf2TDSYEnAhtvVfpnIlILgEVI9HdEYyfuuZGgPcxCszhY+4QXfd58qxMSLnuw+lIhnk7D4311Dl/129lbWLf+92erm3pD4evm/47r2V7S/BS2dejYdzQIXRgOpCOwS9iSj4JjCEwjEI/wvYwst0d2OwPbA9bttt7Nnc3DJtNdD4OMTK6DS19qvvs/TKeAZWPqvkbE9NfN87R2OgoO+VfEj3Q/0xMnS4Jvx8beZPMkOSGYRQ619C0jnHccnvzllEGVq6lXbS0ixWNixEfh8OBfrVKjtnx+zAcaFvH2XqNWSyj4shZbNMkHsTh/cB+OCDjyHg44EUQ5xhGD/3Azm9olh19cIT9PYvbO86I8qltG8Z+5H5zx8u7V+zPVjxaneEY6TpYdi1sDywOwqVYNsSatp2xXF094bd+9GPOVys2/ZZfvn3OH799wZ/5N7wc9xxSBjQnLktYdTa+Gu5P0Zyy+uV7PgeKQ8THBPY2rolrG4yL502Cz/sQgrBctDFKahiAQNs22aFy0S1iymJnWK9a2rYlhG3EfzY6NpukbI+RVmPGIzUs5UjAiHkSfFmCDXhrscYjxkTjFyR5I8kpp1HAe181jqh1QqYC+SjDxi/3mz1fPX/FJxef8/jRBd36ksWyRfxAGPvkiF50HBBTKwcDTdtgpYm/pcCEwnskPUFVZm9+vcugXcPG3Ah+6r1T9yYOASeuaR8PP1P//QZsyFEbp9ud3j/Fd/ybMEKfxvfwq0Hd17f/TVqd05/cxoM82cNjCF+3YWlstRQwk7arX07LHrzj/sNjjCmMLaDOYYYGwSESHaunkmBm8DKfqbxfTOUaHfVzlsooWAJh0kLIvGG8YZwlpLrOQUIsLzHjO2NrFmfBj3GFQqA4bhubIh4MhJjVJeqpTNShigcZsWIQbxit8Pzjz3n9y68ibjGGxlueuY7Lv/Zj/uZv/ogfbP+n3H71FRd3W757d8vN7R0v39xyeLZh/WbP29sbDve3bHcHDMIXh1uaf/HP2b285erjX7L6n/yHnH34Q3osm/sNo3iatqHrWj7/6ks8IKlEkD06X8Vwo7ofUSjJYuxMRi0Ktyz2TeXcpCtNf4PUPIPSwKITroGtyO6pKVFxU/KDEX7mruBlEHXA1hSuytMRFyb7QYhGce99coBO5WlSAGDUVWgvx60dXzrOWqdcfpPJYlLGovaDTBgrnH+qmxpfm7JPWhMaU5fHfNdo0ypJ+W8aqVmkvNlG5/cmOgbdO6NhE7WMVw+/2EyiQ8pMRtMekr6hiPOlPVPJoFnfQUXrqrOtDgh57XJ30XivGVitlF2OsozkLDKFD6sNnQZsTS/Th7QuYz8g3sdSP6aGU2HROs7WS87WC5B7FosV9W7H8xpyKWTVe8esjQ5szHbR+EDjHGdnZ7TtgnHYR14opdhWefaUPPYgXEi9zsd7t7Yt3oDsQ3KAt+yM52c3L/itxYe0rsFIw4BhNwZetCOrw4a3v/gF7ds1a1qe/PYP+egTQ7/sOCBsJbBrLI+Ihk6n+iPjWa1WXF1e0vc9fd8jIpyfnzMMA/v9nt1ui7UN6xDANWwPO+63N0BgsYiR+d0SDmzY7hdw8OzevuFq2XF+9RiGjjZcYIaO/vUtH/+3/w0//uFHjN0at2xZtktgANtCUDNsgbmaXOVjHJINRQTExBrjwSOhjXg3DEhokOCQUMGkejVk/UTpTUtyChJry9sm8fIls6KO5xSPc5pOx4EHhHEUhiHQD4FhEIyNPLAJYCQAtir7WMYFFQ5SeqLwLuSM8lkOMsQ5lxEUmjK53i9q/BsZxmvvfQXupmmS4kLwvp8IO/Mo8VMMeR15fupg6f06DV9tHD96r/44O7h1+nS9agZ6ykyfJllqHFdBLoQYTWyNIwTPJz//I96+fYO1hqvrK4IIi8WS29tbbm5uooJK4rr1fQ8Y+n6gyYrdYuy1ycNoOrciOCmsKpnBlHuYikcwJwBmNm9QJkBom47Lywvu7jY8efIIaw2ffvopm/sNX3zxBU8fX/PjH/8YEXjx8iW3d3dstzv6wyEzkdM2qzFUikVlrKQaQwghrkvfZ0bJEFOQFIZT51oYUVPvvZT39NTVxo76srP1UQJdjNlFEKvvRQY6EuyS6rv6z5a+1ROtaRqcsznqylaR1no1yTBdUkqqITwax5uUdi5+dzGlUUqZGQ1SYKykCO3IyIjE6G9rUqLM2TnLRiUpiEaj8oNIrLdBhYRqWKJi8RQRSVlTNbCqkqV+a9rK7JKCHmOt6YcfjXPU1woDGcG5MGF1zxneqhq2ebxpicIMZoRi6KqHrmNTOKx5msKnm3wmowBR1U0+MbW4JQnha+YFZeplupJz47j+YEzhsLLivhpwqIzd+q6vBIHSdsFDNbOa1z0TrWpdasbTmFTPROHkeLgZPWSmPK2aVil4iOeaKwLrcVZ95GnPfjsCKZHp3dlmFlKdW0M9cGXWhs5LZLr+BVbrKMIadss6TwS+aka1jKTOJwovwQc2my394UC/WHB+ccFisYgplJxjHEds0xBMjCYOXmsNNWTPOlPml3utkGycjkwWt+06DocDbRvNK3P6rw+afL+cJ+89GENIOMuYyKRn2kZ9luo1jPO3NQ5AQGpjSHm+/lwyFdRgVOEw3cP04vS58vzpq+DZOkp7ur9m8nrpLYuXD3cj03OSn040SUQmPGBmbk9kuo7wTFGiKSwrnZvgvCrS/MQqnECP054qPiAauAsgG0xO1RqfjbylerAPo4+pfvOYDa/evCXWIIjZeGqlVGokjrnavHgWdSGEs7Ozau56osl7PkG2ZcmwlPIXE5ymbVH6dM6xXq+532y4vro6Skc9B6xTCs35yn4Tg/hDQqskOH/IOJjxvyqgajKS/757PHNFrRquC0KtcbXJz0n1XRVj5YQo/6cHu9pzvVE61ZFQPZzf16N4esxugtdj5MqUbw4ptZnofGRKag3FSJ6HI9VYUlu1cb68W9Y28+wV35xJcdobNeaMyWlN+cjVcpX5gc1mz5u7e4bwCX/1d/9jPrl7xe2Xn3NmhP7ujoWx0UCotNsWHKDyTw2/x0YQmY43XfP6uJEvPaYRxpgsR9ZOzqfg6+j9ip/Rv7Uh/5RR8ZRcOh/PQwbwU2PSNi0m1tA7xNp2i25x9Ow3uRpzIKQoOMXPGJfoS6IYBhpZ0I8evKT0cjD4gZvNPZttrLfXH/b0/Z5+6KMCN2rsY0fpPDg9piZGtjrrUhRDjOAVU0X5ViWzJoCZ18NiTMGv+bdyZNK7saxYf0iRK4suzt0azldLlu05b1++wjcB41oa12VZp2maLB+JtAQ/MPQ9+32MFneJ3tiUsSOW0wLnGtrlgjDC4Ea6bkHbdogHJw3WOWwTM141Xgj7Hc7Fs9Q2LUPX8urulv3W8/3Hl7SNw5gRv+/Zvz7AOLKiY49BjOPp6oLf+J3fhfWSn7z8gk9eP+PLu1d8tbvnVvYcvI++MGllQtoHkZjNbg6Pp+DQVPzQEUwnhKe6F9s0NG2bSllZRj/gR49IjA4XYlaBmFbfY1NdTNXJNE2XHCOEpk1RcaH0JUZwJqYOH8eYglQkZY+SWtYmnZvIzzXWghOi0SsQgsOYgDeBIODz/BL+pKYP3+x6+IxPaUMQwEbHibc3d3z62Rf44SnS3HN2cc7ZqmPRRQcDXS8AdURWdmpqnClziPPQqL1SUujUeL/pdUqRXdOdr+vjlOFVefV3Pf9N730dPq77fB+l/PteD/NIp9em3H//vk/B2Kk+HoLH92n338T9IwZpNq7677GIVOle/iL2SZtNMoCXWFdc+bNCG1WWS/KgyjN6rxZtMhBPRz/RGlUZMKK8lDJxiWSHL2NT4IBKZyZ3BQiE5CiJIZHTONQ8Gx2vMpER+VuTUopvDoybYrY3weJt4PWXt/xL+YQAbLd7XgXhWz/+Eb/xwRXf73v2b+5Z3x24ennDt27u2Wy2tNueu7tbDjd3yGbD9s/+mPY7V8iTbzOOwjgeMA5cs2Dc3XP3+iXixxRqZI5BotKdZB6h3rf8gil8WhYvyjqr7DXdgyKbRgbbFDwgurYFr2oWRdEtLUh2srs5qEWHVREQfXJ6JI4mPZl/NI6H5NiQDF05kE/XQR9XOaSi3yfwfSUyz3o2JW08Fd+tw6w+FJas8Luh2i+T/lHnjjJNU3QHtdymC5Tk63KvzLuQuMqBwQhiLMaGnEHpNIxMlzf3P0kVMHs0yx0BkRI9qosnac5WVOYrzjyx+QjZqmstwKMDqfQ3KfCvhp3yR/kZS53tMepSQob9LMvN9zXBcx6G6P4Zhr5nHEZMk0oZaN1viTxT1zqWiwZjo3F7wocnvk0z8NpUcqKWx5RnaRpH2y1ompah3xGCymqFb8y2gso2d5JHmO1RHo/RjEAwioBpCCalzLaOsbX86fCWt801nbOc+4bgG+7wrG3L65sb7r44sLtpaZuGv/3U8OtnS7b7e8xuy6UXFs2SO3vgtRG8hcM4cHd7w7DZsV6tGIaB3W5HCIHz8/MsTzZtS9t2LFZLVqslXdNiQpyrNyMbfx932+zphp5F17FYNpguRrVv7vfsbu/ob9/w8uf/Gnn7Fatff4pzEXZC8IxjzyjLqPMSMASCiTXJFeSUfokIPgXNZD5RgODxg2foR/p+4HAYMn+tqop8LoKW3kzzSHpfn5xg6/TkRZ4r5y3TpnTO868ViVRwDwYG7zn4gcM4MviRIYzgAwHBChgxBHGoLiaKqlI1SC5JZ6CUHaQcy+ygYpgGE9QwV314X7ngvQ3jfd/Tdd1RJHataFBlxvsyP6cYYFWWaLvzCHERoe/7nK55rnyp26uFLm1b/6vb1KtW5oRQEePZGMtfCyF63FxfXfHlF7/k1etXDMPAout49OgR4ziyWi359NPneO9ZPnqUjJgtu90eiIjq7PyScfQRmRG9jaMxMzFfFcHM0V2JPigx1zpeQIxaTdROha3Ta18AX0IUYn3wrNYrMIbb23uuH12yWPwlnj17xuuXL3n56jWv39zQti2L5ZLz8wsuLi5zf5otIHuH+5BTj0Rv9LIPmqpNl7km7tkATc2gFhgpRLPsbzZK6+y0rkhW4KTauintuLUGZ12uxQgm12a0xuYa586p0sXlNTOqjGmaqD6QWLfNNclgbW2qeeQmKcaNMbjGpVrZmrZGo8AjQY2IzeKsTZG9UhjuitHIcECpjS1ExDiEOB5jYPQg0ue91vXSq9SiViI5faYwU3V6HJM5j2Lky7tU7SmZUVLFb4HnwpzV79cG1EgciqKngG1hwuvLVNytqGOEEFPazAi2MiEAxpch1I9lZlMZwUlf5L3IzN8MZhVx5yVLDKtJ6xZ15mWdRUpUkDEmE7SyFjGFdq5rWwsVifc3hljvrmrDTNa3mrfRczJTkJg8SiZ7q4uRmP05sanvKTGViKCYG8elGkk+4xm2ayNl3cFkEpN+8z5UwnhmLjh9HSkl0j+KN08pgpR5VpBQR5L5VdL1m4JqtRMhC2aR3wg5SrbwCKLlXqf0UsdIPJPGWozVEieJTg4j+92e+80m1dtclJre3jNiovKbeW3gBBe6V2S26GgNNWUvFi7OL9jtdpyfn+fyKoony7hPAIzkGVVnqURrVhQ4i3hTxXBirOuH0wIWWn58GeqI0OMh1WCW8eBRIycQBrpXc0ciKcK9brCZrnMefI2XTiowTXYimYi9J3mvik7UMFhN6AjOqzG/6/tD12lD6zQ96NRJJs3VVgKtiRkDbu823N3f0fdDPE+ZYU+pqlPpGZMFwZq3meHrOIBCP4ywXq+KMD+ZbLVXc1yjMGjKmuQ5S3lGo+CDDzx58oQvvviSy4uLasZ1f+XugwpKjuEq/zLjg46aP7W/MuuvUh5JdS7LmbMVrQ8VbUzAZaoVN4aT0DjhPaf35zJBfrKiRVPYKjX3alguuGJ6RopDo0n4+8Q6K69AeU7pgYJsvZbWaLap+LJPAeEhHNMPqWlh0epFGFG6pURF13YuoxyvaJYX0vBzanUJAhYsga5x9I1jsejoh8Bmv+dff/wP+d2/9bf5yX/n2bx6znqxwnpPGAdU+M3HdA4r1aVO05k317FWeKvmJd9HRnwfY83XXROFvZQsRaeM2+8yVDx8Ho/HXDuUGAy77Y7gPW37jfzQjy4rhphKPLETkXEjV//WckHGYoKHEJ13bIKDfujZ9Xv2w0Df7xn2e/w4xqjvtiGIBWuiUqix2XFZZarsjJ7kMmuifBozTiVFygwfFrxuMMmjX4ziicrxSP+K4AfPfjswDGDPWgxR4Xd1dobvFnz+i89gEWi6BV23xBmXZTaNamlck/idIeoJvGf0YypV5mhSWknvPc7C0jWYpsGb5LiXDJNGAGuSM7KjExi2G1prcN6zdB12uea2v+c+jFHx2jTYIITdns2bW3o/Yk10sLHW8sHigg8/+oh/+tUv+Mdf/YxP3jxnOx7w6awWGVZlhGNYPQV38+8i0zM4eyC/41wTU+M20aFR64urPAmxxvih30deU6Znyab0v00DbWsZh5HolRdyX4rDVC8gAjYZj9W5Qh3IjQGnWfKUhIvgg+A1lW0yMOW5p2fUOJ7hSdv4miumEi1rdhpHlQa9wP4wcHe/ZXs18OWrZ6zOLvjgyRVPHl1xdrGOWWww0QAgKdDBalaFgoey4SHPpSjNjTUPlmA4Zeiu/37dVeOqI9z3Hm3UzgwPjauMKa7bX+T1q9CU+fv67vx6yFng1FWxTH9h11zm/Cb0J/79FfviGM+8e22n/JpwWrx7iA/8pvNKIlO+54OAD4w+YIVKuZ4+KwpSfj8PufBr+eyll/S78jOZB1S5TBRmTO5LK+Wo3GqAZM1O50l5x0iLjbWgCn+JUeNGbMKa2mDNY6b+QiwloXh5DAFvgRcb7p7fg0lGeud4fXZB92GHWXXQLdg8EZoPnnB1GFn1I+x6urs7tm/esnnxBr8b2D37HP/5z3Degoysr865+vBD6AfWjdCZGI1rOD43Uu220fUsux3vn4IjKe+qEXvyXJqvssWqgwFdVpPpWdzDuSxX7VP6XX+uRK74nO7TBP7JIuPXHqyK7nqB/+5+H53xnBqa6gxUChPKJx3LS1NUPD3bOZo76TjnQT7KjyGVy5ipmsryRVml8ow6KMxGNZl/dZ6yXKRtx9+LflS/G6zCKLOlrwaSj3ueq+496fzNFyptqxDtC1bmP0f+IA2w1pkovJn58/Pp6kBSC1mvJBJ57nouOt4ZzEc4Uvoedf+BYmguWxQnOtl6G/mncRholx2xbBxRryJgQqB1luWiSQbYOTxE/nMYBkLwSR9j8CmLa/ABbz0+RbRb16RSwSq/1SsTr1MO0mWu7z4rymf4tK8WCM5gg4lldxrLp+OWL4ctHxnLJS2H0HCDZxUaxs2Wt27kq4PBdI7fMpeExYq972ll5ALDNR2rpuXGBHojDOLZHnb0mw2HVEpq9B6f+FKMwUvAphKyzpKcPm3CzxZnO7yPfL7H4YcBsYKxwmE40L95xc0XnzG8fUt4+4qbn/4RP3q84nrdEdo1vcSyVEPf0xuPCRL/IwaP23GG+5K+x1PsZvHseqyPBvZhTI7Ohx3D0GfakvGcFHtb8DFl/jiOjL7Y5AoyqP8jq3b0gOd2pcKL6V6mpSY6549+YAwDo7SMMiIp6t0JGLEEfHTeTnjiCH8b8lxsTpWuxL3MCZKuTQGdig9NskLWv77H9Y1qjBtjJn81csB7n4U+HdA3YVJrBr02WM8PnH5eLBYRUFLN8xAqzx0hpZg2EyXIQ4e27kMjC+I9VewfH/AMZOIZPRgsV5fX/OyP/4DN/R1N47i6umSx6BiGgbdvbzgcDjx58oSLi0uWqyVN07Ber9nt94xjwBoXawKoYbvqL3sfzcdenihoPiEbgVJAhJppma+BrkO8F4JBxNM4w3q1wlrL7e0dy1XHj370A66vLnn98lU0tgwD+5vborwTibm8oTIGplTVmrJB1NPEVHvgSGUeEkGxJfU35LQkED1ZXOOq+UenAU1BrnNq2y4qohJDbFNEdZOUJ95HoT8qUVyJyE7R2tZGg7ZrXFYKORdrqWGqtG9ZGWlmY4hXVlbOBBbdsXiwdXciUsjwHDxDGPO70QBVDH+QvPaVtaqw1MTQpTAg1QBmvykC1s9zoSVoGvPqdYFpbfiK1cm8Z4WYVcCL9dp1s0+xgxrBSDpndcx3MT7ofO0kNFIN6IpgFW/AxC4+YzY58TUKelVsmqnu14KaKq5QD8RyPpUhm6xb5ZUcI+lnUevV+qlSX5LSJ3vCSmm75hJrhtImgS6PJnGW9bmHZISPiGxSn7C0Oo08z0xl2SRq4JBqfXQrspnCVARrjlcnHypmcc4N18S4uqJhweR9n69NWSMp4z5xZYOdxB0Vqj1PzkPaTj65aUyqHED7pwgoGSdmHF/hwrQ+Vs90PqsxNVfEnyE7VYBUKUd7oCrDkPDsZrtlu9lyf3+Pc4Zvffvb0dknKT1t8l40BkJSVuZhmwofUH9W2NA5xQhFCcJyueTm5haoowNPLjFZ6qq3SAWsikHKSqEsNBRjdu0gpqPK0JLhhnJwT+2z0tWjgRZTWpn1bH8nU5nxF/nHgt3q9/I7aY6zQIU0ZFPey5qAmatK9a4YyEL2A+Opmk3NTWuW5X19BwNZZ6IoZ3J6purIWir+rh5QxiUJL9mMW2IA49vbt9zcbegPh2QwnzHtRlPsRQeM6CgZ4bFCb2V8JBytnL0R1ssVbddGJ6LjDap4LVMh9EJ7Jr/XtEPhJvOXZL6173varj3ac1PTruqaGlbD7HmZPPcQ3/21AoHu3Qled/q9Ln+SxlDzACJIglE9h6f477kBHCjGNT0T+RmNpim4OMtNk8/VPOr7lP0o7xcaPZl/YhQm+2mq9xIfQQWrYqa1r02INDVXCtAyTRl4ivOSAtUpw5Wu/9GOpjUNFf3R76rgqbPdOIEQomF2vVzSNC37Q+Bus+f2/g0ff/qH/Oiv/XX+7B/9I8ZNoPWRL3YYxoSHdS8fgrE5nNSR3FNj8cP0/9R1ynhxSi58n+vrHEdO9fuue6dkyqkTU0yxevP2LYfDgS4ZHn/VSzhHS0mYjAItxjRI6IAWUlrZxgZ8ShOLifLlsu3oFyNjGNmNPbvdljAOdE3Dqmsj7+eKnOMHP3HKzPNOJ9EYgzNRaWSdLbJfLTcUMCxrRDmPsb2Y5tBIlDOGfuT+9sD9Xc9H19GI3TpDY4Vh8Oy3e5ZtmyLShGEYgIHRj/R9T0hpAxeLBefna66vHzHsDxx2e3b7He5sTeca3m4P7Pc9wzgSjGHcbhnMQOcD7cJjDgO7/RbXrqGDhQQaHxgPe1YWumFkaYSFWzBeP6Y/bNgdeuzKcmUcy9DyZ/dbtgg7EXqEDrgQx4uXL/n7//If89lwx2CEpm1ZjTHdtm8t0kQ5kxBwY2BIctCp81Cvtzpf6/2pwyMTvYriH9e2NG2Xjff6m6ZkNSY6gO/3PsnnFL1P4rmbxrFYtiwXbdqPVK/T+MxPBwn0/YD3JahCedbo2GCr+0nGDiaXTAsh0Ge4CVHJZsocJeOqwiO9H2Zg9vRUnjKmrFusx5icBdqW88tLrp484Z/96z9hs/uKR9cXfO87H/CDH3yHD59+SNO2+L4nBJ/8Xk1ybDE5i5buS9krk5wzyp7V+1fv+ym6+hA+fF88mZdjwieept/mxG/f5HoXLTmF37+ur/f9/X3W4hTNep925+98U4PB5Nn4wq/4/nQT34emPdjSDNYUd8zviXn/M/duGeMYjosOTfWvMasYo6cfDF2IJiat5ZvjI6jlErK+BtIzCT/lkiE5Ejz1KSQVSNpXa7EGvKRoOwkIIbHPVQBHMjhl2Eh6HtXXBdHsH8oSxtKcUd/ji7O9xHqtJiR8pHMJkf9zyVk1BA/BY0Ikxfd/8AUf/8EXCIHGgs86zJRN0hmMdXRyTnO9JqxHwrZn/K9/Pw6dgPzGt/jBkwWOlr/6mz+gf/MnHN7cJ2P+Q/sn+n/U8QfDiVTccZPKPifOoMo+I3lvFAZCKnasDrEGpOKvZcqnZrlNW0t0jfS8vjc/v6ojinYOFQ981r/Vc9BAHNUH6fse4R/cbXDNGpcifE/BfIYBSgTzZC2re3XmKZGSqVSk6IPynPU1A7kUYo0PpjtR7glRI2VMzg6QOizv1NHSeivLOJVAJgoL5exqP4l1yPR6Qm/KKdGuy1SOVpAkoxVDmeqNrcouOp7qfTVQ55IAeSwp602F83TdrDH4kKJupZxnZ8x0/OrkR9EXFfyR+tDlEZnARa0DqD5igEPfczgcaM7WWV8SZXBJkd6W9WpB29jEh+VWAWjbNqUOD1kPEuuKe7x4rHcEH1LGH8Ni0XFvLRJS9qC8tWZ6Vig80vx6J40J0dHSOYsXD00DqTKyD55bP/KLwx0fNVecuZY3Q8NrdtwOPb/DOXfDyL0YlqszLrfCcHOL+bCjPVvRuQYzCmd4jIlBYk3Tcr2+4OYQ8etiuUSA/X5PEGEcBrb7fTKSC7vNLbvtOYe+x5uG5WrN5fU1TdsixOf7+w2HVxvGcY/fbTB39+w/+yXLw47VeMAPb/nuouNyuSQsr9mLY3R7+v2Bvok1vF0IgMcbsOMxzxFQuPbVOfPEPEwHfNgz+i3juMWP+7hf3kRCkA6b9x4/xmDVYRizk2og4joNHtUzUJxFNMp87nB0zE9lG1Sip0ECQUZCGBAZEq0UPDbhFhvtBZnmhYqmJvnESNSLq52l0r+rDTrr9GdwqM/4MJWfvu56b8N4ndpO62Vop+rtG6QwUN/UG7AWDLRmeB1hq32pMFUvQK0ci8gmIFUBeW1b+5kb8OtUELVQqJjuFINWjCINXaq39fb1M87PL9hdbnn6wQdRoGxbnj1/zkcffYvLy4vooTKMPHv2nM12w2635/rRE0jCZtOooqxSMijTViFZpZcTwp8JTTXmydgLkY2AI5l45fkkajVINMh2bcujR1cc9j273Z5Hjx5xdXnFLkUibrYb+n6I3ifjiNYSC0EZOzUOFwWxIUZpt22T0rcBpihYY8rxmDpdIEVKS4rAdllxo0xBrJVdFAJNE+skNM4hxmfBvobLHMEdOdQs/FprU5+aeklhSqbrVBGJeCZNMjiVVHcGwzBLgz1RSlQMg7YTZG6AlryvqaMJoZVkRFciH4dp4/s6V2PJHpcVDEW6WIirtpnhp4raVOjJEHSC2akfFF2fGg8EvZfWQsHPlIbzOqeGTLp3VPOq4hfFhNyIhLkgKmmvKqYoD6Ji4PLTx1HN844fYmJ0LeaC/GS/OBVFNm2jnPN0mFNaxYmCOTO9p1lpbVd50wjmFdNKaVOX0mAKc21MNnDU+ZcnBDA3NFurepzpWVudidNk4ZgRLIYESfLP6ejeMp/q3OieSl7JDF+iXHmFAutWptAj2e3CGAN16WIFoWq+0wwY1RmXiBNFhNF7xiF6fsb62iSYj79Fj86QHZtCle4miylG05gmvOM9JMZG5+hT5E90ILO8ffOG84sLmrbNAp6eq9HH1DrOTUuTxLOQ7okanovDCJmpEZbLRWS0QqkfWeAkvqmwVsOAEBX96iSSDVeiv1K9pwoIyQIpGYZthTvK9p8WppISJ6iAMBENq6fI4ylnb4o7jto+8czRb/Xv+bnpEKZGljKvPCb9NoHfvFLMZz7hk3QNyoEhnziJ3+vna7yoNGIy9upzpp/VOGWOe8w0208+ktYyDCMvXrxgsz0QjAPr0pzTSTRVtp+Eo0r2IPWwg+LJpLhOw0dCxlmXl+cE71O9oxPPlpVKSz2llxN6Xq/XZHtUcRG4ur7m9vaWDz74INH64miUlXAzGK4BYw4T8+sUfj6t4J3R9gdwayVvJAc1hamkWApT+JlfVmu9p33Ss6aKAyjLpscwOw5VsFFGXfGvddfzOdcwWrWR79XDzUSylluUD88ujFUjaQyiA67XPcQ6xkjkw0JAbDJiV7hLMvEAkSmt1O5TL9lxsqAMXc+aF6jwq56DdAUfMAhjP9C1TW588IH9YeDNzWusfMyj73+X7c/3hLGnTZmRxqQAmijUHoA75Z8fqoWcx1PB2kMOAZPvSVZRelPTdDn5DtWRSfjKFhWfVHM4NhSeGNMDcz51Tc+myeWN2ral67r3auOhK9iPIjWU6CQUhxmIYcYtxjqEKIc3yw5aaHzADh6DY7VYMojn9c1rvpKRcXPH4TBggtDYmEmg6Vpc0xBGz2Hc56xf3gfESIZdIybLHMYYSEZNSedF1Roh4YlQ8fATuT1dxtoYiRyEvvdsbj27e894EHbbDc++/Iw//lcfY9pLvvfRt9nZLWBixHHi0LwfCKFDjAOJeoTDYccwhhhVeOi532xgHLm4uGCxWtHYWK7j7PwMe77mMB5ozy7oFmtkf4C3B6xz4BwWaEPgW2dL3twZLkJADjv6QVisDRfrM2Qn9IcDgYaFtByAAeFgYWEXXLkVFvjnn37MV2GLwdJKjFLZWYNruxjN7gN+GGPEhZ3C45z2zO+fogG1saD+zdqWrl3QtC0YcirNkJRoNS83jGPmOaNybUjtWZaLJVdXF1xcrWMpNFlgjFbklrQ/nsMhKmVrHc5RNjWFBxvlWJfk/8jP9hHvpuwIJoRUjiXNEyEj0G9wjWPBWfPyDCIF78Yg0ATdxmBcQ7tYc/HkAzbPXvDszR2vb+/45PPP+K3f+A1+9IMfcHl2xsI6xI8MqRRMqtRZ5LzJHp2mpu8yzv55jNN/rut/gG7nStCvu76JLvKon///dRLHPPwsf2EwcXLf0mEMIRCMSRFoMAZPIz6dmSQf1M55ascVUKqUeVll1iXyYiHLg9lkh4wjamg1JsamxUyONvF2SVMyRuV/HcyT+836FJMcF6NeJOI9hxiHFl7AOUxywhECYxhrCQ0w2KR3NqFElweiU+MoPrEGyaHYGLpgwQvBjIwm8sfOuZR9JgYFyXlLC5hkGAu/eMZPf/GfY23DX/2f/Q7/snHsvCdYzxxD1eJrlpdURlOZ94jf03WOgGOsKcFGlWxa1DmSxDtJex9SZGxxKpr+1Y0tugflJ7OcjUkpeyu5q5IrrTX4YGCUE3JSMoInuunHaGREYtYT76FtY+SttWpwna6aqTykj/ScZTjTXiXJGipHTWQXqbbGpO3X4IvqLJ+gMlnvffKcF2lVl7X+W/hBTSEe53pUrhLVo0s5Fw/g6KhXVypZZaE5MTaVnX3wNOJiMIkxGFfkxlz2R+GjkucUQOy7cJwxiET+SEvxaGbY0sZ8/aSS+wJqFOfE2hxduk4IrTNcPd1wd3fP8uoCK02eAgJ+GOhax+XVGctlx+u3B+pzEEKgbdtoBNZsPybycnXkd0yvHe16Z+tL3r55zeDHnE5ddTcP2cVOOYQ9REstDicWN4x4PIaA8RZMQ0eHNIY/6jc8ZslT29ItVlz1PX9fXvPr3a/zl8aRX/Mdj84+Ynzzlt0t7BZ7+re3yN1brtrAl5/9Arf7q6yettjRcH+z4csvv6Tv+1jSeBww1rI6P8M5x9nFOQCX5+d864OnLC8vufzOtxFgs7nnzcsXPP/8E+6ff8XNi2eE13e09xseDTt+7Hr+8vU5q86xkZ5Pdm/5bPuCP3q+5ezlV1x/9ISuPaPvB3abG7h4BN4jfsQwcJARG9qELys+XmGFkJzPBJtSr4s5MMqWMdwx+nt82CNjjx8M1jUY46L8laLFNZjSWstiseDs7IzlYsHi4oLz80u6LpanaoxmDUulPHi3jFzvtcXgJODCiA19dOpKmUVJ0ffx+Ed8EyTg/cAwjgx+YPRDPhads7QpILXWtQQJ+OQooPCdx5aeDZ6sk67tvF93faPcbsbEtN/auBrIS4dTBVytJKgF4XnKPV3M+lm9V3+3leJfL625VVPliUGmSvGnbWmUubU2L1r9uxpSQ4rUMzbOLQRlBpSwRkFp2a3o91vub17w0Ucf8dGHH2GdI3jPy5fP+e3f+S2ur6558+YNNzc3vHnzJhoyMLSuYbVeZ4ZSGbapp1L24Uje0wlAskZQiaumOagiPDKTVy4RyV6HaWfrH5VFwftYK8U6y/pszWq9ZByiUWexWnBxeZaE1WhUGcehrGVeU3Vw0DkVhWPxFi916fV+TM9n8uiMjWnFVcGVI8pNeS8rxpnCorKT2RidFeQpFVOtQGAkG4uJRqHCUMcnpql5E9GLg4htVwzhVME+NURK9aEo+Op3CuMynYneNxOmPoOD+PK2RMVmRh55XkmEMOq5VpBevRoxXYtMYCOf8fIYxlCtS2UAnylpyr+R2VUHyIw/smJjssJTRkbXWyPtzZThO1KU6nkqfLbOLv4N5ewoAwlmwqTWjOWEPZTjHVI23xqN4qr6zbBU2NLMp1fjmxAe/V4z8lTrWj+rwKhHI2t1ZgZ0U/qrDRDTdlQIKWs24bnTu16yS+2k/TzavM+mwPmEbyw4J88pdaYKKdL882/p3Gg2gezkpCllA3ldtP63roeVBFNikkebZPgP3kdnGf2uBDVEo7X2aZVQi9ZriYLRmIWjkFLpFqFJDeM6B60/iDIcGaQKI11gksk8FQ5i7cukBJB4r2mbCS1dLNqMU9SzPEgT52GignEIHm+EgNBY3csCkCKmgtjjSxWKbdvQDz0rt4z3rSm4TvHyZI+nwg+4KX5NMGitneAx9GzlVms8MBV8a9ypZ8cmgdKHkDIrhNRHMajFkavTTcFRJDqT92zGI2anNlPOqtavmhQxmwiD1flM4/l6Jk7paVmrCsFkuMmt5z3Qy2bco7A8wdIzHqFg/al4Pekv0wZTPWGqNtIeaM0qKc5yGMOhH3n2/CW7wwDWobzPRNjKZ6DGE1VK7TRWc8T7mHzPiOAMnC0XcVQKpBJpfursCKfp+IPMNj7j50KPRaZ7gMDlxQWffvoJT548ySudUbiU1c1OCNXKV6Bf7YBM9+4EzGRlifIj+nxhQKrnqveoIpOnndevoXxNxAHxmTzrRLsmaZlnQpUxRRmhhoGa1tp4HApNUzibo6OMF6tnTl1pwTNfkb5neplnn2SPmubMB577S/+kdJgZi7hkKBYhSClD5VXxGAKl9AvMFUYobDLb2gldrIzpdooTgviKVzaMHppuwXjoMTLSOcs4BG63N6zaHYfrFS7safcGO8a6zAWBF/modliGmpaRadzcwFSX35pf8V4oDiqQ6ydm/JHOZ17uzBYUXG9Isvd8rXx0DLVp3+aQMVfMzeVMndexYfG0ksgYgw8erOHNzWtub9/QLf58qdRHewbiEqwqPRkTrrEgDsHQ24AVi5iYKWtBgyWmrRMJsFzSX1xw2D/m7RgwGlkiggRPGAWCoWsaRmpnvxKFZY2JjnjOZrkca7LSJjqdJR5KokJwEm1lirJ7vsbj4NnejyAtu93A4w8ec3G+pt9v+cN//lN++7f/Gt3jjouzc1bLJWAZxzHJ9Z79MDAOI92iYb3oaJYdjXHIytN2Hb2NMuau37G9jykVt0NP0x/YDTva3YHV+pzWB/abHc3qnGXbcrZccb0644fnj3jyIfR+wevbLZttj3RrNvsdtrcsRsNXmx2fvrjFjJ4FDbuw5yK0PG06FudnfOw/5TD0ONqE6y00lmAM+8NATB8ouMYxhJRu0RSjbQ1zp85Z2s6jtS2BAvG8xnJoCxbdAutavJdk9O7xfkSQVN4tOhpo6R3VmxhjcMawWi25vLrk4vKccddPULPSb41QMVga10zGGkGiGMmbBF+CwQaPDy1u9MXhslBpXJBSSid2+BCb+uAVnfclj6nosYpuQom1tdEgt91t+fTzz3j99oavXt4waG3M4Hlz0/P7//yn3Ly54Td//df48OlTFm2T6jjGLGcqXyqvP7myvJUkowcUkTVO0u9fdx3T3+Pv81YeMlp8k37+Iq6vM4qfWo8jJ5wZrp/j9Pcex6SPh+6bozGdchj7VY33ep3Ojnk8r1N9PGTgeN+r6JZOX/UunVr3d819/psAfhQGPxCMMPgYJe1DKoVgtW63qUXASo+RjHA+Rf+agp+insIn3iwPIOrIGptTsmr9VbGRxnuVudRhV2Icn0aBu+ToFAVCNaCFOE6RyJuYyDcaAzjQiE5jXazJjICPBgddk+CTdGCjg5D1Uc8SmpRJK7VnknNqsII3BiuWBksw4CXQGouXmJbdxTRyqBEv56OUwH/9f/xveBUOGCxyohZ25ply2nPVGUxlsAlMJEZO0zqrjFXLFrXdgKTfVb1m1L8UI31u3VqQYoA0lezgjM1O8QFDjFqvBpT2JZeOybSgGO0zPEpdszdFYY4+6aFcUkPFknVZtqvmMG0so7bJehVdUJ4EKoSFFNmvY7NqcMpnOL1nSSVQqmx7qa2y3pFf1Mj+TIKqfzJNn+AwKXIeNqaVnpW+lLw/ZvL3JBOI4obocGKq/RH9b7Z0KvYIBceoPCwJbDJuPMV36oomPBCzO1YPquwsqhP0Ga9rlllUXkl8jIjkzF2S4NRkIaRe19ncc3+Sn6kf837MRvlsU5FA8EK7aDk/O2Ox7BjH3RGNtNZW5WwELDmYzyYcNyZ9Zdd1rNcrnLP0fcQHbdsRgsl2t1q/X9v+avnwXfQ1mPifCWAbA2Nq1yXbXoBPlsJP6PndYPiOWEax/KPmjt8bnvN3V0/47uUV46Mlz1/3PPMg24B9c8/N3R32fM3rTz4hfPES+fB7mLMzLh5f88PO8p3vfpemaRiHAR8Cl9dXrFYrHj99wtu3b7m5veUXXz3jqcD5co3cb3n9Jx/zxR/8Af2ffsy3d1v+WtvyrUXPYzdw5j3N/cBXP/s5fzgEbs5X3F90HMLII7dnd/uCq6c72uUK0+/xvcPKDj8O+GGPkQP7scc4zSwWoTKXWCMF8WT5r8XJyNjv2Pcb9ocb9ocbvN/GCG1vY5R1gn3lEZxz0Ul7vcZaQ9M6gh9p1mvOzs5iid/UexDBSE5S/rU8i35vjWNhLa2zNDbgGGLteGmIFYVUT5KCoRlARrwMWOmxMmRblQ1pvtZk+q2fJeuekgwMlXNVzN4swf2bM4yrMTlG87oc1Z2ZP2KNgtrrRBdP/6pwBKUmXf3MvGb4Qwzu3Ng2v1TRPgxDHm8RFqeGiVNMq/42bTP+F+tQhYxgjYGLi3Nu3r5if9gzbiJ3Mgwjh8Oex4+vWScAFISrq6t4EH00oK7PziIBDSGlzzIpQqNOaaxMjsljKfNPRnGplLvVmmUlJqrfqtWtxYBeK7KFkNJdx+8+mEwsrbUsV0uWqPFmmlozIv9CgIXidWeSwUrSJIwS5gzY0/HqpQJ4vX8+jKAKaqlJdnlGUw2Vf6bG8nJXifCp5zIEMGVmZtJ3DZcU2NR906lp31G+KwxOaTdUW3iMhGRyv2bopvfJ89KaRbpOeYTawnQqSVDQzc/KLCmK6tzbBNZKz1nQnxH0epRGkgdSqOcxFxZrJqcARoGF6kxOp4BJtdy0DZP6nDRO/Z4KRmUNj+aaGUntZcIqFjimEBVlbPPMhWwwC/U+KSyYfGe6ZjWzp3+rRa8dCopioxh8Z64D0yDvmnnJ71XHMCnl6kHVZ7Wkhp+OOgqnUbhqkoJJIwznp2h2mpDJB51nHaka/zSqKNTfQyD49F9iKIZhSOlZhP7Qp3oyY3L8qbzJQoxKKUbJpNTV+i91ykaKgVedYebzylkMqr2ZpKy25Nru0SHIZqHJpFIOdWmRElnjMm52rqHrumSoJzt7jeOIdZa+P9B1HX2/j1HhwVeQkD6lM+S9R9pUCkIkl4GY4Ia0H1nIq/Y8iLBar9ltt6xXK3zwKVvFw3S6psdS7bXowFI/PmgeuaIYVmNzLcBlhYhMcQmiDg0GsPgwxvIazuXUnsFHRUmNc+I6JwhVYfFrlFi1Q02msVqELo90/n4UAlML85+m65bpxSkaVXCkzMah9+sTV9Dd6TNc7j0037qt6iTXgvWceUYyo14bRAV4+eo1u8MBTMkAY6gUEoUM5Nayw0adIjEPe0o3BEkpTGG1WuKMiSm8KpyphMMUAlIzXQWXzqLKzQlYL1/jGF3jYirr/Z7FYpGfm6e8LXwaJSIuwWKcUtmT4uh3jFfrMRd6Edcqfn13Fo6ab54OMP6xptDZephFQVuUEab6HJ+Lo9R90ZeLgK10repzhjPmY8p0VeWSyXO1Q5ukdaHscekkn/NQa0mVNs+JUHWu9VNtUM9wXDkEu+SUJRrZEJLhNj07cQKiwodSaLHiaV1LQch5H6vxSYiygdHabePIoutoG0d/ONB1a3aHPRiPO/d88sU9v2bPscYXp4TJPI958jLOGs+UtdB5n3pfcZKRucNuKUVUZ/+qL3W6qE05Cn86nvqNCcXKR1ombZ/q56HrXQajkIrNbzf3ydDoj579RpdP0f76nzGItBPeWASct7n2piGhRWeJBuSBlpZFs2K5umSxPrC/u0FsrIPZJicKcZaDxMiR4D3iA6aN7dl03r0BcZaVcXSuiQaDICmCS2EfbEjKLwGDRaxDGONpMVFBLxZELEYCZhDkYBDXcnF9hl0uuLg859e+/ZhXf/Ip45c/582nAzdXl1w8fszFxSOai0vC+SUecM7QYXFAH0aMhyGMhHFk6Edk0bATT2gd3XJB2zS0l+cxcmVrcGtHu4B2bFltOjpjGfYDh+0O8XvshePKr9i+DQzWsVqfcXX+mLvnn/Gis4TDHrvdEA57jF3zr7mH0HFJRwd8Ze75ZPOGYDuMRKWuU4VsMtZI2ksJIepRrav4moJfj+HUl+jITPdiOTDUuVGEWKPb0nVrFt0FbbPABolp5WVEcjpigeCjEst7XNdijNAfBhAfU54HT2sDq4Vh2bXc3O/w0qesAhZDg7OBYRhztEqhzRLrtzubUzlqwIWW1gjBQjD4McKhiGAl4JK8FQLYxGGRAgcylX6/Y8zDD84zx6RxGxgCvNn03B5uMNbSGoMfA36E0TT40fOLz1/Qj4Efbrb86PvfpesaJIwkd7/Mx2kUfgiBJqWWH33IJ3uup5qMaSIzPzxhlQsVNJRHUJpYpzrWsmNf37ZMnnvI8emhazKvWkmSz0Ci4xXSnjd/Sln7rjHMcXaQmjfPs8prBBpQkDmDyVVkhJpdnLVXy9jKd2R9DjWjmGaphivJ7zw0D5WFHmgq73GW6Wf807EcVuOYmpZm1jH+drItJnz4fKza3/H4C+2dP6/0WY2Qow9p7UYQT5CBQw/LBDQqGtWRuOWzFDDLOqC0/5UHovLf0QEsOZAn2TJopG76X4ljTafV1B9N0nkknu2obJ7q1TxGLM42kceTwtE4zfhodOwlQjytGkJgNALGxbGZhEONTbbkCL026XUFckpnyTMBQjSek4wwJuXGN3jMYYzRt0nPMplImk2El1SS1Fb8fzVaKKNXPnuiOMvilqkfziU1Il6IznpBg4CMLbgrORJ4P6ambZKhdJaT9AGpH42gjXeDkIPnMjE+MWMtjaFENwBeYsBV8DEviOsCzsW+S4Itk/F6tPdruur5imqgXHWvEuUUnk2CtcwaRhKfdSqiaTmNyXJY1gkk4xmYCQ3ItE6XKLWlcli9l1nHqIdLEuyfxAdpgNq+UVm0yDWKg/R5lQUVC893whloTXIwpOhcI9ibSmauxoxE/kRvi9p2khEuz73G+lEm9EkubLuOxjV5/hP6Z0zkh/OGFTyqy6w2kbKmNQ5KAUXG5DrMGGH0A2EcMGGMem7vGK0hmIGFg0XnOF90jKnEYl5ziU7mjbWEcYQQcI0lINGhIcmQkkpEeG9Yry9o2zWHwwERDX5Mq1dF62aUV9O4h+T0yagExMeSXcFgTItPWf+sSXzR4Hnhdrwxjo/siqVdsfQbPpY9f+XQ850x0F4s+OB/9BuEj1/z2bM3jDtPdxgwj4WzYY+/eUXowD99RB8MY2dog2W433F7f8vd9o4vvvqcX/9Lv8H9l1/x7Kc/5e3nnzEOO8JHTzEXZyze3nL16WdcfvI5l3d3nI8Hlp2lBQ5WeLX1/Nmzlzy/3WGePMZsBsztlg9XlkeLBfb+Fj9uaZondP6cfrfB2td4ByIjxo8sfeS9tTxHLA6SdAMmGZStxZoQs9J5kCaw6A4sux3t4oDYgB2F0YxJ7i98i3UNzgUa5/HW07hA18USVMa2WFx8PgofEb8GEzM3Bom6sngiU1ClOg4V25RILHPSdZZFN9ItDc3a0q2i7qtkbzNIWETaRcxgZzw4DyEkiBLB2ehYpPTUOlsCOiHKjQqBev4SrxsCyRZAxB3vBsd8vbdhXESid0VKKVN7ykflhAVXFBhN0+SUsLVBO3u7pfuqLNADVKfYqu/P053rM/ng1Qx1UsK0bTsxtmt/ynyp14vWha7HN/9cj6n0HddhvV7z3/+T/5Kh77m5uUUNXYuuY7WKqcUWiwXOOi4uLugPA9vdjqZpWK5WiEQvnZJqJTJrsfbCNG38qX0pwkwiHDURjQ+lz8rMVmA8IfiVcTgTq4jwfWZelZmpCHFZFQwGn9PTxvajASr+ntMMp/dVAThnzKebmpgbJTCZcBfimd/J50kZW5vp+dHaJSJ/2kA9W8M0u9qAXc+7mFhPtTEVvApPczxPnUum1UheJ8UEJUNstZ4nr6lyeDpfvRMbVMOvyXnN89ROMvInEcxsIDW6LM2VvVNlrqbvzs8Yk/fw1CDqva5rGNagqB5/2RA7G/IUbLNrRB431GNXoAI08rN6t/xGqjc6fbu0UD07EZAe3v/6TNbtTp2GZgbbXHOpGkdez8KgUbejR2s+cpFs3JwItzpqUUVpmmFm7iTPIyrjkkE4MXySFGQSSkTSpH6Sjk2Kx5ymg/EptWdMLx7w6V5U4PqUWrzUGfLjmPFgvBfK4Kn6SBMLoumk8hIkhUd9LjRiqzL8JJymSgPFF0Icgx9j3RqRWKLi+tEjbCr74Jyja9qUkimmabMmlo7QNbU2lqCoATAyCLHmmW6kKhWtMbx8+QLvY02ZLHxO4KfAwziOiNTpXs30DAowPWXTcyzC2XrNy1eveKI8QQVnx0bDOb6fXzW8RYOXEXWqi3vfJ29PCaE4EZCMrtbgXBMdDqylSR793o94gf1uj3WOro2pi3IZC9Vu6ZmryJyeIYOtxlkBymyF8gpnuno0taqZCRMzWeW0iBGGUzunDLHxsekeTcYix3txrGictzXvo9DLjOUndGVqFC+KuykOL8qw6Ahyd3fPbrejbVt8oCglTGlRjJTWjal6SjRlooSp1lsxsJRn1+vVhJZl81qR8jJeZLJeis9qWjY1bpf5lfUTBOMDl5eXJZ16CGkfpzgm8zaGWaWK1F6o2jyiqdN28hwmV0XrTh4/zcZRGZOrdmtlqcKiSUuWjTbW5POYsYwht5nH+8D5FxTeY0fqTFHPQNuqca3iQJnhq+zkZ6p2YWqMVQY5g3Z99pisRs1FHQ9eMm9gdf7OZhwaABMS7THk+oMhRIcufSfSyDScGl/OZaByFBMfEn+3BkIqNWORlAErOiVfXl2y270khDHWwhVoupaL7z7i1Wc9H7QNZtjFKO6J4n3KC5ySy+ZXUaSTndAUViKAPmToO77mcljeH44+Hr+rY87/xHsxEivCcMgui++mUV9Hv5rGMYYRayx+HE8dwm90xawtZFKs1Ka4qcVJGbH1iY1nzhYltDWx/FTbLbBtW6X6l4olUiW8oEpoXTxrYl8BAQutsVjrUiRdUlIojxdCHqEq2id0Is3F6zgFjBcYDda1dMsO4yxt13J9sebD8xXBBvabnvDmLYf9Abve0j7ac7ZaIKslXevonEOalgOBhYtRheI9LgQaYB813xBCjsZu7DJmP+qJqWJtR9cscNYwIGBiNh3XB/Yh1q88bx3GLVifLWkvlqy7Bg49bjCIOJ6bwHMZeWxWrFyHtJavZMPb/RbooteA8hf5XEvZOyraR33u7OS8TM4jc7QlmGwwibRLcWPTLmjbBc5G5W7w45FOwLkm81vOWmIEV9TzRL2GoW0sXRvr1yreSqCKKuXHseheMitqSNnhojJasw+ojskYizVCaITWOQZnccEQQspOElJGETPFzBknfqOrYIeTeMiUtiO/CD4IJowx/aSJxrOQdA6C4W534Itnr0Cga1u+/91v0zoXjTZpIZSnnBiX055OaOeveB3NJR+/OZ/55+sHpjTg6wzU775Orb+eAx7EpbXebj6m0ow5eqdqHu3ETPrT28cR6HMGqjZSH0+hGtts/SdjmjT7frTnIR6vfFJe8GGDxfFvysPG96eYadppZp1mS/Mu48i79qvW/dYRXz45wuTsZz4wjkmXYALiQ8rYWmXX0DFmfqnIbMW4k6X2MvbUjxFXeOv0npFkODe1E4PJ/VRLQC3+TJM86r+RolYrmWl9KnCeW6vno3PQhTcmOtRnXJ+ZbpnR3ggLWq4i96vvmEpnOQGHSq56AEeazFHpOiddiqnmldeh8IVHDUHG40XmI2eiqXFNcbos74n4xFoGCr2MTgY+jLmdaiGraZ4IwEs8zalx6pJAsnNKUPYCa6UkChAwJuoPJMuRsVTRQ5gy0sqZQ+dsvSLrUMk3xuSoT5m/oAuewNUk+Y3Mj9cnvUyx7rq0q52fWBZhOiuBuXr51FWJN5M1UBkhlnicPmDNZJhTXin1a3JD+kQ5H7Wur8b99Zy1B+WVjbW0KVo8O71Wa5jfS/MxyuAKUY9ROwyozKxjSpksdUyKmTAko3Usw+iciwFmxhDS2XXOsFp2Rwut/EStP8sw6wM0LqN7CR4RR9stWCyW7HZtrKHtxyiHGD0XpRwEvqIPX4Pz45Qj/KvDno2RQgVXJzxtBe4YeGM9G+BMWj6UBZ9y4Od+y4ebe56+uWP93Y8IT3YsXt/ReFgdPE0QrGvZ39wS7u4I1xv63R33zz7BmCXj3Yb7m9fc374lGGGz3bD/5Se4P/mYqxfPWJiRxScty/USd9jj7u7hfgPe83q3pfENw8Gw7QOv7w58+vYeu1rwvW9/m+Yw0n/1AgtcjB327T2y26XAJfBmZNkmPbgRrDM00uJztoEoOYXE2xoTszMpj9xgCN7hXAPBslpC1yb+OgieACbQIMWZLf+1FX9tMRqElfTGNb5WQC76FfI5mPBIVLhBBGvBNeAawXWGposO1JEuxUNpgiOYmKXZI7FmugGnLJJE/Jlqe2CQiE8TfZqQXdFzFH8JOm8bsGns7yuCfyPD+CkGUyO/o9IpbqganOt0Cg8xqqeigd9nDO9SwsRNMdnzWNOs1YxWRl6mGMtV8VbP66H5S9IILrqOm5s3bDdvuLi4ZLc/EMaYXOfy6grvPY1b4Ucf6xn0A65tWIQFbdvG6PvkZW+bhqLoLOumhKJmIutUf6ZARXw/p1rPg81zLe1Y6qjujH11bhLdmHSeINnYWEq71t6+6R9jSp1iqNJATAlTnQaXOdBmwaHs6dRhISqwjh1Ty0ros55QmqppdBpvJLFTI/cxQSljPw2fUp3NCkVMGEryAS5rOp1mWYsJ305hbWTyRq47LxpxT91S/i2/mf9JrU2eTwR71oe2m5ls5TVqgWiCHONDhbGcvZf+UVg0mOSmWbihsv1aU7ZepUKQq0C5yQ7Ep2edmhmzd2ofZR5dNF0vsKUOUQ0muqcCokrVvN81HEjezwweFeOfFf+izDMznlOyoX9qGK+fKHOrTh21AUjPdaElkTtWZlNN/8V7O9YbHMdohEwTRp0y/Dim0gnRuB0k1TLRsy8SU3SK5BILUcjVcxpSJg6Z7RGZwc3OE8Lkb1n3+LdWCZftSzVSUlkIZf4MSSmXYTxlLbEm1olNzKq1qf5WwnfWuuR5Z0s0YFaWFOZDBMZxYOh7drsddzc3ef+dc1w9usY2bc5qUiuTpsrjSpifMSuBWMtKcQDJ21Xvtd2Cw90B72NqL5FU8iAdt5w2y8AwFKXoqVSy+Zrg/DxKBOi6LmVEGVEHsaniQ/K+n4Ljh5RWIjG6OARhs7nncNhHRUjiNw6HAxJCSWXvo8elCmbGGJbLZV5ray1ewDUNbdtwfn6e97g++SR6WmqQKWGt16bG5+VzkcGUGia8lBGcyfhe+6lpjDqGVIsx7fKILkzXrChVa6VxuqOwVj1/PJf5b5POj/R6hT8J6TzVtaKndEW/B4lnYfSBtzd3EUYx2VBYnwXD9O+ULhS+aX6VNZL8s7OO5XKJD55snE1jL0bWPLHpCuf1LXDykJFXswspXHkJrFYrXr16lfq2+TdJ0RmKtzW6RKp+6hln8pZTzRV+TdIBn+9ezUPW8zzmg7QL4dS5rBfXpP/ZZDQpwkkcowplaJ8VXS5zOzbCm7k8IBX9nA/jhCKrdhyZwKDUK6lns+IVqtnr/NB1A6gdaGZjKLBEFuwnu5cWxUh0csrZp9K4swKYmH1JSIbaIx6C/M50xHHNUpXzmPpT61/qGodA08S1efLkEV999ZLV+QWjBPpgWF5dstnuOGx6Fh5aaxl9BX8nYGHKn58wcM+2bJI6H4OYVMv8KAtDwd+njIDva0w/Gm89NCnwqWchDjnhqFlms8m0Kpib/x68pzGG+92eLz/7HLNafeNxTvpiDp5zvi89Y6o1SiW2xER4FQPiLKax2NZFCDFR2aapsp1rYkRMgGBS3IJ4QkrZGdsPaOSaccn0bZKBU9NdK+8ntUJummFsTl4UFxqiU5vyVKrEXq2WdOsVzeIMGXpkHBnfvMb3A37VwbKDxQKzXmHXZxyco1s3WIhRFulctiEQ+gG/7wmjh8PAol0R9gd8H1NNNmuLuBYPSONwi45l02Bf7Xgz9qyCpesM0sKbdiB865zv2RXjG88oAxvj+SxsGfEssbRdx37h+MzfpbVusxJqnuZP5X7lJWuDMsRIfKMINkFAwf0mA3h9ZjWrkASDOms75xJPbHLmCnWUVlrYLRelDqU1k7O7WCxpWkfbtbRtm89SdIrKI8MHdbxMfCrTc61KulpvFHniiKeaEGgaR9M4fLD4kEoiGZPq0ycOS2vJmsow8BAf++e45niu1hs5l6Jak65kszvwxbOXIIHLyws+fHIVI7aIG2ytxY8+p3vV9r/J9RBOPv4seY9OyfB13xkvzu7X72THtJP0tw5cKXqBB8dtzAQ2MpI+Obay/qcMqw/JMbWM9S6+d3JleXr6/vFjylsfN3E07zzfEwa4rxvPpL9p3yefq/nUb5BO9KG+3nVN9IET/PRwW6fgqtbV1kbxIu9H2SF41TlE/UAIAYMHU/ZegmZeSHjRTLRDiWczhdczCYemKOCJ7tcU+U9lBq0vHELqt3YiTION/KLKDfrvCT52+s8UHyTiXsTKwrOq/sjm0pR6huIZDRJSvXESPEfiqzKthjBgG5wpI5MgKfIh8RVWom5qNs96BqK1aasSQbrmVLTJ1POby7ATflm/xzGXKHGDtU1sR8sFZR46la0zpOiZkDKSkAIF+uz466zN/dTzKDsU9zqcCkLS9CwzPlQkOuLG5DlzRifhiCyfTff6eBQqa5os5cpMrwhJt090qlUY0jJNqbuCa0yNQ212Yla4zEbbakj1HkkVxJKEnUTOTs8hafgnIG+qcdbrFulEfb/QrBj9P22narAebKL9FGf6IxxcNAYVdE7xUeJjtEuVq40xMbNLUwIXs761OtpllTISSOgjQ1bGOzU9LeUdq/EmGBvGgf3hwMqvcRLtWqrHRKJstV4vaZsTpaySUXWOU70fsMHmDF3aprM26836XhIKMal8QOxLg09gTKVpOVrrU/RjooswGmw7tRfq/b0V3tiR14xcYfiOWfOxvORj7vlo07L+M8PqgwuGFi7OO2xj6A49cntgsz7j1c2G8MvPkN2ew/NnvP7JP+XQneF2e/zNDe3mjlXTEj79DPPZpzy+e8NZ6LlsHLs3t1jXMKw77hvDLZ6b/sCbt295dPmIYQ/b2z3bN/fY1vDDb1/zGz/8LrLtebnt2dy/xL0VzOUWsz0QDgd2+x2mgcWiAzzBeBw2ZbCMODmkTCBiBDGRF49OCA6LpcUibUcTPEY6lruGtklnXVNTJLSYK6wlu57KFbFMdNxXa031ny0pyRNgherQxT07xbdk8lhOlka5u+T8ms+wJCdrAe/RzCck2dLmzNxVv/iYHn7SZTrJorTWKClITkqFhh9rxE5f38gwrqlFdCHq6PGxHzIzolHOXqOgmR4C/ayR5dp23VcdzQ3lgNSM8MNChDnKKa99zN+ZMD1MBZxj5plJ/yLC+uyMf/Uvf59+v6HrOp48fpyMELGw/WG/S4aVlqYZca7h7OyMxWKZo90UmdaGMetsciBURnvK+NbjlgnjZSbMY83Uk5W+8U5NKPXRut7uFAD02anxUNd7vkbaRqj2PWP5RPQmhi7towLckk6oGNkj8aiI/WQUyiCX9VLjsd6a0U5y5K4yEszhpH6+Gtus76zFyF+rZ1XpNn2hMCaTGRzDc9zbGm7rtpnAweQlBQJTRqtwQNXKxICSCVJhtopCePpWmcn0tggljf1p/r/gg4pZElTITmsxg2/yOtaIkuOx6XjDKdhLbWRmi8kzkzFXMBHHUSVU03nOotBCPowKrxWiDsXkURjVCj7zWpVzNl9tPdMKD5ltljJGXd8YNV0M0NGrUfJ4wCA+Gr1jPcGI06MH9kg/9Kledqy97av0WcXooGc4OWlomh3K3sV/wmTdajjIZ7WCjxr3TpVniXlMzK4q0wwmM/dOU467Un+7cS4zhdbZbNQ2ifkjMabOxfpgdbRjBKUps6bP628KU3N85n1L27V0i47dfke/P0RFWPDYpsW1Lca6WE/RZD/rAseSAFHPf1r3KAyafL5NYowNkXaICE1Ksx5SKrcYcX+M92PUeaqV5YUQHTfr3aDeuFogr/4AZGevoR/oFotyphJUzL2ZTinncuR2gh1VXIgIz589Z7/b0e/3vL2JEWOjr9Lhp2wANU6dtF+fRxNp9AcfPGV7ecmjR49YrZZpXBUdQwp+z/gjrrs1JZVQupU/5/RlZbZT3H7EUCqeMvWdyZVRuZmu3WSqeV9k8jcrhEQdBiqaNDmYU1x5guCn4R8jdjWCRPwamPNQSq8yPk+93W+2MQNEijgUqohxyp7llGLVqtW/1+evNrQW1Br7Xi4W8fwjqdYcOQpba85NheQaE6czpBuRug7z/ZzwVoUuGGNo2ob9/sBysUSNBVOeNuTuJJ1xbUP5t0w6T4w1U3tRcCmGdh1PyA0w+TyF5elcJoZKqs/GZFpKvUX6OfOhdT+6LhVNru5nA+WMVzg6FZN7deOh8EdSw4NR8kfmIKpjl9eXAleqyDIUfqxOtZ9xxYzvytHoM8KX2zO5ccASrAFxBAn4ENv0VPx0qNqnhonp/pR6zqVGYqxhKdGhyMe1aVvH5dU5b27vubi8jt7sBK6+84Thl69hf8fCFJp0yjAwp9UPXSIxusBVBtKMC4Kg2VTqduvPmrFs3v8p+W9ubJjLfRmO02bM6buxNik2pzhsfqZPyYj6vbEu1ozzgc8/+Yz1hx88uDbvcyl6qiUcnW/dbywzNR2LPmWcwzUNxhkCI4fxwDj29MHSWkPTOKxJZcYCeCuMweNTSRybZDJJ62QxOROL8kUhhJia3VpcwjvRIFOyw02oYrW2elZb22BNgxiHxeH7kc3NLbe3b7mwwqpdcnl+zdoa/N6zWq45s3D39hWHQ89oLOb8HHN+wc3qAroOXKzrPOz2yLKlsYZmvWRpLKvrS87OW7plLNMl1uKNZXO7x+0CLDv8wTO83bF9/YK+WSNjYOcsd27g5/d7lh9e8299+APsF45P5cA/Dm/5M7OlpeVMGrxzPGs8Hw93eT+UJs3hSiTn14zPzs5C/b0oOIncvTnmmXFJ0SaSnFQD0NC2LqZ5NeCl2gv0vEaebnN3myFOMzcBLJcruq5htWhZdF3MikR0PBMTvWk0Be7hcEjvFeNhPU7lyZumyefdKDyJxLqZyucFIkwZSVkxYmRRUiWSJ/ErXO/GLadxXF0iMI7fMwxDisgUNvueT754yXL5MY/+nd9Leq+AV5wDyYflGJfY2X5/3Xje9Wzd7rtx9bSth/Bp4Skf4AUzj6d8YcG58X417vy97J+pdBc1njul//u6OT0819M051drb9rWQ/Aj8+8nnvu6a26I+1Wvh8Z42sj17mP1q8zjoXdVptOSl1PcFNMZjz4gwWNwOZLOarkxlfMS06wl7DIfKGndpILF9LxBcup0CTCmDGRRh+DqQUPSPcTiHco/pDaDFIO4FNnR5Hkofq/PnM0pvQUgFLqYT0h9DlOmFs08F6ORkwN8fApjIh6W4NN6JT5Rayk7G539mwYrAC4FMqSAAhN1Xz6MGImZ74ybGt7EVLpMVUYo/UpjmO5wBfcVPahaLHQtydga6Vrvs+5DCFpCLyB+LPKgytRJ/Anep8woYJtWhacs4qt8UGQVU+7NzoTqm1V2qc9NLM2nMEZ+SvGf0X2fyZazJaLa9YhBTcpeUMsWOiwhRSMXCSY3pHBoIowFG/K+mLw5otOt0PCpMy1H/073TfnVMorytYyjnIUpni97MYMYo/jzXTSvNj4r5WHy32xhj9pQudRU+hir8G2icVJriwcf18xWYTmTUT+wfBkvVO3WzysPNseL3/7gwOu7Oy6vr1i4Bj+mNiTqX62xXF1d0HXNpHPvY+r0pmnwPul8k354GAZc4+jaJtMnYwxiTNLpNcTA13QyMuylaGPX0OIwfsht1ntU24ROXaqfdi5leYY0xhgV70W4l5HXduRHiwWP/YowGG4d3A4e/2LL/bbn8knH6odX+IVjs33FL//4GT9/3LCTe8xP/5Dup4bl85d86yc/4em3v8di3SJ4jIPLheP5v/pXPP/FxzSPHHeXZ3x6WHDz9g2rizOaywU7K9zcbbn74hXm5sBvPv012nXHxtxxe7vnqmu4POxwNy+4uLjk6Y+/zcsvhRdffUb36x9BB84IXS+0g6UbbZI3BGfB93uMcckQHqJMbKKZXNebDJFg8Rg7Ys2YSp9JdC7XLHMhxNI9KZNTLJERo66tS3qnENfZBo8Q8KTMrH6EpA8PYk/igXfRe5FIm0OwOdOGoLqmeDY9Q8x+EHokxDrjwoiIzzih6IG0XS05EW+oswY5AECfneLY9zWKwzesMT73vqyNyNZZQiADcm1Yro3jDzGhcYL2wUi1OaP2EOOmv9WMgx46HYuOYz4W9aTRCHKdhwpmNSMe+7fstlv+4X/zX/K97zzl/PyCq6srmqZhs9nS9z0I7HZ7Doc+RdaTFQPl7yxtjakZnzLX0wJbMv5WlCcrAqt2MlBVjJUyHdppVGZPjbMKYDUyPF71ah0pXhq5n9RQYiEpiuDqbWGyZ6R2lPFUYTd7wpCUUjPvsbL3SXhSzayO56QQItXakRUCmDL/sk7TKzO46bArg1HIaXrqaNGqcyTTcddzycxjZlrK+sV3p/s7bV73qxIGTsxiQsxzu/FOHNc0FbxJOKg2kCnrUfYnISOpmOKqY0GKpg8lwqlNicq0DO+iTIKOo8Cjwlde97SGEx5DitFyjjOiciXFSCdYk3zeo8Ewj7JaIEEjbwOahkhStHQGChXK8iTTWkjI6bxV8FdCpAxhDcOguNEljz6N7ohRPsMwMowDY6rhp235PqbbiTCtTkLFsYe0flEJmqE4R2fHKJ2iwK4FB9AaTHHfNNV//bvCSvbWTP03jYvvujIna10y7tpMB5ymVHQpPZjTGoRNXAdjsuE7CxvZwy1BShXRrZBew39mSCshw+pDyoRLrFykOCAa5othyOWVU1hTcJFo8E7jODs7pz/02imNa2i6RcI3MyGzGltmDfISpjmm+mGie1pNxZpYO6hp2gQT0dgvQXKkNXlv4ovBe0Y/0jYuMxlkeamK6NSO5qyGxHYXiwX7/T4axk9cDynRaiE5U7eEbIyBr758xsuXL9neb9hs7un7A9FYNF17M0M2Dyu3DMPhwGG34+r6CgmeJ0+fslytCMm4oHCalXq1MCqSFSba3pROTM/blH7XafOOMXJ8p16f8ncixFZzyQwkNR3RPtN51++mnOcICjJb8wmynp4Rjr+/S5k8Nyzl9tN++SBsd3tiAbvZXpnZ3xNXNtImBrhOUaarUkqsxQ/rszXRQaDQSOW7yloXBWwIkt+d8o2x3doBcK7olHrziGfk7Oyc+7s7Ft1i0n5N0+rlV1xdlGvTNc5G+bKJZN4Q5U/02ZDhOd4uDMtkbpJR1YO8t81GsbJP5gjmqjFJmUvGcdVnVUjkrEO6JnB6TeFovWs+vd7Pmp8xCSj0+xwlHRkA0mWVhtsMWajRPq54mXs1wzI2mOCR6dg1NWdsW2UPzZQhIUXvJmWryhKZ/zLTcddraUziy5OzcgjJqRm4vLpgf+jZ7+5Zrs44HHqcu2f10VNCf2Dc74BST+4hYfjdRgWZZAAw+nw1TjCZXp/aC2BS9up0P9P9j2crHMuVFR7XdaDaC1W+PUQ7HpJjJ58xMVO2wKJtefr4ycm23vcqeKRaZzNdi7K609IOOjbrLF3XYRvLIAOjH1J9OUtjo5IriI2suQjOtLS2o3UdJilknUm6ACuYYFi6BcvFEpdqLfpxjCWxTcIhCY84E9PlqSJQZdv6ivBuuVyfs1qtkBDYb7Zsb+/od3vO1issgf7+LW/eCNtgOHMtjx8bHm0sjw4bxu09/WbL5pOBsFoTLq4I6yVj29AHw/YwcNe2BNdibItpO9rbGy6uOy67FU3nMLYltLB8vOL8/JzxbIHr37Ad7/iq3eEOjmFo6B28GUbebu756x8+xa4bgtvzgjt+wj2vGPmOueDcLLizwi9lx5f7Dc40MfV28Ee4vBjFvwFMpPVUPlL5fS1JoplJVD4AYqT3YpGcQNRpMskD3sc8sC6en93hQNMmheo4Mgwea6P6aLl0nJ0tWC4XDONAPMdkLkQwiIe+74vsOjtrGlCh57tpmmQYhxBsxqth4ZEQnWMCI9ILIUVIepIco+chE/5/s5fOYxzHOG7nWDaOcRhSlqqooN6PIz/9k094en3Fb/74R7RtQxhjSnWbnHPVQcdaiwnvBwP/pq536de+6SWQ09ke+TZWzyj2n9AaN1UG6xjmhvFTv73v9avM6S/6mvIC33z8D5Dl2YORLr3LQKHtzf++Swn+F3HN+bt5VKPyciJACIRxxA8jQQLDkOQYLUFmqzJk7t38oihPL9OxmLrfJEPHmuaSnXdIEcHKE0Y+vAiwWXdL5WSdoiqNKbx3lGFjWt3Ii6Q+vWY/TVkyU3kSn/l6Q9N2WNegdbZjPJXBNqnecpwQEFLKXAcCo481ihddm+Swkf1mByHQtA3Z6GUdzsaoUJfqdxs5jhh3iR5IkhcnnNAROM9v1GdWYa6IgypXazBA1ClGugYpcMMPibYl/V21/gmbxKh+CSlK3JQI2clYdN9DRlZxLBY7L4uZAXIykzRuyWuhgpTKDEiRTxCSkVSOznCWJhQ+jSFnk0RliQrnKY6FpNMLZSGznBAfslU5uFOZKNMM9EP+dsSvHC9gke9rPlvnMb9MPU+mazdZk8Ldzsm6rYI5jCE7seiaz6WwU7ueG68/SszYFR0w4tm21lW2oWJnEDMz12c5t1pbma9eJbvp+lTyoMJipZRAJBDGnuA91jSQkm4ThDB6jHM8ur7kbN3N+ooL1DQNu90uORkHrG0IIbBM+lUJEsv/dpEHa7sFXbfENVv8OGRDpAh4L3jf45yPety8AEl/Xs+z0m/U9+b2QWNSViJrUzAWjINnOxzYuoawvsDdeh6zJEjD1jiMWXN518F31vDphj0b3jxZ8ub6kvNuyeND4P6TF9w9+5JXP/0pb4cbfufJNRfrK3bbDfe3tyzOLuEH32fbGoYXz2huLKtHH3JwI48vnvLh0w9pDBzMDfdvGt7cvaAT+GjhWV0Zxt05l3YF3ZJWFox94GZ7z6e3X2AegQ8HhnHPeWP51uPHvLz5inHT0y4swQSC7xMTFA3UgYirEMllJ6KxKMTyEKYjSI8fenzfI37EGqGxiecXwRmHMzbDqrGCEPW8fX/gfnPDmzev2R4OLC7W2HVLfzgk2EjQmdKtR2P9w3qY+tzYBkwjiPUEY/BmZKRPOpIE2xKdpWNe5xFjPM7Gs+STk5nVf4VkXE/01ZwKjDb5zCZkVx1xc0Sv3nW9t2EcyAZjBeSmiQdqHMd8DwpyVQ9/NZafYmaPELFIfu4Us1ofnkz03oNhq2udz9OW1ePWCHX9Ple86LvWWlbLFT/5oz/g4qwFYL1esVh0+MFzl+pxSTLaxDq3kSgFZfASMgypPRIStVSGngfWq1amGWOPUyQZPVM1EirKoblySRXl4YhJLP08xLRPFN/MDo4qQzNLUPpJnU/bzYSkMPqFgZjOL/6V/N6E+1IGdTKH+XxIDMMxN+J1DbQZOWauoVJIV0OITSZVqUmsqdpLC58Qf8/TOmaKTk5JmRNlFJkq46dnxhQFRGYOK69tjtvWuUlK32mq+VGNnZkglr2A0iRl1kneS9RZoXiQThhEZRJFcptlaAnWM+NaYKjex2rLslCijatX6xT+I8LXOlCqsLNKjDIvW4Qk7Tf4lO40CSxCiaYwgE/4cUzpxiM+1P8i0TPGpOikKhJ4sjmp/YpJ1c9RkZW8qlPKMERSnVKqekyalsTkNhTmjM6TyiCn09aFTDUqldn2SWE/hgjYy9UK51xWaCnj6Jr4t22aKKgShTyBFKlNggVbAEbHI1IM3YqSTMQkxfgXx5WjdjOTBdQGywQL5UBJ9S8K1OR/ja6xyXARU3PbxHBPPdlsPhOFOQ6k9J0CMhour665ubmFEL2vo/JZ2YQkTM3OvFEclcelZ1zTa6Ya8NlQExXQembars0CpCEaWGJN7gTHjQpVcSLjOELXZdyEMBFC8lnU9T5xnZ2dcXd/H43NM7w5ZYxrmCvP6PmxpkTyv371mpcvXnF/d8/d3R3jOGRaEYdSJfqp4BdK2Y5juiVpzgO3tzdJsRFYLpesz9e5nnvf9xGG2xbjmni+gs8KmCkt1nlWg1H8OzNUTM/i9F6NjytsRqbDFVzoazLZk/JboQs17Zv2U0cukJjKU4YkRbNGGc/Ul1TP1Nd87ye8QggY5zj0A/tDj0q2Nekw/1/i/qzZluRKzMQ+d49hT2e4U94cCiigAFRXNak2Y5OU1JJe1Br4IDPJTPpX+hX6CXrRi/QimaRuk8SyImnVLLKqAGQmkMPNvNOZ9t4R4YMe3Je7R+x9biYKlCmAm+ecvSM83JcvX/NQb2S1rDrQi8Qz1FJbFhqW+JGcH600q76PyocvVUDqfczryjxiAY+K/pZ9EVjW39VyZIHBZr3m3du3+b6QWhHVDnYxms1nFerKUid7NDdk1EGC9bwrXKjGz3w7fSH8rzaOFrm8GLtq/lGenjtBy/hzHMjlvQXGWQgo4xAk8KqCRyUc1RUbCzzDDB+F/hfcO0+/zu1zPXyUHzw66AwXrVXsA64U4ISVzCtJJkBlWpTl4gUuV+/SSXfQShEMqWxoCt710qdbeGMof9drqQIutAopgzHysfiUh+B49uSKr77+FtcYmlZzGAY2Fxp1+Rxvv0OP+wzbuqJSfZ3T5fJ3sp8iG2ldSjJzlnQ8Ou6PcWIsdcjZMyGkQBSKrJPpWvzpk1zzmH55dtzFFbynMYZWG969ecunv/rVD877Q5e3hb9kaiDGtooXymwl+DLeHSDpf26aorO+adn2awZ9wzRZbu0D94cDbdOyWa1ZtV2UGkLE7+BSyXU0RidcsB43OZwdCW5CeZ/Klke8ztRVqWRcLBWWRO5YBlRoYNP1uYTjNI4cH/YMDwdabTCpXYNtYa8VNjj8dMfNfk/nJ4wfCOHI3eGeYX/L7vZ7VBODLi+cYffg2OMZgmIyGtd3mOdX2I8+4k4bpuBwWqH7LVOY+HKyqIsdH9uB5/dHXl5/zOtv7wiqBRrW3vGZGvnEtaj/8B0333zP7473/LrxtK5l5w3tbs1NH3iFxY0Ok/SYBdlMAXmnFRE+VM6/xvO+iQYw55KcRzpzQc0CaVDQ92v6fh0d3AnnY6WogZAzoGPg0DQNrPqWEALjlIIpVGxDt1q1bHcbVqseZ5MzISTakmQLa0POqq7lcJm7OMbr/uKiH2RHgII+6U5esvGMJwSNksTBCEVcIGWQk3XkP/aSMR5L9Ii6mEMlOXDVrziOU6rOEXUcGzz/3X/8O66vr3j50TO6rouZ5arIILUer1LVnKVuf6rrn85zeb9ctX55zqYB0urih+luLXN+kE5nYSE998gzWQ6ozoVayAzLQKR6H5Z0+Rycls7ef4wj/Q+9TuYRao7/OJ8R+P4QD5S+r+WZgp8BOZKis374LJx7V5bbfmCN1V/y9Aff9Zg9UmjeyVpCILiQeuDGhQUP0+Sx1uG1IuDQxIB10eHEbiBzqvWh7Cw8mZvP7d9iFmMtH5fz6pMsaVJAf5Zz0316dpYDQYcifyqR00jjzWVnrUOSL8U57/Apw0/0DanMmjOolUrylYZcZQ8IAaUl21jFcrytRuGZhgPDcc80DqAMzjZo06B1/BeSvLZdrZmSY33p4lPFUJIwIAh0z0i380tR7D/V6Y7yQaUDmqQj5Xck3UngUrIJl+8pSQFRNYp7XgKe1UyHFtuKUnFv5mutaT5Fls9nWgR/lUsUCzxqOb3o+GU9P44MiZ5XHPeCSyrI2sPykdkZUJBsejMFZf6c/BnknSIwk+eedbHZc8VJH9uvnk5lptRmulW/OI0fFs+l8U8BNXd+y8pmJHc2BhmHT13V5XkWz5fXVwEXqrYpiw6Rsqa9Z7YITsAxB3ugBCn6yj6rVOHbIQbhTeNEcKLHOKJeE1uF77Y9u21f4VUpVS42K+ddqtoc4eC9R3mfwTs5y6rr0MawvbikX6/BOyY7ANG2PU2WcRyZ7EiobdgVr3iMn0C08TXa0HYdgcA42pkM1CR/nG5bDsC3auIbY/mpVlyz4rUf+X/ylm/CgU//7sBTfsbv/u433Dy/pv/lT/hn/+v/Fc/e3PD+b/4Dq+GA7lZ01uHffYUyHUcL+6Pn4W5if9jz83/6X/Lkxafc/Dd/hXq45+lnH3N1PKLHA+r9a7rGcKk8P39xzWg0Ly4v0Vc9+/7Am3eO99Zwez/Cmz0HO3Hz+jvuj0f+9LOX9IdAe3vkcHPLvdW8ur3h0qwxOjIArxWqa8BP6IQ2XnR0QTytC1KnPt1aRT7XmZa+jUEMbWOjrcEotJHgAx/bQjmPmyaOxyP7+wdub284TAOuCUxTrPwtQapaG4LWSJB4rpL3A1fMRveZ96ImPBYbFRIkmTfqiKlio9aoEBPkGjn7Ulo/9RTPdJnq7CY9t1ENwnWjHUcCpBI90sKjfvj6g0qpy+FaCpJCEOpofmstbdvOxqiF1ccUFXG8/5Cg+mEDjQAmzP7V61j2GffeZwUlhJAd+fLMfK3x77ZtuXnzez755BO+/fZburbj4uICZx23t7fstjtWqxW77Q4XPC4xZeccx2HEOZsjdIwxxSgaX1QpkIV7nIOb91XJyDxRslCcHhSKXdZB+TsS5Pgm6b0SamodIXVWps6wpYxdM9pQDVOMvXOYZgkEqpLTKuPWfB7MxpC+lmSBKUtNp4d4Of90z0wkOHdPAVNhgnmFAoNqj8qN+e8l64YPZHwDKBGg5eyoGYznjpCQhTMZX1Uwrfc5Q3ehSFWLqfZ0jlcipEZn7lL4qjAmhIy6YQnjeo/kjFUZYjMYEp8tRvaFIJNxquCVGNpRZRxdbs5rkrPmU8kWZ6dSUjOEXDJQooWds7mkeAghz1nuietYRjjHkl8+CUjxp5/DdQHHmQC3uGoDQDbsZpwoQniMYFSxlySq9AZU0qekiqrWOkX7pb+hKs1dDMw+JMPZMMYeucQ1Nm3Li5cvWK/X9F1fejWrgrdN09D3MTv6eBywdprzAaUz+qqEFzO8USJs5VNfgCIMW1ae4CIlCM8JvvV9IugGwf30zlnZZvmscPqZkJ2PXjJQ5LJiRqGdBw1mpVmvNxz2e0zTZtjIaoKfk3tR2AtlqflacbJa5VA+vk8r8MmhYlIJ+fVqzfEwRBovFQWk53tykmil8Vpjp4jfSa8pRpEF7anxsTaceOfo+p7hzZvU55sC5LzfxWEnY9T/rLexDJn1TOPIcBi4u72LJdSHGFWptOyXkBBTsk1m2CHZgKcYYHSck0795Lu2YbNZc3F5wWaziT0zIVZjsDHw5OH+Hp1gel6OOTVwCQxqBymVkjm/eclzy4pUVeJ7eX+YfXGqGJdqG/PxawVdJUPB8tkiY80dxeVd53qvna5tbtyM9wQfeHjYL/Ys0fEZC0hnQbKdZ32HCu2frTHUOJtaPQTPerPGh9jDSHByLo+UkSGchUm1KrKz58w9cxon8lCaqVIMw5BbPoTgYkAwqqrIkgwMVYWB5Xwzj13AI/O/amqFes6DJMtNIhNLJZswcwLnVWf6MF8ryYhUU+lAtTehrD/j7gJe+TOhKUv5Usb1lcIocFvuwYJWnb1ED0j3ZD6kyK2N8hgq8dgQMs+RoJLMIxJZ15mHJSrkfS6tOzOUF9a1WKdkyMi4Cu0D3mu09yh/PqtK1pqoBgWHpB1WDHyExHOAtjE8vdzy9uaGl599yo0dOYy3fPSTX/Dm7RvW1bz/sVcx2iGtr2cy0DKTsNY55YrtYET+eUwnEnpZ9Lv6Z9ySSmHOcBJlPIg4+YF3zOdw7jJa40dLYwy/+uUveXJ9/QHo/IhLqXm5UhKOARLIpqoMckXpnamCVJuIn3dNx+X2EvViYu0V+/2ew3DkOA0cjnsGO7Fpe7rGQoDWpCYvPmBtm41r0zjwsL/juL/DDge8HcA7dDAxWE8lWpF5dZKiMuzUyV5qrdmt17RtLFU5TgPTccBbG/Xy4GjRtHjwgYaYyTb6EDOZbYjvb9eEoDiqGJSqnIX9hP7mHc0w0IR0vrqG9s2O8P4Gteo54DmEwOQMvoPNeo3ZX9FMB26//Yq//e4dxitWo6XVmieblo+fPmerYPz33/LV+3s+DxOvdeDKNqwwHHvDW33k3TTQuNjjXVF0kHg2S1WGEydoJScuSVyWJwi5RGzwwhPj/UEVPVoRy+Y27Yqm7VKVAEq1PGcJ3mFMDGaIbR0cWvcxW9E5bHLGKDR937BatXRtg3dj0b+yJqOw1uX9l/WWBZRqgfW/2DucSKtUrDTVti2dczgXsBactrnMb9RrotNHSgknMWMme/xhR+5xh+Vyr+Qz5zzKKLqupUMxpUpe4iy4uT/y1as3bDYbXjy7wletJYQmhaRvFam2vLee1x/j0P0heJxb+8n7TgTSM/dQdLoPvSv/DLU8V+ZauXFy0PNyfnV1kB/j8D4X4PTH8Lgfuh7bsznvhqWc/sNzmo8506korcD0DwwjcztnW83zS0JdzYnOnYdz14lutND95LNlK8zznxf92FlHCNJLPMrLwcdMvKzHJ/m71qWXBFUM5/FWjQ4xQUPGqOWCgjtQyxsS5B5xVvSHqL+pJKvKg1qpnCCFMjP7r9gAnLNM45hou88yaQipQmE45jZx0kKuVN6TvwFMzILXBqVNlE+Cjw7x4x43DUh/drFtOe/xKrZGMUqxXq3xel61J+9PZjhKgCSfVnJo0XsLvMiys3yeYbzEHyr4IfTW4n2ETUYApZINq5KxNYgzidk+nuKh6Okhy6hFn1nOSNYudsOyvYrGpCCjkJYd5F0ZYtX1eOBJDg4oClWlrRU+P3tCCbYLLpFxCsgBG/mJBb0/w/Ue+X2mZsnrT249OednV1rL7kv8Iu5rgBP3lirSxtlR095k3KseDInXqIy3FGClD0KquFifeZ0q7eTNqPSZ+Cqf8IIK/iqfk0J/ZAFlrBBq3Khtj3GuLjnGvQuxOk8I1P0P27Zhs17NICKt4+RcxEQtR9fpTKN06jcP0fke2hZtGq6un3Kx27Lbbnnz9jt8ABeiY3x/2HN3e8Px4Q47HgkpuHNpG4zLn//MbS+TLtC2babz8hNABc2oPO+U5Wu/5zOzYq17jt7xe0Z+E94zvt/zl18GuLnlcnfFT13HRbfGtjf0Hz2ltw67XbGye/qVYtetGXxA+0CrFMpaOg2byw3NboW2R54ZePbkEnt7Qx8UHYq2aWh7xaQ1x+GIDyveeMVvb+9oVIs10B8PGBRrGlRo2U4myuTeMtmB/aDYj57JakynaYxHBbAuValVNpZERwEScJQQM/30waNUi9YNjelomxVtM9CYLgYzBZvo29xnK/bjXFlW6GfCDZP4QzZkBFW4ZkW/H7/knMvZkjLsHlRqdZGDemqbfgqKrVpCBzQEG+lqWoOcVzJ2J5lFaGp1DjPNU4Lb/4kd49NUHN0ilKgMq4LsEr0mTnLZkCXR/VB59fofLEvCzYm592FmOKnHrAUpmVvt3F8eWHGQhxBKpFMQYZ1IlJOGb7RBK83zZ9d89+1XaKUYx5F3794yTZabm/cxgnCz4XCMgkvTNoCi63sma7E2BhPUDnlRCASZY9aczsy7hvccDvPoyvgTKimM2iEnioYwfUGjkJ7zYuw9cwbKXoZ8TxHm0uFLxuQsl1TEvrC8IiDUnD3CQSFZ7KfrLoYreUrKyWSBOa/6vAI1W0cIswNWL7ree7k3R6HXgk3en+r9lfMqRr5Uhlx/2n+1Wk09SZbKZ6jhludd9sJT4fVSlAthNm9RRPNb5VxQMfATeCgklkneIHhVzyO/L6OFyj8raSkrvEpwJL8uwdtHY2hmlrNMGDKhzrRE7kGyIByk3kRi1IkGoGiIkr5E0lOyxslMC0LIQlDu35lwLdSTyaXHKftWfR2XXxwD4vAR2EeZXmOkx7UShSdlz2oxAJlY4jl938wytE0WbkQIEkOTbIYSAVmEvRAzjGZnLeFFELzwnmEYaXrL3X7P8XgAHWlG03Z0fU+TejYpUh+e5HiP5zUpsd7jk/CrdYoCS0xYVQ4viUAW4X5u6Jg7jDMvygxcvktmuoXhIyRBw0j5syAO+IrhZhjkGWRaI1RgRisy/QwxiC1X8iDD8eUnnzKNY8o+Nlgby5nF9hM+o0wJiprTMuFZPp0LnSMII47GHq4OozV96jF0dXXBfn/PZJMwZD0xPqN2AMR3WmdxXkqNFZp97qoFX7l8CBijY6BJGidXkwjMzxaBcRhz70lRNkTraZuGdrPi8mKH1orr6yuctbx+/ZrbuxuGYcxCHkRcqkvxxzL7KuN/iYKM2fN917DbbWm7ns1mw/MXz2jalnGcOI5DlHeCQmEwWuF87IH07t073IVnu90SvMvnCeq+bpUMmXCx8OWKF1TX3HGs8jmKuBr3LJJfNRuvAL86B2qeSZN2rD4Gab8+zCPrz2sZpEx6Tu8zfReUlNtknNpQoWJQ4P5woLYXyWkp+S2VfFDxo/qsFxpb4FqeTU+oWOFjlQJ04rl3FDV7vi9L3C8Gf8rGioMxyWzye7mnulzEVZ2yBVfrDXd391xeXuJ1Oo+qAC4kOjOTtxIcBJZ5P+QcV3RxyUtFvox/Oaobq80rEd+iUBQaqzOdqK9CT4sRoLy1vPsczuf1ZBiXMWU/6j5+872o4VxV8FiMVUGgnlSRkdKcI0rq2dlqGlNk0IVekWdSGTx1os1KSTZ8hKvWUoFHgo5SkEcFy+z8En0pbVB09iRaqwJag/MK5QPOK7yPAS3euVkbo8jTY+R2vWXex0XHvY2ece/g6vKC+/093796xcXlFdNguec9zdOn+DcD2tlY/UQTHU8KdFApuj1Ux7DwajnyIYTMD0QGmO9Hwu8TcbUEQNdyqZSVj2tY4GMhlBm/C30Jcb+00FeqMyBYVow6wmtrzJrJpyS5ZcElxZDpiBVJtusVu82aP+aaqqAA8rwTPEKZwQxeIucFqQYWT4rRhlXbY3ZX9JPiffsef3fL3k08jAN3Dw9sTMt2tcH5CZTDhshvmzYG9QXvmYaBd/fv2N++Z9jf48YjwfmYZaDaDJdA6ZwkNGTpuCp6KfRtQ9NqmsZgx4nxMGDHMZWBdbTK0PiAIWCUZmU6JgKjHfGTwnhD0+3w2oAaY6nCaeT+YWR69472/oEV0CtF2xi6h3v6KWCuL1m3iodp4uHdQFgrnv7kM1ZNQ7e/wb/5lt+9veXTq2esHawbw8Vuy/XHl7iHkYffv+crO/CV9hx84DMaet1y18FrP3I3DrQYfGrfVIxVkqFWaIDABEIKxqnxq7ry+QHrpTcfoJIMlHrOmqRPKN1g2o6m6TFNS0DhfKk8lUoZIS3yQgrAUUZne0rMNGpR2tD1DX3f0hjDOMXKJyH4WaCLc7FkvE7OmMJyinx28i/LOeSD2pjYB9M5zzQFxinyJB2SXqQUXsXzqJTQ9rmt54edjOev8zLVKT/0IdJlFNnQa22RQ0YHX796w7Mnlzy73kWamLL7VSUrCkWS/V6u4Y9xiv/QtWDjj9gqHr9OZIQ/5Jksh8zHqNsYndsD+SxXnPoRRtAZ/13gyYeuc/dlo+0Zvah+ZunsXd5TBNofN4/026N7dCKfVfP94XEf+SzJJ8WG+OhIj6yxmlslTy3ttsv7om4dS8yGoDNjscFVa4szCxTZIfJAn+WqsJhLDmJ8BFOznUbJPiZngw7MDirikCwyHif7XYKRA2lcXRwYImeqxK+ttQzDEWdtJafEK1YOckCshBWTG2o6anJJeaWbKN/qBmUatDZM05Fhvye4EY2nNaZUofEuwcvGlhxK0Xcd+xwkuZDnhQ+JDnNGEhd5+PQKsxN/NngkyX1FH41zcM6mINkERwDdJJuXKrpUEDrqsI5ZJYraGVefvUyFH1EqZjR5MV+liC1lCInnJY0063By0mv4LM6KQKUS+crnGaAnL5+p4bmS2ofpiZyL83clybvStX/wCotfqjMs7zudq+gLy/lWup+CsKyqKfOXd1S6hZQ4r06hLImCHGUOyzeT4SI6Qzyz2sRgZ+8odkPZVJZHVc0XWV0lGKboKMtVZ1k5feCcYxonrPM0ncE5nwMwCAFjYL1Zzd4T+WHxgfkQg0pAKp5W8xEaHAJaG/qu4+r6KZ98/DG60Tgf9T9ro2O863rea8X+LmDHYrM/d9Uybt0+R2vNqo/l351zTFNJntIOgoZRe976gdHESkdt6LDB8QUDfz8ece96fmU1107z8f1A+8WXvPv2C66fvsC0La71NO82bPY7+r7nwY1oo1k1DY3TbPzI1aZnvelQ+4YLZ+nXK25u36OdRTWKURnug+f300h3d0d3seLOTryZBi6awLpt2BrY9j0mXPJ6Pp5IGgABAABJREFUuoHjxMGNGFzM4DYGrToOe0+/bmlNjwkKbPS9eRXpm/IQUq/xSNmiPzAEjQueBoVWLcZ0GNNjdI9SRrCV7BDOdhyRHwseqsR/tIk2UmlBEAOI5J1k3nSCu+dkhcTjpLNR/D2gQ7E5R7oYbxLdPlY3Vak5QEh+Ap/nE53sRX8QfTbT0SCyQoSASXwVDCFolP9xMvOPL6UeFFqZhUEoCvRGt5CQPITYf0V6ei8jFcQpLdHJS8FUvjvnTBeQ14ZMXUXxCKCcKxkUS0f7ck7LEvD1ofWucEPp0xftSBEW9zfvGPb3bDebWFbYWobB8vTpU2TrTWtwwROs4zgMWTDy3sfoPXfqIM0InbI2UdFpJQgujtGCp0F02Yox5F1CIpdAnB0CK6HERQiYZQHXAp38JymbWXyf/VJuDidjlEjI0uc7VMjsKzyJg0gWZM2u8pwrYUQFspvqVHKpGHBiHPJ3qJyYMzlMVc/KAoWZ5+cXeFkxQFnLCe7Kmn0ReGpak5XfVOKmFiLEUC0ltU+cGYlhe5Wy0JXKwQKZAOZ99rNns+NBzZXDiscX0FTrCrONFiDIvHymiqIs+lQKqvweomDhYynzSBPS7yGk8kipHJ+UD837kMZOc1gqVHUWlQj5IpilOL48L7HYRWErVPJ97POmIFctCrniUwkIEAdvpCXxjNUGHiCV2YpOOUwSrCpn3dJApCD3y4rOvOL0EyXNnYnqNukdsWyhyk78mgbPcEqXdeggpaXKeLncqYpNfGzQoB0XF1eMx4GUPEfTxJJboDCmif3BBY+JDsPjMCX4lhLqpjH4yaZ3JvFTaDASFZeIoLSYKNiYz0IWirN0naLU8hmsgj3SeCGA83EehV4J/a/O1uIsBlUrhRUt9jX9VIAp+BhRnaA0ul/hteI4ORQRLyXiW3hi4UOnLUrK3sVMHxUSvpCM/sTsms8++wSCJzjPxcWWL774HcchZhQ563E+Rn0aFbOnlQu44BntlPs7yvpmekh1/kWBERzy3tO2sZz+MAysVqtKIU0GiyQEvX3zjof7PVdXl1zuLujbNpf+UUnxiEZZx1vt+eUvf4H3nl+4n7N/2HPY7wu/C2Sl2KQ+j0pR4U78vmvb/LeUXXPe46zj7vYeayOdieXaPagm7Z/PgSM+OKbJsVpt4sZnh2YGUIUDwjM4872QkvNO7FpLDUmpKnTvzKWKwaWm+fMzcirM1vRfkLl2PArf8DNDSKh+iGwlUaAh0c/K0S/zyMw2/hvHEeddlCUTFw/pe51kA5XHn5sQzoAzlv2l4GdiapDaZRit6bo2lTcN+f7aERtBOQ9SEF4xZ3c+zzs9HSWDM4oC6XONxqa9Xq+3vH79mt3FJcFGZ55PZSNma/U1bkh4TlphihErODaX3zI6LD4X6115TyLkSn5XGHw8UzlIay4nzfGmgnd66Qm8KtiILLicsvxe09+gyD0VhQaeBG4GUBKyqDLYFvJVhYshRIOJKgGAcZ9dlqVknEiLSpaM9+HM2gUiNQzINsKIXmKgDSh8br8htPPE2B7qMePMJRvOKB0TBHzMaor9IgEnMlYaL4jKqAotCSWsS3nQKuBUQBnFk6fP+Oabb7Fj7BV8N3zP9qMn7N8bttbTeovHMzUKp8AEQ+NjSxXT6Ezjpa+0ZPD5AEo3cb1KetwLPan3ds7jRB8U3TGeIVXw9MylVcjBdkFkJOHrAlEJZsh6RPlfnFKqpKJjqVFVG77kLkEwCgfMO6U1wSgmE98Vxgk1jmfn+2Ovm4c7GT3OpaKjwkeocZmUJFXptEopnLeM48T0MBDGQKs6FA0emLznfhi4efeWlVI8vdgx2D1H90A/rPE6GsoCMRBjGidub295+/0r9jd3+GnCKJ1K2kLQ0UgTlFDJ+XVOP/fe4e2AMYqub2NW+v09h/s9m3YXq7toQ6egUZ4Gw0q3WA3Kx2pE2nratkU3mt702E5xcC0PDwe+PR4ww8RWN6yCphsCrXdstgdWmw2+MUx2xL99i1l5PvromueHluZ4x+D3bLornnZPaK1n8+SCzYsr/G6N++JLDsHyjbe89Y4W2NLSr3p+ayzfjwcexhHTtHjZrig1AcU2Ijgf8T7Kg0ZqhVcwFF5feFPAhyh3m6alyaVwDVoZmqalaVpM26KNwTtQNEignthsYuCNR5sWnZzhcv4c4kCAtu2iUbFv6TuDNqrcFywSfBNCiLKU4KLQpKTvBBezEkUfEpqhdTQ8Cws3QNNoAg0uBCbrGccGq23mv7FiU5ZYkGbnp/z8PC4+9nmE95w+f8jR7oPieBxZrVZ0XYdWimkcEsnQfPv6LS++u+DjZ5dcX1+nVli1TEY6q9H4yeJd55yy/2mvpTzK7P3yTrFLnLtm8EzyQU2L6vtk7OLDmTFWGSK+KskvH2ovcG6uy8+W35FkoZkKRxGLl+s8L+ed4soS77IjpBrndF/Lz3PLe0zGXH43cxIt5MoPjfFjvpc9Xc59yceXsFjOb2kLLjpdpXNXth0gOUgl6y0w5f7SRbwt0yyymsjDeQG1XgWELNPP5yfB1JH7q9QuRIExEHTmW2KzKc+q5Limgkmce/CBkPipUqW1jFRyI5VPt5PFWYd3vp58hgMh2lesnzKspVqeyo4BWWtynJtUjWUcCD7QJZ1daYMj6ktGQexfTOL5KsqYqpI5qitLWLoAOszw+BSRSyuYkjQUQik/L7pNlrCDCNNxr3xwyX6oks0pJovIOkW2jsuP7Tm8d4TxSAxSJvO94jOo8CekNeXyZfU+VnpMpcNHeMV5KGJCXqTvmvpIxaUrpBLcY1dt75W/BW+F/tY6Qv2Col2cXsuKn4sY9w9eQg7z6PVrwnwQgb8PgTr5pp6tQlWBdIo6QSbU46pyfz2G2PajbFL2ItocmCuC81XPJyrl5TNeCrrHzwLk6pWlMglF/872k/krMp8MyRYj/cgr3iO+jRkYi/Ka91mh8M4yHI/YydGtomNcqQYSXVHBx1LqiysESgtAH1Iv6ZASxizaaUwlm2kT7dmHYeDm5oarqyuUboHYOkKZlrU2uGSnU8FzuCfSlQ/I+yLriv1b2i2v+hVK6ziXdI9zDu1i64cOxVF59k3AGlj5nmdBcwv8jluuMfxCdfxicnz05luOf/V/5+Hf/S0f/2//d9iLFRwC6+M997fv2T65ZBtWuOOIVyOrVU9vWp62a8Z2jdUthMDBjfz6/ffYVUPYrHBtz/3R8u3xQG81nzy5Z9dpPv3omhc0XBq4vNqyWm8Zuo437zXfj/ccDgbDxFXfsmm2bMaGu7uBi6s1utOooNBBsVc2VfiKum7sw52Cvb3OtsagQgoCNQTfEHwDPsrzPn2vtELrBvEDlZYVckjTPofSxghUSpxSxKTcVC0s05PTPaXGVdKcgvh5wTmYXEg+1aj5ewIu2ISvsb1UTMjS+KDiPy+BtiYlAMi/uY9X6+j0DiHkaicaRWiazF8jO/sx1O0PcIw3TTMDgPQX994nZcaBgxOn1AJ4dfZ2LVAtndYikJxe5wXr5XLrMWSOTdPkOYQQZqXftZ4rgGLwrIX7bOTxnqZp+O77rzkc9igVs9v6vkMpxTSOXFxcYKeJ9Xqd53w8HolI5zNB8s5lwr40Vmfi7n3M0qiVjCi7ZOIvX0nGWm1ILePVzpzKoRPkqIQTZllfQriXcF5I+XmfaqF27rquhPWFkCxzzUw6G56E+YvyVAnN8wlROGgyGjCPbD0x2GaeWUkGsxvmiy4ZJNXtIhx5P2OOWShfXiHk0vmyvvyVnSsaM8Upe6gW8Ms/kgNCycJUFmCKhhfy7yLIhbiw1Fu9RE8GCqGRzAHnffLyhQxjkHPlkyDo8c6mEldiUC7VGFy6V6aUhQtf+uJFuMb7ZkJCWvd8i9I8VHWWKvwwlWDi86fJcFqDUimaVBmjMU3sgdIYGt1EQbtZZJ6q4syuDVvi6CzCT3yfglI6K80jFOk/C0qxxExD0xSnueCESuVulr2WvHcYk2hciBkgglmxv2OBjbMuOz20jJn2wKcsWCAba7xSybit0dqz2Wx5bwzBJQM0OuKFUrhpygEB0sMpYW/O5pITNE0WcZYWIZEihKJzGaNa/C831p+GIqTPyhvPgz3iV7UknyiSLw4ucfSJS7GmJ8g4RMVG3u99wbmYIWNjifJMd+L5zIhKwCiV9wYPRpkc6VwrNUpxWhpMkQSdhBekPrIqClX3d3dc7HZ0fc9nn33Ker3hb//D32NTZpD3DkIzEy6stVhrcyBWnGfKdqyUv6ztZHiX8+mcZ7PZ8PDwQN/3s++8d1GwD4EvvvgS7xw379+zXvX0fUfTGPrVKpWE0xk29/cHvv/ubYw6VFGIbJo+9d31MVMq+rSYpjHy10SriqyRFAAbI+xJhhVrPda5tKRIJ6y1PDwcMi2IepHGNFFR6PqOaRxoui7vx4Iyz3BrHnAkdF8cl7Xzaz5IPhcJsWfsWRUFseaZ82GWZ6TsxdxQV6oVCG4V1lKdnTy5mveGKlguCiczfgqQFcHSM1Nr2O/3eZz5SZsts/z8IQOwwOTM3EMIrFd9wuFoeMqn14ujLi5EKZ35zmwWQVYpFM3nvwtfKTA8nV85Q1prJmuZrC3nWqkUeFPiYAVe5f0hnyF51XkRI1T7UM1fUYLBKLgYqYmaIYFKipGMp5SUYC94F/8fyicV7mZ6XNPALHDKjSUQQ7Hg85DLyhYQliDL/Fm15gTG9PdyE8reiRW+xtVsFEs4I61JouEhPi9VTuLaK+HlzFg5S0RJYEH8O/q0FThffS77XfOxoozWBjSlkmE2BSerFMCjtcfauoJU4X/nLpVkVqVjuePVasXFxSV3t7dcXl1hnWVqb1h9/Izj777FOIX2MYhKphw0McAk0ZJze5j3UvC3picZ/x67v/yeaYF6fE3STy3qatVa63GR83E6hkr471Mm1lLulJ/zqmfigE944FN5Z6MZp4nvv/uOj//sZ2fn+2Ovd/e1Y3yhB2uFGC5yKN2sekmRU6OsCKtmDc7AtuNhGuiHA+hbHoYjf//bXzPe3fPkome3XdGtelTbxGpLhJmOfzwe2b8ZaNDs+g2Xu0u6tsGiY29SQHmdjJ1Lvb8GbRyvaQxPnlwBgWEcowFwtCQ3P250eAuDnrDGs1YGQ2BjGnZ9i5uOuOMRu3/HAUfDCr3u8TowHY60gO57LIr3Nga5GafoJmh9YLAOOzmM1/TbC/7uwfLl2+/R4zuMP/LkueFz98Dn9nue7tf8/PYFv+heEn7zO/4v7iv+G+N5Gwwv/IoGQ+h73pqBu2BxQdH2PUxjtHNVwb5N02THcHECJTxTlf4srELQMek6CmjXl6xWKzabLev1hr5fY3SHUpqm6WLpdKWYjnvev78FNBLDHF8XgzSDCznYN9otUulQn/poK1itViilaLuGtk2OeNUQszMmpGaGDyr3JM/zD1R/z3WoolsJqhckMVoTTMOqVbDWTNOE9Q7lHcEmDp74UdQ1Z2zij7rqoIXlNXcORsOi9xNaw6rrUY3BTjHAwfqAs4F3N7e8ffOG50+f4YzBTlPVRi7Ce3Iulj4+M59TZ+oft7bluEKnP/zgD497Ym955KrtWD9y+EdhUNPmucx9Kv9KheXaFhPSZ/H+HzH5H5hfPZf67zpTWuZUsZEsfyzH+hD/WwaBqFDk/w/Bczne2b1ffPRDz4TFvUt4LP/Vc6/vL7aj6PiJ1XEiPQqp1UOWx7IMFSrZSZ0uPulVomPlqdc8iWink5B8CZisZdDZGn2AhuwcVypWsMhzCmJ31cS+wOmVyRYTx4iypYaYZLBKmZSZLyRnsPBz4fjVuR2HqAPn9hwhEPyYqrzEIO/GGNqup1+VlhrWldX4FDSpVLSfTXgOwz5VLdKnqlhCXMG3LOefwbo80yyj+Bkszyacqkq2kWSv4FNSRqqoKPqKicEAuTUiKjlIdQy8Nw3eTqmUsASEFbmqto8TpIhKCsSp1yFjU58Fcf5FXcNOU9oLM5Pr45Jq+fxx+/vMOZ50jFwKPU+UE+W5th1mW3RtqEi4LI/l/ThvzKgnVK0lL3v+U36vTXFLGgDoEM0ColuGcL7y3qO2dHllqGlK2UOZj1JFRoZKdqpgIe+rEwOgJAgJHYp0IGZgoxXSTrmekIJkTlLFhJP1twrXKH4K6YscCsDy+nLAn4KffqZ4c/OeaZyALup+CA7FZ3e77YIeS8Z4rFRsbbSFCR+SAA6hGUrFZE+tDc5NTNbSr1b00wSTjbTXe4Jq6Fdrrq6fgrMEZ3He5rZXEdbFt3euOpAEEJLKbre6pW1brLUcj0cOzmHtiHUjoQu8UxOmA+MCBx9waHo0/3Z8x6/cBf8Flp+1io+ut6xDx8vmmgd9ifUPrG3Loe9hHJmaBm+iA9Xqltsv3/L9s+gIPzzc8PH9Ex7e3PH5V6+5frrjUsFKKy6042rX8tJ0/MmTazbrjtt7B/cDE44vvvuG98PEMDi2L54zro68UBsunObt69f829/9HS9//p/z7PoJo3PowdLowOQbDsMRHxwuBaE7CnJFrIn4pNvAxADW448jx8PEODmsVyngSmUdY+kP9T6kf76iYVKpyaQkvlTtlcgLvAunSP7o1TDZwDQGjkfPg5lQbkQxJrrhYyl+73OQWWsajEmBaV5FOTlVMgjJIR6CwjmDc1IZKCXiGRMDsn1qa5sS/Jqmxyhdrf3HCXM/2jG+zACvo/di9EkClQibyYG8jBCdOciq8WTMpdBaPxuvQvTk8+yAItHhheKynMuyf85yLiEEpmnEqBgMIAe8zgANwfPVl39b3qpIBncgRIVea8XDwx4UtE3sV2pM6e0YFV6ZtRBSlZEfUlRXyjBOMRAJChVEIlWNmdgikMyE4XQoQiGyYmhMMlP6LP6yFFA/dJ2/t+bOtTFPhAC5S+UMz3P7HSpOIu7b2ZrqiSgRTOYKgAwxcwyQP8zCcfXCU94r49ZCe/WdvHXufPcnAylVCR6B4uwLRRmO5a4LyyzPiuAe8nRqh6AQOZHiYkRqKkPqxUggPeRc7DHsUq9hCWaR5wI4kUyrNQhuiTISneMChlAZixNekHBqoQzV6FHvcVppNkxLlpMLPpe+zN9TomJJwodOmdVZMFUq9Q+WSNI0rjAJ65jGkfvbO0jzN23LRy9fRkNPG3spmtSPSanYs2oJk4R8eZ9C2v+CF2U9ARaZM1EhaoyJRifvaFIQjzEGIw7tSmhXQErrwNoosBgTlUQfYqa4S0wFxJAvfyc6V/Vojue+ypREFZwJyV2hJEEqwmG12dCvNuzv71FKpwwOh0/7Yp3LQrdkVtWG8yR9Vrbbcg5rlJCvVU4QLDgviDRXtvPH1R5R4aAi92pR8wcKX4m0qqYn9YAxUlkE47iWKFAEaZsCShRXlSOaM49SqRKALopeya5PQreWCHKXaUxtSC6wVBnORivatqHvOrabFevViqYpVV6ePH3CJ598whe/+30Sgi0+tMkoJAZJkwNboKoYkM81hXTKu4XuJS3SOc96veHN69czw5iUbkfFILHb21u882j1ANkpGQBDv+pZrVaYpoEQeHh44O2b9xhjsr7gsjM7ZPoDJUDnHI+vlcMoMC12V6lU/j4wTiN6HPJ5kQhaYyItmaYJbUxqR/BhvpENYNV860uc09UnBdeDzLm0QiApZ36BlydXFqgLbs1gIvBYyAvVxEhArReW93q2VFXWFy9d7km8tp7jZAPjNOVztJQgsqPpDzL8qmp+ZIVZqGfXdXgnZ8qXiVc0POJymJ273Nu8gr/8lBHyDi8Xkn9VsXpQvt/TNCa2Vui6OJZWWZbO+JDJUJqfF1lIFldwRfhrWCgAM3yTNkH5yzS/RBpzQEz6ux6pGG6Sc1/p0rakfkeWiwK5/p7gWEVDygGchRXMpyd7dA4V5e4qiCHjb21hVlGpEqwodKloDhJcFEKBn7T5KgFOxXhxFrYI/Sevu/y3kpMVyZiSTqUCKZcmz2uklUhZk8p7Hc+MVhC0QmNi8JoCRazYpUIq2iPl2EKBTq4hkWAb5bUoB15fX3E8HhiHgaZpOdo96xefcHjznuluz0Z1NHgmYtlmS+ETS+dDfdUOl/reD11iSMnPV3raD71Hnl3eM6dR5y95Z/1+GftkvBBO5ymfJ/n7eDyWALh/5NU0K7QWtPYELCG4zI+y3Kuj0Sv2YqyDzkE3SW5RDegm9tmeJsJWM130vG0Ch1ff8P0377FffsPbdYtZdTSmSchW9NLct1ZrusawWrVoDO1qQnmL1i0Ek+bhiBVa4vNalSo0KR8CO3m23QV/8vwzfvEnn3F4AHd94OHhhuM0QrNG0dOqidAMTF7hbcOoY8aBQ9OiwWkYA73TtK1i58AcLc559kfFanOFvR85HAZGp7E0DHtYK0PXaC5Ng28c+3Wg1Y6uCxwYuR89t/eaw8MrOnZ88+0t368nvr6D/+vnN/y/Xr/izge2Gi6CoqUl0PLtruHV+J6DHVEq4L0FPI1TqLZNGXwml/O11mKUwrelHR2pCoT3UhEPTCzAkAxZLX27YnX1lOsnz9jsLui6HnSUzXGe9XrF7mLHdr0hBMVf/dVf45XH+RREaA/YaaBpIv0P2uC1ZhyPNKpB+YAPUwyEMSsUPds1vLi+oDeGcRiSPDLFQOTQ4QNYOzGGY6xOZGJbGpyLbYSUykkWgUTLxGBqpAKaxyb+q7TKMmBwnu2qj0GQY9x2Q0IxO0WLezKQBRItFEqc5Je6wtOHSMIPOSGXtEypKINO0wREQ3S36hnHMXl9ArcPB755d8/PvMcQ0DqeBAd4pQneRQNdkjVO3zGng0vH6Y9xbMq99Tqz0f4D8KhtZXHYIg+qFPzopUSmipxslnWZnwNEJ1XgFnOspxB0+UpHLVXigU5EREla9RXPFVq1tFfVNojiRCp6utgYhP+U+zKjr5cUcUzN35ufEblIeLGSgPWy4pkYJVUTVc1byY3sRK+ui8afcyzXQVs/9hJ4zT9MPyWIfIE7pzc+zjPlX3Y2GY1Nhu1A1ImzE9z5ote5Cac7cBNNiC3y9k4z+Kh/Sx91lUT0OlBWKWL7N1/kUdnFKErrmewssrB1Y+q9qonho0IvNCr43L4wtrcrMiVKbMbJZkYQL0MKggoZrxSSWJNkNW3Qps3B2QW/SvWymAyuU3u9aOcqthtxBMR/3sbgAUl0SaCIuJpsTwGLHY+zoFutbKwc4hRujJmbJmXQn1xJNlFKVVXUluej7EXGaVF1BFcWTuiM00YywlWyWTSZ1sQxdd6jgAVseqdC6RalddH/goPgkt0D5OyJ3SdmagqdihBzbm69CyFEPmVLi0VFiJUmAxws2KPj4ThhbYPJOnsoikIgyQUVcBZALc7ceIMEXoh+IPgTxyr3+uBj1i8l6DnLv8lGWuZR5LMyPVX0ndncRIkrenZWpWsdhxjoTYiV9kobyijHNG2SK1VNZ/zsDBUaVlPcOV1qjEdr8Jj5M8i7IWDKUkOFf0rlqtFxycsWHMWGpRLsRLtVKu5o5mE5izz+rpzsQ5jxEVX3mSm7GPdaUQyjiUZR7alWCpfgOdk7OvMMpxuCc0ir3/3+yJMnT6iPoCcwektwKenEObxU2jAaZ0doG5qurfQZhW4adAiYtqVfr7loGvT9gXEcCeOIdhPKK1ZNi9vu8NOIc57D8RATYSTjOC3JuZiUCqBNR7tas1qtaIyJCQohyqTWTjRasdusaQ9TDLR1Debg+WqneWYMkz1wYMIqz4VvuLEjv9GeX1r403vNRvXwlz/h7etf04zXTPsjr7zm67f3XF5fsWpa7oF3wx7FwOqu5cLeYx8GlLN04YaLdUv37CXrtWG73tHv1hAsm9U1vN3z/tu3vOkMD87y61ev0N5wPB6ZtOfys+f8D/+n/yO+0Q/8mwF++/lbHr6yPPvZX/KLf/Ff0fl71P4Od5xwJnB/PPIwvSOK7KGSoWKlL6ViOzLTNqiuxbg9ynqGyfF+b3m4t7THIxqPmRp0Y6DTWZ7xhFIhXXihnFetITmZGx/wysfWb15hfMAmc54E+xc6INSgnHtnD4xjwzB0HJsWo0102BOwxAqq1nucHenbjq5raVyk2z6AdTGYKAAqtOCbqAfYKdmmo1+mUQrjDAbF0YldPtJZpRQMpKoikoz5wzYH+AMc48ue4SVTPDnbEmFelr2rr6XhQK5auJIe5eec5XLFpMNiiJFDBmmDKoFODNKSLS7P1M5yeU+t5GhtUvl0NVu3zK/v+1kGuQjDzrtKSElGrADHcYAA4zgmB1YsRRGCOEKSQTTM14EgaDKlRmdEoew+OSfj/aWE4lwwLWPGtYY8XxHUfeFqha9VgrjsmyiUIRSlMN1d78BcuJ/dUwnthPqj8o6yUdWzcX7Z8FsxX2bLFcUmZBhlwUGMofPJFeaT/j6VTQqsytjMGJtEF2dBMwI7wUKEFoFLEsCqaC356as2ANbZIrAmAin9dCT6RdYpz4gSJZG1gRIlk8dI/bZrWDymvMz3bwmWRz6HInSl+dTRYrVApqqzIv2RpOx4dnpL9mjKlDba5DGUUrF6eRWhO1Paqz2KOoL0lgU3TbF/4TAmw2VUMNbrNbqJvZlIZbVc3n+VZLiFWiC4JvijzNwwEcKs+kGtYIcgUX5R2A+JOYTUkzYAfnT53Mt5ldLdokgCuMmluWTAx/1X+c2ErNSFKpozjRFIfZnS/LRJ/ZsqYTKVOLy6vkZpTdt3mKaFlFFiQyo9Fgr+Z4k0H9Y4Fy0OepZydzGqQIGD3KVOaIOsL2U1psz0cl8lwCdjWZThS3UFpSRCXyFBPLLT+b5KYNeVQ09Xe53xVrTt9EN6JiqtMUonI3dIPKzJJfW10bRNzJrRaT2KwuuMMRmCAXJ/I3GOqyQUBOeZRjE7x7189uwpX/7+9zjvYjUHV864To58l8rxGq0XPaXSWyuZPgco1TQZ6Lo2RUlX/CApWd4HbDKMeh9QRIF+1fd0bcv+OPDw8MDxOGRwT9OUsotVNnbIvtRO76xA1kwhzOcuiKySdJid/mnPpHy/T7xcHONKK5TVtG2DUuDsBKwyz605YGHRitpJX/rf1jxyYVhVhR+pan7ZSxcqmJ5cNWaA9KAtczul8/Wzcsbyeyn4D2k9CbaCk4UXp/Pu5dwunOlynhLtH8YxtYMorOTEmDuDi5r9ebIMVRyf8ftkFA/SozU6cp1LSrSTYCCKI1Seq+SUzM9r2KW1ilzhFrxm/qzAsZwX2aGu7TkcjrnSRz2HLNjJh/nLFLxUlaIOVPKUE2PJCTaU3zIZjjMSmiXO2MxHE6/Q8vsi09wT5lG4oYKjVAepgiGWctuShp9FTVXOwDmZM1NppbIs55NH2LliRBT5usg6IeNixhxNCYZLdFYrha9iWOeyHCf7TkgR3nLm07rFyBppDBlfoyNBdJHk8EbhUhlLJTDIeDnn59l4raSEo0uBhArlotE2onqEQbTJhNgexXuUSbqOiYZZYwxXV5e8fv2G9UYxeot/Zli9fMF4+IrV5FDWY5TCNTE6PWrb86y8c44ZMQ4Xg3vhv6f3FppTxpzTiKWTQ+475yiS7yIt0Cf31Ne5dyzlZbked5xHeGsT8UucZP/Yq1MGCdiLvdZaUAHlFaW6iwI8KlVCUkqC75Ih28c9CGEghIEpWJQPjMcj/jiiJh9pQNOiV+sU2xRpgMqVduIZkFjNpmlikJ+qqxtlTK3oGZDkfe+KjmSMYZpipZpnz57x/OOXqN0l3756x4v1lsPrt9i7OwyetlN0zRo7xFLlGg1aM6qAVzGj2CuNdQoOnsYZhsbTek9jPcZ6XpqOtlHYXjF6zwjs8fTa0OgOrRtG5XgfGvAmVUloaPSGdedprGP/+oFnruHn2ydcXl3zb+7e8rfhgZ1p2KHpiOXLaTvulGU/jQQfaFAE68BoVt2KbtVF41WFO7Eql8U5yzRNEW+ci3seYrsmnVs6ReOsMS1dt2K3u2Cz2dJ3PaZpCCmbySlH03U8e/GCp9dPuHl3k7KDPEEnGpks89FhnTApyWnSHs/amAkU3SOKftWwXq1ywH/eZxGCKGsq1Qr8jD5kY7/W0UkeUoVCnSSSjFPlXGqt6drY27wbm5h5ElIPQy32KvA65OpmIjdmWKdzUWSpU3qxvM7RtcfvJensJalEbFXOOYZh4P7+gcNxZNtKYHfkPUppRj/k4JEaRo9dj81j5rz8kfc/JiKerD39pzgKy3zrfzrHSC4GPjeHRauS7KhIvL1QIAGOkknkZ4IoJY/s6Vw3L3POH82+DifTrlZf/XxMrq7GV8n5iXoE/ur0GSo9q/osv032q55/vRmq3Cf6zzneeD5AgpNzmsH8CP6cu8KZuQktyJ9Tn8u0Pj+HfXSUe5x2qOpcByQQw0Oll9fypgqqlGuulY7FtdTFFDCkIMG27WLVMOYJVhIkXnjwKUxzYLMmv1tkH9FfS0HIpCdbCHhMakMTZWEJbiuvDGk+XpK4kvNYm/L+WWBeiLDKjsMq5VV3HcM0lYzPZJfzQwxQiMFNZzLGE9SDwCNhysn5yXpcRdd1ocMhhOoAxvmJHiF0utj5RF9J9JYk22abQMHVgsfJkVn9N/KmKDvFOZTqYYWHhcLW5kvOlT6qj1LVTHJFOud91SqrOo6ZL52rkCsLIOsL52XWmq+FjONCI7Uq+1HvQ970KIylgKJCcxK00zyFUKryiOgi9RmljJFlgjS+BGFEG0usiJBtvXltinl5+ZDV7fncT8EUCKkMs+CSwG75SMj8pNxIZd8Q+FV0UqCVcS/agpVXiQWp2fiyF2KXyksIEZYqq01zG1a2NRYWeLLSqM867DiS+3nLHNI+rbouTylUMJNEnTxaCNHWTazo6F1yvKro7+oq2e84DNGh6Uqv8kC05+mgMKal7Va0bcfh8JBKY5PtgGJXm6ZYQcg0LU3TsNlu6ZqWaZwYxgFvfcpWjzJPv+4x1jANA84dOQTHZBpco3Aunr/eGBQjr+yBL8cHvhpHurbnTbdi+uoVq+OI0op77ZiCYXKaTdOx7jeozZbOeS604qJVrK7WTMbyzAUuVmsun73A6YA3Bm8VDzZwPziGwXLz7gFnNJdPN3z6q09Q728JQ4tfbfAvX/Lvbi3/7Xjgy1vL9vnH/OyXf8k//ef/guAGpuHA8XjA+wMOyxAmjscB7wOT97iExx6YwkTAx0pOjcasGlZGY4LhcLS8eTjy9uae+/2B0TtW2sAZeTGc+UNsxmidWzbXl5r9dh4rE2YCAe8s4xjYH0CFgLUNhy7iwuQLPQwBGuNo9FT0xqwD+Rgo6wKEKZZfr5ISFFGrNSH6x6Z80qS2mKrOVAp0/E/tGIciCEgv1Nr5HQ9q/P2xEgq14hdCiRo5R+iXPWfm1zwac5qmvNlFBkyRlJWTvV6D3CMO/uV3JpUQUKpENMszSinapkURe3EJIc2ZM1W0j/OuMBKSYJdKA4tAp1UxOGbZKq87leQLimxT91JWrTg3fSU05JcVEp/GOwFzeU8AKmYkDKp2HNV7IQhHKHucmUx9jBbCdvysmkx+H5kZ1FlJMkY2FFfPoMjBC/nyvgAxCTPC3nJPcVG8SHk3iZeIsVdV4xenQM35Q4ZZxPtYuiGXdRKDQ8JNayecjQ7LmKVdyuSV8g4lOij3H6I4PxF4V05KmdP89xhJVoSekH+GUPY3w0wUoDNKowgBpfcE5TxpIaIxMs6kSFlxXufe2CnCU/r/mPS39MwmjTVzIOTzGWcxczCIMLO4agdeNnbXCpgMqEQvCbQ6RpxudheMY+x/TVqP0iaVPy2GPhTJaVzApYh0Q5smKb4Fj2t4zhX6cmZkX0OSuGNvDpish9RXRBFy4JGsJ4uuipgVUgfxJMUpLJhIhttCSa1UkPidK4qzSgHMXmhNwsngPf16y4vVhqBVLMHlrGANMeozY1FhvAUqzIRqle/K7C3C05Ws5QCx54nKcBRloYyaYGJUycIOxUkuLiXSXomwXsMgok91BrKCIFHWOiqwiWgZY/L6TMr+UQlXmiYZuohVQ0zKDGqMTtmYBedVsR5l+p0CQAs6Jdojaye1GoBkGLAq/y7j+BBpjqrKVFo7YW0bz4YLURJQUjbZx1KipkFXlWBmuKNqoaM+n3IGTCrnv+TjqcRYKEqmd1FBX2/WrPqe/fGA8xMBl9dmJ5uFd6FZJWChch5nCC4c1Rle1Yeh7O2StzgJOEu936QlgFIqCvWp/FNtyBGYRFqrsnxRXl3xeJJjU/hOjcWhgrMQmwVPLN8tPlreowrNLMaD8r0YdOYGuDD7bGnUql8namRUeKty11nJP51gSDx6msa0hsQHamKQYXBOkBX+UM0LEFmpyIDxp1bxDLRVK52SSSFZGmV9yHqyjBLlLeGzxTEq8F/IqY/wKFUmmq++73n37l0sS6ujSF/TbKp3lhYuKunyCdfS/0iyYSRLhV/62Xrq4JGotKikvCpVycrpn+yAS1ks4nyOjK+WFwVNa1wh8Te5gSyD5FMXQj4HWe5dBHLluVZBUgSSHBUDfJy1ODthrVTDcUVukn+V3Wlp/Il7Xn6R14uSGKu6NJjGYIyma7voEGxMruwiQV4uwXlZztVLn7C0HyptcAZ33MAIx+q+6MgV3cRn/KuKyGRSAFF3kSAsqxRKOXBRZ5O+vxHvQ3yPcyUQWEdY7XY77u/vGYYjTd/y+s3vePbkM8LrLce3t6yDxkAsE9pEfqhyVldZe5FJSGXZVF4zSe55TM8T+jkz0lPO5VJelOtDzqN67KVOWsu5tZOv1lnLnpzLPAyz94cQUCmj7erqKpek/sde67bFh1QFCpBeitH5HaPtIeDDiMKkrGxp6RMN2T6EFBQXWx1ZbAzCGEb8MBFswOiGpu/xmzUKjzYqB+1JpQI5SlL62qiAyf3cangUvix7XmhpxNmYARxLjm63G548f05Y7/j8t/+RCzdx9/otahzZNBqjfNY9mgAd8WwaEZR0wKrA0QesA+00Sk80wdOMlmY4YMaBfhxoXMw76tI5WvlAF6BBY1WD0Q1adXS+YfAwqhbX7VAKvv9uYKLh43aN7jru3JEHLM/oaEKsRON0wG1absPI/TDEDCkdg22bdcdmtYnZOVXWhvc+2TM83he8TnEtmQ7WsFS6oW1j5k3br2jaJlW2icG9zgcaGlbrLf1qi246Docj4ziy3W7jWF5azkTjaNOK8ydWFlr1W6QFXDTERlyLzukuJ0nMLhVpuZTolMpVcraWjkrBJeVDwrdASD3Ta1tTlrMVdL6l71pGK44HRfA6yW0+lbNVufx7LZOJ7F/rz49df4gTsH5mScOapsn2pMla9seBYZy43l3ixyGuYRxRpon8pwochjmNPDenf8w8l1exbfyIcRd8ejnH9Mmp3eHMO0X+mz1f7c3SYZ+D2TLBYf7zDwDFjI7nF8z50mOO4tmlavnzlFfJ7z9+m4TWn861VmeynHUynfQi0VehKi99el/m19UEz63zQ/sYZ33mszM/az4ret2S987GJ+q2Do8JIenzcWn3z1ueOoXxBTdmsnSFJ5WmkeETKkDP7WNR1lTe0SSdpIZhlt3Km2YTntkVFSh0bJeUJlLbRma7GDzeT2A9NBJsnIRFeSYtPlaxIydJhCSzUo2tsi5Zdkh09pCmrrVC6Tb2rrUx27rRMSluv39g0HvWSJXWxbkXnTtASNUwJWBSbi14cxrslICRxtBJzg8I4JRX2Y43c+zJ00rWlNaav4tyi0oV4kLmmzEgtdCmKFNR667ivaz03HqPZ7SglnNUyogMEByMVhIIPbFKRMG+JBGfyJMJStnpqmRfq5XVc5c9SBMtbbFmiM78AdmjJfwr4Mb3EgNLmAGrvE9gkcSw2T/kDJBVerFRGmMyns7sSLViU0Gj7OgjBFRwOyT6QgB0Duw+IbwZH6pXAIUGPk6oY8JKJUss55Fw4tH3ir+l5ls1zGp6VI+f7nHOxyo93oHSc5ApRdu21VNRptI+niuRhUQ+01Vb4Tyd9LdOiVDBe7abDabvULzD2tjGINsBpwHnLabrabs++wTyYlSpqiU2mGkaY+Z5CLRtm4LRA85aUGPUd5yj6QxaNxg8zk0cw8QhxGx9SQvodEwqe8vETbCxklmAFoXaj+jdgF61bPqWdrWi15qdUri2YbtesQrQtYaOwKZrGPqW4GAfAvemYdKKkCrHjV6hvSU00DUK3RiuVis++vgp33m4GRy3/ZY3zZovvr3hi+sdL/7kI37+y1/y85//lItNz7S/odeOwzjx7vaW9/sbnAk4O2CdT/QjVdMKARssTpXA8q7r6NsGEzTHo+X9zYHvX99xeBjiGWoAXePyDMXzvtSymRa+UcsNp0+dXPUZkvGc9RyONv4cbMYHmxKjvA+gNUY5cpWUaryQ+Ij2IfohVPpX0U0CMTDFe5zkB2R2U2hTEDn1R8pdP9oxriqkrg0FOVvbu7wuMRpIqaw6SrYAL8yMKLWhoRaKlgJYCGeEpTNCrXwmjgBZw3JNIIfU5/tjtILDqCY7OUUxq40icRAgpB6IgmQK6r6MMu/y4kIss8CWGciZvQsl870u5V4r07WDooaVEKTiVKx0mRkinvmbmnAXZ3JmJpnop+wrVf6Wtc+EeHnclzfUhHu5t5mmipNncVZrhuOTAOuDz5mq5d6QmZS8S6V3uUR4QzI4EULKmPRVprZP84sOSomity4aZL33qLr0tC8lzL1ECfo4tgjUaVtmjPm8MqDyu8UZVG+Uqko1i6HepbNYMlBjNkcu86RiRYTc003On5Swy9+f6Z+tyxhRYIsGknOGwiI0VvutSzlgwf0QYokPGcsHZnRZSrpIX6GwRF5UFgYinkk2Y4xm09rMq7gRmxI4a0Fr1tst796/z4qDRO6TYFJjXcbvrJNEwat8sJga5P1OU5yVEyonrTiF518VR0bxdZb1lrJfNQ30MRMsD7GklwKFQm2yo7Kac+lhXpzsQRzk4jAl9TjVSXFTqR9XpTBkZ7cqOKGlfFIIsRQ1klEH4gw1jfR3VhU81GycOJbEh5HGqWirCPvJSBV9QPMgp9zPW8kY5MoEsc91gnPiZV3byI5H/pYqHoAEUsichSf45HSQEmypzYEK8/22aQdCRWtzibFq81ShCZlOyz0zoTqho2yW93RdT9MYxnFI0aEpYMf7HLRCUNm5hNZFIUvwL/hW42r5XTKx27ZlOA6sVqtcKhM5n1rTdi3HwxFFPBM3NzfsPvsUlCcEi6vrKqpALMUqBoK0ZuFRZekQZlAtV0X/T85pomXS3iSkqgdxC6JjVPiDMQ3Pnj+n6Vex3E+GeZpRlPdmztdZj2TZ3fwfFddHlaldsysRBc8IdSqcrHK23vPmspo2F1wrVDXMnntkhAhnGac2ile8PrllT0aSqgGo4nwl03aq8zuf2XKcud3vnNQb90yns1siTsOcLtbnBmZGljT4TJaJ34VqD6nOo8hYqjqvcjbmZ0ZpnSNnCYDzub3MTC7MrW8K3Y5jiKOsoiWhdn6XIKMZfonwgcC/hp3KC8+8Ip+x6twvQJhhwvIZKpqmkB6KeW2q8J5aZo3yRKqM48FayzSNKWsxOsWFt5Ll75BxJ34cFttQ8fHZPEtvttzgIpAUUcDBNE65mkSkWbHqk0mtT9q2pe97uq5NDvPi2CgG2hr24kB2iW9UDmCtMn+RfVM6OkCD0CNSc6WqNL7wruCJpemIzmulXFpjBXeZTzJeZvz1HtM0XF9f8erVd0yTJdBw9LcMmwazbwmDwoQSECoOU7mWTjJVwz2dLam2lXlZmAcTwJzPn8OzErh4+t2jVy3ofOBaOu6Wjo7HnAe1Xtkk+dpb+8Pz+oFrt+6wLmb/eyB4cfjF/mqJUxNj43yqXlVkeogGfptkokCgDQnbnUqJtQqlDboxqLbFKJ8NGuIYDyEVsky6cNM0GBVosq6d9lpFuSFHGqvC5zISqlQpCoWbLOtVz9X1NXq15fOvvmV69Q2bydJ7WJkm0sdgo46iQAdFh6ILgUZFPUKrCANnDJMCZwPBO/wwMh4emI536P2ebTCslKFJcp4/HGEcMa2hU3BhGtamYasMk7eEoGiajk7veNWseW0GmhB4Mx754uGWJsC1a9HASEApx7hpeevueBiPBFTM5O5amosNm7bPRj2Br7WWcRxx1iXZQgKXRcZNEqqOZzooHbNu+hXdaotOlZuUVpjG0LUdk/OYpmO7uyKohtu7Pa9ff884DimoUxzgLuOt0Snw38Z+kX3fM00HrIv6bgzm93SNoe/76izPr+BDyTKXnpzVGVkGm2itUYmeBjw6xNKRoXKMCyqhNa2PrYOGySZjmwS/6xQUIjLi8uyJpF/RzFo+nHPy6u/6sw9ftaG/tt+IPWyynsNxZH88QvOcMFn2D3u8OtD1K9q+SzqSn41Vw28Jw3MOzx+ipWfnfmYN59f3ODTKM0v57fz8Qwg/mNAzc6I9Mucsn5151yMzzf8VG8pSIpL5fchxrJbyXih87eSN5bbHZzWzB50R9Cs+9iGbaC2L1QLbh3DpH8urPsSvzznE83tEx6fC2UdgBykZIcxM5Dz5+Qv8FzcwiIgl+slcwq1tkVnzSHKR6JMz24DSKdtaZX0geD/fREWSraPMHsprk6ohNqlkJzAKa6c8IQlKDcleEKcVAJ8DGrVu0otKdZYoPsXg+JrOeKXIrWlFdqEOGy7wFd1C5qdVQ983GONQxMQtOw68e/eOPfesc+n2x8/gnFYv7O+qvrvoe2TJWzQZnZUCRSBoE/soZ1kkI38cK+91tdGptLYk4WSdRStU0KB0TCQKPtsVyuPpHSrEQKuqMuX8HXNdH6WwSvGbIfbTtQ5u7xxff694chUwooecLL+SlWR4rWaJ5EVzKDhb4FlkbLFTLiTjE65W9kH2X1ekpv5v9fKaP1ZEV5GCf2cLSNWv5JgnfTMmTom9RVf63zl+IwuRg3V6Zct4iPdk2lLTuBnvKIElIZ17KhqQtxKVKgnGZ7J+GpcckyaqsWRrZ3Cbwbve4wjQWheWJyvr1pyxZdoV8N5xPB6zbOWRJUbcatsGVQVXtm2D9QY3iSwWbZTWWrquTY5KlQM162Bg5xxt2/LJJ5/w8rNP+M1vPudwODIcJ/aHA/v9A4eHOx4e2thWc5ro9zfRB0jxCUpSbdTlJ6Zx5HB4YBh2XO4u2O52NG10th/HIbUNcgRnUUaj+wZCx2GceAiKDpfah0GLxirDLZ5JK7ba8GSYMCkYxSuDNw1htcJse4KBJnhGA9OmozcdUwM348i9D4xo9i4wDEdu7ITpOlbGsGoUbZjoJk+70TzfbmiaDr1ac2TN36sLvugV3/Vr3rQb3vuWn/3Zf8H/+F/+c/7k5XOMn3j33VdcbVr0qmHwni+/f8Pfffk5ttG0xmOdxSbd2hOwIeApNmOFptfrqOMHzzQ4hr1l/zBhB0ejm1RVyiM6WwygPnd+QiJblZ9HzkzCuxJU9bhcMKP5gHOKo/cMoyMwpc/jGYp8S6GqpOQYRZQPVhxIK7R3saR7JMCRt+VDVs69kAaFii3MCEgxu3z+fzhmHvgDHePGmOwolpKu0zSdGCdqh21d5hzmvdtqArjsYf4hgTwLLT8gWdbClzi2HzNg1O+W97rUB2bpsBcFTmhkFuIoRFWcLVLu+pxeprQmOCE+tYinslCn8phprol4i8O1CHQ5tW+udKZ5F5ZQqPbMaF7DWlVCJCfsMdF2IdIBFVTOpI1OD5VhMH9F5jZyFvP7NGK8rYQbYUACEi+lOFLkuvOxtDixd+hqtULraFwQZTyE6Mh2qXTDNE35b+tsdIqnaHnnbI5o98mZBRWcKnzKvbtlxv4UT2UPTuVAcZ5JOaR4R11SJoKlykyhCkJhji+xH7hiGAbGYcjf9asVFxcXNG0sVxIzCUx2gmfhqcKZuTM7rf6MglsrMfGnngsFocKuWhZPDkaNyk5npeYwzq4UEUxE6ElCVRFyTkUPkS+h4J9WOvfSyOJGCChtcN6zWq8xbYtPuISKcwtKBCEyYyhOJJXOv8owKue4GNszFEPB3bKDc/GzrOjUIRHHKNmA5cPyfEjwU0nRkrJQ1bfUjjeQIIRy2mdlnwMoDCVS2aGCARUIGX8inRPnsOyNqmCkdWHH4jgupCbhoBhZxEld4U0+H9XHOWumwlujFFqFiOsm9gOTDA1R5HRTiwZF+dUpiCIvPMz3Rj4ucPfV/i6qOkRilR/w6eE6+GA2lHyPVBEQ/KiMWov7xWk0GyPPsQBKaGogpEzdwGa94v7+Pmdaehezxk0qW4SK0X6uicqi4IuevSlvKCXwo1IYQmC1WrPfH+hXq9KzLCIVPmXRDccB52Kf1Gma+Py3nxOzGnXCE+G5AoFlmbxQeHCGweMZGTOZoDKaxHMVcvWHSJtTObpkhDBtw2az4/mz53z62adY6yq4zx2TwVc8eAm1ipxmminCBHHtJ4YuCk7+6CsNPuNB9RSSYWdu2PPLHU5DVdHiNW07J6eFBX4qTu4RfjzfqEI3qgVQDXIeBkmu0IoTuKVQ96icKZXbi8Spl/Vkmrc863JLVWpdJbjJjTPcY87zTznUfLWiXDvnMMRoacGH7DBJY5bWBiHzfFl/KTNY4WJ9JqnWpyqumsBa5puoRYiyq1aBItrIxOS8yzzl4zlVE1l1yZ+ybJDnJ8a5ReZkqrQT2zVJFR3B04quVeur+YsCtIlyeqNjn7OoxzSYlFFZDF0JTjq+21mXHC0u44dPJcAUUQ7XSqWghuj82R8OaQ7QNC1d17Lqe/p+RdtJNHxCrhTR4oM4xef/dOYBxF7kihQ1XSpQRKWvZDYU/IoyuMFkWiu8WdpXZPkkJDkmzcs7F8sm24n1esV2u+F+f8Apz+F4j19NvGWi04qVjYZMLfpKRUfEsJJlS1X1RcxHp9b5FnINRWaS38sund67fK6+foxDaKm/Lp0fsg4Joj47txPaA61pCM5yPB7ZbjY/OI8PXbuLDdZJqcjY8mQYBiC+JxpcAz6sk5zpc0m5TK4w+NBg1wobNBwn7GGP7lb41cDUKo52xI8DXXA0bbso9Q2F7hT9RKVqM8sAm9yGwCi0j8Qm+ChXSNaZtymbQEPftWxXPb1SWBR/9Ztf0x8GnnUbPrt8ysuLa/zkaFTAKc2R1Cpogt26xzQtKzOxajtiPo/D2g7rDYfgeO3hQSv2WnFnTAq4GdBO03z/FZdXgSuuWKGwds968lxOGvxEqxVbNLv3e140LV1/wXuv+Ob+nt/evGdHQ0+TWiAoet1xvzJ8f3vAaViZjt16Q7/b4FctIRkHAdq2pW3bjEPOS6uZpOMrk3iOyraYQJRRTNOh2x7d9fF302BMS5PKlLbagGlZby9QpuPhcMvd3R1939EonfVlAGMU0xSy7Oisw002BjkOh9zqKwZkW1Z9n/RuPWsVEHXWVK0o6eEy97qkOpBplQR4G8mqDpH+Kq1RRufg84RaKAVd17Bax9K/U6Xzh1RKPdjUWVHH4N667YdUiSPEQEYxCM+PcVjQnh9nWatpQk0nplSiWOw2D/uB//gPv2V/ONA1iuF4RBvD1fVTPvr4JcM0xloQVWLGctz6nUv71tKmNlPSf+R17l3luyKbLu8plTsEb3/gPdW8l7SVxXd1BcdaBpe/lSojzuTbR9aQf6/40FKuoxqnlrXkZxC58AxvWK7hsT04kfsfkfnze/0pfE7uXa6lPnvn1vrI7x96x4fmXAfMZPtHpYfl8erPqrXNYOzFgUmsZOdLFYo6SFlojciGySoDntQWR84G+Y7ccqc6M0ZFO3ffr/L++5TtVnScyhGpgFDhb6XTFwCGWOFFGVQo7boI0e5Y9wVHpTVbhWrkPk3QMRkpJtq4hHOQu+CFpBMUaKQgtQrzFvQibW6qLmeKPdI7DscDt3e3qCfQd00Joj/ZfJKaEKJsOpPLVb4lvl5kdeENxWYY0lyofuZTU+lfufpnBfuQYEyQkvIS8F8lmAFekW18QWRyAUO2WUVdyBhV9ZevwCV3ZbYU9ZJvQuD/eHsncU18/V3g//zfbvnLP/OYRtYcgFKSXiupf1CPT2WLrvweQc5xHCdX5VRSuZOyP1n2k3NQbVSygWQTRNY/Q6YbOSg7LbQOrq3nGSdbjaFUyjKv7tMq9f+N1TpVCqTM+kjSd8tY+c0Jf4Q+nPIa8cnINePlohSmZUvbQHUy0ulVf58T6GQ+BSnz+kJxxeTAnBkMMv0sfqV8R8Jh0bErplhsAelD5zz39/eM40i3KmXTZe2NNrPVNY1BTxqb5q/TXKdpoA0rbBW8F0JJZBW5pWkanlxd8a/+F/9L/ubf/y03N3fs90ceDgfu7++5efeWd+/e8O7tG16/+pow3HFzc1MqAYn+pA2rrmcYR3yIAbXeWa6fPuFnP/sZ796948svv+TNu7d47+n7FcdpAJ+S/YxmxDLiaVOSkj5a/JSqS3rFMTiObuDCBUatGRoVK9wNE+PDwOtxoLMb+hAYm4Zhs6Jb9eyHI8PtESYI3hAY2bQNv3q64nnXsusMrYaHfcPv9o576/hyPPK74ZbfT9/zH813fP/sJZc/+zl/9pf/Gf/lP/kL/uWf/4J/+tPPeOf2fP7bz7l//56nF1s+efkRv/v6S47e8uXr1/w//s3fcD/BVjW4yRIkAjpuAtroJNNrPIoRhWkj/WiUptMdG7Nit17RGoVyE9CclFNXc1KX8ar2NxV6nShDIRyz66y8EgKEaMuSTii5woqPtMYkOXpyqYS6T37EzLdVrFLooMHT6JACmRR1k/T4wxSVNJ07TaQzeV4qRIPJj7x+tGPcWpv7jIcw7yFeDjezv+ts03NCfV1+aykw1fc9dj0mfNbRufJPFL9aIBQjR53tmj9Tj/egE8ciiaAJWRPaTm3kEbwqst+CTEoWD5kY5nX7gK8yKCJikRE0Z7oXOlsMnBUTSAuORLL+bDHfufFaZRpNElwysUYMthqlxJDv8zjZYeGreWf8kNxYVTKrQ+qZ7UpZehGARGkPoZRkm6bYF3qaxqxkSuZCgNyDO+SxY3RVHQGV9yp4co8OWMAgrjc7ADPckoKvSunweBqj0DSLusmRUorYG644xWv8zM5qLQxQFUdjUipLpYL5WfMuGpHv7u95/d33meh1qxW7y0tM0+RydBJ1I9nZsv9ZnlUVKw2hCGqh7J7gg044EErjygrdamUgCoDZpiAw9WRHqFKSVRmSgEjGmZKNW3B1hshBMKZ2LAbqaCLpW1ZUDlHCwKQeJ/v7O7bbbRGg5YUhCsfEI5kEN5Xhl2FXK+L18auUFRC5pwhXp8wFZvputdSIi6eCaX6vUqm3pJ89k+ccktMxORp1FrbjnUsjgkrGN5WUtHQg4r4nh7km9rbOb6vGK0L/aTRuLSDGDKfi5BC4iKNWK4XRgcZEx0bTNqkPbCrVb+LvGo+pDFwiDwsQ/UypSlmGLiZrC93Kyloo4K9pAiFGZD9qEE+oodGpkkhB0SX9yeqXNLgO1RhA7fzO1RbiF3ks4VUFP2VeZe6l3Lpnt9vx9bff4pzF2mh8FNwVGhPLoHuUcuW8nePFeR5FofHOM4VA2zQ83D/MMpHkLEzTxEcvX3J7e8dhv0ey6nWFRz4bQSKHdMnRkrNIg8+91KqtyWufH5IF/SbMYBuFrFj2PgRoTMeTZ0+5uNjRr1Z0XUfbdZjUMsEFkSESNan3mcIna9yrgJb3On8j+KdAhYoPLvjRH3TlOZyRo87gUQWZ2Xvls1Ah5zlHUj1fidiMC5zTlBBStnj1jLjEZ8vMZD4hTXV2y431O4QBFZ6lErmMeC1BZPX48blcTr1WADIdKBks8a1FWcjGWKE3Ag9qLl1ed3I5coCp9OuSpQlPUUrTdS2b9YZhHBinY5JHdK5qI3DNNDzM31+7j5WsQRUD4HJywh+tX4J07jjIYMmwKfMv7X1quhcyrss7YqsHqc5T5DwxXCr0HPVlyxWIYUkTjUFN29I2TZKpTA56iuOUd86cnoAYHrSOco1potNcEeWDqKu4LNOO44jznnEcGYaB4XhksjaVso9rOBwch8MRwg1NY+i6ntV6FXvytlHJjY4jn+RCcTBGuUscmiJjQ6jkpZD3JAam6owrpCx5WZOUJRbJzlqfSs0XRItVX2LghfMuB7NdXl7wsD/inWe0lu2257vmNaPb0uqER54YtCrwrBRs2a8aBzKVrPa0duI8pncJ/vywKesPv5b07EP3nepKjzwTioFfo7jY7f6oOe6PD7jU79v6wGgtw3CkNbHAvk77KMGNRqmYZaGljGhIOpNlSlnV3jvejbd8bR/44uY1v/7d53z+3/17hu/esF2tME3sU1c7N/L+VgYvgZ4P5OygE3BU2yY6D5S2L33bsttueHK14+WTNc8+esZxPPDNF1/x5avX/M0XX/OTzY5fPbnmp8+f0K0aaDuapueBlnBxTRgn9g979n7gWluuOsXaKVpnUKrnRbvFbBpsYxmB+3HgZjgQug7vJpjA7UfeO8/d/QGrFJur6IRHgZ4s6qvv+P7+FZ9tNrQo3rsJbz19a3iLpfEN192a9mLLG3fgzbjn6tlTLvsN62ZFaDR3dmA6HmOlia6j73vats39vKXSXQnC0GiEpsWzab1LNiKN0g0og3WBoDRN32O6HqUMrW7wKF5+9BFXT57y/atX/PW796y7HmunWBEihNRHfMJo2KzWuOA52imfU6mSRgi0RtE0hidXF7nHeO0YL0cgnuVIP+ffzelD4kVaZUcwYWFDEv0jhEwbdQOrvmdaJae49xCm5LgCVNQrjNY4F3CASb12A6lFCKfzmslEZ3S0P/SqZR9pL6SU4nA88jf/4Tf8+te/4Wc//ZTriy3b7YbhuE+6rJrpDefo1I8J/CkP8Ygg8o+9KuXm7PXHvezHwv6HHMgffDbryaewnC0t1DCvRejTd/yQ7fKD81nolY879E8DIX5g4Nm9j837x8zvD13b0q57yuNDFuPzMT/zvLxbhZidqkLKbPTgXJLvPMRgGFONXsnTSXhcOtKKI722T8Tzp7WJSTTFygNKzQITtDaInYglHGv7TZK9TXLORfIn7f5IdnZJehKZPjrko/0uoKVk+kyPq6F58moqBVVWKdYH0aQgxOAka13WmURybn8R2O1WcO+rSprzPcqytFghKptGnutj+Jz18rNfP3opySyn4Jf3NtqFtEm2p2SLqQ3ogXkbrcQz1Mw2qpC2j0qpZcVfnIvviewq7k3w4Hzg7b3NTtK7hwNv3t0x2hVt1yGSrOyv6GAn9OeMLBxCCt5Nsh4BYkGDytlb2deybJ11wLkcrhaDCz6GpEOG+rus58peUv2sk26KKi3VaGKCUqw2UGhBRAetIKgUEBziNgWVAhgoukHWMxcwybbyat7LS/T2YltPiVm69FXO7FHN3yF4XYEtycGgfXTk6SQjBlXJbMpX80kQyb8WmjZPwitnINMjhCYRy5oDH78w3O8fOB73rDc7QlApIUOCesiVooBc7SwEuSdWhfWp4mcIUZ/VWtO2LaCYpon1ek3TNNzf3/Ov//W/5r/+V/9zVl3LsW05qCH7Z/r1ikt3CXjcdOD+8pLxeMzymw+BcZrw3tN1HZcXF6lyZM8nn3zCX/zFX/Anf/pTfvOb3/Ddm9f06xWaHu8c29UKm4JFg/N4pTh4hwqBJnh8oqUvnecOxz+4O/5vx9c8uXtgrzyub+jGkebg4GHPfq1RnWKz0uwwXHRwYTTaKkyv6UKHag3T2HE/Trw5HPl3+7d8Pwx8O038drL8GhgunnB88pLmT1/w7NOX/NO/+BX/1f/gv89Pnr/g2W7L5aql0fDF17/l1bdf8fbmHU3b0H50heo6VqsLtl7z4vKKz15c8uX337BuLgm9wegGk2wQziY6oGK9U0eU11ebVQyKxmC8ofExGKLYZSLu6CC1mmYHojpAMVBiprcLRoYFjXjkmp3JVEVbN9C1mrY1NC2xvVEQfI6B213bJzpdwlRcqmQQQqAzhja1KA2JdviQWqqE1K4iBCYbeZdWMWDfqNO2aj9Wjv/RjnEfAqpyfjrvQRg1QCo/XSsA58ori5FcKXWSJV4bR2pH+ZzIi24U8ljLxc+V7nnPu+wIJ5Z0UGiMbnIvAx8kW03n+vxCnJxzqY9aSumnCggQmifRiGI7VcLsS6SVOIm0igguIsqMAVEY2kz4qT1moWTG1TDO+1DBTGKNZg6pNMccwR1i+eXscE9zjk7ruFdSxjKE6KgIKXvbOZ/LySuiI1qhYpkayhzjNJPj2s/7azsXIz5jNnb5XidHTajgKEJYFsZQeT2ZLaaNE1hkHq6LwKCMwWCKQ1oMpMl5KE7xUlZZShPqlH2d4KlVdoLnEuYyRjWuMC2l5kKPfDdzrtaMVJam01qD9J0GTOyfugmgzTt8MrIbHftQIOtPTkbJVCeoeWWaLNzI34KVolKkb2UdQZxhJfucSiiJckcgHaSiUMjWzPD71CGTd7KuxrvA9bkEMR8rlq9OTg+BmZzZAJJlN04TT54+4+mTpyilGEabFadqylERKlJRAVl9CTciwld6FHkvxpBo4HGZDs35ExmbC86G+l1VH1hVC4xERmEaU4J6ElcUQbl+hYxYopWr7/JnJQpZ8FUES2lwGjypl2V5x2nUGTSNzpGDkQabGSNW8l6Eb+jFOKCoyiDLf4OgncdbR8DjKhwR/BKaK+pBFv5P9o4igIugXb8sCdW5NDjxPNUZm/KCuqyUzMeHEB0QS82/Qp2ivMcNybOcVRsoWQvZuOfzyatHLYpGCFgby6mTez9arLN0BCSTVimN9ADyvpzj2nFRaMLpOnSiB6vVmml6E3uYq6gs1lk5Xdfzy1/9iu+++47j8YBzsYwoUmJbSkynd7tpiopWVrxK+wdpJyL6cXVkM2xDYtQlvkAXRSor85Gu//Tnf8bLlx/F8kW+OL2t87RdF530CQLlfTWhXjiSKxxQSlH3i/DeZ3mhaGbyu+CiIEi9sxXLy28plLpQbfL7lIxT4fjSQCUAK3pomN1bO6ZkigIDMaTUmeelcliRDb1LQQ/nBNU8fFp3FJrSVzVUl1eYz6wmeVrn6j3Cq4IXMFTWDl/RhEfkCbF2RGdgKR8327rZutJOLJYqym7TtozjGJVRobMBlArsNluury5pjGG17nMWobU2yUGKh/2eN2/fFd6Xz2fBjrzls3eXrI9C82taVa0p0aU8dijrqY0css6crZKVf/LapK2AyHlO5Ms0lsCFpOCQyjtDCVpSxAh4lRzZ0gfNec80HvNcQ4BWHNtB+uMmuJtYQUcmL5nUIQRskkXF0BQS3Y5jNTRtS9e2XOx2PH36JAXUxMj6/WHP/mHP8XhgTFHxzlkOB8d+fx+DOLuW3W7HerOODnJx5BDL3KkUJCROSKEnykcZIoWqJX1FoXIQUeF7tYSiJbgQhcJhAaQcaNo7H1LpsSABCp6+7bjYbrm5v8eniO2L6w03X1l6GpQBG0YMOgdkq4IYiMHPe8+UzqQmyQwmGmmUEI+MU5WTfXZaSmxl/n5hSJzhssBBzeWkcj7q/xZqKrJMpn1yJcajVeG9wpvI5LwYy5VSTM5hGk2/6dHN6Vz/kMu5CesCg/Ucx4n9MDBOA30DfaswykOw+GBptKYxmi5lIjeNwQXPOO0ZxpHRHRj9kbth4Ldv3vHVmzu++f1bXn/+Le7NW7ZNh+470CVAXPjnUrYDCErjqFpFeVKLHMGtWBIRRRwzlwmPAc3jcMQYRd837LYrPnpxyS//7E/pujVXzz7h1bev+PrzL/j3X3/D999+y+f9mhdXF7y4vuLF1ZPY65ojptHgHxj0xPth4E4ZvNO0k0fvD4x3t+xGx65paZThsu/ZNg2r9QYzTbB7gl+1jJPlfuVwbcfOrPBYgndYAt9tV9zeOKx1fHc88A9h5B7FS73BEvsBThrGRvEQHN16zdX1U9ZNi/bRoe3tBCE6jC8uLnj69Cnr9ZqvvvoKmwIeBIdiq4YWRdI70ThvcUqx3my5evKc66cvub5+wcWTK7a7C3a7C/rVCq0N4zBy/eQp//Jf/HNubm746vPf8ObNG54/f56yAl3CL8c0juQgSmfxbqJrdWqZ4POZNo2hbw277Yqm6iVZ40Rte1mv14zjFOn/LDMpRLldxpVe9kajfcj6Qu0YE4dRIPa/7TuN2/p8gn3wDNMRaydUUDQyJy06TUk20LFpYdQZqrN2znG4kKpnDywN8aK/iC3lbECNSpkx3nMYYRg93WrNZr0G73B2omlMbFMn76llyDOffchhme87Izn90PW4k7bo/Y88GWl86qe6xJMZfY5fzN537p2njqLTlz9mAH3s83PzyhJsOIVtsSGcwj6cmfP5OTy+joznqthjPlSrYPm++m9VwzJ++ehz8u4/1qm//Ozk/J57JsmDSziIrTAk+SyWl43rqu2BLiXa+CRLaJFtFDFzNelRiTVlCbmaSdG1alggNqSA6Iwsn0Oyx6OcWkvgwAzmUc6psnDzz5DYY8lwFlk6jlGe9zNdR830OIFxsfNWClp6i7SKkrObnYooAsmB5mOzHggxgCoMQJ9l4uVV1LaQ9ekZHNUS4kWmIL35UTKyvJZ7kMYpNE6yp+Vrn0qmF7lY7HFNUwLcBVzZ/pZ05pDsLX7xXuc8RpN6LcfezT54rA8cJhLtUxxGy+3+yDgatrlw0Fx7j47jU9ySpCqxaUqVVCDb0YyW9iOL86VEc0hrrsG1PIcU3TNh9AK+MmSVNZ71fQBfzknC8djuKvG/OvjXqOyMnk1WXqaKnK29zjqjzHG5/TVuRX3eVGPmcJT5MwLDijdn3TPRlTJ2ovGpysF8BFUCllHR5JuNVIKAIckmaczUrz3TxArAofqvDDHjPXk3o41gHAZ0q6Mc53Sy9YF1E3VRB+9sFXBZ4Ob8RAiOoFX29+R3pXPbdR3jMPDl51/wzddfs98fub274fbujuPxSAieRhvaNraa7LuOru1YdX1ORtBK0TYN0zRhrUXrqJ/0XYs2hn694sWLj7i9u+Piq69o2hYDdJuGkKr9jnog+BbnDxxtPM+GQFARtpv+igd/x41yvNJHlBr42cUOo1s4jPjjEVYNfzq03L+9wd4+sB8mHu4PfPNgGfYDD8cjh+HIW2f5nda8ngKvmzXH9RauPqJ/+pTLjz/mn/zpT/nJz37Ox5+84OmTS3abFZt1Q9dpJnvk7vae928c49Fy8+49x+OECwqlA3u7B6MJ1rAxK/6zzz6l1X/J7743dJdPY2WFVPU0AIN17MeRw+QYbDz/F90Fq9UKoxqmwXO4t9y/n3i4HfBB0eo2B4HKXorsHA9QwjEf0I1G2uv+0HXil6xwMvMgAsbAaqVYrRWrFfQtGK1SZVJFqw0ro+m6nq5tZxq5c57JJR1RdINUAcETkFbH1iusc6kfe0R8qevRaIPWUhk02eB+pOz7ox3jQvuy809XQstCODwVIItjulYMakFp+aw4x+XZ+WaUsR67HhOAJet9TkhBUvMh9leO41dEMmWQhhBieTmt2eyecvvum8JIFDGiTFWCiQ+5/6aYrYL3scSj9zHdP80lQBbGvcBMKXBRaFBKjGG5vkIW2mKQQMh74qqs6dLTOPUs8LEEufTSDgnJnC39ZiV7Oxo5zgi2aX8Q4TTf45OhqxiahNHNjaunThX5TolxKXltlUixVTRLzrymONZmvbBV6l3XtLlfo+y/MAelYj9plaKNaoec1sWxnZEhyNFS2cGTgyDknvyrOiN4VEaDeFeMgq+v5CwouJ2iEKFyMKTsobSvjTE4HKvVhtVqxcFOKJWcpEZHn4jArhZO1VxYWAqyszUloWHmSVdlTRn/Ze1U5TOW4q4uwlUWjIN4v6s6NIhiUhFheSYJ+7IHSqlilMuihRDCiEsqiIEu4p1Pc8uGF88Md5yK5WrzViiyk1reXTOSioKIroIEIUifxwwfXT9bBOQ4vETA1sqF0EWpRqCq++fZ1RIRXQeA1D9rpS3ekuC1yDTTWqfekSqdmSjUxt5ApsAqCe/Sq17oZ1yWvK0od9M0oVB5vvnKShLEPtMOQmSEUWE9VUpDVq7SmmpaXFCmclKHhMIF5rMh0x9a6aQY1leamws5ci2OWAVx5fMguLhcH7FETnqVm531klWdx6nGmPPAR1TIhWIv75VHvPOsV2uU0pEHeJecQA7vNVqnMuL4ODfvU0ZirbZUSmwotEIUg6g0edqmrQT/rDsxpWzFEDztquezn/4kZ4MTPErKg2WYR6PHq29f8c03X6fSvZFvffbZp7Rtl5zrx0gfIiSrfRX5QmSWyumbgpwimmo8gU8++ZiPPn4ZM0DlfFXnU/a2GM4qx+lis0XBrHGspmVyx0zhXrDOfOu5vc6Tylpq3iNd0dD5+xZXfVhqmaoOwlMkZS++p9hahIdXdFaJkWj2kvyOIpMsDbn1+4TGhZPvFur96XLKiYnzSz3MSsR04RvLct+zYRd8Jn8m66b8lHXV/C8s5n7W2K4UTdPw8PDAlg25UEm6r20Mw3Dk9nhgu1mjdbx/GEYeHvYEpWjbnr7rOI7DGblXYFDgKu+di88J1nmORXFX+XeRcUuP8Ij3ZV/lp/DWYlQUeuezs6CUriyzyEGjupQ+LJWqoEnBibHtjcVbF4P/QkglL1uM3qCNpmu7XIYwZml4huGI956miQ5DbST4TYyu0UEkLR6apgGlkpM7Zlc+7Pd5vo1pMI2hMbH8b9d3rPqey8uLWPo+BO4fHri/u+f+4Z5pnHDe4cfA23fvUO/es1qt2F3s6Ls+6wVAlke88rHnc5IXlfKE1BNXJ5qplUJpn2ShGu1KJoRWATQ0qVUlqR1RlpmkfH7Cl+ADGM3l5QX3hweC94zjxMXlFW++fo0yLdYfaFoNY6A+8UInBe+CruckeOYrhp1+rXhJdXQyLauk1/L3Qg+sjcK142WJ7fLbXFSvHFhLur3gSQltkGXWPBtSlpl3MbgKj3Ujf8zlncdZH/v6HUfu99HJPZhA30CjPQqH1rZUUGga2qahbaPR9Hg8MkwD07TnMN7yu4cb/uHVd7z+5o7bbx6Y3tyxpsHsdkzY6FyQPcly0xzW8TvRj5IBmegimN8r6keiwV5lOTCWTOxZr1b0fYPWnl/87GcchsD68gkXz57z7JNPef3FF9z/+rd8/fodr797w++/f8uL7hsuVODp1Y6n15e0WrMdPagedMfYGlCWUY28GQdeP9yz61Zs+lUMdGkbpkYR9gfWytM0mkY1bPoO1TRcKWiNTlkLDdcXO37aXjOZnrfW8do5Bhpa3RKmEeMdBMcBj1VwcXFJ27WEoHD41IYBQsqC2G63fPLJJ1xeXnI4HDgejxyOe/Sgs1zft23UTZVGBYV18fPrqys+evmSFx//hKdPP+biySXb7SXbyytW6w2NaTgcB37y6Sc8ffKE3/7D3/Prv/+POTM9pP603vlMd6JzOmYoBucjHfU+6/hKx6Cirmtye4BzxlSfZa1oWAWdz5NU8JPAGbnqDPGYGTmvOijjex9SZYzo2Fiv+jiAijK1TYFWYiT23qOCptExGKc4NnVl2yHptCSZbs7HAwV3hSeWRZ/+unTwyXqFHsXqTgqVEjMOg2RrxX2ZxhHVrhA+eu7c1dfS8f6YfexDTuf8eVrr8pml0/ScJHb6/kp2WNDjOmgpVH+fndMHvnvs83Nj/NBnJ3pb+mxuH3nknWq+U8s5z22fJZHoXKBD/ILCQ9N/1OyrSto9s7b5WlSlk1frqnhlPb/HxjyZ4w9c58qn12PPbTvhZB4h9VqVCm8xCDoeVJEZPKG0UQhlrMyXlOBd/M7ji+ygVAWWKAeVSpm1ZrDYWyj93QiEnAiRwJxsKyfwDQGkJLPoGIrkvAevAyZVQkuSGyHNdybHZ7DNdnhGfyQIWL7Nv1Y6THGKp7GCB2UqLQqsnRjDwHQ78mc6Bvmd4MYZm+d8RtWeL/BQ3n828KbcdPaj2RuVQufqlPHGrGf4aCNX+eRI+e2AxufA6QynRE+zapvO7PwKxOpNknUc8W+YHDYyDEJQjKPj4TAwTl20p+sSnBD5juyVWg6ffwnJdi++AWNSlqXWmGS/lgqFBTiqWnOBqSJkW2bhd9VPFnClsuGUhxDgZF4Zytfia4j7WiW5aI020X1VbGizTcy8grKNkefn+0+eqOikZMzG/VzeWx3zOf1V53CavC/lHM8nLHTkVKeeTX9uKxDdIi+xkjUqepjpisy5KN3plhDbKSm5V4SYgLMTqi/r897TtKlNTWo7EYi2teg/avIeR7kzPuucw+hY8Wx/2PPu/Xu6rs+73rcdSinG4559CujzzmKUokm6uyRdmhRcPqVKwE3ToEjZykaz3W25ur7i4vKCtm2ZxjG2MpR2TiTZz3kCFpvmZ/GMg2WnVijdMobAu3HPzf0tW2959+6Bu3d33D888DA8MO4feDsOPCjNnXXcD45h1NCu8dst09UOt1kRri9pt1d89vJTds+ecvHsCVfPrnn67CmXl5c8ubpmuzIYFWKwqp94f3vgeDhgpykG01rH3u5RTYf3JsnbLiUDRDvH9cWOP+8+5cnVnmb9JNOdoKIudXSeh2liby2Dczgf6JuOddthlGE4Bu7WE0YdOE4Tdu8xAXSMIIt76v3sTOQzkvhk7T87uX48u484qD1dr9msFdu1Yr0K9F2gMSFXd221pteavjd0Yt8Aoh3CY72iJJyl+REDt7yP7cSss0wuYL040r1QdjoNxqRAs3SGf6zY8uMzxn0pOV73WQNmwPyQcCXArx3e54RGueoxa6EnZ+nyYWG5vuq5SraNPFuXtvrQJY4sca5+9PFPuXv7TUXMImE0uurhbBQhKYnOupxd7Zyl61bp/bGkrRAo6aXovMel+0kM0aVyZnVkpQiPmWlUQpcnnMA4hMoZWBHZRCnz4ZkT65poh6wg1gKN4IYgcYSr7CUzgSYySJOFsnJTPMCTm/LbQbPZbGnaJmcIGmNyiUvJ4sl9Q6r+wwU3VTWXOpKQPLEThSTDIn2kEWk3H1YRJmpBtYJohVOVIDsbr3ogSb7idJ99JvyOJLjmsaOTRykwRrPb7jg+PKT1pj5GpCj5DICyZlmoZL3OnA7V3hQ5qAjRFXbEkQIlkzaEVAUuZAZcA6fg1GwjZpfgqtZF0JHPxWlSixpZWJB/lcKtJfAlLOcRYaCVIrS6CG4L5b0EFRRndiDMomcTBSjKsYq4BhKhXLKVGwr9ysEXcgyq6MN0U96pTPfwlEJgtUGk7IyaPx7noQF06rGqK0Zl8rmK843Cq8nKWRlkSU8UPu+pRHJF9Klpc+V0T7CTLN8KeNVZSjhJUkaipW523gQSQpfyrCo8lS0/1dlO+U4xyoMLLp/pTPdm56EoMYFQZYnJWAUH63dJlmx2NKGS0JhwIyk2xfBWfiZqHr+rleElD1zwXVGoFLFEWt9Fp5APqVxN4jvGNCgV+ZzPrUQg4FFe6ITKZ6rm9QKH7M4MKonZ0REuGYtBJSNlotMh8wuVQKxROmWN6uJN0Sj+9Gc/wzQNv/vyS4J1aGM4DgN//ud/zi9/9Utub265ublhv99j7YSUo8sYmGhTk7KSjscj729uck81lOLp02f85Cc/jSXSKjosfEqErFmFAKGVNT0KM4p3BgcrnpqUukK95I/6bKjTwWq+TaHL8hIvNKt6+cJMNrtfIee5vDZ/7gvPV4oso1STSjgXqmjkerrFyZSVt3OXnP3TWS5+rzn3fL6z4fKXETvnPL6SfzKoQ/3nkmgw/3L+knpvi1xVaHcJ8KmGSY7fuu9o7X47Ho8MxwN2HPnu229RBLa7LQHFOE30qzXOeZrGwDE5pNXMC1nNvDaQBGImtghmRQEXquazfFfoY47bX9K3xJ/z7iQ65kujuCi/epcV5XK2yPRcVXKS0gqjG5yzoAKNic4S7ye6LmbBNiZmShhl6PseyUD13mOSrjGmQCzvFIoWrTzOBqbxODti9VpE3/HO07Qtu+0OdRGr8EixB4l8H4YBax3H40C4u0dp6LoO0xjWq1g68eXHH/OxVkzDyPvbG+7vHzgc9gTgcDhwOB5oTMNut2W93tC1JahIaU2YXM64iM7zxKdIFZWSYU2r0rJGuEcEpirycPoH4JWLJUiDL0+EaHzQKfi5bRoudxfc3N8yWsvFdkf7pMEfDM3U4KaBoAx+4QmVHoJ93xOc5/hwiO/JvYJDFBpzAN8JymYZLn5/wsTPXuccL///uETH9d4C8yDKf8w1DQPDFBgOE4fDyP5+YhhGRhWwbaDRIbWbiSVm8R6tbcocb0ArxmlkspZxmLjbH/nq3Vu+efWOwzcPjN8dUXcT63aF7gzj/g5vS1WBOP+5HFjgW2TYmaxezV/4RpIkZjq3957des1ut6VrW+w48vz5My6/fg3dxOb6mk9+8ifc/MlnfPvRx7z69RfcfPMtt2/e8v37e1b39+x+/x0vry94stty2fdsVj3dGszK0CBZCoo7OxG0xq46+s5gupb7AKMfuDKezqS8OQNGBVpnWRP7uHeN4bJredGsedW2jGrPvbMR//EEN2GCIgTLQNSBtpstzgcm71OLkVTOu4m0arvd8tFHH3F9fc1XX30Vy6qnPttiM2maWFpRS3sHF6AxXF1c8PTJE549e86TZ8/YXe7Y7C5ZbS/p+g2madlcBD799DPub9/zm3/4O774zT/QtnHsWIEk5I1TSmFSsJBPdoau7xJNcMmpr1JriI7NZp0DIZdnNSRnVgix7GOd8xpCKM7xChdqA10IoI1HV/aZYmMohnqtVMo4Sd8nuaptJ5zz2MmlMu8B3TQ461PVuyjDSTnc2ikX8htEvErO9DM2ohNnb0L2OlP8HA0KoseoSDj3xyFWVUrPjuNI0/QnASYfus6954fsWmcv0Vc/QDujTnxGHloORNGLltep7qVOh8vibg5zn41dfq90EXnmkffl+XMKs2jYVT+wrjlc8+8Le9g/hvcsgwU+cGdk69Tyy/yaf1bJuZXudnb9/CfineE0aOZDvy8d44Qom2SjftZJyf+Ja49ZZifyXMLjbC0QPS1HoCZ9daGrRPE46nkaU3Skir4t5ZWkYczWAVUSVpAqSQGtStZtzG8rzvjsCKvGTeL6iX0pkkKR8cjrkUtV9hYlD1VnLQNL9McgCTfz9kXWWiwTv3Twc6Ozjez8paofNdzK5yIDkKl40U0WJ7k8lyTe2bnPNxcZUlogAbmsvk8BYLOxk62PEGKCknypIEgbRih6mUp6TXXp6pxHnuV5ZS1/c/9ASYeDyXoOh5FhnJC+9GUdeXPPaMVF1xI4SdvQ7Bif2QZOn49LUhk/xF4gFoswP1DVVdG0bFs4+wpO9ym9O8uO4hRXOQlNzkQIZLkIKjtJqOgBSUcJImCeAKqSEWTaIckgc2wihPmR4fT3cPLZ8tvC6+WM5fMlP+pBaviGMk5edXUUQv1NKOp8cWmWB4IPsbpQKIGLJFT21kFfzTrJYU3TMFoJEiG3nhWUlHcIPGN2d5SxxmHk7u6Olx/v6LqOvutom/jMNDzgxolpHHDTGFtsKoVTKm+ZUoqubWIiZqoQOY4j0zgwDLHs+ma74+LyktV6zTAM+BBotUGbBhNisk7oe7zWuBAITmMJTMpzJKB0w9F5vrq95f/9xec8MR1fffOe2/uReztxFyYelGLQCtt3TP0Gd9Gjux3bJ8/YffSS7vqCiyeXPHv2hI+eveCnn3zK0+sdFxdrNtuevjMM+yNutIzHew7DgcM4MQbPeBwIk0V5H0vpN2D1RKtXaGcgeMI4ESYXdTJvabqG59unbLafYdQ27pcPuJSgNAF75zk4x+gCNnhs8KyVoUEzttCrCTsp3t3usYch21ZD0v1LgquwAPEFBkyyK2R/mTojN/6ALDDjeSbQdTqWql8HNqvAqoOmFd+DwShDi6bvGtpGOoKLr0fhglRWTbYLFTllTJrzqTKHZrLROT7YVBWEmKzXZ70ptRLj/weO8fnCayJUHOVQhCCl1KzUea0Anwg/i3csBc763rpMejYcLTbwMQOEOITj71J6cP7O5RrrS+YyTVPcWF0yj733yfE98TAMsVzdMLA/7BNhVkzTyDjZ7KjY7nbRCTwM0bgFTOOUy7kHgacQ+FA5rJORIQt++R6fhLvitBUo5/LutSNOxqnhhDhtpFRjWT9JwFJU5RkrhTYEUkSYKYphVe5S6VRqN0en6NmeKaIQ9vbtG9xkQUHbtTx/8Sz2eE0CQSwLPo9wUdXca843Z26J7Of9ZrE+sqEnG2yFqEvmeSYqZdiSmSxjpazu+EcRuGdzkXfLJGvhovxaDMcxWkaImkoSvfOxf4t1ltVmQ9uvAMVqvU19i/RcqJkJQfJTAjLOZ9icKFFZPpG/A9lxIs+IErIYS3BaFJPZNKpZiRPGSzBC9WWM0lRzoSzBSCcEDRWuq1Cihji3RqVyeXCBvZwzRXIgBIVkYJUtqrJJRblRlVM7jZWkgtQHMlROv/kY8rdEOgteCARkuZpoCJVzJIa0pm2zc7u03U1OfCUG8VQuVEMs3Zr2U8TvED/HW2yIbKb64ozQWATFMucKBomYiC4qOJLfJ+NllIy/lEoXAD7vt7xi6XSefV4J8vGz8sZTel9GmJ1A6R9dzUlWHlTISfD1M74+H9V+RZzTWbES5UiyWHOpqBrJgXke3vyb/PcZA0Phm4W+ybnTOvZ0saPwohiwZUwMMMryfZC2HCT9LpzA7mRuAVTiUS45laZxpF+tSgBAyvQpwSZkulPoSFGaIPKa0To++exPUErx6uuvOB6PvH37jv/Pv/4rtrstbdPmdQpmSNaSGGKtsxCSom9tnKkytF3Hs+fP+ZOf/DSvYx5skICiJJBhfg5OqgsUZMy9fAtLUkXRBITB1JisqmGo8Tk/Um2s3Dm7oQSu5QVRzlwmnWSQZ4ffQhyo6G4KgFnQgfxKUvltMRJU5cTEkT4/twvBe/HOU7Pgkmedvn/+V31/4UV1IFM9VKhgOIO//BbKPTMILKYlNCYsXyAzq94h0f8hxMhtIBl2AoRIQ7318RkXGG3sEWyahqbt8M5C0yLUpuCi8EN5aTpbBImOSgp9WrlPc1USvFWtt1LCMxZleaCssf5+hichyaVpbuJckTLNWRFDeENpNRGCTwFbJD7Xslr1rPrY15YQDaLRQT1F+Tm35ZFWPaTy81FpCilr3bnaGSxBNPGzyPMjvZYgsVwlJWVMGhMr8qzXm9zXfLITxyT3H4eB/X6PMSlrt+tYr9c8efKU589fMI4jN+/fc3t7m+jRxM37G25v79is12y3G/qux4fkGKqyv0lyhiYGwMTvEw4Ecr+7GI6hM02WR7VSqdKQAhyxdXCElzECD50DDK4uL7k/PGCt5WhHnnz8grtf33CFog8Ng4Kg5ycwKI3penaXVxzvH5j8ofRoFLRK+660Ti1z5udlqZdpweUPXHXAtehmgmdLfTKfgx8Y8x9zhYpGr9cbuq79o8Z79/Ytk9McB89h8AwHyzDEbInQKFqj6IwiYNJxj7trtcI2cf2TA+cUx2PD3U3D61eW4Z2mvevgYcKPmsko6KG1DZONBpYcYHpGNxAdZqbXB5GzSGxTZOu0D1oTku7mrMM5z8Vux9XVFevVimk/ENYdbWew9/cQPJe7ay5//nN+8Rf/hLdvb/n6m2/46ovf8c1/+C1f//b3vP/2Fermnu3be54Ey4vW8/xizfON5pPdJU90z8+2PcOww5kWvd6gthts13E7DoxXG/abFfeNZpgsR2fxSrE+DHQoVk1graO+7sc7vtm1/CYceODIVjkG98BRjyhvMHpFUJGaNFqzPx5RxDNntKJLsspqvWaX1r3ZbDIeGmNigECu0KdodKnc5EOsbLdaxd7kddnucZqYHh4ID0eUbnj+9BnWOf7dv/1r/v5v/5bbm/esN6vckkNrDU1qNWGjUySEkHt2t00Ts3KcTcHusXfrZrVit9tGh7lzM1kz4r+f2YNknpDosbNJFqztByFVpEpl1rVGGYN2ruhiSqFUdFL7lAWotabr2khHtKbtO6bJMh4njocDh8MBZTRdt2IYxtySBMBazZiqZQgNFGNxcZInWqJEts6LnC26PhlCc2r+Hs9SbfPQWS7fP+xTkJUlOIsbJ/qdnpXCznRNz21XYtuaBSaEuZ5bbEJycKvpnwhzP5IeLuTWU5kunJz9eh2n44XkJiwjyi/FVKIkf1ZE43RnHbgTCv3JQ89thef+zrYf5ryHQC5fLc4XpfSZZyk6zSNrLOMyA5nO+1Ng5tVc7p/pAWf27Yec4+dsr4/N85yDfAmvR5/LsvCpA37Ja8/NZ/Yv2z5lr0vkX63e5HZaqZWX9x6jTCzAl+Q2kYPnonkQ0bfY42TQJKDMcSUlmtRWjISIqjGlDWRF/3JgeFpEsUHO7UdaiX07vSs1XJegWoWOfdiNWQhSodiNIJ8TCaYs2bZn5Cux/4RyT2z9Z/LvwzDg+5DtuLHS5hkakemjqt5R/aKW+59eruZnTnQB0SeK/2Bp7y+O0PiKktQSAvggSWSVrD+jUyeaPMWGGfXWWUu8xXLFyWsni1YK6z1/fTjyr9/dppL9MZDWusB+mHj9buTTj2LQaeqymAZeEIPqfTUMmqaJDkKx8ZHOmPfIFhcUXuxPKDqifDezlVUjVhoy2aZe4zqCcfVcQz1E9do4KbFVlgrAVWCPovJD5FVlviatFJAknMVGGPFkKcUs8S1E/WdGX/LsT+GsBE4zO8FpwIvAQ+iK8sLjCn+QvQhCQ1xyVMqoZ+lnqDZdYFCSf5aX957D4ZAC65PvJ1KJE/4mLSybpmFS41kcydWGCwGPbe+IdvWb21tu7u742c//jO12ZBwt0zhxHA6Mx4FpOGLHAe8sQiIbnSpQJpqotaLtYkn1YTxibyymbfjmm2+4e7in63uurp5wcXHB7c1NhH9j0E6llmGgVYfHM9mYda13G3btFe7Na5SF28nx3et3/P71XxPMBqe2bK5fsPnoU/qnO3bXz3n+9BkfffwRTz96xpPnT3n+/CnPLrc8vdhxfXlB17c4HNorsJbRDjhGpumG/cPAzdsbDvd7/BBQytCse0Y8fpjokg8g+JjC5lSDZqAzoB0cbx7AgWkUBzfQNoH1+oLnu59gnUMHVfgIgNYMXnGwjsl7JhfYD4HWO1pi66YmTBwH2K7umdSIsdHWSdMgvsOaB4RAClKPcqOu/GmKUzqUf5+dpXB6AzFTu+0Uq16xWSku1rBZK7reoLQhBB0rOIWGrutoTU4VTGc3tuYqvrhYkaPRJBuBw3nH5CYmOzFZhZoO2casidnobdvQ6AaUTufox8m1P9oxXiJ1yUqYZBieMzTI53K/KES1s7wW5M+9D+bCVO18Xb5veZ37Xpz1ORpZlyhhyXB+bAx5/t27d7x69Yo///M/5/LqKYfDyM37N9zc3PDw8ICdbI6EbpsG3ZickamUZtV1SC3/tu3QWrF6cg0BDscj9/f3MQJimjJhtVaIXmEcilIKOms4tZImByHdHxmTlDhOiK+YlxXXOkV0GUyKtNBa5h+FoRgQUHppA9jUm0yynuaGdVHOco3QJAdF5qUWBzEETxMC3f6Bg3tII0DTdZg2OW5EwE1Z0IGKcZwIXyErtQkscxgIfPKbZG5VBm42IFeMsu7nSHJ0BpC+9HKvL8OSWwDM3ib7WYTs+nsFqcSPz8J73OoUNZ8Ebetdzm765NM/IQRouoZxsnmuFb/lRCBU1VnLwmMSJOtzENJIS3oYyEJ8nCRxzqoI7WW5ulI2IveMjyTBP+FLIAqeiTTOGLmq9zhlgyvZ19l9WduBLDCViNui3AZyaJ4qMFjE31a9nykCYqWgKCUMqOqxW68v9VsjGbtlk/VSQZKeWEEMR7EiQNMYmralNYq+1aWffWUoqec6dx77ohYECC4KmoEi8M0NK2Ik8wnvqkz9hALx/rnioNJ/onNTEEVVKBIERRYIVOAM4kguSC9O1YSV+bRkMXpO/jKeiGOy/M5szvL6cprLWkMa7FSsnp+JpWQwP2sCA5eP3byUWPWsnMMz8kYxdgkS1k79Jc+bf5ad72kf1usVDw93ENap17grVWCqZ7OgUeFVGbfMo155CLGXjHWWvu/ZHw50qz4GWaW9V9UZCvWESXSdaPiUj30IaBNz0D/59DOeXF3x3XffcXN7wzhZjm/eShxDQpeStqzSeS5BIZquX7HeNqz6FduLHRcXF/T9Oq8/4tKCr6RlZrkl7e2ZXYzrCuX3vCkVXy6oGFgkCWQBTuhGppEZLwKzzQdmg1TGqLl8VNGsrL2prJTOhqxeWI5pxQ+X68r3h1yWNcOCxMsq3nFy1Qv8kdcp1Shcuv4mO2tq2J+86nRup+efCiZCI+awU2fHPj9mbXSUSgqIYUbFzMLVaoUdR7RSmNHggkXrmCENSSZGpSwYPcPVDI+aNpD4XsWTfO4rWFG6UGhspvkZAUVpL4uVwLoCyghPyQ5X6X+N1vVEFsCJTm2IPLFf9Wy3G9brFUbHYEs7WfYPh1hlKZcDj2WmJYvbOhsdbt4lJ3ipxCTZ7K4K0s3zCfNWFlCCNrVWOQvaaB1b1Wid+/sZo+n6nq5fcf3kCTE4yKWs/yOH45GHhz1t6sG2Wq15/uIFz58/5/7hgXdv33I4Hgkh8PDwwGG/Z71es724iAaxBFdvUmCBitHgkaxFh4LgsFbilDE5GC/KrSrDXQywYoD0Lp3dCh9JW2Sahuura16/fcPkHetVy7BVhHuDGi3GiHEoXjFoQaF9wE+Ww/1DdPAEEd11NDiqIm/Hec15VsbDSk9bXiXAo0ajx++X7+vf/5Bs7kedOtV8aj6qIFZo8f6Dz/3Q9ddf/UMaTUNIir6WMwzaK1rVsKbDhiOBCWXAoGlcQ2dadKPwjWfvG27YMLwJjN/eowOoi45u04KdGPd3HKYp7lfqbY0yMXahOrOyTh9GojPCRDyKlk6wYzRqoNA0GBwTI155puCwPtA0K8bDxG63ZXexpt90hLblmzfv+O79A7rdoLXmcLenNUfaS8uffvaEX/z8U8J/9S+ZhpFXr77jmy+/5buvvuXV77/lmy+/4t/+/htu3t2yfv05K/cVm6B4SsNL0/AswNX+hl3Xse1atqbh2fMVF8d7NmqDXrWMz664mxztbsuoFU7HEuZH3/PXXvONU/xuCoyD4ikbhnFgMB3tusc1Gnu8R5s1YdhnOUTrQKcbgjKgFZvLay6evmB39YT9wz3D4QE3HME6GqUxrYmgdBYXHMp5tNf0bYdTCkXMeG/WhtAlO8Y4Yg9HdrsLPnn5nOdPL/n2d7/my89/zes3r5imgc3mEqVMcgZPRF0tAJ62bWObNTcSvIXQMIQRG0Ya3dDrFa1p2F4Y2pUjhJgNrqXCjjZMqe9fUFWginKYVrNp1nSrlv7Y8XB3n3pUxjOlTdTRmiY6jWsa4ION/RCT7mdVVbEr0YBWGy6ahs1KqvE5Hh4eeP8+OhU26x1ApsnWWkLoGVILjVoWFr7hfRVc6WMAgKf8E6tRbXRTxN6zgeKw1koXrUOyGkMaQcNg4e5+4OllYNOtuXn/nvXVBt1EPi96CcTS/tKS6UPXkpbGd1YyfFaElw/OdZxzSSLyU3TDWqg6J3P+4KVKKOS5J8Lst3D2m5ne/yPeHeFT7AL585kpsIaPWvw8vZYtjJZ3qjy/0sqn6BhzHc7kFYSsj9XrKxUhHymBWr8/yTy1vaAOXPlDr2VywcyZfQbuywA0uXeZVCVX/jvZa713uIRjOnhccKmnuMdgmY4t1iV5XHtUqqkXz6tHuaJ4xmoc0baRdR8owY+qhk9A64a8BynjW6qeiCwWg3RioLUyIq95pmnATlaAMNNTmnRfxPwSOB5SxYJMFxcnI/gYoKSTnDXrWa7m/ZtPHBnyZyXnhvQ3ShFC5E1Kx0ScYRx4eNiz2e5odJsz99RSZkpsX4UYyKtpI+8iLM5POqOpemFaUIUoAqoqQCbNWaumnn52zhfcSy3gwryqrehkkmigst04ylMxbiHEJJxs24h4rFWsGOC8hWBnSy76WpTDhyHw5uD4ag9gMIxowAW4Oxj+D/+nNf/7XwUa0ZllMUbjguDBHKZ1kFPTNLRtl9cluqQ2OldBQRe8DCHkxK4ag+bvUbNv5a9zQTT1nOd6bvy8VEgqtiStdWo5ldr0JdonamrByVB0a3m396kEPsRknai/OT/31fxv/uuJoAM3BzJeazkHScdx3mN8yG0Bsx6+oNNyhrJTTnBW6VhFIn2vVfGJFV9XdPiHoFHKZ9vKGasPKuNAkEknuIS87yVoPNH7TCNV/ne43xMGT2sMPnWbDHicK3RdK5j2E65vQBmaVuOtx1qPdzANI+vNKlaLcA4d4snUCec0imAdx/2eL373JX/5T/5zxmnkeHxgOB45Ho74MIEJNK2hW/V0F0/ZOMV0fKCzE3aaGMeRITga3UJvMNaiQmAYDnz73Su+/e41H734lOvrl2y3z+ib71j1DReXFwzDgLubUF7TNganNNbEPtTix7rfXjHpidZrnj37iP/J/+xf8d/7Z/+MF9dPePH8CZdPLui3PSaMrFarvDZCSNWcHd46/HDDze3A3d0dIQTG5N+SfRO4NrrF9T71BA+sAowtqec5WOs53u/ZbTaxLZ7zTMHifOD9sEd1GjsNsWWp3nF1fcVgD7GqSFBZlnAhUq7BWkZrmaxjnAwhWGwY0day6hTbqWPVK7RREMS3Jnq9IwQXM9S8jwGtPvadd0rhjY58K2g0muCI+qUKy3j1bDOQj0tbvHjmVdvSd7DqJnar/y9xf9JjSbKsCWKfqJrZGdw9IjIip5s37/Sqq1hDN4rFXhSBXhEgwCUXBLggN/wN/Bn8H9ySQG+6uW0SRaAJAtXVrGq+qnqv3nBv3hxidj+TmakKFyKiKmrHPCLyvmrQEpHufo6ZmqqoqMwD4elth93NFlKu39pXAJEJXUfoQ4cA6fEmZyUjImPmWeUVqi2esraC1vUQzeg7RpcqXQghgzqAOiDTLLJAJmCxjseun+UYXzpO7KBO09QgiykUVtLQnvPPsyOA/h1L4MsifZY4rp5bXqaImMEjxohxHBG17KKV+zZn/1qkbYyx6YNlBGm73eLf/tt/i9PphGdPn2KGGNOHYcDxcEAgYKcHTjI4JVOkZJYnyVSxXrzMGefLBWmaMc0Tur5To1Xt8XKhsczTBDdZmwhkfdeVXtkUauRH18vnpW+XlRu3z4jKPEpEJahkRjMqEagG0SrYFFKfWfqxZivNWxVLL9Cb4FL5oEZ3mnADSN85ArbbPY5aEhwhAEEjTYhKCXaiWA5ocWY79lNGtfc55accajJrXP2u4lllPq3Bzhl2m/vLoF5eKMK4CbpWSIfbhxo8XCoc9pNNEeIqUFhkataoOovWvIwJIBtThRQV4qVfs4xRHcyNxKz7Q0VIKOOASu/dGqW6iL52u7A8W6aEXkV+6n40KjWhGPHJ7YP9TmocsiaWRFTK8hjuEknkdXbvsPX6iFky4Qy2h+z2iQAWx3Khc6akFmRjICdEYpSy/mo4NzpUGBVX4a+C3K1cy5vGGLUvTA1WEWHcBcpkKxXloVnPQGscUWFM77MsUdZzXY45ABGNDPfkfxkuC4FQyrU0Z6H9X4NnPgucyz2t06/ugQQPFGdNozzpmXWl/JbrBah10NnoV7rHFddvvq0fOUdQQZvrNdY9XWZr1LmWxwqdqcL5ksdV2JiiQmgd+1TORJ1DLp8brQWz9PhNCZvNBpfLKCUmWcpmVl4dKlzYzq3Np7Y2MPi3jiX5kVIGB6AfBpzOEtGKIPxPbqXiJKVStU3+qOet8iBQxc0MYLu/wW9/92dIKWEcR+k1M02yTpNFWAKWrOyYQbmLHfqhLziUlS/5iOUrO5GOdSW36FyvAyWw4BneiNQGNDTPLD6oqLx4httHWrxHeafN1Qd6XdH7hnBQ83nlo3VMZq4lRRf3gyx4qDnQjh6R899T810Z72de60/4Ud3uGN90X5dVep67nFf5dDEiURPsY4LF9fMOKRpcqcaHnBL6ONQzS4RpnnH35AmGrkM2oz0SYhcxTWIYTMw4HE8iD+mriKjFD1OQVd4zWlJx1ynofm7lc3fOC+5xgWf7Xfs3gYqMV4LEVDbPKSOxKGrTLFkX+/1eMyhvwHnG5TzicH8sWX7zNGOeJkyTBGRO04RpHjHPU+PUyFoNAzDZyhttyS9kcT2CUSZP+L9Dbe3TaQY5QsRGMzm3uy3ubp/g9maPlBJO5xMu54s4yo9HPNzfY7vbYr/b47e/+S0ulzN+evkSh4cH5Mw4HI94OB5xc3ODm9tb9H0HzBk5SJuTTOKQlrhM2deaycNAqrwBRMW5brKT9aynlJDgK3qh7BNn4Rk3ux3uhx4IUh4PtxmnA6OLsUScWc/GPElmJHWEy+GMSB1STGBSeaEp4Z9hSry/zLFlsF7rf3b1t34WtWJVcUr5Cj0Lunjl6P3Eq3UOtZnoZVzmol/9Xa9/8y//OzWyaQR9CAgwPVF0rQxgJgAhiXEEJpoGROoUTxjz8YLDq3f47vs/4tXLt0CKGMJGDFZEOJ2PoEmcC6SyrF9z+zs1577AgblUKSsCAwOcqVQ7KwHzOeP25ha3t7fYDBuklHE8HpE5o1PjXBdFtj8cjjicz9jtbrC/vcX+9hZ/9vd/h9/97rfgxMhTwuV4wZtXr/Djdz/ir//wCq9/eoP7n17j/R9f4t+9eo3/4fVrpMs9+HgCHS4AHfD1m5fYU8Ad9XgaBzzf7rAlwtAHDLsBm/0W282Ar+IJ//gffI7f//SXOF4eMM0ZiTrEzRY337xA2m2QxxnhcAEH7Y1J0lpg6AZse1kfuoC7uzs8ffYUtze3eP3yJzH+afB+38tejNOEGYQu9oiBgJwxzxM2+z2GDsB0QT4dELdbjOOI7XaHzWaQ5yG92+d5xvc/fI/7+weAqz0lxqDGUWnbBgB932GaJKvajPGn84jxMoGo9jbd9D12ux3m8yLASK/C8ey8QfDAxtzv96WtwjRNjZPOgu7NcdZ1nWTEWS90ArqgyRfOOG3PmjN+GIaidz08PGB/swWYsNvttMrfjPP5jElpjXeMp9l9ptk7l2kUZ3iSDKg5Ce7mnDEzSln6Im8Z7wRQHbC1HVe1Scg9x+MZp9MFt/sdLuPosutaWtDI9T/nam73tob2fC8d6lfDcKvrtPahn3+ZvFLkCveeZh78+Jw+hcR6G6T7FJK9eF0No4y9sA0Zb1zO035fs2s2n9k4i7kt56pU9YPvqDaVpZ7h599u/dp5/dC1tobruX76tXS6ra/d5BE3X+arZ+1yjdkKPxI4ZzGKO14vVYuUH6n+V5J0nE3I6+A5s5RqZQuk8zqDPBBoRNf1xSEHEGLcIecZaVa51NEF4w0WYKICDEqfRc6Yk1TFMB0WRX9kEKxdgyWMtY66CmsHqMZWw/XMqi3W2vSIbizyds4JcxqR+5oQF2jhGFd5R4KhYn1vqF/DYLuQsakZayWvrwrd8j37LxrMBpiLLVSWpVBzZpNislC4CwupcrNkpnMJplfxuVT1qq8T/UkCZAnTnHC6TG01QQICA/OU8ebdCdN0i83QOx3aL/OaiFk1OmbrBT2CQi2jbnYJ8QdUOyjInOOm5en+OFCJCYS9GW0BcuVNhFK5waoixhjreCrjsdJSs6kAQN/16DrRG4q9uPBHtc+qdTbD2wet6oKOmzPybA691My3+IeytgEoaFFpRj0E7XkwPuq0wus90PWs0laqvEe+rq0Bc6r2ejlbK7ytnGqYiFzGMl5TiUP9HABu9wF9f8TxeMTN7e21ndFNspRkZ0kOyXpvykkq+fqKqc26xd7DJPv36seXmC8T+q7Hzf4W++0N8Aw4HO4RQocQOsGBlNH1EZfTHvN4wXQ+43g6IFwuGHNCThCflMpLkQLylLDdbvD0s6d4+uwptrsdKCbNNA8YhgHn81mXVH140zQhhIDf/O5XeP3jazx79gX+6X/+z/G/+d//7/DNr3+N6f4Bl8sRl+mEN6/fYTwcir5ugRMWaOj5iyUAL+FhcplVL/Y2D1+9CUCRZWPoEEPEyNKGbRxHEIkdJ2oLwr7vkTBpYBFVepASkFXXhtDXfhgwTifMlzPGNOJ0ueB8uiAlCeaRNroFsxyuKi9E5YdWvbnRswu/VN50ZUpf592AhHhlCM5TjKDYg1x4l0m8TEDiGZeUEVxVX/H7iL+BUxL7RMqFr8ya9JDSjJRnMM/oQhSXO7OUoZ8FZkQdCFHX8Wny6c8qpW4Khu/J7f8J4KuAWcqVqtIhfabayxst7D5DpGWGut1jvOkxY4ldphxJ9nWN3GWuRu6C3AvjiO+pbg7ynCWa+p//839e1veP/rP/Gf78X52wG4/IOeN8OummzHg4nZCYMWwGbDcbjNOE0/GMnDNubm6w2WwxTSPSPOF4OoGZ8eLFC3z24kVRjEOMIqgEQfIQ1PgGoGRdUxDGpdJ2Jf9ymdNMDDWVAAPAshwOC+AKHGBOEOu5RBLJ3Ur1LI4GMEJKyPNUHbXa26Upoa9MzuZaBUUUDtNvNgihV6EjijFX381sjBUAJBCAC7Nz+2gCGFUGVJWMJbYoWyycyH1j9R9V2IYbp5EyGm5UHRGmeAoRd+qfboT/WRmsc8IVPseFKZbSpKYswD53cAlVCAFZKW07n3C/t8Aoz/AHMmlU4iO3Z94xZ3FKMIEfLf6JfNxIhPa/BfjrXBQCsD7NZUwY8suYmbXkGVCc3QSLUyqAh31DBXg2p7q3plzJWhlABquwI+dRzl7U87oZthj6mkEmhsVWqXw0N8nJyYTaS6+iZgayhnE5mJT9KL2LTOFB2YMiHKJ9RM6T+8wJa8VhUiEFoEaH+ZGu8Gg5P1CD2/aZKfXsop7rXIQ5muDSnLt2EWXNLRlR9rt8hJfzXcBlIVdS8xurIkFaWq+dk48+b8ugr4nbfuYyejZc1EXU3uWmvK2K7WVeNk+DXYWBKioaxLTb7TBNIw4PB9zd3VVjYEroYm0Pwkrng9IUhvDf4mwp/ISd0gtI4IbQoPP5UpUPI/UEEBttLlovKp45YW51vdrmIwQM2y0GqOyxvNP4lKOhYO1HRy5DxXjHo3KTCw6ytfI1PbEJs0OiQqevhqxjfdSw5PHCnrV32/NKFz8YXOWeoQYuDSAaMBg9Nc5FbjxazLsaSP3dRtNW3uXWvgyUWsf1xz6X71pFgBa/y3dGG8vZZfeMN/Yu56rfm0ghsoyGWyk/Y4v2Rr3d0zu/jGLcIULfSZbe4GRpEDBOE16+ei0OzNhBqndwKXmWCt4GUIjVkWhvK3haA14axPSBRXpWTG4p8s7i7BgUy/fw+FZptfGFYlziiraBgpTlPp8BMPb7Pb744nPs93vM84zxMuL1q5dI84xpkn+X81mc4KMolfM8aRlmiXxmOBlzJXtd2q/ovF1FibrHwJI7F/nCtp6qsmrYZXAuQYeBcDhIEGrXRfzU/YCu63Fzs8eTJ0/x+YsXSCnh4eEBh8MDpmnE+XTCMAzYbrf49pe/xDhOePlKKlERgMPDAafTGfv9Hje3N5KhHQCwRKszS+uKGKMEBjpDa0SU9YegrZFauc1XzgIWzvEgskbOCcOwwZP9Le6PDziPF+yf3eHlH19it9khTzMIhGSyrgbgZiJsb28xpneYcwA6QtOahYNmTJFHr0aPbPRLtNca3Vw3XlHz+5rc2zoarhnBmiPIG2eWz5nOlVPS6lufnpW+dt3/+F5xGyaVqrFBzqvJPLMFcJbjHkCIiKFH5gkpTTifTzg8PODd/RHH04Q0TejIjAvAJU1CVmLVscVw1sLMnwe/bnMABGawVVFCS+ctYMZk6du7W+y2O4AI4zTjdL7oeNreQMukEokTZB4vOD9k5HlE1w2lotkwDHh6c4enX9zhF7/+Cn9/nqUX+/GC8/0Jx7cHPLy5x/27d3j//j3ev3+P+/t7pLcHPDw84NX798iHA7ppRD4+IOQjNu8Dhi5iFwOepwtehwm/P51wyUDoBsz9BvvPPkO6fYIjMtAB3Y6RIhUyG0Gl310mbVHw9Cmef/YZttstjodjk6k8l/LhwDBstNSynO0IMThvhgGBGfPpjGk4oO+foO96xL5HShNev36Np3d3mKcZh/sHjOMoemGsFftMpjEc7vtey3NmbV3ASGlCzpLpIy0kCDf7HTb9BklpuEeA1hDtzpzKoo1zHJLBbVk5FuSPxXkipa2s+l4gWYNVqvH3BmffGYYBt7e3kq10uWC/uy3fJ8WZxNzIwDln5FSziKzyyGYeMGtyw5wT5iTPTXNWQ50FKYtxL6XsMN/kKCupymWuFsD1cDjg/njC55+/wJwZac6IGuDCWkbUYPwhSeixq5FXFzavD9HENXoodrSfOYFPmeCVnvjhefzHCDqydzzmAOYFLn9IXv8YT1qTBx8fj1XnqrZQf/+qjP+BuRmv+pQ5+2fW5/9p712D65pj2z43OlR/1vt5AQ99qtwHIzuNbmZyfrHmNPZdgYm8w4WsqB1A9NEYOwBzCSAHQXqP690ia4mcxBxVj6B6L0mCQ12yyq0pw+wWZmK1upIhSoZqYMl2ra2WNKGJqhy+tmdXn+n//e0MKm13is4SCFayvGQho4i2qm6QZtFfvbjQNbaH3AyK3U9tgSqIrkjUCznDfV/lDW958boVAcjlI7Y3FBrn11+d8AZXyfWQfY6hyqoie12fnQxGpIDEGf+X+yP+1bsDwCanSNAqKS1/++aMcZzAe646uLcDLJai04b1IGdmzCkJ5mlrRAJrzoi0arR2ZibjEyD6gKOtYFZ/AdWtWNgIGi2YzXZTbZ/msF9imrWdtHnEzvssRFetLMjb57jAuQY3Zz1TrIHhWlb9iv89wg3dnIUs1HUYzOu9i79tZD1n1SYvAzftAmBhMF5nJOH1qk/7kZuZ2tTZfWM4LCe06J7Z6+IQfrDZAOM44lZxiXO+3hOSdjwMDTTQM2z/+eoKnvZCaS1FoZOh6/DjDz9iGmfc7G6w2+wQQwciwk8vf9DqxlBbQwZpNbXL6QgAGLQdDyexmdtehhAwjRe8fvMSv8q/w+3tLV68eIHNfoc0HUEQOa44ndXOIZU/qPgZv/7mS1zOZ+xuNxg2Ea/f/Ihu02FgxuHhHU7jEQkJNDNysGB2aU9UyvwrvbUxDX7GB5e8i5Rwex7t77Pq2WILUQmQk/pEtQrenLStkcyJtYCT7WNEBFNGJNYqHJJNPacLxkn6s5/OJxxOZ0zjDM5qs3WIEKpVSLgAtWso/iKHlln1t+tTjoIrq5/pPGG8SltPZw4oATos2fNIoicaXyg6SQhKl9THl40nSyupnLVVJicwsvq3OgmgIW13WSqASJD3I8u4un6WY3zp/H7se6A6s/u+L5+vCWR+TDsgPophKUjJP2qeXY7ro43tpxeCTJn3imEh+M7IsSy1bvdZj3EKAU9fvMDNs69w//pvtVTiAbvNFuMkzm5AiOp+v8d8POJ8PuH58xf48ssvMQwbTNOE73/8HlNKeP78Ob76xTe4u7tTBFHFDwQE6V2TkpU1XsLcPlCaavwMXAU45brGMKsTDJUB63ciRJgQgzK2ZZaWqEqgtHZiAEMISCEumFrNFhd+lAqzY4b+7vY4Z8SuRzcMGMcJsRsABM1upXrAlY9Vw/3ikNqYtnY74MwtHy0CgToWSz8aWXRhqKj32zvdR6s8lu3lbGO1eNbAF4BFINpOmaCkJwIUQxkHbm0VDxzxI2PUCzwx4ZBq/7PmNJMTYG0g+F/NmNVmzlexlsof7J6psOFy5/V1/TknxyHK/qnAVwINuBiEg5tMJdwZHmXtDPixSgQmVfjB8I20LI+2I7CshJLRHTs1MKWycBEccxNpRZCeoIAY+opjQXGyoqVzcxZloy1/ZhJtI8A6vPVCLQqs3EUE1pLu60qtOqvtPcWZYEOvKzE2D1MqZQoVCHU9NoT73f2yrmdf44yfu0WzNjTOD6R4vTzPbnJlTLa5FpByg082V0GjNQGhjmcfcPkCFYd1YvVctPNqBfL2eRuzgUqoz9VTX9d7OZ+ld23OOJ/PmNOMmKIqwVyFE4NTysiRPItBac+gc6MyTytOJkaCvh+QtIdNyi1dLbQE1eG8buTyeFYDe7icmXqqs/uMjUHATpOdF8FL4ydlfLJ3wb3PfjfQt2fqSpnxipc9uVySnVnbnyWO2mWwcHtcUfEaf4nXjZtuQHFu6D5l9kaG9r1Xxi/3fl58DrRzu37r9XeF/vqf5fXVIXa9lvZzG8fw73pmi7+L/GDzqDxZbnPVjfwobopGv6obfklXl6+l5mN70tONEAjTNGGPnTvPEnwTopQ2nFQzIFPMSBS6lFkVZgJpycfmn56HNbl9yRM8vWyd4ljwU7Rwc7ymyg2WIVedm5yzOoIv6PsOX37xBZ48fYKcMy7nM968fqPO71Ey+cZRHBrnC6Z5Ekf5PNW+gTrfDC0zqjTU9yKssllroGUs6M1VJQ4s4KW7wh5lzWEIdUarYU2zLUe9McaIw8M93rx+hc2wwf72Dp999hx3d08wjhecTieM44TLRcpW3tzc4Ouvv8bzzz7D9z/8UAJn7+/vcRkvuL29xW67FbhqFnEgwpwSRKc0R1Slj6SYZwZA27lAtZpNNQaoRM1SkaALhDxPuNvvcTgcME0jbu7uMO0zHqaM7bbHPM2wRwnS928KGUNgjD1hghgdAhgdCMhA4IzAkGyBzGBqqyYVI3CovXiXV8PL0VZeeuwy489yn70e+B/rYgbOl4v2uP/Tr/E8uww6wFNWz2dyhvTiK5QkgEKPFBk5T0hqTBnThEwM6gOIZqQ0SuBuZiQEhG5osuiqwa9C+4qeFB1dg6ItiLrICo5XEmABrTFG3NzcoB96oRGznIWlQ5VJMq8DicOApxlTPiF1I6L27b6oc3yz2SIOhGe3W8RwU5xK05QxXRLO5xGH4xkPhyMeHk44v5Jggffv3uLw/j3G4xEPb99iOj0AlwlpnHA/jhjHI94e3+E4jYghY3+7x+2Lp8idtg+4iGGK+67Q0EBiCIxBnSZK158+fYqnT5+i63tZL6AOVmkTgVD7ihJLC4UYSdvB3GCzvUHfbxFCByLJIks5g1LCnDLO5wseDg84Hh7w8HCPNE2IWmGuKcvs9jEG65MrE09pRkpyti0wv4sBN7f7K0edxwOPH+bUXrLKvu9Lb3UikiwaLeNryqPHPakYF5StKW44Ocm/02hcjBGb7Rb7/R6n0wl5mxBJK+/FiCEE4R+aGZ5d+fSkcrE5y/s0i8Na751TwjxnjNrWI6mNJmUxrgaa1XhXp5gLrEyKIGgNYhxOJzwcT5g1yPlyHtH32ytaXsUZ+Tx8Ir3ytqPl5fdsuX8fH9f2CyiE6GP34xpvPuWZ5Vz/x7g+5vz2c/DPfOpV5P8VOCxllMcl6/U5Lcdas6GuzfkxmC7LBT921h+D19o7lnOx35dOce/Iap5hbpWR8gwAOJudCX9eiAUArVIErYaS88Im4IYWp1IAc0DIocgo1RUm91DQjOIiBGkqRcpADMW+VOGglTTNwZhlnK4DYhcAUocCATCHvMEFtfc1U7g6cde4iVaW1w+N9pefAIgDGEmzjbWyKIktyPRlZohesoCX0SPLLi2KjsHIaLZ+19ot/U8306KiU6kOUlQMmHxfYS4EMUg1EnAzWtUFquRUdp0kaFNEE60/UPSJXIKXlhfp2sZpxl8fz3h3mgFIwGeG0yUT43DUNqm2JP1nyWHFHOHHdnCU6TAyMRBYey7Lmsseqp09s7Ua8XCs+ycaY51HsRaZnV7Xb2Nxec7tt/u96OymcxIhUBR5LUaw18kaCKoO52hAzlnsTqlWQs05laz1JaVpTQleR23fZfNEoa1mg1vQsEIL60IN9o+xhcapSGpDJ2qrJq0w4OJ/KjNykwWK/n7FBxQnslZNLOd4dT5AF23vc4E1SGQtk28AQqCs7clauZ0Coes7vHv7FpfTCU+f3KHvhlLdePuww263wzjeSpsLJMTYISr65pQwjReESwAlglT7VlmOAvI84fBwj0DA3ZM7fPHlFxg2G1x4lASYYcAwDLhcLpKAyjVxr+AMAQhCHcfpjPfv3+D2yS0SCJfzEdN0BgdGxx0YQv8jUanqGjQgE/OMHEI9X3ict9rOeH/i0tbi2+lQIPAs+lFQOTelJO02mBApKm2vCBACIZrfMwtO5fmCeR7Lv3GacBlHzLP5sVD2TxdQ8L7SNsEN31/cox+X5/DRq/JbFGe66e8xRJSWXJAAjcRAZuNrM0wNMQc5szwTKQDo9OzU5Fg7Uma31QYf4EDFpWA8mtQ+8qky2ic7xn3WtHcSG0DsO+Ba6DXg+M88MK1kl41rvaq9M7ve3z7rD8dyTJsrMxAjNfezIqMZhLxBxAtpOecmg9070jMBnDM++/KXeP/qr5GsvAehrKHrutKT5Xy+YOgH/OLrr9F1vY6TMWw2+E/+/j/Ai88/L4oeWTSYKYRWhkC9fiFq719lvMu+RnYuzPjHKlhYL2OCZDcZ063GIHV0WCR/c1Aeiaj1iUhECH2PnIE5zaAUpO4/M2rIh/RoTEk+J0BrOjOQhelTiHj69DOknLDZbjGlBMoBIUqftoJb9s6i3HOZC7u9rMx/gUQr+Lp2LeVqgweoiC7tsMq0CFZ+RyNymLTHCTWCpeiTJibV6Jn6nfwv20EnKncCNVuErKeKfkOBJBJwSQ9WGGg1iPqFm4NwDSCNNFIEjsawuYCZrcO/qWX51wopFeLuRJgMV7UtIwTW1gCSfScGpIi+79GFiBik73EtA2UCsaMvzRpbCdCECBNgr5S1PFXB0q3OGFDp6cpVVCOfeU3kMghNfnJrtvNThic9M6iwdwsoPejRXrInPsvZ1IMWx4v8RoCVqUcRllHwAvY3Ku1sYWDGZ3Iy4VJctbm1cqPBoCozDhaPXP7t3BjIjVcBuHreS77QnmaGZ1z16uwmuATYikK3pDXm/C195Yz+QvdLhWmfdb7s7VJoNTRoAXD7qbRcmgsVGu/PFsAYpxk3+z1iiJjGEZfTWaMaTThWnFChTSKSa6CY9ApvsYvdZIs5R8+IGAxTAZvBwoQoclUusEKqWrja2TNyWQ0a6qov54PZbVI5L1RgXldADd7JJ5WPmGLC/jMDp4dCK5ygHGT7uyiFj+OIzbXQUvcqf5fnZ46SL+jANZ57/LfAq/L82lx5Mdfl/e7Qkv/M5lNupfbZMo12rs19zGVKy3WQn6tfKTn+WebfvPWa8hRh/HqRJi/5EqFlTCeQ21w8nlQZq45rpLuipfCfXlvxlFcTipyWdeyCE8xaUgpISetSuNQttoxRjxkmR1Mr17VnuM7bgRamTJXJ8RKKDhtt/4jKOsRZnHA6HXG5XLDb7vDtr77FfrfDeLng3dt3JWv6fD7jcrmIQ3waMY3Sm4yRtfKTltKFZbK0NKhZG1c8qkafWmaPQGiRoc7fD1rOaJG5rGSuXNKXUB4NMeoeE6zfOxEks32eMF6AUzji3f0DXr58id12h2fPnuLps2cIFKS3+HjAPM84HA7Y7/f49lff4nA44KefXuJ0Ogl8pgnjzQ32O2nbRJnAmpURlPYVGYdZ5cCq+Juhgyggcy03LplR4pyTkpqysMSMDkDXRdxsd3j38A4pZ3z+i2f4evNLbBGQZskal/LMUg2AQIh9jyd3WyAnEAPT+YzL/QF5vEjrJNb+6IEKG84pIafkdKAWRz90VTyu/6pQIftuepY3Glzx64oVDU0E6nlad6Q7HqQyyPt373C5XD469w9d1Pca4lzPsu2lZaYwGJQJlJL0CyQAFIEQQJHRUUBPPXpmDAkYzsDNFJHnGfM4YjxNuJwykAKYOhTzv+k5VGW6Nae4rb84xhe6R7URyDoMfptNj5ubG3Rdh5QzpnHG+TKBwlBbe2mVLCJCiB06BoIaUAMFdBE4jxeMk7Qe67peWpmFHn3fo9906Dc94tBj/2yLp8MeMWqvWRD6E2NKCed5xnmacbxMeH9/xPH+hOP7Iw73BzzcP+DhcMTt93/A23/x3yCd7/H0xQ2+/Hu/wN/87V+DX79HNyakwJg7o0FV74idGHgYku3y7Nkz3N09QSBxCnNmpGku9gOwVupD1WeGYYMQI3ZPn2N3+xybmyfY7G+xu/sMNzc30vvaBaWfTye8ev0S7969w5yk8kOMsbaeQQ1cIj2G4ATjxLM6xgFp8daFiKGLuLvdwXpvGz7IaGg+88ENVqmv2GIoYNhsCv0JMZZsIKg+58uJ13MHWBnW4jQmz/HcFQL6GPHkyRPNTL8IvnR9se0Qz6I7ZyATimM8BkKKGTkFpJzRZS3laBVbNABhmGbMs2b/ZMY4SzboNEvWpcFJWp9U+NiJMe59vow4nE64jDNi7HA8HLC/uUEX16steqeO+6Lhz/9jOY8BI5eeJj+yB1fP8fXfxo6dbHTt4LumOX/K+lr7pbx0+b5PcY6vjfuhz3/ueFXPRsX7Oipa+efa8e3fuXREP8ZX155fcwosv/vQXqzZi5fPervrY9+VeageYxBgiM01c2zVMKBWtSq6hSBazlIRw2jPnCQosNqTq3OXQpDeqyGAoU4EJz+GYPqA8MkQxLHNAOaUwCkhUNXbU7oAoKYNYhEiiRA5ghBBJP10Y2TM8+RanlVbfMURalS4CnudVtFhqpLT2pnRPkwCG+FbofgA7OtlKfXS8rDoU845jlYHqVSCio7gB1/T0WwMv7f1f3XtErkaJEFAdaYrrY/ULup0VQFRq3MKvtVKIi1221oCEAiny4j3hxmnSR3sLEltGVkcLQxME2OcZ0c3ZXNY+7KvaKeu4qQ8wwytiJVLdVdbgayBYK0WJbaNyt6Lc5tx9SZTShWXyn28+GlbQRbkoFtQsserw8qq3sauk3kFv2fVeZfLma/JdLU1qDlp7YxUOWUBpY/T2LLfRkdUv7GvbT+c7NLescTL9fdUqtzONaku4PUMIk3EdM8Wfb+uTPX2xXp1DhJULrqF0a6l34xAWoa7Bh5B6XUM0jY4pwSrZmR0JoRKt62U+fHhHg8P7/Dlly8QI2OaRR9NaQSQETvCsNng7ukTeT7NyGnGPI24nPvqfKYsrkznkJ6nCV0IeHJ3i6+++gLd0GOeB5SWX2RVHSSj2/x3tu7Xb97idL6g7844nk5InDAMPdLpjACgDwGzeVGYS9BPKVFO7X775FhfFczkedm7+r3RS/+9b1EZtAUFM5DSXGhmStrvPUtgKrLZiYVGhyBVohIF7a3N2g9+AqdJglfnGfMkLYDqQVP5HvVsWHBJkbMCpKR8qNVtAWtNYjSq5d0fvdiCLDoJjqGIgICMKsuLU1zbkyDJSdPzKTaVTuioBkJLFaaktKgGbgi+QyuQqt27tX7peXi8uvjy+mTHeO1JFcuhK8qNKxNnZdb9MwVWABLMyC5KFsAlYi7GqOU3pDyW+X2acp3BldACwEEiBPwlIoYIJVkZ75yr4pRSluDlQEha9ipDMiNyTlV+ICkXwwTMOSN2UZBVy3kFMG72N/ib4xEvf3qJaZTSjqfTGdM4gUBI84z9dotpmjBPM77+xdf47MULyaTXrI5v6VdinAoR02wl1HQjsxzerEgQKILZnB56iMkhbEMMocJjq6zYX43zlYwhkMpm7juoIF2lk7KjbHsE06jtWUYfInIkhCTZg5kDWB0kmQMCRc2alsxaE0yEHhCG3S1kWMKUAKKMwAxgljnUjYJlMNr7zclfqRw3SpwxPftE/lxCCuXeUAxDZTj4W4miE0DrcwDQqfRQ3rkU8myOob6fnMDro8FLIH3ZmAKC5S/uWrJzxR/2hK9BHZQy0KVEuY1OKpSh4p3ijcAxFHJc0MuUJqA4/aRNNiOSOvjssKtAZe+LgdB1XBiO9QsOIYjRq+sRxe5X9j0UAsitwL1Ueh1+NIpbEfFcpkpxslUnHivtAGr5UYkQJY0EruNxrkrFVUlbW3izqVzvUUmT/d+NI8R9XjbS9mTRe7xkqevMlEFWoXJZ1YMAqmMYLajs0p+x5fW4SNm+gur6mve4dzEWTt46F/ur+bYs8bpKiZv5OqNPub13oWnbfNprccauFrNYp62p3N/i53LUctTZz95PkQppYfe5je2VG2YGxYBhM2CeRqRJe/PO6nTKvoKEOpWoltBfBhssV2/KEZhLOZ00i5PDyrYxt2fOU636yTU8jE+RnRW9xWhkPbOuV5XCGo4n1DNez8KVYuX4nwP0YqLmAFwEhVhGPYw8Nszial2r65TJlJmGK0Odn7+H14I5rTxhsG/usj0pa4MK8e0+rBpkPfypyhjNXpW56Z3LTV+z6jx2NfuwoDNlf/3gfg4VVpWXLs6mq4Zi7tArVuteXZRX5a6s5co8jvp32kUArIfqOE1lDHtLzSRwcyfCXBwSBjMt42WvXIBwGUhQ5+HOqu5/dryGGY/shzu7Ji8azoRQAmlyTjgc7jGOI+5u7/CLr3+Bvu8xXi54/eo1ziftuX0Rh/g4nnEZJRJashRrxkChYZ5CuE2x35fn17BcdrHlZcvfll82K2ePVY7vOFqTE2t5QxLFFdU4YrJRnjMwz0jTiMvpgPv3b/HD93/E7c0tXnz+OXY3NzidLzhcLhinCcPphJubG/z617/G4XDAq1cvcRmlDcY4Tnjy5A593yHPSQy0QRw8FviamREQJIkm1V6EpHS+yFskAcQWPitdxxladw85EGZm7G92eH//HvOUsL+7xd++foPfPvsG58sInmbM4wWcM/quAwIwXmZ0+x3Cs6fY7++wow49Ii7v3+P993/E5e1rdIGA8QSexHnex4jIhpsSHJJYylGb5GNnw8uLgMrbuiEmBdlRsTvFuRpaQ4HhEVB1znL+bMur4dDa9CwRxR/3PnTomXH/9h3yZcTf5frmH/4O2+0O2+0GfdcDCJjmC06nA8bxgpSkFyjlGT0zOhLTRgJj4owUGDe7Djf7AduB0cVJsjr6gEjA+XDB29cP+MPfvsNf/IcHfP/DqcDKG9o+ZFxYc8y039e+sV503O12uL25wWar5RIRMU4zaNNLwBuV46wOjYxMAWx99EiCOrqQwIGRtFLTdBoxhxPe3c+4XBLGMYPiBv2wK8GyfSQMfYdhF4sxt+sjhgB89XmH/tvnCPELIBIQI7r+C0yXA/6r//MT/Ov/1/8Tp+NbPHl+g/O/P+CSJqQhIgdGxoxIAQHSBqPrxEhsLWBubm7x/PkL3NzscTkJ/TtfLhgvFxADwzAAELtIFwJ2+x02uz36zR79ZoevvvktPvvia8TNHpvtDb746mv803/8D3B/POB8PuN0PuJ8OSNEwu9//3u8e/eutLSzPUqckfOMrBkb8p1krEvGYkBGxpwmAOoY7yOGTcR+v0Map+tKVIYHDncACE+gyiczS6WPQIRu6LGLAd3Q43w8lTEoBMS+Q5clC7tmrwrLM6e5LwVaOGWxj8gcdjc3eP78Od68eSMlSLcDuq7HNCaELLpbUtGNIDairJnlmQghS7l0AIjm6M4ZU0rou4iUBK4pJVxGScwY56h9ynPh2ZadVVgrAzkGdewB53HC++MDvvzsKQ7393j27DN0WzMOVhhXGwb7Ra+fP73VnBn1s0fkxE80IC5lGpOUvK3I62kfNKw6+vqYU/rDn7U6w9oS1p0nyiWW9oGVd/1cB/eH5kv48BqZWZNkqJmPGdlNrv6UuXjH9dI5/jE4f3SOi39ruPMhZ/uaU7ycZzYW7J53/NpYMBEhzRnMVglH8DynpFnh1V7ibdXMrPYkAmXrjdziQSvrVscHWCr0iFBX+45L+dYgVTy0VG7KFhxeS0FL7+VQ5VQW+7PpDxnS9zwHKcU+9BHociklLPTR2XhUdilZtboXoju2To8CB+OrKlczE6bzGcysLdUkOGgzbJCSZDoHza5sL5KywIzyHir6idECoBhJiywRylf6QdF3Hba411DZdLMJrZ0jClGzy3PR/xmoNMHhXJ2crJ9hzigueJI1ucucvB4/SOnq/XHE8SIJMkKrE2AJbSTiAzFjmqSKCGcCBwaphsKuFWKzT6aTuZaomTOIXUtJkGZpioRr7UWklD8VOrwE59KesXSG+0QgA5PfG0bN1hW7P8CJS5DtMAzFbmEtMHNxclsAmgbxpeqQzTlVPpmzVgMrUF/gh1bI0gPgZfklKTKeazovVHcQeYKBoDobFvwV9YwWp3pj12hpFKHSbdmKBT3l5tFigzB921quVvwyzlhnVHRzZpwu0qJXChJd+ymIgC4GnLUX9zSbTV7oX5qlWlSMqPvv4aa0ZLPZ4P7hNV7++Ad8/eVnyGmHl69f4dWrVzidTjifLhinGXOa1dk+gQIhdh36zQab3U1JhGVYpWCU1l8BjPFywjyN2GpFtBiDtB/QigNnbal2PktCj/kkY4y4nGecjhO6cMHlfEFARJ4ZeZL+1B165DyXQEPjVYa/PrnX+zhLMIF+V9tLBUzabseunHNT9t1aOUuZ9E6DMRnjOGK3q9VYhB9JiyTROSPAQqcjdTY4cszoYkRCwnQJAM/Is9hxp2nGOGbkKSEiSNdjZ89d9XBxrWblncc+iEYPfnu+POlYyFMhZ0SWdh9S3UvsCgHCG5VpC24gKhJISfTMWVuKZiB0mBmwGCBSYpo4i2O9ZNYH9CjWXz0fOn8NyLE2IJ9yfbJjfJomURi1T7jPnk4luiSUDGtfpq4gF5nCJKKzEchSDoEzpOxbJfgArqhbcpEba4p4UYYapUkz3dVolR2iF+KuGdjeEFDGJ4FBp2XI5nlGnmf8k//8H2PTdfjDX/y/8Vf/4T8IUvWDZlwwtpsBsetwOp3Q9R2ev3iOYdMjdr06CgicEwICZo0SMeceEEBkpWMUkXR+2bgtGVFd2zVC6eFBlQgUZYYXCkBRYisBLv8ntyWFyXol61opIVBdI6uAmCzrFoD2yyTKEl2npYK6rgdbgwTNEhCk5iL8gTVTyx3kMisnCAgB8wCqAq4pzqaI2V0UnLBGDRRUrtOxmMt7hOmXh9w7a1Y+GqfkQvizMQkN3A33zDjfulTZg7x87lQGVIDV93hFtcBled5UiiyGfqcILffZPjdyWridH7esQ//WaPwuAJ2VPhw2iF1Ap6V3YgyS5Y0sZTBKKb4F/ro+LnX61mfFMmkqfFrB1mDGTn5vlV9hgPUAcBkvFgHSHEgZ0v8isAi9rMJl6XmqeE4gV7S17piCCeZwNqFqcbzASPAYxFxurn/73ub2HXHB2wIXo6Wo76rosECwj3zcwFX3yguRDa22ya/5rsu8FSjK8hCondsK/i8GuZpYcesxry+jTFjeW+iAG2vV3b4KN/ch+8+FMiznd6XgrayLy17WPSzCvT3n1+aOLEMdl0TY7fd4uL/H+XzGsNtVBccEkIZumlQko3DZF/9OO3F1vVmVyZQzesumRIvMS+OM7fbatRTALPrwuk1A/UllkjZfvpqDp4u0MkyBwIL2e/pWRiykpDqhr9bREuXV9bKbVyOQVtVoefdHLlNQHZ9cu2vx+dX+uDHW31LfU5+1Z655J1DhutiV63Ht29UbPT1YnhwT7OtPDflo7i+092oIamhwoc9OFK/BALhGnOWvVuIus2ajVDkTfhy3NLuyfxfJGGsrri91EoXRjMV5W57lK7qpz3rZwWi6oUKMUfFU2pYcDwccT0fsb27wZ7/7HWLX4fhwwP27dzgej5K9d7lg1v7h4zQip0kNiHMpjV4MwWX+C9g2dLXiiBjOrsG5dhoXO18UsMevCu3mVBZNXzGCPK54Q0cA5xmZxXg7TxNOxxPevHmD/X6PF59/gZu7W1zGEceDOD53+z02mw1++ctf4nw+49379zieTnh/f4/9boftbquyhlfghS5nZIQsgUkMraIVAkBZqorqWQ1Bs59AIq+yGOdBKBJV1w/Y7/fgNCN0Hd4+/C3++1f3iCkjMtAxYT8MggeR0G8HPLwfkfmIJ3TB0O/w2bOv8eUv/lN885/8I/zx3/05Hn76AXj/Fl0+g9ME5FmdaHABwAHSqsbB2e3g1c7ocfLOIMtyYuaSHZAXTxNwZQQBavBjM7ibwRXvJonyR8pIlxHz39Ex/j//J/9F0T/BhHmecL6cMI4X5DxDaGxChxN2ISHyjJQmXOYRh/mCkTKePrnFi8+eYL/t0HfAZtODwgzKE+bxgnfvDvjrL18j4ve4XL7H+eEEdoGCrbFwyXO5wOHa8VSfz9n2hIp+vtlssN/vMPQ9mIBJexVySshdBjgCkL3oQkToIpgCsoklBPREmAEkIsCqcZFU5qLEAGYQZnREGMBAYvA44ZRGHNOM7uZZyUpKSdrMIBO62KMYdQKQ6IJf/u5bPH+yQd8xfnj7Gu9e3yJSAHUdEhEoAhvqQHomLBs6dB0CgNgN+OLzL/DVV19is9ng++/+iHdv3+J4OIhNhEiChhVx95stNts9dvtb3Dz5DM+//Abf/ObPcPfiS8Rui9hv8PTJZ/j2228RQsC7+3d4/eY13rx5g4eH9/jppx/UKd4jxq70q2XWPtqaPb7fbjCOo2ZVdxiGLQIxpumClIBIUVpB7HfYbQekaV7F1WvnUtsaj8r66jMxRjHQUcA4jpLRrmPZfb71Vy6iREsHGDUDW9RyMbRFinjy7FmpZvH+/Xvc3t6i6zrkHEEcSu91qzhoKRCG9aRVAb3Dv9P5RAiNiA6vu65Tx7hmHTLK72KDYnASHWmigHGecb6c8ebNG/zi8+eYRuELMXbo+75wG2+X+v/vRQ3BrVTBycVmI/nISOx4qceTT79awavozf6Oj8iuf9frQ3bJT31v8xyrvmLGaqffr8npq2MsLj/W2jl97P7luEun9sfe/ZgzvKzJ9Q9u7EZ58Q++faYF+EoLCdYKbxbgafOvAb/iYBTBotqxY2et8Fb2Tf+fmUupdAkupOK0NEuyhkSWApggUscNkCmBoNmEoVc7o/FBK+mu1UJyAueMOY9g4x+WpY7q1Bb7eax7RFRgaLb2ymtjkan8TktpZStXLc5kQCp+BoXlfrtDGKXdjdjVAy7nkx9F36NnkF1Sis6rEHEyqezTrkbXYUBa2tkiCCKZVj2zrI4IteYXo7HaNDqDTU9KJzPX+ZYgBHApCVznVeXDNCf8n354jZ9OFzCkNUeAVXQPgjtgdJhroG+Q3XnECtXAtrW/ivWQ2VV/IkLIARTEER4QwMG17eCq+pr+axoPs/3kkqRYVGmvPhf12uzggBmdTM8ZR3GwDptBssVDKMFkNn+BqezVnOaCd9UZXh3ibBm3olhWWX4R5GHnB6ikg9bwzOuuZn/wtlAlDd6HoJobGFzn5uwbkvXbysiyH+q2U3pWEtzMZlc2pOITw9NJnb8GtTRSt+K6bc/h4UFa/HbqHmTLTq80cLPp8P7tCZsne8TcIV1sH1pe4O09RkeJhc70mwGnnw74f/zf/xv8+MMf8eTJrbYBuyAz43Q8iuyeGfMsezmPUkI954x+6LG/vcV2K/qhBRnMeUbXdXjz5hX+1X/3L/HZ3/5e2gC9e4+Xr35ER4yo/rzL5YIA0VUliDNrsFKUQItkVfwCHh4ecDwe8dluj+lyxiUn1NBquRq9TgMlanJA3VPrFQ7UBGDzG/rzycwlu52ZcdKy7xK4ENB1QkPGUUqgG83KiaUMeh+ET6jPL7jgISJZZ4gBKY54ACTIfpwwjzPyxECS+QUkwbFY3eFEkH7iJbBOcIlCQOhiDfoq/cbXLbHGW+z35RXAGGKHbegwUEQElYxuQLkFEaLaGIiisnpSHd+SDRJyJiTSpyghZ0lulnty81ZZH5Ah/evBqZyVT2mxZtfPyhj30blARahlFLIZ2EtfOAMmzPnd9q0pJVqdk9y+8z/t8otbi3hsMgDc/IEaJWjj+kiQ5bu8gOsjS+p9hMtlxLe/+jU+e/41+mFAnhOGYcA0SaTMZRzRDQOICP3Qa7a7II0dtnmyfiAAeNY+xoJEphgXZk0akQhjkFwEjXpjWQAqufUCsfsa0HIZ+pn7f4GJH04PCrl9MiORNboXQd6WYL1oUaJ7mBkzs/S0zRnJGDLn2qOHq3JphtYi+2l5j6DGu8IsjVG59QttqYYxb5y3Z3gBEBMkTYBsMnz9wTK8EKlAwNC8x+OTE84dZBs0papW2rtKP1EYUww651qeQ/l6Ncyq4FPYKLk9L+/0ApmN74Qo21dTzMocnc6SJVqnykgaWNKMq+XwSMqVdF2HYTNgMwwY+h6dZnsHJ+hUmOjYJgznhQOCUMqAVomvQLsIU82aZHNUAPHlfyyAgdxGCnwfoz9FkUKlJWRsVyOX2SkczIxMctZyZhDXvjp2vtlgznVPvGhXaJ/ts4OZlb3JxVFSlcPltaSbBXca+Lv7Czy9OFaevP6b0dxLrAEMDTJWWFelZnGVcTTyNbVn0Bs/uEjy5H7Cfwk3oyqgtgPoY9zcswqUBkAS5V3WVEaov1+vj+tpsbm4u/wqmp+LORFzddjaWDoPP15dXjVGByJM44g0p6IElpJVixkXJcLAhXZgrhoSjCiYbDDPs2QQkovp4+bx9j0FQvWceViXdzZ79ggu+sHKr6a4V1wsRq3FulYvRwP8/Qaj5R62i1pkaq/9cXXPIiMdrRwkj9TPHzcAfppgePWUh8/HzoK9Z7lvfq54BG/lZe6uSnuWQTVF8WP3oT/3xgfb4cofnlsYnwRQAjzaMd3Qj6CYd6hT6a1b7+NmalRQlohAKhdZX1dF/Cv4XRlR7L7yt8ONK7pG7U/m6730CqHJH16mAko5XLufKGgPRsGPeU549/Yd+r7Hb3/zW2y3WzwcDji+eYPDwwPOWlJ9mkaM44R5HDXb1aJ/W/pARlMcvEq/OkbpZ7XKPzyc9Pm1j5s9BtSGx1enxeSFx1/BUlaQquHJ8InBauAgNTRUWVRkAMlonecZ796/x/7mBp9/8TnunjzBOI64f/8e517KQw/DgOfPn2N/ueB4PGKcJoQY0A+9jSjzTBJQSGqp5RJoK3JVCLVnJiC6hSjOUeUrMdBwqbwjZddu727x5tUr5JRxe7fDd2//Rlp4ZEaeAigFxC7ixdMvcTz+ANoybrZf4f1DRow9Dud3+OnVX+LFs1/i63/4j/D5b/8MP/yrP8f03SskekCgEwKNmOaLyroBXehURK5Vya50P/fZxwKA/LW8Z00P9WX1HqODnu5agALPCafDEd/9/g8fnceHrm/uvirvZ2ZQz6D9Z2DMmNMkvebSCOov2GBCmM+4jCccxgt4GtARsN88wW54hpt+iyFGdGEApQuQjkh8Ru43ePE04MUXR+z+8BbjSXqj+2BxhRiKcAbASjSKwuXh4k4YC5yDWIthuD9NE57cSA9oCoTL+YLD8YjEGWYSYgIyMiK01RoiQsxiHEtqDGbN4le5GiEAXcTEAXNgcMfQYgngXh0KvAGnTrI3+gGZxMEyzxPmOaDvOnEE5Iw8S0/paWbc//gOr75/jYd3J8wzwBzRDxtMZykFKQY2BpgQGIj9gM12i81+BxAQcsDzJ8/w5O4OMUYcj0fM2tptv9trgKIYqPrNgGG7w2azw25/iyfPnuHFF19gf7PD0AUMm4hh6NDThD//8z/Hfr/HOI+Y04ShF0f827dvMc8zNrErpRwtOaCUQ2dG38dSsrcbek1yOGuWj/Sc7/sON/st9vstkmaSexm6ZF2qbO8d42Z/MbtPiKGxqRARhmFwuohLYFCaVWQuE98yrumB8T9l//K1JF48efYM4f17HI9HnE4n7Pd7fYRK9hGYMHPSDLJqH8ohAlwdT/ZcIKplbXNGF4LKNkntCREpkZbvBDhrYgizVD3UjBgGI6UZ9/f3SGlGT4TxdMK02aLve3eWajagb3u3pqs2js1Gn/x0uviozGfjc7USXNFks9V8bDxqn1nO4U+5PllWdfcuHQOfOt5jTuO1cQRe6/yjGUuFxMaBvLwHaGyY/n1/Chwfs4E+traPXa3NFB9cix+72mddBrndqxWZ/FgSzBJLyWY7E5YgxcYXNPDIdNWcMyhp2015gZGuSqcCgZLcn3IqQYagGvxYKgSyZSpLwkSIvY7dVfrFJm/Z2pO0RcozOM/FHgpWmZE7sSMxFz3E7D2cqdiuhOSZ7M/FVsAMSSwxvFA5FaZXcQarQ55MOGRWx2RC7AJ67rUXrWZprugmgYLFLigCeee4/U/nUOytpsbQtd7rn60qRxmD9B3eRinfc7mDTR7hapssmqXrX2i2dLGpakUTrVpldO761Mrnp9MJP769YJxR9j4DiJwB6jV4IqGPFt+hNr/MbYnxxZGyLFI1VpfkINOSwE4/MvgWFhgQ1Zudm3XrbToH33Pa63X2xPKUF5pmQxHALNVxz+eLONm0rVNuKgu4/uHmTGQXKJbVKZ4sUCOXSrleV6VAV7RMeLBz9q1cZadN59ZFLB8hGGzMH6UwL7J/vdOr2UW2VajJO5wdjdDYZr1douy/s0NUvV3tCba37kzbqg6HA8bLiGGzLWdlScdv9zt899MDtkQSsKC6X7k3JSB2RbaQJFfBj5QFcFK1dcDvf/8d+hjx7NkTCebJM9I0YxxHCV6NXdnTec5ISXw7mbMkN2nABOtaqAtIecbh8IAffvgjTqczLKjl4f4eHUkbr9peORSfY+UTCYf7B/CcNNh8RM6zVH4IkNYKJPhjCb4mSxaZ1XybzbitXxIArLWC2Wy8XmgtJ6zCLRSf5nlGP0glhRijVsVTehvEkZ9mkVE9vmel41FbThIzKDP6HLEJHbaxwxAiOgoIpjFpEqmJvUyAtVaqMNMAUieni+hbdT12Jqg1br8mFxCAAcCu67DtegyxQySZX0JUiiK+oo46ABHghEwdCEn+UULmVHip0HjzN0/qR64BZbLSyo8jBRAlTaJ2lRg+UWb5ZMd4ESxUQFlG0TNzcXymlND3fSF4QI1wszLHSyG+IlZ2wsK1MFcitBQpU0o6FxurdWTb2Gt/LwVXv0a7z9ZY1gCXLQ/Cm1ev8fnnnyN2A7795bd49/4dNsMGN7e3JYqHAbx48ULKgnWdllI5FuKTUwYFQj9sAFDNPjXh2QvHletVasvus6UxlF0G6ApSrAojC4Osilir++HvJ+ihckZNkdFsf7g4xgMRcmdExZTzXAQ/+eGML/aOskSLQnZOcfvdrY3cHNtStFR+fOio+NX6J5m5RBfZXlSQedip05Xkc+/kYVhPC3cO3HPGAMnvQHnespjtoSrItHNBlUVNGLP5+312gudCApXnqM5JkUlWpvcEArpOiFQXxEA79AO6XphA50qegLXHBxEYczVaqHDXohg1U/HO6CLiLwX0NeLXCNZLeFcG5NcsP63knYO/wWTxnmKIZXLRmRFMhvdK27R/XUqztm+ogkguwqBMmKHRf/ruIlDpfCyiT4ROg5XurZW8X5mn0bDGkOTupauzsqIIEwouLGmG/V2FN3I/7fEW1p5pFbXHpmVfGP41++De19zNbqzmVagUbSFAwoa3IIXrNZXfPSh4BdbsT/bKZXvnzqLPSPZQA1Cc3UtHlb23mZHRGKNNufIS2/8nd0/we2aM06RZMkmNwqmJoG/X78p98eLXwpPqd6xZM9M0YbvdrvAgjxe8GGtxFm0Oq6BsjVlseFmmsyrWNfArsF3IJh+a7fKuFsPtQ88Pqd7h8Y7aESvm1qz4hvcu9wa4mvdS7vlTr2JgMvr2CWNS4Tfrc7jGVYXLytBre1cCddxd9n8qyMf1Kz8Hbn40FAkmb3le2Pz92CJW5lYIzNrzQtuLTOJkz0CxGctPrUEwm25ZquF/pW4mk8krlzzfKe3s8Q7l/rIzXn52U4gxFr7EzHj3/i1OxxO+/fZb3N3d4Xw+47vvvpPSvscDLpczpmnEPE2YphFplvLPawC2YIga71xvK8FwvIYLH7jK5P3mrL5+9XoM88v2sMMXMlnAGema4D6q8NW+lWbQTCnjoNHu2+0GX371lfTIvVwwThdxVKnRposRWRVyIkLf97UFQql0o/DS3oTZHzWVIw0XIzTjIUQgp5Ip7iQubDdbdP2AyzTi2fPP8OrlS3QhIKeENM0gANM84dXlD+i6CMobjHNGyJA278zoiPD28AMO59f4n/5n/wv8pze/wP2//lv89MNf4nL+I8bzKwQWY1Jgy4KpZdNNXvrY9akG/GY/qcpSn0r3lv3oArT60QiMpzN++uGHnz0Pfz19tnEGmwyUfpgBOQfMSco5I3TYYQJNhPMF6C4BNEaM1OHu5inudk+x22wQIhDRows7UNhixD0uERiGCZubHbBB7c2wgA0zX31u8Fo6Ttj9z+CpUnXR4TebDXa7LQjSa3saxeFaWqvlhGylAXXsyLWkNWcGTTNCkrLYRgOZgYCMyFKKO3BEh056uLJW8AoB1DEoBnRkwcjAniKG2Akd6iJSIISZ0RNjThMeTgdceEIOwDiNIGJQAPpOepbPcxZHaBADWb8Z0G8GsV0kOVUxSM9BArAZBmy3W+QbLc1IBARC7DvEfkDsBgCEyzjhdD6ie/8Ox9MRXZQg480w4FW3w2azAQKw2W6w2w24XM54eHgAULOyE6hkMnu+QRSQ5gmAzDuQlN/MOSFqK5wYI7bbAbvdFufDBZIrXc9Z2X8ITfFyic8aB9rKDCY/EkFazbkzOE0TsmW5KY0tAexhgW/Nma24aRVIuq7Dze0tYow4HA44nU7YbLegknESQVECGkyPs39i34LaqSo+l0x2e6+uKUCrcUCDMnRSWe0REsghGWlEhDmLwfh0PiFNM/oYpUXfNBVRRNbiZKtHeicuZbaqq6sdC1UufYy2LeXJqytz6whboRXy8AfGcM+KeLIi7y3m9/g4j+sA7efLOV+vcw0mP4eXLO2Ly/c/Zj9YPtc4rB4Ze3nP2jo9vn7Kfvtn1uj62v0fg8OSRix/X77T2m5cvV9pdIZWXWDJcE7cF7mRoQEZzKXCGckLtOS3vE9sIQmdBp6k7OxTzNJypQDW6bkmmpuODUa0ChU5g4JJpRIYQ16XoKwOW1+uOkvLPc5gtgQuFj7FCcuzVUQfDmV9gSTIlkynAKpzXNcOQB3vqcDDSrznVJ3AYkJyrR+M1lFY2NxtPklLWlsbqlZuLLCyz5S+MmqLmxXscT/WaJx8LuJItW8CJLJLlpd4tXupN5fhVU8MGtSWaSWRaRmAAmAiwv/1eI/TpHQ8OLu9OhRB8vnQa394DfbMQEk2lte3b7Q2HEEzYoO2Yyr75iciHxYbuvHzdR2nypFW0VI2xM5k1b9seIMR632se2j3ExG6vgMQME0TLpdReHnX1UrDLBWqTO5L5hBXZ3jJwG0qR1Q6F3QOV8HJH6JpZe4GgGprqPp1VYjsXmuHVm0zNWjC9onZObudTrpKF7kAqsgBRqdsmYVeBFLcBXxZHRvCaIM9N80HPDwccHN3J3vObXYsEWG324q8pXsVAiGTVQ0T53WXMxBio1tlZpDai7uuQ99tMF5GnE5nbDcDmGekNGMeR8zTLAmxXQSnWdvfSD5TCXACwBZ4oiXyiUWGtkoZaZ7BDPSx0wSyrHJX9f95WdJKlufMmKcLJHg6I6UJ03RBvLtFmqnQ/JKMu+RpjY0NZew1n6Hsv9JOx1vNN9kESigvI0gl3BAIKVvLIkg9KtXnpQJIqu0fDLdU/iUGkIEOEZvYY9P16DXg1d6VOIsLmiT73N6fkp41C7xqZP96Ljy+GWJ+so0FQB8iNl2HjTrG+xARQxSa5ypzBwQ1UVjVxCgB0DRjymNT2crmm3lyY3QgaMCoBqpZIFQJ6geXlp6fev0sx/g4jhiGQaMd5vK5lQ2wEuqn00nKaKgjrCCN9hRfGhoMgZroZffe+l1uepwvHdhrl89qNyRdEgwreeUFzaa8AtrS8cWxBOCv/sNf4/2793j67Cvc3N5gnCYcjwc8f/4cr1+/BjNj10tvsRCkV0J6/74Q05SSlMYDcLO/xWa7hQXUi+Bi0cAeOb3ytcLnlfjqYqpA6JS2q3v8s35A/8zaZeMs3sNufOaF01MPcACk8QoT0FEZjyFCH8M7uusBLsbSIuxeEzO7rC8XMxc8Wl5X58XzT12iGDlbvLSbCtssQprtESudcRnnBheDFbgo+9aDxS+G6pP6Xa5Tc0JJYZL6ZZO1bRlLC+UEdSoObPW7gmlUcYIAhEjFQNJ3EZuh1+xvkvLo0QIGlNCTEKdArAK+x0GU8lfMkl1VaEYRaarEkp2T2NPp6zNQYdHeV9dR8FMHKI9QCw3DXzaj2crQ1ZF3fV6KHmUGCWLNkgdCZqQs5UKExsnPOWWnMKE6RY1+MqOa1evZqLDgQjuWRKLA1uFBk+Wjf9s5899VAZkbuC43oKHJXCAJj9BXe0Z1HLb3mh/WcLy8u9JqmW41xhWYu2eqc9HW5wwU7hkz8li5NX8+2jUtJr9Gh5fLW95zVf672cD2M3c1QpxbcyNErb5Q7mJI9KLxpDQnzLP0BLKo90AEyxsvb2D/sxWgCg1rPpE59V2HyzjCgslag06d19Vh1fPWrGNBH8uaFvi9WHLDI2w99dXtvhZ4fmQfrp51823ohLaGKbhbkKpBrmbYwlU8XXHPLSBVn/NtQP5jX/69H0B2r0SsGejIyQvtOI7Wr/zpQeJXX/CIFuvmR6BA8p0MZ/xgYQShxyAMdx5suA9A+xEwFZqleBWD9LZt8cyd8/oyFDlwQe89IbjS7xY8zR40Ptzs00JG8fSETQ5WB6VVerGe4U+ePMFv/uFvMI0j3rx5g3fv3qlD/IJxlP658yyR3FXG9pYh4ZNLOlKnXGmHKfjlc5umKUOo2dpwcqO85pGNWWzl6hn7gIJIa/hrW+Nk+ABCzhaVrdVUdAnzzKoTiDJ4PB7w13/1V9jutvj661/g7skdxnEEz+I0Y82ASmnGzEAXIqjvRJZSWFlQoxh2zJFC5aetSgLtrHWR7rOmtMhHAWDpz73b73E8HHBzc4MpJfz08iWgfYR32w3u7u5w9+QJjscDOERxbs5SHjl2UbIMGMA84V/+q/8av7z7e/j2V7/FV/uAH7+7gOMFfJqBcYbUUiNwIIArbbkyhjGKrN/IcSv84THHhH3ncc3rm3YtnXx2n5XZIwA5yd50IWLbbx7Fm0+5+r1m1LAEN0gwaQLnGQEZnTqQKWdsAwFdAFFEQsBEAR167DZbbLc7DMMAogxkkeMpBikTTRM4DKB+QJKK7Y3eq8ApJKmQDDJ4VQOGfFH+p7w/l7No8m1OGfvdXgLnCBjnCVOq1ZpY5eJAi3MOIDKrskjgNGvGmz4LaAnthMAJgTM4E2LsEKBtH5BBTFIitVRzYERmbIjQU0ACgzVLiQGEMAMhi+EGGZkY8yTO5NgFxC4gJ+eECpIlYpny8zhhOo+Y5qnAilAd49JrM+sCNaEgdgBJsEl+eI/4U8T5dFDxQTKAhn5A6G8Qu4iu73Bzu8fd7S3evX2Dw/17Kc8eNQNeYSn9B80pLedmTOKECUobplnwvusiAgL6ELHbbbDZ9Dg+uP0lf7Zq9Q+7hK2IYVm23tkF3KYSpNe5P8MpJeTLDE7+vMnwVvHOKulV8fia5wn+RWy3W3QxYpomjNOEeZbqAwXPCeIcN2OjiiyB+coWVOdjAUWh6VVM7jvT38zQCUhGqBWbCjEgz0kNzyd8drPHeRbDM/TsoMjQDCBUu8RjMircOYWTX5rvHV/9wHXlOHXArY/6ZAWTz66dxKuTXKPpq1eViT4kphedT59ZE1tL+efVKT3O6x+/dym0wsmyVS/yP01/sv1xosMnvZcX+jg35679fc1JvxzP7vE21k8JQrNxV+f3sXXIw4U/FKeRftc4x93YVsq2OF5CRXZz7hU5kNnZFgQ5LHu764U+BeIGfmRNSlHplM2qSXxhFLmZ1bltIDM5qzj7CAB7G0+uzurCXystTVmTyjTBrNrUCSUlEKqzu+B1CkFpfJU9LRtdbNjqQCtZvJKxGGOAVQC1KnKjxlARQaoKLfSrnGaBlskMfl8BEzMBr8teXZ5mmx5iMATMyX0tuykXFcWqjFVQkQnmgW6dvVRgUuZMJH3pSdqAJqp2oCuzDwEzgL85nZE0iqqq7IRsegdBerVvamWwisemkbRnGIAmKswIDHQdlQTDenFBJzBKgAQrngerQuoItdfzmNuzZtMpTnEjRGVRXGUwa/0KWzeh6yQh8ny+lFYom2HAZrO5kq9LpnhaOMRznZfn5yaPFPuBu0KxLS10QrYM3Epfrh43PoXK+9nTDlfJVVBDKryUvVPjQ5GJPeGmdj6ZuVaraHhYhb3NxT6w7N+CKv4Zfe433wQcz0f1ZQXU4vX12u0G5TMiR0glDCscoX3elRb5hFfDU1K+EGNf3i+lzGelERqklKXyhFQA0L2EBbnWQIAyfYbYHdWZL/2uA+aU0MWIPnZIeS4BOQRSR3mLr0JftRUbJHA4c8I4XRSOxl7a/bA11mAfFULzNe8qDm4yBzgKvbHvHpN1MkszBQpSdSMlSY7jzFpVN4I5ogs9OACzBkfVLHCofVGm2IWAvuux6zcY4hGBGJlnJOOHijte37UgYws8yZb4Z/xCl2O6TkU5s6c4hHI3LOlxFyJ6/deFiBg6BOoQ9D45lfLOoPBmABwYWRq/iW7mzr/QAst6z7rfCVyqKZit36ph6f6aavHJsuXPcIyb87tE0bnSAtKjKZcyCpvNpkQj932vkRwZfd+VDQBaJLNMYm9Qtd/9PUtnel2sjVuFPY+kflz7zkokeIS2cW1N/lpGjkSWDJAYOjx5+gU4CyMbpxlv30kpxGEYsNkMACA9EJiRxto7CyBkTkIsmbEbBmHS2svEGtFPKQvChlAIjFH3tYwZv1bPBYow7ODon/mQcgVTXNyYjWBfpIfFuCaIKvYXw8VCfzBhggBQXM7D/a1ZMJLM0Mygvc/PgBYwcaqHN4qr7AVbohE+Qal27GthaaloPAJLEyacWBQcDtsQFqnGsMQNgvSWdsSCazBCk4HbCJ6K13p+Stlyv0dalq0wGTcHggjgURlpjJ1kgIeATqOfRHaSuQQYYVXiVSBM9a+Sie2mjFB+N2Yqk6jzYdT5FRnbMTqUt7gHyqBuC9z/6/2VuK4J7YXhkds9WjxThOjKGIvgqldU+IfQIeSMaD2IVEBMOYPIMsiFuEu7AXlfVoGPFDbk5lHnTXBaWYHB9aoqQLyiXECuJewf1WNWrqXCfeV0eeTeRp60KTfKgt5RlwM7C8YQbXyH+nJu1j73NIBaJ23LQNnxLU8p6t/MC7pY9r/F8TKenS8nkJRvDb9WYNYsa3HO1+g9iLTEe4vnKQk/FoN/7YFokYTV+McoVsHyvjp3b8Ih906DAQHouh6Hw8FNaT0Lop5H+5Ov1tLSNr7ejkcuhgugWj7jeGE1XFT5o3W+LV7kzlZ9mcN9fa7idbtHttfLYRtFyfMGHZ+x8pC9z82N3DM/6xDb+MzFsd/M64OPXcsWa39fz3/5vT5jMheUHtj4fH2fv6zKCVeErX/bNsDxvPbp9i8l4mQpDqg49QGq2mzINTwWt5I6jnBt/LD3+U+oLgsAlfLfZXB2v8Phgf30dBEVhqUixSNnzwI5I4mj/N37dzgdj/jFL36B/X6P+/fv8fbdOxwPR4yXM8ZJHOLTNGq5y7nIKqL4tPOsfIoqb9d1PqbYmKNc/jBefgVCmLP8Q3zw47TkA58t9o39Df5BqvJE0UnAoMCFJpuhRkCfcT4e8Td/89fY73b45pe/lNLN04Sbm1tM04S+65GT9GufxqBOMFQdCtf8hqxFVhC5MAYpoS5R7doXmawXZkDXAQERFAJu7+5wOp+RGXj++ec4n8/SkiMlPBxPeDge8fLNG9ze3aLrBzy7DcjzBV0kUJ7BiRCHgD4SdpuId+ff4+3pD/j2yd/HdvwCcZNxfAOMOCBdpFQfyHrz1sDlNUO8fb7sK+b1yas9XJFNlt/5n48F/xSdVPluiFI+7slnz67e+XOuaXqL8+UkfRmRESODKCPMIyhLhkAHdRb3AVOaMOYzpnyWkqBEYMyYkNGDMPCAiRPOSAAnXDhgzD3OU4+EDXIYYMHJXt8n4/VUW6MlrmVZmS0brlYBIq4Gc+aMRAkcstgs54ynt0+w2WwBNQhNEIdyAINyAmWhiSkzuk77Z2oAeZgStl2PiRlzlD7jYHFuR5CYV4iASGDKmOiCPkhGsvShy1KGUMsoZALmAOQ+gINUewoMcGLEzBiRJfiXGTzNyGNC4IBAPTZbUgNhAgIhdJ0Y2buANM2YLiPu7++lvyDUgDiPGKcTmBjDdodpUoNYjEonxBg0jSek+YJwCXh9PuBdjGCnRAu+yj51XcQwSED+/f0R7376Cd2wReh6gCKi6nNMCh8AYKDrBozTe5jOnjlhmgLAHYY+oCPGJkY82W8RaJJsaPayHyNEMQKCZAxQVtncKqGYcfq6XYEnlFaB0LLN5nnGlCUAQZzBGmRhlRMKPTV4iFwOFyCEGIs2Gvsez54/x/F4xPl4RJqr/SdY4BekCgABSMyYuLb+q9lAMu9g1RWMj2ZtqUFR4xvEKFmZkQZDxYA5z8gk7Sc4Z0yXjFdv3uCrr77C6e1rzGkCcwK0dOQ8JS0pa04vBrlKMx6ulYeqDPUR/uZtZB8zJC4NpaTLN7mqAMjrMI7nedrJEGOmN2Be93OtsvBSB1uu+/q+9cv2z9scP7b+D8GFi9kwuBmKM4UKjlTaaStoDPCmWX1ItFzo636suja++t1XaVjjW8Y3/XNL/veh62P3LL83niyTQEGijFx6vTLEwF3aP7DasSgjc5LgpRRVLVSHr71LdSiCFHBNOWsLB6EhpI6unCFnKkjGZc0EjS1UM0sJYqURsnfGI60qopThDoVemJ5gsqk+aXNg4UOl7Q4DhJqpXtbi+jUTqoxh+AuEVk9lTbhRGbI4QNkl5MCcVfIvUsCm7zFOI2bOap9mPMy9ZpzyUuMHAKR5lPmFHrEXm3d7j0qgXs9gbro+6qTLveUxZ6dRZcU9wO42ea4VtRmWZMH2u+mVDAgfSTpbe6/Iu9LfWWAUFH/8ciIBeZrwb36QKjKZPR2JEsiZJnRgbELAZruHlQRmv3ajzY2Ox8UemHkCkfphbN+IAWczLdXGnL2iZLg7GwRzLs9AlN96xqm+221ZubLhSXlOp6+vSWkWfno+aZnogDzn0lIvRG1BwBrsllx5Z3OsckWGmjvimDrRot2ZnO9IhMuYsRssG1joBGWAY4ThnulURb9qhtfAtpIMxjAnnPEx79w12KGxKSh/IAsQE5wrtkxracCQIIDSgqHSfWZqxiU945mlb7mU5tesa0DgeJGM6xB6jHMufN/Att126CNAmUFQ+SEO4DQDMWHmGZnEJWmyy6z0xmhKbX/AACVknqR9E0XEfoM5ExInCQgJIusXPkcKosQAk+iRJH6ClBnDdgumKDhGQpcRpRVFzlLBKIaInBJilKoE4uM3mS0KTYkdMghzEjoyTxnTeUaeWVqLAcjQUuhoea85qWVfata8z/yG7o/JKh5vfAKufW7/5nxBRg+gA9EWKWmibEpaNSoizz0itqA4IEAqNRGh/ERUGTcAxAEhDrjttriLAQNmjHxCQkJIpL22AdbqRvUoVwdz0pgqVroZmNElWVcyUqvIufSp2Jh2VXsGwF0H4oyYGTFHEA9gRESMEsjNDEKAVD1Tmq1nJICQAFDYICNi5oSk/FjoQ6hnVkuuExFmzojUOalLAsWMiDBdl8R/7Ppkx/haDxsvvPpSUuZUNgHLAGY9kfzlhaS1SdsYIYTiPF9mcy8vkY3aEl1rgqw51q3hPJGUIzyfz6v9nLzjHACQgD70uL9/wL/4F/8C22HA559/jhcvXoAhvdNykhJklsnlD1Nh9gxwTtj2PV5+/z1e/vQT5mlGjAGb7RYvPv8c+7snSDBfl2Z+oMoM3rlbCNAabFaE0p99rRihbTVG8D9+u0ZOoRKmpQhVpM6rR1e0gCUMnHBIOlgRBArkqtJYFJhmoo+ss8qc7jOqRMG9x/9tGQ9VZ6sOMvmRmvH9enU0WPRaucUJxZYJQODCKELQLAFVOEwosEdLSTYHSuPfRUeBKHQhEAKE4EYr+0Hq6BVpze2hE6zgBC9djxl7mcmthsv7GpGX6y8Ghyq6+aydqnqU/9s0Wgpexy3v1bc6Jb7BBK9EOiGT3GeyXFkTLZDkakt1TiFKPFjOLCUOU0bHjBQS5pQ0qky0tlSEK4vU5DpyzgX/iVAiYBsgeMj6Q2mKiuJmOcLeaFF0Ca6Tbw5AHb81SrRnavmYdyBntymrZMkrz8biG8XfQXp1gIpnLYZdZxJ8Oll8BKb+DvdavxO4Pi2LT6/p4uKNq8+4h50OWR14RBJxaQZHMDDNs5T2yUl4T2flaerbvIO3eafuh4+mt/VJP58a9FZB5Yw6nmcUHGuQ5OpnDfCye9pJXRl9HFNsnNOL9xAAhGpcaM6QKbw5Vzj4MRZ0owjNfg+v5rUyf64wsbN0xVaJHlt6M6+mh7d97ua6vL+5HA9dfWZxlT1ejLXqEF/QRaMYzVqc0gH3uSmSZGWiV486aXBPiwMFZ1aBVt7Q/s6L+2yP4Oan72p+d5pyY2iwH8upEJDmhBidWG776IjH2nJXMMp9ubLXi7+XyyvrcuMTkfJ9gELANI148+o1uq7Dr3/9G+Q04/XrV3i4f5DS6acTpumCaTwXWdgyCY0uNXRQp2nhdP7DRrZbzk33tASwAMU3Dljg1CcT9J99fYiWm7DnQ6uaeRcMIE1qyYVWNbqLCmFpnvDwkPDv/92/w5MnTzCOs/YEl77BnKUPMlHAdrvF/nZfnDyk0fbMGYGC0GX4LAku8EppBjOj6yL6Xko4z1r23socbzYDQgg4nU74/IsvMV6kRD4nqUByOZ9xPJ/w+s0bdF2PeUp48eWXYrwhBnJC3wXsNj2GPoJnYOYZL/P3+Gf/7J/iz//bA2Z+B+QJgTMICVNujbjANX1pDO0NrH/mvhq9Xxlv7fL6obXEoSAVgigQnjx7+rPn4K9tfoN5esB0PmGaLxiRMXQRu75HHwhi+hOD2fky4Xy54Hi54DzOGGdGxozpuMfUDZgyIQx7QPXIlCfM04xxnMTpRjXLeblyDd1Z5QfGui0jodL3xZ4hwHqohki4u7vRMtUZ4zgjuYp0ljnu9f7g9rxTu8A0TeBYz06ll/Xdpu+bXcH+lV6Auo/+X3tVx1FOtcyvVdCb1QjsWxWN44h5zgAeMM+ztkeQntE//vgj5nnCjz/+iPv7e5zPZ4yTGMEDGFF7dfrSkUySrSLnsZ1dylBZXuhsyhkPDydcLmf0m12ZK2vbJSmvOAPMJflhHEeFUVsRoe969H2HfujQdX2Bp2Uj+kvwpsqN3gazdharvNbKm0Erqdze3iKEgIeHB5xOJ2TOpfWDrwR3bUO6tv34jO+u63B7e4vdZoN5ngtcp2lqSggb/uVckyoqjlytpswjxohMXJylxBIkIDS3bc1n8qdMN+Pd23ukWYy3l8sFx9MJT589k2pPMTY8jVTeWbDSVraGuVEevz5GJ6/k9sUz3un9868atP8Yfa9Ok08zcH7K5d/zcxzA69eH1/7Y+GsObODa7rqESdVlsC4YLme30D8+NrcP08JPuzwftTH8GVr2D1++z2jscu1WijenjDRbpjWhSGT2zkKfTM7JSDNXXMtZWkvkGX0cwFzL/nahk5LD2Xg7IQcqZcetf3lldKzldpwcQlicCZuPyVvqiMre7apjOhgspUg/JMEC4IXqkg/S8e9jdYSTVdMMWrZY3hO7HiFETLOW+WVp99GFiDlJUIGVALbkLX9lMJAz8jQhdlFAEaptwOMo6Z4QL77QGxutRBTCovst75e9rp/T4jkwpOpLhgQ0FFsG1+5wzD7OoMhytj/y6uV5BN7dH/Hy5dtS3LDqi5Uvxgjc3gD/x/+DladW+ZAtSMy22uvbJkeJTdEn89V1K1xYKk+CUPwN3o5ick3BN9WJOPtzVdtrLG0z5qS3c+hbgOaUMKeMeZpE1kmS+Gf9uVOacb4k0IWKH2foJXvZAi285dbgys1HpgOhnMPl/j+5Dfhv/29v8b/8L14U3dr4f9Fpy5mgsiYi609utJSqfOloEalD39q+gqkE7lT6tqTt5P5Bk8iowr/h4SoXqwxfHjdccB/Z3A1+mVkCoqcJ+/1+lQcPw1Cct5ksu1tGtM9FzuwEOimDY5sYIsmuA1I+FbohsqDExMQotCIE1ReRrmh9DcwK5dxmh2/er1jwQ1sPlO1zemvQfuOAVHciAJy5yHH23iIzg9Grz89QbMlz15Jq6z6Fshcif1b9OWrSwDzPRS4t59UX0tIBrLpYiBKkOo0jmG8VZ6Wlg6w3NWYoZjmrfT9gt9vhZn+L2/0Ru/4A8Chr5gzKBLaKlQ7+LZ76gJGlXcUCQFjXuC7hWJBJgRc0sLXrNMC3EDiVVauvoryv/GSdkwaoasWTVhbSU1DOBaMPGaAZUIc7kCBaiNI4Bj5Vbvxkx7gpnn3fYxiGBlE8AszzjMvlgq7rMAwDzudzRXSpB9OMuxSul4TFFFkvQPkNeGSy5dmlccOXBrLPo5bU8sLb0vm+FOoAgDigHzb4i7/4S/zjf/JP8NN3/70KazKmKW+AGDxTyg1h1JFF+c0Z83jBj3/8DqeHox4QMZK9/vEnPPv8C3zzq18jDIO2nnDOOVmsh+qjGNwg788RdE2Q4BUH9tVL0MotXhgiKuPYV4R145Y/uPKsLWsl44e57b1byhzaG9bGalyLH7wWtv6rz66ZYZkWWmDYgeaqIJswV3oGOsVHOQERFUG2MHmi8n0IRkiMwbbrbAgQ50p8ak2YIkOCqGR9W5ZHIHXilr+9sNtGPtu6aySo72ddOTzBRdFyfb4pRcMwVufFJgdHm3+lH9dCNkwKb3DPG9ILfj9yFSOfza0g4yJjcIkPuhdZzyPZd4arCkcT3kidiJHECZGilFVPSX7OKSEpN2jgVMZd4Glz9tx3ngY08DDnOFUBmRbwcUaccn6WcH8k1J2bSE9efM6LAam5z5FM1fdWaNwaTSv3GcO9doS77VwdYkk/1taw9iA38NcI6SWBdHSLFz8/NBM/7tXM3H75M0GKIIyMElwVCPM0ab9fiVAu/LWcVQDar2rJn8vv+hajUKZ4SdmgXB2aehCKI73BxcW5dPBpaPVy/4KvPGC0T3HYcHFtC50C5GFXtRA3ln3XEv4rOlKHuXaG+edaqLl1GWwCUEt+23SuhddCZv3SHjsHj10toj4y18cedfTD9srD6JHxrvDLf1b2nOu6HE1dndfK4a08xnEQT6vYD2gfeIjKn2TNRgEId+R268g+0n3LfsQVurB4a86iYKYi/Fe8U6qFWsbD8zp3N7WyET9OzOqeONwl/7n/ncUQYiViY4w4Hg746acf8eXnn+Ppk6c4HA44n044HKRs+ul4wjSNmOYz0jxKBqXbvmqcAazscYVW3TGAC71o4Lc469fr87DQMcqWP47Pj45Xp3f9EWFFIqVmTfb/irqV0hf5jN3amUrJvVLBSBvsZSTkRHj96hVCUIdezkVhV0kC4/mC+8MD+r4rvYVjjFLau+ux2WzQ9T26fpDWV10n8p3KkjanEIL0Qg5Bo/9ZnO9B5cAQsNkMyJkxXkbV2aSP7+5mj9evX+N4PoMRELoeX379C9l/hXcXo2TzBAbtIt68/x5/PP4aYfcECG8QwghgFEXfztljuh8WPOkxhd/v3wfo22MOmg9d7OheBjDrvIft362UesgHbMII7mYgJ0zTiMxB0pY0WzTljJET3h8fcH884TzNmBIAGtB1PWLYoI9bdNQL4iJoWULJcAqhR9dv0PdbdF3/6JqvIVZ155TE8cCDwY7h2zkVXR+sAXoBL168QN93SHPCNDlDvasS1z4LzfYWXjFNM1IkUOgQiaoRiupzS33e7AFmY/DvYGZkArqF5aYYnEgrZzDjfD7jhx9+wPF8KtnGxYBc2rddV7tjZpxOp+KQLZBsHCusVboighqabK5iVPNslqRFwSwlbQVnGMAJXdfLGQ9RYMcM1kwLtmdD0J6MU7G5pCQZGcxAFzr0fYfttsduJ+c9KP8swQeocwmLcwd4ndd9utA/gLblGRGh73vc3NyUvbpczpjGS7lnmdFTxwtl3+y7tRYI1vrPcCKlVJzj9m+eZ5GTU7oynnqjeDY6Xj6vpZ6buak8bbYz288YCciEN+/e4nQZS3na4+GAz54/Lzji5eeCZ3A2jcXR/TTq9fi1tLut0dSf6xS/Ppe42vvrZ4BVCrRy78+Zz5pdbMkbHgvuqHbGRwcv+vpj/GbtvZ9uo7MkjPa5teevba7r621x+9ox/mGbXb2W2efLc+Pf6x0oj81HziLDKlpwktKwyFxaMgpZqg6uYm/T/6rWYec2Yx5n9F3f0G8qvxcog4hK4Ft0+hqRx0r5ojrlgWqbWegY5ex4oAkNWWomMJ1Scc3LjbpQlC4WQRwQBn0zvZvNp0zL6ilr6XAGMGl5ZKgNO1DE/fGC892EaRrRDz0itU4GBoO0WkxOkoGdQwblUII3SasPwfQZClg5ylgR+Bfv8ncVxez6fDJgEUNBdbPMpqBpqEGo8Da4GH8PHMEpS1KaBpT66y+6Hv/lODbzIsh4UsZY6rEMfcRm6Eq1SBGLBK8yA6Dsluj5RCj4WR2XPmAfQIAGxtbAdEULd77aQC5bq2VoM0MrJ3DFWaffmtwDViemlsiuDsckGfOo57acIdRAEkCqUYEt+500SMCXoJZ/XhO0JGvSiilL2iNltmN1aHu5386lOydGCx67ip5mNDtnUCcVfyUgslapkfcYilbvZ9U9/MBUVmUl46/fKht7rafIPcxcspnNlpznGQ/HB4zjWOTH5bW/2WEYOs2+lfadBmuiKElezLIGkqplQF9lCw0CCiHgfJlxuUgLms2mwzxXu7HgatbgyJpxvvSp1SC4ADKfmlvrFT8hs4eQzplAUXTNru+REkvlrE5kbZPZRGYM4BQ0mcJvRxsMtwzWskCO1qHfytxEVf61BFs7q61MQWVdRIRhEBna5PGcpNq02AOC6gy28SorsgUK1PdtYo+b7RZ32z32wxYRBzCC2D1NJjB6swhQsPNGGkzjZUrjE+VZcDFBXeEmuKzLAbf8nY3GyM7r+dOzvmaDhZ3PiBBqAAtzrRQuZ8R8WdKGhNlXtajVlb188SnXz3CMA8OwAcDFwevXYgqWRfgGVcAGLas+T5MCSja4MjApE1An7ogpywG1/lo5Z0Q1znnkNqIq4xlS14zwougulJkQQonSkzIkVA6+KareIC49XixqTfoDnM4H7Pc7vHn1l4UhWVaNMVEiQtcR+g5OEPCsXSLWv//h95jOFyDN6KC2VWbM5wt++u57HB6O+M3f+3vY3t1hytmVxNKT6hGM3E/U+5aC6JqD/ENO80cVDU8tVh5tHG2oAl0ryFRubPfXAakKheUuNx8zgJT5Z/col3G8IOXUuvoZtY77csdiTQ291neb06lVII0gOAavXN7wzXBOHOOsSi/KfjaKaEbrczQNuEruWmK5CjyAi8jSc1WYs4NxcZSROLdCMXzKZzFUJl8Jtj2+FqxQjS7WS6kAPUs5kxY9dd/qdgEFb+wD20VH9GHoXmewJNuV4TqFoBKvgls+S8IYXqEhVcIqa1+CwSK8igCmEYBQYdO/uzr8bT0aiAAxhluJ9agO8TBnjcRLmJCa/ihFGGtw0MNW5+lhdMXcHOTY/c31ePt9L08vmCEc3hmMmj8WcC8vpPpr80L9m9wM/b431/IDvv7ymrZVWK1ObfG8n2b5xikR/uGrccq6/BwVW2zvnWDtz7Xfh2aBBi/7kqtyQws+XR7V8ObYdUjnSxHkcsql7w2rQmk4TZaZ486Qh0c7OVMWrJpMbnEIqA4fR3uv4LQUthpQrmd4LM+vn2ihzaZgLKe+Quh94AEDxXjADlnIfe9RwZ4jkDqcqsPL+iWBoIYE/9raJw4wYQ91X0mVWKU1UvlLlLLKwypvahbw2GXfN3R9lZm353ZxXcHcPefn35x5G6o5G5XOVnex9prFCg1o5l1hJa82ngyttuEXvZiDa91htwiMbTHufJlxxVZeSDEvIEM2qavXGd/rtIxqq0kvwmgWBIDcLzXgRJ7yZQpNIeTlc8ulL2acFQ/tLAUivHv7Fm/fvsE3v/gGQ99r2fQDTscjLpeLRq6P6vAZwTzXc1Tm0EpfwBpdNnq/Bjc9w1qKi5iuAmDs7xJiYfSG6Wp3Vl77OKBW7r9mFe0g12ie6zd+E8v7tUcYqgMkz5od7jJGuCjfQQ0ZJnMFyVLNM9I8FQU/ajQ/4Yzz6YSuH8Qxri2fhn6QXsLRqg3F8j5f7rS21pIPzucRnz1/gT+ezzifz7jZ73H35A6n0xHPnz/H/NNLXMYRr9++Rb/b44thUOMycP9wxM12izAEpDwjbjr8h+//Pf7Br/4R/viXf4UuMyIyELIYC0p1yPU9jMGVIKUaFF3J23XQ19pIyzK+S0P+ki8VI4DLSGUtZT+NI25vblfn+6lX2D7F0CdgMyHMM6ZpBiFg2G7RxU6rVifQNCLwDfo4AgxsEEE0oO/22O+fY7t/iqHfIMYgpWX1fOaU0c8J/TBis9lhM+xLVli7XqNz16dIYJSdAaK9IwCY1fADBjgz+j7i2WdPEELAlGfMOaOh0Mq3TU/yjovaaiwhkTiqrcymSdfL+S2dL3Y2bD5WplK+dHsPhrUWKvKSjjOpAY65Zo+bA8V+X/6bNeOGQs1i93AuujFppTk3f/veZ73IpqgdRgNbMqf6nnJeFSenqRF4zaAHqPEa4uBI0wSTYvouYLcdsNtvNIChsiuRSTIyuMwL7n3Wy/kxEwJQH/CObjtzXddht9uV8uoHAPMklY58xpeV7gzUOsAbmLpzbLYfUXy1iqBGmIecEc0h0XWgELUqwOwyzBPMiC+4Y8716syQMrHQ/o8m2rJ+nkExlPNEJMFGx9OEd+8f8OKzW8zziLPSVnN++DX5dTUO6w+B+k+4PuZ89nP5OZftxzxXu9tyrzxdXWPMfq/XHeofh8aafexjY7T2Mrq6t3wXPjzWx+a3FpDgHv7gXq/pSR+6vGPL//NzWZt/+cypBx8ax493HWhi/1o9b0pS8YLROtTyPINjLoZxsacFN1elLRr0YzYRVnlrnkdMU0TX92qPk3/Z6UStbq7nTT4QGloFdfd/g48BBFCN7lq/Mr1F11Dk+p9xmRNUZGJ7lrTnrOqqqpNbdUNWWzVD12H0lFT+JMLDOWl54qr3XF+GoyLBFkU0EzJJkJfwjADTT8sDa0MVdPKyfPOmCrjmE3b/t7ECQCYHBlutfBlk72pcskrejePebFB13ccp4buX96jL0BGdThAI6GPA0HWaUORmVmw1amQ12cqN1/owEnKO1f8C1vgCsyEruMEFD8Cs9l9zEtVS6oUPMeuZchNn1aH0nvITjJzqeRQnrdiOkN25zdWuZeWMjXdbMuUHaQOjgSsRmQF9RfYWud80I4JbWwY0gq/CXGF2rbeRIaieleqHylmy8i1AwHA2kNh4ibzdtQYByllS+5erTlDmSRbIYHtcT9ay3SzYMpq5wkftE5fLBeM4lnHa6jmE3XbAdrPBYTT5mlVPZSnBX/8E6Fr/CSEgEqHvN+CjlsLPjBg75DxL2wBAWoJyzZT2Mq/hDDlaaTqZ/V63YrHH9p8hOURO7LpOgwellXOw3jeOVocgeNfnHsipBCNmtDpB3YNc16yO8Tov8dWUdUD5i/oFSXFC7IQakGPlvLNoFrGL2GwHpElKi+cUMacZc5q1XVRU/GEwL2yDENssxYCQAxAjhthj6AZ0IQIsrQB8BSEvh/s1NutawF2OLcOSc3DFu+vvQlNMtq06d8rJ6VsAmfIeKs5XnkH1+TJX45N1lkbnDP7WftCCRY3CBnRg0tL4Rc35NF76yY7xEKIetqgLqV57M8ROaUboemvnIQhkVszIoFAjObouFoWNWXpi5ZxBOWOI0qA+W/kwNWpEECgDEdFFEFQCIz+1rKB+sIw8LEieFZEZSNOMaAieGZ32epo1gy5YGq6sGnNOGIYBCQmH0xEzRpyOrysBKMYpJ4gWQ0wluoASBQTM04zTwxE0J2lQHwgBWpI+A5QZl/fv8Bf/3/8B3/7Z7/DsxQtMGuXHhbA54VyJsxcMvFDxmKDslfNVpZK9NFO+qJ+z42bLy+Zgh8ExiHKDm38NSmh+LO6uX5bXcjWrsJNQCP5g1HWUbFVlFvWRBW4ZTBxDsvdZGUPr82nObRMwhVazOpolAtP0O3NI58KV/Pvcgt32+qsEAdg9xuAANY5wEcCMdOeyDyrTK3ZYBpCU8YNz3qswa5BRiUdV+YIzblIFxsLErzfRzL5G+CTgxI1BNQjFnFgqOspP15aA4Z2bDhft0rK7rZtBf+c6EzSw5FYBsGNVnrPpOtwhKiW9KrN3eHR1hkRaao0ZUl4ys2RkDCEgRkLfZcwzYQpATAGjOjKzCn/GSKocaopNXfIqY/Bnws2hfK3/p4ZB1eeac7mgx/U+hZHfmxUFuaGTK+OWsf2YbtZo9leF36vX1GeW4Ch4zf5ugaM51tqpkdvSa2G9fO4GDMtzDW72wNOxZmnLOTNfgUluXZy3ooxRIb0IJK1Ahh7jeJGszjQXYy9IHX665s0wSFki2Lnlwk8KnWKDFQoNJgogVuVBo0hb3CI3ZzS4YfTRjA8FLrYJDW10DMDoFdxDug8ij1BBRZuBVz5FyQlX5br8ubc12P42vIo871rSgHpmSkAgo/ANgaPSaq7PFDpbb1aB3J1Psu8tctxxMcs+D8bzH2EmVIMGHrto8V2L9p4uus8Wb1s1q5D/Ye0iqIgKy9Go/L8hSjAmWOkEGpmGmmdkshVN2lkVfm/wXC5Pe5FVkDwGN77+vqELgnNzmh2Psx7JTsF1OFHKXNl8CsopUhgKhLpiL8uU2TiaveRDBHFImIzx+tVLPDzc4ze//g3SnPD29VscjweMlwsulzMulxOmWUpqZ99P1d5XQO9pGzcb7Odm+19LKHqI2hk0/q2rWDu2cEbLlR7kft/XjHB/t2sN1xfZNgoDWszfWqZIVn0uxitrZZNhsMuFfMrpqsavNGeYRZJDLudinieEcQRpyWzr6dv3kk3uf8YulhKN5nRDMXISEmcM+y2++c2v8eMPP+B4eMDz4QU+223x4x+/x2dPn+DH168xjme8e/sKd3c32O9vBE9m6dG84w3Gywz0HXKccbzrwE+3yCMhjTMmHhGxEQOVi8Zfc1BbZDwrbEvmmJUrdUp+CVZa7gdaOn7ldCpl/q4d7bYLIWeEnIF5xnw8fAxRPniF7QsgZfQ5g1JCTBnQqmXBypqmhL6bsesuCCkhEwEhgtAhhh77fo9h2KPvohjyQNK/u8vIXULXjQihw9BvsN3upZoaKj0ynII7ewA0QEs+rrLoEuudLMpqBAFj2Ay4u7sFQ0p/54yyf83TzsDGOqecM+ZZnJHQ/poEOeIEwrw4eT5L3IyHFkBvJIb9eV3IxvZ50vK9xbDDKO3XzDhZMxscTVvilf7+WBu56hxfN9pZFo99XnkVFJ4Jl4tkVltWiMBNnb1OoiuBj9AM9UCYpxnzPBaY933Abjdgt91gGsVhzq4imJ29MndqccGv/0POy+acOTzoi9NK3mfOYnZwDKiGTM/vHpNpzBHdljJGKQFp3xusY5cxzwEhBglOsdYJOSNwLdtpc8/ZAtHr/omI65wBXOmVTgrTzHj95i1efHaHQAHjNOHh4YAnT564XrZA1VcW5+UR/rW2Bx42/vtVG9AjMPzQex77bvnZlR1Br+tMnw/Ipx/Y649df8pz/hkv0jUwlQ/K/P4u71+9p1FY13nZOk1+/B2POqx+5vy8DXY5lw+949F71U7Eqiea3jnPCamT8r8MuS9EpwK6M9MUX1KdKHMulUNj12vVDFzpYwDc2atytdHIRu9sV9Sirel+MB3C63yGJ2tyr8gW/tyTe2nFNQZKWz8J9goLu31xsqHSTwY0IKy+M6WMt8cJ05xV5lujL1TppQyodoIyKXBOekigeJohvWbLTSg63Bqao8LHA9k/2cyIALPvymtFD2CywAF5iijU9oNF7/QOPbPztHTodJnw/auHKw3UzzgGYDMQfvU1tKLnYt7MondzXV/5XuULs7GklBFjvqYhbk8kIKFae1unuHO6+v9W+IeN25w9d5u1G8g5lwxmn+To95BJKo31Q49eKxHNWuZ6RTsqe5etmhbpfsD93dy7CBhu9LlH+AFzSVKTQZplV51AS+9LC4Fc98SeKWfB8IVhASfVqUxIiRbvqHpm2S2u7U3ruPWSQExnDzf5EoRpkmo//jz7a7sdsN32eDidivorlSMBCp2ureo00kqBK4HTWVvboXk2B3NECFlaFZDIg1n1szVZo9GpHF1du79U9zHg+HshMm3sOvRDj/OlVm5Y4q1so+i4Semt2eptPC+z+TlcOfQd7fdOZLsIEljZxa55BsWeQ1q9LWAaJZAraZb9NCdxjFOQYA4OIOQC1/IypZ+k5yJSRFRnvN1jPlDfsrjwTbQ81fyWazIjNeu7lhPLXhZYWxUyrbbECZHVV8l+QG+/1HOw0HMY1TFOupZQgpoIpfIpESIFN39WP1ZAKZ/OANG1nrV2fbJjnIhKCfVlqSNmLuVXWbkmAQXRfOkpY8bTNJXnmwNjQu2KYixrq0hrfbdydj0/YULO44KcCFcSZSwlz7n0JLff197tIyyMCKWc8PTJE/xUCKLM0TbAG9cfEy5DCNLjdZ4RSExcVi5d1orCrKfTCX/97/4C4zjii69/Ic7xEJA4FYdLeaPH8RWmW8ZuoVMFMmO0JgmtP6BEZn19n6qkNE73cr9jWOVEXU9jbXibT+PY1PW1U19+p0KUHwdaHbUIRTUyzO4LpP1DNAtQjBYrAiKhEKGa1Z5L5NJido3Ai6vv3bQd7K4cG7Y3RQipkXIWwWgGomjlUjTSxgsijKq0Cmxl8Dp2AWrZ9+Y7RxtsfsmTXDdnu9/utXlbDxz3UFlk8/xSkbZsP2OoEO2oKiJcoGI4I9GiNTuD3br8+xsDhdGiwvyTG6/iNjVzV4LtorwyKp5AcYsZiCGhi1Gyx+dZ6QYwa38hZp9dWddb59Ni0NJp674osFApo/l89Znl81fn2dERd9WTXelOfZcnaNdP+eGLg7bBqcUUsByu/XL1VTpQWZLOrfaXX+xnOSOVdvsPTOit2twjb6V6W3O7faaKOPw8PJ0uiy+L0P2Wr0IM2G53uL+/B2XrjSnZLdI2pSu43ncdUs6Y51TGsNk0sC3no6WjPrhMjKcm2Ltzb1O37FanNLnY7rIJRQEv35hDvALOYC1nV4u8K0+26HWPS3Z4PP+oQG8VFlM8TRgsv6syVyrXGC1s4MOFJ3v22uwnVJZwuy8VLWqLlmCThRh2Qlmf/pOJ1Cxpo6llTB/lrPuZ2/2o3+iaqYX6Ej8LyDyPbgeqMsXigBacthWQpw/rZwFGXxe83vNBfz7rM+1Yyzn6GxhtJuLVwnQNS/7dXrR6Lpm5VBdKmn0GRs2Adrhi66o/r+lwA0NVyHhBRwteNTyIyqwF96WHlWTbEn74/nucTif85je/weV8wfv373E5X6Qv7njBOF4wTxfkNCOzc4ovofEYkS1noCpqBp/HCTPKPR5PmnO7GJ+KR7fuF7G7v5EvPvzev+vVDL/gqTWIwBEmVMOIyJyWze2n7uiH0cDyN8McwQnAnDIwzZWeKr6EUKPlY5QSyn3fYzNssNluJLO870v2BwJKVvaXX36JeXqGu5sbPL27w/FwwKuXL7HbDDiPE2IIGPoenBmHw1GDegMIEZdxRp4zdvuAH179Ac+/+hovf/xR5dAO4zQVx+u6g4GLXmi6pvVx8/f7rFugllf2mQPLa+ms845P+2x5X86MLkacpxnf//H7lfl++hUHcYzHnIGcQZkBRMRuEL6QGRQytpERNhlbZslYl1khMLAJPfquU9rMkKDMDoE6hBBBiABLaentdquV34Ra1DzuBZ4qz0MmlW9qtkkFnpA8kzdVLQAzY7fd4OZ2J9nfGqzujWXCm6//Ict7Rs3WpugqBRj87e/F3i/Hesw416wT9YiaUVhIuWQWWssCZi4lHA1HrE+t4Vh1HKv+5Wjvh3DqCi8X9pNqiBMbSJpTKa8pMhg0SzkV+YpZjUjaCg+wjJWggQcjQrdDzhJIud9vsN9tcLkcAUQ3leqgL/Ke8noLZFmD63Jt/r6mrLHeZ9Uqgpuzr/Bnn8s7ZRoWkFnKoIbaksz2TGhrOy8KZoiTecm7U8FlaROUVvuRSy/wVOE61ypf1Tlu+9xWYlIJET+9eo3f/fobxBCRszjGnz59Bs6p0GrDxyLfu71QZaX97BOvtf14jO4u71l+vrxn+azx77VgkitagiqfX3/+EUHhkevnwuaxq+7nYl72nZfBHuVha+Ou8yQ/ftH/nM7zoec/NN7H3vdzYeXH8wZ5z3PXxl5bA5PaVZPSBcj6yxk0edneqTY5bzsucnggrd7HAEtlU0noioixF/WJWcse5/I+dmdPrhZnqzC6QrfJ6TMGE7c+od9On/TKD9zv16Ujy2/Gswnm9NTHLBhO4SFrkl7pIYbK7zXhAgqbaU54/TDhPIlzELzMSHUzIcD6vBLI0SmdCwOMXIPUA1R2ULl9ZV0tvBwAF/L6yqm7Gqc6xUVukfmpc950Apuz7kUMFrTnSp4zcDxNePV+FDmD3P6DIU5/RhcJv/sl4X/7v9KAe2vbAgjusWhoVunAXxIAVedfArCkebuiGGkWc0DwgdoMp+fbT/eOQqtQzozJWkUXc6XWyxiqu2ZOxVlssEkpu70x/VL0jX4Q/aHrutJa1pZmt3JZr82lBj0vZaZmp8mCW80GgzJvD1MLeLDFlyDfhb5JblyojJfShFLpy80RfnRtZ1plw6qDt3YW2YBq4aKCA/Wma+TOXKseU3lKHPw5J5zPF+QiG7TXMEgbnHk+gDuWtymOhBCRJ/PTiW4pAQ8VnlWXimAmrZyTa6lxrSIQuwhQrZzk96gsZUXe9n+bzPaYrJA1k5gCoes7bLYb3N8fyj01YIMLX4gmj2sCdnG6f0DnW7tMnrfEXrs8PbQg86Jvh1ohC0ET33LCnOYi66WUMU+zVIdSulNxx86G3q1HVGw9Tta2OXoa2Ux+bR/8+WphXeSKxTBL2dD0CPs9IyHlCSn3omuQ8Jgi9JqNioQX+HEZue4fWOm00GyCnXNLApLs/UASEFv8cgQQRfShF53WqMgnyluf7Bg35DejgwdKcRiTNJ23A2FIYUaEStQFIQ1xvFEiqHKbTQAiE0IMcvXXrLwrN19XA7S/rg4gEWYJTdeSClwixoxcEVEdm4BJCY6sn0ukcOw6l9lzLXyuCd1eKOacMV0uwjxiRJpQLF2htI8XeSGCwNOEP/zlXyFNCV/96gyeZRIAAQAASURBVJfSw86VLisKyAKdjUh/nADY8w5pqRLh5diVcZY36fvqz08iOrZna8hLrZDn5UUvilQGC3dI/PttTuV8lntsLXVpXpiocq4NFVWYJAK6UJV4E1aatTtmbAYJfxUjxQIcoqi3zHEVt42hKvGV9zqnLozQVSet/SslM8l6lZP2FfLZnaQCV/27VoUx4lqBagy3CCkmeDGXFgF21mxd5R5q38UQ+dmyoYtw3Ai9C0K9wLcrZkDmVnCMzQMZgG8USyUF3ysDde72PdlBtX1iLgbF6lTi5vyUvdIzRoRaeUD/NmHVDE7bKEaabh4xTbMYgrKUXJeggIURw/++0LQ+SUH3B8t/vLitfNscVOegckzRi+z+fCyFTf/65e/+DPup2ndmcCRamZv/fTnIymAV9Vde6MdB3fuib9itDh6fwqJ58bOMo++iqw/ZnQZbdJ0HG35ClLTNZii46Q18YjiNRZC6jBcpc+joJBVBsOwiGgecW3sgQk4JUYPrKJCUNTBlx2EEOfzwKNEYxesry3PNO8ti7SsNWiGg9O0mC97JRZAkPXxFGSjjKkRNKONclVYGWHspwegUkToqXBsJGK2u49n/G9TzZ1aFuaC0NSgN6TrJ6NputipH5VIEJ+VaSSJl7fJkkc6F/ih1cSx3wSKXv5bn2k+u730MZ/197M4Ju5+tGEFXfxMvOWel4a2K6bipWxz53xfzVtTwf7U3PLoYCH1YfAwKDiZ+v+V+Cm1/vSIrUyjl2gquo8pcxalN7ffNXQWF9Kw3C6mHpzlrCzh12kOXAPzxuz/ifD7jt7/9LR7u73E4HnE+HjFNF1wuF0zjBZNWnRCi7MKzVonXBy6uPKnINY8pesvnvNELSurcs7RctxGLlWleY9qnXddmm+t5rp4OsgAP3SHfl1nHDerQYe3LZ2ux568PscBPShwL/wkhIBvt5qyl/FqjTbKSmdYXUg4pYtTAzygR8X3fi8Fru8WwkTLswzAAAM7nMwKgTvCM3WaL4+GENE04n0548nSLlIDj5Yy0IzBLpa/MGQ8PJ+TpB/zm23+G7/4//xpd6BBSLDKtz/RdynreEe71TO+Y8Q5x/7fXAxqD2pUxAVf3r2wogCwV1Oa5BIP/qRfnDQiMSEAIjAgGZ4CSVA8gAIGlSOgARkLWsobC4/oIdMToiDWYGpjm7AxgVHhPCFKe8Mr5j8eP4RJ2xkMrI5dWH0qSwImBnLF7ssd2t9FWLgxoD1CzDayOCz0DKSGnGcNmA+o0wy/XU8TA6r4v/64Gv/qO5bp1NDkbAbV8KSRIn8eMJ0+eAIDQxGkqeGp9opfrsbKAsevQdV2xJWSt3MNgIMk5FBFA1pJZskyCr5rFjEBdo192fYdu6BFnVhkvF6d+jBHIUhUPasi7nM5SSULXZYbYbb8BM7DbDbi922Kz6XA+witNV7hAsbUTsXkPgAa+rUNfPlsmX/i9MBvSbrcrtqjD4VAc5HZ/jBHsSqiKUZIKHfXvIdUtQyGhhMABKTEyKTyzM3KWudX5L9v0WUvBGKvzfJpz6V0+z1aGXUziQVvf2oxjB7x8/RoPhwM+e/oE2+1WsuOZETUV1tvgqoPfXUq3idZp1GNOyI/ZrD5lDK+LL+nn2jiEWub6MXq9Nre1edp9a39/SNf9GAzWrqv5LHvJL8b/lLmvPb82l7pGVNuIEwOWsFyO9bHPH3MYPAaXen/VAlqazav/lu9qf1/Og5ycziVDsplX0e0WjolG4AYCqz6HjMgB0zRpQEuHvhN8rNmPyh6JtOWRDKLaGZhR2jzBFFHi9p36hN1v8pk9VZ1/9pGX/23FNrRKhSUQusJHhqj8HGjbU2Q2uQCIsUOMwX0vrUlymhGQQQEYU8IhAadJkjFyzugWjnECFfolxVvITVb3re6gyC7R7KMmtwMWWN6uqe5ZGdCrBM4+Vf0FrDoYlz/LvTZfoMErUP1cRieE2Cs+TZgXxTmPlxEjAKYIk1lIwW50YOgiuigV6CJB9SqRX7x8YtnA/srJB42IHGf9oYkYIXYCpSx7ajAv58X4k8GMW/pUbayOZkH2wM5unVOV/ljfmWZx7qWUlIdVWzO4yun9INWnpPqY2CiKjuePZNFb/Vm2H4bPBLfz5QrRqvw5fehxaRV2EiXwrZ4zk5+kCpPC0Hw+5XzaRFHpQpl/DQbxNnb5iUJLbJ1+TlTWpvKy6WZQp7hlddsa9NYQIv4nv+vw8PAa8/xbhXOLS30fsN0OSGmWyoEkVQsJHUAdmC+wVolt7r0s0oLvuiBuw5Rm5GRyB2EaL2BI0KDJPOb3Mx55xfu4PeGV1zsnreKv+Q+znhvzuQ3DgP1uj657X5zVmU330czlXP2WIM3o7jpJGlkk0VW8rFnkfn7i54HCIOneYnWNFfZ9mUckk1kfME0XAGbzYVxUNjScYQ7ITMUVwYoXRDVRI3QRmYApZ4x5xqxBlsHhpVvc1R4IXQrF5xPcmZET/3HZoZHXEAAkMM9gnsA0CHyC0amEZatIAEjGl3JGzrP2p6/6/tociKAVC5S/s2WNB3ToEMNGHOYQO0YIn+by/lkZ496pbVeN9hMQ+mhoM7LbRlsfLfvOnO02ti+54/sbtIhGpWyHH8df9t0aIP34AEqPJ3um6zqQ6/elrwRQ+xnY3IZhwDzNhehZLwpj7EIwr+fhjTY2LucMYpaMPLakNtlkIgAxlP4POQlh+P5v/haZM77+1S81y9whmypDQtcfF67NSepugEfYEnnix6pSHRoC1iD64xm2zWltjHkfv1pwtvM2B8uSGKwx27VX2rGuAgA7ARNVYAVKv3mLOCO7d6GMGRM0p643brfvviZBRXBuJkhXRKUaj+V7KZOeTfwufZj8Oqyke6c9JImsRwuV5OoCjSWwmOt82bkl7L7cfl+EqQa3qAhcJkiVOSozbs5sAQih9J1QeDqx1u3rkpijbq2/HK6Yw95w0hh0I5ghNcKzd1IAimulTayL9izv5gq/IqBXJcLGs3LsUv5K1mwRZIEIgSWHJ1CPLkR0MWGcZ2CSkmIV72wezY7qXKn+JHJTdA4wKv+74rLtSWk/a8CcF31z2RnF/AZ5hQaehl6/3p9p+3tN2BQ8QjvWYtyrQa/ms7L8paHHTYJRYSprXBcsbP0F5ktegRbG6xOBe487uKoUecT337MGvWy2W4AsGnRWQ508lrP1Z2ExnGcuCp/1Lq+r8DPWAXQKFAJi7HC5XNAPg9KgAIpcpmmGX6hxnjSa+4o/LQBkFKTQKSoQLftc5qVzd0inf5M7mlxgxwaIxfJ8NYorPmIkUJWIJfn2tJvszK3hotxQ1h5JxM3NZkDf99jtthiGHp0an+d5xpyA8/mCKUkljjROpV1MUMlU3WMVt5ivzlelbQWMV+f8Q9cju3WNxzaeGTMUEB6FbUA7Y5W8674VnuFocXnMG9D8AqkZw4+lh7e8t3Fyri3Avaf5qhgc6l3+1XILS8lfpf1dF43FtzyHKp4DqNnN9aYyQaNDxkUdtXd43BLSyn8kaC0QIcSo2QwZP3z/Ay7nM3717a/w7u1bHB6OOJ/PmKYL5vmsmeJaOr1pB+Px/zGsWLnK9jji/gnPNAERpkgaGXaI29ATozk630KxH5NJ16byCF78KVdx3DfzQ+ErRj9I++emNIO08pWfTsUFGdMr7QwJsLEqBXA0aem0yHkGIBkFYGDKs4w3AaMZfdRJDpUnu77HbrfB0HW4bLeYxlGCLPOM/W6L8+mEt2/eYLPZY07AnBn5PIEhFYviIBklh/kdfnp4i92zz3A+vAOZ0luOMTU/y/qd/ihrqLqlNw57h9zSaX1duheN7mtGE9NpfQa6p0l2vnNOGLpPVrcfvSxgpQRILHhR5ox5ziAmRPSVH7E43mKEGq215DSTGGeCODKDM5CLTtzC9zoQp3wDzyGsz5zxU5PxTRYV45VQqNvbPbZbcYxPKUlx1RCAUi4fC5yUYA6kBGStsNEF1YEF9gGExAxEAmasnuelIwbQrDDmgkMGOytTDojNYSIqCQCdlnJMnLHf77X3NhW7h41l/3wFPcv+snKKn3LZ+RYZzfddRsFFM1ITic2i79XuoAbeeZxdwIgELASqVfi6rkOexUFPxIK7zNjtNtjtNk5Ur3Kuh1nXda7Xr9h+Ss0LB/MPOccfo8H+me1WAgOHYcDxeMTlcilraEqrcjsX/5l8Lpkny/cu+2SOl7n5THTnum9+j223DH+lAkcbpC+ZaJLZjigBL1llkGETcDic8fr1Gzy5vcHt7S3evH+HcRyx2W3LOB5eS3uL8XX9YxWeH4L1n3o1hlK3t5/y3Nr1oWcf++7K1vWBOax996lzvn7n9TNCXT4M4/8Ye1CcLrRG3+T6GLxa29Wnz+mxe/05W/792GcfHAuMPCcgsdhJWJwEVr0mWKYdG9ztf0CV7eTMF/0D0v/aqmoUnYcCiJLqYqZOVfm2qPlO929sAzDOWJNAmC072OQS4ZHWIxVwATv2vwU4itqyBFA579cBr6beGO8gELq+ZjZalQvijGm8CO0PMrdxmsGhx3/9cADGO/yvxwndNi9erS4VRmmB6COnaKkjgTXAgFAVKKNhLslM109EIDZ4Kc0jt1l2O7seyk7HW+pitn8Gq+pEV30wC44Alq0IkDqidSPx/nCypkVlXCrjAh0B22FA30XBr8LfjGY/TjPsytoJSXC3Vqsxv0GtLomFfcNAILgme+zOGKHgRb3fqu0K/EwW8jgPRgkWkUcYnMXZJdW4qu8mxogQOwzDIHgG02Gsmi6V+wvtAhe4lLOl/0yXWdIw46+92kPENm/3tsfHy5OGNsRsQK6gMNxUHUpkCsv2r3TksUvQrgZ5lHfmat9u5mFwdqgbyPR/qXaTcrrS52Vu4uS+jBeMlwvudk9LCx29GzEA+90GOUODWjLEgUnwlX8qKpjykEuVRSJCDBFDvwUAzPOk7SeUjqjj3vY+5XUeanpB5lwqNHu/mAQSZpWN2lYcJVBA9ZOu77G92SMO4ny2hIPseomD63psNiEECSR2FYaWc0wLPDeHdQgdzufzKry8vN/4MJjAmYAouHQ8XsAssmrijDmnJrFYn5J5ICHnCVBnMYEQQw8wgYkwccJpnnAaR6ScQSmLYzxSsdW2x7zlsbWiVNVb9UaYLteYwlZkqzqYtoyIACIgGeCTVHjJEzInZHVUx+bIMYi4sAOwJQcrX/S2Qf3PfHJBy7cbHY4ksnVEByJ1jMOXWv/w9cmaum20GQIMGD5i0YAdnWPZO8C9wuKNCRbl0Wm51jTPKoiI8hlixGzR17ETIqKCXyg9ImzBYqjJqX2f/W5zTKwR00rkQRIdOE5TEVC6XqObtHRp6GJRvhmMyzjquEpUCgV2jM4JUkVIsZlSJa7zLGU6OCd0FJBJjFESYcEqN4hkZgwwU8JP330H5oxf/PpXEJacS8RczrxABG6IaRXU2rmx5QKbogV3UPT+ZsyyWjtsvhf1JwjWa4L68jknHDpSU+VAZdheD7R7ql645qS391cmt1TQPZOtU65MlwjgnJBKcv0yotmhRlmMLanuAahdNwPXcHCkYWWxGk1l99ReM4UZUChl380IRvp56b0D5/A2Zm0Clwefzr+lA1zQn7mGv1t0pHF8R3frc3XVKsRb+Gk9J/LDP2+GYpTv1nFFoUfXgmjZfsNlcjC+et7jgQkL9lxQoaA9T03/SmfUKeeL2URz2dagXTRUMMxsuJvLUSGIzU96ftZ+g4ECLiRRz7WdhCCprHq5xnrZfjeBOwu89JAzOlP3ghfMy8GhvK5uju1FOZ/w93hBo33ueuJU5l41SZmBPeuNURXn8CgsGjpta3VKlpWF4TrIAi/9GhdDl1eQkmRxDBZQry3RP+tvsAfsC78mR3jIRTkWeglgs90KdSBoQIVmK+UEoC/jiLBGZY9RlBbPS3wIAEG7AwAAhqEv/duMtxhGFSVD79UicnXtizN/BRV7tOCpA3pBhbpPlbbZwyuRy8vXGDvPdZxmDvYcLRQmgkbRy9+B2sBCgEvl86XQZucwhIBOz/lms0FnGUgzISeAc8Y4jrhMCeM4Y0ozcqrKFzfwQVGIyzqVxvoz7m5/7NS1vMoU85Xb/OcVVT2wqfxs0NkTcX9GHSJ7R03jNDPaXBZj2ceOpAE1A32BL8ITqP2uvP96gQLSOjgF5yBb0KS1tQg/towvavGRSOepEoPjty0WUl3TFa+W/oJcdpQqLypTkbMQOstCyPjh++9xPB7xzS++wft3b/Fw/4BxnDBPE8bpjGk+iVOcs9tXXpCjFfr6qdfPeJQ9vtQP3dmr+MF+vz3OLBTAq71uRYfFVP8O6yzDewqKqz3MDfqY0cVwAoXeX8/XjcyytznY7VxxHezQvRIMSZDSU6mvMCk/p4yZpRx7TgnzPGG8nBBDwHEY8OtvvwUB+PH7H3B7c4P7hwMODw948+Y1EkdsdjfIEP4yDB0GzVad84y//MO/wZ99+y3+5offI46S2WGGkiYAerFPZhApVZyKvN7ukTd+LO9b6i6PZbEuneIF2kmcjUPsQNOMN2/e4O90aQaL0fUQAmIvumfWrJ2cE+bA4CyBVCH0aiAAmBgzSWYPUgIlyS7wZ5QVJl6GvYKFCcyMFTi5A2VwYM/j7YwSzI6xGQbErsN8vqgxSQxKkrkXEUJE14Wyn2JIqnq40c4JUuElKs3NKSOTwoy52eMPOoq40gdxYlyf65wS5kkyfrPDx64bEEJXHLTeXmLj2TtjjJI9puD0ARyNjkG5fF/wrmQgiQHInklZ7S0MMGfM87TIVK8wsBYZNseUxShnWT5zmpFdlTxioO87dF3QMygypQRPWunDejZ8z9QYo4hCKwEny31YBrH4JIllYgaAYnTv+x7H4xGHw6EprW7PWm9Mv/99L72E52lEzm3yhxk4bQ5E0mLAGz5lbYycJZjAgiH8M/ZOmb+eW+1fzOwqXCjfRwYSocz37du3OH/5OZ4+ewpmxvF4xGa3beBm8C1yltctjScY3MxQ2tgo2vNwpdO76+c4S/1c1sZozgYY2eGqzWN9nvLchypKPLau5XuX9y7vWVvvY85lo5n2jE/2Qbh+5mOOd7+e5Xz8d8WlZ+913z0Gg7Xvl+/90LNr8LmC/2KdvqrC2l6t/1vMkTRTz+kBQodCkWe87cCqmZrz0D5vhDnm0j9Y2gkq7eFaEplVl6uyBjVDiKNdgtKMb65dzFzasDU4aeefq71uKQPWMdop2ESsQpJ3wpOWC89o5RehQ6HY5qViS0JQ+V1aKYqtfEozgIi37884nM6Y7+ZSVciuEKKIBpkKuZFzHMr61sVpWwE5fc2CNZ086/aUuXWm6aIcwnnBeeH8NcApj1JlBxrFWARcphoMAZYgZoTodFnGw+Ekf3QBmBlaDLvsnwQjBsQg7SnNSUXm6IYlDrLSjevsVUu8M94tZ8hVY+Fqv8icESnqezTQT6vPGBzkfFgZbRR5x8YoOmI5I+swrHNxwZm6+tKGMwQJ4Nf2J8yawMcVSi2NA8SZzGoPUL7pzpKpOcvtlNa4Fdca3ODqSLP7SCRFfW8NELdKgoV/6wut3UxJesC1OuhF3GplsHegBCbArZcgjtGyIYbnFZkBllLbbFESipvFtMBamnuaMKncnHObQEdBKkSGENDFHgksfc/LXCH4ywk5d2DXHgYsDlaDaQwBaZ5wPB7x/v17bDY7BOoqHi4CNpd4I/9q9aIlH7CKOtM0FZubl6VMHjY9qOsExy6OP0l1pCqDFWhqQEnZdzdP75f0PGsZUF1bJIVGB1/TK8z/6PV2q/JY5pql2msGVR4Jya7OWXU7KSUNq66BOWDMMyhPuEwTLvOEMSdA9aGuEzrjj63xUg93s1NVf5bTqd32sQ3g9ml52RixI8Qu6Psz5jxBAmCkVRMTqx5aeYTEIDmfmmGk8jBph9S+S6DZytgEoRcSQG7VNknv/DQbzSc7xg2ApnBY3ySLvp2mCaGrkbgmrANolAtAHOEm9FvURSGyQKPIzcwgdZz3+k5hwMr8iVykgESJdF2Pmaey8f6Q2jpsbuaUt0hBKY3dCuSiHKMihdI7CqIodbpuYx71ebmnlLZ2sLHLCPI8TRKhp8zIWsZnZjFqcCWCJp+FzEBK+OkP34GI8M233yKTlCRgP91CPWmF6NrHldhfG/9ao5qbvBvPP3M1QIFP+bkkmMtDthybnZHZSYUm4LY/15WgRxW6xpmMkgmur1CnuPaK9WIRszBxLAnimhDR/CUE2O8FV9Cao8kHLxQhpWT5tI4iT7QyoeCRHhFIdI6VTVfnuGa7W59xu7/ifanf0chIFcihKGCWq9WswwSt4iCv+1mYI/zeCN6wk9gKhApOV/jbXFvc5OWv/ssGvguRRr9zd5lA5J5uv/fRgICUOKkEuuAvuWeN6DeCEZrIV3ICjYzFDh9snPq9Gfw3ZFGNhJEIE0kGsL17zUBnYyzPZPnezltdjj2E5mLG4pNHWJAXgBV2Tqi4EqSofe5qKK8TXd3S0lmd5tXViq/uJh00N/cq5hg+lkccXroRPzQnm5eA1+Ht1RPk/1hIOoAp/baHdjcTiQDIqJlrzOr0lvnHrpOMpWQO8dxETjIXdxwKD/FKgV+uF6rIfQcxjFr/ygqTBZ3RtXo1y4Do6aEJxp42tuf9Gheb+9DcDKM5thdljvWwwQip/1MepXIU6hGSG4owHVAETw8sO6tFXDPaoXzOyyxgxjyNeHiYNXBP4GY8Kc0JiTWjwfFH1akKfyir9ufMFDVbZgOZJaTcJ57HuvuX0F3idDOHxfMtibk+3GQEtEzuEbrQ/LnAkw/MzWZi4Ci02d9pm7WgmXKvBSM+bhhr3hYq5KQXvciyLdfhcp4q7GrAVekfv1gFu9+K7OSJGXNphyDllHMpg83M+PHHH3F4OODrr78W4/zphHEcpdzkNGKcLkhpKpHbhmnkJ7G8PNFcTvhTPvuU65HnRMECnPVt5VlqaBqvYojjk7Y3Bt/6xSfM89MXyP69Oi//dHVgOUcc1yft/DfT44ySqePOkj/TorcovSULeJDvs1Euluo/FAgpZ3AgcAjImBEA/PTqJb7+4ku8ef0a0zTh6dMnOJ0veP3qJUK/BWKHTegwcwfMCaAZgxnSwhmnbkYKpMYjnyHtSm17FunkfW88Xfvc1mpOLXOSP2bQqQ6u0DjUiw5pcwBKoGKazshzamy1f8p1no8IFNBRREfS+ggsTrw5M+aUMM0zRmZIv0nb+ZpFkzGrw1OYBecZXSBQzshzBmYt6xc6nLs9UhQ9PSZG6AgJ1agvOLCg9MzqPMjlrJPiDYEg1axJMyBmMDJubm7Qdx0O6ST4owILEUnPSt1TC0AX+QWlPyfruJwZ0HKsCQACITIwM1/hQs7a8y7o/SlJoKnCjHSeAeT2WNsXaJ9AFtMiTELkDGw3G+SUcAxReHJI6nyYYf1cbf4AqcOB4dsieAlrKeuXf+q88U5xmYManFQHTRnI2e4jMCeAGZGcARNVBzTbTE5JSmVyhqR9BAw9YegJMRA4S0oI0wRi5/jIWXXNHgG5VCsDa4UKrVS0pKvNGc7tGW4Mou6nfQ+IfLndbgt8jqeT2IqAcs7XDLXlPJeKG671DbPqVu6f8bhM4r0u82iGLfOqRtWstgLxj2aCwJFJ8YMb3hwgxssuEt7cH/D+cMYXmbHbdpguRzA/kRKbRrw1c/CKDhorcMRnaRx8zC5i8sYVb1t5dm1Pms/gdQj7BAueJME8VGRQ5de2H+VpAnyJ/CXfomsdo8rllf77OXpesLa+Jf1Y4yHlGW+M97QHC3yha161hNvVXKqYXtj22n2N/g7UE2efm2zD9fvmc3u26Fr1cwaMUOp9pN5DN4erWS01hOV85TsJOKnzz7mFodl7QmCtGCIOpZxmpPkM7jblPXZkJYkoF75d51jXSRQk2xEkPcmdHbjuh2GlH0F5G9UADQWQzsGy1KosX+w/fi9UVivOY6deeHPEKgTtRifDLW7QIyRPWstEa282zxPSPEs2qtLvnCeZCRFyH/DdzQTiGe9OGffnGWNK2KLtIRxibGRahur7yEBpM+r0pQVcoRVXi4gum1duETk0u2x0O596Jn3Quj5fW28t4FIOkTwfKIKznmslQJT0nWSfaSaiA/tlHFWvksoCtq1mwdvGgF+8yPiHv61rLm0ZyxpEMWOmyi/h8B6Wud46yMv6cy7zDOg0C1f9NXMqfpWyL0VmYgcWreCpOORQU86Xw09AfCopSyBmtc1WW0jU7Oqg1Y1gOgSr3NnQHYfRLPJX0aJJbfFF7pF/y+zuECJiR+hCdtKFcx4btSQN1DC5qegPVFoSWOUc1nNDOo4cB7XHFhmXHc77ffVORnPYBYDnMrugFStEbuXFGAC0p7L53WoVibqiCjOB7TzPmC6XArsqSUrbiP3QIYYERg+wBgcQxO5AASkzEjO6oDjpJDXSAOkcE0IXkOaMcUqY54y+n7VtYBKdQM/e2uXPvcGI1f4AXcPlcsblIgH4zT4rHqTk+ClXZ7XBVWRRVpJCxQZvlIOTfsdSSl9KiAfd4+CgW4NIbe6i61lQaruu5dm1IMhpmgpuB11HDFHsJ0U+kBYDKQXMaUaICdBAZvN3MlXbbEZGzmfM03tc0hETZgAdYiYMgQXHiVT7kwBfWuBqZqmGwmqHChogLz4kLnwqMYuO2NBdJ3OBYUmKAQExROQQkEJADgTWiqC1UoqAOILQxU6qvmTbvw6IwJgyMqeK7YWOcT2ziuO5zEN5LkVovyv5aZVLVoIT166flTHuDebm+CZqS4Z5R7R9fzqdGoe6HeClESKX0hVUDIZFaCIxbI3TJIDUzKvAGV3fN3Mdx0sTZWIR0MX5zoxpngEtYVYYx6Isu/XBYBXOQww1qi5E9LFDCIzvfv+XDVz0NxgDAURYZrS18ovgJYsXhcCUMR0Bnu6CwWpI5ywOc0oMQsbL33+HAMLXv/wGCNo/HaQ9+0iUsYJkMno9I4puvuLxAvGrJOGuco8+V9KUFlKdMfOybpSx1mhnERxRHlUcYCdEwgkYdW5rTvBarmcpHPks3CpUWRa1H1sY1CIyjutP8mNmNrmsUdC8MaAQ9cW8vKN3mYUnRCpfKX32W3H46rxK9E6Q/Y+BEKMS9KYMfGX8XAAcFuDixVqEmbLbR3Nuc5maCAXlc73HmDg367Xx1WyiBLnKbq1i1xLm64wWqQJRFmUARCuYwyG8rMeLHP570g+oeY1jNGSCnPxpper9WMJwzVDCzThBM5BR2Jj7vx0lRbRQGLAKispsybL/0UnUbwjIPAos/n/s/UmzLFuWJgh9a29VMzvn3Hvffe7P3aPNiiYzMrM6ICcg5BSEYoAINWUKQ0SqRIA5Ayb8BEbwAxgwLBGgGDAoAYpCqECoqKqMzMjw3v01tz3HTHXvvRisZq+tpnbufRGZJYVIqft9x0xNdbdrr77BKOR5fei4btx7jUyXfXdQjdzAVmqz/dzAdTTqD/vYFyEu7Oas7uAeu+3t2XfaPeqdfx1/2FWIXHOcyiA7lnFFZmSg9scacOLV/Cg8Ihy8YZ7O2mN8T29ue43teiosij3rHFg9GFvtEU0pAa2qoNO9CGXzw6zVC7kPXRa119DezD18nKYJj4+Pu7jrWlG3SdGG7ul37fFn+Pn2ZcJFXCZPARroG4G6JzfHOffnDV8ym1Gx49l4DTWeQjSmEYacQho/ZbS5SWrk1jozboKxPGq8goy7O9+wCNcEaJI+ZxpF0If3C+YBdnzHrpa1n+dR+NOH9VwY3otruXNSr04Bh+cj7bwyHoV+BLaDcNgJjd/rjPrWqWw8of53B1kM9GYLd/F55VVlmQy39tWNijJfmS1eJPKBWVpVp8O0mYc+S6GmVdVUvLvKbV10Qk9b57OiEGGkdHkOfPQ333yDd2/f4Xd+/BO8e/cOl/OTpEwvK2pZsa4X1LKC1RnMh3gFXQHHhRWOsHd9pv8lXLamelZEsOJx3Huo5RPXMPYwqT2D+u47n3kN9DiOm/qvzl8ZTNrm90l2+gyIgsoUAtQxbHw+0g/pu4/dBGcm6koF9KiIKYsj87osAAiHwxGrRqT+4MvX+O13b7AuZ5R1wTQfsdYE0IxcG2pqOB5nfPn6hGmekU8z8lNCXYHI+3mqux34f87YsDWUWyr1bZTq1T4QDf9i+1vjuCgAG3KSaNb7u7ur9r7P9Xj5Dqd8QMoHIB0AVHDLqKio64qlLFjKgkspIJpAIiECbMb8CaUWXJYFpYnCZeKGu/kgEQhrAdWKORNoymiHE9o8yf5WxpSBSt1YxYTB6dPOlwBKc1pjmMfhS2HSFD4vHl4g51myxTXjH7FZ3xDF1zT6QvtoTJKti4wGShp1SoTUZB9i1LHtuTG1jcWpIGXlUhWebOwGR1V1IFJKBiBqAEnacuPHD4cjWlnU6KARsESe1tGM40SEWpoEBpAosPu5NR7I4M+y7GkkbUqDbGHzIccDDV42k4GmClD9EeQuLTInkz9MITzPBzFQcZUoQ5bGTqcJx4OUO+CWwJzASeiVlfdgBlKekPIEgJGaRCDVJvKYiT7M5Eo2N+CaDLWJaI5ndU++t/tmHE8poYHw+Pjo/FF8Lho4+3eJWCGQOibre4Se0ScFHUCUC3vrV3hmzLDY038mnW8mAuckMI1uG88k0YTTlPDhacHbD484Xxbcnw74+PgRpS6gdJQ9bwxqjBa69rNjdC7c3167hthAw4x/vGWwfe5y3Z7vNXwtxgfh9MN/tGeunr02fN8y7g982N6vPBq3bxn6B31SeHY0nMrVGg96RH+OafjOhN20/ubsdQXjAdoiV2pwMz4f9TAKe5u1es4RwNbAzyZHuc96iGO7fXEYw3P/AAukCIYzHiPbGjO4NSSyyNMGrg11XdDqEwhfBHmRHY5tXWNGiMEFiQBAyimY4YyUNnTjKpwHj6tsxnFfCdr5bHz/ALfjd2ZyBxYH/XAOhUeNG2A4qh8qhu5bHLO16IZL6VeyzEgq5FqLZBFiBlFG41UyWIHQJkI7Tchc8bgS3i8VSy1Q97M+c6vJnJPygS3wn9EEGvGkrSd31pOhxdpDxKs+Y47+wyZsZbiAP5i2AEs9a7vjHPYxMUwsaGHvFEdQRg7eS5UZ/+x80Qg2QAJY+kwTgNOU8N/+rzH+6/9A04yTBvyi2xUAS3HeDU99yN2mYgZmOy9S6s7OT4Wlw5a63z0DgMulfpa15SArRxixM4gg0PjWaOeeWdCN8KEJ3ZOUE+Z57gEC+n5jM6IFvOrC4CjDuwEMwgOK7jrtGMYn5LlhziMOlH01e1jnmazt+A8g16FKQGOAJwWaDk5x/SLeHNe0G+p6Wnbo+pDOq7YWcGDfdz/WrUmwoxqv4zj8uOh7tVYsl6WXaItrxIT744ScrVyQlFMiyyJF4mBaxXt1wLlZz1KrjDZJ+eDC4pcENlxZtH604l/H5eM/v2xPdJy1iGNOLQUrSSANWxpenQ9p5iKCsbjU11L/5WAYb8Fhi4f9t+7FEcLeaVaCdkPQjH50mm86lb73MZuROVn37EBat90DH5IbxgHBlQVWtkmyNyFVNYQrVlFZw/a9pYbWFizrBzGMcwEoIzMwgbGmBKaECVI6rVLHH3Y1xXPuH69HvkF4StIendZu1sRgVb4rviZNbU5ATUDTbLY27sqtO+UQIbPIqQKzGoFPQEH1TAoeeOl/BcbMYtO4SUbEbJH9cq+GMVEY66eu72UYjwKFIWpTTOScUdQT2gDC3olR2dM0YVkWN7THtOtEhKWoRw3J0MyDWZTWpApnBUpd2Mvl0kXIlCQduh4kG0f07heBUTyYHZgJKLU4IdpjjBmaQosZYG2zVrx781t/tpbSmRPbZMCRu7VnSu3hnmASHA/HrvAhrSdMwvy6Nw4B1IApiRdPqQ2//tnPATB+5w//0JllA/SoCACuGdnOLF8LBfpJp7HHAncCykp0u9I+Ellr0z7RcH/XqM19tFs+3mlqJFa3PFf5uh8AIWJr9ECybi2atfUphoMZkYO8EFOzXiWN65vd09nqOrH1HxnvMI64P3uXG1DImCR42sHs6bZJU6krE0C2/urBM+xTG/q6EgzJFBtG8Gwq/bs8LH156p5AHIk0u0FgxAx+/K8Py0QQdoLbx0V9rTZrEr7sL5xffmJ0bAEuDFPDY28AP4dBaQOFJ10L90Z0vClEKLVep9xScjc942T9kXmvmYexdEAMNGKYBy4NKWGEUZ4pIdMsNT4o4XI+i2IKqrwlizKnK6cRg10GfGy2fDSsy/XqGUNszPMgr1g7dnOLh/x+aLBv3jN7dv09HKvh6riE/XmDn32c19ulGP6M+PnzxwXotDc4NT7ieGB4veMlH6Pej08a3dkKF5YdwjgOJoAaoawNKSfkaRKP8RA1LsIYg3JQHHE/f5Ezd5nf6JnjNLhOLqXstXNkB2wfIhOqexFwbV+bkVZA52p0bVgJCh8c1whr5S5PagB3WorRaGhrZ+/lJMytnW9AzrrVCI08zFaZQ9Rredq9xdZN602lzYR7FK6mRdRxVZZnha8xsDAc0/fFFFoGMjF9eqSbvD2LV6CXXODH9giEXYn7HrfhCif7B76+F9OsRskvPB+dAbaXnR2nE9B9tVIXvrxxYTbtEHmKaDe0U5zJhjfU89DxfGiWO9x5C1vkxPDfieCe6t4mOmz3OUn6WKk5dp2a1hU8Pr4NLVMeI/IvU548xdj79+/xm9/8Br/z1Y/x/v0HnM+PuFzO4FawrovUFq/rsAPXeMvGvi+K7KL5f8mXn/HNnjsfxBvg/hTLEC7HiwPOuv3s5xjHr7pXz1VyJxiG60qcrxM840afwNP4pgOON4UX5W6RCTgkjqOj6A2+NfTN7OOy9o0nPV8uaMy4f3jA+w/v0VrF4XjAF69e4tt3H5CnhMZFDeOEiRIqAQs1fHwivPv2r/DDn/wAj2+/Vdxa3XkI2OdJDK7NSTvKdFtD29a4vTWiWnv2e3QE31uk3h+0mpHs9zyNDtzf91o+/BLHuxeYjneY6AAq5rzawOuCtl6wLk94bB/ALYNwQEozMh2R8xGMGU+PC56ezrjUMxqteDgckPASGRmpFhBWHHPFiwPwxQn4zZRwSVpOTOvjuaOVzrmnl8QV7NjSDN913aREyIwXL14gZ5mL1cy032PpNVtba6OxpbTWfc7XaZWJErZ0PRqfoo7ikEd1SFTmxZqBPbOHPdfhbJonrFztUPgzhmtjasdlWfD4+AhKwLIu3ocptAF2J+2cpw63JG4GXWYKSIco4JYuWyU1+hoRlEjxnorSnG23Oh5LAZlzwul4xN3dHeZ5CkZ+jSZB54vm+YBpntGqlnOijBzoov3rhvwRVpw2EO2e7bg/8fcIKw8szolPjx9RS68L7vtBPcIoZhSMKTMBy8ATBjf10gyJEhrF1N9tSAMe+7I2LVNi56cB4uZ6KkLHHxMlzDyjnBe8e/cO3735Dn/0hz/Gd2+/w+V8wf3DCYkyWim3A2EC72hziBR5u75R2S/UG74pEU8+d+0ZdWP7t99nx+vPPcdhPFfK9mfGcqvbrW4j4qe9Z27Npes9dozaW1qlcsfemsZzOPSH4Fzk9zRzkPP23ZgRx80OB95Jb0DhwT52Rff1/HYv5md5JdaGeTOmvWuLv69Sr7eGpimFTaSpteJ8PuMwp6vAo3iZoTbqkLrsAkjQCYV7GlBU2xCRhpQkes14AuW5GBbdqg1GgWqY8hapjLgulpuIZ1VwJvdNHGDqGrj9jq+DBksxozCLAUpriZvRgQAUlhKmmQFKCbUy3r//qPq+hI9Lwdu14KtNf8bziE5dI8i5c7udPeaA/41v6PIKmeB668DaugYZbigddSXfUXgvyIEDnx9gwcbK0ZkvISUWo6FeCwj/dFkBJIAlXbmo7cxJsqdRj1fyrCmWPps9cG4rm8SzYtlzLFJVzgapY3QGkWRoKaVgWRYs6pA6TRnm6BGXtLMNfa295r3/HnAnizxhtF+yjJlOyGwrnYcGR5qsDrOt4yczjrHCgy562GdyHQwsQjf1kpHDRXIO5ikPbbIhPdPzmHxD/cw5zoE4wcDupQ4/NPBVgBu8N+czDMZlpUQSMZtSA4ZWxv3dqE9g0nPU5VEE5Qjz9rU2Cfq8cZ2ORxwOB1yYfK4wp1KMwa0wno7VPsENoKx8SvJ5piTRz601dQbWkl+xnv3mX5y7rYekT5eSWvM8u0NxKcUXxnBGpKc5Z8lyFPiniEttXJS6QZuylpFgc8ZtYFQvExY31PjCrSzQ963TLOt71dLP8X0VByUiP7SJzfu1rqgtgbS0crPMDIj1zrtNtpSCZV2xrAWlatYNEucRInJHAiLq5U/36Kv80veIuyaNBxrfqZLQYMUZ1gYzpMYjAdxAXAG1Scl9y55GaKRGbc+4Qo4LCJAqUtzE5gG9AedM9VnlnbPiHjAaCqjO8pmMLid3TvzU9dmG8XUtaFXrtmXZ0HUpHnlqvgwMQV4NJnxZ+lbWVG5ixCUNr69G7AONIso9g4pYd1Arg3kFWFPqETnDYrXCbaHExCyIjFmfU4bb0rGlidzI3RjqBS1CtteaybOkmdUDXop5V8/yDKQei11E0DR1EiVgzgJCJLOnPc0ugBsrYPVdhRBPWRivpojVniQoDQNjgqR9L1XrnzcGo+I3P/8FGISf/OHv6/siDDvRN2K/ZToM0USNB/TQbxnZASGPzHMkFPHxLefMe/ccsWyOXvSeD+MxBfAYyb29xjtmMKDhXh/l8A7bjIJhwJbGkIAzafJA8/d07fsfWXsi/9wZL4NbXK+199sZSA5rvy9jkBo/1SieQl1x4yfYlDTGm7Xhfd81NmZ6JOK9Zjh2fkPw1JKJeVSp9WfGN+0u1uIahbmIkO1eXz9TDsdlj8yEb9j2of1l8w8OE34u7Ch1Q5qFEgjDpWlLHG8RyJVg9owqnBT+KCUkU3YHWUcYKcWmbB6PZjpT8ZjH+ppMPdNEIgLljAMxEs1AKzhfzNFB99YU6ql3bEoEZyg3jIsr5YJyL3Jq22h6YWwNRq9xSFdabDi8uOdbTp7is9t3aXjUXt/w2sNvkfm76i+0OMbZ7rWr6xoYHR8ZR6FL7+4JfY52wlkidAaW6Bp3bwWpuArUnWEMRru3rnxPKWOeZqx8Fm/NWlXx0JUzzjBtcenQaTctu3Dh6wKt/dTxtqxT6mvjSBJSP1ORtCsxxh79aI60Z7s2AWXbmdW+3AkJojyPNaxiN2weUWSOUB13USOUWnpnAUZc5mgMoi6o2Fmw343EVzs8dh4I4dwoDbcxwAR0AiF5JJMZwcx4bzjYRzacHZkoUf9thNqwrmZccNxsxmZ9g+PYewubE/3M1de4j2z7rhm94/BHZ8N+ezxbSZ2MOK5xR2p+Zs3QYAL52FWn8XF9BtaBQns+dtbtNHoaXUJCG9osM2u9yE7v46TtTLXGXg/W+IqIFmUYvHld4d27M6cPrc3GjKenJ/z8Zz/Dl1+8xtPTEx4fH7GuZ3Crkjq9LGIU5yA4h06HfcD48/bjsMJbANlBj3+j65rs9AUPQpLYdPt5Gdf89mB8nwLupmFdYsfbl3dOxUhmbvZIsVtNgcgWaYYGiQ5Kw9h5OwjjlfT9m7w+4p7tr4Vwg1Jf03A3oKn3KuPx6REvXr3Ab35LWMuKUgp+//d/H41+hVmzaxBE9mqZ0Rqwrg1v337E+d0b/PjVH2GpBazpPqF8SmO+Ou/mZW6nNGmkDrifuEQAs2FTmV3T8096jp0/p/6c80YwNbM6crFkARGYEl6QqQGpiSNTBdbz5damftb17s1fIeM15vwKU77DlCd1aGhodEFrZ9TyhPPlCeCEnE44zA9IMyHTBHDCRBUZFSgVBQ10EDk1ccI0ZUwkpRReLAkv0kmM+SmhWNp9qCM7qQIi8k7hijx8MDXIuplMTITjNOHVq1fyrCpaoXKyKL2mq/3VHgAW5epSK2atrR1TnwMAaD/y38ZmjoClFNBpjCa2Z7YGcoZFePWxmBwzzzNqWYEwDivTFg1ezFIr+nw+YzpMij7JxxSdW8xILZ+V3qOv77Am6BHQYAq1hgUu2SO8esRWSpI1SAzdljXPnhGlJ4FxPB5xd3fCNGWs60X4S1U2yemX8gqHwwGH+YAFuigsNVFNsedraQwajQpTi3x77nLHn+E9fTtn3N3d4XA4IBFwfnrCuq6+hluDp7UTI3660lZwUXR2Efm2uaGNqu1TQ0rdOG7lBi2IJCpMpa/qARyufG1OUXQugl/efPcGv/r1Hf7en/4REmW8e/sB8/Eex2NG5QpsDQV/y2s8sf/FXs8ZxfeevWVctutv0hZzd4C65Tzw3FijQ9Z2DEZn645yfe+dob/esd8rHDJT4too7n1oAxa8cYv/InQ/uT3ceXUvsqo75xFON/s4v8+1a1TRdio3LGXF0+WMly9eYZp7LeNaqpS7nOaOK4zfQVhfsKeCtwASWyzniVhmSCpzVJ10Mh7B5FQtpWT6jy69QPeMh71zfgOqR+deF5f6m/JJn3N9wOcvoP5t7iAt+KuqkVWyexivk9MM5hXmGFxLwfsPHwGW6L//7OmC//1ywf+s1G1HUI5I1yGZ6Crr7UO5RY9tWspF78yTUg4Ph7VkuF4Dnmo98r7bKzrJdibX+ofymBKkndGq8NUpRpKDvWyMG+xgIdxATsD//H+c8PLeVgVupGqlSjkIzWZjGXXb5uzYfcuWI2eIkLNkrY04olYGSIIdpimjVkttb/wrRpnHeQh02zjZM+M4mDtuaWw1kcUm1PniuBeM2qoHNpph0HUvhgt0+U0uc7bNdKL6mwUxGq9yhZMD72hldTgEPyTjnYLOtG+74gPufGeiJHWQTYdivB/bEgXdpsLpMCRjbYiABGTk7hR5pYcxvI/NPeM1GFlSgnofrpfz8lbyr9SKy/nc+c5xlfDw8ID7h3usHxflWbvyws+e8oFEWYNXJ1mLLOfFjNFEANeKWsVQ3rgAHlYw4vqbtBnwskBQ3Jxywul0REoT7u7uJABXg2utLeGpRdeVc/Z05ZJxT2lFa2ilZ6UmsvMnhnGvaUOkvGtcfF2bsP9A5/tsfaPdImbKXkMK+Mir1lpV7Tl5exZNLQb+A5b1CbUmpFzBHoVvRnELMBQqTQko3HBZJRPYWgqIMvIMQAOKE+vsktElhatQ43yAknCOuz7CzkjQ8fpSKVzoWaCmMkxhcM3gNqkMwJAY7wbP/owMhjkAE0wnQUSYaELhgoYVlTVDCbNHuY9jTyAWnppJ4FAcfwsashvEP5cX/GzDeKLshNlqH3TvWkEUzHAvBQZcGEnTjFaKpHgrFY0I0zQjJVmsZV2dAclJhMRau1GprGbUUqUvJTSGpguXwxkRTWkqwKvSojEBJN5rpYiBvlRLaQYwEhrLlplXVmMCWkLKExhSu82Q/zwTWGu4HY5ZlSiiGiplFaYtNxAx1mUFCMipATlrmqXJmUhD/KUWmEdQauKdkxXoLJWBCKGy4AlJmLMkf7PeK7XhVz/7KWhK+PHv/x7WWkFJt9mjQigsF3XChB7J0hWrGmGo9xvYhTkzUkbFR6e7HXi7yaT36QfLaQT7b4Z85Xbrz9kYI2Nif5XYdMIX2hu4/jDioFiP3fuYzfhrsE3xIFInSNgTBnQMbPVZbCgc3u7EcMsw2oq68d+HH7xy0McTCX7SlDPurReMnx45yDZHRfhszAkNwrkxRDLX7ojAOh9JbRXGHRgk8zKyujnG59ozlor9irFC94ZiRbjeJrqCqq/VbQ91eaDXpohrFjbF98TnOsCRnhHWqG7zvmzigAONqkxa+9fqoECZJ+j5sdrABnekxmnzliIiJZpVGR5VmDCBU3OiDuOtMBpZ3GlAr0mjRO5PBwCMp/OizIHOrTEo9xQwpDXvEGBMhAfZd48yt7kFYd6eNUW1zbHX5+0wGOHE8I6v1bA1gVO2XdoKS8apbl7zrQvji/f0dAUQiOdKV3TLreOage1D6WsRsFJgojvOhOOdES/KuyMsejuBYdhM5GpdBucRQBRngKY6CmnpakWijNPxDk/vP4hSubaQ9jOOAOp12ftn33/oFnacA2YRmlgMb6SZXghwxzpfNwePrgj2uQX8avgEhBCZg0FohAkrYQO6krNTKltrgcOG0no/8SyN1COMYbNnHQ/HMe/sj/1uJDhOXxvY9hEmsoF/BnMRLMAdNlzxE/CZCYa+X/qc3YsTZYzw5yRDcbgrJPzcw+m5zdUdRcZGI2Eb9yWMP87bBCZjLCj8JyoFtorFK4eJeMXfiAJbZAMMNJ7Gfvux28cJTjuuyBE7DXBBzZtxBsyzeUgUnrzTNrgeJKl5dfJ9ggEujL7L/T4YdwCxdYLWpWagrCt+/tOf4u5wQC0rnh6fsK4Lal1R6opaF5SySroxB3RbnxFPjis0Xs8Zmj/58tjQ8887S8Th63XfDHFAG5yJDadtcLT8tDP+wDfujmXDcmzbHN7dHJ1tH45b9Bl5TJx6O68HiPNcdpwk53gnEi3e2/Yb0PQ4ne4AYDUZG3pKP3BP9Vhaw9P5jFevXoCSlHRa1xXH0wl/+Ad/iK+/fQdQ8jmVKsLzhIylFJSlIB2PuJSCSVP321wSAVu0UU0BrFdCT49HOkbRnV5H6diySrmREaePBgryLD8ZCQmETBmgLOkIIYFlrHWaCYxvf9Mzi/1Nrlev/z7mwxEVJ1zqjMpSR63WisIFnCum44qX6QxCxpwPEr07HZCT0N95OuB0mPFQHlAaY0oNc54wpRm5VZQLY708YT0T7qZXOBzvkOdJ6saDPWVvoECotbkuYDiSVmrJ+AhLScosKRJbQ0ozHh4eUNeiijVzgJLay2Mq6o1xhERmd6VUlAkUNoDbskFrko431m+8pSSKfdfaMOVNmwEHMywl4mhk721qysvlIqUFMrlBJI6l8xuW8lyijohxXSuP4XyAvdM0LWVrDdMUeXTRfcgadAO88X1mtDUSn7IoAA9zxul0RM6iME3IEpkSFoEoIU8zUsqY8oyqeWZb1bSG1GkFqZNBcG8b+Jjvc7msqLJJ1uwBLx5eYJ4mPD094enpSbdo5B3sXvzsfASSBATa/u/AU4XwP9OU0Zop8IF17VkJxkjyBdERXfZDDD4NxZ1SDa7zlHBeFnzz7Vt8+/Y9Hl6+xvv3H7CeLzjOB4+WsrHHv/EajAJh3eLcP3etv+/ve+u893z6G+x9bOf5uQh2H/QTGOHhU2txa26DzOJ/jSmk63voMAV0eeZW3yN8Y5A5xrhFOMxhcw+hP6OfwzOb8e+NYTtuXzeGO+Fc7a9FihqzEp9RmU3+v69H2/L53Sgk/ygR0pTx4uVLTDw5PrF1qLW6cY55LMc00JbGoGxykjifJqP9MD4jiaEI3cGrtablTFPPdhbnPy6i8xtbuBfdDDyA6rqRjoMsgx0BlpSxr9dOv6y8CphdB0AEZHUasPUSw84BtZ7VaaziUld8+HgWnqcx3n644Ju3T1h/PEamcmPBlSEdPCEaMU2G6TKWycpxAiZPmu5o4LfVmd6F0t657EeIeMZAWXh43EU0AyQ27mZcayLZV9FZVBCN+5K0vFxKYrC2PhIBR/EpRKI+B3NovpwvSFkc8kX+xeYUj+dBsoB2WDWeS+BPxinl2CzQRsbcqqRnzykLXOu6+bFzuV11O/qbwx+LHtx0YYmS1P9dqjsV+rj0/BifzSzGcWqp76l27PLvBnY7OJguKGmUeJbgwiSRn1dnTNudc/J5Oc+uexz5eMMDpCHCBOrlZ9Bhy3Cy8UwkwgFSkxI+VkaHwmTISn0QPLKdSXk4n+6424M+jLoOquuFRcZwZZu1E8r0EUkJUStdvOUBWmOcTiec7g548+ECNLExmfVsSkkzuCrfkTMGXM9ASlo3e5pAkExRtRTHtWQBXMNZG8dh38WwXN0RFEiaslsNo9OEeTb8RB1OfT5NdViEeZ4kG/W6Ijcgt6x7ps5tQ2lmRlnX0HagMYCWqtOzYCxTpL/6vDk+7umh5IxWpz1x7hT2sBZGzsA0TzjMRxzyhGU5o9YZ2WRUlaME92iaeJIgx1YKiMXudykFSxE8kUhTmBMhN3iQrCylOC6NestRq2HnKQzcndFs9G4/DXSfSOTiyhUFLGW+UFFZ7Jst1q23tSD0ekXNaqIL3z3nGaVesNZVWmMp3ycOzxBH/CTOXIUniAuvnRUGJ+gZNVzweXzuZxvGGQrIJhy2Bqo1eO9oZDWU4OZJPSdKELwYl8tFva5leWOd8XUtYOo5+Ws1YmBGNYk0R+oGbNfPhUsEkeye4PG6XC7iWa5pFWoTDysbp6deLwU0NZRSvR66tQ1AU68Rvnj5OiwSO4PFqgRomsLYhGTxrjHAMka+OYNI0Pq1HJhOGGMb5G992mtBEABIdMLEhN/89Oc4HY/44quvUJlRGnellQmntrMBJ/sf7s/EI2MKJn/FN4BjEyPSd2VHFw/6InhD4bsxGL0Vit+o80bDgGPPwymHA8pWqRkFhfh6Z6TMyLTtYsO6bgHRtZHGdGGIqB2UsPZeFIyUMRwFiHFd5RUakBIopExXDztLsWnN2F40tnRU/X1WRseEmMgkxWcZ6izJTUr9uXCDzlzpJsmZMEWMLKS125Fzf2dQgCmHMbRrAwOGdN8bKOnLC4PhaATa2St0pqXDdCf0lvrIGSFngJoyJWaoIzeOG8NEBFDTGkPOGDQhBCkwQE2f1WElSuBESC05U0VJ+jXiZ3BmxMbOUiJCTgQ6HNxx6el88bSJSZ/rxmyrsZW1LmKoBRKRxKTMp+6Dr3rnPF2Ac+gJygcgMIJGkMNZuYLv/tKwowNCjIJVPGccWFBSyPcjFca+gwe3OGg7hAHtEK6g72qOV9eIFyOe7Gdu/G41z25eJvT483E+GxxChJQz7u7u8S0zmJvXpqrKrHamH36WB9oR1oQhhnVmxpQzDscDaqnIoaxKY/EoBME9hodlp9i6roHjuP6c0VWB205Hu6OO7gaH/Q33RvJn9zph8XWPS+34uNPl1iffRxxw5nZvelMDkAXB6MYV927rEe+/daHB6Z3hFb0Vz4kcf+60LZw/zwfC6qFp+No8qDZnNZ7Rjm83c+LxbzTGRSXVZsrXz29O0y1Fup1v369IT8P3PR7y1nWrjdjn9RA7szP0w+MTCPOQ9Hj6mcid64jCnIwgOCjoh81c7ERxk3TDgBhmCJJmLynd/9WvfoW1FJxOJzw+PqKsK9aygtXzv6xFhCGZ6B6p/S/X5VuxDx/xOSbuqcD9SP9LmmDEP8Ptbmz+5Pt2BYGeuYEadWVMP9iBHb3ueBCQb62Vg1Zfp2G8G5ppArKkQmNcNFr64f4Bb9+9w+VywdPHRxxP96hlwctXr/G4FqmfrQ0RRF785uvf4OuXP8HaxCiY2PrpB3dAFUQDjbLMGSnJf5jhTsKuOCON+Fa6xKotEsdHiiKOL3sGyXggCnSpfS2OJg3NvxMIxIxf/fwX+2v7mdeLl3+oRtGEygloCUBCbaJuSJlxzMBxbjqf3NOQc0PjgkyMeWIkKihlweV8xlNtmOc75MZYnha8+/ARHx8XgCTibkiHyU34D4WllKhn4rD1dHqtykROjp8YkhHDnNqnacLpeESpa6drBDcwdEVTUMA6T6I0IxiJB2UiNrKEjU8viX5q3Risv8f68nt02dL2ye8CFiOO9tGEcdlvgmCKlq4h9DnGFI2+toA7MEaR0tvVNJiG/geHYe4OxHF+0gHUcbHBaiV6dFoC6ipldcx5rtaK+TDjeDxgmhLWS4FHdhMhRpmJHCpBBVDYYy5IPDkMmGG4r7NElfucnrn2DGVDdJKOKaUEmiekdIdpEn3U09OT92lnw5Sbe0bl5vhGYYjS4Exg/yoRuIryUtoVAE4JbsSIBnfpvwb5RksSskTuE/X5zfOEZVnx4fGMn/7sF/gHf/Z3xTC+ShDG8XjC09PZcXDnq/Zw+Q7+/0zm59ZznzLo7n2/xbMZL/iJkbj+b9vu83PZ4dNi1zuw9Owobs25MxDXzw80pMPxnkF5m0WPeT+rgUT+BZ4UcPjxETkMf948zCAcf3dOYyN+mMx5ax7Dvb1nBDG5wXbv3Vv7m3PGNM84HA6Y3hVMdwxMsraHw8GDs0otahw0QyRfHQXTN/Vzrcb+gT+StqecUYCQvSbIXkHqYL+j/L/+YI7uve++nmIYN1ykaxAFZX1T5DfbKNX/MUbdojWueybsmfIkISW1zTlZNhLbk9aw1oLH8+rtPi3Ah8eKdR11661JndfGVSK7r46xTJw6JPl/HR0o/8hE1xHjLv5RXzACLBrR3+VxvaMepsvbHb7thu1z3OumPK44EBPWssUNhC7zJlgmlpyBec5dVtInzChHLJlacs7Cd/oibM6FQhGHPe6BAJARsukQu3NizOSbIk5lmzt3Xkf3O3nZy74nUd/rOgQOJWU3S+F/nAfru82bhz1KeAPbynJLG5o6PefUI4u366SLkYhwOh4HWUQix21fge36Nm5S41iDiAQ3dMcZh090PQoANyzKVHWW3i/5Xtn5aqln6Nm7ZK31fFgmK1bHitTbGU9NX2/W9WosMtOyLMiHWLqJgdYwHw44zjMEbloP1mKWrEG1Ssr0xkBGhzvDLxD+LNleKCxIxG/InxzmuUcTxq3rdMpejY93Pbo8a3x2tBHknHE4HAyaHLZFXoE7ZZizTynFM+5FPjLyJ9LObZq0fdd4h205nfg3q03GZFJxWp0wTzOOhyOIEtZ1Ef0mmz5egu7Ak4J+gtRxT6i5IqUZ4IRaCaUaPwB1Glc8r/Rp1MFjHH8aeVoi8qBYsy0J3TRi0td60IkBagDvTiVVnXeGyHwGUot4whx34HSC/BSy6Ka5oLKY3AXjJmRMSCSOKokluI9ddqTdMX7q+mzDeNENLyG9UGMGW51wJpS1OLI8HhOWZQU3FqZEAVfeT15PoNaKw+GAWru39OGQ/BlJ9ZI6gOqemDd5TyFkay1Mc2uSeiHWFp/neajxZAJLWcU7pqwFpVz8+XVtfsBSSpImTdu7XM4oaMAPX2Oej3gKm72sCw50cAbMDpE5DjAs4UQXaFmLWQmdl7/OIJF4JgnN6CRfEJqIp0ySUiFpKhcuFT/7y3+Gw3zE3auXYFNqjBwIBjEk8iE7tAcwZix80b+RB2JrdcOQXD1DmztbRnVzwxkl7kjaWAFjdEeEqkjXCOkew7idamDG9gQcDn3vtTUKEWEs2CznvoQy3r9iPOiqH7ndEa/X5cuSRl2QfRgA9xR2WyLWDWfBeGj3A2NhjJIZShijkavLQDzUzjHmxIgtIAjU0qxHASQuVmdQhEAmSr7fBNK0TR2e7bmR8Q0sGu/AAo37vd3FDm1jpPpAzMEeVW5ejUKMJGqf9PxVWJq1Toy3BIk0NTqTMKymfEyUYAlSKwBqFVCBxplwJQoRRuZpxouHjLVULQOhQ2+MxIzD8aj4tHaMQFpvl6DKqsA0+J7B93gUQOAc27DUN87HIPR81hWBmjqvfLXxoU3uhsuYOeJ2+9cD3Gt+aHv7tuHGIDREFmIrLrixAXYOrzu7umPngPVdYsRCoE6H0AWcxj3V0unuZFMYMjXYHtuZ8s57tqRxUoaDG2O1VM/osJJSQqtVPZPJU1/FM9QpW5ivCW+An5uIQ+JAbNzOmHJfU/cIV0IxoAFC31ib8vhRp0n+uQ+QwxrofjANc+t7ZX1v8fxOlMCzl+KOK/jpbUa63vXWbYRfP7MAYlSHTSWsw02hbvgScKbRnvCQnR87E47/0rVydU9RPcz1Bi3evuc0WWkAO7yxC0DGH/QSPrf7vPW940Vs9j5C0XVUk43JeEEfjraxiwO4Cw7RMPXv/Z3/C57yeXfswDX+ikaZ+vtFU+p2PsRp9/eCzf/q+i/quk0tP5eOfu4rhPkp4e/+H3+CrXF8kCEc2QAg9rSG61pQS8Pd3T3evn0n6U1BKOsCcMXLF3coH85aWgu4nJ/wVBaQZjk5HI/gNKHB0sppX4DKTn2kXCNtgNN7FiFIYdpwg2F1Sftuc2UAwlopXtieQZboCeepVanVWgWmDEwTUp5Q1gsYGa2tuDzdPpefcx3ne5+W8JVCC20crDQhU9bxWbaNptHYDYSMRA1EYvk/l4qzOr0kAGVpWGrBWh6xrO9RygWtatL4IDp2mkgdZ9jPIU23K/WdoJozrvDAh8OM0/HoRlnfr7jUTi93jCpkY5Dxddwv7cQMOVvjCmM0HEP1BdEwPvY/rr3+6L81wKObjPY5fdPPEd8Cknp9PhyQU3ZdA4c+TBZj6nxN1IMwR/VtGKCO2/rJOXfeV9v2NOvK+3g5NzIjPTsdkojxCfOckXPC2oU8sCpEfZ+VppKW8GJz/vW11MAIo/ncwEiwkm/Nz+bzNCfS6GgwjDxIooQ0kWceaK2JQXlDt/d4DWarJ58CDPR2orwm+88a0KipIh1Yah+T4RICqEj0m/FWtSZQ68rQbqyScV2WFb/41a/xD/7B30dOGWW5YL1ccDrdibx5fXA6owX43kZEf4vn2l43eRC65ttiO8M52sqPN65P7ftgqKT9uez1L/dvt/spfnOvv4hT+m/X7+8pZvfaivDE4YzF5+Kl6mcYDQN0fcAYSgx6/12Wu7WnMoPAKHLct8jJjmPc4tnQ6DCG7TM38fPm+VEm9UVEygnzYcaPLhPyzOCsEYezlGgRBxL2YKXr/Y3cS9e9Gpx66QlHb1am0MqHQtd/M+8dZUHE1YMsAtbMp5sRuRxAsJIT4xM6KO7ne5BrEbbR2hOiCdLMkj4aIaCoZREDmb67loqPF8WZCVgb8HSpWJZNxLgFyRB5euCrCfHmFgFdoTAukLBtPGQsHRthpT+d5+j6j/3zY8/733C/OS3qvYicVYU/aAJLCM3GLmyMRJJG/avXhJwD76Pt1SJrm8zDU2lTosF9wp/v4CpwMGaXEF2hzD/bqjlPJBtuxuROf42+Ny2tIr+ZEyUwHv+u6eQmQZFmo2Ai9Gxu3M+IjWKb2cbn4Y86YDr5Vh7CMnMmixqnDqN7FIJInMj6iex72P83DsPOoJVbijqj4dFEQO36JTtHbHzxoPfgQO9Vhm/s9p/efdTfCNyS6nq5IeyvlV5RnuwKr3S4uz8BHz5+wLIseHF38t9sH6cpY55sjSSjWIcXqyDAzvv0Vey0kRtLiRflZVq10g/mVNMPxhbPx7/maHBNN3foHvq44mXOpBbhbpk3AAr8r/KctaGWisoVVQNec5aMz4bzrfwzuLNwWz2TtRv5BfsXI/U7/5Y0qFgCEygRqpdYFrvi4SDZvRoDa1k9EwP5OQCIJ4XZDHACtQpKjCmfkNIBhIzaLEM2VB5SOIt0BLZFnV+OpQb8H2xP4eeun7yOR8NB8wPdWgE3Qi/dJDAk5yV3LMXyj1vYN134FstDajqHxozCWmoKkMByB4kECREn4atbHxp2YOe563vVGBfDsHizzvMBtRas64J5lpwhl2XF4SDPLMuCdV01//+kKRgZpTWtNwr1OGMsy4pluSDnCYc8e0qGaZodiXuKViIsZUUpFYfD7MAYr9YYra0Dg0lEWJbFN51ZBKTD4YDLZcHpdAqMaUKtRQ3zyQmRHUCLxEUTT5W/8yf/Gv4/3/1Sa5TL4eOJ/QAt64q7053Bk/8xpsTSoysECsgpsqUAyB0YYXgUJCIlEjEyAa0WTJTQGlAWxl//5T/BH/3Zn2FW44etB+thcKYXQAT7K8pDm3ty0vptI6hAR/cDsRiJGfVJ7V9EId26Gb4DsdkIwb4u2D5iCDwyv+HThmn0uQHOJPPVe33+zqhHZvvGIdwKkp8UQu33sEc9QrG3Ye0mJQz212DJED2gqSw2LqUj38h+z5QyRthdIGUjqz1FRWeujIDJe9sUhfE3faL3Mwg89oeMHfSAb4nOiCaqyHB0RsNT2sh/OhO2hWV/LzIttv7jC/GMENjTSdtLBtfmyCKerw1gIzZGMKOQZko9qwVtkTgAUeu1LIk0NQjJ2VcvR7AwY02Jn4kZ5o/paXhywssXL/D2/TsZG0uGicZS8qGmOsAmI3gJKpwzANFed0Msx7Xp3O14LjbMHLnStu/1Zut3md/rp+yM2Es7Z2d7Pu35Ie8Zbb4HxDAwRWN3AyraGd22q3FOO+tnZ2wfNfR1jZ0Hxwk/BwqyzrxguN1HyJJeyTOlDBHjz+FnO9OBhsR10s4bIJlliJCn7BHjJkwQ/GTGAQ9zcWFNcVLvJpzEIEA6k87jusKpqZUO0rtBqdjp3zVGGT9x7B4OP9xx3dWeB1i8Xlu+/hoEN99WMjgNe73znrdosNSUEhA86nsYAl+TVdo85PvrR4auxwmIc5C1qc8ZlrbXrL1PK791eGF8cZxboeVzrqt+A1025rw/bM/sv3utgN0lLgJPPpetk+DWFcT2rpdy6Rs7GvIppSF94FM+42n+GxrgDoC4W/1X1///X8+fq79Vs7T9PBJxwzukaRgtc9flchE5iEkiyFX5Qmg4HWekxzMuS0FKGR8/vMX7t2+QUDGhiPHwdIdyvoijIDjwseNcTRzsaCpG2HBP+R5wPPUcGehKSlEoJFgEFw9dNXNmVpzfiJCOBxQwfvw7P8GXX3yJ//w/+U9UJmRM9Nni9u6VmT39Jqjzt9wkAsEVRx6VpXyxpeJTHlJ4PvG1J5pQa8JSipTeoYbpSKCnMx7Pv8H5/AFrWZG4SdQyFAMZnWb08k4DDz0aMxxruZwgmdqOpxOO0TDO0GgcclpqMoOlMXU5yuluUn5SJQLqKFPS3XYHd5PjAct4JW32tKSjom3rKEhAiN4ZIY8BUM7IU9bMHKxw0jN1GP2Q2oKE4+mEu9MR09xrDkoptm7oNZrNqb8n9TUsm1WkX2qUIIFdc4BMKYsyzvjL8B6RlDeI2fWiIU2c1pqkq8xJVFQc+FpY9L3y9RQjaaSWY0oKHSzntjXSczXyMszw1OXxusUn7NF+b1HlvkSjYfxJa44bjys11a8v5m50MZxmTgDQPRmN6gKnrQmPxhCdjAp9sifGDyYCUXE+1YNAEkmJLRKYTOhlBUut+M3X3+Hx6Yx5mrBcLnh8/Ij7hwdJ9avlVQaeaLM+z4kW20X0PdmKTp/g2faf4eG37b5F/mmrQLfLea1NW58/jpFv21PUX/W1OSt77Y96Hdrl758zEAz4hXqJSsAkloDNYzsQw7i81+fgbe30aW/2r/HzOKf4fZ/vZT/TV40MvY1z3Jv/rX63NVzNYNPCPBmENE3ILAp3i+JOKWGap9HRiXpgheskmTXzYJ+bRVMzqs0y0CHSkkdi5BjMXVH2ipkHBoY/0moZr3wPJV+o73tfb5OzrlbXmu1yEa6OvtZQJhdXk9WhsYeVZpZ1AbeKpM5US6l4XKrLIo2By1JxviybjTZ8YYZaCvPewkefz3iiNwPfiFWMdv1GhBuT/XtKoLFNFR47Pg/PuC4ycIUeBd/AtWC5XIa+nde0RWWJ1Jwm4H/6PyLMgWexNeEm2SXBKm0prMLo0MBjSiBh8mjO5P8iUDU1vKbcZXSDb2KD325IrK2qsXaMgO+lLLrgzXo+GBJxK3yCRKgTDIZ17YP4azoE08d4hk3TA4Spxvu2h3YOLVKcyM5GGF+4yMZ/Cxc5CjD+eXSSic4X4+c+2uYZIqC45Jq+2uOWFNrW2cuf2eLEYZKdz+5ACP1sfAHXfXoXR/p7Pzng3Udxwn31+vXwlPE682F2/qRnGulrIfr8pvrjUS4a6BwkE/K6Vv9dkJA47PY1uW0Pge1x04AN57nCX+buWMCs/HcfS6kVy6JlmzM5nLCWSWJoXfAmes2mmV9bkXFLtPuIqrbb4/NDp0UxMnzf4UrekQzVqWedZkatVuJowul0wvF4p3bSgsLVHSCEHwDASfmwBKIJxBmZK1ImHA53mKcTEh0gBgKJMG83xmSTjDINpaTR7KH0heKQDo9QABfmnxD5Sc0qwCoP1grUBKoN1DQyPJmcBm9fItnViJ36fWYpwyD1xAkpTchoKCzGb7dNkMg2pDXGRbIX+GCGyps25k/zrXZ9fsR4bWCocuPuHqAk0YcNmJBQljIcklqLImIRPs7ni3gI22ISoRRNJcUN83zUqO2KmTKmKWvkN8BMmKaDACQzcppBWlMPzMh5DhhW0pwzYwDcyJQJkDKAhMtlFaGxisGwVkbO8ns8CBLVLobydV1l/5KkzSt8cQJSW8XrL1/rgdQo9XkWr5pEopEPxNo9H0iJvQlQ6IK8eKEomlSk3HQtjOBTgqbAEESQ8oSJgOXxI/76L/8J/vTv/33QNHmfcIUCeWq84YpUK97zz3Yc9DZz/7zzyhVIhrEP91wwGt8g65N5+MWR66Yfa96YRaeXPq+4B5uHAnENYOUIYhAUBoTR14Zb68/4bRre3RXqArMOHmHQ5uq1HlwgV6Tj98LacmciXQAxtnHgLZV5cq82O6sbQSYQLKsHIreN6dnOrZcGMObMunbliWLZjjTJh++uIdq+pZjNoWaIvG4enzCAxCBGkBiBod73Y61VMVxD7zdlDCQVS1X8oLiq6RorXjFHBQqMqPVvjFGHD1JFVR+dERphgKxtm2saBCMTIlrTCPFGzjiVagQOvk4SwUDatYzzcJhwfzrho9bbM5xikSp9rDoprwsIP2cGn6NRV1pLqcNNnLd68WyONXXGzM6kMfMIt8Ma9HF9gshxaIsM1oChce+BNt9tRgqXLpQhtBHZ0RtjCXjpWkrtgsfecNwhqnPzYTEGRHyNdH0avZVtE0SQbAFZPEgpqaLSPIlbd3pxr3IzwLPBqa5rHIDuTRcmbJqMRFm8NDVrSx9POLdhOygw19F43WmHvWB4MhjNuZ/+bljuxslhfMrdDXTlaj2DAmlYyJtvhNsBH1N3jnHcMTQX9l1xtxgB+vcII7vG8U3/poAR/G5D6YaVAIrj2kT+wuZC6HkWBylYj3JQ4GyveM8UEIMib0MfR0WlL6Z+3wP6/flf3Yr02x4ZcB6ucFWk/7cEIH+S9l+Od6NAsYdBRkWYicvDloCg9MqoSVwvBk7lNLa5WQ4TZIuVM0KEOx1b4B/+q+u/vFekl7T7y9+gMb3KqfXi4Y4rtl70cGxk+MWUB+JwVXBZFrx4eACI8OHjI87nM+5zBnPzmsCJCK0WfHj/DsvlEXMCaluxrCsKS01pMUT38+g8s45DY52EdzQZEMZzSmq9RugHiYHaqii6t3y9NtodlAO/x1JfL+cJlDNomrCmDDod8I/+8T/G3ekOP/3FL/Ddd9+BkZD/lobxw+GlOBKIVV8id7i546PJ22sRxxhKQVlBDMoNU5KICam8fsJ0Ksj1jLV8AKaCw7RgeviA+/oOrf0ctT6i1Yak85aq5sqHMoNL6w5gZAaaIAOYzLCBqdqkZvXd3Z1kklvPMOWxlBvMg3y0rxA0I7DMh6McaP3qP1MIf4puRNllT3cAlU0sFaI90/S3aZpQp6lntbrRPpGkup8nqY1ocn6tVQ0qYkAmItCUlS+T/hKSp3If1kN5Isk0JbBh5egSZRQuV4b+Hn1WUcpyJa+mlDAliSqSQIRgsAcAmlz2Y+61vVuDfwYzpjlLJEtjVfarspIruAJEPSuQyWZbg+EtONi/AnfJ3QBwf3+PnDPO5zPO57NHDbU9Gqc0sbWIEhMqgKQqlLiGtdqakuqX+hpK2vQe4JHU8EYqE9reSyr17Ly3ycfTlNBA+PC04Oc//yX+8Cc/wuPHd/j44QNOd/c4Pby8wUNs5YPREHrLQG3ch7Gvt8jIntE0tjvwWDS+d9U/awmfz97j3tb23N56zn7fwy238M2e4fY5Zb+n4g397MHvp9qya5BO7Vnqjj0iu7chyhmAi9xjf7dxah/P2Ot2fN1BwfjFfd1ff+jTa7nt69ZaR52XpcqtKtTkLPTVspG22gTHHmaPWvMoVNU1xXTQOSeNtlMZLUkIZSIxSrhRDASmbvCwacbxxYt8Uc2QH1avRf0ZO/8t+qQE0SLJGTa9E8I+Wsaba+6ew29yiT6pG4NN5yPZBrsjVS0LwBZByTgvK55W66ICzFjWgg9Po2HcDURgcC0SCS0db+SwLbSMBtWRm9W5wORHXaNN9K1po3wPKIM8wpZDcxs8BWjmEisJOV4pZeRpQisVy7KgttF5bCkMUBYehEU0zhmYM9R5QvliZpiakcFgSlJ3uoqeZQIgRp6wlWQlWKU0rBnEU8iuxjYnQo9WTdep5S1CXDLiMNiMb0F27Gq1axwsMNoDJwDSkrdtaKfLjjJ+1xN5s9zLEwy7a3un/LqWAYr/ug50T7vgErL/l/yfGebDX+qOLdcAoS0GHg8w54MaWhz1L1u9t8knzfgPlvkJ86AjbeFZ3Udba4B0fJv5Kq85IvcuD9Va8fj4iLzBRQTBe4fD1KPBd2iA4UqzQUXcZc941tImQbDOW9vQiLzpaDi+4hcc1+vYW/Pa9fa3Z3HSsagqMGnpq1qKZHAuBSlnb7PWTRp0ZsnaCsaUMrhK0BlS5y+z4n7JlEpSf31vjXb4HaMro96q0wmqGsRbGatm5ZjnGXd3D5jnGWUteHz/EdM90CoDrPY5pQMCCROIJkkgrnjhbn7Acb7HlA9CLbSedyKIXfCqMkyQi1gDazXL8Pas+Rn1Od/iVQJ8tIYjgGPKOKYJR5pwpBkJM8xR1gz4QEFKk7g7sTk7s6RL172eoCWZKKGhik0YFQSRTabU2x4dFdRxR3my9qkaTeH6bEl9miaJDAdwPB49Gvx4PDqTMk2TpqnCgLyhC1/UU6lq+nVjKmqtXns8I2N6MYkhXftNKWFZFpSiXrVZFOzv3r3DixcvcDweHUExzPt2FKyj16CMdcblcoEQheRpxEz4lfe7cdNq1Xg9MhalCHPDP/vP/2PpJByIRGb9Ityf7vDu3bvAFMlPkqarGwEZ6rNGAFEGdL0AQ5aRgdIDGwSZrASlqiIq5RmJGY9vv8Mv//qf4w/+5O+i1AqQ1YvX1OswIVcHF5kU1yj1390zyC797gghMro34Cky1/HaVcIa473tMwyZbQzht5EhDzxlnFhYQ9uvQQgA3AHhOWFoQPqbKOn43O79+GXjwXclSG37VyQQvX1sfwyWh61kTVGxMx/2RUI3epsg7TAXosQd6cD7MkbMFVPKKV3PWOBeUIBwg8mYqLjN0H03hrL11D9rWUGU0KoQxEk9XOc8SerNAA859fRYrgwC+vkhYJqyw7mloTcFWK0FoIRaJPppLUUVK1WnLYwAJWfPdabG1JDPWaLdzSlG5xyA0+pP2TqkRLDsPFxVULNohZTQWu0EmZXuoAlFrHCFLyBrcH9/h2VdJGOHwWRYC1kP8k2zMdpze6dbd3RTd4g28hq5kEKKcPrjnVGyszbWjw/N7OCBq/vh58CDYYTErTAZBbKdc6Z7YjvrnwecscUdcKFv4GPZPENjJ/2hKzwTmzc8DBrSKA/PbWVLHSe449hOt2fklLHWJoypRlnJ3zBGhxX2peuGhLFbpwnoe0kkHsekbTkN25tjaMeeDzd38PD4ve/sNZ3a/XxjAD6/W6Cy7dWi9QJJccGGaDO1wEDbmd+hf24M3/TNoXUOGzDQQGzmG+gmx8f08yCCReejOOfQztDe5t44YN5sRR9ff3zHwcFmOmzVdjOev6LAthXMnj1n8e9m3J3e7Tx09dLeoHZeC33s4RP7LvutzpPcegQj9d07lRP+7X/23w9tQryumZFTQp5EgHz39h3+8i//Ce7v7lDWFcuyACwKgFoLSlnBXnA5lCJAX9Pra3Pyts/tvLfbzPd84vtffZx7qpa/cde7+2rwhoA7+1LcfIVC937WxgG5AWToXJ/V2sRRaLzqZnMuTZll/fzF//CXKPcWgRPfGxm1bjyGITSXVWpruKxnfHl8jYeHezB/xIcPH1TWkawHwgs21LKirheQRi3V1vDm/Tc4l4rM1MtzOAofV29prI6TJM5fBq4cVm+74CmjMKsVbMOE+vz6nIW2M6b5gLUKH1dbww9+5yf4gz/5I7QXD6DTHf70X//X8U/+4j/F089+hvePj1dr/72uTFhbQSvqSa9Xa5AIJIjjJlflsxogaecLgIKcKkp9wrpe8HRe8eHxCe+efo16fIN0+AhMCyhf0NoZND3i1avf4uEOuBwOwFJVdpC1JU1S0eJZ507BBgMHxrUzY06iCceD1Ky+nCv6GWE/KNZGSh3GDfea8sMuZonaBzNSLHnEPVIqRgcbvfNIxE3619Hxo9NAUboVpyUuS0Cc6iUSr69BnLP1Ze/VWiV6ufTUiiBC2vB1yerjkhl19qOc5dnkadJbyPzDLSg9RagL42ANKNjhoZOkJ5zngxu7XfHJjMpQJ42APxDmDsY0zVr/ryI1Oe+iCyIwpJ6iK2PB49oGWNozwsb9cvps6Udrhyv77XQ6uT7Losf3DJc2xxFniqLT4MxwnDxvey5121OScn8982BFKa3LoOjGKNdPKS6XdszYQprhT4wQ//yvf4a/90d/iHV9wrIseHx6wuHhVee5HYdH4vH9rpuk/b8kV9TlXe/Z+P259+P3qNvbPrdnpLVrizc+97oFyzGKU6Ch7+MQ4Rlh9jl2DPvzff653vbNZxFlkDis5yFnb32fG5O1afJqxAemn8k5a0YWKd2Z1t5eThkV1TwJVO7p/JKtW1SkS2YzCVpKOaGUrkuyc1tL86hrcdIiwOqk7k8cijBkHMzD+qYkPHn1cnYKc0rOB17H9DkJatDlYU4YdCtyiUNSpGniUNGaZdTR0qOtqkEXmvG0gCl5mQhi4ONa8L99+rgzxwZQUvpOYKmlIUO+EgLCJ9442Osb28s4YEbPgEMpnqWwn0y9tEXj7nRDvSUe+vVFhuF5Kb96kNI+rWIK/IPrBVQHR8qnpAQkfcxYcwnckcdrY1BqkGBIGXMBY4JmGwn7lnPPZAMQpsn2SgL5BM2Tp4FuLDYUooSsxvm1FHDtGW99LwggJB2jwHFOCdWNoX1/evp1KX1pKatbI19z3yCW9iMMm7NbC/oc5wnZ1lMdC1Lq9FNpaEpZ1RG0gZ7e8T/80xX5v7fi3/+PphFyAm7sjmpW6jKcB3APxjDZxWh7Mn118gatTM9W/mqtBwi5YbdqSZsk2XzNOeDqCjITJfLxdRnVF3hXbhReV+xpWzxMRJgSYZ5ndwiIODwaS80gTht+sf/t52csg8Rj8Cc67t4zjvvZN9nW+BYIPu48VGgDEgyQiDDl7NmApmnq9gEitFbdYJ9JHAtBGq6Wda9qgRigk2c6FNjTALyQNWpvLsBIk1NKwQ7Kfg8QOiKOJQWtioPR4XDA8XgAGuHydMHbt+/wcHzpddT7LhOkjE8GYZJ/LPXgczog5wMoTWAODgnhbAXwUvIzyibxXAx8dNC92bPxr1zt6vcvTvd4dTrh5fEBL493OE1HEA6gnMDQdOdgIBVUJlRuKMHm1MBo1NR2kQCeJGtFaiFzgNUYn0Fej132Lmugl+yPzXWocP7s9dmG8fNlwW+/+RaXywUvX75UL2dlOmrFZREjc7wGI3KtYrBtDWtZB28cQ/7MjLVVtPpBN0g28XQ6+oGvjZFn8ahNaUKtLLVODHYYakDfSUsUhKxlWTBNkyMuG+M8S3p2EZ6yG+2tNvk8z/5sxgwQoZTF6ySD2QUhu0otSDl1o0AAPCLydAHz8YCXr17hkBI+vn+PsvCgpHGlgymP0edsySAYSl3AqHWVWtOt4dtf/RIvXr3GD378Eyx17XsEdo9EmGA28sbXl5+88ICNk8aITxn3ThOhC0OO8l2NPXtKiXDtEYWr8YUh2vbE7/K7IRJd461hOiBze35vLj5G36sRpW2X1Oe8Q7z25ru9ZwREEPlG6clxTK0Tf2VYGEbUlShGxKfu8RY1zd6eMfOdIRiYJzYEqoySr0cn6qZwtfEr2upx1QZCekaLExARFKQexwSasyjU5le4u7uTVHkpI2m6Qhlqc8aEm0W3WwaLUYliDE8mhDSV8DNPFoZNEv1u+1m1jvKyrHg6P+FyWXBZV1S26JSEnCZdH4MjlXKAECHPYZ2UWSD2KCbZkqiEU4KbM1KtfuY8fb4yD+IJJ2uR1VFH1p3x4v4e796/V8ZW4SLK3EHYGBQNxmWGPTPDnDN6jGGv5ZXNCdCDERml8GvHQwGmtWEDOJnr3rkIPbknsePR4ChCfV/GNr3DeDvKTOGZ+MM14pT3whg3eO1KGNybZ+SCAzO/y1hTeGcYE4CdcTSlVfM8u+eneRdHhV8cmo1duWp9hgYBRJGLe+kRM/I0i8IhkWdQiUZL72Q7dF/m672+rbTRvda1kDlw366R2+vbMqxR+OAC9TCCzaBHXHrrivRu25bDg0Xe+QJft2O8hD8ev9tDQ+qiAKt2Rq8W+7oj2nlkS+NvvDm+tHXi2KWK25a3FBT4rEXeG9QA/tfR6dH4cbPr3fFj98HBaaSjn88eb8SLQ6/MOJ6OWC4LuEl6ZY70+mp8poAfI5nqWvCLX/wcOWesZcW6LBAFjtB3iboprhTgOIEd3iUqSXns/nq5DKf6nMY12Oeytk1+ajE/74qK5+8DWt/3Gpqmnft7fRv4XNER+U/kMZ3vcvlAI2G0DjXRpuPYlqMF7nwibekTX73nTjksqkq5PQI6Q2DvfHkCg/Hw6gWezhe8+/ABl1IkG5cqVBlSqstcP8QGmLCUD1ihaalDhoNmZzf0tbaKiuy8T0rJa/Z1uXIEOHMUdg6BNjDJ/VwYL9tAWJkwHY+4e/kKf/Anf4Q/+zf/Daw54btSQET4nX/lj/Dtm7f4q7/+a9B025j5OdflUehzaRL13cDgZLWioWe84qm+R1sral2x1gtaeUIuj7jnAtQFl7LgaS34uK54e/mIfHyDL7+UWm1UgXSpuKsX/PgHd/jyxx/x4buGj+8Zx9JwmBMqA+Is05DTpLJvHc6kK/117VgNp5kICxNaYcxpwhf39zgeDvi2MS6cYaUcpF43aVp1OBx7xnUWmTcRYUoZtayYDzO68lCAutTmirto9Mo5Cy/PQKaEOUvkc1eC9Xa4NYdHAotCO5PDCzPApQBIOM0Tlif4fAFx/Lf04jIOgQOTTYjJlXwJamRWxbC9lz0nt9EFVSIR0CPJNCKQGUBGaxlrEaVT4+o8VC2skUNHcXLghlZWgBmHeRJjfakorYJBSHTAcS549SJhpgPQjgAaKK/qCNs0Y50Y9MsqZfEk7XtGyhkEQqJJVjA1d+wQR3JCg6a8b0CqIrVGp+rmZOe2Y9voaKhymmXM2lzTJIo2yglPj09YLhdto6enlxsTrPa54ACTufsYTN/TsyWQ1AunhFqlcIOp8AilJ8+a7IyIk0A3+umZcdhtKuMm5JTx22++wTffvcGLuwNSAp4+vsPrL78c4MNOIqVYH13x9UZu31s/WXdd42d5oGu+HOgGa3fmQOe7OfbFbJ3J+dsjTzSYCa+GctsQqzUn5SGYCND1FPqXRsWuGX8ij0O0JQjX8+8yrMzJaE7fjfGdPYO+pG5Wg55Qw45Dra3NdJPiMqGzKvtzXyfysRFaK7v9PndtnUacL+Vu3DKDyi6/2oyn6Pw1M3oWEd17o+fdEBj2Xu8TA1SFFjcWXS9aww9evwC/X8S5jQEiyYQ0z7Okfo79K7xZlo9OLQBKM0gzZLBmy2NINF1TxyKE+UuQg0TBmbHJzVlkUddibN7qCI13Go9dcGzBviNjbKOLLOT4/ZrR7CdHQNpkTAIhd3zXWIxDDDRKyGhYvgTeFNGZQUs6MBiXAnz93bbskpxfAjTDkPQtfWr6W+dU++iMW9XagEoTjKeE711831IjeiRlSlofzeYfYTwDSYpgcBMDGCdI1HlttupAykiWmjdlHDQo73J5xPn8iNYq5pC4rrDABlpxfJmYcQLwoP4RDYb7ZGxEGWBS/YqVdmGkpPAdIpgVAoIc2bPIGi8bwcGeYTXMghKOxxNK+eCGOtELBjg1/sGNsOxymak8aIDhBtLijlc4Lf6HDN6aluwZeXTW52xdFBxl/omAlIRvEOu+Rr92B45rXMzIqeL+pI6wuqfs/Zo8odk21XBGqcv/A54h8nvyOikPI3ig12bfFVadrin36nNsuqjEponfeZ1lbywzU1I8UqwdxQ1d7jKAITAaSmm4LCuYRnljxYQVDQ8PCcecsWACIyPnhroKrsuSt9ttYqVVHDTatrWGaZ6Vx6yYpgPAjLU0LEsBszjUmP2pVBmTZCXWwp66ZKznRY55d5bQVF5CumMZUUEMgl9Ibe+JNAi0IhFhzhPACVlxT2sNS1kHnbnZFizmKjGkNGirkvlaHbqr7a1z/ez6dd/f2pBqg1ZFEEOtZpTOpJmbWkMrBZMG8/aa2uLQXCtrhpMVj5d3qFg88Le2igkVTAuIZqAddJ8bkDT706WClxVlvaDUBdQqjgzUBEyN/NwxgKLnkRojNYCqju0wY84T5jQh06QYK6HCsjsA0GzUIp8ZfRTeVH7OEqCXG+ZjxUMmfDnf4WW6x5HuQekIyjMmMvuSrCulg/DqrYBrQeEizrskeJvB4CT9cAUyJpzohWYns9ro/cy4swI31Lb2vQp45nOuzzaM19pwPBzxcH+PdV2RSIGySN3ueT4MBjpmxmGeZUNKEYSCXs90WRYwgFcvX+JwPHqEJpoA01qKe/JaDbJpmlBqxen+DrVUSWuhAsP0zyagAtM84e/9K3/Xme9u6Orpk1uTlA2zEr51La40nKcZDHbDP3T84o3CWh9dmaZWcH864J/OB9RpRmsVp9Mdpkk9nNRrSLyTDxLZ4+MIXCHk64tXL/Hq7h4f3r4BckKeMxat+8VgBGcmRyyeJcZplTIjBJRWkQkgLVb/87/+azy8fIl8OqK05ilRmZRJI2MeKfJT42dgRA7bx8I9uvH6zWvDbPuLRgSNEYiC3aaJ7TCDbLN5NTxJQJT+4nwQ5jR8HowMPCAgb3JnTL4uGyZ5O6qtsGLfYgpwQ8T9zMmTDUFFyaEt+92VTYCl/bLfmyKQFmuKY2wj1lzDIGiPz3bjfWfAtitExiA1xlqKCkRSR+R0OuF0OuHuOPU0H5TcyL2WguV81rQrLSgWeBTMIYhY5teVmy69yCyEcWZLwdnHbZ6jecrIE2GaJ4myzRnz6Yi70wkvHu5Ra8PaKp6WBctlwUX/ShBSrGsVuAOE5UCHV9+3JJ7LIEupFbzVahUjuKb84vCbO5iwZpKoetzVa/o4zzgdT3jUdFidQQ3Mp4+pM3CjWmJk4k350AXeiAs26vLAiBrzHS9XuIcOjDnyRYqM6wYneR/M8JAx3W8Ki+yvhTbif7czZV+P8cxtnzKDr9EhNiHuStmC/WsLG+GIbaPEdw3lzyg7SBk2Jz3qRWrvyfmpoayCLXnvZ9gfIlUQIKyJ0pKgQJg0+o8ZXSBB2IANSRzXQ2HCBAsVfva2fVw0HTP3zzd1XH3gMGQ+PLbd5luDvTGPSHoY6km6OSMUPgP93Fx16xPRz2kzqbgwYcK+P14kNA7acMC2J6M5iu83dNLGOc59S/W2M9hSyr3frun3977iNLUrHtZiQ9+s++dgcfPusw9avwjbxTs/ftYV6KrDpqQMu8bNvX0CNAqgpx8jAN9+9y0+fvwofPUqdeOMbtZS0FrRM8/D+enS7Tj83a2P891sNYdbVwzT32bPtwP6xANb2HXofmZLv+/lc6Xxxs01G4e4+ciutGJbOCGm0mzAKcJzJOWrkjsMj10EXB7oy5XTFkYYo1BaQ8Ah8p3WnrzRWsVSFqxlQakF3775DsfDCYfjEbVJmkozXHZ+gDX7jToBTsBSGal0D37GdaTvCgJa63wcW+prRlY6YpFmNqumChTXumymbvxYN24SKgPH44y/82d/H3/4R3+Mhy+/wPHVa3z8+B44HHBpDe/evMEvfv1rFGYs61aR/P2up3XV1LFiGK8oWMuKZTljWReUsmItK87lI8pTwWU5Y60XEK+4zwU/OkyYCTjXFZfSsKwNIMbdacLL+4zTIWHiI7gCL+5WvGTG6eGMPFOHM2YwG7zEKDoFwWb7vXGeJYNWfZLFoH06ShRyaU2X3QoQGa/R/2t4qPMh1vSWoI/wf9PwIw+4bmAwTOoYrvUpezi484GmzNzKTvE74voEpMONUZVXIiaod6rzZN6vvUVBse06DqA2oNWGWhtqY8f5MhZbM42wAHrZqNY8Ig22TyQ7cpgzTsfJI2niWsgz7Dig1qK6DqhCVOSuHGqjJgvbaUBLjMQCHZw0qsNAhwFLCezOFnvy+M4VdVFx3e23KWfgePS5iE7pOjrIDQ4Ys5pJKZqOf7a8hOxVDW2ZElGfm0TBPvGEaSpoVZwJcm1onjq301lKhDwlPD0t+Pqbb3D/+z/BPM14upyxrguOx7sheol1b+P1HEkbDKb6X+NXBrz/DEP2nKF1IP9bfjTqKHaaj3jgykD77BXOl7U1vGfj2MEVg5w2zn8Lg/vzjshjh5Zu+FD/h75GjJCVI64RcN3fZp/is4PTyIbv3T9P13u4u9YRx++M0T9zH5msCnf6YLQ1tBENVP67lvgyPQBD9FTUGFNK4FZVkU9qcFDYpyACOThwZ8jD/ZwyEgVjsTaQ0gQwUFGlvB7SFQwZQzdIMr7O2qv+tWdkXDR8ps3ad2oXmeT+y3ZbzIQ8XpF77PTL18JgEeoEC9FxFzTRQVOg3RB7wOMmlfowFsvkYgjEeNSr0cQ7zkhu5C9DgKpD6oRfH6Grpq7OhukhU+CRE2vmTHU8ogRKEpVp0ZPL5YzHjx+wLBcQAVOe/IwZzFr5RZBkpjzOwN//4xRgq58JZkhafuNzGUiJ1eGPkTgau21PwlzDefV02+G3Whssi45l2Ul5Qqqm99S1CDYI0xcCahAMZzHuQ2Me8IPxxPGSZeg8isGM49fNRvm5ZIaUdk3uTNdLjhgf4kO5ujq+cFGo/xbmYsEYUU86PriBpg7QYO7ZXSwzZnKw7bh+eD8ykENXPExkO6eu/7lqcXhDhixOxfZUY8ZZMzDHxEKsv52Os5RPpOL4yB8Ieln2vwEmAi5NuleWYl8iduV3icBune6SLSd5YOeIychpgsO4saBxzWwMqfNmnY5EB4cQ3Ge/sfCZpGd+UKOawyOpHUxxDRp3ePI4NnZeWRwPtX58ErrhZUnZjN6SmbXzYuYYI7bFUlbJQAUGlKdca0GpBVMDGhddA3HqSWhoIDSuYFyw1gsu6yKZPZqVi2Ifg+HDYW2b/tP1SIYf9X/9XQNw4UTgexT3hPwfkZjpMgGHPGHOM6Y0q8PZBCJ19UshPbyWUUrcpCqWw3ZTWiaZTYhYnJYCjhRYYwN83R4dX5PM3ylnTf1P6vT26euzDeP/+j/4h6hFPGNbqwIQjQdBooUASECiq03ZYWk+DNkZYmgsdWCINP9+M4Ru/JRsjtVSszQeTVNByuJQQMaE0+Gg9zrzQkTebgsLCADz6ejfCVoTGezEa8oJidQLi5vWsklgTEBNuL9/jfPHt0gJmA9HTdkmefFzFrw1zwc/NClJyh8iUg8SgCjh/cdHPH78gJf3D0CtWGpFOx3ckC+IqCPAKSesizgpnB+fBHC0zawUuFU1gDdGffyA3/7yZ/jdP/ljNAYyUq9DRJGZ6oYPWT4KiC0gdT0zEW0TOi0RnlcNjQjvb3mWeIj18jpjCBEhRowQeCdjODf9Gz2yZ24xYsx83UYUIvw/9p183h65r4wIbSYW+eYrlmDgniOCic90AeaaJRb4Tinr+TA4t5R048AHAYh7WiFb1yiUgXsdmKGVrRA1zFHGT2SIVjzr+hmMRqwGqzvJRZw2cp7w8uEBx9MR0zRhUi/odVmxrBXl6dwjWZ0x0b1jq0fC8lk9+lpg8noUbE8Jamtu40ogMcBrHZ+cJz1zhHS+qDHP6lmJ88s0TZinCfPhgMN8wGGacHiYgYcHrGvBsixY1hXLsuJ8fhKGwhjXAON2CowAgtlr0BnfGE+oeaGmlECtSYoiUmZFvRut9mMjiBAAwV9mnD+ejrhcVtTW/MyQOU0gHNQO8gOT3uHgBoyaIANjvq+v6CxhcGLnca/NkeMNz2yRSnw2Mn/oTBS253yYE8bfopASHro2W+qMuUeWxbNhzxkc9XXYU6zYenTc4PJsENo5rN+gbN22ZmMxOgfba+B4OmmUREPTTA2tFqBV8bIOdMCZ9huKkriqcbxEwLIuwNV4/VaHs531iLR8AxW7V3w9Guzl+/icyGVbR4fQiO/ddb/DWM37JAiH1iEN58kWxnDjDVjchbH+LRq04nhs6AMNieM0CbI/2PeAbpwn7ai79myI2GYc12u112ZgJIYzFGa4I3wjPHHVok1nu3VXz+2c6eG3vodboT7C4q21ioo1w2vbvkwRZdE25vzRlX/6FPV5eeSjO7WxKHTQ03Y5b0SmWOUe1cISDf7rX/1SeNJqAhUgqRUrals73HEf7bhgG15g89jutflt2IFAZ9h+9SXcpR77XeiGN+6ildy/NbDNPHWvJ6O/Wzq4xRHO2AyNDGdke6Z3p7JzzJ+jS3HcrkgYsAUrKZK6eMKPGS2SfxbxNOBD+CSv9yvgdzGKX7vwOM1PqfOTjdEKo5SKh4d7UAJKWwXemPHh/Ucc7r9A4guINBE2EWozXnRCzQ1PrWAi9Gw7zO7jY33XnL2+XGbhPw/HI37v934PrTW8+fYNlnOvi9daA5NEQwCQsl11RSPlwVLScSq/wgA3xpc//BH++E/+BIfjCW/ff0Q+nDBNj1jef8R8POCb9+/xF//P/xBf//wXmDmhLX87w/j79RGlrqhcULmg1DOelg94fPqAx/NHLMsFy3JBWVbUc8V5WdBQcJgBvDiBjy9B84REDcSEiRPuDwlffkH44mWSiOXKklY+V5yoIE9i4OyGDIeQQD4UXynMmLwfcSZBjLaeAp6APGUcDuJQX2sVXYAiuSjT3776uY7KYf81yCvXNGSPrpguo98nR03kJHMwzA/PB5OGrtPWeGftM7NnnzJ+3FOd7tATy0Bl8/V5Z4lGhuEp7crr7Gr6+FEPYnXFm5c/sT1LSeqdC/khiCePpKk8Hg6KT9rADgmtYk3V3o3spufpsqVFYgGk0UyGTwiiMG2NgAQkNsW79GERx80jefZ5lCunHxqN4/bZnGDm3I3Py+WCdV1FkYm9FNmByik/6TSX4PImiCCYb5RtZGjZZVAGY9K1maZJnRkycq4ohTy6zbLBE4ApZzxdFvz2t7/FT776Ei8e7kGU8PT0hNPp/kpnULRs4e4cnrkiDeDN4zcN3ztrv/dOPBNDW8wen3Dr3d33np1HbL/fcZzVfxjHLp2Nr6Lzgt9nDJ96dmiPIWdJabrwL/tz5s37e5eQ+334HxTlw3hi68/PabsWW/kztuK4IOIEo9/cM7LszdN1yK2J3tJlwI5XnF1kwVHrKrqNRAlNs1BGHOksl7FvzB6AIXyBBF5JGbCsY9Va1NwgaW0Fe0H3rpf82OxpnE2gi10cM/zM4OHA9e+DTEPxPd6VecKpCSxq5FW1fQ1GAbq+18azrAXvPn70NqKT0lp65tF++WIOaGZLB69GuBHSrvTPvlg0vm1wN8z2+kx02YTiUyrzJCBBsjvGkkPc8PT0iPP5DLAE0uWcfdhXJ4QEX79+yfi3/7up2zF0b0wokwAJgz1Ga0BKzbM3XuFK0/nT0JWfU1tbom1pCY0sJ2g98DBiQkfsFPiSZmFVyoeZDI5AjMOKCnjzVZOwcxH1DNbSsHABaCEGuqzpsd04vuEFI5z3du23EafbkDvvYXzctZDFw/vXNKiZnjngUlnj6HwWzprT4Q6zG7CPmALbi22yNy4OcOjYUHHp+XwWe1o0jKvO4HQ8qW1u6c4OtD/GyLtFWBMevWfXEV10XzerW22R51saPsKiGUiNJnXnxcHpcHhlszetuTwncNz/geF+C1osw+KcN4tt4JqcVjQ9P7Kwwuc21kADzWqA0nzctv7M4uSKWj3grzEP6cqZWUspFRCx8+nMku2ktoLaNDOV1Q3HpCwCA1zRcMZ5fcTHs5THWteGOZw5BobySeYo0Pd0C2P9LPfTb4t+C/H1d6y5nAhTlrTyedLMDyQZseTYSFQ6MWt5BdFRmHzBmuWKuUogpxoqU1Ia5ng/wEQKdIQlQ9Uh32GajsgaDZ/oX7BhnJrmdCerv80CGNDUXwBmZcANaAfBglkTSsm/1qzwO4FrUw8T2fBmnvWWViMwd2TcT9jgK4bc8DdBUrHZwQw4PQUDc2fUwnCJPZVDku5gXnAESRtnIf9/+mf/DXz7279Gj7YUjzqrR+E1J5ywB8IHiFdKTuA5ozag5oS7119gfnhAyhkMwt39PYCQyr0UnE53+O7NdzjMM95+9y2WpyesT6IYmSmDl0VTLCUwMTIqvvnNr/DVH/weaNYazGpEa449OnHe84i8UhjHdTf+0PHstd9iX+PnGe8rRn7nNztIJjTGRb0eef/ex63sl1J082ShOJntwC0yL4mhozOaoVN9tyMUJY43BBv/Hf3Q7yneI3O3VRz5vJTTd8W57wn3/kmRuI7bFVgBYbIxSxzajqlaGV1RA1W4K2Mj4wfS1JUfYKnnUWtBWVdQAk7HEx5efYHj4QBKpGnJL3h6/IgaI1ZbJ36lFK3TUbVO9opWpE2p5VKHGik23q0Q6HuMjq9sHpItQs6t1bjJOSNPkxrCZ8yH2TNBTErQUkpIWUpDzFo75O50wOl0ADPw9HTE+XLBWiRVITdJJ52CkgXKkPsY2YTYUYkFZfSkNqcQAgNZIoA4QcoVilDI3NCSeYYJniUiHI8HPD49Odz4RX3fTegchbEIyBxfM4BGZKuvJLftCXXmPLRHtDmv1+cam9+uafbIgG0lS2Pstr8POCAyjcxKB4yedBw0OpJEvGBG0c5odMOoPTYyjmHQVxOWsVl6/2GyfY+wibgPa0CkqcwJgu+IcLq7k+8sdSlbKd3bEozRHclwc08Pakb3kekdaSqpU912QhSXwtZyiysDre8M8DMXb2kPqdJhBxT78vVBdLf08F8Aw5zD7wMuVsjfDvHmmJ+ZCz3/+1ZRuBUgt8/4/mz3KizGpxV+GyeX3YM3jnG/TQrvhvVyXMTDkvW9e86JROcd/vY2v8cV8N3e2CN/9JxxfK/zUSFrjOpGWBk4lHF/nbfa7LU4bGK45++G91JK+NUvfo3z0xnzNIkgauecm9QVb93o3jm+PrIr0A6z3MPRn7xsGYb3d85QnJxe7sTHwPrDChz1td9h4HVcz0/gjDgYBuo/zcCq81iAwzeTEkRNweYAEidh621rwr6HHYfsTv2zhnf9CPc2eBiMrp/xlSxcPgMI0U4EXJ2xYa8/gQv8WbaZhvZsX0j65Aqczxc8PDwonyhq/6blqo4PTrzEGE2EWqSMzov7r3A+/AaNSLPjdgX/lhYwSJ2BgcIVhzTjsi64rBf8zu/+Ln78ox/jr//ZX+P9+/f44tUXuFwuKKXgdHdCU95yZfHgr5p6zpRBVUsN5TwBOePbt2/x7t1Psa4rXn/xBe7vHzRyu+DdN99g+fgOzA3zYX52HT/n+ubjL/D09IhlPWNZznh6+ogPT++wXC4SMa71QXltmDgBKSEfM46nE169fonXP/wSc0p4XC7Iy4pDaeAj8OXLI+5PLOn/mEFzxjovmJYPMOeJ0hoqN4loMvkD3bjSt7zz2aORl1W8NJwnmdQsg9y6rqIg3qGRXaF5vdfOd2+idrdj2eoJ2kZ/YOPtSr5beLbz2VF22uLHrQI4qpi8r8YS+ZKSyFuktDoozgBj9Swap69DMsWc1hUU+agClF1GArOXh9umt5azrqlFdY5eU7GpSU7nezhMON0dXS66xctYabqcKrzervL2lCdV/llEm65vk4wErHUCTZHXgsEG6DhVJrvPCzxHl23Nep1VACSK+LvTyRXwve++3h6J7VktCC7WgJCYAIpZEjhkPiBVEitkNOWlKYEhurR5ntE0yrXWhmnq0Ua19rWeFM5/8cvf4A//4A9w/+IFDsc7vHvzFq9f/2DYh60xxHU3z+B0h3UOfz6TdG4V4Hs8/HO/3eprqwu61ff1ZQ7fN/od5nqNV4axMYcTvNNTgJdtG7HL58Yf9VrMYb/6IMfntfE9vsvGuu0u8rTb/dq2/znX3tru763Ffd3QyfB1e/59g8edp9JzSioPUgJSg0fkXhbRDx0U/xlPIA1bZCCM3QMgEeM5q6OLAmROhNYyUtb+E4M1wi+ljtm5NYkaNHnW59a8E5MLrWZ0pAlmaLvix6jvaP+Nhmf6X+MHedOWvr/ZP3fmsQaYYVbb2hjnuuLt+8eBP9fluy3O+sDaRhYO+mOLQKcwMtrKRp93Gb89zJPS5qH+0RxGo/6PUup2DW2ltYbl8igOSjQha5TjAKOsQTqJADSp660wMeAy6rLc3rL53t2Af0qhFjiAHlDSbRcShARY4BERXF9KW1igzqdA3zd666OkcRyjPsl0KTyWYIyDvym+cei3ywcpi6Of1RaPEeOUjN7egAvFISklrFryx3RXXS9nsLjB9WGUxhOAO8/PzJ6y243ioL4HHFqyAMMbiPcmDYv0lvpCSj9yQ2Qpio+P8+/d4OnpSRz8DmEIDNRacHd3wvE4I+eEuhZ/z/oJyBhAL/ljt82pkchK/RSUWjFN4fwEPnVLZ675eelTnutlHOO+MHfHqXHawaEUGjRQDd9qO8yuzks62ayOTp2miG0jKVo2TDmRwOWqiewtk26tVU7JlEGtSFkG6HlKBFR16C4Fi2a+Zu6ZqEtdlUeXaPEc4B6wjE8VjQkVBa0J9shpVaN4Q04NK73Dd+fv8O27t3jz9hGXp4IJIvvFCPfIvwxn2Uo2+Wp3QNzi966zZsT/uiMXMYgaUgKOxwnHw4T5kDHNGUgZjASSJGVIlI2Kqw2yy2+tNVReUbEgWJxAqQfJOn/kGUjFPkNIGlGeMdMRd4fXOE73mKcjcp7/xRvGK0IqDcPfypQ1/a1pDRIjepVFCS6R5RLRKUYmVo9+Y94VfTEjQ6JfjfkhkNYh6IcrBcDFDqJhUikT7HV+APZIcfHC3aaYGokSA2DdiAZIxDVE0KxJ6gCBAWLCF198idPdKzw9vnUCVDWqvunccz4g1veJCLJRQgXh9OJBBTRN2bIWAITz0xOWJ0l5+dUXL8HMSK0CecKrr36AnDNOD/d4++03SA341c9+JhPQSHHS1WJmXC4XfPfNt/jR7/+BpE0hY6KMGF4jdSG6wdN6c+28svkev9jxvC3kxLUZEeo4lpuSij5oP8XHrl4h8nTLvSsa6Z2/GdqPd/eIlbU7Dnxsw4Rtvx8IAeJKbdqFEjFbd2cAHPVJGzxOovmkBNa9jpa9Fb5H4uiMRZeqvE6NDd+9GlnSXsp5k7p263LG+XLBPE24uzvhh1++xnyYJRp8WfDu7ZMYwhXhlyYKgXVdsC4LyiJe/It689dS1XvP0qe34PWKQQnk68ldUUU0rnV/T71FbUkJQ6p6I+JmLE8pIU8T5nnGPM84HA44Ho+YD5Kqxjwep2nC8XTE3d0dXjy8wHm54PHpgvNZ091sGFaJSmoDzCRKWuoAzsgacBheo5R6OnifoxCqlJIok0zJphzYPE+Y1skJvcGXig8OK0RpA4jhLIV34pJeGWa356FLRR39wPB3gDkOHu6h773r6r7BbDyD/tl+SuPYKLAJcW+UW6COUXtb6cZ535x7H7/3s13NLYbamak/ag0Y090fkenZjaC8NSFKBQ174nQ6yZ6RKjGUER3wgadH2x9TZ+L7HB2PgzVyxZSEVc+UjCyiwGHJrevQVne426Mr17/EO1sUHB0ICDTuBw2v9l/MWU/ntTVOR0/xvWtQeu8ob7d0cc/4vUc7P+UsEBXGn3ouGgw+NYc9GrxVLF4/gEiqNtu3dwbGKJeBFu0O8EZ/N65PGbc/6YgxdHXDKcWHteWvRhxhzH8UdjtqGcun2L15ngeaZxBt+NvodU4J56czvv76a3XIMgOW8CIiZCrf/ux56vf3VmYPk92+NryRjv2KQjM76imoqK9V8f07DPzIUmePA3Ja7sh+28v1uMEkQuXfbX1oDKwtpI78TxOwALQS5g+T0Chg2Kybc98s2t4YnrvH2Hyg+MzmTR4/ipOuGshDRq3PGiige3DVi+BBo0n+qNCShOQ16tZ1xfFwxKT8HxqjkWQGGtKbK19DU0JCw/v375CnLA6JqqThaOgLS0GpYSIztrEI1Gj41a9/gd9+/RskJo0cYHz39rdeA/n9hycAhMMpI+HOHSztzHmaOj2f58tHXL4+I2smsw+P7/B4/oDWGo7HI+5f3+PlD+5w//CAL754hdPx9Mxaf/r6f//5/wNPHz+gllWzujQQMw6HE1LKmNOMlO8w3U845QM4A/mY8PBwwMP9C+RZakNPxwNe3E+YZkbhhOO0ItUFnCQanXDBeb3g8WkFo0dtDDTP1jvc2+JiO4rduNGhBWBMU8LxOINZHFpJ1RFRff85eHfPKG4yQFSaRbqxZ8S7NhQF+CdV3mjavqio+1wj0tawbw6nJqdFw20DRKGnI4jp0rfOAD6e1sCtIk9Z5bn+W611UB5KNHfCPE9IYU7Wf9HnLTvJ4XDA8XQSqUBTz66NASSo2ObtS+pIwjwDDBlLSgyrQm+RMZKyVnR43SlBlGK2Tm6QFsTc14+u+ZO4v7ccBomoG//BntY8ZSndNak89/T05LXpbc1qMH5a5GRsN8qdlRmUgEw9CsjHNAsdy8pGSoTMwWmv6IxkzywQgpqk/lwr4+50wPunBb/49W/x8uULfPXVD/FXf/VP8fj4iLu7O183Lz0W0qlfyWn/Aq99nc2nnAZv8Ic3nnsOH+zzxJ/V9H5bKm9uYehvM8Zn+8NIv4loSPdK6HbdeF3xWdzvj2PaOC39La5beM/0LPGXNo5O+BDecMhBfrwaY+yLRRddWbPQ1AasK37w0yccX98LT6A637KuOF8ukv2PUsff1rfrA/SzrqQZCLmJTmTKM8SBaAJNIquuTTKqJZpV9yXBC1IyQlOxRwHH5Ok44au16yvEm8XpxvEIH7aa2+cVjq4EaUKEMKNfKTwnsoDRE8alNDydi64HAzQBICRiTFvrARus2bg6x+qORPZdlVmRdxsX4nNwwufIa9y3tv/a4UnpAUCaehkgSLnJul56H6pv5Hx046i1BbAezIZDnjBl3RNY+ZCtLGN2FFJ1lOp0WdqIl5QOgJaaTW4g3xoday1qdBN7iuB/oVtZMygZe23bw1qyROYd9YY3ljqcaz/nz8nM6MfL1todvb1Mn5zBlCT4aFLnuZQTcpY5u8NaZ0BBm703G8/pOOEv/tPv8Gd/7xW+fJWNbdDuR6cTA1Gnz9vxG00HnI8kkmyozp8wa1BY10mZ3GMY3akumdShOmYy43tf2E6fZT425uszgmG/OLxLAM7nM5ZlAe7DK0nO993xgNN8kIzDRd7k8LY5TRoU11rB0w5dS5LlpxTJQJfuZo8Qt3U1+NvSnKGtSMCUceUrfNnnPNziTouM/zLj90C7kzgyMPUMWESm8VNjt2ZCYm5IFYAa/huARgQkwRHVHDcNm4Ux+D/SewAqNxzmg/PX06SlWXNWp8fueGlZy5pGTcu+VBuh9lXQ2gIqT3j39B3++be/xs9++x2+++4J64WBiQCuOp+gl/Y1Yx+bb2Vwjo2X4aW+PYabjb+2u5LWSLIYJ8yHjJQBghRTZ1QgOCs1dSTQnFJgriJEcAOjoPECRoGkUE+BfrAtuOMkaRDglkE0gzAjpyOO+QGn6QXm/ICZjsiY0c/p89dnG8ZXTVWcdEAtHErz8ADXoLgTrwfAFH2kACmeaHrsJdV9G1knKQesD9t7jd1AvmW0tpcINF1Y3h6mVveY15G5MNSWQt2ArOmhmRs4JaA0oDF++MMfYj7c4/HjGwBCjIpH3DUVcGwc10ZfooT5dML9i3v1GGGUxsBhFt6tzjg/PaJennC8v8PLV6+wngvSlLBWrf9ynDDf3+Hl6R6/+tUvgcpae7gjUGbGlDK+++Zr/Ph3f8/peWeb9Dnbs43QuXeZHjAqb5+/2A/TzSduNBQFfUPejlTjAKJgtunpquWtMGeHb+/yxsLvJuxiJF4cFyUwYeMijaMbldqhzagoZ/Me7J6YxmQ5ptCPRqDNu9bbV7gEUY8MGxS64x514tFHnEAeXW9nSer0CSpfLgvOlydQAh4eHvCDL7/ENE1YlgVPT0/48OGD1NQrReps1ILLWWolrsuCyyJRPB69yuyKisEA4PPqxmCHDTC2Z23cTwrLbwTUjKTKuNf4OLmCqhsnrAYOhLlTz6XD4YDT6YTj6YjT6Q7z+Yx37z5gniccTye8fPGAVy9e4uPjIx4fH1FqgSmquZnRkHRbW89kYOsdiASzEjVnJkQpgyYRGJKiSdkcZcYtzWEiY5yrs3CRobBOJapQ+wnMWHhkPB8RMcSHDY43jZAV62GjF8bAX59pe22UdXYQEEXIZRe+vb4TyH8bGG9/5/oaXABcSac4wL7qPY7thuXYEQUR3gx/wwrT5rudc3RmnzfLvsXLA+Zx/C5tnU4nJC1fUNYC8zp2783hrFh/vGmrtz2sFxGAhmmaUWsJG8ew8xrbG95F34stzY4R68M6+bx5aOdqWTf9hIYxQljHi91rsjc5KmT97qbJPse9ddsafT+P9t5WDP9trudw5qeM9PF3/8335IYx/Wq5tv1ej6fv7ead2BYNDwzj247x1nw+96J40NDFzA5H49ndg3lmRtaoheDKMvKlKmDmnF1pbsYMU+aGh21wUh5Ehoavf/s1lstFjR5KL6hH+w1Kgg2ivQVdW3z8/aDwxtNyuFDBKPcNnBn4V5uw9plBs01PN/qKCYOLEMM2BByxBT6/ZU1Qv8fR2fhf7fViL0sVPuEvMlCA6WPSmlbjZJyH68Mbp4oRZK9o3N76XF0RcnqrFH5lpYHJIpxuNC/0Y/8scPxPoGk+R0e5BONRxTAuaeUO8wFlKSLLNXa+kCGGs5xUQZYIWdt4/YPXKB8/YjaOlNlrwFHWKNSc8OWPvwSlhClPmKaMu/t7SR1IopSoVRybU5L04dM8O832lUoJeZJSYMfjEff39545iEiVqFPCWgru7u/QNEPYVz/+EX74w69wOh5wOM64f/kg51qdJP821ze/fY9aLsjEmDJhnmYc8oy7uzukPIMog2gC0RGHaUbKwHTKeLifcX9/h+PxgEQNmWZQXpDzitImzK1iohkNkrp+XRqePpzRzhWHecbheETOT+7IKzjdHEGADAo6AO6pcVXJ7rLIBp7MaVScMvnTUUER/jhGPgeaQiMNKqV8sj373ZxsAXjb0mzHkRadbfWlx7O2f7lBG31skb9n9KiXWzQ3Udpt03h1p2XoNMzw+bquyGke5iTpv4WGlHIZDOeG/wndy2ieZ0w5wbKNSer0BpA4QUfFp6QilzM7OZ86eaAEAD8PKc06HluDCkpHNQg0ELTuN1mNVPY1A/jmmtl63DpzUYayz6KMz556/HK5+NoKbU5oGyq3pePmSBCN5JmusxxtnSRakwwKdapixGgZtU6icE4ZjQnEUp9xmhPOF+qG8R99hdPxiO+++w7H49EN/+Z03dmATztU3uIhb/H3e79/zv2bz2wI8B4vuu1/0G1snvuc/o0vAroMt601j+/BFw66Cb93Pda98ct+ibwEQHTFgV/crrxzlS045m2e2/YpaHrLdG+MRlEW3hnvc3PZXq5PinzkJ9bzlvzDgOqCNUqcJLI7T0JLWlklq0xj1FaxXBbM0wTMk2cztP7H9RDjQGsNy3KB140FkJCFvgJqBJ/A8yxBG7Uis+h+hNsRAzkze7CGsacJJmvA9QAcDGp9PLY3Ww6xr51jwLZdQ2O89s600bOo626usxMdW1GjakZtjKe14P25eMsObwRMeXsOAXADXc2JOh8Nw33Jf+uHr+P1G1PvfW2fCb/sf+59+wSMJ4c6UWpmING0VazrArDpxSSzSgHwPhj4MgENwhNMGTjMGVMW2hXPR/O+qQckkTgIRLtq9FeJOk9qklW3pxXve9hl2DGVv/CdwvM2Bqj24nmdf+8oN8qwV7JHEEqs3+jI6mMYV9v3WWBD5Vrmq/En1ZvmPElmzpzd4cQG+jz+5ZH3G+ThTpu7MXQ7wQityr8ye4ZNo/WkzmZGV4kplOADwFYyyNaj6+BtfEQkyXRaApMaL7foOKwriIb9ko8GuRBY1uMgIEY4Xy5iGB92AwA3TJkwTRmJING7OWNdGyh3tMEsmbyQ8gDH7hBge6/PresK0L07WfiZJ3LDeITnq92zPmiUF92Ybjy08nSm96DwrLUD2zPtz/QqlAUuWqSnHsTCIFbezVALC69LBExEgJXkQAMTo5XqNgop7wpds1GXZ06KgJbpKvL7w8MDnp4eIaXrJJuul56uTQ3wJuNUAFJ2tvKKdX3C5fFbfPvhG/z6w3d49/SEUhqOWYL0JmJUD+Chq3IEcX2Nv5DMGACgYd0B2kw7TiB1jLcDAB9jdDxZ64K1rih1RcqTyglQnp7QkFRL1sBc0biAeQGwALxCUqsXeZKz0BQdM1vadY80V0caPCDTAVM64DDd4TQ/YM53mNMRmWbVgd2W0+L12Ybxyyo5BQ0px5QScaFTIkfgVuvXDkaipJtPrlwwr/xknrvaKgA0rmilI+rKktLhquZE6gpyZsayViTqbV8f6l7byxDP9mrM4NSQkqQh4cao1FBL8TQfXBsmEN6+fYPL5bEj05RQa0O21DscGcGRiTdEfZgOSElSNeYpgdfSD5emOyil4N37d3j1xRcgIpRVUjCclwWn4xGYMnhKOJxOWB4fe/SMMUYk9SSfPnzAermA5oMj3eTEdhybXf17J5l7dGrQD/u7ff7Wxi3G+JaSPX7v964FqFFsHd81ZOcD3Q56y7wbOnCiZ42Gr1H4Cf0Ol7fP/pkVqcgB15duEEefiyF8V9hwyEzIgbHsDLMpsaR7cYMwtTtaGzfMiIU9S+RZo4HuvZwSDYSK0D3qlsuCy+WCu7sTvvrhVzgeDyil4OnjU0+DXirWZUUpKy7LGeenR40Gt/QipUcQNE05jkA8Nyvsc5aJhzWPGxIED3TYcDHSBBWtKwWwpEeJeIaFQEWlhjFLhk8SSarAp6cnvH//HilnHA4zjocjTvd3eHh4wPGy4PHxEVOecLq7w49/9EMs64o3373Fsq6eEtcFPyic2V7pWSbPrKH71aQWJohAVQwI0kbH1aww56UeCJI6TNesCz529lo4KoqPRgl3A/edYRoXPMC5P9/hOOIG35cdRn0r9sSxDZeds7h/2DE47ozHxuTvbD53PBSZg44/4vO2T46HN7Ab8WL8O+CGkWXHc9ce7vUPLhSGH7TJaZqUpm0dUPp5GnBpoA/+eQ9PhrNHBHUYE2WBGba3Su5rA/jYz7BOVwuwd+saZhH3PozXBDeKz+wte7hHOsfxnGzHr2wljQ100jB2cE3rMMz5lkH6b3PdMmTvKSI/5/ocpZn+YAPYRR82tg5HzyjVtohi7zvg+D62vxUAt3zH3p7Ez9c7sJ2EPXPdr+E7S2vleMXxzehQGffFzis3vsIU4tEOgelEuJzP+PabrxHZXlfetIpayvU84jSo39o5PsNjnwcle+smC1W5obyq4H9QgYf4bDiUm2O9Ha7cENxnKHV4eBjB9Yj3nhqaTgSyQOB/JArE8pGA/ywjfSBMa8hCYytFwoV5G9s2xxmOo3tusWkL5h3vGa/az5iY+6ymM3B95m7dizeZhC9kS42pNPcahkRBUNQwfnd3h8fHJ2GzWsOyrLhcLkA6KOvVZUwG43Cc8e/8O/8ueF1BrYmig5TPrQ3/3n/wP8Dj8lu8fPUK/8v/9f/K8dg8zR6BIsqUjLquogRIPZKhw4ZG7Yr1TUAnjRkZcspAItQkUVUmn9nSWFq8WguY4Qr2dd2ryfk9rqnixcMdHu6OuDsecJxEYcBMqI1QmYBGSC2Jwo6Aaco4almfeZ6QUGS7UwZRlVSBRMjpgJzvkXNDqjPu0hNeHQqOByDPj87jmDzq9HHLjitoWDYncUJk548VK4GIQzSTREIkJ8KMrvjqtP8Wzu8G7JHOD4q1OMQdWnur/X6/0yhXeDJkrKF3l/Oe4RfilczZIl2Poc9r/D4Y7XlUMNu+bA3t8W+PJpYz0GuCq56hyX64TMSMw2HCNFlWsJ35hbaRqus1un7FiB+Hf+ZoYqnVk66jRfBJGwkVlkXQDORainyI1txsk8PmHr8QDY2mG7Er54zjUdLGS4r/vo7F5eq4M2HuGPtrrYETQEiArfsmwwEzME0NtYphXCLGG6ZJdGedVjESGtZakTLw4eMTvv7mDd69+4Avv/gSv33zHZZlwel0Qs5ZHBRU8et9Yty7PT6SN/vrZdV2rj3dzPb3PR7yVjtGO7b81Zbn356Vm2fnmb69LZXsYLRsZ27bMX1qHtv2t2O8NT95Hi53CTohgLZGJ52nN2LfOcDLdZ+3cd0os9zi3Z9b835/225vu+l7Hm23eelz8LAbZYg0haqcK0MvcbdLLeIYlCXa1tpKNheWM8H+IvcMp2rgXpYLDiczqElgyjRphocqhmVQc3lW4CVopRiuCxAY63TTDQyRT0sQnUG/o/x6DPgY4WYrV3ZSxL4H8X1ZvoTkZRXFkG8yf8ozams4nws+Xqq37P8lwjRvnbX675ExEJzTdB5qLA3yV9vu97PHbOfH3ePNm9+DQdRvBecy587N4aCJE7/OVcrIAo/ny2AQhpUnooxEjHnKmCcgkdYY1raFRw4j2OogbszP6Ipl2Ov1ibdnNBrH+7vdaAWAWDI0XS0fDfxMHx82cpKNL/BEbPTThcnNutuMrHxJsN3o/K0kTM4ZaZqEt7cIeXvuBu7cDi2RGU7jcnaYHRZcQXRoj901A9DMPbYcKWvWiaCL8OMb5kzhf2EBHAdsVUtyZEVPOy43eXt7c7WB+Wh0IK8eEh7PC87n80Y+lkC4nDMOc9bSABLla7PuejjlCfOkfPzG0cN4IhI5fV1L2G/FT6rny5TQSLPXqJOp82ra5liKRGE51MaO+2/P2DmQEkKlO5EoPDcNSi2tiZFeSzNLQris69sBhZglIVSLsCalorPPiy3pCLhUUGNMKUmdbCKsrYeako9G2pznWR1VK0CMu7s7LMsFy/IksqKfEVsbfZ+SOm0xJNK1yj9qWFvDh9JwLoxWJXBZ1o5Ak+AzIvj4Bl7I6FFKvXSUAScYW+O4gySHY8XhlXCttYixm9SplSTYingFwGgkTqaktcRLW1HaBbUtaLyC2woxjMfSFOasZnJeAkPO/ISExBNSO4gsSwdMdETCpPp3mc/zXGi/Ptswvqxlo6DrRhJBGBr9XRltXcAMHA4H1GoMA8DU1ANW6nmUUsJGCVBnxRzMzWuXi2tLiEzfzI7biDSfLhdRejR2DwwTZu1585RIBhiKHDxdRk5oVU6AIFvxJKulaYp1Bun4vv36Nzg/fgeCKClzllqqhlzYvRuvo8Wlfd83TNOEwzzjdDzhclkE2TMj1Ya2Flwez+Id6oiVegrDPIEp4Xh/h+XpCSCt507swJ4IqMuCx3fv8fKHX6EaZmYTDzry6cy6IewR+iN9C9OxXQnPXc97ZLAFmXwqomIgYEExYyzYllxyfHbnEnoUTjXZH2Vimcd2/YsSrB0C3R+JBJhvfO4f2Nslb9dwo7VEQE9ZDgyK8KHJcD6B7t3lzAxt5h6Jq152bgI+HOph55yckaq14qw1TV6+fIkf//grlFJxOV/w5vEtailYlsVTp5vxXLynzqh1deWMp7Gy88qBWfURjgowGn5TRhQ0bkGYm68njb+ORk9cwY0RLt9CgtZeMaKeMGmtIS7yOqWEdbngMT8if3iH0/GE41HSqt/f3+NyfsLjxwNOpzv84AdfotaGd+/e4Xy5iLEyZ6+7yNyc6ROGnmEu7jwMzPafHIAkKYusTPcq7eO2VIEDiCtzLHhg9AI2gcIEjAEJxFWOh3OLt21XNjiDhmfsw47CnbZQG18MFDsylyq09iboqomoYOXNmPx5xQ82SMcZPi44ftKbGhE14rA9vLjnENSn0+cRpxqXJG6FozcK82eFA+rlUTx6q0mETm1Vo4jY8cB2XDLWPo/IDm7X1BSlFvm0jfb+HKVTVAyPtKD3Nxg0HeIjLIaHt3zfVgihG78xdsBuhMV9JUFAHLvvKCbbrMVWmfU5a/W5166xl/v3mwrNsB67fE28v7M3/WLHZ4rErpjsbbsAj23HIdr+2vobc39rK8Jcr6a4xf+fWHdS+r07Aeyss9Iox92B30KA9fgOczcYSnpnM9KMfXJ4R86dnL9vv/0W67Loeiv+Z6EtrZrQEc82rtqNs9lb1n3ovn3Fd5gZa2poXzTgTxvoVVcW8LZzi6wJYEsBDcNRe8DZz4pGnzvi8Q2fh+3dCwD/qKJWoP6GMP3FhBlZhxp5F75ar22bV6PdeejWtK5PGoSOogGWTNxpzPPzfO5i+48ax0f6LTyKyFY9atzgWugLsJaCUipohhiSAr0CRFH95Q9eo64r6low5eznhdANPyknvHj9Cgx2xY85idZa1Vkwu5KcIPWBs0Yum9N1K80jxsEaTUqa6ptl3zJBE0WLMY0DoDZNC5cbIzNLyZ2/+RIDAL54fcDrVy/w8v4Od8cDpkQoa8PlInWIKxO4JVBVGSKzGtcaUm7IiTGRrFWjDLQJhIxMs0QU5zuAM6b5gJfHR7w6VNydKqb53RVdtf/ZWphB1tFqaz0z1Za/0n3LGqG7NV4PuGuDhAaapIcn0q1IK/eMcrdw+J4haGuE67ilK+v68wLr5tBxRcMDbumyMruhdM8ZsON+uOPJlXLL1zzQYqCvPcZU857quxakSZxLatVU9mQO/0UiMo1nhehypnkCEjQS8pouedR5NIyrMrIbolV3QuYcia6UgzmlaKr1pOTbEVwn2kRN94NAidE0stb5UOeX9w2KulgjX48OX1aXnYgkKshgNBk8jLzaFla2ewg1jlv75hTS90UixOvcDeOlNI1gF+U0N6BppoI8TVjXgrfvP+Cbr7/Bn/3xv4Jff/sNnp6ePB18HFcHl2vn3O3v/Uv/8znnZo9X/D486/W57+u5lRWeO69bnum5MYfBb87z9efP5bsHWPCZpWGMz+EmES/0s5WCJHNq37/8JyfG3qjzHXswemvse7z6c+/Fd8NAwhBsHHEsAUfDatnulMDDdtxdT5k1s8sUHT/CgpSqRpMyIU0mg/dlinvELEr24kYa+b2sq6SpdjwtDkXTdMDKS9hLVnqX9YwDQBrL/NkI44YF/GYl7rxqGZOPJa6nreTOLmye2eyPzt1pGZGXgWtOS0XnXUrF06XgoumWyZsk5EwSjIXHnTGMY/Gypgj65JjRVQdsFML/fDYrbg/z5t6NZzvS73eZvRmGlX5trnsxw/jT5YLBLh4+EzOS8p0psWfjVJDtfWzGGGWA7fEyp80KQkoVrcXMQ/YmOawKnbJsljy2Hs6hrcO4zJ2X6Nq9DQzpGLfj3MqB/jyrrYIsglieNjxgznmT0jmvLW7OEyzQEmn/1cLrV9NFSfaGa/5r61DYQU1xP43Bc8ZH2TNJIw15M5xRb0wuB/m5DvAm/NkOcNPVB30lruzmlXCGI848nRJ+78cTLpfL2JriqSknHA4HkY9aA1Hua0EJFkhl9ImZNUtHx9c9CloCXNe1OJybvM0WeAfB06wG5CapnweZf4+uxHUd6ca4LlvDuM21adaQBokSBwEtWfYGLXdBZmeQfZOqQpodVQGdq6yxlIyG295QmzpnZqfNNoto6M9J+Lzj4YDL5YJSVnBjzNOEnAi1VCm9bAFs1geblJWQkHSstk+MnCTy+tIIS5Py1KgFtWYwZ2A2OT/5WEbdgsCjlQaw3wl2PsbTvP3kW319FKXUiWBSMElEeGUG1QWgigpJUQ+uaK2icEFtK0pb0doCbgXmQE2h9Flii3BXe63JOCCkpnZaTsjIyJSlprjNbRQln70+3zBeqqPLq/TLRRRvtYjCwohdqsLMn88LUs6hJhwjZajCYlzVqulMmNSTjAhcRFHfJzgyk+OhEsSzFkmhcJwm1CDYGLEjRQpLqUiJMU3k6YUl0r26EAKI14ul7StF/s7Z0ijLijf1aChFEIbU9WBHIGIMqCND3Dk0WC3yw/EwKGkSa81xZpRlQSmrGCgbI88mXIn3eW0N9/f3+PDdG3RPaGf9ZJ9qw4c3b/H6xz/GWhuSFbu6ImsjcvQV1gOzXfcwoas29i5fB9UObwWQPUGrK8SNARYYvB55IOsKR4II6eo3Y/ucedfDyLEhe8bcZQw247psZr/L2w0CWJ+DR55ruwPhCO1FYuLraIgdADTNXbMxIrRr/cd1CeOi4Sz1qEkBo6Q8tDAsrTYwGp4en1BLxevXr3E6HVFKxZvv3mBZFlzOFyyXBWtZsS4XXM4XrFonvFUzvK1eT8PXXhk9G//ezva71J/ZMKyjILmDEbebQ5013L04fuwdWOpIpobK4mXKYb2JoF5ZaiT/mPFOoxLuH17g4f4Bd/d3mA8HHI8nvP7iCzQwvvnmW5yfnjAfZk/h2fGdeC4mE2biZPVra6qAArknmZE+wUUE84kUZ542tjEwfBz+C4UL8s82V4dfezjwi/LnOgJ73IM4j8BCboi69ztSem/T2zZGPOAAWE3xvQNK6N7a8XPsVvGEOw6E+cDhNs57h3sA9u+h48W+3/HxPZzbl367FfI9TDTgF8OjBqvzPON8uXimlegp6niSxj7HdQm8lMGPRssza2Rd3nd+2jea7l9Xz8U+Nwuwb9jVhykCwG365c89++itsYfBxb43wEd0DYxbg/i/zOuTNHrzOcL99tqOO36/dmrQk+ptbxyaeLtG0vnnrcn1On8OkR6dAm+vzTAuJ5v9fD1/jXBJRANv6hKY4bMNrjVDxHP7IOe1e9HXdcXXv/kt3HgZ8Mmt6MqhLdzgacIzPsTPFECgjzZmlKmh/mkF/R4j6hXsKdrwXv7ASPqGdv20jY39S7mkr4AfE4DfYZSHFeW7ivzPM/JKV+hjH6P3367pXr9Jt56xRxUpm8LVXjKu1xShdu52wfY5UN6h904HhgmxwqwoMSSVsqXYs6jxBaf5HmB2o1HOCawGbW4FByI0i4JkIBMNY+bGWJaGVMQzMeeMtVZwrcgpYZ5nrKWCkijhrZQPA+7EOGVRgh+PRzydL/jzP/9znE4nfPmDH0h766Jp2ZLOqaA1xlqkFqcZH0+HA3705Wusy4qvv/4aX3/9Nf6tf+0fPrOYz1+//+NXeP36Fe4OE3JioFWUpWHKFUQHgCYwEloBahHZczpU5LxAlCuMSaPnG2eVrw+YMIFwAOEelMSo9uLwiJdTxcPpjNPxNBjx7Mhdc+Wd1gPmdKd0I8CJ8QKWtrobhHjf2dhRX8d93TE0PBhozifx2UbG3FXMhf4GWfWZNkWJaClLbfwEV4rqeTPe6lk6oYtMJHCNjEH/4SXoeBw/+Vjk+WHv9G8pFVnPkZSyCuWbdA6UJ1fCHw5HKUfQGqqWVUopoagu0ta7lAIONTh7oXlgSuZgOyIHebbrSBImgDQCKYk+h1nGJTYmMRbE2uj7fML1Pg/PBJ6WMK5hUlxhn73ECFt/wYGbx1Se9jk6JHBjcJKIHit9En+XkgKa+lOdUUtpmOcZc+n141OzNPgT1tLw8fEJv/zVb/AP/+SPcTgc8Pj4KKk0NQNU5T6uvfXZrpM/A5Mf+Moge8t4+jlG05uOlv6g4IEr42g8gxgVz/GZ7TU49ITP8W9KecAd23EPfO9zQ9/hd03ujIhqbz5x/hZVB//v6AS6t8oui9pz48B8TW8aITb3PvX91vu8w/zF/WwKTz4WGbSm4G2+D+O/2H5fJ9YzdJxmTDz5j5EPa61iLQWHWqWGMXlVU+3f2tZzS6TReWYoSFjXKsbxeQKljNYs28nc+XCIISBpWxKNLXdNnjZ8Ezk2V9gjylgGQwANxok++Q5r233QD2Q8HcOd6cP6xNZilqpEBNZCQMu64rxcUJ137O/nnPDy/h7Ad3GjfX4E9sCbrmFtMIu/rTmb/DLM5waQh6UjIFSPNB42Xn2Wo7N7lC+lAUZcF9HDe7Q4qBtfEuHpfLkakuFKGN2EwBAzeQr5Yc2dl7C9ZQuov8IH3BoaERI31EqgVK4c6QxerBSJjLU7cbiotKfDiOvqPzF6Kdqdufo62bqR/xozVmx1AASt1Yx+ni2F+jRPmCZJo540WlwOAIcsHh0X7KMjsUNJxk2TdfrY+vcur4wOuGHCkYcwGAnw5t2TfafYi69nIpKAHheu7Lmg+2SDkTAGxtje9VTljTBusnEzwNwkYjxcDIGneZpxOh5FtmoNzAYrXe/o3cS9NJ1gDvuqmY6kZBEU1whs2/4bLJoz4JUjbKCDFPbAjbU6tg5PIy0dgupYcA+UR2u6V6FKt7iFkzln2D/Vk6sDY1JeL7GoYhJleZcCb9+alD7WWutxvWoVe2XKYoA3Z0uwpJ6/XM5AE0zLTepw21oSSIzi+i8hoSEBoRQRESFTBmPC2jJqlfFQg9j1tV2hQWEPN/Bge2hZvK/wzxVvPb5PIDFFuNdLf7YBqGgoXES/wxWoZzAKKkjoihrGKypYP7dWIGW5ZeTUGJTEETZmL2K24OQKZNlltCqZma7gRwf/mdXMPtswXhXgnPEnQqbkEWbzNIEBSVuggE5JjDeScqYOzE7mHSUpBBBFmZf895hWLwHY1ikYN9MQrqQev0qFpUoZExa3jDa0/bWsyHP2eiAVJIdAkRYRgVhqsaSp92t9GKEyJLqui3seT9MsqX1IvG0qNbTEqGioaJgOM9bHVRQYa9Xo9Y6X13VFmiZP8YBkdXPF++Tu7l7TVsSLIcMXA+jT46PTZTswZP/5hGJYvm5/H5+JW/JJowdv93BfgNptJ3zfsuQcBmIMSSTaoG787u1KK6YAitPqhjbevCNtR6P70L/1y9s1ilHZ4fBG4qzwd1OBY4Q5EN3uqXi95n4247rY+Ic2IUyJ1bVx1kqE/MfHj1jXFa9evsKLFy+wXC54890bnJ+ecFkuuFwWlHXBcr5gWcWZQxxUBPkZ4epMSj/fxsD1SPE+sM6CKMJ3Dtkn0gHhGZDrE928d5sVGd+55p+0iX7mScdWJZWGe0I2quA8oawrnp7OeDe/xd39PV69fIW7uzucz2ccTid89dVXWNcV33zzDWqtOByO0MOia5eU0RcvP5+27Xtg2FptHrEs6Lv5efK0RTGK15h0hT9jKLdCVWfGxrMwrBP1v5E0++e4V7EdY/64w8GndmdrJBqimuL4wpiuZaoAk8N5hMKlpZ7qQhcN890yuDcAcQcnDHPZ/W0ccFz/uDfjqxuf2x3m32qpfvjwAQA8RdxYiqTjj0EBwpud8eaNSbf3kysFKTBie0qzK0Xdhlm/Unbx+JujhTg0/xxxPTY/hpUagRyK/XadJbYXh30fSdn1no6G2P15f0ox9be9PkWjt4rVPfp4q51nlaeKc3vt2VtCLwY4jIbk6wYHaLeRoeN4DDDhhu3tfD6BcLaGID/O9h17u30bzmutPauEw5w0TGBHJwbCWwXyFQ8FVZBo9pc3b95gXRcV1Dp6Yrba4lZBdR/bblby6ljxdu3iQHbm31iUieWrAv6CQX/Io2wV18B6ubUfz/z86dP6L+4a9tzoxSsArxra32moPyWkv8qYitW76vC+BcOrcUcUtbm199nH4L+F/xr86F53Jdrt8zcOJWbikBcsYj6moyXHm6LotZrH0zRr5hr4GSylgqE+IRbtrW2fz2f8n//9/xPaNx/w+ij1vt+/fYd1WcCt4Xx6BBLw9PEj/g//m/8d7k53OF/OnoayVcEV0zRhWRd4DVfuEQfruuJ4PAAgvHhxj3/8j/8xfvzjH+Hbv/op/vw//nPMsyjuuEk69VRIHJYhSsKyqszWJGro4eGEr756jePhgDdv3uLnv/g5/q3/xb/76cW9cf3w4Qu8Op1AWIF6QeIV+QS8vGvIcwNyQW0Jl/Wk+CGB5oTjIePumJCypOAjlrSflIDER8zpBKIZtRLADVSA1O6Rlhd4cf8aL16+weF4xPLxUYx2rUH9YwFoFqnWeu3MAVBGhZb8FSWH1L8MkZQuh942RnVcs0EwBkobA+V+O9cAPiqN+lhvGZJuIZtu7Ll62q8Ik8u6ImUJKmDFh2B1zObIO1iksSndbYxAX/aeAc/wulGiGAHnykmlXcuyah3ykddISaJduDJOpwPmw4S2rDBDBmk2BWun1uqGcVOGmoJQRsGgNAljVgsQznfOE1LSSHFKIJohWQSryjsJlnmPqYBaz3bkupa9XdL1uHYyFBprGYx4530iwuFwcF2S6HUMXsWZe1vjPCrt4tg4BlkYTOq6WNYAy9oksMuYplWjvxm1rCgrUFtBTjOK8k2Pj0/4+c9/iXfv3uHh4QFv377FPM+4u7tTpxMM8zZ5aO/a482cjb0B63GuV7q8Tcr43T6GBe/9+p+NXMlKt8YXrsfVz8617mQ7Xi8xF8dJ/TmDLdMZ3rq6uDj2EyfV25NFvebveWBTTX6KDqnDCgz3+/y36xH733vm1rvP/baV33Cj7WGtHWcF2TLUq41r7u9szphxFKUUzCnjeDpiKjMsFlNokmZG0fJApRbMPAHIngUD270yvXJgwvKUpPRfWZCyZrRorPqYA6bpgJwrSl1HHKJ0oDlvbRHl0oEbgqIuzniyDS4y3swGF+E7vtsHj/B8MARHObaxlnppkrklaTQ9ATllNBaHgsu6QrR/GVKmT/p6mGb8Tx7u8H8N4zQ8J/OT6Gkr5UCcQJPqA+x/LjfpfQrDjJsd52V4k284x8WXbL4s7xHFNRF6wg1ikFIjTIS/ZhlQYPSt4eOHj9vOxGjGADeojj8DTFq+R9Kq+ww2fIvh1x1WB4CkcTb5rbWGUqW8azd8G/z2MXa8kq708Dvowpe1c3T6X382ygQiI8iysO9nhDdbb8NdXa0S9l8dCHLOmKYJ0zRjmjUACASzQcBpJ1zvZvuxvQbHPhtzxBuqxx5KAZHJKIqTjPchk1xsn8wR4JoYRlpuczZ7DChkX20BfNHXdry21G17vn0XfONsvj3oSeZ+Pp/lPRfTpJFpmnA6zphy0mDOTh+IqGcotbkB8lxIp97AmHwdtUSi0akEoI1OaMZ3Mgvetr6svRQANdK2jieT2wTHJet6xG2ZAR8/yTmrLE6dVlDW5uV8mZ2ZJJCWWkOqFZkS8ixnHKWK4ZlZ8QMDUwLM+G+LrTbGaeplUQHgeDyitYbHx494enoa5mm6Ud99LY0FnZP1aw4KpTaURqjISPmAwyFhYsI83WGuhIWf0LgClXomUA1IrDE7iwLJNvSs84yddpN/M0qiUEfj26wyx7KusvZIKChAewLzgsKksk63CwPmdNA0STqrAzqLcVz3EST2aKFhADihpoLGFwv8x5oPmNMKmhJA2Q3irQLTZ6Ru+3zDuFpmjSkAJMIMCVrnZULRVMmtNUx5wppFUZBzRqsNh+NBBbHFa2ZcCTSs3ngpuaFR6r0YowFwtUMsqzRNKSAa4HJZkFLCoikjnYiwGJXt4PQu+2H1TSLxEnbDOAP5cJD07JreeF0XMFW8/sGPcDi9wtPHNwDECJ50zsbEnS8XmMK+cUNb1aPEmB6VMSsLIcjzJERWq/GstYITIU0ZpTbMKl8iCLNiaG84Hg7K5ARkrVieWNIOLOcnrMsFNM99zuo5G9fFoyA313MK+2vl+PUzkdmPHmeRgd8iwWeFqt75SAx33rVe+sH3XjdjJmee/ZkrOrYRFqzdLaIPwoMhkigsdKlqv+24Xq6AMmajd4K4fn1JNnvFQTDfW1NlbFKSmtmAeDY1ZlzOFzx+fMQXX7zCj776ER4fH/Gb3/xaUqOfL7hczljXFcvlgtYKyrqiVktz0jS9ivswQYonUGeKN7BjhK4vfYwWv2ZSBgbtxhN79+RO23y/Yh+v7rFh6qtrK8TD07okELymX5NaRpfLGY+PH/Fw/wIvX73E/cNL1LXgcDzid3/3d/Hx4wd890YUlEJsOwMAYidMjHDWBRidmPSAu76glACydG3gPl6jl2gOW8ZQWipF6odr/Hu9FL50V3yN/XZDMOi7vn9dRZ0r7Poco4zEPKRBkntRcoAy7sK025oMRm/7oOM2wcxrrMY12YLL9ryZcLfFIVdn4DbuG3DLeHe8Yt8dtYEbXJl6f3ePr/lrsArM3MyDrwXGu49x3NCwyXEJSDObKFNcq3g1Z/EmuzJuCn28gZP845ZGoQsIgRn3Bq8aCuPcAqPR4931DvGgcar29wY+Fdwd72zXadvQCAO3nAKu3x+f/T4X34DF2+cSm32/Hsuta3BesD7CwVS2bljKYcX2EXgY194cbjUW3+t/o8LxWhi77ituvX2+5imk82v6JuWGmioLrF0GVEgzLBRgBtewsXc57W8Nv/3Nb8DMUvOLTQjpSiA3Ygaa9ollGu/dIpmbqzFjPVa0P26gnzRJ5fiJd3YvhwM5t38zyP+XdG3omsE0/g6D/6Bg+Snh8JeT84K+o3xNkob27LP+GOe8/WztRaWXvM8uQJog+rmLvnVs+5xVNxppkVO1VklNShKZVFkMpaaolaCDwMdRAijh5//8r/GL/9f/F6em0Se1IucJXCvW/+YKnIBaKv7pn/8nyCEq02RNAF4uxMrSDI7RBLwpEln2NVd8889/in/j3/g38eZnvwQ+PGJRXJBSQgEh14xzbVo+S2QnM5xzTjifz/j5m28hZ75hfX+tVP0+1+P0Aa/mild3CfdzRp4zVgLOK8CrlNrKtYL5jDmfMM0nEAGZGAcwaDqg1IpUY16DJzRkpDYjcwZYk8NTwcv0AUfKwERYjg28APf3CY/cUIuBYcFUZ7CE9IeajITKBY0rMhqkDnoThUZdcSDG6ZQx3c/4uFwwpSMqQ7IBKCsukT+W+lBE3cpNyq1BcaJOJMHw6LWxyeArXcFqNzIALE79iTzbgaUiNx5HMkBWkdFbQWFI+voKIIsxRhzxJXVgaav0zUBtPaKry30SJcFgsEb3clVFvJU/a4L154kwZ0k/nwgobBHxcoZEWd1QuOI4zWLIXYvUeYSsyTxNmnKyoHIFaMJSJaMXMyOlCSlN4AokmpBwBGHCcb7gy5czpjbhUisKa3rCVgEqACYwEzTwBZmBVirW2tBKBs8NNEnUBxojZwaCkXEtLPuqysScJlAiqd3YyLOLmb6EtRRCYnaFrEV3m5OLydmNbJ2xr8swHt9L/FzzQJLdQiLIz8tqd53frCyRK4lFeS7ZuUIUU+sKZSahs8SMVIunmkfK6ClwZZC1FdRW0EpBmye0dgQz4VwLDmjATCiU8H4t+A/+4i/x3/lv/SN8ePsW58ePeDod8eLVSwh9L5DUoRpA8Rmo3njwvwlV3TNEx5KGe894X3u6GwDwKHyhBzVsUa/5O4YDSds1NBmjRWXfmRmlwdd9V5Ln0VFnl9/WSDkGA8EQ1uWzGO1la3A9Xl93p9k3ZCHXU4rs1lCueW/WbAsYnYTMSOF9PhPB99zVNLvB8Kzppvae19J/fhZ834xJosEIvmV3AFN3NtSWUVvCnBrmtGKiE5gs2lmemzKhrkCtDefzgpxnzIeTpKBtFSnDErqitQxCBiiBMkC1SUADAfM84bJKoAeBkfOMUipKWR1mUspCC2xuBl+tKt8eS4qw06rOb8tfcSaxAAXp38qSyBLJqojPSZR5aTzXzOgpkRGe0fOf1H7VSLI/Ngk1nCZSf6SCZS04L9Vh6JAyWhNDx/1pwhcvT5sdNmPRgpSy1BWGpMgWfo+6kwA2Bkpjll1Hw+P5CKDSHSZsTqZH7/AF7r85IIUFap51RNKUixpNiXwraGWRTrnzx2slvHm/DDOuMNmwoWDCm0fg9QVgSsjJ9J2GN0inYH9NLojyPUaAJ6iRVY29rWFdV80KorpT1TUN0btgpCwla7k2T5stGQy06WQ0WNYqAYJXo91AYbDzSlrvHOqGksjpqmc8M5KmJRsJjhJdlm4sjpHH0x2OpxPm+eB0Nkb/MozvkjW1qNkr/JTI8clkDiiGCGwuKkokaKYpk+upjy17SQa75+7LMh+2oBiBIWk+uXTOVnPeWvD9VPpS7Tt3+LJnVGlgqF8CS8OzMP6k0wdLcQ7YfNj/Pb3/MCwREYAsJWJevDjg4e6AA00gzGj0CKZJh6Ayzrri/k7azmqY5sqgQ5I04ADmlHB3PKIsDVwS8pRE748VpBHpDZoJSvHb4XBwR2SRm6Bl3IJuQeG4O6Y0tEbgpsgLQILU7K5rQy36ZmngKaORlCCmUkFrEQcTEj4rb/Rp1l9rjIUEL1BSA3nKmJAFLaBJ14lRS8H9fACXCqxFcGRKoHlCCTiKINme13VVWJQNzocZa1txKRdwYsGRKeFyeUKrjwBegHlGLRVLeYPL8h6EA1ppqHXBWgs+1hPevllwenyNl/kEeqhoMyER41KeUFMCKZyWxqgNWEtFbQXM+q9V5JQh6fTF5spk9LHLQiA575LencVZRfEvN0JCRSNzmM6oXPF+WUALYwYjpYZGwKWsWm6CkGgC8VHpUQWrvNhY0q8TSbBwU95dTOSinQeELtZaUMoj1jbjnk5IaUZtBUt7QiozjsckNC0RdIqfdX22YZxrkehoU6RxQ+GGRGow+/iEKU1oteJ4PCJRwtPjE7766kc4Ho/IOaNwxeE447vvvsO7d++cKTOEaAzFWlbZrNQJP5EcToE3S7slSLmWwHQwAE6ohUFqdAOLh5gIuEVSVnGF2Aa7IGRpng8HSTNBnJC5G/KnNHmtmdoakCZUNJweXuCr3/tT/PSf/IdgSF0bq42R/ZAUqdtSG45gnC9nEInQd3c84DDN4NaQmYDKkj6hNhUC5G/KE2ZKXhO9loqMhMQErhJZflka7k5HYJowHQ5qoIRyABWa+QHrumC9nJGn1A+Ea9EUwT7DHD+nAL/1W0RCjuCB/h+/0QlAeDkQlLDX8FdUoTL2vTeWxiYUKU2KSrjYxYZBJ2+vr8swRGZdx+txRC7flJJG+Hs/NLZnBoTI0A0eRTaCLiTFcZuG3gWilERIh/ED5M2QtmWp0gGNNmNhDtZlwbu3UiP7d3/nd3F+esJvfvUbjRxfsCwX+Xu5oBYR6GstgryapHztzhrd8wc+Fp2fcQb2QFiQXWj0/b2tsh13zJq/FoJHfrT7Qfb3uY8de1CgKezDu9aCDVMQOwBuqJVBtXq0QOOGdbng48cPePniEV9++SVO9yeU5YLj3Qm/97u/g2+/+w7np4+4u7uHRcy3pnvvuKwzVMbUidCtOFMZ1sYN1EhTEsr7nsqSZIx9TajvoePqePbCaoZz3GG0r2SPIuvPCFhs4JcVZ3wiii2us0sWqcNO9KwFCPuA1B/p3pi3Hx1QY0difb5XEk54MUxmq3DZM4jeNFriesn2+5QHSF8gpUmGMkTBnHG8P3nqr1qEaZIaRPpeH3QwuHVF22CAcQWcCBRsUeIqDJD9TnrW2BwLrs/llhakDV40Qdjmt1mQbvzQcg0y5y6cu3KcwummcU2tbTNyPweP/RxtYLJvxs7nbZv7/XyWc9jf8LoFi104hs8/LKTP4TlnObvMEByfR4BF+WFEIf1dGygAlnRJ44s3iMXecLb4ajv+SOdHwrDhQ8xj1m4HXEWEq2wmdjviTxaq4BgxCrgtjgvXxMyncD3JnLQ8UKv4+PgRHx8/eLRhd/zRGrMwozxtpv094e1qbIFKsqQyq/9aAX7EKqTcwrDAeEzoGh/T1YdPXDcW71/wFdHg3m+cAPo7jPUnC+g/mnG4JIS8kD5U3s53e22m4zwdAnV9ZjCd92zgK7Ph/jtKSjYGhv5xzzAZW2rMkso84BY5Aw1UVyRUIB2AlCSqmYDKGUtJyEsBLWdRkKhiuZRFU10atDIqn1HWrshrLciQxRQeBFRZc89iQoQ0JbCEo+LDxw/4v/3f/wP1zi8qb8p5IgZaVW/mJIY9SuRRRtQICwOcancC3+Tw+r7Xy9MRr17c4fVdwnEq/z/2/uRXlibLE8N+x8zdI+7w3vvGHCorq7rJ7uqBbJDqJrWXIGgkN73gSn+AAO21lbTSTgsB2gnaaCEQICBBAiFQEKWFBFGLpthqNnoqNrsrq7Jy/L433nsj3M3saHHOMTtm4XHf+zKrGhQoz3zfjfBwt/HYmQdkPGFLT8i8VoMXRSAyIUwF0wzEsNSsZoxkJxxgUWjkXFAoI8Zco5EDAMwEmqniQiKJqhLlovKCLJSxZO5ZdZOBGDD5Q2g+gMLVmGJ8r0XfVh4T1GrAO76HqXGOLcpHd30AV2+Uq+eCnqFNnifT7yZr2f5V8hSo1v41ZazBvTgUDvTE+O9SdK58MY49JzhvyJqmqZZTKvDz4O59IMieZl+yjWqkiDk5WjRvSi0qrjNeqpwQY8AUJxwOh45m2ckmQs0sVP/ljIwWMWx6GgqOjwAQddxhGuXeWEvUBRftwSBwJnDl2QqmaXLRpZIVb5pUzmVd+9rwgNX8HhAqTdxzzra/8zw5nEK64ppKntmNJbbMAG5t6l6VAnCoo2MmFI0wMlixPZ+XWZxKSsGWMkKW1JRWam/dEv7kT36Kx9Nfx939Pc7rGQ+PD3j1+WcoirdsjoH6klkjHI7w18tx+8/swe7Y/jV4f85QXu8P8lKdDPxPbY/22rFJMF9/xutQKn3agYPdeQ28u75wOQLXpvHBe2OtspkAccebG4xV/MBqBN3heQ33+P6JqGtjzxC+t28X62UWq2fesbHXefPlmLpJd5cTLD0ccMv0EGPAMk+gPEROUqMjJUsNVzuL0zLLynDTG1MgTFEyeUrZhoJg5f24yZxSC1b6LjkjTqJtD0wolddiZd9Lje5rAMIdqPTrIDhFptvLYZZZelgwXZ6P87Sy542jtz7MblgYMtacxfzAjF+9XPH+23MTbmqabuBwnLXGuOsjaC1Y49VV50hELptMkx8NP1taY3JzqSPtCUOdS2N9yZUzBZrg2GhvF9hQwcgZ0aGOdWhZQMyZCWT1bYFfMvC//PW7fs6wNkWC23LBujFSbmtrT/rv5N4lnVvYkYeETxL7hemxpFyrcwiwffT8RmHklFFiBoWgpRIJOUmgIYVYeal2Lo2/bzhWKp/YeeXKn3n2Q7a78SoyRvkndk8ZI0EiV81wf3d3h7u7O8zLIudU+eyu7ID2y2DAOT5eBlS29eodddwHRzpM11QFGrR9qGfO9tb2gcTuUy7wlznDWH/uXBo/iwa39V23Xm1s7t4ge3f6kn0lQNs3IjHGDkjDeJR5nrFohL6lf2prZ7ysp1UOBmwMTmFjuLXiXhLeMXn+QNsdM8mQ1oU2p4qOjDlAIwnMridbSl6ojMcJFnDX8Xy2dzXzbd8uDXOtjgaq94zEyBTEmE6KCYoG7QaqcCs8WwZltQFpewWSMjxtCRRF525BuDYOQit3F2MEwoItF5zTGdjOyPQe5/weXGZxDOCCxMC6HrFtG4iAeZowzxsSFyyBcDgckUk9VXNGOK1Yn5J+bVlMgJaxSA6743EUe3pc60icCoDGk7QnREZ5BIeDlKOGpLI3oze0VDERIUTVe3FGcxTW59QJZqKo42PFI5otCkWM4GkF5Qya3iKGE0KeENKMh/Ud5tMRy3zA4XjA8XDQjHB3F0dnvD7ZMD4f7qrHM00BQQvbbykjxIg4zyBI3ZUkpx8UZ3z79h1SSpJCAPLs0+kkqWjmGRQjMkQwCGECgcVQ49JLGXCXUrBtCbkAcRKvYnFaiBUJAUBSb/NptvtcBYnj7b2k/FJvbrATEgsDFBGmuUbKEQiFxJr8dN5wpIhIQIwzphlYnx6xpQ1ff/938ZM//DsSMZsSpnkBSBCGHOACqEE9awqGmk5do0e3rREpIUaWgj3XOiekab0Oh0N9V5T7ulEkdQ3iFEE8OwWCEjUSAONS8PT4gBe3NxLtWJ0OdjyKXdvAc0aa54SSoUlHpISX8Yz9YBSvWhdPvfuhwRF3/4shervnCbyNtZcnxshPNaR3t3oia2MqzK6WHl8w843Qq9m1PuuiU50QcCEk4nJ+9Te3Jx1j4IU5F53p+QV7Iqh3XGXEda5v37xF3hK+/uprAIxvv/0GDx8+SJT4ekZKG9b1jGzp0lnwRMm5WysenQVsUsNcxq/f5fJr1BD63nX917GNfkj94KSVnpiQKoxk6vrdEetmqC6VERWimlFiBBfGmy3j8eEDXrx6iVeffSZ1sg4LXr18ifP5jDdvJP16oFDxy6hMrAqdKmXrnlZjpo5KmQvA81GNYLNjNbhwTUXGUnylrlmFZ4eLB6DV8dmZH7ZAx2yM6Kh02VOi9MY8tz/s5tgJ/sO+74zPmGUaf6xfaef5oa2ds/hpePH6fIkaFO25dVRno7HPYS8aY97aIQA3x9uqAJCoJ0sVqWsN6taxoq82BDjX4LbJDm1baiF7/pLWXNljQ8CKvv38PbzzAEN+TU3x6+HFM/vdOVY8PY6v7UW949bZte3+u0ssuvv9PPbuXaO5e2P7lGtU+I3v+u+XsNjWuCordsYyKtx6RaNzSGhv2ZOunYZWuvMNrywaEczwodKYtv7jkaXxda+JIht/66qtyYhPXIt+4B2dl+fIfTaBPATfr3/nEgeM1+7+s+Dub7+VchxxmmEp0wmSqk/oUENetSYhXTfkeYj+lIuZsb5M4L9eQLfXnzOc3XXyXTr6+Ej2er1y/8/xIgBHgP+rCevfBab36uBK7vfhHADoz4tbpoHLvdygOkXF4w62hSco4BDqw8+hkv3fTMHQj9vGTNSUMiVnqddJcBFiysPUDuTclCLp4rYtgXMBZ41gYqmTbGfG82es2RDsf0UFbGYAGkHrS3UZX8osykQAiAhAEEV1r4STsYpCFzWSK6hR3JTzYEJJjE3rq9V0ir/FdbdEHCepOJfTGef0Fuf0ThQDHBBpxjRPCNOEMEXMc0aMEi0UiEHICDSJg3mJYA6VH+AotdpEhZ+wlhNO2yNyWmvUm6yl4GyLkamK1YGPY10beV6MgLanrPKuRAe3NKEgrfULizbqL2Y1rg840OBx5BmqIRKmBN9pz/GZtfo1t9/930ua2B6233JqBhjfTxtTr2y8kPMcKvJ8iygwewNyx3u4ceWiqRLRjNNmmGUNZojzhHmakbdz5VuCU/LZuopRPuJ4PGq0u54tN3czKLDJfcVSuAp9LIWQs0bs5wJQ7vaCipZQUD7EMhJWpX+N4hKjSxHgAhg1BWd1jmFS5251/OWADjt84hncc1AAgGnSeo4G97oHdr6L22tvhByN46VIBE3JBksEnicHq5oqep5RUkHKGXPOmLeILQVsWQItYojIVPDw8Iif/vSn+OHv/BAFwNPpCY+Pj7i7v8NTdmmpUZ5dgz2e7blnrhlOR371Uz+P/Y1nsN53fYz97r0/jqtv9/L9vTb35tfa8SiQq97xuTmOhnHjw3v8gIt2PHzZdwoMXGxVqLDkry5NuYPT5wz/1/ZhxF/1M+89Y/rNiuC656we7MWYHZ8j0YfiyCd0NWJeFoQ1aKYIqAwq9D2qYbwUOU85JdAyCynSsiAMAKp8J4pg7g0XYE3LziwlxsiS8ToZmMz5Z6RBtr42A6o8uS2Bp3XyXi+3eNgysPoUNFZZvI4+Ks0BuQdQdUAiCwQUBlbesOUEE701gB6fLRH/6s2CZTSMK1+FaHg7Ihqf5ehhp4thwevWRz9+htdR1HdAXbme7qc6lva1Gcf54hmQRt26d9gMtFlKPlIU3P7+vOHbD499n+R5AYm4/uZtwb/7f0r47//bs8CUjYXthX4uOoy2Nn6M1IziVorO1qaULHYSFyhovzG4OoNMIWoW3ogcixCdDoewG487e8QgVruAgxUal9LgqVt3bZd6Rw+C2CeO8Qb39/cCQ6RZgbMGUdkc2OO6UuUDZmA0jFd+0PEL164agEEAUUDRIEkv6F8a16l9NHyts90/j26hgB5Wyd5uBvim15NfNITkAsgJ2PO17+Dd8NH5fL44I7Z2UqJlEkcgw13WrtpIufKqznDM/XyMb2xpubWJEFBKzwfs8RJGd8yBpgawut/bRB0eZXH8L9TKBZg9DbqmBuMjvTM+zGcMq/RPI6GZua6p+v1KJDVL/ogCACGqLVQCiGRxxZRMmjrJ3kHJWBW+t5S6jR1XJXNAISBxBqczHtcHPJ7eIm0S3S/ZrCMePix4fAgo5YhpmnE8ZCTKWCYpjZG5gDmD8wbCiseHM8CEnBkpF+S8wws60gyFwYal/G9A0zoQGBmCg0RWCXREjLeY4oIpQpzNmTFF1ojxgBgmRFrq3hbO6kiW5TMETwUKQkfUeC9nFgjIYN4AliweFA8ATWCakDkgp4Q1PWLNGYmljnmmgvuP28U/3TD+8HQGQFojbm1MHAhUEVaS1HbqFV2yRIMXLjingjAFUMgoWaIXt4LqyUxA9YhmAA8PD5jnGXe3t0g5Y11XPD094fHhCaVIrv5pkrQQDw8PyLcqcDDjT372C/19quk8AAH+eZa0BhahY4dGDNgR0xTx8PoNSik4LAdNAaueg2Dk04qkdcvnSDgEYX62TWrM3N7egU4nNcQDa9owTxPW8xk3NzeSxiMEzJOmLdfDPE0TTqdz9eRgZonqXrdKvGT8M7JFL6gQGSgglYwpRhDJmi6HBTkXhBhBRRB/MeEuSmqIx4dHfPa9WA2/jYFAo9+OfwJbFNu+ot4YwObx5C8a3mkIFx0RGBjroalO6ee7qIp4G4sz+QzI3CZHMK7WNeNTk1dmxd6V9wIG4uTWpC2Wf1kZBGbnZQXXNzsc057vBAhTigwCVyUchtj3OOY9xtTV1jBibB7oQiCA7XzGmzevcXu8wRdff4XHxwe8f/sWp6eTRIdvZ6zrKukDc6qpMMGsHj/KxBrDdsnK7nC3lze1lb0Hn70MdK6/2ROnyhgPbeyPar/tTxmlGTdqf2wZJlpESQmMXBLO2xkPDw94+eoVXr56hbRlLMcjfvCDH+AXv/gF4jThcDiKYhZ2LktlsI2g94NTZbAyJEzDzujZt9pGBrvCAIuyyZ5j1vowI8zaodnb8mekumvKlWvKFPu+Z8hjxScjrmr1jKnCaN/gxYf2lYa//jF2PzgBxys+rs19b957ip/2kHuP+jYu2+pT5dZtcviWiLAclqrI49KEkZpStFuEXpjz46jPKR2gQDWDhkT4+P2iof39Nbm67gM9es6QvL/2+898qpH5Y7Boi20UqI2vb+fauJ8TKnb722lr7xx9iqF9ry0be783+04r47gbnMjZ6Lv3c0b3uaGVj493xPpUj6M5RbRsF35cHa21Vjpa201Xx9WMIyZIOKDcpeUVfAcaThDlQFeTqh1SwFQPRLX93ji0D69EQNkyXn/zrdSL1X6Larksq4sha3YHbESNjlvZvWyLPF4ohZEmRv5LCfQ9Bg1lOkeSsduh7+C7swGfcH0KXP3ZXQ0GIBLYv5Gw/ZQw/eOpxW3v4Ii9ayRJV2nW1eeBauJkfl6pVJveH1iPc+S5C5zGliUstFp29SyJE5axwqzAxKXgvK5gSHpITkXr/Y4yRbu8wsOUITZG8OUzfg51c0qpUcpQ/gdEco8B5myjbDJaMGOdRPYGliiDgHAR1fxdr0MkRBSUtCKVRzxt73HOb7CVFYQJCEfEeIM5AkBCjAnTNCMGrnXaJOKCAI5iJA8a4cUuwpZXnNIjHtYPSNsZ7JSVUkdUyiuZTFxxExoWkeVSJ4UiEY22TiUXLNOMOU6Y4lQNyUFrInu493AD14dXmMkzDbd5ZVg1yGD/lPd0qle4X/Bf9sdFKOuDtY0tbUhp6+CN2RumRwVjm5/QgXYW7fIKvPb+SD9R5bacTOmF6izrz0CIAYtGDD2cn2DyQjWMu3UlklTCZhhvUe/mRmBjEYWWfJfU+Va70sqM5xAkt7lmlaas8mYWpRrIVMJivOdg2FCNA5BU+4HVkGz7xnpWnaxZqICKpNMc19PWo1d+X8EFw70AAgIDWh7AcJfBgdF2cwIyHY2tvxn9SykogVACJDMgzImjdo6UEqZZ0mnOKSNNCdMk6eZpUweeQIhTwLpm/LM/+gm+94MfYJ4WPJZHvHnzBi9fvkKgTZWkbb86mBmuT5FRnrv/MWX4x9r4JPlwOJvP9XftnscP47jH9zwfvN9Gk4lHXDW2abim/74/vuCe2+u30lcX9ND63of7T5Wpx8/jWGnn9+euSg90yWlvXmgGcvL96v8KS6mCwlwdrJZ5qjoI5l7HFoIo1FnPXiotM4lFB5pcIMYZGIGRurHOcQ/MKBA8F8LUYMdoP5zMr2vPFUc6emXcTWUCTXdI6BxXGjKoIDUu8Z78d7nuUPzuyg7YvGHxrGhrEYSGPJ43nNYE5RggVBb4SzcL/lv3NzgsS98RqWFE+bYQLGOr7qOH0W7Myj80wusmSlBvOC+ZoJcTRs5X3+HLR9k/SFCay1riEABLFGLSAB9mqbmeUsbTecW7h/OwuK59krIaTyvwj/65pACeLhydhwF0Tew54oeWyUcd5KTslqvNe0WXwKUgpYy4xArfwktYChaFT/aybHH3SfwZ3XjNqOxzSba2MOzrgI9YdEHLMmOaFxyO4liRNtEdV/4IdjYtEpdrOQF/b+zfz79bD5Morh0Tak9pAzUTsh97x/PBnWTu97N9Ynge2cbYueWrLNHKeFK/huTlFIPf1oLBDqv8ZPsTQ8DD48OAMATHlMKYp4h5jghRIpqJooxMZZcQqJacMntOl+nP8UYhBOSiDleIXRvVnqAHz9MQ+01kzktey3/n8Z7ibAueDWaQDUFS7isvZrKFZfqoWXwc7TSZV6KS7Qxy5S2ZxV7JECN5LixlNjQKnYlQKCMo/EaXcYIBcBT43dKKpNlLGL09ht36JhZnnMKMp4czfvnNa7z98A3WdUKgIyjMYF7w9Bjx7pHB+YBlItANo8wFUxD4lTriCSWv4Dxhmh5AJLa/5KLGq3MCxosq3BpfK14TjR4RzFFAcXQIEpRM95jDF1jiAXMExG4gmS3EoVMygBNPbs8LONh6a+ldNvxk+6Np3wFMoSAgYaJV99tOQwQ4IGfhrVOKOBPApO1+fjHRi+uTDeNPG8OMaYxJ03y3xStZvOxIc/1nLUJGwWrbSL3SXFKtN9orW1Uw03ZLKeAwgU9rrSNF04Lj/YQY5nbgANyGaMWkAACH2zs9ICJceW/eNTOYAlKWvP5xlnRygbIoEWIEgtRETlY3KzcGZE1bRc5p25CDKGlOTw9Sn2KKWF6+lDUojHJzrIJ0jBGn05N4yVsKMBUmRShVrylXf73W3GAGtMZ4UO9xEGrtBDNEhhCRS8Hx5gbvH55amkBNf8csaRfWbcXp6VGQl9UYFi6+pXA0JQp6mm7pZ8erCRZ8cb9n7uz38W9PELw2oxrEvbJ5R9VRFRzthg1CVA7m9njRkR8CNd6MjB1wAg0R1B2qJ8igXW8uY8QvetP2OmbNKUrG5z0RrkvDLAy9znFXOHHMszDD/XSJJHrDr9mHD+/x4cMHfPXllwAD3/z613h6fETS+uHn9Yx1O2HTKPFOWVQlH/P0d2PaGV43VPTjszH+ppdnRR070t3D8NcPcQcyP9ojg1vg7N6b3OY59pdLAXMSQhsjIk/48PAep1UM5K8++xwvXrzAdljw9ddf4+npCQ8PD7i5u5N0XmbwRjuzTdlnkbdOqaDRPI1ZcaeylG7+XskcNLIdgKYtb4zf7uVg8GNGue9itPM4pOGZ8d2mqLfvzzdsj+zgmPHV2iT3zztcNypY9wyWe8qk3eeN2fYC8Qjcu9Nj9OGIHi9Ke9M0Y1kOeHp6ROFSU3KW7A3Xlx2YgH35jOK3Cu/yv5wSeJn3F3TAqX743d9uCs8bwfcUXkR0tavf5Br3r37nDvvtCFHPD+C7GPq9seBjBqPx87VrDxZr+/JDt4h+rFfPscM17ZZhQxn//rW3Z5dnXcCO20fsOAbsjMf+ChtU6hy9kFsfIxuztbYDmGP7OxeDa1pILlxTqV7bJztHls6te26gNSaQvnn9GmlLWiOtHSTD5a1dm/0+XPQoruGPa9fGBfmrAvyNvPtYXb1rRHo8Kr8NI/BfsMuUGXVqP2JsxwT6w4DlMaKnbdd3ZVyaC0jbe8ng18ZhNIWuwOnuuu89O8gKO6MuhZGyRoyq8knOpDkHsrKOEs0cQwAjI6fU6oVzOxN7OMyMT3VUKlv68zIq+8ffnVut4AGfFpoIKIzAkrlM5iUpFkVRE1VhIO1lTcu3mzHpO1yRC0pKSCFBUs5JVEJSY+xKjDwFhCUCfEYJCxBmUIgIkKhxSztImDDFWRWAEnHLpYCpoJQNKa84pxNKTggsBnUEQi4MDqzRY1YPuwDeUKkLV5WatsdKDyRzxRHLsmCKEdu6ohTNFOf2tYvqYDT4qFfPH/k9tex2hueE7+3Xs+evpG2vj7CL5GFImluB305frFcpRR2FUzWKyn2ZmzdmtfSLbW32xmWyWaljMDnaTq7y+065tZWkaY7HyHuuCqZplrJwOVlmvLbmzYAl6zfPC25ujtWJqvFzbbx761/1LqU5snTPyyT1ftIZSW16AoBoEe/WU0SMpoBthgGODEIENGrcn+ea8Wo47yMecDv9/MWiYzFYlv2Tn8yx3PCarYHpu3LOVXkrCtuAHAmcMoh6RSmIkErGnDZwlkwW6ya6rHmeEdZN8Cg00CFm/OSPf4bf/wu/wldffoGb4w2++eY1fvCD38EyL1i3teqKeATc73j5vf7UZ0d+ZuTH994br2v8qu+jf09kkGt9jTzhtXafe79+tzNceUMXKHFFBrgwZO/0Jbq4S1gdzxtInI+8IYG5ZWZouKiPEtsz9O+fjcu1sY72ZKu9eV3Oz/5jO9U/2+rcuz5ZQpqy0r9AhCm0gCpmBhegENf0tEEzdZZSkC1arypf2li9U2CL2iTJNMxcU+TmXBACa9pw1hIpplcpdV0MpwIaNYj+DNgatCVpMkb9Du7Wyb877sWeU09/38lYzgOs/l6j2wNSLng4rTidN4gTHerztzczbo8LDsexxrh109ax8QSsPCfX7m0o8ntQPN3majxgL+y3qYzsqtGP+jQZ/HSCZm1E1l70uEHHWHJCWjekbZUI1BgxTxNyZpzWhO1istyCjtT5by3A47ngzQfG9z6LCNT2kXWMttek51tQvkbMusv4H4vEtNri67oJn+vWYORfGYycE3KOFSfB8cJ1L0wOMXTVyZZOb+WesbX2+1z1jTB+pF8p44mmacIyz1jPK9ZtEx0TS/ki1udk3C0wY8y4EuJguiIJ3mlnrse5Y9BX9+qe3CwLahtUx9AdUW5lWffkfltL3we59runSQGa7BlAst9QvVff73o0uiMDY5ITME2Ev/wXCf+owwOABAYULIsaxgOwbUUDWts+E5GxUwrXZVhRgweBy5zUWaHCj667wi/nUnFBLVvlshmBPJ5yPLvbI9JFI6Jqg7J2omVVcntIMFgSHWaJVOkKo2X47fjF6oTqAvqyFJpjMFJhiUAuBZk1Mr6ZhRGKPFdTvOcMniKYWhBwLhmkY4kxIuYAaMYl6TNjmSekbcM3v3rAP/wHf4pff/sNcllA4YgYj4jTLWgqQLhBWMRJaVnUOVgN8yUV5LRhK0CMwsfHOAOg6hRGWqJZsgWLk4ZhoAu+HuNFgHf4JjV6xxnz9AWm+BXmuGCqMl0AQ9LSBzISFGrD9Wx2iIMrXy/3Y4XlQAyaCmIQe2naTvW0gQMmgsgGCgt5I5zypxUZ/2TD+Jq4MvfAZZ0bhqWhk8XOWT3NFElZLXGpMyqFAnIxzx8FwJQF4LMY+x7PG2hNmqqBq9LktD6BIUqToql9uRJegKaI87ppLn8WA1OI1ctKDmpTQjID67qC6CRIezngfBYDeHaH2IzXUEIWckIuZzAIP/vJPwZD0qNDxcYpBlCcUUrBsnwGAuF4PGA5LAgpSQQPGCgZaUt1HeT5RQRiKohSjQspSWS9pElrXhzB1dMVoSvhcDzinSGOKjBQJTQxBGzrWQ5QYQCx7iMZ5DFqmk1DaoIwB0PrjrLJrl5Y8Yyxktbh9/pb5eihPJUZhYwhH47pKBARDbe4+7kNcLhP/eNUl7YhyiroGKdjQ7YvIwZxNLMqBPy4qCGFOgRqZKGiCS9cMtdogG482GeU+8tm1ODDCG7OGd9++y1CIPzg+9/H+3fv8Pj4iPPTkxjF1zPW84otrdi2s9YPN0I2TN4h1Gsj8SOi4blum559l/tn9uZta6QCVH9dMlLtrr3uAOIj1/4TFYKVqd/vUwh3llSUGkEu3snAu5RwPp/x9PiIzz7/DNu64sXLlwhEePPuLe7uXtRUvCKghcpwd1G5StCrIjA344ixcH5kFR/oX8P7yzJj1YwWDWdcOwOXhsNrV48/ZAS9EnNsp8cffhh9Nx7K+OK99hhd3h+HW9FTw63XIH1UMFzHj+jvK73rfuf+vWaAvTKVbmzt47iu0iawHBacTk8tk0rJFU6MM2VGt+6XgnqrNTTiaYZEVR25CdWdoKbjfVbxNiIJ9/05emS/mQJ4Dwa/i7HYdzwq5j6mOGzPt4kQtb/MPezuwczeWC9p6cfH8ty1rzirN64+s9fv+N2vl829fR7H0T6HC8c8jwOowmnTPwz9XuvE7tfxt6a6dtuMcBUYfTvX+gGqco0IyCVjiYdKy6/hBsPSdd399MdnS8Hrb7+tWK+2SdAUk2pgY1a0N+CK3bFf+VGnX5iRY0H5Wxm4v1yaq+14hmfn+Y+fzP/fusb5hC8Z/HnG9ncIy0OrO95BuqNt4KvbPlzcnmWg1gYjOL7NOylblGl7/aK9az1xv3GNbWgySs8jCB1mi5YqErlT06Pr+6UUl/HAKfc+wkv4yxQnLeqk/fVG2KBRqQFN7qtGDoIoKUMAZUkJJ+sl46pRC9rumjas6yr0Jn6aUH7t+vzlS8yzeOivacKaJzydgfcfClImzAsBISKuYuiMgSR6vDAQMgon5Lxi2wo4nxBKwjzfgDDBKmmy+v8TRFU9A5hJjA8rQflSKF9CKFXDfWnUKRblY0Zv/X3bNszzguPNEfM84/37952zg38/hIBx1Ub5phpSnFHXR2h/F8ThlUHk7gGohnao9G1KNq+wzTmLs7A6t19rH+BujKJQUvh0Ogdro7XXS0n+tBEJzmBW530nX1fjBIQm5C0hxwnbtiKnjBgJIQJFDc4FQNZ3jjcLbm9vRYYgLRtQDElHlJK69PG2F+N62vcQMphjXWMCwGo8Zi5Sji8VABOY5XyFYEpPU6gGMFqpOpmXKBhtDoZD6l45nu+Crnr8VG9d0l9TsgWKYAAlFOTM3ZyJCKR4wOOpGGN1EJDUzAETR6SYgJDFUcrtuZXMC5Dghi0lrOuKzAXH44LTWY3jLE46pwz8p//gH+Fv/Ct/Db/7ox/izZu3+M/+yR/iL/+VP1Dj+IYtbaJ/c/D4qfjzU689/u+79OPhBfg4T35N7/TbXOMYfPvXDJPwvPFlgwKLrl1PG5/j0ffO0MUaeT6hwvj+2uy1P/b1SXIQBu73E+bgr5FtHWmyPXPZthoVKIAfVtz9s/fAq3sQLOpZFOnNSIiqf8hJnJaCFawFS4xLsOwz6LM61v4dvTGcHXpcQkRi3COo3iVg0pTvZPXGR6ZtwEuXF6Fakb/TWW3GKemwRWW2RVXuMtQBw7SO5y3h4THjvKLyAgXARMCr2yPubo+YBuOkrZHj/mRtLmiw0E+LsGdIFhmTewCAYkAogOlxCVB9J/Wym5eRq7wnf0nTLNd2R4ZW+zYdWd5WbGlDKQnTNGGaYk3Xn/KK909ntCT7cgWaaipuhuhkMzM+nBn/8/91xv/4fzjj7mjDbLwSoIZjUlkuUC2L2LUfJPJeaAnVDLg1ypbbXtuyjOVTJLCwSJRrMf2COxtoTijtTIfu7Fkmy/oP7fkmS/T7UQ3RaEZBSVFf8PjwULPTmFhdNPW7GcTbQaF63oI6BxwOR+DBLZQuRYHx+bnBt060wabxq/K38kh1zUPF19aGzbk0IUp4Id1EZjQblQ3J8wOSrqEHHk8LoFlxqEVoo8LHwJrYPe5udVd1cuweCIgQR815nnA4zpjnCY+nFXGKSEgAiwk46BhKSRKIygC5klPmiEQk6y2lKjZMRZxHxdbmHC1LEeP0iN8VRqwEhTkwWKYP44FNrgIkgwMBXa1u/xxNwpuFONW9zSWrrKbR1NyM42BGKK1+fRtT6994yVDERpm5YC3qwMmtbJFFRDOzRqYXsYuSle9SOVM9jaY5IOWAkkwGJeS0gTggnQM+vGb8/CdnPD4GxJmQ+AyKGXFhxJsj7l/cYYkz4nQAxQiQ0DhOGRyBpM5FKSs/TI1GGnzGEOFlDQ+/JjV4eaj+joZzvfPONEWEKIZrK9Em7UgL5uTbSzKexvc9EXk6YzCoeJCASeXqGG8UPwlgNhmqvVdK7zR/7fpkw/j79++rcmOsn1U9dMiYvGYgNwFQwvbFcz4rorZ0vtaOGIGkVoxEcTeCYZvTCETEmrYqVPLSDu2HD++RU2q1qmKsRnDzJI80VSZJFkzTXqUEKFAz1BFAv0sbykQBCGVDCGKYD5oa0AhxqARdxmqMwBQX0UsVSbViDmLCmA1ei7q5MURgAuIk9erO53M1Thf1eJO9bwhrnqaq+JK0Cm2/Si6Y54hNDZ2Is6aSiQ6IBuZjUFxYW/5vr+jeZ+Cacdkh+9qdkQDHwFWekCsT4fvs25aXOh4IXpk4Mmg7FwM+zQVc3cdKoC6E6r2JwjhFN0n/MzXFhc25hur78XD3uTL5e+NAgxm/N50Cye4BWgsiaHrFgKfTE379q1/js1cvcTge8etf/gqn0xO2dcW2rTifTkjbhm1ba/aHa2mQ95ZnH+1df+O3Em3r2l96yHtGg/WJHfbj07rZHedHRr7D0FyujaajLwQYO84Bp6fHGiH04uULrOsZL1++wve++hq/+uYb3N+/kMglTRkMJs1+YrBF3VELqoyTiKwo3s8Ozmwd/eqIc4xTOjJretGdc3FlST9F+Pa0xS8e+QlcXAo7NO6pxy0qXFUmd+8axjY2g4bv2vnqcWBtacCLn6Ks8H2O63RhFHfP7LZp6+VQ6/iO4ATCMkskt9XMqcrbwppCchiLfXfL3Y13uEcUlHa5tHXD3Izj7uZyCQbd52aId+s20jB7/DspGC6v/t3n2jE8ZrioF/Q+ae92rmv0dsT1nzKPvef24PdynPv91nvy4F6n9f6o7PoU/Cu0vQfkTtCvzRvR5lqXto7HKczYfccwnrpl/l1Y1PoVYKx9uF8cDvWDrDSIC8SZtPRlKXYvxcUX6Gn0sJZ9OD0+4uHDw4UQAqCm0qqaCa/duNK9v93tQj3/jPWHCfRXfUap/sW6nPvEs0NX/2W7KAD8bySsfydieYjw2r5uPb4Du2LL7LfD+E22z3pO5CxfG5y+eaVfon5Dx3ZYeZqi8B4nyTrTImrb2W4GqJZNoRu+tbmj7LyYv8O1Mi7qcJpXflgtxkWkoZaqr0buEGKUZ0hlK69MqcYwyPlatxXrJAaxsS7id70CBaR8xlbOOKcNKQWkdI+0FqwpoRRgChl3N0fJ6ENA5oxQJCJ7285ImZE2BspRKtBGxhLuBBYsurswaCuITJgASY3KBVsptZ6lboqeU8E9nfG1KjDknkdpOWcsy4zj4YhpmjoFl9cH5Jwxi4al3tuTQZtc75W3n1CexV0exV/jz6ztEKI4lKvCz56r0TEdbbf2ezgxWJe/BFFER4gBw5RUQf9R/TvKcm4GygOR6ls0S11dr1L7A7LAY1o1gEGy501xQrIUraq3YTAOh4PWun5SGOlRtynN/Tz31s32tH1vPEXkAg7Rnd+IlLgaBcxgDoJGElL17wERKBKgUflkaVnJ0r5XbkWMVLpazH4W6BDWx/gnbyAPQYxr5hywZ+iqSltqKXELi2NaCBGBJNXnRiqbOOcaFMbhsCDnG3G8yEX3S3VTzIhTQOaCX3/zBv/5P/sJphDxO7/zI/z0T36CP/3pn+KLL77A4eaIEAO2NXUwbufG47BPWYNxj6/d8+d2PB+fst7jue8MMzu4vb6Dzhx4Qbcq/O6MwcNs984OcZQ59byxn2dtw+EqqJ5qlMF8H7WN0rczfiaiqjraVWArrmACopD69n6Hp9uVcd1Y2+TFS5y519bFznJbC2Mi5Uyy3Feda6UFLpVyfaUUKVsSCJFRy0Fa85Zy3XCmlW3JaiiMU9TsfCyZOEOshlepCy1RtpkHfEeEAkm3HcICspIKaKl4bRRylAkRAh8cgsRFd1lU+jUj977Q1cbLm0DCfLnGvfxlNMX2FhBzRDOmVhGpkmw9/0pr1y3hacvYuK4oIoDbA/DybsHNMrXAHLexuuKym6XxkjZVrw71xtai0cIyzaC6JK4AxipTsmU3URppbbIKDFWX6uUtVriy9XELRWQZY9VookFjc1xqveuSC9Z1w/sPTxi5ClK9F5MtsWCdzBkfzhtSnmH0XAL4muxX2WVS6j3STmXYDY4AyQhpAX5BjV6er7C1bVNvuERdTy/OY+X5iJwxVwfHPU/FtpZ2Lqqo6HkTKbXScESLJibWzDrnczXG55wdfy/G72XWFMu6NiA5X3GSTDdx6mtybSkjmnMBWbS6Oyt+0gYLlTmDgprHnS1AyPiEIKkjKgyYIRQgcewg1Di7UldaodWOr+6jx282BmroYPdy4OLUbU03SybgkfKC3M5P49W0ZNs84eZmwfE449s3TwjTXIdEyn8YbNjaFAcLTXck7Sd12jvczk4/8jxtq7xfjOCsTrAaxCrZESbJjqMylbXnZS5Jy63vFeWvYkDkWB2R5YxnZDeei7V1+KLSRk25Hu3xIGfYOy9SkHrXzOpOXIrYU7R+O+UCTuIMUsh4A1uHBv8pbSCWYF1CQDqvCBSw0AE34R5hmZDCI86n9ygbMPEKHF4hBmCmghgKKERw1KBjTVtOCGCOOK2s5W+fkNIJW96khrnOoTeMe7xO7q+j8cAFHvHAOwUp3UHBuO2AiQhMs8idXEDEmsn6mmOgvkv9PZ9VI7o9punQaKueDKKeFlxiv/3r02uMv3sHADUtjX3uPJ1JosLFi1cQ4zzPgohKxrqdJdLVDgU1xsoEimnSehisnuYcIDwK1zD/kgpO60PHwPPMxhkibysA1tRxjJIyzmrMA+QgUZTOo41lEi+UOE2IkRApYstJFpKAOIthPZBEqlMgUA6YoqR/r/dgYEVSu9fwn98PEgK/FU0/TxY1Z79pSgcjljGgcEurLl7pCTEOURO2BESI8+yi6Q0fByVMGaRZWNbzGfPdglHTeqGEMKR7BbCeU7JfMtiVix8f3mn48hYr4zM+P9Ka8X5jFq/PQzvo+wIANz/jFUUgGedw0Wn/08W99rmuYVWeDBNywhD8vrcGdhnmTjDV/8YYFO6kr3fv3uL923f44ovPUXLBL3/+C3GcOJ+wns9Y1zPSJoqUki2KtHR9wHrY/7i3vG2cO/f+rC47E76fyvYYk9rzSHWcFaF6wWPn9+uXXwFzhzB2hoZn/FuyeAWszGoCl4AQA9Ja8O7dW5zPZ7x4cY+UEl6++gxff/UVXr9+I7WitbSRwCprvXCtF614QCJMNAIzRk0V1AiJwWs3R/2dWWrggbkxFR62xyPWMVP71/i7KRAvjeO2ZjuItd+16/erJmHYwWtN7oyvUy5cmda1d649Oz5zTTmxd5+vrfEVQPXMqjFIy+HQ5GVWp7ZSdt5v+ywCBV2sU73v3o0xwGpPcoXBRr9ao8Nc9xDJlSHV58btR1ujfVi7/r2tl4ojV/ZlfL8aiW0gSvc6BcgujRwn0Y/pObj6VIXmtec+7jRwSWMuPl+FxX3a7dfUr/Pl2FozBtcV5ew0W33EBZldDL++Q+4cuJvslDN9H9SPpZsJAKccH2n0yBMIo6+pg2NLC7nLDw3tVXiwsbaJK11/h7xt4gDFUOrjjBTKV9f1trNWmxoWa+/S9SvM2Dqj+N7Y6/Cut/df4osBIAD8tzLW/xhYPsQOHwsKGflytG3aWdKR9xofYQDEjAKqqeUAB2cjifzItu0ZMlozotyLgTQFn6Yh1YNcTAklUn2V8UxJabWGfbuW4vCiv0EJUyNpuHT37DkzWMUQsWi01/hcq/NICFx2+7DfeYqYZ8LxMGGrGcx+84sK45xOOOcHrPkJuTAibnEzAcRPoFAQQkY4MFASUnlEyBsgqnmc0wlbyiiZEKhgmQ4oYQWHIyIfQEygwigE3C83+OL+FV7cnnBYZo0SLlJrj9EpuwoxKDekUX05DEkPeKwUqTF+WJbqCF/3zZhxjb7hqck81p9luPJ1KDvF7fD8CBfP8Vd1r92eErXIl1ogW1rq2pZyVD3v4umEtL1zLtwYPPwY/SyFEXs9MAxlVzmCJRKICBpYYNnxLiNB7Hsz4jY5EBBjkB+zKCcJSWnHmFFJnFt64+re2hfOgmcYQAGIcg1ekPUTeCGx3IGjyiuqpmJKCIjiIkAEQtRxmwFcnG70lIM5qxK7yakBjd5rx8NO9tceHvOfKZgingHEqh/LpVy8b2tj0U+FCbnI+L0c4mFuzq283iFnbNsB8emESA4PK58dotTC/cUvfoU5BHz+6hVevfoM79+9QwgBr/AKx9sbyQ3heHTT7DIJvLCmhv4UJeLH+M7xzI0yysd5zb22tIb8R+TJ9mJtoLtd+c2hj70xmyHqmn4FXE3MWmYPVWfQ4aLaZnF8677eBpAzbc43z66lA+pGfxV/sPF8QLiihO6cOah9f25/lB25gnPb3xbBrY1zMxm19dCuzcrApthuta/BrHxK41PFkVTb5JY9s8pf0DPq1l8yZETJnKFOeghwEZ/OpNUQYX2foIawaMbmft+4owvyqui7zamVtdRF48W7BR3WWPB8v05jnxf74vCw/AMAz6/IXpgRodFr2bOUxAFH7ZkAM2IAXtwf8eLuiKWWQutG4v5SK7Hnx6ZtGW/QGc1gzkb2bGNqyZ+xwiBz0qfWp4A8VfhpfdWOd5hXMzzr71wgmRrFII4gerG/Xwj/x3cnSCSbCwysAWdO7w8Cc8CaM/5X/27Gv/PfJvz+73qDjukQ3CiIxq0XnG6GpQp+MjZ/vx1bC5RrbYivhp5j2+NiC2KwEABq7znohdWzbj86hxa7P4y94kHtTxxeMkqRMgRFy7d05UbmCTFItKnQx+iPXDtDulace7ia1WCeCqHww0DQuYOlvavipm5a5I6k4lQy6PZ8gYt81/PfOfKSsbXKTyqPS8pnGWhWMN27WOV0tTGZ3rr97PZT/1OGCPZaPaEw4kw4HGYcDpLR2DJG2dxGGQvcziqzZMqqeJqo2qUms5/FgBCm6izIQ7S46R8s6IYhfPekQazTJI6akmU6GEaBdyBpDsvy+6Rn1ZxWg6eZhZGpNHoz6Gb8+au6SyJQyVJqqkg5Yqu7bjQtRAJKQM5CZ5P2P1n9cwCh2FpZKermMJJyRs4JgQiHw4Lj8Yi7451GVYvzV4yEUhJKOSOtJ2QGmGZQPgF5RWDGpOcwE2lWL9b62hvO2wmn8wNO5wecz09SVidvwucRqqN3JHM2anwRw6Nw4y/24LS9UwpAJYBKAEpUvBcgtb81IBSyJsImX55Njxvrr+SM5MMAKg+mwG+jYf8wEUZ6fe36ZMP4D773PUk3rgLytm5gCLM4TZMaYAVYLBUGETDPE3IuUPgRw3KMmKZZD1EzbtvhmudZvSgSTOCMUVKbzPOMlBIeHx+wLIsYibetegQSEb784hUOh4N6ep2xbVv9TQTPCdtpRcmqiETz9r65udVo2AIOR4nO1kMSJ/FiCiYo5xnHSYiRCEiajs55q1ey3ai9GLoq70AVodgYk6ZNo0CAZGHQyN5Q0wnmnDBNh9aPjglEYC6I0wwEuBRkcDXuSNP6AE9PT5hu7wV2AsE8C4W/aIC1b5xq156y4Tmh6YI87TVtuJ57QuQ6alSz67+/3X4eO/GnjABqXpydonlsH+b0cMnIoi5TpYa2APAraMbRjonWvp4VRrQttol1P/bjtTPlBTqBX6gSR1Dft998i6enJ3zx5Zd4fHjAu3fvsK0JOUlGgfP5hJIStm0FqnF1Zx1Hrr3JL598NfL+Z3/Z+veK5YbQBViCPjfCa4OV32Q+3hjuWKpn5ttzqaUwCJr2NgTwJue55Ix13ZBSxmel4Msvv8A3336LZV7UOcYE8Jbe2mBH+TyXtowq2I6kqtHGZjzqzvzexLvpfFyJce33UZnyTAvP/NZ2vz1LF1+vvsLXx/dct8+N+bsYzcfnvOH1WrsXazbMxwvOImQxbm5uujNRCtcUSKKd9VhsONxKI7yg6ztnBqZpwul0qoobRe5uoq0dUiaKeTCw7y3TMKx+8dqpfU5x+9z3boq4NKKPV//+8HulJ1S/+nb29nXc0+fOym9yfbKSEdfn+zFYrM/JDzAlE+P6+fYs7oXhnOQXea4nPx3kjaxLT4h7BUW7rUJf324jsTKysjfmpqlA9dweGxj6EzyctbyO9r2jiJWfTODVM7S7b4SSM96+eaMCmkzalKQm4FkcQVsDf4iehwdyH7aQkf8rGbjf4YnsMf/CnxeR/zO+vgs/cg39fJervhsB/lsZ518VTP9wQtzlfz+hYzeBj59u3gel73SpxKA8sEWeVIHbdTBNE9J2rrwIAzV9W1CnvcJa14/tXEl7XsGyd43GbKClUk/q8OwN2f4dkNC9zLmjF/M8VzmLmRG8nEfN6GUyawiMKRKmOGGZAgovv9XKEhNK2pDyGblsYCbM4YDjLHIbxxNC2FDoCSUDayLkNCFFUTI+nZ5w3jZxsKQVywRsUwKmGTfTARGLyMKIWMKMu8Mt7m5ucXM8agYyB3BV21zAHsB2aO94MTOmOGGaJBpEjKMWYaSKQ1yncZV3Qa9oG6PEnzPUPbPKkpHOKd+sj1IykqY89A7+oyjkjR3GLzQjU2+wqPClY/O17q/J0bLyni+Sdq1Nqakonu9Wf7Fm6EGDVSur5i9RWGfEMKnegTDPkxigL4ionO/CTenpxzyutemEyHxhABBZNiwITFWaW8CYPJnW/uVFSUsZEGgCU4b49Op6hIDAWtsdRQsD7PMte+u792zlvYSZ9D/Uj2asADVj3i5PY3vr9AeTiziuDgqqCytzQk4JaUtYlgXzLLqwKUVRyBY9gSGAqeDx6YRf/OJX+Mkf/RF+7/d+hCcifPjwAYULXpaCw9ycX0GEYryX8cmdr9InUI1P4EX9ul5bl5Gn3nu/wf/zCs7GZ7bvV+fyjL7KGwM+WX41PRw1ucO3h9reUFd+p70xhfFFX92zIw9OFVdUeMR1nvK5e59ydrqx2Ge5YZ8c7y/32+/Gw+v5Ur48WFYbu6cNS5CQvER1nRV/1syDi6D1AAEAAElEQVQsgi8CUXNSAJzxcMzcUdQpqDn6V8OJBiXZmbUSISISk0bhe1mD6/e2RKTjpRq40EKNzVyiMrTHMxcoZw+nDPKPjZus5Kw6ALRN8NugbbJ1gJQzUuYqpjIDcQr4/OYGv3s4YFFdeD8GqnjjKjNqOKbCo+Iv1UuaEczm2UQGjWa2c6X7UOW+Wk8cTj+lui8/N7T9sXMvMKMGL81MoKE/CCTZFH+5bfj2ae2FRbRd830DBKaAlDPevE14/S7i9+Ac5Oy/bQh17S7X1Oi2wkXdq2mX9/B3OsOuEHMxVqEF5DWY0PVSQLIzQUGeCaEgl8ancJtFt92WmrouM7ie2ZQStm2r2ZOIrN74gmlehKbF2J072zUCdFxyt7jtBICbm1tM04TNnALBGB65uLxOgcx249eOVDvBXLMDuanKfH2QR9sm2VtQtfsw+70hewA1BKnCaVtQ2pmB6UsaHNTubOC1ea7rJVctqcsS3DnPE+ZphmWsqyq5AY5qH2xz9Xi2leo1GWmepWwxUawOmiVLvW0rJWNtWIp9mCw2RQ1OjYhTrMG3hssptDGGYGeq0b6KG7mtkd237M9EJFau0KKNbY7dnLllRWGVQ43XLTnXksZWHrpkyarFpQAxYCYJZJtYXA4omwN3s81YxqZlWfDixQu8eHmP+9vP8Pj4DUrawMgASZr6jIySGTkTQIwpryh5c5nLAqwAAUNw+LqecTo94nR6VKP4GUkzReWSII4vluZdLRT1/LXTxyznuFC/UhVkVYYpzOIYumXklMUJxmgIgGLZxPVfMUirMN/a6+C5G5dtSh3e+EEv81ry/P8+HzNen2wY/+rVLU6nUAn2uobmVaiH3+o7xLig5KKpVrQ2NkUwzzV9yKT5/2t6uQDQFNTZUjwvYmDEacIyz6K8IEKgjNsbwt1yKwJIDigcEbTeRAiEz27F4D7PC5gPOJ1OeHp6wjzNmvM/4fPPX7QDzlwVGpIufULhgi2teHE4qgc3sG0JREDUsaNkBGTEkvCX/8q/hv/kP/oT3QTj1tjhwOadZ4CoFWfAMMN8z8DHKIKhpZyfphkxaAqgokoESNtR1zJOEYWlbsAUouwJiRezERdh7ACmgnSWKH5oXYhIqJHvXF2MzPuSOqRZ/zpYlQ+2BF4IYgeUjbCyv23v1iecZ7H7DDuctT9W5pT91/rsJR/Jw18ok+76sv7R1qA9ynWL4Z65MBYaA+dnP86H3MNo4x+Zi4u57jClbL8bQ6h7aUwPmRdTFGacmfDtN9+i5IIvPv+iGsjTtiGntTqVyPckHv/dUtjGt+8eV43BuNeuBhWXaGuPvSH33702dEGeaaGN0kgid0DTP9kb5XrD9tDrMBrHqFfs3l4Zjssg/NgaKgQYri06e07qcZlrhEJhIdhffP45Xr9+DQZjniQlVIVlFUAYUmO2pfVjMKReXhsqXayfMArCMVfGsk7AwXqdZ782o4HPw/EFHunWY885ZxzZc/d2iGIvSV6+WpmsHs91vYwKCvffpiTsu2n3diZam+U9cAQwGhH3FCZUP1cc5LNlOHzmwBoA4eZ4U8dHJMa1nJLUoZ+p9u/xwGgAr/MyvFMTGgreSltSfIl27hqHhaaZazAI6pn8i6UxoPOSfH3YG2X2sMdAb5zA6XG0kzkky0Ldwx7n78Gi33cBtcsRtGep23+/373CfWhhF5wuuMfdMY208PLZHus1EtAiMy7b5u5zj0d9FhM7X22PbN07xzHXj8FOcy7rvUmbI5KbfgWNca3bhCr01rPLXRPtodZDt3w217EOemu4DrLiUrSzZrXj9h0FHH/gvtfxdM8zzusJjw8Pupa9qqBGi494r9sjXFzjWgEkRvF/M4NuruOz2p7bh73frnX9iazEn/l1Scmff7bCwp/BgCkC/ANGut+Q/knE4Y0YcCtP6vCSdevHbODmh3MxLBrveQX7/kT28Mw+rWr4ro1I+VOIEuX0dG4KnI6MqKCdi/KuDDJDaNI40KSlsoaUnjNEUREp1vSLhmtinPBUHlGI8dlnn2FdV6zriqiGeCoiqqfCyGh4jzhg41xpGhdNUz0wLcZPTdOEZYo4xqCREHN1fv5Nr6C19YhlfoECIi2gOQA4IdMKwhnn7QPWU0I6M+Y4YYkTKAAfPnzAw+mMUgiE94j0gJvlFb66nUA3B9xMARNpOuvMoALcHY54cXuLm+OhpU5lLfMjGiPFwz5pseDxEa70F5G3p4hpslqYjWaT4X/HHT9nkDIFE6PRh6bsJJWdh3fsv67ZEILiX1H01bT60RzRM3IGck7K06Apkzxt5L5doUtcjTMdv+vaqKg8ECJie0Db9HoBOUVGN0Kld/a7GO+V14+hlWkjl3aQWpSPb9eM5WKoCIgxYNGMARXDGX/EQrst8tz0QT6lvY0/BJLM+6ROWCNPEwrAUWAqAJGDKOmNd0MCYQJRrs8QESiq0b9mbyAQIjjoutVaqSxKfreWXj9hpeb2sXyL7CIwYGtuczR0HMwBQrIieeO4X4/qUKFzCyEAEyTyx62JBUyUeca2bYiT1VddkFJGLgzWDA7irEE12vLD4yP+P3/v7+OzVy9xvLnBh4cPeDw94un0hB9+/3c0w2GfQrPWhQcuy2LZPtnvyqsJvbMz5g9az6+6Rjp+qTdOXPK5exxQXUviuoa+/fbspQFlZHVhw+bKRnXz7fbYReB1PKubeW+gZndvoJE8rI3JHY7vZMWvdZi7PGHjYSsOrOtZKW4jvRVPqGN8bbP99e3u9dUWrWBnOLuXNz7I8ZfMJJ6Flb9U5QSiFsfIUPOx4p6oeq1GgrnqSdu5Rp1jG7fcD2q0oJJrTXCG7LEeb+ggBG8WSDAMqSspiwNRQKg0q50DhRebHxvc6LycrCLjC6h0biAfJhKNhp89vUkvRrsV1ewKXbaSgb5a3yIDF6RU1PDTZP1livhvvrjF35zn6iS4t8d+TONh684v2l+i0KUobuefUC2ris/BLEF2LDRFOosgl71T1kLmYvtC2oZtNusmxRiR8iaGnNLqWxtmWbeEh8cT3j88+GDxuo5BabyVKLDyHqUAD09qQCtBgxWFfkj0b+OJqmMAnNMUBDZI4dzgYLxkSnay/Bl2OLRmKPD7Zc5l8j0XKZsj0a8FZoAVto/qfllWp4av2p55HOp1IVwY27pi3TZJXR/EPnM8HLHcHLHMSy3rmLRELtDzchWZX9Aa4MWLFyACPjw8Im0b+Kppy1bA8LbMi9qA26+6XsxaI71k4XNJYVJ/rPjHIEbfM2OlPKM6gYaR2xoC8I4dBgPsH0XDZZUuVKJiDzZ7kI2oQ9D6Pkh4lSlOmOcIWGBnsbVo+Km+rf2RnifJeKNwUOUvwjxpFHoWg2jln1NGcryh570sGltwVGyZu/SfDSYE1Ey3lWCTUQZ1uqw8mJsDN7gtaoRnoPL4vkxWADrYq1iy8omlZtFM24Y0L4jzJKWrdJDmWBOCOBnHWXDbnAryVpD1LJYi9cenOOH+/h5fffklPvv8M9zcvsLPf/YBZ6VNgo834WnLjJIIjICSN3C2uvANfFkdoVLacF5PeDo94nR6wrqewUVsmMFKVKtc4jBndw6Ym+uz8REVeju2i5SnF3lu205I2xlpAognAAGb8tnEul9gIEwV/1R8UeG0N5oHNDrO3YiVf6U83Cv1WyMAn3Z9sqS+0BnxoEAM4NXtsQK3eNNkhDhXBGPeIOIVdKOHIYCZxNCm3ndZI9JCDFjmpS4GESFprahAAdM8qfC6gSgjLIJ05vkIZkY8BSBL0PPLA2FdT1h4RowTlgPhbhID95Y2BJpxPE7VAw3QenDrCiqEw0EisafjLB4fMSLEWJU00PERJuRtwzFk5GlGMx6bV2YzMFdjqqbwjVOsG2Vp02OMWn9cxiKRPpNEjyCAKGpKQU1HGCNKmUTAniYgb9WjhpilNjkDc5gQkKs3hxFvKoz16QkxoNUeIVX8GMFQilwRqs69lyBQ18SM/x0FZjTOsyJ39+MVQWVUiveP0JDGnNuBgjO8oW+nk3z9abfx6fOV2dztW//rKJcsSf+5ptmxdbSDXhllWZBA3hfeSGxjcdgxNJ0nTVucth/GnFN73hQdcVI4C4ScMn75i19iigtubm7xi5//Cut6Ri4J6/mEks7Y1jPWda1egM0E0e9DHQaNv/VXz6615bc29/CWv7fH+o1juESb++3093YcDUbI8bA7wKwf19hXPzo0eBuerXfq2armnguBVerkFYm8AAMbwI8F5racS8YXX3yB16/fIEI8A1N2xvFgkp94uXERh6Awzbi7W/DhwwcA5qHbr3mFeLbsFHKncFA4dk92Lz0TFWo4h9v5tfvuoR7nXFwjwrl276Jz/XmISO0eZ3vkYjz+nXF+HYPFl220+T53NZxi7/R9DGfB8J4f19gic4+vAEANefPhAKEvRZQShVtdSe9ZOvD3fqz+0FRaUfFpQE5ZHMNKrqU+muTnw4ku16J3rLiYWP8XGPYHMM/P9r4CKbvx7p5kwwf7cHx5bzjjfq392jXiOcDiOO9xLS6v8Zmr4xmUD16R1vZqxEwjzrIzbh7htD+ngbL1+HnAEW6s1+Y7GqqNpa+sPfse5Ustg1HnRw4tOZjtBAQ/V8fzkF8Xh6OHN9s42Tei8rSLlLfR6zmrzY9Ew/EnF2uj/AF1Z53w4f17pLRJ2jNNFWkOkEUFpAbzF51e4CYeHmEAKRSUfzOBbvXHHTQ70sMOtOjytr0z0t7f7roAsvaL403BDTpHByTv3NZwR992d3R+43G2tgkA3wP41zPOfxdYXkeFU241CvHMWlVaQPDQ3Z9KfU55avHjvh6RRxeTfI4uoyoV7LIsC5OWb5GsVooUFSZt9mJgAsAfsOVVFOLgqtAY2yYiHOcJBEKIorAIMSJMk9RgY2BGRkLC3f0d8MA4n07IyLCEfQQgE5SfVTqREyj3hhvRyQo9LEX2Q8YlSocZhLtpxu3tLZZlyIX9G1xnTuBwB6IZgVUOngDEgEN4hS3dYktnfMjv8HA+A7ngEALOXJA34NdPK15/+IBUGAGPWOIjXpYViDeI84I4FUzTETMz1qcVT+/f4vYh4+v5Fl987wv84+UnWM6MMG/IQSJxD3lCogTAeEUGctEUtxDcVJWpBatGQB4OAYdDQAjAlmdwABBFtrW0h+KkLroFc8YzHrOgVMNj4aaMrrDM4kiQc9Iaryz5ljz+ShkTBczTjJeHW7x+fCuR7DFW2JqniKyKnMKoxg6CsNukPEukAE4ZKARJwj9p6bemqIuaKjKAtPxalJTyccIcAuZpQtSa60Qt0wERoWAnQwITEA3+ivJTwHk9AxBnjBgmJK0tONEEqc1NiGEG4Yy0nUE0IYYDAiZwFuf4QBMCB8wh4tWLO0wL8PhQUAoBxJLKNheA5yrn2rkY+Qr5rhkgsogfhYrLFiB8WeaMUAImkmwSkym6mEE0a1rLAooRTEVSY0L0Q3GKCEXkiJwzKGh2oyJRKlab1qcTNqUsAMTQcDmjdyKrc6hr3+SilkAXFd4JwGGZquNBKtDI7laCUJyRUXnREMRZRE0/kngyZRwOR6AUyfACwYW32y22LUlGRXOILgnHApwJKERITHizFvwH/4//CP/6v/rX8Tvf/woBBW9ff4s/fPseX375JT7//HMcDkeEaapl+mQaVM8dmGutzrpeURTJW7bIQzXwO6Uls0bm6jUpb7AnMpDBCmnf6HG6d7A3uhAtNApcDX7+nRhE6VuoyZSW8h+6b0bPJ7axKdVT+iZO5xkoQIgCv9kZZ7rUoyTzzpzBYarK9lL3Th1TNOikBK5OKSbP2D+bh9S07WHQw6xfyBj67JF2BR0XB+VXPV+KpvewUg3VAODKhNh9bwSTjYsgR9Z6/q0xdnFqabdt/BwIJN4rdUxxy4iT71PHIxYRkBolQs5AKYgRiLpXohvdKp0gKL8bff1x6cv0ygQCBSl/ESfRFQO2J6XyRLKQUmKFitSDtRTbgmsYYKFltW+gpqwmclnFGWCUCkfVqY/NQUxFQfugOAXKh3SGwg5HtZ7dK/JLCEKf2srq+ogxqeQMZnUyJALlFQ+nFedNTklExv0h4PNlw4sFOCwHxPkGfBH5MjDxtcfS5DLTEZsjVWhOaDbHzvmkKVFRjeQUarpk1mAfSQWuGYIsaCMEBC412rc6SFS8JDSCc0ZAATTIRHKmSkmJkjc8ns94/eERH56ErvYz1LrdhZCV/wlI1Zb/ZgMek+DjCYQJBcW21a8caWDhwHYHQuWlLFOnZYE1ELC/5thXx1b1iOJAVbT0TDP4icGWAS3fGsGIICogxX1FjcGVHrKsTTGcazJsB5tKEwLJVoHx7sN7nE5nxBhxOB5xc7zB8fYWh8MB8zRVHiYX4ftqFktyDu8xaImlxhvZNU0TzucnnJ4+IBepGW8RxYby+ndY8XkS42235lp2EnImE0twJ0NtwFU/aMEUIgcYfinMNdCRoHKE0ph6rqGgDJK61ICxKxAjOlByc1gRI6Yad9VpwfhtrnNzeg2dUctoR5CM3llkIUQc5hn3NwtCzCjICBSrrYBIygennCTAFKj8Z2AG5yz4Tc/fNB+QcwFnBnGAlroWfJuSOhIVIBACRY261tDQQM33pUjgak6plRQmsfWFMCEoDwvI+ki54IDD4SB0i1CdHw0jmh3SjPnbtlVYqIZ5R38r3dOyPCkltbVJ4BmnhEABD6cTwjzhJpDKDIQXt7copWBdV8m6AS3bEYHbeEQkwmk7Y8uS5Wh9Svj6qy/xw6++wtdffoGbeUEMB3zvsx/gw3zC61+fkTJhTVIOp6yyNqCE7fQFMhM23jCVFVMhzBSwbglb2rCVE9ayYs0Zp/WElE94cX+PFzdHbF99D28/vMfbx0fQ8YDEWWh+DLInOaOEKDITWzEuwHBmgzDNRVgyAk2INCPwjDnMCIhAETpPIYJTQl4LOG/gUhAiYToApA7jVh2jarFUpiOVWbwT5Eh5AOUx7XSbzAGHl76DYuaTDePzTFgwKWKWlN5ASy0ARFAQIzdI6lIRZkAFQjGuCRJJE5SpV+aKXN2l4gRinurBAhjTRAjLgik2nqG2rRcRYVkiYlSxJRQcjxNCiIgxIGdJF2cCqBlkxDP6oEyuEMvDvCBUTxYgKSGPjYvErIqQnI3UNGQG9Ew9jOjrbzHE6uHCpaU6Ph6OADSNW05gBtZtBQCczyfklDEXAWQmgAMhoaBMBERCIcaaJL18YGCiAOYMpgAyE7hi+dPphEgBG/fjNOGguypz0z/avvDOTXuBa3PshIv6d+h/BOJLU+fltWeUku6d4LTXTDVyXbT4XGfXmoGjRR3D0BlsFM58H70waIzHjjC5N0pT2Oln67MogYjqfBGIsG0Jv/z5z7EsB0xxwi9+8XNsGhW+bSu29YSczshpq4qLXe/h1uPF+BjXx+ufHbfezei3u5wR4/o4LgBV/984GiPudmaeM2R+bC7jmuyIFVdnXiNvO1BSIZml5MQDa8oaFmXBF59/iV//+tdYcMA0zZpyzzhF8yDWGp4uzY0Jb4VZo0z46rj3V5gb4nMTunY+r30eFuDi948bleuDu+d1r+1PbrN7/Xl4vfb7b9LXxTteeB/6HBUt+ku/HI3HBzOwzDPmecK2bVV4Mi/qit5N8bl3snbxK2on9gbr+TQ4rsIakQhiO/tt7Vdjxd75tU8VF7eJcnFvVGUJYMrMiwn4Z1wfzVGFu0d3v5jUWMfVosHlscv9/Bd1XXNU0YGMT7d7tvbV4HyF7l88S25N2XnfO4DcOxMVVvaxq9t1+T87boEGuuQFbd+cp9GObvCIO4YxPIezL55y43Kubtps6aK3jO54Y08/ce7x2sXaMN69e+fm1n6X2mP4OJH+yFW4IP/lrEbx/YuqZsDdGz5cjNyNa48Nrc+N7X3kGh1C5F3fUf/c+NnW6zru+fSz68Bspw26uIsAlL+RUP7vARM1mad78hO6t9Z3KDbsTDIYiP0vv83VL6Gcg1IK5mWp56CPpEAVgptIkbAcj+AYgCjCdIjiXFVyce0DeRbhvUAMAtMSEJYJmCK2LaFQBCXGT37+C5iSq2T1utf+zGwixg1VlEN5QZbxWr82alNOAfLMRMApTnj/dMLNzQ3u7u5+q3V8fPp9pJSQSgKoiCI+REQUlHJCLitCPmNOZ3y2qHFYD1BCwRfHFYewIZWCaSIclwnHeI/b6RUofIatHHDeIjIxMibQlDHfPGE6bghxBhCQ0oow6XkujMTJARNX9G4GlmooNR4aqDJ0sDqF9jY7Y5odS6+ogqX69o5/BSWn+lwIYgAoKtdLuvVwcdiqo7qWVpsPC8JJnCcoWF08mc+2Zam5mgqK2WpVzqco9TERRK4CW5taYo4IMYo+pJQifFXlv8VpNU6TUwD62olyBsSxqaV1t/FzcUZ3zWoXaxR+AVOL4paU485oBFXysdSLrCnjDa84A8w0awk5kOgbhvPsDfa94aZf7yqTlmZ0643jqlhe1/a5FPDEmpVwas4wRR14rB3lL4ikTmlJGaACRInoMyMWStBDPsDnM9fHfr94Xl5q2SNY0lpuW66pZHPOYmx18F31SrpGBgfLctAIIFHQHg4H3N7eVf6RGUApOG/qQMJiFJgo4HzO+H//3b+PX/7we/jxj76P73/9Nd6/f4/379/j4eEBMUoU+s3NDW5ublxZCXHiMKd8ZlnHEEUHSEQI0+z2nhxdITlv0TkuBQ8PPT/gMT+xGJzV4lnf93iAAXVWGa8GU4Zbouqaalldw+9Bo6ZCkLTJdZ6oxhcOBM4kBgpS/VAw+A6aKl0GbfAXOSIUVHlGznOsc6iKeABxoqovMhxZjB5x6RT2Hi5GBxl5Jl/IY96xxgxmKfX6HKNrBpM5ixOJZc3wfVbHCaWBZgCr+9jh8lL/vv31t9JnaIrt2iY3I+llG2L4yGylf2Tt0nnF47rhZiHcv3wBySZmJQMbHNgZ96KH4O2WKYNAoCi6YQqEwEFoUBmzspHON3ROJBQIk9IMZsCMrm1dDF9bO21vasr3AQeNzpid43L9vcdJZsyvdXyp4Rbb/5oAtOuP63G0O1lxpRhFxThEKHhxf8Crly9wOBw0mGu8lLscmFIv9VgpEpuPpEo2o33jabs52rjrIMV5nhDgo8RbcAWDQkQAUIJE9BcGUtZIcCLBMYGBIPCRVnWCgZWXArbzikDA0+mMh6cTMgiIE4C19knUeMZ6DwAF0TcUlojzbQPmIFlyqg6gtkE1A901nVCjVejmbL/ZWPakoaavaPhTf2gOA2rIlUWD1noWh1Ur2VjPlgbgNAN7a68fj/T3+vVrnM8rbm5ucHt3h9vbW3GumGYx8quzJKEvf+R5BlIhyHAOhX6e5/WM8+mEdV113Kj4vlUQoI4P7OQ864R7tziJ1k2VHhuMG53zTtTmNVnBlKFBkU2+oUAiY7HjQfQvlHaT2mtGRavQ9gFXXOx2vxejTMUMMWBDgqHmZRFeHEAe9m/ke/y+GL0kpVlEJLaDbcOcItSbrPFwfAmz4zx6uUFumKMxM1ecBAAdv6zj8s4Upi9i5cP8fEajuL9GHYyUOpYMTOa4UcVNBtKWkadSszExJCvZ8Rhr+ZuchK7SLA6cMxYAWZwfNWV81LrqZiQ+HA5giri9u0OYJuTE2MqGdd2QuSDyJE4/KeG8PoEREFNCAXBeV5y3Fdv5hNPjAx7evcXDh3cILBnAlhBA98Dnr77Am9MTsMyIYYah3ACRF0QPi3omCEBRx/l2uCTgOYcCRAJHBiYGzQBRRowzQmAAglszZaxlE5mNgYUm3PuyHLqfBQ0GP92gfamDuSaPfOz6ZMP44RBFgIpiyLZacOAAqVsj3rvxMEvKCbLoaSkebweSIN4VZWn1BZZlAREp40/Ne5ckCnFLwkjNk3oMVSRlyCI3IgNgCoRlipL6jVUQ16iESNJWpAKKgoRIgR9ARX6lSHpy81YhR+/rgeaCGGXuli6tGul1j8ZoIttkQ7/EYryMIWCaxHtxWRaAgBwI8zSJB1Sg6k0To3iXl5zFqxeCgLN61nMukva9sHjvg6XmlioCfK2MbV3rZxufHQIvRjMs+s+AtTFZF1fPE/bP0PC3aRq7dWNwt3ZChB2j5AWrHaayKv2prfnuGMfG/CDc524fR2W5TlHxcc+cGzdqTG17A5Vjd734eZDr2xi6+s06tHcHhXodvSMcIFEQ/Oynf4qb4w24AL/85pdIaUPJGdt6Rkobtk2M4sL8hMoojNs6Xv4Zct+vvduza88QeffM+Pm5q+3gJcLc68+JUzWzg3/4sl/q3rs2tnH++4jen4H2RM88cH3Mt1dQwJL3Ew8PUlNCHG0CXr56hTdv3uD2Vr22qnDGAyxJo+ez1PxEYcVtPcw3AtMIThWC6y/00U29NMpd7pFXJuxdn2zItrPi/9qchvGM83UP7OI6P8aPKdBGw8xvaoi/aPNKt6NB3J6vygLD9az4gwviNOFwOFa6wLhkYpujDzqAH2mdPUNEtSwHObpteL4bK3PLBLLDFDmoxQgzl1vscfg+DuhedDOxA+8wsqyXV1q4/fRCabcGdrbq1zZueV/n7+HgE2HvY78/68RjirvrrQJX1rn2Vxd7eHzv8uOzJRnP4sfODy67qu3YnEzARONT/IsVY1/rq2mfpH3SVFM7Z7W2v4unRspndwcYkYFKBiVVUFR8bH9GXgPjfb4YHzPw8OGhnrcyaoY/vvkXl3+8pk8fjeI0fmyH6Fp3F6Ri53n2YDjQ5cuGe4pP/guunItPWQ83rss8HOOIrVH/W4+rrnVCweFG10SYCdu/lkB/b+6iGrrW6foSXTtdl6M2QfhTAeQTFo4crocoGZbFIslYcb18JlgaQlTlRy6MeTmIYWZihHkGWcRW5G5BNwAIhJUzOET81b/+V/DFD76PFAlrSvjJP/wnePtHfwouQWqtJXE+RhFFIZgR2WpNt/Jhpliy75wtQ5bi7wCNZJZapYELHsIZUzpj2c642U6fuJ771+ntpHUeJcKGpoCwzABnYDsCaQMnKYM0hSi2JYYk92HGkYFQWCLGS8aSC2KYUOiA80SguaBMwCECSBNm3CITI2EGl4jJlMKl4ZBSCjBF5+Tk+FVVmkk0vSAz1gwB0zQ1eVnXlEvLVCbkpSkMrT1b7zFiqPudm1HV7runZIRalzkEEsWU6jXauJsxaF1XMRxZxIg8hErDVa5KKSFoWyHECruWWt+y39l4pmnSmtFzVTpeGMaJqgP9SOdKyxxY34uTRobBxbZRw3lUdTjAms7wDllicG6KwkABc4y4OSxdonzo3hgPYHWQ/Vj29makkT6COmsZEeZ21vxFRODA1cgYIoNYy9/FCItcqobESY5FwFR1U8wERoLwcc1IcjHePb5077rKezcDmC6/Gpw10nrbNDVrqQr+3sFBdE4ekcecMM0L4rwhrivmKWKZZ3EASBlUHVcXbJpmndRRJ6WMP/3FN3j3/gN++rOf40ff/x6WZakBKDllnB4f8RosWQtiRIyT/NPvHq6FfXL8uu3nBQ8i8FFYMzVU+knV+NwvG0vEGUzu0HTOaryxck/WirVvVMXa7vk9+VKKzLOWgCDSMxo0I6PhD81YRRKBmXNGyllggmRMUCOpnQPLKil7FxBLM4BXBx0W/ZwZoK38g8FKUcOv7XkprGUbHJ6xNXJrbrBT68zrEtUSDR4IO3aC6/gLq9Eh55odsKYtJdRIe69/k/3WpXSMkX3Of1OQU8kZP//Zz+qZbjV3nQFEYang0kDMLCVNfHmGUgoeHk+gV7cAv1B9tJXFBEiJXrGMenKnnknbD4MD+19dO6izhD5cWLOnyQ05zyHCso8But5BylhQFUQBZg+MjtPVszLyZaMYZHjTq13IzwEGO+jGwxp+RyxrThx1lixwrM5+MbS2TR2ZckGy1NEELBNhmYFXL+9wf3+PZZkvS0UBuk5m6FaaoLTBnB+Knq9ALbNO3ZTajj/R7hNDdPFMjd8qQudMNyoT0T03eqrpmDOnKgdlFFCR9aBJsorknJFTkYCzLA6XN/e3oPcnyScUYkcfZdgSYY441RTBBnNGf/93/+eEX/+a8Lf/G4Rljro+kh1HYEch0J2fBg8CEFbGwa8Je3HO+KieFa5LSxKeXM9KJ3Nxc6AkCC9rAYEAY8trw08VUGxsdaBN5ib5nnPBlhJSzri7u8WLFy9xPB4xz4tLke1wW1DnO+4Nlo1GUz0LtTa6XpamvWhWw8o/Whu6vsHRe2Zuzjp2DwAcX1KSGDYZRk8Hwl56XoXq+vS4zdOj4vPx7whqMtM+iwgBgjszXwzB8FvrxuPQ1jjVccm/GCMOywFznCqdMf0UBbh1av15BykLmmIWI/u2bdi0jrzkUUhKm3pnrguDuxty5a31GQvCNXrWwK2nh3bPZMbWjPHorV9L7743ngtDOVrEuTlymcwC/S3nLIGHREglIRRL0R4xzY2OpWxOqpKVgYvIAId5waS4JaUNyzxjmWdQnHE4HkEUKs9YisIFA3nbsK1PWM8HFASEnFBAOJ9XnJ+e8PD4gMeHB5yeHnB+fEAoBUuccIiS/eRwCMjTgvfrSXjjQpIRig2mKpMj61QYPGXF7cY/G2Dbc+bEWkBBMmAEFKTCWFPC+9MJH54ekErCHAJeHW5wPN7iME+KpwzeuX1Hf8aw892gp+m3e77+z80wHoKEvoegqUhd6h35K4ZvgXJNiQZnlEPD4kQSyRwCac0AYTxDEKG5lE0PHakQrDXmgvc0M2YJtd02ViBEgFkQWqBQU4hUp35I+jd5nbT9AIIIvjESoIb8oIxmmKP2mauhMQQS5lcZR1ICY8rN0VBQFU6OSaNANbXP+3fvcFwWLIcFp8dH8VBJCeUsqRliLrg/HhFLRjmdpUVKUp8kJWRa8fT2PR7fvAU/nsHqmQESxsUQKSCAnlNG3pIQ9m68DfHsXd1d2nuWKoMiwotTtA0Mon/FN9wppEYJlBub4A/DBbLjnpmoHbn17w9Ue64xwlTHz37MyrSMzG2/JLYOcpOYaxTaSBO7cVdB0nbMatF1XDP+/R/9hzhNp9pGG4uuzcBo5ZxBP9TTqEyiEaP293LPR7SyDxWXV8eAXfmdP/G5sf9rqG6Awot3PqWP59r/87w+ZV3p2rcq21HFTSEEhB8FTVt1PT2qH4ERpGM64L/7J/91WQsHH4Dxfg5S2AxJ9vV5xfqlwmkH5tx5fs5A/lz7NOImLznstWdnzP3W9b3z+7XrOUP4aEwfFUqfQsgrzvI3eed3L8AMw27MpjHyYrCo9RG11InVnrSUmN5RqgoCjfu/CsjjmthJM7xrwl7Dxf3EBhGkvtu2hHe2Rk+zQ8X9Yd+BxQsEYELcOMGeZnQjvAqz/t1xPXyXH4G17wCLtecdYeBZWBv5qx0aJPdxuee88159f6fPvXEMbfgnus87PEATUt343PcqEO+Mc4wUJxvL+HwdJjt6bbhG/+MG2vFB1hxEgehecs/j4rtfakXD7TmHf9dtrTWzqlGPTfn7PMyw++C3pTBjfZWBv5ZBN67D4aLnCO1HOn4W9Y3k7tqztHN8XR8XjEfdkut0q8Pfz/Vd92OPw3vukgFFH6ll/CYBYEL4krH+jQ2Hv7c0RcfQCvnmXNvX+IbOScbW5aMM0Ijv9s4E+vVy96uDkJ4liY4z+YRV8UXVsJCzpQAM4gidNWK7iBLTX9uagGnCmTPCtOAv/MEf4OX3v4eVCtZS8P3Pvsb/61f/AX71i1/WunOkEQfibCwbGGOA6O9MWNeIWcUjYYnV6MNB0vaKX7yohYKk68IpJUwTUI6/XY3x9aQRdtCU4kkVGYjIicGZQCmCzzMKqXKLyaFowgwgMoFYU9ICSBTwFBl5TdimgC0SqDDO5wkPK+PxlLGekziLQnkWVj6Ar58ZU4hXw6nyFJGopSs3pRkZTHCVG72R29oDZD8staHtjRlXO8OK/8v9OWGHNBktUrrWQGRUY9C2bUg5azpIriXYTB4rpSAViSqa5kkc3J3BE0Az+lJDONM0YZ6l9rw3itt7nWLHR7I4vq+xpcZHZGdwFhkglbZ2wUXrS8Y8rulsba1N6UwETFPA4bDomWBwEVxRrCYms2ZU2Hcc2/veOSB4JbTbT1Om+oxlHBnRYASoxqoCknScZG1blK6iMku9WYoqhsS4KbzjZSS+7M7l+C/nh2evPh1swBQDQljqvEvJKMkahzOKk6YnnRT/FUzzjOV4wDElpHXFPM9Y5oSSMkqSKN/SBi4YiGW/ORK2lPD2fcbTeUXaCg7LhLu7WxyPBxyWBXOMVacmgSAryK2PlKQIzZAFSS/ObIYsp1T3/A5Dzr8r9m0G0iabqfTgzqgYkktVPIO51kQPqhgeOSFbO+NxiuEmB0/9nuh6q05wNMiM72DgLQ1XTOr4MsVJ8dB+FoXkDOMer3lY8VeDfXTt7PHuF2eLGjz3cmafXrTuJQXE2eVFdwxgKYzQmBrYXgsu2Ak76Ph7UgcMm4ejIfo7qa4iOfzNbCmqxamqOPwECjhvElAVoxh8vQFZePVe5+zlGGatkVssClYW2ZzijN2qrFBhy6Gs4w0IoSAldZ6AwJKlTzYhlvuFFBgmgtW+bvoY2xv0V2WRuLtndNLwrhktm4hFGlSti15IM2UF3532SW2JWHYz5YL/DG+xloRAjCkSjnPE9+KMr+YJ0UorDMNVRVHdX5FpitJ4lTuo2QRoRBRth1BlNcP3NkYtCUCgVhqqyvdGkwlQw1OtXUwE1mwY3kGT1IVsW1esZyklCQhtmaaIZV5qtDk7fnWcdpVb2N3QKP3zxvjV64xUIkohTFPjHfymmxFot/0BRrrz45awp8ONN6+slS1r9yYq/IDIt4icS3UKZHeePO9hnfPQb8kZKScs84y7u3scjseaRcfohDd8iTq64TE/x7o+pHs6rFHS9NtAC27sdooAq6neYL7xrR7vMEuQYy0Nosb2MfBR5IFL/CJ6JgLXEgLXGQVbC6WA7lCZs4Qhf+DCnu7Wm7rzAz0L7Y7gNOWrS6mORMuyYIoRWy1haPsrfGLOudFmbnStnikFiRgjUlIH0jwBWnrI+HjTHxqOBV+6lvPw19bH8wsGK+zma+0LTnE6bn8W+LJNe29Pz2zyiqfK1tdItzfNtGoZdlLJNQtTCAHzMoM2wpY3tzfisBh1D2KMImOUjBgOmA4B8xQxzwuI9LdcwIUk0wUX8LZiPT0BYUJIYsNjBtbzhtPTE54eHvDw8ICHx/dYtzNeHA54cXeP20UzyIYInJ6wvX8HihMyJGtA1nOYWctPAeJIzAAV5bsNVhSnBHW2kSRNmtZfsxSXIlm3zuuGtw8P+NWbb7Fxwt2y4IiovE/PN1YY1/Wqd/x5uHxSH+nxUGv3so9r16dHjE+aDkijA0thPRhcGQ1LwyS1WlCFz7JJ7ZdIJF6QUOAsBRFaD4glzcqkbgZG/M3Tx7w8KuBXQY27FFQAsMxRGWNBSSVpiqkQtN5K5TR17PKbITtDnBbhLvO9rENggidzwe3dLY43L3F6fNe2hKh6enlFU29UaAzJPE14+/SEX//yl7i9uYGk/EnYThvyeUPWlHHnlKoi1ZQ5MwWs5xUgwvn8hHRaEc3LktBqiEOEJUubkVOS9CO3c01Qo/+HGaQ9oFXGU+dXGUp3kaFgQ5wjwR8Ygk4Zp99Jhdne+I2OGo8eIVU5PVDEhvj8Z9+Gwpo7QDY9+2DjkfXxWNalmq573IhlEEpe7wnYOgcF5TC68aOtsR+SeVvW9WPGaTrhcXrCJ1+/nW7u/3/9F+66znT99k03JljOgDF+TUB4zojbcAddPbftknO4Z+Cyfr7LdWHMdvO5+OzaH9FHO5c7bfi2x3sDA+XbujbH3+RyuoauHxnqsEcXQ2/OQFyV3sCiqdKs/msulmJPBSwa97zhu4YH3Z6zefM35tVoCypKa8+C4FKLtdv92Ds06MbxHLtN8Pi5KhHGXGh+desgOikQO4Tmou+6x7tjewa2/Vo8d3G36Vdheu+6bgyni6Y6fqUKEPbRzo2rh+iEQXIbyPq3u2e8wd5ZGM/vxUjd7jpYd5O8fLICDdAVaXZ9eOGynX26BK36GLn3HGyQWxAdBumamVDNEMVyLgWHZWnr4oUAG98eXqy/lU5pLSmGy653dDtruDqn1m//dX2VQRoN1G1Afc6YWhsHV17y+U5cdP9wdVDB7Rx3w3c8psq0Vd1gfVj73uFyXIM9vryByMCc7V1XQLaLHHrmsvdMqE4aXSYTYoAJ9FXB9iLj8CHWM1WByy8/AbUcTF2FywlYG0ykXViUVLyciD/ku/dtHj2uYyZYeT6Df8ON4gUvqW8JFs1gWbrkHKSUcT5vEr1xTiih1LU5n8/V8MKF8fhwRqEzUgB+9we/i9vjrUR2hIDz0wnptOF4uMXpJOWmUk41ujJnkZlyFFk1cK4RvyFIZF6cIihGnEpBIUnn+vKLz3F7f4cvv/4ay80BqRQcjzN++P0vQQBevnyJH//4xx/d/+euh/WhypMENVhtsVPySKQhoSAjEWlKeFGMiwLZ0opHcJG6hQlFUoUXxrkQ1hgQSsZpZbz+cMKbdw94/HCSmtJQhTMBZnyQSLVeBjeYqg52rFHjLI7qZkTqcBMAixQw/mnkxfRDlcHrb+5fYwfEacGT945VAFfcu6atcwY0JFKYsZkxq71WDd/mWMGQ9Y9a096McV7h5hV7QIskN0cYGua1h7M7xZ3GcXuDeUqaRYGgxnRnxGAxLsYpdo4EwfXneUUiNYwvszo4yDk2NkCO7GU6ymsygb/v+V+voJR0xpb6PPX0qttszfka2npa+vtW/k7L/RXB4TFIJsACWToqEvTgU7s3Q2K5GO94XeVbHBTWVPbBSucFjcjWNKPaj8FeS/Mp85qmCblkzMpTc2Fs64a0yb+cJuQ0gUuuziUSOCrGZM6aYhqSxeLpvOGPf/ZrLDNwf3ePu7sb3N7Iv5vDrIYLPTMa1Sx6rtiRAqvrXuqauTUyvO2Wgiz/qD1S02r3OMLXri1FcPy2bsglY9K071OcEEpbq6qP0yjUmvKUC7KOwSv12ztR34PyXFaazA3V74vOxd9nZuTEoMRAFGPn6jJLBBLdYiBCsgh4a8PRTMtu6deOVHfkeZwKHPr+BZ9RPxj+VKxlnzm48+IcH0Jojg8Od9Vz7/tQ3lKG29LS+n/+ClN0Ig3X+Y/9k9II1j7ABA5lMAiRlIQMU3XWIHP8IYhsaf2GltxEosipgz+YPx0JLLasSroPxvfreHqcJsAgJTQLAiVIFWmls042kk+VqZTRGDtXn/U72O6xRr1fikYtvW9zdCWHjxpjS6TR3G4+fY/9/m654G05SUYLAFMAbg8R/9btDb4wGLGxu6tlt+bq1FSzdVhNdZ/ZwzIjXZNT2a2F6Sq4gJVXBLOGdHLlCZTwgUtGCYzAkuFCopFl3JI1omVNBTPO5xXrugKQ6Nc4TYgKmylnnDWD3p4sSkCtZ2/fSccs+Cjjm7cF/+CfFvytv86YHR9z0dJwz/NG8orBI5R2D1DmaLjJ6DyucZVxDJ+g8pTuoCIXRkpbK3tbz6aT2y8WQ6PNofBBVMt0SMYhC3IT+DQDqwzSwhLHy2VNuALDVgq08UPe8OqMq+GSv6qf3fwQWvkdo8UgUoN3N2Gn43F4nbiVpeL2rH33cmk/0+aY0+254u+qr2sUdui79UfogANt5VTGCgHLIjR/3UqnUzO8bM6TRj8ts3IzLkPltYjTmmraeVFJyD7X8g4u6wcX47PbuAPMvuR2jqhfoh1+q7dBugBCz9N1K9Yu7xTp8fuFPqnT8bTLyiNV+SMEpJyQE6rja5wmgKX8i2VXDSHgfFqx3B6krIA6IRQwckyIB3lvmmfVwRZdMxlFyRllO2N9fEQuDJ5O4CCO2mnNOD8+4fT4hMenBzydHpHyinl5gZevPsOL23vM84JMhPzwgEcKyJr6vgAo1NKZF4N3PVPRzgLEOF7LORWVbQoJPZY81chF9mJNBec14e27D/j5N98iIePzuzt87+ZFJwvsXcYrVCB2+9Ffl/hzfPYKpbm4vpOZrORc0y8JrWmLZh4/oyBoRN28u+ABjpvnCYiAGCtD2QRICMOkYwgwpQqLWBgAySPcLk65etHFGAFlTIVDUILSpdBQ7xwjFix3JEJBWRVlmGVcmtIdzWv05vaI+5df4PT0rtVyQUOAVRnnFG3GsFegixFpS3j78IAHCvj8M0mDfPrwiJAVcRdH0I2hZ8ZUNA2J8tcTl5qm3SIajAmpxnrdh/V0wnRzC0CUtdWLqpMQhBkTz+xLrxzbs4bMR+hxaFzH3dpwjwyQa+lLvMfx3tUpe+sYaPdzCH5wl1Hmowf5aDfZj/Vug/frx+C6DzWKoM6rjQFK8MypwLdex1AFOPTrBzlaN/mme9ePspSWhqMqMirTZQDbM2HjdW3Wz71zrY29cXoYGvu69n1s5wIOn2lj7B/D77uM37/g61P24mKklYb0gqe197yRAniKTxpQ0ZgBMjy1c2yNHggYN2H9gsGxZ58jgsNZHN8bn3vu8gY4d3PvwYt2L8a419/AYPcGsv119krMvWe+07zg4HTnQHTG8BGH6Xn3f+2R25sbFVbke8ku6qtRZ1Rc7tr3ghtUeKrMsL5ltJm7cUtbFFqdOKpChH9w73KDV0TpmeOBt21tdWs9EB+jUdQm1/C6teCN3u2X2rfvg3aI286cvJDVvVvP3xX42Lm/d+Z6xfoOjCowEXFTNvlx1mnYMztngJwTTRtMx/td9PvM+apjR7+Ce3TQn2Wqez+sY32O0bWoa9zRCT9O3xbc7lGj37Ye3ZyqoG5npvGYDDFMbNumDp50CRaDIoX8PdtL7ude+SXdCw+n9Sx+jMANRHQLEineC6rjS1Wt26bC2DmDex3t0Gk3BkLbj4tm9o6FvIC2z+RAgdoze+/5Z8Z+xtvW9IA+Luawg6Sd/A7DHaUwCpshYELOpdb+NDjiv5lw/o+B5UNQqOK+C/s4TFPwMrd5FNSohwBZLtKw6Ir+Lia7f32Mr6jcJisMmhGCUOVBq78qohnVFzMzzlvGw+mEkMSQS4EkPa5L88pgnLeEQkCJAf/0n/7nePfv/e/xF/7gL2G6ucUf/ckf40//8D9HfvMekUJNj8cWNU5F6qjNE8I0oVDAfHPEfDjg3bv3YGL8xb/4Y/zlv/ZX8f3f+z1873d+gK+/9z0sN0cgEM7risfTE4gItzcHLJMp3FsE4G96/cmbfypzdHiIoLW6oUolCpjnI5g1C5veIwpACCAENZhOiIiSjpQkWh8k0dwzRQTKeKRH/PTbb/Czn/8Kb3/9GnldQVKzBxFR5H8icEqirKYR7sXAWAoj6P6yphNcpqnVMOamaGV9r+QWyXFx5Bz9AlDLus1xkuxrCkeJW73QDggdXjLF1tP5hKy1NEsujVah1bntx6G8CYthL4A1qgrqZN8bfe1vceOuykX0EaMjjc5ZjJ4j/0uIfTvMWDdRTgJWBgA16geQKN84TSDiqvSEex+qj2EI7EyRsEwz0pYkWgUN1xARMlI17vZb1M9zvH+Nl5e6rEnvS2SmKRPtvRpdjrLTlqxJlXmIQGRR0KR1xoVOM4nRLQ71rC17n69b6a/n5BcdhZ5FMb5WA2rOADJCgChMNeuBweCWU61BL1sh45rnBSEKPgKgdco3Vxc6oaAgF8YyAzFMWArjnBIeTuea4cAHoDwlwtObD/jVmw8gABMBL17e4uX9CxxvjjhMEXMQI9jd3S2meQZZ+Q49r7mQGif79fNnVgwSAfMS6rm1My77XYRXdAZYIq31GRhMCWvKyCkhTAEUJ0zLATNa1Kn1YUboomnqM3PNbGBKfQ9/Vu7ArKfGT457TiTzNCOx3pS/ZiBW+l9YDMHk6orX8lFFUk0j9msFXPKSgNU35apXrc5fO6BXLNWy0lWfTdPgCQByPqPRCtPRGp/dYC7l0jJhDh22+uDtbFb8ps9nrfOQS8Yf/+xnMN7Lj9GvL4jAOSlv4J5jrnMzuWPLgmuX+Bm2+zsgCq5KKp9qc2CI04OMnzQVfx8lGIKUDaB61puUQUHSdofAUhOVqNMd2nlw3Bdsg8yA1W3pPkPl+CIeNtfziaX+1Ix47fla7rM6Qjm4YpHhCwJM7Sh7b0FmqBkYGIw1ZXx4WpEyYyLBDbdLxM3xICl+TT861Hmu+8iMnJLAgPKszflianqJAsXPbV5OvMS4WE2u1uhtghy4mpmU6pisfAyYq4OY/FP+GaGm1U5pw7auIBK8LKm+BV+llHA6nfD0+CR9hziMSc8pu+1VXsZGXwD84teM/8N/mPE3/iDjeJg7GmLP7oobF3SUuvsWzNZUBB72DF7bOQJE/21VBoiaTMVVINA68yUhrRukrnMzZxv+ZphDaxt7CFJWgoLwEfMScHtzq7It22grHTc7zL74b2VqDU/5ALP+hQpvbHWiucKWwbrtd7NLGT69dOipuhPFPTE0rweTQBmDLYE77FHvdXPaFThHF5P9J0q1gfg2fP+OjgFS7sD91hmZszjKzHPENEdgzZUPlMedrqgUzdSAjhfzvVmpIDOMz3Oscp61N2ZgafrEYX0ulkgDTKnfK3LjbQ6I7nw6vtbrnDp+k3s4uLgMp7n2/Ltd9hciHDSoaNs2lM3xukFKJKecAYXTkjOmEHE8LCoLCY3J2wpmcfyalwXTvCCnxscI7c0gPOGJCNhO4DihIKAwkNeM9bThdDrhtJ6w5RUgICwTlrtb3L58hWU5YCuMmxDwMgCn8xnzskjZiTiBphkERgRqJofIXJ1MlUIDxCgckEk/EyEB4BKRVuDECWBg3QpOa8E3b9/jV9+8Ac0Rx2kRZwCWvfXOlOKAwpUmfFxZtbd13/0duz49lTpRrdkBNKa3DUIUNIZEQeIpFUKs3paSgnxMMdUUtk3gwQXQh0bRFQH0QNophFwqMDkoLUWZLLakTwl7hN0UN2i1S0wBYAbTUjQlBKGmaM854e7FS/z6Fw3JVS/DK1jPFKPGkE9xEmKeC9b1hF89PmI7r6As9XJM2VyN+miMRGBjpLXueVHUbUwxMUrmioyMOIEZT09PuPvMkLwRScdvmBLA7u0g8kYQTMDwv9rL/utAhAxHUvud2hclSMN+c2vlux2CfSOB7X0pLdWox5XdmEHDd1snr8TnOhdmBooSdmr717eA2u/IKdT1sIUefr/JN/jbf/TfqwyLMSiBCK+/+RY/+9nP8PL+Hm/fvhPilTIKZ5SyIW0rUtp6eHVgS904dnn7fRAfCY2d6UsAeb49tjXbf2683zMDvi7Md0SUw5Zca+JiZOOCocHC3nOdI4ofqjsno0KJ/BlWhrniTMVVMYry5f7+BV599hm++vprPDw84nhzIxELUIcNhWWDr3/v9/79moWAyIybTXCxMRoo1uk6Brm2ySOcX2FA/LJQfz79e9cMyjuNNPjzn3dgEjt9PMsstYf7r3vtP3NdUx5+13e7yyPiT26sCXhMhNu7ewT1YAwxqlONpUOF0nLzoN/pkCvvVGmqjZlCEAVVN2B0jI+8e4kZuy542Dpq0NivpRlwL4fZnJOMYR46IS+KdbeHz/0Ix70R5Xc7vyO96Z7b29drsPuJ1zVnjPFs1ZnQ2FVHuAUnKO0NQKu51Pha+ToI/+Ocahc7897DAY49qG24F67M/sqaNS3GgK8dcvML8dy5UkWEs0Ubi9rGYN/1xwoBzNUzO8ZoiLbOp5uVvTviLBi/3N6wdvu+AK8kvUrMd34rzMi/Xy5rig/Du7in//kY5O79zrWBj585e56G7bQ1YeMpK+81vHvlbHl+qHU7MAYfYUwcaqqNNHrev1S3noGUMyZo7VJABU6VnSLAfzMh/T8nzDnqPjd5wI+wh6FhjI7nYFhURh3NDl3aY4p+s2tUbgGs9b5LlXWktrJ0RzHiXdrASTKYSDQQo1CjJwzgIRjMF6St4J//0R/jp7/4JbYi0UZ5O4FpwzRNguNjxO39HX704x/jL/zFv4Dvff/7+OoH38PNrQD7zc0N7u7u8Pr1a5RS8Hu/93tAjAjLEWGeYPViKRCm4wF3L1/gvJ7x7u1rvFtXHA8HjQ6O+G2uv/t3/m9tpbid5/ESWdeiM7TEF4JEQsUJRJPU7QsRiMo3RjGkxqC1hJnw+PiIn/7kNX76s2/x7lffgDiB5givpCPJK1DxUQ9vkoozlAzKGRbLRyxRWXOcNC0fFK9BauflhKfzCcfjEcd5AYb63/bXGzJjCDgejyAS54RTPsvvSsPrUfWKLbRUiI9PT9hKAbRsDBR/snvHjOCGfo0fjjFinhasmxgrLVNdVV53kTIWiSztSoR/rgrFzrjo1nRM+Shrf6k/kbYKmCQ6yyL3JG09I4QJIUxgFoX3qGdp8CVjnKaIaQ5IKavNQXimzPKu1R8e17a1MfJj+9cIx1aHOYSCVkO37fcUCzAxgKj8XazwLpae2VYICFEMkgY3CLAkHOIkZJH3DUaMRlwzjuuDz6DBnhe1cQNyPqYAjfCRcccYQdta69mnlGug7KQG8WAw/rnqooiQmHHeVvAmvy9ESJTBKSMy43aZwcuMNSWsmxiZERdheyo8FmzMePP+hNfvnhpca//3dwccj8dKhyIFzLMYd0KMoBi6vfElDbxMWvUg6PeyGfoku+PIl25ZshqGEGrpgT2Y8nBcnRvc+ptzmT9BzK3+uX9/PIMxxosa2GZUv8BFCBfP1d89PyOVQDq+RfBGAy9vNHrOfHIRzPIJ17V3GC1I+2NOIOM21Ee1gVIYv/r27f4zF+PZv/zjZiCrOM/eI5KSKgGgoE5b1WnB5B6J8E4piaMPJFtpDLFbCwEH6vo0vWkpoWakINW3yv2MElx0v/JVVcfMqJHkopdWudTKGRpBH1ZEaI3gEomirxohwW6xjbTOlRpt6IbDjIbK2N6Q/ddHS2GczgkfnuTZOAPLTLi/O+L+7lYM4yB1BtvbrFKdddgZq6R8R2xdD7vL3beB23fBWgCUvopTExFrtgGI40MBoE5+HBhca99w3zqZOFWQ04ZpCljmW404FXmMSGkiFwAZrQTHMHxbO86IBPi02+Yofc7Aw5rFabP02QeEx92H/l7vx929oPBGUH4EXnT0tAcdLiOKCGSOmlTxDMDVqTBnSU2e0qZr5nUYbcMIAEUdh2ZDmSfRLQYiTA5fW91ln0a/8hBcXPveKW0QWJh3HfHqPrE5vvTha2bb6NbBycoXegpu5U6klILAT1sHXXDa0xDpVXWnbbHqvOp+DVlMIDXIFSvUMZoeVnS7VHUNMnkezo91R5gnlRttDTLr+RWb2mFZcLw54s2HD5hjgFQtaaWFzHBpY7D1Ep4SFX8JjkSthb0sEzy8evo4LNLF+pkNwy2j6BD4kv56mp00Y4CdBdvLymNQ++6zVY2Gc4O/sb+xz8wFaUsg5xBm2SaCZo05rWcAqLKmwUCcQ80YZecjpwKKoWboBFjKORwXnFPGIUwgzdyQS8HGT9jSinBYEKYDKM4wrByRMQcCLwsiRynzxYzH7YxlW5Eo1nL1tzfi+DjHCfM8YY6EJU5iFIeUqig5i5PYPFcHM0CcnokJMYgDGaaAjQs+PJ5xmB7xpJnfzinhl6/f4Cd//Cf49Ztv8eLVS+SXjHPKWNeEbSkt/TzMHqE80MfFhz/z65MN4yUzpjhXT/2o+eMBOdzVU42ttpExhwHmNQtI+gaweBvGELRmV6tTFIIOSbG8/E6VwIAxCHTcntdLvOanytCklCpRNgUikYui5B6dGBGVA8kwY3p2nt+ACI1RI9xyzviX/9JfxU/+6d9rh5CHJk3Bc8GQyg8xxppua82Mu9sbnFLWdD1Q5SubCwesTo1Femws0Twi7GREU3TV9TFiQS2QhsTbKoSAi3gGXV8RLqEla8ZUIhfLr7NpyJT3cGHxD7NxKY7gNiRcv9PFQtb5GEL0yNsTnD0jgMEk6hDa3nuQ2DOIdzBDVOHXGvPrW5kgG7aDW4LjtVh7qJwbKrPcCKyLrBiWtc45kCrhCB8+POCnf/qnOC4HvH33TtIFsUQklbwh5eYR2Pwc93vwxOY3upgv4GT3Mfd89y61ufu/Y2v+dLFb54vrzwvh7hwQArV6NMP9TrL5Dn3YDGs6MzBAKiQo80IgPD4+CLGfIr766mu8efMGL1+9ApQZqJ7ogwACuLOjzHNlIHQvHbu+g9d21uGKQsMbwZ41UrQvPXz0D8r43Fi75/3nHcbnY1dn8DN8s9PWn9k1HJrL9dmZo97uSIy2ZQyH4VO2PliEmcMyY4oRKW1iGGdXZ1z3mUBoL+ICf9dbCiXiYNZov6G4/jCL8L9vumpe0VDGrE25MbReOrwwzHaKgpEGKK1TBp/cWral29tf6gRFHrqBY/KsX39+7Pc2lt/y8nDQDYQvBtfoUjN010n4z1ZPlLwzmFDC2k5tiro51t669aQKx1dpAO+sidIAN4Hdd/fxiD8MwwQ9IamPGe9z5RoIUMfCGJ9k56PC9mV7Rm1Lzri5v1dc27iaNs89it/P2Z+aHqb6NZQx8fP0b/gtxwL6/T1GbhhiPSwj/H28u+71jw5r/yx2PEFHoHojr8kPhpcoOL6LUZUv14T68YzD5AV4HOXGcIF6LmfK7mUigAsjccI0iYMbSKJbjF7TBKS/lBH/cVBZqlQY891e8G3djR5HdLB7FeR+QzxVSQVp1JGPPpBxZ80mYvRbDLlJoxYIH5CAmXB8cQeEgC+//FKE6ek/BbCBYsT8xUuktIEoAqXg9u4FQpjw4uVLTPOE+89e4OWXL/Hl977C97//fdy/fImXn73C4XAAYst8RjrWGCMwT/jy5Y+wbSu+OX9AyQXTfMD97V2NhoocwTkhJ1GQfvXyc5wfH7GuK/KWcNoef7N10yu87w1CBpM+gq9odgFT6tlnZk01qOmDEaCKY6AVJ0aFjZQZDw8PeHdKeHg8A6czJjAQNKV4EVo+g0A0IcmAetYKpPUMS4s60d8snXSoEW4NVlPKeHp6qiXSbB94D6cQYZln3Bxv8OL2Dtu2Sa3QlFr0mJcrlUcY5cE8yHQV/OvZ55YiVwdLWoLN6gRO06SR5ZpRT9dE4/Q1MpaBInL7rOmpLcITrr9+LNzTZ3eNxudt25BKxjTNtTyAzbv9k5p/Xf1u45cF0lCKnL3j4YDlsIA5Ofmw0X0PX172/hgfPSoj635Kw/W7rYtFt1dYn9RIVCIYEwIVMEcwghpICIUzQpgFvxPUIYCbfkZTq4/4kYgQQ+zG2NWahsORQDdvm4PR3crxDPyovKCOhURVOTrFSSPHU03hn7R2KgGI84zbeUaYJsyHBctxAUXCuWyISfj0Scc0TxNSKXg6ryiFQFPEHCOeVm+4dnxoJVzC51megXdPZ3w4rTDa6OdMDm3YB+7vdDqjCygevhJ63Ut9hGVE9JQu6Kl7uXuJXPs9tTXeSOUf2nnZ4LwuScbFwIbHjd0jbsZ3hYzGUnbveabgSrs7EzRdWGO1miGB0KLoPUNSlKbuyaueo2/fZVLXeBVbn95QsTOHOsbrv9VnLqfqfrQz1n74oiz43mMEXhjnh8qAV05beW9ZDnGUyCVjXVfM01Sdo4tFZNfXHB+lumI5/wWSyWJPf9zDfP9bW9/ud1wa+Rp8tve984gH6s7xqMPD8q93TBrGyQ5DEUmwcC44rakaTaYYcHtY8G8f73F/PChe1PEMfn5W+iKr11GMAYFEn10D2/xajOdOa3LL2Er3tFs4xREGf8Yys8vUKh+IBL8HQEtuCJ9vEfJsdc8ZEs2ZVnV0EGPgHCaknDCFgJtlAune9ztl+jNHG6Ruj+wXAQgBBYwtSzR+zkn52kHO27uU52EHnO2c6Rmtn3Wi8LBn+gzJFmP8LMMyATocpzSgKA9bcq7w1MOolOYQPp7quQrKCwW1iYQYMM1TdYoQg2PjQYhQdZRte5ujpH1v8KzsV2mGW7uKw7mSIcd4Gp27GuONhwhOZ+HX2pzOGZptV432pbTgyhr04+VJvzE6NklHXTElyJ1H0laq4duG0NgrjXA3fsL6ITeCbvDdWC7QbeWd5ZdSEkJYsCwLbo5HpPQGU1y6V0bezMvANSOJgY8+m9J24fgxttnpTnmcReO35QzLSkn2o4YrzQnU2jFeNGvpGE8b92xCI7/93LX7DKHuJyAG5DVJlPbt7W0NciilYMsJFIPwmhpzySzZY5Zprvyi6eynODuZLeKw3KBkIMwRnAjIGYUTntIHAAHTesC8JEzLAdOyYJpvEF4cIbghgCkgzjOm21u8fPkKdzf3mOOMlBmIEbdgrFnKih2mA5YwYYmSCl00vgzWjDwZpKUo9D4JZE8xgELGhAJsK07rjIfTGWcU5JLxtJ7xq2+/wcPjAwIXzMSIyDUjxzzN4vRoZVXs73CmlOjt80vP8h+fwIC465MN4xSC5J9nTQ2dc1PwsoTchxDRUpgb4WqGXUZGyc3Tj8EAS8qjaN7Zchq0nrL39CmKKAJYnw2xpSuqi2ICKwT4cra06rG2JTWTZERAz9A1ZQ03rxyWeUf1iKIs4BLjjJQziDQKToHeVMbe6CRtX2OsGaGIV8nh5oj1fMZxmvC9738fv/rVL/H+29c6Hq4IThBGi6Kv/KtKAyEI2lW+EIGBiaKmlmrCe2Hg/HQSJK3rCtuHiku5wsAeQFZ0q4wWOQbHK7/qYLgpEUFSd8aUHkZAjDh2ZuAdBtQ1rLBYWh+2B1VTo0S+ChGNNMlZaxGxdXhVAG599/wcuRf0pmZPaIZQE7Ka4YWBzpsZMDhUBS3BRWVYzYdS1wndmFovFKh63aQt4Sf//J/jZjni6fFBGNesXlUloZQEsKG+nuG6RnavopemJbj2hNtTNJi92lxj3i0F/d446gpfMDnPj8WGvPva+CCNX7hjCBxf2WBFb3rDd6tP45G8b5mcN9a1MbvfjJn1Q7RJlQImIDHAKHh8ekR4I1kE7u7u8fTwgJvbO4FmF1FLF3UDnHEZjlny99zYTPHYOS3pnO1ebwjX93xfNg8HKzsLcXWNurHaOD181jPE/Ty8ANnA7xIePP4yDHKxL/a2uz0wgt20DM/a8jqc1vftXtbnG+phfcUP3uZvHVbAbOsLxVUEEAIOyxExTpKisWQI26epfAuDiNuZ5NY3uTl4HG7PmXOtBAG2lWX2a2j4dGB+amrvwdjNGunO3D/fCQIKd/1m1DF3S6xbQG5trxnXq9Fx2JNekBzggm1NbM5OiBiOzIiDn8dmHpxtzQfaWz9QP29fb63+dfOqsFMai9EOfQ/XHvaGwbXndAzd3+Zo09E3cnARRuOy31/UNkY+qxMjqR9/xccXhMXNx++Pm88F8FRYRH+2/KuON7HvDGDdVryMo9JFH3Fj8E551aBRiqTAGubta2fKR/XKvxYBN3ROeo4LM/K/VCp/Ml7j3CpD5efwXFcOJe2NY/8Hf1jsZaXL3X7JM1ZDc9J0yybUNn6TO7Rj9QiNZhlccWGkLKld7d2KNNh1iyuTcuC0I2vr/UarGEDKCRHqhBsmZMPFAMLvMFZKOP6TAwjBnXkzMFQIv1xX7WMcYnX+vMqH9G/sKYF3f6OexlbFpFbCZv0XSFI5Joo43N7hnDPyueDw4h7/nX/nb+Ov/it/Da9evkIIhLv7e2zbhv/t/+X/iofTCS9evcD/6H/2P0XaNjCo1aSNEfd390IfCcjI2HKC1RVlaKQhS01pq4Fda8Lmgu0kmZWmacbtizukLeHdwwes57Mq3IsYo9SId397h1cvX+IGAn+Pj7+dYXya5qpUbHsgBrusUfSFMjICUtmQwKKfNR6V1QlEvZwLaeRKNtqtO1Pps+CKwJJSNYGxlg0UZn2eUAoQzLimmmlxoESFocIaae3wXq0rW1N96pxUhrM17BX7qGmhBaYKQgCW4wH3tzdYlhnbtkq0U8kIcUJGQeDQQWxHZglaHmwHxytMZHOSMfxSCsIUOqN+CKIEJpW7ZXysvFdTZwJmgBYFtTca2jteETc6DoyXfzbGqBHrwlNEy9bHgu8KTBmIGtXr19cUydKfOFcfDgvmaQJrenPApTbWPbhm5PbX6NDhP/sxjM81o70op00BStBIKC3vBs3USgVyBrK0M02xprYPQUoAiGUENcAAgNTo5hZ579N2jutd5wSg/9VWaJi7/qexFEa/g92AOa7MMSDyhDhlhHWVlJxDOutSCpZlRnz1EnGZgBiwloSH9S1WXqUtxRMMYJkl0nsjUUQukbDl0oyljmI12oNqJCjcAlf8JEM95+PV+q68roeN5+BkgPJGw+QE1ajbju9uY2q8uj5bH/B8KSndU5hr5Lbirc7JsE6S+i4rL0euF240Vfknzw+1gQLETfHraW3jRxgMTdU9yJeVh9D/WFkFMDd8X5+n+pd9JKVZYerSuDE43qHr+IJRdlIDN96n4x0q/u3f8fyxrJuMWvBBMAqEEftRITAKbsKEuUhm0pyMjxz1MUVxaDNs5ZSxbVvNxACg8iLNMNdGGEKokf6G0qsBZqRPTq/R8WAVJgzPOXzr+TS9UY1DGPHQsCcMUFQcqavalbrUKwQJLvO6UKNncO2XkrElTWkP4RcO84zfOx6x6HrVkQy4sdUjVvoTpaRA1VPb/rmjYEF1laexANyKGzHAkqxlqA3RYOQ0YyhrgLcYzwIIEnNn9NloitRBn2JETs7uQA1W5inib724xZ++3PD33q/9XCDkpygvopnIUVPfB7GLEDIeT4z/xf8m43/yPygwcY28rLTDPzccSlWcaGqtthYtw4NvT9dB348qA7XsMVqqAQXgUCOALSOu18t1E2Yz2ppTsRjNZL+1fAmEBtXfwwiT7sw4vGBbmYF6jrxTGSuPfkGXi0Tz11Tybr2gNN3rkX3fncMf83jCtH1u9MXjdSi+NtQ46E9rJoMBx3rnJSLhx01vYM9KFuYGG62ZYe61s0a1Rgczhu6ZfitaQmZSg2RXjooZAaE6PVQ8zb1h3GrJt/mglivpnAYcb2dOhn5cXj9Tau1x1Vvo3oEabNplkfdB7XLV6cE5LHl+wPPWz/Gr3hlJ8H3Pu3jjfIxcnyNYBigNco0CySUXbGsCGf5k1JJSgeSdNh6xmZYijngxBhw049g8zSjripwzTusJT+uGEAJujncIIMxTxEQLDlNEnCUteqAJU1yw3N9hub/D8eYFjocjpjCh5IKblAAKWMsGLgUTTbg73GBZjtDcSwLvzIiqN8klgZGVbgDgqHxKQYjAMgfd54xzXrHlDY/rGZk3vHx1hxd8g/v7W9wexBFjywnrtsrcVe4OQTKcNeN4z2fs8ZDkAnh+2+vTI8aZtXZPrmmpzPOIIQBNoShiKjUKVX1i62BzbtHe5iltgN+hSm6pCQ6HpaVoUiaDefAach+L1teWxY2SWpzN068hWVs/83DpvWBNCWsIVpirUpQYUZCaZAUIQTywY4hNuNhRZI5j9QbaoEg3TJr2K0Z8eHwQoT0ESRNkrzKjGMo0PBoGYUEarvtTvbT8MFhqyqVtNWtFh9cvwIud0fq5ywlRVP+jhBqjEVaYCOuxMtCMuk/9aK73boKNUYQmsFSRpbtvrTZjHHYmfdlnrwi0l9qhbEzq+P4lU9wx/uw+o83DuCEu3ujSI3a7Fy2NVCn44z/6CXLKWMsZaRMjuBAcMYrXWr/FK/G5wslH97l1vn9/QFC/Ebr6xJd2lbI7L4/QdK27fVDo2I6dn0iRc3/QKuG3dR3TMeGZJdzrq46POujr8AGxMuwZyMC2rnh6esKb169F0QXNFLEs4GwpfvLl2HYWqhm4Q8WjzP4MAHvQMzIjnYJM5+O4PHee0RQtH7vqS7WTbtxe2eZ/74hphwP3IYZc03Zm+rnuDW686aCN+zv++dFjt/O6HHHFRRtoa+KE63F8Ta4UgWmeJ4m6UkG3ZEklVmlMsTkP60LO8ehiK+SdQLpm7AUTm43fl8v1uejRlFO+MzffSk/cn/rFI7kq8PQ8hQNHJabsBKLhckqNuhbsFVHD4wo3vDu+j6C+Pbi2afm1uAaHvAfR7YXLrfXnwLVNQr+9oHj9oLY15wsDnp2pwYHBK4TYOUF0HT0D+0BV1HiDI7BPM/aHfbFYDdmi7R9plIA5B1WcRo0f6hwFtQnDHVNsyk0TciuHsXf+3Zkm62vnklMlgq8XgJ+9yIZBOH+xgX53TGt37VvPW3XH+Jm+Lq6r7/lV6d8nkETCKmNFgWq0tY8YAKBRhNS/a7xpHQLXJa5OHJFwiBFYpD7WljaNvGiDFn1HS8Vm8KCb5PDKzpmynuuZUFmHWpaqsolxsMLv9wu2f5axrBHsOviUpTdY2322zmnYge96fobu7MpDBCZChEV5Z2YUBCy3t1hOj3g8P+L7v/dj/PjHP8C0RJzXFetpxevH9xLp7Uaf5wCaD5LVLIgj9TklPH34FoDIe5JWPNYSBiZrEoCbw0Fq+gZJdffw8IB3795rqu6A8/mM8/lc3wsx4O27d2BmvHzxEmGecH9/j9vbW2TWzD3MmO9uvvN6+StEQqsl2s5bYJGfRURlgCUqLpiyzaCXnUO11mAMgVCmZhhnQB1HGNMaESkj6lkhAFz0MwOEUg2I3R5XGkI1QtpSNhflL0MgVR6FljYf4lyQsypdxtq/poBS2A8kqXBvDgcc5xkxSIrvzBk1y8mAus2w3vNPJkt7mQz1/NZzrL9kdeZQz6OWrtyVwpBlD5VlEJZJ6wVDXA2DlrrKrlYvAVU5D8XbMphQf5cPg4JR57OlrLoY5/zPatikoMSmSFRYbrW3icz4KevBpWCKAYdlwjxNKGXVOYihztxYTKlnY/C4YR9PUMNtnQKfat+295WXZCj9stqojbdjZnXYZyDKToYgZRyJArhkFJDqVEgz7EXtiiqelnbJ7bP0X8Awnb4pdavCtbLeyve13eilhsordBS99uFpu9TJNqicdY3VoQECv+ualbYtCFEcuFJKKA8btncJXCSldGBRvIpBi5T+qw7Mzhj689HTpGuXwgi1vewEoo6m2u/NOWVUXNr5tnd7NnIcoa7bMNLLAAa9VzuxNxx/ooYSKu6e9tk7tNuuFScf9NqlboxdHWrFL+5n43BHfZwfgze2eB7KHPqqEUR/83q5NufrfDHpxDxUugGOd3QOja8YWtpp/fIp9iu1Kys0o7iV5kQIlQ+rz1NR2JZncilIheScW9pjh1vqHpG1T0g5K1834CiPmxw4E0Wpea90zPhvC0Rpxt2GD5rcQG6PqNJaz3U2HKr4xdWMH9ecgM7IN+oGbK7+anSNK1wIb+mzDAk+35Lo2QMYUwCOC+GwTJiiOOb51M3+KkWyyRAFFyWsNKeebxfNCdM1kjrj2eT08SqT+z1ShxZnBLFyidVAVY3BLPi/MDiKQ7+k8tYyv0XoYM28OqRXjloiIgbgD24W/Ne+uMc/eP8NkptzJVt2WBVsPCqMBC0pCPzqdcGWCw5A0xXWJwfZF42Oit6lwU6Hdp3SXoyaDB9RD0CDAdWZj4dyEZWyhgZ//sxppr8On1jaY9U3UwhSVkNtI0ystd2pGtEvhMEBiEhpcq8n9HNrMLzPczpeB6ilYM242lyhBhRHCjPWh0U4ouHoPXjvxsdtHy/pV8PbezL6qD+t9/U/HvWx33y9SRX++rkZp2F363NVb0uYZsLhMFVjtPXMLCVTJGgRdiAVPjKACTC+Caz4UTINScIIpUfVpkbdv17/qhkkmWHRpaarABquk72RCP5AoZYsgsvoQRU/AAYnVc73a2QwYrDpl7TiYg/yDYb7qP6IggIzyloZiRCUNwOQSsG2bZhryQTN7gVxuvWlAYhInHn0ewxiGD8cbnE4HJFW4ULWLePp/IR5mnBzc8QUCYc54maZcDzMiPMMihExzJjnI25ub3Bze4f5eINlWhDUVrmoXXHLUsZ5ChOO8xHTPKnMUGePGAkzEUpxeELpmAAiIwThlykwctmQ8ybOymnDRMDn95Jh7XiYcZxmgBlpU8M4M8oksvkcJuH5Wfa3nh2j69jjPNpvDuwNQsdfnr0+2TDuvS+ad1lLR1BQwKkpIL3CwZ4x4PFIzZRW5u1hXnyGuL0hfRS0LowcULTEfR3zPQWOje/Skwn1Pf/Xv2dpr1LKiNHGmxHDJIIWXKqqulnPoFY1tiMQlsMBq+0hM4LWK8mj4r/bZ25er+M8gOpRVhkyZZ4CRPA7n04uTfowzouv+yBZx1F/7dsiLxzoYCU9hiFAwhit2u/bQDSu7Ou4b3KwuCqF3IB6ivPM5Q1q+2Pg4ftuK44hlu+dQYTq1jSHD0NKJBOhvYM/jMf+ffvtt3j9+jWmacLT0xMkMhFgizCpmRT6Fv0MKxg+tzh/Ttfza/lbtHvlMw/3PHOzK/rRtTPwCWNwR9nf8yOripd65C+No3Y1YaAXwLNmsyg5oQRR6MYQ8e23r/E7P/odvP/wAa+WLwAKz6a/uey//fUMrCnYPnbtOzHsPTd8VsbZTfpyIT2O5P5cjvTrk2BMBWRrzv7udTuil4/S4j38Vl9099hFzptAvtsG9tcEhtv78bV1kFdCIBHguOBwOOLx8bEybRZNt7dc5rwxqors8KiIVn+TNEMQvKy06KLdYd174dp9Hv/urcm1qzK3+84ne8/6eV0giQuYuISz3qmhXZ/Cto34aoRr1/HzL+9e12jtKKCyo1d8/TV7tZI4daq7isMu5+HX6relBZ965nd/d3xTmzw3GKj44NLD/uNGaDlThqvtnHo6NLZw4VBkPI8ZCPoJiTDHhjp67+TnLiJCQgH+Il8hgkDVaI1nwnX/sWscCdvNq+/7N6h55ZPw0hQC5mWqsoQpazxuNQFb5HAHe2SPUVP4BItoVkWSptcLIeBwOALM2NKGbdNqbgZDrJmbmg9IXSOBk484mTrB1GqjFgDLPHeRhBSA/PsJ+Z/0apdP4lAcXVCUXHmPJvh+2nWdR3G8eL1DUscxGNCQ1AatUV2isJxj1LUmLMsBy+GI12+/xbquePHiBb744oue7yDCzc0NvvnmG0krnVJN17aua5Uxv/76a3z22WcAgNPphC+++ALLslSZlSH1Q6dpwqtXr7AsiyiSNCIckDP79PSEUgpub2+xriuWg6Qn/PDhA7799ltM04RlWXCr9cp/m4u5ZW1o+HJYYwAJCRlF09wBVemmWTbZwpoyWrQtWSp+jYQgMSbWaCwS7DbhAGQ9l5TBinKc70+j9aSK95KAEoESYY6XgQjTFDBPEk0FyBndckbaktQjd6XLvMOxZeWYiHAzBdwfF5FxS0bKCRkMBMniNlMfKSTKM4dDdVk0LLZj7qrhuXAz3pOZTQErX5pzxvl8BhEhb0mcCAGQKp8KSLPtAbkwsu3lNINiAFKumXkI3DKEkOAZECEWc641wxg6/QfrO+eUkYu2QwywjCWngnlZEKNmC8gr0lY0yosASwZHkyxBSWIUOcyIc8TTU1HdhrQdA4sDS2p1ovfkh57etHqczRBulxk4jF6Vfq7FIpwDuFDlgWXaqUZ0yfGIQGBMcVK8mVWZOoEitAZxAKhIBo6cZWTsHMd03YLCfXW4cnNiHWeV2anNuU3Lz1GdCkj23+q1m6NoxbcMEBjLFBBJcL2thUTzJeQsKfoPcUa4v8ccI84fnvC4PmErG5CEH4gkepbEjJAlq8GaM8wIInDW86dt82x9ez7N5tVKGElfJW+drkK2TnBpXRHjb7p+Gs1sBopGjy/6dp89PmzjtxNKA4tDtT0bm0zTySv6nJRtU+dsgpQy6JwaveHI8SMXwszY9iUfP17dPSfv2RnyDuQ0/pd6HuBSNjCWkLs3+zE5xw6/9+Pgr87gmWd2tqT9cRkpyfg2re1eRT5G4Q0TEyZI2bjCBYW0Pi4YU/QQ5zbc1iKoM5J+BgSHx9hqjdvrRntCmMBgwd85iUOZ1lcFCFLppvGWzZkKjn+EnimBT0nRTsi5GaglqKx069A5mjmequn7dFpm2IXBdhuPdB1qJgARryW4S+CLK/47pyQZUgEcp4y7I2NZJkzTDEujXccz7GWggDhNmKelzpl1a3uj1QBKFR499KE9b3MIUXnnUuGRqkE7N5mUGRLViFZaI0csywEhRnGmyBtKkghwCaATY1BJSfnEW5hR+jgRvrxfcBsY79ywA7Nk1qAIcKpwa7gjgBFr4JHo2VbN1hGF6KCwwcjl8arnz+1zL8uqw7LTwwkebeDenAdQS4JsKSlN1XfIeDg1gBerrU6AczwAmSNIbDWBgzpbuSxAxKiG8arjaWBiHD/M9a/B+MUCtHr2li6fWzbVBj/yp0AMkWCpcW14MwQtZ+P4ZJ25rDE7+a6ygdx1YHJRwxHs2mJjimu7/TxsD80OYYjQ6/UFdlur/Z7WhrwSstJnrhleOgzL7i8VMBMCzQqrjGkCbm/mJkUoHS6FEZkQw1SdgcQPtKCUBKIDzHbDzJjnWXB1lrLLMrRLR486LGY1ulvbpnvU2RfWVOnFqhLUK5eiCYI81AQw54vsEWZbajxHgAVKPHd16z3cC6AqKxGAGEhLPgtt2LYVMQoenCahS2nbEHPLWqIWU6w5IZWMwuJUK0HCWz0jMQQcDwvub1/h9nZBygUP5ydkiuAgEdqH44zb+wV3d0fc3Bxwc1wQpwmgCWGeMS0zbueA2xiwBBJHnQAwBUzE2HJCVNl2mRfMyyQ8aa0fLyAXKOAwBQARpQTd+0YLxAdKEMlWksJCAueCUBg3NOFwIIQYMcWIhSJCAdJ5xRoCypwxlwmgBdMM3bcCYALRBH/azDnQ743xqsTu3HS7+vye++vTU6nXA43GoDsGwNJzeEG21mTQ94oRfaCmEbNJjfWbLMLDjNCliBDn00rZvV5R2I6Lb9fa8YJaL7T1BMfu2Rwsst0b0n3KhhAC7u7u8PUP/iX8/Kd/eLF2e/xjVSTpfuWcEbXuDde5Aw8UABH35T1jigbkWdu1OxVx23p4AUKBHUEE95I7T9euIXiDVyNxpiw0UsEmIBgt595gMs7bUr51xmx2Hl8O8P0ejYbq0ThtV3uGKgGsqe1HvMd+PpeXMZ17bVsDo/K9N4igjsM/0+bXaFoTXGxtuI3f1pMu18cY+7Rt+Mkf/QSmqLGrFKkHl5Txq6n5MZLh9vkSuv7FXb+N8flTL5urZ9zG+/2YeiK926ZJQN25uf7s/jPtLNVztPtgMyx6D9RRr1CywMF5PSM+Rbz+9lscb27w+PABd/f3IASpOz/OTc/knhMSO1ht+NRec7jgCu6TNi5/tDW2M+NZRdfB5Ub4F93C7o39Wt910ew39vjJ7+nlOgwNAE4I3AWacW3quM2IONwf576jXLK/e8s+nuW2JvIeA8LoFMZB09yUYl6irErGgdUwXO+Ye+rmXfl/EEmkVGOaNWqzw4NUGU7zZb5YZD9XPx80/Ngx5XVdruwDmhfrLviPeL0KNW5hn8EJezzGxTPXX9+9Opq505dXYPYY/VN7s/fGd3VnLs7e9TEYXd9Tvvq1MV7A1njPyDbyEp0S5cpa+O/jXhi8YRe/7lCFCsztljcye1iEg8VujLakDCC0yD9j9gW9eD7qOp3y8+rh152V2nf//bnLUFz+vIBejTDQ5t7W5JLHrVEgn9jfNXzV/3pJmdmNYV4WzPOseggSow+r7JG54rngfqt8llufUgqyRUNS469ijJKOEC11W2GJNp6nGeu2IaetwkV1erWhNwCp5OEqTqjnRR2HmWspC8nWxTV1I/2oYH2z4fjLWaHOMCh6eNtDAwOu8Dh0b2zjOd6Tm+rOGQwTXXQtymhxJibSaHcdQ8kJMYhCztLN3d3e43d//GP84Ec/rAbpep4dfjgej/jRj36EGCPWda2yZIxRYENxjKWTtn18enqqhmwKUjcakLrNIYSaKtTSvB2PR9zdSV1rZu7k0xcvXmBWB4Z1lfTGZlD/Ta+SucMVJgNy3cIAUb7KSgAWXW4PtLMgqS+1bioz4iRKsMxN2VUzLexIAVUBz2IsqGfIPccsTu2W+pKKvFfTg7PTHdSz1OT7eq9z2mxye1wi5nkB2Grh6bnNRQyHGqGx5/Tp6ZPXKVjb4+fxqlFQDsedTic8PDwgFanR2ZcR01qVqggkaikDQwxV9t7jUZk1teVHhAlmRsl1gpdtaFRXCL38rMNz9Fd1JnPEclhq5JzgVDUoQ3HpR+jJSGNlaJdz7df6kqaPuiZNpI4Ga0Z/GRHs9EvqdGF5bl10sJfpmRqcVWVqjZ5rfIdFJo04MDo4r2O3hR32wy4r49CthcvExGi4ptZWz1kyy5RS9W1TiLg93uCHP1S8mDOe0lMdX8pZHVFiLWs47tHH7vXyUzOkWTCDyZcybnm+GuoqnobCDOozYvysRMILFLs8ZoXZTzijgEQv7cuYjrsIHg7buyBv0EeHty56+kS+6rlx7LW1xzP/pu17vPabjOs3v/bNXrv8tspqpksoJQHR6ZHtdzCmKSBEww/odLPs+jB5zaYd0PSAlUcsShcRLtbH5BGioHWaW8QluQjciiXq++TOcjNKmnPWVFPrtvve0FD7JqqwB6P7RGp4BGKIIlsXdu0MvJfRq9JLES0bgqz5ljJO5xWFgSkCh2XG7e0tlnnRNNl6TAHQkP1qmRfEaQaFCGNwCc042e+3GwdzLfNR3yFUw4w8GkAQZyBh95uTFSvRIwBcimYiMt63LURmqQFcszkVqSceg9XhcM5Z5Gpxs5RtfXkb8S//6CX+E7zt5o3ScIXJTQ3UDc5Q51LTTcMy5arOg54xJXrZjqqbBRRRduJeLU/kUupnzQ4qNKQMcKXwmXNH2+roi5W1jbUcla2VRaLXEp4xVP1Pzcqlw+wcOxw/d8FXVlnW9IktO3BxPOG4PnWdjNbU9fr/Uvdnz9YsWZ4Y9FseEXvvM3zjnTNvZmVmVWV1dXWpW91CUktIbYBMYDIwXsAAQ2aYYQzGH8Abfwh/g4wnCWvjQQ+SYQIJDCSg1a2es6oyK/OO33zO2TvCffGwBl/uEft8596sFiKufffsHTvCh+XL1+xrQfZKKJljz6yd0i1fEdDWZ9z2bqO2bn0M7PQiDoCgKffjtPXFRm/3/UU+Xy87TBW/mANvMGywdjh2YN0wcq4HWa0P8bFNq4xq3+UyvBJ6nVcHaCL9iTTAMtaKbMwYMLj8lXOtcW96V99n/ByDlIlrgFAjN1KUcdftxMue2bJB9bKz4XouUoLCgrEJ4tg23VMOI1b88vTvWoY5kfo0aUTJElCfVA+92B9wsd8hX83IJYMGxvQWSChSn3uUgOxpmmRM+t7hcMDF4QLTtMduN2A3EoZRszukAUshnBYAE2lqeELCIllBnEeK8z9RyF4U1pj0GT8QD2BnFohxAA8JpYzgi4PDc9BT/mlM4DLj9jYjnQaM44B52QF8heEiYZomxatSefkGiTS7Wl8C5vtKMd/pxHjvDF+l8gpEaxgGzPPcIdDaMGknwgEoENbCW9YI7Hia3J7ZQmxJ5VEd8EDdEL3Sb21Ho6x992Gb0UUR3PquShRcOEpJ+0MlXhypJwUlo0pvEqiVgGk3SURjybi5vcXlYR+l9SqVABLVGiiqR8CGx9nSH1GjRqocoKkelgXHuzscHj3GUnKzPtZlQ8lrlw0ziQTH4cbts30TjaEEAGhbNNhSFpp+wv1zRJTjTm5bqBLimeuhylDEodXvzfduTU22ofqY4JBZPu1HaceMrrEPg+Mv/+yXWE6zCibQfSnRV8syS61xM2xgc2XvA8X9V5TI/xlekY70ISKACvqoAso6dsjejfdadN3ut51ekMe6aYcIz3ugSRTRou9dR9TKjv2I6rZicTwOiUxGQ+FcT0EVWf+7u1u8eT1g2u0wH0+4uLiQgRQ4tELz/r3dg/I3nuapc6Lu/Y1Rb+4do5nt/M408P5799CMOM71PvUnwppyv1jNuGOXnvnCN7IjQv0e+Axz9zxUCO+MQKt5xTY6hWMLaitSHGlHSCMGAva7vUZ0ioBUT+xwszmYYdJIq0B0KfllyqZ8S/rhYRpqoJJzJmrA3KxNxDFe76poHDVS6UYRfaeBBdtY0ROPoGiucSjyu8BU772+r+HsIW3ex/8qLLd59JrhIGj3qIByJlHXOq7A+xSXc2Nf/2AKdMUnGdO5vdfyW39nY/2iHNfwD6c7G2M6I7c4nDZoc4RNg6VRXjK8YXG8ibEB9kDHmGjFq9H9bA6NTVijniDgAIf2mXaYAOTU6e+fd+Y13CqA/fvLDm07/mnVaDVQyHzF6D9Ok6RmBukpkoJlsexNckJHjEoK+tLC2rImgSC1aK12YxH5aT4tOGEWp+I4Sp+DKH45i96z203ANOF0OoohwmiE4coGhHrHUXMfALQOY8kFNECdfglDGpBZ640TgN9j5C/lJK0YlUjnrVDr1+g+IWdTKryHZz7gEh1L2hQnIUtkuzp0SQMPwIz5dMKQ5HS8lH65wuX1FZaccTwdUZgxTTt3WkdyFXU6c1znnIMhWh5elgWn08kd5ldXV5UHcg3wBtAElA7DgLu7OyzL4sb4aZr8swVhm1PeDBa/9alxRlNSK6UEWJaIUqQOHAgDBJ/MEObwl2M3UrarFCwo1ZAigJGVIPKa4FBHrgXVWvp7W0sm+Glbob9wOs0EEGkadXN6Q2obJgtYKcCQJiDLaf685EamtJN8pnfb+pmThEmCyBOAuTCWkrUufOUJ9+FqDOKPPOC+95jVyRxkLbMlzPOMYRIDssNE4Sm2kdquzam3Zzgcg77XlWlt1zXYLtweQXW/m5FQHICa+r1IMEfcE02AFiAGuYsDhmEM8EiwwQja1dON55xp1VDN/h7QGkmt/8a5pXCKBxAi/Yn2KLM7jWVE1qwQzAweSOtASg3VpDVQnea7wXYQfEIJp8NV1mF1loAByptB8oDum3pzvU72k7cmn1ZyG1e2YfO3uXuGxZJDTV/57YMPPsDNzQ3ysiDPC/Jc2nbRwju6V953RVnTs3poOuphTJimEXe3M1ISes4lY85S0oBSz/NsvraWcR32KwO6wy/eL/3c7LbSmcJArZL5vtltfo9N9/bAh/K/lRH9/+fXX7we8tAeW5F2Jei1z/v+S6AsXgOXXYnw9OoKT548wp52AIuzb9rtRE5mNHRW2uSqu6QkThdtL1HCAsk6Yelv4zjNhut8AgO4FM0Wqs5UUhNKzi7qVbW/AC6LkTpLtJ73vKi8ojWZU3JekShhCDVXnXJQPTgmIJS/KTWCZpiETZ1XUp074pVH3eQT/i9vf43CCSkx9rsJjy6vJEBKHciFGblkKbUWrml3QBpGWAbCuO51D0SHispZwpzicOVKxe0RJpMSYh1wCWowh24NrJOUypWeFh1zQV4WeKp+W7NSwEXkwzQMGLgA2RzYADRN9I8S8L/58Cn+13i1VglTkiBVhqY2V2coTK8wGIiDMh7+EpvHlpJZr0b3Y3OgO+N1G4bJMJHkuAybWYMn7BRoyKZTtFSN8tRi/4rqMJBAynEYMU4WzBqDNMhrjZvunhJ5XWuSBYM5Y+NFOoctO1yjfrPoYbmUEIjVwsfHbC3r/vY95DCyMcnLjZ8GgAWKEMEDqN2+4PsO7l/RZVF81qDMtWFAeTv5nE3fhGVv59o/gcJaR1wxfAmOfpj+X9+P/ZsMKJ/brEnTbmqCw3y4Qa70/oPcRQSnQ5Y1IOeM+XTCsswrMhRlapNxBbWEHkP3ogUTz0s81Fd1EOvfghRtbBboDGhWqaC7MWsxuffoA/dd53i5yYqWlY6ZcTqdJCt1ShhVv4x9Ew0YhqJOdC1dMYzgkkEYIenKCSkNEoB9fYGnj/bYH4DLywlPnlzg5vYax7sjxmFAImCe76T9NGNcTjhwxjgAaT/gMO3w6OqAadqLrAuRdXMC9uMg9JcAoIAzI3MGkQXPkDv4oRneiOs52gSRAQciDEmacq2SLCik7hsuEjScmXFU2r3kGTkDJY9IYMzDhDLtgEFoL1DNJ015rG4tXUb4La8HO8Yld75GgCsymiJjTjqLoo7KTS9EmjK4LIsL+jaRmDbdrqgs5ZydwPXKcyRqlDQFTynN5o7CRHTqW3q92K7dt/lspQuLjKEwu5HGiB54QyhnNGOtt4UApnEEkqQbON0dwUYcwlo3hIpiCx0tckzSjimuhzlBBHHnecEuwLRfhy2i0BudndihptAhc9J1cxAGae20sCBqhbvG0OwK3TYhj2Ppx9aP4S/uqkzwvDHFP8n/m9z2rIJBeJArc5YlTM7RxSETDSh1FK9fvcI3X3+NQet9SN/CdXNeUDTdUKs0/LbTp/Ui/jO+NoUrvSq6mTKFZpK0gQTcvNm2sd5YtZVzTu9zuG2/Vb1QKb1+czT1/uoJ2na8G/gPO+2RdEl0r5QCUJJIswWYIadb3rx+jWfPn+HVyxd49vw5kDZSFIUxO2qGR6KRiIzeuMFHRnqOUW0bP7rfm+HcF2LQtXcPDVjhznu+2/5sFqe1mrig2b9K3Xsc9vA5Ia06BFeEsbnnjpNmqGcQLvzOdi/QERPozBDrBgJ93hTOwhY974P1MfeBKMZ27DsDQahVQR6t8uP0La711qLT+jeBB/vP5nDq939sg84da1X66/v0jOK2btIBotN5P108N7z7rh6XHf4mfAYFxPvZUHKcuLR6VBic/hh+O8t7z8g2/XObOG/7oSLMJk6tLu7ouck4Z+gYcEZu2ZB1/C86mGm/riivhrRxUhwB9nE+BCzzgnEcvN0tfPRliGNtZABaw5brX+P5jWL6HllouSjAdRjQxtg8gpeV5neM2PnvAy4jb1vkt+9PcFfmvNtJ6rAUaFp0GlTnyeJzd1zVOUUYguB6xqAnDcY0ulFgyRn5dMQ8i9I7TlqHVw20BQW73R6lZByPJx1v4AUbBEl+2rjvIJD7pg8xS43imvWHQXvG6Ycz0q9Cajz/P3vfK5q7AW7Zzm3k/+q5DT2hn1PbbpBztJblOO0gmawAGkbXD+fTEYmAd29fIy8z9ruDOMKXgtdv3mEYB5w0G5I592ympRTs93uM4+gO8Xha257vdUkA2O/3avyuJwbGccTFxYUbXmyM5rQ9nU5SdqQUvH37Fl988QWICJ988gkePXqE3W4HZsbNzc15YD7gmvXkuV0xg5kbf9xhBB+/6XtU6vNSP11OXJeSNYAkBLrr6VTTHUQsaE9vM8PTHDpdQRVnCzMG0pOtlk0uS3p8OWFRMC8zMCRQTijIUnMv2Bei09jX2Ax0LHVlSU/q353ucDotNSAlvNfSvbWOew7PI/1Y4/laCCFKWr++Na2YUQ+h35wzjqcT5mX2YI6u87Njql3WORQ9ZUNccZdNdlUDbl4yipbTYuRQyq4gZ3EaWOaD3Thiv5uQLCaBKfAuuZZSHUzf9dqSxyO8m2BNoME9+83gllJ4rzmpT7qHB01ZPLiBL9pv2HEhaem5Amb5FMeXICUHkIamzJCN3XhQnIesEhqlsGGlm7Kl6gmAOjLIA5xj4I/BRYJ0Bjx69AhPnz7F3btbvH71ptqvdC/HrI02rm2xr12TeL+U7C89f36Njz76AI8eP8U//ke/wMuX7zDtxLBbMtT+k8MBjmaSjuIOJ16adcE5O5HjTnXQgIBxSH5yXwyw4rxvM1L2M1/LyudkxHPy6/e97mvrnL76F9nHfzmXrKPbI+1eVEvb/4VL0zkXlfsAgAmPHl/g6voC05yQlyNyKdg5nKLztR2G6K71QFTSU+Apt04WH0fQi/3gEaoclUxX5YBL0X7JjGqTCTiNEniu4pbxZgKSZrYhdeq5TrwSqINsrnulOtF9CCrLmeeWvfSQKX7MUubjOC84LgAgzparNOBvlAF7zaJTclbnI4NSy+PSsINDSdNvNzaAlX4otJICXlSHJEEyyoUQY6ObJEAihsiR84wlz40s7+dsmWFp14mLO3jqElW9Myt/GYcR4yAyI4MxjAPGMoC44PnlHsNAWHRUnqBlIwDHurAy69PI+O/8a+aJbXUdNvzqtnr0YdT1ZERlrNqYROcshUAk+0ZOdBPMv20Oa3fIIqj/qtvEgDN7glTHyyWDMmGc6ilx4TG6lmhxk5qAB1opBdXGV4HR2yhMd/bAwlLO6vfMGrClEzNHfNWZ/UmFIFU9kOv3Og/ye2y16pkbB2Fvl6DaBeJH1nk29DgqamGfgIV3ruCFMKdGF+ZGDje8jgMoeiyZs/Unc9nvJqlLDwfDSjax+xZ4IPKZwkfhK6eiKw6NuxGcaxaotUwUbQeqwywLUq7BrUSSOXmaJuRc1zE6wYkI0zTJAS/U9kz2ibalmoHq/Txxi21u2dVcv6J2fKUUZBLf4DgMmLogVCJ5LmYiE9jXIOAhES4OIx4/vsSTR3tcLAmneYfTfIH5dI15PgkISYImGAlLYeR8xM1tRsKCMWUMA+HqcAlOojMVZskOpngm+FTnQxbwStJ2Lib7DIqfbAQdIyXhz4mAgTAkKY5l+w9QLu56mwRKZy5YSsGSNZhpGEHDAIqHY7UvO+hsPh076Vt5AzZsEVv2lIfJUg92jJthwU8f9lhDdWD2+zRNnkIgOvH6d6OD26LtW6W1rWMV/xoC+qVN95HHUaGyVA2n0wnX19ce+W/ICVSlPN7v500UhVYxxl1dPxLiU8wBEZSpDS2EIzxIUrYMw4BCMobbGzWGGCwQiErXjjXvvMbaD6SbAa2fBDgfZqkzflkKmDq4rQTaVmGo6xdgEejdFnExPh4Fg/Cr9+EMyTnGuq04li0FYOUI2LxMouJ7+4jtrd9/wLNGaLhbQxdc10zNhLgq+5Cf6OiBy8z45S9/KSd/U11bQIiRCI9nFuX/j69zzpgaTNHhwdlFbnfVtgOo/dXXRe/5p3sVXrhg8z5H0urd9zwvhouixlsVZ6TIEgBCzgBRwt3dHcZxwH6/wzwveHR9jVENuI10HnXEQHvPz1EF9ECj27kHAyOp0x6RjrbPxnnZ120j5fZ44nMPNTC4U7e9GTuqircSOs+Y21lxIt8DAk3bGmtQ0hzG/ltt05AuGqPvxYptCa+fUjsWSjqOGhRmJywr/IOy1igTfZuB/6gwZYaFHt/a/dRdkX/ag2u21PQf6eY2M7Lm6u/1ZGXtsMfFMPHti+/fq2sn5j2MMn7vuwmyw/a+dKlgW+6q0mV9vBnf++lNXVOF2Zm5f1ce7fskKE9VkT5/PdQQ2PfXy5b3tkVVKSYirzXo4+72eNwfDQ9ixjyf5OSmb4VeUNzGAXu8kSPOjLey/fcBDy6j8Oel3dEd+rW/dT9uynbvv6jvkKytqqALma1OcS+ThKqQmqyec1ZZvNIZex/hb2EWZVlpu522JYjOM4ziUKGUMAJYFkbJGcecMS8zpmnSVJIjqIiDKqUBFxcH3B2PYDu9a4J3f0Va1cxdR67ErDEwFDH0ySkPwbH084L5y4LdnBA6bIBbKcI9tNbQ8zvKJ21XFcYi7yh8i6Qtzznj8vIap3lBKcDucBB9sWQs84wxEV6/fInj8Q5XV09xeXmNu9OMNE0ozLi9ufX053Gcu90Oy7KoMcUcZ8kdSFYPupTiac7tVLLpellP1gBw5+E8zz4fQE6Jm1Hj0aNHYGZcXV3hyZMnAICLiwt3wvclv77PZSnbbQy9Y9zw3rIXtIYoBiA1BgHRDxiEkzplXQ4D6r5pxtsG1dgaM9dgSsOu6CQwPJXTLBmcC4ZpUmNtwfEk9ZOREhjtiZA+ZWbs30//ECEzsJwW3N4dcZoXMaqhnrozePWGudjm1rX520oOCE5otpNYa/OL0yVU/DFclNMSeVOuXRt74tja042SJlVkNrJxoejJ/SpDMip80xBtNpKZwoOCRgmeALPX9pRBmczJnrZ2xRzeA9utK65vNR5u8+LIpxv7D0FqKDYwq+tiuCNpbJOD0Iz2Jo+KAyEpfmsbMGeDRYO0zvr+ijgX7/n4UWUGIj00Fp+P8Oh0yx62QtuyZL64vMLV1RXevnnnh0mgaTyjLe27XpF1EQHX1xf4wQ8+we/85Mf44INP8PbtHV6++icqbyekYQQlQl66zBVRhlnNYwaCsb2xAwZZtdrBtD19rinfmACU8zVFo37y0OucrPrbOq+3+ojfv2v738VO1V/3rc/3uaKuuNKdOn156zL+FZ1VV5cH7HcjxgKUTFpaIMpY8BOqbhBVGpg8KAZ6iEqDTkoNyAGqg0wkl1L11creGrInU5C+KPX71gVrmIZgTp+g1Cots8yk/ZpTvRV0rOrk1NGSOsFcN1Q6UngN56ATFGac5gWz+kQGAI/GEX8wTTJOCjpZShj3h3ZsaQhlE8yFUWV4D3JQna7aWaqmLdPYwBXvRZ4ynrvkpZNfSGstWybX0gSPJjJHfLTy6PzV3j8MEhw2n2YwpP44F6m1PCXClBIWc4kTAUygUkudRpAY/ImAcQL+xh+lVscx+Lvsb7LaxsXmUyB/z+lQ1ygzgYjDcrd6QAzSsHf81H3jGCc/Bc4ASi7IlJGGEUOywA3ZY3aC1NFO/+f7RiFuJ3nJ7/fwODd9089aftg/U+3rqPKY2xytj0bZ8t/M39H4nlD5MCnuKhidC1k2Qnb82hycyGbU+qui3Y9VRzJd0+bA+lzDSRXAPmeXF7Rhjt0wliWDkgRwM5m8B+z3k5RnCbAzLDQ96X18wPWmvGjJxcqX++cqfTD/jvJTDXoA2jVLw7DSfftL5rH3+Ud4POQ6P7/3y7VRb+9lWCLCsizIJWPQUkZma2SGBhIsqkNVWVCcw4w0EPb7EU8fX+DJ4wNyHjHnGfOyoCyyhgDUyc2iC2XgOC8oDOynCeM0gBJQeJFMUSDPoKGiLQakYB2p8qcnLFZEZIwVvoWdXjOTOMZZdTnfB64VBvhZdg+xm7Om3x+StKfai0vHDMUL53NATfPJZ5Y5zOP+5dy8HuwYB6x+V95W8o0HUuscj88VZpAq0VY7CahIZAYu68sMFlvKYnRUt3XQZCyWbqXpv8QaUvDUZ75Ru7HH6I/eUW+fa6CAPPeX/vCP8Y/+i/8nMp9c+dkk4i4zKCM3LEhSJzFTQqEiJ+tIIjDsQInRdYUGTERyQSkqD0QoYE0qFYR57dIiOU6nE6z2SiX8FabU9WcCY2QSYYXkmTMy7xYityJK6DfAL8Kxh2tv0O6vqmxCeaKzNLjG9x46aoJCI5D4eLeIdccUpJH+Th1/I7y0j3IwPjX7KvTx1Vdf4e2bN366yYTnUgqW+aTMV099/gUqcv+sry1FUS6LZGxxo30YnfLynhOI4aJIiF3QXNMiW8fKHN8vSEi5h5XccM9g8H78VBy2OVK4H+dcuABZjHLv3rzB1fU1vvnma3zy2Q/W43Fi0+Jq/Lzed7x6zqfRKMbr31cyvrxV+8GGuhj63/r8nXG9IwVE7Vz65jbHTCIsV2EDjqf+6Gr67MoF/D12obD96budXGjm84AnrK4kYPQGmv4rOJlMgahksUGVKjAGau2/kf81xcA1qQ4wDlva2ASd8L/mC/2HAINWoq1z4rDmVNfOX4y8ux9PM//386NtxXZ7zFtXL6/0+9GE061xRFng7G9NZ/pniwY6nM+P9cE8Gi3smrndJ9mGtTHD03175CHjeMh9/71FxjUuomZDAKqsfDydcH11XWXArh3He6Up/SjspIkKB9tjU+fUFj1v+5KP81hAn/Lq/uqK98NzfyHiBdW/skWq/D2kAfvDXpRmU/LUIZjLulaewDpkc4LJyQJXM08anTXjGVijurVOq6WMA1DTRTLhxCfknCVt9jjJidgsDt+LwwVORzkZWk9QbNCN9kOzViY7xv1uAXDDMIbyOED5gwX4O7tG/u6XsBPn24sdONtoEnhqpGPnLrdJ2emnlHA6zbi4uMTh4gJLvpFT+dMEhtSrLUVS6y1ZnHW//7t/iMurS2AsmPYi3z5+/DiMp9bgHFSPNKe46YiWGQyodeBMxxzHsSnV5enqQyC4nTyPDml7t57aTLi8vHQdFajpBhsH3ve4bu9uXV8hqikiiahmKyiS7twM1IY3QnuSnEVgRuaERfX5XKTmeFL6UlhSmpsR3LLF9Bfr/mE71RSQyfV/MgOIZpzJM4b9RQ0+OM4ABCf8NFDQ3e+XNaX2/HGecby9w+3tHRbdBzJuBrcC1T00fNvA0vePgPcpnLRwHoxg5OR6X2omlmYPz/OM4+mE3DnGexl2c7TMnsrd7RRF6qvbHmNI+VOHFsnJLi7wU/xGyyKsEyUkShjHQeTALAFSJv8pAurp442T7u+57qMVjrPakzk1nApyXQcK75hDiSTyt+0nrGtKQjMTD5DYCjnOp9AOY9Oa5Eg1u5EwCP8VSACxnNZ5oJ7RrLHcQD0FY/BtcafiU8Wl5jf9ZxkLd/sdLi4vMU2TlDP07AXt8+8Zqe+HFo5i1zkcJnz26Yf44ec/wA8//xGeP/8IH378S/zDf/gnKGDJSEEDmCT9LQUjqjW8BTNmy+piIvn6kEyEZRikmM8U90UmpWbt75OB71u6c3Lr97GhvFeG/A463Xdp4z799b7rfTL0Q9swiWMluz64lUpfAWA3jdgR1T3MEsiWiMGUYMlXXZZr8ACa5rmWYInBF66LcpXpiVSG7pTcVner9LE90SrPezY+30fUZLupcJY2qqy3BpaLrmC34RLgGTpbmhIm7uMGLNrJ1IZSCk7LgkV5RiJgGgZMo2UVkUGI/DNid7hqYFEJd8xGFeDkVDbSn+qojueSWqcuO0GwdswXkfOCVeBLsRrrFQZWbijqX2DUIHiVzwgAp4SUBlBahA8OCTwOyEXw6pIIt7YcJC6cxNlPSdpCmfnQcDCRZFxPFAPa1HbPAS4rebw6xAn+sELS1L4I8z4gi6o8T6K/my7k5NjL5bT8wWkv2RJoTWRPwR/G1a1nYNB+GE/QLu4ZxDfX9hRvgut+rKgU3oWuBa/l7DAORJzq+nTZmm2+HSw2RxYNPgZmMi5u2F+fTiQnwXOVE4FWtrF7loH5+9BfDmOyqc9Lxn6/A3N2WkBEOOx2mHYT5tzxViDQoBVSNs+ajrUsXGU2Ii8Z0EAsyBOGU0RSPphUtxo1GLkfQ7R1Wd8WFDgMejrc99F5uL2PRzbAu+d9420U8KWBkI6PCZiGERORy+as+osFMtu+xcAAFYBEPj9c7PD06TWePjqglAVLnvWUtYxPSviojRZA4YS7WTJnESVMw4j97oA0DaBBxpsYGqCi+Fak3IelT4+0V3Qp2bKlkO8/NgKqDESyrBFy0QPkqQ0CsrAOBqtoJsE0zANgOigqvXR6b4NRntXYGwltiUzTDb67aNZcD3aMWzRVrMsdLyNIUYjtI34txUt0TDMDw1BT2sV3euMoUDdJPBkST4cDkA3GWI0FBAypngoYxxHH4xG73a7OoxmrtGFp3yPiV0ZUTyQs81KfBZrN2whZxtDCPRfsh0FSy40DRk4YJuDmNGs3VSwrbI4SHQ85toY1qcRZmG+ovaZ9CrwKDocDyMPCDasqgvVKjbVRs0BXCmx4a0ynk0vrt0i7iHx29vy2E0nHt260E/63nGUu7bqAHQWZ+06M90Szxc8HMK64kRHwQme8UuI5CHGaDi7WOtnC+1//+s89mj0q1JJCXVMiagqPbjLr8Uaravx+7upw49zVp8B5n3PannICHG6hEZ7738JXU6gaxYLPPm/fe0ZnxkjDmU3FOApTAeWqcCafM2dlHPcUD/R+ga00q+uuQzBPyRi1JpRjme4BO0VwOp1wnEbslwPe3tzgydNb7A8X/XRg9WzOCWiNAN6NsQdRL9TEjiqjNlxSQdVoXEN7z+Bj91tVJMj/miJx7jIhZ6WYhlYjXWoUb1VaCEYEq+CwErQ2puB92inHaEjq59M185CdRKG9JnBAeZHRmGmaBDeNd0XjuJGEfgDxL9fpyyvkDudmK5oRM3zlvn3jI6ogUkNrWvoU+el76RGjDsbouLEADkEYYekcbwxem4sIp9NtIEj9/ZyxrW1nvcY2hjZojZr7K+NhaMVwO757fgxhITfmgOY2SwrX8HCEjSuA7+HRvZwVAyis39U7vjjtmjwExlUx3jB8birqRkeqswnM3kZ8zOUMW2+062kkYVkWTLtJ223TIJ67fKwKl1juJzzl/3fFe9VQHWu8yhWDptVGrF83ZYjvq428n4L5EywOyt1u3zioLX2bOfSEVxPQOMMpfK7GNQZjSEnSsVvpH8UlkQktIEFOqFDe4vuEnAvu7o7IoxgghmEEkYxN6riRnzrevAJZ53gPAbxcHTEgcU6J0TJpdDeDPmTMe8buNOi61wCtRqZ+z/UALGy+bbHkajiwtI6D60cfffQRbm6PACVM0w7TtAOBcJxn0QWJsRsnzAvj889/gP1hwu3pBtN+505tYC1HFHUc3d7e4nA4YJomHI8nvHnz2k+qT9Pkep/VGo96IEgMwZZZzGSmYRiw3+89YJuZqwOKyNP5mXxuemrURb/v9frta2/H/iVN9c+lnvhZlj4Vpownnoo38dTGOXigufL5kjXV9xHzfMSiJ8sLb/AMy6wG6Ea1Or8EpISkKTDlRPPi47b9B03fvWT2oJZoDzhHv3MpuDudUHLG3c0tjvNJqD8l8EbJKIMDgGY9KqxaufR9xrOUBjfGrR+szzMzlqUo/NSAVcQQbYEJWVMLSrBs4ItNg+t+Yt8lF5Rl8QwHRKmeogS0JEStkUuQ0xnQ1IZgcSwRgHEYsBtHTENCzkqzmBS+QkmLOuKjONrz9+9yGU0DoTao8mJhs2PoSRp9tjeU6jDrGuYCHmqN+2ncxR7BPGg98tpZ7XpAgaUtH5TGBngqT9+yU71vnvKOOdrsvbWzW4KvYo36dUaFuEdyzkiUcHE44HA44N27dz5mZvip2AddLheYjiq2g3FM+MGnH+Ev/fz38fzjTzDtL/Hu9ghKE9IkdZenUbJFLsuC4TCA57nOD3B86/FlwOipNn3QQUaLg3P7KLPKYDJ/ZMkVS5oZ4N614ehQOn/18ui9YIu42MuUW7rvX+D1vna/y1y/zxUdzOHuA9+rgmiDFzCBzKT7AT+fL3F1x6BB0zgXlXBScoeSNux/zd4q/GUQvglNC272nJVex25/EVxT3mH4RVWmZEht6jp3e7fOyexCcR1IBWqi1kYuPKpLRR1esr3kdmSly+Io0W0Bc2zI3nUTpwmVVIO5cmHMs1E8CdIfR+HNQ5IAomGcMNAONE4Yd/tuDX3agJ1YJxhBBlD0XKKtZbVNwewl2oBni9E52vOlSBrtXBb3I4wpgdJQaWERh5DN3eygrOOiFODa0QY/SZmlhvy022FZjsJ/cl0X6VdPXvppS9R5WA3oBCSSxO7ToHXNrf60GkRsTUSHxvrapCeVT7ns4iqh6bMVnkSAOMPtNG/g2SqHLcvi8Ih6N8WFVf7MtqyGSv5zHZ/J/VbuIs6HQh/RdkAEJKaq4zRzjjjdB2oan1C0s3EHWdn1YNvrtmeY1H8Ct+/anrA04H6/I6A1YK4dSa33zVWXlJ6rfcKHLfcKisrxG7xGAe36a7AHGx2oj0qfpRmXBM5dXFwpndN09ANhf9hjt5twuj2GebU+hiiTLIuccJaD3JWfxVIveSMIuNeBXKbREgf6kKQd300ql/HqFHkMNLbx3Nzc4HDYSXaHujFaeQoRj7b5cv/bOftRxM3ODaN40/YHItydjmDUctLCMzgExSpcwBhJ1iwl4OrigGfPnuHZ1QEMCdJfSpFSUsvs8CBKQJJ64ZnF9iF8gDDQgJRGkeHZ8JORIRkRaCn1EDYALlTlyzgX3x8SPEtEmAbyoB/SPVKYNS16DR7Wlitu2dgSazBlwjCMIQua6EcDlMfDCaW3Fa+C4vt9a12/y/VgxzgpHecsnn1mMaKT/jamAUjidDGCOYyDEyoAGIdR5lYWIQ5MyMuCklnqsKnzOgr7FlVnCNorAjF63wHENR1O8QWVyArWehtFjS+GlNHYYScArD+g1pOLhlvxQdqpBKBwxmk+KQFV5dE2kA2CKjwKqkBWVFChAqTDDny5x0fPnuH1y5eg0x32uxF3t3euXENb5QBgv+9MQAJBCtiJoRsMkZABLCCUBFw/vjbxxEYKagREVY9SqCnsowiLrJ9JN3Y8RRCFBw5woead2j8ztzUraweBq9iUtyN6WwMRdzK6Ma3i81w7u03wre+Y/l6VJX0gbliiNr2Pz7aKErE+c5Bq1ECg8KP6WzVoyX8pnIbIOeN4d4sxiWLKXAAq4LIg5xMkjaLtmzaiZlMW6357EHmxsXcK74OvQJjXbVfBwgX7sDYug/sHwDSB6iixn7jZh/F0LLxtuaqQoifEbBwucIWaQeBqeHABGCuBqlWUDJfg/Zy9TMnYXLE1E5DMAKHWkgqDxIy8zOBhwPE04+bmFiUXfP31N/jh55+HFrgCDa2S1/cpy851LyB8DovkQuqmkSIYQxQokWbY2jW0hep7Tr86QVqE36oYOfM8h6MqWLf9x9+7RQP51yqTlSpkMLc/wvB4HbDh/MIj47ZomsyDQjs2//CkPt81wWEdudJnWztWaVqcRMmVAje8s+YfsVTrK1ys69yPxteOK2+XdYTjCOv6NGuIdZAcxYb1qQavwn6KCmJYoDiwjbFWY6IZTLaNPmcucurUgYa9v96h0zz6HoGuNwbHd9bKW+RT7XPVSLt1eqfCqIFt2ON1alTnHJkGV3jd77Sv78agtV45juNk5jWMm/nGgDg4f6n7qvvd9kzlEpXfNDJEfT/SgH4uxit8TgqPYvKLvl60hNB5ZKw0WGgZ9IRlBsByYpxqDW3rtNLjXjEMclkPPkPPJ2d4TD/VjnE9SE5YXdVxa3+ieEcElS0KkjomzdgyLzPykhu5ONEQZCPl0eFEMdlS8ALWIN9cMqgkjNPeeYjwZznlasp7pb8VO5iBYdAaa0XqJhcuOOwlNTgDyMuCYRwBIpyOR5hxKILRt1+DkhVXwML+PWsAM0pmpFEDi7nKHvnnC/B3TAEHTJBucdt+UoB3WyX1Bi0A5hyxq9KUczTR5M0BKU1Iw4CUBjx5+gTX14/w9vaEYXfAuL8AaMCYCKe7GyRNN3h1fYVf/fINfucnP8CcXyMvGTfv3rkuZk7toutYmHFze0QpBVeXl6A04utvXmBWfW+a9mCccHN7BCPheDximiZcXl5iybJfTDk/nU44nU4YhgEXFxdNcPjd3R2OxyPGccThcHA9I+fsdcqPx2Nzn5nx6ec/OgOn91+v37wMcK8GIqClj3mpxof4vKVnLSWjIKHQoHArakUTPWgcJP3w8XjEnBPmOYtjvCzyBAe8MF5cVFdjhqTqlrGIcWMB5QRaCCgLULJj4VyypLNlcaL1KcUtsKBJkazXacko5YTl7gQUln0/QOdTZSMu27xtLYOyk7P3O5ioZqrrjDHDMCANNaOd8Ckzzms9PRIj0DiNQBYa7kEUqLxriy9vXW6QzBlJM1aAoMfUgnFKbQMW6GH1xZlzY2OZpgkXlwfsDjssoaa1BeiaQU/cKPcpbt/xCoSwN6Q2OhS4wYtGrsgh+GBIGHJCzgOmsgczY+RJHRwJw1DhW51zgDEf0pPj1TBYA2vdUKvpI9+XESLiXC8HRdtWCXhTikDYAkvcgeMnJnOzb+zQyjiNuLiQzAxLsJmtSyScuUjFHDsDo7LWYb/HDz79CL/3e7+DTz/7GHdlwJ/+8gt88cUX+MUv/hTL8Qgahua025AmYNc6qqJ9rZWDCQkJnDoaxmFg+lfWr6WB/dzeu4/Vkbq6v5I9HwCz/4pfUTf/r+ZV915HrcNH+Xy43GMckgTy2OlvFAwkwY1gtQMDLvOZ+p/zIkF4Ru+4eK3xvAg9U8tsO4YedKZDENTWJ3SeIj1U1DGdVWTRKhNEmiG2Zwtq6ugR6bvWde880z4yS/3cUpQPB+8YrfZGhTpDUi0f59nTNRPEOS6wI+RZD4GNA0Zm8HIMAGGUfBTexpLaF1ZOtKGdrV5v+qGrxYH2yWlwbvaf2+SVDid1Mi3LElLpU21HoAC3nRLExk4c9AzTGwSWcnL+hGmc5MAYClI64jgvGsgn3YxDwtPHCb9+NSOGuxYASdlYgvgofvZjwv/0vyvygjl52OR4kNsZNm0LjXKw+hERMUXuqo8bnqVhUDkr+brnXFByRtbsSTH7i/kJKA3wzaM6bHXE3R/sGR2Zfs/+Ne+JUitBTBq4UNYHEZnFSWrBDz0UgFjWh/T/1Qlvd6rGXvdWQhjjBj+hoE8yqlpmvVuvUHmzIROK396Ckzmu38n6C6fxNejVZesILrUdROuDnBa2PdVezMDpuKhunMB5QS4SRLnbTbg87PHm3V0jy4qPq8qxRqtqUHK79kltEss8e/asHOC4kn98/u3h2WEcMY3VMX46nZp1MV8cgCbTl2TvmrCUHPYWvL8qfzw0c9e2H6O/V5TGOtwI6H2UIGBZMsDHELgqgfLH+YRFs1JD7QsECXQnDDjsL/H8yYd4dLEHYIFBjIUZp/mIXRqDHCw1xFmRhAkoSfVvJID1lHqRDFbuH1Wbhq81gmO8FPUjAinoZ6Y/EBHGQbO3KDIPIJ+nrF1dawLcnpwzowxsCIRhlEPBRJrpuixCt+qS1DF3l6WFj7QpLtV3cZI/2DFuG8MUbJkgNTpRrE1hgGNmTack0cUUnrOoj+ogtHRzAaH0eftrE+4/95sgnvIGNOU5ScrwUoo6SqoySUR+YsCMIZGw90pPOwZL0ycnNC8uHuPt/HW7fE6DW+Yn8FKBgwicILWZRvk37HYYdjvw6SQG0JIF+UsVX4wtFiXaEvUmxJSJVNEqSMyaDlIK3DMSFjCunzyVtGhcPC1nZXpm2DKGUE+Asz3nElZAPOPORvyAhojb86JkKiNgjbpEK/CZwEDh7V6A2DKyV4M8sKZvirjKkKOAZwaE2m5VnKWd6tBspurtYtVhHUOFqQl87aMc4N4N3g0X6xIDpWQPWLFQMdkHGqmNhxtZzl097vqIg/Iahd3e6Xe+TX2M+nVtHfiGLw4aBvbDWIktgL/+yUf4naePHjAXef7Xb97hP/nzL1bzus2LdmlrbwNkF2Jk/28wWapC1xa8nS4ZM9oEUqeU6b0zovPm1eBj16rhw3yacRqPoDTgxYtv8fEnnzRPs0qAW064Suvj/onwigMJAlF4vxlYS8Q3lIEtpaG+vulIDm01sDtjMDEn6HuNR6t5KK76Vu1Ow3Z9ePubhLGOw9ptjNz2/x5m/nukw90W1HeMf/cCpNGm3W6PNCRPzyowqalA+x7ru3HdKu10gdjnF/ZUpIdxg+uDpEJ0s74931k9E8YpTEaH1CAZaiqgNYz8qSjMo4NvnH5zq2JbxAP7u+JX1MIpXka3t9rp2+8NrlF5re3U+TfG5rBPe4P0Gl/5LO7Kr7xKub41t3thaXRH0WjLqNyvVa/UmjrMYa5Oe51C1nU1vsVxbCYDtIJPg38rXASv4QZrpsowce1as9F5mGz+RsDpdDzDHTj87RDdt2gdR2YG/c6ZhTUWSOG3e/Dg+156UFtGzXIjpYTD/uDrOKsCnovUEbeTIGYkNb1gSKOc3tZgWUPtSWVdk5HEIarOZCF4AAatYah6QkpINAAoDSmxvTWOI0rOWJaM23KH/X7vekHORQ0RO6ltrTglvOvM/CP6UNufDSDn4rUyofI+PWccny7YvRg22EQbwd233T26ub/iZUbH9WVBAwPSMOBwcYFnz5/hsN/jydMnKJxBBFxcXgI0gkDIywl3tzdICZimEcMw4erqMT7//Ac4nW5xOjGGYedGZUtlHoXxeZ6x2+1wq85rADgcDu6sHnnCqIYXcySZE1ueG/ydaZoASAYVSRW4aNkp8rUEYn3KAbe3t7C07ea8N0PRb3N99MmHjd5nqbxzVqO86qKDlVIC1dNzKiPnUrAsM97dHPHy1Tt88+23OJ5ucXm4wOXFBS4u5KSp1Lbb4+3tCRknDMsAmheYXtHrEvVepaesDmrWE6D15KoSEJWzxFBX1FBba6P29S7XTq+idfIY0yQnTfNJAmWYRUcqpQ24jmNfG+va5/or8p+Gz4STK7lktxlYHwJ/WTMwFDdSzVowt3wrplqttpJBZaZIFDfGp0EAMYv0MBDmRU+3LQvKcvK027FUAGAO8wXT7hL7/R6T7pHKp2QejLQJowif76JvNutr8mkng7Ryj7g8qi+k2kSEBc9qmB0CrOyelKmTd7hZLx9AGNM50bCRxzbkrnPza2T5sO7NaXCuGU3EyVXXPS8L8hJO+ev9ZZ69hiVpFoZxHLGozctsXe/VbRQEVVaXtdztd3j+/Dl+9rs/xY9+9EOMY8K3v3mFP/v11/jqyy/w5s0bMBVwEXo6zwtSGuV0/6g0yPhdqvqzOQ4AIIUTmTKtmm2ivVrD7BquSnc2SiranByfWGTE1XqZLcPx4Hy2l3Nreu7aeubc8+f20IPWsWljW0/4bm2s+3/fHq804x4xo9ND2r1ITmMBYEwjdtOkh9fEKc5ccJpnEKTMjuvcKWFE8o7NaWxBTRKIVEADYUgDCim9BVDJMKFk3pCtyeV9s+VVVbPTQR3HK72JNmyDkQR8mj2l8g1XZW3tqMp74GrfA9egNMlIofstQFNbhGS9krs5F8xLxmmeXV9OA7AbB0zjhGkacTwWzPMCUlt+ujsCH1Ro3Lx7LXuSjO/aPCJjVblA/1YebPtVnk2Gr4404WAE4HMrC6OYLGFyrbER38McO0dhOV1IBA+gTVTt2wyoTLVgTAOm3U5o1zC7kw4ADonwb3z2Mf4Pb3+F2zICvHS0n9zOQUlOVIJQT5hyAVPVSc4Feb9vfzX2VwYsxbLZjUrhulcss4/yFwksXjo/jIy9ytQKUkIt39OVqGlkE10to/WShSsEP2j/3rjr1kEOW8lmGuxRqnO87V/Wb14Kfu/3HuPqamj2lT2jaL+tZyPMgTqZpIW42weoh5GBDgApXXKcB2mgNCMlDUQ0nCyhDJLK7oNmciqAO9vd8d3JJoxwj1npiE8dzIyj6i3RHkmUsNtJcC/wqs4w0PYoK6/gwGjWwmgPuPrv4rj6dnx9bNy+TpU/iv69PjVufrucM96+fauZjdgPp1kvkqnMKldXOhzXfFvetzn2wZOrJ5u52UFU5/FhDeZ58bTv4zji7njE8e6EZQlyGROYB5QiCzhNB1wcHmEarT650LAMxjSesBsmDwZjJtCgh4IZWFCE1oEkqwon30tlFJ+fh33afeMKBZ7NqoQgp1pOtnJ0stPi+jfxiFp2TvZhooRhFConJRtk7RmQbFmQw57DkEAh4NGCReMV16P/3OsNW5/fdz3YMR6jhETh3E6VYH9NUbT3olEgpn2MJ76JSBTjgFhReIjOwNVfH8QaaI6wRerAARLRdTqdPOrfDCAtIS4+3hg5Y1evINvJ048/+x28ef0VgDZiARCSasZXAgW7vAgyeRHjzMtvvsHN7S2WnMFEUmtvkFz8gNXMM1SFK8IMReYkUR8sGKknNZITbEkJeMCT58/x+PkzvH73Dh9dPZIIQ6qm20BZbZFbprKaYB2TfSaDqwtx7fNuECY4FTHh+BxzotW30C+MdW0PMXS+fdua6/bRmqD3n7fGSc5kt/rub7sCQ2FB6wBCZOr2VEQRJGUoYqhxiamZXN/n+6/e0SM8vd6LQoU7hh9gKW9gybWNeI0kjO1f/OxTPL3YA2D8zpPH+Pj68vxoOTBeu9sJmj//8Bn+1k/7U9LAf/7Vt7iZF/zff/UFvlWjaUZRpmOCynawwZo2hf4D7IsKTYmsssb5q7W9rNdwEwIu3Og7zPJHDXRcGAVZaeCEeVnw9VdfAT/zBoQDp7Xg0H7fxu33jWtzku+57n1iq9m4/lSjRrdf5+bvQ65mLhsgMcF3653o9FvvdbgQDx2z4VvS09p1it18qH1ndbksz+09hiNaUsHtlE8Q45QaqEx5ZQ7K0X20LcKn0qHeYEAbpUBCI3UD2F/m9TP9542RbV73PGRrZI7VFe72qBTXXa+4Xr7mD7y2jKn9bw95thlyYOmNIqz0YauNRmkO/IyMNnT8shFIN4IPHD6hv819ye3fGGzl820b7l7nzTXpr6290n4PuNngovWpE7wHF+0pAHryl7Ass6b8DIvyHQR4uxKRy7axM8YGjQoKcyWNW332fO2eR777kM9fkSbqWIlITm+o8/s0n7DMi9IjIA2ikZlTaZkzCktK1VwKDuMoqcSsC5WTxmnCMI6wOoVZT02YYQcQpyiro50YoIHAnJC4GvRF38kYJ9ElSJ2ox9MdgL1GtUvdr2EcMQGYTyeYYrgC33rLrMFTJHNH4YKBtbaqDAZIDP7LC/J/lDC48BBlwP9yrpQS9vs9DheXuLy6xOXlJa6ur3BxeYkXr15h2k3InMRAmAvu7u7EsT0RHj9+hLdvZ/w3/tZ/Cx98+JE6rOWE5DRJqt67uzvXawC4rnk6nSSQ4nBwY6YZn8whSESYpslT8T1//tyDFl69eoWrqys8evRIDIgahGH6qOmvp9PJT5xbv3EfRiPO3d3dbwXLTz77nUp3IZhjRqSBNIVsktOWwzh5/1VHlWCSt2/fAt++xts7gNNbZMrAeMDuIPN99vgah/2EeZnx9atb4NVbLPwGxyVjPs1IUOeVygWWZtWNl4qhwl8KUAoGFgdeXoBxkvrVlBLKqYB5xkAJ4AEFhAxGUh038/pUqTvDStF6osVri6NIALjnkdziWUFnXzvTzEhfnR1ZjUem11AaNAhdaTWZsUntBaRtqazN2qftQKIBiQbM8wzOBWNK2I2jpP0uBZyq3rsVlC/T0ZS5XE/1LMuMBYz9NIrMkQvyMos8B+HVhYCFCzJnUGKArfQWyWnDtAfzhP0+4bBPmMYEzgxJo56dWgnY2tTi98koFKy0ptvXZ7oAaEv36PCt70f5qY27k5uFGVRCOT6zs3ABsxyWGBRnU5KgoZIJXJLylk5bMzzggNdFjYPB6OIZFVUWMtxBh0sl4NyWwdhOA0UjudSE15PkZiRUJ4GUJzDju9Il0lOdhz1oGpGPMzJD2lW4vl8ENUNyBjhjAOOjZ4/ws598ik8/fo6LiwO+efEtfvmnf4KvvnqNlPb49IPP8Yu3/0DfKeBFHI5LvgWQmpNShW0vBd2XAM6W0cuRA8n2OfwxRKdEFcF07aKNisXpxySny8xp2uJmWgk35ohlFppCLGVU5PnoEAn6iWNNFIrugfVK3XmIXs9nnnkoT68G6fb1+j0RhVOPdX/3QUZxTyPsS7kVaVao+E3de2EuDAumCfTByg2kBMmSVvDBsx32u8nhJ44PwpxFBqNB5EFrT06OB33EBGPby8hSvjK1h6CqKM5q7Kewd8h/Y3Q0MCyjO6ibJWMYLXO6lmoAG7Otx7aR3xx+lS5VOEZasxL3dH9YNUNiy/6qWWTygqWYXbpgGoFpP2IYB5QCMBGGsdrBaZjipHDz7p2f3ickDSKFz0vBBbNjsNJDBzbXeZRKEvRdmbM93wQXl9YO7/KxfjZwCP4RiOF2DEnlmyzBeKXPDNCOUCiBaMA4VT5vfQ9E+FefP8YXH73Ef/zlDd5AYMQgZAaGAowjYZcYlg9sIGDQsRUkPVle2+SVfR2xjG+z/5z0sOw26uHAVZEy3iL8mlDKgmU+SRChBS2S0MKIc+ZUl6umEyddK4KxaKrrp+ttgy2Fq85pfFR1EnNW14tgqeDrPIPTUVOAr2UNDZwojEdXk6TXR8zgoLuO7Vk7RBFaiHRdSykh/KvBRXFvSnr6ktjlqOqQl75AksVsGAaM6jsTvDS+bXJC/ZeGYBNAlU1XHKKRH0Kf/XNgLKcTxpSwECMToRRCzgPGYYfDBMcXC7gtrFmSJfIuBE9oxpoijkwm0bEHe68IHTaHppRn7Pir00mV9QqDKYEGCZBGLuBFg2vSUIMDdB1M/zVqME07nOaspX1qQBBQs+0I7Ss+nl4Oa2VSlfWEADkse7uVPKuyvekOAZ98IRjIbKWLNFsDn3CaZ9yejjgtCwpL9iFxB2SAF4AS0jBiOFzKYVmN6kgsoxp2ew1GCsFVKTm/y6q/qGqk46l8UcbRwkECh1S+VJ2ulOx6kfFO2NY1u7rvHYg+Z/REf6uBjEIDDUY9bInMnjOi+EEHavc/ivdt2bGGVPnolk/G9KmHXA92jBvgrJPeSByRwdIc1AheVfQsBQrV0+TRcABYdFEvBLRRAVsGYUdY3ug3/LN2ZjWWWCqGGDltjv8YsbDlAIvRqkZM5nnG6Sht23yNKfdGWo+qoho9yCVDDH8L3rx7h7vbO1xeHCSSWwmTKLmWlkVSTwzTJMqQGvqQJOoCmtZtGCZMO0mxlkAe+cWaauvxOMGFvUDUKy+gIIR1InyvJJzBm0aJaHCHnbEasp9ziG+8HkfS8Ngzr2+N0PmdCz46wS1HRocG8ReEBQ74Eo3u5wdlgnbzWMcJGXbqX3GP27lXYl/0JJS+x5pyVZXj83PYvnrj+pa6t+nYuKcf443t/MLYGPjJk8f46dPH+Fd/9JmmMm0bXgkKTcdRiFaB2ehIEKxdUdFfmIA/+vg5AOC/9sNP/O0/f/0Of/erb/Ht7R3+86+/CfXGK0y8FRXmW4Ts+91myvfNRQT7h7pure1U+zQjFDOKiOaaHkqUxG+++SbsU9Q9cYbR9Pc2V0MZdrPn+zZ7oT/M+jxkHrzBu7c2cFf3+RbN6WlAdJI6j3Gm3p0UN0l3i2dypXvyQjelbvL3Omkp8Jh75rnqu+s6/t1NOxzvjj6IWk+Jz6zL9vq3dKnWUGoVN6r3aIOSNHPt+M2aIQg+b038Pl5lw+/XABX2zchcDrw/j8P7HNVbA9neW217/b0eJ87t2W1aw92C1rVsHO66ZPcFrcW+G0NRBJ0ZmdjkoAcypEBvNwMVurluvh/2W7MHDAc31zLyduMXlb7zvbiIZv4cxr8sC6ZQKsjw87651THEr+xy5/pRoUHc8aizVyMDtl02doz7ifN3uhoSSOELBNKWnhpE7ny0k9KDeqKspiglkrrGS5W/SylIUBiY0dvlAwB2cgMCIzO4sS7WOE6alSfpEuteikabkrHMAE2jOP4AzMsip5YJ6hzPmspzBBepP34vn1vJykC7iqx8SxxyQxJnVQGAHTB/smD4YnQcPNdPhP9f1GUBuMziQKZ0i91uh2m/w6An5odxBIoYVggFL19+C0LB9eU19rsdDocP8bu/97tYcsYv/uRP8e03b/Ds2QcYhgFPnz7F1dUVLLWmwctOd5seGnW7y8tLV5DHccT19bWfotztJL3qbrfDo0ePsN/v8Ytf/ALffvutO82B6mAHasDQ3d0dTqcTnj9/jufPn+P169d4+/YtDoeD1yW34Ovve33y8e8AqDgJxYJhSOroU6cTAdO0q7RehWw5yXmHcXiJ0zzi9buM6fAGtwtj3F3g4vIxHj96hmdPn+D68oBTPmFJb7HwiHkpuLs74e7uJNinQXFcihpzzahi+0F+LyhIuTobEouzdRhqNjjWfYWK0YKP2q61WXXtWh/U9nK2nM/M7qSMqWMjD4u0NfKwluZWQcDogRlxiCQlvfCtzqnGLflk2G61Ug4aKMcSmM+lYBiTp4MUA+HaXhHnQWTl0NDQhmWR2oMSBK9l7XJu3wc8vaWgRlIYy6mNgRNKSZimhN1ukLT6hQHLqkYSjGPg6dPU95+3DNhx2DFoo2WQkFSS5+xYzi97ysWN/FYKA5pe2GA6loIyDBgGO2Sg+nSptqkI70b+cR6if/0fe/focKsx7INXuCe8o2h2JvYsTYUtWxNVJ7g57WDOjqJzVDk0pGEdd2ITkqyBGkdi4HkIoecEIIOY8ejqAp9+/AF++NknuL6+xO3xDr/+zZf48ovf4NWrOzx+9BE+/PhjXF5e4+72te/HkiXLBGYCl0GysihdTsHYZPPxY5W6XmIlbW0dROSG35UMGvQsW5vqTJNaxGZjdCT09lX2Y8U71owX1QjW2CMbea0iTIN/8aR/A1r7f3OfWloSnozft8XCNZ2oIIl7bEM/iHWsbT6J9GRlFJjNMe5KQNsvrT5stt8brn0/ENTDp3SVTc5hzUQgtq/nTy6wm0bda8L700CgLE6ZkkQuM9sFmGv2HZ++OWoDrTU9hOrD7IBjf4sZHv3kOlHY/lGV4rDEdd8DKcVTiDUox96MtkNvzGm+/69ps+JoxRFbLmla95D94eJzZC44pow/LTdes3yaJM3yMIwuL5uNR7aluTfq+HLOWKxUKmRdquOmXXOTF+rUItds97sE0chyR5OJrS1FGHANy/D119Zl32pWWp2TB+mQyf9RASFNQU4YBsY4DI1e8uOrC/xbHz7F33v1Du+OxluBojQbLLXIh8EcN4I6dZrdnLvL7zY/U/1n5IYbbSYuSQMHcyzlPKvPpSUmBiN/BwwHsDmsFQe4MDixB767HAVyPVFgobXlIyl0/h8zWsUfOjhEXsmVD8Z5Cl/uoMcRBgbGNsAn7m0Ke7oGsZmfiiqeOA5AHLreMcPsCu7j0WDuQdPZV5qi427GTApihbGDRCbowUWIvi14aQV7lo2XhUuCWmX+ANQRmzCmAbvJaF9ynUH2SWpwKDrGOeAcO2TVab5oieFuFCs5XO+LiJnk8KfCR+ak+MaoclJR52ipNv1xnHB7d6fjqqBo5C+ooz7YF7dsLC5TGE1q9tDqccfayCV0CqvnbO2KBfSWgtMyY9a67ZNlN2EpcSX4k0DjBEwTLGsnXA/QkmdJPkNxsx6oslreopNVm6senuzKbsn+klIYvXzqtlufWMVF/66fTYSO/L4vwUBEocJd3Rc2Qst+hBDwT0WCttDgHoX9Vteq1/MkaONhafQf7Bg3x7UZGexyoSIJcgLwyPox1CkFpI6f1a2zTRbbkEURI0VvROid3dFpDQUQUImB10fVPmLtMiIxyAwsxpC+dnglAC1yWP91TpVQRHhkTshFGGHdpE6V3QBrwoq1XUrBy5cvcH11jcdPn2AaRjx68hTjkPD4+TOULHWxxmnEaCmkzcENZULGYkgZfEr1syrUSQlNts2TEqbdrkGsOh84UtoVRWV0v8X5+HOdsO/3uSfdaBjs1tU0tfVYI2jEv/3MbBSkTFWZqBHCKIgI92s6rJsu3q+b0L4ag7Pofp22t7HSg/rJsawbAZ7SOA1V0MxhowtxsLID2feC19QI/b7vahR9rJls7dE+0hrE77mo+2BrsB9G/MHzZ/ibP/oMn11fbrRL3nugRM2IuFv38xjVjKS5mIMQC+AHj6/wg8dXYAY+/7Nr/OmrN/j7376oqVO4hQHr/zbnifpZ6FKM9gS2ana68LcaZ6VN/fgBFZpMntWRMcTBXoo4xbEsKCwBQ4U7msqVpsYxr/phEzi7DcQu25wxlq3hEukIEzn7O/c8mRQeJeH39He27/Ce/w19m1Aa3zO60bTjKNg6xbfaDI23Cxz2bNyD3o8L6O/ffO91nNvaKV2edjv5zOz8q63t1OKHKRB17TcCCIJWxCxZVsxRbvPsph6nuc1rNta3r6dWG5W9YLi4Beu4Blw/hLFEvK6fg1wosALfi3/nf7sfF89dW8aweL9VeOtsYLKJfX1P28CZcXQwaHjIiv2aYaq+W0Vdqu2EcVHMD6u/Ud0ATZ8VXnXvuPAc9lKzvqFNbhdcn6Hm3ta7ERe5f5XbJhiMeVnc4VbHiBWtCEJDhx51TU/z6Syjq6ToTPBEGOz80QIathatmyutnznz1nsuWn0UUiRjHadaR2yZF1Ei1SluMrAYtwcxQKSEtB9BwwlZs1alNHp0dCJSGcoUtSpRmAwshnoAbMp4bmAnSqjWTVUnBpSfzjOwo0lTfAPzvOB4PInsrkbGvGTsdjuUuztR1hsYirHJDX7G+DeWooJM3W96EpJN/vt5Rv5ixKCK51qsUDod2pP+4Q66967eGXmSCJqlKwtmH0948/atB/BO04RFTwgyZ7x+/RLL6Q5EjCdPHoEw4J/75/4qfvzjH4NBuDhc4smTmmFsniW1pTm0bTa73c6j0/tyXDYfc56bocXW1pzpzJLC7+OPP8bl5aU7up89e4bLS8lSdHNzg+PxiBcvXuDu7g4ffvghUpIU2c+fP8fTp089hTEAb/v7Xh9/9GPBMeOjQS4bBjvpkUAQ/bCwptAjMQoxM25vblFOE+7ugDdPZly8fIXX7+4wThe4vHqKx48/xONHT3F9cYG5zLjLO8xZjGq3725wg3euhwj/FBqbS25obwnlvjgNerJb4DuEQKCaOa7KFilVnOpPi0dc61Ms97r6OaOX/e354X3v+TvhXa8Fq+NKKcnagBsaHu0O5gQppXj6/pjB4Nx4z/3mxnylPbX+Y0vrrfRATU2v+mci8FKdsEQFpUjgzrSTrAyGv+7QUmIRbTLvG28F6f305D7dtG37YXJQyRlM1SgW1yTiipU9MJrQ1y6vf9fp/U0+Xt3b+HefYzznUGd8wzG+6i9quSQGVAM0JfJU6tXRvy0rb8MQMPdSIuDjTz/CZz/8AZ49/xALF/zqz3+Df/qLP8XLl69wd5dB9AIfffwJnj//EF98cYd8ugMTI5cTxjRKdpecUYaMpGUshlQP0IizJoOGEXAYBadlb1DdmMbK4Yq6Z0XWLGDOKJwQT4wRF+GArDqOnVLWcUHTuUeDOrBW1QL0uo/tU+z3+rd5u8F76EK9zhl8z+sYZr9yt4brpfB9Hss6VLz1pjf763+I6xLXp18rAvRwuQmBAd4m/gK4vrrCmAZQdmun0tAR4Ny0d46WD0kylhAFWLDR8Wq3JdT0xQokd0A4HMPgrM+e3vV7vsIloZYAIpWFwoR1Ji1dtH1RT5wKPbeU4EnXtMUxlxmMZ1hQDQAuwM2Y8S3fyHsk+r/Zx+VVPq9XA7i+foTj8Yjj8U6yXeSMVFQ+ScnLdHaaUcOPwmADnARLxe5CoXa5XNX+zb5mm7xf2/WLqu2XmTGOcjpz1HUZUq33HmWtiJ8XhwOePLrCk0cjvpoXcFb5DIQCydKBNODyEB2rKa6Kt2druKlRbdiKt9lgXO8K01iaasmz0OMSHUztPq18xvqt+7rFb/g96d1smfEwjg1ASazqFhZk7PumHX7TtvHIyBvbZ5Q3W+kMU7Z97Ib/8pV1TESCT6Cq+wEmd7ap/e0gVIXTGTsB4DodeVBI8gOgJavz1tEoLDp1OhoHmuG6MXn5D25G0L3YXad5bvipIVRKSQNgBoAG61SyP4W+TZ9altLtrxqAy/peDXg5z7taub4FYL/mUaauJWaK0vAWZ6ucs7bTVr1prduuaDRDjma/Z+zxnahXrOdoNMx8naL7LsuCeZ5RcgaNo/hA4zs2P/u/t8nOP1Ia3CckAQDZ97/8Y1jmFtvLzMCQKkxNhi0ABoffWk7tZVpEf6ZZUoKuYMEkSXmA08FwwruHZXSkxyvFfjsYEaQ0W4sPAXIMbPlVtq4HO8atnpsp9+YcjhEcvRJrg/MJYF0bPCrAy7IAtFZKomFhyzgcU+nFzRWFsbYQPGE3jK7YWd9E5ApSj+D9PRm/CvOWYkUNSR9++BH+zn/2Bk8fXymnI2VAavAKkqUpxqwIzww8fvxITkJYPSiKhgcTFkki9dmTCkA2uxpWldtQgI0lFim2GlSFBY9AD4hlgqBzbCX2IGoFpAZ3WyPfOTU3CuF1IP0z7XeONMHaQDw70wqC5xwJNqUokFQGyi5souvL1qvihbHzihMyp5V0U/vg2H8/MKzgEOdgfQ9pABhY8rIyDAFA4YxcFhBC6mP/ve0kwi7CKhKU/tlmvOuPD79aWR+/9/Qp/ns//ymudhOmoT8qUGFtcODuF6CuRr8G1YkeBLggMJmg4DBYCX4VH4mAf+XHn+Fv8md4d5rx7/2Df4ov3t3gxfGugxH7Cy7XsI2lS4kdBbZGcXj4FXGTa9cql1bEE2FX/pqgYHvRarrZoBIktWW8to1XNUrfBaWwQswmfD54MqHl8IHrb+0owuZqmlmP3eHkoN+SxhWH7G/skDfaCUJrbK9xonaf+35d+bMiSEZ6u2muAgQ68Tg6AB0GRtMo/B7HEJRle1aio+uYRZirPbnBCj3Gyp2Vk7sRGFsYRnoc3rChreilGTTis9UR2sGt4wPEGzjc0d6t9al9BCd1fCQSJJ/neYzf5k3n930vDD70vf45C5TRVvUH/dgsZAWKz3fVTdwblZZxBIY6UM0IoQTJBlT389YcVsJEWKgeXUx2iftRiFoj09jYfI175hH3KjpZYINH+6NRjtF+o9ykULAWQZDTz4fDYb229+BNWBXhajo3i9LuYXJPU+s5NN83+JCtwdZWNfFpmxSf7zqIm9KMrkspSIM4GsEiA5/muXGKW+YjUAIlqRFu8vQuJfBU9ROihGkaxCgKoC02xwqoAlslEfmSlkhKnlLM5HJ5hoBEKCfTa3ScJ5b64sMIZnHoH+/usD8cMI6jpikr2B8OOGqkO7S9SlvIQe0VZrohGy4xC7zgSqL+PALzJzPGL3f1vW0yu5ajAq+9Z/VW6+hN6/hKyeC5Kt9EEpj8/PkHynMy5uMdXr18AeYFz589weXFAY8e/wAfPn+Ozz79FBePDxgmRiJJif/ll1+646fROwnuaATQ1PZu5Vv2vwZzS3dup8lNH3z27BmeP3/uKda/+uorPHr0CCklXF1d4dNPP8VB1zXn7DXIY7kwG8tvcz15/FFrkICd3JL52qnxAWZs4LC3xCl0s9ujLAtujne4uHmD3eUlChMo7XA4PMLV1TNcXj7FxcUl9qXgZs64vbvDzcVFLTeWCzglPVXJmgI8K/tojSaEwWlBItYAE8EvOR1b8Sjn0gSwt3Ot/KHe742jrfFmyxnTr31vZLmPX8dniEhPvlYdfrITHaj7uH/HnCFcWB3jYleZxqnR9SId6NvSBxxu9nnpT4eH+ZUi9aWHYVDDbHFHTIHqiSiQIArG4bDHheK0lSLwMWn73x2f1/zke8s0G6wJ3Dr4ADkoQFwaGNrvOWehxVzThEaDXO8oACTgHB2O216s6Xnb0931tE3xgwvWZjX0cnMqvJSCRTdHPeDIbviXtOqt/DkMA5alliIcxxH7/R7DcKPjWBuDz12kspSdMv/0sx/go08+A8Y9/uSf/FP83b//9/HFV1/jdDyBC+Pm9hW++OpXePToGRIdQFhAJPUtU4LWHZaTZCULr6UdwTMp2HpzUZllPVbjr/H06ZbN0Z4VByb7qSTmrAex6v4HgJwBd4oUoyvRninINsQ0nK6DbjmJ1nRpE8bd99VTWzh+9jq3rtx8pOZu6zxlc7YEWZ44BnOJY7KaCsWO0Msu/aC36Ndqb6tuYTqcT91kSQaIJZD6j26vMBUZo8hkItuNI2Fesu75KswzzFVc+56m0ddTRKe6/8EU3qw6TYSDv4iKlwKfEh5u+Ut1JJizqXd2mkxrNtz1mtYAmdqPqRkr+1wArfCR9RRUIUIuUj/87jgbkLDb7XE4XDiNVOIq8jmLgzU2eHn1CNNuj/3+gHk+YZ5PWJbZa0JXm7HNvcKxryFbB1+fR5ZAjWIw1EeGlDwLhb3CHhSIqouh7sXade0354IhCS8eNLAw56wB2TJ/1x202XFM+PDigP/tDz/D/+74FV68O+FuKchgMA1YwPhv/+uEf/4PVQ9M8Gw7hcUf0GqaPuBteJy7AkraP3LRQODApQbPGTwMlm5XduNJlJ3I+UHkjU33rm/XzEXNzFwX5apbBGK0pn3cfTXdq+pz/e/2iu9zzQQzjkMIeFX9zsZnfesAzcZBEagKBwonxqUf9ow5HDpmhtjRkpSxSsPgOq1kOsstfnLL0+JG3bRNdjTd9gJvP+HXPM8OKxsoazYdy2DGSpNKYQyprrfJKfJaGyhpJTZMH7a1atdmm5834wnPSwadNtjW1jjiodirq85QQl+U6hirjRGbfZ67tsbW6wutf6XlbY18C8DsXiLLATQknOYZd8cjTvOMg5YIERbcyphCizpeQowhZaSUqx5ICUOaHC/7g26O5wjwSVZmh0JgRqtvtXMWHMklr9BR/tYd5PRCkYRSOJAQ1qf3twIhOxjW+NLDe0hjWOv2mb6N910PdoybY5mZMc+zR4/4fd30hrRbg0rDIFER+szW88OQsNvVNHBmYADQRPZb231UQcP7AyDjyXUiAufqgI+Cnc1pWZZVhH8EuHwXQmubNWdBzmfPnuGHn/8MN2+/aokCK6Fr1kaJE6Qu1Ol0xPE4YxgH0DDoyV9IigndTKxEnIj0NKXM3HhNCkSAwn19q4GNR4u64BjYmWZPY2rfaShMEJJ9Ro31rrsiDI0Jc/3coIxzOJxtj0ArPIsN1Hm1Xdrf/nmBSDiFvUG828/aT4RRWF8XKLV5D6JIG3OKC4Wq+MU+JfJSDMJfffUl+LOG2ss72ZRyxjqSuCP0LlxX/IxGJYdDbwz/C7gIhA8PB/zNzz/DT589xtPDHlt0q+JWgjv0uD3NHQfnRBG6zs0TFJbD9pG/6L/003UBM8CPCLjeT/if/PHPccoF/87f+Qf4Ry9fOUxXdCkMJDonbSzRcdriUAcP39+Bnm2sWbz8cYKmYtd5qxAyKOOySEkbKIP9JEIMZFr3dW6Dhjn1+755m8/QlwiIrebD/qbodkIj4HsT74FTdKDJja5fbv96e2fp3ca7Z/o1oTw+T9p/FJBXjr372tsYixisbTdUJ7qd2DJHYDyJFw3OzkfR0ULE3VUnTGG9jXfVMdp4z9PleN9Zxj2CbfPTlgIX19C+98O2PbohGDd/I9dUxY/4PH79Nle/pu/d8xuCOoCaBvcMfmwxXOurGgr9l+Zl2Y+9jFSlj41RNvOTvhD27r1MsvZNaBd+9dpKuvHvzR5qhaV+es0cY2DV1lVpvjTksgFXhWCeZzx+9AggS7HL3TzaILCmcWVwtrzzsrR8Q99/qBIIqKHk6cOfb8YT/j5Q/wCwhU16J0ntsJRE+Z5P6hTXvSmlVSwKWU4AwZXBqkwmSDuG9wR2flZydsW6d9KYkafqOnqaSE9RVsWdAAjvtHIvuRSc5hm73eSGxZwXzKeTOMenAfMsdHYcR5zm2elpdUC5uT4AOCCmG2gqXZVUcRq4rI4yfg6UL+6hl6EH8k/2y9lcxqs1bukMNenUAAIK43R3h2VZcJpnLHPG9dUj5NMJ3379FahkPHl8jQ+eP8U07fH5D3+Mn//+7+HDjz4CpwxOC3KWtOV/9+/+XTx79gw/+9nPBF42YuUN5mA1/XQr0n2e50b3m/QUO7Okfjfn+N3dnQdnP378GJ988gnmecbr169dr7y9vfXP4zhiWRbc3t66k2u/3+Pq6ursGjzkSnKYsopSbMYFgFIBk5THqbGyQqtZ0/eXsuDd3Vu8vXuJN7ev8ObtG9zc3WAuM075hLvTLe5OtzgulzhgApOk8xuIMA4DDrsdri8vtfZg8lq0AvfghGV2PcJrzB8O2O/3uC23OBx2GEbB4VwyjscZu/2I3qEEtI6vKIssy+KZ6eKzKxklyMZb7ZzT6/or6hRxTCWcJo3Z9MzQSVT7aWVrCfi3WoyRJ2/qX8Hucc7JVHLBmMQwhiIBCygs6RZ1/5Uloyx6miRZMKS1q/acAlweDjjs92eyHOjaBcPl+69z/P8Bb56TY4LsaESseYIZGgXZtBX3vDn3DVfNBhSzTbRN5gbX7V1G7tZ54zMXp9XMLJm61RFrQSHuROei9R073dE+qlxhxkX5xkFOFse4nPiMJzUfDHUwi62uMOM3X3yJ0yK2qD/71a/wxVcvsBRz7DBKzvj6y1/j6vIZLi4fI5cZ8+ktaJAU/VKKJCnOZORZ9scwSnm/aF9cLySwOkanE5XUxOsgFCmvwStbZMlLgIKWeKB1SuF2HKZVlrXO8x1kqw68q2tbZtreM71d6pwx/nsNjRmW3zfimqfZBSHRoI6HEvbTVtaL7fHfC0PlISlZ4GoGlwXggnHY4+rioPSQnBdK0qC6Z3tqY3KB7Q1xfFZZm1lsS8lpdm2EiGpAiwcrtkqC6UV2intLb2mM/8kOdAX9GgWJ21TdVcNEW/cera2UleearaDOvcoIQHWERuBYVp+704y7WefEjEnpx6h8rZHuBB2ai9KI3X7AOO4wzidMywl5mVHUGVjcicINfA02dY02MpFowP7S0V/WU6P7wKtYZWBKHe5t6XJqsSil+KnNZcmY1PaRKHld6iENTa161vXe7UZcXV7gh88fg+eX+HY54Q5ieS0pQWM4JKuuOkmbdTO7la5NDMZg1jrfJIFsxrPN1mBr1c/LcLEU8gw8IhdbqQ2SvO+6mOassmWxfdJgUiLVtTrnuMs65mRTB7I6VkGKkyH7acV7zY0feLjgsq7Oyv5UGhxp4Bj2t/Rgp1QH16fciWuZdp1+wnVCywrgvh0ER7qtU9OnBXZwlUOSlDhKw+DZYmOJFNZ9Cq7zFXyjJvDDtT+HA7lsbf3aeepIDzYsOB7gGG1XBsf9fidZHtA6I2uwkHwfhgGznjy3fdzY9DRZewzCizajaD/eslGa7uZyMdVDraXLeiSwlDFM04Tdfo/XL17WDK6dXPDQKzrSnfZ2ax7vbX3emlspC4glq51d0zgh54zjacZxXkA0wLKedKOS30jkvATxUhnulGJ0vIT9yc4TXQdv5mgDFhpleSzacauPFLyaY2JGKoSSg8zle1efg+E5644krX5i2avlBLkxA3J5y9Yvls+tY9+6qBYud9ttpLXfxYf1YMf4fr/3z6aYRsMDs6SFjCnBeqGNCA3ziie4LUo/DbWPqKTEzRB/s40UrygMxw0YxzWYo1nTMmR12EdlL47P3rN/NWKFfCwmaHNhpPGiEn0gCCyVkTFVhjUMI7hkXBwu8O7dWzx5+kyJXmUiBOiGUIJvnmuIg9zXndu/zsx9b2ydVoRxQ9hiESBpyJrn6ruN07nhz3rq0T5Hxh0ELGMGJhC4skNhDvXBtrZyED5Jx9twBvuVLFDANn38sXuNAUuvskXcohOztqXw33qeKtwpbtYOH6WtKgwZnJq5BJwkEPKy4Msvv1ztc0knk0VZZW7G2KsLjQGpW9d675zC9v2vBMLvPn2Cf+NnP8bHVxdBma/jiLhVQzcqbvUBH83cKMzC8Ck8Eciw3jcFxO62fbfOlGhgszuE3TDg3/6rfwm/eXODf/+f/Bn+8atX/oYTaCf6LV10pd3q9T0Y4Ou2/JetJmz/UMBk5aochMFIGmp6yJae3j+WcM8EbMPpjX0qT3b3gwAFDkyzyNNReYijYVq3Ye30Ao0JfP1+jw6sFn6onfXcn9btNr+3IGo+e79xJvp7Q5I7uu24Gfq2+33bq3HbXuMaaWkws35GOyFmAjhzdZ4zrwKm1gaZdnfa33EcIpvRdzvUIB2F0i9WYt73EZ3r9V6k6YzVZogEZ42K7dog4AJtzdHmxdttNePcFqSBmoGneS6StA7WzefzYO94TGTvLUwi7m7BeOvz+p01XXiwka7ZxK1LcL0ZfTEqr6S2jTVO2B4DWtnHKOF5XNyC8zk4rWQj33cb/Bcif47qjKtks5t5J1NUWJuSL7LR5gm+wOM3r27ZChj0w7L529l7HV37zuLCZj8iE4tTWU4nLjlL+xq8WnJBLuJQnvZ7TOMEM36UnFE4IyVNJ2srz3IyJufF5U7XGYOMaJiSSeolihFfTpunQdPipYSszrmUEvJSkEvBMEhveVmwUMK0G/1k82me5YTobsI4DJiXBeM0NTpI5QUt7dkCt4qsaq9lP6kAmHMdoE8L8t9jjDFDzcbyNd1om/1zW3SokajiOINxgkAYLIhhnDCqkfF0vMPXX36J+XjEfr/D06dPsd/vcP34Qzx98gh/8Ac/l3q1zMiFkWc5Af7Hf/zHeP36Nf78z/8cjx8/btiqXb4uIRjb4BxhbZnQzMBv++ju7s6fWZYFl5eXXvZgt9vh+fPnOB6PePfuHa6vrz3dvxl0DodDE/z9254YX/JJZQLVQ8HwAoWEijM8IJeMkhcsecY8n3A83WJZZKwvXr7AV998jZevXuDu9h2GETid3uHFqy8xphl5eYubu0sQGK/fvsObN69xe/sGy3LEMDIGSICI1Qh2J0XQj81QN6SEcRhEb80LlmX2sgNGu2w9LCODpauOer9N0mwA8zyrs784fHsn+n3Ool7/6q+zvDrIkGaYL8GQv3bkV/uDjL3uNMOraL9wA1O4Ylm3fuyt4Th3865BMtEOkosYGNM0AiT6lOsFqnzvpwlTKIXXyHh/0QrhmWtLJqlzU/4n0wy8+wwf7XAhHrLobUR1rUo7bwCxVrndF/m4ddhspltnRg6nyq1cZEwNajjCjKC/97S2nZ6PMaQ+JaDa1NJ2mv6HwN6CfP7811/i25cSCPT6zTss89LKFgTkPKOUjCdPnoDLES9P71RPMOdpDB7RIK6iPH1jfLVtbuYW59w7acweWEpBamRItGsiTys+11P2/dUY2IutN9V3H3RtH96IvFh3c9UBO3n2bMsbOu45ulctHNqB2wFqXVlATtozSAWAOBBSXBo0xXpWvXHrlEc31/fAynCCbZSEZvUYwkuuLi6x301w+Ac9jZKdtjb9iQNNqy0lzwKkCjbMCcaApjVnsjyc0la1KausZDTfIKttsbrQTd6sekTnqKHKPyN8G1tphI3TgnpFmgcfFwNus437QsfMLLKi82s9Lb5knOYFSwYICYyM/eGAw+EgB8UKQvZR0c46jur2K0oDxmmHNCSUcUQxmUsDETk6OGH4U9sR3LNVDZMllq2KiuscaHcpumY65+ZQEdf91uvEDt9SMGuQgAVGyvxHSf9LAJeYNUKWaae88t+4PuDfe7fHMWccj1n4LEbFGcWjTo53nLB9Sy3OCw6jyuNeX8kxZhMntomHrhqrPSfITqYr9O1UUwnB6MTKrk0Ip6kb8PhI2Pei3Kn2cPg9V3cc0QPfzLlmJdZ/W5fQ+DoJIgmgHkb1U/nvBVmDzozeRf2H0aYDN7pU92Dcc8HPo/2Ow+BOcR9blBvAzan3ZrWYu1W1Z2jLjOA6QRz9av0ZXronPmMot99LyYTClU5FfmtwMD3W5PUhVTkIqBmdJStRj5tt23W67eeYNcfeM1mbu3GlROpYhet0ZCXSGpAK3zbefy7cuwN4q2+dGfPW1T/vcwO7A9r2T15En5lPM0DVNmrZI5hDWQa/C7jhIuwfZsai2TkkG4DwOsmkx+6fbfUHCjjUz098i+Zz7g9qSgmQqvP6753c3MvLgOXmi8EoESep+7fW6fqroT1CPBHlNLn1MDn4wY7xKJBaVH1zghvV0R2ft3cAS89Q67pJcXUR6LNHygJFDQgmOCQ9GQKSlDjLskg0P+AE3vuFpDvJunnFCG8EuEbO+sYaEsZpaiKmSikY9JRHRKD14loaCRGAcl4cOX7w+ef4+y/+1Odnht4GLkp8KSXkvCABuLi4xG9+82tcXz/COI0gEsHieHuH3X6PlMaaJohIBBwXBOECrjFbEzDEOaxOLwquQK7CHZEycLJflRijPdkKRJElKKcCqDNEowqx2lEQehxplBFr5GYUFJl9HCY4N+2duWxsgRaFcatAguBcCYK2w1OJac+ujJVGob6Zca+kgOu6oBUAKi+rv0cYMbOnSkxEeP32DW5vblf9WQQ6iBTvbE7WAbfdNfPRO5VGvVc3O+8UWz9HDPylD57hX//xD/Hpo0sfjwlehj9tGYg6UlfrHIejIBDHSvXNM7ixFiFsNcl/r/i2PectKH766BL/9l/9A/z6zQ3+w1/8Cv/FixeNsCr0YN0ec3XgG72672p333seRmQMvr0FR/wXZbpRcleFoe+hN04YE4rzjPNpBG6Oo48jbI0YpijE502IbnCN6j5zRZkiTM/RI/izvcGROeBWM/jwXT+vDWftfpc9TE0/MfAEYc1bx3ftzPYHN/jGoY+1sNmPBc1bLe1lXX62eSivSIM5UhhSn8/q0NyXKnANd2FJdW5pqDw5PtOMklvQt6NX6NkaGBwQ16IG9ZihsM7c6GIf9IJmjb2VRphqIdiyIaNNqDRcH+Kg4IbXA8zivu9gSLG3OBRjVrT5mSjVTdPD79yWiMrgmX3jd2MdMVtfr33VTF9pDQFNMtGN6TjsDZYBj/x/OopAxxDgG8UCg2sN/ADQyEzhPZerKk3zcTUfmoH4x5b/c7tcvgfki4ypYBxGMRZrOkjJHrTFndsxkDdbMTimLwujeM91pi+Da5xChL337h99eK68r5vYuM4IGUSesWJZsjsVE0lt8FIkENfGU45HDOMEQGTywkXqmA4DRPnKyIs6xIurnHABMW7X1X5RZ/upYEkS/DtN4thOROrYYoBGgK00kgTIzsssOoa+czqecDydxGgyDBhKQS4Z025CvotGnTUZcYDGmx3eM7Mq/S19Wj7JmL4a/F2+B8XCymwsy1pqlP+T892oM5nutttNuLq4xsXVJabdXmAxL/jqyy9xvL3F40fXePzkMS4uJozjDs8/+Bh/9a/9NUz7EfMyg0ZC0TrZp5M4RR89usbpdMLpdKrKNjNev36Nw+EC83zyUxKXl1fY7/fIWQIjAHOqyN95XlBKxjhOTbkwo4N2evzdu3e+/tM04UJTjL948QJE4gy333pHee/w/K5X1hTERY0ehYOBWekV6+85L1qD/Q7H4x3ujjeY5yPujrd4d/MGx/kWKAsOuwn05BH20wjGgrvjW7x9R1jKO4AKbm8X3J3ukMuCYSJcXO7rWkP6BAglOMbrXmI/ESCnyzMYBeBqWLMMWsuihuRmTtXhYO1ZmR9zpjOzO9t6A9Z9ukmvy9/nmOv/xrbjZQZDM77ZO60x0Jxxa7nxnOFnZWDDem+aPaYfY9yLER7M7A5TMwoL/2YQM6ZxCCeN23EYFzuXxvr8+OkB/GD7/V4eoVYY2FxDN/p1bW0aLMt2uvUWh4JO0+Fb6XDWgh22nqsOWgBMaBy2er/+C7isskuQYB0YjHZerO+M44hxNEcmrfnHPZfRLCLC7d0dFs2yeDyePB25OEtYUnFmxrt3b/DBBx/j6voxbm7f4HS8AZPY/lKKhnEApcipp6QYzWtcNzlqa92ALgV2WEsr29E8620EbYAIgNgWm7krrNxZReRZ/sjbOSMfR/3I8GlLm9l4rtcutrJobF6UVAaISkZtSR6p0qJDQfeIzVcEI/3OqWuDKh4SwO44f4Aw8ZApoDqeiOo8rJdxHHF9dYndNGrKe9VOVYZraRzUAaz8KMGDKwaVvezyvVYYSBpMRHpKXIVZSqmWoHIcCvQIJn9pm916V4cNglC8QZ+izcDgEeXuKCA2NEBQmBK5bit/Ku80vmP0w9KxZ02JOy8ZS0C3CyZ8Oi9IaQCrbqHQULG5xU3Z4zKGNOjpRkqa5ldKjhbPtFTLFBjcKn80mGF1+dxs7fXhJWdPFU3NHDm0LS1EvuB6XuQv+mdZFhSWkkgu7w/toLLUYUBKhD/aj/gPDiMujiPGOSMXQtekjqeA2NxjpN1ru0anYafeQ9rhaAVwFYUgwVpt+zJn+c36gPGgcLiw1n43Wr/CLMfZSL9lCPLZbPUUxmT7JMo6ocVKe4JthcjGHNcn8sX2pHDf5m++Ivyf/gNguGZN36+6YJRTTFdiAJBsA4ZTZIRCv1dgVxqBxsBg6iM1i0IpSfC082WlLUYVwlpUGaPCtbDY+t3AFa+KxjAO5G1SfIZXJHk+LZL6umlIsh7tdjuM44h5URxQG6DDruPNxpckcBIqTyaX57PyYOf3Pb3ckM23ZFSXjdSXEeUvIgJZkHopnqGLqYVa3Pt6Y0Wfsfk8OV04J3/0c4jf1zZho+kaSBHWcMkSNC94qDJaI2IoLWHFIiIvj2pJkZw1uTwvMoHoTG0gaDeD1ZzMF+qygF7x0DEzkFKwWFM9rGyc4Zy8XXtu90HUldqD03WPGD3sEL6hMxRovwHugWIvgO/gGO8jskspePz4sZyCOJ2wZRSJk9PRImsNIXKju0TBUCKAuuhkUP3H5sRNSDRgSOq45tLU/pE3k9xjwjhMrqSUbMBPKBDmnCiBCRimUVOaCSNaStbI+OTCVLxk0yfkzBiGWr9JDJ4ZH3zwAeal4O7uDQ6HCwxpBIoRfzVsEDCMSfIgCNCw201YlgX/xd/7u/jg+QcoJePNq1e4efsOH3zyCX74ox+DQchK9xIBmlNB2hbAgUnrhqvQWJj9c3S8tc4tZ0dhpjVCJTqv+u/18f4er+h7QwzDtjOh0IdA8UsdG9WXnXB5NBXiK+x/g2gfhJQa9UnhxWb/cMtzVtNFdebXQeknqmO3X5pUSy4zUJh7jDLlqpxCHeMycHz95VcreYNh6e0snXrDOsPfVjA3RujtOK60133ROucvWfy/8vwD/K2f/BAfXl2sxmL4wUSd41Qg3zuvOAiJ3saZnuOXzWe4eyg+z0bLoLSnx+x2jsyaDhfADx5d43/0V36O/9uvvsB/+Ce/wm1Zgk7VzmmdWWL76m0a34HOtyO1vRU2TC4F49gawgoXpETIxfBw24i4RovgJLdBF65poPoJGH0wp7z1ESQ+k5V73LQgGQ+W6UcSNJNNLOGA13zPc80r7SLdx/hXc43fG+beUjlXHOqwmt9WlDcIRPaM6/HNsya0qVDi98mXoSijmnaTpLNzZY71H1pEbBcE4OoAjKAiNd6AJQoyGn2qYgffqzEoqfZjwma3F1afWz7Hob0Wkv2lfTR96/9L7duaajhlrwW7hGPGithLu+4VpOTDiN8bdmiDiA2EPmLgRd1CJpuFdPnh/T7w7ZwQyUqn4zwMlyL+OVdlrnSdAi5GptrJtz5nJVY9P94cVPiNw20hFxweradx3YERZQViP00Rr6Cr121bhSi0t8yg1Rqx5VbyE4bseVJDdiJ/MATpUL/20D3Cmo6KNIJ+i8hwoCUmc3QC2dbnbmvUJV8t1uZzhrpxmbdf2G5RaiYPKMxY8gIulkpQg2R7eYvhdbuZxYg6DmLJLnnBPJ8ktTDQrEk18McJKI7YepMan4o8vxRJuSjGshE02vpnlweL0TcumE8z0l50knGSU+Kn0wkXehrF0vuNWsKJ7JRmA/ceRj64ep/rHiRU/AER6AkDX5OfjCay6O+NwL8U9kboykZgxg/hyyYjsdd6lLTzo6ZRJFxeXuInP/kZaBxxvDtiPp3w6uUrvHzxAvPpiN20w5PHj3A4TEjEOFw+x09+8rv44ONP8OLNKwCEcRzc2SynIIF3794hJcKjR1cVh7jg9vaI00lOeO/3F2owJczzAnMIWsks2V+mgCu9oASgOqvsWdK5WBrvw+HgjpmPP/4YzJJS/XQ6haCOmlnttz0xXnI1EGYufvI3pl/mUrDwnTrGT7i7u5V/x1vM8xHLMmPmI4YBuL48YBgHYJBTgiMR9kMCEmPJMzIyGIRhGnFxeSEnwEpWmq81qZVs5lz5H0Hr+za8Wk6RoDCm3ST1O0v2dfMTs8WC76IzsXcaWqa30hjK7G9vmGqwN/zWG+d62bY1BAY5Mtg4TJZn5pranQNN68bgMnQ3LksHHTPqxb6rYZeqvGsyG9sJsGo8tvHFOVaDkhiOhzQ6w2FU5y4BmMbBM6318j5vwPmhumE0gJ0zNJ67omGvd0yeN/q1/W7dryfnTC4ASumDGaC0oL7X4mjr3I7l/yKc3u8Yr+37GJUfufMSFQd1dI38zCb4QPioBIhZysqHw9rGT0kC0ZZckBiO44BmdBzEaVyWE968fYkPP/oIV1fXuL17hhenI4SWFpjTw+HqbQWZs5dzOu7k89a0r6Sfo1PBfgNrxsUou6ggZ04dYfPtiecqWWhpFn3Oaz+rHrQtl0r2gNpjEHD651fpynVfG53rfwzz32qvyuVBPu/WfEhJ9cIweiLEM3Qipw6t0IugT4CRDcf43JiirtbS1PO0IjwfdQyVo6dxxONH1xjHQegV4HhksQ2SihgqMAd5KOwPyUJKHmQl/Kl4+QJT8OKho6qXkr8j9iGToeyAUO/ch+679WnbKD8ZbGQdrUO9b7m4lbF4pcqAG+7IqDOG6yHaNqu+AJCeupXZlVKQF0nDGyXCvzSO+CtaHhQsJQg8yym2HB4FpSTXSVIawDQAaUBKBZRGybA05KCvGEb5ageNt7/MCWx6W6W15fYWs2WKUCLd1CKPY6XGxez3vCSDkoNcCo7Ho80ORJJW3ucLCc41uYWIMY6E3ZQwJsIxOMajPFCKyMs+/UCfHPUDDvV+FduXTs+tnEXgU6ZTGN2tG6Ce+rRTzWbbM1uPDYDVw2iZGAjtOOq4TMYw2NZ9hw5HNFrFOZoPqiOSkT7FE8RWTmALPb5+MeDt6wGPr/TAZJaA6lnldbLIJpePkpYvMx5dnfuF6/qw0xIfnK0WKEkAjS0ZEcQxrtm5RCflMOYaCNJN2CEB0/0CdPpd0u08p3HbPEmueV6QFy2PUkxukP0jutWAeWl9fPGEcMymbPhV086LHiW6YUbONfiiBqqEoQVZyb5b4IV9L+G3KNPYPcCClyXg5vb2FlltKiYTtLqA+Ypa+apvs5G1sV0Weuv7uj8090wPiu9YdqBF06nnUjBSt3REINTU/xzwyPQvwxmhU8F5zIFeRlvB5jziKtWguLgzjfabDMVgDWyEjwuAZ0YCQ8s/t7xfuVCTFSDSlhjwWEsbVX286jJhbMlaVjqpOGP62XrTnb8e7BiP+f5LKXj69Cmur6+Rc8arV6+kDpue0ojP95Pso+Zjuqo+bVf8a455MAcECf+6Ng2A9n6vCBMBWWs+5Jw3Hd9W8zEqT/GK/ZvzfVkWN6R89NlP8ff/8/8Y33zzApcXl7g4XOCwP2AcNTWNjoGU6eQijqjr6yv82Z/8KV5++62mhJJ53P7ZrzAdLvDsw4+EMMGEqFJRNbnYL+TaiDhpyhB3hmmggacGg+oNwdHM9QQpb5Li73BF0LmwUB3CjfuDesoAoyrrdo0QfafxsMmYm13QRl+r1u/dZEYoKAx7Pc8qnHMzvUpg1EBZ2JkwCJjnGS9fvmzStAAxewJ7ZJi0JQKlTVIEeFMK19dDjBwPMWowA1fjgH/txz/E3/z8U7SUbItZlqC4xmfYcaUaCGJL63ms12tjgNT+TFAcsJ6J3bkYpCHBkY3GerWUCPiXfvgJ/qUffoz/6y+/wJ+9foO/982Lde0jF/hxdk0eMp33X1XhlDmIEGwM2lO56yUBGRVPjLH3xrb7B6pCQYrw64SGTnmQzxU7olLxz/SKCNkjJ1CRhOvYNwUkF1HeM94gSDTDaJTc7eHdd8+VQfvtnLHwzLCIJMhoHEdx0uSiaazWp5Lq7ovCUT8X/a3U2nECv22AVx7UY0Dt8z5UiDjZkPJ+3PHHIEjFmRnyN3gfmrof+3uKUOnY+zHZKF+kguFXE8RRIWfGujpdbp7fGvFqJCYfmHBBqAcDfEGMbgCghnPbSLx1ZTYV1QNurgON+rGwPyeG+8ij69/2igb3yoe7R5reyOQiCrIEhYedMQdhSgV9BYE7E30/NPyp4g241hJfcsY0jtKW8+c1bYl7yGQjDu0aTLl38ppCgn7V/9lcQWw5R3Ie3NA0ScrqkktzWpz0hMOghtsli3Mtln2wk+LgIo7A+QQ5id/tCaDKQzZ+2LoGGdEUsVCqtZSC0/EE3hVMYz0dnJfsPEBOHZGcVs8LhnHEMIxaQ23xzFfDkAQXdhOWB9btXYGXNQAF7HUX4comA58z+E+AD599hBffvlAHPPz0PHdtCb+njr8TLE1drMNrhmZ7tzBwmk/IWTIiPHv+HPuLPe5uTzge7/DVl1/i5t07cCm4vDjg2bNnOOylFm4uBT/84U/x4x//BO/e3brDNOqfkm59j48+usZut5OU50GmOp1OGIYBjx8/xjiOuLi4QNYTRTZ2W2f7S0R+Kvx0OqGUxecf9Tx7bhgGfPvtt7i8vJQa8dqnOc5PpxNubm68T6sz/9tdghu5FGQ1PuW8YCkFpVgq5gwmqYk+L0fMyy3m5Q7LcsSST1peIOHxo2s8f/IcnAbwIEEbiQmJJRQ9JTNupMr3lwJQrfFY01bqCQHHm7r/XRLigrxk3L094vrpIwwpIS8ZuRQQDVj0BDgAWKCC6d3Wlxlwge3TytGAGm0NvSM2/o2fszkBgM21ivTY/kkNy+oYZw0A7U+xxvH1RsDoCIp1L+MYMpsNpZVvjFYVLp6LxU4C+rsWdKBBcUX1LDvtI+/qaX4ChnHENE6bGQCNF/WpLreu1ggIAO/XF2I/dvV0yAJ7VvLihn3GT8wBzTO9DlLKArjx0WSLeDrG1hDNPcdR1KAEu9c/J8beWBIQAG/rES38KPyrMCkqEzGTj0v2Wm1vHEdM005pWwwoe9hFahwupYCVlpHinJhrRwxph2EcMB8X3N28wtt3r3B9/RTPn3+Mt2/f4nT3UuRFdDVdTbJlFTVdpiOXIWI9ThuPvFozT8L4tUGITV9NDU6kRGFX1D3q9tQgP7t8Rb0sB3dANNjmci1jQGtL7O2Z9rwVH674wM1cwBoUSe9fM0Ytn9L323xWOabqMMGR6/KkzbS7qD7PvOjCldX+XO9xs4OtbbvxHeYMKupituf1twTCfpzw5JHwjsVLiJiWVuknhbVgCxZy3FO7MJt9QydGKj83+6PqhjV1M3vWRgBaDsFsbSW8F4N4gsPT5orU3ItOILHnRqdj1OpMzmbEtas4Y2oKo6IRO820JtnfIXEgal3f6BDZ7XYYJuUDTIAdZta2VzSLpE0uBdCMrjEYZygFZcqSOSbsW39OdRvZctX5HvspWlbHAmCK8u1xkmC7kkuAm42r8msCNLg2rHLdDB7YSVR1jyXP4Dul7ftd0/TxKIGeko1qBsqMwovqc+sDaHUP6T5yXVpXpFBQRMwPQa6DGOxJg7j88BtXvt/X5WVVlK1GOTO0/vUYcBJodOeQs1s+kevHLvcEe0hdN503NMDc5ZXupCmxz0G6lCrHpouzPxuCH3IMKuvsIcor2Hm2OG9NFj/eHeH2AgISEsaevwfQV1lN5FPT50zFN58NCBiSzbf+5k5xGy8Q8LmscDtRAmn5Bg4463JT+H/FI0cT/Xs/nzgdjzidTph29TBDQUYpC3Z7y5Q1u4ztY0sJS8mut7a12ROGQctPscxjKYs/2/vV4hXXt78PM174AsNxIueMnLI97GP0cliEFX7E+TDg9Py39XWck9t6WdN8jka3bT9k9d0tS8bd8YjTkjHtCJ6thSzIKGEcJ7sFwIIA2UtK5eBbtSCflEizIqj8dWa+UVZyuqRA5wAnw0ff9Kj9xN/tcIkd6mxtat5rXaseF5QHkNKs1NkdaiaNGtBE3Ja+Xq/L/WsZr++USj3njOPxiCdPnuDx48cgkjSC19fXmJcZKNURXkpZbYpolLA2+ys6oHsjhiGbRTbFtnpQRIIaHe8ANPKlVay3FBoah+b3mIJExpcq0dZ+pmnC7e0t9vs9fvqz38cv//Qf4nT6Aq9fv8bXX36NlAY8e/4UT54+8fRWVgtAoh0ZT58+xZ//8ldiZCssNfYoYZoSLi+vYHqvC0j6mQkgq/MCDlFeWhuGWJ3jdkLVhFybJCphN0bRrdFDCMlDrrXo3H42WUVkpe5pG8N7kDw6U+3q2Gnz/H3NVSce1/43r1awjm0y1lFF5DCm8Bn1u0Z2DWlwQvHixbfNaQu7LJVqCXul4qpPxA3C54jEufsPXXszDP/+0yf47//B7+LRYWrgYYIviFTJ5DouoPkbiXIf5/nepdgaW/8+wopR+7usQVXOGuUbQXjHRsaC0CZA+Js/+hT/Mj7Ff/LL3+A/+rNf4+0yh3nZGDi+dO/VjPvBV6UVW2vJanyLjszb21vsLy40aCetaOCWIUtvbG4ouWW0h8Pj1CyoKUxxgT2QBmj20eZMbVzKfON9x7QeiLxxr5lT/W2LLvZtW8aBcwJr7wBvca8OaTW3jee0QTEKvG9TGD8M7TdroX+bwDLUU1r9s2fnF9bLNAoRXNfrGNFlyzBcAXVOsItKaHiN4zg23rWOGyFc7q1hUxHA8T002xtb4xgcShTaaViRaWWhrzN7CIDXWopvNG11mFWb7pSQ1czqfHxIvoY2H6egYT9H2PabKjYKVKyPG64Gb/VT7vHLlPi1wTCuz+aSbowPAW+iYcCGzBEQANVMDKCQmrrUd4yWrY37qKebSALcxmlyJaABU3h3jUv6TJOadF2b1ibSOA2+r/gmTCPcONPQX4B4KEpuUoVx0SUY1DiUQGkApQH7acIBqpt4gKs4n8EsTvHTCWYwqiREFUbD24rOACyKm+s7RWqbyTtqvCGSVOkncYaNIXX2sizOuxJEpp+XxU9njMOI03zCaZ7l9PMwgOwUh9Z0PXsF/rn5W4B/2A0yl2fAz376U/x/3r3DaT6FwDdCiJuEZTUgtiwvFXcOhwOYhQ/kkjFrO4zKW5PWNNvt9ri8vMThcIGbdzf49tsX+PbbbzCfTtjv9zgcdnj65DHAwP5iAjPho89+hp/+9KdYFgm4bp1vsgbzvOCTTz52XctOc8tzojC/ffsWp+MJ8yJ1LQ/7Ax49foSrqysAUOd3PdVpeuvLly/VmS119y4uLnyPXV9fI6WEt2/fglmMbvM8Y7fb4Xg84tGjR40xaZom7Pf7bX72fS5i8FAAykhcwMjgBEwsJ1yZk/xb9mAqGLFgose4mGbMFyc/8ZESYUgFA2VgnHBcMsZph5FGUJHgDiSps1ry4kRHjC+LHwGI+gUnK7UihhDi6sAkpUFcCtJHCUVp5GmesSx6wsuC1DU43FGaa0Be7ySrKUOrXvVQGMc1iTr/VgB8/3yw3bihxuDDUMeJG9ipwa8tu0NzIqo3ED3gqgGL22mlY/1qt6P4uxlS1132+jAMmJKVoFjL2BacYG0+1NGt33Afg+j1ii3nWfvs+r343Wk4l5XdqdfDOTioW/18zYd73BEj7PbaNUa/Lbmjef7hOJxDa9vGZfkrjvEJwzA2MvKDLhN7LNBKGxZKLKZWOZE+YRgmXF4BN3ev8Mtf/Sk++zTh448+w48+/yn+8T/+z0TcLQsKJaQkdc+HoZofDc6ZVVaKpXw7uBIRhnFYyTtmo7RnbW8yoDGe68qiKWk1aGbPpaS/aKBZaL/5vb2qH6nKwltO4Kg3eMJR1qwlpoe47gokZIDXJXJsvrXdtQNia29msDrkTTe1j1Xol/9EO2zTvcv/SMvYcTZ7TpxnrwucVdnW47UBEdb7ExLweHVxGerNy+MMg5niZpI03lwKMqRkRxoC7gyDGNaL1SpmVMedzaM6swgWRCT8xnRYgD3DCRr6Codblc9lNSsszIEp8mdS/ggyfC+wEmmorwSdBFU1cb2M9RR4cPjXVfalMV5sDS45Y14WzIvYmdXb7zXFTb4uRbPJRdwJ1+jBmMlla2bbewAoYRgISIMEiy4ZXBZJfZy7chKloGbhqL0VK7dSWvv+YX/A9dX1Ns8I+hV3erfhWJN5x4LXrBa9yi9ZyzFF/B6GATPVckr/48sL/Ds3M35dRIZENn1iqE6duul8rrmwp+p3+xvYSwH5u9Y1Jef1SXVLUA226OGQEiFNExgQX43jjuBASoSsGbUSkeg3Qem1Nk13SkOq79t+oKAryEZqZUTnk7JTjT837xlmcV3fKr+E2tPcBvRKqV2RXVPaYZpG7EbCfhL+R6mVvwiQ9cwZRFq2l7QElo7fUulPym8SJSl9iwpfI/lNULribAzeTJRk76i8apvW5ZgVj+ikBaofiBWffXuf0QdbiOJ4Esf4bn+QdQljsBJQREcIbarjsdO6cXylZC1/bDQREqxbMkpmLLOWS05rnlvn2I2xkYUrvW5lWqiTeNRySsUDavf7PYYkGaCTntqP9pFmTUpNBb9FM76LznbOBr4pl7JwlCSOOH83l4y7k9gEHl/sIYFcAGuAgQTtZp8PaSARJWCgCclpl+C0p7IHkBI8aCBmD2rnvvG3k4UDhFYw6GXL1b7fgqPSjEiDfX+g8nVe1vCNTvJBda2U63xi//eO4cz1nVKpm+PXEMdS0ZVScDrNkpZNB2V1yE1ANeLWb5QYfbJt2GuVV3PGxzGZQcqueGLcBOWI7GJ4EiHE+jenj0XEpE6hjYq3IydxMz4bm7X55OlT/OEf/yv4T/7P/64LV+/evsXLFy/w7INn+PSzTzDuJtCQMCSAWcTRadrhyZMn+Pqrr6R/Fob50Sef4HBxiZiGpBr9q/GbufhJvzQkJGM+3CpT0SnRG9t6x1e895DrPiVX6H5gvIRq9AhCUNdgvRsJ0T3I7kIQmVskjL+TGfu+msH2fZzr0wRXF2BjZ5ERVkJtgoalJokvigChwSBDdWN9883XIFqTJ9Z0OHmpafQ3BUUDy5n1fJ/T8b6LmfF8f8D/7K/+IZ4c9oHfCwyCXuj42DjQUJURoGbXXvdzzxj8f+2SAJ2SFmTkoK+4guzvEdDEmjdzIOMhDX71wyOd5b/8+Sf4a598iP/9/+Pv4NV8cgP6Wbx/4JwfcrHuhRbHbG+yRqe2v7969QofqXG4qIGEmvcePliVlX3/r37cWmx7iVFPVeJhAkt9GK4QGv535E6uuHcDYoggTX6vd7avAnDOgMX3lesOYT60gTs293jfhIZeCAu/of/cr1Noo46h0mITviVlbULOi8wx1hx66KXwNKOJR+W3U1O4kP9WN5k9GDb0FpybTd+uj3KLzeXeogEVTwJP9SFVAb3rIAiH3cAIHuAkz6WOV1TcagYXeTTQwWE7HCEKupG2yLAYlua+R/V1azVq2+ZThxkIYPy6ARSi0MPGgO87DUPNGLb4VZ1FlGPssZaPdZva5sP9Paq4GJ8npeEd42VNsW0n00RZW9zIQCTyqKRxLrDUi4ULjnd3ePLkiciSjaLbrgd1+9SMCp76T6/CG/Kz74vItNaP2ZUPZ2paKj42CvyZx5puzzzY3Opo7rizrFNmiILK2/XEuBhCKn6UUjCkQU7gg3FaTliCU5zCxN0hbjB3RczmGJ+pcpvYf2qGJ6tbuSwZDEidtkFOBovBxQyicuIo54xpEkd4yoOeYl7knuoq0zRVx3p38can80BVeSslrw95/OEt/tP/9/8LZbaTuRSmr/sIgJWYklrZVbdiZrx8+RIMXtUfllqSkrZ32kmK+TTISeBvX7zAy5cvcTodwaXg8eNrPHp0LfUNCXj69Akur67wOz/9q/jjP/7n8fnnn+uJ2nUQdcwqVgowDJPqofJcooTHj55iSCN2u72vRSkFeWHc3R7BkNNAKRF2uz2mMeFwOODi4gKffvID5Vex1l7V+1JKePz4sbf77t07zPOMnDO++uorPH36FFdXV8GQSX564vvK1HaN+z0GmOGY1TBVT6zq4qHkiLPV4GxZRmzdbb2r7iHvRycekbUtqdALL8rDw0lNRpPW1uhcAiHF9HbMOAzAzTyDs9SKp2HCUmaR/Qpj4AEDic5KUONdoH3zPGPS7BBm2i8quy5Fzj1buaphGMCQ9M9grcEb5NbWcFLxbKWvFsbgOgohU8FSMpgTEgYMROCyYMknPc0wwU7ZRvuGtxf0YnNKlHBafXUSW/UPMZwnrf7ASGkBDXISmJBQ8gAaBjCRwCLYXBjFjd85Z1AijOOEUmYQFQwYkFiylyQ6YbcjpKG1ychSCO4kAJyz6JlBFrnfRlDnvaU/1O9VJ6nMwU5eGn+P71q78pwMidDKHtZmzewi36VsApHiVDh5LTSIQ9tA5Aetw5Z0SwifMLS1zzorb0JCpuo+6w134vBoccftZM13+wfkPKMsWRzZzBgpYSAJckjjiDRNoDGBA/2/9+L6gYsFa5lTRNIiz+UEXhgM4XdDOqBkxqtvv8IAxuef/whff/kx3rz5Wp1qNld1cBidVyN27951OoTqnBEE1BqszsNYAnY0A98wEKBlElnxs2jWmCjDlJKRNnAJ6ph0fYi0PWbUujbh4IGvG0BoZSjrH1xTp3LASZH9BCZGp0F6QhH1FGRzuYwCH2PsD8zYkuR8San2vcYDrvOGCf0c35Y5EYBUT4VGCTVeGeawrrqTLGGbGQRI4GEBI4MzC10dGEuRk60TMz786jXo4w9RlkXTgcupYZ4kOI5sTzAkpbEGjxa2WquAlVKRMVnabQsSkjTY4nyQUpl+6k35itUnt5OfCHuXHALVHpCzhLEkHqRvEodGFk8zPDiR5CRrdUp2grECjzpdyk2UbOhgtsL2Oc6MDNXj9XAUlwXHuyP+aXqDX+Z3GLAgq6K3S0DigmWeARI79OD4QU0JUwA4nY6+PxOJIxFDkr2q43PHIkicziz2eM6z0wUrFVO0LGSU3G0fRf3C9AGDrXRlWe5K60jnQJD18tPn5wLTlMZQB2giwsVhD0DKPQ3MGNMi+DMAnBO4AH/7P8j49RfA//DfBMBJs7pC5UwCkzoezfkY4mLltL7u53gitFalU1MagagGeoosPgg2JIGNOcxYD8+xOrSr3mzYqzBXe0Z1oiUP+huo6gpWxyB54JHtBVlry0Rp625ZakvJKlMPzteFlWrd8yyZBTgXlGXBkiWIr9HXbIkU128xABqcmVLCtNvh8uIC11eP5KAmwXWxnAuWvGiZRwsEYgynk89/N46Ydjv3daVOTzf9vjD7KVaTz4vhjhk9C6GgZneC0vqUBtRGFS8MlhQduypnkPEPG8aGLYjXWuLxdIfjMuMK18gqy6VCKEvGbhxw2DESGEup/ZYyKquV8mF5ZsWJASWXNgsXSbahnKWWOeeCaT9KCaUoT1PwqcGWk1CQARohEr0EmlRZfYAFPzBL+EJm0fmZGcfTCafjjKJymoUGMao/kGiAoFUG0lB5JNdx+dI29h+5tvyTkU5s/b6SnwHBfxSgZEyQrNG8SLD5jAKkEeAMUIbtxlIYhSXgyPhj4qHKwiSfEw1Ig+0vBrPIgwxCYULOgiuD7s6qD5otRHvcooOohUOqka2Dg5GAYutWedEaI1ubLHW4fl+wcJ9mPfqBe/3u++jd38kxbh3c3Nzg3bt3ePToUTXk6CBMETNHc5/OPDqWI0DMkBTv2aQaRZHXbdmJBbtsnBZtZacw2nrn5EJT3Kj2edztMGi6JuvbxjTPwsTHcQIF5YWZcTyKcDDPM3b7A374ox/h+smnmI9/hmXOKqAzbm5ucDyesJSCcRqBHZBMECXCBx99iBffvkDOJ1xeX+HDjz/BZ5/9AGYsMsYEcHDOtQSSIQYgJEmdUpjV4d+e0IvKZH9tKU/RiNs7wOO9s86zQIgcaVVZ2FLVZL8GohWUya12lQMjIXnNSZC13zphTcEww3pzGk46kb8hKi4KwjBcDLBhX5NIXKvB3rv25tr1oPCeCRWikCXc3t7g3c3Nav4MbgzjlAb0hMj6fwiZ2CIq7yMwRISnuz3+l3/9r+ByZ6Qluosrs7K/baQgtWqA/mTBeBTmEGEZliIwn/oOc12KpjcKY2HUU1NhfGGgDX6t+okNez8V1yJuH6YB/6u/8Uf4T3/zNf79f/KnsbyXGzvea7RoN3A3wHhPe7dtxhEPbGO0dCP2/OrVK3z4ySfaZXVE9DR8c3yhQ1s7UdpbIdAB6fSCKia8Dw7vu6x9n3/r5G6uB22Mrde4wQ1riyjQgnBv8wpI3KxkRO5z74W92jwVBT0EDPGNwuHR6oBVOdXrueZ5CUb47IYXo9mu6cX2UHEZXAXNotlR4l718TkMLYyEwyaNgps8SBv8qsIFvhYGhSZ4QWHH9ixgtUYCP9hwkhJqdDC19KvusXY3mRHJHL2wjC3WDIfBouKKzdndGIE/USKMqqwxM2pZjjqGalyxZqvka0+WsOea7rmdownaLryiH3M0PNdT0c58/fcaEOav6ykHhHWKsAPWKWZ7Z7HhRSyzE2kUgdww5zJjaCdGpNv36MwqWnvrNIuCaHWgF3WKSeruOr6kp+/kZJQYJkjlsEQJy2nxE8N1c1YGFeWntTxVjQyGKmcDVog0M1FYqnsu/phXpKZ+D9RE93TLvdvPZldu9lhFQd9W/rt+H4cRBFKDItQZbvK6RoLr52KnLRgiRxNhmWcs8wz2ky8ase8njTKIyYO8Km8ALHuTfC9OXp2eiVVA+mcxcBZm5CVjphk7PTke8ajoKVhLnU4kuDHPM+Zldsd4CQG/vKFkVyq0xevbVRA0Sc5TmRn0BHi73GC3VLrhvEP/T25YKDidjnIi3GqhMmNeZhCAcdyr/Cp7LJGekiUxuM1lBpZZ9CNIuvnDQYxU+/1OjFYavZ4x4qPPfhd/8Ad/gA8++MBPzNvJgZsbcT5bCnNmrun1dR9asHQp4qyG4Y/O3967uzsqfMi/E5HWK5fo8/1+j8PFBIDdCWtR6TE72DAMePLkicBlnvHNN9/gN7/5Dd6+fSsnbydx2j96JEa50+mEn/7+z8+s2/uvcZwcBzkxBjXUs9M/uYw/NcZ6RlMz2uh5lA3XIgYDJE7uUhic7bRWAcLJZ+m/38xy4iqlShcSEfaJQTc3eDfPqpuaI15bYnXAD9mDe20fRUdKY0QxXIk1e9HvkMqvIh+p/wxSLezic/VzPW0CVEN0myGvjq8nuo2Rx5RABCNVw9v8pQpr1SWr2BxP1Z877VKNTUZb7DSt8GbALBDDQBjHocrrsP2yngPZHLrrITpCHF81ZtXxhml3v3WyUvhs8I7qxxatjP3VcdQ2oiG66uNVjjmnF0c9q51rnVUnet97NfDTvc6hz4hLQhNFhpBMJVA6lTSrhjigge0TyJv96//q+ENwjdHeJYNowTTtMKQBJS+4u73B61cv8PbJE1xdXePtzbegQJfErlZASOoQ4iATUqVpUfYHWicsRTyodIQsiwNRrdfsstOZq1uPxhbZPFQfrJkteL3urltU+sIm3ykqxf3hp6Che0rfl1iPM+PucKNpvGobq2n2tThbuHCzZ6LM3rTjypvK/FVL2ZAx9R5VeJ27TL5NlJBAWHgGZ5JA7ZRwhaGuf6RBPo56opO0trdc62AFw1/BjXqfSwHcVkwVHlyfqXO09S3hc+SLFQYO6wa3Ikx6wMX1Nb2ppzvcjrEZk62h4ars2aLB6aUwlnnB6TTj3fGIpSxIJFkbBgIu7BRpEj4+pRGDZcbYHK/WBS6CY0XrvsuQk+uSdXYJwzA6TTOntQSzFZRUbYjoUadrS/TfrLExpXGI18DBIGtwnYGfQm7gqt3oITlbMwt4tkEMg5SqmKYTkM33QXrGo+qed8eNvWj73WjTxrZwfDFRnTRAyPEJK/oQnUnDUDyIteq5ulPI3K8Ns3S5orUBU82EQ55TX7smQMt5EEEDp+ppXRtecTnP3tMVaPaT8bTK26xEqDmTty5y+UbfjXsBxgcHldksYKLWIZdT+4Y3MyTj1Q7jOGGcxs0gNd/nxI0vSXcdUscvCHCHfN2bml3B9HSSwyM02ZrU/pwnaLOr3bcCTXvDMlzBZcw6D8vS5n1596R8OMpDXQCE8QhUucBsLD6wbnAOy/gT23rZXOs7rneh2m6sb/c9MktmAMUZ4/n1ZHSliz0d7iFW5avSfY9z7uaycW39xswoqKVT/B4XzGZzq59WYQABAABJREFUcvj3OoqWkUDNKOKO6ki3YHQigVOV34sQWphOZ/MwGG3JlWv4EEBb60nNubt1GxtyjOF1FJDtr4lLvG6rP7RMJCVB3D5mtimjl0aL3mcA0+vBjnEzRMzz7MaI3/zmN7i+vsayLJh2kyuoMc1WNCQYsCpMAlKUVtncupwhcz3hvRWRDaABWDS0VOGkHQMgwNvv9/WEAeq4oiHV0hKYQBTHH/t5+/Ytrh89xU9/95/Diy9/KfNT5PMTRYAIYkWiYIgSqDAuL6/wh3/0l/HNN9/gk08/xeHiEhJVOyDYv32zVJaGyhgCoZETNa3iVwXpuKfuR5xNxGoYUVQ627+hkaY9dmIImCHEHrJxEdU6PGao32rPpuRtwuUKnzu6sTr0OEKxnZcJU6ELa7AFRfM9wpji4CocGbpPODxnxKCmlkijGGNfvXqJZZ4xDIPXEbcrEbzmZqBP7fg27v1FXFwY/82f/Ah/47OP3Slugnwb1NCORMlpJzC3V6qginLx5hW2dnPPXjLBwp6zzz4Wqu07f6K2nXPvA60TP7QEc3eyrvfVNOG//qPPsEsJf/sf/cJTo1QGERD/3FwdHtvPnGfY7JM15mFtuBKhlwTwHL1O5znBdKPz1Vj6dW42kgLbnhMDTPOT35chU4sMkSZGLNP2hJd3QTHhsmf639cGytBn/RNKM+v+pSDYdThlxiVHrrDWW9QjDGb9WQUiWc762fsLz65oVhCmVvOkKqyb0u8KCkttw3CeL+g2W/yEnc55Cjf9TGHO0UBpdMFGzojrF4TSOE+/r8+V5m2Zri1CMzSLoLb7Mt5SJwVzRZoM2kK47tvtQLI4MrT7vEIsPlF/4fCxWf5aN44ZkK15fgzWznr70hY6oEZ6kv/WrHCDqJFWGax1juHUjUxCdwjDYW/9sfPFGsxm6bBMJoh/zcBjl9VtZsXHUuTUgQUyMlhP+C5qhEFQkET2EiOynFCxDCyj1uhMRNhpui6J8oYrxBLZXx0zJphXwwabsAdKCfM84+72DvOyYH9QHER8TmERZYVuWe0dLmLMK3ntTK1L1NG1dXPnryi+2PWAl88+Enk0+XQBltM4VrPX0txVJU/rbbkBQtafi6QIk3R5C5b5pKekq1MckPqEJv4R1ZNZzXYxPQVyItd5vCmOCuuqkCtnZ/bg22GQgKJlnqWtwnKyisWJMEyj1MmkWt/R0nsWPVV+vDttsv5O/z17MbOfnkmUUFIBZ8by4xnjP1QYNEuyQq6OLrVjMGcLlE+Pw+gnP/zvOGK32+Hq8gqXlxeSNpMLxiFp5rER+4un+Pzzn+L3fvfnePbsA7x9e4P9bo95mcGlYFmyBGgNE5Y5Y54zDvs9dtMex+MJx3k2pqrzBphrFqaq68gDMmYZYykZp9NRDWby/rKccHNzi/LNDEqMJ0+e4OLiArvdroFBLCtj7X7wwQf48MMPQWSZI7L/Ns+zB2p/38sCoWSeraGgNdTIukWynCx4ulQ6yFzTRrosiLAfiMEsZcdKyShZjV0+7+iYqBdZn0n3q95MRLiYBtyVjHezpHanIRrala+xBgQnM3Z2aVaZq7Gjg8VZmdfxo5UNo9GJ6D6ZGU0fTvMBz4JjdeTrycR6KKBfn+gEV83gbH+Vr671CodZl5HPHQAbbUb931KbIsjm5KlSCT2erduwIa6J1Voe2eYI5xzobsA88/2+q45tHegV26ptVt3Mfu+fOWcsXPd55vfvoH33T9LGvaZlx+F68g0q1w5p9HlFY+h3uXqjqdnBliwG1pwLhoH9JG7OC25v3+Hbb78Gcz304vqSwVKN3RYgE3E92nBsDP2YRI5kd4ABobwBUT0xft+6ue1l3YfjgY6oHUtLix3fuaUV8W+gsqp2ix7k7zst/q5rVPdYFdW3dJEuG8Zq721j2vmAm6oXgerc4s8r81/U3bvR2XgSxA4KBlAKBpLAx8nLW56nb41sRnYfDhObi/NwmMqn+m1KSKy2WGuLbTLWh3cI048RcUD/76Kz4qTpCwa3KM+xDaSdkMu5/kz9MdgN6/yjzGNbSvhMgjjW7Tex1Z+WRU5c6sEtANhPhMuLAyatawuSE+IUxrHeU+Q6kF+aKY0Sg5BalEwEogEjAUwDzJbeOMYcr0jv1awPDuOQYtvmLnV3VS9yYXYtOzFRPfGLjYttLHJJHXafrQTEpQHTuEMZLNtsyEFBwLRnfPrhdpiKBKZzlcdXtDnYdlxX2dhU9kyYn5WMtdrEUTaJ71OEc7+mfque+m53Xr0TDwx4zXhASl8BsPIAAGnMbuBbrotR3UcMpety0r3SRt/McfKOP3ZZsGDJVmbL9jOULyYNWk+SQSrLAc+iOvqoepzp+qAexgIXbILNeA+q7Ak5qBjlIgvg4e7dQTMFRB+TvVPMhgZjf2ecmOEWEbDkWRzjzTNVVrXATk/p77jPdV+i8gLDy77Epv3+vuySrYzayZg6gV7uL9zO1+BnQfKS7l5KEHPi4BR/gBwQftvi3+/7/SHtGu2Nbdrvknn7JJk5kuk29bmSi+hEkiOrOaii4FKYtP32mdeEVsL3AkAYhm0Zv78k0P3cXJXZbMg/52C02Q9bVhHtLxUkTmfXwD+HrMv1Lznfrak63n892DFuDnFLFU5EuLq6wu3tLa6ursBoT+vExY6KZNw4TVRJuO5TsoyBRKe7gMB/rsKs9mW59a3dYRgkJVwHaDNmVCWiraG1nldxomkIF+eYlwXH4wm7wyXG3QXo7uQjzTm7E21MA0ZNdQKqZ6cePX2CR08eIw2Dp3ywNIcudGmmlYZZMGBn/ySlWB37q1evtD58OqMktULtfbrc+xTB916Vj7oAFxXaKNX6psfaudUoHeF1a5zjd++xG4fPte2h74+0vx40jfG6E17rTaqfw3MmxLbvqHGfWQ1igvMvXryA1TtaBZGYgt/12M/8t1y15mJmjDTg3/r57+Cvf/ZxI6/Vz272b0Zlzia/Ezfxqh+cn1TT1/Y71KO1/kbdcjD7wVF/x5+HKRm1/diuv1un3QzVZM94/Ys/lNPYf/sf/aJJJR7Q9+x13zretzXPwQVYp+NdlgVv377F4XBolOMHXyrobirDD2kqkoEgmK22i/eHJoPGvX3FPWhtb9CXzfdCs2FXN221r9je5OaeCZdxvf0zBUTspVzApCZ/1uiSK1gmnGwNfUMJ2npu2k3gt1CHUDxx1AklZ3DD2qEOZqxIyEZzqVIJ7sZt9NtT6SvQg0iwuZbry2BkJ/ntbkscCGgPwIWRtyU/UOfd4Wh/NXc7Y0ZsJ/LAuN8o/L8Zj6Yx8z1t+Lsiqg0Y/HcHm72iDjyjA45LOjfawJs6HMGD5MS0dsSFa2CbtiFBlOGkH7Ok55znarACNOX03BgvGPD0s7HGsBlwhmHwOq8XFxch2t0CI1VgDt/7+RKCDNhtw/5kupWvcTgEWBOEMYgbQvrb7aQOWl7yNs3ZWjZLg08I/JREZmQxIDTLYXIEWnyL+Lq9jl3/K75738vrppp2zvRlXQyDRNAvRSLrRW/QtKKckRcz9ifHIdh7DCynWeHAENtMqns08HCjQaR7mlBxwMbVrLHKXxKRLsaWpGMlIiAJrizz4jhZcgFRdlpFBCwlY9B6g0NKWBZJvT+O9UTyQAMozU7PV1ckUA0s2dMqxr0i+EsgYvB1h2n3sTqCG8PaPsTx+/jRtZfbmMYB0zhhGEcxFO6krq0Zu0QHGzCNewzTFQ6Hx/jk0x/h6dNn+P3f+wM8/+A55lmcdG/evHFnckoJt7e3jW61zIufHj/sD+6AtrWNul7U1/y0DAHH4xEvX77Ezc0Nrq+vcXl56YahYRiw2+8wDBLcfHt7i+fPn8OM6SZ3W+q2c0aE+Oxut1s517/r5Yarrq9o4KjLFOWMGpB93+kovQMgnIplCTbJekKBlQ8TVUeiZAC1kgVmjNDadmQBQmIsPRz22N9NEvTABUOZQCTp31snDfv4bMzxn/etz5hzqZlJKU4b7WxUb7CpgfXnHD91ffv7fspC16CWbiu+d3r7BhuzhTnOg9FvwxbSr43hb0OqSk0NOoyTw5AQ5MINOwaRlFkQ9VPogpzKGcQJgvPy/nlj7Bo349/71IfobNxqt5GHzsk2q3e22+nHGtdlyzl+rv1zuHLfmN73vkt7vdAsdxH3RnzfanaXUjQtKWnAmKTft5qq3/eKBu9qz9O2cy1DSKoEz8sJ33zzJdIwSDBZ1U58nGbLAOva8LpWdguEoPvY3bA/fVyppl3tcX/d7H1MMOCBl7NrgySiQw7MbYaeADugC5ZR55AFHPvYbO8ZzM7gX2y33wubNlQAKeyvfm/2c66/r+mm/eDyT2hT5OnVSIMFqN+XwVlMBHiNapVTuWCcJhz2e4zTWPdIxIFSwOZMsnXXMQY1WQK1NCOPBTsabGQN7SBXUh4m65WzjYVVd5RGOfyl0GejsRG5YzxmSxMwifwusO1QUWlylV2bH2vgX6kZU6udvNoavE0uGKT+j/IoQi5SzuM4Z5xmS6MMPLqYcNjvkIaaaankBaQOmcIWEBDRgWC6vAeSQuFToIc/UmufSBIQiiRz9FTnLA4g1+nZZhOyYupfYZv9WCQ9ue7W5rcIL2sn2XHnAPe6DKYcy6n0+GNKA0AJ0zhhGYRvJrdPyZj+zX8l4V/4y1WOtqAYhiy9OSJB5IEHdgmcASI7WCI0yHI0WDB1DbiwOuTqHC9VLzRcJSIPmnV8CXK6vG00wHRklZ/EEAMiy6AK3xdF09dzLpLNCAOGtMM4JMlgSvBsNaQOTCszUCl7dWYWLs6zPJsWVVrRSwsmv9R5aVaEvGBZZoCAlIubWU0+T0RIo2R2G1lqyUvSCAnWz7bmVIOs5bPiM6UacGrySWdTMhWcWeRgDmf1U0oSYOYZzkh5tsm1Ku/awcZoLXC6bBDY5hVDIvzuj3c4nU6NfGO0fRgGtaPoyWsrC8MM8tPNCldCsANKhoBoc7IDG1WebcfE/aJ1XyI/r3y9PtPzIttPbdbpKmPXzE5VdonvAy0P7OWq99m8v4vMZ4jQ6yxCXyVLm+nKJmdYMEspWdbCaCrj3rnY/o2OcaMNZLo9VdjFds7N555zy/fCcLtNDriwHr/7t/RA1ObYjFazwbW2a3RCyJ6VTLpnAuF6sGPcaoabcr8sC0op2O/3kuZuGlvhDnXD3adYxJpxwHkhLf41hY1onYId6E6GA57a0AluKS40V0WrpmgYhsGNos07Ou9WgV/3awoyiHDz7gYfffgRHj36FLdv37hVzlI9mOw3jROWWepoIMmJhrvjHR4/foJlmfVEEsClP+FVI84UOGCw101ilbuYSA3JVs9CDGVbArU7KNAqo9a+Efnv5SjrriiC+DpbVyY9hnv+PK03mhN6G6fOR2g2h1Z8skroyTdYw2wp4hz8uVZhZRe+m4E2n3nFr7YMCFWmbYmKGfiPd0e8efMWgOFmK/KZAGRzWGHob7dUq4uZ8YOra/zP//m/jDGZQCYjiHA0HA1uO5AKcCt+HvGY61+zmWyAXphx95s3y/XZeHl3YWmaIXS6nY+1a4S773H2FQ/rRJnbUtoM4F/4wcdIRPg//sNfaJqz8wJO391DlrSHmfXMIuM6em73KnVFP/zwQ6e5Le52ozCFJ3ZoxrkHzKm2GgYGI5X9bGt7jU2NAvKY0B0MhE4/2yZ0trXpfpqBVDTGAjMQdCLrZrsRBj3JWDkdG6aP5r4bZP3W+pmtkYTt1QrXAXYmPIGBi8MFXuKFpyezOlVNhouAE+3Ob7NxEPREKOp6Ou9npXsdFhJRTcOwCdrwW79J43fliw3+NroLieOd4YFpkYeYMabSZiNO6xHFZTxHN5rOgwxynp+2uG6PFTXwaKFrXbvIF7iDiUgGdnKerUHbZ8XGkoJixN5MVrnPXhDlO7sz29o4nU7hOaE1kpq8yInsVNc8peQONqG7hHHcaTpX0jTaWlNI02gnCqn5bPi6D+0kZHQ4t58dMhWFrZGObiQvScIO3yqRsPMfOSWgcmVAIFtqaZGaepbTtAuBnS29W11c8Ve2nu8sebNIKrjVa2z0yhxUNvrfRhiIVOQBjxrbN7rpPxoOVR5lzj8zhNi4OWeclhnMhDSfcHF5pfXFMkYNeCg5o+QFgBg/LFUwqxJp8Ip0j2F1Q9Xooqda3JHImqbb9nMipJI8TWNMz296wrIsnka7lHrKFywnBkqRiPA0DEDOWJaMaaoGIYZ8zsvigIkQX/P9cCfqX6vIf4CuGMtYMC0JHAJXti7y/3c9qgHn0eNHuLq6gph5yI3O5hAHEXa7A/aHKzz/4AfIyxHzvODDjz5BSiOef/AJfvyjn2AYdnj18kZPoSc1YCyKFwmHw4XDRoIl4AaDcUzY7ydfB0DqhvfOLXGoZlgZqcPhAp99dgGAsN/vsFcHu52oGCeglNn1V/K5Df45Okb6f4YT9vtfxDVO1Ym7uV6+uaryHzMsxLFKfdbeSWY8pD4vJ6+M5xQwk9bxU34OBLrpy45Rad7QpZkEANKAkIUZw94C5DPEcIHm2bp2pYG3zFKNu1nqUFJhPWWoO11Px5nmYfz7nKPsfQau+HzU9YdUTyKcTnoSHjWzHHUwjTYHZqzmt/Vc1CUjDlhQVs6C3wPtqhyhfTIYAw1uaFrNWU/MAXayahLemzbkyrAmPSzfd22Bdmst7NZ9bbMy7/ueOedo3xp3bzDtf/9t7RzSyJnbnX1r81I+iPBs/SePDOPY8E1A9sBpWXCaT5hnyaZjxv2HzOmcwbXKLSpPqtF5v5eau0SSQeXuTspaNHvAYVtpMzGDCoHHtq8OCKh8bk3fTZasBtVe73sAnO+BAwcH00MM5/GQTDML5+nr+pnkexZSnxnVobzVhl/Dtk0yjo+AzbbubRcQOcGF5fZZq/Ea763m6/zIqHCn34FBpOVd9HspBQnAgISMBbtpxOXFDjvNypGItBa24P+8LCIHhqyYji46PKHVQ6XLPl61XRVznjCIimfxQyIMGFHxVQIvJUuT6DQmnxuut3Ay54SNjeo7zaONotYOXr/2DiMwa7nINR6ZrmRXUMdc1RDHYcFpYcwupjA+enaF/SSyeNZAtKyOcdMvt/Be9DIOiod1pzWlE9A6x1UvI+E/gOo3qjM63jE00E1/C7ochQ+2pokG6VfLdEX4eACz4g8RSVCFzcnoiUNDxsaKH9EGPU4ThnlGGaV0zjgMqo8AhIyCQaQPk30CyCi2bzrdav9RhYXrnK0PwBxAQpIzLNNBSgRiCZgyOWMxB7MGK5mO02TBIp0nA8MIXFxcYJx2GEY5HW+p9W145o8pXJ14RPC9JrxL/CpMyX9PrIEiAT4GkVIK8pLdz2TBTolM5tyiU+wZU2ugANxGwTNAlGFZM2LpG9MzbVFKyTgej6gn7KtT3GwSNTU7Nen2ZV9HfalmUpZT6zvdyybzEYqn0BaauiyLitUhC4rp/taHrV3dKM181vCB1wTvL7PBuIwc7DvuYEQIqFE7ICC4tISAO2bGsrDio9G9eGq5AKiZKCOcqq4cnabVwU0eRBTonU5ncduU0NxY0lmyQG87V7+PHyu2c05G3vrc0PTut1IKjscj5mXGbr8DtAwZs/Ep9r8AkIL71m1v3Vgsu0Dly9RsnS0ddWs+9blglzkjb8S+Ypt1aQ12Bo/+fTTv3xsq2Y11az2i/n5fRvJ4PdgxDhdgCMuS1WiYcFpm3cjiCG42kuuoNd0JERoFrVcaa2S7CbnkNRmUj8GMPfH9eE3TJKkL9USSD5+EyeeStZ5C5aaGapYCJOu7g5lU2U48iSDFqpAWFiPwOI4iFqWErAyIKGFZTri+vJYTFKNE0muYuzMfY9TWfskF8yzGNYkemUBMyFwsE4kIGoZYKhAIU3fxqzG22omX6+srhWNVrttLmbQ6CThG6AWFGxyZufwli9js2wsigBFewyVvJ6IaguizQWDOEbLeqR/f8YZDW9TdM+OPCbmuWJtQg3Zu5A3IM81Mm/FVpZb9XQqpZ7R9ipta8CspTMeU8OL1a5RlQRo0KrG0J4pMuW+Iso+QYCMM6iVWwO+uKoT1BAj4wdU1/hd//Y/U8Nb8iuZkZYSxQlGcYjKWmCp9a1iN8BvnRah7AHAh28Zs+6BdCf2/op4tseFNHDM375zZLdpGq8ZUB7hvMwKIa/BAjIAiIvyNH3yERIR/9x/8U02tw76nrW1XJsL9TYDVx1YzX62jR6sqZsQaViLR4ebNa6Bkp80uyFNdzQYgHbTcTUcBYEGgqcNSWs7wE2+2xvKKUQbUqFxqXq/4agurEbb2u/1t3rHPDAS3aPjBntVVIcFdN7cSOe2OE4oOVUQYOCOrF8Ha6OG4fblwEVowGhTTmTU73mAGC8yyV0XgtPgqga+k9d3tD8rXTbgvnq66cIWftc3hc6T3so4sChnV/edjsaGEdgx+pqKujJU97VrR+h6GVJUN7WcVjKA4WmC0KvIdaLQ5NzBtDdex/3aM7ZLWfUKB2BgNIgh/qEakCmz2cYuyYso9VObyecFw06KRAUuLO88LrF68pMJcsFgteZUPzNgOwB3RoqTCHQJWp1lSj4kinMYBh8MFAGDQk7A+r+DUruOsQrOvsS91xGDbjC2++B4zWcRfNxmjhM+1zUS1n7XyEmVRhYHuMQTY+rgCYakG+Upomt3KRv8tgjXiSAlrbo9znTZbkFk4cQXgNJ8a5cbfZKkH7AKwwa0nV/Hq76+ePffimbYiWevasyWx/S7zEUMGhTbMOU0kTvNlnpF28vIwitFyybMaCQlpUDmdzVFJgYfUQVQFTIJRR60RbvILQfo+zbM4qqFpAgt8T7nBRLlhzllSiw8JqQyq2LGn0SslY0gTJOW4OYItiFgU+XEYa431ADMXJwjCfzbYhN0qIbuU4+rEwA6gTKgnfmo4ktM2ax+t8cJwcxxGJBBG0vSggJ561/0+JEzTAR99/BMc9pcSxElXmKYddvsDfvCDH+L58w+xmw549+5WA6ur0p21XuOySODzOBJ2uwmsp0zE2MeY54zTaWnEDjsVIQ7X6qS2U0QA1Hiz+HqIwUgc3zIPRkoSUB2d4+bENCe6OWX89Ik6zy37WAyu/m2vwejPar0jLycwiTFhSzdOyZz6aGuRMwAatPmIVHbCjVHKIPQHUNmdXVy0lOmJar/JDTnUGCpHhc+SC8ags4gxWusOowahbaVkdDla08GeN2ytDYe9Uat3nG22Ep7tbQ+UxJhpAfhZa7FH/FuPJ8wj8pONNdsaS6TBMp6N4Asba2EMUw3wz6Uaz8HR+SYwkD26Q+qcXs5V+SGn21dD+a2u77t/SHXTc47uaDzvf+ufO2dw+75G1b/oq2gES9JyEUsuuLm5xdu3b3F3d0JhYBh24LJ87z5svoYDwzghDXIQxE6Mj+OIwgtI7VspEfjsQXXZm24nLA/fCz19iM9Xg/kD8KaTUbbmC9RTVXbfrkjfCeTlf6IRNhpsjR6Js7ANpOoNtw9yiv+zvoyOdGNIgW5Vu+/3v1xGKSxZ35TfEYD9NOFiv/c6uHYiWfouXid4v991MCOA7EhGdGaZvUycbS4WKv9jLii5rke0PySYPTuHQGJII6meCJf7qZ4WD/TTTpiazaKFXVBirKGe/6ge6rTYdYq6SkV1Cee7o5SIKqozivy04DRnHOcijnHt+n9weYE/XE5ItEeB4rh8qnpxr6eUAliMdghyM3gxi6NWfImtLOPyLOR35qSmGJNtJGODB1sbPmoT7giHBcgMIC7gQXgcQwMZCkubYeiJazaz6Dx3Jzlb+ThzsNuE5bTsNI2Yl1lrjU/YTQP2Q+iiAZPZtXub6fuvaoft9H3oye5EjX4jvyUNXrEazSELQheMJ5mfRhRYRlvGNE44aCmhYRy9rFFK0/+XvT97miXJ8sOwn3tEZOa33KW61qmu7uqeaQACZwRghhQBiQAFgaIg0mgyPWklZEbSIMOD/hqZnsS/QHqQxFeBImkmo1EmEARsMCsw3T0zXTXdVXW3b83MiHA/ejiLH/eI/O53uxsUKFN03/oyIyN8OX787H5OwV3oiU5YWwynhDyPmKYJkwU1OLiHsifEqAF/otPTTN63HUDJ8N9fc0qYE5DFoVxVJND9FgA76Q5ClYHOy2RShinlZEHugQISkqS+V/tYlqB9tntQJnEYF3lU96c6+lm1CjLAiJw4aG2cJksXz7pJxjD00BP7fGggguaZHeQxAC4I1DsST+MV2cHO9mK9pzda1HURWpnN06d5TtjsBsy22Pwn51wMtTEgNDLyYiSOlq39puMtPL7I8S2vURpXyaVO5nub07dt713ks7c9u/ydFr97OWaaZhyPEy4udBqsO3GGtEFoJ7HdL5d5d12drVt1BKUBgMop6/jh5Zx3lWlbWe1ta25wcevFZKz2BxdbYN2W76dtHw1OrY3tMdejHePKFHgSclJCGV8n6SRsPCKGmIDgjVC1IUEBoye/oyeURNBCDSrYaMpKVfK8oGMAkvcJzLgAicomTquxEOJk3BoB0weuKzHlCQCP9XA4cv3xnDGn2YwfMXItQqTEdfMkTU8UY8omRIzjEX/hL/5lvPz6R5xuRAAVRegLkZ0F/TDwiZKZBZ1pmnF3d4+nT54CALoQuboAAd6opQrtKYReKg1u0q1w07TjP1vbbR8KT33HWqfq21pf7W172nXhBU0/xrYdMyCjzMHGXzhg3WVFhLXDwjBPEcxVRdkLVPquEHOVvINOqJj5RSgwmRwIKmhkxCBGOQKur66YsBGwXGWFk2sLwqBshp6ZLO+Vi1RO8a3DVpWAX7m4wL//mytOcVlyFjrC4l39HkJ5turBParPaPvkXijrA1R2QdkL0eOwG5reKLjs4eGx1uGPQSosTqZHXSvYMtYzDuV+M13UTpGA3/yVD/GnV7f4x19/w+/ZrEP5q/iEdRx46FLcU+HeTvGTpqppNho49RrNM+5urvH06TOkEPgeEeO7wae+fDr6QjZk32pfzZ6sVoEgwUeqNMmek2ey7JMAoKZVHsbKWKXehH2vcTGTc/aj6GwkfagyUq2iw68sC10b2yQwzME0FEQ25RLWquKQozHGQ0vf6rTww6noiL1Z7tsuIE+3ggdUIVPybMoEysBut7PgnMoxnluDssK2FQZJumYnbt9z5hkf7ObXwmO3Ge5RBzvxOAsPWBXi/GaTNWQ8Iot553o5SgN15io5Fhqsa6e0lf1hVKVo8kZSw3NB3nZ8RGUdlRcHRDM0tc8qbZnn0WqcEQjzNGFOydUoZJmB5ZKiZKrjoOt7dEGdj0y7OnHg9V2Pod8gSNozVZSDOL1KvT0xXKCcdK6caSK3RUnaWOGrraV8iQLM4FY3yGSVXwbAauG65VSqqHIlOWJTwCgdm3iovNFzBHEQesKNQtcBQuycDBp0FlTvPdvbZaTlmcKHjF4FYByP6DsOQEFQQyPZ8xAct3dsz4thwPHYw+GwijvWO5XTzct9p1OoaUL5YeXe6dunH6TmeyEZPLWozuyy9xlmct/VF+wkBWuU0z45seGhyLqSQt3EZDEeySIYboIdW8MwYLtlWlei8GWfdx3OhwEp8SmCeZo4fVyicoollJq8ejJjiANi1wmtKzQkpwzqeU/F2CEl3rM+BXh0pxneQUd1cDamC6WrMH4m9x3/LksS4JGDqF42DWzpY8TQcW3FzfYCZ7snGOcjbq6/xtnZe9htLvHxR59gu+XT2+OU8OxbH+H7v/qr+PTTT5FSwv39Pb748ifoug7Pnj3D/v6Avt9gt9tZhjLNvjXPE/Rk7GazhdZOJKrLXYE4bbl3THdykoxpGhuHmSYyj2b4z9jtdvizP/sp+r7HJ7/yIXa7Dc7OOMAnhIDj8SgwqfWpzWZTnRbXcWvNaXWoPDZa/dT1kEHAuy2CBfcVnaaoWk4m9rwp5Oo5vdrTzNq/uVIVXwPTFP0lBB1DkYUAWIkLzTLSS0CC0jgiQugChqHHPK3XKFRep/KIT2VcyYIPSMhep+V/bcrzJc9eNea578Mw8EnGlJBTOcHh5ZR2OiTMvdUzq36onI5v3pZtXM/bMtahrE9JlekOLJCXTaR8CiX0QzRaVOv+ZR4ez7NN5PTl9YAWfx/6fsrA1j6/sOmsvPNQW2vZ807199hrgUNr9yr4rl9BFCBy7yzwELBAq5RmzGnGfr/H9c0N9ocjy4nQffH4y8N2zRYSiI2yfYzYH2Yc9vdWDiUiIBFxNofgzv2orCZQMd4IDnoLqoDpPzduLzoQaeYLF/wU5WSb0j56YF/ZD6dlmZruaWC7GlsLjGC6WpEvWxpTwxWIxHoWSJxE6igqG6XIxHDtunvW3mKsp/dCa99bm68vI1N+LJ1pDXflM6eM2AAsO9RD42m/B0TJrs0v9n1EP0Q7RKGOeRIcCSFIJrM6RbpuHCJUmafKIZKMbNyMquwqSucQAMuQRgToCWSnTwQxeKiuZvPw7dk0qdKJDLZB26gD273B3/5Bx3ba5ksAkMo6910EKFkptEyEcZoxpYQxJX5UytA93/TYdirT8pyiOAzJRrbsUw14vKf5u9ntVHeBOMlNPpA/pgfKalR4KjQ86knTYCnRNSyV/QlAqZEWTWcjABS5bn3RHQt+wZySDQyJ0EHqXKeMOfi1YX9C7ORAnQRF/nd2G7w53+L/cX+Em5zsbbfWNgpNU47aNKVvP6BoMfqbBuXGrmtGrKuQe4EIORVdSZ3O6lyzQCNZszTPGBHQSdDf3CV0YWZ7QtdJcHyh00ojKcPKRPgTre2aArqHIweldr04CSfWt/T0NGbO2kFLDGTHaWDbhQRelF0N26twezIaPXfjIjJneN/1QF/0RFJKEYW7SXud8N2ZZqTMAWK2DlkCKxTvqGSbSpmd4sdx5BPXVHgzZx7oTb/xtqVKmMKp4LGWwPArmhGr2IBhclzXif7p+H35x821mY3Uj6ewU/jqs6u6iueLcHzLHQz0I6/tali0lyXgRT97fPRtMF0q6dQf6yRt+1v7XK1P87v/ayKNk9vbfxqwTQAfhiVCL5kaguhZXC+78LnW+V+PJdbriJqmeNl+bdz+8jqorn97H1Vr1cuL9tssVku8c+PSZvxYgrPmtRkI5GmlR+28H7oe7RhvEeqUEKb37TTLCYF/TUhVI4I6u9toSq/c+NOx1WaFpH9z49WUGb6GeLtp1YgSQsA8z7i+vsbZdmfGjc1mY0LV/f29PTcMpaaXRsyW1A0Zm/4MlDOev/ce3vvwB3j56iVCOEj9DDUKBz4hEvlUTD8MRljG44h0ntB3AzIlFgyqtBX8n1YwBgrTL0hrK1YhYs2oaiRtr3btV9d/Qb1QqIGNQ9ZTF42KzKC3vEHVv2P9rFwtgVp9rmIspf/ljUIwSjtLhoMQ5ASWMgVSYJTfUY+/GkYojwcjFOWUE4hTRV1fX4MNxFSPX2CkuODhX5O8X/Tilj65OMO/91f+JfSxcYojoD1xHFDmbk8FB8V2/gEaC2NCrbbF9/ghZajC7lAIIIzprF0kHa3BpIjkOs5G0ITJ9mVGAeWdtqSBzMeUuaq3UNbMfg/4N3/1O/jR6ze4nqdmdE6Uf2B/PniFIOUJiuCsBiGSxfCpnLy4fXN9jWfPnzf5uFybcFMPYW0L2PiLhWc5PcMBe0AVCLJ9RL5xx5CNP7Q0amWv6Dul+2BwqWcP6Knzcv803BdrQlTRJFOSl8M5yVP9U60TMhRg1XNuhJDaOLsi8DRT1ra32x1i1yFPerqOoxrnlNAbJErwiDdElXkznqkg1PcbjNOEoe8B6OlhdeC10NG18UEC9XyJUKXQM/wTmqxGb6rW3T9jEEDJOqH3WBE3ehTl1KHhYnD7m9dFT6rOKZvTU2WZeZ4scpjlnYw0z0hzrubADnDNmtOJUYLlBZU5okQr95vtIuWvOS/cSb1QCZGeZtYEyqjqyj5h2slOxvKbODLV2CE8wNdLi9HB3PoXoJqBSZfCMwh3z+QHlXd0tLofss2byiwaPsEtqtO6YkCOfzjtBUqzSAw9RV7xNAbuamQGUscVpwwOIYAyYRqPGJ4+QQicoirHAFjAQVmLoHB39KmU9GGZ8fbmZhFFr+P+hfm/FyI8v8Yj2jamuf6bTyVpNMqlPFNNcthszGDSDwOGzYYda72UZsjZ9rniPJEGEMhyCm4gwgJwQ+T6gNvdFiafEVXwJ3CduRC5Xv0RAXPilHSaPlCzKSvuzYnLS3UhIolOQAime+jUOCOWOmpF/ktJgmaddBPWQeigt/pRU4eb3KCoHiDG3JUVfLAjTsXLRqin+O53fwPbzUYcnj32++8ip4y+7zHPGefnW3z80Uf4/q/9AN/+7uecMcTJ5p999pk54eY54fbmDn/0R3+EcRzx4YcfVgb6w2GPvh8wzzPOzs5KJodY+DMRYb+/5xMcxA7PceSa5Oxs14AssmxkXOO9x93dLTabAZeXFzg7O8MwsB46TRMOhwPevHnDzs8YcXl5ic1ms+DTqvcpr/QB4GqU+nmv4rwN7m8Rpmp6s7y8c8mM/nC0uNEXS7/aGxsvObuMl5SpnBTX0ZmYV55TnqFlD+Z5Yp152FQymwYVTOOxshN42cXqqz6k6zkarXJTkQ/KO61OVuZdyxqtrUGNV17fYFqR7cT4Q3qojb+510zByblheV/+ZGmnqmHs5IE2a8FCn0bBCS5pIPJWXo57DW5vu2r9WcdQy2w6s1buaO0Lqw7aUK/tmp3CP9d+b9Tm1Wd0fGvzP/W9wtETz5+Wx70cUcvvy3eDnXSbphmHwwE3t3e4vrnF/n5vpW7WKcPD1yk9U+11IUTJDBQwTSOI+kJnm3a8nc79gCJryalHlQG1b7WtiIFAA47NMW6Kdknna3LeL3jp/O3kHk7hrvT4wLrau4YTmo3JG4HrIADX+MnroX1xyo738LXUt+y+/Q217lQab75K1rbH0Asv8zNRAsDOvc7BPEodXuSStSfJqVh1brd7Wmmh30PKs8yGpH0H1RFYSNVMkkDm1fH72ewdJUhc6WsFf6rHYmoGlD+pvmKTN7iVerT6XXDMy/whWFYrr9eZXhojKCcQSjmVcZ7xo3SNu5S4REqIABI2Q4dOx7bQdUhHtrJ4oZL5OaNZgCYJk0HDopV1j1tTxZmpenq5gZJJgNzhFw0CJ86qkyvdDpbVDESgoDy7lpuCK0tZbCr1Xs5EGCq/ATtXs8iS7BiP+Ggz4L91tsF/hiM7tlwa6UrfdvM9vRvX5Aa+HyRzYX3ft9x+4r9Z95TKBs62kmbOdoMQLAiWD/5xyYCcMlJMCGHEkAb0m8HSqytNUJ07S21wTYNeAvg9HyxB6WVfZvPVpJSsZNVDNK0KGjoBxuCeq0BDjp67ewgasKS/RZmrtzEEK/9UeFuo6oEHrcmOkkkkpQSagTmV+t1+bl2vQYy1zYSEJpI7Qf3Yi1Ac495JqnY5rTHu94GHta4ry6z17g9B9GqxAan/req/kX/kQxndylTW+NS6XFeCuWzfN3iyJqPpc628tzbeh2Tehdz+CLl/sWHlt3GakAEN7yt8KkjGaYBpocNNz9daH5jyo3VZwNO45Vza8a85rSv7on5ehdISPmtywVof7Vja/onW1+3nvd7ZMd6mB6qjyZfCu6/FxYZLnoCPOK4UXnBqE2VEQSaeJA1IJ+nKsjDGTIQudtWYpmm2k+JEJX2Ejofv15vOR/WnlPDVV19hu9ngs88+AxEbsPb7fTFyzDOOI9cD6GKHzXYrqQ+ZaKXMJ+u6MCMnZmJ/4S/+t/HFT/4p7m5vywl8AV3f95YCMGqdQ6mFczwe0Z33Np8ucpoLEpjodQqJyj37ZEaKU8rj2vd3UYZF9q/G45XfemArNLGSaD0Rkxs1WYZyslY5rrrxkrIKxDpQ+VvGXcOyOPtW5k+NGqOblgrzIFJ1p5qkDEeNn+UdkrFoTd7xcMA0TYbzsGdbaagVGKT/CkpLyD3mIiJ8fHaOf+8v/0Vse8Uf1WGDUxBKj97Z7BWBdrhrv4HUTUD+Fq9TMw8/ltJvPffSZ62gl99PKKT2XFGfzNFBelKmngeJIGZL1Y7TN+xW4XzT4+/+1m/gP/xHv4ubeaoYiIl2zd76ea4a1lSvW7s9iXB3d1/GLalkbTIy/tAMrNlapd+1H6qxlNUt27Xg/Sn69DjGWHiVl83UwacC43oTTtVYEdgee8/TpoVhxeFmrcAt3y8CkIM/Cp2uDC1unRa7fuWWrmU/9Djb7XA73fB+zBnTNGKeJtB2C0jaRr9zijzslXx1SkU8ffYMr169xkcffcSPZR4j3FpXQr+j/7Uwq8/DGcNk/tKtOX+cImAKN4/Qvue8TINFOWOaJ567wHWeZ4ti1gwhaU4WkNd1HSvMYkzph76q9xbA6S77PmKz4ZMiUVMSh/afL78AqJGpBOOUOTMOwJQnK9GSi9wFB78lz+N1qrM9lJOAXokNft+LIlgJ4iCjjbZIlCXdG7m2l0Rfxw8zkoh7UvGAlGMCPsracZnymQihcTYrYV7w9EpecXKtk9MQUGhfdZPgT3qYYUX7tSZYQU5pwjSPiB3XMlbarkecCYVxVKRZxpLEeQoCjuMR19dXqB/WfSBci5R3eCg98jLmpgzg0W+uPtrKHzqeGPXkaLbxBRlz7HoMG0n1priIoj+kXNIXR6E1vJe1o2LItWh/BPT9gN1u58DmZTc7uwIgiDGSsNttsT8QQBPLagrjIIEomZ9VB7HPjKU4TDkjSOp0QCPxs9Sq42eiZhPQq0Z0kV9RrbnigOVTELTiPQqACPk845sveE7bLWG3jeh7x49OLCURcHubMWw2+ORXPsf3v/8DAITD4YCcAzbbHfr+DGdPzvDee+/h/Q/ex4cffIDz83MM2y3eXF2Z7jcM7OC+vb3lFI7DgIvzCzx5conf+q3fxDiOePHiBa6vr5FSwmazxWYzIIQOT548QYwRX3/9NS4uLupagOAgk81mgJbjGobe6apsXNBT5DnzSf3tdoOPP/6IT7jHAKCcNh+GAcPAeHI4HPDll1/iyy+/xPPnz/HBBx9gt9tZKuFxHO3v8XjEZrPBxcUFiAj7/f4EZB93ZSkvoMGLtvROZ0Dz1xsqPK1dP2UN+6vPGi8n4VsSmBvg8YTcOywbC6rpq7IjSxpcDhyTQPWed1F29RQ5IP2walxTA+EpoxPcXL2x0hv2HnP5Z72tY2H3CCwbFEPuErZlLLRsv5HXqjk4HZK/rsiTKO14+4x3BLVGprX6x9yE1vOsCYvybD/uU0bGFoZr9xdzoCKHLbJArDzr5+jfX8P99mrtJI8xvp5qa80g2v6z37DEvfV+QrWf7Tla4qS2DJFypmnEfr/H7e0dbq5vcHNzg9u7OxzHkYN2UErEPHQ9Zt3YLjfzqdQwIMYgsnEx2muQ6NpcXW8mz4XsiBAKrWPeKllgHPXx+9BKfTX7YG3cbf+tzts+y4Z/lcf9Pi20s0xP10c/r+ke7qAR6u7ZaUqFID9qDqtPrXx3MrrtZ6AZgfuXF7qh6XInJIV2mR/Syxf7AexIUr6m/XKmK7HrEOSUbjlEEmJEkANJ6hgPIiAV+lnooaZBLvqFzMgEUs0rJrCpaDdBg6X9HDhYQ/lnLM5717/q4ap+WfMVgD3t0L7c91x4pbZreGoOrtZxwTrnPE7Cb7QczIxXaY9JAjc5u17CdjMYvEtweLtPVjaNyM2xOinuD5ww7w6BHcaa1Xwhf4tkHbQUXiCAcrEzqF7veFtABLrAKdSFlwVZVBb3m1O3fhaWMxturO3F8PElBPphwHhk5y8iZ2DrOz753HdAMrwp8/f7zrI2nrhO00zVo7Vtj5tuBqRrYl8EZmpbDgaXLOnT1beiNgmWdxhnMgEh8zqwPYCAvkckceSCbTF2qJGkFFEMoCwp7UmkRGpOugpM/cFCxlvZ65ks/XrZuwKNGAyn4efqIK/rW/ojCbRAec7b0DIhx4xOs7aiHDrQLixroMpwqGsZU1T5ruzJ2sbH+0v10SA6pAb7KnYQaaZgEhjnlUB4f63RWlj5J0DpBoxfdp33CTVOcdL/+PZKjXOzJ0lpTnWMPyQrmp1uMc7Co/zaPOSHilLK6EBkBzJCCEYLdQ5r8t4pnWExVtfvKV/bqc9tf5Z6fuWa5iRwLWxHeRefGM9CArslXWvn4Wid8US/CYKuUTD58qGxrzmsvY4Jo8Xr827fqUqXtu01/Zx6TrrFQz7Nd9H7gJ/DMa6byBYX5XQ4UJ/E1tPZOijdhB45Nc2npVLvImZnlFTmnKSPPgbMOdimSjljlJrnQCGHvh6QnuQOIViaghjJkI3noKnZCH3f48mTZ9juBhzGEUSE7XaDhIzjOMlJAWDYbjmtotQYCTFiGseSZj5GHOcZXeiQ5glPnz/Dd3/wl3F19RL3d1d2AgwhWP1VZQZKEIe+N6NL505bBDgkp9owotcCPSOaCPAaUdeUyndBJi9wtEKj768VxP2G9iTRhOMAw52yOXTzrAjX1Tz03lK+t89Oqzk13brvE32GUFKchlDaffBdR8w8szRYMo7e7/fIWaLvTJxvJlRPpb7f/H33i/DJBTvFd0MhG61+VmCs2FfWadF3KB9ChQ+wGfpf/Ps1JhQFhqjsnaobJdZEZX1sL8EAZ+JrswdUDaRqXCLwk8noi3rpAfXyO12IYULLlbncDvjf/tav43//D34bUyM8GEzDA8a0U5e1VVamFU1a3AlguniQwIxu6OuHBCjF4RKgyiG5v6ud0HJm8sPiuz16QpiyVt5qMFgXigr8/LDc+oewgLft42aSnpb6z2v9nfpc2q8wpuKh9W+wumWt8F0eoep5DxLfnrVPhC4GnJ9f4ObmWpSajHnmNKgpZ8RMlqm+xqdivDYHZAgIBGw2Wzy5fIJvvvkGz58/x2bYFDgjWESzh18xKBVh28sWepXTeqV/gqQ3nmdonS0Cpx0nSb1ksCdyxgUYvvVdcXANfW8p5tXZxjW3Ozut6h3XtaCKJarzrGxXFnSSh3WPAaCFc9lECONBASQHQaXmZNSuckOvndPUGSN4DAXfOCWe/BZquq7wtRkb3yJJWy1zyEkJLbdjooLSAsVFx0GMPpdnitKjNKEweBlxS9HqfRAghlywMtAKBQqpXH83Ok/kcL1ulqiuQWkyQYOjKSfsD3tM41FS784871ROEi/2ImS1pB71OE2Mowh4/fo17u7uamMwCT04oXytXUvDV3MZ7ijOON7mSOGJ1lFLpM4wq3eMh5R9aBkP5J/CNROPIYohhbLHKUh9OHaem6IWACvWFCIiAnbbbSue8QgC0HqddV0ysXP8/j4BuaZHCiciWHp0NXLEECRdJRsOOrCxV+X/nDltfxRnggbphiCjeIi12VCLvCUbUrZkkVjo1zI+vvouPv74Y7x88RI3t7e4vTtgVmOU4EwWfNC9kAnYbJ7gr/21v4Z/+V/+TTx9wiernz97jq7b4Wx3jmEY+KR85HTZh8MB8TBhyoTQlfJX4zjiShzlfd9LjW8eIae13+Lz730Xd3d3ePPmjWXnGvoNciakNOPy8gLzPGOaRuO/RIRxPOJ4PJhe2vc9zs7OsN1u5fkJseM6ypvtgLOzM+x2O4endcYzXceu67Db7fDs2TNrx+uQ6kTX0+lt2sFf9KqCJNxFQk9JCRNCOR1qaw+Djx+TN14Z3jic57qOy5SYC7pq+5nHwBlNeR9rsEeAllgSTpOznPon6Cm2UDiJjeshHTSEQmvVJuG/l1dbObcOHCzPNPIhP1zkChl/eyCAcuagCDmZe+pyr9iN1mBU4Yr/7GSCijIRWcMloKGUb9CrGKuBLg7ougitj5kyQa0oMXpj4tKoecrQ+dDlReW1997mCF8YM50Opji+0AxUbDC+UNb559+Pa3Ol6r7KROS/0xL/TvZg+7g850Tiag0KjhOOxxH39/e4vWWH+M3NLa6urnBzfY1x4pTRemBkoR+cuFo8aOGmwUXHo9rY4MZUgjtXpCWoHqs8SvmXypG695QBErQ+rPyrbIv6TC3DtMZTO6kqMNMt5eUS94BrQwpUuPaq/V9NL/g/Rs+8LYqoZL3kofs9rxltQkWOWmN0vX9cqvrmWhtzvY6yFkZf7GGDa9ERXZuhDo960PYkdE1Tkq+J3baGRLKzCw7EDhLkzA7VLnZIkWlZSglDHyVjQi68m09ZWftdLHV02Smm+CKyrIA7etuQfdSZFvnA8ws7IBGKYyzGyDZdt2+Cla9wtgTPv+HWlojrgbvTqOqgJPDWUflYT+XqHJmG6/YpY5y1jayO8QmHY8aUJN43s9Nlt93y2Gy9SrYrDQ5p19rTLe2cb63QGgJCyKiOQNpflSUkOyayJCELAjf+rei53IfBM3RQDtH2yR1T6dGApE5iFNqDsve5fS4zBpf5ZjNscdjv2UnVse9g6AcMQ4/tEDBNzd728ggBREXXXhE/VrgN2R+i4hzXAPqSSaeWBRCoyARaUkDgqUGlIah2pIcZeY/HECSNc5G3uhAREGUcgAagBC36YjprmX+IWgrB737dYMEI5OF4NNq4kQxN5pS39W+gYvicSjleoa0IRa4qsjDDO4PLcakcRvIegeX+SNFOjbe8UPmO6p8BJeCw+GnAa9Mx/sQQMOfaTqC01OxGBLHlocYJhanQOF/yq/zcCpgORkTmGC/zKW20aa3h5mu8EkDoOiCVtPG+bI9mXvCOcX/VMFwZKrU3FrMwOd+Pexh6bLdb3NA1g0xoomaL9uUB1mSft8mfb7u35tN58L5lsmuDUzlbJMf9yz4KfCC463sUxzjBzE3yXKvNCHBqu5ArecV8J5qZY5Weu8vrkWXIYfFMe5kct/LLqQCD9lprt/V9LG35j5Nx165HO8b9AqrgoQ7nJOkyNNJHHbhqBPHXQ4pWjJK2w6VjzhZByoLLmGYgRISu41PbxyO6Jjo0EyHNbLToug7TNGG73dr4fJr27WYLhGApRPqeawmen58jDlzTO8SAOWfMOYMCMEmdciJmzLOeMksaXcnjT5Q5co4Yseec8P1f/TX88A//K+y2Hba7HTbbLQt3c8J2s0MX9WR4OWmfktQ17zvL1hwCxKm27igyJg/YfuRIq1qgL/i2ttFVCXk7wnpGQFDhtn7mFJvXU3cLEiJKkRLm0mf5qgqYsuCVEZYNc3IOQKlDvEYQ6nbW+lD9wV5ojBvh5ACUQHllQSPHihJ7fXUNrfWrY1wjutQWwT6lrbzlapt4PmzxH/yVX8em93utjNj4dwguhW5YtFVdtP5jzSepRWPDylONrqh8ho/WhincHq+KE47XywnQNtyy0Lr7SoSToSyqslqCmoqqocjfzcjLjcvNgH/t25/gP/vJlxVU/CtrirI3XtTyTe0UL/Opy134WouEMudpGnE8HnCxeVJsFeqMaAwDHqwrYH7E1eKNc6L4Sf2cTG/Z16lTI4Dh9wna4B4sX6uf1gHTGplao0Mx9tR7vHxtlAtpv8jQ5J7RPWrUpVmkMryC1TCcvbg4tzaJ9NT4xIb6gap3auHc7xeSjcv4dnZxjth3uLm5RS9CbZkvO/RS4hPchQ9IymlJPxU7rRfH71gkceAU4/pOCOy02G63JRUigjnAOz2JQio0as2vpYG7XTMNUGsxoKBpgbOCt3pWmquoasUsBL6qzAeAI+f5LQ3EKXol2eNGO4sIVeETEWefUeG7GASowTsNbGBuVcNDhezsmACf0m6NlNWUDD/LWMwwpll94ETBoPuiGKQoa5BmaZwNObXMUvYWzy+GaEEkrXKip/zrAS+DTMjBS/FGT/ySrr97xwc8AsDLly+w2QwYp1GcFUXh05GSGTmyGS+ynIImGff9/R5XV9cCl1oO9vykxqkH+OcBbh1dW5VYEWyd9bvRZ/cq+ZcXV2O4Iio11nUNQ0Fu73Q200aEjYPEwQYEy8a0Sqvdfhs2XJLAP8UZeQTPA+BPXxg8BV/01DPv9yWuWzrZqEbh4vzLOYNCkTUYZzICevmd9+YkgC90HWbArYBc0d1g/2WINBJRAP7qX/2r+Dt/5+/g6s0b3Nxc48svv8SLFy/w1Vdf4Wc/+xmur6+xv98jdh1u4y1mzOi7Dv/u/+p/if/13/l3MWx6/MEf/AFevXqFs8tLPHv6PoBgRpJ+u8G267A7P8f9/T3ub24BCUbu+x7n5+e4uLjAZrOxva9py9Vgczwe0XUdPvzwQzmVnjAe2RCTKWOzGexEdtd1wMxGkrPzM+SUMQw9Us4Y+gFn52cY+kHkanBdXKvpTiUAwa0b0WQO8evra0zThGEYKmOLBg0Skf3Gxg3OUqZBzX3/aFX75JVoXjVWeB16zRjlny3vAJRgp4T4ykZnzcA3zwAVp7jfV76fCM1KgsKrEMQpzgJx6AJS3CFsImI3gBJhPhxxefkEh0QIFAFEzDPhsB+tbTW+VYZeuP3l9paOy/4JCxdKXRn/irMhWSpyS4GpsjR4v6nTmAJAEsCEyLQiJa4vvhl2TCcpI4LQhcjpaPmYFYMhqiGcjegIESkB86R1mJu0w05219rxLJ/UJeY05SgPMgKZeWnsenQd0KFDJCDkDEoTKM9A4MDHzlKtc0aC3W6LjaTyTBkIoYMv85Izp1QN6EDZ02kb8Br22ad159zyevg5QkYqsmwIDZ0rUGN4BagcE6QUhN4DCk7p3l4EKEiLth5WtoPMecShBSL3CF1hvDKpanV+iz6U94NloRx6ln2JwMF3Iu8KvUpzxuE44fp+j5ubG7x5fYWXL1/h1atXuL8/mOwRQmBkPdl3ud62Nq3dp/6szosArMjQRUooPLM8v37lIHl/hDf3EZjnSRwo4grxpw9VZwhlLa2GN4TfAhIEFle69vgqdyLgA3Pr+fjPNWyVvnJmy4CcJ2RzjvDYOnnLSb6qmTZw8TLRSXCVp5uHVp0Cfo42hToIy+hhDAhdlHTVDLtl8EF9JVMviiRVEs6VsfREiGBHcqIZXQTSzO9tNxts+g7pSOi7IjfFCHQxSPZMrtkuZgl0IUgqZ9YFWd/r0fedyNSSUaiiHaKgqSxqcFG6zKVXKCfhdQyvqDS767kUpmxOtTcbHHV/m35ARV+Q39T5DTAv4UdLUBMAcbqL0yNIYHbXM20Lgf81MNZANP5HmBNhP2bsZ5JS5ISAhPd7oN/skIjhx46YHrkbQDkhio5EC9wq+EMV/gTmSSqwq2JHPsNDV/SBAMGrCFBGyYjXIefZPQMV2LhZJydDa8I3l43R2gj2g+rqJHAH1AYbLX2239+ZCIf9HSIyEIGZMmIXsRl6XG46fPqE8IffMO5oVzlwRlztrxpLrbbK/HR4Sm/lpiAfO8T1UKLALcpaE5dgjV1ASkqzyPaC6uBRx2ECcBRHuOCUOMVVTuAU7E4ryhkZs2T00ICWJPczei29ExTl5fBkgNlQlHCkXE59xxhBzjdg6yNO4QpMxOQ/ZUgKeA8vnm/sNJeY7juU4BiPA4DYIPS9ruxhlaGh49f2g4i9yfF7mZsEGBC4Jv08JcxyKKOLHVLI4pNKSHwsHH3kkrqM3mSn8HVOhoULG+FpphADcDyO5hz3NqoQAoYuoQtMBWYSEZIIXRgQwwYhZEz5HmfxHDR7nYCDKVNKSHMGs7aIOXFwO8tAGRSy6eYqk5Txin2EggjZIj/lzPsnBPs9hM7+xsjlGKcpmb7I9FJsPbET+bgwOEq5nGB74Gp1nVM2BbVJtTbcQs9X7IiCTylJFjCTEXocRsKcRuwQESkjTyzzJRoZYllk2rUpeF7cZCsxANjAS2Bp82rTpGsTfo5rTyvuPwBfv4dW5cO3y5+PuX5epzjwDo5x7wQH9HR1iRThKP7aEd6m9QqhbPBW6TGFKxT+QHr6XDb/nGbwKZHB+gQFzHMNXI020o2r/Wmq8hACxuPMGzrIKdzQARmYpyKw6kkBAuH+/t6U8F7Sudspbu2XCKlK207oxTjSJa7N+v77H+D9j76H/dWPsdvtMAw9cirj78zYH82ogsD190KM2A4brncY5LQMsGSmqxsGMFlWDWd+jyxzMj54tQL2anTGgmiXZ13P64L6ohknRJwc5mlH/9rsbMzKHA0npYUVI9TaVSkVyrxpqdIsR0Eqm4jCXhaJiEwAyZlwc3uDgMgChzdMVWt4IhK+vafvL8a3MqcAUCb8re9/R5zinkjyf1XYbwEcwvpSiVwowypjeRsdK6JYvRY+CMPPa9Gcx0elO25Qtl5e2YcT3HRdbWKtKaaeo7YS/MAhdjL/oq4/3Cl0EP71730KAPhP/uQnjXJVel4LizEjvUjjzZQXAw3uc/uQ4iERcH9/j8snTwUU5AfT0JIa1HWzJ+iM3S4CNElaHjP+NuPmOf1iDNSMxDZGh9+6zKt4Se5998AJmqdjPrlH0Qggq+0sKGPz/dQGCvr/etPbfNu9G+ynnBPOzs7RdyUdbc4Jk5yYGzYbS10HEXQKL3HjU5oKdUjyqcvtlmsFa6pHxUdO4xXtpLYa66OkwNUodK0fFoKcNHe0TXGHQb+GL2VPl/SdQbQlN+6azBbcA6CKYAtv3q6Kt+s80AeTFZ6Tq/6KgF32tQU4+LTbGUDI1fqGEMzJXBS+YlQKANecU3qMAOhphIa+to4/j5/FQEJFxgilLrvNn6Adlbm6PgI01ZooW7Y3xQgsCMxjj0DQWnnrmTMM9s0+yiGb4TmKHMn7XJ+jQr/FmJCTnL53eEZEJTI6cypsyiUNeBYlPuVsbeZMOBwPGMcRu90Or168VIDy3GTNPC7P84xpnq2tLMpzygnH41jkx+jlYDWun3AQn7j6rzukX6/xyA2vuYmCuO7W4lJCusp/HJ1doYtenJNETOAgjOzWvOGDwju8oR6hGEWCFDzcDIPRkEIDi1GfeR+vY2xSNwJcZiIcAnjLkvFu03XI3+P0+ZyhoquMnCEGUHIKdNn8OvoCh1Ps7iRbLS9sJMNVpoTrm2sO/g3A++8/xQ/+3Pexk3JQOWdcXV1jHI9IKeM/+Kd/D6/Sazx9+gR/+1/9NxHFof9XfvM38cUXX+AP/+k/xc9+9g0+/+73cH5xgV5OTkcJOOr7jtPPH/emf223W4zjWDmVQwBSmjCOBxvHxcWF6EkDNpszxGe9nXRig2o0IzHAKVY///w7VZC2LwGmGcqIEsbxUNEL/wzAzs5pmjCOI968eYOUEp48eYKzszM7jeBTUuv7Ws9XjeIbqcH+i14BHSwyull6kaBLqvOVvVROdDKd5BOQHSIlm0OQPa08FcIbozuhUhl6ZO/p3oS0EQI7hpWPGw/vOnTglPiJCLOth/I4li90nfjeulGqdYZ7HtA+2zrz9T2fWQ5gFioPQp1rIEJUkZqYDGitxk6yAxSnfUJxsjaBStU8GvokDEfXoR5/2dxKX+Cc48XIqTIS0OUSMOZhBF3XNRlUuuxixycOUeC5qt+vXK18++7y+eNPc7fPtXJWkUkfHqPXT04bP5cn1U7xVtUp6ptYp88NXH3/ASzvAlyWJ+Ts2uU+pinhfn/A3e09Xr65wZurK7x5/QZXV9e4vz84/BaHQKjx4KE1PbWOrWzY3ivPnWx6eVH1Z9GeFhBSEWTpmK4DA22/o8ZfrvUaCp/mtEYnVbbSA70lda2/TNlBu+jqlFT5lmsT834OEKeZm38Icald2G/vtk8eXCv3qcXrEqRT041QIhNNJgqLtVnqMpW6XDpZkQHLnsspg7LWUuXHtPSUftcymwSWs2MsOBClf8vo5f5BcMGc1rpX3JiLYiM7yeZSYKM1m1t7gAUVtPsmOL1L7pnc73BHeS634U6jR3VgMvNlXYdzj1HSsSqcA+Z5Qppn46/H48h6fMrmnggB+NYzDjhQuSIgSjBmcbiHlQ3D8/YysltPItHT5BEhiFx6ORR4rNBr7pfbqEu5AsGySPjnYeOtZIIA03390/V6RTk001nfSrsz8mLeSQJcQgwIie0WXd9hs9ngyZMn6F7dsDMQtf0u6tjCQj1dhykKbA2rnTxBYJ0jVA36gNxk8rLiEJyOabquw3GfjYD/deikPECgwj9UvohSk9yy9cE7vRterfRe8LVYJGTkRkJ1T2RQ0FJbqEoJ6JM39wl//s8/LXCzPaY0ntxQgsGqjLPw3xAjBpPxOWW1woFAZnew3nMJ0jQ7Ljm6K8s3z8kyc9XyYLB5IEipp8DHCzLV9abL6ta447baOi6hzXRUX5ryPth68Pog9LKX+LmojblmiDgYGCT2GWpkqVC3qyvAtKAZJ6md0cFHeR6KjKw6okKED9KUrIidOzFebFitrafud022OaVLeMiuPVPrNbXMpXvR/16Xamp4tds+RhHWxud5PNU6USibahXmp67q3cJQWgjUA8QSjnoVTK/9Nqf9a2tBB0t55m1zeJfr0Y7xaZos6l2NAnxaggfWdR0b6eSUuC60Ko3sWD+dwoCIlWRIRCLAJ6690ZOJESvdSoCyGKj8lVJGDAXRfI0/RTrddOM4VqfdASUQEYkSZlF0p8Sp/AA+IZ5SwjiN6KlHouJ8V2NM13GUYiKOspxyAoWAm7tbfPrZZ/jT/ZfY7rZsNKWSmoc3fLaTKACkfiKfoOj7AcbMg8SOB8fcFK5wqcWcUuZxr14Kz0zXfn/4ahUVLyivbEPry1+h+dUGoby1muCaRLE24BXYOOJkvwk8iaiyPdEK3B51EZUIxhCMmqlDZ23YCyIqv03TiOPhuBAZvXH1l3/xgIkIv/nxR/iNj963sZmCo8qljl/eqYidCgnaauFxVmKDmd2y93ok2uBpZ3Tps/7r3w/NBqiI6qrCXwRIU5H0PVsvR8dWxuGGrnKPl3MrkbA4vPn6G59/CgTgP/2TL0uNYqIaJm5uRRDRtrXDE0znLTfUiBZCwO3tHT76pH6mrHkR3oOdbm037emrHaJuGSVe2n67j992rfKbkn+L16M1sJ0gfGsMeLmXH56vRuq2Rqn1uch6V/S4VR5ao84azLU/mKJQGWWheLekwAHsxBiGAdM42Tg0aCuLo8dLyrw1Tq2N8AQiPjURAvqhZyeT0d9Q7S/XaNn/waVRVmUmRFfLIFcbrcgeKrDCpZUkhHbuoQif9dIQ1raSG56DHxns2zXRdnmKzHAqpUdxTY1x8pznVQse6J8NKHiu70BB4piaU2TKGLO9W/DS08pygrkCibSnzmhW5HRCMs0T24OIMNNseBoCUA5vSzs2RjFdSVS/RY8bDB0DV1yjWpllHMgGf3Zil3VLyUc2o9SNFUWM6/zVdCk0oA0hsEFPnh+nETe3d9id7XB+fl4L9l4WEb6acsI4jri7vcXheCzjU3wNgEZTE2AO+LIsrcLm9/hbLq8HrYtrduOxotHqcxXN97H8rTxZ0ytzOKPM0xRtd+IGECMpZfCB1IgIqVUXBf+Vjnp8NToFozNKa/ikMRAooOs7p1s08nUuBlGlea1cqUAgUl5S+H/nDErW9hrjf+BipyW/OM8z42wM+Oabb3B/f488HxFjQpoO2N9dY7fllOLnZwOePTk3vQ2J1+fy4gL39/c4C+zk/PDjj/DsW+/hqz/7Cjd318iY8fTpM+yPY8nOEQK6IWJDG8sMcnd3Zw5mz4tCALbbDXa7M0tH7vmV6pd931tZLK3rzHAi3N7eAig6q6az15PHMbKzvjIwO16iDm91ft7f3+P999+Xutc1z251TD2Frk51bX+/39cp7X6Oq++Hwi/adaZ157GMFCGgMSproE4GUWfPFGeB0+Hk+dqY58dRnhdbr9SoXDoh+r4HWQYFMp1b9292urTCWNfYO7FLyZTa6evn18KmhdOa8Yp8Osnmt9Ke2BhiRN91IkeU51Qv89mY1pbFDJ0ER/fqOWiK1HXGKdRP+BII1Z5j/salVzgzg0vhGctJT9K5C03ttMal23eLv7bezKi93NKu3WMdeK2s9fB7TBuLTBLQPk4ULIjyoasNqNA19GlR1wym/nuh8/UpnFPzXJf9ve2FA1eICJRmJvsE2zfznHAYJ9zfH3Bzc4er62v87KtXuL29w36/x/E4SnudrLvW3V3C6Z/H9e4BEYCnJx7mhQ4VZ1K7Hwr/dP1TWQfSdMXC61lXiLZeS5vXw3pcO0dvS4rGw4tuFUKQMjhK29jBRMLjDQOi8nw3VtQ4+i7X2wIa3nZ5XNVxnGrT5PRlI/a71yMqQd+1xzKnnAIXUIzThHGagE4CZsUurIFXgDjKo6ZFzsjZBRm5bAHqVGvtJQp3ZW02TLlLxLW9s9auViMLNMMKO6pVRyvONpQ+BCVrfHN8yPQm/VfG6p2awdW7tywogPWtHVpmK8pI82R8IhPhOI6Y5oTk5NIYgN98+hSXocxZDaJWXssDp1pnx8OodWLXMr1pxE6m5aAzcrpoUUI0lbp3pfB4YiVX+0txiexzfTpZxxwkVbd7cdFOrS/apCxDp+4NLan20TDgV7sN/jEguqPTvSoZvujUa7I9Kdw1TZQBzssbhBhlbKHMT+WxOqgCCzlU+T/DgucSY3GIl2ASHq/q+ko7lV+GHFnHApm+vMZ/efhFZ/J4UfC+BK1AS+sG3SNSXqBpM+WMZ5ebqjelvSrbOgAunnGjw9D3CLG3jEflfXkjyOEHKvAl8BgXtiT9TKj0SD9Qpi1kMlzsNONhI6u6dqv/KhkLC/R184Q5k9d0kUHLfulcs2Q7CfVYdZ9TY08BlawCfNp8JZDMwTEEqHaxPmDV60/Mp9DMInfnxAdIEWF+OO/v0S3W9viQ/uD7WuObemtNV/DfT8pEtJQ9k5bVk4jjnAg+uaMvN7nWb6howLLfloc/JA/4vaE0Zhmf/bjT56fGudKrPLtOI9bG966y0UPX41OpSx2qrotSY3RG3w94/vw5znY7xNjhq/krXF9fg/oBaiywBQ7s8M2UihKBUhNjUqPF0CMSR3loulY94UFEyIkQQhIiX077FeQE5pzRR9iptq7v5dRHxDiOIJpAFJETIeVJGEERLuaUEfuI0AeMx5KuaZpmpHlWWcgiozQgICBgTjNiZOc4G9X0ZEvEeBgxThMuLy9xfn4m49WNDTPGpiqKXjc011k/HPac/p1KxEmrjNqaoXW+iO18QRlE4AkAGkL7Vrw4uamcM2blN99vReLb500x9W/qgtcssMCgHv/C8Ox/069hnUCvza8GnRfgQhHSQn3Phu1aqQXmAne9zYJJwH5/j5QTp4wSyuiNQn4uizG5MTe8rZnL+oI/32zxP/q175bpwBN6MkLNv5VPCAprfjY7kADl1LTftw4yrVzsfizr2JLUtXs2ZsAcyu1vfl6hue8HxjzBK1M8gTXl8JQxxvfvKkbw3qT2KXYy/43vfoqIgP/8y5/hKM7EoIIYCg1ZTAprMFnB8UqRX1cKAoDj4SCCRycoVvabzdtPahWn1kUTIr9lClOvhiRMueyVpdFtbXZKi/ytWi4tNx5irqd/WxG2T9HFRoh50IBU0TxUS1MCTtYMXWH1syrqa/163C9zgOBaxPn5Od6Mb6DGVpKMKeqE0lqkujtFh4LVcfYUR3GnQRXd97p/gpx+Y80N9p3ZInEGRFXQSOcgilB0glqoBVq2rVHZuwvG45SboHNRHNFFKQRMx3Ta8LSCB9pt8LD3xLBuK+i4DU6FRpohzvYJWRPBz6U0aMMqvLHgMH/KtiYhBKutyq/XDlj93aYgcyKn9phRqnLeVhub5UGgpM/XiGuQKXRMZ7K0VZwCtfJIxQipPch3O5Eh8/ap03mu0ZMYKL6qg85SAzs+pHhWBHRU49GTscfjyKnZEJGmZE4+DqKUtF8p27jnecY8zZjnxMxB2tODOhqbzmsT/aCrtamMmw+Qm9WrLGB9ORZ48jrFkNebWgol9pcwjSMmjNgMG6mtznA3zDV8DyCfOcHLCyQGUyJ06JoJuIA/wSkNpuAh8H1Nwx87SWFp9VN1RG7fKl6oYSlGqyNf8Xh9WuRcoyOh0OuF8LYK11DdL+ATGOjpljPgL/71P4/Ly3Mc7rOcYg/Y9j1yTuLcjYiRcL7dOcNzh8NhjxwCECPmlLDZbXF2doYf/OBX8cUXX+Lq6g1CeILz8x3rbWB6kVIW/YNPUT9//gybzYbrhosDnIOB+fRyzhnjeECU0/U6h5xdmu8VBTuEgO12AwASyF1OWQ0Dp1Gdpgn393fYbrfYbAZpt6x/zgmgzgLAnz59avqsylqaxlSd8/obCa7qqXY92a41yb//59bW7XHXMGwEnZeyU60v1u+pQbMYw8je0ZNECrvWMW41IT19beTo2sjC/6I6IkJNI/q+B4gN/JSznRjnl6nqx7ergetrTkxvGDplvCqwOmXcosXfUwYuNZLraSIdn7ch8BZxQR9NWyZ3iCxzctxE4uwB2v0dEKHsTF+1EzJQQz6h63rJ0HCwfrq+gzpWoKMWIsrpUhuS49aj1Teo+X3tnZPtNDAhYqN8BaeTV50Nq3xe6jBvb6uMr8WjxXsO5gZ7W4M6tPltRsflOD0BT5IWmp1FmdgGNE0T7vcjbu/vcX1zh6s313j95g1efHOFaZrkRJrIVEHh5JnquwoBbxvzu19rtLvc4TG2+BPc2B/anzV+FbmUhBjx1stmlGhTQq9dYWWcTty2Pvi5wvd8CxVOsYeqnpkSTzfTd8Hdtz1XwcPG7dah/LKgh9r228axTlvz4veC6cXZQ0ILQQTNCqQnbadpwjROoC3LIdngqKe01c7MU8pEiDkj9p1lnpOFL2WUTIfWGuEeAhWQbB6aGcrDBEEdZeUEvWghdmpUT2Kq7lboArnMTlnmX3iM4sGaU7zsb9hng6FLdQ1i3pnTLKmMObD5OE74o/FK0qjz810A/q2nT7BtiZwGlgCiUYrO4de5kn49o5K5Eq+DLwcqt6An3cXtLu+1ggyAKrNpsHG1j5oBIng1IDg8cIzDZkRtAyjEnhshJ4vqUyFIRo/AgVixi3jadfhb52f4v6DoqVqH2+BFOpQity13FzuJVZcvXXtHVEYmkdFFVlNSEkI5FMj718nO5DX0MmXVVaLUxC41tv0zqD4QRAZSfcloSLOnqv3koEhAsdNIIHQjO+q+AC1t37xfWE3ubC7BdczfVbbVjeVlXrMthYAudqWUqchE5OCvtCKLPlnbOqTbZuysT5Y5Aho0IEH+4uyv6KzSaJO5atmrAelbrmJH8Sep9W8/SHZGe9rxK+O7pTWvH6s/T4MpAC1xWH6rdpciE7X3qocKztqY/Lyp+lzzrFDopW/3LbA6pRuckjXK53WeuTovd0/tb+rPIZHxUubiTT7lOgwfVUIo/SkvL/jpYP+ArnxqfP7ZBUyUcC2fXtx5m+x76mdafPNyXPMbefxczvPnuR7tGB9nVu53my2mMWG33eC95x/gbLvDEDvc3d7iye4SmPjk95wlpQu4dkgWp3gIwDxzZD0bJdmwMI4zcuYB5XG2aPuu41TjQQxQ8zwjp6PVB1XF0Qv+++PIzF9Ob4cQMUoxsETMqMZ5RkpkRtjdsEVKM2Ls0Hcdxts9ug2n6NMapgz4aKcJ0pwxHsdCYAHMiZEyhMQpyQbguN9jM2wwU0JKhN3lE5xdfgsp7aV/5gBTSlAFWAUrFcKibIXxOAIZ6PvOBCzjUTzAmvFDh06VkqWMo1aYFMGK4Ma4VSLi63f0FKIQMBM0g9us0nqltCwJpV2h+aL7gQobWSFdzYsq7Kg8szyhqVeuXmUBpBh+VKiNC7hW43BfFqKVvGdE002oEMXyrJ5O6uRkUxeA/d0dgASiWKQ8WqaTYdmC1uG6gBvZlPikhjKTMvrnwwZ/97d+A2eDSwMZiuBVBOVCmBwYGb7ySnS/aTO+BcUba6nhZZ4xqvrh74f6FftNBQ3o/KwfmGAZ3LxKm6FpqayRravrzAv5fqX5WY1KD6a4+Ut7srrkvvaHvPPXP/8Uv/krH+H/+A9/FzfzaNhtWQMEb3Vuni4soYjFL6cuoszKXQDG4wFpmjFslBotWyk8cynkLIfj9lMMCFQiUE1wMi1K2yAXVb/SZzsspXPQ1ZfG9NFGwIfsB9h+baHUYl7VEVT59hMttLQOYPIBO+bAqlurxuiVN09PHmb/YfExtKun8G72ic4ldBHbszPQq5egAOzv7xBCwPn5OVKaOGMLERAi8ylRFHRvkU5EYBuC7HbBWcVxg58NRU8MhGqc/LUWlqp7Njk97eag0BJtU9j9Hle4yvu5pndG36i0pOPT+dTusubUN+kpznLlakHg9oCfVzH+cJQ47wNzqMEZeFT+oho/GM9yoXfLjGT1R10faI1LzxkZTvWJWZmxngRUZzSUZ4nT0aKs4ZRdcVRDlVw9Fah0jgp/VvzPZX5tWl3S51H2X9ly7ORUHhpDELqiKTk1gpDnGLvC62KA1c7id6O1ZwqzjJnToE84HNkp8eT8HNvtppzezUDXd3ZKleR0LjvbArouYrMZMM9Se9kIghrHAMqJ0/ytKAL1etXy4tsuj+O2hzzDfdv7hZyst97IXq3kotNRGAYA4/GI84sLtLNQWhoCmI8Ef79scR2PRrrbqhJn5mE+zcYkO/FKAEWAiDNjddE7/QJ80W/jDiE4AywAqMGg92RryX8ceCrjSMuvmmftQX3INqjjL1B8CLi+e4NhE5Byj5wCDocDvvrmKzx58gRPnz4FCOi6DTKK8ylTRgoBw2bDqQaHAX3XIxCf1vjkk1/BBx98CDUQco3CzrJ1WLCNNMj744hpOgi+lxrLQDAneM4Zb95cYb/fAwi4vLzEBx98AAAYx9EylxVckGAeoTN9zydlUmJH8G43YJ4O+Oqrn+HpkyecUl4MKIfDASEEnJ1doouyVln2OLE4chxHnJ+fYzweARDG44g5zTg/O8c8Tri9vQOR6IYALi4uMB6OOBwOK4v3+KvvN7Kk9T5Zcw63VzHcl2e0zp+njZqe1gxcea0vQNfIxCbLvsJamvG3UPPpvo+ABEdkIsCtnTf2+HH7kmg+JX3rwKxOnzvj4poz/ZST55Qzt+5TU6WX2tullqwYCMUoZ32iXpfiZFNZ6SEpHBV94H0M2+PMK/mz7hef0r3ve+x2O8zzEeosV0dLRVCo8J3gKGzlMFqbz1vG/hhj1boTujAbbWKhRtASX9rPCwfryvo+FheYsXDtWxbJCFwrF0Uklf2xJve3/Zf7sTRPZY2JGJe09upxnHBzu8fV9Q2ubm7w5uoar19f4fWba0wHlpe5/QgiyegUTsP9XRz3/7yuun8yXmXc2a1DcHJk0wo0g1Bpsz1tVmdAMONx1wFrjLW5FVEM0wvnmPHcJd2p5kniaIpsW+T9ZMKKowtFjmh1hTK/0+t6+qITn5tnQvnZ00uz31XC4Ft6XOFJltjL6dnF6ZgBSoy/YqKeU8I4z8gbFuRK+uaIvu+57rdrKxBJAGSBo4IqaxFywKicwdHWzg02ACQnxavSTbbeUj87oMBNYScnSKP+nmHrbQ4VUFX6pzjOpEnn4PEnxQuukQ3UmTFM3k05Y56lrj0V58thmvHleI9MUWBE6LuAoVNLg6YpVv3N80Gecn0VedX4mtpSAhploJYjOFiOyiMm7NahpgJUFE+4rgN5MJR+Kh1aSbPbO14Wr66G58v8NbjUZiwyU06sE8ZIVS1unTaRzMSCveFMRc5R3QyE/H81yAIFrDYO1aWF5mmQQQglu43fu0UvLM5YP6nQ/OO5NHhHRd4j6MnpOoOPhfyTyncVaUGFvgrrCgbB7SkCSOtUL08jZ3KOZbcX1KFdSvABZp+KRQ7TPiybjkcx1SNBhpVEJHokQzt7HGwutZMU20dpu4xfvxaY6dipNGR63BJWsPdOXeWAQfsOoR+KPKv7Xe1ZvAzByll4h64bmuELoRzwXLsKPPnNNZ4ZXHte2G35iXcqe19gCMFOjLuZ1vB0fZ5yip+619LrU7rXqfc9rLyOk6guUw2SgxlZMa/kpDk9Jp3bA/CHh+/6M6fkjIfk6VPzXf3t9EuufTh653He8xBlCX5cK5vskdejHePbYYNtv8HxeMR2GPCdT7+NPnZIKWHoB+w2W4QAXJyfAYi4vb/HmBJevblCJj4RPmx6TokzjghhNIRWBTLGiMM4CZEFIkjShLOhOWXCNCcE4t+0ZjkLPwUhJqnjgAAMXUDOTerXEDDNGSmREbcYZqs3OeUZKRNoTuioRmQVNAK4ZmCMPSgTjscDNpsN+n6wNOjTNKLLGYkI98cDhq63UwRxOEPOBxvPcRrR9wP6qEKeygbKgCJyTjgej5IOZwtIOkB2Knni6TlNEZDcLajz2l/F7RyqDaZCsAlsyjNanREl8s7UamHCCyUB5f4pwhQQJLVOYY7rbt9Qv+ME5AIST8BXpI9KflJIFGITqkm7FhS4knK74fPauQ3Txhda0sZtqeCmMmcMAff3dzJGWRsRWlevUKIndVr1eMjueMHBPum7BPzbf+57uNi0JKKcrLFJAfWauyuGegTVWGyd/Ltl7cLiN/4lL54uTNlmQ9CSoE0/fr7OGC+pjrxuc+ry6LIc/8LtCKh4WLiVddDIX9y3/Ed/0/FcbHr83d/6i/gP/6vfw808mnHAhDo/llWBac0A1EDyBBMjSd93PB6w2W7l9J2HRagZUQPEBUxFabD8MCrUunc9jrf7xrdajCal7fV5NCdz156z/Vx6ULpfBIW3MNpKJ1MBJLp7ct+1RUZ3Vpg5+T+h/CT0ZG2uNX7WAUXrdKEMunJRMQCw3e3AEfPAPM24u73B06dPpGbZzGmnGriY0953LPSncBp4JmPUjZeg2RwNMPy+WwhfVASjAA+iwteWfNJFDVu32QlchqELXmAOZ7C0Qg6ni0zv6awhuejKTvC3zsspEzYIeucnIc2e/fB9lSf0b4G4Co6Oxhvd8KepYePQ09Vax8lOblJxcBORObAro6PO193jU6OMv5YVR099Q58twTH6nq7JP/kbX2LcunSweMRV7WcvJ6w891Azb/txRaQoX0rK4BhvnUzXoHeocaCSWSona7u/y5XO+Nt8Rvjx/+yqGWYju6xc3X3Ah9c1z1/KD0torFCt+kZYebOBmxqOleboTyklBEjQB2VM44jNdrvYY1o3PsSAmCPUEduO3IyaQkPqAAk5/SHtdHZawp1gU/axKvFwT0s2ISdw1VnGE65gx42aULYOpLbZk/2vySES4ALCD3/4RzgcD5wBbJrRdT2ePn2GEDiz13a7xc3NLesyMqau6/Htzz4zvMw5Y54mzNOEYdggxg5bWRc+SV3q7gGcbczrEpq2r4wuIme+YTWpY0TfD3j6lLDd7iyARC+r7+z2LwcyqwOQddTb2zvEGLHdbhBCxJPLZwAFfPHFF/jggw+x2+1wdnaGqzfXODs7R5rvMI4jXr9+jU8//RTjOOL29hYXFxc4OzvDeByx39/j66+/tjTfmt7dp1c/Ho/oug63t7e/cCp1g9OKkaI1jLSfWwOI/layAajxvZzYVbgW58FiJDCHQ+UoKM8ar5Sf+w6I1CF0nMUtza2hmV9sT4evnXRRQ1Lr+PYw8Y7J9ncfLOCvNRj694nKCfEoQTLVuCVov+vior+qH7g2T6xTPZ4AdiDUNEHT+6q3Sdv0tT+7LlTjj5ryN0gKYO2XgNh1sn5LTtG2/ZDh8yFDYYuL9feCf0Vl8nKygKJZp3d3Eq5fp8Z84vbq9aBzVJ+BGkZL23xo1Gn4MWI6TjiOI/bHI25v7vHNi1f46sVLXF3f4O5+j8PhgHGc0ceNrQ238dia2P9iXcUxGEBwJxzd5Y373skD1dUgWSadbqzZSEpaY+Vj/OvC2FvpAaE6iKAyhGotXqbQSzNa6lhLqY7IgZYeR1iJsDGUs+Q1bv+8OL6G09bW6m/cuVZfqG11+m95ra1VkeEdPuoS+7GRBsZmBCgOz0DoME4Jh+OEaZPQTzO6nmse8+GpCKBzOnpGplKvnYhKynWRE228K6mei1lAnWSSzdOlQDZ9ytkeGG1LcMbiIpW+CTlpqS/Rt0PRhXRZ/OlLha06J/WgmPWlfLp8Nb6Z0ixpj5MEIyaM44zDccI4A1kCgWMgDEMASGtS68wKjwxQ+QrLOuOmvzEccgLURhEsiDvLnCMs7TSRg5tvQzQWtRWJGkcGN51vo9PoVnT83+8bKwPm9PEyOzT3ULIECFyqKwTmoSipj1lm7dD3HTZ94VuMzyKXOz27EJJa9jeq5m0AtjFhczf8VT1afwp6atdl6Q1u2t72tsI/23T9QWUdFPqqTuRiB2jAYwPVveNpLMp3sqEY3rFDnkPUCRIon1wq8pXVKvpdsL/6RD1Hs07xJ3JOQLlXyqlEPsFrsqQECackGZHr4H2PbyWARrIeuex2IMe7bG0KYdRnHDDtnfIeHn+FwBll5hmbzaaSr3LOGPoBXa8BKqqb8nh4rwXJ2BwwxM4Cx3WsOSVQF4XW5FIDvJGh2zU7ddUye9GVfVBUCMyXNTPX0PcY5wm6VbwemXOG5TNwcuUavzo1nvZzoTF1e2tttPpHdvYzZFipLyI+XKzsRb+nyL7OABJRvxJQAEe/mH5SbdOD4ou31Zdxn7rWnOAPySMPOdHby8Nj7f5DlxMbuA37jz4A2+FuMG9tF3iXE+P7ewQEPLu8xPc+/xxPLi/x8sVLICVMxwM6Ke85zRmIwG67xeVmwOvXr3F99Qb9ZgMEwpwy5pQX0d1AQN8DiDykEEtq8ZxTMdDI8zmxgSfnjHFOlYwwJ2Ce2SjC8ehs9B2P3E4IAd0wQGuGpJQwHrkeXSBO9xcCgBnISepeymkmynzKvO86pCkDPWGeJiADh/0Rfc/Ct554H6eEKKe7+0A4HkYEBHzwya/iW08v8LMv/imur77mE/UpIcGlJdVldWkRXr18hWfPn6HreidERy/NLTZ7TfDLPRNDHHGTHeVWvo7QWAh9rWwEh6UP4LYREDH4Bs+k9Df9DHqwrdX+T/T3wIvuWZ5A9bybT+M6gqOK/GchHYRykpvo5FiUWGp/+tx+v2cjixunRqqtTxbVOIqSR9X6n7qICP/6Z5/hz3/w3JSNpmkweQ7Vd/tiaOIyCIgYYgqEG3uonqv78QEWPKf6eztuQAU6FsZj4MjsGDQq1j2fOaWUZo3Q0giFBQf333K1XZc5lXnzWJdCgD4bwvIHBZvKi6SKgJOULzcb/N3f+nX8h//V7+LNuOdXnXDpB7eyW08yIugcwgpemWJC2N/f4+nTZ3w7+vUnJSal7VDjmQrrFbDIfil9te+psSP4lagxpZpNtW9dfwZUVcZW9oDyI79IVAIbQnmsgdOa22ldaLAhLHtHQKzaqFqwcbfr9zCzV8raiCumaC3xpNBwNQZsNxszIg9Dj+M4Ic0z5jQjp4wYMyiq40MERVezGaoAi6CtHMk+Ce4YOqgS6eig4aFA2gs9K9hcraHhlFOGQ4WLMBS2r/5ZBEvJxweuC1+itoGQ5CPZ1MtzLS1RGLhVkI1PAjNTKCmXYBit6+n6YWWO29J03MV5TYCeyCbAOxZ0rqqAaDv23Z8abOZS0sQprMUB7h6vaJIpO7AAQKCc2I5Sr55kPgGc1oxAmLYJ01ljmPhv3PVf0/gjkC5aCvNIIeq6fnrB1uXDY1SMls2dfsA5QVD4DcBpq6cxGbuIemrUyYgcsc9ykRqnLENSUJ4a7SQziOV8pQ8xRnR9z05BcvtbL7mnhg6VlVP2xnLdPfyChdlV8hMbB/mUUah4ChuCQunnMZcJ8cufVm8LXc454/nzZ+i7TuqXlRO/egL78vISRIT4O2UVOaiZv/s04sDE+ptcXdeZblfmkzFNszk4o6WIVhrvpAknJ/d9bw5pi6pPCeM4Vqdy9b1xHM0hTUTYbPik9RdffIH33nsPMQQ8uXyCcZzQdT3+2T/7Z/jOd76Dw6Gkbv/pT3+K+/t7XF1d4enTp0gp4XA44HA4YJLgboAzn11dXQFgJ/319TV2ux12ux0OhwPu7+/x1Vdfoeu6xcn2/29dCqu6vjtgVF3xn2oeW0n/IqfxZxT5VdORVRs+l1bigEjsOE45Yz8ekSwNuTKXmlq0uooGl6sRyZ8ib9+Z57k6KV/GXoJdHpKJH2oXxKexh80AjEnS5Y+AjKmXDRFjRFo74XTCyHu6c/4Ps1uGfyZ27JX9wieEY4igyHNLiQPqp2lCpgREQobfNwFARAicJWPbS5YH6dbrq2YEd7UlHzn6h6d2wpB4ck1WiNu7rOPPM57S8eOvtQCAVifioEQgBs5GQoHL+c0Tl2C5vrnF7e09bm/v8PrVG3zz4g1eX19JCT+Wu4ZhAOVkeyKAU/qyTWH+pcLmv76LAEoglGCYIrNLBqEiLcgrKoeWDEN8FXyvHbwiB6B2ZrS0gmViDW6M1i/rKC1OBBsvy+lyGkxPUyKKTF2XVSGCJI9sMvShxseffw0fwN1w4md34sbD7N16bWhf1sDP+oSpbz8AiARMssbTPGN/HDHtZsQYsAtbdF2w1L9dFxFiJw6qwkNYhSE5wRsdriitbLRix9P0XQJQlRzRVkKo/7kZF12OYTjPU/W+OeMg+lCVwQiOHzr5yeMtydOhWRcqg8+SPp1yRj90GOcgh9QS9scRxykhoSx7F4CznhFBT99S8PtCmje5YdVq4G5oG4xGURogtRG4TEvG983Gw+MgsO3UDGOmG7Sd2SuLq8atddnCmaxkNOVZTaGfM8PTcEv0bMs2lnl0fd9hsxmwHTYiA7CTKxOsJJkeMoDYTDjL1fr+1JEwKpGklhTeHTnAgHSbcqO1nZM0KKXY0ULgLLStVBIkS5lmxrJ9Y/tHUSyYnZXfi5I5DZYtrhp9ZWchBbJDW5Vr1A1enLGA7D9nK1lotoQSGB2sRdH75EBjSlBXCafndiUvVFWTPj1XUT+RZu6YU0KaZ6TMJUvMDiYZmDQokvW5aHYRkDtc4OycRXexRWD9UG0FuvhUyw7vegXA5OY1R+QwdBiGoS5VgeCWLpg8mXPmA6lEoJRFny6BqlxG2Z16XuFjMBri91pxhmt78zwv1tv0k1Dz/67rgHkCAqwUVu3fotItljLm2+Drx3fKKX6qrVNtB7SBu9HKVGoqdY4XI+QgB4Yp+3glx5MaCleVnijiUTuUB2Xt+snq+ZNzcnzjMW0/7Jd4HM6vqARLvHlUS+/gGP/825/ieDhid7bDfDzgahqR5hEhAON4wG63RZ5mDF2P4zwBFCSKnusBpjSDpohEAbHbYs4jb4kYLMUEckQgwpxTQZaUME+cSrHrOlb4BLNj5EiegAAaBBBEOByZYHWRME2FaOWUjaTGPFr6szTP0AA8NU4BJYKDPydofbyUEoZhwDQl4Jhwc3ODGAOOxyNCCDgcjghBFPg04+z8DE8uL7Hb7ZDnhKHv8eZwxIff+hD/4//J/wb/r//87+NPfvjbEvUSVN6BN8CpkXi/P+D5e88xzRO0BvXSieQJ7Wlmq1eNlA2Rrtp9AEH8/vOfKzpY+lkguxIXCrYOyhAea8CwdvUdPNDfQ9ca5WjGqkLdg+027agwnZt79o2KAKH4P04TxmniJzWqktb7VYFABlbmL0KTOjpqe6+PpOPRXA4b/Kvf/qhp02ZQz8d/ID+OgrPLR6giYmuOQIKJwECDwy0B1MjRfujlBFG0tDlFcXDv2/5YwjAnrns4zxNH9drei4tx11fZN63DrZ7rifd12eBwQj6Y80xevNwO+Hv/yq/j//AP/gnuU1G43soVbHzl+wldwj2vKef4pfv7fWF6hoftviw4aDRFYWJ72Jdn0JGIMqQ00GWK0GZ9F9yLwD0s4r7LhPW7CeRvIWQ6ToPrEkoF98tea7FDaXhLF3VLWcTz2u91LzZnzUxRI8rqLOyVIlk7gdKmmg3yOk/GEWdEAiQCukfOGZthQC+BZWmeQHkG5WAOqxDk5DJkx5AbrCq5VI/L00onptpG8FHWlkJa5yRY4LddsACP0h+jrNJEVRbd0IAaN1Sxd6nUdV7GpIncUpQxknvfB4FZO1JPjkjfK7TGp9VLOTEdgj+x7RQHh9PqpA4hyKlXdd6TgbusR5OOkqjKQEGyTgEuWEtwoyyXUGkxyOesTkg2GPZ9b/S37/qSUpmonFgjcmVxylrknCQ1HRuzMmVREjjoYDcO8NdpuuyuB4mw0ygWdLRhbGuXe6bl6WQ4EgyulLM9a23bnkCphe6GvDad9n46I8sE3+3XKGLj8G3fe+Bq+b1XMN8G+4d/V7qTgUCW/QBgOPRdj7Dhcfc916Tm/kn2NcvsOQTJaBm4HQBKGKLINxaASaxw98Ng/L139XnVNGKwqngm7/1se1N5nwk+UPoQBFA+eIUAq+Hrw5XUWW5b+nHAW/89lPWWIQiMuVU9Db3bbtkhY7S7OAy7jg0lvv2+7y0Kn2uRsyEo5/Ku6lV835/sA/p+AOn+DsVhSVTqaKrxZrPZSD3we2ubHdJsAFFn3+FwsH7SnPCnf/oFpomd47vdrnKg/qN/9I9xeXmJ455/2+/3ePHiBQA+5fPy5Uvc3t7iyZMn+OCDD/HZZ5/h93//93F/f48YI/b7PS4uLnB7e4vtlrOD7fd7S8E+DANub2/x9OlTnJ+fI+eM169f4/7+Hp9++ulbFvLhK72rgcAbfPzvoVACvSrdAbKnIpAToe22CpTV/R9LWKu163QQ3acaFKFBC8dxxDTNlRGFmn6U1+lfnz6/DYywObp7p35rjVjalp+fGvra5+d5FiMyz2Wk4oRmGUGDvGDGu9ZYxDJBdicFPVxDgcWKYclkOAUuA96Msx5+BUa5yJ0NjPh5trN3XYdOyuL48TQDeFD3XbZd+qwMlSuXwvyU3v4ujsH2/cca6E59N4n6ofm/zX7g2srqB4DKfhlTSrg/HnF1dY2b6xtc397j+rqkTb/fHzHPyXQ5lsMTnP3Z5F/N2sFyGuvF7anHUwbdf1Gc6EQJqE6OF9lIw3pD/YKwYOG5RGBHeXSPOAe5yV2ClyqXqT4UtCcyGubxs9q3YEuBntRS56861EKMyPMEkuA8XTTyLYRs9IJifWL+lC2j/e0x9q5q3amhmQ7PdVz+71pfq3uiaZejFTPUEba2n0Jgw78Pd0qZ7TJazmmaZy7hZWMAhr7D3HVIUrYzi84FV5u74oOonbO145/sv9lSAhf9jZ9vnV8yEMVR1WWonZ8GW6CqWe4dSNqPd4oDocAsKI/2Yy5rUdK+M4FRWTZTxjTPOI5jyeCFgEDsGB+iOm753D75HUY69iJD+CuUQTQ3BA6Qk46GUmLrARCya1M96c7uQk6mLuuACod0TRX07Qh1Xv6+t3m3z9q62Wn7Iu/7iYUYORZe5h1jlNO3E9C4nkkc4IIhdmBKtZOFbmZ0zsAIJfxLPhos6EDhko3B9PaM/VU6V7XHfCLoCfEYygEjzSSkzwRYGyEEc9inZk2qz0ZfBHa6rnaXyvNBYRIkoIDbDyhO6tJsbuwZbbdsn4hBneU6dsXuUHQzXQeHGhqAk1LCPE2YZgnMzJwda04cYhLEPkdZAo1jqdGue5Y8DNTZTRD+EMyp3k7F7DK2jo+RMdzjCFUq9Va+7vsew9Ch6wMmck5tlesNt5z9SYI7A0r2KX2vonf6d41urIgZqhMSUQkoo1pOVj7c970Foap9LCAidkWvNXn7Acid4pktf1vTH05dp+TXBXwaIKQ5SbBUAMmhPoCz5QJiqmllAuVNRn9Py6GP9Ye1Mo7KnI+5flly5Nv8dyVw65cnrz7aMX623WE6TkjjjCly1F4MEVOa0fU9ON0EMOeEnIF+MwBdhydPn2FKGX/yxU+wO38KxB4hBsyznAbq+GRHyoT5OJtAo5tMI0ZSSpgmUQZixwRMFL6UEqgnwQnCfs+Ks24KPb1dkFkVhoS+HwAQIiU+sZ0S5nECABwOe3GM86Icj9zuNI5IOeN44Gj3nAnnZ2cASvqbJE70buhwd3uPw/0B52dn2A6cwmLoevzohz/Cxx99jB/8hd/En/7o97kGmCjUtQDCqbW1djvAJ9KHfkAmTeEdnOG5EDF/tUyX5fJaOC5CnxIDr9AWmc8uoTK6eYzIP3DZhkGwGjzVfc88pL1TRNW/Z20ai1v+XuZpU5VbZUxO71rvg96yARVQRXOtBOfgnqEQ7GQxtW0AmMbJlF5CsEIkuYl2JdTpxfwPBRoOptXc+LcQgLOux9/7rd/Ak92m+V3eV2FqpR/VMQt414XntQRvFkVbmXtWCGtgYYqIU5UNw8CnMzqmK2rgYqUhVnhTlF3XQy4MkwWnjK7vsN1skDMrEfM08cmwWlZyY3bDa9akEtDdWgO1kM5Csnyu8NJ2ZNXz+TDgX/vOr+Dv/+hPFzW3ue32hDCsFfv9bYykkm0ZRvv9vt7jTjiu33P0oPqxEvHLXaeUtkqQfeQHrRlN5+51mxZWp2jhw/NuFtqtwkIYASQlVUapNVs7x4rtxdEDa7pZbA83++zaoWKoVbq4LvwoPfPvotAfT+QI4m/XPhU/yNrKOaEfuBQIgU+Qh8ABbznNQN+B0sxpOGX2hQYzvy24J5Vk3cS8glZopEIyG/6Z/gXdSwF8/qk4/Jn0Jmgk8MIQ7GCmJ69V0SJrk+HjU1ib6d+EbDLep4rZ8hS2pFB0zm5AnxPZBW05GLJ3zZjtDCkFVVRR0DkveZ6O0ZBBUNnXyQuQiHfhFbEraQrZyU4SFS9GupxlnZ0MkUvdcnZ+9NVJPi9/cfYOl+pV6+85MSRScYoTEbyZfjcO+Df+y79kzn8+GRWdXlD2aEoZKc0Yhk21r/p+cN+LAUqjzpU36Al7zirCbaeckGY+IThX0eJeaeR0iSof+prrwJJXF+WmjR6GKYaFUkSjieTXFsAf/8+vkS4I/T7ge//nZ7anAiCp8IBpnhd860/+F7crJ8ybK8DRuIZZrbAScmSz/llpaf1DUdhL4Ivy5s12a9Hf3mlElBFix/iYEigDXR8A9Ag5YSZZN4WXypuB9YJhGJjeuAOrthbKI2Wc6nDXdLeTnBpYv8S5bhHfQne0vmUoRlrBwFISycvjDYxOXsozV39QIR0GX8p8Evv8/BxpzpUj25+wVaceZIzqDPfp7LjNIm9tNhuM42hOUNXf9L02vZ6uac58Yts7wrWP169f4/Xr13j+/DlCCLi7u7MU5lomC+B9+kd/9Ef4+uuvsdlscH5+jhcvXuD29ha3t7c4OztDF1m+e/nyJY7HI169eoW+7/HkyRP0fY+nT5/ie9/7Hu7u/gQ/+tGP8Md//Me4v7/H2dkZnj17hnmecTwe8OGHH2C322Gz2eD58+c4HA44OzvDE6lbfjhw7fTvf//7uLq6erQx4tSVSU42nnqgFkRPyF3yE7lVrXQrz7NDdUdxWoVar1MgqyGtvl/kUP5vzpntBTGCSE+wNLpMY3Rq8UUzBiyMXs17lQ6Jsq9POWbVqOZ2jH2XB4wmpJzRBxe45ei5lh5pg9YL/JcO8rXLG6Nq8VNlFLmnz6P0p+VNYuSAH6ubKWvHz3qYQPiEGma55VN6QuU4W6X9tSPoXY1klb7dvGMy3M9xrY1jdX7NvL3s9tB1Wh5v26nXklkDYZom7A8HXN3c4MXL13jz5g2ubu5xfXOHu9t73N3vJT5e9SVmErYO1bZfBm39giTol36d2h8rT7qxF92Fn80o6dFLGyY/6z3wacqWRnD2BXeQAmXvK0EzkcDTtcZgqw4ApVF6FQclEOT0YUYCSNN7m5Ymp0Z5LuZkcXDy/PLUddrAD51ZbWOTH4vzgNDieUs71+i1ZqsqjcpHva/0tcmeUeQdAiT9vMlsMk6Wt9n+G2PEPE3I240zq7FTinWXgExFRgwB1enWIhMvaYDfvjWfoEqXZHk6VHtLBXJqYKABFZVcpzS4gnEDbx1jtdeDk8lC/aKhawmSFupgcleWAINpSkgZQOxYFqCADkAMJDpU+ScI4qoclZPD1ToC4uitsyDpGJiliAxNZbxeZ+N3VCIW3DL7UpFhi9mkGYUpwwU8OiG/v+03AsrpcOX95cecs2VY8kEMdZfleR1NjFwugWUXteGs7Fmdm9NF/YwKb3fPGl6vMV75j9A/dh56flZsZt5mELQ9WQ/OXBUN18xp7sBse8HhqrZWaI2nJ62MWRiW2nSX8LEKMRx4r523DxMq20jFrQ1tyD8OXfkajoq/Mnd3+FAzRWngLjuZXX3rUHapZuwLFIAIc9LGGNmZrIErMgYJFUJELPqXwyely1TxwbIL/Zo+dHn7VAU+YrtPr5m8rNRD3Z/ne5nUj0bldLa113Swyq+KTNLSPsVFzxuIyNZY56KOcS2pRW4trHwGnA5R0YXT/Kz9/JCc3r7zLldrp9d+kj/0sjLGk201z4SK2L19LG+7OJ4vmJ63bL7t/+eT05fzWF+fX0Zfa9ejHePzlNF3gxEDHdpxnND1hP1hRAiRax1tBuz3B8RhwDERxhwwzsAAVoaRgRB7S+sCIsxzlnql7IhmHGaDbEolRYOmmZjGCSHyvXlKoEseDwG4vT8gzZwanYhKOjUiO4UEktorFJBTwp2mhp1nTEdOh8YO8NmEsaHvBVnZETL0G/TEG3Oz2ZQUEzGiiwMToTkjIoIycHdzj3vcW8r22+tb/OEf/CF+4y//Br77g38Fv/uP/lMcx3sM/YYN1SJ4RWGI4/GoGMBEuh8tXVYIVBGjBd9wCn5wfz2hq4zogLWrAi+56MrScPnoI5FObjI/xhNKJhOLEqG7RqgW0XVOCF3rq0xqOZaqn+Cczivv+wiaWjlaUNz683JBTNBRxYQZZD3HcRqR0oy+74TBF0Jdu9/ARv1Ay3HrsjVDrMfDbf/Vb3+CJ7tNpRx4hl9G4NSKhrGJfrN6iV/fCS6lVRWsosG+Xncl8l0XsdlymiIdBQuisUTvkp6odI6q7Oo6hfKP0wVxHT5QMSrllDlwZzOUkyrT7MZWROrgx1nAruBxRLsoMf6qmWNBGfsrT5Hr87/7nU8wp4T/5E+/QAxhseyry70mm0OZHS3Q1BONEIB5njDLibBKoXXMEjpfKo5Kfj/YnCosaAxnVa3y6m9DD9yp85onlknURrklAJYGOFVOqDKWoHqu2dI6T7chiuDd0qlTAF4fU2tIU8WoRMx6NQCVMFntWUJzr/5eFBlpXyaqimBOs9WP7ayuG0A5YZqO6PqITgBDolhl3kwmPPlxKRxrGDjBV4tLBZKIVDlJKkYSUM0fQtDavSr8EuBqXmk6LM/jsqVIK8YaViZLbaRi9PF1tIPB1Cs3Ssf96bZM5dS98lFVJLW9AMLojEplzIXmqdFeaRfPg7/7Wr2szHH6caVvvFZBjBCFa7BsUVJ92fyE5utYvEMyWWR02UchRE7bR4Rh6E2h5nGLYz9GEGUrj2NwDJoamwy/lbIqH1B4VVs3BHRSdqfvOVBSlSKVUQEOJqRMmKc9Us7m0CaI41sddfI+y5qprJ9f9+B4nuxr0nedwUTTz5nip2/YxnOGbOXiAg+iktXIcMC1YbSJGnrfEHv7LZQxBELt135XPcIakXff9v6p31umKeO0dJIBHOTmDKqZMiJFczQrP8k5o48RXQyYIywAJXYRnegYWYLaCiAziLiWuJ4q1hTsbjjQc+MUdB96Os6nrksKzHLqoLC1aGvrcRugIuPovg7cRnLrny2t4Pp1+pcV+CrM5Obf/B/8TXzrW+9jnjnY98WLF5jnGU+ePMH7779ve76twRwCn9rmQGXWsdhBGc0hPk2Tvb/dbu0UdkoZ9/f3ePbsGZ48eeJSPI+4v99LauCMw+FgzvTtdovj8YiPP/4Yb968wU9+8hP0fY/dboeXL1/i7u4OV1dXmJ5NQOQ1+eEf/Qg3Nzc4HPasY44T5jTj/v4ex8MBwzBgM2zMwKX9vXr1Gp999pmcCL/D69eveI2JSm1x+f7hhx/hcLg3x//d3R2ICC9fvmSdVHROlRtDCLi9vX1oxd56kZ5eXvnN6ytCept7noIwfY9wp35U9iGtS6dmuGC8W2U3C0LzMlAu6RnVWWVIhyK55gwMgPHreWRj4263K7KanihEzX+zyO8aTKZ9tenIW+dnXZ4qGu3KVM7DAaUmbSsjSaP8R38nIHQclIUoRrqo/ZGd9nj4MulsrcfqOaYtwcFc+QUMRqbHe5oH5q+9SykJQMZaTt4pBQPgDLPLsXo5YU1/f5sh8UHbwDtdAt9WmOXOF0ayVmtdWx1vWPSyXyXvFDC4TlW+Dv5W1cYCP/WeyDcEpl23d/e4ur7Bq9dv8PWLl7i6usLV9R32hyPGcZbg7V70vexwHYWPBO8U9rKYP0GIBYx+Wdc/P8MlVX9Wf+OebN3cLVS6EmnGJHaCkMN/lfVKu7Kv/C0IhXNyoTnwcjK5UBqs5TgSuuru8xhVdghA6KRtdSIqNS7039RV+VLD/aE9tmJT8zh6inR5/djGLe/mBJLgqJZukOhvRYepnyhgLTqB8S356GXxGDvj3Rr0o31HtedImuMSxOsc4Z5PuX+6hfy4VM9aOtFdQJmjOx7vjEwDQNAgS6GbGSgHzct4at4VCh66vR0Q2DZcVqPADeBU9ZKpgCQzWdLTnVLK9JBm/Gzec2BXZvkgANhKa9X+URgJvSWQkxlaeC0vlYvVBm0BplD9pn2zDSRwnMb0l1BuuH39EO/mlms+oO1l2WPe5sP6ZII6/wymrukY2HaY3N2AICWbAtIsM65A1WwuxceVX4uty7nrCZIRU5fG4a/Ns52+51FFlvNj0HtmFw01jgenPxT7fGxwgQ9UFPsEoCqR0ouavCjuFhw5eYUi07ThoYoBAUxGg4NrNRaFjciZ8PqNgVrnzTblgIDjdMT+fo/jOJbydM7JrM+rrUcXI8hvXcdZBMY4iU6aXIY/9kcBsDJgBjdyOKDfobKXwzkni+vnlt2GUBzEbXCV+q36nlPocw3iwDCvAuy4oSD+NB1bNL/aUiqsA3kcTTOCKzr7inwQADkSUR949P4Xy2ymtAu6ByUTYQBK5hyCZaQwuusWv4FnLbtRtR6Fdj+uHFLtLyproSUI3JMSfM/Na+ycBsrZ7tFFVrqq9rLFbOoxPPa+h3EZmXQJgbajPYWOBaOlvq2H+lz7/VTQwik58rR4+e5y56Md49OU0Pcb7Pe32B+v0fU9ur5HIkI+jpiOE0LoGWA54DiNuNu/xg9//GMMmw1m6nB/nBAkvVhKGXOa2ciNEuHWBVTpHmIXLV1D13WgQMijbNQYrNZXUciA/fEI5IRxmkxxHgZ2bpGeJJcT4uM44f7uHn2M2AyDnKTgFHnbzRbz3FmET5olQqXr0YUOKZSNcn+3x/FwBAKw2WzMKZ9DZqMESS2jlDHHCbOc+P7DP/hDPH32FJ9+9jm++upfwo//4L/AZjsjdj0TZWGwPQIOR66pd3t7ixii1TFj4zahcwaOgnRum8hG8sx27dINXysXKgw3jp53uYy+r0fbts165zgPvwg1xbCM6j0v2Nh7a+Nt3vUK/amrJRQ+Yu6ddP1mo/t7RGTR/bGLOB5HNzZ18IpgE2uQFaNsMxgL9Tw9HCLCf+/TT/Hf//zbUHqnM6TyEIpg5QiU/8nmBWjkJ6kg5popQv0awfRz4v+GAMTYYbvdoB8GFn7EQadO2pwyxuzgJcZuxS0CKibUOr8A2J7q3AkqPaGy2+1AG8JxPGJyDvLWXeLHroKSx93yrJ9jIxg3go0JfU7JCAD+xuffxjf3B/zuy1cLOL47OxDnuLtjnwXHp4kzZpydnUOdOLquVZ9rezvAnJtOChUm6o7s6TvWTIGd7TwT/oITsFC16fsvs6ppTwyapsmvkc6JbJhrdGhxLe7XStTjrlqsWSqNviudpwtIyjX+IdQ4pz1os4pHClcYONWQw39TmnF2dgYQf2bFj9dxniYcQMA2Y7vZuhpkZeglbXmscFsN7vqwzqtEhnIfSU+Ay+UjdTmbw9KIroYvLx9IL3ZPneOmPNqYyHC2/azwZKe3tJnVkA8RVGtjtRfmtI4xqZQJPfVcBPrqWaiDW1KzmuJEZTHJ1QmuFrs47CgTYh+RZpavYqenwiF14qPUlyop9ihn7A8HbDYDNpst1IFrzn5xfGficjN8Qi1KFgUghB6WHjtHdJ13QidbfyKpAYZggQlKd1Ue1DR2KWf82Zc/LfAGqnXUMSEUXqnwKuTE0TlVzjzcGpxB0GAPoIvMI1LmDD7mtEBpP8NFt8PtOUD4cS1DVF0v+J8ziiyfLgN8NLFRxXD9otcB4VsLYczI9oKDNby/+fXkEFyPCAiWJhMAQoh8qgpFpKmMRKS0m51lsesQQgRBUhlLcELXdcXBDgIJ7APxCs3zhHHqsBkGIGuEOQnuKm8CYKdnSZy3e6Q0F3BWyqPoMlYLnelfshrTakTh9NgaGW41t5Vm6qmDU6ruAu6tJCF3V2SJaZrtS9/3eO+993B/f4+UEvb7PdesJbJgKIBPY//e7/0exnHEzc0Nnjx5gk8++QTs9OVU4zc3N9jv93YCu+s6c6SH0CHGDr/92/+EU1GHUs/84uLCdLzLy0vTc87Pz/HFF1/g/v4eL1++xM3NDVJKuL6+tnaJCPmSa67llPHFF19gmmYbf98P2G53GPoNXowvMI4zhn6DnAm73RkHccdOHPd7/JN/8rs4Hg/o+w7Pnz+34Inz83Oj53wCPElNvoinT5/aafthGPDq1Stst1tcX18j54ztdov7+/vlGr7DpWWmgBrfFrqTBFSY/Bna94ox2mwrKmk7PRrSiqeMpxyeMdRym++rtCslDzLX5UQGxv2I2+sbXJydm2EsE/P7PnZGc3LIGNMIJOAwcXCDZohqnTwtv83KwzNxqvAQS9XzXPYMoU4HaUZPmUWu2maZtes69EPPgcuBO8sTgRIbiBEDyAy6ck/HGfh7DCTZANhWQI2so3K/Ofp17NJOVntJA/uSTWFruoym/wQiUj4iSOr0OIsBNCR0ketdl95qfdX0pkCYaUYM/cLIurYO+pvPMvG26+QzImdVzzbcVIOFs3Jn0pNE4qiQ1MqctnlZR4TnoPWno/VBRJY1jsXVDgCfZvW7xTuiK55u6XhZnshS8/f11Q1evb6Sf9d4+foN3lzdcEYmIfYsD+aCtia9k31juNXzKARiTZdY3lsLYHibcfNt17s8W/XLbzc31vBiOcfQ/oS8/E1lNd+H6S3L1u19E/4d3az6dPKM6z4ECZxsy0BQsReAksQFd7UMqboLD8ANBkbvq7EtLl++JNdgFV06EAc1k8hIIYq8GliOsfHmDPi97vQf3zDlaQV67cVpto2O+cDIkIHIlco5JIpPwc7TzDJe7JFCtuzbnM00IIFpdiSSAOhcZcHSU6GqgykPCAoLyuJwTwrwshbemaGbMcAQprVtFr28BEJkkpI6LpBYeUzRMsn6DSpnhlIaiJ8VnFaalDMoz8hpkmC6CKQAShwYPE0ZL+cR/2y6xsV2wJv9jByAsz7if/fec1COLssB86SACBK4kQTBddEnu1e9lOqslojwQaPmVC8GCCblWj5ADp3xIRbJE+ZtQURizpR2xC6lgSaGx7ZPyj11zC9ph8hCtmcY9zPNHPChznFko+f6XpTADNVJGA4BER0IAccUcJwJ00zY9uVwX01X6OT28HRY+akehkMQ519UG2gto4TItc5zSozTooewLYvlFVZtilPc7EFiC+DyG111ilm5DQf+6t6BrVHWrFgIADHvJOKda4HEUex9ZEsF6BpVsmwZk3TKOpwbB1AScck3IPSGd6q8BqFRzMMbHUl1raABBxL0SMBhPOL169eYJy5bqWUZ/LMkk9cxDD2X+2J9oMcwbNB1He73e9Mhcyo2AlK8cWupHEVJKhmfIdSSRuFTZocNHjqw9VjyYJYpUkoYYodt36OPEZgjYr8FaAQC40FIHRKOmHNC7DujN5XMrPuyi5KtT8db9rYbjqyr8MBQy/OUs+j54ECgeFr/0dJ8oeu4BEQIZt9SuqXzZfzXURR8q/WIAmtf6iIID2zT0T90mf4MxkENLDbZQHDJrMUxC53l/dN1DIMYesmSSQZH3bhlF9YUTufxtnH6LHH+agMoIHbOwjfLGHxgQ4hLeVrbs88oGFoor5Nh4fZW8347J/4s0QQBlSZQ1N/Hy5+PdozvDzO22w6IPdJEOB5nYEyYcxIDRcZ2c44Mwu39Na5vbvCzr7/GmDK2iVOlH9JeCG1cGD0NSbJGujEC6OSVSFPImDLX2lZjsda+UIDNc0IX+DQI18TrMI5HTDPX+em6DnmecHFxwU7srsP+7h5aZyGA26VxRugiZpoBUShTzsgzmXGb04IG9LFD2G4BBK6rLka7nDP2hxvkTEjjDQuSYYecMs7Pn+DFiwl//+//fXzy6bftlO04TYiZ0KNHoCIE3d3egAAcDkeOkDkcZf4dhsAivydSqgiuKiShNrcV56ESioKytVFt6dSGb8NfLdZLh0EYYjDKuBxja4zx7ZvDQZmcM/K273liqmNSQaRiHo31cG1+i3teLzkBE/dA+egYqDlOZCREfCJTicLxeEDF0OjEeuJxRNrG7ZoIIeCs6/G3f/A541pQcBQB3Y8xiLJUhCmdF7etvk8VFrRLHX97kbXqv8MyJSAAm80WG0nfrClpABbCjsdju3ysDMTc4HIBADNTPzJmVLOcIPKRaHoqKiWuMXR+do60YQOyP0FZ6vq6uTncPblu62Cp5rQQ5XUvBeB/+KvfwY/eXOFeDfXvcHmGQVQEw/YJ/aOnvC4uLsUB1TKnE30E2GRKwEr7Xi3ItUpNGWP91wt9ywAbQUrftF+HQoKW8yYflY2C6GvtoN4LKnS97VpCjKofwin8EcUddpqRxxfk1ORij1fjRkUH+T+s1JrySGTOvSQnIDYbLq9w2N9bm5QTUgJynpGmCcf+gM0wiKOKe9WaoPM0cWaYLEbEnM2pnXO2etop+WAVVuSGocduu2FlJcDGy0MtE9VAOD9jT1u98sLvllPlZf2WAjIrmlHQwhlYhVajC1ZexgtzAeDgna4InlVghhmJ+W9KWQy6ZPdZoWQHoDfu+DGygSUYLKd5RgA7vTQloeFUDOxkdrxY1zpon2VzYrvdFWVN+Q9l4wE5Z8wTp5Xe7zOAowQuEFKa7RR2ytkMVHxyPNvJtgyyGuwkuMn4VRanZP4g3N/vjW+UtS/vFrwWo8xiKxZZ4tRGMUMh1KhTC9wkJwOLkhwEv4hl9KAG9HLaT/lrrGpm1uMKWjqgJgXusyNaLpV5+5ynXYSGP+KBAMc/C0DrGG/HovANTcc/7yWD1ACNLkZz4lCkYuB0ChHX65w54ENSBo9JsjSkDHQwZTZrMCEARHaQB7Bj+ng4ACCWqbO8o2J0qPFk1lPO42hZCRRP1CGu99SAlQT355Q4TTGCU0T5P6oXGd0LvEcfBO3JH3nV/e7wfCnNwFc//gr393cMM6nbvdlssN/vcXt7i8PhgN1uh+12yzQaTJt+8pOf4Pvf/z622y2++eYbxBhxfX2NeWad7eLiAtfX1+j7Hj/+8Y9xdnaGy8tLPH36FN988zMcDgdM04Qf/ehH+Pzzz60m93a7xW63w93dHb755htst1vb7x9++CGurq5we3srfc3YbDa4ubmxAGRyCLrfH2QNuCZ4jNFqoz9//h72+z26LmKeEy4uBnBdcz6tfn19gxCAu7tbfOtb7+F4ZB3r6uoKx+MRm82GYZIS5pnh1vc9vvnmG5NLx3HEOI7YbrfYbrc23o8//vih1fy5r9pIcFpG8UFaa3Kp4p5/J3lHyANXQJFDWueMfz+GHps0GB/h4HSuB89inLwr73Ri1MrzjPFwsN9KPo4lLPxnIkIkxwmEBgQtbeAZNUp6xrZN/0+DMfwccybEjtuZU+JyFSsGKQ9K36bqe/5fO5dgNVmXczTjscwBVE7xaP1Fn15X+6iDCGGnbBYGav4VROulI3QMvoxMez2kny4McNW8H8dgVuVA02eXOO7bTpSgwQcqX/F8WE+0lLQgZPlfQZ0AdCoc8V6glFkmk6yk3DcARARJsXs8Trg/HHBzd4eXL16bI/z65g53d3vsD0fMcrjj0br9L3i1TpjHPPvQtUYD/v+Xyqhvh4nq2EsjcNveI3tdSQXdtmL6Bkx65rGIfcH2OWWWyfim/bZsltaJ9dp1yoZAJSW99qBBdZqxM4hdGeBT5R1gWWc6oYEakNd1fVWiSO0GZpkgCQwwOlGybtW6l5v3iWkWB4ubosnNmvFTfiMPAio2mVA7xk0T8GNBWZucXPr+EKyu9ZxIDjdM6CNAlMzmEwEpqcY6t9qvLZhJZFUdYG7WOvuyQiSBSQRkf+I0oKK9pjeJA131a+4rI4fYSLKyPAIrtf0GFN2deWGj3+hH0/dMWHF7goqNIEv5s1xg0KahNrxxF69MMB5LBPxH/wnhiy8J//7/1OECCJnYhhNRAsWK89616eUCGXMMAZ2c7vX2UJUCYuQDfMPQ87oQJENawjRPmGbOQqq1s1W5j1LmRvngMAw8J33OgFlw0GwqqnsLIGpc9lfxMaheWnBXA+9g/Bjym2XU8P3Ysjo5ymvpTgGqeH6A7A/NQFZ090yECD5odRyPuL+7xzSOgMBcD1cRSLJVsG7XDwM2mw02mwF914PAp4E1k2mSrHpGIwNEf3dpvvU2afk9D7UGL9y9JZxp+TBgPrey/wp+WelRsZcorqltQfHCy7zznEpJMltDoT9R4d2OreyNh6+C9wjia4uF3qpd3rKXhsC+FedPbDOeeVg85mpl8Hd5ttWl3I5Zb7dZ7DVaYG01epu/v/bs2uc1v9qp9/R6KKhVdacFTTwlR6rBDjW2FlNF0VXWrlaH1QAx9U8tn18fxtr1aMf4T1++we5sh34YgNBhfxgxpRkEjfKLOOyP2O/32B+PuLq5wUQBoetBQdKNEUldWK77aDVPRIlkRblEFKeUyglPSgBGrrEdWNnrpE5kdsw6hIDt2Q5dJOQQsBHHVkGkgO2wQcoZXQx49vQpdtsBX/30Z7i9uUYMEePxiL4bQLFDREQXIijMQADyxGOIkI1qxrGIYeiE6HDK4eP+Gnl6ib5jA0oOCTlk5PQGiQJur17zXCPw8uWX6LotLjZ7dH2PYcNT6rqILMi2PxzQWXq+I6eL76I595UoqWIbQoPsxXLBIEW9wbDyvbhG9Y3160FhXblmUGd2+xtWsFaZV4nQ1/Ujxxjbv4tx5Xr+aw53E/YcHinzL2P1wlkRBPz8vaBkp1BRMzD9JDMyBhRCKARdhN8ATpmvDgh7S4W71Vrnj9j9xk2VCRP+5uefWYBJCw51CRhEgr0OlfE9r0dzr+1YoWrPFnWk4FpgGA59j93Zzmra9hKJN8+T1JziNjVdcE7igDGhnprx6fgDuhjk1DkLmLHjcgnoe3PU3e/34FrmvMe6rkOaOfrx4vIC0zThsD+YIOdhUE+dKtSq91X9jomdMm6l8baNVFUVpeDZbou//Wuf4//6hz9s9YfT43FPlXVqFBAdayCbGRFhmkaohdEMctW+0cHXTbXjqL/71S87xk5oGM7UTvJ6slS+VH2Xfd7CZHW3EMQIuU4XVXDV8a3PifdoOEVzVq5igtDxO8GhoTX+RHUNB52rU1qoQNOoGTkDeQgAJRPOM5wlLwSMxwNy5pqem80A0Bmnqc0JHGvGbSVwsIgKSLo39vsDO70z1WN0CqTBpvJpc7vDZkAMwNx3iLKPggS9lDnAThjoacxS8644BALEOSnROzH2Rms5Erg+MRpj5wSwaGgegMr5X5URgVPMCSBk+251j5zmltKMUZSLru+sfcMJImS337KcUobwRRBAXWdO2BAjNkMnDjkOtELgdIOH8cDzDQHznDFNR2uTcSVIcILIaERWa5vEgJ7mucqyoIosQEJv6+Ag236O5ulpe9vfjsa1fKa0UamC5ZuQLV4Chb2/AlbLRNTD4+6krVqe4YAHNaRlInMmIpTxV85zXZpQ+JztQ2foKP0XmqXjJzs5AU7TaTKG/seNXn+rpl2oU7Rfa2lmFSTfOSFLBWBZY9zLTI+8HiDCSeiMGmzYSEtAUOe47nuu/ZYCv9NLBqs4J9EtUm1IDAEgzvyEGTbmEICUA9JdwrDhk8V915uDXKWfnPnE91FPKWu65CB0we13oET+I4DlBTHYeiMEoDKfyC8hVEaLlLKtIbVrZ7LZqUWsAc76Ccs1hzczPvrWx7i5uQVRxt3NXaV/7eVUQ98PGIZBgv94jN/+9mc4OzvDNM24uLiQdOb3uLvjYKlPP/0U77//Pn74wx/ixYsXOB6P7ESeZjx5+gyvX7/G+9/6Fj755BNsNoPU4z7DZtjgzZs3+NnPfgYCcHd3h67r8Mc//jHu7u4wThPmeULfD6I/nuH87IxPuN/fG08JCDg7O8PhcLQ1CCHg/JxTob989RLbzQa77Q77/QEHcaJ3kVPXPnv2DM+ePsWLl19zprHNgM0wSDAXU6c5zTjb7RDC1k7E6+n1YWCYbbdbc46HEHB9fY3dbvdu++ShFW2IWS2rrP9WOVzJy+rlBIM35rCxoUgvD8ku3mxq280pBWzkBBISjHUB4iBkuwFREwhCZCcPNIDez6GVods5q3NUjX1Gc434UdVXO7vW8OLvEXGAfdd3iF1Eoow+chD+LCXZ9F2DZWMoM0cP1byp4g32A9lzBE9ynUwbirM7AEZnyvhrPIihx5wPJTtfjIgxsYy3EN9ryTZ5G4HSjuxK3qHGq7c5d1sjnd57F4dw20dQOW/lmfZZCyZ18ylrIPMPgYOqstBjy8xQl10BEUJKyCFK0AGgNbAz8cGG/fGA65s9Xl/f4urNG3z9zTe4urqxkhLTxDpmbE5lPjB7sIG9lV2WMPp5r8c6t9eMr/88+nnXsTzQ46ps2M6Dmt/edZwt3tlJ3/opeOlfRQq/hyrdrUzBvV70xtVx+PmpnktCSbL+m4EgpZYc7fKyPs/gl7dW1QgpAFBHK9mhpKRyVIzIxIGKIQZsuw2T9Ky6G4wWcnr1OtjIZ8XiLopEzHMtNiSdr7ZpDsoyOigO+SyOa8tjn4nQhU4M+EUQ5iCcYHK/6pw+c1gj5Ysu5u9lw1dF4ZTZVj9OCccxYRwzNgPY0RSiSz/t6J2Msypl5nSQNulUzjOE00O5s5+zyrzwdP1kySnVoWQ95PGoQdtBHNpC74JfO3AGG78l1NZa1kT2Ezl6Iw+QnjyU9tk5Xg7xtZfii87L8ETm5U9SEtwYiACS7AUR9nwrA+nCBMAc1KwflXnzi6VP1Y8YvuwTQA9Q5uOnFuRS2cc18J4zoqnj0cYTCk605KXA0N1saS/VKwKRCUnWoC2Jow2SjjOUO5Rremx81/ao68atLxGZ7UIMEIZD1hsxniWxHyPAnK8Kd5U9Q+CsL7sz1kfOzs8w9KwzjRNnyiBieqM0Rx3PKsO2l6rUhBKowYhI9s5DTtMGfNUXtYnz9GsZqOs6DtyWvqusGNADmkWG5cAZ3hcafGk6V4wgmgWfQtXfzyXTKX9Ckc90zCGWcsuDZlWUNfT+GNN5yKPyGvzpwd8ecpYv9CffltDwk+367yAr6ar8/zFXKzM/5BR/VzmNiAMhfFt+Tf2p88fI7m/7Xfmkf3YNtqUdpSehJHEJKHzoHfDu0Y7xf/KnP2GCHALOdmeIIWAcj7i8vOR6cBKBHbuOI5NDBz6UlEHjBAgxSHNC17Oxue8jZqkrrqfI0fUIHRsp+tgjgJXirovYbXcY+g5dzxF/KRN6SfkX3ULtzi/QDRFnT5+BMqELPUCEod+gix3maQLX8EmYCRjnGU+eXeL9D7+F1y9f4e4mYH93AGU+RRIpIOcRd1c/xTwfkXJCGC5wtn2CAQMDPydMiVOuHO5eINARXTxyWgpS+iTUOkQgz+jjbOkeYpcB3GOawCcRKKMLWyD0vLB9j/F4wJMnTxG7gDTNyPOE/T7gbLdFHyNi37MhtnPKVCjGWrUFFLaEIqTIBszIhRE7wYGUmhAZkTF8E0RFI6yT+y+kL0DSbTxmnxNcWl6H1KEguvW90p4K/sUQoj/4YTmhyHpRxi8CmRpT4OaoSykcODinTwjBErN5kaghoe4vnzZWATvGklr3cDhAOzMBD8xgM7VC2uOIZzEK8ejOuwF/7TufGJyK8rX2Yv1VmbiTnprZtsCvx+mNW17pCwHYbrfYbNiw2EV1Ss+Ypgmj1LcMISLnhONxQk6ltlflbAlF6PTG6ynpmivtinZKvOs6bIYNqOeaxuPhiCkGTuXeR3QUJeqyx8XlBfb3ezv9qvvHxuBQMMAn2HaOlBUoFwGp3M/N75ou8C99/AH+4x//BLfT5BSix+BDsGeJlhGrBJd2RvDmfn8vQh7Td68MlRcdY6z21olLcU+VKjl9D+1fhV4BpqpdfqxRIaTMEzWtU4FvtW/93cYBl/Zd8Ekf9nTHj8PoYpDxsjBrGRSIKhjYOVRbYBU8Ie0WOtcKZAZXE7R1zvJegEvvXWCmf1kRSeb04CA0VtJKimuy+33PxtK+7xDDFiFCareW6loBnBJ0mmYcD0fs9wdJ2RvstJKdbFaYhlAEdR03ZjNmbLbsxBiGHlECvmLs7DRmFztbU3M+x3L6sghuscosw7+r4MlwYeOJCneamtQ5HEPZH0HaSKI064nwopzKuhIAYtlmTomVpkxOiMzgwxcaFBhM6QuOjgByyjtL+s1clHSO0E3szJ6LQcdSkBOZAX6uot5J0p6VOT188foExaVyF57GFzw1SuW+lblpO0aqAurnyLdR2imAhe1PJU/cgKSrsleE4rrSCHDPhna4gMMp7YYKhXMCeaiG0VBy+0I2n6RPkUv57h57fwc83SjdC/hLH20xdAG/+/WE33+VpI5lkQVOK5rBlQ1xRI2C8SQd4gIkT2vebUtDCsNQXny8rlEDRd4PgZtTeKeUQIPs4S6asYQoAxmYp2w0axgGPlE6z0CnpyciGxaVdlmEs6yCnRRVXJWs/4FrUac5VTV5CcRln+ZJsgNEM64wSEuwDKgYBDvJPMVBJUxDSdPxxmiGvpw5zaHSsyw1DKMb49rVxie8HeZkAcghAPd3d7h6c8UOycRZPe7v7+100KtXr+z0c47KI5jX//SnX+Hu7g5ffvklfvrTn0omn4D7+3u8fv0al5eXOBwOVlLq5cuXTG/TjF/93uc4Pz/HOI64u7nB65cvcTwecXd3Z050TUPOwTtswJvnucrkcyuOZjY0OXmSMhAyhoF5wLDhsljTfMQ29/jgg/fw+tVrdD3w/PkTHI8jdvOAqQOOxxkvXnyFeT7io08+ws3NNeN7BJ4+e2J1z4/jAdvdBpuO06jrKQzNqHJ3d4e+7612+5k48F+9Wpa7+Xmud3XIkEN5LW/E8oUSL5U7/D/AC0Zv67N1Iqu8o/dYr2D8Z2dtOXWja6v4dcrQos7o1lh2ypDlv6/RyLU5rTnB/RiqdwUXtWSCP23N5d9qxrLoToziOWdU/HSVpq8T2hbOlk1m1fjmW+L/Vtn6pN9+GJzuF6BpR5WGZrceKp9wsIrWAC5r7ce/cEYvDFtFJqzH/TDutUYzv4Yhw+R1/Wsc1Hi3h73MEQRQRiApcWP0Noqjm0/ymrpHEVH1J5EJESVIkyBOvBn744g3bzij4qs3/O/65oYzUhyOVjs5kxjh3TqswWIZQLEOn4LTpb1iRgnuWX3GyVhvudaMlv+iXKfg1TyFFSnoxDxqnVYaPdl/a5guDsFTIT3tuHz7RU5f6rHFKabyfNWS2/wNleT0qCpj6d6WdNkUio7E9/283zqBevhvuR7CGpI5cP9NkKipAEyTi9E+2rus35WMPHoAK7isgawHUoGBZktR8Vn0sWo+TkcJprM8ZmYa/AogeLgqDeP/6ClNILgSWq5lNVjIf03vq2yDJEHO7BgfJz68NWyAidh2HgHEuMIzDDLldK1Of41OG26KmqAvsL1BM2YFE2C9OlEZX6zNvOjDGVz0/9U7rX5KStQaXUs/FF5W1t8xh3Xbi2untj+btcD2GhFnDPOkQ9eU9L+qOzT9qH9AW1b4mWnNfgFUElZeRe4JY2JRbQ89AA1uB0Asr3Sxw9D3GPpBUomzguSoWFkvfbeSv70zV4Ege4ox1JYueLpGpZyuDpdkP1mac6FrlJdwEgpVK0WyhxcORskk4+FatWbrpHggspKXE2Q91dZ0fnaG3dmO/UWBbcOGnCJzB5S67bZ6AgdWzd39B2Cj6HYSJf3ri99qWU+XSmVry8BMGSH0djBCA37Ubhhjh+Bx3bWvGd+8g9TLqX6ca2PTz1Y6lho7aTsPBKPVMZRsu1FS02tb5goKMJn2lymrnKITxTYLQGnkWr/ufcon6E6oOP1Cvlj7fOr7qbF6Oc77ZJZz0t/4sx6K8XJlFQjo2ql9PQ/Lj28bZ90m4BFFS+Mpnjw2KOPxNcYTcDweEQDc7ScgEzabASFO2Etay2EzSO2vCCCiH7aWYqFgJBA7riNJxI5nHWuMkZ1RskmNxklq1L6LQiSZUKYMdH2dVC2EgN12QJCaJXPOCHlCDB06EPJ0xNB16LvAp6kCYdofcHNzhXmc8ezpM+zeex/X4RrH4xGHwwF3d6+R9l+iCzM7OSIhz3eYjl/hkJ8AIaLDHbogBrsoAxcOUnhEqAxgnulSFQ2fOV0tZVxeXgIBuLu9lZMJB3RzJ6kA2QFxf3+HPkZ0Ui/MhFqRGAw6FGBCcyXceYqjYy1CScs0ilm2MAilsDWTWSK4ETJLgeOF0hbr/EnplcszCN0cbjpFACEpyUBe8+PnVw0mOtZYM3idnGrPKn4R1/EpwsJbiK20w3K2jJuKY1GNopxNITmhsTSwcES+62XzDvib3/vMwSHYGIpIUBgg2TcffYuipBhM+FMV0QifMYBEUPD1iAuh3O22GHquI9jJKaHD4WAnZfu+Q04J03ysToby2FnhUSLNeEAO1xwh1nUkNYCz472LnZ3+4dNofBJkvz+g73tst1sMwwZZTnteXFzgfr/nQB/KJvKaXIoiRDrxp4KqwsQcHg7+phDYVU4jq0D8b//a9/B/+v1/6mXRikn9XEJARRt4bbnWjq/JExpYo+wT+C1XZlwggBpAUfdcPd9imGJIqfBTz0kjQb3ghOK8gjjBHO0hB0ftsqCFo0mObhTDcRl7oTWA1dFZjYB1SpPSfkf7GvJkAp+CS5WFnLXkCD9Tpfd0DRVhNpf1EwO/OkrMae2cSGpU6PseZ2c7q7cUYwfqiPfDZsb9/T2mcZJU2VxWIM0J+8OBS4KEzqUgY+XMYGuwENhLQFDfb+10+mazRd9zSjBN573ZDDwOkAXUFX7HgNJMEV5oAopxBCinwStDaggC22DsQseswmoIwaKJgyj5FOoaOykz/4gd1/SGRP7PcyqGCwLmNFvN7ywOlpS1vAxKCreUrVQDAHMOBnMesBHXX5Wi4RBMDRiCUgW3FjcLyhqdIt3FZa6CZfJoWNx76HqbmPrW31uBXcfYHGeo5ZLytO/ESZHGp6ofmzS2JcVgG1igch+VXqjsw2c98K3zgN/6le1ifl1wrNldv/HRgM+edvi///gIdBGtoF/zb5EjYrBV0WGTHDVmHKhmuLwacm2kMxRcepyaceIKyzVRR40GvaTEvFQNG6M60AIwCd8FeD8M/YBOar/n5AJAGtmm8AiFW3D9E4hmpDSbHEhZ6/JFRMmeoPTKG7h0vTW9IUJAmicA7PhW3OykHnqeE3Li9YixEwOOyiUlAJWUKRlfLethE3rLVlNZh8DtXl3f4B/8g3+Ap0+e4vWrNyAivHnzxvjAxcUFbm9vORjxwwR0zDf+5E/+BDln7HY7bDYb/OAHP8AwDFYu4/Xr1/jZz35mjvb9fo9pmnB3e4uz3RmeP3+O+/t7k6umaTI+5B2LmgJdvwOw9OrqgGbdsZYBNAMQLzuvz2azkfrps9UMv725Mf1z2AycXnKazJmfUsJ7772H29tbCd4up2HV0T2LXHbQFN9u487zbPXHlc/f3Nw8vEhvuR7veHK02esvIjsUOV1/83LNijHmEXJjS4eqNXEGkvYfEe/dcRyZ4sbOTvcpL277aOf2WIPKmhFmbQ7ttdYOCSCjc4wDJdWgr/VZdFinR5lsVvb7Q2NYuxg+Zc0qQ5TS+yYVfhAZTEO3K+OSyEuDBvVAxy1t6bit7dKHd7Arjunv647+crUymB/T23C90jmqNt2oSees8ymHAQCW06EnSvWdDKQABBS7DJc/EQGIYDKiQYkCAsk54MA1L3MCppRwOE643+/x+voG37x4iaura7y+usXV7T0O+z0OhyMoKQyd40NsC2W+vxDHFXgVfrjWHj/zuBIKPMbHPfcvwtUaU/295skFbE5JO6dWpNUr/H358PYBh7r9Esy00ntYzmW5pwrNt0ddpgNzDqvMRcs2SuPrYscviKKl8dKi9L/CV1SnlGDiGAKyyOQRUpbK0SzlxynXDlffpwUBUIGFhdQ4HYma98xAASUtrbBWvlfOAsDBXeYlp6v1hHChVyv71Voowe5sT+bf9PR7ShnHcbZTf0MH8MfANWzNMR6MximeEBHXaNYSimvQa3FddAW1vRJl5BgRCUDMQObUyK3e5Bp0n/WPHsRAkV/ceExNqwcmj1FZB4cXSx5ZGFzOyRyr2n7VtP3HKW5iM2A7d5tyvuanD22VANYV+q6zZ32ggGnaqn8a+Ix51IEs2koIJYU61PHK+DVsthg2XHpA/RQdBcCCMmobf2uvkhYNVUOznu22kNsCX82617TlPlXirLv+6E+AH39B+JWP3fSBcijA+iJBMycnhVDKm5LH35oWQnSoNk2zZogaei7LlMSWk3OxU5oZwX32Ct0pXLBt2FhUdDhrtLa6V/2+5EfB7YM+Bi77F529mQo9VBKVswY/hkpWr/QHge3DskFN86pfXFvFTo/qWZUbtY44oOVXS2Bt7ET/ykX6JgQr1fS26+e2m6+8385DfzfYufv+WSvZqHODwyssYbd27zFyo9e3Tuuaa+sE+Im1eLHWz9pvlb1yTQ994LdT/bR60S/dMd51O1xcnGGQNMN5Ttht2fG9eXaGYbMBgtZ9IfTdFhcXHFGtdV9SmsVhxUY7rj85lxpYaca2jwiUoQewkAld12MrpxLmecZ2d4ZxGnFze49+iJhTLcQ+uzjD8XiHnBJ2uwHTOCHkhHS4Qxc77DY9ttuAeSbkPCGEhI/ee4Y3r69w8/o1YhxwcXaGaTwgzSPS/ZeIYS4bnaQiShfRd/fVQpkzUBylhS/xe1mYrZ5I84qsLR7YiHY4HDCNfAJ0nifEyKcyAgLOz8/M6HY4HLDpO8QO2IQNhHojuFQShZE5yQ6FqakD2TZbEQ+ggoQKAGpULQLdihKgyq62QEUACiE4Z1WRJ2tU90KlDbLmwjbWMkFq52in74LyOPjNTYQ6JVDFyOVGKH3BzbcwmlCYvm/KbUyOCMz+R+7KpYhRwq0pQHLOnEq9GpJMokaud7oKO+Z/nz65WDxD7jl9R4Zd4YYXyHybKr4WB0PTDtSYnC09UhA4n52dlTSFscM0cxR9FyPmDEnNOdX45vCdEPj0cGCmMk0Tcpp5nDFiGDam6phQRhkdstT9ITllNKGfuH7VMGzMmDuOR9zf3+Nst0PX99iGiGmecH52xsE0x6Ptp9YopbDR707UMUHVnEsqXKKcfo8maBdDjwqMf/79Z7joB9zOE+oNoWsXGuazLli1eOD/goSOa7MyBWXZpngvtipVz3uhy9YQBFCqtxvKtmf8KMI++QdsnKV/iEDEY6mjmau5UXlmwYx1fi5wxfa0XHoyyPcFwSl9Xp1iDoySiqh2jFPzjipu/j2dhz6jTm7Fnc5qR0kNSVcrjYikBAFwf3+P8Sj1prqI5+89s1qsmkpLnQ8AyqloYj2p7ztcXJzj2OtJF3ZwcLRxj92Wa23e3+0roaRgPc89xoihHzAMPba7Lfo+2inEEII4kiAGQl6FlPmE9G67lVPjAEmdSISAvo8G7xIZHGy9KCdR/jpBHy8IRt1V7LgSWGvNNT1BqkqSOnfaGtrl5D33mbOcrjdh0qNYUTgr/DJcJeExZHMJQU6Rh3q/VHscZHuTjQGSrtb4eSNg2n9+sethcfqXeDUNBwq1Uzw4eOh8DVgip/iG9A8t79XdBjEScdtd7Nz+FgeUlzOEbn16FvDXv7vVrFrlUhHrAZb+/Czi2086/Nk9mfwQNJAo1IEZCO43JRpuMg+ux1cR+CTXtHrxzs/rFFdiWzXlfiZLSa0n5kgMPNSkw1fa1/c9Z6KS0w45JYx5EsMOCf9kp4bR5hCkBmys10nXjlBOcqq8R67MREBF00j2ZgjBSjepHKFyBgskkrYbfJJc3+GAVjYeRnBKdY+qtlUX8imhDdiooF21wfM/35zhN/7cr2O32+H6+tqCi37wgx/YCe/dbofdboezszNOPS9zvLq6wtOnT/HmzRscj0e8fv3aTnvf3Nzg7OwMRGSO8V70xcvLJ0jzbLW4Pdw2m40FaymP6rrOTot3XYfz83Nst1uWhwXG4zhiv9/j8vKyOCfl3b7vsd/vrY8QAm5vbwEUfnB/f48YI87OzozvKU5lybbx9OlTbLdbHA4HHI9HOwlOOWPME+ZpsvZ0bJvNBufn53jy5Alev35tKdV/0VTqbRrPh5y7b3cSL2W/h4wRvu21e13jvFN5xxskrIZh8I4/KnpO16GLXfWcH3tr3LAgqJNGnPUxt5e+5+sRvg1+mo5TT9m0BkeWF/ieBgUuxq+0CKd2r58HULSrZu28fuxeIAneK/IEyzIBQYyfpWOVCVj26+wHHWsmlT+0S830o/JNrp5fjr++3zq4PPxKoCOt4kB5TwM9gv3VZ4t+HhZ9AKdryRs4K4NaRIxASoROsmd4dhp035DuISBTh+M04rgfcXe/x/XtLV69ucKLl6/wzctXuLm9x/4w4jjNyHOq+mNcqQ2Uj7TnnbwKbOyG/7F+WG03D/AVnbyVlPpFB/hf8/UYY/cazq1Jtss1ehwsHjOG2kZQf6zoKDfo9meRdfy94Oopq17j6ZD+dkqfOMVfHr5aweURb1TNczpomA4rWeEkZa/KeWpT5QxtYgeKaodlHbiLEeLVKbAkOJ1BiWI2nS+I3BbcuBYwM3uGn3P9l2kUw6Kyyy7UE6Y5Qcb5KElbxqolSsugyjCP04T9ccQ0J8QA9AEsO1LmoHSnF5WsIDp2UkDZXNph8clSz6NKNhGbYQaXBs0RIWQEOaWsCOclcem5us9OrXKf9VsChfgWODlmp3o0+axdMiHriKSk2CwB/7A5tUK4ifYhwkNeQaSyAMNM+JIbldos13RvrfOt/DyluWQCtMcdjIIE4Abb4TYgpSWqu3obZQgRXQdcXlxiu9mac5RyZthWNgWFRb0m2cG1ugxm5XCG6Y+KX5W8seRHWiavEKa6k3/8exEvX2Z2jDcjVee4vq7OaR2rBZC3fFxHRcX+014xBrZZDb3JLnrAwQLu7Ig9C90hCPyz0O+WTgNCy4qWXa3lQtx7G5+uQVZg7OEcLKg4WhZGJ4PY425vy3fv3C3lBrzsu5SPBaxl9Cf4SdEjig5e2RJFZiU3LoSSvalzpRA1R1bb30My65oM2o7vMe+T4XD9e92Y/1h0MT2Br9kGYsOfT/XfwryGfT2vdq7+fa8XrtVsV92gvuLquNac1F7u9TLJmtO9jKe+z3uvwGWpby5h8ND1aMf4s2fvcdq4ietn9buOlWGiKqVxEICEjhF6HCdEMVhxElCODucBZnRdxDQeECPXB95sNvjOp7+CTz7+mFMp9wOePXmKDz54H7vdDuM0Y0bAF198gf/yH/5D3NzcojsbEOdgRO6DJ5fIFwN2uzM8e/YcQzdg22/QdT2ePX2Ky4tLnJ116Ht2zs9pxlc/+wo/+uGP8c03r/HFT/4MN29e4+WLr/HVz/4Y7z9TBwUZUVOSFeTEqwkj5ByBgU+PKKHLmdNBhhg4vTsgNXzKYgZj1kKghTj1XYe42wFEmKYJx8PeUkfv74HtENH1gWW+foPQKQmTtHUslRmZJYTasbqi2HuhpJIBvXKKsNiAACSCR5kkFWZEKwRGCawbB7nP1RhD/Z3bLRH8nJbGv8fM56Qc3/DxQE68Ck4tsYcaBVMnFQzEvmlUihPcQFQqCCoYFcLJ/h/GqTTPFd/zRCqfnNTbLx3mruvw3WdPbE6+PiHpmB1z1kyMKlMHkVcypGyvwWYZKKD3GnZcQBICzi/OEUPkWrshYJxGm+80zZzaM2VhEtFSC5H8jSGCUFI2AsCcR9ajAFDK6Ico5Rw8PmZQmkCJmbCmbU5zxn4+YOonbLcsAO22HJhzd3ePzXYrjvMB85yw2W4RYhCj7FKpaVSW0wukSEdFiPZE3xbMwzIEfHp5jj98/UaetTCdBzpxe/nEPmmVoJySfQ3g9LKxSLlVe9UHx0DbrRxAsHpnUKEi27MAlmmfC3mRNsq8yA3aG7wssMQkpIKpZMhbHNJ28gdFySNHM/yp7VqJBDp7xu0FVZIkIIbE2buAuRo0BX7avq6R72+W027Kn2LuTPgj2bRkgw4mRNxc32KcZhBl9F2Hp8+eou+4znXf9XIaVvdVUdx8emM+2b1hR8bEqdU5TR1hxmzGm7L0CnjmVbGLuLg4x/n5OeZZnR6dCDZiIAg+rapmhGDFmiDprODq9ho/5pMEs4uCpJwt0CYldlwpreXaoMnqyaphWfHB8MLRaq/mqRFFU/A7sa3Qb9R4Tx4/3fPeKNny26ZJpr9EIjB7Dl/ojzn4YpE31MlntHyBhdqp7t96lIsxOXgsJvqYq206uPYeeqcmJFJr3X2HBLW4iXq41Cvl4IXSdh3kFYxXsSx2wCS4qwELlZOaMs4C4V/+bMCHF0orm/k+ElZ//ls9fnpf6K/JbShKoV7MCzMoOBmkwrUTsH0RgE+Wt40P/Txru96SfFXCBiBw8Ktli+l6qWmfEYiDfmhSHhCMTqWUMM2T8eJMZMFzlAHEbApmySYRG0WvlcNKxiBvR11z0BnN76TMAyDp9JyMQRzkG2IEZUlNTrBAJg6s4VI603GuIOXBVYHvxJ5sX/F3xt/ucPz4gMNmwOXlJd68vsLVFf/bbDbIOePVq1e4u7tjWv+r0m3O+Prrr/Hll19a0NTLly8BwIKpxnG0lOhnZ2cA+KT3JHKbpkMfR5brYoyYpsmc3n3fg0Sn1EudWJqufL/f2++bzYYDH3MGOl4bdbSfn58bL3jy5ImNL4aAy8tL7HY77Pd7DMOAi4sLfPrpp7i4uMB+v0dGNkf3mzdvrO69nm4fhgHIhF4c+HraPOdsJ87v7u5sbBZk8AtcmiXkoeuxir+Iy498NtQ8aOVzF7vquwY3tG2Y7tcYYOZ5RkRA1y/nsGbUaI1VXi96yAjyGIPYKae4/2slD2I045vKX5ZdAAFBMubUfZUsAm0wwungBL/5y3pYqRSRFUtfYtq09IYs82kJiK7rhbSx04lEb+5iRD/0SyOwwTsYPTPnwkqAtjeyrRnb/P0146Nfy4rW2vteT1g38q31ofBtDXzFsR8tMJ3bkAwAGSxvUslEpNPKYKf5JLXlj8cJL17f4tWrV3jx8hWur69xc3uLm7s9DvsjEsEMyDZ2tz80kAugkzj6C11FkVwlAibRumxup4zDa4bSd3Oa/jfpqnHTX7x2CqclrNbeSQ1dOE2v6ncf2g9oaMriM5yTspIdlrrGQ+N6+2/vKtwyzWKzPwDk5a86Fx161sNF/AyXcuCDFtxltoA3PUwRAmfEoBDZGe6Habp/OUHPM5GSU6H0V5aTqj9OPauhQWWtAtjJ6ctpaXtan9dSqC8NijVcRDDNREjzhDlNgAQ/W1kNySB6d7/H4Tgi54yuj+gkqwUocTYM6FlESAmgLDaYaHaIajBtVq7QsS0IEYlmZy8pCgNR5rmR1qplOhfRm7xdZcho9TGvr4k9w+yQRSlyy6H4In+rcgHFvcw6m2IhIeWEaR7ZriK6Y1Sns9OejN+SHBzQ8mZgfwY/xzVvK2ipzp4DKAJdJ7yyWeMsp507qxfeI2Gu8I9QENLroEaJTLeC4W+I0XQndSJut1tst2ci3ySTb4iyZMATewxaVFRZwI0hBmgVdBuClPHSZTKdyhoLWJKTev0DBAy05Dugsh/U9lWXlUuIJOMKwWxwtZzCNFLlHJ1WFsd6psx7RXxAfddht90JbhRYEArOmb0hkK2P4WTDU1RfIcE3dIRIGUhlTgoHQuE7y2uNr7f8qOisbGMD28aHCG+L1csf2NP9U2cKooUsqHv/F5Fj1H7ajl/luBCDnkHi/Ug8VsVvhpHns2/v713Hp39PybqA7tSlbmOypsNFPdCkz/Dp904qe5Hsp9M8u73/Nh7eBrbqmNoT5HNKhceZHIkKqCGwp1fpbDUGqk9wdyJjcplLhaOSEtmPVNbbYLmqJ9FiDbxzfE1WPXU92jGe54kj9IjQBU752EVOL9V3HYgSgIS+j2bc4H+9KGEZlCO2w4Du2QUoE/b7OxARJiQMmx5d3OB7n36ED957js+//Qm+9d57OD87x5vXr/Fnf/rHSGnGRx9/gvc+/Ai/9vln+PrPvsBXXcCcCeGax9nFiG89fwLQGdI04fnFOX7vd34XP/xnP8SLr1/g6bNn+Ct/6S/jb/0bfwPP3n+GrtsidhHPLy7wj/7BP8Tv/87v4A/+4I/w4sVL3N3fYDMcEedLPH/vWxIZDqVIUCofg6afcISNxDCtjEAZCmVkJcAiqJKcSouhR+x6duCpI90RgwAWVroYMI0jUk7ou4g0z7i7uwURO8rPz4FN3JWUH4osLLmXyBXBRWUIglryHFx9cacYOQYFqPK4vgEANJFmtEKu3RikX4IKCLrxWSApzp0yfJ2TcbBT7a/c9gp0RXRR0iuXYZBy9yJkcCPQzVv+lvnY+46QQcetH8X5EkCgnOQ9wvF4YEHS3i2wroxM73gVmYrw17/zbUfo5C9KSrlMJIZ8xeVGUBf8VnywNWvEp+KoacAnxmhN36lRayFw3UsVlqdxknrFQBBG3glBn9MMQsB2u0OIHf8LwRSknDPGw73002HYDIjdYOujpzz3xwNIaib3HTvHIemlpjkh5T02idPmbIYNYowYjyNyTtjtuA7yNM1WPkJTbC5w9sSaFNjUO0XJjW9DT6wYtHkz4G//4HP88B/esHBPTD+W9f6knVBWTVQIhEYyZ/4U3DfBjJxFIBGGOvDqFvxX2kGydVoFvXZ5ESBKC7hdBziz0Ykiy4JrgYNBTU7ccR9lT3uHtq55znoiL9gY1bFZ3uMxBUHyk/uNGiGFCT2SNKLKTXmYP7GsndxcK43bGQGKMOGFhFIPm/fPOE0AEbbirA6h1EdUoZXpUcA8lxrVQQy14zji4uICXdcjdtEZGNiIEwPvCXVScKDCbA6nEAJonBACoctc72fOmgoy2XqGEDBsBmy3G/R9J84qNRQU6qDrlSgjzcnwZhxnqYVeUnjmlDBOkzuxnUrUuzm3i7KkYCYq+0DXZ5a+ui4a3y447Z50a86fRHHOsP0brA/Y9xZ31hTCtX5QD9MIb3D/898rnmwwbe7puB7NSkIzDJfhQhHbE3j3XqFW0o6KJ2g6PzmWQiG1frYaLfy+XWju+nujfFRCtOwz5bM5SdYibaeRIbquw0ffeg95f4uPn02Ncl3D5/2zAZcbVYbl7socqQBnHRaejzj+z4aIZYQu2wiCq4Oeq35P8aJwJ4pmwzZODe0XUHnrt+VjlpMRMXIawSwniXPmPbndbgExcPZ9DwKh73pxUDL/3QxcfoXmWXiLRJ4DVcBNwYUyI80EEMSQY6nMgcrwpPKv0pWu7+y0eCYOauQ1EG4XOGU6z5Hpr5aKQSjZPaIEGdfAd0jd4veD4K3lNSICZkiK8xHffP0Ntpsdcs44Pz/H8cjZcABwIPI4WmdEnA58s9mY0zwlNrqWYGdYtg/9TT/HwJlAiMicvIfDAfM84/b2Fufn55wZSIx0wzCAiJ3QObNTXQPANNW61kFvDUsFj5LVsNa1Oo4T9qlkMdHfAYbLBx98gDlNuN/fI4SAjz76CC9evDAw9n0P1am0j1KGJAjv6MzgqEEDCtef92pPjK8ZO9ZO7no816vIEA8brVrH5Kk2W6PPmn6i36MYZX3Ke/876wA1jfbjVUMe27hPOZIff1V64Im2bJ+juJai6Bjt+5r5oHMZLxYwpuX6PGw8VNlF+Vxw953sqfNpUqzzvkh8qg91CSuijCxZ94bNBtvNluVWrJGZ0q7J2E4vfBueKIx+GQ7fSv5qPpd7y77WxhO7KEa0aFkLYlTzWNFw5zxiGifsj0ccDkfs90fc3N3j6voGNzc3uNvfY78/4P52wt3+HvM0sVNEjMiZIn9O3GZs8EPtLTzOxxvy3vV6G86xyl/gWpx4zr5lbZT33raP/n/9Yrgs4dDSuDVj+tq+IGpPq6ooUnCybU91HH9/ZaSLO76S8L9oq1dkuKJDFM1fA8fz8qUQLIgupYw4z1weJqtjtt4Dms3T7J5QR3hGIsX1JlBs8aHcKDpjLcizxpgl7bKUCu179BIQWjfolLTV9WTaPs8TKLPTNLoAn3GecDgccX17iynNkrUoYJCgU1aL1P7g93mh82wK8DhMCxl1uz2T0RCQRN6OmsnHFsTGzFPRkmEJAewg4Sdq2ldskv4mmdxRdD/ZF0SAO9hg/ZOzBcFQxK4s85qmCdPEtj0KQFTd3q1HgDoLOaOIqglq15/SLHqj37cFCkQcnE5ZHDfdkt77kiyIbPMMMSxK55W9YK2DKIj91h0syARQsFKR/TCg7/nfZrvh8k5iryq4T2bECGC+VOmSNq9C66I50B3MXEF5LuUSCszMyYoCKwJAzpcSlQYGaAbKFieKY5EQQ0bOzG9TTpgF9xECOhTZU9uH2kMcUrBNoGSPoEwcgAteh34YhBS3c0nwdKLyo6jJgUjOJpbfYtTDXmyrhqyFx2Fd9dMi1PpvvM9LRqb2ih3rZ5thcLK8kxMCLAP0mrzr5S0+de5LM4aVfzV/8rK8l2VNlqP6OYVXQLBslSSH5vq+Qz+wfaDrOiTf9iMU6JZvtnNux/uYq3WK6/yKPL2Ehf+Xc5ZclqjG/8uSp3U87Wcv8/0iVyvzxBCQBTfqbKrrcF6TLdfG5J35aoNQnH+sc/zRjvH3np5Z1IyQJkzTiKeXTxBDwDyxEyvljL6P2Er0fDKjVkCaApCPGGiDJ08v8fy7n+D5e89xeXGBp8+egCjhYtPjd377t/Hln/4xfvLjH7IzOiUcD0ee9DRiPO7xwUcf4Xuf/Qq6kPHm6hrxNgCJldVf+/y76GLA8XDAf/R/+4/wH//9/xhpztj0bJT5nX/82/h//xf/T/w7/86/hV/9te/h5vYG3/nud/Ebv/4X8Tu/83t4+uQCh/0NAgjPn26Q5hlXb17j6dNnchoFdrJDN71KQJXTWRdJmArAKedCAJIKX+3pV6kXmxMT8iS1RUlgyennWSDZDAOmAGyG3k4X397echpKMcgwsQ+cYtQYQOE+ASiMgByzIRM5a9ul3DcugHVnt4k/utGofk4ZgSG2MN8azZWJMAy9cx/t5mg3SAgrXFM7LsK0jkXfN6dY+3KAnLCvhSO9p3YOE1L8eBxRbw1GlWMuZ6sZGwAOfkgzpwdlrmbT/EXpYACw6wf85q98uPiliFbBnOI8DzhcqPFC7z1mWDUe8HqenZ1ZTZAAmKE1zTOmceK6SDHaadEY2aA5T5MJCillnG3PRKEPhhebzUYyUszo+h5ARE58ki4AbIgTI+YkhDTljF4Ms0Ra+ppwPIycwnm34ywYu4jj8YDD/iDO8QHTRJyuPROO47E1/y9AufY7z6gI4PocoFtAkYHc0wEfnJ/h44tzfH04FAE6k6Sb8a34jko/9TYiqDE9OPzuu44F1gxQnpEz2InkhO+sBjsCWhObCom6Pt5AZ+QgZ6sDViuqSyFF92/ZV4XGedrMjL48r8JsEWoJydESL4C166SBCdpHJdBJe5YSUsakdVesP+gek3tB00gq5SUgs8Ba00pUCuF+zxlUkqTzvry8xLe//W0TBszhklnYDgDyRmElNCcAQ79BThlzmAH0CL3sN35DTkIDgBgNSephiyM5pYw0y7oRrF0v3BJxurUucu3taRwLxa3ouCg4FiBWISybFvxayZouDUtVc/VvluRF146/RzlVygS3Yo9Vu4Ybhb1DGYEfht87Vf/+nvtCZDNazJv/GyT9xcozTnk4efn2/z/c/dnPbcmVH4j9ImIPZ/rGO98cmWQxB5IqkmXVxBrJUluy1HLblqBWt2G4bcuAjUYDNtz/QT8YBgz7wW8N+KEN2IDhFwGNRjdgyZJLVrFQVRyKLJLFIZnJZA53/qYz7CFi+WGtFRF7n3PuvZlkq2Fv8uZ3zj57iGHFijX+1q7C4vs2l13tI+Xho0fsfcCQ242d6bmz/qlH1uyocNBYFsgnLIfNA14+MDis7c5xIjJ44bDC0SQ9d2j8VaXhHswUIGIxWmkk8UszuOepfaHR9+c4dilDZvQt2omylAXzjFcUS94HYXc0ekCw+mm4T33sY0c/2q7HZCIZKJKVa0S+NjYpOrnhRzN6reHav1VZAcTlnZRfRHagmStKeELTStoEktIYiT4VfjAZupL8aB07P/NAPiMbKsVMcIeiUCSaHgjE8NHOSTZnECVfjF4qw46XqImNHA/kU78yHSBmLnNGtMXV1RWurq6wXq9BRDGwTx274/eoI1ozqp1zGYQej7c6nIkojkvwITqK1cHNSCE9Gik/0zQNiLiMlEK8e+9jfXEA8Rnaxnxo8ntj7WrpkzrWU3mvxCdV+W/bFu+++y42zRqLgwXOz89jLfS2bSM0PM+hT8EZRGiaJjptubSIj07xuq5/YcOCKvlxOjPjkR7aj2cbAURvoW3n+Pi5Y2NV/q5dDviBMWt0v7atKFwMgI3PFnnRgOUD8oHXCITHyzbjbKLJcRt3tQvYuRSi7Key4LacMeyrDls0TVoL4ywUAoSQyYKEpH8PnqNyZRy0ve8c9i/dp7Lz2NA2GHNsj4mi34iAGX8PElBq4CIShIh8okvljCeNt46DOmDGbRnS1e5gsLyPu86P/w1/z4yje+mX/+2CVdTDC8pRNPAGrXvPCGVdx0hCfd9j2RDapmHHeNuhbTt0fUDTe2yaVq7vAN8jkIEtKhgyCH2AD10E6WNZmrM7oXXEjeqZOmJZX3UUR4P4sQ2iImM9bVzzd+r7csf40JDJPETLUIx5kT7/aWvrv65jH9/6ZTzzae/aZTB/Gn8a6Jhju5YcYx1zy1AsTlPSdTaQgbO1kfOMgdyZvqheyu/K1YWsPdaw7rB3SxtS7zOnQG0FdqRojZ44GBNk60ICfpS3GZHXQs92HEU0gWF9u3BpH9fMPJL63FDETnmJrpekWmQ6RtTd07yo7M/sR52JQ/5kdU2IbYb5bs2ySWbTGA7RWFHg9vm+R99zuUCAAz+tIIUSEZq2xfn5OTabNurfxhqUrgJRn40uQLAp4Cxo4HmIMmeCWCeQGa7pqp4wulPwcGXFdh9KzyIZrliWQ2VuIiBey45MYwI4NdgkvZAADN6ZEydL8irx6H43yP7foRfmorX2jYMpu2hnjzqp0kJ2c1EUsM4h2ADqCTCa2AS2MYJSfWCT6McIUizvowFe5m0w30Aae9UnDTLdJ2RrYP8CY3pL467w7K5ITnEOFuHflT4JvCaIpG0kdi+jwZfZXpUEcG05aNCmbPyl3JmBiagEnAjoByQfSw2SlvFTPrmtwSZxSuReQ1CbWtLbkI250rs4HBWhZUAXrG9G3TnKYGlPrKoylfKLcyQ8QWjSi16Xw3pHuxilkjsaMFqWJXrPJZoib8r5/aCNOg/KG1Lwzq4BUp0ulysBtlU6a1EWBZcYtIn/67iy6JgCf7n0PH/v+1TCIe75WRmb/BjwQiSevr23Jr1eeWieDKRljFT2SM+3sNYl9La49tL4pbFLbRw7YuPQZTxv17mn6Uf5X5Pxj6fpgrksoKiVIQSYTIbKX7Vlfx49J2/D+LNet0tGyuUSlf/yFK9d1+3SHZ8mM3nSABIg58Zxn830wvGztvRM6LrO9hZ+ESNnwQDjhIM9x3M7xtv1OcqihLNc17IoHIz1MH4NYy2mpUHvOzgT4ECwIcB3HU4Oj+AKh+lkiuPDOY6PFjg5OYFzFodHhwi+x3q9hrHAgwePgaLEnVu38M4776BrW9RVzTDislCb9Yqd5j/7KW7fuo1XX3oBZ4cHKB65CDfx8MF9FK7AX33nu/jn/+yfo204cmvVbhC8x9qs8Y0/+xYKW+Bv/91/C/fvf4RvfevrXFevamHtGQ5mVzicTWTDCOj7gIuLc0ync0wmU4GhUeZPwhV5olyRoNWoDzE7Uacu1aHoUz0KogjBlqBqhSByYswWQLNZo3ALOGdx7fQUt2/fxttvvy3wgBWC7znrlRANg8gizvONGvq7SUSrQnHMJpNNKdYp3bPIB8Zuvmzn+fi+ARGnewhBkkQlh1bbPl5now1j+MVk7URaZMgUjF1CvEpxlBZarpwOFQwzbIOJg8jviILdUFSIgnQcI4mxImIob3WsyVzkCALPE/W079A5O5lMMK/K0S+jb5EIhr/uejPlO448QVeICglp+0bc7Oq6jnCiANC0rTi+PTZNw8YxayUbXGGmLAg+Bl4QgSFKhQn6KBRLUAUIsBY+EDx1aX4BgWEGXFHyJuQDXOHkuzjmyAh0F6Hveiz9CrPZBGVRYjKZYLPZYLNZYzKdiXO8j8ZQzroajt2ADkZjks9EHDMa/maQ6rgPn0349bu38J+//W508OW17RM9pQ0sbUq044njVgLOWa6xjMSzrEUUUHKjs/7zUenU7zquI6EvU06YL/J1hRsKbKlVZnROo0lNUiziQCqv1gFOzvKc8SR2NjS6RYVXlARr9N1ZRC5I6turRJnmT5+hwl2szRIvNdA61FFpMJwlmQQfK7DCiGMJGLRtF8eu6yQKXPh11/Uxwx9IRirnDEKQKHljYg1V23v0jp0bEIHS954VFR/YGS4BW77nAC7+zmtnaMAJEeKO+XtA2zTo2nZkOE6KjPZLHV9BHAwp0CutoOHWw5BlGsxDRPlU7zhG+xYlYYvtKBlf38tqE93s0kf23kVxO91uWr74x6+Se5hqx2v/uV//Cx0m+68quNkp5vk7sp1I5aRMQdjS8rCtYOw6gigMoIDbM2BeqAAPfOFGiQg+8Lx75Hg7HTHg8fzrvhYoxppHVTv+N5dvzGhac6afvw/5RduH07bIOhmM1T4FlCjRyw5ogKeO0K52jdsuxBxp+hc9SDN3mI4KcWSqIZFf7sFJd0aCCaVON9jhWxrJ7JXJ8b2P5MDGYwJ5VsqeLtgko6fyQ+ZPiSaccyhLRcZih3Hvhedmz+c6dALrKU7OoijgrEMnQbCFs2glCHjn8bHFviFX6M6Aa3QoNcRrnJ9fcPmql16Ke7f3HpvNhmHHrR1M6sHBAVarFQcgCE9WtA/Nutax0trL+rnzbdRtYiS/1IgHWH6o6zo6gPO637nzRQ07vUAXR6MXvxwhBDRNE53TVVUNoItBiLDqWs9e61wrrPtsMYtZCA8ePMB0Oo0ZzkVRwACwVR3nX0tx6N+qqgAgZqNvNpvngkJ/2uHJC4pB4qEABqUjeKxYMlQY7aFkmdMFBvftNpCkc7v2wPgbdmV0DZkbr1wpDVa4WDLFqBxm0q5WuJJLC/Se13h8khUIzLQL6XvV6a70QBlDYj02a2Hm6FMDlJZP2nUMjE8iQwbP69sK32EUCpF1Q48STtD0cnk758syqPIv9cgM3ikaKJRXKZoaOz5YjmRUUJ2n3IDEfyPtGQYrdtaAgkPcvWWoKufgChN1br7fCk0FqDMacDJmZuQYT7KbsylrMVCAsTSg2yTzZW3NZG/ti47JeGpUDPQm1zdkOMURw/pPouGg9VlljIJkd7XBRAQiDe7s2l54eUDvxWYTmAdtmgZt1/MasxbeAyALkAPIog8ESLIDBQJJEoWOqTG54yCjhx0SnEFmKBSK33auSk3SkTyZy2ppHQ2DBHLa5stk7AMHP2tJE+V/GiTEK1fhwDM+oX2E6jbJoP2042nG4h1XD+4ZO5ZzvpfGTs9vG2vHbG9fU57dQhUMnn5lHtjM78v1bsL2x3yuh42mEESPyISSzCYVF/fg5u1eDcTlrcs/ltDxzGP3XJts7AzSpwADQkeEn5Ut7kjbAhEsZZnJOV81op+LvKaOPZVxrCsACN+U81GszjsvKkuyGyoaBdJ6yufDZDqnEQe4JDbF82QAKw43a5JzsixlT/BMG/peGRpjAAo2tQ0U604H38c9CJDgbvJomw7L5QqXyxW6XsoEWsAaTl4IxLDffSB0Xmqxi/sjrWJZRyCxx4jNdBTs4pyFsVW08wRBLAQR834dpoGzOogdS0VrtccOgykShSovS0OOkfyj4xNlAOWXOZ3t+Bgd+OJEcVIiVmv7xvrpmVxTlFxGrmtbbLxH33OZq5Ux+C8bD4IFkY00rPJKyPg3EWBCiEG++RF5MwnvymwfLvJU4eo5BL0VnURRA62DFX2KHeMVnDjEFSklojFE+RLgNG1djzxfvIMP9YLYjlhqRfetnBemuYs7RbQRApp5H0LaN3RLZLpOpd+2321hbInCMrw5DFC4AkVZoCwrlGWNouL+GqvJHsl2MeBHmYwWZSlZiyQ0rU7swhVxTzEmb282t5mQmtOg2l4NMd+zBnCFRVE4RhQT21n0B/GQ7dWxh5bbXJZCXGCucOwTkiYNzAdwgrbmYA3rWb73QveE3HbAfo20ttQ3of3l+WJdl7PflYXmcscwwckYIzCa3HZFZHLOwRmDXsiftzYuw8w8RxBDggcVjmUSkVmsLZhW4SPNIQQYNxzEXU7xXQ77Xed2OcTHv6stA5RofitgQObDgktYBuJELea7HiZ42eeREdZQtosUrUS3g1Z0T8xaiKh+IdEZ/9VRU/k5ZM8cBgnlto74y0CoyE5JH4ZywKhPKlNmDdJW67vi+kXuFKed7/g4AZLP7Rh/9aXbsY6nc6yc9n2P0HscHx1hUlfg4GmD6WwGjdRSeNbgA3zfoF1d4uCFWwje42dv/xBd1+DxkyeYTmoURYlH6w3Ozy7YcDKZRihF3Ugury5RT0ocHR5is77CumlRSV0M7XzftVivNviLb3wTWs8LYc3RF96jDx4IhO9+588wqc9hC6453LYNR435ldQB5wWnmdyBgPVqjRA404GFD1VaUvVgooD1ZoOu7RC6DuQlsy46g5JypuIHz2FW+0o39p1CMomwZ9F3LV588UVcu3YNReFw9+4L+OCDD9jZ6FyEH2F7YuKqSl7R0SzEl9MpJ1ipwGikiwYQhVyhjRPXF8FWISj1/JYMTIOuyFNFGKTsXBJWLbBd9yxj/jsd5rpQ84WSCZu085YUwTXYzKQhueCWNyOv487apIlrXJ3i/E7dZNOQaVv4O2eWWmuwaTaRrmMtbRU8xu3+BMff/+yn4rtN6qR0SRS3HcIaskszktpSyoHBKGXsLh1FWXCNYlFs+q6DNUbqiTe8QYrgpo5xCA9yxQxt08B3HawrUDiHrutjPR9rTYRqtlKjR8lLmWfwPqIxgCAGTSPRaDY65ryXirwUpJh6wGq1xmzK90zqCTaNOMclm7zt2ugc7ySzPWf7tGdM0hzs+539A7njIx/3T58cRqUrFyKjEhE3sSySUidvz96RKxgMId/AGKD3vSBb9Ij1iNTAJDCmGnWc159hGSjxuyT8J/h7vdcYw8Yv76MRmIUII0JuguyxNkVDDkbUbBt9jc2gMOPWL+OS8cLdUXhM+Bz5nfaeZPBIYxmd3EGioEXoh5RJ0Ktyvphqc1GsPcu/hwhfDwDBM/T3fL7gzLqqwnyxYMHKA33fRhhyBCAEji6/urxC0zScxS6s6+zsDBcXF3FtqDIZDQEZ41JjU/ptSDxEQVAKeF5DFoVvtgjNALDi7FdWy79bGBinblQZo8F+myshqgwjuw57aXp8frgzyudcvkOmSA17mz2Bhj8O2jA6Kddl28FT2xfFwD38fzCiI2Pn4AmZrJmMmaP2fsxj6DiIhJ+OPXOx1yibC7NbA0S4WQXcnlu8dlrx6jf5mD6lE/qscdvGt9Cez/GcRr0TiDRYhgb7YS4agcWiwThE2+WuDWHPcTK1OCx7rIGMr28HMxn9mcwgytdk/x2ee84j35C0MP2uMf24x47NrmvZSalR7hxcIzwQUitc+IATB67CprVNy3KFK1BXBp3t0n7CBdyydw+NmflazZftUFZO+01RlrCOeZ06xX3PcoXCblvJLOEgWy55YZ1DWbADUB1XsT6xrtFsbNNa2Uff23JpPp4goECN13/ldfR9j7OzNZwrsFltGMZcAniLosD169dxcXGB8/PzXDiNzmY1hiyXy5hFDXA2uu7dhWRTqyxQZShixqRazNbaeJ/KZOpM1wxyGDF4AdGwkJfsyudS322tjfcrRLtCFZZFGWWzqqpwdXUFCpzRfnh4CGOB23duo+96XFxeYLPZSAAEowhtNhuUYhRTmPg82LDvexgArijgez+AW/+kh9akTf/bQQcEJIPkMMNifAz2zT1Gg+RgQkZ7TJS69+vfoDIU7XOycwOJuDZ74azwKDV4cgaNAdhxYQIaauO6ZPnKwEe0NmmHPlkQt3JnX85y8xHQ80rHQRzj+8YgdzSzY5wRcmAsB8QoIzSAF5kYqFEWjjOIkWRQA2mfwmsHQlRaBoahOGLCC0y0i8d6qCSBwEQM9yr9oZDqYSv96xjDAM4SOioQdC5BsASU1oGHgY2JKs8GMoBhFJEQAtbrFut1i7K2YnxX+TUZOwtxjGvwjCkIyYCHAV/Ru5nECGMoXaIR/RHitV7u07Hk4GY2Ync+2S+CD+i9Rx8z0SjqJo13orfoRg1QbhSUPhZW6rMbD2OBwjGfQtvy3ISA4C1a4jGMBjsTOAESIbNjkDxX+6gyz5gCE8/Pr01Bvfoss3Uzz14q85D6ZUa6Um5AZIWAg2aJjdGlReFKQV4LkVZVXxusrcwomxyOzyMcUFxrTzdmJv6WvTXJU1D+wwZmdegNn5XLnE9rU7b2d8nw2XUAv19lkqcZz3lQQqLj/NE72jB+Hp/Nx2ooJKt+H53l+3i8yd6/9Ubsn4eoQOxr8/DiXe/Ych7k9GzUjSiICvLL1aSQMeM+Bfnnou4n60D+OGvhg4cjx/QQCL33qBw7PZ2UeAveS6C7leHSTFaK71LerbQWR0rHMFAUiSP7EnoOwUfeThSEn2ZO8aIEYAY2zmgKzZe1NWD8WZIM9x7Bd4jJSpKJbC2Xt1mtlri8usJ6wwgWzgGt7bE2LVrv0Xt2jrcEdIMMa90Vsv0fJHZsHZOhPbb3PZxjOHjvAyM8gbhqvLZfsqgh9xORZEIKpwyEYDjRwuhgkr5dSE7GMcrr8bfMrq5zJvdIynSS0TIFLLdN8CMtXFGgMEwjykti8J5JNOvKCs4YNKFB03LWfmENlkWB+6EAWQfySZfQ7qQSlbo/BxTBgUYyoo3ONH21BWlKzEhWYDs/j7UrHCaTCQpXxKAMPVSOdZpoJDSTxjOOrpI3Ym126IBSXIdxW6ahRBr3bMrX/yAsDnG7NxbOcpAZdb3ISOBsbyUBlXnNNj8KcLKeEUuhFJU4xesKZT1BXVWZvTHAUEhleQStMs2xibQ0dpoaw8mPisyrc8HjR2J+UF1A5300rvpNA/iJSw86QU0FjNhPvSSWpDFLTkfKzikNxKmJoxbnAwRXSAA3NzX2ix2QDlVZoiotjGHdNXS9oE9IqUmT9TVKphowMGyNgWU+YAiwJPWx0zowoJRlD/ZxEAV2XBPfz2NS8LjIG3l6giDMGnG6B4A8y5+GpESZgxU+D0hZL4LwnbFMNHbSDsdml3M8P3KdI6eTIZ1KMt+OdyndGWvgBLXDC/IqJwMChTUcYCQLLqILj96TBzwCimCy1eI98snTN3S1x4/fNXjOaHhyvgIg0e1obY3bstvujr3XpQTAxG+S3+Kp3do6ntsx/m/9wVe4VoP3sQ6dsxaXFxeoqhpOnFAKkVdXE1jn0Dbs+J5MJnjl5RdAFPDjH/8QZ2dP4H0PVzjOwFxewrkCvQ8oqwp936EoCo6St5C6wbwX3757F8dHR9g0G0zaDk/OzgeK63RaoygDLi7OcHx8DOrOUBV9zHLTTMVA53h89hi3bt0EEdcqbhrO7iwkYxfGoO96KCwMjEfbrADqMZnOYgarZve2bYvLqys0m0YEMweNMFfnpg9+0F5SRyrPZGTMg9nUTQgUCY2Ihbz33vs5uq7FfD7DfMGQ9MvllTD9STLI6A5jECHRTbZpDZw6iJQFvZmU4auSMSa2qD+YbMdLR96/KMRKX/Rakz1Law4zF7XS5lyLUAEuiW5bL8wXnkF0rOmCyaNcYjtEAttWBpKoqIph3KpoPF56j0bYybWZUEWDvoS4OerYNg0bhdSImPZbWez45IeBGUQYKtkpExkIkLGNem0aU2vSyLMhKjkH4/UYkF4cZ+scJvVEIE+YVxDYsNS2La+ZCJ+usKoFjCvgRGAyFRBKMbhK5HBVliy0aN2fjJZHVAYjNUpBnAnbdwyj1PU9QmAYV+sKGAv4voPvWwAcuOBDwGq9BgxQlhXqeoLNZo2maSKsetu2qCd1zCAbbzw0OpPGKqcN/S2JhwMDSbyTj0VV4rXDA/z08jIpCqrUGaklFuXejP7j6jeD5+l7VKFZr9c4vziHMeDsmN4PMrtywUDXWQ5jHLtFCRaKdRfOuNHe9L3HxcUlyrLEfD5nQ7tzEV3ACcxuCibCwLg5FmoS30y/azRwZCfKJzCE5+Fbx4KObszJODEOIiHhExphm0fS2VGdI87I5iwzRRJRo21ex4fHvBehmSEfSbK5u7bH1dUSH9E9ACLIINVipyxjRhEFTCacsiCb0SFldKfrJz+XXQeT5t1Gnq6mOYmABwGa9YbReKogp7yVRHAmpcq0d2TSf1Tko8KkimTq1g6K3rcSx3Oe3R/3Bd6LVAwLBLhMSMv3z/h9tJyV16YjQQLHducCtDGCnr7bwEVZ/9WBl18X+XvsohkMQB68lStW+RJIPGf0brPrJG0N+Hi8Kfsc/xv/o46N4X4NAJPC4PdeLrN1A+kvv2Qw3uOD9nx+nmNAHrR3nHa+fxcB7muTztOO54xnPg9s2KYKRFpgmTKtk33XA0BfhgxGXXu47XzPsxcGnz/WoYO4fW/f9yhKzqh21oFsQC+Z3ywN+XQXEe+xwteMMWi7FiU4S6AyFYyxHBjbswIdg23MqG/jsafhVwBcXy5DMSECuq6NsHtEQZzlgDGWa0eCa6F5KQvjigLGcUkJrmnPga6JV+jaRzZhzyLaxC+UT+vUBCIUH03wwm/cQdexDnfj5g0cHMxxdXmFruswnc2wWa9xfnmG1WqFi/OLFCgK4PLyMiLkaEa5OrfVIU5EMZtb4cU1q1qRYNTxrZnbXdexo8ZZeBJeTwRYRgwoihJd17LxSyyKCnEeRE9Lc2PRiyNwvligbduY4W7AvLowHAztvQd8wOF8ARMIofewxHrC4/uPUJQF4AmTskZHHRCAZt2gLAp0Deu6XduxLisZ8LmxpZeapgBimz7xIcBFSgcjUNFIx0MbBG3tGc8yOOTyvcmCjIbP0YYEkAZCZ8agtG0Nn2+gxhXpkurCIQBipDS6j+0wmuixDZ+YofZQQi3S38bP2CXb7XrPvvfnRpk8KIJre3PGnDrviSg6qlWeygNHeymBE3RP0X1f2dNYBxtsNrovmqgnxuB7ikxj+EySrCyoc1h+00BiLd0TCPCMksXG4AJd3+Ps/AI//slP8ejxOepZFcs0EeUOeZb5onwNxPkdj2u+hw1kHuke20qzTEWRvULmeOb+pXHSGqY8hin41Ue6EMepzFFhECGWy7JGXdcoSw7KYt2TSxA1m1VEzNCxXi6Xsc0agKC0aCg8k2M/61AZPdc/FI1Dx885NwyAMwYGbLRPx7aBMJf9415PwntNAJc59Wi7DXzg0hmaBQYToHaovC27gmIM0hrbaRTW37U10f4wPOQtcU3kerCWP+KSJUWcA+89fFD5NtGnvsAgBVzl4xKdJFHvSfx7KBc/v9yTS0mjhFvkgt84SGKf0X74/gHjj2dyffdpBub8+9MDE3a3Y9/z9h27DOCIrQZy2ZDAwT9930dHH8m7GW5WeXAav0AMo24Mw40rvC7Aspq1NuM33AdrncjJYs+ICG6pbfmc6FLh7yHagQ04GUN9rkFg543hoB1LBmVVoywrGFuAguGELRAHefLAAEFJUGC5M525Dx591wmyTZJ7SoGJX61WuLy8QNs1sAaoKi5/9sCs0U88NsseTScW5awfgUKy14geF7gTjBDXa9mcoTzz6OEDTGdzzGZzWOc4o1mnUPdAm1XJJcmMhUHfNTEoINolDSCh8Xy9QSoJakhKIYozXdqrfL7vO94BLGeUWhjApfqzijIYdTX5YGDEl1Gk4DvRnxJ/yqmB5bq2bdDJOzl4z+NyuQLBA8aByKDrDcpC6EAHPFMWh6X30gtCGPIDhciPAQZqd8psLtZaVHWNaT1BkD2JuyHyyqiOfXRQktg3jMpqyict06K2AUbk2USPgfxAttNMh3F4otIb0wC31Un7WRRso71b9wK1c46DAbRfvu/i3PrgYR0HLJZlibKsUFVcQ13hzNkB6yURiv0oWlIl0tsgUCQlqrhCbMwV63TsvBf0hcB7xZZ8quNkEFEJAHZuhrYFDNMc8yt+vwZZp9KRBtHGlvV98DcnngxJAcT94TEp4tgP9wSSZLJUm3sXL3esTApdmfiMQeBvpoYmW5+eUxlhuJZkoBCJD4mPJ91CoeBtTNLVAD/d85XP5yW3nufQfW+ffrTLOf403WB8LiXRpjEY6Fqj80rPk8kEi8UCzpaSVyVr3BVb79veU/c5xp/d5mdd9yw98pm/qTqSyYS7nfX7ZYVdTvqnyUrPezy3Y/zs4X0UzmE6nWJWOZw/WqKYTjCblHDO4P79+/DexxpuR0fHmEwYau61T72C+XyOj+59iCdnT3B1dcUMH+KksRYQWC+ub8fMRyNUrEBjBCIYZ2GLAuVkgsOTE1hrcfDkCcrvl0DP2ZtvvvlZvPfe+zAmoOsalCVvJpBI6hCkrgpZNN0GAQGFc2g2G65lLFAqXjIBOdtPObnnTa5rQBRQVROUVQVDXHtquVqhb1sUziJ32KiCq3XJvRcYLhhgIAikTSNtOroJ8rOU31ljQTC4/+ABHjy8j8mkxvHRMY6Oj9D3PdarlUDWlaygCmONha6kcQOiMSlzUhUkVpLHUnzm5DHZxg0WDNL3UcSt6lzaXcgGNH66SPTCUlkpyYSI9DCkB+rzRhtS1A4ISDBJId4Ks5tRZTt8fI7+bjONIzm5dfEO26QzaOyQ8Q5i4USoYWg6EXwl02BoB8kZ3XjU8rF52mHgjMW0VMdc/vzREyI5JtO4Mvm8Tdm3rbZpL1XIEQk2wlMy8kHHAqXv0TbqFHcRytNaC+McZ15ZgVb1HuTZUeiKAnXFsEY6NyowB4lyzaGrVaBROFBrncCvOFShRN/16PoeXddHId85h82ajaFqQPK9x3q1Bk0hMDQVNmIMLssKRVGg73s2Jq83I9rcnsGx0E2JYrPf2AiUghIIGklKohy8cnyAn5yfx+fE9TYSRozBaNPIP6c3K4QQgXC1vIIPvQhDJtu0bHpepk2qzJ7Xt9G/VgKLQAzFpTGFRITVaoP1eoP1usFq1eDmrVNMpgecoaf3itAVoQQVMg1ZhHe2DrmBPLKaYZOUnrQWdT3m9+nzCKoQM3S4CvEk+4SP+ww7CrT2t/fJmEYSud53yfmd/zMGCGEYUGBMmotU43w7mjE3+ijdJAcZAIXtI0QaSnOYUcLWUk6KnL5bidiI92VocJIPyko1olj6MZRxCEPmQynD1iKjWBr8yR43aPQuWWyHuLp90VOu0fHXTlgj2WtSF07rxmmUc9yegt5vIuxh2wJtx8okz4vF4YGFNSQ11rgrqw3bpjWjrCiA+ZQGyrGuQw16UB4bDTbKwQlx76fBXpr6ysuJX67XZDub3EuD6/eP4scTRhM3kwD/YHCxJEwmNQrXonIGPbbpPs6L9tnEr0Mmm3/O+NPg+76/w0ZunY874NNIavS+vaOz791PedzAQjd+FoY8X3/Y+/6CdvRT6ID2TPgz2jps9VPoQshXr+jaFm4yZUMHMWSx9x42cNa4F+PcZtNyxrM0ZDrhgNCuaxECy8BVWcI7B2v7mKW9JStqXwZN0jUgiFnWwRZOjKiCbiIBwbxHaJAX72VlVcEaNsj0vdaBdCirSrIbPTTg0vc9j1EWxKB/P55uR/Fe5f0hAJOrKbquRdd3mM4mePLkMQ4Pj2CcxdX5Eutmjel0hqoq8fIrb+DDDz5McgYFbDab6AjXmu6agaJw6mqg0JrcRFK3sVXZidXOqqrQti1KMQb13kdoYpULnfTZWovZbB4d4SEwUgpgUFV1Jq8aVGUlBjeD6XSGrmqxXK4QKKDvuL2TqoZ1lmVNgGucw6DZbLC8vIqZ7iqfdC2PWdd2WK3XMIAEO1I03jjreL/3noM4ZT/QMfpFM8YBDOHAh94ZZnujjU9pcp9TJN1uBvekz2EkE5hMDuG/2pR9DpUtRxkR6noiyEpllrWjGXAhGoXydu8zRunvY2Ok/rZr2eTjEq97xhjJE6MxV+9TI5x+DyofiP4SjbyjcWCD5/B8MoLKNbt02azPKovmhyI35WWAUhmB4RiqkZhCAByhKF1W2iDJFQgB5ICiqODKGsEU2ASLB/ce4vJqxfxP4GCBoa0g8kNbRYPoUK4a7uUuM/jt5XnGgCEKXdQrnCtQuFICbgBjMgepFaeGZKUxRK7Ur3QWFfVxbDgjfo3lci3vEue4MeiaNdbrNaqqis9WPUaDYmKwrxjSB8EHn+DQUkpqLM3pRc8xPVqM9bt8FlQ/Y0j8XGbndvLzIJ/THGrfIuqA6kI71lYeHJOf+zjHc12tAvLYUAqgkMB43W/jGtK6szvkWOyTa+R3I/fr63Jeka8zlRX0mgHP0s8ADCwMjfaDaEdJwhTtWk97+OyuYzz2z8fjnv94nrnN972nXc9yXyb8sUIfFagQArq2jQht0SluubyYM2o7SPdXZQnnikGJr3gvQQJ5slraqtOonQr8RzND4wnkpKc8mB303gf0bQOVTQ4ODqHOWg2oscairqeoqgkAtqdZ2fMsFIac0RG5drjYHkTWoNBzokZgpzgIoEAoXcHleJoNKHiUZYHDxQJ1PcH51QZty576NhAu1j2HlpoCBiKD5mMUqZHi+50rYWDFWTWk3/V6hb7vsGnWKIsCZVHEvkHGOi8TqpDtrPpLvWwNhLQGliwUvVxl2LieQmqb8lkDkyFBcbkLYySANdqWEO3vaXoz57rQjYPq2MIbRJ4erh1C2zZsK1T53zKddD7g7PKKs19h8d6HwH/6/wD+V/8jG0tDJtuejcFo45WpNvvkxLTx3SJU8MxoUKAE2LFuwzbJoBlCUHsY822VPzKSBoiTv4g4+JjErmGN5UohpP8EEZASn1PTQRBbnHPsQCbiIA6orIN871C9Pe1vMQkkIuokZzV3X9El0rHZcGkTGQTpkNIF/42lSIXoShYSGEHKWJRFCRiDpmmxWq0AICaCahBwVVVx749IpERj1jDYA3X8YBADS2AYFSnJTMk+aq1DK2Wd1NGeNh6T1s2IWkjmL5vKwWbqPSRQICUVjB3azjmGny+K4W/EqyLvG8fGjXkqxblV2VYTcHLeyucshzaaVN5xq1t2d+Bdkq85gEV/0/F2zsFl8ll+jMtx6r1jXWO8z471kPHnpzltgbG6tkOnGciOPpaQnM1mLBOT5RKPskaxox+73v08+/0vUyZ43meLWQnAtm6Xj2uua/2bOp7bMf740SOsVivM53PcuXMHt27dxGq1QtM0mE6nOD4+xtkZZxl473F1dYlbt27i6OgI9+/fx9nZGT786AP4wMqDZlUC3PEiW4hKlGPDlV774YcfxjpHi8UCR0dHcYBDCHj8+DHOL87FINOidAGpxBYzqSDQGeycBtquRdNsYExm7PJ9gjKRjZf3+ADyvNAJDQiEqqzEWcG1tXRRZaK3vN/COYgw5oc/5odJf4yYzcgynHtyPJFAvzPfXK8bbNb3UJQlbt26hUcPH6IoC8xmBnCOgxDyg2jIzEiZlzrCAN20xof2zWRWTF7cERsE0SgXnxM/xm3LiNAzZki6eRkMF0ka0HFk+W6BmwUqtRAmRUrnEzYxdBLnKQtRwwj0qC/qc/N6Lhn8uwxryl7QfooAMBB+jJStzuq0xsxbEDab9UBAT0LkkMkOj+djHncWMxxN6oFuGQMndNwyFdsgn8tMDlCawTat503UXmjWaSX1Xpw4lbwYO7u2gw8Us8h9NDQ6zOZlNDR5z+edAabTCUfagddV13l436Hv+iQM6dhpe7I+K99xZRENvFXNwk8rQi9n0CUnNRtB2GDig0fTbPgZBTvWN2uG3ixEKavKKtawHI9rPlZmMPLjSc4M9EbXG4A8U0Lm7zdfvI1/9s57w2eo0cSMn5i1YGtzH27iVqL1fO9RFA5qUFAeHo2TBFgJDnKquDpB/UByyEbKEEERgZVQ75PxnY3gHVZL3n+s5RphSfBjhUSViwCSWpwqHIoSrHMX+riOgtQ+JyBmafs+lb5QhUnPjYX2VCudooKVC3LIPu8I/5GI8jzTage/lXkbl3jg8iLZXI7vi5ePI0N13EfXDh621QQk0smELjk55Bbb90U+kykOz8Wr/o3JQmn/y88pDGU8KAU46ZheLRUKVhVEgjWEtjMIwcCZkoP8ILB+NsE+O1EMfAh4/MTDh4CqLGAtG/iKwmBR17hz5y7qcop3330X5+dnMVrbOqAuCZMJO4K07jY3lQc7pIWCuN4GzDpxIV0vw5GRsRgZO58tpz7/5KlSp/ujDwZnFwGfe/Mt/E//Z/8E//v/3f8WBo+zRxvxHaYgAuj+tT2No/7mL4UKWcP7Pgnd7XpH/tu+No2PXZvDvvakzu99Fu+LukvLI/WZO24tNg6dZoXt68O+z4M+PKNte9obeYWBZFV2AjdZREOM1hvny5LBTRsUQoi1pTkjm4Nti4L3dyfBS8y/c3hIvj/yMyMBeiY5uphXcyAaI8wwbLbKJpDPBIbSdlYzhgXK3VpUlTiD+154gkPbbOJk0U5a/BhjuePSfglcP77Be6QPmM2nLJc0Ldquw3w2R9M0WF4tMZ/P49+YXSPPbNsWToITKQT0RLGutjqXi6JEWZQw1qDZNLxvVyZCinOGOPNWDoaWeZc5hScgeFiV3T3rPg4GINaxXOF2ykl900RDQt807CivJ1IqqwP1HuvNBgDFuuht26FtGqzWK/ieYdeXqyWCDyjKIsoBfdcDxiAEj7KsAKLoOAo2RJotDO/Xk8kExhjMZjPUou9+4kN1LmCHnGayf3Z0HlD+veWkRpLvclYycBrpasj2iky8kePpEHu6V4YQ0LYNysLFcl8K+WF0NVMqo5PLLbl81Pf9MBs568cuXTA3cuVtyu/bd+ySybQvxjBkY3SMWwtL7FBW/SYZjfOgAn5eUbAh0hbDMgG7xi6KygOZL9NfY38QLxo6xpPjxzmL4Ed0ACN2mCEkO6T2JFkPE9g5Plsc4bZbAI8qLDcfcJAyDO/L0ViaDNFkLQidLFUNMtVO5IPNvGkXnfKdLo6D7QMY3t0CQYzMwcMEB+9LWNuj9xr87NK6kLEkw+4g5yx8Vgte11AskSQ2AkPMr8uyjPOdO4vVeZwHdQQ/DHwdEdFz7Y9aPg3IA5FJ7Ax63sJrIE8MykoBEWnf4tqbiV6S035M5yEfD2tTnWQ5pwG8DO+ZrTuTIaMZnWANis2c6nvsN09bjwZDek/rSvvm4vwoD5HesCy0g0cYk5DH9HedR9WxjcxValviHda6eC6WvIp2kYRWECAQsUL7ZEaLOT42BQ2rA3ff2Oyzez3LSP+0+4cOuNQeotRvPW/t2HnA5z267DqbLFgi2O3awxRpI+oaKgQJrfhADFcdUl37uB8FAsVsutQvzX7sQjcYS2NMhuJB2Toc0bLKgpo5q2Mw4MHpOUxzTFNFWaGqJ9E2UZRlLKnmDCMg+r5HH4Phxa5jdL9inm2dASClhAgZ8inXIldoZBh2bLXNBr3vMZnUqCc1vA+4XC5xtWRZJwSg7QmrjueGM3YDCoUgtnbEm42MZYmyNJEezEg1Pjo6irpt02xwcX4GtSOzHckOaETXLNuICiltx2OvfNWRjeVRQCT6eApGVD10EJxCjPiKukbbNGjaJu5tbNtNNMC0aBg5JCbPBJlDxHWgNh9X5IiEjGrV+xaBBKpZZOWuD7hcNyDLA956QtdbCbAQvgkT+6bOveA1UH6f2J/WxzgY24DlDwQvpWuzgIrYaZ4MA8Aax/ZvJft83cvekMw0BlyWNmVO6z2pBrasbxIbGxy8BArEjPaoj4oFXp4d5Dmd2GyFi8a1qWPE/mWzxTs0yVD3bgNuB8RGwEiInLSp1/XeowAQzDiYDairOgY7cIAtl+tVvUblOpWpNKuf7TzJj6Uzphnpm0bK9RKBPKOU8lwYFLJvqTOeZD6NlB9I9imVyZXXZXMoY5ubePJjMpnEwEcCmO6tifuyonhtOY+VZkRni05852KJq77v016MoWyU/iHKTkSek08p31/T+yAytN2TuW7V5mtT4CCJfc5l7UIcE4rrbtfYbPmg8nuf47pd1wyd60C+Z20/P/fFpaBYRjWwoGCiY1wTwfYdH9eJ/Is4nffJIB/n2clerjvu/vv+TfTtuR3jm806Ltqf//znqOsK8/kc8/kc5+fnsNbi+vXrODk5QVWVmM8XMAb4q7/6K6zXa/R9h7bvIoyDCqz6V6H2otIrTpGh0xYAuI7fvXv30LYt7t27h6qqYh2vvu/x0UcfYi2Oqb7rUQwIE8KcOXq2bRka2fds6Og6L4KHODmsGotZkE2CFMPOFp4wqSdiIDGo6hLe91sKcIy+i8K8hTE+CYgj2jKpobHthpxAn4d0DymclUHfBzhn8cEHH6FpWhBJ9poB6kktED25gSNXTNKbt40j2obElPN5GSo4AcakSLJcwM/fqYwwCau7GRGJAhhpIGsSxX04G9uRwqUCphoWOBjBxBlRZ3hSxDNBOdYNlYg1k9oWQjLi8+UGMGlz3l3TyqS/Ivw6l5isGvmNQSxbMHwEaaux+3hOBkCE33/lxdGdJv4dzlR6qv6N503e9tErdl0vf521mExqFlKNQd8yZHzXtezsjg7REDOsKHi0XY/aORb6vEfhHCZ1BSfRl70EyzAvSEozr7k0NmbQKDEMBK792TYNZ37X3L6Jq+CcFWh3huZq2kYMtoiKcd9zNtVsOkVZlfCBM8nnizmKkuFCp9NprPc8ooatmdNo0nwM9bvqjJG+xBlkpNeDZ8V1FqQ2lY1jkPRcSvqeyelLIzZ9pGdnLcqigCtszNzmDFkrAo9BCJIZTQSt7QJwRpVm1toiCW2lfuUAAQAASURBVKjJeKdwSFK+IhAWBwusV5vI7larNWd9ZZloGnVpDCK8eO89SJECJAo1GawS3wrex/WvQv5eA2vSqqPiQCMJNM5TYnxprrNFod+Ha2jItxIdZDOaLab0jnRPMk5h0K5nCwcGOfTSrsutUR6oLdN3Km3ueYdJv3kiXK0C2s6icITZlFDXuzLpKBujZzT9Ex/7OJx+s1J6QwbTBGxaSKkFh6btAAu40mJaVVgs5pjUNU5PjzGb1Fiv11gtV7i6WoMC1+etJEuUCDhYHOHatRsw1uLo+BA3bl3H4cEBjo4OcevWLUwmnNVYFAWuX7uJxcEhvv71P8U/+2f/T7zzzju4uLiIGZyXyw7Bc4BRUQBFwYgaMFkm+ajrBDaY1iXgCgifGI6HAcRQw+uGRYAxl8m5/XAExy9NyoTZbhMgCivh8VnArZvX8R/+R/8LfPlLvwb6j/9j/M9/9E+GT84IIz4tb8rT6Ga8yT3r+vF9z9Pd8fmc3MakN94w9z2LgFlhsOoCYLdCHYeXjofX5D8Q9mVJWQD4oQU+N4J+HvdjoKebX+o6jUNgDNq2gxXDmSssCI6bTwEIFgFSH1hqojrH0OUQRR/GRDSrvvcJcq0o4IgQaOgoSKKBkcFIUeoqOfa9QFiCnRMGYmgNbLQkcOZjVbHTNwSPruthLNe3LlyZak8bCyIvsilFsX/H6tg6Oyaj3QffFx5ZvPrCK6yP+Q5rSYgMPTtUmqbB0eGR1NsmPHr4EMZYhFmA1HGIsRJeyn1QYPQcYwy6hjPEy6LAZDKJ9ciPDg9ZXssMP5rRp9kL3rMuVAoMnhXnXNu1bAABB+OBCOQ9rCvgW9b5BtlgROg2Dbzto5HKGDFM9R5d36FwReSbmuGdjHvASnRdRrIhtIKCBmNQVCX6vsfB4SGuX7+O2WyG09NT1HWNtm1BRDg6OsLR0REODg5QVRWm0ynLlFX1LLJ/6qFOsbHTMDc6Rc0xGmaG53av0V0BdjllqXFYf99+iBEdND1H1kt2XuWdIBCW0+kEVcmISpXQvZUUsUFm2Q5DFREJlOo+PTXJQ08324xGItoKRuhho3FRmgW4XFruAM/1owh5PTIOqvF018odz23WOJjIcOPJwV/NAssNyiEEBJHTeIwFzc5Lf0wU4ITugSjUOcPXmfT8vufyPYEMrGMoUrYMI2b45cIumSw4GUhZiTuJkd81DMxOfdaSdvE88bkojYuCZKzUJQ4k8n6AOoyNNbEOKOvbjgPdVZY1yQYyGFN1XoldSmHwtwMT0vrUudhJy0IXzzIs5kdyKkPanpzMA0eTK3bK/Mak8gV5MNm4/bveGaTNg/6B4swMbD0mvx8JcRFPW1vPo6cAylfy/uu/suSazToeKVgt1QiOMq203xona0Id/hT1YA0053slEMvE5QB1xMSxsOKwU/o1+iICNF5A+29D7Eeibzn0QzAg4b85BHJuh1R7006JIeOFu87H1w1seMB2cBVfvxXcsfWs7YCWAeqFyfq5k+6VHobPZ/mKuMSd2BBM9lvsg9o7IDuXZSdZorMAzXyE2vmEXrXMIj8ujS0oG59BkymuIw08CiGI3DdBWdUoipLtVWJD0Xu60EkZtA59BgPN/U2OXk6k0pJnAnPsGI6cKIB8QBc4oJr1OccBhcbCFdz3FlqajVExAoDGB3TCA0PwsAWhKDiJwVjN+KTosOSARi8ZrQZm7BUHlxPUYDXdl/u+A0kyHIw6N1Vv4Sxaa5Izc2in1S0orVsdv8RvTEQPBEGcjpyRXxUlO6XbVuT/gBBc2v+ESLQUmPYZ0Q6k8kgKqOApTETASRO9lJeQ64nlzVUjgWBEaHtgI0nqTpFDbQoUUPtPGK2Jgb3XpLP8NUvYEl5orYXPeaqRJgTZawBEC6/ulflTY3a8IlKawfsSP000ktrJ89b3TI8gAyp50AgsGxgj2FiUsuVJyltw4omMpfA2xOGWnSYQ15AeJSzI9p3WrlHxQufTI3gT6ZvbymgTOp/Kpq1zqCdTbDYbNE2LxjUIntdnVXHJzKoqY0CZF0SHAcIjkeiCLDfwWm/RtBqgo/Z+poWiLKPT+upqGQOo4zBk+zOyGWO2obQ7pJqxbGmdkexjF9cQgMhPtfyXk7URE1Mz/q/jHpFWjY1rPWTyUaQ/KJkl/0rar7mWeS4T5QikgJFSplrKJt0HQAJPS050DXnQkyIIjYJNhYYTnew+BjbZkXwyvib/LZfB9jw5jvmuI8rt8VrImHB/yBiRzZnGdqhhO9v3yzx2Pfd55dd9bdoXiPA8fdh138d5977juR3jmuGs9VSXy0s8fvxoEB2ri6Oqqmj4UHiponAMGyrHZDKJTq+80Vp3S6HntqAQRPBhhzYfm80mM2cxwyuF0XR9DybGBFtmjYUXeKK2aUWgtRJJy7W0IJGJYwgpdYSowh0C4fLyEov5DAZspFF0DVUi+JZs4dqstm48ibRm9uiLupdBamvx97TK1SHd9T0ePHyIuq5gDOAKCxjOah8s3LQHxrYlWA0aLFSODN29KBKTVSVN6+EOdd+ddKvKVBQMcyNK9g7ZTPPh0mfmG0LInpP6IeJAvHDckLGSJpHRmRN9eDWB600xpIsN2j4T6+CoIVVvT9FxusUPFRaiFAVEYINgJxFY+fvHwQGf5LAweOFwLu8fj4ggI2RtVCUjtWGbRJ/1PR/Hqq5j9pXCxbcdGxm4JhAbJUMvWQiyC1gjUDTeo64ryVDiTKy22aBru0xRl7YGjbZL7dCIXJWbbK6oh4Cm2aDvOlRVjbKuUZYM19I0Gxaaas780awpIMBaA9/3aFpGwqiqCpv1Bk3ToK5Z4Ak+oK5rbDab2MZdSz0XVPPrtudhOwtYZ8wZgxcXC7y/vBKDhtK3z8kyWzy6GVkMz/D6sdZmmRIGCmVqrYXxgJF6cwaIUYCKxsDr0qMjzrbK62UPIcRTkIJCQWnmeAgBbdfhyZPzAYR8Ep7HBhtEYUj7mX43A6Y33oj3G4kkWlmLGvMFkQ+TCOEqyLNCno8lhN+aeGt+2MzAMlh/GdPTPShX9of7Y0YFWfZsplbGe+KeSXzjYAsibmB6h47z4FUAgK4neK/jO+xsrkD3PdD2XOu3KrkNq7WH9y0mEwNn9akjPv8L8rt9x3h/MkB2gmm865gm1xumcWMI1gGHRwVeeulVvPaZV/HGm5/B1eUFPve5z+HayRFOTk5AweNn776L6WyGJ48vsVgcwgCoqhrL5QrHx9ewmB+jruao60mM2iWh881mLfC9PR49eoR33vkJ1psWxnj84R/+Pk5P/3vsEL+8BBHh/v0HePDwAd5//0N8+NGHOD87l4DEHl3fgSLkP8P/R6UsEJarPmqF1hjMZhZ1aZBQtFTBkXkZTYruGMMj51hqFM7uyzdwGXd1ip9fWJyenOKf/JP/Cb785S/COYPf/K1fh/tpDWC18y3Dic2eP5jcHd/H58f35sx43/Xj6/Y9c99zzY7vT2n7l++U+C/f8XCGBuOXO4GYQ+X8aHw8w5Hd7Di3Y2xis3eOy64X71vMoukNxkFoB8T7al3DwjKfKADfk+glRiAYC6BIEekxo1NgcIMEG7Zty3KxKzIF30QDWW5czbYYMa7kAVaBg2OlvisFimWBtL4diDNgW3HiOlegrMqIegMKMM6i2SR9ZtdQxzGO+92OC/bcZwzz3vqDA5hbnK29XF5icbBA13aMaOHZEPjo4RMQCH65jlnddDd/gY4LRX5RZOOtR9e2KCsOWjw8OoIxBus1O5w3m03MxlgulzGrq+96mAB4m2rDGmPQZcFqqh8CDH+u+1OsL+gDnjx+EqHQo1MnJFSBoixhJSjTe3bSEpFk8wDTCfPjup7g5Zdfxmw2i++q6wp97/HSSy/i1VdfhbVcXqzvuxj4N5tOsVwtYS0jHh0cHKBpG3i/7VT4OIckY2X/mHGMPwNpv497/4Aonr6hqo4vb4XevEt/SjLT0PnN+laSc0iI1xiKYz6bTBlOXyAwkxtUdKH4riRvRQ4ne1CUr7Zk4XQ+NmLQ3qePwfj3ZABOcoIiBVnHmSuh7+O60Hftgs/ntiYZLGT3DK/jl2m2bn4MZNmRHBz19my+Yvaz6OjGKjPRAGL+LTo+AtjYTIaz3qDrnZ8YAqHrCWVZpwxDQcVhVT2tWfYxcmcyytkx6kkni2Ow4+pcj9aLvPTXBIK3AVb7L4Z0Ul3dBthgRVch7qS2i1LfmGZlzg1igK32f5wdPkAsyWT8JPvspreP4xQf3zeGcR86NynW39Tv+k/b/SwnZ75WnmVYHBooEx+Iz9gKpkz3DZ6/8z3DXY2dVePsU0UtY5QS34sNx2r24DC4Ld4nnwmI61DLrm2H1GSCWuSrGawvxR8ij8hGJeuCAUyA2oQoPy//JaN9timIw+ZOB15jattyuX5HI7rStuarKZ7TU5kumCEg5kEH+v2ZvPOpvz79iFrD4D087oEIfeeFrZmh3JyvN/mU0BNS8AhkDWil66RrZ/KV8m/5r+q0ugNkswTN6ta5YKd4LYiDHBTJaHM9et8hohNJUB6XWuOgSM1W1sdzHV1OvOBnO7atS9Zy1zScca7rmQiFBGMqep7aWFoJUgwg9ETYCAIPYGCIkRcLm5XnkyBPLbOhCKpxnqR9+WGti1NSV7UkjHSSPYy4jNP+k6kvUd7nI8T6znbLjhPHh9hRZCMPD1Hf4YAX5gda25drsVMKYhvQttFi3iLjEri+dm6XNtE2HNspSRghJKciIwkS1p3CtRt0PaHpCD4AheNrIsVm6ymEnE+kQ/dnNf/mCb2UXwThxZkdI+qF+TjK9RpWElUvEiFOVsXAFp9fGEWLxCeJCL5X9AMrUNaKLNVLAoqN8qtyOJI1pwH8GhxhYyaz7F8hIEARCIZcJtKU0rRJ/EGfrzxfR41AUa4SLB2mG1twsmXbgSgFz04mE0wmU1R1jUICfHnfV3oSeckkWSeIvtJ1HZoNr9co18W54sRF1lkITdNmMjTzlZDp9olupBdKFKlrUc7LD2cM6skUzhXizNfnJEe9swbWsX9J/V46kLqn5UFncf2MbZFjgY2UZ5jEA+K/nO8zXzGSyR7pSIMa9XeDrA66jcGLxjACkJbW0f6NiCUj4GcfT9vvPo4eMdxH8uboXje6FrkMlcYqzsdToNT/TR5jmfHjyrRjOs2f8TTH9677flnHczvGY6SQYeevZngDkg0hTrwuRsSEKJTnEW/589RgoX/1/HQ6TTU7smuY8frBmouO8zhmLAg4W2CxWKAoSnQbh6okWdQsUCqBqkPGWc4I4CihBk3LNQtJfs8kRYCQRQZxBtl6s+FseApSq8Rg4AzXTUY4WCTwkQCb/UFaRSadjIxEdxbdlHKBnY3fzWaD88AQwDAG86nWRtZ6OdqW9DlG6plhNjjzSL5mGNWjsoRC2vCzvB9nTGcbLLTbNFBYougZlfvhzWm/V6E0l6XybUMNK/xjCJSM/JRfb+JGzMJXGuc8Wk43IN4aWKCx1kENzwG64UsfjF6fYLQ0Yjqvw0wAQ0dbI5ssR3qq8a/vuiRBRCOAdvqTqx+vXzvFLIOvBEYZI9rXyKCGAlL8nI3neNPWI22a0v8IuS3r2StKhECMm6Ts24rXZPCeFV7D9DmZ1KjKEgCjRzTr9SDCFNl4U2woRBAkWb+ULamcnvl3Hzw2m7VAUk05Kwo116I0Jtan63tWdEAM4c11NUsUBUO6NZKBrvxS62qqk0oFjigkZmOYi3CACm6xiXKO4lykq/nXlw8X+NnlRabIydxSUgrHdJQMknz4EEDUSraTRADnyomMcYTjQyKIXOAaLuZ4ib409dbkP/La8TK3Kqj5kYCvwUHKh4ajkY+qSb8NBJbtDXX3Jru9WY/7EgXyrA+Jz2bXZ+tqSH95n2TOIyJAFphl0n5qjIn1sWyurOp12dynnxJNiUYUlSRtukGuTBACGagt7fKKAyCsAXwQp1QglLaIAlxUPsWwa6xFVXJbdY0XhUPXGfRLApGHcx6TCjCGUDjtn40KQNw2B4OOSG9x/FQA1zHLxiQGBQz21rQ/hwAsVwE+FJhVFoULWMw9JtMKMB6/+qufw+/+3m/h+OQQx8cLFKWRGrVrjiD37PR6/4O/wptvvIlbN2sEanF5dYFpcYhbt2ewpkVRrHF4dADfd9g0DBfddR3Ie1BoAfQw8Dg+OgAAnF4/xeHhIQB2/p2dnWM25+jlN996HUVRovcB6/UKZ2fnWC6vYrT8crnEw4cPOYt9tcJyucRms8H9+/cRQsBqteb7nlxgufRYOxOVp1QKwePooBDZDnDODGjLioKSO6N0P9S9kYj3494zws7VEuh7gnVGYIsrHB4e4d/79/4x/u1/++/BSF3Huq4xm89x1ayEzo0oizzDIdesxkxSaSQR9vDI6WjMhPNj3zP2fX7auX2/7XrHaHON3FsU5r21i0k5fNoLbeQZT2kTAPSGrQVaGWfcVmWj2R62dQzElHFnRk2N/TKjZ/MRgkfbdairKvW3SJCnNgSGhYNlFCBo8IeNpY2cY0NDkDJIuZPVqJEoG8pYGxGU7JVGAulAaFvdC4dBUOz8rqTGtGbNEFzB5/ndPXzfoygLdG3LBhodr330t4ue9/w8/oEI+JUXPyuBenNMplOsVisET6gsGN5TIOuC9yishS1KhtXTVxqD0hWc8S3OZH5G4FqCJsCC0be8CRzYSIRLOmedqldoQhuNTepwNsbAGQffeYaANIjlaKx4hDUbSWUpYww6gdTORJIBpN/p6SkA4ObNm7Hs1t2XXgAZRvBom0ZKVrC+WNc112WU8bh582Zso9bybRqOGimKAk3ToPM9ur5HVTG8+9V6haZlmckWDk3foRfD6S9yRGOgSes3yQ880aybjLJposiT6VfPfBvFv7noNjb0xHE3iUnkRg2WyZLs40OPvreoyhKz2RSTSY3leqXdguzASCmZBM4gFn0uGldt2ntEzhw4QOL7x/LtbhnueYw5A0eNYdkYhgNDnHXoQ8s+JbnO2iGkZn7EPVLoKl5hARNMRJ1QeSXpyOrMy2VGM3iujmJquNgr4l6czdfI/hAzbVR/NsigbAPKomSI3rrGquESCZN6gnazRidZ49rUpFJpm2zclnN+OZgLY6Ivggb9yZwYwh+DXM+v43qw7HRSFAzh19bCBgNj2CFWWAMrz7N8RuDfE23ksnVUaURm15IYAGIATtd1UeZR+XafXpEHWTzPsYuGc5oHxD7nE/qFtR5EnFGl7dKMVratpeHmtqaEiLzdqTZ6+usliAoy7uPNKP0GWaeATaimyfazq6+Z/jS21aT2KjS+GY6DMQhGnVU9IrKiyAW6dtJjeY68JHKANGNT9K2YhigvJpPRIaIOM+w/oUwjEcctEDFSAqmIynoGxfnUVwmvVP5mEde7OnphACM6N2L/E3qQ7lVD+1g6H81Ug2kz2XXpeuU6KRg9tXmvIfpj8NKBUR0Jvn/rejAPawQe3zkHlbzyd1L0bjNNR9nCuQw6ndGWYvBQth8S8jliijEmz3oXWlTZOq4jtutNZzPOnLZOAvx7aDBKI7ZlLtFpRB63wqeMlIsRp2xEwSHAWBQFo81sNmtsgpT/0cxcHT1rYS2JQ9KAAsu3TduhaTr4ELChgDYQNo3YyyzgAqG0NgtwZOQxLRPHtBpggkeQdeaswfY0aaAXYG2BelKgpJqDsilIn7K9Tlmr8l4RKHjOguxbsm6iIzmtR+UFPO8J8QcGoEDoAyPPVlXNctuG/QcBPUJQG55D1E8p329kXYa8fERKGlFa6LsOnQS9siO+iBnTbZ/khT4A6zbg5/c8PvNCGe0TcY7F4TyWzOxokHXtAkm+SppVLpsZII6N6lVJhsjnTO0kRkuzkjpbVScR/mJt1FF0PRBS0BiRlJ+1TrKqKzhXoO1aeNFxrDWwEpDMdw+RKTRYWYNH8n3UhwBSO68djRRxID/rF6IrZH011sZkLEDswyLDGUBKAPB+Zi3rkG3XYbla42p5BecKnF67jtlszgEvxOvSFSYmPfVZwJkR27b3vN9qnXIdWyvjSSGgKArMpjNeq1rPPCKjBuROXyKS2AX1kWTyeaQFI2NgB2t00wRcO6w4SVVQHKLvQ9aeZieD2AYexzErmbnryPcolnnD1m9GdLhgaPDdOBvXPduVbERhMlZKDdnMvxJpxcUyZbnfSoPSizKh5uTO+2dJXrvk9Vzmyr/r58g3nrL3sS33Ka+n4XOjdG9SUEKa5D17747zu7bpj+u8/m/q2Kev6W9jp3x+zy9yPH/GOAK0dhDBs6JlAFcYWGL4reADekuACRxtbElgbROU9SDKBNvQPKpIara2wh6me5ip5YMwfAZvFj70EaomE/mygeaolK7r8e4778JadupfXi3RdX2Mkssd40lQGjyRBaC+R+GswIDwLya7i88kJqGwOgxbky8Es0XbO82OyvMpOXe1RbrwAnFNnu7sHG3bYSpQHWVRxrpokTll2fnq+Bus4JGix7J7Bncv3zmrDhG6RY2I6TFjY0Xe9mG2ubx2R8d3M6RcUdI5S3S2P5IlP5uUnZwRpsWZanb5AZoB/wmDBnsoFHrG2CidU6EDcOj6Fgm2mtA0GyiEu+qRBHWmEvZQxXMdxqRmaluGSpTQFA0Fs3wujMnHfKwa6lMQyVEdGXVVxWjWTgygfdcz0oJzEilmAcMZynVdcw3yPFNcnOJt0/A4iQMmhMwNKpsJ10xyg/aLfpqtb41CNBnNcuO7rkXwXiBoCtQToNm0Upeao9NAFsEQrNQQbpsGzk25tpUIRbPpjI1nxLU4N5tmLJ4O/qZvw0j7wT0m8RRuLQ1+++prL+FPPvgoqzFstp5FOiAZ+8iPEBhbgxqKtZpy53d6H4/d9u80aON2j0e/DiSHEV8cvdTsGEGDfJ63R/OXdowVlh2sJV9P44ZEnvcce3gesKOO8vHq38cN8vNOIs89Wxl47QJoWkLTjBWw5DxmHcuCwLXAAKAsASuQuN4zxFrpCkwiioNHIUqOK1wUuF1ZYn64wGK+QFmWaDsuh7Jer9G1Hep6gof3H8KHHkQdjCHMp17g+lOGlRqVAQl6yow5gSBwcxq9i8FYD5zi8TwhkMdyTVitAurJBH/nb/8hvva130LfNShK4PTaEZbLC/67usCPf/xDvPPuCtNJiRdffBHWAt/+5vdwsFjgrbfeQOF6VCUrPnU9xWZzhq47R9ue4/69J3jhzqtYXl6gquaYzg4AF3CwmKIoK665ZgwrRp6wXG/gjUVdV1Ehun79Wox+55pUBnVdA0jZlimT0sd6ukSMSNJ3PZd3EAfhRx99hP/sP/u/4O2fvIOLi0v0njMaQBz8V9U1VmsJhqQeWjIhZeiKQ8paAAxnBwICKPpXWb4oY9BkVRnMZhz5e+vWbbz++uv4B//wH+CtN98E0AHwaDsP37cxoxMwaPuAskjzN1h/T1ta443K7Dk3/jw+dt07Pk+jc8868ut2bQ7yvGlp8IVrFt95RHCGy0EYY7TgaDwGsHxqe5JM2We1qVo6tJsemD67PTCEIYzy6PdB556mGQIqiOx6VN93sAJFzgGYTA/WWPS+T/WpFaowGFhLMbOzUQc0uPZ3XVXJAEYJTYG7qDKA6i0Gyk2JgjhLg9B6HF64okSh8OCB0ItcZwuHsiphjBVY7w5F4SIkexyTUcdp8EHl3nTdrmmJXyIsItA/KDCfHER+TUSo6xqGLPqNl73SRhjQEIKUj0kOLADRUb1arWIQMYDo6FZ9re97FAVDluu7uqDZ+qn+MgcSsnOprmo44+BKhravJjU/sypxcnKCa9evo5Tnz+dzHB4e8nVVhb/ov4sWLerpBP/d//6/g9OTU5yenuL45ARlUQAmZbZfXF2JsYv1n4ODg1i+S9vsvcfdu3fxwQcfYDqbYjFf4Pz8HJPJBNPpNJbvWq1WLKNK0GNd16iqCsvlEl3XRYeZ3vMLHQLvS8ThueosZfEtZcShz24ZLcqBDjTKONjp6CBFzdrx04DnDrNsdz6TiE0IAKbTQ8xmM0ynM/iHD5N+n92/yyE41L35mZ/EEPJUx87T7gMhBvAQZ5+VVclBsJt1FEAZzrHIYCv5iP2UV2uwh5bOCoHEjzwci9xBG79nf1WmHOqjiSdTdl/SwVlmZx7INMToDQ7ep3JIVVGjKgr0HWfCFSBU1gAUsJgdYj6fY71eZjDH7KSmyLMo0qpBpqfEtklQ5mhsskHnP+I0igERqvsDcCYFd7P+34PIccmlyMvlN8h+BSMqe9L/ct04v14DGBJKGKKtQGWgOLZ9skmNbQjDfj0f3erzlfcqPeWlxpyzQjdSh7gH+t5CoV+Ss4NgXea6NXawDvIkkO31B2wJKDbV+BzfY9SoDsAhN8Lv7ufg8enM6CTTVSyxlhuSjUlB55QcooDU093xIiIDa1JNVb1HUUxi2RVrUVaTwbtyyFi1n+TrUm2YmhmctzcQI2Wp01T3ZLZJMJ0TkdjU7Pb7ROhlexEG48r2Ddn7dXHT9rw+lW/mDoCRzU7paOv+OL879hx93vg1cp8GGEQ7wiAbOYDIwHtOPPAhoFROQlrX14FIkS3TPOg6rOqKS2TGhB2R+XLbSKTXxJ+GQQvijIrjqIFAVmjGoSrrKKuqk0wDIw0IzgLec7uddShLl5DiSAPJRU42DCVclTXm8wWIAlbLS1xdXWKz7lCWDrWtUVY1Z7GWUtaCCKHv0PY92tZjs2mk9AXwI3OGcwSsG+0iobRAZQ1cHJMMYUdRkAx/90azSMdKF5+LMOlGKnBAMj6JQI5SZjw0mCOjM/JS2jLxzkQ/0AUmIrmJ79FSekpjxhiQyPHBCKx6WaFwDq04HkMgEHwM7le91cAkeGhtl9DHmNyJgE2zQddzibSicCglk7jtevj4FAeCx+Uq4P/0f23xf/jfMCpLkPVJkOQokiz+bPkoCmwIBGNJgnzTFFgj+pIud6WhLOuWEQeGzx0qcTaes9YiwIEkyIqyRDAT62mzPqWJgz74WBbKFSVmU0bBs84hBEYxCEXBpTJl/p3YeI34lFLgjwGRRUcsS2ipQ5J3JnlnGORE1uJXP3+8w+YmCXvGwjoeOw788IISxvKKs0ynBgZOkrDOz865rJSxODo5wcnJKaxzMZkrTR645J0xMQCk7bro6G6aDdq2lT2AxzoQwUowwdHREay1ODs7Q9u0cJIJ3bYczKJlIuOeFVKwFaUlEQfDWsBZhuzXw3vCT366wa07RbRLM43IBZbtaYMa4ym3EFFKkwFWuSfn9c6Ykb8g8XNFdTCG+aDy4FiyWBaXcwZVXaOaTFBPJzCWE8wiT6T0XCf+AiLunx6qxxWuSG2Q9kSxep8Mku97oz1u/D2/Xj8P9JORLDQIYnjKofrA4FKjNgmKY0D7OjFs4XNc88s7Yp8z8UOPtDQz3rMlQuyWIfS353r3M849z/HcjvEohIQEfRuJU5gaFbRDQTNRsLciQOhzdgn7eo9CseeKnEZwbTkFBsoy/88aVmDW6zWmZRgSteFaE2qQ+eijeyAKsS6TMRY+aESOCEK6YKJCa2EdG5MYboONdkXBGVWc3ZhHLQ2Zm0Z75k7hwYY4JvodXym7NoqdA12C3+094fJyidVyNfg9vkPnTBaelUhZmzHWKDSa9GbNmlWIJ62BlCJ7pP6Lc7E+bc5YIzRG3nedIoG33DfPsU3iMElMb6iEa/Q2okA7HDl+pc6vic8MGv0eIX8y52lsIwskUXDO6D7W2on9SBq3zbRvA1byVus1QiC0XYPgCVeXl5kAjij0qPP3kxh1+FmElyUDMT/ysSZktBG/bx9bClBmtDCjc1rHpKoqqENOx7jvGWI7BmeIEy3CwIUeffDRUU4EtE2DzXoNnYwYPS1rm8dblBqB5NHloYKE1pDkOkFZ1HhGV5B2rpYrTGZTFGWBqq7QbBoW1izXQNGMDGsM2q5F2bOxrKxKtG2LST1h5a/nOjVsWM/HDoNxS2M3mj/oqsbg/oyLRKXYSWZEMJQY13gOgVircasB8kZd15qJlySL0cVRidg+dmxZcZ3ubhViTyJvHAsl8lRdxcNRkCnf2hh3Q/o9va0YT8zWc5drhqtNlxspqbFLcBq+vygIs6nRi4a8eVdTMh6kz80/995gvUHcvzSC0zkD7w2MraLTmojgSoe54yxBNopyhHcpCoJ1FgeHB6hnk1gvta5rLOZzlFWFyYRLC9y5eQvXT06jMWkmDoWiLKPiUc+nmB8wkgvXZwzYbBqcnZ3h3XffwYMHj/D//ud/jJ/86CcAWPFsNjwmfc+KmCmc1KPy4oBhBYMhlQwIDmWhCDRZhk6uOBNwMOcsUmOA3gdcLllR/vSvvIKv/dFX8Xf/zt/C9Wtz3L/3AX7ykx+jcEe4dnqMs7NHeP+D94AQ8Nff/wGsMXh4/xFef/11fOqVTyOEHu+9+z4++vA+Pv/m38B8coTlco2XX3gVq/UlHjy4j+PDQ2zWG6yuPBYLH8vSLOYHmE5nePDgEfo+4PjoGIuDA9iyxvzoGN73UqdXMxE48MY5h84HXF5dwEhQka6xqqpgrEFVVzEa14isos53ooAXXryLN996E33X4/3338f5xQUePniAs7MzEAE3bt7AX377L/HHf/yvcH5+CS1ZUxQFDg4OcHx8HNExptMap6enmEymIKLoGFosFjg9PcV8PocxwGw2w61bt8QhV2G+WKBtGixXl2jbDX769k9w/fp1qWvKcNPelug9K9WFy6AsQREFcq88nDNa85RzW4tuz2e9f8iAx6xo+7rxdxqd33cvsT/rs9ccgB5vn3sse5Gn1IA0eM5okyDE2tDzMr0jf1WEbQu8h+48Bn0xqrMOjqdz2VwOy681+wUOIDoanXUChw0EBBQoxOgWpN0pKFPhfXWvB4xCICVdJUI9W3ZsSwPatkvZEZSyI/i+lLUGAGVVM3ybYYSFru844M+yYY4h7LReI2es+66DaLppXLMBGeFd8OfnEv10z+QnVJsJjm8dwTqgqgq0HQf9+c7D9hZt22HtOXM3hIBNs4l7RPiVhNjy8/fei85tdYbz2EjZLMk84gydTRyfpmlgCoYdN8ZgsVjg5OQEd+/eRVmWODw8xOnpNcxmc9y/fx9XV+y4Pj4+xo0bN/DCCy+wA26zRrNpoNCVm/UGrnCo/qwCOobw/MM//Br6vsdkMsHl5SWatkVZlugpYDKZ4Kg4wmQ2ZSNWCOw8M8BiseAALc9oTQ8fPURRlWjaFq7Y4PD4CI8fP8b5+Tnu3LnD95YFjk9PUFyxvvrg0UPM53Nej87CkQMZwFPYckR/3KMsc3VdnXjbz3RGA0FHwcz5tdEAj/3XAABSduizjmT4GRuQkoPWeAtXFpjN5lgsDjCbzQZ6vhWFamygGrdLYa3NKOMov++T6kjP7CcSkIa1FmUWDGNhQJbrwqpjTfsW9VKTdAsrtex98OgE7lZtKsA4g3IHkwUSHZiEgBe8GrTFja8OHqg9JY2ZCLQgULTHeIh+FAL6rsOsKmGrCm3H6HNslguYVBVmiwNUV5dYNxxEDOuQIFkBTaiA6RjWnFKSQRzTqC+b4a6Ql9dA6qeFgaN8vi2C1OMFHIwt4SwjiRhYfo7aHOCjPhgAmFDClpP0ToyC6GV8VUcuigTRmSMdqkM2BeeHhKS1w6j6vIfSg/JYRb4AuIzgcrnkTNTQRSfuoM4nJccq2+zK+H1crjCXkQGtV+4Gv+VrMiAk1INRH/Nn+q5PItHIeJw/N2yplOldOT/jZPAh38rtiErHka9YK9mIqURjUXDJR645/QxeYYBgUzC99lIhsaPBmggkez7TAEBk5L25rZNANJe1a2PgnSbaMBJdgLEEk6GDjaH71anufbc15kPHoqALhX5Aj3sDGkxKAsmd8nkbxnOi11hrsTJsvzLG4vjkJM1vFiyQlx/gLE3O5GU72rYMT2A9LSJRiU2PwYICNEJa+aG2p+s61kmNgRUY8r73g2cPZj/uQfri5KxNY2yiGYQzFBlC3QeSet5eshgDfM8Q6s461FWNsijhiQPpdL8z8l62lxacJekKOFvAFezU54C9gKoqUZUHcNbCGoeiqmFdAYDnrCpLrFdMQ03Tsn4HIJBBT4z0JsMM6D6aBRaBEB3ijFwSRD5mCClGnkgiqx7seLTRmUckSEo5up01sCTjrSVbdH3DIliCk/WiZRC5PVpzmZJN1pjkuI97DRANsiR9MIJQZywmE7bDKZIah20b5ifEyU4hwrPn2+0wKCueo1SSSe3BwXNQaYBhmS8wXfY+4GLZoetLnnsAQWyUgUjWBOVJ1DAG0R5TQMpnwPCcgHnLYKsSW14+Nxp0oibAeP0go1zlGg0mIhBSIMnAFil9JGJkAQ0mnkymmC8OYK3YkDoujVmWVbzXC2oUB7Mw79NBVn7WiBO577qI7OlDiLXk1dmaH95LEAcpX0Kcc0XZoBCirWDgwIU6qgFbsB/jarnE+cU5+t7HwNiyLPl+VbO5bioHZnhFZGEU06vlEpdXV2g2TQqMsSYGHDpnUdUVFosDzOdz3Lt/H33fo6wqTKdTtG0z4I/8R2h1QJf5WCQeZc22/6SXPVPtc4rEqX4LIqYvRUACfBa0g6RLU+b7GesYYAd5jvBjrUKgcxJLQEIu8SojSV+LopAAYw4ytq5AUTMCR/48RT5W9GM9r3qhAcRpnuQZA+XzT5fDcrluLPN80kNl3jhOu3QTk+29O+V8E5Fw/3/hGGfHE7b3jF/usY1m8Enf9zEd40zEea2OaM+R6LtS4AvUGM/E6qG8TAUuzWjacq5lQnaudIyVXhV6tuokEde3qyo24sMoHHASdGK9gkzYy4X/yJCy2jFJEmYGZ5wIu0YYVSA22FRJMGMCV4uALkyDQCI0mWFWysBR/azpMGPXiQgRmdJNYkXjDcjEDQzGwBDEyTUce253EoizYdWmyaYQpRsMrLbCQOPzMBRyeY+SuUzEk94h581W/3YNgTB0pPGKn1UQi6/I+jO02UAVEh2tXMFiZR2xXlcSulNAiELLG5FI5M2wzkZBhv8v5hQxRqgwCMNZ09ZatJtGoG5XiLXDZNqiIU+f+QkOA4O/+cKt0ZnxNU8/hlMXZxsaoMG9SxSjG5J1joV5a9F1PQwMul6MQYWLgpITJZadNh5d72GMjU7xrm0k+zFX7kg2RM2ACFxfDkDXEWet7qg3xcqIAzkAovCSCNR5YEiggPVqjdl8xhGQJRt7Awk8kLHoAzvnDHGdmFTnhJ1X9WQCVxTou46zZds2Ctu6inJaHs/DmM71GjWWm2g407kgfOn2Dfz5R/eQfhpZ3p91kASXqBAEI3V+0rtyQ1JUgAb8evuxapwzGQ/J6SquE0pft56xdYKykUzXjESS3Q97xqGrZN0Q1hsLouHWOc68ADTQKPHYQfCJ8E8DoO8I522I+whMj6IgLGbKU3KeiahsXi05UKZtTabkIAq3aogpCoeiKAXayuG11z6F1157LToxF4s5DhczHIlzczqdIgSG3+77np2fVYn5wRyHR4foeykz0Hs8fvwYCtH4m7/+6yhtwXWUwHOsdWp5/Vt4w9RZFA5E7ByvqgLXrh3jU596GV3X43d+4yt4++138PDBA3zrW9/CvXv38OTJEyxXK3Rdh03L8Lfe9zG4TfmAtSrEliJ7IKJwpGsYKuvxE+ZJhYPUlC1w/cYp/oP/4N/Hyy+/AGt7fPtb38SHH/4c6/UaR8cHeOGF23j48AE+/dpncffuHTy4/wTOFjg5PsLlkzW+8ju/jccPH+H+Rx/hcHYdjx4sUcBjUh/iJz/8Edp2haJwaFuPxw8fYVIfgm46vPTyXTx8+BBPHj/CmXmCa9du4PLiCt/5zl/irTc/h8XxCS7OL3B0fAwiiNGDoUxPT6+BiNBnwrzKWSFwDWSTKcFFUQAGaDabaLz98KMP0Xc9rl27hvOLMxgTcHJyiIcP7+HVV1/Gm2+9CeccvvbVP8A//nf/MYwtokGjqmpMpwyLC2PQtS28b7FYzIHMwNY0DdqmRS/R6M2mwXK1xPn5kwgn9qMf/QCFGIYOFoeYTw/w07ffxeXlJUMsAyjKEm+7T+HV7m0QAZIQykYCJD40UGR2sb2PyQr3HlvCx57n5qzHYPd942fsehaxxPL6tQJvXAMerQNaT/jhox4/ilaGFBSor7WGFfPPnRrcnFe4MUvy7zvFClfgfe/D+x0mdYHy20D923vatm9zkr/bXdg1MLt4sewn+7pOhLZpOdvZWtkmBI7SGkDg7AxxgBuCkd/YgKWGFieZHbm8BgPUhUMptd6CGDd5WbEBFiJrGJNQhaxzUrdashMDO8URtC5kKcaiBN0OcFYRpY7tGDhKW+xoF3vmETdTQt8B5UWNh+4hNs0SZekQQg8fPPqmh+kV8r3PnP5mS8cKIXDJqKLA7du3sVwucf/+/ZgxPZlM8NnPfhZHR0eYTqec2b1YoJLgqZ4YPePo6Ah37tzBYrHAtWvXorzd+4BSoMx5fHqBpuxTQKWsaTVsanvtNyzQMQ24qoQHAGdRTmo0fYflZs2zXDhGWLCc2Xl1dRUzKK6urjCfz7FYLLBarTCbz9GJrBZCiNnvzjlcXFzg4ICNWmdnZzFz3BgTs0MYGWiDqdCbInZ80uOlF26MzmwvNDZMjaDU43VJJ8qds1Fu2ckHafCHP6Zz+jmH2h1fP6BdYr3o8OgQDx7OUJUFqPdsCDc2odmEEA14qpNrUH2U+aW9udNm7OxR/VC/xzEZ7w+7ej5yGkX5NzAqjfceheOAv6qqUrYtGVV04YpCoJzVOZfWVFWVmJQVKgkcVzrLGa0BkBCsTNRtCZB9nZd6EKMwKK1X1k0ZFnPYBwsiy44AAgwcQB6GAqoqoDCANwWcoLcZ40DO8JyUDnVVoawmgNnATUpMJzNM6ilWxQqN96DgQWL4JhCXC3MctDggskh20ldifh23m0wfiEEFyPg1uPPJhiL2lgCwgYMLpRsSmwwRrGPHUE77FAim22RO4GL4XmXNst/kyR0Dp646EmEAL04GkZPI5LIpZ0cis4s87dD1qvui90A1OZAsUsPBQk2H5eo8QsSyDlBIQDOg9gaGHy1juxUtMPbB+7heOLg/JTtE3Q7qKDGSTZ9Q12Lpi0H7DTpxzhkAucXUkMyq6Nohg/jPHTZK90bsKMa4ZODPoO2jnp9lmPHdqtsLSpy0ufUBDh0gNsmu78WRGWKmYpBMVo/M3pG1jSIUO9O7EadhyvzO9VpEO4TSLCfZsG3ERCeCRekcgmO+KC4JFNExFIeJaU70vohAEQ1u6ULmT1pmRG2q3Ik06zxfWisZRsoOgPvGDijRM4wBQdouthfvuXTj2n4fhB7WOVy7/Wpshu96XF5dYLVcMlIOafBygO82sFDoas4eBIAcCZDHWFEUlB9CeKKFruyxtEkhIGRlDEG5EynZfofit/JMfopSPzvj2QaiZfPUGeiDF7kxMF1oIIX4lq1lPl9bhTPOMnuNZZhpsRsZw0F1fd+hbdbwfQNQH4OcrClQljWsqxAABPKMqiVZxj4Q+uDRBy/rz6DtArrOM3skGQ9nEGDgiXXzIKtF++I9O8S5BFGAcYAlRgXJjziuA1uQ8K3MVhTtwdGuLihWBrAq/4eAiJcZxQ1Zc4EyF2D6Pe69g4lPCHMkMq0rCpQAjCA5BC/IT4YTeEzwoCyTOeqWPqGj6cFyqcA/iz7wXVfiv9gAZAoY9ChMy6iXILQE/Cf/aY//6H9Y49ohYMRm5QOEfkcBG5LVy1nOBEcSgKAjJXZMtaeT6BFEBPKefwu8uhV9Irn4c6VN5sNwUJsmJfGzQjYP/L6AICVFRP8pOFmC90aZc+HlgYCiqGKAcde3IAoip6rtKiupG/9RpKUYwAXO8B8wVO2B0b0Sab8yKkPxOguRPrXPHDDgXAFjLZqmxb3zB3j85AnatsFkMsHB4hDTKdsy1GNpIKQmPDSA0HuPvuuw2TRYrTiAt+s64aNA6BhivypLHMwXWBwsUFYlHj95wvqT1C63Mg8hojVk68uwX037a2V/gU2lQjhglJCXvCUYeGMwO1qg9Wx3VjQwYy3IB1AJOAeUhWGUrTUhFAEWzCOtsfChAVwRmWQIKSAaxnCJCnC5y+g3Uzu7NQAYPp68j9nu1lrYogCIA4rapkVZ8d4xm81QVxWMU7plmdq4zM6vNGqU2DhlPtmsk8uUlCXF0rZDv+IunWDX+V1BZc/SKdSdQEjXWbVhQJEqDGAIxplsvTKfCNRFuqV83aYVIMdwB8uDmHJdME+8jP4ruWm/teE5BFZgyIfz04PblQflv+8Y/10PGncfkJ3rl3N8jBrjGoXOTi0AAhVWSAZBZijK4KaKIkU/M/RPgn7i61P0Wd/3cK4AkY+CBx+s2ITg0fcehniDUwNK13WxnSr4OBGaWQDSqCdZIjKglSii1tiYMZo2BEA5raHEnPRe5okGRhRP4xg+tmm7aFRS6A5Aa1gYeN2Ms8iPXNA1+bvjsYM0togiqYz6sz42CvJRSI4iH4Z/hIkK1yV9iNxgVHCIuuJueJlcEd9aYEHPDoXdbX2Ztu/NhPzcSaRvMcg2AqL8Yan/T9NE9SejfUvPGEdO28HgJnbFzUyKR4yqsjmslyq5FJVC3ci7luEXT05O4UNA13bxOpDABhvaNTq7u5NNO4AIFwQoW9oRvR/biOyXpOBl5JoMB2noxnfF6a1rdpwYqUULsNCf999aVd6NCOdsbJjPZmzY73s0m01UbILAzReO4VaCCIMh+MjgeX0LrJK1DBkj/QukBiWFyLcSiRqkJk4GlUoezWaN6WyOsuQMtbbtYIwTuLSO65pYNr72vUdVltEJXku0KhlwJnnXcUKe0GWqlbl7c8hnKI1vtuHu4AlHdTX4LckpKhrzuyPq6ng/E2OgRjxyO0TMsIgbYIzsjcbIPetfnplHoMZr4rtFehndaslE3Yc/8p0JDcjGSNRdtJ/eaeXOBOlDyteI0HYGfU9oWs404SwTCYxBiYI4UzVHfojNV7oKPZxLgofyD4ZsNTDGwXuuxRUk4rTre661HBxCG3DeaKXcZPwNwYtww2PERgwf16bClsMYnJ4c4fXXX8fv/O5X8MqrL2MymaAsK1y7dg1VVUYjHtc840xSzQas6zq2mYhwcXmJJ08e4y/+/M9xcXGB09NTnF67hlpgRGfzOR4+fIS6nmIyncD3Huv1GlzTsE2GYwOp/8dZxF3Xoe99rHkNIhwdHuJvfOktFEWBP/ij34W1FhfnF3hy9gQfvP8B/vqHf40HDx7gwYMHWK3XaJsG6/Ua6/WaeabIAwrpS4GhfOfzOQvtfY/gPUoLfPmLv4pPf+Y13Lx5ir7f4HOffwO3bl/Hj3701/Azg5u3r8O6gLMnZ7i4uABCwOnRdbTNBm//8F380Vf/DnwfMJlO8OTxY3z9T7+N+XSGl1/6NB4+WeH8ssNkconb8zmIHN577wG+/GtfRuFKfPrTC4AM2q7Hg0cXWK56lGWNo8NjGFeg6Xpcu3EDxln0gVAaBwIHS02nC0ymC6Fdi054T1WVHLDjAyZVjaZt0DUtPnj/A0yi4krRkcOBDYSDw0MczRe4eHwWs0LrusLx/Agf/vwDfOeb30bfe3ztj76GJ4/P8f3vfR9vvfUW5osFbty4gbOHD+EKh6OjI2zWaxA8/vp738P9+/dx7do1vP7669hsNnj8+DGs5SCnw8ND/Pmf/qnA0BX4wQ9+EB1ll1dXWK82eOHuC9is16gEIl6Z2O/90d/Hv/zP/2/4jH0AF4IgfCRFn9mqru1tFjRYtCP5Y3BkMkH8PhbNzOia8bW7rtn1HoPd7xm9k7JPRMDJhG+8tbD4dmFwCUJlCX/j2CdjtvydOMLtRTl42LpJBn5nDW7fvI7Pf+EL+JNvfR3dZolS0Swy+XFwmIzRmn1DStkPAw1sq1/RCDPgrWm/0yALdZZ630eEl8I5BGtjBD9Eb0DgAEfN9jOGoQuNyLraPUIB70nKMLWDzKKk51OUK8qyYEXdGDAEpUcf9SOFgeMsmr7vRJzmMjCxDpvZPXA0/A/k1h26wvaRDCJAf24weeJwv/8IQeouAhJcHAhWavNyRpUgScDg+PgYVV3Buu8DYEfvF774q7hx4wa++tWv4urqCt/8xjdwdHyMyWSCGzdu4PT0FM65yI/n83lyJMGg2bADarVpAGvx5PwC1hqsV2ssDg4wnc2gzmUKgXk2EWazGVbrNUPTS9YUO7DXEYYWMjerJcM6n509gQE4S11+W15doa7rSD+adXB8fIzLy0sQUQxeuLy8jOPonItlKiaTCdq2Rdu2mM/n0Tn/5MkTzOfzRF+S3alOs60g7o95XL9++lzXWRWntoS5Pef4h/0PHBmGoj6JtGbHzrCt+7N7jbWYL+aYTiZcFikzYtLomSoz8WNGOnOm7+1+7bCN49+eNj5PdZrHzkiQjbWCFMd8MAbhGxPrHHKmXFYb3ZhoTK6rEoXArpsIOTlsR3IyRNFv+1zW/oF+FnU03QslIFuM8Kw3c/Bi4aR+rLjDrPCl3ntYBFjrYjk2hSQtixJ1NUFVVOjaFsnpNDbfjdqWcbBcJ80HOj8/DmzPIdLjoMg/5je8NVkZR2fEyWYAxQm1DOsEIwEJmhigrdQ5TWVJzM71PAjYgOgaQtfGWlhIYBVkX6J0374j7d36j51/Xd/j8moJGIeyrOFchems5rqrITmg1eHt+z7WIiZCqpEuNhSIDhjhk7O+RueC6IEw6pw2elvU34wxEqyRZphryjqZq0wWyW0tOk7GwJjEKfKRGVwDA5giIppwv3oOgA0Ejx7wrEuT6KRc9oedtiFoljWfs6GXetAp03doLJdswGy95YeWRYzGbkpzNyjTNpzd7FlGdMIUXK32TXIlyBZpzPM7s2dapIAAk9m5ouMVSaSK+qPYYtixPuKtWss85x/E2esUx4EDPNhRaaNulcpJ8ks3TRPtA6HvGWbae07UMcQIP+rQi89NiQkmGz+CZI0TByA4a5ItTq7W67kb+R6hth6xUVCWJZ3LVDSyrhlw0I62gHhcnQQ6adCxD6k0H9NMtpdF+xYnfXBAt0OQklMJLdFJ9ncKCAt9z8loAl0N0dudK+CKEmTUYWijfSvVJg4RXe1tXKENAX2f9ieeb4p7r3QfeRnRPBiEQgBpqaIR6yIJRMqTThKF7uBzmeydT4TyLp6jEOUPtY3RaH6Gb0mlkHLHqCbPBMmaVZkdQEJ8yPI9DHK7GtPkrjUc/RsGMMRZ+g+aDo8ul/FhucMmEHDvSY/l2uP0kPcmtTslnTV7g6A+Qvtg2DEel2vgvSQgJaHpYmdksIw3yZznQZHDcZRlaAEDJ3sjEHwPkhIdSv9EmsXNGeGlIGKxn1J5UC6DSSKhK2CDBlvwPOVtyPdRpSMDSY60No7l08RVI79bYxJya7x+SDckzw4U0GxanJ9f4NHjx2jbBkVRYjqdYjadSfnOod1SuZNmjPddh6ZtsWk22Gw20SlOIFDg8aqqCkcHh5jP+ZlN23DSlOgihhDLhgbZWzUAJRDTpMrI22vLRFnBWoPC5TI5wRYWh0cHUZGN8mO2NK01scwuqE/rIY5lLuOOdIKMRwNI60LmQHkJgFhDHdbCIiW+kqAjqI+lrmsURRVRjPW5itDAY8t8zjkraC2CUqw6ifKqHWO3zyn+PIGz+bFPn8iPoSw8uBvJf5dfpWiI2saxLDFcN6nto/eanFK2+fZ4adDw7KCdz388fSz0ec89zrseNz73cZr3jONjOMYle5WGWdwKp6fQ5wqtp9E/+o+d1DSoe5gzwARRmLK7VDBiqHJxXiDBVmnWuUI1ADw2RVGwggawUJDJTSoiGgOBjTXQyEmNigkiDO884mapdT8QHRGFKFBBItqC5zoWujGHwLXIw5jAc7nuuShgT8PiGhpCMG/d/TyPk4NCQNslhziPG2ctEyGOHT83CeTKpONmmj8TKgTrpZTzAugdYzrPhXd9eKzHJodmBKX2Z/dERTB7TGpU3sBtwYsQ66bHgIBMuR0rxtzETKABoqRlRo1IAlxSuq09Z+OgMm6BHVLH9kAXyJ6zxWRGFxWR0WYCCSHWLY6xhKT6UB5dH+XdrWO4Uafv8d5BFrjUqokZP0kI7rouq1kb4H2PSqCYiQibZgMfuHpPCOIULwoJqBHIqFy5V2E68CYcs58IUXkxQKx71EmWkhrkGM5MIhvBMDl2s8F0NmN4zr6XrDIPgGuhF0WJQEDXcdsLV8SAh6qqUAqMtHMckIOoeOh4bx/7luxgnWfLT+ftczev4Z+/8x4CUl9V8SCNxNad0mAYcGsMFvM5VuuNCB/Ze8aTni8zUKZIIgpHKiiTljcYGfGGYtaejTme5p4oFJn+MwCahqJBBLI/KBSXdnCzKSGBnFwDWRxrvJcQCD0mdQUQoXAVSlvAmJIjxF2BqnKoa64Z6wQZou/76AgoCovpjA2fWpdU/964cQOHh4e4OF/ipz/9Gd5++208evSYs6KXV+IsJgAOwbBRknVvhkEEBErUqkHFCP0Bx8eHePnlV/B7v/e7+NKXvowXX3oRzhksV0sAEJpt0TR9BqXdAY6hiaezacwk1/3VOYe7B3fw4osv4Atf+EKsw9q2bYRy5Iy4Bh98dE+gtzkzWaG2FUIXQJQT9PmalQ5w8My6WcMHdsRcXl5itVrhzp07+NRrr+DTn/kUvvpHfxDb10jNsNVqhdVqhfV6HWWSpmlSRqE4Y9frNR4+fAiEANM3+L3f+wouLy+wXF7gxo1T/MnX/zV+/t4RfvXLX8IH7/8cTeiwXG3w1lufx9HREX70wx+ibQIMKlyePcFLL76G+w8e4sMP38P169fx5pt/A3VV4wc/+AEurxq03Rlu3X4JXSAU9Qy/9uu/jYvzC5ycHKCsp3BFievzQzw5vwIePsJrn/oUyqrCxcUFTq7d4qCD2QxwFQNGqwEeiHVxiQizqkLbNdg0DQxYtgGA5eUVPvrgQ3zjL/4C0wkXjP7xj3+Mz3/+83jxxRfx6OFDznyzDlfnF6iqCseHRzg/P0dVVCAiTKsJPvrgIzRNg2/++Tfw0Uf38K1vfRvf/9738MILL+DDDz+EMQZ37tyJ+9fJyVFsX992KF2B5XIJay3ee+89EBF+93d/FxYGl+cXaJoGb73xJn72s5/BGIPV5RUePHiI0PsIcYwjRPopixK/9Uf/A/zs//N/B7qH4Jgrk3E+3XfNUL7IWUv+l0afxwJU2tAG7Oip7Op55axn3buvLeO/2eGswWvHNp4fBD1m9xFRNJoDgCeDr/7h7+PGzZvoeo9//fV/hcM/4P02apfjg/Q3eabZlnGgcprRi3YNxPaxewhZdmzalmUD5zhgVubHGgtb2JgVpjBtUfZX2ceC96lMU1ytNjAWEZ4x35eTYSlBuVmbagB638P7VGKqrNiYokZ4AwiaTANE2hx1NJPh41iNB2SXDLZnavoemP78EEcHB6jrEpPJAay1eOONN+Ccw8P7D3B8cIhbt26BiHD37l3MZjMsFgted5s1/vjHf4am4+yJ/87f+7soigKHx0cwzuJL/61fQ1kmNBI2ePeYzmdYHB5E/lwUBSb1BJPJJNbgripGAOr7njP1vMdqucR6vY4ZIhcXF5F/r9drlKWL+486qweB0WA+MJ1MQJLlrfKgZnBrcIT3PranKAosFosYEFHXtUDeWzx+/Dju35vNJgZZnZ2dxe9VVWE+n+P8/JyRysD9atsWx8fHKXPkFzgWi+0SSOODSUZMGzsE9XwP3qWrbB2yBgZ6hcrU2WXP7Rg3gDEMKVtVNQdeZMYfZJ/yus3aZm2ryfTqZxmk8vfrse+eZxlpVKZkdmaiQyOijGXZtwDLW8oP4nuFR5VlycEBtUCrSoZIDm0ddZlo8db26zjoX4XJtmKDSf3gtiVjJjfTZPdbhmy2NvI05U/a3rZtURXEjnNnUZQWXddis+EyLlXJtW5ds0bfp4Af3Qc+Ce3nc781X5lzRHWJTKXYui4aXjO6Z7k56c3GaKJGGNAzb5mqh5stGOid9OkMGBQwH2dVU8RYPqK18XrUf9w2dcDx+8/OHqNpGkwmU1T1hGV2A8Alh5rvW/jeo+u7GCDK7+2TkTpb34oICVL9KY3trnmJbQMG60DHHUL3zjmQdTJHYmCn0fP0c8xLyZwZhFHWugGF9D7v+xiYDpDswWqjg9TBTXq6ygUcHBCicyl3lOZ0x58D9wHDOde28rlEcwld0EbdLLdrjB2O0ZdMCemnKErAlewslXJw3vdA5rhP7XTRLhSJFpTmRREsTNYnY6BB4lG3l44Yk+wrRmS3GCQgAc6cTJByzYko1nsO5KWvPR7e/wCKpAOSmsESHM2vIy5BoTq7rLhdPIOI8BgtZmYabTMuGiQGHBKKVDa+H5GukfhI6gR/zOQwIkZ/iPDgwmcLyTI1JqE5Bp/s1/pQhbK2NsmMnDjlon7KATRCM9C1yHKj73oYMlDYbDJgpJKyhHNlzPDWufIdB4AozwqS5X9hO/gAyU5Wek3hRWw7o9hPPwqUUXpNNt0h/1KbhF5rACnTR1v0mmYrV7zk4RmNUsh9BgLtHulPeKrsMzrmJPoIqX1ILg5EMIJia43lrExpT9dxAlK0XanHGin5Ji+DoC1OKDY8qJ3vcXG1xIOHj6EoFWGk7qw2Ad/9UYf5pMD1I91r1X41pFhrjNgtdQ7U/6G8yvJay9Y7hM/7EKSWNnitapasdQJLn08hjylnhyuypgVQyLoGYLj+PDvJGcNCneJlwf6fQAJlbUTHyvZcI6V0Q+CkIlGIMtkkK0USsu8AEnqngRnRXZyMbH9Ie5QicIz10fTdOoe2aXFxeYmHDx9hvV6jFlvdbMZyP9vKcnI1QmtBgp57tF0X9Z225XrqylrUHnZ4cICTkxM4x3D+l1dL1lemU4RA6LsWffBou07KGEC11Yw/xuka9Msa/ucsl8tjtFIIDRPqqsDx4VG216W1oX8jlLrQtQbARdSjTB5IQQ/KSjP5BWltpes1CZZ1OIKi4ervWl5XkwodqrpGUZQpwVAeqcFFakvk8S3R+Yb7UBSMQmvMoJ3a7pwantcBvkvOGwQHjHSRXd93PVPlsu0jyWfDvXBIyzl/Hr9nGBQyfG88bfQes+Ppg7uwZY/4JRxbfrIdb31ue5HZ4QP7BMdzO8b1ZXkEZN4Arhea4PiqqorGbhXUc0UnPw+k6PDERM3gmnidRKTlQqa+B0gbZO97TCYMc9L1XAPYGnGASRN0o8vrFAAA9VwfPNZsYMlHXxDbpUqUcQw9VFY1R6x6hWoSwg4Bnnzc9BNTGzwyfdqS5nbNyJjRIz14DO7/CQ4iQtsBy5VFCOz84QjxXur0UIQgVMW/bRtpioEhwsHCMEztVlPNiH4S7EparnlGaWpT3PhAWW3RXI6lZ9RM3nNkQzZgaNn9gUiSZLOTo0U43gzSo5N0FJSucqFE/qtZr5dXl3EsosJpErzZLkPU88z4l2/fjHVDtPlpnIdOcG77KErORJ03/tU+DsYhe54xUhPUsiGpbztZlz0AE9vTNi0IHDF3eFTE6Nhasp7btkHftbwyJTK+LEpRNgy6XgwCqvxIg0kYvwNiFD3LZE7qi/dRADOGs9KtGKrYsE4C62WkHS2Kkp2kZVmiaxtoyYioXBug7zr0fcXRa86iaztUVS1zCIEJZaeDcJ74OakC2+OZtrCkTOs86FyRKHInkxqFsfCBJNpQIIu8Zi4T866ilJo3C7xfbODRoSwLvPbpV/G97/0QvWdjjrMuRvSR8nQJ1qDM2hHnPjJMxM1/15LM+2tGn/QIRrP3lF8LIggRui5gdeVhMIUJdYKfFCJlZ1oBmB6wHQriqFUba9kL3ZOFKw1eeOllfPazn8Xt27dx48ZNLOYH7BCvK8znC5wcHmA6naasQGNi8JgrComy5axpIsJsPsNEsrAZdq1HCMDfrmcgEK4ur3D//n28/dO38Z2//A7eeecdfPjhh7jarECUkEyMMZgv5pjUE1QV12adL9jh8Oqrr+JLX/oSPvWpT8G5Ak2zQQgdXFFJGQKKTgwA0TkNWU+FoBvob7kDWzOMG8nOVlhYhY1t2xZN28IYhj+aSeYfgOjUaBpeJ+fn5xFFgYMAetR1jdlshpPjYxwczKPz4vbt29hsNri8vETXdZhMJvjBD34QoWoXiwWcc5hMJrh79y60ftjV1RW89zg9PQURZ0j3fY/pdIrDw0MsLy/x9o+/j4ePH+OFF17AiT/F+cUZPBX443/1Z7h15xWcXruLi6sLNGvCnduvoO89rp3exeWTM/z4Jz/BW2++hfv3nqDtPG7euIOXXnoJ1jkcHBzAmAI/f+9DFLMa8/kJinKB1z/3JVw7OYXvWdFerdaYzRcADA6Ob+HTn3kDq9UKjx4+wvd/8CPcuHEDFxcXeOWVV7A4PEZdz9AFVQS4BnzbtDKOLdbNCmXJysLx4RHWzQpdw87Dr/z2V/DkyRNMJhP8zb/5N3F0dISzszMYY7Ber2Om9mbT4O7dF2I2/2q1wq+8/jpef/11PHz4EH/6p38a4ZOn0yneeOMNlGWJi4sLfPrTn8ZsNsN3vvOXWK1W+NrXvoYbN27gT//0T/FXf/VXuHnzJpqmiXIiAHzuc5/D48ccFFIUBT772c9itVrh9PQUx8cn6Lpe6J/nFRXT6l/8xV9gNpvhPfsijjYXuGNaFKUI/JRzmswRqox1zEANhqxmqCumc9jxffx517Pzz7vuf9ax75n53212OWgvOwf4GlV/yLCMlxtjqqrEjRvXUVcVXv/sr+CHP/whzj/8ALO7z2gw5U3YcW00pu0/nvYG1dvM6MK261A4J0Gukj1BIUFTFhKQK/USoQYYAPBJRhi0Qo1Q8h8DlhusszESXbOENKC3F37JCruT7Ak2bvaejVMU2OkaO/ssWtyn4O0aqB3nQiCUPz/E//If/Idxr7p16xa893jllVeYBzcN1ssViIBDcWQDbIC/vLzE4dFxIjNrcXR0BCLCZrPBbDZDURS4uroCwDrg4eFh5CkA1+3mOtKIY3Z+fo6u66IDXHXDi4uLgdObh4BwcnISndjWIu4XWupDA9+4zwHr9ToaTabTKS4uLuLfw8PDGDyle9f169fRNA0uLy/jOFlrMZ1OY9a4toedURP0PUPSzue8VzVNE/XXs7MzLBaLGGAZM0d+QYW9LKtf6H7kepEcz2zRnjZ/0r6os4jhNwvUVZWC3K3hmps+6Ya5HWDLfoAdescOI8u+lo77sM9AkztVx+eVNpTerJGcJtEDFHlH5So18DrnMJ1OJcDWoSwrWFsMaiPz9ZKQwG/Mzg/bwUGSNrVXnAfsYCsQJDtcDfu5w9U5K6Wj1DGuaw9xhPu+hzOWoTbLApNJia7bYHV5hcIwPHBVllDnbb4h5Lr+M4MYdozvLgMkYGSM5beB7p4Ya+7IyO1NyaEYxCA7DG4f2qvSu7WcS26n0rbFkn/gurYA0IU+1j5VOo+0pM8f7Y363pwOFPaUwEG8IfRo2zWIevT9Bt4TENgWo+/RmvV5ggpAUHv5rkCBNMb8zryM4S7HfT4O4/WZf9cK49YY5CXK5Mo4zvkSG89tvk/mAWjcXoGxln6y4TdP2tAPaf6TqcZl7U9jM+xHEeuf76JJ7oM0TvY6nsOcDrOgGSNfKbtfPjmwfcdZrhFkLNsfuI8d+q4DSSB+tPtlejaU5gfNEzoO43P5wOZfaTfvH8xPOjEeL72XiLC5PBvKWJZlCSN0TyTciVSvH66v8esfTgNuW6Ds1c6T060g3+R8J6fLuNY0THIXv+dBoGxctUqG8stCeB3zCs5+D6P1xM/izEbV+3U9ebFbOzcsBab2pyCQ9AxlzoHAUHq2Bq6qUJQVjK1gEWDIxxKdXNPYQx2Ive8BY9C0Ho0n9JmsrsuLQDGA1Acua+N7H9dUdLoEAlnho3Z3sFNEIbAJRTa39aYLmRiizcuovsYHI0CkNR2l8pwGdU1FOpSHyR4Yd04WPJg36x4g6JRaCqjvGdpfA2YjbQjf1UD+vP3Kb0MgFM6yg/Vqg4dPVoApI8nlFOYB/Bf/cg2LQ/y3vyJdEqTLoV2X26yBgxpUZI2VsTcgqZ+uI6AshaQ/fcc2R1AnS5Kgdb3V6cnzo3snYpshtmbnGNUn+B5EXIKJCJhOGTnTWif7GwFmaJdO/JQ/W1ugKEjou5c2ZHWs5Z/6T4I4yNnmp7llZosvDDeOoeygpQW0Y0bmlQBJlmFExLOzc3Rdi8PDQw52rbned11XsIqWGcda/DohoO9aNFLec71eS0Ib65o+cKBBWZU4OjrCjWvXYKzDar3E5fIKBMLx0RHKosRqvUHb9VhtNtg0Hfdd9xUmBbHXa2AmZExYhjDWwlkO2nGFizY0AKAAHB4c4OjoCF3HCBQQFExAgrak9FchfEn3qcGeLkmgyXZoRKce7gOEJOtyIpxeYyOVOlcgmIDg0/3OORjnJFHHYTKdRz7Jjn6+1llOugme0HXJMd6KTlkURUz8SfxHEXITX98l1w/6Mfp9n26w79jlHN+St4YiZv50XvMZz0w6CgY37XKK7zt2t3lbLs+X2MdX957vhl+GE/t5nvdx3/OxHOOaFaeGCe99hJfLM8NVqFfDeswIM9sMLUEhUTSS6PdciYhKiBg6UwZ7tiHKfb0s2MOjQ4YWXTe4WBWy+XSYTyhGNamTkZ+le6oKvixgBWDg9AEQ68JwJBZDHjhj4eoiGsq6rkPwgeuMceugTvuBE42fOPgzfBlGdLaDiOW/yQC8d7U99eDoJ+BqBRgUIsyRzA/h+OQUL7/6Et588y28/PJL+N73vo9vfvMbePToMdcfIoIlCx88Lq8MiDzqOmA6UQcp4orLo/xSH1RoTXFheX2ILLZ4MH66WQyc1pmQtf9QAZniOPNmmj03290Znm0YuLHzGJ+nbRqKPyDNVEQqkOuJpYRo6E2R0+Oaxs93iMyYvsuY5k7xYetSppV2KymU414MKdNm0ciukJpKPtWcDZL5bQxiRKQBQzv3XYdAFDe34Ht0XTtABFD4QWsFGpt00xxmbajCOzY68dgCcIU4aoTOHdc7L4oCXd+LwpApzWAoVIYULNB1Lawr4LLNSZWf3ntUjiP4uq4TuCmWdApXAGgGY6grY7gmclXu6fNpcyMUlI71zgAnwsriYIajo0McHB7g4GCBo+MbOLl2HbP5DN8x/2c0oQMI+NnP3o3GIH620ieliO2sydEJBQxoahgRZ6KygWgYGvyU8YJ05CBGbFcgrJsO6+UGL985xKt3FiiLCZpNC1cUWCzmaJoGfe/RdS3OnjzC9ZuHqBcVgmehuyhKzGaHmE3nWMwPMZ8fguwCf+/v/0O8+OJLYgC3qOoJgIC2a2CdxUSyaZ11gAH6rsfP338fbdtgPpuj9x7OWcxmM8znc0wmk0gXIQRYLw4BxzBMh0dzzA9ewYsv38Uf/a0/BAB88MGHuLi6lBqWJYLnaNyDgwMOyBCDu7UGdc1ZeN73+OijD3D9+nXMZrMovDpXD5QuNZhNp1N477FerbCSICc1qq1Wq+jM1us1A0QzwXOBrK5qBAI2mw2ePHkCdUxMp1MsFgvcvHmTjeF1HQ3GKqR576OTZbVkZ0RZllitVjDG4MaNG3HsXn75ZXRdh8vLS8xmMxwcHEQnBMBZWgcHB+i6LmYUqgNd31ddO8Vv3v4Kms0aTiAZT27cwuzgBK986nW8+bkvg8jjtfmMo2+tRbPZ4PGDS1w7neHXfu0ruLq8xHK9xL/4l/8v3L59Gy+/VIE88OjBOebTY3zq1dexaTb47Oufx2w+x/Jqhbb1CIEjrQ+PD0CBcHZ+DmM5+/7k9BTXb93GzSdneO+99/D40SN84Ve/JAEEHZarZUTnOd+coa5rnF+c4/LyEnVd4mcPH8Aai6PDQ3z6tdewcWss5gs4a/HSiy+ilKzJzWaDW7duoe97HB8fY7Va4datW7h9+w42m03Muj84OGA6vX4dd+/exVuf+xx+8uOf4L333sM77/wU3/72t/DGG2/g+vVfxc9+9jO8/PJL+I3f+A0sl1d49913sF6vMJ1O0TQbWGtYObxxHc4V+N73voe+77FcXuHi4hJFUeD8/DwiEBhjcP/+A5RlicViDvtSot/JpMJms8YLL9zCz6nF+/ffwRcOr7CYsuIWjW7KMcyYm2QMdN952vO7GV2z67fxvbs+73v+vnuf9/o9R5SRAXAWfaqL2glbt5br3X7w/s9xdHyCL7z1Jv74ew/gb3UonBk8y4zamPauZx0Ggyz+fddg/yW5vNELb6qqSgx5LDPpPssGdAvHVQDFGMjXsIGEBs81RjK0VDFVmNNMJg0UIlylGiXKsoDWEPa9QLIioHBWguS6aPSVSdjV5UEHd8lVzzqUxzXnFr9z4zfwxS9+ER9++CHu3r2Lpmkwm83w85//HDdu3MByucSTR4+Zv1qLg8NDQS5Zovcej588Hky0Zlcr33/y5Ek0LmqN5OVyiaZpUJZlDIQyxqDrfNw/mqbBkydPosN7Op3i5OQkoiS1bSvZJQFN08Sa3mXJ+iYR4fDwEJPJBPfv30/DRoTlknmkwprP52xcUWe9Bm+rI1Az2i8uLmLAlQZcExEODg7Q9xwoMJlMsF6vMZvNUFUVZrNZ3HeWyyWuX7+O8/PziByjddJTttEnP4x9bnV9MB7x/v1X7XujWhF3/pQfOwN1d9xnkIzLjIYyZ/mcRKcmgCgF7OU6/tiuwNkxbsv4tKupAxHzE+hN+/qkbVLHtytY/1feo9lGhZxPDmn+ra4ncM5Ep8kg6xYSvB84SyvfxFLGtzovU+3ycaaltZZrP8am585cddokND7ld6yZUyyr1XUeznoUhcPBYgrfN7i8WuJwPhNYeEYbYqMrUq1xs00bv/j4U9Rt9Ks6PZLTGyCBLufgaxvHfujITefUQaDvMsZI0U7ZR4oqGpwp2z917L336H0f2xAC1/rNHdMA7ynqBIjaXQb7HHVU1aBsgoVVvkpSd3K9abBarYCY0JGcPyoXs06s9jVF7EqG2qGuPDTEDrLnx4Zkk4KK82O8xsod5+K1kcYSXGpuYI/6ZJZlbSXbU0mLdd00dpotbDKa50NRdIaBSnm/c36S9z/u/4Zblq/l9CwLazFAsyyKYouP8ROUHuTpg/UsMosto34SgsJpe84QpoAxLmqSZszWbwYmZeRHVmIwrgeqjpjBNOdjo+MNE9f2uG9dZtcwQoOlyEa8x2stXIAoL1UwPMa8PYSA+w/PEK4fQ8tihsAB7hhcm/iCMdIuAjhDVWUwGSvKLkRak3ofl5nRwMjEnxV2P/EAyuTiNEowZou3BwpiF6+gqAJ9p/KhlFsAZ3MXjiGkAxGMdXClQ1XNYDVL13t0XYO2a0A+oHAF6qpG79kZquWALtct1h3BD9ZEQO8JvSd4w7XGVXz2UteaHXRIpCr3Khz2mEbSFSbrC4RHp7WqY8PjQcwsZQx9EOddEHQNUJbQkyVcjN6f1hZgjM5HrkBlvEUcj66wmEwmYivimuNktgPx4jxnWxDzw5RA17Y9lpsWMRFW92shvwAArsLFpsW69fDBSYkPdnQbk1C+8pF0zopzUB3EfF2gEb1DkE8CBDWvxWQyhVfOEICAHiaAy8AabWQKnA4UYEiQSSUgGLpf9BzKUDiHup7I3AmapIyV8j711wAazAUA7GgvK6BbXcGAg5jTwchbwaf9kohiKcd41YhdqApsIh1ktnK9IkW3RHs6ESdodR2X9FwsDjARm9iknohjvIYij0X00EBS6pTRCtcbrinetA26tkfbdiAKmEzY9nV0fIzDo0NQ53G1WqLtWlhnMClqTKoafc9ztVpvsNw06Pqk1G/TuomiuZYeMQYoBD69dJz1PZDJjcHNGzcwmdZYXl4JbDvLeL1PMlJZliiLHJlQ5RgJOIw8UQPQhrJB+hwiMizAsj4n5UywWXNQtAZRBvhYtoBpRmWtArPZAvV0Jo7+VOaY98dCykb4QRsSeo0iumUySzaU+5ziu/rzrGOXDjJ2QO96n/KTfO9P9vthO57Vnl2/54GgY342vG/c/vF1H1d3/cV03f+mj4+laetCa5omQqPmAp8Kgaqc6N/ciK6wjXl0c15DTCdPI7hyQtF3OVNEIqqqCk3TDIx0Wmfp0cOHqKoSCAFlWUvdU4Ozix5lbXB6rQZMA9PyQi5E0NC6HCZKiAolqatXBGaNvJLNpPc9XOFQVSX8RqFL8vgUvq8oHPqeYYbiA/W5e8wXu8hMm0MgKLrM+PaBQQAqrFC26njzaluGeOm6wI6AwsXxvnX7Fl7/7Ot4/Y3X8cKLL+Dw+DAyoxs3ruE3f/Nv4mp5hT//sz/H977/fTx58CQKY0QFuq6Hoh0GalEWDtMJUBYCfW6yyGPGfRnBbakEnQTcmMWsTEUGhM9RNIAm5WV7cIbCvolKFygJYRpRps+O14yeQ7mlODJhs+PzkB7Gc6R7UQwCMZohnBRnY3nTx5jJjY02UJFnh6yVjV36uu0cj47O7NFbRvHsfdofFUZ07AvnxJDcgaBrOWXAg0IcI3U2kg+YCCxlJwE5xoADBcDRnlqLyCvsuSqyMicKpVTXFcq6grNFilgnjkpt2xbr1Rpt16bxYK2IjZsqFDkX5ciu79F3PVxZcK2Y0KAW+M7e+0i7XG+LDRmBOFPSZXUHVZDbFcEVaXw0f2Y0VzofuVKW4p1FuDVs8KIQcPvOC/itr/wOZrMpPvMrr0idLH5q23Yw76Uo3MvzSxjjkCt9/Ao2puWEoO3JneM7iWSkWIwXw9AAkY4QazTyhZt1g26zxld+41X8o3/4VRwcWJBZwfs+GivVMN22Lc7Pz3FwdIBN12G9bvDo0RkQHI6OThG8gTElPv3pNzBffBavvPoazp5coKom6H1A1zcoSoeyZmN927cMkR863PvoHjabDYw1uHP3Dow1mM/mKMoSIMRsqL73HCxiGL7JFi6V1iBC03Ittq4HjDWYLaY4uXaCsmJUhCdPnuD8/Byr1RKLxQLWGrRtB+cM2pZX+mQy4fa1DdbrFSaTCSaTWYQRv7q6illuzjlcXFzg3r17aDabqNCosV+zmjTzBEB0eFQVBwao0xwAqrrGyclpFIIVkled6kXBcNoffPAB3nnnHdR1jYuLi/j70dERFos5FvPZFpz7bDZLdCAKqsL/qhM1BdyEGFCjzg/9rvSw2ayxaTocHh7GfhVFjdt3X8btOy8zHGDX4+qCHUnLZo35bAZnJ1ivlvjJj97ByekpHtx7jMePL/Dp1z6Lo+PrCDIW3/nOd/DOT98DAVitWlTVHCFYtG2Ht99+B7PpDPP5QhwDDo8eP8Y//af/FGVV4g9+//dxeHSM1Q9/hB/+6Cf4i298E8ury7jAb926hcuLC3zjm9/Ea6+9htc+9SlcLZd49IizsZfLJQrr8P57P+fng6Hi3nvvPdSTCa5duxYdWDdu3MCTJ0+wWCzk3BWsdfjpT38a56Suaxhj8N3vfjfKY3Vd4Utf+hJu3ryJP//zP8NPfvIjHB0d4wc/+B5+8zd/E973+MEPfoDv/+D7AAir5Qqr1RKT6QSbNcMPvye1zFfrFY6OjjCbztC0a1gHPDl7JIYAg+l0gqurq0HQJDv317hadjg4nOHw6G/gu+/8CF90jzDJypHnnFCYS9oUd/Gl7U3s6dftu37X56wZUYvfuznvee6u63OeOj6PPb8BaDuGNvvZlYN1FThIi3B+doaycLj34Qd46/VfwTvv/ATvffBTLF7KjU473m/ir/u79bS+ji8aCa9PU9sCMUQ5I7lYQW0iLr9jjEA4K6SlGNactDLuQXlWQJLJtR0JYlJ0BMOBBEWRjBDKf4L3gq4CtE0jfIHi2NGuPsbv21Yfyprz1JETWaJbGky/fQ3/6D/5Rzg4OMBkwnC7Ch2uQc2b9Rq379zB4cEBFosFet+jrErQElI7vIb5aXp2zkcvLy8HzmvNos4VcN1zDg4OUFWTOD6TyQQ3b96MOpxCnOtvRBT3AK0lrw7Gtm2wXC5xeHiIoihw/fp1mLdF9rA2BoR573H//v3Ix1THUMf8bDbDdDrF+fl5rDl+cnIyyLTYSE10DbTSzPCqqnB+fo779+/j8PAQBwcHuLq6AhFhsVig6zq0bYvFYoGzs7M4B7/IQfRci2ewNtXZp7SX/ZJsovz08VN2ftx3atsmQzvay3CmzhIg8zufz7kGMRHcyCg8CGAFBlm8W3Jjdt12Y/dp1b/YEeVdoU11GlnJlGM5tI7BJCzL2NiHuq4xqScg7DBekWrrRoyfwrNk0tIaS20Ako0k6qpjndAkR98WioExkgGW6gsTiR0HDiCP4AmFA+bzCsYSurZDcVgCNZjHFBVa27DzyWQQr7uMEzuOXQbGfTDsJu43aUae+mx4GLjB87n/ASHkcOop+xuAlNvY38bkBGebVdd18Ej1bK3lQOsUWJxpyJnRc5AhjjR/472FA6zE6YQg+rkHUXJIsE4HFIUdPItpySLRjY5hsuGpLpjD90Z+Ef+qw8IAJtVazp3/RvZcY3I7A0VesStIQZMrhnSbt1WCoo2FK7h8msKSG7IDqHBFNkvtHjq/mScOszT3GY+1AQYZn4lrRPkTP9PZIUS2PneXkVqdD7mDISE3WFhTwEQzrYPxFhZihzCakRugyQskFMHNk7k0wj1MKrk1kM9GCIJxXuLaSvxzIIOZIR0NQwzT4YxF6QqUJfej7wNCr1DK7ICz0m6lvbFNRL+HQHjw+AnWB3cFSdDEIDctW6m1hS2SjXlokxC61u8RrZIPLaunPdYgSUjWqBf5TktW5E5x1jE0uCiXI4c8xIge1fe9wB6zY5/XdjbuxsI6I2UCOFivqieoygkCgK5r0Gw2aNsN3wugWhwAcPC9R9u12ASPb9EDbKJTXPcR7S/Q9QGXBvg/PrrA//rGkTjHE5x6kAB7bwwcaSLKkC8zzXPQymBNjcZ+oCokZsDvEVsIlzzw8XdeLywDpTUlz1PToUGCTieeh7zEUzalkaJ5DjwKx7DNMEDXdjHIyTkX226UDrM+K2+E8KF102G5bviauNZkLRmwZ9zzE//VNzwePSnwP/534tMxZnuMfKiOcaUrRF5LFKIN3RiwA9mkgCFNOPCdFXh9KR9hggyN0iht9S0teiMJMAVsacFO1ITum0YnJTDq2LKcFmCMi/zPWhPRNr3vAEqyogY9MqJiiPyRsglkdp61VO2IWVtjkJmqWcSUl/iYkUSPAm3XRZkJYKTPoiglc1pQRTWRUYLcNOFTERRX63VEP+w6RgU7Oj7GyfEJZvOZoOu2aFYbdH0HgBOjgqABbRoug9e0XXQo6xKN64XJLDmRoXzdRpq22n/5q8NijcHNWzfFfhPgDKORIADOAn3oEUIBZx2qokQtgZ75vq3ywM790iTHro4v8tE2ktiHXMYxwi9EJovJtQ7OFiiKCvV0hslkCi7DqngI4hMkE4Pl2A6ZZAtuS7Kvax8iu1H5ZbTHAEO5eN/f8ef8GOstz3vEkkxSCkYeEnVZ9VOlPWV3WwbvJV2Zo7lCPi78yAHrMTlr3tYh/v/9+Fg1xhU2W43lGrmqi0GzyTV7IxcK2TmQBJU8kkM/G2Oi4YGFezfIDI8LMiBCsXLduTJrKWG9XmF+cICvfu2rePPNN7BZrxEC4Vvf+Bb+8i+/A+8AV9U4ufEaHj+8h3X7kQi8XgRDhkDMiVN3cmU+HASQapIDYGgNcZgpZCjfPhQYrSguRDZ7tjCTXTRHAzkmnmxaoGkNfDDwwcGYHoUjlAUwVeMwEXwAlivOpNVgA0AiAn0BwEhEMcG5FlXFkIuf+9zn8cYbr+OFF15AVdXcBssRdkQMg+3qAmXlsDiY4vf/4Hfxld/5bVydL/Hhh/fwzk9/isePH2O1WkW4xaZp0DQNNi1wtebappxh36OULEyiAGu9MH1VCKV2cwgoC8J0qkYDIxsGyUqW7cJItj+FCHG478ijEa0oMHqON6REx/kRhXWixEXisJNs+CkDWZU1ozSFHXapuBnS4HyW+watA/I87EmZ4t72qzIytsVm0mtirFvdlOcAGmCRYjkpMmMVxBWWvHA2jg8kMyFGwQNcHxIMQ+acg5doWpGAQOBMcivKvw+BYdmJItSLbsRFyfWNB7AyqriD52Y6naGqayyvrrBZr6MSq7WjrXOxdpSqWCEQ2q7FrCzgigJGIgSNZcVBHXrxPon47/seRcnOee8FKjEkxVaFwPEw54qstj4f/0CIpSKSPMvPctZg3XpYqvHbv/nb+KO/9Yc4PV4AJoDQSfSyx6ZpUbkq3l+WFabTCZbrBP8aV5hJNdNiW7MG7gqwyL5gHGyRK09R1M4MqwSwMM4iLRBaWOrx7/+7v4M//P3XUdUrGDToeo/SahBJC1cAxrQg1+PkyKEPS/TdBufnjxE84fjoGiiscXmxQj2Z4efv/Qj1xOPa9VcAGFxeNQhkMJnNUE9L9MGjmpYoUMao3PnBArZgY/l0PkslQQBYZ1GVgkhgDDvDvReDjIERhacoCkxmvK8ypPUGF5eXuHj/fdy/fx937tzB9evXMZ1Oo1OaiAS6FiKMm5jh/s477+L27Vuw1uLqaoXJdIbvfe97MMbgpZdewtHREQCG+lytVnjvZz/Dyy+/jOl0Gh0out8rLKw6xHVv1v1aAxDu33+As7OzmOn98ssvx9qZRBRlhldeeQU3btyImXnqhAc4UMVHwx/TgTpj9Jwqe7qXdV0Xs/K0bV3XxedrYERVVXHsJpMp1hvCvXsPMZtNYa3DerPEROo1FtZBxHgsr5YoixLrdYMXXngRX//X/xr3793HZz7zGVxcLfFbv/k7eO+997D+V1/HSy+9hHv3PsJ3v/tXePz4DF/4whfQtz3ef/8D9L1H2zSYVDXOzy/wZ3/2F/jUpz6FmzdvIIDwta9+FT95+2385V9+B9dOT3H99BrefPNNPLj3AA8e3MMLd++gKAr84HvfQ9M0+PIXv4iPPvoI//Jf/AsAwKZtGG6+qmF8QLve4NbNmzg6OsL9e/fw1z/8Ia7fuIHLy0s8evQIJycnODk5wZ07d9C2LR48eID1eoObN2/G+u5t2+LrX/96hF5+8uQJ3nrrTVy7doo/+ZM/wXq9QlmWuHv3Lr74xS+i6zr8+Mc/wsXlOT744INo5Ds7O8ODhz1OT0+xXq9xeHiIs/MnePjwIQ4ODgDw977vJZCBDTvHx8e4f/++0F3iF2VZYDo7RvCcYbpab3DjxU/jrz4q8Xl7H3XBwShsMEXG8ffIAdsMdvdvyueedm7X/c/6vO/Y9bxd9xs883m5Q6ltPXoPtMHibPEZWPeX8ZrgGa7TIWC9vMRvfPnXcO+/uofNjRXqCRtDB02i0V+jfNzEpg3b/KyOj39XQ9f2IIyHs2tblo/KUqDMWZYzZBA0O4HUoDAcNBZjRvC7mqWWGV+scyic1D0TuTnCPYp856xF71v0XS9tT/sd5YOX09zgQ24Eej5S4Wfzlf7dCr/+xd/AzZs3o460XC4jf9QM6tt37iAQB5rce/hAsqcd7r74Amd+Z/W7tRW6nq21uCH8RPcHzajWbGs9xxkRTdQf88BoIOlzWq+bUSIWMetay3iE4LfQRi4uLrLho5j1vdlscOfOHVxdXUVdcrVa4fbt2zDGYLlcYrVaRadlVVXRuKWO8jz4erVaxfrhjx8/xunpaURcWa1WWCwWMSjMGBMd6XVd4/LycpDZ8F/vMV4nuxnIUJbfrU38f8n702Dbtiy/C/vNudrdnfae273bvSbfy5fdy0xVVqcGlRCWkBAIWVaZMo2wZTscmAjC4K92+AOOsAkTEBAmcASGACMLCYXATVA2MqLUVJVUVaqsJjMrX5v33fbc0+92tXP6w5hzrrX3Ofe+l1kCYbwy7zvn7L2aueaaazT/McZ//CigyMt8Lf+xsYIPx0ksSXieKc76SlYdkuwDWOTsnX7ya38oVwVUrxrPZ43/qrH3bZH1gKj/hTX/QoIcUFXy7vikFG/b+fGnaUqWZ0J1Cw7QddXfuvOklGevcBWSfhweDH9ZMM/bSk3TOJaz/r4dCGhcE1TBJeLgD0oSqjDcKR2hiMN+WRYzyGPmpUWpiCQWf8HPg7/Wxky+cu6vGv9Vv/vn0Q+sdvt1CRSyr97Y317yPXyyzPq8qsvzasU36b/Hndy3IcFTHDJFpGNUAlHkqiat9FgOAQWnCzfvxf/dp+7tfyZV+P4zqRpWzve9auy+V2s3d6LDOz+RkHile8dJ3ce6Ftf9+VCb1aesra11KvgNgMPjDh4tsISAbneey7/LPOmQbNI0gg20tn8NOhBZdQH99c3f1eV3e/25K/eMunUnP8OV1o6j9yz9OPz62HwffJBP+pF3Sl7prjpU2ejSGIRi3QUnsSHYjbNbQthifem6MeveVyrYPP5w1cN8Nqds7TP/CukuMNytgfXjLJI00DTGyQWN0h3+FdarNZfmaO36SuzORdXwSVLydpKx3dJ/lf2OoWrw0kSEvz2utSlj1o3qDtqzQl+vZKK8rde/y/66WEv60D5xpJtna61UnbpzezZIYZLYbLsin2lH4R5HCdZCWa4oyiVVKcykqG6NVXVFUVaUVUNtLUXVrrHoyzpt5Xo4xqgWbG1DUNxYSQD1cs0HY30bg00mEAlqgWca9bhof45V8JE2PTEZj2l9Yo3rO6/6T3BT9/pP/WK0rguSX8jd5/7dIXzcXd0Yg1Gib+MohkTo5024Ty4v6o3NuDXxn9eG765KrFZSAa8il6Dbe3+crF6saj56pPj3/pOUn/tjXTLPmrnmMGjlki3C+6v69+Xfb+vwvjjIVglGa6I4FazP+yi2dS2nnC7wMsxLD+/D2d5b4pOcrPaPbO35GWNDQsiaTHC+V9jTSmvANM0oSuPyK7wOdYkYm3aYE2BeXlze1nWH6t1TkDTW64P+d9axe5nOPvUMrc7uNF6v02OFcQlwRVFQlEVoy2TaljhJmIwn7O3tSjKsUoEJq59o0nrGVK0oXSvCxhWMybPoFUeF9SsLqcOLcX93DBzKLZC1BB+l2N/fCzaDoZVn7e20ltCOql9I0tkj7j3bmH9v561JK/lwzceTYp2KprG0rY/lmXCfQCjgiuOEJM2IHTtPkmTBF+gXv3R6Wzvqd0lU8vE5XyAX1oB/r1Tn16+toJf8/Xl/bs7N5t/9QPza5/6Z0dkYURThkzd8XNWvg6v07GVZ6s536bvLNi7g/I31Mbxs+2ED/v3r/v3afthr/9BU6oPBgMlkEnqyeRo6P8ketPA9x/2ANoGQdedlfdB9Gjt/rAfpvXL21QmbFHVKKd5++20+ffQIHcccXL/GaDAkjiPe+cKb/P4/8NN877e/w8NHT/nSu+/y5Mk2R8cXzGcNQv9gqWtoGtfHS4lyCEapy4yNY81okPP6gwfkueLi4pjV8hxjDXUltMzrCJgNP704kH5k7kXx0u1zbMvCsipioDP+tDZASmugKQ2L1XrmbaQjTKuI40FXeR9FWCM091mWcev2db70pS/w9ttfYGtrO4BUogxqV+GqqQvXJ7SVTDtPKWKM9C3e3d3h2rVrfO1rXwkVgUop0jTl+fPnHB0dAXByckLTNJyengbwKIoioUKMMpbzJZUDE5q6dmtADOzzc88y4OZWKbLUIFnT6xQicWzIUt3NcZAabv1ZFdZ3a1pX3WuCwNe+apzLgg58Vl/Xs74fnPSDFBVlg8I2OApOvzbUZQG2dgpjXW8ml1EcxyHRpHcZrlpGL1tWoerYdkq4N229/bq/11b0hrPrTaj+itcox5DmQBy3p3EVV/4d1lqT5TlxLFVWxWpFGvodG6GZQrm5lWNMK29PoFxSiigIe0WapQwHQwmQrN84YojJnwZ59pOtLaI4DsFxeee7qlhjjCSQOAOlqWtM27rgTxcM74wv3yvHhN6kddOQ04EGSZJgyrI/unWj54pn2M2zCsu5yyLsjKnw01oOrt/hf/hn/xx3bl+nrlbEOgKlKcqapjGBCr5c1eFqcRRz/cYdPvnBx531rXqjcAbauoP4Q27ByLu8dbmo/j4NWlnapmY0iPin/+mf4atfuU6kzolMRVGuiGLp74zpkmpaY7CtoljWxOmA2cWCpszI0xzNUHpvFYq2btnfGfHBB9+ntQOuH9xjvmgoK8Nke4fX33qDONWUZUWrIEsyhsPcVUIvKcqCtjUkPinMEgJ91koyh8VR+rsM8SzLUUp6ulprOTk9JXLBxMlkwt7eHu+880VqnxhCB2b2s1axQuMZRQlV1TAaTZjPV9y8+VqYg2984xtr/bT8Gnzvvff40rvvhspwTy/rt7quOTk5CYC/p771lO4AOzs77OzuYgyXdLKnZvdbvy87EAxeH0TwlYJKdWwy/ntrLVmWBWPRG8w+GO73iaKI5XIZ2GqWyyWr1YrRaBRsh7pqGOYjbGukmjnPWcxnLOYzdnZ20EpTFtLDO4kkuF5XQgP1/e//Di9eHPLk6RPy4ZAvfeldVquCv/E3/iZnZ6d8+umj0O/717/9a7w4fMFyueTOnXuOWrxmMb/g7/ztX+Rb3/pxfvXXfoV79+9TVxXnJ8c8efQpZVny2u3bjgpT8fz5c3Z3d9jZ3ubk9ITlcoG1ltu3b9G2LUVRsLOzizGG8/MLjg5fcHx0JJTqyxW/7/f+Xn7hb/wNlFLM53MePnzIj//4jzMej3n27Bl/62/9LYwxDIcjDg4OuHXrFjdv3uTLX/4yWZaxu7vLcrkkTSWI9bWvfZVf+IVf4N69e7z++utcXJwHRoCz81OSRCrzfe/gKIpdf9+aoljxxhuv8/bbXwhUyaPREGMMRVEwGg2JooQ0Sbl2cI2z09Oe8LGcn58xnoxJE0lOTJOUQZ6wf+0bPHv+Kfebj6mrhcugFjjBZ9Z3Tj9cKXq8+FW9v9cF00tl2drPV52/f51XbZvjWMfLrt7vJWP172RZinP68YXmYvw6b771Br/Cb4ZTFsUKjSWJFeVqyfWDA37PV7/OL73/t7HvtOSpC46/zGQNY5Ff1q2EH2XrzvOyc3hZ3znhZbC1dM8eFEo493sfiLXeIew7/S6z2jns3v71g/AJm8ZIZYu3ZdqmoWoq5+PY8Nwu2SC9mwm4+EvWw+eZuwBiFJp/5Kt/in/2f/Bnmc3P2d7eCjKyD3ZMp1MZs5NT1qEr8+WS0rWhSLM0gFQKFXSBD0x4ZpaiKEJltLVCP14URWiF4WntRqNRSPwajUbM5/OQrORldJ7njEYj6rrm/PwcpRSz2YzJZEIU6TXdBHDt2rUA6gDh+Pl8ThzHoVWEJETlXFxcuLVgyLIs+BzGmKAjlJLAudaa6XTK9vZ20Fm+2t638rDWBn/XB9AXiwW7u7ucn5+Hefrdb58TkLCbv/5oQMZV1+yCJ1z6fO2KV15yXRJ4VpmQuOzXmev92V+vcs71IOKr3orPAneuHN1L9r/0+Yb/CEIt6sfqn7VvdZPnea+Nk+yvtRZbJ00xpQDB3TvaUaNbB6JLH0lfIdP3Q18RyMXLKMPm6uvjMAGsc8n+ygUVfDWSwRAR4ZmjtFZkecJ4NGC6bALQHccJcZx043Y+wo8KpF059y/7zslY/9z9fUm8uxeUwvQqwF8OYm6C515eC81sR3fdf69Dqx4IAZq2FZta+gU3EvxpGvFJHM3wZkV8H7fZ/Nz7pR7gDpTLLmjRBaP7AeEuKUJ8WdVbw/KfEFzy9y0KtVdw2T3PMD+XUIOrQVffbqT/rPrhdv+7+LF+3Kwf4Ebh7yGKEqm4M6B061qnmKBnrVO7l9+H9bH6eb1q/PTGJX92unNNvqw55wrbmjUfaLN6PCRFqM4+CUE7JxsiHRNpaaMgAUbBtjxmgktakXfP9/e1PYylf889udn7dj1x4Oqts4+ueg9t+Cdzsv7e9PcT/7aH+ep1JhO/nvw1L81xbzy1gWlVsMpGbBF35rG7+TCOcA0Zvl8Xcu/9JdlPVPHn6taQtWvhcwft2nCGbnXaNVsTXKuKaJ3S1/fylnNIK04fyFdK0RpXte6ur11boFj7PrvCQlSslpTlSnxu1SWrW2tcwE4KBVoD87LDu7yt7GfComisxTQWYw1/bb7iD24PyXx1rMMbpA2xYAnaOMbA/lO2JtjPSilHg97NY2/H3qT5pFOfYNSG9XG5uKIb/0Y0KZwHaxwWu/7+ds9uPWjr12PrqjS9Pau1prJVz9YgrNf1rfu7aVt+UDacrSp8lbh8qwltE8LCUhS14WIuwfHWupC3Nb6ddji1Xxdexvux+PvwNp7YCsL6opTGhurmxuF7gK0dfuTm2bMwOlYTNPIMrZP5yj/Tnu0W5t87Nb0kr95TC9Ol1vWZP18cJ0R1jaENrB9tKy3cPNsuSjBk657dGv7Y25YrL6O7dx+6NWTt+ujCf23XVtDLeV8s1rU9sMG/6LPClGVJsSooizLY/8KCNGZvf4/xaIxF2kJVVRXkk/cbrWO6aNrWvasNbSvrMnScDe8T4acKf3fPpd9ax698Y6VFghwnbewCRm1FX/g5wK4n+0Q+WStco4/s9zcVBrcWKO45Ct5mqU0LjSRqeMaMYPP7+baSYJmkKXGSkMQJuSsG8uxk0Nl3Xu9IYLyzl8Xe7lon4v3bvtx4xfYqu7Ovl15mp/X3/czz9/TLekxUEkXquqapmzXNLbLLrh3zqjFcpUfX/l2RNPKq8f//2vZfWWDcA9vGGGazWZhAT2/ngfZ+bzkPQG9mS/oF7alSfSC8aRpGo5ETkG1wcPrXssayvbtLWZYBPBHwXM6vdRTOY9rWAfeW6fScLM24c+c23/z6e6yKhmvXDvjFX/wlHj9+zCefiJCztqOER9lQ0eY37+AK7Z9ltVjyv/lf/yuMt7b4D//8f8Av/eLPU5VnIcjayS75xesTg6WoFE0LaQy+6H3dYLu8lZVlVUToV/Sb89llfRBBDBUbAg15njOZTLh79y5f/OIXefDgAbdv36BuFiyWAhItVwuWq0UAhLTWqEi5HuliyCxdgMIDW0+fPMPU8MYbbwXqQA92lWXJwcEBd+/eJY5jTk9PHVDePXdfkVgsSmbnss6yLOP58+fM53OqqmI+n3N0dERRFCF479eRrxSUdWbQka/qbsOYoyh2AIBGJxHD0Yi2afn++79DGlfs748pi1KC8t5BdA4vGwLHB3n6VTBN0wjoqHXIuLTWrAk/7TJ+g8KHACF72e2XTXBIlVCIaSVATKT1moz/od794OjbtePWTRt3Xv/dpoHb+8urzQ03FEBaFKyZiuLUrzlpWrleNhpM4+RDHGSB9Hny+/artKwkMyBVWt6pj+OYwXCIB5iUM037IXLvkBGcFMtwMBDjp+7o6iRwr4JzFcwFayXQnWXoKHLZfnZNgVkrjkXUC4xD5whGcQwuMN43Kdf196ZU6ELnVznC3bdyllGW8If+8B+VCmIlWbG2NSxXS1aO9sm0FU+fPuf09Iz6oAYtlFJpsk9RfkyeCSike4EBWbqvklYv3xSqO9Y/V7u5ejowRgF1JUHgr3/lNv/kz/5+buyDsqeYpqJctURxilYVxpZCo+cyP9umpaxKWlNDYyVr0cBisaIqLYPBCGNaFsWcs/NTvvDWAz7+wfc5uHad+/fvsywM1w5uMd6asKpWkhVtI4qyom5aBoOcyVZMcyY0+qtVSdPUAfxsnVzyxpyvqlksFiHA6+Xg8fExcRzz9ttvkw+GKLrK/OVSgopZmpHEMWmSurWZCAWSk537e6IDq7p2VIfS180HJHwbFNy5vezM8zwkqfiqGN8P3OtBHxjoaLF0p8sdlVo/qO31t6+6gw4o8ucoiiKcf7VaURbLrvWKC6qXZRkodh8+fCj0uUqFftlN07C1tUWWZfzgBz9w/TszJpMJjx49ChXwvmd2HMc0hfRgW67mpGlCnqdY2/KDH3yMsS1bW9tYq1kulhw+PyTPM14cvuDxw4dsTbZ4+vQRh4eHnJyd8ezZE37yJ38Sa1tmsyl1XZIkEc+fP6VulpwcvcBay8cf/g7f+taPs7ezzRsP7vLkyVPK1YLhYMDp8RFaR2xvbXHj+gGgQhXj/t4OSium0ykXF2dEWnH04lCC9S5zWUcxZSlB/POzM+nZfX7B/Tt3KcuS4xdHDAcDvvvd7/L06dOQ4OCDQqJbF9y7d58PPvggzOnt27cpioI8lySOJ08es70zYbI15h/9x/4Es9mMb3/720yn0+AETiajUOF5/foBN2/e5Dvf+Q5pGjMej1zfYdja2iKKNINB7qr6E6zrvxdFitY0HBzsU1UFnT6J2d3bEWcTeQe2t4ZYBVEcsf3OVzg5ucHy099gpz4hUdYlbECaiMMmzmUP8Oor3c/So31xbDc+66MC6iXfbZ5rc/9Xjell53rZmHvnl6odmK4Mh+0Edfdd7m1tUaxWwa4xxjDMcxaLudCBZ4pnT58yHo7Y+8E1zuoXrLAMUjn5pvRXm/fzGfP5Of3Uz9w86GsdmKJUR7MmiWnaOcraOaL+fp3d4oCULoi5MTIHrBhrwPRZglxQQou8axsHAHs7INiOfcuBS8/9dxM82gxAtacx3/rpH0friDwfcHJyQtu2bG1tUfuAd5qGJCFchZKvagXfn7Bc89uMtZydnQUd4XtsV1UlrRCGw+ALnpycsL29HSq+h8ORW38Nk8kkJEO1bctsNmM8HrNYLNjZ2WGxWASfYTabsbW1xXA4dFXuC7lnNy6fVNuHrr2e8WPzusyvheFwyOHhYahSV0qF/uh+DjzlvE/C8nPlk8eqqmIwGOCD4d7HiqKInZ0dRqOR9MHWmvF4fCmY/6Ntn2ONbAD8r9x103ZUV6QoXnJI7UuG8XKgaH3rEuTTNGU8HnX+mjuH0l1vZL/WXkan7c+1+fca5tAD39ZG/JLPX7VdBXopRaDdDAFwLfS33q7qjifYSIPBgDiKKWzX/iVJhB64fz25F+v6g65jIn4cl+9B9Y43bEbGu8quzqUVH99VqDo/ChcE9sFha4UqN89jdna3ePzsmKZuSFPBgaTtisbTel+e46tBus+7XQXy+ft0v6393baGKOqDjYgnaEXG96ua/TxfCkyrLuEhIgoVVf3EDY+DdThJ7BJtlhRFQVkW4oO0DY0tsLahDUGh9fswvq+v7QBjPx7/LnTBZvEjYx27RK8otOgK9+zwBl/UUTc9ak7Vrwpz71i/52vf12Nj7auu4MUaGxLNtO6CvcLYcnUlsMUn160hHt16dh95Xy48fyytNWj302Cl33ov2b0zyzYZAlQn51T/dpXDzTbp7DfWZ+95eH0C68wFns64v47UxnHWglU+cKPC9UEFO0V6b/s+1hZjGrlH5eyOYDv4ofkA2vqaEqzEV5Z7tgPt8IMOc1oT/g5ceJU0D6kRzp4Sfi11ST8oh/eEYqYo7j0hf/0+RtzNX8Bn6D+HiBfHp7yZTjBRROTuJVhYm/LQg65hPNBVM3tZ4Z9VJxf9Z7KPozf2Y6VbiwEXs0qCmqZbD/0kJ49ZWdNPiLFr77Z29pMbktxH64I9cYICqqqkWK0oyhXGNMRx6pLixf5om5b5fElZ1dTWMDM187J7e9eDve5ulOst3sLfXhTczxK+mMSkrRszvWfhAq7rvaG7c7emJbKx0xdewF2RgGFtSAAwbSPBRy+TQN61vgBywSJ/vjDx7ll5HE+mrjtSuSXZBZLdeMKz81X6gkF6PW6tDWsWnBzqD5/uPdNaUxYF57MZ00Uh5wJaa8WgscrdG+CCzQ0wrxqaWcOjFylZHLG3BTZZfzcEL5Y50U5m+DXUX6/GGPI0I8tytNLUtVQgr4oVg2xAFCVIcmtB0wjDoHIJqxqk53j3wvTWSm+O1x+fHyEoE+axxRftqPDMrGnDOf15JQkhFZ3Y1GG+21YqqYVRA/oBeK8t+kvPWqhrJ0PpdN7LzAovc/177HFkvwb6CTr9nu+t81faXrX4crWkrEqwinyQS6X4/l6w/5uqoW06lhjliu6sER9Ra0VZlazKkqppJEHSV+a7d8bfuszFpm5WzlTzP7t9LIJ14tbN1tZWKNTB9XsHQvymbTxjQ0fr7XVJYG7YsOk6E3t9bRj3HhrceLQkjPm9Iq1CQpAXzXEcg1WOdSslilOSJGV7a4eBS6CVyvvumiE24BJa5Nw62GPQT/70NsW6/OvW0WXb/mWfXaXfN2Oc/cDzy/yXfoxuLYHN/e0Ln5qq7iVhenvh8/kva4F8/26GteP+RZfZhv5eB8U/T8D9ZZ9/HnzkVef8YfGVzx0YV0qqBTxI7anzPPARnCwjWQ5pmriFqkJQIFAGbZxXQHBctrEs4KbpDHftBLZ3ON98802+973vhQpjyYKR87Vty9GLFyQuWAqQxK7CVslLMtmaMJooVqslt1+7xc/93D/B4eEhv/mbv8WHH37EcrlkOr0ALPkgZ5APiOKIJE6CU5TnOaNhDtby7/77/w5/7s/9j/lf/Iv/Er/2Mz/Dv/6v/Wt8+OHvkKWdI5zEbmEaRd3CsoxByYtelC1x1DLIOiW+WIG1PqsGUI5uni4LRgWpKduGuykCwEl1rTRJqrm2v8/du3f5xje+yYMHD4LTu7e7R9NWHJ/OyNKUoliIQ1dI31utNMPRiCQT2sHpxRQULJfLAACZ1rBcrsiTIU+ePMG0LauiwFrXd6+qQCnSJKEoy5B9NZlMWK1WDAYDjo+PBVxfVWRxShRHzOdTkjRm/9oedV2xs7vF9vaExXLh+nH4KkQJDEROqA+GA9JcKBmzNOPawTW2t7bZ399nb3+POIqJEsk8rpuGf+Ff+BeYz2a89YVvYM2MX//1XwNlQ1DUr1cPpHla4z7dH+BAWB3ANt9PG7xx1ROmHtTEa58eFfYGMCvHiALx1/1htiAc/JJi3RfqLuVAZq+M174Lqyvs97ItrD0dgQepLSjn/PeP9HPhDRVA2g1gaZtG2BV6NKWyjwqZd1brMF6tFMPBoEf7thFoVshcewfTK3/3Tg0HA2Zts36U0s64IzgsvnWCzTKiSICWYAx6B9XRbZMk4mj6CnLtaWxwxlDPUHvZ8+vNO0irgKueUV8SWGv4/Xdu8St/51d59MlD2rqgKgqaqnQBPENdN6xWBVVZUVUNy39mBWNJaPk7f/vXaLQm0i1pojG2JfI9x9cvtXnpMPP9NbKetdlTlP5bpfCIrXMBUMBy1ZBqy5/8h9/jD/3Me+TJjLqao0xJrFOUTbFNTN22DjhQzigT2uDFskLrmGVRMMhzitWKVbFkVl2QZUOUiqjbksMXj0FP2JrsMJst+Np7t0myCUUpCQ5pmos816kESIyhaeSJSSDVuoCg5fDwmQtIbDMaDVFKcXp6ynQ6ZWdnh/29a+HOd7Ytq2LFrZuvEUVdP/o0TsizoaMPTzGtIUmTwNRhjSXPPWuIyKCqqkjSTAAIC1HcySS/xj2zizGGqiwZDYfkaR5aT8RRRN000qt8sSDSEbj+k7ULJkQ6AuvkW9OC1tRVzXRV0JqWyXhC3dSslivXT6plMMyp6iokArRt69p4EBIIVos5TS0tBzwFMECaJCitKVcrHn/6EKWkerAoCgCOXxwSRRF5nnP84oXIBmuZzeahorqqKu7fu0dd10wvZtjWMBjkpGlMUa6oqgKlDS9evJBgemNIk5TJZMJiMWMwyFDKsre/S1VVnJ6fc+OGUPN++OGHnLmA9Hg85rXXbjMaDRlkKffvvcZgMGQ2nfHJRx+AhTfefItqteDDjz6mNsZRma+4ceMG8/mcN954g5PjFWUptPppmlJWUl3tAzw+0cI676UuxYCeXlxgrWU0HPKLv/SLvPfeexhjuHf/Pm+/8w4ff/wxf/fX/y7vv/8+TdPwm7/5m1w7uMadO69x+/Ytvv71r3N+fsav//rfBeBb3/oWi8Wck5MTzs9PefjpR8xmM5q64dnzZ1KxYi07u7tUlQDEu7u7pElCWVWcn59x7dq18Cx94oJpDXVVB+dstVyRZqmzNYXN5sWLF9y9ey8ATN7RuX37Nsv5ws1HS1EVSP8y6Re3941/gI8/+oT62fvcz6WVS1FZ0tg6sFz15GlPwMJlxWg3Prvqd7Wx7+b57MZ+/e1V31/191XXuGpz3xtrWRaGslX8xuoGX3rvG0RacXZ2SprEa0DqYrlkOBzx7MlTlFpiUZRVyyjb4vi7p+ivtKwqGKSvMBDC7z2bw+ndH83fssFugctOUF+neLCy/zxMK+CHdrJNqh8RunV3YmNbaMBGOpxPbqF3vmBjdGuxbirpweiAus1Hbq9W0t1Ol5To59l6C6YPWtRwt36LBw/ucjE9o6oKimLVA/gkAH509IIkSRmNR6zKEmusUKc73050gDA89AEBYbsQIOjxoyesVqVLUE0CGFQUBTdu3AS6Cm2tFdPpjLIsA9OJryC3VlhAbt++TZ7nvHjxIiRE7e7uUtc1w+GQ+XxOXdeB3cMDmI8ePcb3vwNCoL4sy1DxXRQF29vboSo8yzJalzg9mUyYOfnaZzZbLBaBGt0nfHt566vGgUCl7hOIDw8PKYqCra0tSTyaL6SSJ+63/PqvalOvlgdAeJHM5XX5MjH3WSu0y3F8dbuKtlc16P1on4QeAizWUy32QTiNUp3t6JNdrg64bYzN79Obms3A0aVflXrFva+DYUppkh4e4u/H04L6ZItQkWPFVhNafhuS+6MoIsvytWoYHzD3bd6UWvcOrgKyNgsR5NYvB0A7v9VcSnD1QRCQ59Q21slKQ6Rj8jxjZ2eHpnnuktFjlygzcO9LE8A32xPGVwJUG3rv8yQs+CSUy+fz1dM+EEnnb11xDl+l7+dMKKzjwIgRxzFxKv1GkyRhMpyEz7386bfoETynoqga6qoI8rBpWuqqoW5Kof9uWvEnfYWk6iagPy6fbCAsO0Wwk+T59atlJcjgexWbDdDWIn2EpZ96sxYYX5+bbu0Ys8742AeC+z9Dgr/DMax1QWoThML6c9588Ep5uIrWtpL8rzsKfNOajorXgrYRNBXWtiH5Fgxa9xgYg3/fG8BGxWFXz+n7oF9hV/TeK7PxeX8O+vOkk8428FsfpJdj5HzG4JI21dpzB1fJaKUvsP/n26zK8U5mKkKrNg9m9Fnc1oImfjpsb24uCXx1yY679C76P00X2l+vlu6MU/FnvfwCaDrwSan16/WuexWg7RMmjk8vWO4saQZCLW5cUDVgL6heC2yHrPTXrJexeAxoveVCCKKa3hn8ML1Jqzqr04LI/EbWoaZjlfC0yRJ4w+GynTz1PkhT15iylKIndy8KaI0iy9KAwZeOiSfSMB4MUW5tWaS//Xy5ZDafUzcNp0nNR8UFDVdvYptqp7el6nmxtPwn6oyf0YY/lESYNgnvsuB2BmOkZeDauYyVdWprwQb8XAXx79eadWtUAqY2JG24CnutXZVui3WFQH6NdHa5O4fZWMf+mVg6ubQOWrp11L9/Z184QM2zQA4GA4qycGyo68loa2sS0UWzsuZitpLWg0qjlQuMay22VhCHDv/UGgMsa8u//h9W7A1T/sQfUvDl9efjr9tP2mlNc9m/QhiQRqMhCsViYSmrFfPZAmsUgzwnimMsCW1TiXy0PunGEmmJL8h89LDMNWHgX1z/cnmfp2erdU9IaNcdzirJFJ4i2jrbyOksLFAGSnKpWPZLZx1lVoGPf231uXFfjUgHN6v3i8f1xSdpwvfW2jX2BeMSoT2WX9XCGjifz+U9jCJ293bZ3dllPBkTaU1VVrRtQ910Qf8ojrEKYRQrShSQ5TnFqmBZVLStTwrxvcKVmze7psu8vAj7+XWpvP1AaCnqN601W1tbLOdnna3eW89xHIu90mMQAlGZho1WAL1jlXs/TW+d+u/91rQN2vqkL41xmHgUacfq4cYQJa64IQ4YZJ7nXDs4YDwah/Zffuva2Jg1e8H7+ILJ0ws2yw1sYgibOubzJG5epftfFUwP45Bf1j9fu5euLVvjErCNaWiqJtxPl2xl1q5xpWxSsE6gvGYEBDNAu3N+VnD8h4059cfWn3cbBvfq4wAPonzmtWwvW+aqJIUfZvvcgXHvPHgnz1obqgsk+yfCtFZ6vCYZ1viXwIR+fCipAAKfRQGgXXBTnGHfh0v0ifTibZoWocMSsObDDz8Mmf7D4ZDVatXrSSFB3KaqQxVaWdRoHVG3Yjg0BopyyfHJMVVTMJpk3Iyvce/BH2G5WlKVJd///vuMxkMePHjAYJCvOVmdYwRFseDo6IS//H/7j/ijf+Qf5ps/9h5/8k/9Sf6Nf+P/KA6QERG2rAsB39DoKCHKhHJR6RZlNW0bMV85Wm4noJM4pq4rVBSB7lE1y2zInLrAsFFdlkwcC42EVIUMAcVkPOJgf5vXbt1iPBoRx4rjF89Cf8Bnjz9FRZrZahEMxuViGag+Vsslo/GIYZ6TxL4frKEumgCeaa3ZmeygrKI1LVuTMffu3SXtAQPbO9vs7OwyGk/IsozxeByEmqc1jOOYJIpoyir05lgul1IF6SpAZrMZ8/mcxWIR+sdub28zHo+IIgngHNw4IMliRq4qwVPRtK30NFco6qKmqcR5HWUpt6+/wf/sz/1PWS4XPH30v+Xps8cMx2PQiuVy6cCuhDSqUdo6AWW73uFKFK7vI22RLETjFKwY206oQkfTGRw1TxvjjBMfzHJZ2JGCRCvyJJXq3d7mbZjPEiH97NwrBYbywr0vXC7bSHpTeF1xIuMUuHHnk4z89UF7Y8ZX52MJTp5tHYCADfPr7cHaGRwyPpfxh+vDFHfZj5YufzTQtvnf3G2GczujKE3StYqpSGvpF24MeKNfqeCQad2B6TjHyxuWXiH65KHWgXoWRdsDH9ZVZT+Pfr0afy2gvPn43BT6MyqlwCi++9vf5zvtdzFtS5pkmMZXJMj95llGlm8x2RrwJJ7SUpLnA372Z/8MB7eu8Z/8p/8xi+lzUdqWkKyE7cbVSeCN4LcKQ7sUsOiG7Yw/qzFW46nisA1lWXB9K+Mf/+Pv8I2v3aFpnqGAolqRpjFEFqWd41kLkIC2tLQ0pmW2LCjKhrJa0TYZ84sV8/mSqm6pqgZrZ+zs7RNF24wGO6TxDV6782Vu3nqNo6MLtncikmyA0onLdgflAioeYPcgu68uy/Ocvb19oAOVVqsVt28Pef31TORY04pR6YE7a0nSJABDYoQYmlaqgoWCHaqqoFZScdXaFmOElrS10os1TiVZzFtE1rTkrurby+EWaJzBmMQxTdEwO5uT5SmresloJMwJkYWmbihrCW7HLhGucs5iPhhQFIUkyNUNh4eH7O3t8ezZc87Pz3jrrS+4/q1iA7SFVCeXZUmaZZwdHRFFmiROmM1mkuwWR+JYu3XiWU6UUkJdVRWcnp4SxxHn5xekaRIccR1FDAY5F+fnVGXFzRs3uHnrFk+ePKFZzplNLzjNElpj+NK773IxnbKzvc3R8RF5OibL99ne3mYyfMjFxZR8MGZ7eysY5YeHh7RWcz6dkyQxv/8P/AM8e/ac27dvsVpJX/XHjz9ltVqxKhZYdrDGsCyWPHv+TMBRl4iyKktAMZ1POTm9CCBoHMfcv3+P5XJOFEcMRzkWCWxdu7bDvquWfv78OZHWtFZ6rqf5kJVjewHD+fkZUaS4mJ4zmoz4sR/7Fq/ducd4MiYbDBhNxvz1v/7XefDmA775rW8I049SHD59zve++9ucn5/z7NlT6rphPBqwWkmQ7eT0BVXVVfmPhlmg+Ls4l57h47FUjCfDXNrSKM3OjQOeP2sYDXOxCcqG1aIgiiMO9q+HynWtNXk6QOuY4XDAxcWUi7Nz9E2vs+T7s5Mzbt26xv61balwNkN2dnZ4+vQpTVVwdlKwu7PN+N4f4Tu/+rd4M35BqlrqWvRwFKkgKz3w1XecNsTx1dtLvXAv8Db+3jzv5v6f55ovu+4VuxgLdW2pG/juieJps8MbX3iT5XIBbYNtaqbLRQCmmqblo48+waIoamlbYxyg17aW8XyP1eIYM3LB8UyvDebKYXeKDJTXO5s67/Ns3dmt3VA8PUWoHIhmA1jWm4+2pWpah596OatAK7SKgr72B6jupPK58dSSHQWu2nzO7sMuVtvT2Lb/S0/DbwB2r9wuKVLCnJQfRfzcn/5Zrh1MeH74HGtbtrbGAdR5//33sdZy9+5d6rpiNpsyHE4YjUZkScZ4MKZtG45PThgPx8Q9F9HrqtWq5OT4nChKSOIBi6bEJIq6bhkOh3ifzldeZ9mAuq7Z2dlhPp9TFEXw27wfOZ/PGQ6HFC6R9saNG6xWq9CqqwvsK87PpxwcZOzt7TKdTrl79x7xsVRBKFctcH5+HnyGJEl47bXXAptFnz3Fn9tXgntdduPGjcBOlaYp0+lU/JudncDq4nW/MYbxeIy1klwwGo0EKJ3OiKOI7Z1tqrKiWevX/vdvE1CCqxebumLfz8YkMJ9nJ7UePPFV06PRiNliSZTmaBWhVSTVJGiwOtjTxljiWKqvrFFrQMiV94j3Y9ZCWuFH8EU84mdtd+QlmeJ8Nzz4K9+1Rvy+bDggcsHTNE0D5awiQamIxfzcrW2kZ2KaUtQNZ9MZq7IiHQxJy4ra0XL2t7ZtqY1Ga1BtG+5Nu8pg2xps26IjF4QykaP+FPu/bVtpnYRUe+tI0zgZKR5aK+EZpUl0hsaiVAOxgMWm0cREtFRS/GYNbQu3Dq6h7RzFNYSD1RDpRK4Vp7TGV0Vr4igVxqYr10lPSFuwdDhHeJ49cKvP4BfHMaK6BIPSURQSJnwFEkoTRx02EkVpaLHjzxVnefDRoigOrBqSaCfPNUtTBoNxAM39uNqm4ejknNlsxqpYURQriuKc5VKSGj0rVNM0IUDWtkL/3fXDjJCg9XrfYmMM8/lF0DcdDa6rttIdeKldoAOkIsuvWpFRHWArb1Ykuhh8WZf7v3Kn8NTYEFjXrgBK+75eSIhxeEYINCK+8FUVppvrwAKRinpsL3L+iBitO8A8iiUpVllJpPHqNHKYSFdo4BaVu+8wVo9HuFsXm2S93aPffIKtbwcSRqs6oN9awRgiR5sssioJDBJeT2gdhQpcgChSLqGqw9T6a6DPOOgTFbQfo8OzmrbBalyfZLfpnn3Vs0O0TunYC7uwU5gp33vVYTH+mXvA3t93WP+hmlOKPq4y6KQKM7qkbvzYLksE/4zWBu9GbFFaKju/t7rAbA35ihq4/rpStS6MDTqYV1JQ1KMv94ESAtzk7otwr2KTWYdPgTJeP6zrFtMz/DQuob01KGVQdRXuw2NlSilHm67CqjRBCUUoJQkQ2gUNZN4bytIEn8sYQ5KKXdYCSZCfVjDc2UWw56vacniywkY+OHuV/O21OlAwtxlmXvI344JDFfPPxAlN0xIngkMa5Vga2ytktBah0baNyKcwryA9xEUf+znu01QHKnlXWSoYQK9gxhUV+aQeGa6fV0JgR25J8CTlxYDtGBawosOcESD2BFb0qF/LxoBSRDrGRobG1pJYG3e6J9yzkwPTVUlRNk4CWFqPz7vex6DQvYKg/nteFHBmKv7y/ytm9SYwkEfVGEsMIufdkpaEKplPlEajscqSJQNGwy3ydAhYWmMpy4LWVCyXM6qqIE0jsjQljhOpkg73YWhNjSlK4jhBR6nEHXAJik7AqrBWemvGOnmrHBOq7S2mENCNUErWn7FteNfqpiZSYJqWYrmgDIm4TrNYpFhGeVtFY7miwNIxiBBo4d074V8NJZilcpi8X1N101A5xmEdq1B8GUW+fY34jNJnXKp35/M5i7kUDm5Ndrhx4wb5IHcxMjmnJKatBzxta6jKgqosMYh+MFZxMVsKhbq1RFoRRRJDMJZewq/IDZ+pE25Lia6PtdMLPlnESitMdwtEcUSqYYUOGItyTclVFFYkPsHMtwFUju1AVq3Y40r1K6BFPmlETkaOZVnZRopBTUMex8RJgjXQNBarFSruWIU8S4MxOL8qDfGa1apkZ2eH4fYeKslpzRlZJLjo1tYWrYHZfM58PidLUpSOhVkjikAroiSmcXi7t9+Ve2/7iX4/bOD0quM2g+V9G9Fakc22bdeOEzzd4b+hfYQmyTKsVdRVi2mhaQyqcfpIg9Z9HMWvEXNJvHtMqwt0Xx37Udbi2WT63/vjw+equWIfH8PpAJO+bFuLAWzYkMqun6N/7pclGLzs96sqCjf3/bzP+XMHxn11lw+KQ5dx3GVBWtKk6z0XXiy6/S2XFYtfSB609y9uv8LN71vXFVXZfbbpRPoJ8Jm1fmw+cGGM4fj4mMEw5403Xud73/seRbliMMhZLBbs7e2yWq34fb//964d74ETT1crYM6KJFLsbu8yHkz4hf/yF3j86TO++Y1vcvvmTZ49OxRloBTWjoICDfNpXJ/vtkbH2lUu145OVIJtaTYK1e95LqD53s4ueZoxGAwY5gMAhpMxAsaZEMDwvRZWqxXDPEeZhtVyCbajVEdJ5etgMMBqRdU2pA6cv379hqNGE2MxTVMGeUaepYGmdmd3l4Gr/krTlMFgQBRFFEUhmdRZJhW/7lmathXa6casGzhKUZZdxli5WrI1GhPHkavOSMM5fL8J7/T7hA0ggGHWWuIsRbBO7XrPynUS17vCWkthJMgyHo/Z3dtjMpnw+huvMxwO+bN/9p/lN3/rt/gf/U/+HLP5nH/z3/w3mc9d5VmxpKleOEUv9+XPbZCqtbpuQjWk1qozRHp2A8ZilAkOpg+wepPFGhsMZK0VUSyOYRKCv51gVHgj8CUvcU/whEC3//tKD+VyTbg/5qosnJ4KX/vcWOMo6DRNazYEXhC74rCozij1Z/S0LBYx06wDpzczu4xpUVqTpcna/fk78SOz2JCAIgxHXqIqvNGepCllWYQ1E2QQ3n331zSdnHPvSenYEPyaDNnMfiw9mrwuM3Gjgn7td3XpSfiqOL3xDK56/ForXn/jde7cvkldVhSrkjhKMcZy/fo13n33Xd555x3u3r3L7u4uP/n/+Ad4vnrO1vYW/8s/+y9S1gVZlvJ/+rf/1XX2BDcu03+ebCi+PhDhjOGeL9m7V8kctDijEIOxDctFwVffuc5/9x/7KW7slSxWzyXZqW6I44iyrYiJJAZsLE1b0zpQsGqhrKCoNOcXcHy8oK4Kjl8saBpLmuVCJRWlNEeG19+4x7d+/Kd58PrXqOooGNnT6QwVrVBRTJoNyNIU43oHrlarkCDmqaaDrHNZxj6I3Kcpj6LInUdYB3SPvivSQrlvjCHNEowVOs4+FbsH5OI4oXXORz9praqEOQOlKIuVZK+675RSgUJba6l2KhYr6rJmsZihtWI2vXDvoSVJYjk+FvnepzlfLhaUZUEcJzx//pzlcglI0PHo6AWDQc61a9do25rFYuGC2WcURcFiseDu3bs8f/aCJEkc5ailrioOHUXuxcVFeJ+2t7c5PT1lZ2cbrGE+W7JczKlK6SNrraWuSuazKQf7+yR7cs6L8zP293a5f+8uZ2dnwl5S1zx+/IjFYsHh82fs7u5SNg1HR0e8OHxBURTS7z2eB6p3n4SVZRlnZ6dcu3bAhx9+yAcffMgHH7zP229/gf39/fC8Ly7OGQwylvMpg0HuquMMaWNYLJZ8+9vfdkl/wiIjNMdSIX3z5g329/eYnwgzi0+MuH79OmdnZywWC65d28daK3NUlVRVy+7unpujnfDeNU3Db/zGb2BR/L7BiE8ffcpgMOCb3/wmN27c4OjokOfPnzGdXlCXNfPpnIuLCxaLBXmeUZYVH3zwAUpJhXGSaLI8DfT2vm+w0KNL//IokqrKJ0+eBGaV87Mz0jRluVySpTnz+ZzJZCLBslURKjCVEor8s7MzgBC4aq61kDoGDgxlueLps6dsbU3C+1XXFaPRMAS9lFIsF1O+9uM/zbd/7VdJZ095Y1RRNyJFI+8cgnMArxDCP5zP1G1243d1xd9247u+bdD//bOuoy5/tFwJIL6oFb96FFOm+6hY8ejRI2grImUDUOsdcAnulQJGRAnoCGUlKcw4+375KwPstxaYkaUoLXmqUJ9rjOrltsnn3non8BVgl1UKsKn/ezaL8gDT5f6ul4ydtfHa9V83FbbTcesWQmc3XH3vtr/b59s2xuR79tnDnD/zjZ/lrbfe4vjkRALNqzIka7VtyzvvvEPTNAxcy5jhcEhdtwGk8NXWWkvFS56n3dK0Utmzt7fLaDRikI84Ojp01R811hpOT0+Dj+Sr5Dp/SYLfxkg7LhDbyFdcDgaDQDnudZP3l1arVdC3d+7cYXd3NwTL5ZhuAr2u9InT/t59QHw4HIbq+LOzM+7fvx/GsrOzg9Y6VM77ZGRp+RAFHerZOtq2ZTweBx1xcHDAp59+itaa7Z3twB4ytVN29/d+iIf8I26fZx35JfeSl7YLFKjemv585/w8m7+uVIwPyPOc6XyxZjv2/cJ14KSrnHoVkLJ2Pb1OJeiPWfcRXn4D4qbZDRvd+fWCUKMQ3y/LMvI8p2lbSufLWivVgJ4ZBWSNJmnqgps6tOQSbFeHisYw1lZhHfKTaAHYjGkkYVp3WIj4uwofUNC9YKTEhBw4qBx0rBQ+YVy5nbTugCyrXJVI66tFWqcrFJPJhP29HfcOJ+SDCcY28jyr0ol8TRSJXa6vDIzqngiU60Y6CePvCR/Zw/fSdGsliiKIhEp5jcref6cdDqL9dzGJC3THSUwcJQLoJknwT6Rq1wGpltAfuW0bimIVZElVlZSlMBatVkuWy5XDsBqsrdfaJ/n1afsBOjxleocz9QHbOiTSiP/odZh/RpLPtQ4qXqp+8mu4B3BqFCpeB3RDtVKPDj2KfBXWenV0PzjcT3QJ+/TWH4DpBRVfBUwGzCPMgbuGC0hHOg7BDZ+M3K/k7APd/lr9zzfB3G48bm2FOezmSylCwKN/n/3r9FlG5F+EMDx089qv0F/fV4X5ZkP+9YsTgs8dQOgeAI+v2ANcG0WsXyt9OdKvOFtfK5vz9jJZ6re1ClovKy6hReHsl66zNg/hnJfH0h9T9528N+fnUy5GE5rhkCRPhE0tTgjMpLZ7Nsba0PNauSFJIN+3NXS4TG8NdmNXa/Z431QXu86xF+Io0q0NIH0fK980/7ULIvcerjNn3fvj1wYO57bdHHs5aH21bywFNmVRsFquiOKIqmwoywZXV7Y2j5vzGv5291NZuFjWnMYlxaQla4TqXEWRw31wvuv6uVRPJvU3aQfQ9TD2c9MlncgzkEXQ6WrtJr410n/aGJ9c1OFnUmFuUK1x+tA/T88KEMxyfNKsPz/GdnPq/QKP3SBBOx1pEpVcwi7lnsVOxsJyVVJWtbuaBO+8W+CQS6DF+iH0Wge2WMoGIm2cbyrjq+uGPE9dn/oIrXDYedMlRSkp3BmPxgwGufg3RnAk71PHSYppGlbLkrqqGOayn3J+mVKWqqld8msLqpF3I+raAHh96Cnou3fFr8tuT5lu/646qvIe64evwDZtS9PULBdL5oulw9zWm2t4b2p9XW3KCOfH634VtZcvXcDbI8DGyvkaR+HfyVq3ppQOQcu2aWmNoakbFq4YD6U4OLjO9es3AsNBa4y7tgYaGtcv3d9n2zSUrtDP67QyMB5aV/jStQMNtrf3nWFdXrj1J9X1PRmilNOREncxLtGmqiqwLpmwZ5d43DGO4k7n43WQO6f3te267lx/HuvPpG0bkiRmNBoKTtlYkUfGiI3rbS3XOkRHyvUXz9GRtIapmlriXKMRaSYtl3yiwnA4BBXRNC3np6fUSFGtJM7FYY6Vmxdr/VvF2hz+MFtf979MT70s0GsuyQ5vH3W6VGkFDpPROnIFJ3JcHMch7vEqXfmqcV31uxvElWO79JnqFQPQvWNuj0vH9KVBt4TV+tc9mybI6GCXEZIuNse2Geh+mW25+fmQ0ZX79bfPHRjvZ6xql5XvKfH6hlS/L1jfMARR7k3bhH38oPuAA3QBd2/8BsW54ZymacpqtXLVdvKZtQRqMn/tyWTC9vY2s9mMxWIhFBirOScnx0ynU27duoUxhtFoFAAYD24vl8sArHgqeU8HOhkOMSZiuVixWpUkKuE//gt/iWv7N7j32j1ODk/Rqu3onZCK+TiKmWxPgjIejoZsbW0Fqj7tFJrQdGj29/bI84SmbqjrijROiSLNcDCkcRUQ+VgodZJUnPM0SUkcnX2kNZPxhNxRvSVJwnAo9Lx7u3tEsVBWWCTzP3XOff8Z+eetsa4iXbNcLgP47AEAX5FhrVR5e2ooT7ee5zmRkUCi711rjAkMAP7+B5MJK9dDvG0bkjTBGiP9kRVYLc5AixhXbSXPunYZ9flggJg8JqwdqQhZCnDh+vqmac7+jesUqxV7169R1zUvTo65pq7xB37mD9JiGU8m3Lx9m4ODA8pSqCNHowln5TmaCmxHs6KjCO3WdFmUbq6UOIfOEOlEBXhjA0Biqx3Y4iZfDFE3L3Eck2YpSeJ7aPScDn9e70SwIap6Tsi6bLJr+3t9fJWguSogHk7PpmqUNS/+mqfqMEExSa9weY5lKZT9WZb35sY5L3ajp4czDjqV3AWJFcI00XfW/B+qN6ZunixYf+4W6e1lHN2qpmm7xBsLLrNqfe6MtURKOUNLaLOCYxruY9057MCdbuJ6KiRcz19lMygeQAc3D5vB6H5lSxQpDq7v897Xv8qtmze589pr3L51myROmWxvkaVZAPHqqgrOS9PU/N1f+xUm2xN+8id+gr/4F28yu3jmADZ/TYU1jYxR6865MDZkJHag5MYaWVtGnQEjwfeWomj4h/7Br/IP/oEvEplz5qsL0kRTmxYda0wk66CmxbYW24rMXxYVdQ3GZJRlytHRimfP5rx4saBpFFGckqY5tk7Z2bnGN3/PT/DGG1/g9Te+wNbWDuiIuK5ZrgqU0mxtjTCA1okzXKWnZC03RzZ0Pb56QW8fkETJnUVRTNM2lCuh/U6ShNZldlpjKKsKrXQIWERIIs38Yoq1honrD6tQrMqSzAUfyqIAdOh56mVyUQo1/nK1RCGJIJHWnF9cUBYFr925ww8++YSyLLlx8wa2FjaVolihlBi1ZVUyHPoAipx7sViwvy+V8HVdkyQpxrScn59zenpK2xoePXrIrVu3uHfvDmdnJxwePkNrzfn5BdZKT/Y4jnn+/DlPnz5mPJ6QpglHR8cMBtJXdjAYuOCuYWdnK+jEPJe2BWUVEyeawdBR27vAurWybn/w8SckcczW1hagQmuXsix59OghW1tb/PZvf4cvfeldTk9POT09xtNNnZ4e89FHH7FaFezs7TMYSIV/ng+YTs/RrmpqOBzw5Mkz7t+/T55nPHz4kA8+eJ/MyWelFGVZMZ9O2doai11R1mRZTlEUso7iGFBUTc3W1pZk32pNHEcS4N7dZrmU3rsvXrzg8ePHQV/6HreeCSBz9+j19u7uLr/zO79DlmVsbW3xyccf88knDyVDV2veffddvvq1r/DB+9/n5ORY9GdVh2Qbay1FsWI0GnF+fkZVVdy6dZOyWlFVZdDdp6enjEYjjOn61Psew4PBgNVqxWKxCOtHKgWH1JXh4uKCnZ0dVqsVFxcXpGnqAusRdVOhEGrk8XjckxyWslyRpgmrpdhirXOUptMZe3t73LlzlyPHRrCbSoueB6+/znJ5i0/OznhgHqKagtoYVGRcX6q+EL5Cx/UV6st+7//9qn37+2/+bq/4ffPcG59bA1W9DsK3RvE7Z5pPFgOibBTk06oo0MZgHY0etktuMsZydjHDGKiaBuv0rrfDw8+/laAeNKi3YVkYslQRR1fM2abfrK52n373m4Nm/DU2L9IDFzwI4nUVtvPDelj0mq4P+238LTuy5miH767EDF7hkF8y2D5r6w5Yfgp/+Np/hz/z3/szZFlGVUtiyHxecHZ6zmAwxhjRYWW5wlrpEV5VzVrCbxRFTKdTTk5O2NraElpzV30ktk6D1jAYZGhtGQyzELDObRYqI3d3dynLktPTU4CQQCPJUbFL9JVEsqIoOD8/D/tYa3n48GEY09HREbdu3WI4HDKZTMhzSarxjFNZlnXViNYGH0cpxfHxMcZ4iskRSZKwXC4xLhl4e3ubi4sLJpNJoGv3rFVD19fOJ+z6BNz9/X2Wy2XQt+fn5yFQvlwuuXXrFi9evAjj9wlEn376KV/9xtd/mAf8X8n2quBUf/us4MiPek4flNY6Is8lodq3PZN9WMMNXgp+9AJe/cCJtyO7Y159P+E6mzL1M+6/A9DF1s2yjCSVamSUonYJXeD6UzraWKUUeZ4zGAxIkpSqKtd6IioE/OsH9IyC1vYSg91caBf4DTa/dxvpEgn8vPWnbo0SMfgiElDot7xTQW764IVLZlea8WjEwbU95kVEng8ElHe2bpImGOOY0toWpe16NVnQBf0kBxcIivSl59inkZWPNVpFDn+Q5AJJLo3DvtolHXiA1FdmR9E6Fbrcj/epBE+oyiYkQ/Rpl+u6oKlryqoSuVBW1HVFXTcOZBdh78H8cL8B8EN8V6drrgJZ+8FxmQdH47yBj/UTRDZBwqvWb3imXA6m2413yc9f/xT9sb76fV9XZFp3lVJXjWc9CWa9stiPRYptYreGhGZ0s096f5ybyTMvnQulLt2PDwh48Ff2u/pO++uyf70+LapSqpdA742Ly8+rf/3+8f3n042o21c+U2DV5e8CjOSTBMyle7+UHPiSrY8H9hM5Nu+/HyyXz9ep+rvPrzLSunH1dgz2lQ94K6UoyorZbMFKl+RZQqha7SXUiegynbyx0G8l4YNQtmcDC7bkMRj3Xtj+yLvAoA3Gnk9QJAD860vOrr3vEhhcv3+xv/Ta+WR4qkcZDmh53gH37q2l1WpFY1qUijlSc56XUzeOq5yJl20tVinmteHTeclfOZ3xc3nGcGCFIUDL+TZZYvosDf2AmZed3Rp2uIe7T8984hMXUEqYmdqWxjYSVPXf0Yb3E+tCrbZD+aR6WqSvBDY74/tyEkA3J3K6nqzwYzZWKpC1Jka5oov1TWnt8GQJjBscjbXpWAnw74RVrgWCjLabO0NjLEXT4cGrAqqkQZLLPNupSwxAYi0eQ1URxIlro+EYJjwdfNO0tK1xPbINbVsKg5+Kgq9i6ZKIWiMsMqjIsaKuO7f+f2He+utAgbZ+PuVd8wxb3sHy71rT1DR1I726lyuKqnbzpL03F96jrtWkXz9XyU4VsFD/XveTSDakI6Coq9oF7S3asU14tkLv97QuqaMoCsqqJkszRqMxu7u75INcmK9cn2sih2m3LU3d0DYNjQvkSi91SeqInL/iY0o+ZhB5FqBNUHjzTpVrO+DwUlFYMi2unT2fPjXot1yChlIh6Viqs03Qk8EGihPpQ6+rNQbmMKfOZ/aydVMv+c/CAK2XsT3WAS+fozgkcXrbE62Jk4wkzYjiBGNtSNQejUZkee4YO12BUJIQJynJIpV33QdttV5LovA6I7QLusLmujT+z9helby15ov0da3p9PdVvk04N0K7n6SJYzTr9xd/ta915bPojWXT3gnn8vb2K+5PDujp7wCU0JPnG2O03afe/g12sNysw2v6ulOtnbvjViHoOm+b9W20zSLB3832Q1Op+9+n0ynT6ZTxeMxkMnEVsx0d0KbRLlu3IDeNbB889S+s70Hng6f+mKZpiJV2WT1y7rZp6GeitU1DU9coVw03GY/Js4xitWJrMuGdd97h8PCZgD/jCXdfu0NVVRweHjKfzaRyu6wwxrJaFNy6cYsXL47Y3trBWsNsOqdtWqbVnNnZlLZpOT09Q6mIs+Mzvv+d97n92h3efPA6R6dHlFWJMS1RFDMajbh58yZ7e3tiYFpDa1uUVqEnndbSe6+uGxaLBcVqQaQM470dRqMRO1tbDHLpoTzIB+zv7THa2yYbDcnSLCy0EJxxU7893g7CylfhebCnqiqyQY5VEuT2/fn8vh7wNm1Du6hD4N6vhziOKYpCqrGzjLqpUUaRpplkndU1TV0zW0plQJZka9TpaZrSNA3j8ZiyLJlNLwRsy/PQu027ClwJonbrLIrjkJ09nowDOJckCcr1DItjGI2kesNXmOQ5Qmsfx6g64nw65b333uPFyTE3bt9CxRF/+I/+EWzbspjPL2Vaxek2bXUECIVv27aUZUGeD4ijOCgBEW6StSW5pTYYDkBwyltXCe0Fh6cWF7tKKhLyLGM4HJDlGWmS8CqDd1PQhbcwOH1rr6U7kw2K5FXb5wHCgkh0gs44B2XdQOnYGEoXbNFKrwlOu3ZOOiqxcF++Z4Xv1UUQuN44C8oQV73vEihM62lWRI74Km8VZEuL1V2FxSUP2Rne6gqBvT7nnbwLRkcw+jQt7cas9MPb67ManlNvr82n0V8VSmm+/t7X+O//7J8hScRoWC6WoFoupmfSB6dH8eKvqqOId7/8Rc7PLzDG8o/+iT/Ff/Dv/1toJQGUSHuQxfcR8vMtRpoHn0zb0nh2CD+Pa3emwjjFJzKsVoo3Htzm+u4OFyfnjIct2WAb4+aqbS1t2YCyQnvksoaLVcnZWcuL5+ccvnhG0+ScnzfMpoa2SUjyjDjTFLWhLBecnlsePftr7O1+h+s3bvHlL3+VL777Jvcf3GU8ln6CyvXzlsxPMVJaPJWlQkfQNCW1lQxfsCFIKAazo9OrZLwiv1pxtp2xtFwuiKKYuikBCfSa1tA0dUjGOTo6YmtrC6UUMyTRLI5jWizHx8fkec75+QW7u7uuj2pKmmbMZzMKx6Rxfn6OtVBVpaOuXXH4/DmT4YQ0SWiamsNDYQs4OnrhAtERcawpiir0/G7blpOTE5SSCuHG9VIaDgdkWcb3v/89J9czMWLjmO3tsetHmZLnOd/61rdCVbBSips3b1JV0n/89PSUJEkoioKPP/6YPM9DQGSxnBPHEaPRiIuLC27fvs3p6ema4VfXdZDZwjCiAy1uWZa8ePGCGzeuU5Yle3t7wQD39L/j8ZjhcMT+wXXOz88ZDAZ8+OEHwtiytyfJC5FmtVpijCVNE9566y1+67d+C601164dYGkl0cBajo6OmM/naB1zcO069+7d4/z8nBcvjqmqOsiLLMu4du0aRbFkOBzSNA3D4ZAsy7h//z6Hh4fcvHkTa6VqcTgccnBwwGKxYLEoqeuaW7duMZ1OWS6Xgb5Y+n8OefzkmUsmVCgN88WU+XxG45hqkmFO25jQd3e5XCJAfkaaSjX7YJiFKk9jDE3ThF5bdS3rNYpiZrMZVVWFwPfu7i47OzucnJwAMJlMODuTgLtnO2gaaQewWMxRCsq6ZGtrIhnya+Cls5m2t0LVqW9hYK3l/PxcgummpS5XzOczHtx9jQ/e/4B79+5i1H0eHz6jOfyAIQsOBpaqtsSRIo7VJTHfE1NBt1z6fPM7//vn2XfzOlcd2/uurq2zgaSawn/pf6tb+PO/VaHTIVHUUM+OQ/KeMQbd08PWSB9PENl7cnwRHGzjqdvUeuWVahTmd2KqwpC+ZyhLILOXg+Pd0JxyUGv31P/6pdtnYXpXfLf5kdp8BranNVVni73MrFn3YFi/h00DxbFErT3DDUezS1y74iKfd3P2YbmybL24yf2v30OSpGo++ugTXnvtNW7dfI1r+zcCZbi8ryb00I0iTVnOgh+wWq04OzsLsmV7exseeicXphdTTk/OaJqWe/fuAlJFub9/jfPzc5qmYXt7OzBrPHv2zNGpi70/m82C3pC5s8zn88C8cnx8zP7+PtevXyfPc9I0ZW9PKq2vXbuGMYazs7MQSPXB9b5s8AnGW1tb5HnuKjpXwhTm2Cv6dvzNmzfD923bhupwT5/uE6VPT095/fXXybIs+E+vvfYa0+lUEmpfvODmzZthHHVdY5UiS9MrjO7/dm2fyx/oATIelEvTbM3Hd18i1MEdXaPqTuJjAS8dQ1+symcddfHm/pvA3qZv4sf6ss+MEQpr6Q+eBZvXU6w3TUMUK2c/2uCbD/IB4/GELE0piigEaUH8m7bRa4UIGC0tyhqhJxfMJA7VTYIDa3xFB7157iiQXduuDVxGgVT5IgFp7ZKCw4woFaqOpHpYKJMHecb16/uYo9JhA5KgFyUp+XBIXUvvTuNBPbMe8PJjiNz1PGZke/JY/GDtkvmiIEsVWlo5JAlKR0QObNUuMC4+me4qxVTXg7mbAwd6ty0mtAWU6sbaFSH44oy2bWnahqKYY0zrgg2+V3c35SHAb7oWSuF++5W8EIJtVwV3u/UIHkfsB6yvCsj2AevNdevH9bKgdv94pVRINFLBh74Msm5eIwDlOnjklwHYKz7b/C4Ez+jsjchVTALYdj1x5qpzbM5Jf3yb+/eP2dxvc5+r5uyqe+vPjd/vUnB8Yz//rl4VDN8c5+bnm8GK/nlRKoTg/Hu9OXcvu9/NZ7Q5n/3v+vMeTDbVa7u2cdzlcXSfqU0Qpz/HKFQkLEbnywXPsynbWyN8nDk8d9UFVJUC5Umure9l3bXr8gkMl2xyt/b71bFgL1X/ubPg2wj078n6iVDub9OtbX9O2c/PsU/MUKHYox9M6PBBjce8QCj1V6uVa78Ix+2K89XyinG+YvPvXqQpDZysan7peMqXtob83vGQVKkQRL0UiLDerpVEsUDLbzdp7E2YRxl/x5Bi/cOyNiSWNU3jmFBT4kiH+7XWSv9io93cSmKXd4esC4zLeiJgZX0MsVvj1j2IjXfM+t7Yrt2Fjq4005umoahqqqb1ikCqtunZ+kphrVBI+ycZ/AREx5Ztl25QN/Dt32n4mZ908t5a2qZ12EPs1q/2Z5KexLXD7ZXgclmWY8yKylWyC55f0DTS3g4rLCHG2WNSjesota1nKllv7+EHaMN/VHiWawEx1zLEWNN7vmIHtW1DVUlQeLkqAvbr+05376HCN7gONt0VeGefuBmnv3T4uS6j5Vloh4NVzj6SfSOXTIeVlqsKkQ1t01KWFVEk7ITb29sMh0OWiyV1VTqMz8k9awIeVte1C4q3nQ3Ymz8ft4hctXZoJ9pN4yW/UPXWqMgHFejmRccLg3/EwNmUgp107ajcWnTnC3o/kVgISuxVbzNs+t8+Ya7/z4+rv0xk/NaxTbukDKOCratCEpAbQxwTuWB3FEtsQ4pvEofHDWV81rFBY4Pt520bHw+4rMvtmmz/PAHwzxsk9/PZ/9k/Rzeubhr9udfsB9vpvjhJxA53ss4nM7Bhp1w1jpeN+1X38zLv7dIxtv/rZdvv6nP4sXVXU6r/k43F03vXlWfK6tsa67Zy349Rl87wo22fOzAOBOcPCJU/PjPfWKnY86BECGK7imIxPDRad1UnfUrW4BS5Y+u6dlRrech0McZIwNv3s7y4CFR3axl1bl8Na1n/BwcHDAYD3n//fYxpuH//PhcXF1xcXPDkyRMJYkYypiiKSNOE8/MLHj16zIcffkhRFGitGY/HzGYz8UFrAng8Gk64f+8+d+/c48GDBzx48IAojaS6yhpGw1Hody0UlpLJZZRle2eH27dvBypyn0G+Wq04PzthMT0jTmKssZSrFXfv3KWpa9I4IU4SVk0lTp5tyTMBixaLBU3TkLos9trR4UdRRDbI3Xw21G1Dmme0xlC46gj/3JRSIRhTlmVQFFVVsbW1FYAAa22o9hqNhsRt7CrzpUJb5jN1SltjWxtopINRStfDfXd3l9293dD3r24baCxZnpMPhT7eZ9gXqxVxmpClArAkacJgOHAVmzJuf98ytwlxnHB+fh4UxMV0ytHxMbP5nKIsJVhuDKauSdI03C90Dkwcxb1XFnSkKQrpGwuWLEt58803efzoMXV9Jr0kQIANH/YMMrEnZJwQlyrVTnAmSUySxsTh57rD4U/2UgFo4cdu31iTQT6I2RnzYpRcNiT8T7Um6Kxdh5zUhhZVzrHx+64Nx4NLPvPbQlmUDIaDYHD5NWgc0GR7c9K0XTBZjCDHVOHHRmeceaWoAOlG4wWtHN+6ynDlPuyErHWGS0d5vjGlndPiDJYsTambjX6StnOmgknSB0mcgbwZ5O652Wun69zG9WpyX0Hu595n6tZ1zfnFOVpZ6rqkLmviJEFFqZtTT33aWTrWWFaLFVmSoXXEH/tj/wh/+S//p8ymT4h9+yF3bGck43r0dO97655J2zQ9L7C7K+0cE6UsiyVgU/Z3hhTzmr/513+DUWYZDRKG45TBeMDW1oTReMRwOHAGX421EpxrasVqFbFcblHX21SlZZBnTCZDQLIUo8ygdEzbWpRKaFpN2bQcHh/z+D//q/zyr/wiP/17f4I//sf/uCRPbW/LOm+E7aR1IJo3KMtKejzXZUnt5G21WjGfTteA9vl8jrWW05MTxpMJtjVurcjYB3nOSutAm62A5XJFkiY8e/pM6FqbluVySZplIYi7KleYtuXMBRwenp0SJwmpqx4+OjpiZ3vCYrGkqkrRDxgOnz9z2YgRh0+f09QN29tblFVJUa6IIs3Z2Qmr1QqAqpKEqMEgZzLZ4saNA+I4CcF7pRQ6UqHVwXA4YD5fkKYpz549Y//aLsIaZXn67DHnF6doLZTy09ksJADEcUySJByfvGA+m3NwfZ/T0zOaRc3+tT226jF1XYX2HaJ/RT4eH59w48Z1kihiNhUKc0+NubU1cZV+uTg1jpHlBz/4hIcPH/LGG2/w5ptvEkWSzGSsIY41g8EWZ2dnRLFmsjXm/EIqpK8d3OEXf/GXuXHjFnEc8+zZMyaTCVUlFZDXb1zj4OAadVmiNXz00UfUlQSSTk5O3FwOePHiiKo2DEc1g4GA65PJyN1fTGvakHS25ZgDvF5cLpfcuHEDa4UVYDqdsr29HarjfVXjxcUF0+mM5WKBtZaqrJhNL3j4g0p6qMfyHObzOUmcUDeV9HNVlropKauCra0JceLWfFkyHo9DMCnLsvDshGHHhN/rug4yvG1bJpMJSZxSlkLxDOIgSna7JEROJhM+/PB95otpSILoOx+TrQkSYBhijHUOqGU0HDvbs6VYlWRJTBKnjIdjTl8cc+fOXanmzHLeeOMNVrdf49GT5/ytJ08ZFc94exeyVsCcJBWavFDF4R2rV9nc/ju78fNlmz/npgOswLQdZVZrLE3bRyToOROKsrF8eFJTO8ylai2LskVV815gpHcBI/pBq8s35DWITzbtB8TXmJuUon0YUVpL9p7QqqcJJHF/bG6EtvtlIzeZzWD5lXO06Z2HY/13vYuszaW6pEO9jl//1F/Cdr9vbh5cs/6gV+xrN57V5RvaPPUPv1lLXVjKX0q4v3+DX//1b/Mbv/Eb7O7uShJOpPix3/PjKBWRJDHXr18njhNOTo65c+cOTdMSxZrt7TEA29vbbG/tcHx8ymw6ZzyaAB0QiVJMJsLeURQFFxcXSEA94vi4Y9zY39/nxYsXrFYrrl+/HgCZKIq4du1aSHj2ts/169dZLpfBF/RyrizLwNj18ccfc3Z2xmg0CmxXWmuOj4/XkrYt4vPNZrPQMgPg4OBAegCvVqRpGpJy+2xlnoL92rVrHB8fB7vJB9Ynkwnn5+chUP/w4cPANnZwcIC10mM8+DlaU3pdrhTbrr3F/79um0EjCYwnDAYD54d11WVYgzUNWsnfSlnpoez6FVuDY7P47DenE5ef/y3btPVfCvoYg9WSjDEYDMCx6LVtg8WiY0WSRHRVihFGKQaDETs7u4FVwF8zjmNsFBEnxvU8lTmp2kb0clVRlSVoTZJGrIoygExRFAlY2EVj1mS1BOx1AM57N9vzs0ArCVSr0Be011sY7UNERJHi5sE+L06ecHx8RGta6rpiZ2+Xi6mlXUjycRxZx/4S9S7pg4p6jf4cpbD68n79fay1xFFElogfr1zVeJ+JELrKOz8PxrS0TesShCS43bQNTd1QloswV56Bx+NU62yJPX9ZeZB6bUU4fzcKujJUy3E5qKlRLpm7h39hMTgQFOViH52feFUwtv9vE6SUhADt8Pbu+puVwmtV1qq7powvCuuov143A9TyTlhQLkjo99X6apXaO5+/om9xshm8jSJf4dyt581Acz8gvglWbwab/e9XVZf35/Gq8/fPexW7RR/49jiVt3+7mWXtGH9cn1pV7rEL8PuCoC7Q5BglWJdRmwHsEJTvPye5OD6Q7XbGV0/6dR7G53ERN67+9nmCCJtr1K+/zYSB7h25bPN1wX4Zz+l8wbejFzzY3kdnyZpp7J+txXbVyHjGhQ57NMazErp16sxKuZYbYx/n8vPVs/XXkxG6IgkflOnfjuBTPiikkLiOp0VvkSVinQyWg5IkDs9UIS0VtYrC9YSNrKSqhMVttlgxXVYsCkexb3rB2FdsXp22xoBVtCimZcN/8Olz3hoPubU1IUISZtuN1hgWqYTVSgVKdOMqnN2EhkTbPgDksT1fuauUu5+qZlmsqEphMRwMh9ISVLm4gTGhTackAwg7CRDw65clgBgXMJV+zh19dHhQqguet21Xea4jvTaFyr2LVVWxapuOnl8rdOsKiK0wm8qlW6KAF7oaaD+uDnqTMVr4v/zf53zxC9eZTGKiyKJjSWrWUSSVyFZYaKzxrYIk6Y4oAgvFqmA+XzAej10SbMlsNqWuG7LcJYo0gk3qXnDRJzjgbDKtOsy0W0fr/pRy+srbcUKfL3Pi37PWtQ6s65qyKqmrmtpR8seR2EnWmOBzeDaeoI4s6/IKv17DSC6PSbninfDMuuSgqq4d5ursotjrbV94J/qoKAqiKObGzQPG4wk6kgrsolwFv1H8aU1rulYrTd24inORvcYaMAZjNcoF3JVSEm9wOKiDzHsyBTxVup8VCYprl6woiYo6JIZY2taQZQNJJuyt1SiKgj/mEwdCfMG1qAWXFBCL/Rfwbet1Yyd3bG/NSrKBCmO3Viq+l0vH6oxG6Rh04toJuIp1HRElMUqn6DglSlLiJBU6dWOcP7jNcDBCKU3bGmgV8/mC1ihq06KiiDpUxPvEwZ6+CP56xy7xu9k29f1VdsGlTam1hJw+S1bfzh2ORxRFIaygbsSR1ykbyY+fZ7scy1m3N8DHCi7vc9W9fNa1X/79FZGNl9xPn71l3QbY/HvtwkE+/G63HyowDl1P7/F4zHg8DsHbKIooqjIEqn2Vr/R2tq7atg09oAeDQThfHMfSE7UXKPXALsiNFkVBnufsbO+wv7OLtTb0NL1+cA19EkErL8WX332X99//gDfffJOqLCmrkjwfsLO1zfn5GW3d0DQVL54fYozh+cUFWZqyKlY0dcOqKJhOpzx8+JjDw0OOj44pyoIbN6Tn9ptvvsnN6zfZ29nn4NoBN65fZ3d3l8lki6Io2NnZIYkTR+8F4HpsWB8gJPyO0jTGULsAhVROVS5QJ5Vo129cJ33tJs+fPyNJEkbDIavFkq2dbZpa6LuiOCbLU6y1a8EFv7WtwSpH2as1L46PmV5cEMWxZKF7qnhHiT6ZTBiNRkRRFMAoCdZoUkTgff/73+crX/0qIPczdBV8ZVmSpilb29udEe0MmbIspa+LA3nbtl3rSd/1Pgftqo/iNGU8FsC7LAvquqGqStqlKJzpdMp8PqcsC9rWMBoNuwQD3VXKeAfFb/O50DoqFA8/+YQvffGLPHr4kLf/mT/LarFAKUWaJAFsOzg4COOUQHtMY2K0EspXAfykD4Y1ljwf8IUvvI01lsVygfRiNN508Ld5aQuCu6dgvCkgjrh1FCr6ygP7BmBfSGgU+8PcPS/n0G8M4GqM9+os8zWj84qju+C/ckCm9IK24eLOPtQa2laeucvW81m1OAVu+kauUqF/ctM0Ye690hDUzGcDK5dZa3tBWEe3jsUq52QHp8P9V3XAgXITdsUMdABJCCYIzbYc73rPWxt6XG3O45qDS5cd/DIjlI1PZRS99UFXQd4dZVkVBc+ePufi/JQsS7m2f0BT1+QjqdjRWui4y6Kg00mWctVQlTXnFxdcTGdMRtv84Aefsr0VMVBt14Oo5/gZY6RvDOvAnHEGdt9L9FnPbWuZrSxf+dJXeXDvvlANmZYs0tTlkmI1J0o0URJT1bA8qmiaGnAtDLTCkqFshjGKOM5IRjFJWgv41bRYI/+qVUvTFoCibi2RTrBKM51fkCQp0dLyEz/10yyLkqY1/Prf/btkacrdO3fASrVdkmYsF4uQ0RzHMefn52tyt6oq5vM5J8ddtaZvP7JcLl22qVBi13Ut81+W3LhxA/A0Sw0nJydCJZRlfPrpp+E7XxW8KkX/+n7NaSp6YDQaMZvNqKuS50ksvXqGQypV8tFHH/Hs2TO2trYkwSlKSHXCxXRKkkTEccT29hbj8ZA8T9nZ3eXjj4R6XdhCFjx79pTJZBJAjnyQ8fz5M0dbnnJ0JPe6s7PD7u42z549wVoBd168eMH29rZUtxcrimJF0zTkeRZk7GAwYDKZcHFxQZ5noYpRAvFi/OZ5StuKXtnamhBFGmNadnaElnxvf5fT01MWy5Ib168znV0Ine5qQd3UJEnEg9fvMx4POTk95ej4Bbdv32Z7e8xyVfD02VP29vaYbE1IUrFp9vdfd4HqmP39Pc7OznjjjdeZzaZhLeSOEv7mzRuQ52RZwu3btzk6OuHohayHo6MjplOh7l3NlpycnrK/v+sqqMUpmM0aklScpqqqODs74/r162s05Z988oljJxAQ7vT0lKOjIy4uLqQX8GDA0dGR2GmOrt+2BtPUKJMyn16gtaIqCpI0xWI5Pz9jMpH59MF2XwVqrWR2F0XB1tZWCDj5faQquWv9IQGQ1NHRS6JjWVXs7V3j4uIiZAWHYGvbsr29zU/+5E8xnV24qroiyE6tNU3dkmaZq0YRWuTZbMbx8UkYg1KKSEGqxRmczWeMJxMeP33qRJCjuzUWnWScNDf5q0+n3BsWXB9abmgBPRQtSazoq9soUpfF8oaCEJFv+6LxSv1atxbTXpbvfoz+GIWiMfBk2obLHs5afudIqgjLRgLi3fEvoTlDzmsDSNdpG4v0uxMD4bINsX4++c48jClpSL8mVQ5Na8mSzn7z573yL+ewrqd39ba1iVM9B3dtptwPdekjlL1Cc7od3Pz666jP8pht363unfVzOKk9k6cbn3r5mvg8W9NaqmcR0XnGw/lDnj1L1wCBJEl4cXjGvXt3GQyGPHz4KWmasb29zZMnT5lMttjd3eGjDz8KCc5gGY/HHBzc4Px8zqo4CmwCWMv29j7Hx0eUpQT/JpMxs9mcyWSL6VT6hnvgxSe6FEUR2EpevHjB9evX3elskAf9YLc/x3K55Pj4WPwpFywfjUacnp5SlmWo3MiyDN6XIfo2Dl5nzmYz8jwPjCKe8WS1WrG/v0+e57x48SJQoa9WkrTk5bhPBN/a2gr+iU8GzvM8+E3Pnj1DKaHTnk6n5HlO3TQMXPJemqacnZ//iE/6v12byHlJuIgiFZKeTOsCj3Syq5+I81nU0a+4Yvitf8ylCs7PiTX1ZaCxBmUUUSKAqvcbW9c7dW9vD626Vls+kJ8NB+zu7tKaKlSFb/qn3s9UxtJWllhHXUWRtURxby70hs/QE1F+7qJIoxvnX7nAa7gfN8dNXbtqSt8Oz+B3lWCt9zEUpm24dXOPX/rV7/Dhhw9ZFSt29nYwyjBfzKjrShLLnG+hXS/efoBbKeN6ePeA4Gjdr90EHX2AT5LWpMe4yP4uGNUPVvYD3q1pOvC/9/klv6znP/vgdKS1+HC2CwJsjjPMvQcyvd5CXVp7yoHgxioUJoB6XVACB+53FVH98a2N2VrXIxl3zvU1L36qnNv05mVz64Lf9Jl+X6riLgW2PZDp2Al036/esEcuXRvkoloFjMMHxBPnowrbzXqf876P6QHm9fHIFoKgG/e7Oa+bwemrZM0arrKRLAiEAMNa0gdcWpebQfdNGSftbrqAlfYJBr33wQcWN8e2GaS31joabqTCcONZ+FVnrbxb3TNx/+3hIar3Dnu7qP/OrJnFvarNzQSEfoX8pbHibeBOPimlXAFphNUShCrqlqKsGeRZ79wip3wQrVXCDuhlR9vWrvVBN3Zvo609aYc/rc1UAEjW59xfE3wLwP768/cQThuO6x7FejKPzIv8nmYRWSZ+vTXuHda44rLOFpc2ajXzxYrpoqABLjcxeNXmkCOF4GhKjj+cNfyvvv+I//k7D/jaOCeOI6q6WT/SyzolTBzFauWKFuzGu0RYw17H9RO1LAhjhyukUFphWqjqGqxC65r+8lWOWrmryhX/1AfItPKsIY52XIEyCqUMdatpmiIwksmalKCuUpK4Jz2Q3XNI0p5oFmy7qkqyNOOv5CNMNoNlhXF059qCjrvgj4aAfStrwbeWVFr+oWh6T+zkwvDv/JWGP/hjJb/v6yVt01K7qvG6qQVvjGVtJHGEvZhRNy2DXNq0zFcr8sGIwWBIUwtmZowlTtKwblCaSHXBa++LhUDtmpNymcdyU/53LCsNvrd864sAHf7V/2ed/JK+2B0TpnJrShgFLFZ1rTc3LT/jGrfbDfkOPvjLhstmqaqatjX4djRRFEuf7ViwY1kLMojxZMxksk2W5Y4Vrw6MMlLpLYkudV2xXK2YzWahIEuSOFqHjVpXBawcPiBFV3EUdZi3m3JJxrnsISrVtQ3t3RCVK8a6mCmGo1vcfXAPHX0n3K/XSZ0tvT5TWT5AxQlNa6ldnEjai8Imdb2Xay+j+FZKo4ymrU1g740ihY5kbpVSXUW00ghtf4yKY0nq0BHWBeDzPGc82WIwHBFHCa1p0Fpx9OKIbDB3sZaMWVkElsp+kP/SZl++fj/v1o+xeFt583Mv77x+i7SmbVrAdhXgdMlzeZ6zs7PD4+eHfO+7v82br7/BO1/4AtcPrgldPxbrcK1NNqLf7bb5Tm0mFP0wW2fbr9shl87lbYzPvI+rrn+F7drru/67DY5/7sB447J88lwCa75Ps68U8wP1lbmeosJTma5WK6I4ClXXSZIE+kwPLoTKZpfBPx6PWS6XQucH7O/vc21vn6YsWS1XvPvFL4bKxOgDDa0EgC/OL4gcLYinIZ3P5zz69FM+/vhjjDHs7GxzfHRE0zRcXFzw6aefMpvNGA6HIUhR15b79+7z9fe+zpe+9CXeffddRqMR4/EYYwzD4agDgSNHkeKMRGMMpqlcFmBHoyZ0vMZlAIrC1ZEido/CWhMCK97J0Dqiahpu3r5D7WhHWwPzlVRwDwdD4kihk5jI0faiFG3bMBy4bCQniEejUajsuHnzJsPh8NIi8sK6H6wOBqdpHIjhAKGnT7l586YkN5Ql48mYKEmkT4kxofe4V4Kto2qpVuVacoTP/vWZ91EiQrPfy15rzWA4ZICwBdTLJWfnZ6HnexTHKG1YrlaUbp7KpSRX+OBf3xgfDAYM8pwkirlx7YBPPviIL3/5y2RxwumLY+ltkQ1oHbBx586dkAQSQBuidUNJR7TGUjcanWzz9W/+QW7e/iLvf/ivo7Ws6wADbza1c1vfRPTObtefrXNc4zhiTUCoy0LJr6Pg4G86eOtXW//7FQLGYoMxq3prtfuenoHjndV+ANc7YZ3CjuNIAFLvKNl1A7q7N/ks9srFOlPNOU9t69gplMvG110v9vV7WgcWNqMXbduE8epIqAJZm98NR89c7dyhkJ5JpqN097PkqZ606irxDXZjKFevk/4cX/Vdt8kzuHbtgCROOD+7wLQR4/EW2sak8Vhkr67QdiWyCiiKgn/73/o/8/DhpywWS45PjlmslmRJTlFAUZbsbmdI1wBnAOCD4NIHzic6BPBJOQowvBMCy1KRp9t842tvsTWZMJtdiOFf1cQ6oa4bZ1SXWGuwLhjeNjWRy2oUmhkwZkWkEwYDg9Yxpm1AGZRq0dq1KbARSZQ4+igx0OqmJU0jLA1/9B/+o4wn21SOLvVXf+3X+MbXvkakFfP5kvlsStMaBsMBy8WS73//++zt7bmAecJivgiZmTrSTC+mFGXJ6ckJSZqwt7cvtP1xwuHhc6IoJs8yJpMJZbHi8PkzrLXMZnOiSFhCHj96RJZlnBxL72YdRezt7XFxfk6epTRtQxxp9vd2QUFVVuzt7nBwsM/jR48YDaT9wnA45PzsnOEg560333DB1zmkBHqtOJYEradPH5PnGfNFxCc/+ITpdEaappyfn0twsmlQ2jnwxmDsgJs3rzsad+nLnaYJ8/mU3d09Dg6uMZvNQ5AzTRPSVAKiu7u7JEnMcrmirivG4wltK/3IpbJPu8rn80AB7OXGcDggSWIXeM3w9Jm3b9/i9PQEYwzz+QzfZiHPhdJ3MpG+38fHR+xf2yfNJAA7n89Is5S79+6hIk8vfCrGqTWuF+2M+/fvk6QJWZZJAt3xsauAy7l54yZxIhWNaRSxWM4py5Lr12/w2mu3pVozilmtSkZjzfbuNaGJX8zRWjOdXoieQWwVIFDYJ0nC4eEhr732GrPZLAS1ytAHfRqq/M/PzylL6WHqg4paKeJYU1cVcbwNCCA+m80YjkZYJzenU+sqwVesHCWf0JYnoWLcV3efnp5ycnLCnTt3AshUFEVg/vF2YZIIU0uaZpyenrK9vc3p6SnGGKbTaaDN8oEmoX0TG6LdNRDBXC34tw/+I6cbBSCygNoGu92JXA/qhSop7+e/2UnPPsDi9//EeF1o0Qpi3QGFnUT97O2HcVucurtyaw00PUYk86oTj7uf5T9ffM6rKxj3ADy1CS70x9l3mPxPCY5XNMSvW/RYsbJS4ZmlPqGgh7SGyevpXCzWVY6vO/wvGe+VX2x81nfIrtpDrQ/Iqv6e/dNuXsu+5PfuL7X5mdq49d6lrfv5eV05C6wWhua5Rv9WRuKYt+q6CcEsrSPatuLk+JSyqIiTBGtF/02nU6lU1YqyKEPlTZIm+MrLyXjMgwcPhF79CyUkwlrw4vCEJMlIEpheHDGZbDMYDHn69BlnZ2fcu3ePKIo4OzvDB8dfvHjhKlai0JJpd3d3LRlMZPSc8XiMDyR7+vVtl2Cre2wq169fD8kvi8UigHW+h/PZ2RlFUYT+1YvFIgSyPY289w13d3fDPl4+AaGt1fb2Nk+fPmU4HFKWJWVZBj/KV5f6MSuluHPnjiSAG0lEFjn+owEw/23a7IbtKzJPByyhD6B7X3FzWw+ueJ/D4Lpvc6Vc8EESfw6nDzShY6WTKC8XrN732ASMPJzkA0U+Kd2YFrRid3eXpi5796+6/vU6oaxWwnylI9I0g55/KomkYJWn+XXJZklC61qWSCuoSNq/tUYCX8oHQrtx9oPRxgXtfeBRYR2VOhKMUBqlhKJdKvMtceLAaXSYK2VbdrcnXN/f5tFjxfl0znRqWZaFBOqtEfDfWrAtxmcetT3dwUblKe5h+Hug8+38Ed4HlgC+CoG48M+KLrHOvpelEiQEfmKU6v5pb0T4zfXttAGodutHC05zOUnDraxgT9jgE3XPvr+e/HMirKs+qLq+eaBV7nAtaNh7vv3kOtvNXFg7/r5flgiwHgzuj7kDYf21+sDspQCsG5xZYxp4+dY/rm7qcA0/z1pHIeBivB/du27/3fTPpR8A7we7N7fNefD31X++/fv1LAKbwb7Na/mtn3zjA0bKLbr++WPHeuCP8fvK8d0akmCLDViHH5fC9eH178LG/frrBJmqOtygPwW+3YDHgvoysftbBXyF/rN3vr1SippFOEcSdwU6V82/x9OuSlrwYt7rz3CvWotNrCwtirKuQxWtr0TEGKq6cs/EYwYNTesrxDtMzdruTr0Z6K/jW6H1Br2xnv17oAP+ge3pE+v/o8JcB5llCRgQVs6BIgT4LIIXLxZzrB2S5TlJJgmQSSw4a1GsAo4exxHlbMGvN0dc1CUtYK1CReozHIe1p4L2GJSVwywxR9OCf//xIX/4zk3+6CQn0vGayFy5KkespaorFvO5kyndxPr1EYLWjgHBJxBbJzfquqaqJXBprbCYWCN9qZVbf/5B+bUjGIQJc9qaXktX/0Ct7z0umHzTtGuMoiFoaSSQlaQJSRzhWRG11kGuWStt8ZqmZjwacffmAU9enDFflq5PNzSIbpECeuNwW4/vd3PnMXusXQuMG+C3v/eEDz6M+Hf/kkYZmZ8shWyY8aU3NX/yZ1rKqnEJ5DWroiLPC4bDIaPRmDwf0DYVq9UyxF/iOL7kcPjK+M4uCEvbPb6upMu700H2ubltbRviOcZ0gXFjjDC09ALibSP947v3wwd8vb/eJTN43DXYjRtjF9p+4xgXuraQuiefxObxdpAkWgimK++dL67SWtqzxrHYVb7YRSupuJfYUCWJNQ5vbowU3/hWgBIX6xKiRGQ7uaTcO9+2tKaVhDuPn9u+e3z1++rfS4kztS6oKdi0tMzL2N8/YG9//0q9G/QZMmd+jFmWYZSSljFVhVYxvg2C1Hv7/3T6xMeJNquf+3Z8VdXoSKOimFhrdJwSZ8J4q3VMFCXoOCFJB2T5iCTNQzKKRa6xNdlmPNkmzQesmpIkTVgVBa21JEnKYDhkOZ9jrBRJBSa8vj5eW6uX57Zvx/jxb+rz/v2trb+X2G/9v4N+6c2PL2ICWBUrnj59yrd/+7f59OEnjMcjXrtzm327H5ifoWNe/FH9yatsTNX77+Z+a/fQ2+XS9ft4S2jFc/nM4WwvmdvPt13ez3qqF3q270v2/azthwqMg69iq13P0G1OTk5C8KPvGAKhd7XPjlBGh6DvcrFkMBywtbXFarXC03PnWU5ZVq6npVQZ1VUdgJVHjx4xP78gTVJOT07Y3d3l8PCFZJO57dnTZ+R5xpPHjzHGcHp6irUwmYxZLpZOeNbM53PiKOLI9Z7b39uTKrTBgFs3b3H//hs8ePA6WZY6BW0DxaoCjG1prBhibdtQN1Lp7cGpOI4xTesMAE1d1bRGgG0VO8oK09C0Khjcnh7Wb174GBf8yZOUJI5JU9/zuw1Kdb3vjSWOEueAaff8rAPQ6kDV7l8yX7Hlrwldhu2606HxqRnXrl3jww8/DOwBgPS4cX0z/Ll9r3BAwK/RKKyDnZ2d0BfUV19Op1OKsgBHUecrBf24PJhWliW7u7uBljHLshBkB6HlXkWytoqiYHd31xky8oyKomA5W2Dqhtlsim2F5qRYLlEWzk5OOTk6Jh3mHNy4HqgXq5BNZUmzLZpyiUc+LRbDmMFIehneunWHn/7p38/P/7//Ku9/71cA75BcFpjyXe8JbiCp3qDz/kgcb2RE2Z7RsKkMNjalOkOnC1arjX3Whdvad7gMWdV9si6MOjejNYZYx7SNCUCG0toZshBHmswFFeM4xlSVzKNT2iHj2gapJ9dVygHAdQeiWDGeE+FzxVdPy6hMt35fJtRdsoKXdzrSwQD0j6OvQLXLFhSD3jpdbLogOdK/tTRVT+HqziFyWcH+8p1D6ufw5UJ9fa1sZJ+HO5Y18eDBW9y+fY/Xbt3DGsVqWXB4eMyTR5/w8NNPefzoEc+fP+f4+Jjpz0xhJDTe/5+/+gtEOhbDr62xxpDEMYaWNJ9w++6bfPDh+yRxTZYIUOWfU13XYe5b0zoDylK2GYPBiPlsymi8y8/+43+Ct15/wNHzZ3z04ftcTM8wRlo8VFUjfZ2iGG1boaLx1GMojBbwC0fhvaqmZNkAGsMgG2C1ZGtq/NqLUW2GQtG2tcvslmocBRxcv85Xv/oVHj95Sl2VTEYDbly/zs///H/GfHruaKAjpvMF29vbIVB4fHy0JheKouDsTKpulVKkSSp9xMuIx48eCYVrVQcnxD/DyWTCeDx2gYEE08LQBXCHwyHvvP1OAPCfPXvG/v4eVV1yfnHOs2dPATg5OeHmzZtcXJxLwlmScHZyHAziPM9DG5L9/X2h5V6VLpCdUhRLtra2SFLJ7pxOp4GBw+s2T0W+v78XHMS6LoURAsPJ6TGR1ozGI7a2t2jaijzfZTi8zqNHj3ny5DG3bt0MBrWv2IvjiMFgiyRJQs9OrYUOfjweOwpcqQqfz+ckScJsNlvTZ2maCkuDMezuSgX248ePQzClr2+qqmIymbBcLgJAPxgMePbsGU3ToqKY5XJJXdesVkv3bCQQPZtNybOMp08OWa2WnJwc88Ybr4dWK0kqxr2vwpe2KOfs7kZsbW1xenrm1sk5Os5chbYHYcSWsralcLbQ66+/Tl3VzOazEMDx9s1yuSSOMoyxgRkgz3PX71uunWYpbVVxcXHO7t4uW1sTmqZ21fgD4kTYfwajUajMHAzy0L97Op0CFfP5LNDfzufzUFGe5zmHh4fumSoX4J+ilCJJUi4uzkNC5IvDIyDigw8+COOLk5iqrEKwSeSw9PDUWtG+00Aq+m2Vli+Vi38vtxaoP3Ov/wZuGtj6vDtvOkqGz0VR3NNbITj+ENTEkHy5hWuWlbWksSJJerrMwhrtud+uKNkOVoTdtJLWbahX3pbqO2OXLrE5iPWPnZ3RB2+uPu7S0VeOZ21aN8Gdzzre7bNcGMpfikkuJGmoA4I80OuARmuZTmcsFss1Cr04lgQkz9DVNL6iVWyetm05P5tyeHiCtZbqXgWJ2O7/8r/8v2Nvd4e33/kCX/vaV1ktS6I44o033mS5XDAYDBiPx9y8eZOmaXjy5An7+/uhctwnSi+XS7TWLBaiR7089u26ptMpRSGJHYvFgq2tLZd4lLJwVbmhlVLRJYAYa1gsFkGfeNnl50hkGEwmE87OzqiqiqZpyLIs6N08z3ny5AnD4ZDbt2+HBHDfmmIwkOQjay0XF5LEl+f5ms4aj8eyblzikI50qD7/+7VdBeb8/dokCCK2j39W3cC6wE4fmOoHpPzW/WrXPvMgO6y/U10wqP+e28uf9Y+5AvBaA8dUVyFaN02wARU4DGMVjo9iCYAPBkNQuF7VxgUL4uAPaFc1q5SwZaVpSlu3KAeaW4cXRI69QPwO2yVwbQRvvN9Bb27CPQT5JrSxPiAkwK6fG6SHr3crET8niuDGjT22twYcvmio64JIC6CvPIJufWTLguvxK8m37h5d0ML/FCpu1T24K5ep0Okb2w+Mb/o/FoQROIhxhQere+uKy4kEL3vmfidvS4dgXT9AiO39vu4v+mCfVDLK55vMBS8DY1+lHfz71L+uhwdtAAW6610F7m4GePuX62MBnxUIdl2d0Upfea3+32tgNJC5NoCbr6IvtGnbNlQYbm6vmr/N+9v82z/Lqyrg+kB2Xyb1n9kmiL75dz/Q7/EPH4Txvstm/+9+gOeqbTN47/cz1gbmR+jed3lfu6rBzXvrbyGIA2tz6fe7xFa4Oadrp9t433rz19+uSmZwymDjIoJreAygbBq+w4xbHNBnVzDWUlZ1qFzt2ih08tZdrZsHlMPPZN5Ma1DGEOk4UDr76uNNs1DEiisF0b2kGB8U701MH/3zCb4iU2EzCcS6dV/XNWlRkGe5BLFSS1lVlKuCpq0xjhmvrCqKtqVFGo8AAY/6LPtSuf/I84/cc5Hn0BrL85MZvzwYUEcxf2LkqX5lq6qKNElDYCpNUwmAGlfYYMQv9PIvdi1DfeKgtWCNcdXitUsOcUkwWgW/2OIpqXuz6J63cfomUl2bVr98/LsrY+nTe7fhHMIGQsDsgdCSU9ZIV8VvrXXtSmvaumFnPGZ7POJiWVMTE0cRkVKgE7Gt25pYGax2wbBe73Xl15w1gPdtFWmeUTQNq6p0MlKeYBpZsqLlV5YRH34quPR4EJElmp96r+Crb69IZwtu3tQMRyOqQpJCFCoUEthNhi2XOOvbDPi1uCbv+//Z0AO+6K9tm/DPOBpxY0wvKO6qx93rrtx7jDVYtOtJ7k7fGpRjERK6d8lZ21zHwdUL8jBy/cJ7OtHpNBm2db3rHXuRSwj2rVbTNCGJY6SXu7Q0aJpGWs3WFU3TSj92l8BYVxVVVdM0EsNwXpgzmnDXlYtbKy1s/fpTSod125vQNXvGb36deCa01goraRLHDAY5s1VGml4Ttt8k6Tno3Tk2k9pCclaSUrnnU/u2kb03XKn1E20Gjzd1pJdZbdNgrRSsaKfr4jhGR9q1tU2F4XMwZDAcE0WCr2lwrICara1ttra2yfKc+dTgrSwLqEiHKvGyWbGWkNCfO5Rgx1bRT/5ft90u2yd9RpOXxUQ2v9+cI6UEn44iadfsE8QXiwVHR0eUpbS4tK0JMqsoSoqiRGsdYltyTn2l/n1VkPlHD0D3zu//o7pzXq3vX3LsVWPZ1O2bPpu3w6/yATbW41XjsL3//jDb56dSNwJECPWFwhrp76g4QxExnc0YDUfSd9mIsk8TRVVWFKuSpm2k10AkvSyjSHq8Ti/mAjxXEswqy4q6btje3hYqLq0ZjyfMpkvK8hlZkpAAVhsMiun5lGePn0qGnRZj8oP3P6A1PmglQecsz3n69DlKKZarJWDZ2pqws73LvfsPuHnzlqN83WU0GmEtPHr8hLKuMDhKZKWYLeZYY8jynKKuiFOp/BY6tEgepDGMx1si9DJ5WtZasny4Rhfvg2DyPwk4dC+SGF4+A9L3PW1cZiBKjAMdSbaOsZYojvC9LKI4EuoglBgkSnp4GKvQOsEnMviFE8cdcGZdNp0XelEsfR2aphalpMR4VFrz2p3X+OSTH/DWF94iz3KuHRzQuOw7H4D2BmIURdy4fp1yVWDaLjDhASrJxJKgutLSRydJEqqiQqEYDUdCHxTF3Lxxc3159rKgfZJB0zQoKz3gq6ri4uKCoij46KMP+eSTTzg7O2dxMcVUDaPhkK3xiL/zy7/MxdkZb7zxBnfv3uXOa3eYvzjkv/yFX+DFi0OUhQiFba1kJ7XQ1poo8Q5/zCAfO+GfhPX3p//Un+Zf+d//Jm1jAl3+hqi6/AKvYQMuo9Z2Jrbu9w/BZzOyfp6+4PFCPRjn9srf5bB+hbZaO51SXrhtKIEr/hJF7sbt6f4c8CM9njujxztw2geOjfRx9/RhVqkQ8PKKIdKKtpX3KXIKX9gnMnS0KTtljtUaDUlHodUX+mVRiuPqAAm/pqTvU0dV189Q94arClfrTBvJcreBXs4/Jq2kbsW659oP48sZXkoy2z2TK00ooT7UKFpj+fa3f5PjFydMLy44OT7j4vSc07NzprM5i/kiZFq2bYP5g11GbG1KinpBlqakmWL/2g2++O47vPnWm3zpK1/ip37yp/g//Kv/Gv/Ff/HXmM8X1NUCiyKKLKNBN+1VBUVZc3D9Dv/SP/fP8VM//dO8//3vMxqN+LEf+zHKokBjKauSn//P/p/8/M//Z2g0OlakufThtqYlSSRpSDKHZS21TYsxQuseKYVta6rWkMYRWTpANTiHWCpXTV2SZilxnEi/9apmMMgxtLz1+ht88sGHREmCMYYnxZIvfuFtrMtunV7MmM9nWGt5/vQZp6enXFxcoJTi1q1bIaN0OBwwGgyYT6dEUcQCy2Q8oqkbbroAbaQj0jQJyUDT2czRcu1y4SqGj49OsMayt7/HxcUZx8eHHL04onZOhtZakqvc703TMJvNODkSuu4sy0iTmKJYMhyNyLOM8VgCorPZnLoqXcuMmDzPKIolWZagtVTMLuZzZrMZZVGEthfDPBdjPIr49OFDlFLs7OxwenrK2ekpk8mEYT5gPJ6Q5znXrl3j5OQEhfQT+omf+HHeeP0BURwzn8+5mE4pS6Hxzgc5cRTTNi1lUbKo52xtb0niTBzRNjWrpfTPjbRlMEiJY3HEJ1sTVy09550vfJHvfue7Qje+XHL/3j2ePH7EeDxCIdReSilu3rxOUZQ0jQQzptNzPvjg+3z88ce89tpdbtx6jb29PT799NOQnOCDvcZI246mqTk7O8GYlouLc7I8Jk0jZvPSvfOKJJ2wvbOLVhHPDw85OjpmOpuT5QP2r8WcX0yZz6doLdWOWSbOQZan0ts9zTg7PpO+XHVDmiY8f3rIeDySFjIqpi4rsBCPJEktShKyJBXqQQt1XZEOckqXAFGWFU0TOcdGsZgvGU/G1HVDWZRYYzk9OWU+n/Pk8RNJnnN69rhteZ6m0i+saTg7PQMsZSkJQKuipCrrzkFqapfVLawwjZF+Y5FLZmiahjhylGZaU7UNkU5QOkUpx0S0iojtOr1uZ5gHa11kn7Ov5LMuQSpow55e9GL/hzef/xu4jZGguAHmP/zhatGzOK6YkMsO4eUqLDtTlL8cobYMyRct1Q1LayBLnaMYdnRzf5Uz4+2LK1Xfurt7+bON/Ta/Cn+ry4er3sD8B5cm4vK1+odfuY7WPcNu3P3F9zmcy9XKUPxihD5PUJGvtBEbwYM0WLFP4igGpWnaltZKEl6appRVLfZ+XTsAKgp2vlzH0LSWtijXknStsRy9OOPk5IKPP3nEX/trfxOlFUkSc+/uTfav7XLr1i2qquLWrVvcvXuX27dvY63lo48+AqQK++TkhCzLSJyObZqGra2twCRSObYn3z6kaRqePXsWWMV8Eo4PoI9GozBGYwxxkjCeTPjBD34QwNK6rtnd2WE8mYRkW2EkGXB2fs7QnaOsKlpjGI3HGGu5mE7RSrGzu0vp2nmNxmPu3b8PiG/hk8R9sCyKIqqyJHWJVmmaBqD379d2ZXKruhz8+69rLOJfis3uWQK6wI5B25dTBb4MnOqDYZ06CA5L+PuqwOemn7N2vs8IsvkkDaWUVEHFcQDyLZai7FrMxVHski8GoJSrcHNU53FE24DeCDSKv28xjQvoOJ/DJ5lEVwCdXoz5rR/IXZ+HcBeAwrRdGMeFgfCVykEUhvEZTFtz68Y+B/s7fPppTFFXJFlOY2zv8i7gFD5ZE4b4hCgb5K6lyyC6HCTt3ZW7l+4Oesi3O7bvka2LWB+I8onIm4Do5jpTSoU+nqGqbmMdheIEpcJzhT6Nt11/RqwD1VcBmDJG2+E1m+qvp3ysWZ/1fp08vTX+WUBpf/+XBbX9eTbfo87W6s2LG+raXPYSC/yxUZKG5Ftru8KMtm1CUBNrw5q/Kqi7uW0Gpy9vbrX76sRw3Po5tN6YI7teZd9/B/u411Wguq9KlABttHbd/tz0728z8O7385iJcpWHgiP6VhWR64ssuJ6mqzi7Csz3Y+7GtZ640Q+sv0wOX57/bh6uCor3saartktyGUVrccUVlqZtOSsWGFeMJBXI0qN6tVq5Vg2uv7FP2lUKR+Lp5rE31z2z0Tq7SWtXpKFU8FH660Gp9ecbwHz/L/yQD6wLwHq6ZB8ct5a1oLhnDGjblsa1uqxrCV41rfjIdeWqc634WU/aGXXTIAQSXhGabqCfsUnnaeWojEHC6xJinxc1nx5fQBRxTe90zxBhqauzmjxLHb4SUdW1BBLrGmFGt8En9EyqSUJog9i0wrLjWySGNSpokLN5Ta8FYdcesbOjRQcILtStNz+XElN3/iO4Z6nX3jlfza5Q0sfbCldKf/aslbVnjGG1WjG5sc/WaMxo0FApYTyKPCV026CMBMZrLX60/ydy1oRnv1AreQJKMRpt0ZjG4T0tTWMwTUvZNtSrhmXRcDYVm2CYteRpwnJp+ehTQxwV3H+wxZ/+YyUpJjDLxWnsEg5UWNPGu1tOjihRJrJOe6yona5RYcJ9UkLbtC4g7pkZ2l5g3AfFTcDr/L23Tqm1rXX9uHvJB71LWmuJNMRaXWq3ArKG4jjqBV6jnux0uLezYYxLwPCyU45LiBOxqTxzokIS8Kqmdj3Fi8Bm5NlvpVK8pG4aF3ORNWV6ck5pCfRaY1yVtwmtHbQPjHdva0+Pevunjypb6S7hZkdpaeE0HAxpzBbXr98kzXJhCQtHdToqyCfVySo/Z1XTODkpsSVp49G7eu+Yvv7bTKTqJ574WIFfW5FLiFFOP8VxQhQnRHEMOnJJlR1rS1XVZHkW/EFwLBbWOnZZiS3lwwF1UUrcr2fr+tlT7j/SwuZqObhp62x+5u/vZce+yl6yWmEcFj2dTinLkuPjYw4PDwHY3dlhayKY6XA0JE7itXMEeadtsC827bmX2ZGfNe5N2+Kl53Ay9vL0XZ6jz/YvL9O3r5m23m972Sk2xvH3EsP7/IFxq2lrS54NaduGsqyYjLbI0zOyLKUuGx59+ojFYsHFxQVbW1tcv349VGdVRUUSuewQLdWcxUIyo8qVC4ZawyAbc/O69M/ECdxPH37KixeHjg7UsLc1JklEuKepUO0GRi5rKasGFUXMZouuN91kws1bYw6uH3Dt2gHb2xMRJsMBaZo5SgOvqKVvy70H96mdgk5SMdgHdU1rDMPBoKcjOjqXblPywkfrxnbnvItisFiUMRjrKY5cHwYrBlyspRJczm2ItBh9fsG1iFBQxgaw3wKNq/6QIKMEmr2C90FvT5ncmpaycn0QvOHrjDRrLaZxGXUYGmMd5YwY4WmeMxyP+L/+hb/Azs4OP/7jP85rt27TVrUIJ2OhNSHj11qhCJZ5lmo/X33hs2c9JSFArGNMazg7OaMua/b29mT9mA408Jk0npJptVqhtXaB9tIFAaQn7Ouv3+eNNx5grVR1LqczpifnfPzRR4xGIz76+CPefvtt3vvae1JpYgxGK95594s8ffyEH3z4McvGOEetJYtjClJsuwSlSNM9kliCXVppqrKirRu++Y2vc+PW6zx/8l2axrpkChsUlF8jlwD83uazyzw2cclRoyf0+2BQWJF+v87qsD069w2xFJyGDWxpbX+1Me7+VfwmwI5Qn4tBZqFHaeMzAa2x0hpcibFr2hYVJ6EXiV+3gfZI9fp7GSN0gAZaWopixXA4AOUd6N64N9AFf28eKGlbybrtO559AwcHpKA6WiRjhG1AuzXor2NBaKPwFO8qvDu++h86GbKpbzw4dSlxobdOOuNJvumDEgbLByfn/Opv/1Ui5egQjZHMNDc+Y6X3njyrLtMcwMY1/9Q/9bMcXL/O06dP+Lmf+zlu3bodmDG0tvxT/+Q/wc/+mT/NdDrjz//5v8Df/uVfYbUssGZIkqYMRwNuT1K+9OV3+Yf+8B/my1/+ClmW8s1vfIW2bXn86OMALMZxzO/51o/xW9/5bc7Pz6Vvt4qczFNoB5ilUUqipedzWZYU1QqIaEtNNpSqrkjH2NYSqYg4HUp/oKrCxGJgWwxpFqMbMKYlS1Lm8zlLV5E7Ho95/PyQ2dk5f+kv/iUePHjAm2++yXvvvcfF6QllXDDKB9y+cTMYe8vVkjwf0NQVSkNTScXudDpFW6nmnc9noSJWa81qtSJJEiYjqZx69OlDsixjsVgQxzF129DWJavVikLB7s6E6WxKaYXKHKPIB0MWiwU3Dg64eXCdjz7+SCjdM0XbiLPaVCWzspC/8xzT1rRNzdnpCaPRkCRW5FnMxcU5W+Pb1C6AmsYxq4XQw5umAdMBENuTCcPhUJhfFgvKsuTibMp4PKIuz7h27YCjw2OhniWSavvzM7JUaOCUhr39XZq2oawqtIoYpAOiQSzAgRFn6wtvvcUHH3wfrYUuviiWmDQmiTXKSnLY6ckRSZIQa8jTTJxppbnz2muiV5KI1jTEscLWhroxnJxIFeJ0OuX8/FScIQVZlnB+ccbu3jVOT07AWga5rB9QDAdDRqMRdV2ztTVhsZiRDwaMJ0PyPGM0HpC3jh1nWTBfSD/uuq45O7/g4mJKWdahZzqYUJko+i8NLWWwM9I4QyUarGZ2LhXypjacn1xgkarK2vXWns/nQs+FtBfJXAW9bQ06jgHNdDpjOp0RRbH0J0sStNYsV6eA0MsVq8I5veLMRrHINnHQ61BV1jQ1WEn+UUDdtOg4QfxeD0omWG1o64ZyUdBaQ4vFrFZiv2GDo4oHiBqFgN+iC4b/3hBjDFuTCfPFQuwdX21gDErrXqW5t3/UJb11KYvcyXL/y9+PYNHfq6385wupFJ9D9m/kn7l//17XgeM+JCHb1SD0S5wtgKmm+jsWvWWJ37aY1wxprIiTDnwUAIbe/HuEBvdsVPiU/m6fcf3P3vw1Nk4c5sNfexMResXWG/rax2v3569tA4i3hnu85LTWWoqVpfilGH2eOBvc2xquisafxp3LOMA1VH9G2tEt646a39lTIEHhAHA4G9In5vphtxhJam0ayqpmNBqDgk8++QFFuQxVAnt7eyilQjKqtJ+Yh4rwKIo4PDxkf39/reWCTzjygXHPUBYAEcf+1DQNi8WCxWLBfRekBp8cKsmP9x88IE3T0LKpbVt2XBusJE0ZOt/w5u3b4XjfykmmRoVks8ViIYlljvmqcEFypTWrohCQuixdLz1XebJYYNrWgcbCVHX9xo1Xr6H/mrdXgSC/2+1SsNkDaD3AJIo0k8kWifP5vEzuV3D2gzV4gLM/fvdvDbPtXU/1fr9qbH1A6GVB8HU5uR4Q8dVGnrHGOPsoSmKaumI+n9O4d0xrYc0b5Llr9eQqlRxQ2D+vwiXkIolFxgj1pnfZ8nwgNrFj3/KVXnJTl++ho9CU730wCDrg0Cdfy7kiB9groUHvY1RWAnBVVXLrxgF3XrvFxz94yONnh0RW+nB7DEFZS6SjQBHrA/JqA1wPqjhQhktQftMr8iNW9LCV/nNTHpSDSMeB0UueoQk3YZ3fpBDA7yr9thmk1H37QCk2wT0BxH3VfwfQdvTYHUbkGcP6CrAfOAzPy0gFka9YXZ+Lnn7cXLp+vN5LdPd2CbRX6+D7ZwG/fX+4/24GW8891/WgblfR3g8+oVRgg7H0Qej1IGq/agvVS0R/BRi9Gbi+Ksgs7UWcDdnKutuk9A7zFm9Uj9Fb42q9KrwvC3zwwxc3bI7HhDUgZ/VrRloQydytzbuTaf13WpjwXJWnAaU0+SBnNByRDQYSFNOKwrFfNXUtut3dqzHS+oymwVhDpCPXv9r1QHbYk46k4Ma4NgmeGnizqKInKALespYq03vOXg5sJi6I7O6wDTmNPKPWSNtCtMXUDRcXU1ojPprWUJYli/mC+XyOtJbpzq0dpur7tQr+01WAd+vfVSG3LT5Rxz+zyFUU694ziLTYWD7Bx/tO0Jmz1vqg3/q7ZFwSSAgahjkQimsZv3X+V0NZlXhmLWPaII/rpuHQnFPWDcZ4+QoCOV0OXlx6Hm59RXHi1p7T01phjNiYRxdziqrEVss1kVOUBdEiYjQYSGKhaUmbhqp2lbStVNlWZRXYQa2tQYGOYhSCP1VVResSCoN+chie4Ok2BMYEw/Rvjk9e6cnbpg2yzrfZkWpibzWLbOz3OHdPxz2zfpDWYNU6S2ccxcR5zlnbkmcDqeZPMyAnz4eup3KExhIrS6YMS52gbCsvqrVyb255tm3LWXRCi7A7bO/soZOEpm1Zrirm8wXlaoltC9pWYhHKWBQtZbUkAmazhI8fKUnm+Nvf4+03Ir7w2jUmo5zBoKK1lsVyQRwlZFkqbWBpUUaHwh2U6ztsDCrybWq6OeraIYosEDxcqoNbJ0vatsG4AHIdgsm9av1Wkj9aRw9vjTAg+LazEvjsFYRp0V1ppDBJtMa+1RpF0yhh48lz0jTpArV0dpp/5zzWglISDM8ysjwlTTPyPCeOI7m31lBXgicXxYq6qXtxBwn6V1UdEhz9LBnrdZ5bmQbawCRqHf7r9LIW3DpYQz4xoDfl3k7pvb3h3cvTjPF4RBzlJP9f6v7s2bYlO+/DfpmzW/3uT3/P7W/1BRAFgAWAKLYiKZIZ/GDNAAEAAElEQVRSKNTRUoRCT7Yc0ov/ADtkP/hBjnD4wS9+sBwOR5hqSFFhKUQ1JgkSogDRBFh9h7r9Pf1uV79mk5l+GJk551pnn3NvFYogOavO3XuvNddcc2Y7xje+8Y2sAAe9oqDX7z8nd/c8gUvFWEySJFi/3khyYubtndZHd04C8TbUgu8EZ7t7q7W2vffuHuXX+SRL/T6ZeSn1FIuoTjhv42dZwmaTcnl1RZbk5LnMKUmmEBzKUgkBvN9nMp6wmokKdJIkEQMLTnFY30N7btv97WtCoOjuT51WjybIth2olfIB+aR9b8eOct53nV5e8vDRIz7++GNWqxV5nnNy4wZHR0fUTUN/NObk5ITjoyNGw4HE57xvaYyMIeMMQtqx2yiFFTvL4Xae73rfJ75n27HbHWiBTNJ9/hgv2bpud31wW+dut9s113YvoMx2fLfrkgOft9X11ll/GJ/2MwfGj46ORP61rrm8vGQ+n/O7v/s/M5vNKIqCuq4Zj8e89dZbvP7669y5cycywUP9E2mo1mjc+Cy0uq7b2tJJFkFaELno6XTGw4cPuby8pKkrilwcTgFSxSEsftRjXi3o9/v8uT/+LzCe7PkaG8NYry4E1QQ8dXHxtNbKIolI7X3zm9/kK1/5Crfv3iH30njhCABNlyXjnIuM8C4rp2UCt+yJLotUqcBUbQ38rgEXsil0kmBxkTGbF8VzxntwKoKxFIDhtMtK3QUqIEq3WmtjYLnriHQn0G6QMPy8d+8ev/EbvwGIJO4HH7zPo4ePYr1BINbhC6CXUlJv/sMPP4xA2sHBQbxGYBQG4EApxWq1itkhoT9D3yx9UKaqqph5ItkaIg8bniPUk9FaS/bJnTvcOD7hi1/5MtYY/uSf/dNUPihqcOT9guV6g3WOu3fv8o1vfIP/9m/9LZGfDyUDkiFG91FKk2V5bMtQvzDx9YD/5Df+NP/5f/o+abJBQgF+o3TglGRoRkyHzmLnAmjh293XU+mOS4ffUNndQMM1pHbN73zymF9/5fbzeO/ughX7dxusca7t92Dst5/Zdn7CZyMBgJApbr0B6+JnWna4rBEBkMxzFxmdonygvMFkSFWKxdcY7zjBGiFFCMki6wAw17VLhAPE4TaW1WpFkujIqgzMxlj/ptNwoQ/amh/B2W5bIElTyYKsqvhsARQJjOGX4e7umje3x0n7+bDJe9gHh+O7T89ZLRMvPeU8pCTGb+MalG/bPM+8vJjvq0Tz1a98mT/5p77B1772NVnr84L1ekWR59S11NMZjfrAgL3JmP/g3//3+Df+tX+VTVmJA20dR0eHjMYFe/sTHnzygNPTpygl8uKbzcbLcNcMh0OqqgLgz//5f4HLi0t+//d/n08efAI4Ur8+hTUhBg4hGg3BMEm8A58VIosUjFmdJCgnGQihL4oip2kM9+/f560336QqS7Is9bJIomSSpgmvvnqfolfw/gfv4aoapUReNvE1I50VGddHj77P4dEBg0GfstwAiqKQPUjaOQccq5WQN4TZrzGmIfEZRcYYRqOhlz2fsVrLmJTaRYo0TUiGfZZLkaTt9QoGwwGr5SoyXXu9grLcUPQynJM1uNcTqcJQJ7yua27cuMHJyXEcW6G0SViv+/2+ZPT6WkvS1gJyhj1pNpvxpS99idlsymw25/T0Gc9OT8mylF6vLxne6QhnE5pG9pWyqsgyqXU7GAxI84zZ1VQyrFPpX2Mb8iJlPp/y1ltSE325XDCfT6WEhnXkuZAI5rO51FC/uuLy8pJ+vy/1Z50hy1JOTm5wNb2gLDdY6zg8POLx4ydUVU1dS/AD4J133mE0GjObzlgtFpw/O2X/YJ/x3h6b1ZrFYs4rr9zHVDUnJyesN1L6YTweMh6LzfPgwSM/Lx1lKUz/i4tL1qsNDx48ZDyZBCENBoMhqbWMJxPSNGU+n4NSJGlKVdcsFksuL68Y9oY4hNC1Xq/Z39sny0VSvSgKsqJANQ1pktKYJhIuVus1pjEsV0vyXkHjiW7WGg92CUM8Av5hjW1MBHZwLva78/sARhxya/HEJTF0a+tYz1fUtaGuq5idEljaxjQ0HfCnazvJVwVSnrDVu1lXAOeXl+15xsT3uoGU8NN0gMi4nnadhLiOXr8//PN87DoGzwe1/8kfCgVzTf37DleCe0PKp+R52HW9I9q1Q3YdGocEO6Jdsu1g/WxH2DO3UNdrTvuMztXLTlM77wfv8zmw45rLOantXW6cyKfP++i89SviJTsBnG5AYTf497yzKLbRc8GHcE3PvrdI/co//xd+k4ODA5bLFTdu3GRvb0JdN4yHfYpCZMuDTRQA47B/HB4exu9JkoRXX32Vfr/ParWi3+/H2t6r1Sr6lAFEWy6XnJycAHB4eEhZirTkrVu3YgkTEDvgi1/8IpvNhvF43PpQWvbOohDga71eezsvYTgcxnZbr9ekaRoJSuv1OrbFYrEQop5/P5DyuutXlmURdNMeQE+SJJae+MMc/zTm76cdL1pXgRggDu8pFJXKwW3IMyGHNpWjV4zYP9hnuVmhNORpD40jSzS1NRKUsY7Ez5bEabAOqzRGyd6VCENQvsepFhSjBYd2g3q7cya89qLguPzEB6YdMeShpIbocDjEKajqkjTVDLICUxlOH5+2vop1DPsDTo4OyRNROzIO0jxD6yJmn0XwGEVjhIyCVtjG0lQljamZ7B36IJjC2pokgVTlGNcS58VWTlFJhtYpGrGhc6WpkwanU3AGrSxJZqiahrJK6OUZpqlwFeBrpBoPEjpCxp2iqh17g5T7d2/y5quv8OjRU1yjaBBlOqUszjYY5dgKZG+3rrRr962XjfXgh3U/s4XAhWCQAmUxzmwFcLfmkfM7kPK7y4scaDxQvzWetu2GNjCsYzDaBdDfg4+qPRmpOeu21nKl5L51V/K9c79b8w22S3PsrN3hvQjGKxW3Iokfda7b+U1pDcr5oFC7j1y3p+xiRED000LwQynlSyyBjCX5rfFKhyCy1rJWSNJN8C8EP9IkeNKHby+LeU4WPOw33XsL2JuKnduOAcElpCTi7v7dXRvCERQVA57gXAgQ4QNpLUbW1LYz5jR40DbYOtY4rNsmg8n96vhav9+n8aUko4wqcQECgk0sGZlaBcJ9TVU3DCZj8tGYwXBCrz+kV/Sfww1DuzVNE9cdcNS1kNxCKcugVBnx3LLE2RqdQK/XE6LcTl1d//DoPI3ZsUkSVgHBPaw1nhgMic7jfIq2uxbpWSHvW1AO7bxqqJH11AJl05AVBdY5Np4wt9lUNHWDw4mqmO/PLjlFe7KJoWnV/CKeJIFcY62HTlp0X+ZpCIgnEUfViSb3mbk4sLbxveZxPn8JEwk6Kmayh+81vi/DOEvTVEpwpKn4ebnUO16tRPkUsxHsUGckac7l5YbNxpNrAOfX789iPjjAKoXzfRL6MhIp/Unzdc13PrnY/mzTsF4tmS8KeoMxitzjrAl50SfzpR83mzWblQQaZXxVOFeTZiI/Ph4NmS/mVHUlKoBpSpJmKJ0gyqoG5TyG1eVSKAVOxlnTiCx4mqSxzUO2o3WCuxljaEKCR4hM+6CYVhZqFYkR1orqUhib4edstSE7OGL667/G937rd/nhg4c8e3YOSnmsWoFTkWiSJRlWu3a86IREt8lgynXXYiiyXNbFNKWvNf3EsUgNq9LRNAm2riGMHYS4UFcNrpJ7zbOc/83/8SP+jb/yBnePV3zjj13R1A2JgiwtqUrBSHt5RtHv09BRN/GBqcTDp+E7UDLmnXPUjfj4oojUgBN7u65rIYVaIdxKGVkXg+ZB9cBYg3X4dg7KstIuQjppu9Y0cs2ycZjGQp/YWGfTin/8kxV/4faxlN2NJLI2AI1SJFqyojdlTVVtKIoe4+GA0XhMr+hJzXutqRshaJSbtRB3q1Dz3vjM+O2MaNvBYNuAfNgzQ9DcYRpHlovEeRevT3SHwK81KhJqAjlItXaFAqdkHdVOkfkx/uAs5eBggCp6DA8OsK6hu7FpvR0wFbKIJksz0iSj38u4uFJsNg7ZfiufTOUXj0Rj0Vil2NQVRVGgdUJjpWSVDdfUoFMNRmEBQyJ2pi/5ozNNr5BEpSQbkuYDcp94qpRCp0nsB60TpquSw3HOaDLm4PiY997/iZfUt7iqpnaOMpMSWGkvJc1TEqVQxkDSYJFSrsH+SXAoLdi+dQFPUFJTHXzSpcO6BqXNVrhXK1BaR9VmpRSkKcorFeR5jlZiK5SbDcvFkqurK87On/Hxux8ym82lrnySMF8suf/aq3zuC18kLwqWqxUfPXnMr3/lLr/xS7/E/sGENEtYzi/9vOhhre9Dq9DatGWHtvwabxu+BLt47r3u/O68pXaxCxfsym3CQLBVlcc2Xoi3bW0jzxldz98n2zb288Hw9u+E1sfbeqbPiuF0js8cGP/BD37AjRs32Gw2XFxcMBqN2N/f5xd+4Rc4PpbFaDwe0+/3Re7FB6ZAbi5KJiSpMMKM8ZNBeYZOkNQMkgzOB2phMplwcHAgBmdTIUTT1hhP05T8/RwqSLOMX/njfxxFG5APtS0i8zNJUMrFetTBEFVK7uXk5ASUyKLlvn51CMjgRKY81DqyHqXbdbDlkEVRflXeEOwGCb3xo1SsV+GcYz6fx/ZZrVYMRyPyXsF6vebZs2eSeeCz8WOQonMPidZYDwSt11LfLM+yWNcA2s0vSZJYX7y74e8OqG7gPrImPTPHOcc777wTAahhr8/+3j5XV1c456R2vFcOEIMgIcukzsprr70GCFOo3+/HmjMB7IqSJVZkIANYBkRjItxrqDUYzhNGexXbOjxbeIbFYsEm3YCxJJt1fD3Lc0BRNzX1Zo3zY2w8GPIv/8v/Esvlkm9985vkWUa5KTk4PKRsKpxS0Zmw1vLOO29zdHQoNTvKij/zp/4Uf+f/+z9wfv4+ib8XcfCfzxSOC1SLxMTAcJCHlDrt7crlPIDc8YPb6/lxOi+r2J/XB1x3F57nTnnuTrtYQjeDXAJDftwbG43BkE0fnNNUdxYw15JKmkb6MGyQdDIOTGN8n7bjMowLY0WmerFY+Fq7Ree+Oot9e9PgFE1jfSDNbjl4Jji43TnuiLI9DhcdV6kLLGUNnHfKW6airB1KaZypt25kl4G2BXK8JGgTNo4WFwoPpuJ7v3jzmL87uxLD0wkBw/q2JBWJqMFQgrh37txiOVixZMneZMJ/+L/73zKZDJldXXJxcRHlTMOaGchNYghITZQ8Lxj0Eq6uliLvU604fXrJfHaJMYZHDz5htVqxv78vtVV6PWazGRfnmuFwKKUGyg1VuaauNtTlhqauyYqeOHpOmJp1XXrWYUKa5p4M0fNM+7DmO3HGtThURSQVWe8kNzgnKhyHh/usVguuplcs1yLbk2YJKMfJjWOqusQtLKPRiI1noidJQp6nLJdzFosFWmtefe0+SsHFxXlc48I6tl6vyfOUosiYTMaeKCSS4sYYhsNBDH5L4BJOTiSrTmvN/v6eDyA4lssFdd1QFD10oqjrkjQTibe8SBkMe3z1q18lSTQPHz7g4cOHsdZrIHOFbHYhRch6HvYVpVSsrRoIZQHEAZhOp3Gta5qGZ8+ecni0z8HBITqB/qCHdQalLc41lOUaY/z4SaTObW/QJ9GJ1DTKUvr9Prb2dapsTWMq7Ebk2IypqGuxKwaDAQ8fPmI49EoAdU2v14/7RH/Q96SYPovFwj+fgE4ffvgEYxoePHxCvz+IAdt+v4+1hvl8wWAwRKFZr9a89uorrNZr+oXIueMMOMPVxTmnz57x6PFj5nNx5Muq4vXXXyfLC4xpePLkCcPhiEePn9Lr9cmynDQvMMb5sgAC/NWNwa02ngGqfK1ShU5Sir4QHdbepkrygv3+kMViTuHB89lyhUL20eAANMa0r/ko3Kqqo6MjLNckEk0C27StYaRpGrEFqroiKcUZWEU5MZGkD/ZVW8LEgE5a9T4UxqvctASqlkBobSA+tftYBB2VL43i31AqyM8KKSlcN0mSOA4/awBpF9j9oz5eZLD/sxIA+3neh0LRfC+h+RDcr1nc0JFnOgLmavvkzosdp6pziuuc+oc7XuY0/RQO1ctu5Jpgi3r52/GojWXzVNH8MEVf5SR5GwwIBJLnSSVhXG9n3V0rJeucB01bkmm3tqmAvpoGGI9H/Lt/8d9mtVqy2ZRMJhOquuL02Sm9TIihy+Uy2l1HR0fs7e1xcXGxdc2Yoe6zqAPJDYj1uQOpSSnF3t5erP8tNR0bRqMRJycnDAYDVqvVlj+Y5zmTyYSmaTg/P/dZCI7xeMxqtaJpGhaLBbPZLMq5h/UDEAJ2kO31bRqIN2F9Wa1WTCYTgEgaC3tj1590PpNc1sXmJYPkn++jS6wObbUbuEJBrpSgt2jOzi754Y/e5x/+/re4e/9VHj1+KEGYQL4CyVZSgG5niaH2oFTiATLtBeOC4GsIxGs0iQfPXxz4bgNlz2e/ht93CSaEu/H2fSBCh+voJKHoiYpPIFdkWU7R6zMcDrl7967skUggcdgbUvTENk11ymazEbUx25DpFJ2BZDA1hFEkc01UCWTuKr8Xar+Huq17FlnlxGeXS7AxTRNqHSSYHeuqwjSOVMt7ugl+Vcis3A4ughApT05O+OKXvsiP3n2fx6dXFL2hBBJcCKoatO4Qua/pg6333I4D221zOUnumRfv3wqwjdn+LrUNyIVgawhSRWCve6GguQygt7/L+bdetJe3hCPbkgzj826PrfD6bn5MF0d7Odh5/evbY16hVfDPwysKVCsU/PxlvKSu2pb37gbMw/1BS3QMgcMgmSz34tDat4lSJEkWCbfit9Vt3eEQvKrWXuo1ofG1a8MRviNm17tWphlCYL27P/q1ITbwru/cthnw3B4QvjPgduEasaWsxbqmM09CBqYPkNBmESpaMpe0b4ur1bWhLOtYukiyt0N2sQA8bbvjS6ZJll6WZTitWM6nzOdzCSjqFJyiX/Qi5pmkKWkiwVYZY4F0ntLLRjSqociG6LEmUTqqD4SSSMbUEhwPOJ1rM3Z/kF7QUJHohJPDe175pYpKiwrJeEM7Ui3t5Wyoodq2fRvI933ogbE0TambNvBT1471ekN2fITDklYNSeOgquUM7aWxtRaFAufnQAjKhb51PmGh+90qaSXPnSN2IUJsUcqitdgFqdasdRUzygXzIn5fOJwvN4rfL1oSL15WXLWyw1lKqnXEyXGWzXqFNQ2j4YD1SgJsWdFnbzjh7WzD9Hs/odqI3xcwtG7283WEsDDOX7TfbR1OZM+D8aqA/nCIc4ZNucY0pQ/gQ+ISj5k3VGWFBnr9HlmWsik3VGXJel0Kpucx+DzLWK5WHktLSTMp/7larzsYsPJy+rZjX0rmv2lMVHfE97NxtiU62FZa30VQMPQTcV45Z31A1/F+WfM35iumPoA7bQz//jf/AKUU9X/3O2xMQ9mYOIeXy4Wfm+JLK6VIUBhMxDSVaok8SSIYTCBuGNPw8OED8ixDa5kPVV2zKTcRk4wb0A5mGPaWsq6o6or/5L/4W2Qa/m+ZZjQsuH3rhL/6F1bcvanJc8kcH/T67I9G9HIJ3jce17OqIUklszlgoImyVGVJXZaC01pLCIpvNpKg1jSG2liqSmTIjbWYxmeYB5KYVqRKkWkFkVyS+D2VOL+11vyf/7MRtrHYphbCy79Xx6V3U8PDx3P+xt/6A/7VP1dydHTIoN8nz1KvuiuECZ2CqxqausQ5OD4+Zm9/jzSVGIhpjCRZzOes1mvBNRrrk2RCTfFWdSbeQPihvCw91ic+dBQhTEg2MXENCIHv7hAMAzFReAVDr5Jgrcwn3z5aiwprYxr+0Tef0hss6PcG9O8MydIeZV3uWBIqXieMOaucj8cUZFmBqS2bTUXVNFKON5b39SomSR732jDXtswrpVAeT43KEF4BIpCulANnLM44VGZJtCXPNP2B4GN5XpDmGYmWNcNay3DQ4/jwkJs3bkTYXOZM6v0tSWp1Vvua5TlKpTirgKAqK22glRalQa+G4lQgldTeXqVVcKCjwuTHq9YJeZYKrmUMNBXVZsPV/Jz5fM7F2TmPHj3h/PyC+UyUIctNSW80oD8YsH+wz+3bdzg8PGS5WbGcbxgM9vjKl97htVdf5c07t5lOL6mrmjxP2ZuMuZpOWSym9PtjUSKu6pjgsk2s88rJbEvbf9rxMvt1628rYzuSAtj1kSTR9+eBzITjD3OlFwXoP+34zIHxv/pX/yqj0SgGQXq9HlVV8cEHH0Tw/OTkJNaX6ALvLWhZU1Wlz3DLCdnNM19PVQK3qQ98C8AfAIUQBLHOUnmZlQDE6qaOTodzwvo3jdkCLAIw1Bq4Ulc7ZBKGwO1wOOTLX/4yP/nJT7DGcPv27Rg4DiwhXBaNa9dhm8aG9z/9+kdkYuAlon3NmPA+piMVhzAwN5tNlBMMLM0sy7h//37LrOkAXVvZ3EoWTFUUKC/9F0CKcASAqq7rLQem6/jsGkfdoHi4RnivaRqKopDaenlOnueMRiPm8zmffPKJyAwHQyeRQFYI/ofXFotFBKpC3wYZxRBQDX0V+ivIVg29zGG4Vq/X888nm3TI7qiqKgJyAcSy2jKdzUhCfaLlgrEf6+v1mqauuXFyA+elr//Sv/gX+OpXvsTJyQnleoPSmlW5IclSP55nGGO4e/cuz549jW10cnzE17/+df763/iYPG08sOIiATgaZLTYcCfuHZ3LAAokSbKzanQdu63OJlzKh1GfC4pf91r34i9cOK8L7BJstVCfRAKQiRN2ZBg/OkkwdSNOgpJ5KQFAYXqC8v3fI83S2GdK4etGNmSZsGlxkhEbsqetsygDq9US0zRSuziARz4wFDM/jJA31l5pQHmWnFYqyo2FujvOO6VKEeUfrTewQ70hhyMhQRzNNM5NkOdqAaa2nEG3PbvkgtA3z59zPWwvV93+3GsHezh3KfetAwtUHKa33n6DP/Nn/wzOWv723/nb/OIvfpVH/WcsKy+d7Rquri5xjlgvcz6fR9JLWZbM51Npe2t59OgxddOwv7fHdDqjMYbRcMThkShCnJycSD1xranKknv37gn5ZzBgU5ZReqnf77O/vx/JLlmWxbo6ztc+SlMh2YT9pSiK6CCFtSWs/4DP/m5JQEGJwpiGngcsjTHcunWL07NTnHM8efKEz3/+c0KMGY/J85yLiwsGecbJyU2vEGEoCllvQgA7y1KGw0FcV0PwMGSsaa3jehcMm7C2TSbjWB9tPB6zXC63zr916xbGNFxeyrVWqzXn5xfkeR73vLt373JwcEDT1IzHB3z9618nSRK+9a1v8cMf/jC2z/HxcSSlhYyBJEk4O5Ma5ScnJwTSUXiWEAy31nJ2dsazZ894++23Acd0OqX28qE3b96kLCufLZ97RnEm2RSm4dbN21gFZSVEgKoymCbU3TJUTS31k/o9BsmAsipZ1xtOnz3lS5//EllW8ODBA6pK7JGyXNPvi7zoer1iNruiLDf+/tecnkqfTqdzVsslOi0wjTjipnHMpguqquLs9JLhaMhqucR16mZlOuHkxg0uzs6ZXU0BOD09wzSW6XRKnuecnl1weTnt7JGgVMbnPvcFPvzwQxKd8ur911guV742lcijJUnCei3yeCgh5YWSDkHuUKnEg0sS/A8OTiCkhSOymCOwQ8ycCLJWkdXdCQYExY6mbtViwnyqa3FCrXW4REn2mt3JiiGUCFE4E4J28k9k/YKNo6PDqADrJNs8XEP2PUcTpceInw2gvk40jW0dg24bdMGdTwV4/giPn+UervvMbiDgswTYd0H162y4l33HH+bYuv48ofwfFe5XLc2epVdoEi1Zcc8FxyECVVuQffe5rvnIz+2+4zU7N3Pt+y8/dpvS7XxW8fy1nIXNytE8TDDfzSTE1wk8tiSTdox3neMQNJcg2fP9HoManecKr4X9wDkXiS8UsF6tubi4RGsJgIt9YOj3exRpj/F4wng85oMPPmC5XPLOO+/w4MGDKJ0+n88lq9aPxfF4TJoKKQxEBSpkj4e9cDqdcnFxwd7eXry/9Xrt9z1RS7l161Z8RmsMT548AcRfWa1WEmSsKubzOUVRRAWpq6urqICyXC4Zj8dRcWo8Hvt9PIt7H8ham3mScfCX0jRluVxGfyJkP3QzxruB138WjxfN909bs3YDyMGOSdM02gtdv9jYkn4hdltVGy6nS65mK7JhzmA4ZumE+JDE/UQLwO3AIkpTTrXkecJep71UZpyx8rvSymdQh3nYzpnng2PNS9fSMOeEcKJCRDSOZ1ECEqWlYOedX1wyny9RKkEnMlaKXo/jGzeFlEZCqgp0YkhIwTVkSY5NHa5xNLWRMkeqrcdoM/Edq6qKRI9Qmgvwqk9tYCmMuyyTgGNQUQnYjJa6QmiVUFdS0iYfSvah1o3PevRBm876EfwaIbUPuXf3Dm+++QaPT38PcD4LSoFTZFmOMdvrzIvauO2VF4w5n2kV/DBCX4S+lF4gsK52g7nPBeVRWwtw8F2v/3LXLui7uM9zp7ZrdfAbw3NGP9Ntz6FuUPzT9uAYJ/T30vqZz/uGYf1S3u914Vn8ubobPA4BQOc6ygshq17H73M7vmvXpgjB16BKVfnSenHMqQTr1045L8FKNTKMcV5mOYzbzAeFKmRNkDncxaO63x2+vzvOwvrbBgV277t94bqs8xYDU3EexPayDoclLO8BtwwNJfvEtk3qwBPStA/KhPkqmcqhhEiilWS/hbEreXnPj2Ht+9W1ZBGtFNoH95ypsdaxrNYRO4w4zFaQ1Len1jHBIE1TsjQV6fJO/yqVgJcgDwk2qMRn9oZ21wyHY08Mb/z+IOW48L588I2d3UR/A1rFTMkSD2RasHUla6lKpQ6uSWjKFX/n/H3+ZKbY0yLLnSaaPPXkozQoT/k5pbsy5hK8tNIJKL92JUkaJbaVjwA53552d25b6zPXQ+lKkVaXsa1A+3b2e41yqjNuAtlA5nSapH6uaBKdkuVSDkvwasFH0iRhNBhKLe8sZ1NWLLRjfW/E9IMSYzySpLUEY42JvtjuyrprH+4SXcIYec6vciomWDigGAxItaKpK+bzK4p+j0T5sVD6ORZsIq3IPCHGDoYMBhXrshSFhLpBaRUzdHXTkPoa26uVkLKbYFd4TMi7zYQAnsPFkg7gJfG9P+k/hnOOTyrL35ytfbDc18q2Lsp8i2wxOKVogHXTxH3WOrha1ziv6KLDmNFSjq0xkvSQ6hZ713jFm7A2+a6Q0gTWB9E7c9s1sr85BeEcBfjsYYdE8RTb9v9WXyrFuqrZAMsKZmXN5aLm//RQMRoU9Ps5k1HD//Jfu2Lfq94NfUJRbzD0d+TnvF8b1+slm/Wa1bqkqSsJohtHXVVsylICd8ZQNZa6Nvxf/p81zZYwhyLNMsF5bdMZWw6QdUISD+XsRCtmdSNxDWulpF93DPtyKdN5zf/ntx6xP5nyuTf3eP3ukMloSL9X+EQymedJmnJy4yYHh4dY61gsxE9Yb9YsFktJ+Aky/DgvYe0Dqa61EQKxoTPUCAlcbX17G5PZ8jSJ5ZXCJhSu0bVVkkSTKME4HXjMWuzfPJXSorLG+yS/9YrD4xMOj485ODjCOFBk3ZEU53T7D5SyBJUSnaSsq5LleiUJO0lO01Rbe/6WHSGNwHZpodYPEMUAkZrfrDfgkBIetWGzLkW+vj+k6A9Z5XlUZ26TGH0sp9+jWa+o65LhsE+aaMrNijzt41Rr40q75SQ6B5VgUaQqieo4Go/5K+XneliTnF9DDImW5DWtxB5WSR7Xj6qsWK1XrJYrVqsV09mUxXzB8vKC2eUllxdXzOcLqqqhqR1pmglB/OAGw+GYYtQnyzP6gz4HPjh++84dDg4OGIS1PEl49Ogh4/GQw8MDJnsjjK25uroSFbIkJc8K8jyhriR+GvxLiSdYjBGcL9gC8Dz58mcNlkuZA9cZu9v2V+fTL73Wi2zb3fsMl7ru7K5t96JrvMjX+LTjMwfGA2Mx1CJwzlEUBW+99VbMWlZKmPSXl5eMRqMohxeCG1FiL9GxQ/NiW+Y8Brs9C7EbeM3znESLg2mahoWvwdptdOdkQ5x5oEKA8la6RCmROBH5njawGoywwUAy9l577TVWvl56AGqMEUZb4hmtWiuyPMWERVqFLKeQxRpWy3bNDG2lvfFpraVuygjCADGwHNrhcnpF38vChyBv18HrtlUw/NNU7qvwgfGwcITPb0nc+fvtGqWhrboZ1rvt3HXohO0rUsWpTiJQfXBwIHXBU5E0F6nhR1ITta5555136PX7Xv5G5Jw2m028vxCEAQHOJpMJWZZFAKuqRM65C/IHMoHcl4BjaZrGwNTe3l5cgJXWpFnK4UayUp8+e8b56SmNafj+D37Ak8dPyLSmyAuODg/547/yqyxXKw4PD4W40B+gtGJoGlIfdLt375537Byr1ZL1esNiPmNvMubrv/rL/IN/8A/48KMPGfYtaZIS6siFAHkESpV3PlXrZMc3woLUnaTeeH9+jWoNyLCBK3f9YhECs7tA7ZbB3Dk7BnGvWUSDoW+dOLq5KyDM7UacLqMabyTIHA8Z/lmWkucFVRUylDPStGmzH2nlftvFGUKGegRKrZXM/3njnTdfc87fs/ESYMaP89wrGSilYk0kggHUcY60TuIcDbU58cZPEh0wJRniWmObBqXkuZyTwG2iFaVfC7aC4K7z+1bPsAWchLGyNQQ6IfOW6CAGp0qcJx1oceSs5erqnPPTJ7z99tv8u//Ov80Xv/hF/stv/S0A6rrig/d+Ql3VPH78OAaVg+JHCGAba5mMRxwfH6EV3tG33L1zi/39ffr9AXkuoLcLckt1zWyz5urygn5faoJfXl6yWCy8nLRk+c6uLkmUd8ysaR1L5TwAYeSplWTKKOVi9plz2oMs0gppmrBeL6NjHzAfpRLG4yGPHz9kf3+f6eyKTSk1RI+ODths1oxGA9JUc3R0wMnxIWfPnpLnGRcX5+zt7ZHnGdPpkstL+Xu5nHuZdMl40ka+P0kSTk+fUtU1B/sHrNcryrKMsq/44LK1Ut5De5lxkXDVDAZ9Hjz4mF6vz/HxMZeXl6RpQq/XytK/8sor3Llzh4cPH2F9fZq6rphMJnzjG9/g5OSE3/md30EpxenpaSQWDYeDrTX08vIyluWYzWYcHh7G+TkcDtnf3+fmzZvMZjMhIGjF5eV5rBV9enru9xRFVYlKxNHRkCRJo8R3r9+nyIVkl+cZLs3AWmbzOYkfb5uyojENy8Wc8WREVdX8/u//Pr/8y79M0zR88smDWAf22bNn1HXD3Tt3uHHjmH/0j37Ps5dl7aiqir29PaxVrOYrZtMF+/v70XYRpZLEr9lzFNAYkSf/4OMHpEWf5XrDJw8fcf/+q9TGcHZxQd0YNmUdyRzrTYlpGr78la/yG7/xa/y9v/f3OL+4omnOweEZujmTyR51U3E5nXecQak1F9YfWXuVJ+aJo7VYbsT5blqbSfl9Qs4TVYVIovFggIlZSy34EbFev7dcX4vO7yFOgMsWFFUBZYBw/bgVeHmwLhjdAYjDWhrW8l24mrimh4WuXd0CAakF4K43kj/t+HkGgH+W45/k939WUsAfeRusNeXfV6Sfs7g3LEmhyDNa+bsOTr1lh8Q/XHuSH7P/JJ6g41698JxPdy8/7dpbT4OzjvWVo/pWiltqdCllWLrAfhzrWkewOmTJBSKYrAmyDsTyLR0STNd275JmW7lRL8/YuPiQZVXzP/x3f4/Pf+HzDIZ99vYyxsMx5aakqU0Mln/uc5+jLMtY4uHjjz9mvV7z1ltvURQFRSGlLwKRLASmA8El1Bu31nL79u2oUrNarciyjOPjYx4/fsxmsyFJEi4uLrbA3Pl8Htf88Kxd2yX8nWUCXFz60gxB2Wo0GgHEvS8QlYOvGe45/N00DcPhkLIsY//0+32sMfQ8qffy8jJmmP/zdLwIKO++v/uzq861GzhPkHq7ddPQGEiyHsPJAVfLcxbrDev1hrqsWCN1qQfDgQDcOshTu+hYxMofcncQ/JuOlRz2FwnCyK8d6CVECuI9XgcadX3dMFcDKCjBGhuTAJTWZJlXYcNxeXUlgKgnQKZZxmA4lPJo/lGaRuaBSDo7j0UYrPPAZ5pBY3A+2BIyhsIYdwTAshO06DxXGJOi1JNgfAmiJE2ktqtOUN6nqaqasqrYG/dI02wLCO324y74hLMMBn0+/87bfPPb36Vqap/51dJ025qb1wNlnwWs2z6kN7btADo/XSQ06501dLfPd/t79946f7AbwA5fet24ifepdv25568ffZsdm2ZrxHb7AfGDXPDtO754Zwv9lP1dbX1fxIN8qa0tlRF3vdpCB7GIP8Oeo3WC1oY8y9E+KC7kcI2hLeUnoK7sVUXRI02bWG9ZEcDvNhuTbiDfbdfu7oL/3ee6jhQh77dtHNavLpHBuW2Z9vY7r79e96UuDhGuH9tMKZQSxSjZq13MYI1YnAsZ4mBsszWHtvqg+4wWke1PpD+Ut621amXjg41vncOENrIhq921ih0qBDJbuek2MJ6CSmL7pKlgK1JWqS1xtFjOvA8i63OQKMcHjYwR8k8gxbd9ZkVxLNp6LuJbMi6EfOa0IskyPn7ylH9IyuF4yKTfY5RpBrMGhcJYv1b4fpVM4xZxj2Mj7C3aqxD6704C5gaEWqaS5BTaPATQfKdYh8UrnwmEJCWr/NoR7DZnwzMJLiOqZpJhnWqZK2mWkmeZqIoai0ORZjlKJ2w2FWd9OLUVp5dXlN+74tGzM5yvBx/6MJSPfPEa2w10SFJHOLWd43HExVWj603+XmX5tX5OvzfAWFGNNToBGxTDAkEhacesFfJlbSSAWtUN+POaxv9Ng9KSJVz5us6BgGd9bdz/ZlWy8QSDMF8SpWXQOxcD3845L0MtMs9zYzmtKiHr4/y1fWAvtlXYTxXNLrnRr3FJ4jPDdbv3RtIPoLR8p1YheBXWA7/mKC8drrZX0yxVJFowU41GpQm4jLoxQgz3a1c3uW2rV2MnapyxNNZhGthUa6YLKIqaLJWYyv/1ryn2xobJxHF8mHDjeMTNkwN+46un5FmKbRrquuHiquHv/qOU+dwxX1Ss1huqqqFqrLcfxB+ofca4MYaHZ4ZE0QZ0tSZJDFqDccKTkenXkk1ifyElAYwSzFQqpGw/p9TDBpzhdFpzMT1nvlrz4MmYw70JN473OT7YFyn2zYp+XjMYFcyXa+bzOcvlinJTiuqft+NdwNpjO7bGY5wBDkJyW0jcCetMKJfZkpU0gdyzXX98a8NoJ5RWERsPe3GWBsKZjLO6gU8e1/T7A27ducvB4RFJmlI3VviC3emufJkX37YKSWSQcSqqJavVhtV6E21Kay1JKIGjVJTQD2tCiEF07UQJMstzayVqyFVZgnOCxZe196FysmJJWhSkvoRy6jOxAx7U7/U5ODwg16LyvDcZc7h/wAfvnaI65T9l/4HGed/DtATd+OxaSi5J8pzYN0ojSXnOUtcOZxvKTeUD+A11ZVhv1qyWK2bzGbOZ/FvMF1ENqt6UNLUoKCqVkOc9huMBw+GYvf0Dbty4wdHRDcb7Y4qioN/vMZ6MOdjf4/j4OCZtzq+mpGnCuJ9S9ApQ4mvWdSXjttpIuw4G9PoDSRb0saP4kO2GFjE/1THh4lD4KTCf5/YM1+6b4f32eh088QVH1+bu2mi797X1+0uu9aLXftagOPwUgfHRaBSDpEEuWmsdWdKhLvNms+Hs7Cwy809PT7m8vOTo6Ij9/Qm9fg/njHSWEmkNh/N1wDOaxsZJFoLty+XSZ8NVMdvJWYtG0ZQCdofFJQQURqNRzIYOGYUhY1kAFc18PovnJknCarXi5s2bEqBdrYSdpBS1ryeXpanH5cTY1EphKsmWt94ZCYHcGzduiGxMDMLI4lJv1pK1BTjToJyLAEvMBPGGTJCUunFyA+Xry4rcqyyqIRic5zmmacgSYXU6RG+/yHIwNrJPVdpKn4fgUchYDOSB3Y31OlZuOF7mzIbNL3wugHbHx8c+CATf+c53+L3f+z329/cl27wS6Y3T09MYbMnznP39fQ4PDyPAFAyOoDjgnItZmCFLRDI7UrIsjYCbUpJtErJQLi8vcc6xXC55/PgxSZLwJ37zN/myr/lw785dqZ9UlZTlBuUcjx895r1336XIC8lgrxtUolls1jhcHHPOOtIsQylPKjGW9cEhN2/d5Ne//se5vLzk8uqUgz3JYhaGJ0QHDb/JtutNlNs3TePt2J1J/zJcwZ9qbMjUaxeP7se0d7h17NtrFqrObt09w3X+G5x8G8dza/BopaOcUCRfKDGe8UZEXdXCJlRSi7jIC/I8i1njWqvI6tRae8clin3F59JWrq9QGOciicU576AF8M5v9MGRcIHxBjH7p31qIWkkIRu4rlFKaiFp06CTRNYIlAdmvBy7UlvyvxY6kkjb3Rj7v3ULPcjUnri75Idn7kBW4KCxhqInsjLOGUajHidHh9y6dYOjoyOOTw750pc+z9X0ApSJWQI60bz++mukSatUsVoJm3A2m0WizkcffczV1ZTFYslsNuPq6gJjGl597VXOLySj1jkB5k5OTmJgXTZ9qXt9eXnp1UhEIaCpaxbLZQzEWmsp8tzX92kdaCCeE9bNkJWw+5rSKmZ8AVEaPE1TDg8POTw8FJlxnDdg+nG89fu9uOdVlazrIXNNKcWjRw+5desWaSoymPv7e1T1hnW54Ud/8EPmswsOD27z6v1XGE9GLJdLzs6e0R8MsLahbkRutd8f0Fc9nLMUvZyry0tWa8mo6/f75HnKnbu3AUhSxfHJMVmac+fOHay1UXY2y3Pe/tzn+PD993n06BFlWTKdThkOh/zqr/4qr776Kr/927/N1dUVUgO1F9st7JNhX7x586Zk9Q+HzOdzxuOxyJ3lEoy/efNmDObvTQ4YDodsNhsODw959913USQcHx9TGanlLbXVB4z3JqSeKJZlGZtS5K1sY3BWoRIhQ6zWG5bLBev1iidPT5mMxugMvvWtb3Pv3ivcv/8q3/72t3FOmL9FUfDKK/f44Q9/wHgy5M7tdxiPJ/z4x3/Au+++hzEiW6aUkLGurmaxb995520uLi559vQp09mMotfz88mg05zvfPf7vPHGm2xKw+Onp5yenvvxidSCX63RWiQK//Jf+ZdZrdb8jb/+N/no4w9ZrdakSYa1jjSt6ff7fPLgkZDklHfeO+TAuF56gMYYG4EYaB2XAIQG4CaAt7tAoKML2m2DrtEf8xkr3eNa4zIuNOr5hahdkNprsGNg72It8aK7x871O+twd/95EWv0pwfbn7/Wz3KNz3Ldn9e1ftb7+6dJClAomh9pmvcVxW9a7NCKrF4CSSI/t72viEGEwbTtBz53/Z//sb23dl7k5Y7g1ulhnqn2BQdUjcMsYPOtBHeaenAwjUCSfMeOHd4F0NnOGPR3tXV+d050ybW6Y6sHPyTY14kHV8Pnvv3t7/Nrv/Yb9Ac9qsrQ1Ev6/R7WVDTWlxnZbFgsFrE0UthLV6tVLHMEMJ/PGY1GlGUZs7KDDxLIWuH+g68ZymONx2P29vZIkkSI1y2Ky2KxiD5OCIgHhbFAWA0KMCHwHaSwR6MRFxcXkWCQZRnj8Vj8wLqONsFwOERrHcm6oRQUiK2SZRmJ1lx5WfbDw8M/kvn2816rPu16MZDWCap1ZZC7fiBAlkoW73Kxom4Mo719Xnn1NZ588ylX0znVek2zKSkXS9aLNUfHBxRFLgTTRJOm2q8DDq2RDCbXBpuinaw80GpdlL/uBj5iYDE8B9fNn87zd/bjFhyVee8g2phaCYk6SVPKqmLuVX5C0Lzo9TnYP5Rx7GtuGmco6zImC0QQsjP/q43IcTd6N/u57S/JZtU+W4jn+iVk5JT4+u86E1BfS6Bd+eze9UYyUwLgGK5xHfAOxNJnSiW8/dYb3L55woefPBIwWIsvFGQfXzSmuiDWTztPrlvjwhESEGI5K9x2Vt7uXo/bslVUB1UM0ry7AezrniVcLXxFN7jUff42KA67V2zPC8+2W785nPP89Tof27YBXZdEoPC54lufV35gB/8VQuBv+3pa607wvfXlu8Ff6VeR6w3re5uRjT9HAgUB8+r1eig8aX2zYb1ZRvn0di3ZxqPC3AyvdeVid9ey7rlbZICd/bX7nN2yga0SgwTmuntU8DdDW7ZBHvvc96VJilaJBAeNBMtstPE9yc1ZnDU+Q9nstIHPqtMaEp81GrAZH6gJC0RYD9J0O5M+HF01TWMtTkvQxOHkotb47GCfkFCDU4EY1LZpwFICrmGt4eLiqSetiwwtOJqmDrMh2jES6Gz3jLCHJJ3121pLoiRpwQuJiK2U5azWS77z4Uf0cs3RZMi9k2Mmi44CgG3LGegQ4NEKnfiZp2TT0Fr5BCzfzs5FciJq2w5zXn7BaWnnBsvQKNLgNRohu2t/HcK6kYZEMdX2TSLZ4VmakqSSLZ4moVwfXrY6Rtm5siWXV1PevVjw5OyCx8/OmK9qnFYU/SGJ0hgjCRlSTi6JxOpuQGJ3uZXzbCdxQG3NhXAoOnuBg//2wVPG925x9+YJx6sZdWMAh/OKjI23B54lGZuI8QteXzcivdw0NVophsMBq9qy2TRCEHeSBOOcAi3jvmmMEMiAH1aOsq7ZlBVVWeFcm00bgpRSSTCUahQbwWJ9ubCtR2mfUSm0nwMtLtcemY8LYMFZLXLt3lERYpnCWePLlmmpCIOQz9vyEh31V2W7X06WSnZ9ohVoKZEqz1XhaitZryoQVbYllbv+v9YZRjmsM2itaOoaC2xqy6YWvOH/932NZQ3ugv3JU+7cOuKt114jVTWH+/uSzDJb8pP3r/jb/7BiuVwzXyxZrUs2laGxyO6p/bLTbTClSPzjKSWy6w5RvnFJgSWJ9prYPEncr51PGJBMbIMG0p2SJmmSSdDcSmm5uip59GzF42cL8uQpd27u8+q9e9RlyWYz5+Zxyt4BGDPl7Oyc9bpVq3AQ16sQ+BWbUfu5su2PybRu95tYPtR1Yjpay7xO2tdC+0TyYBeL9zatPKbzczihX6RkWTBbHKsS1mvFrVv3uP/a60wm+1KWz+mt0i1y1+04MUYw8TTNfImGjMbAYrlmtdpsYUgin+8l9JNMSmF01kDdHb8EbF0eTmsZDE3dyDpqDCZpUFVFmmTobIVKNFoJGSjzZEzl12A7HtHrSSmJLM0o8py7d27zwbs/Zj6bSRkQn1wIkOUJKCtEK9ugdEGqpGRblkgmuDUyn8P+3RhDWVes1ys2XkZ/MZ+zmC9Y+ED45eUl89mc1VqSZ0xjZD5rTdEfMxxPJE51cMRkb5/hZMJgMGQ4HLG3t8f+wRHHhwdCDO8V9Hs9sJKsc352ymwqqqvHx8fcPrkHOK6mU5wN9ewbrDUsljOMrdGpppePyXLBMGW/VXSVbUP4ZtfevM7Gafvu0/xHxTbb4rPZ691zdm31l73X+dbnjl18M3zuZTHJz3p85sB4ACwCWBCYGF0ZW601x8fHHB0dcX5+HuV2QzB3vdkwnU1pmibWI0/TlDwTSeL1Zo01YUPRMcgNbR23pq5Fqt06Uq1xiaKhjvfZNA3LxYLX33hTmEoPH/L06VMODg6o65qyLDk6OmI8PiDUiA1ZCr1ej6dPn8ZnKwYDnHO+dq28NhwOY/ax1P+RIFkAXNbrNR999BEgtdGdUjFjOdS3XUynUcpWiAU6BlykxogsPCEoY51juV5tZceH94JsH56BWJalZKV3DNXwjF1Z+XCtrmxUF9TYAuDoGhQvlysNxmsYiLsSPIERG7LF86Ig60g3hmvVTUNVlr7mc5vxEd4Pge4w/gIhIc/zmIEqgfYySnGFzJPhcMjJyQmLxYLFfI41lldfuS/3aSyffPQxxl9rbzLh8OiAwaDP5cUFP/nJT3jv3fe4e+cOx0dHjA4OefX11yCVjOIAwgUJ+JCZ3lQ1+EDrX/krf5n3P3if73y3BrVGK4dhOxgB26ANSoKo4ixY36/XUIF2juA4hK78vcdP+fNv3SfZAZQ7+30bMlHPZ44/d+3O77tGo/VOuPeVoopAawSKbFQgN2idYFWbcZikAhLVdU2eFSRJSl7kUZZFJzqyO9t6K0aYldpvAtGpwgeoXTBDiIF/b5x0CTmhHmS43+D84USGpyhaQpBzjjRJsE6R50V0nAM73jondQCzDJTGNrJemabN9Owesf3jnb64/aXNXYvzdN4VgNDxX//oAX/6z/wpXn/1Pr/zO/8jf/kv/0Veu/+KB98z0iThxskR+3sj6qZVaMA5Hj74mOVihfbg12YtctXr9YbvfufbHBwcsF6JHPTh0SGb1QZTG4ajIc+ePGU0GnlQWLNer3n69DE4RBrVNvz4xz/kzu3bOOeYTCYsFpbFXNbH6dUVWSr1VERpw8uqJbTzqmnafsTFmslK4cF9L72nZM5kuchcpZlGq5T1Zs3+wSE3b50wn89Js0zqwztYLiVrXWowFazXS5bLOVprRuMROCHkXFxcUBQ5y+WC2WyOc5Y8F4nYXq9PnhegLKPJKMrHjsfjuNY/efIk/r5aLeMavNls0ImO8vXL5ZKiKDg4OIhBhjTNmIz3ODo64uTkhDRN+eY3v8nDhw8j0Hp8fMzp6Sl5njOdTnn27Blf+MIX+Et/6S/x27/925ydnVFVdVxL9/f3IzFptVpR1zV7e3tsNhsGgwFN03BxcREz4N577z3yvGA8HvPo0RMSfUGWZzx48Igsyzk7veDjjx9irY0y8ePxSNiUt25R1RJUmOxPuHnzFkmSe7uhR69XUFUljx495MMP36excHk54+aJPO94POb+/fu8+eabzOdz1usNN2+eUNcbXn/9NX7pl/4YRd6n1+vzy7/8K/zH//H/A61Tri6vePz4lLpuS678iT/xG7zyyiscHh7y1//632D/4ASdZcymUx4/ecJ0vsIYw9nlnC996Uv85LvfZTqbsqmkjhdOYU2QMtX89b/xX3J6eoZD6iIqNMYuI/AgGThiaCa+DurWmur3flfXEDJLwix3YtCHVUBryfIRRxKkLmRYJdr1AvXyNQXA7TidLXP+mgXo2kOhdz/jdp5N/MdPP152zs8QA7rOaP6nGSD+tPv5aZ2OP8w5f9SHUgpXKTZ/R6NvWoovOZqxo2kcpYJUO/JceSed542MaJy4nb9Banb+nO/3RS/+FOMw3JN1jrpyNAbMDJqPNDxOodI+SPU8GfW6Pgx7ddeu6oL0uiPjeD3AKdkqXVnwcE4gfXWd1Vfu36OqS3QptVRv3rzBdHrF/mSf0XCEUor5fM6NGzckCOcVTML9TCYTNptNzC7v7mfBfg8lk4JPFHzOwWAQy30MBoNIyh4MBrF3rC8zMR6PI3FYKRUVzLq+kHNCgAOxTYPvFALyzjmv2qKZTCZxjwai3xX8ktKXkCrLslW7qmsGgwHGGIbDYaw1/TMfbmct7xw/81C/bm0PgFg85eUDPAQwgj8ZfPcQUIJW1lunBXW14vzsguWyYTIc8/rrQ9796A+4unyGto5NY5lvKn740Q8wpmY4HLB/uM/JjRNu377FYNgnUQlOpT4zLvik3eCDb5Uk3uTzbbYznxKlI5AU/3lQ0io8mOu6F4ik2eCjinpPLxInQ9CjaRp6fZFQfP3119Fac3r6jAYYH+xzcHLsxzGe2F0TZHPLsmQ9S5jPoKmrLX83ZOcIZiDl54z3jcO/qLiWezlR74sVqieZoFpKUTkHm6piPl+SpAk5BWmSUyuD5JVeX55Enk+SHQ73J/zKL/8ST56eUddGPBilMI3Y7T/tXnXd2Lsuiz383L2+Q1LRnHKtPbQF7LW+YPzs1nV9GS0VXvaBLFrgON535/6Nc7QJi88/c7ftcJ9i5jiLuibtJ9iHu0dsBx2Ccy3REhClESW+dff1bvBWKb1Fjtfd4KQH9ZVSEXzvkpG7CiRdxcHwt3ejaazxMZP2PWMMCYrBoE/RlxrF09klZVnG/Qi297tu4Dl8126SR5gH4V8Xp5L3w0+NUua5fdc5F4nUYZ9MknRrrQifEUJJWx4rPHOeZ9Fv1TohS0XN0TRGFOVwUg/XOhrnyLw0s0P2nbp2sX0D8B0Sb5Isw3SI/kLebp8Lv04kEY/r2CIdG8I/MajMZ/aHMSLAe+IDQcYYnGpAmbiXGlRc88/0DEuwRfw8DJeOuIzz40zmlwUJQPu7EFXP7X5IEu2D19pnPUoARfb0HOca1rXlk7M5n5wt/VcqvAhyd5IIhiScAt8nkAY1QRueuVWri3in7ih3+PU/jL1eYniNPY7SHmmSSAZ4oiVpyYFyIkysPPlPAqdyb0miKYqcXq8vWeNa+6VKsS5L1nXDpizZVDWzcsO3V4/54JMz1tZn/aNI0pw871HkhWRt15KEUBSpL2VhcT6rUuu2z7tzI4zvXVy3Wx4Fa1DWUHeC47/7/Xf54OEp/9Kf+7P85VphqpqqbiTTu65YLpeUZc3/a1VSJwmNsVLPeblitRIsPUuh38t4/f5rotRjLevSSBanNVJ6USGB9KqhqmpqazEWamOi9LaM+KA24AdeoGJIM/hgZmcNYDvxJDx7osVHbyzP2RDOWlFnQGpLK5WQJgqlQ1KQA6U90UFhagNoH3htg9haB3JIZ4gi5QC0TnxQLwGnSLM2+aM2BktLdH1RYEirjF7RlnUsKykRGhKXQp9XtciUz6YV8+lDfvIHD/lHv7/HzZsnLFcrLq+mXF0twXXVAhTOy22rzKtIGCNZ1H7+x/XU2ZgApZRCJYoskcCrtVYIPqotPxRsS2OQGIcTBZFEKcpO3+VpQuqfw2iNNY3sM1ZUOT98dMGHjy5QiJy9+rHcf9etpDMakrgf4LGZQDz0u783COIe6Qz4NRLnsWRfxkopSQoaDHLW5Tri3cFH7e7BMaBpBLO0jbRVkmgG/YLRaECiN942BFPDejPn63/iGxwf3wKlqcqKNNWYeltuPpS70MaQaEuSpBRFj+FwTJ712FQ188WK9bpEqYTG+ZKjqYw9WdvTWBYlkAaes7s6z6N9UB3n1Ry8PYARQotzklhogWrj2Cgpu5P52NhyPqNcS9lBUZpMuXf3Dm+//TY/+fEfMJ/PpURuWZMVOfdevU+WJSSpkIF6RUqv3xcbtaqpNhvW6xXL6RUX51ecX15wcXnFxeUll5eXzC5nEhRfLKmqkkCH0UqUOyeTCTdv3pNEqoMDBoMBxXCP/mjCZDJhf3/C/uEB+4f7DIfDNj6XaFzZsFmvmc+vePhgyuxKFFKzNOHw8IA7d25y++YtlssFH31yLsnCvcKXJHIcHO6xXJ6yqTbU1nByXNDvFazXji7hG5K2nVWL332aXf0i23xrTRFwomMvPU9KfS6ecQ2G8bKg+PPfTwz2v+z+X/b6T3t85sA4sGX4didyABSALSDj8ePHlGXJYDCg3++jtSLPU5bLBQ8efMz9+/cZDkes12vSNKXf79MrhlEiTHsG83vvvQeIw3i4v89kOBKgIy9QWpElScwEbeqaH3zv+5zcEInX9Vqy07Is4+TkJGYrBMA/yGaEZwmgiTGG5WIJ3hEwdePrTUudC8lG0CSpigZDryi4eXLMyfFhNDiapqKuSsbDAau1AOtNVUYp8f2DQwaDITrLUMD52RlPnz3jlVdeodeTDISr6RSdJGRZmzXe6/XiAruYL4QlZwxNXZPlGRfnF5yentLrFbz22muMJxNwjtpnUssG2UotKtU6MaEtwtFd5Lpt5XYmXHhNu/YzXTn8MIkGAwkWBaa5OBACTAVmUqhJFMZcYMOHAGXY4INBGgy5btajgGt0pJVdlGAP95YkCZlOaLKMsqwwVQ1JIjV9dEK12bBaLtnbn9ArCv7Mn/0z/PqvfZ35fEFT1xzs70smwKBP4utgh3YwpmG1Ekl/2xhmV1PSJCHPcv7YL/wi77/3IYvVmkSHRUddg3ipjh8fpKeEIZSmyfYqFIuHdY4YHJGASGNNdOwD6BOzxwNIgAv40s5iSgQInOvyzF3H/OwsdCHo7O9J5kzuA7Ipje/fpmmwzqJVEp2sJE1i/WZbG0ovbZ1nuUizVNVWMNg0Rti/SqHTsIm3Djp+3Kid8WiMIbDznCMSXgDJpNCKkLPtkDnQ7/dQStMYMfiVl7wJnwtgY1gTw+u9okAcE+tB3zJee6u7eB4o6bav67R3fN/fP3Erb438u6/c45VX7nDvldv8K//KX6EoUj748F16RR/nCciPHj9kOByw2awjKaCuax4+fMjlxVWU0Z56Uk9d14zHY5/1bcmzgvfefY9+v2A4HFEUOXfu3MaYhqurK6TWWJtJfHV1ya1bt3jl3j0eP37MW2+95eel44033uDx48cRPHeu3GK6h3UoZul4kCSA6dA6+0WRR7AgGNsRiHECoh8dHUWwXWpViwLI3bt3ePbsGbPZFOcsz56dc+PGDdarFVmS0POlQubzOWmacvv2bbTWjMcTUHB8coJpGo4Pj2mamqMDyRo7OzujLMsovxpA+ZDNLgC7EC56vV7MOHrllVcoyzIGxQP5YjqditSOJ5GFbL/JZMJsNmN6NY3ts1gsWK1WzGYz5vM5JycnPHv2jPV6RZLIvYf9O5DF5vO5X3fl+xaLBWdnZ/T7/ag4slqtKDc1w9EeWmnmi4WArommLCuS+P1L+oO+gMY64fD4iK997Wu8+fbbZFkqLPAaT3oQIKrfL7h79x6f//wX2Gw2bJZL8izlxskJp8+esV6V3Ll9j/E7Egz54IMPWK+lfT/44CPu3L6LUgmHh2P+9X/93+C73/0+dd3whS/9AkXRwzkXM+f/33/tP/XgRI8HT55yMZ1L0MZItoFzDvPkGR9+8lCUc5oyjjsBmBWmrEh0yoOHj/y8bNBaUTUVWiU++0X5dTCJgSBoM8C6ZVisl7B0ynUXgq1VwqrtiKELb2+Bsu6FQGpcfXy9pe5nnmNlfkoYRl2zPl0XPYz3+JIrfcoJ/1wdP6vR/mnBhD/s+/80D7E/NDzTbE4d+oYhe8ehDyVo3GwcqXaSRZ7SjuftYd3um51fXEQ8/C7bQUD+SbZIx+TaflHJPdS1pSodzQea5icJrvaAqW4lPLcyc17kWDoIkb8A2ITPy17ZAZzYkcWlDS4kWjKSYua41gz6fYbDofhx+fusaBiNRvw7/86/hbEVe3tjFospaWYZjnKyNBH/yNu/Yd+4ceNG9LWCX9fr9SiKgtlsFv2Ybvmk4Bcsfamsfr8f98egyBTKXgU59faZFK+88gqbzYZ+vx/BoLBXdT8f/L1w3UBm7b4/GAyizaC11FaHNsMt7KsA6/U6BvOttRzs74ucqDHRx/3DD6zw+85asuUHfMZrvWQ9aneEz7ZmdevSdwNsXYJpv9/HNfBf/Vf/DSc3brEqLR9+8ozpquQXvvIlMm158ugRi+mMSX9EkuVcnp8xn8959uyc73/3R/T7BcfHx+zt7TE+2Ge0N2E4HLK3tyd+fpFHMmzj64Faawjpb+0a7Pe5TmDLqOd9XyD2vezlyvvKgfgrR1A5yL06Qr/fR6tSgi3eb08SxcH+Pp//wjvcvHnCw0ePWJUb8l5Br7fHZDLy322oa+XxCUNZrr16VYu5hLJkpS8nJqXmipihY11LUgh+b6/w2ThIxpimLQsXSreUpeHq6koA+FTkLQMJXwBhKVck9ykRBslalXYpN2u+8Se+zo9+9EPeff8TVpuaNBOQ07pmK4B47bjbee+6IPxnIQx1jwCuv+x7uq/vBtp/+v1TiI7Wqt1wnLyrQj+2PnL3XruHJth2O9dwLgaVw/2lulNirwMlbPnB+Aik2k5yCM+rfaasw5fnCNnPBHNSxb+MtX78tOMM2hIK3fIerqMQJz6wo/Y1p7sYTqo0VbUBrM+u6nHr1i0Wi4WM9bLEWEN/MNz6vm67RL/eP3sbsN7O+g7PHMZ3m0n7/B4cbPNAGpC5IO+YxvkMuRYnS7OctJC5lfpayoFEFfadsiwj8aWrrmGs7EUOs1UaJTyfYBQyfsLzrTcbDg+PogrKJx8/pLGhlIg8V5ponzW7XR7DOVDWCS6YpOhE1MhCTd3YDH6989g41iWgUoq8H+8xBI5bQ0uR5YPYLyIF3Ca5hHau65qs2sS+qesK1VH3C5mkaSpY72DQp6nrjlIoaJXiSLGJBHgbW3vcx7T2mPJGGA4ShbUK20AbEuuKg4d50ckG9WvedYdSgrl8pBbxFA0Ms4ThoE+vKBiolC+oEamG/qZiNBRsWmtF01jK+YrpfOWDz62vVdY1j04U5+UVDx6f8vDZFYEWbdBoncb1OtpROkXnmroRTN5ZS16kbYIUJto/SgWSQIJCx4BOdz/v+bKcdV1jmhqRXG+T0pzKeXg+4//+n/+X/Cd5TpJoGlcLAcY56koIZlkeyv84KmNJEmj83KoaWMxqzr73E5Ik7LPExlSWiJhZ2jWuXTXD/PQlA66hEAqG6Vu2k1kbNTt3AkiVDT0ZjrB2aIrBPlhRt8gyUbVBifqlaSqSJPVJGDLupLx4q74S2rab8b19u63KRqBkZTpB5VImtLEijx76BU9E293HUiWJeQGTLCuvdhkSS/wk7+d9kkTqWOeplnFaFGij6CcDBsdDXr2VMl+L3REU7KyzGCNqBSjZ90zjqCupjb0bN3DOoZy3EwWZJgllQWyDCTwaH3zWCagklwCtn5vL7thzBiElQD+xFOOM9aahrAzOIsQhY7bHUxdtDX3ux4Jk4iOkh7i2X4edtJcKKLocrb2hAJYll1dzGrZxdCmj8byqCa4tFSSBZFhNV1wty7jWOuvoFzm/8ktf43Of/xJluZY1ONFUTU2vX8CqvdcwxsI+mOc9er0h/Z74eefzOYvlmrJu0FnawbUkozsESMOeHrLqQz/RIU6GfTIodfqi3e1egtjlymkSQKepkBE8YaoqNywXczZr8fuGo4GPD/YosowskdK888Ucaw1nZ6f0ej2cdmRZQlluuDy/AGCxWHB+fsH52Tmz6VTqg5+fs1gshDztfATDaYqiz/5kn9u3DhmMRgz29yXje3+f/f19Dg4OOPLqopO9PXq9Hr2sENvLkyhRlqapfTmxSxbLOdPplZQ/1Jo8yyjylJMbR3zunbfY29ujKAqcs5yePiNJEkaTPerasFiW3j9eUdY1OoWqbjg9O6WuHEdHR5Ksmw2oq4aqrLAY0rTFva+zLz8tSB7O2T1fhVoPPF+3/EXX2H3/Z7Op/2iPz+ypdw3JIGcXjN9gWIbM3LDYv/HGG/EzIrvkcNawv3fIvXv3Aclw7hV9HFBXhqZebLFPsyzj85//fPx+awzDwQAdaqg4y8XFBYFR2x8M+Pqvfx1jGgaDHoNBn7quaBrDYjFjvd54Q6x6LitUKRUz+qL09molG1OaMson3nC1JFkKGJbTKcZI/fNekaMVLBdLil6Os47vf/+HvPfe+3zhC1/k85//nDxXVXI8GTObzalmU9KmZGMt/eEITEWRaGaXM+qhyLIUxYjBqJVQVzrDAWkqm1uapyidUVc11ioePnyEcpbTJ4/4h//z7/L6q/f5lV/9Vb76K7+CTkVuGuslqZUC7aV+FJjGxgB5qGMhYKTDGkCZrYkUJk930XQ7m31gs8t5UFUbmkYW3ZCZKABYQV377Dol56ap9oZEa+BnWUpdNyjdZrqAB6ucY+1BtEG/H4OQYbwGQyAYIU0ttY2sgsPjI7I897WDLL2eGLN5TzJ9B2MBLoajEYv1mmdPn2CUEonn2Ywizyl6vfidvV6Ppmro9QqePH7CdDZnPl9wcXnJ57/0Fb7wo5/wD//RPyTTlsRKfVa3Fdz2xhRExoxzYpaJ7Fi2NUefi4N0Dud3YwecLjfcGg1eONe7gQ/rXJQR7wZd23hu8Dh2keD4EeLpxtfQRaGTFNsYz7xNPTvYiXxVIDpokUPSNqGuK5JEk2V5zMqu6qb1v7zz5HAoK5nSQZareyshu8RaJ8ZHx+B1nY1Ed4LiQdoMFHmvR5JmWOcoN5vonDprifWJnNRHlCxyaIwhSVNSvz6KPJgW5Qvw9d5bE3+bXHBd//hmVcHICptPR0rNf3JR1ty+c5vRsGC9vGI+nzEaDsjTlNnVFThYr1ekWca9u3c5Oz8T9QLPklzM51RVyXw+8+BbTpZJJvZms2YymXB0NGS1WjMc38c0Dbfv3CHLEi+7vd/K4/m1IBCpNpsNr732Kuv1CoXj9s2bPH36lEcPHnB4eMiTR49IlGLY70cmubEWrEUjRIPGtIx1aT4JgCdpirGWwtcvTZOEflFEAN4aI4aUE+WRVGsW8znz6VTmITCdXjHoD8izTPxonVLkPcpNyeHBPpcXFyituHnrJr/0S19jvLfHk8fP+OSTTzCmpjZrVpslJzeOOTo+pC5Llos5x4eHnJ6dMp9JKY+D/QMBPpIMTcL56SX9/oBBb0hWpMznM5yznJ09oyh6UZYwTXMWizn1pqZar3j65DEH+/us1mvu370jNVKrkv5gwHvvfsCdu3epyprTZ89YHi7Jsozp1Yx+b8DHn3zCcrnh/PwKZy0Xl5cMBgO01l5a3Xqiko5M09VqDay4e/cei8WSumm4mF5x8+ZN0kr6FyPz49nZGZO9CbnOmS2WjIYjqsZw48YtXnvtDbJEMhSwijyXMgmJSjg9e8ZcawG9XcJyXZO4jF464uzpjP29mywXCx58fEpdP2qBljLn+9/7A3784x+j9Xckax/F48eP+YMf/wHL1QrXalL5uliNB7ATjDUS6FYdeVUl96WUZrEWEoLy5xgHxnhgDiVtpROauhaAoLGghBnrfJTO4TCm8vO468IHoK2zDtPuq/Jv2+l3nXqHPwOOe92vcbW5zojdivm59jtDzbfW0XTtNvHcBdR1X/jyG33ufP3SQJBSaocMcA3IzEtjRLSwMLHfusDoZz+2PyDfa1sCmYcIdu0r1d2jcLgdYC6CPDvftU1PeDmd4foAmN9pPMD0szgz0XLogBHBVmynVVi7wT5J2Dx1qAyydwwU4E4cTWEpK0gSyDMdM9jiBzuwhAq/xJ87TxdAj5ccHcjk+fd2TZ1rhrHDYWoXTGfqBuzaYU4VVJr6x1qywztzOU2ziL/EsWBboopSCp1qP9chywqapl0TQhkcXMhukJsLdniw6Z2DXq9AKU2aacajAYeHB6KWcXTE66+9zngi9dCqsuQ/+OD3WJklIjHqGA3HOGPZGx1gbMN40AenWa8X5HkuGWNnZ4xGIy4vL2NNbtiu222MBOHSNOXg4CAGm8P7wScL/khVVTFzPHyPlOAqYjBUJ0ks8xGBeu+zBnWfEBzpyskHJRTn2izyrk8TrtE0TQx2dO+1HRsuSqobY6ibRkrsEIJKf7ijS0jefV21aNtnus6LFr1ta/R5IOW6o+tXReKhDf6aEPuWyxW/9Xd+lwePHrNalVxNl/zkvU9YlDUkFUf7+xwfiMz4ar7ixt27nJ2eMr24ZDqdMp1OWcznnJ1NefTwGULUE4nw4WjAwcE+k8mE4WhIfzhgOOwzGAzpDQakfryEurDWy7M66+eqdRhb+yYJbaw621h3TfYZE9Z6I1z6OvMZoULqTbGmYb1ckOU5m/WKflHgbEO12TC9PGfQ7+EwVNWG0ycLTp88xDkXa13WdU1TS81OU0n2X1lu2Gw2kkW+brOPQnBSa02SJrQ1TKU/yrLEDKRkQJqlmKaVe9ZaY5VvCwvT2ZyybugVGVmW0zQmYj6q+xmfCat9lqt1FkxNkfT4jV/7OsvVhg8+fIipDUmRfaZx1D2nCxZ3cYZdgk/32A28P7eXvgTM2wZ11XOvtee1e5by4Hl3jwnrbvcaXUJGcN6utas6ryX+HOvaEl9b7aJ2XrOCkdjgB29fOd6XUzauE931RH54lSKgsc4HHMUPVkqhk4QiLyiiMlrts/Nch0DRjpEQFJaNsIPTmFYWPJDY8zwnVVA3NevNksVyhva2/954QtOXNbqsSparVfx8lxzd2hZu6/l2x0233bKsaO0Ev7cnulUeC7W/URKNNo2NWfNaa7I8I0tzn9GWRUJWKNUW5NbLsqYsN/H5a6/+4JyJwbl2z5EM8YBRhmcJ9qDUhk0idpZkOb2iT5rkmMaRpjlFb0JRZB5GsnSV71qso51XUv4jwdqa5fyMsglKfqHvXAzQBTwEp/0+m3jJVw/E+/bXSnF4eESQ8MaJsl+3/0VZr6HoSfKU9Qk+pq7QCZS+lFZd1zSA8j6pRupyh6BjY4yUCkSBsqQSWZau1W0bBtcqBNjap/MYUZxXasuv8rO3M6N27D7ncKRbtq4BlrViNV+jFhu0UnygL8mURV0m7I37jIcDX85Fo9DUm1KSdILEt9bMFnOqjxpqYynrhgrIciHtFZ7cpLVGI0RyZ700v1UkeZ8syymrxu/FUh5BssmFxKO9WorWilQLxhPxXNequMo+ILLkO8JiJKkvfVhX1FWNF+Lf/ucE5/ezD4eiNtIhzm17NtaTP2JzWj8Go53brrlS8scHVrEShyMQudpAXVgHWiUbR1XVcZ4p7zwoJVLrWKkbrJXMOQs0rONcHY1GOGPZbDYo4zNstdgIKF+m1IJVggukiRDNEp36pzdYF+ZCKvtKsDnwA9dpnI3sFFCOJFNol5JYSH2kN+vMK/Ed2vKVQe1IntOSJgm9Xp+qLr2SREKeZ5BIhmqeJvSzjEG/oJ+3ZSPDv14vp6wqKf/mpAREVVdY065hdWKoElkD66aOfq7zbSK2i5RZjBPK14QPkyhgCcr7LrIndikRcuRFjwSLspZcQ+Ms/aJPnss4aowlz0QlJRC2gt0S/IRwaKVoTLBn2zJ13fEhw6+9T9uxk7dcQ6UjhtRYw7aJHpKZdBz/wf5UWHq9AYlX7bDWUVYltTUi2+80w0GP+3du85t/8jdFOtz5uuYOlJLSme19tH6grPWCowspR5OmGReXU2bzBcZIotO6WkQ1DPEvdWw/Ic6IPa19ANyYNilQKUXR65FkHsfXOtqoSorNy316NYGgfqOs9K8vRCoZ2UVBXqTUVcXZsyc8evSITz56gDWGLE1xTmzaGzduMJ/O+ebvf1Ns1sbgjPVkCBVJVKlOGY4mDMZHDEdDxuMxo/GY8WjM/v4+x4fH7E0mDEYjivGQ0XDEYDiQ0ieJVziJCXOwKZdUG7HH1+uV1AJ3lixJKDIpEX20d8DNmwWD4ZBBvy8+q1KMhmMm4wlKwXq9oWkseS+nyHts1iXzxYLZbEZfJzw7u8DphrxIKYqMi6tzIf1yzKA3IMsSrE0wtSSEdm2xMF4/LSC++/7zNqqmq7j0We3pFx3btvH1R5gTL7rn6z/zAt/2M/rHnzkwHgzfXYchBAADgAFEibzAwg9Z2AJEKOq6rVWTZwW62JZF6hq5IUjebeTu5DPGcHR8TJqlUMl9rTcbVFlGYy9kYyVJwt6eyL8Gybsu8x+I2VvhvZ7PNAi1Y2ufyV7kOf0socgSzk+f8ejRI+qqZG884jvf+jZ1U/PKvXus1hs++fgjnDU8e/KYe6/cYzAYcHJygsYyX0xZzs7JiwKFY3E1ZzQYodKM/f0DGoNIMGswjdTSXS42GCsyMSFLQycJe5MJJrO89fbbJApevXeHV+7ewdma737nW/T39rzEvJyfeeYm1uJUCBgCtBKMYTHxo2BrgHX7o/t6kqZRHgkgz1Pft/igt9SKW69XbDYbrq6uqOvGZ5LnLJdL+v0+RdHz/ZZ6RqWMjfV64wkBBWVVMZvNcM4xHo+jFKNSirpp8HTQ2Ie9Xi9mjwSnogvotKQAvcUktlZq1FdVxWq1IisKXn/zTV+fIwXnyLMsyu4XRS8+38efPOPmzVvc8WSQ6XSGMZbPff4LvPv+B1xdfEKipa2Na51sFc3Hzhw0htyPf7NTC/azLBlKwd//6AF/9UvvXPt+BMLoygp1HPwAGqn29fYzLTC9hR1H3NtRVxWFV0JIEpHcCUabdcKSTZTyUjFNzGjAtbKWaZaSu0Kc96Zuge4YlDIyP1SX+a08mBGF1NtnciEQ5ce1VtEZlCxReT0vCnIvob7xDm6WiAyhjQC2fIdkriSYusZaR79fgAq1XUJmehe8CJnguwt3C/iz+77vhjg+vJPnCIQG+Objc06++DXm0yuc6TEeCnt7b7JHqmVeffLJnKZ2lOWGWzdvkpwl0emXbJz9WE8b5PU8z9nbm0S1B61hf38iYHpVstm0TPhQc3Q4HHJ8fEyappyengKOyWTM22+/zWq5pMhzXrl3j8ViIWUltBZyQdhblIq1vsI+oYyXGtIa5ZnQXbZ/nmUk47F83nnJ+45TfnwsRtBkPCb32TGrzZq6EXWDcP+T8Zhv/uNvc+/uKzRNzTNTsdmsSZKUX/nVr9PUDd//7g948+13uP/q67z77o958PgjUGtWq7WwC/Me8+mUJ0+eCEhhLa/cu8vZ2TlZlqPAS8UaZtOpZLsVCcPRkIODQy4uzlkuJaDd6/VYLEoPgCpW6zWDwZBNWTKbzVFKs9msyfMCYyyHR0dMpzPyPOPuvXt8/PHHoBQPHz2ibhqUSlitSqyTz2R5j9W6RAxhL4eYpKw3JUpJgLwxliIvOL+44gtf/DLGwQcffMTFxZWQgrxU2mAwYLlas1iu0FpzcHhIrw+vv/E2n/vcF1nMV7z37gf85Cc/IU0SRv0BT58+pWka3nvvfQ4PDxiNRpK9P51xeXnFfL5isVgyHA6ZzWYsFou4jzvnKOuGhc/SaxqpZSWsZhkHSisqSiwt8KGUAp1irAMSGuNQ3ZpfATjr7ne2nYERjPPv1UaIO8bFBbCdyVuvsfP7i4y3XVhm+73PYvN92inqM521e7gWcAsgdnwnXPgaEPin/J4X28QvN/a3nucPG5tS6jP004s+e92f26xr2cZ2HI9dh+O6743ndOG63S98yf2+rG39Ja9r2k9zNAKAJT+2g2yCZ16vSKBqRfN9WcOrtMFpQ3ZXkd4FcyD1Dx2QpsrXm3Me2AtQJ9tGiP9dTIBryBoveIzntA+i7dMeAcAzjcgthvPMXOE20DxWmEcKZ0A3qQ804DMH/T7m5cxTz7APQadkB/CXwFeQwkxJEpExlmCulNlJEql7KHLsUpIiOOR37txhPB5zeHjEa6+9xnDYZzgqGI2GXFxcMJ1OfUAxp64rRuO+BJ096We1XJGlknk9GuVSV9E6mqakKIqo4rK/v890Ot2q3x18FSD+DBmpQb3LORelzIPNHUpxBeJ1sO+7dcm7oz9kL4fs8FjjWakY2O5mFAbfNPFB9eD/Bf8SiDK6Y29LBAJVUHTp+pGhn3q9Hrlvk6AG84c5utk24W9ofTEhZXVm/wvmZpv59uLv2f18FyR5EZgRnr37+fDM5+fn/OAHP+QP3n2fPM1QCga9gls3jjmfLjh7+oyrPGE8njAaTTi8ccJob4/bd++xWiw9aXHGxfk5Z8/OmM1mlIs51UZ8sqvTc6ZnF2S5gGRJntLvFQyHQ/p7e/SHknEyGAzoFUWUagxjI8s0ziVbbdxt5+4zC84hmWFK+dq+3t8Ia3NT16xXKz9nlmSe/DHo9/jgg/f5g3ffZblai9RulkbVucoHvCsfiDZNQ91UVJURadyqolyvpS6r9y26vqvcq2R1d3104+3kULpu05Sx3+J53jdarzdUVU2vaH3kqIzggdCuKoD4VlIL2VjxI9588w3e+vAT5osNT08vow+1O8a699C+KXtD9H994Mv512QN73g9XYxiZ/vbAu6QYAl+3/HatyhF6yP6M7d/87l6SpI71M518Vj+1iPsgIoBUJfHfh5A3Pqcfy2A0rLlPA9Adk0RyTDdDgqHG5LxGuzN7ey04C+JDH8rD+2UIveBpTCHZawhUqdZRl01lGWzlQzTJSmH8dF4/0LvKDKEUnChbaxtcEmy9VlrLavlmmpTobVIUxd5D6V19C93JdPDcwS/3vlgrQttp2RfDMF+VBv4D+3XZreHfgtt1ZLMuhm6WrfBeefYIpOEzwa1QrlfS8jYVbpdk8M8UR4DkXm8Xb5Qx/5vCSoq0ZRVRZbljEZ7vP76kKquqZrKg+fh/jPxgxrBW7pJDmGeu0bTmITGaE/o6pQn84Gapmm8H+2wpkFpn8qL1ETtUhFrn1kaxoh1kvXtPMaQpbKvt0QPaee012fQL1jq+VZZFKUVOlMoj3EoIM9SbGlxPnFJ6vyKgkaipXwarkXW0KKYqbxhG30XrX3Sor9fDWmWYulgX2GshTmp2r8T1y4GKmbPeqwuPJ/SNN6eWjYJzcqQVZIsUGQFTZ3SGI1xggc641jZlLL2AaM0pV8kpFnR4uT+OUHk8kUUQuaAaQyJThn0hUDoXMgUNxLUymK9ERxSciOs92Fd6PV6W4o9SqU+7N8eWmtqZ3GJihm/oLxk8vbaZbs2SEcdDaQERVBECM3btcNDELI1+pTv0lYdAtvWPt7ep3Scsw5RULXRh1f+/y5cAhJH4hwayVpOkpRZcC+cpdmspfxOv6Auaxrb+ICf7hQ+k+/Vysvoa8lgThw0psE2xASPUHe+RfxkLQ5/yf7gaMtzqLinoRMvGur3mSTMJeXLDLR7gVZi+/a0x9h94DJLNXmeevn/hLxQoA01BpVJ/MYYSFRKpiDxmK01ljTJxBey8jyKGq1EMUBHBS+5b6Mc2ATnFa+c38ddZ5/v7pPKqxlkmSZRIBSKRXw/KwqUNSjboJFs5tQhZFSd+PW4QTmHS6XvnBIstvaS8s7vYyjxu3CC6T5n6Xb2hdj0+DU8zP2wl3TGnWRem7iPdnESpUJSk4zZ0aDHcDiiqqpoCwZ701iL1gknN27wtV/5JY5ODqiaDY2T+ZrolKCu2zUSks7eKnt4TtpRgb66mjKfL6jqmrQQnyvp7I1hf+vGSLQf11uBcW/A5b2eJK+GBlKAbhVPHU7W6edsEu/z+mx6UVdZ0nhlsfVqRe1J0rWPifW9wllZNqzXG4qsx+HBmOPjG2RZIQlFaUGe5RRFj/H+hN5wwGA0ZDDo0+/3pHRjv0cvz8lTTyDyfBTrLE29ZrOqY6JtSNR0EIP/eT+lGIzJ0pxeUdArevQKIaEXAyEjFEVBkecyzpI8+qtZVnBwcEyvn6N1ymDoyHtDpEyBo7E1q83Mq3I78qRgvVlyfq6oJzWjwYh+v0elKu+Ha2np52Cgl/mFLzm3i6e84Brh5a7v8TKMaPc7r/M9W7v5sx27/nF7b58ehA/HZw6MbzYbuoHqrkRR+NKucwZ4eYCW9Rje32UydAMZ3SDlixzUcB/h6N6L1lIPbrVaRTntPM/jd4cadVprNpvNcxnvw+EwZiQECe4gn1cUBXt7exJ8rWuqakNa9MkHI/R8yf5oj16eMz445saNE06fPsVY+PN/4S/y5MkTHj5+zHKz4Wu/9EucX17hrCXLcuazJZODA2pjMdYyXy7YO+hzfn6BU5q6MfT6IUtCU5Z1DDhkWcFwOAatSLIUV1WsNrWX59a884UvspzPObua8ff//m8znoj8Q1VVHB4e+qAufi/eriUVnI4uIIJqAfiuVFvXyQqOSKj/bIxkagRgK/WG8Hi8z3i8z/HxTZ49e8bl5SU3btymaRwnJzdFzn65JEky9vYOyLOcqq48AxmqpsYB9+7di+OuKxtpmoYs1S2rNrIE29pP3c8FME1q4ZQxGBiy1otcat8eHhygfOA869Tiqeqayf6+z76X4OhoPObVN15HK0252aC88XZ6esZf+kv/Infv3uM/+o/+IyxLksRhTTB+YBfgDoZNuP90K7D6gkO1n4/HztogdWa2nfvdAHkXKBAncxfMvuZrrznquibv9fy48kPPM8vDgm+Ck9QIiSJL0ui8rNcb+oM+eSZzuiwlkwfnHRGxBnC+xm7TGJQyPIeYdO/UeeniAGx5MKJbF6vwWUgKqKqSppYNObANjTW+horUIA/sWWsNOtGkkWFv/Nqz7rRg4Mc9302t+bt93wE8gedBGPCGlrXUKH75q1+l3CzIUkWepayWK3AwGAxpmopvfOMbfPOb39wGBPxYuHnzJpeXVxhj2N/fpygK5vP5Fnhd1zWz2SwC42FNODg4wDkXiVNVVXFxccFmI7L4N27cYLlccnh4yGw6jdKpk8kk1o4J8qdBOjw8b1031HULNsvc8PUgrUFrF8+zNqhcqC2DZjab8dZbbzEYDFksZD11Dvb395kvFj4zp8IaS68/4Pj4hDSVeuO22VCVNYvFFb1en3t373Fw4xbnT59xdX7Jm2+8yd7BiG9/+9tMN1esVxts3dA0lqLoC6kiy3j0+KGQw7SiaWoaH5A/OppgGsOmKplN52w2JXnWI01yGtNwcX6FsQJwaKWp6opHT556JzlhOpvLfrdZU9eGsmpi0CLUWl2v12w2G0+kENa4sRYQic7QT0B0HOraM2m1oqmbSM557/2PGAzHvPrq67z51j2KvGA6nfLt73ybi8sZy1WJs1IiwZ1POT+74oP3P+I/+Wv/Of1+n/liThlkcT2gVXtGcjDGW8azgLONb8NdFRDnHFYpjHVURso0pGkqJJcgFe4dsK351jGargvY7Z6zPd+2bZbw2ss+8/xFXvLepwDL/zSPrl3XzcIM7/08v+eP8nPXHV0b9LP0x6c5BVu21Wc4ZDsXR+lTz/0pnvvTzg19/LMeL3JSPouzomohatXvOpr3FWroIIHsHYfZc5TKoYcgAESXICJB8yisI3hp23TdDdbt/N3eeOdG5IdpoG7c1imuAld5O/B7CrfW2DlgWlBBvkZY/UHusuvLdH2osJeGz4bgaze4qpWmKCSzejwekaYZx8fH3L13l73JHkdHh6RpQuEDhPfv3yfLMpbLBavVmtFoxGx2Fclfw+GQJEn8Puhixl9okkQnHB8fM5vNGI1GMTgXpNFDORKlFBcXFwyHwxiI3mw2sSZ4UGoJfwfydHi2LMtYeaWu4XDIarWK9vtwOIxrjdRiFilQOmtt8DdDXXEQ/zWQVoO8eiBBd22L8F5Xura7poVgR8hgn8/nce7kPtgagI5gv4SsyZdlun6mw4PJKgIFrn2ZLiHp+bn8WfaLLes44GnebhL/wMVniN/lup+SupmS/ehIEwFjz88u+OCDD/jB935M2dQcHR0wGA0YjKAYDBlcznh2ecZ8saBpLE3jGO9BnmbsHxxwcHAg5ZM2FYv5nMvLK5aLBav5jNVsxnR6xenZKbPZlHKzZrXaUM9rURbSmqRXeLnyHsPhgEG/z2DQZzgY0h/0ZPzmOTqX2uAqZLGGbNRAzKerIKDRzoPuzmGs2O9FllOtS9bzBdPpFU1d09QN48mY/b0x4/GQstpwfnnFppLyZ2mSkOdFVDkoy82Wndo0NVVZxyzTqqo6gSIi0Ubs3C4oJT2TJFqyV50jzTLyomCzWoNzJEoyOJ2VQLFTiuVqzXpTMhr2I9aTpqmQQ3xXi43fgtchYIW1VFXJZO+Ad955i6vZgsurGcbUpFnSgokd+0D5wbe7p+rO753h3r7iX9zyRTtr+JbP2o7sreuEMzQBwN79ROd/qpu53W4cjnDfLUGwjd10v9tvMsptR306R2iP3W0q+KJhDIYAgpzgKdkmBIF09GO1ViRJ515dW5YutLfWor4YE1KCUqCSYFuaZh2cTAgW1jSYpsEarxqgRII94j/x1pxkC2qH04m0o1YkKkUlfl0JOFHTSNDDr7nBj6zLhnXdJteE8bgrz9u1T0JmMwqcbtco59o+V8HXDXuH74/Qz3JdjxHhKPKCNM2k/nOS+t/TrXuQ+SsqUEKWavHQsF9KPzuUdtRNJZloWvJHg4KQ1hrbRhf9vakYrLGhVq9PKE9QVGVJmaT0ih6DQQ+7qFmuSl+SSsZQmgZM1mN7up0lTSOlDK01NMaBCiSAJI6XNsLhkAx6wTSSxJP9sFjbxMHrnGWxuKITM5LM20hOT6gTn6CjBAsK8zpNNU3TqruEtk7TxNf2NXEeKZ1KFrMD5bEYpSRBJ/VjKbSj8mu8fGeb+BIwYK2UH+++lNdg6KWm2/kd/EwX1iElczP1ZIE4p5IEEwjZmjg/MaLcmRfyfVZBYxMyUnSWkyWQOEfjs3ELa9FZJWtDKLeT+tIANmS9y5wN3xHUgZxPdkrSBGub+GxSvtAnG3Rw3zRJo0S2lD/NyPPM97P2QU6NpVuiAfI0p3EOqxNioyBkpOBzt4STgLmaGPR97uiAkuFKMsi21XHCNbvBOlxra3VJLkpp0kQCgs45rIYkCck5rYy+w/qAsyKxFkUor6gjJipzek2iFYP+AGssppHVWisdZdNlLUvkes6iO3ZU4usB197WT31purYN5D9dv6XVOAh93l03Qtu7OL+yLCX1cyyUgwNLmiVoUj8GEpSGPIU8z3wZPFmfrbM0+BKpKIwSAkmSJmincRa0dmgtagnGOFQjyTKpVdTGkCiF1Lj3faIs2qb+Tv06qyS7N2IdKqwp3roMsSfd1k1um8kHm7VGk5AkGaksNqA1jfbZw875fk1wTua3sxJ3kSQJtTW+nHORiNHa0M/77O0O4tr1pesvK8l2l/dtnK8qGD/eFkvShF6v4PhwH0kiFfKj4HLh847Dg33eeP1VPvf5t9GJwpTyvtZJLIcQAtDtPEi87SZlSoPKiVIKi+NqumS9ke8TQNWh0/AZUSuLcTbV2TtVG5MTeXREoXNQeLl1v2fEPu20n8K/7lsxLqcy76211FVNU22iKivx1LZmuZTmTUkTKIoeN27e5K133uGdz3+JRAvhqF/0KPKCLM/I+z2yIifNMtm7lGAHQhprcMZgTI2p2uReYxq/b7Z2NjiS3JdQGgwY9PrkWU8k34uCPC9kf1eaNE8iPhtKUBrjYvJdkqbiQxapKEXrNJ6nNSQpnJ4rVusFm02D7qdUTQ2rZZxDB3uHFL2c9WoT92xx4WQsBGUagj0bp9H1/uFWbEF13L2d+df6tip0c7xu2Pc/G2TZ9Wmv/65rTpdvVi94Y+u1z4aJfebAeL/fj8Zoy0xuHZnwd6ijEwCLpGOUdAGi8Jmus91lnnYBw+tAu10gdvdeAxs8TNhubbmuYR0k+8J7VVWxWAgTKQAaASwKoFWQ9Bv3RP7vpDfk1t37NJUYxMO9PS7OLxhO9rGmYbNec/f+q+wdHHFweIBTCav1ir3JHmAZHRxyNZuzqRr6gzHDwYjZfM5gNKGsNmRZgVYJ0+ksGod53mOxEDmpQX8Aqaaez8mzjDxNGQwH1OWGIk9I8h6/9pt/irsff8jf/bu/xa//+q9z69YtkiSw07y0dAeYC33VdZ5CYNy5dsEPfbPZbJjP51Jnz4lhGRj6ARR6+vQZWmv6vYHUWaxKNhthrkuN2oaPP3qA1gmPHz3rMHMcZ6eX3L59m5OTEz92LJnPrAltEgIkIZAiclR1W0cFGAxEQjyMuQAwBMd/Op3Gvh+NRl7mSaT3V6sVg8GA9XotdWetjbXtdJqSa82mKqMMV1EUaB+ASpOENM949PARw8GQ+/dfQeuEo6NjfvKTn/A3/+Z/QdksyVKD85vHLqM3bATGWJrGkOXsrgbPHR3fOf7x8XRGZQx50hU7uv4612UxR5ZU/I7WUOw69N3vt4hB4pyjKkuKouezfJU4xGlCYsVI1D472DQWRY3KhKnsnGTMr1YrBv0+edw0NFVVY40lSIiqwER0YUNw/j79mA3OjNKEIDBKte0RnlGLoRKD4nVF6VnfdS21m4LygvH3necFiU6o6prGWPq9HokWpQxjBdgUpze07fVt33HXY19wzdlKBTZzt08ArfjIFvy5YY80NfR7OaZu6Pf6LBcrRqMR643j8ePHvPnmmzRNI0DyafzCGPTOskzqvPlMqQCMB9D+lVdeYTqdRtY5ENeRAGYPh8NYN7xb43O9XnP79m02q3UkYD179ixep7uPhJqpWiceaGhiVjC0WUvBYArfY4zUpV+v1/GeRPJUMZ/PybKMp0+fYq1lNBlHicosyzi9PKOqGqbTKd/73ve5desmWlmKIuf+q6/zd//O3+Xg4JBf+/Vf58tf/Srf/c73ePTwAV/92i9yfHTC//QP/ifOTk8FNC1r7yCmODYUPZH4Xq4WNI1htV7Das3l5SVl5WuD0QZ8nXMslkuRe2oaBoOhZIJnmZfs3ETSj3OOxWIhY7g/xFnHptpwcTn1WeIho6P2WdJyzZgdBNRmFckPKkg++bFmTEPqa/00TYO6mPPhR4/jNbIsYz6fR+c9BKhn05XPcvBGsnORaJQkCeggdxVsAxez+Ora+rigyFItlwuKPNTTkX0hgkg+gGhxmLqK9x7AuRb8aufYbnD7045ucK8bHP8ndfw8g7w/ryPYWCEIVPm6uv9MHD+n9toNgu/apdcFjj9LIKxLPAzX/ox31P76fNTg5378rGNbgDx97Rzr/vwsVwr7tlvI+dXvdYCWY1AJqAnk77T9UDpHud65VOKXhu5Ndg/BjRCFw93nFfui+p7GbTofmSqoPPjqszg1bJUm1J3MGAlYJHRBPSAScnNPwhyNRgwGA8bjMTdu3OD4+DjujV/4whd49dX7lGXJ/fv3o49zsH/AxcUFk70J67WQzc7Pz5lOzyUAnec41zCbXUT/JxCP6rpmMplsqX21gQPHs2fPGI/H0hJKcXJywnQ6jTW9Q6D84OAg3k9QcQoE5SChrrVmb28v7h/Hx8dcXFxEUvNwOOTo6Ih+vx/3lGBXBzsikp07EpLdvbtL1A7tHNoX6AAPOga7ga3ATBj7gagQ7JaQvZ7nOaPRiDRNKcsyBvJBgiFhfdxsOgPmZzmc6QzVEGmIcJyMzRi4+JQjglHd6+9C1D6QpgQIa2z7/BGcjQ5GB79QYuMmieb82ZTvf/dH/PhH7zKfVty4f4v9oz1Goz4OS75Zk48L+nt9zi/nzGZLLs4vuTg7J89zJpOJyKMPh4zHI27evgHe76sbw3pTMru84vz0jPOzM64uLlnMZywXCxbTGReXFyxnU2azGRfNOcbVKGvJ0oQiz+j3egyGPQa9HtnBAUWvoNfr+wyUgcgoDgZSvztJozKRtRatRJrTWYu2IgM5GY54+MknXFycs1jO2ZQr9sYTellKlmj6vYK7d28z3h+zMYZPPviIi9OziCkMh8Ot8RpJM9bhTIMzTQRuhbiiPfjo150k8YSAYMdYb29L5laW5+S9Hs4YrBVit8szcI6qrFAq43K6ZDpbc7C3R5FnpKnM6U252poP1ibgVKd0mkIlmto0rNcr3njzVdabDZ98/AkPHz8lzUYeIPMYgpYAggKUk+xUpVRUr9vdc7ZsLBwOASi7gfEAtgbQUqRM24Fuu+cGMrRSolSmn8eaulmHIPW+u5iXgH7ag4ZtIof2dq0jBC8IvxHz0JT8204UEbvUisY/SoGJBG3/6U5gLnxOaw0q8QHu8E/F4O1uIkvI1g77qtZaAnjhXhCpaeccTVVSVeJrNaaJgQsJlGXkWUug2CWXih2vsKoUsrtOSXRC4jOXtdY4IzU5QybrVpBLa7LMUhvB+8qqotmsyVPtgec8ZmUDcQ+TvUbH5+z2Tdf20FrjFDGjGdjyOUQOXQJng+GInieiAXH9DxhSIA/InNO+TVQkSRlTd0gKErC0xvtBfh44P26yNKNxcm+h9FJ3PhhnaGqDNkEiN8E2NavlnNVSMCzrGpbLpd+3ZF8USexWkaarcNK2fYJTmjzPOnauzNnaJwTIHLQxqSL3e7EQX1r7y1rLfHrux1kHqEcUb0KApTsHQqwEHLOObSQqLlB43NKpthRWYywFCXVTk7gW1nbOoXx/6BB0d84HQzQWGfdhPgV7qKlrSv/sw+GQtJONHAhyXUWAOP603LdKU3SakaUpibWQSCZ0kOFNsD5AlW2NJ60l8O8cWNOQGItLHKnKUboXgxtS1kyCnk0jmc+NTyQhCQQ1P9ezBIehrr2KgW1wzpBoqWNsrSHV7fx1PkEr7CdpKgEvY2qKTMdSAjrbLsfY7w3EuzbgEr8uq7asT7AlghqPtSJB3viszzZYIwH5XQWaNE3ApR73Fywo2HlB2j+qXqhWMruLX2sf8A0B4lQrrJZkgc1ms7WOhLrKJNLm1hqM3Q6MN8ZRGwtJIv2tk7jua3/viSdJKMBYQ+aslJV0ISCqpYyeUqJAGVpDQRKcEaWDHJbMnXCSTrBW0di6nSOCFAPSNkVRSJDYCQYj624GiZD7tEp8gDRBJw0+NR60xjpJQsiU8gQmQyJJ4iReQcVpIWlpL9+stCVJFdZmWJOSNg2VUjSq8XNfkTqHQVSWjFMYpKylNJ+L5K0w32S9EJbHddBCs1nFPQgacMrPWV9+0RikZIWnmDl87fBOMB5PJvFro3SCbdv6Jf5vq2bRDR6H8+V7AvYsCVy++7TGGalz3ctzxqMRB/v7HOzt8/jZqdybSuKYbaqaQZ7y5S+8wS985XPsjYeU6w3KJR11MQAjQe1NnFmAqPmmSY8s6ZFqkUMnhXVTcnZV0lgZq9ZUKAtJkok9n0CSaqxx0k9Ki+3nRFnBImTvclOhlSMrcsbDnpDItJb1RSUkyJwKKu9Ka8ki93ab+BY2kijE1jEURd8n5ogP0pia5WpB3TT0en2SNJe5WNdkWcbtV+7wC7/8x/jiV36RxXyDM5Z+L6fIUxIsZVn7dXxFuapjqa3NZhPX9eBZhWSioigYjwU3DvFQsXs1WZaSZaJElfm4YZqmMu+1ivGI7j4X7AWlvDqQXyfrRhJJ88wx7GdMRrdwzrE3GZHnBY+fPOHy8pwlG5RW9Hs91psldbPBOsPtG7cpisKr0oJSiSeOiI0itd4TQHvSlAYVnvfTjpaMGJ6jnR5d21gmmdjHXYWL7vGi79uNIj0fUYp+RNeet7v3c82VPyMc+JkD48FBi8Zkxzjf6mAPPJRlGRl4IRDdDbruGkPhul2wqGvAdo8QwFytVjFTIVzLGMOTJ0+ek8zufl8ImrRySzbedwi2h+w6IMofBSMmPKdFYVWKUwqDI+sPscZw6859jk5ukaYJdVWSJlIjIlx/7aXQyrKkKkuWyyUKxa2793DIZnRz74i6MewfHNLUFp3kvi5EHu8x3DdKYTA41UoLOeco+gOcM6S9FN1kvPHGW2idcuvW7eiEddERreSZdlUBtsFLcea6pIa6rrm8vOTs7EwWkKzg4uISpa7o9/toLXWinj59ymAwoKpqTNPWF4IQ/EoxRjZFYyyr1SaSE5yDjz/+hGfPTjk4OGA4HOC0GOUB2AuyjeHo9wc01SbWFgRiYC+M5W6GSADqdh0oa2pwqcgba810OmM0HHJ0fBzBNG0tWS6Z7IulECv2k33w7emsOH+j0ZDJZOIzI2qKIuPf+rf+F/zgB9/nBz/8EefTDYd7ASxom9zhUA7P0HZRGm/76PTRCw7nYFqVfOfJGb9892acf4G9do1wTAQfuhJeYVHaCsRyfYh9F7iIwKTT6ERjTNi0M2xV+lojYpBYA5vGRIdM+7UkZvNnmXeA0+ishBsJUCGqzaqId6Lau44gkjR0NOiDUam1iCJVfr5qJTL9zjl6RSHtY4MhWvjsVKhrGdN5URBq2SRas14tY6C+22ovarvnMx+gW+ejS1ToMpg/vJzzyiv3uDg/42B/jAYqL83YL3qYWpyrhw8fcnJywmAwiKSg0EZZlrG/v8/+/j5XV1dMJhNmsxmPHz8myzImk0kkHgWCiXMuZn93A+shWLparRiPx5yensbvtMawNxalj8ViEUGP9Xod1zoJgmeAQ/tMhuDwVpWw4rMsjyCF64C1y+WS6XRK0xif2VVwcjKOcqxNI+z+stywXK8ZT8Y8efyUBw8eonXC/v4BFxeXTCb7zOcLbt2+SdM0nJ1f8uCTj5nP5vzu7/7P/OJXf4F/9d/8N/nud7/N3/zr/wW//hu/wVe+/FX++//+v+fxo8cM+wM2640HKkuqpiRNc7/HCDhZVdIvjTFYC0onXhVBiBlKiYwsDqazFWmaMZ1d0RhDUzfoRNaPxhhZL4DpfCVMeL9XNk3jHSUZO9JeXvnABelYaOpQNyjQODpZ2U5qdYb1UyFSWyGTabkSkoOtW7DEYbHGiPFdW+88gHMSRKlqQ+OsGMw4XBPqP2nqqiZNUmrToJQHlXTCuq6FAY5rg+HOYX3wXPYH+XaFsGMjiWZnxn1a4O/TgnifNXD40wZD/1kKiO/eb/fvXWlL4Fob7tOuGT730x7XfmbntS7A9bMcL7qvn/b13XvZDba/4BPXbO8/29jY7Zfd7+46P91/153zki957jO77f9Z+tk5IqElrEFee1P2vTPvxj51ND8JUuOt5O9WUGXSkOzxvP8FPqinMBcOFs+TbuO1UNt+CsRusNqReYJYsNFDcCIEh5VSsRZ1kiRMJhNee+01iqJgMpnw+uuvk6Ypd+7cIQRigwJXlmWs12ucs4wnI8bjMcvFgvPzSw4OD5kvrrA0zOZXEvzKRwyGPfI8Y5j2vQ0cyo4o8kyC8Ov1msFgwHw+B2TPDNnd4dm79bezLPN7aiO1Fr0/MJvNYvY0sGUXWGvJ85yjoyOMMXF/7/flvkLWerhWIFYFP6JpGk5PTwXsS9PoC4VestZGolsIVIeMeCDaIcG+78qqh4z8oKiV53ksA1PXdTy3W8M82Cjr9TqOhwCwBh8yXDdJEl574/VPHesvngO7Np/zatBdS3I7S6QbVAz9tjuWX/Q3EEvXdD/rnHtuTXUWlG5AOTSJL7Fyyv/wt3+LTz4+ReuM+2+9hk1TKgvj/UO0cpxfnGHWG/rDEa+M9zEGAd5Nw8LX13v06FG064fDIYeHhwyHQ3qDIXt7exweHvLWW++Q+vJfpjFs1msuz8959uwZ52dPuby84OrqisuLM+bTGfPFjOV8ztVyxdOLGdY1WLuJz5kmKUUhWeaDwSASVAbDIaPDQw4PD9k7PBTid5Gh8hSlYelWfHLxgOnFFYnVrFcL9id7vP7661jr+Me//4/55re+wx/7la/x6utvMvnCkOUrC6bTKRcXF8xms1h6LigoRDlmWpW28A8nYHieZ75EnVdL69QYD+MiKCaI3SxBryzPMNZ6/08ClsvFgvOLC+7ePmZvskddS7ZMnufRl3auDTiABJmdduBLOTSmIk/6vP3m6/yVv/wX+Gt/7T/DKSj6A+9PuSi92VQmKgUFief4fP4IayiEpIhWBaxrw6nu/5TaUgXqjuPd/Ux9RlvA2paA214z0KmtBCQkbdVPjFD3c0flAYczGud0mwW14yeL7apIkwFSf1Ztqd9t1db2wE8b8G6TR4IfFNa8qtpQ18T1OPhLxhjKxisREJQpWowkBIwl01ST5ZKJmCQtLhbusRucquuasl77utwKlBaQXIkvb1TjayJL/2nVjm+R/k/o0+7ndV2xWs+38Losy+LeGnCASD6/pt+7z66SJO7dEVvx58u+JfvFZr2hrurYtuEIbSQl9IrncE1rkzjfAkF7U26oLfzSr3wday2PHz/e2mOOjo488buiW7t1dyxHe9sSMVcha6WdvhcFrr6v0R6QEckGlprkYX9USrAMlbZ+XAyr7E4RpyLWsDunVHhLSaJAd/wFHECkcltMuTuvJDtQ5lqadrBIa1E+CKoC6UEagnCnIajallhRrfqEc3GaKaWkhrRDVAkB50uTaaXJvdRQtSmZdUhtYYx0+yT0Ryw70BhqK/tY6u89UYnfTz2elgh5wRpFolNvLzmqShIOEqXIMo9dZ63CUJtA5jPTQ8eEtcY0vta6HNrbU0tfykwrjfILY5ZnnXElQR7bGKq6ZH9/n/5gAAqWyznGWDab0tuoY0aTMY/4uB0PtmHYK8gTTWUa//3iu8t8VpGIGO532Be56MbWcc6L6kIZbefuOh2SKrrB7jRNqCpRWEFJRqxzbK2PW+Qmj19kWUqR90gSUWEJKk0BCw7EytCvQb1woWbxkWV85yRJwsnRmHKziTZnsNudNSgfYEuThNp49ZeqitdP0xTloKnKFrRy+IQCg3DwVEvuIOD8kqGbRVKXieu3ThR5qunlKc6AsdJueZL7gaHIs4JECdGkrmsSLRm0LVnDYWm8TL98q+s8uzRpG8AOSRSuM8+6JYramFE758HFevXX+eZdkv0ukXz3CCVchWRlQGmcV0/I85yqroUU6Ky0nVIkqQKfua+sJVgWcj9trCAc1/m8SSKlGdpAuKylWoVEkjZTN8QDQl12DexNxuxP9hiPx/R7vahSnKZSxkEbK5L0WvP6G6/zpS99mTu377Ly5XqSJCHJdCcw79i6TR/qSdOUfr8gS3LZZxNN2st5en7KxcUFdd2IgoUngwVyQlhPrbcDJdDkbQO/Tsr6LN+bJjqqTQZyXptcKbfT3We7bduNvYQ9GNfafV1SklZSiqMoCk/iScmKnM2m5IMPPuDRk3NmsyUKmAwHjAZ9+r2MNM231GeC33d0dERRFB2lryTaXN1/QRmsGw9MPJkk7B/heZqmVdZs69sLASHzNgudvSQkRJm6oU5T+n0hHvZ7PV65e4/RcMTjp0M+fvAuV1cLenmfw4M9nLU8fPCQal3x5utvYZqMzaaOCUd1LcrTLYHP+IB9p9TOpxwvmnsvwoGUCkS4nwZre/G12u8DOkQq+VQL+L8IY/qsmN9nDowHsGQrYNgxDruszTYw0TrlASTYNe662Wnh7y5oERbb8GBN03B+fh5rhAsLMt26btdI7jbItjPzfHH6VpbXxWsqpRgMBlsAWzjHGkPtC6hkqU9DUY7aOFSS0liHTrPgC4ih5RzFYAjO+UBGzWotGYB7Bwc0taHxLI8gaVH0+jjbZi+EQJ4wbLyDqmQDtX5RCs6n0n4RVgqdpLz99jve4RCWWDBYlPLSs3XT+Z52UQw19nSyHSgPWSUhgJimaZT3LXo9BoMhs9kUrRMG/YGwL5MKa6UNe77e9MXFBQcH+6SpBM7KsiQYiSFbRCm4vJRsSqUA7cjyjKOjI7Rua92H+vZZmpImKrJnAlAXxlcYP0Bc6JRSW5nnSikSJMt5PByhlOLk6Hjb0HJSC0j5xbuX5SitMbUY9sZnl/T7cn+hlqLI41nG4yH/3v/6f8V/+L//P7DcrKmbDXlqoxxLXFcU1I3BGL/Ymp0ARIfJuHvENcU7Ot98csrX7t7YOicEYXevcd1S+Pxr6gWvB7AifIm0fVlKhhHOkWYpta8pTZZTVaU37oShHxlcsptGg3ez2ZAaQ5HnZHkubLg0FYln03DdIhiw8O5z2jingzOcUXhjV2uNdeI4mrrqMFkt/V4/EiNEQt1v0FpT+z7u9XugFNazz6Uej9lpp27g+/ls/Phb50Nu+yQ0qs2K947Stx9f8Jv/5l9kbzxivVpgspQ0SZnOl+RZwWKx4GJ6yWAwYDqd8uzZM7l2Jp9vGsNsNqOuax48eEDTCAPdORfn1NXVVWTUHR0dReJPkBk9PDyMGV9hQz46OuL8/DwCXavVCo2izEv6/T4ff/wJH330EeOxKDZUVRWD19Ay28M9hvYQ8oGNjlWY23Vdx7rlshdZtJ5z44ahqmRuTiY56/WGq6srNuWGs/NzRsMRr732Bj/84Y/48pd/ge985/ue5DPk29/+LkWvx9HBAd/93g9JtebOrTscHx3x7g9+wK99/df4vX/8+3znO9/l1o1b/Lk/9+f54L33+Hu/9Vucn52J44ehbDaxtES5qeNc32xK79AKc9b5YK7SPujtGeLWy/eHNbL2tevD+cYaGu/sia/iM052ZPpcN7URv4d3A5wu1K3Xcc7IUqKwtc8+R2pvOiUs3W1Clb9uLD0g1246mS9hjjuEoR2M6LgeaU3jrK+5ZX29ImRM7IKLnWCBAI8d4wmfvel4yXr50wcbd8GrlxlhP2tQ9p/VI9gKIavyZUHWP6qjDQps//2HuYeXffa69z7ttV3Qdve4fpxsnxfBROciINm99m7Q/bp5ed29ftrf17123f1eR6TYDbrvnrd7Xe0BisD7Cnt1DIB0wId4TSdKM5LFoKLEq5qmmKuW4LvdLqL64owhTcU3kWyPkL0p957nBU1TbxE3j44O+f+z92fBtmzZdRg2VpOZuz39Obd5TdWr7lUBRRC9CQdNSiGTMhmiSEoh2f5ghML2h/3p8K8j/OVPW/pyWOEPh6WwadoUCTYWwaBpEiAAkgALAFkNUK9evfb2p9tnd9mutfwx51y5cp9z77uvCqBoh7Ki3j1nn9yZK1euZs4x5hwzBGA0KuCcx8nJMfb3D3BwsI/j4xMcHh7i5OQYTdNgyrYkINnjFkVBmcdK6ahORCBAA2tHUYFDKQKLnfNYr5ewVmO1XmI6m8D7DsvlGuPxGE3TRHBC7FopVSIAvbUZqpKI3LZtMZlMUFUViqKI6khp/xwdHbH9VkeFmKIooJTi+uTT6C9JQJsAh7Ifi9KM3Ov6+noge26txf7+PtbrdfQP1+t1tNnFD5MA1/l8ntiXiDbIer3mUkiWbTQfM817kqWN4IUAeNIX0ykRr9JmyQYXkH4ymWC73cZseVGtEZ9IiI75fM5lgn68te82MQ72AZN5E//z8u99nnakgeypzyMARPQVjQeQcT1Xh/Pz5/gb/9Wv4PzyCvuHhzg5e4CDwzNM9mYoCotPH32CFy+eYr1eYv9gH3k2wng0QpGPIwB37949CNFVVRU2mw1WqxVWqxUuLy9ZgUmkFEfY3ydgcVSMkNkMR2dnOHv4MJKFBKp1KNcb3CyXWC0XWN4sqLbicomLJ4+xWq2wXC2xWa+w3ZbYrissrq8RcMl+toZVHuPRFFmRYzqfYTqboBjnsFbhenGFsc1x9qUvYzbdww9/8H18+umnUMHjp3/mZ/DVr3wFT54+wz/4e38fX/zSl3F0fIzJZBJVmKy1UfY/Jf4kGGEAwvEh4F7T9KSt9zv7StCoqxajArA2h84s6rbBaEr31oYzNxGwKUtcXF1hW9YRGDbGosjH8M6j7WgeG50BxiFIlpUHtLJA6AAPuLbFfDrBT3/zJ3Dz7/4Z/M2/+yswViMv8rhutG2HIqcgR6M1MmvhQl+iSZQZUvym38/0Z45ls7Ov9vttnBH0u2wvim3cxLcKKkQwlxJCU9VDBvrD0BfvXO+TDA/J5GfZU5MjZ8IklTNPyRxrCh6//b4pRLtzPZFbtT1GlyqASL3eSKb6Nl5bxpPWGsZqTPNRvz+HMOh36b8hyST+Vx/IIJLLIiGc5xZKT0gS1TkEcoOhFKI8uxBMXduyegBnmGkbFWeoSQpKm7g3ydgQ/1La5nk8AjvrFnosUIKVqMYsZWUqJWtrGnBh0PkO6/VyAIQLSE6YAMmd0r89liTkkTFkJ0iglc0KFLMZfvGX/iS+973v4aNPHqOsWozHFlk+xmK1IR+NVUJkLNG+pyE1zZUi/9h15OMaY3Dv3j288847+OEPf8DluSgYnvYnTTaREtrSwJiA6XSKvb19aG1QlltcXr2ANWP299hn5LEnmZhaG3ivkzFAoERPotGhKVU6npPnBQdTB8Zq+sCY+J6MisEg8VkBBK0RS1vzHhhC4CxPycKleemVglGEdaroD3J2nlKA9+g8rXlDGzQwxqo4qK7k4CAX55ZgHjKG5PvWEDGiVL/2ZvoubIxKBFLCCclS5xmpDLquBYwlrBVDZSGaX5R57L1nBQeDTCvojILG25aCB7TRhP8GkP0RNIyyCc7ZwGg78PyV1qhAGE3OQR6iFjcaz5BnlCkJpbFeLgZPZC0Rc3kxRt62aGL9bh0DSTNDWIfrWsp61wYGClkxiSVLuq6D6wIcugSj5jUALuJG6fqVBjgqRTXnU44i9TPStS8Ej8lkRLLJruW9JfCYo7dmbRbLBW2322TvYAVMVkhr6hJd2wLBEW+oFWdj0zqoFPnHhktJpsqJYo/uBpULJ5Gu08r3yXwRO1SyvhtOLu/7JQQPY3OooOJcnUwmnDjRMcHZcx+uA2A4yEoHBN5j+v3IwiMNuhq2mZ5XwSsiwFPOqM/iDzGAqnEdOt9zQDLHdknStG/SPUnaLeu2lIOlw3PACADfQalAyfBewfuewJT3SRt9GoxB60GQwJ70nujnNC07inzHHX9X8edyuLaLdvW4GGE+m2E0Itx4s9mQyqMnae3pdAJV1thsS7RNg/39fbz77jcw39uDQ4DiJBhtLWOHPQG/+16yhMzVmtZpm2WwWYYPPvgYL16cszJjhrrxA+JX7M2yLDFiP016QRsVx4fzDpbl4NPxkCpw0fsbcmnxbSV4YMrBSMCKYJ3it1mbIR8VyNnPq9BgNhlj72AfB4fHyPIxAINxMcHDe6e4f3aMo4O9mDUtryWdXzIuaX/P++zvuG4AaSmaEEiFoAMFeVJQHvkmYoO1bUs80M6zSpJQURSYTqY4OiAF4qau4TriB+vA6tWjAtPJGFlmUIwoKezTRx/hxbNL1BWVqHrrrS9gcXWFH374Ph48eIDRZIy2VthsNiiKEeqq5b2QVEQCqC79j3vsBjNIn/43gfulbUp//jxteG1iPCUj5CZpR6Qgk0RwpkS4nCNRWOLwiOzcdDqN15BBGKX8QMBEGvUvmdO7EWVaaxwcHMTNUzaf3YVUnuMugO6uc2SxHm7SXK8J9LvzDq7rSHpO86Kqh1Jeymiqw9W2ADSy0QQHkxHJuHceNsuhRRJHyWADvEQjgz7XWkPElwDVS0MqzTWu6XPJqkQgWRbDQFNvZNE1vSeyJM2mFnl0ee7NZgOlgfF4RBH7DCJJtrZkdaigMRpNaPNtO+zvkeR8E1ps1iWRhWxs20zxGABubq4BkNEnoEAIARYkBTwajTCfz6MxMtubc+ZMP+5SSS/P0V91XUeQUYzwdCwTWeYGRpTcu21bkqHhsWW0JkkxBhnjHPAkrac51lr5AN8QoDNm+faq2qJpqJZiXTc8nono+9KXvoS/8lf+Cv53/+l/htYpWFuCtTzpLfOeTRGIZJSI7GMcq3fM27sOpYDHmw2+++IaP3l2mNLWg3rjemc+SDCG9NHgO3dQ4mI4RPsiaWPXtuhsBmOzWIvJOw9jDbKQoeP3D143pE40+y0xerNp+sCMzGYwDLoE74kQ5HXGhz5yX1qik/dKwEBfP0wer1e/CPH907jN4UNA15IMtdIaxYik813XoW4aZDlFmQZ2Low22GzXtwwnag33oUzdO96ZOJ4Bw0U+MJuaGmmt8/i0VRhPCmgdMJ2OKVLSORzsH6DjoI0JS8I45+LcChU7wAzStW0XM6TkPAGe5/M5ioLqSdO4rrG3t4cQQixFoBTJlY/H41gXdLPZxLqmIVDbG4603dvbG0Tfk7y6jsaI5mAfyjpxcT7KftJ1HalxNG10lqUkA2WRNdDa4Pnz53j29BmcdxhzJF3bNAiasr6kPlxVNVgsboAA3CyWqOsW14sl/thPfQF/9s/8GXz/++/hi2+/hZ//+Z/Ht/7Ft3Dx9lt450tfwk/98Z/BdDZD1zR48vgxjo9O8Rf//b+E/+L/8l/gcr1A0AHaGNQdSTxNp/uYTmf46Z/+GZRViX/2z34Lz58/J5m0ts9UENCUMn00XCCyXwxI2ZulX6F1rFElxPitxUKlZr6QTzvzH6AAoPj3wOOud/xV8PEeaQTfzkAejN1b80Hamqw3txqSuPMKAbdqTu1+d8ep6Zvzh0dWvOqz/6YNw/TYBQlf5/i8hPCrzkkN5s9zjbvO2x2jdxHNgwCPnXN/1Oe/i8TdvVYK5L/MQUjt5tchnvnTO++TgvA9UNJfZ9dh2X2Gz3oHr/OOboMC/ee7trb8X2ytuwiM+LNSSJ/bmGEGHq1zZvBOU4deKQXFMqZZnqFt2rg39e8AnC0x9Gn29/dxcnISFahmsxlOT0/x4MGDqJqyXq/jORKA9eDBAzx//hzHx8eYTqcAgJubm0iyKqUGUubj8Rg3NwtYa3F1dQXvPR4+fIi6ruK+eHp6HAnaosihtIqZ0dZabDYbzOfzmOGntcHV1QJgkGG1XOPo6IjLcEwiqGeMwfHxcdybhajuAWU6RGElhICzs7PoW9V1jdlsFoPYsizDcrmEMQabzSZKxI9Go5g9UpYl8jzH2dlZzCSS8ZDWPO9BwH7sCnghQbDpgKuqavDeN5tND1xbG20E8XGkTJbYJELaX11dRbBVbEwBeEQlS/wMkcIWHyPLsmgn7SqW/agHm8OgUS81vsF7asLk8fG6a9srz43BZ3TldK4O11oDYzSaqsb583P85m/8c1xdXePk7D5me4cYzw8wPTzA22/fx/ff+wCPnr3AzWIBoynZL+ScPci2rQQq53k+CGIQmf2madAl8ofbbYntZoXNegnvApwn+340GqHgMVcUBYo8hy0KnJye4vTsjLqOwbbNck1lssotynKLcrtlO3eF9WaNbblFXZZwiw3W2y2quoJ3DqvrCtcXN5jNxhgVI0znExTjgggXrTEej7FarfDD99+HtRY//7M/h+l0isdPn0MpFYP7ZZxIUL8E3aayjnJEsgSImIrWFExOmIgGMJSRlWtlRYHRaIKqKnHIQGBmMzhL9rTTwGpdYVvVcN7DZDlne3u03sGBgxgDqA5pRyGRBGRSsJI2QHAOXV0hzwr80i/+HP7V9/4Anz5+gvWqhuH5G6BhhOAOTEgkQGqWZREIjcH5kRDwgzGYjuWIB8k+QycNd870l/T7iU2bYgJak1w5zXnBhai0mfNCnvNeFWT9IfzFaEPlwkxfWlCIC/E/+wzvfk0he34b66CKUpzMFbBPSAGkw/VFyG2qFd5nbUabKZGOl+kvWeIU6MBlyDyBvOB+tdYCWsouBWg9TGKJS0f6fCwVrgPJrjpWfaLX7mPbldYI8Oich/NE6CqlorQ8+R2ea4F6fqekyOi8A5RgWCTLKzLGaftIHr1DAGUNUvcJ1mbinkOqNDyeoOL8lEOIUrl217UAFIzJB4Qp7Vl0HQnY7pyDblv883/+z7FYLDDf28MsKVEigQ1acArVKwBIvxpNKllZXgBdF/d8UXELAXCO6rIqGCqbEIikt1axfWShmDwmtcQ+2AEJ9skTo99/GE/xXuwwHfGqdCsJHL2l2H4zprfJQkKCyFrmmeAmW0zWuMCKZDS/LL+fuC+xnWd9UnOeJi+CJoIvkuHcFhUCrz29j6oAKJmfgbDSTqnkHQ+WCYhUfx8EQm21CYmtoGAYC/aBstMVKNDTgLK5JcvVdw7KeeSsYKACkbQU/Kkp74oJZu2p5jdCQNcRxUFrFieJkSAcfNdxjXOHosg5GMfwmkRe9JBIpExqIou5/i0AbTOooEiRj0s5DjoDwHhC4zdoBW0d4diB28wS8sFTXW+rM4RgibQ0GkGkThFgNDAqcjhnElyMsoo9B8bImi5YRmYzWM1S8D5Aq0DjhOI64lpPc5lwE8VjZ8RENSVcqTiPhPNwrkVVUenPNOFPxmjTUNBJmQRxydjn1ZXl63kcGwutLXSmYHQGSW5TgVTsYr8qBZjeLtZas+w6jW3Bwmg/ocQ4hBD3mb6sIWH8GhpW52SnMdaWZwUMBzoUdoSOn5HWGtqzQgAC469a83t8Ce7Rr+kggh4K3g19vv76nt+3jmt8CMRDBKlzLYs+dtSDdwLOdv1Xol2SrPeO1xVwdrrug617Uo/5HKWToU1rRtzbwmARjPdM97278JVdf1YCqidM6IYQ0DGGx9MAoXVQllTGQrR3KHhmu60wGY9RjCyMoYAUWVyUUlSasB3aA+PxmDFuC8trgDIaXQCePjvHpiwBsUV4/LkQqGSpIRXUum0wnUqwNfmX1N8a3ndQCMgzizEnKco4THkl6dWUk7sLT5F+DSGwkkdvz8k7M0YTuc82iSSymSzD/uEBzu69gcePnmOcFzg9PcXJ8RHm0xEUY/09fygliVT8Pf4twXE8j10nHKZzcGLTeFI1pbKuQox3sQRNarshBA5MoYCCYkTEeNu2ePjgBJnNyK6R4MZAvoQ2GtZo7M1mePPBW6jLCjc31yi3FS7DNaw2ODk7w2JxhYvrC+xN9zAZTVGMcnRtB6WtDF2QkkcAKbO8Osh0Fyu7C0PaPV5GRr8Kd3tVG/p19SXXHfi+w3/T77/O8drEODA0BNOHS8ljWTwHBHLyIEJ0y3dFMldqkwsoQsRGExfRtF5dGrEn58n1Ummo3Yzw3WOXHN190dJuaVf6u9aa9ft5gDgHZUh2W1uKdtVGwyl9K8oIWiMr8kiEee+QFZYiAR1lfavQk70kDUMSSCngozkznJ6igVIkfSEZgxJp61keq2m7uNmLDKE4zE3TsFNCz900DW5ubqIhLkT1aFzECMzFYoHlconZbIbpdMr1vxVc4+EurxnAaGGMRllWkM2N6hZShkZVEWhFBJ6OoB6AgVxFmikiY9CDzhdHRgyUTpwEpVBXJB8kxB11vx6MDSH8ZDxIHzcN1ZPOjYHhe7f8OQCo0ShmhRhtsF7doKkbjMZjlgajRa0pK7RdC50b+OCR5yOOQjLoOoeqIom7P/2n/y18+ugJ/vp/9dexLWvMxgEePhoGCIhR1yTTPSTGb7NdLz9C8Ph773+Irx7vIxf5tR5p4197shaghWcYSU2HyCHvHj0oDua6+u+GAFR1hSmPQ2ss2kD1ubS1sOC1wlM9oV7WSEHks/MsR9v15QkaUyPPaXwGY2G49lDwYTCHA5hWUyoaQmSQ9ht113UciU3Ar6gwULRrL21GWa6kjkClABzqikDqMashdB0ZDE3TkBTYztsa9EvSb/I3WfLFwd49c3d1Uwp4vqrxE3/sJzEeFRQ9ioB8NAKgSMLPBdRljW29hc0kMlvjyZMnwL68N1JkaJo+SGW1WkVyXMoOlGWJLYOI9+/fp0x+BukXi0Wco2IAPn36NGaHrddrHB8fkzMDRKL8nXe+iEePHmGz2aAsSzjnUW4rACYS8DJv+5owfbvlSIEm+iPNc60MyfRXNc/zNio57B3sxWCI9XqL8XiCjz76CHXd4MWLF2SY1jUu/tGv4vGjx/jG138C985OCOALAb/6j/4xbm6W+ObP/Tz+xC/9EhCAw+NT/Mav/QbWyxW+8Y2fhLE5vAoo64rk5csK69UaT59d4vGTF7i8vMTV1XWUTu+BOAFISUJMaYW6jSH0ADuhULQHSM06cjoETLsdcesxJJ7oPsORFRQ5BgH9vke/BKjAY1RsgrsGZmxlii7cPi9C8WxA9icmX0r39KCgby1A4dZyuNucO8ve/AjH5zG4/n/h+CzS+kchUO8yrD/reJ1z7hpkL2vvXc/1evd4xd2Ta3zefkrP6QH/2+28Tbjbnd9lLtP+KANfANuUyErt2d37v25bX3W8ihjfPSeSFztr0e37UIRzetwOdPUEHCb9aK1F13WRfBaSbTqlOmGiZlKWJabTKe7dO8Px8SHyPMPFxQWOWDJZ5JsB2k8kMDe1AUR+ezQa4aOPPkJRFLi8vIxZ3kLAivz29fU16rrGgwcPSDFFU5a4yKadnZ1hOp3GkjFiqy8Wi1h/uxiNovz52dk9iMxcCIHtQ5ISLfIxZrMZE977UIpqolVVGzPSxeY/ODjA6ekpZbVxwJwEHSnQfn10dBTbJEFwdV1HVSbJEB+Px9Gu7roO8/mcM256O178Ovm96zpMp9PoB4psuVIKZVnGLC0ZI6Jco5LxIGS0BDWmxJN8X/zEg4MD7O/vo6qq6INKO4REFyJe/CHxn0TaXkptyRgTyfzNZhP7RXzGH/cITISns0xUE+S34fkvAzBv++/xejsgXrxOJM8EvAtMligYrdHUDZ48eYo/+N57+OSTJzg8PsH+wTHG8wPMDw6wd7SPZ+cX+MH77+Py8hrOdRgXGZrWAapGgIHzwCj3BOIzCGmZZJoAmM1mMTvUdx1c26CsKqxWa2zLsrfnmpbU17oG7aZBVW1gbYaMgWYK3s+jRKo1BvsnR9gLPWhLtqOLGet1XaGpa7Q3LZbrFckhNzXqpkRVrWFNwOLqnAF0j9Z3MQtOa43lzQ2eP3uGpm7w9Xe/jm1ZwzvyXWRNSfcA+V4IgbKWpf/Z/KEAYKq9GQIRGi6EGNzjfb/mU3anZ7Ukjcl0ivV2vQNeOjSNg9IZ1tstVusNqqaBMRY+eM6eKUjq3tccuExto3ESo/OhFdlXgbMDD/bn+KU/8Yso/9Gv4tmLC1RlRSCfzeHZ7zLGwAcgy5BkNvWkU0o6KNUDYbf28WSvG1iNd4zrOCeUTuZDOid6+1PARCFMyTVmAiL0AVUiSR/JjIT8TueT86RsRtdUcAyeOtdjWLS2cdbbTkbhYM5KTdawY4/EvgAUB7/K3Jc5HCDAfojPJ2RwvH7SEyEEitIJREJ59CUK71pLlFKkqAjOrFaKMsd5fitFpAQUB/cyeR2SduzaDD4gKub1QVMcOM0SscZQFry0WUjxmLXoFfxO8KJWHjaRhpV/tdaD5/dcl9ojkCKk+JnBw2qpAZ0Gc6uItbVtAxcC6mqLjz78Ia1tkymM0XHN0YrKAEighbzDfoxRwo1WGlmmEZTChM9LVTVFOY/muR1IuabPFwKiny8ly7QycazTvSnAQ+ai4iAca6l0Rg0OThi8f+kzxPEl9omUBYxzIxmHISTzmiZkjAGLbU5+TzFCSYCQuWKtJfItGcnBEWmuYGHQ28gpbu2cBzjpQRTMZE6FEKKao+ofEFZrWLNrq/KdmaVVoABMcNCDZE/SWoCY1AUEKM1EipLSQRxUo4iwIYyXvufhKYlHZUDo0ApRi14KHADVFjeyQIfYf7IuFIaCkbTJMM7H0JrKurmWskjjexs+JiazPW4HvcfWdfBNDbAss0hZu47WTVLEZHyfk1eoLYYVkVz8P81PMMmeSn3TOmSMoZKmMrcZKzfBRMwjgJPbuO+0sbBZzhnhY2TZejAeae3WUCIV7hzSGAKlFKaTCZq64TZl1CeKxpnif0m9gsa1NTkT4xrae9jQr5kyx1JbzmSj+Fkf5KXieqOMyGeDSwwgJhrJ+BB7AYHaUVU1yvWGbKwRJQL52O8Z26t+gIkTKsN7IPML6TG0M/sgFK17dUKlqY54ukcoRbXKFQC4XilQx0anwWm07ktgFAZ3HM5D2gcFD+OAHNAFpMyAJDkFubggT2HIBYntpaAGWDxHZvCY7YOfBu3awR4UAMuJo0WeRxyUt8L4fj14PjgPbSgD24cOTV3j6bPnONg/wGg8gs1myDJO9JMukzGyM1aNzWm8S+ChIhJ5va3w4uIaLngYkA1GewQGe4XjyFzxtYyxkJJcsb640cjzLKrzCime+j7yPu/CO1KMot+zOSgPiJyXfEcbA2OplrfcT1RDrbW4d/8+miZgfzbHw/v3cHQwg1VA0LovE6VSfL3nCdquY+VL4uWcp9KUYpu1HWWBu4C453SdY+n0wLYG8QUdB8bI+AmB1DMDEEtcOg4I2Z9POIiBxpvn77ZNA5NllDxoM+zt7eP05B6881hvVqjrFucXV7BZhvFkCuc7VHWFjN+T61LV6xCf+VWwzu74/Sys866/R3tz51qv+n5qn9+Fh6XXi+eyvZTa8T/q8drEuCySu5nh6QIyIG2TidA7Z71sumz+Al5dXV3FLAp5+BTMk409gIxxkSSSTIr0aJqGan+xISBH2unRwB5EePUTcWCwqV7OZkCwBcAHqn/cdR3yLMOoKGBYgkWF1GHsQQQx6gIbfEob3ljBNROo/kMfUWWQWTPI5qXvkbMTvIdrGnRdjcASHMaYaESVZYX1ZoNys8X19XUi+ceOWUCsNVZWFfI85+xvImT29vZI6kMpTKZUb81yYMLBwQFH4hfcZwZtRRI5dd3wItLhwYMRimJEEa6ZgbVAlvUS+NLXkv0hxrd8LlHzgaPqnOtAVJoi+S1e3PIso771HmVTo6lKfPDBB/jGN76B6+trTKdTqADUTU1kHJPCBOplJOXO9T0kS6RpG4TOQaT45B1WVQmAszR9QMFSYMuqitFAeZHj+uoa84M9NFWL9YaML9f1mREAZaiUVYO//Jf+fTx79hi/+Zu/DmAVx4o4Bi1Hz1OU73B80yBGxMaGpsrOaSFg1Tb4eLHEV48P4kniDEs2tRiVQpDvkuK794n2AhDHam9a9cS64ndUVRVG4wkEfOzaFgEBhklU13XxvpoDEHwIlPElmQ6Js1tut1SHnMEurTUUA8RifKT90Tu7Pr5fJ2oFIONJpMEcv1PZqH0gp4nIeIrGrusaARSdJ1H1FO1Mcvy7fSL9cmdnvuTdyad358DSNf7fP3yKP/s/+pMAO6GzyRjeByyXN8hMgVExpox2nyEvyIiZTCY4OTkB2v5CZVni+fPnETw7OjpC0zQoyxKz2SzOKd853L93DwoKW64vrgDMplPKFmta1HWD589fYLvdYrVcYjKdxgy1rqX1s+scLi8vsFqt0HUuOveU7baF94gytvTeKGpd5GhjvXj5PxRLWvEarDWMtViu1yR/IyCr99GIW67WADSatoKxBmVFWUQHhwdYr9YoywqN81hvS/zWb38LmdE4OTrCF958E01TYb28wT/77X+B7334CX7t138TZyen+PTRp/jOv/o2nj97Bq0Umqalen6guoo0XwhIscZyKQkFH0g2XICC1IrpXEDoWoj0k8w9Ae8Jv6Jrx8yv3jYbDDnqq12j/vbAihHkiuWLQaR4UIjR8DJoVbxIYuQg7Fgst6MOlcj3IcRnSq+hcAfBsNtYSZF/1Sm3r/K5j7uMr88iEHf7v/9iesKrP7vrDruXvKsdYfdSd5wjcv1y7Gbj327XMKtQrrv7nHSvl2dP7z6YOIm7T9Bft18DY3MSo1mCO2QuxO+n+8DAAB8CebdBvXQ8pu2UMTs8UvJ5167tHWHNDnxq4A/vEMUcQtIvPaaVOAi77UpA8KQNQEosv9oxSq62c97Qcen39p0/85qgBBzkjMIIVoXAoD4781F2UsXhQH3FoCI3IsvyGKCbZZbVWQwT3PdxeHiA+XwPXdfh4GAf0+kUb775ZnyX9+7dQ87ABBERJAF3dXUBYwzvP11UURHi9PT0NGZ9lWXJqjVEKJdliYuLC0yn01hzW7IdxYZtmgbj8Rjz+RwHBwdRHYXWe8oon0yoDm/Ftnhd11EZ6eTkJBLurvPIbI6rS8oyL7c1kchaIfgWXetxeHiA9XqD7baMqiiSJba8uWSAlLJrpKTKbDaLdr2UJ5IBNp/PoZSKvprI2UqAssijCzEucz2tp962bZQen8/n0ZcTKWkZu3mex4x06b/FYsF7dUbvPcvQsvqNHHmeEwA1HlMm//Ex6qbBdDKhEkccpX+zIKK76zpMxpP4fVL5oRI/AqhSXXaD8WgMyWomVRmH6WQapU3rmmpwbtYbbMstbm5uoprWrj/6eY8ewJPXoQbvRoCO17pWsqa/DKhI14/BZ0AEAYX08Z3Ds6fP8fu//x6+9/vfh84L3HvwFnQ2wt7hAfYOD6CUxm/99u/h/fd+gDyzGBUZ28wNmrZD3ToUTYt2PIILDpkj6UHnPYo8R55lKIoRxmMpccU1IZ1D05F9KUHeddtSsOF6je12i7Zp0LUOVdPEYNrgWRKZ/YXxbAxje4nkLM9Q5GPk+R5nZpH9FXyOpiHJVOc6BN8BocFmucA/+dV/iI8/+gBVWUJxTdW6bXCwT1mcq+US7/3BH+BP/uk/hbfffAvPLy8oaFprAtnUUFnA8DrdJeCwUgTE0jiVfUAhLwqU9bAMmpBoEjwuJXUm0xnC+XMABIgba6F1ixAAYzPcrDa4WtxgsyG7V3kPbWi96TLKgGk5axw8BgCyN7UyEZ8ACCCsqhJ/4hd/Hk+fPkXTtnj2/Byd91Aw8Goohy22bkpQKO4XUYYCk0q3SPFk3MbP73SEe+KCTnkZANiDbyEositDWleSM/0T8psIRM4ujj4z+YtOgFPn0LYVOkfqVQCYGO/rlAYBqE1v6UjwVzovaX/lLHqRlgNu9Q3ZRr3stdQZDkAkGqL9hOEYSoOXUhIRSb/tBtqk/3eOszotAbtOzo+vqM8+FvLaeU8JJ0htHHo+H4ZgqygFpu01VjNW5GKQQZqtuAvA0/U6mgMx27uXT+0ko5GxGOIVAwUJyHN7DxUaeN/2/c+2G93LM4gOdK5F27SYTieogkia0vUF12A6QF6gDHDyiTkLFwEIXRufZ7Va4uKi4T0agzlEpHQ7UFZUqpeoFRsly0j9znct23UaWveqFkp56ABoQzVrRd3NdRKkPUQ44tjwRB64jskOnWZbU6anxLgH7+Nl5B0oxXY1/y77oeY0UPEx5HkCCBMkYpxsnRACnKgxRol3H21OzaXLNIDgKADdx8DM3rD1uk9CklrQyMxgXCr0WahQrMKgeiJNfAEZg0Lw098iOkX/C4CGOA6g59UGVB7dxf612qDVPq5pRtNe1vsCANHoPmYeK90TrxmXs5zv7WM6IaXOTVmiqRpYY0EJWIoUmFTfLcV4Sn4JrymddyhXC7RVQ++hsNAGcC29O5I/58ANLguXcgkyZyXxgez04VqQ4sSDeczjNdb6Bc1NrwlPJ6WlDFlRwJgMo5HBwcEhBa0wEU8YOGCUoffraY6mAVl7szlKUyIzFsV0jxUAJNmG5nMtyh9QXNN9SP4BQyWItK7zbO+QbADpWFkDQ2AMnPZBSlbT/ViT16JJ+twYwHctqu0GNzcruKahYBxt4hoXQNiaUprfS98uTYOMsIB03Q7p/1M/U1L1ac8SX7yfy8meIvNS6fg1WQ8C0jK9AVAki36bGFeEP4UQn1/mGgVJaGTKAF2fJBL3FZXaArIfCH7Yr/UCnoWAGLQU9+Cg434dOQ3x+WUWc18WRREDdIc8h+kJdn7HtP8T9joqRqi2JR59+gjz2RyjyRjjcYHxeEzPqSX5h/6j1XDc0HVIWUErkbYPuL5e4tn5dSS5+2CqnuuTsUr+JStqWAttDRQCrDUovUfGKk9ZZuEhZU97O0T2aI+XE+N3kqsYBmYNiPHMQhsi+SlwJ6AsK5QcWH14dIT7p2e4f+8U01GOutqi7SjRVALcJAiv6xw617HirOdyEKQGI7YD7fMBnevVaNPx33nHcYN9SRviT3eek9dAzeOIkrE8zi8u8fDBA96jbbQv2q6jkiSKOL48L3ByckrKw0phvV5isVjC+Q5f/vKXoDwFdNV1ifF4CptZOCerc2/fUn/endyYHncR1K86b2Cj7tjoL8cAX37tu+4/tIOHnMiryPXPOl6bGN81rGSAyKIlsntADwhKZH8aBZUuBiJHJ+BBLwmm43WFlFZKReKidR3qtoEyGkWeoWGjUNpZ1XXMRBSyVSJzpJNkgkbiKjo6qcHYb7zpIf3gOnKMjVKRXKLJlUR7OwelaZEirJ6uZbSJTp7SGnXXomtbznSmCFC5nldUh0ky5cXYbiuqo601RQr7RrG03Bpt12K1XKJuGpYUDjGSL5UxyTIiwff29rDZrlBXJZpqi2q7wcM3HmI2neLk5CT2Y5S26xwMFPLRmAx4R78bpWBGGSaTYgAMp8ZiCB5aDSePd1RPQchox+R9xbKT+/v7LB9ZcAYp1RsuihEb8lSnusgLVFVJYy4AyjlcvXiO9cMHmI/HePL4Efb39uFch6qqUVUUrT8ej7FoG8xmM2w325gVThKYPgZ0NE0T5XPScdBxNv7x8TGePHmC5XKJEKgm43q9Rus7XF5dcK1DB6rlVGI6naGua6yWS0idya+/8zY+/eA+Hj/dwGgPaA3H9bK8D9hsKihl0bZ9liz9lXb711kCZCx+6+kLfO348PaCwoBgJNIkYyE6+ul96T8iqa4ictafGXb+lV+ozqUlSXVNsijStzajTCHJuNbQcHDQbISkwSvaKNQN1a7XOqCpajQgw1AMYb1Tky467RzZhdBHUQVPCgRkLObQRkfH1/OGpzQFh2ibAaC554NHMR7F6G/XtlAKKDdbuemtfpBggdiXg769DfzIdaLBwlcRAKZqO9R5gcl4hLom2e1yS5tunucweY7nF+cYj0e4vrnEw4cPWJ5ni9F4DHSIjrw2BicnJzELq65rHB8fQ6leAvLm6hrwHpcvznFwcIDpaIxtWdI8KStU2wpV1WJxvcDl1SVGoxHa2uGmXtL7rT28Clit1+iYROi8Qlm3WK238Azmd4Gi9quWjBqwUa0UiWMFHxIZegaIhBAWBxiAg0I2GqPpPBnZUFAmg1c0v1ouf6CtRetqmMziF//EfwdXV1d4/vwFfvd3fw9V7TiykkDLRy8u8eT8qn/H6hm0+TBmvqR1cagUAmcdhDjBosPaOBp3IYh2KtW29cn4iZNO1lbypPl74fY4S6SnejgrHYO3I3AHZ7HxF2e/j6NTLjC8n/z8mYtRD+QNvpd8HtKmSHdhuPbJVwQ4Ez9qeN27jbAf61ACRia/c1sGDUvbEbNz+j3+VtmK+E3pg2R95veeWrJ3/eQHQ+WukKbbn6frdA/uyF4tvzkQwKrY65VxoOI7YHwqyqOlYL2AU0pL/cLEqR42Lo7n3uFWAAdn0DrtBrapPEFI2puCFKmDHkeaSn8Xp71vBZFzFKAiYF50ekPfY0rtlg5KyXnEz3dB+9giRdPq1pSJ45pOjiMiCCDU19ZLv2SMjc5ZCibR0Lnbeel/1jBcDxDsJEfwiUFEpTQ815ATQjOAxneUwDYqrkfee2RWAhcD76lMcuheykzWS6UUxuMx8tzi8GiOg4NDnJ2dYjQa4+233sJ4MkZdNzg9PYG1NhKrk8kEeZ7h5mbJxDdJW3/88ceo6xrz+QzX15doW8qGpBq/PbD24sULAIikdVVVODg4wM3NDS4vL5HnOS4uLgbyx13X4ejoKGaXSia3qKcopbBcLjEej6NdTPUrq+ifjEYjHB8fExC52aBtW5yfn2M+n+Pw8BBjJnrlHiLdvtls0HVdvJcQSIeHh/CuxTi3KPia1hg0Fdkis2kRyx8BZOdMRiMYY1CXJartNhL2coj9L6oxUrt7Pp/HdxZCiBmwo9EoOvzy3FL33DmH5XKJzWaD6XQ6kKn0nsqizGYzZGwTUpbFCN5TdntmC1JqqrYDxRgVCIzMsgyz6ZQIx7bFlgnxLMtRlzWuL6/hvccXvvgFwAMGJB3pvUfXdqirGnvzPaxWqygF7xVlq7RNG7P/rbbYrrcx87cNLdq6hVUW90/vk8+gDDbLze7M/nzHYA4P7UKVSnAOvvJy2TrgNmAwJKB6G1l8Zg2VrOkaRZEDCvj440/xq//4n+LJ0xcYTyf46te/gefnW7zzlYd4+NY9NG2D3/j1f44/+N53MJ/PkecWGn1mPkJAW5ZomeQu6xq5zWDthvwizrARKf7cZsitRmYVTGZxMJtGRSIfqOazBK/41kUlsbZtUTcNy6TXqMoqBrpsVutYvi2CYCyRnWU5ZcIUBbIZBXy0dQWrFfb3pnj7zYcYW4/Q1UBXQ8PBmFFfgih47B8eYG++h0+fPMZv/rN/insP3sD+/h7KqoptS0Fjeefik6T/p3GsuZ3grM0cdRJYLqSLYCd9pkuH2XgCazM0TQepkyxAnNIGi5s1zi8ucbNa4eTsjNZ5D2SZh/OOgcIOIThYlcpoEygue6X4XqvVBkfjKf7Mv/NvwRiNf/Ib/xTL5TaWgKBNyaNzDUIg0h/J3qWUGtSEDp7ruO6M190xS3KpO1kkIWC3/qZDGPTtsKZk8rkp4rVlT9TaUOZeYkc4X0ZMQMbTAFhNbSJ2Wnxw1G9KiAHuy+gfiE3cG3bpOkDB3HeAyvF7sYdurR8aOn6X7LBeQjodO+JzC37mopT23UffdwGd7+BaD+NZoSwhvzrXoXOOpIKB2DdiIxqVEvPUBaImkpZtlP3Ue4+6kYz8tB8wwBRj9rPqS7p0XRufU6n++bySLEqRz7YQm1L2NmMNST57P9iTBucYQ6Zc12GUWbR1iWqzSsYokQ7eOSibc53oIZidXi+EECXXBRtUwEBdM8VU41jhNVKOqiJlNihgPGWbiJ9FRopnX0VpCuCmQKVxsr8rDgpJxgB6H0lBU0AGj61USc6zmpsxhqWUEW1Luh7jNfysqXIpvUPJxCbinnMqSBGE55P43yaSh0K+9xnIQk6RXxOI+NGWZXHbiFFnWQaTkdS0vO/1et2rkFiLPKNgEK014CmxQnyfgc+nDGV+Jlg5yZ7ruNZAJe/Be7hAkuC51fDaoO0cXN2gakmxRBsDnWX0PkwvD032TRttN+99bLPmsguuadHWFUpr2N4kG65Fy4EDQNMNffC6ojI62hrYIscsn6Krttgsr7l8HSl8qjyL4EDbUnvG7BekY1rGhuyhVCKvHayhd2WkKqWoRrsd1n+Xv8UyQ0rISI1ilOPNN9/E8uYGl1dXqCqyPZ1zHPhGXpp3adADybDL+jif72PEpQlT+0nWAaWkTEpS3ikZ1zIfvmO/hRaEi77z5a/s+M2A4WvTvkJgHamr5tEPS4PIaBwqdG2D66srLK5vMD+Y4eDgiLPDAWszypBVATojwjNwwHDsU8g6FhAS/IVKeO3KG/f7lMxv51y/x/BZ5FMiOuwaGrBDie2Wg08cHJTqg2DSg7J/CcdSyvbIVIJjm6DgQNpjpFLSK6L2OAujWoZa2QdbEGfTBzOwnZGgr7TMDRNz5FmV1oDWsbykvFPhnkRhJngKBA1KQVmKEpIghTzLcHR0hMurS7z3/g8RQsD+bIb5dA6d01gOvK77EGAoR14GPhQMtMqiD28yDe88njx7gSdPzzGfH6Dr3GB9o2fQMRN6NBoBiks96LT8RUDoHPJJgTyz8R3F97tjX6WBeOn46sdUn6CqVJ/cJCVh5G82o+Q4gLYYzXtyuS3x7OlzPHv2DD4YOPB6VVZYrW5Q1y3v9cNguV2FCtlyfQhx7ZbxJEEikiwkLzvwnBBcqw/s7JMq5Zlpv6MkMpkjT5+/QDGe4HD/gMqfOMflWnmN9x7WBxSFwcHePpqzBl3XomUuZXF9he999/v44jtfwP5sEu83GuVYrbc0wnXfBqKB7wBMf4Rj9z3e5aumPufrEtavItDvIt13P0uDKV7neG1iXLIexICUG0kNb/lZjLHUKEwbm5LqIkF3enoaIw5TKRsAEXQKIeDi4gLHJ8cYZZTFQCBXX5cHoEVwOp3AaBPlDnc3TmmP3EM2MtlUJKNAJ5MQGGYAARQRlGe9PJHUmAMQa2N1LJcg9+q6DsvlMvaR1OTz3scMBHE6sizDwcEBxpMxbm6u47mLxQLT6TTW912v1lgtlqirOk4uay2KvMBkMsFsTjXErWTW2CzWJhQDztoMITh85StfGkQuIiBGtE8mEyBQDfBI/AeOltwJaHBOZC36cZA6hgo+AmghhOggx2ABpeJ7CCHEPhN5ffnOdrtGxcBC13U42D9AWZFsu+8cCpvh3a+9i0effBrlLF88ex4zgE5OTvDxRx9FkPPq6gpvvPEGsizD1dUVVqsV2rbG/sF+ssCMcH5+HrN/2rZFU7cot0TIi3yjUgrvvfceByuUuLwkeU6lVAzUkJqVRVEAwaGBx5e/9A7me38Zf/vv/r/w6ePfp4iroKIBUlU1tDYRPOgHNRgce/3F5pObVbRhIiGeXlOlNAKR04N5BMRFXSJ2QkD8+TbVoYbfVeA67OSYG2M5S6qB0USOA4qAGO+T7FQad1rTWJG1hAIVDCYsx0ljsQNE4YvXocDzl8h8NrbYWEbwKMuGQbHAxiGZQI5JTWMMitE4RojWTY2ucyhGBRvy5HxAAXVVMRm2Qzzd0Sd3vCU6P76SHvoI3HbFf+fYRizLDl/82teo9sjG4PmL5xhz1tJoNMJ2veKAmQrHhyfoGsr8mIynWG828WY+BFxfL7A3n6NpWjx+/ARNQ5nMRD5Q1l7L607TNPjk00dkPAUy8FarJW6WaxTFBA0DlYHnd8fBMMZaCohom7h+ytyntUBzjXAdnYp0bKpI2A2nAyAGSrLpK8KhRMLLsbMqWYMhBHSujRHLriM5zL/6V/8aKUkohc55eBhIrb4wIN2S5nUemrPZUmcu3XuG7/i2weDZcI4bvQDdbGz2o6J/+JcZAHEe37o/EvItOe64TjpWXzVqX37c8a2XXeiuzz/js+G7/tFa+HkOBcQgttgGJI7WANAaflNAHQKzBkhSXKeAIfg5AH1TMOCOn9L7RgP1dZ4nDIHTW9lCWkEp238jqW9L35O6ZsOMnqFzncqi3h38kwL76fUpM6QHTwcO1A4IIuf33+8VFVQCtlK7qM/EZpS2ErnawnOciurd7viMovaQ3pv+NuxdyTiQNUsclHhG6mRRayDBUQHpWiZnvbw2VODsMbFj4xVDX4NNqX6a75LkCDrWtwRkv9YxwllrsgaU7d8xRWCz0oo1EfgRaUR6ZybJcNB48PAeMmsxn8+wt7eHk5NTbDZrvPXWW3jrrbcwm8/QdSUODg7gvcd0OsXFxQWur68xm01xeHiAi4sLzOczjEYFzs9fxFIox8fHse72ZkPZo2+//Rbbm5JlRs/cti2m0ym+9KUvoSxLjMdjFEWB5XIZ++/Zs2fY29uLGdXb7TYGSkr2uNixAOL3RSK9rmucnp5GQnuxWOD09BSLxSKOZ7mmlIvSWkeiPJXqljrkb7/9Ni4vL6N9LHtzXddQ7Ge1XcskP9moh4eH0beSTGYJ5pxOp1gulzHTOQUCd4k7Ywxms1m0v8SeF9I7nUdynT4zNER1KgkOSOejtEuAx6Zp0LQt5vN5lGXvuo7IfSFUQIRAWZbI+P3J/Xu/lGyMk5MTeO9xcX4RM/ylLrgAp7JuSTZc5asYJCzzSgLeBEgV/4uA3BonJycIIcSAgB/1GGYB7+wXfwjHXSSj3CtEECiwj5rF9/Lk08f423/zV9C4Gvcf3MPhyRv49OkNfurnvom3336I977/If7lv/ouPvn0Bzg8mMEowCgBgnM0TYNiPIZzHtuyxKason9jtYFhX5QyxinbpmDQ21qDLLMYFyOMJ5SFYzhQNstynMzmJEcZSbakTBITvJJl3tUBTd2grqXEQIvtpsR6vUZV1aQmVXfYbC9QliU26yW00SgP9zHVCq6tAR84q4UC3iVAZLVc4vTkBHuHByhGYzy/vIBnBQKxNdM5soufpACTBB1ZS3tMYEIqy3JondZA5RJR/H1rc3gPNE0HNbcYTSZYr9eDUkcm92idR+tqXF0vsFgsqK6sZ0LUSq1YAmCbpoJSgHO9TULPYahGtCeCJp9McHlxjrN79/Hv/Nv/Ng72j/B//b//P0Ggq4fNiEDvOoftZo392RxFXsS+kIAFay1GWQ7vHdquLyX2MrCtalv4MMyaNcZGgFX6hsiSPtvuLjDPe4+mLflnATKpH8Lg3h4hNAMMSSsFbWlPlu9KVmO0s4yK2fNAssPrPotQQPp0rAgulWZmDW2aoXmZAvupXRiSz2QNF8xO1jWgT25Jx2S6dqT2nfyt7Uj1pG5adM4jBIWiGEd/hnlIFGxLZJmNagmAR16MkizuPlAi1mftOpqTvE9aa2GzHo+UZ05B8P799/XQ03Ol74Qk8AicadavkSLbKjalVgpOMsuZrFUs7S57lFYGUAHBkhSyb1uYzA6Sctq2hY5kZpo5jeQQ+xUDWzaEADCR6nwLH2iPz3KLel3GfTWEwLVbBdelrDalNdW71Ybkd/luihtgOBABPEa2HEAngT1EKPGbm3hc/ifP8KrjLsQq/UzF/wzP2P2Ic0/p/ok/vtCXt+45JOjU4NN4b97venv9lts9bPDwBrf+TvNM3XHCZ2zgKv1n2NbBJ4n/En2l2Hnp+rjbyN4fSfeTeA8G6lTS9Lu64Nv/7m/1rVS9f4FAa9S5v4SQXLdblRx3DYbYDsa6OOv37i8qaL14qV8kvtnufYSwo2Bg3PLN6BYB3YgVV8ctvvWXfif543fuvN/nPvi2pdnib33x/7b7+P0icNfi/qrLKkC9rYCfHn5t2I98l1vD9PVJJVnP+UUNgj36+4Wd79x9j93PB2f0sACe/U+ucetPyQDbvfLneJqXfuEzr5G8H3lvJZqkgXdcMH5OA71/54hrq/cem7DGc/0Uv5X9FuzWQpea1diGbbvxy3i7LC+gVIbgmohXVFWJ997/AG2noVQGznhhPiSHtRQgLxxLUfS1w+N92EZQKmAyHiMvKKEt44Cg1AeUsSF78F22Q1pCQQ4rKgC8r7ZtC6UpMTJNetUuwBY52rrF82fP8N577+H09A3U1YdYXF1iPLLwXYOuY3w1wWX71xYG95IgxWHQIZ8j6xwkgKzHfejZ0noTJtoK8rwZKw4B5Je0XYfWdXj05Am8DzjY32fFig42N2i7jnJrnQfqElmW497ZCTJ+X48eP8Lx6QNU1RZ/8P0PcHq0jy+++QDjsUJdl5jNR2hbSuT0ntY81wUeXy/HjtP387rHy3C9tI9f9vcf5QjJmn4XOf55jtcmxs/OzuLPREhuY5289Xp9C0icz+exxtt0Ou1rwTGo0nKGYpZlGI1GvePB9cLTySIgg5DnZVXFjF6J0o8vLHA9gM7FLIM0c12MTgGwnHPYbDZwzmEymUQZwzRLfDdjXA4xDuVnMdal3dvtFtc3NyjLkuQO0Nd9lLqHIkssE1QyE6TN19fXuLg8x2QyjkEAR0dHcQEBgP2DfRzuHxD5zZHOkTRNBod3LkpRyHMZQw6p6xy0sZRYGZgA7CRqnmR5qA4X1d1xroPzLhr7q80W3nuqPcgZFZ1zkXzMuOYfBQ8Q6VlXFUWeWovxeIymqqEAbMsS5ZZkKoXk/vDDj7BYXOOdL76DvCiIzPIuAoWXFyS/fHZ2hqqq0LQtFICLF0RGv/vuu/jt3/5t3Nzc4Ktf/SpCCPj4449xcXmBw8M9VPUW7arF9eIaL86fo20bVFWN9XrVE6OBZOWLgojxrmsxGo0wmUwxLsa9TN1kAmsNJpMxzs4IFOsdb4XxuK95KY51nueYT6fonAeUwdtffAdvf/GL+D/8H/9zfP/730PdUqb53pSitcpyS9lY6YD8HOuA2AyVc7gqKxyNGEBEuLWopCQ3OV29W6Igi5waXDtuHK9oFmPmCMGjKkuMJhNSYODM+ZYzx7M84ywyCqqRjDWoACEnRWofEPKaZF2gEGuMB1C9G1ljSH41I0pV9bWpnOPIe60ImFMUWOI8ASB5kSPPRzGavW4adJ3jCPaMN+6GjOiuRdd2EEJFDAPp/9QO2rW06O/9WZEkASCR7ANyDZTV8cvf+xBf/6U38OTRYxQZ1YfybQcVgOXiBsbSWm20hTnSWC6WePT4MZq2IXnxdxxgAdc5fPTRJ/A+xKwpiTS/vFpQ7RTnkBmqJy5rvHcOUIpq2ViLqqqxWHJWV+ij76BYpqxzaFhOXKh+pTk6nbMWO0+qAUJoe+fi+6LO6Q2u9LiLkPYKsT4YtcfHwAUlRlDjIUEeOgSUN2uW+qds9RQgSYmCwfhWvSzmywyv3eMWuZ6AX6+72d913Vd97y5T5/MYQP+mHC/ruz/SYwB2fJ6vDZ2BVzvxdz/L6z7fqwzU3WOXYE7b138umUmKPQPEtYgA3N49U7LI87zu2zQEoJWSyHMMzrl9f3GqxO6yUIp+HxI6iPfzjpQvyK5xsCaL8vCGAUshzQTQob8Raeq8h1YWw9LeCaoQnSMK7gpAJJSHmAOvbdy2u96J1vrO+RjXd7LEuAV9/a/dTDEFQHPwAqmm9Corac20BK6AlB/gVpIUruol7cRx0ppAa6p/SoC89x6jsY0ZvsZYdF2Lo6NDtpkKTKcTPHz4EJPpFG++8SZGoxFuljc4ONiLxKhSlIVRllvM53vwngjWrutwfX2Ntm2jv3F0dBQDGCVr7OnTpzFLYjqdomkaHB4eYrVa4fj4GPfu3YNSFNgl5O9ms4kErTEG6/UaRVHg/Pwc2+0Wx8fHbNNZfO1rX8P+/j4++eQTKKVwdnaG1WqF2WyGDz74INrtQq5KHXNjDCmlMMHjvedseMp4E8l2AQvERhHSSq47mVAE+HQ6jRLksscURRHrZcc6lXxNyd6WmuWbzQYnJydYLpdRBUnqpBdFEWuqkxpViINKiPfRiAAJkapO117vfayrfnh4GAlvAUmEzG6aBnmeU2Ak95GM5+12G217pVTMxGrbBtfX17E/xJdL91QhqpuGzh2PxzGrTdYSyTwVmyWVrJcAWjlkzIlvKPeMBDwTNEKWS/11IWi2223slx/nSIk8+Tfcmvm3j12C766/7a5Fd31HwE5jDIwluc3LFxf4B//gH8Bo4I17X0SwOVbbNX7iJ9/FvfsP8eu/8S/w0YcfYHmzwGw0g1akvmG0YhEfD2spsMRzJhrZXQrK94STcRT43LBaAtVIJKWpvMhgTQljSDbXZkyYWwosGdmM/V4FZbgsmtIwmUGWZ5jMprS3BFJmcy7AdR5d59A0HZqafMG6adDWHZqqxWq9wvnFObTRODo6wP233sCzZ4/QaIvW5HAuwChEJby2rrAttyirCpP5Hub7e0QaNw1JuSdZVbuAYf8O+izjnkQDvAOMAdUM1XUsP9CTFEKo60jkGUNlJxZXF70v2gWYzqFzHlmmsdps8OLiIiq0aRCpZ22GPKeal953MZg1ymRydovSBp4laAMURqOciHZb4Cd+4ifwF/7Cv4df/jv/NQDOnOJgfYvszkSGmF3F60SR5TG4NfgeaCPpWMq+HGsDDDL0hkRuT5h6yooH1bZ2LvEzYxs8XKiY6BaSlmZGL8lMhLfBBNFL9j0ojNCLYyutaX9V/fWJpJTgcv7cdxBlLPL9ECXV074JwQ6eL7Wn7vI5+uHFwS8+lbHnWuBdr0BAKmiyvop6oaE5m6yrKcAtQVBVXWK2t4+3D49xcHgE5xXNscgdiB9PuI3m4IumrlFut9F6FHlf79tBso48m9gB1A4AiTKhJHvsBmb2fdGrWwZP5K6s54eHh6jaJglC0IMxmWa4ab6s1IyXTOoegKdV22igrCqMRyMK+jcGmhVq4k7heyl56te+v1K/U5KHpGwCZYM3g3PEviV5+T4xBRBfm3CXohjDKxsz4iOhy7a3jGfOJYh7+3y+D6VA2IccGvCzO9S9/jUeHj/evvvfHq9xKKCbdJ993r+mw9+lKPeHfQxd2j/8QwNu+m9On/7oxx/x/FOAm/2bPMf7vPI/zMPBoUzH+Su7QKwOQCkDpT2ausXFxRU++vBjzOb7sXlpcJu1ObIsZ0WjjoP0ekUi2lPJvs3Yx5Q9Vo5U0c9xaRQJqr3LzxjaMLxPMzGVJt2KmoTNMwStEJyHViaqMW82GyyXSxyfvYmbmxtoHaD1HsajAsv1TV+iQHpI7DBuA1RftPGWlyW2X0hsu9jTpJwM+X/c+/v+JX+jv1xUIDEGnQ/YljVublbIswIHe3PCwLs+mM97B6cC0NJn87053lBvAFB4+vwZJpM5prM9+LbCxx9/gtVqhfv3z6BAwQ4IBk3jhNmHUv3gGdpFt0tpvQ6pHbGnW0E2AalY022YWeH2ZYVrSpml5IjUbxhc8K7g0dc9XpsYF+NHIgSrquL6ry5mNohxJmSzGKgScSqAlRiVIp+32WwiuJLWpZNJUdc1siwjaUDvUeRFlA5USqPalgPDf3mzjIaqyP8657C/vx/bKc6lyGg3TUO1yDhrJK2fnkZ4pL+7rovyRdvtNmaNyOQlEKyF9w5G8WDuHEtv1zGre7S/h/l8jiwnI7WXedEszUQynrLASL0SGQwEYiomVZkI1BT11nZkHOc2g3IeTdsi1kpRClmw8MFjs9kizzOSGbIWFA3esmOkqMabKmKmjfchSjfw28K23KBpK9R1gxA8rLFRug2g+g1ZlsG7DnVJkebrNdXsvb6+wvHxcZRtLssKeZ7h8ePHePLkCR4+fIjNeo2nT5/EhXdbbjAqqE33H9xH09b4+JMPUdcN5vM5tNa4d+8MZVnie9/7Lp49e4qrqyv85m/+Jn7hF34eb775Js7PX2CzWeL4+BhlVTIQezPIKKfa4zSORb7r8PAgOlrj8RiH+0dxnAtoJpkjBNY1EUBeLpeDebC3R8Dwi4sLemfOwQcFpQ3+h//Rf4hf/js5/tW/+jYWiyWuncNkBIxHFuUOIHnn5iu/quFH5M8HdHB4/3KBX3zj3vCrfNIQOhdidriZyby4iwTf/b0nhXuSN4Dr0HGWlnNUoz7jGpPeB2hrkTMY33Ud15/qyZIsy2iNCSFKM1KNqTCoM0RyYUTK+spBjxM5X4S4gVmbRULAeQ/niVwZFQWMzej7nuZT8AHj8YhkYkOAa1sCpJ2LdcUR+s1V7fZN3JCHYs96Z9MeEnBSpzUMPts0HfyIMrzHY4umavDNb34Tp6enuLy8xLNnz/DRRx+hazuUVYX9+SG0JnADWvVlCiw52x9/9Ckoq6PjwBYLl4AD9MUaIXh0juqOEiivoIxFgIaxBTw6tJ2HNprk5bWhDPHORZl6oJckSyMK6X0HADpmW4SQEt49cLi7sfYbI32HpNMDREpRIu2lj4PrYAzVbrQs76WVhjIEtNPnFtb4OF5kHuweKTH+OkdKjLzs+59Fjv8ohLaM8/9/OP4oIhFfdRCe9tnEw53ffQkZcSswaQfE3SWuX3X9XaJ7dzy9ijSXz2+D1LsrmKzDAlKmtezSv/dt2FUGovvdbtsuuE/tMTBGRWfirmeQ9cP7AFgVgXdxPsSWkv1EbNhdp0wCFdu2pf0mATgl2EolZDov9LHtaavSHfI2iS8/a+x8ie/BY0AHGN33o0oiqeW6gS+a5wURJwzM0muUseQH9033cXIKAe9bJm0oqI9kyqdRenc8HmM+m+DBgwdR3eidd95hInmKzWaN4+MjGEMqOjc3N1FVaTKZIgSP45O3UVZb6MojLzTatsNyeYXxZIzr6/PYz1mW4ebmJtZq7roOq9UKe3t72N/fx9HR0SDj2TmHgm1D7z3W63X0L4Q4Fknyvb09BLYbuq7DdDrFzQ3Vn55MJgghDKTNF4sFbm5uIllaVRWur6+x2WxwfHwcSXaA1HBSP0IysIV8H7F0uQAFZP+QjyUggzx7XddYLBbRRpbnubq6wuHhYXzG0WgUs2JVCL0iERCzu7XWeP78OZRSg1riTdNgtVpFAnu3BJX4e5JlC/TlcES2XoIRxBaQNUcIawkIlhri0lY5ZzQa3ZIdDiGgLEt0rY/9tN1uo43d21DA1dUVxixpKQR+nudYrUSutkWeFQOp2fWaAt82mw1Go1HMSJf3lNaMT20UmXPi60qt9el0Gv3Vuu4VdX6cY5jBpFioQw00nEJiZ6bv7Y6r0Xf17T1i4FPEsoVko2eWZCq7tsP5iwv8y9/5PdRli72TM7TaYDyZ4t7JGU7O7uHb3/4Ofvj+D7DdLKGVgzUayCzZtdqQ7CTA8pO+B+agoHyg/ysOy/UeXej7XisFrS20adG0Ut9Z8XplOOOFaocXljOEjYY2BhnLr1p+Z8ZIZq+DzTJAATrTyLMM+Yie3rkO3jFh2pFC1dHlIeq6Rp5bFKOCfGZWabDaUNZ7QfKmba3QNi2auoZWQGEztK6D1wpehX6/UDt2gO6zTB3LC2tlkWWU8WMtkbqa59V4ZLHeNLyPaCZHqZyUBmWIuo7WvdlsjqvLSwQoaGNhcw/TNBzIXqCqAl5crHB5eYGTozm8z0gpyQSovEMeOqimQyk+q+egsDS4SwUowzXIfQHXNIDvMB7n+OZPfg0ffvg+/uAPfoiGJV01KJM9z0cxgw8BkWjX1sY9UgUDKoRkoE1Sk1ypROpaxdJXREyTD0D+g+c2h6GiF9Us4uAyVroJPGfEdkD/vgQADcn4tQMiVGYQ+ShaKSD0IS1aGyZ9ASh/aw57Zsk1E+KB+1mkYCmIm34nAEhI6l7RL2bTKIBKM6U+exJsp3r/KfX15V/Cooj8R1BJIEuIGdcpThZl5D0HVWQZKRv4QPYFNRwxuK+lwBk4CkhUnmTUu66FdxwY7x08WNbdEBAOpShAQhNu4gI9kwrUfyaxN3sflQPqe8S6n3uKnsyHDm1XY7VagIoFsn2o5Tnpd2sySBlqqm2soK0llcYsQ2YtmqbBerVmrLCE6zwyY6kEmAeCowBw33HwSrSPKfAilekVzC+W9HE8fpWLti4CyR7DB4RkP22bNq61RCCyApDSgAOtc8qjbat+b6DeoKCXAA4aASsIin0TYp/qbZopt4N1hF1/8y7k6Pahkv+8BDtPASbqO4WI//TnirHw2V6v4FS7rU1vO4DYXtfvfJnTLQ+Ztu2l12S84xV/fd3jju6744IhtkXOb/MGQQWooJA1+R2t47MTDGzw2Wc0VO0OnLh23vUML7tmmvmePN9ue9ITBtcdHk1W8/rwR3uooFB0o77tGPwwbNngxwSPSNb14d97ok5O79HYWxM0nhe7t38Vt44UE0t947vt0LBzjd3f6bP0R/nNjboY5G2r7CXTRN364m3c9GXfQdIXO2Nulyzkz3a69NZ8iX9VO79LG+86kq07oH+XYrNnbOumijGCuUgbDiwlTubaAbqGzQtcXW7wyZNLXC9KTMYjdJEbUiiKEe/plpRPQ0CRZbBGw/mut7OUhlEKZdtib0olzIxRCKEnwKncREBwAdCa92Wyg1LcXfpVSmJqtok75xAU3bduemUSpbjmuNIIHlAwgFWAIVvJty2uzs9xcnIBbSwWS0BbS4Gp0w7L1Yr6TOwHx8l0PsCwKqHXPS77WcctHEolMyp4IChoZaJtIW9cAia1ovIyWhNXWFVbrNdLzCYUXFvXNbQXm5O+7DjRT2uDyXiENx7eR9dRieq8yJEXU4RQ4HKxhrYWpwockE+Yf102sLZXVRsMO7E1EjwsxQJ3AwLSfgjos+dvzScVJ+KtaZiWOOrH+e52+PL9mGzSkMzFH22dfm1iXDpGanoICCPEYJ7TpljXdZTnE9ASQJQLk2sJMS2SuSI5lkbFy2AUg04IbZKmriLoICQ2gAhAyEtLo0tms1nMQrBsqCqlYkZB0zQxa0CyACQbXa4vkmcks7ZBwzX4tNYoiiJmFUQZYPT1F/Msg+LPsySqxgcCONu2jQa0tZYysjkrlVSdPdqGSGbniXiu64pr3Vg0TY22IQmmURihaRtkNoMLHo138C1lrxqtkRUFNps1VpzVAADLxZpAqa7tJRYZYF5VZQSJ8zyPIORsNsPy5gbaGKxWqxjY8OLFC7Rti6OjI1xdXUXQ6M0330TbNHj29EkE1/b39zGfT/H0ySN8+slHMbtrcbPA8maJN998E3/8p/4Y1ut38MEHHyDAxxpjdcU1E0LAg/tnUX1gebPEzXKJBw/vo20a/PLf+lt49OgRvPd4+PAezu6dIsCjGOWYzaa4uVkgyzLs7+9hPp+SFHbX4eBgH1VVci3yMYoi5yCLPSwW1wA8utbg448/hHMes9kMWit0HYETm82aNxrKDlcKuLg8xxtvvIG2aTCdzVDVJTsm5ITXdQUoAomDd/iP/oO/jMxo/M7v/C422y1W6xY3yxanx8XOwnSHSfsqO53n5m98+gS/8MY9+jUMF57PykcZRDHv/m3XHEial/5NfvKuo8xxBodFTcCx1LXWGhnPX6px5xgEQO/sKro2ZbNxdBV8BAAk61sx6OQ5Sl6sD5dE2Xt2qrXWyEcWNsupzgwQI+igSAHAWqqL1bYUFBK8R1WV1IfcRvbTbh879vir3Z1+q1E7r9v7gG8/XcDZAt///vdxvDfFX/j3/jzyLMMv//Lfxs/+7M9htdrgZ3/25/G9730Pm22Nq+sl/vgf/2kcHh9jMh7DZBZ/5/o3UKEhgMcUqJoGnQOgDJxXAIgsAcCZBQRgCSi+LWtYm8E0JCVa1Q1lqghA3rUQgilu8CxjHh3axECm3/uouwGhM/zPrU0zBRkjCDZwClwEO/gK4HLzCJ2LUvtijWhj0TlHANVLDIP+fQyzEl6XJE9Jqrue5WXf2Y3se9lx198GxinudmLuImZ/1ONlbX1dYv+u++8C+z/Otf4oj7vGqGRbyd92pVXl5zRD5q6gCbnGboDAywIGXud3scmGYywluxW4chd6L9v3P++cr7VJsMj+HVFGUlKuJiggkYNNHU+tieAYj8h2E7m2joPTVNJmBIW27WCtYXlsAt3rusKLF+do2y6SYamiz3K5QlWVtBYEDWuI7CDlIzHiU+Of1i3Zj9JARgFlxdYS4lH6JLWN0/edrn19sKZnMkdxsKqH1gZpPU25BxHgKpb8KIoR5vMZuq7FttzQOm0os3k6meKNN98kcrLIoY3C4eEB9vf3sd1ucXZ2hq997WsxQPb582cYj/L49zzPsdmsEYKDtQrWKpyfP4/Zbd4TQK50gLGA90DX1UTYq4DNZk3g8XqNYlvELGciscjueuONN3B1dRXJ3JubGxwcHKCu64Hy0/X1dVRjSslyyfidzWYAiCiez+f45JNPUNc1xuMxnj9/jqOjIxwcHERJdKlTPhqNsN1uMZ/PI6l6fHyM58+fc50/8o+ur69jjfK0FjlAkuWz2Sy+/81mEwn/siwjsZ4GfRwdHQ1Ifsn+1lpjOp0yQUfZ1xLYO5lM4DgrWoKAZVwslxQMCvREslIqZo1LFuluuQYJLJagA7HPRP5dnmm1WqEoiihvK32d+maLxQKHh4eYTqe4urqKRLX4ZfK+ZG7keY48U5ShwH6IEOnpuiVrqfxNAh4kSPXq6hr3zu7H/VkCCabTaSTPhcQHMMgGT7PC5V7i+8mcFUJIggBkzpdliR/ruGvPS9fY0IO8qd2ukt8H4DEIXAqByBFZw4aBWf3aC7Dcswu4vLzChx9+hI8+eYT5dB96NIW2OfaPjnF8eoaLq2t859vfwXq1QGaBLCM/VsWyZj15Snwvrfdk1yoIfrIrDy1jwSsFHQAdPJzr11rxvcXHl0zXwedMiGfG8t8Mr6WUdS3koLWGyjlZ8stMZmBzC2sK7Ot9jKYjLFdL+K5DUeSoyxJtVUMHQDEJr3Vfqk0yaBUCjCY7MngPz88nc032CgHNBASMJUQ0EZYy9mgfIj99NMqwrRQTmCp5dQpGA54KIKMstzg8PIQ2hkoDBSq1JkHvWllUtcfV9Rbn5+d4eLaHsiY1M+gMOs+hfQttHUjrqUEbqJa6zIFoc3BijoeG0gZdR5mrJ0d7+OPf/AYuzi9xfnWNpu2AAEwm0yRbVUMFAlS1JYWAaN8pBQUNpTwTnyYhBMEAowTISSALk3jBc4a0GCIiV03zwCjNxCN/wqdpk3GfI74jbSg7X/Zqts7Il4mXpWAP6g+qJer5BCMqO4rLewmkF20tDbGyYhMBCLEDmTPR9lJ0P/4sKL/jYzKZmVwjBfSlhBiU6mVwFSAlc4ig1zxnhUgJoMBlF9cLURdTCsiyHM47bNZrBPazu85FUJraCaBqKYEgyDtzvJ426HzLtacJVxN70HHj5X5aGyr3x1iGD6C+535QjBFI/3jHZX+ilD4HXvsADwfnWtTVFsqM+qAIJZlwNCdFiZH6i7CKXBvkxqIYTTAaj2DrBm3Toa4bINB9NQxcRyCyC54GjCfC2WgLqD6cUoBeFR+C5rhSgDbD7CjCQiSJht4XvI+l8DSAvtQCKyRpDWMtlLJQ2gKBFT4ZaFDQyHOS9Zd1WHMwrGb/OXgK0nnr7/8EjTelYFSIY09zll7wHh0re4piogIRAqLmpKV9SsVEIfq/hSjZUK3aMBgzSgEqKCiv+pIJilUQrEWWFwjKoGsdfOgIxGeAxid+lqwpQEDQGSTwV9aUOGFkliqx9/vEAbIHJUCJ12626zvX3fK5LStdOA40Aq/9suaL1HfwXKrDWihr4nwX+zMNKJQkrZyVnmhf8bGd6VptjEGWjwYB+qJ+kwY0U7CEjwGBspelOL02hsrWRdtBAopoREt5Aec6KBj0gdWIYFk/r+jzNrTRF6JntRR0Y3R8Ntc5dGzDGs0qJqEPsNWaAvs618EFKvUR/W/0awM9Z5x48ehYnVLzxtaxr26MjbaEgoKxJr5/pftgIeFKFONZwbMCoqM1RwEUwMfBdv0eJvLxXB7WGAQEeB5rMtcz9kMUEH1hsatkznedi+80jmcFaN/1EtaKiLeK+RAp6+S9p6Q4w8FFvrcZhS/pOlJxkXfatk3ERiHjzztordDWpK5pDOG33gmuMdyjtEqSsEKIgeziL0QbUPX2lihDuq6F86SY23YNmrqGb+poazkvalIceM9rRlc3qKuK2t9RGUmxK5wjHGAynaCqajR1i851cV+K6y6vi9GXB2HPNEds3GO9D1HtWHOQm2KZugAicDNrqUyQFbwFeOuNe/iFn/1JnB7NMJuOkRcFcQnZGNrkUMZS+Q6vyF5WDWBGuF5u8MnjF6jqDgcThbZhxRMuY0QJAxZNtQU8qf5qAA6s/qU0JXJ7Ciwcj8ewmYXWvQS5tRaGy6jFknu0ANHaIPaY4D6Cv4dAJdu476SsZV1XUaFI9l8J0FPKAFpGTYB3Ha4vL3Dx/Cn2j0/ROg+d5dg7aHAwHmNbbhmTDogKhryfDtP/Xn3s4qHR7u0/iH6ZBAAGUV1U0geISbZaAV4Rl7DZblBWJfb39m9dWxJUuq6FMQHWZjg42EfbNtiuN3CtQ9AGNp+gaVpcLZYwVuEweEwmUxRFhqpsZYINrp+S4p/3oGv4aNdBsKwdjBns56Xf290PZb6/bjvSa3wWPv+q47WJcTkkAlSkuEQWTzIDJHNTNhoAsda3AEkpSCQLejo5Uic3/V028CLP0dQ1prMZtFJRqk46Y7NeYzKdRsBC5PzS7HXnXAR2pOMFTJKNQtqVdrQs/BSdPYLhjUKyjjRntcbn9w7GCuAbgOBgjUHXNQAURaLzs2ul0AYPqID1ZsXgF0mJV1WJoigiaKWUwvLmJmZptOsW3jnYjAzbZ08fU1ZFCBiPxlisVwBLrVMWfYXVeoXLy0tkNsPxyTEuLy6xv3+Aq6urSDCLOoC1NsowCggZAmWsCAgoNfXSheJ73/1ulCXcbDb4zre/jflsFgEDyswgdYH5fI4sy9A0DWazGX7qp/4Yrq+vsVwu8d5732fwL4tBC861cK7jQIktrLW4OH/BSgIKo9EYT58+wWg0wpe//CWE4HH//n3s7e0hzwlcOzw8wHw+Q5bZWP99uVxif38f4zEBZqNRgclkHA2D9XqN1WoZF/5tuWVJV4WGN1sCNwsURY7NZoPOdfGZy3KLuq4wn8/ZaaS+taMMbUNjZ1uWsRyB0gr/4//4P8TB3gz/4lvfwuXlNTZVhdW6vTU/A1T878uWkh3ICzd1jarrMM6y1OfuATV2MGMMzh0LVcDd90s/l3pNsR1sdIZk8XSuw3azwWg8JgdYarcqH+eIthaFNfCsRkCy+uTEgp00pRTgfAIkUEuE0CW/UkfnAGKkCiAFMmqyPIdNaqqRk9BRYEpGUi6GgY6uawAmxcvtlkCTCCpgp2/TPqKI22hMSd/s9mWQPqMfUpIKIaDrFH7143OMDw7xhS+8ib/w5/8cvv17v4df//Vfh80sTs4e4Mtf/iref/8H+Omf/QUUxRi5HeFP/NJ/F+tyi7apcXhyguJv/2+BZoUA4Op6ibpt4TpyBmRNlHXbe3Is2q6F1CFU/GLTLO0AdrCjsyVEeBLNO/BAdp4PkvWdnMHvMD3nrj6T7zBtBQ+FQZoV1PD2/AWf3ixehJ38JJsNuJ1VS6d+/k35VSTxy8jN1zk+qy2Mnf6RH3eR1n+YxPQfNsl9a53bfSf04Y/VBtkv+wjJu2v5pH13V3CCEDB+Z2y+qm2v09bd9X5AiCsC1ihvUVavgBAIYBxeJ73fcG7LQVJdifRU+h3FsEqgPcn7gO22JKARSMCDdIxRTVFZ229ulvEe5LB3yPMCbetwcXGFjNf0zYYUgCSYTSmRotQJWdM7tBJpLcBIun6RuAnZSp1r+ekd8tyQGknXxgw3712cjIHBF6V78BYaETiz1sBYg0JnDOqR/elBJO43v/l1nJyeYr1e4+233kLnOrz77tdx7949GKPw4sVzFKMR9tjOODw8xOXlJQ4PD7Ett2jbOgaNKkVZzpdXLzCdTKm+1yhDCB43Nwtst1vs7e1hNpvBe4/9/T2U5Rbb7QbzPfpsvjfn2t0jXF1dRjvt6Ogo2pPL5TICfES4lnjx4gXund1HVVVYLBbRDhW5NKofvon2edu2ERzc39+P4KD8KxLYACkWXV5eYrvdYjKZxH5wzkUZbgFghLQVP8EYE+trin8hgMzJyUl04CXCPfoNfM0sy5jMoqzm1WoV7W7JVAcQgR+R+xaCbTabxUzmzWYTQSsh8fM8hwp9lrNIhgPAvXv3Yja7tRaLxWIAbomE/JbtGJmrs9ksStvLXi/qSE3TxPukGejT6XTgI1VVFft0uVxiPp9jNpthMpng8vISdV1jNptFqXPpv7IskdkC220JxX7fwcEBlalK1jrJEJfsbVkXRQ5f5OZDCHHsCIl6dHRE0r+cVS9Ar/wr43I2m8V3IQHUy+Uy+rryt/F4HP2EVJ79RznuWjF7wrs/R8Ddfg3sfx+eFBACZ0wyaUTrpI/fkEBuBIcsM2zblnjvvffwgx98iHw8w2T/ENfbBt/4ia/i4PAQi8US/+gf/UMslzeYzccg3J7X0QQXCLyGR8nnhLBKSW6g3wNSXCAlzNMgegAxiIF+vn1NoylTfACoRiKEyL/M0FpuM8N/J5J8Mp7i6PgIWTHCqG2B4DGbTbFYLOJYlQx2BKlT37fTOQ+j+wAOWRfkX5FId85ROTKdlvagw7OUNZVkoz23LKu+7rKn/Zhkkx1jLzQOfegTCvI8jyXnehwHXBIJWK23ePbiEr/w0z+B9XoLlWlYo6GUgbcZgnHIlJRBauG53FVvqxKA57yDd2Svh+DinHrrrbfxta99Bd0fvIfL6yWszTGfzymAJnFiZZ2SNU5AbGUUVGCpaN8hOA6ekAzapB0DU0cFKgMi5Vr4XjEoI84YDpxmefMMOdHUSlFJpnRusZ/nEdAFFf3WuDKlNUAVESPwDr5L/D6toAORuaL0YliWEp78RMnI964n9rVW6FRCPIKUzhDIJlHsIwYEGM78FV9GGi/jM3A7lNHQlq8XentK8bOLr6t43CokhCHPIWs4s8tatG2Ny4stzs9fMCkgta7ZP7RJlrHq+4N6zdFn1sAoi9x7eEdEKEnNU3+aQAkGCAoMeSMEhdZ7KA9YTZluXUp+dz3RpQ0NFhXYBvUhSvUrTWSkfC7zXLA9pSiQIHgJpLHIiwKj8RjjyRgGClVZomtqJmyo9I7W2QBfyXMT67jDZgjQROJ1rl8TVR9EpJgkTgnEVDJeKyG8AddRAEDUPFDUv7JeKSb3PWMlxkgpFYUss5jNJjDWoq4qBADGmgT3FJXMDhS8yYE2DhGz0GwH+RD6kgXeMakopDOtJv1zMqnNa7YoExiuwU77bcnJEDQJjTYYWdqL03UWSpEinDZoWpGfZ0UL9PsHSdLraNNBISGwPCl/JoE1Mhbatq+NK5hyundRoICCBaLyoRPih9d6YzS8JvLEp7qz1CuA5oAcLe2zgCJimOw+Vr5Cv+d0zkXFFPnMM04fEPh5KCPAQMf1VfrEQAJwE19VBWSZpTU0tOiCgw+OlCGknEVwCIHUQIzmBBFP645WAVrT+qEQYAxiEBu1kQIe5D1orVG3lJhCqjAZtLacWMY+l/dwRiGf5NBKw+4ohFlrOMuypgQI1dsY6buUIBGtFELrEJyQhkPlBu8cq0Z6ZHlfUgMArNHQhp9RaSoPqBTgmt7nB9lb3ndA18U5Ce/QVv34BI8bbRSUIlUcY2xfE12BAty8h3Jkb1ljURQZssxisyljchFgYRWgjEYXPBrfoa0bdG2L0Mm41REf7epAWKrroj3oADQNJQaltpVvZO/XTHcENE1Nqkks+x2CjwHHeZ7DB0t7bqB9aqD+woGMeZ4jL2ycy5IYaK2J16KgjhwqpwxYSbzrug4I7GeNCnhOYGrqKuI3jueD46ATCIbZObimRdPW0ffLMhvtKlHkbbcVBfkwFtCyz+WdQ9c5SuTyHjp0rIIT4r6nDPnxgbFlNC0yHZDlObK8wHg8xXgy7QONtyt0bYuuadA2FS4vz4k/sAexNJeCgc5ofkCTyo4OgAsUnO6bDueXV3j69Gmc40JmSx9L0IvsLZLIKmu+leAk1yLLLYpxDmPFxjFxTEhwCtn7rreHFGJZDu6MW/ig2HpN06DlQHcJrhbORcIQjBEqndct53GzWODTTz+FzguMJzOsl0s8fvwI++98EbO9faxXK1rf2O/1joKEPRzgQyzDcTf+NTxSMnkXf5PvDGBkuU5AJI211jE4S/CG1XqD6YRVrHmNJvWWtKSLh9YUEHd6eoqqbPDJJ59gvVojH41wcHCE68U5nj4nfuz05BSnp2cYjQq0DZXES58jfeb0WT5Pcpf8e1d/9OcNf9/FPl+Fg37W7z8OQf7axLiQ3Uop7O/vYzabYbVaYblcxuxxAQlSSUqZTNKhdV1H4CrNxpbzJashdXaFSJdshMB1fUKgKJb9vb0oKaS1xrvvvgvDYIicJ1FzacfLxJU2iGEibUlrJewaNzKZBXTavW68X3Cwrq8DRAs/OajSb21D2Q9N26DICyxuFpjP57i+3FAmZtfh6PgITVPDaIq+omgoh816hbIscXJ0iKqt4XyHdVnBdS1WVYmnT5/FjIkQPK6vr2FthpOTY7zxxpt4cP8eHj9+hO999wlubpZwjp5rs9ng7N49rFcruCRiMMsyNHWNbVni5PgYSgH3799DXVXoEDCbTSMBVuQ5k84ULLFaLlGMRhgVORomhknCMOP+osWvKrfQCnjWkkTEzeKaAcgmvq8333wDWabhvENdlTHoYltu4Z1Hx9nHzjnc3FAU0OHhAZyjqCPLi3ueZ2iaGvP5DIvFAlVVoiy3tGC0DW5ubnD//r2YUX54dIQ8yzhL2LIk3RSZzdG1LaqK3gGQQRuFcltib3+OEDyyzKKuG7zzzjtYr1dwrsNsNgfAtag3HtZmKKsSRgPBd1QPAsDV1Tm+8qUvYD6f4ld/9ddQP32Opt1ZEHY5h9c8uuDxf/rWd/A///mfQi7OKTsvPbGMSJRLtm8/J+K+huR0BvbJyZfvD9r7knZ6T1GKxWhEdXa45rfUq4fr2Im1KIyNYDBJqXt03vcGJigCKzDzKfuZbNL0c99yAccMR7pJhngIAQ0H1WilMCpGDLhylB+DcF3boWmq5D67wKXI3/WfSRQtU0r0l6R/7yKmhgt9QNsFfHy1wdYFFN7jv/en/hT+5t/6u3j/vR8gBI+iUPj//OPfwEefPEVZbvHBR4/w5S9/FavlGv/lX/1ruF4sSDJ0b47FL9wAY4qMvVzcIE2MjHKo0XjS7OCKI0NG5UCakJ/Xa7BBGKK8X4gDJwxqrtxFOEa05GXnqARJk3MSkA4Agtodg2m+hFwmlYFO7t1/afePn3vj/TzHj0siv1bb0on+kvv8YZDOn9WW173Hq877Udv5Ov20axQLvpj+/a4gide5d2o/3EVgpzbRXefcZYi/7Ble9furrkn/JpH9YIJ4hxg36vZ10vVMapPvtCxG23sMM7jk/rL/A0Q4U41TCURUt/oRUFwbS+pcoQ/o4c8IlJMMJ6Btu+goCsGaZaRSEsLQRiSbyCAECuoSiXcooOtofxmPCwacOwZJOEu8a7nuNK2jRVEg4yj8EALynEiC6XRKGaqKpIJNRnW99vb28O6772I8Jrm9pm7wv1n+r3HVXWI2m+J/+j/7T5joCByEJ0GkAdoAD9+gMjOz+Qh1rdC0Wyjt8Oz5o1gyZr1e4ubmGgDZ7vP5HAEeVVlhOpnAshLQdDrFixcvIul5fX2Nm5ubaFN77/HJJ5/ETG15R8+ePUNRjLC/d0iZ2LNefvurX/0KPv30E+zvHeL999/H/fv38fTp01h6RuTNLy8vMZ1O496UqlhlWYb1mlR7pA96ELONBLKQmCLvDfSBJuPxmEv+lDg4OIAxJhLRIo/tnMPe3l7MJAYIWFgsFlFFyjkX/y61usXRl2z3qqpwdHQUa2rLnBHFJRnfkr0OIJaAknqnQnZtNhuMWGGnbduYhZ5KoGutMZ/PAQA3Nzfx/cgzXVxcDBzM1WoVSTXxKyQYWGuNi4sLiNS6fHZzcxNJeQkoSPtOApQBqsksBHZd1zHoWQI01qs+IFf8QQJ301WExrlkcYvf6r2ntrQOdU1KVW3b4vj4GOv1OgYcyLhIgW2RWhfgvyzL+HwhBFxcXPSZWXmOw8NDXF9fY71exxJeP/b+yTaYHHFtDn0wJ8fOAHiZDSXXUtHGUUBvewW2w/ianasBBWRcs3u7XuNXfuXv42ZZwuYTFON9/PDT5/hzf/EvwhiDH77/A/zut76Fm5trHB7uQxkF6AClpVzA7fb37eiz0QSIS4mFvunDLPJoD6sk4zw5OvbVlaKsXQUHhXbg19B3+n1NM9EgfoMAdForjMY5jm7WuLq6gFbA4f4coyLHRx99hNVqhdwqGJ0BUInqHBPdXF7NsPqU9wK6E1ANcH3lAISgoRkIk2AuIMAHB8e+H/mwBddDdxgZ8rvrmqXJk8SDoBThIo7K0MmatVwuo3IbXU+j3FZQWYHWAx9+9CkWyw3gPVTogEB+kTIZ9NQgNCHa3i6QRHbc72UsOcAHCiwDyI9Yr9doXcDbX/giPCxenF+iKkmBT0IzaE62g6CeFDOS8SCfRZA1DhYPpdKAXRlvMn44C098h2iX8FgCScErzuoOHRD4HAU6vffZVBxPxvRjlAJLcOvItIZl5zliUMHH7EYiA4nEBQeIBx7PIYQ4XoRo1EAM2I1Zt9pwIIP0kUeAh9KBJePpQeL05zWG5L0dlOH5xk8GuYb0sQLAhKb44LK+9wSXh2k9rA8kRm40rCFlBheIGOy6DqFpERRlS8p6Lc8ha0EIRF6UcR3gIEdN8zW+dhhAG8D2EGdUkVCKSfU+USc9ZN3Xtn8OWZMiMRpJTBMxQLmHVjnA76ZzfZ11GIOD0wPkWQarDQKTaLLXyBgQu8U5h9oFNK5XIJH1JCX7pM27v6eYpmCoOo57Dlp3HTQo+CclkL3rM/k8r0FkW1BbR6OW65L3144YTBKcpLWmoM7QB4/3wRx9nXaA1Dp2g1t3n42eRceAN2M0AnwsAZdlCRHN2bdCpNc1EXSN6wAfWG6f5m3X9e2g+9Dz94pBzWDPSQmCQQY57lLX6n8PgUjgPFGcS+dOup9RjfpucK/dpLFICMt0VEOiMj23DUM/UsYGgFjSxrkOFsOgohBCxH+HWFSvgCUkZOpbUQCPAynS7GDnybN472E5Szcdw+kYkiAJwEY8Ln02w0Q8GwBQplcW2e0TgINVgx/4qbtchBE/jQMLvBCmCnHcis0XQqDM2eAirpXaLr3/6eBcov4Gsr3iGhI4E10rICkxuDu3hZ+I9hr6MoRyvgS+WWuxqWpAqeg3yPohzy0lK0NH/rAE5sjYloQ6gBNGMhPHA/V9//ehQha1c5qNYp+R3S6cTI0874Noq6oCgBhYK2MPAObzvbjeVlWF9Xodk/TEl5iMx0C9jvij7GwSkCzBfzAGgRWqaPz070rmR1Q+SILxsswAGFECYhLcqGyBLOtViqQf+vceYIxGzoFXsjLQ/SmgRRtWc/Ae0zzDZEZlywI0mrbDixcv8Pz3v0vB44GCzkZFBi0hYNpAm4wCmmwGcMAMl5GGUZTANZ7t46NHz/DBhx/h+fkLHBwcwIc+UIG4No+iyOJ4kn2S1tiCxjnbWiEEHO7tY39vD65r0LY1nOuQ5yOeFz7aZGlfklpIIBNEXBmkKj9JKZauQ1VXqKoqvusizwFFChFBU8a0UjqqGxhjsd1s8fjTTzGeTvHg4RvIrMXi+grnR4c4PjxCMaIAg+DFnmLSmX8S1RmZd+n8S9eNVx0pVpbO5/77/Tjl0xhPI97tZnmDowMKevAgm1VOp+v0ZQHFz3/zrYewmcbjx09xdX1NY2U0xmKxQVNfou088oyCLtq6IXtJ3Z2d/arne9W5uwT1rSMEpPvlq+551366+/Nn4ZqfB6N/bWI8XURlUT45OYG1Fh9++GGs13f//v1IGEp2RlEUMbtcc1SbADm93JmJC2rbtjHaXxbG+JAhoK0bBAS8/4MfIMsyPHjwsDegeSFLFzWRv0uNT3kemXzymfwrC7A8b5zMIjMCitg1ybnpfei+Dbq6jOdI5gdJihAYmucF6qpCnmXQABbX12jbBpdVTZk8dY2ua/Hs6WMURYGLiwsCBdeUhSyyJt9vmkjOLRYLerlscEv2atO1UR7xk48/wpPHj3F0dIRHjx7xM/eZVW+88TBKic9mM4hcIgDM5/NYm7GqKjR1hfF4FLOjq6bG3t4+6prq0G/WjgnkGfLM4unTJ8iMwYY3tvF4HGUhxaC4WSxi3XZrLV68oCjjBw8eQCmFx48fYTIpeCHvVQkODw6w3W6gFGXbr1ZLvPPOl3B9fQ0gMFA55shBx9KfNAYWiwXXs7c4P38Bkdt/9OhTdI7A9/FkTLYRSzfZjOrLNVWDvMgxnoz5uhuU5RZt16IsSVpyf38vymiK5OfFxXl0eJS2yPMC+/t7+OH7P8D9+5TVszffwzjPcXZ6jDfeeANvvvUmfuXv/wN8+7t/gJWv7p6wKfP6GYdSCuflFv/573wH/4uf+2MwEqV9Rx2dlNwOgofw5zGjHEJnRHf6s5u0syiHQOR4zjW9A/OnBLYoOB/gAs0/aMpisIEy2CRqz7lh5qQXI1Kp2BqpR6dZmghinIOsCecoMMUzOS+KBZT5wBt310IrhaauoiO1S9EGiSgPwz6Jf4vkuIoA3+0FPxAoE+lm+qnrApom4P/8rffgjMGLFy/wv/9P/zM0jQOlNQQErKGUxovL34VSZHj+7r/8XswQMJalHRHgfqYPGNiWNRB6xyJm2LMMmDGG5ahYxsoRqewToymAwA7e1eNarXgMBdBQS+Vr6Nlvj5Y0IlDGVP9Lkn2UXCd1dm51/i7afPuqtz9TBJy+bvTcj3N8ns38j/oYEJt/iNf7w/7e573uXc7n7t9edm2pg/Tj3H/3fncZp3LdFMTbHX93Geyf1f7X6UuxidRgjRbwXp6/7wcBLF92LZGQetW9tTKAGQI+PRh093WVIiA4/Qzg4J0dh0SAgdSeS20/cQLlO861KEZ5tAUza5HlBL7kWQ4XJegCZrM5Tk5OILJxSik8ePAA0+kER8eHCCHg6ZMnePfdd1GMKHN4u9niwcMHGOUFvPNo2wbWZphOJiirKpKAxyfHqFva87fbLbIsh7Uk5/3ixTnUip7Fe4/1ZoWTk2O8ePEC14tL5HmGq6tr7O/v4eh4H5NJjizXaNoSxpKNMp1NsH8wQ9u0uLi4xL179+GcQ1lWGI2KGMA4nU7gug4N/221WuHwkAjd5XKFPC+wt7ePx48foa4aLp9BWUVN3cJ1HpPxBF/+8lfhuoDFYgWqCT3Fo0ePmOx1mM/3WPKbwIqTkxO2ockBFBJVawosWCwWuLq6wmQyiXW5hGiPgbUhRCl2AfLH43EM4hW5cLFHu66L9aKF6JZg2JOTk0GG8eXlJQ4ODuL3ZjMKDK2qCldXV9hut5HEF/9kPp/HmuZKKdzc3MAYE0s6AYglirbbLW5u+PQwCQABAABJREFUbiLwJNnOMp7Fd9rf38f19TVCCKiqCuPxGG3boizLeI/pdBp9mtVqFQMbJpMJZrMZyrLEdDqNu3IIPfAmQcPiF4ia0r1797DZbJDnOY6Pj6M0vJRVSgF7IeRFhWq1WkUgREg6qXfuvUdRFBy8UES1qaqqOEOin8NlRWpLMucl81wy1ifjKTabbXz/QorLeKHsCxvl4gW0S8Gz7XaL8XiMvb29SPwLOdA0DbbbbfQfRdL/xz20kFjpmi4GFB9S9RcASXW+7GL9abSght5mk8M5Bw/OkvJAtW3xN/7G38C2dpjtncCjwKPn5/hT//0/i9YH/JPf/DU8+uRjuKbG4cEMQAeT5VCG6ol3XiR8OStbByglZGZCQBlNWTQC3gYmH/vNoA9wlMdX9OxesRSi6u1qCeLk0/rHl+sJOZrsuwqcSR/6gCqlFDJjYUcjLG6WeP78BWbTETQ8rs6f4cmTRxQYJZmMfK+0nnHbthQ8MSIxRQkybtsWGTIoMyyxIWOS8fi4D8qaVvHe4L1HnmdwHpiMiSj3nYvSvbTvkU0tKlzr9RpHR0eRVBK8ppEMEgXUrcOziwV+8P7H+Mmvf42JTEf7rMnhjIO2OUwALDQK7mDP6hGx3xWNYCFfPAfTrlZrZFmBk5MztB3wuHyKLSuJCFlDGaUmkhTyIr3vbtmk5A4a6NAD3ORv+PgO+3/7sa5DHkcHgaEyFpjwAI2roAGv++DmdH6FOJYB7QkjUD5Ax2Gb2iGUqdkoUMavUnC8xznfZ4pqrWAUSYcrRQoLHQdAGa5jH4MFuTY1BTCwXGsAfMsZi/w/7chPC15IeMHFaJAJCdXBo2u5FEuSKSrKXdZaBKUBLdmbamAzaaVhC8o8DlbqZ+rowxtrIkYVPElLZyaPOGAkw4JCwWs+IMpzmkhaTXKuShH+0LWUkUfTmWxSyXoDODM49JloNqOMusDOaBwSogqk+jXDiDyxp2x1mVed6ygLVua7ptKG0JQRHnyPOWaGStoED7RMtsmzir1ujYXSCnVVYwKPqRqS1HLflFiOpDbfT9QJDL93sHR/17TQWrYNkp6n5BsF7ztSdvAewStKRFGImdmSwRaD8DzJpkspNe96GXSaNqK66QDVqx+FINn5rA4lhCuo3I73Q5XOdN3XWiHL+mQr2eG869C0RJj0pB/J8ZJKhkPbtKhZBYqII6pN6z1hEqLAoLg8XIoXKxUG6n9QiFLSPvSZ7wVnqwo5SliU5/6RtSjAMrEoa6PgrvLMcR5BcdmH21iDfMcnmevpeAtxc+y/kJaY8ryOgN+BDxL8tWtj3CY5AgdoRRxdgmXCrh+alsCT/gsyHZPuvDuYXMKT6JcALco26PfPHfk/KChkPCaHQdyy/4FxIg+lbmeE8q3iN4Khtd17IjeVyKVH35+lzcOIAuW5L40Q/4HGjmJcURsT8VH5XPq4J70COs44BhDfW4qfGa3jWqR1Lzsd97zAexAQiT5wi7uOZeQVKWiI30vP2K/TgvERPq0TTC8ZW0rF+siZzVlOmwo9K2swnkwwHo1ACq8uXlMphbquMRpNYQ0nx3UtMptBeVLC8T5Ee+jGUSD5aDTC8dE+3n7rDcxm0+g7SHDx1Frc3Nxw0HGNru0Yb9DYljW6bktJUcGhTko7yRorP4svEryPSgshyK5P/xe80TPmESX9eb2nEma07llrkY0mA6xCFH4G/BqA+WyC07P7CKDST89ePMfl+QWyzODoYB9FnqNrStTbazx858t48OA+prMZ+0YZlDYISspxSOmDAOcDxpM9vP/Bb+PRkxfwQWE0GWN5c50EnwUO+C+w3a5hTU/4C3+n4OMaq5SHtRqOgz5pbQ4Dta6gZK3iPnQ9Wa54DMnzp4S473oFDnkngrFneR6z0XlqQCWli0LwyKzGarXB08ePkOeEtUwyi08ePaGf8wJWGdR1ha5pYXODznOJC5VwGJ+Bk92FtQ3Wk8TuxCv8Mvk7NGCURfAedVVHVToKLAD3O/VemuQRQoh++71791AUY0yeX+D8/BkykFpKXZW4urrGuCjw5S9/GXlhyR7EbZ43fbZdm1n+dvs5Px8+/Kpr3kWuv6yvU77k8+Kcu8fnqDGOCPRJI5wLmM9n+PrX341GU1VWaJuaam8rYLtp4boWbdNgPBljOp3E73teICXSUwy9PLOYjEdUY5jlJeWlBeegeIJpAL/2a7+KMpVSB+DaBlmRo2laNK5DkRfwLBnXcpZEU7PMmioA/ptWiJkOCkBmswiQAYh1FLuuw2q1wmQ8Rp5lKLsuLgJ13cRIrRA8lssF2qqG0gqr1RrTKWVUL25uKNM4y/Hs6TOMxgTSPH/+AqenJ5zZbXHv7B4+/uRjtGz0XV1dAaB6dSIDOJ1MUNcVisyiazvsH+xjuy1hLW1ewQfM9/dwdnYPreuwWa/7+okBePDgIW84BZq6Qdt1aOoae0cHLI9OAN3Z6Qm2ZYmbxTXme3NcXJwjsxbb7Rab9Qp7+/vIM4u6KvHixTPcO7uHopgxUGrRNBXKcoM8y9C1Neqmws1igePjYwQEtLzg+eBQlltcXpzH+i3eeWhlcHH+AkopTGdTIATszWdxMVWKyMmD/X2cn59zVrhCVW3RtR2+8+3v4MGDB9BK4+rqEuvVEqPxCEUxIiDaWIyKguU8gYYJ/q4jMKMLJN0pGUqT8YQ25qqCgsFqtY7yoJvNJtZdpEyiAtvtFkqpWF9yPp/j4ICk6ymbaIyqrrHZrPCFL3wB6/Uae3t78F2H5fIG680axXiEUZ7hL/6FP48vfuEL+C/N30QHR1m9Dr2BBJofnlbjZHYA/XI/mOE4327w+xfX+ObZUfLpDlEUjavEQ4jrg5iJ9DkZT7sUcH/dnhCWNUbFLPUQFJQKqKsK1joUowJgp1wZDc0OEzk1noECNk6sgkUW7ygGu/xORgK4Rl2/kPrEaBYZw+DJeMyyjKMEyTjsOlrXnKOo667roMIdzosY41DRoE8zxvtggmEkbkoy9c4I/Xf33dVtwF/79gdYNh2M7gB4hMpDm4yD9USmvoEoVjTbEsFR2QbvPVTXcv96pNu2Y0CSDHnNDpHnaGCQEcFGSBopHti4l8aK3FN0APoXwn2CWFPmrkP6ISW+X4cIvL3J3k1kSnvFOVGDoJDeQFBsLHkGXl9lAqR7ceyP5HqfeSTgb7xOvNawdYHPjwbMyxry0nu94v53nBuxiuTjwSPecW0FybxBJEbZT965bfJOE2ducEGVBFHsfFfFmRWGJ4ihq3CrnTT/dohxJdUdQ3y23mCWJ6IZqdI+GYxJDqIIQ7UKyDqk+ivJGiB11UTWi9651NIjyUNa/hKpNb6KgCW3g2r4LjuEtRo2ih/s9ksUCXE6TSOmFgmsoaXmVZ8VkY4fyhxxO4a3/Jy8B3Y8yUkngJqcTAORWqRrKO4PurcEWUo2k7UZr0kh3l+c1WEgBBgI8rBWAA+S6ptO5/jCF77AJJtDlpPDtbe3hzffeBMHBwfQWqNuauzt7eH66grjyRgIwJSlde/fvw+lNEZFgdV6hbZrcHx0hKYlO7HcUkDg8xfPgUB1y3Jr0bUBbVNhw5HZJWcF3yyvUVUlTs/O0HUdZ3IW+PDDDyJoAQALt8D/6vH/EnjcP7vYSXqtoZ/2gT2yrompIOu3Ugq44H1ZsngSZzF9ZyEEVlfh9/Wc+1tp6A3t6xLgKsCutLUnUFRcX5VV8E898HQ4htWV4tp+uDOoQQbU7pog82RwLb533G0Hf1O8zvW25V3X2P1Mzt0lbAb7ePod7vOQXE/aFvqbRPBM2oQn/fxK+1IxkCqH1MrbXRNuObqyJl30a4ns81ct+RxKa9Q1jXWJ2ldKRRJYwPnxeIwVS9Sdnp5iuVxGElpsYwAxm2W5XMb2hdATyZI5JyQgzXEisIRQECn5dEXOshwhAEUx4kBXqYvaIc8yZHkGXWlst332Oc1HjdF4BGP64BkvxGhFGVxKawLbui4qAUg/yPPP5/MoNz+fz+Pv+/v7+HGO4HsCl+YZj4Von8mKPMz4uvtivHbzXiZZqjLoSH6VbLuiKNA1Df7lv/w2bpYbHJ89wHJTYdtscXLvPurO4Z/+2q/h8vw5QnAoxjlClFllWegAQA2zlGTgR5A4BpWTtGScz2I3orf5+vmF4fV2HxP9/AX6a/Tjvp+TPrTQIEJPbFr5kjEZRkWByXiMIi/w6NlHNJ4BbDdrfPzB+9is18jzbBAsR3uRZb/Cx4wpWVeMUSDxbQa0RR1L67jXC+GYEmLpnEjLGwGBSrDVHVxoEQJnNbGNGxSgjEaW5dhuSZ1iMplEdYb9/QMsl0tSg/AeVd1gZCw++PgRvvKVL1GNeR+gQ4CxGbwBjM+SOchrugQNSyCt0mx7dJzdLkp7GmVZYblcUYkEKGR5FsuySVZvkRdomVCncdLPO7GnaLiwEgLXvdTaQjEByFOlt7mkPrJWUCL3LGMs5tamA1ABJvm+/OXWfOR2hN5XkzHrkvkaz1OKpdUBFRQsSB5ZsY9lQD5JcB7wATpoItycR9AB0ARoV60HYABwrXWeezS3uP6tMVBZBsP2lzEGxmZMVPS1irUxsLnUzJXyA5oJGg6OUJT5bUxGxAGT+ukeRhieQbB9NnLg/TmVHRaCr8hHRM7wM1HSiYvqO0opmEC4ulc2ElyyOTrHGVRiIkKRXDIT0kSkK6iAKIUtPpXUC4fMyCR7OYQA0/QqE/zm4hqjVUIQao22IeJJyolJnza+X2eVosz1OvYBnS9rRdu20Oh4/Ab+rAPYV+lL9vRt7LNGacymtlUIHk1VJx4N0Yuav0/BnTRnfSClPq3BBB9J07aMhTnnEDoHMAEoe7LYkrK2++ABT/iqBD2JHdOD+TxWVEjGR4jYgBC9PAAQkBDGYrPy/i42S0qMK9UnHkSPRfF4v8uWjZtNst+A2yvTNvpdKrYRAFy9HdwrcQqTlSSg8VK2oLe/ejyMiWQoUCmAu/25fp51gOr9wJD2Y/Jdnfq/ALwJ/fPopH9Vv5ZJ/8rc6JX+AMDy+Aqw/YTrbdQQ0E/Evn0ilS9rNT2rjm1T8d329kgcw94BmlQgNcQW2M06DAiujuNC3mEkeKBgDenGOEU4IbWyvz8G7723N2Qv3bVDjDHQMLFEQOBkEQn2iHXilYI1GZHlvAbEclmy3nialyYosNhsP/ZCr+SpDd1P7H16Pj145whIgsNovEpJmDieguALCto4moe+D3bwTqNrh2t3CEzGBzWYnzr1N9i50czxpHOLgk8UqxZkEZcgn5Gy1oEQn4/6iJL6MpuhGFGy5cHBQVSuEv/SnZ1i67aoQo02NOjgYI3FZDKC8RbadfCdg/YKYw5cpnHp++z/QAFoZI8pDq4fqowGVvPtXMc1wfv1VoIgfdvCcb+1WmPFCry0J4D2OTtURdLaYLt/gNZ5UoMLHidHh3hwdoLMGlydv8DV5TngG5weTfHwwT1MpzMKTjOW6paDAjjIDtBA8Aiugy1yXFyt8OjxOTZljXw0Qte1VO4i8alFlcT7AFPYOH+stRRspXheUINhDAUP++DQth26lvBkwwlnQbHyAhPdUktc7CAZWzHgiedRqkARfK/SkLZRcQkQagrJxsteGDyR9pv1GpfnL5Bllsq6OODq+hr68Ai5MchsxiVV4lLDK8LrYcx3+VqpnzHAA1S/Hgbx3Qa4CPlwxOUQTtNyIhpdC8m+0GMUabCcqLpNp1M8fGCR5wbnVy8wmsyiQs9qvWUlJouy6mJ5GEkQuNXu5Hf5bJdwvoUrfMaRYiKv8527cc3h33aPFO943eO1ifGy2ibOGnX+arnCs2fPcHl5ibZpUSXE32g0wv379zGdTvuMjtEIHUf/OueQieMLWlCbpkFhs7g45XmOriX5QMmwCCHAdQTKnJ4d4X/w5/4sGZjf5QXLezjXorrZwjmSE+sayrqW75NTSZLIXcMyIsGjrVkyQgPbzRaNp0W6aRpcMnl5dnpKjmnwqDcreGtwvVggsxnOz8+RFznqqobzLjoSlxcXsTZf23UxEKBtW1R1jeurRaxFp5TCdr3mbKAM5WZL0eCWZMS+9pWvceQZAUskxdmiLDcxiyHtT3EsHz9+jJubJdXXzgrUFUVKLa7Pqb7hDZHXzneYTMbo2hY/fP8xmqbF/v4eJpMJurbmKCcNaxQO9mfYrDfwvoXWFuV2RbV9RjmKwmK9vsFyuULTkNRmlmUInh1iDYTOYf9gD2W1ZelOi6ZpUdcl2qbGdDKO2ShFUUQwwHsPoxVmkyk0k3UiVVhtK8ADJ0cnePT4MQ6PD7BZr5DZDA8fvAEA+OjDDzGdjdE0FZxrsWVZzMlkwvKStGlvyhKeM0pkDF+Ecw7Q8Dg7OUWe5bi6JHn6UTHG0ydPAUVylt5RJOlmvcFsNsXBwT7quo5yo5KBL3KeIQRYrulUVSXynOoWOucwmkywf3iA68U5ptMcTe3wS7/4c/jrV38PKxDQuDh3sCPAZL2BP50Y9Lncrzh4zfiHH3yCr58cIotZ44hGe48g90c0dJSS9T46jL1VO4B5498HAHu8fO9ACGjsXIdyS9kMNs8RvNTiABACLF/eeQcQvc1GKIMbLE2kInaWOCniULp+M5YaH9ZoGJYilcXVOapp7r1H13boupYi9JFs9OidHDX4JO2O4fmp4xT/q3b+3enzAKCqA/4f3/4A/+LpBRmFDAgFBGQ6RCfFexc7VbIuolGiAASpMTkcKT4BByE/K8BF8J2dpMSmcM7fvQlF36uXWk+fK6nGN2hHTyAoDIdMT372jvPOphn6c+WnXWKHHCvZmOW8YRQy9SH9zRhNAFfa+DuOMPg5fZ7406svcMf1X5alnhLO5PjfdqDv+r3v0zDs20FfyDPcbtfwjNvPk4JAcYFAbwjSz8NnSYke3Gns3CaeBCSSdUhkydK2iuE57IO7goTSWw2BidjY6GzLFfoITq17Z917D61IOpGIE2mviZmQpIwjZWMyFAURO1IyhYJ/OkBJTQN5zsAOqhk6pvSE7GCkvaZJ5nHwxAJypIajH/wdDDAIIRlYm0u+J89M/UpOs9nJOtDkSUGytIlEpbbmuWW5NMlOJ8fYuQ5am1jbV54vkidGo2lKUMQyAOWQZxnarkUA1zm0EgHd8h4/hjYak/EEnSPi6uzsCIcHcxwfH+NLX/oSZrMZnj17iv39A9y7d8YSXYrlwYqoPiP1jV+8eAHvGhSFwYP7p7i8vEJdbYDgcH11jizL8Xh5E22ZcZFHWeyYfRMCurZBZg3qtgZ0nyVcVRXyUQ5lFJOBU0zGYzRNg7qqUZUVgpNxFOSt4tpdU+cna3P8ffez3b//KEc6bF52jfAZf/9x2vCjtvu/PV77kLrG4/E4qnrN5/NIjCulomS79x7L5TIGCgNU010UokTyfrVaQYIvZK6ndQMlOLksS0wmFEwi60Ge57G+vBwX5xS4ev/+fSho5BnNt7pqYLTF1dUV8jyLmYllWSKEgKatYTzJcUqZJbm2MQpNy4T4dBwzF9brdcxmV0qhqqpYWkCeWSRGnz59ip/5Mfo+OJcA1rQ/pwBonPlClPDnAJCY8vwfDwlIBNATWvw9yZTJihxVWWJxvcAHH32M8WwfjQNu1hs0Djg8s/jhD3+AJ48/hYJHnhHQZw0YlJN9gEldw8FLXuwCur/gCrJHp7ZvCmrs/l36I/37LmhN5+2UJpI/qOFeqLQQAaBs2MAKIbnBaFwgH+Woq5LLFFj4rsPNZomnT54geE8ZOr1VCqCX1KR+7olsHzxU6MH3AAJadw0iY3S0PYd2UwqO0f+VAvI8Q5Fn6LqArvPxcvQaJOPcsH3hMRqNY3mAs7N7PC8MXEN1xl3I8fjpJa6XSxwe7EEbDd8BBpqILi9KcxxMoMjfIO9HatfSIAyQLDCHzhExTioYK1RVjSzLKRMuAUjJduyTJ4SwkM9uuxpq8COdbZJPQ2yPBPkplZJx1PKhz0t2pYGQaenV+vcdlbIUBVrHUjthCJzTxOB2MZ6jPJUA00rBGkv1UpVC0NFqpvM0ByYqUTyjjO3W8xwbjBHNimg9yR0yDjBnAoIUR0hA2TtOQlEambWwLE8cAnpi2aiYpWoUkRrBU6kxiGx/vyCh9QG27e1o8Sk9eqJBjta1FMxtA2BBAXLOwzVdfB4ilAM6Lz4/9a3mPUQpJVr8CIoSLYwmIl9rTdl9oLJnVVUhQMjm/r3HzH3J3g+gwPeEMINSMetWgqKkZCECorqC5/FPfiwH6gSStk2J91RCts8Od1AcdJ7OCaid9c372LdxjO348wGAa6l9PUVMQS6UOe74+wEucXc0P69kLksbPBM8fQ3Z4RoV2+dDnEZUEoLHExOFgcc8ufm7vioiniHX917BcFkBOchn7IOI49pBncMZrUwWKXAWb98HqU9FQzfwmGBCUzZObnxK3MsKIDbMLm6WYlly9MRvgkyE/joyxnpdCunb/tze96JNq9/fhbzsr5+OFTkveoq+X8GICOrJVVl/peZ0HH98IVFlpGBCurL4gCH6/f19xceL/SLrFK9nEeMSG6cHveiZnIZkwMpFJds8mjoKCL6NG2KKn8nzUP8aKJgIfcQ+l3UufQ+y1lob1690jGttYBh7oWf3cU1wLgnAUqLMGiIeKQEWEVNRgX3sXrVEss0DArTvpdgD2JJLMv75hcvboHeUYAE9RpDaEDK3Qv+OYvB7ek4/T3mG9O0OoQ82StadllWX4vjgMSqqm0ANBcmu79fKdI5JsEIIfR1say1ejMewWRbHndEaVzfn7FezDLfzsKz2iiDKSIBGFrF3qD5wUSnFZW48V1bhpAWtoLUEWwCAgXMauiOsWNZGBSKBjTGJAgf3r3NQul/vXdfCO9Xv2UrBK43FwlNNdbVP7yt4sjVXW5w/f4zNZoPjwznefvMhzk6PkWWcma409yXjNbxuSbDGeLKH97/3IZ6fX6NpPWxecOlXMMZByQtSykNrLpvDdny0L7QoEBFeQ7ci+wWelVvAWeNZBnCihygZpTaKjBcJGJU62rJ/9XZDGL4jKdmiSDVWgkwGah+e3r13HZY3C+R5hvF4gvlxgdVmgyLPMJtMkBtLKi/w3G+37e1XEa93fXabjFXJHjDEPwd+CxSXL6V+VUENAg7juow7/Br+2bmO7FVjMJ6McKpP0bgGTVPDdQ51RaWJy22J/fkcWrkE0+/n86ue8WV98VkkdI9R3b7Pq677We3YJc3vCkx43eO1ifG08WKgjUYjvPXWW3jrrbfIkNckJQFQbR2jub4MvUE2YhHBj7QejUyMtqqjfJgAJQKs0PcMECj68+Zmifl8BiiFtqEM8KZt8NGHHyAE4Pr6GqenJ1TjbTTqs8U5U3Jb1bi4vIjOwHQ6xagocH5+Tk3uqG3Pnj2L8oi/9/gxjDF4+vQpuq7F3nwW5fZCCNjb28OTJ08AIGY8dJxRLvUzjo4oI3c8HuPT734PNzc3+Omf/ml84QtfgNYkN1mWJdqWpNe7zrEDodB1LYpihCyzuLq6xHK5glLUp0VBGRgCwEo9d4DkCpumwXK5jP39/PlzHB8fY29vj6X+fCTo9/b3UDc1fvu3fxuj0Qjf/OY3o0O/2Wxwfn6Og4ODOJmFhJdI7yzLMJ/PMZmMUXNtCMk22W638CxdOJ1OY4S6UgpFkaPrWsznc1xyvcLr62vs7TE5zw78fD6PgIMslCK/sdlsMJlMcP8+Zcg3TY2GJQ7rusYXv/g2Nts1xuMJHj9+BKUMHjy4z31OTlIIRLZ776OsZCrHWFVV7D8yCj0WN1cYjamuobUGD9+4j9GI+lNqpmRZjrZtMB6PcXV1xTVPshjQEEKI7SyKAgcHB2iaFj/84fuYzWZoW4fF4gZaZei6Mho5k/EY737tS/j08RMsVisCYHzAcm1gDLA/z1AUSVTnziGfXpRb/OBygW+cHsm0jYb9nV/d/Vz131GQzOjw0q/vXiY1bvs/khlW1zVarjVnteQXB2hloA1F2pNDKdG4YqSBJLx8sonwf6Oxp1lOKLPIeR1jkxTBS/ZDB83OUteSpBgCZ0fe6s/dp6VNkRzMnazvxHC/u296MjeCDgCaNuD5qsLvPL0cGLji4qQSNC/r891DnHg54fNEce0eu5tZauT8KMdLnyO5Zmr0v+51Xrdddxkg/7qPdLNPP/u817j94ee/z139tdv/wzGgYoS53PTupvef3/1sfcZp76iLs9IDggRs9NfZNXClbuRnHREw2WkDPW8vKW4tORFeyjkEyiShwK7RoA1i2ItCTUjKFTRNG22jQf9FQIA+MyzT1TdHgplErlBRdH0MEtLopc/pSOvapVkod/dBT7rLs/d9GGK2C6kApXO+r+NlTCIByU5u29a09iaR03Vds4SXgrEZxqNRVPAYj8dxfJ6e7WNvfw/WGEwm0yhV/bWvfa3PbAkB2+0GJyen+Mmf/EkunwIcHBzg6OgIVbkB4OK+TgFyNdVA5Sj01WqF0YhqZo1Y/vzJkyeo6xqTyQTT6RRNU+Ojjz7CaDTiurI+lhQKIcQaZ0+ePElksTzm8zmcc7i6uoolh9q2xYMHD/D8+XOMx2PMZjNsNpsImErNPwAxI3d/fx/7em+wj6bvT/4NPgF403nOQFLqgKXZ5gSAmahiEJ0gYCDRGOGUO9aQ9Hr9uFJxLu+usXEcy0ROgL5b8wMYtD0FsKWv71q70zZqpWPZHInCTu9D56jEThk6gmm75d67IGN6Xvp+1E7fv2z/fNl30nPj7/Iuknei0GeZKQlCCinoKyUieltFKYUDe4gQKFBDsvlEIjwlgUVqXojnruui5PtoNIL3npSzNEm/S/10n8xtKalVFAUuLy/Zds4omJTtEiHei6LoAXUFPHz4EOv1Ovo70laRTW/bBqenJ/EcyeKVd02+VIGyLGPkvYBFbdvGe5qsz2yV2uLiC8nckTVFKZLd/3GO4AU4EjnNEEFdz3au+NnRDuT/DEgUHkues1ZCCHGNon4N8f1lAbi+usb7P/wQy3WJt975Cj769AmW2xLQFsvVAp9++ilU8MhzC2sJPMzyDJ131D7e24yigCbvFUjCtJ8TadD9ACTamS99NmAPKt1lpwzskDvmRHrteH2QsoBSPSjuPc2RYpShGGVQKuD66gIqeIyLMar1EufPnuLm+gp5ZtE2gQHCfh6Tn0ogOQVLD/tayr95lpM2xhChx9+n8ds/W7rGxD0/EIGodIBlvKRtPbxrITWg0/4x2qAJdQzAzrKMyywQsd40Fl1HgRg+aFxcLfHk+Tlm8xkmowJN5xAcZWkrk6EfbA5QfaCI1g5dK+pb5Mn4ELhuK/lqZVmx6oRDXoxIFZDtI1qjRAVDMrcCA+vDta9fOxPSJ1AP9TLOQlzI3xW819A2DQwOrJQlqyZnHGsD5UzcXIlAUSyjynsYg95B5PR1FklLAJRpH1+mAVQWVRNlf9JaI8/zWN6jNQoqIbDp+70ErmZJdWsL/hut4xLgnVkLJePPe3i0SZlAzcC2Rtt1aDu2KzzPWyaOvOvgGAQ3iqTq27aFCx2cb9G1Heq6QqroRSOCgv9yHz1Ynh9CQHdxPgIKntfMtI52TxL354Wg4JSKoL5kkEo9YwDwmhTPRCJb76wpTdNgvV5D+QoKPdlFALyLWELcWyj9HpH4BOFumjPvA4CubdBUJalEgWvGO89rMifm8hhTkfCVMRliVpxkSUKByS0XcS7ZzQULEAoVr8BZxH5XSlRykrrVwOB3oI9x3L0WJSAqnttiUyR7UQT5JVgZIM0DBQSRZe9lZeVdELkbV/XBkt1Lq8sel9ac5v7zIjFvIt7smRAPwQ3mCo1CIjmFxJR+HNpUvV+EkJK2jMkoFdcMIfHkGvIAUs4kJZ/lHSklqol83TgGZR8MAHxcPwbYlU/J2Qx91nQS8CYXVrT++WSv7Occ+ixnXvOszgbYj1IUVCBZm/FzozlAplcmkoB0Wa85/CWOJjYx5Sm4bbLHo3/H6IPdpXdofvBn/A4ijodh33t00U/ZPeJ7hkLmh1mbqV+kGRcUI0vmeedFoaX3iaP6GIDAyVoSMCI+cm/T9MoUvVvDb41LPag4E3Q/1gRR1UBK2iMAHg7K923t/XXak73yg+ccZO1rReom/Hk/b/ttnQjpEPun43W3t8NUnIfyNrSiPYQy5vt5JbYpT9P+WZW6E/eIvpN2POwdgneoyhKbzc3Ax1Fawz/5FCn2Q+NJwVoJglMUIGMpONZYwz5RiPaazTIeJ/06JaojkgWtlSRLORhbQEqSxJJLRgIiQrQ5CiOKILSvOeYb+j4n5aL1covJyMIwhl1VJTarJS4vLtDWW5wcHeLhvRN89Svv4PjoEJbLP4AQal6vxFbyQKBkxCzL8f33PsT1Yo0uKIysRVv3QWcILiqktm0bJfQVSFnPGMvPpOBdhwDipWh9ogx4ZyjYLzAf0zYN1XQPnIDmSVUlDSJKlZTYQRn4zbQXuzg+eml3FdVxev+AcTFNe53VGi4olNsNri81JpMppofHqMotbgy9YzObw+QWXV1zP/brZIpZpOMytT/vwhRuY5cq/jconXwq2JuO64wPksg2xC4COHAAPTYjdjKAaCfFfY39r+l0grOzM1xdXxN2FDyc7/D/Ze7Pem1JsjQx7DMzH/Y8nPmeG/dG3IiMzIzIrKzq6mJXVXexmmyyuhoCJz1JgARQr3oRRAjQK3+BIIIg9CY9aIAoCA0KIFpkE2IVmt1dJVV315hTZGQMdzzznrfPbqaHZcvcfJ99btysKojyROQ952zf7ubmNqz1fWt9a7tNMR6O7PrVBORxnzeqLg9jDPuOt2HpzWdvzyzfxUe+6bxvwna+qV3+8e5S6nRVly1JmcgBIitDYTTVumaCUxiDoqD6flVZueibII6QJgm6vZ5zAoqiAIzBfD5Dsknw/tOnDjRmOekkSeyEUDBVhfVqhSzL0HEZA0TAF3mB2+sbfPzxx4ht1sKrFy+tdAhlM4zHY/z8558jz3NcXFy4mn2UtRxhPp+7bG0mmkejkctSWK/XGI1GODs9xdBKeY9GI1xdXWEwGJDMdq/nQCCuuf7q1SsopVyN6TAM8emnn2Cz2aDTifHDH/4FTk5OoLXGZrNx4CkAxHGM1WppM423DnQ6sHLn3PaqqhCGIWazGcIwxMHBAZIkcROIgVgpJY6OSLL96uoKQRBgMhkhSTYAgO12i5OTE7z33nt4+fIl3rx5g0ePHrXkDTebjScbTwPOf2YGjWMrT851Azmz3ZeWi6LIveeiKCAjgeFwCK01Dg4OsF6vISXVY+TscybxGdyK4xgnJydYr9dUKzDLoMIAWZajKjWCIESa5ri7m0NIjfl8ju9857u4u5shTSloYTCg+oO9Xh9pmlK2QBg6h5Sz1wGgKEpcX98giiLEcYhOJ8bh4YGr8cgAGdV4nIDkHDljAJjN5jg5CTEeT8CAmhACvV4fLHOW5wVub2+htcF8vsByOcfZ2RnKkt4zKrswS4F//bd/HVc3t/iTP/8LXF1dY72ljPSyMLidlQhDhekoQBQ2jp1bMABUNhDk//aTn+F/3v0BzgY9z91qsNPdg/8uLOgh2FJBc5tvWkrvnWf2fAjK2M7SGlIVznmmyEA4gyRQgjZeu5m5TZalXwTBVizXJliSzBqajnCzUeOwkeJSGNRlibKsnLHnm+Y+Ge4cVNE8grl31k4/PtBXPilO/5Kj9Xqe4D/7//yIssSN+cZN4F03hV/0O/fAeG+jcoCQB1Q+ZEw8dM2/TLsfOvZd66EsbP87u6TGbhv/f3k81N/vev79w47WndPuGRk7oBcDN80J+4jmZmb7gPVbyRx2Ah9oN/3duqDWONw1WIHGGdt1yhi42VUFeNvxkMFFEbWBAzODIHCBTbD7oDFUhoVrAe62+b4D0AQLNgo9BET5bTHG2NpnBEa0wX7PQQY7TT653X4WfjdN394/p3mH7fHP70sp6xBbqbvmaKQWuQ8MjHXGNQYDItKiKMJwSMRut9fFyckJgiDAkydPXDBhJ+5gPJlgPp+jriucnh3h8OAA2hhMp1Pc3d7i/PE5Li4uYLTB4dEhjDZ4+eoVDm091U4nQL/fh1IKm+0C280Gw8EAi8XCEXlsx7GzxjWaV6uVI9yTJMFgMHBEIWeJCiGcvfjo0SOb6drDaDRyQZJBEOD29pbqpR0e4s2bN/ilX/ollwHLdsf5+TlWqxXSNMWHH36ITqeD5XLpMs75vTHR+B+f/ceQUmI6naLf7+Pzzz9HVVU4OzvDdDrFzc2Ns7cGg4GzIxeLhavlttls7hHiR0dHVE7Gtr8sqd4b1+oGmlrONzc3OD4+xmazcbZmkiStDOGJfYccbMgBCWw7LhYLZxP6ktss+RtFEXq9Hnq9Hq6vr12G8XQ6xfX1tQtkGI/HrgZ3EAS4vLxEHMeYTqeO0GQloiiKkCSJ6z/OhK7r2vVPr9dztrlSyj0zB1H6tenZLi2KAuv1GsfHxy6wku3C4XDoACEebxwUOZvNMB6PUZYler0euOb2drt1NjgHXDqC2Nr5URRRO8MQRUGBmFVVObub53qWZY6oZqJbCOFs3JubG2dvc3CtEMLNC65nBjT2F5c1YFKZ+94HNQDad/M8d2tcFEWuHrk/tieTCbTWmE6nqCuDm5sb508YQ4GkDlzVBGydnp5iuVy6clN1Xbs1RErh3g2VMOrYoNjS9Z1fa4/HOvtM1GcGuqbPeV6zfCK/S+4nrt3sS///ZY66Khvb1M5LrqXs7x2Fld17aI+lz4jnaWf/GQf0CUH+12KxwFdff43Pv/gKx4+eYnL0COp6AY0Vks0GRfEVpATiKCSASQnIQCKvKkgZoK5qRGFsS1swCdS2qfaR4v5eJTyHYhdk5ud5p2MPcOLAZSGBnTIjTPLFcYx+twslBJJkg7vba5yfnaAuc1xdvcHzr79CniXodrpUK1nXhEfomgByb8+v6soFqwNWutIwWUqkoTECdWUAoZ3ctN9s4703WNCX2qutXC4QBQHKMERZUmZa4ztYCXcZIAxDrNdrTKdTR2Qvl0t0uz2EIWWTV5VGUVSAEfjiq9c4P3+EQX8EJSlIX6gKUoYQKoCEhoRCKGksUGBIjUqRdDoHAVZWnjQIAmw3GcqismAm1bSmusYUNE8B3trNHWMoSxEGNvhOeOOjHXDFQRgQBOhy8AHbKExs1bUBJAG8DelpgwgtEM6Z1dt1Yn1HafdOm3XGtbKNgRECYSdyEq3O5pQSkacOp8MIiK08rK1XDBtcGFhyWAqJvCiJ+LaAc57T/mtsmSxtOLBFoKo0aitVn+eklMjjpa5r1FWFuK5QVpWrXwvBBFBTv5pS45TDNoIwQKACyFBAVBpaV6gyClTXNtAuVALKlptRivonDGndK6xio7BMDmeZMfGn7T4pg8gGR9G6niQJsjIDlxqoqwp1VUOVZCNXVl6frmFtk4qUPZj+LcsSVd7UvHf+gNa2LnUFDmSRVl3Ot33cWvGWpYXtbG1qkr4HsM+rlI03v/P3hgTiQwsBSOXKOgjRlFIie5pJRAOfRHzQb5I2U1pRwAORfz6hyjgFt9S2zZKDu/uJgQ0n8IhinlfS9zOEcrgKZWwLR9CxP+hBRjt+DCDFLrbh0BX611Dt3CaA0sqBC5LUl1CWfGiSBmRgJX6NJR3qGhpWGUsqKIsRNYSDd3djM8nt9Y1V6XOZxIBHxDfKYW5teoBkgXc/XtOM0dAggp+xdb4ekSDsFDbvy1/rd9dDfyNx9wfcsxptIMx91RYiyIRjSgVsLWXbo8oLvGn+JXl+bdqyvH4bAZIEV6IJjgXaCjL+s2gPY2D8rampLtzz1aZuPfsuBkDvoYbiwBrvPJ5T9ss2GsTrC90EbDUSzhLQyq1vALyM8XpnTO9mZnKfeuPc2kpyJ6DN9ZkfiKy1w/Z3sSkeqxyMR99VrnxC630IARXs4AscvMMrpP1KGEQug9e1D4DxlFkogLN2dbZJfcNYvNjWIAejDWTLBGHggoP4OaTiMmgKftkIpUJvHMCpUAoZtmxtIhxt+RFHuteoiw3qgm0if66wjdq8I+76h0xNI2Oag4LUeBq1Uh5zRAIHqr3OKyERRjROyrxwvrVQEovZFQDjFDtgNCSAp+cn+NW/8Uv45JPv4vz8lBI6O1QSVihF8VvaAKohdaVUUCGpZf3kp58jLw2EClwmchCE0LqGUqHD1bmclYBfwickG18BlSFbVQIwpoYQDTcUhqS2JQRlO0vbF0JIqMAmtdR2hxZeGYG68Uc4SJnHIim0Vs5XdwEI3nvWwg1R+pvdb5UwKGuNZLvFzdUlhkfHUAcHEAlI4cpiEzKgoKCAA5lEu/xeMx7uryduLOxgce05yeVIvfHp26Pes/DvPP5rGCqnY0uzwJZN0EI3+6hbfzgY1tpJBWFai+UKKggRhR3UVY4kIftbqQCy1q0a7vwe+Dl3Ceh3wei/6e/tObYf197996Hzdz+7t779Asc7E+NZkroNUtoIEmhynNjRM3W7zixARunt7S0mkwnGkxFW8xmEEJjfbh1AwtHKqGv82Z/+KTbrNR4/fozPPvsMR0dHMIaylA8PD7FZr1HlGbbbratFR6BO4OST4jjCyxfPMRgOsV6vHYkLAJeXbxBaab3JZIJf+7VfQ57nmM/nuLy8xJs3b/DBBx/g/adPsV4RAc7ZAgzw9ft9zOdzbDZr9Ho9ly1xeHjoAK88z7FarSCldBnZn376KV68eGGdz64loyc4PT3Fixcv8OTJE6xWK0doM6DX6VCtvCiidnOfca0+IYQDk+q6xmq1wmeffYanT59iNBphNBphtVphYOtpsHQgA52TyQTdbhcvXjyHNpQZy8DSr//Gb2CxWODu7g51XePo6MjV1jSGsnhZzj3LMldLsCiKVoaEsIsfA5FFUTgwcTQaOWlGBj7TbUKOoH02Bgv5fsPh0DmeDMKt12vEcYxer0dZ5sMhSl0jDEtcX12i0+lZMC8DUKEoSnz11dcO2A2CANtt4oDGTtxxANnR0ZEDF+fzOaSU6Ha7GA5H6PW66HRiLJdzTCZjpGlCYFEcYTDo4/nzF7YmIwGOBJpJPH361PUjGzVZlmG5XEIpheVyaWXmljZ6PEBZ1njzhhQMer0eUDWLRn8Q4wRT/Ou/9RvQGvhn/+wPcXs3w3qToK4Fihy4utUIA41OV6DfbaKBFqsSaU5Oea9T4TZJcDboNZuMx5txtDf/7K9P0hqrvqfDdLClVsB/dRd+y0EECqyBwZc15CB7BqeUCtoaom5TMT6Tb5p2W0CpttG1yhpzDBTCNBGvSjbjtqo4Q9wGdho/87vt7gr/MUWTedX0m/fx7sYqmkw503Si6w+tDdJM4z//88+xyct7mwAf30T4upb/AhvM7rHPMPCv5zty/Pvb7veLHrub9kNt/EXv+S4b6UPn/CL32neNh77/tuf4JpB4n1HRvDsLMOL+Oa1DtT+7dy/h/q/VZv/wSeHGUdtPUDNAbq9079oc+W08Z7QNqjfAu98W/psxAEyjZyGaC99r+31Dlxe4JmqYsyf5nMagbqIvAbi92gdOeJ8hJ4UAEF8yiiNA/etTlClclPeuo7BvLOxmhPtGvzPEZRMxC9vHjV1HgUeNdHrzLvn+UlKEKgfk9ft9kjZ+dIYip2Cx/qCH4bCPR4/ObZ1Tyo568uSJtdWEDVIj9ZfFYmlrfWus12s8/cGnJMccCuRZhl6/j7rKMR718frlc0AQ+fX1VwvUdY3xeASgQl3lWK0WWK8XGA6HGI1GuLu5hgDVBk7TFGmaYjKZ4Pb2FgAF+11dXeHs7AwA8OzZM0gpMR6Pkdja38PhEIktJVQUBQ4ODhxRuVjQvbIscyVyOp0Ovvvd77ps2NPTUzCRlmUZyrLE+fk5rq6uHCmdZZnLPtVa4+nTp1gsFuj1es4ems/n+OqrrxzZ2+/3XfmWzWaDNE0xGo1Q17ULCAXgCM/tdovz83Pc3d0BAAaDAV6/fo26rjGZTFzQHxPa3K40TR040+l0HBkkBJGvxhhHtmZZRoELxrigASaI4zhGlmV49OiRy7ZvMn1LrNdrZ8cWVgGKn5Htp9FohKOjIxdAwNnH/X7f2Zlpmro60JyZt91uXf/MZjNX6sbv29vbW0dwG2OwWlF5os1mg6qqMB6P3Tvh52XSiYl0lqnj9z0YDHBzc+PI48ePH+P58+cOJFkul8iyDJyBHMexDSIZOvuQbWD2RVarFQXB2r4pisIFGKRp6p672+1atQMqT8WBC6xyxLY5l/9hsI9JbX5vvG4IQTXHkyRxpD0RNA1BzGQ8B5GwI87jiEsIcPks/t5ms4GuKQj58PDQ9Tn1cxtkXq/XACijbzQa4dWrVy5ouChyTKZjt/ZR4GrXrWEAnNQ711Nnez/LMvI7LKHGyg08p9n34XsXReF8x3e1xx46Mhsw4wBkAyffyEEHWmsUHnjoH/6ea0xj7/rt4mux4tfLr19idjPDZHKAb3/nE8zWOW7vlkjzgrLIFBBJgVACURzBSIlKg4BBoRB3YqqlWVMt2rQlB2wzPZWEUNKBzO9ki+z5bJ9t6ds5Bm07lHEMJkNJtcUD4+0eOOgOEIU0/m5ubnB8OEWvE+NHP/sJnn/5BRazW3RtQLiBad3PcBCKbOyEylNy0nXtkg0YW6lqm2kvBSSUG0/s50jZlHby3z2/W5JRFFZxRVE9Zs11hDU0DAIlLPiZYTymDG9WM/nudz+hYBZFJcOKskIU9fDl8+f44INz9Ls99OMBPZvwSTEJBQUNbW0BCSk1lKwBSAS6UTthJZbFYoHFYokwjCBUhDTJnB1F5GpIpbJsf3HQjYCANfxaa5LLOLMEM0TlzB2tDeqKZH+VDC1+QIH1otNFEEaIIgr06nT7CIMYMogQRhHiKEYUxVgXK6u0YDO2beYY13ut65oA3LJy6z+DjSSjKqEBCtrXGirPkeY52UU2qx6asozLskCZFcjyjQvEhs0C4yB2pYh8jqMIYS9uZZVLKRFCIAwDRHEXcRQhCENkgjPZmkxHXdco6hJak5RqIBUCQUoedVXBwKDUNbI8tcEddk3PUxhdNfNJcNYhEQRSKSTbrcOqaMxy2cMSZVmAZdlrXcNkNTqdGBBAUeRIki3KKge9RO1mpQGnK+vGnOVyA1YJVRgOyWyCbRiJNQCElOiHCrUIUaNNKPrkLR+cpblLOLb+RQhpNMHRdAF3Tf4T10bWlrDaXa/8dYvvK13faTCFLYOmNi48Hwh71kp+fuO3CVSrnQ4KuoB9blMbtx6zOokQfnYv4SkBFCD9Pt65LwSVVRIg7MQ7h5UyiPA0VJphxxd0uaXepbWp4J9mDBCECqSGRb0jIRBYP0YKQPElhIGUAaRNlIKghAh+/74PZWxfCgAI2n6qv2cqBYhAQYgGTveluOn5hHt+IbjEwn3ilq7N/R0AInC+YxRREA2MIXUHi7sL0ZTL8FUn+D0BNkgJbSUVJktdViCotEEl0CLh/YgJh0eBMjh575SBJWYM3auuaK9RQQglolZbdvtQKUVkPASC1hhiErWRmq50AYO276yt7DCveTBwaq/7SCt3fwHUFsfjet9AG2WQUkJqDcEqI7JRqvKxLSEEBN/fe6eAhlSNzUHv9T5uVsNAai4FQHOL5/xDGBFjnNznu+fyfggFIBauNERDLDeKHJygFsbNuCGikrBSv1yC0Rqi1giFAJczMcYQ0S0borkSVKSihkGNmtYJDuqxkukQlO0OxmKFgggFRKvPiFuqTQApAhrrZie4BHBxjdrkjmw21sYV0JCBgIIlyI2EUgMeFNSUHayS5xoR7vuDMflvdZ1DwIBUHkrUlZ8lDxijIaREUUtAN4EzKrSkeFkiLwuq940aqq4hASiK04JSEt2wg6dPzvFrv/LL+PhbH+H49BidQR8qCMjvUy68y12XbcwoDhCEAf7oD/85nr94ienp+xChQJZtkOUpDkfHmM9nLvGRx7SUjTQ5/xcEAbShkhxCCHQ6EXq9DjpxCM3jRSlSwZWkzCGllf13/2d3dE3JZ3wvrkHuarTbzxoMvnK2Mpd3oDWokdeXUlBAZVUiCAjnq7VGGFCZo8V8jtcvnmM47COKQyRZCiMEDpTEIO4ChV1PhYEW9YPvfd/x0FxlzJDtCohGiU7sjC2gsWlhjAsy4wAuIeDwQcJvmsBRItibtrCCiApCFFVpuQjiGMIgRG1L8HV6A4chsJx+c423P7P/2S62u9snbR/0Pqa7e59vwrvfdnwTd/G24xcixsOQCtSzs8/gCjlIAqYm2YK72QyhzWaQQuD44BC1rpFnGaqSMmAHA5Igf/ToEZJkCyEkxqMhfuu3fgs/+clPMBqNXNbtfD7HmzdvKEJXKlxfXSHZUtbx7PYOv/G3/zYNJA1EYYQ/+5M/xXtPHmMw6KHXJTCHpZLOH51hPp9hs1GIghDJhgz2UAX43ief4oOn72O1WmExX2CxWDjghDKNOi5bhUjyLcoidxKbTL4TkEvgWBiGjux+8+aNA1DKsnTkcFFkmE4nCAKF4bCP29s7xHHkQMYk2ThQjO2aqioghPEyr3ULpPnBD37gshYYhOOMGHKsmkwoNo4+/vhbKCsCDTlrqdft4nd/93fxJ3/yJ+BsczaaOMOIM8A5O+j4+NgNSpbNn06nblNmmVFuaxzH2G63UEq57JDZ7R3msxmKosCTJ09wfn6OTqdjM/CMI8l5AjAoxdkfk8kEaZqiqGpEYQfGAGVR4sXzl3jy9D30eh1EUWzVCmiRkmHgDIxuJ7SS9RQJPh6P3Zgf9EcQAkjSFEoGCGzk2pMn71uwVSNNcwsklzg+PkGWZgjDGLpmU99gOCAQVaDA3d0diqLAdrt1ANxisQBA5QGSbUbZQ0WNXFco8lvcXN+ielQBAW28NA5BcvBK4d/8u7+NNCvw1VfP8dXzV5gvVijyEkVVo0qA5ToH1xMC4IDt9bbG//6Pfor/9d/9G3g06jsAgg+fFLd/gPGkhl1MNDtD8KVHnW/qXa/5DLBOrXc1Pkl4f+E+JAOJamtTfT5YKbbI1a0C3F5sCfAGHDQ1ZSTQRkCNo8h0AgkKzdF+JIPncr73rLeGn8G4BrbavvuVNr3mf9AYz7sBBgBQlsB/9fkrfL3YuG8+tBHtHm8jzpzT/+C33369/z6Ofc/6tr74q2yW++7xLhv325yzfYbBvuuycbgPYN81JByw85a2+fI83A6zc87bjEEhmoHZNvx2gI2WUQR7jv/7/vY5AMG1sWkPrScNWEIOJH+veRa+t7ZpDT7wbQxgtL1HXRPRK+iaymYWGWhbC9tYEsLYUzhrw97LNM/mPTkA7uc2IMR7mL/uMjjBAAiTaEIQ0Uq2Qtd9j6V/ASCyTqAzpr02UP/571A68Ed7keY8tuq6QhCSQ1gUBfqDvs32s8opUkEK4OBggo8+/AjbZItPP/0UvV4fYRjYmsMDTA+muHjzhogRKfHRhx8h7nSw3W6QphmCgGT4gkA5oi5NU7x+/RJHR0fo9/u4u7uDFBK3t9eQUmKxuMN4PMZoNECSkFpNmiQ4PjlGWZZ4/eolyqpCv9/HcDhEHEeOuC6KAq9evcJoNMJ7771HpG5RQimJ8WSM0tawZCloJgWNMTg+Psa3v/1tR5yHYYjNZoPNZoPxeOxIQi5hI6XEbDZzP/OezoGA3W4Xy+WS+rffR1mWLuAyCALEcYzxeEy1xaPIKfpEUYRHjx45Enez2TiFHFY14qxWzprudrsYjUZOGi2KolbG99HREW5vb13tZ24PO8h5nuPDDz8EQM77ycmJI1211ra8S+kyx1ktQUqJwWDgzlmtVo6cnU6nmM/nTpGHCUgArVI4HLHOdZyjKMJ4PHbOOZef4XZyIMJ6vUZRFDg9PUWWZc5OXS6XEELg+PgYBwcHGA6HLquZCdZer4dut4vDw0OyhdZrLJdLhGGIo6Mjp2LV7/eRZRnOz88diMSfnZycoCxLF/zKct4cJMsBDhwwe3V15UhurTWur68dmV6WJQaDAaqqwnQ6dSpEdV07srrT6bi+pzIAhRtLwhgXSMrEOcuKc6CvH3TqE/YcGMBr13q9doEAHKDqk+w8z4RoFBN4L+L7+iQ5Z8Cfnp7CGAqy5Wdl294HaMqyRFnUKIrSfd6sdMb9W9e1s6E56+Djjz+GlNKOhxJZnrqAZ6Bx6Hl99oMXeA1mf4xl3wMVOcUFzjbn4GAmxRrAQu5Zn3+xY7nZNOSIpiy5qtKo6gp13WRZ1LVxcrcMXAshndwp2eQE4mkRoqpo7wkk5TMoWWM8OsDN7RJvrm4BFeHp0w/RGYzxx//sv8FicQclBeKYMkuECiCDADUkhFGW8CCg2LImtt6yQW1qS/hKB/CAwSJjs9UEIJQnNbgHKPFthF177yHbZ18AnjbG1pGE3e9tJiZs/WVJNfq2mxU2qwUCUeHk6Aif/eRHePHiS2y2awilbHs1pAQCSFDCOD2XU5LJqb6fBFAkCWAz7phMB+CAPZdBY7QFu0JqV13DSJZPhNvb3fdliKKuEQYKiAWqukaS5pACqGHBaCOgQcEPta6x2STo9rqYTA5xe7fAepMgCGktrbWGqClA5eYmwRdfXeLo8ADH3xlgcZtA6gmgCptxrSBMiCAIAVSAKSGUhpLWn6pylGVOxL0kULOsamRFiTiO0Ik76HT6CAePEYgAyWqNPMlRFSXqUiPNUghBQSZQAiYQbq4yJsHzjPs8iGOoKEJgVWrq2qDf66PT6UIIiWS7RV6UlhQybm+RUqIqqmb+VyW2aQJjSmht3FpXFDmqsoQxTbZNXeQwRepAXGNtRyqxQ3KmURTCIIZGiCBQCG0mFq3nPXS7sQtuKwPK4JZKIVCUualkQ8KwzxYKjaLIXX1VYwyEpMysEhnKIgNyg3S7gjG1yyCvyhJFSeR85crPaMDU1k4qvHEKwNgayXAD0IK9uz4LAFgbXrdljXm+a/bh6UkAI5FkDVEHw8FKwq4ljAcQ6QSwtL0Bgh0/xWaXkjSpF5jtOebG1k9V9l7GI/98PMIYDWmZF9/Ub60z1iXSMM4PcnOTFxkQEcuPq6zk+u7xdh++TVRQgI8N9N1zLZ/oDbCj3gbnvDQB+kIAQeMj8uGPN9naW4QjT1wL3LXo/1rtFZKCobx12hEED/SBu6YAAEu02qw+KagMEwzVnDfaEB4lAClsEJGTjgYRmDYg1IYBWPJSeGVyGn/J0pl2zRIOQ2KSkPuMnq0h7IQl3mGojjvQ7E2CCTuboc7KIKTm4d6c63fy+UovIJn2Bcat/OFC5Bz3b0NAGKka1UR7XX6HjFFJFdggAg50AaDhaiXTHLD+MBq5cJcAKQR0RfcLVQQI4eBDv6QEBNsH9t7SL+PFfcjjrXkfgfQoC8Njrxk/0oJwOgigpHSKFsauUZqfWwgow6Ln9JocBtjclPpHcngN3ceXLmaCmf6lZ+D20l4StgLXpGzUYxxJDUPrjxccD28q8n2AHYzDquS6NupGOY7Orl3fwnAAhPbaR+9f2fVDCgVjg4+oDrcG7NiUommzRg1I3QTOeIS7cgoGGtIIhGgIvuYt2v8XvLYEFnrVtE5qCgj0TkUgYQOqqOxtq/76zr6jTET9w31u3xnvRRCNQoA2LvSGFOw8O53uAxjZtIWxIA4GciUGELq+J5tWN3iRNw8DGMhAWJslhIFxZXZrW9JXSoVA14gihUAqhGGA/qCHx+dn+NVf/VV8/O2PMB6PEUUdBDJGFEbQuoYS1pcRgAhCVLUNsAgrVKgwmxf4wz/+Aqo/ggoNqiIDihzH40MEKkKlC3SjGCoUyNLc+faM/URRAJCVj7zIoKTBoBtjPOwhXy+Rb0qcnh6jNhqrTYrCSFR5iSJvZ0Dzuk3KAFxShyTXOUhOCCCUBlpY9YC6BuoSqGvUlYYKIsggBux8CgIFKQwFRwQCQksYLVHp2q0Puq4BQ0T96uYSd68n6D/7CCKUKLIa222BQWcIEVYw1n6CVMQPWJ+EqobsBKu4rV24ffE+ii6gtZ3PQkChUSQzgsaVFhqSlYoMKDscgAollcOxc9mNKQlb0sCWSJCSfwJAfSssngkjEIcxorCDMEhRigJ1VWG5XOLs5MSuOcbOC2mnfuDWA3+f3ne0CW87CHkSuZJEvAwwjgsrF8HrHe/vja3U/K2xbBj/dU2539XNPSiDsQ3NvsPxzsQ4E6XL5ZII014PeZ67+odlUSCQBNhlWYbZbIZPP/3UAa+vX7+GRoXBaIi7uzv8wR/8AZ49e4b5fI5ut2sBuhtstgRYXF1d4eOPP8bnn3+Ou7s7B4TkeYYgCJ2M3scff4z/4h/+Q4oyDkiC6vuffB9xJ3RZ5QBcfW8GwA6mU3z99XP0ej1IKZHnuQPOGERaLpcOIGQwiUEQMraaKO/FYoEwDB3QMp1OXWY2G5TsODX1twjs2W4JJJvP5+j1ejg5OXZSfzx5KFuKyHeW8Oz3+062b7lcIQhCDAYDPHr0CFVV4c2bN1iv124zL4oCJycn6Ha7WCwW0Frj7u7OfbZapej2YtcHDCYPBgN8//vfx2KxcGAZZ3MwGMtgqp/lvlqtWvU1GUQjafnUgW++lCVPsMFwgMfn544wB+ACMvi9MshbFAU6nY7r3zRN3fOlRYnlYoPlco0wiLBYLDAaDQFoBGGIXq+HZJu2Mv440yXLKDuqqipcX187g5ezQvhdl2WJXr/rjK9a15hMplgu1y4IAgaulhqDsXxPJkN4jrEkvpTSAXIAbaxlqbHZbNHrdVpAW1lW+Kf/7z8AjEGgQmhDUeyAwvHhEXRtMOh2sU0yrNIt8qpsZXn5tV2klJivKvzXP32J/9m/9h2wUdg6DGCEn4UNOo8NcdEsYLxw8zPQ4iqa+pWw66ddv0SzjrKZfG+zEfDqe3CD7D+1MdAWDCeHRVonojF4LAcGrqcIu1E7Is5tfM1ybLwNgtruAXZNY5suYgPU/ZlNsPaxd83mx9lxkIvCYJFX+BcXMygVuAAX31DfjdDa9/MvcryN5H3Xa/9VCPRdgvZtx7ucs68t3/SMu/3o/8ffeYiQ55/vRcN7RsLuffz7+fPf30++6fne1uf3xkgLMGpfax8AzZ+1Iwvv3+eb2rqvnXwvflb+2fW3AcSO3DdformWghB+AIFonSOlhLCEGAVqscQoZzoZQO86pO1+5XXs/gz2wB4B1w53X+/5+O+7BFBd126fMMZYlZXS7RthGN17H8Y0JHtTsoPb0M4U4GdgBReWEFdKQOsCvV4Xv/P3/038yq/8Co6Oji3R2UdVUXR3IBQGwwFub24wny/Q7XYwGo9xdHiI+WKO/qCHOCZibLFYYDa/RbfbxXQ6xXq9xGAwhjAkf/7q1St04xij4RCbzQaDXg9pkkBXFcbTKcJAOUUYJSUG/T66tgZwFIYQBljOF6jLGt04xt31LaANppMpdBihLkqMhyOM+gPc3t6hKkroWiPPMmxWK5SVxvTgAFzbkvdkVvPp9/vQmuqFsyx2v99HHMc4PDzE5eWlI7uZROW9m8lNtptWqxUODw8BAFdXV+h0Ok79hcvh+MQ1k3lMrrP8NwdbXl9fO5I1z3OEYYjT01NoTVmAnKnOSjRCCPT7fUeWc3b6wcGBfTf0bNPpFLPZDMYYl+XOBDK/U7bBB4MB0jTFzc0NqdgAmM1mLrObA0lZEnw2m+Hg4ABHR0dYLBb0Xm3fDwYDxHGM169fO2lxth3Z7ubocbYdAbhnYVk5fmdaa9ze3job+MmTJ6iqCpeXl+65WSadAxw4eJPnGtvirOS0XC5dRjjbokxYTyYTl53OZZg4I3o2mzmVKH6nPE9Xq5WzLZmo5sBRViKYz+fuvflBu2yDs/3LGc5aa8Q2EJczqH3lCs7454zxIAgwHo+x3W4dQc19zWQTk75FUbjxxO+cfS32U5gQ948gCFr36/V6TgUBgLOP+/2+W9+01i5YIgpjpGnmPud7sb2kpMJoNMJ6vXblldg3YBs3tyW+hBBOBYoz1dkXzLLMBcNywDH3MV9PQDnlAr9/+J36QQD83b/KsVpvYTQpHTEBXtWUcaFr48B6ATgJe95vhOCgLtonJNvnBq7+sBCUWcfg7d3dDLU2GI9HGE8muLi8xMXFBaQAwoAIcKq3SDWMmewUUoHrFsMQMe78gLqR8Weg2SdWhG3XQ3brLjG++/k3/f42O4/nH5MVSil04hhlUWC73aCuK3TiCNvlEpdv3mBj/Vu2UVi1BaihDfV5pbXbv2ueTwWpTwVRBA8DB4xw8tiulqugoF5py5RAUH1lrTl/lv7ThojXoihtPeyGJAYo48jUhrhCNNkmSgUoqwpBWSHoknw5B3xJFdC1ggpZkUHKEBdvrvHi5RhP3juksnZlY5vRuhIA2kApyorSuqJnDZUbk0opV/4pimN0Ol0YAyKYoVAVGgcHAzw6OIEUEnWlkaYZtkkKoex4UZKeCQ0oKdov08oPewSyJjlqDYG8oJJYi8UCeV6gzrZOhYwCoylwjsg1mie1C0Y01m+0PjMEwkg5kkgJCfQnCO1cCjiDW1HZHe4DIyWMlJZQIXtV2t9VwIRTBVFXMKaG0SUqQ8GLTgHAK99Q5wnyLEVRkmS90doC9FxvkkZLlRcwxsra1jVc7c66CcagYPB2aR9HwjCzQJNor//KmEAz3xjsRPP7zrsTYClUz95vKRzxdzgAVzpyiO/Ks4nIIQFjyXQhVIu4cHNOylYWtK8o4T9N88C7z4HW2CM8WDXn2T7ncQSvP1y9bv8+hvET0cJBqK0CSnp+A9eVFT7xe3/t9P+r3fprmyYbApKJccPPJIRb2/z11u+ffWuwe0uur0WrXXRd1fpdKeVhLnDvY9/Pzn8SpnU9fhdGchgHGsLecxcp25ihb2PHBVrP6/cd/dJur+CxIlXr/Puy735/+ZgBAzztsS2lR46iwctobFbQ2u9HHk78Ps1b35fzV+2zCjTvzfiBI14JEwHhMnH9rOGm3+/LDPOAlhyIZ9tm/P7zvrvb3/7vfDT32B9c6D9zI28uoIwEhM08hwBsQAFvHNI0c9J/N8b4fdfUBL/fnuZ3lkPmueXjDW+bOw0JbqXh7f8ewlyafmpf0zQ3dEQZ/MAN6hXcwyFd33Ab6NPGdmySLaQNYKh1ZW0RelDpSH24h5d731+DDwOiNb6NbPfLvWHlkq8M2Ur2JJesxN/la3vzrV2Wpzl4TW5jyfB+Fq0/iNafKMDFaAqK8IPfACon4nUxhACU0M4uN4aCqbM8syV1NJQgxb0okIjjEKPBEAcHBzg7O8WzZ+/jo48+wmRygDAKyJaQIVQQ0l5vAKEklFAguW1Sgun2OtgmKT7/4mu8enON0eQIRtfQdQWlJDpxjPli7dlK1Gfs8wRKQlrJDSkldFWiLkvE/RgqCJClGV58/QK6IoK/P+wDYQQhApRViSLPbaBFMykEyGatqhplSTaiAFCWBWpdQ0mJThxBWcUjOq9AUVJpGKlsHXgpnVIPl55RUqHWbMs1ihhcOlxrjSxJML+7w3hyCIgAna5EkRfIshz9bkxEtQtUkDT2DGDla1tzwgUI8rgFgNbcbMYPzy3e86RdW6RVIBJSAJr3c1pz4yhGGEWuz9zIdEvX/XkmhC1/AUrsy7IceZWgripSEIpCpHkGA4OyLJwdp7WBUm07Zd+82T12MerWhvsA70H7kF0z7k882AWp9Vzue7i/PrTa2boGn//N3AAf70yM/8s/+iMcHBxSLcblEhfZa3z6vU9JonG1xng0wnw2w3w+x3yxQKAUbm9ucHh4CCEEkmSL/qCL9XKBj559gK+//DlWixl6nQhBv4ebq0tskwQqJDBvNpvhZz/7GRaLBa6vrzEajRDHMYJOF6+/fo7BYAAB4PLNBR6fP4ZaWbCnrlHkGcoyhZISy+WSgMKKaltnqUKZ55AqxHuPH+P29hZ1VWE6meDHP/4xjo+PCZC2wCgAV4uxLEtMJhOXFROGgSOIz8/PHXnPcnvsVHDGCmdw+wCfUgqHhwdYLOYYDHsIbN0HtvPKskIcRcjyBJ1OF71eB3EcIs0yCBs5niQbm3EjXPDC7e2ty5xigCvLMrx8+RJaa5ycnKCuaxwfH2Nrpa7yPINUtDgxAMYSjlQHvYPpdOqykxiA8zO3GQSYzWbguptE6HIkssGrVy+d3CZnkhRFgdls1mQa2XoHLPs5GAzw/PlzbDYbnJ2dIUkSzOdzR2ywNGeSJC5Tf7Pd4tWr10iTHALKAlkRbm/vMBwNICCx3aQ226eR5t5uU/T7PdzezrBcrmydrRhJktqskByAQZ6XiKIQ6/UGsDJQnFF2d/scgwFlFTEYTnJiFMnDoClnrbCMJgOsJJ0mHbjGzn2el22i/DFljNe1xtXFDIBBKBVJRQmByXSK0/ffx0cffYj1eo2buzskRYnlNnEBLOPxGBcXF7i4uABgZX0B/Hc/v0SoJP4nv/pttw44Epxte7cOeUaeaH53Dph38B7iolX5Mv51W4dztdpGEO5HZrGDoGGreWgAokZdC8CU7nINQc8bWSOfRpuELxffNM5zz7w+afYR/ly657hnXu25wsOH3w6tgdtNgf/sj36C1NZbYWCO1xP/eBcCdRdgJKCngRj8fvrv+3iXdryN1N7nMP5l7+Pfb9819wUn3HdyvAhle+y+M9+B9J3ev672NzJqotUWaqoPtDDBSqODohH5O/S3+yN9H9V+r7U755BD1cj3ca0mry171hRuX/OvIVDMPVDzvICN1peUFQZwP/OcaM7l6NXGQYR3n3af+Yf/Hhmc3gUD/P+YAOfP2UbwszZYvYRJ7PuBFsbZGj6w0n53beOZA6M4oE0FBk+ePsLf/53fwS//yq9ASZJ2lVKiqnMsV0sMOj30BkMs5jO899454jjE3d0d1qslyiLDcDREf9DD8xdf4/b2FlEU4YMP3sd6vcarVy9RVRXubksoKfH555/j2bNnLoBvMZ8j2W5bxC1nEXe7XQxsMOB2u7XZmwXmdwvkaYnBYIQwCNDrDpHlGVYrkg7vxB2slxtkeQ6tgbvbuatFbIzEo0dnSLPU9QkTv5whykELV1dXrWzvuq4xn89d9ux4PEaaps7mYkKRSTFfDYD3eyGEI9Bvb28dUccELZPbk8kEi8UCq9XK2Uk8Xqqqwt3dHZjQHY1GLuCBs1sJ0JA4OzuDEFQqhuVNOduZn3e5XDoSb7VaOQny7XaL09NTRwRWVYXtdouLiwtwzfVHjx65Z2SbkWuJM4F6fHzspMyFEC6INM9zN+bPzs5Q1zUuLi5c1jnb0hx4AJA6kz8X2P7i68RxjNPTUwBwWf48T1hWXCnlCNper4ejoyNHbLI9yzXNWXab+41JW5ZXr+vaZfBzySCeX1FE9VM50ICA6hq9Xs+RHEKIViZ7HMde5L5xQS8swb5er12GPmdocyACz3MOpOV1hKX/ucQUj3F/XWEVKA6EYCLZD5QAGjKcAxt4fdpsNq49nMHNfhP7QFJKp6TAyg6+KhS/a78muxSBe1YerxxozAf7GdwPHLjAe12327MBQI0Euq/awPOTxwhnuvtS6mmaIQpjp1K13W5RlqWbe/76yt//q9YY32wyIkSNpuBPrSlJSJsmsFSQ/CKvOz642foPGrb4tAWKaZ+TisjEvChwc3uLMAoxHJFc/pdffYEsSzEeDVxAuMvGsShNG5wmoMepuxiWAuc20O7faifYL/CBpfs/79o4+84B2vZZy+bfAzjT2KHgMAIEFaIwQJKsidwNFMJA4vLVc9zd3tIejcZu5udyVxY2gxEGgVIopIDWNQonH63tuxOufqvWTIrD2WTGAMaSptRsktqGtPluAo4IKqsKkZSodQ0I2HJkgFTKyibTO9c2u4xxDZb6Ho9GWNlyFVJKBGGIWhOwNuyNMZsv8fLlBS6fPcb7j8+RliV8MrIBpq3dIwxEXSEIQ0RRjDiKbGBAjbKu0et1MZmMkaQ5qqJGpWusF0voWuPo6BiDwQhxpwvZiREMukR6GcpGC4QkApuJYStTX5WVDWapoUA1GbUX9BwEEWBo7VpvNgRo56lbz3VdWxLdzl8O+ABQqcDJoPLaEAQKURwhsmuVDCLoTt9mgSuXVca1ynWtUVYlICjzzmiNuq5QWsBZZ7auelWh1iV0lrvam4BBUbCkaG0BY3r+MtsSsFxXtn6nsR4rA7fWwTZ+1qVpvz8IG/BuHFHik5jOt3cg7wPEuCN7+C/y3pzdd7h83R1yrP07B/Hy9Yz7NtfUbPkm7Nf7vi63St6vY+yvMT5xs4+o8q/J1xVC7Z5Cc9DNX0+WXLRDfIk/sGCuAxWaDFohdstB0Pyucb+msv9zsw9ol53sE3JCtJ0qR0Ht9Ef7uR5+n+022Plzzy/Bvf2p6Yf2Wv3QvR8iDgGbvGB/bt+nIX/gCGHpPvOGuiNZOXjMb08r8975q/vb9dBhQAFtcgdH8Anj9j3uP//uu374vfjzpDnYnwUMOIGkIQpp7vhJOJxIwvt2q60812DxDdlcm+/N5CqrVTZZovxuduf+/rbv66vGvrHEeCAhXYC7AK9DtP/xeW3Z+TYOcj8R4aHxuPt3DrTZ904eek8Pvbvdd9w+11/D6T/Tmtv8TKbVl82cpz2VyHi4dR+4L9HubCnI1hzm5zW1dmRii8vyFEWbfjbee2nvQ/ws7TlAagVuNBkDY1VwmgzS/XbgQ/3JP++uS61zW9/bo4hoDPE1EpSkb3zyu0GihBCQiuS8ORktz0lFmeaYQKgkoijEsEuljM5OTvH48Xt48oT+m0wmCCLys1g1RkiBQEag8i5kk7OKM4SGEArLVYKfffYFsjTDyVkXyXYJbTQCpVDVNdabNXrDDs1JbRBYO0VZNRsbD0j+Z55BGANTG+R5gU2eYbXNkGw3SEuN49NjTI9PABkBooaGRq1tBrawCgVSUoa+0pA6QCAChGEAaX3Euq6wzSpoTQmIdVkhzQpkeYkgDNG1Ca2OjrDrsbJ2OwyasjJsM9i1hfx0Kss2m91BhRGCMEJZFOT3dmI6V2iHzdksGetjteeij+PtjqH7fokLE3MBam3fDDDC8heSCOxut+P87eZa9K9TuvR4F8YsOciBA0sXq7XLOA8CqwQBCnJpTA0Ot22eq/ns/rrnP7P/c3vOPDAPBeDvmb/I8RAO/tfFV7wzMX4wPUBZFFitVhgPhxg/eQKjDcIgbGUKj8djRGHoIog2G6pX1+/1IAUQhSGyNMX3vvc9zGYzhGGI5XKB29tbxHEXQuUIoxjL5RI3NzcOBHvz5g2WyyUenZ5ivV7j7vYW04Mpbm9uKeMpDIGaXgJll+Q4OTl2IBLLfA8GlJVUVxVSnToJQAb3qqpCkec4ODjASUiAb6fTwWZD5DNn81JWT4HJeOSAJN5EWQaVAaHNZuPq893d3aLfH7jah0WRIy8SdDqUIbLJSDaS5cA7VopU1hJhSItqrWsMhwMHUgEE+vV6fQcAsewnAbQFpFQuu4QzebbbLW5vbx0YOpvd4tmH76Pf7wOgviT58BKdTuwkWMuyxHw+x3Q6de9dCOGkJHlTYDDMlx/MsgzHxyeIotCB/7y4MKH95s0bmFpjPpshyzKcnp460PXHP/4xjDEYjcbufTHoFNoMcAbdVqsV8iwnB1WG9P0f/Zhqw192IKTBeDRGZTPwptORk+FcrdZOzrOqUuR5YaUfN84p9gG37TZFsk0dsEhjP6Ho+Ap48fIV8iy1IFlBC6KUqMoKUgoLBgJVXUFJhTAKrdRIZa+pUFYljBEIgwBlWUHX7UU4zwkEKEGZWefvneP0jORE1+s1irJAmmxwdbfAJitcmYLlcukA4kZmk2o2/ZOfX6OqBf6nv/otBGq/c8KmsCOtDVw2uT1zZzVpbzBsqxlY392dxY5m84eHqLbdvwp4xqG9sLu0fw9eSAU/AX25MfStq21a+48zPn33HNxW0/IxdxrmOTQPnML34PMgiBTPco1/8vUbzJO8yVbwHLTd6N132ST2gQH//3y8rX1ve15/077v0P6i9wGaMdz+TuN4tIlacsYa47+5R9tw8t8htzUMI2SWuPumYAf/HGOaLO7W04imrRylqE07Alkp4WrbsBMC0dTCFsJ3Zq1j4UVfN531jc3d09dNDeum8W2nfycGpHUd3wBtPuT3JRHHVEtSa+PknO87rvvBFweatECI+99lWc4mO4MbzEQ7Zx4RucFAAe+5URQ6NRuSHQ6wWCwdmfmQLK8DDi0IypKrvtOppHJrnBBWOlQIiDDEJ59+hH//f/i7OD46QppSJu9qtbIBgyl6vQi9bgdGVxj0O1ivlqjKAkoKGF0hSUqEocKXX96h04nw3nvnODk9hRAGi+UMQghEYYS61kAFnB6fIt2mKLISg0EfSgbI0hyjgcDdzR3VID88gIDE5cUFojCGrjWKssCXX3yF4WBsVXZOcHN9jbtkjsl4jKKsMBr1sCkTJGWKk9NTxFHe2HgFRcnqSmN2N0Ne5o743G63ODo6okDKLMPt7a0jspmsY9uFZaw5wI2zlbkW93K5xHQ6dfLjLJ/NtbUBOBuGM4g583S1WrnM8H6/j/l8Dq7dVZalI5dZ/pvbyBLSrEgTxyTLenx87OwxDtxkEtH/nUng7XZrbVAqFdTv9/H555/j5OQEvV4PvV4PX3zxBYbDIaIowt3dHRaLBaIowsHBgRv/HLzFpChnqbPtBDRyw2z7MsF9fHzs5MF5LjI5GUWRs9c4wI8JfJas58xklhHn9vA9OWOas8W73a4L6mT7nYlOlow/Ojpycvbdbte9dw4YnUwmuLq6QpZlmE6nbq5yMCRfO4oiF1QBkCoXl+thmfH3338fxlAt88Vi4e5JSlNbR6rzeGRyncnd0I4Jru3NpZc44JICaxNPySlzJDz/a4xxagS9Xs8FKDCZLgQFWnDGOZVTGLpMd86s5z7gEgFCNJLtfra2L/vOeyD7T2mSQQjp2r6b4cfjg9c19gV4btBYylGWlZPpB+DmCH+fA0OMMS6Il9W++NxARUjT1M03HrucUc/BIrzO7mbP/6LHOslbtkez73BGhLT1CI3ziZ18Otq7FGUda2ijoQIBBn4ACaEElusVrm+u8eGzZ+h0upjNZ/jiiy/Q63WJILYZwGzHG7tHGzaAARgh2/aAHZfCvq8mh0k2gKNFdt8G8D9EpOyeA+wDvduf+z87kAoCSgiEgaI9bbNGJw4QBgpZssWLr77EarGgWsGWeCYbQrnasRrGyjeTPLu0fVzrClVVQBsOgqZsEQQBkbHGZotYuwzgaze1QbUm8DkMY6/ttk8UrVMETgcIo4Dq74JUcFiuE8a4daEqS1S27vd4PKayXnmOuNNFFHVRGw2TFxBSIs9qXLyZ4WefvcS3P/oIyWYOKQLKWLfEc8hKVkJACh4nVDKt1+2iKmsUZYU8L9Dv93B2IrBaJ8iKElVRIXn9Bp9/+XN8IRUG4xFGkykGwwHCgHzgui5hKg1RG7d3FgXVq2afvMgp8wio0ZClNBaUCFyAhpQKg8EQIhog6oROmr3T6WAyGtH6HgRQVlVnbbQFopXL+DHgoCbYjB+N0qrPVVWFvLDPVlWoagJf0zQFqhKyLlEUOdIstWtv4UjvZswyyU2D1BESbAvb3wNbx16As5Hbvg6NFQmfGLczFWLHUN8lphtf3fejnTdM49X7rm8n7x7+nYTzk+hQe4gYvz3OnzLcLiJLmJh0GaU8HyDu+Ux+mxi7Atp1o3fPfYg42beO3PcH9ilFNT5OY7NTlxqjrRy7XSPtXN0lInmff8jvvU+iEVEIIYjYsHvJ7hq53+9pP+c+4nb3XO5P6fUx7w78XQ7aNLqRZn5bH+/+vktK+HiI7yQ274Clx60imVsT2v2123/w+oSff7ffuD8fAux3fxYMKJn2dfcdu9jOPkJm33vzf/bVgprn4zYDu1gEXWBvc+hcYQCnRNOMs3tEMp8PuDHszwcuA9O0p72nwZimFKJQ7c/cM7YxRQ40UEpStYWdPmK/Z/c6u+e1nsNbA/x+bQXb74xNTn7j9+dk3YW49773tWOXkN49x5pLretyrwth0LwKvs7OvLXYhIGGMbWt4X0/iHCfrbX7rn28iS/e/L6v5nuz9r9LP+y+E+pPca+PuPb12+xHXon89XHfGv9NeCh/T9dcl1yQ5DaPZe9dK6WgRIAsT8g/qEiyW9nrdIIA/V4Xo/EQR4cjPHnvPXzw/jM8OnuEw8NDG6yoYITxgtVoP+7EvWb/4r3QAN1OhM0mxdfPL/DZz79Gt9uDqTV0RZLogMB8uUBRFDjuHVreSiMMIlIVsupJXLtaSom6olI9m83G+YhHj97D9eUVtkWBTmbQNyH6vSGGcR8Di31ZVBRBoJzfSJihtP4UEfpJkuD29hYvXr7A9c0VBsMhRJ1hk6QoigrjyQRHR6eoDancBCGVvQUApUJIGaDTiWy5HOESFJp9qUaZk601u7tFGMfo9HoIAyqRN+j3EIUkS85jiZWcHtojjDENTrp3vFl7jTY/a/ebpuQVjxEhUeoSURBQeaFOF70+2aCmbvB+pSQguN54e32orQqQLSZuk0xrJEmKIFQuEDqKAlR5DinR+BrGoDakguR8aykAbfbMQTd5YbDfHnjbHDQtpuPtx347674t8Nd1vDMx/vjRY5cVwJH/6TZFp9tF2IuQrDdYzO4QhRGqskAoAiwXaywFEIQ2E8EWnN+sSWZv0B0gS3KEQYDpiGpQ14IjaxVOT0+xXC6RZRkODw/x9ddfYzwa4dNf+h5evXqFMAgwHA/x+7//+6g/qlxHESgHDIcjrNcJwrCD5XKNm5sbjMeZzRiQThqTvkeZzGdnp8jzDJeXFwR+bdbIMooiKYqMNhZd4/joEGmauDp7DMBwJhOBpwWEBEajAdWHUcDh4QGkomgUpRTyrEQ3jhEGVCcxkBIqjFCXFaANtus1BoMhAqmwnC8syKOQJQmkVAikRBTFdrII6ArYrBeIQpuJXRUIA4m8KBAECrWpUZsai7sFup0OwihAmiV4/4On+PCjD3B7e4mqKrFer9Dr9UF1QEN0OrF1/qimdq01sjRHVSc4mE6xTRLousbhwRHyooCyfRFGEcqiojrcoUBZLtDtKphaI7T1srIsw3Q8wVquSeIyL+zGUSOKYrx+fWFrFtKi9/z5SwAvAUmS9XEcY2DlJBObBT0YDFBXGlEQI9mmyPMVyqJAXRWoihyb1RpZlmK7pkx8rWu8efUGnQ5JNQJAlqUwBtCa5CfqWtvsbq5XUpMMmzHIC42yrFy9SyKcyBiqqwpBFAIwLUfGGMrui4IIlYbN9lMwWqJMSwfg5nmJqkpR1SXibh9ZVdmo8dqSbZQx/vr6ljLNQQvuT75+ASGEc7KdMyIEjFBUW1c1tS4kSG5PClu3SwhoAP/sq0tobfA//pWP0I1ksx4yEQ5HKdsoXcDVlRA7Brv9s2FD1jfGd67pPvH87xapDfq+c5nZsfSux+ftfs82yBLojcykxaT48a2x3Vxjdxl39zK7f/fdgZ0viP3bAT+7cH1E59baIMsM/tsvXuP3vnhj++2+UU998PBGs+8z53Dw9+XOOTsRktjjvPnv4KHD4H5dbP9OZMu1FQBIuss3OO7fh53LBzfZtl9L81FzPzdRy3xuM57tuLBfbm/GaP2dnt/2nx0oHoxD9xYks9Zu2m5fE0TF41wIgTDishsBgZ3WoDDGWLkdASHUzpWcziH1GDuw9tqCgSznCAjAUJ0pdkylaEAYARoGQsLWD7WOoDEUmWrB7rKqUWndvA9D44kcLytrt9d4ac1UGGMjGoVwZJ3w2mMgIAIGiOCcD23BCgNAgozMykqGknHL9aVCCKMgTAUJgSCMUNeVAznp1Urr6IKyygVQlSQfRhJZwq4XGkHQZARz/ypls7HrGkJqdDoRer2+I8K63Q6UCnB2dmoJQoUPP/oQj84eIQypzvSjR+c4PDrE9dU1Li5u8X/+P/3neP7iBZqVD24+Mp4gJe2pRlupTG0AEOgk7bgIBElN0WMY1FWBg8MD/O4/+F389t/9TaiAyKE8zXFweIBEJghViKAf4MXzFxi+P0S338P11TWEIEfn9OwESUIOnwoU+qqPNCNJ8ss3F7bcSA8DGxTY7RCBeTA9wGK5RLffxWq9glQSHz79ENfX15CKMt9uZ3eI4wiTgymEAPKCiK+TkxOEUYhABdgmGwSRwiQeo9vpIJltsd4s0esTqZukG3S7PWw2OXr9Lqq6gNYG/UEPvX4XBwdTJGmKPMvQ7/XQ7/UwHo1QFgXKokAUkJLPcrGAEALr9ZrKzWQZIIQjltM0xXq1ovdu/z6zxHpV19C2trJbO6zDPJ/NoILAXZfJXD9b1hjKgmWp6DCkqHKWGueyOkopPHr0CJvNxtmmvV7PtYczdLn+OGeMSyldEKgQwpGpQRBguVwijmNMJhPKwrdkeRTFuLm5xfvvv49PP/0ewjDCcrlAmmZYrynIs9frQmsqgzSbzXF4eAgpAyyXawgBdGIiZ0bjMfr9Pno2i5hrr+Vpk80nBdXNjXs9dHs9hEGAqizR6/ZQFiUCGWDYH2IwGBBxrtcwhgJ4e90uJuMx+lb6XQC4m82w3W5dcEhkVQokKNtSVxVGgwGkUlgtlzB1jbKqKDI9CKCrCr0uldEZDYd2vlOdd5bg5gxzzlZn0pkznnlvGY/HNnh3gMVigbIsMZvNHInN5YpYSUkYqtVc1RWMNm6+9Xo95CmtM2Vdoq40trZEVZJkgBEoigpVmdqSAF0Yk6EqqX5bEESu1qbRGpW1f7nmOwMBLLdO6gQEpNxc3+Lw6AhlUUGAIvrDIIKhkts2OIEI+6IoEIQRjAYCFSLo0hzabBJHrm82GwwtICSFRBTHKItG2pxLDzlQy9rYTNxzNjwAV0edyhZtICWRmVII9HsD5DZYxhhBoBVIFaooSLWLFKJse4MIaUKlsjhYhUsx8fzh+RQEgQue+ascdcuEEm4fBywpLiWUFAhCYeW0G2LaATdgW5GJcIDrIda6hhQGoQlwN78FpEDUjXE7u8PPvnyOsizx3vtPsZzNIAUF6Na0sSNQYQPOSAkhA5uxQlaIsOC/tLdspNMbyc37RM79461AiwdcPUSm+ATEfWBaIgylLYkWQAiNxWIFmAqD/hCb9QpffvE5Xr54SXLhAdmnHATn3otQMIbqJlJGN5Hdftkj8rcq62tplLY2NO8HUgUQluSjGosUQE32K9kxbIsJGCgJa79IVBXXdCa7SymFqrTKAAicTcDkAAeYcOA8B0VJFSLq0Nrd6XSQFik6nR42SYU/+dOf4pd/8CnOjgfYJoS9SKlozgsO8KSiiiqMUFRkh3W7XdS1ptqSVQUIhW7PIK8q1FojCEL8nb/3O0jzDNe3d7i4uMT19RW+fv4coZAIhbRyxXZc+aCzUuh2+hgNJ4jjmNaabhfSKllwcE0cdxBFsVOjkFJCqKhF1vDBQXR5VWFbFJjNXjqblNe+dLtxto8xBrosUa3X9l2V1qbk//bMYXsoQaBlKGDLadtxbGuH3idF2qAg+ar7MrOboAoAXm1XbsX9eeSTfu5693w20zhW7Yu4a7k2cyLSbg/cI+7Z36aTHyK1fRJ71wf27/3QOvBNa81Dnz9EkDfnCcfHuvVNynvX4DHLAVitjFzTaF1RVpwBwGU4BKRsPxuB9/fJut0sX0YkaI56fmzTMncP//d9QLQQcO1gUq65f/uZWYWB9yPBY8qOJ776vgDltx27xLD/933nkqyu/5zNMz00Vvyx/+Bnflt0g0N/00HXsEHKaO9Nu+cBcIF795+LSbk9suZ7rsM/+8HnzfMwyNa85915K9zAaQhtPyN/5+QWWeSrXbZ+t+OzNa69Njf2nW75Tvc+Z9AM+wjTt4+VtwXG8M+7666/RrwLBsf34XVt3zX3XWNX2cJvvz8Gdten3efjuepdwP0doHIh8PqL/+7qbhvjSrT5hD/91w68YFzVPgH8fWhfYMFue/l3HmP7+veeYgEAYcse7Fu3/WAk/tj//r755x/73j31W+H+xt+WspEg11qjrHKstxtUVQEuhCMBxKHEeDDA4cEUh4cHOD4+wpMP38Oz99/H0cERojBGM55J5VDY2u9C0t6qa4DKB1JQnEGFSpPS7l/85If44z/9Ma6v7/DBx59iu01B2eUBdEU+5tHxKYIgQlWSYii/kyCgeu3EO5GtCV0jT0vMlkukeYFAhViuM/yt3/xtfPeT72JyeIhuv4dhf+TwBj8wBMZ4+74ALOdXFpkLGid1wVf4l//yj/B7v/d7uLt8BQGN0WSCZx9+C8cnZ9gkW6RZRmuHBlSoWiW4/HeUl4WbZ2EYIup0UCUZtps1Fne36HU66Hc7qEpgtVpiPB4jjiKoWliC+YExYYwLABaAU1DftwYoxl/tf4r7wDRrvxACB4fTVgC2EAK6ZBtbNvvozlj01yJnv2lCQw8PD13Qf5puoHWJOFJI1gWUxdkquwaTalWzjwlD/JIGoNDMLX4O2sCajeIerr1zuHa6b7z9eMg+e5e//WWPdybGOx3KUshSkrasygqz+RxVdUM1ErsxDqdTLJZLABpFkQOg6I9uj0C0bm+IZJvajKEaEAL9LtUqX6+otiE79OPxGMPh0IF2gAU2ihxpkaE/GqATRlhv1iQJIBVoz6TMPAICJfr9ATqdLpQKEEUdNzlpwOUYDEia8/nzr22WVtcNSMqKntgoFsp4oLpZNTYbyqb66quv0O/3XRY2ZwtxbfI8S1EUBKD0e31keeZAdJZKLPIcia3rJ0BykH2bPR0GgSPwWEaUQDgigjnrIc9zjEYxKiXQVbGtN1hDKZKxN8ZAqJBqStUVJqMRtkmCQCkkVYX1aoXReICOJdmHfar1KBXVhlRCEpguFMq8QLdHsu9SSBoTZWWzo2sM+wNkWYY4imGMwWa9sRnpM3z11Vf45V/+AQIlnRTYZrPBF5//HEqRBGNdVwQ8pSR9Stk5Cb766jm01uj3CdicLxfIsgJSSQRBiOFggNlshuVqiTTNEKgApgKqskav38NysUBR5BgOBjiYThFFp7i9m2G1Wjvw2ZeU5HqQEMCjszP3+/sffACWS0m2CZI0Q9Tto9MhAJQz2LlW6M3NDf75H/4BamNgaiv7pjXqqnZGEmdQEZgCJyXfclYEUJulAwSN4awEciQbF1zYucBSI8p9YgBH4kqpnL8udwhQ7S1ZBgJ/+OIGEBL/ox88Q68jW2SgT2YKSwy5yHLjRYRbG9lCee7qTPP4pDi8TwV7Dg8c7kqm/fu+w6dPWz/73zXNv/B+95vgO3TuDwats1ogAppnxAPtdM9umj7NC4OqBv7J15f4Rz97BTKQyKgin+MhB33/0TYW759rzG5Xu92vOWHn8Gi6B44HoqjbDbPj1bT+xlc2DwwAwWSm/zJbn+/+se0sCSGcbCL/3Sdb94Fl/nWdge0sIr6NuXdekzXsP9/ep3LXqWtNl7J900ieGxuzICB2tvFG7olmoRAGJKm04yx4RDSVgmiiKskBavqlrmnMVaL2nscac5UHUknp5qwBGcC+WKDc/xpbB/V142hTDcZGVry2cqPs3PM7E9JKmgqJUFHwVRzFFlAGBZxZyU2aRyVJrUkCKNhQ5eynKArgS6QGKqb11lBGnlQKg0EXYagwHA5djehut4uDgwNXL/nk9BDTKZF+SZK4EiakIHMHpZSTOl4ul87umUz6qMoUUSSwXM5wd3eLOKIa2KElg5Rs6j4bC5BzTUkpJYwApAyJxNeA1AbCGERBAGMqjMZDfPq97+Dv//3fwXQ6hqkrpDkFPg77Q/Q7fSywwHK+pIyyEWWEpmmKuBMTmC8lXr565TKNV6sVkiRxEsW9Xg8ykhgPx64u8cX8AoeHh3j1+hW22y3G4zF6/Z6VKl9gMOij2+2gqilb9+aW6jr3+j10e11cXV2hKAq8d/CecwLSjLJpVUgO6ZOn70FAYLFcUPb3IoUQAlE8RBAqbDYphAS0jrBarbBcLhEoZW0DykaOoojIV1tbWAiKyD05PnZ7vNYayXbrJJN5XrDMMisIbTcbV0t8Y39OkgRxHKPb7VJ95zR1WaY8njirl6XHATjZZz4421lK6bKV2T5kCWiut8wZ134w52q1wsDaT5yNzRLm6/XaEXzz+Rynp6dQSmGxWOD09AzD4QjGAJvNFtoS0ZxRXhQF4riDm5sbS1IaJEmKwWCAg4MDqiEeU1vY1i3yHLkl5JUk9aP5fA6A6tDmWYbO8THWq5ULHpiOJ8jzwmVkr5Yr1zdFUeDo6AgHBxPkRY7lYuH+LgWRoEpKHNmyT/1ez8mTc6Y0jHEBC0xqG2OQ2yBhDlTQWqPb60FZEsgY42qDMzm62WzcHOeABgY9hRC4u7tzgEKWZdhsNjg4OHDO8mq1cv6EFJJqwxqNMCACqCpJdWi7aTLn66rGJt04SXupNdViqzWKguZF3OmgrhPaUYKQJOzqGlKSJDTbxRSkSv2w2Wyo1FCknAoVDJAkpJ7U6/WQ54VTJMqy3AYMWWK71hBCoiwrt9d2O10qKVXViEKSCCyLErP1Gt1u12Wj8/xj5QUATuZYiCZjXAjhyPPABp+QjLpxYz5JUqdYVVek0KGUQqBqq+ZA8vFxRMpeLJXPgA+/R58MYWl9IYTLcP+rHBqNrS/sswpHilMpEK69zHvlXvDeApYcBFnXNaA1pLX6q6rC9c0dRtMDVAZ4c32Nl69e4fzJB+hGMVJLKAZhiFgF0DL0Mr4oK8+wPcf3RpuQJgCvDah/E9ixC3TvnvNQ4MHbruv/y/OQVNAkiiyB0QWOjqZIt1u8evE1vvriC6ccoDX5cRyMAVgSWmsYQSLTVV1DgLKMOXPSlQKJe5DKviMhrWQ3lYMzFh+BDdw0VUnv27NF89rrF0FAdV7W7t2XVYGirKBURISQkK7NXP7SH5fcrslkgtvbWyrXpkKbmU7kMCBQ1gJ38wS/9/t/gP/wP/wPILI1BVRLCSUpoCsIY2hdweiaAlGFgBIB4rAD0yVyTkmJpVXviwKJxJRYrTa426zw9MkHOH98gunRGOfzE1xeXOD26hK6zCG0DToPCX8gdYSAlOECqunNpLcWQG1ovS7TwgWTAsapqyRJgghU57IsS5RFgbzw6nS7MQzIuvBcFM6Qs9l6hl+ZglEhjK4hZGTfG0DSnNqNfXiSzs6/8Bhkwz+ZtsdsnWz6rEH3YVVlnRtq3McWRGen1jQlHfZ5IA1B5vvuHvDKf5IPE6d8IgcgG3GfyN9HGPv/7lsX+Oc2MX6fNGKbHWiIWx/QbYgGkiinz20m1r2+aNryNuLpIaB693o0TxSkDFBXjNgomzAjILz2SvvO/GAvv198omu3fT7R6ohIAyjVXivFnufYt9buI6b2vavdtdVlB3p/20davq0//Xa1gjz2kFruGmI3KME0GepM0gjZ7oud991qh9gnn95+Fg5p4NnqxphdK9zv0n8+Jhn24wH+Pu4//9v6arff7me3N+ugf12Hf7iHxL1z/Oty8o4jbNCW+qe9Tez9fuswD2clt8bM7jvZcz6/87rWbj43hG6DeXCfU7ua52w+Fw532O3P3d8Zs9jXpn1jlde/3eu1bTQim9mG9Nfjfe/P//7uugA0WeX+Wmh2g1p25icfu+S0CyjzzhfCQ3WNaY0J70pvHbu7n/F16JlavbvT92j12+69mfxv7wE7c/eBsen31742Un+QzagCBak4qIAUX8uyQJ5nKKsawsqPSiEQhyHGowGenJ/j8fkZzs5OcXh4gOlkgt6kj/FwiNAS0wKS7hFSwKSQVKZASIMwiKFLQtmEAiA0aq3RGw5xdTPHv/rTH+PnX7/GaHoEACiyFFEUABoobaD+aDJGmeUkQ64UYGglI5ViTQpRUmC5XODy1XOkVYVVkqHTG+Bb336Gf/AP/gf4znc+QafbRaUrZGWGoixQZAXW6ZpKvZSlLaNDAYVFWaAqKwrsNkBh1crqqkYQBRiPR/i1X/81DMYD/ME/+T0kyRbjyRST6SFKbdDrD9Hp9m3pmAqBVAht5jiXTSOOLWzhMmVZOg5E1xW2mxVub64wGA5weHSCzXYDFUVQQYh+HFs/TrfGlKm9IBC2x5rlae96HCpPqceOaxWQLRAGAaIwRBhFiKOgtS/WdQVjakgZeIS3BmQTYMfXpGzxZq4KKMfTjYcjlEWO7WaO+ewOZZljOOxiPJ4gSXNkmVUkMwJ1TUmbsNgptZd8UGH8NdGzefyf37IfuT54y2cP2pQPnMPP/9d1vDMx/skv/xJQ04QzxuDu7g7JX/w5rq6u0Kl6QA6s1ktymG1WgZQCaZ4hCCh7miP40zTFcrnEe++950hkrktnVIjj0xOsS47SJynsw8MDkiWxYFWaptgsqU5isk1ahjJnwWhdIwwDJMkWUirEcWTr61EGdxwTcRvHMb773e/is88+I6DORv9HUYTlcolut+vkwBvDm7IBer0eRlZyi7N6WG5QWuBJGKATd0jKIAjQiUNUdYWyrLDdJAiVctkxlM0eIM8LFEXporcJXKXMMgY0GfCRUiJNM0gLkrOc2MHBAVaruZNUz7IC5+fn2FQavX4PqDTyIkc/7kIFCjeXN5iMKHOiE8WIoxhKKuiihoTEdDSBNiSHr4TAeklgdWGJfmEMLt+8QZKmEBBIkgTbJEEUkkTF5eUlXrx8ia+++BKTyRhHR0d24RWoqtLVFKW+jyGkQLLdoChICiOKQmhtUBQFZTPlOcqY7v3rv/7rVio8Q5GV+PjDb+Pi8hIvX74hyf84wmgywVGa4Pz8McqyQJKmCOIIHz55ig8//JAUEYIA54/PcXh4iBoCR9Mp1WOvCFCAocj/u9kMVVkiSRMAEs9fvkSW53hz8QbXV9fI8gxZmuHVq1dIkgSzxRyVzdzmxYsXas4KA9obeJsMNDAaTnoDeGAhEKJFLraMMT5lx0jed+waCtoY/MHzS/za4yN8fDRCJ3at4h9aXnZDdDdZ5P7Gsfu13exz/vkhwvVdl8C2+XgfCNj392+6ttjzizHtv+/eh5+Mf37bPRpSXGO2rfB//9FX+Ont0gIA1kn6a9wE/qrHN22CQoh7HbI79ggEeFjS7Z7DBm8sYT8Isa9tjZ/WACSNfdM4H+wY+QBE+77v8Mz3ft4/Kvzz7m32mm4ohSJg3NhAEs64goQvgb7/ek25AMGk+66TaRpA318zGGSln5XXd7Q+EKFj1ywpW3Xd+FZEjluH+f5Q8Pr9fp9JaVrtIsDLEIgEz28XsHJ8AkoKmifSQCpSeFFKwaCECii7zcCgLGuQ8mVl91GFMAycVHEQBDg6OsLp6SkePTpHv0+E2fn5OeK4gyBQODiYUCa9ki7D1hibcZ0XGAz6WK0WGI1GyPMcg8GAbJYkwWw2c+VI0pRsg7u7O/T7fUwmE7x588btiT/60Y9sZxpEMRNWArUuEUZkxtF7qgh0AQDUCALKQqrrGkoYW+5miGfPPsB3v/sxPvnkOxiNBwgCiRcvn+P4+NjtSSzXfXJy4shRIYRT8YnjGP1+H3d3d464Y9skTalMzWAwcM++Wq0wHA7R7/cd0crS1ywH7tfzZSnri4sLl+3FMs5MMhrTZOIdHh5iMpm40jWff/45oijCZDLBYDBAYcFu7qvpdOokj6uKxgA/E2f239zcuLasViucnZ05GfTLy0tHXnO2GAc7CiGcfHqWZZhMJoiiyIHxDNxzXXKAJHCrsnSS40xSsBT1eDx2c4MJ7X6/7+ob8xEEAQ4ODtz7W9uascramXyNPM/xwx/+EI8fP8bx8TEAIkqm06nrcyZS2U5miW+qpzxGmjay1TxW2ZblutpCCCqxZEl+doxJIYcilMfjMRaLhcv84/fKmfPr9drVnY+iCEmSQEqJ6XRqSwGtIIVysuRM/BtjMBqNUNc1rq6uUFalew/8vg4PD11WvF8qicctk68sM86gEGWWhhgMBnj9+rULhjVCuAARDgzJssxJebPyljGmVa+d+4dte77+cDh08t7si1RVRXW8rWwxn++v3Vyzm4k8bisHOPBYZYl3PyM8DEOs1wRoBCH5TnmeI45jJz/O7Q+CAN1O1xGL0gYzzGYzF8xRFAX6NrCX5eIBIuM4SICBf267L7vJvtZqtXKS81JKB7i4/RKwGeFbFxzC457LPrEvFwSB862YEOUxw+OD+5D3QQ684DnObeF3x+sJB0rz3N6XjfSLHlKxgotwxDjAtTTtMyhl60pbq9pukAxuNOAhLKkuYGqy05WV2dumKWazBaYnpxZpUxAysGMlRBx3oSSVeFFBiNJIhIFPKBDBY9iHMFZ9AIaU0CAgrL0hIF32uG8cNNY/2ytAU6dSoG1FCGfY3bfj/WDbHSPd2kDCtlsFITrdmIK2a5I8H/S7kAK4fPMKr16+wHq1AARQ6aoFtDvyQvIzWFBbGwitoQ2gawpkZmWGSlUIBKnR1HWFWheUTW2IpJNSQdls5wCC6sqbxj8MDAPm7K8BVS1R5QUA4zCGIBDQNSBdVj+pUFHgi7GJBQG0AbZJhsl4jDCMkWcZBIDJdIJtqiEDjbKm4HgVxPjJz77CT3/+HE/PHsEojSIvAN8W5XcipFWGoMx5HbmwadQgWVBKiBDQdYX17Rxf/9m/RGHl2CtobJMU29kdtKmg7PVCHUEDKCFQAth6weICtoyH6zNr7lrC2CcQ6rqCEhSMTuQLncQKQxCsnmFQQbkxKWDBaaGagE9ri0pJqmzcDYTEUiFSaqOB0Lb2qGxkNs0OuQJjYISxQ7wdPN5kolPbXLSDP+8F+zNNA5WQTqqbx47zUB3h0oC3flb3Pt/MPx4CNAlIbRMSTV1neOtUm+j0AeLdz5pzdgkarmltWsSK10r33YYParf7bfdjf3T34L8pdT9r/x5xJ6W7jhBMqDQy0S67U4hGpUsIlEXh/DZtrHqEfSa5867pI+18WSmlCyjefWZ4hNm+97fvaHy0Zp/mZ+W5xVLSu/3Q+PQ7pKF/f7pJc68dXKvVv/YZIFgZrFnXeex5V3XXqLm2spR2t2EFE5rjvvLjPv98NwO3RfLZJjnUR/hzS7t/efyy3ce20S4R549LP0v8IdLu3hzVdt0VEgYaRjTt8B6g3cfetfz78t92gzX4e/7zCLd+WlLUe1fCu/busY+Q3NfP/t+EfV/8bvwx6WdG++3bDX7y+1sK0R6TQnhjqr1WsMz7Q0frPUgJLRuFPrLrSIHOuPdkXCB/e71rB4D489Zft3wM56Fjdy0QXkAl+wE+2cbYAK9Ru/cwO+Nj9/rGCGvH3X+Xvi3lP5dvs+4+G30frev5c9wfW28bM/vG3761cN+1yMewOKIBdF0TKVzkqCp6f9pohIISzvqDPibjEY4OD/Do0Rk+ePIejg4PMBoNXeC8jBWUDEF7JgUcBkEAgPxDqQJAkG2jZACtBKQx0KaCqTVUGCLuDvD/+v0/xPPXFzBS4eDwkBI6A4FOFGKzzrDdphgOx/Q+60b2H8YgUKR8FEUKQaBQlQVubq4wW8ywSlMcnZ3jl3/1b+Lv/du/g0dn57i4ekO+f5mjrArA1DSWjXbJJjxmOLm21rVTqxKG3n1VlqjXGvP5HbrdDgaDPv7G3/ybuLu9w3qboNAakVXFMgAkqG/6nQ7CKMJwMES323Mqb0VhORYrBw5NdpGUZK4XeYblYo753S0m00MAEkmaIY4ijLpjO0Y8m8QARjXzYC8H4NkuvMaRnU1JvEGgEKmQxo0NZA4s9sHBI6wGzHOObEprs3AteWNQV8180TYhUgpFcZdWSn2bbLBer7FeL5GlKa3FtcbB9BBZlmG1WqOujSvPRL6MtOuht9fo9h74trnlf77/2PHH3jLv3nb8dRLifLwzMV7pGlJJCJvFcfToFN9Xv4zws8+gjUGoFKaTERaLhc2ESCAEMOgPUVcV4qiD0mYy3N7eYrVaOaCLo/8Pj45wczdDv9dDJ44JxFES0aBvgdcIURRiPB6TrKAKcHh4iKOjI2hdA5Im1na7gdYUOc2gljEk01UUOYqiyQbhyP6PPvoIZVmi2+068CMIAoxGI5cVtAu0JEniAOwgCFwd8zzPMZ/PLYG/xXQ6hR4YB/xqrdHrEkg0HEjcXF2hLEtMJlMLCkcwBjbbKECv17cRMInbKBlIZzCMMoWuHciltcbNza2roXp3d4dhf4S6qFxmO0lpjpGmCcn/AbjcXKITx0DXIE9JErzf7yPdpkg3CdKMgho2mw3Wmw0G/T7V6A4CQAjMZ3OkSYHabqRJkjigd7PZIE/o57XYINlmCBQ5BIXN/IniGHVVIS/uEIYkWV7XlQWiaOdRKkCWphhPDvHv/nv/Ad5/9gyRUths1vh3/p1/H3e3twjDEF9/9TX+q3/830AqhaOjIzz78COcnz/C0eEhxqMxsjxDklFWOiwINpvPkKUZ3lxcY7la4Z9eXiFJElxdXuH65sYtGsvFAnlRIEszGBgkeeqyLRgg5ECGqqKab67KrLFwjcvY4FpMVNcCrjafcaQxG9i6ru8ZBv6xb9Hiv/v/Afvq0jx8kLEi8H/4V5/hP/o7P8CpiNGJpCO9Helm2+vIKnbk2QGFaBPlaP7+UFbw3uf0fm6R2/eue//83WvsYBrfeL5/NPdqIAu6jntzHjDXvr4P3PlZtgDVE/9vP3+D3//qEpvSj3R1nrzX8r/k4b2zX+hrO+PlXcbP/Vvfv8augeqDEA+P07dHW79L+zizqZkbvjwUnSOl2vnOrqF8/7p+m8m4ue+g7LZt14mxCcq0xrPs2s51/cys3WtT37HCgO+0m5aEqTFt6UQ/WKeJDG6MPPc9zsCxtTF9Y5A7he+qpNqNn2m10zmd1pGGMa25bdyiYeeVJylojIHR0jlsUhjEvdDV0WSCbDQeI1AKk+kEcRwiCkMcHB7iww8/RCeOoQLlgtyEkDg5Psb1zTWUUjg4OEBRFBiPqYbwbDbDl19/jvfee4QwDLFc3uFudodetwdtKFP0yXtPAMDVdmbi8fb2FvP5HJvNBicnJ+j3++6cuq7x5s0b9z6I6Bzj+OQAq9WashWd42KsnTJGGApLitP7G42GODo6wmAwxMHBFIcHh+hGHRwfHyPuxFguZ+j2YmhdYr5YI0k2mM1IfYWDFYuiwGKxwIsXL/Dee++5+sBxHGM4HLrgQgCO6P3666/R7XZRVRWGwyEWi4UjnsIwxGKxcCScMRRIeHBwgJcvX+Lw8JCkxedz55Q/fvwYy+XSZagyMQXAEfbspGw25AD0+31H0PO5TLqT6kzf2YdMrnU6HRRFgeVyiX6/j6qqcHR0hOvra5yfn+PFixd4/fq1I7UfP36MN2/eOJKMCb44jnF3d4c4jt3444xZtkc5yJKJUX7XUimcnJy4DFQei9PptDV/B4MBjKFMVc5AZvJuMCDFnvV6jSdPnjhwkjP9eYxxuSImsYMgcONQCOGyk/k9+Yo62qoSMBHKawZnivsEKKkfTLBcLl02+/n5uZXxjpGlW0fU0jyigEsOnBBCuDrtWZa5YIJ+v08qVnausj3DtrG/nhpjGrlpRfXBOWt/NBo5YloIgefPn2MwGKDf72M4HDrylPuVr8HzmevJr1Yraud67WqBc19wAGuWZe7+YRi6timlkKapkxDneuA+ECqEcOQug6f8O48lJr9ZYpxlfznIgeczZ5JzzW9eQ7ku+GAwaCT4JZwCBB/8LPzui4IizvmebPPzuAqCwJHzsY3C11pjs9lgtVrZwNfIBSbwmKOad7XzafhZe70eNpuNKwHg9mNtHOnNf+PAmSRJXCkwrjnOYA0Ha3BgBreD5dd5bPHc5/WLA72571k2nX1GzrL/RWVi9x1SKgdWC49k4hIovh20C5wCbRDfAJCG7XKyJQMVQADYblOsNxt0JweoKvKbu70+Klvaqm8z9FUQWhUyKh3CVyKwiEEVOPqOtu77ILNPbD1oWwr3f/ZXwTfbOW/X1mbUyp7j+007dkcUhoijCHVVoq5KSAHEUYjVaoGbmyusVgsIAUTdDiAAqZW1O5pACvZ1LP4GkuXXYJuyrmz5rdqgLCvkJWVU11WNsq4sUa2I+A0lIklAfxBE0NpAmxoapIoDGZOkprNbBeoqR5aTygODa1VVQddAKOxaAYGiKGFApbJIYlhCKlqva2MQxh2U2xXyLAH0BFIGUKpCbYNwlIywXK/wJ3/2UxyNp+h3O1T6pKo925HGgZCAQggTwIHEDPxXuqYAAEWy9HVVQKYZrrYbpOsNqlqjhkFWFjBVhdrUKE0FVVWoqxpSkLQoBI3vuqpR1VapAVyduw3g0Zhkxsr6okKCJfEbks+OHa6/KCjDtDVCeRjyLHL30c4X5VRunyRqV0WgyWsap9kbywaQ2g5rO/dlM6bB9xQGTeBIM/ab9cB+wAEpRrTGDXUCnC/v1hnZrgfsrs9KTXoXixDeFGw87F2J993MZ8H39Mh+Xs/az2B2rr3zHN69GNAmgLntKwu7npBv1F5DhO1347L3/Te8C9zev+bueXvxGv6bgMtK5e+T3K9wwDjNIQlp7UP/Gs3PcOsZ4N+v8Y+lVIDQTeCsH2hkySo3b1v92j52caT2O7pPzO3+/hDw7QhTv0O9azTn7vzr/EKeX7u4l0+M77QRBkYLKH9sguq/wpDPKYB7z8vX2dM5zc+mCQBq9i+etM05NHcf3gN39/Fdv/xtxKd/jcaD9xGvHQl7z+d2JLLXpt1M5HYWdvN3DkbhfvNJ6d1jd21ptXlnbLXnsWh1tyPiNeGSu5iR304KEqEAin396wh89h+8tvrPxgc928OS6D7ZThuAbkoK8DX8eWLX+33kt/8893DBPff1f/f7avcQbER657Af5T87+5n3lTgI2929/u58b5p6PxBnF++7T4C738BkOf/Oy8DbiLJ2PzR94zCknf5qlhx/5rjdtWk3tC1tWqMsShv4XbgxHymFXifCeDLFyekJjo+Itzo+OsTx0SEG/Z4rwauUgowoy1eAa3wru35TtrgQApACEgLGCAhIGNi5qIAgjnB9N8ef/+hzJFmJXn8AESgUVY5Rvw+hgbIoUFU1joZDqittgzqFAIQN/Na6hFIhtK6w2axwe3eD1WYNGcf49ne/jR/8jR/g6OQYi8Ucy9UCeZ6irIn/gdbNHgbjSi8aAxeQyP1dWdU2nkdUXqhCUeQYDUcYjsYwQkJFa5QugJpsYyUEAosdyCBAd9BH3OtCKInSYh5RGDi80xhDpc0BW3KwQpYazGcznCVbxIMxyqpGYUt2UUKAcDYlLwaMOe0u7Q7HtLY7B/6qQFhbl+ZVqEjJh5WgBHgOsb1oL+wHnFncE6aZR8b5cGTxlmWFuqYECG1V1TabFZLNFlmeIE0S1DbIfjo+wGK+wjbNLO7HY9rWzmQ2Q9Df/PIb/vG2tXbf8TZf+F05qbetfQ+1512PdybGjRIwVLwAtSFn5eTRGeJeF9c315jd3GKx2QCS5LQhSF4iy3IMB30MhwOkaY6rqyu8efMGnU4H6/Uah4eHOD4+xtOnT1GUJZ588D6ub26wXC7R6URQkkkjDRiN7WaD+YIA5UBIB2BobQBJk/329hb9fhf9fh9XV1cYDPqYTqeo6wrz+QxRFFtynAb2drtFnud48+aNAyWLosBgMHCyhgyoMGDpZ5RvtyRV/vLlS7eRMNi62ayx3SbQtt5Dvz9wkowMlhUFZQldXV6hthMxsW2KOx3M7u4QdzrYbNYQQiLPMqggQG0zWyAEOlZmPlCBrdVFwFCeZRhPJlTTc73BerFyABRnNtR1hbu7OwLLOrHLApxOplZKvSLAJNlSnc310gY+0AAkwCS0shg1BEIUeUGOf55DSIFO3MH773+Ak6MTykjvdnFxcUkRQxXQ7Q6hAgoaGI/HiOIAUgqMRkMXIKC1Rn/QR6/Xx3A8Rifq4jvf+RTjgwNcvHyJxWKDFy/+FcaTCY5OT1FUBr/12/8GLi+vYIzB5eU1/vRP/xyLxdzW6C5xcztDmma2/qem7KuKslUoE0VQpL8n3cuywjz5tDHQsPVn7eJe17wp2uhV6RlgsFnUaIxNABDGj2i8P5nfdcHYPfY5ON+0UNw3EOjfTV7hP/nnf4H/xW9+D+fjHqLI+STt78PZdiSj5hmxUjTkuG/nNmTpfQN477V3fnZ/8L6921v3zkdrT9v7nYe+558rvJ9k693ZzXiHLhfuZ+E+YYO4KAz+Hz98gf/2y9d0PSnvGaHYeT/Aw0Zw6zm8c/w+fNdjd9N553vuZDU3QIb9He0xud9JvP/m2HjYBTraBvNbHFnvfs216O1oBqJwn3ymU20oA1/3ntF9v32+sd9cw3e8WDK9aVfTx/tl3e/3k/9M3Hbj+lyIJhinMeKUG2Ps/Ow6c7o2DrQRAi6oTEqFIAxQVqXrgiYIoBkvDcBGxrGU7Ux8rt0dKqpPyRKcLjretl8FCtpULlsUgCtzcXR0hE6ng8ePTxFHIbbJFt/59nccycjkx2AwgAok0iRBUZQ4OTnGZrNxMslSAaNhH9pU6PWIVLq+ubRlYEpUVY73P3gPn332E7x8+dwZ0FzjeblcYDTqQyqDwaDviJe6ptIhnAW5XC5xeHiIqysKwJpOp9hsNu5frrn0m7/5G/i1f+3XcWvrVUdRhCxNcX1zg29961tkR+RbDAZ9QFB/xFHsiFApBapKY9DtoaxKJOkSvX6E1Wph61YPEYbkfPX7I1xeXjrZYWMMPvnkExwcHODFixdYr9fo9XpUm+roCCzZLYTA9fW1y07mDFvO8H7+/LkjVVnq6ujoCMZQEAFnGt/d3SGKIgwGA1xcXLhzpZSI4xhHR0eYz+cIggCvXr3C8fExsixzmb9CCJfxzyQ1yyRz7VHO/qyqqlX+hsEAJuGklJhMJlBKuX8BWkuSJMHBwYHLBGYSnokwDq70s2b4vXO/BEGAy8tLHBwcQAiBwqohnZ6eYmbrXw8GAwhB2RlhGDp5byaKuX64L5UXxzHef/99FxTJpN7h4SGY5K69ILvXr1+7cgCNBDZl7rNCj1/jmvoATumJa47zc/JcYDI9TUk+vdvtOiKUpcwBuHZtt1sXMLvdbh1JGoYUEMtqTpzFXpalre9aIgwiR0bymEySxI1DIQ0Feaapq81ujHHEJ3/nww8/dOsVy9pvt1tHiLNk+mq1ciSolFTbez6fI7RjgAMOlFIuwICDDXxFBD8jYzqdun40xmA2myGOY0ynU7eGuOAENOu1MaZVm95XVjDGYL1et+Ypk+dZljmi/PT01GVRbzYbl0Hd6cZuHABEkvOYdDaJtVF43jFpzAEYrJTA8vCsyMCBA6xuwIG/PG84OIavw8ARZ6LzvNjNoGKJaJ4TPJf5+f1Mc3/N4H/LsnSKDUIIK52t3RrOwQasFsEZ40IIN0f5HfLc+asebh9HA81ZA5u4t9rAgDKOd49dwoJKngh2T2zZFAUY2p+2SYrNNrH1CBUG/SHSlN6fBEAlnwS0jGCURCjbmUKG7V6XLW7bYd8JA6j7SBZu70PEjHcjC+TtP8dd0zPe99mtPNfjKIISAkVdoqpLRBEFnV++eYP5fIa6qtDrdRHEsauJamzgScXlFSqN2r4hA5vFrSm4QKkAZVFZVY0SZVkjzWtou46GYYgoDhFGMaK4S7Ww4xhSKkSxDZKx91VSIogiBEHkstq01giXS8hNgKLIUJQZqkoDqAEjARSIIgJfy0rbmvUClTZQ1mYQ2iDLS0RxB0W2RZlnSJIMYdxBHdixbzSkMRBBB3/yZz/F9z5+hmdP30MUxUjK1K4blbVvOZhdwSjdqpMrpKEEBkVgIZNzUhtUUiDs9rDdJtgmKWRZI+70YMoSVZmhKmuUVWb3eLI/pQwglAaqALBrAturvj0NR3wYMGmtRACpGXhkkopJIAYGASWYCLL/eba/YD7DR0/BPxMZLQVl/UiaetCAnYv2cu5fz2dohq/lP5vMcOd8G22ng50zgj3MBghmJ1YICWl2cAFhyxGJxkfh5BImOfwsSWGzok3dziLdnXs+icd/3+fn+XNx93P2GRofbzcw2Cc/myxsxlCEaAgUl43oiN/9baD9uFmHpFQWs7l/vvvX+nKU4WndQUHv3cAjYo1xZTGkhK1D2yZlaNzywtWUzHN+mR0sQvDn90mefWQY/8n37YSgLYSfl3yzJiCCz/efdfczGi9t8pOfx7dL/e9+4/q+c/h+sPPTH9gv6FztSIOHQPJd4nGXkPPtin19ujvO9+Fm9wD81vZsx83O2N/92W+vv2fttuEhfEBrjUBS8BGTX/vabYxxqm+E29Aq2chZ69Y1/Xb5c93HD4xpS/zu67d9fXo/E90rM7HzLniNoLFlUNXa69MGbyCbjF+Dce+iaT8nQ3j9sjPO+X7+MzCh5wficl9wX7p3513Lv05rHXVrdTvwwSem970DPsdv7+482zfv+D7aex/8N3/s+/Pen8P8Nz9Yg9+7f/h9uA95NN6Warx3Q8F7bTvx/nw0MEa0xtnu87YDAvZjl+39B4Dwz/P6zlg72GjkRWbL11aoihKwYzEKQnSiEMNeD5PpBB9/52M8On+E6XSK4aCPjvUhoihEGIWk9iQlAkV+ioKCtNnBApICoyRFNglQso2pQXuM0TDCUHnAMMCf/vmf4esXl+iNpugNB8iKDJAG/X4P85s7lEWJOArR6/awrXIEAUtnGotdCBSFgZKkTnd7d4P57A55nuHbH36IX/7Vv4H3P/gAt7NbXLx6jdFwACk1YilhIFFXoMQZ0cwRV8pQCBi7R1MKtrSYK+GAYaBgjECapkg2W9RGIwgjHB4doapq3N7dAUJAQtp5LSGEggwCIsctZlDkOV69fAld1wikcvcwsHPHvj+jNZbzGRbzGY67Q2hDa0hVVRiPx6hrhSIvyA5Be/1lkSjeS2kOcBA+BzZIi69JS4bTOuXGGBhL1pCQgGI/ij4zhoIH2MAUoklKauxRoKpqrNcbbLdbkB9cIs8SpMkW0AZFmSFNtlBSYnBwAKUC3N3NIZUiBTDeU6SydmmjOAOQnw9zf97uzp9vwtrf9di35+5+/tB3dj97W5t2j3cnxu1/PMilIjmm8XSC0WSM+oNnKNMM8/kdXr14CQBQUiCOWT6RjKZOp4MkSTAejzGZTFzGymKxwMuXL/Hsow9R5jnVwq4qdOMY6/UaeZri6uIC3V4Xy/Uak8kEgaDs7MjLWjIwWK9X0LoEYDAcElD96tVLm9FTY7GYYb1u5Ccpu/oGFxcXuLi4QK/XQxzHmM1mKIoC77//vstsYCCKwVYGZRhYZQlAzrrpdLq4vSV5VGO2uL0l+VQG1uq6Rl2UduKETiKRAfCTkxMH6PDBme7cdiEESknOb1FUNnJauxrXi8UKurZZ6lWFJEnpmnGMJEmx3W6xWC7R73axWW1cPcGryxsXOS0VRdjVMCjryvUdD9pKV1QnIY7R741QFBURzEKi06FMERWE+PZ3n6Hb66EyBr/522NICBxMpzg4PLQ11mhAd/tdpMkWcacDrSl6J7Xys/PFAstVgr94/jP8w//iH0EIYGklFjc2i70sS2R5gdpoVy8MgIt4hxDQdY3aNI6mbxQ659lwbRMB6UV10pLkG6YKEMZKtxn2YOlzWBk87W24Utp69UTkscNkdzx7Xdk2lsAO3/6F4m0L0u5n+wx3/9zdw7/nOi/xn/zzv8B/9Hd+CY8sOU590hj+7mzhlnznIIK7xi645HB+w6LlIQPC+100t/So6W++DH/H/9u7fs+/n9n3mXPGYEGO3azxJkOcTrEQjQHSTOO//OlL/Hcvrh1Z6cs/tdq0x2Hin/nzhxxCe4JtzX1jkIfvvmvsM7TfdvjZFw+BIr6R+pDhTjWc7jv7/Lkf4cpGmN8vb1NIaN+TrhnIthPnH7wP8HX3Hjtf4zb6zoJA40RQprOiYCHXz8oGDO6CJk079oMC/jM1fdr0l26du9uXu/9KKSBM3WSKGAOja0QhZd7BCERRAAMDXddQUqC2wKQU5HAp1TiIYRhAG43APrtSRE7EcYR+j4DnKI4xGU8wnoxxenKCyNZiPjo+gpAGhweHCKMQda3R7XRQViXqWuP4+BhhILBeU6ZyaDN2l0vKVD46OoJBBSkjqEBC5xWub65sQBYRMav1Etr0MF/cYTgcYrVeIooIcB6NB5AKKMscjx6dIUm2jkjkrOT3338fQghbOqWP1WrtMp6ZlDo4OECn00Ecxzg8PMTd3R2klDg+PsaXX37ZkqderTfodHo4Pz/FcDjEaDTCzc0NhqM+BgOqvX17k+PwaIJABVgsFkiSNW7vbnH+6By1BuIoRpKurbFOtYsAQClyLJarJc5OH+Hi4sKp8nD9a2MMLi4uHFEMwJZqIcJvOBzi+vq6RWYxEcY20tOnT3F3d4fT01OcnZ1hPp8jSRJH7HKQw3Q6dfPk8ePHLsuWa22zw62UwvHxsZOnHg6HAOCIKmOICL28vHRZpLuZoSybbQyRrIPBAC9evMDR0ZHLejbGOPnow8NDpGnq1hom+AC0ZJk545xJRCZVx+Mx1WG2h9baqRJFUYRnz57h8urKZRzzsy+XS9cebvtkMkFdUw1kJupYKvsv/uIvIITABx98ACEEbm5u3PzudDpYrVYuKzvLMnznO99pyWtXFQVLHh4eIs9zVFXlgiRYWjqOKeCC+4IJYyaJhbVveByw3cz9sFwusdluEUeBWxeYKOVa1j7RKQSpF3F/GmOczPpgMMTtzS2ePXuGPM9d/fZer2fHcYTNdgNg64IemcBlwtcY48oacD91u133npgAn8/n7v2y4gBLt8dxjLwooCwhzvvQeDx2/ccBGCyFz0EOHLDB6gWc0b9YLLBerx3RyoEWnU4HYdBIsnM7eS7x8wONtLwQwo17lmY/Pj7GYrFwGdi87h8cHLRqs00mEyRJ4q7Hmdx1rREo7f7OxDwHBfiEMfeHEMKVxBoOhy6Qxh8z3W7XjXcm6XlscsADB8vw/siBIDzeuP1MjG82mxbJztfj/Zx/5qBh9ucA2PIVDUmUpqmbewxWcrBLp9NxASHcf37G/V/mqEqiXKVVlBJCuAxsXZM1WQPQVdECNXcPYQ28qmzA3CLP0I0DmLrG0pYA2G5TXN6Q+lan08FytYXRAoPBiJTXqgphECGSEQJTeRa8tUNEYwv7966qCtVb7FpgP8Gw+5lvze4+pw8WOYN2z718u4hKoaQ22E+iE8dYr+Z48eo5tps1lBQUVG8z/AKlSLZSKcRc0mxDygZVXTu/MghI2U4Y4E7fYb3eIgzvUNcGkB1MD07w7NkzfPq9T3FyekYymbaOpLKEL2QI6ST/lb22JBU/P+AwS3Fx8Qo//OGf4Weff4bZ3RwqEIijLspyg9FojF6/CaDx12yao1QOZjQaod/rYVuXuL25xfsffAijKlSmRpnXKMoKw+EUF1df41/8i3+FXhzhow+/hTTJUNckjw5oS+hZENuQapCILJBZ2XcgCdwMggBxN4aOSuQyRTgQ6K1D9LcRtltKslhsSoRhgLKqKeOpLlBZJQinThFKqECAcE/KqOIxodm2hksEh7FkPIOQwhIjTrnIDjYK4gp5gHk+nYHRNgucHVL3L0jpySoGVM5eVxBCQ0FD4n7tYt+nEAjdWJIw1IdoE25aNKSRb/ez/+naIimDvzW/hBf4KwTsCQQa75krgoF5IQBJ4u+7vqVPXDzkM/q+i/93/2d/vfWftwmAJtLax3AAadWpNLQhEF7aWpm+rysEIJQE82MMbru1VTRkipIKuq7YKQaD4Lv+FQBo2LrLqiGApfbk0UHy2aQAZvEzL7iLg6yCIARQ0zO4Ws420MjAktnkZymlbN1y6d459zH7vXVdI4xDNweafiYpYCucSHNDNvv2vnfr74m7n/HhS6j7vvc+Qldr7QWk7D+az9okHF/Dxw5ojFDwF5Fq+9Z+iXtS4t7Bz72bJf228/fhC34beV9yam1yZ+zsXIMDInjP5mNXxcHtkzttZKyMoEX7HAbUN97YaOZWjao2rXeHPef5h0/U+m3bJSh333+7T/y++ua+Btq1zH0CTgjWCaE578aeDCCkcvLORhuHQe5rCz87LH6lNcn36bpujVW6voYQQdMeZ3+01QillFBC7r2XW6OEsEu39sayaQWU8Nz0A7X9eu/c/w/NT+7lh+a2ELS7aa2dBD7bt7x/CuvTwrsO+4Lsv2vNNUzQwtQZyOXxyHgp24vG8PugkhDGktC7OBaPFTqfbiVl8x5295/2/tJ+1e5zY5z0t4Dx1vnm3bKfxqXDior9JGqSEgLjwQAnx0d4dHaKp+89wZMn72FyOHaBuOwTRV0KbpQBlc5RKgA0EeJKBY4Xcc8thduHAFsCQgqYGo6I3SYp/st/9I+hgj463T4MYAPdYxR5iqurS/Q6PRyfnDnsI4oiS8ADSgBVXSLuhJBKYrlc4PWrl8iyFIEK8Fu//ds4PT3BZrvG3d0C/UEXdZkT7yYouDAOm6BvbYNThP2PagvZQEQBKKGgtYES7OPSHA3DAGVWIMkydPt9jMcjGAhsrbJZXTZqXGEYIup0UVUaYQj0BwN861sfE290ewNl7ZyqLFFLOzN15bpzvV7i8vISo8NTRN0eDJpSWkBE88EG3Pjrr5LEdTLGw74mvwuWQWcWlecdTwOyQxs2gq/Pc7qsKxhN3681daAQVLoYgEvkLYoCeZ5TmeskQSeOEQQSNsULm82SVIyFcP7xH//xH0OpAEcnx5ajU6gqmpuUme6Vu7HBgthjE/hrwLscpjHG7n22b18DGtvE/X7vB9eF+y67/9wHjneXUrfOou9s1zZNnw3HuNvFe8MP0O318dXPf45ks0JdVrQBaYPb2xt8+dVXDgyqqgrPnz93NboPDw/x9ddfoz/oYzabYzaboSwLLJcrjIZDvH79GtODKTqWuK4KmswffPA+xJLaqbXGbDbDxUWKyWSCMAxI4sJozOdz6jdBxhIDlHVdu/qCZVlivV5jPp+7Cceby3a7dWBPlmUOvOEsDgZdOLuCwEfKVs/zHLBG2mxG7ZCSwKHISpiVZYmDg0McHh7h5OQUt7c3GA6HWK83Nks9A9cvms1mLkvNGMoISdMUQkgrUUHXp5qnsIDeEjzxODtPKYnJZIqjkxPMrIw9X5Pl4RmQC8MQB0dHGIzGrh/7/T4ODqYWZOqg2+kiDGNIFWCbJICNCO/3eqg11Y+AkLhbLXE3m0HXNZ6/foMf/vRnKIocZVnixYuXqHWNu7s7ZGmGzXZDGU5VjSzP7MYsoI0ApEBVVs0EEgLXs7mNFiqtPEh7pgi7EGnD0i/GzVH6VVuzijcgS1wKP2KYP4M1YuwPsA6L9Ix+Q5FsuzsxTYsmKoicTt/YMuSk+t/xjM1vWojeZsz/IovYvmNTVPjf/rM/x//qt38Fp8PYSXDsW3iYBG5JXDmwAh493F74+HIPmcc8Dvy7NBcVD37PtWHPPdo/c7vvt+Ft1zb+eHrgXBfN7wBdIMk0/tFPX+CfPr8mw9sDFu5fgPrMN/x2o3R3v/uQo+Ebmg+SvN65bHQDbcBi3/X4aX1Qn87f96bbUem7hw8ktO6HBgiqKlqrnbPt1a+U8oG+dPdlsEM64IkNmF0JGd9Jpz7Y7Se0npGNa7d2wDhDnuvh+c4k96GUoXuWff1CS5ve6e89PdS6931peL6vP4Z2nYkwaMsqMtAYhdY5ggakgRZAp6MQhl0iv63aRxAEqOoKo/EY/X4fH3zwgcvkPT46Qn8wwMHBFJ0wwHazRrdLhG+328VoOHIyy5tkCwODxWIOXZNKTJ6Raku328VifgulBIoyx3Q6xYsXz53UNGe3cgbo0dGRy05lwkZrjV6v50hezmZkJ5BlhdkGYGeu1+tbR4D2+PPzcyzmC9zmc0ipXHYoAOcwTCYTl1m5WFD2Nu2pB45063a7yPIcQhqUVY40k9gmJNec5Qmevv8eXr16BWkMXr94ibOzM3TjGPO7O3z0wTNn5xgV4PKSSG/udyZ/bm9neHR2jiTJcHR05Eg0Jou4RjfXXvaJqYuLC1RV5bKnmXSkYEDjMndHoxEmkwlGo5GTy55MJi6g4ODgwEmmn52dtch1dib7/b4LsPTXIpa5ZjKKs5+VUuj3+66uuS/JXNe1a9NyuXR2lDHGlaDhzOdut4v1eu3eXVVVWCwWGI/HLjM9yzL0+30sl0vkeY7JZOIyw1kCnAnQbrfrgIZ+v48kSVw2NNcUZ+c7DEOcnZ05gjSKIlxfXztSg+XPeW3lMT6ZTLBYLCCEwHe/+10EAQdMJDg6OnJ10v35v16v3ZifTCaOPM/zHOfn56363mEYWBJEuszt4+NjJ0cf2vq4TPgyqc7vSUrKnk+TDUZWPpzrNXP/c4Yh15TmAAcmpvM8x8nJCbrdHkbDMQaDgcvi7nQ6LghASiotwOpQLFvHNcTTNHX1vFk+m4laVozijOYsy5CmKQ4ODrDZbFw5KC4/kOY5BraUAACcnZ254Asm87XWzi/gQAImpTl4QmuN4XCIyWRCwTmrFYIgwPX1NdnlsXJ93+9TuSVem3k8LJfkGHFwQxiG6PV6jthNksQFk3EGNwMl2y0F/FR16UoE8dwxhhQTeHxHoXHS8Bzky+PGr+/N7RJCuDICXBaAs8SZsIvj2GVvc1ALjyspqb48Z+X7ii6+f5qmKcbjcWt94OdjOXUOuvCz8fkclsEn/w0txQAOMOCfuV+4Hjz/zEAJB1z8pQ9dAgLQUsFIgUrXSLYZTF0jViGiIEAYEnHKgdR1rVHXTf12BlOlVWKrIQAjoE1N9ZyNxma9RpKlOOyGKCAgRIB42MFBt4ebxQwHBwfo9XroSoWqoJrsSsVEMtnxV9eUUb7rq9B8Uqjq2hrHEpVTBAhAoCgDzfsDOxvA0xJfHITqd5VuMr+kUPcyLhvbhjI2O50YUmjk2QaBFOjGIUSt8fXPfobF9S2quoIQQJpmEMagRmPLcpZVFIYYDgcwRqOoSggl0RvS2B70eoi6QxgV4fPPP8fq1QU++ugj/M2//Xfx7U9+CeePHiOOQgLSpMUs7BpZVRUCCdSGJBKriq7PtkZdEysbhgFG/R4+/uQ7+NYnn+D65gY//OEP8Y//6/8nri4voOsCRbLFwdEppqfPkOavgaCCMfTedUn2ThBFyPIEKgwRDsaYJ9dYrm5pPVUdyLBEludIcoOjk0f4F3/8EmE8Qdjv4vHZCTaLjEI0JAVxaChoXUBGAQJtA0OlRCwlpAggRYBABSjDAp04RCifoid6uLubYROt0e1u0e93kSYJOp0QWZIgzQukAa3feVGizEqUooZUFNQfxiHCsAehQAAsz2fTAN0+LGA8nJ2zeWnAoD0OdQ3PjHYn3QfsfPuafRq+FoONQSOj6c0TIkHuT3/ydzmjB42PQpr9bTLLJwDc/ZuGu4+tL0a+RuDWTmM0oJvsZGviOmhXGwJKYcdoYNf+JhhZuqDXsiwRhLFN2KigDUABv80zk60pSCGyRaA0PSiFpLYYm2kPQUECUlrcRLps7SCUqLUmiVjBRD6smlu7mwyITNZGu9BrISUR/tpY6gEIFQWiEE6k3XOSX6lbsvK775T/xu+I3qNPKvm1oiWMoSAcXVcAGlWYXf9cVzUCEbTWNWnVulikjdcoIQSECuz4064jSE1AUI16+zdai6mDWuPKjSP73iR9xyehdglRCONIPyUVVKDa79jwdZsa6z4OcN/nVa2xwe/RJ1UNgNoIKCERxuQHwBCpCdB/dV1ZgrF5R7z389reBAfU7m8NBs6YQZuA29dP/LufzSuEYLEXaKMhtEWw/JJruiERVKAgjFW7saqWQRAAtYHmcoxCAqicTcNSvrWuna0ONOVluI1Ur97adyIg8pc/2xlz/Hfem+7jPQ1R648JvpaPZTR9xPfzF9eG9HT3RvOR4Rq8bh0BoI2t2Rs4+9uVoKuBGrReGbaFbAA/30Q4QpaVkAS0rrHbEFZuceOUehW1rrzxANRl4QgzShAAhAidPeKvc1LS+mYX2XvrIPcdz68gCCAUPRujif4//nvZrZWujSF8cTcgy5YnEXQStK5ofmvj6ocLGO4o9+SEi5M6jNYVKPALkDY42DXLw82aownqcu/ZU/lg1RfppJ3RvBOL67kIEAC1xs6aRSqvSkk3Jn3yX4hG4ZD61yDmhA97sC9RFJnzGaqqAqP3EkCoBLrdGNODA3zro4/wrW99C8fHxxgMBojCiDKFUVtfoQkmj8Oo2ReMgKg0jCD5daXo2diWBWDfmV1HNKxSTY4wqtAbDLFYZfi//F//EV5dbPH9X/02ZFUg324Q1MB4OMaPf/wjSBVgeDjFYDpEkiToRxG0BlQoQE2hffbw4BQvvvoSr1+8xPzuGhIVfvVv/Rv49iffh9HAerVCGEsUZYFeJ0In7CFLU6zmC2yWF44j1MYg6nQxnk4Rx32stlsYGUGASgooJVEUKcJQtdYMrSts0g3Ozt7DaEyJAJ9/8TkmkzH5tGGAygZ6mThAtztAEEeohUBea0SdDj789BPoHwPz61voMkOv00Fd5i7gxRigtslH89kNNvNLDPsBoAMsEvJvP3p6iu0mxma7RVaUEGGMUADKaAgVgKXula0XTq/LJ7ubYW4AKgsp6N36gVfUConaldCU9rXTXDN1hbKkhNeiKO2YpODsIs+x2awQBBLnj06Q5ymyZIs0SZAVOZabNZQNHk1XS7y4vMBmk+BbH34EKUNIEcBoq3gLQOgazWwVqA3u7XH7jnfmlswO0/3AoWvLxgnRPv8dyW/jrYfverx7xrg2qE0TbevfuyxLVKgQxx2UVYXpwSHkx8DVqze4ePOapAxBda2+//3v4+c//zm+973v4e7uDvP5HFmW4eyMIleWizkWixkA4Ec/+hHevHmDo+NjhIG0oMrQAQ7SAC9fvkQURs0maYnhIFTIixTbpKn5zABlWZbQdUPyc0YCy1YyQDMcDrHZbBygwRlfjx49ckApb74sadntdh0wNJ1OcXNzi8ViZTMets6YYMCnqipkIAAuTVOs11t0Oh0LKpX48suvHQBTlqUDCdnwSNMmo4MBI0AiCMjxmE77DpAcT6aYHhwgiiOMR2OEUYjJeOIGcr/Xw3g8pmyXIITUGlEcYTQcIQhDZFmKrKhQVBpZnlMW/XKJV2+uqf42gNVqjZvbG2y3G2w3WwKabd8BVFet1hpJUbakPOu6iUwLwxAQAmVZWUOWDl5wyNCjzUPUFIUtQPUUYDe9VZIiCkNnALVIQs/g0BacaQw0AB4ZSn3LxvYO2Wg849dzpvWee/oACh8NwcQEl7c4en/fd+yb5AzM+cbUvkVq39/ajoxHN79lkduWNf43//TP8L/8O9/H08O+c+a5n1r3hP9sQFPfqjGtWsYdGlK5nXFtHPjWJn49et05SOLetdptasxw/+emXbsgwgMX2Tnad99PjbMBbGBQFAavlyn+j3/8M1xuMkil3Fx4OLiBJb7vO2K+43LvPey+z53v33dCv/lvu07R7uf0O8l4+Q58u101nOH3wKD3DULAGzG8fhg/mo8UGQg4ss6rI77vX7/ddw1Kxqfu64OH383+7yhFdQyDoAGP3ZMICbmjUsPPwc74Q4dp1Qu875AD99+hnyXkR3zvOu4ucrEqIaXNALfBRrrWGI0GjmQ/f3yG3qCLTreD8/NzR/p2O12ogDJRhRQ4ODhE3GmyUk9PTpEXOdIkxXA4AHSJTmcMIQSSZIXtdoHVihRalsslaq0xm8/xwQcf4PbuFkEQYnowQScmafJuL3Jk6+3tnSNelFI4PDxqkbNM3DKh2u12EUUR1usN4jjGZrPBkydPYYzB1dWVK6nCRFFZ1hAQ2G5SBEGIk1OqF/7ZZ58hS0sIEWAyGTjZXaAps8Iy3ywV/eTJE6RpitVqhYODA2y3W0eAHh0fYbGcI003KIo+JpMJBoMegBpFkWEw6KEuCpgwpEjjQGE6mVrCX2OzISnlR48eOZKEMzOFkOj3h6hr2DrBFE3KtZf9bE3OwGVCmuWGOXPZz1i9ublBURQ4OTlBFEV4/vw5xuMxbm5unCQ31WwfU5b+auXqEDNhF8exyy7m2tFMXjNpxbWTuW08npns4szjm5sbAEC327Vj4dARulJKjG3AhtYat7e3ODs7c+St1rpFqq9sVuVoNHLkMtcYPzw8dNnw/Dxcr53f/3q9hhDCkZRMvHImJUuID4fDlgy/lNK1f7VaOQKR3+V6vXZy8xzwsdlsXG14zkBOkqRVb52DMvxAhdFohE6ng8Vigclk4jIQ2G7r9XqIItWSuKbgzGa94XIBp6enTv6as9S5hvjx4dQR00yO8/gsy9LZ1HVdOxl6zlwejUZ0XlEiy3JHavMY4FJIJN+mHYHMc5EJWQqiDV22Awd1MCEKwJHGfubveDxu7bdSSoyGQwghHLG8Xq9d7W5eb5RSbk7xOObxy7WtOfiDQRgmGThQI89zrPO1I3gBuPv4fcUBNtyHXAaKCVtWreB+537gd03P0XXBROzDcIAz1RNvshhZjp/LH0gpXX1v2gfJTuVAkM1m44AQBov4HXPJJ5aGY9+M+4b7xPPg3ZwAgMFgAACYzWaOvOZ3z2OM+8UHefM8d+Q5Z0xzIAbPQf88BrZ4L2FfjFW7OEL/r3IUeU5lROoaRVVhnSTYrDeIwxDDbh+IY0t2a+RVibo27h1SbWdDdbQ7HYSBgpISRgaABqQIoLVBlhVYbxJUlSbyRjfSuhzAVRQFYEBEvArQ6cRggNLYOVV5WS6wGCqVptEQgUKkQwL8IEghRzOISpkivv/BIFPL3hKWGEdDpvD5u/9q3cjl+6S4gaYa1QGtX8l2CyUkOnEEITRub65weXnp/G4GYHVdIwhDoleMAex+fnx8jG7cxSZJIIREFEQIAnqmIi+hjUGn1yP7J47x9/6tfxvHj5+irnL8+Md/5tQFlE9Q1jWBVYGyY5xsUhkou2ZGCAIKQKrLCkJoSBVgMjnA6dkZ/tZv/E0cn0zwv/tP/1PcXd2iyhNACsSjAwwGA6y3SygVQknOwgWqqoSSQBCEiCMKXHlzdYlnT99HFMcQUqKqSUEjimOIIMDPfv41Ol2Bf+/f/bcQRAa6sO9SGBihSQK0RUhaFSLBgfrCBlrViOKuJX1CdDsdbNYdbDcRIhs0lff7SLMcW1uSIUlSFCWpBdXaoCxzWzojQyeMEIYEXIadEEpTmbhdP9mvQ+yICOxmM8KRjr632PapbPa1aPs5D5FknA32/2XvT39sW7L8MOwXscczDznnHd9YVa/q1dBd3WyRIAzTIEXbAiXIkmUD9ifB+gP8xV/9xd8MWLANGzYg0LINSoAE0ZQlCiYtmpR6rK6eqrqqXr16w313yMyb05nP2VNE+MOKFTv2yZP3ve5qkYLEDeS9mefsIXYMK9Zav7V+y831rfl7V5ffBpTuZmHWPomvcDT8FBrGoaneazrb+q6fgg0kHwyVQriMWMD6bTQFwkgLONe+j7r9gQUCXGa1/73dWwQEjLRgtWiCOkCT7jeQIUToZbkbrnNqM0bta2g7lBKBC3EQIOe1COCYApXxxwnup8YNiRpW8hhq23PC60G+VgBS1sE7Na2qgbF+Vt+m9ce4AS5K2w+GwSkb8GT3NecTYkCtqiigACwDQXJUG5s5R3ZzKCQqXQeZ82jyfumAJVmXefMBRoi6dir5MmywuTao8sr5LqTwKPbBdMk8zwCtOZCC573NiNe00/mgIgTXZ7VJFoLodYWpAE17YFmUbp+n3YcASyEFpAS0qux+xD4+Ysl068v6xtjXZFwA1tb6xdYhYLFEXX8phc2g5MATQ3OOXx7EskhjK2wpBgvKSwuoVNTvvrwwNrEHgGWvpHkvYVyCG+t+bFcw+0AQBAhE4PRJ1rkA9uHCW2PsH6nnI+kKLJ+0XRvG3ZvmkF+OgtaM1k1Z62dH89GQgdILMrG2KM9/3idpSkhvLmnrZxL2O5pogayTNlxAnaA1aurbwWtKY1ylbQ/LAxovLjsnaQwVldvUWkPGwhcaEIYYVsJAEoup/S6OmOGsqvtECgrMUxUqXVrKY7vOrF3Gc5TfWQiByvMXCvulYzC18on6o87w1lY2kQ5mUAPw9nzPr8m+NZ6fUlBmcxgGUEq7MWfZyffVugbnmz6sesx9v72w+xHNI3/e159HUeBYNIy1pZOY7GsZBM4vK60OwvKsbp92ADjbT2VZoawK57OF1VHTJMbe3h4OD6hm+OHhAU5PT7G/v+/KNvFPGIZI49CTcfWz/flO6zOyr0wsktJmHwthk/mYMcUIABUqk6HX7uP19Qx/9KOP8cc/+hm+/o1vQApN7ZbErHV2dgalNA6P9htB6mTDSxs4RjKq2+5gvV7i5dkL3E5uAJAN/L1f+RViRiwLaKURBgE6vT42qwX+6Ec/xheffYbzszNMJ1MIIdBqtci+jBO0u1187esf4PHTt5AVhQU9aZy73a6ry84+ELb/T05PUJYK5+fnzh+laIN19mq700EUBIiDEEYASpMN2m618PjpU0gI3FxeYrleI20lYJ+wm0AC2KzXeH1xgeFwhPHoEIPBwPoSDNqdLoIoRlKU0EYgEAYhNIwkRiAf5WD9wfjyVwSkD5t67rtser5OCJT5uuFnIXklobVygeZ5Tj/s+yiKDFVVQkpmBJxis1kj22xQ5Jnz3WhjkGWcDJAhSVLHQsXzkGupN/GVeu1/ZeB7x7GNM32ZlsrvX/+9/d3uZ2xjaXztfb767eMrA+PCKQEEAQqr+NjS3iBAWiMKCAAZjvYwHu3h6VtP8cVnn+PZ55+jUgppK0V/0MdPf/oTRGGIyWSCeRBgs1nh4uIClapwc3sLKSXOzs4QhiHWyyWePXuGVquFSim8vvoR0rSFQY9qAXTbHSdJlVI4u3iF4WjgKb8GvV4fSil02h0UZYn1KgfV/CpQFEShGcjAOWIAgcWC6uxFIRnxgwFl4JydnVPGe6mQgSLCBALMZ5TNs1qtyAgIqH44BLBarlCWhXXAKIpQEoKovT3FigUjO1aoHlhlaSISBDJA2kqd4zNJUhweHiCQRLt4dHSEym6k5FTuk6M7CKAMEKUphBS4vbkhJ6ah7JLpdIqzV2f4+JPP8dlnnyHPc8qusYEEG0sZUiqDzNZEL6xSxYfiul6BrJVp+47aKvjkaI9QoVm3hhVjUjYVVKVAdD9eZLeyThNH+2UsRS8Z1CKMrGIBBHGCiiNerHDaaYCCsh6FJCFpAAeoacPUQ83aL43MZ3vPwBrW1P4mBRK9211wqlYS7AozpqGQbi9wOqveaO8DLGvB61EN3aewe23Zutmd77bBThiDVVHhf/ebP8b/8q9+Gyf9FuLIU27gZYl7O4bfau8pqJ0Nxn3ni0U3p3yHg7vacO9sAenw7lV/Xm9EfifU93L3cXOmluNOacNdR4HY+h+uD0TjJnzJOtP4ez/5Ar/74hKbsqbk9I2dXQ7VhlLK81Vbp1kjCtS7xhq+rJQCwrv2frp2/yNaSsYqabDP3DJgsDXPTHMO7dqchJBORojtSeLeV9wdV3bG7FCu/b9rwJf7i1ta38Mfa26Tr3A3+7Gu6XvfOzWz6RlkVg0lnJ9LxkTtWOZ7VmVl59ndum618SBrJwSMzayAU8qEvNu+KIw8OUY0575ccTVTQQZoK43x6MEROu0Wer0+2u02Tk6O8fjxY2SWTva9999FWWWOuni+WGAxXziHen/Qx2yxgNYFypJAqsVcYjK5AgQZOstlhUgKpBbYaKUxASwiwmazRL/Xwe1kChcioTQ63RaqvMDPP/scSZJgvVwiCGN0ul1oVWCVbxwovNlscPn6GuPxGL3uAFprvL64spnmcyRxi55tVghkiP29Q5yfXaDVaqHb6TvAhQGQNGm7TEatDfIshwA5MBgYm02nODg8xO3tLV6+fInT01O0Wi1XsoVBS6bdXi6XeP78OY6OjhwguVjM8Y2vfx0rC2gyxXiv20EUx5BSYHKVA9og2+SYz+fQRqPX7SGMIiQjqm38znvvgMrJTCFliH5/CCkCrFZrCEhoDVxeXjqAlOcaQNTKYRi62uK3t7cuM5kzIjmobz6fYzgcOkDq+vragYBHR0eOKpyVcQagGAQsigLL5dIp9JytbozB/v5+w1lDwJxwdceZIvv169cuC31/fx8HBwe4vLx0maqsdzDtelmWmEwmaNsAQTYci6LA9fU1Xr58icFggF6vR4xAC6LH/+Y3v4nz83O8fn2JKKKMnNlsir29PVxdXeHo6KiRdSyEQL/fd4Af1zgvy9LJziiK0O/3XTkfdkhyFrCf1c1U3hxgwMEM/BwGJlerFabTKfr9vgOmOft8O9NaCIE8Z1AvRadDNeUZJGdwPssKB0Rydi5nVHNwBGd51wGfFMypFdUzLsIAaUpzI0kSGG0cU0Acxy4DHoDL/r+4uEBVVS4YQQoKdGB2BJ43AFytbW3I4ckg32QyQb/XR6UIdOZ5xKUXKgtSU3a/caA5O2jJwUpUZjyGWmvklpZusyHWKmOMC7ohULmuUT2dTtGzQDpnhPNhDOnwHPhgTM0GsF6vEYf1vOX77e/vQwjhSg5wxr8fWME6+nq1doxXAFzADzuOOSA3iYlBqmWz4DmYgOcP2z8cLMR2C2eYMyjMxj73IYP4/H+SkLOi1+u5Nc+Bx+zIZQCfA0c4wMDXwViWcLAM751s27HTxc++4ZrkXAqDSxUsFgu3powxLgAEgGMI47XoZ5lxWQYeF9YHfpkjCIgxp1IKWZ4jW61RFgUSppu3fVTYIJkiL1zmsbF2EoIAoQFCu4NKkBwMgwhKGazWa0wmE2IsqBREqKGVgrbvyWuAwBQNEQoEQQgp4X0fwFi9V2sNrWxmNQyBt5I8zsbaUkpr6zgSUNbH4IIat5ypQK37GmHtRc9+prOM58C0AJWsSzLQ/KM7UaBEBECgLAu0UqIf3CzXuDg/x+Tm1s1Z1uEDF8FItq0BMBgOcfrwIbJNhuDW9oN1UAtpg7cFBUI9efoUJycn6PX7yLMVcstIw0CYhucE1RowEtCUrcpe+lCEkMJAqxKVtYm11oDUUHkBNdUoVIHleoH9gz184xvv4fdnV9isl5jOJNLJBU5PHmG9jmG0gIaAEBqVyiEFIIOQbGEp0e30MJvNMF8u0JM03iSTyHfQ6nYwW67x04+e4a2nH+HXvvcBVjMFU2kYKAhJFJCBDf4EWJ/1gXGJ0IJXIcvoOEG33cG8PcM0SRDaBIYkSRAnBeIkRZ7nSKIYm5zqthdlhbKqqHSfqlBYECEIAgiP5rKWsRxg3bR3DUxtCHiHMLU+7z4TZJvwHBGCILddtkFD5xfijTJh247ZZUP59v6ua3fZ+2wDbd+T2tu0eRv3rG/u+mHbp8JWmv+ufqAi207Cw4bos9o+dXXh3fUBJHwgpAbMyaFQO7drgI7bx5mBdJ6EgZEGxmwlSqAeE2y9G9uj0gU7AOwIr8F5cadPG/cQtX/LH5XalqztOcDP0qUrKs3ykUAmGOPG0WjjwPttf4kbL26bt/+SDwcWjLV9LWpQ0oHWhv0cLH6MBf9gr5E2294A1mZ2Y2Oob6TXl0qrnfY9ZWU3+43AO+PNWenYBiEMhK2BShn77Lvh6ymTuiw44Kdy+3QUhi6bVevar6a0ov2K72NtdckZsFLCBCGCoC7/47u4djnrHcgAb53Yuch+KePNQbg5VK8mY2mHpbXTA+vHqVd5bcv7/g4aN0or5YAQbZrAc1OuSOtjhSefGWCFk9X1HuoDD/669CnWGexjv4f/TLpH6FgE4K5lloF6/OG1syn/fP8PBDOi+uvYr1Hd9I/SteQHZrDYByuJQbReWdt+Vn534Q2DEPD+tnoITQAKYOfR4hcODCBtEImiuscKlWXlqOy5AtDCMXUYAEZTeQfhj4O/b1j/nHaOy1q2ujIC7MiEcJ+5melNZ2b4ECBw1gCMnpMM0fTSVJeY6mELTx7s2gs5aMf3qdMzuCNrUaE0l8+o9YdaxPn3tkE+br2Ebv5VVQkjKQQKwqDIK6dnOT1fK5RVRWOgNbEtVARgpnGETqeNbreLQb+P/f19HB8f42B/hEG/j26365Irwb1tA+CCMETgrSmeZ4HLOKb1xxTcMIJ8d5L1QZv9z/1tJAWMiQJxmqAyEh9/+gK//8M/hQxT9Ps9rPOV07+VUri+vsZwOMRg0IeQpPOy/0Xy/DMUONNqtfDFF5/h5uYCm2yFOI7x+MlbeOudd8g2UxXCIEAcRtBViT/4wQ/x8U9/iqvLS6yWSygb2B5HIbFCt9vIsjV+9KMMQShxcHiIMApRVvWiob3OBvNqSsB8/PgxoijGbHaD2WJeB21bfSC09mbaaiHhoGfjUq7JT9Dv4+jkBDAGF2fn1p6XCGRkx8LQc4sK89kM89kMxycVet0elNKYzRfodFoQMkAYgvRZwO152s1n7UrpGidnaI5XqiBMSdfYkt0e6/OMhilVg6GN9R4/oVYpwshkECDbrJBlG2ijEMchss2aklgzKvWVW3+MkQJxkpB9ZgxlmpcKlVJgyndeS7uO+3Sb7e/edH3z8IT6Vzi299ade63Xju3/t9v/puMrA+NKW+eDMaiUcJQ4QShJIGoDYUiAwFD0t5EBwnYP7337u3jw7vv49NOP8KM//gOkaYRPP/k5jvb2EOgSYRRBigJhpFBWGkkUoyhKjAZDlGWFXq+LOIxQFSUmNzfYH4/Q7fXw7NkzGK3xoiiAU2qnlAKV0sg2hc30IUq31xfXiOMIKgVF/+Ql1gU5KcMwhC41QhlhMV3AGHLALTZrzGcrS3FIhe0NDDbrDVHkiQhlrkgx1BpZnjnlmQYCgFQIJFzNCm4jUaDZ2nYBbN1GMtLb7TZ6vR7G4zEODg7w9W99C0cnxyjKkrK3wwCdbtc5dPMsh1HAZknZZlfXr7FcLvHq5UtcvL6wmTwZlqsNsoxqMk6nU6ckclZDqSqUhusgoRE5UlVMISbtplg7KcgBQlqAEBIB6tpDQgjvdwMDCqCAANHp2XNgmrWQ+M52ugP2GUxbpS1FuzDGgugAjLYOFVKSOYZHc5QmK/eiNsqNASwvWL05i4AMKM/xsg1+NhQituoATzHajrapAwDc+VtKHymdvmPUwGzLDSGsvXHnC6Jm95U9+ximjRWwxiVsRoanTDSj75qGrf9ZbVDV9FyZMvi3f+tP8d956wR//b2HSGOquaG3Wyma/5s7ctFYo6A+rTbydAMwdSB53eVgIFs4g8y/swGrW6Lx+d32sWHfBJ+9O22N8X2ivQbYBZwlaS9W2uAXr+f4j3/2HJ9OiAJVyBrQ3FYi795b8F29Bgo7pt7LoFbEeOMFpKPi4/NZSb2b/Q1A1PXchJF23AKrxAFGaOjtDvduIMz9m2V9RDUlFr+j1k6ppEwDS3nnQPx6DtXtp/njAwyAvzmC3p9XuzHgrOxAkuNZqzqznceCnxmEIcIggNIVjKmcHOHn8XM4Up+za7lv2dALAgq4UhU5ipkmsA7cIGcHQq4zpSkS1spG0sesU8TWiFaVcs9NkgRFWVoHAEXR9vo9RGGEMAwQRhHSJHE0veywjaMYs9kUT55QdlAQBFgtV+j3e+j3OlTOI6Raz0EQoCxKyFAgL3J8+tnHODg+xHw2hzEGaZqgUCVaQRvz2QSbIoNRBp1OF0krxma5xsPThyjLEudnZ1hvNtgbjylzSNOaX28KBEEMY6kGlRYYj/cRhjGKokIcp2i3KYNaCAI14jjGYrl0mYhZlmE4HGI8HuPFixfg7PCTkxNHh66UwnvvvQdjDK6vr+14Cpfd7NfiZOCWHRBch4ipqv36yFdXV2i3WtisVjBK4eHpKbrdLm5ubnB5cYHU1jA2SqEqCiwslXgrTVHmOfr9Pq2OYITnz16g1+ui3Wrj7AUFDd5cX0NrjeOTY/R6PcrAXK8gwwBHB8dotVpotVq4urpCR2sURYnZbIZOp412m2i/12vLaFNVaKUJhDAN4JiBgel02qh7zVm1DPww0Ht+fo5er4fra6pPyzV/l8slFgsKlGDQ2M9Gp1rRXVRVhRcvXqAoCrz11lsQQjgqdAapGXjlTM5+v+8iojnoYH9/39Gac3Y1A2Q8zmlKzvW+NWrPz8+dzHj16pUDguI0xde+8Q1sNqT7iSDA0fExlX55+ZKA7OEI0+kUgKLaXQCStI1SGcgQ0KXC9S0B02qxwmw2w+npCSpNjs+Ls1d48ODU0am/fPkSVVXh+voaRVGg1+u5DFimbecAhOl0ijzPcXBwgMVi4cBuYwwODg4oAOT1axwfHzf2egZ0Gehmeu0gCDAa7aGqSiyXK0gZIIpidDo967yUKIoaTOS1xvOF9bjVYok0SSC0QbHJEAchZJsyjWfzOZI4xnJBQShRFGK2pEz6XrcPQCAMQnTakc08oMxSo4EgiCBFAKUM+r0+NpsM6/Xa1X/v9XpOfjOQmqQJVsslAhkhDGIkSQtFSQZoEidQRmE6X6CngaIsAAjkpYIMCIRdbygzsdNu105QYyDDGHlJtgsZlwpJkqLb7WOzya2zpA8hhKtJTf1GNNebTW7XkERVaQc2E+Ba2Xc36PUG0JYmcL1eI1svsFouMRqNnHOj1Wq5bPqiKCDDAGEQoyo0KlUhkhGUdUaFSYy8LBCHdbmObcOSwWiWcwIBsmyNKIpR6ArCZuwy3XpVVdhsNg6Q9ino+T5hGDqWBv7xs/yd4W/7ie0UXv9cysIHxH3tguexCzK0dgazKjAAXxSFA3M5CIDZxfg5XGOeP+d7cYkDztwH4EpQ8TONoSwI/pyDNv68RxTFBCoYRfWagwBpkqDVaiNJUkQxMW2pqkBelMiLwnP0CgIGwwgiCCjTSBD9n9aGAqc1ZRPw3pmvNwhjBl7INmm3W5ZmWFiwmX7CgDKcojhGFMbO/mBgXFuHkaqIGcguHXL4cICCHSNtHbXkNPVBPz/bCIw4WJDIB8k9pALkUGZgSgqi89VGIZCS2htF2KzXkMKg1UpQZhmm0wlen5/b8mk1mCogEEiJygWvAnGa4ODoGKO9Pdxc3yCKE4RRBG3nDdtKrVYLo/EYrTTFaDxGqSrk2drpFWEcgOiVWfcXYFplZSx1quA5DiRRCu0SEAUgAkBoVBU5c29vbzCdTfHeO2/jGx98A598/DNk2Qqr9QI3N+c4OjhEmrSR56Vd+xqmqpBa+WMMZU3HSYJ2u4P5gqgYO52uDTLRyIsCrV4beRHi6maF3/vBj/DhB+8iihNoXVL7HBBCjl+KKzDwmY6klAi0ggoUhM1CSqMYrTRFyzJaxFGI+XyBLNsgyXIkcY68KCiTPIuR54ULoMvy0iYiUH8QFb5EGFFADwdKCAa72EMJC9wIopqtbT07BRlLcHOSQaCgEbjK7HAOEEATOBPed/cdb3IwfiXn4xZg4n3s7uEHBDBoZN/QtlM0hattPMNODHg6ENvOW7bN+L5N8K1uh/8ZJbLw/Gfg2c57AwB11iHAwSpesLC93x1q0jvvvwXQeH4u3/dRn8O+D7zxPs1+vHueD6ax7sA2rxReEkHDlvayy4DGtdxOrTVE4D+T+9j6HO3vUgibCd2Uj9LKUQ46gAWbmVLV+aj43vRgD45lMJqjXugfdz9TY28cWODcZVx7VsAFLu7qz4YvythSYKLuH2hhs1Jr0Jd9rqWdjI0sPKMR6MAyCDTZHrXXvzXgyrV8CcgKg+DOenYv/4Z5UgeQCBjLvOaAceOvS/LTSGHLk2ir+JrA+SvYP+IDyP4zqd8p2AreXmqEpuQpY5xbStsa3cIyhzDwTQwGnBGurd+HxtVob43YQeTgfve3lA4c5H5i+VNPlZqZjvu9pvjmucfOwnrWOblq55knZd38r/tFuDUO23cMTrEO6yc6UICIcPOcdQyA2Fr4PbVdY8YGfjmhh3q8/eUshYBSlfu7Xs8apZ0HygLjnDAnhV1DHPyh2X9rH9d8RD0bjVsijfnJeldjczO8iu8GGrq+dsyqBqi4X61n1V6vbW0ALQSk0aRfcpIYDWy9Huw15KPndzTuvtyi+mBGEwGWL76c5mu5DrTioAFhyySpClVVkM0mJSopXIAsg+K1rUD6fhiFSFuk06Zpin6vg73xGHt7e9jf38PBwQGx97VSxDHZqQAsXkIZ80EQ1uWLTDOJh1hjAsjAY66w/wsElsmiLgfJ/Wjz/yENlXiNWyk+e36Fn/78Gb54dYm9/WMABlVBc03ZIPS8KLC3t4ckTVFVFBDNNjyMgjZAIEPEESV+vHjxOZbLCbQu0e6M8d7730B/0Mfl1SUMyCaREHj18hX+6Id/gJvXryEB9DpdpJ0OloslNpslsfkajUAKXF6c4ZOff4ROK0V3MEJgbftKVU5mV4rGIggjnJw+wGKxxmxOvpxut2MDRuu5GYQh0laKyPqxbLSTs1vbrRZGe2NopbBar7GazW1QgrCButqtk/VyhelkSgxSUmKT5bgqN1B6iCiOaWba8jWEplC/OWBc13s8y06tjQu2cGteCCo/BWKhKi3wHWg0mL4YEOe5Wu85ZE+t1kvkeQbAQKkQq2qBosgJFLc/6/UaUUpsT0kSuDVRqJICToOm/sr9+lVAZoeDfImPf9f3bq94w7HrnK8KcP95j69eY7wo4Qt7LRR0ReC4lERPka83KMuChEEYwqIviOMY3V4L3/zWt/DgwSk++pMf4fXL11guVmi3EuRZhdvpK2yyDGUJLOZUL1TKCGkaY7FYY73KIGWAJIkxncwRBCE2G3qeVtoB40pp5FmB1ZwcdYmt+yeDAPPJFEVZIgxCCCOpZqSApWHM3MSg+mhk0CmtyRBWZEgTJSNTt1DtCt7oyZmunAJKwEICpSizpdPpIooo4ihNU4xHY5ycnmIwGuD45AQALD1ljE63Q5RGUYzleo2ryQ1uJnO8PH+N25tbTGdTZFmGy9eXePnyJbJVjmyd2Wydug6G1srW3aVFWCtgAEAKl9IWbBFA6S1cFtxGk/PCGAMhd0NgNfitYTx6O6pds5U9bcwdg42dcg6YM6TKsOLfNETtIvUU2sbCsQLOsDZv3NR11/oba30Bt6WmkLoPpLxj5ODuYm0qxE2hQsqiABDUz3AGYd0n2n9HuhhbH8ApKOYusNmIfEQtvP33A2ogj9vMtVi2DTr/Pf0+WZcK/59fvMIsK/Cvffg2AmkQBkAY1AafgK/A2/b4yjzqiEVnYDiljxXu+q3dnTzd/D6B6YdZuBkgmtMGMA0h/2XCt1biGrdozCXjzy1raBalxrObJf6Pv/tT5JVuKEr3PXN7XN/UNl7fTHFdz0Omttpt1Nef1Q2ujV1bac06QmkG2/pcQjXGkcaMDQyr7KHZfnba1JfUih/sb9LWqHXn6uZ65P5iKiACsJmWTsAHtBuKpRDOoIAz0u1zBBCEHCVOBrEBnFNcCgOlSkAYV5eI6pJx/U5mwVCQkughAaZRpzpHXOtIa40kpcy2rq1FWRQFpBSIo9hGXAKdThvj8RgAKAt3covTk1MABGAe7O3h4GDfgQhKKbz77nvIsg329vYRRRJllWNvbw+bzcZlOHY6HRckxXWPr6+v8e6738XNzQ02a6Jl7vVa2GyWiCKJLM+wvFni5ubG1b9dbygzWumKMmC7lNG5Wq+w2Wzw6NEjrDdr3NzcYNgfYjadotvpoCxKfPHsGR48eIC9vT0U5+eOnvr58+cOlGy321iv17i4uMDbb7+N2WyOIAhwdXWFQ5uJPZ1OnYGTJAm6NpOUnc5ZluHZs2eYTCauZrgPOK5WK0flzbTKDDbu7e0BqGtLM926n3UbRRGWyyUODg6glHL1oKUN7OBaxMYYV2ea6yRz4BLX+2Y6aC79wk6D4YDqKrXHLUhB9aAPDg5we3uLzZpqMnN/cMa31hqTyQRXV1fodrt4/fo12u02AIFPP/0Uo9EIrVYLr1+/xuPHjzGZTPDkyRMHCi0WC1dfmgE53uuvr69dBDJTKkdRhCdPngAgXWY0GuH6+hrtdhuHh4e4uLhw1NIMpMVxjH6/77KrW60WRqORA8q53jHTWo1Gowate1EUOD8/d9HanB3N++Fms8HBwYErp/P8+XO02208ePDAZctyXWAOcMmyDAAc6J/ZLGdjjOtbnjvL5RJVpYhK//AQWmuXsbt/cIBXr15hMBhgMBi48SFZQU7g9XqN4XBkdUmJt99+G6vVCqvVytXtZsr6o6MjfPHFFxiNRojjGLPZzK2TMCSduN/vY29vzxp+FOCQ57mrYz0ej927cskfrr3N9NgAcHNzQ0wPNsM8SRIX8BEEgZtnTIGulMLLly/rNdjtEtg9m0Ep5ajrOZDk6PCQqM5su1arlQOFC8tKtL+/b8FSphOnOr+ddocA2FbbUvVpN0d4nDhDmLOOZ1Oqa79arVzABK+Z5XIJbajUz2Q6deBpp9OBUgp5UVCgURQhsPOI9+AoDNFut0le2NIADOQyUwDTx3P/sY41Go3BADIAl63NLAFJkqCqlAOB0zR1medJFGHd6bixZ3r9MAyprl2SYLVZuwDU0JYoStLEZcenaQpjHUlaa5cJzsE/xtAew4FAQggkCWXv837FeyyXMeB3AWq9ngOH4jh2Ncd5nIIgcCUFeF/ktccgO9Ofs7zgvldKodPp3DHoAbhgJh4HZpTgNc9yl+/p08xzZjjL7dFo5NYXO9eNMY4NwZia5t4H37lkBAcr/DKHDEJoA0QhIFoSSZrSPIhTxEFkMwqVk3tJkiIMQoRRhDAIEdja44HLPpEW0KsZkpR1Ui4Xa0xvJ4jSHFEcIdtsoLRGbIMBnENPNulMy6Jw2eVJkiCyNN++zcBjTKo+Uycrp79rY1DoZikhclB79IPWLmeKZGeb2HPtw+y1bOdqxCE5IJVRjo1BCIHFfIZ2K0UriTG9ucb5+RkuLy+gNWUfc5YcrINYa3JWpe029g8OcXLyAIBEEMZI2l3Emwy5zSZnBqiDoyM8efIEaZris2efo1CVDTio5TQgXB1j+xLUV4IyKjnzSZsKYSCB0Gbna5t5D2KqC2SIKlAoiwKfff4Mjx49xqMnT7FeL3F7c43bm3NcX53g5ORdKLVCXmTQUkOaOpuOM3c1gP29A3zx/HMsl0sEQYhOt4ckSVBWFTblBnG7DZXF+IM//Bi/9qsf49e++x0oLVBlBloZBGEIoVjhBlx5MlPbPlpLSB3AiApCG4QycMEnvV4Pw/4Ak8kNZvMZlsslVqsVjUErRmvTQmEZTrIsw2K9wmZDlO9VRcE2VZlDVQWKgKhJOXs8DGh9sPlBNk3tfG+sQemXK6Px8f0Wzpbzbf0dNjQfDBTyc7fBWL7/l9mid8BD37bb8V0zo7R5jQOarMnmwC6/3QCMpCARgdrOajzbe6ZquGqMe9dtwFDrsmHrcluZhrp+TOBsOh9k4ydSMKfYeic4cMfZfKBQlNoHAyc3atlDZ2rTfEf/HruO+h397FrOlCc/DNeMp+znuneFNym22Qc0NGBqoI/Hqz7HpwZWYC5yKaVl+6RnOIY2ISEkAUrGBiQbNOthAxROzp9pXTnoyn3vgZssy40hCm9/7teBKFs+QO893Hei9gOyXIKpa3/7fe0SjSxzA5VVKJs+PE9vYHCC3qfJrujabnVdBwC69X637jrr9Pf7Vbz31Yao1L21yc/jvdSAqanrIOUwrIFxpRSEhAXjGNSsf7QDZaz/lAMflUGpNQpBLD0wxN5kADRrrhOg49N7071pz62ZVOr39OcMA8zUxzwvTA0688ChzoLlv10fsN8ZLFdq2WtQ6xPCyij63+6Xnv+U2iJq1ltd1wj3dQxOYwFMXX7A1O2gmwFUGdBAaA1w8Js37AZEg2881JplhoGCS4Aw5H+vVIGy9PsSgAxsUogN4FAayijrW6KgCV/muWfzWmu65MBAOgdicNCTsHt80xtb61J1P1m2VgNnM9jbwpfDzC6gKtFI7BLWn8b1zt26sIEF/Cxal3d9+8a+gOZ2WZ2QT2HftlFVc/6AysMURelsGwqUA5I4QmEZdmn90p7SbqcYDAbo97sYDCkz/PT0FKPRCP1+H512By1bQqiqCmhVQusKWsPaQIGzpfw1EYZRA+iWtiSAFHVAGAHoxtGn87XcfwCov3RFvRIEKCqBf/SPfxc/+/g5knYP+0f7WC7nKAuFIBDIihxXN9cYDAcY7Y2dDcR07xTAWkCICHEUo520cH11jpcvv0BVrBElMUb7Y3zwzQ+x2qwBIWDLn6PIcvzeb/8Ozl68QCdJ8ejBAzx6/AT9vX1Mp1N8/POPMJ/PoJTBoN9HEsX4xc9/jvF4jCfvJOgNxo4hjA/2WZyePsBgMMBnnz3DdDa18o/krzREwx/FCeI4QStt03q0gUDCkIxVCigrhSiJMT48gIbBT3/0Y1eiIAjq9DUK5M4wm04xubnFcj6DgEKRr1AqhU6nTaV5jITRFQVeauWSAHn++rgV/0SSbA8pKMAKgXQsMJXSqPKCki6cjFLO9idbnMuYUCBDIIHpdIrZ7Bba+g02ADYbCrblINGqquhZNlCc7kv2fRKl5EuydpCPefGa2IWH7MK6duFC/vf+577+DCcL7+q4vGfv0pt3nburDbva82XHVwfGM6JckEGAQEhL7ULTQUOjqhQW8zmEFEj6PcShhAHValhupmi12wjDFnrtAX79N/4qkjDFH/7whxDCII1CtLoD3E4m2KwyxKOWi47INhlKVIhDoibUpXE1v+M4RhK2kBWZo/2RQmCz2KCsCqIX0IZqZgVhwxmolYYUsuEkYcc6O9OFkIhtlhFnXrGi1G63IUMBEZBgC61zbDAaodvuoNftYH//AIPBHgQC9Ad9dHtEayqNcY61oqywWK9wc3OLPM/x6tVPMJlOMLV0dre3E9xMJ5h7zmRuJ2dSkKIEGAWqvSI92kJbt00KqkFWK1yijspzNEwUBehne/vUVKxE+8YAL7QoShx9p1KkjHKfOoUWtaOMNzLWVZ2wk5wpgHrz8yZ7Q5HWuqGY+efV0X+757OvjDYUZ6DxznzsUnb98950P1bwA0uPt/3D53Cddb+N24DovZm5W+3ke3OWnC/0uI+3BbdP3cG0Gr4x03hX48U323M0gN95fok/fT3B/+LXvo6H/Q4KoRFIII4k+0S8xm6NybZa5kezw+GYjfMFo83ed6TI7egb1PO47q8aSN5u0E6BapWxGtZ1anSzgTsaXBQaWWnwt//gY/zsagql6znDz7vPCbJrI9pllPN78Bqj//m8plPAf7163mzfj7JYnBMC0n7GzzdWjjQ3TZ5nzhFh3ty3As26dLAOQj/AQHBNLlE7OGg863pqbCTdfS/hvXtzzW7PbQNyqtRGqAZgEMWhY85QWjlDMAhok6eSDHB7RpLUMpGys0cIoxACAqPREEkSo9/v4Rvf+AZlglqZyHWXl6sllCKgdDwe4+bmBgcH+4jjxFGCKqVQZGsMh0NkG6J91lapEmKE6WSKOOkiz3NHa8372MXFRUMGLRYLDAYDV8O52+06AJrr3hZF4YDLLMtc3WAGdmVImcVFUbj6z5PJxMmiOI4BA8znc7ePn52dod/vO1Dy8vLS0ShfXV257GCmtmVAeTgculrUnC25Wq1IqbYOEQItK+zt7Tkj4MmTJw7gGA6HeP78uasLvdlsXLbp/v4+ADjQj4Ht62uiYheipu9O09TVcz4+PsbNzY0LROj3+zDG2HrfymX6chY0y2LObNVao91uY7lcYm9vz40Hf88U5h0Lir3zzjsO2OGaTAxo3t7eIkkSHB4eIssytFotxxBDVNiZe2cGxrj+NWfW53nuzmNHNWdkM0jN2eFcw5fn2s3NDdI0xWKxcPoXt3U4HNoa5wRAPn36FLe3pAeNx2OcnJy48WXdh+or5Q70CkOi6er1yFHP4CoDYN1u1wYldhzw+/TpU8rYv7zEYDBAFEW4vb2FMQQ89no9ZLZ+KY9rbzBwAQv8DM7Ef/r0qaXFnjuwPo5jTKdTcC3zdruN+XyOoijQ6XTQ7XYd1TOvsU6nA4DAttlshj/90z/Fhx9+2JAlWmscHx9jOp1aYHXk3oujg5fLpQOsmfLfl4NVVTlwXAiBLKNs64cPH+Lm5sbVjx6NhshzMlYZRGJqaa01BoMBAHIyDgaDBojJMnV//wB74z03f1mv4ACd2uFnM/NtSQEG6FnG+w4+7mOmV2eZORqN3HplMFwphVarheVy6WSQc47YDAEOVDHGwIjU6XWcycxjxKB6lmWOPYGBYNazeAwYVGYqfh5Dzi7ebDbodrvodDq2DEMNIPtjxW3hwCwCygnIjcIIaVpneed57tgG+v0+KttHTNPP7BMcnGAMRZzHdo+KosjRmvNYsaOX9xvWDX0acx4/zujmPc/fW/geft1uDsYEaup7fpfKlo/ifYD3BjdOtm85WKf2WYpGkC07CFh++0wwTA3vGLOsTPSzyEejkWPCCILA1Tr3A0d5jJitxKesZ52EmUZ+mUNrDUiBKIyRSAkpt1hxNOmlrShFGiZO1oYhsSts6/mwwE0oJLHkBAJpq4Xx/gHMRx/j9dk52v0+klaKJE2hVAWtKwwGQ6SppS3k+RnELkiCx5TGObRZM4G1k2M4ACG4n05amaYd5DubnE1pfIeouXNurTNTADvQDGbs9XqOXeBWCoyGQ6xXS7w+P8PZixdYLZcQQrqgEACII5qLi+UaaaeNh48e4+j4BEEUIc9LCBGi1xugzHLk6w16faLTH+2FSNI2lAHG+wc4u3hNzAdJTIH6gmgO87xEWTJtfQSjAVXliOIAaRJDAiiLAmW2wWx9g6okQENIiThOMN4/RBgn2GQZpBFIY9rvl6sM3/7Or2C92mAynaEq1njx/HOM9x4ijkNoE6IsMySdBKWqQGwC5COQQiBKYgwGQ6xWSwAzxAmxtaQqxWQ1RbsVkn9DPMG/87f/Ixz8r0Z4cHKMNGhhtSztPLH2ggMDAabuJhpbDmQM7BxVbj22Wi1i/dmnchmr5RKr1QKr1YrK8S0X2Gw2KPICeV6i3W5TOQytUdhyK1mWoShLyqgvK6iCZFchqNYi1WuVzpaQUnosVsY65gGjfJ8EgeW+vNv2G9znmGO7omnHbdtJFo7zfQlbh++85L8b39uGMsBx15fRvIZYJuxY8T23LuDPnd9NenTp/H5sXIOzj+8+17e9aF3fzfY2WtkAE+VdV9uffqA/TE0HLwTb9/79bBJIIwi7uU/5fiD23UAIRxvMoB7dt+mjaQYIMCDe9Gs42vI7we53x4JrHJMjnM5XVR08JoQgJkzlAYCoGciUZjZFCzpDQ3l9LG1mPgRgBGXN0TwJoaFhVH2uAiCU9562r1iP5Dngy38AqDx57O+dfn8bY6ChHeDn97+T4oKYSvkD5elpMqCa8pzUxCAHj9P2+jSsb3hAND+jHlu491K6tFnG5CNFXUHStqdeB/fJAv997/uMMwiJ4ZHGkXVmaletI5G8rFAWws3zeh9UjbEAwOlKTtcCAGEqpxPQSST3ci+goK4NrmkO+P0YBARWemOx/V7b77zt9zSmTrzanhO+L1oGxBKwzcbhj5MbO60QClBWPj/HX5tOYawZTf2D5BDtR6HFPfx51NQv6KDMUeewqn2oaJaUKYqs8e78nuzv5R9smrLR/3HP3ApIonevJW2j3717+Yd7Hysf6j6ogefG+WAq/+YYb/uMAVg6irqtu5K9AhvI02xv7Zt22IF9+q6+537m93Q/LKM0B+8W6HW7GA720e60nK+F8Z1Op4OxzQgfjYbo9XtoWZs2lLR26szduhRbGCQu69b1nffDeoyUDJQLwNRBdc6/KgQxQVoPc0OXsG9lNDMvaUSxxN7BCf7dv/P38Fu//SfoDMZ4/PYTrPMFVusleq09vL56havr1yjLEt///vdtP5QAjCthQONj0GlF6LRSwBj8/Oc/hbFJQEdHx/jmt76Nh2+9jdeXr8n/kSYosgxffP45fve3fxujfh/7wzFOjo7x9pO38I3v/hqKPEO+KfHRRz/BZplhNd/g4eNHWK4zXF1cY7x3jNHeIQC4oGnYMk9xnOI73/kuPvvsM1zfUI1z9v1Vhtgy2u02OtbHE0UJyk3mgqcgAKGN9ftJFKWCDCMcP3yEcpPj459/hCrLkCYx4jiCMcQSUGqFosixXM4wn92i1+thvlyRX6TdRitNEAWS9gMFyv+VzcCoIAgQWJnF6yJwY8jAf4GNZ3u6zHBdNhgMfNlKrFsV8kJBlSUuLi4cC53WCtriinSNRpzESDsUdF5Y21sphc16g81qjZO3T9FttYkB5Z515R+79FBfbv9XfbypfdvYzvbxZ2nfV68xrgUpZEI7J1ZVligN1WusFFHopa0Y6+UCG2kQhRIyAMp8BV2uEEY9dNoEDnz/L/0aDo8O8Fu/9ZuYz2dU41JIaKWQZTS51ysLBCuFbFMhzzJkWU7Rm0pjoRQS61hmg5ecKhp5USEIExil0G1R1keUUHZHp9NFmiRI4sQ52NpWMAZhCMAgjGLESerozIfDEcYHB6QfVxXiNCXlw5TW4U0C/+ziApv1CuvVCi/PzvHy7BovX55huVg6R9JsPsN8Prc0rjnm2QZFXrqMBaaNBIhunOsZaq0RxZGLDieDR9poKxK2utKI4wBaCChDwWyARGVAdEuSFBllDY7a6DKApnpy3I/bCiUL7+3JxvV2aocQATN8PW/0vPnX4LhxxgBHYldVTbvi0yptKySszLIy4S9qf/EK7F4MviPFnespWfy33wf+tXeUOGtR7GqD/aURTcRHcyOtjbR7hZTcfp/a+cPX+Y5adqazAUPOum1j9C5I7isv2wJHCI8uabtPhcCiqPBv/9aP8Y3DIf7F9x7h4aCLTU4GYRQKhIHnDtjyC/B8oK/8+99Fmv2x3cak7zuoj+pn0GfNvtw2Zt35nvP1DhC+68ECUMogL+jC55Ml/v7Hz/HR9aLRnvo591Oo3/3sfgOrnnvbxv5dg+JNDhUAkCIE0/bwdVKGzilQ0yHW17g1QDe199mmaN9qu5UR9Wxu/iJEDZwbGwHPThgT1GMVWdpLrbR7NreV7xOE5LBho1tA2IxuAt+jSCKKaZJyBjEAHBwcoCxLDAYDtFqppXoNoTWBnUEQYjQaOhCWs7IhBLqdLsIoBAxQViVKGwHITp0gYGp6ifmc6nALoXB8cmAphYBur4U/+MPfxwff+AaKsoSyANZscovFYgqlKoqcbLWgVIUoChEnRBd0eHjoQK3BYICXL18CAPr9vqupyooYg88MHjPVOoOYDE5w/VytKSt5Mp1gtEeAOYMsnH18eXlJ2calwmg4wnK5dH3JWdNSUu3fly9f4vj4GAD1PwPAVVU5yt3xeIz5fI6qqtBut2GMwe3tLbrdLoFOnQ4KC9pMJhO0Wi0HpjKdd1EUuLq6cnS57Ejp9/v4/PPPsV6vMRgM0O128eMf/xgffvghFgtywM7nc+zv71sKd+Gy8Pv9Pl6/ft0IQGBgf39/32Vqaq1xfn7ujDJjDHq9nntHY4zLSgeA9XqN4+NjV6Naa+0A8IuLCwLCqgrz+RxPnjxBWZZYLpdEuZxlrt7tarXC0dGRk+97e3uO6pzvPZlMMB6PcX5+DiEExuMxpM1659rYnAXMGeWcdQ/AgVGccc7BEzx3FouFa2+v1wMAB1ZyBt9qtXJje3t7i6qqbLZa0JBf/Mxut4vFYuGAsuPjY3S7XecE4mANrSkL9+HDh5jP51gul26tpmnqMv0BuPrMDx48gDYGuY1oHg6HDkzVWuPm5gaDwRDr9coFJHCWLQOjVNdrgCAIXFsYaOOxHw6HKEuicE6SBO+8844DsHlNCSHcGuB3ZR2LAcvhcOgCLgC48eT+4QAXDqxstVouM56zwwlMVe57BpAY5OW5yWuKaa+Bmj2oKApUZQnhyRmeA2z4cSYx6X6Ve16v18N6vW5k4cYx0dmxDFsuly4imtvN64bXHFNdCyFqSnVbs5vf6+rqqpE9ynPMpzNjun2W1aPRyAV+MoU7A2jM9tDtdh1I7rfBz+LnfmDQtNVqufFkhzPbKMYYRxHO/d+xcplleBzHjmGB9W4GsbntvsMxjmIkXpAJADe/fN2aAzM44KTyDHDO+PfX5Xq9doEZ3J8c4ML3cIFdReFo1jmwyWc6yvMck8mk4TRMbJkPp0uwzmjnEctkfi9uy2QycXYKzzsOeuj3+y4oiOc194WvI3HwEdOpc0AEvwPLBXZqcDDAL+04sBlEu5z35AWSEIFEK4wBCzpJIQFloEzpzgtsKR2m+hYWJDcQCKIQvUEXQghk6zXCOEYYhTBaYbNZoapoLvd7fWJ9iSgYabOJEcUROQeDABLCBmrlHigeQUraFwIbBA0YaF3ZzBhPJyPlEUIARN/Kv/v6cm2CbDsid9mD/LtSFdrtlguMKAuDfq+NXreDzz79GK/OXmA6u4UQQCgljAndOGptyMHUSvD07bexf3iIOGkhy3JQeRyDbqcHZTOUy7JEEpNesVguYGDw4MED/Pqv/zr+4T/8h5bGkL4vigpBGCMUAtpoFJWCMQJBnCAKDaqiwPT2Bq+ev8Tk5gbPvvjCyRAjgCCMMN47wPe+96t4+vY76HZ6yO1avbmZ4PDwBB986zvI8xw/+dEPsJrP8PL5J3j0+C10Oy1M5znynOa0kBIaTP1JY7k33nelEq5eX+LkwSmSOEZf9JHlBVZqicO9B1gupvh3/85/gP/x/+hfwdff+wakaGG9mtk4Z8+Qstq3EQLGBekLSLB/IIDWtQwWoi6pMhj0Udq5uLTU/xxstVwuMZlMaH/IS+RFicx+l+cFSkUsAFVFmZBaKeSbjcuq4z2AgmNCytxieyOIIYSBlGwX1gCsD9LWmcl313zD2f0G28s/HOix43AgJ+6Cz+5awHF2GdQ+HhjPIS9qwA2wmeK7nI3eZw64sp/7QKbfPg6w2G7XLmALaNYTV7qyWYa1zS0tkxczZGw90fUCl/jb6hErO8yd9/MBHpKQfK3cIX/84AguoUisZRQU7s8LBtu8tjS6g57FlrOw2aDsRzNaED2xBYZY8PF71GMioI2yVMcMEFnwsVAwcivzSxDYuQ2iQuaWktY4P42xYBDY7rbz3WgODmA/ErFWKPYLaqaq53JYFvT19rKyLGAEl4qw/gQh7gydEEAAW8pshz/DOtEAwJbjsuPvbxaC/Rne2rHjx35V/56VqbMK4fUTJbrAsnkQgygB0qZ+B9z1pUpJ/Hl+cIHhv8F7O90vkBIV34M9MbZvuGa4dSy6vqjnZp1lKoSAETW4G1h7QZcFFDgznoLYqqpAkvi6hrBzV7i+A2htsV7Dc5+DqWD/JvYBkiUEim4lK/F4R5GTH25uGkOMk56fmPubfUsCddatnaZUw1dXDoRVWrvs7/p3678CGpnl/rM1yzOtved7jAIw/opF5bxJPM1sP3n+J3IbNic1zcNtXxwAzjjnjnKydbdfu7EG3FyhzwIhbRmAZqCF75/nbGVixoFbo/y7+5/eqrEnNQD9uw3bKfuZgScU9f5K2bAU6OLawmMiAvcM1illECAKQ6rfbYOHwki6JAg+tywrxEmMi/NzAAIPTk/xV//KX0GeZ8RmY9+BA3wd+A0DI4ipiOnRAykRugAYu3ZkaNc/9Udo9YfGeqTqCKDkIumBqbYMo5N9pLdzIAfvncLUiYVJkiBpJYiSCL/9gx/hP/n7/wQHJ0/QGw5QFBmybI00jrBYzHDx+gLKlHjnvXfRarUwnU7BfnC2tcjGayGKQmT5CjfXl7i+egVVVQiTBI/fegff/PA7KIoSMgygVIko6mK9WODF8y8AAwSC/KhVWeHq6grZH/4h8jyDMZpKlakKlSZNpN3qIitKrNZrlGWOKApQlsrZbUmS4OnTp1BK4ZNPPnFBxv46jaLIBmi2kSQtxwDHOASzPPlljBk0f/f997DJM1ycn6HSCqEdf6UU2tZvV2QZ1osZWu0E0/kC88UC40Ef0cEY/U6P/OCQiKIQzAjK9jzLiNIGZRpjoLKcykrZ4ArSQ2s5xWU9ClO6JBf20fA8ZjuEnqEQxhFkGFCwbFGgNISFOnlr6tJeeZ5btsYNtNLo9/t45+lbTuerdZi7+uaXAebb32/rjF8GaL/pu22s7svacR9+8mexv78yMA4r2wmo1q52HFO3hlHo6q8Mh0OsVjPMZ1MIYRBIAxNIGLVEISUQEwXX6aMj/Mv/6r+E1WqFJE0hIHH+8hWKnGgVr6+vsVqtcHl56Sb9crGE1gLtNtGRhwHVuvwvyj8AKiBttfA//Z/9zwERuCwBBoUMgDAI8fDxIyRxglF/gDhNKALDOtWmkykm0wkKpXF7c4PVao1PP3+B2exPUZYl5os5bm9uKTtsvUJeWWDcLgai6VBWUZVUl9wZ781saVJcAhR24wdI4c83JaRdaALSKtoRwkhYWnTK2uQNG6CaFqSMBygr7UAOzvInyobStoMnC4HpPqjLm4k/idhpbYyBCEIS7Fb5cQAhYOtj0GYB1PQ/LHC4PUJId08WZMrn2rLQo2+A+c6ObQCQ3qUJJm9/7xRCLzJm+3o+rxF5uHV//37+c4zVaX3j0jc2WWnka9mgbC76u++zS8DcJx58I5OFrU/56UcfNYHfeuPgc/0I2l3vzsbDtrDivlXG4McXE/zscoqvHQzwt77+FEe9FvLCIBdwdci5Kazw0T3QVPxEU5k0W4phs+fs955SyUC275LhUOy6/buVTT8r3W8jt6vRCNTjU5QGWhPF/B+fXeMfffoKN+vc1U/0+5av8w9/3Lc3LO4jdmjUDsSmxRHIpgLsK/J8reRkb3u93wcCgDECgXXckVJKz1OWrsgYjUDWUXFlWRLFk11rWtP3egs44RrONM/ICGEDpygKyAYARiMXWBp3paqtyGRyWlRVhVY7IYaQOCaFV1Dmd7fbs4E5CkIadDtdPHr0CA8fPkSr3UISJ045ODgckyEsgE63i8FggDzLiIrWwGURLhYLJEnqMvkYDASYiplkCdE7rjC9mKDT6aLVakHbqECmbb+6vrZRjxGSNMR6laPTbWE+n1pAYYX9/T08efIIQgL9ftdS92a25mvkambP51ObtUmZ6efnr9Ht9p2i1ciAimNXgyaOY5dZybTiDC4wyLlYLFwGj1/nlcETBgvYsQjAyfkPPvgAURChLEpH381Zere3ty5DcG+PMkwnkwl6vZ5r994eZQsxaL9er4nC3cq1Bw8eOKCTlVJ2pAohcH19jSRJkKaUFcqZv/6+sbQ1e0ejkZOhy+USJycnjqKYM5mXyyUGg4ED16fTqaNePjg4cO2LvfrzDJow1bWURPPOY79cLl32MANObCgwzbqfNccgIAPzANErzedzly1qDGVXjsdjpGnqaPAZqIrj2AFqUUTU/peXlwiCAOPx2O1Vg8EADBoJIbBcLtFqtTCZTFxEtF/jmdcyQAA8g7G9Xg/T6dQBSkVR4PT0FJeXlwAIeGbAkTM1OXOT5xVTpjIFM2eEjUYjDAYDB7DxOA8sDT3XMGeAl8FLIShwjKm4WW9h45bB7F6vh6urK4zHY8xmMzx69KiWc0HoAEwG1zkAIwgCvH79GmEY4uDgwIGhXOdYa23LARAjhZQS+/v7uL29dfOeKZ5ZznKNdaZ/TpIEygaWvn79GmmauoCI+XzuZO90Om2AyVprN49msxlGoxHa7TYuLi5xe3uLhw8fOkAagKsXz7TgDHLyOuU1EAQBwjRAHEWuXZxBy6wMHGBRFAXSlGi91uu1C9bg4ALuI+5rZnHgjOuiKHB7e+vmqBACt7e3zqDk/1k2M9g+GAzw8OHD2nisSidbtCbjcbVauVIBvV6vsdY4M5wZM4Da2cDZ6pvNxq09ptXm4GKlFNI0dUESy+XS3VsI4d6dAyg4o55o0CKXgc7vxrThLG+U0c4O4vVujKntIkPZ61mWYTgcot1uOzAYgKs3z0EiHPDk04+z8c4yifd+P9MosnOA1ypnmnMfcWAWB3KWZYnLy0vn4PIBCwasWW9tGM8wbk3xvkAByFnDecd7F5/DcsYHxbmNrE/z3sm/d7tdZ/OxXPJLX5DuETaYQH6Zo66L3LQTBCxjmAVgNAw51gxQcea1oX/oeglICQgDXWlIAFxLVAiBtN1Cq5XCVBXKIkNZhIiiADKgzF6xmEMYDa1KpCnVki91ijAPnUMwimg/CLSsHUFl6YIqtQ0qJCpxgdAyWUshYGvYNPVjaw9qv64pPIerA1K2bDrRwEqszhqi1UoQBAJaGcRRgIP9EebzOV6fn2F6e4uyoNp7ABAFVH+dwNQCYRTh7adPcXB0jDhOKHNRCJRFhSAIEUcCadpC2mkju52Q3yEMXRD/L37xC/y1v/bX8LX3v4azVy+R5Rna7Y61UjQgAsqGByADyiSXpsCzTz/DqxcvML25hioKLGdTVFojDCMEYQSjFC7Pn+N31ytMp7d4+733cXB8irIUMEojL3KM9/bwzrvv4ez5Z5hM57i8fIn+sIfBcB+ddhuzxRKBjMifEFJud2WI/raVphgOR5hOp1iuV7i5ucF4vIdIhjAhrcvp8hYnj5/g/Pxn+Ce/+UOUhcH3Pvw2ylyi3KoffMfRZR3owgZVGOtD8X3tvk8hDENEYYw4StDt9Oz6LKncjw1gXK9WWK2pLMlivsRqtUZmdY6iKN1PEpEsU9qC5dqgssGnzi4SAiIqAWd7MRBAWe71srzfCbftePSTBHadQz9MIV77iZr2O11D9p71CXmPp+Dlum3bQe98O87kZ/segsGtGswyVo5As80pLTDYtE+FvdyDhHb2hZ8RykCD9UCA7ELAKA0mDea1TACtrUvd6Bf6zrDfwpeV9CD3vgxuOZlhbXPlaP7r1rusdBuUDcDVKIYwMLbvtCEwRRvB3ed8B0zry80QHvey73/hMefnMfBtQPKR1wi3iwK67cOMBeJswDqDWULUwJ5udhY925uHBgZalQjtnJJWTzBCkB8y8OprCzh6W1XRWEghie0N8NZxXUfaD8LjOWCiEElKZWO4L8KAauxqpV2buYa91kypy3/TfGEfhTYGpS2BEcg6K9L3XXG/G7CPRTtGOKZ85vf0KcaNrcfNpZBsN4IZ8lwGMvtkDM0LBhql5KAHy0wqua8qGktL5wxjILT1jbC8oI3elYJQVQVezs4HZIwtjwkL2hEAyUwDUtjsaymo9Il9v8BmZFe5QmyZXnh8nH+ZIH0opaEqDaF9hj5h1x37AWt/GAdXUd/UyRTbPlp/nOofWpzG8Pl1+QCAZcddRkttaiCeZTXTeFOX28UpAiD0qfHrdxCggBQH5PpnSU7OsOBzWJc04nHdBnLDMKRyLlI6O0+6IEEC83iNFta34gPO3D/8DC5VyNey716iCSxL+/5Uz5rKX3D9amcj2XkhhLDnC6dzOvpzB5DXPkX2H9ZtgTvP9y06r+6Wr5GZGXksic327hyR3K/e2hTwyoVK/ty4oFe+J/dZttng/OIC69UKWbbBkydPsFqtUBQ5hCCwtSgLV6ZHG011twM797f3OZLgXmcAAQAASURBVME+ZgkpAkt/Lu4EgsnABuLCQMi6njPPS21lt5vPQa3ru7HXGtBwNoXSwPnZFf7uf/wPELf6GIyGCCKJLFvBKCCKI3x+/jGiUOLo4BTHx8dYrJbONqc5bu02rYkhUhgsVjNMbi+gLV708OFTPH36LsZ7B1hnGc1VLQCjoaoKZVFAACiqCsvVCpfiEov1CurZC0gJrNdLlGWOJInR63URRgGSdopSaRgJ58/xWbv6/T5GozE++cUnyPPC2ataE2tWEiYuy5++I7+wgaFAXm+tCMBS/1MwXakVVBjhyVtPobTCbHKLqirRShIKmLF2aVZkWK3naK3bWCxXCATQ67YRRxFSptFXQFnmyDPVAMYd2O0FSJtKuZJOlceQ5AfHa62hUH9ey8ymzqiUQqUrJNa2NHZ9RMy4bICiKlHkmbN/Ier13ul08ODkgfN3bR9vAsV3YUL+ebswtPvwrDc996t8/mXnbOMrXxUc/+rAuKRIEG03yrJSViEjgTrc20cQh9isV1hucvT7Y/T7Q8ynt5je3iKKBUxQYj67RZTEyMsS3X4PQkh0+13AkNJ0+ugB8oyoIcMohgApDIBAVZWgut8SsAq5KglE/1//v/+3QAVEcYz3P/gQRVFz7Od5juvrawcA/OSjT3F9dYlsvYbW5DSezSiLm5w+JYqyQlbQxsROLHa2V1VJm1kQQkM65YqEfQCtayAO8EE9qpUE+PWKBGyVI8Aq1DKIQE4MGwMsLdio6R6+QeEfRtcGwbZANbZu2TbYCzhZv3uCeBs9LUpBJYusocgKCIPDlVEIQnofH5yn57CCzBsCKZbbwCxFS1og0xkKzQm963MWnEz7uK14bS/oL1ss/qJ6E3BZL3jhvvMNAv+ZPni9fR+KOLt/LFgV3N3uug/ZabjrvXwgePvz7b66r532gvsb6t2z0sCfXkzw0eUMj4ZtpEGAf+3Dd9AuQrTjAEICSSScwXP3ndnI8/6Gv6Zci73fRON/H0j3Rs06A3Yb7vyUO0Axmo42//7GGGSFQVUZ3G5y/Ac//hSvlxmmWWHngL3P1tzZ/sz/btfnrFBxJPB917OhDLDhtrsuFh9+lhb5foR1TPt1sxjADt1644hHAGiliTPghBCILeCcRLWRJSOJMKDaKkkcUq0XIWBA0edpEiGMIpRFgSSJ0e31CHROUqS2tjBlfsb4/q/9GgIZ4PziHKPRCO+99xZubm7w8MFDVIqMucFggE6n48Di5WqB9YroesuqhIDAcrnAcDhCpSp0uy2UFWX9qUohjSPAUHZsmqSQ0mA2nSDLcqdQrlcEEq5XS0trrl1mbLuVUoZpFEGrCjBknBaqhAyoljVgMJ/P0O/3qd+S2DnsGcBjwPXy8tLVh07iGCcnJ7i6usJsNkMURbaGNI3VbDZDEAQOJGNq7Far5ajUGdRmamcpJW5vb6G1dpmRABqZdZyRDMCBq3mZu2zXOI6xt7eHLMvw+PFjCn5LEgx6A0xuJ1gsFvje976HL774wgGyvA+3Wi0HejI186efftqgL3769Cl+8YtfuPZWVYWXL18ijmMcHBzgxatXAODqNI9GIwfIMnh+fHzs+pfriAc20I6zUz/77DNHjc1gWavVQrfbdWtiOBwiDEO8ss98/Pgxbm9vndJ++fq1A7qvr69xeHiI6XTqQCAG6qfTqaNYHg6H6Pf7Lmufwc3Dw0Pc3NxACIHZbIbVauWyzhm04yzqLMsc3TSz1fC7coADB4r5lMs8bgzMCSEcSHVyckLz3I45g/WcKc1AMgNpPOd4HjIoyFn+TPfrZwRzMBeDr0wfzWVvODhACOGCJ9i4YNCOQcQ8z20mdumccQzmAXD9ywES8/ncAWNSSsxmMwghkNh37na72N/fd2A0BwWkacsFMXAGLM8PBooZ3Pd10iAIMBgMHJX/ZHKLKAodeMwgN883rbUrQTCfzzEYDDCfz3F2dobxeIyjoyP3LA5yaLfbri0ckJja+sQ8/lISJfj+/r4L1hgOBzg6OsJms3FsEzwODEh3u13MZjMH0vNYMYjN+i7LHK61zGPAgUQcdMBgpZTSZeWzI2Cz2WAymbg68svlss6YNFT6IMsyF9zDNdAZ8PTllh9UwmPPY871pDnamwNUuN84EIrBVA528fVEBm44k3u5XGI2m7la2Szz/LnP2fzMjMBU/ix/fAezEAJlWSGyNesYxOXveF63ux2UFkjnvvbnZhgEaNlMaZYXo9HIBbhwljjXgue2+s/y5w/r3rzued3xvGOZzMA1B3vULAWlo1Hnvua/fVDMDwxq2DQQzinGIDzLPn9++rq5D5izs4IDfdjmi+MY8/nc7cNMmc8OTx4/Pzqfg8Y4qGmXzfZnOZrBgBZ4McJlNvHhYC8PiGHGHgIuwCgR1fu0nxsYyFCi0+2g2+1gcbtAUWQIixBxHCGKQxgBZNka5BynfSmOYihjKOMsCBAGIeKYZFjoHK1sl1YoixJZnFH98yBwGRcCsNk/Qe34Dbh0V+0gZwCLnJIOanLAF6uqzv4ztfOWxjuAhEFVZCiLAjAKrTTGi+e3mExusdmsYbRCGDTp7znDrz8c4OT0AdqdDpQiuuEgCGAU2QGBJH2r0+tisaBSLoF9NwEKXLu+usZ7776L9WqJ69sbVKq081Z7dgI536M4wtXZOV6+eIHb62tAKaxXKwRSYDgYo9cfIE5TZHmGxewSi/kNPv3FR4Akavx2h9g31ps14iTG8ckp3nn7ffzBH/4+NusZrq7OEUYxhqMjrFYFCCfTjv6cnbzaGLTbHahKoShLzGYztNsdqnEfxihVhU25QDfoIG0d4NPPLtCKf4y9YQ8Pj04wX2d2nm471bbseDSBNNiZy/Oes4CUDoj+PAgQMbBt95Vup0vyO9u4bPHVao31ao3Vmv7eZBmyTY7MlqAoyxJlVRGjU1k6IImc45x9U5GD3APPfDusfp+6nIR/NO09mr9v8m18mc/C33ME70FuPaNxLv9f6aajle4DB4xzf4sdbXMGsG2jETXLF99T+OfZz5So/3bnm0Y+JD1L3mV8sD3asLmF9UFp6Ma70n2pxi39U8s9H9Spm+j7Buw3d1j5eEy2HcbsBL4b4N70D6DxnXujLT/ALt+csH1t+IECCGVAbbV2NgAXPGJAwG0gpQ0mACUsWTBWqGYZECEEoDXRvpLAhDEayhCbTBzH1rdB+2IaxXXQmdEQgXD2Cwdc055ISUEcNBZYOe4HVzIQzYF7rTRBacueQAjEUQQI4fZRKQXCgGwmpbWtv2wBLKUA1LXHtTGolG74bnlc3Phzv9q9kPduf73U+lzoxp+zjX0wFsaCebCB4HZeccYtJTnVuoaj6Q5DAiMBy2ChKPtVMlUvJVmFUUTnKAWjiQI5svaXcsC4gAxoXrjs1iCwADeczSMELQKqbcs0+IED34teiTiKnW1AZS6MA225D4yB629/TlM/2L5jEJR1K6VqwFjUPmRsy0qWAY21RKNHSVm8nprAcfMwbv47cNoCqw7ctWPWeDavDZ4DtsSGL899XxlA45vEkQ1ArUsQcQZ0IAMEIQHjSRhYH7mnf9r7OLYqo1FWhTfPAzePjB0LnvvchkBSEhxgyah5XzKG6tlbIJ1BeGH3MB/gl3bs3Lu6teDJRyFc23fJrO2/t8/ZlnvSJrb4/lFvSoG3Didn7XeU/Qs3x7ypc+fZLAPC/X2kaYrz83O8ePEcxydHiKIQ2tZup2AKDo6hR0n486X5HnyOQGhZkJqlFPz5wsy6glkVuI8Ege6CdXIpYQSoVK/XT8bdh+bXxesr/Jc/+EO8PLvCycN3EEYBKlXCaIM4SHF7c4M8X+Dw5AGOjo9dYLTw9jf2KSRJAikCKJ0hz9dYr2eoyhxhGOHp03dwfHSKMIyxyZcw0G4+BEGA2LLNAcDGJgRlRY5CAQAFGIZRgF6vi16/iyiJUGqFVreDfp/YKCeTCQDyA/T7fQwHQ6hK4cWLl/U8Bu1vSmm04oR0zyR1fh3WCzkYzp+NFDBRT6q8KtHpdnF0dAQBg+nkFkobRHGMIJBQWqMocmTZmnTnbI3A7UUaqipRlApFqVGVVGMegGVzpj1NK13/bgO3iFlaUekIrVFpTZn0laLAKENBw6wPaBukyWwzPJ+1IdytrEooq5sqQxT7nCSS57kNnKLyIolNngCAVtpyvtPtuboL79oGuN3c3XHO9u+7/vbn3/Y5XwUEf9NxH0D+Z7nvVwbGu4MBZWtb6paqqsCVEOI4Rrvbw2y1wDovMR6PEcQt6LLAePwA+QbI8w2qvMBkeovTx48w2jtCpane1KYsUWY5qqLCdLbAYrnAarmyaf9rXN9cI45j9Ht9lJXGOtdYLVeuluFsNsM6zAABrNcb/D/+/b+LbFOgLAuwEVYUOX7xi08wnU4RxRHyzdpmedd0Fay0hTZCXIgIGgR0wda/MSKClhLKGKIrEgJcg5d0WA1jatIq4awEOsig86NAJLgmEgs9ctw0+7/O6ub6aroxoSXgnJACrJCw0mZgFCNk9hwhGlTlACAMR01WzrHETkdWBCy7kruHv6D4f1WU4Boh7GwCvJorVnHTSrsAAjbKaM8lqjK5Y8HyfXhBMxDODgz+zPXE1oLetXh3GbCNvt+xsfv3I6OpqZjxRuyu3TKqpL8xutY2ax3dUTTQBHHZycDawfb52xkq20b2ru92HV8mVO4z7PmgiDjgiyllK/1v/vEfoROFeGfcw9947xEOOimSkCisw4CDSraMVTj9uQZ73fPvAuVNM3o3+H2nP7ecbMb7zH994Z3Pz8kLjU2hMdnk+I9+8jk+upw6cPiOQ3Nr7jSNi+Z5vmLlrzOq8+3dd8f4Q9QGBLfjvjngf+/fkyhDyeiUUgCCnENRxDKPnkHMFsrJu4B1aGiEASCNggwlel2qr5vlOcbjEfr9AYbDIZSucHRygrIoMByN8M7b7+CTT36B4XCEDz/8EAYGoSDnO4MjnMHHGehSShTFBoeHI2htsL+/hzRJcX5xgc8//wX29/fRaqUWsEuRZStkm8xmtm6wXgVIWykmtzc4Ojqkmrn9AS4uLkj50gbLxQJxHGPQHyAMVpQxaJWcly9eYDgcUsmPzQYnx8eUYaYUlJVPUlCUNjv+p7OpqznMIA+DA0EQ4Pj4BNpGO/7oT36MzSbD22+/hQ+/9W2XrTi5ucZgMGrMDwJycgsuE2DZ6XRgDFGOl2WJ0WhkZTEBD6PRyNXBZkrfLMtwenpK2fitFsbjsQOaOUOz3W5TPWUZYDAcYDAYuIxcrqv8ta99jaIwN0QNPhwOMZvNHO0019E+Pj52IA3Xae71ejg9PXWZzHt7e/j888/x+eef48mTJ24OcBY6BTRUyAuipR6Pxw3wlAPkut0u3nvvPfzxH/8xXrx4gfF47N6PAxR4XjEtd7/fdwCNz3gCAEdHR6REW3prrZlme+AoSPl+TAXPYNLV1RWEEA26X64bDdR73vX1tWvPYrEgQztJXCYng/dSUv0lBi+ZZpqZd9KUysQwaM11u0ejEW5ublwAAgNaXJedwUgG9eM4xrvvvutkWJZlbvwY3Lu4uECn00GSJDg5OXHA8XK5dO8vhHBU1T6jgdZE07+/v+8iihnYY0cPU1czoMvjwwAXA2jOaaY1ZrOZA6yllI4SHoCLojXGuPE+ODyE0tpli/OY8BpM09T2I2XLX19fO/pwlk+cZc7Ot/39fZyfn7v67qxr8VzmrHelqB47ywSmoWfgbm9vD4eHh3j16lUD2Gfgt9VqOTYIljXn5+euvjpntBdF4TLPr66uYIzAckkBLUzH3+v1XA15Dm6QUjoq226364IplVKIghocZmYFKaWjymeQlecwg9ZCCBwdHbl1w3OanbBcM9sYg26362p/G2Pc+j04OMBoRJmgnU4H8/nczX0ppQucAOrMaCOFkz0cWKu1du/Nme23t7cuQ5iZLvxs4sFg4IBfdlBuZ1SzjsgBJtz/vvO43+/j+vraZSJzkAPLHl+mOFvA6tyUoQBX5oDtJQZ7lVLYrNeoitIB69Pp1AUH8frzAX5fF+H163/H9+H9Qwhyhm82G7fO/WCd5XLpgml4/vNa4rXIdeW479lh4APnTmsRcLKAs/F9QJ31LQ54mE6nFEBg68hHUeT2X6aPZznDQSgczMPPYPkzGAwcsM5y02c8+GUNfiE8oJD/s2W1eB1SfUJjsxn5OkEEScIpZQ5oCaRsOKGDMMBg0Md4b4z5zRRFWSAsSssQBFSa9tWyqlCW5HTptjswZeUCIIIgRFmEKJOa3pJqpQrAEGAuJGUKRVGEOIqdDRxHMZI4RhwRPWZoQQLOshOSaOD9bD56JQucs5/dGsAGFucy9kdSNlVZlFitlihKBnMkrq+vMF8sSKbbDmYbSll63LTVwpOnb2G8v09Zc8pYoB0QkUBl6SDjNEEXfbQ7cyzmRKHO4I6UEj/76c/wN//7fxMnp6fY5JkrX+NAFOssJ+ejwBfPnmFycwNojU6njZvL12i32nj76ds4Pn2AKElweX2J2W2A89fXuL6+BKREt9fDt7/7q1gsFfI8QxgG6A8H+Oa3voOffvQTbDZLXF+dIUlb2BsfodvpYbVZEuBm1w0EAdBFWSKNE/T6A1RG4/zsDPPZDONxjCiOISRQmRyT+S3Ge6e4PP8MP/noU6SxwL/+L/8riKOQ7H7Ovt3KwBKogcraTuF5a9wcB2xWrAXQQkEAbc3cUge1GN2D9jJy8rzAcrXBZrPGZpNhvc6QZRvcTiZEs15yMkWBIs9RlHau2yD/0mb6VKqC1hWRkps6OcJOMgjYDHJRW7LMegDU2XzNrMMmmM3z3R2mPsNzmbu1XJqaVpynO6/3GvwRqHQNjMIFnADwabKNAYxfag/uXOH5NSx8DgaOhaCAHd/3QfY/Z2fXdrMfBMJt1Jail3W1huMU3jzw+pTX1k4r3zSZ0u56OCzIwz3KsnHLub6jV50drU3zrhKiDk6qRe7Ws4XzE7qx3uF/EYJxes+f4p0mBRywxH4gI2wGsB0XGUiEQWiDdwAdMDVrDSiyzgYeF5TopG0kSQwYBuQ0WpaRpixLaKMgA+FKUvglfoKA6F0rG0QoA+kAW1+PYz2m3W4jCgNUln1GCGJuMTAoixIQxPYZxRHZ01ZvZz2KgGjYbFjyUXImNMByxfo5PF8tpA/2si1XzzP27ZG/hejDjQ2W4ftqzdijV4OYM8Rtdi6DxAxMUr1pjTCKKLFAgIKsjGUACQLAaAqkB2xAvrRyR7tgvKqqUDEwzpTihkoMCEGBBGFkSxUpRQEKgpISqqq0a43rHhPgHdjAixq0gwuuYD+mgEAQRnf8v0IIl5UMe10dDFDL8CCQDYBbBgyWWx3GmBr0hHBspDBe8gYJPjsHglr+CAEIDb+cBet/JHdrtgHOQBYC7n71u1h/mKREPG4LhAeMg9mECqRxjCgK3f0BLmdj+9H+RHacankItw+6JDJoGGhbStV+btehsiVQ6b5w81AKGlv2+bOY0FrDyC1ZusMXTrwXom4TPPzAc7oagBL4GoFr1Dcsi2n+0KeEGXGQQ7PNtEfrO6JbeP5y3ltcKQq7h+gt/ILXrJAhtEvIq2VgVVUIpMT+3j6MMfi9H/wOnn/xDG+99RaSJEZZlKgU2dUwbKtZWnNDCYpSyEaQBGXmk3xw7+z0NlmPu7+e6sjUut/t3ixtEISGLWOllaP+19ogCUlezBcL/PSjj/GP/vHvoDfYw9HREWbzW1RlTjIGAZ5/8QKDQQsnJ8foD4fOLyWCwCujS33d6XSQbzKoKkeer5FtlijLAqO9Y7z9zrsY7e2RbQcDpY2j5k9bLYz39hAlZA+VqoLIbDCNID1bSIHh3gH2D/YwGPYRRBGyPMPjt57g6PgInU7H+htIBo/HY3StD4X9f8b1mHD+lDRtIYpiiIDkv89SIu1aqm3umjUkkBJlVSEMJPYOD2CEQaVKLGZzdNIEsD4Y0gNJP8w2GwRSYJMRm1wkDDZZgbxQMKrGQmlMad0yIE6MJxpKECjO4LhSGqWu64jzuqksy6K/RtgPxOvIgAKbNiXtjVoplGWF0vo2F4sFiKktRCttodvrIklTJHbPkDIgYL0sG3LzTTbqNg7257FnGziKaH5ef7eNzPzZj1/W1v7KwHgYJ+j0pVOyhADKqoIAUdVWxqA7GKA3GEKCKAaMiaCVQdIe4k/+5CP83m//JvJsg8H+GO3+AEpILJYrLGYLLGcLbNYZ5qsN8oKikUtLZVWpCnt7+3j77bdwdPwQy4wmgRBrrNcrAALqoQFCwBiBy9sNinzjMjBUVaEyIcK0Cy3XWK4LABIaAYQM7cTSkFZBKZQGOBJWkGAPAqrbDQOiLdIaxigy6MFR+6T+uyh3Y5V5b4yMAIQMEYcReAII1IpnpS1tkEUBWYQ6ZQH1RuHUdWMgjPaAcRYh2jM87cZqV1VDBxfC3a/hbLAn1ZGDVGdGiKCh6LDzgBWPMAxAwfV3I8qcsYsAQRQ6hdwHtum5ym1O/I6+gGAnmv8dt4HvQQp23Q6+fltR84XCLuPEV679Z/rt3QZifWW7HpPm8/zrtfbrC+3OkgdsdsfOtnrP8u69/T8/axcw2gBFRd2WNx3+vbcVrW1FrP4dWBYV/uRigh+/niCSEr/+cB8fHI7xtYMhAKpFHoWkvBoQNTotKC8S1fXXDiHbMGCpf7bPNdt/m/pc/ztuuvUjWJouchIorfHp9QJ/fHaN3395hUIbJzecUb21nrb7m5X27X51SrIxdxwFQoRglo377lHXAq+f7WdG8Rj55wRBUM9lAbe5aq0QxwG0UUiSjgVmCEjutvrIsxxHR0fUb9rg8PAAX//61x340e91UBR0zuHhIdFFtzsQUmA8GuPFy+fo9rsuQ1AIgYcPLdC4mSNNElQGEKgQxxJluUa320ZZbiAEsNms0ev1MJleotNuY73eYDKhLOr9/X2cHO9hsVzg8vIM49EIJyenyLMN+n3KPmy3EswXU6zXlLE0nUyRJAmmkymyTYZevw9VKbRbbXS6XWSbHEeHR3j+/Dmeff4MR0dHaLfa0EpjPpujLCvMppTBTcAJORSM1uj1+lguFpBhgF6XKKc77Q5ubm5dpuh0MkUUx0iTLpQyWK+XODw8BdHIx3j16gJhGEHAYDAYYbFYuCzEbreLToeyTcuywvX1rQN8B4OBmydcN5czrqlWKNWZHo/HmE5tH0ynDkw8OzvDcDhsgAKcGT3uj1HpytEcM5ChFNXBTpIEy/kSUUi0vvP5HKPRyNHSlmWJi4sLGGNc7WmmPp9MJtBa4/T01O0Xjx49wrNnzzAej7G/v++ywJkq+ej42AGvm80G19fX2N/fd0CXEAKvXr1yteAZEGFQhoEpzn5er9euTs/+/j7CMHRKLdMXp2nq6mqfnJw48JBBzeFwiFarhdlsBmOMey6DvcYYHB0duecwKDgYDNz9hRDo9XoYjUbI89xRkPtA6v7+vqMQp+wM4wAazqjkKF3Oys+yDM+ePYMxBqvVCgcHB66OOQO8nBmSJAkGgwE2mw2m0ylmsxkWi4WjkB8MBlhYkKHT6bi+ur29JYdNGLqavsYYB0BxVjHTZDGwu1gswLW2WU7leY44jl0Gar/fd2AmZzbv7++7rG+Ooj08PES73XZAHQd3MKj56NEjLJdLLBYLl41fKYWlzXoviqJBeU0A9BrHxyeYTCYu85Ypy4IgwP7+vsv050xhrpPM8j1NU8QxGe1lWeLx48fOAVgUhaOIj+MYNzc3LtiFabDffffdBu0WZ1bz+q6qygHiHCSzXpPc5NrKWmsHdGpd05wxu0CSJK5mPO8lDNozGM911auqQhqTYzVJElfqgMFQBvDTNHVMArzO0jR1gLafqc39zTLAL6nADloG8pnlgYFjpgn39UE/EzuOYyCg8/x35nnImeJRFGFvbw+z2ayRgcxZ051OBxcXF9jb22tk5DPlOAPD/BnL0Far5TLnsyxDkiQuCIVrWtd7u8321zXQLoRoZNAzeM3yidcOByYIIWC0Rr/bcwECzBDC/cQ/nC0uhGhk/e/t7bmgCB98Xi6Xrr8YLGeZcXNz48ByDt5gMIvp75n5hGu/8zP9gJAsy9y1TtszcONlrIODbQLumyAIXMASz2kG1Vg2+RneHGXP/bNardwa8UsmcHANB5Hx/GHWBh73P+9hanOOnJO6Wf6odiYbULkt1hXv6qASBkIYQGhbR9ZAKAo+7Lf6ePe9d3Fze4P5YgOtDeKYavldvL6y9awps7Yocmw2a8g4RhxFCIPIOdpbNrAgkJQxFYYRAaw2mIipRcMwBAJyLhI9dohYhk5GRGGAKJSI7PlRHFj7WTp7lcmQGCBr6M9BRTUgRQRdaGRaYZPnuL2dwZgKnW4LlRG4eH1F89auZw4YyssSeVGhPxjh7ffexbe+/V27bwFRFCMMTP1OtjSORIg4baPbH2CzWkMaAhqFoCCaz54/x8eff4HHT9+BECF+//d/HyoBZBgCoBJq1Gch1osVbi7OMeh2IS3ryiov8eDgBI/eeQ+PHz8FILDclFhObjDo7WG1KjG5vsUvPvo53nvva4jtmtlsNoiiBKdvfR3vf/Bt/OmPfg/VZoXZ65d4nST42jd/FR9/PkMpgMQIBIomUCVDFJrs9qSdYi+Oka3WuL26QBgHGAyGSJMUcTjA1XSBm9UU/eOHWEyu8Z/+f/8I3e4x/o3/4X8Xs+UM66KCMhJGxFCmQhwqEE2phqkAyACBs9WFG08/4E0YjUAQwKKFhJaBDUpRTjfVWqPSAUQEhHbedwEMdZOqUmsql8OlXpjtIc8yx0DDgFeCAJPJFBeXly6IKwhjaA0oz+bUunLzcZtNpJ6bAhBMEl7PX98f0QCPvXP48G3C7UzgXfYml88TFrS471x6qL4TLO23gQI4mjS4u9oIAFLY+tRo2qD+30IIlzHW7/fRarcoU9bzRbCfDKaub77th6L+r/u8ztjabXdT9nnzu52ZVPZEd92WX6X+CbY+p77eHgc/meLOs5xvCmAfVmN8/DEQRA3tt2vX+bx2ahC8fg7rVHxP3o85QxUgMGR7Dm/PjV1zTguq2y0haA8Qd8feGAMFYrUThAA2EmoagX9b/bT9PPuH+3zbV/dl7d2ex9t+re3nOoDPEHi27Xe7795+QoQBIDhQwQZMBEIglLVuE0URjIDb8zjTnsBMH3S+W0MaABCi0YfcT74uz7WMt+fS9juxzumPo98f2/4r38+0a8x8n6T/jG0fb7CVgHTfsS1zt58L1+t3fZ3bshreexhjYFTTz0q6rGWOgIHRVE6Vx2O7XY0W3OcbBGVI3+d/dTJvqy/vO7Zlxn2Hq3e91Xfb7ZXSXyPbJ6H2hsu76/DucXde7D5/+5nb72vfsaqZigC44DIDgcqW8Ts+OMR3v/Vt/PCHP8T+aA+9fh9RGAJu7lLAuAAQBNQv9d4QwGeJedM6sRsLpGXdNKAgCz+xr5aB3t5gJITQ0NBUl1xIVCXQ6w8AGPznf/8/w3/5e3+EHCm++cHXsFmtkVc5gfHa4OXLZ1hnG/zGb/wGkjRFnnH5KirVYIyAtvsi+4eKYg2hCuSrDa5fXwOQ+Ob3voOn77+NdifFermENBqBISaPQhnEnQ7eev99PHj7KS5fvEQEoCoyZOsFKkP3fvz0bZyePsR4bx9pq4PL2wlacQ/vvPV1HB+dOn1tsZjh4PAYozExFn708c8RxhFKpUGlniioJUkStNIO6QaSyjspY0t1VgYBmuuZxsLAcdsIwBiJvKyQpjHG+4cIwgifffopylIhFICuFIqywrKo0C1LlJs5lAAW0xhX7QRVOURV1AmuBjULHq8v7e1hAKB0XXaS16H/4+a20ne+5/dhP05ZVsisH4oSAupSImEYYjQaodVqObtTCIHK2LrlVQkpFEpVQkEBoi6V05i796xJXy5vH9s60Las58/oh3pu172aiaYWtNzxrO22bf/ut/dN7d4+vjIwvpivUFYKBgJa06acZ2QYr1drbPIc6zzHcrlCnmXYrDaYTSa4fn2Ji7MLvHzxAvl6SdEaWkFEEYpKIQip5ijX2ym1gYsnlgG0DqG1xNX1Aqv1Jzh7vcTJo7dttLpGWRrkeQbzgNqptMb17RwwhaV4o3q489kccdrGw8dP8OzZM+jKacOkZGiKYw3DAGEk3VAYAEJrqleLGsDm+GABjs7XLoKJs8C1ZkDPF5aEtgWW2lzriqJ3tKJIRm0g3CIhgNzAOMoXY0xjO9A2osxo7X3uRf0Knqxwyqmpm+EicQSIgk9IgTgiRxAL7bpenyEwO4gpClEbRxsEGJsVIAFBfeRH/jUjyagl3F/GeJFyxl84LBiUy253QQNgajtYsNIDoAVH8mpLg8L9Ufcb1y7jBcprrPG7PZezE2Cjwt0YiDrS12hv4fshd/4Gyfc0pkGlYoy9l6FNkRZvHWFWN5zGkTKRt4Fx2jRqY0p4l9b9zN/fVSrefNSGurnTroYxYjvQv/ubhJE2QK40fvP5FX7zi0uEUmCYRvhLjw7x3dM97LVbkBIIpHMduGuDwAZzuiAUO7/8Z1swve4luHkIez47l/ksngMCQFXZyEQBaAW8XmT40fk1AIE/OLvB5WqD0tbAorkgHSUV1Xwj5TXw5jeMZ1QKgcBGPFP7aNwcFZOoHUJhGLr5FAQhuBqDkES7JW2tb3YG8/zmXtNag4IYDbRVtpiGhuqjUn+cBxIKZIj96q9+B6cnJ+gPBhgO+4hiojxL0hhpQtlwe6MDvHzxAg8ePEQQSAJ+l0sEAWVw7u3tQykCrM7OzvDixRcYDgbIiw163R4qVUBKYL1aoJWOkW0I0Cuh0e91XAbYarnEdLoiCuH+AFoTLWdZlWi32phOS5RFgc7BgZPHSRwDIMP/YH8PYRAiSVLnWBHCZrdBYDQcY7GYA0JSJpAIkMQpRsMxyUIRIE1auL66wXi0R/tgpajOYhRjuVhhOOyhKkvkeYFOu0t9kOeAAfIsR5qkKLICy8US/WEfqtKIowTL5RrCCOyP97FcLrE33kd/MMB0MoUQAYx1aPS6XeRFjuFgaJWwunbveDzG+fm5M0rZic+ZjaxkcZafEERFzXTDXN8njmO8fv3aOUvYSXJ0dISLiwuUZekyrOfzOa6vr5GmKdGWb9YuE5cB3UpVMNpYQ0O4jDs27pliO4oiDIdDCCEctTcAB9qxI5KBvVar5WpHc/YnG+wMurYZeI5jAhaXSwdkhWGI6+trjMdjnJ2d4fDwEGsLshpjMJ/NEMUxNus1ZBCgZWm+BYimXAqBkMG9JMHJ8TEmkwmkEHjn7bextFmx4+HQtVsphVevXrl1WlWVq+e+t7fn5iSDZp1OBwvLUsDZ90JQZmee5zg4OAA7vEejkQMLGXSiWvd1XSoG2NhoZ+cKZ4kyGDAej92c4P7a29tzOkG323W1qhns48xkNhB8qmghCJji+vDsgDbGNOo1c5YnQIC9AO2PgQxQmtLWCyQ5OR7vAcZAtw0KB3qFSNPAAooG19c3UKrC3ngPcZw4SlWtFdIkhVIaWZZDa4UkSVEUJc7Ozl1Aw+3NLdJWC0krxWq1dlmjWmtLJ5/g9nYCIWDrnZJMjJMYRU5sEmnawovnzxF4lOBJkrh+uL6+trS0bQyHA9ze3qLT6WC5XKGqSgDCgXBCEEXl8fGJ7dPMZdPPZjNIGbhxKMvKgX5Ery+wt7ePXq9rx432Bl5rNHcydDpUwkApjSiKG8YeZyhzoAdn8QtBkdwMxA+HQ4rslnQOhMBqvUZRluj1ey47hmushVFIJSXs3N9kGTE+iRqo5IxtrhXP0eVruz4BA6ElDAx6lokizzMURYlyNkO71UIYhijKAlJITGdTRFGMLCNwVWmi09tsNjZIIXZBNqznMK089xv/zwB0t9vFfD53LAAcQMF7OAdvLBYL9Hq9RtmAMAxdfWwOlPGBYIqST+tM5DWtcc4YTmwWc8FlArIMRsBlePH1DEoyW8D1zTXW6w1ardRm+BBNO2CB5UC6ABRe+wzcL5dLnJ2dYTAYuIAGLi3BJR2klK78Ac1R6WQ865U8d4ZWVjLlPPe5lBKDwQCz2czJNKbvb7fbjiocACaTiZsrURSh1+u5eckA/v7+vluDLAt5biVJ4mQjBwFxoIcP5hpjHIDPgVe9Xs8FuXAgBu+HPsD+yxzbjs1G0CQrro2jCcrQJ2wfUMaOMZpoWAEnk7/3ve/hxz/6GZarNebzOdJ2q84WLCuUSkOVFbLNBpENBAglZYgHQYCyRRkdgc1W5ICLGpyhz0VQ004HQUCBcxYYD21WVxhIR1GaRDQG2trWYRTa7H6/zrO1S4SBMpQhASOhKoGiqDCfzpFla7TaCdqtBOvlArPbCdbLFQqbGSOtTCuLCqPhGO9+7X188K1vOfYDwJZDt84o3+kFoxGAymSsFnPkmwwQdQZTr9fDb//2b+Nv/vW/jqdPn6IoCvzgBz/Ag0ePLJ0n7bOdTgfPnz9Hnhd4cLqHKIpwUZZot1IEMLi5vMByMUNVKaxWS+TZGtPbGyRRhNIQbfvr169x+vCRxyajUKgcv/FX/jJevXqGyfUlJrMZys8+QX90gJOjQ1xcX0MJBR0F0JVGGGikUUQUkkYhigKcPniAPM9xdXkDowUO9iPEUYT94QCvp3ME0BgO+hh1U/ydf/8/xKib4zf+8n8P7TjAfDGHFBt0WzGyjQWDpAFCBaFqQKEOgG+WbuC54oMwBIYECII6cJ6K0tVOSmNtb5anfPilSlgP5hrz7l5RhFgE+PjjT2jvTxLLuiRQaoU4Th3gHnhryT+2HXbbgIXvzK3BNr+W8W4HobC2t++g33bY1z93g/O35QP7E/izXQAOyU2u84w73+8Cavx2sNzlH9hx4uAz5xMSTcY0Yyiz0fdHvAnAbPgtdo2BB4xv90fjXZqVyO49d9f3d/++WzZvl6N3e45sv4cPjL/pHnxwMOj2OT6IuQuMDLy15z+nIfPuabuQzfsJbDHk8T28fvDnsBT1vevknLvO++b8hfOp7Pp++/ovm7fb5913H7ljjviHO1/bPt+m7ReAUTVQzD8NFi1jUFRlrauY5ty446uzbSPPunHPJ9egpeH12rc95/z32+6PXX22zdDzJv+fe6ctnWbXHOW5+GX38s/f/n77vbaHetc7CVmXi2C545/D+isxsjSDTihBrL7XNth931yDeLPflK+lPP/dfeAfu4IUvkx23ffML28X/3LP52j64r/6s7/KOQICzcQ9/1253Fqapvjggw9wcXGBH//4x/jOd7+L/YN9FwjHTHzGsJ3KD29S6AN14tx2O8DYg/BqvUMisGx7rFPwd0S1TvpGlAbIViVCEUFVBYAKxwdDlDD43/+f/x189ItniNIevv+rX8NiscBisUAribFaLvH69QXOXr3C3/gbfwNCCKw3ayjNLFaUXKc0+TejOEan3cbr1+c4OTrCxasvcH1zhbwqMRyN8P1f/TXEcWJZQy2zgg2kXa0W6Pa6eOfdd/C3/tbfwn/yd/8eqiyDUQpREODgeB/vv/91DIYjJGkLShtM55Q08v2/9Ov47ne+h9Vmic8++9T6ggS++c1vYjab48WLF5hMJuh0OhBC2PJyFHDS73WdnQUQC4fWsCWLvkQAbx1FUSCUAYbDEd577z385Ec/RllkaKfEeJbnOfmlKgUjDfKCMrLjKEJVKBcwqbRuyBb/p9Y7Aa3rGuS7dBRjDKqqcAA4J3gwGyRfS3OMfLXD4RBpmiBNE5dIxP5F9t8JIaCFsbosAGEZmfn5b1hPvsz4sxxfJvfv09m25dNXAcX963a148/a/q8MjP+f/g//F1zdTKCMRFZUxK+fV6jyAvl6Q0ZqEDoO/igMiE6gKuwASVRIERiickJBGY26IigrjEMCmAty4LOyRBEQdK8s3+D29hphkqI/GFpDpoBSBTgaNQtX+Acf/O07yha83823jDMi7p8RNYjJf3+V7P77h9KCnTs+BQOp7hk1EGqhvXthzD/r/sJukfuXwo5rvvLG6b/97jd942Gaf5j7v9x9+R1DY/fn299/lXv9szq2F3TDOIGA6dgwko7G4t+6/Yp3/afzcnfG4yu0QgBYCOC5meA/hMXa7XeBEEjC5sYnhUDQMGq+pE1bD77vfAOgUnUgRFbV+QDmm2+6+9017ta18D+w44e69tmuy+7epG60/73blOHT9NcOUK4vxOc6aioQQH4r68VS2XopRZzjt37jH9GTaAcFSgGVqfoZAPQXtl03XMvSRurbyHNfKpBhDODcozqzgQjGGJhPvL4yHNhAsiCQQS0Vbrhul38fuy4+azoOuO6SGwYhXBQ8/82OJQ5wMIDrH95HKNhHNu7FbeMajOK5NfSUBj6xDhf2WhjjFGV2fDYMFPss8Bq37XGOI6dICKes+86EO4ag7Rt28kshXBCFP/HNF7WCFnpKO1GFwdV8C6R0kdACgJjVzhJjKPhDbUWQc7/yQjZoOrLkpXT3he1HZcdVkEVp+5PmnL4xLpDE9a333lzbzS0pfj6Eo7fzxx3GAGf2M098NncyjwbTGz8ywrbWriHHq/5ENz6Dbasxpn5Hngf2PX3FWgjRqMcGQ0Fowo6JG/uP6mdIuwb84DHuQ55Prk99hdQ+k+dHzXJC/cdLn2RV3ad83fYcrvsN9bO5X71nO71ix9rzv3fXG1uyhC/b0mO29bmGBvEcbrw4SM+NpzdMjfuB5YBXp1I0y53w/8YYiFdNNhOeb0LUTjr/8J1CYnnXSUHNq5lvuNaW2qoRuk1T6OQmarpSWiv+vT0j5CPT6EsBYSOx6zksud+Np7M22tmcC1LIxlrfdfA53J6GA9Mf260xvbvmeJ6jMRe5H7h9jfXl7b21nWC8Z/ODhZOjYvv+/nsYszV3hOuvui+FC7IUAuBaldv3glsixl3vZKfvmBM8B+r+r8ektm+0sZl/DK5g67zGXPXmAcs3e41zeHIb/Sj35+7FG/1P5xlHGezv6Tw/fdlX6wL1eDf62fZJHXxK95lUE/d8Zh9hpg9m3+BAnSAIHKOAMcaB48x44DM9CEFMAhwYwNT4Wmu0Wq0G+wGzC7DDi4MeyrKElFRW5Jc9fGcKO9y2S/FsMfvWA+MdNB+1yzBQCghsqRwhiF2DqPIpi2ZycwMACJOYQGY7D1VVQYQhTFXBCAEdGBhNJbk2G+NKqggbNM1ztdKlJ8sFpAghLcVoIENENus8kAHCOEAcRUiiCDKQWC5KohiVEkEYuUASdkrzFuf6JwwAoQAjUBU03jc315AB0OkmSOIQk8kMm80G4PltyJG1XmdIO228/42v4fHjp5BSYrla3tHf/HIASlEgdyAk4ihFt9tHWZSWQl7a4EOJ6XSKn/zpn+KbH3yA7373u3jx8iWWq6Wj6eegDtbJpJRIkwTDXhf9bgfr5Ryvz17CwLhAFl1m0KqEhoQ2Vmf19gmtDYqyQGXmOD4+xoff/hX8yR/+EDdXl9hka3zy6Uf4zncHGPWHWG02yMoKrXYbWlfQiukpAa0l0m4PJ4+f4OXzF7i9naAoMhwfHaHd6aGTRMg2K0BXGPZ7ePzu1/Hv/b/+IVTYw4ff/AZGwx7mkwnyrEQYxoAICKBREkJUDmz12a04+F0KARkYQDSdj3wuU+QaU0NBfvaNsbrGtrxsMEQYs1MOvPj8GbTRePrWW1SeR2sYu18oQ8GztAc3Wdl2gTa+w9xf275e4fQ1X7HaWtZOTjfex98TxJadq3d81rwpzZnd2eKNfVRSNhdg/Mfbe3vvrIW7L1ADYT7IQMG0Cnm+QZ5v3HtQYois22vg3nX7/Ro6hPDBXB8kBPxMfHFnH97d2drrCh+E3AYThQfkbutK9RMkcAfW4r7b0nshvLFsto91xF332XU0/Edb+qv/bhwgIiEQemvAn7t1SYvaLq3ngd/WWg8km52CmXjOGqvXp2li7Ru7X0jp3puv9XvQby/3Qz3v6vno9kyrl7PtJMiQojv5OubODZTnG7w+d48CaypGb4/drkEgXcbVMxesZVo5pOn/SlVQioKYs4xLalFwlVIKm2wNbSpEMqSZZIeA/Bt6awTgqIbh9Yv/w0fg7B248fHncW1fe2Nge8DousxnwNnu233h2Vz3CSHnJ3JPrfW++/zR27r5rvN26e/NpjWvF0LUe4UBjAcw++dRwGDhPvdLJ/mvfx8Dx67D9z/5a9V/lzeBWrvO3/7cl1vb120DVf7RZOCo73/nTuLuH8Y0M1SdHN5qq7833tfOXe+GXTaa1btq/ZkAzV/5lV/B7/7u7+Lm5hppK3VsXb49LUTYsEm25b0UISA8n4CpA162zw2ixNkDzIRBcoAC3lknyLIMSRyiykt00hRpK8I6y/B//b//e/jRzz7H+OgRRqN9lHmOYpOhnSZY2SDl5XKJX/n+r6LdaWO+WIBXZ1mWiMKY9O9Ko9VKkEQhJpMbdNspwhCYzia4nUwQhjE++OADPHnyFHlRoqgKp1QEgdV3KiqNmLfb+I1/4a8gW+f49OOPURUlBr0eHjw6wYMHD7BaZ1gsllgsV1hvcrzz3vv4F/7yX0GpKkymU6zXG8xmC3znO9+BlBIvXrzA2dmZy3gGJGbzKSpVIW210Eo7SNMUpaISnwZ31209z3b8jjpARSkNKQziMES/P8Dp6SlevXwJpQ1URWxa6/WaAPRQUlkeGzCtSip5rGxtehjy+7KPlGWWNtolAvj2GwBXgoR/iLUob7AZ8RHHMXq9ngsIT5IWkiSxQeSGAgc8tquqqmnaaQ0T+0tDDnhrZtsH4/fnl8nN7eNN+58vT950XlNe1dfuus+bPrvvvd50fGVgPMsLfPb5Fyg1UGkBiBhhGEOXJdIogTCkbpc2+7LISxhbo6jSGkoAYZo6cKEoclTWaAYAaSNtNbTNwCaHTRrFLhM5kAEgiP702RdfuCi6OI5RfaOyPWOQx+uv+lr//Phv8PFlpsJXMyX+2R7bbTT3fScB07ufIue/DsdX6e/t9/P/rmBQ4Z/iO0Z/nou+SshJ01z+ZzYP/Qbs6FYNjavi+pd7hvqS76tf7vZf6Tlf1oa/qOf8V/X8v8j2/0U+a3vOqHt+/4s6/mn2w39dju13fpP4+4taS//8+G/m8d/G9fPPj/92HRaU9mnMtdbY398HQA69LMvQarVcNjcz0nD2BkfbG2NcxH4QBOj1eu5+zOjR7XYdQw8Db8ykwPdiYJOzjP+8B9fpNTC2ZjgoMMwDzshxv8sBuvW3FBacQf29dapz9jPXtjeaHCp5nqOoSkgZOHYiLr1jFNUUFEbbADBJNWg5mEsIW2cWdbCXA3SozimDFlIGiIK6fmkUhUiSCGWcIIoCYgkqSwsyc+Z53dcyCBzdbhBQyS4ICaMMqkJjvVpjMp2i10mJklsKFFmGqipcn2qtUCoNGUi8/c67OH3wEGmrhfV606BwVlpTnV9ZU9j6gSs60Oh0usiyDTbrja0vSI6aVquF169fo9/rYW9vD9/9znfw//sv/okD2dkpdnBwgDgiBgVm1RkOBri+usRseuucW1KAWDZA8xYyJEeiDdagQAQqAad0gaKo8M677+P68hJ5nmG1mOP25hJXr89xePQYOm1BZRtiTYhCqi2tKEBYmwCVNugPxzjIC9xcXWI+X0AK4MnTNh4/PMXV9S3WWY7lOkOn28d8s49/8ts/QL5Z4Ve//S0cjPZxO10AkXCgdxQQQA5mAgMHfhHNujFEBSrsZDeCwBhIL1jU0pBSsF8dHMrgGv+vPbCtGXzXDH7k8ZjP55jNFzg5PiXq1TgCSspikkLa+WuBDyM8BsHm2uOgkm1nfxNQ9H839xuJxgJ5QmyBe+aOLOCDXG53gUP/EOIuaHu3zYQSulAqD6Rp4iE1o14NjCvbDwxea1SVQiCo37Ztf2hec/RcH0ikRzT/JkCjHlv/2duOUsNo59Zxx8Eq7zp0dwFMftbwvY5fgzvBDH5/1S/Lgtm9PGqaUR8Yd580O24LwKyDG20/WcYeBrdZBkMby0YpYbxgWQeM873ldp/f7SO/r5yjv+RXqq/VlSQK5DC068nWqlV1TW+6/26A8A54dsf5bsd/a0/cDrJ0/ei+bp5g+LOt6wwMtJuXfDM/AKW+QAsGSYx/C/su1E9KV66mOPu6janrgcMYot2FgvYCJlnWbb3Snaxs/7gPrNgGzbkHtoOSG+dauaOhm+Nxpxean+0CSwHGGOtg1d3BPnyXNwEgvsPrrqS6DzQRDOSLbWCG/ua66P4ew8kMLvjB3md7bHYdu8Ae146tNrLc/SqHsI2+r/95/u169p3zvbYIixqbHffe1bI77+DkyT0TQNiAYsHA++6x5SXnZBiasmE7s7uqFA4PjzAe72E2W6DdnmJ/7wBFXrq5S4xm9X7nB1y594cAmF2F22YVap4jQggKHLWZ2zwX6FQOluC9USOEhK5K9Hqku529vsZv/s7v46c/f4HxwSm6gyG00VgtF4iiENlmjYuLCwgh8PjJIxwfHyMvCkpCtVTZ0t6/qjTSJIUUAuvVCjfXl/jae29jMbvF5PYKWb5BfzDANz/8NrFNWqZHtjUkgEopSoRRCtPpFGmS4hvf/BBHR6eoyhJhIJEmIeIkQRCniFsdDMYKEAEGwxG01nh9+bpRPvLk5ASvXr7C1dWVs62klJhMppgv50jSBK1WixjchM+4Qus5sOWCd+szPmBa75H8OSfmHJ+eUo3u2RxFWcJo45J9tSLAOcsypHEMrRRUpWtgHDsCMC2uycx6/LefDe4D2MbUwcpcfpN/mAmwDgD2Kflr586uYCcXWObV4+J1sr1qv0w+7dp7m59/OWC93b6vAljvCn7YFcCzrQv6x5e9Gx9fGRj/1/8n/wbS7n+GH//sY0CmWK0LVKVGaSqYSjl6lzAIbR1tAZiAFCdoxGGCOAqxWi4BKSEBCBmgrCqqm2o4qlBA84BJiSCKAQiEIoIUEoVWoBr0xtEsKKUQZokXDWgayh8L3nor9BR7FrXifiV7VxSCu++OnWD7TP9p2ycY7/vtk5vf2b+2FNtdx52Jjnoh3Glbs2O2W+POefN82v3GwrV1+zyx42+z4xRzz3PrLCAAjd/dGU7w3f3sL+Jo2C64v492fb5bofvqBxswEIBuKwo81oBc363r8Ka2fcWn7Wjnn/Fmf45n/wUOVWPt/7nvIXbPqfoJzc9pfOoFwI4zym6uHYQCaGRTsfLNGV5En84vQCc4o9bLWGHnLEyz7pAxpqkQsjPPu1a4O5MTaVJOSDGEwCgceYaB50RgxdDUmaO1ougp7Oxg4vZ67eJNWQi4NgnQJs+OHRflzNfw725c6ja4CNut9sAYoimCcdnS/BwhKCKYHam++OG/+Vx479dog+0bpZT7jjOZuQ0V1zqFQKUqV29cSIpCNLZ/3PW2XW5stvoaqEs8cL/4mdYue4ajZO2eYYxpUPdLdjRIu49a2uI7NcPsO233q7RZ4jzPBLzap167BWet2//5vkxnyVnUsP3A8929L8851IcQsvlOWjf6JwyC5rh4beH2u/H1HC/+e3PUMK8rKSS00S7LnXWDQNa0Wc4BwX3l9Zc/Nx0LAOqaaD4TA68hZkRQ1hjhNnO2Jd8bdg5EUeTWufvOM+Tce/nzZ0sO8LPdGhDCZZ/5go7Xk1+zjue136+Ne3kyzL+vdjpgM0Ke5RK3/Y7SZOe2z4jBc0dw14haL2IKb84I26GFNRY5RwP7a4LLxzij1zM2/LIu7l1c99yvS/oZ1LUD2cvu2mqmsWuE+5ON6/rtm+fVz7+7hzXnBn92t82OKcFzCiitnHOoqXc3VUpeG/X6rnVi1me4vzizyF17563uHvxe9xlH/nv4Tlyf/YHlSTND/q5dsN2H3Cdam0ZL3Zzz7sFzpGHoee9fzwXUMmrrvdw62bq/16mNUkbbi9v1+z0GaWMu2bnOa5fWqvZkKn3La43noq+2NDJ9jP8M2PnjZXKhtuF2L8u7beY1OorGyLIM7XbbRc8DtXxlina/th7Xq+e//Vq9TH9ujHGUdL5zk2U9l45gynr/Pq4sjic//ryHgbevslwRtc5DbeK51uxnficheB7a+rvGA5A8MH+9XrvyJIktLZCXhS2dQKB0FEUQBghDAaMjmDCEDANIQxmRRhhKtRSCyqWZuq4svHfxnfZCCJQycu0PiwB5ESFJciQ2o5+zbKSsGu/HTiNe30EQQIYRAEHZHEWFzWqDxXyGKABUVQFGoyxyVIqyrrk/lTEY7+/j7bffsdnBBnleOB3dGNInjc0QbYyzAKhkkkKattDt9qGUQbbZuMygNE2wnC/x6tUrDIdDfPDBB/ijH/2JKyHDQRynp6cY7+1TFovS6HZ7ODo6Rp5vsJrNLYBF45pXJTQElNJIWwn29/fR6XSprTwHIGCEwnK1wv7BER49eRvz+QzLxQxFtsbrizMM+3uIW12kSYr1agktRV0OSlNflqVCu5NivL+Hqipwc5ljMpni8HCFp0+e2nqGFTZZjiBKMNh/iBdnHyMWP0UiAvzlv/SX0Gq1UGhFezJsJg8HbBBHsJ3mNnPPyWpAGJqzWlBwgjF1dnCdMW7oNmhmRzoHJv9tdQHWNXkuhWGIQFIJgJubG7Rabezt70HIgPQrwfpE7XsyxkCYuqa28eTdfXsIjw/Le7cWdsg6Pt9fL3y2v9fXpzR3zVoObesI/p52H2jfBMb935vPbN7L7yNuP62hWvaQ/RE127Klj/v63JsOX3/a3uPuOFgF7pzTsHP4sy1gfHs/5n7Yod7tGC+DnScCW59zEEhzPJ0eZ8939rynW9tTm7oef+XmmYawkIkRtT0OQZnDQRhABrK2E4Vth6EArXqvEY2fbSc4f+72Tns9zytjAF2V5Ds2BIrDKCgbeMLPIHtzN/W7Pw6svXypA54712vr9u/+vPXfZ/ug/t+dUbzr2XfodO1g1cC4QqVKB6L4zCFSSgsEUWCQkzvi/nc2jhmhaY/UqmHTbtp+t+3jy9bVdr/ddx199ua/+bOmTLvTyh1yrH5mUzaJO7/fqwsDtc9g655OnwIs845y49qwk+7R/3bZKfeds/P5W/vFvfegC2qdfevwMZJdfXNfm9z3ti2uXTwP73mPOz7qN3xf7636DXK//kJu0Wn7Nt+2XysIQpycnOLzZ88wm80pOCsIIVjPkLBMawYwLB+lY29z66jBBMBBG1bvZVtKUoCYH0DJ4GZj7WqDOAghZQAtgFfnl/ijH/0M/+R3/ggy6uPw6BSFrpBv1lBViUgAt7e3KMsSh4cHePjoIcIwxHw+t+NKAYIGtd2SxDHWqwVub66QZ2u02wmeP/sEs+kUgQxw+uAh3nr3XRRFQTq7KwMECKEhYCBkAK0NVqs1bm5uMRyMMB7vkz6vKuTZiijIAQyDEDIIrf8MuHh9gZubG1seDnj48CGCIMQXX3xhy3AGrgTcdDqBMhq9QR/9/gCtdqv2K3GPs+1zj6xvrDNTm8PUHgr4lKAa7gcHh2DXWlVVyDaZtesNqrJCnmXIbWmwsihd8BL/MN052ykMgHNQNes6bJ8yNsCsV0mSuJ84jh0wzmxlvv5a07LXZTLuyH/bL1pvZYxbvUcKBse39T3uO39Ob69ToJbFzXv4x33y7avIGv+9+Lyd+5u3hn7Z4ysD4w8fPcCv/Oqv4JNnr1CoEO1eB1mWI2l1IIxGnCaI0wQwGkVh6z2GAYJA4vr6Cuv1CggCBEmMNElRqQqVrYXHxomqiELL0ZEZgyCJYbSpa1rnBeKYJgpPviiK8K3f++ue0iBgUEdhuMzyJIG2td5CEbpacForF2kdRiGkEMiyDVRVIss2aNn6adPp1NXlS9MUAgZxRMrK0tYu9Xn9ASAMSMlT3iQGmkoIR4m0Wi2XbaAURUoSbSY775oULcJqCtoYF4XEAgWAa4PbwGWAoigRJ0TVVlVVrScJor6RMmwsvrpeMRcxqoMB/MgY/xAGjbHxFQbnDLP9xAaoX3eBzjOAqO+/vdj5vfzFAuDO33zwpcY0HTD1983F5/fb9jPvO3x6MP9634iiGuK6cS47vwOvltiu92RAyb928m+eQ3cV5CrA3v/tASAMtC53CpH7+nG7n4SdD7uoPtmJ5RzcbzrsJvTm59014v0+I2dd85rtyFejBYSgvvOVVV9JJvaKu+9y12lY/7CDzdVqkwJSGud8i+OY6uAKiaOjQ+zvH6Df7TonyzvvvIM0pbq1e3tjvP/+1zCfz4BAeLUnKwDC0UGenb2i9VDkODk+xmK5gFIanU4H2WaDXr+PzWYNgCLZYI3TNE2Q5wXW6xXStGXrkJIMZcrQPM/R6/XcZ0opdDodzOdzl0WVZRn+zZ//W7gpb7AXjfF3vvf/hBDUPq4xmmVU19anB+Uaq0IItNttlGWJVqvl5vdkMsHR0ZGbw1988QVOT0+R57mTeWma4ubmBt1u19UxZSe3McbVa+10Ori+vkbLZsMEQYDz83N0Oh2cnJzg+vrancv1tKMoQpqm6Ha7uLm5QVmW2Gw26Ha7mM1m6Ha7OD4+RpIkOD8/h7Ey9ezsDKenp44SNE3rKL7JZAKAaiGvViusVit0Oh3nYO/1ei7bjCMGmR7o5ubGUpVG7t25VimPz83NDfb29lxNVR4zAO4zXo95nrv+uL29xXA4xGw2w2AwwGazwdHRkatTs79PyutsNkOaprZWcuzqqQJoOJgBylTy67RuNhvnuGWFrt/vY72mGuOXl5cYj8fYbDY4ODjAq1evyIlu5xKPp9YaR0dHjjKU96XJZILLy0scHR0hyzKs12skCdFQcc1XIWgdtdttJEnidAZjjNuDB4OBq5sthHC1XpnCaH+f6kpxnW/OHuSx4HW+Wq2QJImbj1mWOWCV+4qf74OHPj3vbDZDv99HlmWNWqtcF4jnvFIKq9UKSilyHNt35ev8bMg0TTGfzx0wMxqNHH3weDxGkiS4uLjAfD5Hu912Y7DZbLxa1KWrqcy1pnlN9/t9K2fg+of7l2VKnueuvjnLFymlq+3LgRZcX5vnEUB7GNdez7LMyQvSR0IAwkUl8xj2+31Xd7hja8gDwOXlpasPzI4krtvcsvWl+fNGYJDdA/I8p2hgu8b9PbRQlduDid4LWK/XUEq5vu222hBCOACNwSUhBPVBGEBIqtfMspHnI9ct55rS3AdcE4370tfveBy5LjPLKJaJXCOb6Z55/Hgu+/OWwTyuX83zmuUXy8PVaoV2u+3qQ7OsY9nH49hqtTCbzZxsZfrqVquF8XiMoihc9LWfpcv6HtfAzvMcZVFCGOMyH/k8HnspJSqtkNm5G8exe1emtOYMX55zQgi0Wq1Gn/P7r1YrVyOc5wzLOda/+Tms27ZaLVdTm/uS64Rzf/MaKMvS9UUQBE6WRhFR1PBa5hrmRVEgjmOierb351rZvkzkOczygec6r3XWx5VSjfttNhsHxvFa5HtISVlculJYLBZuHgFw8o8BYH/8eH3zfOX1KqVEv993+j7vJd1u1+1xSZK4tVhVlbXRSOdL0xRZlrn1xfqIv6b99VdH1GvX9wyC+33OMo3nMM8Vf33w/7weWIfgcWUQmecN1zJkObOrFuGf9fBBedbRmZmtqfM29VqfwpOcIfU9ycaDAxoB0mnIEbNBGAbodLvoDQfIywLL5dLK/Q3yLMNaSKRpZB05CaI4RhTT/LE3pX1Rsc1KNaW1AbSxAEbU1M1LlLbNQF4AMpeIshBJFHs11SV8umRfZ6+dOQIijAhY1RpVXmG9XGG5WqCVhsjyDHleoCpK6KoEtLY114EoTvHND7+D/YMDbLIcRVlCBtLNbwJW9R0WFwr8EYC2VNxhhF6vD6W0pZ9c2/VYIYljTCZT/OEf/iHef/9r+P73v4/f+q3fcmtpNpvh61//Or72wQf4+c9+hul8icFwhHfeeQ9RGODFF88wuZ0gyzYQEFABUFQKRgYY7+3j3Xffx2A4wnQ2hfYAJgiJzWaNbruHJ2+9hfn8Fi+efwajNSa3V7i6eIW9B4/R7nShqhzZJoMQQBRS1e6yLAERYrXZoNdKcXR4jEAEePniC1y+vsbpyQSBANppilJluJnOcHgwxtHJuzi7eo3/9D//AZSQ+B/8i38N11dTiu0WBoXOEIWtHdmNEkEQQYjKOTfZVKY1IWwJAbJZXXAW+w9AjAvAXTuY1zIf7LtIEspQWi2XmN7eYj6Z4le+/+tuL2MbmOccB3ORE79e7/eBSsboOw7eGvmlg15TYpdfYPvws4buP+pM9u32OAe+gPVR1NmOTcAQ7jNeg7vuty2L3LhRMxyoa6wPq+lv8YO+3E29+9U34rHkkkR8qpOTqHvP/e+d688XNL6vzzf2pr6s2T74edtBPo37ei1hP8ubfErGCK8fGB33z29Sun+ZU1hYog6tUYPTsBS+Xr8aaAhpEIbWn2oM+Smd39KuIfh70T0Zwt47uv2r4Tc01gdbryejKiqtUJaoGHyXEpLZBHx/namDfvxn+nXo7/MLOpTkTr83+3G7xM1u/6INNt4GJnaMC+tL/vMMGISrM4/ZTvX7jvcftwcJsTMIYBsor4MJtN+QO+8s3IJp9ue2TN72v+7yp7l32+r/Xb7X7d+3n9X43za0sT6NF1zEjkyvnfeBw+63XW3y7rOrjcJ7vyiKoO2+raoKgQ3C9NvtyyRsvcv293feeedY3Rc6tbUe7rnPnffZkm275P/Ow/ZTQ55ty7777rU1h3atHyGEU7PeJC+Bu8A4P9PXg/n3xWKBx48f4+b2FlmW4erqCoeHh279QRhiYzWG9Na6UTvA8Ob7u9IbgstDCMioXtuwOoIBHHsy6bASsQD6e3v4gx//FP/gH/8mfvhHP0HcGuBbH34Hq+Uc+WoJoyu0Wi1cXFzg7OwM3/rWt3B0dIggCjGZTEg/ceNAwG5Zluj3eoDRmE6ucXN9icODIYRRuDx/hc1mhdHeAb71ne9ivL+P25sppC27qbVGpQ0CUQevc78uFisURYXhcIh+r4d2u4dWi/woy/UKYRhBa4PFYoFnn3+B2WLudNw0TfH+e+/j5cuXlPUupfO1nZ2doaoq9EcjjMd7GO+NEUYRsiz31STQlnIXLL1vPwKAAFZN11xyM4SqNA4OD9FKW8itL265WKIsK4iQ/EpZnjvfz2azcTYlg99Eh17upEMPw9DZuIPBwKNFJyCcAXCW9XwP/gFq3I3HgLFBntM+jgZjg+VMM5PdX1e+LcX6M68ZntvbWE8t+zWE4BIFNTjO3X6fbN9e37s+bz4PO8/Z3oPu07X/rMdXBsajSOL45AitVgvrWY5SKyStNgANYYHddZZDCAJqKlVBlwVlR0qJdrcHKYBRp0MOJBGg3SMHcyuO3eLVRrlsuqIsXW1RgLKhunGKSITOeciOFwYKjDEIQumiOKSkQScHmrDgtYYM6ZnrjABxIQTKqsQmz2GgocoSwpCjez6fg52UWZahKAqKdLHAeJ7nDSWEo0EAoLJ1sNjB0pxgtKlJSQ6coigRxwyeck1jNmSIYo5+akHPzoAgkPRekindDIwR1skWIAhCVDYiN7DgdxjUkYnCRgNRrTJYB7pEHAdQqlZ4gzAA10pw4LrtdwYGoqCmgsvz3AkJoHZKbgsNf9OiRa1gzP+fuf9oti1Js8Sw5e5bHK2ufPeJeKEyMlJVZnVWVVZVK+tu9ABGcETrEc1gxIAzGP8EJ/wBNE5pxIBNIwcgCjA0CBAgrdpQorNYVSkjMjPkiyeuOlpt5c6B+/Lt59xzX7ysaoqd9jLuPXefvV1+7v6tb63P7UQNmSu7UccAoJRweSKkz4VLeagdI8AWdwciAWsQPTMFAGVT6o0jDwvBxArPZMFljZNlTDLayDp9yJ5xLGFh8+wZbey7tPAHX7ZzuDm4c7ASe0ZqryzWyNc1ttWvDyUAF7S7+Zrs++oDL8dZaGy0NrAyipGNohK732UDGWOj/+/bsPPIb8eR8M+iAVeKpske0KWqx03tGBNuzAGRSnbeUY8l6+SKIiuTKZVEVVbefjDghlJISZx4cKHRbCBNUrz33nsQUmAw6KPX62A0GqHVamEwGKDZtCA0nf+RVFBSehBhuVxCSoksy3B9fYVOp4PFZo5ez8pyVmUJFUWYL5ZQa4Vmq4FmI8ViVuFnP/8ZtNZ48uQJsmyLzXbj8k5ViOMI8/nMgz/NZgNC0JFboiisVOJwOAKAHVCBmw6CmATll8ulla8JxtzNzQ16vZ537LO/Q2Cs3W7j6OjIHw42mw0WiwUA4OHDhztg93w+R7PZxNOnT7Fer9Hv97HdbnF+fo7lss6vSMDj5OQEq9UK5+fnGI/HyPMcWZYhiiIcHR1hsVj49j87O/MAsxAW+BBC+FyNq9UKn332WZC7xoIC3W4XUkq8ePHCg8MEBvr9PsbjsQcIv/jiC7z99tuoqgqTyQRlWWI4HGI0Gvn3vHr1ygMl4/EYjUYDVVV5oLfVaqHX60EphcvLSxwfH2M+n3uQUimFTqfjQY+ytBvOECwjWBDHsQfmi6JAkiR4/PgxsizD6empz3tK4DiKImy3W3Q6HQ/iz+dzX19GLjJHDd9FgI99QxCUgOrV1RXa7TaazSbm87kHRJmvqdfr4dWrVzg6OvL5X999911Mp1MP/iVJgufPn3tA9/T01ANn3W7Xjy2ttQdwjo6OMJ/PkWUZjo6OsF6v3Xxo+mcT1CcQU5YlRqMRjDF48eKFD5DL8zpHGO/jfymjKx2wSRB7tVpBCOFB6hA0IXhNoIbtwYCATqeDJEkwm82wWq0wmUyw2Wx8lGiaph6EvL29Rbvd3gE+uRe5vb1FmqZ49OgRAPh6TCYT38cXFxd+TjMYhWVl+69WK9///F6WZej1ehiPx36z3Wg0/MY9lBNO0xSr1Qq9Xg+r1cqDdOFGniBSuJ4xQIRjkaCodT4bf4Bgv87ncxsotN1iMpn4Oc77WCcClAysSZIE6/Xa/10Il4bHBTSGIBbbkVdeFtDO3jGQIMsyD16SybZcLv28DcfLZrNBlecYjIZQSmGxWOzUM9wzciwKYYHvdrvtgXEGWmw2GxwdHflDFe0Y7TLtLFCDXKz/yckJZrMZsizzwT5sj+FwiNVq5UH4PM99kEi4znG9WK1W/nBXVZVf7xaLBZIkwWAw8GOf63VRFBiPx94G0zaFzjeC5lEUoSgLpFHsgUYCDgQltdbICtteHIsEJ4E6mJS2kHYtz3MfKMK9KkFxBppynWRwGdcwIWp2KgFySr+FB2GOv5BNSlvLIAyC7wB84C2DEjhX+b2wnYwxvk24NofgPcF31oUsagYKhJ+v12v/fq4xLJOWCpFSfh5x3LAeDJoDatYMbTzHI4MQhBA+wI5jnX0CWJA2LAvnZxioxaAFnrtoL+lA5jmEwREMDODFvuT5hTaVAUUMpg6Bc+4ltNa+Trx/PB77tY/jjcEFXNMZdPT3uWSg0bsL7NFxICADxNuOt9oJGF48A9ixQjDEARauHxuNBqRaIM8LbLZb9MQAJycnaLZb2Kw3yJ0tzPMCRVEizwsAS1vWSHlgMY4TJ3euoJTb6yvUZTWALsraSSMd09yfEeocfWVVs/aFOxeGOdZ3z4fOCcoAP2OZwVm+RpatsF7HWC7mmM872OSZlX53gfXNVhtvv/sevvHBNzEej/35dd9pTH6mD+QnML93fhNSodPtwUAgy3MURYkkEjCOiTOfL/Ff/9f/Bv/xf/K/wKtXV/jyyy+xXK7R6XQwnc7xe7//h7gdT/Hq5UtMZku88847+NZwgIvHT/H8q6/w6uULTCYTrLIMzVTh4ePH+Oa3voMPv/MdaAObLxG168odlTGdjjEY9vHeNz7A7e01fvGTv0GRb3F19RVKaXB09hBnx0e4vLzGarVGq9VClCTu3FxB5xVyYdBstvDwyVtIGk385K9/jC+ffYF3330Pp2cPMBr2YKZLLK6vMDp7iOHDdzGbTvC/+z/8X7FaLvE/+4/+JbKywnybIysj6LwObAHq3IxSKUgov5+wSdQd5O2cgF5Tyjj1JwEIJ3DMozullMPzIgOJ+F4Gh6VRjKvFEovFAu+99x4GgwEmk8kOe0dKidVq5dUojNbeOR+ej325OX+VrMsbXLyX40dBBoAqB9+eE1EIqGhXkWsHPAy/uAccHAJCpNh74wGnY+1CvXuFY98YA7VXfqr7WMABUM526SCA3c5+j0bWAJIQ8Gm8Ra2oErpKpLD+QlOVEJHLZx08C4Bj0N5zBYBHWCcc6K/6K/Ydcq+dwpasQaO93++9tAd9hXWFwecw9++p/VivA7B22icAWff9TFzj7CvINNPQlaYOv/fbCKle+87wGayvd58L4drB+GAkrSu/VxPCBjWpqvJtb1DnwGalwqCGQ4DIfQ7zulF2v3+Q2RswwQ85+EXQn/vg3v79h4A/1woQIQhR1eQkXy9jJZEjaa1CpTWM0H5+0ue1Xz77sz7w2aEmsWuSEGy7ur9367sLoth9iLjz3MPAx64N/pohVD8LbzJn7qmcEDWAy1sO3L/fP/XXA8WpYJzws0aaAsb487f1sSu/RuyPw50xGpQx9O3zvkN19nP3nsa7DxS8r/0OrQP77+PnVXDG2W/n8B20Xa+9/Jg6DJD5NQl7ioWvfaTrJ7nLEt8pm3vW0dERzs7O8OzZMzx79gwffvih9ysIaReWnXXbrwPC78lru86FSHjp8vCdGgZSSbe3qRW9hLJrd5zEaLdaSCXwf/nP/yv8l/+3P0VmYjx699t48PABZpNbZKslOnGKPAdevXqJL7/8Ev/wH/4xBoMBsizDYjb3dgIABBS0sf6FZrOBZjPCp59+grOzI/zxj34XSSzx43/3Z3jx/DmkUHjy1lN87/v/AKt17oB7uyYLKWyqG8cCp32QgE2NXGSYTMb2jY4Qas91AmVZB01HUYQ4UpiMLfHn/fe+gSRJ8Bd/8ReQzi+VZRlmsxnyPEen08Hx8REGgwGSJPU+f4C4y28Pfvr+MLtkxrwskCYJ3v/gmxj0ejBa48c//nd4dfkSAhrz+QzX11eAMNBFiaKodp4ZRZE/99E3Q8ISfe38R/8E10diYqEfMvz7fvl5ZrZ+PI3KYQP8bhRFNid6WWNtIR7GtS4MFgnnxv+nrn+fz36dPXjtuv811xsD40pUOD0e4OnTJ7j9m18hiWNs89weJgWdehac7fW6SNMU6/XSFtw1fqQUpADStOErRTl0pZRlhbloiqosUWQ5kqiWELCHHIkqK/0gCtnIvPI8R1mVzvGhvTMdIIMhwnK1QVVWqKoSpS7Aw1WlC7v70BVMWfqIYzpI6MDVWiPPtp7h1263kSQJptPpTsSGFqidE2R7aytxK4Swm3MhUFYWtCrKevBGSkFFEaSTSdDaDnLp8gsIIRAniXUS5aVbrLmRsY6UOK4/kyq2kgrCSYJEMSIhEBm7sRbGIBJ20S+rykWFWjmRsixsZFMFf4CkA4hOA7+BcyAnHUjchIdMOvY/N+G8p763AkHNcNKybULWFCB2FkBO+NDZ7Ad8VDNE9ve/XPSkjHY2J3cm14F5uLuRqWWSuIBwDIT31w+6u5kPy/S63w/9bZ+ZUm/GAQaBWIb1bvkPH6R3D/espzWmdw8UfJePnseeBG1wQAr7O0mUXxykrKXsrFxwrVLA+c4yEdwRQljAO0kAY50oURSh1WwiSVMIUasq9Ho9z1p6+PAhZrMZ3n33XZwcHaPTaWM0HGE+n+P8gQVrj4+PYbRxi6h2tmqF45MTzGcWBBTGysmu10sABnFkQbyizNFutRDFLWy3G1xeLXF8emQ3MIsFGo0GJjcTv6AeHx8DxnhQsCwrbDZbnJwcO6aUhNaFcyYXnhGrtcbl5RWazYZv1+FwiPF4jOFwiDzPsVqtEMcxbm5u0Gq10G63sVxapw/BiTiO/aaXTDiyXIUQGI1G+Oijj5A4u0Mn9fX1tQerCExXVeXz3pCBCFgmKvOtkO328uVLH0l3c3ODs7MzGGNwfX2NBw8eIMsyDAYDDyJx4wEAs9nMA983NzfodrueDU2gbbPZYDgcotPp+PGdJAl6vZ4fm41GA19++SUWiwXa7TaUAwN6vR6MsfZ5NBp5AIX3NJtNfPXVV3j06JGP1KStI8MuZKgC1obO53MMBgP/DMqw0imxWq08sEsHO0EIPpsBGARk6IBnX/Kz6+trz3Ah8M12OT8/99GPBORCJh4dFQRFzs7OsFqtvNIAWXxkxUspcXFx4cueZZkPuiAg9vLlS2w2G/T7fQDw3xdCYL1ee8Ykge48z/06Q3CMARLMDUu7wP4hgFxVFc7Ozjwr/Pb21j+bwI5Syo+h0Wjk2282m0EI4QMRQvY2134+i/2T5zl6vR5ms5m3fdPp1DqVowj9ft87Yglo5nmOdrvt5/PV1RVarZZn3E6nU6/UsN1uMZ1OnXTWKZ4+fepBz6Io0O12fTBHqPhCIIhKFxxjoV3mfFytVr6/h8MhjDEetCc4vt1uPVNcCIHpdAoppW9f7unCnFocx+Px2KsMJEnilSfKskSr1QoAxtrJRKZ1GBCZZRk6nc7OvCKQD8CDeBwfBAtDIDzLMg/Ess8JDHEPU7l1s91ue4nhEPQaDAa4vb7xShocE1VV4fb21oKwaeLryv1kyPwN11DaA9qnoih8cAzcmkq7T8Cz1+thuVx6e7tcLr1t4/gimMdxyucQ6GdQD5nGBFnJXuH6u1gssFgsvK2iugDvoU0KgV/uiWg3qC7AKGv2IRnStLm0RQQgnjx54qXjCORGSYzIAce0vWQ4s105ZqjcwT0I244At9YaL1++9GAsA0QYJMC1Qwjhy0qlBdpy7oHCQyfnPO0Ixw77nwFHfC6VC3hxLHJdop3heGB/83AspfSscKUUJpPJTqAG7R7tIL+33W59vxtjc7dxbZpMJjsqUFxDGMDBvmbfRlGEVqvlD/wE91kP/w7XNpz3tEPCOaXYHrRX3OOG5weC+VyrGMxFsJJjyTstAyCctoMBE2GeZ/Y/21YI4fuFQXVh4AL3tzwn0saErNS/yxXuo/cd7PuODX4WOqBDh72Vrq5ZNFVVAMZARcrvK2yQhUSlK2TFFqWusNqsbUCKkmh3O4CxcuRsq6qqUJUlqrKCroDVYg1g7d+rVL0OxEkCFceIVLQzTylbqoGd+ukDzmKeg3fPV7sseX9ukRLCAFVVwMBAmxJFWSAvcmgY6LICjEF/MMT5xUN845sfYrFcWke6OAx28Jnh57Q/cRxDSAVAotRrxIkN3NluVri5eoW424YQygeDfvTRR/jzP/9zfO9734NSCh999BHKssSvfvUr/OD738c//mf/Ap9++ik+/+wzfPrlVzg+PkajO8TT93s4uXiCm6trLLcb9IYDvPfe+zg6PoYBcHN1CRVHVjYeBkIoSBNBmwp5scFyKdHpdvDd7/0An33yBTbLKTbZHIupLZdChaOjEa4nM2RliQo26BRViUhJlFmOtQaiRhMXj9+GkAK/+Mlf48WL53a/ePEQJ0dH2M4Ubsev0Or1MTwZotv9Ef5Pf/KnuBqP8R/883+MJ4+fol1KrNbLQGZSwQgJretzvJTS5xy17S18EDdMLe9sO8QGnteu7GBcuXnA465SMWBsDs44SpHGMV6+fInVcoNed4C3n76D1XqDNPAhaGNQ5QWaaaN2Cygr+7pznjdOcczwjGxBPha1Hq8OrPGfA+JAauBDfoAKd30F4fwJ/2v/zheRJR62mwV073M6ejsi7rLZTVgBdwmEwCxBN3hfFe1xVZaQog50MQHguO8stp/XPodDjt0woGrfZob33XsFVavLX0s2h8Dg/le+Dmji9+4DhMLfdz8/YOd1daAuNbjp14Gdst/17dxXxp2hwV8MYKo99b4DzPudfqmsHLKKIkDY+VdVjgXuyDlWicNY6V1oG/+inVSswZ00NIfLa5ic2pYp7Mcw2GG/PWADJuoyGzdG76oxCFvBnWf7lE8MVjjULsFk8ONSGx+owX1vVdWBNPzcx/2YOnhmf50Lx/qbAEavAxb43/ued2hNDH/+ujmwv2f52vLtDsQ7gTkC2GHyvm5+C0HC1WuAXWP2mME1KH5o7oTKUwD8HjDsl9AHet+1b9MOtfv+nuR11z44fF977NixA7/zv7ELOj+0B5W1efCs6dfZlkOBKIfK9ibXofF2aCzwXEDSRK/bRb/fx3Q69QHxVvHI1mOXtFeD7r5v9tRed94tBCh7Wqty1P26Xq/R6/XQ7fSw3Wb49a8/xX/+X/4b/OTnv8Hjt7+B4fEZVBLj9voSusrRTFPcXF3hdnyLrCrxz/7FP0er2cJysfCgqhTSkSUrbLMNpBTodjro9Jr427/5Gzx5/ADvvPMEo1Efz7/8As+fP0dVFHj/w+/g29/5HvrDI9zc3iKODXTuVHocMRPSzpuqKOuxDYHKlLCZLy3GVRqHKwlARRJSA1WlkWWWONXttvH06VMcHx/jz//8z7FcLtHtW58Vz2VC2L3mYDRCu9uFjCJHPAxt012Flq+b//4sGPYtgEQlMAbo9wZ4/713cXzcx3h8i/VmZVN9uBQ5BhXSXg+NJEWz0USSpN4nTf/JPuDMPS3texh8xmtfdeV185tn8H2bIoTw2JeudL3JclfoD/R2CQFmdWAPct++ZL/d9/92yG7d9/1Df3vTeX/omb/t98PrzRnjqkKaSHz7w2/gN588x2pr8xQUVYayyAGjEUcNREqjLEoIARRZiUYzhUyaWG/W0HmJZqOBRtLwjgwANi85DNqNFrQuUWQ2aiNNLGMzL3ILlAIwukBVVN5BQakZShoopSCkQKkJ2ApULsrcOs0YlWcdUnESoyFjGFNBmxJx1ESWb5FnGSLAOwnYcSw3318E8um1jFudVw6wzBVtzI5DKHS8wEUjEjgKAQxGg9gNWi35FQJZdTsqXz46j72To9FA5vL1cLDQEUVnYVlkaKQxICTKMgsWeIGypFNH7kzCMLKZ/610uTOZ7hvoIZDN/+5/Fh5CKLNvf1b+71FUL0q7hkUijtOdcawUN401Y8EezGpJDf7McoT5Gw7VIzxgsr5Sqp1y2+fwXRJUMti9jH/PG296AmxduFP1fnS5dYLV0i82z8SunJLNN1tv6rlx970QbnTdhlJI6Q4s9c9CAJACkWI5dg+snDc8rPFnpaRj4kUAjGfl2YCQwua6cmObYCXnmVISx8cjvPXWWx5Mefvtp2i3O3jy5AmUkogi6YEdLl43NzcWKGm1rFNQCByNjpDlOVQENBoRjo4eQgiJ6XSK1WqFxWKBwWBgwdwXLxyII3xelG63a+efsQfAkxPLBiYol+VbFGXhASrKCne7XQgh8PLlS4yGI8hUIU2aUKrC+PYW08kcSRJbSexii80mgxAKL19eotlsoShy9HqWMTmbzdFqdSGEBcebzSZub2+9M3y9XmM2m+Htt9/2YFMcx57FzDkolUK73QYA33YE6kIn9tnZ2c5Cy+g42stut+sY89eeRcZ607EOwDNWaXdoD+mMD+ViCQaR1dVoNLBYLGCM8Y7t+Xzu+5qAVqfT8cxjAmt0ylxfX2M+n+Ps7GxHQpfjjQy0sixxdHSEbrfrgfqnT596YJfy33Ece2Zys9n07GaCV2x3gkSr1QqbzcYDXAS2KTMrhPAADNtGCOEBnTzPsdlsPJP55OTEz5d+v49nz555kJ+scbIAyTxnpCwZ+dfX1zDGsnbZVsvl0gOZlJkno3symXhZoPV67SUnX716hQ8++MAHLZycnHi5+JBpORgMPCi7WCxwfX2Nk5MT5HmO0WjkgYs0TdHpdDzYQrCSYGGn00FRFDvgGCV0Ly4ukCSJX/dCqbp+v+8Z3WQSEtThmkrAhfN3Pp/7eU/m/p/92Z/hgw8+wPHxMaqq8gGAWmtcXFzg448/9iAagWz2CRUUms2mZwmfnp76gIdut+vHL5lK3CTHcYwHDx74ccSAAgYREgwl45LpFSaTCfr9vm8nji8qNtAO8H0EfXk/5/9wOPTzgIEVs9kMrVYLv/71r3F6eopOp+ODFpRSXiadQBoDQpSMsFqtPahVFAUuLy99oA5BSaZc4P6KKgAcx1QXIGi6XC69bQol0/kOBt6EYDmkQMMxQoWoQS/2bavVhhnZtZCAG8f3gwcPrHKCgGe2M+CC76WN4LgnUMp+oN0bDoeYz+d+3NOGMSiJKgPsf6aVGA6HO2klALtXopLD9fW1D+Dhxf6jsgftLwC/N6XN1Vr7eTGZTPw8Ho/HPnAhSRIfBKK13hm77HuOI44NpRTyLEN3MPSANoN8yNDN8xxHx8fIitwH1YR7DipwCGGDNwaDgcttJrw6AtUkWBcy5xngEYK0APz6TRsSjiEGHbENOdY2m41vw/V67VOXMPCA9p6BPmREc90JgxT230XFLNoQgsVck8P9Bp/BscPxxzVJCOEDRABAuT0j1xK+m/OSa4UQdaAAbYAxxoPm7Avu4bm/9fsNWZ8tOBbppGLAAp/BNYDvY+BG+D0GD/CMSBUBzluOOfafMcYHQLENKH1HG8fPWS7ONwZ3HFIqYLlD1vrf5dp3+r2JQ5RnnTCI1Riyay1gHwXsTaM1DIw/fyZpCrnZoqwqaF2iqiIUVWVlCAHoqkISWwZxEsxfYawClg7YClpXyIoMZVlhvd5CbLZgjkV7bpeeMaKUC2hQ0uW4rYPBATqzADJnLVhaB8nactS/C0GgD8iLDGVpg+eLqkRO2cOyhFQKp2enePjwoVvDXL5vY3aCfOsAiF2nOe2HEAKRGyvaGDSMQemCQbudLq4vX2K5XKLZ6EI4ILDZbOIv/uIvMBqNcHFxge12i1/96ldQSuHTz7/EyckJvvXt7+L8wUNMbseOjWbPtMcAHj55GyqxZ/0ojpHnmc2bWRlIU1q+pbHgkpQxdFVCKiAvtmikTTy4eITvfPd7+PGf/ymybI2y2KLMt5hOxkhbXfR7fSxXG78Ha8YxdFFCRjZVjM5zQEYYHZ/j/fc/wKsXzzC+vcY2z/H2ezFa/Q6qpUG5WWORZ2h1enjyze/ib371CpvsT/H737vC733/2+j3LSs7DPCxvKRdP4LYyfnMsa735oZGrTjnzrDufGvv2wNcYSAcGhtHMdYru6bZPbhFcsOAHmkReUhpx4gUNrBDmz3HrAAUdtm19AfQ/2DH0v68FfBIQ2ADDs39O96EO6CFLYjwyEVdNuHYuNYu8G9qZ2zf92yW5HVOSOHLUJd/36ErpQSk2r0Pd2WygV3fUQjQhPMz9MUdbo/XlHfPvlpPHoiGov7q3WdIff9zD73H1pNPM4EnScBGRdTStazH3QftAb6GvqTaj8b/GOwCbvtsNKAGbH0bCTtIwwBkoPa3hf/CMlqflPE+owoE9QAIyu1rCzZiN3iB/b7fb+ZAeYG7fXbv+rgHku+Pobu+vd0UJrvj3uy4Bg8pizg3mPOduQ/2ymmMsWxS+vFEnc5y9711oB8Aq06oIp/iY39+he3i++Juw9U/B+0egoFhvQ/ZoPvuCX++b87dmWuHxhDqsfQ6AGT/+QftZAhoHrjvzjP2vy9qPzW/Z8+vFaJIwZgINg0FWfbcfzEdqtu4IGx64d9kHxnecxccD9v7UJu/7jrkW+bz6RcOpm29TAS2TwiXjgH7/etMlquLVHL3u0E5vNvcU6gOlzX47Z677N/qoJG7aT73MQqOAdqywWCAzXaL+XyOy8tL72vSxnjful1HdjEPv7aIu/58zmP3gGCci51zzvn5OVarFX76s5/hVx//Cj//5cf4alzh3Q+/g2a7haLaYD2bW2A513h29SWybIPeoIfzR48RpwmWq6U/f9i13AYM67JEEidI0wRxEuGTT36DLFuh024iUsBqOcNkcovLl68QRzHeefsdPH78FrK8AKTFgSLJID6DSpe+/GzjssxRj1XjyaQk34UrENO95FmOb37wTXQ7Xbx8eYkvvvgSjUadXo5EnTRNMRqN0Ot1kaQpjAEqXVqCaLAHCINP9vv9vvFU23HaVXtuGwwG6A+HkFGMycSmyfvWh99CpGwAcZ5n0Kb0vgEllFfAuW8tpK+av/NceHe9sWmXJccVdlPnegBbayi5i8WxpcMzpx/zAdZijIGSEkoIrw5r5/39SidvEsxz6NpfB8L17P+frzcGxk2ZoxErvPfOW3h08QCffnkFaYD1aoay2qLVbEHJGBBAlm1QFiWUkn4hs2C0sIfjTe4HCun+y5V1VmabDZS0Uepe5tBFJSZJYqW8tT1kpmmKyWTsDxA0VEbY3FacJFEcW9DYgy4V4qhhD9suj44QGsvVAmWZoZg5pw7gQXCyOTzzQNi6EHymgzRkUZdlCakEGs2Gfw7gIsm5QUJ9uLaMA+tAqKqaFWWNiRu4bvKrSEFGLt8h5ReC/HchS4KggXFy6lzYyyDapCgKVGWO7cZuWouysIc8IbxTwA5ya0T2DzXh5kYpZVmnmlm96sjVGhS+G+EYGjZO9Dq/kfFtFW4E6Nxm34SGJjRG9XU32s8v4jLc+B8+/Lna7GwmbVfejcgLNz3M38CF8dAmkRuTsC3u5gO736iw7/mO+nO2qau3PLy5DA1i2A+HFh7fB6qWAwkPtSIwuuEVRWRSCSvr75yzrVbLAWN9N6+nODo6wmDQw/vvv4PR0RD9/sA74p8+fYo0TVx+4Riz+cQDZQTGmKNSKolWu4n1ZonZfAIVjTB5eQshgNV6AQjLuptOJlit5oijGI1m00nDbAAIrFcrLJdrPHz4yAJQUYwqSTAdT1A4h/GgP8Dt7Q1Oz87w8uVLz/iMoggPHjzAcrnEaDRClFjWtu0rgUjFOD05w3g8Rpo0kGUFZuMlqsrmsz05OYcxdlMxmy2dLA2QZQXiOEVZVsgyyx4fDEbYbu1Gpdfr4erqyrOvtNZeknyz2eDFixceBCZofXp6unN4mk6nnj00GAzw6aefoigKDIdDTKdT79wnU/X6+hpHR0c4Pz/Hq1evPDOacqeLxcLL0I/HY88eqqrK5w5+5513MJ1Ofd7lTqeD5XLp832HsvCU0zXGeDCGthiAByRYVrYD60bQtSxtPmqyEofDIciID3OqkiFLwIN2h/K6x8fHHqwg24y5oQl0MGiA4AHz/R4dHXnJ9izLMJ/PMRwOPSt7PB7j9PQU3W4X0+nU2w+CFQweIOBOcI6MS4JbdHqHG6hQNppOpdls5tc0O3ctaEkgazAY+HWN0uWtVssDAAxCIUjJPOF8P6/lcukVDAhEErw4OjpCs9n08s/MaTydTr10PZmjlNnmPcYYn7+bIAqBJ4JwoVpCVVW+fs1m07ONafd4D8tvTA1mMo+wMTYw40c/+hGMsXnUOR6ZR3o8HiNJEpycnHgW82g08uoNfOfNzQ1OT0+xXq99G3E8870EoSjvqZTCZ599huVy6YNCiqKw0bhO3YHgGccefyfgRACNjGn+HErCMzCFQAhZt9wXEKTtdrueoXp2duaDUsJAAYLpDNzhWGu3u0hTKys+HA5xc3MDKaVnxpOVzOcwuIj2RErpAw64LyPjnEEU3CMIIbwqBWXQCQTaPFlrrNdrJ+eV7DjG8zzHzc0NdFn6ucd2Zz2TJAEEdhSGyrL0/RQC1gD82sV1MQR8ycyl7eTY5vikYkKj0fCpKpgbnG3GMQtYwI5y/ZRl57xn+5DlzjV2Op16W1FVlQ+E6Xa7fu5Q4YP2g3aNe12Ct+wrqohQSp7gLfcaoSIJ5yb78fr6GhpW6jx8B0FNKkhwvrCfCNoReGbf8n7WjexoAsxhsAznBW0vgxoIxtIWURbdGONtKIMJyKxmxH/I9A5VD8LxSydsWF+uWwxmYTlYd7Y3L44hjkuqfAghvPJLttn6Qzhl5WkPGHgbBuPS/jPAqaoqvzZwb8t24x6Te0i2pRDCqwQw/QeZ8hyHnDu8l5dyAX0MbOE9XCMB7Kx/BMeFED4VC8FyrbVPCwDU+Yc5XjebjXeuhfORAWphYPVv61T4uus+h7K96nONbVt7brFjUfs/aW2glQFcOicDCUAijmIkcWpTECmFqrBy6So2tXqStE4wRA6+kgIqsopsSljQ1ud41m49LnMfTK6r2jmkjYGpSqAqISCg3BlRSJ4ZHTgeSMNLKQBp66UiBSUjjwURoBRC2DRMQfuURYHKBacWubX1VVFBG4HR0TGOj07R7nShq8rWj83KcarrYG2ea20b77a31gZKGiRJDK0rGF0hUhGa7TaStInJ5BZaR2g2mj745vb6Gr/59a/w9tO38fbTp3j18iU26w0mkzESF7x6dnaGo+Nj5FmBqqygpPJqdCqG3zsul0usN2tYBg88OBVUBVLaoH1tgDRN8ME3P8THH/0Um+UMWZ6hyDdI0gSr1QLt/hEaTbtWFXmOUgjEUrozawVUBbJ8i1azjZMHFyirAjdXl1jOZ3j57HM8fO89NBopcmOQ5wXW6xV6R6dYrTf44uUEovoIpqjw3e9/B712G9usQF6WKLSGihS0LiEhII1wQJ31VQgDGDrGjQSC8c0UZoYAlvPG05UhYJ3ahtRkaEgBKCmwXC6QbbdoNJtuX1DecfQB9nxtyxEEgQd+ivDenbHCIrmfa+AMsFLw7oxtgnntv7831QE/F8LLl+HuI3Y/3ANQ6RYh2GFcu9XPC9nt9zufw+fzYwIiOugn5jEVqmag7/h5nD+OlwUC74Jl3l/lxrpUqvZDCKvauOsdOdQW/MjcucPXYc99cseXg6Cudz5zHR+uCcb1tndku28EDm9BcFbs9rJvm8DvdL/v2eWFD8rM9vG2wf1Tru3stFIwgmCQWysM2cq1v27X50VnuC2TFBT3DdQahUCtXkgFBzrP63/1XHKf+d8JOu2sdnbtYVvtgXI77QvjbAlgdIVEWSUTCAny2Kt8CwNV941r3/sc/PsA++vWfmPqf1YewT8cTCvIGwVs29MvzJzWKpJQUtmAh50ywH/moJE7ewbfW+HngQ8vHMd1uyH4dPfXemwHto5tEHxL8D2+AIH/9MDTQ2/r/cD4/QEr4XfehD3Nv3kQ2T7Ef39/zef77VnHoCwL7+fk2sJnhSlxXl+Ou2vNob3G112HwMHQ1xs+O7z1UJE4lwBAynv6QXA9g1dt8HUJOlf4m0RtDxEC5sH9eyvbrsWiT90+Qxsr+x0+y49f7h2Fcu8TMBrotLrodTZQQuH68hoXFw+x2WyBqrSYixAO/BSAlF4ZAiIIsjCuTPXmyu2n7Z+kUNBmi0hKxHEEJQV0VeHy1RV+9ZtP8dHHn+H580vMVxXaR8do9rp2n5oXqLIcRVZgPp+jLEsMRyOMjo8xGI6wWMyRZ5nDieo+yYsCSZSg027CmAqTmyssprc4PxkBOsdiOgaMxmw6xWQ6w1tP38HDt56i2+9ju91AChv8YIL5wr2K1jrw74fpLOr1ygYkCrsfc9+1PtstRqNjHB+fYbVe44svP0dR5EjiCEoIZFVpFYqNQavdwej4BM1my6fLJfOa68qhqbC7F98Dn924M4KjygZlxTKyQaZHx+j1etC6wvXlFXSlcXZyDCUF8iJDtt3CQCOKYxi4QC0dBHQd+Mdz7evKtxOssvdfjt/QDu32d/2ufZURzdy+xpJnLe7nusWtOeH+LizP11379ii0h+EzDu2bw36536a/3kYHzbH3u5/9OLyivP56Y2B8XWwgVQvdXhtvv/0QH//qN6i0RCIljFYo8wKb7NZF+bqOgMGyyH1jV1WOyi0YoYMEgGMkCwhTQMkYaayw3a7t4dZVrioqrJcZbJ5tie1m6fNuAi6qwZQoc400bqDVaKPZbiNtNSHjCEmzASOtEyVGDAGJIs+wWi2wXK2QFUAUN9HqR2h3S+jtCpv1Gtl2CxXFkMJKwZemjoqRsdukiBRpo2HLWxZAaQ1kFCu0mi1o43LFuAMcnQVSSpsnRhsYbaXcbL4sm9NHwPiDKGA3x5FS2K43HpDP89yyUB2ga/M123EgHbCutQGEdE5g6YDzWt5BqQhQEQpj+wdCwQSRdf6wod3myBsVOAkg40KWBUoDQChI5lBwE85K5AmUpkIshdssW8YvFzCC5rYp7Ia/0lZiPo5jyEihrGzETCRtlGVeWYauMnUEq1QKlbHbQgYKGGO8A0H4TYzNQwUBt7kEjDC+r7Sxsu7SjUO/ADgZNxhAKLsx9RE9LuCAY5zSgHRMAThoNOyvygP09tJ791X+u4eA9ZrBEB5cbJvSoaerClLZe+091miWzvlru8JJXO5FZis6Ed1d/vlu/kVRBCEl0iRBkli1gziOMRgMPAv26dOnaDWbODo+9sAJAcjT01P0+308f/7cAiKjIZqtFHluc9nSkXx7e4soUsiyLZJEQQmJbLu1jvCihBISkVQwUkMY4PLVJRrNJuazBYbDERZzK9uSZQW22xwCEr3BEMvFAt2WdSiv1tY53W63IaRCkqYYjydIG5YtN5vNcHJ6ap1Epe3zdruDyWTi++TmxsrrEnRYr9fYTjLH7LZy3420gdvrG9w6dl2n1UYSxVit1tC6hJCWtVVpiU6jjevra1TO2R/HMY6Ojjzz+Obmxkuw3t7eehZWyB5j7pZHjx9jMplYB7i0jsQXL1/WS60bYwSxCRY8evTIj+88z7FcLr2DmIDHfD73+YfpVE7TFLPZzD+PcquU2S6KwrOJydyirDOfxXyPBLRp/yjtnOf5Ti5aSsD3+32s12sPNEkpPVOZDC+W/fj42JeZYIgQdW5vrjlk/5LpTRl1siAJdrRaLS/tTACYgDLlwI0xPsDn7OzMA6EEHYQQXqrYGIPj42MfPBCClXwe6wzAgwNh7qvpdLoTSBJKfxEUaLfbmEwmXiWAYBwDT8j0JSjT7XZxe3vr25msPYL+URR5BjeDsU5OTjAejz0Lj+Dj7e2tP/zneY7JZAICRpQfpoOAsuZk+xLcAeBljslOpQ3iGAmBS621Z78TqAwlkglM5XnuAfVup4vxZIJut4fZbG7XJRWjKCxQvN1kHoThmGQ7lmVpQdgsh5IRlIos81gbB/RILBcrbLMtpFBYLlcYDUdYLla+/ttNhjhJ0Gq20WjaAIDpdIZup4fZbIHlYoX+oI9Bf4jZfGZVE9oddNpdbLYb5FmOssjQajasMkMSQ8kIkYqhVIzZzCoD5FnhxprEcrGEkhGy3K4D/cEAy+UCkYrRarewWq6gNbBarrBZb31O9iIvMRqOkOUZtpstkjRBs9lGkdv6DwZDjG/HNuCiKmG08VLsPt+xrpnGBPBqdR74/iJYSGYugTuO31B+mXuMUmtM5zOrMNG1KReyLMM2z9BygQjb9can95lMJ1BCot/rW5CsqgApcHV9jcHQgsKtZguVcc91AEilNbLMSrq3Wy1EKsL56Rnmizmur298IGUIEDPogQEsBLyNMT7whoeizWbjQUgGDEwmE8vyc2BvmDOZ+4RWq+VVMGg3CEayvSiBTzCR5SLgTICR/UTbFjKtCSJT/WA2m2E8HuPk5MSONUa+uz1Lu9NBZTQWq6Vl4zvpYwiBOE0RJwnWW5suibaK6wfZ12FKnTA/LPs43CMZY3zebtrVMB0T5zPXsMVisWNvNpuNV5DhOsq8Ymwvrt205wScuddimflf7q14P5VeeC/B2Pl8jn6/j+Fw6FMakO1OBQIGA3BPzLpxbEwmkx1JuFJZcKnRaOyok7A/9yP312srnU2mO9uW8vjs/6IofAANgxwILrMtGdTF/mS6DwafkL1qjPEqFHwfgzs4xjkWhJAoijo/mwXIDZSSKMswx5uAZf0oRFHsngMURX1mqiqNoijdmiux3WbI8wJp2kAU6SDwQzllq7/7te88OAS8ycARueNosd+wZxgTBiUraFM7MixoopDEDcSRzQ3ONsvzAo2mgDDCnX9d4HKlLR4J49LwVNDCAStxFDxboClswCKDErgPohJPWZYwlYaobAC7rso6MFvSqSnt+VOKOk1bFEFFUeBHtc5M5YLFhaxdqZR6L7MC+TZDvs0htEC7O8Cjt56gPxhCQLqxa9tZCuGdrkbT8UuHbt3CtUPIncMrq2JQKYlKSSBWECJFtz/Ai1eXQLWEgHD7K4kkjvCzn/wE3XYH7777Hj74xgf4y3/3YzRbW7x8+RyLxRwnp6c4PT9HntkAWQFAVwZZtsU2n2EyGWM2m/l5vcOicfUw0M6pqyCMRlFUECLHwyeP8fDxW/j017/GZpuhsV2gP+xjtZxCRDHanT6kbKAqCmyzHKrdBIT1uwgDGC2RZVu0212cP3oLcZzixbMv8OLLzxG3mnhwem73ETLCfL2Bmc5syqrxLX7zfIIXL/8SAiV++Pt/iDRJoAHkurCy6fawbR2uxubWFdaJAFDSWdhR7rtF2XzvBJt49qf/WmgL0BrplPmcDyKNInz54gWqqkCnc4x+v4/VamNBSDceTNCm+2dx3ufP7hA+qMOOf57pawnLcPxwfhtjfK7Q3bl/wA5IsfP93ftDx+V9IJ0FTf0wMeF4rtdw+gz2AaJD9uhQGeD2G6iMbzu/huwF3jN4gfOPxRfOwWUZtrtAV1mWdVBMMPal2mXA121ysDnuXLGU2LfBdbvVz9WoDr7H+9K84zrsq7Ad62fvsxDr8VTXF4D3z4WfHfoe93pm9yX1mHb/FQCSPeUdgP616I4j/G5dA2YualKFDSIRcPx75+9Tbh9eQZsKWrsgHxfAIoXNzau1hpA1m5ztI0QNRvH9GhqV2+M4z9vunHFy6dYOGu9njoyALjRyXaLQJZqNBAk0cpeOIQTh9uu+T8K5A8j4++txZ+eVU4eAXVu1CzTamU8Qnh1uz48CaWrPtsq16yHH/44NCtInhp+HcyT0le7bop16GAMldsc2QZudz4SAdxj759wFT6RkQMyuDTEBSlrbrkMTdh8Uv8vavOtvrVUm9oGc/fKFbXAIWOfeiaxTno9251q9nzx0fR0AtP++192z31+H1pewTnWbHPIp7362O+53A6f2Pw/3R7tfC8pnb99p73qpqMeuQFWPgQB/9mUWod3ha9yHbn8ghfRBkwYWB0GlkcQpmmkTkUwwuZ0gbTRRMJe2W7s59sTOWHMBmKhtOqRyYKTyGIKBTWUrRQ4hDCIFGF3h8uoaf/mXP8VPfvkJpvMCSaOP00fvIBpK3F5eQeeFxTXKCvPpBMvVCg8eXeDBw4dI0gYWqzXWqw0k7EaQKRmM3aLaIMxEYT6d4fLlcwx6TXzjnSeYTm5ws1mgLCtcX92gKEu8/93fwdHFQ8g4Qu7O2gIKVSBdDlMHepckRioF7YOtbXvbPZdtt8qxxLnf324zfPvbvwMhE1xefoHnz79Cq91EVRaQwkCXBXRVIk0bGAxHGIyOEUeJJYwWhU1F7AIyQ1n7kLR3aJ2ux6/Fg4WwgLiEDeaNowTNhiWstNstbNdr3FxfoywKJFEXZZnDlCWgNaSQKPMSGja4AQdUCliWMDj+EGYTjnM7Rv2E8nufnT0i6n2jCObW/ruMsaB4pWsVJU/c1brGxwJg/HWqNPs2Zd8WHdoL3GdXDz2Tf7tr2+7auv1n7j5vd0/1uufcd70xMC7iCGVVotFo4v333sJ//38HlustjAZ0UaE0BfLtemcRoTNHSYn5fIFsu4TRFZj7wDvmgFqSWQBVYZ3SpVtYoihGWRbIM+2dDHTIjLcr31CAM3wyRRKl0I6VVmhtD3JSQEug2WpCVhJKSMgkglYCcavty7zZbFAVW2glMZ0tsC1KRLBR7EYbG1+ihJViK0o/8PKiZt35TXBeYuHqVkfHW6eArrSLbLJl54ZEm/p+KSTyLIeujLtHYuuA6CqykR8w2JV7Vza6yRjHTIGyrHuhdtYuYwyUrHO0bvMNlIm8chc3f9bQWiOnhAQj0P2gV+7Q6Sdkzb6GAKqyZlRIIZFGCaSwA7iqrDRHpCg/45wd2kaxG2Nzf6kogZAKpdYQSkJGAIw1kj6PgqyBYSUVKqUBY1nXKopcPncgSVIPcHO7S8NaVSUgJKRyhxIHIrsK28OD1r6PjCB4bJ1HMC4AwFhnDp2j0Aa1fDo317sGhRtBY6iwoCCEdgdJpxzgdhv7hz4A3jlnAW/49vSyS0qhqjSkNIgcQyEvcq8MEBntorJsoEAUxd4AA/CMRQA4OztFt22d7yfHJ+j2ulit1qiqEj/84Q9RliU++OB9ZPkGlEmPohhSCsRxgtlsCjp4yUwkQLnZzNHppMgyII4Frq4u0el0cH196dmem80KjUYCY7QF0YQFDpVUkLHEYr6AUgrddtdJbTexWq9wdvYAz796CWMEtpsc7VbXg2fNZhtaA5ttjk6njUbTSqxOp1O89dZb+Pijj5AmCRrNBm7HYxhYFtx6Y4NUIIDN1krYMrfqW2+9hfV6jTzPPZut58AHHj4bjjE86PddHs+xc8rnSNMETScT3m63UekCo6OBZ6iSWUaHPJ3odG5zXJPl/ezZMzSbTbRaLSsZbQziJIE2Bs9fvPB2hHPi/MEDbNZrXFxc4NWrVx4sXK/XODs7w9XVFTabDU5PT73srhDCO+WZ27zf78MYm192sVig3+97AOfi4gJXV1doNpuebUZ2IAMLlssljo6O8NVXXzkn1crLUK9WK8xmM/T7fc9YJuvz6OjIs9kpu8x7yNIB6tQUDx8+9GkxuB4IYZlkZLayPtvt1udy7vf7ePTokZ+LZLYCdf5d2lmCJre3tzv5bsk+/eqrrzyIECphkPE5m8080MJyEpghOE7wl5shypoTcCNbkszDZrO5I5Pd6XQ8+5osWeaYJUBfp/qw9otqDnRODYdDLJdLvHr1CsPh0LMuCaQRZIabR1EU4fj42Mt0k7lNUIfju91ue0lm5iYmeHd0dLQj0w8AvV7PBwwQEGo0Gj6IhIDYer32466qKg9kh0xXfh5FkWPNCiRxijhK0Gl3fCCGUgplUaHT6UIbG7BGwJasU45RbQw2m60PCrD5l7rodiwbPlI2+OXy8tLlMko9a7XeV1jn+PWVZVX3ej20WhbkmU5mVqlCxRj0h16Ro9/vo8hLJEmKqtJot22gCJm+WZZZsLvVcnnNZxgOh2i3rWM3jpyksAGaDQsezmcLu+9TEaIo9vNKCLJMbDBcHCeWkagiZNoCYtPJDJvNFmm6dVLJlQfPWq2WB8wodU62MgAvEU/wmHOCQQ4EfDmfOAcWiwXyssDJ6SnixALNSZqipPS629c0m00LqDgQZ7Ne4+zkFAT8bm9vYYQNLhsdH9nxtNkAbi5oY7BYLiAdCMIDT7tp6yWFQBLFuHh44QFlMvyZuoDS+GxTBnKE8tcAvFx2KA1/dHTkD6ZUACG7lTnrGTDAAC7mWWdAXSjDz7WF+aMJwPA7HuRy/RA6wIwxHnyn4gfBatpq9ju/Q8Ca29fIBUnClZllIyBKYGiz2XhwOMsyr8jBctJ+hME0LBMDABjMQ3sSplKgwgL3V2HwEZUdyITnPyqsCCF8/zF9BoFzro1CiJ0gnTDdEsd+mI/dGIPnz58DgFeFAODTRTDoKezXECw3xvhgNq4/vV4PAsKD2GFf8jMGKBHg5r6Wa2kYxMu9qpRyR5ac45VBSKE6BNVQuKZy7HPtIbjOVFMMaGPQHAFzrudCMJ2ETbvS6XQdMG+dJLTRbNeyZEAqfEADgyG1tvtzOy+1rxeDGqzCj/ay3H/X6z5n565jt3YY7jgl6CnD3RRWd1Wp4PssjiMXCFF4exue8e05Q1t2TOCMoSzuIbCAdpqBbxyD4XlI0/a6d/If57pXcctrVYYQgA//MVhXuqByCYGi0liuN1guVzZg6/gE/+Sf/BNsixxFYW1XUbqAaeUcnI56FEp4h06cQw5pwKUXSFMIKZFltl2Ojo4wGo0wux27oD+NXq/rVW9+/vOfQUUKf/QP/xifff4FprOJV525vrnBx7/+FZrNNpSMUOQFitwGemTFwpeFcyh0yrEuRWHtnUbNaNG6QqvZwPd/5we4fPkKs8kNFvM5Go0J+qNT3Lz8CvEjhW53gHQ4wM3NDTabDI1G6lNs2tAEjTKz55124y30uh388uc/x6d/9bfIPljh+PFDtAdDDFsNzF+NcTtb4PjsDJ3eADfTMf63//v/Cn/4m+f4D//Df4K3H50hQYzxqzGkSGGaCltRAtog1ZEb7wrapXgzxkAF/VIZDa9bJwyspG0Nulp5W+eL0HaflsQJGk6ppt1uo9ls1oEtgWO47ne60Wo2qXb+uX2HIPtDSOPAAeNlOO1N8P6gYCDdmZ+HLgIM4fvqcXjY2bn7mmBMO3sRPiMc3+H8eqOy7ZUhtEEhwM53HAoW8KCJ+58FXev3h85x7kfC88l+u9Rlu7/c+/P7dXXjz1ofbpt9h7Axd/to/9K6TnNy5/3Bd2oC9uuBs0PO+fD9O35bpe60fQg+HHrPQQf4XpCC/VzX65JmmWqAi88Kx4Ztj918sgbmjrS6cYsg92taa8jA32b3OiyHgVDW19ZKW5jfLvBv/+wv8NlXX0FL4Pu/8238iz/6EfJsu+OjBsSOQuN+ve+uA2H5AICs9vo7YTtXgZoKX1qTG+DXNXueUR6Q/W3n/KHxsrtPuuun1L4d7rJ4jdlllau9/jsEWu2P7zcaU6+py6Hf7wNR9t99CNzaDyQ59B77GdO9KERRAmNs0Af2fMyHyiJ2xv5h8J/2LoSU7+tfrikGdt3bt6VcqHa+fahcQZ/szMPKldPvNQ/Xp1YxsEGUrNpOuWWwJsP53X2RCJLb9mX3hPYk3GfaqUU/uw184VjmnlMIG3xSmgxx3ACURqbX0KpAq59gPJ0gqzYwqoI0sHF/xsBA21IImyZHSGlBYAEUWnp8QAqbZ12XuVWfUfZs3m4pxMkJXry4wk8//QQ/++gT/M3PPsLV7QyP330H733vHCpWmExnGH+5QrfTwXpb4PrmGvPZFK1GE7/7+z/EYDjEZDbFze0NqqIEBcu1349bFcIHDy7QTJv45c//FsvFGI8fX+CH/+B7yLYrGJ3j+fMX+OyzL/Dxrz7B2ekDfPe7391RYwttLc+uDCSu++buGBRCQCiBqqrHHM9iRVHiwYMHeOfdd/GXf/ljPPvqmd+bV04ZCkIiihO0Ow08fPhwJ1XWvv0/9HM4dg59zk84LqJEWR+8inF8fGwD9E2F+XyK1dqStrxKW1mBGJNdD5wy7t6YDf8LYGcfft91n81+/VpyV5lkf/0BsEMMsOWpFfW4Dt5XtH27HNZj/937Y+LQ3iUs5/758FAdD5Xn6+75+37njYHxVy8vYYzCeq3x0S9/hfVmieVyC20kiqqCgPFgd1jhMP+eEBZMFiLyi34ox2kPFhJFXrPM6UwGgk2bAiyoanX2yZQGAEgDiQqrzRTbcoVMZ+gfnyBuNtFIUxSmlnWDc1bneeHlW+nUKLItSg20uz1keeEdHMJomMpKGBgHPuvKeFa0JPApLDitJbDN1n5B0EZb0NblQJfC5lBTUsFIuyGS3NSZCloIyCiGihjNb52vcRR5OSkpbTQhc2Ezyp+GTAgriaEBVA5Ut44hK+1uWT3aHv6kc7TA9mFRFt5QWma4tsz5yP4eOkoit7fVxm42o8g5QJoNyyZwjjzLzLYgfRTbPNLWaW7l261qfIU4Eu5wactdlTnSRgoDN9G1gJSRn9g16Oyc7woAaml5qN3Nth1PFSKZeMMlAUSyzm9pn2ew2axrFpOuIFFLFykR+8UWEJapDHhg3DrXrUFV6u4BjuM6zHlO5nwkI0hpo3yUczqEG63QMPl8LrDPYt4hmMpvqKWSSOIEkbIMkJOTEZSSTt7ZyukppdDptvH7v/97zoHcRLPZsPKKaYLxeIyLBxcQpkKj4UDIIke303FBLnYuJGmELF97J7yUda5uAH6xZE7WrcvxQtBMKYWNY1IR0DPGYDwee1ZZ6AilXDRlq9M0xe3tLU5PTy2Y6BzYZCAZYzAcDtHtdvHy5UsvvWmBk6aXrz4+Prby2qMRpLNpBHAJ3s3ncxhjvHR6mKt2NBp5dt1sNsNiscDDhw+dXEstU0snIaO6jo+PfD5c5vGmJDIdvlVVebCbgMVyufR5nikFG/7t7OzM98cqyHsax3ZjYMb1AnJ7ewuj9Y4DfLFY4Pj42OXWtfmrlVK4vLzEdrvF6ekpzs/PfX5bAjAMgnj69KkHWZlPOI5jz6RWSuHm5gYAPHt7NBp5iXPWlcALWXtpmnqmXL/f98BuKNPcarV8/tiwHyl7HK47ZCcTuOG4YV5izmGCnUJYEIOOeDKLCYawfgSdNpuNz9deFIUPAiAgopTy+YSHw6G3w8Ph0B/66cBn/5J9zXFO4CqOYyyXS5/fmFLcBF0IPvDeRqOB+XyOm5sbXFxc+LY6Ozvz4DjnK4FUm9bAMvypBsC88SFjGqhzVW+3WxwfH+P6+nonH3WSJDs5vJmrPYoi3N7eevsQ5qUnkJGmqZclJ1DO9wMW+Lq+vkav1/OAUL/f9yDNcrncAVkpkcwgFMpaNxoNFHmBVquN1WqFrVOs4HpIdnqSRh4c4zxjG7TbbSwWSxgBdLtdb8vJdo3jeCdXM/uB4JwQAkdHRz6vNgAvc357e+vluDmuKXVMNQkCcATaFouFP4AwvQCl1sO6M50Axz7zNHMcGGN8+3Is9no9dDod3Nzc+KAMzheqQxCo5b5xs9mg2+36AAU6hLTWaLfbvv/JbKaEONmqdPBxjhEoD4H0Zhz5crItuDbTbgnUTGZKl7PPvapEpLx8NPde2+3Wz5f1aoVep+ttCu05528URYjTxNsr1rUoCq94wUCgfcnuMEiAgCWAnc/4M9cFuDoppTAYDHbsCe8XQngp/r4L3CIrmDaKQR6sL/eE3GOxrWkzKWPe7/exXC4hRM0gp921oFzsHSAE5tleQggfUBfHMU5OTmCMzc9OJYvhcIjFYuFtP8vN8wTLzj6j/eccZV0HgwGklLi8vPTvZHAF00NwTHA/xvlAG0C7w3ah/eL8pt0gUE4gP5xbnDOsO8cexxvPUmTpL5dLLynOcvE5XA+YaoL7KNoJpreR0oaOli6VFMF0AuDh2hc6GhloxD7kGsu1lXVh8AfLxXHJtvCBpa7sPMyzzgwIZNBV6MA3pmaJc/zQkWwM/PjeLxvXd44T2iemD6B9Zh/ug4/czzJwjffQhv5dr302AOf1vqMidJb4+3XtsN792y5j1RjtfTzct1nQGr79gNq5ZIxV7RKGqnAugEXUTNCwzLXjv87Fyvt82aVElNgg2ihOkXhAYDcYuMxLlE6lgmOK7wnHU1G5gKa8wLbaoizc780KhTboDof4vT/4A4zHt/jNp59gMp3a8SSlZ5ZY5qqVX4S5CxDxCh0wLGpRFFCR8kEtxhiMRiM8efIEn2U55tMZxuMJSlNZMLnXxeXNNX78//or9Icj/Ef/0/8J/vW//tf+TNNqN1Fpg6LIsK3W3qesdeXfEfZ96JiqFeKUZ2Gyj5hK5r0PvoFnX32Jj37+U0zHt5hNJugPBhi0m3j17FPM2j1cPHwLjx8/xhdfPcdyY9fwRALZdos0NShhsN3a+Xl0/hDf73bx+c9+ii+ff4XJdIKLh4/wzjvvovvoDNPpHM+uXiFKGxgeH2P0T/8p/uqnf4vPP/nP8IMP38Uf/IPv4nd+50OUwuD6ZoJICyiRQKoUeZ7B+jxiKGlgUKGqShjj5PqFtn3oCAjKqdrxjGp0PW+EFo5raM9f9ixzjmaj6dZzMmUJajllvhCqcH8XuCsTedfBeGCSmxpsqMfUXadrON4O/WxL5d7r/+4ADHEfk3XvvXsf7zt2w/q9DrDav/iMEKgIfYaHnrvDBnM0cuungu/DEHgNg6v2HbXhO8Lvfd11H2C3v/btg7m/zbX/vXA+77zXGM+u958f+P7+73cUJA48O9wzhs/YB0rf9Nr53o7ttLLpWmtAVxCBk3y3PRWEqO6Mj9df9Cm6fncz2/sSK7LoBFAZKGjEvQ7+6m//R/yb//Z/wO1sjpOLM6SNJr734XfR66aQql5XuMZ8bSnMXTtAG6G1lQPmFSoMVS6NB8eWUtIHpysVgekRec4IfYr7bRj2Q1iOQ9c+uBKO5XDPEb7jdc/eXyf3f7/PNv5drv1n3Ddf7/vsde++z9btzwf+nT68cH2t3/eaOvriiJ3vHbrPmN214f5niloxJ6yjm4/h7/vpL+99PwPM/Ebwzitt2+zc4G6SsCoo/lUi+Lf77t223t1n15+HbSUgEBEhh4CEUiycI/gJASljRDJ2RHKFvACiuIWzi7ew3JTIC6BEBDBPvCumAaCd/DT/XxiBSNQpapVSSJMWmq0GBID1aoXrq2v89G9/ip9//ByfPXuJq8kcuVE4f/w+3vvdMyyWEyy3a5hNAYESqtT4/DefYLtZo9vv4Vvf/jYeP36MrCzw8uoS2zxzzGkDUzkypTYo8gJCAI8ePkSjkeBP//R/QDOV+OaH7+CHv/sDHJ8MUORWCvzqeoyyMqhK4B/+o3+KJ0/ewtKpX4aqEQD8WObZjv1z3/iwY7PuIx+8riL84R/9MT755BN8+eXnTrmx9j+XlSX/tdptjI6tpDlgFaW5d70PZA3HzWttnBQ+UCpR1s8YxREaSYInDx+h3Wzg2bMvcfnqEhIC7U4LxXaDKkgXJqVEZayis9tU3Tmbhf/dL9P97XZ3b7b/PPeXg886tK8L91C058oFcjPQXWvua+/uj8Jr96z4epWa/TqE68qb2Pn73vN1Zfz3cb0xMA5jAcNGGuHb3/omZvMV/os/+W8AGUPKGFIqwETeMUZgCKglFKALwAGkdGpwsANA5SSyIYR3zsZJAl1VSNMG4iSG0QZ5XgIGSNIUWWZlzmHg3qmhzRZCG8gqRnaTIdMFHjx6C7oqoaSVh5BSQiqFRrPpnVyZA+TTNEWaxNjMBTabLQajY2SbNbarFXRZAsoizVIRzK/zkDj82xpfIQBp5dQjF3nvo21cnjYpJbTLJ54kiZWeqGwOY4LolG/jgOYzLOhqZdilAIxjCCtKtYhazkQbAyPt4UOHA8s4pre2wLgoGQ2kAUgomSBNrLy3dbDZCCjl5DOkcrkWPCPGwIYwuVxGUkLFrt6COdOBorDgu3C5qrQ2ECqybSclJKzRlw5Yhq6gAORlYQ8FsKC1MQgOt9ZI2XyIBlVpmd0C8NLocRJ7KXDpwtyltHnrtTaQKkYcO1ZOVQcOJLFBUZZ2MYyMH9d20kZQEg4qdxM5GAcKxh5G+bsbe0ZrCLcAKQaGhIEJxkplSOkc7VJBu1zzkWN0hEbvrbceoSxLDAYWgEjiBM1WE48fP0HbOTkbzQaOj48AY0Hc87MzGFjnH9lVNjjEBlRYILYHsl+iKEKcSBgU6PUsI0kbDVFWgCgRR9YWTCYTrDdmR+KVh2AeALiJIPDIXJhhbk9jDObOeR4yps7Pz71TdLvZoHCO9qqqMB6PPfDNfKyUVCRAORgMPGA2dY6wJElwcXHh60rHLFnCRZ5j0O+j0+l4AMmYWnYVAM7OzrxDleDn8+fPPbubjuCQgUqGHNuKDm8ycMmcK4oCo9EIWZb53MMEStvttmdUMb82xwedmV988QX6/X4NAAM+p3Or1cJoNPJAsTMCVorYAZplWWI0GuH8/BxXV1ceKADgn0GHOwE3glQEBt9++20PfoSRicwjWhRWsvnBgwe+fQiiE0g1xuyAg2R2EFwWQmC5XPp3EuQhG/LVq1fodDqehauUQqfTwWw284fPMCcrxw3/ke1GoHs+n/tIS2OM7zc6a8/OznbYcAQjwhzWdHrS+UxAjsDmarXyoBxg5yX7lWOJSgBkNTPIa71e+4CDEHC9vr7G2dmZBxY4/wkODodDty5Xnh1JO8F3MOc6x38ol1tVlS8PxyMZ1cxH/erVK98vQogdMGy73fr8x8YYn78dAK6urnB2duaA5YW3I9zsca3N8xyj0ciPI5u7uk6/QvYsgyi0ttLT3KPM53MfANJut5EkCW5ubrDdbt06LKEc0Mp2ZUAEJcTni6mfH6vVyjtWQrCvKjXOzs48mMQxzfubzaaX16fdqaoKvV4Pz54980xT2oGyLHFycrIj6Ra2/9nZmbfJgAXpw5z0tNMEwDudDjqdDj777DNfz36/7+vJ8nIvRTCUqgAEB2ezGYSwrF7ac4JttJH9ft8rToQOlfBeSuET1DPGeIA4zA/McRGOhzA/ehzHVlbKgSjz+dzbGGOMD1xRzqYQLGKbEuRdLBdouLpScWGf1X98dIzKBcaw7RhEQOB26UDvKFivWP8kSbBYLPzcpz2iAkLozCLYTtsXgoqhI2E+n0MI4YOewvWu2Wz68cT9IsFM7j8JNHNtp7w1xxQD2vaBTwaTsdxkmYcqFBwnBFGpxALYvf5kMvF57KkyMRwOYYwFhfketkEURbi5ufF9yDYJ5xTLEqb/mE6nHjBl+4T7Ia7NDKQKAV2uS1TQYBtyXDOdB21dOE75jCzLMBqNvD3ieOG84lrDtYWgNcddu932KiW0DWybUEUhzKMdx7FnvCtRjyEy5GkfaCs5lzjvOee4vrOsLCdBd7YH1y4GJxLo5t6AwAmDUzimCPqzH/iPdoDrKtdW23YSWVanKIDbB3FN4Pzn+sB1nOsK5wnBb14M6GD7G2MO9uff9eIYPeRM3neahG1BW0hnkBDCuSntua/StZNfGelAbQUZKXvOcOXmfip0EhtKCJoaZNXaMWKBnTL40u05he44O3XN8t2/OLaklD6AmWsOx1PoMNFau4DwChVZ/mUFIRUaSYKjo2OoOEFWVWi322i321i7/Q3gGMcVU2K5s6XZlUo+dAmx67gp3LinUsVms8FodIT1+QpaG0ynE7++0P4sFkv86Z/+Kf7Vv/pX+NGPfoQf//jHWCyXODo5hoFzuitYL6QLpvY5Lff6f6ds0rKbqNZGn4GADXxrNxv48FvfwnIxw3w6wWKxwHY5R6HWmE5mmNzeINtu8fZ7H+LRo0e4vR27FAQZEqVQFVswgNsAKAF0eiO8+70foNkf4eblC1x98Qzleo2H772H7kkfYhFjs9xi8vIF0m4Db7//AbaLJX7y+S1+/fz/gf/xr3+B3/sH38K777yFZqOFvKwwX6+BxAW2mNKloDNOOc6e+SSCYBL+nWw296MQqt4furF8dXXlgvm6aLZaHkirwTaXggy1c5af12PcegGMc9LvdgOZ6q+/LLhQX69z+GJ/TPLWPSyEAfR83n1j+RAwvn+FDs/XAVH7jtF9Ruo+oByO3fDZxhiPoQghIQygRS3LbdMIct9n/VbGHHaWh+V5E2frfX87ZM927637nmNkvylDW77r+N99h3dMB/ti2vM3vV4HLITBVyEwt+9cv6/u4b3hd/mPa4Rtd5JznJqhLv33mKrSjotde85y3Fc3Xz/jgpnMLm4nRAQNR6hwzy5KW46y1Pj+7/wAxxcXeO/DD7BdL7BebdBsWLZqDQzcBWN82Q+Mh7ttRZC9bqN9skx4NwNFbcCm8vdyLxqufYfmDd/Bz8Mxut/HBHX5t/vm9906fX1gRhgAFz7/dd8Jr/sYo/vXfYDZfpnfNChmf49y6N3h++iX4l6an1dVdSeg5dDzPOh6z/sOjbNDzxLu/0xgzPf7fe/bFjeAX8kA79cO6rkDtL+ObVp/z+MODhRn/erx50u8UzZfH6HsmukmtPHPsjiH4PsqtzYIWMa4cSkZpLJtoQ2MqRCZBLqyJDIhJJqNNk6OYvz641/j1ctLnJ6eIY4cc1o4XEIql/bO/ayclHqZW5WzLLcp7DYZbm7HuBlPMJ7MLAt8NsVsrdDqdHH+zimiJAGEwGY5BYoc+XKD9WKBzWqFLCvQ6/fwzjtvo9PrIopjjKcTrFeWKCXKyhHggMpUKDKLt/W6HfT7PWid48//4t/iyZMH+IPf/z6ePnkIKQSKfOPP2PP5Etc3E/QHI/yD3/sRsiz35IMwMD4MSArXbWBXPYL9Zlx7a02SkcZms0Wz2cI7776LxWKBn/3sJ+68n+w8x0Cg0W6j0WxiNDyGclhMVel7bcV9tulwuep74zi2JEGpEElLDjg5PcZiPsdkfIsi36LTbQPQyIvC9r+wwbFm7x1vZvO//m/3Xfvz3Y7nmuzAchwKBAzxQv6uXdogBqVLaQ7Wg88I15VwvQj/9iZ12P/e6975ut/317A3uX6be98YGE+iBBARIm1wenaEH/7w+/g3/81/i/liCQOFPK8jtoUQO9H4dG5ESkGKeoAShKFjP01TaGOQRhEiFSFJYg8iJUlqcxVIoNmyTvTNdoOyCjrZbSYkNIoyhylzpNLKZRd5hmFyDC0ixHGKsixQkBllkVpkeQ4YC4DmZYG40cTR6TkipZBvtri5eoXpZIJGYhm31ilQ15EOH6PtsV5KiaLMneEWflNfA9fwEuIVIzkNUFal/dxov3gwD40d3E5SXlkpSUp1GmMseCqEN/hkdWtjsC1yJEmKNE1gDOUVLfhsYI+yZIJrLWCEBe+jpnW6myiBkAZFVdo860pARhK5ACAp6CEc2Ouiq4RAISVkZHN9FZVGo9tCO20jSVIP/HDjVzPQ7eJsZfCAOImx3awxm1k2ULbdYjOdYLNcoNKlC8wwtt6RBZkrB/ILaWUvhFQonSOtqjRKUyBJUghY+XCtLUBtqpr5kCQJdGUQqQSRSp3Drs77WBQloGFzdgcb23BhsI47m5/e5h+vAPcue6ihcTeIIukXLjLs0jT1LN922wJN7733Ho6Oj/Af//R/jkllc13+r/7T/xRxEqHZTD3wYB1VNrCkHjslxuNbJOkIrU4DaZKiqkrM51sIoR0AmWG5WqLZaMLAqTyYwkqIG2C+XCDfLhHHCV69eolOpwNjSu80TBKFLCt9Xt/RaOQj0ZiDmKAJnYyc62RSA0AeBNhEUYTRaISyLHFzYyWDLy4usJjPXaCD9M7pTqfjndLj8Rhaa88kHg6HHpAjW6vdbmM8HvsclgQDJpOJZzV2HSDOXNYs78nJiWd2k7FM5/Pbb7+NLMtweXnp60UwYDqdwhgL3lNqej6fe1YnGWetVgu9Xg/j8diD4r/4xS886A/ULHY61+kU1lqj1WoBAE5PT32u6JubG4wdE4SbHQJPvIS0sspKSs8+Y3tSYpXgRChFTtZmGLFPAJCMfrLiKLnLwwNlqpvNpmffAxZA2GxqmXrOT27kuOCz78gkJGOw3++j0Wig3+/bHO1V5Z31HJMAvKM9BHjp9BdCYLFYQAjhgQM61ouiwGKx8GualNIfWpmDnGNKKeUZ0gA84zKKIj8e+QwCC8YYz3QlIGGM8TllF4uFZz7SgU72Ltn2BJUp70v2ehzH+PTTTzEcDj1YOxwOfXt/9dVXGAwGaDQa+OijjzAYDHYCAUJwYDabecDryZMnnhU/nU59Lt5QZpnPoorEYDDA1dXVjgOcoOyrV6/Q7/eRJAmGw6HvMwIoBOjIhmY7hps5gpEEVa+urnbyrId2iP3O8UbpdrIQZ7MZer0+jLHrxWg08jKv7NPb21ukjVpqmYAcDxmWmdlEVe6CW0IIz0Dn4draWOMBc0ols4xSSq82QFCLoDbBHrY7A1MIoJ2cnPj+4bxi+oVOp4Pb21sfNBBFkQ+eIHBJQFQ6W8EgBNoJppOgnWJADucr5yztyOnpqd83Ulab6SiklDg/P/djnGoczDtOEIssccpQc19KaWwvSw3j5/N6vfYBIWFAUmWs/eQ8o0OFLDsAGI/HPpBmPp/j9PTUK3wkSQJTaWxd3lcqXNBGhTnEi6Lw9i6KIvT7fb+vMMbg4uLCv5OBRywng3U4loQQOyx41ovzg/Y2POBy37FcLjGbzSxL0alBEIAm+EcAlIcuBpRxXNIRxv0d7QUDqEI1mEajgcFgsGO7CehyDvMZDCjbbDaYTqc7dpzrCNcFAq55nvvguSzLvOQ6FUTCFAd04DLYKwRoCYoz0IBMdNZRSumVNKbTKU5PT/1az35hnWjTw9zvtDtkHjNolux02g5KvDGYZb1ee+CewW/cpzLIhG03mUy87WWAB20ObSXLyf4cDAbeVmqtfdBGGOjIq9Pp+LlBID1McbBYLPyejjaINpb51rkP4BoYBtGxjHQOkLXOf2HwdchK5PzkmCSQzc+4HofPCZ8Vsn4ZpMF1iHLvXPe5ptBe7svZ/bZXGK2/7zCtHQfmzv3+X/AsY4xjDBvfn3wenbdh+4Rt6p0vwbNCdhsBv9/W8bPze1kh8M7Wn4sKWkoLUEtd5xuH8DmchaiZSgamBnNcgKzQNk1UmqSIkgRZnmEymeJ0NECv38d6s/EMFytdGhTigDPmkMM8bPdw/IYBI41GA4PhEOvNBqvNGpmz/RxnVvXlBn/913+N73znO7i9vcWXX36J+WyGVrsN5uc1Rjsgie112Il+yIHIvML2Z9uvq/UKg9EIbz19itn4Fl989jnG41sXcA5EiUKRbXD56gXOHj5Gp91Gtt0izzNkZYGmbNhzZlnCQMLICrmq0Oz0cfH4KRppEzfXrzCZTVF88hucX1yg0+kh7baQbzNs1husZAQZxTDNNlZliY+eTbHc/gzPL8e4OD/GYNRBq9tEs9GGEBLbbYaysOwpAQkY2iLn1IaBlhowTo7WGAg6zSEhpbEB/9LKpRdFiW63h2azhUhFqKrc2Ww6CC3wH/b7LthzqP3rz7QmEPD6OSKEwJu68/afdGj+CQci1OW85+nmLs6+/zvr9Dqw6DAAVrdFCIbT2bvvOK7rIcAlJgR6dkFBKvPVdmvfobvbFn9/YHz/CoOHDrXH6wCtu47+3ft9++yX9zVtf+gdYX337QLXce5Rwu9yrdyvxyEga/8d7D/m8+ZYpH9Tl/nO8+rv7yos7j7zcPvxGfSv2ZZ07SQASGHTUwrtwUNdVmg2GhgO+zg9PcaDB+fYrFowm7W1sYZ+hsPzO9xjf52z3wJ2JCkJKNsQ9fNcmVgXBlWFKgv+eQfHzV3AO/x5v5322y+ch/e195063TOH7htv961J4TP223EfyH6T+frvY06/yX37fcC9aQiMK6X8eDxURv8es7+K407fvm5/dWccHCj+obY3JigLDvelm0Ae4PaMwJ0b4cBrzpX6me5B/mchaxXUuzYDO5+DvnJ5tw15ychD+YBxOZsF/D7OSANhBKQurPJupJCkCRrNJoAO2q0G1os5uk/fQqSsamlZVSjc2Ydz3Z5XSpRlgeU6w2q9xXK1xmy+xDovsFhusNpmKCsNSAXZGqHbaiBNI8SRhDEV1ssZtusNyqJEvi2gK4NG2sPJeRvtTgdJmsAAWG/X2KzXqMoSSkgoA1RaIy9zFHkFKSMMBiPEkcJyMcOzZ59jOOjgd3/3ezg9PUJZZFguFlivV9CVwaeffoYXL16iLCt8+K3vYXR0hNv5BMYYf8YJ10b2B/ex7BO2x+46Llz72DOZVSZr4PT0DEdHx/jlL3/p0sXtpmqttEaSNtBOrWJswwe1l26/hZ1yvemcBALg3Rh/Nkji2OKMcYxep4uL8wdI4gjPrq+wXq0ghUCaRMi3GYo8B5UDjDYwolb00MFc3J+XO3Y6uA7dt//zztnt4L2Hg5t43uDPQE1CDFpmp12+7jq0R7rPRh+67rNz+/sRPu91z77vWW86Jt7kevMc4xAoiwIwEkW+RRwJfPc738T/80//DNooF/lWb5r2O0dKCSUBrQtfeDr3uHDQ6OZlBSMktqu1P7Svs9w1IABTsyDt95wcuYIDye3kLitrAGfTGSqj0Gh2MBqdWFDSGcOyLBE5kKXdscBPghTD0RBVlqEqS2TbDaoKOHnwEK12D0WeIY4iKCFQVWQrOYe5UqhQ2lwEKoJQtaEwwk5K4+RPmGNcqRQGVS19JQW0cUxmY6NohHI5DaSCLisYIVAZARUlSJSBLgsgsoO3KEtIGWHu8xA7p7AxQFHCQHjDXpQlIifpqIVEASBKI6jISp3neQ4TKVQQUEkKFUmgLCCksNE2jnHXaDYghcR2s0WadiBg85xWWiPbZpDKGs7FfI7+cAiVhKxo4Z2Cds9v5T2MlojiCGVZIE1iqGYHqtFBFElIoXH5aYkyWyOKGN0kAVSwED+QptbwWseZZaBA1M4ArY0NL4NAkkhUlUFVZRCwMuS60qiqzC/8jUYDq9UGSdKAMTbfu5KRzU0mAcDl6Eys81LEwo7FOIYxGmlsmV2dTgePHj/yDNKT4xO8/433sVzOMRgO0G61ACFwenKCJE1htGWKVlqjkaa4vLoEGQJKSqACpuUE/8tf/ycQQkJXFqDQe8bULyj2A1RVCaVcVjhvgK1yAEAGSL0JF8EmiGPX9+GN9DI8xhirfFC6nOjGQHwaMFWMsX3gbYuT3xfOofUc9jtB1Jo3fr/aPWjzWdKxG0MnVL0IGv98oA5i8cE7xgWHmNpx7B2gQZALvxs6aHVVofq4ZsNrbZ11UgorC/NVLfnmF6GgHwwA+amEdgwpwG4Q2C4G3NgJr6YhBAM96s1IVVW+zdzudicyk/OMbefb/4u7tn5STPx9ZVlCxjHee+89D1JRTpwMP8rwdjodH+TCA9zGORkJGC+Xdc4WBgAIIfxaANQ5XOlENMZKP5LdR9tFUId9RllcIZzKgwPKKM9MKfkQnOUYInhIR32WZb6sZL8TgKWMMgEiSoSTBUlQmWxWAuasg1LKSwhzrJGFT2BTCOHBvmaziaurK++c73a7O7LsBBloWwjSGGNwe3uLTqezI9MGwDtgCb49ePDAgzFCCA+GKKXw+PFj336PHj2CMVYmm4AUATZK877zzjs+6ISgAAEGgk/T6dSDTuxfziGCQGwz1sMYG2AxHo9xdnaGsiy99DrnJwEuMnEJUhHII3hGcIvAbpIkePXqFbTWOD099awugrjhnoVgbxzHfpNN9q4xxssS0wFeVSWKQntpcYIlDBBppA0oZcck1SPIKqYaAQ/YlPjsdDoeRO33++j1elitVlitVj4IhKx2zj+qECyXSzQaDc/AXy6XGI/HHkS6vr72edypQHF0dORl/Wlv6MDfbrc+8COcSwSjQ0CIdjcE/qhAwPcbY9VMaJ/JRjfG+PLzZ6ah4HxmkIUxtTQ2+4U5WmlDCGDlZYnMgZPtdnuHLUsJe7LZ6ewIwbR2uw0VRchLC0gKITCbzbBcLj2YyLHLYADakhB4M8bs5HDm+FmtVojjGL1ez8txE8wliEd1EtrskGlNYJj7jTiOfSBDkiRotVqYTCY7/RSCZSw/25d2xxjj+5GS9gR+Ce6SwUxbwjWBfUSglfOCSiy9Xs8zdQn0MpCE6zyVGTqdjq9nGEjBscO/sa1ps2lnQzl31pXqCQB2ZJo5B5fLpV8vyEAPmfXsx1D1gYoxAPz44nhgubimnpyc+OA/AF7ZhOUmWM4y0M6S3c4AH64DDBThuCXjmvaW/cz68zvGWAC4LArM5/MdNQP2B99PdjaBd66LoRoO1zfO9aIo/Ge0mY1GwyvC8P0MOOC+j+3H9uZaGqYCYJ25DnOesI3ZX9w/sO60QQS+Q6AgVBYI1y3OXwYLhPaFf//7HtoPOYn3nbFu63fQWb9zH+jU2gVO+R0pxc4+TkqJsqjcGZTOaUPv6V5J73Fq0DlpXOCzgFfVYpn4WAT7dZ5X/N+0PadobVBC3H393mfcJ9vzUgTKjxoYFGWBxXKJm9sbnAz76LlUFZvNBnmWg4ce+h78+Qlf75wO253llZJOqghKaXS6XQyGQyyWC1xfX9l1qNVEpJjbPcff/u3f4J133sFbb72FSlf46OOP7ThP7fpgeQGU5b0r8X7Q6Yb6vBXeq5TCertFq9PGg4uHmE+neP7VV5jPF0hihV63j2YjgTAVxrdXSNIUw+Exmo0EUmhsNhu7jigJbQSUKIFSIkeGRMbo9IeIGymSThPV559iPpkAZYWLi4foDQZotRuAANbLJZrtDqKkCcQtZJsMv/5qjOvpGBfnQzx+eIxHj89wNDxyez0gUgoqiiGhLOgFg1IHCnl04lKSVQgr3ywElIhtP0sJBet7GY2OnG20fikbQMa2FXttDBirs1+PE+/wEzwGB+3MtG+HnP91X+3Mga+5vg4Yv2t/XjN2xZu8czcw4JB9Cx3GvM/OG/t3+hfqe3ZzxwIHWKICYI5qAeycg1mOMCj7kPN153k41DZvft1X99e1x/7voR0Pn2fXjcPfCQfUHVl1Y+60PRD4Evac3PwchiDHfn72mrlt2Zgm6MfDDmmmNqSP1tbHBZt7n5LNy2wMUBU2yMc+MVRkvAum3jdX9sthbRzcnHRLi7A+1coFFAkByMiu0WmaYLNZ4/bmGrc31+h3W4DiMxhEdjgVwX6b3ncZ44LSXPsJAZ9n18F5COcm/SBcj8mGDW3DfhuF5dgpj+/Ouj9DG0WvE33x/IIQNfEHBjufh/uHg/XfW39e9/f9iz7Dne8fvrEubTBmAyT24Gt+m3n/unsNO5L3ct9n7qpjhJZ1f232v9dN738N6yjqD3f2I4fKadswDO87dJ/zk+rDwQr79xojd8p6aA92qEzhNm53+eHI37vvwB7Sl++e5UtKoOKYlLa9PbaipCNoSqhSQwiJoixQGY3K+YvzosDV5SWmjx5ByAjz+QJZltvgRXf+LJ3PYLPZIttmmKwrrLMCWZZjm+UwUgJQEEohTlI0Wy1ESYoKAvnGgtxltsZ2tcR2swVEBKlSNNsttDs9DI/bgAE2m7UN/s9zmMqqPqHSQFVBVyUKbZnMnXYTzUaC5WKOV69eYDK+wR/+0e/haDTAYjbFcjG3+9r1GvP5Ej//+S/x6uoKjUYT3/7ud6HdXph7ffpeSJTan+chYHtIxcN+XpOXzh88wPHJMbbbLT777DO3PlNp2f5PKIVmu41m0wbhq9gqCIeq0jt7onvW132QdWf4uD2vlAJpnEBKhWazhdHREc7PTpFtM1xfXaHIc6RJBCk08myLsqoQCYuJUYHAk085evfeu1++150VDs3d1+9XcOf+8L3h/qcOXK/XdyWlJYz69X7/+a+3i6+7L1ynw8/e5Nmva7f9NX7/v/fZvzc5o+1fbwyML+drDI+GEELBCImHD8/wz//5P8Vf/81PcHs7hxCRXzjpuAF2oyetU7XyUfWhLKFnJkQxqrLOZeejSSqbjyaOEwghvTyydAtNksRYbzZQRiCKW8jyDaQwiOMGhIyxXm1wc3mNXneARjNG0mpZlrayktZlVTk5cellEbUGyqyEgEJvdITJ7S20kKggIWzwMbQWiFSMNI2cgw+QMkGSWClxI6yckzAautLWQAvpEC8NbSRghP2vsAdTbgV0ZaOdrVK4AKREBQERKSjUhqgsS1Qigq4KxEkKISPESYLjbh+NZhNbl6+y1Wo6GR6FqrIsazpAhBAojYZMEjQaTe8spOPP9odwLKE6702aNpBlW1RODl6qFbabwoK7sGzlzdYyQk5PT9Hr9RFFCuvtAnmRQTsneawk8sw6wsqixHpTQSBCmqRI0wjL+Rovnn+J+XSCJIlgdAWzWUCYClIAKlaI4wjr9QaWeW2dCkZYZ0SaKuiqsJHEQkNEApYFXcKYCiTKKmWsOkFV2u8lEfKCAFqOViuG1gWaDcsi0ga2/xuRl9t98OAB3n33XaRpWst/Go0kVj5fLXPakqVnAYYNtK4wmU7R63WxXS+RRBJGa1y+vLHBHHEMJZyRCw5MGhq3xW09YWvi7+uvQ/dVX/P33/Yd/9+4it/y/v2y7/++/7xDbRJ+9maBV79dmf5/9Qx3KaXwjW98A1IIn5e62Wx6md3r6+sd4If5oOfzOZ4+fepZppRY3mw2Pt8rwSoyEaMo8gAvWXhc1MmE489UHuBzALvmUI6WrH/mYieoc3Nz49mbrB/XKTIXCYBw3SEzL89zRFHk881eX18DsDZ4Npv5OayUlbPm2iaE8BLklHimogFBToJELFMI4pPZzedyo3l1deWZwqFc+WKx8OzAx48fe+AilGdnPwwGAw/MMwCA7Xt+fu7ZsWTnhmzWUPYfsJsPphig/Dhznqdp6qXwAatUwrzF3W7Xy70zSCKUkA+BVMAG0V1cXHhA3xgrXT8ajaCUTT9ARwIB0263i9ls5vubbGiCVPP5HADw5MkTD6ITSA0Z+0LUMssEpNvtrlNYsfuc29tbz3hmvZI08gEiIfB0cnLiQVGOO5Y/zBe/XC49a5zAE4FkMv6Z1oCqDxw7bD/KxDL/MkHIEDgj0HR2duadYlz7KW0cSvwTtOTzCVaSsc1+I+uXQBrnW5iHl3L/3Du2221vI2hDCP5yLPDdLOdwOPRgNZnh2gWVaa0xHo/R7/d94IKXQV8tsXEpNgj0s4263a5Lc1KDxQyOEkJ4UD9NUxgpcHV15Z1YlJTn/NdGI99kO8EnVESgraCTi6kWyNIn0MZ+J3AOwPc5xyXHD5nt4Xxg/9zc3HjbR7vFYCN+J8zfHsrTk3EuhNgJuKhzOEtfR44D2jGWNY5jv3bQnhNYDRnFPCssFgsvCc5A2hCEpxQ7wVS+hwFALD/HC8czVRiYViVce8JUKgRmCfwwEIp9JITwgUFk1nMcUEGlDpSpfJ/z2VSIIfucbcXxw7pzXeKcmUwmXn2HATFcazj/CVqHTmamImC/8HP2QRgEpqsKzbThwWymnWD/k9XNuS1lneOeag1k6IcBzVzfeeZie4c2KZx3rBPHMtuTAQVhVHwo787v8r3W5pqdwAEhauUNAuyhcgDLEcrBs69C1QTaTY4vzhk6K/4+1z4rIwzO2QULDgAikqmr6HGsgd7dy/j7IxUhdv8iKZGbcud+ujFDWU37b9dBteuo0IGLlsDsfk2F3U/TCbLvDDcMdHUOnX3fafAZ90tC2vRTQtlH57nxc4vry3r9AI1m0yucrFcbm0ew9tLa9GZBXs/7nDzh51prwJ2ZGaCdpg2UZYW00UR/MMRmu8Ht7Q2yPHNS5/Dzazqd4N/+23+Lf/SP/hHef+99zOZzvHz1ClHcqVtRKFgJ6WhHcp/raejIJChuKgPjGNVsrziOsdlWWCxXaHe6eOvtd/DLX/4St5eXaDZjNFotRHGELN9CyxKXL76A0RWOT04xGg4xixRub8ZIdRtxYksnXYdkmw1UGiNptvDgyVsYHh3h2Se/wVeffoYv8y8wOFrg5PwcJ2enmE8X2Ky3WK8yII7RHQwQH3cwvnyB24+f49e/eYFRJ8XZ2SmePLrAxcU5Tk+P0O63kcYRqjIHYLDJC5SawfcGZemkQt0ItsEKEpFKURQlpBBQAn6PrpRC6Xwb3Efb8RoEhwTzzeIjlPRGcI8DwPyHu0zl+8aSBQBef4//m3vJawGS1zzrzt9xP7j+OsfnffeH7wgduLwOsVTD7+w4Rl1aQLpAwnt/G7DrUDvcd93vqA7Leb8886E2239WWP6vc/DvAxEMMgrfcxBINnVwD8kMnk1mDKQLflIqujOWahCY/w731339QJ+jtQv1s23glUJVOrDd1CQFKaOdZ+3WBcDea3bbytoeY9zKYwy0ESi1DZqB1tZ/qCIYIaAB/ObTT2G++BybYosf/M63cdS2invch9izdgAK4nBbH+pHXjXzvfZDeCWWvfvD/UW9B6jnD1NjMEBEsIOCfjEO9NvpE84d1sX9rl0/ISiL+7b72fiWDZ9/6NoFqncBpNcCGCHosf/se+aQ/34wJ3fvr0Gl3Xvf8DowX4OXo25QS1hK3fmvcuQarsVCsCzBd8D14x7wiPsqXwwBq34SvvZ+e6z33nPnchhDFN1vn8JLi5rg+Dq7f98V/tVUVuFl1/ZVB+dR/dxdqD+8qkpDOKlz+z2bEofBxHESQ4kIJheYTKd4+eoK0/kCeZEjL0v85jfPsFmvcT3ZopIRFpsMmVOyyjObskXDBdgYq5ZUyBaipIFGo4t2r4lWmiBSLtC0LFHkGdbTCdbZGsvZHPlmC+gKSWxJJb3hEbqjEZJWCxrA+OYSRWaZytCWyKQgAK1RuTNbZexe0qr6tfD5Z5/ixfOvkOdbfPit93F+doqf/+xn2G6WVr1Ha6xXa1xeX+Pjj38FCIUnH76Hb3zjG7hxane2/SpPXALgfWA8F9PXGCpY7YyNIKh+sVhgMBzi8eMnkFLib//2Jz4dW6UrMBCq1BrdXg/trlWElEoBQiLLS6eye1/w1ZvNX97nSbpJjCSxQeb9Xg9np6fo93v46Je/tKrQzYbzSWyt+rSwwRZ25AFS12cc4xG73XNPyFK/E9z3W16H9g0+jZV7R+i7Dv9bt53wJD/lfBPE+BicxutNz6qH1rhDdmjfVty3Nh7aox5aL15ne75un/Um1xsD41IqzCZTxEmMvKqQNjqIY4mLizPc3k4hRC0dEjor6SSpqsrlwa6do7vUfnsoK41AFKd3NsyA3cSpKIbWBnFkmbqNRhMCsDmE4wRGa+/g1cag0Wii1AZGSOjK4ObqCt1eD3LTgEprtk2UWCaIhEGZZw5AlVAxoCsnD6kiJI02tLGS2EpKKEioSEG6ztBaI1KRjeA2GjBWCrzMc4jI5jUrXMSRVJFzrlgHsGUoCH94Fipy4ECE3DE1OajLokCv34eAY4tKIIpjwBjvfPK5hmMbQLBZLTGbzgAh0Ov2YCXBbWSQZe4Bt5MJik2JJE1sPYxBIhNoaGTZFrIE0iRGpSvk2wzV2ko1zmZTG8FfFCjyLRbXl97ZV1VWKuXZfGzrXmTIMivJaZyziU4n74A1lo1dliXSJIKuMhhdoaEAvSmBqkKspF+clAIgNAaDDlQUIU0SDIYDbLfW4UmAmkB/r9dDq9XCdruCUhLNVhMCAipyEUSjIabTKRppA1lWYL3Z+nQAcZCHddAfoNIlzs5OkDoGXaPZQJbljjm3wcsXL9FoJGg1U+cwLLBcTXz05zbbIptnaLc7iCKBdruBLNsgiWPMF1NMJhP0ez0AlslO5/10OkVXdKAj7TfE9pwgfDSQO6l75rNw84JRQlrTEVZvHvf3osY5oZgPKjR2VWkDLIyhLJ0zZu57UloGsz+/CAFd7ebZ4X2GB7agLoxk9pItQvoNUVVV1tnFCDdff+wwp+lIC8vu38XvuEOGruoDSxUE9YSHduvM07XDzv13537XBqxr6NCG+9xv/oMywNgtX7jg0a6w/O4PQHC/4uFor0537ve9XB9a2NX7rKaj9AiLxQJVWeLy8tLnc46iCPP53INP3PCvViucnZ15hiLlYTlew5yyvhyiZvVRGpr5tCn5zb6eTqeegRjK8dIJ3e12vcQtc3+H4A/7kWzC0HFNgItrFVlsw+HQ12U2m3k25mAwcFKXFvw/OTnxzEaCACEQx8+ur69xdHSEk5MTTKdTz3BnDlq2Bccac4CTJUvnHNMRcOND0IIABUGtk5OTwMFQj0P2dcjY5uE7zGfd7/ex3W49i5+ANp22IbBClh6fd3t768eFUgpHR0d+zISS87PZzIMeHPdsfwJAtN0EfAmysy+Yd7nRaGA0GuH58+c+bcB0OvXA43A4xGQy8UAX+2W1WvnAJqoiEGxpNBoeANlXBcizDGVZ+TWXcvQE2LlmM/CDzO75fO4PH91uF5u17XOmJhgOhx6A3jrQljLVBO3m8zmOjo4wnU4xGo38HJ3P5545y9QU0+kUs9kMg8HAl4MyywSICaTleY7r62v0+32n4mI8gMd1OgRZCUByX8d+JXhO+XU67JnXOooivHjxAs1m0wLQqpZtJrufdWadOP/5jHa77fMebzYbAAzAtAGDVB0giEZQl6oNWZYhaaQ7AROhvaUtpfOK6hMsJ21cpStUVS1rTbWKxWLh50iaJGj1mjtS43wfWf1Hg2PkRc1cDfdEBAR5P9ninI9kc3P+MyAhlLbnPpM2msAfn8vAnE6ng+Fw6G0CgUvOcR6OWV+uj7SzHC/hmKV94oFsOp36QzjHCvucz9u4oM71eu3tNgHdMDiK44UBRxwTnMfMOc71AYAPuKISAAFcguqtVssHcDDQgSA+xwfblP3NNS38uSxL9Pt9/y7OI45lznHOM4Kd7GOumewzIWzw0GQywdHRkZ97V1dXfi6T8c7vhvnuhbCy6GSy025yH0bwmWolkVIQzglOhRCuTxxDzBHONZXBHAB8HzDwgP3IAALaYM4ltgMdLKx7mAOdc4pjl/txfpfrIfeNDHigzTCmzs+57+DhOAzHNW0aA7j4XSozsG78PstEW8R++/tcocShd4rv7aVCx8z+nhWidtJUgfMqfKYFm4WbWymSJHXKIDG0dvnoPYiCHUnL/euOg8K+qN5/v6Y93sQxwxRqh51GtWModu0GbVDoHFLW87corG0Zj8e4urrCw8eP0O/1UZUam/UW0/lsp31QR6rfufbrs/+7PWtVfu7Tfne7HRhzitVqicn4xo6tJPVj8OjoCJ988gk6nQ6++c1v4o//+I/xX/zJn2C9snZaGwOjDaIo9vtl2hC2xT7gYlmTFQAJBaukpu1hwq6l2y3iKMLR8Sn+0T/+Z/g//x//M2hjHZWlSzUmRA4pDbJsgevrEs1WByenF4jTBl6+ukFZapikgtQVlLZ53GOTwJQ54iRBrz/C9//gj/Hknffx+aef4vrVJV69vMZbDx/g4sk7aJ8NsM02WK/mWF4/gxBA2uwj7p1CGoXVOsPPfz3BT37xEs2mQq/bwKDfQq+X4mg0wPHJEMejEXrdrlehUMqmNbOxDQba5RYucgdYGIN8u9mxIXGcQhugLCskyV3np3dAUvXPAGTIhufN+67XAUT2zPt3sxtv6kg+6ES8B7zav+919QqvQ7YKqOW69+1B+HtoC4Rwdgwu2Ai7YzxU0eB37wPl99/3+qtmPYfl3//ZHcN3yhTedwfgP1Df3Xa7L4Bp9936wN/DPhJ06uw5d7iO8B/gAA/cZSCHZQ3/hU7qQ3UL/7YPbgHWVyKEsP5Gx8hmOex+rZ5L++UQHmQ80DaolSFLTZY2LCheahSOMaq1RrZYIoob2OQ5Lh49RmfQx5N33kZeFri6ucRg0Pc+NXt2cSqnjo3q11xz/5zZLbtvGN/2QtSpW0KfFPc4dVoTW7v9vQ/7L5xT++0RguPh+s/2dDfu+Eb276OfKgR1v87Gve66b4yF4+rv+uzXvfNN77vje7vnvv0ysm9CxuvXXV4x4U4sgAj6OLQ9O7/eOweVNZo7+8ZwzvO7Mop3vh/e658nAI3d/awPoDhQz0P2YucdiCECpRt7ht2iKHJ/LmQ/7NvJMDg0vJK0AatGIiGEgkoSZHmOzz//El988QW+en6Jm3GO1XaDxXKJotIQ7nzfanUg4jZ+83yFKopgoghR1ELSG6AXx2CaDkmfq7OpZVmgKHIUeYbb21tslwts1itLHCwKqEhARgKddg+d9jEajRYG/SG6/R6WmyXWmzWmiwnyMkeVV3bdL23wl62ewWK9sJLjSYJ+f4Sj0QjT6Rj//X/330HrDA8uzvD0rW/i6GiIL7/83PWHJX9uNhm0Fnj25XNkeYFvfPM9/PD3fohmp4nV+BZJlIK5vNkX4Zp5Z18SrLWhTTHGoKxKFJUFlL/97W8hy3I8e/YMz559ZYk8RrsQWeN9A/1+3wZDC2n/SYEqL3b2IofXEdwZV4cAV5ZXubM8A9JHoxH63R4W8zlefPUMaRyhmSRQQiDPchhoKCm9f18I4Um0ArXCyf44358bb3odtN2BLQw+3fkOg7Z4PqZfhIHcrVYTcRQdfDaDjPdt/d13Hq7P62zj/v7r0Jk17LPfxt4faue/7zkb+K1yjMdYbVdIGgkkJMqyQLfTxltPHuNnP/0IVVlCGwkpamk5OsR8JAM04jhCWZU7Up9CSgip0B/0EccNP8g4mPl9u1jDg7llWSGOIkRO0jRNG1b/39hDonHhVaYooWHzim1Wa2TbLZJeDypNPAuPsq9kKcAAUkVWPg4CUZwgTZuIoxhxEkOXFSJhAe8sz5FlORpuUmspIIVEJGMIaORFgcQ5nraFddZ2kgRaW/nvntYe5FBKotloQjkwiU7IvCiR5bUspgFQOFZdDIFCW6B8PB4jcY6bL54984BCnudAmaPVbGKbbTF/OUWW5d5RaYyBMEAEhTzPkCapNW5FLTe8Wi5hyhIggCZg2XIc2FqjrApIkSOKJLK5XeQipWw/uD5UQiJ1EVzSbfiazSbSJEHqDJaQwoEKwKOHFzBVge1mhfOzYyRJBCmAqNFGkjYcY6uBOLb5OPv9gWPltCEEsN6s0Wl3oJREluXI8wxFUaLdbqEoc0SRddKPx2MIYZ2GBgaLuWUtKRUjSVLM5zO02x1k2RatVhvaOWCFFFgu51gvbcDD6dkpkjjBfHpjWQnZCkqWSHpNZFu38dUlmg3LWNSVxnDQw3q1gdYGSRwhdY7VbLvFkct5qrVGtlmjdA7WXqeN/82T/7WLgrPOynarA2OANLVOXOnGExmCQtq88GmjgbIs8OWXz/Dhhx96dh2dh8YIpKllRFVViePjY+8MnE5ngKkwm449O7LdbuOLL75AkiQ4OTnZYZWRvcZcpc+fP8doNMLx8bF7frXDZCRQpbXGYrlE00klr9drPHjwwMswa6197u8vv/gCp6en+PLLL6GUwmg0AlCDJBACg+HQHz7CPLFhjvFQTpsOeMobSymRuXzV4YGBTDHas0ajgV6vB6UUnj9/bhdjt3kbDodoNpt4+fIlhBCeaUewCc72FUWBR48e7QBjSZJ46VgCJnTiE/DIsszngaWjNmQICyE8I3IymUAGjv1Xr155YJCO9NvbW1TOsU/ZboKfURT5tpnNZjg/P985jBMwJXuOMqx8Nv8rhPCAIR3MrLcQNchAhzQd7fz7ycmJfy/z9RJECpnFZLkRjFoul3jw4AHm87kHTEKWd5qmPs/u0dEROp2OBzx5D/uZznCO55BReHR05NnD/X4fUkqMx2MA8PLas5l1wBJ8JZMyBM7IaJXS5n4PgQzmO6cjiEDHxuU05hgJ2Y7WttVMUQKbIWiz2WwhBHZY86wLARke2rne8xlHR0c7DE6yoYFayj10kJFlGAbWURqX0s9sGwJ2xhjP+Cabezwe4/z8HFobp/whfSADwUICfQR5KJFsDHxOdo7P5dIebkKpb8ppKWmBd9aFkuIE1BiBQjtIgH04HHpbsdls7V7GseHZftwj9ft9tFotFE7OeDQa7aQNIMuf72VktJQ2R7I1f9buEdghkM/9GecqbRHtPYNBhsOhZxkPBgMPSIaMYMobG2M8UGmM8faRssks52q18ht3StaH9pBlpHx6r9fzebxpL9lHoTIEbQWBqbCsaZruvDNNbZ7ZjXOGcz9E0M1LJxsr1co5ylzVfK8UEqUuvU1nQA6Zv1rblDJJFHvbdXp66mXo2YbT6RRkCxZF4cvLtYjAItcdzge2F4OQAPg1MgxAZX+HawZBf6ps0BnBOcE9QRRFXlqfwCTTAbAe+4Ai+yBUMiAwzKApjs8QcBVC+LpXlU2zQzvAdg3tAEFnAsxcazjHw8AHridlWXo2tzHG9yXXNdaHNilsM86Zfr/vziJ1P4ey6Ayq4hmDtja0k+zHrgNw8jzfkWkPpdZD5xCl9Vk+Bq2QCR3aI45jzhcGW4Uy5pxXXJs5D7QQ0GXl6835zTHGvSXXjHDMhBLmdG7x91DJgvsj5q0PD8wcS9xzsb9ZXz6LwQ0cd2G7MADEBr9lAIRf0wjIU/EgDB7j90LZerYVGe60reH6Gb6PY5Pf/bte+9/fd36+1mFhDIwOVC/uOEcUlBQuJVkd2GPTucSIopoJf9972EeAzVd9+BKB8/eeXHICKEPpIwO/hu44VYwDxkTAKA+cSh5+MZWX1HSR1PZvjn2TGWA5X+D5ixfo9HrouX/9fh/L9coHaRj30DAv9+ucRhwD3qlFWU9nayIVQxsgbRj0xQBPnz5FkTNti/GOKiklut02PvroF8iLHD/6wz/Ev/yX/xJ/8id/gvV6g2ajgSiKUZW1SgHLEpaT84j9JIRAJCPoUoNAi9YaMo4QSYFtXgBRjLffexcffu938Olvfo1iOsGwP8DpyTE67Zbdz6BEpARgNF68eI7e8BiPHj3CbDpFvt1AVAVkWiJuxNB5iUInqHSFTV6i3emgOzzGD354hs1iiauXL/Dqy8/x8S9+imYrQafXRbvbQ/f4GIUGyqxANrtBaQATN5AO2mglA5iqwjTPcf1igeLzG6TxJVrNJoaNBN1GA41mA0kcQSogjhWiOEIcK8TKKs3FqUAcRxCOGDFxQa1ZlkFIBaUiCKEQRfDnudo5biDlAVZMAJrtO/CMm4/7Uyl0rHrAXes7fboTuMe/ud/3g0ruG6OhM/nOJWoA9T5H476Tk/ceeh/LtA9qhI53CzC44F1jWb5huwZP9MC4krtqCOH4P1Te/TIedjgfvsjmfN39hwCi0NG7D2Lu1H3vOeEzwvYTgb3zoB3q/t93PO/UPXjHDljg1jH7e/2u+xzP++8IPztkG8O/27oYD4Dz71GkUFUSNp83YNxeSqldYJK2q37+YWlz+7NT1DQ2nkkbyx4tSrePKUtkZYWsyhGvVlgXFb7x4bdxdnGOwdEAL776HE1jfa01cCBQVXqnL0M7v9/34VX3NwOl6vEfAhthm3EfWKvDwLej3c9p17O7oFH4aq0rCHOYvbdfVhkpv48M90PhuA3raYyxDc1/4RwXd4Gz/Sv8al0W+DoFd+58dqj8h+b+ITDm0OeH7mf77wfchGN+t83rv3tlhL2gICkPt/uhOoXnhLC9fTuaXTBun6XK71Sl3rkvVKoL/5uX9X6Zn/M8WH8O6CrxPcL+19qRAX25sBM0sn/V62QBKTVUJH1qxn6/61UHmdIojpR9nytXpbVNZak1yqL0PpmiEMiKa2y3uSW1bbeYTGZ4+eoS19e3NiC+MlCdIxyfnaH74BxRmvqAz6oyqBzZQVYllN+L5qi2G2RliSIvHO5ToChLVIUl7nHNMsYgThI0Ggna7Zb3f7b7XSSNJowQKMoSq80Gty+focpzSF1BaINIaxglgVJDGUuiyosC22yLqJHg7ME5Wt0Oss0WH3/0a/zm179Et5vig29+E6PRAEoK3NxcuT27QJmXMFpAl8DV5Q1evbxEfzjC++9/A++8+w6WmyWiWFqmfbAm0Jfi9/RS7oyN/TWK57vClXW+mOGHP/x9SKnwyScf4fnzl2g2G0iSBrLSnvO0sXL3rU4HUZpAWIaje69Lp+r8Mjt76b31Zn/Ohp+z7FznIuf/jOMYw/4A/W4PgMHz58+tf23Qh1ISWhcWo6/qtdXPQa2hXLpY4+Hxw+s2y0Mf234Z9+f6/ny5f69S29T9OUocgOQPq8QXIXbncCHgFUDsurK7j9q/Qtu6v9963dq/X6dw33PIfoZ/2z+/hNeh/e9915vs7favN5dSz9cQkcTaHxRsJOvZySkGvR7mi40FP1FZyXANqCgGhECSWmdjZSpESeSdBVGz6yLpbY7wrBKoUEAKWManBnSRW5lzY1CVpQVAlTViQkQw2qAqrZx5kZcQQmG9WaHVjtwB3EV6ao0ys6CKMBKzyRQiUhj1BzDaoNtuY7vZosxyHA9HmExmiKVCpzvAq8tX2G7WiCMrgdZud3B9fQ2dSGSigmy2cdw+Qa/XRVmV/uAfRZEFgeMEQlhnQV7kOwdUUxkoI1x+bhu9JGWEVquN7TazTvnNBpG0x6zNLHcgSRPz2yssxtZJJYzASw0rT6ENNps1iqJ0oJCdOJGokCSRc1pHqKrSH1oEBJJYQRjLvFXOeSeqEkJINBsNdEcJjJaIowhJanPdxpF1Ond7Xee0kuh2Gmi3rbQjYCfD6Ghkgw2kzT1OedMostKMp6dnaDYtY3673TgmhoZSjsW02aAscwegbHB6eobrmxukqXWUzmYzaF2h3W5hs11gOBhgu11aIFgAi+UUutKIkxhlVSJJY6xWC3S6bTD/W+Jk5BeLJTodm+uCDvLtdo3z8zPc3Nx4h2RVVTYXudYYDkeYz2cYDIZoNVtYrzc+2IJMydvx1DvP4jjGeDL3Y6Xd6SOKnXSlsVI8SimMjk/QbDTw6tUrNNttzOcLxEJidHyMoijx0AUBzOdz58zd2oUmasEIjUazBa0rK1sPjTRO0et1MZ5MYIzBaDjEerlEw0XUNYIctKbKIUyFfreDItvUjvA0QZ5rjEYj7xTP8xwPHz70uVjpMA9Byu12a/ONnJ9jNBphMpkgy3OMJxMvLW+EgIwidLpdLJZLDEcjb9jIPj0/P8f19bV3VsMYNJpNvLy8RNpooNvrYePK1O12ESnlA0qksM7a2DHNhRDIswwwxue+Ho/HGA6H6PV6CJ27nXYbG8fEoxx0eGAhqGmM8SAPQa3PPvsMZ2dnNodtmuKtt9/GdrvFbDZDfzhEI00t2KJtdFoZsI9HoxHG47EH88nEDZ3YZCYy0McYg5ubGw8mLJdLbDYbz3QlizJJEpvTXGv0HWuz02ohimNsHODGHKoEjgGbU3kwGPiAhk7HyjqS1U35YAKzYf5XOrd56CK4S9CBjEVGgxLwIKDAPMIEysmEI9tuPp97QIEbNQJ4i8UCxhifQ5mscgJt2+0WrVZrhznYbre9ZO1wOPRzmIv3PihMljNBKtaP9oCMXSGEB9PJCKak9WKxwGAwsGoR/b530oVywwT4CBgSgKRDno705XKFNLEBUnHDBtHkmQXTVqslut0eyqJCHFkJIwGBPM8QRzZtSV7YgCohLJufrOhwXobqMASvmDdeCOGB3fXKAgTWpa1QFhqtZtv3ubVJRy74RrjDToUitoBGs9mEgAKMzRdqTA6jLYhWFiXiCGg0WoCRmM+nSJMUkUpQ5BXyvE7bkiZNJHGKoiyhK40kbmC9trmcJpMpup0u0l4Dy8UK/f7Abj6LElVVYjg4sk5uk6GqtD84MwjAGAvQMi83DNUkJDrtHmbzGZI4sVGolcFmvcVoNMLt7a0fewRdyChfLBYe5ALg5eqFEDg+PoYQws9zziuriLLd2ciSHUoGI4EOHjwYjGGM8bmtCX5xDnPcEQwi4M15FI5rPnsymWCz2eDJkyd+jjJQpCxLH5TDVACUzmabDgYDz34nA5rMe9oEAlzMR83yh9JgBOPJps2yDEpIlFkJA4NGywbdNOIGojhCohLkRY40if0cJkAYgs5CCHSaLeRFjiLLUQmBDAAqm/6H7EZK3+/nvObnQB2owLQQ3CsRJCYITvCVQTJkI9MW094S9GZ/hSxvssD5M1NEMG0CLzqIaON7vZ5/PwHvfcAXgA/aYJkYlBYyrUMmMQ95HJtsX9pz/mu1Wmi1Wj7Fh1LKR4HToQPYQxPbloA31z7aJ621D/yaTCZeFYNqD6z/arXygVn8HucU7R1tOANSw1zlDGAgOM96MIc9lUCoMiKE8HspBqORhVIUhVfxILDMtXS1WmG9XmM0GnknGAMvQrAuzE/PsRyqcazXa1tubRVp2P+bzQbz+RzHx8e+P3q9gQ+yWixmaDZbkFKAMqhCGCgl/FrAiyA9HWA1W6yWRq8qOvw0bBqoyu8r0jTF8fExjDF+3RdCoao0tLZnlyiqVWPq+u0ygdgOHHthCokwDUo47+mI4z6K32ffhs4Ygsx/nytkP3Jse8A2uAI3a+CYgAfYtKHsLuBzyWrryJWKDl3HRoslZKRsACWAqioANK3DyliVDCiJyPCNVgZcRnYfC21ghLH5nCEgjHHsdbplhAW9nQ6UdbIGdQmdQQ4gDy8DCxwKoM41zPUOdNwCpgKYq1dDe9ASsMHci9Uct5Mhrm8niJMI7WYD56dHmE0mmOcaWhhoUUGjgq5qJ/mO42bH/2KlbY0BhFQgdLnr7LFOVCUV4jhBt9vD6dk5Nuu1rQMAqWwggVIR4ljg5voaf/Xjv8If/dEf4ne//3189NHHKLIcUaOJSEpbTlMDhDZ4T3ofihACEhLCCMDlCXZdZvvNMVQjIVBWJbLSoNlM8MPf/V1cfvUMmVNUMkKikgnaozbWixXKzQZCa1TaYHK9xmB4gn63iaKZYLXaYLzcom8MokRDaQOjK0BmWC9zVGUbzbSFuNnA2eMn6B+PML69xWI2wXyZY7m6tcoFaYI0idFIY0ApVDJCVRXYbHM/GmQaodFIoOIYlZKYamC+zoF1Dq3deZHtriwwriKFWFhSgpKWOVOVFV4tfxUAXwpKSsSysEqCXtrYSq+rSPnfpQASZVXWVOjMdf8IqlufEHx+4ZoNasEl6wOwrDTplBwkrDS9Z60J4VXVbHq4AIgK3gs+F7C8dmOD/eAcpHZ6aRjNkWqD47lvCQ2LMRZhtHNV+L+HwEw9b52jE2pnzksZ+TFurDCttUnS5nev96x7jk1B0MmudxUb1YS5Pl397ZLhVOyktUOhfaFzWJZuLtRtf8iVKkwACvrmCAR93fdN0Pb+u87H5t8phG07mHoehpV0tTHS+O9QPFiEvzu7qr2FCS5T9z0ZmSSzsHOMHYAoYXNDGgnIJILQdg0Qok4JwPax/eGAVzeItCEI5wAxfxaWkKIGNQys0ocQwgNRHK8qiiCLwu4BXNmrSnvAxuciNxpG28kjhbL3GZd/l3bdNisqY1Bqm5ZXG2MBcihoSAfaFZb9VwnoUkDGKbKywHK5QJpG6DRb2CxmKIrc9oq244PnfggJaQBp3LqpwsWrHgbagf2uM2BznFeIpISUth2rqrAKjELAQKLSBgISjbRpU2SKfRUQgShKoKT1uetKe/ti6g4LxpwfVW5M1uswh74VBgZ0WbmfrR2Cgbc9fni5vbE2GsLNZRDgoG9A7LKcjbFqBL5MrEs4xaXwf+O6yvEey13whTbT6FqVUgiuvcaPV/8uvsPVm6kYfLu4sWvHhnBtKP2YNlpDG20BMe6lXJpUGLG7x3K2j33P5+tK2zFsaqDfjmm4PaZ9h4Hdt5Rl6cpji2PPHfadlTaoNPeBzr4TtIRVSNBuXQ7BvbKs6vtMGJghdkDxqtKodFXPb1eGknvLYLhrY9cP339C2BHkjJBi6hvftxyeGsaU0LqCBNBMG2g3G2g2GmilKZqNJpLUSqBXLFdpUx1leY6iKHeA8VIbbLZbbLMceZYjyzOs1xtsixxRFCNJWmi2G4hbLVRFjm1VACvp2y7Pc5Tu/CUMIE3drlrbNEzGBZcaYxCrCGmzA6Uiqx4cKSRJjDhJECWR86nZftzkOZabjW1Hr7CbQQlh92RuzdJVDqMNsrKw+7lYYTQ4xqA/xHazwZcff4LJ7SWy7QzvvfMADx4+QNpMYIRBoStLGCxLmKqCqDRQlcjzLS4vr1BWFb754Tfx9O13kDaaWG+3MNoGK9Xnd8AYAq0hOFkHVe7vZbWuUJYVtluLFTw4e4jR4Ai/+MUvHaGBad8K9xwDSIUoTtHq9O2eoKq8TeJeKFQ2eB3I6UoCAxesKAx0VSKKI7ePUJBRirTZQCtuoJmk6LU7SOME2WaLly+eo5nGiGIBowtoXdpnubVT2SayNkxUdu7RrvtiCcDUASnaaEinSiJhbMP6O51VM9xPOBstpQ8wEbxPOltlDQC0ATI4P4s2WGcFtusVsukMl7NbXL54ju18gSRO0RsMMTq2OEoUx6iK0npfhYCK7L6IfX8fYB+ed8J+3ydehCD3oeftn7n3A47C7+5eh3PV1mUxvp8OBUmE73yT642B8W6/5xkdy+UKMAa9Xh9/8Pu/j2dfvMRPf/4xoKwUg4piFGUJA6DRbNqBLuwBjw48Fl43NLI8h3Kb/DLPUQmgLLbe4cSDQ54XVp4LazSaTRtRArvoJkkDeebkWCOBXOcoSuvMYL6PxWKBCgVOTk/RSgeI0yZaDeugFBDIt9ZhVSmNSEZWNr4sMBwNUZYdAAZJmsAYjXa/g0arBSEVGs3UHbrcAqbt4SuOImTLNeAWoKIorDGsKizJ0K0qVJuN3djoCtssw8uvvkCaNpxzMocuC0gYMOg9SWKMr0qUlWXstVpNCK1R5pYJ0ev3MDrt2jnk2rzTbiOOjAcxGo0GLi4e4MGDCz9YIiWQRBKD/gAGFigcj8dotVro9fre+HV7HWw3WwcAbRDHkXOax4hjhZcvn0NIYDAYYLPZ4Pnz5zg9PfUA32Aw8OBet9tFu2PzlPf6R3biiBIGJVQk0G63MJ1OISMJYSSa7Ra2eYb1doNttkVZlTg5OUGWbzzrvtIlKm0PO2TVHR0dIc9zPH/+HMfHx0jTBIAFD+lwJAAohECWWTYogQWySeggHY/HODs78/kvW60WHjy4wNXVFVarOgK33W47Vo/AbGZZNZ1OB7e3t5jP57i4uHCO8c1OXs2k1UKj0fBs1vligYbL50jWC1mlxti+iuIY+XyOVquF8WSMsrRM7+XSBgi0Wk0PXDcd61YAHihtONZzv9/3DJdGI0FRZJjP5w74TtxYzlGWFnwjEDGZTLyUKXNPAsB4PPbMHDqfhRAYj8fo9no4PT31jsc8zzEYDLwUMhlxBN1CpilZisYYn6eazMZWq+Xz166cg3fhpLyPj4/x6aefotfrIcus7M3Z2RmePH3q2bCUTB6Px8iyDMPh0DtFj46OvFOcjnKy3DudDqbTqW/3s7Mz5HmOH/zgB96xHAX5dckgX61WmEyndkNalsgdqEQHO9UMTk9P8fLlS+R5jvPzcw+AEkCZz+c+cCNkVlGmhgA5JVYJHhGYtDkNp7i9vcVwOLS5YBygTLBmOBx6KWgAngEZRZF3epMdR4BisVh420P2ZlmW2Gw2Xg45BOn43dVq5ZnhzE1D6VullAeL5/O5b0+CKxwXVA1QSvn81ARkuMkLWW50uIcHMLL0V6uVH6NC1Dl06fzmWG2327i5ufHgunLBGVzTON4JkBGUlFJ6ZjWVDAD4POah44vP5uZESunSN2y9w57BAZQjb7VauLm+gZRWorPVagcqAEBZlF46NcssIzOJEw8QEJTgmCMrfjwe78j2rtdrD+6SoWnzUEcQqMEYy+IsAVibayX3F26OxwCEzz1ORy8PdsbkgIFXBrDAp33v0iy9czhkFxMk5DjM8xyr1QqDwQCNtOHKZsu72WxRVRqLeT3212try2lb8tymzKAUO6X98zz3UvkMduC4TuLEg4rG1ExHBnwAtfww5yzHRFEUmEwmXt2GP3MsE/yiJD+D0KbTqWceU0J6H+jh/KSN7XQ6NpDHgXHsc76LNiMEn2ezmS8b24dzlMohbH8C591u19trBneQJd5yaiHGOfu1tjm3yWgMVQs4twiwhnmtQ5CXtrsuW+6BSIK2cRTj6vLKg45cz5j/meAq7QODobh+0L5xTpiqViWgPDjbst/v+8CaMJ8WgXiCtASXCf4KIbzt5Rin7WMwUKjKwf0I52cIvPL7BPdoN0PpcDLlZ7MZNpsNut2uD4RhIAJg2fpkovNiGTqdDhaLhQeJWQY6NXq9nl9TgDonWBgQQFCb8uT8LAQwWScC0yFrnHW29kj69anRaPh94nw+98A125DjmqxmAt9h3mnvMA3qQKUGqkWMRiO/JnCvFOYa57PZZlSGYaAVxzX7kSo7fD/XYCoHsJyUqyNIzrkQBhIwmI1XURRQDuDheGVbc3xordFud/1Bt9Pp3jmY2jW4PixzbeB4tvWoHAAYA4h9mTim7fjoQms7jmjLwkA1rY2f78Y5MehQtufH0qkMSB9swjbiGsd9SZh+geeCsPwM/GX/MB0C+4dy8uG+4t/HFToZ6IRF0N7KH/6Nv59AMZzTmI4nD4wLOg4Aenk496RbGxi0Y71M1mGjnaPUBA5255J1Dm8D69WBBV00oTERFjH8ZMexEYJurF/4XwML+AshvAPTf+6dOLZkQTMFjizrAMxz8/+m7T+bJVuy60BwuTjnhI4bV6V671W9KhBVIARBBdqQ3dbTMxwOR3zl17GZH0o2DYa2plE0ARQhC4WqeiLF1aHjCHefD+5rH4/Im4VHkB1lrzIzxBHue2/3s9dea2O13uL+/gHTcewROZ/NMJ/OsN/VaHwrSapPzskRIBaBHGFQAUeAEdI4aaUQWKxXVVgszqGVRl0f4H2X2l4pKBgU2uBwqPH1V1/hF69e4Qdf/gAP9w94uH+QPIBP+wm+tI49aJX3EbAD2fwpGY48idQDfqkjPZyP+ZnPv/gcb968wTdffx3ZUnWDahRQ2qjW1yZlsaIq0DU1lk+3mM8vUZSjJPe+w65uYZ1HUXjYwsEWad/iPHzboSgqFGWF8eIMuiwxGI9w2G7R7Pfo2hb73Q5tG/MytiihdXxWCojt4oy1EcA2FsEoBB/QhJwV18Ui4AS2ElSOgHOaPoLNWuNudQMBAMHfdMlntDD/VIigegTKYnquyIpiCGDTPKw20ad0gFGpRaAh+xzEzmCsgbUGhdYwSksRhcmAeq178N0U8TvSazj5N8EjMU0dQRcDJeMQASimlnvgloX7BJJ6J2eBCzK/JejZg1YkXSADxwicCSCWgWpGJS3yLGadJjdjHqxXTskTtWxhBkR2cAQyc4fvAfAUxuCDQR4r88Qswaw0cL2v8xhggQF//3x8+DhupcCZ/Oz0V4KZC0B9fKyYUkcWiwX2EpATIWPsxh+moigv9w6vk0Q447KBUYG3mo0b7ScvvOg/Di4b5www620xKVYoxGKFbDz4GYoKXecAdALIhARGGWOljWBoHVQa93gJ2fnSmIQQhCXOtSeCp0qmMnbD87DaA1phUBbQGvjw4R2260eEbo/z83ksdoGDCrHdhEogn1EhATCA1rGdozbp/nlfyiSsRKd5ief3waBIzxmWqjOdE6UVJvuN1ZifzWNBJ+N6to5wHPNcS2SKZmuNimCsqKbQZ5OfsWABPCaND1yzvORlVALJgR7M9p4+2NsjXyatJEAcf8/5AvcLcY51Ar4VFOATNuAS2Cv2HnDoLfzIOoMYfX/y3od7m+hZ1PHepRAz+8yn973nbyDrlPOxCOGYQZ3+7RKjNo2XB0FpJyBqABA6j+5oX6DQeZfOE+Q3Dg4hRLvovwspFPEugrTeJfA9+V++5/CK+0Q6a5wnl3yr336xveSxhL73/qg/uVyHzpU+jueA7XigtPibUnHfEf9TqQAq2YZBX2zQdVCbBiYsoRFglIpEvEwNsQfyQyrMTnuIFCsal/JKXQu2uWvaKOs9GioEXQA2AE0EznMFo3jM+OxQFHE/Ef04rs3GWhRpLebaWpYlYIr4XR3X0fi7NK4JRG+aGk1bo03y4NHWfSoeVWidj3PiPZqujgV7ZYmiirmrQVFg+fSAD+/eYfX4BK06vLhe4PMvXmN6NkPdNOjSHkcl3/bOoWsbHPZ7rFZL3N/f4eLyEr/+4x/h8voqsuMdFV0CRK3jI3+JtiU+JXOvUh6JioNxHzgYDPD5Z9/D/d0D3r19h5bPx8hAY+9hixKDYVT+1YnA2vv0MYP9OVDzCEANCT5N6x1XWkXg2cTxrAZDFNpiMhpjNp0CIcRc3WaD2WQIrWPPc44FsqgS0hgBoS9eSeEyizYS4QJYkOXT/jqgH87oHbG2sH+eMT4VGqkYEYPu42RwUU3HeY/loUa7PcA3LTa7DbZPS+ze3+Cnt1/j5vYD3P6Ay4tLVGUFrS774gIAGv2eNG2CPhrbXzXW+VwcPa9ln/0qsDv3Y+4Tc9s6PsfH1xbN++PYc7T4PHus7/b6zsD4y5cvJYkwn58B0OhaYD47x2//9m/i628/4GHVADpV4ykNU1h4ANUgAsdwCsoHdNrEyXWxwqjSFkrHBFDXOoTgYYsCZRGBusLGhNEmbLBvDui0Q1c71IcW5+cXkbXc7OFVgBloFFWBalRiqCtAKVSp2vjsag6tNIaDESbTCxwODdpDA+8cJtMpXl5dYzgY4FDXmI7H0IlZ0DQ1gFQJpYGnp4cYDNoWoW2wuX+MwI7voLWC66KUxGG/B1wHnyQbgfiww+om5x1c2wBuDwSfEisjKAVsDksMBhUmwwJGVQguJl/OzuaoqhLWGEznE1xdXuLVy5f49ttfYD6b4IsvvsCL62sEAG3b4OLiMiXQtpifTXE41JjNpkfsHLJO26aDclHed7VaJbBRiaxq07Qoy9GRfGbbNphOJ5JwnEzGWJwvsN1uhJ21WCwwmUyEjUM2JRNwOYDFhCmTn5QcJjhCiWMmAw+HA+7v7wVQIhBB1iYTjY+Pj5IcJNBHAIBgG3uCMulLVnJd15gnmXoylinhOZ1OBQR6fHwUNtHT0xOaphGQ9uzsTGSXq6rC+fk5Xr9+LbLWTNgR2Hp6ehJGW13XuLq6kvMw0UkpZ7KEl8slptOpgIbr9RrL5VLYvRwTJpXzZO7t7a2AExy3Dx8+CDBNAIxMaJ4/l1XNGVaTyURAYyadWXhAIAAAJtOpzBnBSO+9jAOviYlgMsd2ux0uLy8xnU7x8NAXAbRtK2y23W4nwK5zTpLaBG+YuCZYQKD75cuXmE6nqKoKn332mVxrYS0Oif0WQhBGHwsyAIhdMglKaW/OcV3X2NzeytzynA8PD2LPm/UakyQjRJACgKgCUH7bWit9u/k55XkJRBMsIWBGRtNutxMGEyVfGRNionssgAQAkUIdDAbYbDYCKhEsINhzdnYmbFTKPrNogP7NTQ6Zh2Q/kvlHsIus8VgIchDgg/dAgPvp6UnsjgBXzqYn4ED/YczLFQHy/rUEIAkeMClOe8mldDnHRVHg9vZWihXYP5c2TfAzhF4inJvOoihwf38v0q4AhB0K9BK39AECPjnwQaUC2gULDSaTCVznUdeNqCbQ99lrm/bBuM7z0gcj6LVB2RVyTsZjgvpkzCmlBKxgHKYEU9M0KKxF23YC2DO25LZGGaD5fJ5YhF6YwG3bYjKZYLlcHm3eeW4Czrx/2iOLA8hUJVi13+8lps5mM/l8NBrh9vZWlA9oA1x76Cd5LOb6wnHMmZgECrnmcVzJ1O0LsnpFEdo6E6wE44EebCObmPbKwgQWLFEumrbD1hB57KeN8r4pl83vcDwJBjMm0b6VUhJvuKayyIPjScCTxT5N0+D8/PyI0UyAlbEpby1B/ySATMCTvsDzMC5wDFlIkYOmXC8JaIUAKbaivbZtKwVQOZOXMZOy5wTNCUZznQP6Pq8E2Dg+9Hv6R16BrbWBKfo5ztVp1uu1rDm0d0qCcR/BeSGImqty0DY5lxx7FucwLvLvvD6ObQhBAPWyLAUgZ0yjn+cFCQRji6LAarXCdrs9euAmsJvLWZNBzoelfO0iuD6dTmX/QV/JpedziS+uBfQBtlOgLTHGMI577yVuLJdL6U9LcL6uayilpGiD64AxRmyL0vIEr7mGMy7UdS37HKWUFGDmyhN5IQgLIKbTCDpTPYbr0nq9hlJKvkv2PoF6gsgPDw/w3mM2m8lY0P6iGtNB1mmJ6+l5LV9fuM+MxUBbiRX8nHZAf6rrA6qqL/TieNF3Y1HQDtZ6KVpgvKXfcgyAIHGIxWa076Kw6Lrj/u+0g3wt4sM454NjRT+iHQB9f3CC8/RdjhvXHQLtjPksGuC1/7e+8mTCUYIwZrIEAOnZUv3rucRSDpz5U1wXPTDOoimFPmlrvYJWQZJQQakEvCp4BbQJeNWKfXdjYpEJjbxI4PTaJFGf3Xf+2emY5GNzOlb5d44Ar9DL9MeXx3a3wv19iflkjOlojIvzc5xfLLBcL9Fu2wSkmAwEO+nB6EN2vFMW6PErvz5eR3z+i8UUeqNSbGxhTBHHL8Tx3h8O+Pf//t/jX/2rf4Uf/vCHcM7hw4cbDIYDGUvaHfcLWuse+AAPdQzI5Yks/sZ7j/3+gMX0Gj/6jd/Acr3C4+NjVHSZTtHuLbRWqFsHNB3KQUziLldP8C5gfnaB2ewcZWnx4eYRh86h8R6Fc6iCgrWAdzG511oLW5RANcRkNMRk+hq+bXHY7rBcPmK5fMKhabBrG1hdY2D7NjjWFLA+ASgpOey8i30s000aHZ/htNJ9b+q0j4NJ7RqcQ+sjIKMEGOmBAsckLYCAlJB3Ltp4GuM4fHHvQpA9AgEAlBKoyKj4X5x/2n2Q/J5WMUYOTGSlQ0X2pjW9tK/O4k9pY2JeqcQwghLf7ZPLQKFTn+QEqsfPYrI/AvY6+m1K18Y4oI4SzhGQN1AmILKKe7CUbHyb7VmD6QQ4VfEA/bUKWKciqyrLRsd7Uz3wme5ZByTCTM9wBIDCFin5HOCUh1MhAe9MmvaZ1EAf7iwz6mAHCAH60AO+BFCgcBJbgsQEqGPgjv6WOxpBi4Ag89RneCE24AEor6FDDy5yvI4AdgBepSQ+jwsFaBwVfygoNMEhsuDiOZRSIrGdn9/rrJVFdt35f0hxOgJq2b2hj286FWHxGoKCMMXz41qtYdOaqnWb9qIdXNMB8FAqwFqD4bCEQezBzYITKIJ6PQjiEdBpj5BY/sojAhGMuyEgKA+lPawO0DZgMiqB0OLt17+A0Qq+28OqzzEalCi0QggOykdo1ygDq9P6rz20UrAave0iCMNaqQj+CSAUgAArMT/aAwCtoGzf592WGsNxhel0hOGojMByAkbiPafzaY2gDQKVP1IcEptJdqK5J46DLufpzZNIdw/ehKSkEGWyI/tUYpTEx8Rg9sf7EiAy6eFVeob3Pf4ioHoqHJR5gdhPlxRN8/e27vjavXPSypPfic8K/TPVMajdM6Wdi2zreH+9PLcjGzv1W3YCVsf3470mxrCPQJlzDp0z4g8cI5cD5QlA0yEkC+6v2TkPJ6YTQbfWN9neTGWfhaSWF9coTpan/7H+gXuyAJikrJADmjIRKoK8AGDMM4UF6niPplRSnYlmHs2R504VNVrp5IfJRkNyQsZ0ZaQwyyNEFeJCwWsF33bY1TWaQ42ubeB9F0HTLraeZYFM3BeprPAsxqO2i2uNLUqYMqD0AbaN7VugFeq2QesdbJOpruhe2UXrXkGSyjDGGJhUnGyP1tP4fN+GEPEcFzGd+nCIYLxzYKyNpD8lz1KeaweApumSLHcslkTQKGyF6XSMwaAE4LF8esRf/PmfYLV6wtXlJT7//DN8/4s3CBrY1wdEomi0r65rEZxD51ocDnssl0vc3NxgvVnjn/79v4/vffkDjMcT7A9J1U9pUEuJ7YiPXqEnWQIfF/kyl8K83+XlJc7OzvAHf/AHMb+f8qpd10HZ2PMcAIqykGcw2hZPyOe0ozUnv6SPngtCdi/cn2uEEFtEscCiKivJS4xHYyyXj7i7u5HnzRDafo5SEQqP1+/1eyUdBR0LUFzyalnrUpwKIY4rToD09MyFtC6KbzepbYcCvO7bfxwOUdE6+Khe+fS0xOHuCc12j/1ui8PDE3bffMA3t1/h0e9goDAajiTHwefyAEhhioydElM8mYfjfx/Hjo/f/xQAffqslL++S8H4KRB/+l585vn4u7/KZn7V6zsD47FKSaNt2f+uQPAGwVtMppEV3nmgblrYwsIWFk3nUO+2qNoaAQEmANr3bDkmh+PmADDGogsBUBpt06QkYYlgDNoA2MEQl4szFKMIohlrMZ1McahrFEUEi60tInBcaGEAxH7j7IuQes408ea7/R7n5+c47PfwwaPSGto53N89oA0e9SEmN/aHHer6gOXqCUrFe6g3e8yHE3Rdi7o+pGRjHXtV6dR3UAeU1gIp+VrAolMdinGJ4C0G1QSTUZQsWiwW+OKLL/Dq9St4HzCdTKKEiLGwRqMoLK6vr2FsrFherp4wn03R1A32u1+PfatHsQ965xy0Vnh6fML5/CUKEyV3hkMDrR2enm5lQ+aDx2bT4eX1S3x4d4OiVNjv19hul5E1+3iLxdkZqmqAu7tHGFPgcNjDGI2qKqFSjy3vO9zf32G7W+Pi4kLYNEy439/fS9J8OBxK31c6C1lzZKdSRjqEIMluSqwSMCYIQEYaE54M1EyGAnEj/ebNG0mkjcdjLJdLSZASyM8BFwZzSsEyiXx1dYV3797h8vJS+u2yB+sPf/hDYSiSdX9/fy9AHHvS8hyUg/be4+rqSpy3qirc3t5G+zwccHl5ib/4i7/A559/LsA+A97d3d1RYv7p6UkYZ8PhEI9JOp0LzW63A9lqTOBR0vPm5kZYX0x+ApCCgcfHRwFOb25uMBqNJEHtfez7SIlTgqxVVeH9+/cCUlIC9+npCY+Pj9KHua5rAdKZLOYckm2ntcb19XVk0ieGNH/H5P7Z2ZkwdobDIVQIWK/XuLy8hHMOr169wosXL6RfuXMOo8RC4jjmrLWmiVV3u5TYJxDMhDmLJpgsZzJaay2sf/boflqtMJlMpMCAjPHdbofr62v4DAQkOHB2diZsbjLjef7Ly0vc398fgb55wvcUfOFmjkUrLNohAEFA+d27dxiPx6ICQMCDDNvD4YC6rkXK9+3bt9jtdtLzm2BTbHPgpSBjMBjg6ekJX3zxhbBEHx8fxV445lzICL4T2KNULZN+LBhgIp8AB8FWzkF+fDIf2b+dwDXHiT2oOQ/shZr3BCZgTTCPABALPXJwnvPARF5cU53I3RPsXSwWOBwOWCwWApCQjU8AjuAWCy5YRMREdg5qxdYPcxRFKfGAAMpsNjuS/+ZaTFCYG4sYL+NYE4jLpbhp7znYxDkDeoYrgToC0fwNN8WM55Q7Bnq2IOMBi3u4yaMt5zLFVVVhNptJsQfQS//zfr2PUuO0RYJTZPjmyTYAR+xXgiKMdexHTmA7Zy/zHvnAwPWPcWw8HgvLUOvYY4txgvafKwUwBvLBLS+2oL/Th0OKeQTBOBcsLMnBTPoGgXOO5akMdn4dkaG/FaY57YDsy91u99Eaz7UuV1cgs73rOgEkCSjm7QgIjHJPQdskWMzxJlDMucj7A3OcCADHIqaAw6GWe+ptvldx0Dq2sOA+I4QgxSEE3QCI79Mv8mIF7m/oVxxvrrFlWcKFAGP7a+DY0BdYZEEglDZIxRAyV1loxd/QhwhesriM9sVCiM1mI3sN+g/XOPoq4yrviyAMAc1c+YPfpww5i582m40kNdjeAoD0leO6T9vPizwYB7k2UgFpuVxKsQYAUYNgMRCLF7lXoY3nsYbjnhddsICH6yfXi1wRgTLuZL+z0CiXdKc6DNe3ruuwXC6lSIEFlI+Pj5KMub29lSID2hDnXGst6x7Xb8rG52Ay11juvSiFzqIO2gT3Y+PxWKTqo1pTkfUmUzL+LFYZDgfik3mBE2MpgMiE1ZBCDQLfjOM5CMvCM67D/DzudbX4OfdNOUDNZCbBbfofgWrGKu5n8rHi8wJjC8eFNs5YctpKRSkl8YfjmbcT+e8BitNmjgDxo6Q2Exx98jJPIJwmNpkFIbtHC6GzT2CQLc6Yyvno2gaAT8AWEFxA8GVEHrUmEg4n0swpcQkFr2KRhVx7llh57t/5e/nrFPQGev997jufSqzwPgGgaXe4v39AZUuUtsJ4MsH1iyus1k/YNwc0hw4asQduflyuoSGNHfMMlG4/vQ+en2tED6Yj+UWcCue8sJeUimwom/pj393e4V//63+Nf/Ev/oXsK7/99ltcvXwhxZX5nDvnYE0vUc3515nN8DecG6ssPDzatsHt4yN+/Td/C+/vbrH+yX/B+5sPGI2GmI5blMMRRpNxSvA7VGWBy/MFtvsDbj98i6fHe7x4+Qqfff8LPDw8YrNaY7054LDvMJ4MURUWSjs438J38dm9OezF38rREG8WZ/hMKWxT38T9ZotmvU1I7aJqAAEAAElEQVTxd4f1eiv3oHVMKmutYQcmqs0l+zNI8uUhCCiufGSss68o9yg96JPYOj7A1enZJMlPOucQUr/h+H0HFxxQHO8fI4CmAPhevlcXgIrtBns7CMlulMRDpEI5WpM5iQOSdCw+9pMcQIeKl121BAR6QCFeZK88pTUZ5xlokMBroFcYMgKKhCMAPi+osdbA6g4KmY+n+Nqz1eORi6rI4hTPbwRo0imha7VJEt3cq0f2ENWegAAbPGx2zhwAUZnPVTaGLqViYQCPq7VJ9xEZ+pQV51yqDPjk+7EwAEfXj2R7fSI6Jsf9SXyIH8YxFj+llEEGjLN3cQQCUhI+9KxdpSDXDkTwjsBnlSTEkb7L8x3FphBQhCIdz8sxeR98uRD78XoPBH0sk8xjCUjoAwAnYHz8PLETFeC1QWmBygDGA10AGufh4aADYJVGUSigLLC3PfDIuRacIiTgGBrAICp0dg6t8+h8gPNIhRMxX93WDXzbwNoSrfNomg6HtsF2vcZ2t8XXX/8S/5f/+f+MolVwqTDO+4BiEFCVAUoZKPT2EhUpgsxFCErYfpSm9iEg2DICHF0XGb+u79vLZ8vSFhgNBihtmfZVXRZTsnkAgeteNrxXekg+wjVPDDD+NmcX8zNHkCcBNSGBwlJQkP5EDoTLtYejY/qg0IXIwIzH7G1Djh08HChLnkDe7Bk2t6dDlxRRUt46Z8r31xKBVqUiyOd8z+7Ov6e9ggl9nsmF0IPYEvcVUNpooycATr6+eh/lqhlKuRZ2Pt1DP+Rw3SGNgxLA1LnIKpVjB8A6I+txDhBGBYm0z0gLWg5yqUw1JKTPCqVj0Ugaz6iukoBspaTdAWOXFHOdgMD8u1H6OGagX2v4d6Rr0eh/x7Hvug71Pj4ftYnEIJ93af31kT1caIvKFOgKyLrBZ1El192fe2iNFHgZYyTW5/ss2k2es+Cald8ni2ykcMI5NHV79G+lFDo4uC4WXiAEGFDRIhbsaERVGgcltkGfbH3C1IoCg+EQs+kMLy9fQwO4u3mHn/3Fn+Obb36Jx6c7vH7zAv/T//RPcHl1EQuZ9zVc49A0sRg8XrCHa1t0TYvteoPVco1v37/Hz3/+S8zmc/wP/+P/gNlsmlQOHIxS6No2FkUEgr7Rx1W/VTwqguD4xILz+AxNssqrV6/w5vVn+LM/+zO8ffsW0/kMtsiIK8mvx+MJxtOZELtCCFJg4X3v9/nc5Xv5U5AzhB60Dz4WJFRJnbGoKlSDAaoyki5HwyEuFudo2hr3D/d4enzCZBqf6w91bGkRspYevH8VwMqmeK0hridUL5ECDcbENHxaa6g29EVyAaIawXAcizE99r6NoHiKR13n0Oz3eLi9xePtHXbLNdq6QVVZFKsa2jkMfcB010F3BR7tAOt2j+ADjDYYjkc4v7xIecYu+rsxR/7wETLOd/P94cl73xVk/tR85fP5KcC9f1b99Lmeez78m+7hb3p9Z2A8BKDrUn9Yq2MvBVWgqR26rkHratRNjeVyBVNGJ2i7Jm4K1kDnOhijUaSNa1VVKKYjzKbTo6TS9XCI2XyWwKmhAH9AgC0KWG3Q1B2Qerpst1tMxiqBFvue9dJFoLKsoiysMQbbzQZQUYJkv1xHyRYAv/zpn2O728UqXibcARz2W4Tg0XYtjIkPxColD4CAs6qAVRtcXswwn1/FhG9p8eb1qyg3fjhgUEQnpCzxYrHAaDRMYAlQFAYhtFAhVo01bVwkRimxUpaRba9VTCrtNo8orIGxCr7ZYfm4TxILAReXF9BKo+06qCT5MhqOsXxcwliLuu5QDQd4fFhBK4v6kBJ61mA0MHh6WqGqyijfHjzKqsCr1y/Fgay1KKsK69UGw+FAkpJMXpFNfHZ2JmDh97//fbx9+xYEY8g2vb+/x9nZmfR1ZkK5rmsB0JiI2Ww2eHh4EBlIAoAvXrwQuWsmtZj8ZU/eXPaUierZbCbAMRk779+/x+vXr6W/49u3b3F1dYXtdisMZCbUmqbB9fU1AAjjiWAtQSuO18XFBT777DM8Pj6K9OR6vcaXX34JACLLTCbWzc2NANZ5D8n9fo/Hx0d89tlnAgIbE3s7578h0ENJzBxo4oaEG4umafDLX/4SP/jBD0SO2lqL16+jJDxZh7uUjGBRAYHWs7MzXFxcSHKfQCGBbSad8yQuk/TGGFxdXeHh6Qnz+Rz39/cYj8eSkH/37h3evHkjwEQuicr7INBEEI59wckUz1k8wTksFgssl0v5He1ov99HQCCx1ay12O12Aqox6dnUNc6TVPfl5SXev38vcsaU2+S1MiGvdS/Faa3FfD7H5198gWUa6+VyCa2jRC2LQIzWmIzHwmy7v7/H9fU1mKw9HA7Y7XZ49eoVDocDvv76axhjpP/1w8MDLi8vBdBn0cXDw4P454cPH47Yny9evDgCKJhwDiFIT18WDIQQhG08HA5xe3sLrTUWi4WMKQHnHBBm0Qd7gTrn8PbtWzRNg1evXgHAkRQziw8IetJmeS/CRkgbzclkIiyy5XIpRRDs20wQbzQa4ebmRkBJLpxcg+bzOULoWaYEHAgqEzSnakbej5QFKCEEYWbzM6ouABGg5HUSdGLvbsYVgl0EFPknwYMQgsQygvhxzSiP7Ha9XmMynkoBj9b6SE6bLF8CegTHmAynvPTYxr6x9A9JnuteCodgR13X0h89ZzcaazBIDzM8H/358vISAATc4jXy4eU5sJQPq6PRSB4W84ce+osxsa81N2GMSWx/EPc4Qdi0ZDSTUUmAifPB+8/ZkTwfAdmcrZNLiJMxTZCI8YH9swkC8j/aMO+NhQaUbWcxDtm7HC+yZMkwJsBG8I+ADf/NuSDgxWtn/ODcMCZx7cyZ4nk7Eu+9FBFQeYXA4iH1KqWiB+2UALtSSh6YeF0EqnjcHMhmsRwLYBhrc0UAxuacqXo4HHA41Aihf/giUE2f5Zpf1/WRT9J/ckCNgL+1FldXV7GoMgOtAUgM4D0QVDTGoKkPCOjluDmHLFwg8Erf5P6LQBznlWscbZPqIpxr2gTnkPfEam8W7w0GA8xmM2l/Ql9ngYZL6yrHn3PChAHBdRbx0EdYCMGxohIPFXjoz7miDuM75y5fw7luU2WGc8gYzhY2LGIhwEl5fymgU0oUYZiQAiB/z1u+5AUaa7ZGSsdhrKf6En/PvSH3glRHoo3t93u5B6rP8PovLi5kveBeirGOTG3GYfrw9fU17u/vxb7YniCEWDRD5j3vjUpOjMmDwQDwsWiUz2LcCwOQPYExhewRaNP0JY5X29ZHyk9ct3OmeV50wdjItZmgQNe1skcJIcg+l3HC2r5VBddaFv8xHlEOPy+EYfED/YjKLtyv8t54nfQH3ifXEEmKpnjL4igWbPxtXyzgyIHxEEKUECdAE78g60AOnD336pMVqs96pVdRFCiNRVlYFKUVtkucnwjQFUWBwhroEJU3ggcUPJQxMDrKNeug4p9KwwFRdj1LyuQJ8b9NEuP0Xp5L2pwC7/k48n1jHZpmj/uHR1hTYTQa4Ye/9jlevbrG7nCAv1+hbjoo1bffOQbHezAVZMaevPJr43dzOwrBoywjKM9k2X5/gPYO1vbz//L1K/z0pz+FtRa/+7u/i3/6T/8p/uAP/gDfvnuLi4uLeD0hwGUFekfnfOa6+JKEWYgAmy1iIXwwBr/zD/4hQgD+1//lf8Ff/9XP8KO/8+swZYUy9diOrLwOZVlgMZ+g6xz2+xo//6s/RzV/wPXlNc5eX8N74OH+CU93Tygri+GwQlmaxCbV6IKHdy2a+gDK/Q+HQ5TVAIvFBS4vr2BMUgdKfUTbOqraca1uuw5t0wC1O/LJkBK+Okuy+6KIDOTSwA5LlCfJdhkb34MwZCIKmEJWYtchpFjR/9fBdf17AODdJkpj5vYY/3Jkl97H9Ho+V3mCVaEHZgXkVCoBpAlo5YQqBZPaoSWs88QOCBBbKBNjOAGzmPg9thEHBR9RU4nPZG4d+ZyJ6wWeY6MBct/DlGHmV+I95HEsPWskgMEkAIxMxByYMSrEbtJJgj4fF6Xie1qfyMyDIDrbSPQFW953Mr4EoHrQCCDxO084kw0v88brA2CzcUohHAQyaV9GIypzII9hLFzok8dUPmJhU2FsilEEXKOd+SLFGYKaOOkfmhi02vatxqIE+TFASVnsEHpwNQf0hcmeg5EJNJVxCJDv6gAoWwChZyTHZ9NG5Pm1iczWwOeWnO2aAAper09EKAQVQVfPa43/Dl5FfqSKTOimaVBWkQzR2Sn0uEKjgGVt8Pv/4U9QGi2FMy6wgKRItt6Pu9E2Ae/p/Wzt9WQih4CgDXzjYq4WkHahBASjDLVOxQd9zGBhgsibKw2v+l7OCkrOA5Xkq03qEa51P7acz1SoIHEH0aeErZ3OKP6ndSqNCehOC9HSsWV+FaCDj5sCAEqZZNtkUSZAVakMtD22M4i/pbtv474xP08OostaHIzYrxStIStiCwHet3C+FWbnkX3TNhVQ+MjCzdft5/YXnW6O9k+cMxAkTjNoVSV+GwuUDApjMEzFXACikoTtfTwylQsY0zOYcyCR7TTIGs/nJa7Lncy5xK807wExpiil0NbtEQRFQqFzeUxXsNoe7Sl4HrmutMfTJhVIKcAqFl1pyaV476GsgTL9+yzi4jrCxaCwJmMzH6tX5OBbMaj696EkLgB9wYV3DhpKnh1zchqPE//O9ehYVpw+z3+TMQzv0z4tFaMBURo9qU/WjseKysjGGExnE3z/i+9F1UfE55q/+umf4K/+8i+xWz9hMhrgzasr/LP/0+/i6sUFPBza7oBD44Gg4QGUNik/Ng2a9By+3+9x8/4Dfv6Lr/DwuMTZ+QL/n//v/w9f/uAHWK436FKRSRyr4zXmk6/ko01STQshKjvUdYvd7oDf+73fg7UWf/GXP8VPfvJfsFgsYktiFh8XFk0d8xPT6RRVyvFI0YmsadEmaa/f5RVCRK7j/iXt3XRsUzAqSgyqCsOqwrAqcHmxwGBY4qc//Snubm9S294x6v0aHVsXqLiXyQt0nn2u8Gk/CQCpK0twvapEX7ls4poJrk+d2JzrHFzKwR3cHs1mh93dE3b3T9g8PKE9xJbFxsZ2H8MQcLFrMHWxolm5gNJpGF3g56aAbYEOsdD2xYuXkUgI4LBcQgNZYUm007zk5zmA+lOf/Y328szv8t8cA+DPv0dw/PRZ9vS5VveiWEfH+tS5f9XrOwPjy+USbdugLAtQ1cu7GqvVDvOzKawBxuMStpjD2gKX11cxwKaFC1phNB3DVj1z6Ww+RwCkf+ZoNELQ8eaZwGqaBrs29gi2oQU6hfXtCtvNFkZrrNcrPDw+JKMx6LoWZVFitV6iqRtJ0Cit0DatVFGqrkaVKnFl2LRG18VrmwyH+OLiGsNBhfFoDGsNxuMRBsMBgIDPPnuDF68vMZ4NcThEIK5Nsh/GaBRlgeA9rNGYTqbCGHNdh9F4jNvb25gcbA/onEOd5AvLssTZYpYmNUoQus7F/s+71Ct6OELdHFDY6IW2KlGVIzzcrVAmNuX9/T3OzxfYbfdwLjL+Dk0LpdaYn51hNJijOTyhqT1Wq2WUDXUBg0GUvCTTiwAs2WGxyKBI9xqr2NsEDJ+fLxBCwM3tB5ydneHly5fChMnBg9lsJrK+uYQwGbHD4VCY4fv9Hjc3NwLqDYdDAUcJEFK2m4lUJrMof06Z3PV6DWstPnz4gPPzcwHBfvazn2EwGODDhw/CIp/P5wLukeHMJFpZlri7uxNwoixLYYIRRCFrmfeRs/4uLi6OgJK3b9/KGAwGA8znc1nAR6ORANZMErZti6urK0lGcyxz6Uom8Lz3uLm5gXNRlpWJZ++9yHDniWky8TlvHOuiKHBzc4MXL15gNpthuVzK/bKggclf8TmljvraUgaUzHsmiefzufTn5bxMp1OMx2P5DRN9HOemaYR1RpYhmf18n8nqp6cnFAkQZYKzrmvc3d0J+8n72COdQEMuXT0ajQTEZvKX8YnACAApyuB3b29vsdlsBPAkcL5LPc+Hw6GASLkEeJGYnwQCCOptNhthczLx/sUXX+D+/h7OOQGWeB6yJPkf/eXx8RFXV1cCWpJ5T4CFrQXYGzmEIKAH7ShPILNNAkEUth5gscsq9b3ndXJBI0NuuVxis9kcMWdXqxUWiwVubm4kNhAQJHDOhDrBBUpfn52dyXgTJMuloQm4ExDK71VrLcUT+cJPIID+rrWW3tz0Odo/CwMouUt1APYJzxmWBOsIVHBtDCHg4uJCZKXpSwThCO5xjPOCFSb6vfepcCTGHrLlgLhBYHzlvQK9agBB/Rw8i5Jh0a/J+NtsNgKo8P45P5vNRvyjqqqoqJCqFhmnOZYscKFv0564buayuTngQGCFoCGTWLx/At0cFxZHEMjlgyj9PU+G8r4IgtNXaPMEj+bzuYCOBJh470e9xVO84DXHLUcv50vAlLEzl5EnkMSEPIH9EHppcrYjkSKEBEDmLP48ZvPvjD2ch1y6mnbKF+fps88+w8PDA6bT6dF6wVjCQqiyLCVWkk1MwI9+sFgspJgqV1MgoEYQlNeXt2DRWsv6r7WW4hAWO3EOWejBBxGOf8887v2OPsmxiffdP8gDEEUQro1MTj49PeHs7OxI0p2gZK5ew70KYypB7M45tElJiePAuSCTlvGN88k9Ti6JTqA7B/v4YtEGz0kAkmNxOBxwdXWFzaZvhzOZTD66HyrMMBZSrSaPs5yvPJbSR6mkwl72TdNITBXQT/fMbCqP8AGJsTEHLNlahWotvM/D4YDHx0e8ePFC/C9nAsckbCt2kku70V67rsPd3Z34dV6gw+IrzlcIAdfX1+IXtBEWiFDdgckz2uZmsxEAnQWjPBcL5Qi00gZ4fZxD7lOdc/jFL36B6+trKfbKCyW496EvcA3kPfd7SUqbOmHh560iOE6bzeaolQDXnwhqDbDbbUXNgT7EV9zPNNLKgQk0xtu8GIb73Dxmcf5ov4yV3H9wr3UKiLNAhH9yTcnXZY43/ZWxl2sHv5ez4fN2KUze5nH0b/PKi8/4Z56sA1KSEzj6zt+UWIoJ1o+/Q1srrEWZ/gwx15RkGjuo4GBQwZYDQKkovaoiOJ60fAHEJHjsyXecTP2bXqdJaEkcq2OA+fS903N8KomTv9+1LVSa56flE759/w5X1wuMJlNcXl2h6xTuH56ilHxKKsn4Z+P83JifJnMkoep7Nlj6Ztq7DgBE5kzbdtDqGER3Lu47vvrqKyil8Gu/9mv4J//kn+Df/Jt/g10mXUm/aZP/xqShQeiOpZJzWxEgx/nYA1MrWFvgcbnCfHaGH/3dv4vNao0//k//CXf3t2gBjMZjVFUp7FphTmmF8ajCcFDgfvmID2+3GA4nmIznuLqYYzGf4v7xAdv9AZu9hy0sqqLtZbhtAWUsPDS6poU1UfVBFfE/Ywy0USiHAwzSXkspIwxN33XCfmy7Dq5pI/mg6+O0UoBve7Zfag6L4F0CE/oih7aNyoKRmBpk7pH+NIjFBG44gA4BNiVG6ZMyywpQIUAFAu2ZvYYciCRjhh8lOV/0H0thSce0axBwnQAh+5xGhmasYHEhxPsU+mgPECs0UceTfhRYpuGjxDxtJoFsURkijhUZsswPAYAjU9nzu5ntcQBSjOC10290AlsIPioV40oISAQdJb3hWXBjtAYMGZORzatUDqay8FNlMQliD6dMxDh3RsZWCRB/3P87grwmvzN5RbAwgTXKw8ElFYHsq+oYYNYw0Hlv8/w4YnYKNhF3CBrpBGAG9hJO/i1gTQhHa3deABgQAOV74Dpk1igxL9mg4j6cIFAQJqRSBBdZsHVcgKBV1pYgBAQUoK/FKdYIulffUDox9J2PBQo6SjIrbbIY2oNpGvxekriOpR2AjgzrEIAoYOLQNB3atoGyBqPxHBjGb1ur8bTcQzT2lYJSEfgKwR3bqQKUbo/mKn7GYofYjzuOXyPAvVI6DndwOKQ8llIAnIeXguVM0tcH+M6Jb/mQ+TAgcuG8LqVUAtuV2IL4LyeEcxwCitAXfTE7ntsWzTVXPODt0i+gUl/mWOcke/loZ0raW2hlYvEJdO+fgLRZ0Er3867Ypx096B8rf/r1S6f/vIdSHsYEWKshfa/R90SHUoC2Eg9iP/jTohctlpOv8QLS5IUvDh+Pp8Se9L0QEDJ5Zt4j70MKHxDQIT6nBLg+ziQFguiuKhYihsQQ1xpW9WxxvozRsCrJ6Os4nnJ9cWWS7w8Ho6N9wHPAFQAoY2FS8Q1wXNjT213v730haSxIKoxN6hxKCgd6MJwjINYVJaZp252Tgh/aKeOZ9x7tZiWFEMjiC48akjR+SC2X+PyTH49zrAEpVIpxBdlVcapjn3C2XnE+FeClWBqCT/L3GsVwjPFoiEFVoSgLFFrD+Q6HzRY3377F/cM9bm8+YLt/wvligR9+/0e4urjAdDqBNQr73RZtcIDEzoi/WBg0h9i+tz7Uidz3Dj/96V9hs93h1as3+Gf/4/+Iv/OjX8d2vwOVtbgH4nPP6R45f94W0omPhUld69C0HZq6xnZ/wN/7e38PShl89dXX+MUvfonJZAJb2ChtD0Bpjc55WFNgOpmjKKseH8xs7Cim6mOlgedsMX9RnSBZKUJQKIr4XFsWBYw2GJQlLi8vsVmvsXp6Qte1qMoCbX1Iz6bZPSPKmHPvLfZIoFYBsYfGcVFYUApBayD9tu06tG6P1vctHbxzaA977DZb7DZb7Ldb1Ns9sN7Eqw+xxUQJj3FRYK5LVG1AODRw+wNsU6PoAKcCTFGggkapY56288CwqjCbTTE/O0M1GMA3/ZrDeGl0AaiohvPMI+DRWJ8CzKfA9Onc5b/71LPXc39+/N5xQc93sYNfdR/f5fWdgfHpdAbnOgAB2gRU1QDeA9PpHKPhBP/v/9e/xF/+/C1CULGqwVg4B+wPDapBhc1mi4fVE5oEemmlEZzHt99+gxAClstVkkCPjIDdboembdA2DbbbKGPuQ4DxGraJm8u2ayIIXVisV/u4mdIKoapQhgBjHGxaqF+8fIHr6+vUj0pD+RoIHtPZFMPBEH//7/8uFokN2rQtXNPi+69eoWs71HWSDR9UaJoaznUYjYZoQ4PtYYNROcJkOkBdA2UZE3yda1BWJQblAM61GFUWm80SRVFC+RbD0sK1h1hhqGPfqPFikoKPT8Hc4XCoUViL5XIF5zzOFnMc6pigadMGKu4DG0AZ7HcHxF7gFVarLbwLCEFhOBzD+Q2sLeDaDkZp1Ps9xuMxri8vUdcNBqkX/H5/wH73HpPpFEZbTKcRCBsORvhwc4Orq7kUMxSlRQgxkfT49ICnpydJor158wbOOZyfn+P+/l6YjkygEazuug7n5+cCXBJMfHp6Etn1H/3oR5KUIgjoXC85HQsT+p6sZOMwUcZkHwHuh4cHWRDevHmDv/7rv8ZyuTwCXsk6J5BOB2PiDYCA2NZa6XVNsJZAqdZRhpXMFSbhmPgkq+n8/FyKEZg0zWVfCUqQBbzdbo96qgM4Yo8xac1kLUEKyoT/8Ic/xN3dnfTrpqx4URQC/KzXa0ySxDjlUFloQICKQDITjnliFoDI0zHpzeRnURS4vr4WZhcASSxyTMia55yR9cq5CyHg/fv3cr4PHz4IcM9+md57lGlM2L94MplIsrpKMiur9VpAWAJCBD4ACHDbNA0uLy+PwGImXmkbi8UCFxcXwtYikLLb7dCmpPPDwwNms5nMNZmAu+0WZSZ7ShCSc0OwhoxaqhSQJchxp+oCW1bQv7jIr1YrLJdLvHjxQljhXdfh3bt3qKpKwKucWU87YiKaCw7tnRK+ZVmKr5Et6b3H69evobXG+/fv8ZOf/ARv3ryRJLQxBtPpFNZavH//XuxxMpmITbNNwNnZGTabjdj+hw+xGEcpJUoQDw8PRwxCytYSbKOiBAESAg+U5V0sFlIQBACLxUJ8KAe56roW5h2BWNojk//r9Rrr9Rrz+Vx8mmw72k3eU5mxgYUIBIg53k3TSP9hAOLnvBaCPwLIpc0hN7cEnekDOQigVATzN5u4QeN7togA2N3dnRQ45f2aee30Ifpt3tdYKSUyxqvVqk/WZg9z6/Ua5+fnEu9ZXEMfYrxhzKHEMtcCzslpQUGuHML1gInjnKFPUHq9XuNwOBydbzAY4PHxUfyP8ZAAHQFKfpegHWWFCTYzPvO13+8FVOI9KBWLsAiWcU75uzw5z3uiPzARweImnpe+zzWEcYVFiKcgPICj4hPayamkeM6ezfuws4Cq6zpMp1PZB3D9IIBJkF2YEWkDfHl5KUA9i78IDrO47OnpSfYFXPtzaXcWPbAYIoQgcToWLsS1k/7H8c9ByBA8qqpXmOBDZN4ShfLmXMd4vq7rpB+5914KLZxzUqTGcbOm743NB/28ACSPX/T7+XwutspK7OVyKfbPuSDgSjCRc5nHFP7JazfGCACdKxAQWOa9MPZxfLjHYHygzfPanXNHDPDFYoGiKGT9YPEYfTpXLMljIQsKp9Op7E+oOsPzSnV6irN5QRD3VYy/VPKgHeXFAF0Xpf5ZWEOZec4lCy64RhNgJUDFQjX6B4v+drudFIVSjp4FA3ligOx5grvsv801bzgcYjweSzHrdDqVOEPQmHs7suQ5dnnbI8Y7iT1Ie6Q0jly76F98eC2KArvdDrPZ7Kg9SywycantUsZOY/I/u8fcN/gZ4433HsNhJTaTA9z5OpKD0VRS4TUz/nPvSLvkWpKrOfTJvL54isVK3Hfn/s85Ybw5TeywIOBv+zpNHPE9SdeEHhDLv/+p36ZP4mch9Z3NmCNa69iezBhYE4sGfIjPpl3Xojkc0DU1NBRGZwtUg1i0XJQFVIjFRlAGQfe9aA2Okyt8cYzzOTm9Vs7paYIm/zvHOr/f/L3Tscv/7Z2HQ4e6OWCz3eD+/h4fbm/x+WevMZ+dod632G13WO/qozHugcNczv27M9/zJJPWSYWkiD0KR95hd9ij2W+PfuO9gynievLhwwcAwO/8zu/gt37rt/Cf//AP0bWp4EX1LVDy+yaA6HE8xvnYkWEoCWAX0DQtZtMz/Pbf+108PTzg5v27yCxOpjMYVPA6sjaV6dl+SmkspkPUdYvusMaqqdE2e4zGc8ymYwyGA7Rdi65tUW+3aI1Ba4uoEljEYnwoBadiiz1lNVSRFQmpCEiblLCPAETaSxgLrWLPUQwh4FA+9sEdM+Uihpsxwn2Ah0foBkmaNxzZKqU/CQqFLFEqoEpKkpM1TbCcDNM+CQ0BJYHY6zuX6GQvUpHLBeQaQyCkkIBsibNJtjoEtDn7L31fJcBAwJCQgHsmmQOP58XW4w3rHkDNBq9nGhK46LJr6eMUmaJ8z3dxHnIATysl4H8cyxSmEqYSEvAfAKgQ478HYnKaRQ28p6wyQUBi1ff4PPIRlfmwUkAwH8XXo++kMbe6lHiXv+T7SAVEwUnfZ3D8snFMXhj/U5D5EtAoROnqCBIex065Jt/bhVLI+pumBD7xQZnnCPQo9K3X6CcEI2lr4vQqMlaBWKSBk2tw6Y4IAMZ5DyJZrxLTSpuBWG68pnhjMucqApbB+6OxV0r3igD5eLOQAhpBSXo9jmUq7tAAEGJBqrUWLsQWltYauM5ht44KTV26qB5g7f1UJisAPpy0TVF9AUAPyjnAsy1V1vcbgAsRWOP4quAjlq916tscbcBYag4A3rW9fHkI8EHFEgPVF09475Lt6v7axWbjhSoOtAswwRB//mi/1v8q+22ccJlP/sm18NguFVHU+F0VC1iQxiE/r5LvRX/N+12zncHp9cTYG2MBkH0vzTsCQXgTy3XkpLw2IMqV67Qe57L08bdS3JP5v6l68hP3flrWp7QuBI/g26OCG5PAfxlJiREq+Zvr5ybNnTHJFmCglInqF4bHZLP5+NJKQyXlDK1N8iGu/Qp5MY6WIYj2oJX+KI4FQCTaObeecvXi/xJoAPTrExygVIdWx+cWxRCCPjYB8dpo6zGWxqIvWSMJQrvjtdx7jzb0LQdUftFAbwshILiQbCIdO1uDebwAheBw/N7JOhZVHpLNagXl+bxQoigtTGFhjI77Em1gtILzHer1Hu3+gNXyAcunJzSHA1zXwiiPN2+u8ObVa8ynUwyqQYyFCmibDq130JzvALimQ9vVqOsGh0ON7WaLu7s7/Pznv8Ruf8CXX/4Av/33fhe//Tu/g6ZrcagbpDoZmXfvYqGNFBSA95zW/VjaCh8cfNei6yL+VNcNus7hi88/x3g8wddff4ObDzfwPmA4LKVIKqo4xPVqPJ5gMBzE8UixX56zxNa4b/zUc8vHQC3owoiYF9K6NhqOUVgLqy2GVYWz+RzWWPz822+x228BxEK3JuFqtDO2p2BOivsFAcXTCT08XFo3vffwnZN8QGSDd2ibFvvdFvvDAYfDHofdAV1dw9U13KFGd2jgDjVc02JkFEptMTAGFTSKFvDbA6pmj7ILCG0H1XUYWw3dBbRw0EqjNLE4poFHUMCoGmE6nmI4GklMCEdjlakiKRzFjOfG+VNz8avmKH//U8+lz/0+fw75VEuqj3/z8Xt/29d3BsYHgyFihZyHNnHT4l2A1gUuLhf4p//sH6Ma/xf84hdf4/b2Ed98+w7OazinYEyJ5XKN9WYJ1zUCRBhjsd1u4kOGj47nuj2sjUlg13UoUnJPdx3OF2cwSmF0VqIsCpSVxX6/xevXr/D9738PTXOAtQbX11cYlJWwH5kgXiwWkvQcjwdwrpNgaI1BURZwnYvG3nbwoYEZKGgVcDhs0NY7DAYVQuewa9cJtI2gS1t3QIhVNIUtgBBgdAEVLNpDDac9SjNGaQusHncYj6dYrVaADlDGIgSNmw+3klixNiZXjLZwHtC2gC0rLFdb2CIutKPRFNvdFkZbNF2LxsUihLjJVGj2BxhrcNjtMdEjTGcD1IcDbKFhrMPV1RlMkieJEvIOrgOmk7OYwN3GBPM3X78Dk53D4ehIZnC/32O32wkgc3l5iQ8fPkifYQKgZCWTkcykFgGP6XSKm5sbSaje3t7CGIPXr1/j/fv30FqLdCLZZzmLlwktAh2j0QiPj4+SJGXiP5cbfnh4wM3NDS4uLkTGlkzcPDlJJhuBLbJQCLqOx2Pc3NygbVu8ePFCZLjv7++PmDVk6TCpy6Rp3n+WD5NkylD2k4l/gro5U4YykOx9yU0Bk9/L5VJYq/wtWY0EUdbrtSR5n56e5Hs/+9nP5Nqur69lfFlwQMkWSt0x+crr3+12WCwWcM6J7DoAXFxcxKRz6FltZDx7H6WymTx/enoCALnPnA0PQBLik8lE2K0EUml/XUpShxAEiGdxB5loSMAB1RKurq4kQU95UZ/ORxnZ6XSKEIIAX7Tpp6cnScLPZjPc3NwIMEsJKsrgE+AkAF1VFbRSuL+/FwZ427a4ubnB69evRWqW4DPviQl5AiDn5+e4ubk56qvKzWNUAGnFrq+urvDzn/+8l2FMc0Ag5fz8XMaUNnB3dycKB7e3t9L7m0AX7Xg6nYoKxbt37wQQef36Ndq2FTYbgQTvPRaLhYw77x+AxCHaF+3w/PxcilS22+2R7zGhysT9qQoB/Wo+n4tE/IsXsVcj2a9kgK7Xa5FXByDFOAS96Oe5LGzOZjyVm6LMMOeHADJt83A44OnpSYqAQgi4vb3FeDzG/f29FFOwJzmZmrPZTNiMWnkBirTWfYFGkugl2Coyk0qJHfaM2RIBTuI+AAFT+DDBuMaCg5x9x89jkVLcjOXy1jweYyHBUBbG0E5zYA3A0TrCGMYxJWDHY/M4eRKSbSlyVijn8eHhQeI/x4CxmEx6+kNeCMDNHjfHZJ1zrGkrtF+T1Cx4LAKytFkCLrQzzgF9hf8xLucgOEFtqivkBQp5f2jGERZzAT2LnsoktDVeB0E6FojwunPwlaonLDzJe2wTCPM+tuVgARtjgXMOy+VS1mGODYvnCNzSFhijeb/0Q+4ZeD2MvVyDQwDatjtSZ+BvyMKvqr6wgQAqx5nxNmfsE8SlvfK7LKLgHoPAfQhRkUAZnarUezCO6/N4PBa27nA4FIUZqimwiIR+z/sj+EufYBES/Zg2QzsKIcg+KL/XHJSfTqfw3kuxVL4nITuWLNs8VhNQZpEW5xCAjF0IQQonyA4+Lc6gnXIPwmsmO533Td9jnCZAyRhD26H/eB+VdOIzT9/77HA4SBETixRWq9VRsSDb9DBuc47oy5wDtuTgfJDdz3tgTMhbIPBe8qIFxiAWiTLW5eC89/6oJQHjUq6qwWI/zgP35MJsd15UbDgnHDNROuicnJf7Sj7AxuvvMBhUAkoDkPvhNcT5rI/mhsVQBJ69D0f7jLygkMetqt7vec2cg1zCnf3AWWiZA9v0C8ZRjiuvO1fiyOMoC2F5P/zN/1EvpWLvQvYXJWDyHCj+fEKCoLFGyAT1eC/xv6jGRltUKrUj223xdHeH/XaH6myK2ewMs+lMnjVsUSAMB9DWQpko+apz8O0Tr78psfGpBEr+7+eSMfnvTgF0puOddwAaHOotlkuDDx9ucbGI/fnO5nOs1yts9huJG3Je/NclY06vkfYdE4gGOijYQmEwHGE8maJrDhlw2l93NSix3x/w9u1bDIdD/L3f+R28evkSd3d3aNoWtkit4fRxL3MBqLJxOx0fpWKi1yUQwGqLw+6AwaDC5198D7/zu38ff/D7y/j8pw2MUjBaAcEi2BKJlSBsxclogMJo7A816nqLx4dIeJjOFhiUFarSom0sDs7BB8B1LTrXQjcGtiilJ7Y1FsoYqEYhWItO68QM1ZIwZvIcxsTvKgWrDYy1sIUVJmKCq4Ej1mUP0HgyfHzss6s4X/l4BaResgQ+ARMyoIAWwgR0irsE+zj2vdqI4NAIAbIf0LRZExPYWuu+wCH7nXABVQ+gEu8JUKAsrpg9CJwHuf6YCvc94JgOzhjB73lSQtO4RYMiiMF9tkcILQjGyrFCBN+PgNq2hYJKQEocv5i8J+gSr1f5IEBal9hXtOt8HFU4lonOPFDsHtonlYssJuWxUgYqZAArgdePWVM6sbYI08kcICHTClE6HJFQK6Bdyi8wfisCoXCStPbwCYBNfdXT2uSF5dZfvvgADUMpeMWx6P+M8fzoFmI/dklYoweppOlsb6RaaWiBnUM/lgIWhwQQJ6YrVXPhE0iZ1ldFefZU4OHjd2XaJXn/cdzWyqR7VjJ1Ab4v7FAZmC3nCHE9Ssf31qJxHQalhQolXNthv435n1YwRB6cA82hiLbehS4Dd+J5e1GAHkzTKSZH9nm/HpuUrxAwVic5am3TuXqgyaRnFx9aYacS4DVJmpq+JOofJy9ZH3VieCuF2vV5gBw864sp4nlUsmkCWFRtiOznOFIqaCBE5RO5vgwY58tnIFg/dErGWCE9q8HBmJ4BngNi7G/ufXbt6hjxYeGa1hoaSgpsJOYmAJogsjE6O4eWc/OcAkQDsYWs7pUm8sJqKYhJ/2NcpZ+x2CIC0mR2WwAK3nUyZBLFlUotBqKkP+8pB5nyvY/y7mhugo8FKx/vj/rCjjhyCUTO9ioBIfVA9lls9uhcF+0s2TrVQRiLCDYygoa4wAKpH3RcZ2LhgQ+Zv8h5qc7D+BIxKF4rY2hsnZCK4sKR26S5YTCNb3ZZe5R4ndl6GND3kaYfIBtXFQsvDOfdaBiroYxBVVYRGLdGTHC73WF7OGC7XWOzWmK73mC3WaGpDxgOSsymU1xeXuH6swvMp7OUB+nQ1Smf5gN85xF0UvQJAfWhRr0/4HBosN/t8fj0hK+++hrL1Rqfff45/sE/+sf4u7/5mzhbLHD/9ICujeud4b4JEPyNgK8U8rBEIfhU/BBxuf1uh6btEAAMh2N88fkXeFqt8e2336I+NBH4tkb2tTyu1gbj8Tj1uNfwIYsf3GdkvnX6+lXPDUe2n6zX2CLmbqBRlgVmkwkW8xl22y3evf0WnWtRlBbOtXBdCyCIGoH3PrZ+SmtcXJt6JRwWgXTeofNRxaDrWrT7mIPp2gZdG5+Xu7rBfr3BYbfDfrfDfrtFd6hhnUfhAOsDjAsogsdsMkEZPAbwKLuA4tChW2+h2gbGxzEyChiqmG+tlIVSBgoKtQIOqRRtNJxgOp4llWscFa0opL2y1rLXPY4Dx89Sp89Pp3PxXcHx/O/5b547b/brT875p17PPSP+Kts5fX1nYPz+9jY5t8NqvUpGHDci3gOXly/w/c9fYj4ZQpsCjw9rvH9/i7v7J9ze3cO3G4zsEMpXkqAeDAeoDxPU9QFlWWE4HGA8KjAYVJifzfH555/j+uoaD48PuL+7x/e//D4WZzNoEzCZjOBch/1+h8X5GQ6HPZSKiV2rDbbrTXRr5zEax16u7WGJ4SgmQzbre5QpIVUfDqhmM9zd3EpyvywrLDcblGURq2R07LmtCoW7u7skOziBtZFtstvvMKgqtO0BZRmTiYd9AzWoUDdJLtFaNG2N1WoTe6AEA3iFwmrUXYPF4jzKZqdkKNljbeew3W1xcXmOgY0VbE3TILQdAhQOhwaT6Rjaaux2W8TeETFge+XQtAcc6h0Kq2GMQtscUBYGzjWwtsJ6s8JwGJNhVTlACANYWwhjtywpz36H4SgydAjO3d3dSe9gMjavr69RVZUAFUx8U8r87OxMkixVVeHh4QH7/R6LxQK3t7fSOxyAgD8Et3MWJKUgCfAwecoEI1ljZH3yXEVR4PLyEq9evTrqf/6jH/0ISikBAcnyZlKXcsBkzzgX+2ve3N7i6uoqgguIAagqSzw8PmKQEswEA/nQxuQfE6u8HyYvCTi+ffsWl5eXYOKcoAoTesbE3sT5OPB6mUR98eJFVEFIyVNu1nJ2pbVWeuoyCb7ZbPDbv/3bqKpKWPMc+81mg7qOPSPZS3W5XMq18x7zBOZyuRSgi4zQtq4RErv/7u4ugu/OYZdA8zol1tebDYzW4huUXmWfw/FohC7d33g8jpKnCZQCIoB5SBLuTFoTjCdAsdpsUCYA1HuP29tbiVXD4TAmhxMIkCfZrbW4u7vDZDKRQgEy9tq2xWq1OrKjQUpqB+8xSGBW27Zxc8UWE+naWbjB3sqUZiXArLUWwFprLSAfwU+lFF6+fImHhwcpXnl6ehK/YK90JorZG5pA7Xg8FrlzJr3n87n4o3MO69U6jSflxQcoywpFQTDK48P7D5jNZ8lWHawt5NrX6w0UKK2q+AyLsqrgnMdms02y6h9QlRUW5ws8Pj5huVyllgITNE2MVbHfucFsNsV2u5NYHgGUKBHuXOxhvVnHe1lvNggB+OUvfomzxRkGgyEOhxpN07OOI+OsgzFWYgHBISZJQwgJZGhhjEdZFFDoGezBB0myxfemsNbg/fsPWCzOJPGplMJoNIZJ4xOBrsjcHI8nuL66lqpyNUwsOeclaR0C8PQYJT+HgyFCiIVtBE4YPwhaSrJVawyrCi4DW+nvXdehKK2wmne7fayEbHtmXF2n4zuHDl0cx/0+rrM+KqGwHQeLDfigmssaE8jrug6z2UwAkhzsyBmAXB/y/s4sLOAawHhNMJCANX2P8TNnGDN20JcI8s9mM/k9gRDK/+bXkCc7R6ORyPbnUsB8cOB8KKUkbrOgL5frp43RVniNLLYgoJG3tsgVPWazOQCk+zMC6IYAxJYrPeOS40fgjoAR54n2wUQAv8O4wDWAc0AFD6oFsDAkVxnhmOVgLQABrSkpzYIXpZQUz7D4LS+Uo19yTDjmOfBnbYGisEc2wHthEYy18foI5jrXH4P3msvz044IjrZtC2NtlOtVGmVZpVgS5yYmwAxc6FuxcKyHw6HIp7O1SgTA68RojipL3ofMn2OiKCoceakmVyoWeMSeVjHhaq1F18YedGUR91jWWNihlb2UKFwMByKdX9gCw8EwFo+FyC7Y7XbQSmM4GqKwsUBhNByh7frCJmtslCM2ti/+K+LcjUYjGG3gk9ygAPTWihTsaDiMjEitYYfDo4IgJpystfDOo21alFUpDI+QHgxXqzWUikonLPqgAgnlE2Nxw1DiSyyMcHh4uAcQFWRim4AKSiUJXVH3qQAoYb8rpQSANYbKF42A+vGcPaBPX4tqLwFlWYj0/HA4xGAwBALwcP8gyRkFhcP+IPvAKJkIrJYr2MJKEQULTF3nMBnHPURVVnCdS9K0yVfrpHo1jOfabreYTMaICgtR4hlwsuZw7crVI+h7ZVkgBIh6CGNEr54UBMSn/+eMe85dVCWID/pN04K9VqO/lgjBo237YjTGfRZvMlZOp1N0XSdKAdyz8oH6FNzm8XhdXBdyyXn+Xtgqqmc4cz7/W16SnM6TnjoJ7WZ7hxxs4++YFMiTpzrRg+L1JmZd6JPnOsUkYyJznL+11sIZA992eLh/wM3bb9GGqGyzWJzjYnER2yONpxhMJyhGQ5iqAooCPnSyFuWv5xIr3xU8/9Rvvksypv8cEXxAQECHzgHb/Ro3N/e4vnjEmzcvMZtO8OL6Ek/rtbRr6sc7jmfvzx9f+69KLAG9rHrcAGsYpVGVGtPJDN1hK3t7rs38zXA4RNu0+M//+T9jMZvjH/7Df4j/8B/+A7755ht0Lu6hWtkbEgzvQdzT6+rtJtlziP09FTTqxH6pqgr/4B//HlbbDf70D/9IFCi895hMpygKB6VdAgqAQVWhbnYoqgJFVaJtO6w3WzzcvsXj3Q3G0zmm0zNMp3NcfPE52qbBcrXCervB9rBF2O9QJAnWsij6xKoxkVWqjQA7RKKUUlAmSuWGbM6t1n0P6RQ/LHTWvzT6FUwEn6BUZG0HBRTRDyDgT4rZIQiIq7WG1VTmSsdLmFBsR8Skewvl+/1oTMieArgaXVBAktINARGACPTZeFwXPHTj+sR9yONFUgxIWKXyXQaYRov3oS+MA4DOezTOIYKWqU9rcCCqGXwEd73XAPoEa0yo+3TlfW/eVtn+/EpFYJjgmdyFQhhlPcUTQCHSwGlfw7Q3Xz0QHiRWhxCirOqn4kqGq4Z4UXId+ehHwIWMVQMCU3I4lfXMFgfq14L4X8/WT4eL39dZPM7mTewPATr4CMCjB5cCIFL1vJ/WdXJsoE+Ce58jy4DRx+0jnwPSoDS07QsWe3n0EyUOQEAhnMSy/JgeoQdKtYYO0Q+QQCdwvTo5RggBXefgOo8uFaYgBAzYXz1AxpbgWwgqTqj28LoDJahPYy3HUqloJ0qnnLQdAioWSBkbn5c2mzUqa45/d7K2RH8OUNpK3ORAB/ge01dxnS1sARd8vF4xNgWVFUWroKKMfvKXvL+yDhoq6a9oZQDT2xb376IocXrNz+AMcU2JYGNoDke2AWQ9gPn3kIG4vHYCluk7PiRP1ZERzueS52zEUFI+7WO5p9WqlxjXRkMH5rbzfUxi0xO0Ch5I7GkytfOXMSaCgsbIcZSK4CUlybWJKq7a6KR4E2OGSXuio/YN3H+aYyUDk4CnjyJKGAvbN58MldkytILT0e+6tkXsnZzbbhcVUbwW4Nql4ghROcn2itoTsE5lS4HFVKcFNScVMoBIhOdz5lWMu3L/mY1Q2SB4fyQbL7EIONq/dHAIaZ2JTP0YDwXIY3xt2xO1CNPHwBSX2bs+BKqsaAaHeL6uXyOjusPH0swxT9SCKjA5csgcQFEUKAclhoOhPGewrQe/7L3D4XDAarnENrUle7iPCq373QaHwx6Ax8XiDJ99donF+RkWZ2eYz2OOZrPZwVoj6/th38BYE3N/XSxC6JoWh/qA3XqH1XqNx4cn3N3f4/7pEd//wQ/xL/+f/w/88Id/B0VZ4vb+IV4XgrTY0GnkvPcIun9eyJ9lmJPhc3CbWji2bYezswW+//0vYa3Fn/3Zn+Gwj1hekXqes5i587EdAIv6XYg1EXmRwZHNZX6V/zu3wfw73BOH4KI1KA1tLMqSyl/AZDzBYrHAaDjCn//pn+Hp8RHDYQWtPGrXxrUge45jaKYNCWHRdei6RvI6oe3gEwB+OOyxfVphvVphv93hsN+jSUzw0LbRZ0MsUqqCwlhpDGBQ+oDCRXD8bLtFVzdw9QH7pkXjAoaFxXA0gC3jftd7j902EnUnw9QiFgErX2PvHULQmIynmM5midTcx4I4Nr16ZqpCORpvvrz/eH/z3PPNqQ/l8/jcc9hzz2P99Z2C5MBRnHzmHPHPvgDm9Fz/hwHjTw/3kticTqfQRsN1Dqv1GpPxGPe37zAdlpiPrzEcDFH8qIBzHu/fv8dkMgUQN63ffvMtLi4uACD25WtqvH//AQgBl5cXwj7J+/0VxQF/98efQaXE4GG/h9EOhTUo7BDBtRgkMPrx8VEkHQFgOp/FRMhsFhmDKTHddR3KaoDBYID9/oC6bhJQEZnNWsf+AIeUUDHaoK07WG1xNj9H0yRG2z5+t6wKFFWBzW6DpmuxWCxQDQusNyt4BGw3G8zPzmKvynEJOzB4vH3AfDaDMkDnalgfq8S1DtgftgK+DYdDTMcD+K7BbreXjZ4LMTAul0tUTMiqAtNZ7CPddR1c5zGfzjEcxIQpk/CHuoEthphMZ9CmQlkWKdGkoxR7ZeBDi2pQ4O7uFg8PtwgA9jcRGCZb7sWLFwBigvH+/l5Y0XVdiwTwZDLBcrkUhgYTymQokxnIhFnOAnTO4cWLF8JAAiAs6FPZUMo2jkYjYR8zcd00jfS2JuObibicmcMHFbJlc5YgHWuz2Uj/6/V6jc16jelshn1doxwMME89r7/8wQ8EYB0nuUoyndh3lbLiPCbvhWMJQPp0kjGqlBIghgyps7MzDIfD2K85yVnassRgNIrSoAlYJZg8TOwnghxM3F5eXkqvY4734+MjFosFDoeD9NgMIQgID0Rm22w2E2CBzFvOF6XZKRfPea9SgtS1LS4WC3QJqJmnxKVzDmVRYJAxJnkfw1SgsNlsIpNAa1xfXkoSf5yke9sE7FGS3DknSXACTUopjNP4tQm80YiV065t8W3qR14UhTDwOR/r9Rqz2Qy3t7c4Ozs7ikGbzQavXr2C914Ykdv1OjKzrcV6tYIKAeMUr7ouVhyTbU/ZV7YLYBKACgtkXXNMBoMBxuMxPnz4gJ/97GdgMnk6nQpzjPLEXDQIODEZTFB8MpkIwEaWHZPVt7e30kdca4vCFmjqFhfnV/KZNhqDwQjLpyVevHgl/j4cVJiMp+JLF+cRaHx6esJutwSAyMiqW3gXMJ3McNjXKIsBnPO4u32A1hrz2RnKopJ2C8unNSbjKE1vTYngd4AC9rsDttvIFD/s4xg1dQfnArrOw3U+Ff+M0LUeChqbzUYATeccmroTGX5K/26wS/Eqsge5QYaBAGOSbA8a+/1ONnBVOcRhH5UzppMZvAO2m20EtnzqHWUMJuMRvEOKlyPUhwj88XrKshT2mtGF9HCtqmHy7fKol3EEdzqJr7KpMAbWJOmvtDFhTNwva9Rdi5EfxE1tF1AWFVBUohpCu4gxQ8N1HbabeL+7bc/iJCiet3kYZrZPG8wLofb7vcjQ8j5y9upoNIK1VmTPadMEYcgaZVHRMTgQN8IEVQluU76fICD7ZbMYi77DDVcuqcz7IggM9BtMsor5e6B/2CIQQ2CW986NIoudCNZwrnleghY5OJ3Lise4q1CWBboutmmJe6Foo+zFxDWUADz3S/l1U0mBDEte3xH7WSlZuxhnuR4cgSyZqgJZ5QS7Oc9c8yIoOBDb576AktdkmHLt4LiSTU0QjOA1vxNVRKJE/YcPH9Ix+n7K+33ci06nU1EhiYxwKrsMBNB0zqNpWjgX0roXH/g3mx1MEeUa266DVwq2GmDfxAK5+Xwm6z1B+aIocHt7i6ZpknpBvJa2jQ+abcuCpsi8Xa8jk36xmKc5MrBWoW072SN5H3txzacxfpemRDBBbIpJC0rlBx8AD1RFBassvPZwwWFQxr3MxeJC1DXOpmfi60op7HexyIyqIOv1Gg4xOVGMCpQ2KTvUDYIPR4V0UcnIoLIlgCCqHd77mEgxBkWhMR4M0TQtKlsdKcFYbeGCg28Zg2MRb5d61CmlsNnsxO/X6w28R+yNZi0+fPhw5Mu90kWZwGWFshzIdcU9TXyu2Ww22O02ab8e/YAge7SXCJw7d0hFiFtU1QDWluJDcd80E7+bTudJ8SS2+GHi1OheYr+qKlRlBe88qrLCrtvhbHEmscqquE+ISUCF5hDtysEJK7iwBVwb5zcmUJD2eCVCUBJHrVVSLJcXx7CAj/tL/jbuvTyqqu9jbm18vyi0xBjaH/ektEnGy7IcJICQcpc6FbX0Pk+lAsb5fD3mPobPKnksyn/DF+05B3P5He6deT+MOwRnuIfPQfe/7es54J0Jd7m2lEzMk1qn96IUWXUZgAgyxnuQSimNwkQwkgUnSimMBiUG1sAdDhgOKrjgUMGjW62w2uzRvn/AbjLHcDqFGQ2hqgqoSphBienZAuPxWPbSHPu8OOo0KXYKauXJk48B7o8TNPl3Pg1aR9UQY1Vko8KjaQweH5b4+S+/QVVVuLo6w+XlOR7XW1GukmtLCSf6xnd95UljmTPVzwvXs7OLcyitsd1sjpQ1+HtTWEymU/zbf/tvYa3Fj3791zGZTPCTn/wE6/Uag6zomgy3v+mlTYItu8gMOxwOsYDGO9zfPeDi6gL//F/+S1zPL/Bf/uiP8fXXX2O92uJ73yvhXEBRlSirElVVYl830EWJpnNAkoadz8aYj4fYbg/YbVb48HiPt16hOrvEi9evMLtYYHEdi8K7rsN6ucLq8TG2iAsB0EaUIkxhozIB2WDaxJjT1gD6vAeQ2J8fvewxHK1jH2ud2SRCgN600u4k8qKZcNP971UEglQ2j0hSsPx3D66noh8oeBX7H0Ol3rrJPys4GJ0n9mwP5hL4SafoAQ6Cv70tcu5DKoYJnnLu8TIIjHvvAQ/o0Bdb5kAvAITEKvUqCGE8BCfxL09Wx8/StYUgUvL8IF7mcRLzNH5xny6AW1aE0vcgjy+ybr138K5L8S0H7LL4qRWUhzBHESD96fN70FqjcT1gqAQA6a+PEtJd27dxyf977sXxYRxUOgJdLl2DNhZa92naPvYDUFlRqtHH33EO8PFZFgrQpi8uU0qlgidzBFD14x1gtYPWqVhB0S6S/aYLiAC9QlBGCjHya2CuwmRrIFmrCqnftQ8I6XtetbyxZAM0i5jbKVMvV9e2Ik8OSB1MVuSTbMnHlgrOkUEakXiuNdYaICkKeAC1B6zSMVYhAv5d56F0wTqYJGyftf3wISplJGUVB/Yvj/4u82v6NU5rA7jYHsDY1PpBAe3JnkEbQOn+uSlXnxHQF4CyPQhOe3huTcyLp3PfOlobAbx2+Oh9OSftJQRheTO25uflOaxRKGxma1oh4Hj9CSGCn/n+is+T+SvmTSZHBdOn9yp7sdDncj/pf8FDs3BJHZ+7P6mC9oj93rNiFPleQJKh9oiE049VWHJ1GaUVYJ4AxFxGSKxfiZOOkvhAZE+rI5+Xe1HHRUP5eEnhguLuMMBpiDpuPFZf6BGB4nRad2wT6MN7Nm7h6Hk+B5SPxyYybfnvfL/EljpxDfFSTHW6/4vuzOKLIID/0TWib+fhvU+xibEqgey0d98XTwTljp418oL2wWAci+2rAUxSoGMeJfch5prX9QbdrkVT11gvV9isV9httjjsdmibGi49G9jg0CUln/PZCOcXZ3jx6gqLxTyC4ArY1msMzQyVHaINHTrfoXMt6q4F9h0M4n10rcNu0+D+/h73N7d4//4DdocDprMZ/q///P+Gf/5//xcYjGJLxOV6DW20KNiwGL7tWpTpuYjjwueXfD/AZ7PD4QBX1/Ah4M2bN3j16jXG0wl+//d/H8v1BvP5WVRMRr9mN02LoiwxHI0wmcRcb2y1nOwh82E+y0Rlht6mcrv41P467rMAqFjcQjINSX8vXr7AaDjE7c0Nvvr5L9JzvkbXNYkkQXJG2isgwKW5Jhl0u91it9tiu9tgtVrFYvWnFfw25ujRubjMOA/lA3SS2LcAzmFRKBsLlJwHdnuYXYuidZEZ3sXvDSejpA6g0XoVe8gbDd12UflBa1itcagM9sFh1HYwLvrGvm2w9x2gDQajCQbDCWxRoMvmlWoiuZoq+tKtYx/OYsRzwPmzcwB89L3nfvupY+Xnin8e72Gfe8ZLnyJ/62i/+snfPP/6zsA4E6WUj3u4f4hJ4hQcV0km2BiDdlSDrJzhoISCEynRs7Mpdjv2EG1gjcKb1y/w9PSE5fIRMen6JHKNj4/3mExGGI4opweMJyORz1uvY0KOCTEAuL6+RlmW+Oqrr0TGk5KpAKQno1KRMUo2Zg56MZl3OByw3+8zxq9HlCCISecXL17EaungRf5vsVhIYmswjL2Zh6MhnOtQB4/pNLI0BoMKh/oQg1NKZJNVNpvNhFW8XC4ju28cZUjJXiuKQtjL7Ns9n8/xzTffJAAy9vUjQ/vDhw+4uLgQsNhai/v7B6zXa5kvSp2+e/dWWLWRHd8zn9jD8OzsrK+i6WL/RQBH74UQBMTmQ5NSSmQpN5uNMFKBuHnjPDERzmMy2cVk9XK5xHQ6lR6JQAT93r17J8za9XqN6+trkVAvigLv3kVpePbR5bgQiCcjcDSKSgPn5+dyvavVSooCCBp+9tln0Nbis88+E1Y8x5g2UicpToI1dV3j4eEB3ns5Ps85m83kHGROci4ACADqnMPV1RVmsxmGiTl1eXWFK60lwUwg+Pz8HOv1OoImRQGjtYBF9OmmabBcLqVQgMA7AJEGJ0DOHu5kRLE3JM/H8WHSkvZN4EqpyKbabDaSCN5sNsLkobQ9k0DchPDeCX7d3NxIbMptp21b3N/fS+9rLgTcoDN5TiCOAZd2SiY/F2/nHC4vL+UhIAfC5vM5bm5ujlQMdrsdVquV2GnTNMLG//LLLxFCwJ//+Z8fJdIiONUXKdB2bm5uRHlhv99Dp7ljf1UucJRuJ4hSliVub29FOj7vn85ClqqqpFf0er2WIhSy07gZPD8/h1JKpOPfvHkjYJ+1Jfa7vfiXUj3rlUAkWfkEL2kHecEMFQZYCMCkOJmco9FIpFcpr0xZ0xwo4xwSOCQzlAoW9CnnnMRS+h4X08lkImsWY6VzUTqfdv/09IT5fH4kmcXrY4zjmDA+AxEAZn9f9osOIbI9yRDPwVed/Jm2mD8853LnlD0GIPbOF4+ZM3Nz22ElJO+Xf4YQUFaljC/tlTGec8tNK+MAWaancs1k0dLv4sa5OdrwsgAkL2ji51rro17wBI0IJudxgmNJpjCLpSgNzv719Eu2zKB9US2AxUO8ZhbU5MVUjIdcq5g4zxmHBPX4Oe+BgCGBZc4HYynvG4gPvYyTp+0FQuiTPixWoFqB97F1TdwLNXJ9LIph8nm/30sM5nsAZM3nA2be4iF/UDwcDunhYSc91geDgah08BxUBuC6Rv/Ki8EIcOV+khcY8DOuH7nsPWM3ix6qqjoqLKOf8joY81lUMB6PBTDnPFLVgGsz10/6aS7DTv/j/dZ1jX19gEpzTD/Mi+6i0kb/G67D8/kc9/f3Em8Yv+jPIURAmcU8vB+OE31cay1tBkprUZWVFJVQjYbFMnwg5trLop+cRcv9D/eMBIgZyzlf9H36KdddFl3kcfHDhw8Shwl6RDvsFW8YL6bTKTabTdpTaoxGYykIpU3l/e6LooRP+zJeG4sFGF+5zxyNRjg7O5NnA8Zg+hjnh3PNdTKPIRw3+jUL2ADIvoqS/t57YV2SydwXswRZ2xkbB4MBVEiFe+nffLnOyZyzf3q+/nB/MUvFwrQZ7i3YGoFxTQq+0pjlBTws9qO954XFbJPA39FXch9hEVKugsEYSjtmbOE5OW9M1vAaqbLRdZ1I9dP+8nYAuTw/n0dYhM0Yz3mkb3PMeA7GKN4PfZgxhoVd9FN+77/H6yjJkJLKin+PX5D5ey4pHP+toI9a+vkjQB2I/mxNCWOK2BvRKnRNAHSB4XyKmdKY3ryH/plHA+BKVXiJCuetRbfcoD0cAKXhygKutPC2wF3xC9xZDVWVMIMhyvEIo/kck+kZykEFrQ2M0rBWAQVlSDVUULEQJCXXO6Wgg4IKpwxbRLAOXnI9xsc+nhoqJhRDZIOEEIT5FVkTDt5FFlkIgHc1NmqJu3uLb76tYLTGixdX+OLNFdbLFZarXVQAgodTDgodjCoAn0BS86uTQ3mxB5V5WCTgfWRIMrYrpeCdQYCFWy3RtA2qsgSSxKUOHoNCI4xn+P0/+F/xm7/1d3F1eYF/8Lu/gz/84z/Ezjcoy0FSkdOwupBx66GkExvxCQDUCs572NJCacCoKEu5Wa7gDw1+6/f+Cc4/+xx/+pOf4H//D/8BP/v5X+Pq/ByT6RhVVaIpLYajEeywbyFGgNYhYDgbYjQboWlbbNdbPLz/Cndf/QzD0QjzswXmi3OM5nOcnS9w8eoarUdM6u5q1PsdtpsoUel9l/qFelidWJNlBaWtyJFbm2TUxQ/SfiBoAZqPimCyhC0AqOCSv/Xy4TlgFAHpAK8EXXrW75WKfE+DHPgwMh8+sYdV6rF8DDI/A/QoABlwhvw3KgIEPSiRgdD5PdI+U7zzWosMvtEE4Pld2wOcgdLy/X2o7L59+j7Afuperst7lw4bjx0IUCWgmsfhXk4lFrh2EdCUoQ2ILMAk3SvAeGiz2esBmyDFP6nfLsc0gUQR9DwB5tsuzScEaI/37uX8AGAToyskZrkcC0hMyh62ye+1B3t7Zjg0+zarfn1UvU0gjY1VKU6qHiDqAYQ+YdzWhyj3a2xUATkqKuhlhLXJwO50v0oraCgBp3yynbw9VQ5qce3tmXcfA5hH9pwB71Fiupfkpi0AShivuQ/kf1cqHqrrPFxSQiKz1SgFqy2s1WID6QCA96ibJrZM0ArGahhrUQwqKGX75TUQvye7Obu3rH80p5b+JN9RQJGexfJMPsdBisS0RtBIe6MQC3J0VBKI6hKpeANRVQDJvjhvPDdfGim+8DISI9tn5wYCDFjAEFnUIUQWckBWkOaBEI7lu5GPZ2LtwigUhcWgGkQlua5D13ZJ9SI+QzsAqungyftN19zSH0M/U37cs1cZE3p76ueBrWXYfiLvH63TxkdWvyyU5gAKZfhNmvPnCg1DNrfPAXb5/PO4LToQsKYd874FDALQhNgXXK4rBCCo4/c6iBLAc3vCEGKRTV4UEYKHUtzz9HtGpQDlg9iVvE82tu9tJJ8nnrv/t0rfSW1+st+FFCdbz7iqUn/mfMxyJnsPcKvg5P7icDBvykuN9tjpSo5tTFzzy0F8zq4SgdIUFt4aYc4abeLqFKKyQhy3Dmgd0Hbo6hr7lMet6wPqwwF11ka2bbfougO6VDDW1g1Cut7InHexjUtZ4Wxxjtl8hvl8jul0gqKw8F2ILTZ1VNhp2jUCemVE5mu0Vmg7h7qpsd3s8fCwxi+/+hpt0+DLH36JH//Gb+BHv/FjvPnic3TOYfX0gBA8ShOP631knysXUCgA1gDBoypKON/GPUiRnv+UjsUv6IttOu9gAlIBd4nNbos/+qOfYLPbYTqdAcag41YhBBzqGlUVCZjD0Qi2KJMtp4Iq1a/XtPsAwIVYvI+0J+rDdJB9M/2x3xspQJdQAMqiwqAaorIFysLg5fUlppMhNus1fvbXfwVbAIPZEKppYYKGgsVKdZi0BvAORhkErXHQAW63w5/+x/8d3/71X+Ow2UTp/+AQugZlWnO196gaB9t5DKAxtCVGtkSlNLrNDv7QYrpbwzgX1zcAzjfQQWFQDQGr0akOddtAdx1C1wHew0KhKAt451DvdxiNhrFoAAFVE+CLFspUcE2Arz2sC9gPA6p1i9nZBOOzKWwZlVeVi4C8KRSs1dA2zxGH7L/4b6WoJJGP9XHrj+/6Oo2bjNeAP/J9aXMge9SkjCTninuA06KpeMzjeJzvmfL/vsvrOwPj7OmolBI5aSZFCDISWCXARnYNASMmNA6HAz58+IC2bXFxcSE3wB7EeYJ9PB5LXz7KquY9TLXWKcBMheW73W7x9u1bAJHtOp9H9sxisRCQigB018VewlxomeyhTG5d19K7lgkUSiP2DJyY3CdAyYQZk1HGGCyXy6Nk23g8FvCFQBb7ThLkXS6XeHp6EmCLLFyy7fK5uLy8lOSatbH39ng8FvYVE4VMngJ9VScLBQjGORcldqfTyOq8vb0V0CmXCH3//j1CCLi4uJDEGe1Ba413795JgvnVq1dgspNBnqywvDfoZrMREC7vD8vEl7D9y1J69j49PeHi4kKYut57uZ7r62tJqOabTs4JE92LxULGn8lkOt/FxQU2m40wg51zeHp6ErB3uVzCA9Iz8o//+I9RVRVev34thRlt2+KQwDwAwvK8u7uT/qAEA5hoAyLw9fLlS0lo58k+JvEIErKQ43G5xHa7xWazAcENJvn3+z1WyyXmqRcmgZ68n2rXdXh8fIxMc6XE/gg8k8XA5CKZeBwzAgYEQsi6pzQ9AXNWYZGhzGMwMRwlmyMznglMsr0Hg4HI8XLOCUwSPG+aBo+Pj+LTi8VCQNSrqyu8ffsWk8nkiJlJkJZABxdisvyZ8FytVnj16hU2mw2enp4kYUr59dlshu02qj48PT1JAQj9pigKXF9f4/HxUew1T9je3NxITHh6ehK5/BAC5vM5zs/PBXxiXGABzN3dHbTWEhMIAOVJ+zwJTtCHPlEUBbbbrfgX4zHBdvouAZyzeSmgp7VW1AFub2+x3W6lYIYbPNoubSDKn/eS8DkYzfklqHg4HHB5eSlzEeVdJwJecb1hDNFaC3BDkGW1WgkDmXOcb7AIpHLuCPAxscb4MJlMZDx5npz1xvWLsRaAjCfvn2sJlQFo4/x9nlRnoQB9nraZF32QHc4xzDcJeasGzpeAIAhA029g+DnPwRYEbKERQhCwnP7RF0pYKdhigRB9Pgcb+GfOFCcgxJjNdZ72yHids/tYOME55joN4AjMynsQE8Tj+slYx3vnxpvFTATLCKAzPhFs5HXQhgHIWsc5z/0w7yscQhAAO9+HcN0zxkis894fMex5b5yLfCwYhxjP8o0s2ZwEZrmnaprYZ4nx+P7+HiEELBYL8UXaE9fk7XYrfYlZbMFYQJvj2PFYBKEIHMUix7X4I4snaAu0MSZFCL567xOLdirjSDscDocib85YxX0BxyCEIPsp+nHeM5h7vPF4elTUxu8y7nD/koP1bDvAdWw8mUTGeLJtxpq8+ECpcOTn6/UaIQQZv81mgxcvXh0p7BBcZMygfbBggr8zxmA2mx0nIdOcMo5x/PI4xRjB+EWb5fjlTBbaGWPoaDQ62qdQvSFXz+Hc5IoNLKCKcT+yfejzLFbI1xO2BaBv8zmCewGqXXGd4R6U+0LG4dlshuVyKUoEvH76OL87HA6l4ITFaJxLFoawCIu2Rp/mmOZrHGM243weKxmH6T9cz+D7QiA+m9HemTSkLXIvQdtWSklv8rxveh6rch/vEzNa9isEpGnznC8WCEiSMj0f0Wc5P2xDw+PQZrgX4TVx7eQzZF6wwbHjHiaPK3nRCgsiy7LEZrNB27YYDodHRSP5PNM3+CfvL/f3XL2DSk+Mqbz+PHH73/ridZxenyReM6CBf34qkRvXt4+r6k8BjthfvIBOagI7t0NsBTCEUsDFxTk0YmdKo4BhUDgLEVhu2tj/99AGdI0DdIdGu8j2tBqdLdCUJXbDB6xGYxRVBVMUsIVFURWwgwrlaIDClrG1gzbQ2kIVFsEYkUqO8xcTJkoxpdIDWJ0OCCpAq9gXE6rfC8YEb+L+PgM8dq7DarWKBabDEcbjEWbzOa4uL1E377Hd72PbIx0TjB4eUB8nbU7n8XROTufz9HNjTGR9+9hzcruJfm8UMinjgGpQYLM54K/+6qfYbtb4/M0b/MaPf4w/+bM/Q9usUZQliqJKycteOSDhPEen9ydMDZOxvxAiWHIIB3SPjzibz/GP/tE/wsXZGX7yR/8Zj/f3qNsag2GF0WiItuswaIc9w9sY6AS0qRDBZOOB0ljMzybQ6x3a9oC7u/e4u78BtMXobI7F5QUG4zGKYghtSgymYwymYwQX++g652JBARlPLvafdt6jaTqEuo6S6P3oRhxB7Oe4vyzBOAI9XnuI1G9i4x4Bfmk0jeoBR2H1pfPx1WqVQCrOf8aujjAUtFZH8rGftBkAZTAfAfk8uvxbAThKhh5f+xEgkscZ+lW6X/Zoh9gKARcFpSLwIiAaABNaOacXaXcFwAtAFxBgYGTMVTLKABUZ6j6CtA4KXUhsUZ3fKYFcSud7IlNH95hgFknIB62Ewfjci0PcFR1OY+9HCV9AwDg6UkAC1VQGhrHw4SSm5/chz266X0dPbYDrH9AD65+6NgAIbizXzyP57FwCqJrjoiqOlUIG0Kf4aYzF6VpDYMsY2zP0eUYFKciQAgMEaGvRf0XJcTwBPBXv0eoeGOc49nPVJ9BDQM/8T75klIbR+fyl3tTOxWKBKqoxKN0Do0Er2YMCEVjOWiUnSex0394Bgt+Fo3nkfSJkNoIMSg4RwOWzjlHHQLFT8Vqdc+hcF4+jI3gVpOgEGZic272CVdnaRmBfKbkA3pKikoTuC4iOe0P3c61l7ZGpze4VMCoyxhu7R304IPiM2Rx8jIEAQuckGhFMjq2Tju+jaRvZA+bs4d5mWBCQgTcnoIiSsVdyQhmHQDAIEt+CSvE49EWD+evId07OczrvSikgqVXJ9/nd3qTifHsHr1RfTJPZsZL57sFolcYth6eh4vrh0R5dn6b/Z0sAx4otq073hkf363rfo62dxhsfesbt0ToZ+r2FVgqBcS7/TxtoWWuiLxa2kHUlgt5RpSGPyfEZOLbziOt4zz6O3+n7z3dtB1/XqIOLsuRti7Zp0DYNDnWNtm3Q1nu0zSE+Z7Ut2jayt13XxX1FxwLeOj2fpfadqaihKkuU5QC2sKiqArP5PD4DlSUKo9HUBxz2URof6PfxXZ0IWd5FhbNU3M08U13X2B9qNHWHH/zgS/zd3/xNfP8HX2J2doaijMrIXddBWwOtLOADOjKGdVKtSHapEMlNSpdpzxwLF621omqjFRncHl1dwxiLpm1xODRwLraxMtZEZZJUeOKcj0zx4RBl1bfmSLtNiekf7W2QxYGTdTF+N4L8gENa7sF4r62RZ+eqKjAcDLCYzzGbzbDf7fHwcI+2azE+nwFtG4ttFOAQUDiggUPhAppCo0aH/XqFv/rf/iPu/+LnMJsNhl0L7R1KKJQBGFQGlQswHYAWQO2AuoZRBwyMRaUsUHcooRGVX+LYqODR+OjHxgeE4KBcBMJ926X1IRY8WWNgbImgA0pj094yAt26jMUnKs3v0jWouwaVthiNx6iGw1T461LRaGz5FovYjYz7cVzLfV0iSR8j+K1n9qDPfe/j+cuP9/EepY/P+bH6df303M+dK8/nn8bl7/L6zsA4EwtXV1fy97ZtRUI2T0QxcaKUwmKxEICTQAD72jLxQ3YhgcmyLGGsxePDg8gRW2vx9u1bkTwluJWzBO7u7qCUEnCTjN/1ei19cclOIEOX1/z4+IirqysZ7LqucXt7e8RcZcIxB0cICpId8v79e0mYExAga+VwOAhwwaTUxcUFbm9vj6rgCDyRnUzmBhOdlAE/Pz8XtuxoNMKHDx8QQkwgMiGb94wmiAxAWO0EJlmYwCQWE1ybzQYAJKnJMSPjkaxVgkfT6RRv377FfD7H5eWlSKM+PDxIYo9JqTwRThnv4XD4EWuIIBwTBPP5XECHvGcpnYA9rwmchNAze3n9TNI9PT1JYpB9TPf7vUibG2Pw9u3box6Fu90OT09P+LVf+zUpnNglmfHXr1/j4uLiSJK0LEvsEkBorcVqtcJ8PsfFxQUWi4WwhpgUvL+/FyYqgCPGJMGam5sbubayLPH09BRtrK5hs7Fh8QmTtTxGnhB/eHiQZDNBjZcvX0rSM2eLaq2PmL1kGDL5z6SlMeaIfUnpfCZv6S9M2BLMYQKdyXImw5+enjCdToXZnCtYMBnOpPN+v8fr16+lZz2TYLRryr4CEB8lmypPFhOsItOYzL/1eo3FYiGFIV3XYTqdYrvdCguSoPKf/Mmf4LPPPpM+4ZQHns1m0lN9Mpng7du3cpymafD69Wvxt9/7vd8TYIwMR+cczs7OcHNzIw/HHEcCaYzL1lo8PDzg+vo6tq/IpJK7rhNFBwIdLIRgUQd7ktMv6Wccp02STWahg/cei8UCV1dX4lf8vtY9w9g5J8U7BCjyRY3ABW2SPsyxIEBFhlpZlri+vhbJc8Yjrj1dtrk8Ozs7YgoztuQg7VlqicBYv1qtQECIih05YEEwh+ACAUvK27NgJAd0yOBncRDXE4L8BPz4gE/wm7ZBv+K6S3CBmwICpTmQ3DSNzC3jvCkLSeYT9GA8YIIxpMRjXlCRM51C6Hv0EBDni+Ak4zbnhD7IcScoRsCCmx7GDgI0/B03dFzrcmnc9XotzOpTYDWv/s5Z9ARDeTz2wAZ69mvOkgQgIBCPzSIjgijcA9Bv+FsWEnE/wvHLj8n9yGw2k4ciXk++6ePvea9UychVWur0QMN7zh+0emb7sbrHfB5lm7kG5JtMznNeGMXjMZ5wP5EXcLAghkA6f8u4Rn/hXFM9iPuwuq6FOZuDiSycYJEJP5/P53h6epI1KX8YWC6XMtZss0JbpPJHZCUHUad4fHwUv2csY6FbVVWx53aan/v7e4nb1mi0aT64R6T/MW6E4GTu6KcsUmAc2u22CAEYj8cYj8dSBMYCN+6/WVRGm8jXfKVi8QjthvbLPReLM621GI/HRz6U+wr9nXtOjguLlfKiGF7bdDqVeJQz9cm2ZbzPbblta7muh4cHWUfH47EAs13XyjpB0F2KbYyBQYBNRV+0Zz4nUBHh+KGtB9nz+z47OxOfYTEBr5OxiXLRtKUccKQf0Dfob0qpowJTzhP3UHwGYRyq6xohAbHcm9AfyJBmHFRKCSDFe+UcK6Vkj8n9NZ/VuIdj8WC+/tE+CNSzMIjAMfdCvFe2xOA6lq9rAKQgj8Wa9BPGAt4PiwE4ttxr5YzbPNbm67pSfYEYCym5htBuadecM443nxlp8zlQwdjH/QvnkzbImPvf8soBlE8lHvi97/J+Hss/AnhkDxGTaDrJhLvOQUHDFgWMUVgsziMwyyQOAoZQsEGhdkDjPGzw6HxMguzQIRiFoDW8cXC6Rbc54GDWOJQFtC1gSgNdWZiqhB1UsEUlMbAoSuiqhE5FENZEm7bGQpnIGsnHSCkFb4CgIos7CA6QeteFlPDPci8CDsHDeYf94YCn5RPG92PMZlPM5m9wcX6O1WaNzjc4HDoobSKRBAB0TDZCHbPInkviPDf2whZNv6GdFUWRwPEOXdvisN/BZ8UBkempUSYltvfv36G0Bi9eXOHVy5e4+XCT+h26OI66B377xHH/bw/2Fk57Dagjn4APaIJHs+kwTq1nfvhrP4SxGr/467/Gw/09mvqA9XaH/b7GpO5QVWxNFmO8NjoDV2PPy3JYYYSA/S7gsD/gsK9RNy1W6wesH29RDYcoByOUgwmGoxFG4wmsLVPCr0ChYy9oHwLgGiCxuJzzEVDySsAX5yOgroWh5hEcZW6P5am991DmGIhLgxbHSLEfuYIOtk/eacpkq6OfBh0QdA4SZp/FH8b5EGBRTigJ7Txx6dgxNDuQgHMZ0KxMcZJv/ujM6d2MeYNjljX3qYTwg6BRManOu6ElW8YuBaQusOlae9WGEAJsOG5ZIWfI5dcTQBhZtQm8QpYohZIe7L2396A4h4ggBLPrnAf5dzoWFBB8QAf3bGKY5+WfVumjzwh45gDfkc+r4yKUPM4D8dynv8lBV4nh6hiEPX2FEGAUr4d9zyPwrJWS4hAAqd9xkHliUQSgJMHO+/KOga9nKTNuhBQn+vmGgHrxaP21dqloibYaAqSXOsG1COiFIwAQPJdcfZrHLF4ppN7HWsMrjl1SBkkxwNikKqKAEBTg457YBQ/n+lYI+fhnUyjnk89CD3qeTISwUsUYOW4+skZj65LeThnfnesl6rXWMFrDgV3okYHAHBEOh4JBim/iRz0wrqASAAzAP2ODz9peJndO+0/noh1YpdCmdjfN4QCjzdGzcJeup3PuODZ+Ym/SNlmbgueA4fxfMq7x/0Lo56KX5z3eK+Tnk38rFg38CnAlTWX++1zx4KhIwUFiCu8jV4tIQycFUVyXeAjpmx5SJE3zp5VCzs4Gern9o2sP4XiscvtU6sh2+r/3hUSASqo8tB2dbFVJj3iewCc/ZozP98jpdFLgFPcjsR1FLJZKx0tjqG15NMs66+Geq3uEtob3Lha8IMYV5x2apkbXtSJ97xqHtm3QuU6kzruUM2/a+LzRtHu0XS05sL7g2Mu2EYiAcfCxrYc1VgqVi6JEWVYoiwJFGWW026ZGUx9i4YDr9x0EiaE0XMd9Q29fSinYIoKklTIoq5iv+P4PvsRv//ZvYzY/gwsBu/0eu318tquGQxit47WhBZSGMamFEedPaRhtoU3oAemAWJQRkOwsrtmuc7HlkE95TwBFWaBoCrHNuF+Ix62qCoPhEEVRyhp/dFOfeOU+yPlPBpr92e9bxT513CcXKZ9ZFBYX5xew1uB+vcZmtUZhLeywgkvt51y8cBQtUCNAq4Bae6y3K9z95V/g5g//CKOnA+bGAsEBXYfKAdYHFI1H1QG281CdR+gcVOugjUZhPArl4JsOBRRcmREIEGCQCvRcAvi9RwEFlVSpkWKsDQqltVAmFaf6uB8yUIC18U8X0DiH+1CjaT0uBhOMJ1OUovR2rJhhMuLn3/Q6zYnk83P69+d+8+l/f3r+f9Ue5lPfz6/t9Jo/9Zz7qdd3BsYBHLFHmHxi0otMaCYciiL2RiRrgmzVnLVFNh2TamSqnp+fw3V9H1Qm95jQ4M0/Pj6irmt8+eWXRyA7EAE2gmkhRPbi9fU1zs7OcDgchPnKjRMZwzlTgtKcBHtyQJUJRIIyZG4uFgus12tJxKxWK5ERZtLLGCMSkHniOgf79vu9gPm5TDpZT09PT5Kour29lar2H//4x3j37h32+z1+/dd/XYBUHpOMmIeHBwHgmbghUESglnN7fn4uCS0yqICY/GMSnCD6w8ODMN9oF9vtFkCUsHfO4eHhAUyAnoJwTAAul0ucnZ3h7OwMi8VCGNAE5jgmZBuzsOJwOEhynEk3ShRz3CnhXtc1rq+vJUHP+3p8fMSrV6+kr3LXdXjx4gXOz89xf38PoJdDHg6HmM1mWG+3cg/n5+fCJmUy93vf+x5GqX/ry5cv8fXXX2O5XAr7lUlsBqvHx0dhyfJa5/O5+AqlzY0xmE6nIKvTGIMiAwuWqcUBQYoQgsi6k1XJa5zNZui6TnpELxaLI8YZgQEmWhkTKI1LAITJ2X2SmmFBCX2TssHeewEfCUqw2IS9cZmY5THJZL+5ucF0OpWe5bTPWWLCE5C4vr4+YlmSBUagIS+uYPKX9uicE/9mzJrNZgImsCiAADOPzetfr9f4wQ9+IPGT8ezy8hJ3d3dHvXJZQMQ4Q9n+q6srAUmm0ym++uorzOdzKVhhUQzBcMrw73Y7vH37Fl9++SWci+0ByCYPIYhELGMbAQylFJbLJUKI8s5UuiCYQRlnjttsNoNWcfNJoIXgFWPafr/HYrHAbrcT8JhJOcYOgswsmqDd8X2CKpRu5vyRRc5kOwEf+gPtkjZCAJDfz1mpHAfaAhdRzgmLf7hmEOx2zkkBE4sA+AohyHm5MBN0ZHERC3a4tlGdBcCz/ZkZtxljyJYjiEhQj+NK++FmPS/AIiDZ7vfoEpDB95nUL8sSqijg2+4ItCbQTFAtZ5pxA5azDHP54Zx1R5YdAbEQghSZsGiCQFDOpqf8LWMd4xtjPpMHVVUJM5xrGwu9OA5c83ntjHe8plx2PmfdE/zieblXITDF+wEg5+Dax3GhrfJ92vSpndKvZrOZzAOBel4br5lrN0HLEEJiuU7x9PR0BBDz2ouiwHL5hMNhj4uLCynk60ESfdTS4+HhAUopKeLy3h/FVd4PAIkNOQhKoIhxljGe979cLo/WO0o/r1YrOR/vi7ZGVRnuC56enrBer4WpyvNz30NQMS/ioq0CEIB/tVqiqgZSaJIXErF4KI/FWmu5/tFoFONCenDmXpb7Tca3OB4B5+cLiUObzUZUTeJ8Bmhdiw8Q9KPf5sUOXAe472maBvP5PPp/26Ueip0U1tBnQghHbQpyZjULU7lPIWuWcY32xvWFds94RhvmfmswGMg+myoMvHYq+njvRLGIQGjeYoG2GQJkj0gFAtp313UohwMc0h6XID9jK2MI93x5MQmLXTjenLdcrn8ymQjwmwPqPA/je140y/WCv+E+lMVU3Fvzt7naAb/fprgEQIpNc0CecS4/Vz6XLCzjvF9eXort8wEzt6dcTSNfx7nX5jXy3JwbjiHXPapJMO7kChn8Ddcu7iVYrMjx430SuGdM4/Xka4wUeCUfpx/nLS1yhZQcgOffWWjIuMY4kxdq5faUs93pv/8tr3w+TmP3KUiTrznPHedvShTkfqV1z9DpOi8Mw7KqsFgsUJUV9s0eDknGGgEDJKAWAYVHSsx5GHjAaKhIsIZTHnXjsPcenVGAMXDWoNEB3mp4rQFjIou8qFAMSphhBTscoBoOUVUDFLZAUVTQhYXSUW42SlJG4ExXFspqBKWj7GhQcG02lglYkzHNxsj5yFRdb9e4e7jHeDLB5cU55vMZLi/O0HZ1YvAFABZQCUBR8Tz5XJzOwa+a55B9h/OutcagqqAQ4Jo29q50DvAEyAClPKpBBe9abDZr/OVP/wLWaPzaD34A3zrc3Nyi3h+ggjqyydy2jDE9EMZkv4sJxCO7MpRxVtisV9huY2z+B//oH+Pz738Pf/UXf4m3336Lx4dHHHY7GOxRH2oUhU0FScOjAhalIpjdoIMtNAbDEloFGA0YHbDf7XC3fEDnHZQyKO0Ao8kEs/kCw/EERTVEWQ1RDscYDMbQhUVpFWyKuVqZyGCDSsBDZOW5zsGn/aP3Ds71YFxMsPcMRdNBgD8pEEBKLpsoZ+2hYiEpwZeU+P/IF1VMfAoge+yAkiTXAPBsb9UEQCSMos36TPfxAfIFAhs2tOgBMU50fuwIPqqAvud1xkPUlFVPoE5gkQkASm3yrD4BMpZFdVonIKeX0OTYhBDgkNbyZGsCioYMvEbs62tTb+a8yJU9bb2Pyg1Rwp32zXtlfKO/0WcJyHIstIxM8B5OZfMUehC4n4p4H4WxR/4dEJmTMs0E8rPxPX1mVAkUynPHuZ8wPnGeWQjQAxvPxxyjIeMZQvxdSGBsBPJi6DIhX0N62FGleQciy86dAK0Rs45Aj1Kxl7nyHxcQHAGQ6f87y6E8Xt8EqeGr6/CRL+FUDr+3F5/6NhutYY1BQCwGMEoJ+KNCkPmOvhGP0QWffJ1+ClkveqCRNyGTe/RiXOvvNc1PZtOcsxhP+hYIHhC77ccs2bqOqhtwQcawBzRz+4v/l0umC2Cv+1/y/z8FADM28BqUzkXc0R8hs0+HgJbDlPawXisgKzx0zqHOisH64WEc7t/XjDvpPxnXbF+k0Pc3Ph0L8RffyzCfvn/63RD6GN3jcP1nefFkfj7609H4qghS8Xt53uA5m9fJPo98UWIQImiv8FFc4PctAfdTieKjeI/+vLoHsI+AadVfH1RsV6PANg86PedQcjsCukZrWG3BXugETQEc+YPS2X6T+yXVo87Bcx2OLV1ycgOfQ7qui+u4d/CH+IwXGdKR4R3VrLaSC/SdA5xH2zRwPgKTsafGcYGGCx1ciOoMzvftC3BkU0DwGkr1iliDwRAhuNiqAvHZ2O0dNutl/28XwXtrC+i0FzPGJIWmCqUxsEUZgVxrYdIzU8wVaFTVIO5Dr65gigKPyyXazsH5WDABZRB8ak+iFIw1MIDElliMwWLwWFjFddd5h6Zu0HVO9hAca+UBnSTqjbUYDIfYHw4SBhlDC1tiOBqjGrBYOvq0QtoXZN899bmPXidxUmJY+k1eoMNcojYRr7y8vEC932O1fMJhv8OwqtCGyKA+dC2cCtDKIngHFTw6q7FzNe7ffoNv/7d/B/OLr/HSTDEcDhC8R9e0KBsP37WAMTAhdk1SIYLVpSmSMlMBBYVD18J3DXyrExQe7UcjJLa3T78NMNpG0DsAIcQiywIKpbLQOsaCzjkE51BoC10WsE5FZS7X4UbV6FxsRzmZzVAmrMK57ogYZvh8pP6Gnu04ji2M//81zzX87mmsje9nBS3PxOn4nefB+NPjPXfeX/Wc/Kte3xkYPxwOklSj7CD73m23W5GSY6KOSZT5fI7lcinAERPV7GU7HA6xWq2EAQRAmHlM1L17904YU9ZakT6nlC7BFoIwTMqRTXpxcYH7+3sBdZhMpdTxdrsVpvpkMsG3334rTKDNZiO/897j8fERTPQxMDMhxkQ92ZwET3LGLceM7B6CxpTqns/n2O12OD8/F8ba5eXlEaBMkByIoCYZuwSZvvzyS5HRZrLncDgIqJfL0jI5TaCeYM94PJbCA0ohk4nFeyKgwQQYAXvKqt7f32MwGIh8NWWmz87OxEAJ0iwWCxgT5apHoxFevnwpjDGCJEywUaaU8qI50yefMybXmGjMk3R0FhYaWGvx5Zdf4unpCZ9//rn0XQeAL774Qhg54/EY8/kcr1+/7kGJosDr16+lOIQAFMdoMBhgu9vBJXCO9jKbzYTRfMp+pF3Qz0ajkdjwmzdvZP6ZiH98fMRsNkPbdVimhDALB3gdwoZBD77VdS1gEf2CIGjOlGISkonCh4cHSQAyEcl7JyBBoIOJdNrJ5eUl6roWSUsmkWlLTHoCEElTAimUUlVKHbHcKfXMxPKrV6/w9u1brFYriSMEoskmy9s8EHQjazsHqUIIIqNP9q21VnyJm/DTRPv5+bkk809BP/rS5eUlmHC/v7+XGOlc7B9PYCcHmmnzVElgEvjq6koKi87Pz2UTxetj0ovtLChjGkLA/f09Xr58KQxQbvCur6/BJPpisZD5p79HYKlXj6CPrVYrXF5eQqme7aqUOuo1DsQFnCAgk+NMKHM88+R+zrAjW/D6+lr63FOBAIAUhOx2O1xdXYEJfqAHdHJmV8585jlDCML0p2/y+xz3nKXJZH8OAnB+8xYYi8Uitj14fDxiAdPuCMYy2U5bJKjW9402kuTntRNMYJykf3Ju6Mt5YUBp4/l5HiYsyYLkeJA1lyej8odKbrRyhQ+CYIzhOfs9/10ORvH8BHFoF/ShHIRgr3COCeeYYBbjD6+TsYYPtQCk2CCXL+b6xD0LC5U4//l7HAcCWLy+vDCANqlUz+ikrRMUYqKA/sF74hrFmErwkXPMa5WEhOv7rBPMpNw0x5bXw7g5Ho/x6tUrtG3fH52Fgbl8O22aRUDWWlm3+XDHe2BPbN4XY+1ms5G5ZDzNW3BwfeLehQWVg8EAi8VCbJ/XyRfHir7Mucxlx8mazeXeGYOoMkAZ9H7utMREFgUxzrGgkXuVoiikIPDx8RGDwQAXFxdYbzbQ1ksMpx3SryMQqI56TbN4lOesqkrWIRb70Oe49+RDYp4Y4r3TTq21qNL9cayUUuLffHE9ZeEAYwvvmf7FuVRKSRFPDljm8YBzwiILzmO+l+Q+jzGpLHtVAYK8+XpclhXqupHzrlYreUCmn++zdg6MhbQRFnPw+MPhUJ5z8vUoj42Mt3w/B39Z1MN747jze4xzAI4AXu7B8gIyxrO8MDj+GcTHef0saOJYci2jCgbXzVwdgGOw3W6lLQJtJo9rvNe84IH/5vNYXricF2Jxr8n3Tl+M5Xym6AtBjhOOHEMC1fm48vv0a95TvjbyOPn6ljPg+Z2cEd+DZF4UTVjQxcI4/ob2BeCIKc5z/vd40XbzB/3TpEL+ndPP8yTBp5IKvF8eR2sDW8Rx8s6haVpoXWCaWjgt7w5ogscBHk0CwBvEHqpWaRTQKFOSzjuP4HwCzhRKAKUK8NZCFZH1VLsOTgUcEOC1gjIG3hjsVMDBd0BRoByOovy6tYlBXkWGeVWhGAxQDUYoBhWqvUmS1QoqyQgWOsYlbS1gdJQt9X0LCagIZsR9j0bdNHhcPsK8NRiVI/zmb/0dXF9dpoSTw3K5g1IaMBo+NKkPbdZ3+mTs8zl57nMfggAM+Z5Da4OqGmA6ja09tpsNnIsynFprON/CKI3haABrNQ67Hf7oj/4I1lr8+Ec/xtXFNd5/uEHT9uthfj30E+ccdGGhba9OY0TGtC+GORwOcHUDIALlnXe4fbjH688+x49/4zfhW4e7mxv8lz/+Cf7qz/8Utzc3WC7XMEZjPB5J8QvXhc45tOhQmD42l2WJsjCoSovDzqJrW3T1Ad3+EdvdI9YfvgZgEBF0C2MrVINYaF2OhijYKmw4RFUNo50UsUemLQsUpkAxnkKpY3/pfSTZjlLo0McRxqH47N6DLcF7hK6Vz/M5Pdo7dx1wsl7H3r29H3sEWK2A7Dj8TOyE15zNJeeMcyVJwhDg0K9Hud0dxQ4V2Un5HlmpCJpA53ZJIBEJWH4+xrW6hC9sVG7RvdwqACjpm6vQwkUmVfLBgBgPfNb7linx2jVyHd57YtvxfhDBXRuOwarT++6/fRwf8+/JOQQ8/7jHZT7G3UkiWOaW/hXNKbKTP3Ft/K7m5Z18Lz8n0AMN/N6njln7j+XYT6/11M5Ox+xUdj63j+d+mzMr83McF5ZE+WOgv554/yfJbe9TbP240IR7FB6T65+sY0ajS8UGfC8oBSgNq7UwQmnPESAGTNFLxat4IUfzkccK7/oiplP7yecswH80toy7/XhAYgZCSMVex4oKIQTo4ECJ6NNXfm0mxH1JbsfPvlSXbvFYgSD/ewgRDIzf+rgYgOesE8CpAmK8LVIhZopdSinUbYPG9WB9nk84BW3yfc9RQUw2NkrFePkcMJ4XPco4PzOP/C7Qg/H5d9KP+0KdFLtlCNWxb9MmjDFweRFe6IHxfJ8bFOANUGgj+y9+50jZSikow9YfJvaGVzr1iO+/a8zHoJTWUXEgssrT8cyn95P5WnZcBBCkHiR439us91CugfcOrvNokn+xgJ3zG58b8oLbOrK607/5rNzVWylqZZ6YPsP3fIoPLGg7ipkqFXSkcYvPVplSJYKoc0iMT3IBfTwyH7XviEbCv3g0zQHeN5Lf4TNSjEHxmcKUBUozgNEFBqO4JxFVpLKMe9v07zxPl6sVe+9xqGv89Gc/Q9c5FGWFwWiM0Tiq9wQV0LQbWGPFfngf8briMsw9jLGnjP4YG6kq0nUOddPCBAXlNZyPuZvzxQV8iHmaruukn/ogqdmx1YZPthFflEHvQdfn1hoZ1ZO1LzPOtCdJ/m+0xLaqqvDq1SsMBxV+8bOf4vH+Hq5rURUGbrXDtqnRwCG4AO0UjLVQuxrddIj7v/wWt//xj+D/8E/xQzXDounQ7WPL3CE0KlholOiQMdpDLAyGc3BNC7BtRAgwKvYuh3haAsURAfWQ3jGxZBA6xEItoxQKaNgQ110fIIVa2ihURQnTBNStx9p1uCljrmBxdoHxfIZiEPPWscCB61BcS1jIchpjT8e/j8l8/3lQvLebfv9yOrefmt9f/QqyJ/7UefPPnjv+r7Kt517fGRgncMSeuGdnZwJM3dzc4IsvvsD9/b0kR5WKyf/VaiVykS9fvjxiWYYQpIciL5hJGwa1ruskeUFp8V52MsoazmYzkQjPE0Xsp/2LX/xCAK/379/L5uPq6go3NzeS2CUAS9AC6BMrdV0L2HN/fy/JbL6Y0Nnv98KkGo1GAtrlUqRaazw+PkoP4NVqdZTMZYKVADNBXiZQCfiTEbRYLHBzcyPgZ16YwF7wFxcXIsNORg2TyEzK8uE0Z1/xfSaEmATMQfrFYiEg+Gg0ksTv69ev8fbtW1ncmLTLpefJ/GUijfYDQFi1ZOISJCCziIZOpi9BI7JsAAgbiqwySmlfX19Da43JdIo2JXYpnU2GOkEdAJJkZSEFx4qFAOMkIQ/EpG8OulZVFe8lXfNoNBJ50hD6XoWSkEhBfr1e4/LyUpjcRVHgs88+k4Qw0IP7LARxKXlHtifBxDyhP6gqdFnS9f3793jx4gXathXGq1JKZGbJ2uTCRwYyk4M5SEMwhAAo7ykHwZjA55izHzQAkc3nb5VSwlR///69nJPAT1VVuLi4EICcSfzD4YAXL16IjTrnsFqtcHFxgeVyid1uJ8UrObhM8JzyoGQH5iAzgV3KzOYynWTeLRYLtG0rvV25KM3ncynmYd9wFl0Q1CUjdLVaSTI8B+RZcMOkEmMDgT3GTIJ99K3hcChytfSppmnw1Vdf4eLiAu/fvz+S7iaLnHGCNnR+fn4kYX/YR9CS8YhsN7aNkIf8tFFnopxg13g8xnK5hFI9iM5CAN43j8O1iInBvDc35533qLUW8OlUPpcKDUzcn7LfAMjGlkl2Fl7RZnI/y/2X6xDBM37GdZB+xGIDfs4kJX29T4YeAwQs8mD8oB/zIYhrD32JYNcpOEWgJAKWA/k31wDGDcYZJqx4jTlYkheFcLy4PuZzd5o4qapKwD8WyvBY9Ceu84xPtG2Ov/exYA3opZ+fnp6OWJ7cV/A9xulTYJyxgO/xXti+hD4IRFUP9junwgV/RztiIQ+LTXJb5p8h9IUPPDfXwaOkcdofcIwJEOcgMPcMtAfuAXje/b4WFnbbtrLn4XWPRkM0TS22RZBNKSVAIdnEjMEs5CBAT19ioVy+XvDBjsU5vEaeazqdih9QDv3i4kLWXzL5c4CVDHCy0geDAZ6enqR1Ca+Vcur0H/Ygv729FcY+2dk8H21ns9mJj3Ks6d+DwUAKC4uikPGaz+fiiwS5t/udzA/vmWtPHLPiqChjNBpJ4SjtW+t47MfHR1kDAMhej3GDxSRcA/nnZrNBSPvX8XgscZJxhqxj2gT3RUxisPUOP+Pvc5vmGs/rYkIrX/t5DI5pDrAzPkQ7jb3b8uMxjufxRSkl40S5cBZyKBXlVX3bK0Ll+wiuGfRhXiv3ISzOYNxkzM0LWng9nBPu1fk+ixnoL7myEtArMNF+eAzu6wnwyrqiemY6mRD8Ddc3rhu54hMVVWhzXG+o/KC1lkJnno/PG3n8YRwEIOsk/6uqSvYOLE7l3olrWJ7kZKzNVTtyYJbf5xjkRZr8Ht9nzGP85HPqaZwEIApTeSKbx8kT7FzPuD7Q11jAk6+XjLUsaOC9sdj1b/viWJyCMs+BIN/l9SmgnsfLC//oc845tK5D23WoUGA0HuPi+grfPNyi8x6tioxc6/qkaQTAA7rEFQE8DACTmEZaGTTeRYZPF+UZR0qhCR5VcPApkaONgdNA6Voo2yJsGwRl0KmATgGd1vDWANZCFQVUZaGtRRWK2FexsDCjuD4MBwOUgyGq8QiD+RTDsxnQ9DaltEahNequg3ItEDz2+6iS8rX5BudXU7x8dYmLyws4H9C2t9hsD0BKPPkAaHwMOD03p/zsNJmef54n8JXSGIwmOD/3UiTUNI3IVvuQGChpbdq7HX76059hszngfHGBH/34N2BHQ/GRpol9Ndnmg0UuhTEoyyh3ThYnC1SRnlsPdY16t4PzLiYnrcVmv8Nqu0WAxnQyxZvvfR/lYIT5fIZvvvnmSA2tcw0CgC75sQsByms0jYcPDj1jO64BQRvoUsMYBVcAvmlQNw28bxAcgA4INaB2qT930AhBQ0FDGQUgsuEjyGRhi0QoKAoY2ysERQnU+Gf8d3zfDKbxe2nPa4xBKb0a+wI9rQfZ/OUytACLCCK6BED1z8YEwXqbUcLyzT8LCdwj4xcAlOuLhvJiniNw3ju4Nq6jHuHo+0dAUxwxdGn8Kd+bg1ZBfQz8AMcYWYzLBjaYxBiMjEKTepx6hcSSi+0aXOhVRvLEaggJYMtA8zh+sV+nZi/iiK5Bq6gG0Pi+4OlTSVUVjhO6+Vpw6ofH9/Wxv3JyQgi9NLmCAC6n3z/26+flQFV2/lOAld91WXL79DMCvMF7aPUxCMhzBUnQB4SsMCUjbx6PQXb9+ZqdP+8756QH90fX9dH5/UdjY3OwkHOo+2fS515iwyoy6eJ5+6IJnebbOwcYE/sZa43QObRtLTagjYYyBmFHIPATBU3JDuO1mY+uS8YEvUQ0VT5OxyMfPxWi5DqAWFBiDKD8R2oVXnXIFU+es8sQArrQHs9fdv78PZ21DPjUnwAlt/vj83hHtqAVYHSKJ8CuadFmzMWiKtAqBReivrhCZBorpWBzAJjX+8x15+ftP/vYNvi8lStN5Hu802Myn+LJaNY94KxNH8+Q4qBW7KEMMbbT+Ki1hupYqK9TGPsY0PEI8DrzhXiwo3v56HfCRAdYYOJ9iAoJWdGIANOulwcXokGzSZ936LrExE7rjtio8/CHBgh9KxKu02Rqe+eSakN/TllnQjiSPo/y6ywM8XC+jYzkZPNaa/gQUCDuAaJcfF8s6BxVoBx8EOi7Z8XjxFZ0hCQ9PKCR2LN9wUT+PKFhoMKxEsuz9pdQTqU0gvJwAVBGQ9vY3sUWcd9UDAcYDkYoqypKrJdRec5oE2XY0/7DmOPnEf6dearoY3FdUUoDGthst3haraGNxWg0wWx+FttQhT6XQ9vJ1x2tYyG4brU8x1VVhWpSJaUmm4ooU3G9CyjKEvvDHkVZYDyZ4N/9u3+HP/vLv5DcUjUYohqOAa3Rup70J7YMgEpU+etTzy/P+cjpPgEAhsMRXNehHI/x8sUL/OB738df/+ynePf+Ldq6htbAdreB8Q6Nq+OTSOvRtR0ONkCflbh/+zVuf//fAf/pT/EbGGEIC4+AEhZamRS/PTQ0vAuIWkoKFsleoOC6xChXCiYEWGhoY5OqiU9+EeO2MPeR2ksgqgRpxB2lCoBv2riXNQo+9ZwP3Iv7Fjs4PGqHB+OhAUwXc4znM5FSzwuutIoFMXze5nPqc6/n1ohPzdPpuvfcnJ1+/queiU7//anj57nxX/X9/5pn4+8MjN/f3+PNmzeyaaCk8ng8xtnZmQDKTNLwVZZlbHyfwJ//P2t/1iRLkpyJYp+ZuXvsketZqqqrGg0QwMxwBiMjpAjn8oGvFKHwH/A3UoSPvKQIhcLlUoaXM3emgcGORqO66+wnM2MPX8yMD2qfmXqcLKAATHRnncwID3db1NTU9FP9lAcv0qyzwbvdDp8+fcLt7W123t3c3AAArq+vM4UyKRfpfKKzgfelo50AKKPA6RBi/WFjTHaeG2MyCEWQkVmvVJLe+5zpfHt7OwJPmHHALGvWQtZjwoyJ+XyegW5mC7569Qp1XeO3v/0tQgg5gICgLoEBALnerzEmg/8xRrx69Qrv3r3LAqIjq1gH/PPnz/DeZ/Arxoinp6dMZUkn583NDd6/fw/nHG5ubjKgzACFruvwzTffZNDw48ePOYtfO8x2u10es2EYcm15Oh/YboIOpIemA+7f/tt/izdv3oycujHGnIU2qIM8661TJgm2LRYLvHjxAjHGTM9OgJJjwAw4ZgkRRKNzUYODdLbSebxcLnE8nRBSBhprUpM+lbShk6bBu3fvcH19DedcZiUAkLN/mf3PebPWZrDo5uYmZwsyo4yf05lIme+TQ4sUwswGHoYB19fX2G236Lsug8CkRieAY4zJTneCIBwnBguQRpbyph2O2mnJIAJeDwCbzQbL5TLPtTbW6HTlnLAGNR3QdI7e3t7mQJlhGPI6oAHGLN+mafDp0yc8PDzk7MCnp6cMVujIRwaCMKORhxSC7cw2f3h4yGvokOpr0+lL8Pjp6SkzMzBogxmmBDwImussucVigY8fP+bABwAZfGH7P336lBkfAGS5JLBHkDmEkOWQIH2MEdvtFtfX1/j+++9hjMklDm5ubvK6ubq6wvfff58z9al31ut1pmzPmYFRKOwpB1VV5X7rMWSADjfi8/mM1WqFT58+5Q2a+pfzMZlMcv12yoaWQQL/GpBh4AId/qzLymdaa3NgCu+jGUYIKuosSU2zS0YSglsca531lw+tCUzVWWOUfbaXRisd7AQgabDqZ+nncR8gSE9dAghoxzq/3Ic1OEUAiLJlEvhA0IXt5xy253POcNCH98uobd6X1+kAEzJK6Ihnfp+6s23bvKbats3BLQxUYyAX76Ez+qirAWSWCIISnBPOP4AcvMQDFseIbSNoyXVJHcQ+UK8xO/Qy69AYk/Ubx4oBNRqkovHJ7GEAGSzkmqYNQp3GjGfOqTEmgz3U4TprlMDZMIQR8MUgsqZpcDweM40yHeaaBYe6hEE5DJp6+/btKBgtxpiBo9lslmWTYDkDgyjP/Jx2I+eSQWJ93+Ph4QEvX77MgKdm49B7BZ39BJQJeHK8OKdkMWiaBldXV7i7uxsFVxBMZEDDfC5sK9xreWDf7XaYTqf4gz/4A2y3W/R9qXUeQqmnfT6fMZlOMAmFZYBZ6ewvx4R2C2tZ06YgKHg6nXE8nvK6YuDL6XQaBTdSf3Ff0/K/WCwQfMg2KYOY+Bn3Jj7z4eEhzx9L61ButB6g7UL5p7zqdnEM2RaOJxlYdBCL6EdxvNBm5P1pXzGoIYSQM/Yps3odLOcLnNMZhO3T+oH2BJkxdMYv9wvuMwSWdTAIbQTqJx0UxbmlntDOQzrMWLueNpe+B20aTdXft10OfOLexs+0LaIDqjQdOvUc+2tMAd2vr6/zGmQQDeVfU45zrDlW1Fu65Ah1nd6n2S/OAWWDz+S5TYM6nCfqF+5X1B+8B2WkOM4KWwp/dDYHZYDfvQTk6TjU7+vAQgLhtHE1AM9+6ICPf+pLM2NcOtIpz/xMv/j3Jejw3OvyGldXklWrAH99rp5OatzdvYAxFn2ULG8Lgxms1GZNeYABHucEcJuQQBWUbLfaRDjVF0SLHsCcQEMEjAeijzgFAcPi4BGM0LV6Y9A7ocX2toc3Z3SJDvfYA8Y5oHbwTrLWm7qBqStMlgusX93jZ7//u7i/fgnWoQ5JF1aKmnkYepzPJzxsnvCb377BYjHDfDHDi/sXaNseffce59ZnAE+DFfr1HIBx6ahMeVj5OspenhfnMF+uhOLaGsQD0LetYK7WJbrfAFgj9OLNFKe2x+enDTanE2KyY2CAoR9Sn8szvPdwxqAykiGVHcbWJqd/TA7wABsHoSQPwqzSp7Pch3cf4QcZy74dAAy4ur/D8uZ6lOXlw5DPfmHwcL3oy953GHwKmPAdvO/hkxPehgncdI4mDGjSXh6GATF4AdSToxxxSI5ygziUrJcAwBtg6Cy6UwK9THEc8vfLH2enMDAp24b6uc66hI734Co4a+Gc2P7WpQBHUpA6l75XpaCPBEUbO9JTyHS1AMA2FGDGWQj9rTGItQVMBS1yBElkXgmgIMso5e9y3RuIQ3aI42wiDaAbY1Kt6lSHOsaU4U2dzWdbBJUR6BPQHhERvQSRRCNawkDWcE5CjQR9kwM51bC1vqwPdjTGkkFvrIBtQxRmFbZFt4u/24yxP69HTQI8kHUT/5Pm5XKN53NaAr7UvdKTc31hl9Z6vneGDSKsdSBYLFT95VzGWrx5DxjdI/VBUDfpWxlQkJKVY/Bjzu98L/17LP1l7j7MRQADSq3ZwfsMdH75HJPnJsaAwfgMHLPmcjTl/iav3QJA5qABfe+oso/T861zfJrIVkxlMrgGQoCpKtSNQd91gLWoJxMsFnP0XmrG5mlHAnXYRrkhSIvMsU0iIrLDP9JarC1ptlWbY8zribJFKm1rEi39xbk5125WYKC27bIsRMA7hj2U0ednJgVwGGNkf76YKw01l3EuuiGPd977ZE5DjBAiFZcDAvI9rYFxYnP5IY5A78I8MW5viH7UttKWcSOtanse1xSMQDvKB9m/uGdeBgrSHuyHHkIHHiQb20Ygyn45eC9U3IEsREhrVhpVgo4SIBalpAz7FaPogsGLzxRRAttCCDn7WuxPeZ4PCcQOKRgjZ0ZL/fnUAPU9oYwWuvBxAJRkVoc8TzGKPSbrp4w6dZA2KylnMT3v0rIVGY7quxf7i/qRPSAIgE8bMFhEm5gS4OBMwCDFoBPgTv3gACsAt7ESTMK5516hZYX2O4zIUgqLgIlGfiDZ90XyIiKG0r/EXW8MMuW86CYngZ7OIsIgIgXXpwB7/jSTGerJVKi2mwZVXcNUDayTwDz+WFN8KXIGGUbrL5/pvNhhQ+/hvSyCofd4enzC4XDC3f0d1ssV5osF5rMZprMZJk2D6WySz9dVVaFiQD/3V2NSAIMf7TPDMODz0yO2ux1ubm6xsEt8+PAB7z58QlVLstN0NkPdTIQdKq09rl/2iX3gvvH8/jC+/sdetJWqqkIFg8Viia9evsKrly+x3T3h17/+VfIVAcYCw9ChDUKljyFKkBIAmIhdPOPj/+c/Yfo332N16nFtFmgRAWcEFA8GNqQyAumnNwbBJNkMAQZF7owxMFHes1LLIrNXRWXzq86C0lf22hQIEiXI0DU17LTBbD7HpGkQXMDeBTwMHfZdixrAfLlKmIETvaGCExjY86Wd89MA8Ms50/e4/P1ZXZ0/k3HQc/z8taWchPat83vUaRqLeq5d/5Cdo18/GRj/+c9/nkGuEAL++q//GnT8Asj1/EgjyahjgrvWSt1fUm7S4U+qxqZp8PXXX2fgiFTR7Pi3336Lt2/fjgCBRaJqYLYWHZ3GSOZh0zQZDAbEAXR1dZXbtFqt4FyhMCatOwHYFy9eZHDr6ekpZ/++f/8e6/U6Owe4gXrvRzXRAQkoYNYHM9kAAQS32604eLsOXS/RJXXT4M2bN3j16hX2aay6vsf79+8BIGfvMOubwQUhAi9fCfjZDx6fHySz/8WLF3h82sBAomk2Txvstjvcv3ghdJP1BH0nkSt13cBak+sKky7z7u4ug910bG02G7x69So76y5pZnUW5mKxyE72b7/9Fo+Pjxnkc85leaFTUBzJUtvxF7/43SzUzjkgAqfzKWeX0ZlPCmM64kMIWcaenp5ytnAIAZvNBr/61a+yQ7zrpKY5s20fHx/RdV0G8UhF++7du1zn9Pr6Gn/1V3+VnfR/+atfSdZ112Uadjqc6aS/vb3NARKr1SqDRnTaAwIOaFp77YwiMMca1pS5uq4zODqbzWCTsy7GiKaucXd7i8eHB9R1jU0ChREjPnz4gLqu8Xu/93s5MOT+/h7OOfzyl7/Ey5cv8eHDhwxGLZdLLBYLbLfbDF6R6YBjtd/vcz1Y0vAyk5hANNcqgdCmaXIwCYMkWOecjA5c28xiITgOFAc5Hdt3d3c5CIe65+XLlwCQdQ1LJTDogwEGdPhToXJsNWMAyy7wd4Kl2gGpwUqyRuia9QweINhAQO9wOCDGmPUqWSgYnLBer9MzJUBo0kzw6ZPo1boSfdCeO8zmM8QQcNgf4KoKfTdkEPirr75O8yJjvt9JTR4Di+1mh/3+gKaZYL26QjNpEvgyw6SZwNkKh/1BDu0hou/EYD8cDtm5zPXI9cfAD9ZhJQjJYAjqGQGgBOTgvBFgo6OdAKXO0Ob9qEM02wXlgA5wMo8QQCMYyY2Z4Blry+rACQCj4B+CtRrE02CSBlwBfEHxTICHewbnmG0gCKEPwwQiNF08a1bJ3uhShu5VAvDtCBDnvzqjPYSA4SwgVxgC+tCPShuEILWYKsf61R2sNWm/YO101pXt877IDF8GB9zc3OT9XoPv1AUM/KHeI1B6mW1IsCvGOBpr6iPOAUFzlgcgYMXvMjKWc0swXRvtGtAgCE5Z1CwqlGeClJQJyiOzkzVgxYxTaQNwPEok8NXVFdoEeolO2ACIeb+jLqIMacCZsk3QnfJqjDD4nE4ENGsAEW17VmuDmbBCe2dM0WGyzzSYTAL6fkAIEfv9Ad6HdK3JYB5gMijNYETaTqxvzuxYrnXu/dzPuI8zG5w2G/Wt3v+oYxkwwwOf91LegwAu5YGBdQxsqOsmAf+SCc2APnFqe7C2ONcuZYw6L2fhVg6zpkY3iHwc9gcsV0u0XYdz1+Lh6RFX19f5YEFZ4l4tctFiuZSgq2Hw4jg3FovFMu8r0SegsK7gB5+yGFKNdyd7Zd922cFt00G3aSbo+g4WBpunTbaZuL9QhmnX62Ac/jBbnCA798jpdIrNZpPngno7IqLre8S+Q13VRR6tweAHGGPRDT38+Qxjhc7snHTbar0CItD1HWJyAFqYvM7arkUDwNU1gg9Sg23SCFVzcj5XdYWmbrDZbnBKgRrU77St6CijPVFVVT7P8CzAudJBPbRvOXcMduBap76mHun7Pss9P6fuZ4AHAaL5fD5ioCD7EH8XJ4bFfLFAn0De2XyOfugBa2SNJqfe0A+YL+ZYLOYSwV5VqOoSUGRg0Hu5h48BjZUQqMGX/YlzyvZo+nEd0EKdxT1M20LsM/ddjj/BcY4ldaQOkuBeqoMeqT9Jya8dm5RX2iPUDzowg3qdGRikm+dLB3PofZn7DtvFoBIGGOhzLZmqGGDwz3lpAFX/XF7zHAD/5XsFaNBuTTrKbcrslEy1KmfTwpjcd8Dkfd0ZiyFEtCaghzh3JrDwCBgiMECyoFwQtyEfGQHAS6XSatTGdJ0RZ7M4lCMsLCZIFJeQ+nMBcv8+RPhhEMATER3E4TsEyYAMvUVvBBesbIU+BhweLM5PHxFPO8z/3X+H2WwOZ2yunStLnawGQN932B13eP/hI25ur/GVfYnpZIK722vstztITctCl3z5unTMXILi2Vms3mcgh3YQyvsO08kMfh4QAhINd5eccoDUe7awPsDW4nztfUR7bOFNh6ruYI3NTm7EmJ29MQhQEhGAQD9MRPRDdqIz+wu+T9ndQiU89D1O56PU70wOOT8ENLVQwVfWwTqpAe0qqUHqqh5VLbU/Q9uhtoANNZz3qILHMDTouw4uBS2EEBCGgBAHVGhQmQ7eCjAeEeBtj8EOCJH020jAYQpZiMykDUD06Xvy8kU8n5nA3ZeOTzOmLJeiqa7UarU2g7owQuksQFG5RhzS+h4FeIMpzyIQ5qy9cMyLo5V7Sa7pmgC8DLQbi2jFAW55TWqbTY59Uuua5MTlvbheCchZawVUiwUUA6w4oFNdUwNpA3OSKEccr+zjTLJejRyf4hQOISZ5NnkeAzPl9HKKRZcZJIDK+zFmpmQhKj2EH9GZMaI8OxDEpY7VAQdf6uEUfTBqF/sp602yFaXpF+ARRE4EIIsC3qX9j8ES1lh1dmUXqEcY4FvaYVDKfYxARKuzZQkHlXvpV941+DyuKVOGkA5vY0hZbhVIhdGY8o0QAnoMJSv3AtDSrxBNfk5xdpd7F1BO5ISUsWMgPiLE5C8IQWoORyB6A6GdiLA2CFuDAVztBIxLd5ExK6KT7Y38ZhkDPlvrWSvoM4UD0aTscCVbsAbRCjA5xAgTfZ4FIK1NAC4Ucnu24wtgHFIv+dIO0NA3gekwRCU7yPITEytD0QUMBMfoWj6a4C4AOGeBEBEZfGXknp7riPaA8qHpoEi+LyCbehb7zXHkmlb9ZIay9wwqwRf3pXxSPviMEESHKEUlYxSDBOFlwOlL26w8P+RAmBgjYIXqu6ifknlNuRU5YWmOOLpHSMC7MB+EAqTHONZzIeRAi9E9kbKk097PdhiDQu+c9gvH4NCUOR5DYgqpSvYx7zFapwaJubyMOQC1piW4RM85wD1PgncM0jgljRTCBVMSaPMYwDrYSjJtJZs8NSJdGULMa5fsHTHGxG5d5D2y74Z6TujPuefCurSXy17pKrFpnK1RuUpsZSs2c9VUqXY4A+gkiK6qJPM4eIs+BvRDB2t9+twlP1vxaVjjYF0pW8XM7aauUVcNIoCmmaCq6mRjyCzyXL5cLDCbTTFpJilz3WEyqdE0ifFyGHA8HBGGPgdTCOPnCX3Xguyfx+NB/CnR4vbmDufTEdvtBm/evRcfzXyJ+XwBV8s5gftlEYaydH8KQEndTp/cc0DuCBSvKjRVhZf397i/vUNlK7z54bcp8S+mM22A9z266GH7AOPl7OClSDge/vJvMPzpr3D7eMBVFPvZxQALk1gOAMCiNoJFeUg9cAcj2d3pfx7JnoasqQrpXAUpDxNNFHsv2x/JBkA6JyWfjksBcHCAcQ6mqVA3NWxToZlOUFUWfVXh4ICN8eh9wM1kgfXtDZrpFFIeyOcA7xgjXOVQJ189z/B6zMdrsgDh2ZaAXsflvFKC9r4Ezn8MYGf5oi9B8/J3vNAtPI/rvYL/6rPUj93vp7z+UTXGr6+vcwbw+/fvszN2vV5n5wcdPAQOKLSkTP/6669H2WqXmdF0pgMYZeeQApw1rzebzShjhY4H7z3evHmT6/bNZrNM48nBfPv2baaQZP1e0m4SwCLteFVV2G632ekaY8n6IDBWVVWu/zyfz/H4+Jgz3QhWMhuRgM3xeMT79+/FiZY21+lsBmMtvvr6axnLlLG9Xq9xTFnCMUqWN0Go169fY7/fwxiLqq7hQ8R8scR0NsfT0xO6fsD+IPSzOJ1xfX0j4OXjJjm9RTibukbXdzkDabVaZQpP0mPzM44PFZMGm3iAHwahUmfWtZ7zr7/+OlNO6yw/jq84XA3ac4eh93ns6dR8+PyYpD1kqvUYJeOH1IZN02QnvKZ1Zhspx4+Pjzm4QFM6W2vx4cMHGFPqaxPQnUwm+OGHH3I9eO89vv7qK2l3FDD6dDrhc8rsjSHgNmV8932P7XabgVwdIEAnG0sNOOfw8PAwejZrohPc5WeAgKpN06BOa885h12al9VyicPhkOWFGZqaSvJwOGSQ+/d///czbQvBZILz19fXOVOO8kDa28+fP+Ply5c5g5nZi7z2zZs3WC6X+PTpE25ubkaUz6S8nUwm+Pbbb/MYAKVUAZ3aXdfloBU6qOlAuqxTzUANrkfKHR2c1krWLJ23XKMMnqH+op4BkIFTOlW5BgjcsB/8jN9lpmLXdbKuVU16rm8C+8wy47Odk7rogGTdV67Grt1j0kxhjUuZ7gdMpzMsFyv88MMPiQZeHNrr9VUO2pk04vDv2h7OVRgGj1evXuPjx49YLoD2LEDJbDpHU3v03QDvA25vr9A0k6xbZUxLJpemqmbJg8lkkpkaGCRDRzKBPWahxhgzmKWzgnWtbIKC3Iw5fjQk9e8EnawVJowYY84ypEzwuYyIzM6DtKHqDEDOE/WappNlFhp1EoFy6j3+UA4pJ3wW9RhBPeo97XRjO8dAAwEGixAi2rZD1/W5PTLGJs+J3qOpk9q2SwezZHDCYuiG3PfFfJmCn8QhK3rQ5Ta2bSeHXxQjh9mMlA1m97G/uoQEdRDBkhhj1tV8sS3MDOUca3CFe4+WLa0jtexQlhjEph3ROsuca5iBJWQQ4f0YXKHroOuMKD6D658A6/X1dQ58aRqpxSQH7YjFYpmDCtbrq0xvTqCa/3IsCDTRZgKQ9Q73Nll/85ylTl0ge+4xg3vDICD41VXJ4Jc1ZjGbzdParNJ+0GbgicEmEpQm+wLLQhC84j5C20cHI/AagrSUAQCZ9YF7BYMerbV48eJF1tc6413TQ3N/IvDO4DWRm4CqqlO/a9zd3Wc9GyPw+PiUg9gY3ET9Tjr6GCNs5TCk96uqwtNmg3MCO1frNeqkp+q6HpWzoc4ptZ+Rgl3E+WutQ1UhrXc5NDUpoMPVdJ6Ls8MPQ6aG43qrXZVlhs7RJgWOcly0jUwdpSnDjTH5X6432v2UfY4152G5XKLtO4QofXRVBVgDm2rd11zfRt7T2ddVVWX6yEGBFnRatH2PtktBOD6xQiUZ4B7tvceyqTEEj+VqhUbRjXMf0ow1XJ+a9YiyxPMFD1+0K621OaiQe4O1wgpC/cG5pc3AudB7D9eyZhChDUB54jUMMuE8UO8AQD2ROV2uV7k9lHnJzuyE4s+5BEoVkNcmcJ1zbalbL/Y56litw/Xn3Kt0pjX3AO6L3B+0045zR7nj93k/DWBzvyTrEseQZw1+l2PN7zCoQ2e9c7/mvFLHFP1Q9mKOM9usM+BpF1C3kllK3/uf89JR8brPl//qebh8lfcMJPOlIBrZKQICiDY7+Vib21Yu7Wup387h6uoKlXHoAHQxohV3EZyQDdKVggjJyinAC/KzJc9GuzIls8omV69JDqjaAA0ELCdMEQAMMcLHWDLIo+T5BAT0JmCA0Fv2aY+v4NH6Aacw4Lx7wsf9FuuXP8d3P/85qroGDIRqF8zgFhB18B7H9oiHxye8ffsR08kUL1/c4uZqhd3tGm3b4XCSklYwY2f55RxoR85zDintAHwuIELs3BrT6QxR/HDoziFnwSEBTPXUYLZYoplMJTvXy3gGnzBc60DWZwJ6lpgVncrWwjiCHYWy1McgvweTAyi74xmn87GIGQA4A+8TEI0S7MPxtcbB2Qg4ocQ3TQ0bHaoYYLyHGYTy2HcdovNCJxl6hJBAjcogmCoD4d5UsM4nMIggRBq3DBYwADogmCp9LsIpDv/nXgJoRc4P/b2eUs6XZBjH0bsa+FT1efN7yhmY30nolwbilUzAlCxNoAAaBL2pb/MZwlqESs5SkiVJoF2y2gni5zZZM/o+5TED7VEFCTAAwBRA3qRnDLYEXSCaBBiIA99Ye6GX0pymjGtnExAJAZl8DIiO16hxNwIIM+MfPiB6J+NjCpCZx5hOegUKls+eWa8QuyxnQQKZYh4KTKOzV8tPRFTAMDWszBe4ptX1HOOYAa5klyVgnECeDx7M8CuaGymLWElW0gdenQXZRc4tnd8RQnGfx0A1zGi8NMaUAVyySTmEMY6/mHUYkl4144xBP/gsRwJKjYOFoPReRQghAiahw8YYiXiKBVBElF0nBoOgnPSazjamzMHoRadEHxC7FiF4xL7FYZASFbZuSqBL+skApP6XAOpozNTZPZU+sDHmwdL798jhb4XGG1EFIV0MdIxRav6m8Y6x7CuXc+ZRgPG82iK+kDtJkjAq09Nk1pDRXoWS1fockBJDLGUeTAq0ST4G7gtDAludU/tbCAWEVWtjpLNjWVPIMqcDV0rbI6QtkjWtP495PfLFewAl+Esws5gTELRdncEgaxLzxHgtyFjku6d5LYFu1Fm4GMMkvKO5Yn+IfluwME1MY4G8hriRRfX9SPkxBsZUsK7oXNE3ad2hMBRUzslcmIg4RATqW0f50wqBzykyVwJ0ngGmkgwYa5Mc8j4h2SLjuaQ86oeYENTtRE5jENuEarls04QpqWcEhOe+BUM/XAVXuXQ/m8ehqmqYSmivGYzu6uRntA3qqk4+KaFCty4FvqX7W2tzzXhjzXiPq1IpKidlRabTKaYqIctVFZqmRlM3aCaCb0wnU0wnU1gnZSzrpgbBRlcJE40fBlQMDIqyBoZ+AIJH9BYBEb7vsN9J4Hh7bpOPusPxuMcpJZ2dzye07Rl+8Lh/8RWqO4unx0d8fnzEu48fMZlJbfN6MkWMwsaQz+wUhshA01LGifrkcu+9BMJplxqjg6to67jsd1vM5nh1/xLL+RynwwFv37wVX+W0kuCTIL6WDgOmXmRlsBGdAdB3ePr//Smmv/2I1dljDoc2BtQwMAHoYwpKgwDdPq08iwgbKVkBXJmiRpJtQW2VfDWBK5OBv8lvao1DNIll1DrkJeokK91Yg6qp0cxnMI2FRQQqh2MFHGyE8Rb3qxvc3N+haSajcwPPs1VVoU5nbL73U86OedGqa/Q8acD6HwLEy+/l/dF+/yPP1J/rdl/uQT/Wj58KkP9kYPz+XpyF2+0Wu90O3333XXYwkPqcYM/hcMDNzQ2urq7yAiD1MB0NdHzQoaJpdVerVc4i/fz5M7bbLV6/fp3pHJmBRZADQMpkE6pjZrvMZjOsVqvRQDKC/+HhIdMmrtdr3N7e4unpCavVKmVWnTIYw1rXzO7QFH+smc4a2Mx4JOUonZ4aGGDQwHfffSdO0kSVSXCIdS9ZR/fx4SFvnHQa00lMA/p8PuO82eRMK46t9x739/fiCBpKHRBdy5Pjt9k8IUIWymq1wosXLwAUyln+rFYrPDw8ZKd1VVU5i9Y5l6nzGVBA8IKAINvGutRd12WAmfS/h8MRzops0OH+F3/xF7i/vweABGgXCvs/+ZM/yfOss/aZ9Ujgl45AtiuEkAMASB/qnMNut8sO4/1+nwMgCFBrKlfKIp/V9z1evnyJp6enbGhS5nh/ziWA7JhkrXZmyxCUYwCKrntKOWS214sXL/K8kClgv9/n74UQRtnmGjzc7/cZRJEgCxnHrutwfX2dqf81Va92PuqM3Ol0iqurK4QQMssCs8uYccMse1InE6AnkKepqgmcsGwAZYzBJgSjKT98DuWAa459IFBFsIbrk/NAJ2YIITMM6LEjKEOnKNtorcX9/X2WZWZ36QwllnioKqk3yf7QEU82iRBC1lsMTKHzlSDdZrPD8nY1ogSNMeYgi67rxGGZ1uZlRnu5zyavMeoyyhX133Q6xc3NDXa7XZ4bgjiUVcoP27per3MWcIwx6yI6vQnMMhiDa5wZ5fyOLhuggx3yITeBMhwbPYd6nWtnDlkfuGZ1prYxpbaUrsWqAVyuP8qNzl7Wzk4NnBNM0MaEBnZ1ljVfI+eIMm4IiBeH/ZD3Yho61LPyXKECYya1dkhw7KYpulBTw3J8OCbcjwg6sh2U3xCE8utyvLnn66AD3oNzSJnNjhI/rh+rjTgtw1p/UqYpiwxy0YAyx5DjyXbo+rFkiQBKvXA9r5RNsn9oinXqe+7BBGU4b7vdLu9hbI8A7rN8781mk4NBKH+klGb5C+4dBPmYOX9zc5PbQNmijLOmNIE8yjvLz1CXT6ezzFzCACruR3rMdEboJdsDDX3nXKZlZiYsM8P5XbJj8BracsMwZJYivs+91lphASGNOueCa5HlK96/f4/VapXndrVaoUtlRLjHGeMBtCO5p966DLzROoGsCxnIg2RK8prvvvsu2VWb3EYGkjEYg2vYmAL8UT51QEzWSzAICbRjcM7YsVkOGLT1WN6EwYG0gwmKc39m37m2KXe0eTQwp7OXuU/pdXg6nQQktBbz5SLPC/Uggwqoh9l+2koxSgAo28M+cg+n3GudqvU0P9N7CgNXGazHOSb7AMeO9el3u122c3SwjWa3YKAi28B1F0LIQTCcewZgEhB67sDKe+SApMRsw6BUzjfnVh8IuSY5T/rZHCfudbyG+zv3G86DLkVR1xWssRkspizFWEqAMNBL067rvZpzzEAtyifnmmwOOkhwnkB6DZBzfhkwoO/DDHzu3dxftc7mOUTvg9QN1DmXGQpcp4+Pj5hOpyN9SxuA+yDnSjscNLD+z3n5C8d02UMAOnIBXABN6ZX/ZkYXnXJfOkW0/hDwzGWdX9e1UDcOEigZjcFqvcasqnEyFh0CjnHAGSmoPUo2BQBYuAxmS16vuNaNARxIVRzTJwJYIopDXZxRQA3AQjI3TPTJ4QRMQCeoQaAzHAKStzGi8x6DF8p1Ew0cPCIsOjgcwoDD4wZ/9Sd/guv1FW5e3gvLUnsW0EmNZ4RHN7TYH/d4+/Y9ZpMJZtMGr1/f4sWLW5yOHfp+i3PXwVg68Om81W5qPTVpDtQ6QXLm8yVMQJcMHkBVlfXnnMM29DmA0SAFhF7d4vVX3+DU9YghOeJhBfyJGMlpP/SZFhaICFGozF1krU/AAwmkAbwPsK5ChEff9TjsD+iOp/S+zOYQA6q6lmzyoZSICoF6KKbfk31Wp+zCCEQvVNcEbIcIhL5HcBGmNuiHBP67Cj46cfwOgzgenYUNFtJpybAbhg6INssZYkAMBrZqiiM+jf2XjrYI+F7JggZU6GNKfxuhqL1E15N/V8nEM5+jiMkYKjGjethfyJH+vn5f2cyjm/8DLw2sqp5eXFVonAVWoc0CIkOiYyHZdAJwW5lUIDu1rU0AtgL2yxnCoa7F0U/QDAzUSfsHweAqBXwBIqc+6TsC8aT4ZrsMDConWXQ5q589M2PQPti0LrUj26XvEYtChLWVgHoy+FkmNOV10lZAKIFjRTcTDDYpqxPwYQACAyZ5B6n3K2OEUWBFOTd+SYMMAKzVGxLNK9+LCY+zQe6f7QsCkUr+QvAjimYZhPS9UGr1kg4dAGKQ4KI8vkn39MOAid6z4hgIY/ZxjAGV1QEKuk9p/0jtlQxvXbtcxtdH0WsCFokOMDEF+SU9E1NJjSGIreIvGSDw5To0xkh2MTg+KYsuFqSQbVM53kWfp35Tr4SUDWwdaZPlb93pECJgyjN1W/S48CusF881amIph8AGeFvqUfNeWp7SHQCUIMGyLhQwHguTQQwBTpUlkQuBaAyComsu9mxhYzBqDcmeldaOAnSJpJZSCmWutP7jj2cmskFmhM9r2GT1lKcu3RbWQvRLJP037doKrhpnNHN+dTuskWCitpX63qVvEjjIOZCsUgUuGa7vshZlHELKPi0yle+n5iP4xPhCIbMGpXS2jEMw0nHvvWDTMcClfcpb5DI0AFCPtq9LezS10RgEJ0FKIj+pb0keyTzjbAKhsyw5ZLg/RsTIMVIBbnl/LnuTgWShB1Pl4BWOvWtY+qTK+wv9Vq5uRgFkthI7VwJ0Klgj54i6qhAtEAPLhiAHk1W2Qs1s8Mole6yCS/XF61r8vFezOepK6nbXk8RGOmuEoXc2zWeo5XKdfMPF/rbOZvko65t+AqBL/jXWe2/bs/go2hZte0bbnnA+S7C1DwMm6Uw6mU7QtR0eHh+k7GbXQeq2dzgm9trpdIqvXr3Cy5cv8errb/H997/B3/36exy7Dne3d5gul4imRu89BrISXC6q1F7tY788Z2mdqs86IUQJ1nTp3GKL/1R+alSuwd3tHW5vbnA8HvHDDz/g8fEh+yy893ndRx8AU6GPHr01OMNj+/49uv/wX/GqbVFFk1iuDBoYVBGo4WSNGCCkfWGwQBVTsCUADw8DK2vXSGa4MG0EuChVyCn7QYzxfA5z1qFyNYILmDSN6EsG7SPi3HewDsCkhkv2gwkBvTM4VUBfG8zsFN989TVevn6NaTORwLGL8azrJvmsxFdgrBVmnYuz5RdnSCj7No7veXntaCunzsFz9+b743n/sZe2j8plY/niM8s5VwP4P35v/frJwPiHDx8wm81yludms8mHfToGGW2/XC5HtLHa6aWdQnSmkI6bFJpN0+TayiGEnIFKJxFQsvOYFUQ6Vjr96ODgc+kA5CKhU46gsnaMa8XJzGZmPNJZy/rnk8kkZxw8PT1ht9vl4ADWPyd4Smctn0mw7yo5HzmeHz58wPF4zE6dq6srHPb7TMdtrcXV1RU+fvyYnUchioOCFJbWSiYVszRDCJg142xpOs4JDDjncHt3n+tZ1nWN7Xabgb7pdJrpt5m9TMcYnezn8zln4VtrM80o63ZPJhPc39/ncfj8+TMeHx9xc3ODuq5zbeuHzw9YLiVA4sOHD5hOp9nBzvv6EPDmzZvsmKUschwJLi4WCxwOB/z1X/81vv3227xZ0skOAO/evcNyucw1qOkc51jyb4ISdPpxXimTq9UqU2kyM48yzgy6x8dHOOfw4sULnE6nPDbz+TzTtBLg0WuJc9Q0TZ4XOmk/fvyYQVG2x3uPV69eoWmaDPRzDZxOp1zSgBsVmRqYsasBezr+DodDBn9Zi5Rj3LZtDiTg+uSaYvY5ARjqFFIPEzRhJjhLHlDxWit1L4/HY86iZcYbUMBJrnWCUVpHaUDbWjuiu8zGOgpAQwc15Z2gOJ3PGvSks5VzzqAP6ojPnz9nUIRZXwRH9H0JvrDerbU2r3E+g456AmgE4QiyU28yeIDBAtrh3jQNPn78iBcvXoyCCTTIzbXBduo64pPJBJ8+fcpr49Lpy/mn/meABmuF85nUqbvdLq9tzuNltjSd3xogZZCNNrY0uKLvRznhvUj1z/c4j3Sic341kEcHPfcatkEMjjrvSXwu5URnCmpQg9dpBzvbzzkfHzTHzxZ2DZtlRWc/8p7isMfoGgIU1GHDUOrxascU28TAIsqbboNeN00zy3OkM/EJ0GTnvRmDXJQz7aRlG9hWnT3J79Z1jZubm6y79NrV648Z4ATfuVa0zGlq5cPhMAIDnCsZrVpOOD4a3KPc6MMW9fRXX3010heUr0sqatbvZokSySAtgWXUHwT8qD8I8PBzgjcxxlwbmiUxyNZD/cuxZtYjdSLXF0EvjgdBNb6v6xl3XbnfZDLJ1NTUMQw643rg2F+WpdBlE3iNtRJYw8zrtm3x5s2bPObz+TyDVMwmZ5CUlinqwMVijmEogRvL5TKv+U0KNtQywrFmNmhd14kKz+fPrRU2ovP5PKprz0AK6mfqDY6zDuDQWXWcx/1+DweTAUB9iOCcsZ064IMBmfq+GrSjLuSeqPcA6hKOP3UUwWL2jfsb6ZXruha3itI9el+4urrKdg3XAnUk7W+2n/3k+3yPuoH7OeWDMsS5oj7gWmJggdYR3vtsg3B82F6+WNuagXicN+pyncnN4IHT6ZSBZLZJs5BQvjXjFoM4aG9S93AMuSeyvwwQo77lPkC7Vdsq2QGUdKU+F9Fe4ncB4HxuUac9jLJCncH+kh2Gex11GNtB2aTtzD2Xcsv+G2NGbB0a5KfcMrBBB6xwnDULSYwx609dsoBrjv2jHHGdc3xp79K+YjAxg3A4trwP2TEYcMKgCu4RHON/zitIg/OYhRjhQ3ENGmPgTHEWJvdJ/n5EypQhCHixh3E++J6xUtN4WtVCgV0Z9H0HEwUkOR5bTF+8wN3qBvvujNPQ49H0qEODSXTo4dBaue9VsNhjgDEOTjlsbDS5rXQQD8nBNCSnEgAMMDBxyFnkITlPA4GEfMcEQgiUiAkcpsmJjygu1yGB5g2AuXG4Nw6HX/1nfKwqhH//77H+xbdAewJggaEBTI/B9hiMxyRMcG4PeNgauDcO3ljYeo77u2/QHgOGrsXTzqP1BkI3O6A4ZIT23FoHgxoBQ3aup8EX574xMK7U9kaqLyggj65hilSrtcJ0vkBlgYeHRxyPJymxAMBWNf67//W/x3F/wMPDA9q2w/r6DtEATT0pshFjdozHGBGGgDiEvG7btkXbd2jT71xv5/0Bu90J5/0Rp32Lvk9gH9jWiMNwRESf761ljzIXEugZq8LWBDipVWkCYmXgVk2irARMiMnW67J+8D6d2QhQ+QHBU3ekEmM+tYvgQkhZuBxTAtpG/mYfgvdwphpl4F06E2UdAQY1jNVMAAUoJzD13PdHspDfY6BIWsFGO/7YlgTmGHGei+M+ey8Fsk6ghlf3+ml+wpgDWtjG9G3IairrLX/wxX0N0P9DgPyzX3z2lf3tF79/8cy/LwjgR774nHOYAA0z//TrEnwDHFhX+tJpXIIYU011JQeXz5O/ea9/+FWepUDY9Cr3G79XnNb4Yk0CCsTMbdNgebHJNIjKexEsN8bnafiyf2b07+XvP9bPy7ZKc8Zt+Pu+p/3Sz7Xr8vrKja8vozb+jo0MUIlffMa/yzPHLAbZ5klrOaa9cKRf8KWs6FrfX/a5XOczMCov50ym8tf7P++df2Aw9CrQIZb7UA99SYud2qua5lHmOgdxpMuZza3bLLJqyt8Q9ggklS3PiqisQ9OU8jghRgRTyq7pczh9AH3fS1CIxReyq3+XtX4B6PMaKwEgMgAOlaIXv7w2j4sBAAvraoRoJMgnPi+zNqq5z18vuiBEAcVdbifHfOzLtFZCEmvLdghoJwZT6ltE2id8fkJEROgHMPipMlXaW4JEzuR2iObXMi/7j9QAj4hZRsf6MIFbwUOan3x9cLBVkwFh0J61ZnSPqpIsbp0oAwCVdagqYbgzSRfT3uKeIP4nN0r8yEB5OuNImbU6n52n00liFpVrm0mDZlLnszYTKugTIQvpCMCtSpBEMfn4exm/NtGa79vjKMFD2B1TAK/3idVI1q6PtJXLGS+ExNhEOxKAcUDlDHrfod93mAcJgj6e9tjvd+i7HsbYlBz5KmN+xlg8PW3w//oP/wG73QHz5Rov719hulhh8AH90KPzvbCbGCN6TMklg94KG8iXpa8u9TJluDLl/GpSoJCtJCjNWYtJVePm6gq//y//ANvNA377w/d4+/YHGATUtUPfdSlBKCKaiMF3OPQWsTaAA+LnB3z4P/5f8fXxEyZmjc7MEaPFHF3Ww3UKXImRowzMQpk3sThtChyVdW2NQZWC2wak040xUsppkD10upiintRAZeH9gPps4dsBfQquM8YAtcPy9hZ2MUXvgKcwIIYGDwb4u+aMD6sai/k9fn86w+/+L/5X+N3f/TeYzOfYHnZSnnYYMHQ9pnWD1XyGxWwKaw1638PYRMH/95heet1S78ZY7HbaHaKz9Y3kvRjH+kHvL7yO9l+82M9+zBzQtsylLazPW8UO/Onn758MjK/Xa9CZXVVVBrkAqc3J7JXNZpNpR0m5rR3TBIHoNGIEP6ltr66u8PT0lB0U0+k0g7DW2gyO8z48tG02GxyPR/zO7/wOfvjhhxFd8mw2y9nCpCGk4+7h4SFnOtE5vdvtcHV1lR0m0+k0Z//SGUxAeTqd4u3bt/nAd39/nwFfay1ub29zxA2BdlI4TiYTDOk+Hz58gLUWX331FV6/fp0dXfP5HDFlQpCmmY7Jb775Jo/rzd19pjhmFnaMQnn/9u1bXF1dwXelfiGBKBEkoWu+ub3JTkc6x5kRs0/APGu604HHrF86gKnUKAMEJJnNMQwDPn36lMHex8dHvH4tFM7X19f46quv8PHjR6yv1pjPJEt7tVrlgAOpdXHE3d0djAUmkwYPDw95cyNgQacfQYjr62v8/Oc/F6FPTjs+83Q64fr6GgCyI4tOXqk1KmDBZrPJbASkEtdgHOVyv9/j7u4uA7t0DjKT+uuvv85yv1wuUdc1VqsVAGQ6UjrqhB57n9vGDe/+/h6n0ylnIOvsuqurK3RdJzXPE3U7IKAgKcwJ1APAw8NDvgcd4Vw/zLIyxuDp6SmvXa6Fuq6x2Wyyw5KZ2avVCtfX16OMXzovOFd0ThLgJSA+nU4zgwKBe2a0MSuQcjafz7Hf73PWOde3DiwhOENnJ4N6KPtcK6x1TwcsdQwdv/O5lCdYLBZZP+z3+xwIw0AFGlmsn/7582dUVaFjZwanduxeAoQMtiFw0fc91ut1Hr+b61scj2XuNe2tzkRmcMdischZYAQhbm9vR5mvGqTV60eDCQQZCOzo7FvOM+dJg2wEJVjLXTvu+VqtVlmWCKLqABvOqc4U46GHL+4rQKFqpazqzEg+Q4PYBC0ILFEmdbY490BS8GZgTGUWUwYIaumxpT5iuzSAzrFk+wja0KlvTMkEp5yyzjdQSlGwX9TlUqcJOWhCHyIoJzzgcqwYuMTMTuoKDfCzrQWc8flZuv1AAXRYqqTv+5F+5LjoMWD7OZ9aPrlu6lrKkmimAPaVICl1JEEojqcOICBQTFkdBimTQuBZ95nzxjWrwR8C77STdEAFr9OBSF3XZYYa3ov7JXVpjBHn8wl1XeUgNe7fV1dXI2Ya7qsEmyk31D9arqkT+UwJuimZpFynnBNSyXM+6GCgvBPglLE3mM/n2G63Wf+Q3YfsEDzkEYzkGDCwcRiGrPM4bqR2530IyBOIZODQJRsD9RB1Pg+JAmIFLJerLK8Et9gWyiBZTTheBJw1awflVMsAmTu0fuDeoOsz634WFoYwAghvb28BX2wpMjzo4AzaxLS9uGb54r30d/S6IYhK+SboOXLgx5idAbT39B5N5h9jTPLDmFGwDDNwaRderm/qYK4pzgODMfUaBMr92XbKQAiF7YXtpd6OUZidWO6Bcz+bzXIpGl5LpwQDFwFk0F23nW1mwB71DseVey+pvXUAE/cy9kWXFLkMHtIHUp4r9PP4OQM0OC6UQepLjhOD/3h/AvmLxQKw4ui43E/1s6jr9BrRewjHV9sI1FmcC013rgMl2G/eh7Yp9xjaBlzzXI/M+KdM6XJdnFu2SzOg8Ix1Op3y+rbW5uAajjXXPPU0dRH1Mc+v7NM/l0rdcx0nJzHn0gjaC8AkNsgEbGe7rDgmuO6tMbm+XQZfUQLWsvPdChVkM51IYEBV4XBsc8BGX0vA+ld3r/Fh84C+63BGhDcNqhhg4YTe3AAmAFNVV0+Rf2LI8La0v0LK6jXiYBWWbQH9BXiQ60jUXuA5qLsYGEQwH4naS8gOBVb3EMArAoihwdNvfoXtzQpuYjH/+hvUj0f0oQUqwBmLJhqhaR8GnE5HfH74DANxNE4n/wK39/cYfI/oPuHz0x5dl0BXZVvJnADWhhSgcNFuY1K2eBz1hZlXAM+pSQfQ0Q3AuBrXt3doJgecUymrDx8+4D/+x/+IVy+/wv5wwod37/Cf/8f/hMVyKQHI01mqPVnBOIfZdIom+Wycq+AmNWazCUJYwlrJknVWMl+6vsPQSQ3SYfAgVSVtPB2k057EPuh6Kb1zOh5xOBxwPp/zuuq6Du35LAB316MfBvhB6sN675OTHYCJMA4JVGjQ2AlgI4IL8C7ZpIhwLibHHM/hA4Jwv6fazSL3bXtIVJsBwnzkEXNN3+K49X6cUT7KGg+C2BhEVEayEr33CXWQbMMR+CKQhrq/yAPXN/L6rhQwzfraGhwzyffXg8BlrvttL0DPiLwaNOD6BdiWAwLGwBedjMXW0Niy9mDyfvluGEv5868YnmG7yB8y4CeO5obri33gGrHRwMZMYgqg0A4DEGpnAOMqm2NwbwQWwkoWr78AIi9v8OUb5R5fzD+fw8/Hf4t8Pgd8FmBFrjejz/L4UzYi5+DHQdTR/MUomdMXMs426gxfeA1kELyK+S/vS4BCzk5/VhbC6JrLF7/zY+0a9+TLLDbp1vh7P/as/Hm6R99/+awAfPEMUp9fAsR6TUtfACjwxKZ9NtrEigDARAHag7qftcK2oEF56wptvuwdam4i9/5RU2BTwBvbr4M/Y3Cj9+u6AmBywB+/z5IB6Vv5eaQ4jjHCVeMAgS/GBdQtDN5XZwwlw5SeliCyKxTpQwT6gZmXMrgWxa9g7YDCTGGTzjIwwcCEZB+YrBWlCSGNe+9zu+wXaw6wUfZBB4Ou1TryMlhG3h8MAJv8HAYZ5FNCAerYoMfiUpwARGNhooOLQPQotPUqk1+CBIAhtmI/pPIWarLHY151yU6xKGu5BHUSWLdmmss5VOr8OGL8AGBjYXvUYBjfs9YBoZH5T+NGS5B7vag2hzgImF2ljGvnGLBf57Nu0zRoZpKl3TQNJs0kg9VVygSX62rUdYXJhAB8aRMxn3Juq5NfqIKtWLos2RAQ1o4cLJbWG22ew/Gc2ZWMAU7tKdkZHpnNI0SEWM7o1thEy5/mmrZjGtNcZg0S3BKjUHdLk0ze7UxMIbExjNaf+OSLz/Hp6QnT6RQv7l/g9cvXeV3N5gvMZks8PT3hb3/9G3z69FmwsRd3+PYXv0AzmSFGi3PX49x1gAGaqk41733e7ke2RdqH9Hv5HHMBlup/c8BgCvybzmaSTW8s6qrCYj7HH/7BH6A7H/F3v/413r17h9P5iGkzQX9u4VFYMEKMCKGCCWdUkxW2v32Lp//vf8bd978Chjm2OMMhYoYaDRI7CATU5goNRkjTvYkwuZRFsXDymUOZPRKOC7keTq5xVgKZfYT3Pbq2Q2g9ljfXaGYTBGtw9j2GyiFer3CugKfTAQ/HPc5dhV0VgNtrLJcvsJ4vsLy+xf/mf/e/xVfffofOD9ict9jttxlvmqWgDR3MH5KcPLdf/th72u+v5/jye8Z8qbvKOvkyQ31kb108+8um0M4Z+6V+zHwkmP9TXj8ZGK+qQvULCIBHwJS0u+fzGV999VV2iPEQTmcIo/mZMUO6cA0M0LlGwFBH3jObgSA2wTgNZH369Ck7XFnH+fXr19nZASA7cuiopbOVmVCsK6wBFF2H7unpCYfDAd99913OoFqv19mZEmPMjkH2gcDC7e0tvv/+++xQWq1WOLdtrr1Op3Df9zlr9nQ8YpqcwARhCU6yD58fn2Ctyw5KCsmnT5+w3W4x9D0Ws3l2yhLUpQNvMpmgPZ9xOOyys5UAHR3bdK7xGXSkVVWVM2I1xaoGH1hj/sWLFzgcDnj//n2mUN3tdri+vs4Au8wxsqOdIDvlRtp9hLEmAxjr9Rrb7TaPPwHIr7/+Gr/85S9zhk/f9znzo23bDBBrKlg6P5k5SCpWOkzpKOYc0wHYNEKJQspcRpDputLM/tGgEJ18zKIlEKUBIRp1BAOY1c5alsaYnI3LMXp6esrZXwxaWCwW+bn7/T7XsSXAx4weOgLbtsWnT5+ybJIVIoSAq6urPHYMWvFeMszpUCeQwntdOurJBMG+0wDTtKAE3mKMOUiC65S6AkAGftk+jjGDduhkZ38pawQCt9stDocDFotFvv7Tp095E2EWJ53NBF0+f/6cAbW6lvq1pCLWdYc57gRF6Mins59GG1BATvabbAaafp9jSR1D3aaBeY5jdojaQknOQA4NGJDulfqW1wPIGcPUiRqM1HWBNVDNdURHN7PCqJ84tjFGPD4+Zlmh81xnxurDG3Ur2833CHJQb9CxzX2Ea5X7EUEujgnXKe9D8ID7hNZ/nFOuOX3NJdWw3hMvjQhmWXJcKO9cJwRrNKDDtgnVUpXbqGm7CSbxIKvBUp0VByhqoBRYoYHI4swtmd8ahCdgApRxp3wx6IJ/83sMbtAG8dXVVQa5qes4htTJuh2UBy3/1EPU3ZwLrdc0QM5AMQAjRhqWBmFAjAauKdcMGiMoQvCD64oypg1+tpWBesJ00qOuTbZzYoyjtct10vd9Do6jfGnwnPK9XC4zYE0wifqL64o2DTO/OG+73Rar1TrJRKEHppxwv+ecM6Oa64FrYzKZ5zGkLUbAjGND/R1jzPLNgEraNyy1QFnZbDaj++oa4pQZXgsUoJCAOftlrcXbt29hrU213ktZCdoB1O/8Pl96D6Gs+hAwmU5y36qqygEVBMMp93VdZ+aQS/pr6tzLtaUDLfS65Fqkbc0xpr7ROq+qqqxruM45HtSd3Aupg9q2xWq1ynYVZYcZs5R1BgBwD+U66doWs8U8yzyZcJhFzaAB6lHqGq13CGpqZiK9lvW6JKirmUEo+3yfbZ/NZvj06VMOItIBrDHGPDcccz6b9+V8ad3OsdPP1uvlUj/owyHlhHYAbRQ+S2eZc574O+0G/Qzu5RqY1gEKGuCmjiCorPtSOYcYYg4K1SC3tlHYL72H6fGh3uQ+qe/DtnPfu3SOUN9pant9HqKNzUDsEEI+W/J5fKbWN2wPA0vJosQAXNr92q5ZLBa5ZIW236kbGTDDZ2uWjf8WL33ud2nso0keROVYKnMuzonLMdXX8H1z+f3kkKuqStZuM8Fud8LQJ+ByUmO+uMXt/R2mv53gdNxhZzwODrgexD3k6CzMoJQ4M8ZQTsyOp+TWgwVJNcXV6yBAF53krObHEblwzeR7VYisLKmejlT6IsFFEbBYYDgd4f/uV9jPZ2juX8PUDq7vxEmdMKpoGdQJOHvCdrfD+/cf8OL+Dt9+8xXW6zXavsep6zEMLWBcAidkHARUSDczqV3aeYiShSn0kQ5h+NLxVJxT8l4GWIxJjsMKk9kMh/0Rf/LH/xUPXz9Jibvra1QR+Pz5M/7yz4Vppa5rTJLzWOQ8wjgHW5WMp5jkrarrXOfSGIPaThPwYLNdMZnU2ZlLJ3kckMeB63ZgJlTy3/jBwyf2lkG9r38PIdEcD1128Mo5fEDXiQ+hPXfpOp8A6gSK+8QkSMA+lf8x5pBr2obgC72wLIQChjuC5wl0wiWYKVmEJrYSkBJCAsDoRIxKFlhMoDgKtaORtOHWfrkuqTNHr5DYZhAlcEAB8YVSO4qrN98vOeYzsMX+JKDuAqzRzkXqlNFKNs8Dr+bHqOMv/iZttMlAtwIZLbKTGvHLvVO+V3RcMKXsdJ6jZx6qEo+eAbMuHLIXAOOzfTVjKmkCdhLQAOQxDF61l20rgLIAQ/ESr/6yIbnden6KEx+kIs7jFS/uNb6nAVL92zCqQc3MLwGRBMQCGFjFfpU9h+NgrSW6VcZXt18DKGYMao/mQQ2EXg+Xn+Xgmcve5bF9BjDXIOwzDvpgxg54vpg5iPSpYbTOj4L2Mv5GtSdCAkwS2gnAZtmBSftifoi+L3+3GLEKaHwWRiBdA5SADZPLU+hx4cs66QP1IwZkAEUAKtEfPg7Qo8nYDKk/LdeGRFWfBjL1yZTQDd4z+4w0WKLnVP7b2BRcGFNGcgr8MREw+TnyhrXcbwKGIWAY+pFcWWPgjBOwLgVKEYAzRkCtEKQ2O4zMB1k38npFmqdM75+7qtpP3Z7esiGPQf4X1NtK15tiL+YRubDhLMaMEjx3fGHLGQY0UFZ4H5tLRsg51iLXBeezokklJkzZ82Ipb6WVq1EAs4lSyqSqKjR1DaeSEypXoW7IxqdB7gZ1kzK3q0qC8JzQkjdWan+zXEaVgPWqqoSuPNGWV9MpamZpVzZlljtYl8qyuMTagRJIrv1K/HcYBnTDgG44Z3vFJ/vBx1JGIsYIhAvml4s1lffsSrNdUFiUTWyAiIDoLwHCFMgx0nnpvj4gRDLxMKxAWEl49tLnL2GmlbM+z1Lz+Rz3d/fpnH7E4+MGnx7fwQ8Bx5NgEfV0jm/vXqKeT9BMphhCwDBIsGJVuZSRLXu9RURAYR3MuibZG3zvuTPJpZyz/9HogAoBlGtnsV4u8e3X3+BmtcJf/OV/xefPn9C3LZyxMDH5mxznQEoDVaaBnRqct1sc/uZX8H/6Z3h17NFjjh0AhwCTyi3BmgRmJxlHzHrLJj0UuAAA2BzGKH3gHuGS/nXGoDJAdOlIMXhEL7Ze3w8wiznaWYM4rdBZg30I2PsB5/MG/aRCW0X010tU1zd49foeWMzQWYPJYomf/84v8K/+6N/ANQ1+88MPOByPOJ9OcKNA8kkO9rDGCTB+acf9Pa9L2b6cM/35c+vg8u9/aO6LLWWe/a62/Z5rw9/X5h97/WRgnNl6dO4SyNOUxcvlUmUe+Qx2M6OSzilG5JAam44rAiF0sAKFppbOazqUP336lJ/3+fPnXJec4B8ALJfLnBXpvc+gOVAy2pipy4wiLmBNhweI8UfHHgFAZgff3t5mBwlrcWr6Te1kZ+b3bDbDq1evsqOXzyDFNf8+Ho9CTZ4cqZwHUo7TGbPZ7rFIFKnv37/HdrvFz372M7x69Qr39/cYhgHH3T47r7SDqzhMHSJkzpiB673P/WMGi65LS6FbrVZ5XAj8UVYINDGbzVqbHdq3t7f48OEDlsslTqcT3r59K1lR0eBwOGYn8nw+zzW0KXekojLGZOc+ncN0dNFhv9lscHt7m7OsJ5MJfvazn+UAhA8fPqCqKtze3uLdu3e4v7/HdDrNYPvHjx/z9cvlEpvNBnUt9Vfp/GMWGR3mpEjnGjHGZLCH8sWAA9KoEyjgd5ixSplldg9LFhBsApADOgisa4cq28aAk+vra2y32xwcMJ1OsVqtcl14DViQVpjyoiPqCJgTAH7x4kWeY51RpWvF0onIFx3BIYRRXXo643kvnaFU11I3nOAOFSQ3ef7O+2v6buovAkw6y4f95ZhpoJnBMxoU0aAc54EA/6tXr0ZrjeuFY0J9Qyct/ybIwedSj46ylWyVAV/qSQ0+Nk2T9Qod7JcgiaY61cEClwAg1zzbop3rbJsGv7kGeR3llrqH80dwiMAB78lrOQacPz2fDMLhGqOjmjqLID83Suo4HSjAfUpn9fJavdnSqNXZZwRyeB3lgIADwWDKms5a1tmgQDEadYYx18P5fM4AIgEQjpkY8MggqgY6uD5ljPZgPRlN76rnGcoZodcm9zn2UYNvOktZ9rZCc55LfKR54FomfTHlRTPLXI475YpriPPN8WFfKCtcd+wn9Q/nmQE4BDa7rsv1vjkmtFPqusbnz5+xXq/z3q2piqmzCIDsdjscDofMFMIsRg1Ma0fEYrEYUU9zGrim1us1CKrJuumxXq+yHqNdorN7qTdYHoB6RgNPOqOXNhx1d9d1ea1Rr2q52mw2mSmDNOzr9XpUTkeAtZL1DSDPPzPA+ZneuxikQIYgyjf1IfXScrnEcrnEdrvNJVLYHl6vwUG+x/tR1gDgm2++yeuSIDvHjgAhad+5v2u99PDwgLoWOvcQI85dO7LlqC+4nvicGEtAG2WcwRe0rQDkrF0GM/R9j7qqE/41ZpvQWcW0I0kdz+Ax2ki6NARtJ9oezrkss9wvdrvdCNDmmuf3GSgWY8znAILbIZayGHyuzt7m3F0Ge3KfJzMH17kGM6nP9Wdcl2y/3ku5DnUAzOvXr7O9Q9Yq2hO0CbhnUp5LBkIpkaH3Be6ZOtiJ80PbL4SQ78G2a1klMwgDbxg8pwNb9EFwBAhcAM16L2c7uQfTXtRr59IWQSX19tg/nUXN/VGzfWg9x3WuD7lcQyMQKJayI+y77i/3K9rdmnlAZ8tz7+dzaHPogLgYYy7togNE+Pfj4+PojMN9iXPBABruNzzP6GBGvvhsBsT8c1687+W8Z0dbBLQzmdeFIE7iy+8WwCs5ppNeyY5O+UaShZRJM5kghgjfDxj6AYOPqJsJ1nfXaJoa3gAHG/BoenyNCX3UACQLztOhG5PL3ph8zaVbxsKU6xK4TZduzDB3Ici7hCN4P5ehdpOv4190WgUADg2W4YjjwwO6v/seh29+wPLnX6EJRup3hkRbb4tsd32H0+mIzeYJHz68x+31GrPpBFfXVzi2LdrzCf0gdppPzrQCPgZkalS1NvR8cy1KzepLZymdfTJ40RjYBJxUdS1zVnkY4/Dx/Qe8//gBXd/j5voKy6slhjigDz2OhyPaocV5e0ZMdW0FAHOwLjmjK6nxbI2BdRYunUOrqkLlxNfhrEuZWDWMRZaZyjlxmIdEaWrEAWyMga2EBnMCrg1x1uVssRhTBlICrH1iFAqSpR6C1J0NQwmQ6doOXdcjhIi2D+h9AdtjGDKYHrxPYHuPtj2BdYuZMS4Z8AKqs25nCOdsD/A9ZrOHkEI/gsfgT2VdhpBB9zEA7gHjL94vEkoA3joBxwmilIwzZKACgNRTZ/AJZS2DMqSPT8S4pqyFGCSLihmH2UFvTA4g4LM1eJtfI4zTXLxJ+Oj5oKACvKZ1kUB7kfEooBqBA8O7EwQeU7VentlMUixjcBVKvxWH66XuMQQVifkk8Kxkzhc4VF9DYK84bE3+jjGFclTeCKmNRo1pzGMdom6rbtePt1Uyx8cgLj+X3zUAKY/V/7JP1uTZzuMj1NEE77j3G9k3LCeSYA//E1Wfi4bmPBoFMLLfZQ+KoxqpfOX5vJg3Pp6PvoSy5b5Q7xbAmdVIchAPyqDIWNiL76pnUlch1Xk2eh3o8VfwuyHjTwG+2C+bAlIMQfGy8mSf0GMAPaelVRro0EDoxVWlZrxaw8EMMCZRdQehORdgPDF2cLNObQSK7EvbpFhDCEUH8enGjseldCPmOUCMYEY6P4upnbVN+kzJGfcT/QpWWE1kX03BTL7YhQSI8zNSoJPcT/a5iAh4AchgAOcsnCugs55b55wU4s6dQw6yyCOTFbXLwU7I88QgqyRv1ko976jvJTeOyfqR/1eQ0g3yt82gNrIMGCNWBvtt07gYjAN85Vw1ye/lz2wFq9psYOBsLcC08smaZBtUCeS2xsEh+fCSP8JZC+uY9Z3sh9rA1QTQG9STSoDtysm1zsE6izoF5FCHm6I8ikqFwWCqVCIgCsgcpZxNgBeZ9GLfBNoXISQZiflMwfNYsbMC2r7H0HcloC7t/zCACWPmNeox2kzGCG2+My7PZ5HfMUjMfnz5CnkdxCj7NpmFYmqjBhGtCqKWPkhQy3w+w2w2BxDRth1CEF/Bw+Mjun7A8XjGYX/EuesRo4FrpljOJfnw6uoap/aEc9+hb1PwH8XaGIRAQvFkP1zYtFzwZQ3K6uB75bKxrRtNCshKfr66crAxYrlY4OX9HV68uMN284S3b37A+XiSvRoQqvlkI+dzoQwlTN1g/9d/i/ZXf4Pqw3ssQoPWWPRmggoeNVUdVU1Re3Lv9K9X6eLc6cqOp+cUeY1YZwUUj1JhJhogWAtMGhwXE+yrgDZ2OEfg5CJOtcUwqeHWS1TzGRaLGWY397h9/RKxcrB1jevbW/z+7/8h7u/u8bTdYvPwgN1mI2fpxPBSV9UowQDGwMRQ9t0feelzprazLuftn/Iag9Zpv/iRez8HcD93rcar/rGgOPCPAMYPh0N2aGrHEwEsTQ3IBl5dXeHNmzcZ+CQVJ6kNr6+vsdvtcjYA7wkgO8OBQr1J51kIIQPUzDYmwMmsKtZApqOLznrS4fF7dLrQoakdsk9PTxnUoEOWgAMd6xp8qqoKd3d32dlNB6h27GvH52azkazolM1srVCYPz09YbVaZUDKABlYoCORjnfWDWUwwfF4xOvXr3NGPTPC2TfSqNMJ9MMPP+Du7i5Fek8Qos+OVQYLbLdb0InNqC46een0JRUtM+SYOTtLkevcCEl7znrbwzBkgLeupV786XSCgc3Zonzep0+fskPRWouqtvkezPweBqnzTae2tTbXMiUoQqXgnMO7d++wXq9xe3ubAx9YS9l7j5cvX+Lt27dYr9eZPp2BAzoIoGmaDMQTDNfUosz0Yz/JlkCH4vl8xna7FfoXVd+TBjTpRElPS+ckQR+uJTqvmTXItUSgQ9chd87h5uYm94XGAMERYyQghffSgK4OkuF64T04drvdDvf396MMOwJ3dBKyr8fjEfP5PD+DzmM6gAlCG2NyNi9ZHNbrdQY+6czl/TVwxMw3Avm8loCZBt1Z/3S9XmdQloAjGRWoUwgQzufzUaaUBpk1gL7f77FarSSzJGUYU1dtt9v8fa4v3oOApDFSg7FrC1MB+0hGgBgLRTx1E4OOOIe8hu8RION4a0eszvzS2ck6G5jf1wFCDFLQWVOUM9YHXq/X2eGtg0gIkmngjbrVOYfNZoObm5vMwMDsUp3dRwc+gJSd241AeD6PL52hq53+GoClbieAkqNgL4JSlssljsfjaN1Rluj8Zzv1/WezWQ6AIrjDQwrvXUCOUgOXYBUBce+91JdJFOcEPwmEcY+QNnnMZiVTlsADZYNypIFSrokYI25ubpKD8ZzXuB5j0vkSgGOQFcevqqrcZ8okgScdIMF2ca3yXz2+1Mtsvw5WYCAPbRgejLjP3N7eZp28Xq+z3aGzKjVgT6Cf+zWBGraXr8t1x/Ut9kyES/VEqad1ZjD3P+oAygufV9d1LnWz3+9zwAntjuVymWWGWfSbzSaPO/cvAtJdV/ZcgnDc25xzuL+/z6w8DC6iXIvNIwFszPKnHUE5pt7m3HF/Y9tYcoJ/U56oZ8keQ/uzrmvc3t6OADANUHK8qIMYWMba7DLfMds5OnKc9h3XOmXaWilnQl0RQgBcySzX/dOGOdecjnxm6RCyuvDlvc/9pqzAlLIEbCdZaqgD2E9m6es9keuW6+G5GvEcP44nM2/1vYBymNcBXBx32u4ujQkp8XlPXqcdM9w/uU+QPUIHGTCYg/PC/lJHaVYAsuHoOeLeQVlm3/l96nAG3WiZ0bT13FsZDMPsYo6LDijj/sy+cq+jbHDdsO8cJ+552qbm3zqwlXuCZj6hbuT64b88Z+nn0oajfPMenIfaVRjUutJjTJ1L3cHx4XN4X7ZBz4G2NXgtM7+pLzgfeq+kDXU4HHLgM2Xx0lbQ+wvlnmcfnkO1M0zXiL/c+2gncE+jTUw9qdcNr2M/dSDAP/XFGpZ0pD/nrCD0cOm8DeHC0RQj2dcBU6hYYQpNa4gx14/kOp9OJjCIKYuXWdMVVvc3aCYTRCuOnI++hcdECDKjh0m13gYrDi0ACXAwQAywKM/lSzLGJZecvxdgnP+Tv+mS1tWYNVygYAIFriGD4+z/DA7+1OL09h22v/xjTH/xSjKOBgEPBwPYmGoohoBh6HA+G+yswbt3b3F7fYWf/exnWK3W6INk32w2O0Q6vwhEGNYZLjTPdPZyLQAF+AtqH/nSEVSAA4L2zljACcCyWCwQX77Afr/Huw/v8bR9ws+//QbXL+7w4utX2G132Dw9YbPZiA3tEzNFqi0qHj+CgjHpxRbtOZ0LwlYBqwppg3aASuetc9lRbJ1FXbPsj2SFVVUFVzdZl2hnuq0saueSQ9+hMlVydKasSKTHBpMBrSHaBJ6XkiRAcZR67+GHAV3ry3vBo+8Sw1vfYeh7DF5qeg7HvexhOYtd6C/PbYsh7VU+erT+XJ7pS4a6XquSXT0utXPpSI4xwlihSOea9F6oWXOt+bRGXQbCJRM9+AAfSoZ8/GKFFaBb5i8BQ0iAj4l5fL74XnqmcPjG0fuUxwJMxASMK0Dy4h8B5yKiV8AOYccYEA052xPtp6V/xCa5LOBhBBJgILT2GvfTIBrBkQKYllcB5UyWlxg9rK2yeDPgSM7n8jyZw2q0Rrk2Q9BZnFFYPkYgF3V3AjaiAN267frf8XwUcFJ3xihQVr53WR+9zMkI1EkAHO9mEr1vMKT/lQy+CFL58rFKxpKOs8bkMRvtgUXtPfPvlxlifPkEYpbrjexVvlD/G2syg4aMT9FHGiii/HMHJF0xgxp4rWXWPZEsNfCUuhgBjDI9kXV6Bj8jIGwOFkEDmZBgHwConKyVgJKhn9uc2025MchZq9KcHAQ3Hmj5KQAtZzYCo/mTQCNhotOy61FVY1CY9oh8Z2yHAKl0hBsH8XGtFrnkOKKUp4gshca5Ex0QQkTtCgAoOt5mSu/cNmMQUErJxdQnP/g8xgYJuMttE5ButF+Be25h7KLNynnj85yzcNGNSmEYI8CoyTKA1PdJ3gP5ExFzX6xJdPmJql6Dq5RbCpiJFYwp9i/lWesMZy1srISi2wooZy33VQloc1UKfKxrec9J/e6qSgkAVS3XpL142qTs7OSnkc/kPnVVp0xvCXwzKGfF/KNYUGyFzG4i7xckMi85AMF3mUUlJKYXnpWGXkq5eD/g2A6IEelzCXwTqvIU9Jcy+61psl5iIIYxsjIq9r9Ocw4D64DaOsRoESPZTAOMjSl2qwBxl7rLWgMbBay3pPxP8mVhMhOBBrZHekr9MBDP+wHRp2SiukaEQUjnLqRzjvjLxJfQD2LDyFkE6Loeh8MR+/0B5/MJbTsgxAhXVZhMZri6vsZ8eY3leo3FcoXZTPzzD48PaB8eAPQycZCyM5Wz8Ej7dDQIFzLOdW6MDgQY2yQ/pvNhkJirUn33ysECeHF3h9evXmHa1Pjln/0ZHh8eRHdFSIBiDDAmSt/TurDWYYgBvgW2f/5niL/+W6zPHSxu0bgBC1OjihZViAoYL7bFlw2TTwyMnA0yHF6CCSPSnuQcTFUh1hUGGLQxIliLYA2iNTBVjY8zi7P1OMKjswZxNsVkvcb05hrLuzvMr9eYrZaYza8wWy5Q1zXu7m7x+quv8bOffQsMHp/fvce73/yA3WaT1pS0trA0uKwvjLUjG+5yDkbny4vrRnOrPtfXld+fsVtGzyHrX1Sj99PBcb3PPLd2/jGvnwyM393d4fHxMYNQPLhpIIxgIF+kJiRoy8wHvqc7pbPv6JzQlMZUFjprkU5F7VjRDnnS4dHxSyCyaRrc399nRxOdWgQl6cCiQ4uZaprOld+7dLDQ2cf61aQ6JUCtI3joWN58/IhTyoqeTCY5m4GONTpOq6rKtNEEDEhzvdls8j1CkMxbgm/MrA39kJ0/BORIM7/f77E/7LFeL/O8EjB8enrCN998kx31FDQaC9oJpzNcp9Mp3r17l7P/jRGQ/fb2NssKAxpI2amzkk6nc3a8E/QiZbr3HlUtNeEpg998800OeiBgStlgu7777jtsNpsMTBGcY1AFQV4C+CEE3NzcYL/f5/k1RjKZ/u7v/g6kEKUc3t7ewlqpzU2givLMetiUM4IfzAwiuLPZbGCMyQEAGqDa7XbZWUs5pWN2Mplk4IfOOlK5Pz4+5qxnZr2HIDTgBKdZY7frOqxWq1xXnutQR9DRscw26OwprlOyMZABgSAqHet6rums1s5PUoESLKQDgfOp174G9gnYsl3akauBfK5tOmD5LG2Y6KzJy+AZzh2DXugkphOxrusczKDBXN6H+olgCYMoCMKxT9RFdMb3fY+mnuQx4Q91ngZvOUcMZGG/CETq7H1t0HEcCK5pYIqUu1wLbIfOBOTc6+xljhNljcEADILgc6k7jDGZFlVnbVIPM7sMKPWONUCj9yJjzAi80E5lPpPObZ0xrQFOAhK8jv1jAAyvYx+ZWcbMVu6JbKPOYmONVF23XY8FZVjXhebcDkPIcqjbRiCr7zsMQ8kU5dgCJTu8rmWv0xnpBE6og3Sf9doqQF3M80V2BYK8OiNYGyoE8Qn4VFWVA5M0qE6wTcs854zrmqBfjCXjXgN1BNvZb64t/svAKQJmDOziXkmAivqHc0HQ8fb2Ns8Dx4cyQxuAASHs/3a7Rd/L2K1Wq1EZFK4tGZsWw1AChQjeEGTmvr5er7Fer3MWrgYvj6mm52w2yxnEm80mA98A8lrV4Nt+v8822vF4zHsuWWD4YuDkZNIghHmWbQaIUO/RvuFYUkaoixm4pWWF8joMwtIzDAPev3+P+Xye7SbaJpRv6lCuF8ox9wzaShLQU+UgOx3cybV6WcaCwBlplyeTCU5dmwM3uEYIcFLWGbSh2Too38858eq6xmKxyH1u6gb+Yr9he7iWuZ/qICnqTs38wWsJAuusfx20oAPfqCOo+6kr+AzuZcWBJI4jXapIM2NYa0d2Adt7PB7zWFAu2F6uc22ncX+lPqIMc+/lWYHP1Pub3re5zzOgiWuA+yRZrjh3zrlsG44OnOogRruI/WFwsJ4rgqwMKGMwog6G0XsCgwaaphmxTGnZ1XpEA9pAAbXZN8qeDkzLAQ4hZKclUMqjMMCJ92ewBmVXH1R5TtC2hpZFjinvrYPtOEYxxhwMzSAOXq8p1mn7cVy5N2i7mLqZTAYMBuU86GBRHRDK/U3vixxb7i26bMTleP1zXjrwQsZwrCv4+tJRMXYK6P33x5xv/LztBUisqhpNsk8QIvoEGsYI9ANw//qVlKhyNYbQ47Nv0ScnuDOJVjNG9CHC8NlRO5CSE8kkcDWOAW8Hk38AoUHn55mFFgUCyGPBPue/i9NFwwXy/RZDtKhMhenhhNOf/Sn2//r3YX/xHQbvYRFgbIUYpWapseJ8PZ09IgI+fLKYfz9HM5ng1auXeHF3j/bU4nxs0XY9KmcRIbWnYUa+qHG76SyPes2NHafaASVM3Vx3iQY33cfVYs/O5kvMZnKe3+22+J/+yy+xXq/x9ddf4/72Br/7P/s90d1djzdv3uDcnnDcH3HYH9J3dlknUNfms78LMpeVASlRtdzRP+BjzBmDAu4E9GjRdWeEc8ggQ9eJjtABapegsYnI5ZKttZKdlp5duwKsV7VFVRWWJtqaXJMT0ra6JS4paS9/rLVo4lSvJAGqB5/3LkDA63Pfp0BRyV4fUsZ66IesH4T63WcbRN4v1w5eqOXb9jgCARiEqMclxojgeyUfAcGlLDgMRWYMEE076qeeI/bVOaCuQ36eDh7Wc4Mc9JJGRGWtRYLjMSKksgGXDlNty8cQEX0Br+VH5IQZ+jEGIBrEWI3l4ULnhSAUztQ1uv25XYiwLgmTGbep6EUkOQ4JFOc6ZOAK/V8F+C56uTj+L9ct+yexCAXUjFH1O4PdJn+Hcpf/q85R6s+L9pd/vwRNx/3mdwuOQTA3iJY0It+IiVI7gbN5HgB1DwN4D+vEDnzOaa6fj2fef25fc8p+5XdNCKOsb9YMvrSpeZ9Rf5Xcj8eg6KrKK7BTtSmvvwRkD2UEcoDBCEwvA0SESMDZGFPpgogA0g5bRGsAYwvVeGSmv+qPI6uCBAhpn7m2T6wtvjVjJJRIn8P5Y5xBnYKTjClBRfSNh1BYoET2WdJN5EED9cbWMLaC3guoa0pwsENlSkAyUIIKs25I66kNY90VM2heSlE564C+zDuZQLS8xBjhY4RHwRL4XZPkJ9ttfQWggOK6nVpebGDQQZFVLYOUCpPoyjlPZT8SwNom8LlqBLh1rtTU5lkmB1XXDtOmUgx2hZZcs9qZeoLM4FLJ/Vg2xdoSXDCpT0q+RZ7KeCcBNkCPdqxz016o96MYB/jYIyTfnf7R+0rbe/SDzOHguwL65oCuZAeosb3cr/R7VT1ex1VtE4CrkikgAXPahuf1cjb1gDp/GJsotVWf8/x7oDJ2JKs6IQsoiZNNXY1kEDBiv/nx/nDu25Hu0mevEtAn41PVBk1em4XJUQD0FsfTGV1fSlx9etjmZDVjJHlpfX2LSTMX1uHlEovFCnUzgalqwFiECAw+oBs8FqsVDqcThuATpTxk77NABYcYJFDJGfdFHxjQM9a1X54XL/WwcRWaZoJJU0vQlg/4nd/9HXz3s2/hrMGv//ZX+P7Xv5L9HMk3OAxpHsvzA4SByN5e483//X/E7n/6T7j9sMO1vYYH0A4BBkeU4k3FNqdFGw3gYTAgSgxmsjPkPGJRAWAIbwQQnOiU6GoBxJsaflLhaA02JuAIjyMCOhMRncehiahXSzSrBZZXK6xub3F9/xKzxQpVM4GtKlSTBre3L/DNV1/j9ctXuLu9QV3X2B/2+NXf/g3+y3/5z/j44R2871A1Ui6COEJdVyMfMVyVg8EufReXr8tg+8u18Ny5Ur/GOgMXdldqA2Jm7IiII4ajy31N62GNrV4+77n2/n2vnwyMA8jZkXQCsVHL5RJ1VeNwOGEYekRAIsuNRVNPAQP4IaBre1ytb+D9AEQDaypUrkYIEfPZImUD9TiFFtYYHA9nAKU2JiPbTsdz2iAqIBrU1QTr1ZUcXtOGczjs4YPHzfUt5vMFqkqiZPqhx+l4QtPUAETxVa7GanmFqq7Qd9J+iQCWKOndSZx6fTfg0J0wnU5wOp1BWrAYZCGc2zMW8wZt22E2nWO33QvlWFWjrpo8Xk+bDQz2WCzmOB7O6Noei+kCQzfgfBT6TCRlOaknMAGonGxwx8MpKVsaIIA1DuvlCnd3d9jtdlisVzju9gj9gO7com9bzCbT7Ayi84xOIp2B7lyNGOTA0NQN6mqCxXyJ3e6ASdPInFUO3st8xihRKO25w35/wM3NDdr2jPOJRlOFupqgaWocjyfc3tynqKUai/kch8MBu+0ek+kUztY4Hs9o6ikO3SFTszNzdrlcYjKZ4OHhIWXIiS19d3eHT58+5Uz41Wo1qitNJ5cxAsxz4xLH9hzv33/A0Acsl2sYJErsaHF7e4u27fD2zTtcXV3JAQAO7blF8HtUrkHlHIKPOQBDKxYaL9wsn56e4L3Her3OwDMdbQDyhqaz/3U22PF4RIwxg0PMECaYYozJ9T05vwQhSDVNgIIOZIIoi8VilDltjYMfYs70aiYTdIlKxhjJTLy7v887RURMThkgBqBre9RNg773CMnBKNfJGA7DgFhL9K+1lcixtejaXvRGUzKqhLZHDD5hE/CoqwaHvaxFPwTY2iUKPlkrgw1oJg384FFVNfqhRN1zrjgGdMobWHgfcD63CCnyt6pEfq2z6BI1rLUWztZwzqJtO0yaGYyBPMs1mEwaHI5HWOPQdwOsreCHiPPphBiAc9dmWRLjBokuEKicUCDGYFA5qQcSY4QfBjS1lCKYreYATNbB2rFNg4w6WjvWCcbGGEdBTMwO1XXCNQBBwITgCAFGOqx5KGHGvw4u0ACLdiDrzHsAOciBlLzMemV2Lx32BK51NiX7SUc+jV3tpM8bXlUnQGGSDjol4j+EFtY6TCYOMYZRkAODMwj+a2c528HnaerU3W6X28150ICZzk7j+DNg6nw+43w+S2mJ9CwGPvDgQ909mUyTU9+gqmoAkoV8PrcwBpC6MlWWGTrjtIFBI5RgBYMxClWtVPzkS2p3dXlcYww4nfoMaklgkhxypE3F+KKc6YPhfD5H1/Xo+wGTyRSAgffilGdEunM1jIlwrlAEE2S6DMCgnBP8AsYlB5pmkoDWQz7sW2tSQJOBczVOp5IBHyPXzgTex+R8KfTE7DcP0ARkqOOpj3e7XQ7SI/A5JD3F4ArKvw7qEflxCMHDGIth8GjbUiajbbt8+PU+4nzuMktC33t03YCqahAC8PS0SboF2O+PuLu7Sw6GEqzATPAYhfmG9Ph6fTGDm8C0ZFIKxamse6DvB5zPLeZzh9lsgrbtUFU1tttd3sNk/Ht4HzCbzdPaCCnYxeF4FIr76XSeMm4brNdXABiUZzGZzBBjyP2S75L5YIK2PaOq6mQDCZxCx84l1bi1NtPdb7dbXF1dZYafxWKRHeE8+PrgxcsZIqwBdpstqrRGfQio6wpD1yOaQvkMlLHO4IEvdNzU6bomtoy9Eydc2ottckoNwaMbBkRE1E0DZlk4a+CiZALMEqjRDz0QJTq873o0TZ0yVQDnpb6bg8lAo2aQYNvaroNxFn1iragnDfrgMSR2islsCp/kXtc2p57hOqSMUk8zQI9Aqt7LCMaQHUjbsgw+0ePZtm3WYWRVYCYxbUrKINvAADIy7VAXcn/heDAwRIJb+tFexWAafoeZz/ye3g90tvJyuZTSSandfMZ8Ps+6P8YSgKTbRv16ue9pKn/KE8ecQQ3cp9l37s/GmET5FlFXYl/13sMB8DFIXUmT6H19Ycvh82hzTKZTnM7n5JCr0A+9OL28OKZjcri3qQ4kZcg1NeAtnLWYTKc4HI95jmMs4LoOXOY46D2TwDcD/ejk5bzwb84Z9w7qXR04xzmjDHN+NVMI14m+7r/Fa3zAL33U/aUrgvIhrzEicukAGTugFUCU9pMmZfY2dSlR4b3Y9KfTGd98/TP8zre/g8fPD/j8+Al9U2NT1Zhai9oY2Bhg2h6LQUAygtFGIDMBFgzADMlMk27EOesiJPscKM41PJcD++VLHDAE45G9XEagh3RNBDDAuwm60CHGDvO2x+H/8v9A83/432M2X8DaCraLkt2RgAxm1dF2ffPmDWwqc/Ttz77Cz3/2LYbe482bdzi3Z4RI+mT3hVNWz8WX75vRWZJzaK3NCYDee7RJx/R9DwOgchWsKRmsi8R89/rFK+z3e/zw6zf49V/9LabTKV6+eIFvv/4KX929kqC/yiEY6dvpdMqB7P3Qo0tBcqfTCaE/g7Tibfsl5bt1Ak5H22THvzE2AwGIMdeANDBYTWdf9F872mKMiDYg2kHkJUq2s9CVD2hDj3MHoAPC0CNGD2blZjA5xOS3kSy1fvCUlPQ8m9upQaPZZFnoYitX/k212KvKybmtmsFUBotJjZWdpDNjoryNOttZasTqZV3ArJBABZ25WYKEaXdKZrhHdx7kdwU++GGQc3vSez54DOjT52Jryz4qQD1rqEYfEXqfmWREvxeaedmzIvzQIoRx4NdYhkUe+nBIi46gN0GN8j05w3HvQv6XP+O1wDNlXuEQe05+CyHK3uRsYqbgGbu0S7IAHWLXiWPbiGIY60G5v+g8r+SyPJO1VXOwcPgykEBkCfCewJHcIiYgPGaAj6VGUha68cgZlBdjPB7nL9fLjzmDnwteu/yudpLHqBH7AiReAszPPTvGCGtqcP95znnN68wz9+G4UWnHCBhX7GTdJ++91I1mprA6017eNz/TFEBNjwNlVOQhwroqBwAYY0oGbxHgZAuNHfEGYt/kJJL0nSEHVohtY20pIZD33iCZvmUsJLPUqv6EEFLNat2/sS2Yf7z0yVmbQXj4EjyeGX8SCDydTuCcgNrnc5t0RJ8CfcoZj/6Iy2Ba0XUaGEuBBMyoNLKLF4BTFoXck4x9iZrZStunxqasdwZsyE80hX7dwsDWBYgTtWNSAGWdAWGtf5x1kgGd9LlQDk9QJz+ks6qPas40uN1M69F7OohMg7gzdZ2c1wvjoA5+JGZQ1oGFVZnWUuu9A0w5U3GNIFlRfN/HLpVIET+X9xJs1Q0DfPLR+hBwTmdjmcOo9hFfvh+jnDPV+GZ5VPaUQbLZ8phwRVysRbWOLKhHp1/ofePc6OuXthBlCoFsl1a1zaByDYDEbOqljMmlf5L3Y5BsflY6h+Z5dBK8wHXuQ0hZ5qWcE1CSSGi7Hbb7cvZ3Dk1dw5oqn3NN8in1PqK2NpWhGTM1DMMAE6XkDAB0PuD8uAELL+g9eBgGWCdYmchkA9gB13f3uL29w/X1tZzVJxNMqhlgTArejOgHYYQyXEOp/03VpGSfPYYEuE+nU3TnlhMFx7Wo9Kr3fiQrRQZclg32kXLO82TdTIQePwDTSYNvv3qNf/kHf4jDboe//fXf4W/+5q/BKize9ynQKMIPQWzjGLNsGmuwedzi3f/5/4RXn1u8qG8xrxfoznv4tE+FVLgpIJWRsg4VpK45IBTtbejTWpPw3ADxjp5dhaEyGJyBdxbeOZi6wmbZ4BwDzr7HYTjj1PcITYN6sUCzmGO6WGCxWuH21R0WV5IVPpnP0UwnaGyDxXSBly9f4/7FC9ze32GxvkJjHfq2xcfPn/Dx8ye8+/QeP7z9LT5+/IjpZIqpmcH7Hn4YYJ3BfDZDXTcwxkoAQwCMkXO8Bsd/7PVje/c/dH2MX545Ze1ffn/sj45pXzVq4es28FqdwHG5p/9TXj8ZGNcUkDpLhtlaQ1+cS1rZkCa9bTtMJtNRFoZstj45tEp2sHYyy7PEWTOfz1NWZIvD4Qihf51B6hoYNLVkyz49PcEYi6+/fp2zBy4zna0tdXD73uPh4SFv5lzEzLZlthA/a9tuROnbtl1ysPlMJ1xP6mzkErThZN1c3+BwOKDrxCEzaSTzjP0/Ho8CvgY6hqvsuGnPLa6urnNGl85YPBwOOQvqxYsXQn96OmE6maJNzsDpdIr9fp+zLI6Jxj3XchxKJs/xeIK1pD4tVJSn0ynXXyXQPpvNcg3xruvL96zLjkgaXufzGXVVY72+QlWVGryTZoKhH7LzkAaFzqrdbrd4+fIlptMpjqd9PqSxpvLhcMgZbovFIgMNpAQlqEYH2jB4vHzxMmc0CbXoJB2gZJN+8eJlBocISi+XS6xWq+SQazCZSlaYpsamzNDBSup7ZkixpiadaTHGHMkl8tHledcZ1XSqUq6ZWU3AHyg017oWpbVSC5HjobOIOY90lIYQcH19nZ0sm80Wu90ur+3pdCpBJHFcx5JKTtb8fgTEAQVIZLtCEGqZYRjyQbGqHOq6GIU0UHionc8XWRFuNtsMohCMYvQ9nc3ihBEDlNTpurYx12hTN/C+Q9NMch1SZruawaBtE+14RKbz5VjO53NsNtssI3z2bleyyUo2l8FyscTV1RV2u5JJxPbwUFfXTZY7UfouAYxmlMktcjyMHLqaKj4fUtJ96ADnuBI81FSsBB30xsOMUMq1porX8w4UcJDtlFINU+VUCXld6PVIoIhZuJRxBi/oAAB+j2Ok1wDli3sUs+uEgWNW5lxlFocQcDqdxZBIa2G/32cHvwZbs8M/MT8w+1tnMs7n85wVz8MnHU2cZ2aoaVYVOtZZS1pny3C9cRy5T9KwZv/1QZD6Qx9YSzZ5n/a4RTak2VfqSspIjAHOFUpjtpM6umkkE1JT27KOdtkDSw13ziEDMwSgqtH3PsuzgDd1bmvpY6Hup7xpxyHHSIO4ZF+h3B6P5wQqO/R9mwMHOK7DUMp8iN6Z5/GPkVmtEXWKAmapAmNMzuJkqQ626xe/+AWenp7y+uCaEaB2yDLETGLqNPaRmawMBuB8eu8zc4hmcrgMAtJ1kyXDd4bFgiCsHQViaZYL730uXUB55PwQxAMKCwj3HgGrKtzc3GZAmod86hsazXXdYDJhRKpFjGU/Wq+v8thcXV1lHc7+U94YNNg0pdZ0ybgV2VwsxNahDUenP/emEEqpFOrYp6cnhBASiF/YQhg8E7wcjM8MVEkyTb3gB4+2a7OTjPfQlPBFz5ea4jy0at0CAwy+sIlQDzUpmMYPEUiZBqs0n5vNBrNqBmMNBj/koBcCeARd0+BLGwefgWPa/TrLdzqZoEsUs001LnvAIB/Kit6LqJ+4dxEIp4xTX3GctL7QuouBG9p+oQ2nwQMGbQ3DgMPhkHUv26kzsodhyGuorms8PT3lkkv6oL7f7/P86DXKuZtOpzgcDqMsRR1sFmPMLFLsM8eM48Z7s2+8L2vP60x9jifbnYP9Lhx0DAag/Uf5LlkGoicOh0PW/bxHl8a6qirJZvQeE6VPrZpDPf6cg9k8saHQDszrPwE8UQIAnXOAMTkDZRgGNGn+6koYmmgrc1+kXc41Tf1Fm0DvabRdeB6JMeb3aUtJkFY3KuvB++hsdR0Up/ci7jeUEYIm/y1e2vFlTHE65L7GceaOOJzGGRiXAJa24SjHMUYY52CdgUnyVldCrR+jwTB4CYKKBqu7l/jDf/PvcDz1+Ku/+HN4eLzxFZoAVNGj6gdU0ePldA74QWoyhggbJNfOJse4h0m1TAF6QUmfLj/mwvXK//74K/lfimtF1KPUQczfTkG7URxcA8Qp33z+gOMf/xkW//N/jXpxJQ4mK8FeiMw7twjBo+077A5HfPr8CU0tzsHvvvsOX3/1Gn3f4fPjI47HE3yQIGJxK/tEqVzm1kCB3urs9HzfBDCJoQRWiX5JtO0Q38ikrhEG7hkOs9U1ru/ucXp5wmF/QHc+Y7c/4pd/8udwzmI2mWK2mGMyl3P9fDHHcnkt4EHSw1ybp/MerHkdQsp2Ztbz0KfAvBZdJ+tsaEmDygrvJbPOGIPaFhCKdMg2O8VlxEM0iMzoMYCRBJ88wVmWU5BcGdsoKT+RYKSApLNcw72gLQQYYroeBjh2O2iQLoOsyYvP8gBxKO9R5hIMn5I3TKa4JKDDQIGqIgiTAoxsA2fVvljJZ9Ya1JXJyOrVjQNgEVHnrCyrwXjKvpll6nvapSGEnAks4+RgQpVBEmZllnrronsGH+B9yu1RdVcDwZUoWW1df5R1HSRjS9PBCsWx7BcYpBZrzi4cBrF1chulZmw0JwXgjMH6nLGaAhWNlfEJISKmGsUh1dW01qGtzkmXika4BF0LODXWMqQh7/shnWvkDNd2+zw+BbiROS+giU0+tZjvw7Hhfsv68mNfdOT/898yvyhAFRJFdwKjGBRCIDBT8Oc+FCBcO5SttZm6WDJuRUf/GLhNfcSgB4CiafO6zQAPP+dFQKKO10E/bAsDFtK6tmIb6GemiZL7p/bzbKB/9DONKT4l9iZGBm8QNE1+E2dyxiAnwJiUEUh9EyNcLG2JQMp4hWqD3DNg3H7+5MCdKPXVDdI+nOMwStVx1vAOnu1BBsaERYQhZLQ7IpCIfmNIOgxRQGXjECGgeAwCzMUY4KyXcYoV6mqKSWNglnZkz2i7mHYmf49ps826K539jC3fsVYKqZgUjECgWHSXyDLpvydmkm0W/dwMgnCMK5btKBTpZU+R95xNpTmU3HOtUP5Fnjwkcd8q2SlArEnXevsjrBrqJWUu+hzWJ3M1IMQeQ9SBDDHTYo+CG6i3k7z1ISLFeIPBB0h6oOxfwqhgRoVmkLLE5bu0gqKxqQxFkX1Zwxw/sfMnVZMlatQ/9buBB1DOTVlHZbuU82LzfpV1RL5ZoYe/LNuBvJ9jpBOtSayRgfuBfG1wQeQ8jYs1EX3bCV26sdkOq1yFxWye7RzOgXWVlEBQ8+G9nOtXy1VmJ2vbM47HwhBM/d62HYbYIuSABYdoKkTrAJc6kErgVFYCHtshIHgJaMvzkpWVmDKil10Bxo3MbWUd3ET0JtL+1jQTxBAxnS2xWK2xvpKEuRADhpjOpkH0gTHuYr4Cog/ovcdyNsdxsUDXn3E4pjJ6BrC53r0Bq3QUsNvCM0iRc/XMXqLXYz7TVlI3ftI0+Pr1a/yrf/GH2G+3+M1vvsfbd2/QdWcJ9gniN4kKb4gA+gQMV3UFeI/f/vf/N1w/7PDd8ltMjMWx3aNPvkjrFrBJvxtXCQNFjBiCMFUhRHQmou3SeDcVQi106EPl0E8rnC1wQsApDDj4AT1aSZJrGrjlHG4xx3I1w+z6GtOrJSaLBSbzBRbrJdazJSaLOSazGRaLBa6urnF/fYvr1bUkPBiDLgz48OkD9k8bHLYbfH54wMP2CdvjDrvjDpNpA8N93pT9fZqC960xyf6WtS3X8UyIZ+aDS+7vO2mVudZnTP4e43ieL+9EbCR/Tp93UEENz8iKBvMvQXXuC3r//ymvf9RJnVlwBOwIDgDA8XjCYr4cHeLocCBFNAESOn7qus7AiXY2MgOKjgw6wXhP1vumAwKQrPWnp6cM9DnncoYu39OZN/ydDg+24RLIkIyyfc7yorOVbadT8sOHD8UBlMB5ZubS8ahrEGuHjAY7jDE5M5q02wRpdL1DPpcOLTpi6LwvwEiTqTtZT5JABR2A7Ccd7wRsT6cTrq+vIcEAY+qUb7/9No/t7e1tprQ8Ho8ZTGD9YBpJrL/N9rdtO6pLroEP0tTqe+jMcV3Le7vd4vr6OtNyF0DU5HGsqipTsLPmKgA0tcPZt3j9+nUG6Ek/s9/vc5aWdh6SuvX7779PFJYmgyk0hjjXup7hfC70ssxsp9OMQRicA44j20gHJevDcy0SbOcaoUyRjl9T0fI5QMlopbIglSQNzMPhkGr0inE3T5n96/U6r0OOM52wmtqV/dZgg1Ze2lFIOh1uhHRiA4UKmo5zOpMpQ5o+lQ5nnaFFKnvJFOqwP+xzBhZlg9+fTqewpso1SzVoQvpz3ktT0b569Qpd143KKhCs4PzSiUuwluuL2f0A8prQmU36oKQzuwDkDCUN7lpb6KDpqGdwj94s6KhnoAjBbvYtAyRpngl6aSp2DcjpzUfrUs4ndRjlhLLMcWcgC7Ok2UbqHY4RHXH6Wbpfbdvi+voaAHI2HMFT6kCJgEbW8QSW2RfRhyUIKGfNpb2OGYTc9zTLA+ea8snMNurvEvBQ57ZxHHU2t3bUUz9z7+P9gUKNowFxAizUUwxi43OoiwnOsz/GuBw8wPnktfP5PGfTcry5tjRg0/cDmqaUIuE6InAkMiyOHi2jnFsJguigKdl18BDlfhj6rMe49hm0wTaTcYP11Pl9UobLepzmuechiHqE+pxjTNnj3sw5trbQvvFZlPXHx8cczMd1xTaS5uz9+/e4u7vDdFpMMfZJZ9XHGHPN5Lu7u7xXsQ461yEDfrz3eV9msCH1AfcYzVbCMaAeoB6MUeiL+77P9dc5D9xXeC33a+51miHBe4+bm5tcX5m6QDtYNIsC1xLtx+yEVyUYNCjF71Km6NzkOtZBFKR/5prSoDMDEnRdZ2NKGQ3qWMoIx4K26Hq9znpSHypjFOajmNYVn03dQjBXzwPXlmb20ACttpN5LfdnjgvXPoF+grEcf+re6XSadXze35IuL8Gr5bsAsD8cMr0cQWDOGdtEXampynXmOIA8Zxrw5rhyvjj2fOna4AyG43e0rosxjoBmyjLbwQAmZkVyPNnP5XKZZYC2Cu9PinwGfVEfsf9PT0856Ge9Xme55/xNp9Nc8kAHYdEe4/mCbaUjhs/leLGfOqhGl+RgmzgXvLd2hhNQM8Zk/TGdFpYprimekajLaGsPJ6rn/gABAABJREFUbZftHOp/rm2Zx5j3F71W9fmFbeUccMw5H9TNVbIzOd+8lnNewAdkm3GxWOQzn2baod6HWpf6LMbzFOeWMnEZEMhxoM7RezfbQn3xT30ZFAAkOzxVlgWf7ZVzneMGjAFxvrTjldeOnFV07MVio1RVhSGETBFdNw3WL17hX/zbf4fuPOB86vBhOOBwGHDqe6BtYU1A0wNVFWARUSGiihG1iaijQWOlZqCNHgOE4lTad+FAIdCT+zGGxceOWeKZJrMla9dLyaUnSODgogABERVCNKhCi/bP/xrt7Su4n81gqhpx6AWMBsSZFANiLOwam80GtXOY1FJS6O7uFvf3d/BR6KCPiRXOWgG/xiw8iZLRpBq+eY9Anp9Lp5PQ58rnzlixsWIZP2OAru+L7BgDM5lifXeLed9jeT6jO51wPp2w224QBskk6/cH2NNJbKq6Rl2VuqIMPKuqGs7WaCZiW1trc8gCEvDkh0FKwSTbghnKAo4OUvc10oEd4I1kgBcwQGplEzhElBGTROUUwD4CmlTohHa2GVPWC8GAmEIkDClbCSQSrBw7Cq0fO+EEqBBANRKURUSIaa2HxHKggPEMZmp5Vk7kEiRgi8yqdcl6pAXsTI7nhCbI/VKGoXHJyW1z/10CnJ53SDMD0sHaCsYZVE0J4kSU2SUzUQiWTxz1KSMVCrApekvmWVi6vAK4A+CBwJrwsdRoD0oeBEwKGSDivsj9SOvk6CWbNjBTO/WB90cEfOCZsmQec+0w8EGWDYOI5D0Aec/l+cW5Cl1/Vuu26NZ8bWoTWa9MpuFlgKwA1vI9AuE6M6rof65vIKr6uTHL+OX8WoMchEbBjig2nc36pbTBp7FWyyIrWqMpOAAUUFydzXM7ioMd+TZjwDyXFzYStGCdTYEwERZpvjOIavI9jWo3AyMISGWA8wt5t3DuAqgbtZOBK3ZcA1iBvVlPFIHJ+kM/LgN/Jn3mxoB9zq5MMmoThTrXLOfF5p9Cfw3IGqfeYFM4LvK+k8gDpWey3rBWQDRmwcaxn47yKJmGiga90mCypgR3JajBCM170Snj52ZdB9oyIBKrgGwZH+rNqABfPb4EfWOEPBcm3yrPXVrPXEPGFt+Sj2VNIUbBYYPkgRoj7cvPTCKfM9KtEdYwlGflAIcLuRvikMHBqNYxGy/7SkhZzWktqRrulEHZDwFy75SXBriiAlDLZQYRJqR9MOsQBguWRZjlk6Oc5NoEru0LsEvrFZOqLRv+QIKVRgC9Sbo0jSPtvZAst1j2axsY+CLy7yjfqja7tRYhsT26xmWblbYZg5ckiP0spatgR2xf4s+piv7LAcPJv5fsGLLOOeMh1OwRQ+/RtQOGPvmko8/z5QcPDwNYCfwV6m4PYxjoIPNlQkjsSWmeAcBYxBS8Z2CK7sm6XnRBKXNhEA1L2pTxDgl8P3c9jqcWi5QoFr2HHyJCwGh9Ud5FzoV9DhGoXYXZbIrpaYrTmQHelcxhAsd9HMZrlLbLM2vi8jXSM8lfNZ/NcX97i59/+y0A4O3bt3j/4T32+x1gTLK7QpbLEOSs4WOQeIPKwQeP7edPiP/ll3hVvcDM1eh8h33oARMxjwaE7o0xiM5hMAZ9CBiszIuvgQ4G/bxGrCyGyqEzBm0YcAoDOuPhnUOoKkQ3RawdrKtQLZeYLheYr1ZYrCUjfL5eYZb8tLPZHKv1GtdXUjt8MptiMp1iNpmiqWpED+yOBxzOJ+wPB+x3W2wfn3DYPOFwOuLYndH6DogRFkBlGMxV9C0TNowtwZuj4OBko+l5EB1G38v4/Hg5j+Mz5xez+sV1l9ebdH4ZXRcVSP6M7JQ9b7wnXOID/5jXTwbGKaB0NIoTW5xRw1BqfxKIYb1MHUVPIJaZcARheQ9moVOJEUigI4JAE1CoLrh5f/78OTuKCK4sl0t0XYenp6f8HU3JyExPOkKYPUJnFuu+GmPw4sWL7CQiZZ7uOx1FzOCls4aOIjpa6AR9zjnD7NXtdpsdeYDUld7v97i5ucmAEp1QVSV1366vr2GMwefPn3P7qOwfHh7yWO52u+yMenx8xM9+9rNMI2qMwc3NTXb0z+fzPHYEe9kuArwEZ1m/j3VU6dwi2KUBATqJOcc6q5vOdb5HA0MHNdBRvFqtEYLP4M3hcIC1Fi9fvsxZbqQj5/fp3MogcTfgcDjmNnFOrLUjxgAGXpzP5wzMs9776XTCsppnMIDOI847HZfsC//WEWn7fcmupiPy5cuXeHx8zOuP/eeL1Op0ZjOrvm1b3Nzc5PVHRx0/10AEna58CSAek+xJ2/Q60VT8POjpMbsELvk+swdDCDmbUjsKNVB+OBxKJKkx2bAhCHPp0KUDk/LCNce20lnDNhAsoMw1jVCuR8TsFKYc8t6z2SwD5Dog5e3bt7i5ucmBHk3T4PHxMeuES11B/aTnHigHU8q2zm6igV1osyeZUaFt2/wdyqwGIfT8MtONuo6giAbXmUGsKYA4jwT+9ZwRYOX9gXGdU30opVxx3hhYw/7rNU/wRNPBZyf8MK63R5lomibX4mWABTNa+WxhGZmPAOXHx8cMmByPR0wmDaw1OdCGeoz6k2Ah5RIQQGm5JAvALssoKWsZ0EGAg9/jGuD8c/3qgJnFYpHngWNHHc0gD/059QuAnD3P4BkaEWT7IEBNOdCZcXpeJMiqZIVSVzDgSdoyHX2X4BhBBJnDonOoO7i3s7RE00hGJ8s+UB9S//V9l8dG2wyUw0+fPmVA63Q64Xg85j4CpUby8XjG4+NjBhhXq1Xu73K5xH6/z3aPtcICwN+ZVVjXEiFMoIyBg1xPV1dXOfiL65IMNE3T4Pr6Oum9cXQ491/OG3UL50iDcnp8l8slZrNZDmRYrVZ5DWkAj22hLcJ1QjkikDaZTHIflstlZmShriBwRJlkW87nM1arVQ6WYqDUarXK9gsDTbhHsk/UFzpIg/NydXWVGW+45rlvUh9qG+USNNKAGZ9L8I7t4pxQV1trM6Cvs7u5n2lwkvYCM4+ZmQ0AtW0QDbIu4T5HMJ6BUxoU54tjwr38kiGC19C2oa1FXRxjzHaxzkTuui5n4PKenNsweDSKFYI/HJO6qhAM8vo/Ho85u5q2LINTTqcTZrNZtiF1PXPKLnWB3rM4Z5xnAiu8jvsi50CDxZQ9rjX2g3N3SqAPgyAYxEJwixnph8NhFBhH+0LrLu7/1HtkptG02pvNJttC7Pf19XUebzJLUDa1ncM9jHuIlm/KEINSdIBn0zQ4HA55bjnOlBPaCxy3GGPe7wDkM5GWQx1ox+Ch+WSar+c+Rl3HedBZ6wyyoN2gz4mcI8oA14G1Fk4FoFF38OxCPcc1yb5esiKwn7xOv2iXsbYg+6wDeKi3uIdRh1BeNYhOXaP7+E99aWfCpYMWkSBdBDNxYxz5mEffp6MzOw9UP40t2f/R0lltUVWio6vaoT/36LsO7bmDMw6r21ssF2t05x6fnzYYHt6g3p/hzycMxyPC4YS+OuPD0MPGgBoRDSImiJhGg6UV2k3JXjC5awm2VFnjzJgzicCQf8nvxeGc3DDJsSzfjfgxdw3J2esY0RgjdOnBwpoOePMO+19/j7BYYPHVV0APGOPAKniBDt8Y0PYtzEHqqk+qKRbLj1ivl7haLzH4LmVQ9+iH5IAyyF5rAVyUExpATCAxs5kou+wXYnJUJ3DcwcAHcShDgYTD4DOYb42BdRWmiyV8P2AynSGu1xj6Aavra3Rti/PxiPZ8Rt916L3H4bST9WCFfrpK+/V0NsV8OsMk6VfRsSmIokp1UV2Dup7CzHsIcFxcZARHCXx679HFZN/3PfqhUH2LTuRaAPxQ9nXpa5L75MTNzAMKDAKS8z2WTDIAmSY2v0HZuchyIchMgCByCulIDqmedsUbowALJklhflYpe1CAFEjNzsj+AMFT3xJ7K5Tg+hUGn2U/17hIK0WDiM4O0DVuDWlLjUlr3wpLhJXszcpVAlCqMyUDiA0cWE/TuvJd0jWb1GjrJhJEl+SPoAuipPpnB2mMAIrdlv+FzXMmGf/NCHgPIYHCKuggxpiyeYXJQJaNybqQ420NwUxkungKjQa4JPE8ZbsHoYW11kqWfALeYQA/CAxhTJLvvJdbtS8IPTS/E0P84j6SrY0UnBFGa4V6u+wD8WIckEDWkjlKEcwsAEFloJbIm7QupVyTDkbIS4KU74jIQSj58/G4FeStyGleZ2pdiFyovdjI39wzc0BEFACT8sr2UnYlkKJQFbNNo2Cv9NIgbVlLGtBO68U51Cl8Ki9YlfGsXz76so5sCTQxhmOT1k+VGEQJcKs25vtaCSogyMzrSePtnIOxBs7UCRgvoDQnSxg3Unk75wuYq8bFqWcbk6pKmzIfETHPRWEOAGCCZFOiyLHougLQReMBEzJ4XgA3DmPSP0qVxRjz+kJugdjLPQZZG/xfoC4sZRVijIBP9tDljwocDDExUCT5CgwYUe2ICSk0oO6NMBeyLLKjEHj5IN+rBA9QRlDosbOoqcCJ3OdYKPvzy2Q5iibkz0c/+Q7lFaxRYD4AXJahSG3FuBtFWjSQDbgEXH9hUI32T6ntbVRGOGwE4JSdA0T4IpN5C04AsLGZ/cIiUc9bm/Yjyfy3ik3FWou2P+F0liSF5WIhiR3nEx4fn9BMKiwWC1RVg4gdzm0PYx1s1aCZCDtOVdcyf0lWBg94DyAF87E0XWBgVjQ4tR26RD2e65JT1yZ2EkCAVh280odLOzANQCrRY3IADABT7mWsTaBnYkQxtJv5LnJwYZ6aIO2x1uF8brHd7hLL40zG1QQg6dC00coaUvrCGJNK7VpMmgmm0wnqY41hkPsGT5YOC5NvU3S9sUaiGvl31hdePcPC2IQJOClFPJtOcHd7jW+++grX6zXevX2Ld+/fYbfdYhh6WCeBKT4GCHIhIxGQ9l8HWAu02z0e/vJXmL59j+v7f4UhnHDqT2iHAGcM+ggMYcBgJcgNlUUwEScfcE51wDsX0TpgqCxi49DbCr0x6KJB6wN8ZVFNp5jMZkKPvlxiPl/CXK8wWy6xXK2wXl8Jo+h8jsV0hvlkitl0hsV8ifnVCs1sClelAIphwOF4wNPTFpvdFrvDHofjAefTAe3hhPNxLyw7KbKkqSrYyDrdDPyVchEsIcqFa+yYPUz/m5exuQSkvzxFXXwF3CPGOmZ8L33uHN3L6BII5ev6e7n9Sj9q37PGVcZ69ae9fjIwTtCRLzqE6KivnIfUCo7ZEU9wmZ2ZzWZ4fHzEy5cvR44VOi/oaND3ZwbWbrfLzgWCVwT96Ihi55ktttvtsNvtMsUonVLGmAxgaEfU9fV1dnAxu4SfMXONDis6t0h5W1UVbm5u8j3pAGTAAJU2nTF0ptExzfGisxpABo/pPNMgDseOztnHx8fcntvbW3gv1KcxSoDAer3Gw8NDBn/5HsE01g/js4dhyFnvdJjrPpM2hBnZvK8GH3a7XXaeM7uVTmygZC5TvugcJ1hDxyMdWgQD+f50NgUQsVqtAIgD7erqCsMw5GxYnZVD4KNENcqBbrVaI8aYAyEIQHDemQ24WCxG9LTauU6HPIMntttt7oPO7jXGZCYBgh6kx6SDkw5SBn7QmTibzUa1FLng6cylwzKEgIeHhxEgRkckHYragcmxA0r2Y4wmRykyY//Dhw+ZMp/AJNcqs//ZHw1qahCTcvzw8JC/WyK0x4EDALIT+nK8xbiR2pLULQyO4PM45tYKJRjbzXqdzGY9Ho+YNBM4V/SIPqTw2QwOMMbkzFM6yvu+z5mMd3d3GVjjmmHQhK7brLNUqUsvnf4cT2aKkcFAH8jI4EE5oJyVw2QcjYcOhGA2MwOVAHwBSmhdSDCUIITO1qIO4H00aEvZpIOe46yzxbjuGPxBsFlnXekM7cfHR3z//ff4oz/6ozwm1O91XecyEXyPQUu8H4NReM8YY8oMFXpsgq0Ef6lDNAOCDhQ7HA7Ybrc5W48BR9YWGmICbwx24r0Y2Uq9RDBcl/Cgc557is6QoA6iXmCfqfs0kEJgi+NEhwP1Dz+jbITkdLS20BTrDFud+c35pG4g4BhCSCD3OesCQB3OncPNzU0K3HEj0F87yUoARcwyoqmmnXNYrVa5Dzc3N1nPcF9hkIIxyDrh6koMVept7nEEXQhMaz203W4xnU6y04PP0MEjbDPBUsqJrkNM/UcgnvtcYeM5ZtBYG4eaZUQfgCjzlCNtV2mwVDPpcJw1tfRlsBsBW35O2nwGPA6DlDphUAIBIvaF8sj9gTaSDqjSYB91P59/Pp+zPcI1cDqdcHV1BQbPaZp57rGcA11HmO3juBG4JYMC9TPHS++5XIdaP+tgCK1nKAPT6RRPmw2qps7PvHTYUQcRgOazdSYr9wrulcwizwFgypHL9yg3OtNY72eUWx1kEGNEsMOI8YJ7HcfHVRWqph6tIdqx3BNpt3FOudb1vs59RgO6lAcN2FLGGFzHcaQOoq7i/scxo/zxDEA510Ap97LPnz+P1qD3Pmfb0y5ZLpd5jHge0cEpxpis92ifU8dTVhhQxnMV1zr1Nsf76ekpr0P2XwcRlwzMUpLCe4/9fp8Da2hnaJuT604fHCnT7BcDa7iuaIuynxmkSzYI55i6gXs+7zXEUGjXbWEC4r7NfYLri9dpWWhcCajiWrkE3vUcU19y7+bYc+/j2OsgFB3YSt3IdlC/a/lmOwsIOWQbSAfSXDoc/rGv4SLj3NI5FlXAD4FiTSGKL50eApdFmCiE1DbNbXZ+0b5BSM5HqXs7mU1RTyzaPmDoW+y2W7T7DtPJFMu7JU59i4+HLdr/bGHuPNrjEf25RXc643jc4+nNW3SHI2Lfo3IBEx/RDD2ubMACDg4eFQbMgkcFI3X9VE63gU1ZKwY2SJYv4VALA5Jzk1ZSXLIFMJT3ykucZ/Kvg8cMFWw0qBBxth7WAxMMePzLP8dp3qB+/QKzeoK26zFBhWAjYDyAATYGtH0EAmBDDRu2qJt3uFpP8dXXr3B7dQV44Hzq8LTboo89DCrAsBQV4f6oah4j0U9iDPAacZqGFAhB4A2IcMmxGEBACeLsRbI1YkQFAxcEMHfWwVQVmnqK6XSe13Y/dOj7LgeyiM4d8j6wPe6xb0+I8SGPp0kyZmFQ2xJ0xjOGBD42qJsGTQo0m8yXWfYAAfczIEdP/gVAJHTcUsaDOtH7RL09CKjuvdRN9Tnz2Jf3BqHx5nfhxWErYEoJahkDZUBwNgMWBDOsctIJRmyz6zAmUDBCOfGizc5im8IrECMcxkE62ZkXXHZO68/o/EVMID+f+YyeIRgp+qLY61FuJnVjvUdkrfUOQChgEsEjfR/pSwBCsTlCCBmQY/v5HkEdbc+Lbi01dCsgZ/8RXCQoRz1rrJUSDxl0VFTOdZXBOmMNwMxc/pu+X6n7OedyCAGMg1FuUe1QdQntfk6Ll34ZAC7Lbfm+zWsD6Vku9TGPJ4GmKFnpon8NhIq8AG3MrJWpoK1TnN15vhVCxjPeJeBPgPDyvoNnpiOyYGUZjAQ2E2p/IXMFiMQXcsvv/9TX5f6l33vuOvUGrBv7qzX4W36Q9jeGXqkOp/EgsDmqK67sdC3nJlGPU9Y1VX0GbQFUlkGuci3nXb7j0rVSB1kHKMAWvVOGswTRXI6V3veHgddy/oXqOstCmjejZUMFRtA+y36lBKBdsjnIdSWAQ7+0T6qAynre0jpQL31dsOXsJCwYX869MSB9xkg2LvVOAZn1PUoQA/WGjUXHAyVD8VI29VnruZeei0uw5kv5NjlrmMEMJgWZmAsx5XxaowOwxvc1UMEtXJcX9xaxVvot6oAxPcCAMfVoLtnu4jctdaads6Pgau1/F52sg83MSNdrP6yBxZgpQeup0sDjscEQrADdM6nTfB6AYI/og8OpMzD9gHaIMPUUQwjYHs7Y7E95LdAuGAZfdHEQ1gzuOyNfxakTu0C12Q8+9aka9Wd0HlBA3kguFGAJJEYDiF0LINX/Lox4omMu1gakH85KoKvMY4CBUIOfjic8PjxhNp3j5uYGs4mcrfrUb+q5IQi7kXGSWBRjgDMCWE/qGabNHCd/QswZ/YAxqqxEkqVsM7hyxrDJ4u39AFsZmEoC6+rKonY1JtUU02aGn728wXfffoObmzt8+vQZf/Hnf47dbgPEgNoahDAAvsVgDGInIbLRWoQAxD6gd4DpTzh9/1vs/5//ES/dHGbaYbc7oxsGOBiYusK+MujhEWsL0ziYaY0OAYcQcQwex+hxgkeLgCFaxN4jzhya+RzL5RJ36ytMFnPMlgvMl0ssViss12us1mvM6gZNSmqbLeaYzxepJO8yn/FDjDi1Aef2jMPTFofDHvv9HvuD+ItPp0NiTu7gQ8I8awsTxWqpjZHYE0T0TFCLYvfPJlPMZgspNeATw5wfGIIDA/OFjrrUXyVznDKLi2sIfidFAQa/yv6nz8ru4v6jlym6S5eaevZC0NdT1or2h3JN8Nk/5fWTgXE6XOhkZTYdwVEZ/EKvG2PMzhk6wejUp4NKO7Q0oEPForPnNEBI5zzBLbaDi40OC2Y+8DsEIJktQlCEbaODkQ4xOmN5MKQzWztj+BxmzPD72+02K0DtvKQjOx8+FVBEIHa73WZgl9mtBBmZ8UWh4d+A1LUm2BeC0HrSKRuCULDWdZ1ByUta4Pl8PsrYoOObc0LnHkH3y4w0nRVBpxQdhRxP3pP3YtYqM8qYLU7nmq5rzXngPdP5J4OdBDzpnKbDlo5OOsPo4GJEEueCGT50/tJZph1xdCzqmpZ1XcO6AhBrRgDtFOXY8Htsp6Z2pRNWO225yAkCk7ab8kOggU5YriO28ZK6lC+doUZHIOca0cI1TurUpzXDzBiODYE9nb2qDSAGjWgnNeWHMqzrlhKE0Vk9bA/ZHgjabjab0XxuNhvs9/sMNjFTOwOljctBKwxMIEhdVZVE8GJM83o53xo8Ip0yAzHm83nWL13X4cOHD3m8NEDC+WH/KBt0HPEZWhfqoBzeh2NK4IJrjc/UtKU6o0oHQFCuOJ9sK4Ez6jkC1dSZbAvlTmeIE7hgG3TGIkExXe6Cn+u+0xFOMF7rKLad1M5XV1cZsOB3KX/Uuxqkresmr2e24dWrVxnMkj7bnKHC/nPeCLrpIA+OrTGFklsHExGQo35m/wmeaf1AeSRwwsxuMj3wdwJbHB/qQF6n9RfHj7qXOoPAmqyVVAdO7bsEV2OMaNsedV3lsecewXbL3ig6X5cjIJsI9fswSCYlazbzM+5xIqsSDKUzmbnPChDUo2nqEU0+s3AZfMD9h3quqqocbFD0VoPlcpXnmdcQ7Hr58mVeI9fX16OgGc6LcyaPB9eFzn5l9DADAHe7XV7PHH+xf/qRbFGO2C/qWO6jXCt6LvhcyhRBLB2swN8J1OtgOG0UU39rOeI9GQjBNhJwYt/4fe51Wj+wTVpfMNiAwR2UTY6pXj+cJ90+jgHXEb/LPYb2Htui160+XGr9wX2KOkQHBFE2ucdTF2h7arfbZTuH+1Hd1DBJJriv6z2O7xEkoM5jQIcOJqItqvuq54jzw7EnmEcdRRYLrh8NnlJnxBDynklbSu9JIQQ8bJ6yXqG9z3Hl2DJYRQfvcE9lkAiDPEKQoNJPnz7lPnCMaM9wfHRwA+WIwLMGWLlnMtAmhIDtdosYYw5g04EomolCB3cxyEIHXPJMQz3DvZh1zDebDbquw4sXL/I9eGbSgWhkZqIdoG0Q/k2b1jmHjx8/5jVGFiUyAnDfpu7R+zvHg7YA55Yyo88wtN14zqEu4pywLA3ZFNjWy6CHYRhQ1TWiL4Ax9RevYbv1gVaz51AufQK4aKdxjVM+9L35O2X70u7i9Ty3aJ1EOWV/aLtQF+n2Ui/TzqAe13qa1/y3el32EaD+Nqiq5x2uWi9b5ejXzjqgBLeFEGBSpmgMEVXV5KAna2Xsuu6MP/7jX+IP/+hf4xe/+zu4vX2Jf/Wv/y2cqfDp43scdhv4YYAfepzPJxy/eYXDbovTbovTboftZofuaYNPQ4eZMbAmCtW6NWi8wQIRS1jMAUyjwSx6WB9QYYA3NTwqyRxPmTTuEoiJBXDUztPkys7vS06aR0QAokUdDayt4YT8EsPuhOFvfov94k/R/C//Ddw54lwNUns9ABM47Kw4mMMw4BwOgIlwHwMmf1PBVRPc39/h5csXCAYIvwnY7U9CU8zsKNU2UkSX9iZ9GkOuaUswnfLoeb0K1APGDlaRl7K/8cU1yP2VZ9SmEbv29evXqKoKnz59wMePH/H09IT1ej2y8Q0d85S7EDEEj6HziO0Zw2bIn+m+jR3qFk1Vj/wq1FuTyQTNpM7rNQfCuApN3QjQqNaDMaWqKvdX2g7abvbeI/TdaM/iZ9K/AYOXfp7T3hLVGtGBXfp3OZP5kqHIPgs6nQHzS1DkEjRx1mQGh3RRckBL8MsIEE2ff/FSQRX8WIMaMUZEp0Ch5CjN970As54DfzRApNsvsvVl3e7L+ZdrC8gfojh3AQBDGRt5vrJTLsCZ0t7Scd1P/VzafJf9IRg0kiftazWmOPpxoY+f8b0K04CeFwEvtKNWjwP/lrrzY13/LMCbAFn+PQKUjPlibnRbLq8FIHofBjAXgHICcR2BKgXI6+eP+3n5d+mffum/f+z3H3s9J4+yj1EueOYwwGgfSPKc/r4EbqHe53M0CMz25e9wiV/I2whQjhEIfnTNpU4UO1KxRoSA/oKqW9/7uTG4XK/W/sNjL0P05do0JtEgJ8DCQMp2PH8PylBh2Lh8XdovIQyj7+rfL9fsc30dPduYS6KP559dcMln28+XNSWo4blr9Pz/Qy+twzhv+j2Acw9ovX6p54C0buN4P9UySbvT2kS7rewCax1cdQFAWymzcQniXq7pGIVplclIPP+x7WxbjIVJTn9+CVzpvvF3HWTBPrVtP9qzh2HAue/yvus9GTdSIEjw5ftJh3rEHBw4cSX57nLP4hhOphPJKKfdrMZGz8PgfQ4s4TzwZ7wXIgWNjG2Cy/Uf4EfPu5Q3GV/AWh3ExYQyk3/quklBluN+0cZjIshyucRiscC0bmD7HsPhgG5IuFryJwXvgeAlMzvZfLTDsn/HSjkGaw0GGABe6UrRvdm+MBKoE0zEdDpLdprDpBGqe2ssptMav/idr/F7P/85nDF4//4dfvWrX2G7fQD1eIwssymlU7wHorEIUWjUp9MJZqsJfvtf/wxv/vjPcXrc4A/+5b+AXa7QdD1c0q370xn7oceha9EOA06hx+HQYYgRvQXQOFTzKaarJe5ubnB9e4PpfIbpYo7ZYoHleoWbmxus1mspLVTXcE2N2WyG1fUVrhdXmXWQa6YbJGD/abPLibyPm21mgm3bFl3fpiCNLslIlHMKwkg+ytqXAJeCN4k9OllPckJrCAFd30s9er1/Xdho2p7Q8vP36brLvenS3/alPnn+Xj+m6/++l7aJntsPLwHzH3v9ZGCcxmPXdTlTmdk7+/0egMFquQYdEB8/fswOF/4Mw5CdOATD6SAbhgFXV1ewVpzij4+PedFxMPf7/SgDiGAA8KUxPorc8SXLm+0AxlSY2tG/2WwwnU5zxjUdkZvNJjvuePih84jALIHOxWKBx8fHnCXCzCoqYgK2dV1n6vWnpydMp1Pc3NxkgA9Adrq+f/8e9/f32fFNBwydVbyOdJ4xxuxw40a1Xq9xf3+fnYd0ul1dXWVQOUdRozi2uRER+CS4QEcyM464kXK8eQ/Kj97otPOSbabzk3TUdV1nOl2CLPv9Pgs5s/h0pi2dmnwe20Rlw0yp0+mE3gyIASPAXA60BURgtkmMpX5mPsQTfPMFbKNsaqXCz8gUsN1us9zpTDZSQXMBlwNjoplT1NUE/HUEHmWBMkaDRIPylHM6gikrAAHlCn4IOUs+xkLBzzrqpOylM0Ubdbw/N2ANOnDOaTBpIJB6QdMjU+fEWKjEeS8+jwEGfF9TQ/OZg+/yWOoSCXRu0lCmQ5lyqQFQyoVW2HR0UxdcOly6rsvBDvyeppUHMAKC2BbKbXYsJz1IOafTiHqMskW50AYqM9m1kUY5oQ7RRrAOqNDjzueyjzpzkeuFMqTp4qkDGSihdbWeZw16Achr+RKM1UEDlCHNYkD6WGNMBpCqqsp6m88iWGtMyR4DpHQFIKAJx5XjSJ1CdgI9XsYIk0CO/ktGQQ6+SOuUABWBPu5pxpicUaMDCjiGlxmtfDaNLQIYeuypEwDk+SIQyTETIKgFKdf6vs9ZkdSxcq8CCnFd6+AhrjkNqBOMpt6vqgq73W40XxIBWTJNJ5PZCNCjzO/3+8ymwb6t1+s852TVMMbkjFLek/8CwM3NDUIIOJ87dN1pBKYSbKWsaApiZr9y3kWuJwAKwMW+E9DnvHZdh7u7uzzXem8a0gFE63fu/4fDIWdtch2R3YHA18PDA9brddZRGvwmSEVHM9cp+6WBIs4P95LLPYzrVNfRpm7QdaEZAKIBKQ3AaqYDglvU+7SLLgFzrnG22zmXwWeucW1XUL/qrPUYZU1rmmQNHutyK9QdnDvKOPdctkEHBpGyX2f8M0Cr6zpM57Oc9cn7aFpuvYYuwSp9eCHAqjPn9T5AW4k14UMImSVBB5jqPYfzxTFn9jj3VtpeNgH7DNLTdr3O/qZtpB1JlEE+j3LhnMtBmcaYzBLy9PSUZVbvd3ocqId4H83CEWOhj6cNr5lRuE9cX1/nOWEmMO0mrmfOMW0g9pf9p66hPA3DkMFxtpuyGGPMga8sUaCp2hngqR0OPCdoW+Dz58+YzWaZoWa322V54p5waaNz/9D7C887utQNbSgGXNLG5jgyMGK73ea+cZ4519pOs9bCd+NAaB3QFkIppaLvx+9SxuuqRp/mk/JKfablWTvadNAD7RfNYEVdrpmqqEcYEKBtER0Qq6nmeabQIDttfAYR/3NebNePOfEApGzWMl78nnYYGJMoVlHayOsunf4xmkR9CDhXY7FYybrGHkBAVTk8Pn3C//D//h+wedri66+/wv39Syz//QqPDx/w+PQZ++0Ou90WT49PaE9nHA8HdOcz+vMJ3fGI83aLdrfDeb/H+XBEfz4hdh1C16LqA5oITABMjEUDoLEOxjjMQ8A8RFSwqFFInR0EXE9WpGSRGJMo2U0Cc4CaMgKhXNw0HuhT1pQxgBFYvIZBNfQ4fXiLx/8aMfu9b7CaX6HrBzgfYQME7HYGTQKiB9/i2Hk0hwZv3n3CZLaAsQ4vXtzg1at79IPHm9++w/50QC+pfDCuEi8fBJiiMzKDNjGOqF6DZxa1YocygNCrS5aptXEU2IYEwbNGszgpUZ6V1pARYUJMIBgAvHn7Fp8+fcDheEBIVKxVU8O3iZbVIGWeJUjVSlZaiAKkTOqq5GIqZxszkglCxhgRLNBHj34IiH2XnckxClopidiXoBtyFpzIOeCqSgBkCLUy121VFephYwxm08kIIHRVjaZu0MzmyIwMMaCpJmkc01imtVSyfSVIY/Dp3BhYIzuB7UGc8nTmhuAzjbauI8trpTRCn2m2ffAY+gGDl1rVIQMNAgTkDHvlNB47CCMiig/GmAJojuYvOy8vMihHn3G4FagWI1i4wKTxMMaicgqSzLolUhgyBORtNZrT55ybclPL7iSAusgVH2FgYeNlhtMzgJo148/zJfr3lJP9RSBCGsfRTZ8DMLXOltrAIc1TGQbKVWlbQAdmLGq7Rz1APktt1ZnqMd9bATZGrU/dZGbYpnvEEBUV/hj4y3sIYqK+1zdCCaig7fflCP3k1xfrG0B4JoPsUmYuneOj+0Rm6Jc26vuM3uf39ZijZMAVoJ/3+fJ+zBo36p4mllrk+sUgiCiTCNKiR2vQoDAMsmnGEMf+EjzmNQT/M8sF+xcvwNk03wOeAanTd/L6ieO18cUYsp25pINqUB5F5P7bqgJVqB57DfPBGCS88HLYxs9HSRjPj4sl+MEASW7NSH7jyO4pARN51cbnx5ivqhqzNlxeR30qZ4Ix24XGK4qNVo38cpf3NcbAmcQ8YUw+A+mMatL0V3Utg0Jdk1g6mP3Ml5SBiHmPilGC8UjLLUwtHj6eEGDQDR4eHUzX5/MLzzjee7R9J/T1vrC1hPRvvjZQd+kxpq0yfgW1nq21qdSAKpkmH2IynaKOEX3yL5jkWyRAbo0EeoQQst0h664IjQa6KXCZhUcFHMu1hXGB+ifrnrTzhRgFyE42Atde5ZLsK4YLl8biOVsfoI4Tuu/n9jUtIyF4wBQmUCDZ/IlxaLPd4oc3bzDc3eeyxbaqYXzCIDgb1qCyFeaTBXa7HbbbrfgBfAmcj8nW4x40fh51T/E5mRSsM4QBzk7hbIMwiPU+X0zx3bdf4w//4Bfwrce7d+/xww+/wcdP72BsBODheymzMwwefgBqAKGyoiai5EF3CIinFm/+9jf4/m//DtVwxq9OZ4T2jG7w6GNAFwK27RmxqlDNJqiaOexsinqxwGo6xfL6CovVEovlEqvVCtfXt7i6vk6+UItm8v8n7s+eLMmVNE/sA8zsrL5GRObNqlvVXT09MxQKhyLDRSjk/84nvvGRDxThkNJTXd11t7wZi7uf3cwAPgA/QM3O8cisqqHQUiLd/RwzGKBQVSj0U1UstN1utdlutVqvtVwnP13TdvK+SewzRl3OZ317fSlJQ9/eXrV7e9N+v9ehVLJ0eT+bgqPSXMJX8LtNMImyVcM4AqMGJNXEqGUupV58e2bd/95l9aLlr/n3XLRv95Jz3rR+x/l39rL2zrwfFtO4tQZe6fMbfbl1/WZgnMnCiWVLCDdNyrbks7u7u+IgxZlKxgqOLpyv2+22ZJBTnhinGmAGCtSWuLNOH0t8HBlkNM4dNThDUslcTfqMw4x2cBByJjoOW5yRgAA4WnC24AT+4YcfShbc6+trpZVzenp6mmTPQFf6Sulr51xx0t/d3V05lK2DDgcPDnbGyYK1WCwmmTg4AG05Rhx9jB8gi/a992W+cIaT2cF7ANYZG/OFQ9k6yHGU2nnCocrCwzmxgJbVeT89A3G1Wmm32xWnHfNCu1yAE8mx2mkcQuk3TnCckAAtZAhZJx2g4nq90jmXCAbEs1nYkwg3w0vwQ4xxkhXJBW/RZ0B06+zDYQwdLODKomrBfOdqxhn0scolzX+v/pIWOYI5cMYCAlrwgP7bygEADSW739dy2ha4pX+2b1aJYWDRtgWrLKgIrwHSOucKkJL4b6lUDroCPBaE6ftB3tUy/bRhHTjweOWdargCuDhXM7PREZTUthlmVmHDG7zHAtQxxqvMOPSDpZVUHbnMvTXckEOMI3QHc2D1ALIDf9qoUfiUhdYGDljwEN6DF9EJyBJ9Z15xPvNeSSVrGbmz4Co6XtIExAWUhh42Qy/pqqO6blnAQ2Qjxqiff/5ZDw8P2XlWKyhQlt2eO22z8JFbZAjZoBw3VUesXrQboHlgi3VOkyWILmY8vANdhxygwyUVAKdpata/BaFx9Nsgk9VqpcPhUJ6Fh1J1hPvCd/YZeODu7l6bzaZUtAD4iTHq48ePJeBAigWgeX19LaASazNgPfT03pfseBuEgxFvM7aRp/v7+wLa8vc4jsUgTXq+lvUCMGNeCeSwMkf1DCuzp9NRp1OS63kGFXyF3gZ45R9AcKq0sSyygy3AWoSdAZhIhiu6Av5HL7H+ICsEqHFciXNuopdthjsyjr5HzggcAZCysmqzrO3REcwX9oG9F9ler9cl0IR5AfRl/uEPaIYdxPdUxWDNtpVKrFMBfkRW54YydKuBIL4Egtmy713XlbXNrrHoUgukUlVjtVolSMLX0uUEuBDQyHpC2za4hrWdeSKIiPUeubeBFwR2EkxhQVvsRgJ5qLpAkEHTNBr7odh5vIO56LouOQu8KzYW+oC+MUfoMdZbZAO9QT8Ijvzy5ctk3hgjfGrXaBskw71tW49YsccNsH7YtXqz2ejl5aXsM9DB6DXmZLfblWM0uGgTgLTv+xIsTKYxAbYECRNkuVwutV6vS/AV9tPr66teX191uVy02WyK/gbwhh9++ukn/fDDD6VPh8NBj4+PklTmh3UB+5u9ETYcY0DGsfWhIQGbjNOuSegXgvycKaeJzc76nxxwtaoKQRfwi+VL5hW9D9/A23GYVqBhDbXyxxpKG8wR4yFwzwYfW6De6lL+cdmgWGTc8roNBiJQAp0Ezf+1l3WKS7cj6Z1ccR7ecjiUNvK/GFNWRRjRhfln8hZK5XxIL+eSnbZarSUnjWOvtnUaRuk//8//SaHv9eWXn/XT3/ykp6cnPTw+afvwoKHvdTmftdvvtf/yqpdvX7Xf7XQ6HnQ+HnU67BMofjjofDrqdDzoeHzT6XDQsD9ouPQaLoP2l17D+SKNg2KUVk5atan09so1WkSnRYhqQ8xnmDu1zmsTpSa6DJe7XHw9OUebplXnG/mm0egkN0TFmEoY9wq6qFOjqLWCwvmi0+fP2v0//z9a/5/+R3mXzkgNLqp3MTlTcobiqJDOBjy+yanRn/70Z7VtcjH+8MNH/fjxo4bzRe6LtD8cNWS+HsKoMGbgL8+BU3YIZ9CpAm15nqUM5F87z9OM+uR8BvS0Z+uGoOinSQTFNmh8cWh+/vJFv/zyS/FLNE0riUoUdc+Kb6oCddVdxdnZUnLeAVWkM5TT+HzhS/ZaSuP26WzdSTlpMQbjTDcgVZQ0RidHSd8x6NwP8u40pVVxfk+Bv2tZC1r4rpRz9d6XDLumadQCNJgS3ui+RM9GXdtOS4DLlYoBZPSVd2dQK4xDKWlb1mHA9liDgGwABCDD5PzofIVYs+P5V4B4zi8PSSdIlOq3wUY8l857hn61yoEBmzJo51U/n6olAz25dOdcT00AdcdfMydolGAWgDTsrQJQuNuZTpPHozNNV4drjFIz44lbgEXlwco36Z2UyAZsiqiKdx3Dzkkxtub3+n19NWiiL7SuY6Vt89lsZOatRR6lmI8BNsEHuc8qviKnxkutn/b9lsO67s0MjSbPpM+m8sZ9857G6SewzkSeMU3d5EZLw/TMFRHKffP7w+RBMMYpOOycU3TDrDXlGA4DkmU+Q3tP3sOQfAK+8ElNTzI3/fcuVUmJlVcnhJn0xGuu05CJiT9Cleeu2jFrzkTOU4Plj0iXDP/N35v/SL+PFYB0zrzVVSDflSCdqieLvp0EKETdZJJ81QoMKUhMSuvLrfO606vr2urM3/SrtGs/5z4zBtqM3vQ9D7asKeYIHFteHLrN/UNefhqYpcRMY9bPGhJ9z8P56tnJv5CA3Us/lACBYD7nbHY+H3JJ/jm9rL5BhhHlOOMDKVXDgHXn8jShoRI/OWQ72yxBsdBKUi7v7zM7Ofmm08I3GpVlOKTKCUHSMPRmvarvKWuqDRqxysLYTmO5p4K9xc4y/JPIksqTx7ziC55rrjPCnQlmqrS0vA83XtNp0k7pR1rD0r4lH3fS+HSOdXQpUc95nYdBm81aXdtptUl+aqdYeDWEoNdyTPFOl0viq9an6gUh5GNTXE22Yv+EzElGnxLAqbS38s5ptej09Hivv/v9T/p3f/c3Gi4X/ekPf9Zf/vIXffnyWePYyzcJ+wk5QDCJfGprUNAwBilIi7bTmCvurFZrdZs7Hbu9/nA6qFku5BadmtVS7XqlT6uVtk8P6Uzw7VaL7UbN3Urb7TaVQt+sc+Xpte62d3rYbLVYLtR0ndouBVK6nDwUYtTpfNawP+h8Out0TBXdjqeTTqejjsf083Q+69L3JdAxKuZqIva4PSfnYwmcHEPItk22J0Ksx2Dc4AP4aLPZyDeVTxPv1eMzWef/l7hsOxM9qmuQ2v5u1yP7jG3X7u/5LPH5bVtk/uxvuX4zMJ7KoI56fExOtNPppMfHR41jdsplYOXx8VG73U6Pj4/CCcJ53zZzB8cQzlqc1zabA0ACx451hOH4IXvdgmA4RHGC4sCg/BeljqUKEJOlhTOLUtZsEgEH7u/v9ec//1nr9boAXDhmcGzj1MQpwqQAivE5jtP9fl+cymRGAVjgZAYgwVluQXgL4Drn9Pb2VkBoHHxN00zKGEoqDj/r2OSZIiyq4AeOJJxwBDI458pZ48w5jnvAjmEYynmKOIRxdlng1gLzvBsg1wKyfd/nRR8gyuv19a3wiXXe26gr+hJDLOdRXca+0LU4faWrsqCAYNCBfsQYU0nQ5VJ9PyiEGi0zjqOSrgvqL73atitOM0CBAsLK5eeT0WHLRFZAyCVjRbmN1VpjSM6JaGSD+ev7QU2TNuPDOBQnVwJwQgHI6A+82DTTagFWrhh323bq+0GccxVCBdCZ15h1B21ESW6sALUziyaZkwkUIzt41GKxLE5bAg4A9ayjmvm1YELNfuzlG69hGHU4HLUm075NpZ7COGqMtbQx827PGq3jrtlkNsPZ8ikOf8CxpmkmGcLwhnUQ40SGHk2TosIARMnIQ3ZshgMOANtndKUNVgD8weFsg1AAX+gPtLSg+TywwFYBsJl7HA9AYBB9Qs5fXl5KBh/rAvNm24qxBh0RcMU46BvlX6EzzjtoCViY+juqaWqkHXPY971+97vfZb1fwa5xHPXt27eSnQmIRXYo8wIYZwFLnP4WoAEggX7I3fl8Lnrb6sAQQgFaMAhYp8jghBbM9zimIznu7+9LEAL3ULHFAsxJ9gaFENX3lzzHvaRY+AWQ0DpGN5t1pm+jEFJVifP5oh9//PFqvYIf0BUAcYA+jDVlRm5KpvRut5tk/7NGwe+APMjbL7/8Iu+9vnz5qo8fP2qxSLokgfWjzucEmCYZ9mUthh9p93A4lMxosv3ILLXHmwxDr0+fftAwcNzKslSx2e8PhY9ZC4/Hk1arZZm/vh/0+fNnPT9/LNVMJJX5twFQyCU6Bx1L4ABVZwhKjDGWc9KtQQk/wqPICaAqMogOtMAYNomtOnA8HosNwVpmjV/mDgDRgvzwFkeksHbRf/qMjMCvMdZjOObANTKJ7YSuXi6Xen19LTYZNB3GUX0ek6VvzPe0XSdlXsMGRO8yrlQ1qToBWS+g7ziOGodeztcqM5Im1V9s4NLc2WD1O/cREMB6+/LyIikdQbHMZ1lZuwkbFNpzvBD8BS8VR7/zRcfzz/KhbxqNw1iCPliTOJMaMJJxQHdrH7PBYR9A9jL2JgAsdGRu4FN0gp135gX9ZisNENQQQtDj42PRQ5SUo4IF1asul0sBqgm6RAfQTwI8aJcADXQy9vznz58ngUjoYKoMEKzGc9AGXoNnV6uVvn79WoBvG4hjg9uQZ+aM73kn+gP5hMbwJPx7a+NKf2zgsvLnydlSHfHjOBZnkg1wY/zw3TzrfE4nQDq7D2A9wI6x+xd0tA2oJghqu93q6empZK9jA7DOI1/2+AyCewlwhT7Q1PIntpIN2r7ltPiXXMX5F7OT5EaYf3FIT56rTgbbB5vh8p7TIIYgOZ8ysKK0WCy1Xm/yfF3kfJT30mn3oj/94Z90Pu709vJFP/z4Oz1//KDt3Z2Wq4222wc9f/hR5+e99m9v2h/2Oh1TUNl+v9fu9SUHnh11Pp10PO51Ohx0envTeDppOJ3UH0467N50Oe4VxjGd+RdGKQS1GRD3GtUoqI1RnXNaNK0+jFGdlAr/xkZNTGB6G9OZxgvn1TqpiW1ySGYSpTMSvaKCOnmt4igdjjr9v/9Rx//+H7TcPhpgXFpGV4BxZeDkfDnJ6VVfvrVaLDt13UKr1UaPD3f68dPHVEEkSsesk0P0OUs8O0+Ll10VD4yuyFrMmUhRKfumgsRTp+kEqHJ1jzF3yHJ574sTbb/f6/Pnz2Wtqc8BXubzeXM/yj61NJx5qRImlTgPOMaykz1KkZLHLmoMuRUHWOJMexmsiMoV8VkvzX1pUPmR2i/eDQicdC2li3Hk13k0rnn56AyIApiRQXKXy157L9/mRIKyjvucpWZLE9fyxJ6S1Rkc8b46++ViBWQkqWnT0W2FFC7DXrd1zBz4kgsFqECXhBg1joNCPl89jrEA5EmXkjmYgfOcIRdC2jdInDVszqY2dExHFExpe+v3qJlTNQO26FHGF0Io/EYDlvMr1GEAmxiL89dCIbWVKbBXGyVY6BaAMaVz+qIGbQrdmvvspCKvQLxWj9N3xq4M8JTPstxF3l/6Mxu1A9i9dlDfvNzsV1cEq5ChQc/ksIPGSw3yVohp5ji/r/FNltVr2arKIdas7Pl9s2s09KoqwU3m0EnlCA0+cLNBFlrH+vekn5YuN+g43ePkXph6+5YH62exzGlht2i/q4EHzqUQrpvrMoBgrvviMvBV+2h/L5KQ58qBzVeucRW8bb274nN+vgfAlX4ZGZWVj5mszP9+Dwwhi92J0uEGZC660tf5dbU9uQoYl7ktYwV4xkdUgWiA86p/p1I5v5i3yTTlR+rcVSbjKBQpmwshKrgE5JWUeKODYlKKaS8ccwWSvFbVMCADGpHhHUMep5M9Bz6EMNW9MZagpnpmtyY8X4ByPsu2bZXlyhslQMCsdXad0uy+QjCjK+cUnhCV98tpjGMGRUNZOxrFHGhYebbY4c6l4Ly8dk3ewpzMbHZXusBn6BVjA5Wf16Wi6+c+6bgY5W37E+A4fxYJmLH65bpa1HtgqG3P+g4Sj1e/TNN4xSANY6+Xt1eNMagfB91tt+qoCBlD0i8h6tL3+vw12eppv5tLqrtGvs37ncyzvkk2Tl3Tq1+ocWT8p6AB76Pa1mu1WOj56VE//e4H/d3v/0br1Vp//vMf9fNff9a3b990Op8UlWyVYejrGe1KrBhi0Ait5NREKXiv5Wqtf/ff/ket1Ojzf/2Dmm6p9f2dltutlncbLfN54PePj1qtVtpstlpt1uq2C63XmxQssFioaVu1TaOuadRlYDooBVqcLsnvcToedT5fSoXiw+Gg8/Gk4+Vc9tzDMKTy+6HanIlfvWIcjI5DNIrxn2UR/sOesRZN5Q38ZxZ/qM+ovsfaSUYW3uOpX/v81p53YruZe27tPd9baxjPHBhPfqubXftX7bt/MzDe+E6jgvY7wOaDYnC6nJMzY9E1urtLQDGZUzYTSUoOse12O4nmhyA2K4KsBRxFOHJwfOJQxZFizwHEeUs7nFl5d3enl5eXknlMJhNZ6YAFOGRpgywQ71OJd85E3G63cq5mEttMTFsuEqCpbdtJVhPjBtQBzAD4ubu7SxEm5mxM52r2eFJqtTSlLZNqyyDivMZ5g3PUOo+YI5xlfIdDzxqCzA0MZx1SZIpaxt/tdoXm8ICkkgljgSkc/Pxt59hmVeKsBXRaLdsJcGSzL1kAYowaXC4RH1NkkcsRlDYziz7xPniB4AIysw+Hw6TUaoxO/aVmkLFZJNAixqCuq9ncYZTGgVLhQ+HTpmnkXasxDOovnPvcTsbRLBv1Q68w5nM1Yi4D2vcahtR+16Uxvb6+FYddAcaO5yIv59NFznldzoMUz2qbhYbenNkS6vn2yGxyti4UI0EJACfpbJwEwqYg0CYD3fDcer0ujubFYimFqKZFD/hMz2FSZjYB7pxr67LMr5WC09LiPgz9xBCYK8O2XSRDwzutlmtJTt63CmPUIo8FnuJC78BXyIg0PQYA0B4HLPxjgaa50W/BIgs2I9fIIc5/dCqZbgTRWKc3QIR1NltAH4e5pFJ6GjmZBJxIE/DdBuHADylQqmYxWiDAOqptSVjAIOs0Ri9Rvp6AB+YRpzVBARYcsyCSPTPbnnlEiVT6v1r1OSvyonEccvkrqWkWahqn1apWUkC/bDabQn/kiLkrIFqME6CDYCV4hew2dIjVtRzDAc/ZShDosHnQFusAgBzj7Pt09joBA/CpzRAGeGd8krRaLfO4z+r7cwa7TjnLiQCyMclMCGrbTpdLAub2+72en5+To9w5/fGPf9TpdCo6njU1gVYqpZgB2gAboM/xeNTT01Phr9PppNfX15IRmeRjLEFkTZPc3qfTRcMQFEKSpf3+oMPhmM9JHvXw8CjOYQpBaltfs3ldzb6PMQHjX79+1ePjY5Hjtm0LgDaOo+7u7rTf73NwYFSMTpdLX/Ri31+0Wq0L6Ou919vbrgQQdd1SMTp9+PCpVDvZ7/dl3YUP0nNvRS4sb8P3ZKNjzzjnynEdMaaMfWSQYDi7PgJW2dLfds1Gp9rSxQDk2+22ZPxuNhttt9tSYhmQm+Cevu/18PBQAus4rsM5VzJX0TPYSqztyAQ6BXm0v9uS89gQ6EZ0C/oY3vdNAsGbrtPDKoG8bdbhQVHtotPpcJwEYAK8E0gG4I9es5VBWB+Gy1mXPE/YGXYdsVV7sF+tTYuetWeU26zvp6enwjNUHECnliNfMr/D46wHlN4mkMV7r/FSbS/sdtaHEFK0/GK1nOg66IEuw/YDkOZ37Km2TWeTE0x7d3env/zlL/rd735X5o5y4+wj7u7uJFXbmTXW6jV4lsAZ1iN4v+s6ffnypQRbkUFM8AZBnOwN0EPO1Uo4BFGgl+2RKAShWjniOB70NnrZZiuTbW2DVrA3kT9semSDbG8u+A/9ae0AG5Rrg9js+6BzWhdWJSjYnnHOxXspDXg6VjlQdtLJu5SVbDaz41iPjZiPlWAi5h4+di4FhVqbyc773ElkbRZkAPrbqjYpQKkvY50HViKrBOihe7GFkBFsEatzsKlsZat/7eXkswOTTB5zZnG5yZU6ohMwbHZNAfHrd/HdOOS9ZkylcxfdStttkpnj6aSU2RC0bL1O+xf95bzXy9e/6uc//0kfPv2oj59+1POHT3p8ftbjw4MePjzr4cNzsXM4iu3ryxe9vLxqfzzocrpIp0GX41Gn/U7DKZVXvxwP2u++affyLQUpHVIWxuV81uV80mnsUxbQmAKfvYvyTdDnYVQbE6jZRq8uSIvgtJTXIvRaqNcieq3kU2nVmHaHo5MuuJ6d1MppMYw6/Nc/avdP/6zlf79VbBYaM1DtXAa/fMoclm80DBedFLQ7tPrypVPbLLRcbrRZr/T8/Khzn30BMep4PqlRDhCN1Rmd5qNOdfLvJmAgnW1pj91iMnMQsqKcqxUQpOooDnkdYr6RT/RydGnt+uWXX/Ty8pLWpaYVZRudywGgZHzPHFzOJ6cnEIh3TjHazKrqoAMniqqZWum+es6u5ef0XwWVJ05458rZq/JGBsw9dsxJbyxmMoFjbwrYpKNQ6pyMMUhjVBwjCNME3IyxyioZP0VOQwKoC3hOCdzcBqBQk4MUsN2bpkmf8a9pUkZU/ul8rQDgnctnftb726b6b5JDlAnLvB9Dgj+dn4IVzJkyRBGjYkyO8+l8TZ2iMUrRoWdu/+RZhXGig1kTp/o9BdEHA9JH9GLJbGccFZAv2Y95TirII5PdqvJ8biT5clycnR1uUEWjQxO/+wJ6g4PGWMiU6VH1dOEHwzcO3HQGcMb8JfwMqBJjb2harynMBIh2rfAB2HKzE7krc1lwRwab5dnFIuMpEzoKGFaSAln4EZsb4LTqhqQAnAiEqKCxRXvT/dGZoyFipRXgQZoDyYTmZNrF2k50Ob4o1vHnhuDHcjsCUvQPfYMWxrfjqu3rzLOMsvaoVsywbYYwfa70pQBvuf8zfc7MFqAD/sj9lqTGtRWwtPpwNsauzWWPnWr7rla/4DtoNve3OUOn9B3A34yemSCVXwyhxDpX++C9y75bPlMdo32Bob/9zHJ++i71rfJYnPzgGnMQEO3e+jcHnNE3YwhF1/CeoGnwpvWXV/A6Kg6htBMVZ+sHjKBS5AKeLUC9VAKx5Lz5rvJPsasZW5nfyicEpJZJMVfaRyeiWX+Cy5nvlvJTnk7VRkIIJThsInv0x7wT+yDPStoPmz0Fz3QmkWmOXTjv85yMcoryPp2HbeeW/U969rqMs+V37+0xF5V5rH8B/m38tIJJ0ePzv1WrXcx9x/af9Utb/rJ9rPq2zg0+7TI7PrV9Op8VFNUPqcLTcrnMR7UMGodRw6XX8XTU675WM57YFdmfCHYgSdHHHAhSA3GtzyOqUYhOTqMWrdOnjw/6u9//pJ9+/FGPD/f68ss3/fN//aN2ry/q+3Nek0Zd+lxJrNAJWy4oZjov5KUxyKvRZrvV3/4f/vcK/8P/oJ//8rPG40UPz8/a3N9psV6rW620Wi21XK7k5bVoOy0Wndrloia3+BqkNw69DrmC5OF01imD4Pv9XsP5or6/pEzx7FeIMRbAvvCWr3qyrIIulPmovDstR85cs5+0+pZ55kKfeO+Tr6Mx+EZI57F77+VVeX6+j7a8f2sveet6b89p+2//tsEodkz2ufn47d9pL95M5G4uN/Pnvnf9ZmAccBiH53azLY4NXswE1GzVflLGEDAG0BVnJ44Em6lknTBkuMyJZrOdGLh12pLF4b3Xy8uLHh4eSqYfwALnDVsCWzCBUoWciwoAxlhstrPNdLZOGOecPn78qJ9//rk4VC1QhXMFJxpOOe+9Hh8fi5OPEpH2PSXraRgmiwFgEA4cCxABSMydPoyPQAMLuIcQtN1uy1jZrEg168mWVCfTApAKJuV3HHrwQNnI+XrmONl6OPFw0FngCH7DmYhStiA2dOF7HIPJKXkpi8U8i5IMIJtdY53XOHfmwCY8yRzClzxns0qto42Fhax1+ISqCACFxbFheNWWcITvmB+AE5tFZR3INpsVfvn27dvEKQ/gwjw7lzaMjG8OsMJz3WJRHNmUxIZ/nEvlXBRjyWjmube3t5IRO48OsgqTsdpzwaGtbQ99ZMGkuaK2Wcos7AC30NE+wxgsQE0ZaZs5abOyGQv9tCV14QG+o7wuTnn0ijWu5otkcWiOtewtfGov9CQX/adddJwF+KmW0Pd90Z9WN8HvONq99yWjD52FvrXZ/hbMR2dbnUpZZiubzDm/2zUI+sdYz8ClD8Mw5PK1Kv2mbDgOeAuWoucPh0NZA2kH5/3Ly0uRH/iBksQWILMVJ3ByOVeDFpbLpb5+/SrnaiURKwOcvWuz7G1p9Pv7+5KNC49YHnAuZerbDD2qVrAOe5/O7aZkOLyw3x8kOT0+PuoPf/iDvnz5ohhTMBRrJDQHbILX//CHP+jx8VFPT096efmqH374QTGmgIPFYqFv374V+r+8vJTsaav7LGDH+e7wkM2cJlsW3oEHLR1YuwDrkFGrJ7fbrfo+HRdgg6A4+gUgG6CZzcZmsynyulzWLFCyYZ+fn8vaghzRH453gWfsWsv6R8AQayaZ56wDVASQVILrxnEsR6ig02xVEQuwffv2TY+Pj0XebOAa7wBsJTgGoJVx0i7rJhfGOfYEgCT0ZewAV/Cs3WwxB3ZdJ3P68fGxVD2xwQxc0MquG22bzh0LRv9bW4F1a2XKq1tbc7PZ6Oeff9bHjx8n6zyArAUi7+7u9DnLDTrYBt3RR3Qves0CbLRp27VHFrG2YbcwD6xd6FlsMwswMl7n0nnpi6YeBYOc8AxtsC5aYBZb39rndj1jDWCuCZg7Ho96eXkpewwCvSQVXUukOvoT2YdnAImZW4Jwttvtlb0DQB1CKDqFaguLxUJvb28Tewn6US0Km5PAH+Shgi3VHoO3WFf6vtdut5voHWiF7AMKU1mFObIBM+hJeAX9wN7J2j7Y26xd9pghO5/oQNYL6I8ushtbu94R4GQrZFj55bLBAKzNyA26DjryN3wZY80gr59NHVZd15VgHHS+DVqxWftUvQohlJL99JdgNmjJeoMszO0w+J79kA0iseP/114xZwQnuKe6CCfgR4xqTOHVWw4OnHghXDsJ7NzGGDX0+XzC6LVoU0DserUpgao4ZJompJLVodfxmCqzfP7yRf/lv/xXrddbbbd3erh/1O/+/gc9P3/U08ODVuu1Hh8f9fHjR/179w+6DIPOfa/L4ajTt9d0Bt/LVx33e13OJ10uJ51PRx0OSb/3p7POh6OO+732b6/qT2ddjgddDkddDkedjwedz2f9rIPGkLJLXBzUOKe2VTo7PDq1ushF6WNcyMVUcL2VTxmHLqiR1MZUztbJaRGDdv+P/0l3f/O38o+PkvNaRpcyGV3N7gFQG8eL9oc3xeDU90F9P6hrov6b/+b3+vThWYuuU+O8/vzzzwoh2WLDmBzqGiWw2BhdPYc6z5fN4nKuyeBdBWOqnHqRERei9Lbblb1ZCcCU5NtG3qUg67fdq75++1qC8tq2VYhj8eOOY7K5Gu/AeK8cT1Y+587qOY9anSIB9CPrU3Ac/nVyqZzpzNl2i6fn76zORBXa2P4kfaLybjkpeKecxpk+8l6umQI9hfiayp8z399y1M1lLwowIIHvLgTFrFNuVfKQsbXmbZmRaxziZPxJfpsEvpsMdmsL2cQEGzy1aLzaxpdS93zXNE3JrJekpu3KeZbWoT7nBx+n6+d8/XAugcEhXIMBjLvQ1wVFXR9fcc0j1+dgMldWX04SsmIsiHdMzFh1ZtH1GZ419mb5PcYa2DTr12Rvr2lZ1flaWm2wofZT1V9hfRbf4znblnOpUt/0XmBX+0w0oFX+bCIKsTwZAWcma9VsGsb3He/28xjHK55O30/5fVC44q98d9U5pY+1tDX/8V5rw7pczcH2a/qvk9Ujds9gL2Rrfp9tdwrA5b75ClzyGerH9sO2VWkyTam7ResYo1p3I3jpHb1q33m73QxnzniutJt5KAW1TPt7Cyy5jNUOf0/HxZiOh5m3Y+XBfnfrnba9cahrXu7IJJiAIwbs2N/jYymfpz4L2qj3uwISl7Wp9VkfxbKy+wz+jTGX339n3mkfO/jddSECpvs6a/kzF68Te8Klv+JrC4gylKhaDXPO09xv15M5H81lZN53AsF4KkoleBYa2D45pSMxoqeipjdzW9dDS0Nrk8z7Uvg/ByJKtVKl/b6Mzyeg035u3zGXpVv6ef43+xpsAj5j/2mf4bn52sv6H2LU226nb9++ycVcDt3ylKRm0akRSTa++HO7rsvBj2mPuc++8Aj+YnCgOr4UdLtaLPTjD8/6b//jv9PHD0/y8vrrX37WP/3TP2u3O2gYz4rqFTVoGC7J9sMOHCvW4RetwthLIR0nEM69mkUjL6cff/+3ev70Sf9NHNS/7LVcrtUtF3I+J0Y4p0XbqXMpwDCOUf1p1Oly0bf9i/bHo06Xo07n5Pt6e3nV8XjU+XJS36fEpeF8SfslT9Wf9K91TuUcgDwfyZZ2IuAr0cZN7pnbPvy0olvlCRlOQavWB+ycK75k/oUc8FNs9F/BjK0tb/lz3o/5vb9m56a+X+vdW/xusbV5397rz3wN/S3XbwbGyT5CyUrVWWSBYgYJoGPL89msJKme10ZbVuHMS4fGGIthvt/vJ4qW9wKoAECQpYoDmb9xzNlsCknFGWsnAeft3d1dKRnZ933JEsfBbMFS51zJ5Nlut8UZ9tNPPxUHGcrscDgU54ykSXY1peAllWdw0MwnmcWnMH2o5/ZKmoAjONClWj4VxxHf45yyoLJ1ZFog0ma8OOfKHNi5hqZ8DqhlBYSsSK75XNA+YAKgIoEWAGzn81nH47EAjtDEgoE48GiL9+Eotmedwr/wEGOwixDORcuX8AVt2+guFi0CDgBgcZJaQ85mRk0MYuOA5HtpGpRhgReAb6ojwMM4lclWxPEaYyygm3M1m7gGAtSzve1clg10Bkk+f/48Ad+gY9/36nyN8rGO0LK5MQAn/DTfqFuw2Trtrc4BIAPws7phroPIyqUd24akCYht2wDgsA5ZwFQLLs95g3ttIAKy4pwrwTCSJuWnAQ3IoqY/LDLoJuaMn/Y8eoBRnPzoJ4AqwIlS/iWDUDh/a0WEWq0BvYP+siAVpWuhkY16m2d3U7oRgBmehI424xI5AEy2Bp/N7kNHMN8AU/AYnwPswJvQ5+npSSGEoj9fXl5Kxlnf92WtgNaUmrbAA/NssziZN+jKT9Y0GyC22WwKfWymvJ0PAEvKs5NB2nWdnp+f9Ze//GViXKAb1+u1drtdAWkJmkqVHt70hz/84Spwg74BwL2+vhawDt7gH6DUMKTy5QDN0OXh4aFkZads7KmeJ/AEOtjAF6tT52Aick079/f3hXfInnbOTSogoKPgC2QWuwEg2B65gX4HWCWYjTXI2jX0hflHvvu+LzRApgGr4DMC9ZxLICZHI5BtDp24B51GgIWkSZasDQJzzpW5s+u/3Uix9qPPCDiabwop8f729lbWdmwYC3xaEJVgE/Q0vAWNL5dLAQ2fnp5K6WuywmmftQPgFtAePimbhOjLhg7dyE/0cD8MWmV7ljbQu8/PzyU4wZ5Jjl4pa0PXTsZq6Qq/QF9bnhmaeZ+CjjabTQn6gNfgG9ZJdIw9h5l5Qlfa4BW7fucJLP1kfbLzh1MLnoGfsfmpjgSNbeAWGdjH47FUvCDo7unpST/88EM+lmBR1gL4IsZ0ZAPfvb6+ahxHPTw8lCOeGMtms9Hnz5/17ds3ffjwodiDHz9+LAEa6BDWT4JwmqbRhw8fii223W6LfNljSKBljDW4hr6ii1jbyLqGPtjdMcaynmAXSwkg//r1qxaLRQkOo38E9gDkW6cUehz9+fb2VjLfyb4H+KafjIWjMmxpfLvPYw4ZG3aYzeqDNqxRBOfYo4PgIYIR4Nn5GoztWWzLbEvN139knv4RRER72ObIGUEJ6EH0rLUNLNjPHo19ADJu1yb05lyeeS9r+r/lsqDR3O6eX9apYv9O90syAIF1TFg933aJft6hixKvtk2nMNZ18sy4Wy/vW0lOUYOOx286Hl/07avXX9pO//RfV7rf3mmz2mi1XGm9Xuvx8VmfPn3S/eOTlquVVncbPf94LydpHKMu5179ZVB/7nXYHfTt26vOh4P2hzftT6kke386KwyjhnOqynE+HXXaH7Tf7TQcjuovZ11ORx0Pe50PO42nk+KlV7wM6odBGnv9MY6SBjVK54Wvg9fKNeokLeTVKso76bKQPv/pj+r+6b/o+T/+R63vn6Rx0OBSOUgX8rnQTuraRlHpCKf98U3D2GsMvVbrZGv//vd/o6fHRzVtqzFG/fzLX3Xpc2WBmPWypoAZnwXDBzh1YYOpEy07qfJnYwg6Xw4KX6IOp2M5cqNtW7lRej286du3bzoeDwphLLrSOrqkahs2rlGTzwx3LmdR633H1Nzhx2WdW9YJlj7zBfyre+wcMJMeLs+iS1J7UyBkKh+ZyDfkRkrAvwVVYoxqupoVldyY08yW+ftvObsVJ17Nq/FfOe+yr9RlwDrGKOebq2diN63uZ3/a+4qznPLo9FvSmM9pHDWqH7M9MvZX40tZjErBJqb/txynMRrgKAM/1tenPA2pB6GWmwc8z3QqfOS8GhOYkwD5ppz7Xu0dJ198zf5qLvi9yZn2ciYDjhzqcq/kmpqZK+/L/NN/xth5pxiu537i4HYSvDmfb55JfA6LVLqGfIwGtFSUQqw6AHS6vj9T3jnNjuGcyKMrdJJCpKRzGfHV5XyQc7WE8XvyDB/ceq8y39m1Z/7svD3b3zKu2XfKZf+tzuF6DzycymkFatNcEFw05dv5GO0J6DGStVxFnucaV32S7wUvXOkNaRpQEVO/+nEaKFB1HXp2Wn7W6t/574q1rPakwsLsH/fZ/UIBU/k5++zWvFp9+b2rPOdNFvwtm2fWNs++q4tvvsxmO0t+0UzWYBvUY8dg+2p11vx9qbJoOxnzhAeyUA9jSOBaVOYhc4Z3iFn2/I0V7Jrm47ifzM18faiDba++t+sZQGnr/MQmmK/X6Vllm2AaoM5lbfhbPDKnHfo2OmmMFRgvL+NZV/3Jc1vC6mCbsMd9NgA4td+ktcXI/C2725s+233M1A6LChqvgM5rm6VWJLVzNNc7c91jaTzXB1zzBD0boH4ZBjknNY2Tc400zhOmEs3GrFe8psl/l+xLYt+0yHvV8zntkRJkW3nde69l1+p+u9ZPP/6gf//v/l73m61Ox4N++fqL/vSXv+jt9auG8aRLf9Tlck4VoUJUGKVhGPOZ8hUIDsMon+cyNpIWrcIw6viy1/5lrw8fftTf/90/aPG30vGYMrrBek79Wd+OLzoeDjrtjzofTzqfBp1OR73sX3U8HXXO94ZoAsdCkHNRbduoW3XFrpKLalKhBg0KmYHr+uKy/Yktr6hie9g1cX6hA5y71h8xUqa+VtCGt/FtFh9F26knAC4Hmd7Sz/b39/hq/vfc5rk1DsvDt9Zk286t9db+nX7eRvbfe/Z7128GxsmKcq46BAE4EAwL+OBkADC0Tk+bhYmDB1DOgn32OSaFknc4kwHbrDKjL2SosnkHGEABWuencxXYsqUmAAXIZLRZVji7GAOANX3o+177/V6r1Upd1+n+/n6S4RFjLEC7BT5tH8ZxnGRIAZ7gaLROY/6hzHBYUq4WAID3MXc4tW3pdxQzNGVOeZ8F8QD+4AOc+Cx8gGqAWzZSDEeZ3bBZ49NGQuFgYq4AGgAo7PwAuuHcn0SyqYK7OO0ABgAS5mCydYgyZhZBC2pY+sYYb5bLZow4JJlzW3qbhY4F3Gbi2eeheYzVacplF0DGbDf6NmoVPgGEBFCEjoB8AIzjWDPWbaYN7bVtqzHW7F3GB59jPBxPR7VNOxkroC/yaEECQDDGnBb1UZdLDRSA3oBekkpbNsvMnhGOrhqGQV++fCm0wvnMHNmS97ZCArRibPDHXD9C6/c2A/C7DeqA5wAzrLEHbemvzXq3QQ0YQVZXWcc24CtyR/lPaID+gV8J1pg7rgGQ5xUYkG2rT9CN9rx4dAQZlwAGrBWW9+2iiSwgp7TL0RfIus28A0S8XC7abrcTEARZ9T5luRIgQ9DN29tb+Q7gQUrOwg8fPuj19bXoQhsVu9/vC60ALgicQt+EEPT169cyB5vNpvABMm7bZBzMvy39S8AL42nbWv2kaZoCTMAjZLpTuhfZ58xvACb6eLmks99tUAvr5ZcvX3Q+n0sZetbp0+mkjx8/liCZp6enCaC/Xq/18vKiDx8+6OvXr3p4eCilsecZtvAqgDs8iQ5Crpl3gjWg4dxonDsKAB3f3t603W5LUIzlO2sT2U0gfAovsq4x5/QBXcT9FgxkfWJ+mEvkEtDX6me77rBOYmfY4ADWadau+bEmNkMZ3cs8PTw8FKBr7sRB79SjMNJ47u/vC+AmqVSFARxEp+12u0In7BmCssiIB1RvmqYElsGz6EvGZXUrdh+6arVapfJqcQrM24DHrusU+qFUCrDHGdiKDtxr+QegcRxHhRh1f39f1h94xc6J3SjQDvNNMIZzFVCFz6AFthG2BbYV/Mo7OaLH6mf0XQhBvklgB/wITyFvhU8XXdEZ9NMGhjHflqes7rVgPRnalO19fX0tPO2cK4FSzCFVMviddyOnl8tFz8/PJWiCTGUCmQhMslWXbgU10FfmhXUKWwmdbqsHYTNCBws+s05wBhkyA88SZAEdpRSYjH5nLwId0GnofgIooLet2sJabUFsG7SFHK1zNm+1sWp5ccbPHou1HprFWIMX0MkPDw8l+Jb32f0hwQgxxlI9hHZZu51LWV12fwlfc8FzyIvdD9lNOnzO/oSgHmtPWb1GG/AA+1P0MN9DRxs8a+X733JZmbW28HuOxfmY4cP0WQIW5/tr6/xL9EsZLjGyZ3Mm2Nur7wet1xsFD3ziJReVsury6Xs5GWEIvU6HXpf+rG/+RY1v1PlWy8VKy/VG66xP15u17rZb3d3fa3u/1WK5VLdYaLnd6unxQX/zt7/L9B906Xudjicd9wcdDged9gedz6m8+ul00u5tp3i4aLhc1PdnnS/p/PLzaa/z8aj+dNJwPmu4nNQfT7oMR43DRerPGk5nHc6DXB/kxlEujFIcFS4XfYnS+o9/0dPvfq/lc6fDOMoNUWPncvnG5KAaR7IknZwbdelPett/088/r7ToNooh6McfP+ru4V5/87d/q34c9Pq2UzydFeKg5I8ci88HfkxnjY55Hu0cVt8b2VDOhQlw7FwNon19fS02oNXZae12appuYndLNehjHJOsuFj3MQnI5O85eJLvoQRv4xVjmPqznMsl2K8zpSTj6Mvj05VzzuU2g8KY+HDuXDOvkmZAVr2mvoiiD3Lfm6a+O0ZmeArSC5nLv0uySUMJBp6NcyK7Meay8lkP5VLrxUHuMjDvU2DfmOVa5n3RtFv9KrmSB2CPgqILsmdoz8FoGitAsJoEUsRY2iHDusxj6UpUYzDTWw7K4g8MuUJI9nNWAMTweBjkQpINdKGz4GOGJxO1vJnnOGOXNJ985FwFpQpQX75UuhPZUi4zXLKL673Rp1LIkgHQYi7JLqV5dE5yCXy0mfXMFwEQiqnOe1QsJfdTJQpK8KdgpZgBdKsL4FvLV4n/5vwwBWK9d6Vs/KTMMXpMNXs5Dc3wsFwZXzpbHJC00lh5fMxVzEA/gUDQ+3vXZL1T5TWCBtL3CViET1I/qgCmv/kd6tf2J6X5wzTYxQIRk3XVx5vt1XbTz9a7YttYvxg6mLEkQD7rctVAFggUwliOXIgT/q73aE7b0rMMkthbJWlWXpxZL3yAbjHyfXW5zJBWhgRwKSN36f9jnE74Tf3jXJL9rFsYd2ml8FlUSs0NVf+iE6KsxH9HF1XdntaZpDfRycEVNiq8QuDgbBRT2kapHwc5DUUWoK3lKSmBsgBkdaky67im7Vb6Gro7QPo6n87qcTf7mdcT3lTen3mwrKexVsah3ZiDabATVOQwHV1n12J4exzxpV/7Qq/W/1hB6cZX/28BFjWtbGV1XJkR54q+cNkHfcvWwG72rpmuPapHn9g+2vbZP5RnYsUxhjBqHDiOZVpaPZXRrvM1BxWt7z/pbZXjORJN2mIjsC4n3qp6DPpZHEDKPukwJO3uvdquk7oEkMcC4jrJt2pcto0yDxbdl/eVJYFwsVTTtFoscnW8MVU/YQ+72dzp+X6lj09b/fDxR60Xa+2+7fXt2zd9e/mmw26vy+Wkfjjq0h/y8bFpXZVqpj/6YBwHudFpueg0KmWMq2vkhqDz7qB//p//Sa/f3vT8z3/Usk0ANqD40Kc95svLNx1yItM49oph0BBCCpLMILZz+Zgm5Khr8lnpqVKF8/UYh+CQjSiX1+1qbzCPrujSxlENaX7OvZOiy/qHZez62BoCV1JwQ+VRaC5p4j8sySI3FlwrF/+a63vPzn1SNijE3jNZsyb71+v75iXnb/Xj1wKwuH4zMM7m3zp6cFaymSI7DFBrt9uVzCwumzkZQsqOpaQqDh0ccDhWY0zlWb9+/VqcFzj+pxEtmmQw4zgAHEMxzKO9bHYkY5uPE0dTjVaeOiRwxuDsASQA0Njtdnp9fS1KCYczTmToQtu0Z7PxLMCIg8pmRNhsIds/MlQsQMxP+kOGGXShfzjwuHCezx1POGRxJM6BYAAWmNNmt/IZfeayAQJszmmL76wjGMedpOL8TOV7X3R/f18c52StMnZABZx48DWKg7KWNmuPzxlD27Z6eHgozgbGJKlkB3F/WdBjPb+c8UuagB4WTOXdFrCFhwlaQAZw8DIeG5DAHHOfdZAiCyjFtm3NWbr1WTZhzDPzbp2e59NZrklZoAShzAHc+/t7HfaHoj+4oKtzKduRIxCgG31OvJmUq82iAli2c8zFd4A3Vu7W63XRRTboAX60AD4loxkvIBZ9w0Djd+vAJzCA/tnsKLtw0V6MsWQozYFM7oX2Fui3Wdlc6MV9PiPFZhtLqWoFwQk2AIe+bbfb4pRHj/M+dNAt+gIIhjA9PxgaINuAoHYOrJzBH3bhvLu7K7IBUGr53+oHgOgYY5Flex/lJcmm/fbtmw6Hg15fX/W73/1Om82mrDM4vr98+aIPHz7o27dv+stf/lJkjgAh3mXXF85W5js7B87V40QYG3IUYywgI/23wAbzwvrZNI0+ffqkn3/+Wff39xNZh9eRXTLjCJL59OlTOYv37W1fgGuCQzj7l+AkgBL4lfFRnr1p2lJy2PKMPWd6GEY9PT3Je6+ffvqp8MDr62sB2WNM4IvNMPTeF5CU9uFZaANPMWa7tsCPrC/wjPe+nA9sM5z53oKXjIFx0bYNEkFWAXyQV2sP2E0QNhI2AYCg5Wf41a6xzBXZ0racMHYPpeJtlR10ADYM7wRwtqAh70LWGYflY2w6O1esVQSCALIhH4CCzBO85L0vtij2JnLImODPl5eXwn/WXmEtBlwfQ9AQxkIbq88Yg10/ATwJTuEd9oxiaGWDtKLqukDgAoAy/ME70T3wEvxCcESMsehhG6Rl+Y730A8b8GL1KqWwsaWg+3CpgVVSsv2o7hBj1KXvtVl0k4pH0MQ6KJgzqnlAO4J+0FcEWjDXtDcPnEB32SoJ6/Vah8NB9/f3pc25vY89iw0x30PYikPYInadod/WkUlwBcEOtpoT+oB12VYwIIMYXkP/Yp+gc+weg3VKqvYt1QPoi+VV+yzBCHZPxPxbOzDGqKenpyLD2BboV34nQIuMe/Zyzjk9PDwUvYF8Y3PZqhLQCXpyL/plbqs653S+XOSzTrQBSNZJjU5EHxIgHWM9ugt9hJ0MjZAfaI0OtM4k59zk2AirB+EZW6ae/s3tsH/pden7Ynenkqoq5fAmTpSJf6GefziOUSNrWnZezh18jTnLGMd5GrekdMyettu1NquFGi/1l17rdZMcvVH5jG4nhZiyKrNDXxEHe9AwXjSOvZyczs7peN7LH76pfU22+6JbarXYar1ZJ7B8tdZqvdJqs9F2s9Z6vdVi0anpGi27TqvFQk+PD7oMycE1jKPCOKof0r59OFzUny85EOuk0+mo8+mg0+Go8+mky+mk/nLWaX/W+XLU0CegfDgdNByPGs5njZeLxuGioe/VXy5qw6ju/lFN0ybQPIYEUsROwSXXuylKmtzEubzjWSd9e3lR0/xRTSPJO/2u8Xq4W+r3P31S23j5l5128axLDkaIqVB7cTRfOaZjcrDxGdmNjfeK3qsfBsXsUXNSdn4nh+kwJJC77+v6V/jMuQLeSSpOOcnJuzYBNfn98BvAg/O+QuQZU7x2fqUvYwGSnJTXSgCgimvOgjdc5VvrDosxlnO9vXG4x9nz9iqgZZGHqVzgiC7O/miyQ50rfbMoiAUWZNtRduIVGkydf0yik5LDlSMPghJT5eYKL+RziQstYpzQIzlWK8F5nb0/7aGnmWx2FHV+psAqmU6TyxkgrbTvJ/PI97n1Ov78n0dv5O/Iki3zF42T3wRXQIeQ3+EV6vzM+hhz3/OJ6tyW5MT2LE+JM0CP8ogKqA1vSIqlNLuv+tgAiir0A4BxBRAxt6h40SMtV1Bq2o6rwJeRhwIu2p/5i+Jsr0xqeCO1NweWouFxy1OVn1TmND3nzTtd6VeMcQouqb5f+dkUYCMNxU+Z+lVkr/S39iOEUIArKSq6eD3vt67I2AAWVXQSZexjMI56wycxz02RcQf9s6zIjgmauwSqGP/QHOBAtsbAPCQ6TUCBzAuOsgiGXyvHqP6/yHX9rqjCLLPplt927AtzUPWH6UfhE5W/oe/URpnqFmQBnohmvMWmlp0Lq3tV2yiyxTxmmTX7NdqMEeBXRdYsn8voHudcps5o6InN3sxoUH3bPJ90cyw8VGbtikkzn2HDI69FBzMHmqz70SJvhqwuGnkuZ2pP6S5NM5+dq8EL07lLwY/MjXPm/qIDUuBQI1fmgUDMNDeGPlk2Cp8WAN2uwa4c1WHnzxdbQfnv9FzbtHW9sTQ1H4UYFcZclYN3lXPc0ztjDBo1BaiDCtsZ/WjlNyiEaWUcfALBtGPHYddlMzmiZzGmkuFNk4D6ZGVxfrc5Pqnod3OMSY1tSvuFEBUcfmVpHIIa32rhm6JTCY6hHozlq6r353qFrkcNY6repKzr28ara71847ToFvrw/KTHh0c93G+03SzV+qYc3fP6+qK3/ZuOp4POl6Mul6OGPiiMUsjH2BS9nHuUZMQr+nRUEF+6TMfz2Kt//arX414/f/5ZbdPIKSd8hrGUYz+dThpyFrVyQHBqqgaXOqey5hceM7bMhO8Kzao9VO2MKseVgryjBpeiHuAlfs7XZieVYA/lY0RiSEFdm+1Gq9Va/TgojHnPOAzyTTogKppxWPaLhrdjjCWwTno/y7uMxPbtBo9YW3y6f53y1fTRmOk3fd97dv28zd96/WZgHMcQzqXtdlvOnwO4kmr0yHK51G63KyURMQJsOUYLANYo5LEAtZT4gmFxfAIC4kyy4ACOVBwgOBPt+dqAmgAh9AknCL9bR7J1gmLMWEerzYy2TmAyKLksEGyzNem7zVbAyYxTDYcZQmGdX9YJhvPMtmcd+XwO4IsDR1JxGkm1xKANBgCIs0At9+Gg5Sd9xAmNI8mCYHaM8ygmnJo2EMBmVQPe2YAGK7Q4cgEJcKTbgAJLR8YIP5LtjMOPvttsMngAoJF7aN/2iffhXGWObdQa4A7zbfuGYw/6MA+0a53A9n7eSXaafT/OXuv84xmbSUUWj5SUUPp7mDgdJU0qOtAHa/xbwGocR11CBbgAz2yGpHWi3t/flznB8UiUJrJklarNHrXnQkoVHLb6iuw/7muadCY2YAGgO05zeM5mn/I5P+1c2NKf9v1Wx+AojjEW2WQ8jBd5sWeJWgCddvgdfsH57FzN+OZ7gnFw7BMgANDK+NGf6A9ADZy+0JyfZPxBQ5zfVt/DhzbDzDqULW3svI/jWM6Upnzs/f29vn37VvgWPeWc0+9//3t9/fpVMdZIQfpyPp/1/Pysy+Wi0+lUMhFZMz59+lTKJOOU//DhQwF80J2AcvAsssB8EhAQQi1zDPDTtm0Bf3G8A0r+9a9/LdnvZDBbOiB3McYCoK9WqwJ89n1fsrThRX4nYOHu7k6fP3+e6CVK4TIHj4+Pk5LelPFl7m2wjD0nOoSQAxIq7eEJdBnHj2w2d4rxUkAN+Pv+/n5SDWW/3094hExL9BB9tvwJnQFrrc60eszy9hwcQ3+gJ6ARZb2HYdDXr18LuG/XAwvCo58BraE7Mg/v2r5gg5HlBShH8BqZ6MMwlIxmG0w1XyPRCfD0vLqLDfwB+ON3+muzaZ0juKGCuFaWuYcqAdhyZPWy3lsQE10Or9p+2o0y/GgDAe26zvrD2Eopb58cnIzN2gboaRdqoBG68ng8lkAQeB9dig6FLsMwlGwPmwXN2vT09FT6RqUHG2xRnIUunVU+juNVhSILbqLT7JqCHCADFuxERi1YzDgZ8+FwKHPQ933KtB/rsTrMO/TlrHeCBGKMen191YcPH4odhw5CZq1sUu3i27dvenh4KGsy+of3oHtjjAUQtUGLNnjW2slSDfRkHpAv1jgbwGmDDVgXbdsE99j1GhvG0p42oCP8slgsij1l7fzValX4ea5nCSah39ir8AX7HPQYY4NH7Npq1132TNaugHdtdiljh995Fj5yzk0CHeAf3m9tNGQFnrSBBfB7m+e/2n414Im9JsEx8+A5ayuzz2HNwFawewCrr3gPfEFwgbU555cNkGCO/k2XU6rk0MwyUoqHRqAS5qHsGBaO9Zy56J3czJmQMoRrBYcxn3OdsvCyc8dLm/VK69VCrXfqL72ivDxtRT8p15syeFPHvPPCDeNwmEsa4igN0mXA3vVqHMFlrRZdp8ViqdVyrc1mo7v7B23WCSxfbpLdvtqs1XStluulNk2rpk0o/jjko0r6QUPf63K+qL9cNFx6XU5nnc8XXU4XXfqLjoc+Z5ufdLmcdbmcdDrudDoedTmnUo7n01mX00UfXNCnH3/QcrtVHAf5MGrMWSQjPrCYHe7FmZMcr33otdvvJCe1bacEYkf93d/9qE8fn1NZwwx0x+NF/ZhOSnYAqpQ5Lj4r49FSzZpq21Zt02QH3lnD2CuMqXIJfjdYJQHkVT7KPyk7z6qDuoIcvoBqFhAAULB70XdZ2iVnm9Ux0Tezu27sqyZ9N+BX7kKI6Wx4Kxpc8zVAug60tX6I+bMZOikATenDJNMy21n8XTygOOCn64QdnyFOkit3fW9yejKOBARzHMzcjpzQh2dvOCXt9xXcunY6Wv6w333PUT4aPTq9B81U6UtG+7xvdj9tP7MBS00RNOPFj8Dt107SVPLUFb1JiXgAFmfe27g4oW95rpw57cpwgGAsKWxWVupHIwm/gUvvLyCrckBMKslaZK442OvfOOmt/XeLfszXfH7m5dWlFCxg54mfE5mIUVLIZ/zCM1JBZ5QSqAEvZPZqEx4i0MBNfS+s05VeJlNbKZPXm3EWv5FPma3R1fOF7To+59c5D8/5K8lxVZjvQe2JvuPVZ8V+V+qvi05jyH0u4GKi4Fj4L5XIDh565n7PQQJAZNOnqKm81hl4rxJHuiX1wRUwafKm+XPwmfc3eWw0AHbpe75uzYV9XrHqlls6eM7DN3VTvK2/gqvHndEO3xmcp3xmEz+szWn30bWvVMrBDw+f02YOwCqsdF2S34JN6fNrnpzQzuUjFAxjJKB9ongS/2YdR5CbbvACgWTOuRJwAT/N96HO0OXWOt/4Rt4RzBuzTLNfD0KFeqUs3PJ84Y+aPctcvEsHc6FD+P3WWghv2f0683qLv269gz6k/VQoczWONVgEfVgCAWZHeth5n9Av5Fl1rtCJgFbO/A5RysZTfldQjNlm8+nM8GR31yz3oOwTRgbyu7vFQl3mFfh0HLOt49DurtheMFbqcv7WjslJw5iP6c3Bq8tlp/VyofvtRh8/fND93VZtt1CIUYfDQV9fPuvb2zft9q86HA86nY8pY/zSJ3spNlIMxUZAzkKR30bBBSmY+co/hzgq9L3C+ajwmrK67TxO5MDXQDUXGfONTGOnqnvpw3dsXU1sPYItNPuZ91CZtqx11s6x6zy6DF0bCzY4tZW3m42Wy1xpO4yKURpDVBs1m7dqlxmtWsdwY528slulKzmd23H8vGWD3rJRyhrm+P7Wd9e0f88m/bXrN+/UyVrjfO/9fl+AA4AtnKVkbTFpOB5wfjvnCqBqywuSARFjnJQrtoA2IKx1Ci6Xy0nJ8hgrAIfBhDPJ/sRJRKaGVDPBrNOG+1kkAS9RrDYbzGYJWWeVdXYxUSwy1klqQUvGjVPSlvuzY3Ougpj035Y7tAbx3NltDVXrPJ5nMSGMOOBxVlnAk75ZUFSq595yxjOOeuswZA5w+kAfm2GFc4xncWpa5yx8ynzNF24LBNpxStPNsAXvnKvZyDZrZ55hTfCGnQdp6iCDL+iXzT6yPATwQdvwtZ1PnHRWWcI/PIdTkrHYqgDwIbyJ3FmnMt8Dwv7xj38smWqr1UbPz8+TDFDkvO9T6ZFmBmxImmR1D0OvDx8+FHraUtzIJ32xWbU2ay8ZDWPhH1smFPrYzD2bkWkDU3DqF+PeAPT2wokKiGGzQpFnnrc8xXPMA7rB8qlUM/kBvrz35XxQysQCnNiMPviJ+QM8sPTn3bbP1uFrA4WgMWfR8zlrAAFA0NWeHY58WQANgMSC67b6wvF4LECGDdjgO7INbaY0Ohh+R95ijFeZt9B+vV5P1gh0Zd+ns5txlkN3KyOSytq03+9LuVkAOXQ1ffv8+XPJ6rPljlk3Acgp5w6ovd1ui75F1tEBh8Oh8A464unpaXJWKjRAV1FFhSAX5oLzmQ+HQwH5oBE8QmUE79sCltzf3+vp6anQlqvve3369Kmcq42u52oaVwJQALnQ68ypBfHI5mPudrtdkRebcWllFp3BPJMt2zRNySx1LpV0X6/XZczoRgvcAJbRT2uUcr9zCazc7XZ6fHwslUXs2h5jPV/dOnu2223RIdhTMcYCktnzpO3xJAQtAIzZzE30GRUDrN6CXwCvkKXFYqHdbjcBvKRaXQOQkGf5ztpQjBf+jzGWTHt0ARn3rG82IG8uu+gOggPshteuaZbXGct+v9fr62uxJ5EfbAayrtu2lbxTt6jnWZOdP6FDrMA4/Xh8fCz6jMoJx+Ox8AX8Q0BRt1ykSOqsd7AXAPIp/w2/2LXK8jf6Chm29EAvsI7QXwuW2qA/1hoAUtbvJHQ1y542bfBD07Yawlgyre1GibEQBEBAHrqIcby+vhZ9IGmiD5Bdq5/t0Q0EIJ3P5xIkw/6CvYW146Ef8m4rIbFOwifWjmGtsqAoazMBRjbjO8Zabp7gFmhLXyw4w/xbOlqQFj6xa6qkkrXNnGOflkAMA/giu6zl1q4muMbaEXM7oOu6ErRonU52vwV9GKtzNZCI/qFbGaMNwIBu6Do7X0WnnU5qxhoEadcBm9luy/nbwEF0Gc8zT9a2hnZ2PNzPnNjvrW1h91rWhrzlPPiXXqyFXHZ/YR079I9/ydmi8r2V0+oYdGrbyt+scQl4IV9ZaprE96v1Wm3T6nCu9p29YozFScM1dza+76wIGsNJY/RSH3U8SVICFuSc2maR1+SVlouVFqultpuNVptNCgbbbLS52+ru7i4FvG4XatfLBJjkLEbnpDgmR9IwpJLsh0PySZxOp1RO/JSA8vPxotP5rMvprP5yVmjO2mxWGsaLdvudDoe9hswPLko+XIMYaQ7qnrvonvgXXS69zueLnBr9wz/8Xj/++IOarpVrpfGXbwqx0WXwGjRK45DP8M4Bw41x2IWoYYhlnUN3eu+1vFx0Oh3TueHG31H6doM3yBRvvC9VCbjHBh3a5+aOXjvHtwDpEHK2r3WShevKCol+OAkrP1nem/AXOLT5v7UdeI5nbwWt3Ap6me81LN1smyHUQMy5fFj9MO/31ZhVgzDnTvtb+3jFa1m81e6v6aT03a0M8uv+2b/LHM6+s0FJXImW03Kg8z0D91twxO4vrQ/Ke5+AccaY4SLnaqnSuQ6KMeYMwCkPWx1Y5sHPneP0e5rVOv/+1nfJBz1ezaml3ZRnZm82fyfShJu8Nr/sWmE/mzu5nZuC4PRxDtzF2Mh7Rz2Am+Odz73dS2dIR1I6d9vqGPaIPFvkDPzMZJTa9Tv9S5hhlfl6bvRcD831SPqd3mWgDUBPt/nb8uktHivj4vNg+NS5UgJ5wvf5fXOf8XSerun+ngzOP7vVlgMZu3GPpdtcz9trDCGDL4lujeEZ1o75WMq6EsME1J3zs9172uem11S3Wlm2/bD/8ttkZZbPLQ/SJ7uWVJma8iOXHW/TeA1hKPqpZmhO+zvX7bfmXkoxOXMa2Gm3/bNyNW+nfB6qD20ub7aPc5/orbnwjiMhpv7NdNXnXQaVC70KrafrNvvm+XVrHbpFq1vfW3B8PkZLm/fWy6mNLxWNdoO2zrWTdaj8Sx9MNWia2Lp+5X3MhFCSGiepabLcUsEi+yu51UVTFSXxoFcKarE4Ud+nioQhppLgIYPuwQ7bebmm1TTgEOA/r8Heq20bbdu0n99uckDrZqO7u62eHx60Xi0VY9DucNTrbq/j8aTdblf+HQ7pSKR+uBR9PNXPsyA11SNK39PN/N40ja5iL227Rh0AYPP9967v7XXea2PObzFGBbPHLp/d0L2zhormsjYqvG5xncSzodCUQHSesXbQ5O/yv99GD0lXcmV/+tm6cD2k6z3irfXGXrds4/fa/971m4FxCErWJs4eHPhSKu/3+vo6KbFLWW2bwT13sJKdgGMRx93csWYdsBZgkFTKbbLhnGc/UEIWY9oKFaCP3QhZgBYHsHUEx1hL9tFuAgtXE8cECo3MLQx5AB4mDSZkw4nChXZkU763qbIKnnFRXtO5mg3CvEBHHII4rpxzxUFPhqtUSynj6JMqOM782aAABM05VwIqOEMSZ789r9U6umwmk6UDjlGyQnDk2zGTicjckU0HoGidwxjoAI04j3HC2jkBRLBl2PmOObOBD7cUIOOymwzLb/yOfNlAjrlxw2aDPkw2DrGWEOYfDmN4CGc04APneQKScTGfjOfjx4/quk7r9Uavr2+TqgIAaoA6rqnZaDgYbSBB27ZqfaOurSVK5wAIsoAzG0AFQCsFzqSzS+YBGfbcXGiD0xM5JXvVZq7a+RvHsfA+c4Jj35a3ZR6gN45S63TlHpvxhMwCdtInC4KiQ9B/diNHm1Yf4lgge9UGWFjAgjGNYzrvG0caDnqr+1Mm76ZkfMOz9BE9AFCAo1qqYIcN2IFO9N2CQhZwLHySZdLKGmAEJceZJ2hHZjW8YOWANWSz2RSeQp99+/ZNv/zySwGAnXOlOgrncwP4vby8FCCUEr6At+hP9BLZgPY4CkoC4+jZbrcF8Awh6P7+vlThIIOS841Z8+BJQJwY6znpyJwFdWwQDWekk3EfYzq2BL5G9zjnCkDOnLOmocsnoFq+eF+VwVqlArkGQKSEcQgVXCLoDf5GBuF99DV6E1raKjVsXCzQY0FBypnjdEPPUEWCdYT1DDlEnuw53YDcd3d3kxLQZHLD78gx1UjgP6k6Qrfbrdbrtf7yl79ou90WWbSlz62cULHAlnVmLWTMrCkWGKXf9rxmq59Wq9XEGYmehL/oi7WLmCfmzgJrjJf1AlCfCgfoMNqvfFGrAWCH2QCazWYzAaP/5m/+psw/PA+v0l4IKWPI3oN+Z+5CCGpcXSvsegyPW6CddtBHTdNot9upfxnk8lxst9tCTwuc2sAsu/7wHutYYn6svQb/oyOQDdYVu8ahFwhk2G63hXYhhFLC1W5uJmvd+aQh1OMDLG8DLmH3Pz8/lyAgePXh4WGi+/q+L32Bd6HD6+trmQ/0KME3cznruk6fP38uYCv7FNYJWymJedput5My68wddOYsbyqCwDvoPXjKBkSiw7C1WI+ZA9oehqEcEQHf2QAM5NaufbTPmkNf7Jpu5wyZoy1rI7O3gI7YiARy8Q5LJxvcwByR1W5tCHS/tTWt7uYe9B77PXiJ/mBvdN2i8qfZv6FHrW3TNI2+fftW3m/fZ3+yVsPr6EjscdZQgkwtEMM9dl21ezNo/2sb+t9yOUkxTM9Zq46AfFOIGsZ+8gwOWOdjOrcyTsEG7zWxD+Ab2k1utKwLotN6tdL93Z2Wq6W+vu4UYw0K4Iq5LwnL/n7W8PUVFTXKTc4dzSWog3QJvYbR63g8SLGZ0Jk1oes6bTabFLyyXmu5XJb1fL3elu/QB02z0o+/f040cLkPMWoYLgpZN4UxaAhBb5deCqP+y3/5z/ov//Sf9XLYa5SkEBQGqohZx052mrsMyAcphEGn06gQnYYx6nIedD6PGoaov//3P+jDx0dtH9a6e9jqn//5L/r21stdlM4pjCmT1PuoGEeR8ukap+1yU44KkjSr+iC17UIxOvVDrZyHXpnbbvBz13VyqtVupOtjpWymjHV+zZ16071qBqCMvMQYpVnWZW6s/oyZntGXv2PMHOrcxHk3hmtw1+5t5s7M+b7dOizt/nt+LzKePouS5gDi9x36lj6WblLNWpzLvL2njGNG71/rwy061M+uQdR5O+/JtqWTpKuA/OrHut0X6+CEtlL12zBuGxxks4fTd2OyYby7ap/7YoylcLTdV9t+FjvvxrhutfueD2g+Jjvn77V167rNp5IFZL7Xv6s1yk0DRiTJNf6Kv+ageLqMc1vSDN7J76OU8ux5N82+ts+72VzadSmY7MRUKvY6AWVOH77DHpzTaa6z5jSatOen/DmVhzSS+RzHGDVBmHx93nsvjdd9sLYIY/g1AO+3Xreec47qA1M+5X23girm96X9VPUNUY1gLjff0yF13by+bgU12CvRbpS3wKtzV3xhfQjzNm7159a9E/A4RrUtCWQsV/beVAHC+0ZN8FfvmduMc9v4Vh9tG/P+Xeuo27r2io7NjfH6a17B3oauliaGcHKqFdjm9C97WdWMZhuaEONUH39v3uefvad7rZ1q7fK5PFi7/lZ7fMbnjHG+ftB+tf+vA6GoADKZINfIlsUpetWplE+Xoupp8JVu3kmtM6EHzrN4pffGqHEY5ALnnme/dZjqvNanQFQvZLIGm9XxpbL1rZPazmuzSvvjzXqlu02rzWaj+7t7rZZLLRad2jb1+OXlVd++fdPxfNHpMujt7U1fvnzR29ubTqej+j7brRxckEuCW164tc7OdbedB/tzflyEfa4EgRq6f892+pdc32sHGz1GTfaf832ldEPvpQby/TVZguo7VNvEx0AgA/4xqa4vt9f58uIpn159/f569N7a8WvPSbfn8lZbt2TZvvu3zuNvBsYBFcm2wuGB48JmafG3zZAD3LYZUwAeDACAJMZYMrC89wUUT4DcupRa5MxCHE5vb28FnJUqWGwdOYwFoaIspXOuZP0Mw1Ayf1BoLPQ4n3CAcp40Dlr6P99A2fcj1NxrS4GzIOIAc84VoMwCcyh4xjF3JqWFenq+sO0/G1tbypJ30W+bTW3fZTcjOMIAFmKULmPQ8fimu8VSSY2HVC4vl14b+16uHyQF9WHQOIZ0XlOIknMKTooG5GTj7lxyfD4+PmocU6YSgRg2u5jnhmG4ysaDpoC/iUaj+n7Q8VhLiEpOfV+BgwQ0LMrnyamcnB4h1PLsMQ7yPpWyQEYS7avzgXmir9YQgp6r1Wpy/qwFs+yGmedpk2AN5lJKmSZk0zhXQR7mtes6ffz4sZzJnD7jaIBRp9M+02GRadZpt9sVZ3BVtjWIYrFYqFt0Ol9S+b5F12lw1REcoxSUDqwD+KBvcwcMfIsOcq4CSpKybHTFmU0wDu0xXrvJwNBHN9AecuOcK/RHjna7fWmnabwulz7LY+WtNLZ0bpj3gNmDhoG5r/KCnkBvWlmHTwDQAKCojIFjH53z8PBQ5AQ6wUsE/Vjwlbm38rLb7UoJb4A1wBroBo0pW5wAPeSBDK1WbSsNw6jFYqm7u20BbtF76HZbxldyWixwqKfSQN5X3rcOa1sGe7/fl4xLZDYZVkHOAZw67fNZ9uv1KmfbJb44Hk95PHeJL0PUYlEDB9Kz+5Kt6H2TIxpTFjLrBvNG31artbxvtF5vtN3e6XQ6ahzJ6l1os8F4ST/rGfKdvn79qsfHJx1PJ7Vdp2EcdTydtVqvtdneab/fSS6dubpYLJMPumkl59R1jc6XXs47NSWDPBUxvVz6/K61YkxniqazbGPOUF4rhKi+J0O0kfdN1gfTIJvL5VLsgaenp7LOwcPQxK5Nw0BmImto1PF40na70WazzYE2tYSz5T9kk0CBGGumdIxxIvcAMfCwDfxCv1g7ZV6JgKoYtEPgCMEOdh2ljD20sUdtcM/b29skO9OWgPbe69u3b9put5NsVQu4UbnBZtRaoNt7X7KjAZsBogBdbalwu9bwDmwRO25AZ1uqHV3AOFnj7Pr28vJSAi3Qt8gJ32FnAIYRfGYD1HgXYwH0sKAZfbCAGc+h56ATa5QtWT2Oo+RSJHWIUUOPjVqDEGPTKhhQn+cIkCKwjvmmHDmBDG3bqlsstFylsZ5zJaTlcqnDfq/lcqVV5t9Dnme76bZBkcwZfMJ4T6eTLpeL7u/v5b0v2cE2ut8GKcGDfI8dVdZ0P6g3YDpyV/iobdV0rgDUBO5gU2KfPDw86O3trbS9XC6LvNh1H1AbuYc36CMbIviVgAF7dFHbtiVox9rkNuiMc8HZv0BLxml1DQAv4KjN3rMAKWurBVuxOVmz0TXz5+ATSWX/xJpNEAW6tTiTZra/pSNBJvPMZ3QpupJS/wR8QGsbYDaOo8ZhUAxB69VK4zDo5XDU+Zxon5xfrgSX2TPPbSWAuZxiR9lqFNa+ZT54hs8WXVfAL+8bjWHUpb9ILoN9Zn4kTQK3seNtICdzRXl8aGP19y1HKX2zfI6usPcwditv/9qrv0yrr9xy6uVCkWqaWkkIekxByWTDKpfsu+UI9ukQ5+wM84oZ7F10S93fP6S985//OnH02XdEdxsose951yHiYvL3xQQyugwqu4DDNsq1GRiO6SzEGKLGUbqcU7uHXaO26xTiUs43anyjpkvVX5p2UXhxsVyoWy61WG60Wa+0Wi21WC60XKT1ftW1Wq4SsL5ZrfS4Wuof/9N/0tcvX/X28qLL6ZTSNtsUZNA2lLrkrOI6O845uUYFfOjHi/anN4UCcI86HF/109/+qKfnJ/3+p99rtdzoD3/4RS9vex2OR52OZ/nRqw9RQz7z23mntmn0+HifA7iTTA8mwKusZZo6cllT7L55yDLPnDSZVlZ3leCdG84tK1/Xjsugpknnz9+a+1u+qysHWpQcTkxFBVdyOS2DZb+ym3zuXJy1iSzz7jijWe03z3Eff0/oOxvAtaPPjiPLQP7bO5dKyRp6ldK35rK0xb6hvfecw7THz/echIzV7pVvvV+6fc6kff9cf0Kj+jMfmm7asCAmbVqAwgYtWh3onFM0oKdvGql5n/5j1ovtrG/Qdv6cLc9s3zm/z4Ju9Jl7LL0munLWru3nfA7mn6WfUfas4UzN/L3y9+ab6MxnzIctkx5mc3gbwLcZ/957c9S5BeqieUemi7fynt8RbwOAc9nvxzDRXzEmANb7aXAJzxBIUefXzuO1rz+ECmxW/ZFFtNge/ibvVxK5yU/nJN+6UiI3aArm0+/ah+m51nb89vdbvP3e9R6P2XaiVPT+1box40HLt+nZpIPtd06ugJ5WhudtTb5zevedlibv6t2okqVux4pcJpr7wgvMpZudKWDfN+cn2pvPnTfvneuBoq+Mzk/s5YreLu/N+mkOrM51VCqTndbBoGDonQgR8qIW5UsJ8alslpWmfIbvLfUnt+WTzeiz3NpAJ6tDQjDymp5+F3wuNDHzlKDjesV4uzrALb64NW92nvDR2s/m7f5aIELt1/u262Q9Np+lz2+kKs+uZPLeDqSdvEde3ptqMvlohcZ7ubaTmibZF8208k2Mo1yKgNA4JN0chiDvk6/TucRXjWsy1yjh9M6pdV6r9VJN49S1rRZtq+VioeVqoc1qkY44Wq20XC606rwWi05N49UPQafzRd++paSfwykdP3g8nbU/HPX6+qqvX7/qfD5O9GCMrgQDK75vv3xvfbyer3l1kNvtWLB5IpvfmZP5VdeF64Qh+319b8zBAEb32AoEeU+V+narLzVRsvrUF3p8fJz40ZsmBetgS4EzVD71Ri8afZ63ZXY8761FVtfAo+/R79aaVNtJdLllC3zvum0n/bbrNwPjDAwCWgAW5xGOLu99cXLifKZMrc38wdlhHSMWJCYDyC4yOBOt09dmCjGB1nCyYLUF88mU2m63+vTpU9kQArJYB7d1EDdNUzL6cJ6QkcWYJorf+yvBwIFl+8vvBAxAD5gcxrBZSThbeDcCZ7+3zM0YbdYa4wRIBXgHvMV5R8YXQCzO0IlT0Dkdx7PaGOT6k7oYpMZpvWgVcr/88aQ2SH3sFVyr6JzCMGrh2nROl3cax3p2PGPabDY6nU4FZID31uv15Bxcu+CRPYKzHSc1oHU6i8FpGEY554tRkAymdCbKOIYM8jUFMHPOFcdsAgQToEYbbPi8p/R6dT7Aj/TR8gv9t6AFc0G/LUAICMLcvb6+TrK0nXMFRMX5ieyS+coZyTjXu67T62vKtLVBAsvlSl231OFwLBnEyLitDIGiHfpBLkaN/ajG+RSZHKU2Gwc4m3EEQ1cctFbv4Cwnc5ZM6jS+XstlBUXgf7IwkS+CN3DyIzdpDpsyp4yBfzVAJMq5xAPpuWT6xZictFUnVVllrpE1gAkCM6z82ox5m7HL3AEWontsQAU6BvABfrJHMOz3ez08PBR9ttlstNvttFqtyvmo6AfAd+j9+vpaPufIC0Chh4cUqHI8nib9SgB5q93uIO+tcegLAC/hiPdFhnCOMzZ4JIRR63WtyDFfJ1Jp8kT/y2VQ1yXw++1tV8Dfpmm13x/15z//rPP5rP/wH/6Dnp8/FMCnaSp9k75I/LBcrrReb0pQhMtOYsATgqRijFkfndX3g1artcYx6HA4ZjD+qPP5rPv7B51OZ0lRyyVrotP5nPjk6elDplertus0ZuOwy/fePTwWWp6yjiigjZwWy5y5H5MuIojj/v4h6/o+866T9626rtFyuSq817ad2rZTOmfIqWlaed8UXoPHmCN0FWegszYjezUDkioxVJHpc1/qWeLDcC46G+Db2gUcl8Hf1si0ay28jC60+tPqKkAb7BPWWwt8AiLB3zZLFbvIBrxUfmpKJrcF6OkfGd42cAW9y9rFOy0QbQNoGNf8qBVKTbOmQyPsEqtnGS9t0QfGaau30F/uZb2C/qxzXOhdxkbWKUAu92ATWQCff/AawQDTLNKu9AH7BJ0JXW1FEN5FwBQg/dBTYSFFS4cQ5J1X29VqEikQ6lx09zxQiwAKxktVhy9fvmgcBh12NSu8a1q9fnspDsVzjGq6TufLucjYHBC3F3qS9YSADgI00K0cJWCDqQBTyaqm0gf28m6302qxLDRjvNYpbfkpxlgyhi2NYoz6+vWr7u7uJvJJYAcZm1QWgJ6XmU4D1CUox9r4IYRJKW4bbEv1GviE9Qu6WrASWQPgtfsXa1czrv1+X4LMLpdLAYWRV+YCu5lnkUvAI4BpstpthjMZn9yL/YKORfcy55YmBARg+0J3bGWrC5CrtEbcl6z/5XKpy/miMI7q2lbnYw6OaPLZ68Oopm3L8RzwPfsgK4M2OIW/6QcZ7FammQsCe9q2Tefax6AxBDWN04C85zkZQ9DZBJTSHnNtdRc8YNcM6IyMsE6whlg9Z/m/BpR2V8412rsNLPz2yzrc6M/cARfzel+dv9Up9J6zwz6b/pHh55IDTc44K5Me2m62ifdjVAhjOmvU2GTOuatMTbuH/dWxKu0VQizQQnrOJcedcz5lzrhQsw6jyVCT0xiCwmVUiGfFnK7tz06+aUp2sfdNsnUWnbp2pUXXqW3yv7bVcpnKtafqU0stlwu1S69//uf/qr/+8U867Q9yONdzlg/n+3H+J2Nn3nAAy0khDuqHoBB6NU3Q4iU5rYZROp1Gffz0rKeHR0lO968bvb7u9PK6125/krsMaZ+Zx9G0TSkF3/dU75k698ta0kzPTnXwhnNa5rUDvmWtpO82EERScb4zPkmTdaL6QqRxfM85RSBE+P45jeX2CoQ7l8oqZyzLtlj4ecp3du1K+/+502zq6AaosRmT13Lzflevv0P24kwm7E/uISCvPBOnmYTl73f6MR3LNZB02+k79cW9N6b5++y6Yt95CxRLOjqfY2qesb4+e+97fZ3rlFu0nPRd83yx677OxxxjnIa43LCB5u3M77N/22e+pw/nz7932VLh9tn8myaCIVcALkklk7m8x1XutrS97rOzYqAUwAQQLtVzg+t5sKaByVymf5ZuqXn7d6KFruhnxzuRJcoRl89cARYm8TOCPBnKa7I+M31wJqMTvTINNLu9rtmPXFnDrskxp4X97BYAf+tdt3jqlly897xLTo10ZvwNGXqvj0U2JTlf9VIIFqi9rQPm+sj59+h4OzjRtjeZe13f62b9SH9X4NmaUnYPbNvns3mf7HfzsV6NZfZTpu+39Oqc1+y7m3J0eJSP075Esy7Hsl5e84Z9lw0on/KdpJihd+fU+CavwSZIIcuXSkCJJEWFOE4yntMtzImKLDjnJppqzs82EKGMaUaneb/nz1/bJO+vHXNZe08P3pwXgz9N771tJ0zGJaXC5+/o/dIPpeAJSXJNo8Z7Nb5R630KCsuBTyneKdlXyZ4onCAnZR/Hshx76r1Tk8fQNk5d26nrko+wa1qt1wt1OcB00XVadq0Wy06LtlXXting1qVA5d3+qMulVz+MumQ//+l80ds+lUs/7Pc6HHY6Hk86nY7iSFRoByhO9bry+Q0b4z2bxH5WvnO3gfF5e9+z627Nya33Wf3xvfV8amvFso+YgNCyVVZmNupsnbcJM1TM5l96xpe98Xx/is+O34v9E+uZ7rbft+TlFj3e+/7717Wd+l57c1q/14dfu34zMC5NHWQ4gqwjGIVgN1N8Zx2mOCYlTbIhcO7iKHLOlcm172diMZxx9EgqTlOb7T1fpAAzcJrHGMt5r2Se46zh97Zty9npOP1wYEk16wLH3S2FO2ecudPXtmdBIUpSYmxYR491LtG2zfJmHGTkHI/HqznF+YdTC4c4DkToiEPJAuaWrl3XqVt2WkSv5nDU33ZrPftWcRwVnOTaTu2q0fnU60+XXsE1eh3P6oeg7XKlVq0GpYjB9XqjVlNnFj9x4lrQ0J43a0umxzg9/xxaV2ddAjbnzjobqGD5ys7RvNS7dVwinPW8rORAmjv5mUsL1PC8BRigPY5SW/ry7e1tIitkRZFZCA+QdU17AOXMMwBByu5KWa+n00lPT0/65ZdfCogKqGppYfkDJWsN0blzl7mbG53MH/yN89LqkePxmIHORKfVainvk1PycDhMgm1w5uOM5nmcxjab3DlXzvNE1qZBJaO6rh49YMeNU1iq2VHMrS2RjAFuS9QzlwBV8JLlKRa43W4nSSUbE3AJuQBw58zrt7c3PTw8qGkaPT4+Fh2Fw/7+/l5SPRaBM7PpE8EoHz58KPx/Pp9L6f1UwSOdTU35SvgPnlytlhrHoZTR5ax0nMgWREFWAd1w0icgvi9ZkHwP8JH0UuU9qyM+ffpUMnJtUM/d3V2pPsIaBMiNjN3f35d3IJPoBOgBwETQA/Pw+vqqtm1LyeBxTKXLyea1Z7Q3TSr7GmM6rgRdfBnSvNgzv5EF9CHZiIBzBAoVoLlPmXbMHXMAT5GFbQEAe8YrzxFUAdBkz5y1QCNyTYY9MknwDPKFPrIZx1QSeHh4mGxibFUQxoDOXC6XRd9hG9hKCc65oufoG+se88m40ZPL5bJkOCOTtGGNSfSEPUIFHgOcslUa0Fn01QawIU8WLOq6Tl++fNHz8/OkZDY2lnOulPgFiLLgot0Q8n4yUbmfz9HByAe0s1nhAI9Wd1q6OucK2AjdkS3owjjs+opM2HV2vp7AI7Rt54y1lndh48Gf6Bbmu2maEtzDGmPnxnuv3W5X9BRjRk7sJgJ+YOysAxz3YoMLGHsIoWTUsr5dLhe5cVRUnFQI4J1SrTCAjcua8uHDh5JtD505bgS6fvjwQZJKYOE4piMyWB/ten633ep0OBZ+sNlj8NVylSpV0D/AfOYdANdWfGK9+vDhQ5E16AZND4dDeZbAkjkoD3/CH+gCq4fnWcrwCeNgLJZvbLY490AX5MHqWauTy9nEub/0E5CduYY/4WfmizUY/mYNJWgthJBBrxpU+/b2pqenp9IG40WHW7DZBqFYgFpS2ThbWxA9GscxZSG46VnafC+lDB3mBhrYIGgbBOScm8ghNJ5f0BxAf24PYifa6gJt18prei4kss1aiTxyj7Wz0ZvzgB8bpMF91lEHD9vNt6UT4/i3XFaPW5B7epEla53y0yyn8ox1FsXkXMVxiXMuJY3XbD7n0lhW63Xmkahh6LXoWo2aOiYmvbrh1Jg7iiaOC0DlGIqzNZYMiVxWXYAaxgkC8OFcCriOnPcc831OY1DONM5j8o3cyat1qTqOUz6LPAfBts1SbdupaVu1TaPGR72+vmh/2CmMQz5LUwJJCTG9y8/HJAN0uTqSGAcNw0WHU9TrrpNTozF49X1UCNKPP37Qw/29VsuV7rZb3W13+vLtVa9vR50uo1IVokSq0+WY9RmAjiulISkOqVtAMPyQ+dj6G87ns/bmuCS7d4OP5o5HuweuPFp5c+IL8ZkOinX+5nTT7HJMqat/ZrxrwmN5THN/DGO1zs9JW9bxVn7J4EUIRbicS3215Tc1430797d+t3/P+xJv9P+WA3Icx1JSekImN3Xaz5+7daXvk6y/50y0/bX3vAdK2HunbaYEAj6Ht1ib7B5grivmc2ft1/p3/hlVM1qVf8+IaNWXN/SQGS/yTBtJjg2vGv5577JzMB/bNW1uX/Pn5u3f+uy9PijGSeIZ343xdnaXfbeiFF1aG7LKzeOHpte6JtEsO66zzkRXJbC+KAgeUJX+pMMA9ctaU9C2Wf98mdgSRMP83aJyGe4cd3AuB97AQdMuVrpZQHAqI44+sNb63wa8WDtjfn+dH+ZTKvyuW7L/PmDEPVGanAlePjey9x7v3WrfctBcx93sh8F23uPtuR61NofVH7f4dw50kzme2rw9LqvTbJvXQG1QKpdu1kfmRIl70xJ3bRtB0/JcjJO+Wnpwn/c5HGwW+MUzFhcIsRJ2rnNmnSnrjR1HsV3z7U3eQ2SzqgZ9lHYqP8YQyrnhpY82qMQ+G+OEi2w/bq2B83lJtMw0N3q96qNU/jvxyG0gj3fOZePWffPP+fs9YBzL+pbYO8MrQZZPjK1a7vXZBs574RwY2fhku6Z3p7PbXciygQ7KIHr6LJ0Jnmy+lLDSNk2yc9tGi67NQaGdlm2rpm1TSfSmUVve55K5HqLCOGjsU3n2U5/2q6dzquR5GXpd+l6n81lvu106FvJ40OV8zHva6RE68N082O57OvO9PdY1v+imbEnJjszRTzfbem89vWpn1vbcZprrmlt7pzm2d8suTWx1bTeO46i2SUH+d3d3V7RM5osJwAzTY3yu1g831Vzfs5fm9LkVlML47Njfo+t8Xf01G/a32FHfu34zMG7LVDrnSllBMqwBdqwjwRIcAnBGM0CVc/XcXxw/zl2fZT0nIKU/AbIAw3DQ0Q/KnwJs8Jllkq9fv2oYBm02G0m62vhZgI0NowXX6K8FFvhHezjXYAwytOmTLcNps8iccxPa49jgc9qwY+ZvHKK2nGaMsQAyMVI+d6Pj8VjGSB+Z33lWP/MxL/fpvZcbg/T1ReNff9H/9P/6R/1dt9HDKp/ndv+g8/Gs//rli17/w9/q8R/+TiE26kPQh8dn7V53Gvpei8VS69VKGgadz6eJYx6Bt7xDH3CyWoAYmtose5xzCexYqW1rwAHjt+/iXpuhZR3280wZW5axZiz6wst28bS/27mC1jbbx2Ye4Xiel+hnfPf39wX8tIEMjMM5V5zCfI9DN4EZNbvZOVeAaByEVjHNS9jaOWGDa0vZA7ryOTLCHNjstbnRCI2gQwJSk+HDOYLMAzoE2tE/QC6et0AF4LQFxeE1K7coepuFis5j/p1zRU/RjwSuJWAPmby7uysBD9wHP9hFkUCG19fXAvh+/vxZ2+1WT09PE7oDICKjZPNyEUwETSXp06dPRXfMQQcCl2w2IsDAer3Wt2/fSoYjWZPMdYxRy2Utf8z5jsxxKsne5aoNNQMX0Kvq+Rr4Qt9eXl4KXZfLlbxvSj8BGcnGe3l50Waz0Xa7Lbxuy7qSdYkT21ZieHh4kKSSNS9F3d3VjMC5vl2t1vrd7/6myBbVSfb7vRaLRSlDz5qIPgdYSjRbarXZqB/6EiA1rxZAn+x6BRhLoMLQ9wrDWIAXm4XqnCtza/+xTtq5t0cOoBcAi1n/5oCPDbqaZ1465yaldwmEsOuzBTiQYwuaNU2j/X5fPmMuJZXSzPA0uor3EVxCxi3A3vPzc6EjPIq+seso9AMcQ3dbIxBdafUJ8gUv01cLAHvvS1l2QCoAdnSwBYstT0A/W0J6HhkKrzBvFiSDl2wQFWsMNhZ62q6p1ri1YwXAZd4JHsRuJBjG8oXN5rR2FPNnK/egS63eogoJ8s8ZztAshDA5zxo5eHl5Ke3sdrsSdMDF+sJ507wbmUP3z20xAoysjYWtS9+aptHmbqtdLk0OTZkTgF67llv9xbgtAExggvf1TG67rtpS5ZaXebYeI1P7bUHMtm308PAwWc9t9jHvsUEY4zgWOUZ3crEGMkbm8xZPwHuW7+052QQyWNCcQAAbyIuO896XNc1uEC3/os9suXYCaXiXPcrAVs6CFsg6feLccvSADUJBru2xLvSXwDV0FfrH2sDIIG0R/GUr/Mx1rbX7U5b+UjHLLUdYobsJklquVwrZPmUNg7aMF7uL+WH+AL7hR3S63QPZACb4Fb5H143jmDIgjHOUdYyL+USHw3vokfleC3rAy/TVBtlaHmce2AsjC//LAOOUcJ5mqVkdoeJWs47U5EjjnhiT41UhznR2KgUuV8dKhkKMMu/0Wi3X2qw38t7pcr5otVxMdF7uwNSRM3NmzJ1DZd8lSTG/y5SerM1GyTvFnC2d8PxUTju/KTsOswzHsTgB0/uCXCnPnsYXhlF9OZuvtnE+e12VvxxxsCbsJTonxZAde744kKz+n469wnMupiyi6IL6/qjXt2+KodUYpL4f1Q+9Yhz1008/6m6z1f3dnZ6fn/T4+KLPn1/0ujtovz/rdLqkI52GlJ3VNl7RuXI2o1zKDFKm9zjWyjRzPw36Fj/BZrORb1rtdjs5V6uIFUemc2WuacvyQfp5GwxJ/JTpMfWIm2dvObpcyi5knykc9BW8jDFlP948kTD3ucyLdQCa/mXGz2/M/DIDjqKAd1XbmLWTIL2ZQzW/l1vDJCuKs2pjLaUOAOETL3uX9ME4DhmkuAFMmX7w+1wPzWXUOUDx2+db2mvuuP3ez3k/mHs7x/DPHAyxvkf7t7WXvXNyEz3rUhUH+hqn0GayHRKtLfPdosd747e0Kf2Nt9uy6xfXLfBpfs+tfty6x977vftoS3nUzl2Dc5YX3xuncMgXB3tqMUrmbGlJcmX9SB9Og7x4N+tt+nv6bgsmNc0so98A2rVvNrMuFlmy/ywdbD8seFVo6ZscJJbOOJ++3GnOHvM+237IJWDx10AceAMbyPrRLT8415jfrzNY688wecctfiw67gYP2/vtZyGEQhN7j3MuHScSbush+57yvrye2z5CCysjc3rZ/Ww6J10zfprKT9pnejk31V+3xlfX7+vy2em7nDg1XnI8X5IJ/FXJxsh9Vap2U+2qWD4H0CTKi3dWADfTx9h/VOkhKz9E48cx9h+nulg6zPnJ53+WFox34ou8moHpXNSLd5k10MnQMtmc8tdyaJ9nH3GL9+e6uuoO+3n9l26/1o1uNu5bwDh9s7S5JW/vBVKkv+cltG1fqy3gkSMUxnw+si0n59U2rXzj1fgaaJDWtGS7tk5qvU9Hn/lUybPrUpCnzz601XKprutL1ndLMkCX/Dxt06j1lGTPwWxjrig0pKSYSw6I5gif4Fr1w6C+H3Q6X3Q8n3Q8HHQ4pXLqx/NJYRykMCqE60p08OhcR9zSTe/9ffu7eMscvb4vVl6f88d77/xe3+xl8dH3np2Pd66b5LApq31p+zcMgxbdYgKMZ2FMQbIcDeT9RMYs1jrRD9nut37C743zlv03n9+5HWCvKmv12Vv2zG+xif6l128Gxm2WNpt9HOYQlFKyMcZSBhRHni0JjfNQUjkDmvM32ZiRWeKcK0AMmYU4amnPueTkxilHeUabyYSziXNRrfOJd1hjAWCNyQNI4XscOUwKWTEWhGQice5ZcNWWCIQpcS5WoGepw+FQnDUALDi5bXYQgIUNDBiGQXd3dxMQkKwhMk+6rtPb21txmDnnipOPAAbGOS+jz0Wfx3FUHKO6bqk///xN//f/6/9Nz+dRm+jlGq/FZqO//4d/0ON//A9aLpbqLxf1sVf0jS7nc9FXTZPOgmu80/l8KiCABWfsWZnwBoIBTzIfztXgi7mzC95mXLZNuwmDLgRZzJ1nzCm/WwclbUj1vG8co9CSuYCvuGKMkywzeHHO284l4JTzM+EN5sYGU9BvC4w650rGU3IkVkPk27dvxdFtHagWDLdlRC1Ig1N2v9/r8fFR6/W6nEdpgWQAB5yx8/Hi3ASMsRUlmmYh7+s8Mvc4pW1f4VccrTjJcQLZsqR8Dy/w01YKwBkKTcicBeTEMZzOTm4VYygOfMZsgUNbLtmCShaQA9wNIRTAlkxOshDtebHW4Q2/U/qUvlnQEXpxZrEFuAlagE5J7qtTnhL1FthJa0Bf5mBerjo5qk+6v0+Z1WQ02gW+BreMBYiAZmSvnk5HLZcJrHh5eSnjZ47IAD4ejwX8RM/Bh5fLpZx5jy59fX0tgQfOpSCR3e5Vu92uAEuXy0Wn06nwt3MqlRyYSwKe7DvIpragOrIcY1TMTi9ANBsgBGgHMLDdbrXb7bTb7YrznioKnFqInqR6COAgsmTBJbs+Nk0qVc+c2+ovljctYGUBV2vo0S+7mWXtI7Bis9mYEvqhyAp9ZE0j8x0jzq6NPEMgC8EiAC+2/C/yczgcCiCMXANcHY/HSfAJY6B95AKwzK4R1oEHDWzpY+YRebHgi81wtNnyttS2LYtOEJA1dAGDmB/4Cd2PzuF3xmV1DzS0ZZbRa3atnINGrAU1SKwpgTq3stDoowVOoQuZ98dj2lw9PKSzbuF5Ww3D8ihzCr9DcxsIJ6lkiJ9OJ338+LHYUofDoayR6/VaT09PhVfg1b7vtdvtSvAMeprAS2vjQS9sXmuj2WMsHh4eCg0A75gL5N5uNuwcUe3IOVfG1XVdWTtYt5lrbAlojW/UOqFjrKCmnJPLG9pxHHU+n0uWvQ3gg9/RXVVf1/Vmu90W2wVZBFykIgjzBVhvgfGmacoxMvAa68YuR6cjA9gQVFex80H7jIcAYJslDi9Ymsz3KcgpcoJtSRY/a6+tXMWah97BHkCHsreBR7D3OKqB/gG4QwM+t/LH/PCPPrFX4x1JVurGdW6bwA/xfC7Z5gT00DbrFnPFu21VKu6xayE233wvZrPdWVeQaS67P6E9G6wxd0IwFqvrrF60AUU26x3etvtCSwer99nz/uuvKM6BjVFybroPw5E4d13aW0pwiVzJGilPGycEf2tCK69xCApNqpDy+PCg9Wql8/ko5+7N+yqYyPx/z6lx7WDJoMsVACHFWLNKXPCTwfnUaeF45XHvuwKKpysB4zGDsS6hqPJ+Wd+Zz/seI4FIsQCTPtsYQySIPPMV/C6clrfAAkhDUFu2+7qFoqT9/qBh+Ksu/VmXy0mX/qRL32u/O+uHHz/q+cOD7u83enzY6Hc/ftBud9Tb20Fvb3u9vR30ctzqeEyyeL5cFMaLnKSmqfuZGKN8cy0H8Mfb21sKvs0Z8ylYcZGDVwcNA/vJvCcch6ssr/kcp5/B0KECUJo9a7jgXechJXfL38a5Ztyfvzljcc6fds5ujeWqP7N7nbdOQOR12n4MIQ+/8oZpQQAxBc6NrgAjkkqWeohBUUFNcVzf7uu/5LJrm3WQlt4Z+X6Pnvayzlb7fcH83TXQYfW1rVTy7rzcmD/bXtA1v+e7r3jM6iwLdMy/T3NrfAvOXTnT7bjt37cc3vY+23+c0vR30m5Wdd7IhPVl2uta16qUUrcBPD5Mz5ef938OOl6NM0rzWTKsftUv294t+kz+9l6NuwGqKh2p4H2qLx2vgGA6MF/z5vrqumy4V1N102xg0+eTTkv8PgPNkFwnNW2b1ovfwAPWPrWBeJV2zXWnTFv8s2x8i//yFxrN3E/19e3nhjAN6J7Q1mTzz2k2l0/eX/XhdI6tDprbFFe6w9L9Bn+yfgFUzi8L/sBHzs3G4lI1G+eTHeLCTL+/IzvBHuSQ2RGQvPTVmf1cO61OlOz0QcNYqyUEE1iWjpjRdB3MZ4TflP8yNldtPqvX39Ehc73IZzfbvvE7c+rMO0KMRiauAbi5vN7mz3DzOXulz27P/S2+uXXPfPzXAZD13soLktVBiewzfSTJxWmiAvs2u49pckJY8Wdk+4p942q10mKZSp132S9F+XOSWPAXtM6raWNZQ4psx3ys1DDqcElJeJdjrdQ1jKOGMGoYgsYxaBiHupfyvQ6HQ8kOPx7TueJDGI2NFyQPWJuCOK3OsvN1y1613/32C9uzPj+fL27zus37t5691d+rN7+jr37tWav/7D4m2mc03cOFMKrxTtv1Wtv1WsfDWY2zVZKznIWopmsl5yY2n/URwO9N293cz91at21f35Ol9+znOc2Qk/f013uf8fy/1Bb+F5VSR8GM41jOBJw7Ga0SwrlHpgAOZAuYIOSSSolB6xjjXutcAZTHEWWBd0nFAYHT8e3trSgtnFY268VuGHmGUrcQFGctz+HssuVjAVhsRgK/M1bux4EFGMPzON8Xi4VeX1+LExmnKqXcycbDSYkTEGejBVkJBLDZgjjGnUtOU8qKMne2tCbjwNGJoxkQNcZ0ru7xeFQ/Bu2aVv/YX7T63/yvpeNZr5ez/Hqhv/9f/ff6m//xf5R8o0HSeRwV01FyOp3PcspO8/NZw+WsJuaIMtWz/7z3xTkuqYwDENRmgE2MmxgnQCRjtxs7nGB2U8Gz0OXf//t/L+ec/tN/+k9XoBLvop+AX+nz9A9nI85uHH30jQxwQCAc/dDf9h1H6el0KuWaGTNAIDxq5cwCizGmjF0CMLjatil8CO8cj0c9Pj5OgBeb2Y6zkz5DT0kFZJBUyiTDT8/Pz+UM0n/6p3+alCvGSWyNDmSqOnQHOcfZxdOsVBys8AZ6AjkAgAIAsjScK/40l24C/lldhUPZZo465/Tp0yd9+fLFLB7jJBOONgDordMZWjFvi8WinM/tfSp1fzgcShDN3d2dTqdT0V1kL+Kstk75L1++qOu6kkUHrxOYwDxQVcIeX4Cz2tLiy5cvqZypAQbRHwBXbdtOMnzJPvO+0cvLS5Fbsu3sHL69vert7VU//fTT5HxigNa2bfXly5eSXR1CKO+CByilKiXgmuNAoO3lctEPP/xQ2oSnoIP3qcRy36cy68jiOpcWZdxdt8jGRzVmAJ+QvZeXlyJHrC3oWn76PBfIoDQN7LAGySGXu3SuVhlhnV60XVm30IGr1Uq73a7oTPgQUMg5p5eXl8KDBAZxARBYHcr7qGZCX9CV8I0NbAIQYe4Bomx5ZcZ1f39f3kWQEvrXZnfDDwCSGHf8vL+/n5RRBoBkvlmbCXQh2IX5sn23a+XpdCp9wpawASDIINnI0NsG1zA/1v5hTFYH0Ad4G5mBvtAIWZ5X9EGmobvVtQTZoId5DvuEvnDZjHJ0CEFJXMjAPHvcBn5IKus7RxEAAr6+vpY15enpqcje4XAoQUiM/XA4lOAYu0ZRlprxAjYjy03TlOMOXl5e9PnzZ93f35fzn6Eh+gearNfrAmymwJldAa5DCKV6BXYBOo31HFou1yvJ1WpAVImwQRzMnz1CwQZVWnDOOqShO7KI3UHWMvezObfyyhyzRhEIFH3KHD4cDiUj/XQ6lTl7eXkpm3TmnDlkjMwb7wM0t9nCyBprOGOkXWwVW61nHFOVDI6WwI6zDgZJxebabrdl3UR+kSv6wHqCPW9LDsPz2Bc2MM2CvsgSunzuTLJ2D/OJTLZtKrGPbLBWQBMb4MZ+AhuDtm32OQC4DbCY61zvm0IH6AdvkwGOqwP+tMFsNjjUBuugo/mOuaef2LdWf0gq8zJx4Az1aBvFONHTFgy3Nj7rBu+xez3sa2SNdYQLG80C9oyDfthgcuj2b7nQW9aZcMtRYO9JP/lXHaxe0+ygqHH2TL5iKiHsmlRmfLwMGsdkRxCU9JqPXPie82PuSPn+FZXKumcHVlQGBukXOqqXyKwlCyhmRzGOFO8VQtSQbsrASSMpTED1xjeKzWvKcCsQRuYl73KSeM4MdDGd7elzvkYkcMOlTHTl/V7mvzp/ZC7WPal3XopO/TmobTs1jdM4nrU7fNb5stP+sNPxcNF5N+j165seHtd6fNro6Xmjp6dHffqw1cenO/V90KUP+rq/aLc76HQ557XjpP3xpGEIuuQ1ITnV+4ltwu+Wr8KYgof2h0MCc0wAr53LtEevgM3cSVYd6XNn+m1nWimjX/hTRaah4RxQN0SWN7pm3gfGd/O9N5u7dv7dkrmJLM76ZulhdazT9KxnaHflqDWlo+cANVfTNJrnxt/q+63vrN4ydxRdLd0+a3euj75Hy1uAHs/wETS0+3dbwWZOn/nf4zjKWd+Nomz1jFHxnTmcnq1JW7ZPyfdyfYSO904hVCfzqCgfaf/2eJMTO733PR1e36tU8SHWIAJAFW6P8RqFvsVzlmblHvNo+dzcRz9u9THk/5qrs8WnfWl8crpb/p33yTWN4lgBWcsDkt79+3uX0+wdhm+tb++WzF3NhQEe59/Z/tggCe4tfK1Kw7GvSSTw/CS4KjsMg8JV8O61vI2TMb137zw4ZU6L0t84fe49WoPx2f5PAhx8opltz8q37WP5jMXT9G2uc27x9uTe0rlZf+163zRqmnT8XuWBaSnn0l7UhKkt39yi6fy+7123+JDPWGfnen8ajOQUA8B6aVVy2CbYftPn7P6DfuQnK+litsH4aeho+/n+2pJsqDTn7wcxTGhxY42Y0+qWLqp/T8dln5ve937m65xHJ2u2mwaq1PEAdk+rjNp22IPbdY55RnZctl+WXTuRKbv/Yx/cNU7LJlcAblu1zqttG3Vtozb7Frz3ck2U8ylYpHEp27sE8yr5o/v+pMuh0TCMBW8YYw7CCClYZhxzELiyvRhTIMMQgi7nXofTWcfTUZe+13i5aNi/6Xw+qg/oLyfFIIVeYo8ZQ9k7hhA0Dr9eFeLW5/M9xnflztVn3wv44/eUff/r4O2tfv3W7ye6dyZPc7599+9Yx8XF3pdE4d14mPF4rc7DZX1zMcaJD8l7r0bX/PovpYfda9gxzmXl/5/XbwbGKSvKICzwY3/iEKJkOpddNHGC3d3dFaOTLB2pGupk11mwCyeXdZxbYAEHe4y1zHqMNfMT5WQBTZvhjRMcRxgKiewuW+KZd1A2kQunFI5fBBAms/0ex1FPT0+6XC4lq4V/MdYz+HCqEGxgmZa+2+w3Ox6cdRbc5/7lcqnNZqMQwuQcROvMh0Z2zM654ozkfNcYo4ZxlGuW+t/+H/8vuv/f/Z/l+4uOw1nDolFYdvqL81pEqbsMGlspeK8YpeP5pP54UbdYanG/Vde1Ory9qeuuzyKkfza7wzq7bGZSMTLNvFBKOf29Ut/XQAb+AZgybzjwL5eLPn36pP/uv/vv9I//+I/F8UjggpUFC3IulwuxaHMGI05hgkFuKXcc3BOhzYsjbXMOqXOujM2em4wSgobwMvO62+0KTc/nc87+rk49HKIWRAZk+PbtW+kLcsX7rAwwVutAxOH79vamr1+/FqczcyqpnM+JoxVwwjomk/ycJ+2TCYdDl3ZsEAL3WdklmABwEH2EriIbgwXFOVdkCBrgpIZWFtAh+9BmctsS6R8+fCjO9s+fPxdHlNUH6Dvk4eHhoYC2BErYRZaSp8xJKonoSrADc4QuA/RBf3/8+LFkH6I3yeJLdO1LaVn0OAC8zZScB2nAVwlsCiWYAz5CD0LXrmv1ww8/SKql4OEjKWXwPjw8XPHi169fS4nuX375pehb+kFwwfPzc5mj5+fnArKjp+GpxDuarA82S5DKAKvVZnI0COCmczUr0JbgBaBi/u7u7jTmjTbBXABkrGlWN3hfs7fRVQBIXVNBFO6b3w/PA1i8vb3p7u6uyAA63wYr0B4gl12PoYWtXkE/0ct2fYYPAb9tFj2Ap23fgn/0DZ3CmGxQDOsjfIgu4ULHI5P0n0zyxWKh5+dnHQ6HMq+M3xp1AOX0yW6koDFjtkdJ2IAFKQHD9D3GBN7e398X4JA2bdUbGzyIfKO7eQ+8hgzwXsaNHQUNkTM7f3NHhV23oCE8YQPsLBBv+dcGKmKPoTv5/sOHD6XCAhnh8ITN6I0xBXtxvj00Ri8R6AMgaJ11fd+XIDFAQ++9vn79WsAzeGm73Rab9e3trXzuvS/rAVnQgOkcowDfAgDTr8Wqnv2OXcCYWE/tGcisgbXSSy3BbXWAXQtjjJOgBwv81cCeTotuUdYt55z2+72+fv1axnb/8JDsttxHgvPQk5ZHbMYXY7B7B2tf2mBANkjWZoHmzLsNouN5bD346+7uTufzWY+Pj0UmbGUkZAT7Gn1FwAA0xFYg0IzKS1RBYV43m03RLVTFsnJoM/PtMQToNgKx4A+CK3gf1Ue22+1El1s6ELwgqQQ0QH94jD7ZwBbWZuT+YgKY4f95cMEQq9PIBoAgk3ZfhtxaHXs+n8txFtjtdt2Rpo4A+x4CImKMCmOQXN14W9t3HpgF/edrA3OB/LEOzeXlVt8sT9v9iN2H/Gsv76fb9dpcKoGe3p+y6YrzJ8SUoYSfwdestehcytDIGRwxpoyNQAlQOTkf5X0j7xqFURqidBx6tYtG988P+vDhWd++vJg+AaomvTGEcUoPkzVXkrqz47V8TjZNjPX7KSUUQgbB1cgM1zh182PZuWUpP9dN9YFGLrKOm8xPMgir31XRSy64dMburIvRZed8yBknhUcqWBZjmqvSpIsaY3UghjHqEi4K44uGcNHpstOXt63uvt3p8duDnr4+6fk5yf9qvdRysVS3aPXpw6gPz3cK452GYdTlPOh07tVfgs7nXn0/6NL3OvYXnU8pMHAcovoxqO8HDf2gEFKgST9eNIa0HoyK6cjenEEvxuicnFpJrZyvgORi6TSGQalEJuCB1xigrjJdKv0hYeMq4GodopaPUkDENaBZ5tdTNj5M25k4EA3gFRNCWDIcY5Wd8ohL4JaV5bkjtTj0aFPTrKOYAdTGXYNDtDHXE7Upw4DzyzEe+5npW6z0jTFU/aAZTUhMjlGhgMO1uciB1Hnq3JjG55zLZ3NGM5O1R2McEv/Mxzcbzpjd5M65lHUvSgnnTuY5SoHwaaImpdC9rwAkQTVRSe/NgE3n8vEUo5mLzFKNmtK/GKNSq0FeNRAnDEHRV/4p7/MEC7hy/nZ67zX4YsFR+mb37jHPW4hBYbR0q+/zTaM4BoWx8ml1mJv5cE7jWP2X9KOwv5GLKEqzVq6zU1V1Y0xBVRPZMWPJfQSko8oBMJzLPOHDmNYiWVm164KRIXmNM8c6dg1/p3kLEzpAF++coss6pLQLL1kAkTXdy+sarFEZatQYKBOtlIFv5D/GkDN4bfBMyvdz3ss3Va8NOVubYtspPqwCNJV2VbZcCa4pi16mQebH/HnbNIW+k8nMuoWVMijKNQb0iAnASmcJ+yqKORnFR2doPQ+SiKLkb23OzB3yo2hA2VpWPM7mXq5RzQiu+ijNE+PJgXXwwuyC1ukoEAQUkCwxq/dOcqlMeszlvuVcKq5Q1h0nxaAwpL1L27RmDhgrIKwr72l8tUhKlqzjvb5Ut/Gu6gcrs5JdCyXlwBz0hl0nk70bJHNkhZPkGyMXUpoj5zP7+LJe2GeckZW03kL7PJLSvTwXMYGoRXmYNTNNO4GCrUJZeOqhJN4ZXT5GyadM+CCOcKn6MhZel3zT6io7PsIfrvBGCkzyaiYBR1FOIcmed0oQWQ7Qblw+msXligS059T4tsydb7x8k8/vbgC2GzWNV+fHch5421ig25s9ldOiC2rbJn+XSqB7g7mhx7yZb8bKvzD26seo8ZTW0HFMx60MIaSqEDEB2+zNxzHdB7+NISiMYyqLHmp1sctwVN+n/WOf95H8G8dQy/n3vcZSTQL9Oi2PHmJ6J3Jg5bPMndAZdT9QeEdZv+T5QDSvbCgjO05OLgbFEHMooV1jomIwKsfd1iFz23T+zltjmP/+vc/sO+bt18/ass4pJl3aNakSSQzSeBnVuFabzZ1isH2rlTIKQB1YpHMlwJhsVNc06ciqTJ+gvK6GWCoUlHVfmqw3yLylnrVpSn/4Z/d7zk2qfvBxen5KJ24JIRqZtPeao3X89Vzeun4zMI6jyTpQpHr+doyxgCVkUALC8jwOd/7GICQiDsc0zj4LcACK4eghIwXHK44unDoVoEgTYTOFbaSQjcjBAWKzB2zmFCUUAR/7Pp3ljDMbp5EFUm1GAc58xgHQjqOcyzp9cLThALSAPgpy7pzBUUTbzAX34agB9GE+oRcAvffT7ARbnheHqc0kadtWLkqL4NRGr0t/kjTq3ES5hZdvW3XyOr/tFTqv4KWhSYLVuk6tSw6z6L0O+4N8U8ues2g8PDwU2pAJT7+t4yrGWEAoayxAJwuiWhAOPoX/5tfPP/+sn3/+Wc6lTDX42PbDOr1x1Pb9RcPQT+YMZxzAgXV0MwbuBRyymZFzhyiAD45le4YqbcKr9Nvyk6Rynm0Io5zzV4Eju92u3MPn88wYxoyj2ZbtlmqpXwvCMAc2i6wadjVbEl1jf/b9MAEXjsdjccpCH/QXWXr2TF8raxaMszKV9E49S8oCksgM2YfIig1K4B3JWX8pTmrOmg4h6OnpSTi0LVhlKyHgzEU+LcAMyGv5H3DAlp5G9wD2wA8WYGbOcHCT4QoIc3d3V9rquqUeHx9Ladfn5+cCrCfn8kW73VvpDzTinqSreq3Xbcn2tlHSzHvbdpMAiGEYSgYowHXb1ixfzvTmXc45PT8/TwIaAIkAKOC719fXyRnKzIfVh29vb0UOyALHYZ4yKBPIwjmw8CG0ttU2Xl9ftVqtSnZ2OaakqdVW4EN4ya5jAOD8zlEcwzBou9koDBV4tpmnBEUx1zj9JU1KLtvAI6u/kHX6DMgwd/ChZ3kOPcd30IWyx8goMmADtWgbIJj+so7yPQEH6MlhGErwBoEcFixCd22320JbdBDZ1dg5lgexP8jYR3/ZoBtbusoGNljAD1owXnQV65UNrrBBIxaQpW0bOMb6ZGkzfyc8gSzYAAEuG9wzl0/eZ9dqAiS5D7vIOTexZ5C9eV94D2tp27YF3EZ+7dpIUITlMXgYegKKY3sx78fjUXd3d+q6Tl+/fi12JUCsXefoK21DV/jvr3/9q7z3xSakEsx2uy1VMqycwL9N02i322u9WU8iy52rRytQNtvagvaoFf6GN+Bx5oJxzEFCC/gSJHU8ndQae/b5+bnoa+Zvrg/IrCfwBzvUgtH0k3UPutp1EpqUTX6oYOd83rF94CP0ETqTOWIPMY5jOVYDfsGehLeQT0klsAxAGt6iKgD9kaTHx8dJwIft0xz0HYahBFTYs+Cp9kC/d7tdCc7BDsDWs3K43+8na5YN6sHecc6VvRPyDCBt+01Q4GKxkEJQf6mVruBVa7t5V48B4XsCgG1lkbmusDYa8m/3cswh821lduIIz/SS02RNYI21Og/bU6oBOfSHOWMusIlssAZrrH2v/Y6x2Guecf6vuRh33cfUseMIxFFR7vGxArvmKiCZaunKGCnPLGWPUAYYVRxmUnLet12qhvD09JhLQr+TXTgDo5IHJzv6VZ38OENm0N7EyTy/Iv9z02cmoA80umr2Bj3iNEMkqoIsfF6aSUc4TmhZnrHtu7kjBjfQjWdjctTWrkUNYy+d05ngp/Ne+9NO+8Ner697fXt51d3dne7uNlpv1lqvVtpuO3Vtq6ZttWhbLZqFNmsVx+g4jhrGoMvQF6B8HIL6YdSl79X3o8Y+qB/6nGHeawij+mFUGDMfxKAxcAa2SvBmBUPS2c7etQquAthj+A1HCcSUuTfll0y1Ij4462eOM57PdE/9aIuD3wdzPnBxwknRxQLWFJ6KTrnGvpktV516md81e7+b8PDciRdLOzyGs89AjXJuyvYO52/ulsrdM96as1qek/rWCnJMXmD1iCF741x+Khb5iG76XFAGxC2f4xOVCvDoVPcqVzrCXiHmQfJcI++mYPtchpDz9LutF10GW+6zmo8+XDlLM0/g5HWZKZyY71jm2JX/qeg0SpXCK9OsM5WfsQR3pIzDSkKc7nWaYmFM000jI+gc61i29KGbY7ideSeZ0qq5bzJ0vbrcjAOhVRZW69SPwZzKnQeFhkU/hwk/1oHf0p6/Bi6EEOy01yerIKjil5VW82atHp5w34TXo6rAWk2hK5mALqxHTtPs06ga4FMCg74ThPPe+GejmNKwqumJDBZ+ds7waFU2LrgqToaH09CdYgkoM4FMrgaZMaZ5X4uPGbDb9NM5V0F/+MspgdTz/lu50vXaMH/vHKCr38cySMw1F1u5mEIVChDlqgZopFKqPMK7+fuoGlzhMp8QFFXuzXNU9WLef4Rcaj8D9AUyjoDWyoGN8Woc16BcM2HHcta14ex0BAzMUWVt7vdJz3FUQJ01Z9eGoqK9SsBQGWNmw7zGpqCAGjFX+TGW9cPaimUYpT9T3neuS9WQjNnnzRy4LHvOJ/Dam899nse2bdRk21fsUTI43eTfm+JbatQaALxtGzWtn4Dd3Lfw2XfXNFdguNUFrQ+Gb6quSgEQGfiMUX02CEIGemNMPBNzQETIIGkY8x5asQDd8FhNAJwC4DZJs2ISQcfLsdiS7Bnt/hye4x0FfJUmf1sevcWzk5/wE79XQw1W0NzemtiG0fK5lT30mOWuWNqPs2fnF76C+Tt+7XrvuffasGuAtRfRWc4pVwDLgdv9oMY1Wq/W2qw3E19fWW9inOpkaz8oy4xvZAsRUXVnQk/3vq79tXVqsne3n0sinMJrPvbpVW0/N/lsajuZZfo3XL8ZGMexY0sHStPsIFvaHCc8DiacHXZgAGFc1mmC08pmw/A7DjkczTg9AYnoB05rzjwkq886KHBM2/fajAeyQayD5vX1tSgxMitw4r++vhYHOg4UxpYmKRbHDcrHgnC2DKTNZrOZo1LNOIFGON1w/gN6WKVFmxbs4Vnmz9LQBkHgALMRbPas60JT79T7QeNSOg0nNZ2XWy/TAjf2WsVW6+1SbtHq7KKiy+e9hVGr5VLeeR3PFynWbBCpZkNaJytzPAdYLKCCo5jMIPgWmvf9ReNYo6akaSlJAEbojBPRZvkwp7aqAjSrwSSV55AHC/DzDhYieNw6wwD/qJjAHNpxwheAJ7YcNUYofbd9wWlIPy6XYdK+DSywJbahG7zqnCtZjdZ5SgAJ2enMmT3WYLlc6scffyxOxLe3t8kxCM65cpYmjvcESJzUNL7wPUAA/cGJTYYzsg54boEm+oROQ48dj0d13ULeNxMeCiEUfRBjLBmGh8OhyKcFIJ1LYDiOWYIDoLGk4oRHH1mdZ+WQ8rw208mCxTilvffa7/dlvGRCocsZ+2q10tvbW3FY2/PZ7XnG6/W6ZLMnHThkYzIB21+/fp04xheLhVarlV5fX8v8obOZS6nOA5nAgPYxxgyI1fOOGRtgD9mKq9XGlGf3BZyHzwHG0CuHw0EPDw9lLbGAmM2Ah/fTfa6UaabctQU8ElDitd8fCjgNX6JvCWIAqADIZq4JQuhNFrF1+AN+sabaIBdoiFw2vlEw5dYIkIDefI7sE7hC27ZErzVOCP6glD9AjAWrKL3N+mZ1rNWv8CnvQj4JvLOf25LpgKUPDw9XupWx2Yzb3W5X5pG11+oqeId+oQ8IzkDW7LrPeACN0NXWyWGBaABS9DL3zI2+z58/l7Lp6PVv376VChjWloBGtioG/UJW0Ee2LDw0s6Wb0Ue73a4EOEEjeAwegRcJOgL8spUQnHMFsIPX0Gt2XYFO1i7ZbreFl+aBkjaYgSMS0AfwNmXG+Rs7kPfbcs7w4OPjYzl2gc8AQcdxnJRdh6/v7++LfSCpBB8xnru7O93f3090gNUZ0LJd1vPk4eW3tzetVqsSFICMSSqgKuA1MscauN/vFWMK9EHG0e0cu4ENx78SIGiAQnQKY7tcLjqdz+qWi/IMthBZzLvdrvCVDeoCmGfNmu8BCHhFltAr6ByOf0D+kXd7vjyyhdwSyAVfMq+2agABB5a2tFGD2qp9hkzCu9gC6BeqtNAmOtTKOfoNXkIWbWALvIUttNlsyryii1i/4HPk1Mq5Pe/dgr42QAP5QvfjnEUHwAPsAbzPVRE2a8W8llt73O61WPds8IoNrqCvjMVW7GEM2CF8Nl/vuq7TqFptBHlD/yFv8B40pD3uYf3gO9t/5BVdaYOXbEAnPDh3wP5rLxtwNv9363rPkcB1y5lq20vzNJaskpR1UJ0ii8VST0/PN51fZe+SPkjgOY5G/boT6ZbT6MrRZXxk1T06/X8F4G/TiL4Wp9B3aPRbvis0d24KQL4zR/P2Sn/MZ2nd6jUMF136k07Ho3a7N72+bvMxaFttNut07vv9s1arpVbrpRaLVl3XqOuSkzbpyuxr0EopQ2hUGIOGMTlGk6M0O0X7UX0f1I+j+sugSx80DqPGMeb7g8IYdQ6nnB1ez9ZNPCGFMZRM0GE8VEc8usWMGyefzay0oMGU7iloYzIHszl0zsupZp0FnzLBeK+LsQCghWPM724GwJqWCypkfWEuf5buiIX7bJ+5r/LJrTfUjBdLg8kdbnr6peX6+ll2HF/hFQaorW+cNebkXJMcjBUa11xKUlCBUgAN47RO1vLimnUkS6eZPvDwZ8kEnfaz6h+rF+wdt/XF9y6ORChviKA4Kj+zSKvOjQURXeXdaMdFA9GIv+3n3LE/VROVNlNd7ma0k/AzZCDN0L4CRzCaM+Oa0ccZOnyHdjfpyrOu/k3nQ6zVJbjvFhhQsoed4cdJn5R1vjP3TMcaowHQbqyN132vsjhfLyc6xwxt9vh0vPDIO/cSXOHcFKTgmgDlIagUCSi8V1e6EoQQ5nJfe+xcBbRDDJqJ72TeSt8mX7ubPxlysvGmARTsy+oRG3O9V/tXsvcnNhJ8zt7QSS6fR+3q+eH0ZQKqRPrlKz/GsqrUdzjU/m1QKq1fKWvYUQEg48ZklDqXwdW8bw05W1ZychHa5yxu4//1LidYxHqci3MuH6uSbdAYNZqzsgtf5PEG/NXz+YzxWrZc0uWWgwswXqptUP2mHqXF8xO7MH83hDGxfNGBiajpXv5yUp6HJJeu0p250WQ5yLSrvALALfm0kjtWsEr/IkdFL7SFn52Us6qbmnXtSIhMAb2A0gn8TsB22pN5+Sbkqklencn0bppGbZP+TgD5lBfalr1O7lueP4LNqhq+tnMlSSH5Bkr2dZ7zEb9ZDpoYw9SXVtqJKs/X4Il0un0KjhxLNjh7p7TvTyXThyEFTfZDr3GooHgIUZdcdcTyxy35qXJ0Gwi/9cytNr532X1bemb6ub3KviTGcuTK965i+8zW3ffvn7Zn+2Dt+vnnv9bWzTUsMtZUDQKdGLINcLmctVh25VjAeeLNrTHN6X9r/YQe9p8d19X9v2EO35tz9tRB8eqs91vXfGz/lus3A+M4gGOMRZAseIeDwWYa8xmOA4SPDT734YjjHn5axwgZDtZxZUFum0E5b5/MYgu0WECYe6R6bmpyeiVCn06XvLHscunoTt4rOwMBN4/FyZ6UlIpznyyc1FbKYuS91kEjTc/otAYbzirGR3u8g8ABsgUt7fgcJxwOOwtg4PAax7E4l3HM4eyy5S9x1lOWGefcctFpiFH9MKhbrdS06Yy3y9DLhahTCOp8o3aMatpG/hwU46BxjDrpkh23KgvXbnfI40ztJGDNF6Fp20THy6XPNGs0jkHpXEQyVdLCf7kMZbGKsYIGMU5L51rBYh5spgkObQxAwG/kAmcYDvR6b1TTtJLIHklpB+fzUZIr0WBtu9BqlbKQklO2USr743IWqlfXLeW9y3M3ZGCq0+l0VghDiVBLxkqKPPO+kXNew9ArxlrSX6rl6Flk07sreIqjn6ADWxq76zq9vb3pw4cPulwu+uWXXxRjAgLJjru/vy9AB3yUfkqLRZflyOnl5ateXl61WHR6fX1VjNKHDx8noAjAqQWazueTdrtdAQUo6YrOADiCzwF90Fnp82RArVadQiDye1DfD6JUEfJtS4VL9Sxfsi4BLtGZOKXZwB6PJy0WrS6XxDMfP37Ufr/PzudBXbfI5WpGLRarrLeCmsbl7K96DjsO7VqWByd70HK51vF40DimM9ISnw9q24U2m61WuXTv29tbcQSvVivd39/reDzqT3/6U+l73/d6fn6WJD09PRUg/MuXb1osEu9wTqst69u2SXd9+vSp0Aa9CMD1yy+f1TRteRfZt9A5le+tWYY///xXPTw8ynuXszrPkpy+vvw5lbVtGvVjOqO76Vrtj0fdPTxoCLWkMWAF5YHRkZTNJqDAnt96uVxSZvoiZwl6r+3DgxRTKarz+aQhRF3GQe1ioW6ZsjHbrtVitdJu95b0eddqjEFN06ofB8l7XcZBjfcaFTUOg2KsAVCU+LUZbqxj6HkLHsETIQTtzweFXNJ0jEFDyHSNIdEpAx7b7TZl1HinpmlT+TeXjKGgBP5xhjaZoLyPtRfwyJbiJVgE/reZ+TxjDS2bzYreYWMI2DEH2AlEsesiVSYw2ABOTqeT1ut1WYctMIh+A3xBx3MeuF2bWfcs+ARYYrMbbZY1Y7P3ExBlAwFCCAX85m/aQhcyB9CHPkvSy8tLkaV5UA3zAGDOnBHYZSsohBDKGm/Hb7NFsUuYI+SEdQSZgm9YU/jZNM0EMLSg2P39fZljdDfZ/vQHfQ99qFKy2WzknCsBXIBq8IgNmpmf8U5mu5Rt32wzDEOvrluoabyOp5PGYVDbdtod9pkeaVO+WC3V94NiGLXO61M/DhrPQb6t/NUucnCK0rrs+uzk8Y3GMa0DTw8PyT4Yaklv5hvgFl6A9vf39wWsRm/Ad23bqnFep8Mx6YXsQGibVv05VbYZh1Ex60jkzgbhdV2XNs0ZnLbBH1RWQj9ha8Nr6AJ4xO4XCHqBv1hz7+7uJsEuBDraADfstLrJr5nJu92ugNq2Qg88Mw+GRDaxNdC38DMyCK8yXkBu/rbBTOxBWBeRfe7BlrTzy7i6rtOHDx8KDz88PBSdx5zYQGTrjEBfov/QgSWoahjU+Eab5UqXvk/OkWGU806LrtOYnUo2aAbZaNs2BwSl8+ta79U4r0XTKsQg5xv1/SVVamtq+TbmHN2FTNJ/9DYBRHZebOA0cw6PJodh3U+xPlp73a5F1kmBfrbgN78TsGbXnLmjw37P87Rteexfe9lx2oAie1WnyRTkt85N54pX7urZuXMjxJRtEmOG2Vz6n3Nei+VKHz9+0qgawMe4ucr+VjWrsfTzvb9n31nnC1d1cIOWTJ3eErBTTKVedQ048970zqlT7b2rOOrfuUpfo4FsXG38Vh/iO/SwNpFvRkUNGkOvy+Ws42Gv3dublsuVlst1qeSxWX7Ver3UZrPWer3Uat1pueq0XLZaLLvk9G29lou8V+hauSXz7iXfFhAlZqB7DFFDP6Z1YYzpX4gJSB9HnYaL+mHQOIxKZ1QGjQMAe8pcSkGe6YgcMppC5HzzDNBnPqV0YwEAZs6y4IKiRsmFZJtCM0mprGa61zufyj0q5lLPko8yQF3+n5PSyWHp2WjnYTb3UdiiNpOLvmWnvVPqH3Nv5rPoDJ9BkGDrds54LwmMwugnsuoyUDBFIqPsGblVxinxXOXaQWfDa5b/6tgTEgRMEtxMYUhqBPAyff7a4X19tvStq227Kz15u+0x07PS4LZDlPfVcppzvV0AGNPfOS3S/ZKztdHrE4UXUjMV4Ps1GtvAMS67/jhngaM5wGj0o1fSy4GsuSkA6PI+zjVOzoB0t+eDsspT53165/S+m+1kISrykdcO+BBle4s2Nhjhlq7kFlfmcRowEM1/7gZtDTFnMjWVQcsjN9uYUSF1Jb0/o3ZXz8cZHW6vR77SyRs4dXKvea9cnlP46rpPE1R/qtCu1jPnXAGQnfm+aWoD8/6z7jMO+Det/b6UNwa8sSzk0FEefTrli6kspEAjJ5UsX9qYrv0u+y00+cwGwFTekdANk5CAwic5QEGjfM6aj6H65F3MpbUVNYYh61t0bxaA4FICGPRSq5AtIiwAQNwQYw0ScNNzwSu/RNnS6VN7bW7U8XMsOiQ9kwF8zYI2M88k2YGvKvtxHEYbloVXir0V5/rAlaNpnHcCrJ7eoyLr6GFr49pAkU7TCmUV0J6WGG9aAijy2dxNOk8++S3qMVBtB5DdqgPozqB28vEkwLttst+prdXwJjoiSs4zk3XvmGydXBUkJi/aZVCxd2rG9ahx7IsNFELUOExxIehl7cJk59djGu1l9979cNE4DmUPdblccjWgYRLw3g8XRQPE231kaTfz2C39aNfn+T/LH7fsA2h2m4/47P226jNTfTZ/F8G6v80eqfr06pt3vrjaV3znnvnPW/e9911a/0LZ18CXSW8EXfqzfnh81IcPz7q/v58cg1313nU/57S/3mdWjPa9/s1p+u7e7da4ZveGEETsqpW799bP77X5a7anvX4zMG5BHn4ijDZThqwN66SKsWaeAmbj0CJTDketLYOIIwPnmS1PDmFwYuIQtIByjNWJbftsnXkAXTiNcCbgWMfBlgDjk8YxKMaa3UZfYowFQGua6oTEucbEWMCAjESysaCnddjM+28n2zrZLXDCXNgMB+vwBrSCvgAVKEnrOASIx3lOto0NRABYKI4b59SEKMkrXILOuQzqep3L0Uo6HFL2k4/JcXe8HNWul2kFzke/jGPNeE2AXT2zOmUV1SCG5bI6yc7nS3JKGwUeozSOQzHWnPM6Hk+FLpavmYu5YwaeguY2Sw9aAargcMeRmJyKVFtIi3kyOJIiT3zTaLFYF7CeRTvxbPqsOu7qRi/xrXJAQC1ftN3e5f5eyruTI7bONYABMs7z0BUn6vPzc8kA5Gxx+A0wmGxFwAmcvgRb4LCn7UTrGnF/OOzzGd9Jth4eHjLo1haA7XA4lHPAv337ps1moz/96U9aLFJACOXtATmTXPYlEw0gzpb0Xq/XmY9tBhNBPMmATMEJtVw0oBqOfPSB1VfWyY9+gl+apla7CCHq5eV1AhjvdvsSxAPPMX9JHwXFeCnOXLIb0QXpvnQ+5DgGrVZpjJSZt0FGnMPLfF8ul3Iu+mKxKGdy0weyatE/nz59Ks7s3W5X9EKMFaiEryiJDBDNPD48PGiz2ZZs87u7u5IRDTBxPp/18vKa9XM6f/jv//7vazCSpHUGMFfrZpL9/emHTwXUVqhOidVqpb/+9a+Ff9nkOef05cuXieOeShUxRl36Xh8+fMiA5qVUFhmzHK/XmwJotpS+HfpyTtAYgha5RHqah0HOO+1zudwkI02hK3ODDNBH+M1mXdry3ejx02ksRq1vGh1y2f+u6zSGUfvDXqt1DhoLQb3JQG3bVqMBXeegITLWNE0pL8/5y6xx8A6VCeCFQqO2LVUw7NpNYJ0Fd9Ef2B5UqJBUgsIs/yWdW8vvAi7B18wxazO8bUE9dAlrtO0na4XNZLQ2BeAZ60YxYFXP4eYdztWsS8Zvs6Ap827XZfq4Wq1KZjMyRvAO6yZl5KWarQrtqEARYyxZ+PTl8fGxfMdcYOsBdKEPAJwJwNvv9xOdAa8kvjwVPuT7xWJR5J45AOxs21bPz8/FJptn7dJfjtzhsvS16zfrHnrQbjABm51zKXrfOTVtq0t/0XiqZfDP57Pedm/577SeRkn9kIImvJMeHh/LvayzIaZtdJPtLd/4XL01ln4Nfa8h02vRJV7G4YdcwLMEYznnCu2XRsfA4zFGxbGWmxyzTG7W66TjJHVtlVnWHcvXziW7o8m6DRAbe9JWV6CMt60qZe1M5pU5Y72zOposcObP8ht/o79tBQj0p7X5CdRhveVz9MUwDCW73LkaLGP3JbwD/oCXaCOEUM64n1c5IEAE3Wz3PHPacKFvOa4KObP3Wv3J98grtOeZu7u7qsOGcSKDMSZH3el00iVcyufoXYJh4FG7D2mbdmIjt52X2rrHsZtqbBkqc0E/m5GPvcC6bNuxe54CdjunmPcNVp+i59CV6D/0o7VnrC2PnpkDGPDLvGKVXSO5z+qqf8s1dxTajf78b6lWbkOWqm1bHazMlQXdLcAdxuRVb5oaGON9oxCdfNPp+eOHpCePp3I8wSnbK7SBE08uKvrvO4vyH6Vc6vccHu8+P/9O11DW/y8vnHilrHM0nmUZ8FwTbMY8O/07/XNK0xgU4pCCEfqzTueDCIJufKv16ucSgLNYLLVcrIrcp2M1llosOnWNK2A6DmPOtIQH2tankqBeapdObrWQ90rFz3zqS3L6PiqEqrdjcGU/mkq4A4y3siXdkb3pOh91GVzKjJqt//Of2ATWzwTNilPXV4dqCPmsXzfNdJGkpukmdKf90q5zCXx0fZ61em4mB6fTXJr+aelw+mWdv85JTUtQmATAWvggJnCknAdb+MOJw6ujUtZgpAMzXuOzyDsF9nFbIv4lzkPbTzcBqpxsSfPU5+aK5pYu1aE8DVZ6z/fFnM4/nzvy09+0VR3Bc6dquPHZb9U98/5VGtwAgTQFu37tsrqesdnPaMeO235+7Xz3+vUpzqBWue8WLaLqedLT/tbvacOcAW+uOcD0azQvPHH1rmvnd4z12ITv8fT8/dgBv/XimfqOWwi0rr5DPuZrcZX/dA92J+9Kz1T9MTk6IIeCXb+PsforOk2/v54L5/xN2ycBJHUvbOdyag+pHv+QsWbAVvrssjqzPA1dLTBuecr26dZ8MfdT3XJ7zHGiq6Fj/d5bsy3mIBRFBTcqxFF9f5H6er/ilJYpVqJ+Pg6jae5WEFFBrQyNpuBUjqvK8+8LfZivuf4Joc80rYFSkko7ZazqJnam7U9pV+moFKuH7L8KHvPvhi50gHsu2Rkmaxt734La3jktF34CnLOvsfurlCxWq7ayP7B2TXqPcrDA1JZO058SG1PJ8hzcYXw9fd+ngL3RnLvdB1ExJwHcMYPdYeojCj63XYPFmPcJD2gKdBe6yZYoTwGKVMRlf2PtKpI3LeBt9yxWNkIcbr7PgqNuxqO3eNd+d8uenf+ct3HrivF9MPb9Z26vJyGGEnB0bVf89ut7Ngr6670+/Nr6b/GnW8FzqHYnp9alwCXvpDAm8CxIev7wrI8fP2i9Xuvl5WXid7x1Wbvh1ndSOl5n3s58LudrzC276pbtdov+xQ7WdN/0Xv9uzed7bX/v+hcB49bJGmN1XFvH2fF41H6/L5suK8woPhQWZXURZoBoCIBTGaCa91hnA4pRUgEQcEzh0LBOHdou0TQGGLeMnhxg9XxhnM22JCi0cM6VrG0Lrien90nOTc+yw5ltQXreC52sAY9DE8chDjvOKrcLg6QJXWzmG4435gMaQx+bscb47HvgA8t8CC10wXlCyW/nnH744YcCHmPoMQZoZbPh6Zs0zUZEsVOe1zr/2BjYspTQFCXD/NMveHHu+LILCPMOgBNjnNCA926321LeEkewbZ85sErBgrM4ze25mAR9cLblvMw+JbdteUkbzEHWnVRLB6f7F7q7u5NzCeQETAY47LqFiCpyzk1KtZ5Op3IuZmec4qvVqjhmv337pre3N4UQ9Lvf/U5PT0/q+15fv37VdrstGWXwzP39fXFqA85AO+eSo/2HH34o5zDv9/tSTpSywodDAqp/+umnwi+AZOfzudCPM5x5h83UjLFmxlkDg0w3+IsKEPf39/ry5UuhOw5rdAGyiiOdMXrvC5hnz2Bv21T69uHhYaJb0KucgZt4udH5XGWfc8CZk2RgNnp72xX+Iiv47u6uBLMMQ+K37XZbnt3tdtput6IEMOPiDPTHx8cSJLHf7/X8vFTTLIrep7Q2PEx/LK0BIT9//lzKoC+Xq0mwEWNlHcFRfn+fMk/IZOUM2AR6rgvt7+7uSvAVAEXSI2N5jsxa1gKcu9AVIBonOiWIOascAAU54Hd0rdVrAEDzjR86hjUDXYPxSuZr0zQ6HA46HA4lM3/uyOedFuzx3heQlIAIABJkxJaTf35+LrRF53tXHTO2P4zFrkHH41Gvr6+TgAr4gPkl4xddyvm56/V6knFuA7ugHcdZEOAC6Gt1JnxGn6E/c2OrSRwOhwJcs2aw1kua9M+WYEa3k7Fr7aA5qIi+I5OcNdpm3UMLG7THRaWN/X5fQaDMO5IKKE5QyX6/LxujuS5crVYTW4P+wMPoMrJKbfYm6ylzBC/Cl5R9Pp/PJVMbmjw9Pent7a2M1Z53D43QnxaUgj7WMQ6dJBVdhJ63IKGdQzaQtEXgD/aOjaoFHIV3xhjlm3pcBke6sOmmGpEFnywgQTY+Mg4wCp2Yo8Z7XcxxCvCsDbQ4Xs7FviaoAplG91mbAlsDHde2rZq20e5tV/gIvrLzBX2sXBEol5wbbsLj1q5k3lizKAdPn+knckbAFiAxbTK3c3CPecceQ7dgi1oQluAd5tLabvSb9QaetkfDMNeUWscmQ1aqoyKU4AToiPzB4/Dv6+trkTPmtlabSv2z+yPG3/d9scNqkKTKHsnun2xQLfYEPF32F0pneGHnWzvS0p31ErqgAziSAzlD50KDso4rBWVhd8Cb1s6DPwkCsvsD6GJtaesAoo/eOXnVyjJW/8dYK5hh69j27F5zHnADjZnr+R4Dm9PKAO1Cl3/rZWX73cv4NeayafsYM5qG/Ng9l91/tj5XhVPy04Y4KshpHKO8S0fYPH980vHQV5qEc6GRdYDYd8yvd50iN37n73+tI+vfcqX3fr8f6T3J+Vv9/9VRZh1QExjDOHfm7Tq1mgIdKUN4DINCPhvdOadz/5LnvFXTtGqbhdqmU9ettVws1XVpjejaTt1ioa6rmVRtV53RbdfJu1beN+o6nMtOvkmO7C6fo+l9qhThXHJa+yY9771T05pADCe5pk25nLGOPOKAjvnzGBXGDPEATmd6hHHMmemDxkEaxxRQ2veDxjFX9QqA8KnqyRAaheAUQiobOg6jhjg9SzMB92R1VQB7DFSfyP2TNMShlC4uMuSCGUvKDOOzNId4MaOCQt5XI5/5nWS55tlO2GSiSWguqc1Yz7tODdSzWEuCsJtm8dGv+odTHPPazSzEWPmwOBFnIFusoLptro1+AgTNZaw6h6cZWvV+eNkex+BmMla6VujpnF2b0jNJZup7+BtZSs/eOFeYsRn5u+VMvS3ntW/18/Hd561tY9u0enIi97N7547f+TNzP9Z1P2842W+M7b2/nTP67cZ93+vbfIz28++9e/o5ubX1s1v3Vx5+/5qvj7aPts3vAS+0MR3LbdrcGtb8eewU+znzaAEqa5tgk8xpfrtvt+h0zXPzIIz587fk3dITv8OtsaL/0me54uulV4yMkcAAKQG5VebfA3fm4/DOT/htfh+2r7MVB/K7Ae55d6kCoDlPxLJ+hTBqQRVBe0+MZs1T1pVmTDIvlPK51/ldoak6z1Wur3Psiw1nh1nKi8sAvi7tJbzzcrnSaF0nqmx7lwIffZPO0Hbe53Lm5pxt77TIGfCc013O62682pz0472Tb/NZ3PiHPOdrpwztdGZ3UONT1YDGZ4C74V3p/O60n5nKELx2zefu6ngB9gtjf9EQ0zEvlyHp6jjWMuWp4tSocj63VNZna/+n9cqcUx+bVAHA8lyUglJ7FUSXyPZnXWT+UpBbyPukQ35nLHbQGMguHyZ2CYlzNQgs6T77HtHnWO2PqR1Wq5NAW4YxB9HHaCbhnYv1/NZ6ZWn0Pd1qf6a5uAbTJzo2Tp+fy//39gu/dQ2at/m9/t/as/zadavf712NU1kLmVuLgz08PWq93SpFsTo1TZfnMgXIJP5IlYhR1dfjJgAU5rgNNk/tN119N7/s87fWIPvc/5e7f+2xpcnuO7F/ZO5d98u5P0/f2E2ySXHI4VDC2DOSMTBsj2FYNkYG9EX0XeaNP4NhvzJsjCUYkDEGjBGkkSiJpClSvDUv3c/tnFP3qr13ZvhF5C/iH7FzV9V5ujUDOLvPU1V7Z8ZlxVorVq7/WitCH3Lg1Fyb7d5VPdvohudez35bdyeDZ9W58wNno5+H2m7uDlq7s4BNFGcPL9bubABYYOIACq2zS5Kd7Vzu9YygEEKVIYuBgaIlQxcHCY4WxuVZJGQ8JOVdHEPJuXOUGR3HIMAm4/VsKQcEmBN0wFmFYw7nKHR2ujkQitGEo5N2cWbjmGLsNzc32UHkTh4HhN1572WTQwjZcQctoQ/jS6Wiu8qYA6jx7Dt3QDlg7s5+sg+5h7V1xzo0ODpKGeue5QjdGBvj8ayJnGUV61K9McbKcYtj1deNjYv2PAIyhKCTkxN98cUXFfjv2V04fz3riTLAOEl9/eB91sPLDqMcHh5KZtL9/X0G9JDb5TKBxPD+9fW1Xr58qYeHh3x+KIBQCCFnRsPPZ2dn2t/f18nJSXbcS9LZ2VkFLCXap/lcXV1lOXXZDaHTcnLYUOIa+Xv37t0EvmxyqfaHh4eclf7+/XtdX1/r9PRUUirLC8h5dnamm5sbDcOQwWjn1XFMFR28/C5OVa+eAe979pqDGPC1A4BefWGz2ej8/Hw6omExgfy3mc+RY+aG3Pd9qHRo3/d6+fJl1seJb8oZ8yEEvXjxIoNji8ViCuDYy7wNQAKveIACfeCMdp6megOAKcA3Y18sCn96xhlzGscxB2p4kMf9/X0uoXt8fJwz7QB+37x5o+VyqYuLi5yZHLtyhjbjWK1WucrB/gRIsR+cnp7mM+IPDg629onb29sMliyXy7w+3bKU040x5oAO9KvLvu9x6BzkBV53erNeAI6ci359fZ3nDR/d3NxUIPgwDBlEJWiK8RBoAN94xuzBwUHOiN9sNlUmJP/W9w8VGO0gBhUZQijlbwkoK4EaizwO6NzyBcBlG2DggVHMlexo2oRvvHIMQJAHrLHOzLENekAekFsHSVyPevlj9kSeo0/uk0o1HQA/zpa/ubnR9fV1zmTNZe3NIcLlfcBjrJcD15Jypi37KrLK3kMgTt/3OTvcgSbsjaOjowrsQlfEGHVycpLP5H54eMiZ4ZvNJrcJzYchHYlAAAo2EnqDfU5SFTRYory3zyhmvwDwJwCP9camYu/2NeEIAfqGl/l+uVzmIINRUYtlCmr4+PGjXrx4kWXe9bwDt+M45goabovCa8gBNt1ms1EMBShED2BjEEjnASXYbFQBgEfog7UDhCRoJA7bGUbv37/X3t5eDh5jX3dbh8ADwM7NWBx58Dhr6NkurDf84C/OrCdBFb6voUuw3RivZ/MjH8i10xWbplTmGPKaLBYLHR8fV+sSYwrgIPiSAAYPZoUHkRWqMMBnblMRDIPMMmaOZnBed97hc9/f3Q6Bp5B53oWYtwdgwYtul/q+FGN5p2Mt+InuIPgDuWfd3P52W5m28jtWjNoMvBMVnuZdhTEyh9YZA78gE+y56L+y/41a7C01bIZcDUpS1guSsk5kr/ZgDmhJu8wDHnfnDrzonzvt+N5p8fNcraO57T87BaDXlDmA8zMG5UxsCk7xrtQGnpf9bspw0aB0tFD6exhGhUWng6NjvX79Wn9++VeFRlKuyjPnHHrKSZHBuiecWrPOsdkG4xZE8qmOkk/vt3FuhW1QvP1u7sr+k2EClycgtQtRIls4PxvUxVQpKoRBXbdWCOn9qwvXk97o1XXpyLG0t5ItXhzXfR+03NtT1y3UdSmAZLlYJOd2l+5dLpbiSJFOJDyQ8TUB5n0C0ruuU9cH9Uvj1ewEn4I1+FzSaO/l2HHOl8kuCgnkFY7jWM7TNF0xKFU3yH9vBg0xOZnJZB/HQeOmPDMOY3VPcpon5/Z6OvszWn8JvPfS8wmAdyenjynLQEh8MsaYzmKPsYDtimUu/WICxlOwADwTpp8FoFH+rHwHgJ/dygoLz0ytebXokdY5Cxif+Cxf45i/koLi5Hi37qf5F/Alte/9pPa7rgZ4cs9GQ3d8zoG8XVcD43XJYakKwmBeY6zolvecdhwyPRIlhVq+Q/PxdHhEhiqSDg7zZ2lz/nP1WVrQSKBAF9LZqMGc1KHQtC4HLxEUoCrQYNtJ/Byd3N7/2N+FJJNe6ybKRF8LnOxlbbuZsdFO/XfPBCe6wxMT70007HbMqZovbRhfISv+NHLXOuF9n3ebfW7cuS0preH0k/OHE+/EPLegAv61/bU2iPsV5+wQqTmLe7raAI1Mk9SYpl0mVeKZPgMq0VT2Pd0X0pYfEzAZQpC6XmFa95YC0YCOGGMGYD0ob57G9Tx9LcrPVOExfR8nuWoBnRRkVAHjwQHDNM4Qgjaj8nhD103PGC37NJ6+offc1dpr6M3SP/tgJw1duSeEih+7ae9Mq5OqmZFNrekZgOoudLn0fDftu4vJf+WgtkLQ3mIKoOynBMYJJAcUT/t20F4/lmdzO8UG4OzuvidYop33lP2NbigUSoQwUJc7xk2dWDba75F3yhi12QBWFz4ZxjGdqz0W/T8M6VhLzuuOCbXOe7AkDQJMLkfADG5f0KbM7qaPMaZA0pEs8lFxY/3ZveM4iMzuBIhvMv+yj7XAPPvRnP6tbY/CY3HST61uHMdRobelaJr0LnJ/rjP5aTfG2BxzYfdVz8yMvf0uav6ZWpcrV9xDV8n6VyzBMEzQ5dXHOo6jqsDWZtwtcfJuFrfpAKli2K0bHttD23FOU7UAsekdVlFDHBWHhF2QlJD8lNt63l8n/R12bkxZDpt7QsMDbTtzenp2z5npM8+dfzN2yy4azb5n7ehz7no2MA4g0jpuQigAGpkkgL9kEuAw4eXGs4VDCJWDy8F0/rnjiH4lVSWwQyjALWALfeDQ5SUL5w2AAM4uP6dxb29fDw/1OcEhlJKJjBcQmaxPiRLYJXjAgSB3tvtC4ejifsbnGRzQkvn5/X7molQcQW5o8KLZZqMybpwjtM+cHJTwctW0GWPMwKpneHuZNOebxWIpqWRysybcM2fAOb+5Ew/gGwcqDkocmmQwetCGg5WtE4vNCgC8BDjUgQHwrG9uXDhD3SHvAR+sbYxRFxcXVVZbjDFn4cD7h4eHGRRGDsjC9uxxZJSMWl9/xpoyJG90fHyUQTR4ETlO8wnZmU42IqA8ABrrhOMdBxv9tHP3LGTApPv7O11fX+v169fZGe3A6tHRoVarjb788ktJ0tdff50DGxaLxeTMX+rk5DiDIWR43d3d6dWrV1kWyCwjWwkg4/z8fGrrYw4eYXyUKM8Rh0M5sxK6OngGgIRjnGxAD2xx4ADwCp4iy9+dQmTFAxQmnVD4EPnjXrLCV6sCcDH+5XKp8/NzDcOg29ubrH8BE8dxzLzlWYYOPnhm32Kx0O3tXd6A3claHPDpRQJeQu6c/8jauLu70+npaeYz+JeMwxcvXmS+Zkxv3rxJGY99r4f1qtLvkvTNN9/kbPb7+3stugL0Q++PHz9mfeF8hOPeM92QrZOTkwy0EChCCXp05+3trQ4ODnRyciJJla7ybEIAYQ8oADyQUgldgrEAGn1O6OIQSql7gtVo2/WPA9HoYT9f20vB3t/f6/7uTp1K0JO/gPu6oxNijHk+rmMp4+8v8uheL4Xs58BDIyosYGOQsYg+gN/6vs/7MnuWgyqAR4D879+/z32TwXtwcKCjo6MczOZBHMwZeTo6Oso6BjlzOedar9e5kgZrzJ726tWrLGvofjI4HciCF9GpZCPDV250shbwAXqCttBRAMS+B8AfgIrYeewxx8fHWSe5M4gqDW63wK/QBPk6OjqqQBh4hb5bWvM59iR0Zh18fcjgZxysP7aYZ+67fco8oAtAq/pSfpm22d9YDwJS0Mv0yf7gQXRuC/Ny3fe94lCqI3kwIfwfQtDDuuhqfzFk/AS9XF9fZx2G3UiW8nK/193tXcXb7HUER3nAKe077yyW5bgS9kR+OihOyWuvHoKNBlgOz0ol45sLPU77tEU72J3Q2c+LXyxSSX/s3PbFiDl6UAjrCQ/CQ/Cg25Pw+OHhYQ7QYP08aJV18mBgt3n7vq/sQObL2rsudZ0IraE3n3uQDPwFzxFEM46j9pZLxaEEKhCkBH15J0JWkCnsOX/xJVjK5wq/r9YrDdMaoDOhjQehsib07e8frCty5QE/2QE2DOpNHrCP6Af97ME2vh6838GH7XuOB0bSrwdz+L7mPNC+O3+ba8s5EuaBhKiUnT/iPIsJCMN5lx4u77BtJjq84O9ho2JygsZO6YzpUWFI8vXm7Wv96Z/+pKZBLM7FXQ6Ndl61I2z72uU82tXeY1flUJs6jNoBXH9Cu3Y3zdLhfNuh8sRX/dRORVqDqKU8cXbGla6kmJxkIUQNQxlJmBzxMU7HpXWhAqg7JRB7uVgoTEB66JKDfNGnY636bqnFYqm9xX4KetUEuJPl1Qf1XUhl2Pup7T7kDPPkeC9neroshiBp2ExO9r76B2+lTLhRoUOn4WwzoAxsJyS3WgU4xxQ04uC2RpI/psybWJzbgzm2N8NCKUOwlE1NSRTls2EYNayLzVGc6FS+SEBGjJOcWvtkgpVstDFBH5N+Gwd33OMA1pQtpIbn0n9w6ONM7/oh31Q50OERcVbz9vmixkQTfS1rO0pVqe5gPwK8G7Lukd0WgZELqmwwdF2lIX03liAf/8plKUYlDBpZL7QtsjNlyjHzBhjz5jbivMtYo6Z2BUkC+LZ5idmbs1emgwg4klo9wwCCup2O3qBF1xXwPYPNHbOy8c5XuJgDCJ66HgM3qnsm0dzpUJ/+dTNEnd3jQrEt/fs4KoMUCgn82eUczz4x7mXftoDB6pmuHl3rjPdx7NqX/Rpik20+MV5g75za8TlUMhNKgJ6/t7g9VtEmbmdwz40VemzTPGTAKXNwALIYWUJuVi6jnfVKqm7hoFRBnkIGlQFQYyx7FVciza7gRPqVQkj7WKyertc9t1nRNFOgonfKkE1zSra90p4RmnVXzGAxQE4O+lIBiPM+Z59v/VNQN4bMm/Uc0zF7XdcrhEGhG0U2fW9BZgmYXuRgty73X/bSsn+mvpa9qnGmQDrW0+aguqrGHM+nKcZsj5TKK1ExbjSMUdpEDXGKr4opnjLGKA0GOk9rvRk9C7rslezjee8cKIVeA+jDOFRgerrf9sBxnJSIMr9uYipX7vv4ZqokM8ZxCmgbNcRBnsE92rj4XDEqboaJFi24XwLpbDcsMpXpVotlRJxadRNLwFmGFoMBnLHsS1me3H6IFgTWrKnbCVJtQ5T+JUr8P7a/tHtC21b+Psw/6zZ1mF5y8j02x1029uNjkNRtH0vSPk+fAR2+RTXooe118lusn137R/4869tJt8aQbd31ZqOzsxc6PT3VYrGsMMzUxvZA5nRji8MV2Y3bn8/Q97G9t5pLM/+t+x+xM9y34p+113NtGq5PyhhnADibcZTguKBcsaSqxHUIIZdO9cUHhKJEIQ6XtoweFw6nEEJ2PErKgKc7TXFyuDPMgVjAAp5x50dyzvYax2UGKXEWMUbKluLogT44yEOgNHnJ5CNwACcX97lDkcvBdeiFg88ZC2cWzkHmTzaeg+Fdl7JuXfm4o5yymzh0cKaFELbOMsXJRBYWPOCO/BjLGelk0eCsC6GvDLU2OtyBjBYQZ+7utAdE8+xE5gTQyfpCC7KfGKtnypWS1SWAgbF5RrwDHDjcyAyClwhEWCwWmT/ciUb7lCmVtOV8d0c/c4R/AVjhv8vLy5w1jTMPuWP8gHmA7oAe3NN15ax0MgKvrq50c3OTz15us7pc7lmvvu+zrDCOq6ur7EA9OTnWZrPO4AkZ5q47AC+9nDiy/fr1az08pEy2y8vLzKsAFQTPMFacrQCCkqZszcIL6IpxTBl/rDWZdNCF8qrQFP4niIX1Qn4d6GBMnpm72Wx0e3ubnew4Gskevb+/zwEwKSujnIvq4BmATowl+5f5A3Qi4xhtHmxAlhVHA+AcJyOP+wq/lD2C+9gHAF0eHu50dnamy8vLkh05yQfZpl2XQKeLiwtdX19n2QA8BwRxkNCDKYbNRldXV3r9+nUGjSkLT+bk3WqlZV9nCIeQsrPRNYB4ZMO53kLvwfMxxqqUNHwXY8znqAO0oD9dL6AvoAH7CWOCn9AnwzBk4Pb8/DyPD95jXOy1gJjwNGvie+g4jjlzGB3MhX7bWy617AsY5zoaXYmuhbfYY+EXxok8ML4YY+Z/sonZ71LgxW0OAKLfu7u7DJTwk3OxAZgcNEHfo6dZ+75PpccPDw8zGE9JauSXtUfO0Z+s5dXV1ZYxRgCJZzzHGHV2dlYFEAA4ffHFF9lGYp++v7/PfOnngvveisyhq9CNgMTQFJnziifwGEA2a+SlxT2IhTXzAARsLQfioBN7AJ97ABnrzd6HLMDPnp3OfgkvZYeDSjYn4A62ArzHvJxfCfJiHaCjg/EETWTgqAvZsengmYNsXvGG9qH77e1tPl7GbRPmwn43btK54nzO/R6ItZj0F44N+Bx6sLd6oCM2WgqMu1UfCi8jWwTlsHZuXxdnwphldhzHHDDAHHzfZw0Zu8uC61IHGuEBZBD5cJuO9tx+8rPl4QeC25xX2EPYdxywRP+5Lei0ZU5eAp0xcT/0ozICvOJ7vr8zMB+3C6Ahehq971UQ2ncaH4MHb7nucVA970njqGHiF/jM+QdQ3l9AaRdZg3eYv8swMtQNtZ3tvEtVj+IADFmGkc9cvn+6/J2jlQ/mCo19Ld2e9+BW9IvrGOcdaOwBBi3N2TvbPRJ+9PeXb3O1L/9zzsg5J45f/o7ZOik8kIe9utOUSb6Qui5MZ45Lmw3VW3q9efcu63gPrNA4iuH5+3zroIdWZWC1H2uXk2hunnOOEnzxc46tTC/am3EHbjl8Z2j+qGNmznHZPOc+iNl7JiA8/e1OMe4PUgyK4+QE7Xwc01ngU2ZJmuGQjsaO23zVaXLGc5Z4CAqasse0UMok77VYLFOp/W45gec40hOQtOjTkR1935fsta78o2xqzjrrpkyzfgIhOsquUlK1V7+YQPQwKnTD9NliylDzzPUEYHRdVOiUM9i6qb8QprLv01mpHW7eUBy+WT4mkib//ibTPu/Z0DROju4haBzSe/AwDiWT3IKUpAQCUAK1lHEdc0lMyq8Om85Ad8q71+DAOMaU2WhAwpgd9X5e+qjQAQQ0c5jKuAJKVxl5MU4nRVs2lpTOa8+4XnHcBwOqErXMybrl3I8cmV5kNBTndCVOMSqGlF2+Sy9AH4XY6INE2w7wfeovr31ztboljsPs5+1nXT+jg1RkOYTJgT/WR0vQhutl/2xrPKYzeoWtz3muaj/EBIJl4GUbbNGM8/up67H7Y9gdSOD7Vb/jppaOo+ZB6gpEbv6eazOEGWA8Fp+zr0Fnz82Nzfdj2vI1q/S8ytq3PkB/pgsls3Nu75Lq40l8j527ngLGs/2p+pgun5fzcAGpi4w6HcKUghqm78tz3Kv8N9nOYfqC75xxim3nY1bmZ57pQqdedVai23PlM+W9R/Q06TKy1xXqo0L6vkfZpfF2Xc6mD6FUuU3HivQJwAZUnoDrxQIgPUx7UZeB9LTfBHUqoH2q1FKf1c07QNprJ1uf7O4wtWn76rKLU0l0FfA+rxP0nXgzWpRDpnOpBKIobTY1IDqO5aijEig25t/5vADM5e/NIA3sXVP/wfYmqjUMcTo7vtJZk10+7WdSVB/QKWUfy4FlZH+PgzZDCshOfcRydMs4KiqB6+MoDUOYxjuVMo+D7ZOJRMOwnvbe+viXlM1f+HdC/iucdE5HcQp2+a619esKViOl4xuzF35yYNl1pGLBvZLt+Pg7RNKZJakyjyZu7xlui8ztc/63tzfXVlIy9TPS9vtMF7crZ7R9YqvMXdUYpK2S/LNzSEw7+y5S37vjRcDabG2A9rOydq1tMdm4IWizScfTnp6eJf/zap1lqejfgge1ffv4289L0N3uCmo+fv+s/X6Ljt/ymut7jocfe49sr2cD4zjLAF1CKGfYoXxxhuNkdIcfTqUQirPUHbA4cxww5EWACRUDvmRI8kLuWRStI5cxci/OLUm5PGSMpQQqY+q6RS7v6POUVAEI9OEZHGQSrdcr9X05txiAh35w3nqpV+giqXKsObNJ9RmE0I+MrDdv3ujq6ipnXuIApS83cnASxpicVkdHqfw7a8kZqlISpOPj44reXqaQ9nGYsw6e3SWVjQa+8mwv1rrruirbr+tKFh59bDabvH7wD21AF/iNl4hWoTufujONZ3iZ9ax9/pFxFUKdOQwt+Q5awEuAjV5WGxkCbHU+hg884xZn3M3NTc7uPjk50f39fQaT2/HjnGNtGTNyA5/2vaoKBcvlUq9fv9b19XVeM/gXRzFn0cdYSktLygAhQRmcD57ArLucVevOZByvg0UOAhhvJgC073udnp7q5OQ4Z4x7diwZpf4CCVgFOEa7XZfmQvlfSdl5/PLly8yTno3s1TD8M3eutsAAgCsBECHUmQUOYF9fX+cMcC9TncrSrpXONdrLfAXtAE5d38RYMoIdcGqz+OAjdCDADroNvuTs4cIvIYOU33zzTc6S5vvT0+MtHc753IvFQldX19rfL+MDfCTYysERL3+M/CVjtgT6sL44zdFjZ2fnur2+zmfqwq8OZvd9r4uLi7xuXh59uVxqb39fYyxBKJwjzLnV6/U68//h4WEuX+wyjc5Btgg6YO3hC/YbBwLQ2ZeXl1XACff3fZ+DNqAXupD1ADSCfsiL60faOzg4SE4/41H0o7ftWbi0X16c6rmx7zlYik5kTQCxqJhAFiy6n3UhuIE1onwytHbgjX16s9no+vpal5eXOcsZnm8dIx8/fszHQgC+ezUQ9h2AfA+y8HK9/gKAvgRI8OffvHmTdagD2PCWpDweghH4jn58P0ReWGsAUGg8jmO170BjaMXFuiDnnvHuAYb0CajrwUEOCnsmuu/l0I65+TEWjBm9RBAAlQSo0oEtij5AHxIMBs9jr7meQMacp9frUq4euWVc2EpUimlLNZPBS5ASazGOYw6IAUBcTPIHwAq9nI9XQwFnpQLYerAlexw8xTiQtb7vtbTKFX3fZ7pwDxnQR0dH2tvb04cPH/IezX4QuxLciVyzntDY+2Y/dH5FZ6FT0Hm3t7c5IIhxOjjM2rH3wn/wLDyB3BHs4NnPLivIvFeDYE7X19d5D4XGbZUF1pXKAax1+6LGnucVEuBN9JbTIoOUk+x6Bj7jg6ZzQLZXF0AO4JUuBHXT/Z7hjo3gAXesC3sVa45egBbugEUHL5dLxVAfF8K6uw5Cr/Iu4zaw8xc0Y77QNoSguCmfI2MeQOCgvtOaNt3ub3mXvllXl5fWgcGa/qIvDyDwy/dtHB/+7ss92YagLKli5gmCeocJBFqE9M6z6BbSdN84BK1XG0mDFv1Sb9++rWxe9vbNMKhb9Nlp5PZM6zjxd7/sbWwAsXQ1zo0Wg44tGKacAZsfecpB0nYVY3aGK9QOwcfaq0H2HRkU1t2uaxxHdT22FKU4pZSdm0DrKYdLUStJIeHoNXw0/eumHlNB3CBpzPZRAthGJSd0DKn8fspwLqC5t9iHTkM/WEnVxTSuTn2fAPRuQthDZ8DBzL/Eq71Ct1/5cpzfC6i+UB9q/xO/+/v+MqTs9dC0xe+LxUJd32vZjeq6UPUplQSFvu8VFr36MDRjTnNbTu/QkqRlVOw4AqjWh5l2Ia1FbPjCeSmtt6QxOTNdJ/G9v08Nm+3P3KZJe0TUOBxtAfW0nfbR6SzUmEDmdM+gDQC+/VuNqTQ9fOrjK3OIihr4IIMfbvsz786eow++L3v1qKhyDKLv3z6OECgBXXRB22fUoBBL5mZ7ebsLbQPjbj/kdm25fe3HccxgWALGa5+ej6t8Pu/09Xeqvu+lodj9BDYESl3P0Mjb2Zpz1g/zz85dj30/aHsP9Llm+Y67gaLM85L6UKpxzslO5pkYZ9d0ultdF6aqKhPNFRQt4CJ/pqh+Zr+tWgsAxKFZv+15xEjp8G57O7M5dCFlUvtzkiod5zLSdenMafbuOd4q40jU9D03koY4Abt+bQP4k04P9RnobvMnKgd1033oUR8b93ahzxuh37tNS6rTTRnpzj+B8uG9OlsLAqxqva20R3UehDp91qfEuGTLBi26EkwD7X2+8GEXpL5v9zOroKGSbZ2eL3ND1zOG0Ekx1OfNOw9lGqpTiPPnqVd7wRCznl6P6+o9zM+rXq+6R/ePGBO4fL9e1+2bTsr6cJTGMeRn3NAp+0LUGFaKYZiQ7O1gwfLQWEqmWz+SqvEG9hgVf+MmV2SZ9r1xTGB8nDKoq3nakUemk0Ybc4zpi3EKyOjiYuqxfhco65caG7EuUokAAQAASURBVNWrKsNfyRQ2b8yAbFlrEpDQD1E54iRmwdk2JmNUjMPEVyEF5Fimd/C9K4QSIPqovi/nfbfr5Da31OV1H8dxW9dpxzqr2M7ZBJ/m4mNrn0trGfIa8bu3mT5Lf2U+m8mAT/5kpeNLHrELYiyBdbvsuLnnnnPNyTP7UVRUpz6XZyewiD3g+ORUJ6enWiwXerhLtqj7TxItGhBZxXaYPqj6jjE2K1+/c8LrrY5s9+m59XY9v/29BVg+0k7ra6notmMf3HU9GxjPZaxCcUC7AwZnB6U9PYt6HMeceY1zkMHSjoNybdk5BwT4218S/GXGM6UgHM6VdpPlRd3Po60Nz5JtCTDMcyy8O7ViLFkX3h/jjTFmZ3bXddnJA73asrg43NxJF2PMz0slOzSEUM2ZOQKQ4vyk/K+DwAgLmaL7+/u6uLjIjjuAfuYKOAKI4JloUhE2z9x3enVdrwSOF6DNAQTWmHYcGG9fMsl48+wwngPwhadceAHKcJr7eZBOU3/Zw3nP/HEmOZjJ+NzBxlqO45izUGMsZViHYchlZZEN1jjGUpIY/khA42leX84bx2kHzzgoiiM1lRm/1atXL3NfZAnjeE1nvpZyroDhfd/rT//0T/Xu3bvcJnNAJjjXkXEvl8sMlPp546XsvjJwcH19ra+//lrv3r3LsjGOaa7oBNb48PAw893d3a2++uo28yZ6iDOkvWy68y9gfZKRkOdAOVR40l9AXD+QtQ6okMGCGDM440AQvwMqMQYA4vV6rRcvXmS5IiP45uYmA+5tyV/WG94jKzbxadTBwd5WFQvXDWSeX11d5bO40XmsI2uPHN/d3VVZvFR/WK1WevXqlW5ubrRarfK53Pf3dwoh5gAQwCoCLK6urvTwcK+jo2MD/pO+evPmjd6/f68PHz5sgTesI3pwMZW09Sz7EMqZ1ycnJ7q8uNCbN290enpaBRBAH2S9PaZjvV7rw4cPev36tZZ7e3pYlUAUMqxirIF1+Bw+ctCYtl13SOWs+q5Lx3TA533f50CBEIIuLy+zzHtp9nEc87ELgGW0F2OswEd0m+9jrI2P9+DgQA/3D+pDCYZjHwSU5px2XmgB1NGz6Dz2fNr2rMSHh4ctul9fX+dsf/QnmYjI6MePH7W3t6eTk5OsZwD5pRLgg37LztVJ1ilvzos49Hbw7erqqjoOxZ1ybhM5EORBX56x64Ee2CzwEnKEnsI2QaZZb7cnsE/QW1xk3CLLUgG3GTc8slqtcrCIA2307+vKWjPXYUiZupSUZ13hEZd1eAfeoFKFJJ2fn+fxce6409SrcUAf9AkgJPYOlSvgZwI1sPEYYwt+0ReBagQwrcehOm4C3ri5udH5+XnuB1Dcs8qhcYwpAMePGlosFtW59sN6o9X9vW5vb3PwJ7K0WCx0cXmp0Bd7kjl4sArrR8AHegI+PTk5UR9CzhhzuwvaZIfVZHt7iXDaGcYJXLFnfJ9jXP6S5PraX2zcXqM/eASAvgU1HIxHRzMHbCD2TQIQWGfP2HabknF4HwDR2GjMB5D848ePmb4FXKizBLGF2oo4ed1NH/Ac8+V319WshesptwtCKGXb3dZv+18ulxqHTSWv7BOsU2t3M0cCR9zmdTsd2Xp4eFDX95qOmc3fsX+jEz0AoOtKqXZ42UENeJ0gA9bSA+jY1z0Q2IMYWDOnEzzTAkbOd/CaA3BuQ9AWc0FGqfrx81z+XuxzLrKUnJysCQ774g+YHHkKGYRaDYNu7++qAIJuAlWWy06LvlMYpWE9qu8WUthobznVx9VCn739JZ2fv9DDpPv2D/Y1KJZsN7JPlTLv/P1UMudSnBx9UkGMW+T4GUH/bftjLE6gloa7mp18Z9vdxahRxXGa6Jyy57g7tR/NhZTcWfNj5fvyQR6/Oz2HCbyLvWLszHkVpTBoQsJ99JpzwFZ9hsk91hnQlL+PIke40K0wUnKuScO4mTD2IGmQtJ6lc4xRIdb6ibN1gzm+QujUY2M233UAHJyZqkUBF7pyRq3LaQi91AAoXejlpWFjjNrfXyplmYc8pq5fZgCGfsiW77tyfnoCPHj/9/HYmatear7rpu9T5nPXhZz1HgLOxQQ+JR2zVlA0GhXAZ7EI+V2dZ8s/B7MKZwyxvA+U7ymnOvFtTDzt+5SvZQERgkYvQ296swZV9hRj0YvDwLnsY342KpXVRQZiNDCiAmAkaZHOe50y8v2dIfsBQqzO9YzWbuVUzT77WneTBQkBc+ZzhP/doY4dle6JFc3C1mcFQikymcaUT3Ce9LSS7ogmT6H0yQebEfA5Go2257wOtlcYzWKM0ljswEXo8nhGo69fIUQpjLPflT5HdWFP0cZd812hezejIsueVv4eFMr/3GEe04bRTfhSCMWmpY1q3WNQHwoADm2lOrN4HEd1i0X+bs5ulKYM34jdz5ijKHPt+jCEBkzKa2r7VNR07npdPZS2s/4afX/n80TcnD0cUhhODnCaQPkMPMUCHHXdotLLSSeniiFpj0h7+7IrOpTM5wzQ9FTsCNNxHUmvd92UHT2da50A66BeBbzL1Ub6Lut1BrtYDMrlyLuuolnW+11aewfMWYPOxxyUAG/jgUw7Ywa24ZI1nfiM8RY+7bStY3zN0t+DFkmm1mOjA/x86lHjpgBWVB1BL6X7UhDEMOlPApjmjuOIJs9kaqcM7altxjtQTxvtBhhswS2xHO0h04PMgXnGqUJHoh/9OIie9otU0SZO53cXGvOToy+GoaHtmAK1attXuQ0+m/5fzQubPcaoRd9nEB3bK7+HIIddCmdYDXVgVZiwaLcJXYY34yZZycupqpXxlV/olEzgULcXo3JGd/kwKESvGDSni4OoBJP1RQPe575j8WVVuqlZ28lcLHuZ9dnaCvVI6vHH/LPmn7rfAo3P70H1fkIQVlRs1mnS5dGOn2v7Ml7mXdVHjL8hTO9OkfeD6DPYphk/h5nxzNkjc+8nue38b9r/2Su6Tst+oT522tysdHZwokXsU1BlN801JDsh2d3TOzvBAAGZtbVQPa5Eg/J+gs6FNj5ft0NbWvgcWx6cfTdr3wF3XC0+gz71Pts9e9f1SWeMoyykOtMQRSIlBYJDz8/CxvkAuCOVyH0cYQBFDsjSNs4mqThFQggZKGQsuazuUM6mc2K7k4f7AB88WyM5V/a0v7+XNx0IC3CFA5SxZsUxtUF/ni3OvAF43KkOKAXgRolBniNrJYSg8/NzhRByFtMwDPl7nKSejUG/7ojzDcDPn3z//n12CEMXB/u7rtOHDx9yhq6DIMwFoDDGOqsuORrv1XVkBBfnGUBHGhdnExdg2YHuYdhoudyr+AIg0mkKPeFhgGnWw50o/CS7SyqKy3kRhyRZdjj15qJk4F36ZQ739/f5LGBAHldCzBtnGllxzJGyzQcHB1vnNp+cnOju7k4//elP9eLFizwnstSOjg61XC708uVLnZ+f6/IyAZPFMbivh4cJaJgAk/v7e52cnOjN2zdVmXjKsDttoC+fAVIeHR1ptVrp5cuXur+/n0DWm+r4hbOzM11cXOjo6Eg//dnPdHhwoNev32bwh7X8+PFjBrbSWiXQ4e6uZIy/evWqAgUwJtfrVQYsk8N6TyFINzd3VaAOfMA/1gjd4452BxM2m00FUq1Wq1y9AZ7zMv7wkINS41gyqMg+DiHo7OxsAjzudXNzPTn8Vzo42K9002IxnQc4BcOwJowvtec8fzDxbTHuyVQ/PDzMgFMIJQAHfvJnrq6uqkCYvu91e3unh4e0Lg7QrdcbvXhxPtHmKAcAXF1dZdkiaIAKGK2uvb6+zuDser3S4dGRru2MXEkV+IZsUDEBPmVdAEEIqCBwgYoJy+UyR3JvhpLhh5wD0FG+HN2GDgCYoF30DCW84Ze2NPVms9E4DLq/u9Pe/r5+9rOf6eT4RHtne3ktiC7vJl4n8xc95MFVg1VNWa/XuQLDerXWar2qypbfT+PcmHFCqfCPHz9uVUjwbG10Xtd1OYPTg4lYFzIsyZ5HL/Ld7e1tdRSB01yqs1XIjOY+ly0yeaEFPM4+COjsAVAEgWFjIO+M0+UdGnBO8/HxcaYzQSnIEnqb/R6e9kojLfDE/uvHsngZbGSu6zrbS8seTxAStoPvbW0woY+fvskgxu6iIgIgNetNMAPBcdgggJxehcaBKPZG38c9oxOQuetS4MjZ2VnO1mbcHtBAUAZAs9soBBOgC8Yxvcgz781mo4fVSsvFQosgdRPPc/E7xz5gz2DH+p7A+AEVfW93J/Vev8ilvr1KE30cHhwoWok8DzBhHZAjt2f8xWW5XEpj1GZYF9stFkcStHNbcrFYZJnn6rpO/bJkI8PnbgdAV7dt2BvQD/Civ+Syt8cYMz94oB909jV1PQSg7lnZ6CSCK+ANAF5JtjeWClCsAevrdiv9+UsY64Gcebu0iU3BhVzzGTLM5fYna+LHA7G2/t7j4/N1c3mipCfyTzs+J/8OGkJT5yvazCD8eq39iU/jOGa+dZvJAx4kZduBtWnnlZ07sQ48gI+7kJxZc/Y7dHbAxqtWcC+fscZeKYp19EAllxvnd+hFv/DYt73K+3eZl+97RXZCtYbcz3hilEaNOWMRGjL2EIKWe0vtL/e06PoMcIeQMuxSdaU0l8Wkr16/eqW//Mu/TIG1x0fVmHO50qitcdFuRsGzt8mQvApiLs9EAwjmruykmRyj7qhpHTPlobqfPMb6660+0jfdjrEUB3n7fSy+LUlNadyZcZXxtO1kL11ud5eDko/bvtv7Kb9exh3K8vj9W3OK8z+Huuxvuxb8PlrwbkuvCmAatx1wSY8CBoUE/Od7pqxA9XYW7OQrWBRfVphAGLK9S2ZnyO3zfC6TG6JlzXfqestmp//2rNbpPYISu8lhWYArQPUJHsvt8zv35WCAvuzhJUDA+0xrBaAfWIfOzqbNn4UpSzIU4CgY0KZOfRfV9y6uLiUNT+TvASoMsIhF6JJJUHhYsQA0PBdHpfNppQlsrh266Jlxxpkeo4E501djIyutszrb5RmAbB3GtTM2jKHaA+iqfIY+IGiJs3fLfCkrPIWqZGCslYl8lm3oCh3yWFLbowVArnPifroP3RhjyR7Mc6pAs7HQP6/XqDogp16v7ETXYktf1dcEME1g0GN3QkeX+TyfqsVOin3l42DtSp9JbhWakuUNeBzjFLjV7BnYZFy+1zPaGD2zuHQfugL8hCxfZBfzWUxHRtj4kFG5PHamgkPdXjfJsqQUMGD60vVEpmfQdEyF6S3u6ycgOqTgg0VoAp3mdHHQND6fX5kj69D38o160tMhqwzoHlQCjn3t271GOfQk2RTjGLUZRsU4ZNni81ofuZ4peiLGWGRtLHmTLvepr/YzVW0k+amruvnYq79Nbh2kymOIk2xOmc9zoCSfj4qzfdb9esWOQsMx1md9xxgzIJ31lX1X3glGRW3PNY8JINp0Flnt8+PbtjPmbJzRvp/jFam8bw3DoM0wVJ9LRVfHCQQdNfkhGpl3v7D34XhPVMzvuuj/x6/5e9o+AEf9nch5yT+fo0f7eXsvbfjlPpJPvR5bj12fz4Hm7X3t2hXMeHdVlNk+G5q7HmtpUQLT5qtRzdH9MfrP8fvOcTDWGKU+HWkUorRar7W5T37K7333e5KUsZWseH09m/ewucv3PHREOxdo4/Px6qPtXj33vPfVXtOWXF2t32HXuNtxIYdPXc9+U1+vixOrRDXWoCtRcBDGM694sRqGKKnLL9YhdBqGUfv7KYuNSHwcXjmCvdsuiwrQAvCAsxpieTa3EwsnAFkcOG8dzEnOuvuprU4xYox16vugzWat5bKvskC4/OVttbqvnDcOrlESGmcLTAxTkX2P00VSVTaccr+Aj5SBBqzEUYkjHYMSB9zd3Z2Ojo4y8IOTeLNJ59I6qJDBmTFlJDqgE2M5/xwACOAHwOfu7s7ovphKk94rhFS25uBgT8MwarNZTRFtQwYoFwuyovYU46CDg8PMO+MYsxPNAVDGTCleeAjnKY49eAonLPQCgOcZL5HtWdnweAU6DaX8P0ELOHqlYqwAbA/DkOfA+gKWAqjjbMRBzFnNONdfvXqly8vLDFThAL67u9ObN2+qlwkCCsZRurq61mq11t3dvaSgxWJP799/0MHRYVqPYaOzF+cp4mzR6+zFizT+IZ2Hms+Q7Eq5JOYMj7sRgnOdoJLDk2Mt9vcUQ9Dh4ZHuVg/axFGrYaPXb14rhCQHVAQ4PDzUxcWFhiFl2ScH8cHEW9JyuafFYqnNZtT+/lLjuNZqtdHe3lLjVF5wudzTarXRwcG+9vb2xcvj+fl5XktkFLDBM2UvLy8z2B9jAQTc6Ds9PdVischg1OnpaQapycKENl4Omb6QPQ+8IQuYgJmTk7NJVyyyMzkEyhUnPY38Mo7Dw0N9+eWX2tvby7KxWt1Pc+i0Xm8UQq9hiLq7u9cwjLq9vZ9ArOSkubu7n+apSZ8WkMvLuSMTZKwm+nWTHHQTMDxosVhqf/8gA2ZnZ2le19fXurq60vHxsV69epWDQvJLwVhKI52fn+v29lY3U5Y6Y2Ed+Hs0IDyEkHlIUhWMcHV1lfW5V+ig7PFmKKWoUtWClH1O2W0fnwOXbkSTheg6dhzHzCOr1UqdpOViqXG90cHefg6i+aXvfV+bYaMQ0wvqwd6+wv6BNuu14jDq/v5BB9OaHJ+c6P379xomntByT1eXl9rf2886arE3nRM7jlp2vY4PkpzFGNUtFnr/9TeZ9gRPUcHixYsXGdAkQArgFB7zuQ9GOwJE4M/FYpGBMAd5yNZkL2VfocIFutKNLPb4i4uLXFkE0NxBew/kI+OX/r2Sia9dCEEXFxcZxGQPQVezF9ze3mb9RRYsdEQfe4b46elpBjYJFGHvJ2MZfYpOoEKA7zfcj/0ELb1UvOsugHaAO76/ubnJx8mwbxIkwF7Jvs+zBBd4YArzbIMbCJhgLRzQZc8lOKbN5oTvKJveVl9ArlkLAhNYT2zG1Xqt1e2tlnvLFJz48KAxSJs46vD4SDfXN9oMmwxWo3+gTetoIqixNcjJVifYCJsTkLzrOmlvT0GlZHRrM44xql+WKiE3Nze5SgXrSYAHNg5j42Wdea/Xay36fsrCW+iBqjP7SQcuptBwL9HPFWPUYrnIGf7ehweqEgCHPPLT7V0uZJ19Dj5kP4YHWUP6IGguxnLEEgEU2PgELfHZer3OGfUEQ3nVAHcqdF2X9Q/BI4zJ+d4BRnQBdiRjgj8o6+5XLm9u7xLoMJdJr3rAuniwMDYrNq2/2LszdDUFffShzh5knq3j2e0g9DlZxt1ioSGO2qxXWg2blF3Ud1ptNuqWKbBob7Gsgg3gA4IuoCEB1QXcKYFB7nTyQCHkves6rdZrpewijnFIzuHNkLILcXJ78KYHZkALxuDvh63zCbuLdXJ6+e+t8+zbXm27rVyGsPss0bYdHKzrzXrK3ClVHfaW6QiLzhy9ISQnM+c30+/BwYHevH2rv/7rv068YBlyMUYpAsopO4gfG1cGyHdceZ2CP1M7Q6o2VYO57ix57lWNudvl5KnXoe1jzsEGeDLXjz8zCkfo42PblSW+fe0IDNhqt3G02hiy0+yRdoqsaEufzP0eQirlLnOGRftvGALEVYhjAYpKA3l2IdTAeLnQ7yXIpO+DfYbD2cDygIOuAYAy2OSlcaeS8pMsAvDwbPm9S8Xrg4P5sjPRJ/A+LlSdGQsgFcrZ6RlcD6HKnidz3c+UBXD3eaTMeBt/F6WtsvHbYBok96zYMAFezKnrgmIogdgtH6n6vMuf2WrVa9hJi+wtJX2tPFO1Pd0XypdbV+WCn+HjDKKpV4xFLsqthcelqD4WMKtqh70jTk+Eecd9cULjeJ90/TCAG2aeyiDZVF6cMeDErtuKGodmfswnTgDVNJvB9LT/9PEW+Y91ew1o2AWqarR6vw4YihpNVqTZxWI8odHz7bKZvM3pnUp+p7WAgLV8T3ueqIBS2vJ9tjyzzT+tTQez+tjm9q4QotTFAoQ3P6t+jb9bfZPbVgPuzPQvKZ9ZXfVnJE7fxVlZyTxRfed8VGSl8JM0bhblM4IvYhMsEqPieFPxYZYNgMwM2FpwoIpfDrA73UsG5PbYZIEdhU9pp3zmsuUJIi0NKtkJm63PWtmaelMB0WVBLwbcjmWc6Jb6eQOim3H5WpXn67mmbONRNZifsrJzAMEjcwiqj5GjP2x57mHEoz2bxzb9LDWOdl/ZfmjoP3ef2/utXVaNV8nfjb72ACXe69o2JQJ40vP5/ezJGWgyP+pM17n5sDu0tHX+m7evNftZO/+558epPAUf77Kl5z5r23qsn11je/rd4el5t2Nu6eefu97O34Wivx4b69b8Is9uy8ncONsLm5bWk25LPxd9r9V6o8vLK50enej1m9eKISQf8SO0Ld+VfcDnUe5BP45bbbRzluqKacXGLFVP2n3If295uLN9jPf1OVuk3c/Yd9138hh9/Xo2MO7R6pR2AfwuYGPI5wjj4Njf37ezbcfsvCDL1kstJuVRHGHuPHbQyMERQEscdLk8xqKUKGdRvNSkZ0/65gEBndA4ZMmQpnzf3t6+Dg+PsmOlLcHNZ/RJZlMIKdMdBzPZ1Tg6PfLQwZpxrLMAARS8PLpnqvg/zp72Zz2r2zNByOrE6TcMQ3bw43RzxyuOI88MBwTAScy90ASgPDn9EEBpGEqUOg5EByVw6PECNwxjlbEWQqgyxznLGqBfKpl7CC1Zilw49OEdwH7mQBs4fAH0vIqCO6UpVQtvkb0GCEtwBWCYO9lwoDMe1oWxAYz4ebWUkX3z5o0ODg70zTff5DUFHMJxenOzmZy0B5lHV6uV+sVCcbPRwrKrkAvGPa77qqQ7a+ROWg/GkJRLpkPv66trLZYJALi4vNQ333yjh4cHffe7302gg4L6UAAXglDevHmjvk/lpd057ICaZ2nFqByIkGhQAm8SXUvgCo5X1q7KpJnWS1KWPxz5rIFHS3lmEbLgusizNSVlOeI7dBy6AX7jOcYsKT+HfkWHkI1LNrZvUmxEnJ98fHysg4ODqUrAw5TxfZvlv58i1AB3oLsflUH/8Nlnn32W1wneDiFkABy9Mo5jzqq/ubnR8fFxBj3u7u7yevkGSLY48wuLUiXi7Owsn+eOvh/HUYuunEvq+pnnbm9v9fLlyzwfqQCHMaaM5P29PQ2Tbr69vdXPfvYz/fCHP9TR0VEGuQgQcpDIHUroAgfBPPv06OhIR/sHWe8RlJRB0eVe3mfhvfU6nUlP4Ab7wtu3b3NFkXEYdHhQzq9m/yNIYLPZ6PLyUl9++WXO2j89Pc1nZ3/11Vc6ODjQ+fm5rq+vc2AP+gFA9uzsrAIxWHsy5z2ACv0NwM1exTOMK4SQ9xfncWjnZwgTqACAg9zd3t7q/Pw8G0lXV1e5dDf08MxNz94MIeRjBPibsaHTHFhCdik17rqBvRS7g2AQ5ArA1CtGSAXwRu+dnZ3lfQ66uM7iZ4wlcxJbCjn26hbMmz2H/uBB6MY6OE9DJ+TRwUCyyMl2ZWwOECKrjNf7I1DA9SX2QakcoiyTjMUD4LA3PfCt6zt1Y8m+xuZDDvf299RtCih6enqqy8tLvXz5MgOs8AR096x1KgPA077HQLNXr16lftdr9V0dnAUoR3uecf3q1auKFwiQiDFWeg97xHUo9gJXCQhNtsj+cm8q11pKnNcvJsUpBU9jm2EjsI+yFyPnruuxeTyowu18+BW9B08iM+gvP6PaHfrIPXzmtEX+mDcy4sE8/PMjENzW972lfRls14x90fdmD2Kde3nzIAG3pVwneEY99IYOPhbaKQHLpaw6bbVBQLSBDDEGrxwTu6DNQ8mgHmN5F2EN0Nfwn7+n0BbzILCBIAvWkPWDFl4lg3cu9owsy+OgYVPeDckq9/0R3UbQqwPzTmvkkb6hSRtM4AGWLnO/iGvL+Vg5BIrzJNsZ5cHsUKeNHDgeSnWS5WKhvUlPBctO6rpOGsYMormue/fuXa7AEVX2geTYTA5bt3u2HVEZDUmfmQi0dHNHU5xx9tftFpCF555ymH6bK07OZNqYW6P5/oOqyap2NuV2Jqeaj29rHlGp3POTF+BlO4e5cTx9Pl985Dt/rnVst8+EyeGY+aDqIV3jRIug5KwPBhy2Vwjk24atOaS//Tgcz2xhreqyuzGacz4AHDnIpfyMYjmjvKxZTfd0PmwBfYNCAaVCyBntpVR6AZoziG5j7sKe3Vfu2QLBu1S+WNW95V+6P4pzvHcB413XSZEM9TqIoIx1ui80x1E0C08WfnkvldHV/02fd+VczXbN8z8pA4YVrSZaZyyRWIjEDHltc4Zr1unTLdMYyjMhy2aQ1IeNOGgc3ZP6VQaeYnAeCnYvvxTdTUhMtoUnPuvg73E7QCTLUYy1blKs+5lsuID8TH1vosuttSuXtU5BbcBX9G1mGm+0QdE3nZd2w1Q4PtSEmLla/en90XxU6KajfuaeCvOf811uGV6KQw7Q2DW6wJzaa25tFG395x+L03e2Q1YTLeCBM/BuXRzGeSAmRiulHaPCmI7qiGUU2VZgPlI6atT7i2Vy075f5uXPl71xKqc9jtK4KJnPdpY07xgClNaDWpA2tUllhPRTMVUp4rgOxenop1gCjMepGoLTsqVLNbfypd1j3079VJ/NtBe6wcZtoL2PI6QVGKfvlOmZvgfojmNUHLCxGJcMRJ+AdK9KAT/YmpVxTIEDuez5UAIV7Bpt/Fvzw9ZR0tH++ZxtVEC37SsqZiguxO3gQDMX8hrM2QNzNmT7ezuX3H9et84CL6LUlSOj5vZQbN/Ek2MJkpu5qvFFpSChJ2zRNM7i26k/L3bOvO2zTYtdMtB+Zie0PPrsc665Pnbd5z932fEthud9zNHC25+j9+z8Kr20bZM7j1cyYfvd3Bgeu0II6v1oHKWgyM0km33fa4xRV1fX+sF3v6+TkxNd3d5M2f3bASW730W2+63nuV2the/ae3nv9XbaKiuP8fhT9HHfYHn/dRu2lsXntMn1bGDcQSMpOWvI2koOpXTekGd9OFB2e3urcYzq+3I+cNeVs6UlSobXJWk7Uz5kYXhGHg5XgHaIgdPWnT1eQhUHLePAgedOK490oj1e/nGyke0k1edXuvNHUnYMudAArOEs88xz7sMBiFOJ51gDnOI43VEM9O/noTJ3z7xyRx/OKRxRAPer1Uqnp6eKMWanJGdJ40z2DExKFZNRCM0opY3Ti0xSxuoOS8aJQ5l1ZB1ijFP55z47N92JijN5rnwpdGA9WqEKIWQHm5flBbRi/R0IxAHIWjt/Mg74GD6NMWX/eBn5k5MTXV1d5XWhnDPAPPTzsqXLZTrHe29vT+fn5xnghodfv36d1xrZYf4YrLSNMxoQlvnzfYyT8z1G7U9ldFk7B0lwUkITeA7nt4M6oQs5i+3w8FBHR0c52AOHJ2sAuIhscPbv6elpnjNAlGc3+QWPe9Qicnp5ealhGHKmMXRfr9e6vb3NATjILONjPjha0ZleaYB/9MsYkCHO0cSpSkAKJah5NoRy9i56gDkSWANPs8aAR7e3tzo7O8tjvLu703q91meffSZJevHiRcWn4zjq7OwsgwTo8oODg6z72kxISWldTY4PDw9zdYyTk5MtPUxWLTLlASO0A3iJrLLOZK0Nw6Cb+zSfzz//XIvFIgP2jH25WEhjzOsGbQBq0HW3t7d5nPC4VzEZJ0cI8vmDH/xAMcYsfx4AgMywtlyAQuyRvl/AHwB8DhLAf8gx8gl/+bEknKHNnnt4eJhlG/3GngKwSkYlx3W8ePFCX3/9tWKM+uyzz/Td735XNzc3ee/1cXVdl8uTE8yBMeQ6nTkQJARfEGTFvNjzkSvoyd5xc3OTx7tcLnMpf/r2/YwsWUm6uLjQ4eFhBisdSGI8DiY6cIfN49niyLuDCA6Gsb7shwcHByVQwcBhL9mLbDsghOyz/1xeXma5Amjy40I8qxbaEpiAHmKv870QoBme97GzVyGnfq4043Xbz4Nw2Acd2Awh5H1ZUg5QQQ8dHx/nwALofXR0ZC/zpdwzdGHf4nP0HevJWq1WKymk0sHIEPxKJja8he3BWkO79+/fVxms8JsHULEPsCe5bQrPjeOoMJbS1+yJGcDv0vEN3aLPdpMHOkBvdANzYQ3gceTQ6cP6OMCOo9rt/krXTHrM9yIPaiDoDFmmHdbLs6pZa/a9NsiAEvzcg8wDZhIEwBjZM6lW5GMDeGXv873cdbHv084/0Aq7Dv5yMJCARmwqjhlgnl6RgmA95usgqut32iNQBr5ENllPrxrg+4vrJfj/4eFefeiqvcrnR3vYVrTpVQSGcdRmM2Tdvlwus3yyb8HLbiO7reTywnsGNOKCN9DX/n7mcsk6elUe5h5jcq4BHPvLM/Tn3YTPfO8i0IV74Ae/z+28ds//ea5dDhcHrroQFMx50Tpt8r8uORCzvbm3l88RzaXTG+da7VgqbQ7DoO98/nmudrJer6rgzxiTc5GjXniOthUTSJDHJmkXkF7NRSrgVvnCb1L+1oGaGbp+6uXtzNFYM85kly9raWf/W86cOP+9X+NMplF7hbDbQfT0mIsrOn8+gTe7aMIax/h4GcMYVYFIGQgIjTt5cvwHOY3SFz7UECaAIEiUF8j3ByD1dI3RHXg+z1qGdnKK6Wt/bk4O8+8TAOSfpXs1PT+Nr6lQ0ALV2Z8UDvIISxtT2wGQfYIfG9C/+r5L449xe/y0x/NdWChUZ7arGgNAvqztmi99nwvqsl6QCg3rPlEZc235ve33PuccZBJVMu1Dndnbrl+3KLpobk15nr1m63mzD9Izfd6v2rayndUNCt0oqnSMY2zuSfzad+PEzzXN2ivambT5a7Pl+LzLYQUT71S4TQu6uI5wOcjNP3kluu4acwtitCWjy/jyTGJQHOr9KkSHe8lELQBTNe5Y2uq6TnEcNA922ihCkB31Lqdq0Snpwu6x1rR9lvuki9BZskzhWO4dx6GiSYwx99/em9f6kTbjWIJTij6rz2BOH+8Gtfi863p1oVe7H0J3Po/aqAa8a6AY+nV9maO/P5X1mOY+TAHhdlyGgzQJWB40aqjnPgHK4xhnad3Ozz9P61DzRPtMsW/Kz9k1jVGD6pLjvr/ltZhWZ24d6ja3x+VzyPd1nWpejJIF2xV5n+S8bUsFvM6BO27rNVexL+p7phFXEldqWjwCcO2w72ZtpXEbfI6xDgQlMKHve8WJf/ppXhsLtndfIu9O6T0u5r1mHMe8x87ZWdU4dgCQzczyurmtvItX/fd5m3X7c/8MHZ1+r0cyJw/t9Snf+ZycXrv4fG7+c2v7qVetg4yOO4KMpFq387wD9k+NZ+69p5vM0cpOVNAihFw1YrVK/tTv/9IPmv18e62h6VM0clq2do1/137G+5+/4/OdV9/ddT3HDmg/d59Wa3d50sJzrmcD43TgGSi10i4OM89cxfkuJaOu6wogcXx8rOvr68pxOI6DVqvi2Henqp9bCRFwYNAHzkuIgIMeYAiwixKPzAkHmzun+Azwyp28ydEV1PeLXH6cBXfjOTmkV1VGH/2iQB10Yl44z2jz+PhYfd/rpz/9qUIIOdsGB+rV1VXug/Mx/SxowFcHj3HO9n2fnYcOjnRdl89iXiwWuYQ0gBWgNczGT8BDLhyAvARQWrWceX2U6X5zc5MdgIAEOEIPDg5y2dgCzpdSxJTWxeEdY3FqAkJ0XSmn7g5hBzekUoYVIOH6+jqXqgfEK8ZfyRzGqYnzHxDBgVOyGQkYYONFBqA3JWQ9U9wVlGcJ0cc4jjkDE5ASoGe9XuvP/uzPchavg37Qq5W1GGN26pLNJUnLvT2FMebMf6kANx6E4rKEHKIncHJSgvn4+FiXl5cZAOn7XsvFUu+/fq++T2XIXanGmLL3aA9wwUtaIoPoDQ8qQAYvLy9z1iS0h4/d2U6QCA7aUqqztOWAFjyGsQRw5ZstussDaR4eHnR9fV2tqYNpbeYfjmepgErwFHLGOHCq932vi4sLXV1d6eXLl/riiy/UdZ2++uqrzC+07boeeV6tVnrz5o0uLi709ddfZ3Dv7OxMl5eXmR9wqK9WK11fX2eQ6/r6OoPwrgtdLgF4WGuATZ7xs4FjjCkzM4657DJltjFSN5tNMtnHmB38jNOz8E9OTvT1119rGFLFCsbM3L/44gu9evNaCgXoA0hlzwCABUwki7UFCZkb82WNMqg01ufG+sbvwBhrj/y/evUqA+BU7gAwhR88Sw8dSeazV8ZAB5+enur9+/dZf0M7f8Ho+z7zqOtG9C5AoweCsSdAX4Jj2Fs8K7TsqWtdXFzk/Rlg9cWLF9rf38/n0ccY8151cnKi09PTDCTPAazsGdgfm80m77EEAbi8u8HFnND/DuCwr7I+2CHwKQAkx6DQPoFM7GPIPO3wO1nm8DC8y1iwT+iP7FqAQzL34bu+76eqEfdZLzqwhS1EYEKMMetOl2fX7zHGDCgBSErK6w0dHXDsunIWN/wh1cemsF+1wW/sk+4UgfbIc9/3iiolhPf39zOo+fHjR+3t7eXgjhhjDp4BmEWfYn94xmn9glzsLPriQkayDBnf8j0VZsZxVL9XQHoCB9jb2OfgA7fD2LewTaC1g5ysUZC0t3+QdYDPBf2rIC32SrBlrtoRSoWntqS422XoPM9OJlClfQGDV+B7zxp2HvBgN99/kZH1eq3Ly8vqBRN+RBcyfn/XYQ7IBv3Ci9CwDYbhXt5FoIMHqbKObtf4fgDtaRO9zvjhcalUUPDAKddrHsCwXC4Vx6jBSoVzD+vgso7+gcczncdSEt3foVg7DxzwdujLAzb45wEZzpseaEEwkesSxuw8Bd9wxThKADvmVGXtWGNfuxBC9V7Dfuy2Lfsqc/BgFdbq57nGcVMFBDBPeHbyWU6la+dLqnOFkACPru+0Fw7ULfrkUJ7mpCFlJKVsyuQcjRrVddI4FuCq75darwd9/p3v6O3bt/r48WMq53d+Vo6gaQCPLefbI06aJx0oUbuz7mqs5hdyOaiw8x5zIPpn0qfzwFPOoMrRBgj8RJ/uiH6sr7mhRgN4ir5S48J+fO3m5pTvjZMHsHQ2oVptW0FtJkyZV0WE6nlAEk2Z2iWwos9PJVaK+f6tfufWZBp3AgJGqcn4mqfF/Dq0YIS0TKDAjCOyzFsK4XaLTJUjdZKzcTNstVHuBVTtFRr34NwzshLp7VW1rV6+Lt6O37fo5mnWziOEbd22RZf04aPjijGqj3vqZkDqFmQIoQ46YV/wvSvpu8XW3Nr1ioo543BOT+dgYvXq1G3Zc1V/krow7Fx7n+sYu2ZOO3gp7tZVZQxpf9jWG9tz3qWE/dm+n89sa++be3Z+fDNlcGee8z7atS9z2H6mXYt0bWfEzuq7Jkhs7p4uRPWh2D6+72O3uv9kbj7+ewpQqcedA+q6EnTS9XU2nttI2RaTqqNM2nXis13r1j4zjHdqwf32X/rCSq7bvwqLmPYjt6nHcazssCQLQ6Nna96lT6eF02FrXvJzpHdfQXuP0iy1Fbeqv8zy0TTfuTk89tzc9+k92cqCd9uyW/bY6egGxupBICrt9fasB7nWgdSaeNPGpO2dcY7mXI/NuZXr9j7e81o9SIIG7ynX19d6uH9IxxXGKE2BV2fmxwS7Ya5RpbKJz7+9tuw4leTJR5+J8/PaRYe539v7W7/Bll40ULi996n2eWbXtb3nln59/Z/D4895f3hqTHP8EmNteTIu1zXbz9SBvI9dLb27Sdxcb8dx1BCT/0Wh1/X1ja6vr3V0dKTf+q3fStjFOO7s71Now+X7RB6H7RFte9zfJjW19PL7+Vl9N8bK5naZdN3sv8/ZJLt4de56NjDuTgL+AULR4d5eKWPM/ThEuykSCSXkGTEQLzkzCiDcNcYDTmoH0nHwApbzk4vMqKOjo+w4w6GJcxxnLU4HxgWI1hIbED45SEuW1M3Njd69e1dtwOv1qnKckkECaBpjzACoVDLxW2cLzsnXr19XJdpxiuHsxvnXOmP4W1LlsMdZzrqwUZA5SbucR96CIFU25gSSvHr1Kn/PGHxN7u/vcwluaI2gHh8fV1lHLnAAlSWzfZGzDjmjUFIuLYwA4dSHxji2HZAkQ8XL8iPEIaSsyRBCLg+cN76J9gB2ONTgKdbZgw9wct/e3iqEUqXg4eEhg4qnp6fZyQavhlDK9ibeWuesISll+3711VeSpKOjo5zVe3l5qRgTGPi9730vA5lkW3ugBjSHr3B0A1zl+XS9lsu+cgBjnPI7Tk8HSB3Yfnh40KJf5D729vb07t27zNc3NzcKSmDxzc1NxduAhw58AM7Ce9Dfg2jIPgNEYd1PT091cXFRZSs7GAwt+N1508FawCjvM4SQZc0DVgA1vBw85aUTf/c5iAd+IujDAZcQQnauw++ApOhQQBtkjRLAL1++zE5wP7JBUgGTQwG5ABzpE9oRxHJ4eJj5Ff0G/5Ohe3R0VAUnjOOYM4cps+805ALc87OKHQxaTG1ynjv85lnHcUxl45BfpxW6+f379xkodDASoJY97e3bt5nu79+/z2vpewR6jQxjB1HgBcrBQ3fA1evra8VNAcWZC8AWwUJXV1cZDAfwcMDWnefwKHs3sgng4cANwUzjOOrly5d57/Cgi8vLywrIhP9YFyppcJYva+gGMCAdgQOc9U1gDzqYAAUH+LAD4DFsCz5nL4Nm7LXojaurK61WK718+TLbB+zTjNV1+t3dnU5OTvJ4PYM0VcUpmeXwS2vL+Hm68CV9eKCT78kAV17phfGxRsgEMsde4aAV680aMGaCN5DJzWaT5dqDANgTCRKiCgz9QRO3DZxvubqu0+npaQ68YK6Xl5d69epVbp99gn3KHYLjOObsd/ZweA9egP89g9X34BCCYkgR+ux/BPG4LmROq9Uq04zAAmjjuhJ5I+gGe8TLxjuIC59rGBW7utKI60L2zo8fP+b96/r6OusY9jPfmyRlvQq9CcrADkc/eYWU9Watg/2DHHThLzQhpDObOZvYbRm+d4CetfTAIfqiXejXgqgE5LldwLw8gNbfARxY5x92HXs/uo41QCZc77FnwvuMD97wdfL3ohhjpXNdtjx4hfcP5uwOI28L3nb6YtO7A8UDHJmL27LuAErtLrScZJf93IF2xsza8a7WOk729/a1Wq8yf3hgHfa6B+qgw5bLZVXi3sfo9jc8BG8yT1877GH0k/MIc+q6Tpv1Wpuh1hGMm3cWB7WpjMa83fZH97WVBNCHzNV54NtecRhSEML0M4Sg0PfqlBw1ZHq3zq05JwFlSyPPTM6HcRgVh9RH0KSjVDsNNWUUpbVMcvXy/Ehv3rzRX/7lX+rrb77Wm3dvdXl5mXhmAjzGGHM5QHd8xBgzOO6fMQd3mFTz8HsrOLOh2xNOuuc4iTItZ55PP+tRPd9Z+LSjJj3HWj7e5tz45hyNT49rB4AUZ9pt17L5Pn+mOaB52xGWHYkzfMv3IQQpn6vc8nlLqxb4myJIpFTKXMXBnxzN3BOrDLj0/LjVZvmutIRjm1ui0a080CmfkV0+LNh7fqj6kT6fwJ8QbHTT8tR08zMiy5XkNy2d05p7Y1xnGvh8QwOCp3OLW/9r4P/TcIueYYxlX65mpn7mM6db/i520zhlY2pB+2bWM22HELRgrHlsU3CRLV5UVN+XYLzSSihBFFP7Q/SgiBq4ip652ZVzwRMNC9FC6KbQj4U6SumTEz7NN41x2v9nyqXOyno3qkAvyhmM0CUqKsS0DlVbvqBO4Orndv9JTuts60oEJpmJUYrj/BxaPdB1YVqTXde0Hp3zdN1m+3sGe4LtJBOxQwiKlllcxo4eKnqN4ImtsU2LHFoCTDfPzaYLU7GIUO6BXiEELfrpGNLYKzZrkMc50SnGqDCOW/tHF0IuN575oE9HWsZxLH3GUgGTqiTYVOmd1zOT+Ycd5bo76VDKnhe92E/8XXRb9TMSTLIDHPV5Suo7+IYKE3W1xRiLDJRrfm/0/de6q580eXeeLt9rWv8gaaXH9jbmOsT62EDf5/I7uQ2tNFn2wULfWPFRNeMdNkHF62Mth11XZ8XmXv2ZEKf4s1DWr4xMkjRqVBhTsCXXOKNOkqx1c0Nt5q7CRzPfF7mQpO2Akvb9iODuq8tLfefdZ/r1X/mxzk5Pk29pHHV5c6Xf/4M/0Np8Zl49LvFdAQVDmHTdIzYpNoC0ndVePReLHfOLumbtNtavsiPr8czZa7uu1t7e4v0Ze3XOFp2zbdFJc+20nz9m88/tO9Z7xW/+jjrnJ+Geoszr+bTj5JkuhN0BavkdLgWUbTYb7R8c6Aff/4E+/853dHF1OR130G31savf51z+LjY3h7adHLhnfh7e/dHF7Rrvet/zfqGTr/e2PV7zZhvg9Nj1SWeM4yjwCH8cAsOwUdclEM+ziwAyEkA1qu8X1bNkN5dyh2tdXV3lDGmcUzikvLQ17TrTAxS6QwLie1YBTjHOt2Wj4ZxnMjcBygCp7u7ucqZW3xfgE+eYZ9glR+Uij8GzdBirA284iz3rCLpDSwAIz8jr+15nZ2dVdAZZRA5IxhgzMMhYyao8Pz/P6+yBAdAWIGAcU2llHG44ox4eHnLml2ekAcCxfmRloUxw9DnAyrwQBLIdmUdx+g7Z+eIZKDhTOWdXKiVqyWoCZKR91oD1D6E42qHbOJaMdujJuo/jqI8fP+YM1TbSC0ce/QIo0Q9AFZ/1fZ/B+L7vcwZx16Uz4OFPp9XNzU0G7j3YJMnVkIG/s7OzLCdOO3hqf39fo1JWuDtCcQJL0rAp54+5AkJZwUN+Zih8RJv7+/tp/bsSAQRYJ5WzYVd3KUgDUOv29jY71rmPjN855zRjAyhzIBvDxwMZGB9ZgdCY55Bb6IZeajde52XAXxz5fB9jzMEgzAPZhLeQ6YODg3xUgZ/Lend3pzdv3mQZw4HtOsKdw/ANfSHnd3d3eZ15Bl1KO4eHh1knkHkHUHx8fJzXnmf29vYy+AgY5YCXZ8BSeYMqCa2+RzfBZ+5Yd0DSndsA3pR3HYchH5AEoLRcLvWzn/0s617ocnh4qOvr66wzKXV/eXWl4fpGy72PVenz29vbrCscgGb+8DZyzhq68x1eZA440x1oRkYBCwj6gibulMeh31YAcCPC+RF+DqGUpvaMbc/iRh9QsQQQkLYBKV1/AO4CNNIWPOGZ41QH4ZgEl0fKtgKis7c4+MDRARzLAK96QB+2iu+5lOdn/ujG29vbfKQI7UFvpyFglxtj2AMOmrAXxBhzlj36xfUf+oQ9FVmDTwEE2Ut9z/Gs148fP+YMdPiHbGiMVd8LCHCBHxwkJvuddYUeHO1C1nYLgra8yPjhaQ/OIEDw/Pw8253IO3s58uZBQvTppZf5zgMOWIPFYqnb+5J9j33H35TPR995lQHkGB3tBv84jll/+F7pAV2+V6xWKw1W4Qj+CSHo/fv3evnyZQpOurysAiKQVfr3Sia0w/4PfQgIcn2LHpOkRd9r2ZdS1thmbaBSt+jz+NFtfvyFZ4Qj+94OutxtXZdF+vEKHOhs9iR/UUJm2qARqbxUwT+Mqw3su7m5yXNiPZ1vqKIA3dGn/PT3lfYl0Ncence9znMhhBxc4xVi2BfQKehm1+kEzcIH0NSdgtlOCMlV5y/k6BrmxFrRhr+PZJBbMdtzHmDs9oTzO3NynuMnc3UecD5m3/Pg4Nbuc153mnddp3EYFZwGNkcfN+t1e3ubP+PytWbsXuGGtj1wwysZfZsr25PmOGA/cbmcc1jMOy6CRs5pnuiaMs6Tszytl7UXAA1UrQntv379Wufn5/r6668rGvlYKBFZO2UKOMS4pBqwnnNo7HJqzn0/14Y7WXbds325s9mfK9/vas/72+XMme0xpiKi48z4Z8f9SJvpvvDYLTP3P/F52P5sdr0mfqs+2+KF3U6xun9J+fTRR8CIqWc+Z/7cG/LYx+l3H3esPtvFGunzOV5wOoRtPjfZynw+01HQaOPKsF2eV8jgA7LiUupzLnN6nM+hj68V9Gocn7OhDnV/UvHhF9nx+fAZr2Yhf2XfVj/GhnYhf1dA3krThQJgtjw2dBvFOMhLWac9od4TOwGMTzPbwWvjWCkzI0sslAlBCv2jvJ+CMkaFsK3X2v1a0XIzbU+vxhGjQpiO/qj4vBA6jS9mmD34f7fmFKVQzvGe46gQQrptRq5bHhyzDDY6PBaYK4RybvHs5bLlbbRj8gdiLV12Y3V/jGMN7kV7ZhpnOj96O5jLbdS5MbXzSTq/E+X/+cxtqNJeAwNCL/bm6dluZt+aHUuY9v4x5/5mysRxLMB4mM4ijwU8h8NZxgSwT3PvoPU0h6nZMA21Amxn1jjZDyR4tfLAdFOjw9SX6+7UXtTGkrSiiiy1ttJT1/Z9ocxdKsEVeZwTm4hAkVr3Mc7y7LRv2VTitLYERtoUnxirCqHtkVrcYvWTNWr3N2m7XHSaQ8vT7Kvba7kL8I22R9RtJVB5nClh3bbR+t7n7kmsMG7Zzf4ulQLHV1KUfvC9H+jXfuVXFYdBdzd3uh6utVgu9erFK/3Of/K39Ud/8se6vr7OiT+8V6AzmOs48eDT17wtVdMxKJdt0ONA4nOu9l63VWs9VtsCrV76Nv1szy393fLJU9ecvT33fauPH3sP2LLRJl03p+N3jUXatu1aXc41IV9ZNqu9v4RgSdMxKin4uNeLkxP9+Mc/liRtNqOiHSOxiz7t9an80s63fb/x+9yP7/TftR9lX0MI09Eu89n4j41n7vfnXM8GxunYs8ncWdB1S+1NZRU9G5MrOaOkZDiOuXQx0f2lJGtXlUz2f9yHcwwnjzs+yLjEIULZVLIdJWVw1p3bknR8fKyXL1/ms0lPTk5ydpkDdwU4HrJT8fr6OgcF4KxJzyrP1zPTKfvtTlucKQ7y4lAGQGiB3tYpx/dkKXlGP84snIzHx8eSlDMZAWVYL8rZujLB2czfAPCvX7/O4Dlr4uXbybIZhnSWMqVMydLD+UgGJCACc/fzznHswouScuYltAWsw/nL2pVAjmLAetY8GbDuaHdwg8+ZP30/PDzos88+q8rX85O+ADoJCDk+Pq4ycFlv6Aevdl2n8/Pz/BlrTBbu5eVlBnxw2tIGDkhKvkJ7aEJGso+h6zr1iz4rN4BbD+gYhkGxX2Q+TjqgGBQA0J7l1zoHl8ul9vb3tFguMi0PDw91fHycwYn1aq3jg+Mqq5lsN9YCGrZADICFV32g5C4VEAD4yARFz8FnrTL3Up7QGIATer169Urn5+e6ubnRhw8fqtLeDq4DuKITcPQCWrnT2wNRQgj5SIM///M/17t37/I8nQcAdWjD2+u6cn4zjltkFN7iirGcXQt/xhhzUNFqtdLx8bFijLnMqwcj9X2fv3/58mXOHOb7GEsZfKerj8nBAV8XwNJ8/MDqIetg36Q3m3TswziMWs5knr5+/ToflbBarfTixYucqQpICth3fHSkg+NUkeHDhw+5yoOvEUFXBBvc3t7q1atXOdsNOSBLHtlB3/D3ZsrcQs/4+d3I08PDQw7aWiwWOTOUNUePsA+iQwCp2D9p04HQy8tLnZ2dZR0Bb7LfkW2O3DN/zv8mmAA94nsJ44e/0W88B6+yJsg4a+Zg93q9zoEODrS7Ho4xZlq1L3aeIQ7/e3AWmcKMAd7lb98XGANjizHmqhCsowOZDpqzH5Gdjs52Y7Lv+3zGO3KBLkfnMRaO63h4eNCLFy/yuK6vrzN/cw9yg3z6eAAboT97MLIBbzw8POQXQ+wswGwPmEGfUA0EmXYwz/cNSpDD2+zzrCsZolQdcDlA/glIgF/gxTGWQCL6dXowXvQdPAOIz/c877ZBCCHvP6yz39N1XZbbvu+1Nv2BbGJvupwSaORBXJR5Z/4ezEqQoGcrtwA9e5TvmR7QhE2OnPLyDl+jp9lX0XM8w9oSmEKwA7YxMuUyiM1HIAb2C/TBJpFKlrUfh8L8GCe6g2f9c7+gCe0wLt57vAKB9+92m7/Yu07yjALX0R4ITJveJ/zkwU3+j70WOdnb29PHjx8rPcs4aSuE9KJN4C9r5H1AL9+XoUl+b5le4B3shvczeD6UzHv4y7Pe6dPHhsy2R0G1AQ/8hJ7+fugA7jAMWvSLyUcYK7r42vMT3nCZQFfAx+x70N7taJcvgr+/7YV9606HWfD5ESdA1kuqn8n2kiZQXMn52nedxljWY4gFLHdHyDCkqjIvX75UN61Zli8bUwLbWmdIUFT6vIypHnfrsJl1qjYPPeVQc2eY6+snnShNs6V/73t3f3X7Bjo8sW7t/H38+fkwB1Rutfak02g37eL22mh7LebamcuKnJvTY1f5vgVuHRhJo6rHnACkJKs47sr32MX1tGvwIv1a2o/R5z1PL/oIk8O//CSrzXgnt1/6TfRzgKXlnelrH+Z0e5nLDKCZecAdw21G3jZf7lyvmtxlbBPwNcYySGjg7aVpBg0N0pPlkyCI6asxjNVSe5ZgzoKeaEE7AJjtz3VzvnG+v6OdadzRypXHws8V3WLznek6bzs90Kla6/o/Sq2MUhjzeFsWT/o6GMksMCDUVT5ilPrJ5WucpxgTUF4757cd9ltXsLXTvOyGwNjmwPxGI4SyB4SKDvWVEsZn9ETWfYlSuzC0egih7qfSoSHzbwEYXP5jNc70d5wCGqZ1oLOosl4h5C4rCpiMR2RYTeUC4y3XhXN6wUkUY0zgwjSGWZUwTSVa9YEM7oYwnRkdc3Y9Z0jndYwl8KP1nSpIYZhfzxCCxjg0+6fzQZlDG1jFvSGwR6bPupFqCjOTjIOcAIUvzbap5LfqrVAmNnw4Hc+Brqn27FCyPxO4X8tCXZ5aigZ6ZvuC/0R2jtL2Y/vmo/vqpIwDayn3i6T+yr7qi7G7rLndJIXtUtPMKY8pKtPrsVZbG2jXnJ5nR22Dhn4P+EVQSlb87ne+q+vLa73/6qt0bO1qJQXp6PhYv/4bv6HXr15rGAbd3NxUvmB4n3nO2UA7Rvr0HZOSmN1fZu6ds5n9/pYWczZxjLEEZTRrscs+nx33I5+349wFjs/Z/e08P7W/Xfcx36wbHmlzjjbps3r9/f2peheZqvlkXVKNr9hRlOjfTO/kZ2dn+vyzz1PC2chxYe2BQ9tjba9d/DB3PXXvU7LYJmpV9lemY5iVhues3645PnU9GxjH0cjLLs7OwjCj+r441nEYkc2VnBRlo8ThBNOTTRJjyS7DcdKWIvVsZHd2jeOYx+ggimc6uaOXhQkh5BLAnqnAOd5kM5NFJWkqDXuvdG56pzdv3uS5kQmZxp0cWQALDpI6aI0jAdAPGjoAgCPeM8twLHGOpzvn3JFEOUyyu8mOXSwWurm5ySCZl4n37LZxTGeBX15eZjAGkAtnFONx8AXginmQAbNcLvXx40fd3t7q6OgoZzDd39/nUuuLxULX19fZAYwAAS71/bLKuvVzgwH5OTMUAPT6+jqvDRmPy+Uyl9FmLXCueRZKzpae1hDeAugOoWQWuYNXUs703WzSWbesPRmgd3d3ur+/z0CFA4Q3NzfV+YUoE2hLNiyAN+PGQczcPVP69PQ0ZykSpJLbH0dpM2gzbHIbtJmrLlhgBg55rzCAo5/fmSvgG7pjPZbyv6ytZwfdP9zr+OA4ZxAiG/Dc4eFhdb77zc2Nrq6u9Nlnn1WgCQ5drwJxf39fnclNUAfghStrd/4jW75+0ALe++abb7KDGZAf8Lfv+wz8sZ44aKEjsktmFAAFFQkA2sgqOzk5yWNqs5WQeXSHO9MBN5mDA9CMdbFY6OXLl1nnotdZy77vM+0IEsKJ6w7SEIL+8i//Umdn5fxJaEJwAuA7IB8852NHvlgf9DQ6Gn3F3gJt9/f3tVlvtLAgKmi5XC51eXmp+/v7XLL7s88+0zAMWTfAnzFGHR0d5fLv5+fn+bxr1gc9AiB1dnaWdYcfo4Fu4G8HCRNPlXLwrAW8i1yjw/kc5zlgYQvSQDOCGNgLWD9+juOYz4HnOfYXdBSBMQBFvueSadt1XRWM46AG68X82AORUYAHP17EQX/AiMVioVevXlVnFHtGOkAc68b4PcgLG8TL9DpQQwl19JP/JFiPMUJ7aP7w8KCTk5McMMPZ877P0w9jQ54ZC3ztmZrc77YUdEWftBmsfIfO4Gx59ksvGwz9HLSC3g6Ks3/Axy9evMi2kGdmellu9ALBTsj7YpHOAL+5udmqjOIBWv5ixHOum/04CQdkqXqR9/KxnCtPkA1APu1RCYE5YgswNufl1gajhD97B+1IdVDSarXSuEnlydHF9PPZZ5/leRJ44EA7fI9eR0959it7MjzBXsfY4R/2pXRcSgEOfb/CCcU83D7DzkOefM/2o4EI7AP894Cf1Wqli4uLShcQuObzdqDf+Yf5uvzCM16Rw20V1g2b4PT0NOt4l3sPVuVqA7rcKQi/I4ceyOV7PnKMHQ+9sb0yv8YSyMB3rb1CZSsut2FY7+VyqWGzqfSUB+f6cSAesMt9vLf1fa/1sNFmsnXY+33c7J/wPusMT/v4mB+87/ucB0QyBp+37/fo1nbM+/t76hSyHRZCyLYg43Q6eTCO74UeSOh63wFx7BQPNPy2V6lKJEnF8Tb3rziW551hE1ZR+d9w6CYvdnIc9v1CnYOQjaMDvt4MG52/eJGrWhBEFmM6uiZqcqQbD1bOEJwggUHNO1yecgK2csA9bTvPva96pvlly8kZ6/vm/DExWmluphnrDL+qr/LgVldhbgx+bwg72gyVYzu2z/B3mBlJ5SSfvhtx3DcOQ/YS67e4+Kfn4/Yaup7afbVgUBlrYqMEhgdAO02VIMaorqN8YwJaNptBi74HActnq1LdYPJSpnXK82Oxu/I7DegZzlagDVDsNPNtcDQEdXEhgDgHbAoJ4zQvAxqCFGIBfPzyYs84HufpyRC2ZTHPL6SM5hppqzOjQwjpiJj8nPFYaXH60dnobJzGOVLKpM5d8ii04MNpSmF6YqvL6dFN7KbvbS8Zo9KRwSGrpKD1rM4IoS6d3sdSOjxuObantYtBnq1aTdd1k3qNsc/rHWPUMI4ZSAsdAGWdqVzGViGLGjVV2MxdpSzMOBEq2xshVBTnV7J9U7vbGc3cWNQJ1I+Vo39Lz0bltWdd8sd63lV4EsGoK9IUMtQ6qoy/7hHdIUm9AcIKBCkAgE/2QIwKsVfexpyfsq5L4xyyFNp+kMUiTrQe87pU8zReSH93SqBsSxHXS0IxFtpO+47bCiEEqS+B1UmlJ70+dl2958QGMNuxV9P3zp212TbS7e0axGyzxFjomT5KvxOAF2NMxw+YjiwBAaHZ20YLplDmcZvipDBzI83Q7V5pihWZeFwNWGh9TKcgFNqNY60zFfLxCFt0zZ9F+e66y3bZ9bm/6+V1rFYJnWifxvLNY7bSNI1i1xWhmNa7BstjbHiosevbecztRfm+R+wHdF5gfLx3BOO3IK1XKz083Ovt67f63ne+o8VioX/6T/9fur64VN932gyDLi4v9Vd/9Vf63/9X/5V+7Tf/ll6+fKnVw4OoPpOqMdXk3BpbqLivltha9ebba7K3K+ZyU9N0lw2c9fmWrYgesk9jLPPa8W6xy46esyOeetb9cO0Yk+Q7keL2O+E4Gu1CRed2r5y7nHZFJxo9w3Tsysw8tufarIP/ND7Yop3ZFtPWkI7Z6Dp1fa+Hyed7fHys07NTXV8nX3wcnBZz+0Mtls+52nfLx3QL99e2Uv15HMcUEh3C1nbFfcM4VjZRe3VdY7s9gxefup4NjIcQcgljmM+zGZIjIkznGZeIfu5LZTBGdV1xQOFI8HN0Q5CdHxy0v3+gEFJJluTgXGdHGk4MB0FwhtIvbQ3DkB2+zAfHPgsGMEvWUwid1uuNHh4ogb7Q9fWNxjFli5dSo8MENvfabIbJkbOUVGcs+tm5OPtwVJNZhnNQKuVzcey4U5n5OdgJY/C8Z8zSjjvopFJGFwfher3W8fFxBuSk+kWVbDWAWJwgZOYnAPheBwf70zniIZdWxRl7e3uXS50fHBzo5ORU9/d30zijNpvBStLvqet6xThqtSqlE3FEEaAB+Md68jv06LpOV1dXOZMTeuEcxvGNQ0eiykFxdjqo4HTG8YWzF6cePA7YTcappBww4g5GL8frzk5AbD7D8dj3va6urhRCyAEKlA3mcrnAYYrzHh7B4SgpOx2jovaWS/Vdp7vbu8lRuizj7TptVusM+jIXeIzNDJDj5OQk6w6ypLuuUxzSRus6YbFcaNEvtBpW0pjOL0WOAZMcJEOuKed/cnKSwTNfU8828oAd2oAulP+/vb2VpOr8XZz8OEUdWKdteBHnvMugyzXr6xnivm6A2oAbgJzMC97wbDT4CFoiR8g6jnjPrqfsqAM0gFWMgfLtt7e32XEPaMAahxByFjLADGAWwIekDEzhbAYIQVbI3IZe0Jtxt6BTdqgr7anjOGrR9xo0OeYnQ3i5WErjBN5OjrBhHHVyeqq7u1sdHhxpjFGff/ZZLgfqAIyDh/cWEARo48c93N/daZiA+mGz0fHRkW5vU2Zot99pP4OZKTpwM8nG8ZRtqZgMrnEowAVVH9B7yMJiscjHXLieAMyArxi7VMroA/q0Z9f6fuAgELzKOhLMAyjIWcMEy6BXAd4IYoEvCCJjPdElZJ0TgAEPjOOYA2Kg/Xq9ziAqYPrlVG6aoIv1ep2rnxwfH+fMYr5HJ3iAAPKMnJIJi85nnJ6Vz/nUyAGgCwES79+/z3YJOsgzgZHVDDhNckRbDrgDTjsg6QAac+v7vsr4p23Gv16vsx5B7yC7ntkOMOlHMQB8kvWMzkenoHeQW3Qx+zj6lX0JPRBjzMcDEBSEjoHW8BBGNoEu8DZ6oe97nZ+fZ5C+LfUeJd3fJ3kdx6iHKVAoA+zT24OvE/06eO6AeCuDrSyxlwGcIW/q+tzvou/V9b2GcVC/WGi9XqVSc7ZvoQtoxwNvnCcc6ISP0OPIrvP6OI66W62z8yzNKQFl68062+NRJQCTdYUmwzDo+vpaR0dHeQzIMkEmjBWbDLlbLpe5KkquHjPJmvfltPMALM9mbsFCAijQc5KyHdj36Tx6SdmmxabzQBUH19nnfU/zwF/ec/ib/Q9bgzEz3tvb24pWBC7St9uu/hMZ82Ah5oitwzwYz2YzJPdgjBoAhWPUweGhlssEyIxDOleyn8rmrzel8sywTu8Ji0mHOg/5+wv3o8O9mlVrR1NlhbHCFy5TzA9dha5jvvSHDQ8f0I+isj3DeJFdAmwd6HZeYy9hPK5/kX3nRQ84+Xmu1cNkH05rlGSzeGUnN73A4LecEN5/mI/CV5ic7grS9K4+juWcxK7r1XWhonEIQfertQ6OjnX+6pWOTo71xRdf6Hvf+54e7u4Uxqg+SHHcZIdU68QY+HxmSL5u7e+to2buucqpNfP9XNtbbRmdQ/mwcdQBVExnDc6MyfI+UzvjuOWkixlYMjqF1tkGmF7GrxCksehr9zU1M6/aqpxxzcNbTsw8jvI559Fv0Rj6T5OFW/15+q5kMz8+71wtn9eOzSQWE22mW8Yp93Ucoq6v7vX27Vv9rb/1G3r56pUWe3vaDFFffPGF/ujf/mvdXN9oubfQ8WkKxFaMGgcH/lr39XbZ1nbMLZ/b6jgFJr7qqzXl11FD1RbtVPzbBS8sX8oXNxJVHJBtHhFlOetPd82nPNVtJQ9GX3d7Lmf6+ribnxManY+LyHzR3peBsx1MDtAiKXQ12N7qwqAx95c/69wZnTjX13qXrgmSxtBVgGn070NIUFwICt203nP6a9JBvaTO9JjilGcemMeYzyL2cfB7q8vWQ5IPVeOfHOfTV1GS+i75ZSau6hTUK0jDkHzsffLJbTabCSTJ/1H9Z8jrYFMzwtk6qXNx8F9yKdU09mbB2/anTmLo8/e5Y/ZMPurSWjy9N9cVxrjfbTFJ6qUc2Jq/p4S4jWMoM8y8Eqa9t9Akakchiurq4kIFGB+zLvQxhxA0ria7NIRk7w2DYpC6bpHlpO97LZKSzmNKPpWoOA7pPPKJBnU5/u3r0+ydXUfBwC+AUmP255SbSgt536yYWVYWvtAj2xDeyOMzqv5Cv+a1RgbHEkhY9FYQZcUlSUMsIO1E46Lb0tjHJn96jp5R9RFFrW312H661V6A1llTzt8fpWEGtA/tuigqbkxuhu3M8ax2WvtUkbikrf5bnVY9t2WTbU0xg+K9pveCcUhHgmGrK+jy4wcdHR3p9PhI97fX+if/z/9Ge4f7+pW//Ws6PDxQp04Pt/c6+t0D/V/+z/8n/YN/+H/Qd773Xb04P9WXX36pk/OzBIKHgv8sl8sc+5NtV5U9osxHiuOMDTqnR0Osnk6i29lRSKkKx9ZST21X2M609lv2MssOn/NxYyxkOy/W9qVUYyX+PjJn983dE6bjSeq1r/ktxqhFPgaiyF+AqNO+F+yIFKfDHL15P42xVPENIeT9N/URKz3gzzt9YzAgf9rHs90M34bybKaHpv2en3FUp6DlImQf/8npiV6+fq2js3NdvP+gvuvUKQX8DVNyVefROHl86K76XHR/L5fqgHxfp7n3Ktpu7Q9+5nZjTO8rRqdkJ5b352EYCA+rrtJmq7MK37W85z6Ap65nA+MOoHlmCs7dBNoGDakWkvb2lpUzaLPBaZgccJxFTTvn5+fZsS8F7e1xtqnUdb1Wq4fJeX2n5XKRndyAN3d3d9mJ4ecN+xnkDtrxNw7yg4ODqlQqGclpLpRC3kxOsF77+73W65VOTo4nUGKjw8NUKnZvr5ynjGMIQAJAH6AeBsRB6VkLOLVRrA5oMXcyLHEgexlhQA8c2TjTWU8usrVw8DlD4SjH4QQI7Y5OQN9SXnBPIfSSusnpeaSu63OpecrZsvabzaBxlA4Pj6YM6M2U+ZiU/P39Q3Z8eol01vju7i4LroPhLYjtFQ8QLM/kODg4qLJ6cXZ6Bi/ORoIO3JFKX17uECCHzG6y0fwc0zbDhPWJMVbVDXjOs5QBdWgLngJI9MwNZMYzt7nPs4FyRs+y07gZdDg5Cod1KRc7bkoVAw/UgFfgHT5jfKwJwNXx8XFyoA6jupCU+d3NXR5rPwEFTuuLi4sMEgME0yfnwOJ49ezREIK+/PJLvX79Oj9PRhq0hq6eGQjY3Zay9GzE1WqVeRqZdV0DUIVuGoYhly71oAQCE+gHcGgcU9YxNPfgDkASL1s6Z2jAR6w7vOQ0al/4oBP8SEZt3/c6PT3N/TCeGEt50hBSmXvP4PNsPzKg4B/k4PLyspITLsZPcAVzv7q60uHhoY6OjrS6T3QY1lN27d6e1quUoRcnOq+HjUbFDK7ePdxLXafQd1rsLXVxeaFhSMdwoAsI+hnHUaFL5Ws8qApnOhmui8VSRweplPrx4ZE0Rp1OvB67Lr8kbKbswU5BIXTSmEqejQaueCl56AbPe0n+jx8/ZhAK8IN/0A4gAd0JOIYcoludv9tnWEPP8APA9cCN8/Nz3d/fb5XmxmACBEEO0EXwgwNXjKXrOr179y4D8L7XoTsptYxMMmbGjS7xzHsHLNl7GSe0Rrff3d1l8BX5RGf4ec2bzSZX5XDDD/lDzhiXB6J5cJHvLez5Dqiil1gn33eQKzL6/WgR9r+XL19mPQav+37HOD58+JD3G0pu0wdBknznDiNsHmw1dAbzcD6UlG1DB6qgKzzogRLM14NA4Ju2qpDvn+jkEKYzjMaoPiTbE3tqjFNm9tSuVxPA7sUOcl0GH3llIOdtD6oBNB/HUf1ykeV3vV4rDhuth0Fhs9YYoy4vLqqznD0IAVuMvh3U9X0ePnEbyMeWg/v2k67HAbZebxTYK/em40lsP3E5ghfgH9qFv/0Z9rdxHHPFC6mUjiZbmD0EeXDQtXppNV3FvQTetseU0Ibvmegpxt/up9DQK5SghwkEyoDhZMegG3gngV8Yq9tSbjuhOzx4yKtctI4wfvJ7a8+zH1A5Cf3RLxdSV0qXawJaYhzTi+nUhh9RMQwTUNuVo2Go4OO2sAdMMC+nNWNEH5Ah7na4r5XTgLHQj9uabhe7Xg0hgf0EJiAzrpfhM/jJx+N2CHzpthN7If8Ym79rfJtrNUwVUiZvQDoTd3IFdIUHKmfMjCOAOY3m+HEecruVNfOLta31XZKFly9f6fPPv6uf/OQnkwz2GuMEpoQSnLrlfHvimnOg+Xef0tan9hVjyVb7udqM0jYo1YK9tYNxaxyPrGc7xJ+HLnP9ZP3SjOnZbc58kICh5/X/ZPuztJFWq7Ue7u71nc8/03/5v/hf6f037/XVX/2N7h9WOj8/02/+6Jf1n/z6j/W7v/uv9Mf//o/1s5/9TG/fvp34PB0TMI5Ri8VS0ijvBhr72rRO+8qZ2GTuwBdB8+u1a70fm/tjtHuKJx6Ts/b7GMnmedxJ+ou6Kjp+ou54SoZ2PdPS9al+C8wWM0BTjXsCHZPptJltz53T30YO2nnUjT9yM055KdsAKfgxahxGDZtBGgd1y4WG9VqxC1IP4FGCCXwPkaRusi2wF6shBWVwaBhLJiIOcugzxAS8SR0IztQOAUJbyI+dRZ72ywlzLveGMOFKBUB1HY2shhCksQQtT4uX28htx6i1osKyVNoZxqQvOsY8Pd/lShGTnRAKQO4Y8DiULmmztfNCWGuMg4Zxo2EgaBFCRI3joHEY1Ws/6bIYFbqgxXKp49MTjZv1BIwH9bHXoQVht1ec4em561NltQB4T7U7A67+j3Q9lxbtM0/tnXP7fvtd/jsdgvDo2Ob02HzHklfu39WeR2+1dksTJjbfzQwNnkvDp9e9rVZR9+tDG6YgrOVyqWGydXm3W61WOj051Vdffqn7u3vt7e/pN3/zN7UeNlo/pMSVRb/Qb/3Wb+mnf/0z/c1Pfyp16YhL3u18zLxXua09N+/2u8d4JX22vSehez9VRmjvOX0/r63y04HnXXN+dC9UHtqjtum3Ga+/q83Zbh7s3bbdTYFC2EA+X/fhdV2XgqGeGJo/4++tvN+l9zWvvJbG8PbNW333O99JCas3t1qvVsUWiap8M20wJ/eEmaAG99e2PD13n1/t9+3nad9Mz7DXtPc6JrNbVninZB6lX6ejv98/dT0bGD89Pc2OZpzvIaQMcUARHPg3NzeSSvYkzkoHGS4uLqpsXxxCnk29Wq1yJhjOkfv7B93dlcxbdxIDkpDhSbuMmbPDcVLigJJUOZ6K0/skZ9qQ2cY51okxlMfLPMhe4yxYd5xQ3htnH847HFX8fXNzo8PDw5ztAPABME6GFUJE5ibO5FwmcXL+kAFP+VYHiRESQGt38OIw7bouK/y+73PZYC9ZSCba6empHh6Sg//u7i6Xnj8/P8+0x9EIL8Dwl5eXuri4SJFap6d5LF4invsBHACrHJhzYGVOgL1cIrzD/F3gKAvJOuBEgrbMARrxrGcBuROfe8m052xND54gO5c5uEOXdcChjOC7c5gMGPgexQLQyNw2m03OMqdt7sVJ6ACJVzLAEe9ABWPBuAB4oj8CJyRlgASns5cWhv9TtYG6BGcLpEFf9AS8DnDI2cQEPFAym5+AHJ5F62N2EJj1dOPGAXfABneiu3M9hJCDd3CuQis2K+YIUMBmQPYt6+pZoF4qu+s63d7eZv3p4Ik7iQmUOTo6ymu4Xq91dXWV5804ydRED6EPAXPcSQx/UNbbs27hZ8aLHoD3edaziNFlR0dH+vjxY9bV8CXlel++fFmBSzHGXLo6A0wxVUsYY1S/SLxNhrDvL6wZesWd8/DG/f29NmMp0+ogBrLh4A60J4DHecIBPcY6jmOWc+7xQBZojv5Ct3GcA7zHeUceCAPdnY43NzfabDY6Pz/P/VNilooC8MTd3d0UvKYsr/BbC/Q530ADdCngB8EktEPfXpkBuSOAaxzrErnQz/VP61xyEBf6I++uywFJkD2eYZ/14BVkx8GiueA29m0y/gkm5EKmY6yz9KGBB+ZUJWqn9j34ag6MdBuJ7xg3v9OPn2fsdgDVODwQ6+joKAf4tc4w5sI40I/oI+iLXLEWJbhumUErrjbgCBq1+of+Y4x5jaD38fFxtg1ZN571lwDXbZI0xLKf+osvum2u6gH9eiUY5sfPVvc5eMxY0E/oFvgfeQkhVNWIYox538Mm4IV/GIbqyCCCQzzoBR704AvsjeyonHjT5yYp2zauG9gz2MvQz4wTerNn+N6HDmV8LQDuti9jQbd6GX7sH/SeBxoxftaOPRL6OF+5XYNcsxfRF3uEA6a060Ez7PuMHXlFV/PuMPeC6XYuF/Omb6eTy6NXoWiDR7GvCEhD9zJGD0hgzC5rfkwBtHG+9vnA57QPn2EfomfdtvZ5O4jtYC1854A5feXKCYtS7aHdv6FVOzb4iMvtUugOT7lN7nvgz3MRtMuY0F8eACqlzH8fY/szTl6QyvGiGtDgH3IOf/g7c3XfmIKfTk5O9P3vf1///J9PAdmRc1g9W1hb46uvp0E5//vp9naDWq1Tx9uunG3V6Lb7bx1qTMP3w2clpUmajsPecjZ5W1vraQNt5/Lca46eW33rW8YHxMQBWw42I8ucc23nOJo5euChr+HdfXqXPjs70a/86If6J/+P/0b//o/+WMN6o/29fS2We3r76rV+6z/9Hf3SL/2STk6O9bv/+l/p4uKDXr58qc0G3g+Stp1qLgP+meujak6syQx/OTg+t+6P0WPXd3N8v+uZOR7e9WxuIz6XHxpAdGas3t9TfPBUO3Ofba3FjufbMcz5kD51DPm7dMPU7vx+sGvt5/qeG2vbls+/7EE79GHz9xgnB/8wpuz1fqGPHy91cXWpu9sbrR9WUzZuyXz1NroQNHbk7zZZgpoym9FlE6yWwfHpp9wejAWAd2WU+g7V3+q6Uko3FgA9tZWa7mhn+mxszpqnrTgUfqcig+t56DuMBSyJkuI4TuD4RIGpr2FVB/CWzmwtRqV+pjYY+0ibU7tjlVme9uI075EBa1RUL2mIMZOt7xd6++6tfvjDH+nt27c6PD7SuF5rM/ly/R06t97K/47rMTmsppv5t+Wcx9t8Sg7bvrbW8xm6YHuM223MjWfX3Odo95iub+fYPh9jVKTKwhNze+56IAdz867tjHk+2P5rnsZP0Wu+vSfGbmObsyXav7uu0xBHxWHQEIs/pVPQh48fdLh/oL5faBhGvX39RqvVWl3fZT0UQ6nCCCbm/rh2DG4TPDoPA/g+dR+c458Y673XeaS2QeqM2l3r7zxZfke/Pj0WnnPd8qTtMdZjaOnyXLshxqgwe+xEPc72s7l/9DvGYrv5/Y9fceca448qNtZUWaDrRAARe91ms9HpyYnevn2r87NzDavJvy4pxHQs7noox6y4T87pRfl/3qvdd9rSeO690e/ZJXst37CHtu/F0M8/39VuO65CsjpjfY7PHrueDYx7mUtKJHpJZJxvdE40vjsv3AEaY3npBswj89azMPgdR0wCFqSTk5MMbOC0xwETY8zgNIAYBgVOEzIbAHMZM4C0JC2XJXMIoAOwgbECintWmIPeOBtxdh0cHOTsHcaOM1JSBkRw1LgA+rnr0GJvb0/39/e5xPHp6WmeK85d5izV52WyDsvlMmeiUVIaGuAooXQg8yHDsHX8JIBy1PHxic7OztR1nb7++ut8JjnOVNYe59/9/b2Ojo7yWdw4SBEGd9h3Xafz83NdXV2p7/vMCw4wUfa2jXpkjs4PHpXi2ZBePhs68tOdiswF4KYVamiDc5kgBfrD0cg5pJ7ZBM/A/2TfAWKwRjj9GAtONAfmfXMKIWTwi/a8gsNgytTLHV9fX+vq6kr7+/uZl1snLr/TLjS7ubmpMm6gLXKO/HZdKQHujuoQQhWkwHjv7u4yuI5sMm8HB6A3P4+OjrIztK2E4WAK8uzVJzxLDD6Azh7sQVvwG98jA+489s2DvwmiAchl3hhgnjXPerM2DhxxdjXjPzg4yP28f/8+9+FnugLixZgAjbu7u+rcenQ6PIi++uqrr7RYLLKTnOApl0F0H3rF9Rb0QmYYD3oG3chnlK9Fp/l56lx81nedRsXsTAa88ACH1f2D4qQ/2WA5dzztC0sN6wKGugyy3yhK4xS0wTPOG5TbJmsdWcIwQX4A8eAnaALvQSuAMAJMPPMSutEWOhxZAyQm856saEBX1pigHi+7zpgJZmHf8TOGucdlHLln/Oh2wFanK89iLF5eXma9iowhu/A7gVIeeOKBN9zressBGAeAaIPP0cnw6GKRStmfnZ1lfmUeq9VKp6enlZ6BH5BlB2FiLMeptICQA0xO/7ZsOfP2IB5sDPrgO553GqB/0X/YRJyVje3j525DK8bH+sL/9MH3HjgAj6GDAMUJJHC93YK2zNV5yvdc3/vYn6+urip6eGUBxuxHstzf3+vk/Cxn9bOnwI/oLXQKoDVjcrn1lydsP/Q6QV4O0rutgU5lb+Rv5Ij5w9tUT0EO0Y3Ys5SsZt/w8v6r1UonJyf5XoIU2BfhPZdvfno1otVqVdna2GkOrtK3v7h9/PhRIYRcRhwa+osdexF0QgaoNEIgLPLlL3z87fY56+OZ2m7L+f7N3htjzNV/4F9/D/J19IAe6BhjzEGlzLF9ifVxeHCUB1S0L4J8xzExnmnv8uLvE24ru62IrvKXdWjBM+wRfhyF20rMhX2wzdBmPASioluwK+iz1cPoEmw96MUatYGHIUzlL1X4wufslwcA0g/6GlqiJ2mLcUEP9Db88PNcwzik7NdJhjeb6Widvlc3Dhpj8qhF4/PWMdBebpe2TifnKa4WOPd2Vg8pUOTdu3c6OTlNAd57+xVA3DrA5pwd6ZZnwm2NU2bOkdP258/5+1DbXttOpssT41AevqMcEYxidlzVeCfkYjd9HgE64+7nHrvm7p19PmYXqI03oUwtr8y26c/GPNXd/emJ+dpnc2s5bjbq+k77e0t98dO/0b/+3X+lEKXjo2Pt7yd/ytfffKl//a9/V5vhP9bJybG+993v6g/+8A+mfkbFWPaMuXG1cvDYXDI4VjWkrerQj13PXiv77ind86n84s89R1Kf4uFd9z12b3v/U+Nv12YXrz6lU74tneY+29VWO8Zda/jU2Nq/dzm9t8c62bWx7AubYdA3X32lP/qjP9L1BIqP62G2jbpBBrOrL37fUVFl2teUaVKXxs8AunWlkICDMc4A4/ZcKKh2/j7vo9UY6t8r2gVrZ5xgi65Th62JDTDpyaAgxfo9rqYDTvyUKJj2XO5luL7unbp+OvYldBq01jCdc4+tlM6iH9X1ncbJJru/v9NP/uzPdXd9o4cf/bK++73v6ez8LB2NYTakj+sxOWk/c538XNlsr5rnH+dt/+yxfeip/b7tf5dOf+zvT9XRs/fQ98RfxA5wR5Sm4IcClMUdwVtTg0/1/vw5zsw1hNDs54zyeddWX6Hq5tN0b2PfbbWfhF9BCTyMIR1d2HWdxvVG97cctZlu70Kvfjpal3Y3m42++vobvXr9Wm/evNFiWR8h1/br709P6X1Z9YTnvjfs4rm4pcvglSj/Br23qw3/u91D6pa2n3/OXjd3ZVoa4++y8Z/SR1zjpIfb7+fG2b7rtD/HMZU1b2k0Z7NGly/eB56wzTKtp2fQB7GTQlhoGDZ6++6dXr54kf1bktQvFoqbVIGlC1NA1DhqGCTFVGr/Mbva19gvp+tzbbq59qdPZvvlclulvdwWZ5t6TuD5c2Xp2cB4jCW7B8cGQFeMMTsDcBx6hpKDRzhgcE57RigldPu+z85YHElk0i6XC52elkxAz3Yi2wHHExnaENLvwSkOgBhjAljIbE1zKdmfOIMZY3J+roXxwfnrx8fHmV4x1ufqxVhKouN49SwggE6cSKkkb8k8dCc4mTeS8tmfMaYMGi/n6GUzoRkOXJ737DzWNYSQAbaTk5M8fjL4JeX1h+EKYFCMPc6gpVzrl19+mR2wBwcH2WEK39ze3ur8/Fx93+urr77SwcFBpgvAC5k5x8fHme8uLi7U932mK/T3agLuaOXMZDYrADrPMIO/oJE7xNyx6EESIZSzHv0+j65xoB2n3uXlZXY+45j1bDhJ2QHLZ9fX15k/HTjyMp8+91bRePUCL5lI+4wBnsPZTzY38s3cudf5i+xJglEk5c+gAWuKYkMmoRv6xTOBPOgD2f748aPOzs7y3Po+VZAgk9Z1mDtecWrTlmeNHx0d5eMWhmGojgBgLp71T+AP8tlm9kNXbwN+wFnMd7TrFQiQXwJYWAN3MNMvQUd93+vy8lL7+/tZP93e3ubsPniG8UvSV199late+PjhsaOjowz0oSsA9F68eKFXr17p/v4+V8JAZzowi9Pegw7QF643yUqVlIEbgFzkxc9rhoaccQ1Qu7e3p8VyqYOjw0wfgGlodXZ2luRuLJn5BFUAVg/joK4vpYDJLnfAarHo1SnkcQO8cTGuruvymeoAAwCQl5eXevnyZZZh6IF+gJ57e3s6OjrKwFOMMdMb+jpgA838+As3dOAtB6V9H21fdtm7rq6udHd3l4McmIsHKHlGtusCaOPZ14wB3cZcHURvsyORjVbvotfQlYCi6A72IweKmQPyxNiZM8+iF5B19jXkxktdA9CgN/gMmfIgGkBHvnfwL8aYgU3078nJSfU5PIvuduCPNXEgzvdL7nMgFBD29vY2B0ewL0mqMoXRa+xF7J+MwQE+xoruQed4xQn2TXSgByuwbtgQrPE4jrl6BbJB0Bz6mrY9yxjwnMo18Gi7n7o8D8OQbRnX7dDQM7adPswVWwrb2e29k5OTKvgHIBP6QDe3AbwdB6W9Cgrl6bkXHYrN51novqezpywWC11fX6vrSgUiqgQhJ4eHh1UVE/gAu8Ez4aETgQIhpKA37DyCSbEP0Cfcj54isBF+Rob46YEHyBo/eYfhOw+YQ+5dRp2P+R0ecNsT/emBl+ypDqi7neU6mD2TsXrJfB+z6/NW9l2eudBf8Bd7GnNG10IveBD+lVQFcdEv9/KPsaKT3R7yYB34k/v528Fn1oQ19fclf+diX/D12Gw2Cgtp2Zcz4RmzB6D5eNGPjL21u/gOvsKWa9cNen3b626qSoA+kqRll5ziUdI4prFyLEvoigMEf0A6U67eu9t9kou5tZ9J246Rrgt6eFhpb2+pV69e6c2bN/qbv/krHbzaT44jPQ6itU6T6jxOPQ5Czj0/d80553Y9t+Vw+4SYhtRm8mIX4OX5z++6MvQTaK9kURYnUxnDc5yRn+Rs3tEG3von6RuUnbLytaseqPvY5bybcyi2nyXajFp0CwVF/bt/94f68OG9/qPf+I9ylalxHHRxcam//uu/Vug6/fCHv6RXr15pb7nUerVS1/fSDJjNXHc52pCTXY49p38u2Tzb0m4n73OdfDz7lAP2sc/nnt3V3tw4o/HoLp57bnvP4Ve/5ykeb+9tv3uujJR1evz7uX4fGwOfzY1hbn2eGutj32e+tqiVtJ8Ourq61h/+4R/qD//wD3V6eqqjoxPtH6ZKkl3o0ED5uaCgMY5aUCK8aMMddO7lOoVfA/8CGrAv9+yepUZNwP4MoJrlrkw8A+yVXqvGW/ZRezDLeAhBiyHd0HXpyM1FvxCZfdIEvvW9usVBtkWroD3roO87LRZd2rODtOipvNYpBM4v78rZ4IuFur7TsFlXdmO/6NV3nUI3arHoNcaoh9WDLi4/6l/+q/9ef/1Xf6XNMCgser149VIbbYNBbv+2+qjlzbnfvw1PPqb3ntIJz9UZz937Hmtv1zh/Lr0VynnEBHJOf2ibO7ftky3JiF31xO4BKLe1c/wzACV/BzXjeqyrR/aWGKcZ7NBrj+nLJkRmdqzSBJBKUzH6EiCz2WxyNYb0TjP5HYdRm/VaIXSK46D7u3vd3T/oV3/8Y718+VK3d7f5HWZuvK0s7OahEhHgvL4td9ttt/fMyl9ITNTa8KVyxrfbU8Ytfbn9bKvjtsbQPJPvj5iNny7HW9+N04rvoFV7edBw22ae9xi3xuztO324r6uWpNy7006LMf0LkkI6EmMcR71980Znp6fqu0539/caSRBODStVO0pHbylORwGN0d4Nw7Tv6ekx2Py31ugRGs49ryg77mT+2mVH17JV78/Pead76vqkM8bduYbj3QFvnwx/41xhgp7NtFwuc5Zs3/cZwMJRg5OL7OTkACnl92gPQuDI+/jxY5XtS184zhifZ5LgoGI+Xdfns61xGh4eHmYnbMmqHDLIhiPGMxtwOvo8oQnOIRgRxxVOtI8fP2bnpWcDx1gc2GTbuKOdUoTu1MKhCB1xbtMe9+MwxdGDA87LRrLuOOI9q05SdR/lcpnjZ599VpX4pW3GRPYWAAmAAyB2C/AMQzoLOIRSljjGkgXjjlFJOfPWs91xrEIH6A0/eYZ2jAV4wGHnABPZLr5mONxw3pM1dXp6WgH2p6en2UmI86/N4oZPGR+AVAu2wsc4xdtoGgej4Bt3HAO8AzTggEXmPLgFpzVZaJTddQcmjnDPSsJhyBw9y4b1j7EGcqBj15WS6ycnJzo6OtLZ2Vn+/q/+6q/06tWrHAixWCz09u1brdfrnEnXZqbi8HTQCzpRJUFSdk76HOC5xWKRM9Yp88rnVDZgU3HAyzOgPTMJ0M6zn6EL4yQYhmeQRz8a4e3btzn4A/48Pz/PpecBHnEUn5ycVIFJ8Cj6GxlmXGRTcy+BKvAoY0RfwKOcjY18obNbGSCD0IMXAOJ8HL7neCnvg4ODBN4sFtI0Fy9pjX5Bl68sMxT9hd7ZrDeKXaleQB+MYX9/P0WLR2Vg9P7+XicnJ7l6CaAATm4AqhBKiWr0IHzPXoQuhW8cRHad4QaO8znAOzL88PCQ5wiQAU09+zXGqBcvXlTyeXl5mYPN2CPJoiNYzAEWz0iF5z3AzgET9Bll9GOMGdRELthbKZV8fX2dgUT4ERn48OFDPlYhxpgDP+BdL9PuwUnQDfoC0DE+5n97e5tlpNgRXd6v4TX4Hr70zGuqpXhgFIF+rKcDTdDF7Sr2atdx7oBBRgi8c52BvmPcvOixZtgJzld+tAV61CtesJ7sr55tzb3ofuwAB5iHYcgl5H2eBLZ4sI0DVQ5q+hiQZe//+vo6V7g5PDysMtRjjFp26eXBs/5pi/VirwuhBMTQhwdctcEIgNHcD40ZL0eeQA90IHsR6+l7OdnkHz9+zPsWtOdebD1+Zwzn5+cV+E5wE+2/evUq61oqTNzc3OQjSgBK4TH2Ig9CZR6M3e0TAjI9uMVp5rbL/f19Dmpx2iAvrBXBFPCI2+jM3/clB33RDdzrNoEfG+Xfw7/stewPtIeea+UZ3oUXpBKU6brKXxjRcf4uxO9e+Qk7jTm6HYJMuV3hVwihynbnfYXv+J6x8rzb6+0Lt+9lHhTgL7bsf36vBxu2gUMeGMf7R4wx8yHPDCrBWR4sQF/YQ9DDs75dlzqfuYz6+jGu1gb/1Iv3FvQSFWe8ssA4jNmB7jzpPMM7dD4jXnW0/WNOD//H9/Ua7uvs9Fw//OEP9ad/+u+THdRJ2hETUDs4cBxtOwR3OaYec8A95iB57N5dfSeXZdh2Os9PTIZgbzll+CtWjxgSpMbRFFmL8lBsHJk+fp7ddqZuO4xj04bf85TTCwfXLid41e7kuApk2GQa+D0On5U25tZ513j83i6kAs3jeqOvv/5aP/jhD/T59z5Xv+h1v1ppMwYdvTnX3tGRvvrqq2nf+3WdnJzo/fv3evn69SS/JQjSeX6Oxi0dK9rPkCkqViXl23nOOZLbvp977VrnT3mu/uJpR2SMUZ4S/xx+3TWGnePYcf+cbP88NJsLFqLdXc+1fLBLFuee92d23T83z6euXe1VY5zA2OXenq4ur/STn/yl/u2/+T29fPNG/8v/9X+p3/yt39a7z7+n5WJZSgyr7JG8Dyy7CdCdmXNSHRNAhX1un4WQAGyyr1PbiyfnOsZRm2G9Zcf43EMIE7o0BaaEsJM/FstyBEyrH6VSPn0ZO8XpvX/RTxWR+gRuByllknedtKjtiLm+Q9crdMUW7fou04M+0/NrBRW+zPfbe1+MCQD0NdpsNvq//d//r/o//tf/tX7yxd8oHiz1w9/4NR0uamCv2gNn9us5+j73ekyXtzT+lGeeGsunjPGx556Su6f6mdNpYdrkH3v0ufMqf89sMHNXQh9tHNvtIp9b49Z2F750j9kgj43/sft33bPrXv/cbXY+20x+gf39fd3d3Oizd5/p7PyFfv/3f19ffvlVOm5wk46dvL6+1q/8+Ff1P/1P/yf6/T/4PV1fX2uz2aSqvzFW75j4AXhnepQv4vzazz0Twm552PX3Lnp/yq7YtpH/aoIq2v3rubqkfc4O2Zi9b04n72orKmocng/8z4Gz7fvSo8IqaOTHiMzPp7WFss0vKWoQgWohBK02ay339/XZZ5/p8OBAw3qj0XBCTQmqi75UXJvbo9t+676318zb8H+eYOC+nbl3COyL5wYMt/2W9pUbmRujP+/zfOp6NjCOw4FsPhxfDrqFELLjmHOteQbHKY4dz+y+vLzM7eDU8NLdOFwAmcjajrGAsiwITkQM2DZ77OjoKC80bVSGkkqmE9mEOMouLy+z8zA5wOuV9Swc/r6+vs59r9frnImEYw3HCqAUYyCbUyol+wAe3Ok9jmMFfpJhISk7Nx08Yq44SwGmWROcfjFGXV1d6eTkJDt+oSPZJfzt2asJYCoAqTvryOYLIeRz0rOQT6WVHaADmJIKCI5j6Pj4ODu7aB8nuTtO4TGCDRiPZxlCN5yI8Hrr0AIEksoLEn8DiAD4AMqxDsyTTGI2X8bIhUO+dQh74AZ8QNlK5ugZkFLteAQAZcz+4uIyRCDHZlOOCECmPdOac9CRNYJGGAfz43sH2VyJsgZzyhca46hlLjjayWoDHEAWoB/zRObJkvbS8GQoI4fQyDPgPXjD58PY4BPkhOePj1M0NQEgjDvG7TPo0DMehOMOasCO/LI5OfgvLy91fn6urkvlyAE8mQt8f3t7m8dKWXAAQJz7ZC7TVuvU//jxY67kQcY4Y/MXPGTbx7hcLnV6epqBUddh6CcAIvYRB+rOzs4y4HpycpL1DzIvFWc/MuwbNv1FSf1ykYOHPnz4kIyHydE8jqOGcci6B9CTeRH00S3rSgkAkvDowf6BgmIFbDswCs08exOHPCCyV2hBPhyYY10IPGAsBIg4QE7fThf2GvQj4/RMO8+OI1DN9QYgNPwPjTyLFb4leMNp6S8NnmnIC4SX+eY7eM15OcYEIPoeR1ASQDiBR+OYsrEJ7OECHCQwATn3PY6Lfviu7/sMKCLfrW3E+Bk780J/oP/dfmEeni3Mfu9gTowp6xi+8iC3vu+3zkyGt6RyzEAGjab9z3U5gLfrI2gH36KDPTsY2fSqJG6MOw97MJRXAkBvOUDmQCg8SX88By+zp/oRJtDP18iD/jyrOY+hr49EoQ3sU7+gNTxCpR23OT3gCNnysaCPoLH36XYr/OFlx+FxP/aANWZ8McYMervORXbRbx6QgP3ithi89OLFi+konVJdBznxozw8yKPdB6gicnl5qePj48oW8vcAeNMDCKAb/HV7e5vHgI3DnFh7lyF/2WWcbgd4dr2kSr+gp2nr5OQkV2nxPZ/1dh7y9w90jmdHI1OM3UH8NojH9SN0Qedj4/l7DnSlXexvd+hAQ7fTXFewjk67NgDC54f+oFoAPORj9H3K9wa32+Fz5uL7LPzU930GlHPfCtqbZNPXpQ1Ggj7OWy7f6C740vcp9BVjYU4/z3V0UI6jafeXVDOvlxbzTia3ofl+Dsjn3uxE2uFQcDkrn3UKoddy2enHP/6x/rv/7v9Tfe8lDNvx+e9hJuq/dWI95eDw59t7H3OCte2XdxKJ8pPPKx49PbRjnPhzYv7j6bZGkyfW6qm5+Bz4/bm0Y/133T/HZ+06feo1kfnp+3bwpf/ddZ06dTlA9d27d1oPG92vV4qboM24Ube3VByj9g8OdHR0qPX6QX/xk7/Q/X3aO8bNRnv7+wqh0/192Z+fouEcHWJMWTpz8yAcYI5mcw6/x+Tjf6grxsTAv8ien8Of/2O19xy94Zfrz+e0MTfO5/b5C6VbjAKY29vb13K5p+urn+n3f//3JUn/6B/9I/1v/3d/Xy9fvtX9w1Dt3a09NY5jquW6Y04ux55xGGOsjhfYNTd/l2jfa2ln1xqEENQr5H7m7s12RhhyAE8rg5W+DGXd3X5zeyWOUX18XK5jjBrGQZvNWuMYlc6W3R5jCEGLkEg8Nx76HIZB3bJ+d3n58oX+wT/4B/p//7f/rf7FP/tnWt/d6v7uVmdHpVLgXHufwtO/yOt/qH6ee/k7GNfPu/+VZ1Xx288t2xgwj9802SzPaW4G1AxbIW2fNsatPvSL3Vza9pVKTLd9HBwc6Pz8XF988YXOX7zUj375V/QP/+E/1L/7d3+kr795r6Bev/SDH+mXf/lH+tEv/1D/4l/8C33x5Re5Yl2S//r8Zd5NPpUnHrs/7b/zRx35NSe3c3vT3DM/zzWnJ5yX5wDnXc8RvLTr8vfKtr/tMSgdS6DnzfMxWrX7FJ/NrYOP/xHKN32nn+OYyqL3fQq4ior6eHmtv/07v6bvff/76iQ93N9LQ1SnJDvJXxWmf7Xfpx2bv+/P+fh87Xa10fKh781+T95PZj7boobxhge51WMbqjHtejf4lOvZwDjOHDZWnBnLxsFQotJjBpNwiOB8uLu70/n5ua6vr3MmM+3hbGodDzj/Dw72JfXVQgG4AOgcHx/r48ePOdscR7Kf34gh1/flPGpfoPR3XzlHvdRnOVux0AgnDi+uZI9eX1/r7u5OZ2dn+axHqRiPgK9nZ2f6+PFjzrbEOffhw4fsDMQh4iCEZ++TXQqw7EyOw9IBHHd2sW4+Lge/oB+ZjCGEDPpJqrKCj4+PM5iFk9udOXxOFpFnu7qQ+BmXAErMy5Xs6elpVfbZwQFAG5xt7vhjPPDoarXKpdGZozu/4Hmy2s7OznI7ODX9nHH6Yj39bHapZAN5G9DZnXOAAw78woc4ZpkD2Yk4VwGaHAwgQAF+ZZxeNhYZw1kO7QBXoBuAMFULuFgfaA8f8ZzTAWcv/cGXyAoO+eVymcEND7qAb8lY/f73v5+DS3BwE5iBDqJPQAQHBOAreDmEkEtqk9ncAlgAPF3X5XsZH/fBb/CIBw6xbszVx804Qwh5zQFDpFRW+uLiIoN96GWAeeZ4cXGRS5CjX6k4QYWKruty4AMO5fv7e7148aICBfJ5Jn05pxsQnDUGqHKgDr7AYQxohmxAX2iEPiYwJISQzwmWlPmvBQXgD9dxt3d3Wu7v5aoNlCrm+yRvg7pQzub1IDDXKasJUGDfCiFkQD3GqH0rzw8PQBvW+vT0VF1XVwXAOOF+MntZd98joQ16knVFr/je7C/pABNON9eJAPAe2IHOdUAXEMhLppO17lUzANU8AAS6HR8fV6AOuqvrOl1cXGT+932KPZ3ABfZb9mf2dioFQJ/Ly0vFGLPsxBirACvo6lVCyJplXZB1z5iEZoBg6GHGC33d8GTtuDx4rQWh4XvkDb3glSvgU+SdttFJ8IAb7vC4A0LIDJVUvD94wnW4G6nIqGfVUgFjLsDBy1TDt8gc+6/bJP6iSaUBgifgM+d7fmcOyJoDebTBnuDHGpR9eagyogGA4SGOZqEiAXyMHiIY0vdU109UIfGXAHS+B6e4PQOdCVRy/USAlb8cOLCHHCKLDnSid4+OjrJ+Zp8mOAmdgK5lXvTNmlMxBHDS7RrX1eh7Sfm9gGAJ1gpasse7zkWnwttuc0Fv/gFu87wHE8wFVbK/8rfLMnPAPmKdoAVrwj3oC++XeXuAmL+PIC9epcKD1tgPoFN7zh28xBwZo5dL96AJ50HoCM9AU9aYcUP7OWC7XROpHB/j/bndwvN8jv6Ab9rAUX/vbHWuB/04//ta0g9jgqfdfvQx0Rfz8IAm9hHachvw57mgfQsAeLu7nLTt5fNmjLscHfTldGrXttjj6Ry7X/rBL+mzzz7X/e2tlosSnBxt3HPjw3EVQg3OtmN6zKn32L27+nyq/eqvhgfm+41ymLfqYyotn9oNxUu344ox5kzqVjZ23c84/P3Iv/e1f7Tfpo04990n+r/LWJ7OvW/HwBUCvDKodibW3vQxRq03o6I6/eZv/qb+zb/9N7q7vdXB4aH2+4VWD+lopEXYl8ZRo6RhSLrt+vpa5+fniuOocRi0v9zTZtymfUUf0z3td5IUYnLEu26XSvLMc/j6MTo9drkj+jnPtLru216pnbrSwrdt7ymZnmu3lYc5fvqUcXl7c8/52n+Kvppr91Oux56f49n2fpfLEFPW9XJZKg9eXFzo7OxcL1680h/+f/9Iq7vf083VTX5Xa/eL6l3nGTpzUM2fIZApWM+h3UdLe1NFiqovbX3m7XUTMA49sr+gHXMGntmfKNua6MU1arJJVCq4xDiqn45uSTSJ6kZ82JrabAEcKYZRMWwH3Pr4QwgKEZ92p77rVCqOTCDQONmBcTXZX1FRo/b2lvqVX/llvT491+nhseIwqt/Uxwm19JrbWx67nuL/1hZ4TH4fa6dt77E22vt32T3P7fMxmjz27ONy/u2CD3brpvlwvq12DX/8Njr6WfD7J+ju54xjm3e2q/o4XfL9k43WdSXYnNG8ev1a4zDoiy9+pn/+z/+Z/ov/4n+u/+w/+891f7/S3nJPCtLV9aX+6T/9p/rzv/xzHUyJWry/SKUSlf/9rDmGkG29x+ePPvp0Xpmz912VtTy9y0auZDPUz/v+Nyff7e+P8cKoqBC33xt8DHN7+9YY+f0T99gWWK7ekaeKJny/KzhhnKF3q1PTes7s1eNGXd8rhHRk1hhTcuiv//qv6/jwUOv7lTYhKCz6aS+NImOcvbkNqJ2zAZjrHO/5vj7Xht/j7/b+nLc5mcJb/c/ZUu24vs01x/O7rk86YxwnloPFDt6tVqucmYgTD2eNO2TJxJOUQT0yGP2sxa7rckYLzy0WS/V9AS080waH1IcPH7IjF8ICPOBYIcMD57eD5Ov1WhcXFzo6OqnKknr50wS8FucOSg/n1mazqbJTcV7hiBrHUcfHxzo4OMjnYAKIA4AAyNGvn98aY8xAJM4b6OznsMYYq+w9QEXPvHFAz5mPdnCievaev2SwPjjLlsv9zA9kl2M8U/o2xphpTUlA2sPhjJPQHcKM3QF7AgFYSwcUWGt4w+eIs8vLYXtmCg5iHME4keEB6ITiAaSBzjiDQkhgJln6nvWDwgKM9I3EnW4AIzHG3DcghKRqrFIpmexZKmTr0m+OJDUnsjssHQzD6dcCrg4EtWerAKgDhrKGzM+zkPiM/miLjDec7NAT8AEnEXO4ubnJ8gX4eHd3lx3byJ+vNXIUYyml77LkQAnyxJp6oAHzhR/QZawvgDzADDJIf+58dDp6tipy5KAyfBmnzTKEFCz0/v17rVYrnZ6e5mx+ggNwkKOr+FySbm5ucia+Z0t7BlqMJcsLPicggDLs0J5qAl61gfZZRwCr6+trHR0d5Yz0o6OjfE6tgxmU1GYeVCJBF3vQDY5tgh+W+0mvwReetb23t6chlHJljBMdt1wudXV1pf2jw8yj6CjA3b7vEygeShltd67TnvMz/It+RiYAidC/zkvsMYBuftSD3wMwhz52PQtPhVDOW3Vgh6AI6Aw/cC88SJlynnf9yD2A9sgyDhf2YS7PQIafoYHrN4DKq6urLD8eQIFedMCc8ftxIW2wweHhoa6vr3V7e6u7u7sqQ5U9jH6wDQiEQabaDF8PVEK3MF4HjNA1/jLlWcbtUS7cB9BF8IGkHDTDONC17OnoNy7WoQ1M9EAF5Ncz2L08NZ+xRxPwQnuu2+AjnyO2iB/h4QFUHNHhtgjr20a6rtfrLHvMK4SgFy9e5PV2cBq+ubq6yjRi/0E/cD9HCrCXSMqVSXwMzAn+Q4egr5BD35s8YIv9iXO2uZf93dtvbZo2GMF5LMZ0XEbfp2AyMtovLy8r3YJ95qA79hafoyMcOIMffL/0lyb2aPidf8fHx5lGyGfrXKDClNsObgewnv5O4PaGA/0eOMYcPOgS2wWZIKAT2cP+Rj7Rb4DT6KbT09O8dgRvoNPbl0JkwYNQPEiztRFdz7a/Oy+5DmI+Tle39ZhHq5uxIZA/18eMyft2m86/b5/hb75vgfU5oAl+5z4fD7oF/YSNFWPMjgzkgT44SoNxwB/oCkmVrDnd2oA350t+uv77Nlc32SVhOmhyOrk7neE90WPUmM8cdR0EjebAMV8L5sx3/n7ifOdrltY6ndfMur169VqvX7/RX1z+qRZ9p8Ui8cwYYzWupy7G4D99/L/oa+eYMthQ83h7fzsu59eg4giK7c/ojkHzME7fdWGb/30d5sbe0mxOBp9zVTJnwFBuL247+fxqx/ipa9c+k/opwRPSbqdqDNL9eqXu9ka//dv/sdbrQX/y7/9I6/uHKQA+qA/S5c2loqTjw0MdHR3pyy+/VAhFzzgPtnPyfl2etsc8fR+CYgvuPbMSwWO083m34/TAoXZMO2nXyNrsfWEX5FKPK3QlsGOOT3eNaReftrz8KTzVygPt7OrP5WwXffzzDWs7037+e8dcdo111/zace2iR55z87ePJcl3GncXR/WLXovlUuls0uJP++abb/T+wwet7h+0XpWj/tDrW3yCAzyUsrBb81DQEMY8njDNJdgI556NjuZU99XOeH82sy5jNTnnyAr4Ok5lPaK6UkLaxlZTVZKmCpNRGRyv+mrov4sH0+fNd1Pf7CXQM7A35P+GAlDZ8FKTCRRXiFou99Qte21SXWHFEBVDqeg0P6bnX4/JDN/P8feu+x+7r/3sOYFfj11tP+1+u6vv9vu59X3qSnvEp423tQv8Z7IfntWKZPv7Y9fOvf6RsT027kdH9cg9c/Ru757j5RCCggWve8LIMAw63N/Xu3fvpqTGe/3Lf/kv9cUXX+ns9FxS0N39nT58fK+v33+Vjv7aP9Bisu+j9dXKD/20nzt/IdP+HrqLBv5+5e/Y3vZz6JZ+36aXt/HUXhQ1v1ZP8dKcrLTPpaMoHq/O4PT1z+bun+WbR+xjv79dQ2TGx9A+E2Pcin9t34VK/7WfrB1X8hn2+qUf/pK+853vpPeqYVDf9WLfU5DiqCyQbTs+91381b63P0Z7p/ucPTDHb4E9dsbObPXtLD1jnGSFvX57b/i2+9ezgfHNZq2uC+r7oPX6wRx8tznipus6HR+nLJO+7yQFLZdkqS4y8yyXlIM+sCzcE202a2026+xE32w2evXqhYYhnVf67t3bSXElxy+Arzu3AA/SGPqpvwJsk2nB5VkIPJec6cutyLkQQnbE4Nzb3z/QYjFOm4l0f58c8fv7BxqGUff3t1lQyE50kM+zUhyoROGRLXhwcKDj4+Mpa/4gAwoOMEALz+QBgAGEkxLQBmDg2SA4VHGK4QzySgFpTfe0t7eUFDO41feLiX6lNCsOYByoUsnuJLvKASXm3pYzDaGU/8ZRDbOz7qyVl+j1kpmeBR1CqAIB+r7P53TTP+2SUXtzc5PLpXOmJTRCCfgZopyTSWY28wcIaJ32UgGooAV8R2l5zxTIWal2bqe3I5Vy/DwDrV1OAOpwxrL+yI47w93ZXQJVSklpABvAZOjOGeysmWdqeeZKjDGvQR0MU85QdICsLYmKjCPnAB1ffPGFLi4udHJykuf/7t27DAK0jkDPkD06OspZuwTijONYncF9c3Oj9Xqdy0rznKRc6QK+RQbhVy/jztnFAFYOLDMn+MMDXwAyyD6+vr7W+/fvK0DawTyXBebO+t/f3+vly5d5jdrjJg4PDxVCOb8T8It1evPmTeYH9Bb6FnlGr7GhebAGdN1sNvnMX8+Og2+99Dh8eXBwkINuoGubNbi/t6dO0sHevsbNRof7B7qP9+q6oHEKdIpKe8fDepXKEy8X6rtey75XjKPu7u6lcdTV9bUOD9N+F2Iq0Xp/d59AkM1GVzellC+yjD4m2AbeZU2RBwKIDg4O8p7h4Cxr4ZmC0Ja14ncPiEFXuswS/OXObzfwHPgHPEB/I8cvX76sQESCnsgcdZl1UDWEUI0PoN+PAQCccl3BmLnHjShvH13J58iDl+3mHs4cRz7ZI6gQgj6Bjj4W9jkH2KG/B75wD/fTFzzv53jD28jSZrOpAhuo6hBjzLJwfX1d7SU8x55DpRPnO+wer1ThwUGAS9wLL6A3fF0A6OEZr2QAoI494LoL/YpucJ3ghjZl+uEv9LFnA9/e3mbdvr+/r7u7u3zshu9rOTtaqUztEEeNm7X2DvZ10B1qHEZthiGd5dTt5f2SebD2c8AYcwHUJKinlUfkFD5we8WPBlitVnkf8HOmPfPcX/IItmTfpS//nfYJ4ru6usp6Et6Db/gcGUI+2KP8mBfk/fT0tAqG4yfZ4Og01oh1wV6Fjuv1WopBJ8cnurm91XIxncE+8WpQKhfmGboO9MHPbk95UB50oJIVcgNYju0Lnw/DKGmjvktnRw6bQUuqHDys1fXlfWS5mLLAh1GHB2nvXK1W6rtFeXay0cKUPRoUNAzpnWK5XGrRL7ToFxrGUYrSMA4ah0HjGJNjuuukGHW7vlUIKWsXZymAWnL4dhoHnKuS4lTJS0H9sleM0mKR6Bm6oIP9hUKQVqu1NptVKj24GTUMD+pMv4bQ5XeitN7pfLNx4GU5aLlIgQ6rh3XKQguduq7XZtiom5xAY4zqAtm0QeM4vUdG7BPKkkt7Sw/+TWBwHBNM3Pe9OIutm9ZIMabMKUlDHDUoaj0MGoa0V/heMo6jNMas8zyLHF3sTgr0r19lv19MtumnOZXnrrw35xKbCRyP5v0OE+if/k1Ol6nvOafRY44zdC52wVxwglSXtRuGUSEkW/Dzzz7XX/zZn6YSuaHTGJX5PMQCOpBB+9TVOnJah07bRvvdpzhGHmsv8r8Yq8wkYJz8SfRn7fetjtq+olJN3nLz3NjbzyZSPnrPLjrPOa5Sm7HJcJ+/Hlu/p9ahPPppoG99f+2k5OoXC63WG93c3urm9k6/+uMf6+H+QR8/vNdq2pO7rpNC0IuXr3R0dKDNZq2b6xudn5/mOUejQTuepy7n1+lhYwhz5u3IqHbg+XExKW2GpPBz7lwIQmHkMT02l6ec4HWvs5xXMUvmISOB/VmNvPrA283yV77OdI3ztMvtPiL/QU+v52Pfb/UXC8A8db79ewhTydNWSZjQz/TTrttOkGJuvHNOYm+PsceoUVG9NPlxpdClsuOS9PHqQkFBm81aoyVedF2X1q+ZQsjdhPKTL2Kz1NNn6Zl2bjy/g9+2gHGnQzBeK3ulABEigGCrX9Dz/fazmtOvxeYxqtb9KSqqPVal0IY+FTOrzBCLLqZ5ql7XOb0f1GszZbCHTtobB13eXGo9rDXmQvZpjEgax3e08hZ3yNsuvfKkfNnPui+nidQ/sY/znQdZ7rrnqTbK2OpKKeXT+rdOnamhCeyy0A5Cn6Km42JoIWzLvJl025fLxZaOCVnN5/WcfrYAXHosVDKyu9P2KkfelOFkZi18OMZJvnZNBYq4nDBeZZB5jpfmwE21rTl5THdk+sYi+9OsFMd0bNrh0bFC3+vm7lbffHyv+4cHnZ+/VIxRD6sH3T/cqes7HR0datmV49sKOcqKa/o8B7GwKVc2Xpp8Dgf6FN1u83UzQ+i1bAnEaQxWAny6p211juZRu9dy+/M0oTweFR311Ny2bCbVARtzz2dAmPvl+7+y/RGbSczpzDwOlYfyc5l5gqnkGhTf1V4luyGB41lC896IDhvy3pT4N2gzDIpj0NHxiX71R7+qg7193d3cSuM4ve9N+7XZIHFMYx3jqK4z5pj0RBc8YDpNLRrWo+kedUEx1GC37wc+Xw/i9t2Q71zlVFua6/vMP+l91vtp14wtt9IieW9PdB7H5DN5zvUJGeOjQiil03FKlJftqGGoMzHHccjKEydhcpwnZSKViHsJ5/TR5IgbxTRXqwft7+/l9gBhcAgCZOHox2kH4QBS3OHbvvgDYOLQTY6tmJ2pPv7i1Kdk+jJnwNP2ONZn+VGWEloAIHi5eRwsgJWemZ9f4KR8JjDOSqk4VWkXkIL5UiaUjBypODRwgOIMlVQ5Qz3DRirltCnVeXt7Nzn3Rm02Q1W61jO8vHQv4BrAsjM7zlRKk3z48CE7cx3wzI7tWEBTryDgwQ7wwcPDQz7/GKCSzNHlcpmdvHd3dxWg4xlCiSdXmfdYCwegAZN9nNCcDF8+p23o4PIAoDDnBAKEoS+cdAC5DmwBaLK2jMX/OcAJIMvnnsnG/CVV5WUBZzzj00Et53EPXvEghlrnFADeaY4sAlp5ZjvOTIIu7u7u9PbtW8UYs5MbcPKLL75QjEnGX7x4kfXGV199JYBHMr4AK5K8l4w6+uU8U74nyKTrugpMRr+0IB36Af45OzvL4wV0Bwx2fttsNrq8vMz08WoR6AOCV9ADXpaeMXEvY0ZfIAOeOQ//3t7e5jLY8EXfp8oW6LyTk5MKPEH2nYcBP9BdrDG87TLCGnklhuvr6wqYA0Sifeg2DINevHhRMi37hTbrtXrj/ziOWu7vab3ZJD0bEkjysF5pfChVJYYJ6Li6vEzZrXEqvb1cZgsXUMxL3BZwJZVmLoFhJcMTOr579y474z0TzUuUxxhzuwTdeHUD9jhkG95wXeF863qYPnxdkBcPlooxgarL5TKXmGaOtEklmb29vZxtC2/1fZ+z+9B3MaaMVrK2WzDaj/NwmsBj6JzNZqMPHz7kIA3nX+bo2ZuuS6Aj+6NnT1OKnz2TcvzoF2hWMur6qr+Dg4MMSLLGBJS5PSApg8G0nwLySkBYq8PRi8gQNEOnuY0GII9N5y+bzGO9Xuvq6ioHFnl2LveTcYzsYk8gqwSUOUCLjvKgPS7Pruc5+NntIngROYAnzs7OcpAU+yzrRXBABv3393Q4BRviJF30vcYYtVmVShPwL3LtbUAP5ACaoKfQsW6bsVdCMw9QOz4+znqLgA1k17OO6csD9AgS8kxoL/XM/c57zkfItO9j8I8HJrK3MH/ags+xiT2j3/mHoE7kmnl5sIBndq9WawEa9/1C43qtYZN04HKvBAB6oAZBjB5Ihhwg69g1VASAn9Atnuk9jlF912vYDFI/vcZGadgMU9nMqHEYNWyGfEwU8ljs+1HjuJ76SEA7eiPNeSzz3ww5Kwt5Tz+x7/dyu+WFtWQLbzYlwDIt2pRNMzkZ+q7PY1ZUBrMpW5eqV5UqUvlluCsv4aw78r96WFXVKlLlFJxCg4ahvEt1oVPfLyQNktl6+3v7VVAbex8gvK/nMIzq84t/CeiIY9R6UzLj8742DtP7rB25ohJQlf6VM+Tpy6sjeRCs2/QFjGcNyzFiuxxKz71G97WbY8D3+S4ELbopWKS6vRzPsk3TbSeT7ymts5tns9OkS8EY6bNRm02y9374ox/qX/3uf5/ouBk0RmkZOvVheufHVzR5NPq+1xinYxnm/WbVfP2am0PrQPQ9dZcDf1e7McbJORY18NmWM3tycsWYXUKl7VAcdS6OoQaBIg4rc5jOZVW4YwiHXwil0tHctcsZOXfFGDPwksGgLmydp5g/V9iiN33OOR7zHiI9OubHr7D1O13AJ8vFUsNy0M3Njf7N7/1b/f3/zd/Xf/73/mf6yU9+oj/7sz/Tx48XCl2nd29e6rPvfK7V/Z3+5I//SJv1OldiGqM0KmWYaWwBre35Mp5oTmq/kqNycqxmt+ru9QkOiFW809yfjx/gXnNqJiZTnOayNaZHZIDPWucngFmZgTeoqgx26TOIwBJJ5cz1zCM1PFPJaQVFWX87FKs7xufkvppf+7fJ2Zwe2XUF+xmbz/zzIkfb3F93F6d1KzI0N7ZdIBHfhYBz3x3+mnRVM2Z4ZZMyiftFOtdUY3p+Na61t9iTulRuHcBcIQW3RXM+dwqK3fweE0y3JDthIYD1WZ7KclBn5G1dM7JS0SFPfUzrMNpaxR3thrFqzjmx6jomBG5uXy0waVnjei1dX0wyWyhUPt5qd3t+87o4qg9BY5zeT5e9+r1eozaKGhRipy52GpX236ShAPS2K/zMXS1/zl3+/sA1CqmOcoGIcrCkBpIeu3bZCXP3PfX5tKSz+339d5HmqARk1fMIeX7YZFI9v9L/9mdVY/ma+huj/H4fS9C8/DHPvF7W8Jy+LHu56d+m2dE+n0ymSsNt6dKZNljzZM/UfbfP+/jLPKwf5CXUFSRi2gjzO0zi86BxSJQbp/aWhwc6O0y+z9X9g95ffp3t/cPjg/weEDHspneHYqNnQU+fhy4FOE+6rOs6qZMi9vQojZ2oT7HTTk3z1gyPp5LjYRrEMLaaNEphzIompEVLbXfbcuu0zTZwy6tirsp0lqI0jgpdmlPbtvOXr8vuK2SeqD5t+borgQdVQItTIUiqsIZpvNl2HPPnWTKG/GU6DidKCsWqiXrsiI9iK+U553uKrZ2CmlP/6bM0g1ETrjFKq9Woo6NjvXv3ff34h7+qh+s7jZspISCMWi6nJFurZKjp3TDt/yH3n88iVwlemGarOA6Kk38EunaxU+zqahzOHz7/TkEpUj2Il5xpO7M9PqqgvOyPocxfSRIXISVZz+uisneOwQP+rD2lpJeN+b+fup4NjLvTE8etO9EAnW9ubqozr30CAC442G5vbzNBUTA8w0s79+O4BSDgvO6PHz9W2bWe8UpWHo5Rov2luvQiTlfPkkylLIpDxRfeM308aweGwYkGEO3ZBF7S3R0zxZGSnJZHR0fV2MkexFFHphLOU5w6tM0YAGa8bKNn5bTAdJtJyrqUbJxR4xizsxqHqmezMa7Ly8tcwpo1whnptGR8PI8jEUDAnbSeXd9mBbnTH4duW/YSp6ivuQNHAHuA+jjc6ZPxk8FN9hsKHj7o+1TWO1VGOMzfu5PeHfwAHm3ZdOdVSVt9eIlN2uNZHHnIDc58ZJE1cRnEcQ8Q7EEUtOOBJw6cMjbaZW3dAQ2fAgS6DmGdXX5Zp8R7sQKqmI8DZIAxvuHS5vHxsR4eHjIo8PLlS63Xa/3kJz/R7/3e7+nv/J2/o9VqpaurK52fn6vrOt3c3Oj8/DzzxocPHzJfefb3ixcvssEEIOUlcwkMAbgCbLm5ucm87cDEzc1Nzsodx1Hv37/XyclJXq8QUplWaEWJV+QCPX04lQa8v7/X2dlZlckPvVyeWGd4mjl6xiOZmV7ZgAxnsn2hvQcMOa/d3t5W2fIAnWR9u2OW+XlQVoyx0jc4aqEtc2LPYZ4XFxc50AcehB9dF3ddl0tAe8Yx8rDXL/K8yTJEr1K9g9LWZAe7EYvMkOHarj9AN/OADwDDrq6u8lyvr68rcNYrkXgWJXrCAWhkEF1H1jJ0d5CXyg/oQ/YQ+B6dQ0CFZ9VuNqmk9vHxcbXHEGABTy0W6RxwgGP2F+hPGV8c9gAw8ATjBYBz3XV9fV1VL2Fe8LuDna63CFJzIBGaoje5WDfGgD7kWejiz8Cf6AwCHFznHx0dZf1LEB+l3Flb1tQDsdDpvsczb9ph76WU9PHxsY6OjvIxNqw1etZLRzuYdHd3l9eX9XAd7mP3IA23a7Aj6I/9yCtFIJPwxvHxcV5b35d8bAQ4ovOY297ensaoyjYCUAawh6+xuQCD0V/0gQ50sIy2PFgA3mnBp5Zf+ZyKBB48AD/xXEujm5ubHIyCDKLP3e71KhPYGfCr72GsoYO97fpht7GGHuSDnjk6OsqBnwQouR3ioLS/Wyz6UqUAeYdW+YXd2nJbEb2d75Wy/UYbw1DOi3dwFTrx7Gaz0d6yBO94sCBr7nun26uMA35k//J5tX1jo3sGOzRt313cnkT2WseD7/foAdacvdltL18b1gO+bJ0mzJH7PCjIaS0lkJm5tFW5slzavu4BoOhKryriTlsPNGvfO7qum5x2BUxm/E6PEKM26xKI4mXlfaw+z7kXd3fm7XJOPvfKdtm0vm5nZz1itBjHMTu4udfH4++srXOK9WXMrdOHy8H28rt0dXWlH/3oR/r888/1J3/yJ7q+vtbbt2+1eVhVOtDH446c1gnYXj7edm9rr6edbvW9Pu85mtQP8GVx/GRA45Fu23Z2zddl7LHnd/rQn6DdY+PD17uF5tic+bsFCR4d6xPf7aL9c9tsaclxVT/72c/0T/7JP9Hf+3t/T7/zO7+jv/t3/64uLy+1Wq0VQ9Dv/8Hv6U/+9E/113/z13rx4oUOj44VQ8Cvp3HYTL+3ANucfMPT9bjSveiq5PDb4v+WDuM8Hbb4fVqrdjy75GKOXm0/c2vR9j/7vP1XSgFXjyFaIYRMrLnxbuuI3W35uOeuLTqnBx6959tcu8aQdeqMzGzPW5kuczz3nHG29zh92/0pfz5JdLpXybnO9wGQByd/ve8572Q+2LEcz+Gzdu6Pze+p9rb+nobnf0fN7NnxcV2V2t45xN39P/F3+9lOeXtEP3L/OI5TgErIts5ikar3PCc4ia3gKX3y2Fh3PzdvI1X8mT/bvb4/j421a7+Jtgd+G/ti+5kExLX2Im1F7/AXdD13zZ5q41OuMCP3nzKGVgbbd5m23Tk91vabf0pSqM8s3mWnd12ng/19HeyV928fS4zF+kmPMu8CmKd3VEkalGtihQlADFLoDFvW89Y/jbcODJiT5DKv8vecPR/H7cCDtp3U19B+kX8tOcIqQW/Ts+wn+d4d+vSpMfjP6vf08pP72fXuFaQqwBPTw/ULtJ1/69neNx+7tu+N0x5qgR9TtEwcR+Ol9HsXJMVOd/d32lvu6/vf/4F++7d/WwcHB/rw4UP2C5OwwXst79WeENEGO+PTKPGJ28GP/AwhTIHL9Xt/+wzteHv+ffZHKgXWzb5XWTubzaAujJUPxseU+wkpcGraIJK90pckAfwzz7meDYxLylHxOL3cmeAOwExEAyu8dCEOHc7DdKcG2bw4Ujhv++uvv9bZ2VnOrMT55hlfvPxDiBbA5HtnEnfmuNMoxkEPDyXbCoejOyNwKAGI4FBiLpKyk9zPOsVx7OA/jnzmEkLQ+/fvJdWOYxzCZJtCB84r9zKjZCy9ePFCx8fHuri4UAjlfN4YY6Y1GdI449zBx8tl3/e6vr7NpV8PDg50cXGhly9fZloCpHsQAo69YRiyg9cz6Mj05j4EACcrjO+Z0Kyng2c4wuibDDLG5iAO6+5BBPv7+xlsZO1ijNW6kYUcQsjnRrLGAMGsFfwLX1D6lnsZD3Qgk9Ad4yg4p5c7w0IIFYhDNj1ntDsok0t2NgYGf7elI6EjPM3YPOAC2rIuzA8wDOc3a8rcGTugkwe0oNAdSEAuHXSBz0IoDn8cupz565Ujrq+vcxWCzWaTS9P+2q/9mu7u7vQHf/AHOZDjL/7iL/T69evcN7J3dnaWadOCWNANHgQIg3ZSOb8b4Aoego7MxTPD1+u1Dg8PM5jAXM/OzvK6n56eVroVx/JyWY6EIDgAHkK2fLNgnQB07+7u8hm3zHEcU6n409PTLN9eChodwxo6kEbwFAFCOJwBfqGZl0pHl8J3XpoZXeTZ+8zdy2zze+vsl0omN3PZjKk0rssNz7reJtPfHcPoBQCl6+trxRgrMNcdSgT/eHDQer3OIDEBEqenp1me4XlkZX9/P5dVR2eQoR9jzOeW4yCET6ALbblD3ctlw++np6e6vb3NcoPOhIYuK8vlMvN2jAV0g6e95DalymkHXnd9xZw9SAlgHr7lefZ7twXgN+YMT/oc/RlfKz/iAP2DU8GBVNd1PI9Ow+5wfc+4fe9EHgG9AYcJJuBZzrP2DF2AW6e1831bEaDruqoEPPvyMAx6//59ll/kFJ7wfZGxeyAZ5dyZN3SnAgm6FF1FEAT6wYEoaIjMePAgPH1zc5PHAP0dRGMvwDbq+16vX7/W3d1dAjr39/WwXmWbwY9kAHxjX4Su8I/LCfPgew+6IxgF3mVd3V5yHem8QuDI8fFxlkV/+YGH2GM4sgdd1Y4TWrlcMR8PDgKU3d/fz7Sds1l4zsFfB909CAm57fu+OtPbaQZdyj5fbI7W5oMGDw8PGZzx7HdsFnieew8PD6t9j3XzlygPMIOfx+F+S1egk9gboS00h6bwMmuIbqQ99lcPCHId5vLq7ypSseG4l3WApt5OK0tux7EPwVf+ou3vdv7eht3Z6hkuf851qvM69yOzbfvQzN/HXHf7izh6kHkis8WejBrGcoY59/p7ocZxi9fcXkY2mANr5bZcoruqdfl5r2EYsgMFvvJ1jTFlAuS/NTkLps88KKx1SKB/3I6ELq3Dqp2LPzeOyUb5/OVn+tGPfkU/+9kX+vrrr/JazjlSfA13us5tHm6/7XKktXPzz/35x55r+00faAsFCRWAvGMCTZs+/nYuj43v570+ue1d88k4+bcf63/IeUq1o/Wzzz7T5c2l/vE//sd68+aNPv/8c7148UJ3d3f6d//+j/XTn/5Uq/t0FNLbz94lPSYpTuB1yo7tnvRZ7+JHYLdvMYmdqFvVF4e96+cDiHZdu+f17a9Wt3QzXWw5Xb8NDf///HpKjvyd86krKIhYjHGM6rqUecXeke8K377Ww45R6mlA6Bnj/w+oT34RV1qDX6ze+2TZDMUGIFM7ZMhuZk/6Fmvd7mmP8ucz2pswxtlx/IfeRx67sj3hASL6Vpq+XPEXB44/ly5B1Ad4Guh/Fr/93ETYvh7r9yn95/clXqo/e5xOT2UsT1W4qjUDFEx6NMaoZZ+qXrVXV3KTaXhrrvRVfOIp5zbb1MN2qFUIQTHEUolp1oaf7P5xmxZztvqcrTp3VW1Mc2ovf/ZRnooeqLVt94eQgOVhyvb2cbf8GqVS5eSRa9fcd70zPdXW3D1z/ASfpdfRpAduLq+0t7evX/3lX9Fv/sZv6Luff67Ly8v8bu/+V97h/T2UC3vLg6L9vbrMN6jrHBdIfDuMQ/Ve7u/uvDOGEHIFBPcNOa1CSBWYQt9trZX7RHnHxp9Cv3NroSHmIMcQ00YxjhsIm6qp9b9gYBynV9/3+SxdHKd+7iiOeCbiBpmX6uR5z+pxJzJO4nEcdXNzo5OTEx0dHWmxWGQnOqC3O0FwqrozRyoZJk5Q+sfh6WcLJ0YpmYQOstM2WZ+ME+cTbaTPo7pOeW4AhrSBI7A4NhKD8FkL9sB8jMPLrwKcvX79OjuXKBHumasEJDiI4tlgzA3npQOtfV/KiCJklDKmTRyfjNGdyNC5OI5iph+84dlmlBJF+B14duHG4cn3nuHoa+OAOH2yHjc3N9nR6o5nd/yxNi7sBwcHuX3nNXfcutONdaN0qoOZDroQMNBuQMjI/4+2f2uSJUnOBLHPzNzjmrdz6lTfuwEMGgsMuLvDuUC43BU+LGdHVoSvFD7wN/DfUfhAUkiRIbmCGZnBLHZuuAzQu90Auqu7us4tMzIyItzNlA9mn9nnnpF5sgozLpV1MiPczc3UVNXU9FNVmzvz+DeBAMon30fHuSoW3jcPLKHT2zlXwXZ1riq4qIqX7ZPXCcwy847vUkfonNdTShXEY+CHOpLJJ5QJzj91As/jNrNaMlXv//DhAy4uLmrWUggBv//7v1+ByNVqhXfv3sG5DKj9+Z//OX70ox+V7IKWxahl1vf7PS4uLqou5JgIWBJUZTliyotmPXLuANQMUfIoHfkfP36cnO/MeSL4QN3L95N+FxcXNShFy5pTpxCQmmf58mxl0pPv5RwoCKDlpcmT7BNBTJ5By+Ad8sjHjx8ruE7gkg56BUrIt+w321SglwEdBJEJ5BJYIahI+rFP1HfmHBYF8FVARkH1+/v7KhscK3lceVYBKdX5GqzF+dK5oBxsNps6F5QdPaOYban+1KAb8pfKKGlBXmaftU29T/XEZrOpepbzSt2k6yL/1mAm8vg8k4901LWN6zznkHqE/Eh+V6NO9Y/KBfUvdY5WpyHv8GxzrilqLzAQhXOilTio57RCDtcABbC0jL4GGmlQDfWR8uO8SgL7zYxJ51wFe7WMva4RGkxFGrI97SOr+CggxoAVXf/mdgrv997jw4cPVb4VEOOaSv2sIP1ut6u0VDnT9VN1gGbKc+1W2nPNpC4hjRXEpD4DSjnIEGp1i4eHh1punRngCqaQ7lr6nGsLdQB5nHxHgFLBda59vI92Ge9Rm4e2KccTY5yAu4vFAre3t1WGedwO6aKAnYK+1EtmVseqNi/XNjpF1aYPIVSbeG7rULYoqxpsp0Ff7MMk61U2QQ8PD/CulE5Pqa7bDDIkb3d9j64LVb55ka+GYaiAswZOaXUe0karOumGMYSA1Xqdj+AoQWAKKpPXNeCStFKgV0FSte9IA67FlA/KMO9hIDLXBR2rypvSmGsH38F3kj58D3WfypZ+r0Ga5BFda9hX1V2ka814Fv7XgAl9h9qQrLzAd1LedO9FPmZ/2Xed57a2GdystJ/KBoDJ/Onnul/hXJDvKccaxJr3f9MM+2968XnnAOdboPmkXYdSnr5UHCgl5FTvzJ/RtVHfw2uu/9TZoWPNfMUAjRzE9sMf/hA/+9lP8fCwxzhbh885mVz2CpVz6M5kk8t955xWzznX9Dm9Vx1t5Jlzzrd6Lz/T75xjIsjj+8+0c65vL/nsXHt6V0zp0b3n/j439qfeda4/z333qXte+vlz9zxHT51j/sx17u3dR9zdfSy6w2N/PGC9XuH6+hKb9Rq+6zDGBOcdzCKMwOATr/3U/BIUz134enrA5JkKXJ3riIljcPY3JvKT/1V9MG2m6cRP9u2MfGqb9XP/NL/oOlfPsGz5qe2+/1SA+NfUy+qDePkrXnb/N2n7pdc5HXr2e6e0lmM6yj7SuN6W7ONn3/cEvjeX53O6iddcr/PWp2TuJZ+fe8endMtzeqo9c76Nx22eB23m7Z9r51PfP0dbSpYlm9hvlrTM+2OZPlcO+yk+nffxm/Lzp3Xq3/76lM3wqWeB6Xi1lPqTo84oIQi2ts/AZQIMPDn7+AvWWn52zgZ4aszt3qfnKz8LOARMNDKjFjRLvH72icseRzs8Zw89J39z++2p8ec1ZhpcrPfUf53BSknreUa10tc5VzNWs97LxqBzDs47dKFUh0kjmE2OWpej6DTnKz84V6p9V3kufaj8ATTg3QCpKjOX35hiPesdcPmoBGmI+r2uuM/oyXPtPzcP9fNCy3O66yVzzZXm3J5g0iam3/H+Oc97NweCPz3Wl9in8+vcmvLcmpff0/A/GI838/jhD3+IH//4x3h1c4OH/X2tbEz/Dvft9J/PccXJ+CWxQJNqdA894W1zcCXNnhVVuH5ocKNZSWi0qX9AMbjWZsI4TCtIK7hOfxf7dC4QfOI/mu2HJ3alGcYZDZ67XgyM8zxUliNOKVWQxCw71Qh40llNYtB5o4NXx6hmntGZQqcIHY8KOqgjik4udfjM/z7nVDazCniwT5o52CavnXOsTjQ6TggwKdjlXMtsC8EBaP2gk33uTOeEMRObzh2z5nTle5mhbpbPYWUbzCS/u7ur46KDUkHjDx8+VKemOoQ5VucacEugm07f02nAatUAZjohzQzX19cAspP248ePFQhUoeCYSAcKoTIyM7PJMzoP5BsqBQoLaca5NbN6TjPBMI7HuQzOE4Qk/zEIQ5WGKnd1nqmTnbxCXqVi4lhJE7Y/jmMFYlJKuL29xXa7nZSC5XhJe/IBHawECNgW+6ugPB2nzD6dOJKlNDDHxPGQxgq88TMtQUp51edVubJkvQKK6njUQA9dSJVuWtaZwR8Eu+kYpSwzg5NObXXgsq/M3iNfkI6k3/X1NcwM3/3udytwu9vt8Ktf/aqC1WZW58W5XNKc2Z0AajUHLeGv0dYK+FJ3cF6p8wiOMSjh7du3k7NuGThB5zLHSdCI4+Mca9l5ggPONQc638k5Ut7bbrcVKFOgUcFozinpwOcZQEBwnvOgFTz0zHAzq5no1A2MflOQmDzunKtrQghBAnjyfLLUNh31u93uUQULDQoJIcBclvXdbofr6+sKWBGQ3mw26JyvgQaUO3Xua9AP+0JdTEOUIJFzruozXuStlFqlB8oRs0F59jbXOTUASV8NRgNQdSDpyn/Jk1yD1PGtxgZ1z+l0wrt377BcLiuP6hqt6xvXGQbsaDlg8iz7QL2nGZQsSX9/f1+PpVADS8dHuhMQUWCSwQvUGWyb64EGfKlhyPdwTshv/F3XdQUB+YyuIewPA0Xu7++rbHCNZrCB8hANXQ2SIBjDdwGogQmswFI3PdYAMgXOAdTgAAD16Bddr7lWzTfVpCE/Z3Yx+08gjHTTfqi+0iMhGBCjNOPY7u/vK49Tdy4Wi8oXBGJZQpw6imsqdZe+O8aIdOKZyS1YQoP52CeuOXo8CiuesE0CsBoIRfrqWkA5mgejKVCuWeW6uaBcaZAI13nOi9pmGoTD8dAmpO6fB6cBqLqU+oT/Up7JR+yr6g4GObF9VsGgDULZA1pFIQVXyT/eeyz6BY7HU6XD7e3tBOjIeqP1WzdstA3UjlXAltV+VN9ybpSWCvrHsZUd55xpZLPaR7xPbTTVb+w/+R9oxxaQTuRDXQ8ZCMp2uP7QLiA/aCCFrgWUMf6t+xddR3T/prpGI9IVOCe/8mJb87lVkF51EYDJmqYb4Rq4JnQmfdRuYV8ps491t4Olacn8+drt4Zp+SOnR2sw+MRj80fN+ekSQ6r1vetU1j5DEzOlCOjs0IJBln+eOIe3T3GGi45g7//Q9pIV+V1rJwPjxhM8//xzf+ta38atf/Qqn0xGd+AXmV907eP8isErHPf9Mr+e+nzu7lPefe+f8/c89p/SfPz+3MZ5737k5zF/U/31yfC8d57m2zj1/ro/nLqXRf8zrqXc/9Z4aKDpGxBqEZtisVgh9sz/MrJ4Rmx3GkhHoBMew7ASXYqpwrgBQz9BPRgAFD+b2VdZdzwNR7SKcXMAL5z6JTZzjf/19TtOnxqTfUe986r6z3wkdQZor0PJC9rFMgCffU+8pTZ6TT733XPvP8bq2/3Wvc3rt3Dv+tvL0rI6zBnxT33vvMYzcc5igFZ98E54DjBtPnG9sKuPP6/2X0ORT83KOB+a6/ulnCt8+pavPjOM5Hf/S/unn8/5O7in/M7S1v67HbtqvyTtB4Pxvx9val2/ynHtGdzx3PdffT8mZaqVztK80tpeMa37P8+/m9ZI19tyzT/HG2TYcntTbU15tAHpTze3zFhzwNPD5+L3n3/fUeJ7qH++Z+4Weff0Zeantws7S/rGOL+M3FHsANWsVxgESZM8gYzYdtG0DWKZ6Yts9s6bWfcUU/EwpIcUEs1QrRk3HV+wOGUcGnp+n00uvR3p+1s5T/HxufQBaRr1+Nrdh53Nybr/T+vMYLD7Xp099P79ees/c3pjvwXQ/CQCfvX6D3/yN38T11RVSStjd72Bj26OZtUQQM5tkjetY2C738PQDaBKe7r11DN57+C4Hh9LuRQmocoXVkQwJEYCbjEH3iXXODDBLsJRaxS0zpDHm9SmmWlo+B6jSL9sBmB5jxox255rZl2mXf1jFTBMJnrteDIzTqULC0wFDgqkjW7ORgSnQtlwuJ6VH6VzU0npalk8d0Cyvy0nTTCc6PZXp6HShw4n9IzhApwidUMoE+bm+PkfHJQmuzKZOImZztmzAJiB0pBH8IpBA5yppo0APnTI8r1vBAzqh6HhjZjU/oxOTwC+FjO1uNhsAqOAOS5L2fV/PM76/v68genYItfLCmnXlva/lR+kQp5ONn5FeBKTo7KJjjM4nOiFJ87u7u4kCnGc/qPDRCfju3bta0pj8S35TpzjPSqaT8erqqvIW58HM6vmpmllP+qqDzHtf53O73dYMPQJwn332Ge7v72sZbOUnOvq1JDzPEmYWtAIrBCLObQrIB5Q7DQjRs2hJM3VGMuuW72VFAQZjkIc4v6QV+WxufFFOq2M5tooKBCpUGZM/b29vAeRy4+QbLa9sZvVsWWYecT45TtUzmp1FmSFYSt4bhgFXV1eV/47HI37/938ff/EXf4H9fo83b95UvuP50MzYJM2oG81skoV6Op1qJrGZ1dLCzPRUnlbHvp65SwezAsF0zDPLnn9TD6xWqwoqqJObcuOcq2ClAoo3NzcTeaOeJw0Z0JFSqvPA/m6321qqWLPb9/t9BXDmARPqhOZ3c0CJz1HmyLfUYfPSxORbLooMZuJcM5iCZ/ReXV3hUOi83W5xc3NT2yGP7Pd7rBfLOl9cP+bZywzS4HhUXtgmZZV8Q7CGY6aOVGOGoOfNzU0FAx8eHmrGJ9dqvsc5NzlnnbynYBhlS6sI8MgIrpHUKXzHzc3NJGvy/v6+BuuQtwgAc044P5R5DTYizSirCoo45+ock0cIFqmxR72ueofrs76DvBVCzq6l3tIs8HMAj4KPCggBqPqZAYS67jFgZLPZVH3K9YfVEygn7HtKuYKEllTnfFBPaN9Up5K3uU4pgEN6UK9olQ0NUFEbQ+eU/SO9dA3WtZwyqlGfvFSeWUWDOp7AHt/B+ST4TX7SIDjyL+0j8gH1CCvPKPBZ1x7nANfWMdpi54Kr9MgOBgtohitppaCflghngB71Adu9vr6e6Cjy9/F4rAEBbIfgIOWLoK/OmeoSzj+Qz/6l3ZdSqgEZKm9zkJjVGngfAzi41jCoRI9VoP7SAEjyCnUEdRRpofqHNpBzDsfTEafTNOuXPNaylBsf8DkCo6oPVMbZln5HO20+FxrgwnJtcwBU9x3UA5xHrsX6Tn2vgrwqK3P+Jt8uFotqA/K9Oudsk3NK2eTvXMsor3ofP6eO4Vzyc12rNcCR/Mcxzd9NfcDPKJcKslbwd6YHda08RycN4FL7kGPjxftiGid95HdVf3RdzqJy09JuFbwt+1byCOdXbdzctzYPL92UP3VV2lhzcqgzo9Kj+Fjy+DGZx/leVHlX6aS6RPcXOj8TJwfU+crjIoZclvrzz3F9fY2f//xvsFhv6n28tE8AsqPETUvsveSa39v6cx5wnju/nvr7Kcedyvzc2Tcf31Pfnfv8ufvPP/8idOpR28/R57k+fur++T1Kx3PPnrv367znuf4lOtbQ5ovrCBY9PDZN7/hy7mFKmYmdz4CQQ4acLQEuB21UGkrWV373OfyWDrr51eRlfm8bk4MO73n6zUHu8898iq5PfT+X9+eeVTe+WXGiPjO3T7WrcvpkH5+RrblD/mxfX8Bnz10vkXu9Z76+P3c9Jw9P6aVPfffUfbzXCHrLPSE0n9goAbvPtvdYED5xfb0HzuldXc++1pufWDs+dd/jz58HxXO/zmcxPtf+ues5uXh67SJqQDBMABrn4GfnLj93PR7X4+/mLZXRy1/8LYOHz/GVy79MOOSp976U/1925WCnT7bz8mX46SaesFW+7nPP8f853UO+xCwQ6fwsPqbvczaSXuftnSe7evaZc/ujub3/lK0hrcJMg+8BzvPknpTBbAA1I5V9mIyTtmvulASRTPvuZ4kmOqb6O1CAwinPq/jWCJdkk30Y7XYHwGJCSlbHxO/qgGtFdkMyQ0CTffXz1DE+sT7P+/+kjpx9f05Pf+rZ+X1zParBGM/1N6b45HfP/X6+c01Kztk6AP+08tU0i1v3TeSN7NsCgg9Yrpb40Q9/hO995/sIzuPw8IDhdEJw3SM/GX1nCoxrko9iLxrErj5U9QnoFULAwvsMVpcf8rqj2jBDGtPkbPbn9pjOgOA8nJ8mXxEU9wxLMiv3ALCUw7Qs28oOlveMna+2eq7ckMQ2zH+P4/D8XJbrxcD469evJ8RS5xnBBs1QBB5n2GomBh0zZlYzUzRCn0A7Hbl0oqgzlM/PM2+4+TGzSRYY76HDDkAtKcvMQjruWQJPHR90CAIt+4h/M+OP/WolPFGdP+yHAjga4eGcq47weTYpHWoEvThGLZ9M2rFd3se21WnLzCqOjf1mpiqd0JpZMgwDLi4ucXe3q2Ae6UiH2TAM2O12k7PgKRCcSzq36gYVDZCjYB4OB1xdXdVsTdKX7yEIx7YY8EBgmTxD0It8xvNrzVqgBh1XmlFGPme2oplNAja0lCtBRM7JZ599VsFlOsEJgjLj2cxqFhH5XrNhCerqYkfnKBUXx61/s88EWpj17JybZI7rwkfQ9ikASx3FdHqTHzQqyTlXgUjSVcdP/tJIJC4SmiGtpXNJE9KSAA7vJ93IiymlCsjqok1AURU/acnMO56jrYEdl5eXOB6P+KM/+iNst1u8efMG19fXtfyvOv6p0xQ40CMjCIQpOMP5Z580a5sBNpQ/1ZvOtTLeyr/UR6yGwDHynXyGYIvZ9Axg8nMIAbvdrsobeVLpNndic+6urq6qXlIeY8Y1x67BAuQ9AqkMXtIFlU515Tt1DOv6QnCAOp7gufIL0LIi9/t9/f5wOOBwzGXCf/nLX04MmapPvYcVfaGOetKXGZ0KzNDxThrrOsf7yPvUU0oTyvp6vcbHjx+rDmU7WrZY5ViDKBhgoWsDacSAHj6razv7SP1NemuFCwbcKBDE+ae+VRCBz+laznOaOQ4GdsxtDzOrgVhKP66tCkaovuFar8Abx0zd33XtjG8CHdT35AUNhNJKGaQ1x01wk+1y3jVYkPpBQSst38/xcOwK7JPXh2HA69evJ7LFMSm9NCiK46S+0qCXYRhqOW7KL9cEDSpg23pEjOob/q02mcok1y3NMjezWolAM7zJn3NwT+nKOeF3CiiSRxTwjDHCB18d4iGEKiOcb8os+861OMZY+WQun5RjPS+a8qjzrv2fBwkRBKWNxTmlHJMndNOjNgz7xsoSfd/XgA2uDSoXqkf5ozYSA55oy3Du1H7UNjSIRPWE8rzyCMerG132jzqDNCSdY4wl6MfBhwZIK8249s+BYravAW2kI2lN/dQ2kx1SbLytm8/7+/sJTfkM1wWu7dQ3HDcvBY/VpuB45kETnG8F6FVedS7ZR67ftJUZzKM8yj5zjrhHWS6XE9nW+eal8893qVzyXn6n9NV22dY5Bxh1EPvMf/kezrUC3dNNf3MCqJ7S/Qj7xDb0It/rePg+0of9NHtcqvGbXo2vIuLYKgDQfgRQSia2YKIkz+refE5r5RkN9iBN+cMx8mq6sACIxQEUY5bt1XqJN2/e4Nvf/jZ++tP/BVg/HtcjJ5QZkptAWhMXozv3zBO0Ovf93DH8vAP1cT/nTre5k3R+vXT+Hzn57LzD+ZFTtniwWR3guTGd6+fT9GuBFUr91i8Fdh+/d+4A/hSddV7m+8M5vc/de+5KQKmgcC5Dx4DgaqlRZ54JW3A+wKruzE5xSwku+OYItfPO1+yvnrgGwS6e02nPXW185wGTl/Du/L7n3t/01vOZcueu+XdOeCLicVv696foML1vCjg4NwPhX3Cd6wOvczR5SbtPyetT937d6+voq6+r2x49W0lc1m0JJIxjhBVg1ZLAnGfo5Ga/fZP+fLKvT3z+Td815/1v2tbLZft5gOlTunx+3/z+id5jbm+Rcx/UdsPsb1lPvl6EQ3uvw5Q/5Ptzwzpn+7/k+jo65JteT71jTqOn+v+Urn3pe57q07nfn7vv6c9y1mXtb60SkP+a3Tq5XmpXPHW9RFaA83p7LjNP2U/ze7lGt88f25Tm7JGcnrNFklQs4/1qT3Nv1y96eAmapx9VfejeOWCcVhnUn7kfgvviamdmhLZiQHEckWLEGCOGOCCmUgmK+5fyTkOqen1OY6XLub8/OX8l6OKc3f6U3prM16xf5/Qz9c25eZo8Y4aY2l753BifkvPzvGUNgOVes5RTedSMDFHnMrdf9sZoAeOb9Qbf/+4P8Du/8zvYrFa4v78v+9uEh/Ew6dM5vEh5kPtd9Vdr0sp876fzw+9eEkyt+199p/aD98+D1jkO55z4IoCuaxVO5z6C2p9CXudyZZEkeCjM0IUAV/xCn7peDIwzq4mdp8NVS6ASzAFQHXsEq8xskrVKQhGMIpCoRNNNuXNuct5jSoYQ6JR4HDV/DpDX75m1oo6mEAK22y0AYLe7h1mqDjP2gW0DLROeziP2n/9mJkpYrZYTkDSEVvKZIK/SiP0ymwojo+jJTHTesi/ZwbVAjC1TkcpRy9rSkWRmAsoOcK5FlLCkuILqx+MR+/1Ddb7S+fjw8FBLupPmGgxA2mtGpZa0NbOJA5flWFNKuLu7q5mwzrlJ2Vc9g5u8+P79++pEv7m5wcXFRaUhM7A5j+wvM/UYKEDAQHmQzm9mLRLkY+a/976WaSZ9CD6QZwgAksaaXafvo/Khk54KQMFAjnu73VZwhvzAjMdxHGuG4nzxXK1WNfhBy1OS1nSs0bHPzGo9V9W5BqYyo5Yl7QlcU0ZY3l95guAPzw1VGdNMS9UjpGNKqeqO/X5fA3fI38zmA9q5nGxTg2eAXD54u91WncUxa9nrH//4x7i9vcVXX32FL774At///vfru733NdhBzzbnvPFz0ocZquR9OqY5b8y+U6cugR3yEp3aWuIcAD5+/FjHy5LC6vjf7XaVnyl/XPBub29rsM/pdKqyo853jvd4PNY1gbpst9vV7HTNPCborJVCqOPmgSgEzMhXmmUdY6yZzhw/1yG2O3dskwd4L99Jmtzd3U0yCDM9gVB0JeWbPJFSjkJLsVV7MMuVAW5vb2uWNftL0JT6mWPVABUazSyprdmkCgiRnqQRZYjlmhnQpOfJUxdfX1+fBcy5DvA9Co7MdY3SVc/pJS01u5L38qIuVNCJ79N72TfKB+dWs3K7rqt6nO/TtUeBDg2kY+asHsFAmyKlVOnFii7UP9TbPPpC6cB3a4axZpvS1uCcsQKIc27Ci1z39TtGfSqIrOs9ZYBZyDymQwMkqMd4DITqZwZvMEhO54IAOoBKCzWMdR3jGBQgpcxRVikXlEe2Tx1Le4H/zkFE2iIMFuGRPgpGusKDPHKBMsV+3N/fw/mcFaGAeYoJ8A2EVLuC/eNao8EABH+powiIb7dbHA9HMAOCthgDOXRMCjDT8Qigtk3bi+sI/25A7bTqA/lRgxg4BwrO0r5i1QDSXue37/oaga18T96mviZNSHPK8RywVf3jXKuy0+y3HiH4SfWSKvOhBfBoMA9tlOVygVgAw65vOoi0oU0z76Pahmqf5gz18Pjc95QmMk2aw7VKTBOHYuFBjc4mv9Mpwnmi3mWgCHmB/EIZtOL00Eo4l5eXdV3lURvkNdKQeob6j7qPfE96ayDJHOzVdXUeTKA8zbElS5MAjtAFxLE5c8jzub+57B8BvonzwbVz4aivVderDFC/cMxsJ4QMdpnzVbfyqv3lWjuO6Lu+riG6ds/3gHwX7QddL51kYGkFkm9ysR3vPXzfzqJ/FFgjNhAvdSCo7qjzIg46oGXv655B29A1INMY8J7tNT1xe3uH169f43d/9/fw85//Ah/fvT277vN353LqwZMOdANzaidZqZ+i23POvTl95/fN+/icc++p93/qnqfe+VRfpw/hHG76ybZf8AQeOcQn4QlOfj//Pl5z+utnT9H5qXG/iCblCj4ArmSCxxYwFuOIcRwwjsVPBJTywkA0Qx+Aru8RI2ApIllCCIU3P0U+hxygkntb+PfrlXedN/gcLSZ3fqL9r/P+b9bX823UzJ8X3Pscf57jX/eJ77/udfYdL2z36/DmN72+jj75Jpf3PoMkaHwcvFTOIaD0qELBOXD3PAB6/vpPS7f/WNdTeu3l/Z+CcPO2v+68nlvnn/p+0ouij7J6coBrK+o5XfVNZsdkbfpPJRva5nPtf913v6Stia2vFLLH2u6l/eT3z83b1+nrc+94aTvzz5+yLb++jYGiJF52q+49nur/HKxTW+rcGB4DlA0odN7Dh1IBC6389PwHyeDdFAxXH5HayiklpHHEMR6rD4/Vp2jDj6dhYpMrdlV5rtjKHEMeVKZnjPmYvt1uh9PDAYm+9z7vU1zXcK+u7oUe01Nt/6culeun5j0Z8NwZ4+dkY9puOqsy5+9LT8w1PzMrIHZqgdFP2WXn7NT551l/2iM+O2uXFV2ruKZ+z7/v7/foQo9Xr17he9/9Pn777/wYr69fF39+2f3YiGFoSZ+KKSn/PzUe7nPpQ2ESBYDJPpj3c3/L/bXu8YEWpEGsUelDTEMxR00O0HnWvWjzO2RQmz5D0o/PaHCIjpU+kvkYXnK9GBinE4YdYllzoJXjowNhOUPl1eHMMsUEQbmBbo7P7JBKCfC+g/fM3u6wXncYhubwMaMzjZnimefpoCWA45xhuVxXJ+5isQLgsFptirNoUTdLu92+MEhzRDH7kkxIZwiACQDKydcsITOH+/uHAoAv4X0oTrEOIXSI8QTAl/F6hNDDzGEcmVGYgdGuW4BlzDNdPIAR48iFgozmC/B+wm53j9NpQIxjcfYTYG5nRx+PJzjH8rs5MoMCQAd73/e4v78vIMxldeJTEAhK0FFIJ6Q6/OaOEDrxeNb3drutGSkEpN6+fYvLy8vqRKQTWAEnAjTMIqYDks5f/k7w4OHhoTqWKUxsk2WvNaIGaCWRmTl5Op2qQ57OI3X+UfEQ5KcSpKCzz/f395VvtLS6ZlIpuKFAIvmbZXm1PCqBY/6rILP3Hl9++SXevn2LH/3oR/j5z3+OV69ewTmH169f4+3btxXU1cAEZttfXV1htVrh3bt32G63FXxV0Fb/JvjE9kgDzUjl/BKAvLu7q6AwHbUcLwEYOjUJuqqzmeXw9cgEBQw4TwSrqXAVrGX2eoy5lP93vvMd/OAHP4CZ4U//9E+x2+3wu7/7u7XEPsGh/X6P6+vrmpFNvUG+Zj+4ydQy3AT1aZRRP7JPBKoV7OPfXHQI0p1OJ2y32yozzADt+x7X19e1PwQECGJwDmKM2O12FaABUM8KJwjIOSY/x5izrclvCsBR5nQBJB1YzpmyqJm6XGu4+PPS4xUUlGGlBAWftOS69/ms8o8fP9agET3WAgAWXakaYvms0TSMsBiRStRiWOZjEjjfXAc0c01L5yowpAAy9SDp8erVqxpkpRsAjk8DVjhnrKBAedKS72xX+YwleM9VGZkDn3qpXqWxTFnSMuR8n55bzLb4rBpTvEfvJR/r2BW8Zn/ZJ86rgjuUGco1x6z3ci6oN/S84an90I4B0LWRuozj0SAw8gRBMcoHZYnrJm0MBTK1MgLfr/JOms/fzR+uKXyngmKk3Xq9ngTOTQEqq+8gj5JmnDeVXwXDSDvSnPOp81SdpQIK8l18jv2iLUUaUAZYMSFagrMEizlQMjkgxQTXBXjnsNpmGX84ZZvi+uYmj3MYEWFwXZ7/j+8+ou97fPbZZ5MADOpf1bvab+q7lAzDKQcdPewPlYY+eBwejmWNcXC+6T8FmHk/dSVprpnWlB8+o2CkAnsAMMyCNQ3AaRjgiz7iGswxEjAnz/R9tjdjjDgeTkgpwrsA7wIODztcXl5iHIdaHUZBVXU0mCFv5gzo+wX6rh27cDoNlbbjkNuPY4RD5pMuuEkfGShoZlWfcT6SGYILGMcTGJlOfjmdBiwXOTh1HNo6F0u5LsDBuyBgBhC8h0Oeu5QicjS3KxHpCWNMCJ1HjKWiVOixj0WOUtkj9GXdP+USvIu+h/MlICh4wJoOJC9w7eS/1KUcPy8F9TVYinw5DbBtepf0pv2toLs6ipxzNeiDvKV7HLWpgJx94ZD3ahbHqj9izOeF5fcU2nYeaYjo+lJBJQ6As5ahUg4sa1HmocyBa/IIwHnAUsLxdJgAw4vQIVmCh8FZQnBACB7OilPfcqn0GBPGU163LSYcTg/NpimgM+0PdVxR31KOaQvpWtl06Vh15VPO8JdenOvgPbxrelT75DoHi+LoE6e0OhS4bqg9pjygf6t9oGs3f/KcNPvOOY+uW8AsYhyz3fr9738ff//v/338v/+f/486Hq61+r5zv9e/TcpWz0h5DqzQMcydL+eceefaeKmD9xwoNHcCnmtr7pDTtf65+57oBfjYS0GIl7zn6/TlKefzOYeozu18PtRfcG5+nhrffO6dy2tDShGh72BxWpml2pzFcRk6j1CeyTpYx6MZ9E/Tgrop93NKiyaXGmBwvs0GMrTfn5LTp/iG352j/1OXyuQ5fn6qLX1/hYqkDXX+nmvznEzO39cuacdNM8bPveel17wfL+vL17/MLFczcA2Y1JYZkuLKzzfVQ+ec+ee+52eUu1jWSYLg3k+r22RxKaBRskft1/u+Vp+fvmfKh4/16XPjevbdQD0CuD7h2JkGPJmdn4e5XD53TeX3Rd17NMZz8vMp2X6KJtXeswIW2fT+aSP85/mM7k/J3kvWpSe/f2J9/tS6fW6N1f48994sn9OqCPXzR7zuJgxvT7zrHHD13BieArqe6vNL75l/rusu/35Kd1cgVq5zgN9TOn3y3vzlo74995y+X3WcjkH7rntk/k3fhSZG8vvaJlAC5lK1q/nDJKoYI4yAd0zFpzpUn5z2P6DYGb5VVuz7HqvtNveBVaucr8lEBC11XGaltDT1dbFpFBi/u7vDbrfDYXePu9s7vHv/Dr/85Re4vbuDDx7L9QrrzQabzSZXxt1sH49/xpeZpnbOauFkiI2j1QfaXD0lj/xOaVb3FOm8zpn3M+Fxvx/dbwZEHpeT9/QW06P7rJTk1qCEiY3jJMP/TH/03hpQbTbZNyk/Wm4UIQTc3LzCj374I3z3O9/DZr3Fhw8f8n475Pc55PtY1VUTlF1pg/tS7Qt/6GfUJEP6GhTfm9N8vu9jW/O26Q9nsDiTHRQvpN+TcnduX5D/NoTi45gD6uqzpA+AfePvVTbwvC7V68XAOEEivmDuAObndAQT/NaShrvdbnJWplkrJ802nQPGMQKIxZkYkBKdRFaBsUKyurHRTGjNEmgAbctsy4BinigCcs3J3aKFOA4yjZboJqjGcVOxMttCyw/SmdR1/aQPCr5xMhXkYmkFLXeotCNDkfFUIAgK0nF1ebmqTksCvMxgYp/zmF2dUwU0Qgi1DKcC0EA7Y5dXLeEhDhstm0gHPsGF/X5fs5p5XnMIAdfX1zCzWlaYDnznpiUmSWPNoGc7BJaZ9ccsOwJyVE4KVikYQxoTWKQjk07xEELN0CTAynnnPGv2NAVVo1so6M65mulJxye/5wJ6e3tb51Ed48wC4lwq72n1gNVqhc8//xz7/R77/R6ff/451us19vs93r17h67rannp29vbSRlnBjGwP6oHmOFM3qfyIz299zUzTTMJSWvKwTAM2Gw22G63VZkS9FRAjLzEftzf39dMKbZzLvKJQPo4jri/v8fl5WUFg8lX5FnK5Hq9ztmGLoPpr169whdffIGvvvoKfd9Psnxvbm4qD5C3+Rz1BHUFaU2nqxo+XFDofNYzxukwZv8I7pPX1ZDimC8vL2tbnFulP/UlMwups0lb6vGrqysAqBmgjMrS6hc8a5o6UAFV51zNrqcuov5Q+XPOTcBqzg/pSDqRpnyPgpO6FvB9BGUYVEIasQ8a0JNSwqqMu+/aWSzDMOD29naiz9RQ14Wb46MOVD1JXaKBAAwi0Qg96iDNGjfLwT6LxQJ3d3eVDnOjlrQkqEz50LVEdSNlmLzgnHu0nnKedG75O99P0OX9+/d1ztmmZqZqdCB1MXlcszg1wMDMauZzWytdBRSpE2mcUU60HDrlxXuPi4sLAQT7GnzE9UaDabQvWk6d3ytwyfWCpacpU5xjM6v8TLrpOj8/J5vVKFJKde3RYAa2z6xxDfRhEJpuAMlLnGPqcfIS5ZeyTd5hkAZljX3k+NVQVSCc8sX36LnnrZpOW7MZVDPnfdWRYyk5tli2QAXNLu26ruo+zhnXMq473nu8fv16sm5wLORpPjcvwX84HFqFAWsZ2pwLS22+xjii6xo/6dzqhob6VCtgUKdwU6Ib+3OBLVb4l3qUa1zVk5IlPNdjeVMx4n53X+1j6j0GJD08PGT7ddlPgjfIG3V9SgkP+8zvy7TE/n5fbSP+S1ngXGgVEV2T5zYlMA060yMN1J7gGqhBJFr5h8FJ5D+d/2zLaKavnXV4jfHxETi05Uh7BnweDgcsF+24GcoYacf5VZ6lTM/XMtJJgW/2iTylm28dI/mP864yRr7nWjAHRdW2yuOflqnnGsB1cRxHwFJdXxgIyHnTPgc/dWBRx3Cd1+At0ojz3nc9Ft20OgvnQ99Rg0W7DkF4bmSlq7I3IL+pjlV9zbGQf5Te1KHUFwosfJPLF4ea96E66dX5Up1DMQI8L7H5u2u/6dxqzxrMeL7i3AHUnDecx+pcMqDzIQeROA+rZVit0GMBlzzGIaHvFvjP/rPfw1/99V/hz/70TxHHEV3wCN5hOJ2wXK4wxAjA01MKwhWV7NbarmVLZWznnGGUgbm8zh3rajc95Xx7iRNa237JNb//3Bjmn+szjjSZIGnnHcpPjZHgG2qqfplfJDgYnLly/rYDw1ccHYopIaAcT5AMrCDufCsjaSjBf96Xsu8NanD5MM06m3kYKQdIOdewqYZ85n8ckHwOwnDFUUgntis8lMfbzkHEzFZjfqQLIYNDfJ/Lx29yHYWrd5ZqFpWgeDxdHNeZszkLTVHSzk1oCGTwEc5l+jiDJQfzHkipOJxRx0XhFsgGPuX5sxJY5Gq/c4AQn4tnWKzKQ6W1m/w8ZmnqF57jmHmwZpwqRczyeJQ+bAMEOpV2+tn0c06Tx7Qs83wcn7pUb+YIKxmT6L8mUg5emp478+tndg40mL88t+kLiEF93KiHxudoAPpknC8aZbu4Lqe5fvJyNAB7YQYXHazIsHM5wNP3IYPIo8EjZO5LuTcm/DOZe8rvWbXW1hy+vf1dW2h3l/nPcZZOnpvraz7ZMqIJvk3Wwpy/l+PwJvSdopvTPhV5akpA1s0SUFARZkzBUlc0nFmbad5aCeXK+cJljFVuXJMcxwBClaYzBC50coW3Pe2Bcm4yz3V1CVXHjwGADwB8mfsio4XuzrmqI7w7+0qqtyktq5pyjd7SZV2btK2ml4p8WMr6wRp9Va80BE70kOo22hMuz5fne2fkqzINcmazIyY+lsIg3nnEZO19ztU5qlxabKzOGk2sdHU6znLNgNB538wsA6OzMTzSgQ4IJsFDyEGslSEqyRw8/PxRNjq5dwwe9Yxua2tlStSbXDu7HAxuBrOc/emqTkiFVxySFbC7lC73LgDIWdghdPDOw3cBPmRae1+yuZ2rJcHz762faiM51/pW16uUcsJLHHE61tWoBsVpokWC5XOPLdUEmfYOj0XwWPQleW7ZKr2FELLuDCEHhfeLyT6s6/JevNowRXbGmFrwa5mEZKgVuFJKwFieMQBFH9c5sw6LdcDV4gIX1yOuPz/gZrfDzWef4Ysvfo4vv/wVbj98wIcP7/Hq9WcZ24kFf+m63Jb3NQOb2rYwipwhbaIjxXws8ztZG3mDWRUKrm+6x9D9TLXf+chcR8ztWePhOflltCsmtkSR/9yVNLHhVEqqKpn1R16e7ak28naPWdazlhAj/WChrGEJY8pYZwgL5MrX7ZiYm6vX+P73foA3r99gtVji8LDHcDzBYFj0PfquQ8fgb5+D81MiVpeyj6nLvuYhxsxL3mO1yAlM9MMN44DjkHGzMSas1iPW64TlYonlcoExZn90jKniT0MccSr+xDhGwBJiSkgxFr2adSrMEE5j3X8PY0IcR5yGj20NMQM8qo/Eu1BtkOB9qXyWbVfvC27ou6rzYECK2fcSx4hkESk1nwBpWuUFxcZ+wfViYPypaHkyLgEXgip0yHEiCO5SIfBSANOMgEtzPivj8z1zZzCdWHSE0VlNh4+CXQSS2Vc6Xgg68W86OajcNHODY6IzRcsEKPBJIEQzteioVgBGzxSkM0oBeHVO8x28+AwdWby0lDOBu91uJ1kY08j/nGmas5rUmURwoGXIt7LMbEedcWxL2+BYOV49e5JgLR35zrmJA5RZK3QS53Lue9zc3FSgnkCsljFUoHGz2dTIK/Igx0ZeoROv7/ta7nZ+vjOdXsxYJggMYBJcoSAHeZh8wHfReUyeBFpFgkznoZb1p3OXZZ/NrH53e3uL9Xpds8aZrcwz4NlnXuTfbYlQo2OYjmp1PF5cXFSlQiBZ+fX+/r6C6EojAuCkC4EFOgrVcUia9X2P/X5fz08lr8yDAFipgnSjY5X3sm/kJ83kZYlygmEKwpE/TqdTPc+e41GAkm383b/7d8HyuG/fvq30ePPmTW2P0VwE+PU4AAJ7zIqkHFC2NLCADnOW6iU/qKOY41SHtIKKHCfPvaYu0eoOnEOVaedc1SUEIXiMAnlLzxemfLHPc8ejBqNQBjVzUoF/tkfQhPpKSwkTZNQqEAQzqefVia96HmjgFHWsrl/kM8q6Au2ahU59RTBG1zzV2/NKFeQ3AlYEx9m3rutqljLBQ/Il6U3wZb/fVzrpvJOWNIboxFfZY7AQ6Us66fqq4ImW7+H4CbxT9swMHz9+nGSvK0itEY2kCfmEoBvXYAKw7B9lXQ1pAr/UzSGEWuqf6+9c75B+5H0GBrBNZitzThW806wjrtWkF+dGy8HzeQZUkeaswKDBW+Rf6jeVIc5hjLEeX6KRyeQdLdvLyGTVv9qOAiwq+zovCgYrsMv7NPNUeYa04N+17HlpS/UE54pHMqiOoI2gc5FSAuRcaQW8FFgj/TleDVZR+0b1jJlNaD8H4KgLqLtijOhCi+omnUlLrv99386kZjlzpZnyjQZk6EadPMYxknYMZOn7PjtrRI+obXs6neDQwD5W2CBtuQmy1Dac8/GQb4ehVahQW7eCojYte0eenp85zvPCNaiJ46Xe43qgvKX6g58rPdkfzhH5lUG61Ptsh3pf12Dqvtz3A5Klif2may3Bdq4lbJNzzYouKdqk+g+DlvjD8VJeNGiMc6oyT95U/mQbXKfmtrra5PxbAXlgeu4X7Y75XoVR8LxUDkk3M0PwjY/VvuBY1DbkM+wD+6VrNZ8DMAmyWHTTADS1F1RXkif5ne5fNUiGwD37RF7RPY7aYrx3HrikwbDf5PKuZIoLneeA/8SZdAY+mTp2FVR/nCWqPMK/67rH/hAU9076kd+lwVLOeby6eY3/8u/9ffzqyy/x7quvcBoHLLoAOMMYh9xfjsG1bNnJulJ/q552Gc/00s/Off/UvU99pjzzkutT73zumo9p7hivtpk4DLMjeoJKvKhvFcx05/vc3ld4gU6p4oRilo5zDi6084hZZcOVY0qCVEthO670dwJcJS3XbA1bkczU7FBNcPDVyZqK09WsOFIrVpB5PUaD9woWW3XwWkVzrMpCfr+CWxmGac5oOtkz4JF5w7V5AJ3U7T5MgLzSOoFZswr4eOTzzpPgbDJ54vpt/0uln/WES85VAeQYlODrQeoyxzb92/Q397gLjp815ATnRMPYDwhoZM3R7vnsFBKi77r+lenY3lFncSYXj97/hCxMZWsysvbepmIKL9sjGj2mi2Nv+egTl1MGLQOWSSDPT4JIPq171A9z9jsdrCs0PHNvQAO7vc+VFFwX6nc6jkfsea5feDwX7I4TgpvhLB8puGEE71z934x3ikxC5PFMv9pdnwhmqA9Og8ceX2c+c1M+pt7wcq8VQXITvnFwM6GcyJubScs53geQg5DaexwyHsqzv53zrS/OwfVd0Rmu6iPnM1w6pli+y9VZp32Y08HqOEC9RL3lHlsmbraOt5GLrnRW0XhrikAGq3PMwzGmwRdtKqnTC+2kWlQZXGkv99nPdDzHw5Yn32kzOg43/ZzzUWV9OgB4iA631vc6ZLXNOJ7SaNW1bKv2rQSOkZ7ySufwaF7aZRVUci5X2EoKjMMQ4vSYsRjz0SRW9Xeu3GIWK3hmlldxBgd0XSg+9iWC8wUY7xF8gPOcGga8uCJf07+ZSGkxVbrRduUxTpYiLM4rvRa6WHuHh8uBqN7D9bRbMigffEDoc+XfZddjuejR9wu4Unp9sVjkymBlDvuuQypHu1AOqJ8yzTKYGlNCREI0Q4q06dv53zXQ14qe5pwLfznn4bsF+n6Z6b1YwvULhC7Ad5QJw4cPH/HVV19lP01M8HBYrpdwXQYhcyWwMsdmdb04ZxvP/6Y8O8q7yb319iLpdR/C72b36J/nuJPPJxP5ssm/vBxtItmr1P5i+gzHoG2plm4hIO2elBKcWbVXm3871cANQ8p85VqfvA9Y9Eu8+ezbePPZt7BebRBjTiw4nXKia1yugJXDctnlai3eIxb/c0qxgOddBqtTwmkYcRpiDoICA3hi8b0mjMkwpoR0PCIaEJNhTIZ+uUSEw+E01CScxXKJIcYKjNfjRFNOpOBa7oNH5xwwjGCAaE5qjkjHIpsGxDRiiBlLWK/WCKFrHFECwPNeM+Y1usioa4oAloCx+I2cSyX4pQHj+V1SyeKF+7cXA+PnnE5AAzLoPKBzQTOhCTSy9ASBLzKagj3OtawDApd0mNEJpY4qANWBqW3yR7POuEnXMoNaUlAdG3RM0pFCB5JmEmv/5uPhPVpyns5WVRhaSpefM3hAnV4UOnXIAu1sAHWOqdNotVphs9nUkh90xut7CHydTkeYtef5vYIpznmkUipSMyVJ35qJIVlDCgpoBkYIAe/evcM4jri+vq78w34TnKYj1TlXHbJ8vwIJnC91RBLsmI9Dy9QS/CBdmdWoIJCOk3PAOWP/NPOX76LTk1mydAzquZOUCQXBFLSmk5WghIJdBKYZwEEQdg506EJFYIb8qGV86URUxybHzsw7oIH1cyBCASM6mQk4aLah3kdwULMQKZ9KE9Ka87rf7ysdAdTzcmOMtUw96XZxcYH9fj/JPue4m9P7WPlCA18YUKJZjZeXlzgej7i+vob3Hj//+c/x5Zdf1gCJGGMtt60gPuWUck8a6wJK8O3h4aGWuSGPkE/Ju13XTYJnFNDhuxRg0kxyzh//Jk9opiJllTJAvqPTU3mMepVOfAWkeVYrgWz2laDX1KBuoB3pTfCM7TJzkU508iT1jJYX59iYDcusPdKO/KQgWN/39X4aBqQXx6rOd+pTdbKrPCggruA2eYw8w/uof+bgJdtXpzNlijqJuoPrkAYqcf6pizVzmvzPtYyywsAqrnNa6p3tcC7mjvo5TThuBT8U0GHwB+eLgDuf0bYV0CHIpbpO13zKqx7hwgAPtsM1nf3iukjZYpuaYQpg0q9zc67rBnkHwETPEPzj2kbZor2jICD1CftLHiKNCbIDmOg4yhPlQsvuk59ZUUOrMDDgjPOhsqh6Uu0rDaIk/ynfU5fMS4TxPVzr9Bzn3W43yXjnxflXoLCCcWFa3p36jXNKQI3fkZ81m1x1BOeX88D+M7iF/Zqf85znoiuZdE2OVbb5buod6kb2Zw6Kkg5a8YeZyYey1vAezid1mPKMBtLUvowRZgnDECf8xvllcKOW+Z6XnM7vDdWe0ndqsI/OGWWGwQEaxEH+1mAj6nFdxxWo1kBU1QecG7bDNULXNO55lJdTGSvpqcEJ7MfNzU0NQOP6RR2gIL3qTR7zoAD7fM1jNQvq6HPBH7qOkG5cE+Y6i4FurNakgK/SVYFhrk38Tu1g8jDn8BxooXyr6xODZHRfcm5vQdtdbULSRnWm9pfj1jVc7R/db+naxL0B12LOl8ou9b7yHIMsOSbSX22+b3qdc0CR1mrz8/fqNBSHgN4LOHEcAM6pA6I4H0Q/1Xl1LVcLyI7XKAEH5GF9b0oJ/8V//p/jFz//G/zxH/8rvH/3FilFLBcLPBwOWK+22XlqCQhPl1YGmhNagaCJY92ec6PN2/k0nZ/6XN85v0fbfuo9vH/+vY5jLkf699yZ/rJx6z3NG87zC/PcNk+r8w4pJiTEHJhhBksR46lU1vEG33Xouh6LRVeObMvV/rJslX2r515By5p6qNMXZvDRAZjakdRPdXgply9VOys7llnyNI8zImdxZmd4moIJ1uxPgvawBtI776fARY4Um8gc5yTzopYOLUBqRbNc/YdjdcWx7VyAQ/EjFXo7n7Prx1j6LPPBZ/M8kR7AMeR3ZfDLwTKykrOrU4JZBAxYIXDm2+AqnF6ac4bo6VycAsLKNzmr1UszM/4rtAlJGiiAcJbZ1pa3kllexjcBgqjHcm+qA5v21lN8f04++bl2R+C3Mlwem1L6CZeP3qnUKrypHvs6H4/Xvfnf1L0Nh5mhZpwd0+ziOYDrzv7a2p++17lccWT+yOOpdQjBYwDX0VDs7ly9oOvK8SwSQFLbOafnRE4mumui90p1B+2vgJN6eScZZ+euZ3Tt9LYmK9PuUvd+vWbNbJZv2/hJbnrU2FQO23eugrrTfmHWpp1lA/fo1pyxW/ZOntWGGJyUwbTFYiV4tyv6o/An9bP3ZR8Taz/nTFTn1ZoNoXaIlXYf3T8d2mwoDq4LT8j6lLd80e02oU8DIpX5zQwI5yiXhzwJBCnrCoFcAvoOJVElNduqfjezYeIsa5E6JEk/PYAQy36y0H6y1uuaZKnIddFZNaiM73a1mo+hlX7OYWHUKZnXgpO1wZFdadMFeJ/Btd4vyxgh61Jed6tP43TE4XTE6XgAim19Oh0xDidQusc4Inkg9Ll65nK1xXK9wuXlZbYhnM/nd/sO4/FQ902x+BBoF8QYkWLMNmjKumlypBBoKxcw3jLNvfdYLBf1mNkQOgSfq+OuN+uatBBCQF+xBP6EksUegNTWpiGOGIcRyVI+0mwcMJwGnE4Rp9MBKWVQMv+MGFKkaGV6Gwqt/WSPpz9dOSquDy04OFeAQPlp+63DacRpjBjGCLiA65tX6LoeF5dX+MXPf44/+w9/noPakWVmTBtsLi7Q9yiBuOJ7dB7Ofz0bm/ees3GdK/yYF9SprVtvPKMTnniH2sv6r+6DztkEKqfqwzz3L4Ba9SK/rwVyVjrlsgL1b+dcOfbPwftcgaXiaQZ0IWC13uD6+hW+853vYb3ZIhpwPBxwt9vhNAxY9QvABYTQw4UEuICYHE5jwjCMiLHwXDT0kfhnwlj2rQffquimlGXA4OB9j2iGh9MJpxhxjBF98bk+DAPuWVn6cECCe2T7mlmpLVVkqlQkaf7xHEjaAtJzcEiEwykmxMMRp7FhClnxsHqClTAeTZIORSeW6g4xwlKu9p2FMMt5KhULaC9QL7zkejEwrlmXbZNiFcih42qUzQqdnDc3NxNAWRmMThl1HBOg00yOCYMVxcvNFftBp8XcwaHAOh3uCl7zPoJPdMjquX1sk057jpfOE32XCp4GDBCY4nMAquNOHXv6HNDO2qNDWQFr51p5YTq6eT8dj3SC73a7R1kfdKTmYIUp4KLOJDqkxrFl2ivQSQcz50aduEADUvu+nwB8XZdLnTLrWZ3NAOoZngSpeR42HebkAWb+XV1dlfIPLUN7DsgSNCVf06nLPvP9dEISVAVQ38U21dHO8TLjkVnJ7Cd5mVnpl5eXNROOTmN1wpMHSDvOuZbJP51O9ZxPBX4pH6QzFweeo04+JJiuWWNaQpnv4btDCPjw4QMuLy8rYEJgk/KpmfHkc3WaE9R1ztUzyhUMUh5liXTyl5lVGqWU8Pr168r/1BHL5fIRAPvhwwfQaciscNKJvMcAHma+Mtji3bt3VW8RSJw7jl+9eoW/+qu/wj/9p/8U/+Af/AN89tlnrZSObwE8lA11/KoOobxrJqOWhadDW7MntarFHETu+77qWDUaCJ6Rz8inKnsKyHGc1MvkJ9URGrDEM+/Jf3Smc574fjWWNDuOpesp+6SbApRmVoOsCCwoQM8xnHsv55IBCJwHvl+d7vyd/KNBAUoDrotKP5VF8iPvI38pIKWBCpRXZnkSQCVwyEAAAFV+tUy5GtZ6DjC/py7mukC5n49DA1XYDtvgfWZWg3KAXKWDPMDvFdCZB15QVyhYy7WRupcZmJptSh1JvuDc6zrMfvA+nR/qS7VLyJMMEqK+YFa68gH1s5ZV1+AevoeVccgLrBihPMff1Vbid9pf9pP01iAhPkca6RErAGqVDwK/pOk4jm0DWOwfyjnXZTPDw8MDttttXT84ds2a1yA0tq9gtQImam9wXjhHBKT4LrUfq41RnMiqhzQgQW2deXlt8p0GAmnQmdp/mpmv8sl3BZ8BANVFDGii3jKzegYZ339/f19tAI6NfdCS4rq+cp75fuVf2kWqt2h76jrDeeD7YoyVxxeLBZLPEc1mY11f2U+uM4tFj+PpOLG5KTds0zuPcWzlwsnnyitz20nnY74B4+/UVwwu4dgUFFQbX/UNxz5vX6sXUO9xDZoDVHxW11X2kWPjeCkn5B3eq3zNeQIwOc5A+UwDC3SvQ1pTbua00kBZ2k4qj7xX9QL7q84G0pnyUR0b3pcSopiMR50hdFKqjaN8wOfIPxy36ox5AICu6yoDnfOP+EbXSg1s4PfzIEndP5LHNCCDfWmOqlZdQO0WtYU5v9/0In10P6zBebyH93H86vRpPOyLI65k9dhjgI/f63N1XgSULl9MeIlzq3M4DAP6o8M/+cf/BF3X4V/98b/CX/31z2DOY725wHA8YRE69KHDABnXTO7ki7NfqTye67veN79Udj51ze899/en3vXc9+cuHVf+W3z87jFA8UxL7d8K6Opn2ZnEsqIhBPiU8LC7wzgMcACWxX7edosMIidDPBzwcH/EQ3Gqp9QCVVZdP6ERZVblBt7jJHa8Hm2n97nQISz6JnvFLW1oQTHee4zmcuFYR3yhOSsTA3DHEf2pnCdu00o5DXTPDkaWFp3rTq5/Zjkjr/c+4xPViZh/8lgyLDA4wwERDqXiWqeO21K2NRhCRmHavBtqP9psWgafHZqjeYwV5O28h/cLwAODSwXzmmapzi9fqr4DyKWWgYLltmdKLk8DYSpgI4AEkEH2iiq7Cc9WOfXAnIEdJ67wolkB50QOHus2VECPv+v3k76ZlWN3nqZDfa6Wtea4CHK211juaO1Xltd2EzNQJ7pz9i4dF0v68wUT/TJ57tkh1Llu79WRTFqCATilsa7XVfa8B5B5J++NctblU++TPx6N7dy9rpa/nvKl/q644FMas37nHvPSYz17Ll+85g0+8YLHYzAQcpXeUlbOzYuSx/vH65irqOSk/2e7I2+d8ocrGYplPQZgowFW7CfZw6WUs3hrlSEfspy5DCxMbI+UK0F1weNTV3Jnqr5Q5mcymjHYViQfoNZsM+Rcs311nNRnfEh5PVl6xO1OOMgR1JF3Ou9y0JL3AO0jaaMGZ6C91zsP89Zs3dn39d+CgCc0fQAAwVDLgufvUz1DutriDAiqa7bL67fXarJlHfEegTar66o8d12Hrve1nS4w8CVg0bVKWCH4msFNO5ZAfZrZ57RFj8cjdrtd9t99/IDDwy1uP7zNZ10fDjgdjhiLj6pWiwSw6Lp85vV2g36xwtXVFRbLJZx3iEMJtnWPgU/2jb60ruuwXV6gWy4qqN0vFliUv9frNfrFAr7r4XxX/b3Vtk+G02moe9OUIsZYMK2Y1/jjOGI47DEUG98MGEarmavcL4BHFbjm6/BlfWZQYOjXWHLf5n2V1+AaCK78oz9ZNuf70mZnkG/W28vMIynieNjhlz//a9zt9lhvtvjBD3+I1WaNf/kv/yV8NKQ3b+BCgAsBY4y1wicgNk+aBjBxLs5dug98av3VS/eb2sa598z14eRZm63VNgvMkTGYtjtba+d7NlceUBuRGeNqKzKgberrcnAhl9YPPp8jDxewXKxwcXGJm+vX+Pzzb2G9ucA4WvU77h9OGFNCtBEDjjhEQ3c4wbkOx+MDhuOQAzFSrPusEBKAhAjLR+ckw2nMe2OC4qn23Ep1ooR4OuHj/T3e394CaH4LAPCnExjopHZBmyNf9U6OlZRKU+YQ/HSOQtfjUvzJJZYgHwVUbPFcft7XI6PyukH/Apqt5QNGxLrmRcthjM61yjfmDcDLjjN7MTBOUE/BLjrv1FkItIwgOmVJCAJOvNRJ6tyUiTgpCkCT6fRsbAWY+BmAieODgAEdTnTsOedq9iCdccygYHu8F2hgNR0d6iDi/dwgqXNVnZ7skzrumU2spTs1Y1u/o+OawBxpSJCH/SRNSD8CnnTIa3lKMnjfd2DGODMOWbKb41wsengfJm1ryWIF7MZxrO+jg1gz0DR7j5kZbJfzo856bqK5GHIjSjCI80u6zbPa+R7dmAOozmkCzXTybzYbxBjx8ePHSZlxAsPkM2aLkVZzZaqAHsElygPBQQJlmtVHA4Xta8nz1WpV54dAIkFhzikNBQaCcM7nWV6kJx36nKeLi4taPp3zQWCEY6ejkvTUQAClMSszUJ7IuwRAKVMt0yy3fXl5WfvLwJLLy8t6jjUdxpqVBaCWUeZc8F8GTVD2maH661//GldXV7i4uKi8wiznH/7wh3j79i0uLy+x2+0q0Ea9AqCWjb65ualtD8OAjx8/Yrvd1gCCu7u7+k4FQmjcsa88/5rBDjQ6KQcTR3AxrBQc5qJNelD+adwQ5ANQz39mP5hFO69KQX3GUvMqc8z457zREU2doNnZvBaLBbbbLWKMNQNcDR/lFf7tnJuUMVe+4Lu999hut3Wd4Do1B3NZPWOufylDei/lUbOFOQcauEJ6cy1Th7qef60BCJqpt91u67wSyCBv80xx8oLKKtCAXPa9gnayfumaO44jdrtd5QHKn4IolDGlBfuqQCTfeXt7i9VqNQG4SAfSlmPmnJJ+m81GNiSthDZ5ohpQaZo1r+sobQbqWy1fr/yqYBq/YztaQUSD0HgPPyPfaVamZp2SjpQn6vjr6+vK0xpoo0dQkK+pCxoY2SqYqG1k1oJEuL7T7mB7MeYKI9wIatCJczlIiZnApBFpoOPk+xk8qOCPWQuQII2OxyO22+1k3vR+BnAxeIZ8M+cBBQoJZB3HduwK54C8TTlkH/k9+Z96Ids1zUajbtTv6+ZAgFbyonO5fJTaFZzrzWaD0+mU196+w2LRVx3Ks+cZoEDbj7YS7QT2TwF/XfeolymLMSWksVXHYSCnyrcPOQ9CQVy1X4dhwKJvx8OwL9OAzRExTY/hUD3Bv3VOKEMcB+1jvnce0KjtktakLXUZ55+8Tt3FexhcoXsRdVZof3SNmDskSMOUpsGwwLSqCPW78o0GopkBXWgyw37TPtJqPuQ3vlvHq7pT9Sz5RO0mrV5A3aHAJWVP1y8FopVuCg6zTzAgphaMwnvqOuk9vJ8GrfA9pC3fx3mZ8yTHp3spXSvZJ0aKU0dpgBptM+om1bVsj3LDfjGw4FwAHOmse1e1yTgGlYm/zaXOl7lees6JxmvuWFKH0fz+c/NUdZxlBx/vJ0+qs4R9bGtGxP3dCZfXV/iv/+v/BtevX+H/+z/8//CXf/mXWTcj7/kxAr7PDljHsQgNMviU0GprPn3Nbcr59Zyj7VPXfB/53Hs+9e5zz87n7j/W9ZL+mhlQnLUpjri/u8Nhf5/LJ6aEFBM+lKC4cTAslytst1tcXFxgs73AcrXKWVhdX+XH9zyeCuBxeaqzU8pni6d9BGCIxzGfHxjHkhHTnOkRCRERQ62Oksuw9qW0KRBzpkzo4UNf91fMVq8+Ap8zu3ervIb7LiD4XAK1KxnvNasSqNmUCnipvJixhCYqrsZMlVx6vpScNMDFDM5rydS8fkfEccjnQacxg0sFLKz+MjyW1T5Ng7+iMeBFJzb/eO/LmbcNsNVxaRb1lDFkzAZ0zgPusV6jw7XynO8e6aHHvG1gFirfcVZnOifAENogzSZgotn5Etkvkamz7549ZpiDEgV06+YO+3x3eyrf6Wb5xWd1M6Y6rOrCJzHbTwMImD8/4w8HIPgeo5XqNc6h73pstlvAORxPJyREPEqP/sR1ThdXuYKD83N3tMLgbex6dMO5tnglPNZxj2nh5S0U6Pn7+VkDTc5dZtoa6tnGk/fXAIlPX0+vXdOwAB1TLTV75rvgAtzC5WN8UsSi7JmZuehc1nnOOXQhwNnUr819YLQpOPbcVUtJp8egGJDnSAMJuOaj8sX0qhrOSYKdmwLhmUlUvxR7EVaBZoLwDPTQy8wa4GI8osLVPlUojO8vuuw4Szqz1mBui3uO8m83s9e897k8svMZVF1Mjyvlv13XldLiDqGAuw4MEM+gmw/TqmqdCzWbPQSPRddnO7mppbIvGFqp5TFieBhwPD7kBLrTEeMwYhwHjMc9htMJh+MRh8OhJtgNpxNOxS44DQccjg84Hks1Ndf23nmtH7FZbbF0AWkY8fDhHof7I64/e4Nw0+PV9Wd49eoVLi4uMo6wXtdjWvq+w3K5yomMXT53mEtAGgi+5azsIUYMpWx6tIRTSkiHAWMaEMeEYXyHGGlT54zzMbYs9HrOdmbMNlc+g4EZ1A5wvsNi2WO13k72UuQHBhfN7bpmX0zDQeZ42Nze9C6DjfqZ7tOoP4aYg8pccLhcvsJmtcZms8Evfv43OB5P+OyzN/h7/+X/Gn/5H/4c796/QyxH5GwutlivVhMllveMbVyfsnnV/p/fb6Jf5j4EHavN9NCzOl2ORHD1fyRpCyyZHANR9Bnb5ZoXzTAMp0d2RDYzWqUCX+wx6gFnRvwYyZVzrYOH77KNGkIHVwKTF6s1rq5e4/rqBpeXV/DdErcf9xilfXM9fAASHB5OEfvjPsvyaLUaxoSuMQFDytPmWqn+mBKGUorHMuHgQu5o9hc5dK6HecNYSp4H36ELOcA1jrEGyrS5yuzBQI6q/+DO8jrnL1encjlYoOwfDU1n0o8RQkAXOgRP/1pLCKBc1mNWRZfTv05/Cfey9Lt+6noxME5nigIDWhJZgUo6KOgw4CaEndRMHRKNjpmU8u8sIUxgjk4IvkszhPjeh4eH6thVYIaOCTpy9XPeywk8Ho81o3ieucD+M4uZThl1yGoWA51lHC9BLc1GVwcUGUGzl9R5RWBTy2sDTTHQeQqglp/VMWtWhDotWhYo6v0EXPhe8gBLqavDT0sY0ylOR0mNCgutsgCzdQlmcM7oaCNQR0fsOUc6N5Hq0NTgDQIOLGn55s2bdlZCyTSan/FJJxiBiK7r8O7du0ojOtDW63V1OvL3zWaDh4eH+g5mV5F/6FDTrFgtgc1+kdcJPtKBRxqQ3gTLyQP6Lp1rDajQ4AnOF8FhnuuqYMh8XkmH0+mE29tbXF5e4urqahIYsdlsqkzSIaIOdZ3rlBKurq7qOeEErRTUIKikzlbKDt9BYJOyoA5iKmvS/+HhoTpG1+t1zf6/urqqPE6QkPJGYIdzq85mBtasViv85m/+Jr773e/CzLDf7+tZ72/fvsVv/dZvVXCIDlmC95Rn6kPKM2VlDgCS3zmXuggALQiBvLFarWo2XEqp8r1zDrvdDhcXF/VvnfMQQgX1yYPL5bKCt5R1zpNz07KrSiv2izxMHqTDW0EgBh4oPVTWqX8ZIMKL7+aapEAK6UbeAjDJpFOQhUFHvIc8D7Qseg3eUHnjHGh2KfmWOkT5nM57AkLqSOff/Iz9oRyyMgJpSL0yNwY0O5P0IL0V+CNPk3dYPWWelVYNcwFp+BmrYMwrI5A2pAHHoZUEtB3+znlnIAbbU5lQXmYW/Ly6iupK8qG+j/TmGsVnqdtCCLi+vp4A0lwXvfe4vLys/Mz+cP5VfzdwrR3pQj7nHKeUapDLer3Gfr+vOkzBPs1gZPAK+8c1nfzH+xVM0RL1GlCjgYHOuQpMa1a/tsO5IY8vl8tHuoF8QtlnUIpmWipgzbWe69HchiBf+C6f/0U55fgJ/JFmvJ/zTVrouksazZ9RnUXQWG1GXgyGUqBf9YVDK3XPjGfq0fv7e1xeXtYKKrQrKJ/sq24+CABzriivwzDkDdFM501AveLoaRuVVu2F8pBSqmsUdcV8k+v8dMM+17fJDM6liU6i7KsuZL8oq+QxVqigriVfU24oX8o75DulE+lAxxI/U97XdjhnCgh677FaLtEvmo5Re4vtaJADaUn+qOtimgbSkr5qH1AOGMw3ByepRzl/DLLUgDvOO+VWA4I4Ts2MZ4Abaa80VSeeBj4Ow4DQt+M6yKsKquczzyTDXPQF55/tse8KsFYAHlPbR+fPe48UIzxa1RO2pbKqAddsT+1VzlUIYRKAqcFduv/geLTyE+13XZc/5UT61KVZ7zp2Bcl1vnhVwE54kv8qMKn3sJ35usQrO4MEgMe0rLHq27aHDgjO4e7uDsvtGr/92z9Gv1wCBvzNz34K+B598PCuyQzCtKQk2yfuOKfHfJxzZ9w5R+P8+XOXvnt+kV4TB90T9z53PdVP/e5RHxWoRHYG5/vly0l7bvY3slOw/D7ZH6ZcCvR+d4fD/Q42xuwMPxxwPByxXKzwrW99G6++90Nc3WTH3vX1NbbbLZbLddE7vpYvT0nPDncIXWh2CstxW8HbOJflmbpOxRExJiBG4DTg4eEe+909xmEAYPUMx9NwwjgMGMZcpYWZ78PphDjmkq4pxuroT2i2QXYcTp2kKN+l4CeywX2ABsWaA6zLeYiulJ7NznOWJc4ZNRYA1wWsug5wJYCfcoUc3HY6POB0HHA6nnA6HfFwytmdZkX2fJO/ISxrlmDf9VitN+hXK/Qlsx4uZ0b6ceqE1mAbjt0sB9iRS5LKlbWz2flu8pxJdmYGq/Jc+oRMD8dcTVd80wLMG+BCBnAyLwMuUraAmkvqGuipOsnJPGXwH9VhbYbqDJ9Abu581Qld66rslYz8eg+DI/R5s8yb2tbj5jMFHgFy7X7SqtJydrObv9dN+5zbm4EIghua/FGBSLN2dnPKn8WUy/t33qPvQrkngywsJ/vUdU5nPnV/BS0bmogp5RzOTNPZdisdnnjfY71MWrjpJxNdO0O55/NRPnNIZz6b3ljZ3rkGxpubBnVUPXBunAaNSpja32EyZl3vIyI6t8hAjTPAHLL4UI9JtU6HDPblh5t9IP1gYNy0b9N/IwqAUUqVuzTlhbpnSKnyos5f7jzZwirupfPDtW4KXiWpBNGCUQIEYKuLjQT5wdWAALhyJm/RK+qvdxUUbSXGA9r3ik/Mf2rV2AKUep+B8GpvIeuWLpzPbtQ9G8zKGb8R43jC6dj2y9ynppQwPDzgdDxiOA1IMYNm4zjmtTFlAPh0OuE0jiWIK38eYwbL1f41S+gwlvOnm06knbtZBlysNnDhAp776cUSrTx4KDzncHFxieACTqcR++MRfrHAm+98D1evbmpSnTdX1k7uWYHTCAzxiN3+2NawYi8Mh1KaHDkrNpJeZvlYFbMS/BMwkU5Hmzqg8x18UPu1lBV3bgKIa0Ub5d8gGf3euxKs4MEVtS1VDsG5GujA9THHm7kpfeFaBQig6IzyTtkrmchqjBGhy0HLY8z7Hh86vPrsTX536PDzv/4Zrq9v8K1vfRvv3r2tFVJXqxWG0wmBiUmiS56zlckL8+/1b9VLc//BuUvX+bkc6Dtr4GLVIc2+mOx/0BIMyD/8TrG+cZYYUd9VgHYUPWJA5QPvPVwJCGI/qh1pmX+zL32Di6sbXF/dYLu9wGKR95XHISKmWFDnHCyTUnmPFVsMKIExrbrXhC4llJKLiJllHpS9IdtwzsGFVg3AinzovsZ7YNH38FzzaZPRDg3Ui9nPlY9kIA+wcwmunBvOyhpA5l2o7i6HAAEAAElEQVRfAncYzWA+J+lmHTmtUBbr2RjFUir6D6Fra67MRcU7U6vA8anrxcD4brebMI4Cq5pd6L2vDiuNpOc9BMH4twpCdnjmQ9rp3MnjPHNGidmkDCovOk3UeUKHAt+roOHc0c2/Qwh48+ZNdfrGGCugREeLAgZ0nKkzjI4rjoGZQ3yWm0UF6/isZkXQ6Uua0nlGoI7PaFY1x0G60WGtDl1+zkyzYWjAEkvO73a7SWnXfOZzO0OY9FGnMmmkJTWZXcvM/YeHB1xfX0+ytEhDzcYicKIZ5ZrdMQcY1CHI51m6HMCjs8C1rDezSp1z9XzZi4uLqhjpkOfZ0WbtjMu7uzvQOa0bZpaqVmBAHf3KH/ye808HrkYLqmEFNGc30Jz95HXyjALEOu8E1/nD8a/X60rvarhKRsjpdMLl5SWcczUDmmNVvvPe18AW0ptOY3XgMVOUtGEwhGYKki48H115jjzCvioAok5x8sIcONQAEPIHL/KNgiyqQzh3rC7w/e9/H+/evav339/f1/L/f/M3f1PPaafuI79QN2h7qm/NchAG+ZV8TrCAdGKABDMeyRd05mrmGCsOqG4kvxAo0GAn6kmW72c/tBoHQTzNXOOcEFifB3lQPyioqMECmkVI0IjZdATX+KwCJ7yfBjsvVqzQICYCeNRRlLfNZjM5BkD1kxpMBOJ0bRnHcVLGm/RQx7w61zmG9Xo9WZc0g5VlmvhDnuR9c8c3ZYJ91XOSY2xVCAjEEgyhLlcQt22MbMJ/bJtgn2ZSKw8ryM81Yg6G6TqoQUHUWeRDzVR2zlVak7bq4CWPUu+wH9R/XBc0OIT3qLypnuY8kUdZsUMDQvg+rapAXmZWMHmWPENAlnqG79cAo7nji5vw+ZpLXck5Vb4Gmr1D+SQPaUADf+d8aEWe1Wo1qTyz2+2qDuU6Qf6oUZ2FT1QXz4FbzrPafBpcSX3onMuZz2V+OB6CkzW7TGwxnRu139g+5UvXaF1HlI9Ie7Z3iIfKw+R5tSf7RV91PgF+DSwxs5phrvLFcXBdJj8DmOgKgqOj2A8KfCoIrRVLdG41+DWlhP1+X9fZR2urJTjZLyp4pRtCjkf5iLxGHnAuVywgbbWf1FvUQaxCoGuSBp6QX5QXOL8M/GSFIAaecS1S24rtUF9l+yVnWsx5h3sD8ibllDpKjy3p+x7HQwu0Yvsq/9QTGhzLPrFNDXbTtUADREhnzgXQ9ibKw8rvpOGkjJroWdVPqieo49VubGswKkCkpdopB2rncf3n/HGeaceQNgAmdHYunznmZX1TR4AC7Ry3rhP6ftKJgRfcW6nO5XupdwHU/RSP/6C86B71m14aPKD/kufOOarUiXrONpjfd679+TN0QDl5zvnp3lx1t/4gZpfNMESsliv81m/8Fv6r/+p/i//hcMTth49IccwOTSnNT97iT+ube+QQOjf+yU2pgKcmjnQ63qtj5sxVcBpnLWPxm1xPOf74neq/2n/txuxvuv+mn8/GPHkHBGgQB6bcTz0/nAbsDwfsd/fY73YYy1FQcB7r7QW+890f4Ac//BG23/oOVtsLLJflqI0QcIQvcx0rmGFjRD3HHHQknhBKlpwrzrbel+ztAparLkG3QAjFsb0BwsUG65tXYEBABqJdA9PzEaxZZ485EztGBtYVYDxGuHGEpZytPY4RMY4zezeDLeMY6zxURyKQxzqWEpWWMNpQz0ElCEqe5TzwjNcQOsDnxITsRHfwDrA4Yjw+YBjyMSf39/saJAWCzAWcARxC1yP0PVarNdbbDS6urrBYLhC8R9fnKjHwDh16aIalCUO44phMlmkB50TO692NV6reKE7bqmemgLOLDIhofJyMjmX5uzqw5dx50LFN3sbEcdt4f5aRlkdZgmhaf4zjpBO2wmYidy7/TVk36otzYPCTIv20rE/fduapNqQ5/n1eP7iKtNR/nWtg62O9c+bzOtc5083Blb1f3rf3XQfACi/54sh+Zoxn1pFnL+eEZI+faevX7I7ZGOp7X/TKJpOzb/AYnD8fAKVP+DPVE87dBylxbubq2873b/LBo8YKbFC+fur9Dj4ws5HZyQF919czp73z2eeGlMvsWkLgeOlzKjI658v5ZWYtc3I+eHt8L78CeAa2q8F3eqVy3IJzbgIcTuyMCkaeCeh0uUKIWeZdBlJVPUodQb8FXC1vTpoxG7v6VEs/CBopjxiQg7sk8DAOQ62uVD9LeW2stlqMQGzgdAteausT/7ZSuSuOuez3OI7l91jXilgCxVLM0GwIoU2DczWYFMFVPUC6LnoHHzp4v0QIrbpsMqsgMdfuhlUEdF2PRZ+zutebTeZNx3U/FH/lEsH3iAk4jBGHMcIv1/BdwDEmxGMOZHNApq/4sQEgyRrNKw6SMe2aLjefM7u78nfnyth9sT+UTZ34y4ttG0pARHCzYLdy7jZDGrx36MpZ7ZB9j/MOCQ1Mp03gnWTXVn62Ng9ljhxQgod0cfBNrMoamu051H1TBMu8OxzNYCmi63psLy5w8+oVPn78gNv37/HmzRvs9zmZ6+7uDtvtNp+/DuQoM5HSc7Z26+rjzPC5HpvvReZ7Bl66b3Fl3mjDNmOCvzfbRIM9UW24ZmuYNZlSnyb7z3dzn0+aUi7ILWLR1WdpqzrRP7nSgQOQQeDlYoXrq1e4ur7BarVBF/pSqaAd6eNYEcsBzmV7yMGqXVxiMQoJWk8qUF+IRnp5uGJru2ZblVi04EKrjoF85nnVhaU/Pnj0UhMl07Ls05xvgSPOwyPLFGld3lJs1cYDCdlmNwPgm9xxvYHLxwV4iL+i6H9fqhXFFDHUU+Zc/ce5XMGF+jkakJ44+mV+fa1S6lyQYlW4wDCMVTnSgNIsJDJbdtREDMNYgO9MuBhHdF1fjXuzdo4nHXR07GTHpi/OfV+Yuwnd5eVlcdyw9HMm/nLZIvmp2On0oLNDI3/pvFRhZQYUgaQGrFlx1hEMdKVUaUDfLyaALh3tMcaaEU9HkwLeLDHMszq22+3EMaUZJQQtNAuH99BBy/liuWKCUxRizRLNoGSH/f4Bp9OA5XJRyxITnKBTjIqFpVnNcqYsM6jpwNVzUdUhS2c+gEkGtpY+VZBcx6vlWtVJ2fd9dRZzTlmOuOtyyXFmc3CTSUcWnV9AW1TUiUbHFJ2pdIbOsxg5PjpvSV91zDMTinPJuSBPqPOftCWwoWNV8JFyRucex0LnHseq/MsSnwShGAjAMtR65i/7ptUROA4FXuhYmQMrCipqoAyd1LogjuOI+/v7KjcEkvid/q4l6amfdIHie8lbbOv29vZRFh4dmvos+0a9oZUkyG8fP36s9HfO1ezSb3/72/X3rutweXmJDx8+VD2pQQM8h5gZu3yGIDKdr+q81kwn5S0CKMfjsVZAUFBOg0q0OsFqtarl7fu+n1R5UOCN9Kau2e/38N7XdxGQUx1KJzIBOzrH2X8Cagp+8J3zzDLK6u3tbX2Oz6o8afYcQTyWrCZ4zcAf1aGq9ykDCpxxA6P6neeBkwfW63WdK3XU83vKDGlNXcq5VYCQPK3nC2spWH5GwIQ01YAQBtqw+gPLaptZrRqgACZ5hNUUGBxHWvF+Ar6siEBQhveS3gRfuCZRtz48PNT+acCKgj0ct2b6KRDF/lPPUGb0nQw+YXa1GvCcR9I+xnxkhpnVYALqUPab+l+NavIZ6QHk4Jqpge9wOg1FJlh1ph1D0gK2cqSo8ky+F2WcoRidHjGmKjfUi1pBhtVAyLcKOjEQjmu3lhqer615HetxKvI5FP3bdV2NZD0csgM9Wa6G0Hdd3synrH8YlZrMYJEOgexUXvR9sQsT+kWPkCQL0uUMFkM2pjvfVUeRrtW8P4RchmkYh1y6utiEpG+2RTo45JJr4xhxOp7gQwNzde0nfQnuOecQx9yf4H0NGNRy/THGFqRkAm6BgWE54tU5X2y2ZeFp1HWhXywAl0G/PCc5k88h298EesbSP1dlLSKlbLfnEl4MIsgbmmafO8SYcCqOE6655FWeU+cK/VOy6nRKMAynU+Vf5/IZbZeXF1kXHQecrB0hoRWEtLIJK834kDMKssOnAdKn0xHeBxwOD7ACIHRdX+nL+VFdqPLG9xCcZoAu54O8Q/njmqN7Gc7p4Xio65XyXs0Ece1YDdp4GiAQY8wOSR+w39/nTIYxZkdkaLZITMz4ZpZFs0tijOj67KgOwWO1ztUCLFldz0k37tv4PB2Di+UCDu5RkIoPreqJlY14Lrs4zXzu+yzX6826bmRPpxNORVd3XSuH3nUhZ3MM07Lu1NWqyzmPGvCjwLJWNeBcZZ2aAyottbYVVOX9PL6F+0u+i3TX9YfPsR/kJdKSz9L2AR4Hz1AXvRggeObSeXyuvbljau485KXg37xd0kGfa85nND2eEpwLtcyp6uB5m4acpTIOEYDHer3BP/h7/wAf377Hn/zJv8OHd28xnI7wch4d0AIzNEi4OneELufoZJJmZi5lIGF+f+74095+cegrNFjHJTbjU1dbv6fOIf17/t1T49OOWesYnH8CENdhlLV3MpdyL2Xw4eEB93c7HB722O92OB4O6Loe1zdX+M73fojf+Du/g9effw5bruFChwSP/XHEOB6Qq8pZAagBmINL5ff6HtpOHHseZ4+UHYkT8MEjeFQ7wHcBoZSa7UKoJWUzeJ7PRw3F+U6wKjvKmoNVfGi5PLwAC8yki7KPtZQQD61aDvduWmkpxgy+Hw97nE4DxtMJKUUka9UrUszAU4xDcdR5GHI2mYMBlmBpRDwdEIcjhjHPxX6/x+F4rE7f5vhsZzl2fY/VeoXNxRan/T3GhwNWm3yuaug6+C6g61eT/XG1l7pQs4q8Ayw04L3yisuZTyxdC2Z3Q0TEpqA3ZnzcwKCmX+jQr/Y0AfJkj8AlB6CzVlJzrtsmMlN8gLQxz8n39H5XgQftu5khuGkgzvl2DGYdMJfzdlN7wE0BBIKNNdurPGcioBNMwMl7jYD/eV1SNw2ckyf0iclPQqZ/CB2Wy0XdH/ddV7IfpTT1OcJMbI5PX7WNCoCIbi2jprM806oBR8x0dyj0msAV0/E1sGmqByZdR+Pd9tkUdD43rslHAty0NeN5msw/nwLLbtJ33u9QAJQZqFuQtExLOCAAzrjfKLpCEhwIjCckHI4HWLIC2gV45zDGWNosQDD766RnpD1lqujrJmOQSgPzNbvYt64Bji2TO98+FuA26yDeq0k/pcR08AW8ssd041oN1Z0MfrK6b0spwlku3+7LT8jKKAcEWyrn4mYcwjSQKuWKGxpkTd0fD0Mu7Z3yURpjjBhOxbdgPFJkxChJEHyHAuUZsIoAYmNsrqdCy7ynKjLFvc0yYykuBISQ9zqh67CQ8u3tJ6Dvc/nyrutyANZi/SjYch5EG1yHvlvg4uICl5eXLXGr3EOfVxeW8KHHkAy/evcB7+522H3c43Q8YowDnOWzkeFLgDwDFMRHXkuaO4fey5E+jsC2hwvM7s/rm7dU9jeh7q+aPesmewLvXHkny0ZLBQHn4ZBlg+eHhxBqhrsrzJtZPpRy+Y2v69xU2Rf5FbblMwR38zOtRD6zigHkDFwg81HKx9GMY4B3hsMx7wlD6LHdXuDzb30Htx/vcHF5USvA7nY73N3eYbPZ5DF2pVy9BJh96lLbdr4+zO1a5aM6TtoJMRa6uqp7JuRx8nxKzfaQdZ981z6fAeOzvlUbq+jVbDu6+jflq+omoM3LbI9WsUWfgdxFv8T24hKvX32Gi4tLAJmP08hKe83f4pzLZ26zokgZf9Zz+a15uIWOhdfqelh0s3cu67JyVIah2FouVxMoarwFScm6ThvdO18BcwaAJkPVY67KRCjAuBP7qVRvxZTWyQxwuVQ79ZMr+j+r2lxx0BUDh/qRgQfOExgfMA5xMs8Mks97+hx0oEcBPne9GBg3a4YxHYVmDsdjftFikc9vonLUUtbNmZI3wiGwc9mZSIdrBmYa2MMJoqM2O6dP1XnkfXaY02hjWdmuRDYC+RzEEHxxDPqSVZT7wiyUqsh8O7uaoF1KufQws3VI2AzMeIzjgL6cHalgAsBy7608K4VdS28RfNEzegHgw4cPFXQjuEyaAizF0Er60THE7wissD81a0lozXvNWuZN3y8LYGXwPuB4HOBcNg1SAhaLlrWjDkf+rQA/71PHFheTq6urqjRIG2aCAqhn1XJcBNqZkULBVWCXIDgNeGYGcV7pCFXAjn2dAzPkY6CV2udc8CLQqMqczl861NQJTKcb53C1WtUyqgQumE03z0BS0E/nnU44OnE1y3IOsHO+1MlLxzLbJnBJWnPOFJgkD5FOGrQxPwuVzk2OQelO+SP/8lxi8kNKqToxybvKy861jGuea6zgCJ2Z4zhO5Ov169e4vb1FjDk7/u7urjrCNVOegOl+v69VApTndPGmPA/DgIeHB/zGb/wGfvrTn+L169f49a9/DTOrZ7Z/8cUX+Oyzz+C9ryB21rFZZ2nGM/lWQVl1JrNPdEpTV2hAAME6Zrgq4EwAVflNF2XOK+eRP/Oz53ktl8uJXmV/yEcajKHZ/0A7ykADPfgvHdkaGKJBOZwzfs77GAhAHiZoxSxfzqc66XlRNymd56AL58PMSjWNUHXz3DGvRzeQR/UMbQVrGexB+lJWNZNb2+e4VaerXtB+MzCKtNf3a6AOdRUd/tTheR3OzsCbmxu8efMG7969q32hLFInc33RgLq5A4BjUV3FPlBHVrCzBOSQXxjcQF3AMt1ce9QI13Vcy8mTf8h7SmeC8pw38ijXaD3OQueW9D6dhhq8kXkpVt7Mc5bKxq7Dx4+39f3H477yeLYx8xlYrTIMy1an4qBtYLyCRhpUMac9ATEG0vHdnG/ShMfU7Pd7hL5HSlbPJLfjCXY41iAS8rRzDsmAISa4YIjZisbDw0OWrWQT/gUAQ86M9kDOaFi2qkPH4xGLboGUxrLh9bBUeDVmeyWmiNNxQIpW16O+a2XmAWAcIlI0xDE7oK3YSJle7biRChqVrLNxiOi7lrnsfSuLRd4MIVR5IWBLuVZAjbxO3UF9McaI09BK1lOW899D1SVmmT4pxhxpzMzprmW86rqU3087zGCWzy0NXQnOLJvImFogW85SX8DGEbGUJnTeI45jcZjmUrk+ZD4eyjqRN015U6NBjvMAPn4+xojD6Yji6sHxlPl0UWQ8wYCUQQuCttTXXc++trPPdI2kzuH6qWubyiv1itoNlI+pnm9HxpBP1M7iGKmbtHw59TjHDmcYxlIRw+fzvAxNv1jZNKreTSkhFsCpc61CUIwMUM6exzGWrG3fxpmzPa3SMDJ6utSfSxZraXxuyFOMGOKp6C9X9zl1PSib88ggji7g8vKiBXWlUq0hLHA8U3mAwaPUlQyWIz25F2NQI+eCa7Laoly/mLmjdrMGdPIdnBPyEi8N7GL7HC/XRPIxZZt6mnzGPV/bt06PDPkm12NnxRQQ4nh4nft+/p1WlKD+Ig3Ujp+D+ymfBTAJIuB9akPO+9ot+uLoCohDxEN8wHa7xX/73/7v0fUB//bf/hv86osvso6XvqrdUPvpfAZH3BSE17nMHwLMoFHem9sgz10TJx8eg9Vzx9+5tpXP9VK9+JJ+TP6evBNPzvdTz/NBvZO28e72Dru7Oxzu97jb3eLi4gI/+OFv4Dvf/yFev/k23HKNt3d7hP2ARb8oAYdLLFyHFEx8eSWYxz/m0XnAoAOQyrmOCSjnbyekiS0n+TEpifMzf6pj6UIuA+mcq2B75/O/oQtYLPKez4WuYgu03xfLFZZBSuJ6D79eVOBG9/zNCYis8wogHmPKmZMpIaah7NFy8kaKI+I45ISRERit2Lq7O9y+f4sPX32J/X6H0+0tQr/A9qrHZUlAoR5KxREcxxGnh1zdZf/xFvcfPuLtL35Zg/UaiJQD3Qhmec+ggzBJsEAXYH1fss179F2HruvR9V3+vc+ZptWXVdbPvusLEEPQoNBouSyOdVfXqc61MsSZB10tuTwv02zWAikcgN6mpaTP6UMCzeQx/Vfpd27PoaB7Kk5ymAL3qOD3/P3zfkw+52Ag4D9Rbcx1wyzIL1l1eNNpX4Fsm5Y/pTzN5Z6lTgn9G9CUiAqOYaL7vS97/+Jb7fse0SUcXL39sQ4s/9byq2cu/Twy+6xh320eCS47TPT7c3pzrudr/5w+97ikfaUfyHdGGPjZ/gNAcvb4c9GD564K30pf29yKbqzfAXASeFHK8ypC0+7Nc+ecQ0KEN5/zwT2wudgW320GVim3r998js1mmytpWAbM6/7JoWRQN2Bcg2vmvJffPV2PfcnOVXoozZ21Oa7rOm8MrsqMytlcXsfxVIKURsQhlwgfhwHDaciZ02ZI41gqhuTvsh9hwPF0xPFwxPF0hI2xBK02WYyWJsB3HMcSlFwSwIqcz38ngLkudjsz0Vk9oOu6fOyF8xngCi25I5Qg00W3QBcCur5DF7oMVhfAuu86hNDlewNB7FwuPHShyHCHfrnEYrmAuRzXRKDa9x18PQte7UfKCIFAB4flI5rXnxgLbazw5gJ9v8XF1QUWpWqaAYDPtsbS9wiuwykmfPX2FvEUEY8jvDlsF2tcrtfoQwfrXdOfYrtPqjGZwYcsUWX7VI5aCzXTtjyO3rs6DzmwLkz418sxKN55hE543eWqLtxfG6bHBuXhKYRb+FXLpVu2W7w8R9muMkHbzLUS7jLUciQX17KmZ0iXHEwx5n3cWKoLjBEx9Di5E0K3wLe+9W188cUvcffhAZcFGP/VF7/E7cePuL65Rug7LMoeKesEPLpUx87Xvk9dTY+hArb1+QL2p2JbzXUo2696oCSoztf6c/dqX+d9pq4z79GVbOi5fnPO1SAf51wN9NNxefEHd75D3y+w2Vzg1c0bvH71GiH0GMaEGFtlVkMs9mVZB83gXa7i0giVQynz5fNe3XKCh5mr8lH/9b6UfwdoIzvkQNU0DhhMjs1J5cgjk3GU/Xgse+BkLYBofzyURJicnd11HXosYBanc2mGYTi2hC4AY5K9Xa0AwgqnwBhjyVEn3pX1tWFqI8YYcX//MPH3qo+N92Qf6P/lDBdOr68BjDcFyL8JoGVn7DRrTbMo6CByRZHQaUDnEjfo/FwznWnoNdDpgGFogKf3ORODZzNyE+1mROMEk0lz1FUmINumo3zuyKCDUw2tvDlvjjI61jUTkw6WrjgfgZxtfHFxUR0S8zPU+TsBTzriFWTabDZYr9cTB41mPwANXNNNp9JZS/JyYSGgyzO+6VAi/Qnevnv3Duv1GtvtFh8+fMBut8N2u60KWR0jCsRnkOBUs3wJrhDAuLu7w69//Wt873vfq3MAoJYXpaOJ73CuOY+ZQd7ABtQMoZTSZEwUFpauZNl0BbK1JC/BDwIH6hy7v7+vfKxlf51ztYQt50Cz2rquq+ef03k3V7oppcn58HxuHmyg8kkZnYNmzjXHvNJHg0mcyxnTpLcGC1xfX9csKx0TgS/Ogy5ICuppCXXyqwJ9ZlZlg4Ag+0hAlG3Rcc33MAOa2ef8nWCPOvWoHPXcyFevXpUAm2Wdj/1+X9u7v7+vv/Mepb/KsnMOFxcX+Oqrr7Ber2s2LAB88cUXNfv6dDrhBz/4QaXHZrOp862BGpoZrhlpBLjJO3xGZZCOYjObBCFQLwOYlI8n3fhZCAG73Q4xxpbRV3T7zc3NJICB/ML+aQAIQR/+zWxwyiB5hXzMvmvQBbPZOeccFwMn2C/yK3Uf/zVrYDPb1coZ5DX2hf1XeWbQCPU7Aw34/eFwmJwTTB4nAD0HARXA5lzoWrBcLmuf+ZlWb1BZJ4hL+aOe5EX+0YxwyhDXLv7OeWQZZVbgoI7kGBis9PHjx/oc55ZBD3oOsOoTjp06k/PCNsnzGvCgTiLOB0sjk39Ur5Ceui6rvXFxcTE5x576QunMag8Ez6mDlecJPpPuupY75+q6qYCO6mTSm2A9q7OQBzK9coZOjt7uH42VuphHe6h+U0ef8rtmPFEnzAEprjXkhZQSTmMelwbBsV3qc/IJP+dcU26oB1JqAVIK4gPAw+GA5bKBempL1mx42Zyqk5K6RnULg+bu7++rHToHulR36Hqq8kUHsgZ6aHZx3SwLP3CdZFCArp/8exgGDOOI/cO+6kINRqL9SX5ioB/bV9CXdjHlljzAuVKgeK67eQ/7xXmcbyIVBFN9Qr3eddlpE8d23joDp7hm+YxaTKoKkZ5tThMMbqIr5+Bo6Do4uYfzSZ5Te4j2lILec3tN9avuQWJq52JrVQy1LbUUPb8jn/OoET7LNWi+eed6qZt7zgl1qupizu38vTomjkPpoPdy/hk0N8+E5/qn9ymIz7Z1zSTdlO58J9ds3buw0gzlUPlyDnhqwDT7k1LCerXGfr+v68J8H6g8zcBQ/j4HSmi3UtZV31Kv6P6SNFMacSyr1Qp/m2vuZFB50XVxDqDz+3lbai/omPk3g9lUr1fdmrLjpOq27Omu79U1R/nrxEAQIJ8dCYe721u8enWN/+4f/2N861uf44/+5b/An/67fzOxrZT+VUZCXx1P6nvgT7sECrIpOD2ni15z+r7kekm759o/50DUNlSnTdqQvMl8zwv6KG3GGGu5XNLl4eEB7969w/5uh8N+j8PDATdX1/g7P/5tvH7zbSy3lzglQ+8Crq5fY9FNs7vhZU5KSUUgg9TzMWVHIAqonJ2fybYZOE5TWiabHhXEMy8dgHxeLtfrIisGmBthlvk8poQI4FR0b3pg8FGCL88rGKj+rspbsckJP5/7JOA9rPPVxlgUgJksmeWph+s6+H6JHgG9y2XOrwEgRsThiNPDDg/7HWw4wbt2HB7Xbsov5213/xbvP7zH7cePuN/dIw0JvQ852y4hA6uW8JCOE71U7cB0wrHod0SDG5rtwKwgBUDMDLEE2Km9NJcb5xy6kg3knQOCL1mdYVKa2HmPUMbHH9p8LRjUA8HDFl21w+byX9eE4OvZl3pPHVOhwXq9xqLPNmgXOsl8mlaW8F07eovyWPskPH3u0nby71arCCjN5nR0KQPipHelaRHkOb3n7TySNdEP83frmu1cQIwDPv/8M9zcXGP34SN2ux3GYcDD4YDXr19juVzh/vb+yT5UGSl9fY4mmcCPwZVz6/7ZZ8+8V8d07vlMx4oWPHs/7HEfzvXFdVM66veTdvWs7QK6c6x8Np+PPM3CbT8m6zwmzzebqIH52fYKsJjPml2slthcbfGXf/Lv8e/+/b/DL3/1S1jo8K//9b/F//H//H9C/93voiMYMuaMzeNwKlWECknG5qOm7aQ6Jf+dql6dfBcz4Fz3xWP5rNxDP1gs+9CUEmyMcKzOQYBPnmmZ2SOG8YQxRqRhnOqvoZ2NbZazNE+nUwbBo+j64GuwF3zWJV3R85R53+VAkU5+fMiZobyP+4yqw7oOYVmORe0X6PpiVwHVP+N9BsajT3Uvr+9lH4MPADrAeglizwHCvN85h3EY4H0OZh9jRIJD8j26csyGZYgM5hyC+RwIkHLAPUQX8oop4YhUzglGA6pLv1KMGI5HBANWXYcxGn75q69wPQy4ubnJPh5XjhHpe0TncHfY49dv3+NnX/4cYb3B5rNrLLoOq9USry4v0XsPi2O1E1T2VDZy4EzZo/upzs+lpKf7Ba6dczxIbWiACV5F37tqcdU+RPgaYOYge4yy5rG9LuQM8WqnOlcr4VQauwZoPqtDABhS7f84xAqwOtfBF+DfYr5niHkP+uW7d7mKXr/A0gy3tx/xwx/+EP/h/l32/V9c4sPyPQ6HAz68e9/WQi+j/hp27lOXWQ4Y1EAelM+aje8RXCiV6tIj+0N9NGaWs/TP2CGP3num/3o/93icA91H8nMPV4PMgVw1sFY1WPTNjim64c3NG2w3F1iuNlgs19jvD9jt3pV9lANcwjAOGJK8B2jnpjfDHZYiTsMe5pi8FnEaBhyORwyx7cEZnBFCTqLQMcQSwHI8HnEcp1XOKB/0U9T9QRxKlnfm0WT5uL3d/r7tFUOHRbee+EdyYA6q3Zrx4rxXoJ+WAV7VZ+mKHFkuP19l3RO8z+sj+cEnV/cN5FnFgnXf96nrxcA4z9Clo7Tve1xdXVUntzoTlah0GuQFu6tOHXWCE5Th/cw6AloZdScbA18IoxnS6uhQBwyFhoZ1y1B0WK9XEwdMCGECRGrGNZUWnSF50cvKRwF8LoZsF8iAyTAMWK/XkxLtXEw5Pp41Tic8N0EAHgFIBPjUeUnQI8vO1FDl/ev1utKK4yMYRicHnUUPDzman6XczQxffvlldW6mlDN6WUaaYDIwBW4IWNHZSVqSZ+h86vseP/rRjyp96ATk+d01A6xvJcS1/Kw6CumEZR94H513BEZY5pY0b9lgmZ4Ev25vbyufqNORdNBz2AleE0ghzUkbyoOZVbnSxZptLJdL3N/fT86jpfFH+pLnOOarqyt472vpa2Y260bPuel56hwz54BgHjNtU0q1xDjQzphmG977mu1/OBywXC5rdiydhXoWJPmNWdgx5qxUDUDh/FGG9Wxdjoe0IFDCuVHnppbPVtBTFwGCv/NMeAA1w1xl3LkMTjCIgvJ1c3Mz0ZFDMQQpuzR637x5g5/+9Kf4yU9+Au89Li4uar+p5zQrXY00Pa9e+ZoyRxCSPHk6nWoQzd3d3QQsVYcjM+qZga0OBMoqeV6dQKqT1KmqjnzKMkFO51rmLrP8GQRA3gNQZY9rAnlPDRVmrXLs7Afvoe6mjD88PODm5gYAakl751zdfBDUZvtcl1gunGAlZZ1nS7PPh8OhltZXvaxZahwvA3BIFwU0SX9+TzqyTf5QFyoAqvNGXaN6Qs9vpc5fLpeT4DLqMwZs6Pm3CsQRPNW+EQQjXXQMQAM0DodD1Yl8/ng81mMtOCfzjEytkmHWgq74ufe+yidpMgdd1+t1rdQxdzoQYKY9wX9Jy7a2o/KnZrFrEE6+v8kQ17vD4VDXe9KRckjaks9yBZEl8vliLYiBgQfNydfKfvOHayAzM1kxge/ks+QFguCkJXmT9Mw60Fc+Jcistgzfcy5DWnUPj47QjFbq7Ezbdm666lsNfrNkuUSga0FyutZy7rQ0utoIGmimMkReoJzrexnYxzZpp8yNbsoN9Qt538zq3HMNqzqiZOOorB6PR1xcXEzGpkecMHjFzOqazTmmnn3//n2VIQX4NUhsrjO5dqt9zEsDIHjpRrWWk4ab0Jy2oOqfMeWsd9KafNbkNZ8LqE4OttFs9MeZUnwH10jqFN2b6JqloCbHw7WD/MJ7eRwF5Z9yxHVI1zatakJbkO3rmk/6kEZ66ZrXnDlT+03HAzTAn+Pi/GmGNAM21AlDuqosqn4gb6kNxe9oi9HeV1uEfaadoYGhbI/9Vv7QH3X8a8CI0pI0Jx8pwKqfhRCq/le5n9s/8/WLQQN8p+oN3tN0WDt26JyD/+tcus6SJ7RdQy5/6+zx+ekaZMF/2QZ5qzpSq2zkEposG8k+VP3oHeAdBitnuZV+ah9VZukIM+dq9g6QwZ/3799jsejxuz/+u3jz6nPc3LzGH/7hHwKxZOK7DmYlyO7IbNwR0TlE76HnpvritAneo18uYGnq3DWzfIau5TQ75zI8svBNvg3I2Zn5v3watE3Bqfml36UYW8lY52qf6FCE5awPlCPk3LShmtGZHaRALjfIs/oAgs163rmDgzdfHIOFto6ZJ+1AwgLLwQxwoUM0FKAmweKIh7tbDA87HPZ3OJ0iNleX+PaPfhPLqzeIiw1sscZ6e4n1dovVqvgRChi+6BflPNISIO88nAvwXQBs6qSqc5FSHbOZoZwgMeEj5ds8PxHmCCwm5CZyVl4yq+k1CbG0PQMei2Ot8qlJNTP5vs4X+50y9aZLvWFkVlhCDhoZIsxO2Nm+ZMFU8iOmnHGYMCJhxBjzUQRWAk36rsNmucBn19f47rd/hOvLgM1mDReWuH8Y4H2HNJwAxDKTwGEYcby9Qhc2CP4K600OJAw9sFgAne8QfJe5pPBHo53+MIM5AWks+9ic4V7lQkr6xjjUqiDc8+oaGmMuE+yR+TKZlYzCBpw1uyEhnnY4xlid28xMcihrTnl/Zloyvpvc3xzrRXBA4IE8R/7K9y0Xi4lu9j4f96DrDwBgvcr0K/LE+yZgWfDwiz5n5vtQqxQwCIBnyRJs41m7BElq2d/yDq1MoL4A51zNhnTO5bl15VmgVAho2Ya8kpuBAaCd49oZod5j0Qc4Ay42F/j53/wCf/pnf4bbux0uL6/w//m//7+wiA6//Xt/F9ubV9X2UPq5orTyPEyzKZufGDVD7LHTeipj1GOAK6XlxWZxLMXa5tWZQ+f7Oue1lD5KGwUs9c7gnDVs3CFnVJcgG7hcftZ8LLqFVQsYrNOAdecc7NiVYCVUGvD7zPv5iIYACR5LNhm72jg5+CE1XuB7U6rj8cnVs7CtyFf9vch0npMgto/Hu3dv8c//+R/iZn2Nqx9fYBgH/NP/2/8Vv/7zn+Dm1Q28a8lY6hdLKYPMiNPAOn5HwCX3P1XwjuPUdZK8GB1lts17m/PGrG7Rg2WzKdMZrCyyF3JFjOVmCR98CXZhtnSpjFGyrRE6IOQ9AX1ItFtXq1W1DRfrJaLF6q8IgUcptlLjgMFcN63gUmTP1YzhHMjmw7LwRMsS1lLgoFyErK9pf1UZKouJGeCsBJ8VOeIJwLnAeqHfArBgeaVICeMw4BgjFmNE6PK7GGR2Gn2O7kBX3mGwcR6UF7K94DJY19bWbI8Et8Dl+hKb1RLX2zVW6wU+vvslPrz9Ci4N6MObPAeLZdH/CTacMOx32L39CtevPsOr71zj6uoaq/UKofh5NotFzlyGg6UIWPZbpImiAJxPjU6Z8lWWqg1kQOf6sg4Xf19wTW+XKiadB0Joc5Dnoenq6uP0VnWu96FWX3AyxwArIIiyIWOTjuXfmEq5a1mnKRjU2YW9+DhcCKXUdbEby2uiz2BhFzy2fonX8RLHwx4WB8QBCKWq2NXNZ3gXf41uucTrN2/wv/zkJzVRrV8u4UKowWGUz3oxiJGfF9vehD+4/hvtA65PaPasWarPxjHiNMQcAFLthmwDO7RAaPbFFWKo34l+uEL8wtMp85DsGed+drNceaDvfbFHM/Nwj+Wdg+/y33EwpGhw3rDZrNEt8tF0oeux2V7h4vIVHAJ+9e4Wx1++K/vJU9Wdee/Vqhx3oYdzaHucMeZjHLpcxjymhDEOOI5HdF1O1jyeTjgcjzicTgA8+kVf+YtVBQb6LEM5RgGuJRZZWz95qT+nXR48Bpt77RzEdMoZ40VfLcKh6jFufQDaH2Xt9h7mHMxCWefK/CMnHFu0cuwAABcrv/jyDjOgs5I3Tz9r6Np+B4boVWbSf/wzxjWLhA4XdRCnFNF1LbqfDg91KJKIFxcXFbSjg+/+PkceEhDiAkXHLw3vlHLJEjpXCNDRKUEnnwKHZlbvY3Zk1zXn4dXVVc10o3GvWXLqgKETiuPcbDa4v7+fnIvO9/DZvg8VnFJHKDPu6XCj445OlWZATsvc0QFFg5rMreCjOrU5bwQ53r9/X8fHMdFhO45jPWsUQDWK1JnJuaET5ebmpr7n3Lna/E7Hw/Nq6QAk/RlRMp8v0pz8Q3put9taCpvZWKQdeYxjZv/ViCO4wAz4w+FQgxc4djpBNXOG/VKDn8Ec5D11XDKDUp3zdDzyb3U8arYeeY08wqw5Zt8xsCSEUAFs3agQ1NRS4aTBarWqoJdzrgKk7D+dtB8/fpzwEmVbZU8BB2ZsU3YJhtFxqtlIBJbokKMsMZtdnbDq/FaglfexjC3/5nvp4CTQRECKRjHLal9eXlaAJYQst8zy5lxmfZcddqQXs+5SSri4uKiZYXd3dxVEAYCPHz/i/v4ev/Vbv4X379/DzGqZaAVayOusrMANBy8NdCCfEVTjRpW8ttvtKu+Tp8hf1BXkXQXJCHyonqd+phNVs3XP8bUaHtR9qscIMhHA0DkGUAMmyFMxxrqJUcCGa4Ze80AU6nqVS45xDiiQZ+gAZ/8UNCcfkXdJX9JJs/VUX3ON4X0EgzRIinRTmlK2zDLQudls6maNsq16i3xKnlAaMTCKY1PglOPgOKm7FETxvmX7c63nM5zT3W43AQYo01wvOS7KD/me5cDnOghogByzCqnHqTuoKygLejyHrl9ce6kTaJusVqsaQML+kY9JR75f7SHVhdpnHt3SdV0NguK6QT2noFbf93X85AHqpAx0btH3S9F1uUwYMGKx8Oi6Vg6ffaHe5lpHcArA5BgUzhPXAvaLskN7yJe5JLCkthFppkCWtgOgZp2y9D3L7t/f36PruirzfZ/PB+e6p8AWZdG7x+VYqYep47TiCHlUDf45kKMBkZQV1ZU6NxqYos/w/ZQF2lZzoIh955xpP9m+Atq1pCFQx0YaKnig+pT2C2VTdfX19TXu7u4mmeQ6bzqPau/Mg3AUGOT8hxCQYnrEC5QT6k3Vu5xD8h/1R4pjcyCXH9pBdKgx8lwdsNRhui5x/BrRTHkinTifSk/vPWxIdaOv6+w84I4Vjigfqv9JJ9q8WjWA9OEaqfzC92lAAnlc1wfV05R/pTf1APc5aluxHdpR7BuDC9V2nIOpZrmCC21MlmSmntDKNAw6ZcCZAukqFw8PD/Uz3jeXQ32GaxrXMtJQ7W7lV6WN6gHOAeWL80IbnkEvCwFVJjqy0Eznhbz3TS8rTnVDc8qRT6oOdDnLgvSa67ipDW1wLpc6bfvrJsd9zywJBjjLmZK5UcQU4Vw7L1jlX9dOPhdCKJlOqP2i7GQnKXB5dYV/9I/+AKfTgD/5kz/B6XiAgyF0HSyN6PoeKfnqoD8dh8qrKHsdyvFpGLKjSR3LjmAM8r8+V61QrI1OmDrW+VzYuU9n97jiTjNDlMzu+j0adDd3qLvJ77lqhiMAg+Zo0m642tkpoGAFJKd+NBAozgBRLklviMOI4bDH4XDA/n6PYRjRLxZ49eoVlqs1fOiwWK6xWm2xXK2xLEfMrddbdKFHV2xKZioqr4UQaundqZN9TktXkynPrc8pMRQgAy4VXOIQjetqdqTCFyetNeC9guIVBLbiMNMMJL6zBRlwUpsMELiyye/5lzxnKTXgjFeg/rEOhoQQc6JGSoYQHJZ9j816hfVmgeWyw9XFBuvtFi4s4bsR5jyCGYBy9qwlLMeIX3z4NbrFFpdXS2wsnyHqu4SuyyCBR4DzAYZSNnMGOs0mBZZaYGmzr9qDWWYHIKUKxMVxnAAV1CvBt1LflPXcNvephaLjkEtlljlKkZVQbKJPME5Lpbbzd1uAIwEDDbzIQGSaBD9kYFTaMsNohiGOsLHwkiW43X0FLsgnZgJqcH59plEDs1DlYQL4OtdK3Ks+KvR1vmSluaIF6vd8vH2evG9A3OSnvdshlyt3bqoLjbrJNWAjdD6XYw4BX331FR4e9vjN734f/7s/+N/gn/+zP8S/+aM/wv/y53+B9fqy7ZMn7ZS5snJ+KcUQyIENsNZXNBmtznwBibTNDFyj8EOjG7M9yXMwObOUck/CO1fn28HXs4B5drEVvotxrO1619qofcJ03h0cUpGtCvizP+R9K5UCXAvkqAxRhl9lgWMw8lLRb8J/Dq4EvWTwl6rVF4BMbTWgVGzwrpTRjrheX+Af/uO/j9B1+Ortr/Enf/InuL3d4XDIGde5jHjzRTifM6d9COXgbV8qQXh0EhDBefHBl/UV9SimUAJIgg+1xLcVPa17RwLeNTgEDkEqQBLsrudGh3Z0A0ILaA6lj7ovyXZrpgmrFHWhq+3QrhrHEYvVCgYGBVo+8sgIbJe9TdGqnB9dmOuc1eCMIF+b0GtuH7wsw9FZ84nCTa0JV3mbegRYhVh9ALTf+XxKY5UZNSIY2MfPvWvttZcV4Mr7GnzQBY9FF9C/eYOH/R1ub2+RUsSbzz+HweFwPAHItnQcIw4Pe6zXG3gY1quyRyi4wDoAoc/HNTHQCoAAcr6An0nGjso7NVioANvBNb1CHqv2q/OFbsWEcG5Cl4kOLrw+MROqjKasryoPPK6ukibrEdc1PL6v6Ioa0Cf6rAZVCS95V0BM7yZVUK4uL7NfahxxfHjIAHoyXF5e4WF/j4f7ffVf3t/fY7Pfol8uckn1IpPksKyDtCtajamAkalVQ5voYUxtPwW6+Tf3u5AAOqDt6XipjaJ7MP6dUuJEljVuWg2G80D9wHGMQ0TXLaqfLyUDvENfKkPk/WHAou/Q9T7rYuexvVhjvbnEYpEzw3/+N1/gw8dbDKXqRoxD01k+FN1TEj5CnsdkqVbRgFk+5qzYtfmziC50MJePdB6GEUMs+/zFcjp2tEpxqezBHDLGcBpOdd1veoi2ytT+TQB8JDDe/FxR6I8EDKOVSkBNJ1mKOSi6Bvp4GGK1m6ue9w4OAWZjsc+yzAbv4UIuucDgx5QSrMzzRMeXPZ0v9mjdf0ry8HPXi4FxOk0VGBrHUTJe25mUdArQWR0Cs8OyAry8vMRms6nZunRiM+OY0f50oNERRNAJsEkmFEEpOq/oHKEiIAhH5m4Cmt9BUIzOJmZweu9rVgMzb5hZnZ27hmE4VccjM4jpCHp4eKgKgw54gtOkzTAMuLy8rM8ToNhutxPFSZCONFEggw59PdeVpUcJ+j48PNQ5oTNJSy+zL13X4fLysoKmZq38OftChyTvpxNCHYjqpOU96iQh36gzZrPZYBxHXF5eVocTM6Y2m00FRYAGejHrU6MaSUvONzOP6cADWtlZM5uAawRI6DhVYJf04/vN7NH4yXfq5KXTW0EyAmnqnNNMKc4ReRFoWfDMZqTTm0bO3d1dBXvZJh15PP+Y7e/3+xoQQfnieChXpDWA2i4wPWObY+PFwIoYY+W5i4sLHA6HCpQtl8tamp2BEJxrPUaB9CJfa8l7dfrSuUbHP3+nXuEzfd9XwJoAFQEuzgUBfX7HoAEts66OVcrb69evcTgcqtwy2lQrMXz++ec1W/nLL7/El19+iRACrq+vJ055LthaAYIg6zm5YhaaLu6+LtotE5nPU3fwuTnwRbmmw1n1OnlEM7l5Tjp1PZ3vlDdmXCtAwn4pqEZ9pwCzljvn/Xw/+9Q2fo03+B59n+q8h4eHCgrwp4GP69oHpSPHBEwNurnzl/yqcso2yXuURc3mY8AN3zmKk5c6gPThGszvOG7ykIL+Cryyj6QD55v8wGNJ2D55V4FppcF87FoBgsELChSzTxwb+Yz8PY75SIL1el3BT+pfXnxGs7WdawA75TbGFuWt67raGdR1qjdVZ3At4L18v8oMwWVdQznODGRa1bs8kkMDxxQc4zq33+8rcKTrzHq9QdcF5POmA2JM8D5gsQjouqb/GFDDwB2dM+p8rinke7WZSE+lL20pk3lgwA/ngjymfMp1jRUg+r7H7e1tpT2P7mAfWaGGDlYFLRmg9+HDh7zOL1Z17WT/KHe0IVWOKBsK0CpoSFlUPau6XquEsL+cOw3EUZ3Ee733+PLLL3Fzc4O+7+v8co0+nU5YdDnTgTyiAV9sn7aFBoLo+9SxpHaKBrtwneb6qwGKGmBEWVV+od6hXUwdTxrzd+89LLXzp8kTqv9jjEixZeoqsFtLXI8jwnJRn9V/eS2KnJE2zAyn3LG/HEMIYbLmUieSdzmfDCChXUj6cgwqm+yT6jTV8dSHzEDWgA3ep3YOx0keIp+yDwCqDXh1dYXFYlGrK1E2OVbSVPmA9NB1kvYweYFVfZQXyF9zO5P3sM8MYqPM829dawnS6zrHcVI3XV1dTXiqHqOAtnaRJ7nO6zETej9pxovPqi5koAHXPy39z/WZoPs8uEBpo0C/rqHf+DKCm6iOyfkanPudszkJJnG8Wpralaj6zH9TXQm0oCXvW7Zdduo2RDYlQz7OLk3KkKoe0gAatWH0Yh8rfwWPb3/72/iDP/gDjOOIv/qrn2F3dwuznDXgQ8t+zpUmBDS16ZjNMshRHXc+l/qjwxTljOXsVA2T8x4BZIf9hGauADtlPohmuIYzNsdgcQjJ5xPnN0GQmX/5zMSD2YH1eb5D3sf/q6Nb9Ye0VoFxFCDHYsJ4GrC/3+Ph4QGHQ7aJNtsttpeXOSC777FYLIufY4nlYonVco3t+rLoQI8uNId1pRkyUBOcgGCzSx1yxhCA2bjMms1JuiZLbT4KMAGIQ7B0wASwsMkPwdtj4fHZO4RV22dT23/+0/pS5LJ5y1vfLJVMntw5HzxgCV0AFp3HatFhtezgMCDFERYTXMhAU3I+Ax2WM2tiijgNIx6OBt+tsbnsEcIiOxFdCR6MBmce3ncY3TAB7viv8k0mBLM+ZwCga4FnKZXziX12wBOkhgCaZgbvcgANwWqzBkzXdgEA48xHVzLATII6Us58NAXFmfkeY83Ib/Zba0/BbwJVyVIFJer3sZVfroGd4pznu0b5vu6/0yAjmvJtzpYr706Zd6PFRhOb8pc35KxM+XyiPy3PzJha0DxEx7jZZxbTRJdVIHrC79n5T5/HaRjw6tUr/Pbf+R38w3/0D/BwOuInP/kJ3r19Dzu9Lfb30NaX8j722cEqKm4iP4/0dColrkVY8vNNZzjnCrhPEGg63kaTvD5pljXBdn2nQwbZXLGXu5DLWnNuuaYEH+ocAVaDGdhTyo+5mEE6js0KcEe1jRLS01HWpoCEtgkzOHO1GgeDDawQmTQIAfXHFTAsmAMrLZn3gMv61woobt5he3GN3/7xj/Hj3/tduOBx8/4dustr7G8fmj8ypUob7jHyWtBNz8CWLNmave0cXNfB+ZCB8QqKl8QLOXID9Hs5Zt1OK1zWvVZoVUcn99RKCyUYwUnyiAZeOFfBdg8HZ2j0rcBnBkvHcSx78wW8D1guOFdBbCn6tHJ1kiaburA3uUop6+HG4U1eHCaPwMBzfq2Brq7xGh+uzxebrrXTaNcTWKqAllQerPRzMHdsvMt1gffwM9fKf+tQSf8MfAXElHA4DhhPJ6wutlitN/jq17/CbnePxXKFzWbE/nBATPls9wzuDXg4POTy73BYdF3mQTOsFgGrhceyD+i8A1xXp9UXOw4IcJ56yE14I49XZM2jAeJSUUcnxunZEziz3tP3ZVwP25pTs+HF1hjHx/ZC8zVwPWr23tzW0D4IZxQQvPlpW/CIR9exYokvgQsdLrZbHB4esN/d4845wBLW6xVWq3ysCP2gu90uV+Xc5EBILJa1pDqDz+b0afz7eP3l97QR5ut8q27hGj0ApHFasVX3e+dssLntS3DYFf1D3pjTU3VK1t3ZZoJZrgZkOZTKu1ypIfgOrWpMPh5hvd1itdnAzOP29h6/+OKX+Ju//gKn01BoEZFKtYO+6+oZ9yF0ADxGxGo30RbJZ34328RShDdDCFm3p5QQUxZE7wLSSHum7Y0rv7iyn0PeP1k0RFd0Y5V1UUZZCWR6J63U4kqANnLAJeloJfSyy0B2C1BoZ4lznYCch96FdvRBTLlSEddaHk9R/c8zfjKzGuDMY3o0sUHX6JdcL96p0zFAQJMOFDqAcgR3cx7QUazZR3lQK9ze3k4csgQxtfzycrnE3d1ddb60stgGs4jdbjcpn0zHC53MVBDqCCUBsxMgn5vL5+gcYnuM7o8x4vLyEkA+c1WdSCm1aLoQcsbTxcXFpGzr4ZDB1vV6jbu7u1o+nvRRZzGdOVRoLMFOMJFZHHS0AKglOTebTXVsEISqzkmzWp42pVZmkA4oAvucX/aNipZ9oNOEzlQ6q+ZObdKNdFXDhnykjmrOk0YMmWWnuY6Pc8gsFLZxOp0qCMrnNWNVwRmdX+VVbojooNXM5hgj3rx5g77v8dVXX02y2tQhRnrQ0cy+AdPMPDopqTA0e5T8qW2pQ4XBJJy/lBKur69xf39fgd+Hh4cKsJCOmt3D4Af2kQAS72c2D0FUyoX2S2lFpzGfJ401c4lyQRCPPLdarSq4r2fWqiOZtCNfEBB49epVBaOBlk1K2lB3sE+UX/K/OqS1nCwzvcxsUkIbaOfEk27qrNXPyOvqrCO/UJ6+//3vY7vdVn6jHuC42T/KhzrG1enPi2AkHZPMUtXjK5xrZwPr3LESgYKcCgpo0Acdz5RZ9o36QQFVBW64kHGsWkqY3xPU4py1bKJ2vqeC++wn540yRdqTFgqkUlbZ9yCLN59TJy77ofTmHDOghgCkgqakhfIJHc77/b4G7GgAg2b/zfmNdGR/NLuQ88txqYNaZZUyqSW4nXM1sGZuWJLmmjnH+VM+r8YkUMdFOhPwZf+pW8gblEe2ydLDKjecZw30IV9yHtlHvpMyO9eDHJMCJ1wzWRqf/WOpfrN2PvQ4jhP9yN/JY+QB6jENalG7SGVFdQX5lsdS8HsC3ZQZ3suAj4eHfV0TyTfkB7bJIBa2o8dVELTnXLBdNT6HYcByvQZLYOo6TEcaeYg04D2kn+pyrpHMeKau9z6fS5TPTGu8SH5tDqsW6EceVB3GDZ4CNLQFKEu6nlEH0RbVwADyPvUl6a+BGtoe6cO+M/COdOS57QyiygExR3gJaFF9T17hOGjPaUatBtyQtlrNhLpisVjUAB4Gk1B/z3mXPK9gqgaTafaxgmGn0yk7mMv6St7SdcC5FjSkgQSkXXkZuq5l4yugzH9zFmqqumK/30/seQ1a4dzzXRwzx0k681nlq5QS+q6dv801XWVYj6pgW+R/8piuuaQDdQLlQvcCXMOAVo6fevjq6grb7bbaUOSZzWZTbV21hbh269g1yED3YFzrVC9xbaENx3ml3tFqWVzD+C/XIe4rQgjVtudekHQhD/L9fE7tEfKjgs669mnAB20Syv38d459vt4yOIqguG7I+ZwGTnHu+KM0/NtczjmErulbJMOQhsl7AcPxOFSHNgFLAEjlfDjSp9EsZ8dxXVGdxS43e8hN1iqgOKELAGCWA2GC2H5AdtyZa3pJ7QXyRt2H5zrn+N3f/V30fY9/8S//BX7yl3+Bd2+/KmPh/KDuITJfD2A+IentnMNwOuUsVO7xu1Ly1LVMmuADYtdKslbnqXNAcejTQWxOACoCLTq1uWOYFydUHpg65dzkszSbz+zLaq2d46X8d3aTevgn+a3OGQqeZKVk4zBiOB1xf3+Pu7sdxhhxdXmBq5sbdIsFukWP5XpdMocW6LsFFos1+n6FRbeqwK4Z4C1nt3Q+A7jOo9DvvFNKaZ3HPM0GIrBF4DJ/52Bg+Ws65ASoom1qlsvNGx7TTByzY1zUUr+1XDL7JMCcWc7urmBHvR/I5U4J/DppCxWsM7P2nuJoDcFjuewRvKELQHAJzkZ4i4jDA+4+RsA8lhcBQyxOxxAQnMEbYNFwd3uH0+DQLS6wXG6xXGXf1mgJaRxh0RVBdRhsXk7yMZ84FFCAPFICEKZAtjWwicBUATGU1t45pHSa8L7LxETQdzrAB6CbBYGoE7y2CQEcSlv5n/beZLnCpE0cw6hO1fbeaSBGpYoR6Mhge+czMSagetKjNMpn8VDJWt+ncw9kWYlTEJ7gfIypPoNoAPc5tGErUF6y6lNCPA3tGWvHLpjwfdatAq6IXKTKu+2z1XKF43DC9vIC3/7ud/DD3/5trN98C//Nf/9/wHf/5/8ZX/71L3D36/fZthpbuX2gHR3hHOp4KmPVuS30LAGNKcYK6OkckDea3DUfSwU4CPQLHtmyzaS9+v/cN+p1ABW0daSP6uFuIcB4qYDheCZwvicDjCW4yvumX8uZ1pXPHODWfb2P781tugb0pxwU0fU9clWwFsjinct9dUBCB+e7qmM9gd62fCCEHLTE94e+w/byEovlEkNMGOKI1be/j7/3o7+DhWuAQgbSJHGizKl3PmfcYnr+ucqUcw7m2iEr59akOo+kZZ13oAFnbeY8CHJqZmMjGd+bLE2DF2by7pxDOaG7gotFlZXvPToXYGhHJoSQ5yEfJVG4r+i+fJjM6dHYlCZ8iXft6MH5nDZAO5/87QpIT+DZ++n4S2Jz7TcDAeZHMPRlDWa2Pm2Xxrslqz+kab84v5K1D5dHOz+awgk47hzwcBrx7naPt7/+Cj502Gw3OP0i4t27t1iulrh5dYXD6YjD4YhxjDidBsQ0Yr+7x3G/RxwGLLqAi80rOGfYLAyrRZezc7vQzuYmr8EhpWKTVz3gKg01uCuZIYL6BlU361nW+TMHi1P/A7+f/giwndIkOEt1yTA+Xqcaa+i90+pp54JEDCXIJiUE15KWeD9A/2MG8H1kZagjuhBwsd3i4fIC79+/g3e5xPa6VAIKZS/21Vdf4fDwgOPhiHE7VjmEWQvYqryMsgahBH1NaUWeM1gFe3XMNbmnBKnksJ4cwJJm8qR+SpU32vhV/1jDZ+Czzuy6DgFtf6e+Gt1v+xCwDAukGDHEEbmMeG4jWS6nvlqv4bt2VNfq4hKvPvsc+8MJX/zyV/jZT/8Kv/jiC3jfYdHnI1bMSsKAGbwZfA2qiPDeYRh5VGoBsMmXNjYbIuWgCw/L1Uwc8vhcjpBKwSEll88g77pmH/kcWFmVBufMIuAMqRzxMq8qw8CTMCp4ztL0Ug2o9C+FEpDRdZM1tswUvEeZ41ADoXgvXD6KahgGGLKO7lw5AqPL1VGqvnMtMAKulGAvvLBcLNDRp1KqQz2qcvHE9WJgnJtmdXbSEZOdPF11xLx9+3YCxFChLBYr9L2fOMGHIZ/7ulqtqrOIzlrNPqRjA5hG6dN5yIh3BVkVVFCQJDvqF7VfBEmZUaaOLS1PSyFqANyAENpZjHREqmOUjoZ5Bi7QAB2lgWY6aZby/f19zTShA5YlmM0MX331VS3bTACQzn86I9VBxUw1nUf2U5UPs3bUGazfs22OhdnrZlYdwepYVNBgruh4n5nVUut0Wu33+wo+qXO4KlM3zQjSQAg9l1j5TJ3Y5AvNEqSyvL+/x89+9rMaIOF9LkHKrGudT3V8KwjCUtUEU+h4Z8CCjoNnipLnOF90RAKYnOU4jmPt82azqe+JMdYqBvf399jtdjUTkzTkYrDdbivdKAM1OrRrJYT5twabaFbecrmsJVjoiKTTi7QiD1EeSAsuVCzvTgCKcq8BGATXOUfkKwbGaAS3Zrqr4548o2Ar26AsKhDMftFJqgAb30caqeOXfSYA8Pbt2wpM/PVf/zW+973v4bJkZahMqB6ifJJX2Db7TsCRznjqD/IB50nlkIFNCgrMgwZowBGsZxCKWc4Adc5Nzp8nsM12FLin7uJ8UOa9LJp0lJMHycMK+AJtE0BdSRrpmajL5bJWoeBRHawAoMCWBrWwbfIowQcFBFhlhICvgoGUHz02QdcCnmutBixBAHVg1M1baFnmupZxnePfCg5yzNSh83WM6wDv5zlCzF7lGqS6MVc/mWZHsl+aSTd3mlNHkeeUJ5ihroF2zrmqDxQ8mq8LCrCxffK3AkoafMf5UeBDs7UVoLu/v88bSik3RnosFoua8ZwB6cdHeHBeyU/aPwJgWpmEsjAH1Pq+x4cPH3L0pDksV0vEGtTRAeYwnLKzdhhOtQ9cp8jTnKPb29vaLwLS5FfNZqVsKyjENg8PBwzFLlObSudXacz5ZfUafb8GdGjp45RSPlbITyuDkLbe+1x6rayJ6jzl+KnjqLcoM9QBDJjQTZYGk6itw3YJFFPmOFekn5ZLVluR80s9r0GDWnVlHCMC2pnOvIe2hdoytC+037T3qFNof2rgD+WftOG95BfyJ+1CtaW/9a1v4d27dzXYg/qR/K2ApPceFhuYT/uAQG2lE2zSP87j4XCogWnr1bLSnn3S4LDkMgChQCTnnRnYXBeUX3WeKc98nrqI9hyQN8tqN3FeNVqf9FV+1OChEAKurq7q/HKNVhBf+Ydt6JrS930NNuJ4OJccG20XXetUr+u71f7mvM/3V+pwUZnhv/O1gX1i4AQv3sPPKCPkaVY34n1qB1Du1K7QNYDbXur76uCVtVbliXPF4x1IW5Ud3q+6it8pv6vOoy5l30iHv83V9W1NqQExKcF3rZKWCW2cGUwAeq0A5BcLQPQYUsSy67DqF5V38uc5KyGEgLHsV3Ikf3PYWcqgNOc9OYc0xmqfOucAZsI4POI/2hh1X5Ei7u7usN/v8b3vfQ//5J/8d/it3/pN/I//47/CT/7iL+C7cqQNPNIYcTyVYyC6HuMwTHgzFaDOW8mSctm5forjhC9qjqdztfyryit16BwEeOrfueMu06A5Q+lQBDycoxf3MXDLi+fqaft6Zb7LrZCe6tiavteQs0ZKkOhwwul0xPF0wH6/x8e7W7y6ucH1q1fYXF3AnMNiucJqvcFisSzHT62xWqywWiyBlJ2G3gN9COj7BVaLHn2fy9hmX5eb7G9ynwz22D+czyNHs/F1zM1hDZhNg09bllbbt4wVsDz3gwr2Jr9Cy/aarv1tPgDz/aRfc/rmec7AuNL83JX5zJDiAOeA9bLDetnBw3B42OPjh7d4//YeD3aH0C2x2F5hjBEI+YgZHwLgHGI0vH/7AaFbY73e4Pr6Bjc3r3B1dVV9DK6ABjFGIMz4UPYd7bM8YF2/VFb53EigV+ZS9W6dN7uAAp56n9LHezx6h35fbbvgHn03b7ug+3Ve5rL56P4n2uF3BPP13sc8Qtl63Hd9xrkzpYgh/EPZPyPvynf1c2cT0PmsXjID0uN+8Z4abOg8Vq7H/eEB/aKHeWAYB9w/7PGXv7zF+mKL3/hf/QF++78oWcgCXM5ponxAufHiUCdvcc82l6cJba0EYmB8dJ/6DvPnRAumz9e55PM+oZZePkdXEHz3E/U818N8p6V8jMTcTprTRXGCczq6/FKBaQX25veOKYOC7PdUjtszviv3FDkeT7myWzqc0CEDN2u/AmDoF/1kDPM9RjKD68OkP4/0IIDgPMITcq9XEHD3HA/ws/AErqHPZZBlCgzrd03+crUZtWu5xk/9LgOcn9qA+Z2+wsfOOThvdQzn5pWy7Z/o90RukcHRc/2etp+D0PLf+clzNOxcrcPyaA54b0oG57rJPU/RWv89t4YAQLdYYbldYBwe8OHtHbbbS6xWG+z3P8ef/dl/wI9+43swG/GBpfvHiLuPt/DuHvff/R6OD3vYGHH9epvHiQGhDwh9h77v0BXfwBgjAO5FgMPDqYGzYmNOgpgMGFLTT7q+cT8EAJaLk1S7f25D1LUKuQ/Prg3WonbO0UtpaTbdQ57T6ckMY5KjybxH3/XtaICyL+i7UHGqlBJub3eTgN6bmxvcvv+AcUxYbza4urzEW9kHHw9HPJSscR49OrHFOP+lzHcqQQHjME7G9Gg8QAsiUD0lupxzMge75zpO95yKyWgSijmUQKRQZZDzpzYH5d+rzncJuRKCgw/FFgTQLxYYkeCXPW5uXuNie4Of/OwX+JM/+VP86stf14qIwWWwN09dA7yPKSGEfAx1QAePBO9YVS9XS7GSzR1qRYYCbHeSfCZrfxcWGTBG02fANICJYwzF3+CKXnKi/+b/hhDQGcqxHW0vpO/gnHXFv6Pvg1Qa4N6r8w2/4Jxyb1uPGUYOxJqv8fxRjDMWHhxjRBoilks57q8EqL3k+lql1Glkq+NcM5RTGmsWt5bco3MmBI/37z9U0IJC5n3O1NKynARVd7sdNpsNnGsZDDzHjllP54REQU4SnmBX3qznCDx1RtEhQofN/PxyAirNMWpwrmWSzgU5M1QDPth/PXOY9FHnJOkLZIf23d1ddQzx3XQaEvTUbF7SW89MX61WNWNaHapmzentXAP2ScPdbgcAtQQ1gVfnmtOQjiA9G5rKm1lkmj1BOnJ++J06vmiIke+6rqtOdYKYms2mwRBqyGk2ppnVjEDSQx2pE0cOmnOcYB7b4fhIZ11I6TDTDDiCTqQZaUA+5zwTfCXYwqATyh15ks8rfS4vL6tjlP2gE1kXVM2OAVBli059DRLg7yqX3MjQMc7+a1lqOhlJI8q3lp/ks8xoJv8DqHM0z4zkPGvmtXOu3q8ZRTybksA6QW8zm5wNyTllyX49O5hVHgg2mrXsVpbCpaxTT5BepDsdzAAqrbbbLS4uLtB1He7u7ur57V3X1Sx48goz38inml1t1oBOygz1E3lws9nUMeniA0yzEOfZbqRl3eAUWeJ7SVfSRYEx8ib1D4FJGigauKKAYSvf2cbL+UopTRz8nEsaBgxwUmOdvKGZ7ORbysHhcKgBQqpPFOTRzDU9KkMBDQ3OID04NuoB6mLqOHW8z+mtYCs/17PWOe+USa5bPFJD50Gd8vo+Ajyn06lWZzHLjnMtAx9jnIBLCijpeCl7nGvqVzWweI9WL1Eeps7j/OkxHpwbgvnb7Rbv37/HbrerQRAKTJI/uE6pnqdeov3BtUPlNsZYg+VIM9KSawjlncecqPOgrbFxImN8NzPgD4dD5S9dK8nnVcecRjzsW9UYOnLzd0Mp/Rdrv8i7fBflkTScX4fDoWYR0yjV0sfNCYcqT5x/9nde4YCyB7TyvKvVahKQSJuENFaADmm6bmmJZDjUM6zVSFZZ1kAmBlgymIm6hnzH9Uo3Dmqsk59UpjTzkjqW9FUaqI3D+zRQsRr7YZrtR11J+dfgID6jAVAaiKUyyrb4nIKSDEQyM9zd3U1AUAKE5N+7u7sqy3d3d7i+vsZut5sEfdL2NTOELgBjs/loJ6ouiDbdlFJOtfqJQwv05BxSj2TZjcX537LpyQ+039TxSptHbVLSTG1A2r1V//c9QtfKhrGflAUFnrUqAW3sthdqayCDNdWBzPY0UIM8TR5Qh45mRHOuVIeojOp+Se3ouoGd8Y6uT5QB8jLb1aBH2p1cXxg8Rj4iL6pzZS5Pc+CbtNN+zNeElFIu9xy6ekwPPyfNdUOvAcPKW9QBpAnfocEspBF5aq73NDiI9J87yr7utS72s1nONkghZAdhkYVxHHO2dpg6rHlV54YA32pPdYsewXcT2igYC74jtnHTZrRx6sSdA8gAEMcRQ4qTY3ZUD3GfFGNEv8x2zRdffIHLywv83u/+Hn7jhz/CH//xH+Of/bM/xN3dDjAH7zuEYOi6Ik8i31y3+LcGOPqS7ZKdeaX6AKYOF+dcLrXuxDGNVqrPF8eS3u+DZP055P54D2fWMjTKlaGUXOLRNNWxZuWgAWOY4OqPHLBVps9mW54B4PivGSyOGI4H7Hd32O1u4b3H5dUN+sUKyRwuthss1tkOCM7nAIpFjz54XG7XWC17LPsei77HcrXAer3Asu/Rda1UK5CQkivDmfdRnM3IGZbst6vPPwZUzABW7PM+VxXJ5+zm4wTGMdsPBBoJCOV2CNgyUzfU9vQMz1xOWzLDrGWJorSTEvUqasYtSV6aqZ8DwgbBYMFgySM4j81qgc16ncv7Avj49h3evb3FdhlweTzieDjibr9Hv+jhkBBDh3gacfvxDvuHB6yWN+id4Wrb4XvfucTnn79CjCOOx1XhgRKgVZAUB/eINxof4RHYpmNo+jeDB8yQ03bU4Zmsrxm3Nsta1kz9pNUCZI500rPcqt+PPZ5eyVx9p/e+noM+ESS0She5b9M98uQ+yTKb86LSLg6xjrP2vzrYM93PPa/tVPtiZg/Or2r3lkoZbF+/00ttQG2jfZbn2CKwXl3IPnuB5XaF0+KEruvhUwaLc9ay6vvSCRnHXKc+Hgtp8RhYndM2C1fOrNNzxecgrgdqRqOjPpas/WbrBGjFjjxeyqvaF66+/qkr6//Cl6654NWuzaxq6EyDGlxZLs6Awb4d3ZHLk/vHtAEe0VYzz50rmXUu1rHnCktAGhKQwJPWARjcOh+HkefUV31VAWPvJ2FcbF/XN37mkMoaJ4BqyTquvwMZpK6Z0e0+59pnDg6TxHLX7sny7ep9es505T3Jos5fplz63gnYZG2sQAnURUTwrtqsZtMS/Xr//HrE6266Rqu8TKbVslWgc03eod5VmpavypVaZYrSh2PyYIAYP2v2KffOCcA0QeOpK461R7X/Wd/nIH3vPcLCo1t2+Nab13jYneDQ4fLyGn2/xF/85Z8ixQckG7A/jBjLGvv+/Ud4F/Du3Vvc3Nxgs1mj6/J+5uFwAlxC3wWsFgv0XT5mqwKrsnallI+6YEWNmr2tJE5+skYp8elfabRt+wzlIdIRAdCAqDlorPpev48x1uxp9gXFJpu3o/Y6186oa4VzueS0DzUZjxjbarXCou/rXB+PAzofcLFe4bPf+THubz/i7he/yM+V5Dkzw2LZ4TQccHi4x/FhjfuuHZ9XmW4WUFjHmh7zz9wXSICZvDyn65wXdY/ccLiGGZ3bt7lir5caKjWwhzKrPnO+n22fTkcQEA99y1o2lgAPHq+vX6NfrnA8nvBv//W/x09/+gvEmPD5629huVpisejRL3ukYSx61aHrcsn/lDIQ3nWLDI6HUMr3W9N5aL62rH+zbu18q7hsxTSzottJX+6HfNn/OI4/laAr+hfGoR5tk2KcVgEo82xmSF0OxkwAojXbWOc9pXwskyYvVNvIUvUpcc6Ifel80x8wjiOiA5LPekbPrOf4zKwkC6WqwlM5xoB63dc9wssg769RSn2sTlM6Sy8vLxFjxHa7KRO3rAAXmY3O/9Vqhdvbu+og40STadWRSMfmMAy4uroCnU/OMUPF14wuTh6dyzlzJ1YgOpdoMfR9PifEDODZD+wbHWecMDqxCPBReAh4MZs1g2RcSLjx7tB1GpUxPb+PjMJMNc2gJNhflS3ywkzwks4v9vvy8rICqBm8WCHGEZvNGuv1Gre3txjHnAkfyvkvdIKRAQm8UXkCmACkmoHJ53mpQ4h9ZmlZBeLUKaFKi4CZnvVI0ELPLARalIn3Hh8+fMhROKGdja19Ugefc66COkp/go/q0CNvMquOfb64uKhCzEvLUaqDlc570onOYDOr5S7X6zVijPj48WNefEpWJT9j8AEdgZQJ0oQKgw4oKiBmomoWF4Mn1ut1BTN10SAYQicf0MoacnwKctEZxqMMOEdzMJV8wYtgAsEjs+yc//jxY9UnpBNBDIKY1Dvs2263q5Ul6NSkY9Asg9fb7bbKiy6qpBl/2KZu4DgOgoN0HtMJSPqp/lCHuDpWKRfUizwWgMaFHoEQY6yBR+rQ5xySzqQlx6DzMHfC8hnyOGWAbVBO6SzVoAb+EBRjBib1M/mdfMTFjbQjD5AnyRekMe/leBlgReeoAhma/amAAOdB5xmYnsE611mkA5+jrHOs55y77Cv1EAFx8oS2ze/Z57kBx+/4u87DHAwlbQgiKvBBueLFNZLgMueHulaNUjOrgNh6va6ZyeRlghmr1QofP358FBDmfahlmnmmFIBHvEjQh8CUOsI537yXdDkcGODAjNqxtLUsQUOHXHYr3uJ0OpVqF8zO9ohxxH7/AOeAEDqYsZyvOsd5TnMSsDQBoDEHAK4AJSNC8GW+aJShBPusCt19ocmAxYLnimeHyjCcsiEqRntKCff39/UIC9JAdSDvr4asBxZ9BziHOEachhMWfXY4hhBgzuAtYLVe43DIZ2aypO1yuQRcAe58Nmz7xbLy6xhzmbxUNphWdP3+Iffvbper0ZgrZ7SK01Rlj0AlZYP6kfxMnbpYLHB9fV3XA64JqtuqDZEM45hLYgafz3fLZ2p1gLWjHMh/GrhJED7GWI+iUXCOcqHrPZ9VfUJ50+AWBco0MplrkeqaBpyUcochl4ofxxF9l21LHzwMGeRxcBjjiNPx2JwwZrkcXheQYip8ljdvWdd08M7jNJzyuXldyBmSPpdQ9C63CQCr1bICaftSxSJv0sqmzTkcHg4Yxb5aLhcwS+hCrpZEe3PRd4jhMfieIxeA1XZV54h2NPmdOvJhnytSJEtY9IsSJBlxPGb9wv2ARqtTtwG5TKAB6EMukzzGYscPAN38octAFnV5BlJKUODpgHHMc8hzJr13SKdcOj10+Tywrm+OgdPphM1m88jO1XWa/Eb+ZlATAfd5RLbShnqCOkDtaK6XlBkF5XVt1zWNNpeuAxqgTPqyH5rpreuT2gK0gwmSc/wMmKYum9ssCrirHUD50TVCS7NbyqX5PbKjMxU7J8VYz4ykDaNBwJRNrmEKynLfQr7lj+5D1J7QtZR95zu4T+Mc6hE7ag9/00vngL56tR8zn5zPLiI/6D5oYucglx+OQ9NfQfZHALBcLBBCdn6atbnSbGAN0Jg7zDyAsfD4MLTM+84VZ3yR1pzB4BD6HikakkvYrDf4R//wD7Beb/A//U9/jF9/+Wvs9w9ACIhlva7ViBKPGFlgHAckEMSLQIoYxiEnWQqdguzTqxM1Zj1gtfxg6duMj3lVm9W7UvJPnPLipFfHINsFnYKlLedcdi4WFIIg33xtqva++CHVwajB39V5WIDdcTjVsoX7+3s8PDxgu71Ev1iU7JGAxXINjyyPy0UGwPvO49XVFp+/vsFms6ifZ/3EsVkdWjKHWPm/OPbFDyGjyfNUnZppMhYnwIkVB3amOXm8zJd1GZi3rBPaWx7njNjk/6Yftj1cKfsZTar+GftKHhdAjbekKdDOZRHIlVLyutTlzEqfAfLj6YT7ncPDccSHj3u46yVudzsMcHj74RaL5RLLRQeLCfv7PT7e3mG9vkTXBSwWHleXK7x5tcXltsM4Gi42m/K2zEs+NZ2Qf6nDafYKHP7/xP1Zky47lh2ILQDu3xjDOffmzbGKlTVlFUlRRUrdktpag8naTM96kP6afoZMpqfWg0xmahmbRhrZ4sxiDayqHG7e8ZyI+GZ3AHrYWMByjy/inJtFSZ55bkR8nzscw8bGxlp7bzgfRNYaGcMOMnD1udOCllPvza6OVz0T3jWysqYNzV3rq/I0yYI6LFKuykqrY9nvZ4ukbd876JmvSqbO26Cf1+9c19qQZ/eU+pqsKInVZEKrznLaZ/ouHYc2Ptr3dJoxteHgZ0vLBNRWfJsEepVDIXC1bS4g5YSea3JZW5BMXl02chCBhKVWcubgU+vDNSY9/9zx3NlZlZ0TWci13q7KTrtN3++dHemgtrercp7RzoaeEovtPie6xiE5iwhln0Pu4/sdmjyzEa44PSnulnO2tObTCVXfyQJJD1cbN3hII9r6XuXEPesH/tfWH4uUNaLEIxcdbXvLUMnlzkXE1GzQiR1R3uPh0APS/8+dnuyZBFcHTWqkqkfWrol2VvK8jEWuY/JCv8HBMrDoigIO3ezS+Z9QF1oAFq0JyyhA56oysV3Z15jDS5HNAKQ405FX5BZwGDGX/6kOqt8le7Z91PQbV7IMh5RdXUvrG7m+iq5IVacUbDDF1reYHic2l02WYz8dcm5OyIo10u713qPrHVZjh83mFsvlAofjDqGzvcLlfMFXX32F4DNi9nZGMYD90yNCt8DXX3+F+zf32N5u4YLV793jASkmdMHSJK+WfY2MraRetkjbuR3npG85Z9LYUoPz3Hn2jR7bkl2u67vqBK6BOdv5zg3ja07JDQPmz+dR5+0fj2QpNc5XCHa2Y/a3zlMjTUPNaLtcLiu/0/c9brbrpjdG24Pd399j+c07XC4nODS+rQsdTmc70jfFiDyOOI+0J4toq8yW/3q4GiHMPlc9Uh2fXeNqJvKWW3Cjchx8F/Fa3ZfNn1fH8BAMC0llPPWN/F6DjFowQsmuiwQfHPpFj8Vyia5fYbFYYb3aIsWM8+6Ep6c91t0Sf/i7v4cYM3wIWCwXuL29wWqzwuV0Lhh5wT76EnyYXdmzlSMrir2lfTUMtl8p3l6IKWFMzVG5ylvVC7nKTz3ixNFhRMjlIuuXy6UE1kyzsVlfGu6ZUkLuiuN8ziU7WUJMsdm2RU+4Mh9iFucG8wqqZ59nZEv17kTvmqKvc0Hlqq4xdQ2zdcwFD3R9wca6KjN1jaz79emRca9dH02M55yw2ayx2WxwOBwKAd0i6XQRVcCKwAjA9IqN9CWBxHOTCSSQ/CCYQkKP6c7H8TIB0hn1wsg/O2t3UcBoj/P5WMCkVMmmlBpYopG2rD9BGQI3ejHyVYnABnyY0hxHS8HCi9FBjFZl1Iyel8h/LT19i5AkiUBgTNOOLhYLbLcbxGhgz3a7KYTuFuv1qrTNGYiApqQYYUkwi2e/kzQiOEJyiYCcggKsI9t3e3s72XioUlcjgM9QUDU1J1P+acpvPqtjRYKYABX7R9MfM1pHCa/tdluJPKBFZWnqznm7NGry5uYGOef6PJWwpjFX4otjRIKLSp5kaUoWEc5zwXnGKYFG1jvG6fm+GkFGGdKUsVxYFAxVxcdFgDLGOcvf6SihBgX7meOpqV0JSHIslbAmcMuo/4eHhzqu/McU0KpHSGZwPEIIuL+/r/3E/uACyX4g6KuAJceF8qP9xPZyzJWw0cWVuoBOOApIKxmkqc41ClFBczrYvHnzpjpJkNCnflSnHSUXqBPZtxXwKmPlvUXVqixTntiPagDPSVoFVFW26IjD++hgogCcpoDXOaR/U1YYRZpzrpHGBKRpCFE/6XyjzKaUatQvYJkL6NijjlyUERITKieMEmPdqJvnwIg6UFB3q+yRPOa8ImDNMU4p1YhL1V1cP/SoAJVPyi/7gk4HWo5GvGo/UYYZcUt9pLrp6empeefFlg2C8hdCKASQORTxc47r5TIgpVzXVSUpqZ8oJxxTPst5Pr907qTUjmo4nc51HlNXO2fe0M3ZbpoOjaQ4x5hjyKwhwzDicmlOSJRl9WoEXH0H7yGZNAzA6XSu9gr7ko4cOo9Saucgq7MPx5ORltQn1KccS2bmGIYB3TnUdPSLxQKHMjYp27l0McY6Vy/DCDiHpWR5ASyKz1ddQEeCjNAV58UQLFVZ2Vg71zIEsF26RuhaofqG7aQemxOjOjYa7cuIhXFoR7bkPIqDwjRimuNOO2GxWGC3201sFWamUd09js3xkzbENduF64rZmM0m0o0YZYTHoVDe7ZyohPPlXPVWGhIu57KGFqJ8ZPRvsCSElJs6H73HOAxY+B5xHI3ILcBAv+wQop1Bl2JLq+6cgw8Om8W6zvNNcYhh/ReLHppybbEw+avHogSmC3fofF/7PNTPm63Gs0iD2C/UtezPakskS1MGuAoGjSMzCJhsMoOG6ki+v659KSHmZo913RopmQNJ13XY7/eTjEdAOTuV4Ii3SMNutSyOtg5932GxKNmNhksF6IZhmGTboXxT7ylput1uQQcqbtoosyRlVScoict+ytl0L+/jverMS73A91N38z3UL5yTnDs6d5XU5XqsgATHkuWyPfOxANqZ6Jy3XIvUAUif45hqGdSh7C+UPZZzrkb6eu8xnK1vL3F6zIyu82ozqKPBw8ND7VO19XRMCSqp3AEtilzXNLUR/nMR4laX4dm5fClPMwEQuFO9pf3J+k/ALPYPcj07l5/rMwCqDojJzi6s+2VGVru2N7T+JmBT4UnEsUTTI6PvQ3XqsfI9xjgi5VRIeDl7NQM32y3+3h//XXQh4C//8j/hl7/6Jb795hscj0d03hc9QoDUyISUW7QUoxxicQIKkHTdzslZyg08StkBJR04nEOOCdknZOeRpG8zMkauE1fOKme0XyXNvZsAstk30tp+NhtcAdD5VT9zriDiz++ZXBXAyhiHwdKon044FQfpzWZdwKQOoSsOD/BYLZbYrNbYbla42a5xf3eD+9st1ssOXW+RoylbWn2uManYFTHGlloTAu5qO+p/Gjhcz+tl++mMAMOkFDxlZA/PYCVBVkG10ke6t2n/msMj9QvHylpv9k6Hj4wMxNQemn9vc5SchQNSyS6UMi7njGG44Hg64XA6YbHICA/vEfYHfP3Ne6xXS6xXS5yOBxwOJ1xiwk9u3iDljOVqie12jfV6AYcIlxOcD6Y2CzE+EY9K6NWRKfcVchwOjISrYkb4209oMMzPCZ70hrPyc1YbUfuvjG8lq1ofsv8m+7Hyn0r8lLbUz+oHJeK2vKtFTdKGdY3EflbpUufyvUfLINS4qlkdAUTnJl2cSWjVdwhQzDtm8sH2u8axTj5vLSwEbm5kzQQcn7WlRpZrCTN1kYFyDinK+zMHqGZwsjnFik2J50k96zg24pTrC2o/qfxNL86TNp/aO6/dzzbZkRlKGul7uOY1p49ay6on2Ld8RsigCasr88cByKHJhNTTF8eqio1KTnC1rbR++p19ZnshyqMruhEpTp5rz7Z+A1DXUHCtQ4YP3siLQkgAGYvZnicXksbrGa659e9r61KGE/KjNrj9yj6l/F6Zh3w/ad9nd1CnZLl/9rzqhdrfpR1J517OE50YY0ROZS0RAi9DskZki+ZP46xmz+pji1EUmZtf1CHaJsroZDgd57iR1C+tM+3vRppzLJ4TYBnIz4nxDFyJuDb7m+Vl5Eq4mZ0ELBcdvAOWC8D7zoIZUrKjUhyw3x+wXfdI8EDKGGPCYb9Hv0p4fHrEw+MDHh7fwweTn3fv9gCAvreI8fO5gwdtI9bPwXkurBzlOhCtXTkhF35GHRbZDzGVSG7+LzW7sJZV7GWzyRs+pPa4yXNb91Jse4T5eE1/b3PruW0xfX5u63tvTnbdYHbR4XjEYrnAdrPBarUGYMfwBe8RzmeczycsVgtsthukOML7gOViVffmKUaJDLa2qig2iQDgfLW3OFud8wVXMP0VJ8Sse6brtLk2516eK5Q/xfH158SB1VvK8ZzKWdMOdVxjShY1LX0ZOmYK9kiICJ0Fnaw2W/SLDYZLxMPTCafDEePlAmSH7fYW2Xkcj6ficGQ2ZEoZwzjifL5gHAfAtTWg5DdhbyC65nCTCu5wPp2KzKWC60RcBEslOW3rl6tZaqw9qcmzOLNUiyFnDHG0dYBncVc7u+2nbL8/dZSemJJiM4eu6BHaI87BwfY8tME5bouFnQVe14iyr2VmrpBLD7mp3HH94/7N8Csey0ZdLbZJXTw/fH00Mf7ZZ59Vkmqz2dR0z4xyJnDB83kJGpNcZhQazyILwc7xBFBBQkaXkeDm50qQWCSDEZgkOLkJJ6D/ySefVBA/hFDJWhIzBPO40BF0JFlJ4IudT2CL7SPRz0hbPc8OaB4empqX79HIaRKWl8sFy+WykqQEac0JwADzu7u7Z2RWzrmStefzCc7ZOKl3Dc+ONgBpCvYwFTTrRbKNk43njAKYEMUE7zQKhKnweB9BQCWyKQfqmcaJysWE6cRVdvg9205imuPV2tcib1arVU2xrVGSbC8wTedIgJv1YgpWLnAa0XZ7e1tTNVKW2H6th5LWHFPOE37G3wkAalRu9XQqMsK+Z6S0nqlMGVYPK80wQDBU+1/BQ843XWC1ngSmSVaRZOT84/gSbOXYN9B9MQGESe5yXrOfJkCSn0bz8h1KODE1LcdH662k+HK5rBFMvIf36T/1MuNF8FjlxnuLtD0ej1XuqQeYvYJORDpH2EbqG8r2v/7X/xr39/fIOeOTTz6ZEJ/qPKLkK+VmDrqzbQTJSULzOz5D/cZx1+wQNPA4l/lu6j7qKXUuOR6PE6KY7da0/2wLCQ5NoaJyoOQZ604wnY4GJAlYz0ZUDvVzjh0dbtSxgfXQNM7L5bISZ3w/5Z1lsd3qwORcc47Sucbf57LHi6Sozh/qNM4hJbvHcazk+uPjI7bbbV0D9vt9bTPnNglktoHyvN/v8fT0hJubm5qhgfqehDb7iWv86dTWPs24oZ+F4CspPAxDtQfYdo4NZU+9M2lTcIxZBvuBMsr5rw4kJDhZroLzSsJoH9AZgd+RaOdYUG+xDJYLYLKWcB3le+abFK7XnJNcRzS9Nx0bOEf5HpJhJGXo1LEWUpPravAesehlTVGvzk+UPdaB71GnH85ZnufONY7rhs5J/lPbqmWwWU8cPigv2sfqwTnf4LBe1A0alahrAtvG+Us9zrlG5xtGjXN+6PrOf+ogMt9sUa7VIZJ6hvdRv3PN1Ohf6kFde9RJC2ggPuvGsubrh/aR2oR01tHjejSLg5KelBsl9p0zhxE6F8UYqw3JPuQc5P3qzEaHLzoKxrGdbUxdqrJm+vqCJBmc2CbaF2wPZYdto+2hTqKsI4B6xAL7Ss/kVluHayp1DtvBcaLNRPmh/fX09FSJdl7qhEQHpvP5jMPhMDl+RtO3cc3h3NY1fD426mSmxwTRkUczdem6N/ewVxuTtqJmV9C1l3NVdQltBc4Bzj/OOTr/cixVJ9MJlbpV9TZtQj0qhPu+EAIWXT+Zt5XULM9zrijxrfqcspBzfmZL6e9ze0T1sup6lVm+k2s317fmXPW3u8bY1k72AWVTwQbLmhKfPf+SzlAdDFhmkq4cNWay12xFdZrMmWkzLRojCEiRUsIYmVbWQHmbmxZ+FYJHWDQbhePEPj2fz1j2i0oe50JoDznjk7dv8Sf/4H+MN/dvcHd3hz//8z/H559/jhxHsJtt3CwjROg6OAKWAg5lwMhn2Xv47JCQKiGV8gzAzNmcM7JDclPZzbN7K6k7GZsW1eNkfwfnAN/O4qvrizPgl5Gb9Vk3I8KcUwh4gjvoxfFIpR3jOBZS/IDLxXCXxXIJByPvu9AjJyNlln2PzXqJ2+0G97c32G6WWHTe6pbNceN4POFwupQMRxEx2bl/4zBgLJFGBP20jhPSmqCbb44WKJ97X9I3o/3d5JdALGzsgwGx9s+VqNZCJKLZZ857hNlYTgDVydhRvlDHoB03oN9nGaNCtLAeBSB2MNJvHEfkMcJ3ASmOGIYzDoc99ocdLuMZu2NERELKDl9/9S02qyXWywUeHh4wxIjt/Vu4LiDGjM1mi9V6DRccTucz0mDpghmhAyekkXPV3qBsqF5wGGuf2Wd50hbA2REB0metaDf5+YyQh/KHZUyc0RxNV+rcsvHlM+kF+dGrwrqyxmj7qi1PcrzV7BmImnNGl9v3Or3muj25Z1Wp9a+/F6CWt2X5r76X5J28GUog2rszMkjyXydaat0kWjXreM7akct4DuMIBwv+45EQMSYD/LMMqcwpvnuuD6+ugUVpFUprwmM9qxNtN3mYX1dZcq2AKWj//MV2LyPB66fPqphzRkBXaAtUYvqahnUTSL2MTZ5mJ8g5TyLsKRoqctWxgTaLNrI0iDKf7baJTkIlgwHKq3fTaLmYEzrnkVDySWRbH31Z+x0KNkT7IhQnk2x5B0bkdvSAyrLKOqtT1ych+nTc4Sf1fT4IeN4H9X15Sn7nmdy8QIwDHi676kTX3t8aYva3a7LtXCGPSmJmqQ9V5FW5UAHMz+dmnce5tUdtj6skZP2tCc41qWy623RHnTMkerOMS2YwW6koFOuQNUD2WbwUWwCAOFr23MVygINlMhtk/zKcT8irHs7ZGnjikaNdj/3hUMlxX6JUn3YHhOCxjD1cHjGODq6sa1wPPLycud4UMR0+p9lbxqmOt8pPyW2jItt+LBXSMtMx1chEO6YD0OwxM+8Meybx3fOxn4wYUmLwGmvmWnkyNuz3mJLNIu6xvEcsjpgxA92lxxgjLuOInMu+KvAoIMMI1psNTscjQuiwXDbMBGxXZIY8cRCRtdWL/reGMVU4AOergwNlO5dOqr4Gsj9jv9ivUyyNtpg6UXNfotyS8hLee7hgDhkIrd/zOCKmdmRr5Rz6Hn2/QNctLPOed/B9h8VyidAtMQwZX3/9iG/fPeJ8PqELAbc3d1hsAy7DBfvz0dbOk8NxOCHB4bDf4XK+FJ0SkZHA9N6NHAdyceyw/Z3xYOfTET7YPak4mV7SWO6zDJfeOyOGXbMD6HhLMt3aaLZ9KLavBTqE6vTpINxQcWigYut9X8XRe48udAglw6EeVeE7NxNbB+eCpXnvzDYPPmDR2VGXy7LnoEPyBCNMqHZmQnNuzGXdpsx1XTdxPtb1JSNPyv3Q9R1Sqcea9pfAi0YlKBAPAO/evcN6vcbNzU1NG25EwlDBs/1+PyFjOalJdu33+wnoYOnRF5Vky9mI4e12i6+++moSHbPbPU3AI04Edo5GKWlkA+9T8I1kC8FrKgwCc0w/SACbhLmCNgosK9jFurBeSvZ0XYfD4VAJKQIhCi43UjNWUuLp6amO2zAMtQzvp2m5WQf2A4Gdm5ubyXm/HHMFm9gWTZtPxwGWpaAv3zEH6tjfVGIEtjk+2l4qLcoE28B/3vva9+wroEWwsr9JZml2AtbDOVcJZ/7unMO3336Lm5sbrNdrfP311xVYI4CnUanDMEzOGFeQW0FynrtNpwQlMzinmFqTQJ2C+pRZvlcdVxTgYz9Tlik7jB7SFM26MFEOKS+sxzAMePPmTY1s14hW1t85V0lhjSAn+XRt46RkDQFFBT4IevKqxkmapttTUJl9SDlgH9IRheOsAC9llfVmZBbHU8kUzt2UUiWSmg7aPZNTfYdGnP/Jn/xJBau/+uor6DES/EdnFRIPdCTS6EaOBa/Hx8cJWUT9ShlTRwmSv5zfACZjew30V321WCwm5JU6vXBcqOM14p0y7b2fyDt1B+cLZZeyrYQnx1fbTtnWNO46d5yzNP2cuwpmTwAiZ9kMmKGAskF5pHzM5ygjVdlW6kM6TnA8SK6QkD8ejzVNL+fC4XBASgk3Nze1bSxLI51JtipRoX2tJNV2u61jpkQIyS/KWs65vKfpTPYVCUDWgf3BbA8kVOZrL9/LvtAxVTlT4pbOSOwrdb6hflLZUX2i+oJrMUl4JQi0LiyTZJ5eGj2o528rgcg+VV1EncK+U73G9rD9PCOX93Czpk5Q1G01OkvqxJ9z8oZrI52T9FgQ6is6+iihxL6nAwXrQV20XC5ryn/qE9ZD5Z06VcdFiTquz5rBgzKlxzrQzlAyUO0ifqbtXywWNY0126Df0T7guKlM836SxpyD2hbVPbQfuHaErskX55hmFtC1Y25vsb3U1ZQ/fk95c65lQuBnbCP1DI8hYpuoM2lvUZfSmZXjr45cShTq/GbbNVMA18ZKPs0ItPPlXLPlXC4X7Pf7ugZxflKuVObVxtGNMPv9dDrhfD7XYyGox2in8322r1jWftOjW5QI5drJPtdU4hwb7hnorKQOPNQ9XC90raR+4MV2KligG/8K3JS+oc2s+rtGWZd20G7g+sTyaYdQTtWBde7UwLqxjMPhMNHdqq95sW90rVYnO+6vVIY4jvy7ziM3LYf9oWS16lbqdOoAtfXZT9zDze0n3s/xpTxzXeI8+JBzD8d4DoZ+1ysYGoGMaZS47jNzthSZatNV/ZSNGGng0jRCv4IasuZYpo6mT+v+yzFayXRGqGt12RsfT/U4A5tvC4Tgq2OS4gZzXZ2znWUdi73LfUsGsFwt8fj4iNVqhT/82c/w49/6CX784x/jX/yLf4G/+su/MN3tPPqe+jjV81SrDdqFRjY5JplOWPpe+tHuHa6kxURM0lckOqfAXb03lzPECZrzF8JFvgE53nkgWLQPPIGmkvJWQR/ZRypQaOV00Ih//afAe0oRyBExmb47Hg+IY8R6uSxZPiyNeheas2ZGQtcHbLZr3N5sEIcBu6cH+NtbxJiw3x/wzbv3eHjc4XIZERNgqV6ByzBgOMrZlMCErOBgONf2g963SHA4ywii0UdGSpMobzLtvJDSBW/UtcGR1HWulhUQpn3LaH7BKJwDujCd07qmtXsrF1TGRMatRLM754Cc7Hz3yxkheNzcWsa0x8f3+ObbL/Hw+C3GeMLhaMfxxAQ8Pj4gnpc4OIdvvv0W/WqJT37wI7iuQxo8tjd3dt7lZcR+t0ceHYYIdJ0d95MQkR0zRiiR32SWasrlVlfFWSYylY0gYlubjmtlT7EwJTO1L8s4x+Lg6hppr3PSxMaiUOf6VPd+Vv9Geet84XFB9X7vJ4ScYiYTcQ38vt1b60/HBzj0sobN+7iWVcrQ9tVSZf+SmPJg2jJo9XLOcLE5PEzrPr33hXwHZSxbm0I20qAS4gDSOMJ1HilHBFgWjyoXkQcD2Du9b84/mdkKrtF7lcwUclL6V4nqXO71oJ7l9xaFbm2we1NOyOJRoGna2WelpijnSpTPn2d3MZlpc5ufXVvPHU71t+KVMcOn7Fvvn8uX1qvNjbaeNGKyRbvnnAHnkQvtrDjWvNzsOov4h9kSOY0WMR1HhOqAlvFOdOW8LLUr1K5TPTmpf3YvyOWUHL7W78/qn3M9CX3+/Lz8fL17JzonZ4eY/aTP57hPzhk+T2VXbUiQOk0JuIJNXtMjXt6pddd352zHx0wv96r8vfaZz6HK3rx9c91+rYw5ZgukqzKmcnE6OQyXC5B75MxMSyNSjuhCwGkYMY4RoaSUPh/bMbKn8xHvH95j/c0GYdEju4Tz6YjOB+S4QI4XBJfhi8ynbA54ug+s7QdK2ueGDaUMDKOOd37WP9ZJuToNXOsXOo5kHrWAtn5M9X15PgWxA2ejO1kHxok+zpjPlyv1gUUYm69Pbkf+dAsjFA/7guEkLLqucGk9+tCVINeu4CwBy2Vzpue63fYKqHYkr9C8EWq92R6WMbeXqNPmGarmWAptlfmz3DMqjqGcU30f2uxlP/JZ7jm4zyN+anhUDx8W2G7XuLm9Rc7A426Pn//iC/z1X/0KD+/3CN0KYeWxWPU4pIhvzzsMlwGXoeBeAOL7hHG0PZFli7L2DcMFoeuwWi7RdT3opLnMRuCnbKnIEzJcb1mxewamjRHdKGdo+5Z9sQsBdB/TwELuY5yjK1LDMSyn9FQPzPEhAGV/UcbXOztmjkEEqr98rmtfMbdoidVyLeU/bG9YbLAUI8YYMRRn2jxGnJJ9lnLGmCJ4FHZMSY48AIaLHQuldcmztTeWjA0fuj6aGKewMgpDoxMZaUAAlIsl01gSbLSF3dXN7u3tbS1HgUECdCR0KOBG0AaMY0snfblcauQGFfjDwwM05J+ThSAYSUQFmgi8MrI0BIsM1ohIggwkjddrS0up0YCMWmTEo3NuEqWkRpJGgTEtI/uOdV4ul7i7u4P3HofDAQAqcUtgz8iXVQUa7u7uaoQvwafVal0EqgFsGqnI9ivBMx9/Jb9Pp9MkFT2VjQLKHEcFJjW6SvuCMkCiUSeopt/UKDuWQ8CW9WD/sM8VNFYCTL2E9DsFxwnwbjabSlzzOwA10ob9w/doumFGl2qUkHOuAuKq1JjOnqTRHDxSGebc2+/39X3sB5bP+nAx4bs1Motlsf05NzIi51xBZL6PfUKQmBdJNCX8CUKzv1kvEsP8jOOoUbb6T5W0As3qIaZypLqEMq4potVzSBd4NeyV3OI40RlGCSBdRCg7BL+VNGFZBGP5rB2FsK1k3d3dHU6nU3Uu4vyPMVaClIQQLyWwOe/5XsoO+1KzcqisKamqacApAznnSVQt68C5zXWA/UFjg/OA8qU6l8Y1dRGdFZiVRAF1TSOrJBjL0shvygzbr4aBjjf/Zj1ZNkkPrmccM41OpP5Vcm0cRxwOhzpHSVrxey2TgJHOWfbfdrutssiobhLNb9++rfONeoOyzT5R/U59yLnAuX17ewvnXD3WgHM7pTRxwCB5n7PJ2Wq9wn5n2Thub2/ruxaLpifmmwPOR62nyiuN05TakQacR9Rfl8tlEoWsupGyw/dyLOcy0jZt05TwStaxLC1ztVrVSH2uxbe3tzVynv3M8kl8kWzV6G4lcXW9ULKMpB7Pfta1im2iLUbnEqbgVoIdwETns8/5U49TCSFgu93WeT/XC+ocxT5jOafTqWYs0KMe+H72m66/lH/acnR+UN2goCpliDqL5C3nM+tGwlkjpSk71IG6WdB1h+sUj+Gg0xodgbhOkgSlTPF36jO2d+JMWLzz2X4AVdZ1PUgpVX1bn01T72jqFK37drudOIdwDuj6St1I+Wb/cj2nfuNPOr9x3eJRKJRZzpu5Ex/HznZDrtrMtBHmdaIDCu0D1p/jTEc2dWygXUJ553rLvuV4085S4lbXFY0Yp6MR+11tBe436OxLfc7x4XioswDv4TymLiSRrWUrUKWbWF6sO9d9vo96g7qVMqokL+0xlSPqHPYBbQLqJq0P+4F9xTayXtQ17GvWn99Th1M++H6Vd8qrkt3sK+7XLjFNxpDPcp5rH+nRLLrn0PHfbDa4ubmpTm9qM+uapeu2jofqVZ1r3DfqPor99ZteD/td0Xf0mi+2a2Z0dIlUR7PZGDXJs6p77otTAnKCW0iWITpX5ebkMcQM+Haky5gGMBWi6hqXHFI0bDhnB+97LPwCfdchjgmn467IV4/tdoPhknHJAzIGhN6ybe12O4wxousCbm8treM3v/4cp8MJfdfj9vYWKwQ87vf49v0Oy2WP9XqJP/7jP8YPfvAj/Kt/9a/wl3/xZ/j6q69wOOwLSOeRU0SOQBpbdrDVisdvlCPDssMpZoTQjsDKOWO9XM2cMukoYWC+6fSImDCRgSojhZl1bkqUVFmUAIY5COWl359ecGB49q9rukHvnV8+e1zGAU+7PR4fH3A47JHziNXi1va0t7fwJb29AxCCw2q1QN8H5BxxONk+ZHcK+PrbHQ6HE56eHvH4+FhszQtyGsEIKuu/odaFJE+1D60DSpsFfJu1YfK3F7BVIqrqZ84ho4PSgbrOtn5pziP6rI5lXXuh/W+ELjADw51Ddn42ViR/JeNLGpHjBTle8KPPvoebm1t88+4dfvn5N/j6m0c8Pjzicj4hxoTRO6QckYYnnNIR58MFx+MFy9UWm/Ut4pCwXVzg3YjLacDDmPHunTnK5yhnHCMjeyAOESm2LA8A0C0CYhxLZJdHzgHIcTJOpYfRhSXGMcP7aKlrX7jaeA+Tv6/JJIqcXQP9dQzmZb94/+w91+7Rz1+bL4oxvFTOS226/n0GMDtHc7Zf0nq9VGdeHMNrWMbkOSf73/y8j9qzU0fglzAS5ObaMq9va0/6qD5z6XXZ0P7/UF9b775cXq2rMSVXv9NnxyvHi1y/frNjU671T127r97znMjT76+VNycy55e1LSO56+VM2p4LFT/7XmVjbr/Or4+Z4x+q7/zeigNeifznVfFlmK3C5z40v6/dM7m3OGpce3762TXi70obvCu23nVnDbvPgQvfvH6T3wvBq2Upvsp5PI4nOCzK8TMO3mdEXNAFh5wccg5w8Ih5hPcOw5lnRQMxDuh8AFNFw3mEsMDpbEcJnocRx8uA4+mIOOwxjgeMcYvsIuJ4QR4HpPMJYwiIlxUu5yOOxx0Ojw/wyDXDMG0iYpxK2nPfcG3MnrUZz9eQ53PI+veltaatb40YvzaubUyfB3HlnAHXjioBihOslF8MzrkUTI4BYAaPOu4oslP2vanr4JZL7J8y0noNnh09dGZzewDr9RLnzQpd57HdbMQJpKyBKcF3HqtV4+aIT8Vo7w2CcXkP2FGF9n0LajWy2PpEHYunmXraPmOAc8RVujomL9nEk/HJwHg5QaOcc8EcnPNYLlbC7/W42d5YgNNygdV6g365weEU8esvvsI3377Hbr/H5uYNfvCjn2C16M15zDkE34I1XHlPCAE5OQxxxJBHdH3jWFJpf+eDHVHlPVKMcGBgRcFxL2Y7Kc/kncOm2Oen8wmpOOt2fYfgJeNrkQPiH0Ahk0X2YrQDVogl2J7a+jiONk7U5cc4lOcS4FomZfJSNdA0N86BGNWY4mSesY4o9cupHOmRgTFGxOrlBmQ5pkG5DNVxUZzmKbd9Z44fwT8PXnnt+mhi/Ouvv8b9/T1SSvWMcQISmkqWERcEMwgW3t3dgWeS1bR4JRpXvfrZkVR+mjZXQUcCYQSAFEQcR/MqAPAs8pf3sxyNzGPHr1arybmVfE4Hkp8BqJvt8/lco9BIovB5jcRhdBQHUQFrkq68h2ngKbBM18yrEQe2IDH6RYFEEpD8O+dpFBbBRgWcWG8lvbTOSoIRXCUwqwQT36dRFxwvJYt0bAgqMhKboCzrRuBbgXWVGwJ4VUmJAcUxIcir6XoJAgONTKJc8r0kvbbbbU11T7BXgV6geSYBqMcOKFDL/iJA+e7dO8QYK9mhBB8jfZgGmUAux4/KgopjLqsESylbBCYZ/cvxUrCS48/PSM5x/ikJzXnDeivJrnOIcqngsxoKVOAEy4FGQiqJynpRZhh5qqnq+ewcqOW4qN5RxxW2R512SDYr2Z1Sqlk05gsz6zDXIbyHoC3lWkFbRtkwYwb/KWjPOa1zSzfvDw8Pk7pTPxGg1ygxoGUGUKcDlqVHR3CM9Rxu5yyimu/QhUn1G+cG+5lgI/u6GZktHTn7XeVC66XkCWWN3ytZAaASv0yBvtvtanlc2NVYVbBLCQgS9s65epyH6lE6T9BQUL2uZSl5y3pwjs4dWdgnCtyt1+v6PZ1oOD/4OwlW6nrKwpycVxI0hFBJV7bvs88+w5s3b2uaZerCr7/+WmSnpRzWNZw6SOdkjLFmuOD4qyOOEsYKWLJftCztGzpiMXOLOuBUcH9sZ9bqWqr6RslC6nc+q6Qn+1TnL5/n3FYdp8aizjONPtZU9ow+nbdb1wbaVJhtEnSdH4YBt7e3VT5YB7UHcs6VdNQU85oVZk6us03USSSkqG9pr7DeXJs1GwxtNMpCbU9p59ypzntfiWqWo1k5VAfQluB4sV816lhJBDqbqIMYCXiODwm4+TziOGtqbOqh5XJZz85VclHXBtaFMs3f55ltaBepHFFH8zPtK67xIYSayYbR45RrOl3ONy6cA7vdrtoNHBOOO21Vzmd13At+molDnZ3YxyThVf+zXpQrEtAcT83oxLWHckD7UMtindguOtJq9DR1MseYekn1gzpicG3lXOA72EY6U7EO1K8ce643bDvljXYebZ6UUnWUokwBmKzBvNS+4P2ce9qeEMIkO5Mei3N/f1/1szopqmMaZUUdf6j7+cw8CwR1BeeU2jbqJEr55Xg0UMnDw030NGWL71enNnVq0HFg+0n+ql2sc0Kj5lWWdDM+d07kOqryPO/73/Ta748yP4EGjtv+L5Ro4S5Y1q+6T760dO5tnZo6p8QYy/ph7brU7BFWdtcFnIPBdUaM0xHe0kk6b6lmvfcl5R8wXM64DJdGoKeMm80tjscDCl6FmHl0mB0Ftlgu4fwKx9MRX335JeIYcX97bw45fY9vHx7x9ddf235jvcDxyOhmj9///d/F/d0tPv/1r/DLX/0SX375a5xPR4uOcEBwQBoMwL1cLDLbuw5d8JZiPWcAVk+UlJfqnBdCALJHF5gtZZo6lLaUyoeufXqvysccQFWSi06svptmWNM1WIlxoDkq1fcWwN57X393zmMYTrgUEjuOzXYDCq7gXXWW2263E1s5pXb0zO5xj8PhgOPxhPP5hGG4WLRHqtCWAccFZ1b5teq5knLXCGQN95uTH/a3pf+Ea2nl7R7X2lciVnM529ddAVKtMs1pwbsrpHntr1mfuxYJrmNoZc2IcfvC6izEicsJwQHb9RKfvb3H09MjHh4e8PD4gMfdE46no53xOUYglDSTY8QlJhyPB6TcjhpLKcH5JS5DxFdfv8fpeML7d++xWC5KumMC/JYhIYSAHFPpfSAjo+u8ebZQXmD9nPIo/WJODd4Vh4NJPu2XSFbG9aLW4cV7PeViGumsQPhr75pcMq9QW3qtrnxfG6N2z0sEHJ+btilP3ittuFKGk8wR8mEtaF6XKw28/ld7/ZUn8uRr96xXyjfzDzPqk9N++xgngTwfinLP80q65zc8G0eSnq/1j8Xx8vFXiDFpCd/Tfp+O38dcH5TJ8oaUXshKIPsqB0zS6L/+Xj7/ylvz9eNV5nMqXynEudmZ9azgJIK76PFMp72ij5+1001ELCM3KSzPMsJ/vl5eI9trvTLvF6dB3iFVn8qDm8lEe1bX8edlTq+cc122VJbq+mATyK50Pfp4Xjf+/ZJDg9XR1TTi9dncRqrimf46Ya6f5ZyR8og4OjjXAc4hpRHLlcd+PKMLCwTfA9mIcdsPTZ17bI/XWRvhELoBT32ue4zL+YTL5YxYMoNY9glXSdxxHOHHEcMw1v39+XRCTrHuUdUxfk6SzbGJa+M1mf/P9Pr8/rZyzZ/l8/ZOs6lfLscudc5+af5DSprrrtnd15+9ou+IxzSi29o1kXXnsVj0WK2WWBTcho7His/OsVqbkwGzWMqKsenRTsR8WA7Hivaq1pe2re2rOnhPUtT6nI7vlPHFYoHFcoVjsUvNTrMMQxkrxDgipYwBCTmNWC4WcIsFvAsIXcBiscTt9g43t7eGPWRgPEc8fP0ej09nLODw47ffg//kBwjBosQ3yyVc8Ig5Y7gMOJ3OGMt+Ed4VT+GyJ3eWor0LwcjqYcAwDkAyktyhjFHZG1kK9NGOILhc8Lh7AjIQuuIYsjQc5nA4WGYvCB54vuB4POJ0OuJyvpRskrnaVyk1wppR1HUs4Sw9unOIMSOOEXGMlnXBm7Vo9jJKRhiL3jZiu2AQ2dc+mMpKhgve0tMXfZ7KeAcf4EOwDD4+ILiWuYmZi0LgcW12PJADqrPBsjgMcHHJ2dVzyqd7pA9fH02Mf/LJJ5VMVI9aoKXnJIDF6Gd2PIGr4/FcAT9+lnOuqR2VEGG0GoAKNsTiTe59u5dgpE56AkwK1hIsInFD8J3RTRw4/sw54+npCd77eqY0J6wCXiT9SVYqgMyJrmm2tc8UpCLhRsCGfaoALQkYlscoQCMcDaAhcYUioEzLq6SKRoGRIOL7CMRzg866MDJOFZcKGwF9pi7m+/XieCjQwH7luDDqjFHWzE6w2WxqNKbKH0FfTXVNgIobeCWgCHwTyNQFlPVgP9O5Q9P2an2ccxOAOYSAb7/9tr6f5AgjjwiyUPbZH0r8KiDKflWZJDnN8VLnAQUomSKX4CDL4jyaRwYp8E6gkX2iMkm5UHnmPZQBzj3tYwUNSdaoAwTlQp0c1MlEF3u2hQTMbrer72BbKScaRaURpaw35wTnGOtG2STJoU4XHBsCz+qkwXFgGwjKE0TlfefzGU9PTzXrBHWrkgB3d3dV5tfrddURPKOUZdHY4PjtdruJ48Jnn31W54eeUcx+0Gg6Omaw7ygzCu7zu3fv3tVxmKel5nybO4koKUayRqPUqQ9ZHp1PNF019S71khqaSp5Q/lh3JRV1vaBjiso71x32meowRjBSTwHNAUuJSsqiOmtQj7LvFbBX4576kOWxfE3vz40DZZdrRQihZhZg/7JflAhg//GoDep/jj/1wziO+Pbbb3E+X2pEP5/VdcvWn2XNekESTucs1y7nXNUF7J/D4TB5jnNTDXI+q7LG9fOaM47qFDWMODa6mdK20OFCiTWScKrfOT9IEC2Xy6p76GRFmdVL360Rp0qAkZzh+LJ89hHncHW4yC3lMW0djVSnTKhDIh0I2BbdqLBO1EscY/YT15ftdlvliXLDPlYHIX5Hu4X3c/5QpjlWul5pZD/LBqaObtQznKcaha91UEJIbUbKEuXtGtmn5VNG6bTJvua4K0nadR2WqyXOl5b2mm3leABtC87+0frxdx7rwIvjNr+PtqeWz3VInQeod6kbqdfouEedQptAj6ZRkptOEOr4ammMW3/SRqReNP0y2JlTYeqoqiQpx56bdPbvdrutc4Hzgv3BdlHnKFl+OBzqvKP9SzuN8s9x5jNKfLHdx+Oxzlnac/x+tVpVh0gFA1RHKYlLPc85rMSvOuRwHpEEVjBI7XMll3Wt51zgOJLwpo3B9tLmUTKfdVcbX9+reptrPdd53TNRNvk957TOM+0nymqU9WRCVM2Ib/YZbVU+o0dLqM2hzijUHXqUhtq7tEXUQUr7hXKiTj1qy/+ml9mfjZRue7RYZPuM4D3WpV+559BMDnXOwsB0znXnHPrFAqH0P53K1iUNukOu5yPGVOoQDRCJMWLIZc32Hl3pl/P5hMtwaWtN1yPGC4ax6GqZW94Xx4LOolbfPRxwPJn97UNAzBmH4wn7YheGri/pMEcAJboEwM2be/zWosPN/R1u72/xq1/9ArvH9xjHAS4acD9eRmuLM+DEO4/oInIun0tKzHEckaOA8Q4VTFQ5ZDu4LlwDJ18DZNUm1Lms9dD79F7dhxM0VKxhDmg65+DhcBnPuFzOGIaxOi7EaBErdvZkO/aIGT+GYaiRW/u9pebcPT7hdDZAcIy2bsWB9roRTNam6To1qZ9z9dzdZitdIyrljPXM/tD+FIKTPz1J73JWOYnQcr/1VSOOCRoDc2K0pWxu/4w8trGVsaznmbv6GfhqkiwpIwQPh1uczkfk9wm73RNOx0NxMBiQ4oDhMlhEUcBk3en6Ve2PnBJcWOB8iTgcnvD4+Iinxz0WfW+OK5IWPsGj74KlUpYkoyll+NCRnYaHRXDHNAKgnnVANkDd+wA5sfwq+cvRY/Mnn79wP/sdTklb69NqJbXpiHnJkyKzfj55aEoJu9k9vMOJw4RvZ51frfMzQplOEajOFa1aGUizrFpCnl3tm2tlz7530455dqVK4Lh6f8vqrb09i2qd1c1+ETLoJT44z750+o55/fPsO6VOtUyS2trfz/sjY6prpk4LePbZS2SWVfulBupNzyOVXyoz5QxcK7N8Tg3krsjatbXjY+p67eOJfprVeapTX372eRM+HH3NMvW+6/8A6kvaK9N3KXEt90/Kts/0menv195n8p7RPrvuHCLluNb+1/qkVG4ysvY+/UzalJ65JNR7zCRztY/0OyvSiOsJMT6zk+vbUgKCxzgkODeWbCJAFzqkmLB7fIfT6YJxTFguF2VfswRgx6VYtiElyRzy2IIzLpdmj47D1HE5FwfJMUaEOM0+HGNEig2rpm1/DRtmma/J82t2mF5c85stNpdH2gTswdd1CL9XLKjVozlWOGASCT6/l3UrNWqfXblX28r9DvEt70O1C5xzQHAIXYflYomlHE1omNOUv2I7OD7OTY/Gow3KfZDinYoXVscNN3VQmdpYemRQq4PiHuzTMSVLjlWisDMcxpgA55HgzZYZI3yX4EPAarXGcrXGcrVC1y1wGSK+fv8eMSaMQ8T5eMF+f8TpkuD7HsGHSgb3i4Db7QYu9BhTwvFwxP6wNz5AorI5lsuVBcMFb3ZoSiVLV2pn1Y/RjqUyDNZhjCPOxxPOF3NeRQb63qLZgzeC+HQ6lzEAQolSvwwX7Hd7nI5HjOeSrcc7hM5XXa5jSClqRzuVPUXw6LpyX7RzOBoO4eA8yl6K6zH3VOXc8WBHMnnv6oklvsjfouvQB8ukGMdo55mX/nWwd5uTa65OEZodLkU7BKsLdhb6ZtGh77pCumtg2twh9sPXRxPj3DxrNIpGJRBUAlAjE5mGkkQelcjNzQ32+31VYAq+8TNupgnKMJVe7ZRC/uWcJwA9QXYlzueAqxIpBFX1fEmClufzGW/fvp2AGgQ7lCgmOUnAjZOWUdUKSGgUBAFEXew1EodEBpUPFcA333yDnHMFhe27jM3G+vr9+/dYLpc1hfnt7S26rsfT064Szl3XTUg9nhHKzxXA4maf9dPUk0p8sT8VyGO/sCwlqZ1z1TGBJA9gAAnPmSTRqtHIQAOONdW9Rg3ye7ZHI8Qoa5RZBSBJehG4JWlERwQF0/iTkdAkaAiUMy2/Ru1R7jQKjOVTRgiWMv3rfr+fnPn59PSElFJ1FmAqf5JWOZtTR4yxph5+enoCSRguWkoi6mJEwJhzSqNnVH7Yj3NgSJ06gBbhrY4cBENp2JAE4TznvCCIPz9bls4sHHv2r0Zlqa6gDGu9qCMIiiq5SPKXgBT1DIlltpvjPgeqCCIRACYpSoKT/aGkO+vLdqxWK3zxxRf45ptv8MMf/hA3Nze1ntRtHA9+RjCYuocLCduq3n/UKex/tv18PmO73VbdzWeo21hHfk7dyvEhwUFZpy6lQ4CS0pR7yhcXXXWMIWE7dyDiHFdgWmWadWVf8W/NIsK+UWOuedK1NMX8fBgGrNfrZ6Q1IxhJ8LFt/EkDjiSErkdcW6n7SJIoIcDPNZKWMk2SROtPfcVx4Rm/umawr+jww37iM+xzAnHn86XKB/UcZdt0SKprCck4rhVsy/F4nIC8mp6bY6EZGNhX7A/WV9P+K1HBNlEWFotFzerAuUhZ5lzmZ9S98/WBOohtom7Z7/dYr9dVBwAtVb6Sd6y7ZtihHeJci/ZX+4o6i/N5HrVNWXTOVectFD3GflRbhrKi4LgC7poRhuPGNVqjskmQz+cFbRXOc7ZD1wjOWdYxhFCzYlDmdO1Qon1OWnG82A98p+pCypiuS2r7sQ/4vMqlEh/6DOce+5e6aL4G6DvrfB8zfPB1DrHfaAsuFguslsuJI43aTnrxfYx8VjuM/cmyacPQiUidGFgX9hnXHeccDodD1Rea3WRuV6s+4brOteZ8vsChZVfiuFHn5ZzNM1psXM1IpQ4QlEuuJ9QdPGrk6empOpjpPNQzw/lOyk3OLYPROI71CAnKGNtH+5jzg23hmsLxUHkhuUrnLso07RmOAXUIQQjOe2aN4X2MhuffepRAzi36XeVX5ZG6nTKlupm6mO+mranyRjnk/eoow7ZSB+r85DvUDqeenttmXB/ogM3v6ciA3Dzd1VmHaynHknpSM4Owj+icYWBdiwjmu+hswDnI93H8ODYKFPFSRybqD10H/jbXMHAvaYBKxtQJotqecBVsGYe2F8rISLFkwCogbAadnAP6mBE6S2l3PJaoC3ikBIxjc/Rmf6aUMJb+OMcRKcUaZUx7N8YRXd9j6RwCgPMwYBxGOzfPMQW8RRDAOQzjiGEcsT8eLYocHofuhGGMyHBG4qaMNI6I2WEMBsLknHEZi2PlYoW3n34GeI8IA5KOh4PpL3cC0sUiwsvFqMn6X+csGBYGPOWcoFHMMT8nQn0hkk0/AMjpeYQdpoDlfN81/67Wz7kKrs2/42cNAKXdWzkWkIQYRwPFnHMI8IUYvyDGETEmuGzZAAwYs4gO771FuXQdcso4n84Yit7Z7S1S/HQ8YBxbqvmcElIcn+kg57oJiKztc74lDo5l7sA1souP2b0lArz2f2uj/gQA+GRt9q5EOZf+KlGKzc6c9jdm/e9KXXIW4sozQoVllvuBCuDW8pW0LPennOF9h2Vw2O93OJ0OOBz3uAxnjOMAywA4YjidkBY9OgSb8ynhdD5h5YvzerLP4DyOpzNOxxMen3Y4ny84Xy4GRlbHCRhY3Ad4JAMdi0wMY4Ibk50Nn5NFtAePnIt9XrulZGkKwdJVV0S/RcfPL39lLkD6tfYLR6KWhSouHPdpEc/f9ZKe/U0+V3tfgf/Xyvmo92QAV+by/N0vPX/tu9e+5xVzfPa9c4WTrmMxnQ/z9tZnXYZzJevA7HWc5zZd6HiCF+XDLnUenvfxa8Qtrvydaxnz4Wq3kVC8ft/rZV+/5hbBS7LyWlLzKkdX73Q6JZ4/awVM75D58/x+YeMas1vrMdGl1182+3AaWZ3tD63G5NG278/1XupnlSESk2Z7tM+h9+rvXtZTcep4dlFvX/k5r/NEQNxcEwlZKW1mGVUOyjxrVRLZm7wzQ48geLn6SohPZVT7jeKb0Ugu510hR10lY53ziCkheI5/xldf/hq//vzn+PKLL/H0aE7En376KX74wx/jzf1bLFYb+K5HysV5CBnZA3QkIDbAfcJwuWAYzQnRiMOS0nsca+YaI/Sbs8DcllCsQOdms4NevvT712xytQ2ulav21kvlX/myjWWxAZAton/+vnmZ83oXCamfeTSx0/v5U/Ec2/d01f42GSjnPvc9+sWiRfKGUJxdzcl9aqs2Xa927Pzdc0dz/j4nt6/1HctLabp0qKMEbZuKB3Nvlhkk64sdFIx43nRYbbZY9Cv4rsMlZjwdd/jm3Xs87XYYBsuGMFwixpiKbIdagZQj1psV3sY7ONdhGCL2+33dr8ccEcvewTnDPzbjBj3PEq92IbV8O75qETvAO4Rge8/zOOAyDojjaLrfAxg8+mDzlvstoGXXdc5hXI6WjWFh3KvZ8tMjI2WTUElxHq/jy5jbPqjs5QuWQzLa9Ex6Zps5lGjvinP6uv7ws77rse5bxspkD9rTrgUJZ7TjfDRwkvOf16J39ThP5xyQ7bgg25OgOip8zPXRxLgCpgQNCFoRYNJobIIe+/1e0jwacPD555/j008/nUwikilsvBKQuoE0ALGfpEJUMt2AEWCxcBXs5IbeuZaCke9TkEwB4Bgjbm5uEGOskWwAJkQawcJ5OkG2V4FNAiUhWMSwAqPsU4IqjJZU8oiRpAT8GI1CB4TTiRGbFt2fc67Raw8PDzgcDlit1lit1hNHA41IYT0JsrCv1OAnYUIQhu18Bs64qRODjiHHm+1jXQhsEyAkaM26kRxguapUWQ9Gr87PfmQbdZzYtySdeGn0GQkSOnJo+g4CiQTaCBbrHOCzjPRX4JPEDMFDjepkP5IU5IL27t073N/fA8DkXiWDCOixLl1n5xKzTAKCVCAaycLnCJZzDhEY5NzXeaXRMSRhVE/oNScglEDQ1KK6SPLd2kYFiKmHVAaBdsSDOnsoiER5nEf9sP3zurCuJAYoWzzjnWNEwpjj8vDwUIkB9k8jDlpkML8jIW1zdlUjq7bbLZ6envCjH/0I3nt8/vnnVd5Zf84hkmKLxWKS2pPv0Uhrto3RmZRfjfZar9eVcFBgX0moeYQ120gdouQBySSC8zrf1AuU0SlqjHE8SILc3d1VeQghVDKd+oO6Q/WSzi/KqKZJp16eO5JcLpai5v7+fkJGc47QGYXrizoR0MGHcssy2e5qIIhuIkHD+3kUQc651pdEP9szl3+OE/tO52RKlvGE6ZRJoPE97I+UMrxH1cscPxI2NpfjZPzYD5ybWk+uuyr3jWBvTlbaN/MoesoZHXVIAMzPnuIYaKR63/f1jHXWX9ehuYHO+aT1JnHEn5Q7tQfUsajruppuWgkd6k7n3ETvqHyaXtggpVg3NVWmCxHSdx7nMtc43upkoU4ZZjcxwlG95VHvVcKXcsVU65RBddChTuHaojpeSUG1k0iGcR7M1yO2XUl72kgVsC5zWs9xVlJN9T77WecYZVbbq3qeelDtTOoZlQeOFddr6j/q1GEcsPDtCAuSdFwvqXdWq1WVHeoQ9iXnyXq9xm63m6z5tFs4N6hr+L069iixqDLKo2JIBtOGJ+lNRzs6AN3c3NR5SDtZHZGGy1BJbh4zwXHkWLJMRiDS6U11AYk2dYClHtW9Ah0o1Q7l+NKBSZ1ndL5z3qhznMoj7+E4c/4pUKsy6r3Hmzdv6virI+b9/X1dl5l9iHPqcDhM+pVrJB0CKFuUe3Vu1IxI6mwzz7ii9jn1EX/X76k3qaPYFvYn127ag/ye9+p7KKsce7Wz1R7juj23Fxi9G2bruJarelTrQ4cZrqPq4MnyqSupz/i72oWUHT2CQp3UeB/li32l9stver1/94AQuoLnJ2TQeYrrpI3Fbn9EfNoZQZlaBI8v7biczxhiRIalTvQhICWHeB6QTwNistR53jvsTxccz6MBH84XAg6176uzWgEwrH9jlUUA6JNDzg7DmOEicL5ckFMu0Qg9FoseIQIxmkPKMI4Y44in3Q7H/QlPT2aX+NDBd+X4o2jEXN936LseDh770xHDOMAH06fLzS1+9JPfwXq1wcO7d3h8fITzj3A4IA4DkGMB4suZedAzoIEuJaT03DlpHDUrR4Jzzek0FfQue1fHB05I1dl1TfbhHFyWlLpuBsIL8OhcAUjFbq91zRm5zB9kixZNyU7eTS4UQrxEXuRczhDNNWLD+QAXLLW2rU1DidxK1Q4+HA6IaYClqSxZDJ6RTfybOhdQgNVsGCAzki6lSdu0r+CEiM2TH7W/IH8nF43Ag4NzzcmZRdX3kDy6gpNbuVPyb2571DGs7PHzKJX5/akQ1nuf8fT0gNB3OF0uduRKtBSXw3DB+XwEEOH80voyRQyXC/reiIThckFY2Zzb7fc4Ho84no/IAMZhRECx1RNTp1pdugD4bCmnu9Ch6wodUzJQmA4ohLAr4HTWI7IsQ0HpEemb6d+vXSoL7Jf5GKiscxwcw49aSVfG7nqk65VavHAf7a02nqVGV2jbj2tvu/+F50Qm3dzJA0pKT5+1rmnEtnNt7sE10DrmNCuz9G3W56cc4JxYrPJcEjDM5119rhYyi6N+8f7YajTTlfqOaw5pz+uQi05/Tsbo36+Spi+U/9o6Hmb8+VxSqj58RTDnOmV+zT/T/ao++zH1vXaxd1VvPasDSKROv2t6f1qfl+ox/+yluipmoWvmtedyzlNi/BVZcvnD/fOSfF9bb3LOz+RXZSyjOShck736mQMcZuM/nbLP3nNtLOrz4hQRCxntkmvHgRQdkcG9b0DwwH7/iH/8//rv8M/+6X+PL7/4NQ4lu9zv/PZv47/4n/6X+OGPfxvf++yHuLt/i7BYAq5DckZAuuzgM0nZETzqlf98jrDsR3Q4bUcPtna/rFt0H6mff5fr2v0v9eN3KfsluVa7jjYaAKQx2TpTxuLa83k21nNifPLrlfmhc7KSlZJJxuWERdfDB49egoZsf9TB+87IYekj08UNE+F+eI7Vqs7W/bYG47zUd9bW5pTrC9ZCDCJ0HUIoGVNTQo4jYkRx7AtAtgxXxqNZwOjm7T28Dzidznj3+IRvvn2HL776Gu/eP2JICQ4lmt4bOZyzHWWTM5BdRug8cu+wSiNcyhhOI07nCy7jUJ09aP/3ix6r1Rrr5coIZe+B4pTS9Rbh7LxHgjmedmPCZrNF1wWkGHHsF7hcBniYzvXOoe873BR8lc6ZKed61jgccDmfLStR+dtSks+ctGl/+ylhbnPYxp2p8MdxRHDeorLLWFukux3DVfeb3Pt7LyrLbGN1rkZxwHNF7vNoGSNSssxjIXS2FxwaBpZyArI5h/M9xN5THhGCLxnGEk7HE8YxFWfShgN/zPXRxLiSJQTSCHKSfAihR9dZOH/ODovFCjEeMAwEJ/pJ5IVGYxLQUaCfYI1GARA0UY98gvPcwBog0iJAAUzAQwrAdrut4D8jEhTgJEFGIE4nPEFLJYsIbhFEZ0rNOchjuf+NhNputxPShOAj20YhWq/X2Gw2z853Z3RPkXFcLhfc3HyC0+mM0+mCrrPo69Vqg7dv304ifAh6acpq9gHHhe+hYlMig0CRgs7qFMD3rFarmu5ay9LITraR/cXx0oWP0X8EodgGEsQcR7aDgBUBSQCVqAOA7XaLzWaDx8fH2lYFzThm7B+dCwRkQwgV4Hx8fKwpSEnO932P7XZb5XO9XuPx8RGHwwG3t7fVSUNTTKusPD4+1rYPw1DHX8eDcvb+/XsQJNRo9rlnnQKrHGuSaM65SgJoFCF/brfb6hm12Wwq2UI5pRwpKKoAJf8pgKNkIAk5nXNshwL5JJjU6aLrunqsgcoVLyW2lESk/tGzcdULixH7b9++rf3H+UuwmkSJgq0EatmPXhYfEhTaJgKJJBxOpxP2+z1++tOfVqLq888/x263q1Fmb968wW63w8PDA96+fVvfyYVEow9JWClIzD6iTuZ4aBmck+xrPROWfUUnDwWyKROqm+dRb2oIbzabiYwoKK96QIFKLoqcO0xry/ppmneNBibZpZGQfIdG3en9SiLo+UZ8h5LYWhZlXdujsqvkMecPn2F5Sr5RdkhQca3heHadpc3WvuE8IjGjxijTqVMuWDbJuePxWOYizyYFQrCze6wc8/jlnOLcp+4hyUCnII4n5808krqRGe38VtNxucrw27dvJ0S2RlRT5wC2xjBiNMZ2PAP/LRZ9kXdLF8kUllZGqGc5Uz4oD9TzpjdRx8+etdQ/XReQMzAMRj4zSlHHXR1L9CzzOaHifMC794/IoMEKpOIFudyYA19MjVimPiTxake9BAxDRAgdjsdGlIVCjBiYFIud9DiRS9aZY6m2zFyvq21InadENfUS9T7XPrXjlKSjPHEeUnfp3FEbRG0SzlElO5mRpureLmCx6KtDQF0DvMfpdES/WGC5WkzsVefMs5ZjR/1q6arsTF5rcwHmPbBcLmpEct916MS5pO97nC92NqtmCWBb1KDf7XY1sw3QnDaoF9jfmulGI/zV2YJr5e3tbe0Tyl7OeWILkPQHULOpPD09VefM29vbSi5St6/WSyAD+8POxpObW+eRkQBn8r7ZbLDf7yfEtUbys89pv6v9pdHh6gzH+ygX6ijEtZt9qLYA9Snfy2MJ6DDE6AfO0+12W+cJ68W+pE6g/cb5TKcGAHh4eJjYQxr9r8Qr30nbWIE/1pdzQu0i/lRnSJUr6iHOJfYbnRj4LOfszc0Njsdj2Vesap3URuY8VOcmdYSivud72W86rylHbHedd2F65BT7jGsHy6BMUKa5HqitrzpDnXM0O4DqDtoplCP2LceB9+hPdbb521yP+8NM38XJnrTrrF/2h+Zcpbqbsn48npAy0HULYMwIOSNGk+kxxhrNbQCLrxE71MnaJvZpgTgKrkfCvDjCxozj6YKUTug9nQbMhuj7jP3hUp1enDOgJLnirI6I05mOH0AshE9GBpJHTsAQR3SdgU8okYLOZfie+/xPEdway8Udttsdjocdnh7f4XI6II5npGhOAB4dgHYOe84GKrnZP810oKQEZcYAo4JTcm8OIDsHJ05f9rWrzgv82xMc5U05TwFVeZ6RMTlnpBgR6yMlO54TsqsAhyllZESknOBzgZ5zi8zqQl/O5rN0iZfLGafTEYsyX4lxjOOIy/lUdLoR7CjxHc4pCWXZhHJu/Ta357OF6EPBYgXFmx4rxC6uRA/zTNvydyoEg/XllEjNJA1Lj7Ke1y7nzOZ1dSD5DGbPNHa9JoN/hTiMJWuBSwMOhx3W2xs7rzFGnMsak0b72RWAl/M95YgxDjhfTjgeD1je3iDlEefDEcfjAZfLUPTWgOQjmP4ccFguFhiGE3aPOzw8fIuHx/cYhgE//OGP8ZOf/BSrlR0XdDwwc1Y2oNyhOFHYOA9jZPdOrtcpjas93Ajh1r1CHLUS2ecaqX/tyvk5aXe9loCmZ53Uavb8x+rvjyFQKP9zsuNj3/ld1hItl/LjXug/EuvXBk/3Qc6V+Zef3/is/S5fcSV4fjGjw9V6uVqzq9fzfgOmY3y9njadn2foeFY3vC5vrNvstdefca9HjOszJPevf/c6qTcnmz5GZl7SgteeTVe+e2ncXiO++Nm8jq/V97W2Z2RcOU79SiHTtj57H/V7SuSq5VFlp9uv/Hw+l/X3GKfnUb8w2TCREtcypKhdkG3RfqZLpkVlWww/1Lc5I6aI25sNXI74xd/8J/xf/y//Z/yzf/KPQX+vjIwUM/7iz/8MP/7hj3A8nLHfH/DDn/wWfvjj30KKA+BKlroMBOeRs8cYSxr1QorHy4CIhEUqZGO2s4xpZzIT0RgNw8qyP5tfc/02/+67XPN+VKzoQ8/N/Baul5FzWTPnuj4XuXi5zvN5PyfGXZGFD7WpYQnFamddsu3HnctYrhZ1r9iXCPK+7pGAGPUIn1Y/3avP+SHFZLRe3L9pcADLIJ4O76pM5JzL3wk5OSBl+GA2l48RvTdbsutC2Z8aX0Z8vu8XeP90wq+++CW++PWXeHh8xPkyoOuX+MFnP8FiuYT5/zosnK9rXN/3CJ3ZxBlAv+iw3a7h0SGNufKACYxktjYwg+a6X1rEeCgOpwBcMMwrlL6+XC4YdsxS3AI6h8GI8XEgCZywulnXfgMa1sl9ft5sy76jYObDCOqUOs8k6BGu7X3Guu5Y0A05tjk+PgwDLoMd+UPeYBgswr2Ob0rV+Xby7pwwOh7/2LK0cq/uvLeMCgk1u8RLTmApJQyxZCCrDhptj+4LYU5s5UPXd4oYB1qoPsENkqEGjLczy9hpTKtu4EcDXhTYcc5VwHC3200Abr6bZa5WSxgQHytxRnKAfxuJ0yYggRBGH3JgCLAQ7GNZGhWhqV77vq9AsILOjAamInj37l2dhPv9vk7mFlmXKgCrUSQacU8yg+eaKjFDQJcEBhWUCazH4XCsJBQAO0ehpP5TwIlpvhVU0ihJChGJZF5KGgINvFagiW0isKWOBnyfyhEVANsFoNaPY0W5odwx8lWjtyowkVqUL5Utx5v/FEijLFL2VNmo0iaZk3OenM2qID/TmDOCjpkHCFLnnGskEUFhjSCnTGp7CHoqyMd+ZSpdArQkJ1gW+5ftYL2ZgWCz2dSx4EJIBwkFnruuq1GRm80G6/V6QhBrPdn3SqLo91RqKncca36nkXKM4OW84Fm/Dw8PNaJa56RGc+Wca9/o+bYcY7ZZZYx6RCNN+TtBYpbF9qzX69oOgu7e+0k/cZGkE4XNz9WECKLMsc3UP4fDAd///vcBmBMG201wXp2L2H/OuZrC/ebmZhIZxbJ1bKhHdRzqQlV0l+ox6i+SFuxHjj0zW7Afdrtdna/UDTSC5kA3x5NjwTFg+ZRxgqosjzIP4JlTiwK8vCjTSvzwnaw/P2Ob1GBhf1OelRjX5zRbhDqYqQxSv3vvJ5kIOH81ak0diJTsYrnsJ4455y/7mmsdy1dnBZLhlC+Oi+pSTbXOtbKRyr5GArM+1FPqYEAZInGixJrqEOpX+xyTfiHxxPmtDi3UZepwRAN2seirziXxoiQLAWDOWXWIoNwdj4eJnk2p9SHXfsvgMFRirjnvxUkbtQ5ce6qjRXbYXU7FwDcSLHR90WUJXdcjpbGmbgZQj9ygw4i9N2AcYyXqra8czudLeecFJPaVLOP6RH1wc3NT1zPKL8dtrj/Yv0yTrEa1jj/7RmWZcsJn1F5Q8lPlTjdkWjcAk/nGuUMSm33PevmlnXM0jkN1kFB9SZtQNxckkDm+nHfsx/P5XOcW1xXat0mIQ9Z9GIZKFvM4BCX8FosFHh4eat/rWknbgGsTZZbzjzb0MAy1bNaT6yV1IvUt601ymWOgtoo6kVI/XoZLbX+dX4ehjq+SvbR9SPjrZox6TdejYRiqDaM25XwDVQHdoou5XgOothrXptVqhYeHh8k+gBkwlNClbp8fh0EHv8PhUG1F2tNqW3MsdH9FXcN9COWMepx2EGVeHUnm+oX30YmX8qEgZIyWFYuEL205jifnsmYG4B6Gepjn0eu7dW3RNWEeba37B9Uj1H1cK1erFZDsPDK2U/eKaivzb9oulGOd99yD1PnumzMjj0HSY8HYLxwTtpP9PnfS0T0Iy/7bXN++f8AYY01FmVK0KJ+cC7hfskTBYdH3BdMtzk/ew+2PsvZ26LqMdDDbJhZPfMz0SOhXBlCU88St3Qne27nFbK+LTH+J2h92BnFAKsBSisA5xXpmb0wOw8VI3/MFiLGQLT4jIcIjIDkPq3Ih632HiFRAxALj+w4ZHufBwFhvfD7yMGAYB8SLAULeL3Bz+wlWK9MVh+MOl/MBl/MRp9MBnaOOHwqA6eFCgE8RyKkCmhxPtvMacGrfc19psDrvdQVwN3loeyTKqpZVbaEYJ3OW71DZn9u2czu36kEU7wJkixHz5f0lCqPrenSi66tzZbElLuczhks7xkjBKkBTu1p0i2db3TTzS70r50L6gl4Pz78HZs9Vhrrdx7ZpnEq2bAXt/va9Dpn3L0cX51ynRn0P5C3Ta0rX89kXC0bCODqcLmcstzdIsIg+2rspATkxso7YxwCXLTqIDr6mwyJypiOeRcr4YEcYsMIOCbuHL/EXf/Ef8U//6T/BL3/+N9jvnmxdWy7x27/zu/hH//B/gp/98d/Hj370U8QU8fj4hJgsHakPdlZnztHONb/KBnxXalz2ZxMHBinUTe8nIXCNcK3rfp6PhhQng53S8/TiVs60zN9Ef+szc5nO+flc1z3j3H7521y1XBmv+usVAf04Iui5c8q1Omf3elm8P+ePi+b6mP4olM+L9zZyqUmQ2onPyvsQ2V0/v055z+9/rQ1zmfjQda3Prz2ne6oPlf+h8Z+Xce3+5/Mpv9jHlVSeTLpWjnPuGZH9Yn0s1vrDffeR04rLh7ZQVrvrz1ybB2zbvK+u8fFXbpu9YPLzJf3U3olKoAfna/+4DCAVfZrtvN4uAP/qX/4P+H/+P/7v+Bf/7J8AcHj75hPcv32D1WqJYTjjr//iz0rrI379+a/wtDtgvbnF/Zu3yOXs33L0sGB7A2JJCT3GEd5lZDu3A3Y2eVvjGH1q/yKy7C3ml+rNSZtf6otXu7WNm9od196p34di30hB9Tuzz1HaOdU3ar/xYh+8VPemuzD1S3plfszra/s2O/+5YYUROUX0Xaj73b7v7Qzu5arstQJ0JihmYDxALHuOKaal2D6zoNJe1eAo5QwANKy07xBTqg6Zfd9j0S8nAWeLxQKLrsNmszEMtesRAp3MgWEYsTucsNt9i8PjgPEy4rM3n+FH3/sJQtfbfiZ4hK5HFzpz0C2OGT6X7IKFdE85GRHvPcZoNlfoPULvAXSIxYnRwc7WPg8XDEM5AjUYeRuIe6YWVHQ8HvGweyrYnAVfuNIPcRzNYfJysXcGw04WBcO4DAP2ux32+0N1kqY8DcNgwVvjpZwBXiQlmY1uWSQ4D0vgmbMsYQ52lJOlhgdCF+o56bT/vXOWQYZyWTJ22C5o5iRUxqvzHn0p3wWPRVjVOZRzRmBf+Q7BT8+4JzdFzKfr7KAh23P4EqW/QsrOgp68fbbZbF+YIdPro4lxCh+9EeaROUYYtpRyBJoIDiyXS9ze3iKEUNM1EiBREIbgm0ZPMSLWiKgR2+26gpFzYIRnoW63NxVkI/FIhaCAC8tWEoHt1SgDRpQTOKfAkfThwsR2Oefw/v37SgSpEvDe1/SrCnYCqPVhP97d3VXhIxjKd2v0M8djsVhUMFRBGQKNVMZaHkFrkghUPlRsBJPYhwQpCUCR0Key43dUcHwHAUl+v1gsapQ8HR+ccxXAYr9xfEg28G9GsLA+mspVx5AAHCcTo1wUZFZSIqV2bi3HgsQe+13rpbJKUoIKnkCgRskokc6IcSXPVqsVzudzJTOVtCSRwGjR5XJZI0EU9OdnBJkJthJMZf9qlDzHRIHNuYGn0adPT08TBUUCkXLD+3WMOOcVUGIfknQlUMoxYF/OI231GAOOpUZda6QO5Z9nkFPWOW+2220llb/88stKcFBe6wJQwFT9SZJd38828nPqEZLZBL4J0rJdrPcwDPjxj3+M3W6H9+/fw3tfDYrj8Yhf/epXGIYBP//5z/HmzRvc3t4CQCW/qfM4NnTUoR4nUcZoWuqI3W6HxWJRiWtNfUvZZ1s4tuw3AmnUs0yLqwQw66KeYYzC06howAD4p6enStIQnCdwq+TCMyLmcsHj4+PkrFIacdTRLIdlKolMMHwencdxIOE+jxjSuapEDckbygbHW+VVyQFN9cr5wL7R9YLy+fRkxhSzgqSUsNvtqhML9aX3vpJzJIGU0KDO0jGkfkopVbJZ10ldn9QY41zm5zrfKfuqe/VceiUZeOmRLHwHx5Rl6trA95Pc5nc8eoAG/vQzTHRDjHKeqpDzShR1XZNZzhPO/dvb23I2eyN4OY4ppTo/lDBWp8O6qUyoMqngGTNJmEwIkJ7bGVw3Nze1/t53df3VLCGszzhGhODQ90tYil6LHAsho+ty2SC1s3ZVNiiXanvohl3bOHe8YTkk2pQM1/WC7Z+DPCxTI0Gpo9mXHDf2hcodz0OifFKf0XmAz6lTHddCtoUOV0om0iblXNG1kf3Duc7PGKGsumW+VnMj+NVXX9X3qY2ufcKje3iRuOWYaKQ3HYOAdlY0CVW13+iAwnmidlRKqeptPYJAs2zwWWZF4ZEf6uygDk6sjxLv1G20WzQamBkz9H1zwIH23H6/r6nLWQadMtV2Z7uV9FWvetpZqrNzznXNp3xwHuscJdlOHcK5zf5lW/geri3cS2lENf9m2dQJlFfdN7FNmgafa4Q6PDAzFseX66BmkFDdrXsydabSucSxZJ9StpSo5l6g7jdKJjDacKoz5u/nGKjTDOeS6hs6knK8tP6qX1g+L7V9OHf5vc7/l0DL73p9+/BgYxotO0hOBkA6mDd8CECXPeA9xtQij51zyM4V0KpkkUrAcDob8OEwiXDNMKIwdMxMZSk3CYk52C/1HEjA2Ogcyneunl+Z0c4PTdmAPBdKJhRY5IVzDmHRA6OzlOA5AwiWbjY3R8OMEhUSOvRLmWMp1VR5wTsAJXX4GBGHS035WqlRH7C5vcdys8UwXHA6HbHfP+L0tEMeI5wLCMGIUu8cokvII0pUd57Ijjo/6JyBM0CM44/avy+TX5TZub1Zbp7IIeVtTqbz/VovXm0/ZB0RUzS/ApHZqmeKfuH7U0oYCsA2lKiVcbSjDQwEBSWj1scBcJmMshLWnBcNS04xV9nyuaSj55dsszNCv1HizaHdItoM6J885ubzVgnydqUUn7Xh2uW9ttHBOToCvEQG2z3tmXavtb8dT7etZHhGShlxTBgHA5stVX2Ed+XIsJTgxwHjcMZlKGfFE59xHtlZJic225XnTscDvvj5n+Fv/vLP8fkvfo7H9+8Qo9ll59MJ/+k//gd8/cXn+Ku/+k/4r//X/w1++ru/h+WyQ4wGmuYSTVwB/8w2q0MEe1rk3n8Hgrc+5sr/Xf2TEeQ5633zR19/z2tk4Gvkkn6fZ4196fOXnnmtDvyZr8z5l64P3UP9Nw9rfI1I+VDZ16NmywiU7A3z31/qt49pgzwlz8wqMK1gq8MLLZ0Sm0oszz57qQ/mn3+kiF9zSpj0BfWUjpOUre3JpPeFJXOzyvD5XNgzPn+d2HWTd73WxfM2sESHNjaTHs7Nxvi48q5dV8ap/YJ5inIlBZ9fkqL9lfroWtU+nz7VMk+0NYGvzXkqQpOy8od1o9l6r1/XbNRr12tE8t3NBl/++hf4t//y/41//2/+lWEUqw1y9lj0a9y//QRd7/Hzv/or3Nzc4v7+LR6fLIPo6XTEXX6DlEb4YBGodekr9tg4jDVqvO+YSaasdxPMWe0kXLVn5k6B2j79W/G2l/pj3g8v9dW8zFp2NgfPa99dWxOe13taN8WT5s/Vv8u/ef2uvW/eR6V1AJrd6XqPcQzI5Hx6ZtNb1qhm1k33W43/skyGiv8oHjTpr9TSbjcHCGvzfJ8YYwS87UGWyyXW5UhgYvYco77vAV8wv5QQzxHjeMbhcLLz66NFLo/RjomJOQFjQioZHU3GXCGIs0Vae5Nbh4zOe4SSWh2hHeF2vJxwKY6jdbkALEI5WKp0k29Ll2/77B6r1dKwxnI8VhxHHA5HHMtRtwCPkTMHNL7P9kgJLid0obPjsLwdjXQ4HnE8HOuetus7BB8A7+uxCU7GrV8YZ+iLjZ5dmYvFWdCHzv7REdgX/MsZEW5SZGNjnxXH9mBK3js9Z9zs98o9hQ6bfmGpz8exrBuW3t+I+RKIHbryL9TjwDjm9k7DkpZdBo9jgHNYrZZwBVuNMdnRReF6dqD59Z2I8ZxbdDbQUjgyVeM4NmByuVxWEIXgbc65pq0mEEawTYkSBXQIbHKTZoDelJAmmUHlud3e1Im72WxqZKyCGASvFKwj4KTRPyQ2FQhT4JukGYBJHRQko5Ig8MToFvX4VgWs5CeVlkbLKvCtSoFAIvuT0e3b7baC7xppR7CM/cOxZJ8SjFLvHk447QNN0dz3fR1XJaip5HQDr0QEwSsFeAkWK+DJi+Au+0nTaVLm+Dkj/kgkK8nhXCPuWSftY44rZYNgaggBn376KYZhwPv37ytQyefYlwSVdYNEOWcbuRDQKcHS3vpKaKmcqxxxvEkKsQ0EYdlv9PxS0I7vo7LlPGQUEOWOoPp+v58srARGKBuMROM4U6Z1zDkn2PeMquZ7OIacZ9QZdDRh3RmJ1fd9Bd+VuGD9SIxpZC/7QlOIcn4SGFKiWuWBv9/f39c+ZP8z3TrnIYlokosE+jUDAuVTjQvtO6bn1qMVOD//4A/+AOM44rPPPsPT0xO++OIL/PCHP6xlEuTnua4EnTUdrMrWOI4VoFZnHiWQOI/5b71eT2SCMki9QNknEH08HuszmgpcyXqOL8l9rjlKohJE530sU6PJU0q4vb2tckWdoaSAEubU46p/+C4l4nLOeCgANeVMSeeUWtT5zc1NXQc1ipL9zLnDuU0d8f79+1ovPa9cnXkY7clxYV9zDM7nM968eVPHZbPZwHtfnabofMM1i/OABDL1CIl+yjPnCMeYsqwZMzh3OB+p4+ZrnpLZmo2COpcXCSXKgEXG5CrD7KucG5nEtnIucdy32239zvtmeNMBT9dvRttRf+haRZkhUKpGPec0QWa2j21VgotrKbNGsC3sc+q//eH4LF0+NwWNzIw4n4dK6nG+PT4+VhmJsTm0USfPgfRxtKgxyrs5B1gKOLOXFpVoZbvZHs6TOfhPOWH7KZdsgzrBqXywDhxTrTvLZ5+pcwb1rK5zlBnKO/sRsLMzOf85B9g2rsvsQ6bSVj2ua4muFZyTIdjxGJQLjZZXYlt1jmY9eXh4qGse044zlTXbulqt8M0330zsVer9+WacemCxWNS03jyqRvWZOipxbFRW2A7+Y6QtyWnLlnCpa5iuCYyGp+6mTGsmCtoCeqyL6j7WkyQl1w/qKd7LtvAn5zxlS9Ojcx7yc5UfrnvUS2qfU/drVh+VS/Y91yG2hT+VZKYcUe9sNptqY7FNHE/KHmVW1yvOJeotPbOe6yj3VXNiTnUan+F4qB1AZwzOZ/Y/x3nu1KU2AeWS36s9wfWDTpPb7dYADnHq4RizbuwXyoLKPeuiDg/aN6oTOE7cG6jDhBKG/F7tRPat6lV93296DePQvPnrlHSAC+Vfh+wKcOMMvGH0VM4ZcBalkB0sNR1a9FDpQMA5lGXP0v4BYCRKcoUASwWKL5+7AlqZ3JIULQRayhVoAowUh29nGzpXotpzts8B+GyEuHMOHqGCLXAlQjH40u5cwJkCsKaEnDySN5Ayp7GkQS22Gyw1X4KDDwt0/RKL5QbL1S2Wq1vsw5e4nM8Yh3Jmdo5Io52f57yz4x9SMsBH9u2Uac3gk4HJuZ5qO1Mea5/InJ8DutSNmhJdgdC5buZdvoyjL2NSATE0VsLGCXXcePycpVEvx0F58tHJUlmyb1JEHAe4DCRX0kbOCAuXG/nicpMrbVsl3rPJlHeu8kHTKE1laswdJDvpQyFP533IurHbcmUIXeNaYU6AU4x5xiICyLkBa+y39p7pZyTF2z2lN6pOKjXoPIah7Ds5qeCQSwpJ22uXLFyhgM4xIvrioBAHjOOAkuEcDkVWyxxBmY/jMOLh/QPeffM1zqcD8jCgcx6L5cqIi5wwXM74+ovPMY4Rvuvx5u097m7f2lwodiCjgaDtl/6f9FolRsocF0Bdx3Pa527Sn+0+Jak4ck6em/OSeXZPe93zcZ7f11rR7Kf593l274dJKd6fpXN0/lv9rhMq3+0d06vqCecmtc5ABcW/+/VSimE3nbyU5w+sf3lCDs3ro8rjY8l00XV4xTnNUQT1HGv7wn0o2t29XoeXevXVeldWWfQOpmT49e6Zz6PZ8276/It1uDI3XhjlZ1eV3Ynum9bjevXlm/mXbv7+eTtR1oRZPazRdT2Z1501/dDV1uWXU3azDY6y5Ob1ae9ycPjAVHjh/bM2zOVZ75l9x73LXK9quc459J3H7ukB7779Gk+P7+FcwHKxQt8tMI4J798/IuWITz/9Hj777DOs1hscTxfE5NCJjZtTsnY6DxTbzPZmFvEa41jvp52cYnq2B2AdXyK152146buX+vBD18eUDUxn20v6+3W9/tz248850Q+09a/a225q183fc+13w/FapuKQis2XM5YhmA3n27G0jQCfZvSy/Warv9l0Tc6Ia+geiPsw3f9pYB9/krMLi75yT0bMtuO0dO+2HxxOp7M5Dmfboz8+7TCmCCbFAoCUyNUVgj4ls6liOx/bCHA757v3Hn2wiHGLLDen38sw4Hw+YBws+MUH2vkeXd/D0rgXR34ASEAo+4NF7BC9N/us7tmBVdejc9aHlcQOAcgZcRGRcyo6zXC65XIBO7464aYEVDIwaNFbCnxkWKax4Wxzs9hQi4J7LrriKF8w0TOd04NFbHvvjahGc661bFON8DYVV376XPYstKnLDKkO3Xbm+WLBQOiL2bD2sI3rOGIcRuQYEcOA0Ye6p2zrTHM870p2x3EYEVOEC3Z2eyy6J44R8SP0PfAdiHEabwSvNdWcgfYLdF0De9Vrn2Szkq4ESSabyZwnACNg5DujuYwMXVTCUdPmElwygCrC+1ABM4JwBLUYiaogWc4t3QNBUNZZQRa2n/cwra6Cg9zskYTiZyT4CLxWhYap97cqBQKmJMlIIGiUBPuZ/abnRN7c3FRgJ8ZYUztSYSmZTHCRY60R4gQQSYauVivs9/sJSHc6nSapOjebTW2r9q2dg35TwVP2MVM5WtT/udaT7VRAioSAArUE9wBU0o0RtN573N7e1vOAgQbGkVhgmwnOdl2H+/v7mpKWfcA+OxwOeP/+fQXWSGIxtdnc+YLvVJKFcsdxpPw34qVFRGoky3q9rn3KMkgyjuNYjyTg2BwOhwpccp4ooDrx6gE3+C0qgmeK0tFADSuClAQxlbxgX3GeKiFLWVYAmPVTgk7lnAAUwVaNuNVIbMomZZYEmDrfsO4E4tk+PT5huVzWowweHh4mfc7yGIGs0ZwEinVOEnBVRwetOwmynI3A+fbbbyuRQ2KTjkKcG9vtthLKJLVpyDw8PNR3U58+PT3hk08+qWVy/hKUZxtojHLus49YT5KdZ1mIta8JFtOphEC9yit/cuz1vGLKLjNZAJhk+2A9SWYCqJkglGwlWK6ELPtX9QXnDfuJ7eXFOU3SiPqAMqZguuorJWh0TqhBp7JJXcLzq+kMMY7jJMWwOskomavnt1MHLRaLGkGpzkrsSzoMqa7JOddsFerQEGOsek6NWraZZBHrtd1uaxoflq1ypmQx26gGuEZWap2pY2jUU2cpIQGg9i8zWvB9NgYtOpBrOMeT+pEpxllf2j2cv7Z2tdTdlEmuT+ags5zUi310e3tb9Rnngjr3UJfZ/aESUJRhytY42rnwXbcAU6ArQU2SahwjLpdYCclGfLdoau8XGIYLYrR0tc41vdt1dHrIVWcAqHYN20e5oA1CWSFJyPHgmLF/59kz2M45YUV5oR5n/XNux5uwDP1M7UDWY7GwszPHsRG8ClQqOc9xo4MGbRRdUzkPdX2g3HAek0SlvmF9KDc8HoRR3c3G7ispy3RhuglSUp3zbbvdVtuATmQk2X/84x/XftJMR9T3dLBjOTrXSBoreUr9xbbTkYMR2dRP1Mmqx0iYn06nqms4frRnWD/KjDps0RmNOmi5XOL9+/cTm31OOlMfUH40awkvTf2uexfqkeVyiYeHBxyPxzp+JNnVpiFhTN3B+lCvqCMH60SZ04wpHF/aqLS7dO/BOcI5Rkcm6jW2kUcb6F6C76Wu5lxlndseq81P6mM9eoP7LraTDkOqH6j7dA+kzsZ8F/vueDwiwE10DXUD56baOtQTnCfcK2j5atNo9L+u1/yMYzs/MobtUvKTfTK3e/5WlwMUcIIrmRV8B+/tGC3Aw/nOAItydBmyect3fUDwAcM4wvmMzhvQY/qK5RNU9vDOAymhphHPqZHs5XYDJAKyK4ARGpDZztlu+IHrLNog+FDST8Ii2Ut6fDuDO9iZ2t5XctXaa4RfcijnWafCuZTYc8sLauALMlyOKIELBuRUkoNjZNEUy4XHenWDbe9xOh2KvrV/5+MRPjl0IVn6xJiQx3ZcSigpFwE7/49zJCPb+YfIZWyek1+m+6cDrDKqMt6VMsgbEIxSBxjnHDkoIDvj5V0Q2ZkLk/5DBQnhSuSHL9Eq3r4bBwO0UyypvaNFWWckISZKpH09lbdwoiipVZ06AGQQ8uDTeVK3ieADmVH4SmpU5mt6e/2YWRXmaZ+nhGrORX40N6kTWoiAao6TsdT2VGqWe2h5jqBhquMPO9LTlTSV1A8FTMxAdSqhnZdis5soF1w3YoxF3lxpQ6ljIfu884jDgKeH94iXC9arFZaLFVIE+kUPB+AyXOzc8vMJ3379Jf6Hf/ZP8Pf+/t/Hn/zD/xIuZoA2bCxODCEUJxlU/WHvbFeLKp79dErsXKPYnn+Wc/vXwNZ2/wSABaYycaWsZ+8rdXfzz4EyLvKpm5fxceR4WwOmmUTmeuG169r3c13CdtQ7SbbO5Ju/PK/zlDCbv/NaHV5ptpR3baKS5Mnt7+e5yxt1+lHLaHNaLo9fr7MnESsk7mQtRNOruDbu889EJ8FdO4LdrjQtZK5PtB3zdrFefDef/9Cldtc18oy1ZwfUskF+OWM+p1R+tfxmp9SX18L0+/bepvlVkGQEpWY6X1o9rrXFPa+yfcd6a1uu3Me2Xftd/642rMrQvJz6legnB9B5cX61rtOxKmuEK+niJ2WWAjOd1KbCOl+vJu9yhazPGXEcsVwucHd3h9PxXNrmsNsfcHl4QIwD/sHf/X18/wc/wuF4RtcvsOwW2JY0xQ4o5JfNwZgzxkjHugvGyxnjGLFcdDavKzlpkbBWn7ZeZFk3XxqXa9c1/Tq7A/gIh52PeldRAhkv6/Amt8+zq1D/XdMB18fK3pUKSUodNZ0bL+vsXBbscRxwudj+pEMP54AAICyXSGUf2HUWqWtHKsUSuduwuGuXc8RoUfd/fK9hbbIH7gO6ss8DXHW8dXBgSnDf2Tnn3Isej2fs9k84HI+FdzojxhGPZ4fLxdLEh9BVTNyOinJl7gAJdk43tQBlbBgvSCmi7xdYdD1CKll6+34618yYNdyh69GXeey7lv7bMOwl+sXCJM0M8oohrVcrdKEzG5v6Y5uwcA3jZ0aFrusA5xDHWHVFcnaE4mJhKeOda0cedsWJYNF16EuUd4ojLhdz/E2jZebqQoflaoll2c8SBz1ezgWfclXfxJzhEyPqmzNs3e+VOZyTReOn0tf6PWJzsE05A73HclkyJJ9OGKPJc8oZwzBiGAcAFonvi61c8e5k9WBWz+xaFrEYE0bhU2v9XjjqZH5951TqBOYIiPR9j7u7O3Rdj8fHpzq5z+czbm9vcSyCq+AIgQJu5g6HQyXCSFIS0AAa6AEAl8swIQG1nEZAOtg5aL4C7SQzCE4S4CZopKQoiSZGyTHyBZieYUqSQok7TR97d3c3IQoJvrx79w4AKlhIAC1XRTQ9944ADs8mJjCrwBOBSgJvHCsFAEkoqvcOCffFwhZCRpoCLbKY6XT5OcF/tr8pq2OtvwLdlAkSXASqCAzPI5XZJy1CsDlXcKwIqCnpRXCTz5Eo0/rPwVSSErzPZKwR2b/+9a+rwtDsATxHfLfbwTlXSQ72G9tPIJPtVXJHQUUAtX4kHZVM0Ps4RkoiaGQLgEKUdJO+ojxzcZo7PpCoozxRJudANNvIzxT0o2KdkxhKZpJQYTSvEtgaSaWgv57LSlnmuZ2c5woWaNs5viml6jCgUdiqQyizSuqM41ij+DkfCHITDCcJonKoepKLg0aOKQmt0e1KJhEYJimgxDDHYblc4o/+6I9q9gZm5bi7u6sRhYzMu7u7m8gey1KC8ubmZkIccfxJBlHvExRuKaW7iXyQVKFsqUOIkql8N8/K1fkxDAPevHlTSRneS53F53XOUXewn0muEEBUma6GhJDo1KlKXjESmQ48zKBAPUG5Y/0ZEa8ErpKnlFn2G/UmnSPUQYbriupm9jPnthKqdE5idoTj8VjXMGZs4JrC3+kkwdS8rItzrhIzmpJW1yS2n+9UR5eHh4c6npQZnQccuxhjPVJDyRB1oFHnLc18Qn15LbKR+pF6jvaGRcyaTN/e3k5kgv3sva/9wmhS6lHKM8tgnTieAHB/f1/KGyaONtTTjOpmlCmzkdBeYjsMMG1E7HyDYzo9YRhGhNCOeGBmCLbd2pWrzuVYcSxVnkPokBKj9m2zYXOXZ+02GIE6Qe0g/lRHMHUgcc5VMpRyRluLOg1ATbPNOUB9zjaxr1Sm6Lyl9hH1Lx2BWNYwDAideUdT5qlrNEqddh7nGOtDe4qX2jtc00j0Upeo/GoKbK5X89TOnM+ch3TmYsQ4x0/HnHPmeDzWjAHqbPfJJ59U8lJTnp9OJ9zd3dU20imG9iTbQdlkmeqwomuGZvGgY+Rms6kkaN/3VZfq2s3yVDdr37PPtS6Hw6ESS7qG08lJnWzUCaISD6mddU3bSh2HqL94j7ZP6049RedK6gMeG6QOvdeI7Hl9Uko4HA5VxmKMk/T8lAklrVkuZWPuQEVZUecOdXZRgpz9oWsG5yH/VvKcc4jON+oQrMS4plHnnNMMS13XTZzd9vt91eshtLPeKYPU/eqApf9473K5rKnjuWaklKqNpOsF+556n44m/F7nvBLj7A91lvwYAO61K8WxMkM5Aw4JwS3QdyTqCgmYF/BwSGmcOKWGEOCzBzzXx5YWb4ztPPu69sSEmNr8isgYU6xkvJ0/ZykDExoxbuB26RNA0ux5IFua7lCAxBhH5JzgQmcUZgXjC1GQBORLCTlZuvTOeaTsDehIGRkeLhRKMcFYxxDQhYBQnWLIDZlTHAoI43xG7xw2N5/C3X6KmEYMwwXH4x67/SMulzOG4YIxWlTD5VScWMP0mB0XOsTLAO87ZCTETIfIpgt5b3O4mmbXsXlbQCfn4LsAj4ycLRUi0FK6u9xs9rrHYBS1e4EQyBbJ1ZWImyH6EpGPUlZxAkoJDm2PEIt9N8aImOxfKpioT76R9UDlBZ6B2SWKjvxlThaxQ+CtVBDwFi1zdbZUMqHsTet77aU5z0gi1qEQO66+qxF1Nia+cWKzdihlYmdtOylHmsc6vfJd6TF4b6S1y8AwJlzGjDEZaO4QgXTBMJ4Q4TDGjHG0CBoED+dKtNJoZ06Og83RUxrRe4fsEjJGOHiMKaNzQAgOSBeMhwd8cvcGq9UNVtu/weh6rDYbdH2P+P4B7nJGHB1yOiKeHvHP//t/jH/0j/7nzVECEYiWqtIlZ3M2CxmYUQcoU1cB4ibRiIMuPD8uh+M+6z7rQ6ckZJbPp+M56fQX6K6XiAst4Roh8TGXPndN9ytWcu1vfc+HympXgrY1CQBcyzPGylxEJu9Ik3nzUjuv1WVCXb6wvFGfXf/u6qfIM+J40uaPGAeTk4847ztdHwOSM6abGmbAR6+NgekjLW9a5kvPtTrPCetpO22M5u8Emg57udx5PV+WbS4chZoiKw7M2obqdDO/1IaYD7BDO7pD6+Dh2636yLOxzi8z2Hg+jik/HwMALe2xjs2V5733cC9wKc/m9FUvCF2LMFmX6WjgCqk2nd9m75TKtM+ctT8VItxlX9xKzFGw3l8dpLxFeWKa5nk6lz0ys7vEjPX6Fn/3j/4Ey7DGv/93/xZffPEFUt7D9wvc3N7jt3/n9/CP/mf/Be6/9wl2v/gC3XKDm9t73L39Ho7nE2Is2EwhgEfXYRyzkWHDGXk4leOAmizGGHEZR2QPuGDJdnzOcInODddlWIlZlTu2b+6IOykDz6PTn13FySwXh0HaWfauNr5J3smxsuWvYeBW0jxlep7MR9oO1+ao7km1D9TmmJelfaJ9YbjPWB0d+0WPBMsK42JGgMf5PGCxXKNfLtH1RuDmbM6pne/McRamE4nZqbO8YumKS7FOMfZwISP0Dl2/QHIe3pmTb/Bml/a+g/MJp7PD7jDgcHrC4+Mj3j88Wtrx0wmXoWG0280brJYbwxa6DsgJ68UC4+Vc2911HULf9uW5zB7vPFK2mRVCQOcDetdVnEMxFJT5WvfVKcEDRt57b+dj95bKHM4h5gQ3ptKuMn7lPZm2rgOW/QJv1jfIznDIyzBgTBGLvkeCZQ3LKdc60MHKAQjBw288TpeLRcgDQMyIcUAeB9vTHPZmM44jYgKSM8zGB5sPMTHoL+N0sQAZOjGYs7Mr5Hdx2hXOCCkjJTsuYUxGTLvgiz7KhiFma20axpI+vWSNRMOiDb9o+9acI5j1q9rWmfJfXF69Q3Id9HguV4xFl23N6ZxH6KbH8710fTQxrilvOTH5couQaAQDQT9Nlc5oQAJg7GgCB4+Pj5W446QnYK7pDK3s5lVD4pEAhwHFdj6mEgoERAlYEdRX0BhoILdG8zCajiAygAq8KojKi8CUkr8si2AsU1QTkNLIFRICp9MJX331VSWO6UCgIJ+CkgSwCBzp4s46kUTQqA4AFVBjnbhRZ//f3t5OHBCUOCIQtN1u67iTTFBwmcArx3lO6DA9OgkIjRCicmK7KEMEdAmuEUjTScb65pzx9PRU5YtEuN5PIDrnXM8EpjyTYCd5FmPEj370owqAsgy2mWPKdrKOet4zI0QJFKsM6iLHcdP0nSyX/USQU1M062JK2eJ8YnsV2GdbKVtMi6pgMiNZWTe2m/KmJB/fyzHm+cUkqVkGCVyNGlQvM7afxDZJhYkyE0cEzikFg+fGFOe8RtLSMYGg/NOTOfsMw1Bli/2ppAYwPQKC9abcE5SlflQjSucx+15BVuoU3tN1XSVeqWN1PHh0Ap1/SHwQ/KUcqy7nXNcIsnlqa5Lmqo9vbm4q4O29x+FwqPqec0HlgPOCEYAc2+12W8/E1uh7kjSM+iSwrWSPkl/sb+pZOkCoHDCaUYlmypPqtTlQrH2uzhSc2xoFTccZHWfOI/Y51yR1sGG0o0abK+g/32SzzZRJ/iRRU9MkzYgRkgBMIc7ydA2eE37UuyTS1UFHHQ8aaewm8qOZOkhqkszieUGUD85hzhcSMDQItS+1Xnw+5ykpwfYwSvXu7g70VNY5SxLXSKAOKZ3qM0q8k8Q1ndBsE6AdZdJ0SjsTmdG/1B+M4hzHEU9PTxMjnOMVYyyb+OYwovrW5GZEzkZYq+4gWWz9k9B1y/oM138lzuw7Izns3KKIy6VkAfAGXtiROS2DiZKFuu6wXK7RlLE5AMf37vf72re0M7Q8jY5qstD0rK6n1HE6d9QpQTeIQDuuhX3ODCmaAUHHlM9Qp3Iuq63Dd9E5RdcnOtioncn1m2XTbqVdxD7S+Uybh/fTnuX9tHVJpvK96gBE25XzllHddD7ie1jPurks7+G84vrHjE6aFYB9ykh4HU+VF+pYjqPqTxKzdOBh2Wqr0sblfGcbdZ2gbry9vcVut6sOeLQ39H6164DmNMlxVeKbdgLXaO436Dym+4m5DGn2IM5d6mja0kqC61xi+9VxUZ1vpqRbnsx1OgbRIUPnAmWa87uBw7nOT87XnHPV79S9us/Q9YE6r+kbN7FHlWRne6rDSAhAbraWzg0FZXSto13J/qReYh35TjoOa3p/3kedo+PKtU73MKpXtE1qi/+m1ziaPK6WjBBoZDRAUtr+F4JFMsx1bUzJUqQ7i+bpQsl0Exyyn6ZDjDHCZwNiXfBYShuzprNNGX0AUlJgoxDg8kwczV4YTzCAJCU7BzwNGAuJkcEMFpauO4uMeG8Qb820k1MFiH0GgJJOvQKTGR5OogQMQmYdWS7/9U6O1kgjLoMR4ikVh4rFEtvtBuFtczYch+b0FmPEBXTWcQiYZnLQ9arOJUOHJ9+H0JX6W3pHJ89onT08UmpYyjX5Yr/VscpG3kTfMiLwfPZhGNCPxTZZLEpEcEIskfDs90n/yX91bZ+DukYCJFTWU77n2Zz8LL9Qxrxdkza98vekHlLmtPxXUi1P7n/5nmvfqg6DczOixyBZl6bONbovS2mEyaNlK6jAMhx8NoJnjE0G6FTAyCabfxnL1Qrr9RqLxQKffbrEze09fvnFL/Bv/91/xBdffI63n3wKHh8Qs2VHgOtw//YNHh4e0C23cN4hJ41mM3JAaWlM+qBEvmOa2aDK4zUgf9aH+j3v4Rr0/+vrJbl6TW7+tvXUvvnYewkMX5uP7hX5nZfzoc8+/vr/z1jNx+taH871wTW9FYsOdvlaZP11GX2pTq/V9/nvGVzX9buPkYXf/P02A+0VJPd4V4sABCA66rkTxvxd6nQyxoj55X03Kful+l1r+m/aHy+9g7/Ttp7nGnn5umbfKVla+pJ+KpVYfU6kzvl/4h4k082eNCcq7wq+6jxibMcYed/BAUhIk7X3eR+nas9tb9a4v7/BT377h/jRjz/F/+H/+L/Hv/t3/wa/+NXn6JdrfPLJ9/DDH/0IN7dr7HdnPDw84Ps/+DH+8Gd/F3d3d9h/cZjIqK5/Y9k/Gy9yAdwaGcURONqRIJxL838vXbon4fv4+Uv2ttWtOBlIOfNyAXPocjJwWTE9YNJOll1tbgDgcQI5ThwSFKNhH7EM5QymdW51u2bzzedBLSM9b2dSbHm0CF4cHJarJWK/wOGwr3tkZq8kxhlcOdIyt33hPOCLGI46EZM3YFDGZrMx+YwJ3ncYYzaMK1j2K8MSTjgeBxyPI46nc5Ed4NObz/Bbn63hO4sy5/4sB6AP3QRbyzlOgjNW/QI36JBc23+nbKm/U9H3AJC9R/QtQEuxYs5H5xxCNieOlMzRMY8JLkc7PmhMOJ5P2O12GJBq6nH2nWLNxKAX69UEbyJ2oNHScOZiQTzM+rilrKcj+fFyxpBG9MHjfD7iuD/U8ej6DsM4Yn88Yw2gK2a5c14cPcoRWUU3u37xzNkozRzSu0UHpBHL4C0FvDMHpcV6ia4L6LseXReQEzCeCv6FaVZkmx++7Ms8Ot+COpzzk3s5/7rOw4fyz3u4LiDAbO7iT/SRevw7RowTNCf4pZFevhxKP4+u4j1zwEKjI3LO+OSTTyrQTnKWAkiQrQGjQ406qZ7S5XeNLiHARgWx2+2qQpqn1uM9KqgkPBVM7WSzT3CMkxJokYwk1qi0VWmo8OqmmX1L4me/39fz2UlAMQqfYBX7UM9Q5yad/U9wjqQu33M4HCp4Q1CMxCCBZUZS55yrYiPIxAgOEuB939dIDBLSCjx3XYfb29sKJHVdSwfJ/iFZnXNLGaxn0LPfNMpVI501VTpJQL4fmEagpdQiVEjUadmciJRHgt3z75UsnSs6bnapODj2CtQpSMgxojJUkoCKaH4UAMnrEEIlmtjfHFM6hLB+Gm2rqSRZpkb7Ag38VBCdYKgS7CQj2FaVUbaHMnlzc1NljQaORvQTIOWiBrSUxnOSnuPMcWCbqHNYb/5kZCLrRJnjOJPYowLmnCIoyvElGH8NtGakNucI+3Vu8CkIq/OJ9eFcr+Cm6I25IajONRybu7u7Wj7JJ6Yop+4j0Mv0t2rocGwJHrPvWScSM9q/1IN0hum6bqJHFotFBbT5Pp4pzjHl2PFe9h2JbSVH2eanp6c6vzXqmX2sICbbpoQedQ4vJRGYXUNlU8tSQl6/Yx/zPk3nzHmi8sd5xbZz3jKdPuWK+ovnBVMvsc0EM5Vopw5lHXkOuXPmnMZ6KZHDeUBdt9/vJ44KHAOuKSqL1BvqcMGyOV9oV5BEVWKY/cL72T+Usfk9nK9Kzus8pn4xMswIvbdv39a1gTqo2QetD9jPAGr0LN9Nvc02zNc/ypnaQnSG4FjFaFHB6mhAWbbzUd1ED6jTnx0f0zZZfC9tsc1mg92uRVzqcSxKTuaCX4+DpSPKGdist5LBxiIouCZr9CvbwDWb8qfOC5Qp1aHsc46TRpF2XVfXNOoKyqs6prCfmIWBa56Csawb76u2nPQX9SplV2049jsdY9TupF6mHGj9SV7HGHF/f4/T6VQdjEhC087jeHrvawYB1bXM+MG5SD1BvbvZbKrzH/UX9SffRT3FPufY6nxleZoem8eMaJ0412hTaBm73a46J/GdtOFp64+jHc2jDnnsY10/+W61w3WsVEeobUD503GkQwg36JQ71U+q+1k/jQqnd7xmSeL6Qh3NtXE+T6hbWL7KMsdHnSRJ3KvOzDlXWafNqkd8sG/oaMB30EmF/UibjXLE8jjX2Gb+rX1ImdW1nnWkflD9O9fFlEcl7WmDqFxxD3l7e4tYsm+wjjxSi/OTtrDuq9gGOgyyLzhWbJNmKuC8oF3E+9UBhzKkezfdk2o9XyIuv8vF+pxxkbkyJT2N+ujQBQfnCvksds75dAF8QN91WC66sn84IqVs0RJl/FZLk1uXE2IcC1FtkRVjHGvUQlf6a4wDLsOlAUi52eokxlJM8MFSJSKVSITICOTRzvnLqQJARkaggsFwBlLWjAWw5ju4cpRyRkY0dCcDTMfZUupN9+JzKrMP3tLCl/rmkqrdIioN1FouFnh7/wabzcb2L30P5z2GywWHw6Fm3HGwo9Av54tk2mlATrYBQ/JTRxzro5IW33mEMj/GNLXxAZQzOYvjgmvZJ9Qu0fsbYGvnV7tQbG/fIYQOoWuZi0IIFbRMSFWWKzBnKG+JBhGS/SUMm+Mo1wSkmtVbZXoOWtfnBdzV9VnLuEpVzMqzZ1+s2ZX3T8mfnHOLgpw9N5nzOSM7pnjWuiaM42Wy79N2cQwbpmOZilJOdm4io2+yRexwEGK0cxVD57Fer+DffoI3n3yCcXzE7/z0d/Ff/S/OuL17gz/9sz/HL375S5wPe+QUcXu7xQ++/1v4O7/9O3jz9lOkbM4adrb82PaGENZMGs40qK23XEUaE9r5lo0hav9STJNxrWU8+3syQvjY64U8BFe/y9NG2Y9yDr3VcXb3FTnlZx9qj977ofuuf9b2GZWE9B92MPnQ+/Wza/PrtWflW8yrPC/3Wpv03mv1+Jh2zefS/Nn5+HC+VnsMLeo443o9rr3zpb9fkod5G+tafiVv/Lx8N/e3+cD9H7peLitP9LvW+WPGsPwy2cNxPVGs4dqz7T3P15hr/f3SetDa6J6N50t15py6NmbX/v7gfVIH/pWupNbXCP1p9hWja4PzdazGMSPnWI4/YSZKICU6tOYalX4t+po/T5cLfu/3/wAOGX/zV3+JX/3qc/zdv/v38Ht/8IdIcAhdDx86PDy8w5/92V/id3//9/H3/t4/wPd/8CP8/Oe/xHgZ4HzR8wCCs0NVLuOAYTjjfD7VYI3K3ZQ1bBxJOqdncyHHFqQyGZcXdMHUztP+lnHyz+2NZ2VoHxV75zVHkJfqwd8VZ1CdM3GgKxc/u6a/9P653D3TI7mtx/qc8i4AEPoOKSeLBM/GNfE8pHEYAVeyfTo7y9k5B++MND2fTwihw2rFINIw4bp4rC6d6He7Hb7++mucTmdcThekCETncXN7j/Vmi1D2cMMwIEXA+YC+WwDZYbkAVqslgvcl5bbtw/f7PVIe6vpse2yLQB+GATFFINs54AgW5GF79hE5l+AwNJw4hIDleoO+X1Re0u7NdX76EMyRsNhC3Cc652pk+Pl8xv50hO8CQhesfx1sH+RaCvzKmwQ7Mto5y1TAvbodyVQlDzkERCREb3sL13dwqwXWyzVu1hscDgecdgcMxzOADGzukO5GLAv+3i16nE7m/Nv5gL6SzaG9w2kENnCz2pbxdQiC09p8Dlj0HVbLFbarHsgZ53HAMA4YS392XYeuOC44D5zjuWI93pXAQMCySxDHLls1Zh6Ds6wFbrbwpbLvzMiIOSMmPUYJtt/6yD34dyLGL5ehgnkk0bgRNszH1YhYAjfXIncI5CkAo2cikqjVBY5n/Rro3DwkUiIon9F1GUx703XdJNUygAqGErTUaEKC2gSsSMYr0clU4wSqCHjROYAgFJU+y9KUEoBt7B8eHipIlXOepAsFUEEngqOMWFUwSRUbJyOBmxBaagIqQW66uDCRhK8ARs4V8Cc4RfCIypN9QUBRwSXWm2SOkmsE+mgMkUThxZT3enY2CTIlxFgH9itBLwKRu92uRqWP41jJf0a0c2FglCv7hTJJkJDg+TiO9exzJebZViWVgQam6lmnavCxXhoJSllhG0lo0vmDbdZxJujLeTMHQvmZgu2sH+VWSRvOA8oQ66wyBbTzTtkeypRGT+u85U/OE3qtc54Q1CUIy3pxzNWJYp62m/3MOUoSwHRDmDhvzIFY/iRJxLrOnVVYN03j/oy0yi3lKOtBmbi7u8Nut6vg8hws4TwlWAygRvAqkUQ9yb7VuU3nAnVu4fOUczpQELBWWVCCimMFtLNaWW/eq84hKvvUJzlbtgUlz9i/1GvUUVxYOd4kBdgvOVuWh9PpVI0r1clzIFr1okYysv/ZVoL5XCtYXs65evU57zCMA86nM0LX2ZksXUmNEw0w5r0o8uC8x/lyqZFOOeeamp46rsl0y9JBoMjSFbUxbinYq8hgsViWOdBX3UGZZF+PYwSQJ/Of/WXtNgeb9+/fVxKThqKSfev1Guv1pnhuHst7zGtP+5Qyy/mrZ79TRqgr6FhAGSahwXWcfUD9QPmY6sxGZHHMlRCj7On6R/mgHuo6k7Fvv32H1WpZSUDKdtf1VT74+eFwqM4e1v6MnDt0XQPsObfMSE64nI1YYJSbLylocyrnhDnbzObsMA4WAWT1HWFd2M7q4nmlcYz1LCXnMkJYAkgYhhZ1rPWwubyoRP8wNPIPsJS2HNucyzmS2aLWLheYIW/WKXJOE1lWRwzqK84nEokkAzU7DscNYPpoa8/hcMDd3R2cc3h6eiqyFOHKmboEZMc4wsHVcYuxOIO5qUf2crVEF7rqtGd1sk3G5XJBygmLRV/rxjnFeTnfsOp6oU4qfJbEnJKBdE54enqqdpHaweo0o8447DtdM8/nMzabzcSphk5C79+/rzqUMs/faUty7eIzfDc3snTAORwOldxWRzotQ4lB1TOLxaI6THGdpmxwTWBacdq/2v9KQisRqVG8dKDQ73mxfymDlFXvfY2Yp6MTAHz99de4v7+vukZt3pyn6fm5t6GNS/KfbdfsLCSjVdY5vqyjyhqzQ6muVAcPzWihdiCdjRjBT71Hu4G6Wdd02je0P2jHaL1UftVhjv1D/at7HT1zm0fNqD3HNYHzjH3MurKfnGtHEBFU6UPLSMYz8MZxLDqzRVty3NlXmiFBCW7OY9qV+pmS4eoYeC1jFu/jvFd9MG/Xb3r9+X/4D6WfWgatLvQVrLOznzN86NF3HkCL1h/jiOADxpiQ4dF3AYvexvJwONRxYbk1rXzRqzWlnsuIsTjxem/n8IWAoRDjNQtPzghdV4EM2jSLRWe2UW7kakpJiPGaWLD0WbN523zkWdglDThKcYnAaq6gnQMQCUARSM7TVMNWbEbf+RIV24BoG8tGCjs4fPPVV1iu1ri/v8ftzU3VJ33f4+7+3vRp+bdarnE+n6osqjMXI8tNbqfnLhJUc7DU2d5zzohAVIS9AVfONd03B2XrvCKTjtIvBUDsu+b4jWzjnNBI1hRTcWqw9beti68TLyQhWn9fISmknnPA9xq4PS/r2jqdc55En+uzz+830udaOdeuSZ3sg0mk7hyUnz5rMszacM05n47IxSFlHuU1d6wJwZdjBe2fZVcYkV2YkdRAjAnO2fEpP/vZH+Gf/5P/DjEG/MEf/DFWmzt8+tn38fmvP8evP/8Fjoc9fvyj7+MH3/8h7m6/B4QFlqu1zbFYUoaGgOQsrSrn27xPnl3SL8hAx7GQ4XyJtFb8JBf98JIqfU22pl+8XNWXLtO85b8z2Xnp/dc+V1zkQ9ek3YKr6Hf2PUk2RtQDLucyfyUFqexLn7+LZV2v92udNpf3advys2df6qeP6ZNr8/y15+e41LVn53Kin89J0Wt66WOul8p/uTwjCZ/3+7Ux+XhngXkfXeszlbuXLsWNPvbdep/aHEzn/3Kd2Ecf9Ypnc+Xa/CshvR8qqL59Pmc/Zq4/u8e5OnyTVP9litjaDAtmdlfmFe8Fv9d6FTK8Hl1QKLd60HqJSncOuJL9IOeMd+92+OEPfoKf/ex/hJvNHf78z/4UX3zxDvCm+WhznS8X/OxnP8Pf/wd/gru7exwO55LxcUQIhWCFEZrVji62M/cHDg1XjONoRwWV9pVRA89YtvtL1DvaeejT7DJN1yEzqXLrXJcnVghyhHw/GST5rz0zldVZlpMX7JVrPzsfqlMkHT6TDaK+upwdLvXNrIN9Zme4Y+KAVms7eW7mzEI7onpPlfo5h4V3toeIEakQwIvFAl3Z1zkv2ZWKnWh2qmGm3O+qThiGEafTEV9/vS82tBHZDw+P2O2e7JjBMSKmDL9Y4fbuDRbrNeDa8WQAMNIeLTqn78q+oOyziJWi3G8mrocPltIcKJhtKoEpwfCfWPYizvvq5DpGy2DQhQ63jg5w5SiZPA3M6PreHHlLRoY+hDrzcpnqy8XCnGiXhWMspK4v++/ga16C6jTYdz1CMCI453Leegh2X7b9SXQoxw84hC5Y+vbgcbva4Ld++CO4lPHw+IRvvn2P42GPOJwRfMZqucR6uUK/6LHb73A8njDmDE8OwgGxnEGeRZYcgK7gLN65mS5MGFNEGrI5Upb9+amkg48xwncBLl+KUzUA7zC4XLDUoQp/SgnDOCBF68kxRYzq0FEcS3PK5ciTgu9eTL5StrPEY8rlWPky9/P/F4jx83moAEqMlmqMoNp6vXlGVhDwI7lHwJ3pIwn46CKpkRUaOQpgEvFBsIxKtYIjY6x1HAY7/5cAGoAK2gCYRNEoaUaQhEATU80y6kXPoea7nLNzWEm0cFMaY6wRys65Cq4RuNF02gQiCKQpMAO0tNIKFrI9BGA0pSNJQraLABiVFsdu/iyBPhJtfK+SxwQGY7S0g4zaaKRLrhEaT09Pk8hQJZcpK0pQE/hj9Pnbt29xOBwqCJpziyBmOnq+/+bmBsMw4P7+vgKvGuW6Wq1qClwSypQzAs2MpKUckLBk3dkW1oVjR/JTI/HYd5RPRupwjEj2XAPd2OeMzmQ95hHEJIA1IpN9yYgioIGgnHdaFyV354Bo81KfZkWYg/cEbSn7Xdfh6elpQubS8YBt5Jyg/CmITFlXw0Mjxwn0x2hpqym/nJs8G5hkjPaLgsYk59ivKpucw1wEKf9KHPIZjTI/Ho84Ho/49NNPsdvtJnOAuofPaoYLBacpN5fLBev1euLUs16vK9HEcpSoITHFPmM7lCx0ztWzjanDNKJ6v99PohcU1FfjSPWTRm2SAO+6Dm/fvp3oe60vQWu2Q/uUMkZQnnVk+wjGU2fNo1QZRcezq0nWktTjPKCOpLycLxck5MlcpaFYiQNzPawAZsrA19++M/nItiFwOaPrfE1FTVLTCMo2h1NK1WHEMhk0sN3u8cV57FQcvvaF5Brw+PhYyRgapprlg8cq2Bh1AGKJ/koIocPpdJ4YnCThrL8yQugwDOPEwaERY8sJSJNzmhBujEqlHCmBSrlU/cr5yH1CzgbqhUCyJWMYzFGJRLUSZ0pocf1UXcbPaTMsFkvsdnssFn31Co0xYRiOtR4AqnxQfrn+8feUeFaq1ZdOhDbXl8jZYxgyQugRhwHJOaTk0PerOl9D8HDBjLw4mDz4GG3Dwqw35wu6QBvEIr00onGM7XeSo2qvmA6KoncDnOOYjPA+w3vr965zSAkYhlidPoyIf36GOOfIPJMK+5ljwLExO3CNMY44Hk9VP8MBl+EMuIyUIxbLHvfhDuM44rQ/FlK8pD8um+Z+sUBGQr/oJjbLOI5YrZfN8Wa8wHlgsezhg0O/UCc4m2u73a6upSQreWY37UC2kzpPnec45+YgNokmHt9wOByqbuF6xzWV9pPODfYdN4p3d3fPnJL4HupS2p3bbYv2p6PoarWq5yYze4cCSVxrOIc0k5E6+wGY3Etbmk6Bag+0qElfiU6u082JpGXr0Shyrkn6T9POc26qDqRtXDewEg3JOa0Oimwrx0XXYq5H1FmsI9dTzgHOu3EcJ+sqnT1pN5BI13WOtgnbyyNJWF9dizhetBs0i4bqWdo2c2cxtkEdT/lu7bd5P+garPLNdVfJYEZuq/5lnVg/HQc6HXAcc27HerDeAOCCx3FnDgl91wPBY39q2VVcOcuODpysA/cIzrmaLUjnzdzu4+d8t9o66qxAeVSbFmhR96oPOXd+0+sXf/1XppydeevbGC6rfMQYEVOCX/S42WzAFIIXHt8RAng+cfAeIbi610NuxySEYCCLA5CLFz6cnUM+xLHOlb7rsewXcN4h5oihgCCVGA9Mi0jGBTh1rhKrgAF7OVtUsgF2rgLWzjF1qxBD0h/OM5V8LunAp6kOvTcHtJR4lJQBYATUdM7Y7y1VrJ392GQgjm2/nMYLEB7w+PiIzXqNzXpjEeS3t9hs1jbfsoPzAcvFCv1igcvljBYVVvRhTPAloMBg3QZuT0DVMSLz/HbnEQLPIZe0nQSI0eRtTgoogG6ZBhKyS9WRrOtKtHhXHDvGwfqWfR8bUJ2LgVbEsbFqr12K0NZB5AAT1MWVcfkwYTYnLSbvnPXDnATT51973zUiRPDlyfMTMmMCIBLA56g3LOB8PsN5j6TrXZFDA18luit0AC7mtDIOSHG0iJkgGQkK+BpjxPky4NM39/jeH/4Mf/Ef/xS/+vxL/OQnv4W/89s/xf2bT/B7v/eAn//8r/H48A7397fYrm/g/RKbu7fYrDc4ntoxFbnUBZx7aMTLlW4354sy5Ukyqk3eHkJxdJmSwc/6caYHXrv0+Y+VpRdKqnrwmhxcex+vawTUNRm89tmHytbyc4bog9bfGfM6XJfR68VP+2+uU16q23w+vtau18qZ1u/DZbykB157VnUo3+Ne+H5enr7vpfa+Jm8f0yZ9/Pn9tm69VM53lTF97qWxZjn8SRl76d75M3O9Tuxg+uy0T7kuf6QYTdrxYr3ytG8/VMbHfDfv32ffv/Csc45DWdfCSkyJPep9iTgFAN+CAWpZZa0odG7br2UZI2QAHnMlmnPG0+6Ip90RP/je93B7cw/vAn79688Rc8QYk537vFjge59t8Ls//V188r3P8PDwhG+++QbDUDIBci1wzYZLKWIotv1lKGtJhpF8Zd+QxljlifXJuWVLCb4R47X/crtXOlMbNf1I+vND+rQ+mK9kfilrkKtzrzgdCDGtY8KKDnGa4fClOqTG2leZ4j5Yn5/X92q5Mm/Yp3o/QG6mtyhoZzZ6Kvvw5XKJftFbWmxYFgDietVBujhOkI8yR4gRp/MJ79+9x9PuCefTCZYVINUgW9r8zgf064wxA273VLIjSpaAzlWHAgAo4RGo+Q8yAJfhg2uOn96O/wtdQN8vkLKl8x+GoUY7Z9j50+RRuq7DmCzTjvcO2+W6cHaNN9D9Bff+qRDsnQ8TezOh7KtK+bof7soeKnibi6m895xGOx6h1N97j1DShzugOgOchxFnP1g7F13Z72SsQo9Pb++xWSyx6Fc4DBHncUDMI2KKuKQEFy0S/zKOOF5OuKQMhOZUfrkMNbhL5UTxCrZbud+cM4IPWHZLZFci8pNFbvsQgNSO0s4AcrC9dIqpTdLcslfa0Nr/OAcZOZ94BFEJ9smp6MOcEctZ8S4w88t3c976aGKcwIJ64bMTDexvxC6jWpRMIkhBEoBAIIFygo5KzCpxxKgXXiQDGKnNSG5OJBJRTKutkcWbzWYCJlHIeR+AqhAIPpEIJ3nEZwgq8V0kX5UoJmDPicHo03nkJRUgATOCspyQmmaWyof9mHOekOCcsBrJwvKUOLq9vZ1E6QAt5TcJEpKs2mcAKsiac65gIIAamaWAm/e+RiYQCKe8MAKK/a9k+fncUi3c3NxU+ZlHQTKihHUnKXa5XCappNknjMRUoI7yQVKPoCLvzznj4eGhynHOeZLulGOjqbk5mZVQJDHB+nAO6JwCgK+++qrWjf1FeSJgRwCWm2tGiGlUEMtmpCNBRsoe0/OT9OUizOdIinMu8DuCrATl+JlmWiA5ppkJKKN6VrNG2Gs0D/uRsj/fZHC8KYdKYAHNAUaNBeoZfRc/472qL3jxec53TeHJtMgKfFP+ma6afaIRkyrDBNapXyifuklhJgz2K8si6cvP1EBieQqksz2sLy/qWnUgINivZ9hSf2iEpb5D/1a9RznWbCJKJCkRQqIk50ZGUA4pS9QNbKMS54ww5xjyfayfRrFxzJ0zDzXnW/S/zkn2afAei0U7S10dtQzQSuhFt88dLIBGMFIWqZf1eyWoqON1rrNOdAQBjBRThxb279zxRSPnVAaZup1kGvufPznvSbxS91cvUucm48HyOX/o3EUSkuVS9iz7S1f0xzhJW6vkKnW+je1FxpEER4vaNceJFbxvuvd8PuN8vlSng75v5wVTN1H/krRhWyhTLJu/q9xfLheLssoXdN0CBL1tDWTkZTBiIbV0V5ZJwMD5xaKHcx6n0xE5t2NTVE8pUbZYLKtTGGWR9WF72lqE6qjIaHE6G7RI5uZYcXvbjinhOM51MeWRY6FEqjofDsOArg+TdUXH+Xw+V2cXtQX5jzKoax77nrLDtZI6jHXm/eqQxrnLcumww7WeckCnSR5hwDGgXcW2U65J+GnmCsox1y1+zjnF+uomkzYr7Uodz91uV8lXtWWZkYd9xjFSeeD7ANR6UFdS/zCyW9cjzQjBTArM9sTIZEaa01bn8xoFr3OHdaN9rHJEudL20VlSU8JzLaJcqGMVsxC8f/++yhj3Jre3t9UWZJ/o/oXzn+sf7+FYqqOCzk22izJEpyDaRGyL2v20d9TeY7v0H9cVHkGy3+9rX6gtRGc6dZbjWsw9na6HnF8cQ6556rhGeaIs0lGIcq19ojYf1372Ce1tzjcem8C66fpFIEXXPq7R1FfqmHt7e1vnEedojBGPj48AgDdv3tRIA9UvrEPOFk292WxqJi3Vpxw3zgHd07DfOJdpE/9truPuscpT7gJy7JDGS5EDcwxPyOjcCt1ig3hJcHmEyyOQBiSMCP0Clso5YhwTLpcznDPC2HsH7wHnzDnMe4/VYmFnknuH0/mM8XixyIHOo+8D+r7YzujgcoJzQOcNtmKadQh4nuLY0ltnIJe/vHPwXQfv214nxmigBxwsSMAjojFsbV/UyrHPOEdsjHyZyz4EBF+Oh3IlMqbayUCMCqK6AuDRSaSQyS6jK1G9h+MJh90ByF8BzmG9vcGbN28qWb7dbnGz7bFcbtAt6DxiOnZMGb5rQGpK2Zw6UI7VQQZKZPw4DHBdX8aIe6ASdSFrbi6pteHM0a45HCp1YW1LyZwZXIrVGYFAn3cZMQ5IycFhum+a6GJiAaEduTW/JkTBtXsEsGdc+YfmyWtE07N3zz97qR5ovATB8GuX6rNrpPi1umnfGGAu2RnK9+M44nI+w1KWt8yK1scmfwm2r6COdc4ivOIwIEVLVwnXomOAFujw+PiEz97e40e/+3fwX/8v/1f4b/9v/y1C1+Oz738fP/zBj/H2zffw9u338fT4iMeHB9sr9T1+7w//EMACu90ROSUEbw6YKWf40LFFU8aHLXXSQ7nMQxdq5JkSB0xFrynBtf+0bxUg/00uLXuux6+Rge33PJlGrz0zL//au7XPXJV+1J/1lfk5+Tov11LaTj9jH2dxbnHPdMHHt+Wlzz/23pfm7YfA6tfm1t/m0nUczrXoPJn/dOTIs+e03nzmY/vhNfmbf37tuw+V/9p1Tbdek9FJ37xwMSNLecjKwpWzxymHsh/ke7QP5z8/qEt/Q/m6VsZ8Xl175rUxnpc3/8mytZzX5MDmakt9TdzKnEV7MN1xjCMulwHHQjramuLtWBy0zE81KpkOMy4DmGbYAuyYnL/6679GFwJ+/3d/B//N3/nf4Rd/8zd4OjzhdD7BeY/NdoNPv/cZlss1/vzP/xw///kv8fDwYFkVk3nWF5MCXB9ytIhxS6Xe8CVkeydtc3L+lWAWzNQXK++ZfOH5GvHa+FwbG+QWearjQdJ1vg+d/5yP57Pyy1VxxBfWkkasT/caz/bCKdeo8pq1MoszBfFU33ZoSQABAABJREFU75Fjue/KPG976kJ6dxZh7b1H8AF3d3cVZ+u6Dr4LyLEd/5WRMQ4j9k97vH98j3fv3tdAxvFiGW2ZxVdxj/V6bbLcL+B9wHpzg+X2FmPMGGJEggWVcO+9XNoeJDOrUi77tYq3Fcf0roNjJqnSBt/1WCyXcPCIZf8YEkq/mc3RhYDFcoGuK5j6aDYOHa1RpKE6p3hn2J7KT3F8TeI8msuYuBLR3eQL8M6Xfy0w+HK54N1wALjv8QWzJ6ZeZHEcRhz3R5zjYO1c9BZJnTPu1xu8efsGd5stvnx8h7959xUeHt5hPB1xOh6QxhHeA/2iw+Uy2PGq3DM5yzZqTi4W+a1yQ4yuHh2UTWYjMVcwKyDq3s+Xs8arg35MxfkTpY0zbCME9JKNd7PosewsE1IdU+9lXtgRQouFnX8eU0JEhg8llX6JvOeZ5R9zfTQxrhGLmhZbgeDFYjEBDEm2EhAjScvNZk3XllrKN54RrekECWISwGH6ZAVuCBgAJjiMEgRatDNJVb6XypgkqgKL3vv6vG7UlawhGc/IdEYg8l6CP0qI8J03Nze4L2nX9OxakgMazcJ+nBM0BIW4+SGwxmcJrLENzrVov5ubm1o2+1BBJgUCSWazLJY/DAMeHh5qtDxJbraD5VEYmW6XEZtsD8cXaOAsiZWnpyfk3FK8A8Dt7S0eHx+rUwSAyftJmnCDyXSOLJ9OCjpWKsMKgDrnsN/vK2F0d3eH9XqNp6enWs/5O6hACOQpGcF+1ohX9jHHg+M/DEPNMKBkIQFrjfTiRpn9yjroGOhc5fdK7FGuODeprDk/OUacZwTNFSjl/ayjcw6bzWYSycf5ybor4anvVRKT806NU+oWLtyUYzpZsHwCwpxHGsWqjib6jI4/36fANj/TCHIqck3lrOPAMkny69gp0cbvANQjCxSg53spP+wv3qsAOC+2l21mu1ie6gh+zvHmM9ofBJg5l5QMpwGnpItmBuA8I2nN+Uf5UWKf7aA+Zh+wzYy+JPBOwifnXLxYG9jPucUMD5R5nl9b65scBnGuoFONyokr+oDf6dpDYiAV+aQuYF+S8NNNWTWiUstKQB0wB9XZZ+wL9pkSEbqGsFwlwNkf1OnUYew7tpWySP03jwCmXuZzdFTQ1MfUf5RDnUs656oOShkOAevVEquVGd7eZXjHtEkRyB67p0OZ95dSbvNidM7Skg+XJlv78YBFv0BO5vxgm0+PcUw47I/YbDY4Hc+lDiWtOR2+vEOKPKoFQEmp5EObx6pjWYf1ZoM42nOWOcCifcbx0tYd76tnY87ZoshcgvMZKY8YS7rvEGxruFobuWGesQlwZqBb31zquzUqn7KmJPpyuZyks+YzakfM28U5RkJprsc4L/kuOrHt9/uqg0nKjXGoDk0kVHPO9QgMTf1N2Zyvp9TpnAcc/7nTCWVvvV7XyPC5viW5TVvSOVcdOrm+ULedTna0wE1JpcvvqKO897i5uZnMa9aPc4i2BucLbQKg2UGqP9TeZf24yWQfkSSnvtf2sd85j9Uhh/qGtg6dQmlncNxvbm6qXuJzbDez91A3UW/RAYAZbBhpv91u6zgwwp1t10ho1Y/Un9SxbJeSppQBXhxbHl/Ed3CPQRmj3NAu5H0qJ2rbaCYfjgntaTotkrxXHa46UB3hOJ7cp3BOUA9zbaODydx+V/uK/b/dbnF7ewvvPfb7fR0D9h0dA7iPYVs5D3ivOoOyHpwnXEu3223tX0b8U/ZJwNOepf3H/qPsc94456qDrcqC937iRK12ItdvzTTAtnDNXSwWeHx8rHNUHXHpjMBxZ1tpr7LP53ahXtRRanNwLJi94ze9ttttGZ8G3DHNN22C0Hf43vc+xe3tDb7+9a+x3z02x4psxK7Jsa0VQDsGxeo+TuzJt5+8xaK3rDu70xEopFZMCcfzSeZ0kw+im0PMFnF+5XLZqCAi6w62ruZcwJ+YEGMux4dMI8AbcRRg+QqzpScM3WRe1P2OkMSUe7Uz52TB3M5Vm7PZ6RZh7Z1FenHcD8cLnnZH9N0jtiWS/O7+Bjc3N1itVlgt1/De4fYuVyzDnMAuGIdLnfOICUA70gczgConVPBTnW68L5Fg2SMnV8eCHW1gJkrAeDnSJ3TmjNeV9bPoSwO/ZjJug2R1cc3eeulSgJlA+RTAnhIhzj0ns+fXtXn30nz8TlRazo0UvwKg1RqnVMdDSfGX6lY/d4xvaiB4Kt9Vh6nBnCkhn6M8kWLGSPyiOMSnFHE8McNRBFKs+QAs/ajZRvvdDj//+S+wWS3wv/nf/le4uVvin/+Lf4k//8u/ALJHigE+mPNmF97is9+6w0//8Ldwd/cJ/sOf/YWR7imV1JRGitm6+XIna18E3zXwOAHZTSPeUs4GmILn5DaHymt9+/Ex48/rdA0cVTvjWv1zJpHxMjGs+wDWfV5OvU++r+251iTpIzfXAfJepmDmpWs35UijEK+18docekmeX2vbtfs+VNZLc/q1566942MuHZ8sj9b3CPZQP5O+p8jb81faN6/vK/W7Jm8f02ff9Xqpj/mOeR/O5eLad9dKu1r3PD1yB2hEUM4ZcRyv9pFiQB9zzefexzw7n/evjcdLfXLtPa/Ni2tzZK5DbA13CJ0vx8iucbPd4v72Bje324L3GhZ0PJ7wzTff4Ktv3hVuJJcjE4gLjPBoDnRwJOgzGDlunwO+B46XJ/yHP/s3+OKLv8Ef/cEf4oc//AF+9/bvmF0wDDicTvjyi/f4y7/8V3j//n21m83utmjnnBKys8xGgNXzfDzidDjgUuxgrm3cf3DfZIS5kV2Wfv2EGBOCOE3NZWP++2tjn4sN89y0ee6soLikjtW8DnPdPy+zzZnn56c/e3+meZZeLFO/876thu1d5uzpaGJLGXN5Zju7ELDo+/rvpz/9aeWoxnHEZbBA1PPpgG+++Qb7/R673Q6Pj4/48ssvSyr9tse9v3tb92x0UlaH9xACVv0am9Ud7t9+gk+/93243o55hGvBEn3XWdak1HB/h4Yva2BBDENxPmz9FWPEcGI2P0vJvhunR3upQ3eKdF6NGMSJ0fah6pRSMFfvAN/4x4FBOjBSfByjOTrIuyqWX8aH4zaOI56GU61X8B5d6Cq/VbH7lJFHyxCG4NHlEX3Xoe87nD3w1e4B7w47PD7ukM8XbPslltstECPOpyPGsQTHvjGcxyVzZK59kBLS2LL8cY99u1hV56fKP+Rc8XL2U79cYMztaFLFjJHJgQ1IaYAP031E4wlsfNZ9j3XB4Lhn577d1g/LJBr6DmOyIxbHGM2Juk0aeLhnc+ml66OJcSosLm5MW0mCg5OMFed52ASNPvvss0qIkyQnIEiScU4gnE6nej4rU/sCqCmACXgRMOCmlROKSozgj54jzs8JrjQlY989PDzUiA4CLRopShALaGAz38NLwVD1/OLf79+/r79T8AlwKOhMoeI4kFhiNJWOD0kigh00RBTAZsQIJzbbSBCb40Pgjm3n3wTDuJCxnwmScIwJMBIc1Kiwy+WCm5ubiaIchqFG8+WcK2hK4FKjsmKMFSwnqKdgHvud5C0jlNhHvF9lmuACy1bAnQQYZU+BSrafdXTO1ahNRlaxDUAjCVknRoGSjOLxA1QE7FOS+TRElABgv7LvNDKO8s33qjyrzCrhRgCdZei8UVlS0kT7RRdvtlUjCunQQOCXY0OZUZBZI755LwkrRvhQltk/Gt3GPicoyz7jPXq+pBKMbAP1BOVa5YtlcYxIKrANSjblnGsdqC+orzgmagipg4A6pahcKOA31xcEdZV013EkwcHPKacsg2Ax20HZoPy19MxT56G5/mW/6mKm0e7sSzpNEThXWdI5r4A79TDbyrmkThXsP/YDQXk6L7Cdqss5j3Rd089CsDSenIOq1/kMM3Swf5hinn9z3l4ul5qxQdcOyhPlWvXNvEzqT5KRrING02k79LgO1p1EKaMnKWcknbh2aMShzru+73A8XqrhwvbonGO9qcs10rzve0sNHx1iPD7T5exrylGLNvU4ny91bHS91N8pQ5qtI2cj3tvfqLqRMqbyybbw++AtralukFRnxzhijEbAxzhOvuOZ013XwYUG2Cuw39YxypdEEzmNsu2xWHQ4HPb1jGhmseAaRwKKz1PfK5FWgfnS3u12W0nA/X5fn6/pz9GITNUxAKoDI+codYa1z1WvaHXMo47TqFXaHirHuqGkTHBcuTZwrVanJP2pdaKOYJvG0TJOHA6HSUYiJUhaVP2UYGH5ShTzftpX2+22yvDDwwPevHkD51xNoc0xUMdS6gsAlahjFAGASaSrrvVKOipJS32p9i9taa5PfK/qCsoB5yOdB9R5j/KmTjiaXWmz2dR2Uib4vtPpVB2eNOKe71MZVb2vMs31su/7GlFNncd1WNcwXZsoW+w33cirnOuc4e/sb5Uzbrq5nyEIRLKathPHVQl3PqsOZKzLfL1lPdmO4/E4iThX24jjoVk3OLdo/9N20fWG+uss4Bb1IecxbQcS+OrswfHj0QIcb2ZioA357t27On5cn9lutdtol7NPnXPofVunWTbrp3sn2l1zm5qyQRth7hSg+of2CfddumdSB4vvCt5fu4aGfsG5bBFuACJgZ/6GgJiBr79+h4d3D9g/PiJHy1yz6JaA97gMEcOYLFVft0LXe/SLBVKKyLB/XQCWq2AZIHLA4RxxGTK6xRY/ePsZusXCwKOhnOk2xhqh4V2JEPDNHqIMBO9hR42EkiIQLe1htrfnnJBiQhqiYXneV1vLCHIP35XnCXSU9aR0DQgKtrWcNrJRGlOwko5Lbb5yfbJ3WlYXRkXonkJ1hXOukoVWHp0VEo7niCE+odsfy5xudthyucBivcJqs8ai69EFj3EcSjYby5Y2nM4YUtuTeO/hvEcXpkR/zhnJGXHLcw/Hsek0X/dqHglATCO8d1gsF8xLaGUNIyJThOY2fpA5wLVH58RLMs7Pw4y4033O5PPQ7GDt65fKne+b5s++NvdeI4SuXvw+t3Poaz2AmvUH/oWzR53JFWBnyjtmOgAm9hhg0eLN7h5xOjmsL0ukGOE90PcBY8w47g+IwwVppFO6gzMfGKSc0fcdMjJ2ux3+zb/5txjHA/7hn/xD/OyP/gF+/esv8Ytf/BLffP0ei+UGfb/Ej378W3jzyR3GfMG///f/Ed++e0BwgM8JGQld8Mg+FKD648in4Tw2QDVYCtGu7+CdRTeOw4hzPJsOSg3b0H1t7cffgBTXcX1pjOefz59hOuIP6XLK4jX5a2VmfJTbhjOZ+pAM1xS4Ds+yLug+IaUR1IHX6v2f+5qX+V3WwWtz+m97zctT0ojf+NDOUPW52EWh2YHaJnXvIcHxwTpgOmtek7sPXa/L2Mc7F3zXd+cr+k8vXfOX/cKOGrm5AYC6rtE2SznhucvG63V6SS7mc++7yvR/jjnwsfoFaPuXa58753F/d49Pv/cp3t7f4uZmg+12jfV6iX4R7BxyACllnP/OT/DV1+/wN3/zN/jyq2+wPxyAbMTaZRygWofZYeyyyE1m1/a9w+l8xDllXI5HPD484GazLRiFHadzulwwnIH9fofQBQAZzhtGEaNluKGdwXZfLhfsDwcLpIoJ6wWPORtxPh1wOh0mwVeuVJYRvjlnDKAN+Fym9ff5HH1pDNh/ag/O587cRlE8cv4sv3+tzFCieuv84XO+KO5ikyaIU1x+Pr9z1kyy5ezxapuxndy3NrxYZU3Jyoqx9IZrffPNN/j6q6/wp3/6p9jv9zU789PTEw77JwAW6T8UDFkdMy3D1gZ9mPIGGTAnmNJPfd+jWy6R+h6PhyPOX3+J7PRIq2JvdB6nZGnW2Xb2X4y2X4gFF4suwgdfMwMZ/iDOYYm4aIeaqt2Xo6l8V3E29mUXWgBR13UIKVrEcihHTXmPRQjou0U5krFHXpfALjhkZ86MOWcsuD/yAX3XIXSdkeWFVA9dZ+eO5+lxONzDkJcxWXBIPC8dll686zss+t5Sw3cBw2XA8jbgfmF80mrRY9l3ZV8QMYwDsrcI7JSSRWp3HUIw/H339ITz+Vgcl2y+PB1PovfNNhmKA4uuByknxLIPya60o7QpjiOGywXnMeIy2jiPschRNIeCUB0NSsS9c2Yvel/T8Mc41vHMGXDokLi/A0p96ASTUbxQ8X+6ohfm10cT4wT6gJaakYCckqDv378vhnxL181njsdjBfQ0Ko4R5hoF8vDwUL3sFewiUOicq+Q7AQ+CHEpGcvO2Xq8n5KeSUwQuOQEA1EVbU0ATICHgxDSk/J6pGXnpWX2cmCQ4Cego2KdRdwSv9HcFN0lGsE1sJ8dGATwCS9xAqyMDFTfLJKnB9OYkBrz3phQPB3z66adVAfZ9j91uh5ubmwnAqRtoPj8H0VSutD4sQwE19uN2u60RTwS5KEsECFm2nvetG3nWhek/NWqGjh5KePMZOhM8PT1NAHqN/ua4E7AkmK5EDcsnKawRM5RHLljsM9aLfUsgmH3EyG0CqkpUsm+HYZjIKB0Z2Ocqy5xvSkQxhSzvY1vYP0qkEVBnfdl2ElPb7bbWUcFOtpkX66WyrOmZSaCyfP5UYFKBShLwqgeUxGXfMwqNZfH+uTOFRpz9f3j7syZNciQ7ED0AzOxbfY2IXCqrqqubxaaMyMwLRfj7eYV8J2dIXpJNcsheqqtyi8WXbzMDoPdBcQA1c4+srGrKtRTPcP8WM0ChUCjOUVXYjRzlQD0E2vkcdr5R96z+UKf4u80o49jaYA4+l/bZEhJsl81at7IFGknGeUeZsx2c1xxnfoa2xhJE7COBbAuYW/mQYLXPt/boc5sbtpN9pBxo/+3cpY7aqhIcS2sHrq+vq3xyzuiGXoHFPD8rmOPaMmlbYIIlajjPViaDjeulndeUM8eUARXsOwkSzj0GdrFNNmiDBBzt32q1qs+z1VC4NluSkAECtA3Mqqdd5jrM+U2dp9428ritL7Tblkyi3DheJPBpy56fn3G5jNisdxhHVktxmKZWbv3h4cnoNjQaU9qzUiJh3NX+rFZDyZzxOJ+1XCU3bk1XPEQ016breiOLJkfnSJ41HRI0MJN2nPLnOuoQ0HXzs0F1A5ixXq8wrAaMUdeCzWZVHXaRDO+h0ZBlc6M2TuVyuYzoOj0rdJo0+8/6Hwzsy7mdD82/GYzAgCFrRzmeJG3ZV67jXB9os9frdS2xznGgXV2uIcvL+o7Ufc6n4/GoG4oSrGJJJ841Vj0JIeD29nZmyyzhtd1uq+8J6Nq3JPr5fOrl+XyuZ4czO5zjS5mQVCfZR8Lb+rdcD3meNu0q5cRnMFOetuT6+noWMGoD2qxfQjti2760l5Qr28xxoo2k38ugR47/MiCLY8J70VaQEJ6mCVdXV9UOppTq+FjbnVKqpd6tD2OJfBuUQluVc8bXX39d28nncI1txEJb37iHsHKgTeMYsIy3XWPpr1ji2G5OlxVRKK/tdlvltiSHCTAwIMgG4VGXWH3IBqxw72F9GFvRhessP2t9CRtka+2xbT/7Q9lbn8+OHQM5GZBl1xG2mTIj6U59YbAt5yP3UiKC6+vrqhdPT2rjd7tdXats9RvOP+oo9UhEsNtuS7ZxK6tOmfC7tEk2cJRrIKtDMNjDAl60gbaqEeVKmXE+Lf0YC/r9udcv/+IvtC3lb657XFO817Ps4AO8ZHRf/QrroWRpQJCSIEKArqvAI+2qDY4JXsnyvu/h0IIsxXn0qxJcnDQrKLiiK5JLJq2WCAxBSyaLkE1SECVnXQeDa/SAng+u5+DFGCE5ozNl7wjmch65or++ZFuQKAbQsj1S0gxJcUASuAK4AC8znCt4eeHZd/Spydkz0Jhrvb5ugTbveZ65ZjulnHUdrznCDbxkJpcDEIpf0HcdNuu1VtHoe3RdOyKq7zqcSnC3PZKDpRarX+2AKSWkAgQ1YLX4ss7BZZZWBaY4ou+DlrguJHsqYwGvgXy56Hi3ICc5f+waxHlifXdezjmw8KTdI4lpp77nS7b8nPi291leDeSfXxaDeO37r7XztXu8+vorzyHlJUAtN/ra/QhaO8nl+AFfz42kTPkZgYK+cZoAp3ooKQEO6Iq/y+C2nFvlNwuYXsYRHZQkiTHhf/2/32G8/Ed8+cUX2O02+O1vf4u/+ssEKcUGYkr48cMf8Ps/fI/ff/eDzmXRYBoHp2fPd44danO8CbaRf+X9rhuwXq2x3W5xdXWF6+trDB2PwxlxOp3x/PyMHz79WPG+Ja5i9a+yGovrczJ/8X3MAyqWurD8XeRPyzha7mFfuy9e2Yu//Iz+z2KWvCwmuFmvEZjJllO1F7y3nUt2H/65Ptvr5/b5s/0097Hr6R977p/bjtf69rlLRG05z5ntug6rEjg39D1C2SM+Hw8Yp3ZEEPfvyz682m/TLt0z/rTcl2P0ert/Oohjeb/Pte219jtXhFIWKRHqDwPOyhhKw4SWdnW9LnN9u8N+t6tHizjvMI0TTucTDs8HfPz0EQ+fHpBSfDXgZTlnbX9+qi8Wu11ef6o+f05nX9iMz9D7wp5J66Er/5N61HYh7Hw7jvP2+g3evn2Dd1+8wX63xqrv9LzkwWPotbyySEaOCX3nsVp9jd12i+vrb/Hdd9/h/fsPOI8XBF+OyCSJxNgt2hNBwT6AGD18WMF7QLLD+ZSQRk08qkE3xZf0nsfbqb0nLss9AZ+B8t7lfMYUp4p1heCQytnjS3xAbVaRWdLS2hEZPs+Jcfs7n7kMcH5t/EhCL9eG5frAZb2up86XgP5yE0EpaW4GVlCD/qvv6zR4yVaDmbVNrG7pvR3b4H1bT4EaEAvT5pTmsqMcsogeX8J2ZyWSnW9nWIegurTdX0Gy4O/+7u/w7//dv8PDp486ptYXN7xa1/XqL5ix4742hHnApmkcAMUZVsMA9B5Hd8E0neAen5DKHFFy18Mhw10E3pe9iHda7j10mFJE8IB0HvClEqnrsF6tNUi1lJq/vr5SQrj0XSDou9V8rIEaXObK5HROg3xVj1vlQW2/9rHJUknlru9LIFvB7nPGZRyL7yvliAMdo5QTzuMFIihlv/WoJw8mhCm5nLjWeFdL5UMYGKD7MMUtCrcWI8Zpwhgn5Cxlbmc40cAMV/Qn5gxxvqiowLvGnVwuZ5yeDxjHS7PNWZAnaWsY56cIfCHU61zKhVNxzd6gyNaJ7vloDWn/dL9W5ofTcvV918O7DgJX91tDv0Hfrzn9yvrdIbisp12xlD5K9nrXoQ8d+sU69VPXzybGCUwQZCA4x4wHRv9bEiSEUMHEp6enSrCQlLQEqSXFRQS73a5mWdjMbrbBkh8EBlky0DmHx8fHGSFGoK2SH938jHESFwSWb25u6rO5IScATDCZ4CeJWgC1DDz/5r92I0kgz4LIBCcIMBHws6XQLaHCMbEkKNtviWjKl0TdchPANtmMH5tdTbCIxvD29rYSTKfTCR8+fJgFGVjynyQ7wUaCeg8PDxVsizHOSAS2nSASfxeRmsm43AgTuOCCzHG2GUp2vNlOZleyb7wXAbWnp6cqe5JkBCqXm3obBOKcq0C8DX4gcEZCgsAHN4EELTmGJIw4FiIa9U25WcKdm0lLXhBstwQw3yNYT72yBLEl2EkchBAqsD+PXGpOgwW1SZ5Qj/m3fY6dF2wj5wP7Y0lr+y/nCv8miEvAmAQd27rdbuv3G8GESgzSbn3OtlhSYgnYWAB1GIYXWWD8LOW+dAD5fM5n6iizvSxpzLlknTib3crX2W6OBd9fZszaLLSUWrUC3pfttvPJBmRQz6wDxHYQ0CbpZucn/7WBKzbAgO9bPaNuWHLeytHKmZ/lmFC2/D4Dn2wgCWXQDX0FFi2ZxHnW9z1g1gSCldbGd6FVmmBQFu2sdcj4DPab+sg28pmWWOEz+Xmbkco1046FlRfXBQYvAJjJgpm2NsjE6httCNdB2gMl5MfZfKQ9pA6wrZbst5m+Or/CzNEW8bN7WgJM+6iRk1ZflmsICXxCFDyTJoTWP7uuWp/BbuwsiKaXQHHw9jptBOfPer1GF3rEmBBjW3cp055Rnl2oGdabjWbJkri9vr6qfoN+19f1lJsPJb8cdrsWzMZACs5xymy9Xlfyreu6+hyrz9zkUtb8zjKz05LC9sxnXsfjsa5ftB/qh6BGJ1OvWGHBVtWw/pQlyQhOrVarGRlsfSS2heu8tX0552rrbNUd+/n379/P5zxHXVqgHO0hjyThZ5fBcDZymvOS97Z2hud0r1armgFu/WRLgHKt4r24VtIO0S+nP8SqFNbv4TE+1k7Qn2JwGPXaHpHEy2ZhU69tBQDOcdof+lYcm+vra+Sc6/6A9oT+rPe+BugwMJEENoltO9+5R3DO1fL9NvDSBi9St/kv54P1Z/n3MqiMn7fEMOVH+XPtzjlXnaZ/wvnHjHh+jj4/j6SgflPv2F7ei7aG6zP1zvrPtA/r9XpWZcpmu1u/geAG/RjKljbbOS2pz7HmM9hG6gvtkw3EYqAAA1E5rnacKXvKxa55Gjx1qfsQ7r8YkOAAuNDG1R4PwrXHVovi2JHwp6/DOWX3Z5YM5xy2e13rq9ofrl2fI/B+7vXm/k15ZgPJrL47p0xuhGDrHO42O2zXA1xwOFzOeL6MSOIAFyCi1UckZ0xThHfUq5K9EDpAgFQzUzwECbFUZyIxrlnSAsmG0FuskRYXExRbaIBB/kwxIqYICErmQgmoW2ZLBy27HuAKP9YqsaVEglHvJaXEsBLUXKNrYxpYJhkpl4CLIheBlDP9WEWqlHN0JevH9M05zYRVv7EQ0ZAKBvF+IgIpqacCQXAOwbWyhKteiRkNhNZAq+vra7iy3oRQ5lqmHS5+fdHP7BKc07ZSZxUcbQEODpq9LSGUdjg43yEMK1xKpY7gPSRG5BghzpYM1j6Jc0hF77LzdcznuNMchAq+/c05ZffQ1GPUY2LcYsyWpaTL562CmRxO9Q7n3yUY5xyh5/nXLCZkcZLaNnO9ANHR+i+f+Zx+gBltBhxPLSlBAz0CfNchiZisOS0JGlwbT5GMcTwjlsDKIpQKNnon8Cjn0YtDFuD5cMLf/8M/4vHpGTc319jvdxiGDuI0M/358IxPD0/48PGxnnte24qSeJMTeGK1W8qt/J3LOZnDsML93R1ub69xe3OFm1t9pgbVZEyjBhIfT3usv+/x/uOnGiBY8ZXga4AMZcbxsM+2vkgbDxpMgeMclHYv5xkUW7RG7JiR1GrvodjZ2hzqCb8jjdQBjJ6ivbacG1LngKNA2/NFwe0G3qufsVoP2O122Gw2WG/XpXqVVrY4HA54eHjE6XSuwUZOz2iq65HFVGY6uriW79l58VPfM98w/xYY3sikjd8ffzbv0z47x2JeucOL+3E90297eNjApC02mzXW6xVW6wFDCJjihN3jCqfTGafTBYfjCafjpQRRSQ16gpOqRzDjPdNVvCR7rf7O+yyv6M3nu/hzRmL5zNevNocb4WfaaypFCJT5qLbAO2zWa7y5v8ft7TWur66w324xrDTYwIG4zw6X8x77/QqrwePDp2ecx0vJrmxdLhQMGGBG3QF+muC2fsXn+m7l/bl5MF9vPn8v4PPyr3MF7f6aBVkwCTF+RAjYbne4vbnBl+/e4fbuBtc3e6yGvp7rC0ghNKkWHp3T4H5/dwMHoA8BDg7ffv99CdZzs+fbdZc4CgAglaNboKRWFsGUE1KOOh4OZjoXXFFVHxkMJvTFP3LIKBhCHDGNZ+SSoDCsVtCs3VTxBpTvB198NsnIOULdHc08tSRtsyXMIi7+iHAvAtRqfoJSUaPWdJmRjE3X9IvOFUK6GH/KKiPVgdbAT/UPuf7XZ2Z+qJwljbn8LdZk7UO1raJ+r9eGqv8lDSukJc25rFeZuISDC8T5pB6tIpAaxJlF1P92Gkjry7pwtd/i6fkZ3337B/zDP/wdLuczQujqsS0kb/uSpKH+RtPvyg14PdPeiWhgpSMG4qFF4stzuw6r9Qb7YQ1xGpUXk1afIsnrCsHc+76OfSh7gym2QEIUkt9LOaoPbX+23+2xWa0gkmuGewrU3TJWIjUZquoEHFBcKvWny/vQjHMGw6LghJpJ7qvPitL2KUao6EtFu1yqNIjgPLYER4s3+CLDVPYjDl5J5tz8F55NDgDBhzpGUwkwTqLBfN5pdS5JOr88sSnnwCAoba4vwbYaGC07YNis61yLMUHGqRyTgOpPe+cxDH2RSTEQokc0leiOGhyCsqdyToMQNBDIlTahugjOoepA8D2cC6UqgMx8bfpD3gV4r4HZLN2O4id3nWKsfehqAPUfu342Mc5zFAmyaHbTpgLVBMNUTxox9unTpwrkERwC2rkAJKwsOH5zc6NKU0o5W7CKGRd8FkERAoA2M9KCpKfTaUby2QwE6yhachZoCwhJx+fn51mmODe0/B4zkAmWWFKHE2BJ8HITZsF3S5AxS8eCAyQ32FaCWZZ8Y4YPAXK2GUDN8CIxZMGi/X6P29tbPDw81Mxxm03B8aTcCZbvdjt472uZdYKhdgPM8aMsvPd4fHysIBeAWZYK5UiwypLHJE8tgUEQmLK3ICB1geBeCAHH43GWGcznW8LEEoT8Hu9vS02SINtut7MzUVmKlXMipVSDLtguAo+WIKSsbfYu+8f5QCDegvBWFuwH5Q60TEKCuwQNqRvUQVu+ksAhx6ku0GZ8KylojDtlYs9DJ1jKa0neEhTl2C83YXwGQVHaIAsyp5RqFQOrI7adBI76vq8g+zILjCTHksDk93hxLvI+Vp85ZwmwEzC24AvHgjrC/hE4ps2kLbKOLceT7VzqEW2MBWapO9YGUh8tKUagnOD41dVVLfdq22SJVPaH+kZZsE0kJSyxx2e8tjl5DWhm2ygLG7CxDMzgv9aeMGCEZXaX4ArlQZvItrbgrwmQVo7f2qactSzNaCpb2PK4NrKWY2htA+9nwXmrt5zbXOuAdowIS3CS2L1cLnh6eqr6R/l437LcLTltSSFLdlSAyreAoGU1CKARX9QPEkB2btCG2cxeXtMU0YUOzvkiewZ2aXR0LbXlQiXupikV8E6d2BgjdrtVGXMFicdxAjAVmSXEEk2p93PQ7mnmXQgdnAsVbExpLH2lbWwbUoeXpfQtAeq9R8qaUTdFXQNWqxX6oRGQzgPrfoWcec62nq+6Wg1wDohxQowT9HwjJQVSanZ/u93j7dv7ej60DXyxJahpU1JKr5Kc1EvqCL9ns6m5blgfxAIM1ldjYBdtBKsYUM8UT29rKtCqEXEebrfbmX7TnvN3fo5zxh6XQ9+HfoBdV6l/dn5zbsYYa/ay9atoO6yvQBkyu5UyqWWdi89kg99YgYA2i7aQ6/RQiBESwXYdZ3uYBcx7c3xJ0PPz9BVILnLtZbAK7TPtk5UngxKs70MbZHWea58NRGG7KTP7OvVomqZaYYpy4dpH+XJsrMxDCFV/+V0b3ER50sazfdQbkv426NSe223n7uFwqDoIYKbL9P/YRuvjWOCZlUyWus33LXlOH4QVK+y58JwfXBsoVz7DkrOcL/SPbIY27bYNErF7Ho4lfXvqFl9nsBfniN0HMgCKz7DrM31QBmUs551dgywJz9dswON+v5/1jbKNMcLleXCstS1s0+l0quXirS9s7biVsz0Sxa7ZltR77XvWH/l5JMLnL8miZcazNMJX2nNFBEkyRsnY9APW3mHjHRIychpxOD8jRg9kPaMulSzvmBIyCXZzvm9OGVFahluOLSDJzm9fAcTiq0GzaKycah8KCeyBGag2k5EDfEddbmfKpaRZS5RrcOU88twCRGywgoK5gikrYBJ8QNeVigmi2eUpMgtckHBRgtn0TbMbMlF6bVvJ3CAphmI3emjAZMqlDKQTwGRkKCPtC8BdguhQQFMRTGPE5XACiq6v12tcnUeMMaN3LIXuELzTsutdp9lbWeDo9wcVrI4Rs9znZTcla1ZgCKbSUXDoBiAdjm3vnjOQIgR6XrX1u3nydQih6OLLTK4lcZEXeIe18TPA2DHLaZ7p2v4uxFqRf66fAWaEYwEmCVRaTGcJRItr3xRwv+Sqjgp03GVB6C31t4LmZr4vP2dtP8FCSVL1PIROQWsS41LA1SQYzxeshq4cDas6HqczpssZWloyA8UXF8lwOaErAQlZVB8dMp6PBxxOR3z3ww91LeSefxxHJag8S7+W43fMOJKMoC4vL/Z3Nazx5s0b/OrXX+Htm1vcXG+x268wDD1yFkxjrsEscdpjt9tjtVrhw/sPeHx+wulcyDLnGjlm5LzcL85k7Vxhclq5eoLe9QckRNyr96iqVJx+qYo11xXbZ4L/sPeoytX0fFnKl3fk/oJzQZA1kSoDQ+ixXg163vDtNd68vcf1zTV8H+r9c0o4H4/44fs13n/4iOfnAy7nETFpRpXtE/XwRXDKT1x/bB177X07b+evA5bc+uPPbvcrphdA00H77KyRT+b57LOC6XAOwXUY+gGb7Rq3t9e4u7vFZjtgterRDwF93yFOF9zs1jifRjw/n/Dp4Rkf8iOO5xNiLtl0TgcoS7FbbC9og2ivGgH3Gs7xQpdk7l+8fr0+B/+YLD9/N5J8rXJK2/s2m4ggqAolSm6sVgPub+/w9Vdf4f7+BrvdGsOg/nvoHFztz4CcN7i+WmO37dH97kd8/PSAw/GIaYo6Yzk/neoGHOBEy+su5bW8WNb3p3TVvve5+/zc71Nyr32mWhkRYDn2Aog4uBJMs+rXuL+9x1dffoEv3t5is1uhH8oxMKJBiDk1QhdAPTYDOaPvPO5urtU3csD5fMHHj59QPJAW3MO2GbsDaBUe0Yg3/fEOuRxU7fRLKnfvkBGrmROU4Mmqrg6A16A5ACleMF2OQC7HTg16VvM4XjDWqr+FEKsBf+qfcT+lBNgrfoXxH7z3sOd4N6ITZQ33NYCBZxAvffiK1/KDWUzgkvFvoJVeNOjIVxmRaNXPuEJOqu1LZj5/bl/gnINAy8yL41AU+2iwJSnZwPqvWdLEaWCd18QN2hwpjKPn0UQhaIUpp7qxWa/w+3/8HX744TtcLmfVx5VWL6I/pP5n4z5SjJDUsEEboKpOtmYC932HpkTqsyVxGLoVbne36IcVvHOYDD7gu6BHrTgNLuD88iVwMlasNEFxu4AxjXC+yVMScDqftYoS1Mc6Xy44YULKqeynciXI+bvqTRsT9c1UY1yRgQ8ko0M9Ror23jvXCFqoGQ++JTByTSA+yTLmfcHBu65TIly0rL4ObmONvfcIcJUQt8kYQx70Y96hcx6dD2A2t66brDTDvXXQ4NzgEUKHru9qdjr7QLwmX06zYGwUu7zqlRgPpfKUg0PfKY7L6ap+Rqry8d6jh0foArqhL3pFvFmDFpxzCL6D96EcT1QCBXiP8h8AiJ9zHRlFzt7XKgPOv27nl9eflDFOYoGbUJIflrwiOElj8/z8XEvEstS5BY5tR/h9guhd11Xi3BJmBDgJfHz8+BE3NzcV+Ms54+bmpgJiBGtthqAF++3lnKtgPjcMzGYmeGizJ1imsUZ5GBK4KUOu2T8koJfZ6AROAdQsG2Y6UuYEvgm4sn+U9/PzsypIkS2zedgGAkxAAweZwUVwiaAOgVeClQDquAN4kWEBAIfDAavVCk9PT3BOs0oYsGDPGefF8zRZDpWAo81Y5HcI3C0XEgvYE9BlRpHN3LPjS4CPfQdatBOf6b2WfqT82W4LdlqSiPcWkRrtXA2g+TyfRaCUgC1BO7bPkrQW3LUlQflsvk494fsEWm15VptVZgFaS4qRUOOzbMCCBcape3RUOA9sFjAXS/7L+3EO28wgvmezswhsUn+ca0EunKfskw364FmprM5AIJj34TgTgKJ9soB2dcgWpPoSiONCxs/Y7G97jrV9H2jZXBwLysfqOEFjS0BxPKhjvBfHkfIVkaoDvL8NHLHnj1q7QD23AUYktChnkja23WwbP2NJAr5PgJv6beVJebDvfI1zi6UkOd5LYpltpgwpA647bIclkggE2T50nQJT1g6z8gnXg/EyYr3eVH1sDmELIApmLSE5Ym2AJYxEWqUOrmskIWyADPV7CTpbOTFQgjaAcuFYs2QzP29JfZIGXA/qOZeFJLRzwNqQaZrKejCvjsJ1j+POPthgnpzzjNiJk55DmrOWiAqhVdtQ0LbZbtXxFcZxUsA6Z3SdZsQx41FJm1iClgY4Z49sYJSvmPkjxYFDIdwJiLbMe+1fKWFbAAGucxwP9qsFvaAA81qmlHZSAeoRItpXJcZz1RnadxvgozJmoNSEcZwTwLZSiCV7bHCItS3M1lweyUGdoHwsSUbbT51ilinXDwZT0lZzLmw2G0xxQgjtuAmgVXagzlN/Abzwl4ZhqAGUh8Ohfo72gWXTqZec1zw33FYRom9oj76om2PzGdpF71uAE+VlA1G45lg7T/nR9tm12/pQnJPUbZu1bW085571GWkfSfjS7+Tv9D3ZD85Dlo6mr8YjhGg3aP8456hjlCnbY9d+S4BTdnatsaS5zXq2bbM2kXaKa4YF8mmD6LPYz1hC3K4b/DwDnqwu045TlvQdeA9LpLL/fJ99o3/JcaIu2mAi+tt2X0S5U09og22/6hqFeeUB6gHnZ7WnsVXyYiCxbQ9lzf4wqMTKioEI9Inpo7OKEOeQ9WE5V9gX6hLXEI6pDV5cVlvgfODfLM9ubaENgPPeI8VWUp72zpL6bU1AXbvsWNIW0o+iLtg1i5fdGwCY2UwrV+rVP+X6z//5P5d7Fnl4N2sjQZ0RgrfrLR5vr7Ffr5Ah+HQ+4PvnZ0yjQHIhZkuTrM9r52vOGVNMLbPGZG4v9+9dIZvr3HXtd3tfEuOOxCa/37UjwJx3cCKQVM4ZL5+tvo5jJoEvAHDzBZtfhPqAS4zwZS71JdMj54w0aSYl25nAACsF0ZxTYMleClCX8tciFSjrug5daEcboD2++p32h+to8F0h8JSE55rehVABydPphP/29/8V59MR3jnsNivsr3Yt2KYfMKzX2Gy32JZqM4AG1E0lC88Gm6i+m0DalOF8O2qK+4MUJ8SoWRqcy1Zf1M8SJKFs/Kz/n9N5O5/5+Rk4XIhxazvn806JJ++K37943/5OiMdiHxXYNj8pTbPn6Pwy2WmiIHMSvGg7/7X9tXsee1kQ38qCPoXiLhMmEwDIzDmRhMvljODV11GwdkKcRpyPxxf3Xsq2ZjKhZZxnyTXQeT4GAOB/+n5mktk9c0oRzuna8Mtf/BK//e1v8fbdPdaDhw+lKG7xvXXOFzmueni/wX6/w/uPb/D99z/gD99+hx/fv0ccNfhVnENG1ooH8jJYet5WoFCTpr3tTSW17edejim/RyB7uT+3V3u9sBH1cUq8q70gqZHhXcOU7LNtIIuuhQEJGjS7Xa/x1Vdf4uuvvsTbL+6xv9phtR4wxVgDB5wI4nSNq/0Ob97c4Mf3H/H99z/i++9/wCQovkmAQwm4yC1o/YWcFmP/512vZ0iT0H0x/xcX29M+04igNh6vPDXn2VjVz0lGLnLYbgbcXF/j3Rfv8PbNPfb7LVarHlo5N2tggqwh2x1SFFwuEY/PR2y33+Mf//Atno/PyFGUVEEuJZE9Gfva7s/r6Fw3Z3JiKu5PyoJylNkzX7NRf+zi5/Irn3/RB9dIlhwFXedxdbXH27dv8M3XX+L+zY1Whaj7WV1Xh65Vn/Pe4/pGj1XY7G7w+99/i2+//R4/vv9QbEiNfChtmwebfG4eLvuztLc/9dmf+szPvV4+l9Vlmvy6LiAnzQiVkvW72WzwxZdv8dVXX+Ltm3tsNyuELkBJUSlHzmS44qd4eCWLwMxNV4P5V+sBX3/9NZJkHP/TAdP5pHiFTppZW3hGNaDrpTPv/5S8fkqf2W/O/Wkccb6cALSqicQ1xqkdKUofsFW/iEixlHF3Xo+DcfOqTFw/qw1zDaOq+xrX3q9tLBV+Xmu75IxEmy/zYwHbOpdm+0+gVY5d+gIWL2uV/xrGb3FPfsdiEAAJ8oZLl0moxKl3rYqM0+M0BFppJYsgoCXxcJ9vuTC+99233+L7776DA2rQMQP2iJNuVs3/SClVsr/6TkWRYszY7taAqK9OAlngMU4Jp8sIdzziguZXZjS9ygByqcAxSaortMUNl2vHOV+U8HcekBKkmjVRqSsktoeDHyOWtsPqkX2t6zoMqx5uzdLcPYZhjVACfoa+VbfSzHxUXbBYzbpvFWS1VPz8yGPqQ1f2/77X4BEp8z3FPPse289xtHOgzl/va6a/nTfLPg9dX+1t13eFmHcle79VAojnI0Ye3ZMSxrPyon3fo+uV2M4pow+D6b/uNVNKSNPLIxOo40t7Uve0ZR3vh0GzxqeL9gslWCiWI82K/AFR/XclYCcLckyIudaE+KPXzybGbfavzUQZynksJFItcQwoGHZ9fV1BGQ4ov0sw2TlXQRsCLCRMCGhY40NC6+bmBimlCrrZTSiVhm0mSQSoEbSl3W1WEIEqZnJYQjKEgKenJ6xWq1nWAYn85Tnj/NtmgBJMpZLaMqSUsyXaCIA65yq5wn6RsGJJTH6XwB/BaMrbZgkRhGOmN0uc2/Hc7/c4Ho913ELQLOtlth/JSJ6zSbkQkCUgtgS+eZGEWq1WuLq6mpVZvLq6qgA7M1ioAwQW2Wdu8kjs2IWF+mCJAps9zfGwuk5dIojKMqSsZkAw2AK81FHqL8eVz+QP79EWukZskdAiwM++8J7UXStH6jhBUuccjmXDbIkAe+6lJTA5pnbOs80AsN/v6+cof75vqx3w2V3XzYJVlgEO1lEgoGuBVQID1pacTifNpLi6qu2h/Pm5EALO5/MsC4+ODeVjHRU+i+NsNx82Y4r2h8Swdcqo14CSOJx3/D6dKJ5bW7ObzGJlbQzvQ11q5aDnWXTsLx01fp+2g7psZWAJaQsQs38WvLZkvojUjESO5dLZtM+kLtOWWoKCQBD7Zxdu2x7qFm2gBWBo0/jZJRlDnahA6CsEn81S4xjGrCWCYowInZZYQxY95y8LutBh2PWFvE16vlto8hYpRNTAIBSNPJ+mWDI+O1wuI7hJyLmVYFZdjGA2j10DrK6Q+OSaY52LJZHlnKvrA8fCnnNrAVFrE23GHuUcF0CKHX+N+G9ZpNbuqi3Y4Pn5GYzwpGyGoREr0zShCysAGcMQINICNpxjtQxgHFt2bs6A9+oQec9qEhOgxT6R8wRfzp6Z4gUQ3chPkw2qiEUfO4i0KGUFkVTufd9VG9FsXavgQt22PkYoALfKSjc3HGvagOPxWJ3fXPRsGHp0IeDm+gpPTyozPTdJESHNYiu6nTKmsaz1UIfy6fFR++McBkOoha6V3yZBXAM5Asuz0452JbNHswpTSuo09x0u5zN2u62WeooRnx4+VSJys16j67tSRWZbz0IaJx3fbVk/V+tVJZG5Ib66uqp6ZoPSGBTBftBOM3iAn99sNlWu1kZSl6mL0zTNNn0k1mmn6FtQB+iz5Zyrf2LfY1voU3FusQ8McLDzxfo41B/aKdqurutqWW1rJ60M7NykjGxmPrNs7fO5NvOZNgCS85+EOclCVnzgfe3zuI4eDoeaEUwAhJclNekPc12j3KmDdi/B8aTNyjnXPjPYw57fzqAE5zQI48cff6xBAfShrbwsuci1gbaN6wRlzrWdxLslwvkZ2llmZ1MH1+s1NptN1Tm2n7bbBnUxIJivsZw6KyJQf9hGC7LQpvGiDljQhvODdswGf3C/w3nC1+z6bgMxuSY9Pj5WXed8436FfZ6BVcW/tAGT1g+wQUacDylG9J2W+UYhMCVnjOe2BrK9lrDm+m59AxuQanWac836d3YvQX2xPr/tF/vE15d7kD/3sn690lztmC7qjfMeK+8wdB2SczhnLXuXQ4f1eothFdB56uo8YLHew+6ffQucsCC9cyUbxjVij3Od30+LrPEQQiU87U/1PY2f470rWbzzAF4poJHdK3DuWXDRuVJ+WQR5kQ1agUrTfuccxpTn+ulMxofxj2NSux2nFpTKuaT2UMtIOljwubXfBhV1nVas4R4kOwDBI5Q+ppRwvujeeIoRHsDZAeN0weV0KlnADl3fY7PZYtVrVZbNdo3Vaqjr6jAM2KzX2G/V5l/OOq/HYVVteMoZ17s9JCY9v10ciKUz+95WXdA1zwRqu/nZl1YXlqAXQTgYuegbmumpIO9cJ9ta0ohx3kvKoL98nqvyXQKD88/NAz2XbW/P9q98FxWwX/az9vWVizQp58Z0udTss5SSnj8OAIVYSnHC8/MzBnNeZkqanPL89KAEgzln/LUnApQVKnGbS+UIwbzi3IziMPsye+WyV+I8VrvrcXt7jS+//BJ/9Ze/wVdfv0POEeN4hiACiMXn65GlEBhZCZ/ddoPtZsB2u8LtzR73dzf47//v/8S3f/geTjRCJrzSrtfa1gjZeank5XccGln08h6fJ4F+7vuvt21eXWppJ/h3jBqg65zDF1++xb/47T/H11+9w83NHuvNCr7TLKzQZ83cEy2z3HUB6+EGb95c490X9/jiizv8w+82+J9/+wddm9HNsg//WPv/d17z+TR//U+9lvPZvr58v14ZGDYD3rx5g6++vMfbt3e4ubkpPmQZh5p1WjIlux6SBZutYH+zw83NHrvrNX7/j3/Ah48POJxO8OLrnBJlGF9tx8/xBai3MG3/vHwKafy/6eLdlvJc/kQBIAnb9Qrv3n2BL7/6El9++RY3V1sMQ4C6afKK76APcAzwc8DXX7/DsOqxWg+AF3z37Q+IRYbNEjn83L6+pl98/f8ful7Hr1p5veh76P6HsgG22w2+/voLfPPNV7i9vcF6XbAgSYCTkunoS+CFYJoSPHLJ7ARy8TnG8YJpSoDzWG16fPnlF/jhh+8x/eE7nM+54gdgtKEojlDlEl7rh15LudV5p39BZEEqQlfLmEaczmdcTmdA5kdPnk4nnE8n5JSwKpgpnyUiiCmqzxiWAYotuJptqetP97IyDYPC7DqQYwKcQ3BzQpT3STFpOXWzB7S2xlYyI38BzI98pL9njwmjHnDfsZTpkjgs71SZOuLWxQeweymLbwJtHyTSuATKL6VYcYx/+S//Jf7X//zv+Pu//3t8+vRJ8YFhhc4HwAtcgJaidvNEGJtwR/6HMul8MP50AFyADx12VzcYtnsAHpMIHk6H9rng4UuGsPcevtjj3g/1PHTKV8lYzQSmrLfdoAT4gmwNIaDrB/QlqSYM870yf+zYBadVA7q+LxngzAIP9ZnOOfguwAWjXxmzsSBG4WWOi9o9t9WpzOq13aDP7kLlPiwG7kLzHZb3rft6ESTMg1yW+xDvvcaAOU3yCa4DslYW6EM/qyjUrdY4HA7tiDzfI2dgGkdMF612qXqtgZyhBCSQA3WuYVIplQx8l2sfrL6z9P/5fMFYSs53Q49+NcCV9xQHBSQJfOhftVfOaYWrP8Xs/2xi3Cpay4BqJA5BopRSLR2dUsLNzU3NLuYmjfcj6WEFsiQa+TwLpLGM4el0wvF4xP39fTVO1vjwuwTO2CZGzHBT4b2v51wDmslss21tOU0SvUtjZLOZLPBFI0sAjmCo3Uhb4thmbNFwEsQD2pnIjPC12ZDMFOKkYJABjRbHh5+12SXsFw1eW7xzLZNOUpIkis3MIWDZdd0sS5Zg+el0qn1cgsYAcH19/aKcL+VtyRg+m0SK1SECafv9vmbDzxZq52Zjbx1VGgkLnNiL37Xkrs12ZalKLkQ0UnY8rcHieLZywFMBGqaZPlqShf2jHBo40cDpw+FQgX0aWpZ5tQC2JYYBc1aFCXrhfSwIbklYCyIycIG6YAFOS7hb8pa6R+AReFkyl0Sec66SytfX13V8OVa2XDd1kIQhZWXHwGZNWbtGfRBp5CPnN/tPfSF4zGxG3sdmBdrsd2B+1j0B9eVnKCfrNFmHh/PC2hD2m7K183cpc44z72PBSxskQB3gmFgdspGS1vZZXbFyYts5LygnjrmVlV3ELXhgs/vZbraZ5J6tqkHZsH2UtSW/bKYS5ZymQtg7Bw9U0B2ipCXbLYWspIPCkpv893xukaG8xlHXwc2mkVJ2rqpO7ep84llodi20BBz11cqMwUscV54ty5LJx+NxVn6WAVOWiORzlgFaNsKR40BdZdlTlWvTayXoJzALWvuqFTksAXm5jNhs1tW+XMZTtZGCiJhKlhJigUYzppId6Lyr551mmZDjBOcLcS8TQqclyEWKXkqCD3oKlr4POB+wWvXVLnQuoO8DUkyl/JS2c7Vu5FJKrby7iMwqwjTCtQWZ6JxLmKZ5xnB1kkXPHmM5108fP6rDX0hMa/NsmWudq5ppJjnjUspgxxhxKT6OiNRNFcfYVkPQkvtOo3lLVQLqCcf6cDi3iOfnUAOPAMHpdCxjy0ooEedLC3BU33Ct58i6tqY+PT1ht9vVdf58PuP29rbq+9PT0yzAb+kTMaCFn6d95/znHLM+B+c8A0vYV9qXp6en2hYRqYQmg64s0GXPOaf/ZKuW2MhX6gnXTM4j2lracfpLP/74Y537bDtL0jMI0B5ntCx9vtls6r1Z9WFp3ytRVNbKGCOen5/rZyyYQ3nR/pAopp1n6fHb21us12ucTqea8Uw9smsDSRuuq1yX6PNbYop94Ty4XC7YbDY1U559oE/P+9/c3FTfkv21PpwFO2jL6GPzaKSlX2LLgdtxXQZBcuzomxNM2G63szO1bSAH5wH7S53iHGr2tvks1qe04Dp/+r7HZrOpgW3Wv6AvvQR+rK/C+9o+8Zm0X/TB6Jcs/Uvro9m1y5LS9HMpc5uxr8R4Qhzb8UWSczmDLyOUIGobtMdxtn7fcv7bOWr9RLtZ59hQZ7jOUgYWBLO+mvVVliDYn3r99V//dZVdLYvoDUDjNSsjQtBnQQ89YzhDsBfgTgTOdejDoOChRwPeXSEp0QBP71whR7WCSiXScq7AuXetosYSlEg5I6a2d/Pew6HttWZ+nglarGObyjnfztVShUmk+qHW/6NP14D7XM6AFEypjQnHgiSSnX9jutSzEUn6e+9nBK4eiXIpc31O+ueYWtvK+NgKExbIrYEBQTNCUkqIJZvCMfunyGW6jPA5wjuPUM5fDN7BrdeazV9IzThdcD4cwLwJUB8h6Lset3c32O132G332Gyu6tzjnPHeI93dAWjBY3XeJyCarGrOydf8esrZ2p8lGWT35faibusZrJ8rI+wqYTy7l3Mzcpyf5Vsv7mJeXAKp1g6+/JtlnOfYgls8WwTmc0po8DVLPksWJLM2ha4zWZtSwMaMOE04Hk+4ub6ayT2lhOPhCXGakFOGhNfJXUGh9V2jbKqIgm8VDphlLWyhJRrba7UDaJhCCAHX19f44ot3+OLLd1itBjw8fFA9Cw5dB3R9y3iy66d3DsgTUooIPuP6aoPd9hfqg08jPnx8RCzZQSX+FlrAQaouSBGwW5Bnrf0m0xBNL6w/Zz/PsbV2afkZ+779zHJP/+qYLOYKr2YzgK7rcXNzjd/85jf4i9/8ErvtCs4JxvEIl4Gu80DSzCmwilWxfcF7XO03WA9f4Pr6Cl3Y4G//4e/VD5giuq5HMvZYZ1+qQVd2rf6nXJ+bV8v3X3vPfu+nrvkYkZAswSCiZ9g6p7bt7bt7/OpXv8IX765xtVsVAF8rdqWUkVM7Hk3PZ86VLHcOuL3bIQzfIIRSVeeHDzieLiXwgzoGnTCefc9woDz9i7b/nOt/9+deuxwrHswCSuy5zUW2orjd/Zs7/OKbr/D27VtcXWlwgQ+ASELKQIplfxGAiKgEk/LhYCa5IGK7XeGrr94i5QnH4xGfHp/U9tUAIoGwnPDn2v4z5t/Mx1h8ZjnX/xw5Vvng9fVLfd1C6JRnbbdrfPHFO+yvtuj6oMFKSYCcIS7D+VBCmlz1T7RktgnsqxU9Vd5Tisg54t27N3h4OiDGVP1o7V8Gq+PY/n9Ohq/ZQADVR9MDmZvdUP8QSFPE6fCsx/U4PelD/Srg+VlL53vv0ZvgUwcH4b40aDUiHhMjZR3NQv+QASmukuIVpwKA3LAri1mVTulIGRu8DNpkf+xe2D6jknzSCGn6o/T5lpi+Ja4tpsF9C9CqsWmbE+KkpctrIoFzGKM+A05JTY5TLqRj6Dt0Qc+bt/s9AHXffHNzA+8d/uN/+I/48YcfABH0QTF0D6BzHqHzNSwlieJ4kc8IAZvNpga+A2VfpjnfSKLVDoIP2Kz3+PVf/RZf/+LX8L5Uh6IGej3mwkGPTuz7vhLYPunBheqjeQhacpPFe0PQc6tnfiiC+hw+VPzL9YqTsRoW/QH65N7RBy9H6qCtg9Q/gGeea1lylmJXffNwLugxEJAa2KFt1bPhLYbNmRTjBcEDl3GEjxF+0uoJOev56LUUvwCIrSKxzw1fhHOVyJcMoBy9YAN0qh+UBQka3BhCQDCygNekm5wyYklEiuMFk/H7V8MKuy92uJzP9Vjihq+Uyto5IcaM1QCs1nOsJ9m5ODcq6Pseq2HA9W6HaRzx8PiI5+MRp9NFA1oCzw/XPbx3Dr6US2/rFu1DC5D5OdfPJsZ5caIT0Kby2UgOlpalcSEgZ42qJU/4Ho0Js13sJtJmBlqgkMTi8XisgJPNXrXkDM+3o0Gg4SH5y4wjZspww2z7RcCKCgC0jTEVgyQ00AgN3o+AIg0pgVZmxnOyU1ksQUvQkyCfJaqWmzoLuOac8fDwUIFNAHXTW6PSz+dKJJJYZL8sYEzQkZtpjj030iwpWTc7ZgEQaZlTBOII6loy93A4VCDNOVfbRdCNekPihqC5zf7msxkIQYO93MxzLDiOFsijXLbbLfb7fb0Hz3y3l10cCf5ybliZvbbJ4t9LAJb6ZjPRbYCEJabZV/6wD9RLgo6UBdvGawlu8DXrRFhw3vbDez/LuOv7vgYKsK12g8XvsXQuP0fHzpKW1kkgyc/ACutI2GAUCxITtLVADsEgPssCQNaBsiS0lRHBOOr6a8E9vB91g+Nrj5WwgQ38Hu0biSI73my7HQ+7oWdbK/gn88WXbbTnQFsCgrrKeWbH3+os32OVC/Z/WaqW5Yl5f44ZdZd2mbbAnqlrg474XBJ5BK+t7SMhQhnweczotJ+lDaLcGlk7PyOXF2XJPnJ94HPZX+sYWBvD9tv5Q9219khEamZgO/91DrBbQsTaHDu/SLBTRrSffOZ+v6/vcd1ju6yTybHnOO12u6q7lAvbwnEnKUy7TplzvefnYox4eHioGwb2xZ7pa+cHvzNObd2G03NDtd8CcV7PvjJEn7WD6nguSmwV8ocBAmwr260bMCllewBAzyA/lSjn7a5lqiq5f6n3s2Wy7LpiA4XYTmY623XA2jKucRbY41jZ163MaCepEykldH07UmC/3wPQkvPUkefDAdPUdJgELX0UAJUI5ZpPgpK6QvJvHEdcX19Xu80MV7t2kbD79EkzzrmO2KNX7DEOlrSyvlnOLWDx+fm5znPaHAa1UUdpv+gzkrRj6fHn5+c63xmta9cFBjRSzpYQ4waUc4v9tcGXlCefyeoOVieoizbz2Fb7uLq6qr4o7ZLNyrWBj1Z2tLn7/b4+k+sAjz7gGkD9sr9bP4fjRR28urqqc/t0OsE5DWC1fi3bSx2iP8Ws72WfLZlKWdOn4nhRz9lH9tlWZ+Lr1BvqlvWjrH7e39/PfFxLpjMgzq7FNms851aNxa7jXC9o93kfuwewc9qW5qddoC231ansGsM2MRjBgjZ2baLuA3ix3tojrCy5zHtaOfP71AX+vfSD2F8baGP3QuwX94FLfwoAXNdK9/Oye8JlcIAFHmxgpG2DDcrk3OXrdp9mZWz9beoln2H7xvtZm/9Pveoa4AQiETm3I5Ccc0hQMthlJUoEggwgCpBFz5zz3sN5zMGSQoBbwleyVMCnll5PLQebOmL9D5j3SODz7xTn/qRzPH/RVpuywR0NpOQzUp4Hc9r5NANEPDO0GiEJFJ02wCVtQkaEaxhVvXcIQcFTEUhOEJm3n5+H8cV1fICUlJShj+ILGxe8Q+gCQt8p3B1dBc+qTy+C0HdYbzfoJSNNE1IckeMIgdT1I1P2oqQNz9FLSUtwj9OEy+WMmEY8PHxC36+wWu2qz2OrBlF/h2HQs/n6DpdS0Ubg9JziQuQTgIPxp3gtgWa7T1nqyCsaDriXn6/PEFeJEr7OIagAmFuCY6/PPX4upzT7Xn29yLUGjBhdXrZ/pg+L1yw2A5gzySmrFJA7W52h+OApgTR2lqyZOTHV0qTB67EE5+NptvYv5c3fM4kEiCHpDAHiGnTIykGz9628RTP7JedqMzabDW5ubrDb7dF3HabpgnHStbDzPbzvwBL80xSREoNwAPHQsv/Oa1lqB/R9wNdfvcPDp2+QkuDp6Vl9eNgxnfe3hCCU3+ZEmpWNnbp/yvWaLKz9e80W8qo6+Zn78TMtmKrHfr/Hl19+ifv7OwBaPcB7AVwudsor+ZgIaFOnM5JEAA59P+D2dsBvfvNrjHHED9//gMPxVKXU5GFtJV7qx595fe77r73+T3lW+67KR4T7Nj3+ogsdrq6u8ObNG9zd3WC7XaHrSShkCFxZA1uCQNAFSW/LstaSsF71uL+/Q5wycga+//49zlNsH0XTLa49P0cGn7NVP2XHygfq8z5na938hZfPnflML8lhMcSMDwG3t3d4+/Ydrq726PsADeJxAIKW6U+ClLSyhBcguA4eWg0GQMn8cxgnJTuGocfd7S3u7+9wuuixTVpSvpCICJ+dX/X1xfuv+iU/oY9LrLLK5o9cM91bWJXZ84TEYTmGbBiwv9pjtVlV4tFlXecALYzEihqArrdaWsZrkFxolYySCQKcChHedVr18NAfq58EoPhF8+Cyz83HpVyWgW7Wpnqn9t2B+5GIw+EZKWd4144tPY8XnE9nwOwLOvJIrpBY0u7v4eqkEtGKPzzbm0FcPhQSTOZjZ7Fci2vxsr6K7RPlskwSsfsW7te5L7LrusWO+XnLA1g/1sp1+R6PD+JnQggliFNDbHLOZU5qpnPofD2j2XuvQZXFt+O+2DmH6+trfPXVV/ibv/kb/P73v6/7au/15GbvPMRJrayUc8Y5RoxxKnsCV/1H9e9bYIaDoOsHiCTAB6y3O3zx1df49V/8Fb748ut6pnSNz/MOOUkl+kPoELpObUqxE7YdlAWDZgEgugQmE0EESAkCB3QdEAJcKGR3Cf+BpDLBRCseCSApIzsPeD3XPqbWf4FWaNBgsrIvjiV4R6TOP+5bqu/nVZeTlICYrHsyPbfdJBEm3b/G0naX27Gv7czvQtTnFmjr8stAVOdaYPOrdkzavLVBH557b+cQpwmXEqgrokcbaGXQxlf0XV/3/hbb5348lQSiMUa4CwMJvJ7T7kKpSiVw0o4DAAS979CHHle7LYY+4P7uDt//+B4/vv+oVV2z9i1NEaELpmQ+fUyUOEFnTcTPuv6kM8YJpjDLw4JqObdsMBoQe56v6mkjnpZlJwhW2IvAqM0Q4oRg1g6fRRLVPoOA/+PjI7bbbY1q+fjxYy33R2WxkQ4kRqhEJI256bCZN+wXAfHb29sZcElw0wJ8JN8Jfluwl4SiBUkp79eIS2a1sh02m6QukIXIIMC2JCPYfsqN97GAki2ry3asVqt65qQlIeymlO3ncyljm1XCvtrSotykL0kO209LpvNethS2BYhZChRAXYTrJDDgMdBALALyFoxlnyxJRXKXC5YFi+xZnTbDhN9nm6wOMYiDBs7+bkFpG0BB2dr2E/wTmWc/26MKOKbL7/G+FrS0ZDKJ66VzwddZamNZrpP3tIAiZWiJaxKPBG66rsP9/f1MnxngwrnM+3LMaANsIA3QqluQuCAxZYM1LKC6JMT5N9tO0oXtXxK2tG9WBrw/dYlks3XG7OaMP4zOY98oL44R9cvOXQvi2nmxnFeWNLbEuF3gmQ3JvnP+Wfmwnfacd85RGwjBeUCbR8LZkhRsu13wSapQXhxTEgcE1vkszj2C3TZy0lYk4P1pn/u+r2ds895cK6yjYW0dZQKgBhPxs7PNdpiXeeVPSgkPDw/VPsSYZvOMBI3duLFPNmvW2jPalmXpX9qF18h1ALOMReoq9Y3PsySyXa8pG1Y0seWzqHPUR/oU+/2+6nRKqZI2bIPN+rVlsvlsnglsgzXsnLL+AYFgZsja+ckAFi1rniAeGPp25IA6dZ1mv6VcCUC2k7rCMcw5zYLtbGWHpcNq10w7P18DWGnLW+CE1I0Xdc97X7NeCRxTP0gqsv+r1UrP8yoX78NjRDhfuq7Dw8PDzG/gmJEsjzHOjox4fHysbdput3UDRtKf5DOrG9BP4LPtumPJYQbLcF6QqCchz7Wfumh1kOsUbSbHbhkUY0twL6uDcBxEpJ5pz8/bIChrY6y/wmpK9j4k5VmtyG5oOVYppdlxLtRdazvZFsqI9pu+D/0RlkinXeV7NkDVAgHcBFmfi1nz9I25NrPfnGuUDfXDzlf2xa5n9mglS0SP41jtE9dejretUJVzrtn+zPImMMPxpV2swTfFp+Az7dpFO01fkPeifCxJyKxz2ji71tLGWCIqpVQrANAu8/gp+oS0ywxqszaLdpD2wAbRsX+00fQ7ltV8aD8sKcw5Q32xfgzlRJtvP0tbttyTsQ3LTGve21aFsj5Y13VAzrqh9vNsbDuvOFb81/qqtKlsA8eEMrEVvOx+c7mn4O+2r0vbTF/aBmL8U66PHz/O2kBwWWRByjgUsKcR4wLFU5M4eGjWgnNtT259mJk/kHVdcQ6laorTbOtyVZ9BxJAAbcxCCO17AKaxkXfMyLZrnI55axdLKta1z6xffAaJbX6fV9M/1KA27xWAkwKouqyZFXpGY2eAGdRsmK7rtBx9Afx8aV9n9FNSydpZAMYEh2umSkFonNcMKdcpwEm95JpIICx4r2cK5oQUR5xPRxyfHyG5ZG9LCygREYQugE3QrNEMFyfknHA+n8q6e0AXjlqmsYxR3/Xoh77O8a4L2O2v0A8DcglUdz6UDJtWktUZH8b6jnYO8FruFfmv/YxwsCx+Z+8LAKUEr7hXnrvwk/j+a76T9fmdsXN2v2exldLgeR/crKEzEI5j7/286sCs346ZTrn2nbpQAUagkASCKUeMYwmUcpod5b3D5XTCNI16tqK0o41M4wzJMA9ksTYexTagjO9C8OWfeqOSSavPCqHDdrtTUrxfISf1D0PnkWIqxL8SOuqvR4jonBBfxikJXFeeJSrF/X6Lb37xNQ7PR+SU8Pj0rAS6sR3La6l7L/RENNBDx2LJZArmX9V2VN002f/z13i9LFG+1L0q0kXbrB2mD3F9fY37+ztsNuuCFyWshoCuL0FcSTBNWgFDM91cWROU/AIAH9Sff/vuHs+Hr5BjgsgHHE/nOpbwgtfQYys3ey3l+7nrc9//3L3+2PN+6n7tPUELnNFXiHve3t6W/UELRPGeQYAZMabmy6VSTtnaJdEzTCHAbrvB/f0tYsw4HE4YH1sQfm1PsQu1jWjasrSddo/6uf699t5Sp16T0TxE5CVNzzX6tecs26kZnQPu7u5xc3Nd9vda1cLDI0Ygxgk5UQ8L9uczAA3Ka/wxq3+ppVuvN7i/v8PHT4/qLxbSzxL2Kqel+WXg1OtBWMu+/JSMf85rLz7TpAcr6Rd2tgQbOifoQo/dfof91ZXui1KCmyLEC3z2GqzheI9C3EWtCuJ9jxC8sRlSjsXQAKNxnHC5jEgpYxhWM6wcxWZXP8/Y9J8nN3nxcX0/IxcCE4UPjDnh8HzQ4LPqEwacT+e6LyKGpT8LUrHc26EQtZqDCzgTCF0IRCXPPXJOJfgA1ffKOSOnNrftvmHZT9pgi1XZ/cjy8+yDxeHt5+1+Z8nPvLZPYvtyzuh8KH5o45By1iCeLuhxgzFGtf/lNbbD+jkOmsOt/n3GdrPB9fU1nAP+w3/4f/D09AjJbf8XY4Tr56W+AZM45No56SEwAxuVsBUIfA+40GGzv8bbL77EL371a3zxxVfY7fbtvpkVIdRfZSArCrks2andoL9VdEtEkB3Ao1C8U+JaBJWoLt4bpqzHFAWUrP7c9hEzX1XUh+QxUzxuhHo5J8b1s5KTzjvR88X1Xhle5kG9ztoAgA4ifNf2oTIBOU3UrGo7UypnxjtAxMNBavCH1L2X+lIqs1yyo9tzGYhjfZflnM4lOJrBk/oZjj/XLlficxrGOfR9XRO8D4DTwMspRsSCf3EeCQRd7+DK8Za6z2zz0Zc50AU9m77vtSLzZrtDyg6XMeE8jhBJxdYnDZzw+szgNQCuDFDNEuc+6+dcfzIxzgHkudMWDObE4VmALIXHs3X3+30FxZgRB7TzH7mJsKCyc272vnOuln212dh0egiM8uK5fgTC2Q8aHwK8KSXc3t7icDjUtpLgIBBGAMRmJhLUFRG8efMGObesMbbFOTcjBgjKMCv4zZs3OnCVDIlmMoYKaPGZ/JfAms2W5QS3hJYlk0SkEtHMYiKwSeLQkvaW4CRgTWPYdR2en59nxt1m6nJ8mU1RzyUoiyCzeSgPjqctr2vH3QKO/BGZnxVZo9HKeHE8LOlHmVqQi+CCBRb5YzNYLBBPYpsy5ve5UNpACNtvC7gxeIP3t4us3VSxrZbktX21ADHbw8AFtpsgob2W/ed42D4tF0SCjASueY8lIUSdt0Zx6RAQNLR6y3bwO/yXZDZtAOXHucN+WoO/BMpor2gzbm9vX0Ta87IgN/XZgs60cTaTi+CvJU7sGNrAFVv21gLJFuSzOse/rW7Q3lI3rMwtCQ80AJdE3pI055ym3aItpp5ZgpqEA8eFZJV937bV6v6y7WyH/bFHc1Df+L3VaoXn5+fqiFoHVGSeVcjv20ACjgP1lPOP8lsGt/D71oba51lCgVmCJKJtBvkyiIs6QPvCOUY9AoDttp33zTFcEh92sbdzh7/zWbaUNNdPfpabJraX/WXfmEFobciyHzYwjnpLO7EE3KlTdn7aii/WRnPMbRCLJY+p17wfx5G6ZjM57XO5xtB2UZcsGcr5o5GgCrJP0xkxTmV+tE0P5wJ1iXbPZrNSt/g7bdJrRCvlYO0uA0A4dzh/dOxaFjPHgWs3ZTXGWI8bYL/5DL2Pbj4ph8PhUI/isD7F3d0dttttrcjAecQgJQYLcd2lHKZpqnPXBupQX51zs4BKjvfSD+QazDlOX4VzsOu6mm1rf+c9KR9WEOJFu2dJTgbSUW6Hw6H6TfbscfbBrrskaWlLqQsMxLLrA4nl+/t7Mx4qj91uV+VnCU+gBbRZvbK2mH6iDYLk+HRdh6enp+obc8zYBz6XY8z78qgAa0O4jqSUZue+c52jnWV1BLu+9H1fz9CiHG0gxvF4xGazqb4k/T8ee0TbST3kHGFwE31dGxDJzPSrq6s6LrRvtDWch6vVqp6XTdv36dOn+nkGd3EOU0coF65LfJ1z6uHhYaYXdk90PB5xOBzw5s2bWXAZx+Lu7q4GfHKN4Fy37acdW8p2vV7j4eEBV1dXL7Ih7FyxfgttnbVfvB/3DDxWgPsgttuWu+ce0AY0U7+4RvKZbItzWi42uxYIYPcG1r/h3nMpD/bf7q0YGGKDq9jnJXFv138GYrBtnMv2M1Z2ds7+Odc//uM/1meIgWH1majtULtBNMOAtFlBQ1eIG2aUvCDtRSoAkjMJaocOHYKbA2UVWMyFFPTz8WjjpEALA8yoW8GMifV5nePa1PFhpq9tbGzbrV+s/dM9jy2ZuAy2gNNAgpwzfLZnExauyHu4bl72WdeHCcGZ0nwVgNTsOCealaJzH+i6gOBb6c2q76JnezvnsFmvETq1tVOMyNLsqgsJHlushhW8czgenoA8VUCR/pb3BiwzvkXOsY6j9x6hc/BOcDkfq1465yrhA0n49V/+Ja6ub2d7ENXt+X4cC7/FXhaLsGud3dva/YDeQ0twLl9v/xLXWJK6qidSf50/Y7mvpw64Mtg24NQv9NK2Zdk/20brM1bZm++/CswVG+tTQs4JPpQqaOMISUlB0AKiMkCq67paMrQLQYMeLiclozIrFTUsBjDEWEYNkmyNLx8As2ylZGktroW8bXnpYRiw2+7qHB+nCMkOfb9GjEo4xpgRuow4JcSpVDhw0MwfiQjoIEgl6EFBTyDj7bs7PD9/jfGiAZSX8/hC1zgG7fWXwb6v6ajYksevDHP9vApt5qcXkUCnAcd4rkPWJtU2YE6CLteMnHWNu7ra4+7uBpt1kek4AhLh3Rpd18PB43QaEWMBrD2QnNSMVAdfgnoEMWYMfYcv373DNE6IMWO8/ICp+AXMICMgbtv+2euFLP/0y85Pysdicz/nWo4xkAtB4yDZIfhWcfD29rb62hefNCAqdIhxwjimquMCgcSsx2zlrGupa8dWTeME7zvsdzuk+4ynxwc8HR9fEFI5Z8AbYhGYrd7Ltle9eLHK44U+N10s3/+ZMvrcfX7qOxaT7fsB2+0WNzc3BYflkXmqc7p/itBDq31pn2BCOYYGAV7PQVD/TqBrXlay5O7uDtf79ziUSrCtPSzzzjm11FG3+PdlP/6c64/OAwCanmhtY/uFwUMiWtlB26T7w5vrG+x3N5jGBGDSLPsQEKSD8wku6DF1IqhljVMQdEPAUOzROI4axJ91no/jhPNlxOUyYZoyQkdfjDZqjpMaQc3Wsc90tK7DNmBKRO2O8wJ4D+fUvuc44fnpESkndMVnk5zx/KzH/XUl2J17T5Jl3jnNfl4ElNp1nXgl+HwRBGhgwHI9nqZJK7AImt+GeSCctdXWDr3mNyz3BnyOxUztPS3+bZ9hsQZLsKeU4KRVS/UBswTOruuxWa+r/whoBUUb8KsVn3IN6gQUN9rtNaCn73v89//2N/gv//n/i+AadsZjF+E1czw4VnmZXlRF5N5VFutedlqlare/xtff/Aq//NVv8Ktf/wbb3b5kEqdq4cT0vx0zkbU6vwiS0Ffw1W0prqfODQfAeXRoAQECtTOAQKIAKSF7gfOCZNZc+glLnc8ikBR1rfaafV03BqKByQKpstU9D20d21jmkwlLWj6LeyXuZ87P8yB6cepD6pETAin+ehf0fG8BMV99jivHI3Dnx+aEUpGqHr9k1ihXSGVXg3AYEG7dRIEr53gLNIs/luRCYis+eA24DXqUVl8qYw3leVM5K5z8hPd6rGXMEUgCnzRgOKzWOk4p4nA8IqYI7zXrf399jb7geTFOiNMFUyTe0SoWAEAoa4UOs9RgmT92/Wxi3DqDFhAhgWGzymiEKPjT6VSBI1u2lRMc0DOmD4dDzYSwgAUnJEt/ciAs+WOBDn6ebR6GAU9PT/j06RPevn2L//E//ge++eabCojelXO1jscj+r7H1dVVJVG99/U8b4JSNOIEF232OKPXCSCxvKfNhLPZMgSseR6jiNTyoiS8SbrZ0tMETLlpJYlhz3+kISZJYLNiWf7UkhvL4AcafnvGOkFOZrfw/q8RepTBOI61bK7VI+oLAbv9fg8CaFz0CGwCzWlkNg3lTZ3hokLA1gJu1tDkmRHGbENsDZQF5giu83Ub6MBsOgK/fJ/PsIAigBpgkHM7Y5rfYT/tBtoCnASKvdcyogQs2A5+lzq6zDalXNlnm0FLGbINh8PhBTFK4mVJJBJMJlHFTKKlbnI8ACUhCHhzzvJ+HAcLoHM82G7OFWBeYp46ys/Q7tisbOu4EAy1hAiNNm2fDQTgXCZwT/CYBARtD8ecsiFhxAxC6gZtmUg7asHaPhtkwTlG3eNYM/CB841ys9mK+/0e+/2+khrUVd6Xc88SPZSBJRtY/QFAJVa22y1EBG/fvsXz83OVuS2zHGPEzc0Nrq6uMI4jnp6e6lnYOedZxQA6LRaYt6WCl3rLcbMbS+uYOtfINI6pJW6pQ7RR9l9bIomvUV6W1OY9bEluEuQ2YITgFtcGS6qynXydZBX7zLGwOsE+E7hkJiwJPdpQbiAoL85XzhPKhvOW7WFm5uFwmJEFlsC3hInN6LVHoFjbxrlLEmO73c5ktyQRrJ3hffhM9tMSjfz8MlOXfaW94FwmuUaiU3XCIfgBXQdcLqOxjbqp9V7PB5XcMpftusbn59xIbeuT8OK4LkEy6hM3H5wnfM3a75QSVqthRhKzX9w8ni8XnMtaSn/De1+r4QBQP02af8HjZ0IIeHx8nFWuYRAhS6EzINJGf1uynHPdEiYknFlG3QbhUYdsZSLaRv5Lv5LrHIOE2KfHx8c6f66urqpfSZ2mTtj1XUSztne7XX3fBlDYtdauKcfjsdoYHoPivWbsM4iB9pq20QYu8N9hUNDJ+3m1GHtPG8RBe8ZMfM5ze/QOyW/aIrbfBposAwdyztW3srpJm8R5z8AKVhjg5znW1u/j+kYbY/WXc5S+Ktc3+rmWAGc77d6D+mP9J+qPjQ7nxb8twU/fmyQpZUvdoO7SNvN4Cfqo9O2sflgbvlqtZoFbXddKkLPvHOMQ9Hx0rnucWwwAYMUHVnCh7nAfQXtmAxNoN/ljs+UpN/7QvpBEr2CNa0E3DPywerr0Ae0cpp4zmNMGxdKGLvdQNviw70ItDWfH1AZIcX5ae8I5zjnI51m/Sm2oZvlzvO18eAGcGL+a9tvunahj1r/6p1w3t1cFZClEs5+DK/wJrmTTekU1+FoASeq5L8Pxt6RxBfPM+YxdeHlOdP1+uaciKXMZsd/OOayLr1+zSmROgjS/i5m2DeiywUd2jtDH4fOoF+OkVSOeHx8xTc23DH0LqoBv2EZKE1IywbSuwEMjZnOi7hOmQl5LruhTmiKmWIIhDQZD+VoMAAByipDMffoAKVkWqpelihAyIiK2mzX64Mt9m3+IUmqS58DnnGa2yvrNKnMghKTZaV4wFBvMOXE6nfDDj9/h6vYW290Vdrvd7Og49YU7iKTZmFg/z+7z7ft2LViSMW2MK0s7e6/qZgHmk3mt3oc6pX+AoQvOuRlBXeeMKNDoFqScDcxbYgcWv5gBmK/0f0mE2+dbna+YRIzwIcD5FhAkhXDhPQ8nDQZj+dC+75DGC54enzTorexDl88pIsHyj9qmQuAQaLdYwGv30nlczhn1PdbrDbzvME0JwIi+D3CrFWIEuk5qFqNIxjSl6lN77xACELwAHtAqWcVHDA6n8wkOHnf3Nzge3+J4PuL0vT3L8vWz4fX3n0H0yJJ+bGM10ysoofI5O66vv55R+EJuIvCFIHK8f3kGdebm+hpv7u+x2+0xxQnn8xFDF5SUnTK6AHRDwDSyPLtogBIAKaSUC1pmNmfB5XICsmBYdXj75h4pJpzPIy7vPyBLVJusOXezbiznqZXby/6/JCHt3HptHHQtwou5+Vm9W46WmNcMuQ9XzlAWrYix3+9xc3OL7XaLlCbEmCCpg+QBOfOoGGJgzDwEpjHBu1zWJM4Vj5QEIhNyhpYAv7vB9x8+1H21tY0umzY690J2r8oRAkj+Sd2lzknr/mc/b7XT2qWlrJe2+zWfcLPZ4P7+3gSeapWRYejhRNB1Dl23Qs4OKQpiHJHyiKEP8H6Dvi/rzajHgyBrGeUpJkA8QuhwdXWNh6enip0xoIB69Fo/6xz8qfmOlzr62vWarf6jl7z8rMqSgfUtiEEJyBWGfg0R4HzWwIDcO+QAdF4gTjC4RrjFKMVuApuCHwG2CigwjhNO57FU7dLAPAh9NQ2atMfl2HG1Z8kvZdA6VLUIjcQ0XyrEnCsE9OFwwOl4gIPAe90HHY9HrYzWd+j7doxsCKGeJa0+TOMSUpzmc2qBlbCtnH/WxxCRWumI9iblhnVx/bV6ZTFCW/XQ+gDcN1gexQY30+cchqFyOhansrrFe0/TpHZ6GLBarQou4JFy2aP0hY/xaoOOJz2KrCYgni8VB+C8ZRvI5bx79w4A8Ld/+7f41//6X2tDvNPxGBoGn1ICglY9ZFIDZcWk06EfZqse9wHROWy2O/zlX/0Wf/nbf453777Cer1rfE6pcJCq7XboRH2BRuxn9S945IqfB55odrGDz+rnRQc0ul2TPAAHBJQqRwXbr41tdxNmUudGZofQaRUWuBJjnOuxBg4AUi6JJHbBRJ0XzrnSBn3Fmefx8pLhJaNzHr7vsL65heRGHidpCSTTNCKlcgypxUips8YXav3SK6MR+Sk33905By/tSF5BO16486EGYOYsiKlUCygugvqAgstxAjDHhPUeWo0leA/khgWM46h+Zq/zPeeMVM4xhwBD38rzZ2SM04jj8YwMVwMvHQBf1sjz5QiBBtl0XY8+kP/TqmfaXl+Pmfpj1590xjhJSRqMlFItH7kEKkiaWiNl37fAQUoJP/zwQ80msUSFzVTg59frdS03aUlDEnbH47GWDyX4DgBXV1c4HA64vb0FoIT4brdDSqlmMdHYcvNqCa6cc82SsplbPK/Rgpzc1BD04kaeYBkJ9u12OyvTTqNZN71ojsr5fK4AE8FMC4o9Pz/X37nJJfhmCT2STBbwtUCJXWg4ySxBZQkcC9Dt93sMw4CHh4cKlKaU8PT0VIMjLFlJopD3IqhtM8ztQsSzOJckNOVDYgtoJVZ4ViV/LDFK8op95UWjsFxc2V/2n/phs2kJzi2dTVsFgM+j7Akgsg32uVa/CURSJgShCZYSIK4b6MOhLogWOFQQpq/jaZ/DNnOcl2ffEvTn4ka9ZgY35WMdbxpL2g1mbw3DgPfv36PrOuz3+1lFAktgWaeFi7UFJGzggwVy+aylo1oXgDIXSExzTnM+sg3W/vF77LdzruoY5Xt1dQUANcOQzhBBJwBV/mzP0tGiHOyz+VlLINg2kmiiE0fba6sEWFvDfrDdywANK+clMWTJEuqk9x7Pz891TlmbQefxfD7XKh3sBwNhbAliG3zFcednmcloM+CWRDrbSdnaM8GtLvMZ7I91hBnMYQMgKAsSz5awpM2x1QxsFQ5WCAFQCQzqtg2caf1pOse+UBeoD7SVfP5r5A+JdEs6UBYkHixRRr2zWdOUH9tnyTMAL+YZiSU6N9QlErscV9oWEhFPT08zm2TbaUszc87zniRLbfvYNvaDemoDpyxxsdxkSW5ZqCLzYBUlahKcA0I3r4xggzRUR7pZFiJtH/u4zOSk/aY+2Y0an8G5bvtJ8dNuUzc5drHo4m63q89hxi0rZ8Q41SAYrkvUL5t5P44jnp+fax8YUNj3fQ3YsuCQXXNIWN3c3GAYBnz//fe1ZDrHxwZA2ABI6lEjUDRgg+eJ81kkwHPOlWTl/e0GmtnY1oddrVZ4+/YtAMzGwPou1Hlbsp42ioS93WiTKHTOVT/O2nL6NDZois/nsxlkYINQ6WtSp5+enqpebLdb/P73v6/z/nw+43Q64fr6umYac64fDofq11LXrZwsiUkZXl1d1fnD0uX2aAYSzNY3ozyZrX1zc1PnNcfK6l4lkBbzgAEdllSnHlriifOIAINdn7gGcCyor5T3arXCw8MDAMyO1aHeEGT4XCUd3ovfpY5RXpQR1yerLxxbW22I8rfr0TiONVqb9oW2iIEaHDsS9JQj9yIW+My5lZa3lbFor6zdpY5zvWP/lmefc9xt9QDrl9JmWb/EBlRSZ0IIWA2rmX2189mS7LzsHsceB2X3VrTBNkCAbbK+C2XBZ9v9HuVJfbPrNm3FMtjrT71++9vflnaVs9lcO8ZsBoYUglS8K2fSeQQ4eCn76pTg4GsG85Lc5O8AtDS1LxnUZd5yTs/2Em5ecSlDqm/B10IIeC7BtmLkaP23+m+hNnOaE67im+7m1DJqWOGCczHnjCmWo5JcA6VDCIA3x2qU/gHQXNXcyoTDOWRHEFYzU7z36LsBzgNpLNW+YtQeSwNfxTugZE84p2S33lPBOiXOM5zkel40LgIRB/hyTmbJBuuHAcCAy2VC8kDn9XzXJA56jjj9kA4pRaScFXSaJu1DzqWPZY2TuV9L/ZymqQZlHQ4HfPz4Adc3dzXY1Qb8cgy89zXIwa71r/3LcbRzlpcde/vWEkD23hegcU42eqMXQKsK7QsHRZ3l3LQ4j4jAm+/WtjmnYGbRBwUpX2bT2v3b8j07V/h824ba5pQQ6UeIoExNY4+09C7ta0oJ0WuJ56HrcLxccDwdq89j15uZLOXluNiLa58dr9fGwoxQ/Zd90izFiC54OLSKSd7FikPHmDBe6Ms79EOA7wNSFKw3a7iSMa5jNGEadV29u7vB+fIl3j88zgLAXusH9Z1tt/2dQ8c/fdUxfeU+r8lD5c69BElLPsUB5fz0nFP9fM6t4mPOGkB3c3OF1XoAkBBjwvmcgWHAauiRYsb5PMKNSYMM4hEQQR881usOQ98XflBKsJIg5QiZMpxLWK9WuLu/x/PhjMfHJ5zGqHYPudieP369FgawXD/091T7L/JS77JkeHjN1jbXazZCFXhBPM7+T0avlJpNGc6p/7fd7srxXKW6VOcRU8b5EpExout6wPda/jVp0FPf9xAfMAQghB7eO1xKJm7OJovaC66ud7ja7XA4HCo+aX0ABi3Avya5V67P6O7yYoUCGHvy0zq6fIzFuNo+0tpkXvTNt7td9V11jTe10Tut9KJ+ODCNE06nIwQJw/U1QugBOEzjiPF8KT6WQM9TUIwqiWLt+/0epxJULJLgfTeza9anNj36k/r9OVn9qXL83D00i7HJUvfXSpRuNhvAORyPJ4MtAjlkZO+QkJBzj67T6gfjJeJwOmM9qE+WUkaWhFzONtZ9nWaP5+yQkuB8vmCKY5Gftov7FLYx5QQvDl7CTHpL+1p9uVo5SKqtXV6u2JHD4YBY9y6KtTw9PeneZbNG17UkqJrMYZJRpJKz8yq4r/kX3Oewj1LW7uBbIhT7y/G1WJPVJ67V1m/gXttyDwyOZvssTkAfg9UQiTnxnjaBjvvA8/mM6TLWgHbea5x0/x4cMbGE8/lSccXDUdeA7XaLX/3qV/jmm28AI3+29d27d3j/4Qf8p//0n/Bf/st/KVi+1OOGvfcYpwmrzRo5tuMOL5dLLVm/Xq+x2+3acXmF1KTv7UPA7d09fvOX/wx/+c/+Gnf3b9EPa0w5wZeACYeMAI/etaO7YowaDNR5LRMPIKaMFAqpybHOzc8WD2SvutiJw1DsixTyWARK7no9X1wARHl59NJyD+IAuFwSgZ1mQFuc2XkPyQVnAGY6QJ3MAoxJieg+aPa6xcVWqxWmwunVtTP4MqeT2nanfmxKCVPSdSULkMQbe938Cz1CCeqD5KyZ8rklVFjd5HOtTw/MbT/72/sACe3YXcViNalZqxbpkdMxRd1/SkbfteOpFEfQIzfO5zOejwcczmfc3t3i7vYWw/UGyHqO+TTpj/ceUZLqXd+h6waIC2oTRADvMPQ9bnc9DuczfPB6LFQ3FL1NiJcROWmlkd7PKyZ/7vqTSqkzy/l4PFYwhCAcQQQC0ASbWerSOYeHhwd0XYfr6+tKsPEeNBYEonhf3ovG5vn5GXd3dxWU4mSyUTi73a7en+ARjVDOGb/4xS8qYPztt98ixoh3797hdDrh+fm5AoTX19eV9Hp6eqoAKo0fgApEWdBvvV7X7B2CUyTeVqtVVSB+P0Ytb3o8HuvCybZaYBRo5+KS2F6v1xVoBFCiIZvxopGnIbcAN4EiToTPTRyCqgS8OCZcJAikUQdEpILABC3oRDFTxJ5lDKDqDRcj6teSgCXQYp9ngUICYfx3GTnNwALKwBK2/LHAGoFAS0hzDG02MMeN8qZcANTslyXwSp0m2D1bWAzQnnPL5rLghF3Ya3RNbtnOrLBAENc6glwQltmq1DHqD7OD2TeSHpQn+8i2WoKJ/bOAIKPWmEV4e3s7y57k85YkEPXVym1JvtgNvSXfbDYVSR+OuZUHHUuSBHzPgp/LMr92TDgnaM9IsrDffd/jcDjg22+/xc3NDXa73ezsd9vfCjDmz59jScKC+kBSgrYAwCxb284/kgF27Plc6gqJA9oAS8Ly2bRF1FdmANPeUk4kjDkvLXBE/bSgswXqeX8C37aML/vE9lKGlqi2oDv7bftmyVbqMMePsrc2iDaAcuP3qS+WBCZgS/nbwDDej4Td8Xisc7g919X1i30iiU59pj2jPbaBZFwbOIdJmlKXbYCG1UHqPefYZrOpcqf95v3s2jRNU13XLThHAonjaW090I4DIGlq7bwlg+zcXwYwsb0M3BmGATc3Nzgej/j06RPevHnzwvFju62dpZwlO+SspZ1S0vN3vHdwTiPaRYAQHAQN/LcVXWyQGrPGaactOeecw9PTU10j7brFPh2Px9nZ3JzTBLQZ0GNtBceePhfvR3/E6jB9pa7vsVq3EtAM+KPe2ioD+/1+FuhkiXSOFceJR+/EGGfHy7CSDCsG2AAU67BTDz6UjAyWcs851w0nfS2Sb/v9HrvdrlbR4ZhYop1jJWVDaQk5jiePACJxbW07bT9JRxIOJGyt38V7bTYbPD4+1oA2rgGUIZ9rbcOSzKSttUTgOI61csfpdMKnT5/QdV0t3304HGaZ2JyLtC20XzaYwGaRsx92DWZgQdd1NViJ9pcVmCgz+iOc19RJO+5ch5aELUtfLtdGEtvWt6G/aTeDvFg63wZUWhtiAz3tfobBuHw+ZWCzsDmXSSjbZ9g5bYMIKG/aPx4bQH2kPK0t4Dp8OBxqW2zgF/0fG8hC/2NJdiztv23rer3G8XislRZo+23wj/W9rO+5DATls6yPwHXSVjziWDLLlfsE2jhBO1OZ64L9nf3gfLBVuWwlKuvX0AbwHhZA478M8qKO2QBXrrlWt3lZ39UGKP451+PDoxJ0JbOB+wW2g2OtICgKwcHSgwpSTikhpghJAvB8XzGAUNacQV9KWIoBWXLOSJn+vUKhzqs8hwo4lHsCM5sC6lVnyp1DiQzK2P5kEp+in2F7XPCIYwlqgGZA5ZiR0tn4DZpl4n2P9aov2X4tuzyLYBytHx/Q910tdjgjLKGlAEMIhaj26Fdq+6ZS6hqu7D0kIU4l0NoH+NCjHwY4Fwp5zk4rmb0eVui8R5ZcS38mAeAB7ztodpcCXSFs4BzgkAFJmC4nfPft7zBNCd45JSGdZrZowIPUMQseCEEJCmEdbUdgnIEoLXmBduTx4QE/fPct3r19g/1mj4f0BAUcgSQJMY4Yhl5Lc5dzIVVkSm4zk8Y7zfyKyZbEbXtXBarLHshrKUW7F3hxlfML9bxRvubMP2VvmAS5BAToGxlJ9BxSV0ssFvLSFUpNpBCEqPMF5nW7FgOY2fU6D722K7/Sdtoauy41soEsvpKXXgQuJwTfwbsOTryW548jTucjum4PHwJydIAPuDw+lTQ4LR8NeKTpgq7TChPZeWTRczbtOMxES7vHv4vKcnA1i7WR4ZnjWIDicxwRyjwX3+EyJXTjCIcOKKRLFocpJpwuGiwyDAHOA0PvsVl7DWSBIKeMKWWkElOSk8p6v9/h/u4OvytEQM658DKaDeW9Vz3/TDll55yRgDOYMn8vWZ0180v77Oa3++yVqVPkcJ3aKrZBm6HzWnU8wyGXTC4BELDeXaHrN4gJuIxaKSV4IMYMYIKIgziH3gliOuNyESAnSJ8x9B5hXTAe0UzcFFMpyx8QowLuwQHX1zvc3l7h/INmk0OXBYh/mdwx62OeB8FY+aqetMu9uIclhjXjTMu/m+987tkO2sCSsmb3c8gmgAoCSEISYNX36FcrhL5DygnH8wXroYfXGvPwEEgHJEQIHGLMmMaEOE1IQ8KqC1itBzhkpJghWedmzvp3TBq4kBJwtb/C49MjpvGs5CRUb1KSYs+LPWL5/tpHZ0Tyst/WF7FSVNPWiElK9kXAAgBIgpT1eSZSVwWr99eFpgQ8paqzKWX0wxqr9Q6r1RbOKTkn3lXbCHg9ooPHU7mAlAUxisroSso0y5jSiMt0gRMtTR+THlmWsmZFAw6r1dok47UjNpak6FJJ9PxZ238bPtEk5WQ5BG4uPEHJDZ0HXr2u9/NS6rNH5VyMmFaIsPhuygmOwa+xPDNkpBCQZMIUE7wfkTPKERQTNqs1phgRLurfTZNgGidcpoQxJUw5qizThGk6q41xprQ/bNUA7aHuV7rqd8GhZFg23RAxvlsl5LTPsyCQItCUgMePn3B5fsB61SFOCcfzGafLGcOqRxc0QDP4Dt4r8VWDarnGO2C8nGsA3jKpxeLm9jXOGe89fPDV3wQAHzzWfVu3vW/7B56xHIJXfGe2R6QOapUI5UIE3mnRZjgNGtCT1lFJ7L7rgCxwOaPzDkkAiRFj0n3QOI4l4EZ5lsukRwAl4ulZA5u0ZH4sZ8kLctRKQfurNd7e7/D27R1+8fWX+Itf/xqrvkNKE56OVxijgw8B3nn89//2N/iv//U/47vvv8PlfIJDxmazxnoY0PkAOIe+6wGR2f69VqIbBlxtdhhCAFJEyhrYckkZ3bDCZrfDze09fvPLf4Zf/upX2O73cNIhjZpd3fedqcaWIS4qQc5kiPJfFq0KlMDKHw2fqIEdKWE0NnEQ6JndQfsRY0TMrQqIcwWP9g6Ssv5ANAA4eFwuI/oQEC8Fs3WqAznFGiAMSAk08LpPqadseLigPoTafQ8XGs+S86jreMlmzikBZ9e00gFwmuG8GgbddxQyH86jXwWEHBBj2Ut5h64v1RmL/jpfKlnmjMs4Ik0jkkl+Ij7EKhx1zxu6omO5nlGvYx4xTaPaGu/x7v4Ow0orXMQ44TKOOJ7P+OKLN5pgOEU8Pj5gvRrQBdfaBSClCd459F1Zh08nfHh8RNd3+MVXX2uVRDikFHWulPH2na+BvSj7Gx9C8f0KJhU8pnjCZUxw6LDb7tC5CckBlyQ4XSbEy4Sd8dV/6vrZxPhms6kg//PzcyUQLfG13KgvCQ4CpyxlyXMauYiytDIBTZbDe3x8rEAqy3ryGff393j//n3d9PJeLNv5+PiI4/FYgYn9fl9KjIyVaLm5uamAKEFW3p9gDRWIGxuS/vv9voKjlqyy4CtBIgvyvX37Fg8PDxXcenp6qplGlhC1JCEBQ5slRLCLgNkSrOKPzW7i/QjcETTivQkOkfAhMOScq+3j823fSdYwe4tAmiXuLehEIgVo5BNLa7PvIlIJP+qWBRxpTC0QbwFRu9Hn/SqAVAw+0MhUq7+8D2VBHaUs6LBZwoD34r8WyKXcCTLyNWY6sI0EGSlj2w5GhO92O+Q8z5Tkwm4JSZt1bwkT6j4BcEvy8R4EESkX6iDBYxI9HGPK2gLFtm2WfCXJwDGinlpC3EbWU3+tfJfjS1lamXNu2H7wSAFLqPGibG3mG+VKB8YCGkvyzrZhs9lU8kakHelAIoT9pX3h0Qy0TZx/NqvDArGUO8fAZoRx7lk9897j4eGhytRm89r28Nk2KIH3PZ1OOBwOAFBJppubG0zThMfHl+drcR4xuIZy5e/e+1l5Xc5L2w6OAzP6SfbYOU+S1dp16oUtcU1SpG0Kmh7RBllinbK3hL4luhgYQEKWc4yO5Hq9rnOWJARlYslrjsfSXnLslkEcfI6NjqW8mZlnA584J+w6RLKBdt/K0a6BFbgzBDXngiUQlqSmtUdsnw2YYntIJNFuMMiD0ajUN85B2kMbkc9IV64XrJZxPB5r9RrqoZWbJTD5/bbB0lLqCqLHIheSIRO8DwCabeG8JAnFjJZxvFT9OZ1OM9tKnSV5azPUrUz2+z2812CncRxroALni8q5K3vv5nOxJPc4jgqiitSsWeooianr6+uSQb6q/sRqtaqf5zPZbrsecxxjjNU/ZCYrg+noA5KEJ1FLG8N5Y8fDrr3MSqdu0WbxbxKzdq7ZiG/q7O3tbQ3g4FhYf8SCfpQxg//2+33Vq5xzzcam3lgbzTnBYAaSgvS37HpHW8i+8vMcpxhj9U25qaFtop9rSU5LAFPf7fEmt7e3eHh4mPm9u92u3u9wONRAWAbQcB1gYCBl9vz8XNc52zfai+12Oytnbu3s4+NjtdHTNM0CP7huc35sNhs8Pz/XucL1kmPM71ni0toW+m7UJcqebWPAp/WL6ZOnlGoQKu9rwRkrY7aLayjnOPWVumvJH9o0yowR+hwvAkLWx7SBNqfTqQbW2GBPuzYs1+UZcLTQN85JEvU2+MCu1WwPZbZcL2z1GZshzn3L0l+xemP3F81XUYDRft5mf9sgTAbscO6zv/TP+Lr1UyxxxXtzT0n5W7/P6h1lw3ZYv/h1APdPu374/od6HynP4pnQFSx25XxFAjZ1vEsQZy77qNzOlCOw2UB3jy6UYNAFMV5JZ6dpDCwtnEVmekTdsATgUsfLYgo9a9SA19LObfQhKLHCPbDzZsy01LpzAHKuYKHqQgOvHeZt4zpg/ftW4aB8QxoJOgxabYJErLhC5lRb7dD3HXJKGC8XJcacgw8dutABcPVsS6AQDjlhs15r9nhKGOMEcQ65AILeFTCoyCWEoOccopxR6t3sPHdfMmacD3oWYtES8Rl6DnTWrLIkJfjByklBJ2uL1Fc+49OnD/j44T2u9rc4nI46/xzJ7g4pZXgp5x8amWl2T5NlSi0Y1tqRagdRfFszD62Pbr9bfV0xr78gJMqclkaQEsdX0NrNPsvrBYW3sHnLPiw/o+1SWlZEKiloMYDXcII6f6FzDeLBcp3UdYL14zThfD5hs1kr2B2UcD4fDnqGY8pwPc94be1V3X1J6Ni2Vb9T3+AHW39FAy7MTfSejkE5ETkA8A4pe8SUMMUILxlZNLBJS4EnnM4XDeQIgHM8Ik6JiVx0JqWMGAthFhsxst/v0RUcisEpznMEWQqVYOrrV6X3yy/8ZM3AtWSh+cBrY2/3S0ZtK9nG9xlUpE/nXsmQpCJwQQNvszhoVSq1j8EFBKRSytXBB7V9YxxxPmV4p5mRGthUAPqspHhKqZ43S7lmEQx9j+12gxA8dFmQNkeMTtbuOPdq/1+Tq31hdht5+Sm1268HMry4uYMyEbLQYaObbb56dF2P0KkdnlKGjGMJQgH6juMzapUG3yFOWatzTCOc6+qRBTlnpEnPxlVSPCkxHkuQ8lT2TMOALnQY3QieiZ0zfQBX5LGce5STeyk/Iw8rf8YHwFizz2m7A0oQy2u8e70RaqlytKoHQmIKelZ7CD2cD0gxY/ITcggIWloFPB9aSmYpXEZKgmmK9bk5ZyAK4hSVYBLNCo1JZZliwjhG7ZdvAYtNXjp3ZvbqRade/m1f0T6+8pUmivrSa+Px+hyQV4RLvWz/Sl23dN2cpliLCYjZG4SsgYj0SXIuAWxl/jKj0gEYx4hx1EodMaUSYJCQc0JKEdm1Pe2r86q5DMYwQpXMVdNk+vy6LOzfIkBMEcfDQYNMgujadToV7EkzyLm++fJDP8+Ve2VmvqIleizXU7vn4N7bYs6O2D/oN5WgPT+vzNbsBjEstaUpZ8Q4KWkHoO8C+oKPTNMEj2B8mRJYvFrX/dTlfMExHZFiw3YtBsMqcjXwHloRKU5RqxBJbuMAqfNi3XdYrQd8/fU7fPHlO7x7d4+397e4v72BE/VRxY14/+mAD+/f49OnT/jbv/1b/OEPf8DpfCw2sC9cRuO3AonRGHEZL7iMI7JowNt2pRxcjhqEAecA79H3A27v7nH/9h3evP0CX375NXa7XbnHBAcNMo2px+VyRs5aBcd7j37q0XUFS0HzeSijjFzHS1CwcFB3igp7jwigcz08Gs+QRdD5UPcwEABdUF8zah9jTkAXMPQDbq93yH2H0+mE43iBwMP5jKHXAE9AcBk1wJgTIxc3c9W36m0+BPRDX6ucTVHxphWD1LO0fUgJQvHBI4jHUBJYWFLcO4fOe4i0CqzBByXQC9diA0Y4T6bYkjm6risVU1R+l3FEqFhyS9JNKWO1Giq2xaPSUkq4v7nBerNFV/Z44xTxu9//AVfbNe7u9GiNw/EeQ/DYrEvCbFlLUpoQDZeaJONwuSDFhNubG6wGLcmfcy5l6wuP1PcI3SL41BGrtVWjJ4xjhmSva7CP8EPARRwuY0S6TFi7ZfDO69fPJsafn59rNnWMsZYgtwSbBZW5ESWZRSPF30VamUQ6YCmlCsZZ8B5owCSf672v58VxoGnYmCGz2WxwOp2w3++Rc8b19XUl4wiaEsQmAMMMI0uAAFqGfQmsW8Ao54zn52cADah+DeAloGPBrr7vKznEPrDvzHjo+x4fP36s96dBJ8BuS3JY0sz+a0lNeyYGfwgyU5YE8ghs2xKsbD/BWEssELwlyc1nkwzjImRBLV4kV7j4EWS0IIYFJG05H8p2KUsLEBJss8+gHlqQden42Ig0G+BA8NICatRxAsp2vC3wamVln2lBOtsO9oMZMATmlyAlAfBPnz7VcbHkI+VAw8cx5vhZII/kPEFMyo06YWXDtlmy0IKHBM2p2/b1Zf9FZHbeLwk53o/AKvXPkiucvwTVbXYkdc7OTeod+0BbY/vOMSGAr8BRK0VrdZc2kTrJseN8f/PmTc2ctMAqSRnOFWYTMhMx51wz0HkvkkC0RZzLy6AVEhc//PBD/ZtEC2ViAd1ltjffo22gTaWc+OxlhQ/qF9tNebNiANtrSQnqOYk42kE7l0l+ikglC6nDXD9IHpEMAVrZTQuCWz1d6iHHj/1e2ksrYxLMds7arDUC7I1k6sx8iKVdunHSjOSmd7R70zTV4DAGBgCNALLVDaxucn5wXopIlbk6xe2IAX2/nYelGUtdcUwDrq72+PTpE1ardn649qc9l4Qa1xBmSVr50Omy1V9sVijPYGYQDseeY1LLOJW/SYCzv9NUSojHCZvNGuN4qWPKtcNm2U+TRqkr6a1R7BJIgjh4LxCh47hCynpeYrwkBcZzRt/zvGqN/o2xq2d/0xZZW9V1XV0XuQngOPOymaUkdayNI1kbY8Jmo4GEUsCnaWpBV3AOnx4e4KpfJthuN+iHHk9PT3j/4cdC6LfAOmZ3cv3gRdvMuWvnps0cXs5rzhPaB1bJYcCMXUM5VtY+ciNK+2ArJVjbwMxtypP6ybPOuZmgHjLIB0Al8MdxxPX1NVJK1fel/tkKMiRJnXNVp4Zh0BJm5bNcXzabTQ3qoT8LAO/evUNKCb/73e+qface00ex8qfsbak16gjtG9f9pQ/OtYm+FeXP92lHeWY8SXfq7PF4rEGZHI9lGV4GKNBnYPBUSqmeKU+70ff9LDjW6hP7zYDM12w3+2TXUr5Gu8LKKdYf4Y8NArVnUPP7XEttcABlZAnc8/mM7XZb+2lBGnuUAoBaeYv2muszgyXsekF7aucE+8SxtyXKGbRr/XH6S9Qd6rENHLH+EeVogxv5LL7G+/Key/0G0IJPl7KyPifJZ5a755y0vkcN9ILiGpb8n6ap7k2WgSU20IYyYrALbZwlsK0fQLvC+1EneHwY9ZsX54wNyrGBXJbo+3Ouw0HtljeBa/SdrV8C5+GBAoa2CidK2nXIXdZzHJ0lVRtY631AFxjkZkjW2VrvCzHTQE3KhzLhPLMEy3Lu1bXQ9IP9qoS1aPao3WN5r5nWWUp2SdbMDw8jB3Cv1sgHkXYGd9uToQClfL/hGDr3evT9AO8VIL1cGCRCQkJB65wEKSugmSGQNCo5VzIxagVgEUhOiPFSksmKXSigXzJ6wpLzPnQIXYCDIMUJ03jCNJ3hvPa5yTZAUusTXKi+XN8pKR4RZ2Op2VJzohoAcln3fve73+H/+j81I+RUqzMpSKhzaU7yNF2anzEfupekbH2e0yAIESnAfvMFONc4rgpulqxx4hHmOXx2lbVGiBgdkEKCuEo8m6bP7mH36QBezGOr1/Z1/mZhOPtZG8Bj58lSPg3cZ+ZbAKYWoN93PUKxWafTAefTCTFOWLkNUAJCHLTaEcFXyfPOyrLzRnb2/eX+CGhcEmATY0oCgG+VjSRqVmkWgQ8Rl0vE+XQpfjOPBgpIMSFmzWhOmVhFwjSW8zZTC/xj0LGIguZwza9urXv94li90BWgkjDVMLLfRiesPHjN7vVClHM8ybZTpMmacgO03Pw0xUpWBR/gHZDFw7kE5yeIKDh9Oo/og8dq0AAKoPjcUck0JWw0QCelhClxvW4Y6Cz4zcy3z/VrOd/sXHlNpz6rZ02CM9m+JmMA7ZwEe2Wrm+13HxpupJnLCcgZo/Nlr61BQylHuM4hhIxpzBgvI1Kc0A9tT5wLURSnhJgyphgxRWKK7Yiyvhu0hKz3tRJI65OuyUvZ/XHZzGUo0ohe90pY0OfuvRyfFzZHtLS9c05lioYZahUTX23IOE2FrNPKHNKiFpCdEs+5HANAfEb31xHOKeahZG9ESlKCDGL5KZnquWELvhBDLWBlccZ168nrsnuFLP9jwRgiwoibz15V15wsxhoA8iw4SsdNfaYspSLJOKLLmmGcQih2M8P7hCypLF2u+SVJlAifJnhfKgFNE8ax7INrMHVLLHlVTItrrhdAk7MNSLBhGC91a65XgjhpGX0lE0ecL0qyVj+wyNZhnjxF/z7nVMuwA5a8S/VzfB73rta2WzyBr1kSnDaHgaN8TYTVgHU8JAvSFMv+J6Drei337j2kZNvyHG4RYLUalKiNU0kmOuJ0OiJOY20/+8L9s/UfNMNdkGOuVQZC5zGsegyrNYbVCuvVgM16jZubK3z19Zd49+4t9vsd1sQ/zxPOxzPef3jE7/7wHf7hH/4B3377bcFNk8reK17SdwNENAhNsSK1A8fTEedLweFDwRPKcRQZSkb7XsnL/f4Gv/jmF/jyy1/g/s0bDKs1IkY8nw5IsXEXJEXtPj2MAd1QKnKVgDYBSiCCWpKu0ypMwWswaco8hoj7Dg/pNIvaAeWoJUHvHIbgkWLGOCrunkePq90OfR+Q4gWX0wHZAbdff42vv3yLAE3ceP/pA7oQ0HcBm9UKfa/VmC7nC04lCDZLKfdeeNHddgvJGSF0WK9W2O92gABRRnSha5UG4HA5n2sgM7wGa6zLWHShw9AP2GzWCEErUknxjfTcbMUV4IAudOj6Dn3XV+wFAGJOGIsMvTMB5rlUt3Ja2WlKsfgbI56en7Fer3F3d6fvxRa44aEYFzFtAfmbjM1qwG5/pUfJpojra620WDZVyJJwPp60rHzXoRsGuK7DdLmoL077IW3f0/Ud+mHQsZ0FFNHf75BzCZQPK/QDdN3KenxUP6z0uKGQgZUG8f6c62cT4yRLCODYrJDHx0d8//33uLu7qxkGOWfs93sQ4ObEX5JOJAZIrjPLkudwfvjwoYI9FvzjxpbZR3wOwU4SFnzG/f19JU1Yrp3ZVNyc2QwVbl7YVoI5BHpodHmOMPtKQIzGmP2lUbAgGo0CMz1tthhlxTPIn56eZmAu70ew3QJfJKE4Rnyd4J5thyWGqGx28dntdjVTk2NlichpmmYlXuumuoB1Fnjj56lPbBfBMEsUEgzk5ocgiQXR7Wa5luEwC/WS0GXb+T2COBaI5RmXJFnsxhxojiRlyCADC5Tbi6D2bNEzIBszz9geq1sErym3rutqqWH2d1lenIAeSSUGTbDtFqAkMWnPJ7dEIPXWBgXwPeoTZWz7xE07ZU8inkCUJYAom6VeUYfsfLfgJQkJnovy/PxcCSbKgHpBGfKZLCdsgXcLAjPTjhnAlB0JBhu4YzO81ut1tVnUax7FwPYSWOZ8suebigh+/PHHajtZeYHE4Nu3bxFCwMePH2d9pE0SkVm5agYfWMLxL/7iLypRHEKYHR8x36xLtREWpOEYc+wpCxu0wPvYYAZLQlk95Fjz/PFlaXmWayZJwLnBjE9+l3rsva/ANfvI7GFb6plzhf2xZAH11VYxsGcCs22n06muIZZgpe6SOLLgAtcg9sf7VkaaY0eyiTppsxuXFTcoExJbAGZZtJzHfK61S9RfPSbjPNNlC25bWTIr2BKd3vtqQ/p+qP2zY8azcr3XDFORFqxBW2LtAwkpGxzCUsY205YAIwMoaENU72O1zbSVdp2k/vC5Vje4Buk8L5uIslFTuCCBJbUsyG5tH9dhG9xD+S5tPslB9p/2abVa1cxzu8Hb7Xb4/vvvcT6fcXt7W+TSzkTf7XazrHjOv/VmXcahnE8qebYW0MblnCuBTP1nwFPd1Jb5QBKZ9p62kEQw7Sz1nZ+x6yrbQKLKBlDYzay9D+VBm0o7wHG9vr5GjHpMzadPnyoRfDqdqk9DEpFt5z3YR9rUYRiqjtsIXc5R51wlO202OOXO+9sqDrSDl8sFnz59wul0qhWSAMzKSDM4wTlXS6RfXV3V+dB1XX328XjE3d1dJd2Zsc2Lz6TttH6hc65mZ3N+vX37FiLzyg7W/2OJdNoFS67yXwZ+MLghxljtAP32cRzx+PhYgwQYeGbPG6dd4DrCtTUlzei2ew5+nlVxOM72OA3OM/aNRLad0zHGqsccO1Y+sPsE2hnaQ9oP6g9trrXjrP5A4tcCPrR7XJNsAAg/Q/+F6z31imuoDXawVaEeHx9rEAc/b/UY0H3EbrfD8/PzDGSlfKzfZP0E3o/jR72lbGljbDUV60PTZtn1GQDO5Xw9zjtrpzm+XHftfsWuoTbAxPpd1HXrj9BvoM6xX3Y9Z7+tzOkb2vXE9vvPvX7zm99omWzfMvPtOFMWoZDaGa2f7D+kEYTOV0qrtlMvD5b+ZaAeP2fHx/rpfA7vo0CxA1zLwuFc4HdElESmL4vcKhjQtiz3o12vWdjOOcQ01dLuMzDUOzgnSkinhCmm2gd7P9oNfp8+CjMquX+wgWkxTojpNPN/7CWltB8c9OzDVPQhmSxlJ5CU0XW+koWAqwEPlI2CRAJkoBu2ZU5kpDghTROGrpzN3A0IvvhCIq3SsNOMfmZze9/De4HWa28BIzZwwu6ZgQmXywm/+93f4f7+Hl9/9Q3ev9cSiKkC2B3EBJZbnaBv5gvgpx+T2fxjufho9oidn1cDEikgp292B8Lzwwt5mtPsvtXfLjo4u7jPMWMnRv+tj7/cL9g5zssC7VLGU9gOvE6YVpJkoT+82AfaHw1M9fVIAQZaroYV+l7xkOPxgNPpgGkakVI5A1JKxh1KdYfc1iDblmVfgTllpG0tFSNmbSZJWRIMpgkMRAneIQaP81kwdCXgqcyNy2XEOE5KsomWbE4pIk8ZUzZJCAmYRu6Nmsx4XOHDwyeIZGRx8DKvWLIkyOwapp/RqlDOKdnT4lZKoNHsLhpcsJTb0vY5t6ApPxtzsCByS7CH9yWwSJwJEoZmgfsJDkCXAZFUiLWM83nCeBnhV3q2Kv3WOJUM3KRjFyUiTXomeUws296qgTIIVsBs2naOcCOtX+tQIZNM1vGy80vdem1clu/P54fU/0ueY2wOKEc5aClrHRf9Wfcduq6HiAYaABNyFwDomeqSE1IK6CTAJwdAs5XjFFUGUoLtSuY9ycYxZaRSHrxmjJd1ZpZoEufJX6/JZTn3rDw+Kxu0dZmZ4MvvvJini4vyfTEvNFUXHO5KwLtSpQBaiUOJcT1awwfN1AOTWz37o+W/L+OIXQjICRinBCAiRbUVccrIWUu1U5Zc+22A3OVi26zZ6d4DUn2anyA9ZvEvPz8ogfNzmUm+vJcU+2CDMih3V+Z3nfPQajIC4k2CKQsAjxDUb2LmNFxupzlk9Sc001SJ8OBY9WqqZ7NTF5XoKhitn58ZXP1Y3/qhaxcTQPhQFPtqZOZ8DViYyUBeBnzFOOF41Ip/p9MJ5/GCFBtu2oIz9Uxp+u7VnsIVb9TVstTV75J5Nc/KS4WuZMvPz1DmD9td9ayc4wyoHeHxQCIarCFOSkCWrwEvOQlOxwsuXgPCL+OpZtaSROQPKyGfz2c9m93xmBlv1o0WpKuVgQQheHReifngA/peA6g3uy3W6zU2mzU221LNyDt8+PAB5/MFu90WyMB/+Hf/CX/zX/8GT+cTzoUT0P2U05LTzmE1rGp57Rg10CWJw5R0P3U6n4CyJ1yt19jsdvDrLbohYLPdYrvfYbPboe8GbLc7vHv3Je5v77HbbJCmCy7TBTmP1U+/jEog72+usd705TxoDTAYiGFKqbhT1pzNZoNd3+mRGKZKaIpRs7I7JU+7roNsejgxVRNTQig+03i+4PD8jA8fPuDjwwH/7C9+jav9Ho9PT/juxx9wPJ/wF7/6Bf76t3+F3WqDaRrx6ekBwTms+g5DkZ0Gp5bjIrxDdBqcdim40tVuDye6hnY+6JFJISAMvdptclC5HP8ZPJK05M6+JMuwumCQjJtdSQAdL1XvNZaW61OCTOp7qk1QnzkA2PT2uDydNw4afKEyivDQs7qD97icL0hTRBwVq9ms1tiuy1HIxxPWBdeMKUFcxl/86hs8laqSj58+wgHoy/6Z+8A+dNhsV5CNYDyXSngxoi/znsGxXAtjwSYlxlqNjGuoQ6sk7JyHHmGVANdhFQK6AK1mkAVT8kCe4EQrBeTPm/rZ9bOJcZJLj4+PldAjwMjsQwLi3EiSEGdJTWY5cTHebDa1FLn3euYgwTQA+PTpUynt2YgtCwAwkg9oZ6Az44SbWm7QSFCJCN69e4fn5+cZicGLACRBU0uMWQKPxD1BML5mgfneTGRLojnnZmd2MwOQYLIFwW3m6BKEIkhswSP2ZRzHSlaToLOZeVwkeHYpM35sNhQXlePxOANX+LMkmgn+cJFalvO1xC9l20rYtVK8trT1qZRdYf9sFggBFWssa9Rm6eeSTBKRCsKRbLbAFv+lrC0J3Pd9BYFZ0nMYhpq51oCGRtbbUqvLDXXOuS5KFgQUkVnghIjMCDbKh2NojQbnmfeapcX3SVxQZkuZ2Ig1m71ZF2v3koyzjhY38PwenR3OqWUJawtYAo0wZZ+W48KLsuRY0fF7fn5+kZlMEofjyQ01QWQbPEAnibbDkroERvl8Au22r5Q7CQeCoMyOo/5aApl2je3lmcjUZ+oybQ3Lutqx4IJHvaYttUE1p9OpgvM552pnKENbTYD3JIhOe0Y95u/UKd6X79XF3eioiFTZ0EbysgEddKytXlAHd7tdJbUA1HL3NuuNfbJVJ6hXNriHtpPv27O6ub7YTaN1qnlfjqclQe19OSa2JD8JB8qdZaT4edpdPoPkwjJ7n3pn54wlDPl5ypbysaQsXyfhQn22648luuzG3gZzcP1VPQl1bbMkNOcZ1x2Ond348h4kgy0ZwfnI8aZNOhwOs2M7qN+67lyQUgPY6YdQLva5tGeUD8dRCdw4I0v5O4B6VvR+v5tllFKeS3KQfeDaStlxfCh32ngbPEUbw3Xi+fm5Bo7xHgzo4vxm0JZ9nvUTuJbaDE7aMWZBtxLGLdOV8j+dTlUHaTtp+zgPGGBmA604r7hmU/e5aV1uaK0OUB+5rtiS3pzL1F0Sejw+h+NugyMIugB6jMtrkegVhC4BKzZohjLlHOd8pw1hkJOdNwzkYpZOSqkG8zBo0q5DfD7lt9lscHV1hfP5jKurq5qF7pzD1dVV9aNp9ylLO5dtMJD1m0hC03/lv+M4zvpB2XLNvbq6qiX3aWNsVRBb1p1ts2s0f968eVNJcUvOU48ZHMMKTuyDtcf0rWkvSNByzvOe1AHaUuoq5c3xo+1gnzgvmB1s11MS4sv12+5rrP04Ho/VPtlgk/P5XMuyE1RZzh0GVS4DMXgfyplVtuzehAGvDJKwxDaD1Giz6X/zu+yH9dGoq1a36D/QH6ANYVv597LCE9vBNY22KnQdgvOzKgW2+gT3lPTDrd9q59CympElx+1az3Za/WJb2H67BrNv1m5Ysv2fer25f6dtECnn+s2DA2iTrJ8yJSV6JaNG/hP8ZrNE7PmMCsAyy1DPnmYLmr9vQVECUJQPZcu1yQZ0xMyztgm6KlqRs2ZWOecg3iF6DZROMdbSit77mlWcYoQTTR5UeRs9NHvU8uZs32r9nKXvyT5xDJ0T5NyCZ1OKCH1pbyklb7+jJf8CxDmIUyJg6Do4cD0pCWhZ4EtCPjPIvNn/eecU4IKDR0DXr+G8R07Nvq6GDj2Dby4XPD8/4nT4oY1RLiRZajZSM0wE43iqvlnOgq6T2Zqnn+0R04Snpyf8x//4f5d1R4+4e3x8QkJC5zugV3LTBhpYGdZLAOe0fKp9TbKDdx18VwI74BB82+dJ1jK7iEAOHBcArvn8yZT3tvppX7PXknCygLnFPpbf573tHgHAzB9IKSEZ/+I1AsYtdRSG5De4Dv0Tzmv6hgTcvQ/YbnR/cz4+4enxE6bpjNB5jAlATOh47iWPQXhFRtb+vm6vGulo+5Eh8CKVcGfGnM7Dct5qTpDkkLKgywxsLpVDQsBlHHE6eThEhLAyexQlgtTWRyRh4kZGzhGbzQp6XmkBPWMCOhSbSIK2kGaW+GYKNlSHLOulfWtZkiqL9pq9rCy4LvD7lsgFrJ1o5xDP9AuoraWfN00T4Hw5rVZJEg8tTa0l6jXT7jK1/WbO6stdJodpHJESkErFipQjUhRMUcnxnIs++G5WyVFyhpjSy3WhcE2epdZp6UPrX+vN/K8/tgLqfdLi71c/OAs8cHXsLCnOEuDNL4kxI+cRIWRgs1KqzWnQUEwZfRa4oCTrOE7IJUBnmiY8Px0xDJ2eAV/md05QnUw8hzViilouvO/7StScCx5U5eQafvZTsvhj74t2vslNbLb9zyCKl/czuuxdC4gQtLFwQc97jinicpmgy4VH7jJCCsgkWvKcqNf9RSqY2xlwHbzLNXghxoyYpMpynFrgWgs8cbO/uTYDAuc+f25skwleKGHOYqzCy++YT8IGfli5fV6OTQb2dSWYPeADcoYG7TlBzznuNGjdew+PAN+JuQeQswOy4HS5YDMOlQSbpqn4ei1IgwFF0zQBHjOZqv8CuDw/Nsa2metB9dNaT2evzdYDwwVIzjg9P+P9+x9xvJxxfD4gA/BdBx96pBQBp9VnuM6tDfdiuZ6cMzKx/dD2/5fT2ew9miVyglqhxwlq+fk0xTq+XGvZZiUtSyJdqeowpqniPjbJ0CaRvH//Ho9Pn2aEuE2QYB80UH15jIqVatb1FHpkyqrvsBpWWk6769WP7AIgGeN4RpwuOB4CVhsNYN7ur+C7Dl2/wn57jX/21/8Cv/v9d/jh8RGXOGJ3tcfpdMT5fKrY0Wq1an5BVyr2FFxljBP2Nze4u7vDze0Nrm9ucHd3j5v7t9he7XFzd4ur21ts9zvo0esZ626FVT9g1Q/Yroa6T6NMeBTnL3/5S1xf32C7WmNl9q456xEArADU93p83m41aBWsag8K9+dcDahwziHHMtdcWVMd4EPAGCecxgtO5zO++eYXQPZ4d/9Gg7PHCx6fn/F8OmKcJhwfH9HvFJO6u7kBkLHfbKDHGCUNat10kP0WzoWytibkVHgGoGY/i2jw1Wa/w1SOeopTxLlUSry5uYHLAqQElwXr1QpTznBdB/EOl3HCeRrhSyXKSMzQefihw5QSJhS/e8qQs1S+YMy6R+rRAjdt4MrM/8x6hvpm1eP6m69r6XTkWANzHICrkqgmIgi+VRW8vbqeYyolMIXBupPovOj6AN8F5JQxjRNOx1Md+25oyXnOchvOw5Vg79PphOPxEd5r1YaawAWHh08HrDtg1wd4AP/z999DXMAXdzvsSln3/HNKZ+BPIMYJnlxfX8/KEloghhlPLI/JbAESNAAqqEjQhKBOzhkPDw/VaBN4JzlAQ0kShhswnkdNAMIS0DR49sD5h4cH3N7e1kzEJYhN4okDbstFknDk8wjA0ZG/vr6eEZsElLgBJUDMjafNIKCRZpaqBYtIFKSUKpBoQWDbZ46BBbe5OeMzCLpZgBfAbPPFH46FHWPnXM1Ur4tWbmVwSOYswTS2g6/xnpZwo5wtSEW5UZ52A2fBRC5AlnAn4Efwk1kylBnlyWcwYt6S1ICCd9w8kNTl57iY2Iw3Sxixr5YIsQuBiFTg1YKKliAloEMCiP2kvtrLllPmJtvKi0QhwUIuXtRH6jZ1whKe/B7Hh33XiPVjlY3Ve2swSUpzg8/XlkAbf7eEK50Tzj9L7JBwsPPCkvgWJGVmHfthwRzaJM57Avv2Xja7nqB4SgkPDw8aWVfOYGUfqJdLkIR9IelCm2n1lTJ4fHzEzc1NnVs2Q8ySPhw/gpHOuTrXSZrtdjs8PT1VUoNZlQSCCfZTJ+g82uw0kgQ2upO/E7BekuW8LEBZgVWC34X8JplBu0Bby/nDvttMPMqE+p9zntlxm91l7RZtuAW4+VzqjM3Cps1lX609JDlIcp7ja23wEoQi0LWswFCdjGl+Hra1iZZw4e8kyvl5SwZRf5c2yWZ5WlKcNoztoV1t5H6TxWrVzruh/lgfwQYpcMx4P/aL67K1m1wrvW/Z5s4p4clgB2ubtQ9t/aI94HrIeU19Ymkg6sLcVnczW0nd4zxgwBLbxzUlBM2uf3h4qPOV+kr59n2P6+vrmgHMgBTnNOuZfocF7s/ncyUM6WcsCTnqE+2QDRSUknXFM4kJZnL8mcFpyWHq5PPzM1arVT1GwfoMHEvaihBCDSCizJf6y80i/Tvrd1jA2eohbQlfJ8FqSS4+32Yncm7wjHQ+z9pNbsJWqxWOx2P1Qzj+ds3nGFkygPrGZ9oAP84n2gXabWu3qKPURT2uYDWbM1wjUkrY7/d4enqqmxiS5CJS7Tl9KhLelhykjLfbbT12hT4Sfc7D4VDtI8ej69pZVbQ1P/74Yx07DRbZV1nTR+A8sEGRdp2hr346nXB1dQXnHD5+/Fi/U0m9IrsaUV3sA9cL6pj1O+kzUZdpP7kW8xk2QISyssGe9JU4dhx/ziHrp9C+8HsMpLRBCRxb+o+c3/SnKHd+nt+pm060iiFLYk9EajUSVmNhGX9miNmADs4RG0TJ/QTlaG219U+sjaJ948W20jezQU9LWXDuWxvEe/d9j4B2/jdtgSWM7BpLf4J9ylmDVLiO8Jn8LHWH/eC9aNv4Hucn9YOfpd3n/sLukfn5f8r1v/7X/1J5SkbK84Bku0fjM+0+OQuqDoo0Ylz9UUsqAoAr5PjLjOg6PpXgKRmX0sqd2r0b58Y0TaX0eUYXQjtL0nsFS3wpCC6CJBmXFNGXQBzbP5jx7V1A57mW+HoPJcbpA/gGLmNOPLqatVMAImklPC3BYnUTBUoP3qPvVprlbeacD3oueMwZU85AcuUcwLbHAQigZYSg56RbEofAGs/Zk+wAP4KEE3VSRMuz6xwYEJPg6fkPmtGHDJeVJFFwW6vcpJQgOZq2aCalLIButZEqtf1uj+fDCf/P//3v8M//+l/g/v4t3ry5w9PTATHOZWT3/E2nGqlogXfqm+pj2RdlwXm8NFBRWnnF+fdUB+sYKSo+s+t2Dzi7l7lee335GXtZX4OfpW2h3vAn5wwx/g4/b/ejS5tnx8XuFbouFL/uotnR3HvgjOA7rIYBl+dnPD18xOl4qDY15oSu75GmhJSllGhdZlZj1jY7nvp7fiGn+jcE2WmZ9BhjIdV4TqzD5Cbk7JAi0OcOfe4Qgtcy1GNEcCPGIWBceQSvmUzVZlVcqZRXT0qKx5QwmWpQDbfJADTzSJyfk7VOAOH4ZMPdloz1n5CD7fcSa7Ey5Jr1ghjOgvwKqab7m4UOmmfGmAEfawl3nnXtvYdPDj4kzfAaR0yXDO+B0yVgfb4g5wiJmsWbROq5wzGyUkTUrKxi+vt+hRDa3s67AOcEjiRrpbdnTE4lnwQyOyqiCKv+/fkZ9bosP7fuSCG/2Sp98tLWkOB19ZgBnSsZXafrD0Qgoj598g5TnPR81xAQJ81GjE6wOnfYblpAu55pmpseTixBO2EcG/HoXUDw3WJPkMAArhmBKI2QhOkXSrUP9v+FXKpNbH/o514GcXxOvp+zdTmX1G/RUs45q26mlHAeR0QBuL3JmVUsAlJWoojBaZCWmHIeR5xOF8AJQlB55JgxTRlTzbxP1V+bckJOESnp3Lbr8bwfr5fvn83hV2TwOaV8cR+NQGjvfUZmtJUt8KUKc2bPsivBznGCF3Muu2j2afDMGA8Iyd6/HPmRM8ZRyXFAtNzxlDCN7ezqmAohGUdMaapnLlMuPxWp0tZ/o3NMtfRK4MLYSL0vjyPJhbTySGnE+w8/4He/+wccDwctfd11CB2PLwoYOo+ulJZmIlnwWkmn2chW9coGqAJtL6I2wSGmiHE6z7BWlQdxfd2D9l2HEPoX90q5JVDp8zwgGX0fwHONvXfo+6HuOZ8POxwOTzgej3XPxjbRB+e+M6Vppgt2Hlpffr3qIeuNVlECyvEaXTW4IqIBU9HhfIpwfkQ3jDVxqOsH/J//1/+Bv/rtX+L/82//Df7dv//3+MMf/gDvfcU41C/Rs8FXqwHjFAt+1WEYVri6vcFXX32lxPR+h+1uh9ubG3x5/Rah7zCs1xg2a6zWa3gESEoYfIfNqhDuvUcswUOplJk/F2L8qy9/oQmh3peQE6m2us4bp2eSa+Jh0PLf4wXTFOEhEOdKJcdSej2LkuxS9pw5IccErWqU4ZJg1Q/YbXbY73YaVCvA0AVc77bYbFZ4PhzgcsJ0PuF8OuHj8YguAHj3Dpv1Ck58mTu+2sOclW7tQofn84jn46FW48o54zyOkG//gLdffInNZgvnAyR0OB1P6C4TNus1XNcDKSNmAC4g9B776x6breICx/OIfgC6XvcbqVQUgGSEvoPvWhWh86iZ7C6U872hQdEC1COpUCoU9H0P3wWElOqeEkCtkAigVvUCgPHSjmmrFUhFK385tH3SarVSP8xgH4qtbjAMPRwScm64QYwR8A1/R/HjT5ezVszq+nos8zCsAMw5nYYlqLx0vnhAAoAeGV7J+NxwiZ+6fjYxbjOHmH3Mi8ZpuSEhgHg4aCkNEm8WQPXe43g81u+pnJW82u122O12leC4urpCCKFmrTvncHNzowNWAOXtdounp6e6WSFIReCXoAw3NAAqKESAXEQqaEzgn31gu1kCkYpAENICoMxQO5/PNVigAtTSyBagbSoJ3BDEJeBJwIwLBftPYNVGWRGUttmZPPfTgsExxgpykwCzxtyWrQRaZhvlYDOuCQ7xGRwTjqklKOym0JLDluC2bbQbRrtoEXik42uJfd7TbjiZmW8JaAKZ1AeCWdRrAsrOtbMJCfrw2c65OvE5RnyuBQgpUxtMwrZyDvBvPsOWIOXrvPg65bjUAQJ+S2KdYJ6dtzY7mCQtf+dn7fhwPCxxbkuU2jFge6iLDFSxRrhFOraMUDrUlozjv/b7u92uzh8SW0A7r5TAJmVg9YnjsHS4+EwuAB8/fqzyseA2SZ3D4TBzgp6ennB1dVUJlv1+PyvJaAlKypRtX5KsJPRCCFVPaO+oOzZrW0QqKUNHiWTINE31zFgSHn3f15LgvCfHkTJlFQ3qmwXw7bma1mbaTGQulhwn6vryX44ViZHn5+eq99QFLoY2SIpz0Xtf1yfOPdp3GzRjgVsAdV5yXHLO1b5zjDmvLZnL1+wZ2rw4FhxjSwDo+6GUxBrb5r3M5b5vJfRtYEF1Isx9SH6JSF0/OPcZYGFJOupwzu24C44Vx9HaY2vnLJFjs7RJxHZdsyOcI9QTzllbkpm6z+cy0tZezDxlFiPJNDsPluu693p/Vhxh1RQed0D95lzh97i2cA6mlGe+hV3b379/j9VqwDShZnZSxw+HQy1FbO3LclwfHx9ntpJzhVcD2xoBRkKQGaUWmCWhKiKVWLdElfiWhWxlXzP6inwZoEAH2a4bzE4mQWqzkGljuBbYOck5R1/SBjlZUsc5NwtIWq7jbKslw+mXMJOW1V1yzjidTjP94LpAW8sjOWhPaIO4hnB9tJmptHlcZ+mzibRsXJY1Z0kprqu0FbRtnKuWiFquVZSVnY+0c7S3XJeszec8IyFPPbaBmyy5TjtPX4Y6QwCagQJ23V6tVrUftDW73a7OZ84X6pZdVxnsdDwe8ebNm6pnt7e3lbTlXOSVUsL9/f0sy5kytfJbr9czIp1Be1xL6D/S9lEW19fXeHp6qsRp3/e4vb2t96a/9P79+zovSULSNnIeU59p3+2aEWOs578v/SmuaZx//B7/pb2jTvP4KW5YSYbzrHfOXc4VzpFlwBifx3WIdt36Rvydm3AGNFgQi2skn9t1XQ344N/jONbgH36H/jzXKq6JFfha2APaCXv8Cu2dXds5JjZYkDbL2htLjLMv7Ldd+23QDe0RZcv9h7XZ1kf5p1zPhydtjxRyB/PzEhuwNj9yi8AlYI7jmBHj1g9jeTpXARSnb6qNL8QtRFkRknZOtKw2Cequ67FaDUipHQEgooT8YGyRc5rx4bxHjqlmXuSc0Q0d2HSS2AAUQPFaVtqZttd1kza0vC4u1iNDuGcC8GLNiRMDAHMhYBRc00xnVzPEJXs4DySXKimj2WcOXpTEnVLEOI2QnJFSD+87tOYJpjgi56TAlWt5az54iDgg55qFm1MGnDlKCFqSepqmgsFL8Z3OUBhVx5DtVSq0oo0AApxvgfIi8yOrtD+lmKUrVVWCx+HwjL//u7/F+XTGu7dfYL/f4enpoBm7mAeN8qfpnwmqIBsHk1Fdsh8F9igcW4p9Pu/RuHL9278MrLZ6sfSp+Fm+l5MtzzwnNhznSwk4sPfnZf0pu49a+tIWCA/ew/lSKrtkE7kSaEKwsZYlDx36vlRvyy2gKGWtruIAvL2/wXazQsoR5/MJrgD/MbLqAvT8Ra8k8avkSHldm9Bk2giQJmORrOC0tKCo7CKUGEfJGHfIGUAfgOggThDEF0IxI3aFDBsTgneAMJNUCUj1IRQ4V2K3Ae3BtapuzT8sOCLtEztJ8rDMTzE2YtZ900erM5/7zPJ12rjlezM+eSZH1XktJ6+fy4WITClBIinpUk7YO80W8w4+eySfW5BBaGcNOwiklFDX89qJryi5G5OU3+cYTV3Ls+Yuqq6U3HtjpxYdX3ZR5bfo72uXnROfk/PsM2IfZEnxFlhQA5Uc98uTEvdOs8i7KWp2ZtZy8sEHuCDoynhMU0SKCd6jrt2cozx+KiXR88ajyRgv65zK1Ab68VxsgNnH8/4VtTT9bZ/5rOhelddP6S33Dz81HrVd5vx1MeObc1aSEQ7O6Zn3gpJkEHIJVgrwvszD3CrPAOXox94hJSXG05SRIjBmK8sJU8qY4lTsQAsAfa3tPGt82W9rswy3XS9n/j/r+08L58Xn2nNfDzyQnIstL/a8C3rkSio4jg/IOUBkgndAdsW3cSVwxYva4pIGm3NGFwu+Dg0AoZ5yD0YyOJWj32Zk7Gey2YUGSJR0fFXWWUqQ0fz7zrX+133P5YLHxwd8+PABnU/o+w6h6+FdgIiSvV3XYSiEOPfXIlKDgKxfbX0APme5pipeUsqvFx8IgUGzKMR4hxA6OHiM3I+a/Q591WmakFMEzw6n/2nnOfd37z/8iIeHTziWoLSua3gD56QI59TL9ZR61NayJgu1U3pcTCc674IP8KGDd305jsRhHCNCN6Hre5wvJxwuR9ze3eJf/at/hWG1wr/9t/8WP/zwQ10z+37Afr/Hmzdv9RghkZpJvtvtcH1zi+vrq7pPXZd95tWw08zlJMiXBHEJYQhlTYmYnOJvwADvAvqSMCOSMW5GbNd77Ld6DFzKGvSm/rUHgqt+O5z6W2OMJeC0VBbyjIPUgFhdtwKmacQ/fvoWHg7b1QbbzQZ9vwJch67TfwUlYNr7Wkmg+tk5Y7vZwAvgcjlH/HxBcA6Xy4ShHFnEIJAk6ts4aXsmEYeYMpx4zYz2wOF8wbfff4cfH5/w9u073N3cYrveYIDHaRyRBOj6Dt7r+eVaOEUrB8B16LwgSdJKAuig/n5CjhG9D0gluM8D8L1isxJTqQAATMXP975UVhUNYnNZ4LOUYGNoDBQEl7NWgR36VfW3XCWiFbe+XM54etL96Bfv3lV/t9pqw0HZAO3m8ziE0GO9DtAAMK16IrkkjgaV8WpYI0d9Plh6fnD1KAdWYBHJ2O9WcGmEzxHBA2/v75AxYFj38EEgmIDp8tP2vVw/mxi3m32bxWAJBRInzFQikcjUfqCdI83NhQU5bekoAlsEX66vrwG0rB5rCGl4SM5N01TBPhrpZXlXlry4uroCQRn2xZKsHFxmLVqinu2xxDsXJYKUtexZIRgJQjGLyxIelAlJq77vtUTGdjsrtUlDajO6bAlnGm1mbBGEsuSEcy3LzQYIcIP3mtGmrO14E0BntjSDAQg6Um+4kbMAMx1ygsoEXm02k83CIdjK+9MhsTLk85YEJ+XGcbMZahaA5vctiW/JbU50EgEWZLObNDu2lvCzGYdWPy1xRTCShAK/ZwluLspsM0FIO06UL4kkjivPkqL8bCabBWgJxocQKhlGQsbKl88kSErwaUnEW1DVOgG27L8dL36OADnlZoFS6h7vbcFM9p0AOb9jSeQlWUnihjKxQDfnrS3Dz7nN8WcGIwHfN2/eVGKFWWYMEKIO2OzvlFL9HAMjWDaWi87z83Odu977Sr6RWOccp04vdZL3spH5Vp7UUZLibJPNfLVBJjZQwAY1kBwiiQS088D5PEvg004wEtMSbZxvNvuXJaYtQWVJ/SWRbrPPlvN9aeNI0lqSjnKzwTWUKe0A3+czrS2hzoUQik6i2nQ+n9+zx45YMonjxnbbYCnqss2SZL+tLWUGJI/QSClhtRpwdbWvNsfaRNpdS/qHEOoZ4SS8YmzR8xx/lvFlFinJnMPhUOc8HW9LrtlNLtcG+gq2zDKfTRlyTnEceVRLSgk3Nzc1wIPBB9RlrkEkzFSGTRdJ7FowVfV7wmYzD6qhHaAfwnnFs5632y3ev38PEamZuSTMmTG7zMy3ds4G1HGNoVxIEnFcttttJaIvlwu6skmx1Wpo5xiARz3jBpCfsestZU9/zvtW2p6X6tWqzk9Lwu92u1kgGgN+aB/sekIfhWvJdrutQUIMsmJwAADc3NxU+8QqRMwwps7aADrqhHMaiGP9Vo4BdfJ8PuP6+npmP2xWNnWUZDjXC14kyhmAYe0vAxVpoznPGAgh0gKe2HYGY9BG8ofH39CWM1N4WVabvqw9xoHrD6vkcO7xXhxHViuwvhRtFslmVi8g6GADB+lTsILJbqdHEjw/P7/wEWx2PTdk1udisA1tIp93c3NTCTHrM9l1mOPDQBW73k3ThI8fP86CxPq+r8fnWHv+/Pw8069l8KQNIqPt5dzi5+lHUx9s9ST2z9ourl2fPn2qdoRnny/9F+dcDYBbrkm8D3WDaxzHmzpFe2b9KetfLP0wS5axfzZggoE+IlLJemtn6E+wnTZogLYwxlgrC3Au2zli1yy+RplzfbdBLyTV2QeuoRxr3pvrKPtn12D7/CUx9+deq1XznUhUUA+sDwf40j8PzUYCUPIyYirZks6C8LbN5dxnlD4Ftl1m/Wj7l7IHkHJeZMnSpo7mnBCnWEoACoLv0PV9Ac7afQUNcJQs6ODQ9wyaBo9G16Z7LTUJuJpZhAL4QBoZRBA7Q7POaJMIWNr9k3MO05jgXCFAWKo+z7PUnHNA1vPAQykBKiBg3OST0oQpjkgpF4BW2+sU20acRmTRcwalkP8Cge86uHKGp+RCNMQM55T043hqwMGoWTW0aZLhvdqyULLgHQROVPYOWpJWAbLma1mglrLIOdeypJK13Ok0RXz48B4pRkAEb95+geCBvusK2D7Xj9dwhCUoTJnqubRQotW3an98364tqgckkR1v8mK+LP18+7q9dExfIUTqsxSEFWdeM7iIDXoJIcz0wBKP1k5SZ0kw0A/wBfVlZqyOAwoAXHCAZANiCraRM379yy+x32/hIDifT9jseBxVRNeFAv6LlvksiviCGK6vOLQAgdcy6lvGuIgGk+ga4+GczqPoSslPX84gThEZDj45Pa85JaQYKiHmnRJABE/rPjU3n96u5RDRoBrHtpp2iunGK2P+qg7gdfJtqTtLG7i8r2CuH58jxa0M1W6hgvRKJKaaLe6clqb33iEXXfJZyYQYtYx3mBymqVT+cno+O+DADOeUIqao5FwqZV+1WkQrV23X9tfG/bV17HNzazn3X/vOT93/hY0wtt58C4alm/+4XO0cnJTEQo8pToArgSVJELqMvtSLlZgQS+Z3F7gPighBdZJnF6ckmKYS1FHkP8VyNvkiMKKNb7NjNcjrj8iJGMFMn5ZyXIzTT8uzLDYz+TVit96mrqU2I7hVwQAcYpzU7IpATKlzSQk+FL8w5xropj75hK5Xm0BiPCePKRf5FTkyCIYBMlZGL+fjsh+vyNT4EJSbvrWU2zzb3r1CqL8m5ybL+euUBwl+EUGAQHKCZI/sHDzU7/aulGx3GdmpH5VFgEBS3JUk/oRpAi7jBU40sIO+OgnxmFo5atoYLVGtbbFtpAwZYDDX3WUf591cruuULQCM4wWPD59wOh6x3w0IoYMPnfpChRjv+w6r9aomLLyK1Unb99rnEBO3AY4igsDYT9fOaud7EC1lHadU9REgfiaYptFUyYrIuR1TwXl9Op1xuZxbRq0IDsfn2dFlNqGQbXltjr52MZyxOHyoRGzOCBlw0COFQggILqDru0IkqqySZFzGC54PzxhWK3zzy2/ggyaU/pt/82/KvkFJ8bu7e3z55ZeaUDOssFqta6D1riQ9dAV3rUccOsF5GpEzEKaELOo3jNOINEUcR49hXKEfNNF0s1qjCyUoAh4OoVYFqMFJoRDjrN5UZD2VvUNwrhwlEtCZatgeXrO4M5CmhP/+u3+Adw5f3r/FL1ZfYbXeQAQa/ORU76TMcbpzuRLjmhDbOYd4GRFCxHq1LpnlxXcC4JwgcZ0v67uU+/qgJb7hHULXAd5hWF8gAB4eHxE6LYu/Wa/Rr1Y4PD0hxhP62GMgDlX3kAKXpZxxPqDr+rIvS0AWxDGiWwfdymUgwCP0Wo0r56yBC6J7vhgzuo7Bsgwo9shaYEf3S+XVGBP6HoWo10o9zrW9Q+gy0vGEw+Gofl5M6Lq2L7Z4wywgx7yuey9tjw8BObFKpwOc1wDsoLYt+QRI1uBeUXmILzOl2PSYBMPg4XyvRYMg2G17XGLAOGXE/x9pf9ZjS5KkCWKfqtpydt/uEhGZUZm1ZGdV13TNAM0FDRAgwJcCAb4T/KPzSIBokIPBzBTJmWFXdlXlGpGx3MWXs5uZLnwQ/dTEjvuNjqqygIf7PYuZqqiIqKh8ssSIqpIzxo+5fjQwTtCDGzudGdpRq8sR8hC6Xq+ffU9n7FxdXZUNgyABnQ4625NKn5k97G3L7BsNRNCZzaxrOjrYm5GOLO0Q0iXUdeaUdg7Tybzb7Up/wOvr6zJ2KmmCvzqLhMxBB70G/umYo/IehqE46wFgt9uVQwEPT5fMxzHzNWMMdrtdce7qstCXGbk6Y5oOSDou6ejh57nO/E1AgfNmhjOACV3oyNJgKZ1/dAryGQTVtbOKPKiNopccnprXmqaZlIgmf+joM96DDrFLAAAYs3j05quj1QhY0NF7eaC/HBsBTO3s5HcpU7w36cPgADoHeenMV4KZdHgAY/YN10gHMxDAIvjPsfC7unemc24yL9JAA3XkY2YM8n7aSNDOl8vnkU4EkjXPaGcJP68d9dpY4ncIRnOMl4cRfofzoyOcjlM9HuoH3nu325UgHcqDMaYA4swyJx+Tn3g/8mAIUoFDlzamHFEfUrao6/gaeZsZWQSCU0qTksuXfBpjLJmeh8NhAirS+U/AQhuk1DUpjWXgL9dPA/jkZwYpaUf7pQzyb+o1HXzCezVNU/Yd7fQmCKZ5mPzI+xPwpAzx0EKZ1hUZCCiQ3+fzeXGekz5apjVgSv1BvTQMw7OMNep2bfxf6mQ9R46Jn9MHAv0ZzotrVg5iioaUIe6vY19gi++++w5VVeHq6mpSnlwDseR/Ppf7oNx3OidAgjj0+Jn1TV7k55k9StpznHw2QdJhGEqvY/I8+UBn5Mqcx4MIAVXyFIE/0px00Dqe9gz7GrNMFjMeyR8MvNF7G3UTIPt313XlPvwhDZm9SwCYdOE4SQcdQHjJM3ofoR3TNM1EBzRNA1s5WOfKumndyTEQ4J04oyD2D/tZU2aoGwCUIASth3VQlrZbCIqTVzebTQEBabeweoBu8UHbjnporFQwrgnXTVeU4Zpo/iJwS33D9whEkxZ6D9N2FMeqKwVp+dY6gJn9DPrUgZPOORwOh0lwEQM8abfqrFTSnnTnPsBglGEYJu2D2GOdoCTBdu5xDJTjWKkzCXxTVq6urso9abvq4DBmsGt9ocFD0l+XuKeduVgsStAAbV3K4P39PW5uboqskb90xRDukdS93C+4TrRLtb7V5xXyCZ0i1A0MwiH9tE3DMwL1D59HO0g7eXSQh3MOu92utILgnLRdQj2lA5nIK3r/ugyq4mf0a+R/vQdru1zbf+QD6hStz3T1Eu3c1TpE2856bRh0Q/7RwWwcl7Z7OQZdFcAYOdKHizHQTmd1p8sgEq4NL/I79TDXh5UWqBM02K0DCjlOPp+f1y1TaAPrz/5Yx9inrs8//1xoBtJ63AtC8Nm5IaAHgyTGc0o+T8QwoZG8FxSNLaytYHPZSFdlMDeOmYe0KwRZy7yaxLFKJ3jwFsFXk3Op0LZFCDmwXtl6gUBtLg8+MxWctRiigNMhl48PUbLYReYMEmiTZtmOSf3OmXt23Jv1WJ6BPNHAqtLGlIGURoDcADCV9GG1uQx68c7kvGz5fgSSR2l9bTIfWAMYyQa21sCE7KAzAvJXbQ1nxwBEYwwigMrUuWwkHe7iuDJWHIrWGjhUcK5BStkJZpL0JO9OEOcvg3/HTEChf5zwRDmXZqcf5atpRHc/Pj3gkHX1mzdv0c5mIHCibVctx9SRmuZaf9nKwZlRD2u7DhiDqf9LcqTtO2Acuz6vj7wOANnew3PQ79lzkjgatY2oP8fvS7YtJnS4DB4zRrJeohmroGk/hr6vVX6Cuq7hQz+eD3KWVnc+o6ocZm0NkyKGvsN8mSsBpIiUMuCeZQMqIOVikvL8jOdq+29KkwzsRiCZ3PcbPgMRHvQWWxg4Z+BqL7mykYH8EvBRO4eh9+gqixg8jJkCIpoPLoHxGKMA76pqxDQQ4gIsx3OZ1/6lH3rtRX74xP3iBT+8dB+5F3thxxEYZw9x7wEYxIyJUccYjEFao40g4GzlTfG7EhhPySiQUbLLY2Swp5SwjkGqdHB6lL+X5nrJ6y+99mP2uZd56iUavQy8l/1Hc3CcVhIEEmL0GIYe1ibYyiAkgz4AxtSwFggmoooVjKmlF7sPCD7mVhaq/VLdTnSZ2GOypwwhA+PB50w2AviXczE5u/B5FQs97un7U9vqRX79BM2e89+Yya4/fzkOE7MvJt+df3PetlQl8UXOYjRwNiBGi2Atqpj9hUn2uhDEvjv3A1wFOCfBXTEAKVh0vpcM5xAR/NieSu/Zl7qI4xU7tGy0Ez4pfyuAe5xv3qdxKauX/Hz5vU8DnZfPjTFKdrgCqUU1BsToYBBFwM0gY7dFmwE5QM4lAbJigoBUMcF7g747w6SEytbFru77PttKzFBn6WSxEb2fJh6MciS6IpIeMsmy5+l5a97Rr+v9OqWE0+mI+/uPiNHDmFb6Zxtkm7tCbS1mbYPVcol2tpj40S6fpTEFYFpdmP4Ra23OzB/BbD02JkOSp3imG33TEUzsGJ8pepqVj0pFI1ZSyICo7JnPA/g41pf45fLfxS9UwGEHWDdF84zJ4LEEolqb0LQV4IC6rWBZCSgExAg8Pu4wmy3xs5/9DH/7t3+LX//616Wd8O3tHa6uriQLfL3G8voW89kcbQ7mr6oKlRUQu8mArjEGJ9/j5HukCNQArK/hYkQXPQ79CeHs4c4Oq3aJWdui6xdY+Hk5nxsL9KHPdghQOQtXVairHDRhUq7wFOCHASFGNHAwdU5WTDazZhLwN0jQaBwivnv/PQyApq7w+u626OJS/SI/05pGzhXZVrOuRu0SXC3tumJImM8d2sUaxgBNJdUvQradqgrFpo+I8CnAJIOqrrBaLeHzebaqK8xnM8yaBk+5OmTfn3A47LCcL+CMJHkiSJZzU0+DuoW3LOaL3KbLDyXQLYaAytUlgFfswwq2klY1KUbJiA8JJhpYWFR2xMeKzGb7QvjJwfshYxRMYIVUzgJgnAOMQ1U3aNoZYgjYH46YzRq0Knl1yOdr8rXG/ng2F1r05axKezMGaRFjITLlGinJ7oPs5TJ2ytRoF7qU7Wcr401+wPaxw8P+hKpxuL5qcb0az1Y/dP1oYJwOMAo0HUecvHZ28zcBJQAFjKYCI2BLYJaOLG3YMsOCfcrp0NOKRjvWGdXCjDfnXHEKAmOZWB5q6ETk5sE50vGujXKdLXl1dTVRvPwOyy/SeU1Dgk6TxWJRwHWdSZ5SmgDk3LjoHAXG3qQEosgMukQoHeF8HmlKQdMlrPn8ruswm80mwAs/ox2cGmwheAcA2+12AnTpbFde2nGsDQRtvHEtuGlxzHy+znje7/fF+aTBLY6bwB4z5rlx6qx+zldno2qg4aUDIddV04HjpwNQ05A/3GgJjDPyiuOlE1o7IHXAgZY/3offI5iis2h0po02Ki8dFMza084Drjvvy7VhOVCuAZ2kWga0Y7Bsgurz2mFBmpJvuD7kaWaR9n1fypTrAAfSnHOlPrqM1KOzk99/yflKpa1BddKEQCjpShowM0wrew12AcD19XVZO9IXQMnq5Fj1OnMM5AfS0lpbwDsC2sw8JECQUsLV1VW5B3UD39P6mmsNjIB9SmmSgUwdTFm+zGzXBzXyDeWL+wB5mnLJbDuuN8EGVqsgMEH54Pf1POgk0gYvZUw7x7XTnLTVThaOM8axlYTWB9pxztfoeNDP4f00uM/XOF6uhwZB27aZyAF5kX9rniRfAmNpfYJ2fBYBMb036uxD3kccU6ODiSDyZrMpThHynOYdAoOk6+l0wm63U2sUitxr0JTgpvcex+OxjEtnB5MHmWWuq8UweESDmKfTaVLCn/YEdYhEMI7z1fsJ9yMNcnNulE9jTK5IYCctALjfycHvBGvHMtfkeU1rvTcTxCWPUJ9x3Kxgw/1bZ91SLvk52j0Ewgjqkn8Xi0WhHeXVOQeX5Y78QZqSJ8jTzHTmPsdgkKenpwLW0VE7m82w3W5LGS6WkWdbG9ohDBAhL5AfKBc6cOV0OhU5pz3HQI3FYoFvvvlmUnmDwYijs9CX+5H2m82m8IMuQU8ZJihL3cI9T++r+kBBcJvAvAb+aXPoTHd96KcuJC/rfZEl2ClLpDPHWhwuaaw4QKCXgaeUyf1+X2RZ2wyX+pKyx7Wl/Opsb64x9yZWMuHcCD5r3a4DaPV+rIMOKSu0q5fLZdEbDBjjnHVbDGZdM7hLV6/hvsxy4gwQoQ5nOwOWgteBTpQ5vR/yeTqgiecYnmG4TqQddQ5lizLK8RAcZtBLjBHX19dFfxBI1jSi7iC/aPmnfqO8sLqVrpSlbTbSjDyr+VWD+drW41h0eXi9t5K/mMHP+fK+tBNog+ggE56xyGM8+2kbeDh3RcdpGuuqOVovaDuHdNMBhPqcwM+/5NTSAT88U2l55Gf5N59Fvnc5GOlfc81muW1CSsUxF5PsYwwA1WfZum4LyFqA4ciM+7G8aYwqCxPiHJE8JnHgIo0VLQbfvQiaII6gKOdLWdS6ra1aVgSVtYgRAVHc2gaSDW4sqpzexd68IQk4njAG5yGO/TwrK84y+bkISE5jpTFtA+kfa0zOjB7b4chcdB9ryZqoK9ptEGcoz22uIRQHAyvlLm3OwFfjoTPaOYc6l4NPSBhCgHFSVp6f51hm2Tah3RKC9I6uqiqXrw3iRIdBGDpYCwxDj/3uCR/efYdh6AoIa0wCTCh7ly/9XX3ZE6qqyn1JgaoCnKsRweQFj77v8Ps//B6Pj09Yra/KOUQHffHSeyL/rXUY15dAaPLT8rmUWa4f6Weg7mHHMub67GIL0AAwGOCSJ4cBk7L8etzahhfHN9Cq9hH6nMj1SSnJOtJWUH4PzX8xSraVtoG1M5+6F3baviQmX4KpuKfFEPCP//ArRFvjp6ZBs5SEE58iGu5JCahcPZnf5cV5Xfo+pte07LxUPpAKAylI1jjXqLJSKeF0PsNa7SRNCH1Ch0Ec484gBgNg3DuZUea9rD3LixPgGemUsgSNayZ7hgK+5MMF5RLQDijAn/JtkFdinAIwmh6XAMgUWNPkSXx6+W7hX+X8VuQsvMDy0JH3TgEmhsnZ1BgDnyL8MMDZhK4zOJ8tUqwhPTYNgk8i33FAjKPvKoSIbsjAYyQIlAeB53zAq5z7+Ukl19N5T7704r2efe8Tr03pHyavGfW8cS0BhxFUs87C2QAE2uEJVaTfMGBIHkBEZSSLLsUA71OuiAHUcaxiILQTXiQoXnxGgQCbL/2KSTPmgnLdqeNfmi8/j5TGwCv+nfcieQ05qGLkq5fIP47j+WtaFyKBu3GWpTxnGCTvkaxHBQMHg5Q6CNheIRpbKhkYY+DNmNSQYsTQDzDGYTbrULko8h4FGI8e6HwvPW5DmtgxlHXvB6TgJdszTvfuETPQtJ7SlWJoLmQRE7kfA9w+Jc6a7Ny3SwCE0iVl78BzX3KM0toFwQMxIdoAFyska1E5qeYirYYrKUWfFAjkpQzyMEifcQODaFPm81CA8ZRSDrLJwfputMX0OXTKJEAiDTPvjXvnFAT/lHzyvRAC9vsDvvv+u/IZOQO1mM8FiK2txdVyBlM1EgSQRn+5xoFiSuU8Qf8PMPowiUWcz2e8e/cOMag9JPvFjscjul56shsjNkFMKqObARUQmo7JKwLUDr7H4KUacrMcqxVyrCFisvYAJj5+jRVc0vKSjjFG9H5APQzSCz3vmTUkENNaB+MsTGXhLBBij6aZoSp+oBZ13eJ09ri6WmK726KuK/zyl7/E3/7t3+I//sf/iNvbO7x69RrL5bJU09vcSkZ/gkUICevFvLQqRq7A5JyDqSs0roJFhboSm2+xXCLZK+xOB3TDGSEFNHUDPwS8f3gP+2RRVxXqqh79Uslg0bZYNi2i9+jzubuqHZwBkBJsCBi6DsfKobcRNo1nQTInbSCYCv+n//AfcN4fsWhbrOsa/nTCvG1xjh7H0xEhRtSzFibUmOW2jy5JBR1XZfsRBnVVw0Lss9lshuB77Pc7hDDAOis2IO24lINHMi/WTQUMgwTE9BHz2Qw//+ILnF+/Rj/0iCHCATAhYNE2mBEMBxDOZ5ArjZMM+pQCTsOAytSSEW4djJESS6d+KOfWyjoMCdleMoB1sMahtQmoR9tL+85D8CXzPVoJnrR1g67vRc9XNZyx6I5HHM8dlgvR6cvVGpura0Tv8fT0gOPxjKETv6urxmoAxHHm83nG92I+R0bptWNH34jGJbVsRC+VQ+jLEL/CbOJvq6sKMQwYImCsQ1M7tK7GYf8e//kf/4CAgJ98cYt//9c/x4+5fjQwTieGBqeoHOjgZqlQ733JBNfO4pQS3rx5UwCQl6KAtBOaTjbd/40OGDqu6WThIY/Oa+3cYQ9JOmD5LGbj0KHHTUP3QKXDic+mkgWA29tb3N/fF+cNAQWt7AiiFGHGmLmngQc+T4OvBNv5mRCkTwCBuraVUq50WAGjU1VnD+ux0FlFBx7nxgMxD56XB1PtRKPDmUxaDqBmBBzpyNb/5ibGeXtlUNJ5V1VVyWTTzmDNKxpg5lpqoIff1bSkM0GX9yQQr4FsDXjzPuRP8vAliEWgi5s25YL34Rx0mW39Wa0IOA9dQpK8x3HMZrMiPwQALoMDSiS+HUu163vxt3Z80knPEqoa3NYGKGlCOuigBtKNQS7aCNMgGz/H9zWwwN6wpC+zqsi3BOwpnxwnwbZhGIpMkuYvBTFw/JR58o5ef4JUpLkue6p7W+pMbtKIcsKxM7iHMsQ5MiOQwBlBQWZCc7NgJQlm+tIgNMaUyhWbzaYALY+Pj2VDoo7b7/dYr9fFGKIjmhnV5B/Klw5S4RgImOkynuRHDURR9+l1fAnopTFMHrgMLNGyTwCCwM5lMALpyvWlk457l76XdnDwu5QJvZa8uDHz+ZxPcVSqgBXyFu/BoC2tk+UZEtHPjFHqPI7tcgzGMEhpzLTnAZTPI6DK1/k39QvpPgx9lp1RXgku8HN8NnW7cxW67jyhGWlZ1035DkFrBseRh30+XHA/pNzRocqew9z3qWsIsFF+CUaxioIOxhO6OTHSlP3BMfNeKUn53uPxiNlshrZtsd1ui27b7/f5kFGX9VyvVzgc5DsiW2O1EO5DuoUJ50Kdw/XVJdapwwneEXghYOecK0AxwTny8Xw+nwRV6ZLSBAwZANW2Lfqs35FlSdsk5BO9zzw+Ppb113YCdTXBbt3PmTLA9SPtWGWDFQYYxEjdTbnjmPg6dSLtCe5lrB5EeWF1An5XA9Y6UIw/PCToAB3antTnHCd1w/l8LmAy5Z78wqAPzhkY2+LoYEdtU3DsemwcC4OvGDRJHUc+IghO/qBOJL25T2rdwHVmT2o+SzvsucbH47G8T5BVg5Ln8xk3Nzd4eHgo9g73S65nCKHQi/RbrVZF/pyT4NXdblf4T7dDijFOqh6wmoVeP54FaGfNZjOsVis8PDyU0vS07bTtEUIoJci5Dgzaop1IW43tjLgv6+AJ8gn1EfU7+YDPom1LetNu0/qMPE+9wbmxxQLXnnxAQJjVM7hf8jf/Ji9oe5T2DC/ygAaiqdtGB+N4Rnl4eCj0Jq/qNdQynJL01PXew+Wz5ND3qOoaMQTMZnN8vP+IxXyO5WKJWEd0rhMHhbVSencYEDPP6DYH5QAdx/L41CWap/k67UW9b2rgTesEbSdcOrc0aE5akcdo93CdLgH3f8n1m1//QZymUbK3tQM2hFAc8aZysDmrxAAFuNVrH4NHCgGuqqTc3uBL9oRR/TqNjZK0wnmrsqakV1VVCD6hbkZnNOWprsbgQgGPnWRoqPNiSOPZmN+/DGRFxgKoX/MnYa2Bq6Tn4jRI1YAZDwYKjE0RzlUX65GdsiZOAkyC9xl0HsEWk8EmABmYrlFVbrLG3ocJiI+USkZGSkDIZ6W6rtG0uaJX36M/nRCiF7AUkl3uotis5+4oIEEGsmJiNjugM8OsEWAGKcKHAefzCfvugBj6ko1jkeCiZIDDOEiZYSnZHaPH8bjPukv6HlprETKpuI9aa9B3PXbbjzgetiUYiuW+WepemEjKps5nK9R1AynxL2NnYKExBg4ChiYDVI1kD2nH/KW9zvLdhWcU4F0+p53Q+W7OqKobBTidZpPzHpon84ARhjHQDUmAETrZyffJDIUn9Hj0eYb7kDU2A2xjZR0DIHiP3g9was5VVaHyDSoX4dOAgACYhLqt8LA94u/+7v+Dcw9sru7w+duf4GnYY/BRyq+aiBQ7RDvK2jOARM3dvkCTjMRN/BeS2eORrGSQh5AAVAgh4YwIFx2cj6gyXyQ39twdgse5j0hGAHxN17zjZB7PvpkQ4EPEMETARKkoYSRoIagA7xACrMl9OiGOXzOyY5lLSoBBblOQM5TG9c7BN5mPUsmUfQEIVmtsUpoAZphC3+UKBCQDz9w2y29AiD1SjHC+BlKAjw7wFqaeVjorYJH3GCzQnS2OrkYMDga+tJqIEfApIpz7sn+EEBFSQAoevu9z1rgEG7FsqZYnUWOjfS0MP4Kxn7xewuA+sRdOQFr1nJEHnwdsMKM1JQEDBdwzyNXoYVwGIz0QU0TjKkQEBOeQTEC0DtaL3A3oR5vcWJw6C3dsMA994S1mlhafcQgSEJL1QNEBSdoWmJiDqszYuiOos+zlXMvc0si/l2Q0SZf8HgPExnuN8ppyAIjcV4PFU1ry38460Ys5yzLEiJiAyjqkYZCxxwRb1dKmJI3AiiW4a9hKcgQGmyq3wLTSAgFAKfctlWgk+zNmeobBIw4hZz2qwCHqwxwMZZKyV5S/ckKP/H+DcR2SlV7nL11U7ULrvB+bcREKhK7FHLk6R4zjDeLz1gtVVSGGCLhU1smnCBdkP7JFF2Xg3KugshgRU8BgG/SVyHhyY/W0kghiUGTYAoiDR+gHRO9lzM94QKqHRFGIiCmUwBd+RvSNqEOb+xHHFCe2XEwRs6ZGHAbsHx+xe3zEar1BSIBJDv3ggZzo1NQ1HrZbeCbEhbF9TUypVF6hrW5z4KEzFpWr8tmywXIxx9P2AR8+fI/TcY+2rmGcZNuHXIofBnAViixYY+BQK5ke58hEwRACYq4WRJ4iAMmMVptEhvsUikwXkD2M4zfGQZew/9RVngEjFTBilm0TkIxHShYxl/WOPiIYqQAIH5FsQHIRqKRSy6x1qCvAJgPfR/Sdx7//9/97vPv+ATDS19qHBGMr1Nl/Jc/P7WwA7I6HcuasnMOpO+V7S8Jr5RyatkLTyJnverGEcxuxU+oKQz+MSXXWwuWM5XN3Rt/1uH96wFdn4Yfbq2ss5ys0dQ2Tz8Xd+Swg7dBh1raYNy0a64DZHD5FJGNkDKnCDA02yzv09VraMpwCznHA6dQDxiIEA++BrjtKP/TZLLd6kKDSGhVcLgBFH6qxFoPP50drEQbg1J3x8LiDcw63t7eoGwleSDClUlXlHEIKBXOy1iL0HWxim9oGIUXsc8s9kyRzfrGo0FqHGGVdYAx8dIjRo7Ethq4DQoAD0CFIFakkAc0S4Cy+5OQs6qpGDYMqAkPwCBFoZoKvWmPgrJzHog8Y0iCAepKqXiYBqfcIsQcQsbBAdAbbwxZtLcERDrXcp27lTFfJuUCCqXNF53wGLzitlT7yolwkA99YO/EXAOKjbdqqVMqQahZGNnNAWnNFCdqOKWIYPGaugYkRyQcMCYhVxNvPrrDe/DliCKjrCgg/rpb6jwbGCTIDoigJQIQQSpYTgJJxwkzPu7s7ACiOWYIxMY49l+lAp+OHznk6WElUZpzz0Ewggs4OnWFHJwBBKTpnNKAbYyyA+dPT0+SZPMyP/UbHcrt89tPTU7kXndganCBASJCBIMLpdCq9HukQ4998NsGvscTqGSG4oriaps5ZcQkxSmmSGMfMFs1odNAw05AOUoLXnDOVsga/6PDn+mn60BnINaNDTIOel1nEvJfOIHHOYblcFtCIzkk6+1iukg4r7WzTTiwe1FJKJcBCR2tx3MC0l6IeNzD2zeZ3OE9tfDEAg2AtnZB0UvLeGnS+BNkuSx5rIE2XG+WcmBXGjHmOQ5faJL/wh/KiI+304VHTkQAqA0joBOFhRZeg5Rpz/QlK0cggYMW1oK6gQ4jz5cUDHmWfekaDIxpIv8xs9upQzHu0bVvkj7Sjc5705Gc5XvInnfKkYVVVJYOKc9UApp6fzk4jEKLXcLvdFmeqDnro+x739/c4HA7YbDYTQCHGWHokEyCqqqqUaV6tVmXsMcbSU/YyuGSxWJSsVz1/Avc0gjQowHUkEKODDiiv+n6kCQMBuK5aZzOQQpcZp37SQBV5lvderVZFN3GuvA9BBsoEQTgNQulAIWYUXl9fT0pYk9fJNzxsUO64j+ggGoJwl8A711brsJfAb/bTRMlyYEnLMUuGQO9IuzrLsYxzs1lnwySirquis4choa4r1LWA2pxnXY/ZUd6HIgN13WC7fUJdjzTgPKtKIlKF1wOslbLAsq+4wpcASs/YEKTH+OvXr3Nvpi7r9TmsNZjNBEiezeaoKocPHz6WPtG8F+WB/M715F7GQC/qBSBNso41CGaMyTzPqjXSa2oYxsCn87nDfL5A25IGo52yWi1RVa6A/zq7WgNxxhis1+uiEwjm6b2Fz9P8S11Gnmf5bga2UO+mNJamZyly6mJjTMng0kEkqRvgWiP9qqxFZSxc3eDpeIKDOPXY0mGbSz8RZF0ulyXIgXJO2dUAIO0H2k4EYqk3GazIvZ12FqvqMHCA+oa6iLrq4eEBt7e3ADDZZ7inkT+oR4AxWlbbOgRdOY7LYB8NGDNISO+HzE6lfqV+45qytB2DYrhv7Xa7okc4TsohdQ95VOt/DThq24J0Jf9Tx+nsXh3wQJnZbDbo+x6vX7+G974EQejgHwaOlgN75snHx0cYY/D4+Ijj8YjNZlN6UHNsDNrg2Dm3lFIJIlgsFvjw4UNZH9oKV1dXZc/V8qR7pxPYZ3UE3eLi6elpEpCiA524ThwD7Zq+70vwBj/D/YcBEgxi0WtNntIVihhgqG1GVlcIIZQAFu4Fel114J7mbdqllwFXtMc4XsoYZZE8QHvo8fFxYjsBY5UMnvE4Zi0vmk+ttbi5uZnoAdKf/EM9EqM4CiwMTA0gZ7Y657KTMqF2DpvlKjs6pY/Yar4oe09MCSmk0k+ZvF9AEGW/FvBXAdmcC9eN9jH3cO7HI7BqJ/LP+1O3anua60baMLBMB9foUu7/0qsAKcbCutHh7UyFlr3EjfRC5rma5x3KHueMNJa1TDAFVIwxIkXA1hJkKv0axWHt/YAU0+hYZpniJP3PtT2j9zcNjAMoZfbYd5u05GdHB93YWoYObW1jMhCAn48wQIgI0QtwNngBe6LIQWCwfNb54rS0xTGTMmhOeY+Rgcspg89Zf4J8UeUy5qMMFFAEgp+T7wqoi+xopzxVYzuhvu8zxJHDE8xYgnAsCTkCREk+BmcFcLSukn6DJhWHVd3MsViu4SxQVbn0OgAbEkIYpDfm8QD0PVKwiBBAToK+YgG6he4AgUFrpQ8g+5aaaGCiBYzk//c+lyXOpUeNAazbjln0ZgSMrbMXZeJTcc5q3hHZo3PewFkDqPY91BPyni1Zffw8IL6TLETgcbw49VX5/ZcAOPIFoEC6lAMRVC7hpMe9BlbpOLdSBjXBwIdYAjeQnewBodA3xoghgxRal5XgQWvB0rGiezvsdlvstk8I0QvAHnJ/RiMldTVk9FIQAF8nKKJB8UtwUnhb6MnfMASnRjoaO2Y+M7hHSgxb+ODhBis6yV2CzjpTN4yymMKEppdjz18tkLTO9Hz2OTOCjCSDvi+nkcCl/IFnFpp8uhx7oSGRp/Je1u8xB3rHAGMkO8wYKauuz5dcc+rPwRv0A/dfI+XUE+mX4GMEyn6XgfFSclmyslhVwWaexTO+CJBc7Ben8PKlbN1PAeI/dE31nr7tD2ShyxezDSDAWILQLiDBgGWbI2ymr/DetEoEg/hsDp4AxkA67pf8m7+lTLbHpEUJs4sv5qXnon/zO/kfkzk9+37pqTylwad4VdP0JXrGLJ9Io12UEgT0MQLWRRPg/Qgqap8jgcTxWVLCeEhyHrLOIFZj0pD2f4bMmzGM7UvIkyMt896qsnyRpvzAvVuPwygilXu9IKOXa6N1EZ/z7DOIiMwY57PyWGN6vu5RCCoZsDGW+QgHmlH+LvRzyoEXwXvZX62Hhdr/YkTeSvOeMq5zSknadwQp+5wUz3F/1JuD1v+aXtaMefd8LmnvjEXTttg+PuHp6SlX0TXFfgghlGqX2r+n10TbrACKzc7e5NaOGI9UBD7isJce38YKUOpjyOXExySncQ6ZD/Ky6LMxMIKiol9FL/Dsy/f9xdhi6pFSrgSg9hB5jLY5Cne8eNEOGO1oWQmupTWmAPKAyAFyoEPMAVIhiO4pviZLrgJe3b3CF198jvfvP4h97hKaRnxYwfuSLV3XtejMEIQro1QxSDGhG/qSCdxknzr94fqsOMccTV2jrsYKYeyTXTmHzlaASQjJY7fb43A8onIVUpIgMcrJ+XxG7BL6tkeYedSuQjwccc6BhE1dY163mFcNuiDB0xEJISZ0fY+HhwfAGMxylbaEhLY/4e7mVnz6FvAx9zIPAUPMpfIhPecZsGgA1G0LV9doGsm07ocBkrAq68WqzMSjtI8sxYS+z9UQXIe2ncPlwFQkOWMdDids1isR/SC2owHg+wF9tnVjiohDRJ0swiB2kHHZ5ooRVbI4HTu41iDVDgECjHddj+1hCxihf13VCN5jMVtIuynv4X3AYCUgIEGSp7zvEZO0fkrGYejlfF5XFWYzOaMP3ucWA4BzCd7HiZ+QcqgTPIrvRCUSkM5d16Hvuhx0XAEJGLzghsbK+HmWkeCqiOiUzg8BcUhwlcPt7U3xG9gfkL2JzvlRn8LY47Xv+wlwpSdKByMzFq+uroqD4LLf6+iQ98WREmMsmSrMkgAwAUzoKCY4tN1uJ85uOj94P+99+Twdn9p5z/LEdCjxOwS0uLA600s7ZehQIk2AUdFqZxUB1NPpVBQWlS0drIysIZDPzcYYlP6OZDDtnBHAR3oSsXcwHUbAWIaboAHnqx2PBBF0xgufn1IqDjMaP8xSo4Objh+Cjt77ks2iHdGcA/nBWovr6+tJOVV+/9IRxSw9zofgGNeJhwaWgiP4SAc5x8zx8LBN5zazdC6zF/jaYrGQ6P0MiLBsMelQFGBeQ150SNJZDqCUm9XP0d8vhrmbZqQT3NPZSNq4I7CtgWIN6gNj9jzvqY1knVnOeREwJVh4mRVFXi1lZfI4KXeUc/IdeUA7KfUYOG4NahBM0fTiffV3dSS7pqseI8FTHbBAviLf7fd7PDw8YL/f49WrV6UlA/VHUeoqIEIrfl0ShDqCvEP98OGDGCc3Nzeoa+lXvl6vJ+Ay50CnNTPUGEyyWCyKbBBQJ2hNfaZ1UlVVpXzOcrksel33nad+1gCLzkjsum5Syo+0oM7Rhq12dHIcBEr1M7Q+YKAC+Y78xtK6BBTI5xpwJ70IJmm54f010MR9hLqauobf0yXddWljAjOUQdKE870MouJBgIDMZYAI76sB+suDHfUi14Tj4pqQLvqgzjU4HA4FdOQYOb6+77Hf7yc8V9fTgCet6wnMU8e8efOmVDYh/xOwo77R9CRoNGa/xbL3MNuU+pTALmmsgw+ogwmGamCKQD/nzz2H68ZM3tVqNQElKcuszMCeXNRzBLGoDzebTdGJGjTSOoIyQlqTj7lWrIKhgTDqKV26muNjNu3xeMRqtSr7l943uCeS1pfVHTheBhRQP4QY8fHjR1xfX6NtW3z48EEF5/VFfrm/8TWd8c+9l8+kXqC8cO/SfbBZep37MwHl+Xxe/ibv0Kbb7XYTkLDrOtze3hbeoY4AMLFZKXfGmElvb/I6KwrQbuVerQNuuLakPYMumqaZBIToYECuN3lUj73QP4RSPlzrkhDG6ka0r/XeySAIDUKTn9iDXPMQAOx2O8zn81J9hLJPXbder/Hw8FDmTiCZexH1OIMeNH+yzQeDjqgzKH8E3Z1zBczX9KIOIJ1oT2jdyKAnBocQ/B3tZpnPfr8v9NRtlXTwE3mMug5AqQ5APUzgl7Tlc8i71HXcz2hvcL35Pu0ayjoD1jRgzn3opWcDY2sYXemGtOL8tOOR80gpFZ3Hsenzmz53kNaseKADYxmseFlBhTzOqj8AisyYOGa10HFAPUqdTDuJckKZ0PtgjLHoT1a+mc/nWK1WMGYMKqVck6e5DrynDmghnbWDWtttXDveU1e+0rYP9QIvPvclR/Q/95rNZ5MxksdpOxQ+y3aGlumUkmSFZJ5MSZx+zkkPw2fAeA4Eq7Kj24cAaytxOAvKAGbsBtVDk88qAHy+yOcxCaDNTOSU+ZzZitLj3BTwXfMCMxx4v5jSCM5jtP11YIQ4kccy+Ma5PIbswDYCGsaUwDK3mqbUa1xbAUukGo0xY1Z0OSubnJGWe3/zXuVsA4NK2VQZfhS5iiGDSMhA6Aj6poxCTUrBMvMp25h1VcMkCZY3BQxOACQLzVW2OJ5MBPaHLT6+f4f9/gldd0LwPXx/wvl8RPAeSNPAbEFgxnNpqmvYKGU3ua4wkpEtQJMt6yM26litjzQiQK75JETJOOH71ko/d+dcmb8xgHMWlZMM9MIPKSl5ECCcMkFwmT08hRZ5rZ1k9pdMX9Ja/57Y48rJjqmdbq2AHVbLKhSQEiOSchhKQIbLYEoGmg0goCiAOAK85DXypQmABwERKQt9Oh2x3W0lgxoEV8jvpvTZHO83wdsyn45tDEa9xYCMyx9JzTX5W1HycSf0SDEiwGcekn9zbwrewxuDhAgbn595pqAj7epxfyg/GGVMZFEFLCQz/k0wgXN6QS9rX8S43iP9P6XLL/X/SOPL7Ps0BaHK/QhIBiAayfI3khkXzfR+OngipoAQAD9YdF2f5WMM+IgxYYgBVpUEDzH3Ks1ZlQQgOR5Dxng234iUfryTWQcoTOf6jEov0pO/xzW5/PfoJ40saZwfHJME7cBI9rYFhDOLrpBKCsYa2HQJmgLDYDEMvXxGvad9mZcAebrIGp/KD6VoXEdtc0zpk4oMTto8PAuoeK4fLmn3El3165qnYwaGDD+TMjCeeUkiuyKQnoOaMeu26ZyyTKQE7wcMw7iPaD/FSEsGoo19gRk0UtY80QZJRT9fzjNRkU4IJ4FumnY/dMn9AS3/en2erWih18VPTLn/PPfUCGMEThfgUsrVSwyHKcFF07nkoKsQEN3Ybs+odZP1mq7JyKcSBJNSBKKRUsZggKPQ5yV6XPJKBAowi4RSvQYQ2ayrCsfjAdvttiTSyB6MQhudxCbfG8+e+nUdGGetZEdbI+A8q88c9gcpkx08nDPFHuX3eU+j7FHNFZc6Rp83GLzJMYYgQVnWjPhNSkn0B+mpZVP9RVthIrwX4zDmIoBG8Y6293mnIl+5r7zxA5yvsr0qQXxih0iwyGw2x83NDZ6enpD6mG1HqQ5E+8MaoK4crJGM8KpyYvlFsZW1D6ppW3WmSApDG4qfgHOjzesyraraYW5mSDbC56SUYehhkKtAGSm/bq1B10lFE4SEtm7gY8DusEcyQFPXWLQznJsG+078h3XToG5q1G2NkCIOhyNOfY+qlrPeMn/HZl7jGXeYzzAMrEYnSUbnc4d+6FG5asQ7nAGi6LOA0SZrW2klI/sqzyWyz7q8ZiFEpNADSYICjYEEwiAhDiEH/1eFl1ICutMJQ99jNm+QkG3kYGByJZ2+96P9agxi7+FNjxRd6bk9xAFP+x28D3DWoalrdGfBHpuqQgwBQ++lTL+rYayRvt5hgA8DEgLaqpGgdmtQWYfTuUNChcEH1JVFW0sZ88GPVZ4pJzyj6griVdZjMUogrXNiz5xP53LeFjmvpHpDktLqKY6Jp846DENAH/qCXZiCoeSg2wSE4DGE57bZS9ePBsYJQuisTjr66YigU1tH2WsQg04MRtRrECKlVJz3dV0XUF07MXlfOsP0a/ybBiOdF8w2osLTWSS8uEFrBUnHFp+nnWUaJCmKUTkntOOUz6RDhX9rBz+/qzPvORYZhyg17cAmzejUOR5HwN0YiaQiOKMdeClNs7i1M0s7pOlIowNag+EE0l8CCQGUTBHOjXPls3TGLh2cACZ00sEBdAoTNNRluzWf0ZFyCZbqNb3MYuB8rLXFsUbnGh3hVPjMtAGmJZB0liqAiZNXz4dBJQSMue5cy8vsTGYocVPR/Mr1pNOUfEfjnPfl+LiZauCYMqHXig4tOrQpq/v9vjhDCSiS33hfjlVn++rfuo9z2SQVz+qABO2s5fqRBjozSpfeJe0ZwEJ55fpo2ae86+ALlnEGBEjZbre4vb3FarUqoAD5TjvIOV6tezh2yg2DXvjcxWKB+XyO9+/f43w+4ze/+Q0+++wz3N3dlYxzbtbaYU0akk9Op1NpnUAeot4kWEXaMUDjdDrh+vp6su4EwCj3DALQQSPUeefzGfv9Hm/evCkyyKob3nspL5Mdx9T75AM64xmko7OnqR8on+QtHpj2+z3ati19bzR4zv2DfKQNagJdOqhI6wF+n5d2hBPU4vdCkAop3IPGEuFj1jKBQ4IPlzzD/YJyqve3UedP+6iPh3VTwFUNqum9kXxvjMF3331XApQIKpJ3SAPZpyRakJ8lgHp5eKY8ErRkP1vdRyZG6ZULoAQksXxy284Kv+jgJsoWgFKqWwOU3vsCODLzTZd6ZqAGeV10YiqyxDUwxpTXuNYM3tFBSeMePe2VznswsISAEQHUw+FQPk+wns+grmX7FYKHHB91BPW+bimi9z6Co5dBXpdgDTNJqdeur69LWXXuazp7tqoqpEx/9mbmWlOPaKcfx6srYhDkYtS1lnPSZb/fF2CVP6xaoQMF1ut1yQh+enoqPDkMQwHgqec5fsozg6kINjJggzRieXbSkfTjnsgsbwBlPPxbBzRoOjNAgnJO2SZgq8F87mOkDW2QzWZT9JLWoVwr8hv5Uwcy1XVd+qRT1wEoAVDUH3w2x0wbnn9zLRkgwnlqvcB9hvtRjBE3NzfYbreTYDvOlzqHepFANeWfa0BdQL3BsenANtpSpIUx04A07iOUqVevXk0ccORjBnlwLRl4kdJYUl3bR9zPKRfc/0kL6mD9DPI11+wykEOfHzgH6n4GgekSiZyX1seXAV08vGt9qHmZOpp2D+08bdPoli48w5Gn9fO4JuQ/Bm1o3hiGAUhSEpL30LSgjQCg8IjWufycPrfpPZXBylofUt+S16ljeJG/ub60czgvyqU+a3EddWUz7vG0cbTscI0ubdt/6dW2bY6SV70tM3AnwJuAalXO+OC4mUUbc2nJvh8yOG1Q1RWssfCJ5SvzuakPGPwAZ2wuEZtyNsoI/kcC0Snh3J2Us9EU/5+1pgArMQTJ1jNSeYZZCaSTrEvODgeKfgo5q1b6xDpk30927I72IdS9KIvCO6IDySfC/8rBLZ4p1HbcQzkebd9f3puYmjHiyLPGwlRjAL/el/V5tFKAdwh+BCANYFWp4gKMg6Cfzn4WOkumimSMS+nz3PYg0UGecjnQEYwzAExKeHi8h3Et5rs1+u6I4Dt05wOeHj7gfDrA+1huM+4nch9jhHdSckj9aEeOfosaztWo66qAbqIbOA7a3roP/Qi0xpiAOIIRI48oexQJTT1T57kRVIYxsEacgqY4pJHpN/oL+EM/C5/HsY3guvzboFJrYMZ7m0tYjyB7dnOX9U+Su1UAyrESwThPrj/P5COoq88KdKKbOJbPBYDT6SztBJU9K5niJo9jKisp88nkNVwCTQoMUrycslxEA5hgBSy7oG+MEcHwHiPYVnSINfBWYEAte5yvBh31a8h8iUxXpIgEg5QUKMd7GZYCNxeg4ktg2mVACEETvUaXoNWn7zV+/wIkTVSTCoA0FkCEiQGIFtFEWMi8gqFsxAKKowDjUTLDhgHOAtamEjCSRJTgY4BNGoBk5viYKZ4Hi8gz+MXqyyUBBwnToJZPXZrfLmml6YhP3K/ITRkE9dslwHQBSiJnDmcqW5MQYSRoIzE71SAaC5ssUpoGsRkDeOQs5wxsXZ6BdFDcJTBOncR7GlYmSElK+wsBhA7yIU64yF/R9EbxdJq+9ozvMIXf0gu0Shhll4qPzxSbIYK7M3moyC2B1TKmkYdNvpcerzHcPyMGb2CHvB527BELjAEbQuOAMXA+TGiekgQ5cHNKJgLJTt9Xe+T4+gUdQSDzJV5U95osjVYCSp+VtdE8GIt+KvKdgXlrM42ZMW5NtmtGvjBGYxQE2EeahKw7TRr9SXLPqW4SenrEMFaFAIzwvElAMrkKAOml1jWN99AX93HKGeUz5X1yt9thu90WXcUF0HuXxmAu10D76oqf2GWADUCKCW1bo+/O2G6f0J1PwkMhosN4xtB7ENeSr2XGLXYD+T5FyTSVkt4ZsFQ60ySUDFSedYyRaifc28l7SemkH3OlCf+kC37KNFKfN5kHRSYTTDDwfpDy9GFAiD6X5k8IfoBBwnq9FqzCsB2QVImsKweLhJRLVDvjUNUOlbNgEEpdOXT5bLpcLbGwC1RVXbKqy9kgRlh7UjwYYa0ruI6cHXNyi5mjn3fYHw5jQoxpUTdSJbCpHY7nhKEfcBJTBt1wxtPTQ7HdwuyMc1Xh7HNL4MqhruaYL5cIweP7d+LfHvoeBoCHlOsGUBLWuq7DfDX6x9qmhkHC6XwsVTFns1nxT5bA9URbUGRb4zYAEEL269VV/pyF9wP6fo+uH2CNgVSklJLs2+02V9GUIMYYgdPxhN73qA41XJP9vUECB3rfoz930mosJlSN+Kt6P0jlcZvPwCli8AO6s/h1q6rC6XhCekqYNQ1iEBoLwzjUTQazTYKPAUPoMHMN6mx7OGuR9nt0fcQQItqmwmLWYDFvAVNJa4Ts19KJbF2uJh68x7ydSTWhEFHVEqRhAJxPJxyOBylxXzeomxZVXaGpmxwEmKuFOYe6qjAMBsPQF3+IrSpp9RAC+tSJf3sY8GPaGQD/zIxxZpbQgcwShnQCE4Tm50VwzTNlR4cFP/v4+FhKdeosEWttycTgxWw759wz8FSDUnT8ACjOHTpa6GzRmbTL5bI4c/XBVjtbdKYUx0enPR1fdPJRQdCpxAO5NrbpENLONjqydPYYlchqNS+ROMMg/cbbtinCNgxjGQvtyNSZnnTQUDmx5DKfw+wyZkvRKcnvcIw6g51KgMCadlzqteRGqMFfOtHpeKdjgk5F7Vygc4vrb60tpSRpDLHEB52dwFg2XYOMdOYTuNIHIb32l9nz5BcNHBIU04EPBAHJN8za0s5YOtt0dimfpcE67TzlOEIIBRDlXCgD5F/SinPiXLXjPsZpBiTnTucfwX6WstXGCumrM8Epl5f35vg1f+ssDM0fujSoziLlPS+NZF4a9Cffa2cv9Y61dpJFRz7UARIcBwENne2tM5s4fgaD6M/0fV8yHr3aIDTwysxMBgNRTnXmJasvMEOL7xEEmc1mBSymLmGWNwMa6BTUQSmkr5Q7QgGBmQH4+PhYAFCCVk9PTwUo0zLDNby6usLxeMT5fC59zwkCEDysqgqbzaYELBBQ0kBEcajkNXXO4bPPPiu6QoOYx+OxtDXQoCmz8KjvKW+ad/QzuGdwn6BMc+6UT2aZpjQGItAIryqpLCElzIcC7ugsu/1+P8mC1fpmPFCnck+OizJCHuPewb1rt9vhw4cPeHx8LLx7c3NTwHwCRdQxei9PadQH3AP5GfIUeZm9uGkgkj8IPG6327K/EQijDiI9GVh1CZAxMph6//HxsYAP1DXU25R5jpO/RZeODmoeknhRDqXKyqhDdDCF7GtDWTPukQwO435F3UHeIq1Op9ME+CyGnJUAOJaZNmaMqjXGlHLUxhi8fv0aKSU8PDxM9kJmqOoAMMoOeYb8Zq3Fw8PDZM/VEZtcXwbhWOcwDKLPWWFAg5P6/lxv3k8DfQTgNQC2Wq1KpQgGiGlQlPskq97owy33POo6yhRlWFfc4fd0xQD+GCNVdVgpiFUGOBYGQFGfMwCL8qMPftrO0kFio6N+lOH9fi+9n5QTQwPr1MecC8dwf39f5IR05l6seRkY2xVxr6HcUeYoO9RZtBd0cAm/w3WjPUd+pg1GO4N7nbYLucaaX8lrpB1tTY6V+pdyfDgcyuu083WgE/UOgLIWXDM+j0FurNKkaU69TNnj/qjBedKJ82Z/c36OdgVll7qV+5Oeuw6s41prO18H/VEeGQhEWui2TNSBWr9S5xYnmbIpaQvqoAraZ5QJ7oPkJe5n/FufSfgZ8iB5hpV1yA+a3zWoTj5kCxLafJwX6cG/uQdoW/F8PpczJPn8MiiT/EHa8jW9btQvWl55NqRtz3XXvMFxMQD2MuCA9+c+9WOdY5+6nnZbcZgCBRgfnS/qTDGbF/ujROZnHqPeds6W7AnSj45uwBR5bOoGdSUOG2cUcIAEWIPK1ahcBevGijtca10xrMzfjU6S4iB1Dk0zVnqwxqB1YyB+cWry3EG7XTx+E6elvsazvWTJLBZLdF2PDw/3k3O4c1K9pMoZ6ZpvaOPpcYy8JUEK1lrUTQOXW9NcAutC94AQvGRixxFw6IZe+uXla3Qaj/ohmZGHXzovlTVJQDLjGT1F6c2KZBCiH53ciAixR4DFYr1GU9cIfkD0HU7HHVK0sOYRw3AWJ6v3GPyYuY8MEvH5de3UGgQMg5R+Hx3TyPZRXfhPwKMEgmHWjsAFW/LoH16sNICYkEKAM+L01+uDHChiYJDMFAi+vD4FLun39U9K039ru1yfjbUtoF8zxjy/P1yxzfS9OB/tC9BjBphphMyXIsN932G/3eJ8PqKqGySEsdd2ylmfL9Dg+b+nwC7/rW0g4UfylYdJkrUek4GJGfyIQYI/Jg7/nBWdJHPSZOA8RvtsPFq+C1gQE1Ia+0wKP3Cds4P+QkYufTiavy6feflejBGwn3aXPl8fBSaOn5r+lSQQCZTVlL3+xsJkQC1GLzC0Ie1zRmU0SNYiat5IEQOiNADGeBZIMFIGN0n5dIKiL9E1d0rNbSpiOYsBKKWXiy9HJvtJmpS5Rgb2vADiTuj26f1xnGPSiK/6fv47Rin7GyMi5TTlABYrpWYlGIffkVYuAmJOq7EAgMs2wEAc7QWe0ecE+V6cVFHRvi+ZpykhACZNWxsAIzT5EjX0PTRNLvlPg+KXNDcmg9fjTRVtJYtZf7fo1Pw+M8mTiblSCAREtzn4JsRn8oSUEE2C9WMCgD6fpJwNSJkRfR6yLmG5de4/Ro03y5qqDsGKES9dU/qpe2naXH6n/G/cP4H0bIHGuUwBc8n4ZRa+KXNMUWWMx5SDeqL0BDcGxjxvyZAKrwEhVIhW9asnveI0CQNQ5f+VHco9JyPyMv5MkpcCYlghR9R3ljFIwCLy2GMEYvB4enrAbv9UzqcSQBkm++Alb77EpzzHCkBns34CrAPqpsIfv/oWu/0WMUoWLNuK8MzI87Wu0sUxhBCQkJRdI890tUVVOTRtTt5Q9p+QZ5T70japbUbcJ02DqC756lN7eXlf8VJkoCppFYK0onKiQ5gVbpJU8ZC/c2WGrkOczRDCgBQHIAUgBayXc6l2a8dqQwKWz6U6VD/gGCLMcglnHVKIxQ82m83g6grff/89Hh8tnDO4vr5Gxb7T5dw8FN8iwIDqhBiraRW1FHMmOnDMftH1eo20WgshogTkGjPa+ue+w4cP7/H4+CCtNSuHED3OhxMW7QqttbAxIvkBrXX4yz//BT67e43Hx0d0+fyWQkCIEdvcQvl4OuF8PmPZdwUwl3LjI8bHSls8azGxxVmHFFECpG9vb0vCFvExmS8xNIvBBzwddjjsTghxQF3VWC0WuLm5Qtef0HVjS1wDoem7d99jdzqibmusNytcLdflGefzCfv9Abvdrvh7qYvG9Z3h9vq6+DX8IJWZTqcT+iiB0KfuJNjd4NFUFqvlEsvFEsu2QbIzmKpC33UIQ07MshV2uyM+Pj7Amoh5W2OzWuL21efFh8Ex6ASfp6cnaSkIoJ21sEaw3sViIf6T4PG03QreG0S3V1WFu7sbbDabyZmeGHHXDTgc9jizMlVdIQ7iX2JlAJ3U8EPXjwbG6YSgM5wGOx0XdJZR6bDsdUqpgCl0gtD5RCfGarWaZL9qZyMFjU78uq5LVjkdSHQsUtHSQcx70SnHDZmObjItx0xQj84rCq/OjuFmwudxztrZSKXLTCWteHWGje6DzYvOJ33QGwb2HW/R9wPqukJKAwAx8IahL2vEjYhj1MKhnT98jYYxexQT0GVpXNKKIA9pcgmIERRnJpx2fumsLB0tRqVJOuiNUPew1wYUL/6bz+BrZH4CYKQ1x82oHzq/NHh7GeyggVRNw5cAQQClZKh2hmmQSQNT2kHJrGauDZ24umSqBtTp9NKZ9vqiI5hzp1MVGHsnE5Qh/zIYQoN8XNeUUgmA0QcHzpXBDXT46uAGvV5aRvgax8Ox0QiibmAJdYLcdO4TYNbOBh0hqAMAtBvrENQAAOQwSURBVFNVB1XQiUmQ69tvvy2bCgFigtWXOoF6hrzBUqCcFzfXw+FQSn2SHzU9qIfW63VxdBMEI835maenp0kADsE6nR3EgBTnXHH2k4eZ3Utgk8AXs6voHCfQenV1JSV30th64vb2dkILnWHITY/r0XUd3r17h6urqwltCCJwrciL1HuaTpQj/hDkprF9f38/KTVMPaira1BmtZOKfEUHO3UG58IgL+q+4/FY+Id8w3LWeuxar2l55XNZwppOY9KEnydfck35HWMk6IdZyAww4L2dkxLFDBJgVnTTNCVjtO97/OEPf8BiscByucRmsylGk+jC8cCkARwGAREo495EOdVVRahfSSMdlEawOaXqmd7VepOXzlS9BPr4PuWQ+oul17uOB7Wxagv3ZeohrccoIxrERs4Won7gHqez9XkI41wZrMKgKa4tn+ecKwEj1Mka6OOewL2maRq8evUKAPDu3buydtpuSCmVNad8GTOWt2ImP20lvTeOzm1mhBrEIRZwmvJJviZITBCc60ObQwcOEcTkfklbhOXGSUct95c6oqokm/329hbGCGDK6hWsGMG147z0oZvzpRxyv+Hez3WkTmS0sNY/uuoGXydAxqxeHfxBOW7bFvP5HB8/fgQwVkKgbFPmqUPIh7wXAVHKEuep5VHr+qenp2InUN9QlnVGNPeIu7u7UpWAa8G1495P2nHP1CXQ+Tov7dznOpLHeIjUpcYJiGpgVd9PB2LqQAfqeW3vMWjiUodqO4/ApeZ9HZx0PB7LMzguyoU+K3DtuX563uRzyrAOENayzt8cp7ZRuP7cI1hCnw4ezT+cM3mCeluPiQEP0yj2sfIHacM1ZmArx6J/X4KUtA1IW/2a5tthGNC4qtgopC+dS9q2pA4kvWn/6rZdGqCnvHJ++sx4eWnnJT97qX84Zm2rannSMs597CXQnXsudc4lcPvPvX75b/9qcsYu4817YyndjTEAk3sA+ZF6qW6kDOUx6wMdgOR97ote1wWs4POstagVWML5EjDk+BhQw0yMGCOqukaEDvyu4apphYqqyv3kuJcOfqJPNDitqwlwb9fyyPG8unsFYw32hwMO2S6Xfaop/RSttRlEHp3zcknmcUgRMeTsSjD7aATeuqFHlUbdMi2lqEp7GgOXe6U3TQMmd0lWNeB9/pwL0ns7y1OKY6AFaUyaTJzLti9yGqM4HREFNKVdE6JHNxyQQsDgPfqhR9918F0P3wU4O0c7S6iqGsNwLOcGr+8JAbM/5fDl+UfvB1wjrUP4fe1T0NdLzvOUco/D2gGICEmcnKMXPwMTef0uwa6Xrk99Rj9fPmN/8D76fi85+qev8b4jWFBVFeqqgZSPHAFzfQ9tO4TgMfh+4oQ+n894fLzHYbfFzd0rIMZcqWF85sVoL2ggrxXQRI2V9Bh/hG9Lj/joESV9HECCiYAzFcAMemZ2pwTve0Qn5eKl8sHz8WkQp+jtKABuyuC6jEFlPCNBq1q9tvpvfZbQ+uLy4n1TDNILmNUDXuAZue/0e+P66fONZMUaCMgkwFkGxU0E7Di+kMaWKiFIGd+kbFyugzEGMUmGV2VUVcMMKsn9pOUidVxKBODjs7UVuhPMksiVCfeaWECiH7r+y9Iy0utFoOgTMjnSd3yN+oW0TCnARJfpKZn3SFZ0eDQFBNb2GzDykkGEdQYmhRfHRl07DcyZBh3oOXCsxrjJ6/p+L/39QzQp/Hnx+yUd9GOvlBKQRn5mRjgKz0gMAm0h7WNJSudKht7Yr50+Ufl8KPQYaQekZMD+7DGxqsa05aP8srmMOMFdGXtMU9CasvNjeevyc9RbL9N5+v1SEYWDjMyqloz5ScCCrnxgcklyQPWNthfPi0iRSV5Z/9sASTYfK67odS+ywvYJQXq3w5gccDMN8jJKfylCy9wuAh4IjMOMvFbXNY7HIz5+/Fh8QsWG+YR8v2RDaDuHOrkyoitdXWHW1jgdDtjuHmFtKvqTNq72N1IP0gbWdAGmgfP6/Om9RwpS1cRCWvkwUDHEiM6PCW1630hpDNIyMpkfLYcTmyiD3jCiwh2yzyfKHmqNlLRuKmbUS4Z3XRmY4DF0J0Q/R4otYvAIfoC1wHqzQdvIOvl8xvfewxqDPmMDIqfiC1ksFthsNljMBd85no9wTtohANNEN4M8Vmfg/XgWHGlEWRL90fcdTudT8eFKwLpUQELem0wSu/nQnRC8x5vXr/CTn3yB4AdUlUNKAefuiD9+8w2ul3f4k5/9DHMnfpJ/+qd/wGazyeOLmM9muLu7w2LW4v7+Hk+7rZxxTERCwNV6ic1Ggrv3ux0+fPiI1WqF169fl3M6dd7hsMfT06PwRQ7m/O677/D+/fe4ubmRUvPZJ/X09IRgpEXlbLbAfLlCBLDvBB+oXQWfAlY3a1xdXeHx8RG+C7BGzuPGAaZySIgY+g6ng0HjyCsGXX9GgkfTOmy3B/RD9vsbB2dqzOsG1+sN1ut13rMSvBff08f7e/S+RwgecSUYgO8HpBzIUlcGbVPh7voGp5gwdB380CP4AT4YXN3eIBppzXQ8n3E+H/H9h3u8fv0agNij9EE8befFFzVbtDieTiJPJqILPeIZsH2H8+mM5CzWN9d43G7x8eEeT09P+Ob9HK9evYLLc3fWYZZbvJk4ngGHYcCxO8PBYDZvsZjPsZwvsF5OE60/df1oYHyxWDzLgNXOMjqmCR4wg4gZYXS+0FlMRz4BCGb86WyKlFIpkUmHNv9OKZWed/qZwJg1cTgcSklE7Qihg47gAh35XDAqcmNMKZ9NAIL32mw22O/3OB6PRfFyUQi00Hl5OByKA047o+mQ0IYe6clNTEDACt4LzZnZlRKKQ0ycWXUBfIFpOV7SK6U0cfhxXbh5UDnpzC9dflA7dngPfXAjb+jn6+yPcjC/AIE5bz13biQ6mxsY+wZyXDrzgwYX76mdV7qXMDczfk9v3peArnZI64tZWwS6PuVA04AOs5S0Y1e3FeD46NDid8l7zAABRsctn6kdp9pQvaxSoIMONChCWdaZRHRwpTSW39f0XiwWJUuPRpEGvTlOvW5cO/LO8Xh8VmaUa8cx6XL22nl+CYbQmUrjgvMg348OuTE7jzxvjMFPfvKTQpvlclky0KiDOD86YKlzOAaCQuRX6ictD5RrAiLX19fFuX04HAoYofmBGWgadKUhq3nTGIneI5Cq+Z7ro53fmt4cAzPUtIzTQczseeog7UygvqPeH4ah6MjdbodXr17Be196mWtwgQ5UBuNoGpJfF4vFRP/yewQqddAK70EH/G63w3K5RF3XJQu+9D01Y3l0nVXH++kys9Tj5G/yqC4To79HGukMTtHnY8lr6jtmG/M1foaOdR1IRv7lGvMZ19fXuLq6wi9/+ctSJprZ/3VdY7Va4XCQ3k+/+tWv8Itf/ALz+Rxd1+XSPZjoTY6JAXHH47EAOgQkybfkdxrVOqCJMsXv6MxKOogZEAIAXe4TRNkc98Ex45R8rA9b3HdFTw5l7MAYMc11IN14gNrtdiV4j7Iia2Ama68DlygjXG/SgO9rm4TZsVrvakCfulQDRjq4zhiDu7u78hrXimtE0FUD8JfPoe5l2XveR9PSuQp1PfbP04EOI3gu+7TOMiWARzCXPLfZbPD999+XvZLPubq6moAYdV0Xe1AHOOnnaT3OZ+iscNKdwJi2yzQwRRrFGEvpbB7gtM5hsJf3Ui2JwQK0H8gnrIahnZcEu3e7HVJKE3nhutHW0raptiX0PrPb7SaBJJQdrh/3fv0a9Sx1kw4CpR6j3jfGFL7gReCJmcvcy8kbGoDRdo/ObOacySt8n4EawBiUoUF5/nCt+DcBcO1s4Xv8t15rAqq09XVmMvmMepuyq+1q7qu8r7ZVaWtwXuR58hbtKWPG4C8GwF06LRnMCGBix1IPU7foQDdtK17qIgYDAWNrI1YcIP/qMwD5ksFGnDfljd9nsBjXlrLJ8XDeet20LccqR3petOu4PtyDdFABdYwxY4sZ3vsyqEY7yclXOshD21a8p7bTtfNWO720fOt113zOvZl7kQZPXgJd/jnX3/zX/40CJ0YHpjHSc9Gw5DMsvA/lM6Ptb1HXObMFUlZvznO93AmSEZGD/6pKMomVU9o5h8pVSLlMnfcBcRgAV8HmymW2qhCQ8Ljb4nw+j7ZcDEASXR9slIwF8YwjpAgpBS69nv0grRSclQxxpDEjQ+sy8iZ1kl4nQHTox48fEWK22wE0sxmkQ+74GR3sxsuAfmvJ9krWwBgHE0c9PgSP6IW+OqBNeGisMEJdUFcVnBn1W0pCApPBQRm7yyU8s34NSegC2me8p3xGl1xNaSjl8FPuH8y5GATE6BH9AESPvu8wnI7oTmcMfS/lN3u2qJK19cNFtlQerMxLZ3lOQUB9htbyqfd0zkf/5t+fAoUK4GQNYhLe8aFA4JmYeTgXzugfApp+6DNTp/YPZZ/LKOj81f9OE8BhLJMu/BVAwL0n/f2AthG7ywdf+qdzjNRhGhSuKpFL7z0OhwOeHh/x5u1nOJ/F/oYxUlpezUfrQk135tyXz6nnIyXJ1GaQhAFiCqW8sg2xUCn5AJ/yeqcIRItkLULwCEF6RVrDIAvA2uqC3lMQuwAaCUovTT8n9BkrPkzABrW++qwDTM/Rz3gAKFU6BPi8DCZ4DlRq+vIuZX/CCGanKBnGif2bYeCMQ3JS3thYI72ys9Yay8XLqEQmCNxaRAfE6CZjS5By0yGyz/tFcEAce41rMHfks1C4Arwv/hmgt/77BZlHHtWz+3Et+B2gBOaMZcrlI5fgPgy5MLdYSECKUkpd1jqXOjac5yV4yoAiC4+UqzOYMqRRfgUMl7XIOj+MJcBDGGAvqg1My8vr6Y5BFKP++PRV5vrCSlyQ95mv9qX7pCR9zVOSzNMYmH2PXPbbIhoDa8ZKEfw+nyF72lRHAShZe8JzAVBBCdrnK7ItQFXKZXMvAwuF30f7H0aqgxQ6luIRpthMCWpc+fViT+WNWIcClWdpOVL0luFOZV3rnETapVB4AcbA5eeVPTyKTDskqXACjOg4RL+ObTCmAH1MET7TO6ZU9gmubkDEEBk81cH7/kLf56Asa4RoGYyP6hkv6dAYgrTCiREh6zGXsz6fnp7w+PCA7tRNKzS+kGWv9aPmGe1b1H7ntm1R1Q4+DPj2u2+ynwdIzpbWPvQT8Luz2QyOVUSK0ZyAqprcW9uQPBtaZa/RVxOR0GdblJXvtC+q3CeNe+jlPC91H1+XMY9VdiiHXHuw3UCIMJVFZQ2ayknmt3OomgZVlRMTUoKJQVpxBI/z8YAw3GC1nKPOCS/n8xkJBrvdHoerXNXWWlRubF9If1+IEeeuw7sP75AyT5/PZ+x2W9R1M/ozg1QDSjFkn0ZT/DqjX0toF+kDQvbvIeF0PqNyDvO2wdVyhb7rcL99xLfffiNZxOc9/vqXf4WffP4Z/DCgGzo87p/w/uEep7PH8mYD01hY5/Du/gO+//gB69UKVVWLH3jWYLlosVwt4CqLY9tit9/hfDoBMeL169f5LNpjt3vCu3fvYRBRV05snTDAWYtXdzfo+0EqLHppUeX9UCoDnk7HUnHV+wFnP+B0PiHEiPlygXbWZJ+SA5LsE+/efYfFT7/EfD7HEWe5fyfVV//kT/4E3VmqsQ59DwwBVd1INcP5EjHImQ0AKmfRdT32hwNOOTg5pYSh96Wfe92O1WArJLimhbMWp+6MPQ7YH/e4//gR290OXd/j9ds3uLu+w2q5QO0cQki4f3zA0/6MD/f3cNbg5nqNLz5/i3ffvcPXX3+Nm5ub4mun35d+CFc5zBctNpt18TX0Q4e+G3A+n7K+mWE2a3Bze4W6kbOnrUXWTZIzbVU7AA4ICctmjrqWgOPj8YToPSorPvO2qdG0zTO5e+n60cA4HcNUOroHI51vdKTRyUanLb9D5yrBRJ25PY24A7SDp67rUu5Xl8jgIZlOlqZpJg7uGGMpKUAgJoSA/X5fwBEax1Rq2okMjGUaqfzoANvtduXZ/C578rE8Ix1uZAwN+tGBxnvQqXLpbORnjke5d/A6ki6iriqczidUlcN6vZqAdHpTs3bs2cp50tjQThs6DHVfdg1+crPh6zxYaMcYHZekIQMddMZVVVWl3zydlxQOggrkF24kl2Oho4Y8SKcp504QSRss5D/+mzx9GTxARa7BVu2EI430HLh5ApjMnzzNjDXtpGTGGUtvXIL7wzBMACIdZMC/2Tt4NpthtVpNwGAtfxxTjLFklGpgUz9XVx3gZ0hnAkQEUHXWsF5v8nBKqQCmLN19dXUF59zE2a/vwaw07djXgCHXRDt2+X0NvHNNmBWt+UE7QymHBAroBKaO0WDSfr8vsqD7W1KHaRnRNOY8SGeuOZ3m+t8alCQwEqP0cdU9yLXjjQ59ZqgTaNLZzCWyTzl4yfe6j4p2Is/nc+z3+wnQRmCMGcXz+Ryz2Qy73a6A0XVd4/r6ugD+LK/MsWhHOGnIuZAf+MMqIVwr6irKl3bQc1/ifrFYLCZ6lzLAfUTvF7wv+UEHP5Am5FECIVwLDbxxn6CM8rMaMND6X4M0BPupUxjgQAduXdeT3tnn8xmz2QxVNZZ6ZdWP1WpV9O5ut0PbtvjFL36B6+trvH37tgSrdd3YL5qVBFginOtGYIrzotFMnmBPqUtdxqAGGYeAOHU9LbP+Esig5Zd6hWtHGdKBAXzNGAkm02upD5Syl4/Zvtpe0UF5fd8VueKlA7JID+oTnZXO9dcBD5wD+ZAALA8oLCPEfZpgszGmlNSmDiQIShtGDPHTRBeR5vqgqfc/resY+BLjGMjHPvEcCwMfaPscDoeSvU5bh7zBkujUDeQb9qUnbbbbLZbLZdH16/W60IZj0z2dOFfuQ5wngAk4fDqdJgGblA0C3pRBfT/u4/v9vuh+VmXhfqNtG64fZZb2pwbAmM3KddGBI9SjBC71PnYZWJhSKjaZ5meOnXpbl1ynHqAeYdQuM5G1ziJoqXmdNLVWAnTYG5401ffQWcqXck07inqf7XsYTMU5axub39UZ5zowge/r8tV8Pr/HPWq73U5kXAPhOnhFg87kDd5bP1c7iKjX+VnuFTqDmXYFbQfuJZdtTXTAEPclrgdtMeoeXVGJY6QdoW3EqqqKnab3IM5JV5hh0ObhcCjBDORl8hHpS5uU66wDXzgeHchpAFT16Fzid2ibXtoieu/X9qu2E7gOWgfooBVNB9ofnIsG1vV+o/eWy/tT7+qWDaSrtvd5fx2QTZ7611xNPUPgGVk7K5lhlOlsrIVkbLJPcgaRYAQgDgEhl582sKjsNNCrss0IMlhXHMbkrRL4BSsOx5iAAvYKzbuux363L7QTWkeYKD7JpJzqMgcLY8Zeo8yMMsbC537TIUQBa72ANCyrTV1AGeFZlGtagruNQWUtHCQ7fEgCBicAw+Dh3LTcNWVaj9MaIy34jEHIPduDoh1/O4cCYLtcPt45cToyK8v7gIhYnLUsW2x0Rn4EYOnf12OxMKbCZf/pylTidE8JEdLTPZXSmwmIkinmkkHsA/pzh+58wtBLFsjQ9Tid93lfOyH4AZLNPkFvkB+IlMYy6NrG+tSlncf893hb8+xzn7oiS1Dj0tcumfzGGFy+e3l/fV06qzUPXI7jB4ZVnjd+72VwfnyP7wuvs+94CJLtaq2DhSvlofW+z2sM7nEAEpKPGPoeT0+PGcpklqcAMCaN55yJDOrfGMu0cz7jj86IDUj5s8YKs6ZcMhgsFZxVVIQpmbsxSllfg4QQDILPrRqqabDr9Llj1qruR0w51b4sDaKRPnquEwADI6il6TJZ93SRLX1Bt0/xvf6cfp68LkCZZIznEvcmAiZKKfUQYByQkkGMpgR+cPwE5wV8E3AhRhQwU2QAGQRkqeQpACljknL0pClBHWNEt6dJiXMGnwi4GH9YGOQxFzT6tJ54GSyS78j7+rt8jZes/xgokmKmrct7cNaLJjIT87m+kb0oFVQ5INuwOW1TxvOp+aiKJjnIQPsMjZn2PH7p0nLIj2g+fEknTqslvES7EbTm65f6Ts+DwDhizEEb8po1DsYKICF9daV8szEi82AReImeAHKgHe872kTyvcKGKanPIfNxlOC7og+lP7YxVsU9CTjOOU3lE89ev7Tdtf4daWHwnMTTsZIPp9+70CFAlumQgXEGnDCZQeyAGCOMBaSKAQBkHi3jSGID8G9ZycLn7Ck+lQveaUwU8cOAMAyIPmfpWybZ5EAGDcQn5MAdFL0nIp/5P42BCTFFIGSecg5V5XD/8BG77RbD0KOqxsBFbVtpn/wP7fX6HFA5yST2fsB2+4Td7hFAgrW5pYkZ8YOJPescmmps4yI2loENUn2j+IAzoGuMye2D5J4cW9lnjZn4orRtr880XDOj+EfP61NzLeC4VfIbtc0PxYMplyJPAmjnH+ccmtrBIQEhSH956xBjwKydY7laIqWI7W4H41hNLOLq6gqz9RrLHMi+2+3g1flqNpvheDpKRafjEU9PT5jPF1ivN8WfVPa8/Fv8I8MYlMs9B0mAzaqCDcSQgH7ocDoZLBdztLctwtAjBY+YAvqhwzfffoPr1RrXq5UEIXdnHA4n+Bgxm8/RDwIIO+fgg882qoFzNpf5f0Tsz8UHsFrO0dQOCFKlqbEWs6YB2ga1s/j44QOOhwNqVhxIQPAezlrMWvF1nE9n9MMZw9CLXrIJXXfG8XTA4HtsNhuY3uJ0PuN8OuCw36JuZljMWlytlrBOQt6i9/j2m29gnMPx3OF0PiOmhGbW4vO3n6G+voYfehwPB7x//wHffvMdDtcnXF9di6+QZ1JjEB0wayOSsRhixMf7B7TNEafDCeeuA6zB5uoKMBaumgEh4nTu8bQ74DSccR4CHvcHfP3td3j3/gM233yPN7c3+LOf/QxvX79G287gQ8LHh0d8/c03sAY4nq5Q164kc6WUniU+pSR+5qp2cBaYNRWMsXAGqIxBZSzayiHEiOCltURlpad5DB4mRczbBk3d5ITj7JtxoreGKH6/+aJFHByaupaghgQcDrsX9czl9aOBcWbFaOBOp8hr4FNnTVBx0PmpHQUEHWOMBWDSDgqdpbrZbIpDU2ceMSOcjo67u7viFLvsQajLBrK0Iw/OBFPoXKLTXAP8Wvlx3gIqyIJf9kIkeKpL6RKw4H1OpxNWq1VxGNGZQ9D06ekJ+/0BSGOGiAYkm6bBerNGm/thMHPtsrwfjXI+Q2fO6A2L89BrPWalj5msGojg/ejwJ2CgHYvAtOwkn0/nETdK0pkZLfwsnYYabNeZmrxIA86DQCrXiOC5MaaAEhok1QcYnZmgn02nC4EgzcekCz9DHqDzjLzJZ+iIOh1VQx6gEuE9eQ8NCPM9lrzVzuVLUJQARAhhUrqc9yYtdKUABhvQ4XzZToGgswYuNDioxwkg9/tbFCCCc6VTnYCI/j7Hpel3qU948W8Cr1wzyj6/S0c/70l9QDDmeDxiv9/jlPuPPD094ebmBm3blrLGlG3y9tPTU+mDy5Lel05byqYGbLlO5JcYJZuR7Qmurq4K4A+MlQwon3Ra6qAOrhk/r53JvAhu8t7UUcz0YYCAljfyE9eTwAnXfLVaFSDAe1+i0qjPNRjH+WswVQducC10lhrXU/ODLj/P9SdN2NuYoAQrYtDZTVpTRvRaaOf+arUq9KLcMquUvEheISCvnTI6Y5gyyz0jhDHLlONmCWyOUfOnlinqBzrtAQlk22w2ePv2bSmvTuDVe4+7u7tC19VqhdPpPHH4U644f/Is9TUz63XAG8fH+fR9X/ZgzYc62Ik0ZJAHeUnTgXsAdQSd3zrQZHS+hzIGY0ZdrXUiaUW9w4sVPSgrwtsoc9ztdoVneF+dLcl9jwAfdQ6BOQJ73FeYIU46c77kEY6H+7zOBtfZ7bq6CGneNE3pz06wO4RQ7CjqKu7ZpRJEHEEyjl9n01prS/Yvx0IZpu1EmWfQzGw2K2C4MQKACs/Ja5Q9AlecJ8d2qbPId5QP7uU6IElXVQBQ9nnyCcdMQIUytVqtsNvtir3L+V1fXxf753LeDEjiWnC9yN/Un7QZKcMppcITpB33pr6f9junHqa8a/3LOXFsBF2pXygn+/1+UrWIewttEW2fkSan06kEsLI0GPmUcno5V+69mjerqsL19TU+fvxYqljw0MS9jGWX6XTg3kKbgIAuZY/yR/tcBzMZY0o1DH1eoW4if9Fu1cEL2rnCNSHNuadyf9C2k7Yx+BmdpU/9T35n0Ehd18WeGIahVKjhGC6Dr7hO1B3adqUNCkhwIXuO6TMIx811IU9eZotTD9Ee0BUzSD/acFxP3o9Bwrpkvkl9CfrSYDa/e2mrab3Nz/I1XQlHO964ppcOy8sKOQAm5xiusz7IX4KitDW0bc+xUidTj5B3+Vm9B/5LL+/j5B7MLAFUhq4BjAJr9XkmJQ8MypGfINkK+fsG2WFoDYxluXgHg7G1kqOeSQGOoKxDduTyDJEQPJ2MY3a0fE9Al/E8IH0ODcTBr4EE0d8WBGOsdXCuQoyZ5ysHazN9jYF1Faps+6YEhNK3k4EJrjhQkRJ8n9upGHFcelUul856Gacut2lQZwBdUhzNM1mSnwRgWpmmOIWj5k0LaxhoWfHFiTNWem7nHrhl7W0B8sfxJjgjWS0uAQEWJgExelTWwWX6p2DhowGCZJWnGHOpzR5df0DXHdD7HtFL9g/XUMusyeMcJ3Lh+WWUxuQ1U94aUQz9ocssyfTsM/qRqTjtx5KS4ioene+pgMB6IMzIUq8IOjHRG1DlxMeXX+5HrdcBQMku5fB1tukU2Cs4Yy5DajJgGfMZvYK7ANQuAS1jeObNsmsiQgYPYgilf3XKgREmTYPQSSv9ml5f8tb4M1ZoiFEyGhNBXbBcNcHYDI5FKbUuOmHUVyPIHhCDFYNbrfnzZwvhErPF4zge7X+wNpX10/v45Vw5D+0H02DNJV2SWmPe64euy7Uq8xbNJBhsAaQzWJuBcROD6KZcBh0pIVkCjiNvxhglACEB0UiggQ8ShBPzkyRgARm3jHl9Rj2Hsq55TTNAZOwUQCYwSVr8mEtnn+o1fUafF0h5KVf6uy/RWgPjMWVg30rGPIMLks2AubVFF5GWYGYus6aR/ZZm9CnQv3A5pvF8OfK03s/GiiAvVzCY8JnSES99Vs/5Uie8pJ+Aacb4p+gYk5T7Fh5g6W4p1B2ClPa1yarvZzDbKJooYJxjE/tCBy8YsFQ4yuvcNFLRV+VskgFmRx1fZHmU8+n1nG8u6SO/4iffH+lHmZsC6S/Rr4wryxZB8WLvcI1TBjttyjYR960MTk+qdWDyzCmfZ76+0FsJo/0SY+6T7SUYSfhXQG2t38a97oU5GiMD4WaVAdmxUkXWSRZ4eHjA4bBHCB5tO7Y/0nPS936JJzkubTvWdY0QpYT148M9hqGHqyxsyqW3bTXZA8r9zAh+A9l2yuWvQwglPsIklICw2o2VonimKn5PbtYYE+B4puI+VGhaOOaCP16Q5TJnY9XvHKSQx8WMbmNM1uoQYDw/yyRpM1I5i8a50qM7OI+qruF9j9lihfVqJUmVp1NpZ7Q/iE9gvV6jyf6gwXvEeMxBCQ4JQF1LsHXfdUgRaGrxqd7c3Co7WbJ6mXBAn9AsV2uyxo7BB9ZiCBJUUdcNTsc9DscD6rrCF2/eoLIWdV1huZxj8Cv0XY/DcY/NYgEkaTXc9wOqqsF6uYQDEAcvZbRr4b+2qtFmP8FwPuPbx4+Cna3XWM7FB7NazNH1HaLvgZjLfc9aWBjcf/yIFCPWqzXatkHI6+isRTDSXikEDwkhiiUgpD93MAa4vb2BhUF/7uD7Ht3phHk7w3y5xGzW5nOyQxgG/PY3v8HudMJ2f8D+eEDvZe1e3d5hc3WF2WqFYbnGEAz+869/h2/ff8TV1RXWmw3qWvp411WF8/GEwQ8IORhu+7RD27Q4Ho94etpifzjg9vUrfPbZZ5jVC5wOJ7z/8B7v3n+HZiG45eAT+iHicOgQ4x6xH9BWNVKM2Gyu0PU9IhJClOpZ+4Pc++76BlU1rVojetDDZdmqrIU1YudUlVQ7QN2Iaozioz0ejjj7hNpazOsafdcB3qOZz7FaZH5KSdYtBwCUwMtsm9a1Q+WcZPXn/uP/petHA+ME7VhWlQ4CZq/pzJphGIpzWDsutROHSoR/E/jQzgbtENIgGO+pMwNJeGAsS3h5mKOj0Xs/AeLZm5POPu996dmps/d0ORdmSmlHC3sBMjuWQQKaVnwOjaXr62usVqvivKaCJOguGSgtDIxE7gB4/fpOypikhFnbwjrps8B76tIeLHnPrCRNf13+NaVUeokxI4VgCMetsyzoQCI9SCedzamdaHpDoKOM39VAg65KQIcesyG1A4tGHmlNZ9ll5ikwOtNIe46RgJM+BGngR4P4GtDRIC8dIqQnx8bXeTnnSkYWQTUNImmHnnbKEpyjPOh/pzRWVaDTmLJEOunX+e/LygTc2AnY6O9w7QjaadCcf+vy0hwX151r3rYtlstloRsd5swc5ZozYOUSLKAM8/6kBdfp8nCgnaoEK8jDpIF2cnJM8/m8AD8ppeLQJ6DFjf7m5qa8xnEQUKIcc4zUbfrwrgNJ+FmuK8ems+OdcwVIv9xsSOOUEj5+/IjNZlN0JQNs6LSjfHN9nHO4vb0tPX/1XGKMRcdq/UuAnPLO+WgHPYE07gtcB2bJEYijE1oD5tTPnB/1sgaZ9TwWi8UkIEvvDSlJ4ABL2J5Op0kJWW2Mk5aadymXdPZr+drtdnh6eiqgGel3e3tbaE0ZJo/pwA8drEKQYbValexh8qYG47X+41ip45fLZTHiV6tVCT7hc0hn0kkDLM6xPPCQXw+qoorP45boS+dsAdWleoI4uAg2k3eFJh2A3DsxR/bVdYPj8ZB1EHWGrMVyuULfj7wEjBUxOAfaEVwb6kbqI8otD7PMeGqaFs5ZDIOAhLwfy3gTTCNP0BFOPaEPSrx0sAiDXjh27pt6z9SgG9eGwVqUMfIawSgGdJBXCGTXdV0CMbi/p5Tw+PiI1Wo1AZo1eEt+0sEylKe6rlHlZ5F/yVM6IO98lvJO+/2+yCjtDupYVu95//59CQTSAUQM/GFAh64CwudrUJTVDLhGL2Vm6mxzAIU2tFU0+Et6Ud8yk5prpoOMeD/qX8rdYrEoPc+Zocy56P1cA8EcL8ek91PaEvf39zifz6UnFPmHOpB7OPUt9Rzny8oAvNq2xc3NTangcZkpTd1GAJW04Zg0f1DH6rGwkgVpru2Auq6LjtK6nmcH2ktsFURZ1jRnFQDuwVx/gt0E+VlBQ++Vuow256ntI72uAApPU1dqu5H7BgOVeDbRgDT59TKQhXQin3PNGbxFvqRs102DGMbKQLQF9jl6nXuatn/IE7QN9X7FgA3qAe7dXE+tD7gGxphCb8oHA3vJq5fBjNQ55CdAIuw1bRhMSZkFxhYb2hYg/Vk5ia25aPtrpxTvQVqwQhMdNafTqcyPcs77aFtXnzH12UDrJ72v83XqCv39y4pX/5pLnzuk9GV2mkUF5OQsLY6De+uERzLAXeXs7oBMEyCXQxfnZ2VySd+J8x75eTkzoTgup85UY0zZf7SzLIWAGCIgMRBwVYW6nRXdPDpqxz3dWgMLC9RjNjhpkIw4Y6vaoqrHdm4hSD9gWIvK1MgokDgRlRMZkD51Ve3EqVLOREkyFmIuoUtHdwR8GoqDsuhA51DV2dHnnNzXAZ6Bc7Q3I4OJGxhjS3/slBKssRiCRygBItLbV+Rf+mrDjGW4TRKAMHBtY4Sxo9yamGBy9j0y31bWYgDguwFp8KhthVQ3MNHDD2dE3yPEHgYe1gLOUhdX6PsO7C+LDPCKo1gyhMk3gDhrM2RRMp+QxkxezkEDBQSprNUZVhfgLUx5tmQm5+pm1pY10wCQwbRKg8nA+3O/NF3YGVo3GgDj/gBI3jPHIG+O8jGCNFXuOZnA7D8BrRNQSo3Kc6R3qQAS+nwT0XedtBEwI5h2GdhD2zuECGOkFY41JgPjWwk2SjkjOQHJSOYssmOdv9NInOJ0J+VHWRnBBq1XZB0FaGQ5Xq6P2OAWzJ4jLUmblIHhFCKCDUjheaKG1nsjV7BMsQLPFCgitM1BNdBAHib3v7zvaNsnEHymPWQUuKK/+xLIQca5BNL1DBIy0ER65H7tCZJ9bwhipbEUOEEwglExjoCdOOcjBgDODUjW5VgUVk8wMC7LWr4fgyaQLgClrDNKywkzBpoY83yNfuga4UTFS+ThTCcAsG4KOF/SVo/v8v3J2MkT3HOtA2ABGyHxG7JnjMFkI7cTykoxZYpK2ejoHJBEm/B7kXprIhMChiaVJRyLD1qA5aTop+1OPc88sPLvS37Vv2U8F3qSevUFuvF+L/JlEnBcgPGQg6YiojGIOWAj2fF+BubZmnCvvPQxIokvIUYBxpJqS0HeRwkZGXVbyvt2CKFkRHLd5DNjO4Txfi9MTdly4/xVldpC8cvvMcjp5YAOrQe4P5IuIYaiJ0V2GOgp9ouNAAyryCSU7UqX2jcoGd3kqyJDyt4aZUpep03AM6+2AaV6QoShrfAJftFzu7SR40WlgpTPQA/395Oqdz74Qo9Y7AIUsJc6sPAJxoBA+jyIQzw83uP+/iO220dUzuU9L9vksDmhz8MY1dccDNTOspsB8EscImFsH2mMlao72cfUdV3R5cZKMGepFBYi6qou9OGZXF8XFsK4TuVfKHTm2ULsuPG7tDNdJcGd1kqVFQHDxR5EjEghwCax5aP38ENfSmz35zPiKmBztZHKkCFiv98Lhnc6Yn+QnuKr1QopJbFNDDAEj3PfYR49Xt3d4XwWfCvEafvg+WyGtp3BWoPDTsqTkyurSvpBWyvzsHWdKzBlvKttsVgscDoesN/tcDoc8fbuDpvFEovlAnfmNpd0D7i7voO1FsfDAcfTMfvQFlhUNWbWYVFLmfBF3eJ4OKCCwcxVqCvx09zv93h/OqKpaywXixL0P/QDnIH8WAHZK2fw/XffYrd9wmeffYa3b9+izb4bA2DI/ivnHBbzBbbbp3Lepl+o73pUhqWVAJsSVvN5Oc/OZjOslku0bYPj/oB3v/p7vP/4AR8eHrA77HE+n3G1WqP+2c+wuLvD1dU1Pq/nWP/Tb/E//H//Zzw8PsBZh+vbG/zNv/sbLOcLbJ+e0A9nVLXD3d0t9g87tDPxkTzstvj6q6/wzYd36MKAm5u3+PjxAf/0D/+AP3z1W3z5sy/xxeefo3Iz3F29hk015vMFoj/h4/1DaS04X6yw3lzhyy+/RIwDZk2F5XKJYegxny+QkLA/7BFCxCljDIvFHIvFEvNZjdYZJO+xXK6L38oYh+AjzkYCO9I5wZiIWV3jfD5JGfkgmeSNs0ACziGgjxGuquEqqbZ0Ph1RWYehcohB2g9U7sdB3j8aGKdzhmAfHSVt2xbQTDtmNDiryyUS2KMzhYpJ941br9dFqTHSRDtvqejp/KFDkKUAY5QM9MViUcp+6iwZjkOXTtxut8W5Jou3KBs750vF1yjHsd44dElFgtHsb8gxa2cgHVcETHUWFsc7n8+xWjnEmMC+qfxMjFLuFtkxojPWAZQsWI5fO7k5BzppT6dTcUTRucCsca4LMJbw1s4qHeGvHU/M/tFOIl26keMKIZSNlGAMwVY6yThuXQVAl9il4zylsQwiN9rilEkjMKzLLerspmL0xjHTnc5LOrt19iTXQTsm6Zggj3OtL7OHtDGiD3XcHDVYTgcvx0h5olMYGLOu+Rw+yyrjhwATAx/ISxp4PB6PJfDjeDxODHOdzZVSKo50nd2us4p1QAPlhP8mmMh7kr6ci86M00EpHCfXVoPiBM44Jx0oAaDMk2WldUbmNLp3rA6x2WwmQTukGedH5+fxeMR8Psd6vS70IdDNOWvwmbTgWvFz1IUaUOd8jsdjMVroKKceY/9OXa5UA+p0cFN+NZioeYbypEuHaweB3hP0mrDUsvcei2xs8HksIaxBDzpOuf46gEcDySmlCfilDXkNVuq1u8xopsE7ZvRM2zponULwBUCp+EGZ0aAd9zmCy5wz+YEAAnlTg0y60gCBdzryNcDIMfDS+yj1K9+n7DC7mGtL3QtgwqukH/dvHXwT4wiwCP0M6no2cUzrIA4B8A9YrVZoGhnPfn/K8/BjuZtE+WX/dNED3OOZ5Uz5Im01KEqAg3PWvMEgLx3IQh1C+eR4ma0LoFSNYS9ilmCu66q8fjweS0QtdTH3NI6B9gWzwTWAf9lrh2Om3cH1475C3iZQxvsSZJzNZuWHvHQJelPOm6bB8XicZAizig8/W9c1zl2HkGLJFNZBNAwk43w/fvw4CbriXkV+13qO89O6nEFtuuIBg6IoL7wXwVYGHnG+BLC5z5HmpONqtSprfjweJ3aEzjrVwX/M0KYep21JWeFaUx45B+5f1J36vgzWZBlxll0HgM1mU9pVaBmmTiXduHfofVwDQRrwBUawk/RZrVY4HA6Fx2lL6axq6jWukd6f1ut14Wu9/+kqNwBKwCXHxzXhvUhjYAzaIE2ttXh4eCh6jfqSQSLUB7w/15EVK1jqn73udXAtf6/X61IRinSgXUcZJ/1IW51ZfDgcJrRjAJK2n9kSQe81TdNgs9mUNdS8St7Vgag8J5EG1jnJJDNjRi+DpViNgGPgXPU5J6VUWqLQvqZNwPFwLPoMwuChcsjvc2k45azVNhZlj7ImY6gxz4ELHDN5QQfT8p58bozSmkPvb3of5Gc5Nn2u1I4+7gO6+gbHy8AkriftXwa5aMCW8lTOXnncrHagM83JO9r+/ddcQxT+sMYWUBwJSDZlR6A467neJo49rhMgpS5dDeuqnK0YEAYPIKFtalQZ0B1CQIqAqSxqJ3t5jB4w4pgdgkdIAkqJbVEhmYiqriRrMQTUsYG1ojOtkfvKOHpIBrKDMU7Ks+b7hzAUpzxbhl06ZFvXwjU54DIm2Hz2YunH/jTaNRUkiC+oKh51LX0M+76XjHcDKQFtDGoHVMbB2ho+RTz1Rxz7I9bzFRazFoDHqTvheOonNpwQm47Vajx/hlSC8Y2Ztjb76U9/iqurNd5//w2228ciA9J2qCv6hrytdVkIQ9Fv3dCX84JzDst2bHPBtSffUqd05w59bjXCwKXGJcTKIs3maKsxMJT8LSXWT9D95gGx2cPQTfYcWFXNLNMGdNQCsM6gqsbEBa03YkpS/j1FOJsBBrxg90PKRbazGeqcldYNPfohwphYQF75rc8tAlCTnzjmlHwG5DUYgPw5AZ6sdUg549mYDDYS4Ecu724E2G+aqthK+W5I7O2cs4qQgMo6rJZLzGYzbA9Swj6mCFsZxDhgd3jEcnVT9lueUadnMsDHhMalgqt47/H4+ICuP+exBcSUYJ0V0BMQUERn8cUxIPQlQFfThuV8gbHFgQkeTd0CFYEkm3kBSEYqD/A+craJBc4zDH5RQQ2Xz5yAMLlRQAxjYHyM7FluEUMeg1HVKrgOabr+tH0YgDI+d5phG2OYIGf6XKdfY0WISzBz8r2MgUUExOgR4wAfJJPW1gYxecTcMsKkEZzW96JutNbChCBOd2NgTCoZq4w2MblXMXyGpeKY6RsHBjjYso9ImmqSZxs17gxY6vm9dF36ey7X8JImgLSe0DTTn52+rp/NsefPRi+9hmNCNNKLOEKqiZRaBC5I5QTSDxmeKgi+9PW1CdI2I0lyL5B7FF8O3WS9lSJi8gJyhojoPaLvYaKUyI1GgF1Zs6nr/VO0fIl39J740uc/RWNtl/zglQKi9yXDW4JurLRxjVH422aiGACRpbX1uGQcDgIypVzdxqYEBGkXABW0xMouEj/jIfolIPgBfujhByml7l/Iuk8IENGc7lvlshc8lSvijKEPqhKL3HAEmVOaBN+8RDvNi9yrgFwhKKEE2wGAtZJZaZOFcwmwFvKfk1GEvJdAgo0E8EYBwQHV5scIoGxzq5Qgg5EqIYj5Lh7RnzGEDh4+68wowSHGwCQGok/9upwDX6sqse0QpXx7LMFuyAF5FlVd4fi0w3d//EZKTVcOQxwyAJwpdCn3ZgoMk39q12DWzDBrxee0Wazx4eFbfP/dNzgej2iaGvN2VgDVwAS5ZDFfLIGY4IcBta2xXm7w6tUr3N/fS8tAJGmlHhOGBAx+PIO0bYumbnDI57nxjJDxAGNQVzWquoa1Dn7okJLBMATUtfgK66rF8XAuPFTml4AKFsmasYWOydiaD6isQ2UdxBw1CCkieVoLEdEkwCXM4kzKw8cayQBNY+FiRA0DYyTo1ZqI0J1Qz1tUwaAaDNADx2PCvFtivdrg9avPsV59jd/+7p9w9+YKi/kG/emM0+GIw1ZaYp6PR1zf3ODq6gqrqw2a+RxzV+NqscHMzYqvLKWExlYSaOkDtqcTfvPVH/Hw+BGb9RLLZYvVYYGrzQbr5QYWFdpmDmsg1V9CxMzUqJNFW7c4Vx12ux3+X//9/4T/6i//CvV8hvNhwMOHJzR1jeqmwRASPj7t8fH+EceuA4zB/XaHQ9djl5OMXt3dYd1eIwwex/MZlRvgjMVqcQVEh6f9Fn989wGPhy12xwOatsIvfv5z/OLnf4bP8AYtGjT1AqmZ4Q/3H/E4dOgM8O/+8i/RWIf9bo9Td8L+uEeVLH75sz/Fr377a3zYboFs48IHxLPH7w87HE4nOGvhXYX0/nvcbDZYzudIKYjeCwv89Z//JZKtML/+CvaPX6H7+it8fLjH3/2//w6PH+/x5vVrzOZLPJ0CrlYb/B/+N/87/Oof/hP+8bf/hL//1e8RXY8vP/8palQYYKQSz7sHXC1X+Pj0hLqtcX13i9ubG7x79w77/QHWfcDVYob/7V//W/zk9ga+cfjd118jdj027Rz/5k9+io/7B7TNHebLFfrB4/7hAX//6/+Et29e45e/+DPc3Wxwe7XGq7tbHJ96fPXdd/jdt9/i/mmLc9fDGYvj9gmLxQxffPEZbq+uYPqA3eGMt5+/QTV3EuDqLc6niMPuCU2Tq4XEiMpZfP7Za9xer3E47NF3J3w8n5BQ4Ztvv8M3Tz0qZ3C9nuOLN7f4/PUdzsc9utMRPSxgG5y6FyKmXrh+NDBORx+dSXQQ0SHE9+j0Y78BOkiYGcgDnXZWMWuI32VWIR0Z1toCuFCB0QnJbAw+kw7Kh4cHACjZSCwxQKciHYn6niz9B6D0VaWznYABHegcIx1PdCYR5Caotd1ui4M0xlgccgDKWGV/mEYDE9Q4HA4FnAFQypLyfqQtMEYq0elDOuuDFIMQaFDTWCJQoJ2iJQIyjpHB+r50VNFBcDqdJjxDpxe/S6c46aYBTR7etRMEQOkJSscAHVW8P51eBDi5nnwex1tVVaHn1dVVATUIcPCzXA+OgY6w7XZb5kK+vuRz3QuVDnLtIKOTk3RkJq92etNRoQE6rhOfQ56jgzHGWIAu7Qgnj+k+tAAmdKIDkkAiHdJcc64hf/P5/C7BTcqTXkPyGL+ns2v4wwwmvf6k3zAMWK/XkywjOoDJs1oP8LukDTO/eG/Sk/3NtcNIAyuUpZRSyU7UZY31RdCDYFxxSiqnLf+mXuDf2inM7Eod8GGtgIcEBfhZglakK53B5EXqJjr8V6tVeR6da1xfBmxcAiLkU+pv7TQnv+rKIKQZeZf8q/tVc3+gbm8a6TG8Xku0mHZWcwzkDQIsGgS7dBRp/UlwhsAjeUQHy7BvOfU8eVrTSWelkSacq87+JCDCIAPyD2kGoFRDoKOdzyKPUI9SX5C/OA5dsYI8RDpxDTlfgqTMHn/79i12u13R0ZrOlFF9sB0jVmW+BESKczmOlSa4PtQHer03mw32+32ZZ9+PAKUG9Qg4cp7UM9y7Oa7T6YTT6TQpwRxjLAAiZZqAJeVSy7cOCuBrLP1NYFl+j8EXpBMDATUgr/8mSMZsXe4JGtzRACn3HB3UQZ11e3uL/X4/6c2j+Y17OW0o7uHMPieI3HUdlstlCfBhBQz2ptcBW9wzuL46aIX6iHsnaap53XtfQCbq4Nvb27KPU29pemgQjD8EKHUAig6m07LA8XAM3Nc1+Mk10sE/5BPqa86T+zZ1AteINiv5hc/UupLgftu2xfZLKRW50XYQx7LdbrHdboudy/lpudS6gLLLvZDz0z2e+UP50Hsg9QyrJujqEqxGMAwDnp6eAKD0gSevcd/SAViad5kNXNd1sZsYEDqbzbDf7/H4+DiZI/vQHw4H7Pd7rNfrkvlNO4d0Jj101jF1h7UWq9WqyAR5hsE0GhylvUU7rK7r0tZInxs4TtKRUd68N207XUqb4+a6aduMthf5gnsVg3Fp2+hgSW1/F5tRVZhJKRV9z89pu592CceuW9WQ7zTYrCtxUM55T36ftCA/6P2MepNX3Yw6nOvGwAHaCnxf72u0G2njaF1DWacc0p7kPGinaHmnDch/83xHXcD76apOvMg/2mlInUK9p4NydNAO+eBfc7VuVZy4JvcPD0HKxlkrmaUxRXjfo3YCxBlIf7ba5WpYuaRuCAIguAweOdiclQTJbHAWtq4ASES+q2o4J3bI+XSGHzysdWhnLWbNHLVz2TkO2NpKaeWcjVWCq41B14vDNFMUIdHuAKIP6Ice3bnD/ngodrf3XnpZpnymDD730fUwGCt+UN9rHgaA+awp+/sweOwP+2KnFWewAWZYYH7d4Dj0OJ061An4v/yHf4P/6//5F+j9gP/pf/0t/tv/x9/jf/ntu+wTaItMRPCsKeXd+Tp1ZN/3QOnHCvz+d/+IxWKJ/e5J8ajDfr/NuqJCVblsX8l7EliQCrBbghJzdmeNGofDeL4i37dtk/3qBlXVwC1rzOczdMcx+K3vpeTjcrUSm94JJO0HnwPxbNETQ99DQEPZ7/tOnH1VVcFkfXo8HqVnZ84q894j+YTZclZkA8DEH4MMVfiQ91ugAFXAWG3BOXEgV2YMUtX2r74ubXCtSzXIMQZrXPaCBpAlLqWxQou+twYB+fvSntP35ByMM6isyNgwCLgjJa5tBtyzfRsGCWQxo601BakFdo8xwafACWH3+IiPHz7g5vaVzCtG+MHD5WnrgJ9LMETbg1M/zQga6zNKSgkp5vMSAOeACgY2OhhnS1UEPgtAqSog8uIRgtSsuLwu5yt/5yB23jevUkxCB5ZYRs6enAJaplQSSGmsMsB56+sZfQyDNQpzSAUMsknGTfV3LvkkZZArJuRMUan6IPtegk0Rxlk4V4+ZssbAuedZ2uX+KRUA5iX+kDeQAUndj1mCG2T9VAlwn8/ZZgTMAbAbwoQ+L11aFjTf/9AeeAnacg6aZ/Ld8+emlQwMBMAKGRgHqDWGDLwqmc0VHZAyOFn0kcpoT1NavqQ39Dg5NkB4ahgGdH0PEwNM5QodjXXIpuMz3XFJowkAfCGjz5/9/PPTcVJen6/bS+uSoAJCkOBiBIwVYDSl5zB0SpCIOhUAcZER+xJvarmOSTLVY5QMPznXnNF1p2wvj9US9CWvxfIe5wpAwGYzyqREZxk1v3zWtSyxPSZSlbPUBY0v5doYg8EPGFt3mNKOoNgI2T6oqgEpjS3TeI4wuXLIpCx9XgijM9vTWJFTzpBjVSdjpX0Cl1f8Nl3OtBwQL4J2Rn6R+QSOXxaxzFP24zFIzaYxkFdAK4fVYonf/uY3+Prrr4tdHdQ66DWfBAcbU3p586zinIH0Kq7yGfkR779/h6HrUbsKTSU2+u3trbTMOp+x3+0kuBwJySSY2sFUDj5G3D8+4mm3w6nvJKCzF/uIVfB0YsowDCWZUScp0JYruEoc7Q3tm6DdVYL+TNYrRto7IMtfZehXAkIM6M4nDMZkW7rCerPB9WaFxXyOtmlKtnhdCY+6Suwgg4QweBz8Hs4atE2N2l6jWs5El6eAIQzAKZ91ooerZri+XuPV6zv87ve/xjdffYf11UnAeyfBqjybnU4ndH2H+4cHrK82WC+W2O33uL+/R4rSZo5nwld3d6ibBtvdHr/+9a/hhw6V+wwWEafDEV//4SukCCwXaziXq89Zg8VsBj947E9HBCSYusL6+hr77Rb/8JtfY7HeSF/z/QFICS73K396esLp3CNFoA8DPnz8MMGJ3rx5gy+++EJOQkkqAITBo57PsVwu8XoxR7tcAB8stvsddk97HA89Bh9x7npsD3uc+wHz+QLz0wnDqcd333yLua3QuBr7wxZPhwNCAq5XayzXa3zxxU/x66//gOPpBOcqLOoGs9kc9fkk5dS7Hg8fP+C4fcK3zqGpKlxtNnj96hXevn2LoYn44u1brNYrvL66wV27gIkJh/0Bf/+ff4V//P1vsNhsADPDqmnw5z//Gf7sF3+GP377R/x3/8N/D+ssblYbxN6jixHBVVisV/j5z/4Uiw/v8Zvf/xZ/fPgai9kMP//5z+ERcTgesahn+OInP8FPv/wSv/n+G7imwtOHe6Qht4isGzzeP+GwP6GeNWiaGk1bo+/P+O67b7Foa8TNBodDh5ASDtkHvJjNMWtmmNct7O0N7h8+4LvvvsXHD++xaBd4eNrhu8f3aOc1TucT7j8+4en+hD/9sy/x859/jg/3O/zud3/EH37/W/zki7f45b/5i+y7qVDXLerZDPtTQnc+4BQ8zocnHLaPCMMX+Oyzz2DriMOxw353wOk8TeL41PXPAsaZqURHAMEiOv0IchFw0QpYOy7bti0ObpYQpENlt9vh8fGxONFSSvj+++9LpgHBISoygnn87OPjI/b7/SRjjE5YDcrxQEVFtl6vpW+C6ouqQQo6iVJKpRSldlxyA6ETgI4jHb3NudPhT+eTztqiQ44OLN2jnA4zY8ykJOP0IJcm9yX9deYc15DZ8ZegMsdKsJaOq0sHJDNgmFFHZ57OwNTOZQ1G1nVdMi7061xfzonP5CGM9KVDUxsIOqJP309/V2fP0CghWMRn0tnMagRGbdqkH0GJy2xF7/2kVzAv8i/Xlsqb49dZgaTHJf9wQ9aAO+9DkJ7GBudCkEPPj+/zecaMZQ/pUKbTnQ4WroPm5ZRSAakuD9KUFWYFco24dloerbWlJzeBbmttAW0oS3ydAShiKI9lPAlUHg6H8mzOgWv12WefFdmnvPOinBM0OJ1OuLm5Kdme+nDE+ZBfGQij+Vc70XlRhikD2onCsrycL4CSqVrXNTabTZG9MRPFTIIcyD9aJ7CcuX4e15ElUfhv7QinLr/MVuD66Yx+OpLJjyxZy/LJusoG9U1K4rhmCwety/g+56jLtmva8fmUFd5HH0b4vNHoHoNyyJvaua9lnQFReg8zxpT9S68x11EDrOQvnenLsVw6e6hnNWhGwEYHKxF05nx1Fif1nNaHIQQ8Pj4WcIjrz/fpvNcBMTrg4ZJ/+WwanzpYh7QEUACqq6urIm8a4JnP50XPaICK/Mu9UK8XwSsCgTHGcl+CNJynPohRPtnfl3PVuogA3qVuCiGUz3M8BEiZgUkwdL/fl+9qvmGGMGlLncssx7Zty/t87vF4LPqHQJbeC3WWsw6G4Thp31DnEwz33pfMVR2EJIGFFWLWRZd6XmdE7na7AuRRVjU4xovv6cA72hwEDqinycN6/zufz5NACR3Icemc4PgowwRUtd7gnkma8cBLcJ3yRTuH4CyDk6jPnJMqGGzJo3UFATHeg3ymbTCuC3U7AzG5rsMw4ObmZlJJifMij1wG0/F98jBpQxtGBzpQDhaLRQHCNdDrnLRm8N6XygL6PeodnXXPYBQCw/f391iv1/j48WPRdzqwDRBwn8+vqgq3t7d4+/ZtOQuQD3SgFV/TwKOmB8F9ba8tFgucTqfC17odlAYIqKuBMTjo0g7lOp9Op6L7OR/qQAYgEEwi/Wm/cmwv2aTkw5DbJHDv5B5IQCyGgCrrIu1AJujHYAbaqtyjdTYq10AHaFF3MciJvKr14KW+vOQ57r3F1ogRne+KPa6BCNrMeg/RDidtd5D3NbimaX8ZHEU9oHWf1hF6jwRQdAYwAkTUG/wMx0la6LOEdkprW17bx//SK+GEFJEdtbmkNQACBbJOCcbVCH3AMHRIIcIacXYNxpTsmJjLpKbs9G7qBk1dw2YQy/so+U8x92HNGVyn0zE752qEJOCbOMlr+GFAQoRzBrNZi8qyx3NCjB5d32HoI6yrkGJC8DGPJZfDNPL5c9/hMe+FIQS4SvpBljUwUn56GM7ou3MJrIExOB1PGDKo2rQt2qaBMQkh9PC+k4oofsB83sC5uQCxPqDrzlg30nO9reb42asN/ptfvML/7f/4F/j55wH/9Nt3GB6/wnn3HRazOb788kusVmv4EHDuc3ZRSFgsGRAjwD0rKxwOR1jLwNEGbdtk4P7zoj85v1nblECSIgfWAmYaEApkoBLqXJHGDHPqL8rFxL4F4H2PFBN2+x122y2W5yU2myup3pMSuvMJx6OU2dTAeN938GFAygD20I9V+Iy1aNsZ6qbF4FndTPSe7xlIK+us5ansi7IiItsq2y6B5Xdz8I4xAm6B/pkEA+m7jpQy4GqLiFDWL+3C8Xoum/yYMWPWLPdB4DmYpPcQDaLpdeS6VFUlQS5prOQmPJD7LhoDV1MXcm+Q0rPJOgmGACZ6XMphC/iSYHA4HvHx40dcXd9kmfaTqWpfyaUtpUHi6TzHvT4E3b8csMnAJ4MKFjZnuMUoJS+jEQCy0CeFAljLmvA8EqGvTwFpMQooLmuaxkoTOcBCuugKn+gzu15vguMxRcmMTgBcmnyilCLPvKn1+w9d+nOarmoSOUM/5BK4KQNR0jM4+ABjHCQPVAKHjOo1z3sbK/eS0shjcDjnfDnOIj+lPDTkmSkUGpKOxuTy2YY6w44VIF6Y66deu1y/T12aTvrsccmf0/snlI0wSQ9TOfcAMKn0w0YMpXD3KI+SL4zI56Dci32di/2TAmwaqw2MY5iWnTaJvcW9BJ/5IfO5gGPGJClHHhWAmoMtRpLl++a/L9gmf4901XS7BMafUfi/SHt+kWB4CDEHsORs+RiBXMnAYlqNUuilAhWynrbMBlfreOmzltRRAJEBnTEHy3iwFVplbR7XNMhlXIuXAwzKa1oeosnxTmMFkhQTQm4pYJXdy3LugIB4KZlsf+XqCQZSxSfrB5af55z1viPv50x1CwlGTLnCQLHjsm43Edl8KjzwXBdHxCj7QqmJYmQufhDf2tD3GLpeqvAg7yGZcmWORoKSglHBKWlkopTSZN9gYNww9NL7uqkRo8cf/vA79INUqnI5Fz6lNFa8yAGE0Wc73lYiH3nuPgyoqwrz2Vz6O1uD8/mEh/sHWAO0qrKnrso3eC9BUSnheDqimc0EYEbC/niAf3oUGy0T08DAxrEaFTAmQ+mAYmDa4oz0p46kTaXPSBqTAMZ9w1rAx5h7hAt9Y4xIw4BZXWO9WmO9lp/bqytUVY2mruAcP8+y8AIKOmdgK4PVYoH1ZoVFOxOZ9QOGvsPD0xbL+QK2qlAZCcIKxyP8YQu3cJjPHK5v1livrxCGhNPxJBUbs615fXWFqpZ2iafzGUPwqNsGb1+9KT6wfhhw7s7Zd1ejqhss5gt4H/Dm7hWMSVivFnDWwPsBgEGIEfvDAcfjGfvDAef+jMpVeP3qFepZgz54GCdJNq+/+Az+1GPwA4YQUDU12qrGKldtrPJZH9ag325xPJ9xO18g9j0et1scjicczx1q59DWDZyVoN2032GxbYv/YjFb4E+//FPEFOFsjW+/eYfd/R5t1eIcBmzW0r976HqkEPD+/b3Ymgao2zlmOYD1eBbev7q6QtXJ+f/11Q2Ms7i5vsbm6grBe/T5HGKNwfl0wvsPH7Dd7/Dw9IifvP0TrDZrpCFg6Vp8cfVakmFtg8fjAY+HAw4x4tXtayzWCzzut5jPZmiaOf70T/4Uw9Dj1fUtQt/h+w8f8f7DO3T7A/7rv/kb/PLVHW5ubvDb3/0W//jrf8J/+odf4cuffon1eo2qrvHh/iP22x1+8+0f8fqz11j99CcwIcKkiGUcsGhX+O799zg9HWGcRdtWqNsK577Hb3//Bzw8POGLzz7H1dUarhb6LOYzrJcrtFWNoTtjvZqjG844njscjz2is4jGwNYVWjNHO++wP3/At99/jy9+cod2tsBqc4PZ8gM6H/H+42P2v3oYW+HV6zdomhnWizkAySxfLmY49gHvH7awsDgez9g+7XA8TpN3P3X9s0qpEwSnEb/ZbIqzD0BxklNR0BlTVdIfkIAyM7dfvXo1ieDnAcE5h91uh91uVzJMCJIxKp+ZLjpDMyUp705gm4ANHVoaKKHzWIMUs9kMh8MBj4+PxdlNkO36+hrb7bY4VDXQow9AvF9R2MrhSmXJv2OMz/pna6cwHUAaJCKQo4F5rdQvHUePj4+TrFE6cDUoC4y9+VialY4k/jjnypwJJHN+BCZ0hg3XhOtA57A+MM5ms4nTnrTREaakE8euS8Fy/PxbG0LakUbnHPtIkJZ0oulACL0O5BXNzzrLkeAcacW5kg90dDfvT54DRmCR49NRZzrjnGPS46Khpft5Uj50hvDlIUMHg9BByLFxHVjBgZ+l7NPxrYMfUkol88w5N+kBSYctgEIfYCwVzDESsAJQypySHtoAeXx8xM3NTXHM6kw5yjmBDd0r1Zix5zUzs3UPHJYY5voS7HDO4euvvy49pAki0eFNYIr34W+Cyvw3M1d0ZiN5hGtCh6wxpgDF5HWO93w+F0ebNui4DnRUU4fobCbtqOfad11XsucBAVCYHVhVY/YzgEJfLc+UczrtU5KsNYJH2nmt/63leb1eF7BNg0jkceopDdrynuQByhBlhuAIn3s4HEqJc51RpgObKAu6BKsOeuB6UdYuDWCuqe45SzCFNKNsaABQg9kcL2lLmjHQifTQ60054Zqwsgh5SesJzlmPj0EwlEOCStrJD6CAzhoYo+69DMhg2W4NjpBPGLHMICHSjoCF3ld58OGleZnrRN7gOpOW1JmUOQbT1HU96T/MFiLU6boyyzD0k1K63H9JPx10w7WmDib99Tw0OEZ549gYXAaMlWuYcU266uxtzvl8PmO1Wk0CVygDIYRS/loc2n1Z46enp5JFRx4/n8+wzqFq6hKkwP1OB8hUVVUCGrkHUk65ngQeGRyiK+5wL+V+TvBO64u6rgt9qB9ID/KKMaaMmzqUekvrXup1jo200XYD96enp6dihy6XywLMsy0E+VBnFFMO+By9P3H/1baa3ptZrp3joX2rA1doK3EfJm0YiMdMcer8lMa2GcaYYsOxXQFllK0fqIMY0Ed6828C9dSd2+0Wzjms1+uis3XlER24wZYsHJN+PmlJedJBfvv9vvAHdSF1HHUO14PBo9SNpAVtXVZd0vYnx0e5pHxxnXRWsa48QD7kGPhcyp/W+xq0J010L/RhGEpAC20uXuHivFCAiJQmssZgq+vr60n1I90GgXyg7a0RSI3FtudnaH/T7ud+Qj7XQRjaBrukqXayxxBgcqaE1i2kF21H6hLtNOWYabtzjNzPOC7uTTq4V2f70+7RuoBz1mcVbR+Q5rz0mUPrA/0+x6D3x6lD8192Pd5/AAB4L4536VfNMwN7dBrA1fBDdrwAqJxFVVkgJnSDhw++OCsNElxlEZoWoZZezT4GnE8dumHAMAjIYK045F6/foX1eoXz+Yynpy12u0cgGdROslMMElJlERzgagfrcqZGCkhxQNtWMEZAoeAiKif+18o51FUF6wxCbLHazBBCzkpvW1SVlGOnTFtrcdjvy9nzzZvX6PsBHz58KFU77l7dYbVcyRiQ8l48AAaYz2ao6hoJCUM/4HQ+Yd1YLJsWN4sGn9/N8Fd/usSfvU34/W9/hf/lf/0jvnn3hKu7t/jJX/0bfPknX2I+m6P3HufuLCU6Y8Rms0HTtDJHiC0QYkSXHWZ13eTxO5zOkqFDOaQunM1aSGZ5xOBzNSwj5U6tNYiJVapkTcShLLYAwnjWGRNmU8kstxnkEkAzoM+lu2GA5XqJq6sN/OAx9AOss6ibGgvMizw3sZEem97B9wOYaQ2g9K53rkJIQJX3hhQjBu8x1J2Sn5CzOCOcYfaegOh0S5SzVSQIkTIvWunp7mpxtnvx3xtIeXXKmquc4I0sEe4cTKXAwAyqythRnPPGAulCZlOS7wBGaGjHArwppwlr4BQp5M/YSS9WZ4XPq7rO3ZvHhAd9njBW9t6MFRWboDjh0wV4KLMQcJTnl2HAw8O9CqqVrL9AyO0CTLrUUTH3+57Ugs3rULKsM4iVICXdKxhEGxCjhUnyGwZZ92vwjfp9BMVTEr0wQp4JpWJA4t8AkMG6AlqNgG6MAdawn3oOoPgEWMjMTD5NgL8pMD6uf5Jev8bkezzX53z9JaCYd+T/yU8xSWlqAUpHUDGGgGg9iEQH1XtdfqDke9rvmuO99KOllAE5MwXG9T6dcnBFilH1wk6ZGmMvXj0lTd8Xr5QmGfbjZ9VK58/IlDQwnL+W39f+MPWATFPdS1mCBkyMSEbmbZF5IgmgKPXmTQkouKSVtBvJPBoDkqpmQD7Q9E4xIuSgsxgVHVOCi1aATjN+Xt/rpd+FJmquI3bOfTXLixFgOb2wDnw/RdVi4nJt9L8T2yRg/NtIr3sk2ZdiCPBglceRJy3GsfM3uVCqOdj8Y0r0QUoJJjogRaQ4gtEhiI0cvARhwVLnaZ8qg3em89Ig/CVvFtpbrduEUilBgG2j56CrBo0yM95QAn9Gmo3yZ0zuUR+yfGc+SVyTrPOSET2YuJGNNyp/locBY0BS/ryB7Kk5UgYheCk/HwJCDsYtZ5/MC5N+7ZmuJteS57igZEP7oVPMfdJBe8zgw4f3+Orrr2BtblfCmBXujfk/a0Z97yo32TettZi1ckaKKaI7nnHY7xFCL8EHiiYxxgzanhCD2Eo+83hT59ZACVkmk9h7SUqTS2Z0VSpahuDFhjA2ByEJn1tjUbkKTdPmc4jHEHLiWUowNpd/zmd+ffZEVrGaxaxj1QLRLbU1eHV3h9evX2O9XqOdzeCclCMfhj770UadYgFYJxnjxhq42mK9WuGz+AbursZqucRqcwVnDY6nI+IQ0A0eMZ1QzWZwTULszkB1ROUS1uslrq+v0dYLHM5PsE6CDPp+wOADTC9VL7rs7zidz3DGFX9pk/1lx/MZ1g7Y7nYI+WyxnC+QkodJwDCILA9eAveWyxVc3SIg4dif8eHjR1R1jTezN9KWoveoqh6rxQr1zOF47hBC3odcldnKwFYV6nYGVzkcjiecTscsWxYxGRzPHba7PZAiZrUEylZ1ja732O92mOfS+VVdo61auLpB33X4+OERD3jCcr5APW8xW86xWq4QfcDQdfBDj84PsM6hnc1RuQqh6/Dd998DLvuwqhpV5eR7vZdy8fMZ7GyOk3V4fHxAPWvRzmboOxnndrdHSjU2h70EHiXg7uYW9/EefQyoXI3+eMCx77GaL7DbN3i3/x5XmyssZjPcXN/h6fEjnAXqtsFiNkdjdvjw4QN+94ff45d/9hd4dfcKXdfh2/ff4w9f/wGr5Qrr9RrWGnSnHtv9FufTCcEHzJcz1NbCxIh1ZbGceYQUsN1vMcSAu1c/RTubYb/b4+njIx7vtzgeOnz5s8+w3lwBroJJBvNmhtZVGPoex/MebrCo2haLtUX1uIWrDG5u12ibBq/u3iDFCufjAedzB2NnmM8aXG3WePP6Frc31xiGHtvtHsfDEX13wqu7Wyxai2Ho5KzhA47nASEdEENC3/U4nc7wQVUS+YHrRwPj2snJUr4E9OgYorOLoAsdwOyJS6cfncOz2QxPT0/FgUgnBRUxDwqff/75JMo/pZR7cY09+egM0eXHZbFtcXTQaUgHEh0tjITWGZIadNTZQ7PZrGS68ZLD7GwCPNNhykOqjioi4ERHkHa20fGkS3ZoIF2DJdpxyHmRhjq7RTtmNDhE564GWEgLOsU0OEoartfrMiaCeHTa0imkHW3aMXoZTKAzVRhAQP4iGMEsG01vzkk7NjVYpw0TOv5SdiiQDwAU0JQZKxwL+YlOWTruNNijnX/eS8liAic6Q0SD3rwfx6iBURoeGsznvbhGBK7pYCQ9WAJGr5V2/lOGNeCmAS068oZhwG63KzSiAUPHp3a28rm67CS/8/T0VOanD16AgACLxWLiQCWowDUhyEnaAuJU/vjxY9Elx+MRf/zjH/HFF18UAyclAVurqsJms5n0T+VzCIYx+4yBOrpsqrUWX375Jb766qtJlhT5lmCENrw1vfierjpAemmgjLzL+e73+wJgU/cwe0vzoQ5cIUjPNdMgLgESAivkW+q6OkcEMiNeV3tgKXbSgyAAnXiUc+pzRspRjjl/ZhaSl/l96j3qe+4pDD4guPbhAx3CUz2lAx902VoGFDAYgE5uBkyQRmzroflaA8aXQTGcp65EoB3k2omvweqqkj62lBVWuuBcCAZpvaOfrdfyEsDXvKfBdr6n9wauAefDrDfyoN4jtfyTRpo3+Bnu3RwDMAK7zxxtyhFJHtWBYrpiBulL3UR+0wAIX9OBWARJGSTAfuCUQZ2d6JzDmzdv8Pj4qBxD49y9p4MjFfprfc6S4VdXV0gpTXp46wo5BL0o83UtbV1oI6WUChCo5ZhlrEgHDRZzrVa59CkBYV0tgOvOfZp7E4ObvPe4urpC13W4ubmRwMUw9inXPED9MwxDAYk1wM79irRh1j4zrvXBUX+OewP5RwO/q9VqAj5reeJFurKNDtefbTcox6wwcjkODRQCKHqEOuXVq1dlX2S1Fx14RV3AgA19UT+8pLOYlc4y9zr7O6WxEgrli3s+15hroZ3pWma03aIDSfhdZoqnlLDdbkswms4o53cZ7HQ8HrHf73E8HqV8XdeVwI0YI66urkqwI20a0lpX5dFBYNRbtC9oa1trS5Arx0yblnOm/qFu4di1vuHzqHe5N3Ff1LqGa6bpeRnsoIFY7qmUcwYR0Pbx3mO32xX9QF7QQQvkQ55JSmCUCuDkeMmn5Pcqy4lzbhIcwvtqWaXu4edoC+j9V2dbc45cI9oY5EHyM/WItsdfAq3P5zMaV5XncZ3I39re4euaX7kWen21vaUBaN6Lc9RnF/2dy+9z/S9BePIQ11Tb18BoO1zqs0s6aL31L7m2D/dICQg+5DKOAowKUB7E6WgrBJMQhg7WGDR1hVRXCAOkNGlkL1rp/1vXFdrWoXYJ1gYYE2FNRIw9uvMJXSfBLE1bY7lc4Ze//DMsFnP88Y/f4HjcYT6vMZ8t0dQNjJWeyXVVoXIWrs5nqWGADwFrrLDZLHQuHAwk26qqHCpVGcQ6hxB83g/G84XYv6JjHh+2OBxEF3/x+ee4f7jHt99+ixACrq6u8Pnnn2O1WiOZiGFgNTSWMx1t0cF7BO8xb4GfLBx+ft3gzTrBmUd887v/Gf/3/+ff4f/3hzOO9Rf487/+G/zb/+rfYbPZQACrDPpmvmewvjEJMY0tqLi3OVuJi9iYvHeNQSA8Q1PPDYO8LzKjKukMgzilDYMRpTS+NQYhjK3NqLN8CIA1AiRDnOohSm/VEAUwXiwkGLZuHO4/3uPcnYEUYZHg6loyzHMfR2cdkgOClXtUdgyesc4BNqD2ubx/1nM+BAxNLSXwU0SMDsYKEMd9MYQI4z1cNZ6RKecp73f0M7VNg7piK5oBIeT+rhD2tpZVIwRs1+cEyq7es4mdGMNAF/pdclYgpsELer/VemIcdN7fzAhU6zV2NtsD1GNJ+hpzjcXp3GQAOtPWSG/cqhKwf4iq7DMAaXvADHsAiHh8vM9l8q2AS8ZItjY430+UXs6AhrEWRgFYBYwpmbIhrykA5POxtfITPAIMkjFwJgP8xkwCNgACcVlnq77jZSAERvVzI5MDYgYN+DuMOcQGCtw1mT4aGU/josOA2a4vXQJ0/AD4qz43yWfV36HNQ1pmnjIxg2pptINjjPDDAOdk3JwDgyYKLk6ML+k1iuNvrmV5Jvd0U9aAdCMAk2KUbPwMdpqceV/mGCks6UcB4yPO9+mAjMJ7L/Gipm/m7VTwwzQuqQLGU2QQTUDMcG0EYExAihWSjTkIQ+QqximAmlcJMUl1AxvNlDM0PdLIk75UyZAM/DxCAX1hFPs9z+Y3E159OQjgktbkyyxSSk6e3/d5tvVzOlOmecUCqCID63kuMberz3MRuTaIz8Y2yoOJBjHZ/GNKEEpKSRLGk3RT1qC47IEDQvBwDpNS/jLnqP6Foi6m9FPv5w+llKTOvs30EULBXLDdJf1fohlp/Jy+MpgUI1KQDPxoA5IZg6ZFFoWfYww5cIOY6mW1iZx9DCCXDsrrHbMNIPZbSrk9m/ewkF7bbPdQQFs17vIDC1uNfmPqMgaEFR1kgJAkTIRBan3X4de//jXevXtX9thxPx75mOedvArZjmFmNdDWbU4gMTieDtjttjgfT1ivlxi6MbDXZd/R4XCQwDM1l3Y2w6xpUfH8UVVo60ZA32Eo2eVN3WI+X2T/EINYJQCTv5umxWK+LL4YPwhonFKCrUYf0LgHjclRYDCE5iUrfGJh0TYNbtYr/MVf/AXevn2LZAxOXYen7Q7fffMtjsdj8VWH4JEQc+ujHGJgDVztMJ8v8JPP7vH5F5/h7ZvX+Oyzz/DlT3+C29efY7ff4f7hPfruhH7wwot+gB9OcCZhuZjh5uYGb+7meNx/QNefc0b76JeWik7jXM9dh8enJ1xdXeHm5gaz2Qy7g4CY2/0eAZLZb41B7wP8ccAQRllu5jPMFgtsrlusNhvM5gv0J6loUFU1qpTgfY/T8Yyu7dC6CtY6WFchJo/ee+xz5q91FeY52LTvB5zPJ4g5beCqqlQRCD4CsUeCwdw59MkDvZRVbxuP2WyOpjWwDkjJ4Hjs0J/P2NZ7XF1vULUNVvMVmnmFtIw4n0943G8RLXILBOlV/91332O+WkjwoTWobK6W1nV42m6xDGvMMx2HwaNtG8wXC7iqwhAittsnfPPue9w/PqKtalyt13hz9wqoLM5dh6au0bgKw/mE/njCU0x4//09TjcnvMnBFR99wO5wwHzWYrGY4/bqGt/ev8f/+Hd/h6ul3G+z2eD27hW++uZr4bPjsdjxVV1jPpthu90ixoDFfI55XWPWtqhciy+++ALzxxn2pz0+/8nnaOczfPfN99g9HfDw9Ijj6SskF/BXf32NN2/eSABoAGZVjaap8Puvf4+zl8SOm9U1nK1hbMTd7RWur65R2RazeoU//O63WXA8ahexnFX44rM3ePX6Fs457LY7fHj/AV3//2/vz3otS7IzQewzsz2c+dzJp/CYMyMnkpVFNrslSKpSo6pLggBJgCBAgPSsB/0rCQ0BAvQgQIKepFY10GoWuwaSmSQzSWbG5BEePtz5nmmPZqYHs8/2OiciySyWBEnEWYCHe9x7zt42LFtr2frW0OJkMcH5yQy7qsLdwwoPqw16p9BZoG1aWN7Boi/x76Lf+qZOUIAO0aZpksOTjhSZqUTAkQ5iWfaToB4dnnRqAkggCnsLz2YzjMfjBGhKQJjZXQR5ednJ83wva4vOZILAMpqfY6JDjmARHZMs/0nnMMEWfo6ZRRT+dBLJHqgE0fgOmcXAMTKjnv12WaKVABWw36+KQKgE3KUTi/tBR27XdWkuvBjy+wQomCHF/WLmH/dUa50ABjqseIGV4IMEtVar1V62Dscqx8vACulklI4uCZ5LsPdw/ByTdJDJ7GSuIddGAi+HPQWZ8cVMN7m//Lwcq/c+9XNlX2o5t8MqBXTUckyH0WYSRJbZZIckgQbOTTr65drR4SJBS+99On/ScQpgD2CU4AQd7+R/ZoIR5CN/MPuU51IGoiilktOb4Cq/KwMauB6Sh8jPzjmcn58n+cD5Ui7w/ykPKJ+yLPtWK4LZbIbNZpPOK/fx5OQknV+u73a73XPCy6AGOkhl8AMdKYdgOs8z5VdyCuqhR43cO4JEzrmUKUagHAiGoWx3IZ380oFNgI+AFuUU94T/lhc06Qiic5vBQZSBEkTmczabTVrjQ6c0+YpzlwADgL3S0/zOYQYh38nncS9k0AXXjmM7lCs86+PxOK2NBHwlee+THJUg+CFYIzPvuL8c33cB+zIjkHOUmW+U+dxPyi1+dzabpc/xD88pMzkPQSTqI8psOmslb5N3JBDA/ZTyk+9jZroEESW4zpYNMsCCMoI6lbLpsLwzz6A8UxLwkIETPPOU4ev1OvGLbP/w8PCQZAKz3PnMsA4qyRfKD64LwV/KRgYE2gguy6Ahyi8G7tGe4VnmXOVFWOpFzp9ymmeAe8GzyIxNnndZRptng8FCk8kk7T+DRLQP5QA5Fto8rLBB2coAEfIWz8BhFQ2WyQ7lWEPWPkvIc19l/2oCvyx7TRnCeQNIeoD8zKx4nm3upwwu43oyAIj8QhCM5537y/kwq5fn5+HhIY1XAoI8+3VdY7vdpnYp5CtW7eH68aLNdeE55RxpvxI85zipm+q6xvn5eZJt5Emu693dXbLhGDihtd4D9sknsgVJ27a4vb2FUgpPnz5F0zRYr9eoqgq3t7fpDM5ms73y19K+lzxAvpM8LHUAgWdZVYk6TepKyi3p1JHVqqSu497KzGrOlTL+UO9xn/l+PoMyVWZj0ybkWnO+rC7AwDbaNuQHfkauAc9vcujyjhTBtgG4+XabEcpqymjKIDn2wzNK4nMO90aeMQY2yMAV/pE2Js8O7xSH1RkIZDVVvQdYcy959qVMoz6UgQMuOhh4prkuMqBJBpOQZHAfv8c5SKCd8+e+Uh7I+9pvcu7LNZKfkzpLvuvvQxfny7ivPoK7WeSpoV98lmXorUeWayzmM0zHI+SZgbOxGk+0MZU2UMZgNCqQaYS+0RyvMdhVNe7uVlAqVCc6OVliuZzj4uIcd3d3OD+bYz77CCcnZ6ENUlulfQcA24U2EW/fvkXTtBiNxnjnnWeYzkL2tzHcIw9Yyk+zxztAcCo3bYO6DuXK8yxDURao6waPLs7x7Glo5xVkrcbJcpGqwiR7x3t0ptuT19Za9LF3ngKwnC9w/miGHy4sztUK3eoV/vKv/xL/p//y3+DTG4UnH/3H+PEP/yO89/GPMc2aZA/keY7ZdAJAoRVBaX3foe2aPT5yTsP2dk8/a6OQZbHCkfdo2xosHBEc07TDHZom2JBtN1TkCK2XOjgX1m80Gu4+PKthbYeKfNY5RFwMKsswmc6iE97h7v4W37x+BQCYTceYTMbIjIH2lL8AVOiDmUVbIwWAmJDJxBKbWZSTPO99O0qyKJ0RNbTW4R+jg24MIF6YS9d1wC7w2HK5xGI2x6gs0bQN2qZFH+WF9W7PJ0A7kmOUNjDHIu/b8t4pZR/lb1EMgTzULZTFcm5SlkpQU54R/k5rDZPtt5Dg/gY+iaWhOb7cQMFAqS7qCLf3HoIRUAqXl1fYrFeYTmcAPNq2D6CfAIMOKck4ILV2H3hpAI+99wFydA6uDyA4lAnlJRJ0G/WzCX1LfUDAxHtC6fAAZjpYDBWi5Fjk39Rvzg0+kiDfoh4VWasqAnZQCkOZ9gQ7Bd7DAPBKPvhNgNh3/W5vjHyLuCcB+Jb8D3MJgFnQD+yNHX1d3oQNUEMQZ1jzfUDLORf21PvUx9a6bi/D+VtrGDC1wPsuAI/WMjDPoo89xqEUnNIC3hF0sA7ftSZADIY4GIP8vFzXw30+fO7w/Zjhz5R5xDgH51MGvnMOPUJ1fOUdtIn77XvAxjZhCGCujiWy1QEyKvX5oSyQ+0o/Dm1EKeNCD3kPH0vRU57LtQAOIeuwvlIXfhd913odrrGKwDDbmvw2z0JcQ2stemvhlAWUQZYDOsvhQu1xaOuhYFKbBK0jgJts2/03Sl+l3H/r+7TG1oYe90Ge9nCuh/cWfQ9onQriQy7LHi/xTKd57Z8X70MQEgA4O4C3w3oNfCh9F9/ar2/JAfbnjr9PgS4WzsfqKfDwFoDL4bM82cjhvuygYrZpAL8JpiJVr/DOIxThoR3ew9owD2WYdNjC9l04z32P7XYTx6txeKb21sV5GK9D4J42IaiL9yuhExRCZRbeKVb393j9+jV+/uc/h7U9lCrAKh5ce20IfofgAZNpKDUEsBJ4n8+Cnrp/uMN2s0ZT1zAm+BEgMIFc3Hs8QnBfZjLkRayY6Ty0VhiVAWiH8+j6LpQE7/uwU0p/yw6gPOXd+fzkFPPpDJtqh91uN+BEfmjr17YtbNenpLXT0xM453B5+SbxT7AVgKrtob3C8nSBj95/D//od38Ps8kUv/r01/jsyy/x+u0V1tstoL4rcAb7FM+WWu3w8s018LM/R5FnOD8/w09/+lP8p//kn+InP/kJ3vvoQ9xfv8Xbr77Gq7dXKMYTlKMRMqUxKTJcnJ3C6AmmyxK3dzcB4xqPMJ6Gyoqd7VGYAqOyxHKxxM3DPb788ktcXl7i2bNn+N73v49Hj5/g8vISu7pC7ywmozFmZQi2rKoKu12Fpg1tj27u7rF6WOPs/AKPHj3C9z/+GMvpDNvNBsp65MpAFQUUgGq9wappgVjNCgjtHe7u71PFu/lshul0ivOTExRF8JdU0e9YVRXm8zkWywXgPZQPMqkoCjy6OEVXt4AH8rzAYnECpwB4helkBu88Vrs16r7DarvD6fIEy9kMozJgg+vtDk4rbFYb6GhLeB3u3HXXwjmPrmpx5RW6qsHlzS3M1TVm8zlOzk5xenoa/VYdtDY4PT3D2dk5Xt/cYLXdQCuF++0a9/UWm/UG37x5hfOzM3zv+fshSMkAo/EUfR0qPz08PIQkZCi8ubrCeDrCOBthUuY4O1niy6+/wvXtDU4XIVC/rRucnz3C40ePcXtzi/XDGvP5AvOTE9yuVvjyyxeYzCY4OTnBbDpBuxsjy8cwuUFRFlC1wjfffIPTszMsFif44IMM88ktrq9v8OrVa9zeP+CHP/wx3nn6FMvZAtNyhI8/+ggqU/j0i8/x9voat7drTCZzTIoRMq/gux5OG8zHc3z80UeYzDJstxXapkHbVXj19jVGswLjcoTzR2d49PgcP//5z3F1+Rp/8I//OabTGa5ubvGLX/w1rm7uYTIfbCptkJvQkuu3od8aGF+v1wmsBoZyyHSos5wxHd+yJKUEtAios5zgEGG9n11DoKzve9ze3qbsJoJDdHrToSxBRWDoeXfocJLOEAJxdDgzA0Re1FJUeXRS0YHH7GCZKS57XALBYJegmnTicUx0urBEqMwEZPYos4t4sZOOLAITBJD4XukQJKhKcI7rwEugLMlJhy2d+8w0pFOK2YDJgIn8QCclFRcz1AiMlGWZHG3MDmJ2EcdGMIvPI2/JagEyq4ZzdM6lPsl0TgL7gQQSrKRDV2bm8nNUttI5Sl6k44kGnDQueOGWIDrXCEDaBz6f/UkJJh2WWSVP0lkuHc/kD5nVzrGTDoFNgn8soSrHxnfSSS6dR+Q/rrcMgqGT/rsynPl5jkM6TzkuGcjAuTAghWeUa8Z1Xy6XmE6nKQNwMpmkgAE6ZXm+OHe5JvJvzv/29jaBN+RH8ppSKmU9cqwSSOF76Xwl31Gu1HWdzjE/SwfdocOGhhV5RP5ZrVZomgbvvPNO2jueXzqAyrLEYrGAtTYB0tJxLJ3DfN92u02tISTYRzCFMo+gnhy3zMSSjnvyJtdCgrjcF+69zNLnuSOIJUFqvlNWiJDlfZkdynWhQ2w8Hic5w+9ZaxMoxX2Wa0ggXpZ7JohJ/meGJcfNsfLdBGEkz3Nu5EsZIEQDnWdquVwm2SNlCvdUni15LrnXBGi4B5wj5SBLqPO5vAhIWUmZSDnO7FYpAyVIJAF4zplygXza9zaBJRLsoN6TYAnlD9eeTkVjQhln733SUdQZfC7lMc+aDHDiOXXOpcAtyiCpP7kWBAxlhrsMAiIPyXPB9zEgYwDaB0BMgvi0dagbqSvJG8xYZtDE/f19OjvM7h0yzQYgiLKb+8vAGcl3DGLJsgwjY7CtdmmM5GWp76RtJIOq+FzqwSzLQs8qM5SjBpB0nwyGsNYmoJ7r3/f9t2Qxv08eJt+RhykTpOwh72y321RamxUceI4YOMXzTp1JfuYYKScp4zkm8phzDmdnZ2nPJpNJspuLosAoRuKSd/gOBkPOZrP0c6110nNa673KBpeXl7i5uQmX9/MAVs1mocTx06dPcXp6mmQdWwCRdyTwR95ZLBZJ3tOWIs+H8sAFTk5OUsALAzpYxl9WvTgEB6lDZLUczoPBQuR1XqQZSMLzw3PH9eb55Bhl4J4sLS8rxozH43TGpc1Cnb5arfb0N88y95L7LoNbpTOUQUGcM3mbZ5Dz4/rLIC1p21lrQ+Yl9rPeOWfyN/WndJBzPHJdpTzhWnDO8nskGVxAPqEe49mnvJDySepYqeOqqkJmsnTGOC9+9tDJLO8C/Dn1reQBvmPPoSqCL6TTTz5Lvlfah1JPAEgVQBiQwu+SuCY8q9Q5fKa0B+V6/n3pn/yTP0BTBzsj7KEB4Pf0Utc7dL3CdDTGfDZBlhk416NtY3sJk8H64Cyw1gGxxKwGgx8z6CxDZy3qusW4LJFnsYqSAW5urtC3LR5fnMVMboW+b5HnGkqHXuLOOUADbd/AK2CxWCSnT900UCqUCofgea01rMvgOgAeMAhO9ra16DoF32cBxOgVOijkeoLpIkeeB5368PCwF+RBhxgQfBesNsCzPSpLjKPuKssS5+fneO+958jWn+Fnf/4z/Nm//SP8Nz/7KxSP/zH+xf/8f4onzz/AaDKGcx2qzQ6Axmg0SeteN3XU76HUfd87KGSYTKaplYnWPtr4k3huPIpcw8TymlVVwagsjqlAng8VoJqOgT49ygIoyzF677Dd1mjbYGuNx5PB8R/vjDKwisHr5MPJZIJxUaLxHl0X7I/xaIp33303nClrAe+QmRDwZT2gswImCyAU17L3Dm3ThJKbnYVWGRbzkz3guOs6+HISeWT//lJVVfI56JihSnlO29r2PvSXLIIOU0aHkpVawxQ5lDPInQ/9TrOh/VylhzYRlC+HxPu9tK+l/SoD5AHsBawOMsVA6yHgQSm7JwekrUc5rlTIbJf+JmlrUfZnWb73Pq018gww2eBTkoH+LK/svcft1TXevHmN99//AHleoO/aFIQBpVKvY9IhAChWKf1Mylv25iV4rxCCXrwOWZ8BcC7D+4yGLHnMzFStNby1cFonEPUQ5JPyegAeoy0h7sm+t+iUi1nxYv3VUI3uEBRKcI/0mYQP7K2DFSWVD/0rkg7BTKlv5DqnNfXDHHpr4aCQA8gyBReB8WFcLlWckH4G62zac/KB5GfJP9LfNejNPpQiti2c3w/IThUDFABZTly8Dwf/lmS/48z9XXS4puI3UAIYhEfsJ79/p+Z92ngP5wKYq71KQQZ8FhRCn2fQfzzMjStu7ZDpemh7HNpdIUijQ9+3sLaDx2DTKcWKDRrKDQEgiZf4bPI5gN59d8DBb+K9w8/K//8u2Xd4zgDAqOGMsRqNixnumXXIcofQ49jAa8oLZmbrNAcAexnklKuH9yfp6+v7cM/t2hp1XaGtKzi735YmPJ4RO+Gdh7wn/61jRnvCCABAR0Bc8hKGf/P7WZbBqFhxIJ4ZD59aksh1ZMgQf+rF85wNZfZt1wO5vDuGNjNGBxtOI/p1hsnBkwdiaXOngdB/vYNWMdBKOQA6VgcJQHZb1bi6fIu2aZI8+018430A19uu2vOdOufgrdvbM979eM7u7u6CD7Vp8fjiEfqYPc3Md2I00mdKueV9kGgcT9e1uL6+C2XAoz1gTPDxnZ6cIc9KVHWNPsr+xeIkBbvzLt21DbbrNWaTKSZl6G/cViFgva2bcOa1Ts84vD8ZY1JL0tPTUyznC4y2I+w2WxQx8NB5B+dDQtVoNMJ6tUJTN/Ae8F6lwG4DJndZNE0P7YH/6A9+Dz/+0Y9wenKKTz/9FH/0R3+EpunQ2vDMtDPqO/ZM6hVtoFVMKPLBlu96jzeXt3jzf/uX+K/+n3+Mn/70p/gX/+y/jz/8/Z/iJz/+x7h+/RJ//de/wNIrTGZzLCYjaG+x3W5w9ngRs/TXqNsWbfQFnMV+7UYHnfL82TNsNxv8+tNP8ctf/hVev7nEk6dPMJlMgg/HxozlbIQPP3ofNzc30eZUWC5GWG03+Prrr/HZZ5/h9PQM7zx7jsfn53j27Bnu7u+xW62R5TmeP3+O50+e4u03r/D65hqbaovexqptaoRytMSzZ0/w6Pwcucnw1YsXCcMbjUdYLBe4vLyMwQqngPfou4gzjHL8/k9/H7nJ8OrVK3z18iXWuy3eef4ct9e3iR8Lk6F3Dm3XoelarLZbbDZb1E2Nh+0GpixgnENTV7hfrZDnOS4uLjAZz4ItQ1tXa0zmof2g9aEFwHa7hbUW5+fnmEwm6Y4+m8/QxwpXlW3x8OZVqOBc5Hh88QiPTk7hrcOvPv8MvnT40Y9+iPV6jb7rAOfw4QfvYbXb4ub+Brd393B1FxNcWvybP/13GJcl3n36Dr7//geYlCPsuhCYXjcNenePsixxslji7OwUVivAaJSjcA9WWmGzWePm/hYP6xXG0wkmkwVGRYnZaIbT+RLnJyfISoNXr1/jz3/+c/zqV7/CxfkFZuMxPv/yC7z/4Qf43vc+wWJ5is8++wyFVhjnJXxvUa23UKpB3/ZwnUPf9sjLEc6ePEULhYeHe7x+exdayuZjnF+c4fd+/w/xp//uT/B//r/8X/Hxxx/j6dN38NGHH2I8vkJWhLtm07TYVru9dnV/G/3WwLjsfcgyxLx4SSFJB8ZhJhqd386FSHJGebMco8yEooDy3mO9Xqff3d3dJacds7tkBhcvqbvdDsCQEQkhnOmgI9BzmJEmgWbpdKIAJYgkM8z5GTpGOHbnhmyZJLRFljOdsrLstAQJeFik0JaO+Ol0+i2nHZ1ufD8BUYLfMiuJc6RSYQYvHZ58Hx3LvKxKIObh4SE5RQkecr8BpP0kCCOBTnlhlGABjbLEpBFQkM5Wrhd57dARxrnKy4HM4pfZM3Sq8zmyhyQv5nx+Mq4OHGvDJTZLgQR0qo9Go71MF4IoBDuyLEuZyXRiSCCa/WHpkKbhchjdTGcAx0QeI0mgTIJ65FeuhQS3yOvkSWZiSYezNHro4KED97AMKp2PfKccs3QeSh455AWecwnm8T2cJw1onjkJrM7n873PsEqD5CXKh81mkzKaKAcpRwCk9ZCXTO4JnecEW+X5p9NIBvXIgADp0Cafk19khj2NQumwoIOeWWoMWpGyIs9zrFardK65D9wj7gfPDEEK8ogEnbTWWK/XaSwAUk9brg+BDsoH7j0BLgJwkn+ZMSrBdplZy57MHPthRp+UJwS7+DwCXBKwlGCCPGN8tnMuyVz5XQZEcW34fQIUzg1BSxJ84x4eAtLUUZSnDEgyxqSyy9wLymb+TZ0oA7y41lxDpVSqbgEgyX2CEaz2wGxOyizyEOWCDAgg38uqFvISPAQFDK1SuDey3D7PO88E15V7y3EegqLcH54ZWY1itVqlz5FXqJNZfYLnmeeh7/tYJnrQqZRj3Ocsy1Kf5bIssdls0npxvXlWeUbJX1LOAUhZ1NTThxdYWX46z/MUgCjtLMoPmZU0mUxSYJ1sI8J9YmDB6elpkDHxjHFsMmt/u92m8yXlL8E/rgPPAPUA5QF1FOfCzP2+7zGfz5OMkWW12dJFyhDJO7K6D9eL+pr7y2AhBsTxLMn1TE6A+P1DHUIARdoIlENcU56/qqpwcnKCvu/T+nKM5F/O7zA4oOs6nJ+fo2maBITzXBEwzrIMz549Q9d12O12ScZuNptvBS0qpVJFI55tCfDTrpf6hlnV0n5mgIiUrbTFjTEp2I56jPJN2hWHDn+Og2OTNiHlAHUxn0HdwbWXQZCUUQyQGjJq6zRO7r08O/xbVpWRTlZpW/GcUc4SbJIAkJS5nMN2u036kd891BnSnhqct4Osoczj+7O4D9I2o3w6LFkug1cGR+0+qM31pzwkX9LWI+/zuRwv7QnqTzkmab9JZ7x8d3IexjHwdzJojncK/k7aIuQJrivHK+1faWMezkXeP6RM5nepZ7g+0pkrA7DlXUPeQxJ4IezYvw8V2Rwo2nimKLtKzKIu4DjLskBZZsi0gXcWvffI8wLOKzR9h6aN9yWw9GSBIi9iL+gO1baC9eT5AGZ5D7RNh9l0CTXTCNmNoRxtWRRoXQ/XRwe5B9qmwXS8wDu/8x7KLGR/9L1FbkbQ0FCxrHKWx7uwztB3Fm0bHVclXRM9lNLIshzGZwDCXMoylMa0rg9guw79Duu6Dn3Vs9A/crPdQimNsoyVObIsZDyZoLuXiwWWiwXGkzFu73f4d//1H+Ov/vxPcX/X4f3f/5/hx7//TzGe5DC6gq07ADmKfAyjQw/p9XqN+4cH7HY7PH36BEUxAjAELhIo5XkP/M37SwgmIBmTI8sK6FjxuY37lGUZ4GP54+RoBVwfyoGaRZ76YG53awD7mWDS5imKAkaH8o6jvIhnUcc1zjAZj9F3DTbbDXwsOR96c6q4hhkQQRIT9cbrt69xf3+PareDcw7z2Ryz+SxlkPMssR+scyGfL/QjD2EZzsa2L0ohy0KvculUN8Zggkns723QdhbWVtFPHFoIaM1nhgw0IJRRt84hy/IoG+lnoD0aAkRkxSVpu8j7vrwL8HfyD3Xvob9CghBSr7B/7wD27Ae/ArzD78sYIJydIstiD+ThXuOcS850rTX6rsPrl99gNp3i9Ow8jo2VUADgcHwSLAOU2pdp+/OIZbcDAhR0XYvQCxgeOUoorWFdB2gTS4YPz3ERzIX3sPApSOBwveTaDOsXWxRYh7YbKkG6vg/lUF0AsAa/koM66BEt/TmUp0r95szn0Hc4rJnM75XjDd8nML4PPrFcNx/P+RiF2N7AwvYOvffwTsEVHtrEjGcACg7wodIHtCj/rT2UCDKg7SvBR76PukvaYH3MLm3bJv2xfQethsCWAONT7wD7/dm/TSpmKQdsYIAMh7l/+/OxMvt3rquEG732+3zv94PNE49YC+cCZqg9kAVcPI4h2jE+BOIcnrugxzy8H4IhJTjI8w8gyfigfzv0XYu2adDHCh/StmDe7WG/culjlnNXSpGpDlbYp4Xcs7O5ljg4r/Ah4/I7zpeUUd57OMhWMzEY0vpQGRr7/aat7QCYdK69c9DpHd9dBj6U7Vfp99YSGA9VXPq2i0HiNZq2CQCpHnSHfF6gUOpbsovj+vnwWyfe750bqg2oECCkYgUJ70OwhYvrGM5T+KiUP4cUdNp+Ow3662xvAyhuQ5uH6VwkDCEEJfbeQzuTMk8jJgqAgUMuBjE5KDX4IHproV2Yv+trKAQQ/vbuFl98/im++OzTmF3KfRv2XeonH4Fx77q9M2SdhVEa8/kcBduHRYygt2FeLp4FBoC3sf1LnmfIM4PMzLGrdmiaWD3VGEB5tF2bfMvJhw+Fru+QZ1low+FDEMZ4PEVrLSxCZnwes8iJI3Vth2q7xXYXwOumaaCMjuXcPVSeYTQZo2lb7OoKXW+R5SPo0mA8niKL4LvSCmWs5rrdVtiWO8zGMyyXJ3jWWWRl8GlXsc3QqJxguViirVs0dSPsBoRS54otPHtoBfz3/pP/BL/7e7+L+9UD/tUf/zH++lefoW5a9P1hCxGkKgHwEiyXesfBux7aaGij4jl08J5Vmbf42c/+FC+/eIF/9YMf4p/8p/8U/+P/yf8Io5MTvH7xOfq2A3qPySjHX3/6a2zq0xBgFXXI1dUVyrLEcj7H+dkZloslbN/jYbPGs6dPsdvu8Or1G6xXKxR5jvF4HKoFKwXbW0CFVhTlaILZfAG920FrhYvTM8wmU1xdvcWurvH28i1s26a59daicxa7ijhewMFMU6PvPDob/Ce7zRbb1RrTcoTZdIpRUWKUF1A+lMw+OTnBYrFItq8CMJvOMJtO4XqLN69e4+zsDMoYmDzD1e0V8vEI8A6TyQh5plE1Ge42K/S+R93VgAbGeYGz83NMFnPcr1aYjkbITs+wODnD1fUV1tsAes9nM5ydnGIyGePu/hblOATi5lkGZz1ub+/CGessXO9glcVuu0NucpxMFxgXJZRWaLoON6s7zCcBeFYeaJoW5WiM27sHeKMxmUywzOcojUFmWDFbo8rG6OsGvfL48MMPAQAvX79CpgyenF4gNzm+unoN34aqS3XX4vXlW3z47F3o7AO8vHyDXbXDyXwGeOCb169QjsYYj6dwymC9WePt60v8zo9/hPlkiraqANvi8vIW5+ePoPMMvbeouyZVH+y8RzkaQWmFDz/6AF1tMRmVcK6NsT8ZRpMRqrbD25sbzOZzTMdTPH/6HNWuwtnZOeazKbzzeLh9wHvvvIt/8c/+OT77/NfY7nZ4/foVZpMpysxgMZuhHI+x2mxRxza6vw391sA4ewJLg4BOZToNmKVH5xSdOAT76CiiMGbmj9ZDD0JG6NMBVxTFt0ATWYZagukUstLZJ53g0nEjs9oGJW/3MrbkZ4ayVgMIy0sSwS+ZHSId3zSmJFghnUsA0u9kRotSKpVkJQhFh2PXhdKP19fXKQO/qqqUJUmgj9lI8sLBi7p09DLYwDmXMoRk4EAQxPu9b/M8x3K5TI55jvH29jY58mgAcA+YYcw5ywsmHUdce/KTdPJK4JzAIOckL7CHFyzJD8zWovP7u0q18l3s/UoQTGa0yYh4OrVlGXnuJb8vs7bJSwTAyKcyQ5JjmM1myVEoe2NKJzPP43a7HS7F0ZgnmMuxk/+BfXCda0DH4xD9vh/Bb4wJJTvE3nGNeT4lEEf+ohOSe0x5wv/nWnGMfA7PE9ecPGStTeVd5WclYMuzwlLfzoXgHWYYK6VwenqazhsBHAJqdK6Sb2S2AH/HsQ0X/qFcKB10/L7MkKFDWgavUD7Rmc+9Zl9x8hWff5hJKZ3o/Dmd83wP5ZbMQGOWLWUreVcCUQQCyCMEtaXzjbwkZQR5l7zAM2utTeVrV6sVRqMRNptNyrSUATgMLmAlEq11KkPMedIoJV9xTFwvgtDcF8pVZpTL4A75XM6P5+ew1ynHSYcDzxHnxrmSx8kj5HeufZZlybiU4LwEWRj0JS+zMpBLguKyb7DkY8oDCchzjQAkGcO5E+ykXuactR7K8vPZ8llSt/Gzxmj0PXtF5ul8FkUenaRDhoUMwiEPECwh4Ej7gWAc14AZSJTf5FW5T3L9ZOAXwU3KryBbcpFhD/BS33WD3qH8sdahbXfBmW9Cr1TvkRwAOjq1tFaoa1ZwYWWA8LmyLKC1SXsYnPtl0ntSLpI3pGyXuoFnh2eYskUphfl8nniVTlXKankepC7frNehJFFowIeuabHbBL3zcHcHQEFnQ9WQtm0TOMtzQN3HQB6eK/I/9Zh0RtAGo87ifMqyxM3NTeI/KQupyzgn/ryu6xTtzf02xmC5XCZbins6m81SIBGBembeU3cxKGC73eL6+hrGDFUNZAAHbWbatZLnlsslqqrC5eVlsiMY0KCU+patM5/P8fjxY8zn85QtTj1G8J3PobOf7+T5Z3k4tgugrgiX+SbJK9pwUnZxLLSTrLVJ18kAEtrWUkdL4PNQtvB7h3a9dDDKAFDyL2URA61oh9GW4nwkYMz5aK1R5OHMqeiQCf0nQ5ULIHjFtTawzsOYLGTdxn9rY+ARznUX1yRk5QZnmDZZkiFt12GkQx9l6sWu76GNic9B0u8EnXlH4rk+dHBLOSv1kXS68gzIACg+n/vLM8ozUNd1spWkDcdzyX1t6wbVdofpdAJtMuQmALPW2ujocCnLRuoKBirIexnlG/lL2tqcM21TngnyAWUV+UUGZ3HMEjDkupEfqItpF8hny3sgzxbtCYLx3AvKV1lR5bscqv8+JO/AwWkbZB9U6DsOBKC+yHLkJot9VlXM4jRwNmRk9dZDQSMzQefmWeD73vUIvWc1jDZQKofROeBV6CNsNYoyT+dZWQuYkCXquh7exGBs2yHXBSaTMSbFCKFMrYvgLpDpAH4GICw4813fwnY29uIErPXxPARgw8d+jVmWIS8yeDjsdhXqpoX3DrPZHCaCw2FPM7RdyFIJYHOsrKMNurbDer0BnIdRGhoKb9+8xX/zyz/Bq8++Rpa9gw9/9FN88MmPMF6O4dsqZm0BgEpZPUqFHt3Bt2BhTCj3aCIAq9VwF9jnYR/1QovMmNBXFIjgQtD/gc+H/qEmK+As0Hc22kYOtncIvccZOBJ6bYdz4MDOs2Gvs1A+WXuoLPQ+lL6IIJdZ/QIoizLMUYdsyiwvUOQ5bB97dnsHD427uwdstzt0ca2NyWGyDEpRFmWDHa+GoPDQr1bDK4UsLzGaALm1UPBQKtg1yiPJPlkRhKQAFMVwbyewxnkBCuPRGF7tg0/A4f9bBIB6H5ySvhvKHP4tQUd57gPvDS1lOGae/T2wioCE431jP6DBOYfcZFA6vkPYdAy+1FGPZJlGVUUZJGRGlmm8efsGy5Ml8rzANCY8DO//dsnq4WcDeCXXLPx/WC8FHVAk7eH7UJkiFPZWgDbQMdvdO5f4PO0j34+QWcq1leu2v1ayOgiB8CHY0PZdRH40lEbsYRzhhZTtLUBivZ+EwXvlIa8k0t/e68P/D9/9dkAEPzsA8YGsDQBC+ED4j7c9Oh+A6CzXKctZ62EPNHQ0SQgAur1n0icj58LP7gFf0Z4msEufm7c9vHJwbggscz7mq6f7fRr0d5I8H4djkeNJa++Hfx/+fn8dXeKdBJh7UanIDVnjzjvAAZlSoe+94v6Gr2motI5pfDHjlmsVzu6ge2lLkLiOwc4PQd5d06BrW1jXJ0g/ZYMqhVzn38kj37U+hzzDz/1tvLh/VuP7Vb/3WQbFeC+/62GUaO9jySMeXoem3D5WVwg8OVRi0BF4h2LZ9v3xBplm4dx+5R+bdH6oXGBd4MXNZoPteoVQ1p/y2Hzn3AJwLefKcxHkjIt/h8+RN4bgmcP1Z29i5wL/kM2ljJJyyvvQkmDfr9OiazvkWY6iyON9p4DJaygtgnKiPIVW8BaJP7XQA3AExg+CGFwAVOkDybIM9/d3ePHiC/ziF3+Ju5sb5JkBks2Ob617eF8ITlNeBOUjVLLIsgyT0RidD/Z4VVfwQJIVSoU2KqmdiA93+vl8hpPlBZ49e4abmxt888038TPh+U3TxIpjgDEhOCGsSQHX25ilH2yIelehczbol3h3ZNU3rRSQZcB4HGxh7aB0sOssgM1uF/xYoxGKcYOm79D2NgXAT8YT2MImn2eoqtZH/5KD7S3yLGAdJstw/3Affh7tgfv7++jrUwK7UshMhq4f2hw9e/YEP/jkE1y9vcRnL77EF199HTLjaU/qEP7kXQjKUUqF0t9pN/YDXeABpWxoeyB/Hk4onA9Jam+bSzSNxcOuQQ2P/+yf/Lfx9J13sb27w9X1LYrcQBmgqiuUoxHK6Kc0mUFZlNjudiFYpLeYjCehQkzXYzKe4PHFIzh4LE9OUnu20WiE8WwMDeD+/iH6XICiKKMvzOPi/Bx5rvGw2aDtLcazKTob7sCzxTzYOgDuHh7gbY/5fIosN9judlhtgkzouhb397fwrkc1myM3GRbzOW7verRNi6br4CLQX8We5OPSwY3GGOcj3F5do6lrdM6hsxZV0+Dq+hKPTs+wWMygoLCtRujh4HTQH5vdBqu2x3xWYTafx0BbjaIoMV3M0TmLardDvdtitVqFoJLZDGU5wibySVmUGJUjnJ2FBAh4oGu7EOxlPdarBxRLhWU5xmQ0gRvHMCodKsO0TYvNdoN1XaPqWnS3N3ikPcrCQCsD4z3G4xls79HkJfquxaau8Mw8xWQxx+k04HvaeZzMF6hgMR2NsKsqbOsaTd2ga5lIGAJJqrrG7OIxpvMpqrqFyXIsFyfI8xH6tsHd3T1gLUZ5jqdPn0D5DK+u3oYWIkoD2mA8GWExDaXem7aDMQqzaYknj55BwWG9vkfTdHA2VEMzZYl+69HsdliMRnj3g/egvcVmt8UkL2KbJ416fY/MGDx75zmKPMeoKFEYg/u7ezTVFibLUBY5TpYL1O3gk//b6LcGxgkKMOthPB5jtVqlfrsEDuhIJyggS9DR4QIMfZAJGIV918m5R2Lp1u12m6KDZNadLPtIoEVeHqi0ZEaYvOiwByOd8CyzKZ3NnL8xoeSk7EW4Xq+xWCzSM6isaChsNpsEaBOooUObZeXplDx0clHISnCAjhk6C2UmGS9kMjuR85Y9W3kZBoZeWxwXo55ZCl2C1PL9XFcCf33f4+HhAVmW4fz8PCl9Kg/uhyzRTAPz8P0yc5oGK8csLy8EYchPfAcVEYENRg3xWQT3ZeADQTMCIQSDlBrKojCDmIEQBBTp5GYVhbu7uzQvlqmVwRR0CPL/d1FxEzijI58Gym63S+A4z5J0DDNIQmZPAkPPWwB73+d6EYw9dDofXs65Rjw/Mrta7qOs9nCYEXloREqggOtJ445AhSynyQusNEyNMbi8vMTz58/31oqZc/P5PK0p95z8zTVkL1ueb64RwUZmZvJ88lmSd6TzmiCrbH/AjDLOn/wigzm437zkS2CK67xarfYctvyZcy4ZibJlgbxgco3JdyzjTxnV9/1ehjId4SRmWx6eWfIRgRnKeH6GZ1Ea7pSpDw8PWK1Wqdw5HeKnp6fJ+JWgOoMy+AyZxQkgAes889IhLZ2TEjgIPRqHs0uekzJptVqlNaTMlrxNOSfPCcFlnn+uAfeS2dj8rrx0S7lZFEUCsA/7chM0o+wij9MxwqzBQ6CMZ1VeLmUgBHmYvMggAqnXZGAFicAF9yZdmoQDisDKvhNuCPoJgEyzp/u4n3zmIUBCXSABIwYpyVLU1ENFUcRs8CHoi99LDoGoszn+4aybJEvlfMI8SgGAZAnIVkrv8Qffwf1nOwiC/YeVHpQKwQTODcF5skQ7+ZDnRQJPshoAgcuu69J5lbI+gHkO1W7owU5ZwmCo9XqNk+UJXBxHz8CcuK7sCWa0ScCudCQTJCaQRHtRglAhWnuL6XSa7EGtdQqKkWfv4eEBd3d3e/ocQOoDTjuR36GelZUB5BipC7n2EqS7vb3FarXCcrnEw8NDKrc2n89T5vZkMsHz588xHo9T9Z+TkxO8ffs2jZl7yLlxT6hbHx4eku4hT8tgHoL4DPS4ublJ69c0DebzeTqfrBggZQIwADbcE9qm1Ffk0fF4jMlkgpubm72qGSyFz++wKg71nrRlpQ7n+d3tduns8JxzHJyvzM4/rOQhzyXfxf0lv9ImkkGC0lHLOfOsBAYEmrZJcwpywcO1Q7CbUsFZ0TJTHCJjWOsITg36PmR2eWyjrhmPx2i7Fr4dyv8xYEHKKspl3os4L64vM3MIvlK3y8x73ou45xL4ZTDHoXOWAQtN02C32yXdyP0jb1CuV1UF1/eYRZ4Yj4aAJ60UjA7vyorBicp9pl6k/TSdTnF9fZ3uN7yfHNr+lBuH9iXnLeWy1FPyfsZzzTFJvpJ3FvIGx8u1pLyQAZ7UHdQn5BnJu39falKWfMxmMh5Kq1DlQ7SdaSNY7OWHwQzDAJLy7zwLTogAxgZQKcvyUKbR5AgZwj7ytEmOaTpZw7oYFAF9hO374NTLDMblKDjRHOUEUGQGOjqFw3pZdF0AuKx1KeWttx55qKsNIGSxKQUoE5zIXR8ySpq2w5jth5jVp1TItGhaMBNaqVBOlZlf2+0Gu+0G9w8PyPMcV9dX+KsvfoFleYLn736A58/fw/JigXX1EMB6k0XUdcjK7TpWYNPJZ0B+Di8aqgjw5yo6wb2P1aV8KMsaNhYBLHYe1g6AXd87WG/R9eFPAB3CukEpaBPA1aZtAecDaC3uu1rrABD50LPcRPC+63tUdb3ncA8At8Z4PA3v7Dp0nYXJMmiToesadF0P6yycdWjaDmUxgjGhPLeJd6AszyO4FMCTcjQOWa4+ZLnBx3LXziDPA7gfzo4N4FLXxfGGIIckq2MmMBC2QwbvhTWMYE7MmsrLHCr2SFYH55MAhHNB5pO8C5mSWink2cD/3rkYgBKc0mGLAxrvnD1Y8zzxuQQh0wEWQEvARrT4m7IIybbyArzal3VRFihm5obS1VwjkxmsVyu8fv0Kxhg8fvIkfNgPbvZDAM6ld0RgmePY+3d8fvyYs3Hvuj6V/jUmC5UqtIlZ3AoQoKJyBMZDz3tnA5RBuSX/ZpZn4AFmV1v03VB9r+9DaXcCrCHIxyGB4YQYkroLXZ972jERmNFmH4hUCPJE+TCOPVAM+yT9VYd6NT1PqRS04p2DS2s68ITtG3gfskO1zmC1glZxjNH+kCCewn4mrQwelWNLYJqPPc1jgAF9jG3bBpve2th7ewiQCHvl4aHgY8Af5TqgBEMNASoxnnCYt5jnsBeR/7AfmCLtx/RgRGBTri0xTx9B0ChHbOw7D33YViWerYA2QPsAeuzxXJQ9Olb3iDByBFIH8JP3WmaLd22Lvm1RVxXqukLXt4FvlJwB9oBxGcrCzOU0LwYiyAx9hZTlTpuT65LWDGqA0iJ/MROcY09gMYT9mvjLw1tR9QIaWVFAKR3LkvMP4LyGVjqsi9Z7ATDDYRsCIqUMTvzo2C+7B7zDZrPGq2++wfrhHl3fxncOQf/gGVLkznjU45ohVl1R0b8wBJkFHeKiHHF+aAsWdHTILLXOomm7oKvcIK95bhjcJvmgd62Ytk+BO6PRCNPpNN0VeUfWWsdKEAoqM0EOxgg8rVTIeCaQnYDxwWfinE2yhPeBpq7w8uXX+Pzzz/HmzZvwPZ/D9z0cz2EcoxP2gVYOzgHae2gTz0m8ixRF0GVtW4e2J3WFYjSKYw32Rt+yEpqKLSc88iys5dnJKQDg9evXyQ/Fe2ZIZtAoMgOV5cjyHM5adPF5vQ0tM1brB+RlyIIt8gyjMqwpPJKfKctzjD3QaYs8L2D7Ht55VPFOOslz5EWBoizRWwdngclkjKLI0XUDhhLwjgbj0Qjj8QhQwfYuRyWyLAce9vGrUMY64Aaj0YALaJPBRbtiNp3gB598AmUy/OrTz/Dly6/xsNmk4Kx0UH8DqcHk2JMUKp777/oCn2adxc39De7/YoNNt8X5fIb/+Pd+gvnJOTa7GkYDp/M5eqVRFmNkeQZ4wOQG0/EE9+1d8KO5kAHuEDALeGA+m2I0HmM8n6GzIfg+Nxny8QTeA/f393ttCI0xwRZVCpPJFMpk6JzFeDQO926rUBQhkSPPMqw3KygHjMYjjEdjzCYTZNpgtV3DK4Se5l2P7XqDR48eAVBouw5120SDL2SPN00bNVe4t490ju1mg6ZroYscUVWhaxsYrVGURQgwzvNgc2fBD7derfCwu8Pt3W3YO6gAtmqgHJd4/OgR6u0Otzcau+0Gd7d3mEymyMsi+BaaBrZ3MCbHJGILbddBNUOSR3fXY1dVWJnwbm14H3XolULXt6jaGrs4p912g3pcoBuVcCODddVgogwynUGNRrC5gc408jLH4vwMZVYig0bdt4BWmI7HmI7CfX+7q0Kgq7XYVTVs7+Gtx2azxbZtMJ3PARNaSeV5AaWARntYBsx4F6oHzBawb98AUMgzg8l4hOl4jNOTkHhCW6vIciyXc/Rdi6ap4JxCD6Bpe2SZwXg8gW0bVFUIIHjn6TN89sXnsF2HXM8wHY+xeXhA3fcoT88wmUwwm4wwHRUoixwvv3mNh/sHmKLAdDLC++8++41nTNJvDYwDoeSqBL/kz6jg6JDi55RSCXwi2EsgSoJ7TdOkPol0GsuSzHQa0sG8WCyw3W5FRtWgZGkMEsylM1ACGMw2pAOUGSc8vHTg8Wd0osgym3d3d8lh9xAv2PIiLMEcAizMOJKARFEUOD09RVVV2O12KRhAOmjyPE/9PPkMOtFl+Vo6pLj2sqQlneQEuWioEGjh/KQTls59joVzk85951wCbYAh24XKg+suATI6K7lvEnCXfU35TIJgvHQAQ5Qc94BZXHS0sfSizN6We0LjJcuy9FnuIcdAB/T9/T289zg5OUEXS8nwXVw/CdIxiMTaoccnz4uMiiZvEAzmPJil5r1PWaJ8HnmafMu1YPYKn0meYRYX1/EQNJWZotxTyX90yPJ7dFoyc/YwE4z8JwMYpGOTZ5G8SVnAveUfjk2ebQIbHMsPfvCDPeexHDv3VK6llFPkHedCdhwdwgwMAYby82VZpoAAOnF5drhOfAbfs16vMZ1OUz/rwWmGlK0sS68ySIDPlnxNkEXKVWbBs5UFAwJkEAv5mDKQoCXXiKCJBCMoX/gdynQJjEsZKzPxuK6SF+i4lyA3jeLnz5/vBZeQFyWQzvVmBQueAa4FA4BGo1HKjuTaSWelPGsSqJGObAm8kOcpJ2TwE88TZRkvyDJQgqC4DNaSPCeBZo5HBmdwzjLTPDmv3JAtLLNOJQh1CIhLh4m8DMrgIM6da8P9l+A8/y0D4WQ1Cu4h5SrndRiUxrNKnqBsTJc1cRY4FvIdx0QwiH/zuSwHTXCPupN6XZaclvKC545OIlmqmbqQmc3UpZR/3DtZXYAgt3QIELTkcykrOHfuK2V84FGfdA7fxflKOUmZTpm92WyglErnl4ErXBuOg/pXGZ1sNFKWZXsZ2H3fI4/Bik3TYLlcpsoxHLvKwnO5VuRbGZQm+ZORxpRPi8UiZY9L+c/MbQYUsooEK9YYY5K+DBfVUeIf2pTk/el0mgBaAnwcy2azAYA0N+p+9tQuigKz2Sztr9R/l5eXuLi4SIFndV3j5ORkL0CAMotniWeyrmssl0vsdjtst9sU+Oicw2QyQZZlqfcx93o6nWK9XifQVVZOyPM8BTkyeEqC4jILn8EWMhiHOoHrxTXmdxlUwEAUVt+Rsk3yOfeX76U9zT3hmST/0oEidQz1hCxjLW0Nri3fJQNpqFcoL7kWzrnYfwx7Z5lrIwMndNTbPGc8I3wP94xnU9rx4XMqjZv3C/Kv1K3UWzIIT8p174YqCpQBtBNoG8hxSJuCvEkeSo5RNZQApz3BcXBP+buTk6G/XxudqAyakO2HyA+UqzLwjzxAu5X6mHvHOxr3TK4P9SL1D2WUXA8ZnCfvKlJekg+45tLW5D5JcEvqZ46HulDyPHmOc/wPpV3VIc9DKWulggO4qlsAAdD03kM1HZztkl6VtqpzDmWWYSyqM2XZcA+S9nXgFRMycByzUyRgERzj4TsO40nIOLaZQl7E7F7l0TkRuKIUZlHGd51DF/tmJ7tBKzD72TqPDCqAwhGw17EXd8P7ITyynC0GGvRdgyz2Q/dQsNbDROeN9w59dGbrTAMaeHt9hfVmjaqqcH9/j4/e/RC/8zu/g5OTEyilsH1YQUNBqRIeGhYa8CFTP8syXF9fJ5ufesGIve9jMEEoN9uLQMWB15y16F0PeCArcoQM8BzON7AO0Magdx677Q7W9UAESpy32DVVKKEZ29UqrWAQAgLkHUzKPK01lNbBiVlXWG/W8NbBxPPooTAah16RVb1D23XobKjM0PYd2r5DZ1tY69Ari9OzU5RFMQA18LHKRo+qCpnkvfPQWQatHbJcwTuNHioAmVrD5BkUPHrbo2l6WBfKnyOBNUCmQ7a/zqIc0gGslDa7RwALur5DCLYMJStDWWGTZN9wLwgBDM51qJsQYBrA8Bx936HIMpRFBu9CeWuVmVh5V4XgA2dhvQe0Qt+3Qi4YaJ1DqaGVwyCDQ+UMozR6C/Ts3+xtxJAGGz6cgz66cwfZwuoHXgC1xhhMRiW00mi6Dr3t4ayNWbIOb15/g2q3xXazwvzsFBoKmc4CABO4J8hE6krv4JUXgSb75d6pKzJoqCg/rHfoe4dOtfDOIdMGo7xE1wNmnMUsNw0b1zAA4xZwCtqH6isQlfvk++Sd0nkP6xxcH4NEmw5t08N2DhYEwUJgiornPQQYaCSQ3IfKBDoz6OlvQAwciesQsIq47l5D925v/hH9jYFH++RjgAqirCQ4SX4mNA7vAw8hBD9YF0qbN3UMTlcFtDKAt1A+h46AJ4xPYGsAPWMAgR/ur0OAxaDHCHAHOz5k3YUEgS12VYWua+FsD9XzLjdUEpN7wozaFKQi3gcgnRPKcv8dMQJcj0N9y3fwMyFzdvh/53mPjc+N54rPC9mcXQwuUNB6lIJstNbhLAMBAAwSa8jOtUPgi1IqRFk4D6cCQKdcKI8cxhoA0j4GpnVdD9vW6JsGqxiwG+4ioa9s8mXFXtFDoNQB74jzxTn9bWvH/ZF+CWnTAdGuQeiNTEqBJHoIxA9tAJjxPQTrTyYTLJZLGKWQKcAoIOSPh2MVZJ6GMyaC2Ox9PIDvwaYe7sHhvfHsOYe+a2FtD+UdXr18gb/8+Z9hF9t30VegtPnWPOU68Q9tHvk57z32ClZ7Dxfl8ngUgDeTBVCwaRvsqioG6/kYNDHwhYpBTPLZFpS3lKiBlYJ/s4WzFqOyBNQOWR6Ctbz18GMgRwFl4lppBWdUWF1GNzgZxGCDLWB9qOyDsF+j0Rhff/USv/iLn+Prr78KPsL5As4BNlgviZxzyKPs4niNAYzPoTXiu3hPngDaYbV7wGazDr4wF/x6WW4igN3CebtXeazebfFwe4ftah2CXpyH7S08YhKV92i7DpkqUBQ5ynKEsgz+uy4Ltsau2eH+4Q69s3g2X2I2mWJclCjLEcbTMS6vr1E3DYo8R1kEWVkYA6ccOqdgvY08BzRNaA9RFqGdT2YyPH50gboOrQ8U77haw00moVdykaPre1zfXePi4jHGZRGqAhmzZ1+Xo1DOezYLLWTu7+8B5Oh7hSIv8OTRY/zuT34X/+ZP/hS//vrr2AYyVGJKdrWTsjvakTz7ah8AT9+RAUlyf1NUDOBgAVjYtsVf/fzn+N+1CuP/zf8av/c7n+Dp++/ii69e4t2TR1hpHfuWq9CipKmRTwucLE5RNzXavsPDdotiPMKuCi03MmNgjA5gbdOgbzrk0BiZHCYvUvu9tm2DrT4ZIdM5bu5Cpdc8M5iWJaCBzW6Dtm7w6PQMy/EY03KEh/UK26ZGXhY4nS8xObnAo/kZPn39NTrlAW1Qty3u7x/gswyuc7jbrJBlBrPJGL7tkakclerRuw6dt7C+R91X6GGhvEVuCpisxGw0xnI2R2kyNHUNlzmMyykenz4GtMJsMUdVV3jz9i1efPUlVuuQXNP7Hqtqjaat8IOPv4/J02d4O5vjq5cv8frtG/zVr3+N9z/+CMvFSehzH7ETY0wo7b8LVQMmsynm8znmVY3W9vjq5gpdF8DvIs/w5NEFRmWBPDcwuYY3GUqlUPgOuuth6xZtPsZXV1fwb69CJdxcI9MOp4sZJlWLflOjNR36IkOdGWwfVhjnJU4vlphPC5yMR3CnF/jy7RWqmzuM8hEyr7FbV/jLF5/jo+fv4fHjJ3C2x3r1AN/tcHG6wKNHZ/BeYbur8OrqFt7nKGczoFGYjAos5pNQQaXZYr6YYTabIYtVsNrdFt5b5NoAeYHGOfT9BgYeF+dnuL1b4839Ftfrv8YPf/gJZosTPKxWIVgrK1GOF7i9vcXdN1coCoWz0yk+fP8ZvvfJx1hXPX71qy8AOLzz7AI//cnH3z4s30G/NTA+ZHMF5yGdR3Q2MDNrNpsloCbP8+QooyObzvL1ep2cdMxIYK/RqqpShhiVKLOWqeikw4PObTphCPjId1OI8bv8s9lscHd3l95BRywBEOmI3mw2CWSUgLxzQw9Z6awDkPpC0zE7m83SM1MEMag8u/Q7/kzObbvdJgcdI9QJ4knnHx3Q0qCi84ZOTjlGaaBx/Qh4AEHx02lN0Ec6/oGhF/IhkMlnHTpJpTFHnuDvZclYWbqXwCezyelwJyjJ/SdfEUxvmiY5rqRTlWst95GOLFYi4PouFovkDGWWDdeXDjnuocx+pONdlqtWSqWAks1mkwIVmDknxzxEsLV75SYZIEHDkA4aOhx5jiaTSQLX2MdWzpO8zos7z4nMkuE7gKH8NfmS55DrLzNquM4SROMz+SzpOGBWI/dQAl3S4JUOfe4H95bryjmRDg1ongXyH/mb6yv72fIzlGEEmrz3iW8lf/MiX9d1ynwlAMT5yHVixiCz/Si/yD+MiCfwS16VoL8MWpBOMJmpRCc+gNQvlkAtnyHlJN9BvpC91vl8Wb5X7iXlBNdcfo5jkn3HuS4861wvgnLSycezzTHy0sTv8jzwnMh3SiIgwflLpzefx7lMJqHPDeUd+0lTXnF8/A7lhwTDyIM8pzI4TPIO94kyFBj6VUmg5xCQ4/z5DJ4jri3LOHO88tJNkEuuM9dEgtM8NwQ3eC75czofeY55rnjWE6gjeIp6jzJOBifxc7QNCHDzjBJE41wYlEfZwd7VMsOd/2aAG+fF78h+7nwHv8cgDoJ1h0ERci8oY8lPMgOS55FrLgMYeCY4tvV6jclknEBJCerwbBHI5Xupswkas3T4zc0NHj9+nMbGQBIggNjODxkQBJYIcvE7ZV6gjfKOOoXzz2NUtldI3yXPkvek7gCGUuRcX6VCewtgaI8wn88TuCbL4/P7xgw9sJlVzeAbZr5eXl7CGIPVaoXT01NcX1/De4/T09MU3DidTnF6eoqLiwvkeZ6qaDBoTWabc83kPEajUXqecy4Bh7vdbg9Ans1me456Bo7y/5fL5d5Z47udc1gul4mfyAcEZiSoTNuFthz5X8oJ7j9ln8wIZlUKXm4py2WlHO4BQXFWCZDnkXr78PPcw+12m2wj8p2Uc5QLHIccP4njo/ySa8OgJgbPUJ5SZ0lbjrJHBhBJsFsbA6WHQBzpjJN6jD+jfSnPgbX7AD15ljxD25Fyg3sqHX7GBIe+dHrLzPoBRBmCn2QwLPdYriN1AoNLWDWGclEGl3GO5DUdq0TI/t6H+oTvof0jg3xJ5HMGAUl7QwYIyDmRZ6mPOXc5L+oEzlHyiuQnafNx3gkEEhnmXAcJPB7ywyF918/+fcjFTIG0p1qjrXd79roTc5D6Rwaa8XxyTBIUl2uUZRkcQgYq5YON55POYerR8KyYvap1kndehYwI5zxyk2G32sJEwDLg3Sr0nAzY92CjaZWCmKR9F86txmQyxmyxhHMebV2j61poFfpYExRv2xZdVWMa74kBBA0y7vT0DJPZDHUMgJtOp3h0dg5rQ6k+vldrjZb38gh0mgj8ZlnoU85APK6dDIg5DKAJfCg2VankTKfN4+LeQYd04N1uh91ul3RO27ao65C9lRdZuheYmO0mZbg86xwTsF8hqLcDgEL5HXhkAqM1puMu2Rm5yeAnk7D/5EuxVtS1JtOYzYf2Kd6HcrzkK61Df3l5VpWL9qhzGEf9QJvA+eAcTO0Z+h69HSpehEDGBm036GOAbdMMxqNJBKWGYKKqCgBaWeYo8wLeDkHaXCupG7UxKFS0r92QlR1s86EyIgGzcA+JMsPHDEzfDwCHH4AtKcelnMyyUNVB+lUCENfsBwXEdLI8M8jykJVF+3lUztF3ocTn559+ivFsCsOS0lypWKwBCtBGJ8Dk0Hcjid/nU5z3EQM2mE5nODu7iPfJAq0ukOUB2AqpugrwIRtTaRVLHzu4bj97WvKutEFpJ3Rdh6au0DZ13LsGdVWh6xpopUOpU0O/01BJJc1LyHt5h5KynvsRsIpBtu+NE8SwQvlbfu9QHwz/9kgl1IFkO3Bu3nt0fYMxFErlkSOHyQ1a26JzXdLlSX8xIzm+O4COADDoVudC6rL3Dl0ExZumQde0qOsGu80OdVzLrq725i73PPGCYkb4gR0GtYfVSGD8cE3kvu6tU4Bxw2u4wJwHRJBarOQg9Vm6x8dqJY8unuHJs2cwWQ7dxeozHqg2NYo8S1Uh5By8D33MsyyDyRSMKvbG5uN55n51XYeurqHg8PXXX+HFixe4urqKfgiz1wYBCFl4yQ8aU545AmbbH4LmDNw4pG+vW/y5G/g0yzJokycZQl6Dj8Epe+/UUYYO/uHZbIbn776P8/PQFdt5oFSAc6FqSTgzOXReAMbAuf3kGAZi0Kb03qFthzaLtusAZ9HWO3z98iv80R/919jGoO4itmOodjWgB5l0aGfJn3+Xb1vm5gc+HXxkRVFgOpsm31HIxgZGo2JvT7iH0p7k9xcn8717rAzQ9N5jtXnAttrg/Q8+hlIeru/hXQ+HHk0d9HheZAHojhXc8zwPVXf6EBRnMg14B9v1gf986Mc9nU7xzauv8V/8F/93vH3zBkDop6wA+BhQJ+1YFe1XuQ5a6xgIGOZrjMFoVMQ9AxZ2Ae+D74s+geVymXQT/Uvck6qu8NU3L9FGfVw1NbJ8CE6djMcBhI686JxN1dL6vkdrO3QxyNP1Iaj3vXffw3K+QNs0uLy+SncYHflvNlvgbnOfwHn6+Pq+x83NTbrTn52eYjIaA0ajbXuM4/27LEvAe5RlaDPmth5VE1rW9n1IspjNZgBCL+yiKLBcLjGNNhGz8BnErrXGyckJPvnkE9R1jZ/9/Od7fY6l3Do874f0d/3+N5GPwRyZUeh74C//6uf4z//z/y3+V//L/wX+xX/2z/Df+u/8d/F/+N//H9EVcxTjERyAtm9DxvjJLOzpRsHuQu/0drODdQ66yJGXBfJRCaMU6m6Lrm6w6h28VnjnyTt4/vw5qmqLm5sb3N/fwd17cV/wmE0nyMwY9a6Ctw7jchRs3jq08bp7uI/3XI3peIKnjx7j7PwMf/PySzR9CzMaY1yOMBtPcHZ2ht16B3VPn3WBi4vHyMwIn/3bf4P1bo2zkwWeXVzg8ePH2FbBrm6bFnk5GqqG9j1ub29hO4uLiyd4//338dXLr1E1O5TjES4enUObYDvc3d2htx2AUHnmzZs3+MEnn+D07AxV02JX13hzdYk3L7/Bjz/5AU5PT9FGGcGKjYvFApPxGPAeL168gM4KPD49RVXvsFqvsFqtcPn2EtM8x3tPngFujLpqsRh3mJQZnj/7HnSm0fUWm21op/vnf/YzfPje+/jhD7+PDz58D8orGF3i5atv8LBeIytzPHv+HLPpAne31xiPC8B5bNc7OK9wNp+jXu7QjUewrkfdNvj61Uv8qy9e4Hvf+xg//uGP8I//0U9R1zU+/ZtPcXN9h/c//ADvf/ABttsd/u2f/BmuL99iPp1iVIwwGk2gvMbdwwZeZZhVNTKTwzqF0+UUWa5R1Q36PgSxhLt3i+XsNCYl5ri9ucHrV1/jg3efYzsbo9rt8PrtN0GHWmC9rZDVwG77gFfffIMPP7jFT/7RH2C2PMEXn3+GL1+8QLVb4Q//8A/+zjPzWwPjvORJZwSwDwAzE1AeYJm5kOc53r59m8AgmSHBspTeD6WGqTRp4Evwj9mqdNDR0SWz+k5OTlJvS0ZoSFCOnyeIwj8Ev1lS2DmH9XqdhDZ/TyUzmUySM53rwQwB/j8da7JMt8xK5fjpTKTzgk4X733KguMFmtlqh8KVDngAe9lpLMEpL/F8jwQSh4g+nZzOdHLTwUinKo1kAmvkk8OIdSo7OsK41lSi5CsJXtEBTVCEDlIC4xI455rx2UP/Ep2cnbxIMFiB+05BTWccwUfpwJeZt+Qb7oPsgcuLKx0EBB8I0tOoovGmlMLJyUk6C3wPHeiHJde7rsPFxUVycMkSrDyndCDKDBk6Gfh78h75m7wpAUauMc86sA+UJ+dZPIcE4+QZ4zwlMEV+Iu9x32Q2Li9+ySkhLuYcL3lGZkhLJy4VjwTgJehGQ+gQAJTgpSz9I8+GNMDJ2+RdvpOZJ+QHfp6G9Gg0wna7TfyVRQNXrrv3ARRiaXAptyTAyLNDYJAlqOkk5xgI5klQlzIUQAJpOF+eXWttylQk77BUvXS4J0NVOB/4e4K7lPHcO+lk5vpIYIRE+cJ1kFn+PDeUbTIYhWvB/ZMAtpR71EUSdOW4ZeAAdQPBX46JsoxzlOWCye+cB+UvZbS8RErnPIlraozZm7d03HO9JDDDPaRMlvKaOpR8z7PMdZCZ7dKBJ9eaPMaLNveT+8A1lCC6BGQIHnIu4WLZJ1CO7yZAybP5m/QW9Y2sosL96Pt+L3P89vYWWZbtZchKkF3qX/6Ma0Jwk/OS/MVAJPa6lc5o7o/kNwmsyiAaznU+n8dnDf2h5SWd4Cz3kDzBQCG+n89jSwbyKPV6uDwZ9LHXKPmDIHMCZ0uLIh+cLNxfvlsrBRidAokoW6m/abeQx5RSWK1WyRbj+WbmK3leytzb29v0bOpf2gAPD6Gv1WKxSGcnz3M8evQIRVHg/Pw8tV1g1R1rLc7Ozvb2mA4kCegeyiVmYlPWMVtdgk8MouGZ4/5Lu5P8QX0MBHuN4yRvcA8pk6jXJWBInc9xchwSDD4Ez40x6cJPQKqu65RlTvuA+kPKa8psZs9Tn1DncO7U8zwj/C5tA8kP8kyR3zlvyhrKF9o6lHuUd1I+EeDnc6TzO1XGyAY9Rv7j2WGwhfYhS5VnXX6etpoE5WUVFM5nFMsQUsZQ/sjAXwnY0saUfCn3mrwmHXFVVaXAYsoY2sIygFAGLvAZ0tblvKVdR/lHHs7zHEYNgD2DozlGrgHlO6srSTkmgz/kXSAFJAiQX9obh8C4vE9Ip6TUszJgj+/hOeG/pY3HfaBMpSyVz6VtIAMPJEB6GMjx9yG+k/Y+5VZysB/wpLTTpSNZ6jPadtJe47tCJpBNGQ5932Mc9bJSg66j/OVaBp3s4j74AFjrkB0E5zDODKBDlh60Co4vDxSmAEuMu56VjQj+hAx16nXnHPpmAMrG4ynyLDg5qQtHozGM9dBGx8za0OeQvx+PJxjHyihlWcK7ULYbGIImgg3i05zkWSP/0EY4vKvIu7+8sxCw1Vqj7btQ+jre+4u8TMFCm+0WTRv0YaEVmrZF27TinITM6W7UwM+Ck5oZ5dKWpP7kPUPpUHiZZ3xUFLB90KOr1SrdQ5g1SH+Hdz2UYqWPJgbqU64UCNUMHEL55VDG2Dlm+iIF8Bd5jjLP4Rx7jg/B6lkWMsPrqkLveuQmw6gok9OSZ5t/vB/sk6at4dx+e5s8DyUs6Rw28e7LYNvJZITJZIS2rmGUgopyynYdbBH6l+osg/IMOAmOfC8C1uo2ACm8S2Ymg3YKHsHZn8698lBMIkYEW8S9Vuok6ik+T2EAb11vE66a6eFekHrxGgNlDKBmA1DhWXY1ZBwOZzRm9XYW9+sVrHNDr9O/Q1wppffKOAMhc9TZHsZkWCxPYG2LTz75Ibq+g/MOxgRQxphQLcHF4Bn4eGfMQrsHmdnMc5Rksw2Z4NvNBnW1Rde3aNsam/UKL1++xM3tFYwKpZe1NgkM4zrJcvU6VgHg+yivJaDmXMhS3y9nHYuhH2AV6d4lgE7+K/wu/L/U4+RpCQ4T0Hny7DkePX6KxXKJugl8MR5NABWyxLuuRZHnsYx0iExyHrBQiCnCe7K+8wq27eB8LKPe9gEA6i3ausHt1Q2u3r7F3f114kOpP+Q8lR6Aceo6z+ColJmP+LnQKkDeS9Mp8CwpvreSw+f8PmrsIQIZfOjFTBBqb519KIG83YaS5k+ePsXp6TngLGzXYzQaQ/lh7cM8417F0tvO91C6hIu6QSsVz7SNtvMObVPD9RZZnuPLz1/gF7/4Be7v7+Gcw3g8iqX6h/YZgZ9V6HtOsFthmKMOmbweIYt0b7W+Mzv0u1u0pIoCOpTlNiaD1kMiglZsmzDYV0F/6ChrWW7fYr1e4/Xr13AOODs7A+DRtSHYejSaIDdx/X1ocaB14AArAjpt79C1gNGjkJmtNGzfYbvbQDmHrm3w6tUr/Ot//cfYrFcoywJZVoSAL6VhoOAVvnU2h7URwQTugJsiL3m1D6DDeUwmRWoF1bbhj7UWzltstlvk8R4b/oR7xHZbJTDXe4+zszMsZ1Ns1mu4zsPkGcr5LOimmAkfbCPgi89/hXfeeY7F4hRQDso75HmJPtPwoP7SyDKDutqm+XoP9K1Fp4AyN4D3yLNgM335xWf4l//y/4G7m9sANuY5ECsrBBs6nCMGYykAZfTBKcFrOtozzvbo+w7rdYP7+3tMp6Ec9NnZBSaTGS4v36QELNobeZ4nu1/anru6Sr6AdBdqu4T3jIocNiYAbLcVTk9PQ1a2D0EjRZnDbTepbZqzFl3TYrPZBD42BkYEYNAnQB+VTCKkrcs/bbSllicnyZ9+f3cHwAFq8Jsxk329XsOY2KIs+iROT0+DLnMOru9xf3+fgr3H4zEeXTzCo0eP8Dd/8zd7fgzy5B7f4rcDyf99aPB3+ni+gZ/9+c8xnc6gUOB/+D/453j3o6d48XaL3vZouxb3q/tQLcp45JlGZgzmixnOTk/h6j4Eb2qPk9MlPnj3PTw9f4Rf/+pX+Jtff4r79RrN7S0ypfG7v/u70Dq04my7Fk3XoG1rPHnyJNgf1qJvOpydnmC+mGOz3iSf3sn5OYrJGJd3N/AKuL2/Q7MLdlrvLEblCBenZ8igcHdzi9uraygVW1+pIL/n8zn6Lvhtqt0OV12Db2Yz5FmG0WSCum1Rty12EV+6vb0NfLzewPYWm6ZGNspRtRU+++JTVHW4C188usDFowucnZ+g2u1g+2D/jaYTLM9O4bXBZDvD6fkZdKzKdX9/D6+AJt6nTk9PcXJyku7H5CvA4fH5CbLsArvdDjdXV9iensLD4/b6Oth6zqJ2DU7HI4yKAqO8wKbd4c3NPbQDfvSTH6HtK1zeXyN/k+PpxePAayZDVpaA1lhttiizYNPuNg2ctaia4GN87/FjXJycoO46NG1okff8yRO8uf4GSmlcX10BFnj+7DkeP36KX3/6K9zd3eDxk8f44Q9/gD/86e/gbDnDw8Mabd3h3q7x9NkzLJbnuLq5xvXdQ7jnw6B+9hjf+95HsN5gc32L66tb7KodTG6Q5cB8PsPj8yWmowxlmWMxH2M2LZHnT2FMjtvbO3z22WdYrVd4dHGBJ48fYzqe4Neffoq/+Jtf490P3sfFo3M8eXSBr7/66rc6M781ME4gl86Ww3Lp8m8eRmZCEJio6zpl/tBhxf7KLPlMRwqVAZ1WdLoxc4fC2PtQhpRghtYaVVUlR7fMSCNQQWcm35Uic/M8OdMeHh6Gy2p0zpyenkJrnYQeHVCcM7PjmIXIdaMzhn2TgQEckWAZnYUSQOBlkGsq582sej6PBghBOAB7TiQ6inmp5/P4XjqW6Nik41MavnQWSqcSHcLSYTYYykO5YgJJXFcas3TmEIQmCMU5UXFwbnVdJwcyjTyOVzoyCZzQmURnsIwCpxOZv5vNZkmxHgKP0kEnM8+5fwQT6PhzLjgr2IOUzl6OgU5Jjo17Lssn01ksHV28kBOs1FonMJMGgeyBTod013UpkzVdLOLZ4rpxX+jEPwx0IUDAZ0qwimvBcfM58rLH31trk+Ndgm/cR/KKHLscs3SS0tjhs6RTlA5hnhE+Wzr0+dndbofFYgGlVMq0IxBIZyod/Rwnz/FsNktyh455GmPMyuPaVlWFLMtSJkhZllgul3DOpV61lKXM+OczuZa73S7xCeWXvDAwk5MySIIV2+12L8seGJy7nDP3FRgiZSnPASRZRjCM8kPut5R/UnbISHeeZTrkWYZVfo/rKI1K8iDPL2UdnercK6WGfqYSWJdgLrM6vR+qDzAwhSAH/5C/JpNJcvQRwJIOjUO5zDPGlh2UJdIRJufLsy55jDzI9ZO6iWeC35MBPZy/nKcE4+WZlI5dSXw/z81sNkuymu+Wz+FZJg/wGZRN7J8snbacL8ER8gDXgIANzyvPsgSW+D7yCYNjpN7iZUcGKFHGcH9ZrSE5sIWOGI/HqUc528JwnXnGZAADv8815J5Tz5Bf+UcGupD/5Nj4fL6TOmaz2SQ5IfmLOkwGkMjS6tThs9kMDh7G9nvylQAV92g6mSKPZ91am7K6yXdZlqFuQ2kyGSghq5iQ+FwG2XF9Qqmxob0HgbTr62tYG1rp0I7j3pydnaXAQ9pytEuog6krKQsoJ3h5nk6nSZfzTG632wRGkZd5lii3eOnn3Ag2k38liC15VNpQBE75XO4Ng6Vop8l2LHQ0SGBT2nLkbQlcU17QxqLt1TRNinSnfKTNL8tWU1ewghEwVJxgaxfKQgIa0pYk0MsxyxZNUt7Qfuf5kLpGgsQSkOS85Bg4H2lvci849yQL7b4slHeaPM/hMZTll0Dp4HQfwNVDIPfQ+c29oG6jrOE+UZ6z8gYrJdDGJl8R4Obnqbul7UPbk5/jfUPOkzJQgqzSDpN6Qdrl/CztJvIE7VYpe4EBoD5cX7mHEjjn2PhcGdjBvaa8o1yUYzu0OXhOklPQD5m0MijpcI4MbJLAM38u7wc8lzyjJI7/70tFnmM2CWAuA7w4JpY79t6j64fKQFKWcO243ocgBX8u7X9mN/R9nzJ7An+FteL9N/QTDsBmKMc63EdZPjX0Jw9goDZZwG0ijxVFgbws4GiX9Q6ZAXQmM9yGzCZr2fc1gHHhLPbo2g4egMky5FmB3rWoq9A3UN7jkl2nNRQU2rYLvZGhoE3oi+28w2Zbobd9Ai263iIzOsl98rAMypV8Jdd6cMgPYB+DDpK+sR4vvvoKV9dXya588uQJ8kmBzeYB1a6GUhptW6Nt+wiGh7O+Wq3QNPVeoPBhFYVw7kIZ5mRLqIA2UZ6QV/su9Hy1UT8HueTQNDWs7WE0YHQov64E6GVtn+4bzECnDLDWwuihz68xGsaU6b6qlEKRbXAT7eY8zzGbz3FxcRHvs6GMe9s2qHZVsu9SFZ+2QeiD3onAsxx5FvZex3UIQeqhnG9d19BKYxID3DoGW1IuxCCQru/Q9y6Uou9a1E2Dpq7Rdh20DjyX5TlMZjAtR8l+czx7eqgu4ZyL4KqCdQHozvIceT4kaGRZbFXSx/7FXcjiDGcsgB1BtoWy8LYLQQ8eiH1+NfJMo+9Clrr0X9iuT5m2HkDb97Cuw6YO5YOZRXgIVw4UAlXYNx4WyDLqGqC3Hdare7z48nOcnpxgfnYO7/MAElLGGJPAmq4Le6GRJ1lMHSEDX62NWcLWw9ke3ls0VYWHhztcX13i9uYt2raKYFrITieQGgIRCPqH7GllWJx8KMsdD8yQTe9jmXJRnzbohMDHAA7Ay2/fn+C5kgNo7jH05079jyOwHHydO1jr0bcdMqWwOD2DdRYtQslvzcA+5eBZiSDqSqU8lAYUNB8I6xzazsJbBt436NsWyjtsNytcvn6Fy7dvcXd/CxdL+ys1zBXMiVdxmUK99CTnEtgPlYAqAPDu29nPw1oNP5f2n1xR5Q9+rIZxKRWA8UG/+7SOznmMRgXqeoM3b1/C+Q5KOZyfP4ZSGn3TwDkdeCCdjThWT54IAQTwwTbUWkHp6C9pGyh4aAVUbY1Xr17iZz/7M6xWa2itkOcxy9yHIIJwXhVYrlzpYe5BFx1miGPo1/0b1g/Y7yMfWG2wLfn7YOfqCBiFzE8PFXXnfjs3Bhx5BB7Koz5bbx5C9mCzxdnpGRbzBboiANeepeKjjvfaBPnAahIuBISFSgY9rB1aCALAbrvBl19+gc8+/xS3N9cwsWpFb0N7I5OFDM3DIADpo5ILd2i7JTASQifHwIrhbtaibdnqh/Isg7fDvW0ymUTdUaPvu+R7LIpQcaRrO7iuR14UmMWkQGzDmKwKcqzvarx+/TK2IzrD6ck5bBmA+LIoYTIDpzWcCzY3e6FrpZDlGbK435kx2O22ePvmLf7yL/8c1zdXyPNYBTXOfT5boOt6tE3wtU7GYzjvUnW1cDeyqKodttsdJvMpirKEj8F7m80GNgabaaOR5TlGZYmLs3NsNhv0bajmkhmDk8USRV5gtXoIgUTawOR5kkl938P2NlSGdw5NVYXy9VrDxf1hxba261DVFao2BLXwnn51dYXNag2tFE7OTpGPSlzf3KCq69Dnex7kwMnJyZ6fSCm15xOt6yYEleVDKzD+Hfz2c0xG49DeJfoXvFfpXq/ivZL29Gq9Tj4RJh9st1ucnZ1gsVhAa41vvvlm7+7Hs3l47/0u/9t/CAU9r6GUgfc9tAkZ4X/1N7/G/L/8r/Dx9z7EJz/6Hm43n0LpDNaPAQ2stxu8ffsay+US7z59hg/ffQ/vPHuG9cMWm6bCm6u3eLXdwrYdHp2e491338VqvYXXGk3bIC8MqnqHzWYF63qMRiXKcfCrbbahdWChM2TlCH3bASbYn/frNR7u73FzcwNd5CinY9RdB7gt+qaD8qEFArQO2d6jEc7OzlC3zZCNH238m5sbLBfneP7Oc3jlsFk/4PLyMvDedArrHLI8lPGnvTouR9BK4frqBi+++gq9tfje9z/G+aNzXF5dYb16gMkMJpMx5vMFLs7OUVc1Li8v8fLlS0xmUywXYd+Dfa1xc3MTfI5lgfEovGsymeDk5ASr1Qq73Q51VWEyGmM8LdHZFsYoFJlBmReoVIXHT5/i7uEBm+0WnbU4nY7x3jvPMZtMsN3scLNe4e3NLS6vr/HBe+9gMl6isz2urq6R6RzvPH0H8/kCTdfjYbPG3cM9yrzA+8/fAbzCtmqw2qxRjgrc39+G89e18EpjNBrj/PQco2mGtu2w2zZ48/ot7q7v8f1Pvo+z01Nc31zi+uoNlosJ3nnyDp49vsB8MsP9wxqrzRY3N3e4ePwYs/kCTgG77Q511+Pt9Q2WJ0uMylD5anmywHwxh4NFnit0bRvsY6ORxap0oQWHwnRa4uL8UWih8OolbG+xWm+hdY53338fb64v8eLLL/H2zWucn5yHYKTfgn5rYFw6SXghlBHxKZtIKDsJKNGJSicHhQMVDS8LMjsVGEqT13X9rQwSCeBIIITAhexvynHc398nZRkiv7YJgOIzCPrLHrFAcPTc39+nksez2SxdzOi44xikQ4eGCQEtzkk6krh2o3ho+HkKSUblU3DSkSwzQwmqkKSzVApiOiV5caTjDhhKB0sQQa47wTnOjX+TrB16tvL3HGOe56nnMh180vkqHQsEc+jkpfHRNE3qLy/Hzah2KqZDZ9fbt28xnU5TSXRGQTITUYI45A/+jHzPPeGaSaeS5GHyDp3tl5eXaYwS9CVJpyUBz+l0mjIO6ajnGsns064bIu/IezxDcr1lCW46YabTKe7u7tJFnNm1s9ksrdFhhg7PPs8zP8f58PnkHwkoMluIgC6d3txradDTmU7DQTp5gcEZKR22PH+HQTV05nO8BHjI03RMAwOgTKfxaDRKn6ETkn+TF+igZLlw6fxmv3gCuDLzlYFCfIcMUCFf8BzRCUnDjc+SvVf5NwEK6XgnqCCrSRBYBZAClAgiSPnFdZLnmoCHXHMZqCKBGQk6c+85Fu4Ly2RT/pZlmQKluJcMOuCcqIsoE+XaSPlxyIvkVzrUJpNJ0i8MdjImlMnhukpdxnXhekiAU4LDkg+5TlwbOnukvKEckoAX94LfoyzlusoWBpTz8t101Ev5LEFonlnJ43LNuc4EsCjjdrvdXssTnhU+f7fb4e7uDk+ePEljpZ0gA584Pp6l8N4B2JIZl6PRKDniOQeCrgw44BqR3whgy/3huyiDZCCcBCjJnwRB5UWbtkVVVSm7netO+c9AGOolCcbzzPBs8axQJ/Ndssy4UgM4w73kXLIs25Mt0jkvA63m8zm6rksBKQRAKTuaZgiMms1mqZcw91XaDuQFZkzTFuptj10E4FjGnWdAykDqEilvFosFPv30U8xmM0ynU0wmkz0ZIsuVc70YdJJloRwdg2vkH+oHBlCSn7gnxoRS7Hd3d6nMOefHteIZLooCdV0nW+Tm5iadP45BVrVh1SKlVAK0Dh02XKvtdps+r3UIwlwulykYkzxHucYALupo8owMhJP2G9eRvM2gBNJ6vU48TNuVco77TvuNzlA5D35W2t0SgKd+MMbslV0/DILkWKXu5jnj+aMcl4CnBKrI05Q73wVcy/uFtJVlUJWU5x5A1w/VkxiMx/sPx3FYBYQymDKtLIv0ea4LeYNOJOoc8hV/x585axOIPjg0hyocnM/h2pO3JagsgyikrpB3CI6V68k9A0K2vcJ+YPQh8Apgz+6VgVxcm0MeSCCS+A55+zBojXzN+aaxCfkq90HqVjkGqUtlYAHX/vD+yTWSMlfqXhnQ9B9CWoVKQUWepxKUCsFB6r0PDlTx53Bt5Zi5rnK/5Xx5t6xENRLyxKF+DOcwPIPnj3eAcH4CUOG9Ck4t56D0ABiH9wUZ0LUhQKTvHIrioJx2tGOpj9l/UUf5wZ7DHrH8e+/R2T46iYd2MJRh2hhkyTkcHJ8887TraBenwA7v0Suf1kHqYnl/lXJd2tHhXA82exeDxWif9J3F5dVlKNEoAmQDQBCAGcr62azEyckJtA7nYb1eo40ltmXrjMOz67yH9S4FkBEY53yGAFwXxxfu2tPpEn3fIF45MGUQlds/WwzWHY/He3pzNBqFTG1r4d1+iX9+xzuZfRqf6xxMZjCbz5ItZCoDZ1ldKku+FeccqmqbSs0DQJ4XmE5msVRtkWwyAFDKo6530ArIszxm3IbfNW2bykV3PashBr1FsLW3Q6Yss620Vii01DUeRitkmdmrKhdzxhPv8D4lfTLGGHSI2avOwXsdeXQ/UB8AvD3IOtPhbBBkVPGsKABFNlS0cS6AYNPpGE4zuN6lM/Mb5ZFW8CqA+0oPTv4QgODhrMPt7Q1evPgCH+Q5JpN5yBTVCr73UN7DOw/lHbQKQJTtsBeYdQiM0171fSjNvNuFHrS3tze4u79D33dg7/hUilvtrwtBaPiYIez3A4UG3tgHI10vfi70jpRjYV32e3L/JvIIVSwOfR98Xt/32KxXMEpjXJbIixyjchTKTnvARHvL2R4OobpD0MGA8zoAuhiqj1kbqn+4Pvh5uraB7bpQlvjyNS4v3+D+4R5t28SqOEMgQOKhBJT7IeDg4C6pcLA24nOS5GfCutG/I997AIwjlFIP341loFXIsA3PkvsR7pe9ddjtVri5Cd0ptNI4WZ4D3kHDQDlWXAnZc8k2j3N2zkJHQNl5QLmgR9q6BlQIYLi+vsZnn30WwBw9BLxLe4PZmiG44LvBL8kLngu+xzPf/R0ZxPFdOl8pBY8etrMJoAwVWMaD7o395p1zsC7wkzGs6Jih6RqsVh1C0JuF0UMluNwWyLIc7DUeEs51OOvwCK0lwnSYhU67oqoqvPjic3zxxWd48+Z1AIETL6iBf7RKC/Cb5FI418OaH/Lc/rqEQIghIYyVBQOo65WLY3XQah8INWbIgE52Vd8nG6zve7RNyMIMviID34egsTw3aOoKXReCz7wDFotl0nVZDLAKAUShdQsQ5G0W39v3oQ3sm1ev8eWXX+Krr16gt0H2hc/pND+tNcqiwHQyTvfpvhsqePZdi2q3Q13v4E042ZkWPbRtrNLoHHzXQSuVquS2bQtEm4/Jhqk0ug+BHbSpmqYJfBf/v+96dKYDEMqoBOwjBOBlMQi5tS22uxZd26EsYrVa55CbYF9M5sFH4Z2D0UPlQ+pZqUMopwLvdaEVSxHuUoh3CdoXMkA5L9roB2ixXgdAF2qoFpznebDD4//P5nPc3d1hvVmjyIvkW1+tViFA6m/Rqf+fJq15PBRu7+7w17/6FX7+8z/HT//g+ziZz9F2Fq3tk77ZbdeYjsaYjseYjEpkWqPzNiYabHF7e4MvP/8ilDl/+hTleITTmAUd+s3vAj9loRe5jkHou2qbqkTPxxPUMRAiyzLoeP96eHhAD49TdYEyH8EpE4PJFHZVBbvdojQZxkWByWgM6x12VRMD2IMf+M2bN8izMU5OT1C1O8BbVOt18GGoEBgLpZDnIdh+Op1iMZ8jMwZt0+L24QFv377F4ycXyIscs9k0BMQ4i/u7e8ADo/MLTGOw8turS7x48QJPn3YosjydvUlKPlTIiwIn02nyZ08mE8D7lKxSdw2wDdU2jNLIY597rxRgNCw8mr6D6UNv99zMkRuDcTHC+ckZ2i6MzyFW5Osd2q5DXTdJNtZ1javrS8ymM/zOj34IbRWqtoPTCl4rXN/eoKp3WNcVrAcW8yV+8P5HWORjrNdbeHeP7abC/d0lTk5PYYyJSYUOdRVaskwnY7RtSMJ59ep1OLtKYzIbh2oFSuP+9gFvLy9RZAaPHz1CluUxyFpDZ4AxHn3vYGOVJO8Vus5CKQPngLbpoE0Oa4H5Yo56V6NtO1xdXWMyG2O5XKKLQVhN22JcfHd1lUP6rYFxZugopVKGDJ28APaccwQppNNAOr6kE5xOawojXuro9JAOIQo2CcwR2GAWJp2kdJDygsmMFPbE4KXz0aNHe2D8dDpNTm0ACSihg1zr0FeTl2BmLsu+ERwfhfChg4iOJTp6mVkGDGAswXkKd2AwBuj4p0KXDmsJZNH5QUfYarVKGU0EojJxQSIwKgF+CXRyHvIyxr1n1k2e53uXP66L934vu0v20paOLQDpZ+Qd+TwanMwQZH816aSgo4NgWpZle85uOsrpfJegBJ2Kh1lOcs9oUNAJRwc/z0RwIkzT/GUwAbOjCBgQCEw9+eJYmNlHxwwvNrLHSVEUWCwWyVE9m83SWZLZOlxXCUAfOrLlXtHxJbO5Gc1PQFNmYhJckvKAzn9pnHBPdrsdTk5OUv9fgox8NsdKI52XYRkwQqcOnWYAktFHuUMgnjzE80Kgis++ubnBeDxGWZa4vr5OJXokyM3vM7OLDjDKCukYpVHAz9HApPNDAloAUj9Prif3rqqqlEUmAdDRaIT5fJ6MU+4hzwxBFHku6LCkvJKO4sPgBvKJBJBlVjazzqTzWQJcUl6x9DrlOp2aUmcwKIjrQqDtMENLZogzA5K8Ksthy+AcyjbKxcMqDXSyH4K0Nzc38N6nViD8HOVJXddJlkp9xDXj87jG5BHuJ+WIvLiR54Eh0EaWvueayOAn/ps6l+sqQZ4hmh57v6d+ksFlMoCGJIMDeF4PQR8ZUDWJRuJ6vd5rbcLgA4KNy+Uy8QbPE9eLslqCU3T25nme2ko451KQlAQi27bF3d3dXlATMDiwOR7Op67rNAcZjMXnUt5wzWTrGClvCEzyTNFZy0AnykCeD7mW8ncMahrkcXC+8vfkLzpTpY1BOSmrWsiKBTKLjOeb8yryAize13VdylLN8zxcVPoefuyCczueIxk0stmEkmc393d4+vRpWm8GS1DGrlarlD1+dnaWZFzf9ymATNoFBLOBoe84zx6dyTwv1MeH55T2kCwLz3WSZdU5Xu4R9ZrMRGXAE9vrSAcYbVHKXMoO6iHuH99HnpNArbQtrbWpb7kMbhqPg6ODZ4HySSmVAkXIs5Qne470KPspl/h8aXdy/fksvpdnhzxMXcUx8z0D8DVExjPDWQZdStvtEKSk3JEAP78j9T2/w+dI++fQWSllF+Uw+UOC/ZwD5y8DomSgktQ55D2CxzyHfD9tRo6BZX0pixiowDYr0mbdA4qFDcp589+Up9Jml/Mlr8nqEhyj9z4F6FCvyHWSDm2uu7U29Eb0Q5UPWQnk0MYjb/EP7xmH9gP3mbKYv+e8DoMj5N7xHZKXKOf4ucNxHDrq5TupHwHs7R/39VAOkw8On/v3JerqQxmX5Tls36NjsMLBfHl3ArB336ZNxvUhHzDgkBU+rDjPw03ZJz7md6XM5B1PZxm8Z2B9D7gebW9jH+PgKApnu0O13aKpK/RdD61C4Jp1CrvdNt2jiqLAfD6Pjn4EB6UOPUvpmLYuguZeQ+cZpjFLqq1DluR6vQ4BQNGBSjvfmAxKaZjoLAtA/WDzhOxywLv+W0EODFAl3/BvVrGjnm/b0GKLOosyguu4WW/R1A2MNshGWZIPuS5Q5AXyvIDR4bvL5SmWyyV2uwq73Q6r1Qre7wcGkW8oX5RK6Z7JltUxA7Wu61QFhGcWQKrSF2zcoR3HbDZDUZborUXTDAFodBbLQCZpCzd1jd6GUutFMQScE8x+eHhIVUWoJ4q4T5kZwHPakmGuPslpBm2GrNgOWZYT+0QewQ2eSWOird120Znv0550fEeUs1VdYTKZYRz9QDIYDQh6qG3acBZ3g//GOx96f2dG6CAm+A6txEyWRSB76DUuMxwD0MHg21DyWNrfTdMi9dHVGsaEMst9HyoemBjY5axFbrIhWMM5WOuQ5wUmivqug/cqgYPhxAO0QxUznRFLZ5uYKepj4opWsNahaRt8+eWXGM2WuHjkMZnOkBWx0qQbgHGjFUKVhn0wkTKPeiWAej1sF/wVNze3uLm+wsPDHapqF95tDGycs1LMxNVgpja8T5mnoc1CGLhXAcAjgBkAx4jmwSOG34lnqpi9HL8f10kJUPdbLaG5YPDQ0GKuAwZKWwRAKOe6WuP1N69QFiWePn0HcAoRB0euDLyz8GbYm8CL1G9hPrST2rZB19bo2hZ916FrG9zeXOPlN1/j/vYWXT+0jznUixJo5f7A+1ABRNjrXIPh39h7nrz/y2cNOnII5viuJYQch+CV/bFSD1hkmQkVDNarqPc8tMkCL/oCJuqoEAgS78JgEEBYQ69dPLMhe7dtQ1/2qt7h7u4Wr1+9wosXXyUd6pyH90MChkvzo33wbdBW8r2c699Jv+E5w69V9C21aKPuB8I9cTQO1TR2uy2aukNT7wKYnZ6hI5imoDViFvEaCgqZLtL5LBl0ZOJdm3aRTyEUUGrwSfP+U1UVrq7e4pe//CXubm/Q2w5FXoQqLQhBf1qb78yYlzx5OO/fZHNR3iqlQqUBHQC74PsOvBFs1RxtX6PvQ4UKnQ2+dfpgpE+073vUIknF2lDBxWGortlbC+c8ppMxvFeomx6r9RpAqIAzt0PyUOFizw2fQ+U5tFZJrnjvsVqt8M3Ll/ji8y/w6tUrNE2NchT8Toh+EkBht6ugtcFkFPzOiHYT7b6qrlHXNeqmhvMh4UErnXzjtAXH4zG6vkMTeWc6HqU2Z1wPruv5+XkEP2tsov+aLdSstfDRjtZKB5u1a1EUIRA/ywL+wexr3j/atsN8VqAoC+TaJD+Q1hpFWYZy6rHPAu0f3v/oizk8X866AacSwYy0e+eTaWi1IXQy/eS9HdpzLhaLhBstFgucnp1hs9mkypwAks3+/w1IfDgfwY63LlQf6LoW11dX+NnPfoYf/+77WM4WuF9tUDctlAfOFkucxLLjmTbYrkPG9je3t5iVY7z77B3kxuDTzz7FX/7yl9i1DXKTYzadwszmgI6t5kbRx+F9CkSt6h0mkynOz8+xmMzw+vItdg87zGaz4INBTFxdPWCz2WB0NkaRFyjyHFrFAP26xnI2DzaBszDEFLWB86Fc/+p+heXiAdPz84CP1DtoazGdTBglBWDwqy3mc8ymM2iv0DYtVtsd7u/vcXl5hbPTU4xGI5ydnqFpmmQr51mG5WKBs7MzbKsdNusNbrJrTCfTdG9YLpew1qKOQbFMxK2qKvmA8iwDnMft+g7jchT8KUUZ7nfwuF89oJyMsTQG2Kyxa7Z49eYNpsUImTI4WyxR5iPMlwu8vn6NKt4p8iz45rabDXob7l5KheACowNWlescte2QN1sU4xLr1QZd32Kz26FqWtRthx998gMsFjNYB+x2IdB1tVrjy69f4HQ5x3K5QFlm6LoWb9++xaPHT+Ccx2azwatvvsHNbSiJ//0ffA+nZ6coiwJd2+PN65f46qsO8B6L+TKB4+V4hCxTULDwtkdnW3hoWAvkmUHfOTTNFtYGf/14EYJqdv0Otzd3uL27xvd+8AmePXsG2/Xoux673fa3OjP/XhnjdNwTyKHwkRcpCkmCJzIzipdEXtIYuU0lQ1CSIAIBaGAom7vb7fZKDUqjGcAeuEfnohwDM7Sn02lyPBNQI7BChxCdA8yyYrQ6exFIR2AQPANoSgOAziYCe7KHIn8/n8/3ACz+W4JTfCYzynmZzrIsgad0InIdueZ0VNDpxjnxGQCS049AYl2H/jF0APE5EqCTzkg62XgxleWfOQf2FqUSpSOMQkPOQb6TgqvruuTgZRYujRJmWdNpTgcc9+j09DQBuuPxOO0neaXrulQyVfICDS86pLh/LI1Ow5AlSKmIOP/DLHnuO40EOtuZbcl5cL3m83mKxJPvkdlEvKCTOEY+W1ZykDzG7D06PplNT+ORlzNgCKSQwCblAvefc+cfgjYSHGG/VBo2BJh4FmSGpHS+B8M+jJMBHTY6c2S/dwBYLpdYr9fJMKLTmvOSTkJr7eAoi2f+9PQURVFgtVqltecZoTHGf/Ocs+cwS+kTQJDgC3lVAgrkRzrGuI50RMnMdaWGqEwJXJAkOM695HrJLFrys/c+lSxOfQTjGGgA8pkcA/eGaykDmrgOdCRT5m23W5ycnKTfMyNb6hVW55DBUSk7xAzlgmULBoKDXC8Z0cvvSSch+cBamzIzeVb5LP5NnSAzFnmmJ5PJXiYrzyD1HudEvSBBJWbpUwYOva3aJFN5vqmnuLYMxODeE4ClXLY2lJherVZ7QJvc70M+OXSgSwBFyjPOledYZu/ze/ybwV7kOwZ58cwBwWC+u7vbq4oxgEr5HjjNzFeuw2EAgMwqp5w4BEUYUEG9AgCnp6cpMpVni3JEzolrRpCHQJys4MH9kWAf1wlAqhRDmXx+fp56XR7yPfeOdlCwc0IJTanLGaHsvU9l1KUtJM8le2OxB5i1NrW1Ic91XYfReIy+a5Nc3mw2ePnyJS4uLlKW/GI2xywGfrFcuZQNJycnmC2HSgLn5+e4v79PrWh2ux0uLi7SevLcUO5kWZYywrme5HXuJ+crAyz5DP6cezQej5Pu5j5Ju5Hnm3pFriHtWPI130WbjEFwdJRTzpAXKD9klposq09wXIKCsmWEDAjgflDfyyoI0uFEXcXxUudJm4bygyRbh/Cckk8kKEtQG0CSsXw/KwFQ7vM9vBccgseUMVwfyYt8JmUFf8b15NpIG0wG/5Dv9x2uQ1YY95Q6mXPWagi8437sZXa7IWiRQRRyrtwD2tpSPg78MQQJU76R3yToyfHRJubayTnQjqN+4c+BAaiVAW8yWEM+X4J5BJvIr5RJ1J0SWJbBTBLEOFxXAvaSJzh+rgXPLnlF8jPPHG19aRNSBnD9v8s+SMEEkeQ9TYLfPDvUu/IuRlkv+Uv+XAYXyLnx55I//z5UxwxuqZNk8BPvO86F1hHL5TLdwdn3EMCerSntCdpPfH6WZeCqWRtKSzfJuTi0QyPfSn2Z57FtTwx8oxPcdm1wfGQZTJ4jL0KwZFPtcHtzg6YO96SiKNF2QZ5TTwYZlscSwxZFOQpO0QjSw1sAGn1v0fUdjMlwdvEYq1WYO+/+6/U6VIhRA6hjjMFyNugs7vthqxop4+V5lBUslFKpTCL1gLyn1nWN6XSa1pt/r9drbDYbLOZz6OUSbdfi9u4OX331FT56710sFgtkWTjLo9EolQvt+yHIgZmT1GXSJkhBNACKUZn42Hugi/d26pfA/z2gPHSmg13QdwiZxAZFMYLOcoTewYPD2TmXnOq8w1Gf9X3o0bnbbtFGEGGxWKAsi1St5eb6JoFqTdPELPiQ+XN3e5vmXFUV1ut10oFhX1cp4M5kQZ6EoDiVMraY2UVwKstMyOCLZTi5703TwPr9NnC2Cxk8mcmglYMzIZAwgNdRZlmLrm1xt9lhVBZ7doiHSo7/ruuACCiXZYm8LJI8k/ZwnudoqqBvKaOof6RMCQHqVXLyZ3kOkyPq7w4KLOUeq+BgX262rQ0gr9YoihEUDEJP0oEov/cAKITvGENdQlCXbZEm2Gxr/PKXf43n727w5OlTLE/C/RomljePiHXfa+h8kCFcdxkg3/fBwdnWNa6vr/HNN19jtX6A7TtkxsB6j77uAe8II0FnBoCDj1gT9RUAKBNAAn9Q9SCsbSwXHzPssAfkDlidj2sArs8eqHuY8Rsqe3A/hwxnlzBQ9ms3xgBeoe0s3l5eA8rAmBLzxQJ5kSOzPZTz0HkG7wbdorUOwTtivAmMdA028Uw1TY3NaoXPv/gs9mf1oQS6Htp+fJfeSvKkD3yaRb0t7SxpS+rwg28BmRyXBMq/i7z3e3nrAcAefhD0eOjbzVLowcZRyb+cFyW6tsPDwwpV3cGpDI8ePcJ0Okc5mqAsJaga1zEBbNSZPE8tmrbCdrvF69ev8PbNa9xcXaNre0wnQ4slG0uvW2uhjE53pLatEWKv9tdBUgoqUPu93X/T+jAY7jf+3ntUsTXYvp1tEdKEh3OdAnXMEHTTti1MlmNUBhtwtV5hs6lxcXGB8/NHmM1mKEcjZEW4dzgFFH7wEQS9qVNQHsHHV69e4S/+4i+wfXiAMRplMYFSHoUxcC76NnWUU94HUEcfBGd8BzHL+lvyyojMb+tg+yBv26ZB07QwRqMochRF6MPrXAhOyaO/ZrfbJX/WcrlEnoey2avVCi7eh8fTEIi9i0FdBN9SsLrKcXq2gHehOl5d1/j8iy9xdnaGx48fYzyZIC8LlH3wKVofgoiUUtBVKCf++eef48WLF8GnYXS6r5dlEUrOA1EnbhJmsNru4NabFNSmlEJrHbJyhEk8R7uqgrWh8gTb2/K+t6sq7KoQ6A9nY5/owebnOj9//hzWWtze3qHre+QxAHG5XKIdh7LI08kERVEEv7jtMSpLjMcTNE2bAgcJ6k2nU7R98AGdnpxiVJRgpj+TmIo8R5HnaHd1sjuAwbfPs0QbzjuHXVXBVxVMFtq18B5+d3uLq6sr9G2HyXQCqFBp2Fqfgv5aoaedc5hNp5jNZpjFhKXnz5/H6jh9KI3vXMIApP/20IdLWfAfelfYI54V5wCYwI7eQ3mLpt7g01//Cp//+ksYfYayHKNpW2x3W6zvHoJNWXis7h7wcHOHvm1xXVd478kzfPLxx/j+xx/jd37yE/zqy89xc3cL7TUuTs4wXyyxrSsoGIxGE2idQRuNxcki+XqdczA6+DTPz8+xbWJlQWNwcnKCs/MzjO9maFyP5WKBWTGG6i2aqg7nD8F+dM7h+uoaKgu29qbZoRyF7O+RCUkPajyGjs89mc1CGxcV2jNY51DV4Y7kegvvPDIdgkO+/73v4fb2Fk3TYLetkGWhRcRsOoU5WWKz2eDLr15gMp7go48+wk9+8hMuOoDhTmqMQWEyXN3cYLPdJuwFQOL3IsswGo/g17fYbGNFCecxHivMT0PVwJOLczx+Osdz53F3dYOXLz7HX9UNTk7PkBclqqbD8tE5Hj25wObhDrf3d9jsdnBdi8npOXRRYDyfQucGTddgs3pI/jiT69AeZDLCfHkCnWWYn4WWQdZavL29xmT8DrxT8B7QmcGTZ09we3uLm7s7QFlMxiPUdYXXry7x0z+Y4PziEb5nHTbbDd5evcaf/Lt/jSzXGI9LvPv8Od579hyurXB3e422ZTu5DEo5WOsDOL+uUFUttAYeT+ewzmF9f4/dtkLbBrlQZGVomaUUxuMR3n3nCa5vb/H69SuMZ1NMRmOM8hJW/XZV25T/u7TukY50pCMd6UhHOtKRjnSkIx3pSEc60pGOdKQjHelIRzrSkY50pCMd6Uj/f0z/bwxLOdKRjnSkIx3pSEc60pGOdKQjHelIRzrSkY50pCMd6UhHOtKRjnSkIx3p//foCIwf6UhHOtKRjnSkIx3pSEc60pGOdKQjHelIRzrSkY50pCMd6UhHOtKR/kHTERg/0pGOdKQjHelIRzrSkY50pCMd6UhHOtKRjnSkIx3pSEc60pGOdKQj/YOmIzB+pCMd6UhHOtKRjnSkIx3pSEc60pGOdKQjHelIRzrSkY50pCMd6UhH+gdNR2D8SEc60pGOdKQjHelIRzrSkY50pCMd6UhHOtKRjnSkIx3pSEc60pGO9A+ajsD4kY50pCMd6UhHOtKRjnSkIx3pSEc60pGOdKQjHelIRzrSkY50pCMd6R80HYHxIx3pSEc60pGOdKQjHelIRzrSkY50pCMd6UhHOtKRjnSkIx3pSEc60j9oOgLjRzrSkY50pCMd6UhHOtKRjnSkIx3pSEc60pGOdKQjHelIRzrSkY50pH/QdATGj3SkIx3pSEc60pGOdKQjHelIRzrSkY50pCMd6UhHOtKRjnSkIx3pSP+g6f8F87lOoajGj04AAAAASUVORK5CYII=\n",
+ "text/plain": [
+ ""
+ ]
+ },
+ "metadata": {},
+ "output_type": "display_data"
+ }
+ ],
+ "source": [
+ "fig, ax = plt.subplots(1, 2, figsize=(20, 20))\n",
+ "\n",
+ "ax[0].imshow(image1)\n",
+ "for mask in batched_output[0]['masks']:\n",
+ " show_mask(mask.cpu().numpy(), ax[0], random_color=True)\n",
+ "for box in image1_boxes:\n",
+ " show_box(box.cpu().numpy(), ax[0])\n",
+ "ax[0].axis('off')\n",
+ "\n",
+ "ax[1].imshow(image2)\n",
+ "for mask in batched_output[1]['masks']:\n",
+ " show_mask(mask.cpu().numpy(), ax[1], random_color=True)\n",
+ "for box in image2_boxes:\n",
+ " show_box(box.cpu().numpy(), ax[1])\n",
+ "ax[1].axis('off')\n",
+ "\n",
+ "plt.tight_layout()\n",
+ "plt.show()"
+ ]
+ }
+ ],
+ "metadata": {
+ "kernelspec": {
+ "display_name": "Python 3 (ipykernel)",
+ "language": "python",
+ "name": "python3"
+ },
+ "language_info": {
+ "codemirror_mode": {
+ "name": "ipython",
+ "version": 3
+ },
+ "file_extension": ".py",
+ "mimetype": "text/x-python",
+ "name": "python",
+ "nbconvert_exporter": "python",
+ "pygments_lexer": "ipython3",
+ "version": "3.10.10"
+ }
+ },
+ "nbformat": 4,
+ "nbformat_minor": 5
+}
diff --git a/VISAM/thirdparty/segment_anything/scripts/amg.py b/VISAM/thirdparty/segment_anything/scripts/amg.py
new file mode 100644
index 0000000000000000000000000000000000000000..3cae6ff720e5cb718045ff3f1082340968516d6a
--- /dev/null
+++ b/VISAM/thirdparty/segment_anything/scripts/amg.py
@@ -0,0 +1,238 @@
+# Copyright (c) Meta Platforms, Inc. and affiliates.
+# All rights reserved.
+
+# This source code is licensed under the license found in the
+# LICENSE file in the root directory of this source tree.
+
+import cv2 # type: ignore
+
+from segment_anything import SamAutomaticMaskGenerator, sam_model_registry
+
+import argparse
+import json
+import os
+from typing import Any, Dict, List
+
+parser = argparse.ArgumentParser(
+ description=(
+ "Runs automatic mask generation on an input image or directory of images, "
+ "and outputs masks as either PNGs or COCO-style RLEs. Requires open-cv, "
+ "as well as pycocotools if saving in RLE format."
+ )
+)
+
+parser.add_argument(
+ "--input",
+ type=str,
+ required=True,
+ help="Path to either a single input image or folder of images.",
+)
+
+parser.add_argument(
+ "--output",
+ type=str,
+ required=True,
+ help=(
+ "Path to the directory where masks will be output. Output will be either a folder "
+ "of PNGs per image or a single json with COCO-style masks."
+ ),
+)
+
+parser.add_argument(
+ "--model-type",
+ type=str,
+ default="default",
+ help="The type of model to load, in ['default', 'vit_l', 'vit_b']",
+)
+
+parser.add_argument(
+ "--checkpoint",
+ type=str,
+ required=True,
+ help="The path to the SAM checkpoint to use for mask generation.",
+)
+
+parser.add_argument("--device", type=str, default="cuda", help="The device to run generation on.")
+
+parser.add_argument(
+ "--convert-to-rle",
+ action="store_true",
+ help=(
+ "Save masks as COCO RLEs in a single json instead of as a folder of PNGs. "
+ "Requires pycocotools."
+ ),
+)
+
+amg_settings = parser.add_argument_group("AMG Settings")
+
+amg_settings.add_argument(
+ "--points-per-side",
+ type=int,
+ default=None,
+ help="Generate masks by sampling a grid over the image with this many points to a side.",
+)
+
+amg_settings.add_argument(
+ "--points-per-batch",
+ type=int,
+ default=None,
+ help="How many input points to process simultaneously in one batch.",
+)
+
+amg_settings.add_argument(
+ "--pred-iou-thresh",
+ type=float,
+ default=None,
+ help="Exclude masks with a predicted score from the model that is lower than this threshold.",
+)
+
+amg_settings.add_argument(
+ "--stability-score-thresh",
+ type=float,
+ default=None,
+ help="Exclude masks with a stability score lower than this threshold.",
+)
+
+amg_settings.add_argument(
+ "--stability-score-offset",
+ type=float,
+ default=None,
+ help="Larger values perturb the mask more when measuring stability score.",
+)
+
+amg_settings.add_argument(
+ "--box-nms-thresh",
+ type=float,
+ default=None,
+ help="The overlap threshold for excluding a duplicate mask.",
+)
+
+amg_settings.add_argument(
+ "--crop-n-layers",
+ type=int,
+ default=None,
+ help=(
+ "If >0, mask generation is run on smaller crops of the image to generate more masks. "
+ "The value sets how many different scales to crop at."
+ ),
+)
+
+amg_settings.add_argument(
+ "--crop-nms-thresh",
+ type=float,
+ default=None,
+ help="The overlap threshold for excluding duplicate masks across different crops.",
+)
+
+amg_settings.add_argument(
+ "--crop-overlap-ratio",
+ type=int,
+ default=None,
+ help="Larger numbers mean image crops will overlap more.",
+)
+
+amg_settings.add_argument(
+ "--crop-n-points-downscale-factor",
+ type=int,
+ default=None,
+ help="The number of points-per-side in each layer of crop is reduced by this factor.",
+)
+
+amg_settings.add_argument(
+ "--min-mask-region-area",
+ type=int,
+ default=None,
+ help=(
+ "Disconnected mask regions or holes with area smaller than this value "
+ "in pixels are removed by postprocessing."
+ ),
+)
+
+
+def write_masks_to_folder(masks: List[Dict[str, Any]], path: str) -> None:
+ header = "id,area,bbox_x0,bbox_y0,bbox_w,bbox_h,point_input_x,point_input_y,predicted_iou,stability_score,crop_box_x0,crop_box_y0,crop_box_w,crop_box_h" # noqa
+ metadata = [header]
+ for i, mask_data in enumerate(masks):
+ mask = mask_data["segmentation"]
+ filename = f"{i}.png"
+ cv2.imwrite(os.path.join(path, filename), mask * 255)
+ mask_metadata = [
+ str(i),
+ str(mask_data["area"]),
+ *[str(x) for x in mask_data["bbox"]],
+ *[str(x) for x in mask_data["point_coords"][0]],
+ str(mask_data["predicted_iou"]),
+ str(mask_data["stability_score"]),
+ *[str(x) for x in mask_data["crop_box"]],
+ ]
+ row = ",".join(mask_metadata)
+ metadata.append(row)
+ metadata_path = os.path.join(path, "metadata.csv")
+ with open(metadata_path, "w") as f:
+ f.write("\n".join(metadata))
+
+ return
+
+
+def get_amg_kwargs(args):
+ amg_kwargs = {
+ "points_per_side": args.points_per_side,
+ "points_per_batch": args.points_per_batch,
+ "pred_iou_thresh": args.pred_iou_thresh,
+ "stability_score_thresh": args.stability_score_thresh,
+ "stability_score_offset": args.stability_score_offset,
+ "box_nms_thresh": args.box_nms_thresh,
+ "crop_n_layers": args.crop_n_layers,
+ "crop_nms_thresh": args.crop_nms_thresh,
+ "crop_overlap_ratio": args.crop_overlap_ratio,
+ "crop_n_points_downscale_factor": args.crop_n_points_downscale_factor,
+ "min_mask_region_area": args.min_mask_region_area,
+ }
+ amg_kwargs = {k: v for k, v in amg_kwargs.items() if v is not None}
+ return amg_kwargs
+
+
+def main(args: argparse.Namespace) -> None:
+ print("Loading model...")
+ sam = sam_model_registry[args.model_type](checkpoint=args.checkpoint)
+ _ = sam.to(device=args.device)
+ output_mode = "coco_rle" if args.convert_to_rle else "binary_mask"
+ amg_kwargs = get_amg_kwargs(args)
+ generator = SamAutomaticMaskGenerator(sam, output_mode=output_mode, **amg_kwargs)
+
+ if not os.path.isdir(args.input):
+ targets = [args.input]
+ else:
+ targets = [
+ f for f in os.listdir(args.input) if not os.path.isdir(os.path.join(args.input, f))
+ ]
+ targets = [os.path.join(args.input, f) for f in targets]
+
+ os.makedirs(args.output, exist_ok=True)
+
+ for t in targets:
+ print(f"Processing '{t}'...")
+ image = cv2.imread(t)
+ if image is None:
+ print(f"Could not load '{t}' as an image, skipping...")
+ continue
+ image = cv2.cvtColor(image, cv2.COLOR_BGR2RGB)
+
+ masks = generator.generate(image)
+
+ base = os.path.basename(t)
+ base = os.path.splitext(base)[0]
+ save_base = os.path.join(args.output, base)
+ if output_mode == "binary_mask":
+ os.makedirs(save_base, exist_ok=False)
+ write_masks_to_folder(masks, save_base)
+ else:
+ save_file = save_base + ".json"
+ with open(save_file, "w") as f:
+ json.dump(masks, f)
+ print("Done!")
+
+
+if __name__ == "__main__":
+ args = parser.parse_args()
+ main(args)
diff --git a/VISAM/thirdparty/segment_anything/scripts/export_onnx_model.py b/VISAM/thirdparty/segment_anything/scripts/export_onnx_model.py
new file mode 100644
index 0000000000000000000000000000000000000000..8ec5c2ec24fc53cd9fdf66564cfe163b9eb26c24
--- /dev/null
+++ b/VISAM/thirdparty/segment_anything/scripts/export_onnx_model.py
@@ -0,0 +1,204 @@
+# Copyright (c) Meta Platforms, Inc. and affiliates.
+# All rights reserved.
+
+# This source code is licensed under the license found in the
+# LICENSE file in the root directory of this source tree.
+
+import torch
+
+from segment_anything import build_sam, build_sam_vit_b, build_sam_vit_l
+from segment_anything.utils.onnx import SamOnnxModel
+
+import argparse
+import warnings
+
+try:
+ import onnxruntime # type: ignore
+
+ onnxruntime_exists = True
+except ImportError:
+ onnxruntime_exists = False
+
+parser = argparse.ArgumentParser(
+ description="Export the SAM prompt encoder and mask decoder to an ONNX model."
+)
+
+parser.add_argument(
+ "--checkpoint", type=str, required=True, help="The path to the SAM model checkpoint."
+)
+
+parser.add_argument(
+ "--output", type=str, required=True, help="The filename to save the ONNX model to."
+)
+
+parser.add_argument(
+ "--model-type",
+ type=str,
+ default="default",
+ help="In ['default', 'vit_b', 'vit_l']. Which type of SAM model to export.",
+)
+
+parser.add_argument(
+ "--return-single-mask",
+ action="store_true",
+ help=(
+ "If true, the exported ONNX model will only return the best mask, "
+ "instead of returning multiple masks. For high resolution images "
+ "this can improve runtime when upscaling masks is expensive."
+ ),
+)
+
+parser.add_argument(
+ "--opset",
+ type=int,
+ default=17,
+ help="The ONNX opset version to use. Must be >=11",
+)
+
+parser.add_argument(
+ "--quantize-out",
+ type=str,
+ default=None,
+ help=(
+ "If set, will quantize the model and save it with this name. "
+ "Quantization is performed with quantize_dynamic from onnxruntime.quantization.quantize."
+ ),
+)
+
+parser.add_argument(
+ "--gelu-approximate",
+ action="store_true",
+ help=(
+ "Replace GELU operations with approximations using tanh. Useful "
+ "for some runtimes that have slow or unimplemented erf ops, used in GELU."
+ ),
+)
+
+parser.add_argument(
+ "--use-stability-score",
+ action="store_true",
+ help=(
+ "Replaces the model's predicted mask quality score with the stability "
+ "score calculated on the low resolution masks using an offset of 1.0. "
+ ),
+)
+
+parser.add_argument(
+ "--return-extra-metrics",
+ action="store_true",
+ help=(
+ "The model will return five results: (masks, scores, stability_scores, "
+ "areas, low_res_logits) instead of the usual three. This can be "
+ "significantly slower for high resolution outputs."
+ ),
+)
+
+
+def run_export(
+ model_type: str,
+ checkpoint: str,
+ output: str,
+ opset: int,
+ return_single_mask: bool,
+ gelu_approximate: bool = False,
+ use_stability_score: bool = False,
+ return_extra_metrics=False,
+):
+ print("Loading model...")
+ if model_type == "vit_b":
+ sam = build_sam_vit_b(checkpoint)
+ elif model_type == "vit_l":
+ sam = build_sam_vit_l(checkpoint)
+ else:
+ sam = build_sam(checkpoint)
+
+ onnx_model = SamOnnxModel(
+ model=sam,
+ return_single_mask=return_single_mask,
+ use_stability_score=use_stability_score,
+ return_extra_metrics=return_extra_metrics,
+ )
+
+ if gelu_approximate:
+ for n, m in onnx_model.named_modules():
+ if isinstance(m, torch.nn.GELU):
+ m.approximate = "tanh"
+
+ dynamic_axes = {
+ "point_coords": {1: "num_points"},
+ "point_labels": {1: "num_points"},
+ }
+
+ embed_dim = sam.prompt_encoder.embed_dim
+ embed_size = sam.prompt_encoder.image_embedding_size
+ mask_input_size = [4 * x for x in embed_size]
+ dummy_inputs = {
+ "image_embeddings": torch.randn(1, embed_dim, *embed_size, dtype=torch.float),
+ "point_coords": torch.randint(low=0, high=1024, size=(1, 5, 2), dtype=torch.float),
+ "point_labels": torch.randint(low=0, high=4, size=(1, 5), dtype=torch.float),
+ "mask_input": torch.randn(1, 1, *mask_input_size, dtype=torch.float),
+ "has_mask_input": torch.tensor([1], dtype=torch.float),
+ "orig_im_size": torch.tensor([1500, 2250], dtype=torch.float),
+ }
+
+ _ = onnx_model(**dummy_inputs)
+
+ output_names = ["masks", "iou_predictions", "low_res_masks"]
+
+ with warnings.catch_warnings():
+ warnings.filterwarnings("ignore", category=torch.jit.TracerWarning)
+ warnings.filterwarnings("ignore", category=UserWarning)
+ with open(output, "wb") as f:
+ print(f"Exporing onnx model to {output}...")
+ torch.onnx.export(
+ onnx_model,
+ tuple(dummy_inputs.values()),
+ f,
+ export_params=True,
+ verbose=False,
+ opset_version=opset,
+ do_constant_folding=True,
+ input_names=list(dummy_inputs.keys()),
+ output_names=output_names,
+ dynamic_axes=dynamic_axes,
+ )
+
+ if onnxruntime_exists:
+ ort_inputs = {k: to_numpy(v) for k, v in dummy_inputs.items()}
+ ort_session = onnxruntime.InferenceSession(output)
+ _ = ort_session.run(None, ort_inputs)
+ print("Model has successfully been run with ONNXRuntime.")
+
+
+def to_numpy(tensor):
+ return tensor.cpu().numpy()
+
+
+if __name__ == "__main__":
+ args = parser.parse_args()
+ run_export(
+ model_type=args.model_type,
+ checkpoint=args.checkpoint,
+ output=args.output,
+ opset=args.opset,
+ return_single_mask=args.return_single_mask,
+ gelu_approximate=args.gelu_approximate,
+ use_stability_score=args.use_stability_score,
+ return_extra_metrics=args.return_extra_metrics,
+ )
+
+ if args.quantize_out is not None:
+ assert onnxruntime_exists, "onnxruntime is required to quantize the model."
+ from onnxruntime.quantization import QuantType # type: ignore
+ from onnxruntime.quantization.quantize import quantize_dynamic # type: ignore
+
+ print(f"Quantizing model and writing to {args.quantize_out}...")
+ quantize_dynamic(
+ model_input=args.output,
+ model_output=args.quantize_out,
+ optimize_model=True,
+ per_channel=False,
+ reduce_range=False,
+ weight_type=QuantType.QUInt8,
+ )
+ print("Done!")
diff --git a/VISAM/thirdparty/segment_anything/segment_anything/__init__.py b/VISAM/thirdparty/segment_anything/segment_anything/__init__.py
new file mode 100644
index 0000000000000000000000000000000000000000..34383d83f5e76bc801f31b20e5651e383be348b6
--- /dev/null
+++ b/VISAM/thirdparty/segment_anything/segment_anything/__init__.py
@@ -0,0 +1,15 @@
+# Copyright (c) Meta Platforms, Inc. and affiliates.
+# All rights reserved.
+
+# This source code is licensed under the license found in the
+# LICENSE file in the root directory of this source tree.
+
+from .build_sam import (
+ build_sam,
+ build_sam_vit_h,
+ build_sam_vit_l,
+ build_sam_vit_b,
+ sam_model_registry,
+)
+from .predictor import SamPredictor
+from .automatic_mask_generator import SamAutomaticMaskGenerator
diff --git a/VISAM/thirdparty/segment_anything/segment_anything/automatic_mask_generator.py b/VISAM/thirdparty/segment_anything/segment_anything/automatic_mask_generator.py
new file mode 100644
index 0000000000000000000000000000000000000000..23264971b7ff5aa0b4f499ade7773b68dce984b6
--- /dev/null
+++ b/VISAM/thirdparty/segment_anything/segment_anything/automatic_mask_generator.py
@@ -0,0 +1,372 @@
+# Copyright (c) Meta Platforms, Inc. and affiliates.
+# All rights reserved.
+
+# This source code is licensed under the license found in the
+# LICENSE file in the root directory of this source tree.
+
+import numpy as np
+import torch
+from torchvision.ops.boxes import batched_nms, box_area # type: ignore
+
+from typing import Any, Dict, List, Optional, Tuple
+
+from .modeling import Sam
+from .predictor import SamPredictor
+from .utils.amg import (
+ MaskData,
+ area_from_rle,
+ batch_iterator,
+ batched_mask_to_box,
+ box_xyxy_to_xywh,
+ build_all_layer_point_grids,
+ calculate_stability_score,
+ coco_encode_rle,
+ generate_crop_boxes,
+ is_box_near_crop_edge,
+ mask_to_rle_pytorch,
+ remove_small_regions,
+ rle_to_mask,
+ uncrop_boxes_xyxy,
+ uncrop_masks,
+ uncrop_points,
+)
+
+
+class SamAutomaticMaskGenerator:
+ def __init__(
+ self,
+ model: Sam,
+ points_per_side: Optional[int] = 32,
+ points_per_batch: int = 64,
+ pred_iou_thresh: float = 0.88,
+ stability_score_thresh: float = 0.95,
+ stability_score_offset: float = 1.0,
+ box_nms_thresh: float = 0.7,
+ crop_n_layers: int = 0,
+ crop_nms_thresh: float = 0.7,
+ crop_overlap_ratio: float = 512 / 1500,
+ crop_n_points_downscale_factor: int = 1,
+ point_grids: Optional[List[np.ndarray]] = None,
+ min_mask_region_area: int = 0,
+ output_mode: str = "binary_mask",
+ ) -> None:
+ """
+ Using a SAM model, generates masks for the entire image.
+ Generates a grid of point prompts over the image, then filters
+ low quality and duplicate masks. The default settings are chosen
+ for SAM with a ViT-H backbone.
+
+ Arguments:
+ model (Sam): The SAM model to use for mask prediction.
+ points_per_side (int or None): The number of points to be sampled
+ along one side of the image. The total number of points is
+ points_per_side**2. If None, 'point_grids' must provide explicit
+ point sampling.
+ points_per_batch (int): Sets the number of points run simultaneously
+ by the model. Higher numbers may be faster but use more GPU memory.
+ pred_iou_thresh (float): A filtering threshold in [0,1], using the
+ model's predicted mask quality.
+ stability_score_thresh (float): A filtering threshold in [0,1], using
+ the stability of the mask under changes to the cutoff used to binarize
+ the model's mask predictions.
+ stability_score_offset (float): The amount to shift the cutoff when
+ calculated the stability score.
+ box_nms_thresh (float): The box IoU cutoff used by non-maximal
+ suppression to filter duplicate masks.
+ crops_n_layers (int): If >0, mask prediction will be run again on
+ crops of the image. Sets the number of layers to run, where each
+ layer has 2**i_layer number of image crops.
+ crops_nms_thresh (float): The box IoU cutoff used by non-maximal
+ suppression to filter duplicate masks between different crops.
+ crop_overlap_ratio (float): Sets the degree to which crops overlap.
+ In the first crop layer, crops will overlap by this fraction of
+ the image length. Later layers with more crops scale down this overlap.
+ crop_n_points_downscale_factor (int): The number of points-per-side
+ sampled in layer n is scaled down by crop_n_points_downscale_factor**n.
+ point_grids (list(np.ndarray) or None): A list over explicit grids
+ of points used for sampling, normalized to [0,1]. The nth grid in the
+ list is used in the nth crop layer. Exclusive with points_per_side.
+ min_mask_region_area (int): If >0, postprocessing will be applied
+ to remove disconnected regions and holes in masks with area smaller
+ than min_mask_region_area. Requires opencv.
+ output_mode (str): The form masks are returned in. Can be 'binary_mask',
+ 'uncompressed_rle', or 'coco_rle'. 'coco_rle' requires pycocotools.
+ For large resolutions, 'binary_mask' may consume large amounts of
+ memory.
+ """
+
+ assert (points_per_side is None) != (
+ point_grids is None
+ ), "Exactly one of points_per_side or point_grid must be provided."
+ if points_per_side is not None:
+ self.point_grids = build_all_layer_point_grids(
+ points_per_side,
+ crop_n_layers,
+ crop_n_points_downscale_factor,
+ )
+ elif point_grids is not None:
+ self.point_grids = point_grids
+ else:
+ raise ValueError("Can't have both points_per_side and point_grid be None.")
+
+ assert output_mode in [
+ "binary_mask",
+ "uncompressed_rle",
+ "coco_rle",
+ ], f"Unknown output_mode {output_mode}."
+ if output_mode == "coco_rle":
+ from pycocotools import mask as mask_utils # type: ignore # noqa: F401
+
+ if min_mask_region_area > 0:
+ import cv2 # type: ignore # noqa: F401
+
+ self.predictor = SamPredictor(model)
+ self.points_per_batch = points_per_batch
+ self.pred_iou_thresh = pred_iou_thresh
+ self.stability_score_thresh = stability_score_thresh
+ self.stability_score_offset = stability_score_offset
+ self.box_nms_thresh = box_nms_thresh
+ self.crop_n_layers = crop_n_layers
+ self.crop_nms_thresh = crop_nms_thresh
+ self.crop_overlap_ratio = crop_overlap_ratio
+ self.crop_n_points_downscale_factor = crop_n_points_downscale_factor
+ self.min_mask_region_area = min_mask_region_area
+ self.output_mode = output_mode
+
+ @torch.no_grad()
+ def generate(self, image: np.ndarray) -> List[Dict[str, Any]]:
+ """
+ Generates masks for the given image.
+
+ Arguments:
+ image (np.ndarray): The image to generate masks for, in HWC uint8 format.
+
+ Returns:
+ list(dict(str, any)): A list over records for masks. Each record is
+ a dict containing the following keys:
+ segmentation (dict(str, any) or np.ndarray): The mask. If
+ output_mode='binary_mask', is an array of shape HW. Otherwise,
+ is a dictionary containing the RLE.
+ bbox (list(float)): The box around the mask, in XYWH format.
+ area (int): The area in pixels of the mask.
+ predicted_iou (float): The model's own prediction of the mask's
+ quality. This is filtered by the pred_iou_thresh parameter.
+ point_coords (list(list(float))): The point coordinates input
+ to the model to generate this mask.
+ stability_score (float): A measure of the mask's quality. This
+ is filtered on using the stability_score_thresh parameter.
+ crop_box (list(float)): The crop of the image used to generate
+ the mask, given in XYWH format.
+ """
+
+ # Generate masks
+ mask_data = self._generate_masks(image)
+
+ # Filter small disconnected regions and holes in masks
+ if self.min_mask_region_area > 0:
+ mask_data = self.postprocess_small_regions(
+ mask_data,
+ self.min_mask_region_area,
+ max(self.box_nms_thresh, self.crop_nms_thresh),
+ )
+
+ # Encode masks
+ if self.output_mode == "coco_rle":
+ mask_data["segmentations"] = [coco_encode_rle(rle) for rle in mask_data["rles"]]
+ elif self.output_mode == "binary_mask":
+ mask_data["segmentations"] = [rle_to_mask(rle) for rle in mask_data["rles"]]
+ else:
+ mask_data["segmentations"] = mask_data["rles"]
+
+ # Write mask records
+ curr_anns = []
+ for idx in range(len(mask_data["segmentations"])):
+ ann = {
+ "segmentation": mask_data["segmentations"][idx],
+ "area": area_from_rle(mask_data["rles"][idx]),
+ "bbox": box_xyxy_to_xywh(mask_data["boxes"][idx]).tolist(),
+ "predicted_iou": mask_data["iou_preds"][idx].item(),
+ "point_coords": [mask_data["points"][idx].tolist()],
+ "stability_score": mask_data["stability_score"][idx].item(),
+ "crop_box": box_xyxy_to_xywh(mask_data["crop_boxes"][idx]).tolist(),
+ }
+ curr_anns.append(ann)
+
+ return curr_anns
+
+ def _generate_masks(self, image: np.ndarray) -> MaskData:
+ orig_size = image.shape[:2]
+ crop_boxes, layer_idxs = generate_crop_boxes(
+ orig_size, self.crop_n_layers, self.crop_overlap_ratio
+ )
+
+ # Iterate over image crops
+ data = MaskData()
+ for crop_box, layer_idx in zip(crop_boxes, layer_idxs):
+ crop_data = self._process_crop(image, crop_box, layer_idx, orig_size)
+ data.cat(crop_data)
+
+ # Remove duplicate masks between crops
+ if len(crop_boxes) > 1:
+ # Prefer masks from smaller crops
+ scores = 1 / box_area(data["crop_boxes"])
+ scores = scores.to(data["boxes"].device)
+ keep_by_nms = batched_nms(
+ data["boxes"].float(),
+ scores,
+ torch.zeros(len(data["boxes"])), # categories
+ iou_threshold=self.crop_nms_thresh,
+ )
+ data.filter(keep_by_nms)
+
+ data.to_numpy()
+ return data
+
+ def _process_crop(
+ self,
+ image: np.ndarray,
+ crop_box: List[int],
+ crop_layer_idx: int,
+ orig_size: Tuple[int, ...],
+ ) -> MaskData:
+ # Crop the image and calculate embeddings
+ x0, y0, x1, y1 = crop_box
+ cropped_im = image[y0:y1, x0:x1, :]
+ cropped_im_size = cropped_im.shape[:2]
+ self.predictor.set_image(cropped_im)
+
+ # Get points for this crop
+ points_scale = np.array(cropped_im_size)[None, ::-1]
+ points_for_image = self.point_grids[crop_layer_idx] * points_scale
+
+ # Generate masks for this crop in batches
+ data = MaskData()
+ for (points,) in batch_iterator(self.points_per_batch, points_for_image):
+ batch_data = self._process_batch(points, cropped_im_size, crop_box, orig_size)
+ data.cat(batch_data)
+ del batch_data
+ self.predictor.reset_image()
+
+ # Remove duplicates within this crop.
+ keep_by_nms = batched_nms(
+ data["boxes"].float(),
+ data["iou_preds"],
+ torch.zeros(len(data["boxes"])), # categories
+ iou_threshold=self.box_nms_thresh,
+ )
+ data.filter(keep_by_nms)
+
+ # Return to the original image frame
+ data["boxes"] = uncrop_boxes_xyxy(data["boxes"], crop_box)
+ data["points"] = uncrop_points(data["points"], crop_box)
+ data["crop_boxes"] = torch.tensor([crop_box for _ in range(len(data["rles"]))])
+
+ return data
+
+ def _process_batch(
+ self,
+ points: np.ndarray,
+ im_size: Tuple[int, ...],
+ crop_box: List[int],
+ orig_size: Tuple[int, ...],
+ ) -> MaskData:
+ orig_h, orig_w = orig_size
+
+ # Run model on this batch
+ transformed_points = self.predictor.transform.apply_coords(points, im_size)
+ in_points = torch.as_tensor(transformed_points, device=self.predictor.device)
+ in_labels = torch.ones(in_points.shape[0], dtype=torch.int, device=in_points.device)
+ masks, iou_preds, _ = self.predictor.predict_torch(
+ in_points[:, None, :],
+ in_labels[:, None],
+ multimask_output=True,
+ return_logits=True,
+ )
+
+ # Serialize predictions and store in MaskData
+ data = MaskData(
+ masks=masks.flatten(0, 1),
+ iou_preds=iou_preds.flatten(0, 1),
+ points=torch.as_tensor(points.repeat(masks.shape[1], axis=0)),
+ )
+ del masks
+
+ # Filter by predicted IoU
+ if self.pred_iou_thresh > 0.0:
+ keep_mask = data["iou_preds"] > self.pred_iou_thresh
+ data.filter(keep_mask)
+
+ # Calculate stability score
+ data["stability_score"] = calculate_stability_score(
+ data["masks"], self.predictor.model.mask_threshold, self.stability_score_offset
+ )
+ if self.stability_score_thresh > 0.0:
+ keep_mask = data["stability_score"] >= self.stability_score_thresh
+ data.filter(keep_mask)
+
+ # Threshold masks and calculate boxes
+ data["masks"] = data["masks"] > self.predictor.model.mask_threshold
+ data["boxes"] = batched_mask_to_box(data["masks"])
+
+ # Filter boxes that touch crop boundaries
+ keep_mask = ~is_box_near_crop_edge(data["boxes"], crop_box, [0, 0, orig_w, orig_h])
+ if not torch.all(keep_mask):
+ data.filter(keep_mask)
+
+ # Compress to RLE
+ data["masks"] = uncrop_masks(data["masks"], crop_box, orig_h, orig_w)
+ data["rles"] = mask_to_rle_pytorch(data["masks"])
+ del data["masks"]
+
+ return data
+
+ @staticmethod
+ def postprocess_small_regions(
+ mask_data: MaskData, min_area: int, nms_thresh: float
+ ) -> MaskData:
+ """
+ Removes small disconnected regions and holes in masks, then reruns
+ box NMS to remove any new duplicates.
+
+ Edits mask_data in place.
+
+ Requires open-cv as a dependency.
+ """
+ if len(mask_data["rles"]) == 0:
+ return mask_data
+
+ # Filter small disconnected regions and holes
+ new_masks = []
+ scores = []
+ for rle in mask_data["rles"]:
+ mask = rle_to_mask(rle)
+
+ mask, changed = remove_small_regions(mask, min_area, mode="holes")
+ unchanged = not changed
+ mask, changed = remove_small_regions(mask, min_area, mode="islands")
+ unchanged = unchanged and not changed
+
+ new_masks.append(torch.as_tensor(mask).unsqueeze(0))
+ # Give score=0 to changed masks and score=1 to unchanged masks
+ # so NMS will prefer ones that didn't need postprocessing
+ scores.append(float(unchanged))
+
+ # Recalculate boxes and remove any new duplicates
+ masks = torch.cat(new_masks, dim=0)
+ boxes = batched_mask_to_box(masks)
+ keep_by_nms = batched_nms(
+ boxes.float(),
+ torch.as_tensor(scores),
+ torch.zeros(len(boxes)), # categories
+ iou_threshold=nms_thresh,
+ )
+
+ # Only recalculate RLEs for masks that have changed
+ for i_mask in keep_by_nms:
+ if scores[i_mask] == 0.0:
+ mask_torch = masks[i_mask].unsqueeze(0)
+ mask_data["rles"][i_mask] = mask_to_rle_pytorch(mask_torch)[0]
+ mask_data["boxes"][i_mask] = boxes[i_mask] # update res directly
+ mask_data.filter(keep_by_nms)
+
+ return mask_data
diff --git a/VISAM/thirdparty/segment_anything/segment_anything/build_sam.py b/VISAM/thirdparty/segment_anything/segment_anything/build_sam.py
new file mode 100644
index 0000000000000000000000000000000000000000..07abfca24e96eced7f13bdefd3212ce1b77b8999
--- /dev/null
+++ b/VISAM/thirdparty/segment_anything/segment_anything/build_sam.py
@@ -0,0 +1,107 @@
+# Copyright (c) Meta Platforms, Inc. and affiliates.
+# All rights reserved.
+
+# This source code is licensed under the license found in the
+# LICENSE file in the root directory of this source tree.
+
+import torch
+
+from functools import partial
+
+from .modeling import ImageEncoderViT, MaskDecoder, PromptEncoder, Sam, TwoWayTransformer
+
+
+def build_sam_vit_h(checkpoint=None):
+ return _build_sam(
+ encoder_embed_dim=1280,
+ encoder_depth=32,
+ encoder_num_heads=16,
+ encoder_global_attn_indexes=[7, 15, 23, 31],
+ checkpoint=checkpoint,
+ )
+
+
+build_sam = build_sam_vit_h
+
+
+def build_sam_vit_l(checkpoint=None):
+ return _build_sam(
+ encoder_embed_dim=1024,
+ encoder_depth=24,
+ encoder_num_heads=16,
+ encoder_global_attn_indexes=[5, 11, 17, 23],
+ checkpoint=checkpoint,
+ )
+
+
+def build_sam_vit_b(checkpoint=None):
+ return _build_sam(
+ encoder_embed_dim=768,
+ encoder_depth=12,
+ encoder_num_heads=12,
+ encoder_global_attn_indexes=[2, 5, 8, 11],
+ checkpoint=checkpoint,
+ )
+
+
+sam_model_registry = {
+ "default": build_sam,
+ "vit_h": build_sam,
+ "vit_l": build_sam_vit_l,
+ "vit_b": build_sam_vit_b,
+}
+
+
+def _build_sam(
+ encoder_embed_dim,
+ encoder_depth,
+ encoder_num_heads,
+ encoder_global_attn_indexes,
+ checkpoint=None,
+):
+ prompt_embed_dim = 256
+ image_size = 1024
+ vit_patch_size = 16
+ image_embedding_size = image_size // vit_patch_size
+ sam = Sam(
+ image_encoder=ImageEncoderViT(
+ depth=encoder_depth,
+ embed_dim=encoder_embed_dim,
+ img_size=image_size,
+ mlp_ratio=4,
+ norm_layer=partial(torch.nn.LayerNorm, eps=1e-6),
+ num_heads=encoder_num_heads,
+ patch_size=vit_patch_size,
+ qkv_bias=True,
+ use_rel_pos=True,
+ global_attn_indexes=encoder_global_attn_indexes,
+ window_size=14,
+ out_chans=prompt_embed_dim,
+ ),
+ prompt_encoder=PromptEncoder(
+ embed_dim=prompt_embed_dim,
+ image_embedding_size=(image_embedding_size, image_embedding_size),
+ input_image_size=(image_size, image_size),
+ mask_in_chans=16,
+ ),
+ mask_decoder=MaskDecoder(
+ num_multimask_outputs=3,
+ transformer=TwoWayTransformer(
+ depth=2,
+ embedding_dim=prompt_embed_dim,
+ mlp_dim=2048,
+ num_heads=8,
+ ),
+ transformer_dim=prompt_embed_dim,
+ iou_head_depth=3,
+ iou_head_hidden_dim=256,
+ ),
+ pixel_mean=[123.675, 116.28, 103.53],
+ pixel_std=[58.395, 57.12, 57.375],
+ )
+ sam.eval()
+ if checkpoint is not None:
+ with open(checkpoint, "rb") as f:
+ state_dict = torch.load(f)
+ sam.load_state_dict(state_dict)
+ return sam
diff --git a/VISAM/thirdparty/segment_anything/segment_anything/modeling/__init__.py b/VISAM/thirdparty/segment_anything/segment_anything/modeling/__init__.py
new file mode 100644
index 0000000000000000000000000000000000000000..38e906243d898d7fc071c0fe218338c5cace3ea1
--- /dev/null
+++ b/VISAM/thirdparty/segment_anything/segment_anything/modeling/__init__.py
@@ -0,0 +1,11 @@
+# Copyright (c) Meta Platforms, Inc. and affiliates.
+# All rights reserved.
+
+# This source code is licensed under the license found in the
+# LICENSE file in the root directory of this source tree.
+
+from .sam import Sam
+from .image_encoder import ImageEncoderViT
+from .mask_decoder import MaskDecoder
+from .prompt_encoder import PromptEncoder
+from .transformer import TwoWayTransformer
diff --git a/VISAM/thirdparty/segment_anything/segment_anything/modeling/common.py b/VISAM/thirdparty/segment_anything/segment_anything/modeling/common.py
new file mode 100644
index 0000000000000000000000000000000000000000..2bf15236a3eb24d8526073bc4fa2b274cccb3f96
--- /dev/null
+++ b/VISAM/thirdparty/segment_anything/segment_anything/modeling/common.py
@@ -0,0 +1,43 @@
+# Copyright (c) Meta Platforms, Inc. and affiliates.
+# All rights reserved.
+
+# This source code is licensed under the license found in the
+# LICENSE file in the root directory of this source tree.
+
+import torch
+import torch.nn as nn
+
+from typing import Type
+
+
+class MLPBlock(nn.Module):
+ def __init__(
+ self,
+ embedding_dim: int,
+ mlp_dim: int,
+ act: Type[nn.Module] = nn.GELU,
+ ) -> None:
+ super().__init__()
+ self.lin1 = nn.Linear(embedding_dim, mlp_dim)
+ self.lin2 = nn.Linear(mlp_dim, embedding_dim)
+ self.act = act()
+
+ def forward(self, x: torch.Tensor) -> torch.Tensor:
+ return self.lin2(self.act(self.lin1(x)))
+
+
+# From https://github.com/facebookresearch/detectron2/blob/main/detectron2/layers/batch_norm.py # noqa
+# Itself from https://github.com/facebookresearch/ConvNeXt/blob/d1fa8f6fef0a165b27399986cc2bdacc92777e40/models/convnext.py#L119 # noqa
+class LayerNorm2d(nn.Module):
+ def __init__(self, num_channels: int, eps: float = 1e-6) -> None:
+ super().__init__()
+ self.weight = nn.Parameter(torch.ones(num_channels))
+ self.bias = nn.Parameter(torch.zeros(num_channels))
+ self.eps = eps
+
+ def forward(self, x: torch.Tensor) -> torch.Tensor:
+ u = x.mean(1, keepdim=True)
+ s = (x - u).pow(2).mean(1, keepdim=True)
+ x = (x - u) / torch.sqrt(s + self.eps)
+ x = self.weight[:, None, None] * x + self.bias[:, None, None]
+ return x
diff --git a/VISAM/thirdparty/segment_anything/segment_anything/modeling/image_encoder.py b/VISAM/thirdparty/segment_anything/segment_anything/modeling/image_encoder.py
new file mode 100644
index 0000000000000000000000000000000000000000..a6ad9ad2938842308e482a05c9d35ab08db9b2c3
--- /dev/null
+++ b/VISAM/thirdparty/segment_anything/segment_anything/modeling/image_encoder.py
@@ -0,0 +1,395 @@
+# Copyright (c) Meta Platforms, Inc. and affiliates.
+# All rights reserved.
+
+# This source code is licensed under the license found in the
+# LICENSE file in the root directory of this source tree.
+
+import torch
+import torch.nn as nn
+import torch.nn.functional as F
+
+from typing import Optional, Tuple, Type
+
+from .common import LayerNorm2d, MLPBlock
+
+
+# This class and its supporting functions below lightly adapted from the ViTDet backbone available at: https://github.com/facebookresearch/detectron2/blob/main/detectron2/modeling/backbone/vit.py # noqa
+class ImageEncoderViT(nn.Module):
+ def __init__(
+ self,
+ img_size: int = 1024,
+ patch_size: int = 16,
+ in_chans: int = 3,
+ embed_dim: int = 768,
+ depth: int = 12,
+ num_heads: int = 12,
+ mlp_ratio: float = 4.0,
+ out_chans: int = 256,
+ qkv_bias: bool = True,
+ norm_layer: Type[nn.Module] = nn.LayerNorm,
+ act_layer: Type[nn.Module] = nn.GELU,
+ use_abs_pos: bool = True,
+ use_rel_pos: bool = False,
+ rel_pos_zero_init: bool = True,
+ window_size: int = 0,
+ global_attn_indexes: Tuple[int, ...] = (),
+ ) -> None:
+ """
+ Args:
+ img_size (int): Input image size.
+ patch_size (int): Patch size.
+ in_chans (int): Number of input image channels.
+ embed_dim (int): Patch embedding dimension.
+ depth (int): Depth of ViT.
+ num_heads (int): Number of attention heads in each ViT block.
+ mlp_ratio (float): Ratio of mlp hidden dim to embedding dim.
+ qkv_bias (bool): If True, add a learnable bias to query, key, value.
+ norm_layer (nn.Module): Normalization layer.
+ act_layer (nn.Module): Activation layer.
+ use_abs_pos (bool): If True, use absolute positional embeddings.
+ use_rel_pos (bool): If True, add relative positional embeddings to the attention map.
+ rel_pos_zero_init (bool): If True, zero initialize relative positional parameters.
+ window_size (int): Window size for window attention blocks.
+ global_attn_indexes (list): Indexes for blocks using global attention.
+ """
+ super().__init__()
+ self.img_size = img_size
+
+ self.patch_embed = PatchEmbed(
+ kernel_size=(patch_size, patch_size),
+ stride=(patch_size, patch_size),
+ in_chans=in_chans,
+ embed_dim=embed_dim,
+ )
+
+ self.pos_embed: Optional[nn.Parameter] = None
+ if use_abs_pos:
+ # Initialize absolute positional embedding with pretrain image size.
+ self.pos_embed = nn.Parameter(
+ torch.zeros(1, img_size // patch_size, img_size // patch_size, embed_dim)
+ )
+
+ self.blocks = nn.ModuleList()
+ for i in range(depth):
+ block = Block(
+ dim=embed_dim,
+ num_heads=num_heads,
+ mlp_ratio=mlp_ratio,
+ qkv_bias=qkv_bias,
+ norm_layer=norm_layer,
+ act_layer=act_layer,
+ use_rel_pos=use_rel_pos,
+ rel_pos_zero_init=rel_pos_zero_init,
+ window_size=window_size if i not in global_attn_indexes else 0,
+ input_size=(img_size // patch_size, img_size // patch_size),
+ )
+ self.blocks.append(block)
+
+ self.neck = nn.Sequential(
+ nn.Conv2d(
+ embed_dim,
+ out_chans,
+ kernel_size=1,
+ bias=False,
+ ),
+ LayerNorm2d(out_chans),
+ nn.Conv2d(
+ out_chans,
+ out_chans,
+ kernel_size=3,
+ padding=1,
+ bias=False,
+ ),
+ LayerNorm2d(out_chans),
+ )
+
+ def forward(self, x: torch.Tensor) -> torch.Tensor:
+ x = self.patch_embed(x)
+ if self.pos_embed is not None:
+ x = x + self.pos_embed
+
+ for blk in self.blocks:
+ x = blk(x)
+
+ x = self.neck(x.permute(0, 3, 1, 2))
+
+ return x
+
+
+class Block(nn.Module):
+ """Transformer blocks with support of window attention and residual propagation blocks"""
+
+ def __init__(
+ self,
+ dim: int,
+ num_heads: int,
+ mlp_ratio: float = 4.0,
+ qkv_bias: bool = True,
+ norm_layer: Type[nn.Module] = nn.LayerNorm,
+ act_layer: Type[nn.Module] = nn.GELU,
+ use_rel_pos: bool = False,
+ rel_pos_zero_init: bool = True,
+ window_size: int = 0,
+ input_size: Optional[Tuple[int, int]] = None,
+ ) -> None:
+ """
+ Args:
+ dim (int): Number of input channels.
+ num_heads (int): Number of attention heads in each ViT block.
+ mlp_ratio (float): Ratio of mlp hidden dim to embedding dim.
+ qkv_bias (bool): If True, add a learnable bias to query, key, value.
+ norm_layer (nn.Module): Normalization layer.
+ act_layer (nn.Module): Activation layer.
+ use_rel_pos (bool): If True, add relative positional embeddings to the attention map.
+ rel_pos_zero_init (bool): If True, zero initialize relative positional parameters.
+ window_size (int): Window size for window attention blocks. If it equals 0, then
+ use global attention.
+ input_size (int or None): Input resolution for calculating the relative positional
+ parameter size.
+ """
+ super().__init__()
+ self.norm1 = norm_layer(dim)
+ self.attn = Attention(
+ dim,
+ num_heads=num_heads,
+ qkv_bias=qkv_bias,
+ use_rel_pos=use_rel_pos,
+ rel_pos_zero_init=rel_pos_zero_init,
+ input_size=input_size if window_size == 0 else (window_size, window_size),
+ )
+
+ self.norm2 = norm_layer(dim)
+ self.mlp = MLPBlock(embedding_dim=dim, mlp_dim=int(dim * mlp_ratio), act=act_layer)
+
+ self.window_size = window_size
+
+ def forward(self, x: torch.Tensor) -> torch.Tensor:
+ shortcut = x
+ x = self.norm1(x)
+ # Window partition
+ if self.window_size > 0:
+ H, W = x.shape[1], x.shape[2]
+ x, pad_hw = window_partition(x, self.window_size)
+
+ x = self.attn(x)
+ # Reverse window partition
+ if self.window_size > 0:
+ x = window_unpartition(x, self.window_size, pad_hw, (H, W))
+
+ x = shortcut + x
+ x = x + self.mlp(self.norm2(x))
+
+ return x
+
+
+class Attention(nn.Module):
+ """Multi-head Attention block with relative position embeddings."""
+
+ def __init__(
+ self,
+ dim: int,
+ num_heads: int = 8,
+ qkv_bias: bool = True,
+ use_rel_pos: bool = False,
+ rel_pos_zero_init: bool = True,
+ input_size: Optional[Tuple[int, int]] = None,
+ ) -> None:
+ """
+ Args:
+ dim (int): Number of input channels.
+ num_heads (int): Number of attention heads.
+ qkv_bias (bool: If True, add a learnable bias to query, key, value.
+ rel_pos (bool): If True, add relative positional embeddings to the attention map.
+ rel_pos_zero_init (bool): If True, zero initialize relative positional parameters.
+ input_size (int or None): Input resolution for calculating the relative positional
+ parameter size.
+ """
+ super().__init__()
+ self.num_heads = num_heads
+ head_dim = dim // num_heads
+ self.scale = head_dim**-0.5
+
+ self.qkv = nn.Linear(dim, dim * 3, bias=qkv_bias)
+ self.proj = nn.Linear(dim, dim)
+
+ self.use_rel_pos = use_rel_pos
+ if self.use_rel_pos:
+ assert (
+ input_size is not None
+ ), "Input size must be provided if using relative positional encoding."
+ # initialize relative positional embeddings
+ self.rel_pos_h = nn.Parameter(torch.zeros(2 * input_size[0] - 1, head_dim))
+ self.rel_pos_w = nn.Parameter(torch.zeros(2 * input_size[1] - 1, head_dim))
+
+ def forward(self, x: torch.Tensor) -> torch.Tensor:
+ B, H, W, _ = x.shape
+ # qkv with shape (3, B, nHead, H * W, C)
+ qkv = self.qkv(x).reshape(B, H * W, 3, self.num_heads, -1).permute(2, 0, 3, 1, 4)
+ # q, k, v with shape (B * nHead, H * W, C)
+ q, k, v = qkv.reshape(3, B * self.num_heads, H * W, -1).unbind(0)
+
+ attn = (q * self.scale) @ k.transpose(-2, -1)
+
+ if self.use_rel_pos:
+ attn = add_decomposed_rel_pos(attn, q, self.rel_pos_h, self.rel_pos_w, (H, W), (H, W))
+
+ attn = attn.softmax(dim=-1)
+ x = (attn @ v).view(B, self.num_heads, H, W, -1).permute(0, 2, 3, 1, 4).reshape(B, H, W, -1)
+ x = self.proj(x)
+
+ return x
+
+
+def window_partition(x: torch.Tensor, window_size: int) -> Tuple[torch.Tensor, Tuple[int, int]]:
+ """
+ Partition into non-overlapping windows with padding if needed.
+ Args:
+ x (tensor): input tokens with [B, H, W, C].
+ window_size (int): window size.
+
+ Returns:
+ windows: windows after partition with [B * num_windows, window_size, window_size, C].
+ (Hp, Wp): padded height and width before partition
+ """
+ B, H, W, C = x.shape
+
+ pad_h = (window_size - H % window_size) % window_size
+ pad_w = (window_size - W % window_size) % window_size
+ if pad_h > 0 or pad_w > 0:
+ x = F.pad(x, (0, 0, 0, pad_w, 0, pad_h))
+ Hp, Wp = H + pad_h, W + pad_w
+
+ x = x.view(B, Hp // window_size, window_size, Wp // window_size, window_size, C)
+ windows = x.permute(0, 1, 3, 2, 4, 5).contiguous().view(-1, window_size, window_size, C)
+ return windows, (Hp, Wp)
+
+
+def window_unpartition(
+ windows: torch.Tensor, window_size: int, pad_hw: Tuple[int, int], hw: Tuple[int, int]
+) -> torch.Tensor:
+ """
+ Window unpartition into original sequences and removing padding.
+ Args:
+ x (tensor): input tokens with [B * num_windows, window_size, window_size, C].
+ window_size (int): window size.
+ pad_hw (Tuple): padded height and width (Hp, Wp).
+ hw (Tuple): original height and width (H, W) before padding.
+
+ Returns:
+ x: unpartitioned sequences with [B, H, W, C].
+ """
+ Hp, Wp = pad_hw
+ H, W = hw
+ B = windows.shape[0] // (Hp * Wp // window_size // window_size)
+ x = windows.view(B, Hp // window_size, Wp // window_size, window_size, window_size, -1)
+ x = x.permute(0, 1, 3, 2, 4, 5).contiguous().view(B, Hp, Wp, -1)
+
+ if Hp > H or Wp > W:
+ x = x[:, :H, :W, :].contiguous()
+ return x
+
+
+def get_rel_pos(q_size: int, k_size: int, rel_pos: torch.Tensor) -> torch.Tensor:
+ """
+ Get relative positional embeddings according to the relative positions of
+ query and key sizes.
+ Args:
+ q_size (int): size of query q.
+ k_size (int): size of key k.
+ rel_pos (Tensor): relative position embeddings (L, C).
+
+ Returns:
+ Extracted positional embeddings according to relative positions.
+ """
+ max_rel_dist = int(2 * max(q_size, k_size) - 1)
+ # Interpolate rel pos if needed.
+ if rel_pos.shape[0] != max_rel_dist:
+ # Interpolate rel pos.
+ rel_pos_resized = F.interpolate(
+ rel_pos.reshape(1, rel_pos.shape[0], -1).permute(0, 2, 1),
+ size=max_rel_dist,
+ mode="linear",
+ )
+ rel_pos_resized = rel_pos_resized.reshape(-1, max_rel_dist).permute(1, 0)
+ else:
+ rel_pos_resized = rel_pos
+
+ # Scale the coords with short length if shapes for q and k are different.
+ q_coords = torch.arange(q_size)[:, None] * max(k_size / q_size, 1.0)
+ k_coords = torch.arange(k_size)[None, :] * max(q_size / k_size, 1.0)
+ relative_coords = (q_coords - k_coords) + (k_size - 1) * max(q_size / k_size, 1.0)
+
+ return rel_pos_resized[relative_coords.long()]
+
+
+def add_decomposed_rel_pos(
+ attn: torch.Tensor,
+ q: torch.Tensor,
+ rel_pos_h: torch.Tensor,
+ rel_pos_w: torch.Tensor,
+ q_size: Tuple[int, int],
+ k_size: Tuple[int, int],
+) -> torch.Tensor:
+ """
+ Calculate decomposed Relative Positional Embeddings from :paper:`mvitv2`.
+ https://github.com/facebookresearch/mvit/blob/19786631e330df9f3622e5402b4a419a263a2c80/mvit/models/attention.py # noqa B950
+ Args:
+ attn (Tensor): attention map.
+ q (Tensor): query q in the attention layer with shape (B, q_h * q_w, C).
+ rel_pos_h (Tensor): relative position embeddings (Lh, C) for height axis.
+ rel_pos_w (Tensor): relative position embeddings (Lw, C) for width axis.
+ q_size (Tuple): spatial sequence size of query q with (q_h, q_w).
+ k_size (Tuple): spatial sequence size of key k with (k_h, k_w).
+
+ Returns:
+ attn (Tensor): attention map with added relative positional embeddings.
+ """
+ q_h, q_w = q_size
+ k_h, k_w = k_size
+ Rh = get_rel_pos(q_h, k_h, rel_pos_h)
+ Rw = get_rel_pos(q_w, k_w, rel_pos_w)
+
+ B, _, dim = q.shape
+ r_q = q.reshape(B, q_h, q_w, dim)
+ rel_h = torch.einsum("bhwc,hkc->bhwk", r_q, Rh)
+ rel_w = torch.einsum("bhwc,wkc->bhwk", r_q, Rw)
+
+ attn = (
+ attn.view(B, q_h, q_w, k_h, k_w) + rel_h[:, :, :, :, None] + rel_w[:, :, :, None, :]
+ ).view(B, q_h * q_w, k_h * k_w)
+
+ return attn
+
+
+class PatchEmbed(nn.Module):
+ """
+ Image to Patch Embedding.
+ """
+
+ def __init__(
+ self,
+ kernel_size: Tuple[int, int] = (16, 16),
+ stride: Tuple[int, int] = (16, 16),
+ padding: Tuple[int, int] = (0, 0),
+ in_chans: int = 3,
+ embed_dim: int = 768,
+ ) -> None:
+ """
+ Args:
+ kernel_size (Tuple): kernel size of the projection layer.
+ stride (Tuple): stride of the projection layer.
+ padding (Tuple): padding size of the projection layer.
+ in_chans (int): Number of input image channels.
+ embed_dim (int): embed_dim (int): Patch embedding dimension.
+ """
+ super().__init__()
+
+ self.proj = nn.Conv2d(
+ in_chans, embed_dim, kernel_size=kernel_size, stride=stride, padding=padding
+ )
+
+ def forward(self, x: torch.Tensor) -> torch.Tensor:
+ x = self.proj(x)
+ # B C H W -> B H W C
+ x = x.permute(0, 2, 3, 1)
+ return x
diff --git a/VISAM/thirdparty/segment_anything/segment_anything/modeling/mask_decoder.py b/VISAM/thirdparty/segment_anything/segment_anything/modeling/mask_decoder.py
new file mode 100644
index 0000000000000000000000000000000000000000..3e86f7cc9ad95582a08ef2531c68d03fa4af8d99
--- /dev/null
+++ b/VISAM/thirdparty/segment_anything/segment_anything/modeling/mask_decoder.py
@@ -0,0 +1,176 @@
+# Copyright (c) Meta Platforms, Inc. and affiliates.
+# All rights reserved.
+
+# This source code is licensed under the license found in the
+# LICENSE file in the root directory of this source tree.
+
+import torch
+from torch import nn
+from torch.nn import functional as F
+
+from typing import List, Tuple, Type
+
+from .common import LayerNorm2d
+
+
+class MaskDecoder(nn.Module):
+ def __init__(
+ self,
+ *,
+ transformer_dim: int,
+ transformer: nn.Module,
+ num_multimask_outputs: int = 3,
+ activation: Type[nn.Module] = nn.GELU,
+ iou_head_depth: int = 3,
+ iou_head_hidden_dim: int = 256,
+ ) -> None:
+ """
+ Predicts masks given an image and prompt embeddings, using a
+ tranformer architecture.
+
+ Arguments:
+ transformer_dim (int): the channel dimension of the transformer
+ transformer (nn.Module): the transformer used to predict masks
+ num_multimask_outputs (int): the number of masks to predict
+ when disambiguating masks
+ activation (nn.Module): the type of activation to use when
+ upscaling masks
+ iou_head_depth (int): the depth of the MLP used to predict
+ mask quality
+ iou_head_hidden_dim (int): the hidden dimension of the MLP
+ used to predict mask quality
+ """
+ super().__init__()
+ self.transformer_dim = transformer_dim
+ self.transformer = transformer
+
+ self.num_multimask_outputs = num_multimask_outputs
+
+ self.iou_token = nn.Embedding(1, transformer_dim)
+ self.num_mask_tokens = num_multimask_outputs + 1
+ self.mask_tokens = nn.Embedding(self.num_mask_tokens, transformer_dim)
+
+ self.output_upscaling = nn.Sequential(
+ nn.ConvTranspose2d(transformer_dim, transformer_dim // 4, kernel_size=2, stride=2),
+ LayerNorm2d(transformer_dim // 4),
+ activation(),
+ nn.ConvTranspose2d(transformer_dim // 4, transformer_dim // 8, kernel_size=2, stride=2),
+ activation(),
+ )
+ self.output_hypernetworks_mlps = nn.ModuleList(
+ [
+ MLP(transformer_dim, transformer_dim, transformer_dim // 8, 3)
+ for i in range(self.num_mask_tokens)
+ ]
+ )
+
+ self.iou_prediction_head = MLP(
+ transformer_dim, iou_head_hidden_dim, self.num_mask_tokens, iou_head_depth
+ )
+
+ def forward(
+ self,
+ image_embeddings: torch.Tensor,
+ image_pe: torch.Tensor,
+ sparse_prompt_embeddings: torch.Tensor,
+ dense_prompt_embeddings: torch.Tensor,
+ multimask_output: bool,
+ ) -> Tuple[torch.Tensor, torch.Tensor]:
+ """
+ Predict masks given image and prompt embeddings.
+
+ Arguments:
+ image_embeddings (torch.Tensor): the embeddings from the image encoder
+ image_pe (torch.Tensor): positional encoding with the shape of image_embeddings
+ sparse_prompt_embeddings (torch.Tensor): the embeddings of the points and boxes
+ dense_prompt_embeddings (torch.Tensor): the embeddings of the mask inputs
+ multimask_output (bool): Whether to return multiple masks or a single
+ mask.
+
+ Returns:
+ torch.Tensor: batched predicted masks
+ torch.Tensor: batched predictions of mask quality
+ """
+ masks, iou_pred = self.predict_masks(
+ image_embeddings=image_embeddings,
+ image_pe=image_pe,
+ sparse_prompt_embeddings=sparse_prompt_embeddings,
+ dense_prompt_embeddings=dense_prompt_embeddings,
+ )
+
+ # Select the correct mask or masks for outptu
+ if multimask_output:
+ mask_slice = slice(1, None)
+ else:
+ mask_slice = slice(0, 1)
+ masks = masks[:, mask_slice, :, :]
+ iou_pred = iou_pred[:, mask_slice]
+
+ # Prepare output
+ return masks, iou_pred
+
+ def predict_masks(
+ self,
+ image_embeddings: torch.Tensor,
+ image_pe: torch.Tensor,
+ sparse_prompt_embeddings: torch.Tensor,
+ dense_prompt_embeddings: torch.Tensor,
+ ) -> Tuple[torch.Tensor, torch.Tensor]:
+ """Predicts masks. See 'forward' for more details."""
+ # Concatenate output tokens
+ output_tokens = torch.cat([self.iou_token.weight, self.mask_tokens.weight], dim=0)
+ output_tokens = output_tokens.unsqueeze(0).expand(sparse_prompt_embeddings.size(0), -1, -1)
+ tokens = torch.cat((output_tokens, sparse_prompt_embeddings), dim=1)
+
+ # Expand per-image data in batch direction to be per-mask
+ src = torch.repeat_interleave(image_embeddings, tokens.shape[0], dim=0)
+ src = src + dense_prompt_embeddings
+ pos_src = torch.repeat_interleave(image_pe, tokens.shape[0], dim=0)
+ b, c, h, w = src.shape
+
+ # Run the transformer
+ hs, src = self.transformer(src, pos_src, tokens)
+ iou_token_out = hs[:, 0, :]
+ mask_tokens_out = hs[:, 1 : (1 + self.num_mask_tokens), :]
+
+ # Upscale mask embeddings and predict masks using the mask tokens
+ src = src.transpose(1, 2).view(b, c, h, w)
+ upscaled_embedding = self.output_upscaling(src)
+ hyper_in_list: List[torch.Tensor] = []
+ for i in range(self.num_mask_tokens):
+ hyper_in_list.append(self.output_hypernetworks_mlps[i](mask_tokens_out[:, i, :]))
+ hyper_in = torch.stack(hyper_in_list, dim=1)
+ b, c, h, w = upscaled_embedding.shape
+ masks = (hyper_in @ upscaled_embedding.view(b, c, h * w)).view(b, -1, h, w)
+
+ # Generate mask quality predictions
+ iou_pred = self.iou_prediction_head(iou_token_out)
+
+ return masks, iou_pred
+
+
+# Lightly adapted from
+# https://github.com/facebookresearch/MaskFormer/blob/main/mask_former/modeling/transformer/transformer_predictor.py # noqa
+class MLP(nn.Module):
+ def __init__(
+ self,
+ input_dim: int,
+ hidden_dim: int,
+ output_dim: int,
+ num_layers: int,
+ sigmoid_output: bool = False,
+ ) -> None:
+ super().__init__()
+ self.num_layers = num_layers
+ h = [hidden_dim] * (num_layers - 1)
+ self.layers = nn.ModuleList(
+ nn.Linear(n, k) for n, k in zip([input_dim] + h, h + [output_dim])
+ )
+ self.sigmoid_output = sigmoid_output
+
+ def forward(self, x):
+ for i, layer in enumerate(self.layers):
+ x = F.relu(layer(x)) if i < self.num_layers - 1 else layer(x)
+ if self.sigmoid_output:
+ x = F.sigmoid(x)
+ return x
diff --git a/VISAM/thirdparty/segment_anything/segment_anything/modeling/prompt_encoder.py b/VISAM/thirdparty/segment_anything/segment_anything/modeling/prompt_encoder.py
new file mode 100644
index 0000000000000000000000000000000000000000..c3143f4f8e02ddd7ca8587b40ff5d47c3a6b7ef3
--- /dev/null
+++ b/VISAM/thirdparty/segment_anything/segment_anything/modeling/prompt_encoder.py
@@ -0,0 +1,214 @@
+# Copyright (c) Meta Platforms, Inc. and affiliates.
+# All rights reserved.
+
+# This source code is licensed under the license found in the
+# LICENSE file in the root directory of this source tree.
+
+import numpy as np
+import torch
+from torch import nn
+
+from typing import Any, Optional, Tuple, Type
+
+from .common import LayerNorm2d
+
+
+class PromptEncoder(nn.Module):
+ def __init__(
+ self,
+ embed_dim: int,
+ image_embedding_size: Tuple[int, int],
+ input_image_size: Tuple[int, int],
+ mask_in_chans: int,
+ activation: Type[nn.Module] = nn.GELU,
+ ) -> None:
+ """
+ Encodes prompts for input to SAM's mask decoder.
+
+ Arguments:
+ embed_dim (int): The prompts' embedding dimension
+ image_embedding_size (tuple(int, int)): The spatial size of the
+ image embedding, as (H, W).
+ input_image_size (int): The padded size of the image as input
+ to the image encoder, as (H, W).
+ mask_in_chans (int): The number of hidden channels used for
+ encoding input masks.
+ activation (nn.Module): The activation to use when encoding
+ input masks.
+ """
+ super().__init__()
+ self.embed_dim = embed_dim
+ self.input_image_size = input_image_size
+ self.image_embedding_size = image_embedding_size
+ self.pe_layer = PositionEmbeddingRandom(embed_dim // 2)
+
+ self.num_point_embeddings: int = 4 # pos/neg point + 2 box corners
+ point_embeddings = [nn.Embedding(1, embed_dim) for i in range(self.num_point_embeddings)]
+ self.point_embeddings = nn.ModuleList(point_embeddings)
+ self.not_a_point_embed = nn.Embedding(1, embed_dim)
+
+ self.mask_input_size = (4 * image_embedding_size[0], 4 * image_embedding_size[1])
+ self.mask_downscaling = nn.Sequential(
+ nn.Conv2d(1, mask_in_chans // 4, kernel_size=2, stride=2),
+ LayerNorm2d(mask_in_chans // 4),
+ activation(),
+ nn.Conv2d(mask_in_chans // 4, mask_in_chans, kernel_size=2, stride=2),
+ LayerNorm2d(mask_in_chans),
+ activation(),
+ nn.Conv2d(mask_in_chans, embed_dim, kernel_size=1),
+ )
+ self.no_mask_embed = nn.Embedding(1, embed_dim)
+
+ def get_dense_pe(self) -> torch.Tensor:
+ """
+ Returns the positional encoding used to encode point prompts,
+ applied to a dense set of points the shape of the image encoding.
+
+ Returns:
+ torch.Tensor: Positional encoding with shape
+ 1x(embed_dim)x(embedding_h)x(embedding_w)
+ """
+ return self.pe_layer(self.image_embedding_size).unsqueeze(0)
+
+ def _embed_points(
+ self,
+ points: torch.Tensor,
+ labels: torch.Tensor,
+ pad: bool,
+ ) -> torch.Tensor:
+ """Embeds point prompts."""
+ points = points + 0.5 # Shift to center of pixel
+ if pad:
+ padding_point = torch.zeros((points.shape[0], 1, 2), device=points.device)
+ padding_label = -torch.ones((labels.shape[0], 1), device=labels.device)
+ points = torch.cat([points, padding_point], dim=1)
+ labels = torch.cat([labels, padding_label], dim=1)
+ point_embedding = self.pe_layer.forward_with_coords(points, self.input_image_size)
+ point_embedding[labels == -1] = 0.0
+ point_embedding[labels == -1] += self.not_a_point_embed.weight
+ point_embedding[labels == 0] += self.point_embeddings[0].weight
+ point_embedding[labels == 1] += self.point_embeddings[1].weight
+ return point_embedding
+
+ def _embed_boxes(self, boxes: torch.Tensor) -> torch.Tensor:
+ """Embeds box prompts."""
+ boxes = boxes + 0.5 # Shift to center of pixel
+ coords = boxes.reshape(-1, 2, 2)
+ corner_embedding = self.pe_layer.forward_with_coords(coords, self.input_image_size)
+ corner_embedding[:, 0, :] += self.point_embeddings[2].weight
+ corner_embedding[:, 1, :] += self.point_embeddings[3].weight
+ return corner_embedding
+
+ def _embed_masks(self, masks: torch.Tensor) -> torch.Tensor:
+ """Embeds mask inputs."""
+ mask_embedding = self.mask_downscaling(masks)
+ return mask_embedding
+
+ def _get_batch_size(
+ self,
+ points: Optional[Tuple[torch.Tensor, torch.Tensor]],
+ boxes: Optional[torch.Tensor],
+ masks: Optional[torch.Tensor],
+ ) -> int:
+ """
+ Gets the batch size of the output given the batch size of the input prompts.
+ """
+ if points is not None:
+ return points[0].shape[0]
+ elif boxes is not None:
+ return boxes.shape[0]
+ elif masks is not None:
+ return masks.shape[0]
+ else:
+ return 1
+
+ def _get_device(self) -> torch.device:
+ return self.point_embeddings[0].weight.device
+
+ def forward(
+ self,
+ points: Optional[Tuple[torch.Tensor, torch.Tensor]],
+ boxes: Optional[torch.Tensor],
+ masks: Optional[torch.Tensor],
+ ) -> Tuple[torch.Tensor, torch.Tensor]:
+ """
+ Embeds different types of prompts, returning both sparse and dense
+ embeddings.
+
+ Arguments:
+ points (tuple(torch.Tensor, torch.Tensor) or none): point coordinates
+ and labels to embed.
+ boxes (torch.Tensor or none): boxes to embed
+ masks (torch.Tensor or none): masks to embed
+
+ Returns:
+ torch.Tensor: sparse embeddings for the points and boxes, with shape
+ BxNx(embed_dim), where N is determined by the number of input points
+ and boxes.
+ torch.Tensor: dense embeddings for the masks, in the shape
+ Bx(embed_dim)x(embed_H)x(embed_W)
+ """
+ bs = self._get_batch_size(points, boxes, masks)
+ sparse_embeddings = torch.empty((bs, 0, self.embed_dim), device=self._get_device())
+ if points is not None:
+ coords, labels = points
+ point_embeddings = self._embed_points(coords, labels, pad=(boxes is None))
+ sparse_embeddings = torch.cat([sparse_embeddings, point_embeddings], dim=1)
+ if boxes is not None:
+ box_embeddings = self._embed_boxes(boxes)
+ sparse_embeddings = torch.cat([sparse_embeddings, box_embeddings], dim=1)
+
+ if masks is not None:
+ dense_embeddings = self._embed_masks(masks)
+ else:
+ dense_embeddings = self.no_mask_embed.weight.reshape(1, -1, 1, 1).expand(
+ bs, -1, self.image_embedding_size[0], self.image_embedding_size[1]
+ )
+
+ return sparse_embeddings, dense_embeddings
+
+
+class PositionEmbeddingRandom(nn.Module):
+ """
+ Positional encoding using random spatial frequencies.
+ """
+
+ def __init__(self, num_pos_feats: int = 64, scale: Optional[float] = None) -> None:
+ super().__init__()
+ if scale is None or scale <= 0.0:
+ scale = 1.0
+ self.register_buffer(
+ "positional_encoding_gaussian_matrix",
+ scale * torch.randn((2, num_pos_feats)),
+ )
+
+ def _pe_encoding(self, coords: torch.Tensor) -> torch.Tensor:
+ """Positionally encode points that are normalized to [0,1]."""
+ # assuming coords are in [0, 1]^2 square and have d_1 x ... x d_n x 2 shape
+ coords = 2 * coords - 1
+ coords = coords @ self.positional_encoding_gaussian_matrix
+ coords = 2 * np.pi * coords
+ # outputs d_1 x ... x d_n x C shape
+ return torch.cat([torch.sin(coords), torch.cos(coords)], dim=-1)
+
+ def forward(self, size: Tuple[int, int]) -> torch.Tensor:
+ """Generate positional encoding for a grid of the specified size."""
+ h, w = size
+ device: Any = self.positional_encoding_gaussian_matrix.device
+ grid = torch.ones((h, w), device=device, dtype=torch.float32)
+ y_embed = grid.cumsum(dim=0) - 0.5
+ x_embed = grid.cumsum(dim=1) - 0.5
+ y_embed = y_embed / h
+ x_embed = x_embed / w
+
+ pe = self._pe_encoding(torch.stack([x_embed, y_embed], dim=-1))
+ return pe.permute(2, 0, 1) # C x H x W
+
+ def forward_with_coords(
+ self, coords_input: torch.Tensor, image_size: Tuple[int, int]
+ ) -> torch.Tensor:
+ """Positionally encode points that are not normalized to [0,1]."""
+ coords = coords_input.clone()
+ coords[:, :, 0] = coords[:, :, 0] / image_size[1]
+ coords[:, :, 1] = coords[:, :, 1] / image_size[0]
+ return self._pe_encoding(coords.to(torch.float)) # B x N x C
diff --git a/VISAM/thirdparty/segment_anything/segment_anything/modeling/sam.py b/VISAM/thirdparty/segment_anything/segment_anything/modeling/sam.py
new file mode 100644
index 0000000000000000000000000000000000000000..303bc2f40c3dbc84f5d4286bb73336e075a86589
--- /dev/null
+++ b/VISAM/thirdparty/segment_anything/segment_anything/modeling/sam.py
@@ -0,0 +1,174 @@
+# Copyright (c) Meta Platforms, Inc. and affiliates.
+# All rights reserved.
+
+# This source code is licensed under the license found in the
+# LICENSE file in the root directory of this source tree.
+
+import torch
+from torch import nn
+from torch.nn import functional as F
+
+from typing import Any, Dict, List, Tuple
+
+from .image_encoder import ImageEncoderViT
+from .mask_decoder import MaskDecoder
+from .prompt_encoder import PromptEncoder
+
+
+class Sam(nn.Module):
+ mask_threshold: float = 0.0
+ image_format: str = "RGB"
+
+ def __init__(
+ self,
+ image_encoder: ImageEncoderViT,
+ prompt_encoder: PromptEncoder,
+ mask_decoder: MaskDecoder,
+ pixel_mean: List[float] = [123.675, 116.28, 103.53],
+ pixel_std: List[float] = [58.395, 57.12, 57.375],
+ ) -> None:
+ """
+ SAM predicts object masks from an image and input prompts.
+
+ Arguments:
+ image_encoder (ImageEncoderViT): The backbone used to encode the
+ image into image embeddings that allow for efficient mask prediction.
+ prompt_encoder (PromptEncoder): Encodes various types of input prompts.
+ mask_decoder (MaskDecoder): Predicts masks from the image embeddings
+ and encoded prompts.
+ pixel_mean (list(float)): Mean values for normalizing pixels in the input image.
+ pixel_std (list(float)): Std values for normalizing pixels in the input image.
+ """
+ super().__init__()
+ self.image_encoder = image_encoder
+ self.prompt_encoder = prompt_encoder
+ self.mask_decoder = mask_decoder
+ self.register_buffer("pixel_mean", torch.Tensor(pixel_mean).view(-1, 1, 1), False)
+ self.register_buffer("pixel_std", torch.Tensor(pixel_std).view(-1, 1, 1), False)
+
+ @property
+ def device(self) -> Any:
+ return self.pixel_mean.device
+
+ @torch.no_grad()
+ def forward(
+ self,
+ batched_input: List[Dict[str, Any]],
+ multimask_output: bool,
+ ) -> List[Dict[str, torch.Tensor]]:
+ """
+ Predicts masks end-to-end from provided images and prompts.
+ If prompts are not known in advance, using SamPredictor is
+ recommended over calling the model directly.
+
+ Arguments:
+ batched_input (list(dict)): A list over input images, each a
+ dictionary with the following keys. A prompt key can be
+ excluded if it is not present.
+ 'image': The image as a torch tensor in 3xHxW format,
+ already transformed for input to the model.
+ 'original_size': (tuple(int, int)) The original size of
+ the image before transformation, as (H, W).
+ 'point_coords': (torch.Tensor) Batched point prompts for
+ this image, with shape BxNx2. Already transformed to the
+ input frame of the model.
+ 'point_labels': (torch.Tensor) Batched labels for point prompts,
+ with shape BxN.
+ 'boxes': (torch.Tensor) Batched box inputs, with shape Bx4.
+ Already transformed to the input frame of the model.
+ 'mask_inputs': (torch.Tensor) Batched mask inputs to the model,
+ in the form Bx1xHxW.
+ multimask_output (bool): Whether the model should predict multiple
+ disambiguating masks, or return a single mask.
+
+ Returns:
+ (list(dict)): A list over input images, where each element is
+ as dictionary with the following keys.
+ 'masks': (torch.Tensor) Batched binary mask predictions,
+ with shape BxCxHxW, where B is the number of input promts,
+ C is determiend by multimask_output, and (H, W) is the
+ original size of the image.
+ 'iou_predictions': (torch.Tensor) The model's predictions
+ of mask quality, in shape BxC.
+ 'low_res_logits': (torch.Tensor) Low resolution logits with
+ shape BxCxHxW, where H=W=256. Can be passed as mask input
+ to subsequent iterations of prediction.
+ """
+ input_images = torch.stack([self.preprocess(x["image"]) for x in batched_input], dim=0)
+ image_embeddings = self.image_encoder(input_images)
+
+ outputs = []
+ for image_record, curr_embedding in zip(batched_input, image_embeddings):
+ if "point_coords" in image_record:
+ points = (image_record["point_coords"], image_record["point_labels"])
+ else:
+ points = None
+ sparse_embeddings, dense_embeddings = self.prompt_encoder(
+ points=points,
+ boxes=image_record.get("boxes", None),
+ masks=image_record.get("mask_inputs", None),
+ )
+ low_res_masks, iou_predictions = self.mask_decoder(
+ image_embeddings=curr_embedding.unsqueeze(0),
+ image_pe=self.prompt_encoder.get_dense_pe(),
+ sparse_prompt_embeddings=sparse_embeddings,
+ dense_prompt_embeddings=dense_embeddings,
+ multimask_output=multimask_output,
+ )
+ masks = self.postprocess_masks(
+ low_res_masks,
+ input_size=image_record["image"].shape[-2:],
+ original_size=image_record["original_size"],
+ )
+ masks = masks > self.mask_threshold
+ outputs.append(
+ {
+ "masks": masks,
+ "iou_predictions": iou_predictions,
+ "low_res_logits": low_res_masks,
+ }
+ )
+ return outputs
+
+ def postprocess_masks(
+ self,
+ masks: torch.Tensor,
+ input_size: Tuple[int, ...],
+ original_size: Tuple[int, ...],
+ ) -> torch.Tensor:
+ """
+ Remove padding and upscale masks to the original image size.
+
+ Arguments:
+ masks (torch.Tensor): Batched masks from the mask_decoder,
+ in BxCxHxW format.
+ input_size (tuple(int, int)): The size of the image input to the
+ model, in (H, W) format. Used to remove padding.
+ original_size (tuple(int, int)): The original size of the image
+ before resizing for input to the model, in (H, W) format.
+
+ Returns:
+ (torch.Tensor): Batched masks in BxCxHxW format, where (H, W)
+ is given by original_size.
+ """
+ masks = F.interpolate(
+ masks,
+ (self.image_encoder.img_size, self.image_encoder.img_size),
+ mode="bilinear",
+ align_corners=False,
+ )
+ masks = masks[..., : input_size[0], : input_size[1]]
+ masks = F.interpolate(masks, original_size, mode="bilinear", align_corners=False)
+ return masks
+
+ def preprocess(self, x: torch.Tensor) -> torch.Tensor:
+ """Normalize pixel values and pad to a square input."""
+ # Normalize colors
+ x = (x - self.pixel_mean) / self.pixel_std
+
+ # Pad
+ h, w = x.shape[-2:]
+ padh = self.image_encoder.img_size - h
+ padw = self.image_encoder.img_size - w
+ x = F.pad(x, (0, padw, 0, padh))
+ return x
diff --git a/VISAM/thirdparty/segment_anything/segment_anything/modeling/transformer.py b/VISAM/thirdparty/segment_anything/segment_anything/modeling/transformer.py
new file mode 100644
index 0000000000000000000000000000000000000000..f1a2812f613cc55b1d0b3e3e1d0c84a760d1fb87
--- /dev/null
+++ b/VISAM/thirdparty/segment_anything/segment_anything/modeling/transformer.py
@@ -0,0 +1,240 @@
+# Copyright (c) Meta Platforms, Inc. and affiliates.
+# All rights reserved.
+
+# This source code is licensed under the license found in the
+# LICENSE file in the root directory of this source tree.
+
+import torch
+from torch import Tensor, nn
+
+import math
+from typing import Tuple, Type
+
+from .common import MLPBlock
+
+
+class TwoWayTransformer(nn.Module):
+ def __init__(
+ self,
+ depth: int,
+ embedding_dim: int,
+ num_heads: int,
+ mlp_dim: int,
+ activation: Type[nn.Module] = nn.ReLU,
+ attention_downsample_rate: int = 2,
+ ) -> None:
+ """
+ A transformer decoder that attends to an input image using
+ queries whose positional embedding is supplied.
+
+ Args:
+ depth (int): number of layers in the transformer
+ embedding_dim (int): the channel dimension for the input embeddings
+ num_heads (int): the number of heads for multihead attention. Must
+ divide embedding_dim
+ mlp_dim (int): the channel dimension internal to the MLP block
+ activation (nn.Module): the activation to use in the MLP block
+ """
+ super().__init__()
+ self.depth = depth
+ self.embedding_dim = embedding_dim
+ self.num_heads = num_heads
+ self.mlp_dim = mlp_dim
+ self.layers = nn.ModuleList()
+
+ for i in range(depth):
+ self.layers.append(
+ TwoWayAttentionBlock(
+ embedding_dim=embedding_dim,
+ num_heads=num_heads,
+ mlp_dim=mlp_dim,
+ activation=activation,
+ attention_downsample_rate=attention_downsample_rate,
+ skip_first_layer_pe=(i == 0),
+ )
+ )
+
+ self.final_attn_token_to_image = Attention(
+ embedding_dim, num_heads, downsample_rate=attention_downsample_rate
+ )
+ self.norm_final_attn = nn.LayerNorm(embedding_dim)
+
+ def forward(
+ self,
+ image_embedding: Tensor,
+ image_pe: Tensor,
+ point_embedding: Tensor,
+ ) -> Tuple[Tensor, Tensor]:
+ """
+ Args:
+ image_embedding (torch.Tensor): image to attend to. Should be shape
+ B x embedding_dim x h x w for any h and w.
+ image_pe (torch.Tensor): the positional encoding to add to the image. Must
+ have the same shape as image_embedding.
+ point_embedding (torch.Tensor): the embedding to add to the query points.
+ Must have shape B x N_points x embedding_dim for any N_points.
+
+ Returns:
+ torch.Tensor: the processed point_embedding
+ torch.Tensor: the processed image_embedding
+ """
+ # BxCxHxW -> BxHWxC == B x N_image_tokens x C
+ bs, c, h, w = image_embedding.shape
+ image_embedding = image_embedding.flatten(2).permute(0, 2, 1)
+ image_pe = image_pe.flatten(2).permute(0, 2, 1)
+
+ # Prepare queries
+ queries = point_embedding
+ keys = image_embedding
+
+ # Apply transformer blocks and final layernorm
+ for layer in self.layers:
+ queries, keys = layer(
+ queries=queries,
+ keys=keys,
+ query_pe=point_embedding,
+ key_pe=image_pe,
+ )
+
+ # Apply the final attenion layer from the points to the image
+ q = queries + point_embedding
+ k = keys + image_pe
+ attn_out = self.final_attn_token_to_image(q=q, k=k, v=keys)
+ queries = queries + attn_out
+ queries = self.norm_final_attn(queries)
+
+ return queries, keys
+
+
+class TwoWayAttentionBlock(nn.Module):
+ def __init__(
+ self,
+ embedding_dim: int,
+ num_heads: int,
+ mlp_dim: int = 2048,
+ activation: Type[nn.Module] = nn.ReLU,
+ attention_downsample_rate: int = 2,
+ skip_first_layer_pe: bool = False,
+ ) -> None:
+ """
+ A transformer block with four layers: (1) self-attention of sparse
+ inputs, (2) cross attention of sparse inputs to dense inputs, (3) mlp
+ block on sparse inputs, and (4) cross attention of dense inputs to sparse
+ inputs.
+
+ Arguments:
+ embedding_dim (int): the channel dimension of the embeddings
+ num_heads (int): the number of heads in the attention layers
+ mlp_dim (int): the hidden dimension of the mlp block
+ activation (nn.Module): the activation of the mlp block
+ skip_first_layer_pe (bool): skip the PE on the first layer
+ """
+ super().__init__()
+ self.self_attn = Attention(embedding_dim, num_heads)
+ self.norm1 = nn.LayerNorm(embedding_dim)
+
+ self.cross_attn_token_to_image = Attention(
+ embedding_dim, num_heads, downsample_rate=attention_downsample_rate
+ )
+ self.norm2 = nn.LayerNorm(embedding_dim)
+
+ self.mlp = MLPBlock(embedding_dim, mlp_dim, activation)
+ self.norm3 = nn.LayerNorm(embedding_dim)
+
+ self.norm4 = nn.LayerNorm(embedding_dim)
+ self.cross_attn_image_to_token = Attention(
+ embedding_dim, num_heads, downsample_rate=attention_downsample_rate
+ )
+
+ self.skip_first_layer_pe = skip_first_layer_pe
+
+ def forward(
+ self, queries: Tensor, keys: Tensor, query_pe: Tensor, key_pe: Tensor
+ ) -> Tuple[Tensor, Tensor]:
+ # Self attention block
+ if self.skip_first_layer_pe:
+ queries = self.self_attn(q=queries, k=queries, v=queries)
+ else:
+ q = queries + query_pe
+ attn_out = self.self_attn(q=q, k=q, v=queries)
+ queries = queries + attn_out
+ queries = self.norm1(queries)
+
+ # Cross attention block, tokens attending to image embedding
+ q = queries + query_pe
+ k = keys + key_pe
+ attn_out = self.cross_attn_token_to_image(q=q, k=k, v=keys)
+ queries = queries + attn_out
+ queries = self.norm2(queries)
+
+ # MLP block
+ mlp_out = self.mlp(queries)
+ queries = queries + mlp_out
+ queries = self.norm3(queries)
+
+ # Cross attention block, image embedding attending to tokens
+ q = queries + query_pe
+ k = keys + key_pe
+ attn_out = self.cross_attn_image_to_token(q=k, k=q, v=queries)
+ keys = keys + attn_out
+ keys = self.norm4(keys)
+
+ return queries, keys
+
+
+class Attention(nn.Module):
+ """
+ An attention layer that allows for downscaling the size of the embedding
+ after projection to queries, keys, and values.
+ """
+
+ def __init__(
+ self,
+ embedding_dim: int,
+ num_heads: int,
+ downsample_rate: int = 1,
+ ) -> None:
+ super().__init__()
+ self.embedding_dim = embedding_dim
+ self.internal_dim = embedding_dim // downsample_rate
+ self.num_heads = num_heads
+ assert self.internal_dim % num_heads == 0, "num_heads must divide embedding_dim."
+
+ self.q_proj = nn.Linear(embedding_dim, self.internal_dim)
+ self.k_proj = nn.Linear(embedding_dim, self.internal_dim)
+ self.v_proj = nn.Linear(embedding_dim, self.internal_dim)
+ self.out_proj = nn.Linear(self.internal_dim, embedding_dim)
+
+ def _separate_heads(self, x: Tensor, num_heads: int) -> Tensor:
+ b, n, c = x.shape
+ x = x.reshape(b, n, num_heads, c // num_heads)
+ return x.transpose(1, 2) # B x N_heads x N_tokens x C_per_head
+
+ def _recombine_heads(self, x: Tensor) -> Tensor:
+ b, n_heads, n_tokens, c_per_head = x.shape
+ x = x.transpose(1, 2)
+ return x.reshape(b, n_tokens, n_heads * c_per_head) # B x N_tokens x C
+
+ def forward(self, q: Tensor, k: Tensor, v: Tensor) -> Tensor:
+ # Input projections
+ q = self.q_proj(q)
+ k = self.k_proj(k)
+ v = self.v_proj(v)
+
+ # Separate into heads
+ q = self._separate_heads(q, self.num_heads)
+ k = self._separate_heads(k, self.num_heads)
+ v = self._separate_heads(v, self.num_heads)
+
+ # Attention
+ _, _, _, c_per_head = q.shape
+ attn = q @ k.permute(0, 1, 3, 2) # B x N_heads x N_tokens x N_tokens
+ attn = attn / math.sqrt(c_per_head)
+ attn = torch.softmax(attn, dim=-1)
+
+ # Get output
+ out = attn @ v
+ out = self._recombine_heads(out)
+ out = self.out_proj(out)
+
+ return out
diff --git a/VISAM/thirdparty/segment_anything/segment_anything/predictor.py b/VISAM/thirdparty/segment_anything/segment_anything/predictor.py
new file mode 100644
index 0000000000000000000000000000000000000000..57c089d1fc4a6bbf5786e1ef62c59e22d582f5aa
--- /dev/null
+++ b/VISAM/thirdparty/segment_anything/segment_anything/predictor.py
@@ -0,0 +1,269 @@
+# Copyright (c) Meta Platforms, Inc. and affiliates.
+# All rights reserved.
+
+# This source code is licensed under the license found in the
+# LICENSE file in the root directory of this source tree.
+
+import numpy as np
+import torch
+
+from segment_anything.modeling import Sam
+
+from typing import Optional, Tuple
+
+from .utils.transforms import ResizeLongestSide
+
+
+class SamPredictor:
+ def __init__(
+ self,
+ sam_model: Sam,
+ ) -> None:
+ """
+ Uses SAM to calculate the image embedding for an image, and then
+ allow repeated, efficient mask prediction given prompts.
+
+ Arguments:
+ sam_model (Sam): The model to use for mask prediction.
+ """
+ super().__init__()
+ self.model = sam_model
+ self.transform = ResizeLongestSide(sam_model.image_encoder.img_size)
+ self.reset_image()
+
+ def set_image(
+ self,
+ image: np.ndarray,
+ image_format: str = "RGB",
+ ) -> None:
+ """
+ Calculates the image embeddings for the provided image, allowing
+ masks to be predicted with the 'predict' method.
+
+ Arguments:
+ image (np.ndarray): The image for calculating masks. Expects an
+ image in HWC uint8 format, with pixel values in [0, 255].
+ image_format (str): The color format of the image, in ['RGB', 'BGR'].
+ """
+ assert image_format in [
+ "RGB",
+ "BGR",
+ ], f"image_format must be in ['RGB', 'BGR'], is {image_format}."
+ if image_format != self.model.image_format:
+ image = image[..., ::-1]
+
+ # Transform the image to the form expected by the model
+ input_image = self.transform.apply_image(image)
+ input_image_torch = torch.as_tensor(input_image, device=self.device)
+ input_image_torch = input_image_torch.permute(2, 0, 1).contiguous()[None, :, :, :]
+
+ self.set_torch_image(input_image_torch, image.shape[:2])
+
+ @torch.no_grad()
+ def set_torch_image(
+ self,
+ transformed_image: torch.Tensor,
+ original_image_size: Tuple[int, ...],
+ ) -> None:
+ """
+ Calculates the image embeddings for the provided image, allowing
+ masks to be predicted with the 'predict' method. Expects the input
+ image to be already transformed to the format expected by the model.
+
+ Arguments:
+ transformed_image (torch.Tensor): The input image, with shape
+ 1x3xHxW, which has been transformed with ResizeLongestSide.
+ original_image_size (tuple(int, int)): The size of the image
+ before transformation, in (H, W) format.
+ """
+ assert (
+ len(transformed_image.shape) == 4
+ and transformed_image.shape[1] == 3
+ and max(*transformed_image.shape[2:]) == self.model.image_encoder.img_size
+ ), f"set_torch_image input must be BCHW with long side {self.model.image_encoder.img_size}."
+ self.reset_image()
+
+ self.original_size = original_image_size
+ self.input_size = tuple(transformed_image.shape[-2:])
+ input_image = self.model.preprocess(transformed_image)
+ self.features = self.model.image_encoder(input_image)
+ self.is_image_set = True
+
+ def predict(
+ self,
+ point_coords: Optional[np.ndarray] = None,
+ point_labels: Optional[np.ndarray] = None,
+ box: Optional[np.ndarray] = None,
+ mask_input: Optional[np.ndarray] = None,
+ multimask_output: bool = True,
+ return_logits: bool = False,
+ ) -> Tuple[torch.Tensor, torch.Tensor, torch.Tensor]:
+ """
+ Predict masks for the given input prompts, using the currently set image.
+
+ Arguments:
+ point_coords (np.ndarray or None): A Nx2 array of point prompts to the
+ model. Each point is in (X,Y) in pixels.
+ point_labels (np.ndarray or None): A length N array of labels for the
+ point prompts. 1 indicates a foreground point and 0 indicates a
+ background point.
+ box (np.ndarray or None): A length 4 array given a box prompt to the
+ model, in XYXY format.
+ mask_input (np.ndarray): A low resolution mask input to the model, typically
+ coming from a previous prediction iteration. Has form 1xHxW, where
+ for SAM, H=W=256.
+ multimask_output (bool): If true, the model will return three masks.
+ For ambiguous input prompts (such as a single click), this will often
+ produce better masks than a single prediction. If only a single
+ mask is needed, the model's predicted quality score can be used
+ to select the best mask. For non-ambiguous prompts, such as multiple
+ input prompts, multimask_output=False can give better results.
+ return_logits (bool): If true, returns un-thresholded masks logits
+ instead of a binary mask.
+
+ Returns:
+ (np.ndarray): The output masks in CxHxW format, where C is the
+ number of masks, and (H, W) is the original image size.
+ (np.ndarray): An array of length C containing the model's
+ predictions for the quality of each mask.
+ (np.ndarray): An array of shape CxHxW, where C is the number
+ of masks and H=W=256. These low resolution logits can be passed to
+ a subsequent iteration as mask input.
+ """
+ if not self.is_image_set:
+ raise RuntimeError("An image must be set with .set_image(...) before mask prediction.")
+
+ # Transform input prompts
+ coords_torch, labels_torch, box_torch, mask_input_torch = None, None, None, None
+ if point_coords is not None:
+ assert (
+ point_labels is not None
+ ), "point_labels must be supplied if point_coords is supplied."
+ point_coords = self.transform.apply_coords(point_coords, self.original_size)
+ coords_torch = torch.as_tensor(point_coords, dtype=torch.float, device=self.device)
+ labels_torch = torch.as_tensor(point_labels, dtype=torch.int, device=self.device)
+ coords_torch, labels_torch = coords_torch[None, :, :], labels_torch[None, :]
+ if box is not None:
+ box = self.transform.apply_boxes(box, self.original_size)
+ box_torch = torch.as_tensor(box, dtype=torch.float, device=self.device)
+ box_torch = box_torch[None, :]
+ if mask_input is not None:
+ mask_input_torch = torch.as_tensor(mask_input, dtype=torch.float, device=self.device)
+ mask_input_torch = mask_input_torch[None, :, :, :]
+
+ masks, iou_predictions, low_res_masks = self.predict_torch(
+ coords_torch,
+ labels_torch,
+ box_torch,
+ mask_input_torch,
+ multimask_output,
+ return_logits=return_logits,
+ )
+
+ masks = masks[0].detach().cpu().numpy()
+ iou_predictions = iou_predictions[0].detach().cpu().numpy()
+ low_res_masks = low_res_masks[0].detach().cpu().numpy()
+ return masks, iou_predictions, low_res_masks
+
+ @torch.no_grad()
+ def predict_torch(
+ self,
+ point_coords: Optional[torch.Tensor],
+ point_labels: Optional[torch.Tensor],
+ boxes: Optional[torch.Tensor] = None,
+ mask_input: Optional[torch.Tensor] = None,
+ multimask_output: bool = True,
+ return_logits: bool = False,
+ ) -> Tuple[torch.Tensor, torch.Tensor, torch.Tensor]:
+ """
+ Predict masks for the given input prompts, using the currently set image.
+ Input prompts are batched torch tensors and are expected to already be
+ transformed to the input frame using ResizeLongestSide.
+
+ Arguments:
+ point_coords (torch.Tensor or None): A BxNx2 array of point prompts to the
+ model. Each point is in (X,Y) in pixels.
+ point_labels (torch.Tensor or None): A BxN array of labels for the
+ point prompts. 1 indicates a foreground point and 0 indicates a
+ background point.
+ box (np.ndarray or None): A Bx4 array given a box prompt to the
+ model, in XYXY format.
+ mask_input (np.ndarray): A low resolution mask input to the model, typically
+ coming from a previous prediction iteration. Has form Bx1xHxW, where
+ for SAM, H=W=256. Masks returned by a previous iteration of the
+ predict method do not need further transformation.
+ multimask_output (bool): If true, the model will return three masks.
+ For ambiguous input prompts (such as a single click), this will often
+ produce better masks than a single prediction. If only a single
+ mask is needed, the model's predicted quality score can be used
+ to select the best mask. For non-ambiguous prompts, such as multiple
+ input prompts, multimask_output=False can give better results.
+ return_logits (bool): If true, returns un-thresholded masks logits
+ instead of a binary mask.
+
+ Returns:
+ (torch.Tensor): The output masks in BxCxHxW format, where C is the
+ number of masks, and (H, W) is the original image size.
+ (torch.Tensor): An array of shape BxC containing the model's
+ predictions for the quality of each mask.
+ (torch.Tensor): An array of shape BxCxHxW, where C is the number
+ of masks and H=W=256. These low res logits can be passed to
+ a subsequent iteration as mask input.
+ """
+ if not self.is_image_set:
+ raise RuntimeError("An image must be set with .set_image(...) before mask prediction.")
+
+ if point_coords is not None:
+ points = (point_coords, point_labels)
+ else:
+ points = None
+
+ # Embed prompts
+ sparse_embeddings, dense_embeddings = self.model.prompt_encoder(
+ points=points,
+ boxes=boxes,
+ masks=mask_input,
+ )
+
+ # Predict masks
+ low_res_masks, iou_predictions = self.model.mask_decoder(
+ image_embeddings=self.features,
+ image_pe=self.model.prompt_encoder.get_dense_pe(),
+ sparse_prompt_embeddings=sparse_embeddings,
+ dense_prompt_embeddings=dense_embeddings,
+ multimask_output=multimask_output,
+ )
+
+ # Upscale the masks to the original image resolution
+ masks = self.model.postprocess_masks(low_res_masks, self.input_size, self.original_size)
+
+ if not return_logits:
+ masks = masks > self.model.mask_threshold
+
+ return masks, iou_predictions, low_res_masks
+
+ def get_image_embedding(self) -> torch.Tensor:
+ """
+ Returns the image embeddings for the currently set image, with
+ shape 1xCxHxW, where C is the embedding dimension and (H,W) are
+ the embedding spatial dimension of SAM (typically C=256, H=W=64).
+ """
+ if not self.is_image_set:
+ raise RuntimeError(
+ "An image must be set with .set_image(...) to generate an embedding."
+ )
+ assert self.features is not None, "Features must exist if an image has been set."
+ return self.features
+
+ @property
+ def device(self) -> torch.device:
+ return self.model.device
+
+ def reset_image(self) -> None:
+ """Resets the currently set image."""
+ self.is_image_set = False
+ self.features = None
+ self.orig_h = None
+ self.orig_w = None
+ self.input_h = None
+ self.input_w = None
diff --git a/VISAM/thirdparty/segment_anything/segment_anything/utils/__init__.py b/VISAM/thirdparty/segment_anything/segment_anything/utils/__init__.py
new file mode 100644
index 0000000000000000000000000000000000000000..5277f46157403e47fd830fc519144b97ef69d4ae
--- /dev/null
+++ b/VISAM/thirdparty/segment_anything/segment_anything/utils/__init__.py
@@ -0,0 +1,5 @@
+# Copyright (c) Meta Platforms, Inc. and affiliates.
+# All rights reserved.
+
+# This source code is licensed under the license found in the
+# LICENSE file in the root directory of this source tree.
diff --git a/VISAM/thirdparty/segment_anything/segment_anything/utils/amg.py b/VISAM/thirdparty/segment_anything/segment_anything/utils/amg.py
new file mode 100644
index 0000000000000000000000000000000000000000..3a137778e45c464c079658ecb87ec53270e789f7
--- /dev/null
+++ b/VISAM/thirdparty/segment_anything/segment_anything/utils/amg.py
@@ -0,0 +1,346 @@
+# Copyright (c) Meta Platforms, Inc. and affiliates.
+# All rights reserved.
+
+# This source code is licensed under the license found in the
+# LICENSE file in the root directory of this source tree.
+
+import numpy as np
+import torch
+
+import math
+from copy import deepcopy
+from itertools import product
+from typing import Any, Dict, Generator, ItemsView, List, Tuple
+
+
+class MaskData:
+ """
+ A structure for storing masks and their related data in batched format.
+ Implements basic filtering and concatenation.
+ """
+
+ def __init__(self, **kwargs) -> None:
+ for v in kwargs.values():
+ assert isinstance(
+ v, (list, np.ndarray, torch.Tensor)
+ ), "MaskData only supports list, numpy arrays, and torch tensors."
+ self._stats = dict(**kwargs)
+
+ def __setitem__(self, key: str, item: Any) -> None:
+ assert isinstance(
+ item, (list, np.ndarray, torch.Tensor)
+ ), "MaskData only supports list, numpy arrays, and torch tensors."
+ self._stats[key] = item
+
+ def __delitem__(self, key: str) -> None:
+ del self._stats[key]
+
+ def __getitem__(self, key: str) -> Any:
+ return self._stats[key]
+
+ def items(self) -> ItemsView[str, Any]:
+ return self._stats.items()
+
+ def filter(self, keep: torch.Tensor) -> None:
+ for k, v in self._stats.items():
+ if v is None:
+ self._stats[k] = None
+ elif isinstance(v, torch.Tensor):
+ self._stats[k] = v[torch.as_tensor(keep, device=v.device)]
+ elif isinstance(v, np.ndarray):
+ self._stats[k] = v[keep.detach().cpu().numpy()]
+ elif isinstance(v, list) and keep.dtype == torch.bool:
+ self._stats[k] = [a for i, a in enumerate(v) if keep[i]]
+ elif isinstance(v, list):
+ self._stats[k] = [v[i] for i in keep]
+ else:
+ raise TypeError(f"MaskData key {k} has an unsupported type {type(v)}.")
+
+ def cat(self, new_stats: "MaskData") -> None:
+ for k, v in new_stats.items():
+ if k not in self._stats or self._stats[k] is None:
+ self._stats[k] = deepcopy(v)
+ elif isinstance(v, torch.Tensor):
+ self._stats[k] = torch.cat([self._stats[k], v], dim=0)
+ elif isinstance(v, np.ndarray):
+ self._stats[k] = np.concatenate([self._stats[k], v], axis=0)
+ elif isinstance(v, list):
+ self._stats[k] = self._stats[k] + deepcopy(v)
+ else:
+ raise TypeError(f"MaskData key {k} has an unsupported type {type(v)}.")
+
+ def to_numpy(self) -> None:
+ for k, v in self._stats.items():
+ if isinstance(v, torch.Tensor):
+ self._stats[k] = v.detach().cpu().numpy()
+
+
+def is_box_near_crop_edge(
+ boxes: torch.Tensor, crop_box: List[int], orig_box: List[int], atol: float = 20.0
+) -> torch.Tensor:
+ """Filter masks at the edge of a crop, but not at the edge of the original image."""
+ crop_box_torch = torch.as_tensor(crop_box, dtype=torch.float, device=boxes.device)
+ orig_box_torch = torch.as_tensor(orig_box, dtype=torch.float, device=boxes.device)
+ boxes = uncrop_boxes_xyxy(boxes, crop_box).float()
+ near_crop_edge = torch.isclose(boxes, crop_box_torch[None, :], atol=atol, rtol=0)
+ near_image_edge = torch.isclose(boxes, orig_box_torch[None, :], atol=atol, rtol=0)
+ near_crop_edge = torch.logical_and(near_crop_edge, ~near_image_edge)
+ return torch.any(near_crop_edge, dim=1)
+
+
+def box_xyxy_to_xywh(box_xyxy: torch.Tensor) -> torch.Tensor:
+ box_xywh = deepcopy(box_xyxy)
+ box_xywh[2] = box_xywh[2] - box_xywh[0]
+ box_xywh[3] = box_xywh[3] - box_xywh[1]
+ return box_xywh
+
+
+def batch_iterator(batch_size: int, *args) -> Generator[List[Any], None, None]:
+ assert len(args) > 0 and all(
+ len(a) == len(args[0]) for a in args
+ ), "Batched iteration must have inputs of all the same size."
+ n_batches = len(args[0]) // batch_size + int(len(args[0]) % batch_size != 0)
+ for b in range(n_batches):
+ yield [arg[b * batch_size : (b + 1) * batch_size] for arg in args]
+
+
+def mask_to_rle_pytorch(tensor: torch.Tensor) -> List[Dict[str, Any]]:
+ """
+ Encodes masks to an uncompressed RLE, in the format expected by
+ pycoco tools.
+ """
+ # Put in fortran order and flatten h,w
+ b, h, w = tensor.shape
+ tensor = tensor.permute(0, 2, 1).flatten(1)
+
+ # Compute change indices
+ diff = tensor[:, 1:] ^ tensor[:, :-1]
+ change_indices = diff.nonzero()
+
+ # Encode run length
+ out = []
+ for i in range(b):
+ cur_idxs = change_indices[change_indices[:, 0] == i, 1]
+ cur_idxs = torch.cat(
+ [
+ torch.tensor([0], dtype=cur_idxs.dtype, device=cur_idxs.device),
+ cur_idxs + 1,
+ torch.tensor([h * w], dtype=cur_idxs.dtype, device=cur_idxs.device),
+ ]
+ )
+ btw_idxs = cur_idxs[1:] - cur_idxs[:-1]
+ counts = [] if tensor[i, 0] == 0 else [0]
+ counts.extend(btw_idxs.detach().cpu().tolist())
+ out.append({"size": [h, w], "counts": counts})
+ return out
+
+
+def rle_to_mask(rle: Dict[str, Any]) -> np.ndarray:
+ """Compute a binary mask from an uncompressed RLE."""
+ h, w = rle["size"]
+ mask = np.empty(h * w, dtype=bool)
+ idx = 0
+ parity = False
+ for count in rle["counts"]:
+ mask[idx : idx + count] = parity
+ idx += count
+ parity ^= True
+ mask = mask.reshape(w, h)
+ return mask.transpose() # Put in C order
+
+
+def area_from_rle(rle: Dict[str, Any]) -> int:
+ return sum(rle["counts"][1::2])
+
+
+def calculate_stability_score(
+ masks: torch.Tensor, mask_threshold: float, threshold_offset: float
+) -> torch.Tensor:
+ """
+ Computes the stability score for a batch of masks. The stability
+ score is the IoU between the binary masks obtained by thresholding
+ the predicted mask logits at high and low values.
+ """
+ # One mask is always contained inside the other.
+ # Save memory by preventing unnecesary cast to torch.int64
+ intersections = (
+ (masks > (mask_threshold + threshold_offset))
+ .sum(-1, dtype=torch.int16)
+ .sum(-1, dtype=torch.int32)
+ )
+ unions = (
+ (masks > (mask_threshold - threshold_offset))
+ .sum(-1, dtype=torch.int16)
+ .sum(-1, dtype=torch.int32)
+ )
+ return intersections / unions
+
+
+def build_point_grid(n_per_side: int) -> np.ndarray:
+ """Generates a 2D grid of points evenly spaced in [0,1]x[0,1]."""
+ offset = 1 / (2 * n_per_side)
+ points_one_side = np.linspace(offset, 1 - offset, n_per_side)
+ points_x = np.tile(points_one_side[None, :], (n_per_side, 1))
+ points_y = np.tile(points_one_side[:, None], (1, n_per_side))
+ points = np.stack([points_x, points_y], axis=-1).reshape(-1, 2)
+ return points
+
+
+def build_all_layer_point_grids(
+ n_per_side: int, n_layers: int, scale_per_layer: int
+) -> List[np.ndarray]:
+ """Generates point grids for all crop layers."""
+ points_by_layer = []
+ for i in range(n_layers + 1):
+ n_points = int(n_per_side / (scale_per_layer**i))
+ points_by_layer.append(build_point_grid(n_points))
+ return points_by_layer
+
+
+def generate_crop_boxes(
+ im_size: Tuple[int, ...], n_layers: int, overlap_ratio: float
+) -> Tuple[List[List[int]], List[int]]:
+ """
+ Generates a list of crop boxes of different sizes. Each layer
+ has (2**i)**2 boxes for the ith layer.
+ """
+ crop_boxes, layer_idxs = [], []
+ im_h, im_w = im_size
+ short_side = min(im_h, im_w)
+
+ # Original image
+ crop_boxes.append([0, 0, im_w, im_h])
+ layer_idxs.append(0)
+
+ def crop_len(orig_len, n_crops, overlap):
+ return int(math.ceil((overlap * (n_crops - 1) + orig_len) / n_crops))
+
+ for i_layer in range(n_layers):
+ n_crops_per_side = 2 ** (i_layer + 1)
+ overlap = int(overlap_ratio * short_side * (2 / n_crops_per_side))
+
+ crop_w = crop_len(im_w, n_crops_per_side, overlap)
+ crop_h = crop_len(im_h, n_crops_per_side, overlap)
+
+ crop_box_x0 = [int((crop_w - overlap) * i) for i in range(n_crops_per_side)]
+ crop_box_y0 = [int((crop_h - overlap) * i) for i in range(n_crops_per_side)]
+
+ # Crops in XYWH format
+ for x0, y0 in product(crop_box_x0, crop_box_y0):
+ box = [x0, y0, min(x0 + crop_w, im_w), min(y0 + crop_h, im_h)]
+ crop_boxes.append(box)
+ layer_idxs.append(i_layer + 1)
+
+ return crop_boxes, layer_idxs
+
+
+def uncrop_boxes_xyxy(boxes: torch.Tensor, crop_box: List[int]) -> torch.Tensor:
+ x0, y0, _, _ = crop_box
+ offset = torch.tensor([[x0, y0, x0, y0]], device=boxes.device)
+ # Check if boxes has a channel dimension
+ if len(boxes.shape) == 3:
+ offset = offset.unsqueeze(1)
+ return boxes + offset
+
+
+def uncrop_points(points: torch.Tensor, crop_box: List[int]) -> torch.Tensor:
+ x0, y0, _, _ = crop_box
+ offset = torch.tensor([[x0, y0]], device=points.device)
+ # Check if points has a channel dimension
+ if len(points.shape) == 3:
+ offset = offset.unsqueeze(1)
+ return points + offset
+
+
+def uncrop_masks(
+ masks: torch.Tensor, crop_box: List[int], orig_h: int, orig_w: int
+) -> torch.Tensor:
+ x0, y0, x1, y1 = crop_box
+ if x0 == 0 and y0 == 0 and x1 == orig_w and y1 == orig_h:
+ return masks
+ # Coordinate transform masks
+ pad_x, pad_y = orig_w - (x1 - x0), orig_h - (y1 - y0)
+ pad = (x0, pad_x - x0, y0, pad_y - y0)
+ return torch.nn.functional.pad(masks, pad, value=0)
+
+
+def remove_small_regions(
+ mask: np.ndarray, area_thresh: float, mode: str
+) -> Tuple[np.ndarray, bool]:
+ """
+ Removes small disconnected regions and holes in a mask. Returns the
+ mask and an indicator of if the mask has been modified.
+ """
+ import cv2 # type: ignore
+
+ assert mode in ["holes", "islands"]
+ correct_holes = mode == "holes"
+ working_mask = (correct_holes ^ mask).astype(np.uint8)
+ n_labels, regions, stats, _ = cv2.connectedComponentsWithStats(working_mask, 8)
+ sizes = stats[:, -1][1:] # Row 0 is background label
+ small_regions = [i + 1 for i, s in enumerate(sizes) if s < area_thresh]
+ if len(small_regions) == 0:
+ return mask, False
+ fill_labels = [0] + small_regions
+ if not correct_holes:
+ fill_labels = [i for i in range(n_labels) if i not in fill_labels]
+ # If every region is below threshold, keep largest
+ if len(fill_labels) == 0:
+ fill_labels = [int(np.argmax(sizes)) + 1]
+ mask = np.isin(regions, fill_labels)
+ return mask, True
+
+
+def coco_encode_rle(uncompressed_rle: Dict[str, Any]) -> Dict[str, Any]:
+ from pycocotools import mask as mask_utils # type: ignore
+
+ h, w = uncompressed_rle["size"]
+ rle = mask_utils.frPyObjects(uncompressed_rle, h, w)
+ rle["counts"] = rle["counts"].decode("utf-8") # Necessary to serialize with json
+ return rle
+
+
+def batched_mask_to_box(masks: torch.Tensor) -> torch.Tensor:
+ """
+ Calculates boxes in XYXY format around masks. Return [0,0,0,0] for
+ an empty mask. For input shape C1xC2x...xHxW, the output shape is C1xC2x...x4.
+ """
+ # torch.max below raises an error on empty inputs, just skip in this case
+ if torch.numel(masks) == 0:
+ return torch.zeros(*masks.shape[:-2], 4, device=masks.device)
+
+ # Normalize shape to CxHxW
+ shape = masks.shape
+ h, w = shape[-2:]
+ if len(shape) > 2:
+ masks = masks.flatten(0, -3)
+ else:
+ masks = masks.unsqueeze(0)
+
+ # Get top and bottom edges
+ in_height, _ = torch.max(masks, dim=-1)
+ in_height_coords = in_height * torch.arange(h, device=in_height.device)[None, :]
+ bottom_edges, _ = torch.max(in_height_coords, dim=-1)
+ in_height_coords = in_height_coords + h * (~in_height)
+ top_edges, _ = torch.min(in_height_coords, dim=-1)
+
+ # Get left and right edges
+ in_width, _ = torch.max(masks, dim=-2)
+ in_width_coords = in_width * torch.arange(w, device=in_width.device)[None, :]
+ right_edges, _ = torch.max(in_width_coords, dim=-1)
+ in_width_coords = in_width_coords + w * (~in_width)
+ left_edges, _ = torch.min(in_width_coords, dim=-1)
+
+ # If the mask is empty the right edge will be to the left of the left edge.
+ # Replace these boxes with [0, 0, 0, 0]
+ empty_filter = (right_edges < left_edges) | (bottom_edges < top_edges)
+ out = torch.stack([left_edges, top_edges, right_edges, bottom_edges], dim=-1)
+ out = out * (~empty_filter).unsqueeze(-1)
+
+ # Return to original shape
+ if len(shape) > 2:
+ out = out.reshape(*shape[:-2], 4)
+ else:
+ out = out[0]
+
+ return out
diff --git a/VISAM/thirdparty/segment_anything/segment_anything/utils/onnx.py b/VISAM/thirdparty/segment_anything/segment_anything/utils/onnx.py
new file mode 100644
index 0000000000000000000000000000000000000000..4297b31291e036700d6ad0b818afb7dd72da3054
--- /dev/null
+++ b/VISAM/thirdparty/segment_anything/segment_anything/utils/onnx.py
@@ -0,0 +1,144 @@
+# Copyright (c) Meta Platforms, Inc. and affiliates.
+# All rights reserved.
+
+# This source code is licensed under the license found in the
+# LICENSE file in the root directory of this source tree.
+
+import torch
+import torch.nn as nn
+from torch.nn import functional as F
+
+from typing import Tuple
+
+from ..modeling import Sam
+from .amg import calculate_stability_score
+
+
+class SamOnnxModel(nn.Module):
+ """
+ This model should not be called directly, but is used in ONNX export.
+ It combines the prompt encoder, mask decoder, and mask postprocessing of Sam,
+ with some functions modified to enable model tracing. Also supports extra
+ options controlling what information. See the ONNX export script for details.
+ """
+
+ def __init__(
+ self,
+ model: Sam,
+ return_single_mask: bool,
+ use_stability_score: bool = False,
+ return_extra_metrics: bool = False,
+ ) -> None:
+ super().__init__()
+ self.mask_decoder = model.mask_decoder
+ self.model = model
+ self.img_size = model.image_encoder.img_size
+ self.return_single_mask = return_single_mask
+ self.use_stability_score = use_stability_score
+ self.stability_score_offset = 1.0
+ self.return_extra_metrics = return_extra_metrics
+
+ @staticmethod
+ def resize_longest_image_size(
+ input_image_size: torch.Tensor, longest_side: int
+ ) -> torch.Tensor:
+ input_image_size = input_image_size.to(torch.float32)
+ scale = longest_side / torch.max(input_image_size)
+ transformed_size = scale * input_image_size
+ transformed_size = torch.floor(transformed_size + 0.5).to(torch.int64)
+ return transformed_size
+
+ def _embed_points(self, point_coords: torch.Tensor, point_labels: torch.Tensor) -> torch.Tensor:
+ point_coords = point_coords + 0.5
+ point_coords = point_coords / self.img_size
+ point_embedding = self.model.prompt_encoder.pe_layer._pe_encoding(point_coords)
+ point_labels = point_labels.unsqueeze(-1).expand_as(point_embedding)
+
+ point_embedding = point_embedding * (point_labels != -1)
+ point_embedding = point_embedding + self.model.prompt_encoder.not_a_point_embed.weight * (
+ point_labels == -1
+ )
+
+ for i in range(self.model.prompt_encoder.num_point_embeddings):
+ point_embedding = point_embedding + self.model.prompt_encoder.point_embeddings[
+ i
+ ].weight * (point_labels == i)
+
+ return point_embedding
+
+ def _embed_masks(self, input_mask: torch.Tensor, has_mask_input: torch.Tensor) -> torch.Tensor:
+ mask_embedding = has_mask_input * self.model.prompt_encoder.mask_downscaling(input_mask)
+ mask_embedding = mask_embedding + (
+ 1 - has_mask_input
+ ) * self.model.prompt_encoder.no_mask_embed.weight.reshape(1, -1, 1, 1)
+ return mask_embedding
+
+ def mask_postprocessing(self, masks: torch.Tensor, orig_im_size: torch.Tensor) -> torch.Tensor:
+ masks = F.interpolate(
+ masks,
+ size=(self.img_size, self.img_size),
+ mode="bilinear",
+ align_corners=False,
+ )
+
+ prepadded_size = self.resize_longest_image_size(orig_im_size, self.img_size)
+ masks = masks[..., : int(prepadded_size[0]), : int(prepadded_size[1])]
+
+ orig_im_size = orig_im_size.to(torch.int64)
+ h, w = orig_im_size[0], orig_im_size[1]
+ masks = F.interpolate(masks, size=(h, w), mode="bilinear", align_corners=False)
+ return masks
+
+ def select_masks(
+ self, masks: torch.Tensor, iou_preds: torch.Tensor, num_points: int
+ ) -> Tuple[torch.Tensor, torch.Tensor]:
+ # Determine if we should return the multiclick mask or not from the number of points.
+ # The reweighting is used to avoid control flow.
+ score_reweight = torch.tensor(
+ [[1000] + [0] * (self.model.mask_decoder.num_mask_tokens - 1)]
+ ).to(iou_preds.device)
+ score = iou_preds + (num_points - 2.5) * score_reweight
+ best_idx = torch.argmax(score, dim=1)
+ masks = masks[torch.arange(masks.shape[0]), best_idx, :, :].unsqueeze(1)
+ iou_preds = iou_preds[torch.arange(masks.shape[0]), best_idx].unsqueeze(1)
+
+ return masks, iou_preds
+
+ @torch.no_grad()
+ def forward(
+ self,
+ image_embeddings: torch.Tensor,
+ point_coords: torch.Tensor,
+ point_labels: torch.Tensor,
+ mask_input: torch.Tensor,
+ has_mask_input: torch.Tensor,
+ orig_im_size: torch.Tensor,
+ ):
+ sparse_embedding = self._embed_points(point_coords, point_labels)
+ dense_embedding = self._embed_masks(mask_input, has_mask_input)
+
+ masks, scores = self.model.mask_decoder.predict_masks(
+ image_embeddings=image_embeddings,
+ image_pe=self.model.prompt_encoder.get_dense_pe(),
+ sparse_prompt_embeddings=sparse_embedding,
+ dense_prompt_embeddings=dense_embedding,
+ )
+
+ if self.use_stability_score:
+ scores = calculate_stability_score(
+ masks, self.model.mask_threshold, self.stability_score_offset
+ )
+
+ if self.return_single_mask:
+ masks, scores = self.select_masks(masks, scores, point_coords.shape[1])
+
+ upscaled_masks = self.mask_postprocessing(masks, orig_im_size)
+
+ if self.return_extra_metrics:
+ stability_scores = calculate_stability_score(
+ upscaled_masks, self.model.mask_threshold, self.stability_score_offset
+ )
+ areas = (upscaled_masks > self.model.mask_threshold).sum(-1).sum(-1)
+ return upscaled_masks, scores, stability_scores, areas, masks
+
+ return upscaled_masks, scores, masks
diff --git a/VISAM/thirdparty/segment_anything/segment_anything/utils/transforms.py b/VISAM/thirdparty/segment_anything/segment_anything/utils/transforms.py
new file mode 100644
index 0000000000000000000000000000000000000000..3ad346661f84b0647026e130a552c4b38b83e2ac
--- /dev/null
+++ b/VISAM/thirdparty/segment_anything/segment_anything/utils/transforms.py
@@ -0,0 +1,102 @@
+# Copyright (c) Meta Platforms, Inc. and affiliates.
+# All rights reserved.
+
+# This source code is licensed under the license found in the
+# LICENSE file in the root directory of this source tree.
+
+import numpy as np
+import torch
+from torch.nn import functional as F
+from torchvision.transforms.functional import resize, to_pil_image # type: ignore
+
+from copy import deepcopy
+from typing import Tuple
+
+
+class ResizeLongestSide:
+ """
+ Resizes images to longest side 'target_length', as well as provides
+ methods for resizing coordinates and boxes. Provides methods for
+ transforming both numpy array and batched torch tensors.
+ """
+
+ def __init__(self, target_length: int) -> None:
+ self.target_length = target_length
+
+ def apply_image(self, image: np.ndarray) -> np.ndarray:
+ """
+ Expects a numpy array with shape HxWxC in uint8 format.
+ """
+ target_size = self.get_preprocess_shape(image.shape[0], image.shape[1], self.target_length)
+ return np.array(resize(to_pil_image(image), target_size))
+
+ def apply_coords(self, coords: np.ndarray, original_size: Tuple[int, ...]) -> np.ndarray:
+ """
+ Expects a numpy array of length 2 in the final dimension. Requires the
+ original image size in (H, W) format.
+ """
+ old_h, old_w = original_size
+ new_h, new_w = self.get_preprocess_shape(
+ original_size[0], original_size[1], self.target_length
+ )
+ coords = deepcopy(coords).astype(float)
+ coords[..., 0] = coords[..., 0] * (new_w / old_w)
+ coords[..., 1] = coords[..., 1] * (new_h / old_h)
+ return coords
+
+ def apply_boxes(self, boxes: np.ndarray, original_size: Tuple[int, ...]) -> np.ndarray:
+ """
+ Expects a numpy array shape Bx4. Requires the original image size
+ in (H, W) format.
+ """
+ boxes = self.apply_coords(boxes.reshape(-1, 2, 2), original_size)
+ return boxes.reshape(-1, 4)
+
+ def apply_image_torch(self, image: torch.Tensor) -> torch.Tensor:
+ """
+ Expects batched images with shape BxCxHxW and float format. This
+ transformation may not exactly match apply_image. apply_image is
+ the transformation expected by the model.
+ """
+ # Expects an image in BCHW format. May not exactly match apply_image.
+ target_size = self.get_preprocess_shape(image.shape[0], image.shape[1], self.target_length)
+ return F.interpolate(
+ image, target_size, mode="bilinear", align_corners=False, antialias=True
+ )
+
+ def apply_coords_torch(
+ self, coords: torch.Tensor, original_size: Tuple[int, ...]
+ ) -> torch.Tensor:
+ """
+ Expects a torch tensor with length 2 in the last dimension. Requires the
+ original image size in (H, W) format.
+ """
+ old_h, old_w = original_size
+ new_h, new_w = self.get_preprocess_shape(
+ original_size[0], original_size[1], self.target_length
+ )
+ coords = deepcopy(coords).to(torch.float)
+ coords[..., 0] = coords[..., 0] * (new_w / old_w)
+ coords[..., 1] = coords[..., 1] * (new_h / old_h)
+ return coords
+
+ def apply_boxes_torch(
+ self, boxes: torch.Tensor, original_size: Tuple[int, ...]
+ ) -> torch.Tensor:
+ """
+ Expects a torch tensor with shape Bx4. Requires the original image
+ size in (H, W) format.
+ """
+ boxes = self.apply_coords_torch(boxes.reshape(-1, 2, 2), original_size)
+ return boxes.reshape(-1, 4)
+
+ @staticmethod
+ def get_preprocess_shape(oldh: int, oldw: int, long_side_length: int) -> Tuple[int, int]:
+ """
+ Compute the output size given input size and target long side length.
+ """
+ scale = long_side_length * 1.0 / max(oldh, oldw)
+ newh, neww = oldh * scale, oldw * scale
+ neww = int(neww + 0.5)
+ newh = int(newh + 0.5)
+ return (newh, neww)
diff --git a/VISAM/thirdparty/segment_anything/setup.cfg b/VISAM/thirdparty/segment_anything/setup.cfg
new file mode 100644
index 0000000000000000000000000000000000000000..0eee130ba71d14ec260d33a8ebd96a6491079a54
--- /dev/null
+++ b/VISAM/thirdparty/segment_anything/setup.cfg
@@ -0,0 +1,11 @@
+[isort]
+line_length=100
+multi_line_output=3
+include_trailing_comma=True
+known_standard_library=numpy,setuptools
+skip_glob=*/__init__.py
+known_myself=segment_anything
+known_third_party=matplotlib,cv2,torch,torchvision,pycocotools,onnx,black,isort
+no_lines_before=STDLIB,THIRDPARTY
+sections=FUTURE,STDLIB,THIRDPARTY,MYSELF,FIRSTPARTY,LOCALFOLDER
+default_section=FIRSTPARTY
diff --git a/VISAM/thirdparty/segment_anything/setup.py b/VISAM/thirdparty/segment_anything/setup.py
new file mode 100644
index 0000000000000000000000000000000000000000..2c0986317eb576a14ec774205c88fdee3cc6c0b3
--- /dev/null
+++ b/VISAM/thirdparty/segment_anything/setup.py
@@ -0,0 +1,18 @@
+# Copyright (c) Meta Platforms, Inc. and affiliates.
+# All rights reserved.
+
+# This source code is licensed under the license found in the
+# LICENSE file in the root directory of this source tree.
+
+from setuptools import find_packages, setup
+
+setup(
+ name="segment_anything",
+ version="1.0",
+ install_requires=[],
+ packages=find_packages(exclude="notebooks"),
+ extras_require={
+ "all": ["matplotlib", "pycocotools", "opencv-python", "onnx", "onnxruntime"],
+ "dev": ["flake8", "isort", "black", "mypy"],
+ },
+)
diff --git a/VISAM/tools/batch_diff.py b/VISAM/tools/batch_diff.py
new file mode 100644
index 0000000000000000000000000000000000000000..18a46236f019c4cff5f825060a8a8454ae3c1238
--- /dev/null
+++ b/VISAM/tools/batch_diff.py
@@ -0,0 +1,20 @@
+# ------------------------------------------------------------------------
+# Copyright (c) 2022 megvii-research. All Rights Reserved.
+# ------------------------------------------------------------------------
+
+
+import argparse
+from glob import glob
+from subprocess import run
+
+
+parser = argparse.ArgumentParser()
+parser.add_argument('src')
+parser.add_argument('dst')
+args = parser.parse_args()
+
+
+for src in glob(args.src+'/*/*.py') + glob(args.src+'/*.py'):
+ dst = src.replace(args.src, args.dst)
+ if run(['diff', src, dst]).returncode != 0:
+ print('code --diff', src, dst)
diff --git a/VISAM/tools/copy_back.sh b/VISAM/tools/copy_back.sh
new file mode 100644
index 0000000000000000000000000000000000000000..0634563885d6994bb9d516f38afba9ff79140a46
--- /dev/null
+++ b/VISAM/tools/copy_back.sh
@@ -0,0 +1,10 @@
+# ------------------------------------------------------------------------
+# Copyright (c) 2022 megvii-research. All Rights Reserved.
+# ------------------------------------------------------------------------
+
+
+set -x
+
+cp $1/*.py .
+cp $1/models/*.py models
+cp $1/datasets/*.py datasets
diff --git a/VISAM/tools/debug.sh b/VISAM/tools/debug.sh
new file mode 100644
index 0000000000000000000000000000000000000000..0ff5267d0433e34ebc726151068ba07a6eade412
--- /dev/null
+++ b/VISAM/tools/debug.sh
@@ -0,0 +1,12 @@
+#!/usr/bin/env bash
+# ------------------------------------------------------------------------
+# Copyright (c) 2022 megvii-research. All Rights Reserved.
+# ------------------------------------------------------------------------
+
+
+set -x
+
+args=$(cat $1)
+
+export CUDA_LAUNCH_BLOCKING=1
+python main.py ${args} --output_dir /tmp/clip_mot_v2
diff --git a/VISAM/tools/eval_dance.sh b/VISAM/tools/eval_dance.sh
new file mode 100644
index 0000000000000000000000000000000000000000..67f3b28c3bbe25b379b2284732f5faba3eca94a6
--- /dev/null
+++ b/VISAM/tools/eval_dance.sh
@@ -0,0 +1,41 @@
+#!/usr/bin/env bash
+# ------------------------------------------------------------------------
+# Copyright (c) 2022 megvii-research. All Rights Reserved.
+# ------------------------------------------------------------------------
+
+
+set -x
+
+set -o pipefail
+
+OUTPUT_DIR=$1
+
+# clean up *.pyc files
+rmpyc() {
+ rm -rf $(find -name __pycache__)
+ rm -rf $(find -name "*.pyc")
+}
+
+
+cp submit_dance.py $OUTPUT_DIR
+
+pushd $OUTPUT_DIR
+
+args=$(cat *.args)
+# rlaunch --cpu 8 --gpu 1 --memory 24000 --positive-tags 2080ti -P 13 -- python3 submit_dance.py ${args} --resume checkpoint.pth --exp_name tracker
+python3 submit_dance.py ${args} --resume checkpoint.pth --exp_name tracker
+
+popd
+
+# python3 ../TrackEval/scripts/run_mot_challenge.py \
+# --SPLIT_TO_EVAL val \
+# --METRICS HOTA CLEAR Identity \
+# --GT_FOLDER /data/datasets/DanceTrack/val \
+# --SEQMAP_FILE seqmap \
+# --SKIP_SPLIT_FOL True \
+# --TRACKER_SUB_FOLDER tracker \
+# --TRACKERS_TO_EVAL $OUTPUT_DIR \
+# --USE_PARALLEL True \
+# --NUM_PARALLEL_CORES 8 \
+# --PLOT_CURVES False \
+# --TRACKERS_FOLDER '' | tee -a $OUTPUT_DIR/eval.log
diff --git a/VISAM/tools/launch.py b/VISAM/tools/launch.py
new file mode 100644
index 0000000000000000000000000000000000000000..c8004393005e2c0c679cf1007c756562e5bb2885
--- /dev/null
+++ b/VISAM/tools/launch.py
@@ -0,0 +1,195 @@
+# ------------------------------------------------------------------------
+# Copyright (c) 2022 megvii-research. All Rights Reserved.
+# ------------------------------------------------------------------------
+# Modified from Deformable DETR (https://github.com/fundamentalvision/Deformable-DETR)
+# Copyright (c) 2020 SenseTime. All Rights Reserved.
+# ------------------------------------------------------------------------
+# Modified from DETR (https://github.com/facebookresearch/detr)
+# Copyright (c) Facebook, Inc. and its affiliates. All Rights Reserved
+# ------------------------------------------------------------------------
+
+
+r"""
+`torch.distributed.launch` is a module that spawns up multiple distributed
+training processes on each of the training nodes.
+The utility can be used for single-node distributed training, in which one or
+more processes per node will be spawned. The utility can be used for either
+CPU training or GPU training. If the utility is used for GPU training,
+each distributed process will be operating on a single GPU. This can achieve
+well-improved single-node training performance. It can also be used in
+multi-node distributed training, by spawning up multiple processes on each node
+for well-improved multi-node distributed training performance as well.
+This will especially be benefitial for systems with multiple Infiniband
+interfaces that have direct-GPU support, since all of them can be utilized for
+aggregated communication bandwidth.
+In both cases of single-node distributed training or multi-node distributed
+training, this utility will launch the given number of processes per node
+(``--nproc_per_node``). If used for GPU training, this number needs to be less
+or euqal to the number of GPUs on the current system (``nproc_per_node``),
+and each process will be operating on a single GPU from *GPU 0 to
+GPU (nproc_per_node - 1)*.
+**How to use this module:**
+1. Single-Node multi-process distributed training
+::
+ >>> python -m torch.distributed.launch --nproc_per_node=NUM_GPUS_YOU_HAVE
+ YOUR_TRAINING_SCRIPT.py (--arg1 --arg2 --arg3 and all other
+ arguments of your training script)
+2. Multi-Node multi-process distributed training: (e.g. two nodes)
+Node 1: *(IP: 192.168.1.1, and has a free port: 1234)*
+::
+ >>> python -m torch.distributed.launch --nproc_per_node=NUM_GPUS_YOU_HAVE
+ --nnodes=2 --node_rank=0 --master_addr="192.168.1.1"
+ --master_port=1234 YOUR_TRAINING_SCRIPT.py (--arg1 --arg2 --arg3
+ and all other arguments of your training script)
+Node 2:
+::
+ >>> python -m torch.distributed.launch --nproc_per_node=NUM_GPUS_YOU_HAVE
+ --nnodes=2 --node_rank=1 --master_addr="192.168.1.1"
+ --master_port=1234 YOUR_TRAINING_SCRIPT.py (--arg1 --arg2 --arg3
+ and all other arguments of your training script)
+3. To look up what optional arguments this module offers:
+::
+ >>> python -m torch.distributed.launch --help
+**Important Notices:**
+1. This utilty and multi-process distributed (single-node or
+multi-node) GPU training currently only achieves the best performance using
+the NCCL distributed backend. Thus NCCL backend is the recommended backend to
+use for GPU training.
+2. In your training program, you must parse the command-line argument:
+``--local_rank=LOCAL_PROCESS_RANK``, which will be provided by this module.
+If your training program uses GPUs, you should ensure that your code only
+runs on the GPU device of LOCAL_PROCESS_RANK. This can be done by:
+Parsing the local_rank argument
+::
+ >>> import argparse
+ >>> parser = argparse.ArgumentParser()
+ >>> parser.add_argument("--local_rank", type=int)
+ >>> args = parser.parse_args()
+Set your device to local rank using either
+::
+ >>> torch.cuda.set_device(arg.local_rank) # before your code runs
+or
+::
+ >>> with torch.cuda.device(arg.local_rank):
+ >>> # your code to run
+3. In your training program, you are supposed to call the following function
+at the beginning to start the distributed backend. You need to make sure that
+the init_method uses ``env://``, which is the only supported ``init_method``
+by this module.
+::
+ torch.distributed.init_process_group(backend='YOUR BACKEND',
+ init_method='env://')
+4. In your training program, you can either use regular distributed functions
+or use :func:`torch.nn.parallel.DistributedDataParallel` module. If your
+training program uses GPUs for training and you would like to use
+:func:`torch.nn.parallel.DistributedDataParallel` module,
+here is how to configure it.
+::
+ model = torch.nn.parallel.DistributedDataParallel(model,
+ device_ids=[arg.local_rank],
+ output_device=arg.local_rank)
+Please ensure that ``device_ids`` argument is set to be the only GPU device id
+that your code will be operating on. This is generally the local rank of the
+process. In other words, the ``device_ids`` needs to be ``[args.local_rank]``,
+and ``output_device`` needs to be ``args.local_rank`` in order to use this
+utility
+5. Another way to pass ``local_rank`` to the subprocesses via environment variable
+``LOCAL_RANK``. This behavior is enabled when you launch the script with
+``--use_env=True``. You must adjust the subprocess example above to replace
+``args.local_rank`` with ``os.environ['LOCAL_RANK']``; the launcher
+will not pass ``--local_rank`` when you specify this flag.
+.. warning::
+ ``local_rank`` is NOT globally unique: it is only unique per process
+ on a machine. Thus, don't use it to decide if you should, e.g.,
+ write to a networked filesystem. See
+ https://github.com/pytorch/pytorch/issues/12042 for an example of
+ how things can go wrong if you don't do this correctly.
+"""
+
+
+import sys
+import subprocess
+import os
+import socket
+from argparse import ArgumentParser, REMAINDER
+
+import torch
+
+
+def parse_args():
+ """
+ Helper function parsing the command line options
+ @retval ArgumentParser
+ """
+ parser = ArgumentParser(description="PyTorch distributed training launch "
+ "helper utilty that will spawn up "
+ "multiple distributed processes")
+
+ # Optional arguments for the launch helper
+ parser.add_argument("--nnodes", type=int, default=1,
+ help="The number of nodes to use for distributed "
+ "training")
+ parser.add_argument("--node_rank", type=int, default=0,
+ help="The rank of the node for multi-node distributed "
+ "training")
+ parser.add_argument("--nproc_per_node", type=int, default=1,
+ help="The number of processes to launch on each node, "
+ "for GPU training, this is recommended to be set "
+ "to the number of GPUs in your system so that "
+ "each process can be bound to a single GPU.")
+ parser.add_argument("--master_addr", default="127.0.0.1", type=str,
+ help="Master node (rank 0)'s address, should be either "
+ "the IP address or the hostname of node 0, for "
+ "single node multi-proc training, the "
+ "--master_addr can simply be 127.0.0.1")
+ parser.add_argument("--master_port", default=29500, type=int,
+ help="Master node (rank 0)'s free port that needs to "
+ "be used for communciation during distributed "
+ "training")
+
+ # positional
+ parser.add_argument("training_script", type=str,
+ help="The full path to the single GPU training "
+ "program/script to be launched in parallel, "
+ "followed by all the arguments for the "
+ "training script")
+
+ # rest from the training program
+ parser.add_argument('training_script_args', nargs=REMAINDER)
+ return parser.parse_args()
+
+
+def main():
+ args = parse_args()
+
+ # world size in terms of number of processes
+ dist_world_size = args.nproc_per_node * args.nnodes
+
+ # set PyTorch distributed related environmental variables
+ current_env = os.environ.copy()
+ current_env["MASTER_ADDR"] = args.master_addr
+ current_env["MASTER_PORT"] = str(args.master_port)
+ current_env["WORLD_SIZE"] = str(dist_world_size)
+
+ processes = []
+
+ for local_rank in range(0, args.nproc_per_node):
+ # each process's rank
+ dist_rank = args.nproc_per_node * args.node_rank + local_rank
+ current_env["RANK"] = str(dist_rank)
+ current_env["LOCAL_RANK"] = str(local_rank)
+
+ cmd = [args.training_script] + args.training_script_args
+
+ process = subprocess.Popen(cmd, env=current_env)
+ processes.append(process)
+
+ for process in processes:
+ process.wait()
+ if process.returncode != 0:
+ raise subprocess.CalledProcessError(returncode=process.returncode,
+ cmd=process.args)
+
+
+if __name__ == "__main__":
+ main()
\ No newline at end of file
diff --git a/VISAM/tools/make_detdb.py b/VISAM/tools/make_detdb.py
new file mode 100644
index 0000000000000000000000000000000000000000..9037dd811f8f1287d6aac837067aa493683008a5
--- /dev/null
+++ b/VISAM/tools/make_detdb.py
@@ -0,0 +1,47 @@
+# ------------------------------------------------------------------------
+# Copyright (c) 2022 megvii-research. All Rights Reserved.
+# ------------------------------------------------------------------------
+
+
+from glob import glob
+import json
+from concurrent.futures import ThreadPoolExecutor
+from threading import Lock
+
+from tqdm import tqdm
+
+det_db = {}
+to_cache = []
+
+for file in glob("/data/Dataset/mot/crowdhuman/train_image/*.txt"):
+ to_cache.append(file)
+
+for file in glob("/data/Dataset/mot/DanceTrack/*/*/img1/*.txt"):
+ to_cache.append(file)
+
+for file in glob("/data/Dataset/mot/MOT17/images/*/*/img1/*.txt"):
+ to_cache.append(file)
+
+for file in glob("/data/Dataset/mot/MOT20/train/*/img1/*.txt"):
+ to_cache.append(file)
+
+for file in glob("/data/Dataset/mot/HIE20/train/*/img1/*.txt"):
+ to_cache.append(file)
+
+pbar = tqdm(total=len(to_cache))
+
+mutex = Lock()
+def cache(file):
+ with open(file) as f:
+ tmp = [l for l in f]
+ with mutex:
+ det_db[file] = tmp
+ pbar.update()
+
+with ThreadPoolExecutor(max_workers=48) as exe:
+ for file in to_cache:
+ exe.submit(cache, file)
+
+with open("/data/Dataset/mot/det_db_oc_sort_full.json", 'w') as f:
+ json.dump(det_db, f)
+
diff --git a/VISAM/tools/merge_dance_tracklets.py b/VISAM/tools/merge_dance_tracklets.py
new file mode 100644
index 0000000000000000000000000000000000000000..795bec0349d23e49412763ebd95797201c7241d1
--- /dev/null
+++ b/VISAM/tools/merge_dance_tracklets.py
@@ -0,0 +1,59 @@
+# ------------------------------------------------------------------------
+# Copyright (c) 2022 megvii-research. All Rights Reserved.
+# ------------------------------------------------------------------------
+
+
+import argparse
+from collections import defaultdict
+import os
+from pathlib import Path
+
+parser = argparse.ArgumentParser()
+parser.add_argument('input_dir', type=Path)
+parser.add_argument('output_dir', type=Path)
+parser.add_argument('--t_min', default=20)
+parser.add_argument('--t_max', default=100)
+args = parser.parse_args()
+
+
+class FindUnionSet(dict):
+ def find(self, src):
+ if src in self:
+ return self.find(self[src])
+ return src
+
+ def merge(self, dst, src):
+ self[self.find(src)] = self.find(dst)
+
+
+for seq in os.listdir(args.input_dir):
+ print(args.input_dir / seq)
+ with open(args.input_dir / seq) as f:
+ lines = f.readlines()
+ instance_timestamps = defaultdict(list)
+ for line in lines:
+ f_id, id = map(int, line.split(',')[:2])
+ instance_timestamps[id].append(f_id)
+ instances = list(instance_timestamps.keys())
+ fid_map = FindUnionSet()
+ for i in instances:
+ for j in instances:
+ if fid_map.find(i) == fid_map.find(j):
+ continue
+ end_t = max(instance_timestamps[i])
+ start_t = min(instance_timestamps[j])
+ if sum([0 <= start_t - max(pts) < args.t_max for pts in instance_timestamps.values()]) > 1:
+ continue
+ if sum([0 <= min(pts) - end_t < args.t_max for pts in instance_timestamps.values()]) > 1:
+ continue
+ dt = start_t - end_t
+ if args.t_min < dt < args.t_max:
+ print(f"{i}<-{j}", end_t, start_t, start_t - end_t)
+ fid_map.merge(i, j)
+
+ os.makedirs(args.output_dir / 'tracker', exist_ok=True)
+ with open(args.output_dir / 'tracker' / seq, 'w') as f:
+ for line in lines:
+ f_id, id, *info = line.split(',')
+ id = str(fid_map.find(int(id)))
+ f.write(','.join([f_id, id, *info]))
diff --git a/VISAM/tools/merge_dance_tracklets.sh b/VISAM/tools/merge_dance_tracklets.sh
new file mode 100644
index 0000000000000000000000000000000000000000..58ab8009303a1a8caa95a77eef163a5423fc8063
--- /dev/null
+++ b/VISAM/tools/merge_dance_tracklets.sh
@@ -0,0 +1,18 @@
+# ------------------------------------------------------------------------
+# Copyright (c) 2022 megvii-research. All Rights Reserved.
+# ------------------------------------------------------------------------
+
+python tools/merge_dance_tracklets.py $1 $2
+
+# python3 ../TrackEval/scripts/run_mot_challenge.py \
+# --SPLIT_TO_EVAL val \
+# --METRICS HOTA \
+# --GT_FOLDER /data/datasets/DanceTrack/val \
+# --SEQMAP_FILE seqmap \
+# --SKIP_SPLIT_FOL True \
+# --TRACKER_SUB_FOLDER tracker \
+# --TRACKERS_TO_EVAL $2 \
+# --USE_PARALLEL True \
+# --NUM_PARALLEL_CORES 8 \
+# --PLOT_CURVES False \
+# --TRACKERS_FOLDER '' | tee -a $2/eval.log
diff --git a/VISAM/tools/resume.sh b/VISAM/tools/resume.sh
new file mode 100644
index 0000000000000000000000000000000000000000..e6a64d0f1077b3307cc1cb93a12c9f4d24b3b35d
--- /dev/null
+++ b/VISAM/tools/resume.sh
@@ -0,0 +1,33 @@
+#!/usr/bin/env bash
+# ------------------------------------------------------------------------
+# Copyright (c) 2022 megvii-research. All Rights Reserved.
+# ------------------------------------------------------------------------
+
+
+set -x
+
+set -o pipefail
+
+OUTPUT_DIR=$1
+
+# clean up *.pyc files
+rmpyc() {
+ rm -rf $(find -name __pycache__)
+ rm -rf $(find -name "*.pyc")
+}
+
+# tar src to avoid future editing
+cleanup() {
+ echo "Packing source code"
+ rmpyc
+ # tar -zcf models datasets util main.py engine.py eval.py submit.py --remove-files
+ echo " ...Done"
+}
+
+
+pushd $OUTPUT_DIR
+trap cleanup EXIT
+
+args=$(cat *.args)
+python -m torch.distributed.launch --nproc_per_node=8 --use_env main.py ${args} --resume checkpoint.pth --output_dir . |& tee -a resume.log
+popd
diff --git a/VISAM/tools/run_dist_launch.sh b/VISAM/tools/run_dist_launch.sh
new file mode 100644
index 0000000000000000000000000000000000000000..45546d606af80861413b9d65636776d6fe259b32
--- /dev/null
+++ b/VISAM/tools/run_dist_launch.sh
@@ -0,0 +1,34 @@
+#!/usr/bin/env bash
+# ------------------------------------------------------------------------
+# Copyright (c) 2022 megvii-research. All Rights Reserved.
+# ------------------------------------------------------------------------
+# Modified from Deformable DETR (https://github.com/fundamentalvision/Deformable-DETR)
+# Copyright (c) 2020 SenseTime. All Rights Reserved.
+# ------------------------------------------------------------------------
+# Modified from DETR (https://github.com/facebookresearch/detr)
+# Copyright (c) Facebook, Inc. and its affiliates. All Rights Reserved
+# ------------------------------------------------------------------------
+
+
+set -x
+
+GPUS=$1
+RUN_COMMAND=${@:2}
+if [ $GPUS -lt 8 ]; then
+ GPUS_PER_NODE=${GPUS_PER_NODE:-$GPUS}
+else
+ GPUS_PER_NODE=${GPUS_PER_NODE:-8}
+fi
+MASTER_ADDR=${MASTER_ADDR:-"127.0.0.1"}
+MASTER_PORT=${MASTER_PORT:-"29500"}
+NODE_RANK=${NODE_RANK:-0}
+
+let "NNODES=GPUS/GPUS_PER_NODE"
+
+python3 ./tools/launch.py \
+ --nnodes ${NNODES} \
+ --node_rank ${NODE_RANK} \
+ --master_addr ${MASTER_ADDR} \
+ --master_port ${MASTER_PORT} \
+ --nproc_per_node ${GPUS_PER_NODE} \
+ ${RUN_COMMAND}
\ No newline at end of file
diff --git a/VISAM/tools/run_dist_slurm.sh b/VISAM/tools/run_dist_slurm.sh
new file mode 100644
index 0000000000000000000000000000000000000000..b1f02ad6240de46789419a58b9b830604bdb736f
--- /dev/null
+++ b/VISAM/tools/run_dist_slurm.sh
@@ -0,0 +1,36 @@
+#!/usr/bin/env bash
+# ------------------------------------------------------------------------
+# Copyright (c) 2022 megvii-research. All Rights Reserved.
+# ------------------------------------------------------------------------
+# Modified from Deformable DETR (https://github.com/fundamentalvision/Deformable-DETR)
+# Copyright (c) 2020 SenseTime. All Rights Reserved.
+# ------------------------------------------------------------------------
+# Modified from DETR (https://github.com/facebookresearch/detr)
+# Copyright (c) Facebook, Inc. and its affiliates. All Rights Reserved
+# ------------------------------------------------------------------------
+
+
+set -x
+
+PARTITION=$1
+JOB_NAME=$2
+GPUS=$3
+RUN_COMMAND=${@:4}
+if [ $GPUS -lt 8 ]; then
+ GPUS_PER_NODE=${GPUS_PER_NODE:-$GPUS}
+else
+ GPUS_PER_NODE=${GPUS_PER_NODE:-8}
+fi
+CPUS_PER_TASK=${CPUS_PER_TASK:-4}
+SRUN_ARGS=${SRUN_ARGS:-""}
+
+srun -p ${PARTITION} \
+ --job-name=${JOB_NAME} \
+ --gres=gpu:${GPUS_PER_NODE} \
+ --ntasks=${GPUS} \
+ --ntasks-per-node=${GPUS_PER_NODE} \
+ --cpus-per-task=${CPUS_PER_TASK} \
+ --kill-on-bad-exit=1 \
+ ${SRUN_ARGS} \
+ ${RUN_COMMAND}
+
diff --git a/VISAM/tools/simple_inference.sh b/VISAM/tools/simple_inference.sh
new file mode 100644
index 0000000000000000000000000000000000000000..4dead75868e48b90633a9a7f10ab39f7e16ded81
--- /dev/null
+++ b/VISAM/tools/simple_inference.sh
@@ -0,0 +1,11 @@
+#!/usr/bin/env bash
+# ------------------------------------------------------------------------
+# Copyright (c) 2022 megvii-research. All Rights Reserved.
+# ------------------------------------------------------------------------
+
+
+set -x
+set -o pipefail
+
+args=$(cat configs/motrv2.args)
+python3 submit_dance.py ${args} --exp_name tracker --resume $1
diff --git a/VISAM/tools/train.sh b/VISAM/tools/train.sh
new file mode 100644
index 0000000000000000000000000000000000000000..642da0e764d36f045122f2521ecc358ea3be35a9
--- /dev/null
+++ b/VISAM/tools/train.sh
@@ -0,0 +1,54 @@
+#!/usr/bin/env bash
+# ------------------------------------------------------------------------
+# Copyright (c) 2022 megvii-research. All Rights Reserved.
+# ------------------------------------------------------------------------
+
+
+set -x
+
+PY_ARGS=${@:2}
+
+set -o pipefail
+
+OUTPUT_BASE=$(echo $1 | sed -e "s/configs/exps/g" | sed -e "s/.args$//g")
+mkdir -p $OUTPUT_BASE
+
+for RUN in $(seq 100); do
+ ls $OUTPUT_BASE | grep run$RUN && continue
+ OUTPUT_DIR=$OUTPUT_BASE/run$RUN
+ mkdir $OUTPUT_DIR && break
+done
+
+# clean up *.pyc files
+rmpyc() {
+ rm -rf $(find -name __pycache__)
+ rm -rf $(find -name "*.pyc")
+}
+
+# run backup
+echo "Backing up to log dir: $OUTPUT_DIR"
+rmpyc && cp -r models datasets util main.py engine.py submit_dance.py $1 $OUTPUT_DIR
+echo " ...Done"
+
+# tar src to avoid future editing
+cleanup() {
+ echo "Packing source code"
+ rmpyc
+ # tar -zcf models datasets util main.py engine.py eval.py submit.py --remove-files
+ echo " ...Done"
+}
+
+args=$(cat $1)
+
+pushd $OUTPUT_DIR
+trap cleanup EXIT
+
+# log git status
+echo "Logging git status"
+git status > git_status
+git rev-parse HEAD > git_tag
+git diff > git_diff
+echo $PY_ARGS > desc
+echo " ...Done"
+
+python -m torch.distributed.launch --nproc_per_node=8 --use_env main.py ${args} --output_dir . |& tee -a output.log
diff --git a/VISAM/tools/visualize.py b/VISAM/tools/visualize.py
new file mode 100644
index 0000000000000000000000000000000000000000..06dd6f199dc00039da29dafab173ede039f1dec2
--- /dev/null
+++ b/VISAM/tools/visualize.py
@@ -0,0 +1,71 @@
+# ------------------------------------------------------------------------
+# Copyright (c) 2022 megvii-research. All Rights Reserved.
+# ------------------------------------------------------------------------
+
+
+from collections import defaultdict
+from glob import glob
+import json
+import os
+import cv2
+import subprocess
+from tqdm import tqdm
+
+
+def get_color(i):
+ return [(i * 23 * j + 43) % 255 for j in range(3)]
+
+with open("/data/Dataset/mot/det_db_oc_sort.json") as f:
+ det_db = json.load(f)
+
+def process(trk_path, img_list, output="output.mp4"):
+ h, w, _ = cv2.imread(img_list[0]).shape
+ command = [
+ "/usr/bin/ffmpeg",
+ '-y', # overwrite output file if it exists
+ '-f', 'rawvideo',
+ '-vcodec','rawvideo',
+ '-s', f'{w}x{h}', # size of one frame
+ '-pix_fmt', 'bgr24',
+ '-r', '20', # frames per second
+ '-i', '-', # The imput comes from a pipe
+ '-s', f'{w//2*2}x{h//2*2}',
+ '-an', # Tells FFMPEG not to expect any audio
+ '-loglevel', 'error',
+ '-crf', '26',
+ '-pix_fmt', 'yuv420p'
+ ]
+ writing_process = subprocess.Popen(command + [output], stdin=subprocess.PIPE)
+
+ tracklets = defaultdict(list)
+ for line in open(trk_path):
+ t, id, *xywhs = line.split(',')[:7]
+ t, id = map(int, (t, id))
+ x, y, w, h, s = map(float, xywhs)
+ tracklets[t].append((id, *map(int, (x, y, x+w, y+h))))
+
+ for i, path in enumerate(tqdm(sorted(img_list))):
+ im = cv2.imread(path)
+ for det in det_db[path.replace('.jpg', '.txt')]:
+ x1, y1, w, h, _ = map(int, map(float, det.strip().split(',')))
+ im = cv2.rectangle(im, (x1, y1), (x1+w, y1+h), (255, 255, 255), 6)
+ for j, x1, y1, x2, y2 in tracklets[i + 1]:
+ im = cv2.rectangle(im, (x1, y1), (x2, y2), get_color(j), 4)
+ im = cv2.putText(im, f"{j}", (x1 + 10, y1 + 30), cv2.FONT_HERSHEY_SIMPLEX, 1, get_color(j), 2)
+ writing_process.stdin.write(im.tobytes())
+
+
+if __name__ == '__main__':
+ jobs = os.listdir("exps/motrv2_noqd/run1/tracker/")
+ rank = int(os.environ.get('RLAUNCH_REPLICA', '0'))
+ ws = int(os.environ.get('RLAUNCH_REPLICA_TOTAL', '1'))
+ jobs = sorted(jobs)[rank::ws]
+ for seq in jobs:
+ print(seq)
+
+ trk_path = "exps/motrv2_noqd/run1/tracker/" + seq
+ # trk_path = "/data/Dataset/mot/DanceTrack/val/dancetrack0010/gt/gt.txt"
+
+ img_list = glob(f"/data/Dataset/mot/DanceTrack/val/{seq[:-4]}/img1/*.jpg")
+ process(trk_path, img_list, f'motr_trainval_demo/{seq[:-4]}.mp4')
+ break
diff --git a/VISAM/util/__init__.py b/VISAM/util/__init__.py
new file mode 100644
index 0000000000000000000000000000000000000000..1175245761df5146940896944ea13a78f986b3b2
--- /dev/null
+++ b/VISAM/util/__init__.py
@@ -0,0 +1,10 @@
+# ------------------------------------------------------------------------
+# Copyright (c) 2022 megvii-research. All Rights Reserved.
+# ------------------------------------------------------------------------
+# Modified from Deformable DETR (https://github.com/fundamentalvision/Deformable-DETR)
+# Copyright (c) 2020 SenseTime. All Rights Reserved.
+# ------------------------------------------------------------------------
+# Modified from DETR (https://github.com/facebookresearch/detr)
+# Copyright (c) Facebook, Inc. and its affiliates. All Rights Reserved
+# ------------------------------------------------------------------------
+
diff --git a/VISAM/util/box_ops.py b/VISAM/util/box_ops.py
new file mode 100644
index 0000000000000000000000000000000000000000..5976ad2ecf945843bd79ac654b02820ed99dbd0f
--- /dev/null
+++ b/VISAM/util/box_ops.py
@@ -0,0 +1,98 @@
+# ------------------------------------------------------------------------
+# Copyright (c) 2022 megvii-research. All Rights Reserved.
+# ------------------------------------------------------------------------
+# Modified from Deformable DETR (https://github.com/fundamentalvision/Deformable-DETR)
+# Copyright (c) 2020 SenseTime. All Rights Reserved.
+# ------------------------------------------------------------------------
+# Modified from DETR (https://github.com/facebookresearch/detr)
+# Copyright (c) Facebook, Inc. and its affiliates. All Rights Reserved
+# ------------------------------------------------------------------------
+
+
+"""
+Utilities for bounding box manipulation and GIoU.
+"""
+import torch
+from torchvision.ops.boxes import box_area
+
+
+def box_cxcywh_to_xyxy(x):
+ x_c, y_c, w, h = x.unbind(-1)
+ b = [(x_c - 0.5 * w), (y_c - 0.5 * h),
+ (x_c + 0.5 * w), (y_c + 0.5 * h)]
+ return torch.stack(b, dim=-1)
+
+
+def box_xyxy_to_cxcywh(x):
+ x0, y0, x1, y1 = x.unbind(-1)
+ b = [(x0 + x1) / 2, (y0 + y1) / 2,
+ (x1 - x0), (y1 - y0)]
+ return torch.stack(b, dim=-1)
+
+
+# modified from torchvision to also return the union
+def box_iou(boxes1, boxes2):
+ area1 = box_area(boxes1)
+ area2 = box_area(boxes2)
+
+ lt = torch.max(boxes1[:, None, :2], boxes2[:, :2]) # [N,M,2]
+ rb = torch.min(boxes1[:, None, 2:], boxes2[:, 2:]) # [N,M,2]
+
+ wh = (rb - lt).clamp(min=0) # [N,M,2]
+ inter = wh[:, :, 0] * wh[:, :, 1] # [N,M]
+
+ union = area1[:, None] + area2 - inter
+
+ iou = inter / union
+ return iou, union
+
+
+def generalized_box_iou(boxes1, boxes2):
+ """
+ Generalized IoU from https://giou.stanford.edu/
+
+ The boxes should be in [x0, y0, x1, y1] format
+
+ Returns a [N, M] pairwise matrix, where N = len(boxes1)
+ and M = len(boxes2)
+ """
+ # degenerate boxes gives inf / nan results
+ # so do an early check
+ assert (boxes1[:, 2:] >= boxes1[:, :2]).all()
+ assert (boxes2[:, 2:] >= boxes2[:, :2]).all()
+ iou, union = box_iou(boxes1, boxes2)
+
+ lt = torch.min(boxes1[:, None, :2], boxes2[:, :2])
+ rb = torch.max(boxes1[:, None, 2:], boxes2[:, 2:])
+
+ wh = (rb - lt).clamp(min=0) # [N,M,2]
+ area = wh[:, :, 0] * wh[:, :, 1]
+
+ return iou - (area - union) / area
+
+
+def masks_to_boxes(masks):
+ """Compute the bounding boxes around the provided masks
+
+ The masks should be in format [N, H, W] where N is the number of masks, (H, W) are the spatial dimensions.
+
+ Returns a [N, 4] tensors, with the boxes in xyxy format
+ """
+ if masks.numel() == 0:
+ return torch.zeros((0, 4), device=masks.device)
+
+ h, w = masks.shape[-2:]
+
+ y = torch.arange(0, h, dtype=torch.float)
+ x = torch.arange(0, w, dtype=torch.float)
+ y, x = torch.meshgrid(y, x)
+
+ x_mask = (masks * x.unsqueeze(0))
+ x_max = x_mask.flatten(1).max(-1)[0]
+ x_min = x_mask.masked_fill(~(masks.bool()), 1e8).flatten(1).min(-1)[0]
+
+ y_mask = (masks * y.unsqueeze(0))
+ y_max = y_mask.flatten(1).max(-1)[0]
+ y_min = y_mask.masked_fill(~(masks.bool()), 1e8).flatten(1).min(-1)[0]
+
+ return torch.stack([x_min, y_min, x_max, y_max], 1)
diff --git a/VISAM/util/checkpoint.py b/VISAM/util/checkpoint.py
new file mode 100644
index 0000000000000000000000000000000000000000..7b166ad9689627e2e224fb57d0b58b26d0925864
--- /dev/null
+++ b/VISAM/util/checkpoint.py
@@ -0,0 +1,40 @@
+# ------------------------------------------------------------------------
+# Copyright (c) 2022 megvii-research. All Rights Reserved.
+# ------------------------------------------------------------------------
+# Modified from pytorch-checkpoint (https://github.com/csrhddlam/pytorch-checkpoint)
+# ------------------------------------------------------------------------
+
+import torch
+
+
+def check_require_grad(t):
+ return isinstance(t, torch.Tensor) and t.requires_grad
+
+
+class CheckpointFunction(torch.autograd.Function):
+ @staticmethod
+ def forward(ctx, run_function, length, *args):
+ ctx.run_function = run_function
+ ctx.input_tensors = list(args[:length])
+ ctx.input_params = list(args[length:])
+ with torch.no_grad():
+ output_tensors = ctx.run_function(*ctx.input_tensors)
+ return output_tensors
+
+ @staticmethod
+ def backward(ctx, *output_grads):
+ for i in range(len(ctx.input_tensors)):
+ temp = ctx.input_tensors[i]
+ if check_require_grad(temp):
+ ctx.input_tensors[i] = temp.detach()
+ ctx.input_tensors[i].requires_grad = temp.requires_grad
+ with torch.enable_grad():
+ output_tensors = ctx.run_function(*ctx.input_tensors)
+ to_autograd = list(filter(check_require_grad, ctx.input_tensors))
+ output_tensors, output_grads = zip(*filter(lambda t: t[0].requires_grad, zip(output_tensors, output_grads)))
+ input_grads = torch.autograd.grad(output_tensors, to_autograd + ctx.input_params, output_grads, allow_unused=True)
+ input_grads = list(input_grads)
+ for i in range(len(ctx.input_tensors)):
+ if not check_require_grad(ctx.input_tensors[i]):
+ input_grads.insert(i, None)
+ return (None, None) + tuple(input_grads)
diff --git a/VISAM/util/evaluation.py b/VISAM/util/evaluation.py
new file mode 100644
index 0000000000000000000000000000000000000000..a4fb1084ca22e3bac51f79fefbafb891de177ec4
--- /dev/null
+++ b/VISAM/util/evaluation.py
@@ -0,0 +1,205 @@
+# ------------------------------------------------------------------------
+# Copyright (c) 2022 megvii-research. All Rights Reserved.
+# ------------------------------------------------------------------------
+# Modified from Deformable DETR (https://github.com/fundamentalvision/Deformable-DETR)
+# Copyright (c) 2020 SenseTime. All Rights Reserved.
+# ------------------------------------------------------------------------
+# Modified from DETR (https://github.com/facebookresearch/detr)
+# Copyright (c) Facebook, Inc. and its affiliates. All Rights Reserved
+# ------------------------------------------------------------------------
+
+
+import os
+import numpy as np
+import copy
+import motmetrics as mm
+mm.lap.default_solver = 'lap'
+import os
+from typing import Dict
+import numpy as np
+import logging
+
+def read_results(filename, data_type: str, is_gt=False, is_ignore=False):
+ if data_type in ('mot', 'lab'):
+ read_fun = read_mot_results
+ else:
+ raise ValueError('Unknown data type: {}'.format(data_type))
+
+ return read_fun(filename, is_gt, is_ignore)
+
+# def read_mot_results(filename, is_gt, is_ignore):
+# results_dict = dict()
+# if os.path.isfile(filename):
+# with open(filename, 'r') as f:
+# for line in f.readlines():
+# linelist = line.split(',')
+# if len(linelist) < 7:
+# continue
+# fid = int(linelist[0])
+# if fid < 1:
+# continue
+# results_dict.setdefault(fid, list())
+
+# if is_gt:
+# mark = int(float(linelist[6]))
+# if mark == 0 :
+# continue
+# score = 1
+# elif is_ignore:
+# score = 1
+# else:
+# score = float(linelist[6])
+
+# tlwh = tuple(map(float, linelist[2:6]))
+# target_id = int(float(linelist[1]))
+# results_dict[fid].append((tlwh, target_id, score))
+
+# return results_dict
+
+def read_mot_results(filename, is_gt, is_ignore):
+ valid_labels = {1}
+ ignore_labels = {0, 2, 7, 8, 12}
+ results_dict = dict()
+ if os.path.isfile(filename):
+ with open(filename, 'r') as f:
+ for line in f.readlines():
+ linelist = line.split(',')
+ if len(linelist) < 7:
+ continue
+ fid = int(linelist[0])
+ if fid < 1:
+ continue
+ results_dict.setdefault(fid, list())
+
+ if is_gt:
+ if 'MOT16-' in filename or 'MOT17-' in filename:
+ label = int(float(linelist[7]))
+ mark = int(float(linelist[6]))
+ if mark == 0 or label not in valid_labels:
+ continue
+ score = 1
+ elif is_ignore:
+ if 'MOT16-' in filename or 'MOT17-' in filename:
+ label = int(float(linelist[7]))
+ vis_ratio = float(linelist[8])
+ if label not in ignore_labels and vis_ratio >= 0:
+ continue
+ elif 'MOT15' in filename:
+ label = int(float(linelist[6]))
+ if label not in ignore_labels:
+ continue
+ else:
+ continue
+ score = 1
+ else:
+ score = float(linelist[6])
+
+ tlwh = tuple(map(float, linelist[2:6]))
+ target_id = int(linelist[1])
+
+ results_dict[fid].append((tlwh, target_id, score))
+
+ return results_dict
+
+def unzip_objs(objs):
+ if len(objs) > 0:
+ tlwhs, ids, scores = zip(*objs)
+ else:
+ tlwhs, ids, scores = [], [], []
+ tlwhs = np.asarray(tlwhs, dtype=float).reshape(-1, 4)
+ return tlwhs, ids, scores
+
+
+class Evaluator(object):
+ def __init__(self, data_root, seq_name, data_type='mot'):
+
+ self.data_root = data_root
+ self.seq_name = seq_name
+ self.data_type = data_type
+
+ self.load_annotations()
+ self.reset_accumulator()
+
+ def load_annotations(self):
+ assert self.data_type == 'mot'
+
+ gt_filename = os.path.join(self.data_root, self.seq_name, 'gt', 'gt.txt')
+ self.gt_frame_dict = read_results(gt_filename, self.data_type, is_gt=True)
+ self.gt_ignore_frame_dict = read_results(gt_filename, self.data_type, is_ignore=True)
+
+ def reset_accumulator(self):
+ self.acc = mm.MOTAccumulator(auto_id=True)
+
+ def eval_frame(self, frame_id, trk_tlwhs, trk_ids, rtn_events=False):
+ # results
+ trk_tlwhs = np.copy(trk_tlwhs)
+ trk_ids = np.copy(trk_ids)
+
+ # gts
+ gt_objs = self.gt_frame_dict.get(frame_id, [])
+ gt_tlwhs, gt_ids = unzip_objs(gt_objs)[:2]
+
+ # ignore boxes
+ ignore_objs = self.gt_ignore_frame_dict.get(frame_id, [])
+ ignore_tlwhs = unzip_objs(ignore_objs)[0]
+ # remove ignored results
+ keep = np.ones(len(trk_tlwhs), dtype=bool)
+ iou_distance = mm.distances.iou_matrix(ignore_tlwhs, trk_tlwhs, max_iou=0.5)
+ if len(iou_distance) > 0:
+ match_is, match_js = mm.lap.linear_sum_assignment(iou_distance)
+ match_is, match_js = map(lambda a: np.asarray(a, dtype=int), [match_is, match_js])
+ match_ious = iou_distance[match_is, match_js]
+
+ match_js = np.asarray(match_js, dtype=int)
+ match_js = match_js[np.logical_not(np.isnan(match_ious))]
+ keep[match_js] = False
+ trk_tlwhs = trk_tlwhs[keep]
+ trk_ids = trk_ids[keep]
+
+ # get distance matrix
+ iou_distance = mm.distances.iou_matrix(gt_tlwhs, trk_tlwhs, max_iou=0.5)
+
+ # acc
+ self.acc.update(gt_ids, trk_ids, iou_distance)
+
+ if rtn_events and iou_distance.size > 0 and hasattr(self.acc, 'last_mot_events'):
+ events = self.acc.last_mot_events # only supported by https://github.com/longcw/py-motmetrics
+ else:
+ events = None
+ return events
+
+ def eval_file(self, filename):
+ self.reset_accumulator()
+
+ result_frame_dict = read_results(filename, self.data_type, is_gt=False)
+ frames = sorted(list(set(self.gt_frame_dict.keys()) | set(result_frame_dict.keys())))
+ for frame_id in frames:
+ trk_objs = result_frame_dict.get(frame_id, [])
+ trk_tlwhs, trk_ids = unzip_objs(trk_objs)[:2]
+ self.eval_frame(frame_id, trk_tlwhs, trk_ids, rtn_events=False)
+
+ return self.acc
+
+ @staticmethod
+ def get_summary(accs, names, metrics=('mota', 'num_switches', 'idp', 'idr', 'idf1', 'precision', 'recall')):
+ names = copy.deepcopy(names)
+ if metrics is None:
+ metrics = mm.metrics.motchallenge_metrics
+ metrics = copy.deepcopy(metrics)
+
+ mh = mm.metrics.create()
+ summary = mh.compute_many(
+ accs,
+ metrics=metrics,
+ names=names,
+ generate_overall=True
+ )
+
+ return summary
+
+ @staticmethod
+ def save_summary(summary, filename):
+ import pandas as pd
+ writer = pd.ExcelWriter(filename)
+ summary.to_excel(writer)
+ writer.save()
\ No newline at end of file
diff --git a/VISAM/util/misc.py b/VISAM/util/misc.py
new file mode 100644
index 0000000000000000000000000000000000000000..9033d34e509bf14a33236aa2b7eaf42296d320ae
--- /dev/null
+++ b/VISAM/util/misc.py
@@ -0,0 +1,506 @@
+# ------------------------------------------------------------------------
+# Copyright (c) 2022 megvii-research. All Rights Reserved.
+# ------------------------------------------------------------------------
+# Modified from Deformable DETR (https://github.com/fundamentalvision/Deformable-DETR)
+# Copyright (c) 2020 SenseTime. All Rights Reserved.
+# ------------------------------------------------------------------------
+# Modified from DETR (https://github.com/facebookresearch/detr)
+# Copyright (c) Facebook, Inc. and its affiliates. All Rights Reserved
+# ------------------------------------------------------------------------
+
+
+"""
+Misc functions, including distributed helpers.
+
+Mostly copy-paste from torchvision references.
+"""
+import os
+import subprocess
+import time
+from collections import defaultdict, deque
+import datetime
+import pickle
+from typing import Optional, List
+
+import torch
+import torch.nn as nn
+import torch.distributed as dist
+from torch import Tensor
+
+# needed due to empty tensor bug in pytorch and torchvision 0.5
+import torchvision
+
+class SmoothedValue(object):
+ """Track a series of values and provide access to smoothed values over a
+ window or the global series average.
+ """
+
+ def __init__(self, window_size=20, fmt=None):
+ if fmt is None:
+ fmt = "{median:.4f} ({global_avg:.4f})"
+ self.deque = deque(maxlen=window_size)
+ self.total = 0.0
+ self.count = 0
+ self.fmt = fmt
+
+ def update(self, value, n=1):
+ self.deque.append(value)
+ self.count += n
+ self.total += value * n
+
+ def synchronize_between_processes(self):
+ """
+ Warning: does not synchronize the deque!
+ """
+ if not is_dist_avail_and_initialized():
+ return
+ t = torch.tensor([self.count, self.total], dtype=torch.float64, device='cuda')
+ dist.barrier()
+ dist.all_reduce(t)
+ t = t.tolist()
+ self.count = int(t[0])
+ self.total = t[1]
+
+ @property
+ def median(self):
+ d = torch.tensor(list(self.deque))
+ return d.median().item()
+
+ @property
+ def avg(self):
+ d = torch.tensor(list(self.deque), dtype=torch.float32)
+ return d.mean().item()
+
+ @property
+ def global_avg(self):
+ return self.total / self.count
+
+ @property
+ def max(self):
+ return max(self.deque)
+
+ @property
+ def value(self):
+ return self.deque[-1]
+
+ def __str__(self):
+ return self.fmt.format(
+ median=self.median,
+ avg=self.avg,
+ global_avg=self.global_avg,
+ max=self.max,
+ value=self.value)
+
+
+def all_gather(data):
+ """
+ Run all_gather on arbitrary picklable data (not necessarily tensors)
+ Args:
+ data: any picklable object
+ Returns:
+ list[data]: list of data gathered from each rank
+ """
+ world_size = get_world_size()
+ if world_size == 1:
+ return [data]
+
+ # serialized to a Tensor
+ buffer = pickle.dumps(data)
+ storage = torch.ByteStorage.from_buffer(buffer)
+ tensor = torch.ByteTensor(storage).to("cuda")
+
+ # obtain Tensor size of each rank
+ local_size = torch.tensor([tensor.numel()], device="cuda")
+ size_list = [torch.tensor([0], device="cuda") for _ in range(world_size)]
+ dist.all_gather(size_list, local_size)
+ size_list = [int(size.item()) for size in size_list]
+ max_size = max(size_list)
+
+ # receiving Tensor from all ranks
+ # we pad the tensor because torch all_gather does not support
+ # gathering tensors of different shapes
+ tensor_list = []
+ for _ in size_list:
+ tensor_list.append(torch.empty((max_size,), dtype=torch.uint8, device="cuda"))
+ if local_size != max_size:
+ padding = torch.empty(size=(max_size - local_size,), dtype=torch.uint8, device="cuda")
+ tensor = torch.cat((tensor, padding), dim=0)
+ dist.all_gather(tensor_list, tensor)
+
+ data_list = []
+ for size, tensor in zip(size_list, tensor_list):
+ buffer = tensor.cpu().numpy().tobytes()[:size]
+ data_list.append(pickle.loads(buffer))
+
+ return data_list
+
+
+def reduce_dict(input_dict, average=True):
+ """
+ Args:
+ input_dict (dict): all the values will be reduced
+ average (bool): whether to do average or sum
+ Reduce the values in the dictionary from all processes so that all processes
+ have the averaged results. Returns a dict with the same fields as
+ input_dict, after reduction.
+ """
+ world_size = get_world_size()
+ if world_size < 2:
+ return input_dict
+ with torch.no_grad():
+ names = []
+ values = []
+ # sort the keys so that they are consistent across processes
+ for k in sorted(input_dict.keys()):
+ names.append(k)
+ values.append(input_dict[k])
+ values = torch.stack(values, dim=0)
+ dist.all_reduce(values)
+ if average:
+ values /= world_size
+ reduced_dict = {k: v for k, v in zip(names, values)}
+ return reduced_dict
+
+
+class MetricLogger(object):
+ def __init__(self, delimiter="\t"):
+ self.meters = defaultdict(SmoothedValue)
+ self.delimiter = delimiter
+
+ def update(self, **kwargs):
+ for k, v in kwargs.items():
+ if isinstance(v, torch.Tensor):
+ v = v.item()
+ assert isinstance(v, (float, int))
+ self.meters[k].update(v)
+
+ def __getattr__(self, attr):
+ if attr in self.meters:
+ return self.meters[attr]
+ if attr in self.__dict__:
+ return self.__dict__[attr]
+ raise AttributeError("'{}' object has no attribute '{}'".format(
+ type(self).__name__, attr))
+
+ def __str__(self):
+ loss_str = []
+ for name, meter in self.meters.items():
+ loss_str.append(
+ "{}: {}".format(name, str(meter))
+ )
+ return self.delimiter.join(loss_str)
+
+ def synchronize_between_processes(self):
+ for meter in self.meters.values():
+ meter.synchronize_between_processes()
+
+ def add_meter(self, name, meter):
+ self.meters[name] = meter
+
+ def log_every(self, iterable, print_freq, header=None):
+ i = 0
+ if not header:
+ header = ''
+ start_time = time.time()
+ end = time.time()
+ iter_time = SmoothedValue(fmt='{avg:.4f}')
+ data_time = SmoothedValue(fmt='{avg:.4f}')
+ space_fmt = ':' + str(len(str(len(iterable)))) + 'd'
+ if torch.cuda.is_available():
+ log_msg = self.delimiter.join([
+ header,
+ '[{0' + space_fmt + '}/{1}]',
+ 'eta: {eta}',
+ '{meters}',
+ 'time: {time}',
+ 'data: {data}',
+ 'max mem: {memory:.0f}'
+ ])
+ else:
+ log_msg = self.delimiter.join([
+ header,
+ '[{0' + space_fmt + '}/{1}]',
+ 'eta: {eta}',
+ '{meters}',
+ 'time: {time}',
+ 'data: {data}'
+ ])
+ MB = 1024.0 * 1024.0
+ for obj in iterable:
+ data_time.update(time.time() - end)
+ yield obj
+ iter_time.update(time.time() - end)
+ if i % print_freq == 0 or i == len(iterable) - 1:
+ eta_seconds = iter_time.global_avg * (len(iterable) - i)
+ eta_string = str(datetime.timedelta(seconds=int(eta_seconds)))
+ if torch.cuda.is_available():
+ print(log_msg.format(
+ i, len(iterable), eta=eta_string,
+ meters=str(self),
+ time=str(iter_time), data=str(data_time),
+ memory=torch.cuda.max_memory_allocated() / MB))
+ else:
+ print(log_msg.format(
+ i, len(iterable), eta=eta_string,
+ meters=str(self),
+ time=str(iter_time), data=str(data_time)))
+ i += 1
+ end = time.time()
+ total_time = time.time() - start_time
+ total_time_str = str(datetime.timedelta(seconds=int(total_time)))
+ print('{} Total time: {} ({:.4f} s / it)'.format(
+ header, total_time_str, total_time / len(iterable)))
+
+
+def get_sha():
+ cwd = os.path.dirname(os.path.abspath(__file__))
+
+ def _run(command):
+ return subprocess.check_output(command, cwd=cwd).decode('ascii').strip()
+ sha = 'N/A'
+ diff = "clean"
+ branch = 'N/A'
+ try:
+ sha = _run(['git', 'rev-parse', 'HEAD'])
+ subprocess.check_output(['git', 'diff'], cwd=cwd)
+ diff = _run(['git', 'diff-index', 'HEAD'])
+ diff = "has uncommited changes" if diff else "clean"
+ branch = _run(['git', 'rev-parse', '--abbrev-ref', 'HEAD'])
+ except Exception:
+ pass
+ message = f"sha: {sha}, status: {diff}, branch: {branch}"
+ return message
+
+
+def collate_fn(batch):
+ batch = list(zip(*batch))
+ batch[0] = nested_tensor_from_tensor_list(batch[0], size_divisibility=32)
+ return tuple(batch)
+
+
+def mot_collate_fn(batch: List[dict]) -> dict:
+ ret_dict = {}
+ for key in list(batch[0].keys()):
+ assert not isinstance(batch[0][key], Tensor)
+ ret_dict[key] = [img_info[key] for img_info in batch]
+ if len(ret_dict[key]) == 1:
+ ret_dict[key] = ret_dict[key][0]
+ return ret_dict
+
+
+def _max_by_axis(the_list):
+ # type: (List[List[int]]) -> List[int]
+ maxes = the_list[0]
+ for sublist in the_list[1:]:
+ for index, item in enumerate(sublist):
+ maxes[index] = max(maxes[index], item)
+ return maxes
+
+
+def nested_tensor_from_tensor_list(tensor_list: List[Tensor], size_divisibility: int = 0):
+ # TODO make this more general
+ if tensor_list[0].ndim == 3:
+ # TODO make it support different-sized images
+
+ max_size = _max_by_axis([list(img.shape) for img in tensor_list])
+ if size_divisibility > 0:
+ stride = size_divisibility
+ # the last two dims are H,W, both subject to divisibility requirement
+ max_size[-1] = (max_size[-1] + (stride - 1)) // stride * stride
+ max_size[-2] = (max_size[-2] + (stride - 1)) // stride * stride
+
+ # min_size = tuple(min(s) for s in zip(*[img.shape for img in tensor_list]))
+ batch_shape = [len(tensor_list)] + max_size
+ b, c, h, w = batch_shape
+ dtype = tensor_list[0].dtype
+ device = tensor_list[0].device
+ tensor = torch.zeros(batch_shape, dtype=dtype, device=device)
+ mask = torch.ones((b, h, w), dtype=torch.bool, device=device)
+ for img, pad_img, m in zip(tensor_list, tensor, mask):
+ pad_img[: img.shape[0], : img.shape[1], : img.shape[2]].copy_(img)
+ m[: img.shape[1], :img.shape[2]] = False
+ else:
+ raise ValueError('not supported')
+ return NestedTensor(tensor, mask)
+
+
+class NestedTensor(object):
+ def __init__(self, tensors, mask: Optional[Tensor]):
+ self.tensors = tensors
+ self.mask = mask
+
+ def to(self, device, non_blocking=False):
+ # type: (Device) -> NestedTensor # noqa
+ cast_tensor = self.tensors.to(device, non_blocking=non_blocking)
+ mask = self.mask
+ if mask is not None:
+ assert mask is not None
+ cast_mask = mask.to(device, non_blocking=non_blocking)
+ else:
+ cast_mask = None
+ return NestedTensor(cast_tensor, cast_mask)
+
+ def record_stream(self, *args, **kwargs):
+ self.tensors.record_stream(*args, **kwargs)
+ if self.mask is not None:
+ self.mask.record_stream(*args, **kwargs)
+
+ def decompose(self):
+ return self.tensors, self.mask
+
+ def __repr__(self):
+ return str(self.tensors)
+
+
+def setup_for_distributed(is_master):
+ """
+ This function disables printing when not in master process
+ """
+ import builtins as __builtin__
+ builtin_print = __builtin__.print
+
+ def print(*args, **kwargs):
+ force = kwargs.pop('force', False)
+ if is_master or force:
+ builtin_print(*args, **kwargs)
+
+ __builtin__.print = print
+
+
+def is_dist_avail_and_initialized():
+ if not dist.is_available():
+ return False
+ if not dist.is_initialized():
+ return False
+ return True
+
+
+def get_world_size():
+ if not is_dist_avail_and_initialized():
+ return 1
+ return dist.get_world_size()
+
+
+def get_rank():
+ if not is_dist_avail_and_initialized():
+ return 0
+ return dist.get_rank()
+
+
+def get_local_size():
+ if not is_dist_avail_and_initialized():
+ return 1
+ return int(os.environ['LOCAL_SIZE'])
+
+
+def get_local_rank():
+ if not is_dist_avail_and_initialized():
+ return 0
+ return int(os.environ['LOCAL_RANK'])
+
+
+def is_main_process():
+ return get_rank() == 0
+
+
+def save_on_master(*args, **kwargs):
+ if is_main_process():
+ torch.save(*args, **kwargs)
+
+
+def init_distributed_mode(args):
+ if 'RANK' in os.environ and 'WORLD_SIZE' in os.environ:
+ args.rank = int(os.environ["RANK"])
+ args.world_size = int(os.environ['WORLD_SIZE'])
+ args.gpu = int(os.environ['LOCAL_RANK'])
+ args.dist_url = 'env://'
+ os.environ['LOCAL_SIZE'] = str(torch.cuda.device_count())
+ elif 'SLURM_PROCID' in os.environ:
+ proc_id = int(os.environ['SLURM_PROCID'])
+ ntasks = int(os.environ['SLURM_NTASKS'])
+ node_list = os.environ['SLURM_NODELIST']
+ num_gpus = torch.cuda.device_count()
+ addr = subprocess.getoutput(
+ 'scontrol show hostname {} | head -n1'.format(node_list))
+ os.environ['MASTER_PORT'] = os.environ.get('MASTER_PORT', '29500')
+ os.environ['MASTER_ADDR'] = addr
+ os.environ['WORLD_SIZE'] = str(ntasks)
+ os.environ['RANK'] = str(proc_id)
+ os.environ['LOCAL_RANK'] = str(proc_id % num_gpus)
+ os.environ['LOCAL_SIZE'] = str(num_gpus)
+ args.dist_url = 'env://'
+ args.world_size = ntasks
+ args.rank = proc_id
+ args.gpu = proc_id % num_gpus
+ else:
+ print('Not using distributed mode')
+ args.distributed = False
+ return
+
+ args.distributed = True
+
+ torch.cuda.set_device(args.gpu)
+ args.dist_backend = 'nccl'
+ print('| distributed init (rank {}): {}'.format(
+ args.rank, args.dist_url), flush=True)
+ torch.distributed.init_process_group(backend=args.dist_backend, init_method=args.dist_url,
+ world_size=args.world_size, rank=args.rank)
+ torch.distributed.barrier()
+ setup_for_distributed(args.rank == 0)
+
+
+@torch.no_grad()
+def accuracy(output, target, topk=(1,)):
+ """Computes the precision@k for the specified values of k"""
+ if target.numel() == 0:
+ return [torch.zeros([], device=output.device)]
+ maxk = max(topk)
+ batch_size = target.size(0)
+
+ _, pred = output.topk(maxk, 1, True, True)
+ pred = pred.t()
+ correct = pred.eq(target.view(1, -1).expand_as(pred))
+
+ res = []
+ for k in topk:
+ correct_k = correct[:k].view(-1).float().sum(0)
+ res.append(correct_k.mul_(100.0 / batch_size))
+ return res
+
+
+def interpolate(input, size=None, scale_factor=None, mode="nearest", align_corners=None):
+ # type: (Tensor, Optional[List[int]], Optional[float], str, Optional[bool]) -> Tensor
+ """
+ Equivalent to nn.functional.interpolate, but with support for empty batch sizes.
+ This will eventually be supported natively by PyTorch, and this
+ class can go away.
+ """
+ if float(torchvision.__version__[:3]) < 0.7:
+ if input.numel() > 0:
+ return torch.nn.functional.interpolate(
+ input, size, scale_factor, mode, align_corners
+ )
+
+ output_shape = _output_size(2, input, size, scale_factor)
+ output_shape = list(input.shape[:-2]) + list(output_shape)
+ if float(torchvision.__version__[:3]) < 0.5:
+ return _NewEmptyTensorOp.apply(input, output_shape)
+ return _new_empty_tensor(input, output_shape)
+ else:
+ return torchvision.ops.misc.interpolate(input, size, scale_factor, mode, align_corners)
+
+
+def get_total_grad_norm(parameters, norm_type=2):
+ parameters = list(filter(lambda p: p.grad is not None, parameters))
+ norm_type = float(norm_type)
+ device = parameters[0].grad.device
+ total_norm = torch.norm(torch.stack([torch.norm(p.grad.detach(), norm_type).to(device) for p in parameters]),
+ norm_type)
+ return total_norm
+
+def inverse_sigmoid(x, eps=1e-5):
+ x = x.clamp(min=0, max=1)
+ x1 = x.clamp(min=eps)
+ x2 = (1 - x).clamp(min=eps)
+ return torch.log(x1/x2)
+
diff --git a/VISAM/util/motdet_eval.py b/VISAM/util/motdet_eval.py
new file mode 100644
index 0000000000000000000000000000000000000000..19423d066ba3a166851f080446694db21d60a070
--- /dev/null
+++ b/VISAM/util/motdet_eval.py
@@ -0,0 +1,402 @@
+# ------------------------------------------------------------------------
+# Copyright (c) 2022 megvii-research. All Rights Reserved.
+# ------------------------------------------------------------------------
+# Modified from Deformable DETR (https://github.com/fundamentalvision/Deformable-DETR)
+# Copyright (c) 2020 SenseTime. All Rights Reserved.
+# ------------------------------------------------------------------------
+# Modified from DETR (https://github.com/facebookresearch/detr)
+# Copyright (c) Facebook, Inc. and its affiliates. All Rights Reserved
+# ------------------------------------------------------------------------
+
+import torch
+import numpy as np
+import time
+import cv2
+
+def ap_per_class(tp, conf, pred_cls, target_cls):
+ """ Compute the average precision, given the recall and precision curves.
+ Method originally from https://github.com/rafaelpadilla/Object-Detection-Metrics.
+ # Arguments
+ tp: True positives (list).
+ conf: Objectness value from 0-1 (list).
+ pred_cls: Predicted object classes (list).
+ target_cls: True object classes (list).
+ # Returns
+ The average precision as computed in py-faster-rcnn.
+ """
+
+ # lists/pytorch to numpy
+ tp, conf, pred_cls, target_cls = np.array(tp), np.array(conf), np.array(pred_cls), np.array(target_cls)
+
+ # Sort by objectness
+ i = np.argsort(-conf)
+ tp, conf, pred_cls = tp[i], conf[i], pred_cls[i]
+
+ # Find unique classes
+ unique_classes = np.unique(np.concatenate((pred_cls, target_cls), 0))
+
+ # Create Precision-Recall curve and compute AP for each class
+ ap, p, r = [], [], []
+ for c in unique_classes:
+ i = pred_cls == c
+ n_gt = sum(target_cls == c) # Number of ground truth objects
+ n_p = sum(i) # Number of predicted objects
+
+ if (n_p == 0) and (n_gt == 0):
+ continue
+ elif (n_p == 0) or (n_gt == 0):
+ ap.append(0)
+ r.append(0)
+ p.append(0)
+ else:
+ # Accumulate FPs and TPs
+ fpc = np.cumsum(1 - tp[i])
+ tpc = np.cumsum(tp[i])
+
+ # Recall
+ recall_curve = tpc / (n_gt + 1e-16)
+ r.append(tpc[-1] / (n_gt + 1e-16))
+
+ # Precision
+ precision_curve = tpc / (tpc + fpc)
+ p.append(tpc[-1] / (tpc[-1] + fpc[-1]))
+
+ # AP from recall-precision curve
+ ap.append(compute_ap(recall_curve, precision_curve))
+
+ return np.array(ap), unique_classes.astype('int32'), np.array(r), np.array(p)
+
+def compute_ap(recall, precision):
+ """ Compute the average precision, given the recall and precision curves.
+ Code originally from https://github.com/rbgirshick/py-faster-rcnn.
+ # Arguments
+ recall: The recall curve (list).
+ precision: The precision curve (list).
+ # Returns
+ The average precision as computed in py-faster-rcnn.
+ """
+ # correct AP calculation
+ # first append sentinel values at the end
+
+ mrec = np.concatenate(([0.], recall, [1.]))
+ mpre = np.concatenate(([0.], precision, [0.]))
+
+ # compute the precision envelope
+ for i in range(mpre.size - 1, 0, -1):
+ mpre[i - 1] = np.maximum(mpre[i - 1], mpre[i])
+
+ # to calculate area under PR curve, look for points
+ # where X axis (recall) changes value
+ i = np.where(mrec[1:] != mrec[:-1])[0]
+
+ # and sum (\Delta recall) * prec
+ ap = np.sum((mrec[i + 1] - mrec[i]) * mpre[i + 1])
+ return ap
+
+
+def bbox_iou(box1, box2, x1y1x2y2=False):
+ """
+ Returns the IoU of two bounding boxes
+ """
+ N, M = len(box1), len(box2)
+ if x1y1x2y2:
+ # Get the coordinates of bounding boxes
+ b1_x1, b1_y1, b1_x2, b1_y2 = box1[:, 0], box1[:, 1], box1[:, 2], box1[:, 3]
+ b2_x1, b2_y1, b2_x2, b2_y2 = box2[:, 0], box2[:, 1], box2[:, 2], box2[:, 3]
+ else:
+ # Transform from center and width to exact coordinates
+ b1_x1, b1_x2 = box1[:, 0] - box1[:, 2] / 2, box1[:, 0] + box1[:, 2] / 2
+ b1_y1, b1_y2 = box1[:, 1] - box1[:, 3] / 2, box1[:, 1] + box1[:, 3] / 2
+ b2_x1, b2_x2 = box2[:, 0] - box2[:, 2] / 2, box2[:, 0] + box2[:, 2] / 2
+ b2_y1, b2_y2 = box2[:, 1] - box2[:, 3] / 2, box2[:, 1] + box2[:, 3] / 2
+
+ # get the coordinates of the intersection rectangle
+ inter_rect_x1 = torch.max(b1_x1.unsqueeze(1), b2_x1)
+ inter_rect_y1 = torch.max(b1_y1.unsqueeze(1), b2_y1)
+ inter_rect_x2 = torch.min(b1_x2.unsqueeze(1), b2_x2)
+ inter_rect_y2 = torch.min(b1_y2.unsqueeze(1), b2_y2)
+ # Intersection area
+ inter_area = torch.clamp(inter_rect_x2 - inter_rect_x1, 0) * torch.clamp(inter_rect_y2 - inter_rect_y1, 0)
+ # Union Area
+ b1_area = ((b1_x2 - b1_x1) * (b1_y2 - b1_y1)).view(-1,1).expand(N,M)
+ b2_area = ((b2_x2 - b2_x1) * (b2_y2 - b2_y1)).view(1,-1).expand(N,M)
+
+ return inter_area / (b1_area + b2_area - inter_area + 1e-16)
+
+def xyxy2xywh(x):
+ # Convert bounding box format from [x1, y1, x2, y2] to [x, y, w, h]
+ y = torch.zeros(x.shape) if x.dtype is torch.float32 else np.zeros(x.shape)
+ y[:, 0] = (x[:, 0] + x[:, 2]) / 2
+ y[:, 1] = (x[:, 1] + x[:, 3]) / 2
+ y[:, 2] = x[:, 2] - x[:, 0]
+ y[:, 3] = x[:, 3] - x[:, 1]
+ return y
+
+
+def xywh2xyxy(x):
+ # Convert bounding box format from [x, y, w, h] to [x1, y1, x2, y2]
+ y = torch.zeros(x.shape) if x.dtype is torch.float32 else np.zeros(x.shape)
+ y[:, 0] = (x[:, 0] - x[:, 2] / 2)
+ y[:, 1] = (x[:, 1] - x[:, 3] / 2)
+ y[:, 2] = (x[:, 0] + x[:, 2] / 2)
+ y[:, 3] = (x[:, 1] + x[:, 3] / 2)
+ return y
+
+
+@torch.no_grad()
+def motdet_evaluate(model, data_loader, iou_thres=0.5, print_interval=10):
+ model.eval()
+ mean_mAP, mean_R, mean_P, seen = 0.0, 0.0, 0.0, 0
+ print('%11s' * 5 % ('Image', 'Total', 'P', 'R', 'mAP'))
+ outputs, mAPs, mR, mP, TP, confidence, pred_class, target_class, jdict = \
+ [], [], [], [], [], [], [], [], []
+ AP_accum, AP_accum_count = np.zeros(1), np.zeros(1)
+ for batch_i, data in enumerate(data_loader):
+ seen += 1
+ if(batch_i > 300):
+ break
+ # [batch_size x 3 x H x W]
+ imgs, _ = data[0].decompose()
+ # print("imgs.shape={}".format(imgs.shape))
+ #dict{'boxes':cxcywh_norm 'labels', size, orig_size}
+ targets = data[1][0]
+ # img_path = data[2]
+ height, width = targets['orig_size'].cpu().numpy().tolist()
+ t = time.time()
+ output = model(imgs.cuda())
+ outputs_class = output['pred_logits'].squeeze()
+ if outputs_class.ndim == 1:
+ # focal_loss
+ outputs_class = outputs_class.unsqueeze(-1)
+ outputs_boxes = output['pred_boxes'].squeeze()
+ target_boxes = targets['boxes']
+
+ # Compute average precision
+ if target_boxes is None:
+ # If there are labels but no detections mark as zero AP
+ if target_boxes.size(0) != 0:
+ mAPs.append(0), mR.append(0), mP.append(0)
+ continue
+
+ # If no labels add number of detections as incorrect
+ correct = []
+ if target_boxes.size(0) == 0:
+ # correct.extend([0 for _ in range(len(detections))])
+ mAPs.append(0), mR.append(0), mP.append(0)
+ continue
+ else:
+ target_cls = targets['labels']
+ # Extract target boxes as (x1, y1, x2, y2)
+ target_boxes = xywh2xyxy(target_boxes)
+ target_boxes[:, 0] *= width
+ target_boxes[:, 2] *= width
+ target_boxes[:, 1] *= height
+ target_boxes[:, 3] *= height
+
+ outputs_boxes = xywh2xyxy(outputs_boxes)
+ outputs_boxes[:, 0] *= width
+ outputs_boxes[:, 2] *= width
+ outputs_boxes[:, 1] *= height
+ outputs_boxes[:, 3] *= height
+
+ detected = set()
+ print("output_boxes.shape={} class.shape={}".format(outputs_boxes.shape, outputs_class.shape))
+ print((outputs_class.sigmoid() > 0.5).sum())
+ num_dt = 0
+ num_tp = 0
+ for *pred_bbox, conf in zip(outputs_boxes, outputs_class):
+ obj_pred = 0
+ pred_bbox = torch.FloatTensor(pred_bbox[0]).view(1, -1)
+ if conf.sigmoid() > 0.5:
+ num_dt += 1
+
+ # Compute iou with target boxes
+ iou = bbox_iou(pred_bbox, target_boxes, x1y1x2y2=True)[0]
+ # Extract index of largest overlap
+ best_i = np.argmax(iou)
+ # If overlap exceeds threshold and classification is correct mark as correct
+ if iou[best_i] > iou_thres and obj_pred == int(target_cls[best_i]) and best_i.item() not in detected:
+ correct.append(1)
+ if conf.sigmoid() > 0.5:
+ num_tp += 1
+ detected.add(best_i.item())
+ else:
+ correct.append(0)
+ print("precision={} recall={}".format(num_tp / max(1.0, num_dt), num_tp / max(1.0, len(target_boxes))))
+ # Compute Average Precision (AP) per class
+ AP, AP_class, R, P = ap_per_class(tp=correct,
+ conf=outputs_class[:, 0].cpu(),
+ pred_cls=np.zeros_like(outputs_class[:, 0].cpu()),
+ target_cls=target_cls)
+
+ # Accumulate AP per class
+ AP_accum_count += np.bincount(AP_class, minlength=1)
+ AP_accum += np.bincount(AP_class, minlength=1, weights=AP)
+
+ # Compute mean AP across all classes in this image, and append to image list
+ mAPs.append(AP.mean())
+ mR.append(R.mean())
+ mP.append(P.mean())
+
+ # Means of all images
+ mean_mAP = np.sum(mAPs) / (AP_accum_count + 1E-16)
+ mean_R = np.sum(mR) / (AP_accum_count + 1E-16)
+ mean_P = np.sum(mP) / (AP_accum_count + 1E-16)
+
+ if batch_i % print_interval == 0:
+ # Print image mAP and running mean mAP
+ print(('%11s%11s' + '%11.3g' * 4 + 's') %
+ (seen, 100, mean_P, mean_R, mean_mAP, time.time() - t))
+ # Print mAP per class
+ print('%11s' * 5 % ('Image', 'Total', 'P', 'R', 'mAP'))
+
+ print('AP: %-.4f\n\n' % (AP_accum[0] / (AP_accum_count[0] + 1E-16)))
+
+ # Return mAP
+ return mean_mAP, mean_R, mean_P
+
+
+def init_metrics():
+ mean_mAP, mean_R, mean_P, seen = 0.0, 0.0, 0.0, 0
+ outputs, mAPs, mR, mP, TP, confidence, pred_class, target_class, jdict = [], [], [], [], [], [], [], [], []
+ AP_accum, AP_accum_count = np.zeros(1), np.zeros(1)
+ return {'mean_mAP': mean_mAP,
+ 'mean_R': mean_R,
+ 'mean_P': mean_P,
+ 'seen': seen,
+ 'outputs': outputs,
+ 'mAPs': mAPs,
+ 'mR': mR,
+ 'mP': mP,
+ 'TP': TP,
+ 'confidence': confidence,
+ 'pred_class': pred_class,
+ 'target_class': target_class,
+ 'jdict': jdict,
+ 'AP_accum': AP_accum,
+ 'AP_accum_count': AP_accum_count,
+ }
+
+
+@torch.no_grad()
+def detmotdet_evaluate(model, data_loader, device, iou_thres=0.5, print_interval=10):
+ model.eval()
+ print('%11s' * 5 % ('Cur Image', 'Total', 'P', 'R', 'mAP'))
+ # TODO: Remove the hard-code 3.
+ metrics_list = [init_metrics() for i in range(10)]
+ for batch_i, data in enumerate(data_loader):
+ if(batch_i > 100):
+ break
+
+ for key in list(data.keys()):
+ if isinstance(data[key], list):
+ data[key] = [img_info.to(device) for img_info in data[key]]
+ else:
+ data[key] = data[key].to(device)
+ output = model(data)
+ num_frames = len(data['gt_instances'])
+ for i in range(num_frames):
+ metrics_i = metrics_list[i]
+ metrics_i['seen'] += 1
+ gt_instances = data['gt_instances'][i].to(torch.device('cpu'))
+
+ height, width = gt_instances.image_size
+ t = time.time()
+ outputs_class = output['pred_logits'][i].squeeze()
+ outputs_boxes = output['pred_boxes'][i].squeeze()
+
+ if outputs_class.ndim == 1:
+ # focal_loss
+ outputs_class = outputs_class.unsqueeze(-1)
+
+ target_boxes = gt_instances.boxes
+
+ # Compute average precision
+ if target_boxes is None:
+ # If there are labels but no detections mark as zero AP
+ if target_boxes.size(0) != 0:
+ metrics_i['mAPs'].append(0)
+ metrics_i['mR'].append(0)
+ metrics_i['mP'].append(0)
+ print('cur_target_boxes is None')
+ continue
+
+ # for cur frame
+ # If no labels add number of detections as incorrect
+ correct = []
+ if target_boxes.size(0) == 0:
+ # correct.extend([0 for _ in range(len(detections))])
+ metrics_i['mAP'].append(0)
+ metrics_i['mR'].append(0)
+ metrics_i['mP'].apppend(0)
+ print('cur_target_boxes.size(0) == 0')
+ continue
+ else:
+ target_cls = gt_instances.labels
+ # Extract target boxes as (x1, y1, x2, y2)
+ target_boxes = xywh2xyxy(target_boxes)
+ target_boxes[:, 0] *= width
+ target_boxes[:, 2] *= width
+ target_boxes[:, 1] *= height
+ target_boxes[:, 3] *= height
+
+ outputs_boxes = xywh2xyxy(outputs_boxes)
+ outputs_boxes[:, 0] *= width
+ outputs_boxes[:, 2] *= width
+ outputs_boxes[:, 1] *= height
+ outputs_boxes[:, 3] *= height
+
+ detected = []
+ for *pred_bbox, conf in zip(outputs_boxes, outputs_class):
+ obj_pred = 0
+ pred_bbox = torch.FloatTensor(pred_bbox[0]).view(1, -1)
+ # Compute iou with target boxes
+ iou = bbox_iou(pred_bbox, target_boxes, x1y1x2y2=True)[0]
+ # Extract index of largest overlap
+ best_i = np.argmax(iou)
+ # If overlap exceeds threshold and classification is correct mark as correct
+ if iou[best_i] > iou_thres and obj_pred == int(target_cls[best_i]) and best_i not in detected:
+ correct.append(1)
+ detected.append(best_i)
+ else:
+ correct.append(0)
+
+ # Compute Average Precision (AP) per class
+ AP, AP_class, R, P = ap_per_class(tp=correct,
+ conf=outputs_class[:, 0].cpu(),
+ pred_cls=np.zeros_like(outputs_class[:, 0].cpu()),
+ target_cls=target_cls)
+
+ # Accumulate AP per class
+ metrics_i['AP_accum_count'] += np.bincount(AP_class, minlength=1)
+ metrics_i['AP_accum'] += np.bincount(AP_class, minlength=1, weights=AP)
+
+ # Compute mean AP across all classes in this image, and append to image list
+ metrics_i['mAPs'].append(AP.mean())
+ metrics_i['mR'].append(R.mean())
+ metrics_i['mP'].append(P.mean())
+
+ # Means of all images
+ metrics_i['mean_mAP'] = np.sum(metrics_i['mAPs']) / (metrics_i['AP_accum_count'] + 1E-16)
+ metrics_i['mean_R'] = np.sum(metrics_i['mR']) / (metrics_i['AP_accum_count'] + 1E-16)
+ metrics_i['mean_P'] = np.sum(metrics_i['mP']) / (metrics_i['AP_accum_count'] + 1E-16)
+
+ if batch_i % print_interval == 0:
+ # Print image mAP and running mean mAP
+ seen = metrics_i['seen']
+ mean_P = metrics_i['mean_P']
+ mean_R = metrics_i['mean_R']
+ mean_mAP = metrics_i['mean_mAP']
+ print("res_frame_{}".format(i))
+ print(('%11s%11s' + '%11.3g' * 4 + 's') % (seen, 100, mean_P, mean_R, mean_mAP, time.time() - t))
+
+ # Return mAP
+ ret = []
+ for i in range(2):
+ mean_mAP = metrics_list[i]['mean_mAP']
+ mean_R = metrics_list[i]['mean_R']
+ mean_P = metrics_list[i]['mean_P']
+ ret.append(mean_mAP)
+ ret.append(mean_R)
+ ret.append(mean_P)
+ return ret
diff --git a/VISAM/util/plot_utils.py b/VISAM/util/plot_utils.py
new file mode 100644
index 0000000000000000000000000000000000000000..bd16263a036dace52f862cc15ba92cb7c67b346d
--- /dev/null
+++ b/VISAM/util/plot_utils.py
@@ -0,0 +1,159 @@
+# ------------------------------------------------------------------------
+# Copyright (c) 2022 megvii-research. All Rights Reserved.
+# ------------------------------------------------------------------------
+# Modified from Deformable DETR (https://github.com/fundamentalvision/Deformable-DETR)
+# Copyright (c) 2020 SenseTime. All Rights Reserved.
+# ------------------------------------------------------------------------
+# Modified from DETR (https://github.com/facebookresearch/detr)
+# Copyright (c) Facebook, Inc. and its affiliates. All Rights Reserved
+# ------------------------------------------------------------------------
+
+
+"""
+Plotting utilities to visualize training logs.
+"""
+import cv2
+import torch
+import pandas as pd
+import numpy as np
+import seaborn as sns
+import matplotlib.pyplot as plt
+
+from torch import Tensor
+
+from pathlib import Path, PurePath
+
+
+def plot_logs(logs, fields=('class_error', 'loss_bbox_unscaled', 'mAP'), ewm_col=0, log_name='log.txt'):
+ '''
+ Function to plot specific fields from training log(s). Plots both training and test results.
+
+ :: Inputs - logs = list containing Path objects, each pointing to individual dir with a log file
+ - fields = which results to plot from each log file - plots both training and test for each field.
+ - ewm_col = optional, which column to use as the exponential weighted smoothing of the plots
+ - log_name = optional, name of log file if different than default 'log.txt'.
+
+ :: Outputs - matplotlib plots of results in fields, color coded for each log file.
+ - solid lines are training results, dashed lines are test results.
+
+ '''
+ func_name = "plot_utils.py::plot_logs"
+
+ # verify logs is a list of Paths (list[Paths]) or single Pathlib object Path,
+ # convert single Path to list to avoid 'not iterable' error
+
+ if not isinstance(logs, list):
+ if isinstance(logs, PurePath):
+ logs = [logs]
+ print(f"{func_name} info: logs param expects a list argument, converted to list[Path].")
+ else:
+ raise ValueError(f"{func_name} - invalid argument for logs parameter.\n \
+ Expect list[Path] or single Path obj, received {type(logs)}")
+
+ # verify valid dir(s) and that every item in list is Path object
+ for i, dir in enumerate(logs):
+ if not isinstance(dir, PurePath):
+ raise ValueError(f"{func_name} - non-Path object in logs argument of {type(dir)}: \n{dir}")
+ if dir.exists():
+ continue
+ raise ValueError(f"{func_name} - invalid directory in logs argument:\n{dir}")
+
+ # load log file(s) and plot
+ dfs = [pd.read_json(Path(p) / log_name, lines=True) for p in logs]
+
+ fig, axs = plt.subplots(ncols=len(fields), figsize=(16, 5))
+
+ for df, color in zip(dfs, sns.color_palette(n_colors=len(logs))):
+ for j, field in enumerate(fields):
+ if field == 'mAP':
+ coco_eval = pd.DataFrame(pd.np.stack(df.test_coco_eval.dropna().values)[:, 1]).ewm(com=ewm_col).mean()
+ axs[j].plot(coco_eval, c=color)
+ else:
+ df.interpolate().ewm(com=ewm_col).mean().plot(
+ y=[f'train_{field}', f'test_{field}'],
+ ax=axs[j],
+ color=[color] * 2,
+ style=['-', '--']
+ )
+ for ax, field in zip(axs, fields):
+ ax.legend([Path(p).name for p in logs])
+ ax.set_title(field)
+
+
+def plot_precision_recall(files, naming_scheme='iter'):
+ if naming_scheme == 'exp_id':
+ # name becomes exp_id
+ names = [f.parts[-3] for f in files]
+ elif naming_scheme == 'iter':
+ names = [f.stem for f in files]
+ else:
+ raise ValueError(f'not supported {naming_scheme}')
+ fig, axs = plt.subplots(ncols=2, figsize=(16, 5))
+ for f, color, name in zip(files, sns.color_palette("Blues", n_colors=len(files)), names):
+ data = torch.load(f)
+ # precision is n_iou, n_points, n_cat, n_area, max_det
+ precision = data['precision']
+ recall = data['params'].recThrs
+ scores = data['scores']
+ # take precision for all classes, all areas and 100 detections
+ precision = precision[0, :, :, 0, -1].mean(1)
+ scores = scores[0, :, :, 0, -1].mean(1)
+ prec = precision.mean()
+ rec = data['recall'][0, :, 0, -1].mean()
+ print(f'{naming_scheme} {name}: mAP@50={prec * 100: 05.1f}, ' +
+ f'score={scores.mean():0.3f}, ' +
+ f'f1={2 * prec * rec / (prec + rec + 1e-8):0.3f}'
+ )
+ axs[0].plot(recall, precision, c=color)
+ axs[1].plot(recall, scores, c=color)
+
+ axs[0].set_title('Precision / Recall')
+ axs[0].legend(names)
+ axs[1].set_title('Scores / Recall')
+ axs[1].legend(names)
+ return fig, axs
+
+
+def draw_boxes(image: Tensor, boxes: Tensor, color=(0, 255, 0), texts=None) -> np.ndarray:
+ if isinstance(image, Tensor):
+ cv_image = image.detach().cpu().numpy()
+ else:
+ cv_image = image
+ if isinstance(boxes, Tensor):
+ cv_boxes = boxes.detach().cpu().numpy()
+ else:
+ cv_boxes = boxes
+
+ tl = round(0.002 * max(image.shape[0:2])) + 1 # line thickness
+ tf = max(tl - 1, 1)
+ for i in range(len(boxes)):
+ box = cv_boxes[i]
+ x1, y1 = box[0:2]
+ x2, y2 = box[2:4]
+ cv2.rectangle(cv_image, (int(x1), int(y1)), (int(x2), int(y2)), color=color)
+ if texts is not None:
+ cv2.putText(cv_image, texts[i], (int(x1), int(y1+10)), 0, tl/3, [225, 255, 255],
+ thickness=tf,
+ lineType=cv2.LINE_AA)
+ return cv_image
+
+
+def draw_ref_pts(image: Tensor, ref_pts: Tensor) -> np.ndarray:
+ if isinstance(image, Tensor):
+ cv_image = image.detach().cpu().numpy()
+ else:
+ cv_image = image
+ if isinstance(ref_pts, Tensor):
+ cv_pts = ref_pts.detach().cpu().numpy()
+ else:
+ cv_pts = ref_pts
+ for i in range(len(cv_pts)):
+ x, y, is_pos = cv_pts[i]
+ color = (0, 1, 0) if is_pos else (1, 1, 1)
+ cv2.circle(cv_image, (int(x), int(y)), 2, color)
+ return cv_image
+
+
+def image_hwc2chw(image: np.ndarray):
+ image = np.ascontiguousarray(image.transpose(2, 0, 1))
+ return image
diff --git a/VISAM/util/tool.py b/VISAM/util/tool.py
new file mode 100644
index 0000000000000000000000000000000000000000..2bfc81e654cdd5b19dd72446f696f8921eef7bcf
--- /dev/null
+++ b/VISAM/util/tool.py
@@ -0,0 +1,73 @@
+# ------------------------------------------------------------------------
+# Copyright (c) 2022 megvii-research. All Rights Reserved.
+# ------------------------------------------------------------------------
+# Modified from Deformable DETR (https://github.com/fundamentalvision/Deformable-DETR)
+# Copyright (c) 2020 SenseTime. All Rights Reserved.
+# ------------------------------------------------------------------------
+# Modified from DETR (https://github.com/facebookresearch/detr)
+# Copyright (c) Facebook, Inc. and its affiliates. All Rights Reserved
+# ------------------------------------------------------------------------
+
+import torch
+import numpy as np
+
+
+def load_model(model, model_path, optimizer=None, resume=False,
+ lr=None, lr_step=None):
+ start_epoch = 0
+ checkpoint = torch.load(model_path, map_location=lambda storage, loc: storage)
+ print(f'loaded {model_path}')
+ state_dict = checkpoint['model']
+ model_state_dict = model.state_dict()
+
+ # check loaded parameters and created model parameters
+ msg = 'If you see this, your model does not fully load the ' + \
+ 'pre-trained weight. Please make sure ' + \
+ 'you set the correct --num_classes for your own dataset.'
+ for k in state_dict:
+ if k in model_state_dict:
+ if state_dict[k].shape != model_state_dict[k].shape:
+ print('Skip loading parameter {}, required shape{}, ' \
+ 'loaded shape{}. {}'.format(
+ k, model_state_dict[k].shape, state_dict[k].shape, msg))
+ if 'class_embed' in k:
+ print("load class_embed: {} shape={}".format(k, state_dict[k].shape))
+ if model_state_dict[k].shape[0] == 1:
+ state_dict[k] = state_dict[k][1:2]
+ elif model_state_dict[k].shape[0] == 2:
+ state_dict[k] = state_dict[k][1:3]
+ elif model_state_dict[k].shape[0] == 3:
+ state_dict[k] = state_dict[k][1:4]
+ else:
+ raise NotImplementedError('invalid shape: {}'.format(model_state_dict[k].shape))
+ continue
+ state_dict[k] = model_state_dict[k]
+ else:
+ print('Drop parameter {}.'.format(k) + msg)
+ for k in model_state_dict:
+ if not (k in state_dict):
+ print('No param {}.'.format(k) + msg)
+ state_dict[k] = model_state_dict[k]
+ model.load_state_dict(state_dict, strict=False)
+
+ # resume optimizer parameters
+ if optimizer is not None and resume:
+ if 'optimizer' in checkpoint:
+ optimizer.load_state_dict(checkpoint['optimizer'])
+ start_epoch = checkpoint['epoch']
+ start_lr = lr
+ for step in lr_step:
+ if start_epoch >= step:
+ start_lr *= 0.1
+ for param_group in optimizer.param_groups:
+ param_group['lr'] = start_lr
+ print('Resumed optimizer with start lr', start_lr)
+ else:
+ print('No optimizer parameters in checkpoint.')
+ if optimizer is not None:
+ return model, optimizer, start_epoch
+ else:
+ return model
+
+
+
diff --git a/VISAM/visam.gif b/VISAM/visam.gif
new file mode 100644
index 0000000000000000000000000000000000000000..be71bd288935b328f71a52d3d8dda272bcbebc4c
--- /dev/null
+++ b/VISAM/visam.gif
@@ -0,0 +1,3 @@
+version https://git-lfs.github.com/spec/v1
+oid sha256:4c75f33480d65ff38fc86fa8b7eef556a8066a7a40fef59c1913cb858a4512bc
+size 40634464
diff --git a/assets/Grounded-SAM_logo.png b/assets/Grounded-SAM_logo.png
new file mode 100644
index 0000000000000000000000000000000000000000..33fa9ae14782a2817ad8cc1d8e7deeaec7775b4a
Binary files /dev/null and b/assets/Grounded-SAM_logo.png differ
diff --git a/assets/acoustics/det_voice.mp3 b/assets/acoustics/det_voice.mp3
new file mode 100644
index 0000000000000000000000000000000000000000..0c205c3f60e2bbeddd1226bf60b756fae691e8dc
Binary files /dev/null and b/assets/acoustics/det_voice.mp3 differ
diff --git a/assets/acoustics/gsam_whisper_inpainting_demo.png b/assets/acoustics/gsam_whisper_inpainting_demo.png
new file mode 100644
index 0000000000000000000000000000000000000000..cc5d83c200b4fbd27bbd0e0a8552847d5452de2d
--- /dev/null
+++ b/assets/acoustics/gsam_whisper_inpainting_demo.png
@@ -0,0 +1,3 @@
+version https://git-lfs.github.com/spec/v1
+oid sha256:0f7b6db373d70240849fa4ad2fa22d50f503ebd9d34bacb84d30dd1ca78318a7
+size 1197658
diff --git a/assets/acoustics/gsam_whisper_inpainting_pipeline.png b/assets/acoustics/gsam_whisper_inpainting_pipeline.png
new file mode 100644
index 0000000000000000000000000000000000000000..fa4a5a3afc56d8142dac053a56a9eaf606fa7d8e
--- /dev/null
+++ b/assets/acoustics/gsam_whisper_inpainting_pipeline.png
@@ -0,0 +1,3 @@
+version https://git-lfs.github.com/spec/v1
+oid sha256:09572a0c39009e59bb27bc3a634bfc9f305fea34cc0d3c16b89014fd8ea91ef2
+size 1183914
diff --git a/assets/acoustics/inpaint_voice.mp3 b/assets/acoustics/inpaint_voice.mp3
new file mode 100644
index 0000000000000000000000000000000000000000..ba429b3b1cce108fffd61a48791bb96d6a5ac6b6
Binary files /dev/null and b/assets/acoustics/inpaint_voice.mp3 differ
diff --git a/assets/acoustics/prompt_speech_file.mp3 b/assets/acoustics/prompt_speech_file.mp3
new file mode 100644
index 0000000000000000000000000000000000000000..9d8c0d8ebdce0747bf991d906ccc1882d5cc33cd
Binary files /dev/null and b/assets/acoustics/prompt_speech_file.mp3 differ
diff --git a/assets/annotated_image.jpg b/assets/annotated_image.jpg
new file mode 100644
index 0000000000000000000000000000000000000000..dbe080b9fe152b67fda3fed73e06328fbeddfff4
Binary files /dev/null and b/assets/annotated_image.jpg differ
diff --git a/assets/automatic_label_output/demo1.jpg b/assets/automatic_label_output/demo1.jpg
new file mode 100644
index 0000000000000000000000000000000000000000..4c62079c117abe2e4a58718f868b21b227366d1a
Binary files /dev/null and b/assets/automatic_label_output/demo1.jpg differ
diff --git a/assets/automatic_label_output/demo2.jpg b/assets/automatic_label_output/demo2.jpg
new file mode 100644
index 0000000000000000000000000000000000000000..07a404e423b40112f5b511580b20823285c14f49
Binary files /dev/null and b/assets/automatic_label_output/demo2.jpg differ
diff --git a/assets/automatic_label_output/demo4.jpg b/assets/automatic_label_output/demo4.jpg
new file mode 100644
index 0000000000000000000000000000000000000000..76d34a3496d0caf226da809d533a99d4c1ff5b68
Binary files /dev/null and b/assets/automatic_label_output/demo4.jpg differ
diff --git a/assets/automatic_label_output/demo8.jpg b/assets/automatic_label_output/demo8.jpg
new file mode 100644
index 0000000000000000000000000000000000000000..d858381ef12d4b397ab35d7de613ff5a7e86904c
Binary files /dev/null and b/assets/automatic_label_output/demo8.jpg differ
diff --git a/assets/automatic_label_output/demo9_tag2text.jpg b/assets/automatic_label_output/demo9_tag2text.jpg
new file mode 100644
index 0000000000000000000000000000000000000000..c50f30dddb4fbeca18bb93d3b3e1c5213dc23baa
Binary files /dev/null and b/assets/automatic_label_output/demo9_tag2text.jpg differ
diff --git a/assets/automatic_label_output/demo9_tag2text_ram.jpg b/assets/automatic_label_output/demo9_tag2text_ram.jpg
new file mode 100644
index 0000000000000000000000000000000000000000..98c65355f480ab762c0f922b3352a5feca6634ae
Binary files /dev/null and b/assets/automatic_label_output/demo9_tag2text_ram.jpg differ
diff --git a/assets/automatic_label_output_demo3.jpg b/assets/automatic_label_output_demo3.jpg
new file mode 100644
index 0000000000000000000000000000000000000000..5166f202e7c19784c7154089266a400022d06a8e
Binary files /dev/null and b/assets/automatic_label_output_demo3.jpg differ
diff --git a/assets/chatbot_demo.png b/assets/chatbot_demo.png
new file mode 100644
index 0000000000000000000000000000000000000000..7f38d1fda258fbde345bd700d52c02f956c7bf21
Binary files /dev/null and b/assets/chatbot_demo.png differ
diff --git a/assets/demo1.jpg b/assets/demo1.jpg
new file mode 100644
index 0000000000000000000000000000000000000000..b51fde5fbe4d06c4295270b100f8861bbb02a870
Binary files /dev/null and b/assets/demo1.jpg differ
diff --git a/assets/demo2.jpg b/assets/demo2.jpg
new file mode 100644
index 0000000000000000000000000000000000000000..583f69ec771a6f562e8dd9511b61fb9034a1af64
Binary files /dev/null and b/assets/demo2.jpg differ
diff --git a/assets/demo3.jpg b/assets/demo3.jpg
new file mode 100644
index 0000000000000000000000000000000000000000..83c0c9eb9f5026fdb7a7f49fba081d4764ce0515
Binary files /dev/null and b/assets/demo3.jpg differ
diff --git a/assets/demo4.jpg b/assets/demo4.jpg
new file mode 100644
index 0000000000000000000000000000000000000000..deeafdbc1d4ac40426f75ee7395ecd82025d6e95
Binary files /dev/null and b/assets/demo4.jpg differ
diff --git a/assets/demo5.jpg b/assets/demo5.jpg
new file mode 100644
index 0000000000000000000000000000000000000000..a204f5a7567288216ec7e18a5223e677ab397b36
Binary files /dev/null and b/assets/demo5.jpg differ
diff --git a/assets/demo6.jpg b/assets/demo6.jpg
new file mode 100644
index 0000000000000000000000000000000000000000..679431b782257372a0bbe19ab701c308d114f0d7
Binary files /dev/null and b/assets/demo6.jpg differ
diff --git a/assets/demo7.jpg b/assets/demo7.jpg
new file mode 100644
index 0000000000000000000000000000000000000000..9374e1fa87e3103869e727a8c56fb22525adb715
Binary files /dev/null and b/assets/demo7.jpg differ
diff --git a/assets/demo8.jpg b/assets/demo8.jpg
new file mode 100644
index 0000000000000000000000000000000000000000..20a3789bad40238cc90cca7b8e0049aaad1e1dbd
Binary files /dev/null and b/assets/demo8.jpg differ
diff --git a/assets/demo9.jpg b/assets/demo9.jpg
new file mode 100644
index 0000000000000000000000000000000000000000..3eac841b38ec6d00d2cb28e4beb237184e71f847
--- /dev/null
+++ b/assets/demo9.jpg
@@ -0,0 +1,3 @@
+version https://git-lfs.github.com/spec/v1
+oid sha256:1b2906f4058a69936df49cb6156ec4cd117a286b420e1eb14764033bf8f3c05f
+size 5701095
diff --git a/assets/gradio_auto_label.png b/assets/gradio_auto_label.png
new file mode 100644
index 0000000000000000000000000000000000000000..b9e816acb5cbd17982dc314fc871cfd4b999aa9d
Binary files /dev/null and b/assets/gradio_auto_label.png differ
diff --git a/assets/gradio_demo.png b/assets/gradio_demo.png
new file mode 100644
index 0000000000000000000000000000000000000000..f345d6d49f665f50e25350cb5bac59b165715142
--- /dev/null
+++ b/assets/gradio_demo.png
@@ -0,0 +1,3 @@
+version https://git-lfs.github.com/spec/v1
+oid sha256:4c78e1d44c5d15100aa43c7a9da9b7e30a630321b2cc452d2b6f8187367b5ffc
+size 2938908
diff --git a/assets/grounded_sam2.png b/assets/grounded_sam2.png
new file mode 100644
index 0000000000000000000000000000000000000000..941574de7faaa7f81275a77188fe61ddaebe6a3b
Binary files /dev/null and b/assets/grounded_sam2.png differ
diff --git a/assets/grounded_sam_annotated_image.jpg b/assets/grounded_sam_annotated_image.jpg
new file mode 100644
index 0000000000000000000000000000000000000000..b0378b82ca1b6d40507149b8fa7c0d82b9fd409c
Binary files /dev/null and b/assets/grounded_sam_annotated_image.jpg differ
diff --git a/assets/grounded_sam_demo3_demo4.png b/assets/grounded_sam_demo3_demo4.png
new file mode 100644
index 0000000000000000000000000000000000000000..44fe44671aa13cf9bacec60b1bb18edb5890ca3e
--- /dev/null
+++ b/assets/grounded_sam_demo3_demo4.png
@@ -0,0 +1,3 @@
+version https://git-lfs.github.com/spec/v1
+oid sha256:035473e8670cef7b6e6582bce84927264f587d23d35d049997a5f47c6ec1202e
+size 1734661
diff --git a/assets/grounded_sam_inpainting_demo.png b/assets/grounded_sam_inpainting_demo.png
new file mode 100644
index 0000000000000000000000000000000000000000..3440cfe22b363cf0aca792fed48ac1ab1ede0353
--- /dev/null
+++ b/assets/grounded_sam_inpainting_demo.png
@@ -0,0 +1,3 @@
+version https://git-lfs.github.com/spec/v1
+oid sha256:0ef6cf9abcc4e9e9df3167559ce70d60eaee2db9f5c2355ab7a361b9100615eb
+size 3420030
diff --git a/assets/grounded_sam_new_demo_image.png b/assets/grounded_sam_new_demo_image.png
new file mode 100644
index 0000000000000000000000000000000000000000..54a32814f9286505f926b475e472eb1b99e6bfc3
--- /dev/null
+++ b/assets/grounded_sam_new_demo_image.png
@@ -0,0 +1,3 @@
+version https://git-lfs.github.com/spec/v1
+oid sha256:60717bd52070c041713fe5de4c4ff3625a4439eb5d65ee83cfa31c42f834edb1
+size 1213073
diff --git a/assets/grounded_sam_output_demo1.jpg b/assets/grounded_sam_output_demo1.jpg
new file mode 100644
index 0000000000000000000000000000000000000000..8f9654bff39d8d55b00a8dffaf8e634b1c735463
Binary files /dev/null and b/assets/grounded_sam_output_demo1.jpg differ
diff --git a/assets/grounded_sam_whisper_output.jpg b/assets/grounded_sam_whisper_output.jpg
new file mode 100644
index 0000000000000000000000000000000000000000..975c497f647db9a1e1475f0382509f0a03033b24
Binary files /dev/null and b/assets/grounded_sam_whisper_output.jpg differ
diff --git a/assets/grounding_dino_output_demo1.jpg b/assets/grounding_dino_output_demo1.jpg
new file mode 100644
index 0000000000000000000000000000000000000000..6bd1e7e9030fa463b8196f6d537f03b2a45c2f2b
Binary files /dev/null and b/assets/grounding_dino_output_demo1.jpg differ
diff --git a/assets/groundingdino_annotated_image.jpg b/assets/groundingdino_annotated_image.jpg
new file mode 100644
index 0000000000000000000000000000000000000000..4db80491cfa9f94a8bcdf7adde8aa2e75cd87060
Binary files /dev/null and b/assets/groundingdino_annotated_image.jpg differ
diff --git a/assets/inpaint_demo.jpg b/assets/inpaint_demo.jpg
new file mode 100644
index 0000000000000000000000000000000000000000..e84dfc8554d344a69afb1fe8c7b8b2997d4e5e11
Binary files /dev/null and b/assets/inpaint_demo.jpg differ
diff --git a/assets/mask_3dbox.png b/assets/mask_3dbox.png
new file mode 100644
index 0000000000000000000000000000000000000000..a67fda1398b1e9742381feecad7e93878753d945
--- /dev/null
+++ b/assets/mask_3dbox.png
@@ -0,0 +1,3 @@
+version https://git-lfs.github.com/spec/v1
+oid sha256:ff33c91db0a8b0c1998a9abe537230068819d616db5727b49e69975d8f36f18c
+size 1951860
diff --git a/assets/n015-2018-08-02-17-16-37+0800__CAM_BACK_LEFT__1533201470447423.jpg b/assets/n015-2018-08-02-17-16-37+0800__CAM_BACK_LEFT__1533201470447423.jpg
new file mode 100644
index 0000000000000000000000000000000000000000..a79b1124213e94e247d53cbb3d204aaaa632348e
Binary files /dev/null and b/assets/n015-2018-08-02-17-16-37+0800__CAM_BACK_LEFT__1533201470447423.jpg differ
diff --git a/assets/osx/grounded_sam_osx_demo.png b/assets/osx/grounded_sam_osx_demo.png
new file mode 100644
index 0000000000000000000000000000000000000000..92ec99e4851eb0bf25c85f098d0952ec064bc7a4
--- /dev/null
+++ b/assets/osx/grounded_sam_osx_demo.png
@@ -0,0 +1,3 @@
+version https://git-lfs.github.com/spec/v1
+oid sha256:36db4c7d3a392d397ba86faaac7d358b5fd84751ba1c2eecc6d999a675787c2e
+size 1541635
diff --git a/assets/osx/grounded_sam_osx_output.jpg b/assets/osx/grounded_sam_osx_output.jpg
new file mode 100644
index 0000000000000000000000000000000000000000..7fa457434d8c2ff6d23aaeaa97e8e60cbde8d3e8
Binary files /dev/null and b/assets/osx/grounded_sam_osx_output.jpg differ
diff --git a/assets/osx/grounded_sam_osx_output1.jpg b/assets/osx/grounded_sam_osx_output1.jpg
new file mode 100644
index 0000000000000000000000000000000000000000..0598210a2b5ab54bbde079717f65ed6dec0463e9
Binary files /dev/null and b/assets/osx/grounded_sam_osx_output1.jpg differ
diff --git a/assets/osx/grounded_sam_osx_output2.jpg b/assets/osx/grounded_sam_osx_output2.jpg
new file mode 100644
index 0000000000000000000000000000000000000000..2f74139602d871073a95ce574c1530e7d20b7ef4
Binary files /dev/null and b/assets/osx/grounded_sam_osx_output2.jpg differ
diff --git a/assets/osx/grouned_sam_osx_demo.gif b/assets/osx/grouned_sam_osx_demo.gif
new file mode 100644
index 0000000000000000000000000000000000000000..6c37acd79770d4e75f4763e77c25c814079dbc58
--- /dev/null
+++ b/assets/osx/grouned_sam_osx_demo.gif
@@ -0,0 +1,3 @@
+version https://git-lfs.github.com/spec/v1
+oid sha256:e440e2e27f4b168e206a7fa25a6a9c31d7a4b9eb33101871727d36e2af132293
+size 6104943
diff --git a/assets/ram_grounded_sam_new.png b/assets/ram_grounded_sam_new.png
new file mode 100644
index 0000000000000000000000000000000000000000..b910f91bbe96bcc00c2c5234ca54e400d21cf5e4
--- /dev/null
+++ b/assets/ram_grounded_sam_new.png
@@ -0,0 +1,3 @@
+version https://git-lfs.github.com/spec/v1
+oid sha256:5db61d41be4b7f938878ab4f299c699322470fd94e0a41c9cca29bdaedc93e67
+size 2791192
diff --git a/automatic_label_demo.py b/automatic_label_demo.py
new file mode 100644
index 0000000000000000000000000000000000000000..676cbbf1aa9afec3d7482115c76fc7f882a6eb78
--- /dev/null
+++ b/automatic_label_demo.py
@@ -0,0 +1,323 @@
+import argparse
+import os
+import copy
+
+import numpy as np
+import json
+import torch
+import torchvision
+from PIL import Image, ImageDraw, ImageFont
+import nltk
+import litellm
+
+# Grounding DINO
+import GroundingDINO.groundingdino.datasets.transforms as T
+from GroundingDINO.groundingdino.models import build_model
+from GroundingDINO.groundingdino.util import box_ops
+from GroundingDINO.groundingdino.util.slconfig import SLConfig
+from GroundingDINO.groundingdino.util.utils import clean_state_dict, get_phrases_from_posmap
+
+# segment anything
+from segment_anything import build_sam, SamPredictor
+import cv2
+import numpy as np
+import matplotlib.pyplot as plt
+
+# BLIP
+from transformers import BlipProcessor, BlipForConditionalGeneration
+
+# ChatGPT
+import openai
+
+
+def load_image(image_path):
+ # load image
+ image_pil = Image.open(image_path).convert("RGB") # load image
+
+ transform = T.Compose(
+ [
+ T.RandomResize([800], max_size=1333),
+ T.ToTensor(),
+ T.Normalize([0.485, 0.456, 0.406], [0.229, 0.224, 0.225]),
+ ]
+ )
+ image, _ = transform(image_pil, None) # 3, h, w
+ return image_pil, image
+
+
+def generate_caption(raw_image, device):
+ # unconditional image captioning
+ if device == "cuda":
+ inputs = processor(raw_image, return_tensors="pt").to("cuda", torch.float16)
+ else:
+ inputs = processor(raw_image, return_tensors="pt")
+ out = blip_model.generate(**inputs)
+ caption = processor.decode(out[0], skip_special_tokens=True)
+ return caption
+
+
+def generate_tags(caption, split=',', max_tokens=100, model="gpt-3.5-turbo"):
+ lemma = nltk.wordnet.WordNetLemmatizer()
+ if openai_key:
+ prompt = [
+ {
+ 'role': 'system',
+ 'content': 'Extract the unique nouns in the caption. Remove all the adjectives. ' + \
+ f'List the nouns in singular form. Split them by "{split} ". ' + \
+ f'Caption: {caption}.'
+ }
+ ]
+ response = litellm.completion(model=model, messages=prompt, temperature=0.6, max_tokens=max_tokens)
+ reply = response['choices'][0]['message']['content']
+ # sometimes return with "noun: xxx, xxx, xxx"
+ tags = reply.split(':')[-1].strip()
+ else:
+ nltk.download(['punkt', 'averaged_perceptron_tagger', 'wordnet'])
+ tags_list = [word for (word, pos) in nltk.pos_tag(nltk.word_tokenize(caption)) if pos[0] == 'N']
+ tags_lemma = [lemma.lemmatize(w) for w in tags_list]
+ tags = ', '.join(map(str, tags_lemma))
+ return tags
+
+
+def check_caption(caption, pred_phrases, max_tokens=100, model="gpt-3.5-turbo"):
+ object_list = [obj.split('(')[0] for obj in pred_phrases]
+ object_num = []
+ for obj in set(object_list):
+ object_num.append(f'{object_list.count(obj)} {obj}')
+ object_num = ', '.join(object_num)
+ print(f"Correct object number: {object_num}")
+
+ if openai_key:
+ prompt = [
+ {
+ 'role': 'system',
+ 'content': 'Revise the number in the caption if it is wrong. ' + \
+ f'Caption: {caption}. ' + \
+ f'True object number: {object_num}. ' + \
+ 'Only give the revised caption: '
+ }
+ ]
+ response = litellm.completion(model=model, messages=prompt, temperature=0.6, max_tokens=max_tokens)
+ reply = response['choices'][0]['message']['content']
+ # sometimes return with "Caption: xxx, xxx, xxx"
+ caption = reply.split(':')[-1].strip()
+ return caption
+
+
+def load_model(model_config_path, model_checkpoint_path, device):
+ args = SLConfig.fromfile(model_config_path)
+ args.device = device
+ model = build_model(args)
+ checkpoint = torch.load(model_checkpoint_path, map_location="cpu")
+ load_res = model.load_state_dict(clean_state_dict(checkpoint["model"]), strict=False)
+ print(load_res)
+ _ = model.eval()
+ return model
+
+
+def get_grounding_output(model, image, caption, box_threshold, text_threshold,device="cpu"):
+ caption = caption.lower()
+ caption = caption.strip()
+ if not caption.endswith("."):
+ caption = caption + "."
+ model = model.to(device)
+ image = image.to(device)
+ with torch.no_grad():
+ outputs = model(image[None], captions=[caption])
+ logits = outputs["pred_logits"].cpu().sigmoid()[0] # (nq, 256)
+ boxes = outputs["pred_boxes"].cpu()[0] # (nq, 4)
+ logits.shape[0]
+
+ # filter output
+ logits_filt = logits.clone()
+ boxes_filt = boxes.clone()
+ filt_mask = logits_filt.max(dim=1)[0] > box_threshold
+ logits_filt = logits_filt[filt_mask] # num_filt, 256
+ boxes_filt = boxes_filt[filt_mask] # num_filt, 4
+ logits_filt.shape[0]
+
+ # get phrase
+ tokenlizer = model.tokenizer
+ tokenized = tokenlizer(caption)
+ # build pred
+ pred_phrases = []
+ scores = []
+ for logit, box in zip(logits_filt, boxes_filt):
+ pred_phrase = get_phrases_from_posmap(logit > text_threshold, tokenized, tokenlizer)
+ pred_phrases.append(pred_phrase + f"({str(logit.max().item())[:4]})")
+ scores.append(logit.max().item())
+
+ return boxes_filt, torch.Tensor(scores), pred_phrases
+
+
+def show_mask(mask, ax, random_color=False):
+ if random_color:
+ color = np.concatenate([np.random.random(3), np.array([0.6])], axis=0)
+ else:
+ color = np.array([30/255, 144/255, 255/255, 0.6])
+ h, w = mask.shape[-2:]
+ mask_image = mask.reshape(h, w, 1) * color.reshape(1, 1, -1)
+ ax.imshow(mask_image)
+
+
+def show_box(box, ax, label):
+ x0, y0 = box[0], box[1]
+ w, h = box[2] - box[0], box[3] - box[1]
+ ax.add_patch(plt.Rectangle((x0, y0), w, h, edgecolor='green', facecolor=(0,0,0,0), lw=2))
+ ax.text(x0, y0, label)
+
+
+def save_mask_data(output_dir, caption, mask_list, box_list, label_list):
+ value = 0 # 0 for background
+
+ mask_img = torch.zeros(mask_list.shape[-2:])
+ for idx, mask in enumerate(mask_list):
+ mask_img[mask.cpu().numpy()[0] == True] = value + idx + 1
+ plt.figure(figsize=(10, 10))
+ plt.imshow(mask_img.numpy())
+ plt.axis('off')
+ plt.savefig(os.path.join(output_dir, 'mask.jpg'), bbox_inches="tight", dpi=300, pad_inches=0.0)
+
+ json_data = {
+ 'caption': caption,
+ 'mask':[{
+ 'value': value,
+ 'label': 'background'
+ }]
+ }
+ for label, box in zip(label_list, box_list):
+ value += 1
+ name, logit = label.split('(')
+ logit = logit[:-1] # the last is ')'
+ json_data['mask'].append({
+ 'value': value,
+ 'label': name,
+ 'logit': float(logit),
+ 'box': box.numpy().tolist(),
+ })
+ with open(os.path.join(output_dir, 'label.json'), 'w') as f:
+ json.dump(json_data, f)
+
+
+if __name__ == "__main__":
+
+ parser = argparse.ArgumentParser("Grounded-Segment-Anything Demo", add_help=True)
+ parser.add_argument("--config", type=str, required=True, help="path to config file")
+ parser.add_argument(
+ "--grounded_checkpoint", type=str, required=True, help="path to checkpoint file"
+ )
+ parser.add_argument(
+ "--sam_checkpoint", type=str, required=True, help="path to checkpoint file"
+ )
+ parser.add_argument("--input_image", type=str, required=True, help="path to image file")
+ parser.add_argument("--split", default=",", type=str, help="split for text prompt")
+ parser.add_argument("--openai_key", type=str, help="key for chatgpt")
+ parser.add_argument("--openai_proxy", default=None, type=str, help="proxy for chatgpt")
+ parser.add_argument(
+ "--output_dir", "-o", type=str, default="outputs", required=True, help="output directory"
+ )
+
+ parser.add_argument("--box_threshold", type=float, default=0.25, help="box threshold")
+ parser.add_argument("--text_threshold", type=float, default=0.2, help="text threshold")
+ parser.add_argument("--iou_threshold", type=float, default=0.5, help="iou threshold")
+
+ parser.add_argument("--device", type=str, default="cpu", help="running on cpu only!, default=False")
+ args = parser.parse_args()
+
+ # cfg
+ config_file = args.config # change the path of the model config file
+ grounded_checkpoint = args.grounded_checkpoint # change the path of the model
+ sam_checkpoint = args.sam_checkpoint
+ image_path = args.input_image
+ split = args.split
+ openai_key = args.openai_key
+ openai_proxy = args.openai_proxy
+ output_dir = args.output_dir
+ box_threshold = args.box_threshold
+ text_threshold = args.text_threshold
+ iou_threshold = args.iou_threshold
+ device = args.device
+
+ openai.api_key = openai_key
+ if openai_proxy:
+ openai.proxy = {"http": openai_proxy, "https": openai_proxy}
+
+ # make dir
+ os.makedirs(output_dir, exist_ok=True)
+ # load image
+ image_pil, image = load_image(image_path)
+ # load model
+ model = load_model(config_file, grounded_checkpoint, device=device)
+
+ # visualize raw image
+ image_pil.save(os.path.join(output_dir, "raw_image.jpg"))
+
+ # generate caption and tags
+ # use Tag2Text can generate better captions
+ # https://huggingface.co/spaces/xinyu1205/Tag2Text
+ # but there are some bugs...
+ processor = BlipProcessor.from_pretrained("Salesforce/blip-image-captioning-large")
+ if device == "cuda":
+ blip_model = BlipForConditionalGeneration.from_pretrained("Salesforce/blip-image-captioning-large", torch_dtype=torch.float16).to("cuda")
+ else:
+ blip_model = BlipForConditionalGeneration.from_pretrained("Salesforce/blip-image-captioning-large")
+ caption = generate_caption(image_pil, device=device)
+ # Currently ", " is better for detecting single tags
+ # while ". " is a little worse in some case
+ text_prompt = generate_tags(caption, split=split)
+ print(f"Caption: {caption}")
+ print(f"Tags: {text_prompt}")
+
+ # run grounding dino model
+ boxes_filt, scores, pred_phrases = get_grounding_output(
+ model, image, text_prompt, box_threshold, text_threshold, device=device
+ )
+
+ # initialize SAM
+ predictor = SamPredictor(build_sam(checkpoint=sam_checkpoint).to(device))
+ image = cv2.imread(image_path)
+ image = cv2.cvtColor(image, cv2.COLOR_BGR2RGB)
+ predictor.set_image(image)
+
+ size = image_pil.size
+ H, W = size[1], size[0]
+ for i in range(boxes_filt.size(0)):
+ boxes_filt[i] = boxes_filt[i] * torch.Tensor([W, H, W, H])
+ boxes_filt[i][:2] -= boxes_filt[i][2:] / 2
+ boxes_filt[i][2:] += boxes_filt[i][:2]
+
+ boxes_filt = boxes_filt.cpu()
+ # use NMS to handle overlapped boxes
+ print(f"Before NMS: {boxes_filt.shape[0]} boxes")
+ nms_idx = torchvision.ops.nms(boxes_filt, scores, iou_threshold).numpy().tolist()
+ boxes_filt = boxes_filt[nms_idx]
+ pred_phrases = [pred_phrases[idx] for idx in nms_idx]
+ print(f"After NMS: {boxes_filt.shape[0]} boxes")
+ caption = check_caption(caption, pred_phrases)
+ print(f"Revise caption with number: {caption}")
+
+ transformed_boxes = predictor.transform.apply_boxes_torch(boxes_filt, image.shape[:2]).to(device)
+
+ masks, _, _ = predictor.predict_torch(
+ point_coords = None,
+ point_labels = None,
+ boxes = transformed_boxes.to(device),
+ multimask_output = False,
+ )
+
+ # draw output image
+ plt.figure(figsize=(10, 10))
+ plt.imshow(image)
+ for mask in masks:
+ show_mask(mask.cpu().numpy(), plt.gca(), random_color=True)
+ for box, label in zip(boxes_filt, pred_phrases):
+ show_box(box.numpy(), plt.gca(), label)
+
+ plt.title(caption)
+ plt.axis('off')
+ plt.savefig(
+ os.path.join(output_dir, "automatic_label_output.jpg"),
+ bbox_inches="tight", dpi=300, pad_inches=0.0
+ )
+
+ save_mask_data(output_dir, caption, masks, boxes_filt, pred_phrases)
diff --git a/automatic_label_ram_demo.py b/automatic_label_ram_demo.py
new file mode 100644
index 0000000000000000000000000000000000000000..49ea6179387a886a9597c91c257bcd6b663bd2ad
--- /dev/null
+++ b/automatic_label_ram_demo.py
@@ -0,0 +1,324 @@
+import argparse
+import os
+
+import numpy as np
+import json
+import torch
+import torchvision
+from PIL import Image
+import litellm
+
+# Grounding DINO
+import GroundingDINO.groundingdino.datasets.transforms as T
+from GroundingDINO.groundingdino.models import build_model
+from GroundingDINO.groundingdino.util.slconfig import SLConfig
+from GroundingDINO.groundingdino.util.utils import clean_state_dict, get_phrases_from_posmap
+
+# segment anything
+from segment_anything import (
+ build_sam,
+ build_sam_hq,
+ SamPredictor
+)
+import cv2
+import numpy as np
+import matplotlib.pyplot as plt
+
+# Recognize Anything Model & Tag2Text
+from ram.models import ram
+from ram import inference_ram
+import torchvision.transforms as TS
+
+# ChatGPT or nltk is required when using tags_chineses
+# import openai
+# import nltk
+
+def load_image(image_path):
+ # load image
+ image_pil = Image.open(image_path).convert("RGB") # load image
+
+ transform = T.Compose(
+ [
+ T.RandomResize([800], max_size=1333),
+ T.ToTensor(),
+ T.Normalize([0.485, 0.456, 0.406], [0.229, 0.224, 0.225]),
+ ]
+ )
+ image, _ = transform(image_pil, None) # 3, h, w
+ return image_pil, image
+
+
+def check_tags_chinese(tags_chinese, pred_phrases, max_tokens=100, model="gpt-3.5-turbo"):
+ object_list = [obj.split('(')[0] for obj in pred_phrases]
+ object_num = []
+ for obj in set(object_list):
+ object_num.append(f'{object_list.count(obj)} {obj}')
+ object_num = ', '.join(object_num)
+ print(f"Correct object number: {object_num}")
+
+ if openai_key:
+ prompt = [
+ {
+ 'role': 'system',
+ 'content': 'Revise the number in the tags_chinese if it is wrong. ' + \
+ f'tags_chinese: {tags_chinese}. ' + \
+ f'True object number: {object_num}. ' + \
+ 'Only give the revised tags_chinese: '
+ }
+ ]
+ response = litellm.completion(model=model, messages=prompt, temperature=0.6, max_tokens=max_tokens)
+ reply = response['choices'][0]['message']['content']
+ # sometimes return with "tags_chinese: xxx, xxx, xxx"
+ tags_chinese = reply.split(':')[-1].strip()
+ return tags_chinese
+
+
+def load_model(model_config_path, model_checkpoint_path, device):
+ args = SLConfig.fromfile(model_config_path)
+ args.device = device
+ model = build_model(args)
+ checkpoint = torch.load(model_checkpoint_path, map_location="cpu")
+ load_res = model.load_state_dict(clean_state_dict(checkpoint["model"]), strict=False)
+ print(load_res)
+ _ = model.eval()
+ return model
+
+
+def get_grounding_output(model, image, caption, box_threshold, text_threshold,device="cpu"):
+ caption = caption.lower()
+ caption = caption.strip()
+ if not caption.endswith("."):
+ caption = caption + "."
+ model = model.to(device)
+ image = image.to(device)
+ with torch.no_grad():
+ outputs = model(image[None], captions=[caption])
+ logits = outputs["pred_logits"].cpu().sigmoid()[0] # (nq, 256)
+ boxes = outputs["pred_boxes"].cpu()[0] # (nq, 4)
+ logits.shape[0]
+
+ # filter output
+ logits_filt = logits.clone()
+ boxes_filt = boxes.clone()
+ filt_mask = logits_filt.max(dim=1)[0] > box_threshold
+ logits_filt = logits_filt[filt_mask] # num_filt, 256
+ boxes_filt = boxes_filt[filt_mask] # num_filt, 4
+ logits_filt.shape[0]
+
+ # get phrase
+ tokenlizer = model.tokenizer
+ tokenized = tokenlizer(caption)
+ # build pred
+ pred_phrases = []
+ scores = []
+ for logit, box in zip(logits_filt, boxes_filt):
+ pred_phrase = get_phrases_from_posmap(logit > text_threshold, tokenized, tokenlizer)
+ pred_phrases.append(pred_phrase + f"({str(logit.max().item())[:4]})")
+ scores.append(logit.max().item())
+
+ return boxes_filt, torch.Tensor(scores), pred_phrases
+
+
+def show_mask(mask, ax, random_color=False):
+ if random_color:
+ color = np.concatenate([np.random.random(3), np.array([0.6])], axis=0)
+ else:
+ color = np.array([30/255, 144/255, 255/255, 0.6])
+ h, w = mask.shape[-2:]
+ mask_image = mask.reshape(h, w, 1) * color.reshape(1, 1, -1)
+ ax.imshow(mask_image)
+
+
+def show_box(box, ax, label):
+ x0, y0 = box[0], box[1]
+ w, h = box[2] - box[0], box[3] - box[1]
+ ax.add_patch(plt.Rectangle((x0, y0), w, h, edgecolor='green', facecolor=(0,0,0,0), lw=2))
+ ax.text(x0, y0, label)
+
+
+def save_mask_data(output_dir, tags_chinese, mask_list, box_list, label_list):
+ value = 0 # 0 for background
+
+ mask_img = torch.zeros(mask_list.shape[-2:])
+ for idx, mask in enumerate(mask_list):
+ mask_img[mask.cpu().numpy()[0] == True] = value + idx + 1
+ plt.figure(figsize=(10, 10))
+ plt.imshow(mask_img.numpy())
+ plt.axis('off')
+ plt.savefig(os.path.join(output_dir, 'mask.jpg'), bbox_inches="tight", dpi=300, pad_inches=0.0)
+
+ json_data = {
+ 'tags_chinese': tags_chinese,
+ 'mask':[{
+ 'value': value,
+ 'label': 'background'
+ }]
+ }
+ for label, box in zip(label_list, box_list):
+ value += 1
+ name, logit = label.split('(')
+ logit = logit[:-1] # the last is ')'
+ json_data['mask'].append({
+ 'value': value,
+ 'label': name,
+ 'logit': float(logit),
+ 'box': box.numpy().tolist(),
+ })
+ with open(os.path.join(output_dir, 'label.json'), 'w') as f:
+ json.dump(json_data, f)
+
+
+if __name__ == "__main__":
+
+ parser = argparse.ArgumentParser("Grounded-Segment-Anything Demo", add_help=True)
+ parser.add_argument("--config", type=str, required=True, help="path to config file")
+ parser.add_argument(
+ "--ram_checkpoint", type=str, required=True, help="path to checkpoint file"
+ )
+ parser.add_argument(
+ "--grounded_checkpoint", type=str, required=True, help="path to checkpoint file"
+ )
+ parser.add_argument(
+ "--sam_checkpoint", type=str, required=True, help="path to checkpoint file"
+ )
+ parser.add_argument(
+ "--sam_hq_checkpoint", type=str, default=None, help="path to sam-hq checkpoint file"
+ )
+ parser.add_argument(
+ "--use_sam_hq", action="store_true", help="using sam-hq for prediction"
+ )
+ parser.add_argument("--input_image", type=str, required=True, help="path to image file")
+ parser.add_argument("--split", default=",", type=str, help="split for text prompt")
+ parser.add_argument("--openai_key", type=str, help="key for chatgpt")
+ parser.add_argument("--openai_proxy", default=None, type=str, help="proxy for chatgpt")
+ parser.add_argument(
+ "--output_dir", "-o", type=str, default="outputs", required=True, help="output directory"
+ )
+
+ parser.add_argument("--box_threshold", type=float, default=0.25, help="box threshold")
+ parser.add_argument("--text_threshold", type=float, default=0.2, help="text threshold")
+ parser.add_argument("--iou_threshold", type=float, default=0.5, help="iou threshold")
+
+ parser.add_argument("--device", type=str, default="cpu", help="running on cpu only!, default=False")
+ args = parser.parse_args()
+
+ # cfg
+ config_file = args.config # change the path of the model config file
+ ram_checkpoint = args.ram_checkpoint # change the path of the model
+ grounded_checkpoint = args.grounded_checkpoint # change the path of the model
+ sam_checkpoint = args.sam_checkpoint
+ sam_hq_checkpoint = args.sam_hq_checkpoint
+ use_sam_hq = args.use_sam_hq
+ image_path = args.input_image
+ split = args.split
+ openai_key = args.openai_key
+ openai_proxy = args.openai_proxy
+ output_dir = args.output_dir
+ box_threshold = args.box_threshold
+ text_threshold = args.text_threshold
+ iou_threshold = args.iou_threshold
+ device = args.device
+
+ # ChatGPT or nltk is required when using tags_chineses
+ # openai.api_key = openai_key
+ # if openai_proxy:
+ # openai.proxy = {"http": openai_proxy, "https": openai_proxy}
+
+ # make dir
+ os.makedirs(output_dir, exist_ok=True)
+ # load image
+ image_pil, image = load_image(image_path)
+ # load model
+ model = load_model(config_file, grounded_checkpoint, device=device)
+
+ # visualize raw image
+ image_pil.save(os.path.join(output_dir, "raw_image.jpg"))
+
+ # initialize Recognize Anything Model
+ normalize = TS.Normalize(mean=[0.485, 0.456, 0.406],
+ std=[0.229, 0.224, 0.225])
+ transform = TS.Compose([
+ TS.Resize((384, 384)),
+ TS.ToTensor(), normalize
+ ])
+
+ # load model
+ ram_model = ram(pretrained=ram_checkpoint,
+ image_size=384,
+ vit='swin_l')
+ # threshold for tagging
+ # we reduce the threshold to obtain more tags
+ ram_model.eval()
+
+ ram_model = ram_model.to(device)
+ raw_image = image_pil.resize(
+ (384, 384))
+ raw_image = transform(raw_image).unsqueeze(0).to(device)
+
+ res = inference_ram(raw_image , ram_model)
+
+ # Currently ", " is better for detecting single tags
+ # while ". " is a little worse in some case
+ tags=res[0].replace(' |', ',')
+ tags_chinese=res[1].replace(' |', ',')
+
+ print("Image Tags: ", res[0])
+ print("图像标签: ", res[1])
+
+ # run grounding dino model
+ boxes_filt, scores, pred_phrases = get_grounding_output(
+ model, image, tags, box_threshold, text_threshold, device=device
+ )
+
+ # initialize SAM
+ if use_sam_hq:
+ print("Initialize SAM-HQ Predictor")
+ predictor = SamPredictor(build_sam_hq(checkpoint=sam_hq_checkpoint).to(device))
+ else:
+ predictor = SamPredictor(build_sam(checkpoint=sam_checkpoint).to(device))
+ image = cv2.imread(image_path)
+ image = cv2.cvtColor(image, cv2.COLOR_BGR2RGB)
+ predictor.set_image(image)
+
+ size = image_pil.size
+ H, W = size[1], size[0]
+ for i in range(boxes_filt.size(0)):
+ boxes_filt[i] = boxes_filt[i] * torch.Tensor([W, H, W, H])
+ boxes_filt[i][:2] -= boxes_filt[i][2:] / 2
+ boxes_filt[i][2:] += boxes_filt[i][:2]
+
+ boxes_filt = boxes_filt.cpu()
+ # use NMS to handle overlapped boxes
+ print(f"Before NMS: {boxes_filt.shape[0]} boxes")
+ nms_idx = torchvision.ops.nms(boxes_filt, scores, iou_threshold).numpy().tolist()
+ boxes_filt = boxes_filt[nms_idx]
+ pred_phrases = [pred_phrases[idx] for idx in nms_idx]
+ print(f"After NMS: {boxes_filt.shape[0]} boxes")
+ tags_chinese = check_tags_chinese(tags_chinese, pred_phrases)
+ print(f"Revise tags_chinese with number: {tags_chinese}")
+
+ transformed_boxes = predictor.transform.apply_boxes_torch(boxes_filt, image.shape[:2]).to(device)
+
+ masks, _, _ = predictor.predict_torch(
+ point_coords = None,
+ point_labels = None,
+ boxes = transformed_boxes.to(device),
+ multimask_output = False,
+ )
+
+ # draw output image
+ plt.figure(figsize=(10, 10))
+ plt.imshow(image)
+ for mask in masks:
+ show_mask(mask.cpu().numpy(), plt.gca(), random_color=True)
+ for box, label in zip(boxes_filt, pred_phrases):
+ show_box(box.numpy(), plt.gca(), label)
+
+ # plt.title('RAM-tags' + tags + '\n' + 'RAM-tags_chineseing: ' + tags_chinese + '\n')
+ plt.axis('off')
+ plt.savefig(
+ os.path.join(output_dir, "automatic_label_output.jpg"),
+ bbox_inches="tight", dpi=300, pad_inches=0.0
+ )
+
+ save_mask_data(output_dir, tags_chinese, masks, boxes_filt, pred_phrases)
diff --git a/automatic_label_simple_demo.py b/automatic_label_simple_demo.py
new file mode 100644
index 0000000000000000000000000000000000000000..eab11c4ddffbd0b976302b419453250dac6c3a26
--- /dev/null
+++ b/automatic_label_simple_demo.py
@@ -0,0 +1,166 @@
+import cv2
+import numpy as np
+import supervision as sv
+from typing import List
+from PIL import Image
+
+import torch
+
+from groundingdino.util.inference import Model
+from segment_anything import sam_model_registry, SamPredictor
+
+# Tag2Text
+# from ram.models import tag2text_caption
+from ram.models import ram
+# from ram import inference_tag2text
+from ram import inference_ram
+import torchvision
+import torchvision.transforms as TS
+
+
+# Hyper-Params
+SOURCE_IMAGE_PATH = "./assets/demo9.jpg"
+DEVICE = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
+
+GROUNDING_DINO_CONFIG_PATH = "GroundingDINO/groundingdino/config/GroundingDINO_SwinT_OGC.py"
+GROUNDING_DINO_CHECKPOINT_PATH = "./groundingdino_swint_ogc.pth"
+
+SAM_ENCODER_VERSION = "vit_h"
+SAM_CHECKPOINT_PATH = "./sam_vit_h_4b8939.pth"
+
+TAG2TEXT_CHECKPOINT_PATH = "./tag2text_swin_14m.pth"
+RAM_CHECKPOINT_PATH = "./ram_swin_large_14m.pth"
+
+TAG2TEXT_THRESHOLD = 0.64
+BOX_THRESHOLD = 0.2
+TEXT_THRESHOLD = 0.2
+IOU_THRESHOLD = 0.5
+
+# Building GroundingDINO inference model
+grounding_dino_model = Model(model_config_path=GROUNDING_DINO_CONFIG_PATH, model_checkpoint_path=GROUNDING_DINO_CHECKPOINT_PATH)
+
+
+# Building SAM Model and SAM Predictor
+sam = sam_model_registry[SAM_ENCODER_VERSION](checkpoint=SAM_CHECKPOINT_PATH)
+sam_predictor = SamPredictor(sam)
+
+# Tag2Text
+# initialize Tag2Text
+normalize = TS.Normalize(
+ mean=[0.485, 0.456, 0.406],
+ std=[0.229, 0.224, 0.225]
+)
+transform = TS.Compose(
+ [
+ TS.Resize((384, 384)),
+ TS.ToTensor(),
+ normalize
+ ]
+)
+
+DELETE_TAG_INDEX = [] # filter out attributes and action which are difficult to be grounded
+for idx in range(3012, 3429):
+ DELETE_TAG_INDEX.append(idx)
+
+# tag2text_model = tag2text_caption(
+# pretrained=TAG2TEXT_CHECKPOINT_PATH,
+# image_size=384,
+# vit='swin_b',
+# delete_tag_index=DELETE_TAG_INDEX
+# )
+# # threshold for tagging
+# # we reduce the threshold to obtain more tags
+# tag2text_model.threshold = TAG2TEXT_THRESHOLD
+# tag2text_model.eval()
+# tag2text_model = tag2text_model.to(DEVICE)
+
+ram_model = ram(pretrained=RAM_CHECKPOINT_PATH,
+ image_size=384,
+ vit='swin_l')
+ram_model.eval()
+ram_model = ram_model.to(DEVICE)
+
+# load image
+image = cv2.imread(SOURCE_IMAGE_PATH) # bgr
+image_pillow = Image.fromarray(cv2.cvtColor(image, cv2.COLOR_BGR2RGB)) # rgb
+
+image_pillow = image_pillow.resize((384, 384))
+image_pillow = transform(image_pillow).unsqueeze(0).to(DEVICE)
+
+specified_tags='None'
+# res = inference_tag2text(image_pillow , tag2text_model, specified_tags)
+res = inference_ram(image_pillow , ram_model)
+
+# Currently ", " is better for detecting single tags
+# while ". " is a little worse in some case
+AUTOMATIC_CLASSES=res[0].split(" | ")
+
+print(f"Tags: {res[0].replace(' |', ',')}")
+
+
+# detect objects
+detections = grounding_dino_model.predict_with_classes(
+ image=image,
+ classes=AUTOMATIC_CLASSES,
+ box_threshold=BOX_THRESHOLD,
+ text_threshold=BOX_THRESHOLD
+)
+
+# NMS post process
+print(f"Before NMS: {len(detections.xyxy)} boxes")
+nms_idx = torchvision.ops.nms(
+ torch.from_numpy(detections.xyxy),
+ torch.from_numpy(detections.confidence),
+ IOU_THRESHOLD
+).numpy().tolist()
+
+detections.xyxy = detections.xyxy[nms_idx]
+detections.confidence = detections.confidence[nms_idx]
+detections.class_id = detections.class_id[nms_idx]
+
+print(f"After NMS: {len(detections.xyxy)} boxes")
+
+# annotate image with detections
+box_annotator = sv.BoxAnnotator()
+labels = [
+ f"{AUTOMATIC_CLASSES[class_id]} {confidence:0.2f}"
+ for _, _, confidence, class_id, _, _
+ in detections]
+annotated_frame = box_annotator.annotate(scene=image.copy(), detections=detections, labels=labels)
+
+# save the annotated grounding dino image
+cv2.imwrite("groundingdino_auto_annotated_image.jpg", annotated_frame)
+
+# Prompting SAM with detected boxes
+def segment(sam_predictor: SamPredictor, image: np.ndarray, xyxy: np.ndarray) -> np.ndarray:
+ sam_predictor.set_image(image)
+ result_masks = []
+ for box in xyxy:
+ masks, scores, logits = sam_predictor.predict(
+ box=box,
+ multimask_output=True
+ )
+ index = np.argmax(scores)
+ result_masks.append(masks[index])
+ return np.array(result_masks)
+
+
+# convert detections to masks
+detections.mask = segment(
+ sam_predictor=sam_predictor,
+ image=cv2.cvtColor(image, cv2.COLOR_BGR2RGB),
+ xyxy=detections.xyxy
+)
+
+# annotate image with detections
+box_annotator = sv.BoxAnnotator()
+mask_annotator = sv.MaskAnnotator()
+labels = [
+ f"{AUTOMATIC_CLASSES[class_id]} {confidence:0.2f}"
+ for _, _, confidence, class_id, _, _
+ in detections]
+annotated_image = mask_annotator.annotate(scene=image.copy(), detections=detections)
+annotated_image = box_annotator.annotate(scene=annotated_image, detections=detections, labels=labels)
+
+# save the annotated grounded-sam image
+cv2.imwrite("ram_grounded_sam_auto_annotated_image.jpg", annotated_image)
diff --git a/automatic_label_tag2text_demo.py b/automatic_label_tag2text_demo.py
new file mode 100644
index 0000000000000000000000000000000000000000..671e81f7a5f67c612286f5af6b448035edb27a1f
--- /dev/null
+++ b/automatic_label_tag2text_demo.py
@@ -0,0 +1,352 @@
+import argparse
+import os
+import copy
+
+import numpy as np
+import json
+import torch
+import torchvision
+from PIL import Image, ImageDraw, ImageFont
+import litellm
+
+# Grounding DINO
+import GroundingDINO.groundingdino.datasets.transforms as T
+from GroundingDINO.groundingdino.models import build_model
+from GroundingDINO.groundingdino.util import box_ops
+from GroundingDINO.groundingdino.util.slconfig import SLConfig
+from GroundingDINO.groundingdino.util.utils import clean_state_dict, get_phrases_from_posmap
+
+# segment anything
+from segment_anything import build_sam, SamPredictor
+import cv2
+import numpy as np
+import matplotlib.pyplot as plt
+
+# Tag2Text
+from ram.models import tag2text_caption
+from ram import inference_tag2text
+import torchvision.transforms as TS
+
+# ChatGPT or nltk is required when using captions
+# import openai
+# import nltk
+
+def load_image(image_path):
+ # load image
+ image_pil = Image.open(image_path).convert("RGB") # load image
+
+ transform = T.Compose(
+ [
+ T.RandomResize([800], max_size=1333),
+ T.ToTensor(),
+ T.Normalize([0.485, 0.456, 0.406], [0.229, 0.224, 0.225]),
+ ]
+ )
+ image, _ = transform(image_pil, None) # 3, h, w
+ return image_pil, image
+
+
+def generate_caption(raw_image, device):
+ # unconditional image captioning
+ if device == "cuda":
+ inputs = processor(raw_image, return_tensors="pt").to("cuda", torch.float16)
+ else:
+ inputs = processor(raw_image, return_tensors="pt")
+ out = blip_model.generate(**inputs)
+ caption = processor.decode(out[0], skip_special_tokens=True)
+ return caption
+
+
+def generate_tags(caption, split=',', max_tokens=100, model="gpt-3.5-turbo"):
+ lemma = nltk.wordnet.WordNetLemmatizer()
+ if openai_key:
+ prompt = [
+ {
+ 'role': 'system',
+ 'content': 'Extract the unique nouns in the caption. Remove all the adjectives. ' + \
+ f'List the nouns in singular form. Split them by "{split} ". ' + \
+ f'Caption: {caption}.'
+ }
+ ]
+ response = litellm.completion(model=model, messages=prompt, temperature=0.6, max_tokens=max_tokens)
+ reply = response['choices'][0]['message']['content']
+ # sometimes return with "noun: xxx, xxx, xxx"
+ tags = reply.split(':')[-1].strip()
+ else:
+ nltk.download(['punkt', 'averaged_perceptron_tagger', 'wordnet'])
+ tags_list = [word for (word, pos) in nltk.pos_tag(nltk.word_tokenize(caption)) if pos[0] == 'N']
+ tags_lemma = [lemma.lemmatize(w) for w in tags_list]
+ tags = ', '.join(map(str, tags_lemma))
+ return tags
+
+
+def check_caption(caption, pred_phrases, max_tokens=100, model="gpt-3.5-turbo"):
+ object_list = [obj.split('(')[0] for obj in pred_phrases]
+ object_num = []
+ for obj in set(object_list):
+ object_num.append(f'{object_list.count(obj)} {obj}')
+ object_num = ', '.join(object_num)
+ print(f"Correct object number: {object_num}")
+
+ if openai_key:
+ prompt = [
+ {
+ 'role': 'system',
+ 'content': 'Revise the number in the caption if it is wrong. ' + \
+ f'Caption: {caption}. ' + \
+ f'True object number: {object_num}. ' + \
+ 'Only give the revised caption: '
+ }
+ ]
+ response = litellm.completion(model=model, messages=prompt, temperature=0.6, max_tokens=max_tokens)
+ reply = response['choices'][0]['message']['content']
+ # sometimes return with "Caption: xxx, xxx, xxx"
+ caption = reply.split(':')[-1].strip()
+ return caption
+
+
+def load_model(model_config_path, model_checkpoint_path, device):
+ args = SLConfig.fromfile(model_config_path)
+ args.device = device
+ model = build_model(args)
+ checkpoint = torch.load(model_checkpoint_path, map_location="cpu")
+ load_res = model.load_state_dict(clean_state_dict(checkpoint["model"]), strict=False)
+ print(load_res)
+ _ = model.eval()
+ return model
+
+
+def get_grounding_output(model, image, caption, box_threshold, text_threshold,device="cpu"):
+ caption = caption.lower()
+ caption = caption.strip()
+ if not caption.endswith("."):
+ caption = caption + "."
+ model = model.to(device)
+ image = image.to(device)
+ with torch.no_grad():
+ outputs = model(image[None], captions=[caption])
+ logits = outputs["pred_logits"].cpu().sigmoid()[0] # (nq, 256)
+ boxes = outputs["pred_boxes"].cpu()[0] # (nq, 4)
+ logits.shape[0]
+
+ # filter output
+ logits_filt = logits.clone()
+ boxes_filt = boxes.clone()
+ filt_mask = logits_filt.max(dim=1)[0] > box_threshold
+ logits_filt = logits_filt[filt_mask] # num_filt, 256
+ boxes_filt = boxes_filt[filt_mask] # num_filt, 4
+ logits_filt.shape[0]
+
+ # get phrase
+ tokenlizer = model.tokenizer
+ tokenized = tokenlizer(caption)
+ # build pred
+ pred_phrases = []
+ scores = []
+ for logit, box in zip(logits_filt, boxes_filt):
+ pred_phrase = get_phrases_from_posmap(logit > text_threshold, tokenized, tokenlizer)
+ pred_phrases.append(pred_phrase + f"({str(logit.max().item())[:4]})")
+ scores.append(logit.max().item())
+
+ return boxes_filt, torch.Tensor(scores), pred_phrases
+
+
+def show_mask(mask, ax, random_color=False):
+ if random_color:
+ color = np.concatenate([np.random.random(3), np.array([0.6])], axis=0)
+ else:
+ color = np.array([30/255, 144/255, 255/255, 0.6])
+ h, w = mask.shape[-2:]
+ mask_image = mask.reshape(h, w, 1) * color.reshape(1, 1, -1)
+ ax.imshow(mask_image)
+
+
+def show_box(box, ax, label):
+ x0, y0 = box[0], box[1]
+ w, h = box[2] - box[0], box[3] - box[1]
+ ax.add_patch(plt.Rectangle((x0, y0), w, h, edgecolor='green', facecolor=(0,0,0,0), lw=2))
+ ax.text(x0, y0, label)
+
+
+def save_mask_data(output_dir, caption, mask_list, box_list, label_list):
+ value = 0 # 0 for background
+
+ mask_img = torch.zeros(mask_list.shape[-2:])
+ for idx, mask in enumerate(mask_list):
+ mask_img[mask.cpu().numpy()[0] == True] = value + idx + 1
+ plt.figure(figsize=(10, 10))
+ plt.imshow(mask_img.numpy())
+ plt.axis('off')
+ plt.savefig(os.path.join(output_dir, 'mask.jpg'), bbox_inches="tight", dpi=300, pad_inches=0.0)
+
+ json_data = {
+ 'caption': caption,
+ 'mask':[{
+ 'value': value,
+ 'label': 'background'
+ }]
+ }
+ for label, box in zip(label_list, box_list):
+ value += 1
+ name, logit = label.split('(')
+ logit = logit[:-1] # the last is ')'
+ json_data['mask'].append({
+ 'value': value,
+ 'label': name,
+ 'logit': float(logit),
+ 'box': box.numpy().tolist(),
+ })
+ with open(os.path.join(output_dir, 'label.json'), 'w') as f:
+ json.dump(json_data, f)
+
+
+if __name__ == "__main__":
+
+ parser = argparse.ArgumentParser("Grounded-Segment-Anything Demo", add_help=True)
+ parser.add_argument("--config", type=str, required=True, help="path to config file")
+ parser.add_argument(
+ "--tag2text_checkpoint", type=str, required=True, help="path to checkpoint file"
+ )
+ parser.add_argument(
+ "--grounded_checkpoint", type=str, required=True, help="path to checkpoint file"
+ )
+ parser.add_argument(
+ "--sam_checkpoint", type=str, required=True, help="path to checkpoint file"
+ )
+ parser.add_argument("--input_image", type=str, required=True, help="path to image file")
+ parser.add_argument("--split", default=",", type=str, help="split for text prompt")
+ parser.add_argument("--openai_key", type=str, help="key for chatgpt")
+ parser.add_argument("--openai_proxy", default=None, type=str, help="proxy for chatgpt")
+ parser.add_argument(
+ "--output_dir", "-o", type=str, default="outputs", required=True, help="output directory"
+ )
+
+ parser.add_argument("--box_threshold", type=float, default=0.25, help="box threshold")
+ parser.add_argument("--text_threshold", type=float, default=0.2, help="text threshold")
+ parser.add_argument("--iou_threshold", type=float, default=0.5, help="iou threshold")
+
+ parser.add_argument("--device", type=str, default="cpu", help="running on cpu only!, default=False")
+ args = parser.parse_args()
+
+ # cfg
+ config_file = args.config # change the path of the model config file
+ tag2text_checkpoint = args.tag2text_checkpoint # change the path of the model
+ grounded_checkpoint = args.grounded_checkpoint # change the path of the model
+ sam_checkpoint = args.sam_checkpoint
+ image_path = args.input_image
+ split = args.split
+ openai_key = args.openai_key
+ openai_proxy = args.openai_proxy
+ output_dir = args.output_dir
+ box_threshold = args.box_threshold
+ text_threshold = args.text_threshold
+ iou_threshold = args.iou_threshold
+ device = args.device
+
+ # ChatGPT or nltk is required when using captions
+ # openai.api_key = openai_key
+ # if openai_proxy:
+ # openai.proxy = {"http": openai_proxy, "https": openai_proxy}
+
+ # make dir
+ os.makedirs(output_dir, exist_ok=True)
+ # load image
+ image_pil, image = load_image(image_path)
+ # load model
+ model = load_model(config_file, grounded_checkpoint, device=device)
+
+ # visualize raw image
+ image_pil.save(os.path.join(output_dir, "raw_image.jpg"))
+
+ # initialize Tag2Text
+ normalize = TS.Normalize(mean=[0.485, 0.456, 0.406],
+ std=[0.229, 0.224, 0.225])
+ transform = TS.Compose([
+ TS.Resize((384, 384)),
+ TS.ToTensor(), normalize
+ ])
+
+ # filter out attributes and action categories which are difficult to grounding
+ delete_tag_index = []
+ for i in range(3012, 3429):
+ delete_tag_index.append(i)
+
+ specified_tags='None'
+ # load model
+ tag2text_model = tag2text_caption(pretrained=tag2text_checkpoint,
+ image_size=384,
+ vit='swin_b',
+ delete_tag_index=delete_tag_index)
+ # threshold for tagging
+ # we reduce the threshold to obtain more tags
+ tag2text_model.threshold = 0.64
+ tag2text_model.eval()
+
+ tag2text_model = tag2text_model.to(device)
+ raw_image = image_pil.resize(
+ (384, 384))
+ raw_image = transform(raw_image).unsqueeze(0).to(device)
+
+ res = inference_tag2text(raw_image , tag2text_model, specified_tags)
+
+ # Currently ", " is better for detecting single tags
+ # while ". " is a little worse in some case
+ text_prompt=res[0].replace(' |', ',')
+ caption=res[2]
+
+ print(f"Caption: {caption}")
+ print(f"Tags: {text_prompt}")
+
+ # run grounding dino model
+ boxes_filt, scores, pred_phrases = get_grounding_output(
+ model, image, text_prompt, box_threshold, text_threshold, device=device
+ )
+
+ # initialize SAM
+ predictor = SamPredictor(build_sam(checkpoint=sam_checkpoint).to(device))
+ image = cv2.imread(image_path)
+ image = cv2.cvtColor(image, cv2.COLOR_BGR2RGB)
+ predictor.set_image(image)
+
+ size = image_pil.size
+ H, W = size[1], size[0]
+ for i in range(boxes_filt.size(0)):
+ boxes_filt[i] = boxes_filt[i] * torch.Tensor([W, H, W, H])
+ boxes_filt[i][:2] -= boxes_filt[i][2:] / 2
+ boxes_filt[i][2:] += boxes_filt[i][:2]
+
+ boxes_filt = boxes_filt.cpu()
+ # use NMS to handle overlapped boxes
+ print(f"Before NMS: {boxes_filt.shape[0]} boxes")
+ nms_idx = torchvision.ops.nms(boxes_filt, scores, iou_threshold).numpy().tolist()
+ boxes_filt = boxes_filt[nms_idx]
+ pred_phrases = [pred_phrases[idx] for idx in nms_idx]
+ print(f"After NMS: {boxes_filt.shape[0]} boxes")
+ caption = check_caption(caption, pred_phrases)
+ print(f"Revise caption with number: {caption}")
+
+ transformed_boxes = predictor.transform.apply_boxes_torch(boxes_filt, image.shape[:2]).to(device)
+
+ masks, _, _ = predictor.predict_torch(
+ point_coords = None,
+ point_labels = None,
+ boxes = transformed_boxes.to(device),
+ multimask_output = False,
+ )
+
+ # draw output image
+ plt.figure(figsize=(10, 10))
+ plt.imshow(image)
+ for mask in masks:
+ show_mask(mask.cpu().numpy(), plt.gca(), random_color=True)
+ for box, label in zip(boxes_filt, pred_phrases):
+ show_box(box.numpy(), plt.gca(), label)
+
+ plt.title('Tag2Text-Captioning: ' + caption + '\n' + 'Tag2Text-Tagging' + text_prompt + '\n')
+ plt.axis('off')
+ plt.savefig(
+ os.path.join(output_dir, "automatic_label_output.jpg"),
+ bbox_inches="tight", dpi=300, pad_inches=0.0
+ )
+
+ save_mask_data(output_dir, caption, masks, boxes_filt, pred_phrases)
diff --git a/chatbot.py b/chatbot.py
new file mode 100644
index 0000000000000000000000000000000000000000..cb1e2937e4b00c20038d90b9090142795de5be52
--- /dev/null
+++ b/chatbot.py
@@ -0,0 +1,1460 @@
+# coding: utf-8
+import os
+import gradio as gr
+import random
+import torch
+import cv2
+import re
+import uuid
+from PIL import Image, ImageDraw, ImageOps
+import math
+import numpy as np
+import argparse
+import inspect
+
+import shutil
+import torchvision
+import whisper
+import matplotlib.pyplot as plt
+from automatic_label_demo import load_model, load_image, get_grounding_output, show_box, show_mask, generate_tags, check_caption
+from grounding_dino_demo import plot_boxes_to_image
+from segment_anything import build_sam, SamAutomaticMaskGenerator, SamPredictor
+from segment_anything.utils.amg import remove_small_regions
+
+from transformers import CLIPSegProcessor, CLIPSegForImageSegmentation
+from transformers import pipeline, BlipProcessor, BlipForConditionalGeneration, BlipForQuestionAnswering
+from transformers import AutoImageProcessor, UperNetForSemanticSegmentation
+
+from diffusers import StableDiffusionPipeline, StableDiffusionInpaintPipeline, StableDiffusionInstructPix2PixPipeline
+from diffusers import EulerAncestralDiscreteScheduler
+from diffusers import StableDiffusionControlNetPipeline, ControlNetModel, UniPCMultistepScheduler
+from controlnet_aux import OpenposeDetector, MLSDdetector, HEDdetector
+
+from langchain.agents.initialize import initialize_agent
+from langchain.agents.tools import Tool
+from langchain.chains.conversation.memory import ConversationBufferMemory
+from langchain.llms.openai import OpenAI
+
+VISUAL_CHATGPT_PREFIX = """Visual ChatGPT is designed to be able to assist with a wide range of text and visual related tasks, from answering simple questions to providing in-depth explanations and discussions on a wide range of topics. Visual ChatGPT is able to generate human-like text based on the input it receives, allowing it to engage in natural-sounding conversations and provide responses that are coherent and relevant to the topic at hand.
+
+Visual ChatGPT is able to process and understand large amounts of text and images. As a language model, Visual ChatGPT can not directly read images, but it has a list of tools to finish different visual tasks. Each image will have a file name formed as "image/xxx.png", and Visual ChatGPT can invoke different tools to indirectly understand pictures. When talking about images, Visual ChatGPT is very strict to the file name and will never fabricate nonexistent files. When using tools to generate new image files, Visual ChatGPT is also known that the image may not be the same as the user's demand, and will use other visual question answering tools or description tools to observe the real image. Visual ChatGPT is able to use tools in a sequence, and is loyal to the tool observation outputs rather than faking the image content and image file name. It will remember to provide the file name from the last tool observation, if a new image is generated.
+
+Human may provide new figures to Visual ChatGPT with a description. The description helps Visual ChatGPT to understand this image, but Visual ChatGPT should use tools to finish following tasks, rather than directly imagine from the description.
+
+Overall, Visual ChatGPT is a powerful visual dialogue assistant tool that can help with a wide range of tasks and provide valuable insights and information on a wide range of topics.
+
+
+TOOLS:
+------
+
+Visual ChatGPT has access to the following tools:"""
+
+VISUAL_CHATGPT_FORMAT_INSTRUCTIONS = """To use a tool, please use the following format:
+
+```
+Thought: Do I need to use a tool? Yes
+Action: the action to take, should be one of [{tool_names}]
+Action Input: the input to the action
+Observation: the result of the action
+```
+
+When you have a response to say to the Human, or if you do not need to use a tool, you MUST use the format:
+
+```
+Thought: Do I need to use a tool? No
+{ai_prefix}: [your response here]
+```
+"""
+
+VISUAL_CHATGPT_SUFFIX = """You are very strict to the filename correctness and will never fake a file name if it does not exist.
+You will remember to provide the image file name loyally if it's provided in the last tool observation.
+
+Begin!
+
+Previous conversation history:
+{chat_history}
+
+New input: {input}
+Since Visual ChatGPT is a text language model, Visual ChatGPT must use tools to observe images rather than imagination.
+The thoughts and observations are only visible for Visual ChatGPT, Visual ChatGPT should remember to repeat important information in the final response for Human.
+Thought: Do I need to use a tool? {agent_scratchpad} Let's think step by step.
+"""
+
+VISUAL_CHATGPT_PREFIX_CN = """Visual ChatGPT 旨在能够协助完成范围广泛的文本和视觉相关任务,从回答简单的问题到提供对广泛主题的深入解释和讨论。 Visual ChatGPT 能够根据收到的输入生成类似人类的文本,使其能够进行听起来自然的对话,并提供连贯且与手头主题相关的响应。
+
+Visual ChatGPT 能够处理和理解大量文本和图像。作为一种语言模型,Visual ChatGPT 不能直接读取图像,但它有一系列工具来完成不同的视觉任务。每张图片都会有一个文件名,格式为“image/xxx.png”,Visual ChatGPT可以调用不同的工具来间接理解图片。在谈论图片时,Visual ChatGPT 对文件名的要求非常严格,绝不会伪造不存在的文件。在使用工具生成新的图像文件时,Visual ChatGPT也知道图像可能与用户需求不一样,会使用其他视觉问答工具或描述工具来观察真实图像。 Visual ChatGPT 能够按顺序使用工具,并且忠于工具观察输出,而不是伪造图像内容和图像文件名。如果生成新图像,它将记得提供上次工具观察的文件名。
+
+Human 可能会向 Visual ChatGPT 提供带有描述的新图形。描述帮助 Visual ChatGPT 理解这个图像,但 Visual ChatGPT 应该使用工具来完成以下任务,而不是直接从描述中想象。有些工具将会返回英文描述,但你对用户的聊天应当采用中文。
+
+总的来说,Visual ChatGPT 是一个强大的可视化对话辅助工具,可以帮助处理范围广泛的任务,并提供关于范围广泛的主题的有价值的见解和信息。
+
+工具列表:
+------
+
+Visual ChatGPT 可以使用这些工具:"""
+
+VISUAL_CHATGPT_FORMAT_INSTRUCTIONS_CN = """用户使用中文和你进行聊天,但是工具的参数应当使用英文。如果要调用工具,你必须遵循如下格式:
+
+```
+Thought: Do I need to use a tool? Yes
+Action: the action to take, should be one of [{tool_names}]
+Action Input: the input to the action
+Observation: the result of the action
+```
+
+当你不再需要继续调用工具,而是对观察结果进行总结回复时,你必须使用如下格式:
+
+
+```
+Thought: Do I need to use a tool? No
+{ai_prefix}: [your response here]
+```
+"""
+
+VISUAL_CHATGPT_SUFFIX_CN = """你对文件名的正确性非常严格,而且永远不会伪造不存在的文件。
+
+开始!
+
+因为Visual ChatGPT是一个文本语言模型,必须使用工具去观察图片而不是依靠想象。
+推理想法和观察结果只对Visual ChatGPT可见,需要记得在最终回复时把重要的信息重复给用户,你只能给用户返回中文句子。我们一步一步思考。在你使用工具时,工具的参数只能是英文。
+
+聊天历史:
+{chat_history}
+
+新输入: {input}
+Thought: Do I need to use a tool? {agent_scratchpad}
+"""
+
+os.makedirs('image', exist_ok=True)
+
+
+def seed_everything(seed):
+ random.seed(seed)
+ np.random.seed(seed)
+ torch.manual_seed(seed)
+ torch.cuda.manual_seed_all(seed)
+ return seed
+
+
+def prompts(name, description):
+ def decorator(func):
+ func.name = name
+ func.description = description
+ return func
+
+ return decorator
+
+
+def blend_gt2pt(old_image, new_image, sigma=0.15, steps=100):
+ new_size = new_image.size
+ old_size = old_image.size
+ easy_img = np.array(new_image)
+ gt_img_array = np.array(old_image)
+ pos_w = (new_size[0] - old_size[0]) // 2
+ pos_h = (new_size[1] - old_size[1]) // 2
+
+ kernel_h = cv2.getGaussianKernel(old_size[1], old_size[1] * sigma)
+ kernel_w = cv2.getGaussianKernel(old_size[0], old_size[0] * sigma)
+ kernel = np.multiply(kernel_h, np.transpose(kernel_w))
+
+ kernel[steps:-steps, steps:-steps] = 1
+ kernel[:steps, :steps] = kernel[:steps, :steps] / kernel[steps - 1, steps - 1]
+ kernel[:steps, -steps:] = kernel[:steps, -steps:] / kernel[steps - 1, -(steps)]
+ kernel[-steps:, :steps] = kernel[-steps:, :steps] / kernel[-steps, steps - 1]
+ kernel[-steps:, -steps:] = kernel[-steps:, -steps:] / kernel[-steps, -steps]
+ kernel = np.expand_dims(kernel, 2)
+ kernel = np.repeat(kernel, 3, 2)
+
+ weight = np.linspace(0, 1, steps)
+ top = np.expand_dims(weight, 1)
+ top = np.repeat(top, old_size[0] - 2 * steps, 1)
+ top = np.expand_dims(top, 2)
+ top = np.repeat(top, 3, 2)
+
+ weight = np.linspace(1, 0, steps)
+ down = np.expand_dims(weight, 1)
+ down = np.repeat(down, old_size[0] - 2 * steps, 1)
+ down = np.expand_dims(down, 2)
+ down = np.repeat(down, 3, 2)
+
+ weight = np.linspace(0, 1, steps)
+ left = np.expand_dims(weight, 0)
+ left = np.repeat(left, old_size[1] - 2 * steps, 0)
+ left = np.expand_dims(left, 2)
+ left = np.repeat(left, 3, 2)
+
+ weight = np.linspace(1, 0, steps)
+ right = np.expand_dims(weight, 0)
+ right = np.repeat(right, old_size[1] - 2 * steps, 0)
+ right = np.expand_dims(right, 2)
+ right = np.repeat(right, 3, 2)
+
+ kernel[:steps, steps:-steps] = top
+ kernel[-steps:, steps:-steps] = down
+ kernel[steps:-steps, :steps] = left
+ kernel[steps:-steps, -steps:] = right
+
+ pt_gt_img = easy_img[pos_h:pos_h + old_size[1], pos_w:pos_w + old_size[0]]
+ gaussian_gt_img = kernel * gt_img_array + (1 - kernel) * pt_gt_img # gt img with blur img
+ gaussian_gt_img = gaussian_gt_img.astype(np.int64)
+ easy_img[pos_h:pos_h + old_size[1], pos_w:pos_w + old_size[0]] = gaussian_gt_img
+ gaussian_img = Image.fromarray(easy_img)
+ return gaussian_img
+
+
+def cut_dialogue_history(history_memory, keep_last_n_words=500):
+ if history_memory is None or len(history_memory) == 0:
+ return history_memory
+ tokens = history_memory.split()
+ n_tokens = len(tokens)
+ print(f"history_memory:{history_memory}, n_tokens: {n_tokens}")
+ if n_tokens < keep_last_n_words:
+ return history_memory
+ paragraphs = history_memory.split('\n')
+ last_n_tokens = n_tokens
+ while last_n_tokens >= keep_last_n_words:
+ last_n_tokens -= len(paragraphs[0].split(' '))
+ paragraphs = paragraphs[1:]
+ return '\n' + '\n'.join(paragraphs)
+
+
+def get_new_image_name(org_img_name, func_name="update"):
+ head_tail = os.path.split(org_img_name)
+ head = head_tail[0]
+ tail = head_tail[1]
+ name_split = tail.split('.')[0].split('_')
+ this_new_uuid = str(uuid.uuid4())[:4]
+ if len(name_split) == 1:
+ most_org_file_name = name_split[0]
+ else:
+ assert len(name_split) == 4
+ most_org_file_name = name_split[3]
+ recent_prev_file_name = name_split[0]
+ new_file_name = f'{this_new_uuid}_{func_name}_{recent_prev_file_name}_{most_org_file_name}.png'
+ return os.path.join(head, new_file_name)
+
+
+
+class MaskFormer:
+ def __init__(self, device):
+ print(f"Initializing MaskFormer to {device}")
+ self.device = device
+ self.processor = CLIPSegProcessor.from_pretrained("CIDAS/clipseg-rd64-refined")
+ self.model = CLIPSegForImageSegmentation.from_pretrained("CIDAS/clipseg-rd64-refined").to(device)
+
+ def inference(self, image_path, text):
+ threshold = 0.5
+ min_area = 0.02
+ padding = 20
+ original_image = Image.open(image_path)
+ image = original_image.resize((512, 512))
+ inputs = self.processor(text=text, images=image, padding="max_length", return_tensors="pt").to(self.device)
+ with torch.no_grad():
+ outputs = self.model(**inputs)
+ mask = torch.sigmoid(outputs[0]).squeeze().cpu().numpy() > threshold
+ area_ratio = len(np.argwhere(mask)) / (mask.shape[0] * mask.shape[1])
+ if area_ratio < min_area:
+ return None
+ true_indices = np.argwhere(mask)
+ mask_array = np.zeros_like(mask, dtype=bool)
+ for idx in true_indices:
+ padded_slice = tuple(slice(max(0, i - padding), i + padding + 1) for i in idx)
+ mask_array[padded_slice] = True
+ visual_mask = (mask_array * 255).astype(np.uint8)
+ image_mask = Image.fromarray(visual_mask)
+ return image_mask.resize(original_image.size)
+
+
+class ImageEditing:
+ def __init__(self, device):
+ print(f"Initializing ImageEditing to {device}")
+ self.device = device
+ self.mask_former = MaskFormer(device=self.device)
+ self.revision = 'fp16' if 'cuda' in device else None
+ self.torch_dtype = torch.float16 if 'cuda' in device else torch.float32
+ self.inpaint = StableDiffusionInpaintPipeline.from_pretrained(
+ "runwayml/stable-diffusion-inpainting", revision=self.revision, torch_dtype=self.torch_dtype).to(device)
+
+ @prompts(name="Replace Something From The Photo",
+ description="useful when you want to replace an object from the object description or "
+ "location with another object from its description. "
+ "The input to this tool should be a comma separated string of three, "
+ "representing the image_path, the object to be replaced, the object to be replaced with ")
+ def inference_replace(self, inputs):
+ image_path, to_be_replaced_txt, replace_with_txt = inputs.split(",")
+ original_image = Image.open(image_path)
+ original_size = original_image.size
+ mask_image = self.mask_former.inference(image_path, to_be_replaced_txt)
+ updated_image = self.inpaint(prompt=replace_with_txt, image=original_image.resize((512, 512)),
+ mask_image=mask_image.resize((512, 512))).images[0]
+ updated_image_path = get_new_image_name(image_path, func_name="replace-something")
+ updated_image = updated_image.resize(original_size)
+ updated_image.save(updated_image_path)
+ print(
+ f"\nProcessed ImageEditing, Input Image: {image_path}, Replace {to_be_replaced_txt} to {replace_with_txt}, "
+ f"Output Image: {updated_image_path}")
+ return updated_image_path
+
+
+class InstructPix2Pix:
+ def __init__(self, device):
+ print(f"Initializing InstructPix2Pix to {device}")
+ self.device = device
+ self.torch_dtype = torch.float16 if 'cuda' in device else torch.float32
+ self.pipe = StableDiffusionInstructPix2PixPipeline.from_pretrained("timbrooks/instruct-pix2pix",
+ safety_checker=None,
+ torch_dtype=self.torch_dtype).to(device)
+ self.pipe.scheduler = EulerAncestralDiscreteScheduler.from_config(self.pipe.scheduler.config)
+
+ @prompts(name="Instruct Image Using Text",
+ description="useful when you want to the style of the image to be like the text. "
+ "like: make it look like a painting. or make it like a robot. "
+ "The input to this tool should be a comma separated string of two, "
+ "representing the image_path and the text. ")
+ def inference(self, inputs):
+ """Change style of image."""
+ print("===>Starting InstructPix2Pix Inference")
+ image_path, text = inputs.split(",")[0], ','.join(inputs.split(',')[1:])
+ original_image = Image.open(image_path)
+ image = self.pipe(text, image=original_image, num_inference_steps=40, image_guidance_scale=1.2).images[0]
+ updated_image_path = get_new_image_name(image_path, func_name="pix2pix")
+ image.save(updated_image_path)
+ print(f"\nProcessed InstructPix2Pix, Input Image: {image_path}, Instruct Text: {text}, "
+ f"Output Image: {updated_image_path}")
+ return updated_image_path
+
+
+class Text2Image:
+ def __init__(self, device):
+ print(f"Initializing Text2Image to {device}")
+ self.device = device
+ self.torch_dtype = torch.float16 if 'cuda' in device else torch.float32
+ self.pipe = StableDiffusionPipeline.from_pretrained("runwayml/stable-diffusion-v1-5",
+ torch_dtype=self.torch_dtype)
+ self.pipe.to(device)
+ self.a_prompt = 'best quality, extremely detailed'
+ self.n_prompt = 'longbody, lowres, bad anatomy, bad hands, missing fingers, extra digit, ' \
+ 'fewer digits, cropped, worst quality, low quality'
+
+ @prompts(name="Generate Image From User Input Text",
+ description="useful when you want to generate an image from a user input text and save it to a file. "
+ "like: generate an image of an object or something, or generate an image that includes some objects. "
+ "The input to this tool should be a string, representing the text used to generate image. ")
+ def inference(self, text):
+ image_filename = os.path.join('image', f"{str(uuid.uuid4())[:8]}.png")
+ prompt = text + ', ' + self.a_prompt
+ image = self.pipe(prompt, negative_prompt=self.n_prompt).images[0]
+ image.save(image_filename)
+ print(
+ f"\nProcessed Text2Image, Input Text: {text}, Output Image: {image_filename}")
+ return image_filename
+
+
+class ImageCaptioning:
+ def __init__(self, device):
+ print(f"Initializing ImageCaptioning to {device}")
+ self.device = device
+ self.torch_dtype = torch.float16 if 'cuda' in device else torch.float32
+ self.processor = BlipProcessor.from_pretrained("Salesforce/blip-image-captioning-base")
+ self.model = BlipForConditionalGeneration.from_pretrained(
+ "Salesforce/blip-image-captioning-base", torch_dtype=self.torch_dtype).to(self.device)
+
+ @prompts(name="Get Photo Description",
+ description="useful when you want to know what is inside the photo. receives image_path as input. "
+ "The input to this tool should be a string, representing the image_path. ")
+ def inference(self, image_path):
+ inputs = self.processor(Image.open(image_path), return_tensors="pt").to(self.device, self.torch_dtype)
+ out = self.model.generate(**inputs)
+ captions = self.processor.decode(out[0], skip_special_tokens=True)
+ print(f"\nProcessed ImageCaptioning, Input Image: {image_path}, Output Text: {captions}")
+ return captions
+
+
+class Image2Canny:
+ def __init__(self, device):
+ print("Initializing Image2Canny")
+ self.low_threshold = 100
+ self.high_threshold = 200
+
+ @prompts(name="Edge Detection On Image",
+ description="useful when you want to detect the edge of the image. "
+ "like: detect the edges of this image, or canny detection on image, "
+ "or perform edge detection on this image, or detect the canny image of this image. "
+ "The input to this tool should be a string, representing the image_path")
+ def inference(self, inputs):
+ image = Image.open(inputs)
+ image = np.array(image)
+ canny = cv2.Canny(image, self.low_threshold, self.high_threshold)
+ canny = canny[:, :, None]
+ canny = np.concatenate([canny, canny, canny], axis=2)
+ canny = Image.fromarray(canny)
+ updated_image_path = get_new_image_name(inputs, func_name="edge")
+ canny.save(updated_image_path)
+ print(f"\nProcessed Image2Canny, Input Image: {inputs}, Output Text: {updated_image_path}")
+ return updated_image_path
+
+
+class CannyText2Image:
+ def __init__(self, device):
+ print(f"Initializing CannyText2Image to {device}")
+ self.torch_dtype = torch.float16 if 'cuda' in device else torch.float32
+ self.controlnet = ControlNetModel.from_pretrained("fusing/stable-diffusion-v1-5-controlnet-canny",
+ torch_dtype=self.torch_dtype)
+ self.pipe = StableDiffusionControlNetPipeline.from_pretrained(
+ "runwayml/stable-diffusion-v1-5", controlnet=self.controlnet, safety_checker=None,
+ torch_dtype=self.torch_dtype)
+ self.pipe.scheduler = UniPCMultistepScheduler.from_config(self.pipe.scheduler.config)
+ self.pipe.to(device)
+ self.seed = -1
+ self.a_prompt = 'best quality, extremely detailed'
+ self.n_prompt = 'longbody, lowres, bad anatomy, bad hands, missing fingers, extra digit, ' \
+ 'fewer digits, cropped, worst quality, low quality'
+
+ @prompts(name="Generate Image Condition On Canny Image",
+ description="useful when you want to generate a new real image from both the user description and a canny image."
+ " like: generate a real image of a object or something from this canny image,"
+ " or generate a new real image of a object or something from this edge image. "
+ "The input to this tool should be a comma separated string of two, "
+ "representing the image_path and the user description. ")
+ def inference(self, inputs):
+ image_path, instruct_text = inputs.split(",")[0], ','.join(inputs.split(',')[1:])
+ image = Image.open(image_path)
+ self.seed = random.randint(0, 65535)
+ seed_everything(self.seed)
+ prompt = f'{instruct_text}, {self.a_prompt}'
+ image = self.pipe(prompt, image, num_inference_steps=20, eta=0.0, negative_prompt=self.n_prompt,
+ guidance_scale=9.0).images[0]
+ updated_image_path = get_new_image_name(image_path, func_name="canny2image")
+ image.save(updated_image_path)
+ print(f"\nProcessed CannyText2Image, Input Canny: {image_path}, Input Text: {instruct_text}, "
+ f"Output Text: {updated_image_path}")
+ return updated_image_path
+
+
+class Image2Line:
+ def __init__(self, device):
+ print("Initializing Image2Line")
+ self.detector = MLSDdetector.from_pretrained('lllyasviel/ControlNet')
+
+ @prompts(name="Line Detection On Image",
+ description="useful when you want to detect the straight line of the image. "
+ "like: detect the straight lines of this image, or straight line detection on image, "
+ "or perform straight line detection on this image, or detect the straight line image of this image. "
+ "The input to this tool should be a string, representing the image_path")
+ def inference(self, inputs):
+ image = Image.open(inputs)
+ mlsd = self.detector(image)
+ updated_image_path = get_new_image_name(inputs, func_name="line-of")
+ mlsd.save(updated_image_path)
+ print(f"\nProcessed Image2Line, Input Image: {inputs}, Output Line: {updated_image_path}")
+ return updated_image_path
+
+
+class LineText2Image:
+ def __init__(self, device):
+ print(f"Initializing LineText2Image to {device}")
+ self.torch_dtype = torch.float16 if 'cuda' in device else torch.float32
+ self.controlnet = ControlNetModel.from_pretrained("fusing/stable-diffusion-v1-5-controlnet-mlsd",
+ torch_dtype=self.torch_dtype)
+ self.pipe = StableDiffusionControlNetPipeline.from_pretrained(
+ "runwayml/stable-diffusion-v1-5", controlnet=self.controlnet, safety_checker=None,
+ torch_dtype=self.torch_dtype
+ )
+ self.pipe.scheduler = UniPCMultistepScheduler.from_config(self.pipe.scheduler.config)
+ self.pipe.to(device)
+ self.seed = -1
+ self.a_prompt = 'best quality, extremely detailed'
+ self.n_prompt = 'longbody, lowres, bad anatomy, bad hands, missing fingers, extra digit, ' \
+ 'fewer digits, cropped, worst quality, low quality'
+
+ @prompts(name="Generate Image Condition On Line Image",
+ description="useful when you want to generate a new real image from both the user description "
+ "and a straight line image. "
+ "like: generate a real image of a object or something from this straight line image, "
+ "or generate a new real image of a object or something from this straight lines. "
+ "The input to this tool should be a comma separated string of two, "
+ "representing the image_path and the user description. ")
+ def inference(self, inputs):
+ image_path, instruct_text = inputs.split(",")[0], ','.join(inputs.split(',')[1:])
+ image = Image.open(image_path)
+ self.seed = random.randint(0, 65535)
+ seed_everything(self.seed)
+ prompt = f'{instruct_text}, {self.a_prompt}'
+ image = self.pipe(prompt, image, num_inference_steps=20, eta=0.0, negative_prompt=self.n_prompt,
+ guidance_scale=9.0).images[0]
+ updated_image_path = get_new_image_name(image_path, func_name="line2image")
+ image.save(updated_image_path)
+ print(f"\nProcessed LineText2Image, Input Line: {image_path}, Input Text: {instruct_text}, "
+ f"Output Text: {updated_image_path}")
+ return updated_image_path
+
+
+class Image2Hed:
+ def __init__(self, device):
+ print("Initializing Image2Hed")
+ self.detector = HEDdetector.from_pretrained('lllyasviel/ControlNet')
+
+ @prompts(name="Hed Detection On Image",
+ description="useful when you want to detect the soft hed boundary of the image. "
+ "like: detect the soft hed boundary of this image, or hed boundary detection on image, "
+ "or perform hed boundary detection on this image, or detect soft hed boundary image of this image. "
+ "The input to this tool should be a string, representing the image_path")
+ def inference(self, inputs):
+ image = Image.open(inputs)
+ hed = self.detector(image)
+ updated_image_path = get_new_image_name(inputs, func_name="hed-boundary")
+ hed.save(updated_image_path)
+ print(f"\nProcessed Image2Hed, Input Image: {inputs}, Output Hed: {updated_image_path}")
+ return updated_image_path
+
+
+class HedText2Image:
+ def __init__(self, device):
+ print(f"Initializing HedText2Image to {device}")
+ self.torch_dtype = torch.float16 if 'cuda' in device else torch.float32
+ self.controlnet = ControlNetModel.from_pretrained("fusing/stable-diffusion-v1-5-controlnet-hed",
+ torch_dtype=self.torch_dtype)
+ self.pipe = StableDiffusionControlNetPipeline.from_pretrained(
+ "runwayml/stable-diffusion-v1-5", controlnet=self.controlnet, safety_checker=None,
+ torch_dtype=self.torch_dtype
+ )
+ self.pipe.scheduler = UniPCMultistepScheduler.from_config(self.pipe.scheduler.config)
+ self.pipe.to(device)
+ self.seed = -1
+ self.a_prompt = 'best quality, extremely detailed'
+ self.n_prompt = 'longbody, lowres, bad anatomy, bad hands, missing fingers, extra digit, ' \
+ 'fewer digits, cropped, worst quality, low quality'
+
+ @prompts(name="Generate Image Condition On Soft Hed Boundary Image",
+ description="useful when you want to generate a new real image from both the user description "
+ "and a soft hed boundary image. "
+ "like: generate a real image of a object or something from this soft hed boundary image, "
+ "or generate a new real image of a object or something from this hed boundary. "
+ "The input to this tool should be a comma separated string of two, "
+ "representing the image_path and the user description")
+ def inference(self, inputs):
+ image_path, instruct_text = inputs.split(",")[0], ','.join(inputs.split(',')[1:])
+ image = Image.open(image_path)
+ self.seed = random.randint(0, 65535)
+ seed_everything(self.seed)
+ prompt = f'{instruct_text}, {self.a_prompt}'
+ image = self.pipe(prompt, image, num_inference_steps=20, eta=0.0, negative_prompt=self.n_prompt,
+ guidance_scale=9.0).images[0]
+ updated_image_path = get_new_image_name(image_path, func_name="hed2image")
+ image.save(updated_image_path)
+ print(f"\nProcessed HedText2Image, Input Hed: {image_path}, Input Text: {instruct_text}, "
+ f"Output Image: {updated_image_path}")
+ return updated_image_path
+
+
+class Image2Scribble:
+ def __init__(self, device):
+ print("Initializing Image2Scribble")
+ self.detector = HEDdetector.from_pretrained('lllyasviel/ControlNet')
+
+ @prompts(name="Sketch Detection On Image",
+ description="useful when you want to generate a scribble of the image. "
+ "like: generate a scribble of this image, or generate a sketch from this image, "
+ "detect the sketch from this image. "
+ "The input to this tool should be a string, representing the image_path")
+ def inference(self, inputs):
+ image = Image.open(inputs)
+ scribble = self.detector(image, scribble=True)
+ updated_image_path = get_new_image_name(inputs, func_name="scribble")
+ scribble.save(updated_image_path)
+ print(f"\nProcessed Image2Scribble, Input Image: {inputs}, Output Scribble: {updated_image_path}")
+ return updated_image_path
+
+
+class ScribbleText2Image:
+ def __init__(self, device):
+ print(f"Initializing ScribbleText2Image to {device}")
+ self.torch_dtype = torch.float16 if 'cuda' in device else torch.float32
+ self.controlnet = ControlNetModel.from_pretrained("fusing/stable-diffusion-v1-5-controlnet-scribble",
+ torch_dtype=self.torch_dtype)
+ self.pipe = StableDiffusionControlNetPipeline.from_pretrained(
+ "runwayml/stable-diffusion-v1-5", controlnet=self.controlnet, safety_checker=None,
+ torch_dtype=self.torch_dtype
+ )
+ self.pipe.scheduler = UniPCMultistepScheduler.from_config(self.pipe.scheduler.config)
+ self.pipe.to(device)
+ self.seed = -1
+ self.a_prompt = 'best quality, extremely detailed'
+ self.n_prompt = 'longbody, lowres, bad anatomy, bad hands, missing fingers, extra digit, ' \
+ 'fewer digits, cropped, worst quality, low quality'
+
+ @prompts(name="Generate Image Condition On Sketch Image",
+ description="useful when you want to generate a new real image from both the user description and "
+ "a scribble image or a sketch image. "
+ "The input to this tool should be a comma separated string of two, "
+ "representing the image_path and the user description")
+ def inference(self, inputs):
+ image_path, instruct_text = inputs.split(",")[0], ','.join(inputs.split(',')[1:])
+ image = Image.open(image_path)
+ self.seed = random.randint(0, 65535)
+ seed_everything(self.seed)
+ prompt = f'{instruct_text}, {self.a_prompt}'
+ image = self.pipe(prompt, image, num_inference_steps=20, eta=0.0, negative_prompt=self.n_prompt,
+ guidance_scale=9.0).images[0]
+ updated_image_path = get_new_image_name(image_path, func_name="scribble2image")
+ image.save(updated_image_path)
+ print(f"\nProcessed ScribbleText2Image, Input Scribble: {image_path}, Input Text: {instruct_text}, "
+ f"Output Image: {updated_image_path}")
+ return updated_image_path
+
+
+class Image2Pose:
+ def __init__(self, device):
+ print("Initializing Image2Pose")
+ self.detector = OpenposeDetector.from_pretrained('lllyasviel/ControlNet')
+
+ @prompts(name="Pose Detection On Image",
+ description="useful when you want to detect the human pose of the image. "
+ "like: generate human poses of this image, or generate a pose image from this image. "
+ "The input to this tool should be a string, representing the image_path")
+ def inference(self, inputs):
+ image = Image.open(inputs)
+ pose = self.detector(image)
+ updated_image_path = get_new_image_name(inputs, func_name="human-pose")
+ pose.save(updated_image_path)
+ print(f"\nProcessed Image2Pose, Input Image: {inputs}, Output Pose: {updated_image_path}")
+ return updated_image_path
+
+
+class PoseText2Image:
+ def __init__(self, device):
+ print(f"Initializing PoseText2Image to {device}")
+ self.torch_dtype = torch.float16 if 'cuda' in device else torch.float32
+ self.controlnet = ControlNetModel.from_pretrained("fusing/stable-diffusion-v1-5-controlnet-openpose",
+ torch_dtype=self.torch_dtype)
+ self.pipe = StableDiffusionControlNetPipeline.from_pretrained(
+ "runwayml/stable-diffusion-v1-5", controlnet=self.controlnet, safety_checker=None,
+ torch_dtype=self.torch_dtype)
+ self.pipe.scheduler = UniPCMultistepScheduler.from_config(self.pipe.scheduler.config)
+ self.pipe.to(device)
+ self.num_inference_steps = 20
+ self.seed = -1
+ self.unconditional_guidance_scale = 9.0
+ self.a_prompt = 'best quality, extremely detailed'
+ self.n_prompt = 'longbody, lowres, bad anatomy, bad hands, missing fingers, extra digit,' \
+ ' fewer digits, cropped, worst quality, low quality'
+
+ @prompts(name="Generate Image Condition On Pose Image",
+ description="useful when you want to generate a new real image from both the user description "
+ "and a human pose image. "
+ "like: generate a real image of a human from this human pose image, "
+ "or generate a new real image of a human from this pose. "
+ "The input to this tool should be a comma separated string of two, "
+ "representing the image_path and the user description")
+ def inference(self, inputs):
+ image_path, instruct_text = inputs.split(",")[0], ','.join(inputs.split(',')[1:])
+ image = Image.open(image_path)
+ self.seed = random.randint(0, 65535)
+ seed_everything(self.seed)
+ prompt = f'{instruct_text}, {self.a_prompt}'
+ image = self.pipe(prompt, image, num_inference_steps=20, eta=0.0, negative_prompt=self.n_prompt,
+ guidance_scale=9.0).images[0]
+ updated_image_path = get_new_image_name(image_path, func_name="pose2image")
+ image.save(updated_image_path)
+ print(f"\nProcessed PoseText2Image, Input Pose: {image_path}, Input Text: {instruct_text}, "
+ f"Output Image: {updated_image_path}")
+ return updated_image_path
+
+
+class Image2Seg:
+ def __init__(self, device):
+ print("Initializing Image2Seg")
+ self.image_processor = AutoImageProcessor.from_pretrained("openmmlab/upernet-convnext-small")
+ self.image_segmentor = UperNetForSemanticSegmentation.from_pretrained("openmmlab/upernet-convnext-small")
+ self.ade_palette = [[120, 120, 120], [180, 120, 120], [6, 230, 230], [80, 50, 50],
+ [4, 200, 3], [120, 120, 80], [140, 140, 140], [204, 5, 255],
+ [230, 230, 230], [4, 250, 7], [224, 5, 255], [235, 255, 7],
+ [150, 5, 61], [120, 120, 70], [8, 255, 51], [255, 6, 82],
+ [143, 255, 140], [204, 255, 4], [255, 51, 7], [204, 70, 3],
+ [0, 102, 200], [61, 230, 250], [255, 6, 51], [11, 102, 255],
+ [255, 7, 71], [255, 9, 224], [9, 7, 230], [220, 220, 220],
+ [255, 9, 92], [112, 9, 255], [8, 255, 214], [7, 255, 224],
+ [255, 184, 6], [10, 255, 71], [255, 41, 10], [7, 255, 255],
+ [224, 255, 8], [102, 8, 255], [255, 61, 6], [255, 194, 7],
+ [255, 122, 8], [0, 255, 20], [255, 8, 41], [255, 5, 153],
+ [6, 51, 255], [235, 12, 255], [160, 150, 20], [0, 163, 255],
+ [140, 140, 140], [250, 10, 15], [20, 255, 0], [31, 255, 0],
+ [255, 31, 0], [255, 224, 0], [153, 255, 0], [0, 0, 255],
+ [255, 71, 0], [0, 235, 255], [0, 173, 255], [31, 0, 255],
+ [11, 200, 200], [255, 82, 0], [0, 255, 245], [0, 61, 255],
+ [0, 255, 112], [0, 255, 133], [255, 0, 0], [255, 163, 0],
+ [255, 102, 0], [194, 255, 0], [0, 143, 255], [51, 255, 0],
+ [0, 82, 255], [0, 255, 41], [0, 255, 173], [10, 0, 255],
+ [173, 255, 0], [0, 255, 153], [255, 92, 0], [255, 0, 255],
+ [255, 0, 245], [255, 0, 102], [255, 173, 0], [255, 0, 20],
+ [255, 184, 184], [0, 31, 255], [0, 255, 61], [0, 71, 255],
+ [255, 0, 204], [0, 255, 194], [0, 255, 82], [0, 10, 255],
+ [0, 112, 255], [51, 0, 255], [0, 194, 255], [0, 122, 255],
+ [0, 255, 163], [255, 153, 0], [0, 255, 10], [255, 112, 0],
+ [143, 255, 0], [82, 0, 255], [163, 255, 0], [255, 235, 0],
+ [8, 184, 170], [133, 0, 255], [0, 255, 92], [184, 0, 255],
+ [255, 0, 31], [0, 184, 255], [0, 214, 255], [255, 0, 112],
+ [92, 255, 0], [0, 224, 255], [112, 224, 255], [70, 184, 160],
+ [163, 0, 255], [153, 0, 255], [71, 255, 0], [255, 0, 163],
+ [255, 204, 0], [255, 0, 143], [0, 255, 235], [133, 255, 0],
+ [255, 0, 235], [245, 0, 255], [255, 0, 122], [255, 245, 0],
+ [10, 190, 212], [214, 255, 0], [0, 204, 255], [20, 0, 255],
+ [255, 255, 0], [0, 153, 255], [0, 41, 255], [0, 255, 204],
+ [41, 0, 255], [41, 255, 0], [173, 0, 255], [0, 245, 255],
+ [71, 0, 255], [122, 0, 255], [0, 255, 184], [0, 92, 255],
+ [184, 255, 0], [0, 133, 255], [255, 214, 0], [25, 194, 194],
+ [102, 255, 0], [92, 0, 255]]
+
+ @prompts(name="Segmentation On Image",
+ description="useful when you want to detect segmentations of the image. "
+ "like: segment this image, or generate segmentations on this image, "
+ "or perform segmentation on this image. "
+ "The input to this tool should be a string, representing the image_path")
+ def inference(self, inputs):
+ image = Image.open(inputs)
+ pixel_values = self.image_processor(image, return_tensors="pt").pixel_values
+ with torch.no_grad():
+ outputs = self.image_segmentor(pixel_values)
+ seg = self.image_processor.post_process_semantic_segmentation(outputs, target_sizes=[image.size[::-1]])[0]
+ color_seg = np.zeros((seg.shape[0], seg.shape[1], 3), dtype=np.uint8) # height, width, 3
+ palette = np.array(self.ade_palette)
+ for label, color in enumerate(palette):
+ color_seg[seg == label, :] = color
+ color_seg = color_seg.astype(np.uint8)
+ segmentation = Image.fromarray(color_seg)
+ updated_image_path = get_new_image_name(inputs, func_name="segmentation")
+ segmentation.save(updated_image_path)
+ print(f"\nProcessed Image2Seg, Input Image: {inputs}, Output Pose: {updated_image_path}")
+ return updated_image_path
+
+
+class SegText2Image:
+ def __init__(self, device):
+ print(f"Initializing SegText2Image to {device}")
+ self.torch_dtype = torch.float16 if 'cuda' in device else torch.float32
+ self.controlnet = ControlNetModel.from_pretrained("fusing/stable-diffusion-v1-5-controlnet-seg",
+ torch_dtype=self.torch_dtype)
+ self.pipe = StableDiffusionControlNetPipeline.from_pretrained(
+ "runwayml/stable-diffusion-v1-5", controlnet=self.controlnet, safety_checker=None,
+ torch_dtype=self.torch_dtype)
+ self.pipe.scheduler = UniPCMultistepScheduler.from_config(self.pipe.scheduler.config)
+ self.pipe.to(device)
+ self.seed = -1
+ self.a_prompt = 'best quality, extremely detailed'
+ self.n_prompt = 'longbody, lowres, bad anatomy, bad hands, missing fingers, extra digit,' \
+ ' fewer digits, cropped, worst quality, low quality'
+
+ @prompts(name="Generate Image Condition On Segmentations",
+ description="useful when you want to generate a new real image from both the user description and segmentations. "
+ "like: generate a real image of a object or something from this segmentation image, "
+ "or generate a new real image of a object or something from these segmentations. "
+ "The input to this tool should be a comma separated string of two, "
+ "representing the image_path and the user description")
+ def inference(self, inputs):
+ image_path, instruct_text = inputs.split(",")[0], ','.join(inputs.split(',')[1:])
+ image = Image.open(image_path)
+ self.seed = random.randint(0, 65535)
+ seed_everything(self.seed)
+ prompt = f'{instruct_text}, {self.a_prompt}'
+ image = self.pipe(prompt, image, num_inference_steps=20, eta=0.0, negative_prompt=self.n_prompt,
+ guidance_scale=9.0).images[0]
+ updated_image_path = get_new_image_name(image_path, func_name="segment2image")
+ image.save(updated_image_path)
+ print(f"\nProcessed SegText2Image, Input Seg: {image_path}, Input Text: {instruct_text}, "
+ f"Output Image: {updated_image_path}")
+ return updated_image_path
+
+
+class Image2Depth:
+ def __init__(self, device):
+ print("Initializing Image2Depth")
+ self.depth_estimator = pipeline('depth-estimation')
+
+ @prompts(name="Predict Depth On Image",
+ description="useful when you want to detect depth of the image. like: generate the depth from this image, "
+ "or detect the depth map on this image, or predict the depth for this image. "
+ "The input to this tool should be a string, representing the image_path")
+ def inference(self, inputs):
+ image = Image.open(inputs)
+ depth = self.depth_estimator(image)['depth']
+ depth = np.array(depth)
+ depth = depth[:, :, None]
+ depth = np.concatenate([depth, depth, depth], axis=2)
+ depth = Image.fromarray(depth)
+ updated_image_path = get_new_image_name(inputs, func_name="depth")
+ depth.save(updated_image_path)
+ print(f"\nProcessed Image2Depth, Input Image: {inputs}, Output Depth: {updated_image_path}")
+ return updated_image_path
+
+
+class DepthText2Image:
+ def __init__(self, device):
+ print(f"Initializing DepthText2Image to {device}")
+ self.torch_dtype = torch.float16 if 'cuda' in device else torch.float32
+ self.controlnet = ControlNetModel.from_pretrained(
+ "fusing/stable-diffusion-v1-5-controlnet-depth", torch_dtype=self.torch_dtype)
+ self.pipe = StableDiffusionControlNetPipeline.from_pretrained(
+ "runwayml/stable-diffusion-v1-5", controlnet=self.controlnet, safety_checker=None,
+ torch_dtype=self.torch_dtype)
+ self.pipe.scheduler = UniPCMultistepScheduler.from_config(self.pipe.scheduler.config)
+ self.pipe.to(device)
+ self.seed = -1
+ self.a_prompt = 'best quality, extremely detailed'
+ self.n_prompt = 'longbody, lowres, bad anatomy, bad hands, missing fingers, extra digit,' \
+ ' fewer digits, cropped, worst quality, low quality'
+
+ @prompts(name="Generate Image Condition On Depth",
+ description="useful when you want to generate a new real image from both the user description and depth image. "
+ "like: generate a real image of a object or something from this depth image, "
+ "or generate a new real image of a object or something from the depth map. "
+ "The input to this tool should be a comma separated string of two, "
+ "representing the image_path and the user description")
+ def inference(self, inputs):
+ image_path, instruct_text = inputs.split(",")[0], ','.join(inputs.split(',')[1:])
+ image = Image.open(image_path)
+ self.seed = random.randint(0, 65535)
+ seed_everything(self.seed)
+ prompt = f'{instruct_text}, {self.a_prompt}'
+ image = self.pipe(prompt, image, num_inference_steps=20, eta=0.0, negative_prompt=self.n_prompt,
+ guidance_scale=9.0).images[0]
+ updated_image_path = get_new_image_name(image_path, func_name="depth2image")
+ image.save(updated_image_path)
+ print(f"\nProcessed DepthText2Image, Input Depth: {image_path}, Input Text: {instruct_text}, "
+ f"Output Image: {updated_image_path}")
+ return updated_image_path
+
+
+class Image2Normal:
+ def __init__(self, device):
+ print("Initializing Image2Normal")
+ self.depth_estimator = pipeline("depth-estimation", model="Intel/dpt-hybrid-midas")
+ self.bg_threhold = 0.4
+
+ @prompts(name="Predict Normal Map On Image",
+ description="useful when you want to detect norm map of the image. "
+ "like: generate normal map from this image, or predict normal map of this image. "
+ "The input to this tool should be a string, representing the image_path")
+ def inference(self, inputs):
+ image = Image.open(inputs)
+ original_size = image.size
+ image = self.depth_estimator(image)['predicted_depth'][0]
+ image = image.numpy()
+ image_depth = image.copy()
+ image_depth -= np.min(image_depth)
+ image_depth /= np.max(image_depth)
+ x = cv2.Sobel(image, cv2.CV_32F, 1, 0, ksize=3)
+ x[image_depth < self.bg_threhold] = 0
+ y = cv2.Sobel(image, cv2.CV_32F, 0, 1, ksize=3)
+ y[image_depth < self.bg_threhold] = 0
+ z = np.ones_like(x) * np.pi * 2.0
+ image = np.stack([x, y, z], axis=2)
+ image /= np.sum(image ** 2.0, axis=2, keepdims=True) ** 0.5
+ image = (image * 127.5 + 127.5).clip(0, 255).astype(np.uint8)
+ image = Image.fromarray(image)
+ image = image.resize(original_size)
+ updated_image_path = get_new_image_name(inputs, func_name="normal-map")
+ image.save(updated_image_path)
+ print(f"\nProcessed Image2Normal, Input Image: {inputs}, Output Depth: {updated_image_path}")
+ return updated_image_path
+
+
+class NormalText2Image:
+ def __init__(self, device):
+ print(f"Initializing NormalText2Image to {device}")
+ self.torch_dtype = torch.float16 if 'cuda' in device else torch.float32
+ self.controlnet = ControlNetModel.from_pretrained(
+ "fusing/stable-diffusion-v1-5-controlnet-normal", torch_dtype=self.torch_dtype)
+ self.pipe = StableDiffusionControlNetPipeline.from_pretrained(
+ "runwayml/stable-diffusion-v1-5", controlnet=self.controlnet, safety_checker=None,
+ torch_dtype=self.torch_dtype)
+ self.pipe.scheduler = UniPCMultistepScheduler.from_config(self.pipe.scheduler.config)
+ self.pipe.to(device)
+ self.seed = -1
+ self.a_prompt = 'best quality, extremely detailed'
+ self.n_prompt = 'longbody, lowres, bad anatomy, bad hands, missing fingers, extra digit,' \
+ ' fewer digits, cropped, worst quality, low quality'
+
+ @prompts(name="Generate Image Condition On Normal Map",
+ description="useful when you want to generate a new real image from both the user description and normal map. "
+ "like: generate a real image of a object or something from this normal map, "
+ "or generate a new real image of a object or something from the normal map. "
+ "The input to this tool should be a comma separated string of two, "
+ "representing the image_path and the user description")
+ def inference(self, inputs):
+ image_path, instruct_text = inputs.split(",")[0], ','.join(inputs.split(',')[1:])
+ image = Image.open(image_path)
+ self.seed = random.randint(0, 65535)
+ seed_everything(self.seed)
+ prompt = f'{instruct_text}, {self.a_prompt}'
+ image = self.pipe(prompt, image, num_inference_steps=20, eta=0.0, negative_prompt=self.n_prompt,
+ guidance_scale=9.0).images[0]
+ updated_image_path = get_new_image_name(image_path, func_name="normal2image")
+ image.save(updated_image_path)
+ print(f"\nProcessed NormalText2Image, Input Normal: {image_path}, Input Text: {instruct_text}, "
+ f"Output Image: {updated_image_path}")
+ return updated_image_path
+
+
+class VisualQuestionAnswering:
+ def __init__(self, device):
+ print(f"Initializing VisualQuestionAnswering to {device}")
+ self.torch_dtype = torch.float16 if 'cuda' in device else torch.float32
+ self.device = device
+ self.processor = BlipProcessor.from_pretrained("Salesforce/blip-vqa-base")
+ self.model = BlipForQuestionAnswering.from_pretrained(
+ "Salesforce/blip-vqa-base", torch_dtype=self.torch_dtype).to(self.device)
+
+ @prompts(name="Answer Question About The Image",
+ description="useful when you need an answer for a question based on an image. "
+ "like: what is the background color of the last image, how many cats in this figure, what is in this figure. "
+ "The input to this tool should be a comma separated string of two, representing the image_path and the question")
+ def inference(self, inputs):
+ image_path, question = inputs.split(",")[0], ','.join(inputs.split(',')[1:])
+ raw_image = Image.open(image_path).convert('RGB')
+ inputs = self.processor(raw_image, question, return_tensors="pt").to(self.device, self.torch_dtype)
+ out = self.model.generate(**inputs)
+ answer = self.processor.decode(out[0], skip_special_tokens=True)
+ print(f"\nProcessed VisualQuestionAnswering, Input Image: {image_path}, Input Question: {question}, "
+ f"Output Answer: {answer}")
+ return answer
+
+
+class InfinityOutPainting:
+ template_model = True # Add this line to show this is a template model.
+ def __init__(self, ImageCaptioning, ImageEditing, VisualQuestionAnswering):
+ self.llm = OpenAI(temperature=0)
+ self.ImageCaption = ImageCaptioning
+ self.ImageEditing = ImageEditing
+ self.ImageVQA = VisualQuestionAnswering
+ self.a_prompt = 'best quality, extremely detailed'
+ self.n_prompt = 'longbody, lowres, bad anatomy, bad hands, missing fingers, extra digit, ' \
+ 'fewer digits, cropped, worst quality, low quality'
+
+ def get_BLIP_vqa(self, image, question):
+ inputs = self.ImageVQA.processor(image, question, return_tensors="pt").to(self.ImageVQA.device,
+ self.ImageVQA.torch_dtype)
+ out = self.ImageVQA.model.generate(**inputs)
+ answer = self.ImageVQA.processor.decode(out[0], skip_special_tokens=True)
+ print(f"\nProcessed VisualQuestionAnswering, Input Question: {question}, Output Answer: {answer}")
+ return answer
+
+ def get_BLIP_caption(self, image):
+ inputs = self.ImageCaption.processor(image, return_tensors="pt").to(self.ImageCaption.device,
+ self.ImageCaption.torch_dtype)
+ out = self.ImageCaption.model.generate(**inputs)
+ BLIP_caption = self.ImageCaption.processor.decode(out[0], skip_special_tokens=True)
+ return BLIP_caption
+
+ def check_prompt(self, prompt):
+ check = f"Here is a paragraph with adjectives. " \
+ f"{prompt} " \
+ f"Please change all plural forms in the adjectives to singular forms. "
+ return self.llm(check)
+
+ def get_imagine_caption(self, image, imagine):
+ BLIP_caption = self.get_BLIP_caption(image)
+ background_color = self.get_BLIP_vqa(image, 'what is the background color of this image')
+ style = self.get_BLIP_vqa(image, 'what is the style of this image')
+ imagine_prompt = f"let's pretend you are an excellent painter and now " \
+ f"there is an incomplete painting with {BLIP_caption} in the center, " \
+ f"please imagine the complete painting and describe it" \
+ f"you should consider the background color is {background_color}, the style is {style}" \
+ f"You should make the painting as vivid and realistic as possible" \
+ f"You can not use words like painting or picture" \
+ f"and you should use no more than 50 words to describe it"
+ caption = self.llm(imagine_prompt) if imagine else BLIP_caption
+ caption = self.check_prompt(caption)
+ print(f'BLIP observation: {BLIP_caption}, ChatGPT imagine to {caption}') if imagine else print(
+ f'Prompt: {caption}')
+ return caption
+
+ def resize_image(self, image, max_size=1000000, multiple=8):
+ aspect_ratio = image.size[0] / image.size[1]
+ new_width = int(math.sqrt(max_size * aspect_ratio))
+ new_height = int(new_width / aspect_ratio)
+ new_width, new_height = new_width - (new_width % multiple), new_height - (new_height % multiple)
+ return image.resize((new_width, new_height))
+
+ def dowhile(self, original_img, tosize, expand_ratio, imagine, usr_prompt):
+ old_img = original_img
+ while (old_img.size != tosize):
+ prompt = self.check_prompt(usr_prompt) if usr_prompt else self.get_imagine_caption(old_img, imagine)
+ crop_w = 15 if old_img.size[0] != tosize[0] else 0
+ crop_h = 15 if old_img.size[1] != tosize[1] else 0
+ old_img = ImageOps.crop(old_img, (crop_w, crop_h, crop_w, crop_h))
+ temp_canvas_size = (expand_ratio * old_img.width if expand_ratio * old_img.width < tosize[0] else tosize[0],
+ expand_ratio * old_img.height if expand_ratio * old_img.height < tosize[1] else tosize[
+ 1])
+ temp_canvas, temp_mask = Image.new("RGB", temp_canvas_size, color="white"), Image.new("L", temp_canvas_size,
+ color="white")
+ x, y = (temp_canvas.width - old_img.width) // 2, (temp_canvas.height - old_img.height) // 2
+ temp_canvas.paste(old_img, (x, y))
+ temp_mask.paste(0, (x, y, x + old_img.width, y + old_img.height))
+ resized_temp_canvas, resized_temp_mask = self.resize_image(temp_canvas), self.resize_image(temp_mask)
+ image = self.ImageEditing.inpaint(prompt=prompt, image=resized_temp_canvas, mask_image=resized_temp_mask,
+ height=resized_temp_canvas.height, width=resized_temp_canvas.width,
+ num_inference_steps=50).images[0].resize(
+ (temp_canvas.width, temp_canvas.height), Image.ANTIALIAS)
+ image = blend_gt2pt(old_img, image)
+ old_img = image
+ return old_img
+
+ @prompts(name="Extend An Image",
+ description="useful when you need to extend an image into a larger image."
+ "like: extend the image into a resolution of 2048x1024, extend the image into 2048x1024. "
+ "The input to this tool should be a comma separated string of two, representing the image_path and the resolution of widthxheight")
+ def inference(self, inputs):
+ image_path, resolution = inputs.split(',')
+ width, height = resolution.split('x')
+ tosize = (int(width), int(height))
+ image = Image.open(image_path)
+ image = ImageOps.crop(image, (10, 10, 10, 10))
+ out_painted_image = self.dowhile(image, tosize, 4, True, False)
+ updated_image_path = get_new_image_name(image_path, func_name="outpainting")
+ out_painted_image.save(updated_image_path)
+ print(f"\nProcessed InfinityOutPainting, Input Image: {image_path}, Input Resolution: {resolution}, "
+ f"Output Image: {updated_image_path}")
+ return updated_image_path
+
+#############################################New Tool#############################################
+class Grounded_dino_sam_inpainting:
+ def __init__(self, device):
+ print(f"Initializing BLIP")
+ self.device = device
+ self.torch_dtype = torch.float16 if 'cuda' in device else torch.float32
+ self.blip_processor = BlipProcessor.from_pretrained("Salesforce/blip-image-captioning-large")
+ self.blip_model = BlipForConditionalGeneration.from_pretrained(
+ "Salesforce/blip-image-captioning-large", torch_dtype=self.torch_dtype
+ ).to(self.device)
+ print(f"Initializing GroundingDINO")
+ self.dino_model = load_model(
+ model_config_path="GroundingDINO/groundingdino/config/GroundingDINO_SwinT_OGC.py",
+ model_checkpoint_path="groundingdino_swint_ogc.pth",
+ device=self.device
+ )
+ print(f"Initializing Segment Anthing")
+ self.sam_model = build_sam(checkpoint="sam_vit_h_4b8939.pth").to(self.device)
+ print(f"Initializing Stable Diffusion")
+ self.sd_pipe = StableDiffusionInpaintPipeline.from_pretrained(
+ "runwayml/stable-diffusion-inpainting", torch_dtype=self.torch_dtype
+ ).to(self.device)
+
+ @prompts(name="Get Photo Description",
+ description="useful when you want to know what is inside the photo. receives image_path as input. "
+ "The input to this tool should be a string, representing the image_path. ")
+ def inference_caption(self, image_path):
+ inputs = self.blip_processor(Image.open(image_path), return_tensors="pt").to(self.device, self.torch_dtype)
+ out = self.blip_model.generate(**inputs)
+ captions = self.blip_processor.decode(out[0], skip_special_tokens=True)
+ print(f"\nProcessed ImageCaptioning, Input Image: {image_path}, Output Text: {captions}")
+ return captions
+
+ def _detect_object(self, image_path, text_prompt, func_name):
+ image_pil, image = load_image(image_path)
+ boxes_filt, scores, pred_phrases = get_grounding_output(
+ self.dino_model, image, text_prompt, 0.3, 0.25, device=self.device
+ )
+ # use NMS to handle overlapped boxes
+ print(f"Before NMS: {boxes_filt.shape[0]} boxes")
+ nms_idx = torchvision.ops.nms(boxes_filt, scores, 0.5).numpy().tolist()
+ boxes_filt = boxes_filt[nms_idx]
+ pred_phrases = [pred_phrases[idx] for idx in nms_idx]
+ print(f"After NMS: {boxes_filt.shape[0]} boxes")
+ size = image_pil.size
+ pred_dict = {
+ "boxes": boxes_filt,
+ "size": [size[1], size[0]], # H,W
+ "labels": pred_phrases,
+ }
+ image_with_box = plot_boxes_to_image(image_pil, pred_dict)[0]
+ updated_image_path = get_new_image_name(image_path, func_name)
+ image_with_box.save(updated_image_path)
+ return updated_image_path
+
+ @prompts(name="Detect One Object In Image",
+ description="useful when you want to detect the specific object in the image. "
+ "like: detect the black dog in the image. "
+ "The input to this tool should be a comma separated string of two, "
+ "representing the image_path and the description of specific object.")
+ def inference_detect_one_object(self, inputs):
+ image_path, text_prompt = inputs.split(',')
+ print(f"\nInput Text Prompt: {text_prompt}")
+ updated_image_path = self._detect_object(image_path, text_prompt, func_name="det-object")
+ print(f"Processed DetectOneObject, Input Image: {image_path}, Output Image: {updated_image_path}")
+ return updated_image_path
+
+ @prompts(name="Detect Multiple Objects In Image",
+ description="useful when you want to detect two or more specific objects in the image. "
+ "like: detect the black dog and white cat in the image. "
+ "The input to this tool should be a comma separated string of two, "
+ "representing the image_path and the description of multiple specific objects. "
+ "Different description should be separated by symbol '&', "
+ "like 'black dog & white cat'. ")
+ def inference_detect_multi_object(self, inputs):
+ image_path, text_prompt = inputs.split(',')
+ processed_text_prompt = text_prompt.replace(' &', ',')
+ print(f"\nOriginal Text Prompt: {text_prompt}, Input Text Prompt: {processed_text_prompt}")
+ updated_image_path = self._detect_object(image_path, text_prompt, func_name="det-objects")
+ print(f"Processed DetectMultiObject, Input Image: {image_path}, Output Image: {updated_image_path}")
+ return updated_image_path
+
+ # modified from https://github.com/Cheems-Seminar/segment-anything-and-name-it/blob/58408f1e4e340f565c5ef6b0c71920cdcd30b213/chatbot.py#L1046
+ @prompts(name="Segment Anything in Image",
+ description="useful when you want to segment anything in the image. "
+ "like: segment anything in the image. "
+ "The input to this tool should be a string, representing the image_path. ")
+ def inference_segment_anything(self, image_path):
+ image = cv2.imread(image_path)
+ image = cv2.cvtColor(image, cv2.COLOR_BGR2RGB)
+ mask_generator = SamAutomaticMaskGenerator(self.sam_model)
+ anns = mask_generator.generate(image)
+ plt.figure(figsize=(10, 10))
+ plt.imshow(image)
+ sorted_anns = sorted(anns, key=(lambda x: x['area']), reverse=True)
+ ax = plt.gca()
+ ax.set_autoscale_on(False)
+ for ann in sorted_anns:
+ m = ann['segmentation']
+ img = np.ones((m.shape[0], m.shape[1], 3))
+ color_mask = np.random.random((1, 3)).tolist()[0]
+ for i in range(3):
+ img[:,:,i] = color_mask[i]
+ ax.imshow(np.dstack((img, m*0.35)))
+ plt.axis('off')
+ updated_image_path = get_new_image_name(image_path, func_name="seg-any")
+ plt.savefig(updated_image_path, bbox_inches='tight', dpi=300, pad_inches=0.0)
+ print(f"\nProcessed SegmentAnything, Input Image: {image_path}, Output Image: {updated_image_path}")
+ return updated_image_path
+
+ def _segment_object(self, image_path, text_prompt, func_name):
+ image_pil, image = load_image(image_path)
+ # run grounding dino model
+ boxes_filt, scores, pred_phrases = get_grounding_output(
+ self.dino_model, image, text_prompt, 0.25, 0.2, device=self.device
+ )
+ # initialize SAM
+ predictor = SamPredictor(self.sam_model)
+ image = cv2.imread(image_path)
+ image = cv2.cvtColor(image, cv2.COLOR_BGR2RGB)
+ predictor.set_image(image)
+ size = image_pil.size
+ H, W = size[1], size[0]
+ for i in range(boxes_filt.size(0)):
+ boxes_filt[i] = boxes_filt[i] * torch.Tensor([W, H, W, H])
+ boxes_filt[i][:2] -= boxes_filt[i][2:] / 2
+ boxes_filt[i][2:] += boxes_filt[i][:2]
+ boxes_filt = boxes_filt.cpu()
+ # use NMS to handle overlapped boxes
+ print(f"Before NMS: {boxes_filt.shape[0]} boxes")
+ nms_idx = torchvision.ops.nms(boxes_filt, scores, 0.5).numpy().tolist()
+ boxes_filt = boxes_filt[nms_idx]
+ pred_phrases = [pred_phrases[idx] for idx in nms_idx]
+ print(f"After NMS: {boxes_filt.shape[0]} boxes")
+ # generate mask
+ transformed_boxes = predictor.transform.apply_boxes_torch(boxes_filt, image.shape[:2])
+ masks, _, _ = predictor.predict_torch(
+ point_coords = None,
+ point_labels = None,
+ boxes = transformed_boxes.to(self.device),
+ multimask_output = False,
+ )
+ # remove the mask when area < area_thresh (in pixels)
+ new_masks = []
+ for mask in masks:
+ # reshape to be used in remove_small_regions()
+ mask = mask.cpu().numpy().squeeze()
+ mask, _ = remove_small_regions(mask, 100, mode="holes")
+ mask, _ = remove_small_regions(mask, 100, mode="islands")
+ new_masks.append(torch.as_tensor(mask).unsqueeze(0))
+ masks = torch.stack(new_masks, dim=0)
+ # add box and mask in the image
+ plt.figure(figsize=(10, 10))
+ plt.imshow(image)
+ for mask in masks:
+ show_mask(mask.cpu().numpy(), plt.gca(), random_color=True)
+ for box, label in zip(boxes_filt, pred_phrases):
+ show_box(box.numpy(), plt.gca(), label)
+ plt.axis('off')
+ updated_image_path = get_new_image_name(image_path, func_name)
+ plt.savefig(updated_image_path, bbox_inches='tight', dpi=300, pad_inches=0.0)
+ return updated_image_path, pred_phrases
+
+ @prompts(name="Segment One Object In Image",
+ description="useful when you want to segment the specific object in the image. "
+ "like: segment the black dog in the image, or mask the black dog in the image. "
+ "The input to this tool should be a comma separated string of two, "
+ "representing the image_path and the description of specific object.")
+ def inference_segment_one_object(self, inputs):
+ image_path, text_prompt = inputs.split(',')
+ print(f"\nInput Text Prompt: {text_prompt}")
+ updated_image_path, _ = self._segment_object(image_path, text_prompt, func_name="seg-object")
+ print(f"Processed SegmentOneObject, Input Image: {image_path}, Output Image: {updated_image_path}")
+ return updated_image_path
+
+ @prompts(name="Segment Multiple Object In Image",
+ description="useful when you want to segment two or more specific objects in the image. "
+ "like: segment the black dog and white cat in the image. "
+ "The input to this tool should be a comma separated string of two, "
+ "representing the image_path and the description of multiple specific objects. "
+ "Different description should be separated by symbol '&', "
+ "like 'black dog & white cat'. ")
+ def inference_segment_multi_object(self, inputs):
+ image_path, text_prompt = inputs.split(',')
+ processed_text_prompt = text_prompt.replace(' &', ',')
+ print("\nOriginal Text Prompt: {text_prompt}, Input Text Prompt: {processed_text_prompt}, ")
+ updated_image_path, _ = self._segment_object(image_path, text_prompt, func_name="seg-objects")
+ print(f"Processed SegmentMultiObject, Input Image: {image_path}, Output Image: {updated_image_path}")
+ return updated_image_path
+
+ @prompts(name="Auto Label the Image",
+ description="useful when you want to label the image automatically. "
+ "like: help me label the image. "
+ "The input to this tool should be a string, representing the image_path. ")
+ def inference_auto_segment_object(self, image_path):
+ inputs = self.blip_processor(Image.open(image_path), return_tensors="pt").to(self.device, self.torch_dtype)
+ out = self.blip_model.generate(**inputs)
+ caption = self.blip_processor.decode(out[0], skip_special_tokens=True)
+ text_prompt = generate_tags(caption, split=",")
+ print(f"\nCaption: {caption}")
+ print(f"Tags: {text_prompt}")
+ updated_image_path, pred_phrases = self._segment_object(image_path, text_prompt, func_name="auto-label")
+ caption = check_caption(caption, pred_phrases)
+ print(f"Revise caption with number: {caption}")
+ print(f"Processed SegmentMultiObject, Input Image: {image_path}, Caption: {caption}, "
+ f"Text Prompt: {text_prompt}, Output Image: {updated_image_path}")
+ return updated_image_path
+
+ def _inpainting(self, image_path, to_be_replaced_txt, replace_with_txt, func_name):
+ image_pil, image = load_image(image_path)
+ # run grounding dino model
+ boxes_filt, scores, pred_phrases = get_grounding_output(
+ self.dino_model, image, to_be_replaced_txt, 0.3, 0.25, device=self.device
+ )
+ # initialize SAM
+ predictor = SamPredictor(self.sam_model)
+ image = cv2.imread(image_path)
+ image = cv2.cvtColor(image, cv2.COLOR_BGR2RGB)
+ predictor.set_image(image)
+ size = image_pil.size
+ H, W = size[1], size[0]
+ for i in range(boxes_filt.size(0)):
+ boxes_filt[i] = boxes_filt[i] * torch.Tensor([W, H, W, H])
+ boxes_filt[i][:2] -= boxes_filt[i][2:] / 2
+ boxes_filt[i][2:] += boxes_filt[i][:2]
+ boxes_filt = boxes_filt.cpu()
+ # generate mask
+ transformed_boxes = predictor.transform.apply_boxes_torch(boxes_filt, image.shape[:2])
+ masks, _, _ = predictor.predict_torch(
+ point_coords = None,
+ point_labels = None,
+ boxes = transformed_boxes.to(self.device),
+ multimask_output = False,
+ )
+ # inpainting pipeline
+ mask = masks[0][0].cpu().numpy() # simply choose the first mask, which will be refine in the future release
+ mask_pil = Image.fromarray(mask).resize((512, 512))
+ image_pil = Image.fromarray(image).resize((512, 512))
+ image = self.sd_pipe(prompt=replace_with_txt, image=image_pil, mask_image=mask_pil).images[0]
+ updated_image_path = get_new_image_name(image_path, func_name)
+ image.save(updated_image_path)
+ return updated_image_path
+
+ @prompts(name="Replace Something From The Photo",
+ description="useful when you want to replace an object from the object description or "
+ "location with another object from its description. "
+ "The input to this tool should be a comma separated string of three, "
+ "representing the image_path, the object to be replaced, the object to be replaced with ")
+ def inference_replace(self, inputs):
+ image_path, to_be_replaced_txt, replace_with_txt = inputs.split(",")
+ print(f"\nReplace {to_be_replaced_txt} to {replace_with_txt}")
+ updated_image_path = self._inpainting(image_path, to_be_replaced_txt, replace_with_txt, 'replace-something')
+ print(f"Processed ImageEditing, Input Image: {image_path}, Output Image: {updated_image_path}")
+ return updated_image_path
+
+#############################################New Tool#############################################
+
+
+class ConversationBot:
+ def __init__(self, load_dict):
+ # load_dict = {'VisualQuestionAnswering':'cuda:0', 'ImageCaptioning':'cuda:1',...}
+ print(f"Initializing VisualChatGPT, load_dict={load_dict}")
+ if 'ImageCaptioning' not in load_dict and 'Grounded_dino_sam_inpainting' not in load_dict:
+ raise ValueError("You have to load ImageCaptioning or Grounded_dino_sam_inpainting as a basic function for VisualChatGPT")
+
+ self.models = {}
+ # Load Basic Foundation Models
+ for class_name, device in load_dict.items():
+ self.models[class_name] = globals()[class_name](device=device)
+
+ # Load Template Foundation Models
+ for class_name, module in globals().items():
+ if getattr(module, 'template_model', False):
+ template_required_names = {k for k in inspect.signature(module.__init__).parameters.keys() if k!='self'}
+ loaded_names = set([type(e).__name__ for e in self.models.values()])
+ if template_required_names.issubset(loaded_names):
+ self.models[class_name] = globals()[class_name](
+ **{name: self.models[name] for name in template_required_names})
+ self.tools = []
+ for instance in self.models.values():
+ for e in dir(instance):
+ if e.startswith('inference'):
+ func = getattr(instance, e)
+ self.tools.append(Tool(name=func.name, description=func.description, func=func))
+ self.llm = OpenAI(temperature=0)
+ self.memory = ConversationBufferMemory(memory_key="chat_history", output_key='output')
+
+ def run_text(self, text, state):
+ self.agent.memory.buffer = cut_dialogue_history(self.agent.memory.buffer, keep_last_n_words=500)
+ res = self.agent({"input": text.strip()})
+ res['output'] = res['output'].replace("\\", "/")
+ response = re.sub('(image/[-\w]*.png)', lambda m: f'})*{m.group(0)}*', res['output'])
+ state = state + [(text, response)]
+ print(f"\nProcessed run_text, Input text: {text}\nCurrent state: {state}\n"
+ f"Current Memory: {self.agent.memory.buffer}")
+ return state, state
+
+ def run_image(self, image, state, txt, lang):
+ # image_filename = os.path.join('image', f"{str(uuid.uuid4())[:8]}.png")
+ # print("======>Auto Resize Image...")
+ # img = Image.open(image.name)
+ # width, height = img.size
+ # ratio = min(512 / width, 512 / height)
+ # width_new, height_new = (round(width * ratio), round(height * ratio))
+ # width_new = int(np.round(width_new / 64.0)) * 64
+ # height_new = int(np.round(height_new / 64.0)) * 64
+ # img = img.resize((width_new, height_new))
+ # img = img.convert('RGB')
+ # img.save(image_filename)
+ # img.save(image_filename, "PNG")
+ # print(f"Resize image form {width}x{height} to {width_new}x{height_new}")
+ ## Directly use original image for better results
+ suffix = image.name.split('.')[-1]
+ image_filename = os.path.join('image', f"{str(uuid.uuid4())[:8]}.{suffix}")
+ shutil.copy(image.name, image_filename)
+ if 'Grounded_dino_sam_inpainting' in self.models:
+ description = self.models['Grounded_dino_sam_inpainting'].inference_caption(image_filename)
+ else:
+ description = self.models['ImageCaptioning'].inference(image_filename)
+ if lang == 'Chinese':
+ Human_prompt = f'\nHuman: 提供一张名为 {image_filename}的图片。它的描述是: {description}。 这些信息帮助你理解这个图像,但是你应该使用工具来完成下面的任务,而不是直接从我的描述中想象。 如果你明白了, 说 \"收到\". \n'
+ AI_prompt = "收到。 "
+ else:
+ Human_prompt = f'\nHuman: provide a figure named {image_filename}. The description is: {description}. This information helps you to understand this image, but you should use tools to finish following tasks, rather than directly imagine from my description. If you understand, say \"Received\". \n'
+ AI_prompt = "Received. "
+ self.agent.memory.buffer = self.agent.memory.buffer + Human_prompt + 'AI: ' + AI_prompt
+ state = state + [(f"*{image_filename}*", AI_prompt)]
+ print(f"\nProcessed run_image, Input image: {image_filename}\nCurrent state: {state}\n"
+ f"Current Memory: {self.agent.memory.buffer}")
+ return state, state, f'{txt} {image_filename} '
+
+ def init_agent(self, openai_api_key, lang):
+ self.memory.clear() #clear previous history
+ if lang=='English':
+ PREFIX, FORMAT_INSTRUCTIONS, SUFFIX = VISUAL_CHATGPT_PREFIX, VISUAL_CHATGPT_FORMAT_INSTRUCTIONS, VISUAL_CHATGPT_SUFFIX
+ place = "Enter text and press enter, or upload an image"
+ label_clear = "Clear"
+ else:
+ PREFIX, FORMAT_INSTRUCTIONS, SUFFIX = VISUAL_CHATGPT_PREFIX_CN, VISUAL_CHATGPT_FORMAT_INSTRUCTIONS_CN, VISUAL_CHATGPT_SUFFIX_CN
+ place = "输入文字并回车,或者上传图片"
+ label_clear = "清除"
+ self.llm = OpenAI(temperature=0, openai_api_key=openai_api_key)
+ self.agent = initialize_agent(
+ self.tools,
+ self.llm,
+ agent="conversational-react-description",
+ verbose=True,
+ memory=self.memory,
+ return_intermediate_steps=True,
+ agent_kwargs={'prefix': PREFIX, 'format_instructions': FORMAT_INSTRUCTIONS, 'suffix': SUFFIX}, )
+ return gr.update(visible = True), gr.update(visible = True)
+
+
+whisper_model = whisper.load_model("base").to('cuda:0')
+def speech_recognition(speech_file):
+ # whisper
+ # load audio and pad/trim it to fit 30 seconds
+ audio = whisper.load_audio(speech_file)
+ audio = whisper.pad_or_trim(audio)
+
+ # make log-Mel spectrogram and move to the same device as the model
+ mel = whisper.log_mel_spectrogram(audio).to(whisper_model.device)
+
+ # detect the spoken language
+ _, probs = whisper_model.detect_language(mel)
+ speech_language = max(probs, key=probs.get)
+ print(f'\nDetect Language: {speech_language}')
+
+ # decode the audio
+ options = whisper.DecodingOptions(fp16 = False)
+ result = whisper.decode(whisper_model, mel, options)
+ print(result.text)
+
+ return result.text
+
+
+if __name__ == '__main__':
+ load_dict = {'Grounded_dino_sam_inpainting': 'cuda:0'}
+ # load_dict = {'ImageCaptioning': 'cuda:0'}
+
+ bot = ConversationBot(load_dict)
+
+ with gr.Blocks(css="#chatbot {overflow:auto; height:500px;}") as demo:
+ gr.Markdown("
ChatBot
")
+ gr.Markdown(
+ """This is a demo to the work [Grounded-Segment-Anything](https://github.com/IDEA-Research/Grounded-Segment-Anything).
+ """
+ )
+
+ with gr.Row():
+ lang = gr.Radio(choices=['Chinese', 'English'], value='English', label='Language')
+ openai_api_key_textbox = gr.Textbox(
+ placeholder="Paste your OpenAI API key here to start ChatBot(sk-...) and press Enter ↵️",
+ show_label=False,
+ lines=1,
+ type="password",
+ )
+
+ chatbot = gr.Chatbot(elem_id="chatbot", label="ChatBot")
+ state = gr.State([])
+
+ with gr.Row(visible=False) as input_raws:
+ with gr.Column(scale=0.7):
+ txt = gr.Textbox(show_label=False, placeholder="Enter text and press enter, or upload an image").style(container=False)
+ with gr.Column(scale=0.10, min_width=0):
+ run = gr.Button("🏃♂️Run")
+ with gr.Column(scale=0.10, min_width=0):
+ clear = gr.Button("🔄Clear️")
+ with gr.Column(scale=0.10, min_width=0):
+ btn = gr.UploadButton("🖼️Upload", file_types=["image"])
+ with gr.Row(visible=False, equal_height=True) as audio_raw:
+ with gr.Column(scale=0.85):
+ audio = gr.Audio(source="microphone", type="filepath", label="Just say it!")
+ with gr.Column(scale=0.15):
+ transcribe = gr.Button("Transcribe")
+
+ gr.Examples(
+ examples=[
+ "Describe this image",
+ "Detect the dog",
+ "Detect the dog and the cat",
+ "Segment anything",
+ "Segment the dog",
+ "Help me label the image",
+ "Replace the dog with a cat",
+ ],
+ inputs=txt
+ )
+
+ openai_api_key_textbox.submit(bot.init_agent, [openai_api_key_textbox, lang], [input_raws, audio_raw])
+ transcribe.click(speech_recognition, inputs=[audio], outputs=[txt])
+ txt.submit(bot.run_text, [txt, state], [chatbot, state])
+ txt.submit(lambda: "", None, txt)
+ run.click(bot.run_text, [txt, state], [chatbot, state])
+ run.click(lambda: "", None, txt)
+ btn.upload(bot.run_image, [btn, state, txt, lang], [chatbot, state, txt])
+ clear.click(bot.memory.clear)
+ clear.click(lambda: [], None, chatbot)
+ clear.click(lambda: [], None, state)
+
+ demo.launch(server_name="0.0.0.0", server_port=10010)
+
diff --git a/cog.yaml b/cog.yaml
new file mode 100644
index 0000000000000000000000000000000000000000..8b3c26fc02fbda7e76c48e27a8ec94cda0b341be
--- /dev/null
+++ b/cog.yaml
@@ -0,0 +1,27 @@
+# Configuration for Cog ⚙️
+# Reference: https://github.com/replicate/cog/blob/main/docs/yaml.md
+
+build:
+ gpu: true
+ cuda: "11.7"
+ system_packages:
+ - "libgl1-mesa-glx"
+ - "libglib2.0-0"
+ python_version: "3.10"
+ python_packages:
+ - "timm==0.9.2"
+ - "transformers==4.30.2"
+ - "fairscale==0.4.13"
+ - "pycocoevalcap==1.2"
+ - "torch==1.13.0"
+ - "torchvision==0.14.0"
+ - "Pillow==9.5.0"
+ - "scipy==1.10.1"
+ - "opencv-python==4.7.0.72"
+ - "addict==2.4.0"
+ - "yapf==0.40.0"
+ - "supervision==0.10.0"
+ - git+https://github.com/openai/CLIP.git
+ - ipython
+
+predict: "predict.py:Predictor"
diff --git a/gradio_app.py b/gradio_app.py
new file mode 100644
index 0000000000000000000000000000000000000000..ea24b3241d9b5faaa1f291119363c216ef06813c
--- /dev/null
+++ b/gradio_app.py
@@ -0,0 +1,400 @@
+import os
+import random
+import cv2
+from scipy import ndimage
+
+import gradio as gr
+import argparse
+import litellm
+
+import numpy as np
+import torch
+import torchvision
+from PIL import Image, ImageDraw, ImageFont
+
+# Grounding DINO
+import GroundingDINO.groundingdino.datasets.transforms as T
+from GroundingDINO.groundingdino.models import build_model
+from GroundingDINO.groundingdino.util.slconfig import SLConfig
+from GroundingDINO.groundingdino.util.utils import clean_state_dict, get_phrases_from_posmap
+
+# segment anything
+from segment_anything import build_sam, SamPredictor, SamAutomaticMaskGenerator
+import numpy as np
+
+# diffusers
+import torch
+from diffusers import StableDiffusionInpaintPipeline
+
+# BLIP
+from transformers import BlipProcessor, BlipForConditionalGeneration
+
+import openai
+
+def show_anns(anns):
+ if len(anns) == 0:
+ return
+ sorted_anns = sorted(anns, key=(lambda x: x['area']), reverse=True)
+ full_img = None
+
+ # for ann in sorted_anns:
+ for i in range(len(sorted_anns)):
+ ann = anns[i]
+ m = ann['segmentation']
+ if full_img is None:
+ full_img = np.zeros((m.shape[0], m.shape[1], 3))
+ map = np.zeros((m.shape[0], m.shape[1]), dtype=np.uint16)
+ map[m != 0] = i + 1
+ color_mask = np.random.random((1, 3)).tolist()[0]
+ full_img[m != 0] = color_mask
+ full_img = full_img*255
+ # anno encoding from https://github.com/LUSSeg/ImageNet-S
+ res = np.zeros((map.shape[0], map.shape[1], 3))
+ res[:, :, 0] = map % 256
+ res[:, :, 1] = map // 256
+ res.astype(np.float32)
+ full_img = Image.fromarray(np.uint8(full_img))
+ return full_img, res
+
+def generate_caption(processor, blip_model, raw_image):
+ # unconditional image captioning
+ inputs = processor(raw_image, return_tensors="pt").to("cuda", torch.float16)
+ out = blip_model.generate(**inputs)
+ caption = processor.decode(out[0], skip_special_tokens=True)
+ return caption
+
+def generate_tags(caption, split=',', max_tokens=100, model="gpt-3.5-turbo", openai_api_key=''):
+ openai.api_key = openai_api_key
+ openai.api_base = 'https://closeai.deno.dev/v1'
+ prompt = [
+ {
+ 'role': 'system',
+ 'content': 'Extract the unique nouns in the caption. Remove all the adjectives. ' + \
+ f'List the nouns in singular form. Split them by "{split} ". ' + \
+ f'Caption: {caption}.'
+ }
+ ]
+ response = litellm.completion(model=model, messages=prompt, temperature=0.6, max_tokens=max_tokens)
+ reply = response['choices'][0]['message']['content']
+ # sometimes return with "noun: xxx, xxx, xxx"
+ tags = reply.split(':')[-1].strip()
+ return tags
+
+def transform_image(image_pil):
+
+ transform = T.Compose(
+ [
+ T.RandomResize([800], max_size=1333),
+ T.ToTensor(),
+ T.Normalize([0.485, 0.456, 0.406], [0.229, 0.224, 0.225]),
+ ]
+ )
+ image, _ = transform(image_pil, None) # 3, h, w
+ return image
+
+
+def load_model(model_config_path, model_checkpoint_path, device):
+ args = SLConfig.fromfile(model_config_path)
+ args.device = device
+ model = build_model(args)
+ checkpoint = torch.load(model_checkpoint_path, map_location="cpu")
+ load_res = model.load_state_dict(clean_state_dict(checkpoint["model"]), strict=False)
+ print(load_res)
+ _ = model.eval()
+ return model
+
+
+def get_grounding_output(model, image, caption, box_threshold, text_threshold, with_logits=True):
+ caption = caption.lower()
+ caption = caption.strip()
+ if not caption.endswith("."):
+ caption = caption + "."
+
+ with torch.no_grad():
+ outputs = model(image[None], captions=[caption])
+ logits = outputs["pred_logits"].cpu().sigmoid()[0] # (nq, 256)
+ boxes = outputs["pred_boxes"].cpu()[0] # (nq, 4)
+ logits.shape[0]
+
+ # filter output
+ logits_filt = logits.clone()
+ boxes_filt = boxes.clone()
+ filt_mask = logits_filt.max(dim=1)[0] > box_threshold
+ logits_filt = logits_filt[filt_mask] # num_filt, 256
+ boxes_filt = boxes_filt[filt_mask] # num_filt, 4
+ logits_filt.shape[0]
+
+ # get phrase
+ tokenlizer = model.tokenizer
+ tokenized = tokenlizer(caption)
+ # build pred
+ pred_phrases = []
+ scores = []
+ for logit, box in zip(logits_filt, boxes_filt):
+ pred_phrase = get_phrases_from_posmap(logit > text_threshold, tokenized, tokenlizer)
+ if with_logits:
+ pred_phrases.append(pred_phrase + f"({str(logit.max().item())[:4]})")
+ else:
+ pred_phrases.append(pred_phrase)
+ scores.append(logit.max().item())
+
+ return boxes_filt, torch.Tensor(scores), pred_phrases
+
+def draw_mask(mask, draw, random_color=False):
+ if random_color:
+ color = (random.randint(0, 255), random.randint(0, 255), random.randint(0, 255), 153)
+ else:
+ color = (30, 144, 255, 153)
+
+ nonzero_coords = np.transpose(np.nonzero(mask))
+
+ for coord in nonzero_coords:
+ draw.point(coord[::-1], fill=color)
+
+def draw_box(box, draw, label):
+ # random color
+ color = tuple(np.random.randint(0, 255, size=3).tolist())
+
+ draw.rectangle(((box[0], box[1]), (box[2], box[3])), outline=color, width=2)
+
+ if label:
+ font = ImageFont.load_default()
+ if hasattr(font, "getbbox"):
+ bbox = draw.textbbox((box[0], box[1]), str(label), font)
+ else:
+ w, h = draw.textsize(str(label), font)
+ bbox = (box[0], box[1], w + box[0], box[1] + h)
+ draw.rectangle(bbox, fill=color)
+ draw.text((box[0], box[1]), str(label), fill="white")
+
+ draw.text((box[0], box[1]), label)
+
+
+
+config_file = 'GroundingDINO/groundingdino/config/GroundingDINO_SwinT_OGC.py'
+ckpt_repo_id = "ShilongLiu/GroundingDINO"
+ckpt_filenmae = "groundingdino_swint_ogc.pth"
+sam_checkpoint='sam_vit_h_4b8939.pth'
+output_dir="outputs"
+device="cuda"
+
+
+blip_processor = None
+blip_model = None
+groundingdino_model = None
+sam_predictor = None
+sam_automask_generator = None
+inpaint_pipeline = None
+
+def run_grounded_sam(input_image, text_prompt, task_type, inpaint_prompt, box_threshold, text_threshold, iou_threshold, inpaint_mode, scribble_mode, openai_api_key):
+
+ global blip_processor, blip_model, groundingdino_model, sam_predictor, sam_automask_generator, inpaint_pipeline
+
+ # make dir
+ os.makedirs(output_dir, exist_ok=True)
+ # load image
+ image = input_image["image"]
+ scribble = input_image["mask"]
+ size = image.size # w, h
+
+ if sam_predictor is None:
+ # initialize SAM
+ assert sam_checkpoint, 'sam_checkpoint is not found!'
+ sam = build_sam(checkpoint=sam_checkpoint)
+ sam.to(device=device)
+ sam_predictor = SamPredictor(sam)
+ sam_automask_generator = SamAutomaticMaskGenerator(sam)
+
+ if groundingdino_model is None:
+ groundingdino_model = load_model(config_file, ckpt_filenmae, device=device)
+
+ image_pil = image.convert("RGB")
+ image = np.array(image_pil)
+
+ if task_type == 'scribble':
+ sam_predictor.set_image(image)
+ scribble = scribble.convert("RGB")
+ scribble = np.array(scribble)
+ scribble = scribble.transpose(2, 1, 0)[0]
+
+ # 将连通域进行标记
+ labeled_array, num_features = ndimage.label(scribble >= 255)
+
+ # 计算每个连通域的质心
+ centers = ndimage.center_of_mass(scribble, labeled_array, range(1, num_features+1))
+ centers = np.array(centers)
+
+ point_coords = torch.from_numpy(centers)
+ point_coords = sam_predictor.transform.apply_coords_torch(point_coords, image.shape[:2])
+ point_coords = point_coords.unsqueeze(0).to(device)
+ point_labels = torch.from_numpy(np.array([1] * len(centers))).unsqueeze(0).to(device)
+ if scribble_mode == 'split':
+ point_coords = point_coords.permute(1, 0, 2)
+ point_labels = point_labels.permute(1, 0)
+ masks, _, _ = sam_predictor.predict_torch(
+ point_coords=point_coords if len(point_coords) > 0 else None,
+ point_labels=point_labels if len(point_coords) > 0 else None,
+ mask_input = None,
+ boxes = None,
+ multimask_output = False,
+ )
+ elif task_type == 'automask':
+ masks = sam_automask_generator.generate(image)
+ else:
+ transformed_image = transform_image(image_pil)
+
+ if task_type == 'automatic':
+ # generate caption and tags
+ # use Tag2Text can generate better captions
+ # https://huggingface.co/spaces/xinyu1205/Tag2Text
+ # but there are some bugs...
+ blip_processor = blip_processor or BlipProcessor.from_pretrained("Salesforce/blip-image-captioning-large")
+ blip_model = blip_model or BlipForConditionalGeneration.from_pretrained("Salesforce/blip-image-captioning-large", torch_dtype=torch.float16).to("cuda")
+ text_prompt = generate_caption(blip_processor, blip_model, image_pil)
+ if len(openai_api_key) > 0:
+ text_prompt = generate_tags(text_prompt, split=",", openai_api_key=openai_api_key)
+ print(f"Caption: {text_prompt}")
+
+ # run grounding dino model
+ boxes_filt, scores, pred_phrases = get_grounding_output(
+ groundingdino_model, transformed_image, text_prompt, box_threshold, text_threshold
+ )
+
+ # process boxes
+ H, W = size[1], size[0]
+ for i in range(boxes_filt.size(0)):
+ boxes_filt[i] = boxes_filt[i] * torch.Tensor([W, H, W, H])
+ boxes_filt[i][:2] -= boxes_filt[i][2:] / 2
+ boxes_filt[i][2:] += boxes_filt[i][:2]
+
+ boxes_filt = boxes_filt.cpu()
+
+
+ if task_type == 'seg' or task_type == 'inpainting' or task_type == 'automatic':
+ sam_predictor.set_image(image)
+
+ if task_type == 'automatic':
+ # use NMS to handle overlapped boxes
+ print(f"Before NMS: {boxes_filt.shape[0]} boxes")
+ nms_idx = torchvision.ops.nms(boxes_filt, scores, iou_threshold).numpy().tolist()
+ boxes_filt = boxes_filt[nms_idx]
+ pred_phrases = [pred_phrases[idx] for idx in nms_idx]
+ print(f"After NMS: {boxes_filt.shape[0]} boxes")
+ print(f"Revise caption with number: {text_prompt}")
+
+ transformed_boxes = sam_predictor.transform.apply_boxes_torch(boxes_filt, image.shape[:2]).to(device)
+
+ masks, _, _ = sam_predictor.predict_torch(
+ point_coords = None,
+ point_labels = None,
+ boxes = transformed_boxes,
+ multimask_output = False,
+ )
+
+ if task_type == 'det':
+ image_draw = ImageDraw.Draw(image_pil)
+ for box, label in zip(boxes_filt, pred_phrases):
+ draw_box(box, image_draw, label)
+
+ return [image_pil]
+ elif task_type == 'automask':
+ full_img, res = show_anns(masks)
+ return [full_img]
+ elif task_type == 'scribble':
+ mask_image = Image.new('RGBA', size, color=(0, 0, 0, 0))
+
+ mask_draw = ImageDraw.Draw(mask_image)
+
+ for mask in masks:
+ draw_mask(mask[0].cpu().numpy(), mask_draw, random_color=True)
+
+ image_pil = image_pil.convert('RGBA')
+ image_pil.alpha_composite(mask_image)
+ return [image_pil, mask_image]
+ elif task_type == 'seg' or task_type == 'automatic':
+
+ mask_image = Image.new('RGBA', size, color=(0, 0, 0, 0))
+
+ mask_draw = ImageDraw.Draw(mask_image)
+ for mask in masks:
+ draw_mask(mask[0].cpu().numpy(), mask_draw, random_color=True)
+
+ image_draw = ImageDraw.Draw(image_pil)
+
+ for box, label in zip(boxes_filt, pred_phrases):
+ draw_box(box, image_draw, label)
+
+ if task_type == 'automatic':
+ image_draw.text((10, 10), text_prompt, fill='black')
+
+ image_pil = image_pil.convert('RGBA')
+ image_pil.alpha_composite(mask_image)
+ return [image_pil, mask_image]
+ elif task_type == 'inpainting':
+ assert inpaint_prompt, 'inpaint_prompt is not found!'
+ # inpainting pipeline
+ if inpaint_mode == 'merge':
+ masks = torch.sum(masks, dim=0).unsqueeze(0)
+ masks = torch.where(masks > 0, True, False)
+ mask = masks[0][0].cpu().numpy() # simply choose the first mask, which will be refine in the future release
+ mask_pil = Image.fromarray(mask)
+
+ if inpaint_pipeline is None:
+ inpaint_pipeline = StableDiffusionInpaintPipeline.from_pretrained(
+ "runwayml/stable-diffusion-inpainting", torch_dtype=torch.float16
+ )
+ inpaint_pipeline = inpaint_pipeline.to("cuda")
+
+ image = inpaint_pipeline(prompt=inpaint_prompt, image=image_pil.resize((512, 512)), mask_image=mask_pil.resize((512, 512))).images[0]
+ image = image.resize(size)
+
+ return [image, mask_pil]
+ else:
+ print("task_type:{} error!".format(task_type))
+
+if __name__ == "__main__":
+ parser = argparse.ArgumentParser("Grounded SAM demo", add_help=True)
+ parser.add_argument("--debug", action="store_true", help="using debug mode")
+ parser.add_argument("--share", action="store_true", help="share the app")
+ parser.add_argument('--port', type=int, default=7589, help='port to run the server')
+ parser.add_argument('--no-gradio-queue', action="store_true", help='path to the SAM checkpoint')
+ args = parser.parse_args()
+
+ print(args)
+
+ block = gr.Blocks()
+ if not args.no_gradio_queue:
+ block = block.queue()
+
+ with block:
+ with gr.Row():
+ with gr.Column():
+ input_image = gr.Image(source='upload', type="pil", value="assets/demo1.jpg", tool="sketch")
+ task_type = gr.Dropdown(["scribble", "automask", "det", "seg", "inpainting", "automatic"], value="automatic", label="task_type")
+ text_prompt = gr.Textbox(label="Text Prompt")
+ inpaint_prompt = gr.Textbox(label="Inpaint Prompt")
+ run_button = gr.Button(label="Run")
+ with gr.Accordion("Advanced options", open=False):
+ box_threshold = gr.Slider(
+ label="Box Threshold", minimum=0.0, maximum=1.0, value=0.3, step=0.05
+ )
+ text_threshold = gr.Slider(
+ label="Text Threshold", minimum=0.0, maximum=1.0, value=0.25, step=0.05
+ )
+ iou_threshold = gr.Slider(
+ label="IOU Threshold", minimum=0.0, maximum=1.0, value=0.5, step=0.05
+ )
+ inpaint_mode = gr.Dropdown(["merge", "first"], value="merge", label="inpaint_mode")
+ scribble_mode = gr.Dropdown(["merge", "split"], value="split", label="scribble_mode")
+ openai_api_key= gr.Textbox(label="(Optional)OpenAI key, enable chatgpt")
+
+ with gr.Column():
+ gallery = gr.Gallery(
+ label="Generated images", show_label=False, elem_id="gallery"
+ ).style(preview=True, grid=2, object_fit="scale-down")
+
+ run_button.click(fn=run_grounded_sam, inputs=[
+ input_image, text_prompt, task_type, inpaint_prompt, box_threshold, text_threshold, iou_threshold, inpaint_mode, scribble_mode, openai_api_key], outputs=gallery)
+
+ block.queue(concurrency_count=100)
+ block.launch(server_name='0.0.0.0', server_port=args.port, debug=args.debug, share=args.share)
\ No newline at end of file
diff --git a/grounded-sam-osx/LICENSE b/grounded-sam-osx/LICENSE
new file mode 100644
index 0000000000000000000000000000000000000000..b1395e94b016dd1b95b4c7e3ed493e1d0b342917
--- /dev/null
+++ b/grounded-sam-osx/LICENSE
@@ -0,0 +1,201 @@
+ Apache License
+ Version 2.0, January 2004
+ http://www.apache.org/licenses/
+
+ TERMS AND CONDITIONS FOR USE, REPRODUCTION, AND DISTRIBUTION
+
+ 1. Definitions.
+
+ "License" shall mean the terms and conditions for use, reproduction,
+ and distribution as defined by Sections 1 through 9 of this document.
+
+ "Licensor" shall mean the copyright owner or entity authorized by
+ the copyright owner that is granting the License.
+
+ "Legal Entity" shall mean the union of the acting entity and all
+ other entities that control, are controlled by, or are under common
+ control with that entity. For the purposes of this definition,
+ "control" means (i) the power, direct or indirect, to cause the
+ direction or management of such entity, whether by contract or
+ otherwise, or (ii) ownership of fifty percent (50%) or more of the
+ outstanding shares, or (iii) beneficial ownership of such entity.
+
+ "You" (or "Your") shall mean an individual or Legal Entity
+ exercising permissions granted by this License.
+
+ "Source" form shall mean the preferred form for making modifications,
+ including but not limited to software source code, documentation
+ source, and configuration files.
+
+ "Object" form shall mean any form resulting from mechanical
+ transformation or translation of a Source form, including but
+ not limited to compiled object code, generated documentation,
+ and conversions to other media types.
+
+ "Work" shall mean the work of authorship, whether in Source or
+ Object form, made available under the License, as indicated by a
+ copyright notice that is included in or attached to the work
+ (an example is provided in the Appendix below).
+
+ "Derivative Works" shall mean any work, whether in Source or Object
+ form, that is based on (or derived from) the Work and for which the
+ editorial revisions, annotations, elaborations, or other modifications
+ represent, as a whole, an original work of authorship. For the purposes
+ of this License, Derivative Works shall not include works that remain
+ separable from, or merely link (or bind by name) to the interfaces of,
+ the Work and Derivative Works thereof.
+
+ "Contribution" shall mean any work of authorship, including
+ the original version of the Work and any modifications or additions
+ to that Work or Derivative Works thereof, that is intentionally
+ submitted to Licensor for inclusion in the Work by the copyright owner
+ or by an individual or Legal Entity authorized to submit on behalf of
+ the copyright owner. For the purposes of this definition, "submitted"
+ means any form of electronic, verbal, or written communication sent
+ to the Licensor or its representatives, including but not limited to
+ communication on electronic mailing lists, source code control systems,
+ and issue tracking systems that are managed by, or on behalf of, the
+ Licensor for the purpose of discussing and improving the Work, but
+ excluding communication that is conspicuously marked or otherwise
+ designated in writing by the copyright owner as "Not a Contribution."
+
+ "Contributor" shall mean Licensor and any individual or Legal Entity
+ on behalf of whom a Contribution has been received by Licensor and
+ subsequently incorporated within the Work.
+
+ 2. Grant of Copyright License. Subject to the terms and conditions of
+ this License, each Contributor hereby grants to You a perpetual,
+ worldwide, non-exclusive, no-charge, royalty-free, irrevocable
+ copyright license to reproduce, prepare Derivative Works of,
+ publicly display, publicly perform, sublicense, and distribute the
+ Work and such Derivative Works in Source or Object form.
+
+ 3. Grant of Patent License. Subject to the terms and conditions of
+ this License, each Contributor hereby grants to You a perpetual,
+ worldwide, non-exclusive, no-charge, royalty-free, irrevocable
+ (except as stated in this section) patent license to make, have made,
+ use, offer to sell, sell, import, and otherwise transfer the Work,
+ where such license applies only to those patent claims licensable
+ by such Contributor that are necessarily infringed by their
+ Contribution(s) alone or by combination of their Contribution(s)
+ with the Work to which such Contribution(s) was submitted. If You
+ institute patent litigation against any entity (including a
+ cross-claim or counterclaim in a lawsuit) alleging that the Work
+ or a Contribution incorporated within the Work constitutes direct
+ or contributory patent infringement, then any patent licenses
+ granted to You under this License for that Work shall terminate
+ as of the date such litigation is filed.
+
+ 4. Redistribution. You may reproduce and distribute copies of the
+ Work or Derivative Works thereof in any medium, with or without
+ modifications, and in Source or Object form, provided that You
+ meet the following conditions:
+
+ (a) You must give any other recipients of the Work or
+ Derivative Works a copy of this License; and
+
+ (b) You must cause any modified files to carry prominent notices
+ stating that You changed the files; and
+
+ (c) You must retain, in the Source form of any Derivative Works
+ that You distribute, all copyright, patent, trademark, and
+ attribution notices from the Source form of the Work,
+ excluding those notices that do not pertain to any part of
+ the Derivative Works; and
+
+ (d) If the Work includes a "NOTICE" text file as part of its
+ distribution, then any Derivative Works that You distribute must
+ include a readable copy of the attribution notices contained
+ within such NOTICE file, excluding those notices that do not
+ pertain to any part of the Derivative Works, in at least one
+ of the following places: within a NOTICE text file distributed
+ as part of the Derivative Works; within the Source form or
+ documentation, if provided along with the Derivative Works; or,
+ within a display generated by the Derivative Works, if and
+ wherever such third-party notices normally appear. The contents
+ of the NOTICE file are for informational purposes only and
+ do not modify the License. You may add Your own attribution
+ notices within Derivative Works that You distribute, alongside
+ or as an addendum to the NOTICE text from the Work, provided
+ that such additional attribution notices cannot be construed
+ as modifying the License.
+
+ You may add Your own copyright statement to Your modifications and
+ may provide additional or different license terms and conditions
+ for use, reproduction, or distribution of Your modifications, or
+ for any such Derivative Works as a whole, provided Your use,
+ reproduction, and distribution of the Work otherwise complies with
+ the conditions stated in this License.
+
+ 5. Submission of Contributions. Unless You explicitly state otherwise,
+ any Contribution intentionally submitted for inclusion in the Work
+ by You to the Licensor shall be under the terms and conditions of
+ this License, without any additional terms or conditions.
+ Notwithstanding the above, nothing herein shall supersede or modify
+ the terms of any separate license agreement you may have executed
+ with Licensor regarding such Contributions.
+
+ 6. Trademarks. This License does not grant permission to use the trade
+ names, trademarks, service marks, or product names of the Licensor,
+ except as required for reasonable and customary use in describing the
+ origin of the Work and reproducing the content of the NOTICE file.
+
+ 7. Disclaimer of Warranty. Unless required by applicable law or
+ agreed to in writing, Licensor provides the Work (and each
+ Contributor provides its Contributions) on an "AS IS" BASIS,
+ WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or
+ implied, including, without limitation, any warranties or conditions
+ of TITLE, NON-INFRINGEMENT, MERCHANTABILITY, or FITNESS FOR A
+ PARTICULAR PURPOSE. You are solely responsible for determining the
+ appropriateness of using or redistributing the Work and assume any
+ risks associated with Your exercise of permissions under this License.
+
+ 8. Limitation of Liability. In no event and under no legal theory,
+ whether in tort (including negligence), contract, or otherwise,
+ unless required by applicable law (such as deliberate and grossly
+ negligent acts) or agreed to in writing, shall any Contributor be
+ liable to You for damages, including any direct, indirect, special,
+ incidental, or consequential damages of any character arising as a
+ result of this License or out of the use or inability to use the
+ Work (including but not limited to damages for loss of goodwill,
+ work stoppage, computer failure or malfunction, or any and all
+ other commercial damages or losses), even if such Contributor
+ has been advised of the possibility of such damages.
+
+ 9. Accepting Warranty or Additional Liability. While redistributing
+ the Work or Derivative Works thereof, You may choose to offer,
+ and charge a fee for, acceptance of support, warranty, indemnity,
+ or other liability obligations and/or rights consistent with this
+ License. However, in accepting such obligations, You may act only
+ on Your own behalf and on Your sole responsibility, not on behalf
+ of any other Contributor, and only if You agree to indemnify,
+ defend, and hold each Contributor harmless for any liability
+ incurred by, or claims asserted against, such Contributor by reason
+ of your accepting any such warranty or additional liability.
+
+ END OF TERMS AND CONDITIONS
+
+ APPENDIX: How to apply the Apache License to your work.
+
+ To apply the Apache License to your work, attach the following
+ boilerplate notice, with the fields enclosed by brackets "[]"
+ replaced with your own identifying information. (Don't include
+ the brackets!) The text should be enclosed in the appropriate
+ comment syntax for the file format. We also recommend that a
+ file or class name and description of purpose be included on the
+ same "printed page" as the copyright notice for easier
+ identification within third-party archives.
+
+ Copyright 2020 - present, Facebook, Inc
+
+ Licensed under the Apache License, Version 2.0 (the "License");
+ you may not use this file except in compliance with the License.
+ You may obtain a copy of the License at
+
+ http://www.apache.org/licenses/LICENSE-2.0
+
+ Unless required by applicable law or agreed to in writing, software
+ distributed under the License is distributed on an "AS IS" BASIS,
+ WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+ See the License for the specific language governing permissions and
+ limitations under the License.
diff --git a/grounded-sam-osx/README.md b/grounded-sam-osx/README.md
new file mode 100644
index 0000000000000000000000000000000000000000..a13cd92e35c15d173c96b36fa2adfe4a2be7970b
--- /dev/null
+++ b/grounded-sam-osx/README.md
@@ -0,0 +1,2 @@
+# grounded-sam-osx
+This is a submodule of [Grounded-SAM](https://github.com/IDEA-Research/Grounded-Segment-Anything). It can estimate full-body pose and shape from a monuculor image. The combination of Grounded-SAM and OSX supports promptable 3D whole-body mesh recovery. Please refer to this [repo](https://github.com/IDEA-Research/OSX) to use the full code of OSX.
diff --git a/grounded-sam-osx/_base_/datasets/300w.py b/grounded-sam-osx/_base_/datasets/300w.py
new file mode 100644
index 0000000000000000000000000000000000000000..10c343a2adf84947159f2651b3e918d1fc32ea90
--- /dev/null
+++ b/grounded-sam-osx/_base_/datasets/300w.py
@@ -0,0 +1,384 @@
+dataset_info = dict(
+ dataset_name='300w',
+ paper_info=dict(
+ author='Sagonas, Christos and Antonakos, Epameinondas '
+ 'and Tzimiropoulos, Georgios and Zafeiriou, Stefanos '
+ 'and Pantic, Maja',
+ title='300 faces in-the-wild challenge: '
+ 'Database and results',
+ container='Image and vision computing',
+ year='2016',
+ homepage='https://ibug.doc.ic.ac.uk/resources/300-W/',
+ ),
+ keypoint_info={
+ 0:
+ dict(
+ name='kpt-0', id=0, color=[255, 255, 255], type='', swap='kpt-16'),
+ 1:
+ dict(
+ name='kpt-1', id=1, color=[255, 255, 255], type='', swap='kpt-15'),
+ 2:
+ dict(
+ name='kpt-2', id=2, color=[255, 255, 255], type='', swap='kpt-14'),
+ 3:
+ dict(
+ name='kpt-3', id=3, color=[255, 255, 255], type='', swap='kpt-13'),
+ 4:
+ dict(
+ name='kpt-4', id=4, color=[255, 255, 255], type='', swap='kpt-12'),
+ 5:
+ dict(
+ name='kpt-5', id=5, color=[255, 255, 255], type='', swap='kpt-11'),
+ 6:
+ dict(
+ name='kpt-6', id=6, color=[255, 255, 255], type='', swap='kpt-10'),
+ 7:
+ dict(name='kpt-7', id=7, color=[255, 255, 255], type='', swap='kpt-9'),
+ 8:
+ dict(name='kpt-8', id=8, color=[255, 255, 255], type='', swap=''),
+ 9:
+ dict(name='kpt-9', id=9, color=[255, 255, 255], type='', swap='kpt-7'),
+ 10:
+ dict(
+ name='kpt-10', id=10, color=[255, 255, 255], type='',
+ swap='kpt-6'),
+ 11:
+ dict(
+ name='kpt-11', id=11, color=[255, 255, 255], type='',
+ swap='kpt-5'),
+ 12:
+ dict(
+ name='kpt-12', id=12, color=[255, 255, 255], type='',
+ swap='kpt-4'),
+ 13:
+ dict(
+ name='kpt-13', id=13, color=[255, 255, 255], type='',
+ swap='kpt-3'),
+ 14:
+ dict(
+ name='kpt-14', id=14, color=[255, 255, 255], type='',
+ swap='kpt-2'),
+ 15:
+ dict(
+ name='kpt-15', id=15, color=[255, 255, 255], type='',
+ swap='kpt-1'),
+ 16:
+ dict(
+ name='kpt-16', id=16, color=[255, 255, 255], type='',
+ swap='kpt-0'),
+ 17:
+ dict(
+ name='kpt-17',
+ id=17,
+ color=[255, 255, 255],
+ type='',
+ swap='kpt-26'),
+ 18:
+ dict(
+ name='kpt-18',
+ id=18,
+ color=[255, 255, 255],
+ type='',
+ swap='kpt-25'),
+ 19:
+ dict(
+ name='kpt-19',
+ id=19,
+ color=[255, 255, 255],
+ type='',
+ swap='kpt-24'),
+ 20:
+ dict(
+ name='kpt-20',
+ id=20,
+ color=[255, 255, 255],
+ type='',
+ swap='kpt-23'),
+ 21:
+ dict(
+ name='kpt-21',
+ id=21,
+ color=[255, 255, 255],
+ type='',
+ swap='kpt-22'),
+ 22:
+ dict(
+ name='kpt-22',
+ id=22,
+ color=[255, 255, 255],
+ type='',
+ swap='kpt-21'),
+ 23:
+ dict(
+ name='kpt-23',
+ id=23,
+ color=[255, 255, 255],
+ type='',
+ swap='kpt-20'),
+ 24:
+ dict(
+ name='kpt-24',
+ id=24,
+ color=[255, 255, 255],
+ type='',
+ swap='kpt-19'),
+ 25:
+ dict(
+ name='kpt-25',
+ id=25,
+ color=[255, 255, 255],
+ type='',
+ swap='kpt-18'),
+ 26:
+ dict(
+ name='kpt-26',
+ id=26,
+ color=[255, 255, 255],
+ type='',
+ swap='kpt-17'),
+ 27:
+ dict(name='kpt-27', id=27, color=[255, 255, 255], type='', swap=''),
+ 28:
+ dict(name='kpt-28', id=28, color=[255, 255, 255], type='', swap=''),
+ 29:
+ dict(name='kpt-29', id=29, color=[255, 255, 255], type='', swap=''),
+ 30:
+ dict(name='kpt-30', id=30, color=[255, 255, 255], type='', swap=''),
+ 31:
+ dict(
+ name='kpt-31',
+ id=31,
+ color=[255, 255, 255],
+ type='',
+ swap='kpt-35'),
+ 32:
+ dict(
+ name='kpt-32',
+ id=32,
+ color=[255, 255, 255],
+ type='',
+ swap='kpt-34'),
+ 33:
+ dict(name='kpt-33', id=33, color=[255, 255, 255], type='', swap=''),
+ 34:
+ dict(
+ name='kpt-34',
+ id=34,
+ color=[255, 255, 255],
+ type='',
+ swap='kpt-32'),
+ 35:
+ dict(
+ name='kpt-35',
+ id=35,
+ color=[255, 255, 255],
+ type='',
+ swap='kpt-31'),
+ 36:
+ dict(
+ name='kpt-36',
+ id=36,
+ color=[255, 255, 255],
+ type='',
+ swap='kpt-45'),
+ 37:
+ dict(
+ name='kpt-37',
+ id=37,
+ color=[255, 255, 255],
+ type='',
+ swap='kpt-44'),
+ 38:
+ dict(
+ name='kpt-38',
+ id=38,
+ color=[255, 255, 255],
+ type='',
+ swap='kpt-43'),
+ 39:
+ dict(
+ name='kpt-39',
+ id=39,
+ color=[255, 255, 255],
+ type='',
+ swap='kpt-42'),
+ 40:
+ dict(
+ name='kpt-40',
+ id=40,
+ color=[255, 255, 255],
+ type='',
+ swap='kpt-47'),
+ 41:
+ dict(
+ name='kpt-41',
+ id=41,
+ color=[255, 255, 255],
+ type='',
+ swap='kpt-46'),
+ 42:
+ dict(
+ name='kpt-42',
+ id=42,
+ color=[255, 255, 255],
+ type='',
+ swap='kpt-39'),
+ 43:
+ dict(
+ name='kpt-43',
+ id=43,
+ color=[255, 255, 255],
+ type='',
+ swap='kpt-38'),
+ 44:
+ dict(
+ name='kpt-44',
+ id=44,
+ color=[255, 255, 255],
+ type='',
+ swap='kpt-37'),
+ 45:
+ dict(
+ name='kpt-45',
+ id=45,
+ color=[255, 255, 255],
+ type='',
+ swap='kpt-36'),
+ 46:
+ dict(
+ name='kpt-46',
+ id=46,
+ color=[255, 255, 255],
+ type='',
+ swap='kpt-41'),
+ 47:
+ dict(
+ name='kpt-47',
+ id=47,
+ color=[255, 255, 255],
+ type='',
+ swap='kpt-40'),
+ 48:
+ dict(
+ name='kpt-48',
+ id=48,
+ color=[255, 255, 255],
+ type='',
+ swap='kpt-54'),
+ 49:
+ dict(
+ name='kpt-49',
+ id=49,
+ color=[255, 255, 255],
+ type='',
+ swap='kpt-53'),
+ 50:
+ dict(
+ name='kpt-50',
+ id=50,
+ color=[255, 255, 255],
+ type='',
+ swap='kpt-52'),
+ 51:
+ dict(name='kpt-51', id=51, color=[255, 255, 255], type='', swap=''),
+ 52:
+ dict(
+ name='kpt-52',
+ id=52,
+ color=[255, 255, 255],
+ type='',
+ swap='kpt-50'),
+ 53:
+ dict(
+ name='kpt-53',
+ id=53,
+ color=[255, 255, 255],
+ type='',
+ swap='kpt-49'),
+ 54:
+ dict(
+ name='kpt-54',
+ id=54,
+ color=[255, 255, 255],
+ type='',
+ swap='kpt-48'),
+ 55:
+ dict(
+ name='kpt-55',
+ id=55,
+ color=[255, 255, 255],
+ type='',
+ swap='kpt-59'),
+ 56:
+ dict(
+ name='kpt-56',
+ id=56,
+ color=[255, 255, 255],
+ type='',
+ swap='kpt-58'),
+ 57:
+ dict(name='kpt-57', id=57, color=[255, 255, 255], type='', swap=''),
+ 58:
+ dict(
+ name='kpt-58',
+ id=58,
+ color=[255, 255, 255],
+ type='',
+ swap='kpt-56'),
+ 59:
+ dict(
+ name='kpt-59',
+ id=59,
+ color=[255, 255, 255],
+ type='',
+ swap='kpt-55'),
+ 60:
+ dict(
+ name='kpt-60',
+ id=60,
+ color=[255, 255, 255],
+ type='',
+ swap='kpt-64'),
+ 61:
+ dict(
+ name='kpt-61',
+ id=61,
+ color=[255, 255, 255],
+ type='',
+ swap='kpt-63'),
+ 62:
+ dict(name='kpt-62', id=62, color=[255, 255, 255], type='', swap=''),
+ 63:
+ dict(
+ name='kpt-63',
+ id=63,
+ color=[255, 255, 255],
+ type='',
+ swap='kpt-61'),
+ 64:
+ dict(
+ name='kpt-64',
+ id=64,
+ color=[255, 255, 255],
+ type='',
+ swap='kpt-60'),
+ 65:
+ dict(
+ name='kpt-65',
+ id=65,
+ color=[255, 255, 255],
+ type='',
+ swap='kpt-67'),
+ 66:
+ dict(name='kpt-66', id=66, color=[255, 255, 255], type='', swap=''),
+ 67:
+ dict(
+ name='kpt-67',
+ id=67,
+ color=[255, 255, 255],
+ type='',
+ swap='kpt-65'),
+ },
+ skeleton_info={},
+ joint_weights=[1.] * 68,
+ sigmas=[])
diff --git a/grounded-sam-osx/_base_/datasets/aflw.py b/grounded-sam-osx/_base_/datasets/aflw.py
new file mode 100644
index 0000000000000000000000000000000000000000..bf534cbb756e8c514c2f5e2a7fceedd55afb637e
--- /dev/null
+++ b/grounded-sam-osx/_base_/datasets/aflw.py
@@ -0,0 +1,83 @@
+dataset_info = dict(
+ dataset_name='aflw',
+ paper_info=dict(
+ author='Koestinger, Martin and Wohlhart, Paul and '
+ 'Roth, Peter M and Bischof, Horst',
+ title='Annotated facial landmarks in the wild: '
+ 'A large-scale, real-world database for facial '
+ 'landmark localization',
+ container='2011 IEEE international conference on computer '
+ 'vision workshops (ICCV workshops)',
+ year='2011',
+ homepage='https://www.tugraz.at/institute/icg/research/'
+ 'team-bischof/lrs/downloads/aflw/',
+ ),
+ keypoint_info={
+ 0:
+ dict(name='kpt-0', id=0, color=[255, 255, 255], type='', swap='kpt-5'),
+ 1:
+ dict(name='kpt-1', id=1, color=[255, 255, 255], type='', swap='kpt-4'),
+ 2:
+ dict(name='kpt-2', id=2, color=[255, 255, 255], type='', swap='kpt-3'),
+ 3:
+ dict(name='kpt-3', id=3, color=[255, 255, 255], type='', swap='kpt-2'),
+ 4:
+ dict(name='kpt-4', id=4, color=[255, 255, 255], type='', swap='kpt-1'),
+ 5:
+ dict(name='kpt-5', id=5, color=[255, 255, 255], type='', swap='kpt-0'),
+ 6:
+ dict(
+ name='kpt-6', id=6, color=[255, 255, 255], type='', swap='kpt-11'),
+ 7:
+ dict(
+ name='kpt-7', id=7, color=[255, 255, 255], type='', swap='kpt-10'),
+ 8:
+ dict(name='kpt-8', id=8, color=[255, 255, 255], type='', swap='kpt-9'),
+ 9:
+ dict(name='kpt-9', id=9, color=[255, 255, 255], type='', swap='kpt-8'),
+ 10:
+ dict(
+ name='kpt-10', id=10, color=[255, 255, 255], type='',
+ swap='kpt-7'),
+ 11:
+ dict(
+ name='kpt-11', id=11, color=[255, 255, 255], type='',
+ swap='kpt-6'),
+ 12:
+ dict(
+ name='kpt-12',
+ id=12,
+ color=[255, 255, 255],
+ type='',
+ swap='kpt-14'),
+ 13:
+ dict(name='kpt-13', id=13, color=[255, 255, 255], type='', swap=''),
+ 14:
+ dict(
+ name='kpt-14',
+ id=14,
+ color=[255, 255, 255],
+ type='',
+ swap='kpt-12'),
+ 15:
+ dict(
+ name='kpt-15',
+ id=15,
+ color=[255, 255, 255],
+ type='',
+ swap='kpt-17'),
+ 16:
+ dict(name='kpt-16', id=16, color=[255, 255, 255], type='', swap=''),
+ 17:
+ dict(
+ name='kpt-17',
+ id=17,
+ color=[255, 255, 255],
+ type='',
+ swap='kpt-15'),
+ 18:
+ dict(name='kpt-18', id=18, color=[255, 255, 255], type='', swap='')
+ },
+ skeleton_info={},
+ joint_weights=[1.] * 19,
+ sigmas=[])
diff --git a/grounded-sam-osx/_base_/datasets/aic.py b/grounded-sam-osx/_base_/datasets/aic.py
new file mode 100644
index 0000000000000000000000000000000000000000..9ecdbe3f0afeb19dbb7aed42653ce5efd85cfda3
--- /dev/null
+++ b/grounded-sam-osx/_base_/datasets/aic.py
@@ -0,0 +1,140 @@
+dataset_info = dict(
+ dataset_name='aic',
+ paper_info=dict(
+ author='Wu, Jiahong and Zheng, He and Zhao, Bo and '
+ 'Li, Yixin and Yan, Baoming and Liang, Rui and '
+ 'Wang, Wenjia and Zhou, Shipei and Lin, Guosen and '
+ 'Fu, Yanwei and others',
+ title='Ai challenger: A large-scale dataset for going '
+ 'deeper in image understanding',
+ container='arXiv',
+ year='2017',
+ homepage='https://github.com/AIChallenger/AI_Challenger_2017',
+ ),
+ keypoint_info={
+ 0:
+ dict(
+ name='right_shoulder',
+ id=0,
+ color=[255, 128, 0],
+ type='upper',
+ swap='left_shoulder'),
+ 1:
+ dict(
+ name='right_elbow',
+ id=1,
+ color=[255, 128, 0],
+ type='upper',
+ swap='left_elbow'),
+ 2:
+ dict(
+ name='right_wrist',
+ id=2,
+ color=[255, 128, 0],
+ type='upper',
+ swap='left_wrist'),
+ 3:
+ dict(
+ name='left_shoulder',
+ id=3,
+ color=[0, 255, 0],
+ type='upper',
+ swap='right_shoulder'),
+ 4:
+ dict(
+ name='left_elbow',
+ id=4,
+ color=[0, 255, 0],
+ type='upper',
+ swap='right_elbow'),
+ 5:
+ dict(
+ name='left_wrist',
+ id=5,
+ color=[0, 255, 0],
+ type='upper',
+ swap='right_wrist'),
+ 6:
+ dict(
+ name='right_hip',
+ id=6,
+ color=[255, 128, 0],
+ type='lower',
+ swap='left_hip'),
+ 7:
+ dict(
+ name='right_knee',
+ id=7,
+ color=[255, 128, 0],
+ type='lower',
+ swap='left_knee'),
+ 8:
+ dict(
+ name='right_ankle',
+ id=8,
+ color=[255, 128, 0],
+ type='lower',
+ swap='left_ankle'),
+ 9:
+ dict(
+ name='left_hip',
+ id=9,
+ color=[0, 255, 0],
+ type='lower',
+ swap='right_hip'),
+ 10:
+ dict(
+ name='left_knee',
+ id=10,
+ color=[0, 255, 0],
+ type='lower',
+ swap='right_knee'),
+ 11:
+ dict(
+ name='left_ankle',
+ id=11,
+ color=[0, 255, 0],
+ type='lower',
+ swap='right_ankle'),
+ 12:
+ dict(
+ name='head_top',
+ id=12,
+ color=[51, 153, 255],
+ type='upper',
+ swap=''),
+ 13:
+ dict(name='neck', id=13, color=[51, 153, 255], type='upper', swap='')
+ },
+ skeleton_info={
+ 0:
+ dict(link=('right_wrist', 'right_elbow'), id=0, color=[255, 128, 0]),
+ 1: dict(
+ link=('right_elbow', 'right_shoulder'), id=1, color=[255, 128, 0]),
+ 2: dict(link=('right_shoulder', 'neck'), id=2, color=[51, 153, 255]),
+ 3: dict(link=('neck', 'left_shoulder'), id=3, color=[51, 153, 255]),
+ 4: dict(link=('left_shoulder', 'left_elbow'), id=4, color=[0, 255, 0]),
+ 5: dict(link=('left_elbow', 'left_wrist'), id=5, color=[0, 255, 0]),
+ 6: dict(link=('right_ankle', 'right_knee'), id=6, color=[255, 128, 0]),
+ 7: dict(link=('right_knee', 'right_hip'), id=7, color=[255, 128, 0]),
+ 8: dict(link=('right_hip', 'left_hip'), id=8, color=[51, 153, 255]),
+ 9: dict(link=('left_hip', 'left_knee'), id=9, color=[0, 255, 0]),
+ 10: dict(link=('left_knee', 'left_ankle'), id=10, color=[0, 255, 0]),
+ 11: dict(link=('head_top', 'neck'), id=11, color=[51, 153, 255]),
+ 12: dict(
+ link=('right_shoulder', 'right_hip'), id=12, color=[51, 153, 255]),
+ 13:
+ dict(link=('left_shoulder', 'left_hip'), id=13, color=[51, 153, 255])
+ },
+ joint_weights=[
+ 1., 1.2, 1.5, 1., 1.2, 1.5, 1., 1.2, 1.5, 1., 1.2, 1.5, 1., 1.
+ ],
+
+ # 'https://github.com/AIChallenger/AI_Challenger_2017/blob/master/'
+ # 'Evaluation/keypoint_eval/keypoint_eval.py#L50'
+ # delta = 2 x sigma
+ sigmas=[
+ 0.01388152, 0.01515228, 0.01057665, 0.01417709, 0.01497891, 0.01402144,
+ 0.03909642, 0.03686941, 0.01981803, 0.03843971, 0.03412318, 0.02415081,
+ 0.01291456, 0.01236173
+ ])
diff --git a/grounded-sam-osx/_base_/datasets/animalpose.py b/grounded-sam-osx/_base_/datasets/animalpose.py
new file mode 100644
index 0000000000000000000000000000000000000000..d5bb62d951b71da25e679bd755fe566216dc3f6f
--- /dev/null
+++ b/grounded-sam-osx/_base_/datasets/animalpose.py
@@ -0,0 +1,166 @@
+dataset_info = dict(
+ dataset_name='animalpose',
+ paper_info=dict(
+ author='Cao, Jinkun and Tang, Hongyang and Fang, Hao-Shu and '
+ 'Shen, Xiaoyong and Lu, Cewu and Tai, Yu-Wing',
+ title='Cross-Domain Adaptation for Animal Pose Estimation',
+ container='The IEEE International Conference on '
+ 'Computer Vision (ICCV)',
+ year='2019',
+ homepage='https://sites.google.com/view/animal-pose/',
+ ),
+ keypoint_info={
+ 0:
+ dict(
+ name='L_Eye', id=0, color=[0, 255, 0], type='upper', swap='R_Eye'),
+ 1:
+ dict(
+ name='R_Eye',
+ id=1,
+ color=[255, 128, 0],
+ type='upper',
+ swap='L_Eye'),
+ 2:
+ dict(
+ name='L_EarBase',
+ id=2,
+ color=[0, 255, 0],
+ type='upper',
+ swap='R_EarBase'),
+ 3:
+ dict(
+ name='R_EarBase',
+ id=3,
+ color=[255, 128, 0],
+ type='upper',
+ swap='L_EarBase'),
+ 4:
+ dict(name='Nose', id=4, color=[51, 153, 255], type='upper', swap=''),
+ 5:
+ dict(name='Throat', id=5, color=[51, 153, 255], type='upper', swap=''),
+ 6:
+ dict(
+ name='TailBase', id=6, color=[51, 153, 255], type='lower',
+ swap=''),
+ 7:
+ dict(
+ name='Withers', id=7, color=[51, 153, 255], type='upper', swap=''),
+ 8:
+ dict(
+ name='L_F_Elbow',
+ id=8,
+ color=[0, 255, 0],
+ type='upper',
+ swap='R_F_Elbow'),
+ 9:
+ dict(
+ name='R_F_Elbow',
+ id=9,
+ color=[255, 128, 0],
+ type='upper',
+ swap='L_F_Elbow'),
+ 10:
+ dict(
+ name='L_B_Elbow',
+ id=10,
+ color=[0, 255, 0],
+ type='lower',
+ swap='R_B_Elbow'),
+ 11:
+ dict(
+ name='R_B_Elbow',
+ id=11,
+ color=[255, 128, 0],
+ type='lower',
+ swap='L_B_Elbow'),
+ 12:
+ dict(
+ name='L_F_Knee',
+ id=12,
+ color=[0, 255, 0],
+ type='upper',
+ swap='R_F_Knee'),
+ 13:
+ dict(
+ name='R_F_Knee',
+ id=13,
+ color=[255, 128, 0],
+ type='upper',
+ swap='L_F_Knee'),
+ 14:
+ dict(
+ name='L_B_Knee',
+ id=14,
+ color=[0, 255, 0],
+ type='lower',
+ swap='R_B_Knee'),
+ 15:
+ dict(
+ name='R_B_Knee',
+ id=15,
+ color=[255, 128, 0],
+ type='lower',
+ swap='L_B_Knee'),
+ 16:
+ dict(
+ name='L_F_Paw',
+ id=16,
+ color=[0, 255, 0],
+ type='upper',
+ swap='R_F_Paw'),
+ 17:
+ dict(
+ name='R_F_Paw',
+ id=17,
+ color=[255, 128, 0],
+ type='upper',
+ swap='L_F_Paw'),
+ 18:
+ dict(
+ name='L_B_Paw',
+ id=18,
+ color=[0, 255, 0],
+ type='lower',
+ swap='R_B_Paw'),
+ 19:
+ dict(
+ name='R_B_Paw',
+ id=19,
+ color=[255, 128, 0],
+ type='lower',
+ swap='L_B_Paw')
+ },
+ skeleton_info={
+ 0: dict(link=('L_Eye', 'R_Eye'), id=0, color=[51, 153, 255]),
+ 1: dict(link=('L_Eye', 'L_EarBase'), id=1, color=[0, 255, 0]),
+ 2: dict(link=('R_Eye', 'R_EarBase'), id=2, color=[255, 128, 0]),
+ 3: dict(link=('L_Eye', 'Nose'), id=3, color=[0, 255, 0]),
+ 4: dict(link=('R_Eye', 'Nose'), id=4, color=[255, 128, 0]),
+ 5: dict(link=('Nose', 'Throat'), id=5, color=[51, 153, 255]),
+ 6: dict(link=('Throat', 'Withers'), id=6, color=[51, 153, 255]),
+ 7: dict(link=('TailBase', 'Withers'), id=7, color=[51, 153, 255]),
+ 8: dict(link=('Throat', 'L_F_Elbow'), id=8, color=[0, 255, 0]),
+ 9: dict(link=('L_F_Elbow', 'L_F_Knee'), id=9, color=[0, 255, 0]),
+ 10: dict(link=('L_F_Knee', 'L_F_Paw'), id=10, color=[0, 255, 0]),
+ 11: dict(link=('Throat', 'R_F_Elbow'), id=11, color=[255, 128, 0]),
+ 12: dict(link=('R_F_Elbow', 'R_F_Knee'), id=12, color=[255, 128, 0]),
+ 13: dict(link=('R_F_Knee', 'R_F_Paw'), id=13, color=[255, 128, 0]),
+ 14: dict(link=('TailBase', 'L_B_Elbow'), id=14, color=[0, 255, 0]),
+ 15: dict(link=('L_B_Elbow', 'L_B_Knee'), id=15, color=[0, 255, 0]),
+ 16: dict(link=('L_B_Knee', 'L_B_Paw'), id=16, color=[0, 255, 0]),
+ 17: dict(link=('TailBase', 'R_B_Elbow'), id=17, color=[255, 128, 0]),
+ 18: dict(link=('R_B_Elbow', 'R_B_Knee'), id=18, color=[255, 128, 0]),
+ 19: dict(link=('R_B_Knee', 'R_B_Paw'), id=19, color=[255, 128, 0])
+ },
+ joint_weights=[
+ 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1.2, 1.2, 1.2, 1.2,
+ 1.5, 1.5, 1.5, 1.5
+ ],
+
+ # Note: The original paper did not provide enough information about
+ # the sigmas. We modified from 'https://github.com/cocodataset/'
+ # 'cocoapi/blob/master/PythonAPI/pycocotools/cocoeval.py#L523'
+ sigmas=[
+ 0.025, 0.025, 0.026, 0.035, 0.035, 0.10, 0.10, 0.10, 0.107, 0.107,
+ 0.107, 0.107, 0.087, 0.087, 0.087, 0.087, 0.089, 0.089, 0.089, 0.089
+ ])
diff --git a/grounded-sam-osx/_base_/datasets/ap10k.py b/grounded-sam-osx/_base_/datasets/ap10k.py
new file mode 100644
index 0000000000000000000000000000000000000000..c0df579acbb8cf0de1ef62412ba865ee8710f0aa
--- /dev/null
+++ b/grounded-sam-osx/_base_/datasets/ap10k.py
@@ -0,0 +1,142 @@
+dataset_info = dict(
+ dataset_name='ap10k',
+ paper_info=dict(
+ author='Yu, Hang and Xu, Yufei and Zhang, Jing and '
+ 'Zhao, Wei and Guan, Ziyu and Tao, Dacheng',
+ title='AP-10K: A Benchmark for Animal Pose Estimation in the Wild',
+ container='35th Conference on Neural Information Processing Systems '
+ '(NeurIPS 2021) Track on Datasets and Bench-marks.',
+ year='2021',
+ homepage='https://github.com/AlexTheBad/AP-10K',
+ ),
+ keypoint_info={
+ 0:
+ dict(
+ name='L_Eye', id=0, color=[0, 255, 0], type='upper', swap='R_Eye'),
+ 1:
+ dict(
+ name='R_Eye',
+ id=1,
+ color=[255, 128, 0],
+ type='upper',
+ swap='L_Eye'),
+ 2:
+ dict(name='Nose', id=2, color=[51, 153, 255], type='upper', swap=''),
+ 3:
+ dict(name='Neck', id=3, color=[51, 153, 255], type='upper', swap=''),
+ 4:
+ dict(
+ name='Root of tail',
+ id=4,
+ color=[51, 153, 255],
+ type='lower',
+ swap=''),
+ 5:
+ dict(
+ name='L_Shoulder',
+ id=5,
+ color=[51, 153, 255],
+ type='upper',
+ swap='R_Shoulder'),
+ 6:
+ dict(
+ name='L_Elbow',
+ id=6,
+ color=[51, 153, 255],
+ type='upper',
+ swap='R_Elbow'),
+ 7:
+ dict(
+ name='L_F_Paw',
+ id=7,
+ color=[0, 255, 0],
+ type='upper',
+ swap='R_F_Paw'),
+ 8:
+ dict(
+ name='R_Shoulder',
+ id=8,
+ color=[0, 255, 0],
+ type='upper',
+ swap='L_Shoulder'),
+ 9:
+ dict(
+ name='R_Elbow',
+ id=9,
+ color=[255, 128, 0],
+ type='upper',
+ swap='L_Elbow'),
+ 10:
+ dict(
+ name='R_F_Paw',
+ id=10,
+ color=[0, 255, 0],
+ type='lower',
+ swap='L_F_Paw'),
+ 11:
+ dict(
+ name='L_Hip',
+ id=11,
+ color=[255, 128, 0],
+ type='lower',
+ swap='R_Hip'),
+ 12:
+ dict(
+ name='L_Knee',
+ id=12,
+ color=[255, 128, 0],
+ type='lower',
+ swap='R_Knee'),
+ 13:
+ dict(
+ name='L_B_Paw',
+ id=13,
+ color=[0, 255, 0],
+ type='lower',
+ swap='R_B_Paw'),
+ 14:
+ dict(
+ name='R_Hip', id=14, color=[0, 255, 0], type='lower',
+ swap='L_Hip'),
+ 15:
+ dict(
+ name='R_Knee',
+ id=15,
+ color=[0, 255, 0],
+ type='lower',
+ swap='L_Knee'),
+ 16:
+ dict(
+ name='R_B_Paw',
+ id=16,
+ color=[0, 255, 0],
+ type='lower',
+ swap='L_B_Paw'),
+ },
+ skeleton_info={
+ 0: dict(link=('L_Eye', 'R_Eye'), id=0, color=[0, 0, 255]),
+ 1: dict(link=('L_Eye', 'Nose'), id=1, color=[0, 0, 255]),
+ 2: dict(link=('R_Eye', 'Nose'), id=2, color=[0, 0, 255]),
+ 3: dict(link=('Nose', 'Neck'), id=3, color=[0, 255, 0]),
+ 4: dict(link=('Neck', 'Root of tail'), id=4, color=[0, 255, 0]),
+ 5: dict(link=('Neck', 'L_Shoulder'), id=5, color=[0, 255, 255]),
+ 6: dict(link=('L_Shoulder', 'L_Elbow'), id=6, color=[0, 255, 255]),
+ 7: dict(link=('L_Elbow', 'L_F_Paw'), id=6, color=[0, 255, 255]),
+ 8: dict(link=('Neck', 'R_Shoulder'), id=7, color=[6, 156, 250]),
+ 9: dict(link=('R_Shoulder', 'R_Elbow'), id=8, color=[6, 156, 250]),
+ 10: dict(link=('R_Elbow', 'R_F_Paw'), id=9, color=[6, 156, 250]),
+ 11: dict(link=('Root of tail', 'L_Hip'), id=10, color=[0, 255, 255]),
+ 12: dict(link=('L_Hip', 'L_Knee'), id=11, color=[0, 255, 255]),
+ 13: dict(link=('L_Knee', 'L_B_Paw'), id=12, color=[0, 255, 255]),
+ 14: dict(link=('Root of tail', 'R_Hip'), id=13, color=[6, 156, 250]),
+ 15: dict(link=('R_Hip', 'R_Knee'), id=14, color=[6, 156, 250]),
+ 16: dict(link=('R_Knee', 'R_B_Paw'), id=15, color=[6, 156, 250]),
+ },
+ joint_weights=[
+ 1., 1., 1., 1., 1., 1., 1., 1.2, 1.2, 1.5, 1.5, 1., 1., 1.2, 1.2, 1.5,
+ 1.5
+ ],
+ sigmas=[
+ 0.025, 0.025, 0.026, 0.035, 0.035, 0.079, 0.072, 0.062, 0.079, 0.072,
+ 0.062, 0.107, 0.087, 0.089, 0.107, 0.087, 0.089
+ ])
diff --git a/grounded-sam-osx/_base_/datasets/atrw.py b/grounded-sam-osx/_base_/datasets/atrw.py
new file mode 100644
index 0000000000000000000000000000000000000000..7ec71c8c508a0340139371a651ca2dd56eeae3cf
--- /dev/null
+++ b/grounded-sam-osx/_base_/datasets/atrw.py
@@ -0,0 +1,144 @@
+dataset_info = dict(
+ dataset_name='atrw',
+ paper_info=dict(
+ author='Li, Shuyuan and Li, Jianguo and Tang, Hanlin '
+ 'and Qian, Rui and Lin, Weiyao',
+ title='ATRW: A Benchmark for Amur Tiger '
+ 'Re-identification in the Wild',
+ container='Proceedings of the 28th ACM '
+ 'International Conference on Multimedia',
+ year='2020',
+ homepage='https://cvwc2019.github.io/challenge.html',
+ ),
+ keypoint_info={
+ 0:
+ dict(
+ name='left_ear',
+ id=0,
+ color=[51, 153, 255],
+ type='upper',
+ swap='right_ear'),
+ 1:
+ dict(
+ name='right_ear',
+ id=1,
+ color=[51, 153, 255],
+ type='upper',
+ swap='left_ear'),
+ 2:
+ dict(name='nose', id=2, color=[51, 153, 255], type='upper', swap=''),
+ 3:
+ dict(
+ name='right_shoulder',
+ id=3,
+ color=[255, 128, 0],
+ type='upper',
+ swap='left_shoulder'),
+ 4:
+ dict(
+ name='right_front_paw',
+ id=4,
+ color=[255, 128, 0],
+ type='upper',
+ swap='left_front_paw'),
+ 5:
+ dict(
+ name='left_shoulder',
+ id=5,
+ color=[0, 255, 0],
+ type='upper',
+ swap='right_shoulder'),
+ 6:
+ dict(
+ name='left_front_paw',
+ id=6,
+ color=[0, 255, 0],
+ type='upper',
+ swap='right_front_paw'),
+ 7:
+ dict(
+ name='right_hip',
+ id=7,
+ color=[255, 128, 0],
+ type='lower',
+ swap='left_hip'),
+ 8:
+ dict(
+ name='right_knee',
+ id=8,
+ color=[255, 128, 0],
+ type='lower',
+ swap='left_knee'),
+ 9:
+ dict(
+ name='right_back_paw',
+ id=9,
+ color=[255, 128, 0],
+ type='lower',
+ swap='left_back_paw'),
+ 10:
+ dict(
+ name='left_hip',
+ id=10,
+ color=[0, 255, 0],
+ type='lower',
+ swap='right_hip'),
+ 11:
+ dict(
+ name='left_knee',
+ id=11,
+ color=[0, 255, 0],
+ type='lower',
+ swap='right_knee'),
+ 12:
+ dict(
+ name='left_back_paw',
+ id=12,
+ color=[0, 255, 0],
+ type='lower',
+ swap='right_back_paw'),
+ 13:
+ dict(name='tail', id=13, color=[51, 153, 255], type='lower', swap=''),
+ 14:
+ dict(
+ name='center', id=14, color=[51, 153, 255], type='lower', swap=''),
+ },
+ skeleton_info={
+ 0:
+ dict(link=('left_ear', 'nose'), id=0, color=[51, 153, 255]),
+ 1:
+ dict(link=('right_ear', 'nose'), id=1, color=[51, 153, 255]),
+ 2:
+ dict(link=('nose', 'center'), id=2, color=[51, 153, 255]),
+ 3:
+ dict(
+ link=('left_shoulder', 'left_front_paw'), id=3, color=[0, 255, 0]),
+ 4:
+ dict(link=('left_shoulder', 'center'), id=4, color=[0, 255, 0]),
+ 5:
+ dict(
+ link=('right_shoulder', 'right_front_paw'),
+ id=5,
+ color=[255, 128, 0]),
+ 6:
+ dict(link=('right_shoulder', 'center'), id=6, color=[255, 128, 0]),
+ 7:
+ dict(link=('tail', 'center'), id=7, color=[51, 153, 255]),
+ 8:
+ dict(link=('right_back_paw', 'right_knee'), id=8, color=[255, 128, 0]),
+ 9:
+ dict(link=('right_knee', 'right_hip'), id=9, color=[255, 128, 0]),
+ 10:
+ dict(link=('right_hip', 'tail'), id=10, color=[255, 128, 0]),
+ 11:
+ dict(link=('left_back_paw', 'left_knee'), id=11, color=[0, 255, 0]),
+ 12:
+ dict(link=('left_knee', 'left_hip'), id=12, color=[0, 255, 0]),
+ 13:
+ dict(link=('left_hip', 'tail'), id=13, color=[0, 255, 0]),
+ },
+ joint_weights=[1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1., 1.],
+ sigmas=[
+ 0.0277, 0.0823, 0.0831, 0.0202, 0.0716, 0.0263, 0.0646, 0.0302, 0.0440,
+ 0.0316, 0.0333, 0.0547, 0.0263, 0.0683, 0.0539
+ ])
diff --git a/grounded-sam-osx/_base_/datasets/campus.py b/grounded-sam-osx/_base_/datasets/campus.py
new file mode 100644
index 0000000000000000000000000000000000000000..334316e9c25282508767158d3fae30578ab3949d
--- /dev/null
+++ b/grounded-sam-osx/_base_/datasets/campus.py
@@ -0,0 +1,151 @@
+dataset_info = dict(
+ dataset_name='campus',
+ paper_info=dict(
+ author='Belagiannis, Vasileios and Amin, Sikandar and Andriluka, '
+ 'Mykhaylo and Schiele, Bernt and Navab, Nassir and Ilic, Slobodan',
+ title='3D Pictorial Structures for Multiple Human Pose Estimation',
+ container='IEEE Computer Society Conference on Computer Vision and '
+ 'Pattern Recognition (CVPR)',
+ year='2014',
+ homepage='http://campar.in.tum.de/Chair/MultiHumanPose',
+ ),
+ keypoint_info={
+ 0:
+ dict(
+ name='right_ankle',
+ id=0,
+ color=[255, 128, 0],
+ type='lower',
+ swap='left_ankle'),
+ 1:
+ dict(
+ name='right_knee',
+ id=1,
+ color=[255, 128, 0],
+ type='lower',
+ swap='left_knee'),
+ 2:
+ dict(
+ name='right_hip',
+ id=2,
+ color=[255, 128, 0],
+ type='lower',
+ swap='left_hip'),
+ 3:
+ dict(
+ name='left_hip',
+ id=3,
+ color=[0, 255, 0],
+ type='lower',
+ swap='right_hip'),
+ 4:
+ dict(
+ name='left_knee',
+ id=4,
+ color=[0, 255, 0],
+ type='lower',
+ swap='right_knee'),
+ 5:
+ dict(
+ name='left_ankle',
+ id=5,
+ color=[0, 255, 0],
+ type='lower',
+ swap='right_ankle'),
+ 6:
+ dict(
+ name='right_wrist',
+ id=6,
+ color=[255, 128, 0],
+ type='upper',
+ swap='left_wrist'),
+ 7:
+ dict(
+ name='right_elbow',
+ id=7,
+ color=[255, 128, 0],
+ type='upper',
+ swap='left_elbow'),
+ 8:
+ dict(
+ name='right_shoulder',
+ id=8,
+ color=[255, 128, 0],
+ type='upper',
+ swap='left_shoulder'),
+ 9:
+ dict(
+ name='left_shoulder',
+ id=9,
+ color=[0, 255, 0],
+ type='upper',
+ swap='right_shoulder'),
+ 10:
+ dict(
+ name='left_elbow',
+ id=10,
+ color=[0, 255, 0],
+ type='upper',
+ swap='right_elbow'),
+ 11:
+ dict(
+ name='left_wrist',
+ id=11,
+ color=[0, 255, 0],
+ type='upper',
+ swap='right_wrist'),
+ 12:
+ dict(
+ name='bottom_head',
+ id=12,
+ color=[51, 153, 255],
+ type='upper',
+ swap=''),
+ 13:
+ dict(
+ name='top_head',
+ id=13,
+ color=[51, 153, 255],
+ type='upper',
+ swap=''),
+ },
+ skeleton_info={
+ 0:
+ dict(link=('right_ankle', 'right_knee'), id=0, color=[255, 128, 0]),
+ 1:
+ dict(link=('right_knee', 'right_hip'), id=1, color=[255, 128, 0]),
+ 2:
+ dict(link=('left_hip', 'left_knee'), id=2, color=[0, 255, 0]),
+ 3:
+ dict(link=('left_knee', 'left_ankle'), id=3, color=[0, 255, 0]),
+ 4:
+ dict(link=('right_hip', 'left_hip'), id=4, color=[51, 153, 255]),
+ 5:
+ dict(link=('right_wrist', 'right_elbow'), id=5, color=[255, 128, 0]),
+ 6:
+ dict(
+ link=('right_elbow', 'right_shoulder'), id=6, color=[255, 128, 0]),
+ 7:
+ dict(link=('left_shoulder', 'left_elbow'), id=7, color=[0, 255, 0]),
+ 8:
+ dict(link=('left_elbow', 'left_wrist'), id=8, color=[0, 255, 0]),
+ 9:
+ dict(link=('right_hip', 'right_shoulder'), id=9, color=[255, 128, 0]),
+ 10:
+ dict(link=('left_hip', 'left_shoulder'), id=10, color=[0, 255, 0]),
+ 11:
+ dict(
+ link=('right_shoulder', 'bottom_head'), id=11, color=[255, 128,
+ 0]),
+ 12:
+ dict(link=('left_shoulder', 'bottom_head'), id=12, color=[0, 255, 0]),
+ 13:
+ dict(link=('bottom_head', 'top_head'), id=13, color=[51, 153, 255]),
+ },
+ joint_weights=[
+ 1.5, 1.2, 1.0, 1.0, 1.2, 1.5, 1.5, 1.2, 1.0, 1.0, 1.2, 1.5, 1.0, 1.0
+ ],
+ sigmas=[
+ 0.089, 0.087, 0.107, 0.107, 0.087, 0.089, 0.062, 0.072, 0.079, 0.079,
+ 0.072, 0.062, 0.026, 0.026
+ ])
diff --git a/grounded-sam-osx/_base_/datasets/coco.py b/grounded-sam-osx/_base_/datasets/coco.py
new file mode 100644
index 0000000000000000000000000000000000000000..865a95bc02fedd318f32d2e7aa8397147d78fdb5
--- /dev/null
+++ b/grounded-sam-osx/_base_/datasets/coco.py
@@ -0,0 +1,181 @@
+dataset_info = dict(
+ dataset_name='coco',
+ paper_info=dict(
+ author='Lin, Tsung-Yi and Maire, Michael and '
+ 'Belongie, Serge and Hays, James and '
+ 'Perona, Pietro and Ramanan, Deva and '
+ r'Doll{\'a}r, Piotr and Zitnick, C Lawrence',
+ title='Microsoft coco: Common objects in context',
+ container='European conference on computer vision',
+ year='2014',
+ homepage='http://cocodataset.org/',
+ ),
+ keypoint_info={
+ 0:
+ dict(name='nose', id=0, color=[51, 153, 255], type='upper', swap=''),
+ 1:
+ dict(
+ name='left_eye',
+ id=1,
+ color=[51, 153, 255],
+ type='upper',
+ swap='right_eye'),
+ 2:
+ dict(
+ name='right_eye',
+ id=2,
+ color=[51, 153, 255],
+ type='upper',
+ swap='left_eye'),
+ 3:
+ dict(
+ name='left_ear',
+ id=3,
+ color=[51, 153, 255],
+ type='upper',
+ swap='right_ear'),
+ 4:
+ dict(
+ name='right_ear',
+ id=4,
+ color=[51, 153, 255],
+ type='upper',
+ swap='left_ear'),
+ 5:
+ dict(
+ name='left_shoulder',
+ id=5,
+ color=[0, 255, 0],
+ type='upper',
+ swap='right_shoulder'),
+ 6:
+ dict(
+ name='right_shoulder',
+ id=6,
+ color=[255, 128, 0],
+ type='upper',
+ swap='left_shoulder'),
+ 7:
+ dict(
+ name='left_elbow',
+ id=7,
+ color=[0, 255, 0],
+ type='upper',
+ swap='right_elbow'),
+ 8:
+ dict(
+ name='right_elbow',
+ id=8,
+ color=[255, 128, 0],
+ type='upper',
+ swap='left_elbow'),
+ 9:
+ dict(
+ name='left_wrist',
+ id=9,
+ color=[0, 255, 0],
+ type='upper',
+ swap='right_wrist'),
+ 10:
+ dict(
+ name='right_wrist',
+ id=10,
+ color=[255, 128, 0],
+ type='upper',
+ swap='left_wrist'),
+ 11:
+ dict(
+ name='left_hip',
+ id=11,
+ color=[0, 255, 0],
+ type='lower',
+ swap='right_hip'),
+ 12:
+ dict(
+ name='right_hip',
+ id=12,
+ color=[255, 128, 0],
+ type='lower',
+ swap='left_hip'),
+ 13:
+ dict(
+ name='left_knee',
+ id=13,
+ color=[0, 255, 0],
+ type='lower',
+ swap='right_knee'),
+ 14:
+ dict(
+ name='right_knee',
+ id=14,
+ color=[255, 128, 0],
+ type='lower',
+ swap='left_knee'),
+ 15:
+ dict(
+ name='left_ankle',
+ id=15,
+ color=[0, 255, 0],
+ type='lower',
+ swap='right_ankle'),
+ 16:
+ dict(
+ name='right_ankle',
+ id=16,
+ color=[255, 128, 0],
+ type='lower',
+ swap='left_ankle')
+ },
+ skeleton_info={
+ 0:
+ dict(link=('left_ankle', 'left_knee'), id=0, color=[0, 255, 0]),
+ 1:
+ dict(link=('left_knee', 'left_hip'), id=1, color=[0, 255, 0]),
+ 2:
+ dict(link=('right_ankle', 'right_knee'), id=2, color=[255, 128, 0]),
+ 3:
+ dict(link=('right_knee', 'right_hip'), id=3, color=[255, 128, 0]),
+ 4:
+ dict(link=('left_hip', 'right_hip'), id=4, color=[51, 153, 255]),
+ 5:
+ dict(link=('left_shoulder', 'left_hip'), id=5, color=[51, 153, 255]),
+ 6:
+ dict(link=('right_shoulder', 'right_hip'), id=6, color=[51, 153, 255]),
+ 7:
+ dict(
+ link=('left_shoulder', 'right_shoulder'),
+ id=7,
+ color=[51, 153, 255]),
+ 8:
+ dict(link=('left_shoulder', 'left_elbow'), id=8, color=[0, 255, 0]),
+ 9:
+ dict(
+ link=('right_shoulder', 'right_elbow'), id=9, color=[255, 128, 0]),
+ 10:
+ dict(link=('left_elbow', 'left_wrist'), id=10, color=[0, 255, 0]),
+ 11:
+ dict(link=('right_elbow', 'right_wrist'), id=11, color=[255, 128, 0]),
+ 12:
+ dict(link=('left_eye', 'right_eye'), id=12, color=[51, 153, 255]),
+ 13:
+ dict(link=('nose', 'left_eye'), id=13, color=[51, 153, 255]),
+ 14:
+ dict(link=('nose', 'right_eye'), id=14, color=[51, 153, 255]),
+ 15:
+ dict(link=('left_eye', 'left_ear'), id=15, color=[51, 153, 255]),
+ 16:
+ dict(link=('right_eye', 'right_ear'), id=16, color=[51, 153, 255]),
+ 17:
+ dict(link=('left_ear', 'left_shoulder'), id=17, color=[51, 153, 255]),
+ 18:
+ dict(
+ link=('right_ear', 'right_shoulder'), id=18, color=[51, 153, 255])
+ },
+ joint_weights=[
+ 1., 1., 1., 1., 1., 1., 1., 1.2, 1.2, 1.5, 1.5, 1., 1., 1.2, 1.2, 1.5,
+ 1.5
+ ],
+ sigmas=[
+ 0.026, 0.025, 0.025, 0.035, 0.035, 0.079, 0.079, 0.072, 0.072, 0.062,
+ 0.062, 0.107, 0.107, 0.087, 0.087, 0.089, 0.089
+ ])
diff --git a/grounded-sam-osx/_base_/datasets/coco_wholebody.py b/grounded-sam-osx/_base_/datasets/coco_wholebody.py
new file mode 100644
index 0000000000000000000000000000000000000000..ef9b707017a24a1a133bb28566d212c618fee694
--- /dev/null
+++ b/grounded-sam-osx/_base_/datasets/coco_wholebody.py
@@ -0,0 +1,1154 @@
+dataset_info = dict(
+ dataset_name='coco_wholebody',
+ paper_info=dict(
+ author='Jin, Sheng and Xu, Lumin and Xu, Jin and '
+ 'Wang, Can and Liu, Wentao and '
+ 'Qian, Chen and Ouyang, Wanli and Luo, Ping',
+ title='Whole-Body Human Pose Estimation in the Wild',
+ container='Proceedings of the European '
+ 'Conference on Computer Vision (ECCV)',
+ year='2020',
+ homepage='https://github.com/jin-s13/COCO-WholeBody/',
+ ),
+ keypoint_info={
+ 0:
+ dict(name='nose', id=0, color=[51, 153, 255], type='upper', swap=''),
+ 1:
+ dict(
+ name='left_eye',
+ id=1,
+ color=[51, 153, 255],
+ type='upper',
+ swap='right_eye'),
+ 2:
+ dict(
+ name='right_eye',
+ id=2,
+ color=[51, 153, 255],
+ type='upper',
+ swap='left_eye'),
+ 3:
+ dict(
+ name='left_ear',
+ id=3,
+ color=[51, 153, 255],
+ type='upper',
+ swap='right_ear'),
+ 4:
+ dict(
+ name='right_ear',
+ id=4,
+ color=[51, 153, 255],
+ type='upper',
+ swap='left_ear'),
+ 5:
+ dict(
+ name='left_shoulder',
+ id=5,
+ color=[0, 255, 0],
+ type='upper',
+ swap='right_shoulder'),
+ 6:
+ dict(
+ name='right_shoulder',
+ id=6,
+ color=[255, 128, 0],
+ type='upper',
+ swap='left_shoulder'),
+ 7:
+ dict(
+ name='left_elbow',
+ id=7,
+ color=[0, 255, 0],
+ type='upper',
+ swap='right_elbow'),
+ 8:
+ dict(
+ name='right_elbow',
+ id=8,
+ color=[255, 128, 0],
+ type='upper',
+ swap='left_elbow'),
+ 9:
+ dict(
+ name='left_wrist',
+ id=9,
+ color=[0, 255, 0],
+ type='upper',
+ swap='right_wrist'),
+ 10:
+ dict(
+ name='right_wrist',
+ id=10,
+ color=[255, 128, 0],
+ type='upper',
+ swap='left_wrist'),
+ 11:
+ dict(
+ name='left_hip',
+ id=11,
+ color=[0, 255, 0],
+ type='lower',
+ swap='right_hip'),
+ 12:
+ dict(
+ name='right_hip',
+ id=12,
+ color=[255, 128, 0],
+ type='lower',
+ swap='left_hip'),
+ 13:
+ dict(
+ name='left_knee',
+ id=13,
+ color=[0, 255, 0],
+ type='lower',
+ swap='right_knee'),
+ 14:
+ dict(
+ name='right_knee',
+ id=14,
+ color=[255, 128, 0],
+ type='lower',
+ swap='left_knee'),
+ 15:
+ dict(
+ name='left_ankle',
+ id=15,
+ color=[0, 255, 0],
+ type='lower',
+ swap='right_ankle'),
+ 16:
+ dict(
+ name='right_ankle',
+ id=16,
+ color=[255, 128, 0],
+ type='lower',
+ swap='left_ankle'),
+ 17:
+ dict(
+ name='left_big_toe',
+ id=17,
+ color=[255, 128, 0],
+ type='lower',
+ swap='right_big_toe'),
+ 18:
+ dict(
+ name='left_small_toe',
+ id=18,
+ color=[255, 128, 0],
+ type='lower',
+ swap='right_small_toe'),
+ 19:
+ dict(
+ name='left_heel',
+ id=19,
+ color=[255, 128, 0],
+ type='lower',
+ swap='right_heel'),
+ 20:
+ dict(
+ name='right_big_toe',
+ id=20,
+ color=[255, 128, 0],
+ type='lower',
+ swap='left_big_toe'),
+ 21:
+ dict(
+ name='right_small_toe',
+ id=21,
+ color=[255, 128, 0],
+ type='lower',
+ swap='left_small_toe'),
+ 22:
+ dict(
+ name='right_heel',
+ id=22,
+ color=[255, 128, 0],
+ type='lower',
+ swap='left_heel'),
+ 23:
+ dict(
+ name='face-0',
+ id=23,
+ color=[255, 255, 255],
+ type='',
+ swap='face-16'),
+ 24:
+ dict(
+ name='face-1',
+ id=24,
+ color=[255, 255, 255],
+ type='',
+ swap='face-15'),
+ 25:
+ dict(
+ name='face-2',
+ id=25,
+ color=[255, 255, 255],
+ type='',
+ swap='face-14'),
+ 26:
+ dict(
+ name='face-3',
+ id=26,
+ color=[255, 255, 255],
+ type='',
+ swap='face-13'),
+ 27:
+ dict(
+ name='face-4',
+ id=27,
+ color=[255, 255, 255],
+ type='',
+ swap='face-12'),
+ 28:
+ dict(
+ name='face-5',
+ id=28,
+ color=[255, 255, 255],
+ type='',
+ swap='face-11'),
+ 29:
+ dict(
+ name='face-6',
+ id=29,
+ color=[255, 255, 255],
+ type='',
+ swap='face-10'),
+ 30:
+ dict(
+ name='face-7',
+ id=30,
+ color=[255, 255, 255],
+ type='',
+ swap='face-9'),
+ 31:
+ dict(name='face-8', id=31, color=[255, 255, 255], type='', swap=''),
+ 32:
+ dict(
+ name='face-9',
+ id=32,
+ color=[255, 255, 255],
+ type='',
+ swap='face-7'),
+ 33:
+ dict(
+ name='face-10',
+ id=33,
+ color=[255, 255, 255],
+ type='',
+ swap='face-6'),
+ 34:
+ dict(
+ name='face-11',
+ id=34,
+ color=[255, 255, 255],
+ type='',
+ swap='face-5'),
+ 35:
+ dict(
+ name='face-12',
+ id=35,
+ color=[255, 255, 255],
+ type='',
+ swap='face-4'),
+ 36:
+ dict(
+ name='face-13',
+ id=36,
+ color=[255, 255, 255],
+ type='',
+ swap='face-3'),
+ 37:
+ dict(
+ name='face-14',
+ id=37,
+ color=[255, 255, 255],
+ type='',
+ swap='face-2'),
+ 38:
+ dict(
+ name='face-15',
+ id=38,
+ color=[255, 255, 255],
+ type='',
+ swap='face-1'),
+ 39:
+ dict(
+ name='face-16',
+ id=39,
+ color=[255, 255, 255],
+ type='',
+ swap='face-0'),
+ 40:
+ dict(
+ name='face-17',
+ id=40,
+ color=[255, 255, 255],
+ type='',
+ swap='face-26'),
+ 41:
+ dict(
+ name='face-18',
+ id=41,
+ color=[255, 255, 255],
+ type='',
+ swap='face-25'),
+ 42:
+ dict(
+ name='face-19',
+ id=42,
+ color=[255, 255, 255],
+ type='',
+ swap='face-24'),
+ 43:
+ dict(
+ name='face-20',
+ id=43,
+ color=[255, 255, 255],
+ type='',
+ swap='face-23'),
+ 44:
+ dict(
+ name='face-21',
+ id=44,
+ color=[255, 255, 255],
+ type='',
+ swap='face-22'),
+ 45:
+ dict(
+ name='face-22',
+ id=45,
+ color=[255, 255, 255],
+ type='',
+ swap='face-21'),
+ 46:
+ dict(
+ name='face-23',
+ id=46,
+ color=[255, 255, 255],
+ type='',
+ swap='face-20'),
+ 47:
+ dict(
+ name='face-24',
+ id=47,
+ color=[255, 255, 255],
+ type='',
+ swap='face-19'),
+ 48:
+ dict(
+ name='face-25',
+ id=48,
+ color=[255, 255, 255],
+ type='',
+ swap='face-18'),
+ 49:
+ dict(
+ name='face-26',
+ id=49,
+ color=[255, 255, 255],
+ type='',
+ swap='face-17'),
+ 50:
+ dict(name='face-27', id=50, color=[255, 255, 255], type='', swap=''),
+ 51:
+ dict(name='face-28', id=51, color=[255, 255, 255], type='', swap=''),
+ 52:
+ dict(name='face-29', id=52, color=[255, 255, 255], type='', swap=''),
+ 53:
+ dict(name='face-30', id=53, color=[255, 255, 255], type='', swap=''),
+ 54:
+ dict(
+ name='face-31',
+ id=54,
+ color=[255, 255, 255],
+ type='',
+ swap='face-35'),
+ 55:
+ dict(
+ name='face-32',
+ id=55,
+ color=[255, 255, 255],
+ type='',
+ swap='face-34'),
+ 56:
+ dict(name='face-33', id=56, color=[255, 255, 255], type='', swap=''),
+ 57:
+ dict(
+ name='face-34',
+ id=57,
+ color=[255, 255, 255],
+ type='',
+ swap='face-32'),
+ 58:
+ dict(
+ name='face-35',
+ id=58,
+ color=[255, 255, 255],
+ type='',
+ swap='face-31'),
+ 59:
+ dict(
+ name='face-36',
+ id=59,
+ color=[255, 255, 255],
+ type='',
+ swap='face-45'),
+ 60:
+ dict(
+ name='face-37',
+ id=60,
+ color=[255, 255, 255],
+ type='',
+ swap='face-44'),
+ 61:
+ dict(
+ name='face-38',
+ id=61,
+ color=[255, 255, 255],
+ type='',
+ swap='face-43'),
+ 62:
+ dict(
+ name='face-39',
+ id=62,
+ color=[255, 255, 255],
+ type='',
+ swap='face-42'),
+ 63:
+ dict(
+ name='face-40',
+ id=63,
+ color=[255, 255, 255],
+ type='',
+ swap='face-47'),
+ 64:
+ dict(
+ name='face-41',
+ id=64,
+ color=[255, 255, 255],
+ type='',
+ swap='face-46'),
+ 65:
+ dict(
+ name='face-42',
+ id=65,
+ color=[255, 255, 255],
+ type='',
+ swap='face-39'),
+ 66:
+ dict(
+ name='face-43',
+ id=66,
+ color=[255, 255, 255],
+ type='',
+ swap='face-38'),
+ 67:
+ dict(
+ name='face-44',
+ id=67,
+ color=[255, 255, 255],
+ type='',
+ swap='face-37'),
+ 68:
+ dict(
+ name='face-45',
+ id=68,
+ color=[255, 255, 255],
+ type='',
+ swap='face-36'),
+ 69:
+ dict(
+ name='face-46',
+ id=69,
+ color=[255, 255, 255],
+ type='',
+ swap='face-41'),
+ 70:
+ dict(
+ name='face-47',
+ id=70,
+ color=[255, 255, 255],
+ type='',
+ swap='face-40'),
+ 71:
+ dict(
+ name='face-48',
+ id=71,
+ color=[255, 255, 255],
+ type='',
+ swap='face-54'),
+ 72:
+ dict(
+ name='face-49',
+ id=72,
+ color=[255, 255, 255],
+ type='',
+ swap='face-53'),
+ 73:
+ dict(
+ name='face-50',
+ id=73,
+ color=[255, 255, 255],
+ type='',
+ swap='face-52'),
+ 74:
+ dict(name='face-51', id=74, color=[255, 255, 255], type='', swap=''),
+ 75:
+ dict(
+ name='face-52',
+ id=75,
+ color=[255, 255, 255],
+ type='',
+ swap='face-50'),
+ 76:
+ dict(
+ name='face-53',
+ id=76,
+ color=[255, 255, 255],
+ type='',
+ swap='face-49'),
+ 77:
+ dict(
+ name='face-54',
+ id=77,
+ color=[255, 255, 255],
+ type='',
+ swap='face-48'),
+ 78:
+ dict(
+ name='face-55',
+ id=78,
+ color=[255, 255, 255],
+ type='',
+ swap='face-59'),
+ 79:
+ dict(
+ name='face-56',
+ id=79,
+ color=[255, 255, 255],
+ type='',
+ swap='face-58'),
+ 80:
+ dict(name='face-57', id=80, color=[255, 255, 255], type='', swap=''),
+ 81:
+ dict(
+ name='face-58',
+ id=81,
+ color=[255, 255, 255],
+ type='',
+ swap='face-56'),
+ 82:
+ dict(
+ name='face-59',
+ id=82,
+ color=[255, 255, 255],
+ type='',
+ swap='face-55'),
+ 83:
+ dict(
+ name='face-60',
+ id=83,
+ color=[255, 255, 255],
+ type='',
+ swap='face-64'),
+ 84:
+ dict(
+ name='face-61',
+ id=84,
+ color=[255, 255, 255],
+ type='',
+ swap='face-63'),
+ 85:
+ dict(name='face-62', id=85, color=[255, 255, 255], type='', swap=''),
+ 86:
+ dict(
+ name='face-63',
+ id=86,
+ color=[255, 255, 255],
+ type='',
+ swap='face-61'),
+ 87:
+ dict(
+ name='face-64',
+ id=87,
+ color=[255, 255, 255],
+ type='',
+ swap='face-60'),
+ 88:
+ dict(
+ name='face-65',
+ id=88,
+ color=[255, 255, 255],
+ type='',
+ swap='face-67'),
+ 89:
+ dict(name='face-66', id=89, color=[255, 255, 255], type='', swap=''),
+ 90:
+ dict(
+ name='face-67',
+ id=90,
+ color=[255, 255, 255],
+ type='',
+ swap='face-65'),
+ 91:
+ dict(
+ name='left_hand_root',
+ id=91,
+ color=[255, 255, 255],
+ type='',
+ swap='right_hand_root'),
+ 92:
+ dict(
+ name='left_thumb1',
+ id=92,
+ color=[255, 128, 0],
+ type='',
+ swap='right_thumb1'),
+ 93:
+ dict(
+ name='left_thumb2',
+ id=93,
+ color=[255, 128, 0],
+ type='',
+ swap='right_thumb2'),
+ 94:
+ dict(
+ name='left_thumb3',
+ id=94,
+ color=[255, 128, 0],
+ type='',
+ swap='right_thumb3'),
+ 95:
+ dict(
+ name='left_thumb4',
+ id=95,
+ color=[255, 128, 0],
+ type='',
+ swap='right_thumb4'),
+ 96:
+ dict(
+ name='left_forefinger1',
+ id=96,
+ color=[255, 153, 255],
+ type='',
+ swap='right_forefinger1'),
+ 97:
+ dict(
+ name='left_forefinger2',
+ id=97,
+ color=[255, 153, 255],
+ type='',
+ swap='right_forefinger2'),
+ 98:
+ dict(
+ name='left_forefinger3',
+ id=98,
+ color=[255, 153, 255],
+ type='',
+ swap='right_forefinger3'),
+ 99:
+ dict(
+ name='left_forefinger4',
+ id=99,
+ color=[255, 153, 255],
+ type='',
+ swap='right_forefinger4'),
+ 100:
+ dict(
+ name='left_middle_finger1',
+ id=100,
+ color=[102, 178, 255],
+ type='',
+ swap='right_middle_finger1'),
+ 101:
+ dict(
+ name='left_middle_finger2',
+ id=101,
+ color=[102, 178, 255],
+ type='',
+ swap='right_middle_finger2'),
+ 102:
+ dict(
+ name='left_middle_finger3',
+ id=102,
+ color=[102, 178, 255],
+ type='',
+ swap='right_middle_finger3'),
+ 103:
+ dict(
+ name='left_middle_finger4',
+ id=103,
+ color=[102, 178, 255],
+ type='',
+ swap='right_middle_finger4'),
+ 104:
+ dict(
+ name='left_ring_finger1',
+ id=104,
+ color=[255, 51, 51],
+ type='',
+ swap='right_ring_finger1'),
+ 105:
+ dict(
+ name='left_ring_finger2',
+ id=105,
+ color=[255, 51, 51],
+ type='',
+ swap='right_ring_finger2'),
+ 106:
+ dict(
+ name='left_ring_finger3',
+ id=106,
+ color=[255, 51, 51],
+ type='',
+ swap='right_ring_finger3'),
+ 107:
+ dict(
+ name='left_ring_finger4',
+ id=107,
+ color=[255, 51, 51],
+ type='',
+ swap='right_ring_finger4'),
+ 108:
+ dict(
+ name='left_pinky_finger1',
+ id=108,
+ color=[0, 255, 0],
+ type='',
+ swap='right_pinky_finger1'),
+ 109:
+ dict(
+ name='left_pinky_finger2',
+ id=109,
+ color=[0, 255, 0],
+ type='',
+ swap='right_pinky_finger2'),
+ 110:
+ dict(
+ name='left_pinky_finger3',
+ id=110,
+ color=[0, 255, 0],
+ type='',
+ swap='right_pinky_finger3'),
+ 111:
+ dict(
+ name='left_pinky_finger4',
+ id=111,
+ color=[0, 255, 0],
+ type='',
+ swap='right_pinky_finger4'),
+ 112:
+ dict(
+ name='right_hand_root',
+ id=112,
+ color=[255, 255, 255],
+ type='',
+ swap='left_hand_root'),
+ 113:
+ dict(
+ name='right_thumb1',
+ id=113,
+ color=[255, 128, 0],
+ type='',
+ swap='left_thumb1'),
+ 114:
+ dict(
+ name='right_thumb2',
+ id=114,
+ color=[255, 128, 0],
+ type='',
+ swap='left_thumb2'),
+ 115:
+ dict(
+ name='right_thumb3',
+ id=115,
+ color=[255, 128, 0],
+ type='',
+ swap='left_thumb3'),
+ 116:
+ dict(
+ name='right_thumb4',
+ id=116,
+ color=[255, 128, 0],
+ type='',
+ swap='left_thumb4'),
+ 117:
+ dict(
+ name='right_forefinger1',
+ id=117,
+ color=[255, 153, 255],
+ type='',
+ swap='left_forefinger1'),
+ 118:
+ dict(
+ name='right_forefinger2',
+ id=118,
+ color=[255, 153, 255],
+ type='',
+ swap='left_forefinger2'),
+ 119:
+ dict(
+ name='right_forefinger3',
+ id=119,
+ color=[255, 153, 255],
+ type='',
+ swap='left_forefinger3'),
+ 120:
+ dict(
+ name='right_forefinger4',
+ id=120,
+ color=[255, 153, 255],
+ type='',
+ swap='left_forefinger4'),
+ 121:
+ dict(
+ name='right_middle_finger1',
+ id=121,
+ color=[102, 178, 255],
+ type='',
+ swap='left_middle_finger1'),
+ 122:
+ dict(
+ name='right_middle_finger2',
+ id=122,
+ color=[102, 178, 255],
+ type='',
+ swap='left_middle_finger2'),
+ 123:
+ dict(
+ name='right_middle_finger3',
+ id=123,
+ color=[102, 178, 255],
+ type='',
+ swap='left_middle_finger3'),
+ 124:
+ dict(
+ name='right_middle_finger4',
+ id=124,
+ color=[102, 178, 255],
+ type='',
+ swap='left_middle_finger4'),
+ 125:
+ dict(
+ name='right_ring_finger1',
+ id=125,
+ color=[255, 51, 51],
+ type='',
+ swap='left_ring_finger1'),
+ 126:
+ dict(
+ name='right_ring_finger2',
+ id=126,
+ color=[255, 51, 51],
+ type='',
+ swap='left_ring_finger2'),
+ 127:
+ dict(
+ name='right_ring_finger3',
+ id=127,
+ color=[255, 51, 51],
+ type='',
+ swap='left_ring_finger3'),
+ 128:
+ dict(
+ name='right_ring_finger4',
+ id=128,
+ color=[255, 51, 51],
+ type='',
+ swap='left_ring_finger4'),
+ 129:
+ dict(
+ name='right_pinky_finger1',
+ id=129,
+ color=[0, 255, 0],
+ type='',
+ swap='left_pinky_finger1'),
+ 130:
+ dict(
+ name='right_pinky_finger2',
+ id=130,
+ color=[0, 255, 0],
+ type='',
+ swap='left_pinky_finger2'),
+ 131:
+ dict(
+ name='right_pinky_finger3',
+ id=131,
+ color=[0, 255, 0],
+ type='',
+ swap='left_pinky_finger3'),
+ 132:
+ dict(
+ name='right_pinky_finger4',
+ id=132,
+ color=[0, 255, 0],
+ type='',
+ swap='left_pinky_finger4')
+ },
+ skeleton_info={
+ 0:
+ dict(link=('left_ankle', 'left_knee'), id=0, color=[0, 255, 0]),
+ 1:
+ dict(link=('left_knee', 'left_hip'), id=1, color=[0, 255, 0]),
+ 2:
+ dict(link=('right_ankle', 'right_knee'), id=2, color=[255, 128, 0]),
+ 3:
+ dict(link=('right_knee', 'right_hip'), id=3, color=[255, 128, 0]),
+ 4:
+ dict(link=('left_hip', 'right_hip'), id=4, color=[51, 153, 255]),
+ 5:
+ dict(link=('left_shoulder', 'left_hip'), id=5, color=[51, 153, 255]),
+ 6:
+ dict(link=('right_shoulder', 'right_hip'), id=6, color=[51, 153, 255]),
+ 7:
+ dict(
+ link=('left_shoulder', 'right_shoulder'),
+ id=7,
+ color=[51, 153, 255]),
+ 8:
+ dict(link=('left_shoulder', 'left_elbow'), id=8, color=[0, 255, 0]),
+ 9:
+ dict(
+ link=('right_shoulder', 'right_elbow'), id=9, color=[255, 128, 0]),
+ 10:
+ dict(link=('left_elbow', 'left_wrist'), id=10, color=[0, 255, 0]),
+ 11:
+ dict(link=('right_elbow', 'right_wrist'), id=11, color=[255, 128, 0]),
+ 12:
+ dict(link=('left_eye', 'right_eye'), id=12, color=[51, 153, 255]),
+ 13:
+ dict(link=('nose', 'left_eye'), id=13, color=[51, 153, 255]),
+ 14:
+ dict(link=('nose', 'right_eye'), id=14, color=[51, 153, 255]),
+ 15:
+ dict(link=('left_eye', 'left_ear'), id=15, color=[51, 153, 255]),
+ 16:
+ dict(link=('right_eye', 'right_ear'), id=16, color=[51, 153, 255]),
+ 17:
+ dict(link=('left_ear', 'left_shoulder'), id=17, color=[51, 153, 255]),
+ 18:
+ dict(
+ link=('right_ear', 'right_shoulder'), id=18, color=[51, 153, 255]),
+ 19:
+ dict(link=('left_ankle', 'left_big_toe'), id=19, color=[0, 255, 0]),
+ 20:
+ dict(link=('left_ankle', 'left_small_toe'), id=20, color=[0, 255, 0]),
+ 21:
+ dict(link=('left_ankle', 'left_heel'), id=21, color=[0, 255, 0]),
+ 22:
+ dict(
+ link=('right_ankle', 'right_big_toe'), id=22, color=[255, 128, 0]),
+ 23:
+ dict(
+ link=('right_ankle', 'right_small_toe'),
+ id=23,
+ color=[255, 128, 0]),
+ 24:
+ dict(link=('right_ankle', 'right_heel'), id=24, color=[255, 128, 0]),
+ 25:
+ dict(
+ link=('left_hand_root', 'left_thumb1'), id=25, color=[255, 128,
+ 0]),
+ 26:
+ dict(link=('left_thumb1', 'left_thumb2'), id=26, color=[255, 128, 0]),
+ 27:
+ dict(link=('left_thumb2', 'left_thumb3'), id=27, color=[255, 128, 0]),
+ 28:
+ dict(link=('left_thumb3', 'left_thumb4'), id=28, color=[255, 128, 0]),
+ 29:
+ dict(
+ link=('left_hand_root', 'left_forefinger1'),
+ id=29,
+ color=[255, 153, 255]),
+ 30:
+ dict(
+ link=('left_forefinger1', 'left_forefinger2'),
+ id=30,
+ color=[255, 153, 255]),
+ 31:
+ dict(
+ link=('left_forefinger2', 'left_forefinger3'),
+ id=31,
+ color=[255, 153, 255]),
+ 32:
+ dict(
+ link=('left_forefinger3', 'left_forefinger4'),
+ id=32,
+ color=[255, 153, 255]),
+ 33:
+ dict(
+ link=('left_hand_root', 'left_middle_finger1'),
+ id=33,
+ color=[102, 178, 255]),
+ 34:
+ dict(
+ link=('left_middle_finger1', 'left_middle_finger2'),
+ id=34,
+ color=[102, 178, 255]),
+ 35:
+ dict(
+ link=('left_middle_finger2', 'left_middle_finger3'),
+ id=35,
+ color=[102, 178, 255]),
+ 36:
+ dict(
+ link=('left_middle_finger3', 'left_middle_finger4'),
+ id=36,
+ color=[102, 178, 255]),
+ 37:
+ dict(
+ link=('left_hand_root', 'left_ring_finger1'),
+ id=37,
+ color=[255, 51, 51]),
+ 38:
+ dict(
+ link=('left_ring_finger1', 'left_ring_finger2'),
+ id=38,
+ color=[255, 51, 51]),
+ 39:
+ dict(
+ link=('left_ring_finger2', 'left_ring_finger3'),
+ id=39,
+ color=[255, 51, 51]),
+ 40:
+ dict(
+ link=('left_ring_finger3', 'left_ring_finger4'),
+ id=40,
+ color=[255, 51, 51]),
+ 41:
+ dict(
+ link=('left_hand_root', 'left_pinky_finger1'),
+ id=41,
+ color=[0, 255, 0]),
+ 42:
+ dict(
+ link=('left_pinky_finger1', 'left_pinky_finger2'),
+ id=42,
+ color=[0, 255, 0]),
+ 43:
+ dict(
+ link=('left_pinky_finger2', 'left_pinky_finger3'),
+ id=43,
+ color=[0, 255, 0]),
+ 44:
+ dict(
+ link=('left_pinky_finger3', 'left_pinky_finger4'),
+ id=44,
+ color=[0, 255, 0]),
+ 45:
+ dict(
+ link=('right_hand_root', 'right_thumb1'),
+ id=45,
+ color=[255, 128, 0]),
+ 46:
+ dict(
+ link=('right_thumb1', 'right_thumb2'), id=46, color=[255, 128, 0]),
+ 47:
+ dict(
+ link=('right_thumb2', 'right_thumb3'), id=47, color=[255, 128, 0]),
+ 48:
+ dict(
+ link=('right_thumb3', 'right_thumb4'), id=48, color=[255, 128, 0]),
+ 49:
+ dict(
+ link=('right_hand_root', 'right_forefinger1'),
+ id=49,
+ color=[255, 153, 255]),
+ 50:
+ dict(
+ link=('right_forefinger1', 'right_forefinger2'),
+ id=50,
+ color=[255, 153, 255]),
+ 51:
+ dict(
+ link=('right_forefinger2', 'right_forefinger3'),
+ id=51,
+ color=[255, 153, 255]),
+ 52:
+ dict(
+ link=('right_forefinger3', 'right_forefinger4'),
+ id=52,
+ color=[255, 153, 255]),
+ 53:
+ dict(
+ link=('right_hand_root', 'right_middle_finger1'),
+ id=53,
+ color=[102, 178, 255]),
+ 54:
+ dict(
+ link=('right_middle_finger1', 'right_middle_finger2'),
+ id=54,
+ color=[102, 178, 255]),
+ 55:
+ dict(
+ link=('right_middle_finger2', 'right_middle_finger3'),
+ id=55,
+ color=[102, 178, 255]),
+ 56:
+ dict(
+ link=('right_middle_finger3', 'right_middle_finger4'),
+ id=56,
+ color=[102, 178, 255]),
+ 57:
+ dict(
+ link=('right_hand_root', 'right_ring_finger1'),
+ id=57,
+ color=[255, 51, 51]),
+ 58:
+ dict(
+ link=('right_ring_finger1', 'right_ring_finger2'),
+ id=58,
+ color=[255, 51, 51]),
+ 59:
+ dict(
+ link=('right_ring_finger2', 'right_ring_finger3'),
+ id=59,
+ color=[255, 51, 51]),
+ 60:
+ dict(
+ link=('right_ring_finger3', 'right_ring_finger4'),
+ id=60,
+ color=[255, 51, 51]),
+ 61:
+ dict(
+ link=('right_hand_root', 'right_pinky_finger1'),
+ id=61,
+ color=[0, 255, 0]),
+ 62:
+ dict(
+ link=('right_pinky_finger1', 'right_pinky_finger2'),
+ id=62,
+ color=[0, 255, 0]),
+ 63:
+ dict(
+ link=('right_pinky_finger2', 'right_pinky_finger3'),
+ id=63,
+ color=[0, 255, 0]),
+ 64:
+ dict(
+ link=('right_pinky_finger3', 'right_pinky_finger4'),
+ id=64,
+ color=[0, 255, 0])
+ },
+ joint_weights=[1.] * 133,
+ # 'https://github.com/jin-s13/COCO-WholeBody/blob/master/'
+ # 'evaluation/myeval_wholebody.py#L175'
+ sigmas=[
+ 0.026, 0.025, 0.025, 0.035, 0.035, 0.079, 0.079, 0.072, 0.072, 0.062,
+ 0.062, 0.107, 0.107, 0.087, 0.087, 0.089, 0.089, 0.068, 0.066, 0.066,
+ 0.092, 0.094, 0.094, 0.042, 0.043, 0.044, 0.043, 0.040, 0.035, 0.031,
+ 0.025, 0.020, 0.023, 0.029, 0.032, 0.037, 0.038, 0.043, 0.041, 0.045,
+ 0.013, 0.012, 0.011, 0.011, 0.012, 0.012, 0.011, 0.011, 0.013, 0.015,
+ 0.009, 0.007, 0.007, 0.007, 0.012, 0.009, 0.008, 0.016, 0.010, 0.017,
+ 0.011, 0.009, 0.011, 0.009, 0.007, 0.013, 0.008, 0.011, 0.012, 0.010,
+ 0.034, 0.008, 0.008, 0.009, 0.008, 0.008, 0.007, 0.010, 0.008, 0.009,
+ 0.009, 0.009, 0.007, 0.007, 0.008, 0.011, 0.008, 0.008, 0.008, 0.01,
+ 0.008, 0.029, 0.022, 0.035, 0.037, 0.047, 0.026, 0.025, 0.024, 0.035,
+ 0.018, 0.024, 0.022, 0.026, 0.017, 0.021, 0.021, 0.032, 0.02, 0.019,
+ 0.022, 0.031, 0.029, 0.022, 0.035, 0.037, 0.047, 0.026, 0.025, 0.024,
+ 0.035, 0.018, 0.024, 0.022, 0.026, 0.017, 0.021, 0.021, 0.032, 0.02,
+ 0.019, 0.022, 0.031
+ ])
diff --git a/grounded-sam-osx/_base_/datasets/coco_wholebody_face.py b/grounded-sam-osx/_base_/datasets/coco_wholebody_face.py
new file mode 100644
index 0000000000000000000000000000000000000000..7c9ee3350e3bd67ab1825344849487834c71c82b
--- /dev/null
+++ b/grounded-sam-osx/_base_/datasets/coco_wholebody_face.py
@@ -0,0 +1,448 @@
+dataset_info = dict(
+ dataset_name='coco_wholebody_face',
+ paper_info=dict(
+ author='Jin, Sheng and Xu, Lumin and Xu, Jin and '
+ 'Wang, Can and Liu, Wentao and '
+ 'Qian, Chen and Ouyang, Wanli and Luo, Ping',
+ title='Whole-Body Human Pose Estimation in the Wild',
+ container='Proceedings of the European '
+ 'Conference on Computer Vision (ECCV)',
+ year='2020',
+ homepage='https://github.com/jin-s13/COCO-WholeBody/',
+ ),
+ keypoint_info={
+ 0:
+ dict(
+ name='face-0',
+ id=0,
+ color=[255, 255, 255],
+ type='',
+ swap='face-16'),
+ 1:
+ dict(
+ name='face-1',
+ id=1,
+ color=[255, 255, 255],
+ type='',
+ swap='face-15'),
+ 2:
+ dict(
+ name='face-2',
+ id=2,
+ color=[255, 255, 255],
+ type='',
+ swap='face-14'),
+ 3:
+ dict(
+ name='face-3',
+ id=3,
+ color=[255, 255, 255],
+ type='',
+ swap='face-13'),
+ 4:
+ dict(
+ name='face-4',
+ id=4,
+ color=[255, 255, 255],
+ type='',
+ swap='face-12'),
+ 5:
+ dict(
+ name='face-5',
+ id=5,
+ color=[255, 255, 255],
+ type='',
+ swap='face-11'),
+ 6:
+ dict(
+ name='face-6',
+ id=6,
+ color=[255, 255, 255],
+ type='',
+ swap='face-10'),
+ 7:
+ dict(
+ name='face-7', id=7, color=[255, 255, 255], type='',
+ swap='face-9'),
+ 8:
+ dict(name='face-8', id=8, color=[255, 255, 255], type='', swap=''),
+ 9:
+ dict(
+ name='face-9', id=9, color=[255, 255, 255], type='',
+ swap='face-7'),
+ 10:
+ dict(
+ name='face-10',
+ id=10,
+ color=[255, 255, 255],
+ type='',
+ swap='face-6'),
+ 11:
+ dict(
+ name='face-11',
+ id=11,
+ color=[255, 255, 255],
+ type='',
+ swap='face-5'),
+ 12:
+ dict(
+ name='face-12',
+ id=12,
+ color=[255, 255, 255],
+ type='',
+ swap='face-4'),
+ 13:
+ dict(
+ name='face-13',
+ id=13,
+ color=[255, 255, 255],
+ type='',
+ swap='face-3'),
+ 14:
+ dict(
+ name='face-14',
+ id=14,
+ color=[255, 255, 255],
+ type='',
+ swap='face-2'),
+ 15:
+ dict(
+ name='face-15',
+ id=15,
+ color=[255, 255, 255],
+ type='',
+ swap='face-1'),
+ 16:
+ dict(
+ name='face-16',
+ id=16,
+ color=[255, 255, 255],
+ type='',
+ swap='face-0'),
+ 17:
+ dict(
+ name='face-17',
+ id=17,
+ color=[255, 255, 255],
+ type='',
+ swap='face-26'),
+ 18:
+ dict(
+ name='face-18',
+ id=18,
+ color=[255, 255, 255],
+ type='',
+ swap='face-25'),
+ 19:
+ dict(
+ name='face-19',
+ id=19,
+ color=[255, 255, 255],
+ type='',
+ swap='face-24'),
+ 20:
+ dict(
+ name='face-20',
+ id=20,
+ color=[255, 255, 255],
+ type='',
+ swap='face-23'),
+ 21:
+ dict(
+ name='face-21',
+ id=21,
+ color=[255, 255, 255],
+ type='',
+ swap='face-22'),
+ 22:
+ dict(
+ name='face-22',
+ id=22,
+ color=[255, 255, 255],
+ type='',
+ swap='face-21'),
+ 23:
+ dict(
+ name='face-23',
+ id=23,
+ color=[255, 255, 255],
+ type='',
+ swap='face-20'),
+ 24:
+ dict(
+ name='face-24',
+ id=24,
+ color=[255, 255, 255],
+ type='',
+ swap='face-19'),
+ 25:
+ dict(
+ name='face-25',
+ id=25,
+ color=[255, 255, 255],
+ type='',
+ swap='face-18'),
+ 26:
+ dict(
+ name='face-26',
+ id=26,
+ color=[255, 255, 255],
+ type='',
+ swap='face-17'),
+ 27:
+ dict(name='face-27', id=27, color=[255, 255, 255], type='', swap=''),
+ 28:
+ dict(name='face-28', id=28, color=[255, 255, 255], type='', swap=''),
+ 29:
+ dict(name='face-29', id=29, color=[255, 255, 255], type='', swap=''),
+ 30:
+ dict(name='face-30', id=30, color=[255, 255, 255], type='', swap=''),
+ 31:
+ dict(
+ name='face-31',
+ id=31,
+ color=[255, 255, 255],
+ type='',
+ swap='face-35'),
+ 32:
+ dict(
+ name='face-32',
+ id=32,
+ color=[255, 255, 255],
+ type='',
+ swap='face-34'),
+ 33:
+ dict(name='face-33', id=33, color=[255, 255, 255], type='', swap=''),
+ 34:
+ dict(
+ name='face-34',
+ id=34,
+ color=[255, 255, 255],
+ type='',
+ swap='face-32'),
+ 35:
+ dict(
+ name='face-35',
+ id=35,
+ color=[255, 255, 255],
+ type='',
+ swap='face-31'),
+ 36:
+ dict(
+ name='face-36',
+ id=36,
+ color=[255, 255, 255],
+ type='',
+ swap='face-45'),
+ 37:
+ dict(
+ name='face-37',
+ id=37,
+ color=[255, 255, 255],
+ type='',
+ swap='face-44'),
+ 38:
+ dict(
+ name='face-38',
+ id=38,
+ color=[255, 255, 255],
+ type='',
+ swap='face-43'),
+ 39:
+ dict(
+ name='face-39',
+ id=39,
+ color=[255, 255, 255],
+ type='',
+ swap='face-42'),
+ 40:
+ dict(
+ name='face-40',
+ id=40,
+ color=[255, 255, 255],
+ type='',
+ swap='face-47'),
+ 41:
+ dict(
+ name='face-41',
+ id=41,
+ color=[255, 255, 255],
+ type='',
+ swap='face-46'),
+ 42:
+ dict(
+ name='face-42',
+ id=42,
+ color=[255, 255, 255],
+ type='',
+ swap='face-39'),
+ 43:
+ dict(
+ name='face-43',
+ id=43,
+ color=[255, 255, 255],
+ type='',
+ swap='face-38'),
+ 44:
+ dict(
+ name='face-44',
+ id=44,
+ color=[255, 255, 255],
+ type='',
+ swap='face-37'),
+ 45:
+ dict(
+ name='face-45',
+ id=45,
+ color=[255, 255, 255],
+ type='',
+ swap='face-36'),
+ 46:
+ dict(
+ name='face-46',
+ id=46,
+ color=[255, 255, 255],
+ type='',
+ swap='face-41'),
+ 47:
+ dict(
+ name='face-47',
+ id=47,
+ color=[255, 255, 255],
+ type='',
+ swap='face-40'),
+ 48:
+ dict(
+ name='face-48',
+ id=48,
+ color=[255, 255, 255],
+ type='',
+ swap='face-54'),
+ 49:
+ dict(
+ name='face-49',
+ id=49,
+ color=[255, 255, 255],
+ type='',
+ swap='face-53'),
+ 50:
+ dict(
+ name='face-50',
+ id=50,
+ color=[255, 255, 255],
+ type='',
+ swap='face-52'),
+ 51:
+ dict(name='face-51', id=52, color=[255, 255, 255], type='', swap=''),
+ 52:
+ dict(
+ name='face-52',
+ id=52,
+ color=[255, 255, 255],
+ type='',
+ swap='face-50'),
+ 53:
+ dict(
+ name='face-53',
+ id=53,
+ color=[255, 255, 255],
+ type='',
+ swap='face-49'),
+ 54:
+ dict(
+ name='face-54',
+ id=54,
+ color=[255, 255, 255],
+ type='',
+ swap='face-48'),
+ 55:
+ dict(
+ name='face-55',
+ id=55,
+ color=[255, 255, 255],
+ type='',
+ swap='face-59'),
+ 56:
+ dict(
+ name='face-56',
+ id=56,
+ color=[255, 255, 255],
+ type='',
+ swap='face-58'),
+ 57:
+ dict(name='face-57', id=57, color=[255, 255, 255], type='', swap=''),
+ 58:
+ dict(
+ name='face-58',
+ id=58,
+ color=[255, 255, 255],
+ type='',
+ swap='face-56'),
+ 59:
+ dict(
+ name='face-59',
+ id=59,
+ color=[255, 255, 255],
+ type='',
+ swap='face-55'),
+ 60:
+ dict(
+ name='face-60',
+ id=60,
+ color=[255, 255, 255],
+ type='',
+ swap='face-64'),
+ 61:
+ dict(
+ name='face-61',
+ id=61,
+ color=[255, 255, 255],
+ type='',
+ swap='face-63'),
+ 62:
+ dict(name='face-62', id=62, color=[255, 255, 255], type='', swap=''),
+ 63:
+ dict(
+ name='face-63',
+ id=63,
+ color=[255, 255, 255],
+ type='',
+ swap='face-61'),
+ 64:
+ dict(
+ name='face-64',
+ id=64,
+ color=[255, 255, 255],
+ type='',
+ swap='face-60'),
+ 65:
+ dict(
+ name='face-65',
+ id=65,
+ color=[255, 255, 255],
+ type='',
+ swap='face-67'),
+ 66:
+ dict(name='face-66', id=66, color=[255, 255, 255], type='', swap=''),
+ 67:
+ dict(
+ name='face-67',
+ id=67,
+ color=[255, 255, 255],
+ type='',
+ swap='face-65')
+ },
+ skeleton_info={},
+ joint_weights=[1.] * 68,
+
+ # 'https://github.com/jin-s13/COCO-WholeBody/blob/master/'
+ # 'evaluation/myeval_wholebody.py#L177'
+ sigmas=[
+ 0.042, 0.043, 0.044, 0.043, 0.040, 0.035, 0.031, 0.025, 0.020, 0.023,
+ 0.029, 0.032, 0.037, 0.038, 0.043, 0.041, 0.045, 0.013, 0.012, 0.011,
+ 0.011, 0.012, 0.012, 0.011, 0.011, 0.013, 0.015, 0.009, 0.007, 0.007,
+ 0.007, 0.012, 0.009, 0.008, 0.016, 0.010, 0.017, 0.011, 0.009, 0.011,
+ 0.009, 0.007, 0.013, 0.008, 0.011, 0.012, 0.010, 0.034, 0.008, 0.008,
+ 0.009, 0.008, 0.008, 0.007, 0.010, 0.008, 0.009, 0.009, 0.009, 0.007,
+ 0.007, 0.008, 0.011, 0.008, 0.008, 0.008, 0.01, 0.008
+ ])
diff --git a/grounded-sam-osx/_base_/datasets/coco_wholebody_hand.py b/grounded-sam-osx/_base_/datasets/coco_wholebody_hand.py
new file mode 100644
index 0000000000000000000000000000000000000000..1910b2ced5a8b31cd6f83911e41cae9f1a580222
--- /dev/null
+++ b/grounded-sam-osx/_base_/datasets/coco_wholebody_hand.py
@@ -0,0 +1,147 @@
+dataset_info = dict(
+ dataset_name='coco_wholebody_hand',
+ paper_info=dict(
+ author='Jin, Sheng and Xu, Lumin and Xu, Jin and '
+ 'Wang, Can and Liu, Wentao and '
+ 'Qian, Chen and Ouyang, Wanli and Luo, Ping',
+ title='Whole-Body Human Pose Estimation in the Wild',
+ container='Proceedings of the European '
+ 'Conference on Computer Vision (ECCV)',
+ year='2020',
+ homepage='https://github.com/jin-s13/COCO-WholeBody/',
+ ),
+ keypoint_info={
+ 0:
+ dict(name='wrist', id=0, color=[255, 255, 255], type='', swap=''),
+ 1:
+ dict(name='thumb1', id=1, color=[255, 128, 0], type='', swap=''),
+ 2:
+ dict(name='thumb2', id=2, color=[255, 128, 0], type='', swap=''),
+ 3:
+ dict(name='thumb3', id=3, color=[255, 128, 0], type='', swap=''),
+ 4:
+ dict(name='thumb4', id=4, color=[255, 128, 0], type='', swap=''),
+ 5:
+ dict(
+ name='forefinger1', id=5, color=[255, 153, 255], type='', swap=''),
+ 6:
+ dict(
+ name='forefinger2', id=6, color=[255, 153, 255], type='', swap=''),
+ 7:
+ dict(
+ name='forefinger3', id=7, color=[255, 153, 255], type='', swap=''),
+ 8:
+ dict(
+ name='forefinger4', id=8, color=[255, 153, 255], type='', swap=''),
+ 9:
+ dict(
+ name='middle_finger1',
+ id=9,
+ color=[102, 178, 255],
+ type='',
+ swap=''),
+ 10:
+ dict(
+ name='middle_finger2',
+ id=10,
+ color=[102, 178, 255],
+ type='',
+ swap=''),
+ 11:
+ dict(
+ name='middle_finger3',
+ id=11,
+ color=[102, 178, 255],
+ type='',
+ swap=''),
+ 12:
+ dict(
+ name='middle_finger4',
+ id=12,
+ color=[102, 178, 255],
+ type='',
+ swap=''),
+ 13:
+ dict(
+ name='ring_finger1', id=13, color=[255, 51, 51], type='', swap=''),
+ 14:
+ dict(
+ name='ring_finger2', id=14, color=[255, 51, 51], type='', swap=''),
+ 15:
+ dict(
+ name='ring_finger3', id=15, color=[255, 51, 51], type='', swap=''),
+ 16:
+ dict(
+ name='ring_finger4', id=16, color=[255, 51, 51], type='', swap=''),
+ 17:
+ dict(name='pinky_finger1', id=17, color=[0, 255, 0], type='', swap=''),
+ 18:
+ dict(name='pinky_finger2', id=18, color=[0, 255, 0], type='', swap=''),
+ 19:
+ dict(name='pinky_finger3', id=19, color=[0, 255, 0], type='', swap=''),
+ 20:
+ dict(name='pinky_finger4', id=20, color=[0, 255, 0], type='', swap='')
+ },
+ skeleton_info={
+ 0:
+ dict(link=('wrist', 'thumb1'), id=0, color=[255, 128, 0]),
+ 1:
+ dict(link=('thumb1', 'thumb2'), id=1, color=[255, 128, 0]),
+ 2:
+ dict(link=('thumb2', 'thumb3'), id=2, color=[255, 128, 0]),
+ 3:
+ dict(link=('thumb3', 'thumb4'), id=3, color=[255, 128, 0]),
+ 4:
+ dict(link=('wrist', 'forefinger1'), id=4, color=[255, 153, 255]),
+ 5:
+ dict(link=('forefinger1', 'forefinger2'), id=5, color=[255, 153, 255]),
+ 6:
+ dict(link=('forefinger2', 'forefinger3'), id=6, color=[255, 153, 255]),
+ 7:
+ dict(link=('forefinger3', 'forefinger4'), id=7, color=[255, 153, 255]),
+ 8:
+ dict(link=('wrist', 'middle_finger1'), id=8, color=[102, 178, 255]),
+ 9:
+ dict(
+ link=('middle_finger1', 'middle_finger2'),
+ id=9,
+ color=[102, 178, 255]),
+ 10:
+ dict(
+ link=('middle_finger2', 'middle_finger3'),
+ id=10,
+ color=[102, 178, 255]),
+ 11:
+ dict(
+ link=('middle_finger3', 'middle_finger4'),
+ id=11,
+ color=[102, 178, 255]),
+ 12:
+ dict(link=('wrist', 'ring_finger1'), id=12, color=[255, 51, 51]),
+ 13:
+ dict(
+ link=('ring_finger1', 'ring_finger2'), id=13, color=[255, 51, 51]),
+ 14:
+ dict(
+ link=('ring_finger2', 'ring_finger3'), id=14, color=[255, 51, 51]),
+ 15:
+ dict(
+ link=('ring_finger3', 'ring_finger4'), id=15, color=[255, 51, 51]),
+ 16:
+ dict(link=('wrist', 'pinky_finger1'), id=16, color=[0, 255, 0]),
+ 17:
+ dict(
+ link=('pinky_finger1', 'pinky_finger2'), id=17, color=[0, 255, 0]),
+ 18:
+ dict(
+ link=('pinky_finger2', 'pinky_finger3'), id=18, color=[0, 255, 0]),
+ 19:
+ dict(
+ link=('pinky_finger3', 'pinky_finger4'), id=19, color=[0, 255, 0])
+ },
+ joint_weights=[1.] * 21,
+ sigmas=[
+ 0.029, 0.022, 0.035, 0.037, 0.047, 0.026, 0.025, 0.024, 0.035, 0.018,
+ 0.024, 0.022, 0.026, 0.017, 0.021, 0.021, 0.032, 0.02, 0.019, 0.022,
+ 0.031
+ ])
diff --git a/grounded-sam-osx/_base_/datasets/cofw.py b/grounded-sam-osx/_base_/datasets/cofw.py
new file mode 100644
index 0000000000000000000000000000000000000000..2fb7ad2f8d1fdbe868b3691858a370e26b59a105
--- /dev/null
+++ b/grounded-sam-osx/_base_/datasets/cofw.py
@@ -0,0 +1,134 @@
+dataset_info = dict(
+ dataset_name='cofw',
+ paper_info=dict(
+ author='Burgos-Artizzu, Xavier P and Perona, '
+ r'Pietro and Doll{\'a}r, Piotr',
+ title='Robust face landmark estimation under occlusion',
+ container='Proceedings of the IEEE international '
+ 'conference on computer vision',
+ year='2013',
+ homepage='http://www.vision.caltech.edu/xpburgos/ICCV13/',
+ ),
+ keypoint_info={
+ 0:
+ dict(name='kpt-0', id=0, color=[255, 255, 255], type='', swap='kpt-1'),
+ 1:
+ dict(name='kpt-1', id=1, color=[255, 255, 255], type='', swap='kpt-0'),
+ 2:
+ dict(name='kpt-2', id=2, color=[255, 255, 255], type='', swap='kpt-3'),
+ 3:
+ dict(name='kpt-3', id=3, color=[255, 255, 255], type='', swap='kpt-2'),
+ 4:
+ dict(name='kpt-4', id=4, color=[255, 255, 255], type='', swap='kpt-6'),
+ 5:
+ dict(name='kpt-5', id=5, color=[255, 255, 255], type='', swap='kpt-7'),
+ 6:
+ dict(name='kpt-6', id=6, color=[255, 255, 255], type='', swap='kpt-4'),
+ 7:
+ dict(name='kpt-7', id=7, color=[255, 255, 255], type='', swap='kpt-5'),
+ 8:
+ dict(name='kpt-8', id=8, color=[255, 255, 255], type='', swap='kpt-9'),
+ 9:
+ dict(name='kpt-9', id=9, color=[255, 255, 255], type='', swap='kpt-8'),
+ 10:
+ dict(
+ name='kpt-10',
+ id=10,
+ color=[255, 255, 255],
+ type='',
+ swap='kpt-11'),
+ 11:
+ dict(
+ name='kpt-11',
+ id=11,
+ color=[255, 255, 255],
+ type='',
+ swap='kpt-10'),
+ 12:
+ dict(
+ name='kpt-12',
+ id=12,
+ color=[255, 255, 255],
+ type='',
+ swap='kpt-14'),
+ 13:
+ dict(
+ name='kpt-13',
+ id=13,
+ color=[255, 255, 255],
+ type='',
+ swap='kpt-15'),
+ 14:
+ dict(
+ name='kpt-14',
+ id=14,
+ color=[255, 255, 255],
+ type='',
+ swap='kpt-12'),
+ 15:
+ dict(
+ name='kpt-15',
+ id=15,
+ color=[255, 255, 255],
+ type='',
+ swap='kpt-13'),
+ 16:
+ dict(
+ name='kpt-16',
+ id=16,
+ color=[255, 255, 255],
+ type='',
+ swap='kpt-17'),
+ 17:
+ dict(
+ name='kpt-17',
+ id=17,
+ color=[255, 255, 255],
+ type='',
+ swap='kpt-16'),
+ 18:
+ dict(
+ name='kpt-18',
+ id=18,
+ color=[255, 255, 255],
+ type='',
+ swap='kpt-19'),
+ 19:
+ dict(
+ name='kpt-19',
+ id=19,
+ color=[255, 255, 255],
+ type='',
+ swap='kpt-18'),
+ 20:
+ dict(name='kpt-20', id=20, color=[255, 255, 255], type='', swap=''),
+ 21:
+ dict(name='kpt-21', id=21, color=[255, 255, 255], type='', swap=''),
+ 22:
+ dict(
+ name='kpt-22',
+ id=22,
+ color=[255, 255, 255],
+ type='',
+ swap='kpt-23'),
+ 23:
+ dict(
+ name='kpt-23',
+ id=23,
+ color=[255, 255, 255],
+ type='',
+ swap='kpt-22'),
+ 24:
+ dict(name='kpt-24', id=24, color=[255, 255, 255], type='', swap=''),
+ 25:
+ dict(name='kpt-25', id=25, color=[255, 255, 255], type='', swap=''),
+ 26:
+ dict(name='kpt-26', id=26, color=[255, 255, 255], type='', swap=''),
+ 27:
+ dict(name='kpt-27', id=27, color=[255, 255, 255], type='', swap=''),
+ 28:
+ dict(name='kpt-28', id=28, color=[255, 255, 255], type='', swap='')
+ },
+ skeleton_info={},
+ joint_weights=[1.] * 29,
+ sigmas=[])
diff --git a/grounded-sam-osx/_base_/datasets/crowdpose.py b/grounded-sam-osx/_base_/datasets/crowdpose.py
new file mode 100644
index 0000000000000000000000000000000000000000..45086531a601870716eed15a32c5413c0e24b7ae
--- /dev/null
+++ b/grounded-sam-osx/_base_/datasets/crowdpose.py
@@ -0,0 +1,147 @@
+dataset_info = dict(
+ dataset_name='crowdpose',
+ paper_info=dict(
+ author='Li, Jiefeng and Wang, Can and Zhu, Hao and '
+ 'Mao, Yihuan and Fang, Hao-Shu and Lu, Cewu',
+ title='CrowdPose: Efficient Crowded Scenes Pose Estimation '
+ 'and A New Benchmark',
+ container='Proceedings of IEEE Conference on Computer '
+ 'Vision and Pattern Recognition (CVPR)',
+ year='2019',
+ homepage='https://github.com/Jeff-sjtu/CrowdPose',
+ ),
+ keypoint_info={
+ 0:
+ dict(
+ name='left_shoulder',
+ id=0,
+ color=[51, 153, 255],
+ type='upper',
+ swap='right_shoulder'),
+ 1:
+ dict(
+ name='right_shoulder',
+ id=1,
+ color=[51, 153, 255],
+ type='upper',
+ swap='left_shoulder'),
+ 2:
+ dict(
+ name='left_elbow',
+ id=2,
+ color=[51, 153, 255],
+ type='upper',
+ swap='right_elbow'),
+ 3:
+ dict(
+ name='right_elbow',
+ id=3,
+ color=[51, 153, 255],
+ type='upper',
+ swap='left_elbow'),
+ 4:
+ dict(
+ name='left_wrist',
+ id=4,
+ color=[51, 153, 255],
+ type='upper',
+ swap='right_wrist'),
+ 5:
+ dict(
+ name='right_wrist',
+ id=5,
+ color=[0, 255, 0],
+ type='upper',
+ swap='left_wrist'),
+ 6:
+ dict(
+ name='left_hip',
+ id=6,
+ color=[255, 128, 0],
+ type='lower',
+ swap='right_hip'),
+ 7:
+ dict(
+ name='right_hip',
+ id=7,
+ color=[0, 255, 0],
+ type='lower',
+ swap='left_hip'),
+ 8:
+ dict(
+ name='left_knee',
+ id=8,
+ color=[255, 128, 0],
+ type='lower',
+ swap='right_knee'),
+ 9:
+ dict(
+ name='right_knee',
+ id=9,
+ color=[0, 255, 0],
+ type='lower',
+ swap='left_knee'),
+ 10:
+ dict(
+ name='left_ankle',
+ id=10,
+ color=[255, 128, 0],
+ type='lower',
+ swap='right_ankle'),
+ 11:
+ dict(
+ name='right_ankle',
+ id=11,
+ color=[0, 255, 0],
+ type='lower',
+ swap='left_ankle'),
+ 12:
+ dict(
+ name='top_head', id=12, color=[255, 128, 0], type='upper',
+ swap=''),
+ 13:
+ dict(name='neck', id=13, color=[0, 255, 0], type='upper', swap='')
+ },
+ skeleton_info={
+ 0:
+ dict(link=('left_ankle', 'left_knee'), id=0, color=[0, 255, 0]),
+ 1:
+ dict(link=('left_knee', 'left_hip'), id=1, color=[0, 255, 0]),
+ 2:
+ dict(link=('right_ankle', 'right_knee'), id=2, color=[255, 128, 0]),
+ 3:
+ dict(link=('right_knee', 'right_hip'), id=3, color=[255, 128, 0]),
+ 4:
+ dict(link=('left_hip', 'right_hip'), id=4, color=[51, 153, 255]),
+ 5:
+ dict(link=('left_shoulder', 'left_hip'), id=5, color=[51, 153, 255]),
+ 6:
+ dict(link=('right_shoulder', 'right_hip'), id=6, color=[51, 153, 255]),
+ 7:
+ dict(
+ link=('left_shoulder', 'right_shoulder'),
+ id=7,
+ color=[51, 153, 255]),
+ 8:
+ dict(link=('left_shoulder', 'left_elbow'), id=8, color=[0, 255, 0]),
+ 9:
+ dict(
+ link=('right_shoulder', 'right_elbow'), id=9, color=[255, 128, 0]),
+ 10:
+ dict(link=('left_elbow', 'left_wrist'), id=10, color=[0, 255, 0]),
+ 11:
+ dict(link=('right_elbow', 'right_wrist'), id=11, color=[255, 128, 0]),
+ 12:
+ dict(link=('top_head', 'neck'), id=12, color=[51, 153, 255]),
+ 13:
+ dict(link=('right_shoulder', 'neck'), id=13, color=[51, 153, 255]),
+ 14:
+ dict(link=('left_shoulder', 'neck'), id=14, color=[51, 153, 255])
+ },
+ joint_weights=[
+ 0.2, 0.2, 0.2, 1.3, 1.5, 0.2, 1.3, 1.5, 0.2, 0.2, 0.5, 0.2, 0.2, 0.5
+ ],
+ sigmas=[
+ 0.079, 0.079, 0.072, 0.072, 0.062, 0.062, 0.107, 0.107, 0.087, 0.087,
+ 0.089, 0.089, 0.079, 0.079
+ ])
diff --git a/grounded-sam-osx/_base_/datasets/deepfashion_full.py b/grounded-sam-osx/_base_/datasets/deepfashion_full.py
new file mode 100644
index 0000000000000000000000000000000000000000..4d989069ee7253d3a5b5f01c81135b1a472cd4b2
--- /dev/null
+++ b/grounded-sam-osx/_base_/datasets/deepfashion_full.py
@@ -0,0 +1,74 @@
+dataset_info = dict(
+ dataset_name='deepfashion_full',
+ paper_info=dict(
+ author='Liu, Ziwei and Luo, Ping and Qiu, Shi '
+ 'and Wang, Xiaogang and Tang, Xiaoou',
+ title='DeepFashion: Powering Robust Clothes Recognition '
+ 'and Retrieval with Rich Annotations',
+ container='Proceedings of IEEE Conference on Computer '
+ 'Vision and Pattern Recognition (CVPR)',
+ year='2016',
+ homepage='http://mmlab.ie.cuhk.edu.hk/projects/'
+ 'DeepFashion/LandmarkDetection.html',
+ ),
+ keypoint_info={
+ 0:
+ dict(
+ name='left collar',
+ id=0,
+ color=[255, 255, 255],
+ type='',
+ swap='right collar'),
+ 1:
+ dict(
+ name='right collar',
+ id=1,
+ color=[255, 255, 255],
+ type='',
+ swap='left collar'),
+ 2:
+ dict(
+ name='left sleeve',
+ id=2,
+ color=[255, 255, 255],
+ type='',
+ swap='right sleeve'),
+ 3:
+ dict(
+ name='right sleeve',
+ id=3,
+ color=[255, 255, 255],
+ type='',
+ swap='left sleeve'),
+ 4:
+ dict(
+ name='left waistline',
+ id=0,
+ color=[255, 255, 255],
+ type='',
+ swap='right waistline'),
+ 5:
+ dict(
+ name='right waistline',
+ id=1,
+ color=[255, 255, 255],
+ type='',
+ swap='left waistline'),
+ 6:
+ dict(
+ name='left hem',
+ id=2,
+ color=[255, 255, 255],
+ type='',
+ swap='right hem'),
+ 7:
+ dict(
+ name='right hem',
+ id=3,
+ color=[255, 255, 255],
+ type='',
+ swap='left hem'),
+ },
+ skeleton_info={},
+ joint_weights=[1.] * 8,
+ sigmas=[])
diff --git a/grounded-sam-osx/_base_/datasets/deepfashion_lower.py b/grounded-sam-osx/_base_/datasets/deepfashion_lower.py
new file mode 100644
index 0000000000000000000000000000000000000000..db014a1747ca618f93a7d092d29027015b48ae3c
--- /dev/null
+++ b/grounded-sam-osx/_base_/datasets/deepfashion_lower.py
@@ -0,0 +1,46 @@
+dataset_info = dict(
+ dataset_name='deepfashion_lower',
+ paper_info=dict(
+ author='Liu, Ziwei and Luo, Ping and Qiu, Shi '
+ 'and Wang, Xiaogang and Tang, Xiaoou',
+ title='DeepFashion: Powering Robust Clothes Recognition '
+ 'and Retrieval with Rich Annotations',
+ container='Proceedings of IEEE Conference on Computer '
+ 'Vision and Pattern Recognition (CVPR)',
+ year='2016',
+ homepage='http://mmlab.ie.cuhk.edu.hk/projects/'
+ 'DeepFashion/LandmarkDetection.html',
+ ),
+ keypoint_info={
+ 0:
+ dict(
+ name='left waistline',
+ id=0,
+ color=[255, 255, 255],
+ type='',
+ swap='right waistline'),
+ 1:
+ dict(
+ name='right waistline',
+ id=1,
+ color=[255, 255, 255],
+ type='',
+ swap='left waistline'),
+ 2:
+ dict(
+ name='left hem',
+ id=2,
+ color=[255, 255, 255],
+ type='',
+ swap='right hem'),
+ 3:
+ dict(
+ name='right hem',
+ id=3,
+ color=[255, 255, 255],
+ type='',
+ swap='left hem'),
+ },
+ skeleton_info={},
+ joint_weights=[1.] * 4,
+ sigmas=[])
diff --git a/grounded-sam-osx/_base_/datasets/deepfashion_upper.py b/grounded-sam-osx/_base_/datasets/deepfashion_upper.py
new file mode 100644
index 0000000000000000000000000000000000000000..f0b012fd37bee1ba5ed956a7a5465a8623bf0894
--- /dev/null
+++ b/grounded-sam-osx/_base_/datasets/deepfashion_upper.py
@@ -0,0 +1,60 @@
+dataset_info = dict(
+ dataset_name='deepfashion_upper',
+ paper_info=dict(
+ author='Liu, Ziwei and Luo, Ping and Qiu, Shi '
+ 'and Wang, Xiaogang and Tang, Xiaoou',
+ title='DeepFashion: Powering Robust Clothes Recognition '
+ 'and Retrieval with Rich Annotations',
+ container='Proceedings of IEEE Conference on Computer '
+ 'Vision and Pattern Recognition (CVPR)',
+ year='2016',
+ homepage='http://mmlab.ie.cuhk.edu.hk/projects/'
+ 'DeepFashion/LandmarkDetection.html',
+ ),
+ keypoint_info={
+ 0:
+ dict(
+ name='left collar',
+ id=0,
+ color=[255, 255, 255],
+ type='',
+ swap='right collar'),
+ 1:
+ dict(
+ name='right collar',
+ id=1,
+ color=[255, 255, 255],
+ type='',
+ swap='left collar'),
+ 2:
+ dict(
+ name='left sleeve',
+ id=2,
+ color=[255, 255, 255],
+ type='',
+ swap='right sleeve'),
+ 3:
+ dict(
+ name='right sleeve',
+ id=3,
+ color=[255, 255, 255],
+ type='',
+ swap='left sleeve'),
+ 4:
+ dict(
+ name='left hem',
+ id=4,
+ color=[255, 255, 255],
+ type='',
+ swap='right hem'),
+ 5:
+ dict(
+ name='right hem',
+ id=5,
+ color=[255, 255, 255],
+ type='',
+ swap='left hem'),
+ },
+ skeleton_info={},
+ joint_weights=[1.] * 6,
+ sigmas=[])
diff --git a/grounded-sam-osx/_base_/datasets/fly.py b/grounded-sam-osx/_base_/datasets/fly.py
new file mode 100644
index 0000000000000000000000000000000000000000..5f94ff57ca93d8f562b6a61b9a67198abdcde217
--- /dev/null
+++ b/grounded-sam-osx/_base_/datasets/fly.py
@@ -0,0 +1,237 @@
+dataset_info = dict(
+ dataset_name='fly',
+ paper_info=dict(
+ author='Pereira, Talmo D and Aldarondo, Diego E and '
+ 'Willmore, Lindsay and Kislin, Mikhail and '
+ 'Wang, Samuel S-H and Murthy, Mala and Shaevitz, Joshua W',
+ title='Fast animal pose estimation using deep neural networks',
+ container='Nature methods',
+ year='2019',
+ homepage='https://github.com/jgraving/DeepPoseKit-Data',
+ ),
+ keypoint_info={
+ 0:
+ dict(name='head', id=0, color=[255, 255, 255], type='', swap=''),
+ 1:
+ dict(name='eyeL', id=1, color=[255, 255, 255], type='', swap='eyeR'),
+ 2:
+ dict(name='eyeR', id=2, color=[255, 255, 255], type='', swap='eyeL'),
+ 3:
+ dict(name='neck', id=3, color=[255, 255, 255], type='', swap=''),
+ 4:
+ dict(name='thorax', id=4, color=[255, 255, 255], type='', swap=''),
+ 5:
+ dict(name='abdomen', id=5, color=[255, 255, 255], type='', swap=''),
+ 6:
+ dict(
+ name='forelegR1',
+ id=6,
+ color=[255, 255, 255],
+ type='',
+ swap='forelegL1'),
+ 7:
+ dict(
+ name='forelegR2',
+ id=7,
+ color=[255, 255, 255],
+ type='',
+ swap='forelegL2'),
+ 8:
+ dict(
+ name='forelegR3',
+ id=8,
+ color=[255, 255, 255],
+ type='',
+ swap='forelegL3'),
+ 9:
+ dict(
+ name='forelegR4',
+ id=9,
+ color=[255, 255, 255],
+ type='',
+ swap='forelegL4'),
+ 10:
+ dict(
+ name='midlegR1',
+ id=10,
+ color=[255, 255, 255],
+ type='',
+ swap='midlegL1'),
+ 11:
+ dict(
+ name='midlegR2',
+ id=11,
+ color=[255, 255, 255],
+ type='',
+ swap='midlegL2'),
+ 12:
+ dict(
+ name='midlegR3',
+ id=12,
+ color=[255, 255, 255],
+ type='',
+ swap='midlegL3'),
+ 13:
+ dict(
+ name='midlegR4',
+ id=13,
+ color=[255, 255, 255],
+ type='',
+ swap='midlegL4'),
+ 14:
+ dict(
+ name='hindlegR1',
+ id=14,
+ color=[255, 255, 255],
+ type='',
+ swap='hindlegL1'),
+ 15:
+ dict(
+ name='hindlegR2',
+ id=15,
+ color=[255, 255, 255],
+ type='',
+ swap='hindlegL2'),
+ 16:
+ dict(
+ name='hindlegR3',
+ id=16,
+ color=[255, 255, 255],
+ type='',
+ swap='hindlegL3'),
+ 17:
+ dict(
+ name='hindlegR4',
+ id=17,
+ color=[255, 255, 255],
+ type='',
+ swap='hindlegL4'),
+ 18:
+ dict(
+ name='forelegL1',
+ id=18,
+ color=[255, 255, 255],
+ type='',
+ swap='forelegR1'),
+ 19:
+ dict(
+ name='forelegL2',
+ id=19,
+ color=[255, 255, 255],
+ type='',
+ swap='forelegR2'),
+ 20:
+ dict(
+ name='forelegL3',
+ id=20,
+ color=[255, 255, 255],
+ type='',
+ swap='forelegR3'),
+ 21:
+ dict(
+ name='forelegL4',
+ id=21,
+ color=[255, 255, 255],
+ type='',
+ swap='forelegR4'),
+ 22:
+ dict(
+ name='midlegL1',
+ id=22,
+ color=[255, 255, 255],
+ type='',
+ swap='midlegR1'),
+ 23:
+ dict(
+ name='midlegL2',
+ id=23,
+ color=[255, 255, 255],
+ type='',
+ swap='midlegR2'),
+ 24:
+ dict(
+ name='midlegL3',
+ id=24,
+ color=[255, 255, 255],
+ type='',
+ swap='midlegR3'),
+ 25:
+ dict(
+ name='midlegL4',
+ id=25,
+ color=[255, 255, 255],
+ type='',
+ swap='midlegR4'),
+ 26:
+ dict(
+ name='hindlegL1',
+ id=26,
+ color=[255, 255, 255],
+ type='',
+ swap='hindlegR1'),
+ 27:
+ dict(
+ name='hindlegL2',
+ id=27,
+ color=[255, 255, 255],
+ type='',
+ swap='hindlegR2'),
+ 28:
+ dict(
+ name='hindlegL3',
+ id=28,
+ color=[255, 255, 255],
+ type='',
+ swap='hindlegR3'),
+ 29:
+ dict(
+ name='hindlegL4',
+ id=29,
+ color=[255, 255, 255],
+ type='',
+ swap='hindlegR4'),
+ 30:
+ dict(
+ name='wingL', id=30, color=[255, 255, 255], type='', swap='wingR'),
+ 31:
+ dict(
+ name='wingR', id=31, color=[255, 255, 255], type='', swap='wingL'),
+ },
+ skeleton_info={
+ 0: dict(link=('eyeL', 'head'), id=0, color=[255, 255, 255]),
+ 1: dict(link=('eyeR', 'head'), id=1, color=[255, 255, 255]),
+ 2: dict(link=('neck', 'head'), id=2, color=[255, 255, 255]),
+ 3: dict(link=('thorax', 'neck'), id=3, color=[255, 255, 255]),
+ 4: dict(link=('abdomen', 'thorax'), id=4, color=[255, 255, 255]),
+ 5: dict(link=('forelegR2', 'forelegR1'), id=5, color=[255, 255, 255]),
+ 6: dict(link=('forelegR3', 'forelegR2'), id=6, color=[255, 255, 255]),
+ 7: dict(link=('forelegR4', 'forelegR3'), id=7, color=[255, 255, 255]),
+ 8: dict(link=('midlegR2', 'midlegR1'), id=8, color=[255, 255, 255]),
+ 9: dict(link=('midlegR3', 'midlegR2'), id=9, color=[255, 255, 255]),
+ 10: dict(link=('midlegR4', 'midlegR3'), id=10, color=[255, 255, 255]),
+ 11:
+ dict(link=('hindlegR2', 'hindlegR1'), id=11, color=[255, 255, 255]),
+ 12:
+ dict(link=('hindlegR3', 'hindlegR2'), id=12, color=[255, 255, 255]),
+ 13:
+ dict(link=('hindlegR4', 'hindlegR3'), id=13, color=[255, 255, 255]),
+ 14:
+ dict(link=('forelegL2', 'forelegL1'), id=14, color=[255, 255, 255]),
+ 15:
+ dict(link=('forelegL3', 'forelegL2'), id=15, color=[255, 255, 255]),
+ 16:
+ dict(link=('forelegL4', 'forelegL3'), id=16, color=[255, 255, 255]),
+ 17: dict(link=('midlegL2', 'midlegL1'), id=17, color=[255, 255, 255]),
+ 18: dict(link=('midlegL3', 'midlegL2'), id=18, color=[255, 255, 255]),
+ 19: dict(link=('midlegL4', 'midlegL3'), id=19, color=[255, 255, 255]),
+ 20:
+ dict(link=('hindlegL2', 'hindlegL1'), id=20, color=[255, 255, 255]),
+ 21:
+ dict(link=('hindlegL3', 'hindlegL2'), id=21, color=[255, 255, 255]),
+ 22:
+ dict(link=('hindlegL4', 'hindlegL3'), id=22, color=[255, 255, 255]),
+ 23: dict(link=('wingL', 'neck'), id=23, color=[255, 255, 255]),
+ 24: dict(link=('wingR', 'neck'), id=24, color=[255, 255, 255])
+ },
+ joint_weights=[1.] * 32,
+ sigmas=[])
diff --git a/grounded-sam-osx/_base_/datasets/freihand2d.py b/grounded-sam-osx/_base_/datasets/freihand2d.py
new file mode 100644
index 0000000000000000000000000000000000000000..8b960d10f3538801531dbccdd67aeac6e73ac572
--- /dev/null
+++ b/grounded-sam-osx/_base_/datasets/freihand2d.py
@@ -0,0 +1,144 @@
+dataset_info = dict(
+ dataset_name='freihand',
+ paper_info=dict(
+ author='Zimmermann, Christian and Ceylan, Duygu and '
+ 'Yang, Jimei and Russell, Bryan and '
+ 'Argus, Max and Brox, Thomas',
+ title='Freihand: A dataset for markerless capture of hand pose '
+ 'and shape from single rgb images',
+ container='Proceedings of the IEEE International '
+ 'Conference on Computer Vision',
+ year='2019',
+ homepage='https://lmb.informatik.uni-freiburg.de/projects/freihand/',
+ ),
+ keypoint_info={
+ 0:
+ dict(name='wrist', id=0, color=[255, 255, 255], type='', swap=''),
+ 1:
+ dict(name='thumb1', id=1, color=[255, 128, 0], type='', swap=''),
+ 2:
+ dict(name='thumb2', id=2, color=[255, 128, 0], type='', swap=''),
+ 3:
+ dict(name='thumb3', id=3, color=[255, 128, 0], type='', swap=''),
+ 4:
+ dict(name='thumb4', id=4, color=[255, 128, 0], type='', swap=''),
+ 5:
+ dict(
+ name='forefinger1', id=5, color=[255, 153, 255], type='', swap=''),
+ 6:
+ dict(
+ name='forefinger2', id=6, color=[255, 153, 255], type='', swap=''),
+ 7:
+ dict(
+ name='forefinger3', id=7, color=[255, 153, 255], type='', swap=''),
+ 8:
+ dict(
+ name='forefinger4', id=8, color=[255, 153, 255], type='', swap=''),
+ 9:
+ dict(
+ name='middle_finger1',
+ id=9,
+ color=[102, 178, 255],
+ type='',
+ swap=''),
+ 10:
+ dict(
+ name='middle_finger2',
+ id=10,
+ color=[102, 178, 255],
+ type='',
+ swap=''),
+ 11:
+ dict(
+ name='middle_finger3',
+ id=11,
+ color=[102, 178, 255],
+ type='',
+ swap=''),
+ 12:
+ dict(
+ name='middle_finger4',
+ id=12,
+ color=[102, 178, 255],
+ type='',
+ swap=''),
+ 13:
+ dict(
+ name='ring_finger1', id=13, color=[255, 51, 51], type='', swap=''),
+ 14:
+ dict(
+ name='ring_finger2', id=14, color=[255, 51, 51], type='', swap=''),
+ 15:
+ dict(
+ name='ring_finger3', id=15, color=[255, 51, 51], type='', swap=''),
+ 16:
+ dict(
+ name='ring_finger4', id=16, color=[255, 51, 51], type='', swap=''),
+ 17:
+ dict(name='pinky_finger1', id=17, color=[0, 255, 0], type='', swap=''),
+ 18:
+ dict(name='pinky_finger2', id=18, color=[0, 255, 0], type='', swap=''),
+ 19:
+ dict(name='pinky_finger3', id=19, color=[0, 255, 0], type='', swap=''),
+ 20:
+ dict(name='pinky_finger4', id=20, color=[0, 255, 0], type='', swap='')
+ },
+ skeleton_info={
+ 0:
+ dict(link=('wrist', 'thumb1'), id=0, color=[255, 128, 0]),
+ 1:
+ dict(link=('thumb1', 'thumb2'), id=1, color=[255, 128, 0]),
+ 2:
+ dict(link=('thumb2', 'thumb3'), id=2, color=[255, 128, 0]),
+ 3:
+ dict(link=('thumb3', 'thumb4'), id=3, color=[255, 128, 0]),
+ 4:
+ dict(link=('wrist', 'forefinger1'), id=4, color=[255, 153, 255]),
+ 5:
+ dict(link=('forefinger1', 'forefinger2'), id=5, color=[255, 153, 255]),
+ 6:
+ dict(link=('forefinger2', 'forefinger3'), id=6, color=[255, 153, 255]),
+ 7:
+ dict(link=('forefinger3', 'forefinger4'), id=7, color=[255, 153, 255]),
+ 8:
+ dict(link=('wrist', 'middle_finger1'), id=8, color=[102, 178, 255]),
+ 9:
+ dict(
+ link=('middle_finger1', 'middle_finger2'),
+ id=9,
+ color=[102, 178, 255]),
+ 10:
+ dict(
+ link=('middle_finger2', 'middle_finger3'),
+ id=10,
+ color=[102, 178, 255]),
+ 11:
+ dict(
+ link=('middle_finger3', 'middle_finger4'),
+ id=11,
+ color=[102, 178, 255]),
+ 12:
+ dict(link=('wrist', 'ring_finger1'), id=12, color=[255, 51, 51]),
+ 13:
+ dict(
+ link=('ring_finger1', 'ring_finger2'), id=13, color=[255, 51, 51]),
+ 14:
+ dict(
+ link=('ring_finger2', 'ring_finger3'), id=14, color=[255, 51, 51]),
+ 15:
+ dict(
+ link=('ring_finger3', 'ring_finger4'), id=15, color=[255, 51, 51]),
+ 16:
+ dict(link=('wrist', 'pinky_finger1'), id=16, color=[0, 255, 0]),
+ 17:
+ dict(
+ link=('pinky_finger1', 'pinky_finger2'), id=17, color=[0, 255, 0]),
+ 18:
+ dict(
+ link=('pinky_finger2', 'pinky_finger3'), id=18, color=[0, 255, 0]),
+ 19:
+ dict(
+ link=('pinky_finger3', 'pinky_finger4'), id=19, color=[0, 255, 0])
+ },
+ joint_weights=[1.] * 21,
+ sigmas=[])
diff --git a/grounded-sam-osx/_base_/datasets/h36m.py b/grounded-sam-osx/_base_/datasets/h36m.py
new file mode 100644
index 0000000000000000000000000000000000000000..00a719d8b19f9ff3c5ef98476d73216055bf9186
--- /dev/null
+++ b/grounded-sam-osx/_base_/datasets/h36m.py
@@ -0,0 +1,152 @@
+dataset_info = dict(
+ dataset_name='h36m',
+ paper_info=dict(
+ author='Ionescu, Catalin and Papava, Dragos and '
+ 'Olaru, Vlad and Sminchisescu, Cristian',
+ title='Human3.6M: Large Scale Datasets and Predictive '
+ 'Methods for 3D Human Sensing in Natural Environments',
+ container='IEEE Transactions on Pattern Analysis and '
+ 'Machine Intelligence',
+ year='2014',
+ homepage='http://vision.imar.ro/human3.6m/description.php',
+ ),
+ keypoint_info={
+ 0:
+ dict(name='root', id=0, color=[51, 153, 255], type='lower', swap=''),
+ 1:
+ dict(
+ name='right_hip',
+ id=1,
+ color=[255, 128, 0],
+ type='lower',
+ swap='left_hip'),
+ 2:
+ dict(
+ name='right_knee',
+ id=2,
+ color=[255, 128, 0],
+ type='lower',
+ swap='left_knee'),
+ 3:
+ dict(
+ name='right_foot',
+ id=3,
+ color=[255, 128, 0],
+ type='lower',
+ swap='left_foot'),
+ 4:
+ dict(
+ name='left_hip',
+ id=4,
+ color=[0, 255, 0],
+ type='lower',
+ swap='right_hip'),
+ 5:
+ dict(
+ name='left_knee',
+ id=5,
+ color=[0, 255, 0],
+ type='lower',
+ swap='right_knee'),
+ 6:
+ dict(
+ name='left_foot',
+ id=6,
+ color=[0, 255, 0],
+ type='lower',
+ swap='right_foot'),
+ 7:
+ dict(name='spine', id=7, color=[51, 153, 255], type='upper', swap=''),
+ 8:
+ dict(name='thorax', id=8, color=[51, 153, 255], type='upper', swap=''),
+ 9:
+ dict(
+ name='neck_base',
+ id=9,
+ color=[51, 153, 255],
+ type='upper',
+ swap=''),
+ 10:
+ dict(name='head', id=10, color=[51, 153, 255], type='upper', swap=''),
+ 11:
+ dict(
+ name='left_shoulder',
+ id=11,
+ color=[0, 255, 0],
+ type='upper',
+ swap='right_shoulder'),
+ 12:
+ dict(
+ name='left_elbow',
+ id=12,
+ color=[0, 255, 0],
+ type='upper',
+ swap='right_elbow'),
+ 13:
+ dict(
+ name='left_wrist',
+ id=13,
+ color=[0, 255, 0],
+ type='upper',
+ swap='right_wrist'),
+ 14:
+ dict(
+ name='right_shoulder',
+ id=14,
+ color=[255, 128, 0],
+ type='upper',
+ swap='left_shoulder'),
+ 15:
+ dict(
+ name='right_elbow',
+ id=15,
+ color=[255, 128, 0],
+ type='upper',
+ swap='left_elbow'),
+ 16:
+ dict(
+ name='right_wrist',
+ id=16,
+ color=[255, 128, 0],
+ type='upper',
+ swap='left_wrist')
+ },
+ skeleton_info={
+ 0:
+ dict(link=('root', 'left_hip'), id=0, color=[0, 255, 0]),
+ 1:
+ dict(link=('left_hip', 'left_knee'), id=1, color=[0, 255, 0]),
+ 2:
+ dict(link=('left_knee', 'left_foot'), id=2, color=[0, 255, 0]),
+ 3:
+ dict(link=('root', 'right_hip'), id=3, color=[255, 128, 0]),
+ 4:
+ dict(link=('right_hip', 'right_knee'), id=4, color=[255, 128, 0]),
+ 5:
+ dict(link=('right_knee', 'right_foot'), id=5, color=[255, 128, 0]),
+ 6:
+ dict(link=('root', 'spine'), id=6, color=[51, 153, 255]),
+ 7:
+ dict(link=('spine', 'thorax'), id=7, color=[51, 153, 255]),
+ 8:
+ dict(link=('thorax', 'neck_base'), id=8, color=[51, 153, 255]),
+ 9:
+ dict(link=('neck_base', 'head'), id=9, color=[51, 153, 255]),
+ 10:
+ dict(link=('thorax', 'left_shoulder'), id=10, color=[0, 255, 0]),
+ 11:
+ dict(link=('left_shoulder', 'left_elbow'), id=11, color=[0, 255, 0]),
+ 12:
+ dict(link=('left_elbow', 'left_wrist'), id=12, color=[0, 255, 0]),
+ 13:
+ dict(link=('thorax', 'right_shoulder'), id=13, color=[255, 128, 0]),
+ 14:
+ dict(
+ link=('right_shoulder', 'right_elbow'), id=14, color=[255, 128,
+ 0]),
+ 15:
+ dict(link=('right_elbow', 'right_wrist'), id=15, color=[255, 128, 0])
+ },
+ joint_weights=[1.] * 17,
+ sigmas=[],
+ stats_info=dict(bbox_center=(528., 427.), bbox_scale=400.))
diff --git a/grounded-sam-osx/_base_/datasets/halpe.py b/grounded-sam-osx/_base_/datasets/halpe.py
new file mode 100644
index 0000000000000000000000000000000000000000..1385fe81dc2190684f2142449c0f288f2cb74c1a
--- /dev/null
+++ b/grounded-sam-osx/_base_/datasets/halpe.py
@@ -0,0 +1,1157 @@
+dataset_info = dict(
+ dataset_name='halpe',
+ paper_info=dict(
+ author='Li, Yong-Lu and Xu, Liang and Liu, Xinpeng and Huang, Xijie'
+ ' and Xu, Yue and Wang, Shiyi and Fang, Hao-Shu'
+ ' and Ma, Ze and Chen, Mingyang and Lu, Cewu',
+ title='PaStaNet: Toward Human Activity Knowledge Engine',
+ container='CVPR',
+ year='2020',
+ homepage='https://github.com/Fang-Haoshu/Halpe-FullBody/',
+ ),
+ keypoint_info={
+ 0:
+ dict(name='nose', id=0, color=[51, 153, 255], type='upper', swap=''),
+ 1:
+ dict(
+ name='left_eye',
+ id=1,
+ color=[51, 153, 255],
+ type='upper',
+ swap='right_eye'),
+ 2:
+ dict(
+ name='right_eye',
+ id=2,
+ color=[51, 153, 255],
+ type='upper',
+ swap='left_eye'),
+ 3:
+ dict(
+ name='left_ear',
+ id=3,
+ color=[51, 153, 255],
+ type='upper',
+ swap='right_ear'),
+ 4:
+ dict(
+ name='right_ear',
+ id=4,
+ color=[51, 153, 255],
+ type='upper',
+ swap='left_ear'),
+ 5:
+ dict(
+ name='left_shoulder',
+ id=5,
+ color=[0, 255, 0],
+ type='upper',
+ swap='right_shoulder'),
+ 6:
+ dict(
+ name='right_shoulder',
+ id=6,
+ color=[255, 128, 0],
+ type='upper',
+ swap='left_shoulder'),
+ 7:
+ dict(
+ name='left_elbow',
+ id=7,
+ color=[0, 255, 0],
+ type='upper',
+ swap='right_elbow'),
+ 8:
+ dict(
+ name='right_elbow',
+ id=8,
+ color=[255, 128, 0],
+ type='upper',
+ swap='left_elbow'),
+ 9:
+ dict(
+ name='left_wrist',
+ id=9,
+ color=[0, 255, 0],
+ type='upper',
+ swap='right_wrist'),
+ 10:
+ dict(
+ name='right_wrist',
+ id=10,
+ color=[255, 128, 0],
+ type='upper',
+ swap='left_wrist'),
+ 11:
+ dict(
+ name='left_hip',
+ id=11,
+ color=[0, 255, 0],
+ type='lower',
+ swap='right_hip'),
+ 12:
+ dict(
+ name='right_hip',
+ id=12,
+ color=[255, 128, 0],
+ type='lower',
+ swap='left_hip'),
+ 13:
+ dict(
+ name='left_knee',
+ id=13,
+ color=[0, 255, 0],
+ type='lower',
+ swap='right_knee'),
+ 14:
+ dict(
+ name='right_knee',
+ id=14,
+ color=[255, 128, 0],
+ type='lower',
+ swap='left_knee'),
+ 15:
+ dict(
+ name='left_ankle',
+ id=15,
+ color=[0, 255, 0],
+ type='lower',
+ swap='right_ankle'),
+ 16:
+ dict(
+ name='right_ankle',
+ id=16,
+ color=[255, 128, 0],
+ type='lower',
+ swap='left_ankle'),
+ 17:
+ dict(name='head', id=17, color=[255, 128, 0], type='upper', swap=''),
+ 18:
+ dict(name='neck', id=18, color=[255, 128, 0], type='upper', swap=''),
+ 19:
+ dict(name='hip', id=19, color=[255, 128, 0], type='lower', swap=''),
+ 20:
+ dict(
+ name='left_big_toe',
+ id=20,
+ color=[255, 128, 0],
+ type='lower',
+ swap='right_big_toe'),
+ 21:
+ dict(
+ name='right_big_toe',
+ id=21,
+ color=[255, 128, 0],
+ type='lower',
+ swap='left_big_toe'),
+ 22:
+ dict(
+ name='left_small_toe',
+ id=22,
+ color=[255, 128, 0],
+ type='lower',
+ swap='right_small_toe'),
+ 23:
+ dict(
+ name='right_small_toe',
+ id=23,
+ color=[255, 128, 0],
+ type='lower',
+ swap='left_small_toe'),
+ 24:
+ dict(
+ name='left_heel',
+ id=24,
+ color=[255, 128, 0],
+ type='lower',
+ swap='right_heel'),
+ 25:
+ dict(
+ name='right_heel',
+ id=25,
+ color=[255, 128, 0],
+ type='lower',
+ swap='left_heel'),
+ 26:
+ dict(
+ name='face-0',
+ id=26,
+ color=[255, 255, 255],
+ type='',
+ swap='face-16'),
+ 27:
+ dict(
+ name='face-1',
+ id=27,
+ color=[255, 255, 255],
+ type='',
+ swap='face-15'),
+ 28:
+ dict(
+ name='face-2',
+ id=28,
+ color=[255, 255, 255],
+ type='',
+ swap='face-14'),
+ 29:
+ dict(
+ name='face-3',
+ id=29,
+ color=[255, 255, 255],
+ type='',
+ swap='face-13'),
+ 30:
+ dict(
+ name='face-4',
+ id=30,
+ color=[255, 255, 255],
+ type='',
+ swap='face-12'),
+ 31:
+ dict(
+ name='face-5',
+ id=31,
+ color=[255, 255, 255],
+ type='',
+ swap='face-11'),
+ 32:
+ dict(
+ name='face-6',
+ id=32,
+ color=[255, 255, 255],
+ type='',
+ swap='face-10'),
+ 33:
+ dict(
+ name='face-7',
+ id=33,
+ color=[255, 255, 255],
+ type='',
+ swap='face-9'),
+ 34:
+ dict(name='face-8', id=34, color=[255, 255, 255], type='', swap=''),
+ 35:
+ dict(
+ name='face-9',
+ id=35,
+ color=[255, 255, 255],
+ type='',
+ swap='face-7'),
+ 36:
+ dict(
+ name='face-10',
+ id=36,
+ color=[255, 255, 255],
+ type='',
+ swap='face-6'),
+ 37:
+ dict(
+ name='face-11',
+ id=37,
+ color=[255, 255, 255],
+ type='',
+ swap='face-5'),
+ 38:
+ dict(
+ name='face-12',
+ id=38,
+ color=[255, 255, 255],
+ type='',
+ swap='face-4'),
+ 39:
+ dict(
+ name='face-13',
+ id=39,
+ color=[255, 255, 255],
+ type='',
+ swap='face-3'),
+ 40:
+ dict(
+ name='face-14',
+ id=40,
+ color=[255, 255, 255],
+ type='',
+ swap='face-2'),
+ 41:
+ dict(
+ name='face-15',
+ id=41,
+ color=[255, 255, 255],
+ type='',
+ swap='face-1'),
+ 42:
+ dict(
+ name='face-16',
+ id=42,
+ color=[255, 255, 255],
+ type='',
+ swap='face-0'),
+ 43:
+ dict(
+ name='face-17',
+ id=43,
+ color=[255, 255, 255],
+ type='',
+ swap='face-26'),
+ 44:
+ dict(
+ name='face-18',
+ id=44,
+ color=[255, 255, 255],
+ type='',
+ swap='face-25'),
+ 45:
+ dict(
+ name='face-19',
+ id=45,
+ color=[255, 255, 255],
+ type='',
+ swap='face-24'),
+ 46:
+ dict(
+ name='face-20',
+ id=46,
+ color=[255, 255, 255],
+ type='',
+ swap='face-23'),
+ 47:
+ dict(
+ name='face-21',
+ id=47,
+ color=[255, 255, 255],
+ type='',
+ swap='face-22'),
+ 48:
+ dict(
+ name='face-22',
+ id=48,
+ color=[255, 255, 255],
+ type='',
+ swap='face-21'),
+ 49:
+ dict(
+ name='face-23',
+ id=49,
+ color=[255, 255, 255],
+ type='',
+ swap='face-20'),
+ 50:
+ dict(
+ name='face-24',
+ id=50,
+ color=[255, 255, 255],
+ type='',
+ swap='face-19'),
+ 51:
+ dict(
+ name='face-25',
+ id=51,
+ color=[255, 255, 255],
+ type='',
+ swap='face-18'),
+ 52:
+ dict(
+ name='face-26',
+ id=52,
+ color=[255, 255, 255],
+ type='',
+ swap='face-17'),
+ 53:
+ dict(name='face-27', id=53, color=[255, 255, 255], type='', swap=''),
+ 54:
+ dict(name='face-28', id=54, color=[255, 255, 255], type='', swap=''),
+ 55:
+ dict(name='face-29', id=55, color=[255, 255, 255], type='', swap=''),
+ 56:
+ dict(name='face-30', id=56, color=[255, 255, 255], type='', swap=''),
+ 57:
+ dict(
+ name='face-31',
+ id=57,
+ color=[255, 255, 255],
+ type='',
+ swap='face-35'),
+ 58:
+ dict(
+ name='face-32',
+ id=58,
+ color=[255, 255, 255],
+ type='',
+ swap='face-34'),
+ 59:
+ dict(name='face-33', id=59, color=[255, 255, 255], type='', swap=''),
+ 60:
+ dict(
+ name='face-34',
+ id=60,
+ color=[255, 255, 255],
+ type='',
+ swap='face-32'),
+ 61:
+ dict(
+ name='face-35',
+ id=61,
+ color=[255, 255, 255],
+ type='',
+ swap='face-31'),
+ 62:
+ dict(
+ name='face-36',
+ id=62,
+ color=[255, 255, 255],
+ type='',
+ swap='face-45'),
+ 63:
+ dict(
+ name='face-37',
+ id=63,
+ color=[255, 255, 255],
+ type='',
+ swap='face-44'),
+ 64:
+ dict(
+ name='face-38',
+ id=64,
+ color=[255, 255, 255],
+ type='',
+ swap='face-43'),
+ 65:
+ dict(
+ name='face-39',
+ id=65,
+ color=[255, 255, 255],
+ type='',
+ swap='face-42'),
+ 66:
+ dict(
+ name='face-40',
+ id=66,
+ color=[255, 255, 255],
+ type='',
+ swap='face-47'),
+ 67:
+ dict(
+ name='face-41',
+ id=67,
+ color=[255, 255, 255],
+ type='',
+ swap='face-46'),
+ 68:
+ dict(
+ name='face-42',
+ id=68,
+ color=[255, 255, 255],
+ type='',
+ swap='face-39'),
+ 69:
+ dict(
+ name='face-43',
+ id=69,
+ color=[255, 255, 255],
+ type='',
+ swap='face-38'),
+ 70:
+ dict(
+ name='face-44',
+ id=70,
+ color=[255, 255, 255],
+ type='',
+ swap='face-37'),
+ 71:
+ dict(
+ name='face-45',
+ id=71,
+ color=[255, 255, 255],
+ type='',
+ swap='face-36'),
+ 72:
+ dict(
+ name='face-46',
+ id=72,
+ color=[255, 255, 255],
+ type='',
+ swap='face-41'),
+ 73:
+ dict(
+ name='face-47',
+ id=73,
+ color=[255, 255, 255],
+ type='',
+ swap='face-40'),
+ 74:
+ dict(
+ name='face-48',
+ id=74,
+ color=[255, 255, 255],
+ type='',
+ swap='face-54'),
+ 75:
+ dict(
+ name='face-49',
+ id=75,
+ color=[255, 255, 255],
+ type='',
+ swap='face-53'),
+ 76:
+ dict(
+ name='face-50',
+ id=76,
+ color=[255, 255, 255],
+ type='',
+ swap='face-52'),
+ 77:
+ dict(name='face-51', id=77, color=[255, 255, 255], type='', swap=''),
+ 78:
+ dict(
+ name='face-52',
+ id=78,
+ color=[255, 255, 255],
+ type='',
+ swap='face-50'),
+ 79:
+ dict(
+ name='face-53',
+ id=79,
+ color=[255, 255, 255],
+ type='',
+ swap='face-49'),
+ 80:
+ dict(
+ name='face-54',
+ id=80,
+ color=[255, 255, 255],
+ type='',
+ swap='face-48'),
+ 81:
+ dict(
+ name='face-55',
+ id=81,
+ color=[255, 255, 255],
+ type='',
+ swap='face-59'),
+ 82:
+ dict(
+ name='face-56',
+ id=82,
+ color=[255, 255, 255],
+ type='',
+ swap='face-58'),
+ 83:
+ dict(name='face-57', id=83, color=[255, 255, 255], type='', swap=''),
+ 84:
+ dict(
+ name='face-58',
+ id=84,
+ color=[255, 255, 255],
+ type='',
+ swap='face-56'),
+ 85:
+ dict(
+ name='face-59',
+ id=85,
+ color=[255, 255, 255],
+ type='',
+ swap='face-55'),
+ 86:
+ dict(
+ name='face-60',
+ id=86,
+ color=[255, 255, 255],
+ type='',
+ swap='face-64'),
+ 87:
+ dict(
+ name='face-61',
+ id=87,
+ color=[255, 255, 255],
+ type='',
+ swap='face-63'),
+ 88:
+ dict(name='face-62', id=88, color=[255, 255, 255], type='', swap=''),
+ 89:
+ dict(
+ name='face-63',
+ id=89,
+ color=[255, 255, 255],
+ type='',
+ swap='face-61'),
+ 90:
+ dict(
+ name='face-64',
+ id=90,
+ color=[255, 255, 255],
+ type='',
+ swap='face-60'),
+ 91:
+ dict(
+ name='face-65',
+ id=91,
+ color=[255, 255, 255],
+ type='',
+ swap='face-67'),
+ 92:
+ dict(name='face-66', id=92, color=[255, 255, 255], type='', swap=''),
+ 93:
+ dict(
+ name='face-67',
+ id=93,
+ color=[255, 255, 255],
+ type='',
+ swap='face-65'),
+ 94:
+ dict(
+ name='left_hand_root',
+ id=94,
+ color=[255, 255, 255],
+ type='',
+ swap='right_hand_root'),
+ 95:
+ dict(
+ name='left_thumb1',
+ id=95,
+ color=[255, 128, 0],
+ type='',
+ swap='right_thumb1'),
+ 96:
+ dict(
+ name='left_thumb2',
+ id=96,
+ color=[255, 128, 0],
+ type='',
+ swap='right_thumb2'),
+ 97:
+ dict(
+ name='left_thumb3',
+ id=97,
+ color=[255, 128, 0],
+ type='',
+ swap='right_thumb3'),
+ 98:
+ dict(
+ name='left_thumb4',
+ id=98,
+ color=[255, 128, 0],
+ type='',
+ swap='right_thumb4'),
+ 99:
+ dict(
+ name='left_forefinger1',
+ id=99,
+ color=[255, 153, 255],
+ type='',
+ swap='right_forefinger1'),
+ 100:
+ dict(
+ name='left_forefinger2',
+ id=100,
+ color=[255, 153, 255],
+ type='',
+ swap='right_forefinger2'),
+ 101:
+ dict(
+ name='left_forefinger3',
+ id=101,
+ color=[255, 153, 255],
+ type='',
+ swap='right_forefinger3'),
+ 102:
+ dict(
+ name='left_forefinger4',
+ id=102,
+ color=[255, 153, 255],
+ type='',
+ swap='right_forefinger4'),
+ 103:
+ dict(
+ name='left_middle_finger1',
+ id=103,
+ color=[102, 178, 255],
+ type='',
+ swap='right_middle_finger1'),
+ 104:
+ dict(
+ name='left_middle_finger2',
+ id=104,
+ color=[102, 178, 255],
+ type='',
+ swap='right_middle_finger2'),
+ 105:
+ dict(
+ name='left_middle_finger3',
+ id=105,
+ color=[102, 178, 255],
+ type='',
+ swap='right_middle_finger3'),
+ 106:
+ dict(
+ name='left_middle_finger4',
+ id=106,
+ color=[102, 178, 255],
+ type='',
+ swap='right_middle_finger4'),
+ 107:
+ dict(
+ name='left_ring_finger1',
+ id=107,
+ color=[255, 51, 51],
+ type='',
+ swap='right_ring_finger1'),
+ 108:
+ dict(
+ name='left_ring_finger2',
+ id=108,
+ color=[255, 51, 51],
+ type='',
+ swap='right_ring_finger2'),
+ 109:
+ dict(
+ name='left_ring_finger3',
+ id=109,
+ color=[255, 51, 51],
+ type='',
+ swap='right_ring_finger3'),
+ 110:
+ dict(
+ name='left_ring_finger4',
+ id=110,
+ color=[255, 51, 51],
+ type='',
+ swap='right_ring_finger4'),
+ 111:
+ dict(
+ name='left_pinky_finger1',
+ id=111,
+ color=[0, 255, 0],
+ type='',
+ swap='right_pinky_finger1'),
+ 112:
+ dict(
+ name='left_pinky_finger2',
+ id=112,
+ color=[0, 255, 0],
+ type='',
+ swap='right_pinky_finger2'),
+ 113:
+ dict(
+ name='left_pinky_finger3',
+ id=113,
+ color=[0, 255, 0],
+ type='',
+ swap='right_pinky_finger3'),
+ 114:
+ dict(
+ name='left_pinky_finger4',
+ id=114,
+ color=[0, 255, 0],
+ type='',
+ swap='right_pinky_finger4'),
+ 115:
+ dict(
+ name='right_hand_root',
+ id=115,
+ color=[255, 255, 255],
+ type='',
+ swap='left_hand_root'),
+ 116:
+ dict(
+ name='right_thumb1',
+ id=116,
+ color=[255, 128, 0],
+ type='',
+ swap='left_thumb1'),
+ 117:
+ dict(
+ name='right_thumb2',
+ id=117,
+ color=[255, 128, 0],
+ type='',
+ swap='left_thumb2'),
+ 118:
+ dict(
+ name='right_thumb3',
+ id=118,
+ color=[255, 128, 0],
+ type='',
+ swap='left_thumb3'),
+ 119:
+ dict(
+ name='right_thumb4',
+ id=119,
+ color=[255, 128, 0],
+ type='',
+ swap='left_thumb4'),
+ 120:
+ dict(
+ name='right_forefinger1',
+ id=120,
+ color=[255, 153, 255],
+ type='',
+ swap='left_forefinger1'),
+ 121:
+ dict(
+ name='right_forefinger2',
+ id=121,
+ color=[255, 153, 255],
+ type='',
+ swap='left_forefinger2'),
+ 122:
+ dict(
+ name='right_forefinger3',
+ id=122,
+ color=[255, 153, 255],
+ type='',
+ swap='left_forefinger3'),
+ 123:
+ dict(
+ name='right_forefinger4',
+ id=123,
+ color=[255, 153, 255],
+ type='',
+ swap='left_forefinger4'),
+ 124:
+ dict(
+ name='right_middle_finger1',
+ id=124,
+ color=[102, 178, 255],
+ type='',
+ swap='left_middle_finger1'),
+ 125:
+ dict(
+ name='right_middle_finger2',
+ id=125,
+ color=[102, 178, 255],
+ type='',
+ swap='left_middle_finger2'),
+ 126:
+ dict(
+ name='right_middle_finger3',
+ id=126,
+ color=[102, 178, 255],
+ type='',
+ swap='left_middle_finger3'),
+ 127:
+ dict(
+ name='right_middle_finger4',
+ id=127,
+ color=[102, 178, 255],
+ type='',
+ swap='left_middle_finger4'),
+ 128:
+ dict(
+ name='right_ring_finger1',
+ id=128,
+ color=[255, 51, 51],
+ type='',
+ swap='left_ring_finger1'),
+ 129:
+ dict(
+ name='right_ring_finger2',
+ id=129,
+ color=[255, 51, 51],
+ type='',
+ swap='left_ring_finger2'),
+ 130:
+ dict(
+ name='right_ring_finger3',
+ id=130,
+ color=[255, 51, 51],
+ type='',
+ swap='left_ring_finger3'),
+ 131:
+ dict(
+ name='right_ring_finger4',
+ id=131,
+ color=[255, 51, 51],
+ type='',
+ swap='left_ring_finger4'),
+ 132:
+ dict(
+ name='right_pinky_finger1',
+ id=132,
+ color=[0, 255, 0],
+ type='',
+ swap='left_pinky_finger1'),
+ 133:
+ dict(
+ name='right_pinky_finger2',
+ id=133,
+ color=[0, 255, 0],
+ type='',
+ swap='left_pinky_finger2'),
+ 134:
+ dict(
+ name='right_pinky_finger3',
+ id=134,
+ color=[0, 255, 0],
+ type='',
+ swap='left_pinky_finger3'),
+ 135:
+ dict(
+ name='right_pinky_finger4',
+ id=135,
+ color=[0, 255, 0],
+ type='',
+ swap='left_pinky_finger4')
+ },
+ skeleton_info={
+ 0:
+ dict(link=('left_ankle', 'left_knee'), id=0, color=[0, 255, 0]),
+ 1:
+ dict(link=('left_knee', 'left_hip'), id=1, color=[0, 255, 0]),
+ 2:
+ dict(link=('left_hip', 'hip'), id=2, color=[0, 255, 0]),
+ 3:
+ dict(link=('right_ankle', 'right_knee'), id=3, color=[255, 128, 0]),
+ 4:
+ dict(link=('right_knee', 'right_hip'), id=4, color=[255, 128, 0]),
+ 5:
+ dict(link=('right_hip', 'hip'), id=5, color=[255, 128, 0]),
+ 6:
+ dict(link=('head', 'neck'), id=6, color=[51, 153, 255]),
+ 7:
+ dict(link=('neck', 'hip'), id=7, color=[51, 153, 255]),
+ 8:
+ dict(link=('neck', 'left_shoulder'), id=8, color=[0, 255, 0]),
+ 9:
+ dict(link=('left_shoulder', 'left_elbow'), id=9, color=[0, 255, 0]),
+ 10:
+ dict(link=('left_elbow', 'left_wrist'), id=10, color=[0, 255, 0]),
+ 11:
+ dict(link=('neck', 'right_shoulder'), id=11, color=[255, 128, 0]),
+ 12:
+ dict(
+ link=('right_shoulder', 'right_elbow'), id=12, color=[255, 128,
+ 0]),
+ 13:
+ dict(link=('right_elbow', 'right_wrist'), id=13, color=[255, 128, 0]),
+ 14:
+ dict(link=('left_eye', 'right_eye'), id=14, color=[51, 153, 255]),
+ 15:
+ dict(link=('nose', 'left_eye'), id=15, color=[51, 153, 255]),
+ 16:
+ dict(link=('nose', 'right_eye'), id=16, color=[51, 153, 255]),
+ 17:
+ dict(link=('left_eye', 'left_ear'), id=17, color=[51, 153, 255]),
+ 18:
+ dict(link=('right_eye', 'right_ear'), id=18, color=[51, 153, 255]),
+ 19:
+ dict(link=('left_ear', 'left_shoulder'), id=19, color=[51, 153, 255]),
+ 20:
+ dict(
+ link=('right_ear', 'right_shoulder'), id=20, color=[51, 153, 255]),
+ 21:
+ dict(link=('left_ankle', 'left_big_toe'), id=21, color=[0, 255, 0]),
+ 22:
+ dict(link=('left_ankle', 'left_small_toe'), id=22, color=[0, 255, 0]),
+ 23:
+ dict(link=('left_ankle', 'left_heel'), id=23, color=[0, 255, 0]),
+ 24:
+ dict(
+ link=('right_ankle', 'right_big_toe'), id=24, color=[255, 128, 0]),
+ 25:
+ dict(
+ link=('right_ankle', 'right_small_toe'),
+ id=25,
+ color=[255, 128, 0]),
+ 26:
+ dict(link=('right_ankle', 'right_heel'), id=26, color=[255, 128, 0]),
+ 27:
+ dict(link=('left_wrist', 'left_thumb1'), id=27, color=[255, 128, 0]),
+ 28:
+ dict(link=('left_thumb1', 'left_thumb2'), id=28, color=[255, 128, 0]),
+ 29:
+ dict(link=('left_thumb2', 'left_thumb3'), id=29, color=[255, 128, 0]),
+ 30:
+ dict(link=('left_thumb3', 'left_thumb4'), id=30, color=[255, 128, 0]),
+ 31:
+ dict(
+ link=('left_wrist', 'left_forefinger1'),
+ id=31,
+ color=[255, 153, 255]),
+ 32:
+ dict(
+ link=('left_forefinger1', 'left_forefinger2'),
+ id=32,
+ color=[255, 153, 255]),
+ 33:
+ dict(
+ link=('left_forefinger2', 'left_forefinger3'),
+ id=33,
+ color=[255, 153, 255]),
+ 34:
+ dict(
+ link=('left_forefinger3', 'left_forefinger4'),
+ id=34,
+ color=[255, 153, 255]),
+ 35:
+ dict(
+ link=('left_wrist', 'left_middle_finger1'),
+ id=35,
+ color=[102, 178, 255]),
+ 36:
+ dict(
+ link=('left_middle_finger1', 'left_middle_finger2'),
+ id=36,
+ color=[102, 178, 255]),
+ 37:
+ dict(
+ link=('left_middle_finger2', 'left_middle_finger3'),
+ id=37,
+ color=[102, 178, 255]),
+ 38:
+ dict(
+ link=('left_middle_finger3', 'left_middle_finger4'),
+ id=38,
+ color=[102, 178, 255]),
+ 39:
+ dict(
+ link=('left_wrist', 'left_ring_finger1'),
+ id=39,
+ color=[255, 51, 51]),
+ 40:
+ dict(
+ link=('left_ring_finger1', 'left_ring_finger2'),
+ id=40,
+ color=[255, 51, 51]),
+ 41:
+ dict(
+ link=('left_ring_finger2', 'left_ring_finger3'),
+ id=41,
+ color=[255, 51, 51]),
+ 42:
+ dict(
+ link=('left_ring_finger3', 'left_ring_finger4'),
+ id=42,
+ color=[255, 51, 51]),
+ 43:
+ dict(
+ link=('left_wrist', 'left_pinky_finger1'),
+ id=43,
+ color=[0, 255, 0]),
+ 44:
+ dict(
+ link=('left_pinky_finger1', 'left_pinky_finger2'),
+ id=44,
+ color=[0, 255, 0]),
+ 45:
+ dict(
+ link=('left_pinky_finger2', 'left_pinky_finger3'),
+ id=45,
+ color=[0, 255, 0]),
+ 46:
+ dict(
+ link=('left_pinky_finger3', 'left_pinky_finger4'),
+ id=46,
+ color=[0, 255, 0]),
+ 47:
+ dict(link=('right_wrist', 'right_thumb1'), id=47, color=[255, 128, 0]),
+ 48:
+ dict(
+ link=('right_thumb1', 'right_thumb2'), id=48, color=[255, 128, 0]),
+ 49:
+ dict(
+ link=('right_thumb2', 'right_thumb3'), id=49, color=[255, 128, 0]),
+ 50:
+ dict(
+ link=('right_thumb3', 'right_thumb4'), id=50, color=[255, 128, 0]),
+ 51:
+ dict(
+ link=('right_wrist', 'right_forefinger1'),
+ id=51,
+ color=[255, 153, 255]),
+ 52:
+ dict(
+ link=('right_forefinger1', 'right_forefinger2'),
+ id=52,
+ color=[255, 153, 255]),
+ 53:
+ dict(
+ link=('right_forefinger2', 'right_forefinger3'),
+ id=53,
+ color=[255, 153, 255]),
+ 54:
+ dict(
+ link=('right_forefinger3', 'right_forefinger4'),
+ id=54,
+ color=[255, 153, 255]),
+ 55:
+ dict(
+ link=('right_wrist', 'right_middle_finger1'),
+ id=55,
+ color=[102, 178, 255]),
+ 56:
+ dict(
+ link=('right_middle_finger1', 'right_middle_finger2'),
+ id=56,
+ color=[102, 178, 255]),
+ 57:
+ dict(
+ link=('right_middle_finger2', 'right_middle_finger3'),
+ id=57,
+ color=[102, 178, 255]),
+ 58:
+ dict(
+ link=('right_middle_finger3', 'right_middle_finger4'),
+ id=58,
+ color=[102, 178, 255]),
+ 59:
+ dict(
+ link=('right_wrist', 'right_ring_finger1'),
+ id=59,
+ color=[255, 51, 51]),
+ 60:
+ dict(
+ link=('right_ring_finger1', 'right_ring_finger2'),
+ id=60,
+ color=[255, 51, 51]),
+ 61:
+ dict(
+ link=('right_ring_finger2', 'right_ring_finger3'),
+ id=61,
+ color=[255, 51, 51]),
+ 62:
+ dict(
+ link=('right_ring_finger3', 'right_ring_finger4'),
+ id=62,
+ color=[255, 51, 51]),
+ 63:
+ dict(
+ link=('right_wrist', 'right_pinky_finger1'),
+ id=63,
+ color=[0, 255, 0]),
+ 64:
+ dict(
+ link=('right_pinky_finger1', 'right_pinky_finger2'),
+ id=64,
+ color=[0, 255, 0]),
+ 65:
+ dict(
+ link=('right_pinky_finger2', 'right_pinky_finger3'),
+ id=65,
+ color=[0, 255, 0]),
+ 66:
+ dict(
+ link=('right_pinky_finger3', 'right_pinky_finger4'),
+ id=66,
+ color=[0, 255, 0])
+ },
+ joint_weights=[1.] * 136,
+
+ # 'https://github.com/Fang-Haoshu/Halpe-FullBody/blob/master/'
+ # 'HalpeCOCOAPI/PythonAPI/halpecocotools/cocoeval.py#L245'
+ sigmas=[
+ 0.026, 0.025, 0.025, 0.035, 0.035, 0.079, 0.079, 0.072, 0.072, 0.062,
+ 0.062, 0.107, 0.107, 0.087, 0.087, 0.089, 0.089, 0.08, 0.08, 0.08,
+ 0.089, 0.089, 0.089, 0.089, 0.089, 0.089, 0.015, 0.015, 0.015, 0.015,
+ 0.015, 0.015, 0.015, 0.015, 0.015, 0.015, 0.015, 0.015, 0.015, 0.015,
+ 0.015, 0.015, 0.015, 0.015, 0.015, 0.015, 0.015, 0.015, 0.015, 0.015,
+ 0.015, 0.015, 0.015, 0.015, 0.015, 0.015, 0.015, 0.015, 0.015, 0.015,
+ 0.015, 0.015, 0.015, 0.015, 0.015, 0.015, 0.015, 0.015, 0.015, 0.015,
+ 0.015, 0.015, 0.015, 0.015, 0.015, 0.015, 0.015, 0.015, 0.015, 0.015,
+ 0.015, 0.015, 0.015, 0.015, 0.015, 0.015, 0.015, 0.015, 0.015, 0.015,
+ 0.015, 0.015, 0.015, 0.015, 0.015, 0.015, 0.015, 0.015, 0.015, 0.015,
+ 0.015, 0.015, 0.015, 0.015, 0.015, 0.015, 0.015, 0.015, 0.015, 0.015,
+ 0.015, 0.015, 0.015, 0.015, 0.015, 0.015, 0.015, 0.015, 0.015, 0.015,
+ 0.015, 0.015, 0.015, 0.015, 0.015, 0.015, 0.015, 0.015, 0.015, 0.015,
+ 0.015, 0.015, 0.015, 0.015, 0.015, 0.015
+ ])
diff --git a/grounded-sam-osx/_base_/datasets/horse10.py b/grounded-sam-osx/_base_/datasets/horse10.py
new file mode 100644
index 0000000000000000000000000000000000000000..a485bf191bc151b0d76e48f3e55eb8e2dda6c506
--- /dev/null
+++ b/grounded-sam-osx/_base_/datasets/horse10.py
@@ -0,0 +1,201 @@
+dataset_info = dict(
+ dataset_name='horse10',
+ paper_info=dict(
+ author='Mathis, Alexander and Biasi, Thomas and '
+ 'Schneider, Steffen and '
+ 'Yuksekgonul, Mert and Rogers, Byron and '
+ 'Bethge, Matthias and '
+ 'Mathis, Mackenzie W',
+ title='Pretraining boosts out-of-domain robustness '
+ 'for pose estimation',
+ container='Proceedings of the IEEE/CVF Winter Conference on '
+ 'Applications of Computer Vision',
+ year='2021',
+ homepage='http://www.mackenziemathislab.org/horse10',
+ ),
+ keypoint_info={
+ 0:
+ dict(name='Nose', id=0, color=[255, 153, 255], type='upper', swap=''),
+ 1:
+ dict(name='Eye', id=1, color=[255, 153, 255], type='upper', swap=''),
+ 2:
+ dict(
+ name='Nearknee',
+ id=2,
+ color=[255, 102, 255],
+ type='upper',
+ swap=''),
+ 3:
+ dict(
+ name='Nearfrontfetlock',
+ id=3,
+ color=[255, 102, 255],
+ type='upper',
+ swap=''),
+ 4:
+ dict(
+ name='Nearfrontfoot',
+ id=4,
+ color=[255, 102, 255],
+ type='upper',
+ swap=''),
+ 5:
+ dict(
+ name='Offknee', id=5, color=[255, 102, 255], type='upper',
+ swap=''),
+ 6:
+ dict(
+ name='Offfrontfetlock',
+ id=6,
+ color=[255, 102, 255],
+ type='upper',
+ swap=''),
+ 7:
+ dict(
+ name='Offfrontfoot',
+ id=7,
+ color=[255, 102, 255],
+ type='upper',
+ swap=''),
+ 8:
+ dict(
+ name='Shoulder',
+ id=8,
+ color=[255, 153, 255],
+ type='upper',
+ swap=''),
+ 9:
+ dict(
+ name='Midshoulder',
+ id=9,
+ color=[255, 153, 255],
+ type='upper',
+ swap=''),
+ 10:
+ dict(
+ name='Elbow', id=10, color=[255, 153, 255], type='upper', swap=''),
+ 11:
+ dict(
+ name='Girth', id=11, color=[255, 153, 255], type='upper', swap=''),
+ 12:
+ dict(
+ name='Wither', id=12, color=[255, 153, 255], type='upper',
+ swap=''),
+ 13:
+ dict(
+ name='Nearhindhock',
+ id=13,
+ color=[255, 51, 255],
+ type='lower',
+ swap=''),
+ 14:
+ dict(
+ name='Nearhindfetlock',
+ id=14,
+ color=[255, 51, 255],
+ type='lower',
+ swap=''),
+ 15:
+ dict(
+ name='Nearhindfoot',
+ id=15,
+ color=[255, 51, 255],
+ type='lower',
+ swap=''),
+ 16:
+ dict(name='Hip', id=16, color=[255, 153, 255], type='lower', swap=''),
+ 17:
+ dict(
+ name='Stifle', id=17, color=[255, 153, 255], type='lower',
+ swap=''),
+ 18:
+ dict(
+ name='Offhindhock',
+ id=18,
+ color=[255, 51, 255],
+ type='lower',
+ swap=''),
+ 19:
+ dict(
+ name='Offhindfetlock',
+ id=19,
+ color=[255, 51, 255],
+ type='lower',
+ swap=''),
+ 20:
+ dict(
+ name='Offhindfoot',
+ id=20,
+ color=[255, 51, 255],
+ type='lower',
+ swap=''),
+ 21:
+ dict(
+ name='Ischium',
+ id=21,
+ color=[255, 153, 255],
+ type='lower',
+ swap='')
+ },
+ skeleton_info={
+ 0:
+ dict(link=('Nose', 'Eye'), id=0, color=[255, 153, 255]),
+ 1:
+ dict(link=('Eye', 'Wither'), id=1, color=[255, 153, 255]),
+ 2:
+ dict(link=('Wither', 'Hip'), id=2, color=[255, 153, 255]),
+ 3:
+ dict(link=('Hip', 'Ischium'), id=3, color=[255, 153, 255]),
+ 4:
+ dict(link=('Ischium', 'Stifle'), id=4, color=[255, 153, 255]),
+ 5:
+ dict(link=('Stifle', 'Girth'), id=5, color=[255, 153, 255]),
+ 6:
+ dict(link=('Girth', 'Elbow'), id=6, color=[255, 153, 255]),
+ 7:
+ dict(link=('Elbow', 'Shoulder'), id=7, color=[255, 153, 255]),
+ 8:
+ dict(link=('Shoulder', 'Midshoulder'), id=8, color=[255, 153, 255]),
+ 9:
+ dict(link=('Midshoulder', 'Wither'), id=9, color=[255, 153, 255]),
+ 10:
+ dict(
+ link=('Nearknee', 'Nearfrontfetlock'),
+ id=10,
+ color=[255, 102, 255]),
+ 11:
+ dict(
+ link=('Nearfrontfetlock', 'Nearfrontfoot'),
+ id=11,
+ color=[255, 102, 255]),
+ 12:
+ dict(
+ link=('Offknee', 'Offfrontfetlock'), id=12, color=[255, 102, 255]),
+ 13:
+ dict(
+ link=('Offfrontfetlock', 'Offfrontfoot'),
+ id=13,
+ color=[255, 102, 255]),
+ 14:
+ dict(
+ link=('Nearhindhock', 'Nearhindfetlock'),
+ id=14,
+ color=[255, 51, 255]),
+ 15:
+ dict(
+ link=('Nearhindfetlock', 'Nearhindfoot'),
+ id=15,
+ color=[255, 51, 255]),
+ 16:
+ dict(
+ link=('Offhindhock', 'Offhindfetlock'),
+ id=16,
+ color=[255, 51, 255]),
+ 17:
+ dict(
+ link=('Offhindfetlock', 'Offhindfoot'),
+ id=17,
+ color=[255, 51, 255])
+ },
+ joint_weights=[1.] * 22,
+ sigmas=[])
diff --git a/grounded-sam-osx/_base_/datasets/interhand2d.py b/grounded-sam-osx/_base_/datasets/interhand2d.py
new file mode 100644
index 0000000000000000000000000000000000000000..0134f07de5bf536eaffbf71155a7e6eb33b24f0a
--- /dev/null
+++ b/grounded-sam-osx/_base_/datasets/interhand2d.py
@@ -0,0 +1,142 @@
+dataset_info = dict(
+ dataset_name='interhand2d',
+ paper_info=dict(
+ author='Moon, Gyeongsik and Yu, Shoou-I and Wen, He and '
+ 'Shiratori, Takaaki and Lee, Kyoung Mu',
+ title='InterHand2.6M: A dataset and baseline for 3D '
+ 'interacting hand pose estimation from a single RGB image',
+ container='arXiv',
+ year='2020',
+ homepage='https://mks0601.github.io/InterHand2.6M/',
+ ),
+ keypoint_info={
+ 0:
+ dict(name='thumb4', id=0, color=[255, 128, 0], type='', swap=''),
+ 1:
+ dict(name='thumb3', id=1, color=[255, 128, 0], type='', swap=''),
+ 2:
+ dict(name='thumb2', id=2, color=[255, 128, 0], type='', swap=''),
+ 3:
+ dict(name='thumb1', id=3, color=[255, 128, 0], type='', swap=''),
+ 4:
+ dict(
+ name='forefinger4', id=4, color=[255, 153, 255], type='', swap=''),
+ 5:
+ dict(
+ name='forefinger3', id=5, color=[255, 153, 255], type='', swap=''),
+ 6:
+ dict(
+ name='forefinger2', id=6, color=[255, 153, 255], type='', swap=''),
+ 7:
+ dict(
+ name='forefinger1', id=7, color=[255, 153, 255], type='', swap=''),
+ 8:
+ dict(
+ name='middle_finger4',
+ id=8,
+ color=[102, 178, 255],
+ type='',
+ swap=''),
+ 9:
+ dict(
+ name='middle_finger3',
+ id=9,
+ color=[102, 178, 255],
+ type='',
+ swap=''),
+ 10:
+ dict(
+ name='middle_finger2',
+ id=10,
+ color=[102, 178, 255],
+ type='',
+ swap=''),
+ 11:
+ dict(
+ name='middle_finger1',
+ id=11,
+ color=[102, 178, 255],
+ type='',
+ swap=''),
+ 12:
+ dict(
+ name='ring_finger4', id=12, color=[255, 51, 51], type='', swap=''),
+ 13:
+ dict(
+ name='ring_finger3', id=13, color=[255, 51, 51], type='', swap=''),
+ 14:
+ dict(
+ name='ring_finger2', id=14, color=[255, 51, 51], type='', swap=''),
+ 15:
+ dict(
+ name='ring_finger1', id=15, color=[255, 51, 51], type='', swap=''),
+ 16:
+ dict(name='pinky_finger4', id=16, color=[0, 255, 0], type='', swap=''),
+ 17:
+ dict(name='pinky_finger3', id=17, color=[0, 255, 0], type='', swap=''),
+ 18:
+ dict(name='pinky_finger2', id=18, color=[0, 255, 0], type='', swap=''),
+ 19:
+ dict(name='pinky_finger1', id=19, color=[0, 255, 0], type='', swap=''),
+ 20:
+ dict(name='wrist', id=20, color=[255, 255, 255], type='', swap='')
+ },
+ skeleton_info={
+ 0:
+ dict(link=('wrist', 'thumb1'), id=0, color=[255, 128, 0]),
+ 1:
+ dict(link=('thumb1', 'thumb2'), id=1, color=[255, 128, 0]),
+ 2:
+ dict(link=('thumb2', 'thumb3'), id=2, color=[255, 128, 0]),
+ 3:
+ dict(link=('thumb3', 'thumb4'), id=3, color=[255, 128, 0]),
+ 4:
+ dict(link=('wrist', 'forefinger1'), id=4, color=[255, 153, 255]),
+ 5:
+ dict(link=('forefinger1', 'forefinger2'), id=5, color=[255, 153, 255]),
+ 6:
+ dict(link=('forefinger2', 'forefinger3'), id=6, color=[255, 153, 255]),
+ 7:
+ dict(link=('forefinger3', 'forefinger4'), id=7, color=[255, 153, 255]),
+ 8:
+ dict(link=('wrist', 'middle_finger1'), id=8, color=[102, 178, 255]),
+ 9:
+ dict(
+ link=('middle_finger1', 'middle_finger2'),
+ id=9,
+ color=[102, 178, 255]),
+ 10:
+ dict(
+ link=('middle_finger2', 'middle_finger3'),
+ id=10,
+ color=[102, 178, 255]),
+ 11:
+ dict(
+ link=('middle_finger3', 'middle_finger4'),
+ id=11,
+ color=[102, 178, 255]),
+ 12:
+ dict(link=('wrist', 'ring_finger1'), id=12, color=[255, 51, 51]),
+ 13:
+ dict(
+ link=('ring_finger1', 'ring_finger2'), id=13, color=[255, 51, 51]),
+ 14:
+ dict(
+ link=('ring_finger2', 'ring_finger3'), id=14, color=[255, 51, 51]),
+ 15:
+ dict(
+ link=('ring_finger3', 'ring_finger4'), id=15, color=[255, 51, 51]),
+ 16:
+ dict(link=('wrist', 'pinky_finger1'), id=16, color=[0, 255, 0]),
+ 17:
+ dict(
+ link=('pinky_finger1', 'pinky_finger2'), id=17, color=[0, 255, 0]),
+ 18:
+ dict(
+ link=('pinky_finger2', 'pinky_finger3'), id=18, color=[0, 255, 0]),
+ 19:
+ dict(
+ link=('pinky_finger3', 'pinky_finger4'), id=19, color=[0, 255, 0])
+ },
+ joint_weights=[1.] * 21,
+ sigmas=[])
diff --git a/grounded-sam-osx/_base_/datasets/interhand3d.py b/grounded-sam-osx/_base_/datasets/interhand3d.py
new file mode 100644
index 0000000000000000000000000000000000000000..e2bd8121c281c741ec9b980c7570ebef8a632993
--- /dev/null
+++ b/grounded-sam-osx/_base_/datasets/interhand3d.py
@@ -0,0 +1,487 @@
+dataset_info = dict(
+ dataset_name='interhand3d',
+ paper_info=dict(
+ author='Moon, Gyeongsik and Yu, Shoou-I and Wen, He and '
+ 'Shiratori, Takaaki and Lee, Kyoung Mu',
+ title='InterHand2.6M: A dataset and baseline for 3D '
+ 'interacting hand pose estimation from a single RGB image',
+ container='arXiv',
+ year='2020',
+ homepage='https://mks0601.github.io/InterHand2.6M/',
+ ),
+ keypoint_info={
+ 0:
+ dict(
+ name='right_thumb4',
+ id=0,
+ color=[255, 128, 0],
+ type='',
+ swap='left_thumb4'),
+ 1:
+ dict(
+ name='right_thumb3',
+ id=1,
+ color=[255, 128, 0],
+ type='',
+ swap='left_thumb3'),
+ 2:
+ dict(
+ name='right_thumb2',
+ id=2,
+ color=[255, 128, 0],
+ type='',
+ swap='left_thumb2'),
+ 3:
+ dict(
+ name='right_thumb1',
+ id=3,
+ color=[255, 128, 0],
+ type='',
+ swap='left_thumb1'),
+ 4:
+ dict(
+ name='right_forefinger4',
+ id=4,
+ color=[255, 153, 255],
+ type='',
+ swap='left_forefinger4'),
+ 5:
+ dict(
+ name='right_forefinger3',
+ id=5,
+ color=[255, 153, 255],
+ type='',
+ swap='left_forefinger3'),
+ 6:
+ dict(
+ name='right_forefinger2',
+ id=6,
+ color=[255, 153, 255],
+ type='',
+ swap='left_forefinger2'),
+ 7:
+ dict(
+ name='right_forefinger1',
+ id=7,
+ color=[255, 153, 255],
+ type='',
+ swap='left_forefinger1'),
+ 8:
+ dict(
+ name='right_middle_finger4',
+ id=8,
+ color=[102, 178, 255],
+ type='',
+ swap='left_middle_finger4'),
+ 9:
+ dict(
+ name='right_middle_finger3',
+ id=9,
+ color=[102, 178, 255],
+ type='',
+ swap='left_middle_finger3'),
+ 10:
+ dict(
+ name='right_middle_finger2',
+ id=10,
+ color=[102, 178, 255],
+ type='',
+ swap='left_middle_finger2'),
+ 11:
+ dict(
+ name='right_middle_finger1',
+ id=11,
+ color=[102, 178, 255],
+ type='',
+ swap='left_middle_finger1'),
+ 12:
+ dict(
+ name='right_ring_finger4',
+ id=12,
+ color=[255, 51, 51],
+ type='',
+ swap='left_ring_finger4'),
+ 13:
+ dict(
+ name='right_ring_finger3',
+ id=13,
+ color=[255, 51, 51],
+ type='',
+ swap='left_ring_finger3'),
+ 14:
+ dict(
+ name='right_ring_finger2',
+ id=14,
+ color=[255, 51, 51],
+ type='',
+ swap='left_ring_finger2'),
+ 15:
+ dict(
+ name='right_ring_finger1',
+ id=15,
+ color=[255, 51, 51],
+ type='',
+ swap='left_ring_finger1'),
+ 16:
+ dict(
+ name='right_pinky_finger4',
+ id=16,
+ color=[0, 255, 0],
+ type='',
+ swap='left_pinky_finger4'),
+ 17:
+ dict(
+ name='right_pinky_finger3',
+ id=17,
+ color=[0, 255, 0],
+ type='',
+ swap='left_pinky_finger3'),
+ 18:
+ dict(
+ name='right_pinky_finger2',
+ id=18,
+ color=[0, 255, 0],
+ type='',
+ swap='left_pinky_finger2'),
+ 19:
+ dict(
+ name='right_pinky_finger1',
+ id=19,
+ color=[0, 255, 0],
+ type='',
+ swap='left_pinky_finger1'),
+ 20:
+ dict(
+ name='right_wrist',
+ id=20,
+ color=[255, 255, 255],
+ type='',
+ swap='left_wrist'),
+ 21:
+ dict(
+ name='left_thumb4',
+ id=21,
+ color=[255, 128, 0],
+ type='',
+ swap='right_thumb4'),
+ 22:
+ dict(
+ name='left_thumb3',
+ id=22,
+ color=[255, 128, 0],
+ type='',
+ swap='right_thumb3'),
+ 23:
+ dict(
+ name='left_thumb2',
+ id=23,
+ color=[255, 128, 0],
+ type='',
+ swap='right_thumb2'),
+ 24:
+ dict(
+ name='left_thumb1',
+ id=24,
+ color=[255, 128, 0],
+ type='',
+ swap='right_thumb1'),
+ 25:
+ dict(
+ name='left_forefinger4',
+ id=25,
+ color=[255, 153, 255],
+ type='',
+ swap='right_forefinger4'),
+ 26:
+ dict(
+ name='left_forefinger3',
+ id=26,
+ color=[255, 153, 255],
+ type='',
+ swap='right_forefinger3'),
+ 27:
+ dict(
+ name='left_forefinger2',
+ id=27,
+ color=[255, 153, 255],
+ type='',
+ swap='right_forefinger2'),
+ 28:
+ dict(
+ name='left_forefinger1',
+ id=28,
+ color=[255, 153, 255],
+ type='',
+ swap='right_forefinger1'),
+ 29:
+ dict(
+ name='left_middle_finger4',
+ id=29,
+ color=[102, 178, 255],
+ type='',
+ swap='right_middle_finger4'),
+ 30:
+ dict(
+ name='left_middle_finger3',
+ id=30,
+ color=[102, 178, 255],
+ type='',
+ swap='right_middle_finger3'),
+ 31:
+ dict(
+ name='left_middle_finger2',
+ id=31,
+ color=[102, 178, 255],
+ type='',
+ swap='right_middle_finger2'),
+ 32:
+ dict(
+ name='left_middle_finger1',
+ id=32,
+ color=[102, 178, 255],
+ type='',
+ swap='right_middle_finger1'),
+ 33:
+ dict(
+ name='left_ring_finger4',
+ id=33,
+ color=[255, 51, 51],
+ type='',
+ swap='right_ring_finger4'),
+ 34:
+ dict(
+ name='left_ring_finger3',
+ id=34,
+ color=[255, 51, 51],
+ type='',
+ swap='right_ring_finger3'),
+ 35:
+ dict(
+ name='left_ring_finger2',
+ id=35,
+ color=[255, 51, 51],
+ type='',
+ swap='right_ring_finger2'),
+ 36:
+ dict(
+ name='left_ring_finger1',
+ id=36,
+ color=[255, 51, 51],
+ type='',
+ swap='right_ring_finger1'),
+ 37:
+ dict(
+ name='left_pinky_finger4',
+ id=37,
+ color=[0, 255, 0],
+ type='',
+ swap='right_pinky_finger4'),
+ 38:
+ dict(
+ name='left_pinky_finger3',
+ id=38,
+ color=[0, 255, 0],
+ type='',
+ swap='right_pinky_finger3'),
+ 39:
+ dict(
+ name='left_pinky_finger2',
+ id=39,
+ color=[0, 255, 0],
+ type='',
+ swap='right_pinky_finger2'),
+ 40:
+ dict(
+ name='left_pinky_finger1',
+ id=40,
+ color=[0, 255, 0],
+ type='',
+ swap='right_pinky_finger1'),
+ 41:
+ dict(
+ name='left_wrist',
+ id=41,
+ color=[255, 255, 255],
+ type='',
+ swap='right_wrist'),
+ },
+ skeleton_info={
+ 0:
+ dict(link=('right_wrist', 'right_thumb1'), id=0, color=[255, 128, 0]),
+ 1:
+ dict(link=('right_thumb1', 'right_thumb2'), id=1, color=[255, 128, 0]),
+ 2:
+ dict(link=('right_thumb2', 'right_thumb3'), id=2, color=[255, 128, 0]),
+ 3:
+ dict(link=('right_thumb3', 'right_thumb4'), id=3, color=[255, 128, 0]),
+ 4:
+ dict(
+ link=('right_wrist', 'right_forefinger1'),
+ id=4,
+ color=[255, 153, 255]),
+ 5:
+ dict(
+ link=('right_forefinger1', 'right_forefinger2'),
+ id=5,
+ color=[255, 153, 255]),
+ 6:
+ dict(
+ link=('right_forefinger2', 'right_forefinger3'),
+ id=6,
+ color=[255, 153, 255]),
+ 7:
+ dict(
+ link=('right_forefinger3', 'right_forefinger4'),
+ id=7,
+ color=[255, 153, 255]),
+ 8:
+ dict(
+ link=('right_wrist', 'right_middle_finger1'),
+ id=8,
+ color=[102, 178, 255]),
+ 9:
+ dict(
+ link=('right_middle_finger1', 'right_middle_finger2'),
+ id=9,
+ color=[102, 178, 255]),
+ 10:
+ dict(
+ link=('right_middle_finger2', 'right_middle_finger3'),
+ id=10,
+ color=[102, 178, 255]),
+ 11:
+ dict(
+ link=('right_middle_finger3', 'right_middle_finger4'),
+ id=11,
+ color=[102, 178, 255]),
+ 12:
+ dict(
+ link=('right_wrist', 'right_ring_finger1'),
+ id=12,
+ color=[255, 51, 51]),
+ 13:
+ dict(
+ link=('right_ring_finger1', 'right_ring_finger2'),
+ id=13,
+ color=[255, 51, 51]),
+ 14:
+ dict(
+ link=('right_ring_finger2', 'right_ring_finger3'),
+ id=14,
+ color=[255, 51, 51]),
+ 15:
+ dict(
+ link=('right_ring_finger3', 'right_ring_finger4'),
+ id=15,
+ color=[255, 51, 51]),
+ 16:
+ dict(
+ link=('right_wrist', 'right_pinky_finger1'),
+ id=16,
+ color=[0, 255, 0]),
+ 17:
+ dict(
+ link=('right_pinky_finger1', 'right_pinky_finger2'),
+ id=17,
+ color=[0, 255, 0]),
+ 18:
+ dict(
+ link=('right_pinky_finger2', 'right_pinky_finger3'),
+ id=18,
+ color=[0, 255, 0]),
+ 19:
+ dict(
+ link=('right_pinky_finger3', 'right_pinky_finger4'),
+ id=19,
+ color=[0, 255, 0]),
+ 20:
+ dict(link=('left_wrist', 'left_thumb1'), id=20, color=[255, 128, 0]),
+ 21:
+ dict(link=('left_thumb1', 'left_thumb2'), id=21, color=[255, 128, 0]),
+ 22:
+ dict(link=('left_thumb2', 'left_thumb3'), id=22, color=[255, 128, 0]),
+ 23:
+ dict(link=('left_thumb3', 'left_thumb4'), id=23, color=[255, 128, 0]),
+ 24:
+ dict(
+ link=('left_wrist', 'left_forefinger1'),
+ id=24,
+ color=[255, 153, 255]),
+ 25:
+ dict(
+ link=('left_forefinger1', 'left_forefinger2'),
+ id=25,
+ color=[255, 153, 255]),
+ 26:
+ dict(
+ link=('left_forefinger2', 'left_forefinger3'),
+ id=26,
+ color=[255, 153, 255]),
+ 27:
+ dict(
+ link=('left_forefinger3', 'left_forefinger4'),
+ id=27,
+ color=[255, 153, 255]),
+ 28:
+ dict(
+ link=('left_wrist', 'left_middle_finger1'),
+ id=28,
+ color=[102, 178, 255]),
+ 29:
+ dict(
+ link=('left_middle_finger1', 'left_middle_finger2'),
+ id=29,
+ color=[102, 178, 255]),
+ 30:
+ dict(
+ link=('left_middle_finger2', 'left_middle_finger3'),
+ id=30,
+ color=[102, 178, 255]),
+ 31:
+ dict(
+ link=('left_middle_finger3', 'left_middle_finger4'),
+ id=31,
+ color=[102, 178, 255]),
+ 32:
+ dict(
+ link=('left_wrist', 'left_ring_finger1'),
+ id=32,
+ color=[255, 51, 51]),
+ 33:
+ dict(
+ link=('left_ring_finger1', 'left_ring_finger2'),
+ id=33,
+ color=[255, 51, 51]),
+ 34:
+ dict(
+ link=('left_ring_finger2', 'left_ring_finger3'),
+ id=34,
+ color=[255, 51, 51]),
+ 35:
+ dict(
+ link=('left_ring_finger3', 'left_ring_finger4'),
+ id=35,
+ color=[255, 51, 51]),
+ 36:
+ dict(
+ link=('left_wrist', 'left_pinky_finger1'),
+ id=36,
+ color=[0, 255, 0]),
+ 37:
+ dict(
+ link=('left_pinky_finger1', 'left_pinky_finger2'),
+ id=37,
+ color=[0, 255, 0]),
+ 38:
+ dict(
+ link=('left_pinky_finger2', 'left_pinky_finger3'),
+ id=38,
+ color=[0, 255, 0]),
+ 39:
+ dict(
+ link=('left_pinky_finger3', 'left_pinky_finger4'),
+ id=39,
+ color=[0, 255, 0]),
+ },
+ joint_weights=[1.] * 42,
+ sigmas=[])
diff --git a/grounded-sam-osx/_base_/datasets/jhmdb.py b/grounded-sam-osx/_base_/datasets/jhmdb.py
new file mode 100644
index 0000000000000000000000000000000000000000..1b37488498a2bade1fa6f2ff6532fcd219071803
--- /dev/null
+++ b/grounded-sam-osx/_base_/datasets/jhmdb.py
@@ -0,0 +1,129 @@
+dataset_info = dict(
+ dataset_name='jhmdb',
+ paper_info=dict(
+ author='H. Jhuang and J. Gall and S. Zuffi and '
+ 'C. Schmid and M. J. Black',
+ title='Towards understanding action recognition',
+ container='International Conf. on Computer Vision (ICCV)',
+ year='2013',
+ homepage='http://jhmdb.is.tue.mpg.de/dataset',
+ ),
+ keypoint_info={
+ 0:
+ dict(name='neck', id=0, color=[255, 128, 0], type='upper', swap=''),
+ 1:
+ dict(name='belly', id=1, color=[255, 128, 0], type='upper', swap=''),
+ 2:
+ dict(name='head', id=2, color=[255, 128, 0], type='upper', swap=''),
+ 3:
+ dict(
+ name='right_shoulder',
+ id=3,
+ color=[0, 255, 0],
+ type='upper',
+ swap='left_shoulder'),
+ 4:
+ dict(
+ name='left_shoulder',
+ id=4,
+ color=[0, 255, 0],
+ type='upper',
+ swap='right_shoulder'),
+ 5:
+ dict(
+ name='right_hip',
+ id=5,
+ color=[0, 255, 0],
+ type='lower',
+ swap='left_hip'),
+ 6:
+ dict(
+ name='left_hip',
+ id=6,
+ color=[51, 153, 255],
+ type='lower',
+ swap='right_hip'),
+ 7:
+ dict(
+ name='right_elbow',
+ id=7,
+ color=[51, 153, 255],
+ type='upper',
+ swap='left_elbow'),
+ 8:
+ dict(
+ name='left_elbow',
+ id=8,
+ color=[51, 153, 255],
+ type='upper',
+ swap='right_elbow'),
+ 9:
+ dict(
+ name='right_knee',
+ id=9,
+ color=[51, 153, 255],
+ type='lower',
+ swap='left_knee'),
+ 10:
+ dict(
+ name='left_knee',
+ id=10,
+ color=[255, 128, 0],
+ type='lower',
+ swap='right_knee'),
+ 11:
+ dict(
+ name='right_wrist',
+ id=11,
+ color=[255, 128, 0],
+ type='upper',
+ swap='left_wrist'),
+ 12:
+ dict(
+ name='left_wrist',
+ id=12,
+ color=[255, 128, 0],
+ type='upper',
+ swap='right_wrist'),
+ 13:
+ dict(
+ name='right_ankle',
+ id=13,
+ color=[0, 255, 0],
+ type='lower',
+ swap='left_ankle'),
+ 14:
+ dict(
+ name='left_ankle',
+ id=14,
+ color=[0, 255, 0],
+ type='lower',
+ swap='right_ankle')
+ },
+ skeleton_info={
+ 0: dict(link=('right_ankle', 'right_knee'), id=0, color=[255, 128, 0]),
+ 1: dict(link=('right_knee', 'right_hip'), id=1, color=[255, 128, 0]),
+ 2: dict(link=('right_hip', 'belly'), id=2, color=[255, 128, 0]),
+ 3: dict(link=('belly', 'left_hip'), id=3, color=[0, 255, 0]),
+ 4: dict(link=('left_hip', 'left_knee'), id=4, color=[0, 255, 0]),
+ 5: dict(link=('left_knee', 'left_ankle'), id=5, color=[0, 255, 0]),
+ 6: dict(link=('belly', 'neck'), id=6, color=[51, 153, 255]),
+ 7: dict(link=('neck', 'head'), id=7, color=[51, 153, 255]),
+ 8: dict(link=('neck', 'right_shoulder'), id=8, color=[255, 128, 0]),
+ 9: dict(
+ link=('right_shoulder', 'right_elbow'), id=9, color=[255, 128, 0]),
+ 10:
+ dict(link=('right_elbow', 'right_wrist'), id=10, color=[255, 128, 0]),
+ 11: dict(link=('neck', 'left_shoulder'), id=11, color=[0, 255, 0]),
+ 12:
+ dict(link=('left_shoulder', 'left_elbow'), id=12, color=[0, 255, 0]),
+ 13: dict(link=('left_elbow', 'left_wrist'), id=13, color=[0, 255, 0])
+ },
+ joint_weights=[
+ 1., 1., 1., 1., 1., 1., 1., 1.2, 1.2, 1.2, 1.2, 1.5, 1.5, 1.5, 1.5
+ ],
+ # Adapted from COCO dataset.
+ sigmas=[
+ 0.025, 0.107, 0.025, 0.079, 0.079, 0.107, 0.107, 0.072, 0.072, 0.087,
+ 0.087, 0.062, 0.062, 0.089, 0.089
+ ])
diff --git a/grounded-sam-osx/_base_/datasets/locust.py b/grounded-sam-osx/_base_/datasets/locust.py
new file mode 100644
index 0000000000000000000000000000000000000000..db3fa15aa060b5806faae7a21f65460f77be2745
--- /dev/null
+++ b/grounded-sam-osx/_base_/datasets/locust.py
@@ -0,0 +1,263 @@
+dataset_info = dict(
+ dataset_name='locust',
+ paper_info=dict(
+ author='Graving, Jacob M and Chae, Daniel and Naik, Hemal and '
+ 'Li, Liang and Koger, Benjamin and Costelloe, Blair R and '
+ 'Couzin, Iain D',
+ title='DeepPoseKit, a software toolkit for fast and robust '
+ 'animal pose estimation using deep learning',
+ container='Elife',
+ year='2019',
+ homepage='https://github.com/jgraving/DeepPoseKit-Data',
+ ),
+ keypoint_info={
+ 0:
+ dict(name='head', id=0, color=[255, 255, 255], type='', swap=''),
+ 1:
+ dict(name='neck', id=1, color=[255, 255, 255], type='', swap=''),
+ 2:
+ dict(name='thorax', id=2, color=[255, 255, 255], type='', swap=''),
+ 3:
+ dict(name='abdomen1', id=3, color=[255, 255, 255], type='', swap=''),
+ 4:
+ dict(name='abdomen2', id=4, color=[255, 255, 255], type='', swap=''),
+ 5:
+ dict(
+ name='anttipL',
+ id=5,
+ color=[255, 255, 255],
+ type='',
+ swap='anttipR'),
+ 6:
+ dict(
+ name='antbaseL',
+ id=6,
+ color=[255, 255, 255],
+ type='',
+ swap='antbaseR'),
+ 7:
+ dict(name='eyeL', id=7, color=[255, 255, 255], type='', swap='eyeR'),
+ 8:
+ dict(
+ name='forelegL1',
+ id=8,
+ color=[255, 255, 255],
+ type='',
+ swap='forelegR1'),
+ 9:
+ dict(
+ name='forelegL2',
+ id=9,
+ color=[255, 255, 255],
+ type='',
+ swap='forelegR2'),
+ 10:
+ dict(
+ name='forelegL3',
+ id=10,
+ color=[255, 255, 255],
+ type='',
+ swap='forelegR3'),
+ 11:
+ dict(
+ name='forelegL4',
+ id=11,
+ color=[255, 255, 255],
+ type='',
+ swap='forelegR4'),
+ 12:
+ dict(
+ name='midlegL1',
+ id=12,
+ color=[255, 255, 255],
+ type='',
+ swap='midlegR1'),
+ 13:
+ dict(
+ name='midlegL2',
+ id=13,
+ color=[255, 255, 255],
+ type='',
+ swap='midlegR2'),
+ 14:
+ dict(
+ name='midlegL3',
+ id=14,
+ color=[255, 255, 255],
+ type='',
+ swap='midlegR3'),
+ 15:
+ dict(
+ name='midlegL4',
+ id=15,
+ color=[255, 255, 255],
+ type='',
+ swap='midlegR4'),
+ 16:
+ dict(
+ name='hindlegL1',
+ id=16,
+ color=[255, 255, 255],
+ type='',
+ swap='hindlegR1'),
+ 17:
+ dict(
+ name='hindlegL2',
+ id=17,
+ color=[255, 255, 255],
+ type='',
+ swap='hindlegR2'),
+ 18:
+ dict(
+ name='hindlegL3',
+ id=18,
+ color=[255, 255, 255],
+ type='',
+ swap='hindlegR3'),
+ 19:
+ dict(
+ name='hindlegL4',
+ id=19,
+ color=[255, 255, 255],
+ type='',
+ swap='hindlegR4'),
+ 20:
+ dict(
+ name='anttipR',
+ id=20,
+ color=[255, 255, 255],
+ type='',
+ swap='anttipL'),
+ 21:
+ dict(
+ name='antbaseR',
+ id=21,
+ color=[255, 255, 255],
+ type='',
+ swap='antbaseL'),
+ 22:
+ dict(name='eyeR', id=22, color=[255, 255, 255], type='', swap='eyeL'),
+ 23:
+ dict(
+ name='forelegR1',
+ id=23,
+ color=[255, 255, 255],
+ type='',
+ swap='forelegL1'),
+ 24:
+ dict(
+ name='forelegR2',
+ id=24,
+ color=[255, 255, 255],
+ type='',
+ swap='forelegL2'),
+ 25:
+ dict(
+ name='forelegR3',
+ id=25,
+ color=[255, 255, 255],
+ type='',
+ swap='forelegL3'),
+ 26:
+ dict(
+ name='forelegR4',
+ id=26,
+ color=[255, 255, 255],
+ type='',
+ swap='forelegL4'),
+ 27:
+ dict(
+ name='midlegR1',
+ id=27,
+ color=[255, 255, 255],
+ type='',
+ swap='midlegL1'),
+ 28:
+ dict(
+ name='midlegR2',
+ id=28,
+ color=[255, 255, 255],
+ type='',
+ swap='midlegL2'),
+ 29:
+ dict(
+ name='midlegR3',
+ id=29,
+ color=[255, 255, 255],
+ type='',
+ swap='midlegL3'),
+ 30:
+ dict(
+ name='midlegR4',
+ id=30,
+ color=[255, 255, 255],
+ type='',
+ swap='midlegL4'),
+ 31:
+ dict(
+ name='hindlegR1',
+ id=31,
+ color=[255, 255, 255],
+ type='',
+ swap='hindlegL1'),
+ 32:
+ dict(
+ name='hindlegR2',
+ id=32,
+ color=[255, 255, 255],
+ type='',
+ swap='hindlegL2'),
+ 33:
+ dict(
+ name='hindlegR3',
+ id=33,
+ color=[255, 255, 255],
+ type='',
+ swap='hindlegL3'),
+ 34:
+ dict(
+ name='hindlegR4',
+ id=34,
+ color=[255, 255, 255],
+ type='',
+ swap='hindlegL4')
+ },
+ skeleton_info={
+ 0: dict(link=('neck', 'head'), id=0, color=[255, 255, 255]),
+ 1: dict(link=('thorax', 'neck'), id=1, color=[255, 255, 255]),
+ 2: dict(link=('abdomen1', 'thorax'), id=2, color=[255, 255, 255]),
+ 3: dict(link=('abdomen2', 'abdomen1'), id=3, color=[255, 255, 255]),
+ 4: dict(link=('antbaseL', 'anttipL'), id=4, color=[255, 255, 255]),
+ 5: dict(link=('eyeL', 'antbaseL'), id=5, color=[255, 255, 255]),
+ 6: dict(link=('forelegL2', 'forelegL1'), id=6, color=[255, 255, 255]),
+ 7: dict(link=('forelegL3', 'forelegL2'), id=7, color=[255, 255, 255]),
+ 8: dict(link=('forelegL4', 'forelegL3'), id=8, color=[255, 255, 255]),
+ 9: dict(link=('midlegL2', 'midlegL1'), id=9, color=[255, 255, 255]),
+ 10: dict(link=('midlegL3', 'midlegL2'), id=10, color=[255, 255, 255]),
+ 11: dict(link=('midlegL4', 'midlegL3'), id=11, color=[255, 255, 255]),
+ 12:
+ dict(link=('hindlegL2', 'hindlegL1'), id=12, color=[255, 255, 255]),
+ 13:
+ dict(link=('hindlegL3', 'hindlegL2'), id=13, color=[255, 255, 255]),
+ 14:
+ dict(link=('hindlegL4', 'hindlegL3'), id=14, color=[255, 255, 255]),
+ 15: dict(link=('antbaseR', 'anttipR'), id=15, color=[255, 255, 255]),
+ 16: dict(link=('eyeR', 'antbaseR'), id=16, color=[255, 255, 255]),
+ 17:
+ dict(link=('forelegR2', 'forelegR1'), id=17, color=[255, 255, 255]),
+ 18:
+ dict(link=('forelegR3', 'forelegR2'), id=18, color=[255, 255, 255]),
+ 19:
+ dict(link=('forelegR4', 'forelegR3'), id=19, color=[255, 255, 255]),
+ 20: dict(link=('midlegR2', 'midlegR1'), id=20, color=[255, 255, 255]),
+ 21: dict(link=('midlegR3', 'midlegR2'), id=21, color=[255, 255, 255]),
+ 22: dict(link=('midlegR4', 'midlegR3'), id=22, color=[255, 255, 255]),
+ 23:
+ dict(link=('hindlegR2', 'hindlegR1'), id=23, color=[255, 255, 255]),
+ 24:
+ dict(link=('hindlegR3', 'hindlegR2'), id=24, color=[255, 255, 255]),
+ 25:
+ dict(link=('hindlegR4', 'hindlegR3'), id=25, color=[255, 255, 255])
+ },
+ joint_weights=[1.] * 35,
+ sigmas=[])
diff --git a/grounded-sam-osx/_base_/datasets/macaque.py b/grounded-sam-osx/_base_/datasets/macaque.py
new file mode 100644
index 0000000000000000000000000000000000000000..ea8dac297ea2f0e36dabccccc021d953216a6ac8
--- /dev/null
+++ b/grounded-sam-osx/_base_/datasets/macaque.py
@@ -0,0 +1,183 @@
+dataset_info = dict(
+ dataset_name='macaque',
+ paper_info=dict(
+ author='Labuguen, Rollyn and Matsumoto, Jumpei and '
+ 'Negrete, Salvador and Nishimaru, Hiroshi and '
+ 'Nishijo, Hisao and Takada, Masahiko and '
+ 'Go, Yasuhiro and Inoue, Ken-ichi and Shibata, Tomohiro',
+ title='MacaquePose: A novel "in the wild" macaque monkey pose dataset '
+ 'for markerless motion capture',
+ container='bioRxiv',
+ year='2020',
+ homepage='http://www.pri.kyoto-u.ac.jp/datasets/'
+ 'macaquepose/index.html',
+ ),
+ keypoint_info={
+ 0:
+ dict(name='nose', id=0, color=[51, 153, 255], type='upper', swap=''),
+ 1:
+ dict(
+ name='left_eye',
+ id=1,
+ color=[51, 153, 255],
+ type='upper',
+ swap='right_eye'),
+ 2:
+ dict(
+ name='right_eye',
+ id=2,
+ color=[51, 153, 255],
+ type='upper',
+ swap='left_eye'),
+ 3:
+ dict(
+ name='left_ear',
+ id=3,
+ color=[51, 153, 255],
+ type='upper',
+ swap='right_ear'),
+ 4:
+ dict(
+ name='right_ear',
+ id=4,
+ color=[51, 153, 255],
+ type='upper',
+ swap='left_ear'),
+ 5:
+ dict(
+ name='left_shoulder',
+ id=5,
+ color=[0, 255, 0],
+ type='upper',
+ swap='right_shoulder'),
+ 6:
+ dict(
+ name='right_shoulder',
+ id=6,
+ color=[255, 128, 0],
+ type='upper',
+ swap='left_shoulder'),
+ 7:
+ dict(
+ name='left_elbow',
+ id=7,
+ color=[0, 255, 0],
+ type='upper',
+ swap='right_elbow'),
+ 8:
+ dict(
+ name='right_elbow',
+ id=8,
+ color=[255, 128, 0],
+ type='upper',
+ swap='left_elbow'),
+ 9:
+ dict(
+ name='left_wrist',
+ id=9,
+ color=[0, 255, 0],
+ type='upper',
+ swap='right_wrist'),
+ 10:
+ dict(
+ name='right_wrist',
+ id=10,
+ color=[255, 128, 0],
+ type='upper',
+ swap='left_wrist'),
+ 11:
+ dict(
+ name='left_hip',
+ id=11,
+ color=[0, 255, 0],
+ type='lower',
+ swap='right_hip'),
+ 12:
+ dict(
+ name='right_hip',
+ id=12,
+ color=[255, 128, 0],
+ type='lower',
+ swap='left_hip'),
+ 13:
+ dict(
+ name='left_knee',
+ id=13,
+ color=[0, 255, 0],
+ type='lower',
+ swap='right_knee'),
+ 14:
+ dict(
+ name='right_knee',
+ id=14,
+ color=[255, 128, 0],
+ type='lower',
+ swap='left_knee'),
+ 15:
+ dict(
+ name='left_ankle',
+ id=15,
+ color=[0, 255, 0],
+ type='lower',
+ swap='right_ankle'),
+ 16:
+ dict(
+ name='right_ankle',
+ id=16,
+ color=[255, 128, 0],
+ type='lower',
+ swap='left_ankle')
+ },
+ skeleton_info={
+ 0:
+ dict(link=('left_ankle', 'left_knee'), id=0, color=[0, 255, 0]),
+ 1:
+ dict(link=('left_knee', 'left_hip'), id=1, color=[0, 255, 0]),
+ 2:
+ dict(link=('right_ankle', 'right_knee'), id=2, color=[255, 128, 0]),
+ 3:
+ dict(link=('right_knee', 'right_hip'), id=3, color=[255, 128, 0]),
+ 4:
+ dict(link=('left_hip', 'right_hip'), id=4, color=[51, 153, 255]),
+ 5:
+ dict(link=('left_shoulder', 'left_hip'), id=5, color=[51, 153, 255]),
+ 6:
+ dict(link=('right_shoulder', 'right_hip'), id=6, color=[51, 153, 255]),
+ 7:
+ dict(
+ link=('left_shoulder', 'right_shoulder'),
+ id=7,
+ color=[51, 153, 255]),
+ 8:
+ dict(link=('left_shoulder', 'left_elbow'), id=8, color=[0, 255, 0]),
+ 9:
+ dict(
+ link=('right_shoulder', 'right_elbow'), id=9, color=[255, 128, 0]),
+ 10:
+ dict(link=('left_elbow', 'left_wrist'), id=10, color=[0, 255, 0]),
+ 11:
+ dict(link=('right_elbow', 'right_wrist'), id=11, color=[255, 128, 0]),
+ 12:
+ dict(link=('left_eye', 'right_eye'), id=12, color=[51, 153, 255]),
+ 13:
+ dict(link=('nose', 'left_eye'), id=13, color=[51, 153, 255]),
+ 14:
+ dict(link=('nose', 'right_eye'), id=14, color=[51, 153, 255]),
+ 15:
+ dict(link=('left_eye', 'left_ear'), id=15, color=[51, 153, 255]),
+ 16:
+ dict(link=('right_eye', 'right_ear'), id=16, color=[51, 153, 255]),
+ 17:
+ dict(link=('left_ear', 'left_shoulder'), id=17, color=[51, 153, 255]),
+ 18:
+ dict(
+ link=('right_ear', 'right_shoulder'), id=18, color=[51, 153, 255])
+ },
+ joint_weights=[
+ 1., 1., 1., 1., 1., 1., 1., 1.2, 1.2, 1.5, 1.5, 1., 1., 1.2, 1.2, 1.5,
+ 1.5
+ ],
+ sigmas=[
+ 0.026, 0.025, 0.025, 0.035, 0.035, 0.079, 0.079, 0.072, 0.072, 0.062,
+ 0.062, 0.107, 0.107, 0.087, 0.087, 0.089, 0.089
+ ])
diff --git a/grounded-sam-osx/_base_/datasets/mhp.py b/grounded-sam-osx/_base_/datasets/mhp.py
new file mode 100644
index 0000000000000000000000000000000000000000..e16e37c79cb63c4352c48bb4e45602b8408f534b
--- /dev/null
+++ b/grounded-sam-osx/_base_/datasets/mhp.py
@@ -0,0 +1,156 @@
+dataset_info = dict(
+ dataset_name='mhp',
+ paper_info=dict(
+ author='Zhao, Jian and Li, Jianshu and Cheng, Yu and '
+ 'Sim, Terence and Yan, Shuicheng and Feng, Jiashi',
+ title='Understanding humans in crowded scenes: '
+ 'Deep nested adversarial learning and a '
+ 'new benchmark for multi-human parsing',
+ container='Proceedings of the 26th ACM '
+ 'international conference on Multimedia',
+ year='2018',
+ homepage='https://lv-mhp.github.io/dataset',
+ ),
+ keypoint_info={
+ 0:
+ dict(
+ name='right_ankle',
+ id=0,
+ color=[255, 128, 0],
+ type='lower',
+ swap='left_ankle'),
+ 1:
+ dict(
+ name='right_knee',
+ id=1,
+ color=[255, 128, 0],
+ type='lower',
+ swap='left_knee'),
+ 2:
+ dict(
+ name='right_hip',
+ id=2,
+ color=[255, 128, 0],
+ type='lower',
+ swap='left_hip'),
+ 3:
+ dict(
+ name='left_hip',
+ id=3,
+ color=[0, 255, 0],
+ type='lower',
+ swap='right_hip'),
+ 4:
+ dict(
+ name='left_knee',
+ id=4,
+ color=[0, 255, 0],
+ type='lower',
+ swap='right_knee'),
+ 5:
+ dict(
+ name='left_ankle',
+ id=5,
+ color=[0, 255, 0],
+ type='lower',
+ swap='right_ankle'),
+ 6:
+ dict(name='pelvis', id=6, color=[51, 153, 255], type='lower', swap=''),
+ 7:
+ dict(name='thorax', id=7, color=[51, 153, 255], type='upper', swap=''),
+ 8:
+ dict(
+ name='upper_neck',
+ id=8,
+ color=[51, 153, 255],
+ type='upper',
+ swap=''),
+ 9:
+ dict(
+ name='head_top', id=9, color=[51, 153, 255], type='upper',
+ swap=''),
+ 10:
+ dict(
+ name='right_wrist',
+ id=10,
+ color=[255, 128, 0],
+ type='upper',
+ swap='left_wrist'),
+ 11:
+ dict(
+ name='right_elbow',
+ id=11,
+ color=[255, 128, 0],
+ type='upper',
+ swap='left_elbow'),
+ 12:
+ dict(
+ name='right_shoulder',
+ id=12,
+ color=[255, 128, 0],
+ type='upper',
+ swap='left_shoulder'),
+ 13:
+ dict(
+ name='left_shoulder',
+ id=13,
+ color=[0, 255, 0],
+ type='upper',
+ swap='right_shoulder'),
+ 14:
+ dict(
+ name='left_elbow',
+ id=14,
+ color=[0, 255, 0],
+ type='upper',
+ swap='right_elbow'),
+ 15:
+ dict(
+ name='left_wrist',
+ id=15,
+ color=[0, 255, 0],
+ type='upper',
+ swap='right_wrist')
+ },
+ skeleton_info={
+ 0:
+ dict(link=('right_ankle', 'right_knee'), id=0, color=[255, 128, 0]),
+ 1:
+ dict(link=('right_knee', 'right_hip'), id=1, color=[255, 128, 0]),
+ 2:
+ dict(link=('right_hip', 'pelvis'), id=2, color=[255, 128, 0]),
+ 3:
+ dict(link=('pelvis', 'left_hip'), id=3, color=[0, 255, 0]),
+ 4:
+ dict(link=('left_hip', 'left_knee'), id=4, color=[0, 255, 0]),
+ 5:
+ dict(link=('left_knee', 'left_ankle'), id=5, color=[0, 255, 0]),
+ 6:
+ dict(link=('pelvis', 'thorax'), id=6, color=[51, 153, 255]),
+ 7:
+ dict(link=('thorax', 'upper_neck'), id=7, color=[51, 153, 255]),
+ 8:
+ dict(link=('upper_neck', 'head_top'), id=8, color=[51, 153, 255]),
+ 9:
+ dict(link=('upper_neck', 'right_shoulder'), id=9, color=[255, 128, 0]),
+ 10:
+ dict(
+ link=('right_shoulder', 'right_elbow'), id=10, color=[255, 128,
+ 0]),
+ 11:
+ dict(link=('right_elbow', 'right_wrist'), id=11, color=[255, 128, 0]),
+ 12:
+ dict(link=('upper_neck', 'left_shoulder'), id=12, color=[0, 255, 0]),
+ 13:
+ dict(link=('left_shoulder', 'left_elbow'), id=13, color=[0, 255, 0]),
+ 14:
+ dict(link=('left_elbow', 'left_wrist'), id=14, color=[0, 255, 0])
+ },
+ joint_weights=[
+ 1.5, 1.2, 1., 1., 1.2, 1.5, 1., 1., 1., 1., 1.5, 1.2, 1., 1., 1.2, 1.5
+ ],
+ # Adapted from COCO dataset.
+ sigmas=[
+ 0.089, 0.083, 0.107, 0.107, 0.083, 0.089, 0.026, 0.026, 0.026, 0.026,
+ 0.062, 0.072, 0.179, 0.179, 0.072, 0.062
+ ])
diff --git a/grounded-sam-osx/_base_/datasets/mpi_inf_3dhp.py b/grounded-sam-osx/_base_/datasets/mpi_inf_3dhp.py
new file mode 100644
index 0000000000000000000000000000000000000000..ffd0a70297b24456ea38566ac205bb585aa47e5d
--- /dev/null
+++ b/grounded-sam-osx/_base_/datasets/mpi_inf_3dhp.py
@@ -0,0 +1,132 @@
+dataset_info = dict(
+ dataset_name='mpi_inf_3dhp',
+ paper_info=dict(
+ author='ehta, Dushyant and Rhodin, Helge and Casas, Dan and '
+ 'Fua, Pascal and Sotnychenko, Oleksandr and Xu, Weipeng and '
+ 'Theobalt, Christian',
+ title='Monocular 3D Human Pose Estimation In The Wild Using Improved '
+ 'CNN Supervision',
+ container='2017 international conference on 3D vision (3DV)',
+ year='2017',
+ homepage='http://gvv.mpi-inf.mpg.de/3dhp-dataset',
+ ),
+ keypoint_info={
+ 0:
+ dict(
+ name='head_top', id=0, color=[51, 153, 255], type='upper',
+ swap=''),
+ 1:
+ dict(name='neck', id=1, color=[51, 153, 255], type='upper', swap=''),
+ 2:
+ dict(
+ name='right_shoulder',
+ id=2,
+ color=[255, 128, 0],
+ type='upper',
+ swap='left_shoulder'),
+ 3:
+ dict(
+ name='right_elbow',
+ id=3,
+ color=[255, 128, 0],
+ type='upper',
+ swap='left_elbow'),
+ 4:
+ dict(
+ name='right_wrist',
+ id=4,
+ color=[255, 128, 0],
+ type='upper',
+ swap='left_wrist'),
+ 5:
+ dict(
+ name='left_shoulder',
+ id=5,
+ color=[0, 255, 0],
+ type='upper',
+ swap='right_shoulder'),
+ 6:
+ dict(
+ name='left_elbow',
+ id=6,
+ color=[0, 255, 0],
+ type='upper',
+ swap='right_elbow'),
+ 7:
+ dict(
+ name='left_wrist',
+ id=7,
+ color=[0, 255, 0],
+ type='upper',
+ swap='right_wrist'),
+ 8:
+ dict(
+ name='right_hip',
+ id=8,
+ color=[255, 128, 0],
+ type='lower',
+ swap='left_hip'),
+ 9:
+ dict(
+ name='right_knee',
+ id=9,
+ color=[255, 128, 0],
+ type='lower',
+ swap='left_knee'),
+ 10:
+ dict(
+ name='right_ankle',
+ id=10,
+ color=[255, 128, 0],
+ type='lower',
+ swap='left_ankle'),
+ 11:
+ dict(
+ name='left_hip',
+ id=11,
+ color=[0, 255, 0],
+ type='lower',
+ swap='right_hip'),
+ 12:
+ dict(
+ name='left_knee',
+ id=12,
+ color=[0, 255, 0],
+ type='lower',
+ swap='right_knee'),
+ 13:
+ dict(
+ name='left_ankle',
+ id=13,
+ color=[0, 255, 0],
+ type='lower',
+ swap='right_ankle'),
+ 14:
+ dict(name='root', id=14, color=[51, 153, 255], type='lower', swap=''),
+ 15:
+ dict(name='spine', id=15, color=[51, 153, 255], type='upper', swap=''),
+ 16:
+ dict(name='head', id=16, color=[51, 153, 255], type='upper', swap='')
+ },
+ skeleton_info={
+ 0: dict(link=('neck', 'right_shoulder'), id=0, color=[255, 128, 0]),
+ 1: dict(
+ link=('right_shoulder', 'right_elbow'), id=1, color=[255, 128, 0]),
+ 2:
+ dict(link=('right_elbow', 'right_wrist'), id=2, color=[255, 128, 0]),
+ 3: dict(link=('neck', 'left_shoulder'), id=3, color=[0, 255, 0]),
+ 4: dict(link=('left_shoulder', 'left_elbow'), id=4, color=[0, 255, 0]),
+ 5: dict(link=('left_elbow', 'left_wrist'), id=5, color=[0, 255, 0]),
+ 6: dict(link=('root', 'right_hip'), id=6, color=[255, 128, 0]),
+ 7: dict(link=('right_hip', 'right_knee'), id=7, color=[255, 128, 0]),
+ 8: dict(link=('right_knee', 'right_ankle'), id=8, color=[255, 128, 0]),
+ 9: dict(link=('root', 'left_hip'), id=9, color=[0, 255, 0]),
+ 10: dict(link=('left_hip', 'left_knee'), id=10, color=[0, 255, 0]),
+ 11: dict(link=('left_knee', 'left_ankle'), id=11, color=[0, 255, 0]),
+ 12: dict(link=('head_top', 'head'), id=12, color=[51, 153, 255]),
+ 13: dict(link=('head', 'neck'), id=13, color=[51, 153, 255]),
+ 14: dict(link=('neck', 'spine'), id=14, color=[51, 153, 255]),
+ 15: dict(link=('spine', 'root'), id=15, color=[51, 153, 255])
+ },
+ joint_weights=[1.] * 17,
+ sigmas=[])
diff --git a/grounded-sam-osx/_base_/datasets/mpii.py b/grounded-sam-osx/_base_/datasets/mpii.py
new file mode 100644
index 0000000000000000000000000000000000000000..6c2a491c7b58bc3eaa5c0056d3d7184bdd1d1cc7
--- /dev/null
+++ b/grounded-sam-osx/_base_/datasets/mpii.py
@@ -0,0 +1,155 @@
+dataset_info = dict(
+ dataset_name='mpii',
+ paper_info=dict(
+ author='Mykhaylo Andriluka and Leonid Pishchulin and '
+ 'Peter Gehler and Schiele, Bernt',
+ title='2D Human Pose Estimation: New Benchmark and '
+ 'State of the Art Analysis',
+ container='IEEE Conference on Computer Vision and '
+ 'Pattern Recognition (CVPR)',
+ year='2014',
+ homepage='http://human-pose.mpi-inf.mpg.de/',
+ ),
+ keypoint_info={
+ 0:
+ dict(
+ name='right_ankle',
+ id=0,
+ color=[255, 128, 0],
+ type='lower',
+ swap='left_ankle'),
+ 1:
+ dict(
+ name='right_knee',
+ id=1,
+ color=[255, 128, 0],
+ type='lower',
+ swap='left_knee'),
+ 2:
+ dict(
+ name='right_hip',
+ id=2,
+ color=[255, 128, 0],
+ type='lower',
+ swap='left_hip'),
+ 3:
+ dict(
+ name='left_hip',
+ id=3,
+ color=[0, 255, 0],
+ type='lower',
+ swap='right_hip'),
+ 4:
+ dict(
+ name='left_knee',
+ id=4,
+ color=[0, 255, 0],
+ type='lower',
+ swap='right_knee'),
+ 5:
+ dict(
+ name='left_ankle',
+ id=5,
+ color=[0, 255, 0],
+ type='lower',
+ swap='right_ankle'),
+ 6:
+ dict(name='pelvis', id=6, color=[51, 153, 255], type='lower', swap=''),
+ 7:
+ dict(name='thorax', id=7, color=[51, 153, 255], type='upper', swap=''),
+ 8:
+ dict(
+ name='upper_neck',
+ id=8,
+ color=[51, 153, 255],
+ type='upper',
+ swap=''),
+ 9:
+ dict(
+ name='head_top', id=9, color=[51, 153, 255], type='upper',
+ swap=''),
+ 10:
+ dict(
+ name='right_wrist',
+ id=10,
+ color=[255, 128, 0],
+ type='upper',
+ swap='left_wrist'),
+ 11:
+ dict(
+ name='right_elbow',
+ id=11,
+ color=[255, 128, 0],
+ type='upper',
+ swap='left_elbow'),
+ 12:
+ dict(
+ name='right_shoulder',
+ id=12,
+ color=[255, 128, 0],
+ type='upper',
+ swap='left_shoulder'),
+ 13:
+ dict(
+ name='left_shoulder',
+ id=13,
+ color=[0, 255, 0],
+ type='upper',
+ swap='right_shoulder'),
+ 14:
+ dict(
+ name='left_elbow',
+ id=14,
+ color=[0, 255, 0],
+ type='upper',
+ swap='right_elbow'),
+ 15:
+ dict(
+ name='left_wrist',
+ id=15,
+ color=[0, 255, 0],
+ type='upper',
+ swap='right_wrist')
+ },
+ skeleton_info={
+ 0:
+ dict(link=('right_ankle', 'right_knee'), id=0, color=[255, 128, 0]),
+ 1:
+ dict(link=('right_knee', 'right_hip'), id=1, color=[255, 128, 0]),
+ 2:
+ dict(link=('right_hip', 'pelvis'), id=2, color=[255, 128, 0]),
+ 3:
+ dict(link=('pelvis', 'left_hip'), id=3, color=[0, 255, 0]),
+ 4:
+ dict(link=('left_hip', 'left_knee'), id=4, color=[0, 255, 0]),
+ 5:
+ dict(link=('left_knee', 'left_ankle'), id=5, color=[0, 255, 0]),
+ 6:
+ dict(link=('pelvis', 'thorax'), id=6, color=[51, 153, 255]),
+ 7:
+ dict(link=('thorax', 'upper_neck'), id=7, color=[51, 153, 255]),
+ 8:
+ dict(link=('upper_neck', 'head_top'), id=8, color=[51, 153, 255]),
+ 9:
+ dict(link=('upper_neck', 'right_shoulder'), id=9, color=[255, 128, 0]),
+ 10:
+ dict(
+ link=('right_shoulder', 'right_elbow'), id=10, color=[255, 128,
+ 0]),
+ 11:
+ dict(link=('right_elbow', 'right_wrist'), id=11, color=[255, 128, 0]),
+ 12:
+ dict(link=('upper_neck', 'left_shoulder'), id=12, color=[0, 255, 0]),
+ 13:
+ dict(link=('left_shoulder', 'left_elbow'), id=13, color=[0, 255, 0]),
+ 14:
+ dict(link=('left_elbow', 'left_wrist'), id=14, color=[0, 255, 0])
+ },
+ joint_weights=[
+ 1.5, 1.2, 1., 1., 1.2, 1.5, 1., 1., 1., 1., 1.5, 1.2, 1., 1., 1.2, 1.5
+ ],
+ # Adapted from COCO dataset.
+ sigmas=[
+ 0.089, 0.083, 0.107, 0.107, 0.083, 0.089, 0.026, 0.026, 0.026, 0.026,
+ 0.062, 0.072, 0.179, 0.179, 0.072, 0.062
+ ])
diff --git a/grounded-sam-osx/_base_/datasets/mpii_trb.py b/grounded-sam-osx/_base_/datasets/mpii_trb.py
new file mode 100644
index 0000000000000000000000000000000000000000..73940d4b4827f8e08343c3b517360db788e4820d
--- /dev/null
+++ b/grounded-sam-osx/_base_/datasets/mpii_trb.py
@@ -0,0 +1,380 @@
+dataset_info = dict(
+ dataset_name='mpii_trb',
+ paper_info=dict(
+ author='Duan, Haodong and Lin, Kwan-Yee and Jin, Sheng and '
+ 'Liu, Wentao and Qian, Chen and Ouyang, Wanli',
+ title='TRB: A Novel Triplet Representation for '
+ 'Understanding 2D Human Body',
+ container='Proceedings of the IEEE International '
+ 'Conference on Computer Vision',
+ year='2019',
+ homepage='https://github.com/kennymckormick/'
+ 'Triplet-Representation-of-human-Body',
+ ),
+ keypoint_info={
+ 0:
+ dict(
+ name='left_shoulder',
+ id=0,
+ color=[0, 255, 0],
+ type='upper',
+ swap='right_shoulder'),
+ 1:
+ dict(
+ name='right_shoulder',
+ id=1,
+ color=[255, 128, 0],
+ type='upper',
+ swap='left_shoulder'),
+ 2:
+ dict(
+ name='left_elbow',
+ id=2,
+ color=[0, 255, 0],
+ type='upper',
+ swap='right_elbow'),
+ 3:
+ dict(
+ name='right_elbow',
+ id=3,
+ color=[255, 128, 0],
+ type='upper',
+ swap='left_elbow'),
+ 4:
+ dict(
+ name='left_wrist',
+ id=4,
+ color=[0, 255, 0],
+ type='upper',
+ swap='right_wrist'),
+ 5:
+ dict(
+ name='right_wrist',
+ id=5,
+ color=[255, 128, 0],
+ type='upper',
+ swap='left_wrist'),
+ 6:
+ dict(
+ name='left_hip',
+ id=6,
+ color=[0, 255, 0],
+ type='lower',
+ swap='right_hip'),
+ 7:
+ dict(
+ name='right_hip',
+ id=7,
+ color=[255, 128, 0],
+ type='lower',
+ swap='left_hip'),
+ 8:
+ dict(
+ name='left_knee',
+ id=8,
+ color=[0, 255, 0],
+ type='lower',
+ swap='right_knee'),
+ 9:
+ dict(
+ name='right_knee',
+ id=9,
+ color=[255, 128, 0],
+ type='lower',
+ swap='left_knee'),
+ 10:
+ dict(
+ name='left_ankle',
+ id=10,
+ color=[0, 255, 0],
+ type='lower',
+ swap='right_ankle'),
+ 11:
+ dict(
+ name='right_ankle',
+ id=11,
+ color=[255, 128, 0],
+ type='lower',
+ swap='left_ankle'),
+ 12:
+ dict(name='head', id=12, color=[51, 153, 255], type='upper', swap=''),
+ 13:
+ dict(name='neck', id=13, color=[51, 153, 255], type='upper', swap=''),
+ 14:
+ dict(
+ name='right_neck',
+ id=14,
+ color=[255, 255, 255],
+ type='upper',
+ swap='left_neck'),
+ 15:
+ dict(
+ name='left_neck',
+ id=15,
+ color=[255, 255, 255],
+ type='upper',
+ swap='right_neck'),
+ 16:
+ dict(
+ name='medial_right_shoulder',
+ id=16,
+ color=[255, 255, 255],
+ type='upper',
+ swap='medial_left_shoulder'),
+ 17:
+ dict(
+ name='lateral_right_shoulder',
+ id=17,
+ color=[255, 255, 255],
+ type='upper',
+ swap='lateral_left_shoulder'),
+ 18:
+ dict(
+ name='medial_right_bow',
+ id=18,
+ color=[255, 255, 255],
+ type='upper',
+ swap='medial_left_bow'),
+ 19:
+ dict(
+ name='lateral_right_bow',
+ id=19,
+ color=[255, 255, 255],
+ type='upper',
+ swap='lateral_left_bow'),
+ 20:
+ dict(
+ name='medial_right_wrist',
+ id=20,
+ color=[255, 255, 255],
+ type='upper',
+ swap='medial_left_wrist'),
+ 21:
+ dict(
+ name='lateral_right_wrist',
+ id=21,
+ color=[255, 255, 255],
+ type='upper',
+ swap='lateral_left_wrist'),
+ 22:
+ dict(
+ name='medial_left_shoulder',
+ id=22,
+ color=[255, 255, 255],
+ type='upper',
+ swap='medial_right_shoulder'),
+ 23:
+ dict(
+ name='lateral_left_shoulder',
+ id=23,
+ color=[255, 255, 255],
+ type='upper',
+ swap='lateral_right_shoulder'),
+ 24:
+ dict(
+ name='medial_left_bow',
+ id=24,
+ color=[255, 255, 255],
+ type='upper',
+ swap='medial_right_bow'),
+ 25:
+ dict(
+ name='lateral_left_bow',
+ id=25,
+ color=[255, 255, 255],
+ type='upper',
+ swap='lateral_right_bow'),
+ 26:
+ dict(
+ name='medial_left_wrist',
+ id=26,
+ color=[255, 255, 255],
+ type='upper',
+ swap='medial_right_wrist'),
+ 27:
+ dict(
+ name='lateral_left_wrist',
+ id=27,
+ color=[255, 255, 255],
+ type='upper',
+ swap='lateral_right_wrist'),
+ 28:
+ dict(
+ name='medial_right_hip',
+ id=28,
+ color=[255, 255, 255],
+ type='lower',
+ swap='medial_left_hip'),
+ 29:
+ dict(
+ name='lateral_right_hip',
+ id=29,
+ color=[255, 255, 255],
+ type='lower',
+ swap='lateral_left_hip'),
+ 30:
+ dict(
+ name='medial_right_knee',
+ id=30,
+ color=[255, 255, 255],
+ type='lower',
+ swap='medial_left_knee'),
+ 31:
+ dict(
+ name='lateral_right_knee',
+ id=31,
+ color=[255, 255, 255],
+ type='lower',
+ swap='lateral_left_knee'),
+ 32:
+ dict(
+ name='medial_right_ankle',
+ id=32,
+ color=[255, 255, 255],
+ type='lower',
+ swap='medial_left_ankle'),
+ 33:
+ dict(
+ name='lateral_right_ankle',
+ id=33,
+ color=[255, 255, 255],
+ type='lower',
+ swap='lateral_left_ankle'),
+ 34:
+ dict(
+ name='medial_left_hip',
+ id=34,
+ color=[255, 255, 255],
+ type='lower',
+ swap='medial_right_hip'),
+ 35:
+ dict(
+ name='lateral_left_hip',
+ id=35,
+ color=[255, 255, 255],
+ type='lower',
+ swap='lateral_right_hip'),
+ 36:
+ dict(
+ name='medial_left_knee',
+ id=36,
+ color=[255, 255, 255],
+ type='lower',
+ swap='medial_right_knee'),
+ 37:
+ dict(
+ name='lateral_left_knee',
+ id=37,
+ color=[255, 255, 255],
+ type='lower',
+ swap='lateral_right_knee'),
+ 38:
+ dict(
+ name='medial_left_ankle',
+ id=38,
+ color=[255, 255, 255],
+ type='lower',
+ swap='medial_right_ankle'),
+ 39:
+ dict(
+ name='lateral_left_ankle',
+ id=39,
+ color=[255, 255, 255],
+ type='lower',
+ swap='lateral_right_ankle'),
+ },
+ skeleton_info={
+ 0:
+ dict(link=('head', 'neck'), id=0, color=[51, 153, 255]),
+ 1:
+ dict(link=('neck', 'left_shoulder'), id=1, color=[51, 153, 255]),
+ 2:
+ dict(link=('neck', 'right_shoulder'), id=2, color=[51, 153, 255]),
+ 3:
+ dict(link=('left_shoulder', 'left_elbow'), id=3, color=[0, 255, 0]),
+ 4:
+ dict(
+ link=('right_shoulder', 'right_elbow'), id=4, color=[255, 128, 0]),
+ 5:
+ dict(link=('left_elbow', 'left_wrist'), id=5, color=[0, 255, 0]),
+ 6:
+ dict(link=('right_elbow', 'right_wrist'), id=6, color=[255, 128, 0]),
+ 7:
+ dict(link=('left_shoulder', 'left_hip'), id=7, color=[51, 153, 255]),
+ 8:
+ dict(link=('right_shoulder', 'right_hip'), id=8, color=[51, 153, 255]),
+ 9:
+ dict(link=('left_hip', 'right_hip'), id=9, color=[51, 153, 255]),
+ 10:
+ dict(link=('left_hip', 'left_knee'), id=10, color=[0, 255, 0]),
+ 11:
+ dict(link=('right_hip', 'right_knee'), id=11, color=[255, 128, 0]),
+ 12:
+ dict(link=('left_knee', 'left_ankle'), id=12, color=[0, 255, 0]),
+ 13:
+ dict(link=('right_knee', 'right_ankle'), id=13, color=[255, 128, 0]),
+ 14:
+ dict(link=('right_neck', 'left_neck'), id=14, color=[255, 255, 255]),
+ 15:
+ dict(
+ link=('medial_right_shoulder', 'lateral_right_shoulder'),
+ id=15,
+ color=[255, 255, 255]),
+ 16:
+ dict(
+ link=('medial_right_bow', 'lateral_right_bow'),
+ id=16,
+ color=[255, 255, 255]),
+ 17:
+ dict(
+ link=('medial_right_wrist', 'lateral_right_wrist'),
+ id=17,
+ color=[255, 255, 255]),
+ 18:
+ dict(
+ link=('medial_left_shoulder', 'lateral_left_shoulder'),
+ id=18,
+ color=[255, 255, 255]),
+ 19:
+ dict(
+ link=('medial_left_bow', 'lateral_left_bow'),
+ id=19,
+ color=[255, 255, 255]),
+ 20:
+ dict(
+ link=('medial_left_wrist', 'lateral_left_wrist'),
+ id=20,
+ color=[255, 255, 255]),
+ 21:
+ dict(
+ link=('medial_right_hip', 'lateral_right_hip'),
+ id=21,
+ color=[255, 255, 255]),
+ 22:
+ dict(
+ link=('medial_right_knee', 'lateral_right_knee'),
+ id=22,
+ color=[255, 255, 255]),
+ 23:
+ dict(
+ link=('medial_right_ankle', 'lateral_right_ankle'),
+ id=23,
+ color=[255, 255, 255]),
+ 24:
+ dict(
+ link=('medial_left_hip', 'lateral_left_hip'),
+ id=24,
+ color=[255, 255, 255]),
+ 25:
+ dict(
+ link=('medial_left_knee', 'lateral_left_knee'),
+ id=25,
+ color=[255, 255, 255]),
+ 26:
+ dict(
+ link=('medial_left_ankle', 'lateral_left_ankle'),
+ id=26,
+ color=[255, 255, 255])
+ },
+ joint_weights=[1.] * 40,
+ sigmas=[])
diff --git a/grounded-sam-osx/_base_/datasets/nvgesture.py b/grounded-sam-osx/_base_/datasets/nvgesture.py
new file mode 100644
index 0000000000000000000000000000000000000000..7d5a3df7b9c6ac553ff8eab9428a9a3fb96ef564
--- /dev/null
+++ b/grounded-sam-osx/_base_/datasets/nvgesture.py
@@ -0,0 +1,42 @@
+dataset_info = dict(
+ dataset_name='nvgesture',
+ paper_info=dict(
+ author='Pavlo Molchanov and Xiaodong Yang and Shalini Gupta '
+ 'and Kihwan Kim and Stephen Tyree and Jan Kautz',
+ title='Online Detection and Classification of Dynamic Hand Gestures '
+ 'with Recurrent 3D Convolutional Neural Networks',
+ container='Proceedings of the IEEE Conference on '
+ 'Computer Vision and Pattern Recognition',
+ year='2016',
+ homepage='https://research.nvidia.com/publication/2016-06_online-'
+ 'detection-and-classification-dynamic-hand-gestures-recurrent-3d',
+ ),
+ category_info={
+ 0: 'five fingers move right',
+ 1: 'five fingers move left',
+ 2: 'five fingers move up',
+ 3: 'five fingers move down',
+ 4: 'two fingers move right',
+ 5: 'two fingers move left',
+ 6: 'two fingers move up',
+ 7: 'two fingers move down',
+ 8: 'click',
+ 9: 'beckoned',
+ 10: 'stretch hand',
+ 11: 'shake hand',
+ 12: 'one',
+ 13: 'two',
+ 14: 'three',
+ 15: 'lift up',
+ 16: 'press down',
+ 17: 'push',
+ 18: 'shrink',
+ 19: 'levorotation',
+ 20: 'dextrorotation',
+ 21: 'two fingers prod',
+ 22: 'grab',
+ 23: 'thumbs up',
+ 24: 'OK'
+ },
+ flip_pairs=[(0, 1), (4, 5), (19, 20)],
+ fps=30)
diff --git a/grounded-sam-osx/_base_/datasets/ochuman.py b/grounded-sam-osx/_base_/datasets/ochuman.py
new file mode 100644
index 0000000000000000000000000000000000000000..2ef20838fe583fde133a97e688d30e91ae562746
--- /dev/null
+++ b/grounded-sam-osx/_base_/datasets/ochuman.py
@@ -0,0 +1,181 @@
+dataset_info = dict(
+ dataset_name='ochuman',
+ paper_info=dict(
+ author='Zhang, Song-Hai and Li, Ruilong and Dong, Xin and '
+ 'Rosin, Paul and Cai, Zixi and Han, Xi and '
+ 'Yang, Dingcheng and Huang, Haozhi and Hu, Shi-Min',
+ title='Pose2seg: Detection free human instance segmentation',
+ container='Proceedings of the IEEE conference on computer '
+ 'vision and pattern recognition',
+ year='2019',
+ homepage='https://github.com/liruilong940607/OCHumanApi',
+ ),
+ keypoint_info={
+ 0:
+ dict(name='nose', id=0, color=[51, 153, 255], type='upper', swap=''),
+ 1:
+ dict(
+ name='left_eye',
+ id=1,
+ color=[51, 153, 255],
+ type='upper',
+ swap='right_eye'),
+ 2:
+ dict(
+ name='right_eye',
+ id=2,
+ color=[51, 153, 255],
+ type='upper',
+ swap='left_eye'),
+ 3:
+ dict(
+ name='left_ear',
+ id=3,
+ color=[51, 153, 255],
+ type='upper',
+ swap='right_ear'),
+ 4:
+ dict(
+ name='right_ear',
+ id=4,
+ color=[51, 153, 255],
+ type='upper',
+ swap='left_ear'),
+ 5:
+ dict(
+ name='left_shoulder',
+ id=5,
+ color=[0, 255, 0],
+ type='upper',
+ swap='right_shoulder'),
+ 6:
+ dict(
+ name='right_shoulder',
+ id=6,
+ color=[255, 128, 0],
+ type='upper',
+ swap='left_shoulder'),
+ 7:
+ dict(
+ name='left_elbow',
+ id=7,
+ color=[0, 255, 0],
+ type='upper',
+ swap='right_elbow'),
+ 8:
+ dict(
+ name='right_elbow',
+ id=8,
+ color=[255, 128, 0],
+ type='upper',
+ swap='left_elbow'),
+ 9:
+ dict(
+ name='left_wrist',
+ id=9,
+ color=[0, 255, 0],
+ type='upper',
+ swap='right_wrist'),
+ 10:
+ dict(
+ name='right_wrist',
+ id=10,
+ color=[255, 128, 0],
+ type='upper',
+ swap='left_wrist'),
+ 11:
+ dict(
+ name='left_hip',
+ id=11,
+ color=[0, 255, 0],
+ type='lower',
+ swap='right_hip'),
+ 12:
+ dict(
+ name='right_hip',
+ id=12,
+ color=[255, 128, 0],
+ type='lower',
+ swap='left_hip'),
+ 13:
+ dict(
+ name='left_knee',
+ id=13,
+ color=[0, 255, 0],
+ type='lower',
+ swap='right_knee'),
+ 14:
+ dict(
+ name='right_knee',
+ id=14,
+ color=[255, 128, 0],
+ type='lower',
+ swap='left_knee'),
+ 15:
+ dict(
+ name='left_ankle',
+ id=15,
+ color=[0, 255, 0],
+ type='lower',
+ swap='right_ankle'),
+ 16:
+ dict(
+ name='right_ankle',
+ id=16,
+ color=[255, 128, 0],
+ type='lower',
+ swap='left_ankle')
+ },
+ skeleton_info={
+ 0:
+ dict(link=('left_ankle', 'left_knee'), id=0, color=[0, 255, 0]),
+ 1:
+ dict(link=('left_knee', 'left_hip'), id=1, color=[0, 255, 0]),
+ 2:
+ dict(link=('right_ankle', 'right_knee'), id=2, color=[255, 128, 0]),
+ 3:
+ dict(link=('right_knee', 'right_hip'), id=3, color=[255, 128, 0]),
+ 4:
+ dict(link=('left_hip', 'right_hip'), id=4, color=[51, 153, 255]),
+ 5:
+ dict(link=('left_shoulder', 'left_hip'), id=5, color=[51, 153, 255]),
+ 6:
+ dict(link=('right_shoulder', 'right_hip'), id=6, color=[51, 153, 255]),
+ 7:
+ dict(
+ link=('left_shoulder', 'right_shoulder'),
+ id=7,
+ color=[51, 153, 255]),
+ 8:
+ dict(link=('left_shoulder', 'left_elbow'), id=8, color=[0, 255, 0]),
+ 9:
+ dict(
+ link=('right_shoulder', 'right_elbow'), id=9, color=[255, 128, 0]),
+ 10:
+ dict(link=('left_elbow', 'left_wrist'), id=10, color=[0, 255, 0]),
+ 11:
+ dict(link=('right_elbow', 'right_wrist'), id=11, color=[255, 128, 0]),
+ 12:
+ dict(link=('left_eye', 'right_eye'), id=12, color=[51, 153, 255]),
+ 13:
+ dict(link=('nose', 'left_eye'), id=13, color=[51, 153, 255]),
+ 14:
+ dict(link=('nose', 'right_eye'), id=14, color=[51, 153, 255]),
+ 15:
+ dict(link=('left_eye', 'left_ear'), id=15, color=[51, 153, 255]),
+ 16:
+ dict(link=('right_eye', 'right_ear'), id=16, color=[51, 153, 255]),
+ 17:
+ dict(link=('left_ear', 'left_shoulder'), id=17, color=[51, 153, 255]),
+ 18:
+ dict(
+ link=('right_ear', 'right_shoulder'), id=18, color=[51, 153, 255])
+ },
+ joint_weights=[
+ 1., 1., 1., 1., 1., 1., 1., 1.2, 1.2, 1.5, 1.5, 1., 1., 1.2, 1.2, 1.5,
+ 1.5
+ ],
+ sigmas=[
+ 0.026, 0.025, 0.025, 0.035, 0.035, 0.079, 0.079, 0.072, 0.072, 0.062,
+ 0.062, 0.107, 0.107, 0.087, 0.087, 0.089, 0.089
+ ])
diff --git a/grounded-sam-osx/_base_/datasets/onehand10k.py b/grounded-sam-osx/_base_/datasets/onehand10k.py
new file mode 100644
index 0000000000000000000000000000000000000000..016770f14f3075dfa7d59389524a0c11a4feb802
--- /dev/null
+++ b/grounded-sam-osx/_base_/datasets/onehand10k.py
@@ -0,0 +1,142 @@
+dataset_info = dict(
+ dataset_name='onehand10k',
+ paper_info=dict(
+ author='Wang, Yangang and Peng, Cong and Liu, Yebin',
+ title='Mask-pose cascaded cnn for 2d hand pose estimation '
+ 'from single color image',
+ container='IEEE Transactions on Circuits and Systems '
+ 'for Video Technology',
+ year='2018',
+ homepage='https://www.yangangwang.com/papers/WANG-MCC-2018-10.html',
+ ),
+ keypoint_info={
+ 0:
+ dict(name='wrist', id=0, color=[255, 255, 255], type='', swap=''),
+ 1:
+ dict(name='thumb1', id=1, color=[255, 128, 0], type='', swap=''),
+ 2:
+ dict(name='thumb2', id=2, color=[255, 128, 0], type='', swap=''),
+ 3:
+ dict(name='thumb3', id=3, color=[255, 128, 0], type='', swap=''),
+ 4:
+ dict(name='thumb4', id=4, color=[255, 128, 0], type='', swap=''),
+ 5:
+ dict(
+ name='forefinger1', id=5, color=[255, 153, 255], type='', swap=''),
+ 6:
+ dict(
+ name='forefinger2', id=6, color=[255, 153, 255], type='', swap=''),
+ 7:
+ dict(
+ name='forefinger3', id=7, color=[255, 153, 255], type='', swap=''),
+ 8:
+ dict(
+ name='forefinger4', id=8, color=[255, 153, 255], type='', swap=''),
+ 9:
+ dict(
+ name='middle_finger1',
+ id=9,
+ color=[102, 178, 255],
+ type='',
+ swap=''),
+ 10:
+ dict(
+ name='middle_finger2',
+ id=10,
+ color=[102, 178, 255],
+ type='',
+ swap=''),
+ 11:
+ dict(
+ name='middle_finger3',
+ id=11,
+ color=[102, 178, 255],
+ type='',
+ swap=''),
+ 12:
+ dict(
+ name='middle_finger4',
+ id=12,
+ color=[102, 178, 255],
+ type='',
+ swap=''),
+ 13:
+ dict(
+ name='ring_finger1', id=13, color=[255, 51, 51], type='', swap=''),
+ 14:
+ dict(
+ name='ring_finger2', id=14, color=[255, 51, 51], type='', swap=''),
+ 15:
+ dict(
+ name='ring_finger3', id=15, color=[255, 51, 51], type='', swap=''),
+ 16:
+ dict(
+ name='ring_finger4', id=16, color=[255, 51, 51], type='', swap=''),
+ 17:
+ dict(name='pinky_finger1', id=17, color=[0, 255, 0], type='', swap=''),
+ 18:
+ dict(name='pinky_finger2', id=18, color=[0, 255, 0], type='', swap=''),
+ 19:
+ dict(name='pinky_finger3', id=19, color=[0, 255, 0], type='', swap=''),
+ 20:
+ dict(name='pinky_finger4', id=20, color=[0, 255, 0], type='', swap='')
+ },
+ skeleton_info={
+ 0:
+ dict(link=('wrist', 'thumb1'), id=0, color=[255, 128, 0]),
+ 1:
+ dict(link=('thumb1', 'thumb2'), id=1, color=[255, 128, 0]),
+ 2:
+ dict(link=('thumb2', 'thumb3'), id=2, color=[255, 128, 0]),
+ 3:
+ dict(link=('thumb3', 'thumb4'), id=3, color=[255, 128, 0]),
+ 4:
+ dict(link=('wrist', 'forefinger1'), id=4, color=[255, 153, 255]),
+ 5:
+ dict(link=('forefinger1', 'forefinger2'), id=5, color=[255, 153, 255]),
+ 6:
+ dict(link=('forefinger2', 'forefinger3'), id=6, color=[255, 153, 255]),
+ 7:
+ dict(link=('forefinger3', 'forefinger4'), id=7, color=[255, 153, 255]),
+ 8:
+ dict(link=('wrist', 'middle_finger1'), id=8, color=[102, 178, 255]),
+ 9:
+ dict(
+ link=('middle_finger1', 'middle_finger2'),
+ id=9,
+ color=[102, 178, 255]),
+ 10:
+ dict(
+ link=('middle_finger2', 'middle_finger3'),
+ id=10,
+ color=[102, 178, 255]),
+ 11:
+ dict(
+ link=('middle_finger3', 'middle_finger4'),
+ id=11,
+ color=[102, 178, 255]),
+ 12:
+ dict(link=('wrist', 'ring_finger1'), id=12, color=[255, 51, 51]),
+ 13:
+ dict(
+ link=('ring_finger1', 'ring_finger2'), id=13, color=[255, 51, 51]),
+ 14:
+ dict(
+ link=('ring_finger2', 'ring_finger3'), id=14, color=[255, 51, 51]),
+ 15:
+ dict(
+ link=('ring_finger3', 'ring_finger4'), id=15, color=[255, 51, 51]),
+ 16:
+ dict(link=('wrist', 'pinky_finger1'), id=16, color=[0, 255, 0]),
+ 17:
+ dict(
+ link=('pinky_finger1', 'pinky_finger2'), id=17, color=[0, 255, 0]),
+ 18:
+ dict(
+ link=('pinky_finger2', 'pinky_finger3'), id=18, color=[0, 255, 0]),
+ 19:
+ dict(
+ link=('pinky_finger3', 'pinky_finger4'), id=19, color=[0, 255, 0])
+ },
+ joint_weights=[1.] * 21,
+ sigmas=[])
diff --git a/grounded-sam-osx/_base_/datasets/panoptic_body3d.py b/grounded-sam-osx/_base_/datasets/panoptic_body3d.py
new file mode 100644
index 0000000000000000000000000000000000000000..e3b19ac462415a840ca2e0b9e214bdb35d91b5e4
--- /dev/null
+++ b/grounded-sam-osx/_base_/datasets/panoptic_body3d.py
@@ -0,0 +1,160 @@
+dataset_info = dict(
+ dataset_name='panoptic_pose_3d',
+ paper_info=dict(
+ author='Joo, Hanbyul and Simon, Tomas and Li, Xulong'
+ 'and Liu, Hao and Tan, Lei and Gui, Lin and Banerjee, Sean'
+ 'and Godisart, Timothy and Nabbe, Bart and Matthews, Iain'
+ 'and Kanade, Takeo and Nobuhara, Shohei and Sheikh, Yaser',
+ title='Panoptic Studio: A Massively Multiview System '
+ 'for Interaction Motion Capture',
+ container='IEEE Transactions on Pattern Analysis'
+ ' and Machine Intelligence',
+ year='2017',
+ homepage='http://domedb.perception.cs.cmu.edu',
+ ),
+ keypoint_info={
+ 0:
+ dict(name='neck', id=0, color=[51, 153, 255], type='upper', swap=''),
+ 1:
+ dict(name='nose', id=1, color=[51, 153, 255], type='upper', swap=''),
+ 2:
+ dict(name='mid_hip', id=2, color=[0, 255, 0], type='lower', swap=''),
+ 3:
+ dict(
+ name='left_shoulder',
+ id=3,
+ color=[0, 255, 0],
+ type='upper',
+ swap='right_shoulder'),
+ 4:
+ dict(
+ name='left_elbow',
+ id=4,
+ color=[0, 255, 0],
+ type='upper',
+ swap='right_elbow'),
+ 5:
+ dict(
+ name='left_wrist',
+ id=5,
+ color=[0, 255, 0],
+ type='upper',
+ swap='right_wrist'),
+ 6:
+ dict(
+ name='left_hip',
+ id=6,
+ color=[0, 255, 0],
+ type='lower',
+ swap='right_hip'),
+ 7:
+ dict(
+ name='left_knee',
+ id=7,
+ color=[0, 255, 0],
+ type='lower',
+ swap='right_knee'),
+ 8:
+ dict(
+ name='left_ankle',
+ id=8,
+ color=[0, 255, 0],
+ type='lower',
+ swap='right_ankle'),
+ 9:
+ dict(
+ name='right_shoulder',
+ id=9,
+ color=[255, 128, 0],
+ type='upper',
+ swap='left_shoulder'),
+ 10:
+ dict(
+ name='right_elbow',
+ id=10,
+ color=[255, 128, 0],
+ type='upper',
+ swap='left_elbow'),
+ 11:
+ dict(
+ name='right_wrist',
+ id=11,
+ color=[255, 128, 0],
+ type='upper',
+ swap='left_wrist'),
+ 12:
+ dict(
+ name='right_hip',
+ id=12,
+ color=[255, 128, 0],
+ type='lower',
+ swap='left_hip'),
+ 13:
+ dict(
+ name='right_knee',
+ id=13,
+ color=[255, 128, 0],
+ type='lower',
+ swap='left_knee'),
+ 14:
+ dict(
+ name='right_ankle',
+ id=14,
+ color=[255, 128, 0],
+ type='lower',
+ swap='left_ankle'),
+ 15:
+ dict(
+ name='left_eye',
+ id=15,
+ color=[51, 153, 255],
+ type='upper',
+ swap='right_eye'),
+ 16:
+ dict(
+ name='left_ear',
+ id=16,
+ color=[51, 153, 255],
+ type='upper',
+ swap='right_ear'),
+ 17:
+ dict(
+ name='right_eye',
+ id=17,
+ color=[51, 153, 255],
+ type='upper',
+ swap='left_eye'),
+ 18:
+ dict(
+ name='right_ear',
+ id=18,
+ color=[51, 153, 255],
+ type='upper',
+ swap='left_ear')
+ },
+ skeleton_info={
+ 0: dict(link=('nose', 'neck'), id=0, color=[51, 153, 255]),
+ 1: dict(link=('neck', 'left_shoulder'), id=1, color=[0, 255, 0]),
+ 2: dict(link=('neck', 'right_shoulder'), id=2, color=[255, 128, 0]),
+ 3: dict(link=('left_shoulder', 'left_elbow'), id=3, color=[0, 255, 0]),
+ 4: dict(
+ link=('right_shoulder', 'right_elbow'), id=4, color=[255, 128, 0]),
+ 5: dict(link=('left_elbow', 'left_wrist'), id=5, color=[0, 255, 0]),
+ 6:
+ dict(link=('right_elbow', 'right_wrist'), id=6, color=[255, 128, 0]),
+ 7: dict(link=('left_ankle', 'left_knee'), id=7, color=[0, 255, 0]),
+ 8: dict(link=('left_knee', 'left_hip'), id=8, color=[0, 255, 0]),
+ 9: dict(link=('right_ankle', 'right_knee'), id=9, color=[255, 128, 0]),
+ 10: dict(link=('right_knee', 'right_hip'), id=10, color=[255, 128, 0]),
+ 11: dict(link=('mid_hip', 'left_hip'), id=11, color=[0, 255, 0]),
+ 12: dict(link=('mid_hip', 'right_hip'), id=12, color=[255, 128, 0]),
+ 13: dict(link=('mid_hip', 'neck'), id=13, color=[51, 153, 255]),
+ },
+ joint_weights=[
+ 1.0, 1.0, 1.0, 1.0, 1.2, 1.5, 1.0, 1.2, 1.5, 1.0, 1.2, 1.5, 1.0, 1.2,
+ 1.5, 1.0, 1.0, 1.0, 1.0
+ ],
+ sigmas=[
+ 0.026, 0.026, 0.107, 0.079, 0.072, 0.062, 0.107, 0.087, 0.089, 0.079,
+ 0.072, 0.062, 0.107, 0.087, 0.089, 0.025, 0.035, 0.025, 0.035
+ ])
diff --git a/grounded-sam-osx/_base_/datasets/panoptic_hand2d.py b/grounded-sam-osx/_base_/datasets/panoptic_hand2d.py
new file mode 100644
index 0000000000000000000000000000000000000000..7a65731ba87b155beb1b40591fd9acb232c2afc6
--- /dev/null
+++ b/grounded-sam-osx/_base_/datasets/panoptic_hand2d.py
@@ -0,0 +1,143 @@
+dataset_info = dict(
+ dataset_name='panoptic_hand2d',
+ paper_info=dict(
+ author='Simon, Tomas and Joo, Hanbyul and '
+ 'Matthews, Iain and Sheikh, Yaser',
+ title='Hand keypoint detection in single images using '
+ 'multiview bootstrapping',
+ container='Proceedings of the IEEE conference on '
+ 'Computer Vision and Pattern Recognition',
+ year='2017',
+ homepage='http://domedb.perception.cs.cmu.edu/handdb.html',
+ ),
+ keypoint_info={
+ 0:
+ dict(name='wrist', id=0, color=[255, 255, 255], type='', swap=''),
+ 1:
+ dict(name='thumb1', id=1, color=[255, 128, 0], type='', swap=''),
+ 2:
+ dict(name='thumb2', id=2, color=[255, 128, 0], type='', swap=''),
+ 3:
+ dict(name='thumb3', id=3, color=[255, 128, 0], type='', swap=''),
+ 4:
+ dict(name='thumb4', id=4, color=[255, 128, 0], type='', swap=''),
+ 5:
+ dict(
+ name='forefinger1', id=5, color=[255, 153, 255], type='', swap=''),
+ 6:
+ dict(
+ name='forefinger2', id=6, color=[255, 153, 255], type='', swap=''),
+ 7:
+ dict(
+ name='forefinger3', id=7, color=[255, 153, 255], type='', swap=''),
+ 8:
+ dict(
+ name='forefinger4', id=8, color=[255, 153, 255], type='', swap=''),
+ 9:
+ dict(
+ name='middle_finger1',
+ id=9,
+ color=[102, 178, 255],
+ type='',
+ swap=''),
+ 10:
+ dict(
+ name='middle_finger2',
+ id=10,
+ color=[102, 178, 255],
+ type='',
+ swap=''),
+ 11:
+ dict(
+ name='middle_finger3',
+ id=11,
+ color=[102, 178, 255],
+ type='',
+ swap=''),
+ 12:
+ dict(
+ name='middle_finger4',
+ id=12,
+ color=[102, 178, 255],
+ type='',
+ swap=''),
+ 13:
+ dict(
+ name='ring_finger1', id=13, color=[255, 51, 51], type='', swap=''),
+ 14:
+ dict(
+ name='ring_finger2', id=14, color=[255, 51, 51], type='', swap=''),
+ 15:
+ dict(
+ name='ring_finger3', id=15, color=[255, 51, 51], type='', swap=''),
+ 16:
+ dict(
+ name='ring_finger4', id=16, color=[255, 51, 51], type='', swap=''),
+ 17:
+ dict(name='pinky_finger1', id=17, color=[0, 255, 0], type='', swap=''),
+ 18:
+ dict(name='pinky_finger2', id=18, color=[0, 255, 0], type='', swap=''),
+ 19:
+ dict(name='pinky_finger3', id=19, color=[0, 255, 0], type='', swap=''),
+ 20:
+ dict(name='pinky_finger4', id=20, color=[0, 255, 0], type='', swap='')
+ },
+ skeleton_info={
+ 0:
+ dict(link=('wrist', 'thumb1'), id=0, color=[255, 128, 0]),
+ 1:
+ dict(link=('thumb1', 'thumb2'), id=1, color=[255, 128, 0]),
+ 2:
+ dict(link=('thumb2', 'thumb3'), id=2, color=[255, 128, 0]),
+ 3:
+ dict(link=('thumb3', 'thumb4'), id=3, color=[255, 128, 0]),
+ 4:
+ dict(link=('wrist', 'forefinger1'), id=4, color=[255, 153, 255]),
+ 5:
+ dict(link=('forefinger1', 'forefinger2'), id=5, color=[255, 153, 255]),
+ 6:
+ dict(link=('forefinger2', 'forefinger3'), id=6, color=[255, 153, 255]),
+ 7:
+ dict(link=('forefinger3', 'forefinger4'), id=7, color=[255, 153, 255]),
+ 8:
+ dict(link=('wrist', 'middle_finger1'), id=8, color=[102, 178, 255]),
+ 9:
+ dict(
+ link=('middle_finger1', 'middle_finger2'),
+ id=9,
+ color=[102, 178, 255]),
+ 10:
+ dict(
+ link=('middle_finger2', 'middle_finger3'),
+ id=10,
+ color=[102, 178, 255]),
+ 11:
+ dict(
+ link=('middle_finger3', 'middle_finger4'),
+ id=11,
+ color=[102, 178, 255]),
+ 12:
+ dict(link=('wrist', 'ring_finger1'), id=12, color=[255, 51, 51]),
+ 13:
+ dict(
+ link=('ring_finger1', 'ring_finger2'), id=13, color=[255, 51, 51]),
+ 14:
+ dict(
+ link=('ring_finger2', 'ring_finger3'), id=14, color=[255, 51, 51]),
+ 15:
+ dict(
+ link=('ring_finger3', 'ring_finger4'), id=15, color=[255, 51, 51]),
+ 16:
+ dict(link=('wrist', 'pinky_finger1'), id=16, color=[0, 255, 0]),
+ 17:
+ dict(
+ link=('pinky_finger1', 'pinky_finger2'), id=17, color=[0, 255, 0]),
+ 18:
+ dict(
+ link=('pinky_finger2', 'pinky_finger3'), id=18, color=[0, 255, 0]),
+ 19:
+ dict(
+ link=('pinky_finger3', 'pinky_finger4'), id=19, color=[0, 255, 0])
+ },
+ joint_weights=[1.] * 21,
+ sigmas=[])
diff --git a/grounded-sam-osx/_base_/datasets/posetrack18.py b/grounded-sam-osx/_base_/datasets/posetrack18.py
new file mode 100644
index 0000000000000000000000000000000000000000..5aefd1c97fe083df35ee88bebab4f99134c27971
--- /dev/null
+++ b/grounded-sam-osx/_base_/datasets/posetrack18.py
@@ -0,0 +1,176 @@
+dataset_info = dict(
+ dataset_name='posetrack18',
+ paper_info=dict(
+ author='Andriluka, Mykhaylo and Iqbal, Umar and '
+ 'Insafutdinov, Eldar and Pishchulin, Leonid and '
+ 'Milan, Anton and Gall, Juergen and Schiele, Bernt',
+ title='Posetrack: A benchmark for human pose estimation and tracking',
+ container='Proceedings of the IEEE Conference on '
+ 'Computer Vision and Pattern Recognition',
+ year='2018',
+ homepage='https://posetrack.net/users/download.php',
+ ),
+ keypoint_info={
+ 0:
+ dict(name='nose', id=0, color=[51, 153, 255], type='upper', swap=''),
+ 1:
+ dict(
+ name='head_bottom',
+ id=1,
+ color=[51, 153, 255],
+ type='upper',
+ swap=''),
+ 2:
+ dict(
+ name='head_top', id=2, color=[51, 153, 255], type='upper',
+ swap=''),
+ 3:
+ dict(
+ name='left_ear',
+ id=3,
+ color=[51, 153, 255],
+ type='upper',
+ swap='right_ear'),
+ 4:
+ dict(
+ name='right_ear',
+ id=4,
+ color=[51, 153, 255],
+ type='upper',
+ swap='left_ear'),
+ 5:
+ dict(
+ name='left_shoulder',
+ id=5,
+ color=[0, 255, 0],
+ type='upper',
+ swap='right_shoulder'),
+ 6:
+ dict(
+ name='right_shoulder',
+ id=6,
+ color=[255, 128, 0],
+ type='upper',
+ swap='left_shoulder'),
+ 7:
+ dict(
+ name='left_elbow',
+ id=7,
+ color=[0, 255, 0],
+ type='upper',
+ swap='right_elbow'),
+ 8:
+ dict(
+ name='right_elbow',
+ id=8,
+ color=[255, 128, 0],
+ type='upper',
+ swap='left_elbow'),
+ 9:
+ dict(
+ name='left_wrist',
+ id=9,
+ color=[0, 255, 0],
+ type='upper',
+ swap='right_wrist'),
+ 10:
+ dict(
+ name='right_wrist',
+ id=10,
+ color=[255, 128, 0],
+ type='upper',
+ swap='left_wrist'),
+ 11:
+ dict(
+ name='left_hip',
+ id=11,
+ color=[0, 255, 0],
+ type='lower',
+ swap='right_hip'),
+ 12:
+ dict(
+ name='right_hip',
+ id=12,
+ color=[255, 128, 0],
+ type='lower',
+ swap='left_hip'),
+ 13:
+ dict(
+ name='left_knee',
+ id=13,
+ color=[0, 255, 0],
+ type='lower',
+ swap='right_knee'),
+ 14:
+ dict(
+ name='right_knee',
+ id=14,
+ color=[255, 128, 0],
+ type='lower',
+ swap='left_knee'),
+ 15:
+ dict(
+ name='left_ankle',
+ id=15,
+ color=[0, 255, 0],
+ type='lower',
+ swap='right_ankle'),
+ 16:
+ dict(
+ name='right_ankle',
+ id=16,
+ color=[255, 128, 0],
+ type='lower',
+ swap='left_ankle')
+ },
+ skeleton_info={
+ 0:
+ dict(link=('left_ankle', 'left_knee'), id=0, color=[0, 255, 0]),
+ 1:
+ dict(link=('left_knee', 'left_hip'), id=1, color=[0, 255, 0]),
+ 2:
+ dict(link=('right_ankle', 'right_knee'), id=2, color=[255, 128, 0]),
+ 3:
+ dict(link=('right_knee', 'right_hip'), id=3, color=[255, 128, 0]),
+ 4:
+ dict(link=('left_hip', 'right_hip'), id=4, color=[51, 153, 255]),
+ 5:
+ dict(link=('left_shoulder', 'left_hip'), id=5, color=[51, 153, 255]),
+ 6:
+ dict(link=('right_shoulder', 'right_hip'), id=6, color=[51, 153, 255]),
+ 7:
+ dict(
+ link=('left_shoulder', 'right_shoulder'),
+ id=7,
+ color=[51, 153, 255]),
+ 8:
+ dict(link=('left_shoulder', 'left_elbow'), id=8, color=[0, 255, 0]),
+ 9:
+ dict(
+ link=('right_shoulder', 'right_elbow'), id=9, color=[255, 128, 0]),
+ 10:
+ dict(link=('left_elbow', 'left_wrist'), id=10, color=[0, 255, 0]),
+ 11:
+ dict(link=('right_elbow', 'right_wrist'), id=11, color=[255, 128, 0]),
+ 12:
+ dict(link=('nose', 'head_bottom'), id=12, color=[51, 153, 255]),
+ 13:
+ dict(link=('nose', 'head_top'), id=13, color=[51, 153, 255]),
+ 14:
+ dict(
+ link=('head_bottom', 'left_shoulder'), id=14, color=[51, 153,
+ 255]),
+ 15:
+ dict(
+ link=('head_bottom', 'right_shoulder'),
+ id=15,
+ color=[51, 153, 255])
+ },
+ joint_weights=[
+ 1., 1., 1., 1., 1., 1., 1., 1.2, 1.2, 1.5, 1.5, 1., 1., 1.2, 1.2, 1.5,
+ 1.5
+ ],
+ sigmas=[
+ 0.026, 0.025, 0.025, 0.035, 0.035, 0.079, 0.079, 0.072, 0.072, 0.062,
+ 0.062, 0.107, 0.107, 0.087, 0.087, 0.089, 0.089
+ ])
diff --git a/grounded-sam-osx/_base_/datasets/rhd2d.py b/grounded-sam-osx/_base_/datasets/rhd2d.py
new file mode 100644
index 0000000000000000000000000000000000000000..4631ccd03814155b06687e0b1ba2b83404c837fc
--- /dev/null
+++ b/grounded-sam-osx/_base_/datasets/rhd2d.py
@@ -0,0 +1,151 @@
+dataset_info = dict(
+ dataset_name='rhd2d',
+ paper_info=dict(
+ author='Christian Zimmermann and Thomas Brox',
+ title='Learning to Estimate 3D Hand Pose from Single RGB Images',
+ container='arXiv',
+ year='2017',
+ homepage='https://lmb.informatik.uni-freiburg.de/resources/'
+ 'datasets/RenderedHandposeDataset.en.html',
+ ),
+ # In RHD, 1-4: left thumb [tip to palm], which means the finger is from
+ # tip to palm, so as other fingers. Please refer to
+ # `https://lmb.informatik.uni-freiburg.de/resources/datasets/
+ # RenderedHandpose/README` for details of keypoint definition.
+ # But in COCO-WholeBody-Hand, FreiHand, CMU Panoptic HandDB, it is in
+ # inverse order. Pay attention to this if you want to combine RHD with
+ # other hand datasets to train a single model.
+ # Also, note that 'keypoint_info' will not directly affect the order of
+ # the keypoint in the dataset. It is mostly for visualization & storing
+ # information about flip_pairs.
+ keypoint_info={
+ 0:
+ dict(name='wrist', id=0, color=[255, 255, 255], type='', swap=''),
+ 1:
+ dict(name='thumb4', id=1, color=[255, 128, 0], type='', swap=''),
+ 2:
+ dict(name='thumb3', id=2, color=[255, 128, 0], type='', swap=''),
+ 3:
+ dict(name='thumb2', id=3, color=[255, 128, 0], type='', swap=''),
+ 4:
+ dict(name='thumb1', id=4, color=[255, 128, 0], type='', swap=''),
+ 5:
+ dict(
+ name='forefinger4', id=5, color=[255, 153, 255], type='', swap=''),
+ 6:
+ dict(
+ name='forefinger3', id=6, color=[255, 153, 255], type='', swap=''),
+ 7:
+ dict(
+ name='forefinger2', id=7, color=[255, 153, 255], type='', swap=''),
+ 8:
+ dict(
+ name='forefinger1', id=8, color=[255, 153, 255], type='', swap=''),
+ 9:
+ dict(
+ name='middle_finger4',
+ id=9,
+ color=[102, 178, 255],
+ type='',
+ swap=''),
+ 10:
+ dict(
+ name='middle_finger3',
+ id=10,
+ color=[102, 178, 255],
+ type='',
+ swap=''),
+ 11:
+ dict(
+ name='middle_finger2',
+ id=11,
+ color=[102, 178, 255],
+ type='',
+ swap=''),
+ 12:
+ dict(
+ name='middle_finger1',
+ id=12,
+ color=[102, 178, 255],
+ type='',
+ swap=''),
+ 13:
+ dict(
+ name='ring_finger4', id=13, color=[255, 51, 51], type='', swap=''),
+ 14:
+ dict(
+ name='ring_finger3', id=14, color=[255, 51, 51], type='', swap=''),
+ 15:
+ dict(
+ name='ring_finger2', id=15, color=[255, 51, 51], type='', swap=''),
+ 16:
+ dict(
+ name='ring_finger1', id=16, color=[255, 51, 51], type='', swap=''),
+ 17:
+ dict(name='pinky_finger4', id=17, color=[0, 255, 0], type='', swap=''),
+ 18:
+ dict(name='pinky_finger3', id=18, color=[0, 255, 0], type='', swap=''),
+ 19:
+ dict(name='pinky_finger2', id=19, color=[0, 255, 0], type='', swap=''),
+ 20:
+ dict(name='pinky_finger1', id=20, color=[0, 255, 0], type='', swap='')
+ },
+ skeleton_info={
+ 0:
+ dict(link=('wrist', 'thumb1'), id=0, color=[255, 128, 0]),
+ 1:
+ dict(link=('thumb1', 'thumb2'), id=1, color=[255, 128, 0]),
+ 2:
+ dict(link=('thumb2', 'thumb3'), id=2, color=[255, 128, 0]),
+ 3:
+ dict(link=('thumb3', 'thumb4'), id=3, color=[255, 128, 0]),
+ 4:
+ dict(link=('wrist', 'forefinger1'), id=4, color=[255, 153, 255]),
+ 5:
+ dict(link=('forefinger1', 'forefinger2'), id=5, color=[255, 153, 255]),
+ 6:
+ dict(link=('forefinger2', 'forefinger3'), id=6, color=[255, 153, 255]),
+ 7:
+ dict(link=('forefinger3', 'forefinger4'), id=7, color=[255, 153, 255]),
+ 8:
+ dict(link=('wrist', 'middle_finger1'), id=8, color=[102, 178, 255]),
+ 9:
+ dict(
+ link=('middle_finger1', 'middle_finger2'),
+ id=9,
+ color=[102, 178, 255]),
+ 10:
+ dict(
+ link=('middle_finger2', 'middle_finger3'),
+ id=10,
+ color=[102, 178, 255]),
+ 11:
+ dict(
+ link=('middle_finger3', 'middle_finger4'),
+ id=11,
+ color=[102, 178, 255]),
+ 12:
+ dict(link=('wrist', 'ring_finger1'), id=12, color=[255, 51, 51]),
+ 13:
+ dict(
+ link=('ring_finger1', 'ring_finger2'), id=13, color=[255, 51, 51]),
+ 14:
+ dict(
+ link=('ring_finger2', 'ring_finger3'), id=14, color=[255, 51, 51]),
+ 15:
+ dict(
+ link=('ring_finger3', 'ring_finger4'), id=15, color=[255, 51, 51]),
+ 16:
+ dict(link=('wrist', 'pinky_finger1'), id=16, color=[0, 255, 0]),
+ 17:
+ dict(
+ link=('pinky_finger1', 'pinky_finger2'), id=17, color=[0, 255, 0]),
+ 18:
+ dict(
+ link=('pinky_finger2', 'pinky_finger3'), id=18, color=[0, 255, 0]),
+ 19:
+ dict(
+ link=('pinky_finger3', 'pinky_finger4'), id=19, color=[0, 255, 0])
+ },
+ joint_weights=[1.] * 21,
+ sigmas=[])
diff --git a/grounded-sam-osx/_base_/datasets/shelf.py b/grounded-sam-osx/_base_/datasets/shelf.py
new file mode 100644
index 0000000000000000000000000000000000000000..5fe6e42b3b44e3f65947284efd9ffac58d41d43f
--- /dev/null
+++ b/grounded-sam-osx/_base_/datasets/shelf.py
@@ -0,0 +1,151 @@
+dataset_info = dict(
+ dataset_name='shelf',
+ paper_info=dict(
+ author='Belagiannis, Vasileios and Amin, Sikandar and Andriluka, '
+ 'Mykhaylo and Schiele, Bernt and Navab, Nassir and Ilic, Slobodan',
+ title='3D Pictorial Structures for Multiple Human Pose Estimation',
+ container='IEEE Computer Society Conference on Computer Vision and '
+ 'Pattern Recognition (CVPR)',
+ year='2014',
+ homepage='http://campar.in.tum.de/Chair/MultiHumanPose',
+ ),
+ keypoint_info={
+ 0:
+ dict(
+ name='right_ankle',
+ id=0,
+ color=[255, 128, 0],
+ type='lower',
+ swap='left_ankle'),
+ 1:
+ dict(
+ name='right_knee',
+ id=1,
+ color=[255, 128, 0],
+ type='lower',
+ swap='left_knee'),
+ 2:
+ dict(
+ name='right_hip',
+ id=2,
+ color=[255, 128, 0],
+ type='lower',
+ swap='left_hip'),
+ 3:
+ dict(
+ name='left_hip',
+ id=3,
+ color=[0, 255, 0],
+ type='lower',
+ swap='right_hip'),
+ 4:
+ dict(
+ name='left_knee',
+ id=4,
+ color=[0, 255, 0],
+ type='lower',
+ swap='right_knee'),
+ 5:
+ dict(
+ name='left_ankle',
+ id=5,
+ color=[0, 255, 0],
+ type='lower',
+ swap='right_ankle'),
+ 6:
+ dict(
+ name='right_wrist',
+ id=6,
+ color=[255, 128, 0],
+ type='upper',
+ swap='left_wrist'),
+ 7:
+ dict(
+ name='right_elbow',
+ id=7,
+ color=[255, 128, 0],
+ type='upper',
+ swap='left_elbow'),
+ 8:
+ dict(
+ name='right_shoulder',
+ id=8,
+ color=[255, 128, 0],
+ type='upper',
+ swap='left_shoulder'),
+ 9:
+ dict(
+ name='left_shoulder',
+ id=9,
+ color=[0, 255, 0],
+ type='upper',
+ swap='right_shoulder'),
+ 10:
+ dict(
+ name='left_elbow',
+ id=10,
+ color=[0, 255, 0],
+ type='upper',
+ swap='right_elbow'),
+ 11:
+ dict(
+ name='left_wrist',
+ id=11,
+ color=[0, 255, 0],
+ type='upper',
+ swap='right_wrist'),
+ 12:
+ dict(
+ name='bottom_head',
+ id=12,
+ color=[51, 153, 255],
+ type='upper',
+ swap=''),
+ 13:
+ dict(
+ name='top_head',
+ id=13,
+ color=[51, 153, 255],
+ type='upper',
+ swap=''),
+ },
+ skeleton_info={
+ 0:
+ dict(link=('right_ankle', 'right_knee'), id=0, color=[255, 128, 0]),
+ 1:
+ dict(link=('right_knee', 'right_hip'), id=1, color=[255, 128, 0]),
+ 2:
+ dict(link=('left_hip', 'left_knee'), id=2, color=[0, 255, 0]),
+ 3:
+ dict(link=('left_knee', 'left_ankle'), id=3, color=[0, 255, 0]),
+ 4:
+ dict(link=('right_hip', 'left_hip'), id=4, color=[51, 153, 255]),
+ 5:
+ dict(link=('right_wrist', 'right_elbow'), id=5, color=[255, 128, 0]),
+ 6:
+ dict(
+ link=('right_elbow', 'right_shoulder'), id=6, color=[255, 128, 0]),
+ 7:
+ dict(link=('left_shoulder', 'left_elbow'), id=7, color=[0, 255, 0]),
+ 8:
+ dict(link=('left_elbow', 'left_wrist'), id=8, color=[0, 255, 0]),
+ 9:
+ dict(link=('right_hip', 'right_shoulder'), id=9, color=[255, 128, 0]),
+ 10:
+ dict(link=('left_hip', 'left_shoulder'), id=10, color=[0, 255, 0]),
+ 11:
+ dict(
+ link=('right_shoulder', 'bottom_head'), id=11, color=[255, 128,
+ 0]),
+ 12:
+ dict(link=('left_shoulder', 'bottom_head'), id=12, color=[0, 255, 0]),
+ 13:
+ dict(link=('bottom_head', 'top_head'), id=13, color=[51, 153, 255]),
+ },
+ joint_weights=[
+ 1.5, 1.2, 1.0, 1.0, 1.2, 1.5, 1.5, 1.2, 1.0, 1.0, 1.2, 1.5, 1.0, 1.0
+ ],
+ sigmas=[
+ 0.089, 0.087, 0.107, 0.107, 0.087, 0.089, 0.062, 0.072, 0.079, 0.079,
+ 0.072, 0.062, 0.026, 0.026
+ ])
diff --git a/grounded-sam-osx/_base_/datasets/wflw.py b/grounded-sam-osx/_base_/datasets/wflw.py
new file mode 100644
index 0000000000000000000000000000000000000000..bed6f56f30f7a2f093e44c5726212e2a0d4659d2
--- /dev/null
+++ b/grounded-sam-osx/_base_/datasets/wflw.py
@@ -0,0 +1,582 @@
+dataset_info = dict(
+ dataset_name='wflw',
+ paper_info=dict(
+ author='Wu, Wayne and Qian, Chen and Yang, Shuo and Wang, '
+ 'Quan and Cai, Yici and Zhou, Qiang',
+ title='Look at boundary: A boundary-aware face alignment algorithm',
+ container='Proceedings of the IEEE conference on computer '
+ 'vision and pattern recognition',
+ year='2018',
+ homepage='https://wywu.github.io/projects/LAB/WFLW.html',
+ ),
+ keypoint_info={
+ 0:
+ dict(
+ name='kpt-0', id=0, color=[255, 255, 255], type='', swap='kpt-32'),
+ 1:
+ dict(
+ name='kpt-1', id=1, color=[255, 255, 255], type='', swap='kpt-31'),
+ 2:
+ dict(
+ name='kpt-2', id=2, color=[255, 255, 255], type='', swap='kpt-30'),
+ 3:
+ dict(
+ name='kpt-3', id=3, color=[255, 255, 255], type='', swap='kpt-29'),
+ 4:
+ dict(
+ name='kpt-4', id=4, color=[255, 255, 255], type='', swap='kpt-28'),
+ 5:
+ dict(
+ name='kpt-5', id=5, color=[255, 255, 255], type='', swap='kpt-27'),
+ 6:
+ dict(
+ name='kpt-6', id=6, color=[255, 255, 255], type='', swap='kpt-26'),
+ 7:
+ dict(
+ name='kpt-7', id=7, color=[255, 255, 255], type='', swap='kpt-25'),
+ 8:
+ dict(
+ name='kpt-8', id=8, color=[255, 255, 255], type='', swap='kpt-24'),
+ 9:
+ dict(
+ name='kpt-9', id=9, color=[255, 255, 255], type='', swap='kpt-23'),
+ 10:
+ dict(
+ name='kpt-10',
+ id=10,
+ color=[255, 255, 255],
+ type='',
+ swap='kpt-22'),
+ 11:
+ dict(
+ name='kpt-11',
+ id=11,
+ color=[255, 255, 255],
+ type='',
+ swap='kpt-21'),
+ 12:
+ dict(
+ name='kpt-12',
+ id=12,
+ color=[255, 255, 255],
+ type='',
+ swap='kpt-20'),
+ 13:
+ dict(
+ name='kpt-13',
+ id=13,
+ color=[255, 255, 255],
+ type='',
+ swap='kpt-19'),
+ 14:
+ dict(
+ name='kpt-14',
+ id=14,
+ color=[255, 255, 255],
+ type='',
+ swap='kpt-18'),
+ 15:
+ dict(
+ name='kpt-15',
+ id=15,
+ color=[255, 255, 255],
+ type='',
+ swap='kpt-17'),
+ 16:
+ dict(name='kpt-16', id=16, color=[255, 255, 255], type='', swap=''),
+ 17:
+ dict(
+ name='kpt-17',
+ id=17,
+ color=[255, 255, 255],
+ type='',
+ swap='kpt-15'),
+ 18:
+ dict(
+ name='kpt-18',
+ id=18,
+ color=[255, 255, 255],
+ type='',
+ swap='kpt-14'),
+ 19:
+ dict(
+ name='kpt-19',
+ id=19,
+ color=[255, 255, 255],
+ type='',
+ swap='kpt-13'),
+ 20:
+ dict(
+ name='kpt-20',
+ id=20,
+ color=[255, 255, 255],
+ type='',
+ swap='kpt-12'),
+ 21:
+ dict(
+ name='kpt-21',
+ id=21,
+ color=[255, 255, 255],
+ type='',
+ swap='kpt-11'),
+ 22:
+ dict(
+ name='kpt-22',
+ id=22,
+ color=[255, 255, 255],
+ type='',
+ swap='kpt-10'),
+ 23:
+ dict(
+ name='kpt-23', id=23, color=[255, 255, 255], type='',
+ swap='kpt-9'),
+ 24:
+ dict(
+ name='kpt-24', id=24, color=[255, 255, 255], type='',
+ swap='kpt-8'),
+ 25:
+ dict(
+ name='kpt-25', id=25, color=[255, 255, 255], type='',
+ swap='kpt-7'),
+ 26:
+ dict(
+ name='kpt-26', id=26, color=[255, 255, 255], type='',
+ swap='kpt-6'),
+ 27:
+ dict(
+ name='kpt-27', id=27, color=[255, 255, 255], type='',
+ swap='kpt-5'),
+ 28:
+ dict(
+ name='kpt-28', id=28, color=[255, 255, 255], type='',
+ swap='kpt-4'),
+ 29:
+ dict(
+ name='kpt-29', id=29, color=[255, 255, 255], type='',
+ swap='kpt-3'),
+ 30:
+ dict(
+ name='kpt-30', id=30, color=[255, 255, 255], type='',
+ swap='kpt-2'),
+ 31:
+ dict(
+ name='kpt-31', id=31, color=[255, 255, 255], type='',
+ swap='kpt-1'),
+ 32:
+ dict(
+ name='kpt-32', id=32, color=[255, 255, 255], type='',
+ swap='kpt-0'),
+ 33:
+ dict(
+ name='kpt-33',
+ id=33,
+ color=[255, 255, 255],
+ type='',
+ swap='kpt-46'),
+ 34:
+ dict(
+ name='kpt-34',
+ id=34,
+ color=[255, 255, 255],
+ type='',
+ swap='kpt-45'),
+ 35:
+ dict(
+ name='kpt-35',
+ id=35,
+ color=[255, 255, 255],
+ type='',
+ swap='kpt-44'),
+ 36:
+ dict(
+ name='kpt-36',
+ id=36,
+ color=[255, 255, 255],
+ type='',
+ swap='kpt-43'),
+ 37:
+ dict(
+ name='kpt-37',
+ id=37,
+ color=[255, 255, 255],
+ type='',
+ swap='kpt-42'),
+ 38:
+ dict(
+ name='kpt-38',
+ id=38,
+ color=[255, 255, 255],
+ type='',
+ swap='kpt-50'),
+ 39:
+ dict(
+ name='kpt-39',
+ id=39,
+ color=[255, 255, 255],
+ type='',
+ swap='kpt-49'),
+ 40:
+ dict(
+ name='kpt-40',
+ id=40,
+ color=[255, 255, 255],
+ type='',
+ swap='kpt-48'),
+ 41:
+ dict(
+ name='kpt-41',
+ id=41,
+ color=[255, 255, 255],
+ type='',
+ swap='kpt-47'),
+ 42:
+ dict(
+ name='kpt-42',
+ id=42,
+ color=[255, 255, 255],
+ type='',
+ swap='kpt-37'),
+ 43:
+ dict(
+ name='kpt-43',
+ id=43,
+ color=[255, 255, 255],
+ type='',
+ swap='kpt-36'),
+ 44:
+ dict(
+ name='kpt-44',
+ id=44,
+ color=[255, 255, 255],
+ type='',
+ swap='kpt-35'),
+ 45:
+ dict(
+ name='kpt-45',
+ id=45,
+ color=[255, 255, 255],
+ type='',
+ swap='kpt-34'),
+ 46:
+ dict(
+ name='kpt-46',
+ id=46,
+ color=[255, 255, 255],
+ type='',
+ swap='kpt-33'),
+ 47:
+ dict(
+ name='kpt-47',
+ id=47,
+ color=[255, 255, 255],
+ type='',
+ swap='kpt-41'),
+ 48:
+ dict(
+ name='kpt-48',
+ id=48,
+ color=[255, 255, 255],
+ type='',
+ swap='kpt-40'),
+ 49:
+ dict(
+ name='kpt-49',
+ id=49,
+ color=[255, 255, 255],
+ type='',
+ swap='kpt-39'),
+ 50:
+ dict(
+ name='kpt-50',
+ id=50,
+ color=[255, 255, 255],
+ type='',
+ swap='kpt-38'),
+ 51:
+ dict(name='kpt-51', id=51, color=[255, 255, 255], type='', swap=''),
+ 52:
+ dict(name='kpt-52', id=52, color=[255, 255, 255], type='', swap=''),
+ 53:
+ dict(name='kpt-53', id=53, color=[255, 255, 255], type='', swap=''),
+ 54:
+ dict(name='kpt-54', id=54, color=[255, 255, 255], type='', swap=''),
+ 55:
+ dict(
+ name='kpt-55',
+ id=55,
+ color=[255, 255, 255],
+ type='',
+ swap='kpt-59'),
+ 56:
+ dict(
+ name='kpt-56',
+ id=56,
+ color=[255, 255, 255],
+ type='',
+ swap='kpt-58'),
+ 57:
+ dict(name='kpt-57', id=57, color=[255, 255, 255], type='', swap=''),
+ 58:
+ dict(
+ name='kpt-58',
+ id=58,
+ color=[255, 255, 255],
+ type='',
+ swap='kpt-56'),
+ 59:
+ dict(
+ name='kpt-59',
+ id=59,
+ color=[255, 255, 255],
+ type='',
+ swap='kpt-55'),
+ 60:
+ dict(
+ name='kpt-60',
+ id=60,
+ color=[255, 255, 255],
+ type='',
+ swap='kpt-72'),
+ 61:
+ dict(
+ name='kpt-61',
+ id=61,
+ color=[255, 255, 255],
+ type='',
+ swap='kpt-71'),
+ 62:
+ dict(
+ name='kpt-62',
+ id=62,
+ color=[255, 255, 255],
+ type='',
+ swap='kpt-70'),
+ 63:
+ dict(
+ name='kpt-63',
+ id=63,
+ color=[255, 255, 255],
+ type='',
+ swap='kpt-69'),
+ 64:
+ dict(
+ name='kpt-64',
+ id=64,
+ color=[255, 255, 255],
+ type='',
+ swap='kpt-68'),
+ 65:
+ dict(
+ name='kpt-65',
+ id=65,
+ color=[255, 255, 255],
+ type='',
+ swap='kpt-75'),
+ 66:
+ dict(
+ name='kpt-66',
+ id=66,
+ color=[255, 255, 255],
+ type='',
+ swap='kpt-74'),
+ 67:
+ dict(
+ name='kpt-67',
+ id=67,
+ color=[255, 255, 255],
+ type='',
+ swap='kpt-73'),
+ 68:
+ dict(
+ name='kpt-68',
+ id=68,
+ color=[255, 255, 255],
+ type='',
+ swap='kpt-64'),
+ 69:
+ dict(
+ name='kpt-69',
+ id=69,
+ color=[255, 255, 255],
+ type='',
+ swap='kpt-63'),
+ 70:
+ dict(
+ name='kpt-70',
+ id=70,
+ color=[255, 255, 255],
+ type='',
+ swap='kpt-62'),
+ 71:
+ dict(
+ name='kpt-71',
+ id=71,
+ color=[255, 255, 255],
+ type='',
+ swap='kpt-61'),
+ 72:
+ dict(
+ name='kpt-72',
+ id=72,
+ color=[255, 255, 255],
+ type='',
+ swap='kpt-60'),
+ 73:
+ dict(
+ name='kpt-73',
+ id=73,
+ color=[255, 255, 255],
+ type='',
+ swap='kpt-67'),
+ 74:
+ dict(
+ name='kpt-74',
+ id=74,
+ color=[255, 255, 255],
+ type='',
+ swap='kpt-66'),
+ 75:
+ dict(
+ name='kpt-75',
+ id=75,
+ color=[255, 255, 255],
+ type='',
+ swap='kpt-65'),
+ 76:
+ dict(
+ name='kpt-76',
+ id=76,
+ color=[255, 255, 255],
+ type='',
+ swap='kpt-82'),
+ 77:
+ dict(
+ name='kpt-77',
+ id=77,
+ color=[255, 255, 255],
+ type='',
+ swap='kpt-81'),
+ 78:
+ dict(
+ name='kpt-78',
+ id=78,
+ color=[255, 255, 255],
+ type='',
+ swap='kpt-80'),
+ 79:
+ dict(name='kpt-79', id=79, color=[255, 255, 255], type='', swap=''),
+ 80:
+ dict(
+ name='kpt-80',
+ id=80,
+ color=[255, 255, 255],
+ type='',
+ swap='kpt-78'),
+ 81:
+ dict(
+ name='kpt-81',
+ id=81,
+ color=[255, 255, 255],
+ type='',
+ swap='kpt-77'),
+ 82:
+ dict(
+ name='kpt-82',
+ id=82,
+ color=[255, 255, 255],
+ type='',
+ swap='kpt-76'),
+ 83:
+ dict(
+ name='kpt-83',
+ id=83,
+ color=[255, 255, 255],
+ type='',
+ swap='kpt-87'),
+ 84:
+ dict(
+ name='kpt-84',
+ id=84,
+ color=[255, 255, 255],
+ type='',
+ swap='kpt-86'),
+ 85:
+ dict(name='kpt-85', id=85, color=[255, 255, 255], type='', swap=''),
+ 86:
+ dict(
+ name='kpt-86',
+ id=86,
+ color=[255, 255, 255],
+ type='',
+ swap='kpt-84'),
+ 87:
+ dict(
+ name='kpt-87',
+ id=87,
+ color=[255, 255, 255],
+ type='',
+ swap='kpt-83'),
+ 88:
+ dict(
+ name='kpt-88',
+ id=88,
+ color=[255, 255, 255],
+ type='',
+ swap='kpt-92'),
+ 89:
+ dict(
+ name='kpt-89',
+ id=89,
+ color=[255, 255, 255],
+ type='',
+ swap='kpt-91'),
+ 90:
+ dict(name='kpt-90', id=90, color=[255, 255, 255], type='', swap=''),
+ 91:
+ dict(
+ name='kpt-91',
+ id=91,
+ color=[255, 255, 255],
+ type='',
+ swap='kpt-89'),
+ 92:
+ dict(
+ name='kpt-92',
+ id=92,
+ color=[255, 255, 255],
+ type='',
+ swap='kpt-88'),
+ 93:
+ dict(
+ name='kpt-93',
+ id=93,
+ color=[255, 255, 255],
+ type='',
+ swap='kpt-95'),
+ 94:
+ dict(name='kpt-94', id=94, color=[255, 255, 255], type='', swap=''),
+ 95:
+ dict(
+ name='kpt-95',
+ id=95,
+ color=[255, 255, 255],
+ type='',
+ swap='kpt-93'),
+ 96:
+ dict(
+ name='kpt-96',
+ id=96,
+ color=[255, 255, 255],
+ type='',
+ swap='kpt-97'),
+ 97:
+ dict(
+ name='kpt-97',
+ id=97,
+ color=[255, 255, 255],
+ type='',
+ swap='kpt-96')
+ },
+ skeleton_info={},
+ joint_weights=[1.] * 98,
+ sigmas=[])
diff --git a/grounded-sam-osx/_base_/datasets/zebra.py b/grounded-sam-osx/_base_/datasets/zebra.py
new file mode 100644
index 0000000000000000000000000000000000000000..eac71f796a761bbf87b123f8b7b8b4585df0c525
--- /dev/null
+++ b/grounded-sam-osx/_base_/datasets/zebra.py
@@ -0,0 +1,64 @@
+dataset_info = dict(
+ dataset_name='zebra',
+ paper_info=dict(
+ author='Graving, Jacob M and Chae, Daniel and Naik, Hemal and '
+ 'Li, Liang and Koger, Benjamin and Costelloe, Blair R and '
+ 'Couzin, Iain D',
+ title='DeepPoseKit, a software toolkit for fast and robust '
+ 'animal pose estimation using deep learning',
+ container='Elife',
+ year='2019',
+ homepage='https://github.com/jgraving/DeepPoseKit-Data',
+ ),
+ keypoint_info={
+ 0:
+ dict(name='snout', id=0, color=[255, 255, 255], type='', swap=''),
+ 1:
+ dict(name='head', id=1, color=[255, 255, 255], type='', swap=''),
+ 2:
+ dict(name='neck', id=2, color=[255, 255, 255], type='', swap=''),
+ 3:
+ dict(
+ name='forelegL1',
+ id=3,
+ color=[255, 255, 255],
+ type='',
+ swap='forelegR1'),
+ 4:
+ dict(
+ name='forelegR1',
+ id=4,
+ color=[255, 255, 255],
+ type='',
+ swap='forelegL1'),
+ 5:
+ dict(
+ name='hindlegL1',
+ id=5,
+ color=[255, 255, 255],
+ type='',
+ swap='hindlegR1'),
+ 6:
+ dict(
+ name='hindlegR1',
+ id=6,
+ color=[255, 255, 255],
+ type='',
+ swap='hindlegL1'),
+ 7:
+ dict(name='tailbase', id=7, color=[255, 255, 255], type='', swap=''),
+ 8:
+ dict(name='tailtip', id=8, color=[255, 255, 255], type='', swap='')
+ },
+ skeleton_info={
+ 0: dict(link=('head', 'snout'), id=0, color=[255, 255, 255]),
+ 1: dict(link=('neck', 'head'), id=1, color=[255, 255, 255]),
+ 2: dict(link=('forelegL1', 'neck'), id=2, color=[255, 255, 255]),
+ 3: dict(link=('forelegR1', 'neck'), id=3, color=[255, 255, 255]),
+ 4: dict(link=('hindlegL1', 'tailbase'), id=4, color=[255, 255, 255]),
+ 5: dict(link=('hindlegR1', 'tailbase'), id=5, color=[255, 255, 255]),
+ 6: dict(link=('tailbase', 'neck'), id=6, color=[255, 255, 255]),
+ 7: dict(link=('tailtip', 'tailbase'), id=7, color=[255, 255, 255])
+ },
+ joint_weights=[1.] * 9,
+ sigmas=[])
diff --git a/grounded-sam-osx/_base_/default_runtime.py b/grounded-sam-osx/_base_/default_runtime.py
new file mode 100644
index 0000000000000000000000000000000000000000..62b7ff270aae280268ea528c1fbe99c0052e20e3
--- /dev/null
+++ b/grounded-sam-osx/_base_/default_runtime.py
@@ -0,0 +1,20 @@
+checkpoint_config = dict(interval=10)
+
+log_config = dict(
+ interval=50,
+ hooks=[
+ dict(type='TextLoggerHook'),
+ # dict(type='TensorboardLoggerHook')
+ # dict(type='PaviLoggerHook') # for internal services
+ ])
+
+log_level = 'INFO'
+load_from = None
+resume_from = None
+dist_params = dict(backend='nccl')
+workflow = [('train', 1)]
+
+# disable opencv multithreading to avoid system being overloaded
+opencv_num_threads = 0
+# set multi-process start method as `fork` to speed up the training
+mp_start_method = 'fork'
diff --git a/grounded-sam-osx/_base_/filters/gaussian.py b/grounded-sam-osx/_base_/filters/gaussian.py
new file mode 100644
index 0000000000000000000000000000000000000000..b855f4bde1e1adf71186b3f82f1a3e522fbc53ff
--- /dev/null
+++ b/grounded-sam-osx/_base_/filters/gaussian.py
@@ -0,0 +1,5 @@
+filter_cfg = dict(
+ type='GaussianFilter',
+ window_size=11,
+ sigma=4.0,
+)
diff --git a/grounded-sam-osx/_base_/filters/one_euro.py b/grounded-sam-osx/_base_/filters/one_euro.py
new file mode 100644
index 0000000000000000000000000000000000000000..61f797efdf9fb7a12d40b2d8eee6cb3a5e2e1ea9
--- /dev/null
+++ b/grounded-sam-osx/_base_/filters/one_euro.py
@@ -0,0 +1,5 @@
+filter_cfg = dict(
+ type='OneEuroFilter',
+ min_cutoff=0.004,
+ beta=0.7,
+)
diff --git a/grounded-sam-osx/_base_/filters/savizky_golay.py b/grounded-sam-osx/_base_/filters/savizky_golay.py
new file mode 100644
index 0000000000000000000000000000000000000000..40302b004460699dfe8522c59c9a3e8cf1c35d83
--- /dev/null
+++ b/grounded-sam-osx/_base_/filters/savizky_golay.py
@@ -0,0 +1,5 @@
+filter_cfg = dict(
+ type='SavizkyGolayFilter',
+ window_size=11,
+ polyorder=2,
+)
diff --git a/grounded-sam-osx/_base_/filters/smoothnet_h36m.md b/grounded-sam-osx/_base_/filters/smoothnet_h36m.md
new file mode 100644
index 0000000000000000000000000000000000000000..0901be8fe26468b3603ef77412a4feea16a1f239
--- /dev/null
+++ b/grounded-sam-osx/_base_/filters/smoothnet_h36m.md
@@ -0,0 +1,45 @@
+
+
+
+SmoothNet (arXiv'2021)
+
+```bibtex
+@article{zeng2021smoothnet,
+ title={SmoothNet: A Plug-and-Play Network for Refining Human Poses in Videos},
+ author={Zeng, Ailing and Yang, Lei and Ju, Xuan and Li, Jiefeng and Wang, Jianyi and Xu, Qiang},
+ journal={arXiv preprint arXiv:2112.13715},
+ year={2021}
+}
+```
+
+
+
+
+
+
+Human3.6M (TPAMI'2014)
+
+```bibtex
+@article{h36m_pami,
+ author = {Ionescu, Catalin and Papava, Dragos and Olaru, Vlad and Sminchisescu, Cristian},
+ title = {Human3.6M: Large Scale Datasets and Predictive Methods for 3D Human Sensing in Natural Environments},
+ journal = {IEEE Transactions on Pattern Analysis and Machine Intelligence},
+ publisher = {IEEE Computer Society},
+ volume = {36},
+ number = {7},
+ pages = {1325-1339},
+ month = {jul},
+ year = {2014}
+}
+```
+
+
+
+The following SmoothNet model checkpoints are available for pose smoothing. The table shows the the performance of [SimpleBaseline3D](https://arxiv.org/abs/1705.03098) on [Human3.6M](https://ieeexplore.ieee.org/abstract/document/6682899/) dataset without/with the SmoothNet plugin, and compares the SmoothNet models with 4 different window sizes (8, 16, 32 and 64). The metrics are MPJPE(mm), P-MEJPE(mm) and Acceleration Error (mm/frame^2).
+
+| Arch | Window Size | MPJPEw/o | MPJPEw | P-MPJPEw/o | P-MPJPEw | AC. Errw/o | AC. Errw | ckpt |
+| :----------------------------------- | :---------: | :-----------------: | :---------------: | :-------------------: | :-----------------: | :-------------------: | :-----------------: | :-----------------------------------: |
+| [smoothnet_ws8](/configs/_base_/filters/smoothnet_t8_h36m.py) | 8 | 54.48 | 53.15 | 42.20 | 41.32 | 19.18 | 1.87 | [ckpt](https://download.openmmlab.com/mmpose/plugin/smoothnet/smoothnet_ws8_h36m.pth) |
+| [smoothnet_ws16](/configs/_base_/filters/smoothnet_t16_h36m.py) | 16 | 54.48 | 52.74 | 42.20 | 41.20 | 19.18 | 1.22 | [ckpt](https://download.openmmlab.com/mmpose/plugin/smoothnet/smoothnet_ws16_h36m.pth) |
+| [smoothnet_ws32](/configs/_base_/filters/smoothnet_t32_h36m.py) | 32 | 54.48 | 52.47 | 42.20 | 40.84 | 19.18 | 0.99 | [ckpt](https://download.openmmlab.com/mmpose/plugin/smoothnet/smoothnet_ws32_h36m.pth) |
+| [smoothnet_ws64](/configs/_base_/filters/smoothnet_t64_h36m.py) | 64 | 54.48 | 53.37 | 42.20 | 40.77 | 19.18 | 0.92 | [ckpt](https://download.openmmlab.com/mmpose/plugin/smoothnet/smoothnet_ws64_h36m.pth) |
diff --git a/grounded-sam-osx/_base_/filters/smoothnet_t16_h36m.py b/grounded-sam-osx/_base_/filters/smoothnet_t16_h36m.py
new file mode 100644
index 0000000000000000000000000000000000000000..0cc0c3be924b59056b6b92e1a9f97978cce4a3e2
--- /dev/null
+++ b/grounded-sam-osx/_base_/filters/smoothnet_t16_h36m.py
@@ -0,0 +1,13 @@
+# Config for SmoothNet filter trained on Human3.6M data with a window size of
+# 16. The model is trained using root-centered keypoint coordinates around the
+# pelvis (index:0), thus we set root_index=0 for the filter
+filter_cfg = dict(
+ type='SmoothNetFilter',
+ window_size=16,
+ output_size=16,
+ checkpoint='https://download.openmmlab.com/mmpose/plugin/smoothnet/'
+ 'smoothnet_ws16_h36m.pth',
+ hidden_size=512,
+ res_hidden_size=256,
+ num_blocks=3,
+ root_index=0)
diff --git a/grounded-sam-osx/_base_/filters/smoothnet_t32_h36m.py b/grounded-sam-osx/_base_/filters/smoothnet_t32_h36m.py
new file mode 100644
index 0000000000000000000000000000000000000000..dae59f3b81e2adceec532079a3849de23772f0eb
--- /dev/null
+++ b/grounded-sam-osx/_base_/filters/smoothnet_t32_h36m.py
@@ -0,0 +1,13 @@
+# Config for SmoothNet filter trained on Human3.6M data with a window size of
+# 32. The model is trained using root-centered keypoint coordinates around the
+# pelvis (index:0), thus we set root_index=0 for the filter
+filter_cfg = dict(
+ type='SmoothNetFilter',
+ window_size=32,
+ output_size=32,
+ checkpoint='https://download.openmmlab.com/mmpose/plugin/smoothnet/'
+ 'smoothnet_ws32_h36m.pth',
+ hidden_size=512,
+ res_hidden_size=256,
+ num_blocks=3,
+ root_index=0)
diff --git a/grounded-sam-osx/_base_/filters/smoothnet_t64_h36m.py b/grounded-sam-osx/_base_/filters/smoothnet_t64_h36m.py
new file mode 100644
index 0000000000000000000000000000000000000000..aef2993272cef9fff1d7f8c882507781064d44b7
--- /dev/null
+++ b/grounded-sam-osx/_base_/filters/smoothnet_t64_h36m.py
@@ -0,0 +1,13 @@
+# Config for SmoothNet filter trained on Human3.6M data with a window size of
+# 64. The model is trained using root-centered keypoint coordinates around the
+# pelvis (index:0), thus we set root_index=0 for the filter
+filter_cfg = dict(
+ type='SmoothNetFilter',
+ window_size=64,
+ output_size=64,
+ checkpoint='https://download.openmmlab.com/mmpose/plugin/smoothnet/'
+ 'smoothnet_ws64_h36m.pth',
+ hidden_size=512,
+ res_hidden_size=256,
+ num_blocks=3,
+ root_index=0)
diff --git a/grounded-sam-osx/_base_/filters/smoothnet_t8_h36m.py b/grounded-sam-osx/_base_/filters/smoothnet_t8_h36m.py
new file mode 100644
index 0000000000000000000000000000000000000000..cadd8865dc75d2247a8b4af6036131963aa4d4a5
--- /dev/null
+++ b/grounded-sam-osx/_base_/filters/smoothnet_t8_h36m.py
@@ -0,0 +1,13 @@
+# Config for SmoothNet filter trained on Human3.6M data with a window size of
+# 8. The model is trained using root-centered keypoint coordinates around the
+# pelvis (index:0), thus we set root_index=0 for the filter
+filter_cfg = dict(
+ type='SmoothNetFilter',
+ window_size=8,
+ output_size=8,
+ checkpoint='https://download.openmmlab.com/mmpose/plugin/smoothnet/'
+ 'smoothnet_ws8_h36m.pth',
+ hidden_size=512,
+ res_hidden_size=256,
+ num_blocks=3,
+ root_index=0)
diff --git a/grounded-sam-osx/config.py b/grounded-sam-osx/config.py
new file mode 100644
index 0000000000000000000000000000000000000000..304cbc17d7f620f55e424855abdfb6922779a66e
--- /dev/null
+++ b/grounded-sam-osx/config.py
@@ -0,0 +1,47 @@
+import os
+import os.path as osp
+import sys
+
+class Config:
+
+ ## model setting
+ resnet_type = 50
+ hand_resnet_type = 50
+ face_resnet_type = 18
+
+ model_type = 'OSX'
+
+ # osx_model_settiing
+ upscale = 4
+ with_wrist = False
+ hand_pos_joint_num = 20
+ num_task_token = 24
+ feat_dim = 1024
+ encoder_config_file = 'grounded-sam-osx/transformer_utils/configs/osx/encoder/body_encoder_large.py'
+
+ ## input, output
+ input_img_shape = (512, 384)
+ input_body_shape = (256, 192)
+ output_hm_shape = (16, 16, 12)
+ # output_hm_shape = (8, 8, 6)
+ input_hand_shape = (256, 256)
+ # output_hand_hm_shape = (8, 8, 8)
+ output_hand_hm_shape = (16, 16, 16)
+ input_face_shape = (192, 192)
+ focal = (5000, 5000) # virtual focal lengths
+ princpt = (input_body_shape[1]/2, input_body_shape[0]/2) # virtual principal point position
+ body_3d_size = 2
+ hand_3d_size = 0.3
+ face_3d_size = 0.3
+ camera_3d_size = 2.5
+
+ ## human models
+ flame_shape_params = 100
+ flame_expression_params = 50
+
+ ## directory
+ cur_dir = osp.dirname(os.path.abspath(__file__))
+
+ human_model_path = osp.join(cur_dir, 'utils', 'human_model_files')
+
+cfg = Config()
diff --git a/grounded-sam-osx/install.sh b/grounded-sam-osx/install.sh
new file mode 100644
index 0000000000000000000000000000000000000000..9590f3e371632cb012f459281cf8e78bec99c371
--- /dev/null
+++ b/grounded-sam-osx/install.sh
@@ -0,0 +1,5 @@
+#!/bin/bash
+pip install openmim
+mim install mmcv-full==1.7.1
+pip install -r requirements.txt
+cd transformer_utils && python setup.py install
\ No newline at end of file
diff --git a/grounded-sam-osx/nets/__init__.py b/grounded-sam-osx/nets/__init__.py
new file mode 100644
index 0000000000000000000000000000000000000000..e69de29bb2d1d6434b8b29ae775ad8c2e48c5391
diff --git a/grounded-sam-osx/nets/layer.py b/grounded-sam-osx/nets/layer.py
new file mode 100644
index 0000000000000000000000000000000000000000..a316ae923fd35138971786edd76b2cfd98382238
--- /dev/null
+++ b/grounded-sam-osx/nets/layer.py
@@ -0,0 +1,56 @@
+import torch
+import torch.nn as nn
+from torch.nn import functional as F
+from config import cfg
+
+def make_linear_layers(feat_dims, relu_final=True, use_bn=False):
+ layers = []
+ for i in range(len(feat_dims)-1):
+ layers.append(nn.Linear(feat_dims[i], feat_dims[i+1]))
+
+ # Do not use ReLU for final estimation
+ if i < len(feat_dims)-2 or (i == len(feat_dims)-2 and relu_final):
+ if use_bn:
+ layers.append(nn.BatchNorm1d(feat_dims[i+1]))
+ layers.append(nn.ReLU(inplace=True))
+
+ return nn.Sequential(*layers)
+
+def make_conv_layers(feat_dims, kernel=3, stride=1, padding=1, bnrelu_final=True):
+ layers = []
+ for i in range(len(feat_dims)-1):
+ layers.append(
+ nn.Conv2d(
+ in_channels=feat_dims[i],
+ out_channels=feat_dims[i+1],
+ kernel_size=kernel,
+ stride=stride,
+ padding=padding
+ ))
+ # Do not use BN and ReLU for final estimation
+ if i < len(feat_dims)-2 or (i == len(feat_dims)-2 and bnrelu_final):
+ layers.append(nn.BatchNorm2d(feat_dims[i+1]))
+ layers.append(nn.ReLU(inplace=True))
+
+ return nn.Sequential(*layers)
+
+def make_deconv_layers(feat_dims, bnrelu_final=True):
+ layers = []
+ for i in range(len(feat_dims)-1):
+ layers.append(
+ nn.ConvTranspose2d(
+ in_channels=feat_dims[i],
+ out_channels=feat_dims[i+1],
+ kernel_size=4,
+ stride=2,
+ padding=1,
+ output_padding=0,
+ bias=False))
+
+ # Do not use BN and ReLU for final estimation
+ if i < len(feat_dims)-2 or (i == len(feat_dims)-2 and bnrelu_final):
+ layers.append(nn.BatchNorm2d(feat_dims[i+1]))
+ layers.append(nn.ReLU(inplace=True))
+
+ return nn.Sequential(*layers)
+
diff --git a/grounded-sam-osx/nets/module.py b/grounded-sam-osx/nets/module.py
new file mode 100644
index 0000000000000000000000000000000000000000..630c8d1c721879dafd3e0d436ad6f29cb4675a22
--- /dev/null
+++ b/grounded-sam-osx/nets/module.py
@@ -0,0 +1,172 @@
+import torch
+import torch.nn as nn
+from torch.nn import functional as F
+from nets.layer import make_conv_layers, make_linear_layers, make_deconv_layers
+from utils.transforms import sample_joint_features, soft_argmax_2d, soft_argmax_3d
+from utils.human_models import smpl_x
+from config import cfg
+from mmcv.ops.roi_align import roi_align
+
+class PositionNet(nn.Module):
+ def __init__(self, part, feat_dim=768):
+ super(PositionNet, self).__init__()
+ if part == 'body':
+ self.joint_num = len(smpl_x.pos_joint_part['body'])
+ self.hm_shape = cfg.output_hm_shape
+ elif part == 'hand':
+ self.joint_num = len(smpl_x.pos_joint_part['rhand'])
+ self.hm_shape = cfg.output_hand_hm_shape
+ self.conv = make_conv_layers([feat_dim, self.joint_num * self.hm_shape[0]], kernel=1, stride=1, padding=0, bnrelu_final=False)
+
+ def forward(self, img_feat):
+ joint_hm = self.conv(img_feat).view(-1, self.joint_num, self.hm_shape[0], self.hm_shape[1], self.hm_shape[2])
+ joint_coord = soft_argmax_3d(joint_hm)
+ joint_hm = F.softmax(joint_hm.view(-1, self.joint_num, self.hm_shape[0] * self.hm_shape[1] * self.hm_shape[2]), 2)
+ joint_hm = joint_hm.view(-1, self.joint_num, self.hm_shape[0], self.hm_shape[1], self.hm_shape[2])
+ return joint_hm, joint_coord
+
+class HandRotationNet(nn.Module):
+ def __init__(self, part, feat_dim = 768):
+ super(HandRotationNet, self).__init__()
+ self.part = part
+ self.joint_num = len(smpl_x.pos_joint_part['rhand'])
+ self.hand_conv = make_conv_layers([feat_dim, 512], kernel=1, stride=1, padding=0)
+ self.hand_pose_out = make_linear_layers([self.joint_num * 515, len(smpl_x.orig_joint_part['rhand']) * 6], relu_final=False)
+ self.feat_dim = feat_dim
+
+ def forward(self, img_feat, joint_coord_img):
+ batch_size = img_feat.shape[0]
+ img_feat = self.hand_conv(img_feat)
+ img_feat_joints = sample_joint_features(img_feat, joint_coord_img[:, :, :2])
+ feat = torch.cat((img_feat_joints, joint_coord_img), 2) # batch_size, joint_num, 512+3
+ hand_pose = self.hand_pose_out(feat.view(batch_size, -1))
+ return hand_pose
+
+class BodyRotationNet(nn.Module):
+ def __init__(self, feat_dim = 768):
+ super(BodyRotationNet, self).__init__()
+ self.joint_num = len(smpl_x.pos_joint_part['body'])
+ self.body_conv = make_linear_layers([feat_dim, 512], relu_final=False)
+ self.root_pose_out = make_linear_layers([self.joint_num * (512+3), 6], relu_final=False)
+ self.body_pose_out = make_linear_layers(
+ [self.joint_num * (512+3), (len(smpl_x.orig_joint_part['body']) - 1) * 6], relu_final=False) # without root
+ self.shape_out = make_linear_layers([feat_dim, smpl_x.shape_param_dim], relu_final=False)
+ self.cam_out = make_linear_layers([feat_dim, 3], relu_final=False)
+ self.feat_dim = feat_dim
+
+ def forward(self, body_pose_token, shape_token, cam_token, body_joint_img):
+ batch_size = body_pose_token.shape[0]
+
+ # shape parameter
+ shape_param = self.shape_out(shape_token)
+
+ # camera parameter
+ cam_param = self.cam_out(cam_token)
+
+ # body pose parameter
+ body_pose_token = self.body_conv(body_pose_token)
+ body_pose_token = torch.cat((body_pose_token, body_joint_img), 2)
+ root_pose = self.root_pose_out(body_pose_token.view(batch_size, -1))
+ body_pose = self.body_pose_out(body_pose_token.view(batch_size, -1))
+
+ return root_pose, body_pose, shape_param, cam_param
+
+class FaceRegressor(nn.Module):
+ def __init__(self, feat_dim=768):
+ super(FaceRegressor, self).__init__()
+ self.expr_out = make_linear_layers([feat_dim, smpl_x.expr_code_dim], relu_final=False)
+ self.jaw_pose_out = make_linear_layers([feat_dim, 6], relu_final=False)
+
+ def forward(self, expr_token, jaw_pose_token):
+ expr_param = self.expr_out(expr_token) # expression parameter
+ jaw_pose = self.jaw_pose_out(jaw_pose_token) # jaw pose parameter
+ return expr_param, jaw_pose
+
+class BoxNet(nn.Module):
+ def __init__(self, feat_dim=768):
+ super(BoxNet, self).__init__()
+ self.joint_num = len(smpl_x.pos_joint_part['body'])
+ self.deconv = make_deconv_layers([feat_dim + self.joint_num * cfg.output_hm_shape[0], 256, 256, 256])
+ self.bbox_center = make_conv_layers([256, 3], kernel=1, stride=1, padding=0, bnrelu_final=False)
+ self.lhand_size = make_linear_layers([256, 256, 2], relu_final=False)
+ self.rhand_size = make_linear_layers([256, 256, 2], relu_final=False)
+ self.face_size = make_linear_layers([256, 256, 2], relu_final=False)
+
+ def forward(self, img_feat, joint_hm):
+ joint_hm = joint_hm.view(joint_hm.shape[0], joint_hm.shape[1] * cfg.output_hm_shape[0], cfg.output_hm_shape[1], cfg.output_hm_shape[2])
+ img_feat = torch.cat((img_feat, joint_hm), 1)
+ img_feat = self.deconv(img_feat)
+
+ # bbox center
+ bbox_center_hm = self.bbox_center(img_feat)
+ bbox_center = soft_argmax_2d(bbox_center_hm)
+ lhand_center, rhand_center, face_center = bbox_center[:, 0, :], bbox_center[:, 1, :], bbox_center[:, 2, :]
+
+ # bbox size
+ lhand_feat = sample_joint_features(img_feat, lhand_center[:, None, :].detach())[:, 0, :]
+ lhand_size = self.lhand_size(lhand_feat)
+ rhand_feat = sample_joint_features(img_feat, rhand_center[:, None, :].detach())[:, 0, :]
+ rhand_size = self.rhand_size(rhand_feat)
+ face_feat = sample_joint_features(img_feat, face_center[:, None, :].detach())[:, 0, :]
+ face_size = self.face_size(face_feat)
+
+ lhand_center = lhand_center / 8
+ rhand_center = rhand_center / 8
+ face_center = face_center / 8
+ return lhand_center, lhand_size, rhand_center, rhand_size, face_center, face_size
+
+class BoxSizeNet(nn.Module):
+ def __init__(self):
+ super(BoxSizeNet, self).__init__()
+ self.lhand_size = make_linear_layers([256, 256, 2], relu_final=False)
+ self.rhand_size = make_linear_layers([256, 256, 2], relu_final=False)
+ self.face_size = make_linear_layers([256, 256, 2], relu_final=False)
+
+ def forward(self, box_fea):
+ # box_fea: [bs, 3, C]
+ lhand_size = self.lhand_size(box_fea[:, 0])
+ rhand_size = self.rhand_size(box_fea[:, 1])
+ face_size = self.face_size(box_fea[:, 2])
+ return lhand_size, rhand_size, face_size
+
+class HandRoI(nn.Module):
+ def __init__(self, feat_dim=768, upscale=4):
+ super(HandRoI, self).__init__()
+ self.upscale = upscale
+ if upscale==1:
+ self.deconv = make_conv_layers([feat_dim, feat_dim], kernel=1, stride=1, padding=0, bnrelu_final=False)
+ self.conv = make_conv_layers([feat_dim, feat_dim], kernel=1, stride=1, padding=0, bnrelu_final=False)
+ elif upscale==2:
+ self.deconv = make_deconv_layers([feat_dim, feat_dim//2])
+ self.conv = make_conv_layers([feat_dim//2, feat_dim], kernel=1, stride=1, padding=0, bnrelu_final=False)
+ elif upscale==4:
+ self.deconv = make_deconv_layers([feat_dim, feat_dim//2, feat_dim//4])
+ self.conv = make_conv_layers([feat_dim//4, feat_dim], kernel=1, stride=1, padding=0, bnrelu_final=False)
+ elif upscale==8:
+ self.deconv = make_deconv_layers([feat_dim, feat_dim//2, feat_dim//4, feat_dim//8])
+ self.conv = make_conv_layers([feat_dim//8, feat_dim], kernel=1, stride=1, padding=0, bnrelu_final=False)
+
+ def forward(self, img_feat, lhand_bbox, rhand_bbox):
+ lhand_bbox = torch.cat((torch.arange(lhand_bbox.shape[0]).float().cuda()[:, None], lhand_bbox),
+ 1) # batch_idx, xmin, ymin, xmax, ymax
+ rhand_bbox = torch.cat((torch.arange(rhand_bbox.shape[0]).float().cuda()[:, None], rhand_bbox),
+ 1) # batch_idx, xmin, ymin, xmax, ymax
+ img_feat = self.deconv(img_feat)
+ lhand_bbox_roi = lhand_bbox.clone()
+ lhand_bbox_roi[:, 1] = lhand_bbox_roi[:, 1] / cfg.input_body_shape[1] * cfg.output_hm_shape[2] * self.upscale
+ lhand_bbox_roi[:, 2] = lhand_bbox_roi[:, 2] / cfg.input_body_shape[0] * cfg.output_hm_shape[1] * self.upscale
+ lhand_bbox_roi[:, 3] = lhand_bbox_roi[:, 3] / cfg.input_body_shape[1] * cfg.output_hm_shape[2] * self.upscale
+ lhand_bbox_roi[:, 4] = lhand_bbox_roi[:, 4] / cfg.input_body_shape[0] * cfg.output_hm_shape[1] * self.upscale
+ assert (cfg.output_hm_shape[1]*self.upscale, cfg.output_hm_shape[2]*self.upscale) == (img_feat.shape[2], img_feat.shape[3])
+ lhand_img_feat = roi_align(img_feat, lhand_bbox_roi, (cfg.output_hand_hm_shape[1], cfg.output_hand_hm_shape[2]), 1.0, 0, 'avg', False)
+ lhand_img_feat = torch.flip(lhand_img_feat, [3]) # flip to the right hand
+
+ rhand_bbox_roi = rhand_bbox.clone()
+ rhand_bbox_roi[:, 1] = rhand_bbox_roi[:, 1] / cfg.input_body_shape[1] * cfg.output_hm_shape[2] * self.upscale
+ rhand_bbox_roi[:, 2] = rhand_bbox_roi[:, 2] / cfg.input_body_shape[0] * cfg.output_hm_shape[1] * self.upscale
+ rhand_bbox_roi[:, 3] = rhand_bbox_roi[:, 3] / cfg.input_body_shape[1] * cfg.output_hm_shape[2] * self.upscale
+ rhand_bbox_roi[:, 4] = rhand_bbox_roi[:, 4] / cfg.input_body_shape[0] * cfg.output_hm_shape[1] * self.upscale
+ rhand_img_feat = roi_align(img_feat, rhand_bbox_roi, (cfg.output_hand_hm_shape[1], cfg.output_hand_hm_shape[2]), 1.0, 0, 'avg', False)
+ hand_img_feat = torch.cat((lhand_img_feat, rhand_img_feat)) # [bs, c, cfg.output_hand_hm_shape[2]*scale, cfg.output_hand_hm_shape[1]*scale]
+ hand_img_feat = self.conv(hand_img_feat)
+ return hand_img_feat
\ No newline at end of file
diff --git a/grounded-sam-osx/osx.py b/grounded-sam-osx/osx.py
new file mode 100644
index 0000000000000000000000000000000000000000..b4da24d75cdd4b3217cf9b1efc5ff286b411ae3c
--- /dev/null
+++ b/grounded-sam-osx/osx.py
@@ -0,0 +1,153 @@
+import torch
+import torch.nn as nn
+from torch.nn import functional as F
+from nets.module import PositionNet, HandRotationNet, FaceRegressor, BoxNet, HandRoI, BodyRotationNet
+
+from utils.human_models import smpl_x
+from utils.transforms import rot6d_to_axis_angle, restore_bbox
+from config import cfg
+import math
+import copy
+from mmpose.models import build_posenet
+from mmcv import Config
+
+class Model(nn.Module):
+ def __init__(self, encoder, body_position_net, body_rotation_net, box_net, hand_position_net, hand_roi_net,
+ hand_rotation_net, face_regressor):
+ super(Model, self).__init__()
+
+ # body
+ self.backbone = encoder
+ self.body_position_net = body_position_net
+ self.body_rotation_net = body_rotation_net
+ self.box_net = box_net
+
+ # hand
+ self.hand_roi_net = hand_roi_net
+ self.hand_position_net = hand_position_net
+ self.hand_rotation_net = hand_rotation_net
+
+ # face
+ self.face_regressor = face_regressor
+
+ self.smplx_layer = copy.deepcopy(smpl_x.layer['neutral']).cuda()
+
+ self.body_num_joints = len(smpl_x.pos_joint_part['body'])
+ self.hand_joint_num = len(smpl_x.pos_joint_part['rhand'])
+
+ def get_camera_trans(self, cam_param):
+ # camera translation
+ t_xy = cam_param[:, :2]
+ gamma = torch.sigmoid(cam_param[:, 2]) # apply sigmoid to make it positive
+ k_value = torch.FloatTensor([math.sqrt(cfg.focal[0] * cfg.focal[1] * cfg.camera_3d_size * cfg.camera_3d_size / (
+ cfg.input_body_shape[0] * cfg.input_body_shape[1]))]).cuda().view(-1)
+ t_z = k_value * gamma
+ cam_trans = torch.cat((t_xy, t_z[:, None]), 1)
+ return cam_trans
+
+ def get_coord(self, root_pose, body_pose, lhand_pose, rhand_pose, jaw_pose, shape, expr, cam_trans, mode):
+ batch_size = root_pose.shape[0]
+ zero_pose = torch.zeros((1, 3)).float().cuda().repeat(batch_size, 1) # eye poses
+ output = self.smplx_layer(betas=shape, body_pose=body_pose, global_orient=root_pose, right_hand_pose=rhand_pose,
+ left_hand_pose=lhand_pose, jaw_pose=jaw_pose, leye_pose=zero_pose,
+ reye_pose=zero_pose, expression=expr)
+ # camera-centered 3D coordinate
+ vertices = output.vertices
+ # root-relative 3D coordinates
+ mesh_cam = vertices + cam_trans[:, None, :] # for rendering
+
+ return mesh_cam
+
+ def forward(self, inputs, mode):
+
+ # backbone
+ body_img = F.interpolate(inputs['img'], cfg.input_body_shape)
+
+ # 1. Encoder
+ img_feat, task_tokens = self.backbone(body_img) # task_token:[bs, N, c]
+ shape_token, cam_token, expr_token, jaw_pose_token, hand_token, body_pose_token = \
+ task_tokens[:, 0], task_tokens[:, 1], task_tokens[:, 2], task_tokens[:, 3], task_tokens[:,
+ 4:6], task_tokens[:, 6:]
+
+ # 2. Body Regressor
+ body_joint_hm, body_joint_img = self.body_position_net(img_feat)
+ root_pose, body_pose, shape, cam_param, = self.body_rotation_net(body_pose_token, shape_token, cam_token,
+ body_joint_img.detach())
+ root_pose = rot6d_to_axis_angle(root_pose)
+ body_pose = rot6d_to_axis_angle(body_pose.reshape(-1, 6)).reshape(body_pose.shape[0], -1) # (N, J_R*3)
+ cam_trans = self.get_camera_trans(cam_param)
+
+ # 3. Hand and Face BBox Estimation
+ lhand_bbox_center, lhand_bbox_size, rhand_bbox_center, rhand_bbox_size, face_bbox_center, face_bbox_size = self.box_net(
+ img_feat, body_joint_hm.detach())
+ lhand_bbox = restore_bbox(lhand_bbox_center, lhand_bbox_size, cfg.input_hand_shape[1] / cfg.input_hand_shape[0],
+ 2.0).detach() # xyxy in (cfg.input_body_shape[1], cfg.input_body_shape[0]) space
+ rhand_bbox = restore_bbox(rhand_bbox_center, rhand_bbox_size, cfg.input_hand_shape[1] / cfg.input_hand_shape[0],
+ 2.0).detach() # xyxy in (cfg.input_body_shape[1], cfg.input_body_shape[0]) space
+
+ # 4. Differentiable Feature-level Hand Crop-Upsample
+ # hand_feat: list, [bsx2, c, cfg.output_hm_shape[1]*scale, cfg.output_hm_shape[2]*scale]
+ hand_feat = self.hand_roi_net(img_feat, lhand_bbox, rhand_bbox) # hand_feat: flipped left hand + right hand
+
+ # 5. Hand/Face Regressor
+ # hand regressor
+ _, hand_joint_img = self.hand_position_net(hand_feat) # (2N, J_P, 3)
+ hand_pose = self.hand_rotation_net(hand_feat, hand_joint_img.detach())
+ hand_pose = rot6d_to_axis_angle(hand_pose.reshape(-1, 6)).reshape(hand_feat.shape[0], -1) # (2N, J_R*3)
+ batch_size = hand_pose.shape[0] // 2
+ lhand_pose = hand_pose[:batch_size, :].reshape(-1, len(smpl_x.orig_joint_part['lhand']), 3)
+ lhand_pose = torch.cat((lhand_pose[:, :, 0:1], -lhand_pose[:, :, 1:3]), 2).view(batch_size, -1)
+ rhand_pose = hand_pose[batch_size:, :]
+
+ # hand regressor
+ expr, jaw_pose = self.face_regressor(expr_token, jaw_pose_token)
+ jaw_pose = rot6d_to_axis_angle(jaw_pose)
+
+ # final output
+ mesh_cam = self.get_coord(root_pose, body_pose, lhand_pose, rhand_pose, jaw_pose, shape,
+ expr, cam_trans, mode)
+ # test output
+ out = {}
+ out['smplx_mesh_cam'] = mesh_cam
+ return out
+
+
+def init_weights(m):
+ try:
+ if type(m) == nn.ConvTranspose2d:
+ nn.init.normal_(m.weight, std=0.001)
+ elif type(m) == nn.Conv2d:
+ nn.init.normal_(m.weight, std=0.001)
+ nn.init.constant_(m.bias, 0)
+ elif type(m) == nn.BatchNorm2d:
+ nn.init.constant_(m.weight, 1)
+ nn.init.constant_(m.bias, 0)
+ elif type(m) == nn.Linear:
+ nn.init.normal_(m.weight, std=0.01)
+ nn.init.constant_(m.bias, 0)
+ except AttributeError:
+ pass
+
+def get_model():
+ # body
+ vit_cfg = Config.fromfile(cfg.encoder_config_file)
+ vit = build_posenet(vit_cfg.model)
+ body_position_net = PositionNet('body', feat_dim=cfg.feat_dim)
+ body_rotation_net = BodyRotationNet(feat_dim=cfg.feat_dim)
+ box_net = BoxNet(feat_dim=cfg.feat_dim)
+
+ # hand
+ hand_position_net = PositionNet('hand', feat_dim=cfg.feat_dim)
+ hand_roi_net = HandRoI(feat_dim=cfg.feat_dim, upscale=cfg.upscale)
+ hand_rotation_net = HandRotationNet('hand', feat_dim=cfg.feat_dim)
+
+ # face
+ face_regressor = FaceRegressor(feat_dim=cfg.feat_dim)
+
+ # scale
+ encoder = vit.backbone
+ model = Model(encoder, body_position_net, body_rotation_net, box_net, hand_position_net, hand_roi_net,
+ hand_rotation_net,
+ face_regressor)
+
+ return model
diff --git a/grounded-sam-osx/requirements.txt b/grounded-sam-osx/requirements.txt
new file mode 100644
index 0000000000000000000000000000000000000000..ee29e184451e8303a129ab6837a941de84f67766
--- /dev/null
+++ b/grounded-sam-osx/requirements.txt
@@ -0,0 +1,28 @@
+numpy
+scikit-image
+scipy
+scikit-learn
+smplx==0.1.28
+tqdm
+yacs
+numba
+opencv-python
+tensorboardx
+filterpy
+cython
+chumpy
+Pillow
+trimesh
+pyrender
+matplotlib
+json_tricks
+torchgeometry
+einops
+joblib
+boto3
+requests
+easydict
+pycocotools
+plyfile
+timm
+pyglet==1.5.27
diff --git a/grounded-sam-osx/transformer_utils/.gitignore b/grounded-sam-osx/transformer_utils/.gitignore
new file mode 100644
index 0000000000000000000000000000000000000000..e792015fe7abb9597efbe787d25d0c4d242ef42b
--- /dev/null
+++ b/grounded-sam-osx/transformer_utils/.gitignore
@@ -0,0 +1,141 @@
+
+
+# Byte-compiled / optimized / DLL files
+__pycache__/
+*.py[cod]
+*$py.class
+**/*.pyc
+
+# C extensions
+*.so
+
+# Distribution / packaging
+.Python
+build/
+develop-eggs/
+dist/
+downloads/
+eggs/
+.eggs/
+lib/
+lib64/
+parts/
+sdist/
+var/
+wheels/
+*.egg-info/
+.installed.cfg
+*.egg
+MANIFEST
+
+# PyInstaller
+# Usually these files are written by a python script from a template
+# before PyInstaller builds the exe, so as to inject date/other infos into it.
+*.manifest
+*.spec
+
+# Installer logs
+pip-log.txt
+pip-delete-this-directory.txt
+
+# Unit test / coverage reports
+htmlcov/
+.tox/
+.coverage
+.coverage.*
+.cache
+nosetests.xml
+coverage.xml
+*.cover
+.hypothesis/
+.pytest_cache/
+
+# Translations
+*.mo
+*.pot
+
+# Django stuff:
+*.log
+local_settings.py
+db.sqlite3
+
+# Flask stuff:
+instance/
+.webassets-cache
+
+# Scrapy stuff:
+.scrapy
+
+# Sphinx documentation
+docs/en/_build
+docs/zh_cn/_build
+
+# PyBuilder
+target/
+
+# Jupyter Notebook
+.ipynb_checkpoints
+
+# pyenv
+.python-version
+
+# celery beat schedule file
+celerybeat-schedule
+
+# SageMath parsed files
+*.sage.py
+
+# Environments
+.env
+.venv
+env/
+venv/
+ENV/
+env.bak/
+venv.bak/
+
+# Spyder project settings
+.spyderproject
+.spyproject
+
+# Rope project settings
+.ropeproject
+
+# mkdocs documentation
+/site
+
+# mypy
+.mypy_cache/
+
+# custom
+mmpose/.mim
+/models
+/data
+.vscode
+.idea
+*.pkl
+*.pkl.json
+*.log.json
+*.npy
+work_dirs/
+docs/**/topics/
+docs/**/papers/*.md
+docs/**/datasets.md
+docs/**/modelzoo.md
+
+!tests/data/**/*.pkl
+!tests/data/**/*.pkl.json
+!tests/data/**/*.log.json
+!tests/data/**/*.pth
+!tests/data/**/*.npy
+
+# Pytorch
+*.pth
+
+*.DS_Store
+
+# checkpoints
+ckpts/
+vis_results
+vis_results_poseur
+scripts
\ No newline at end of file
diff --git a/grounded-sam-osx/transformer_utils/CITATION.cff b/grounded-sam-osx/transformer_utils/CITATION.cff
new file mode 100644
index 0000000000000000000000000000000000000000..067f4ff996793aa8b8a5f39d35f43c0e275cfa64
--- /dev/null
+++ b/grounded-sam-osx/transformer_utils/CITATION.cff
@@ -0,0 +1,8 @@
+cff-version: 1.2.0
+message: "If you use this software, please cite it as below."
+authors:
+ - name: "Poseur Contributors"
+title: "Poseur: Direct Human Pose Regression with Transformers"
+date-released: 2022-07-21
+url: "https://github.com/aim-uofa/Poseur"
+license: 2-clause BSD
diff --git a/grounded-sam-osx/transformer_utils/LICENSE b/grounded-sam-osx/transformer_utils/LICENSE
new file mode 100644
index 0000000000000000000000000000000000000000..acab10d9e2ab392bd0839978663306846c56aca3
--- /dev/null
+++ b/grounded-sam-osx/transformer_utils/LICENSE
@@ -0,0 +1,677 @@
+Poseur for non-commercial purposes
+(For commercial use, contact chhshen@gmail.com for obtaining a commerical license.)
+
+ GNU GENERAL PUBLIC LICENSE
+ Version 3, 29 June 2007
+
+ Copyright (C) 2007 Free Software Foundation, Inc.
+ Everyone is permitted to copy and distribute verbatim copies
+ of this license document, but changing it is not allowed.
+
+ Preamble
+
+ The GNU General Public License is a free, copyleft license for
+software and other kinds of works.
+
+ The licenses for most software and other practical works are designed
+to take away your freedom to share and change the works. By contrast,
+the GNU General Public License is intended to guarantee your freedom to
+share and change all versions of a program--to make sure it remains free
+software for all its users. We, the Free Software Foundation, use the
+GNU General Public License for most of our software; it applies also to
+any other work released this way by its authors. You can apply it to
+your programs, too.
+
+ When we speak of free software, we are referring to freedom, not
+price. Our General Public Licenses are designed to make sure that you
+have the freedom to distribute copies of free software (and charge for
+them if you wish), that you receive source code or can get it if you
+want it, that you can change the software or use pieces of it in new
+free programs, and that you know you can do these things.
+
+ To protect your rights, we need to prevent others from denying you
+these rights or asking you to surrender the rights. Therefore, you have
+certain responsibilities if you distribute copies of the software, or if
+you modify it: responsibilities to respect the freedom of others.
+
+ For example, if you distribute copies of such a program, whether
+gratis or for a fee, you must pass on to the recipients the same
+freedoms that you received. You must make sure that they, too, receive
+or can get the source code. And you must show them these terms so they
+know their rights.
+
+ Developers that use the GNU GPL protect your rights with two steps:
+(1) assert copyright on the software, and (2) offer you this License
+giving you legal permission to copy, distribute and/or modify it.
+
+ For the developers' and authors' protection, the GPL clearly explains
+that there is no warranty for this free software. For both users' and
+authors' sake, the GPL requires that modified versions be marked as
+changed, so that their problems will not be attributed erroneously to
+authors of previous versions.
+
+ Some devices are designed to deny users access to install or run
+modified versions of the software inside them, although the manufacturer
+can do so. This is fundamentally incompatible with the aim of
+protecting users' freedom to change the software. The systematic
+pattern of such abuse occurs in the area of products for individuals to
+use, which is precisely where it is most unacceptable. Therefore, we
+have designed this version of the GPL to prohibit the practice for those
+products. If such problems arise substantially in other domains, we
+stand ready to extend this provision to those domains in future versions
+of the GPL, as needed to protect the freedom of users.
+
+ Finally, every program is threatened constantly by software patents.
+States should not allow patents to restrict development and use of
+software on general-purpose computers, but in those that do, we wish to
+avoid the special danger that patents applied to a free program could
+make it effectively proprietary. To prevent this, the GPL assures that
+patents cannot be used to render the program non-free.
+
+ The precise terms and conditions for copying, distribution and
+modification follow.
+
+ TERMS AND CONDITIONS
+
+ 0. Definitions.
+
+ "This License" refers to version 3 of the GNU General Public License.
+
+ "Copyright" also means copyright-like laws that apply to other kinds of
+works, such as semiconductor masks.
+
+ "The Program" refers to any copyrightable work licensed under this
+License. Each licensee is addressed as "you". "Licensees" and
+"recipients" may be individuals or organizations.
+
+ To "modify" a work means to copy from or adapt all or part of the work
+in a fashion requiring copyright permission, other than the making of an
+exact copy. The resulting work is called a "modified version" of the
+earlier work or a work "based on" the earlier work.
+
+ A "covered work" means either the unmodified Program or a work based
+on the Program.
+
+ To "propagate" a work means to do anything with it that, without
+permission, would make you directly or secondarily liable for
+infringement under applicable copyright law, except executing it on a
+computer or modifying a private copy. Propagation includes copying,
+distribution (with or without modification), making available to the
+public, and in some countries other activities as well.
+
+ To "convey" a work means any kind of propagation that enables other
+parties to make or receive copies. Mere interaction with a user through
+a computer network, with no transfer of a copy, is not conveying.
+
+ An interactive user interface displays "Appropriate Legal Notices"
+to the extent that it includes a convenient and prominently visible
+feature that (1) displays an appropriate copyright notice, and (2)
+tells the user that there is no warranty for the work (except to the
+extent that warranties are provided), that licensees may convey the
+work under this License, and how to view a copy of this License. If
+the interface presents a list of user commands or options, such as a
+menu, a prominent item in the list meets this criterion.
+
+ 1. Source Code.
+
+ The "source code" for a work means the preferred form of the work
+for making modifications to it. "Object code" means any non-source
+form of a work.
+
+ A "Standard Interface" means an interface that either is an official
+standard defined by a recognized standards body, or, in the case of
+interfaces specified for a particular programming language, one that
+is widely used among developers working in that language.
+
+ The "System Libraries" of an executable work include anything, other
+than the work as a whole, that (a) is included in the normal form of
+packaging a Major Component, but which is not part of that Major
+Component, and (b) serves only to enable use of the work with that
+Major Component, or to implement a Standard Interface for which an
+implementation is available to the public in source code form. A
+"Major Component", in this context, means a major essential component
+(kernel, window system, and so on) of the specific operating system
+(if any) on which the executable work runs, or a compiler used to
+produce the work, or an object code interpreter used to run it.
+
+ The "Corresponding Source" for a work in object code form means all
+the source code needed to generate, install, and (for an executable
+work) run the object code and to modify the work, including scripts to
+control those activities. However, it does not include the work's
+System Libraries, or general-purpose tools or generally available free
+programs which are used unmodified in performing those activities but
+which are not part of the work. For example, Corresponding Source
+includes interface definition files associated with source files for
+the work, and the source code for shared libraries and dynamically
+linked subprograms that the work is specifically designed to require,
+such as by intimate data communication or control flow between those
+subprograms and other parts of the work.
+
+ The Corresponding Source need not include anything that users
+can regenerate automatically from other parts of the Corresponding
+Source.
+
+ The Corresponding Source for a work in source code form is that
+same work.
+
+ 2. Basic Permissions.
+
+ All rights granted under this License are granted for the term of
+copyright on the Program, and are irrevocable provided the stated
+conditions are met. This License explicitly affirms your unlimited
+permission to run the unmodified Program. The output from running a
+covered work is covered by this License only if the output, given its
+content, constitutes a covered work. This License acknowledges your
+rights of fair use or other equivalent, as provided by copyright law.
+
+ You may make, run and propagate covered works that you do not
+convey, without conditions so long as your license otherwise remains
+in force. You may convey covered works to others for the sole purpose
+of having them make modifications exclusively for you, or provide you
+with facilities for running those works, provided that you comply with
+the terms of this License in conveying all material for which you do
+not control copyright. Those thus making or running the covered works
+for you must do so exclusively on your behalf, under your direction
+and control, on terms that prohibit them from making any copies of
+your copyrighted material outside their relationship with you.
+
+ Conveying under any other circumstances is permitted solely under
+the conditions stated below. Sublicensing is not allowed; section 10
+makes it unnecessary.
+
+ 3. Protecting Users' Legal Rights From Anti-Circumvention Law.
+
+ No covered work shall be deemed part of an effective technological
+measure under any applicable law fulfilling obligations under article
+11 of the WIPO copyright treaty adopted on 20 December 1996, or
+similar laws prohibiting or restricting circumvention of such
+measures.
+
+ When you convey a covered work, you waive any legal power to forbid
+circumvention of technological measures to the extent such circumvention
+is effected by exercising rights under this License with respect to
+the covered work, and you disclaim any intention to limit operation or
+modification of the work as a means of enforcing, against the work's
+users, your or third parties' legal rights to forbid circumvention of
+technological measures.
+
+ 4. Conveying Verbatim Copies.
+
+ You may convey verbatim copies of the Program's source code as you
+receive it, in any medium, provided that you conspicuously and
+appropriately publish on each copy an appropriate copyright notice;
+keep intact all notices stating that this License and any
+non-permissive terms added in accord with section 7 apply to the code;
+keep intact all notices of the absence of any warranty; and give all
+recipients a copy of this License along with the Program.
+
+ You may charge any price or no price for each copy that you convey,
+and you may offer support or warranty protection for a fee.
+
+ 5. Conveying Modified Source Versions.
+
+ You may convey a work based on the Program, or the modifications to
+produce it from the Program, in the form of source code under the
+terms of section 4, provided that you also meet all of these conditions:
+
+ a) The work must carry prominent notices stating that you modified
+ it, and giving a relevant date.
+
+ b) The work must carry prominent notices stating that it is
+ released under this License and any conditions added under section
+ 7. This requirement modifies the requirement in section 4 to
+ "keep intact all notices".
+
+ c) You must license the entire work, as a whole, under this
+ License to anyone who comes into possession of a copy. This
+ License will therefore apply, along with any applicable section 7
+ additional terms, to the whole of the work, and all its parts,
+ regardless of how they are packaged. This License gives no
+ permission to license the work in any other way, but it does not
+ invalidate such permission if you have separately received it.
+
+ d) If the work has interactive user interfaces, each must display
+ Appropriate Legal Notices; however, if the Program has interactive
+ interfaces that do not display Appropriate Legal Notices, your
+ work need not make them do so.
+
+ A compilation of a covered work with other separate and independent
+works, which are not by their nature extensions of the covered work,
+and which are not combined with it such as to form a larger program,
+in or on a volume of a storage or distribution medium, is called an
+"aggregate" if the compilation and its resulting copyright are not
+used to limit the access or legal rights of the compilation's users
+beyond what the individual works permit. Inclusion of a covered work
+in an aggregate does not cause this License to apply to the other
+parts of the aggregate.
+
+ 6. Conveying Non-Source Forms.
+
+ You may convey a covered work in object code form under the terms
+of sections 4 and 5, provided that you also convey the
+machine-readable Corresponding Source under the terms of this License,
+in one of these ways:
+
+ a) Convey the object code in, or embodied in, a physical product
+ (including a physical distribution medium), accompanied by the
+ Corresponding Source fixed on a durable physical medium
+ customarily used for software interchange.
+
+ b) Convey the object code in, or embodied in, a physical product
+ (including a physical distribution medium), accompanied by a
+ written offer, valid for at least three years and valid for as
+ long as you offer spare parts or customer support for that product
+ model, to give anyone who possesses the object code either (1) a
+ copy of the Corresponding Source for all the software in the
+ product that is covered by this License, on a durable physical
+ medium customarily used for software interchange, for a price no
+ more than your reasonable cost of physically performing this
+ conveying of source, or (2) access to copy the
+ Corresponding Source from a network server at no charge.
+
+ c) Convey individual copies of the object code with a copy of the
+ written offer to provide the Corresponding Source. This
+ alternative is allowed only occasionally and noncommercially, and
+ only if you received the object code with such an offer, in accord
+ with subsection 6b.
+
+ d) Convey the object code by offering access from a designated
+ place (gratis or for a charge), and offer equivalent access to the
+ Corresponding Source in the same way through the same place at no
+ further charge. You need not require recipients to copy the
+ Corresponding Source along with the object code. If the place to
+ copy the object code is a network server, the Corresponding Source
+ may be on a different server (operated by you or a third party)
+ that supports equivalent copying facilities, provided you maintain
+ clear directions next to the object code saying where to find the
+ Corresponding Source. Regardless of what server hosts the
+ Corresponding Source, you remain obligated to ensure that it is
+ available for as long as needed to satisfy these requirements.
+
+ e) Convey the object code using peer-to-peer transmission, provided
+ you inform other peers where the object code and Corresponding
+ Source of the work are being offered to the general public at no
+ charge under subsection 6d.
+
+ A separable portion of the object code, whose source code is excluded
+from the Corresponding Source as a System Library, need not be
+included in conveying the object code work.
+
+ A "User Product" is either (1) a "consumer product", which means any
+tangible personal property which is normally used for personal, family,
+or household purposes, or (2) anything designed or sold for incorporation
+into a dwelling. In determining whether a product is a consumer product,
+doubtful cases shall be resolved in favor of coverage. For a particular
+product received by a particular user, "normally used" refers to a
+typical or common use of that class of product, regardless of the status
+of the particular user or of the way in which the particular user
+actually uses, or expects or is expected to use, the product. A product
+is a consumer product regardless of whether the product has substantial
+commercial, industrial or non-consumer uses, unless such uses represent
+the only significant mode of use of the product.
+
+ "Installation Information" for a User Product means any methods,
+procedures, authorization keys, or other information required to install
+and execute modified versions of a covered work in that User Product from
+a modified version of its Corresponding Source. The information must
+suffice to ensure that the continued functioning of the modified object
+code is in no case prevented or interfered with solely because
+modification has been made.
+
+ If you convey an object code work under this section in, or with, or
+specifically for use in, a User Product, and the conveying occurs as
+part of a transaction in which the right of possession and use of the
+User Product is transferred to the recipient in perpetuity or for a
+fixed term (regardless of how the transaction is characterized), the
+Corresponding Source conveyed under this section must be accompanied
+by the Installation Information. But this requirement does not apply
+if neither you nor any third party retains the ability to install
+modified object code on the User Product (for example, the work has
+been installed in ROM).
+
+ The requirement to provide Installation Information does not include a
+requirement to continue to provide support service, warranty, or updates
+for a work that has been modified or installed by the recipient, or for
+the User Product in which it has been modified or installed. Access to a
+network may be denied when the modification itself materially and
+adversely affects the operation of the network or violates the rules and
+protocols for communication across the network.
+
+ Corresponding Source conveyed, and Installation Information provided,
+in accord with this section must be in a format that is publicly
+documented (and with an implementation available to the public in
+source code form), and must require no special password or key for
+unpacking, reading or copying.
+
+ 7. Additional Terms.
+
+ "Additional permissions" are terms that supplement the terms of this
+License by making exceptions from one or more of its conditions.
+Additional permissions that are applicable to the entire Program shall
+be treated as though they were included in this License, to the extent
+that they are valid under applicable law. If additional permissions
+apply only to part of the Program, that part may be used separately
+under those permissions, but the entire Program remains governed by
+this License without regard to the additional permissions.
+
+ When you convey a copy of a covered work, you may at your option
+remove any additional permissions from that copy, or from any part of
+it. (Additional permissions may be written to require their own
+removal in certain cases when you modify the work.) You may place
+additional permissions on material, added by you to a covered work,
+for which you have or can give appropriate copyright permission.
+
+ Notwithstanding any other provision of this License, for material you
+add to a covered work, you may (if authorized by the copyright holders of
+that material) supplement the terms of this License with terms:
+
+ a) Disclaiming warranty or limiting liability differently from the
+ terms of sections 15 and 16 of this License; or
+
+ b) Requiring preservation of specified reasonable legal notices or
+ author attributions in that material or in the Appropriate Legal
+ Notices displayed by works containing it; or
+
+ c) Prohibiting misrepresentation of the origin of that material, or
+ requiring that modified versions of such material be marked in
+ reasonable ways as different from the original version; or
+
+ d) Limiting the use for publicity purposes of names of licensors or
+ authors of the material; or
+
+ e) Declining to grant rights under trademark law for use of some
+ trade names, trademarks, or service marks; or
+
+ f) Requiring indemnification of licensors and authors of that
+ material by anyone who conveys the material (or modified versions of
+ it) with contractual assumptions of liability to the recipient, for
+ any liability that these contractual assumptions directly impose on
+ those licensors and authors.
+
+ All other non-permissive additional terms are considered "further
+restrictions" within the meaning of section 10. If the Program as you
+received it, or any part of it, contains a notice stating that it is
+governed by this License along with a term that is a further
+restriction, you may remove that term. If a license document contains
+a further restriction but permits relicensing or conveying under this
+License, you may add to a covered work material governed by the terms
+of that license document, provided that the further restriction does
+not survive such relicensing or conveying.
+
+ If you add terms to a covered work in accord with this section, you
+must place, in the relevant source files, a statement of the
+additional terms that apply to those files, or a notice indicating
+where to find the applicable terms.
+
+ Additional terms, permissive or non-permissive, may be stated in the
+form of a separately written license, or stated as exceptions;
+the above requirements apply either way.
+
+ 8. Termination.
+
+ You may not propagate or modify a covered work except as expressly
+provided under this License. Any attempt otherwise to propagate or
+modify it is void, and will automatically terminate your rights under
+this License (including any patent licenses granted under the third
+paragraph of section 11).
+
+ However, if you cease all violation of this License, then your
+license from a particular copyright holder is reinstated (a)
+provisionally, unless and until the copyright holder explicitly and
+finally terminates your license, and (b) permanently, if the copyright
+holder fails to notify you of the violation by some reasonable means
+prior to 60 days after the cessation.
+
+ Moreover, your license from a particular copyright holder is
+reinstated permanently if the copyright holder notifies you of the
+violation by some reasonable means, this is the first time you have
+received notice of violation of this License (for any work) from that
+copyright holder, and you cure the violation prior to 30 days after
+your receipt of the notice.
+
+ Termination of your rights under this section does not terminate the
+licenses of parties who have received copies or rights from you under
+this License. If your rights have been terminated and not permanently
+reinstated, you do not qualify to receive new licenses for the same
+material under section 10.
+
+ 9. Acceptance Not Required for Having Copies.
+
+ You are not required to accept this License in order to receive or
+run a copy of the Program. Ancillary propagation of a covered work
+occurring solely as a consequence of using peer-to-peer transmission
+to receive a copy likewise does not require acceptance. However,
+nothing other than this License grants you permission to propagate or
+modify any covered work. These actions infringe copyright if you do
+not accept this License. Therefore, by modifying or propagating a
+covered work, you indicate your acceptance of this License to do so.
+
+ 10. Automatic Licensing of Downstream Recipients.
+
+ Each time you convey a covered work, the recipient automatically
+receives a license from the original licensors, to run, modify and
+propagate that work, subject to this License. You are not responsible
+for enforcing compliance by third parties with this License.
+
+ An "entity transaction" is a transaction transferring control of an
+organization, or substantially all assets of one, or subdividing an
+organization, or merging organizations. If propagation of a covered
+work results from an entity transaction, each party to that
+transaction who receives a copy of the work also receives whatever
+licenses to the work the party's predecessor in interest had or could
+give under the previous paragraph, plus a right to possession of the
+Corresponding Source of the work from the predecessor in interest, if
+the predecessor has it or can get it with reasonable efforts.
+
+ You may not impose any further restrictions on the exercise of the
+rights granted or affirmed under this License. For example, you may
+not impose a license fee, royalty, or other charge for exercise of
+rights granted under this License, and you may not initiate litigation
+(including a cross-claim or counterclaim in a lawsuit) alleging that
+any patent claim is infringed by making, using, selling, offering for
+sale, or importing the Program or any portion of it.
+
+ 11. Patents.
+
+ A "contributor" is a copyright holder who authorizes use under this
+License of the Program or a work on which the Program is based. The
+work thus licensed is called the contributor's "contributor version".
+
+ A contributor's "essential patent claims" are all patent claims
+owned or controlled by the contributor, whether already acquired or
+hereafter acquired, that would be infringed by some manner, permitted
+by this License, of making, using, or selling its contributor version,
+but do not include claims that would be infringed only as a
+consequence of further modification of the contributor version. For
+purposes of this definition, "control" includes the right to grant
+patent sublicenses in a manner consistent with the requirements of
+this License.
+
+ Each contributor grants you a non-exclusive, worldwide, royalty-free
+patent license under the contributor's essential patent claims, to
+make, use, sell, offer for sale, import and otherwise run, modify and
+propagate the contents of its contributor version.
+
+ In the following three paragraphs, a "patent license" is any express
+agreement or commitment, however denominated, not to enforce a patent
+(such as an express permission to practice a patent or covenant not to
+sue for patent infringement). To "grant" such a patent license to a
+party means to make such an agreement or commitment not to enforce a
+patent against the party.
+
+ If you convey a covered work, knowingly relying on a patent license,
+and the Corresponding Source of the work is not available for anyone
+to copy, free of charge and under the terms of this License, through a
+publicly available network server or other readily accessible means,
+then you must either (1) cause the Corresponding Source to be so
+available, or (2) arrange to deprive yourself of the benefit of the
+patent license for this particular work, or (3) arrange, in a manner
+consistent with the requirements of this License, to extend the patent
+license to downstream recipients. "Knowingly relying" means you have
+actual knowledge that, but for the patent license, your conveying the
+covered work in a country, or your recipient's use of the covered work
+in a country, would infringe one or more identifiable patents in that
+country that you have reason to believe are valid.
+
+ If, pursuant to or in connection with a single transaction or
+arrangement, you convey, or propagate by procuring conveyance of, a
+covered work, and grant a patent license to some of the parties
+receiving the covered work authorizing them to use, propagate, modify
+or convey a specific copy of the covered work, then the patent license
+you grant is automatically extended to all recipients of the covered
+work and works based on it.
+
+ A patent license is "discriminatory" if it does not include within
+the scope of its coverage, prohibits the exercise of, or is
+conditioned on the non-exercise of one or more of the rights that are
+specifically granted under this License. You may not convey a covered
+work if you are a party to an arrangement with a third party that is
+in the business of distributing software, under which you make payment
+to the third party based on the extent of your activity of conveying
+the work, and under which the third party grants, to any of the
+parties who would receive the covered work from you, a discriminatory
+patent license (a) in connection with copies of the covered work
+conveyed by you (or copies made from those copies), or (b) primarily
+for and in connection with specific products or compilations that
+contain the covered work, unless you entered into that arrangement,
+or that patent license was granted, prior to 28 March 2007.
+
+ Nothing in this License shall be construed as excluding or limiting
+any implied license or other defenses to infringement that may
+otherwise be available to you under applicable patent law.
+
+ 12. No Surrender of Others' Freedom.
+
+ If conditions are imposed on you (whether by court order, agreement or
+otherwise) that contradict the conditions of this License, they do not
+excuse you from the conditions of this License. If you cannot convey a
+covered work so as to satisfy simultaneously your obligations under this
+License and any other pertinent obligations, then as a consequence you may
+not convey it at all. For example, if you agree to terms that obligate you
+to collect a royalty for further conveying from those to whom you convey
+the Program, the only way you could satisfy both those terms and this
+License would be to refrain entirely from conveying the Program.
+
+ 13. Use with the GNU Affero General Public License.
+
+ Notwithstanding any other provision of this License, you have
+permission to link or combine any covered work with a work licensed
+under version 3 of the GNU Affero General Public License into a single
+combined work, and to convey the resulting work. The terms of this
+License will continue to apply to the part which is the covered work,
+but the special requirements of the GNU Affero General Public License,
+section 13, concerning interaction through a network will apply to the
+combination as such.
+
+ 14. Revised Versions of this License.
+
+ The Free Software Foundation may publish revised and/or new versions of
+the GNU General Public License from time to time. Such new versions will
+be similar in spirit to the present version, but may differ in detail to
+address new problems or concerns.
+
+ Each version is given a distinguishing version number. If the
+Program specifies that a certain numbered version of the GNU General
+Public License "or any later version" applies to it, you have the
+option of following the terms and conditions either of that numbered
+version or of any later version published by the Free Software
+Foundation. If the Program does not specify a version number of the
+GNU General Public License, you may choose any version ever published
+by the Free Software Foundation.
+
+ If the Program specifies that a proxy can decide which future
+versions of the GNU General Public License can be used, that proxy's
+public statement of acceptance of a version permanently authorizes you
+to choose that version for the Program.
+
+ Later license versions may give you additional or different
+permissions. However, no additional obligations are imposed on any
+author or copyright holder as a result of your choosing to follow a
+later version.
+
+ 15. Disclaimer of Warranty.
+
+ THERE IS NO WARRANTY FOR THE PROGRAM, TO THE EXTENT PERMITTED BY
+APPLICABLE LAW. EXCEPT WHEN OTHERWISE STATED IN WRITING THE COPYRIGHT
+HOLDERS AND/OR OTHER PARTIES PROVIDE THE PROGRAM "AS IS" WITHOUT WARRANTY
+OF ANY KIND, EITHER EXPRESSED OR IMPLIED, INCLUDING, BUT NOT LIMITED TO,
+THE IMPLIED WARRANTIES OF MERCHANTABILITY AND FITNESS FOR A PARTICULAR
+PURPOSE. THE ENTIRE RISK AS TO THE QUALITY AND PERFORMANCE OF THE PROGRAM
+IS WITH YOU. SHOULD THE PROGRAM PROVE DEFECTIVE, YOU ASSUME THE COST OF
+ALL NECESSARY SERVICING, REPAIR OR CORRECTION.
+
+ 16. Limitation of Liability.
+
+ IN NO EVENT UNLESS REQUIRED BY APPLICABLE LAW OR AGREED TO IN WRITING
+WILL ANY COPYRIGHT HOLDER, OR ANY OTHER PARTY WHO MODIFIES AND/OR CONVEYS
+THE PROGRAM AS PERMITTED ABOVE, BE LIABLE TO YOU FOR DAMAGES, INCLUDING ANY
+GENERAL, SPECIAL, INCIDENTAL OR CONSEQUENTIAL DAMAGES ARISING OUT OF THE
+USE OR INABILITY TO USE THE PROGRAM (INCLUDING BUT NOT LIMITED TO LOSS OF
+DATA OR DATA BEING RENDERED INACCURATE OR LOSSES SUSTAINED BY YOU OR THIRD
+PARTIES OR A FAILURE OF THE PROGRAM TO OPERATE WITH ANY OTHER PROGRAMS),
+EVEN IF SUCH HOLDER OR OTHER PARTY HAS BEEN ADVISED OF THE POSSIBILITY OF
+SUCH DAMAGES.
+
+ 17. Interpretation of Sections 15 and 16.
+
+ If the disclaimer of warranty and limitation of liability provided
+above cannot be given local legal effect according to their terms,
+reviewing courts shall apply local law that most closely approximates
+an absolute waiver of all civil liability in connection with the
+Program, unless a warranty or assumption of liability accompanies a
+copy of the Program in return for a fee.
+
+ END OF TERMS AND CONDITIONS
+
+ How to Apply These Terms to Your New Programs
+
+ If you develop a new program, and you want it to be of the greatest
+possible use to the public, the best way to achieve this is to make it
+free software which everyone can redistribute and change under these terms.
+
+ To do so, attach the following notices to the program. It is safest
+to attach them to the start of each source file to most effectively
+state the exclusion of warranty; and each file should have at least
+the "copyright" line and a pointer to where the full notice is found.
+
+
+ Copyright (C)
+
+ This program is free software: you can redistribute it and/or modify
+ it under the terms of the GNU General Public License as published by
+ the Free Software Foundation, either version 3 of the License, or
+ (at your option) any later version.
+
+ This program is distributed in the hope that it will be useful,
+ but WITHOUT ANY WARRANTY; without even the implied warranty of
+ MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the
+ GNU General Public License for more details.
+
+ You should have received a copy of the GNU General Public License
+ along with this program. If not, see .
+
+Also add information on how to contact you by electronic and paper mail.
+
+ If the program does terminal interaction, make it output a short
+notice like this when it starts in an interactive mode:
+
+ Copyright (C)
+ This program comes with ABSOLUTELY NO WARRANTY; for details type `show w'.
+ This is free software, and you are welcome to redistribute it
+ under certain conditions; type `show c' for details.
+
+The hypothetical commands `show w' and `show c' should show the appropriate
+parts of the General Public License. Of course, your program's commands
+might be different; for a GUI interface, you would use an "about box".
+
+ You should also get your employer (if you work as a programmer) or school,
+if any, to sign a "copyright disclaimer" for the program, if necessary.
+For more information on this, and how to apply and follow the GNU GPL, see
+.
+
+ The GNU General Public License does not permit incorporating your program
+into proprietary programs. If your program is a subroutine library, you
+may consider it more useful to permit linking proprietary applications with
+the library. If this is what you want to do, use the GNU Lesser General
+Public License instead of this License. But first, please read
+.
\ No newline at end of file
diff --git a/grounded-sam-osx/transformer_utils/MANIFEST.in b/grounded-sam-osx/transformer_utils/MANIFEST.in
new file mode 100644
index 0000000000000000000000000000000000000000..8a93c252bd38bafddc390bc9ae9b7278e3479246
--- /dev/null
+++ b/grounded-sam-osx/transformer_utils/MANIFEST.in
@@ -0,0 +1,5 @@
+include requirements/*.txt
+include mmpose/.mim/model-index.yml
+recursive-include mmpose/.mim/configs *.py *.yml
+recursive-include mmpose/.mim/tools *.py *.sh
+recursive-include mmpose/.mim/demo *.py
diff --git a/grounded-sam-osx/transformer_utils/configs/osx/encoder/body_encoder_base.py b/grounded-sam-osx/transformer_utils/configs/osx/encoder/body_encoder_base.py
new file mode 100644
index 0000000000000000000000000000000000000000..26bdb9a4350e5fd371442113db8eb009d89cb649
--- /dev/null
+++ b/grounded-sam-osx/transformer_utils/configs/osx/encoder/body_encoder_base.py
@@ -0,0 +1,169 @@
+_base_ = [
+ '../../../../_base_/default_runtime.py',
+ '../../../../_base_/datasets/coco.py'
+]
+evaluation = dict(interval=10, metric='mAP', save_best='AP')
+
+optimizer = dict(type='AdamW', lr=5e-4, betas=(0.9, 0.999), weight_decay=0.1,
+ constructor='LayerDecayOptimizerConstructor',
+ paramwise_cfg=dict(
+ num_layers=12,
+ layer_decay_rate=0.75,
+ custom_keys={
+ 'bias': dict(decay_multi=0.),
+ 'pos_embed': dict(decay_mult=0.),
+ 'relative_position_bias_table': dict(decay_mult=0.),
+ 'norm': dict(decay_mult=0.)
+ }
+ )
+ )
+
+optimizer_config = dict(grad_clip=dict(max_norm=1., norm_type=2))
+
+# learning policy
+lr_config = dict(
+ policy='step',
+ warmup='linear',
+ warmup_iters=500,
+ warmup_ratio=0.001,
+ step=[170, 200])
+total_epochs = 210
+target_type = 'GaussianHeatmap'
+channel_cfg = dict(
+ num_output_channels=17,
+ dataset_joints=17,
+ dataset_channel=[
+ [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16],
+ ],
+ inference_channel=[
+ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16
+ ])
+
+# model settings
+model = dict(
+ type='TopDown',
+ pretrained=None,
+ backbone=dict(
+ type='ViT',
+ img_size=(256, 192),
+ patch_size=16,
+ embed_dim=768,
+ depth=12,
+ num_heads=12,
+ ratio=1,
+ use_checkpoint=False,
+ mlp_ratio=4,
+ qkv_bias=True,
+ drop_path_rate=0.3,
+ ),
+ keypoint_head=dict(
+ type='TopdownHeatmapSimpleHead',
+ in_channels=768,
+ num_deconv_layers=2,
+ num_deconv_filters=(256, 256),
+ num_deconv_kernels=(4, 4),
+ extra=dict(final_conv_kernel=1, ),
+ out_channels=channel_cfg['num_output_channels'],
+ loss_keypoint=dict(type='JointsMSELoss', use_target_weight=True)),
+ train_cfg=dict(),
+ test_cfg=dict(
+ flip_test=True,
+ post_process='default',
+ shift_heatmap=False,
+ target_type=target_type,
+ modulate_kernel=11,
+ use_udp=True))
+
+data_cfg = dict(
+ image_size=[192, 256],
+ heatmap_size=[48, 64],
+ num_output_channels=channel_cfg['num_output_channels'],
+ num_joints=channel_cfg['dataset_joints'],
+ dataset_channel=channel_cfg['dataset_channel'],
+ inference_channel=channel_cfg['inference_channel'],
+ soft_nms=False,
+ nms_thr=1.0,
+ oks_thr=0.9,
+ vis_thr=0.2,
+ use_gt_bbox=False,
+ det_bbox_thr=0.0,
+ bbox_file='data/coco/person_detection_results/'
+ 'COCO_val2017_detections_AP_H_56_person.json',
+)
+
+train_pipeline = [
+ dict(type='LoadImageFromFile'),
+ dict(type='TopDownRandomFlip', flip_prob=0.5),
+ dict(
+ type='TopDownHalfBodyTransform',
+ num_joints_half_body=8,
+ prob_half_body=0.3),
+ dict(
+ type='TopDownGetRandomScaleRotation', rot_factor=40, scale_factor=0.5),
+ dict(type='TopDownAffine', use_udp=True),
+ dict(type='ToTensor'),
+ dict(
+ type='NormalizeTensor',
+ mean=[0.485, 0.456, 0.406],
+ std=[0.229, 0.224, 0.225]),
+ dict(
+ type='TopDownGenerateTarget',
+ sigma=2,
+ encoding='UDP',
+ target_type=target_type),
+ dict(
+ type='Collect',
+ keys=['img', 'target', 'target_weight'],
+ meta_keys=[
+ 'image_file', 'joints_3d', 'joints_3d_visible', 'center', 'scale',
+ 'rotation', 'bbox_score', 'flip_pairs'
+ ]),
+]
+
+val_pipeline = [
+ dict(type='LoadImageFromFile'),
+ dict(type='TopDownAffine', use_udp=True),
+ dict(type='ToTensor'),
+ dict(
+ type='NormalizeTensor',
+ mean=[0.485, 0.456, 0.406],
+ std=[0.229, 0.224, 0.225]),
+ dict(
+ type='Collect',
+ keys=['img'],
+ meta_keys=[
+ 'image_file', 'center', 'scale', 'rotation', 'bbox_score',
+ 'flip_pairs'
+ ]),
+]
+
+test_pipeline = val_pipeline
+
+data_root = 'data/coco'
+data = dict(
+ samples_per_gpu=64,
+ workers_per_gpu=4,
+ val_dataloader=dict(samples_per_gpu=32),
+ test_dataloader=dict(samples_per_gpu=32),
+ train=dict(
+ type='TopDownCocoDataset',
+ ann_file=f'{data_root}/annotations/person_keypoints_train2017.json',
+ img_prefix=f'{data_root}/train2017/',
+ data_cfg=data_cfg,
+ pipeline=train_pipeline,
+ dataset_info={{_base_.dataset_info}}),
+ val=dict(
+ type='TopDownCocoDataset',
+ ann_file=f'{data_root}/annotations/person_keypoints_val2017.json',
+ img_prefix=f'{data_root}/val2017/',
+ data_cfg=data_cfg,
+ pipeline=val_pipeline,
+ dataset_info={{_base_.dataset_info}}),
+ test=dict(
+ type='TopDownCocoDataset',
+ ann_file=f'{data_root}/annotations/person_keypoints_val2017.json',
+ img_prefix=f'{data_root}/val2017/',
+ data_cfg=data_cfg,
+ pipeline=test_pipeline,
+ dataset_info={{_base_.dataset_info}}),
+)
\ No newline at end of file
diff --git a/grounded-sam-osx/transformer_utils/configs/osx/encoder/body_encoder_large.py b/grounded-sam-osx/transformer_utils/configs/osx/encoder/body_encoder_large.py
new file mode 100644
index 0000000000000000000000000000000000000000..efd95afa09d8326f2a76c55ca1eea85c6cb60dcc
--- /dev/null
+++ b/grounded-sam-osx/transformer_utils/configs/osx/encoder/body_encoder_large.py
@@ -0,0 +1,169 @@
+_base_ = [
+ '../../../../_base_/default_runtime.py',
+ '../../../../_base_/datasets/coco.py'
+]
+evaluation = dict(interval=10, metric='mAP', save_best='AP')
+
+optimizer = dict(type='AdamW', lr=5e-4, betas=(0.9, 0.999), weight_decay=0.1,
+ constructor='LayerDecayOptimizerConstructor',
+ paramwise_cfg=dict(
+ num_layers=16,
+ layer_decay_rate=0.8,
+ custom_keys={
+ 'bias': dict(decay_multi=0.),
+ 'pos_embed': dict(decay_mult=0.),
+ 'relative_position_bias_table': dict(decay_mult=0.),
+ 'norm': dict(decay_mult=0.)
+ }
+ )
+ )
+
+optimizer_config = dict(grad_clip=dict(max_norm=1., norm_type=2))
+
+# learning policy
+lr_config = dict(
+ policy='step',
+ warmup='linear',
+ warmup_iters=500,
+ warmup_ratio=0.001,
+ step=[170, 200])
+total_epochs = 210
+target_type = 'GaussianHeatmap'
+channel_cfg = dict(
+ num_output_channels=17,
+ dataset_joints=17,
+ dataset_channel=[
+ [0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16],
+ ],
+ inference_channel=[
+ 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16
+ ])
+
+# model settings
+model = dict(
+ type='TopDown',
+ pretrained=None,
+ backbone=dict(
+ type='ViT',
+ img_size=(256, 192),
+ patch_size=16,
+ embed_dim=1024,
+ depth=24,
+ num_heads=16,
+ ratio=1,
+ use_checkpoint=False,
+ mlp_ratio=4,
+ qkv_bias=True,
+ drop_path_rate=0.5,
+ ),
+ keypoint_head=dict(
+ type='TopdownHeatmapSimpleHead',
+ in_channels=1024,
+ num_deconv_layers=2,
+ num_deconv_filters=(256, 256),
+ num_deconv_kernels=(4, 4),
+ extra=dict(final_conv_kernel=1, ),
+ out_channels=channel_cfg['num_output_channels'],
+ loss_keypoint=dict(type='JointsMSELoss', use_target_weight=True)),
+ train_cfg=dict(),
+ test_cfg=dict(
+ flip_test=True,
+ post_process='default',
+ shift_heatmap=False,
+ target_type=target_type,
+ modulate_kernel=11,
+ use_udp=True))
+
+data_cfg = dict(
+ image_size=[192, 256],
+ heatmap_size=[48, 64],
+ num_output_channels=channel_cfg['num_output_channels'],
+ num_joints=channel_cfg['dataset_joints'],
+ dataset_channel=channel_cfg['dataset_channel'],
+ inference_channel=channel_cfg['inference_channel'],
+ soft_nms=False,
+ nms_thr=1.0,
+ oks_thr=0.9,
+ vis_thr=0.2,
+ use_gt_bbox=False,
+ det_bbox_thr=0.0,
+ bbox_file='data/coco/person_detection_results/'
+ 'COCO_val2017_detections_AP_H_56_person.json',
+)
+
+train_pipeline = [
+ dict(type='LoadImageFromFile'),
+ dict(type='TopDownRandomFlip', flip_prob=0.5),
+ dict(
+ type='TopDownHalfBodyTransform',
+ num_joints_half_body=8,
+ prob_half_body=0.3),
+ dict(
+ type='TopDownGetRandomScaleRotation', rot_factor=40, scale_factor=0.5),
+ dict(type='TopDownAffine', use_udp=True),
+ dict(type='ToTensor'),
+ dict(
+ type='NormalizeTensor',
+ mean=[0.485, 0.456, 0.406],
+ std=[0.229, 0.224, 0.225]),
+ dict(
+ type='TopDownGenerateTarget',
+ sigma=2,
+ encoding='UDP',
+ target_type=target_type),
+ dict(
+ type='Collect',
+ keys=['img', 'target', 'target_weight'],
+ meta_keys=[
+ 'image_file', 'joints_3d', 'joints_3d_visible', 'center', 'scale',
+ 'rotation', 'bbox_score', 'flip_pairs'
+ ]),
+]
+
+val_pipeline = [
+ dict(type='LoadImageFromFile'),
+ dict(type='TopDownAffine', use_udp=True),
+ dict(type='ToTensor'),
+ dict(
+ type='NormalizeTensor',
+ mean=[0.485, 0.456, 0.406],
+ std=[0.229, 0.224, 0.225]),
+ dict(
+ type='Collect',
+ keys=['img'],
+ meta_keys=[
+ 'image_file', 'center', 'scale', 'rotation', 'bbox_score',
+ 'flip_pairs'
+ ]),
+]
+
+test_pipeline = val_pipeline
+
+data_root = 'data/coco'
+data = dict(
+ samples_per_gpu=64,
+ workers_per_gpu=4,
+ val_dataloader=dict(samples_per_gpu=32),
+ test_dataloader=dict(samples_per_gpu=32),
+ train=dict(
+ type='TopDownCocoDataset',
+ ann_file=f'{data_root}/annotations/person_keypoints_train2017.json',
+ img_prefix=f'{data_root}/train2017/',
+ data_cfg=data_cfg,
+ pipeline=train_pipeline,
+ dataset_info={{_base_.dataset_info}}),
+ val=dict(
+ type='TopDownCocoDataset',
+ ann_file=f'{data_root}/annotations/person_keypoints_val2017.json',
+ img_prefix=f'{data_root}/val2017/',
+ data_cfg=data_cfg,
+ pipeline=val_pipeline,
+ dataset_info={{_base_.dataset_info}}),
+ test=dict(
+ type='TopDownCocoDataset',
+ ann_file=f'{data_root}/annotations/person_keypoints_val2017.json',
+ img_prefix=f'{data_root}/val2017/',
+ data_cfg=data_cfg,
+ pipeline=test_pipeline,
+ dataset_info={{_base_.dataset_info}}),
+)
\ No newline at end of file
diff --git a/grounded-sam-osx/transformer_utils/mmpose/__init__.py b/grounded-sam-osx/transformer_utils/mmpose/__init__.py
new file mode 100644
index 0000000000000000000000000000000000000000..abcf8693e279f59c8c80f55e1797841e593dbd72
--- /dev/null
+++ b/grounded-sam-osx/transformer_utils/mmpose/__init__.py
@@ -0,0 +1,29 @@
+# Copyright (c) OpenMMLab. All rights reserved.
+import mmcv
+import mmpose.ops
+from .version import __version__, short_version
+
+
+def digit_version(version_str):
+ digit_version = []
+ for x in version_str.split('.'):
+ if x.isdigit():
+ digit_version.append(int(x))
+ elif x.find('rc') != -1:
+ patch_version = x.split('rc')
+ digit_version.append(int(patch_version[0]) - 1)
+ digit_version.append(int(patch_version[1]))
+ return digit_version
+
+
+mmcv_minimum_version = '1.3.8'
+mmcv_maximum_version = '1.8.0'
+mmcv_version = digit_version(mmcv.__version__)
+
+
+assert (mmcv_version >= digit_version(mmcv_minimum_version)
+ and mmcv_version <= digit_version(mmcv_maximum_version)), \
+ f'MMCV=={mmcv.__version__} is used but incompatible. ' \
+ f'Please install mmcv>={mmcv_minimum_version}, <={mmcv_maximum_version}.'
+
+__all__ = ['__version__', 'short_version']
diff --git a/grounded-sam-osx/transformer_utils/mmpose/core/__init__.py b/grounded-sam-osx/transformer_utils/mmpose/core/__init__.py
new file mode 100644
index 0000000000000000000000000000000000000000..87f34c570a66dd58d6fb84f79b45063b89526d58
--- /dev/null
+++ b/grounded-sam-osx/transformer_utils/mmpose/core/__init__.py
@@ -0,0 +1,9 @@
+# Copyright (c) OpenMMLab. All rights reserved.
+from .bbox import * # noqa: F401, F403
+from .camera import * # noqa: F401, F403
+from .evaluation import * # noqa: F401, F403
+from .fp16 import * # noqa: F401, F403
+from .optimizers import * # noqa: F401, F403
+from .post_processing import * # noqa: F401, F403
+from .utils import * # noqa: F401, F403
+from .visualization import * # noqa: F401, F403
diff --git a/grounded-sam-osx/transformer_utils/mmpose/core/bbox/__init__.py b/grounded-sam-osx/transformer_utils/mmpose/core/bbox/__init__.py
new file mode 100644
index 0000000000000000000000000000000000000000..557993386a6c5de8336a92514072c81b48419ba7
--- /dev/null
+++ b/grounded-sam-osx/transformer_utils/mmpose/core/bbox/__init__.py
@@ -0,0 +1,5 @@
+# Copyright (c) OpenMMLab. All rights reserved.
+from .transforms import (bbox_cs2xywh, bbox_xywh2cs, bbox_xywh2xyxy,
+ bbox_xyxy2xywh)
+
+__all__ = ['bbox_xywh2xyxy', 'bbox_xyxy2xywh', 'bbox_xywh2cs', 'bbox_cs2xywh']
diff --git a/grounded-sam-osx/transformer_utils/mmpose/core/bbox/transforms.py b/grounded-sam-osx/transformer_utils/mmpose/core/bbox/transforms.py
new file mode 100644
index 0000000000000000000000000000000000000000..703639443a9f327801b6e6b00ca278b2e22a0ee0
--- /dev/null
+++ b/grounded-sam-osx/transformer_utils/mmpose/core/bbox/transforms.py
@@ -0,0 +1,88 @@
+# Copyright (c) OpenMMLab. All rights reserved.
+import numpy as np
+
+
+def bbox_xyxy2xywh(bbox_xyxy):
+ """Transform the bbox format from x1y1x2y2 to xywh.
+
+ Args:
+ bbox_xyxy (np.ndarray): Bounding boxes (with scores), shaped (n, 4) or
+ (n, 5). (left, top, right, bottom, [score])
+
+ Returns:
+ np.ndarray: Bounding boxes (with scores),
+ shaped (n, 4) or (n, 5). (left, top, width, height, [score])
+ """
+ bbox_xywh = bbox_xyxy.copy()
+ bbox_xywh[:, 2] = bbox_xywh[:, 2] - bbox_xywh[:, 0]
+ bbox_xywh[:, 3] = bbox_xywh[:, 3] - bbox_xywh[:, 1]
+
+ return bbox_xywh
+
+
+def bbox_xywh2xyxy(bbox_xywh):
+ """Transform the bbox format from xywh to x1y1x2y2.
+
+ Args:
+ bbox_xywh (ndarray): Bounding boxes (with scores),
+ shaped (n, 4) or (n, 5). (left, top, width, height, [score])
+ Returns:
+ np.ndarray: Bounding boxes (with scores), shaped (n, 4) or
+ (n, 5). (left, top, right, bottom, [score])
+ """
+ bbox_xyxy = bbox_xywh.copy()
+ bbox_xyxy[:, 2] = bbox_xyxy[:, 2] + bbox_xyxy[:, 0]
+ bbox_xyxy[:, 3] = bbox_xyxy[:, 3] + bbox_xyxy[:, 1]
+
+ return bbox_xyxy
+
+
+def bbox_xywh2cs(bbox, aspect_ratio, padding=1., pixel_std=200.):
+ """Transform the bbox format from (x,y,w,h) into (center, scale)
+
+ Args:
+ bbox (ndarray): Single bbox in (x, y, w, h)
+ aspect_ratio (float): The expected bbox aspect ratio (w over h)
+ padding (float): Bbox padding factor that will be multilied to scale.
+ Default: 1.0
+ pixel_std (float): The scale normalization factor. Default: 200.0
+
+ Returns:
+ tuple: A tuple containing center and scale.
+ - np.ndarray[float32](2,): Center of the bbox (x, y).
+ - np.ndarray[float32](2,): Scale of the bbox w & h.
+ """
+
+ x, y, w, h = bbox[:4]
+ center = np.array([x + w * 0.5, y + h * 0.5], dtype=np.float32)
+
+ if w > aspect_ratio * h:
+ h = w * 1.0 / aspect_ratio
+ elif w < aspect_ratio * h:
+ w = h * aspect_ratio
+
+ scale = np.array([w, h], dtype=np.float32) / pixel_std
+ scale = scale * padding
+
+ return center, scale
+
+
+def bbox_cs2xywh(center, scale, padding=1., pixel_std=200.):
+ """Transform the bbox format from (center, scale) to (x,y,w,h). Note that
+ this is not an exact inverse operation of ``bbox_xywh2cs`` because the
+ normalization of aspect ratio in ``bbox_xywh2cs`` is irreversible.
+
+ Args:
+ center (ndarray): Single bbox center in (x, y)
+ scale (ndarray): Single bbox scale in (scale_x, scale_y)
+ padding (float): Bbox padding factor that will be multilied to scale.
+ Default: 1.0
+ pixel_std (float): The scale normalization factor. Default: 200.0
+
+ Returns:
+ ndarray: Single bbox in (x, y, w, h)
+ """
+
+ wh = scale / padding * pixel_std
+ xy = center - 0.5 * wh
+ return np.r_[xy, wh]
diff --git a/grounded-sam-osx/transformer_utils/mmpose/core/camera/__init__.py b/grounded-sam-osx/transformer_utils/mmpose/core/camera/__init__.py
new file mode 100644
index 0000000000000000000000000000000000000000..a4a3c5526560996791a85f0d84a72a66286486ca
--- /dev/null
+++ b/grounded-sam-osx/transformer_utils/mmpose/core/camera/__init__.py
@@ -0,0 +1,6 @@
+# Copyright (c) OpenMMLab. All rights reserved.
+from .camera_base import CAMERAS
+from .single_camera import SimpleCamera
+from .single_camera_torch import SimpleCameraTorch
+
+__all__ = ['CAMERAS', 'SimpleCamera', 'SimpleCameraTorch']
diff --git a/grounded-sam-osx/transformer_utils/mmpose/core/camera/camera_base.py b/grounded-sam-osx/transformer_utils/mmpose/core/camera/camera_base.py
new file mode 100644
index 0000000000000000000000000000000000000000..28b23e7c6279e3613265a949df91f6ced0413b99
--- /dev/null
+++ b/grounded-sam-osx/transformer_utils/mmpose/core/camera/camera_base.py
@@ -0,0 +1,45 @@
+# Copyright (c) OpenMMLab. All rights reserved.
+from abc import ABCMeta, abstractmethod
+
+from mmcv.utils import Registry
+
+CAMERAS = Registry('camera')
+
+
+class SingleCameraBase(metaclass=ABCMeta):
+ """Base class for single camera model.
+
+ Args:
+ param (dict): Camera parameters
+
+ Methods:
+ world_to_camera: Project points from world coordinates to camera
+ coordinates
+ camera_to_world: Project points from camera coordinates to world
+ coordinates
+ camera_to_pixel: Project points from camera coordinates to pixel
+ coordinates
+ world_to_pixel: Project points from world coordinates to pixel
+ coordinates
+ """
+
+ @abstractmethod
+ def __init__(self, param):
+ """Load camera parameters and check validity."""
+
+ def world_to_camera(self, X):
+ """Project points from world coordinates to camera coordinates."""
+ raise NotImplementedError
+
+ def camera_to_world(self, X):
+ """Project points from camera coordinates to world coordinates."""
+ raise NotImplementedError
+
+ def camera_to_pixel(self, X):
+ """Project points from camera coordinates to pixel coordinates."""
+ raise NotImplementedError
+
+ def world_to_pixel(self, X):
+ """Project points from world coordinates to pixel coordinates."""
+ _X = self.world_to_camera(X)
+ return self.camera_to_pixel(_X)
diff --git a/grounded-sam-osx/transformer_utils/mmpose/core/camera/single_camera.py b/grounded-sam-osx/transformer_utils/mmpose/core/camera/single_camera.py
new file mode 100644
index 0000000000000000000000000000000000000000..cabd79941af5c81110876e94ce6103cc02ea5078
--- /dev/null
+++ b/grounded-sam-osx/transformer_utils/mmpose/core/camera/single_camera.py
@@ -0,0 +1,123 @@
+# Copyright (c) OpenMMLab. All rights reserved.
+import numpy as np
+
+from .camera_base import CAMERAS, SingleCameraBase
+
+
+@CAMERAS.register_module()
+class SimpleCamera(SingleCameraBase):
+ """Camera model to calculate coordinate transformation with given
+ intrinsic/extrinsic camera parameters.
+
+ Note:
+ The keypoint coordinate should be an np.ndarray with a shape of
+ [...,J, C] where J is the keypoint number of an instance, and C is
+ the coordinate dimension. For example:
+
+ [J, C]: shape of joint coordinates of a person with J joints.
+ [N, J, C]: shape of a batch of person joint coordinates.
+ [N, T, J, C]: shape of a batch of pose sequences.
+
+ Args:
+ param (dict): camera parameters including:
+ - R: 3x3, camera rotation matrix (camera-to-world)
+ - T: 3x1, camera translation (camera-to-world)
+ - K: (optional) 2x3, camera intrinsic matrix
+ - k: (optional) nx1, camera radial distortion coefficients
+ - p: (optional) mx1, camera tangential distortion coefficients
+ - f: (optional) 2x1, camera focal length
+ - c: (optional) 2x1, camera center
+ if K is not provided, it will be calculated from f and c.
+
+ Methods:
+ world_to_camera: Project points from world coordinates to camera
+ coordinates
+ camera_to_pixel: Project points from camera coordinates to pixel
+ coordinates
+ world_to_pixel: Project points from world coordinates to pixel
+ coordinates
+ """
+
+ def __init__(self, param):
+
+ self.param = {}
+ # extrinsic param
+ R = np.array(param['R'], dtype=np.float32)
+ T = np.array(param['T'], dtype=np.float32)
+ assert R.shape == (3, 3)
+ assert T.shape == (3, 1)
+ # The camera matrices are transposed in advance because the joint
+ # coordinates are stored as row vectors.
+ self.param['R_c2w'] = R.T
+ self.param['T_c2w'] = T.T
+ self.param['R_w2c'] = R
+ self.param['T_w2c'] = -self.param['T_c2w'] @ self.param['R_w2c']
+
+ # intrinsic param
+ if 'K' in param:
+ K = np.array(param['K'], dtype=np.float32)
+ assert K.shape == (2, 3)
+ self.param['K'] = K.T
+ self.param['f'] = np.array([K[0, 0], K[1, 1]])[:, np.newaxis]
+ self.param['c'] = np.array([K[0, 2], K[1, 2]])[:, np.newaxis]
+ elif 'f' in param and 'c' in param:
+ f = np.array(param['f'], dtype=np.float32)
+ c = np.array(param['c'], dtype=np.float32)
+ assert f.shape == (2, 1)
+ assert c.shape == (2, 1)
+ self.param['K'] = np.concatenate((np.diagflat(f), c), axis=-1).T
+ self.param['f'] = f
+ self.param['c'] = c
+ else:
+ raise ValueError('Camera intrinsic parameters are missing. '
+ 'Either "K" or "f"&"c" should be provided.')
+
+ # distortion param
+ if 'k' in param and 'p' in param:
+ self.undistortion = True
+ self.param['k'] = np.array(param['k'], dtype=np.float32).flatten()
+ self.param['p'] = np.array(param['p'], dtype=np.float32).flatten()
+ assert self.param['k'].size in {3, 6}
+ assert self.param['p'].size == 2
+ else:
+ self.undistortion = False
+
+ def world_to_camera(self, X):
+ assert isinstance(X, np.ndarray)
+ assert X.ndim >= 2 and X.shape[-1] == 3
+ return X @ self.param['R_w2c'] + self.param['T_w2c']
+
+ def camera_to_world(self, X):
+ assert isinstance(X, np.ndarray)
+ assert X.ndim >= 2 and X.shape[-1] == 3
+ return X @ self.param['R_c2w'] + self.param['T_c2w']
+
+ def camera_to_pixel(self, X):
+ assert isinstance(X, np.ndarray)
+ assert X.ndim >= 2 and X.shape[-1] == 3
+
+ _X = X / X[..., 2:]
+
+ if self.undistortion:
+ k = self.param['k']
+ p = self.param['p']
+ _X_2d = _X[..., :2]
+ r2 = (_X_2d**2).sum(-1)
+ radial = 1 + sum(ki * r2**(i + 1) for i, ki in enumerate(k[:3]))
+ if k.size == 6:
+ radial /= 1 + sum(
+ (ki * r2**(i + 1) for i, ki in enumerate(k[3:])))
+
+ tangential = 2 * (p[1] * _X[..., 0] + p[0] * _X[..., 1])
+
+ _X[..., :2] = _X_2d * (radial + tangential)[..., None] + np.outer(
+ r2, p[::-1]).reshape(_X_2d.shape)
+ return _X @ self.param['K']
+
+ def pixel_to_camera(self, X):
+ assert isinstance(X, np.ndarray)
+ assert X.ndim >= 2 and X.shape[-1] == 3
+ _X = X.copy()
+ _X[:, :2] = (X[:, :2] - self.param['c'].T) / self.param['f'].T * X[:,
+ [2]]
+ return _X
diff --git a/grounded-sam-osx/transformer_utils/mmpose/core/camera/single_camera_torch.py b/grounded-sam-osx/transformer_utils/mmpose/core/camera/single_camera_torch.py
new file mode 100644
index 0000000000000000000000000000000000000000..22eb72f23d6eecf1b5c5a9b570a4f142fcf6e02a
--- /dev/null
+++ b/grounded-sam-osx/transformer_utils/mmpose/core/camera/single_camera_torch.py
@@ -0,0 +1,118 @@
+# Copyright (c) OpenMMLab. All rights reserved.
+import torch
+
+from .camera_base import CAMERAS, SingleCameraBase
+
+
+@CAMERAS.register_module()
+class SimpleCameraTorch(SingleCameraBase):
+ """Camera model to calculate coordinate transformation with given
+ intrinsic/extrinsic camera parameters.
+
+ Notes:
+ The keypoint coordinate should be an np.ndarray with a shape of
+ [...,J, C] where J is the keypoint number of an instance, and C is
+ the coordinate dimension. For example:
+
+ [J, C]: shape of joint coordinates of a person with J joints.
+ [N, J, C]: shape of a batch of person joint coordinates.
+ [N, T, J, C]: shape of a batch of pose sequences.
+
+ Args:
+ param (dict): camera parameters including:
+ - R: 3x3, camera rotation matrix (camera-to-world)
+ - T: 3x1, camera translation (camera-to-world)
+ - K: (optional) 2x3, camera intrinsic matrix
+ - k: (optional) nx1, camera radial distortion coefficients
+ - p: (optional) mx1, camera tangential distortion coefficients
+ - f: (optional) 2x1, camera focal length
+ - c: (optional) 2x1, camera center
+ if K is not provided, it will be calculated from f and c.
+
+ Methods:
+ world_to_camera: Project points from world coordinates to camera
+ coordinates
+ camera_to_pixel: Project points from camera coordinates to pixel
+ coordinates
+ world_to_pixel: Project points from world coordinates to pixel
+ coordinates
+ """
+
+ def __init__(self, param, device):
+
+ self.param = {}
+ # extrinsic param
+ R = torch.tensor(param['R'], device=device)
+ T = torch.tensor(param['T'], device=device)
+
+ assert R.shape == (3, 3)
+ assert T.shape == (3, 1)
+ # The camera matrices are transposed in advance because the joint
+ # coordinates are stored as row vectors.
+ self.param['R_c2w'] = R.T
+ self.param['T_c2w'] = T.T
+ self.param['R_w2c'] = R
+ self.param['T_w2c'] = -self.param['T_c2w'] @ self.param['R_w2c']
+
+ # intrinsic param
+ if 'K' in param:
+ K = torch.tensor(param['K'], device=device)
+ assert K.shape == (2, 3)
+ self.param['K'] = K.T
+ self.param['f'] = torch.tensor([[K[0, 0]], [K[1, 1]]],
+ device=device)
+ self.param['c'] = torch.tensor([[K[0, 2]], [K[1, 2]]],
+ device=device)
+ elif 'f' in param and 'c' in param:
+ f = torch.tensor(param['f'], device=device)
+ c = torch.tensor(param['c'], device=device)
+ assert f.shape == (2, 1)
+ assert c.shape == (2, 1)
+ self.param['K'] = torch.cat([torch.diagflat(f), c], dim=-1).T
+ self.param['f'] = f
+ self.param['c'] = c
+ else:
+ raise ValueError('Camera intrinsic parameters are missing. '
+ 'Either "K" or "f"&"c" should be provided.')
+
+ # distortion param
+ if 'k' in param and 'p' in param:
+ self.undistortion = True
+ self.param['k'] = torch.tensor(param['k'], device=device).view(-1)
+ self.param['p'] = torch.tensor(param['p'], device=device).view(-1)
+ assert len(self.param['k']) in {3, 6}
+ assert len(self.param['p']) == 2
+ else:
+ self.undistortion = False
+
+ def world_to_camera(self, X):
+ assert isinstance(X, torch.Tensor)
+ assert X.ndim >= 2 and X.shape[-1] == 3
+ return X @ self.param['R_w2c'] + self.param['T_w2c']
+
+ def camera_to_world(self, X):
+ assert isinstance(X, torch.Tensor)
+ assert X.ndim >= 2 and X.shape[-1] == 3
+ return X @ self.param['R_c2w'] + self.param['T_c2w']
+
+ def camera_to_pixel(self, X):
+ assert isinstance(X, torch.Tensor)
+ assert X.ndim >= 2 and X.shape[-1] == 3
+
+ _X = X / X[..., 2:]
+
+ if self.undistortion:
+ k = self.param['k']
+ p = self.param['p']
+ _X_2d = _X[..., :2]
+ r2 = (_X_2d**2).sum(-1)
+ radial = 1 + sum(ki * r2**(i + 1) for i, ki in enumerate(k[:3]))
+ if k.size == 6:
+ radial /= 1 + sum(
+ (ki * r2**(i + 1) for i, ki in enumerate(k[3:])))
+
+ tangential = 2 * (p[1] * _X[..., 0] + p[0] * _X[..., 1])
+
+ _X[..., :2] = _X_2d * (radial + tangential)[..., None] + torch.ger(
+ r2, p.flip([0])).reshape(_X_2d.shape)
+ return _X @ self.param['K']
diff --git a/grounded-sam-osx/transformer_utils/mmpose/core/distributed_wrapper.py b/grounded-sam-osx/transformer_utils/mmpose/core/distributed_wrapper.py
new file mode 100644
index 0000000000000000000000000000000000000000..c67aceec992085e9952ea70c62009e9ec1db30ca
--- /dev/null
+++ b/grounded-sam-osx/transformer_utils/mmpose/core/distributed_wrapper.py
@@ -0,0 +1,143 @@
+# Copyright (c) OpenMMLab. All rights reserved.
+import torch
+import torch.nn as nn
+from mmcv.parallel import MODULE_WRAPPERS as MMCV_MODULE_WRAPPERS
+from mmcv.parallel import MMDistributedDataParallel
+from mmcv.parallel.scatter_gather import scatter_kwargs
+from mmcv.utils import Registry
+from torch.cuda._utils import _get_device_index
+
+MODULE_WRAPPERS = Registry('module wrapper', parent=MMCV_MODULE_WRAPPERS)
+
+
+@MODULE_WRAPPERS.register_module()
+class DistributedDataParallelWrapper(nn.Module):
+ """A DistributedDataParallel wrapper for models in 3D mesh estimation task.
+
+ In 3D mesh estimation task, there is a need to wrap different modules in
+ the models with separate DistributedDataParallel. Otherwise, it will cause
+ errors for GAN training.
+ More specific, the GAN model, usually has two sub-modules:
+ generator and discriminator. If we wrap both of them in one
+ standard DistributedDataParallel, it will cause errors during training,
+ because when we update the parameters of the generator (or discriminator),
+ the parameters of the discriminator (or generator) is not updated, which is
+ not allowed for DistributedDataParallel.
+ So we design this wrapper to separately wrap DistributedDataParallel
+ for generator and discriminator.
+
+ In this wrapper, we perform two operations:
+ 1. Wrap the modules in the models with separate MMDistributedDataParallel.
+ Note that only modules with parameters will be wrapped.
+ 2. Do scatter operation for 'forward', 'train_step' and 'val_step'.
+
+ Note that the arguments of this wrapper is the same as those in
+ `torch.nn.parallel.distributed.DistributedDataParallel`.
+
+ Args:
+ module (nn.Module): Module that needs to be wrapped.
+ device_ids (list[int | `torch.device`]): Same as that in
+ `torch.nn.parallel.distributed.DistributedDataParallel`.
+ dim (int, optional): Same as that in the official scatter function in
+ pytorch. Defaults to 0.
+ broadcast_buffers (bool): Same as that in
+ `torch.nn.parallel.distributed.DistributedDataParallel`.
+ Defaults to False.
+ find_unused_parameters (bool, optional): Same as that in
+ `torch.nn.parallel.distributed.DistributedDataParallel`.
+ Traverse the autograd graph of all tensors contained in returned
+ value of the wrapped module’s forward function. Defaults to False.
+ kwargs (dict): Other arguments used in
+ `torch.nn.parallel.distributed.DistributedDataParallel`.
+ """
+
+ def __init__(self,
+ module,
+ device_ids,
+ dim=0,
+ broadcast_buffers=False,
+ find_unused_parameters=False,
+ **kwargs):
+ super().__init__()
+ assert len(device_ids) == 1, (
+ 'Currently, DistributedDataParallelWrapper only supports one'
+ 'single CUDA device for each process.'
+ f'The length of device_ids must be 1, but got {len(device_ids)}.')
+ self.module = module
+ self.dim = dim
+ self.to_ddp(
+ device_ids=device_ids,
+ dim=dim,
+ broadcast_buffers=broadcast_buffers,
+ find_unused_parameters=find_unused_parameters,
+ **kwargs)
+ self.output_device = _get_device_index(device_ids[0], True)
+
+ def to_ddp(self, device_ids, dim, broadcast_buffers,
+ find_unused_parameters, **kwargs):
+ """Wrap models with separate MMDistributedDataParallel.
+
+ It only wraps the modules with parameters.
+ """
+ for name, module in self.module._modules.items():
+ if next(module.parameters(), None) is None:
+ module = module.cuda()
+ elif all(not p.requires_grad for p in module.parameters()):
+ module = module.cuda()
+ else:
+ module = MMDistributedDataParallel(
+ module.cuda(),
+ device_ids=device_ids,
+ dim=dim,
+ broadcast_buffers=broadcast_buffers,
+ find_unused_parameters=find_unused_parameters,
+ **kwargs)
+ self.module._modules[name] = module
+
+ def scatter(self, inputs, kwargs, device_ids):
+ """Scatter function.
+
+ Args:
+ inputs (Tensor): Input Tensor.
+ kwargs (dict): Args for
+ ``mmcv.parallel.scatter_gather.scatter_kwargs``.
+ device_ids (int): Device id.
+ """
+ return scatter_kwargs(inputs, kwargs, device_ids, dim=self.dim)
+
+ def forward(self, *inputs, **kwargs):
+ """Forward function.
+
+ Args:
+ inputs (tuple): Input data.
+ kwargs (dict): Args for
+ ``mmcv.parallel.scatter_gather.scatter_kwargs``.
+ """
+ inputs, kwargs = self.scatter(inputs, kwargs,
+ [torch.cuda.current_device()])
+ return self.module(*inputs[0], **kwargs[0])
+
+ def train_step(self, *inputs, **kwargs):
+ """Train step function.
+
+ Args:
+ inputs (Tensor): Input Tensor.
+ kwargs (dict): Args for
+ ``mmcv.parallel.scatter_gather.scatter_kwargs``.
+ """
+ inputs, kwargs = self.scatter(inputs, kwargs,
+ [torch.cuda.current_device()])
+ output = self.module.train_step(*inputs[0], **kwargs[0])
+ return output
+
+ def val_step(self, *inputs, **kwargs):
+ """Validation step function.
+
+ Args:
+ inputs (tuple): Input data.
+ kwargs (dict): Args for ``scatter_kwargs``.
+ """
+ inputs, kwargs = self.scatter(inputs, kwargs,
+ [torch.cuda.current_device()])
+ output = self.module.val_step(*inputs[0], **kwargs[0])
+ return output
diff --git a/grounded-sam-osx/transformer_utils/mmpose/core/evaluation/__init__.py b/grounded-sam-osx/transformer_utils/mmpose/core/evaluation/__init__.py
new file mode 100644
index 0000000000000000000000000000000000000000..5f9378429c8ddaa15f7ac17446bc9d484987df16
--- /dev/null
+++ b/grounded-sam-osx/transformer_utils/mmpose/core/evaluation/__init__.py
@@ -0,0 +1,22 @@
+# Copyright (c) OpenMMLab. All rights reserved.
+from .bottom_up_eval import (aggregate_scale, aggregate_stage_flip,
+ flip_feature_maps, get_group_preds,
+ split_ae_outputs)
+from .eval_hooks import DistEvalHook, EvalHook
+from .mesh_eval import compute_similarity_transform
+from .pose3d_eval import keypoint_3d_auc, keypoint_3d_pck, keypoint_mpjpe
+from .top_down_eval import (keypoint_auc, keypoint_epe, keypoint_pck_accuracy,
+ keypoints_from_heatmaps, keypoints_from_heatmaps3d,
+ keypoints_from_regression,
+ multilabel_classification_accuracy,
+ pose_pck_accuracy, post_dark_udp)
+
+__all__ = [
+ 'EvalHook', 'DistEvalHook', 'pose_pck_accuracy', 'keypoints_from_heatmaps',
+ 'keypoints_from_regression', 'keypoint_pck_accuracy', 'keypoint_3d_pck',
+ 'keypoint_3d_auc', 'keypoint_auc', 'keypoint_epe', 'get_group_preds',
+ 'split_ae_outputs', 'flip_feature_maps', 'aggregate_stage_flip',
+ 'aggregate_scale', 'compute_similarity_transform', 'post_dark_udp',
+ 'keypoint_mpjpe', 'keypoints_from_heatmaps3d',
+ 'multilabel_classification_accuracy'
+]
diff --git a/grounded-sam-osx/transformer_utils/mmpose/core/evaluation/bottom_up_eval.py b/grounded-sam-osx/transformer_utils/mmpose/core/evaluation/bottom_up_eval.py
new file mode 100644
index 0000000000000000000000000000000000000000..7b37d7c98e684284e3863922e7c7d2abedce0e24
--- /dev/null
+++ b/grounded-sam-osx/transformer_utils/mmpose/core/evaluation/bottom_up_eval.py
@@ -0,0 +1,333 @@
+# Copyright (c) OpenMMLab. All rights reserved.
+import numpy as np
+import torch
+
+from mmpose.core.post_processing import (get_warp_matrix, transform_preds,
+ warp_affine_joints)
+
+
+def split_ae_outputs(outputs, num_joints, with_heatmaps, with_ae,
+ select_output_index):
+ """Split multi-stage outputs into heatmaps & tags.
+
+ Args:
+ outputs (list(Tensor)): Outputs of network
+ num_joints (int): Number of joints
+ with_heatmaps (list[bool]): Option to output
+ heatmaps for different stages.
+ with_ae (list[bool]): Option to output
+ ae tags for different stages.
+ select_output_index (list[int]): Output keep the selected index
+
+ Returns:
+ tuple: A tuple containing multi-stage outputs.
+
+ - list[Tensor]: multi-stage heatmaps.
+ - list[Tensor]: multi-stage tags.
+ """
+
+ heatmaps = []
+ tags = []
+
+ # aggregate heatmaps from different stages
+ for i, output in enumerate(outputs):
+ if i not in select_output_index:
+ continue
+ # staring index of the associative embeddings
+ offset_feat = num_joints if with_heatmaps[i] else 0
+ if with_heatmaps[i]:
+ heatmaps.append(output[:, :num_joints])
+ if with_ae[i]:
+ tags.append(output[:, offset_feat:])
+
+ return heatmaps, tags
+
+
+def flip_feature_maps(feature_maps, flip_index=None):
+ """Flip the feature maps and swap the channels.
+
+ Args:
+ feature_maps (list[Tensor]): Feature maps.
+ flip_index (list[int] | None): Channel-flip indexes.
+ If None, do not flip channels.
+
+ Returns:
+ list[Tensor]: Flipped feature_maps.
+ """
+ flipped_feature_maps = []
+ for feature_map in feature_maps:
+ feature_map = torch.flip(feature_map, [3])
+ if flip_index is not None:
+ flipped_feature_maps.append(feature_map[:, flip_index, :, :])
+ else:
+ flipped_feature_maps.append(feature_map)
+
+ return flipped_feature_maps
+
+
+def _resize_average(feature_maps, align_corners, index=-1, resize_size=None):
+ """Resize the feature maps and compute the average.
+
+ Args:
+ feature_maps (list[Tensor]): Feature maps.
+ align_corners (bool): Align corners when performing interpolation.
+ index (int): Only used when `resize_size' is None.
+ If `resize_size' is None, the target size is the size
+ of the indexed feature maps.
+ resize_size (list[int, int]): The target size [w, h].
+
+ Returns:
+ list[Tensor]: Averaged feature_maps.
+ """
+
+ if feature_maps is None:
+ return None
+ feature_maps_avg = 0
+
+ feature_map_list = _resize_concate(
+ feature_maps, align_corners, index=index, resize_size=resize_size)
+ for feature_map in feature_map_list:
+ feature_maps_avg += feature_map
+
+ feature_maps_avg /= len(feature_map_list)
+ return [feature_maps_avg]
+
+
+def _resize_unsqueeze_concat(feature_maps,
+ align_corners,
+ index=-1,
+ resize_size=None):
+ """Resize, unsqueeze and concatenate the feature_maps.
+
+ Args:
+ feature_maps (list[Tensor]): Feature maps.
+ align_corners (bool): Align corners when performing interpolation.
+ index (int): Only used when `resize_size' is None.
+ If `resize_size' is None, the target size is the size
+ of the indexed feature maps.
+ resize_size (list[int, int]): The target size [w, h].
+
+ Returns:
+ list[Tensor]: Averaged feature_maps.
+ """
+ if feature_maps is None:
+ return None
+ feature_map_list = _resize_concate(
+ feature_maps, align_corners, index=index, resize_size=resize_size)
+
+ feat_dim = len(feature_map_list[0].shape) - 1
+ output_feature_maps = torch.cat(
+ [torch.unsqueeze(fmap, dim=feat_dim + 1) for fmap in feature_map_list],
+ dim=feat_dim + 1)
+ return [output_feature_maps]
+
+
+def _resize_concate(feature_maps, align_corners, index=-1, resize_size=None):
+ """Resize and concatenate the feature_maps.
+
+ Args:
+ feature_maps (list[Tensor]): Feature maps.
+ align_corners (bool): Align corners when performing interpolation.
+ index (int): Only used when `resize_size' is None.
+ If `resize_size' is None, the target size is the size
+ of the indexed feature maps.
+ resize_size (list[int, int]): The target size [w, h].
+
+ Returns:
+ list[Tensor]: Averaged feature_maps.
+ """
+ if feature_maps is None:
+ return None
+
+ feature_map_list = []
+
+ if index < 0:
+ index += len(feature_maps)
+
+ if resize_size is None:
+ resize_size = (feature_maps[index].size(2),
+ feature_maps[index].size(3))
+
+ for feature_map in feature_maps:
+ ori_size = (feature_map.size(2), feature_map.size(3))
+ if ori_size != resize_size:
+ feature_map = torch.nn.functional.interpolate(
+ feature_map,
+ size=resize_size,
+ mode='bilinear',
+ align_corners=align_corners)
+
+ feature_map_list.append(feature_map)
+
+ return feature_map_list
+
+
+def aggregate_stage_flip(feature_maps,
+ feature_maps_flip,
+ index=-1,
+ project2image=True,
+ size_projected=None,
+ align_corners=False,
+ aggregate_stage='concat',
+ aggregate_flip='average'):
+ """Inference the model to get multi-stage outputs (heatmaps & tags), and
+ resize them to base sizes.
+
+ Args:
+ feature_maps (list[Tensor]): feature_maps can be heatmaps,
+ tags, and pafs.
+ feature_maps_flip (list[Tensor] | None): flipped feature_maps.
+ feature maps can be heatmaps, tags, and pafs.
+ project2image (bool): Option to resize to base scale.
+ size_projected (list[int, int]): Base size of heatmaps [w, h].
+ align_corners (bool): Align corners when performing interpolation.
+ aggregate_stage (str): Methods to aggregate multi-stage feature maps.
+ Options: 'concat', 'average'. Default: 'concat.
+
+ - 'concat': Concatenate the original and the flipped feature maps.
+ - 'average': Get the average of the original and the flipped
+ feature maps.
+ aggregate_flip (str): Methods to aggregate the original and
+ the flipped feature maps. Options: 'concat', 'average', 'none'.
+ Default: 'average.
+
+ - 'concat': Concatenate the original and the flipped feature maps.
+ - 'average': Get the average of the original and the flipped
+ feature maps..
+ - 'none': no flipped feature maps.
+
+ Returns:
+ list[Tensor]: Aggregated feature maps with shape [NxKxWxH].
+ """
+
+ if feature_maps_flip is None:
+ aggregate_flip = 'none'
+
+ output_feature_maps = []
+
+ if aggregate_stage == 'average':
+ _aggregate_stage_func = _resize_average
+ elif aggregate_stage == 'concat':
+ _aggregate_stage_func = _resize_concate
+ else:
+ NotImplementedError()
+
+ if project2image and size_projected:
+ _origin = _aggregate_stage_func(
+ feature_maps,
+ align_corners,
+ index=index,
+ resize_size=(size_projected[1], size_projected[0]))
+
+ _flipped = _aggregate_stage_func(
+ feature_maps_flip,
+ align_corners,
+ index=index,
+ resize_size=(size_projected[1], size_projected[0]))
+ else:
+ _origin = _aggregate_stage_func(
+ feature_maps, align_corners, index=index, resize_size=None)
+ _flipped = _aggregate_stage_func(
+ feature_maps_flip, align_corners, index=index, resize_size=None)
+
+ if aggregate_flip == 'average':
+ assert feature_maps_flip is not None
+ for _ori, _fli in zip(_origin, _flipped):
+ output_feature_maps.append((_ori + _fli) / 2.0)
+
+ elif aggregate_flip == 'concat':
+ assert feature_maps_flip is not None
+ output_feature_maps.append(*_origin)
+ output_feature_maps.append(*_flipped)
+
+ elif aggregate_flip == 'none':
+ if isinstance(_origin, list):
+ output_feature_maps.append(*_origin)
+ else:
+ output_feature_maps.append(_origin)
+ else:
+ NotImplementedError()
+
+ return output_feature_maps
+
+
+def aggregate_scale(feature_maps_list,
+ align_corners=False,
+ aggregate_scale='average'):
+ """Aggregate multi-scale outputs.
+
+ Note:
+ batch size: N
+ keypoints num : K
+ heatmap width: W
+ heatmap height: H
+
+ Args:
+ feature_maps_list (list[Tensor]): Aggregated feature maps.
+ project2image (bool): Option to resize to base scale.
+ align_corners (bool): Align corners when performing interpolation.
+ aggregate_scale (str): Methods to aggregate multi-scale feature maps.
+ Options: 'average', 'unsqueeze_concat'.
+
+ - 'average': Get the average of the feature maps.
+ - 'unsqueeze_concat': Concatenate the feature maps along new axis.
+ Default: 'average.
+
+ Returns:
+ Tensor: Aggregated feature maps.
+ """
+
+ if aggregate_scale == 'average':
+ output_feature_maps = _resize_average(
+ feature_maps_list, align_corners, index=0, resize_size=None)
+
+ elif aggregate_scale == 'unsqueeze_concat':
+ output_feature_maps = _resize_unsqueeze_concat(
+ feature_maps_list, align_corners, index=0, resize_size=None)
+ else:
+ NotImplementedError()
+
+ return output_feature_maps[0]
+
+
+def get_group_preds(grouped_joints,
+ center,
+ scale,
+ heatmap_size,
+ use_udp=False):
+ """Transform the grouped joints back to the image.
+
+ Args:
+ grouped_joints (list): Grouped person joints.
+ center (np.ndarray[2, ]): Center of the bounding box (x, y).
+ scale (np.ndarray[2, ]): Scale of the bounding box
+ wrt [width, height].
+ heatmap_size (np.ndarray[2, ]): Size of the destination heatmaps.
+ use_udp (bool): Unbiased data processing.
+ Paper ref: Huang et al. The Devil is in the Details: Delving into
+ Unbiased Data Processing for Human Pose Estimation (CVPR'2020).
+
+ Returns:
+ list: List of the pose result for each person.
+ """
+ if len(grouped_joints) == 0:
+ return []
+
+ if use_udp:
+ if grouped_joints[0].shape[0] > 0:
+ heatmap_size_t = np.array(heatmap_size, dtype=np.float32) - 1.0
+ trans = get_warp_matrix(
+ theta=0,
+ size_input=heatmap_size_t,
+ size_dst=scale,
+ size_target=heatmap_size_t)
+ grouped_joints[0][..., :2] = \
+ warp_affine_joints(grouped_joints[0][..., :2], trans)
+ results = [person for person in grouped_joints[0]]
+ else:
+ results = []
+ for person in grouped_joints[0]:
+ joints = transform_preds(person, center, scale, heatmap_size)
+ results.append(joints)
+
+ return results
diff --git a/grounded-sam-osx/transformer_utils/mmpose/core/evaluation/eval_hooks.py b/grounded-sam-osx/transformer_utils/mmpose/core/evaluation/eval_hooks.py
new file mode 100644
index 0000000000000000000000000000000000000000..b35a9c6a990c69b2beac9e73f893f97c237e4783
--- /dev/null
+++ b/grounded-sam-osx/transformer_utils/mmpose/core/evaluation/eval_hooks.py
@@ -0,0 +1,99 @@
+# Copyright (c) OpenMMLab. All rights reserved.
+import warnings
+
+from mmcv.runner import DistEvalHook as _DistEvalHook
+from mmcv.runner import EvalHook as _EvalHook
+
+MMPOSE_GREATER_KEYS = [
+ 'acc', 'ap', 'ar', 'pck', 'auc', '3dpck', 'p-3dpck', '3dauc', 'p-3dauc',
+ 'pcp'
+]
+MMPOSE_LESS_KEYS = ['loss', 'epe', 'nme', 'mpjpe', 'p-mpjpe', 'n-mpjpe']
+
+
+class EvalHook(_EvalHook):
+
+ def __init__(self,
+ dataloader,
+ start=None,
+ interval=1,
+ by_epoch=True,
+ save_best=None,
+ rule=None,
+ test_fn=None,
+ greater_keys=MMPOSE_GREATER_KEYS,
+ less_keys=MMPOSE_LESS_KEYS,
+ **eval_kwargs):
+
+ if test_fn is None:
+ from mmpose.apis import single_gpu_test
+ test_fn = single_gpu_test
+
+ # to be compatible with the config before v0.16.0
+
+ # remove "gpu_collect" from eval_kwargs
+ if 'gpu_collect' in eval_kwargs:
+ warnings.warn(
+ '"gpu_collect" will be deprecated in EvalHook.'
+ 'Please remove it from the config.', DeprecationWarning)
+ _ = eval_kwargs.pop('gpu_collect')
+
+ # update "save_best" according to "key_indicator" and remove the
+ # latter from eval_kwargs
+ if 'key_indicator' in eval_kwargs or isinstance(save_best, bool):
+ warnings.warn(
+ '"key_indicator" will be deprecated in EvalHook.'
+ 'Please use "save_best" to specify the metric key,'
+ 'e.g., save_best="AP".', DeprecationWarning)
+
+ key_indicator = eval_kwargs.pop('key_indicator', 'AP')
+ if save_best is True and key_indicator is None:
+ raise ValueError('key_indicator should not be None, when '
+ 'save_best is set to True.')
+ save_best = key_indicator
+
+ super().__init__(dataloader, start, interval, by_epoch, save_best,
+ rule, test_fn, greater_keys, less_keys, **eval_kwargs)
+
+
+class DistEvalHook(_DistEvalHook):
+
+ def __init__(self,
+ dataloader,
+ start=None,
+ interval=1,
+ by_epoch=True,
+ save_best=None,
+ rule=None,
+ test_fn=None,
+ greater_keys=MMPOSE_GREATER_KEYS,
+ less_keys=MMPOSE_LESS_KEYS,
+ broadcast_bn_buffer=True,
+ tmpdir=None,
+ gpu_collect=False,
+ **eval_kwargs):
+
+ if test_fn is None:
+ from mmpose.apis import multi_gpu_test
+ test_fn = multi_gpu_test
+
+ # to be compatible with the config before v0.16.0
+
+ # update "save_best" according to "key_indicator" and remove the
+ # latter from eval_kwargs
+ if 'key_indicator' in eval_kwargs or isinstance(save_best, bool):
+ warnings.warn(
+ '"key_indicator" will be deprecated in EvalHook.'
+ 'Please use "save_best" to specify the metric key,'
+ 'e.g., save_best="AP".', DeprecationWarning)
+
+ key_indicator = eval_kwargs.pop('key_indicator', 'AP')
+ if save_best is True and key_indicator is None:
+ raise ValueError('key_indicator should not be None, when '
+ 'save_best is set to True.')
+ save_best = key_indicator
+
+ super().__init__(dataloader, start, interval, by_epoch, save_best,
+ rule, test_fn, greater_keys, less_keys,
+ broadcast_bn_buffer, tmpdir, gpu_collect,
+ **eval_kwargs)
diff --git a/grounded-sam-osx/transformer_utils/mmpose/core/evaluation/mesh_eval.py b/grounded-sam-osx/transformer_utils/mmpose/core/evaluation/mesh_eval.py
new file mode 100644
index 0000000000000000000000000000000000000000..683b4539b29d1829a324de424c6d9f85a7037e5d
--- /dev/null
+++ b/grounded-sam-osx/transformer_utils/mmpose/core/evaluation/mesh_eval.py
@@ -0,0 +1,66 @@
+# ------------------------------------------------------------------------------
+# Adapted from https://github.com/akanazawa/hmr
+# Original licence: Copyright (c) 2018 akanazawa, under the MIT License.
+# ------------------------------------------------------------------------------
+
+import numpy as np
+
+
+def compute_similarity_transform(source_points, target_points):
+ """Computes a similarity transform (sR, t) that takes a set of 3D points
+ source_points (N x 3) closest to a set of 3D points target_points, where R
+ is an 3x3 rotation matrix, t 3x1 translation, s scale. And return the
+ transformed 3D points source_points_hat (N x 3). i.e. solves the orthogonal
+ Procrutes problem.
+
+ Note:
+ Points number: N
+
+ Args:
+ source_points (np.ndarray): Source point set with shape [N, 3].
+ target_points (np.ndarray): Target point set with shape [N, 3].
+
+ Returns:
+ np.ndarray: Transformed source point set with shape [N, 3].
+ """
+
+ assert target_points.shape[0] == source_points.shape[0]
+ assert target_points.shape[1] == 3 and source_points.shape[1] == 3
+
+ source_points = source_points.T
+ target_points = target_points.T
+
+ # 1. Remove mean.
+ mu1 = source_points.mean(axis=1, keepdims=True)
+ mu2 = target_points.mean(axis=1, keepdims=True)
+ X1 = source_points - mu1
+ X2 = target_points - mu2
+
+ # 2. Compute variance of X1 used for scale.
+ var1 = np.sum(X1**2)
+
+ # 3. The outer product of X1 and X2.
+ K = X1.dot(X2.T)
+
+ # 4. Solution that Maximizes trace(R'K) is R=U*V', where U, V are
+ # singular vectors of K.
+ U, _, Vh = np.linalg.svd(K)
+ V = Vh.T
+ # Construct Z that fixes the orientation of R to get det(R)=1.
+ Z = np.eye(U.shape[0])
+ Z[-1, -1] *= np.sign(np.linalg.det(U.dot(V.T)))
+ # Construct R.
+ R = V.dot(Z.dot(U.T))
+
+ # 5. Recover scale.
+ scale = np.trace(R.dot(K)) / var1
+
+ # 6. Recover translation.
+ t = mu2 - scale * (R.dot(mu1))
+
+ # 7. Transform the source points:
+ source_points_hat = scale * R.dot(source_points) + t
+
+ source_points_hat = source_points_hat.T
+
+ return source_points_hat
diff --git a/grounded-sam-osx/transformer_utils/mmpose/core/evaluation/pose3d_eval.py b/grounded-sam-osx/transformer_utils/mmpose/core/evaluation/pose3d_eval.py
new file mode 100644
index 0000000000000000000000000000000000000000..545778ca7441c2d3e8ec58449c8ca7b162322e9e
--- /dev/null
+++ b/grounded-sam-osx/transformer_utils/mmpose/core/evaluation/pose3d_eval.py
@@ -0,0 +1,171 @@
+# Copyright (c) OpenMMLab. All rights reserved.
+import numpy as np
+
+from .mesh_eval import compute_similarity_transform
+
+
+def keypoint_mpjpe(pred, gt, mask, alignment='none'):
+ """Calculate the mean per-joint position error (MPJPE) and the error after
+ rigid alignment with the ground truth (P-MPJPE).
+
+ Note:
+ - batch_size: N
+ - num_keypoints: K
+ - keypoint_dims: C
+
+ Args:
+ pred (np.ndarray): Predicted keypoint location with shape [N, K, C].
+ gt (np.ndarray): Groundtruth keypoint location with shape [N, K, C].
+ mask (np.ndarray): Visibility of the target with shape [N, K].
+ False for invisible joints, and True for visible.
+ Invisible joints will be ignored for accuracy calculation.
+ alignment (str, optional): method to align the prediction with the
+ groundtruth. Supported options are:
+
+ - ``'none'``: no alignment will be applied
+ - ``'scale'``: align in the least-square sense in scale
+ - ``'procrustes'``: align in the least-square sense in
+ scale, rotation and translation.
+ Returns:
+ tuple: A tuple containing joint position errors
+
+ - (float | np.ndarray): mean per-joint position error (mpjpe).
+ - (float | np.ndarray): mpjpe after rigid alignment with the
+ ground truth (p-mpjpe).
+ """
+ assert mask.any()
+
+ if alignment == 'none':
+ pass
+ elif alignment == 'procrustes':
+ pred = np.stack([
+ compute_similarity_transform(pred_i, gt_i)
+ for pred_i, gt_i in zip(pred, gt)
+ ])
+ elif alignment == 'scale':
+ pred_dot_pred = np.einsum('nkc,nkc->n', pred, pred)
+ pred_dot_gt = np.einsum('nkc,nkc->n', pred, gt)
+ scale_factor = pred_dot_gt / pred_dot_pred
+ pred = pred * scale_factor[:, None, None]
+ else:
+ raise ValueError(f'Invalid value for alignment: {alignment}')
+
+ error = np.linalg.norm(pred - gt, ord=2, axis=-1)[mask].mean()
+
+ return error
+
+
+def keypoint_3d_pck(pred, gt, mask, alignment='none', threshold=0.15):
+ """Calculate the Percentage of Correct Keypoints (3DPCK) w. or w/o rigid
+ alignment.
+
+ Paper ref: `Monocular 3D Human Pose Estimation In The Wild Using Improved
+ CNN Supervision' 3DV'2017. `__ .
+
+ Note:
+ - batch_size: N
+ - num_keypoints: K
+ - keypoint_dims: C
+
+ Args:
+ pred (np.ndarray[N, K, C]): Predicted keypoint location.
+ gt (np.ndarray[N, K, C]): Groundtruth keypoint location.
+ mask (np.ndarray[N, K]): Visibility of the target. False for invisible
+ joints, and True for visible. Invisible joints will be ignored for
+ accuracy calculation.
+ alignment (str, optional): method to align the prediction with the
+ groundtruth. Supported options are:
+
+ - ``'none'``: no alignment will be applied
+ - ``'scale'``: align in the least-square sense in scale
+ - ``'procrustes'``: align in the least-square sense in scale,
+ rotation and translation.
+
+ threshold: If L2 distance between the prediction and the groundtruth
+ is less then threshold, the predicted result is considered as
+ correct. Default: 0.15 (m).
+
+ Returns:
+ pck: percentage of correct keypoints.
+ """
+ assert mask.any()
+
+ if alignment == 'none':
+ pass
+ elif alignment == 'procrustes':
+ pred = np.stack([
+ compute_similarity_transform(pred_i, gt_i)
+ for pred_i, gt_i in zip(pred, gt)
+ ])
+ elif alignment == 'scale':
+ pred_dot_pred = np.einsum('nkc,nkc->n', pred, pred)
+ pred_dot_gt = np.einsum('nkc,nkc->n', pred, gt)
+ scale_factor = pred_dot_gt / pred_dot_pred
+ pred = pred * scale_factor[:, None, None]
+ else:
+ raise ValueError(f'Invalid value for alignment: {alignment}')
+
+ error = np.linalg.norm(pred - gt, ord=2, axis=-1)
+ pck = (error < threshold).astype(np.float32)[mask].mean() * 100
+
+ return pck
+
+
+def keypoint_3d_auc(pred, gt, mask, alignment='none'):
+ """Calculate the Area Under the Curve (3DAUC) computed for a range of 3DPCK
+ thresholds.
+
+ Paper ref: `Monocular 3D Human Pose Estimation In The Wild Using Improved
+ CNN Supervision' 3DV'2017. `__ .
+ This implementation is derived from mpii_compute_3d_pck.m, which is
+ provided as part of the MPI-INF-3DHP test data release.
+
+ Note:
+ batch_size: N
+ num_keypoints: K
+ keypoint_dims: C
+
+ Args:
+ pred (np.ndarray[N, K, C]): Predicted keypoint location.
+ gt (np.ndarray[N, K, C]): Groundtruth keypoint location.
+ mask (np.ndarray[N, K]): Visibility of the target. False for invisible
+ joints, and True for visible. Invisible joints will be ignored for
+ accuracy calculation.
+ alignment (str, optional): method to align the prediction with the
+ groundtruth. Supported options are:
+
+ - ``'none'``: no alignment will be applied
+ - ``'scale'``: align in the least-square sense in scale
+ - ``'procrustes'``: align in the least-square sense in scale,
+ rotation and translation.
+
+ Returns:
+ auc: AUC computed for a range of 3DPCK thresholds.
+ """
+ assert mask.any()
+
+ if alignment == 'none':
+ pass
+ elif alignment == 'procrustes':
+ pred = np.stack([
+ compute_similarity_transform(pred_i, gt_i)
+ for pred_i, gt_i in zip(pred, gt)
+ ])
+ elif alignment == 'scale':
+ pred_dot_pred = np.einsum('nkc,nkc->n', pred, pred)
+ pred_dot_gt = np.einsum('nkc,nkc->n', pred, gt)
+ scale_factor = pred_dot_gt / pred_dot_pred
+ pred = pred * scale_factor[:, None, None]
+ else:
+ raise ValueError(f'Invalid value for alignment: {alignment}')
+
+ error = np.linalg.norm(pred - gt, ord=2, axis=-1)
+
+ thresholds = np.linspace(0., 0.15, 31)
+ pck_values = np.zeros(len(thresholds))
+ for i in range(len(thresholds)):
+ pck_values[i] = (error < thresholds[i]).astype(np.float32)[mask].mean()
+
+ auc = pck_values.mean() * 100
+
+ return auc
diff --git a/grounded-sam-osx/transformer_utils/mmpose/core/evaluation/top_down_eval.py b/grounded-sam-osx/transformer_utils/mmpose/core/evaluation/top_down_eval.py
new file mode 100644
index 0000000000000000000000000000000000000000..ee6a2501cf1eec1b16f7d58bf9fd62da0fa48ccf
--- /dev/null
+++ b/grounded-sam-osx/transformer_utils/mmpose/core/evaluation/top_down_eval.py
@@ -0,0 +1,684 @@
+# Copyright (c) OpenMMLab. All rights reserved.
+import warnings
+
+import cv2
+import numpy as np
+
+from mmpose.core.post_processing import transform_preds
+
+
+def _calc_distances(preds, targets, mask, normalize):
+ """Calculate the normalized distances between preds and target.
+
+ Note:
+ batch_size: N
+ num_keypoints: K
+ dimension of keypoints: D (normally, D=2 or D=3)
+
+ Args:
+ preds (np.ndarray[N, K, D]): Predicted keypoint location.
+ targets (np.ndarray[N, K, D]): Groundtruth keypoint location.
+ mask (np.ndarray[N, K]): Visibility of the target. False for invisible
+ joints, and True for visible. Invisible joints will be ignored for
+ accuracy calculation.
+ normalize (np.ndarray[N, D]): Typical value is heatmap_size
+
+ Returns:
+ np.ndarray[K, N]: The normalized distances. \
+ If target keypoints are missing, the distance is -1.
+ """
+ N, K, _ = preds.shape
+ # set mask=0 when normalize==0
+ _mask = mask.copy()
+ _mask[np.where((normalize == 0).sum(1))[0], :] = False
+ distances = np.full((N, K), -1, dtype=np.float32)
+ # handle invalid values
+ normalize[np.where(normalize <= 0)] = 1e6
+ distances[_mask] = np.linalg.norm(
+ ((preds - targets) / normalize[:, None, :])[_mask], axis=-1)
+ return distances.T
+
+
+def _distance_acc(distances, thr=0.5):
+ """Return the percentage below the distance threshold, while ignoring
+ distances values with -1.
+
+ Note:
+ batch_size: N
+ Args:
+ distances (np.ndarray[N, ]): The normalized distances.
+ thr (float): Threshold of the distances.
+
+ Returns:
+ float: Percentage of distances below the threshold. \
+ If all target keypoints are missing, return -1.
+ """
+ distance_valid = distances != -1
+ num_distance_valid = distance_valid.sum()
+ if num_distance_valid > 0:
+ return (distances[distance_valid] < thr).sum() / num_distance_valid
+ return -1
+
+
+def _get_max_preds(heatmaps):
+ """Get keypoint predictions from score maps.
+
+ Note:
+ batch_size: N
+ num_keypoints: K
+ heatmap height: H
+ heatmap width: W
+
+ Args:
+ heatmaps (np.ndarray[N, K, H, W]): model predicted heatmaps.
+
+ Returns:
+ tuple: A tuple containing aggregated results.
+
+ - preds (np.ndarray[N, K, 2]): Predicted keypoint location.
+ - maxvals (np.ndarray[N, K, 1]): Scores (confidence) of the keypoints.
+ """
+ assert isinstance(heatmaps,
+ np.ndarray), ('heatmaps should be numpy.ndarray')
+ assert heatmaps.ndim == 4, 'batch_images should be 4-ndim'
+
+ N, K, _, W = heatmaps.shape
+ heatmaps_reshaped = heatmaps.reshape((N, K, -1))
+ idx = np.argmax(heatmaps_reshaped, 2).reshape((N, K, 1))
+ maxvals = np.amax(heatmaps_reshaped, 2).reshape((N, K, 1))
+
+ preds = np.tile(idx, (1, 1, 2)).astype(np.float32)
+ preds[:, :, 0] = preds[:, :, 0] % W
+ preds[:, :, 1] = preds[:, :, 1] // W
+
+ preds = np.where(np.tile(maxvals, (1, 1, 2)) > 0.0, preds, -1)
+ return preds, maxvals
+
+
+def _get_max_preds_3d(heatmaps):
+ """Get keypoint predictions from 3D score maps.
+
+ Note:
+ batch size: N
+ num keypoints: K
+ heatmap depth size: D
+ heatmap height: H
+ heatmap width: W
+
+ Args:
+ heatmaps (np.ndarray[N, K, D, H, W]): model predicted heatmaps.
+
+ Returns:
+ tuple: A tuple containing aggregated results.
+
+ - preds (np.ndarray[N, K, 3]): Predicted keypoint location.
+ - maxvals (np.ndarray[N, K, 1]): Scores (confidence) of the keypoints.
+ """
+ assert isinstance(heatmaps, np.ndarray), \
+ ('heatmaps should be numpy.ndarray')
+ assert heatmaps.ndim == 5, 'heatmaps should be 5-ndim'
+
+ N, K, D, H, W = heatmaps.shape
+ heatmaps_reshaped = heatmaps.reshape((N, K, -1))
+ idx = np.argmax(heatmaps_reshaped, 2).reshape((N, K, 1))
+ maxvals = np.amax(heatmaps_reshaped, 2).reshape((N, K, 1))
+
+ preds = np.zeros((N, K, 3), dtype=np.float32)
+ _idx = idx[..., 0]
+ preds[..., 2] = _idx // (H * W)
+ preds[..., 1] = (_idx // W) % H
+ preds[..., 0] = _idx % W
+
+ preds = np.where(maxvals > 0.0, preds, -1)
+ return preds, maxvals
+
+
+def pose_pck_accuracy(output, target, mask, thr=0.05, normalize=None):
+ """Calculate the pose accuracy of PCK for each individual keypoint and the
+ averaged accuracy across all keypoints from heatmaps.
+
+ Note:
+ PCK metric measures accuracy of the localization of the body joints.
+ The distances between predicted positions and the ground-truth ones
+ are typically normalized by the bounding box size.
+ The threshold (thr) of the normalized distance is commonly set
+ as 0.05, 0.1 or 0.2 etc.
+
+ - batch_size: N
+ - num_keypoints: K
+ - heatmap height: H
+ - heatmap width: W
+
+ Args:
+ output (np.ndarray[N, K, H, W]): Model output heatmaps.
+ target (np.ndarray[N, K, H, W]): Groundtruth heatmaps.
+ mask (np.ndarray[N, K]): Visibility of the target. False for invisible
+ joints, and True for visible. Invisible joints will be ignored for
+ accuracy calculation.
+ thr (float): Threshold of PCK calculation. Default 0.05.
+ normalize (np.ndarray[N, 2]): Normalization factor for H&W.
+
+ Returns:
+ tuple: A tuple containing keypoint accuracy.
+
+ - np.ndarray[K]: Accuracy of each keypoint.
+ - float: Averaged accuracy across all keypoints.
+ - int: Number of valid keypoints.
+ """
+ N, K, H, W = output.shape
+ if K == 0:
+ return None, 0, 0
+ if normalize is None:
+ normalize = np.tile(np.array([[H, W]]), (N, 1))
+
+ pred, _ = _get_max_preds(output)
+ gt, _ = _get_max_preds(target)
+ return keypoint_pck_accuracy(pred, gt, mask, thr, normalize)
+
+
+def keypoint_pck_accuracy(pred, gt, mask, thr, normalize):
+ """Calculate the pose accuracy of PCK for each individual keypoint and the
+ averaged accuracy across all keypoints for coordinates.
+
+ Note:
+ PCK metric measures accuracy of the localization of the body joints.
+ The distances between predicted positions and the ground-truth ones
+ are typically normalized by the bounding box size.
+ The threshold (thr) of the normalized distance is commonly set
+ as 0.05, 0.1 or 0.2 etc.
+
+ - batch_size: N
+ - num_keypoints: K
+
+ Args:
+ pred (np.ndarray[N, K, 2]): Predicted keypoint location.
+ gt (np.ndarray[N, K, 2]): Groundtruth keypoint location.
+ mask (np.ndarray[N, K]): Visibility of the target. False for invisible
+ joints, and True for visible. Invisible joints will be ignored for
+ accuracy calculation.
+ thr (float): Threshold of PCK calculation.
+ normalize (np.ndarray[N, 2]): Normalization factor for H&W.
+
+ Returns:
+ tuple: A tuple containing keypoint accuracy.
+
+ - acc (np.ndarray[K]): Accuracy of each keypoint.
+ - avg_acc (float): Averaged accuracy across all keypoints.
+ - cnt (int): Number of valid keypoints.
+ """
+ distances = _calc_distances(pred, gt, mask, normalize)
+
+ acc = np.array([_distance_acc(d, thr) for d in distances])
+ valid_acc = acc[acc >= 0]
+ cnt = len(valid_acc)
+ avg_acc = valid_acc.mean() if cnt > 0 else 0
+ return acc, avg_acc, cnt
+
+
+def keypoint_auc(pred, gt, mask, normalize, num_step=20):
+ """Calculate the pose accuracy of PCK for each individual keypoint and the
+ averaged accuracy across all keypoints for coordinates.
+
+ Note:
+ - batch_size: N
+ - num_keypoints: K
+
+ Args:
+ pred (np.ndarray[N, K, 2]): Predicted keypoint location.
+ gt (np.ndarray[N, K, 2]): Groundtruth keypoint location.
+ mask (np.ndarray[N, K]): Visibility of the target. False for invisible
+ joints, and True for visible. Invisible joints will be ignored for
+ accuracy calculation.
+ normalize (float): Normalization factor.
+
+ Returns:
+ float: Area under curve.
+ """
+ nor = np.tile(np.array([[normalize, normalize]]), (pred.shape[0], 1))
+ x = [1.0 * i / num_step for i in range(num_step)]
+ y = []
+ for thr in x:
+ _, avg_acc, _ = keypoint_pck_accuracy(pred, gt, mask, thr, nor)
+ y.append(avg_acc)
+
+ auc = 0
+ for i in range(num_step):
+ auc += 1.0 / num_step * y[i]
+ return auc
+
+
+def keypoint_nme(pred, gt, mask, normalize_factor):
+ """Calculate the normalized mean error (NME).
+
+ Note:
+ - batch_size: N
+ - num_keypoints: K
+
+ Args:
+ pred (np.ndarray[N, K, 2]): Predicted keypoint location.
+ gt (np.ndarray[N, K, 2]): Groundtruth keypoint location.
+ mask (np.ndarray[N, K]): Visibility of the target. False for invisible
+ joints, and True for visible. Invisible joints will be ignored for
+ accuracy calculation.
+ normalize_factor (np.ndarray[N, 2]): Normalization factor.
+
+ Returns:
+ float: normalized mean error
+ """
+ distances = _calc_distances(pred, gt, mask, normalize_factor)
+ distance_valid = distances[distances != -1]
+ return distance_valid.sum() / max(1, len(distance_valid))
+
+
+def keypoint_epe(pred, gt, mask):
+ """Calculate the end-point error.
+
+ Note:
+ - batch_size: N
+ - num_keypoints: K
+
+ Args:
+ pred (np.ndarray[N, K, 2]): Predicted keypoint location.
+ gt (np.ndarray[N, K, 2]): Groundtruth keypoint location.
+ mask (np.ndarray[N, K]): Visibility of the target. False for invisible
+ joints, and True for visible. Invisible joints will be ignored for
+ accuracy calculation.
+
+ Returns:
+ float: Average end-point error.
+ """
+
+ distances = _calc_distances(
+ pred, gt, mask,
+ np.ones((pred.shape[0], pred.shape[2]), dtype=np.float32))
+ distance_valid = distances[distances != -1]
+ return distance_valid.sum() / max(1, len(distance_valid))
+
+
+def _taylor(heatmap, coord):
+ """Distribution aware coordinate decoding method.
+
+ Note:
+ - heatmap height: H
+ - heatmap width: W
+
+ Args:
+ heatmap (np.ndarray[H, W]): Heatmap of a particular joint type.
+ coord (np.ndarray[2,]): Coordinates of the predicted keypoints.
+
+ Returns:
+ np.ndarray[2,]: Updated coordinates.
+ """
+ H, W = heatmap.shape[:2]
+ px, py = int(coord[0]), int(coord[1])
+ if 1 < px < W - 2 and 1 < py < H - 2:
+ dx = 0.5 * (heatmap[py][px + 1] - heatmap[py][px - 1])
+ dy = 0.5 * (heatmap[py + 1][px] - heatmap[py - 1][px])
+ dxx = 0.25 * (
+ heatmap[py][px + 2] - 2 * heatmap[py][px] + heatmap[py][px - 2])
+ dxy = 0.25 * (
+ heatmap[py + 1][px + 1] - heatmap[py - 1][px + 1] -
+ heatmap[py + 1][px - 1] + heatmap[py - 1][px - 1])
+ dyy = 0.25 * (
+ heatmap[py + 2 * 1][px] - 2 * heatmap[py][px] +
+ heatmap[py - 2 * 1][px])
+ derivative = np.array([[dx], [dy]])
+ hessian = np.array([[dxx, dxy], [dxy, dyy]])
+ if dxx * dyy - dxy**2 != 0:
+ hessianinv = np.linalg.inv(hessian)
+ offset = -hessianinv @ derivative
+ offset = np.squeeze(np.array(offset.T), axis=0)
+ coord += offset
+ return coord
+
+
+def post_dark_udp(coords, batch_heatmaps, kernel=3):
+ """DARK post-pocessing. Implemented by udp. Paper ref: Huang et al. The
+ Devil is in the Details: Delving into Unbiased Data Processing for Human
+ Pose Estimation (CVPR 2020). Zhang et al. Distribution-Aware Coordinate
+ Representation for Human Pose Estimation (CVPR 2020).
+
+ Note:
+ - batch size: B
+ - num keypoints: K
+ - num persons: N
+ - height of heatmaps: H
+ - width of heatmaps: W
+
+ B=1 for bottom_up paradigm where all persons share the same heatmap.
+ B=N for top_down paradigm where each person has its own heatmaps.
+
+ Args:
+ coords (np.ndarray[N, K, 2]): Initial coordinates of human pose.
+ batch_heatmaps (np.ndarray[B, K, H, W]): batch_heatmaps
+ kernel (int): Gaussian kernel size (K) for modulation.
+
+ Returns:
+ np.ndarray([N, K, 2]): Refined coordinates.
+ """
+ if not isinstance(batch_heatmaps, np.ndarray):
+ batch_heatmaps = batch_heatmaps.cpu().numpy()
+ B, K, H, W = batch_heatmaps.shape
+ N = coords.shape[0]
+ assert (B == 1 or B == N)
+ for heatmaps in batch_heatmaps:
+ for heatmap in heatmaps:
+ cv2.GaussianBlur(heatmap, (kernel, kernel), 0, heatmap)
+ np.clip(batch_heatmaps, 0.001, 50, batch_heatmaps)
+ np.log(batch_heatmaps, batch_heatmaps)
+
+ batch_heatmaps_pad = np.pad(
+ batch_heatmaps, ((0, 0), (0, 0), (1, 1), (1, 1)),
+ mode='edge').flatten()
+
+ index = coords[..., 0] + 1 + (coords[..., 1] + 1) * (W + 2)
+ index += (W + 2) * (H + 2) * np.arange(0, B * K).reshape(-1, K)
+ index = index.astype(int).reshape(-1, 1)
+ i_ = batch_heatmaps_pad[index]
+ ix1 = batch_heatmaps_pad[index + 1]
+ iy1 = batch_heatmaps_pad[index + W + 2]
+ ix1y1 = batch_heatmaps_pad[index + W + 3]
+ ix1_y1_ = batch_heatmaps_pad[index - W - 3]
+ ix1_ = batch_heatmaps_pad[index - 1]
+ iy1_ = batch_heatmaps_pad[index - 2 - W]
+
+ dx = 0.5 * (ix1 - ix1_)
+ dy = 0.5 * (iy1 - iy1_)
+ derivative = np.concatenate([dx, dy], axis=1)
+ derivative = derivative.reshape(N, K, 2, 1)
+ dxx = ix1 - 2 * i_ + ix1_
+ dyy = iy1 - 2 * i_ + iy1_
+ dxy = 0.5 * (ix1y1 - ix1 - iy1 + i_ + i_ - ix1_ - iy1_ + ix1_y1_)
+ hessian = np.concatenate([dxx, dxy, dxy, dyy], axis=1)
+ hessian = hessian.reshape(N, K, 2, 2)
+ hessian = np.linalg.inv(hessian + np.finfo(np.float32).eps * np.eye(2))
+ coords -= np.einsum('ijmn,ijnk->ijmk', hessian, derivative).squeeze()
+ return coords
+
+
+def _gaussian_blur(heatmaps, kernel=11):
+ """Modulate heatmap distribution with Gaussian.
+ sigma = 0.3*((kernel_size-1)*0.5-1)+0.8
+ sigma~=3 if k=17
+ sigma=2 if k=11;
+ sigma~=1.5 if k=7;
+ sigma~=1 if k=3;
+
+ Note:
+ - batch_size: N
+ - num_keypoints: K
+ - heatmap height: H
+ - heatmap width: W
+
+ Args:
+ heatmaps (np.ndarray[N, K, H, W]): model predicted heatmaps.
+ kernel (int): Gaussian kernel size (K) for modulation, which should
+ match the heatmap gaussian sigma when training.
+ K=17 for sigma=3 and k=11 for sigma=2.
+
+ Returns:
+ np.ndarray ([N, K, H, W]): Modulated heatmap distribution.
+ """
+ assert kernel % 2 == 1
+
+ border = (kernel - 1) // 2
+ batch_size = heatmaps.shape[0]
+ num_joints = heatmaps.shape[1]
+ height = heatmaps.shape[2]
+ width = heatmaps.shape[3]
+ for i in range(batch_size):
+ for j in range(num_joints):
+ origin_max = np.max(heatmaps[i, j])
+ dr = np.zeros((height + 2 * border, width + 2 * border),
+ dtype=np.float32)
+ dr[border:-border, border:-border] = heatmaps[i, j].copy()
+ dr = cv2.GaussianBlur(dr, (kernel, kernel), 0)
+ heatmaps[i, j] = dr[border:-border, border:-border].copy()
+ heatmaps[i, j] *= origin_max / np.max(heatmaps[i, j])
+ return heatmaps
+
+
+def keypoints_from_regression(regression_preds, center, scale, img_size):
+ """Get final keypoint predictions from regression vectors and transform
+ them back to the image.
+
+ Note:
+ - batch_size: N
+ - num_keypoints: K
+
+ Args:
+ regression_preds (np.ndarray[N, K, 2]): model prediction.
+ center (np.ndarray[N, 2]): Center of the bounding box (x, y).
+ scale (np.ndarray[N, 2]): Scale of the bounding box
+ wrt height/width.
+ img_size (list(img_width, img_height)): model input image size.
+
+ Returns:
+ tuple:
+
+ - preds (np.ndarray[N, K, 2]): Predicted keypoint location in images.
+ - maxvals (np.ndarray[N, K, 1]): Scores (confidence) of the keypoints.
+ """
+ N, K, _ = regression_preds.shape
+ preds, maxvals = regression_preds, np.ones((N, K, 1), dtype=np.float32)
+
+ preds = preds * img_size
+
+ # Transform back to the image
+ for i in range(N):
+ preds[i] = transform_preds(preds[i], center[i], scale[i], img_size)
+
+ return preds, maxvals
+
+
+def keypoints_from_heatmaps(heatmaps,
+ center,
+ scale,
+ unbiased=False,
+ post_process='default',
+ kernel=11,
+ valid_radius_factor=0.0546875,
+ use_udp=False,
+ target_type='GaussianHeatmap'):
+ """Get final keypoint predictions from heatmaps and transform them back to
+ the image.
+
+ Note:
+ - batch size: N
+ - num keypoints: K
+ - heatmap height: H
+ - heatmap width: W
+
+ Args:
+ heatmaps (np.ndarray[N, K, H, W]): model predicted heatmaps.
+ center (np.ndarray[N, 2]): Center of the bounding box (x, y).
+ scale (np.ndarray[N, 2]): Scale of the bounding box
+ wrt height/width.
+ post_process (str/None): Choice of methods to post-process
+ heatmaps. Currently supported: None, 'default', 'unbiased',
+ 'megvii'.
+ unbiased (bool): Option to use unbiased decoding. Mutually
+ exclusive with megvii.
+ Note: this arg is deprecated and unbiased=True can be replaced
+ by post_process='unbiased'
+ Paper ref: Zhang et al. Distribution-Aware Coordinate
+ Representation for Human Pose Estimation (CVPR 2020).
+ kernel (int): Gaussian kernel size (K) for modulation, which should
+ match the heatmap gaussian sigma when training.
+ K=17 for sigma=3 and k=11 for sigma=2.
+ valid_radius_factor (float): The radius factor of the positive area
+ in classification heatmap for UDP.
+ use_udp (bool): Use unbiased data processing.
+ target_type (str): 'GaussianHeatmap' or 'CombinedTarget'.
+ GaussianHeatmap: Classification target with gaussian distribution.
+ CombinedTarget: The combination of classification target
+ (response map) and regression target (offset map).
+ Paper ref: Huang et al. The Devil is in the Details: Delving into
+ Unbiased Data Processing for Human Pose Estimation (CVPR 2020).
+
+ Returns:
+ tuple: A tuple containing keypoint predictions and scores.
+
+ - preds (np.ndarray[N, K, 2]): Predicted keypoint location in images.
+ - maxvals (np.ndarray[N, K, 1]): Scores (confidence) of the keypoints.
+ """
+ # Avoid being affected
+ heatmaps = heatmaps.copy()
+
+ # detect conflicts
+ if unbiased:
+ assert post_process not in [False, None, 'megvii']
+ if post_process in ['megvii', 'unbiased']:
+ assert kernel > 0
+ if use_udp:
+ assert not post_process == 'megvii'
+
+ # normalize configs
+ if post_process is False:
+ warnings.warn(
+ 'post_process=False is deprecated, '
+ 'please use post_process=None instead', DeprecationWarning)
+ post_process = None
+ elif post_process is True:
+ if unbiased is True:
+ warnings.warn(
+ 'post_process=True, unbiased=True is deprecated,'
+ " please use post_process='unbiased' instead",
+ DeprecationWarning)
+ post_process = 'unbiased'
+ else:
+ warnings.warn(
+ 'post_process=True, unbiased=False is deprecated, '
+ "please use post_process='default' instead",
+ DeprecationWarning)
+ post_process = 'default'
+ elif post_process == 'default':
+ if unbiased is True:
+ warnings.warn(
+ 'unbiased=True is deprecated, please use '
+ "post_process='unbiased' instead", DeprecationWarning)
+ post_process = 'unbiased'
+
+ # start processing
+ if post_process == 'megvii':
+ heatmaps = _gaussian_blur(heatmaps, kernel=kernel)
+
+ N, K, H, W = heatmaps.shape
+ if use_udp:
+ if target_type.lower() == 'GaussianHeatMap'.lower():
+ preds, maxvals = _get_max_preds(heatmaps)
+ preds = post_dark_udp(preds, heatmaps, kernel=kernel)
+ elif target_type.lower() == 'CombinedTarget'.lower():
+ for person_heatmaps in heatmaps:
+ for i, heatmap in enumerate(person_heatmaps):
+ kt = 2 * kernel + 1 if i % 3 == 0 else kernel
+ cv2.GaussianBlur(heatmap, (kt, kt), 0, heatmap)
+ # valid radius is in direct proportion to the height of heatmap.
+ valid_radius = valid_radius_factor * H
+ offset_x = heatmaps[:, 1::3, :].flatten() * valid_radius
+ offset_y = heatmaps[:, 2::3, :].flatten() * valid_radius
+ heatmaps = heatmaps[:, ::3, :]
+ preds, maxvals = _get_max_preds(heatmaps)
+ index = preds[..., 0] + preds[..., 1] * W
+ index += W * H * np.arange(0, N * K / 3)
+ index = index.astype(int).reshape(N, K // 3, 1)
+ preds += np.concatenate((offset_x[index], offset_y[index]), axis=2)
+ else:
+ raise ValueError('target_type should be either '
+ "'GaussianHeatmap' or 'CombinedTarget'")
+ else:
+ preds, maxvals = _get_max_preds(heatmaps)
+ if post_process == 'unbiased': # alleviate biased coordinate
+ # apply Gaussian distribution modulation.
+ heatmaps = np.log(
+ np.maximum(_gaussian_blur(heatmaps, kernel), 1e-10))
+ for n in range(N):
+ for k in range(K):
+ preds[n][k] = _taylor(heatmaps[n][k], preds[n][k])
+ elif post_process is not None:
+ # add +/-0.25 shift to the predicted locations for higher acc.
+ for n in range(N):
+ for k in range(K):
+ heatmap = heatmaps[n][k]
+ px = int(preds[n][k][0])
+ py = int(preds[n][k][1])
+ if 1 < px < W - 1 and 1 < py < H - 1:
+ diff = np.array([
+ heatmap[py][px + 1] - heatmap[py][px - 1],
+ heatmap[py + 1][px] - heatmap[py - 1][px]
+ ])
+ preds[n][k] += np.sign(diff) * .25
+ if post_process == 'megvii':
+ preds[n][k] += 0.5
+
+ # Transform back to the image
+ for i in range(N):
+ preds[i] = transform_preds(
+ preds[i], center[i], scale[i], [W, H], use_udp=use_udp)
+
+ if post_process == 'megvii':
+ maxvals = maxvals / 255.0 + 0.5
+
+ return preds, maxvals
+
+
+def keypoints_from_heatmaps3d(heatmaps, center, scale):
+ """Get final keypoint predictions from 3d heatmaps and transform them back
+ to the image.
+
+ Note:
+ - batch size: N
+ - num keypoints: K
+ - heatmap depth size: D
+ - heatmap height: H
+ - heatmap width: W
+
+ Args:
+ heatmaps (np.ndarray[N, K, D, H, W]): model predicted heatmaps.
+ center (np.ndarray[N, 2]): Center of the bounding box (x, y).
+ scale (np.ndarray[N, 2]): Scale of the bounding box
+ wrt height/width.
+
+ Returns:
+ tuple: A tuple containing keypoint predictions and scores.
+
+ - preds (np.ndarray[N, K, 3]): Predicted 3d keypoint location \
+ in images.
+ - maxvals (np.ndarray[N, K, 1]): Scores (confidence) of the keypoints.
+ """
+ N, K, D, H, W = heatmaps.shape
+ preds, maxvals = _get_max_preds_3d(heatmaps)
+ # Transform back to the image
+ for i in range(N):
+ preds[i, :, :2] = transform_preds(preds[i, :, :2], center[i], scale[i],
+ [W, H])
+ return preds, maxvals
+
+
+def multilabel_classification_accuracy(pred, gt, mask, thr=0.5):
+ """Get multi-label classification accuracy.
+
+ Note:
+ - batch size: N
+ - label number: L
+
+ Args:
+ pred (np.ndarray[N, L, 2]): model predicted labels.
+ gt (np.ndarray[N, L, 2]): ground-truth labels.
+ mask (np.ndarray[N, 1] or np.ndarray[N, L] ): reliability of
+ ground-truth labels.
+
+ Returns:
+ float: multi-label classification accuracy.
+ """
+ # we only compute accuracy on the samples with ground-truth of all labels.
+ valid = (mask > 0).min(axis=1) if mask.ndim == 2 else (mask > 0)
+ pred, gt = pred[valid], gt[valid]
+
+ if pred.shape[0] == 0:
+ acc = 0.0 # when no sample is with gt labels, set acc to 0.
+ else:
+ # The classification of a sample is regarded as correct
+ # only if it's correct for all labels.
+ acc = (((pred - thr) * (gt - thr)) > 0).all(axis=1).mean()
+ return acc
diff --git a/grounded-sam-osx/transformer_utils/mmpose/core/fp16/__init__.py b/grounded-sam-osx/transformer_utils/mmpose/core/fp16/__init__.py
new file mode 100644
index 0000000000000000000000000000000000000000..5cb054810870626496ab4145446b17cf2c2e0b5d
--- /dev/null
+++ b/grounded-sam-osx/transformer_utils/mmpose/core/fp16/__init__.py
@@ -0,0 +1,9 @@
+# Copyright (c) OpenMMLab. All rights reserved.
+from .decorators import auto_fp16, force_fp32
+from .hooks import Fp16OptimizerHook, wrap_fp16_model
+from .utils import cast_tensor_type
+
+__all__ = [
+ 'auto_fp16', 'force_fp32', 'Fp16OptimizerHook', 'wrap_fp16_model',
+ 'cast_tensor_type'
+]
diff --git a/grounded-sam-osx/transformer_utils/mmpose/core/fp16/decorators.py b/grounded-sam-osx/transformer_utils/mmpose/core/fp16/decorators.py
new file mode 100644
index 0000000000000000000000000000000000000000..2d70ddf533c069b26f08ef3a973328790843def5
--- /dev/null
+++ b/grounded-sam-osx/transformer_utils/mmpose/core/fp16/decorators.py
@@ -0,0 +1,175 @@
+# Copyright (c) OpenMMLab. All rights reserved.
+import functools
+import warnings
+from inspect import getfullargspec
+
+import torch
+
+from .utils import cast_tensor_type
+
+
+def auto_fp16(apply_to=None, out_fp32=False):
+ """Decorator to enable fp16 training automatically.
+
+ This decorator is useful when you write custom modules and want to support
+ mixed precision training. If inputs arguments are fp32 tensors, they will
+ be converted to fp16 automatically. Arguments other than fp32 tensors are
+ ignored.
+
+ Args:
+ apply_to (Iterable, optional): The argument names to be converted.
+ `None` indicates all arguments.
+ out_fp32 (bool): Whether to convert the output back to fp32.
+
+ Example:
+
+ >>> import torch.nn as nn
+ >>> class MyModule1(nn.Module):
+ >>>
+ >>> # Convert x and y to fp16
+ >>> @auto_fp16()
+ >>> def forward(self, x, y):
+ >>> pass
+
+ >>> import torch.nn as nn
+ >>> class MyModule2(nn.Module):
+ >>>
+ >>> # convert pred to fp16
+ >>> @auto_fp16(apply_to=('pred', ))
+ >>> def do_something(self, pred, others):
+ >>> pass
+ """
+
+ warnings.warn(
+ 'auto_fp16 in mmpose will be deprecated in the next release.'
+ 'Please use mmcv.runner.auto_fp16 instead (mmcv>=1.3.1).',
+ DeprecationWarning)
+
+ def auto_fp16_wrapper(old_func):
+
+ @functools.wraps(old_func)
+ def new_func(*args, **kwargs):
+ # check if the module has set the attribute `fp16_enabled`, if not,
+ # just fallback to the original method.
+ if not isinstance(args[0], torch.nn.Module):
+ raise TypeError('@auto_fp16 can only be used to decorate the '
+ 'method of nn.Module')
+ if not (hasattr(args[0], 'fp16_enabled') and args[0].fp16_enabled):
+ return old_func(*args, **kwargs)
+ # get the arg spec of the decorated method
+ args_info = getfullargspec(old_func)
+ # get the argument names to be casted
+ args_to_cast = args_info.args if apply_to is None else apply_to
+ # convert the args that need to be processed
+ new_args = []
+ # NOTE: default args are not taken into consideration
+ if args:
+ arg_names = args_info.args[:len(args)]
+ for i, arg_name in enumerate(arg_names):
+ if arg_name in args_to_cast:
+ new_args.append(
+ cast_tensor_type(args[i], torch.float, torch.half))
+ else:
+ new_args.append(args[i])
+ # convert the kwargs that need to be processed
+ new_kwargs = {}
+ if kwargs:
+ for arg_name, arg_value in kwargs.items():
+ if arg_name in args_to_cast:
+ new_kwargs[arg_name] = cast_tensor_type(
+ arg_value, torch.float, torch.half)
+ else:
+ new_kwargs[arg_name] = arg_value
+ # apply converted arguments to the decorated method
+ output = old_func(*new_args, **new_kwargs)
+ # cast the results back to fp32 if necessary
+ if out_fp32:
+ output = cast_tensor_type(output, torch.half, torch.float)
+ return output
+
+ return new_func
+
+ return auto_fp16_wrapper
+
+
+def force_fp32(apply_to=None, out_fp16=False):
+ """Decorator to convert input arguments to fp32 in force.
+
+ This decorator is useful when you write custom modules and want to support
+ mixed precision training. If there are some inputs that must be processed
+ in fp32 mode, then this decorator can handle it. If inputs arguments are
+ fp16 tensors, they will be converted to fp32 automatically. Arguments other
+ than fp16 tensors are ignored.
+
+ Args:
+ apply_to (Iterable, optional): The argument names to be converted.
+ `None` indicates all arguments.
+ out_fp16 (bool): Whether to convert the output back to fp16.
+
+ Example:
+
+ >>> import torch.nn as nn
+ >>> class MyModule1(nn.Module):
+ >>>
+ >>> # Convert x and y to fp32
+ >>> @force_fp32()
+ >>> def loss(self, x, y):
+ >>> pass
+
+ >>> import torch.nn as nn
+ >>> class MyModule2(nn.Module):
+ >>>
+ >>> # convert pred to fp32
+ >>> @force_fp32(apply_to=('pred', ))
+ >>> def post_process(self, pred, others):
+ >>> pass
+ """
+ warnings.warn(
+ 'force_fp32 in mmpose will be deprecated in the next release.'
+ 'Please use mmcv.runner.force_fp32 instead (mmcv>=1.3.1).',
+ DeprecationWarning)
+
+ def force_fp32_wrapper(old_func):
+
+ @functools.wraps(old_func)
+ def new_func(*args, **kwargs):
+ # check if the module has set the attribute `fp16_enabled`, if not,
+ # just fallback to the original method.
+ if not isinstance(args[0], torch.nn.Module):
+ raise TypeError('@force_fp32 can only be used to decorate the '
+ 'method of nn.Module')
+ if not (hasattr(args[0], 'fp16_enabled') and args[0].fp16_enabled):
+ return old_func(*args, **kwargs)
+ # get the arg spec of the decorated method
+ args_info = getfullargspec(old_func)
+ # get the argument names to be casted
+ args_to_cast = args_info.args if apply_to is None else apply_to
+ # convert the args that need to be processed
+ new_args = []
+ if args:
+ arg_names = args_info.args[:len(args)]
+ for i, arg_name in enumerate(arg_names):
+ if arg_name in args_to_cast:
+ new_args.append(
+ cast_tensor_type(args[i], torch.half, torch.float))
+ else:
+ new_args.append(args[i])
+ # convert the kwargs that need to be processed
+ new_kwargs = dict()
+ if kwargs:
+ for arg_name, arg_value in kwargs.items():
+ if arg_name in args_to_cast:
+ new_kwargs[arg_name] = cast_tensor_type(
+ arg_value, torch.half, torch.float)
+ else:
+ new_kwargs[arg_name] = arg_value
+ # apply converted arguments to the decorated method
+ output = old_func(*new_args, **new_kwargs)
+ # cast the results back to fp32 if necessary
+ if out_fp16:
+ output = cast_tensor_type(output, torch.float, torch.half)
+ return output
+
+ return new_func
+
+ return force_fp32_wrapper
diff --git a/grounded-sam-osx/transformer_utils/mmpose/core/fp16/hooks.py b/grounded-sam-osx/transformer_utils/mmpose/core/fp16/hooks.py
new file mode 100644
index 0000000000000000000000000000000000000000..74081a9b73b95ebb20cabf07cfaeab86cc874780
--- /dev/null
+++ b/grounded-sam-osx/transformer_utils/mmpose/core/fp16/hooks.py
@@ -0,0 +1,167 @@
+# Copyright (c) OpenMMLab. All rights reserved.
+import copy
+
+import torch
+import torch.nn as nn
+from mmcv.runner import OptimizerHook
+from mmcv.utils import _BatchNorm
+
+from ..utils.dist_utils import allreduce_grads
+from .utils import cast_tensor_type
+
+
+class Fp16OptimizerHook(OptimizerHook):
+ """FP16 optimizer hook.
+
+ The steps of fp16 optimizer is as follows.
+ 1. Scale the loss value.
+ 2. BP in the fp16 model.
+ 2. Copy gradients from fp16 model to fp32 weights.
+ 3. Update fp32 weights.
+ 4. Copy updated parameters from fp32 weights to fp16 model.
+
+ Refer to https://arxiv.org/abs/1710.03740 for more details.
+
+ Args:
+ loss_scale (float): Scale factor multiplied with loss.
+ """
+
+ def __init__(self,
+ grad_clip=None,
+ coalesce=True,
+ bucket_size_mb=-1,
+ loss_scale=512.,
+ distributed=True):
+ self.grad_clip = grad_clip
+ self.coalesce = coalesce
+ self.bucket_size_mb = bucket_size_mb
+ self.loss_scale = loss_scale
+ self.distributed = distributed
+
+ def before_run(self, runner):
+ """Preparing steps before Mixed Precision Training.
+
+ 1. Make a master copy of fp32 weights for optimization.
+ 2. Convert the main model from fp32 to fp16.
+
+ Args:
+ runner (:obj:`mmcv.Runner`): The underlines training runner.
+ """
+ # keep a copy of fp32 weights
+ runner.optimizer.param_groups = copy.deepcopy(
+ runner.optimizer.param_groups)
+ # convert model to fp16
+ wrap_fp16_model(runner.model)
+
+ @staticmethod
+ def copy_grads_to_fp32(fp16_net, fp32_weights):
+ """Copy gradients from fp16 model to fp32 weight copy."""
+ for fp32_param, fp16_param in zip(fp32_weights, fp16_net.parameters()):
+ if fp16_param.grad is not None:
+ if fp32_param.grad is None:
+ fp32_param.grad = fp32_param.data.new(fp32_param.size())
+ fp32_param.grad.copy_(fp16_param.grad)
+
+ @staticmethod
+ def copy_params_to_fp16(fp16_net, fp32_weights):
+ """Copy updated params from fp32 weight copy to fp16 model."""
+ for fp16_param, fp32_param in zip(fp16_net.parameters(), fp32_weights):
+ fp16_param.data.copy_(fp32_param.data)
+
+ def after_train_iter(self, runner):
+ """Backward optimization steps for Mixed Precision Training.
+
+ 1. Scale the loss by a scale factor.
+ 2. Backward the loss to obtain the gradients (fp16).
+ 3. Copy gradients from the model to the fp32 weight copy.
+ 4. Scale the gradients back and update the fp32 weight copy.
+ 5. Copy back the params from fp32 weight copy to the fp16 model.
+
+ Args:
+ runner (:obj:`mmcv.Runner`): The underlines training runner.
+ """
+ # clear grads of last iteration
+ runner.model.zero_grad()
+ runner.optimizer.zero_grad()
+ # scale the loss value
+ scaled_loss = runner.outputs['loss'] * self.loss_scale
+ scaled_loss.backward()
+ # copy fp16 grads in the model to fp32 params in the optimizer
+ fp32_weights = []
+ for param_group in runner.optimizer.param_groups:
+ fp32_weights += param_group['params']
+ self.copy_grads_to_fp32(runner.model, fp32_weights)
+ # allreduce grads
+ if self.distributed:
+ allreduce_grads(fp32_weights, self.coalesce, self.bucket_size_mb)
+ # scale the gradients back
+ for param in fp32_weights:
+ if param.grad is not None:
+ param.grad.div_(self.loss_scale)
+ if self.grad_clip is not None:
+ self.clip_grads(fp32_weights)
+ # update fp32 params
+ runner.optimizer.step()
+ # copy fp32 params to the fp16 model
+ self.copy_params_to_fp16(runner.model, fp32_weights)
+
+
+def wrap_fp16_model(model):
+ """Wrap the FP32 model to FP16.
+
+ 1. Convert FP32 model to FP16.
+ 2. Remain some necessary layers to be FP32, e.g., normalization layers.
+
+ Args:
+ model (nn.Module): Model in FP32.
+ """
+ # convert model to fp16
+ model.half()
+ # patch the normalization layers to make it work in fp32 mode
+ patch_norm_fp32(model)
+ # set `fp16_enabled` flag
+ for m in model.modules():
+ if hasattr(m, 'fp16_enabled'):
+ m.fp16_enabled = True
+
+
+def patch_norm_fp32(module):
+ """Recursively convert normalization layers from FP16 to FP32.
+
+ Args:
+ module (nn.Module): The modules to be converted in FP16.
+
+ Returns:
+ nn.Module: The converted module, the normalization layers have been
+ converted to FP32.
+ """
+ if isinstance(module, (_BatchNorm, nn.GroupNorm)):
+ module.float()
+ module.forward = patch_forward_method(module.forward, torch.half,
+ torch.float)
+ for child in module.children():
+ patch_norm_fp32(child)
+ return module
+
+
+def patch_forward_method(func, src_type, dst_type, convert_output=True):
+ """Patch the forward method of a module.
+
+ Args:
+ func (callable): The original forward method.
+ src_type (torch.dtype): Type of input arguments to be converted from.
+ dst_type (torch.dtype): Type of input arguments to be converted to.
+ convert_output (bool): Whether to convert the output back to src_type.
+
+ Returns:
+ callable: The patched forward method.
+ """
+
+ def new_forward(*args, **kwargs):
+ output = func(*cast_tensor_type(args, src_type, dst_type),
+ **cast_tensor_type(kwargs, src_type, dst_type))
+ if convert_output:
+ output = cast_tensor_type(output, dst_type, src_type)
+ return output
+
+ return new_forward
diff --git a/grounded-sam-osx/transformer_utils/mmpose/core/fp16/utils.py b/grounded-sam-osx/transformer_utils/mmpose/core/fp16/utils.py
new file mode 100644
index 0000000000000000000000000000000000000000..f1ec3d328328560c7959ae5e77621feb77692068
--- /dev/null
+++ b/grounded-sam-osx/transformer_utils/mmpose/core/fp16/utils.py
@@ -0,0 +1,34 @@
+# Copyright (c) OpenMMLab. All rights reserved.
+from collections import abc
+
+import numpy as np
+import torch
+
+
+def cast_tensor_type(inputs, src_type, dst_type):
+ """Recursively convert Tensor in inputs from src_type to dst_type.
+
+ Args:
+ inputs: Inputs that to be casted.
+ src_type (torch.dtype): Source type.
+ dst_type (torch.dtype): Destination type.
+
+ Returns:
+ The same type with inputs, but all contained Tensors have been cast.
+ """
+ if isinstance(inputs, torch.Tensor):
+ return inputs.to(dst_type)
+ elif isinstance(inputs, str):
+ return inputs
+ elif isinstance(inputs, np.ndarray):
+ return inputs
+ elif isinstance(inputs, abc.Mapping):
+ return type(inputs)({
+ k: cast_tensor_type(v, src_type, dst_type)
+ for k, v in inputs.items()
+ })
+ elif isinstance(inputs, abc.Iterable):
+ return type(inputs)(
+ cast_tensor_type(item, src_type, dst_type) for item in inputs)
+
+ return inputs
diff --git a/grounded-sam-osx/transformer_utils/mmpose/core/optimizers/__init__.py b/grounded-sam-osx/transformer_utils/mmpose/core/optimizers/__init__.py
new file mode 100644
index 0000000000000000000000000000000000000000..906f67c231d9d33faee6c15f5c9b5582af6fdb19
--- /dev/null
+++ b/grounded-sam-osx/transformer_utils/mmpose/core/optimizers/__init__.py
@@ -0,0 +1,8 @@
+# Copyright (c) OpenMMLab. All rights reserved.
+from .builder import (OPTIMIZER_BUILDERS, OPTIMIZERS,
+ build_optimizer_constructor, build_optimizers)
+
+__all__ = [
+ 'build_optimizers', 'build_optimizer_constructor', 'OPTIMIZERS',
+ 'OPTIMIZER_BUILDERS'
+]
diff --git a/grounded-sam-osx/transformer_utils/mmpose/core/optimizers/builder.py b/grounded-sam-osx/transformer_utils/mmpose/core/optimizers/builder.py
new file mode 100644
index 0000000000000000000000000000000000000000..cd2cf49133c57f28261b555d30a5cee18ae105af
--- /dev/null
+++ b/grounded-sam-osx/transformer_utils/mmpose/core/optimizers/builder.py
@@ -0,0 +1,70 @@
+# Copyright (c) OpenMMLab. All rights reserved.
+from mmcv.runner import build_optimizer
+from mmcv.runner.optimizer import OPTIMIZER_BUILDERS as MMCV_OPTIMIZER_BUILDERS
+from mmcv.utils import Registry, build_from_cfg
+
+OPTIMIZERS = Registry('optimizers')
+OPTIMIZER_BUILDERS = Registry(
+ 'optimizer builder', parent=MMCV_OPTIMIZER_BUILDERS)
+
+
+def build_optimizer_constructor(cfg):
+ constructor_type = cfg.get('type')
+ if constructor_type in OPTIMIZER_BUILDERS:
+ return build_from_cfg(cfg, OPTIMIZER_BUILDERS)
+ elif constructor_type in MMCV_OPTIMIZER_BUILDERS:
+ return build_from_cfg(cfg, MMCV_OPTIMIZER_BUILDERS)
+ else:
+ raise KeyError(f'{constructor_type} is not registered '
+ 'in the optimizer builder registry.')
+
+
+def build_optimizers(model, cfgs):
+ """Build multiple optimizers from configs.
+
+ If `cfgs` contains several dicts for optimizers, then a dict for each
+ constructed optimizers will be returned.
+ If `cfgs` only contains one optimizer config, the constructed optimizer
+ itself will be returned.
+
+ For example,
+
+ 1) Multiple optimizer configs:
+
+ .. code-block:: python
+
+ optimizer_cfg = dict(
+ model1=dict(type='SGD', lr=lr),
+ model2=dict(type='SGD', lr=lr))
+
+ The return dict is
+ ``dict('model1': torch.optim.Optimizer, 'model2': torch.optim.Optimizer)``
+
+ 2) Single optimizer config:
+
+ .. code-block:: python
+
+ optimizer_cfg = dict(type='SGD', lr=lr)
+
+ The return is ``torch.optim.Optimizer``.
+
+ Args:
+ model (:obj:`nn.Module`): The model with parameters to be optimized.
+ cfgs (dict): The config dict of the optimizer.
+
+ Returns:
+ dict[:obj:`torch.optim.Optimizer`] | :obj:`torch.optim.Optimizer`:
+ The initialized optimizers.
+ """
+ optimizers = {}
+ if hasattr(model, 'module'):
+ model = model.module
+ # determine whether 'cfgs' has several dicts for optimizers
+ if all(isinstance(v, dict) for v in cfgs.values()):
+ for key, cfg in cfgs.items():
+ cfg_ = cfg.copy()
+ module = getattr(model, key)
+ optimizers[key] = build_optimizer(module, cfg_)
+ return optimizers
+
+ return build_optimizer(model, cfgs)
diff --git a/grounded-sam-osx/transformer_utils/mmpose/core/optimizers/layer_decay_optimizer_constructor.py b/grounded-sam-osx/transformer_utils/mmpose/core/optimizers/layer_decay_optimizer_constructor.py
new file mode 100644
index 0000000000000000000000000000000000000000..1ab6a82548c046483b7c412cefa0762cdbc531f8
--- /dev/null
+++ b/grounded-sam-osx/transformer_utils/mmpose/core/optimizers/layer_decay_optimizer_constructor.py
@@ -0,0 +1,208 @@
+# Copyright (c) OpenMMLab. All rights reserved.
+import json
+import warnings
+
+from mmcv.runner import DefaultOptimizerConstructor, get_dist_info
+
+from mmpose.utils import get_root_logger
+from .builder import OPTIMIZER_BUILDERS
+
+
+def get_layer_id_for_convnext(var_name, max_layer_id):
+ """Get the layer id to set the different learning rates in ``layer_wise``
+ decay_type.
+
+ Args:
+ var_name (str): The key of the model.
+ max_layer_id (int): Maximum number of backbone layers.
+
+ Returns:
+ int: The id number corresponding to different learning rate in
+ ``LearningRateDecayOptimizerConstructor``.
+ """
+
+ if var_name in ('backbone.cls_token', 'backbone.mask_token',
+ 'backbone.pos_embed'):
+ return 0
+ elif var_name.startswith('backbone.downsample_layers'):
+ stage_id = int(var_name.split('.')[2])
+ if stage_id == 0:
+ layer_id = 0
+ elif stage_id == 1:
+ layer_id = 2
+ elif stage_id == 2:
+ layer_id = 3
+ elif stage_id == 3:
+ layer_id = max_layer_id
+ return layer_id
+ elif var_name.startswith('backbone.stages'):
+ stage_id = int(var_name.split('.')[2])
+ block_id = int(var_name.split('.')[3])
+ if stage_id == 0:
+ layer_id = 1
+ elif stage_id == 1:
+ layer_id = 2
+ elif stage_id == 2:
+ layer_id = 3 + block_id // 3
+ elif stage_id == 3:
+ layer_id = max_layer_id
+ return layer_id
+ else:
+ return max_layer_id + 1
+
+
+def get_stage_id_for_convnext(var_name, max_stage_id):
+ """Get the stage id to set the different learning rates in ``stage_wise``
+ decay_type.
+
+ Args:
+ var_name (str): The key of the model.
+ max_stage_id (int): Maximum number of backbone layers.
+
+ Returns:
+ int: The id number corresponding to different learning rate in
+ ``LearningRateDecayOptimizerConstructor``.
+ """
+
+ if var_name in ('backbone.cls_token', 'backbone.mask_token',
+ 'backbone.pos_embed'):
+ return 0
+ elif var_name.startswith('backbone.downsample_layers'):
+ return 0
+ elif var_name.startswith('backbone.stages'):
+ stage_id = int(var_name.split('.')[2])
+ return stage_id + 1
+ else:
+ return max_stage_id - 1
+
+
+def get_layer_id_for_vit(var_name, max_layer_id):
+ """Get the layer id to set the different learning rates.
+
+ Args:
+ var_name (str): The key of the model.
+ num_max_layer (int): Maximum number of backbone layers.
+
+ Returns:
+ int: Returns the layer id of the key.
+ """
+
+ if var_name in ('backbone.cls_token', 'backbone.mask_token',
+ 'backbone.pos_embed'):
+ return 0
+ elif var_name.startswith('backbone.patch_embed'):
+ return 0
+ elif var_name.startswith('backbone.layers'):
+ layer_id = int(var_name.split('.')[2])
+ return layer_id + 1
+ else:
+ return max_layer_id - 1
+
+
+@OPTIMIZER_BUILDERS.register_module()
+class LearningRateDecayOptimizerConstructor(DefaultOptimizerConstructor):
+ """Different learning rates are set for different layers of backbone.
+
+ Note: Currently, this optimizer constructor is built for ConvNeXt,
+ BEiT and MAE.
+ """
+
+ def add_params(self, params, module, **kwargs):
+ """Add all parameters of module to the params list.
+
+ The parameters of the given module will be added to the list of param
+ groups, with specific rules defined by paramwise_cfg.
+
+ Args:
+ params (list[dict]): A list of param groups, it will be modified
+ in place.
+ module (nn.Module): The module to be added.
+ """
+ logger = get_root_logger()
+
+ parameter_groups = {}
+ logger.info(f'self.paramwise_cfg is {self.paramwise_cfg}')
+ num_layers = self.paramwise_cfg.get('num_layers') + 2
+ decay_rate = self.paramwise_cfg.get('decay_rate')
+ decay_type = self.paramwise_cfg.get('decay_type', 'layer_wise')
+ logger.info('Build LearningRateDecayOptimizerConstructor '
+ f'{decay_type} {decay_rate} - {num_layers}')
+ weight_decay = self.base_wd
+ for name, param in module.named_parameters():
+ if not param.requires_grad:
+ continue # frozen weights
+ if len(param.shape) == 1 or name.endswith('.bias') or name in (
+ 'pos_embed', 'cls_token'):
+ group_name = 'no_decay'
+ this_weight_decay = 0.
+ else:
+ group_name = 'decay'
+ this_weight_decay = weight_decay
+ if 'layer_wise' in decay_type:
+ if 'ConvNeXt' in module.backbone.__class__.__name__:
+ layer_id = get_layer_id_for_convnext(
+ name, self.paramwise_cfg.get('num_layers'))
+ logger.info(f'set param {name} as id {layer_id}')
+ elif 'BEiT' in module.backbone.__class__.__name__ or \
+ 'MAE' in module.backbone.__class__.__name__:
+ layer_id = get_layer_id_for_vit(name, num_layers)
+ logger.info(f'set param {name} as id {layer_id}')
+ else:
+ raise NotImplementedError()
+ elif decay_type == 'stage_wise':
+ if 'ConvNeXt' in module.backbone.__class__.__name__:
+ layer_id = get_stage_id_for_convnext(name, num_layers)
+ logger.info(f'set param {name} as id {layer_id}')
+ else:
+ raise NotImplementedError()
+ group_name = f'layer_{layer_id}_{group_name}'
+
+ if group_name not in parameter_groups:
+ scale = decay_rate**(num_layers - layer_id - 1)
+
+ parameter_groups[group_name] = {
+ 'weight_decay': this_weight_decay,
+ 'params': [],
+ 'param_names': [],
+ 'lr_scale': scale,
+ 'group_name': group_name,
+ 'lr': scale * self.base_lr,
+ }
+
+ parameter_groups[group_name]['params'].append(param)
+ parameter_groups[group_name]['param_names'].append(name)
+ rank, _ = get_dist_info()
+ if rank == 0:
+ to_display = {}
+ for key in parameter_groups:
+ to_display[key] = {
+ 'param_names': parameter_groups[key]['param_names'],
+ 'lr_scale': parameter_groups[key]['lr_scale'],
+ 'lr': parameter_groups[key]['lr'],
+ 'weight_decay': parameter_groups[key]['weight_decay'],
+ }
+ logger.info(f'Param groups = {json.dumps(to_display, indent=2)}')
+ params.extend(parameter_groups.values())
+
+
+@OPTIMIZER_BUILDERS.register_module()
+class LayerDecayOptimizerConstructor(LearningRateDecayOptimizerConstructor):
+ """Different learning rates are set for different layers of backbone.
+
+ Note: Currently, this optimizer constructor is built for BEiT,
+ and it will be deprecated.
+ Please use ``LearningRateDecayOptimizerConstructor`` instead.
+ """
+
+ def __init__(self, optimizer_cfg, paramwise_cfg):
+ warnings.warn('DeprecationWarning: Original '
+ 'LayerDecayOptimizerConstructor of BEiT '
+ 'will be deprecated. Please use '
+ 'LearningRateDecayOptimizerConstructor instead, '
+ 'and set decay_type = layer_wise_vit in paramwise_cfg.')
+ paramwise_cfg.update({'decay_type': 'layer_wise_vit'})
+ warnings.warn('DeprecationWarning: Layer_decay_rate will '
+ 'be deleted, please use decay_rate instead.')
+ paramwise_cfg['decay_rate'] = paramwise_cfg.pop('layer_decay_rate')
+ super(LayerDecayOptimizerConstructor,
+ self).__init__(optimizer_cfg, paramwise_cfg)
diff --git a/grounded-sam-osx/transformer_utils/mmpose/core/post_processing/__init__.py b/grounded-sam-osx/transformer_utils/mmpose/core/post_processing/__init__.py
new file mode 100644
index 0000000000000000000000000000000000000000..8076b799b9e405e7ac5a883aa3a6d5dcb84060b5
--- /dev/null
+++ b/grounded-sam-osx/transformer_utils/mmpose/core/post_processing/__init__.py
@@ -0,0 +1,16 @@
+# Copyright (c) OpenMMLab. All rights reserved.
+
+from .nms import oks_iou, oks_nms, soft_oks_nms
+from .one_euro_filter import OneEuroFilter
+from .post_transforms import (affine_transform, flip_back, fliplr_joints,
+ fliplr_regression, get_affine_transform,
+ get_warp_matrix, rotate_point, transform_preds,
+ warp_affine_joints)
+from .smoother import Smoother
+
+__all__ = [
+ 'oks_nms', 'soft_oks_nms', 'affine_transform', 'rotate_point', 'flip_back',
+ 'fliplr_joints', 'fliplr_regression', 'transform_preds',
+ 'get_affine_transform', 'get_warp_matrix', 'warp_affine_joints', 'oks_iou',
+ 'OneEuroFilter', 'Smoother'
+]
diff --git a/grounded-sam-osx/transformer_utils/mmpose/core/post_processing/group.py b/grounded-sam-osx/transformer_utils/mmpose/core/post_processing/group.py
new file mode 100644
index 0000000000000000000000000000000000000000..75499cb0bc4eb96f9255e9c02d20cf7a9c95c402
--- /dev/null
+++ b/grounded-sam-osx/transformer_utils/mmpose/core/post_processing/group.py
@@ -0,0 +1,418 @@
+# ------------------------------------------------------------------------------
+# Adapted from https://github.com/princeton-vl/pose-ae-train/
+# Original licence: Copyright (c) 2017, umich-vl, under BSD 3-Clause License.
+# ------------------------------------------------------------------------------
+
+import numpy as np
+import torch
+from munkres import Munkres
+
+from mmpose.core.evaluation import post_dark_udp
+
+
+def _py_max_match(scores):
+ """Apply munkres algorithm to get the best match.
+
+ Args:
+ scores(np.ndarray): cost matrix.
+
+ Returns:
+ np.ndarray: best match.
+ """
+ m = Munkres()
+ tmp = m.compute(scores)
+ tmp = np.array(tmp).astype(int)
+ return tmp
+
+
+def _match_by_tag(inp, params):
+ """Match joints by tags. Use Munkres algorithm to calculate the best match
+ for keypoints grouping.
+
+ Note:
+ number of keypoints: K
+ max number of people in an image: M (M=30 by default)
+ dim of tags: L
+ If use flip testing, L=2; else L=1.
+
+ Args:
+ inp(tuple):
+ tag_k (np.ndarray[KxMxL]): tag corresponding to the
+ top k values of feature map per keypoint.
+ loc_k (np.ndarray[KxMx2]): top k locations of the
+ feature maps for keypoint.
+ val_k (np.ndarray[KxM]): top k value of the
+ feature maps per keypoint.
+ params(Params): class Params().
+
+ Returns:
+ np.ndarray: result of pose groups.
+ """
+ assert isinstance(params, _Params), 'params should be class _Params()'
+
+ tag_k, loc_k, val_k = inp
+
+ default_ = np.zeros((params.num_joints, 3 + tag_k.shape[2]),
+ dtype=np.float32)
+
+ joint_dict = {}
+ tag_dict = {}
+ for i in range(params.num_joints):
+ idx = params.joint_order[i]
+
+ tags = tag_k[idx]
+ joints = np.concatenate((loc_k[idx], val_k[idx, :, None], tags), 1)
+ mask = joints[:, 2] > params.detection_threshold
+ tags = tags[mask] # shape: [M, L]
+ joints = joints[mask] # shape: [M, 3 + L], 3: x, y, val
+
+ if joints.shape[0] == 0:
+ continue
+
+ if i == 0 or len(joint_dict) == 0:
+ for tag, joint in zip(tags, joints):
+ key = tag[0]
+ joint_dict.setdefault(key, np.copy(default_))[idx] = joint
+ tag_dict[key] = [tag]
+ else:
+ # shape: [M]
+ grouped_keys = list(joint_dict.keys())
+ if params.ignore_too_much:
+ grouped_keys = grouped_keys[:params.max_num_people]
+ # shape: [M, L]
+ grouped_tags = [np.mean(tag_dict[i], axis=0) for i in grouped_keys]
+
+ # shape: [M, M, L]
+ diff = joints[:, None, 3:] - np.array(grouped_tags)[None, :, :]
+ # shape: [M, M]
+ diff_normed = np.linalg.norm(diff, ord=2, axis=2)
+ diff_saved = np.copy(diff_normed)
+
+ if params.use_detection_val:
+ diff_normed = np.round(diff_normed) * 100 - joints[:, 2:3]
+
+ num_added = diff.shape[0]
+ num_grouped = diff.shape[1]
+
+ if num_added > num_grouped:
+ diff_normed = np.concatenate(
+ (diff_normed,
+ np.zeros((num_added, num_added - num_grouped),
+ dtype=np.float32) + 1e10),
+ axis=1)
+
+ pairs = _py_max_match(diff_normed)
+ for row, col in pairs:
+ if (row < num_added and col < num_grouped
+ and diff_saved[row][col] < params.tag_threshold):
+ key = grouped_keys[col]
+ joint_dict[key][idx] = joints[row]
+ tag_dict[key].append(tags[row])
+ else:
+ key = tags[row][0]
+ joint_dict.setdefault(key, np.copy(default_))[idx] = \
+ joints[row]
+ tag_dict[key] = [tags[row]]
+
+ joint_dict_keys = list(joint_dict.keys())
+ if params.ignore_too_much:
+ # The new person joints beyond the params.max_num_people will be
+ # ignored, for the dict is in ordered when python > 3.6 version.
+ joint_dict_keys = joint_dict_keys[:params.max_num_people]
+ results = np.array([joint_dict[i]
+ for i in joint_dict_keys]).astype(np.float32)
+ return results
+
+
+class _Params:
+ """A class of parameter.
+
+ Args:
+ cfg(Config): config.
+ """
+
+ def __init__(self, cfg):
+ self.num_joints = cfg['num_joints']
+ self.max_num_people = cfg['max_num_people']
+
+ self.detection_threshold = cfg['detection_threshold']
+ self.tag_threshold = cfg['tag_threshold']
+ self.use_detection_val = cfg['use_detection_val']
+ self.ignore_too_much = cfg['ignore_too_much']
+
+ if self.num_joints == 17:
+ self.joint_order = [
+ i - 1 for i in
+ [1, 2, 3, 4, 5, 6, 7, 12, 13, 8, 9, 10, 11, 14, 15, 16, 17]
+ ]
+ else:
+ self.joint_order = list(np.arange(self.num_joints))
+
+
+class HeatmapParser:
+ """The heatmap parser for post processing."""
+
+ def __init__(self, cfg):
+ self.params = _Params(cfg)
+ self.tag_per_joint = cfg['tag_per_joint']
+ self.pool = torch.nn.MaxPool2d(cfg['nms_kernel'], 1,
+ cfg['nms_padding'])
+ self.use_udp = cfg.get('use_udp', False)
+ self.score_per_joint = cfg.get('score_per_joint', False)
+
+ def nms(self, heatmaps):
+ """Non-Maximum Suppression for heatmaps.
+
+ Args:
+ heatmap(torch.Tensor): Heatmaps before nms.
+
+ Returns:
+ torch.Tensor: Heatmaps after nms.
+ """
+
+ maxm = self.pool(heatmaps)
+ maxm = torch.eq(maxm, heatmaps).float()
+ heatmaps = heatmaps * maxm
+
+ return heatmaps
+
+ def match(self, tag_k, loc_k, val_k):
+ """Group keypoints to human poses in a batch.
+
+ Args:
+ tag_k (np.ndarray[NxKxMxL]): tag corresponding to the
+ top k values of feature map per keypoint.
+ loc_k (np.ndarray[NxKxMx2]): top k locations of the
+ feature maps for keypoint.
+ val_k (np.ndarray[NxKxM]): top k value of the
+ feature maps per keypoint.
+
+ Returns:
+ list
+ """
+
+ def _match(x):
+ return _match_by_tag(x, self.params)
+
+ return list(map(_match, zip(tag_k, loc_k, val_k)))
+
+ def top_k(self, heatmaps, tags):
+ """Find top_k values in an image.
+
+ Note:
+ batch size: N
+ number of keypoints: K
+ heatmap height: H
+ heatmap width: W
+ max number of people: M
+ dim of tags: L
+ If use flip testing, L=2; else L=1.
+
+ Args:
+ heatmaps (torch.Tensor[NxKxHxW])
+ tags (torch.Tensor[NxKxHxWxL])
+
+ Returns:
+ dict: A dict containing top_k values.
+
+ - tag_k (np.ndarray[NxKxMxL]):
+ tag corresponding to the top k values of
+ feature map per keypoint.
+ - loc_k (np.ndarray[NxKxMx2]):
+ top k location of feature map per keypoint.
+ - val_k (np.ndarray[NxKxM]):
+ top k value of feature map per keypoint.
+ """
+ heatmaps = self.nms(heatmaps)
+ N, K, H, W = heatmaps.size()
+ heatmaps = heatmaps.view(N, K, -1)
+ val_k, ind = heatmaps.topk(self.params.max_num_people, dim=2)
+
+ tags = tags.view(tags.size(0), tags.size(1), W * H, -1)
+ if not self.tag_per_joint:
+ tags = tags.expand(-1, self.params.num_joints, -1, -1)
+
+ tag_k = torch.stack(
+ [torch.gather(tags[..., i], 2, ind) for i in range(tags.size(3))],
+ dim=3)
+
+ x = ind % W
+ y = ind // W
+
+ ind_k = torch.stack((x, y), dim=3)
+
+ results = {
+ 'tag_k': tag_k.cpu().numpy(),
+ 'loc_k': ind_k.cpu().numpy(),
+ 'val_k': val_k.cpu().numpy()
+ }
+
+ return results
+
+ @staticmethod
+ def adjust(results, heatmaps):
+ """Adjust the coordinates for better accuracy.
+
+ Note:
+ batch size: N
+ number of keypoints: K
+ heatmap height: H
+ heatmap width: W
+
+ Args:
+ results (list(np.ndarray)): Keypoint predictions.
+ heatmaps (torch.Tensor[NxKxHxW]): Heatmaps.
+ """
+ _, _, H, W = heatmaps.shape
+ for batch_id, people in enumerate(results):
+ for people_id, people_i in enumerate(people):
+ for joint_id, joint in enumerate(people_i):
+ if joint[2] > 0:
+ x, y = joint[0:2]
+ xx, yy = int(x), int(y)
+ tmp = heatmaps[batch_id][joint_id]
+ if tmp[min(H - 1, yy + 1), xx] > tmp[max(0, yy - 1),
+ xx]:
+ y += 0.25
+ else:
+ y -= 0.25
+
+ if tmp[yy, min(W - 1, xx + 1)] > tmp[yy,
+ max(0, xx - 1)]:
+ x += 0.25
+ else:
+ x -= 0.25
+ results[batch_id][people_id, joint_id,
+ 0:2] = (x + 0.5, y + 0.5)
+ return results
+
+ @staticmethod
+ def refine(heatmap, tag, keypoints, use_udp=False):
+ """Given initial keypoint predictions, we identify missing joints.
+
+ Note:
+ number of keypoints: K
+ heatmap height: H
+ heatmap width: W
+ dim of tags: L
+ If use flip testing, L=2; else L=1.
+
+ Args:
+ heatmap: np.ndarray(K, H, W).
+ tag: np.ndarray(K, H, W) | np.ndarray(K, H, W, L)
+ keypoints: np.ndarray of size (K, 3 + L)
+ last dim is (x, y, score, tag).
+ use_udp: bool-unbiased data processing
+
+ Returns:
+ np.ndarray: The refined keypoints.
+ """
+
+ K, H, W = heatmap.shape
+ if len(tag.shape) == 3:
+ tag = tag[..., None]
+
+ tags = []
+ for i in range(K):
+ if keypoints[i, 2] > 0:
+ # save tag value of detected keypoint
+ x, y = keypoints[i][:2].astype(int)
+ x = np.clip(x, 0, W - 1)
+ y = np.clip(y, 0, H - 1)
+ tags.append(tag[i, y, x])
+
+ # mean tag of current detected people
+ prev_tag = np.mean(tags, axis=0)
+ results = []
+
+ for _heatmap, _tag in zip(heatmap, tag):
+ # distance of all tag values with mean tag of
+ # current detected people
+ distance_tag = (((_tag -
+ prev_tag[None, None, :])**2).sum(axis=2)**0.5)
+ norm_heatmap = _heatmap - np.round(distance_tag)
+
+ # find maximum position
+ y, x = np.unravel_index(np.argmax(norm_heatmap), _heatmap.shape)
+ xx = x.copy()
+ yy = y.copy()
+ # detection score at maximum position
+ val = _heatmap[y, x]
+ if not use_udp:
+ # offset by 0.5
+ x += 0.5
+ y += 0.5
+
+ # add a quarter offset
+ if _heatmap[yy, min(W - 1, xx + 1)] > _heatmap[yy, max(0, xx - 1)]:
+ x += 0.25
+ else:
+ x -= 0.25
+
+ if _heatmap[min(H - 1, yy + 1), xx] > _heatmap[max(0, yy - 1), xx]:
+ y += 0.25
+ else:
+ y -= 0.25
+
+ results.append((x, y, val))
+ results = np.array(results)
+
+ if results is not None:
+ for i in range(K):
+ # add keypoint if it is not detected
+ if results[i, 2] > 0 and keypoints[i, 2] == 0:
+ keypoints[i, :3] = results[i, :3]
+
+ return keypoints
+
+ def parse(self, heatmaps, tags, adjust=True, refine=True):
+ """Group keypoints into poses given heatmap and tag.
+
+ Note:
+ batch size: N
+ number of keypoints: K
+ heatmap height: H
+ heatmap width: W
+ dim of tags: L
+ If use flip testing, L=2; else L=1.
+
+ Args:
+ heatmaps (torch.Tensor[NxKxHxW]): model output heatmaps.
+ tags (torch.Tensor[NxKxHxWxL]): model output tagmaps.
+
+ Returns:
+ tuple: A tuple containing keypoint grouping results.
+
+ - results (list(np.ndarray)): Pose results.
+ - scores (list/list(np.ndarray)): Score of people.
+ """
+ results = self.match(**self.top_k(heatmaps, tags))
+
+ if adjust:
+ if self.use_udp:
+ for i in range(len(results)):
+ if results[i].shape[0] > 0:
+ results[i][..., :2] = post_dark_udp(
+ results[i][..., :2].copy(), heatmaps[i:i + 1, :])
+ else:
+ results = self.adjust(results, heatmaps)
+
+ if self.score_per_joint:
+ scores = [i[:, 2] for i in results[0]]
+ else:
+ scores = [i[:, 2].mean() for i in results[0]]
+
+ if refine:
+ results = results[0]
+ # for every detected person
+ for i in range(len(results)):
+ heatmap_numpy = heatmaps[0].cpu().numpy()
+ tag_numpy = tags[0].cpu().numpy()
+ if not self.tag_per_joint:
+ tag_numpy = np.tile(tag_numpy,
+ (self.params.num_joints, 1, 1, 1))
+ results[i] = self.refine(
+ heatmap_numpy, tag_numpy, results[i], use_udp=self.use_udp)
+ results = [results]
+
+ return results, scores
diff --git a/grounded-sam-osx/transformer_utils/mmpose/core/post_processing/nms.py b/grounded-sam-osx/transformer_utils/mmpose/core/post_processing/nms.py
new file mode 100644
index 0000000000000000000000000000000000000000..86a0ab35e0e26d27bb0bb55071018ffc5ac9af1d
--- /dev/null
+++ b/grounded-sam-osx/transformer_utils/mmpose/core/post_processing/nms.py
@@ -0,0 +1,207 @@
+# ------------------------------------------------------------------------------
+# Adapted from https://github.com/leoxiaobin/deep-high-resolution-net.pytorch
+# Original licence: Copyright (c) Microsoft, under the MIT License.
+# ------------------------------------------------------------------------------
+
+import numpy as np
+
+
+def nms(dets, thr):
+ """Greedily select boxes with high confidence and overlap <= thr.
+
+ Args:
+ dets: [[x1, y1, x2, y2, score]].
+ thr: Retain overlap < thr.
+
+ Returns:
+ list: Indexes to keep.
+ """
+ if len(dets) == 0:
+ return []
+
+ x1 = dets[:, 0]
+ y1 = dets[:, 1]
+ x2 = dets[:, 2]
+ y2 = dets[:, 3]
+ scores = dets[:, 4]
+
+ areas = (x2 - x1 + 1) * (y2 - y1 + 1)
+ order = scores.argsort()[::-1]
+
+ keep = []
+ while len(order) > 0:
+ i = order[0]
+ keep.append(i)
+ xx1 = np.maximum(x1[i], x1[order[1:]])
+ yy1 = np.maximum(y1[i], y1[order[1:]])
+ xx2 = np.minimum(x2[i], x2[order[1:]])
+ yy2 = np.minimum(y2[i], y2[order[1:]])
+
+ w = np.maximum(0.0, xx2 - xx1 + 1)
+ h = np.maximum(0.0, yy2 - yy1 + 1)
+ inter = w * h
+ ovr = inter / (areas[i] + areas[order[1:]] - inter)
+
+ inds = np.where(ovr <= thr)[0]
+ order = order[inds + 1]
+
+ return keep
+
+
+def oks_iou(g, d, a_g, a_d, sigmas=None, vis_thr=None):
+ """Calculate oks ious.
+
+ Args:
+ g: Ground truth keypoints.
+ d: Detected keypoints.
+ a_g: Area of the ground truth object.
+ a_d: Area of the detected object.
+ sigmas: standard deviation of keypoint labelling.
+ vis_thr: threshold of the keypoint visibility.
+
+ Returns:
+ list: The oks ious.
+ """
+ if sigmas is None:
+ sigmas = np.array([
+ .26, .25, .25, .35, .35, .79, .79, .72, .72, .62, .62, 1.07, 1.07,
+ .87, .87, .89, .89
+ ]) / 10.0
+ vars = (sigmas * 2)**2
+ xg = g[0::3]
+ yg = g[1::3]
+ vg = g[2::3]
+ ious = np.zeros(len(d), dtype=np.float32)
+ for n_d in range(0, len(d)):
+ xd = d[n_d, 0::3]
+ yd = d[n_d, 1::3]
+ vd = d[n_d, 2::3]
+ dx = xd - xg
+ dy = yd - yg
+ e = (dx**2 + dy**2) / vars / ((a_g + a_d[n_d]) / 2 + np.spacing(1)) / 2
+ if vis_thr is not None:
+ ind = list(vg > vis_thr) and list(vd > vis_thr)
+ e = e[ind]
+ ious[n_d] = np.sum(np.exp(-e)) / len(e) if len(e) != 0 else 0.0
+ return ious
+
+
+def oks_nms(kpts_db, thr, sigmas=None, vis_thr=None, score_per_joint=False):
+ """OKS NMS implementations.
+
+ Args:
+ kpts_db: keypoints.
+ thr: Retain overlap < thr.
+ sigmas: standard deviation of keypoint labelling.
+ vis_thr: threshold of the keypoint visibility.
+ score_per_joint: the input scores (in kpts_db) are per joint scores
+
+ Returns:
+ np.ndarray: indexes to keep.
+ """
+ if len(kpts_db) == 0:
+ return []
+
+ if score_per_joint:
+ scores = np.array([k['score'].mean() for k in kpts_db])
+ else:
+ scores = np.array([k['score'] for k in kpts_db])
+
+ kpts = np.array([k['keypoints'].flatten() for k in kpts_db])
+ areas = np.array([k['area'] for k in kpts_db])
+
+ order = scores.argsort()[::-1]
+
+ keep = []
+ while len(order) > 0:
+ i = order[0]
+ keep.append(i)
+
+ oks_ovr = oks_iou(kpts[i], kpts[order[1:]], areas[i], areas[order[1:]],
+ sigmas, vis_thr)
+
+ inds = np.where(oks_ovr <= thr)[0]
+ order = order[inds + 1]
+
+ keep = np.array(keep)
+
+ return keep
+
+
+def _rescore(overlap, scores, thr, type='gaussian'):
+ """Rescoring mechanism gaussian or linear.
+
+ Args:
+ overlap: calculated ious
+ scores: target scores.
+ thr: retain oks overlap < thr.
+ type: 'gaussian' or 'linear'
+
+ Returns:
+ np.ndarray: indexes to keep
+ """
+ assert len(overlap) == len(scores)
+ assert type in ['gaussian', 'linear']
+
+ if type == 'linear':
+ inds = np.where(overlap >= thr)[0]
+ scores[inds] = scores[inds] * (1 - overlap[inds])
+ else:
+ scores = scores * np.exp(-overlap**2 / thr)
+
+ return scores
+
+
+def soft_oks_nms(kpts_db,
+ thr,
+ max_dets=20,
+ sigmas=None,
+ vis_thr=None,
+ score_per_joint=False):
+ """Soft OKS NMS implementations.
+
+ Args:
+ kpts_db
+ thr: retain oks overlap < thr.
+ max_dets: max number of detections to keep.
+ sigmas: Keypoint labelling uncertainty.
+ score_per_joint: the input scores (in kpts_db) are per joint scores
+
+ Returns:
+ np.ndarray: indexes to keep.
+ """
+ if len(kpts_db) == 0:
+ return []
+
+ if score_per_joint:
+ scores = np.array([k['score'].mean() for k in kpts_db])
+ else:
+ scores = np.array([k['score'] for k in kpts_db])
+
+ kpts = np.array([k['keypoints'].flatten() for k in kpts_db])
+ areas = np.array([k['area'] for k in kpts_db])
+
+ order = scores.argsort()[::-1]
+ scores = scores[order]
+
+ keep = np.zeros(max_dets, dtype=np.intp)
+ keep_cnt = 0
+ while len(order) > 0 and keep_cnt < max_dets:
+ i = order[0]
+
+ oks_ovr = oks_iou(kpts[i], kpts[order[1:]], areas[i], areas[order[1:]],
+ sigmas, vis_thr)
+
+ order = order[1:]
+ scores = _rescore(oks_ovr, scores[1:], thr)
+
+ tmp = scores.argsort()[::-1]
+ order = order[tmp]
+ scores = scores[tmp]
+
+ keep[keep_cnt] = i
+ keep_cnt += 1
+
+ keep = keep[:keep_cnt]
+
+ return keep
diff --git a/grounded-sam-osx/transformer_utils/mmpose/core/post_processing/one_euro_filter.py b/grounded-sam-osx/transformer_utils/mmpose/core/post_processing/one_euro_filter.py
new file mode 100644
index 0000000000000000000000000000000000000000..325466522dbcbd5f2cdf85276a94269466fe741f
--- /dev/null
+++ b/grounded-sam-osx/transformer_utils/mmpose/core/post_processing/one_euro_filter.py
@@ -0,0 +1,113 @@
+# ------------------------------------------------------------------------------
+# Adapted from https://github.com/HoBeom/OneEuroFilter-Numpy
+# Original licence: Copyright (c) HoBeom Jeon, under the MIT License.
+# ------------------------------------------------------------------------------
+import warnings
+from time import time
+
+import numpy as np
+
+
+def smoothing_factor(t_e, cutoff):
+ r = 2 * np.pi * cutoff * t_e
+ return r / (r + 1)
+
+
+def exponential_smoothing(a, x, x_prev):
+ return a * x + (1 - a) * x_prev
+
+
+class OneEuroFilter:
+
+ def __init__(self,
+ x0,
+ dx0=0.0,
+ min_cutoff=1.7,
+ beta=0.3,
+ d_cutoff=30.0,
+ fps=None):
+ """One Euro Filter for keypoints smoothing.
+
+ Args:
+ x0 (np.ndarray[K, 2]): Initialize keypoints value
+ dx0 (float): 0.0
+ min_cutoff (float): parameter for one euro filter
+ beta (float): parameter for one euro filter
+ d_cutoff (float): Input data FPS
+ fps (float): Video FPS for video inference
+ """
+ warnings.warn(
+ 'OneEuroFilter from '
+ '`mmpose/core/post_processing/one_euro_filter.py` will '
+ 'be deprecated in the future. Please use Smoother'
+ '(`mmpose/core/post_processing/smoother.py`) with '
+ 'OneEuroFilter (`mmpose/core/post_processing/temporal_'
+ 'filters/one_euro_filter.py`).', DeprecationWarning)
+
+ # The parameters.
+ self.data_shape = x0.shape
+ self.min_cutoff = np.full(x0.shape, min_cutoff)
+ self.beta = np.full(x0.shape, beta)
+ self.d_cutoff = np.full(x0.shape, d_cutoff)
+ # Previous values.
+ self.x_prev = x0.astype(np.float32)
+ self.dx_prev = np.full(x0.shape, dx0)
+ self.mask_prev = np.ma.masked_where(x0 <= 0, x0)
+ self.realtime = True
+ if fps is None:
+ # Using in realtime inference
+ self.t_e = None
+ self.skip_frame_factor = d_cutoff
+ self.fps = d_cutoff
+ else:
+ # fps using video inference
+ self.realtime = False
+ self.fps = float(fps)
+ self.d_cutoff = np.full(x0.shape, self.fps)
+
+ self.t_prev = time()
+
+ def __call__(self, x, t_e=1.0):
+ """Compute the filtered signal.
+
+ Hyper-parameters (cutoff, beta) are from `VNect
+ `__ .
+
+ Realtime Camera fps (d_cutoff) default 30.0
+
+ Args:
+ x (np.ndarray[K, 2]): keypoints results in frame
+ t_e (Optional): video skip frame count for posetrack
+ evaluation
+ """
+ assert x.shape == self.data_shape
+
+ t = 0
+ if self.realtime:
+ t = time()
+ t_e = (t - self.t_prev) * self.skip_frame_factor
+ t_e = np.full(x.shape, t_e)
+
+ # missing keypoints mask
+ mask = np.ma.masked_where(x <= 0, x)
+
+ # The filtered derivative of the signal.
+ a_d = smoothing_factor(t_e / self.fps, self.d_cutoff)
+ dx = (x - self.x_prev) / t_e
+ dx_hat = exponential_smoothing(a_d, dx, self.dx_prev)
+
+ # The filtered signal.
+ cutoff = self.min_cutoff + self.beta * np.abs(dx_hat)
+ a = smoothing_factor(t_e / self.fps, cutoff)
+ x_hat = exponential_smoothing(a, x, self.x_prev)
+
+ # missing keypoints remove
+ np.copyto(x_hat, -10, where=mask.mask)
+
+ # Memorize the previous values.
+ self.x_prev = x_hat
+ self.dx_prev = dx_hat
+ self.t_prev = t
+ self.mask_prev = mask
+
+ return x_hat
diff --git a/grounded-sam-osx/transformer_utils/mmpose/core/post_processing/post_transforms.py b/grounded-sam-osx/transformer_utils/mmpose/core/post_processing/post_transforms.py
new file mode 100644
index 0000000000000000000000000000000000000000..93063fb1c1a60519a527037795654b0278a880e4
--- /dev/null
+++ b/grounded-sam-osx/transformer_utils/mmpose/core/post_processing/post_transforms.py
@@ -0,0 +1,366 @@
+# ------------------------------------------------------------------------------
+# Adapted from https://github.com/leoxiaobin/deep-high-resolution-net.pytorch
+# Original licence: Copyright (c) Microsoft, under the MIT License.
+# ------------------------------------------------------------------------------
+
+import math
+
+import cv2
+import numpy as np
+import torch
+
+
+def fliplr_joints(joints_3d, joints_3d_visible, img_width, flip_pairs):
+ """Flip human joints horizontally.
+
+ Note:
+ - num_keypoints: K
+
+ Args:
+ joints_3d (np.ndarray([K, 3])): Coordinates of keypoints.
+ joints_3d_visible (np.ndarray([K, 1])): Visibility of keypoints.
+ img_width (int): Image width.
+ flip_pairs (list[tuple]): Pairs of keypoints which are mirrored
+ (for example, left ear and right ear).
+
+ Returns:
+ tuple: Flipped human joints.
+
+ - joints_3d_flipped (np.ndarray([K, 3])): Flipped joints.
+ - joints_3d_visible_flipped (np.ndarray([K, 1])): Joint visibility.
+ """
+
+ assert len(joints_3d) == len(joints_3d_visible)
+ assert img_width > 0
+
+ joints_3d_flipped = joints_3d.copy()
+ joints_3d_visible_flipped = joints_3d_visible.copy()
+
+ # Swap left-right parts
+ for left, right in flip_pairs:
+ joints_3d_flipped[left, :] = joints_3d[right, :]
+ joints_3d_flipped[right, :] = joints_3d[left, :]
+
+ joints_3d_visible_flipped[left, :] = joints_3d_visible[right, :]
+ joints_3d_visible_flipped[right, :] = joints_3d_visible[left, :]
+
+ # Flip horizontally
+ joints_3d_flipped[:, 0] = img_width - 1 - joints_3d_flipped[:, 0]
+ joints_3d_flipped = joints_3d_flipped * joints_3d_visible_flipped
+
+ return joints_3d_flipped, joints_3d_visible_flipped
+
+
+def fliplr_regression(regression,
+ flip_pairs,
+ center_mode='static',
+ center_x=0.5,
+ center_index=0):
+ """Flip human joints horizontally.
+
+ Note:
+ - batch_size: N
+ - num_keypoint: K
+
+ Args:
+ regression (np.ndarray([..., K, C])): Coordinates of keypoints, where K
+ is the joint number and C is the dimension. Example shapes are:
+
+ - [N, K, C]: a batch of keypoints where N is the batch size.
+ - [N, T, K, C]: a batch of pose sequences, where T is the frame
+ number.
+ flip_pairs (list[tuple()]): Pairs of keypoints which are mirrored
+ (for example, left ear -- right ear).
+ center_mode (str): The mode to set the center location on the x-axis
+ to flip around. Options are:
+
+ - static: use a static x value (see center_x also)
+ - root: use a root joint (see center_index also)
+ center_x (float): Set the x-axis location of the flip center. Only used
+ when center_mode=static.
+ center_index (int): Set the index of the root joint, whose x location
+ will be used as the flip center. Only used when center_mode=root.
+
+ Returns:
+ np.ndarray([..., K, C]): Flipped joints.
+ """
+ assert regression.ndim >= 2, f'Invalid pose shape {regression.shape}'
+
+ allowed_center_mode = {'static', 'root'}
+ assert center_mode in allowed_center_mode, 'Get invalid center_mode ' \
+ f'{center_mode}, allowed choices are {allowed_center_mode}'
+
+ if center_mode == 'static':
+ x_c = center_x
+ elif center_mode == 'root':
+ assert regression.shape[-2] > center_index
+ x_c = regression[..., center_index:center_index + 1, 0]
+
+ regression_flipped = regression.copy()
+ # Swap left-right parts
+ for left, right in flip_pairs:
+ regression_flipped[..., left, :] = regression[..., right, :]
+ regression_flipped[..., right, :] = regression[..., left, :]
+
+ # Flip horizontally
+ regression_flipped[..., 0] = x_c * 2 - regression_flipped[..., 0]
+ return regression_flipped
+
+
+def flip_back(output_flipped, flip_pairs, target_type='GaussianHeatmap'):
+ """Flip the flipped heatmaps back to the original form.
+
+ Note:
+ - batch_size: N
+ - num_keypoints: K
+ - heatmap height: H
+ - heatmap width: W
+
+ Args:
+ output_flipped (np.ndarray[N, K, H, W]): The output heatmaps obtained
+ from the flipped images.
+ flip_pairs (list[tuple()): Pairs of keypoints which are mirrored
+ (for example, left ear -- right ear).
+ target_type (str): GaussianHeatmap or CombinedTarget
+
+ Returns:
+ np.ndarray: heatmaps that flipped back to the original image
+ """
+ assert output_flipped.ndim == 4, \
+ 'output_flipped should be [batch_size, num_keypoints, height, width]'
+ shape_ori = output_flipped.shape
+ channels = 1
+ if target_type.lower() == 'CombinedTarget'.lower():
+ channels = 3
+ output_flipped[:, 1::3, ...] = -output_flipped[:, 1::3, ...]
+ output_flipped = output_flipped.reshape(shape_ori[0], -1, channels,
+ shape_ori[2], shape_ori[3])
+ output_flipped_back = output_flipped.copy()
+
+ # Swap left-right parts
+ for left, right in flip_pairs:
+ output_flipped_back[:, left, ...] = output_flipped[:, right, ...]
+ output_flipped_back[:, right, ...] = output_flipped[:, left, ...]
+ output_flipped_back = output_flipped_back.reshape(shape_ori)
+ # Flip horizontally
+ output_flipped_back = output_flipped_back[..., ::-1]
+ return output_flipped_back
+
+
+def transform_preds(coords, center, scale, output_size, use_udp=False):
+ """Get final keypoint predictions from heatmaps and apply scaling and
+ translation to map them back to the image.
+
+ Note:
+ num_keypoints: K
+
+ Args:
+ coords (np.ndarray[K, ndims]):
+
+ * If ndims=2, corrds are predicted keypoint location.
+ * If ndims=4, corrds are composed of (x, y, scores, tags)
+ * If ndims=5, corrds are composed of (x, y, scores, tags,
+ flipped_tags)
+
+ center (np.ndarray[2, ]): Center of the bounding box (x, y).
+ scale (np.ndarray[2, ]): Scale of the bounding box
+ wrt [width, height].
+ output_size (np.ndarray[2, ] | list(2,)): Size of the
+ destination heatmaps.
+ use_udp (bool): Use unbiased data processing
+
+ Returns:
+ np.ndarray: Predicted coordinates in the images.
+ """
+ assert coords.shape[1] in (2, 4, 5)
+ assert len(center) == 2
+ assert len(scale) == 2
+ assert len(output_size) == 2
+
+ # Recover the scale which is normalized by a factor of 200.
+ scale = scale * 200.0
+
+ if use_udp:
+ scale_x = scale[0] / (output_size[0] - 1.0)
+ scale_y = scale[1] / (output_size[1] - 1.0)
+ else:
+ scale_x = scale[0] / output_size[0]
+ scale_y = scale[1] / output_size[1]
+
+ target_coords = np.ones_like(coords)
+ target_coords[:, 0] = coords[:, 0] * scale_x + center[0] - scale[0] * 0.5
+ target_coords[:, 1] = coords[:, 1] * scale_y + center[1] - scale[1] * 0.5
+
+ return target_coords
+
+
+def get_affine_transform(center,
+ scale,
+ rot,
+ output_size,
+ shift=(0., 0.),
+ inv=False):
+ """Get the affine transform matrix, given the center/scale/rot/output_size.
+
+ Args:
+ center (np.ndarray[2, ]): Center of the bounding box (x, y).
+ scale (np.ndarray[2, ]): Scale of the bounding box
+ wrt [width, height].
+ rot (float): Rotation angle (degree).
+ output_size (np.ndarray[2, ] | list(2,)): Size of the
+ destination heatmaps.
+ shift (0-100%): Shift translation ratio wrt the width/height.
+ Default (0., 0.).
+ inv (bool): Option to inverse the affine transform direction.
+ (inv=False: src->dst or inv=True: dst->src)
+
+ Returns:
+ np.ndarray: The transform matrix.
+ """
+ assert len(center) == 2
+ assert len(scale) == 2
+ assert len(output_size) == 2
+ assert len(shift) == 2
+
+ # pixel_std is 200.
+ scale_tmp = scale * 200.0
+
+ shift = np.array(shift)
+ src_w = scale_tmp[0]
+ dst_w = output_size[0]
+ dst_h = output_size[1]
+
+ rot_rad = np.pi * rot / 180
+ src_dir = rotate_point([0., src_w * -0.5], rot_rad)
+ dst_dir = np.array([0., dst_w * -0.5])
+
+ src = np.zeros((3, 2), dtype=np.float32)
+ src[0, :] = center + scale_tmp * shift
+ src[1, :] = center + src_dir + scale_tmp * shift
+ src[2, :] = _get_3rd_point(src[0, :], src[1, :])
+
+ dst = np.zeros((3, 2), dtype=np.float32)
+ dst[0, :] = [dst_w * 0.5, dst_h * 0.5]
+ dst[1, :] = np.array([dst_w * 0.5, dst_h * 0.5]) + dst_dir
+ dst[2, :] = _get_3rd_point(dst[0, :], dst[1, :])
+
+ if inv:
+ trans = cv2.getAffineTransform(np.float32(dst), np.float32(src))
+ else:
+ trans = cv2.getAffineTransform(np.float32(src), np.float32(dst))
+
+ return trans
+
+
+def affine_transform(pt, trans_mat):
+ """Apply an affine transformation to the points.
+
+ Args:
+ pt (np.ndarray): a 2 dimensional point to be transformed
+ trans_mat (np.ndarray): 2x3 matrix of an affine transform
+
+ Returns:
+ np.ndarray: Transformed points.
+ """
+ assert len(pt) == 2
+ new_pt = np.array(trans_mat) @ np.array([pt[0], pt[1], 1.])
+
+ return new_pt
+
+
+def _get_3rd_point(a, b):
+ """To calculate the affine matrix, three pairs of points are required. This
+ function is used to get the 3rd point, given 2D points a & b.
+
+ The 3rd point is defined by rotating vector `a - b` by 90 degrees
+ anticlockwise, using b as the rotation center.
+
+ Args:
+ a (np.ndarray): point(x,y)
+ b (np.ndarray): point(x,y)
+
+ Returns:
+ np.ndarray: The 3rd point.
+ """
+ assert len(a) == 2
+ assert len(b) == 2
+ direction = a - b
+ third_pt = b + np.array([-direction[1], direction[0]], dtype=np.float32)
+
+ return third_pt
+
+
+def rotate_point(pt, angle_rad):
+ """Rotate a point by an angle.
+
+ Args:
+ pt (list[float]): 2 dimensional point to be rotated
+ angle_rad (float): rotation angle by radian
+
+ Returns:
+ list[float]: Rotated point.
+ """
+ assert len(pt) == 2
+ sn, cs = np.sin(angle_rad), np.cos(angle_rad)
+ new_x = pt[0] * cs - pt[1] * sn
+ new_y = pt[0] * sn + pt[1] * cs
+ rotated_pt = [new_x, new_y]
+
+ return rotated_pt
+
+
+def get_warp_matrix(theta, size_input, size_dst, size_target):
+ """Calculate the transformation matrix under the constraint of unbiased.
+ Paper ref: Huang et al. The Devil is in the Details: Delving into Unbiased
+ Data Processing for Human Pose Estimation (CVPR 2020).
+
+ Args:
+ theta (float): Rotation angle in degrees.
+ size_input (np.ndarray): Size of input image [w, h].
+ size_dst (np.ndarray): Size of output image [w, h].
+ size_target (np.ndarray): Size of ROI in input plane [w, h].
+
+ Returns:
+ np.ndarray: A matrix for transformation.
+ """
+ theta = np.deg2rad(theta)
+ matrix = np.zeros((2, 3), dtype=np.float32)
+ scale_x = size_dst[0] / size_target[0]
+ scale_y = size_dst[1] / size_target[1]
+ matrix[0, 0] = math.cos(theta) * scale_x
+ matrix[0, 1] = -math.sin(theta) * scale_x
+ matrix[0, 2] = scale_x * (-0.5 * size_input[0] * math.cos(theta) +
+ 0.5 * size_input[1] * math.sin(theta) +
+ 0.5 * size_target[0])
+ matrix[1, 0] = math.sin(theta) * scale_y
+ matrix[1, 1] = math.cos(theta) * scale_y
+ matrix[1, 2] = scale_y * (-0.5 * size_input[0] * math.sin(theta) -
+ 0.5 * size_input[1] * math.cos(theta) +
+ 0.5 * size_target[1])
+ return matrix
+
+
+def warp_affine_joints(joints, mat):
+ """Apply affine transformation defined by the transform matrix on the
+ joints.
+
+ Args:
+ joints (np.ndarray[..., 2]): Origin coordinate of joints.
+ mat (np.ndarray[3, 2]): The affine matrix.
+
+ Returns:
+ np.ndarray[..., 2]: Result coordinate of joints.
+ """
+ joints = np.array(joints)
+ shape = joints.shape
+ joints = joints.reshape(-1, 2)
+ return np.dot(
+ np.concatenate((joints, joints[:, 0:1] * 0 + 1), axis=1),
+ mat.T).reshape(shape)
+
+
+def affine_transform_torch(pts, t):
+ npts = pts.shape[0]
+ pts_homo = torch.cat([pts, torch.ones(npts, 1, device=pts.device)], dim=1)
+ out = torch.mm(t, torch.t(pts_homo))
+ return torch.t(out[:2, :])
diff --git a/grounded-sam-osx/transformer_utils/mmpose/core/post_processing/smoother.py b/grounded-sam-osx/transformer_utils/mmpose/core/post_processing/smoother.py
new file mode 100644
index 0000000000000000000000000000000000000000..6b57768c03b48ff84877acbceb6e27b82832c04d
--- /dev/null
+++ b/grounded-sam-osx/transformer_utils/mmpose/core/post_processing/smoother.py
@@ -0,0 +1,227 @@
+# Copyright (c) OpenMMLab. All rights reserved.
+import copy
+import warnings
+from typing import Dict, Union
+
+import numpy as np
+from mmcv import Config, is_seq_of
+
+from mmpose.core.post_processing.temporal_filters import build_filter
+
+
+class Smoother():
+ """Smoother to apply temporal smoothing on pose estimation results with a
+ filter.
+
+ Note:
+ T: The temporal length of the pose sequence
+ K: The keypoint number of each target
+ C: The keypoint coordinate dimension
+
+ Args:
+ filter_cfg (dict | str): The filter config. See example config files in
+ `configs/_base_/filters/` for details. Alternatively a config file
+ path can be accepted and the config will be loaded.
+ keypoint_dim (int): The keypoint coordinate dimension, which is
+ also indicated as C. Default: 2
+ keypoint_key (str): The dict key of the keypoints in the pose results.
+ Default: 'keypoints'
+ Example:
+ >>> import numpy as np
+ >>> # Build dummy pose result
+ >>> results = []
+ >>> for t in range(10):
+ >>> results_t = []
+ >>> for track_id in range(2):
+ >>> result = {
+ >>> 'track_id': track_id,
+ >>> 'keypoints': np.random.rand(17, 3)
+ >>> }
+ >>> results_t.append(result)
+ >>> results.append(results_t)
+ >>> # Example 1: Smooth multi-frame pose results offline.
+ >>> filter_cfg = dict(type='GaussianFilter', window_size=3)
+ >>> smoother = Smoother(filter_cfg, keypoint_dim=2)
+ >>> smoothed_results = smoother.smooth(results)
+ >>> # Example 2: Smooth pose results online frame-by-frame
+ >>> filter_cfg = dict(type='GaussianFilter', window_size=3)
+ >>> smoother = Smoother(filter_cfg, keypoint_dim=2)
+ >>> for result_t in results:
+ >>> smoothed_result_t = smoother.smooth(result_t)
+ """
+
+ def __init__(self,
+ filter_cfg: Union[Dict, str],
+ keypoint_dim: int = 2,
+ keypoint_key: str = 'keypoints'):
+ if isinstance(filter_cfg, str):
+ filter_cfg = Config.fromfile(filter_cfg).filter_cfg
+ self.filter_cfg = filter_cfg
+ self._filter = build_filter(filter_cfg)
+ self.keypoint_dim = keypoint_dim
+ self.key = keypoint_key
+ self.padding_size = self._filter.window_size - 1
+ self.history = {}
+
+ def _get_filter(self):
+ fltr = self._filter
+ if not fltr.shareable:
+ # If the filter is not shareable, build a new filter for the next
+ # requires
+ self._filter = build_filter(self.filter_cfg)
+ return fltr
+
+ def _collate_pose(self, results):
+ """Collate the pose results to pose sequences.
+
+ Args:
+ results (list[list[dict]]): The pose results of multiple frames.
+
+ Returns:
+ dict[str, np.ndarray]: A dict of collated pose sequences, where
+ the key is the track_id (in untracked scenario, the target index
+ will be used as the track_id), and the value is the pose sequence
+ in an array of shape [T, K, C]
+ """
+
+ if self._has_track_id(results):
+ # If the results have track_id, use it as the target indicator
+ results = [{res['track_id']: res
+ for res in results_t} for results_t in results]
+ track_ids = results[0].keys()
+
+ for t, results_t in enumerate(results[1:]):
+ if results_t.keys() != track_ids:
+ raise ValueError(f'Inconsistent track ids in frame {t+1}')
+
+ collated = {
+ id: np.stack([
+ results_t[id][self.key][:, :self.keypoint_dim]
+ for results_t in results
+ ])
+ for id in track_ids
+ }
+ else:
+ # If the results don't have track_id, use the target index
+ # as the target indicator
+ n_target = len(results[0])
+ for t, results_t in enumerate(results[1:]):
+ if len(results_t) != n_target:
+ raise ValueError(
+ f'Inconsistent target number in frame {t+1}: '
+ f'{len(results_t)} vs {n_target}')
+
+ collated = {
+ id: np.stack([
+ results_t[id][self.key][:, :self.keypoint_dim]
+ for results_t in results
+ ])
+ for id in range(n_target)
+ }
+
+ return collated
+
+ def _scatter_pose(self, results, poses):
+ """Scatter the smoothed pose sequences and use them to update the pose
+ results.
+
+ Args:
+ results (list[list[dict]]): The original pose results
+ poses (dict[str, np.ndarray]): The smoothed pose sequences
+
+ Returns:
+ list[list[dict]]: The updated pose results
+ """
+ updated_results = []
+ for t, results_t in enumerate(results):
+ updated_results_t = []
+ if self._has_track_id(results):
+ id2result = ((result['track_id'], result)
+ for result in results_t)
+ else:
+ id2result = enumerate(results_t)
+
+ for track_id, result in id2result:
+ result = copy.deepcopy(result)
+ result[self.key][:, :self.keypoint_dim] = poses[track_id][t]
+ updated_results_t.append(result)
+
+ updated_results.append(updated_results_t)
+ return updated_results
+
+ @staticmethod
+ def _has_track_id(results):
+ """Check if the pose results contain track_id."""
+ return 'track_id' in results[0][0]
+
+ def smooth(self, results):
+ """Apply temporal smoothing on pose estimation sequences.
+
+ Args:
+ results (list[dict] | list[list[dict]]): The pose results of a
+ single frame (non-nested list) or multiple frames (nested
+ list). The result of each target is a dict, which should
+ contains:
+
+ - track_id (optional, Any): The track ID of the target
+ - keypoints (np.ndarray): The keypoint coordinates in [K, C]
+
+ Returns:
+ (list[dict] | list[list[dict]]): Temporal smoothed pose results,
+ which has the same data structure as the input's.
+ """
+
+ # Check if input is empty
+ if not (results) or not (results[0]):
+ warnings.warn('Smoother received empty result.')
+ return results
+
+ # Check input is single frame or sequence
+ if is_seq_of(results, dict):
+ single_frame = True
+ results = [results]
+ else:
+ assert is_seq_of(results, list)
+ single_frame = False
+
+ # Get temporal length of input
+ T = len(results)
+
+ # Collate the input results to pose sequences
+ poses = self._collate_pose(results)
+
+ # Smooth the pose sequence of each target
+ smoothed_poses = {}
+ update_history = {}
+ for track_id, pose in poses.items():
+ if track_id in self.history:
+ # For tracked target, get its filter and pose history
+ pose_history, pose_filter = self.history[track_id]
+ if self.padding_size > 0:
+ # Pad the pose sequence with pose history
+ pose = np.concatenate((pose_history, pose), axis=0)
+ else:
+ # For new target, build a new filter
+ pose_filter = self._get_filter()
+
+ # Update the history information
+ if self.padding_size > 0:
+ pose_history = pose[-self.padding_size:].copy()
+ else:
+ pose_history = None
+ update_history[track_id] = (pose_history, pose_filter)
+
+ # Smooth the pose sequence with the filter
+ smoothed_pose = pose_filter(pose)
+ smoothed_poses[track_id] = smoothed_pose[-T:]
+
+ self.history = update_history
+
+ # Scatter the pose sequences back to the format of results
+ smoothed_results = self._scatter_pose(results, smoothed_poses)
+
+ # If the input is single frame, remove the nested list to keep the
+ # output structure consistent with the input's
+ if single_frame:
+ smoothed_results = smoothed_results[0]
+ return smoothed_results
diff --git a/grounded-sam-osx/transformer_utils/mmpose/core/post_processing/temporal_filters/__init__.py b/grounded-sam-osx/transformer_utils/mmpose/core/post_processing/temporal_filters/__init__.py
new file mode 100644
index 0000000000000000000000000000000000000000..8aea62513b14fdb6ac740c06e82683a1e27363db
--- /dev/null
+++ b/grounded-sam-osx/transformer_utils/mmpose/core/post_processing/temporal_filters/__init__.py
@@ -0,0 +1,11 @@
+# Copyright (c) OpenMMLab. All rights reserved.
+from .builder import build_filter
+from .gaussian_filter import GaussianFilter
+from .one_euro_filter import OneEuroFilter
+from .savizky_golay_filter import SavizkyGolayFilter
+from .smoothnet_filter import SmoothNetFilter
+
+__all__ = [
+ 'build_filter', 'GaussianFilter', 'OneEuroFilter', 'SavizkyGolayFilter',
+ 'SmoothNetFilter'
+]
diff --git a/grounded-sam-osx/transformer_utils/mmpose/core/post_processing/temporal_filters/builder.py b/grounded-sam-osx/transformer_utils/mmpose/core/post_processing/temporal_filters/builder.py
new file mode 100644
index 0000000000000000000000000000000000000000..adb914c5222db967c9cdb56fa9f469ff47792f79
--- /dev/null
+++ b/grounded-sam-osx/transformer_utils/mmpose/core/post_processing/temporal_filters/builder.py
@@ -0,0 +1,9 @@
+# Copyright (c) OpenMMLab. All rights reserved.
+from mmcv.utils import Registry
+
+FILTERS = Registry('filters')
+
+
+def build_filter(cfg):
+ """Build filters function."""
+ return FILTERS.build(cfg)
diff --git a/grounded-sam-osx/transformer_utils/mmpose/core/post_processing/temporal_filters/filter.py b/grounded-sam-osx/transformer_utils/mmpose/core/post_processing/temporal_filters/filter.py
new file mode 100644
index 0000000000000000000000000000000000000000..6c6ce0127092235c370f8e398751884f09a18bf5
--- /dev/null
+++ b/grounded-sam-osx/transformer_utils/mmpose/core/post_processing/temporal_filters/filter.py
@@ -0,0 +1,42 @@
+# Copyright (c) OpenMMLab. All rights reserved.
+from abc import ABCMeta, abstractmethod
+
+
+class TemporalFilter(metaclass=ABCMeta):
+ """Base class of temporal filter.
+
+ A subclass should implement the method __call__().
+
+ Parameters:
+ window_size (int): the size of the sliding window.
+ """
+
+ # If the filter can be shared by multiple humans or targets
+ _shareable: bool = True
+
+ def __init__(self, window_size=1):
+ self._window_size = window_size
+
+ @property
+ def window_size(self):
+ return self._window_size
+
+ @property
+ def shareable(self):
+ return self._shareable
+
+ @abstractmethod
+ def __call__(self, x):
+ """Apply filter to a pose sequence.
+
+ Note:
+ T: The temporal length of the pose sequence
+ K: The keypoint number of each target
+ C: The keypoint coordinate dimension
+
+ Args:
+ x (np.ndarray): input pose sequence in shape [T, K, C]
+
+ Returns:
+ np.ndarray: Smoothed pose sequence in shape [T, K, C]
+ """
diff --git a/grounded-sam-osx/transformer_utils/mmpose/core/post_processing/temporal_filters/gaussian_filter.py b/grounded-sam-osx/transformer_utils/mmpose/core/post_processing/temporal_filters/gaussian_filter.py
new file mode 100644
index 0000000000000000000000000000000000000000..b737cdb15aeb9985c0666afeb26e919893343262
--- /dev/null
+++ b/grounded-sam-osx/transformer_utils/mmpose/core/post_processing/temporal_filters/gaussian_filter.py
@@ -0,0 +1,44 @@
+# Copyright (c) OpenMMLab. All rights reserved.
+import numpy as np
+from scipy.ndimage.filters import gaussian_filter1d
+from scipy.signal import medfilt
+
+from .builder import FILTERS
+from .filter import TemporalFilter
+
+
+@FILTERS.register_module(name=['GaussianFilter', 'gaussian'])
+class GaussianFilter(TemporalFilter):
+ """Apply median filter and then gaussian filter.
+
+ Adapted from:
+ https://github.com/akanazawa/human_dynamics/blob/mas
+ ter/src/util/smooth_bbox.py.
+
+ Args:
+ window_size (int): The size of the filter window (i.e., the number
+ of coefficients). window_length must be a positive odd integer.
+ Default: 11
+ sigma (float): Sigma for gaussian smoothing. Default: 4.0
+ """
+
+ def __init__(self, window_size: int = 11, sigma: float = 4.0):
+ super().__init__(window_size)
+ assert window_size % 2 == 1, (
+ 'The window size of GaussianFilter should'
+ f'be odd, but got {window_size}')
+ self.sigma = sigma
+
+ def __call__(self, x: np.ndarray):
+
+ assert x.ndim == 3, ('Input should be an array with shape [T, K, C]'
+ f', but got invalid shape {x.shape}')
+
+ T = x.shape[0]
+ if T < self.window_size:
+ pad_width = [(self.window_size - T, 0), (0, 0), (0, 0)]
+ x = np.pad(x, pad_width, mode='edge')
+ smoothed = medfilt(x, (self.window_size, 1, 1))
+
+ smoothed = gaussian_filter1d(smoothed, self.sigma, axis=0)
+ return smoothed[-T:]
diff --git a/grounded-sam-osx/transformer_utils/mmpose/core/post_processing/temporal_filters/one_euro_filter.py b/grounded-sam-osx/transformer_utils/mmpose/core/post_processing/temporal_filters/one_euro_filter.py
new file mode 100644
index 0000000000000000000000000000000000000000..b954a97fd79543f243a087510a20c4e0037b9ef5
--- /dev/null
+++ b/grounded-sam-osx/transformer_utils/mmpose/core/post_processing/temporal_filters/one_euro_filter.py
@@ -0,0 +1,113 @@
+# ------------------------------------------------------------------------------
+# Adapted from https://github.com/HoBeom/OneEuroFilter-Numpy
+# Original licence: Copyright (c) HoBeom Jeon, under the MIT License.
+# ------------------------------------------------------------------------------
+import math
+
+import numpy as np
+
+from .builder import FILTERS
+from .filter import TemporalFilter
+
+
+def smoothing_factor(t_e, cutoff):
+ r = 2 * math.pi * cutoff * t_e
+ return r / (r + 1)
+
+
+def exponential_smoothing(a, x, x_prev):
+ return a * x + (1 - a) * x_prev
+
+
+class OneEuro:
+
+ def __init__(self, t0, x0, dx0, min_cutoff, beta, d_cutoff=1.0):
+ super(OneEuro, self).__init__()
+ """Initialize the one euro filter."""
+ # The parameters.
+ self.min_cutoff = float(min_cutoff)
+ self.beta = float(beta)
+ self.d_cutoff = float(d_cutoff)
+ # Previous values.
+ self.x_prev = x0
+ self.dx_prev = dx0
+ self.t_prev = t0
+
+ def __call__(self, x, t=None):
+ """Compute the filtered signal."""
+
+ if t is None:
+ # Assume input is feed frame by frame if not specified
+ t = self.t_prev + 1
+
+ t_e = t - self.t_prev
+
+ # The filtered derivative of the signal.
+ a_d = smoothing_factor(t_e, self.d_cutoff) # [k, c]
+ dx = (x - self.x_prev) / t_e
+ dx_hat = exponential_smoothing(a_d, dx, self.dx_prev)
+
+ # The filtered signal.
+ cutoff = self.min_cutoff + self.beta * np.abs(dx_hat)
+ a = smoothing_factor(t_e, cutoff)
+ x_hat = exponential_smoothing(a, x, self.x_prev)
+ # Memorize the previous values.
+ self.x_prev = x_hat
+ self.dx_prev = dx_hat
+ self.t_prev = t
+ return x_hat
+
+
+@FILTERS.register_module(name=['OneEuroFilter', 'oneeuro'])
+class OneEuroFilter(TemporalFilter):
+ """Oneeuro filter, source code: https://github.com/mkocabas/VIBE/blob/c0
+ c3f77d587351c806e901221a9dc05d1ffade4b/lib/utils/smooth_pose.py.
+
+ Args:
+ min_cutoff (float, optional): Decreasing the minimum cutoff frequency
+ decreases slow speed jitter
+ beta (float, optional): Increasing the speed coefficient(beta)
+ decreases speed lag.
+ """
+
+ # Not shareable because the filter holds status of a specific target
+ _shareable: bool = False
+
+ def __init__(self, min_cutoff=0.004, beta=0.7):
+ # OneEuroFilter has Markov Property and maintains status variables
+ # within the class, thus has a windows_size of 1
+ super().__init__(window_size=1)
+ self.min_cutoff = min_cutoff
+ self.beta = beta
+ self._one_euro = None
+
+ def __call__(self, x: np.ndarray):
+ assert x.ndim == 3, ('Input should be an array with shape [T, K, C]'
+ f', but got invalid shape {x.shape}')
+
+ pred_pose_hat = x.copy()
+
+ if self._one_euro is None:
+ # The filter is invoked for the first time
+ # Initialize the filter
+ self._one_euro = OneEuro(
+ np.zeros_like(x[0]),
+ x[0],
+ dx0=0.0,
+ min_cutoff=self.min_cutoff,
+ beta=self.beta,
+ )
+ t0 = 1
+ else:
+ # The filter has been invoked
+ t0 = 0
+
+ for t, pose in enumerate(x):
+ if t < t0:
+ # If the filter is invoked for the first time
+ # set pred_pose_hat[0] = x[0]
+ continue
+ pose = self._one_euro(pose)
+ pred_pose_hat[t] = pose
+
+ return pred_pose_hat
diff --git a/grounded-sam-osx/transformer_utils/mmpose/core/post_processing/temporal_filters/savizky_golay_filter.py b/grounded-sam-osx/transformer_utils/mmpose/core/post_processing/temporal_filters/savizky_golay_filter.py
new file mode 100644
index 0000000000000000000000000000000000000000..18e0528f6cec71f19fe1c4a1f26560c1438bd1ce
--- /dev/null
+++ b/grounded-sam-osx/transformer_utils/mmpose/core/post_processing/temporal_filters/savizky_golay_filter.py
@@ -0,0 +1,50 @@
+# Copyright (c) OpenMMLab. All rights reserved.
+import numpy as np
+from scipy.signal import savgol_filter
+
+from .builder import FILTERS
+from .filter import TemporalFilter
+
+
+@FILTERS.register_module(name=['SavizkyGolayFilter', 'savgol'])
+class SavizkyGolayFilter(TemporalFilter):
+ """Savizky-Golay filter.
+
+ Adapted from:
+ https://docs.scipy.org/doc/scipy/reference/generated/
+ scipy.signal.savgol_filter.html.
+
+ Args:
+ window_size (int): The size of the filter window (i.e., the number
+ of coefficients). window_length must be a positive odd integer.
+ Default: 11
+ polyorder (int): The order of the polynomial used to fit the samples.
+ polyorder must be less than window_size.
+ """
+
+ def __init__(self, window_size: int = 11, polyorder: int = 2):
+ super().__init__(window_size)
+
+ # 1-D Savitzky-Golay filter
+ assert polyorder > 0, (
+ f'Got invalid parameter polyorder={polyorder}. Polyorder '
+ 'should be positive.')
+ assert polyorder < window_size, (
+ f'Got invalid parameters polyorder={polyorder} and '
+ f'window_size={window_size}. Polyorder should be less than '
+ 'window_size.')
+ self.polyorder = polyorder
+
+ def __call__(self, x: np.ndarray):
+
+ assert x.ndim == 3, ('Input should be an array with shape [T, K, C]'
+ f', but got invalid shape {x.shape}')
+
+ T = x.shape[0]
+ if T < self.window_size:
+ pad_width = [(self.window_size - T, 0), (0, 0), (0, 0)]
+ x = np.pad(x, pad_width, mode='edge')
+
+ smoothed = savgol_filter(x, self.window_size, self.polyorder, axis=0)
+
+ return smoothed[-T:]
diff --git a/grounded-sam-osx/transformer_utils/mmpose/core/post_processing/temporal_filters/smoothnet_filter.py b/grounded-sam-osx/transformer_utils/mmpose/core/post_processing/temporal_filters/smoothnet_filter.py
new file mode 100644
index 0000000000000000000000000000000000000000..c7f8df520ad9457722f738c33b79d69d3a99fb9e
--- /dev/null
+++ b/grounded-sam-osx/transformer_utils/mmpose/core/post_processing/temporal_filters/smoothnet_filter.py
@@ -0,0 +1,226 @@
+# Copyright (c) OpenMMLab. All rights reserved.
+from typing import Optional
+
+import numpy as np
+import torch
+from mmcv.runner import load_checkpoint
+from torch import Tensor, nn
+
+from .builder import FILTERS
+from .filter import TemporalFilter
+
+
+class SmoothNetResBlock(nn.Module):
+ """Residual block module used in SmoothNet.
+
+ Args:
+ in_channels (int): Input channel number.
+ hidden_channels (int): The hidden feature channel number.
+ dropout (float): Dropout probability. Default: 0.5
+
+ Shape:
+ Input: (*, in_channels)
+ Output: (*, in_channels)
+ """
+
+ def __init__(self, in_channels, hidden_channels, dropout=0.5):
+ super().__init__()
+ self.linear1 = nn.Linear(in_channels, hidden_channels)
+ self.linear2 = nn.Linear(hidden_channels, in_channels)
+ self.lrelu = nn.LeakyReLU(0.2, inplace=True)
+ self.dropout = nn.Dropout(p=dropout, inplace=True)
+
+ def forward(self, x):
+ identity = x
+ x = self.linear1(x)
+ x = self.dropout(x)
+ x = self.lrelu(x)
+ x = self.linear2(x)
+ x = self.dropout(x)
+ x = self.lrelu(x)
+
+ out = x + identity
+ return out
+
+
+class SmoothNet(nn.Module):
+ """SmoothNet is a plug-and-play temporal-only network to refine human
+ poses. It works for 2d/3d/6d pose smoothing.
+
+ "SmoothNet: A Plug-and-Play Network for Refining Human Poses in Videos",
+ arXiv'2021. More details can be found in the `paper
+ `__ .
+
+ Note:
+ N: The batch size
+ T: The temporal length of the pose sequence
+ C: The total pose dimension (e.g. keypoint_number * keypoint_dim)
+
+ Args:
+ window_size (int): The size of the input window.
+ output_size (int): The size of the output window.
+ hidden_size (int): The hidden feature dimension in the encoder,
+ the decoder and between residual blocks. Default: 512
+ res_hidden_size (int): The hidden feature dimension inside the
+ residual blocks. Default: 256
+ num_blocks (int): The number of residual blocks. Default: 3
+ dropout (float): Dropout probability. Default: 0.5
+
+ Shape:
+ Input: (N, C, T) the original pose sequence
+ Output: (N, C, T) the smoothed pose sequence
+ """
+
+ def __init__(self,
+ window_size: int,
+ output_size: int,
+ hidden_size: int = 512,
+ res_hidden_size: int = 256,
+ num_blocks: int = 3,
+ dropout: float = 0.5):
+ super().__init__()
+ self.window_size = window_size
+ self.output_size = output_size
+ self.hidden_size = hidden_size
+ self.res_hidden_size = res_hidden_size
+ self.num_blocks = num_blocks
+ self.dropout = dropout
+
+ assert output_size <= window_size, (
+ 'The output size should be less than or equal to the window size.',
+ f' Got output_size=={output_size} and window_size=={window_size}')
+
+ # Build encoder layers
+ self.encoder = nn.Sequential(
+ nn.Linear(window_size, hidden_size),
+ nn.LeakyReLU(0.1, inplace=True))
+
+ # Build residual blocks
+ res_blocks = []
+ for _ in range(num_blocks):
+ res_blocks.append(
+ SmoothNetResBlock(
+ in_channels=hidden_size,
+ hidden_channels=res_hidden_size,
+ dropout=dropout))
+ self.res_blocks = nn.Sequential(*res_blocks)
+
+ # Build decoder layers
+ self.decoder = nn.Linear(hidden_size, output_size)
+
+ def forward(self, x: Tensor) -> Tensor:
+ """Forward function."""
+ N, C, T = x.shape
+ num_windows = T - self.window_size + 1
+
+ assert T >= self.window_size, (
+ 'Input sequence length must be no less than the window size. ',
+ f'Got x.shape[2]=={T} and window_size=={self.window_size}')
+
+ # Unfold x to obtain input sliding windows
+ # [N, C, num_windows, window_size]
+ x = x.unfold(2, self.window_size, 1)
+
+ # Forward layers
+ x = self.encoder(x)
+ x = self.res_blocks(x)
+ x = self.decoder(x) # [N, C, num_windows, output_size]
+
+ # Accumulate output ensembles
+ out = x.new_zeros(N, C, T)
+ count = x.new_zeros(T)
+
+ for t in range(num_windows):
+ out[..., t:t + self.output_size] += x[:, :, t]
+ count[t:t + self.output_size] += 1.0
+
+ return out.div(count)
+
+
+@FILTERS.register_module(name=['SmoothNetFilter', 'SmoothNet', 'smoothnet'])
+class SmoothNetFilter(TemporalFilter):
+ """Apply SmoothNet filter.
+
+ "SmoothNet: A Plug-and-Play Network for Refining Human Poses in Videos",
+ arXiv'2021. More details can be found in the `paper
+ `__ .
+
+ Args:
+ window_size (int): The size of the filter window. It's also the
+ window_size of SmoothNet model.
+ output_size (int): The output window size of SmoothNet model.
+ checkpoint (str): The checkpoint file of the pretrained SmoothNet
+ model. Please note that `checkpoint` should be matched with
+ `window_size` and `output_size`.
+ hidden_size (int): SmoothNet argument. See :class:`SmoothNet` for
+ details. Default: 512
+ hidden_res_size (int): SmoothNet argument. See :class:`SmoothNet`
+ for details. Default: 256
+ num_blocks (int): SmoothNet argument. See :class:`SmoothNet` for
+ details. Default: 3
+ device (str): Device for model inference. Default: 'cpu'
+ root_index (int, optional): If not None, relative keypoint coordinates
+ will be calculated as the SmoothNet input, by centering the
+ keypoints around the root point. The model output will be
+ converted back to absolute coordinates. Default: None
+ """
+
+ def __init__(
+ self,
+ window_size: int,
+ output_size: int,
+ checkpoint: Optional[str] = None,
+ hidden_size: int = 512,
+ res_hidden_size: int = 256,
+ num_blocks: int = 3,
+ device: str = 'cpu',
+ root_index: Optional[int] = None,
+ ):
+ super().__init__(window_size)
+ self.device = device
+ self.root_index = root_index
+ self.smoothnet = SmoothNet(window_size, output_size, hidden_size,
+ res_hidden_size, num_blocks)
+ if checkpoint:
+ load_checkpoint(self.smoothnet, checkpoint)
+ self.smoothnet.to(device)
+ self.smoothnet.eval()
+
+ for p in self.smoothnet.parameters():
+ p.requires_grad_(False)
+
+ def __call__(self, x: np.ndarray):
+ assert x.ndim == 3, ('Input should be an array with shape [T, K, C]'
+ f', but got invalid shape {x.shape}')
+
+ root_index = self.root_index
+ if root_index is not None:
+ x_root = x[:, root_index:root_index + 1]
+ x = np.delete(x, root_index, axis=1)
+ x = x - x_root
+
+ T, K, C = x.shape
+
+ if T < self.window_size:
+ # Skip smoothing if the input length is less than the window size
+ smoothed = x
+ else:
+ dtype = x.dtype
+
+ # Convert to tensor and forward the model
+ with torch.no_grad():
+ x = torch.tensor(x, dtype=torch.float32, device=self.device)
+ x = x.view(1, T, K * C).permute(0, 2, 1) # to [1, KC, T]
+ smoothed = self.smoothnet(x) # in shape [1, KC, T]
+
+ # Convert model output back to input shape and format
+ smoothed = smoothed.permute(0, 2, 1).view(T, K, C) # to [T, K, C]
+ smoothed = smoothed.cpu().numpy().astype(dtype) # to numpy.ndarray
+
+ if root_index is not None:
+ smoothed += x_root
+ smoothed = np.concatenate(
+ (smoothed[:, :root_index], x_root, smoothed[:, root_index:]),
+ axis=1)
+
+ return smoothed
diff --git a/grounded-sam-osx/transformer_utils/mmpose/core/utils/__init__.py b/grounded-sam-osx/transformer_utils/mmpose/core/utils/__init__.py
new file mode 100644
index 0000000000000000000000000000000000000000..512e7680bcce478ca00f79e536ee54cd02de93df
--- /dev/null
+++ b/grounded-sam-osx/transformer_utils/mmpose/core/utils/__init__.py
@@ -0,0 +1,9 @@
+# Copyright (c) OpenMMLab. All rights reserved.
+from .dist_utils import allreduce_grads, sync_random_seed
+from .model_util_hooks import ModelSetEpochHook
+from .regularizations import WeightNormClipHook
+
+__all__ = [
+ 'allreduce_grads', 'WeightNormClipHook', 'sync_random_seed',
+ 'ModelSetEpochHook'
+]
diff --git a/grounded-sam-osx/transformer_utils/mmpose/core/utils/dist_utils.py b/grounded-sam-osx/transformer_utils/mmpose/core/utils/dist_utils.py
new file mode 100644
index 0000000000000000000000000000000000000000..b81f925ad7aa51ce800e27bead8eb8ba021c2592
--- /dev/null
+++ b/grounded-sam-osx/transformer_utils/mmpose/core/utils/dist_utils.py
@@ -0,0 +1,90 @@
+# Copyright (c) OpenMMLab. All rights reserved.
+from collections import OrderedDict
+
+import numpy as np
+import torch
+import torch.distributed as dist
+from mmcv.runner import get_dist_info
+from torch._utils import (_flatten_dense_tensors, _take_tensors,
+ _unflatten_dense_tensors)
+
+
+def _allreduce_coalesced(tensors, world_size, bucket_size_mb=-1):
+ """Allreduce parameters as a whole."""
+ if bucket_size_mb > 0:
+ bucket_size_bytes = bucket_size_mb * 1024 * 1024
+ buckets = _take_tensors(tensors, bucket_size_bytes)
+ else:
+ buckets = OrderedDict()
+ for tensor in tensors:
+ tp = tensor.type()
+ if tp not in buckets:
+ buckets[tp] = []
+ buckets[tp].append(tensor)
+ buckets = buckets.values()
+
+ for bucket in buckets:
+ flat_tensors = _flatten_dense_tensors(bucket)
+ dist.all_reduce(flat_tensors)
+ flat_tensors.div_(world_size)
+ for tensor, synced in zip(
+ bucket, _unflatten_dense_tensors(flat_tensors, bucket)):
+ tensor.copy_(synced)
+
+
+def allreduce_grads(params, coalesce=True, bucket_size_mb=-1):
+ """Allreduce gradients.
+
+ Args:
+ params (list[torch.Parameters]): List of parameters of a model
+ coalesce (bool, optional): Whether allreduce parameters as a whole.
+ Default: True.
+ bucket_size_mb (int, optional): Size of bucket, the unit is MB.
+ Default: -1.
+ """
+ grads = [
+ param.grad.data for param in params
+ if param.requires_grad and param.grad is not None
+ ]
+ world_size = dist.get_world_size()
+ if coalesce:
+ _allreduce_coalesced(grads, world_size, bucket_size_mb)
+ else:
+ for tensor in grads:
+ dist.all_reduce(tensor.div_(world_size))
+
+
+def sync_random_seed(seed=None, device='cuda'):
+ """Make sure different ranks share the same seed.
+
+ All workers must call
+ this function, otherwise it will deadlock. This method is generally used in
+ `DistributedSampler`, because the seed should be identical across all
+ processes in the distributed group.
+ In distributed sampling, different ranks should sample non-overlapped
+ data in the dataset. Therefore, this function is used to make sure that
+ each rank shuffles the data indices in the same order based
+ on the same seed. Then different ranks could use different indices
+ to select non-overlapped data from the same data list.
+ Args:
+ seed (int, Optional): The seed. Default to None.
+ device (str): The device where the seed will be put on.
+ Default to 'cuda'.
+ Returns:
+ int: Seed to be used.
+ """
+ if seed is None:
+ seed = np.random.randint(2**31)
+ assert isinstance(seed, int)
+
+ rank, world_size = get_dist_info()
+
+ if world_size == 1:
+ return seed
+
+ if rank == 0:
+ random_num = torch.tensor(seed, dtype=torch.int32, device=device)
+ else:
+ random_num = torch.tensor(0, dtype=torch.int32, device=device)
+ dist.broadcast(random_num, src=0)
+ return random_num.item()
diff --git a/grounded-sam-osx/transformer_utils/mmpose/core/utils/model_util_hooks.py b/grounded-sam-osx/transformer_utils/mmpose/core/utils/model_util_hooks.py
new file mode 100644
index 0000000000000000000000000000000000000000..d308a8a57a04f1a2acaa841ac2e8ad42439bb633
--- /dev/null
+++ b/grounded-sam-osx/transformer_utils/mmpose/core/utils/model_util_hooks.py
@@ -0,0 +1,13 @@
+# Copyright (c) OpenMMLab. All rights reserved.
+from mmcv.runner import HOOKS, Hook
+
+
+@HOOKS.register_module()
+class ModelSetEpochHook(Hook):
+ """The hook that tells model the current epoch in training."""
+
+ def __init__(self):
+ pass
+
+ def before_epoch(self, runner):
+ runner.model.module.set_train_epoch(runner.epoch + 1)
diff --git a/grounded-sam-osx/transformer_utils/mmpose/core/utils/regularizations.py b/grounded-sam-osx/transformer_utils/mmpose/core/utils/regularizations.py
new file mode 100644
index 0000000000000000000000000000000000000000..d8c7449038066016f6efb60e126111ace962fe98
--- /dev/null
+++ b/grounded-sam-osx/transformer_utils/mmpose/core/utils/regularizations.py
@@ -0,0 +1,86 @@
+# Copyright (c) OpenMMLab. All rights reserved.
+from abc import ABCMeta, abstractmethod, abstractproperty
+
+import torch
+
+
+class PytorchModuleHook(metaclass=ABCMeta):
+ """Base class for PyTorch module hook registers.
+
+ An instance of a subclass of PytorchModuleHook can be used to
+ register hook to a pytorch module using the `register` method like:
+ hook_register.register(module)
+
+ Subclasses should add/overwrite the following methods:
+ - __init__
+ - hook
+ - hook_type
+ """
+
+ @abstractmethod
+ def hook(self, *args, **kwargs):
+ """Hook function."""
+
+ @abstractproperty
+ def hook_type(self) -> str:
+ """Hook type Subclasses should overwrite this function to return a
+ string value in.
+
+ {`forward`, `forward_pre`, `backward`}
+ """
+
+ def register(self, module):
+ """Register the hook function to the module.
+
+ Args:
+ module (pytorch module): the module to register the hook.
+
+ Returns:
+ handle (torch.utils.hooks.RemovableHandle): a handle to remove
+ the hook by calling handle.remove()
+ """
+ assert isinstance(module, torch.nn.Module)
+
+ if self.hook_type == 'forward':
+ h = module.register_forward_hook(self.hook)
+ elif self.hook_type == 'forward_pre':
+ h = module.register_forward_pre_hook(self.hook)
+ elif self.hook_type == 'backward':
+ h = module.register_backward_hook(self.hook)
+ else:
+ raise ValueError(f'Invalid hook type {self.hook}')
+
+ return h
+
+
+class WeightNormClipHook(PytorchModuleHook):
+ """Apply weight norm clip regularization.
+
+ The module's parameter will be clip to a given maximum norm before each
+ forward pass.
+
+ Args:
+ max_norm (float): The maximum norm of the parameter.
+ module_param_names (str|list): The parameter name (or name list) to
+ apply weight norm clip.
+ """
+
+ def __init__(self, max_norm=1.0, module_param_names='weight'):
+ self.module_param_names = module_param_names if isinstance(
+ module_param_names, list) else [module_param_names]
+ self.max_norm = max_norm
+
+ @property
+ def hook_type(self):
+ return 'forward_pre'
+
+ def hook(self, module, _input):
+ for name in self.module_param_names:
+ assert name in module._parameters, f'{name} is not a parameter' \
+ f' of the module {type(module)}'
+ param = module._parameters[name]
+
+ with torch.no_grad():
+ m = param.norm().item()
+ if m > self.max_norm:
+ param.mul_(self.max_norm / (m + 1e-6))
diff --git a/grounded-sam-osx/transformer_utils/mmpose/core/visualization/__init__.py b/grounded-sam-osx/transformer_utils/mmpose/core/visualization/__init__.py
new file mode 100644
index 0000000000000000000000000000000000000000..c87fc29145b1eff15713ca79bc36708a4836ecf8
--- /dev/null
+++ b/grounded-sam-osx/transformer_utils/mmpose/core/visualization/__init__.py
@@ -0,0 +1,8 @@
+# Copyright (c) OpenMMLab. All rights reserved.
+from .image import (imshow_bboxes, imshow_keypoints, imshow_keypoints_3d,
+ imshow_mesh_3d, imshow_multiview_keypoints_3d)
+
+__all__ = [
+ 'imshow_keypoints', 'imshow_keypoints_3d', 'imshow_bboxes',
+ 'imshow_mesh_3d', 'imshow_multiview_keypoints_3d'
+]
diff --git a/grounded-sam-osx/transformer_utils/mmpose/core/visualization/image.py b/grounded-sam-osx/transformer_utils/mmpose/core/visualization/image.py
new file mode 100644
index 0000000000000000000000000000000000000000..0d40cb60115822a5564e165e4eef08609adbcfd8
--- /dev/null
+++ b/grounded-sam-osx/transformer_utils/mmpose/core/visualization/image.py
@@ -0,0 +1,522 @@
+# Copyright (c) OpenMMLab. All rights reserved.
+import math
+import os
+import warnings
+
+import cv2
+import mmcv
+import numpy as np
+from matplotlib import pyplot as plt
+from mmcv.utils.misc import deprecated_api_warning
+from mmcv.visualization.color import color_val
+
+try:
+ import trimesh
+ has_trimesh = True
+except (ImportError, ModuleNotFoundError):
+ has_trimesh = False
+
+try:
+ os.environ['PYOPENGL_PLATFORM'] = 'egl'
+ import pyrender
+ has_pyrender = True
+except (ImportError, ModuleNotFoundError):
+ has_pyrender = False
+
+
+def imshow_bboxes(img,
+ bboxes,
+ labels=None,
+ colors='green',
+ text_color='white',
+ thickness=1,
+ font_scale=0.5,
+ show=True,
+ win_name='',
+ wait_time=0,
+ out_file=None):
+ """Draw bboxes with labels (optional) on an image. This is a wrapper of
+ mmcv.imshow_bboxes.
+
+ Args:
+ img (str or ndarray): The image to be displayed.
+ bboxes (ndarray): ndarray of shape (k, 4), each row is a bbox in
+ format [x1, y1, x2, y2].
+ labels (str or list[str], optional): labels of each bbox.
+ colors (list[str or tuple or :obj:`Color`]): A list of colors.
+ text_color (str or tuple or :obj:`Color`): Color of texts.
+ thickness (int): Thickness of lines.
+ font_scale (float): Font scales of texts.
+ show (bool): Whether to show the image.
+ win_name (str): The window name.
+ wait_time (int): Value of waitKey param.
+ out_file (str, optional): The filename to write the image.
+
+ Returns:
+ ndarray: The image with bboxes drawn on it.
+ """
+
+ # adapt to mmcv.imshow_bboxes input format
+ bboxes = np.split(
+ bboxes, bboxes.shape[0], axis=0) if bboxes.shape[0] > 0 else []
+ if not isinstance(colors, list):
+ colors = [colors for _ in range(len(bboxes))]
+ colors = [mmcv.color_val(c) for c in colors]
+ assert len(bboxes) == len(colors)
+
+ img = mmcv.imshow_bboxes(
+ img,
+ bboxes,
+ colors,
+ top_k=-1,
+ thickness=thickness,
+ show=False,
+ out_file=None)
+
+ if labels is not None:
+ if not isinstance(labels, list):
+ labels = [labels for _ in range(len(bboxes))]
+ assert len(labels) == len(bboxes)
+
+ for bbox, label, color in zip(bboxes, labels, colors):
+ if label is None:
+ continue
+ bbox_int = bbox[0, :4].astype(np.int32)
+ # roughly estimate the proper font size
+ text_size, text_baseline = cv2.getTextSize(label,
+ cv2.FONT_HERSHEY_DUPLEX,
+ font_scale, thickness)
+ text_x1 = bbox_int[0]
+ text_y1 = max(0, bbox_int[1] - text_size[1] - text_baseline)
+ text_x2 = bbox_int[0] + text_size[0]
+ text_y2 = text_y1 + text_size[1] + text_baseline
+ cv2.rectangle(img, (text_x1, text_y1), (text_x2, text_y2), color,
+ cv2.FILLED)
+ cv2.putText(img, label, (text_x1, text_y2 - text_baseline),
+ cv2.FONT_HERSHEY_DUPLEX, font_scale,
+ mmcv.color_val(text_color), thickness)
+
+ if show:
+ mmcv.imshow(img, win_name, wait_time)
+ if out_file is not None:
+ mmcv.imwrite(img, out_file)
+ return img
+
+
+@deprecated_api_warning({'pose_limb_color': 'pose_link_color'})
+def imshow_keypoints(img,
+ pose_result,
+ skeleton=None,
+ kpt_score_thr=0.3,
+ pose_kpt_color=None,
+ pose_link_color=None,
+ radius=4,
+ thickness=1,
+ show_keypoint_weight=False):
+ """Draw keypoints and links on an image.
+
+ Args:
+ img (str or Tensor): The image to draw poses on. If an image array
+ is given, id will be modified in-place.
+ pose_result (list[kpts]): The poses to draw. Each element kpts is
+ a set of K keypoints as an Kx3 numpy.ndarray, where each
+ keypoint is represented as x, y, score.
+ kpt_score_thr (float, optional): Minimum score of keypoints
+ to be shown. Default: 0.3.
+ pose_kpt_color (np.array[Nx3]`): Color of N keypoints. If None,
+ the keypoint will not be drawn.
+ pose_link_color (np.array[Mx3]): Color of M links. If None, the
+ links will not be drawn.
+ thickness (int): Thickness of lines.
+ """
+
+ img = mmcv.imread(img)
+ img_h, img_w, _ = img.shape
+
+ for kpts in pose_result:
+
+ kpts = np.array(kpts, copy=False)
+
+ # draw each point on image
+ if pose_kpt_color is not None:
+ assert len(pose_kpt_color) == len(kpts)
+
+ for kid, kpt in enumerate(kpts):
+ x_coord, y_coord, kpt_score = int(kpt[0]), int(kpt[1]), kpt[2]
+
+ if kpt_score < kpt_score_thr or pose_kpt_color[kid] is None:
+ # skip the point that should not be drawn
+ continue
+
+ color = tuple(int(c) for c in pose_kpt_color[kid])
+ if show_keypoint_weight:
+ img_copy = img.copy()
+ cv2.circle(img_copy, (int(x_coord), int(y_coord)), radius,
+ color, -1)
+ transparency = max(0, min(1, kpt_score))
+ cv2.addWeighted(
+ img_copy,
+ transparency,
+ img,
+ 1 - transparency,
+ 0,
+ dst=img)
+ else:
+ cv2.circle(img, (int(x_coord), int(y_coord)), radius,
+ color, -1)
+
+ # draw links
+ if skeleton is not None and pose_link_color is not None:
+ assert len(pose_link_color) == len(skeleton)
+
+ for sk_id, sk in enumerate(skeleton):
+ pos1 = (int(kpts[sk[0], 0]), int(kpts[sk[0], 1]))
+ pos2 = (int(kpts[sk[1], 0]), int(kpts[sk[1], 1]))
+
+ if (pos1[0] <= 0 or pos1[0] >= img_w or pos1[1] <= 0
+ or pos1[1] >= img_h or pos2[0] <= 0 or pos2[0] >= img_w
+ or pos2[1] <= 0 or pos2[1] >= img_h
+ or kpts[sk[0], 2] < kpt_score_thr
+ or kpts[sk[1], 2] < kpt_score_thr
+ or pose_link_color[sk_id] is None):
+ # skip the link that should not be drawn
+ continue
+ color = tuple(int(c) for c in pose_link_color[sk_id])
+ if show_keypoint_weight:
+ img_copy = img.copy()
+ X = (pos1[0], pos2[0])
+ Y = (pos1[1], pos2[1])
+ mX = np.mean(X)
+ mY = np.mean(Y)
+ length = ((Y[0] - Y[1])**2 + (X[0] - X[1])**2)**0.5
+ angle = math.degrees(math.atan2(Y[0] - Y[1], X[0] - X[1]))
+ stickwidth = 2
+ polygon = cv2.ellipse2Poly(
+ (int(mX), int(mY)), (int(length / 2), int(stickwidth)),
+ int(angle), 0, 360, 1)
+ cv2.fillConvexPoly(img_copy, polygon, color)
+ transparency = max(
+ 0, min(1, 0.5 * (kpts[sk[0], 2] + kpts[sk[1], 2])))
+ cv2.addWeighted(
+ img_copy,
+ transparency,
+ img,
+ 1 - transparency,
+ 0,
+ dst=img)
+ else:
+ cv2.line(img, pos1, pos2, color, thickness=thickness)
+
+ return img
+
+
+def imshow_keypoints_3d(
+ pose_result,
+ img=None,
+ skeleton=None,
+ pose_kpt_color=None,
+ pose_link_color=None,
+ vis_height=400,
+ kpt_score_thr=0.3,
+ num_instances=-1,
+ *,
+ axis_azimuth=70,
+ axis_limit=1.7,
+ axis_dist=10.0,
+ axis_elev=15.0,
+):
+ """Draw 3D keypoints and links in 3D coordinates.
+
+ Args:
+ pose_result (list[dict]): 3D pose results containing:
+ - "keypoints_3d" ([K,4]): 3D keypoints
+ - "title" (str): Optional. A string to specify the title of the
+ visualization of this pose result
+ img (str|np.ndarray): Opptional. The image or image path to show input
+ image and/or 2D pose. Note that the image should be given in BGR
+ channel order.
+ skeleton (list of [idx_i,idx_j]): Skeleton described by a list of
+ links, each is a pair of joint indices.
+ pose_kpt_color (np.ndarray[Nx3]`): Color of N keypoints. If None, do
+ not nddraw keypoints.
+ pose_link_color (np.array[Mx3]): Color of M links. If None, do not
+ draw links.
+ vis_height (int): The image height of the visualization. The width
+ will be N*vis_height depending on the number of visualized
+ items.
+ kpt_score_thr (float): Minimum score of keypoints to be shown.
+ Default: 0.3.
+ num_instances (int): Number of instances to be shown in 3D. If smaller
+ than 0, all the instances in the pose_result will be shown.
+ Otherwise, pad or truncate the pose_result to a length of
+ num_instances.
+ axis_azimuth (float): axis azimuth angle for 3D visualizations.
+ axis_dist (float): axis distance for 3D visualizations.
+ axis_elev (float): axis elevation view angle for 3D visualizations.
+ axis_limit (float): The axis limit to visualize 3d pose. The xyz
+ range will be set as:
+ - x: [x_c - axis_limit/2, x_c + axis_limit/2]
+ - y: [y_c - axis_limit/2, y_c + axis_limit/2]
+ - z: [0, axis_limit]
+ Where x_c, y_c is the mean value of x and y coordinates
+ figsize: (float): figure size in inch.
+ """
+
+ show_img = img is not None
+ if num_instances < 0:
+ num_instances = len(pose_result)
+ else:
+ if len(pose_result) > num_instances:
+ pose_result = pose_result[:num_instances]
+ elif len(pose_result) < num_instances:
+ pose_result += [dict()] * (num_instances - len(pose_result))
+ num_axis = num_instances + 1 if show_img else num_instances
+
+ plt.ioff()
+ fig = plt.figure(figsize=(vis_height * num_axis * 0.01, vis_height * 0.01))
+
+ if show_img:
+ img = mmcv.imread(img, channel_order='bgr')
+ img = mmcv.bgr2rgb(img)
+ img = mmcv.imrescale(img, scale=vis_height / img.shape[0])
+
+ ax_img = fig.add_subplot(1, num_axis, 1)
+ ax_img.get_xaxis().set_visible(False)
+ ax_img.get_yaxis().set_visible(False)
+ ax_img.set_axis_off()
+ ax_img.set_title('Input')
+ ax_img.imshow(img, aspect='equal')
+
+ for idx, res in enumerate(pose_result):
+ dummy = len(res) == 0
+ kpts = np.zeros((1, 3)) if dummy else res['keypoints_3d']
+ if kpts.shape[1] == 3:
+ kpts = np.concatenate([kpts, np.ones((kpts.shape[0], 1))], axis=1)
+ valid = kpts[:, 3] >= kpt_score_thr
+
+ ax_idx = idx + 2 if show_img else idx + 1
+ ax = fig.add_subplot(1, num_axis, ax_idx, projection='3d')
+ ax.view_init(
+ elev=axis_elev,
+ azim=axis_azimuth,
+ )
+ x_c = np.mean(kpts[valid, 0]) if sum(valid) > 0 else 0
+ y_c = np.mean(kpts[valid, 1]) if sum(valid) > 0 else 0
+ ax.set_xlim3d([x_c - axis_limit / 2, x_c + axis_limit / 2])
+ ax.set_ylim3d([y_c - axis_limit / 2, y_c + axis_limit / 2])
+ ax.set_zlim3d([0, axis_limit])
+ ax.set_aspect('auto')
+ ax.set_xticks([])
+ ax.set_yticks([])
+ ax.set_zticks([])
+ ax.set_xticklabels([])
+ ax.set_yticklabels([])
+ ax.set_zticklabels([])
+ ax.dist = axis_dist
+
+ if not dummy and pose_kpt_color is not None:
+ pose_kpt_color = np.array(pose_kpt_color)
+ assert len(pose_kpt_color) == len(kpts)
+ x_3d, y_3d, z_3d = np.split(kpts[:, :3], [1, 2], axis=1)
+ # matplotlib uses RGB color in [0, 1] value range
+ _color = pose_kpt_color[..., ::-1] / 255.
+ ax.scatter(
+ x_3d[valid],
+ y_3d[valid],
+ z_3d[valid],
+ marker='o',
+ color=_color[valid],
+ )
+
+ if not dummy and skeleton is not None and pose_link_color is not None:
+ pose_link_color = np.array(pose_link_color)
+ assert len(pose_link_color) == len(skeleton)
+ for link, link_color in zip(skeleton, pose_link_color):
+ link_indices = [_i for _i in link]
+ xs_3d = kpts[link_indices, 0]
+ ys_3d = kpts[link_indices, 1]
+ zs_3d = kpts[link_indices, 2]
+ kpt_score = kpts[link_indices, 3]
+ if kpt_score.min() > kpt_score_thr:
+ # matplotlib uses RGB color in [0, 1] value range
+ _color = link_color[::-1] / 255.
+ ax.plot(xs_3d, ys_3d, zs_3d, color=_color, zdir='z')
+
+ if 'title' in res:
+ ax.set_title(res['title'])
+
+ # convert figure to numpy array
+ fig.tight_layout()
+ fig.canvas.draw()
+ img_w, img_h = fig.canvas.get_width_height()
+ img_vis = np.frombuffer(
+ fig.canvas.tostring_rgb(), dtype=np.uint8).reshape(img_h, img_w, -1)
+ img_vis = mmcv.rgb2bgr(img_vis)
+
+ plt.close(fig)
+
+ return img_vis
+
+
+def imshow_mesh_3d(img,
+ vertices,
+ faces,
+ camera_center,
+ focal_length,
+ colors=(76, 76, 204)):
+ """Render 3D meshes on background image.
+
+ Args:
+ img(np.ndarray): Background image.
+ vertices (list of np.ndarray): Vetrex coordinates in camera space.
+ faces (list of np.ndarray): Faces of meshes.
+ camera_center ([2]): Center pixel.
+ focal_length ([2]): Focal length of camera.
+ colors (list[str or tuple or Color]): A list of mesh colors.
+ """
+
+ H, W, C = img.shape
+
+ if not has_pyrender:
+ warnings.warn('pyrender package is not installed.')
+ return img
+
+ if not has_trimesh:
+ warnings.warn('trimesh package is not installed.')
+ return img
+
+ try:
+ renderer = pyrender.OffscreenRenderer(
+ viewport_width=W, viewport_height=H)
+ except (ImportError, RuntimeError):
+ warnings.warn('pyrender package is not installed correctly.')
+ return img
+
+ if not isinstance(colors, list):
+ colors = [colors for _ in range(len(vertices))]
+ colors = [color_val(c) for c in colors]
+
+ depth_map = np.ones([H, W]) * np.inf
+ output_img = img
+ for idx in range(len(vertices)):
+ color = colors[idx]
+ color = [c / 255.0 for c in color]
+ color.append(1.0)
+ vert = vertices[idx]
+ face = faces[idx]
+
+ material = pyrender.MetallicRoughnessMaterial(
+ metallicFactor=0.2, alphaMode='OPAQUE', baseColorFactor=color)
+
+ mesh = trimesh.Trimesh(vert, face)
+ rot = trimesh.transformations.rotation_matrix(
+ np.radians(180), [1, 0, 0])
+ mesh.apply_transform(rot)
+ mesh = pyrender.Mesh.from_trimesh(mesh, material=material)
+
+ scene = pyrender.Scene(ambient_light=(0.5, 0.5, 0.5))
+ scene.add(mesh, 'mesh')
+
+ camera_pose = np.eye(4)
+ camera = pyrender.IntrinsicsCamera(
+ fx=focal_length[0],
+ fy=focal_length[1],
+ cx=camera_center[0],
+ cy=camera_center[1],
+ zfar=1e5)
+ scene.add(camera, pose=camera_pose)
+
+ light = pyrender.DirectionalLight(color=[1.0, 1.0, 1.0], intensity=1)
+ light_pose = np.eye(4)
+
+ light_pose[:3, 3] = np.array([0, -1, 1])
+ scene.add(light, pose=light_pose)
+
+ light_pose[:3, 3] = np.array([0, 1, 1])
+ scene.add(light, pose=light_pose)
+
+ light_pose[:3, 3] = np.array([1, 1, 2])
+ scene.add(light, pose=light_pose)
+
+ color, rend_depth = renderer.render(
+ scene, flags=pyrender.RenderFlags.RGBA)
+
+ valid_mask = (rend_depth < depth_map) * (rend_depth > 0)
+ depth_map[valid_mask] = rend_depth[valid_mask]
+ valid_mask = valid_mask[:, :, None]
+ output_img = (
+ valid_mask * color[:, :, :3] + (1 - valid_mask) * output_img)
+
+ return output_img
+
+
+def imshow_multiview_keypoints_3d(
+ pose_result,
+ skeleton=None,
+ pose_kpt_color=None,
+ pose_link_color=None,
+ space_size=[8000, 8000, 2000],
+ space_center=[0, -500, 800],
+ kpt_score_thr=0.0,
+):
+ """Draw 3D keypoints and links in 3D coordinates.
+
+ Args:
+ pose_result (list[kpts]): The poses to draw. Each element kpts is
+ a set of K keypoints as an Kx4 numpy.ndarray, where each
+ keypoint is represented as x, y, z, score.
+ skeleton (list of [idx_i,idx_j]): Skeleton described by a list of
+ links, each is a pair of joint indices.
+ pose_kpt_color (np.ndarray[Nx3]`): Color of N keypoints. If None, do
+ not nddraw keypoints.
+ pose_link_color (np.array[Mx3]): Color of M links. If None, do not
+ draw links.
+ space_size: (list). Default: [8000, 8000, 2000].
+ space_center: (list). Default: [0, -500, 800].
+ kpt_score_thr (float): Minimum score of keypoints to be shown.
+ Default: 0.0.
+ """
+ fig = plt.figure()
+ ax = plt.axes(projection='3d')
+ ax.set_xlim3d(space_center[0] - space_size[0] * 0.5,
+ space_center[0] + space_size[0] * 0.5)
+ ax.set_ylim3d(space_center[1] - space_size[1] * 0.5,
+ space_center[1] + space_size[1] * 0.5)
+ ax.set_zlim3d(space_center[2] - space_size[2] * 0.5,
+ space_center[2] + space_size[2] * 0.5)
+ pose_kpt_color = np.array(pose_kpt_color)
+ pose_kpt_color = pose_kpt_color[..., ::-1] / 255.
+
+ for kpts in pose_result:
+ # draw each point on image
+ xs, ys, zs, scores = kpts.T
+ valid = scores > kpt_score_thr
+ ax.scatter(
+ xs[valid],
+ ys[valid],
+ zs[valid],
+ marker='o',
+ color=pose_kpt_color[valid])
+
+ for link, link_color in zip(skeleton, pose_link_color):
+ link_indices = [_i for _i in link]
+ xs_3d = kpts[link_indices, 0]
+ ys_3d = kpts[link_indices, 1]
+ zs_3d = kpts[link_indices, 2]
+ kpt_score = kpts[link_indices, 3]
+ if kpt_score.min() > kpt_score_thr:
+ # matplotlib uses RGB color in [0, 1] value range
+ _color = np.array(link_color[::-1]) / 255.
+ ax.plot(xs_3d, ys_3d, zs_3d, color=_color)
+
+ # convert figure to numpy array
+ fig.tight_layout()
+ fig.canvas.draw()
+ img_w, img_h = fig.canvas.get_width_height()
+ img_vis = np.frombuffer(
+ fig.canvas.tostring_rgb(), dtype=np.uint8).reshape(img_h, img_w, -1)
+ img_vis = mmcv.rgb2bgr(img_vis)
+
+ plt.close(fig)
+
+ return img_vis
diff --git a/grounded-sam-osx/transformer_utils/mmpose/deprecated.py b/grounded-sam-osx/transformer_utils/mmpose/deprecated.py
new file mode 100644
index 0000000000000000000000000000000000000000..b930901722ab8fe57455f8eaf9e7c1c728b4b4f8
--- /dev/null
+++ b/grounded-sam-osx/transformer_utils/mmpose/deprecated.py
@@ -0,0 +1,199 @@
+# Copyright (c) OpenMMLab. All rights reserved.
+import warnings
+
+from .datasets.builder import DATASETS
+from .datasets.datasets.base import Kpt2dSviewRgbImgTopDownDataset
+from .models.builder import HEADS, POSENETS
+from .models.detectors import AssociativeEmbedding
+from .models.heads import (AEHigherResolutionHead, AESimpleHead,
+ DeepposeRegressionHead, HMRMeshHead,
+ TopdownHeatmapMSMUHead,
+ TopdownHeatmapMultiStageHead,
+ TopdownHeatmapSimpleHead)
+
+
+@DATASETS.register_module()
+class TopDownFreiHandDataset(Kpt2dSviewRgbImgTopDownDataset):
+ """Deprecated TopDownFreiHandDataset."""
+
+ def __init__(self, *args, **kwargs):
+ raise (ImportError(
+ 'TopDownFreiHandDataset has been renamed into FreiHandDataset,'
+ 'check https://github.com/open-mmlab/mmpose/pull/202 for details.')
+ )
+
+ def _get_db(self):
+ return []
+
+ def evaluate(self, cfg, preds, output_dir, *args, **kwargs):
+ return None
+
+
+@DATASETS.register_module()
+class TopDownOneHand10KDataset(Kpt2dSviewRgbImgTopDownDataset):
+ """Deprecated TopDownOneHand10KDataset."""
+
+ def __init__(self, *args, **kwargs):
+ raise (ImportError(
+ 'TopDownOneHand10KDataset has been renamed into OneHand10KDataset,'
+ 'check https://github.com/open-mmlab/mmpose/pull/202 for details.')
+ )
+
+ def _get_db(self):
+ return []
+
+ def evaluate(self, cfg, preds, output_dir, *args, **kwargs):
+ return None
+
+
+@DATASETS.register_module()
+class TopDownPanopticDataset(Kpt2dSviewRgbImgTopDownDataset):
+ """Deprecated TopDownPanopticDataset."""
+
+ def __init__(self, *args, **kwargs):
+ raise (ImportError(
+ 'TopDownPanopticDataset has been renamed into PanopticDataset,'
+ 'check https://github.com/open-mmlab/mmpose/pull/202 for details.')
+ )
+
+ def _get_db(self):
+ return []
+
+ def evaluate(self, cfg, preds, output_dir, *args, **kwargs):
+ return None
+
+
+@HEADS.register_module()
+class BottomUpHigherResolutionHead(AEHigherResolutionHead):
+ """Bottom-up head for Higher Resolution.
+
+ BottomUpHigherResolutionHead has been renamed into AEHigherResolutionHead,
+ check https://github.com/open- mmlab/mmpose/pull/656 for details.
+ """
+
+ def __init__(self, *args, **kwargs):
+ super().__init__(*args, **kwargs)
+ warnings.warn(
+ 'BottomUpHigherResolutionHead has been renamed into '
+ 'AEHigherResolutionHead, check '
+ 'https://github.com/open-mmlab/mmpose/pull/656 for details.',
+ DeprecationWarning)
+
+
+@HEADS.register_module()
+class BottomUpSimpleHead(AESimpleHead):
+ """Bottom-up simple head.
+
+ BottomUpSimpleHead has been renamed into AESimpleHead, check
+ https://github.com/open-mmlab/mmpose/pull/656 for details.
+ """
+
+ def __init__(self, *args, **kwargs):
+ super().__init__(*args, **kwargs)
+ warnings.warn(
+ 'BottomUpHigherResolutionHead has been renamed into '
+ 'AEHigherResolutionHead, check '
+ 'https://github.com/open-mmlab/mmpose/pull/656 for details',
+ DeprecationWarning)
+
+
+@HEADS.register_module()
+class TopDownSimpleHead(TopdownHeatmapSimpleHead):
+ """Top-down heatmap simple head.
+
+ TopDownSimpleHead has been renamed into TopdownHeatmapSimpleHead, check
+ https://github.com/open-mmlab/mmpose/pull/656 for details.
+ """
+
+ def __init__(self, *args, **kwargs):
+ super().__init__(*args, **kwargs)
+ warnings.warn(
+ 'TopDownSimpleHead has been renamed into '
+ 'TopdownHeatmapSimpleHead, check '
+ 'https://github.com/open-mmlab/mmpose/pull/656 for details.',
+ DeprecationWarning)
+
+
+@HEADS.register_module()
+class TopDownMultiStageHead(TopdownHeatmapMultiStageHead):
+ """Top-down heatmap multi-stage head.
+
+ TopDownMultiStageHead has been renamed into TopdownHeatmapMultiStageHead,
+ check https://github.com/open-mmlab/mmpose/pull/656 for details.
+ """
+
+ def __init__(self, *args, **kwargs):
+ super().__init__(*args, **kwargs)
+ warnings.warn(
+ 'TopDownMultiStageHead has been renamed into '
+ 'TopdownHeatmapMultiStageHead, check '
+ 'https://github.com/open-mmlab/mmpose/pull/656 for details.',
+ DeprecationWarning)
+
+
+@HEADS.register_module()
+class TopDownMSMUHead(TopdownHeatmapMSMUHead):
+ """Heads for multi-stage multi-unit heads.
+
+ TopDownMSMUHead has been renamed into TopdownHeatmapMSMUHead, check
+ https://github.com/open-mmlab/mmpose/pull/656 for details.
+ """
+
+ def __init__(self, *args, **kwargs):
+ super().__init__(*args, **kwargs)
+ warnings.warn(
+ 'TopDownMSMUHead has been renamed into '
+ 'TopdownHeatmapMSMUHead, check '
+ 'https://github.com/open-mmlab/mmpose/pull/656 for details.',
+ DeprecationWarning)
+
+
+@HEADS.register_module()
+class MeshHMRHead(HMRMeshHead):
+ """SMPL parameters regressor head.
+
+ MeshHMRHead has been renamed into HMRMeshHead, check
+ https://github.com/open-mmlab/mmpose/pull/656 for details.
+ """
+
+ def __init__(self, *args, **kwargs):
+ super().__init__(*args, **kwargs)
+ warnings.warn(
+ 'MeshHMRHead has been renamed into '
+ 'HMRMeshHead, check '
+ 'https://github.com/open-mmlab/mmpose/pull/656 for details.',
+ DeprecationWarning)
+
+
+@HEADS.register_module()
+class FcHead(DeepposeRegressionHead):
+ """FcHead (deprecated).
+
+ FcHead has been renamed into DeepposeRegressionHead, check
+ https://github.com/open-mmlab/mmpose/pull/656 for details.
+ """
+
+ def __init__(self, *args, **kwargs):
+ super().__init__(*args, **kwargs)
+ warnings.warn(
+ 'FcHead has been renamed into '
+ 'DeepposeRegressionHead, check '
+ 'https://github.com/open-mmlab/mmpose/pull/656 for details.',
+ DeprecationWarning)
+
+
+@POSENETS.register_module()
+class BottomUp(AssociativeEmbedding):
+ """Associative Embedding.
+
+ BottomUp has been renamed into AssociativeEmbedding, check
+ https://github.com/open-mmlab/mmpose/pull/656 for details.
+ """
+
+ def __init__(self, *args, **kwargs):
+ super().__init__(*args, **kwargs)
+ warnings.warn(
+ 'BottomUp has been renamed into '
+ 'AssociativeEmbedding, check '
+ 'https://github.com/open-mmlab/mmpose/pull/656 for details.',
+ DeprecationWarning)
diff --git a/grounded-sam-osx/transformer_utils/mmpose/models/__init__.py b/grounded-sam-osx/transformer_utils/mmpose/models/__init__.py
new file mode 100644
index 0000000000000000000000000000000000000000..641d115a693abff882fa7604811430f8e6b605ab
--- /dev/null
+++ b/grounded-sam-osx/transformer_utils/mmpose/models/__init__.py
@@ -0,0 +1,16 @@
+# Copyright (c) OpenMMLab. All rights reserved.
+from .builder import (BACKBONES, HEADS, LOSSES, MESH_MODELS, NECKS, POSENETS,
+ build_backbone, build_head, build_loss, build_mesh_model,
+ build_neck, build_posenet)
+from .detectors import * # noqa
+from .heads import * # noqa
+from .losses import * # noqa
+from .necks import * # noqa
+from .utils import * # noqa
+
+
+__all__ = [
+ 'HEADS', 'NECKS', 'LOSSES', 'POSENETS', 'MESH_MODELS',
+ 'build_head', 'build_loss', 'build_posenet',
+ 'build_neck', 'build_mesh_model'
+]
diff --git a/grounded-sam-osx/transformer_utils/mmpose/models/backbones/__init__.py b/grounded-sam-osx/transformer_utils/mmpose/models/backbones/__init__.py
new file mode 100644
index 0000000000000000000000000000000000000000..06717917a2dbd08800587d3ffa193149e42a653c
--- /dev/null
+++ b/grounded-sam-osx/transformer_utils/mmpose/models/backbones/__init__.py
@@ -0,0 +1,41 @@
+# Copyright (c) OpenMMLab. All rights reserved.
+from .alexnet import AlexNet
+from .cpm import CPM
+from .hourglass import HourglassNet
+from .hourglass_ae import HourglassAENet
+from .hrformer import HRFormer
+from .hrnet import HRNet
+from .i3d import I3D
+from .litehrnet import LiteHRNet
+from .mobilenet_v2 import MobileNetV2
+from .mobilenet_v3 import MobileNetV3
+from .mspn import MSPN
+from .pvt import PyramidVisionTransformer, PyramidVisionTransformerV2
+from .regnet import RegNet
+from .resnest import ResNeSt
+from .resnet import ResNet, ResNetV1d
+from .resnext import ResNeXt
+from .rsn import RSN
+from .scnet import SCNet
+from .seresnet import SEResNet
+from .seresnext import SEResNeXt
+from .shufflenet_v1 import ShuffleNetV1
+from .shufflenet_v2 import ShuffleNetV2
+from .swin import SwinTransformer
+from .tcformer import TCFormer
+from .tcn import TCN
+from .v2v_net import V2VNet
+from .vgg import VGG
+from .vipnas_mbv3 import ViPNAS_MobileNetV3
+from .vipnas_resnet import ViPNAS_ResNet
+from .hrt import HRT
+from .vit import ViT
+
+__all__ = [
+ 'AlexNet', 'HourglassNet', 'HourglassAENet', 'HRNet', 'MobileNetV2',
+ 'MobileNetV3', 'RegNet', 'ResNet', 'ResNetV1d', 'ResNeXt', 'SCNet',
+ 'SEResNet', 'SEResNeXt', 'ShuffleNetV1', 'ShuffleNetV2', 'CPM', 'RSN',
+ 'MSPN', 'ResNeSt', 'VGG', 'TCN', 'ViPNAS_ResNet', 'ViPNAS_MobileNetV3',
+ 'LiteHRNet', 'V2VNet', 'HRFormer', 'PyramidVisionTransformer',
+ 'PyramidVisionTransformerV2', 'SwinTransformer', 'I3D', 'TCFormer', 'ViT'
+]
diff --git a/grounded-sam-osx/transformer_utils/mmpose/models/backbones/alexnet.py b/grounded-sam-osx/transformer_utils/mmpose/models/backbones/alexnet.py
new file mode 100644
index 0000000000000000000000000000000000000000..a8efd74d118f5abe4d9c880ebe80ce7cbd58c6b2
--- /dev/null
+++ b/grounded-sam-osx/transformer_utils/mmpose/models/backbones/alexnet.py
@@ -0,0 +1,56 @@
+# Copyright (c) OpenMMLab. All rights reserved.
+import torch.nn as nn
+
+from ..builder import BACKBONES
+from .base_backbone import BaseBackbone
+
+
+@BACKBONES.register_module()
+class AlexNet(BaseBackbone):
+ """`AlexNet `__ backbone.
+
+ The input for AlexNet is a 224x224 RGB image.
+
+ Args:
+ num_classes (int): number of classes for classification.
+ The default value is -1, which uses the backbone as
+ a feature extractor without the top classifier.
+ """
+
+ def __init__(self, num_classes=-1):
+ super().__init__()
+ self.num_classes = num_classes
+ self.features = nn.Sequential(
+ nn.Conv2d(3, 64, kernel_size=11, stride=4, padding=2),
+ nn.ReLU(inplace=True),
+ nn.MaxPool2d(kernel_size=3, stride=2),
+ nn.Conv2d(64, 192, kernel_size=5, padding=2),
+ nn.ReLU(inplace=True),
+ nn.MaxPool2d(kernel_size=3, stride=2),
+ nn.Conv2d(192, 384, kernel_size=3, padding=1),
+ nn.ReLU(inplace=True),
+ nn.Conv2d(384, 256, kernel_size=3, padding=1),
+ nn.ReLU(inplace=True),
+ nn.Conv2d(256, 256, kernel_size=3, padding=1),
+ nn.ReLU(inplace=True),
+ nn.MaxPool2d(kernel_size=3, stride=2),
+ )
+ if self.num_classes > 0:
+ self.classifier = nn.Sequential(
+ nn.Dropout(),
+ nn.Linear(256 * 6 * 6, 4096),
+ nn.ReLU(inplace=True),
+ nn.Dropout(),
+ nn.Linear(4096, 4096),
+ nn.ReLU(inplace=True),
+ nn.Linear(4096, num_classes),
+ )
+
+ def forward(self, x):
+
+ x = self.features(x)
+ if self.num_classes > 0:
+ x = x.view(x.size(0), 256 * 6 * 6)
+ x = self.classifier(x)
+
+ return x
diff --git a/grounded-sam-osx/transformer_utils/mmpose/models/backbones/base_backbone.py b/grounded-sam-osx/transformer_utils/mmpose/models/backbones/base_backbone.py
new file mode 100644
index 0000000000000000000000000000000000000000..8787d944d2233955a96d0446d9ead9f8fd8a6a9c
--- /dev/null
+++ b/grounded-sam-osx/transformer_utils/mmpose/models/backbones/base_backbone.py
@@ -0,0 +1,83 @@
+# # Copyright (c) OpenMMLab. All rights reserved.
+# import logging
+# from abc import ABCMeta, abstractmethod
+#
+# import torch.nn as nn
+#
+# from .utils import load_checkpoint
+#
+#
+# class BaseBackbone(nn.Module, metaclass=ABCMeta):
+# """Base backbone.
+#
+# This class defines the basic functions of a backbone. Any backbone that
+# inherits this class should at least define its own `forward` function.
+# """
+#
+# def init_weights(self, pretrained=None):
+# """Init backbone weights.
+#
+# Args:
+# pretrained (str | None): If pretrained is a string, then it
+# initializes backbone weights by loading the pretrained
+# checkpoint. If pretrained is None, then it follows default
+# initializer or customized initializer in subclasses.
+# """
+# if isinstance(pretrained, str):
+# logger = logging.getLogger()
+# load_checkpoint(self, pretrained, strict=False, logger=logger)
+# elif pretrained is None:
+# # use default initializer or customized initializer in subclasses
+# pass
+# else:
+# raise TypeError('pretrained must be a str or None.'
+# f' But received {type(pretrained)}.')
+#
+# @abstractmethod
+# def forward(self, x):
+# """Forward function.
+#
+# Args:
+# x (Tensor | tuple[Tensor]): x could be a torch.Tensor or a tuple of
+# torch.Tensor, containing input data for forward computation.
+# """
+# Copyright (c) OpenMMLab. All rights reserved.
+import logging
+from abc import ABCMeta, abstractmethod
+
+import torch.nn as nn
+
+from .utils import load_checkpoint
+# from mmcv_custom.checkpoint import load_checkpoint
+
+class BaseBackbone(nn.Module, metaclass=ABCMeta):
+ """Base backbone.
+ This class defines the basic functions of a backbone. Any backbone that
+ inherits this class should at least define its own `forward` function.
+ """
+
+ def init_weights(self, pretrained=None, patch_padding='pad'):
+ """Init backbone weights.
+ Args:
+ pretrained (str | None): If pretrained is a string, then it
+ initializes backbone weights by loading the pretrained
+ checkpoint. If pretrained is None, then it follows default
+ initializer or customized initializer in subclasses.
+ """
+ if isinstance(pretrained, str):
+ logger = logging.getLogger()
+ load_checkpoint(self, pretrained, strict=False, logger=logger, patch_padding=patch_padding)
+ elif pretrained is None:
+ # use default initializer or customized initializer in subclasses
+ pass
+ else:
+ raise TypeError('pretrained must be a str or None.'
+ f' But received {type(pretrained)}.')
+
+ @abstractmethod
+ def forward(self, x):
+ """Forward function.
+ Args:
+ x (Tensor | tuple[Tensor]): x could be a torch.Tensor or a tuple of
+ torch.Tensor, containing input data for forward computation.
+ """
\ No newline at end of file
diff --git a/grounded-sam-osx/transformer_utils/mmpose/models/backbones/cpm.py b/grounded-sam-osx/transformer_utils/mmpose/models/backbones/cpm.py
new file mode 100644
index 0000000000000000000000000000000000000000..458245d755f930f4ff625a754aadbab5c13494a6
--- /dev/null
+++ b/grounded-sam-osx/transformer_utils/mmpose/models/backbones/cpm.py
@@ -0,0 +1,186 @@
+# Copyright (c) OpenMMLab. All rights reserved.
+import copy
+
+import torch
+import torch.nn as nn
+from mmcv.cnn import ConvModule, constant_init, normal_init
+from torch.nn.modules.batchnorm import _BatchNorm
+
+from mmpose.utils import get_root_logger
+from ..builder import BACKBONES
+from .base_backbone import BaseBackbone
+from .utils import load_checkpoint
+
+
+class CpmBlock(nn.Module):
+ """CpmBlock for Convolutional Pose Machine.
+
+ Args:
+ in_channels (int): Input channels of this block.
+ channels (list): Output channels of each conv module.
+ kernels (list): Kernel sizes of each conv module.
+ """
+
+ def __init__(self,
+ in_channels,
+ channels=(128, 128, 128),
+ kernels=(11, 11, 11),
+ norm_cfg=None):
+ super().__init__()
+
+ assert len(channels) == len(kernels)
+ layers = []
+ for i in range(len(channels)):
+ if i == 0:
+ input_channels = in_channels
+ else:
+ input_channels = channels[i - 1]
+ layers.append(
+ ConvModule(
+ input_channels,
+ channels[i],
+ kernels[i],
+ padding=(kernels[i] - 1) // 2,
+ norm_cfg=norm_cfg))
+ self.model = nn.Sequential(*layers)
+
+ def forward(self, x):
+ """Model forward function."""
+ out = self.model(x)
+ return out
+
+
+@BACKBONES.register_module()
+class CPM(BaseBackbone):
+ """CPM backbone.
+
+ Convolutional Pose Machines.
+ More details can be found in the `paper
+ `__ .
+
+ Args:
+ in_channels (int): The input channels of the CPM.
+ out_channels (int): The output channels of the CPM.
+ feat_channels (int): Feature channel of each CPM stage.
+ middle_channels (int): Feature channel of conv after the middle stage.
+ num_stages (int): Number of stages.
+ norm_cfg (dict): Dictionary to construct and config norm layer.
+
+ Example:
+ >>> from mmpose.models import CPM
+ >>> import torch
+ >>> self = CPM(3, 17)
+ >>> self.eval()
+ >>> inputs = torch.rand(1, 3, 368, 368)
+ >>> level_outputs = self.forward(inputs)
+ >>> for level_output in level_outputs:
+ ... print(tuple(level_output.shape))
+ (1, 17, 46, 46)
+ (1, 17, 46, 46)
+ (1, 17, 46, 46)
+ (1, 17, 46, 46)
+ (1, 17, 46, 46)
+ (1, 17, 46, 46)
+ """
+
+ def __init__(self,
+ in_channels,
+ out_channels,
+ feat_channels=128,
+ middle_channels=32,
+ num_stages=6,
+ norm_cfg=dict(type='BN', requires_grad=True)):
+ # Protect mutable default arguments
+ norm_cfg = copy.deepcopy(norm_cfg)
+ super().__init__()
+
+ assert in_channels == 3
+
+ self.num_stages = num_stages
+ assert self.num_stages >= 1
+
+ self.stem = nn.Sequential(
+ ConvModule(in_channels, 128, 9, padding=4, norm_cfg=norm_cfg),
+ nn.MaxPool2d(kernel_size=3, stride=2, padding=1),
+ ConvModule(128, 128, 9, padding=4, norm_cfg=norm_cfg),
+ nn.MaxPool2d(kernel_size=3, stride=2, padding=1),
+ ConvModule(128, 128, 9, padding=4, norm_cfg=norm_cfg),
+ nn.MaxPool2d(kernel_size=3, stride=2, padding=1),
+ ConvModule(128, 32, 5, padding=2, norm_cfg=norm_cfg),
+ ConvModule(32, 512, 9, padding=4, norm_cfg=norm_cfg),
+ ConvModule(512, 512, 1, padding=0, norm_cfg=norm_cfg),
+ ConvModule(512, out_channels, 1, padding=0, act_cfg=None))
+
+ self.middle = nn.Sequential(
+ ConvModule(in_channels, 128, 9, padding=4, norm_cfg=norm_cfg),
+ nn.MaxPool2d(kernel_size=3, stride=2, padding=1),
+ ConvModule(128, 128, 9, padding=4, norm_cfg=norm_cfg),
+ nn.MaxPool2d(kernel_size=3, stride=2, padding=1),
+ ConvModule(128, 128, 9, padding=4, norm_cfg=norm_cfg),
+ nn.MaxPool2d(kernel_size=3, stride=2, padding=1))
+
+ self.cpm_stages = nn.ModuleList([
+ CpmBlock(
+ middle_channels + out_channels,
+ channels=[feat_channels, feat_channels, feat_channels],
+ kernels=[11, 11, 11],
+ norm_cfg=norm_cfg) for _ in range(num_stages - 1)
+ ])
+
+ self.middle_conv = nn.ModuleList([
+ nn.Sequential(
+ ConvModule(
+ 128, middle_channels, 5, padding=2, norm_cfg=norm_cfg))
+ for _ in range(num_stages - 1)
+ ])
+
+ self.out_convs = nn.ModuleList([
+ nn.Sequential(
+ ConvModule(
+ feat_channels,
+ feat_channels,
+ 1,
+ padding=0,
+ norm_cfg=norm_cfg),
+ ConvModule(feat_channels, out_channels, 1, act_cfg=None))
+ for _ in range(num_stages - 1)
+ ])
+
+ def init_weights(self, pretrained=None):
+ """Initialize the weights in backbone.
+
+ Args:
+ pretrained (str, optional): Path to pre-trained weights.
+ Defaults to None.
+ """
+ if isinstance(pretrained, str):
+ logger = get_root_logger()
+ load_checkpoint(self, pretrained, strict=False, logger=logger)
+ elif pretrained is None:
+ for m in self.modules():
+ if isinstance(m, nn.Conv2d):
+ normal_init(m, std=0.001)
+ elif isinstance(m, (_BatchNorm, nn.GroupNorm)):
+ constant_init(m, 1)
+ else:
+ raise TypeError('pretrained must be a str or None')
+
+ def forward(self, x):
+ """Model forward function."""
+ stage1_out = self.stem(x)
+ middle_out = self.middle(x)
+ out_feats = []
+
+ out_feats.append(stage1_out)
+
+ for ind in range(self.num_stages - 1):
+ single_stage = self.cpm_stages[ind]
+ out_conv = self.out_convs[ind]
+
+ inp_feat = torch.cat(
+ [out_feats[-1], self.middle_conv[ind](middle_out)], 1)
+ cpm_feat = single_stage(inp_feat)
+ out_feat = out_conv(cpm_feat)
+ out_feats.append(out_feat)
+
+ return out_feats
diff --git a/grounded-sam-osx/transformer_utils/mmpose/models/backbones/hourglass.py b/grounded-sam-osx/transformer_utils/mmpose/models/backbones/hourglass.py
new file mode 100644
index 0000000000000000000000000000000000000000..bf75fad9895ebfd3f3c2a6bffedb3d7e4cc77cba
--- /dev/null
+++ b/grounded-sam-osx/transformer_utils/mmpose/models/backbones/hourglass.py
@@ -0,0 +1,212 @@
+# Copyright (c) OpenMMLab. All rights reserved.
+import copy
+
+import torch.nn as nn
+from mmcv.cnn import ConvModule, constant_init, normal_init
+from torch.nn.modules.batchnorm import _BatchNorm
+
+from mmpose.utils import get_root_logger
+from ..builder import BACKBONES
+from .base_backbone import BaseBackbone
+from .resnet import BasicBlock, ResLayer
+from .utils import load_checkpoint
+
+
+class HourglassModule(nn.Module):
+ """Hourglass Module for HourglassNet backbone.
+
+ Generate module recursively and use BasicBlock as the base unit.
+
+ Args:
+ depth (int): Depth of current HourglassModule.
+ stage_channels (list[int]): Feature channels of sub-modules in current
+ and follow-up HourglassModule.
+ stage_blocks (list[int]): Number of sub-modules stacked in current and
+ follow-up HourglassModule.
+ norm_cfg (dict): Dictionary to construct and config norm layer.
+ """
+
+ def __init__(self,
+ depth,
+ stage_channels,
+ stage_blocks,
+ norm_cfg=dict(type='BN', requires_grad=True)):
+ # Protect mutable default arguments
+ norm_cfg = copy.deepcopy(norm_cfg)
+ super().__init__()
+
+ self.depth = depth
+
+ cur_block = stage_blocks[0]
+ next_block = stage_blocks[1]
+
+ cur_channel = stage_channels[0]
+ next_channel = stage_channels[1]
+
+ self.up1 = ResLayer(
+ BasicBlock, cur_block, cur_channel, cur_channel, norm_cfg=norm_cfg)
+
+ self.low1 = ResLayer(
+ BasicBlock,
+ cur_block,
+ cur_channel,
+ next_channel,
+ stride=2,
+ norm_cfg=norm_cfg)
+
+ if self.depth > 1:
+ self.low2 = HourglassModule(depth - 1, stage_channels[1:],
+ stage_blocks[1:])
+ else:
+ self.low2 = ResLayer(
+ BasicBlock,
+ next_block,
+ next_channel,
+ next_channel,
+ norm_cfg=norm_cfg)
+
+ self.low3 = ResLayer(
+ BasicBlock,
+ cur_block,
+ next_channel,
+ cur_channel,
+ norm_cfg=norm_cfg,
+ downsample_first=False)
+
+ self.up2 = nn.Upsample(scale_factor=2)
+
+ def forward(self, x):
+ """Model forward function."""
+ up1 = self.up1(x)
+ low1 = self.low1(x)
+ low2 = self.low2(low1)
+ low3 = self.low3(low2)
+ up2 = self.up2(low3)
+ return up1 + up2
+
+
+@BACKBONES.register_module()
+class HourglassNet(BaseBackbone):
+ """HourglassNet backbone.
+
+ Stacked Hourglass Networks for Human Pose Estimation.
+ More details can be found in the `paper
+ `__ .
+
+ Args:
+ downsample_times (int): Downsample times in a HourglassModule.
+ num_stacks (int): Number of HourglassModule modules stacked,
+ 1 for Hourglass-52, 2 for Hourglass-104.
+ stage_channels (list[int]): Feature channel of each sub-module in a
+ HourglassModule.
+ stage_blocks (list[int]): Number of sub-modules stacked in a
+ HourglassModule.
+ feat_channel (int): Feature channel of conv after a HourglassModule.
+ norm_cfg (dict): Dictionary to construct and config norm layer.
+
+ Example:
+ >>> from mmpose.models import HourglassNet
+ >>> import torch
+ >>> self = HourglassNet()
+ >>> self.eval()
+ >>> inputs = torch.rand(1, 3, 511, 511)
+ >>> level_outputs = self.forward(inputs)
+ >>> for level_output in level_outputs:
+ ... print(tuple(level_output.shape))
+ (1, 256, 128, 128)
+ (1, 256, 128, 128)
+ """
+
+ def __init__(self,
+ downsample_times=5,
+ num_stacks=2,
+ stage_channels=(256, 256, 384, 384, 384, 512),
+ stage_blocks=(2, 2, 2, 2, 2, 4),
+ feat_channel=256,
+ norm_cfg=dict(type='BN', requires_grad=True)):
+ # Protect mutable default arguments
+ norm_cfg = copy.deepcopy(norm_cfg)
+ super().__init__()
+
+ self.num_stacks = num_stacks
+ assert self.num_stacks >= 1
+ assert len(stage_channels) == len(stage_blocks)
+ assert len(stage_channels) > downsample_times
+
+ cur_channel = stage_channels[0]
+
+ self.stem = nn.Sequential(
+ ConvModule(3, 128, 7, padding=3, stride=2, norm_cfg=norm_cfg),
+ ResLayer(BasicBlock, 1, 128, 256, stride=2, norm_cfg=norm_cfg))
+
+ self.hourglass_modules = nn.ModuleList([
+ HourglassModule(downsample_times, stage_channels, stage_blocks)
+ for _ in range(num_stacks)
+ ])
+
+ self.inters = ResLayer(
+ BasicBlock,
+ num_stacks - 1,
+ cur_channel,
+ cur_channel,
+ norm_cfg=norm_cfg)
+
+ self.conv1x1s = nn.ModuleList([
+ ConvModule(
+ cur_channel, cur_channel, 1, norm_cfg=norm_cfg, act_cfg=None)
+ for _ in range(num_stacks - 1)
+ ])
+
+ self.out_convs = nn.ModuleList([
+ ConvModule(
+ cur_channel, feat_channel, 3, padding=1, norm_cfg=norm_cfg)
+ for _ in range(num_stacks)
+ ])
+
+ self.remap_convs = nn.ModuleList([
+ ConvModule(
+ feat_channel, cur_channel, 1, norm_cfg=norm_cfg, act_cfg=None)
+ for _ in range(num_stacks - 1)
+ ])
+
+ self.relu = nn.ReLU(inplace=True)
+
+ def init_weights(self, pretrained=None):
+ """Initialize the weights in backbone.
+
+ Args:
+ pretrained (str, optional): Path to pre-trained weights.
+ Defaults to None.
+ """
+ if isinstance(pretrained, str):
+ logger = get_root_logger()
+ load_checkpoint(self, pretrained, strict=False, logger=logger)
+ elif pretrained is None:
+ for m in self.modules():
+ if isinstance(m, nn.Conv2d):
+ normal_init(m, std=0.001)
+ elif isinstance(m, (_BatchNorm, nn.GroupNorm)):
+ constant_init(m, 1)
+ else:
+ raise TypeError('pretrained must be a str or None')
+
+ def forward(self, x):
+ """Model forward function."""
+ inter_feat = self.stem(x)
+ out_feats = []
+
+ for ind in range(self.num_stacks):
+ single_hourglass = self.hourglass_modules[ind]
+ out_conv = self.out_convs[ind]
+
+ hourglass_feat = single_hourglass(inter_feat)
+ out_feat = out_conv(hourglass_feat)
+ out_feats.append(out_feat)
+
+ if ind < self.num_stacks - 1:
+ inter_feat = self.conv1x1s[ind](
+ inter_feat) + self.remap_convs[ind](
+ out_feat)
+ inter_feat = self.inters[ind](self.relu(inter_feat))
+
+ return out_feats
diff --git a/grounded-sam-osx/transformer_utils/mmpose/models/backbones/hourglass_ae.py b/grounded-sam-osx/transformer_utils/mmpose/models/backbones/hourglass_ae.py
new file mode 100644
index 0000000000000000000000000000000000000000..5a700e5cb2157fd1dc16771145f065e991b270ea
--- /dev/null
+++ b/grounded-sam-osx/transformer_utils/mmpose/models/backbones/hourglass_ae.py
@@ -0,0 +1,212 @@
+# Copyright (c) OpenMMLab. All rights reserved.
+import copy
+
+import torch.nn as nn
+from mmcv.cnn import ConvModule, MaxPool2d, constant_init, normal_init
+from torch.nn.modules.batchnorm import _BatchNorm
+
+from mmpose.utils import get_root_logger
+from ..builder import BACKBONES
+from .base_backbone import BaseBackbone
+from .utils import load_checkpoint
+
+
+class HourglassAEModule(nn.Module):
+ """Modified Hourglass Module for HourglassNet_AE backbone.
+
+ Generate module recursively and use BasicBlock as the base unit.
+
+ Args:
+ depth (int): Depth of current HourglassModule.
+ stage_channels (list[int]): Feature channels of sub-modules in current
+ and follow-up HourglassModule.
+ norm_cfg (dict): Dictionary to construct and config norm layer.
+ """
+
+ def __init__(self,
+ depth,
+ stage_channels,
+ norm_cfg=dict(type='BN', requires_grad=True)):
+ # Protect mutable default arguments
+ norm_cfg = copy.deepcopy(norm_cfg)
+ super().__init__()
+
+ self.depth = depth
+
+ cur_channel = stage_channels[0]
+ next_channel = stage_channels[1]
+
+ self.up1 = ConvModule(
+ cur_channel, cur_channel, 3, padding=1, norm_cfg=norm_cfg)
+
+ self.pool1 = MaxPool2d(2, 2)
+
+ self.low1 = ConvModule(
+ cur_channel, next_channel, 3, padding=1, norm_cfg=norm_cfg)
+
+ if self.depth > 1:
+ self.low2 = HourglassAEModule(depth - 1, stage_channels[1:])
+ else:
+ self.low2 = ConvModule(
+ next_channel, next_channel, 3, padding=1, norm_cfg=norm_cfg)
+
+ self.low3 = ConvModule(
+ next_channel, cur_channel, 3, padding=1, norm_cfg=norm_cfg)
+
+ self.up2 = nn.UpsamplingNearest2d(scale_factor=2)
+
+ def forward(self, x):
+ """Model forward function."""
+ up1 = self.up1(x)
+ pool1 = self.pool1(x)
+ low1 = self.low1(pool1)
+ low2 = self.low2(low1)
+ low3 = self.low3(low2)
+ up2 = self.up2(low3)
+ return up1 + up2
+
+
+@BACKBONES.register_module()
+class HourglassAENet(BaseBackbone):
+ """Hourglass-AE Network proposed by Newell et al.
+
+ Associative Embedding: End-to-End Learning for Joint
+ Detection and Grouping.
+
+ More details can be found in the `paper
+ `__ .
+
+ Args:
+ downsample_times (int): Downsample times in a HourglassModule.
+ num_stacks (int): Number of HourglassModule modules stacked,
+ 1 for Hourglass-52, 2 for Hourglass-104.
+ stage_channels (list[int]): Feature channel of each sub-module in a
+ HourglassModule.
+ stage_blocks (list[int]): Number of sub-modules stacked in a
+ HourglassModule.
+ feat_channels (int): Feature channel of conv after a HourglassModule.
+ norm_cfg (dict): Dictionary to construct and config norm layer.
+
+ Example:
+ >>> from mmpose.models import HourglassAENet
+ >>> import torch
+ >>> self = HourglassAENet()
+ >>> self.eval()
+ >>> inputs = torch.rand(1, 3, 512, 512)
+ >>> level_outputs = self.forward(inputs)
+ >>> for level_output in level_outputs:
+ ... print(tuple(level_output.shape))
+ (1, 34, 128, 128)
+ """
+
+ def __init__(self,
+ downsample_times=4,
+ num_stacks=1,
+ out_channels=34,
+ stage_channels=(256, 384, 512, 640, 768),
+ feat_channels=256,
+ norm_cfg=dict(type='BN', requires_grad=True)):
+ # Protect mutable default arguments
+ norm_cfg = copy.deepcopy(norm_cfg)
+ super().__init__()
+
+ self.num_stacks = num_stacks
+ assert self.num_stacks >= 1
+ assert len(stage_channels) > downsample_times
+
+ cur_channels = stage_channels[0]
+
+ self.stem = nn.Sequential(
+ ConvModule(3, 64, 7, padding=3, stride=2, norm_cfg=norm_cfg),
+ ConvModule(64, 128, 3, padding=1, norm_cfg=norm_cfg),
+ MaxPool2d(2, 2),
+ ConvModule(128, 128, 3, padding=1, norm_cfg=norm_cfg),
+ ConvModule(128, feat_channels, 3, padding=1, norm_cfg=norm_cfg),
+ )
+
+ self.hourglass_modules = nn.ModuleList([
+ nn.Sequential(
+ HourglassAEModule(
+ downsample_times, stage_channels, norm_cfg=norm_cfg),
+ ConvModule(
+ feat_channels,
+ feat_channels,
+ 3,
+ padding=1,
+ norm_cfg=norm_cfg),
+ ConvModule(
+ feat_channels,
+ feat_channels,
+ 3,
+ padding=1,
+ norm_cfg=norm_cfg)) for _ in range(num_stacks)
+ ])
+
+ self.out_convs = nn.ModuleList([
+ ConvModule(
+ cur_channels,
+ out_channels,
+ 1,
+ padding=0,
+ norm_cfg=None,
+ act_cfg=None) for _ in range(num_stacks)
+ ])
+
+ self.remap_out_convs = nn.ModuleList([
+ ConvModule(
+ out_channels,
+ feat_channels,
+ 1,
+ norm_cfg=norm_cfg,
+ act_cfg=None) for _ in range(num_stacks - 1)
+ ])
+
+ self.remap_feature_convs = nn.ModuleList([
+ ConvModule(
+ feat_channels,
+ feat_channels,
+ 1,
+ norm_cfg=norm_cfg,
+ act_cfg=None) for _ in range(num_stacks - 1)
+ ])
+
+ self.relu = nn.ReLU(inplace=True)
+
+ def init_weights(self, pretrained=None):
+ """Initialize the weights in backbone.
+
+ Args:
+ pretrained (str, optional): Path to pre-trained weights.
+ Defaults to None.
+ """
+ if isinstance(pretrained, str):
+ logger = get_root_logger()
+ load_checkpoint(self, pretrained, strict=False, logger=logger)
+ elif pretrained is None:
+ for m in self.modules():
+ if isinstance(m, nn.Conv2d):
+ normal_init(m, std=0.001)
+ elif isinstance(m, (_BatchNorm, nn.GroupNorm)):
+ constant_init(m, 1)
+ else:
+ raise TypeError('pretrained must be a str or None')
+
+ def forward(self, x):
+ """Model forward function."""
+ inter_feat = self.stem(x)
+ out_feats = []
+
+ for ind in range(self.num_stacks):
+ single_hourglass = self.hourglass_modules[ind]
+ out_conv = self.out_convs[ind]
+
+ hourglass_feat = single_hourglass(inter_feat)
+ out_feat = out_conv(hourglass_feat)
+ out_feats.append(out_feat)
+
+ if ind < self.num_stacks - 1:
+ inter_feat = inter_feat + self.remap_out_convs[ind](
+ out_feat) + self.remap_feature_convs[ind](
+ hourglass_feat)
+
+ return out_feats
diff --git a/grounded-sam-osx/transformer_utils/mmpose/models/backbones/hrformer.py b/grounded-sam-osx/transformer_utils/mmpose/models/backbones/hrformer.py
new file mode 100644
index 0000000000000000000000000000000000000000..b843300a9fdb85908678c5a3fd45ce19e97ce2fe
--- /dev/null
+++ b/grounded-sam-osx/transformer_utils/mmpose/models/backbones/hrformer.py
@@ -0,0 +1,746 @@
+# Copyright (c) OpenMMLab. All rights reserved.
+
+import math
+
+import torch
+import torch.nn as nn
+# from timm.models.layers import to_2tuple, trunc_normal_
+from mmcv.cnn import (build_activation_layer, build_conv_layer,
+ build_norm_layer, trunc_normal_init)
+from mmcv.cnn.bricks.transformer import build_dropout
+from mmcv.runner import BaseModule
+from torch.nn.functional import pad
+
+from ..builder import BACKBONES
+from .hrnet import Bottleneck, HRModule, HRNet
+
+
+def nlc_to_nchw(x, hw_shape):
+ """Convert [N, L, C] shape tensor to [N, C, H, W] shape tensor.
+
+ Args:
+ x (Tensor): The input tensor of shape [N, L, C] before conversion.
+ hw_shape (Sequence[int]): The height and width of output feature map.
+
+ Returns:
+ Tensor: The output tensor of shape [N, C, H, W] after conversion.
+ """
+ H, W = hw_shape
+ assert len(x.shape) == 3
+ B, L, C = x.shape
+ assert L == H * W, 'The seq_len doesn\'t match H, W'
+ return x.transpose(1, 2).reshape(B, C, H, W)
+
+
+def nchw_to_nlc(x):
+ """Flatten [N, C, H, W] shape tensor to [N, L, C] shape tensor.
+
+ Args:
+ x (Tensor): The input tensor of shape [N, C, H, W] before conversion.
+
+ Returns:
+ Tensor: The output tensor of shape [N, L, C] after conversion.
+ """
+ assert len(x.shape) == 4
+ return x.flatten(2).transpose(1, 2).contiguous()
+
+
+def build_drop_path(drop_path_rate):
+ """Build drop path layer."""
+ return build_dropout(dict(type='DropPath', drop_prob=drop_path_rate))
+
+
+class WindowMSA(BaseModule):
+ """Window based multi-head self-attention (W-MSA) module with relative
+ position bias.
+
+ Args:
+ embed_dims (int): Number of input channels.
+ num_heads (int): Number of attention heads.
+ window_size (tuple[int]): The height and width of the window.
+ qkv_bias (bool, optional): If True, add a learnable bias to q, k, v.
+ Default: True.
+ qk_scale (float | None, optional): Override default qk scale of
+ head_dim ** -0.5 if set. Default: None.
+ attn_drop_rate (float, optional): Dropout ratio of attention weight.
+ Default: 0.0
+ proj_drop_rate (float, optional): Dropout ratio of output. Default: 0.
+ with_rpe (bool, optional): If True, use relative position bias.
+ Default: True.
+ init_cfg (dict | None, optional): The Config for initialization.
+ Default: None.
+ """
+
+ def __init__(self,
+ embed_dims,
+ num_heads,
+ window_size,
+ qkv_bias=True,
+ qk_scale=None,
+ attn_drop_rate=0.,
+ proj_drop_rate=0.,
+ with_rpe=True,
+ init_cfg=None):
+
+ super().__init__(init_cfg=init_cfg)
+ self.embed_dims = embed_dims
+ self.window_size = window_size # Wh, Ww
+ self.num_heads = num_heads
+ head_embed_dims = embed_dims // num_heads
+ self.scale = qk_scale or head_embed_dims**-0.5
+
+ self.with_rpe = with_rpe
+ if self.with_rpe:
+ # define a parameter table of relative position bias
+ self.relative_position_bias_table = nn.Parameter(
+ torch.zeros(
+ (2 * window_size[0] - 1) * (2 * window_size[1] - 1),
+ num_heads)) # 2*Wh-1 * 2*Ww-1, nH
+
+ Wh, Ww = self.window_size
+ rel_index_coords = self.double_step_seq(2 * Ww - 1, Wh, 1, Ww)
+ rel_position_index = rel_index_coords + rel_index_coords.T
+ rel_position_index = rel_position_index.flip(1).contiguous()
+ self.register_buffer('relative_position_index', rel_position_index)
+
+ self.qkv = nn.Linear(embed_dims, embed_dims * 3, bias=qkv_bias)
+ self.attn_drop = nn.Dropout(attn_drop_rate)
+ self.proj = nn.Linear(embed_dims, embed_dims)
+ self.proj_drop = nn.Dropout(proj_drop_rate)
+
+ self.softmax = nn.Softmax(dim=-1)
+
+ def init_weights(self):
+ trunc_normal_init(self.relative_position_bias_table, std=0.02)
+
+ def forward(self, x, mask=None):
+ """
+ Args:
+
+ x (tensor): input features with shape of (B*num_windows, N, C)
+ mask (tensor | None, Optional): mask with shape of (num_windows,
+ Wh*Ww, Wh*Ww), value should be between (-inf, 0].
+ """
+ B, N, C = x.shape
+ qkv = self.qkv(x).reshape(B, N, 3, self.num_heads,
+ C // self.num_heads).permute(2, 0, 3, 1, 4)
+ q, k, v = qkv[0], qkv[1], qkv[2]
+
+ q = q * self.scale
+ attn = (q @ k.transpose(-2, -1))
+
+ if self.with_rpe:
+ relative_position_bias = self.relative_position_bias_table[
+ self.relative_position_index.view(-1)].view(
+ self.window_size[0] * self.window_size[1],
+ self.window_size[0] * self.window_size[1],
+ -1) # Wh*Ww,Wh*Ww,nH
+ relative_position_bias = relative_position_bias.permute(
+ 2, 0, 1).contiguous() # nH, Wh*Ww, Wh*Ww
+ attn = attn + relative_position_bias.unsqueeze(0)
+
+ if mask is not None:
+ nW = mask.shape[0]
+ attn = attn.view(B // nW, nW, self.num_heads, N,
+ N) + mask.unsqueeze(1).unsqueeze(0)
+ attn = attn.view(-1, self.num_heads, N, N)
+ attn = self.softmax(attn)
+
+ attn = self.attn_drop(attn)
+
+ x = (attn @ v).transpose(1, 2).reshape(B, N, C)
+ x = self.proj(x)
+ x = self.proj_drop(x)
+ return x
+
+ @staticmethod
+ def double_step_seq(step1, len1, step2, len2):
+ seq1 = torch.arange(0, step1 * len1, step1)
+ seq2 = torch.arange(0, step2 * len2, step2)
+ return (seq1[:, None] + seq2[None, :]).reshape(1, -1)
+
+
+class LocalWindowSelfAttention(BaseModule):
+ r""" Local-window Self Attention (LSA) module with relative position bias.
+
+ This module is the short-range self-attention module in the
+ Interlaced Sparse Self-Attention `_.
+
+ Args:
+ embed_dims (int): Number of input channels.
+ num_heads (int): Number of attention heads.
+ window_size (tuple[int] | int): The height and width of the window.
+ qkv_bias (bool, optional): If True, add a learnable bias to q, k, v.
+ Default: True.
+ qk_scale (float | None, optional): Override default qk scale of
+ head_dim ** -0.5 if set. Default: None.
+ attn_drop_rate (float, optional): Dropout ratio of attention weight.
+ Default: 0.0
+ proj_drop_rate (float, optional): Dropout ratio of output. Default: 0.
+ with_rpe (bool, optional): If True, use relative position bias.
+ Default: True.
+ with_pad_mask (bool, optional): If True, mask out the padded tokens in
+ the attention process. Default: False.
+ init_cfg (dict | None, optional): The Config for initialization.
+ Default: None.
+ """
+
+ def __init__(self,
+ embed_dims,
+ num_heads,
+ window_size,
+ qkv_bias=True,
+ qk_scale=None,
+ attn_drop_rate=0.,
+ proj_drop_rate=0.,
+ with_rpe=True,
+ with_pad_mask=False,
+ init_cfg=None):
+ super().__init__(init_cfg=init_cfg)
+ if isinstance(window_size, int):
+ window_size = (window_size, window_size)
+ self.window_size = window_size
+ self.with_pad_mask = with_pad_mask
+ self.attn = WindowMSA(
+ embed_dims=embed_dims,
+ num_heads=num_heads,
+ window_size=window_size,
+ qkv_bias=qkv_bias,
+ qk_scale=qk_scale,
+ attn_drop_rate=attn_drop_rate,
+ proj_drop_rate=proj_drop_rate,
+ with_rpe=with_rpe,
+ init_cfg=init_cfg)
+
+ def forward(self, x, H, W, **kwargs):
+ """Forward function."""
+ B, N, C = x.shape
+ x = x.view(B, H, W, C)
+ Wh, Ww = self.window_size
+
+ # center-pad the feature on H and W axes
+ pad_h = math.ceil(H / Wh) * Wh - H
+ pad_w = math.ceil(W / Ww) * Ww - W
+ x = pad(x, (0, 0, pad_w // 2, pad_w - pad_w // 2, pad_h // 2,
+ pad_h - pad_h // 2))
+
+ # permute
+ x = x.view(B, math.ceil(H / Wh), Wh, math.ceil(W / Ww), Ww, C)
+ x = x.permute(0, 1, 3, 2, 4, 5)
+ x = x.reshape(-1, Wh * Ww, C) # (B*num_window, Wh*Ww, C)
+
+ # attention
+ if self.with_pad_mask and pad_h > 0 and pad_w > 0:
+ pad_mask = x.new_zeros(1, H, W, 1)
+ pad_mask = pad(
+ pad_mask, [
+ 0, 0, pad_w // 2, pad_w - pad_w // 2, pad_h // 2,
+ pad_h - pad_h // 2
+ ],
+ value=-float('inf'))
+ pad_mask = pad_mask.view(1, math.ceil(H / Wh), Wh,
+ math.ceil(W / Ww), Ww, 1)
+ pad_mask = pad_mask.permute(1, 3, 0, 2, 4, 5)
+ pad_mask = pad_mask.reshape(-1, Wh * Ww)
+ pad_mask = pad_mask[:, None, :].expand([-1, Wh * Ww, -1])
+ out = self.attn(x, pad_mask, **kwargs)
+ else:
+ out = self.attn(x, **kwargs)
+
+ # reverse permutation
+ out = out.reshape(B, math.ceil(H / Wh), math.ceil(W / Ww), Wh, Ww, C)
+ out = out.permute(0, 1, 3, 2, 4, 5)
+ out = out.reshape(B, H + pad_h, W + pad_w, C)
+
+ # de-pad
+ out = out[:, pad_h // 2:H + pad_h // 2, pad_w // 2:W + pad_w // 2]
+ return out.reshape(B, N, C)
+
+
+class CrossFFN(BaseModule):
+ r"""FFN with Depthwise Conv of HRFormer.
+
+ Args:
+ in_features (int): The feature dimension.
+ hidden_features (int, optional): The hidden dimension of FFNs.
+ Defaults: The same as in_features.
+ act_cfg (dict, optional): Config of activation layer.
+ Default: dict(type='GELU').
+ dw_act_cfg (dict, optional): Config of activation layer appended
+ right after DW Conv. Default: dict(type='GELU').
+ norm_cfg (dict, optional): Config of norm layer.
+ Default: dict(type='SyncBN').
+ init_cfg (dict | list | None, optional): The init config.
+ Default: None.
+ """
+
+ def __init__(self,
+ in_features,
+ hidden_features=None,
+ out_features=None,
+ act_cfg=dict(type='GELU'),
+ dw_act_cfg=dict(type='GELU'),
+ norm_cfg=dict(type='SyncBN'),
+ init_cfg=None):
+ super().__init__(init_cfg=init_cfg)
+ out_features = out_features or in_features
+ hidden_features = hidden_features or in_features
+ self.fc1 = nn.Conv2d(in_features, hidden_features, kernel_size=1)
+ self.act1 = build_activation_layer(act_cfg)
+ self.norm1 = build_norm_layer(norm_cfg, hidden_features)[1]
+ self.dw3x3 = nn.Conv2d(
+ hidden_features,
+ hidden_features,
+ kernel_size=3,
+ stride=1,
+ groups=hidden_features,
+ padding=1)
+ self.act2 = build_activation_layer(dw_act_cfg)
+ self.norm2 = build_norm_layer(norm_cfg, hidden_features)[1]
+ self.fc2 = nn.Conv2d(hidden_features, out_features, kernel_size=1)
+ self.act3 = build_activation_layer(act_cfg)
+ self.norm3 = build_norm_layer(norm_cfg, out_features)[1]
+
+ # put the modules togather
+ self.layers = [
+ self.fc1, self.norm1, self.act1, self.dw3x3, self.norm2, self.act2,
+ self.fc2, self.norm3, self.act3
+ ]
+
+ def forward(self, x, H, W):
+ """Forward function."""
+ x = nlc_to_nchw(x, (H, W))
+ for layer in self.layers:
+ x = layer(x)
+ x = nchw_to_nlc(x)
+ return x
+
+
+class HRFormerBlock(BaseModule):
+ """High-Resolution Block for HRFormer.
+
+ Args:
+ in_features (int): The input dimension.
+ out_features (int): The output dimension.
+ num_heads (int): The number of head within each LSA.
+ window_size (int, optional): The window size for the LSA.
+ Default: 7
+ mlp_ratio (int, optional): The expansion ration of FFN.
+ Default: 4
+ act_cfg (dict, optional): Config of activation layer.
+ Default: dict(type='GELU').
+ norm_cfg (dict, optional): Config of norm layer.
+ Default: dict(type='SyncBN').
+ transformer_norm_cfg (dict, optional): Config of transformer norm
+ layer. Default: dict(type='LN', eps=1e-6).
+ init_cfg (dict | list | None, optional): The init config.
+ Default: None.
+ """
+
+ expansion = 1
+
+ def __init__(self,
+ in_features,
+ out_features,
+ num_heads,
+ window_size=7,
+ mlp_ratio=4.0,
+ drop_path=0.0,
+ act_cfg=dict(type='GELU'),
+ norm_cfg=dict(type='SyncBN'),
+ transformer_norm_cfg=dict(type='LN', eps=1e-6),
+ init_cfg=None,
+ **kwargs):
+ super(HRFormerBlock, self).__init__(init_cfg=init_cfg)
+ self.num_heads = num_heads
+ self.window_size = window_size
+ self.mlp_ratio = mlp_ratio
+
+ self.norm1 = build_norm_layer(transformer_norm_cfg, in_features)[1]
+ self.attn = LocalWindowSelfAttention(
+ in_features,
+ num_heads=num_heads,
+ window_size=window_size,
+ init_cfg=None,
+ **kwargs)
+
+ self.norm2 = build_norm_layer(transformer_norm_cfg, out_features)[1]
+ self.ffn = CrossFFN(
+ in_features=in_features,
+ hidden_features=int(in_features * mlp_ratio),
+ out_features=out_features,
+ norm_cfg=norm_cfg,
+ act_cfg=act_cfg,
+ dw_act_cfg=act_cfg,
+ init_cfg=None)
+
+ self.drop_path = build_drop_path(
+ drop_path) if drop_path > 0.0 else nn.Identity()
+
+ def forward(self, x):
+ """Forward function."""
+ B, C, H, W = x.size()
+ # Attention
+ x = x.view(B, C, -1).permute(0, 2, 1)
+ x = x + self.drop_path(self.attn(self.norm1(x), H, W))
+ # FFN
+ x = x + self.drop_path(self.ffn(self.norm2(x), H, W))
+ x = x.permute(0, 2, 1).view(B, C, H, W)
+ return x
+
+ def extra_repr(self):
+ """(Optional) Set the extra information about this module."""
+ return 'num_heads={}, window_size={}, mlp_ratio={}'.format(
+ self.num_heads, self.window_size, self.mlp_ratio)
+
+
+class HRFomerModule(HRModule):
+ """High-Resolution Module for HRFormer.
+
+ Args:
+ num_branches (int): The number of branches in the HRFormerModule.
+ block (nn.Module): The building block of HRFormer.
+ The block should be the HRFormerBlock.
+ num_blocks (tuple): The number of blocks in each branch.
+ The length must be equal to num_branches.
+ num_inchannels (tuple): The number of input channels in each branch.
+ The length must be equal to num_branches.
+ num_channels (tuple): The number of channels in each branch.
+ The length must be equal to num_branches.
+ num_heads (tuple): The number of heads within the LSAs.
+ num_window_sizes (tuple): The window size for the LSAs.
+ num_mlp_ratios (tuple): The expansion ratio for the FFNs.
+ drop_path (int, optional): The drop path rate of HRFomer.
+ Default: 0.0
+ multiscale_output (bool, optional): Whether to output multi-level
+ features produced by multiple branches. If False, only the first
+ level feature will be output. Default: True.
+ conv_cfg (dict, optional): Config of the conv layers.
+ Default: None.
+ norm_cfg (dict, optional): Config of the norm layers appended
+ right after conv. Default: dict(type='SyncBN', requires_grad=True)
+ transformer_norm_cfg (dict, optional): Config of the norm layers.
+ Default: dict(type='LN', eps=1e-6)
+ with_cp (bool): Use checkpoint or not. Using checkpoint will save some
+ memory while slowing down the training speed. Default: False
+ upsample_cfg(dict, optional): The config of upsample layers in fuse
+ layers. Default: dict(mode='bilinear', align_corners=False)
+ """
+
+ def __init__(self,
+ num_branches,
+ block,
+ num_blocks,
+ num_inchannels,
+ num_channels,
+ num_heads,
+ num_window_sizes,
+ num_mlp_ratios,
+ multiscale_output=True,
+ drop_paths=0.0,
+ with_rpe=True,
+ with_pad_mask=False,
+ conv_cfg=None,
+ norm_cfg=dict(type='SyncBN', requires_grad=True),
+ transformer_norm_cfg=dict(type='LN', eps=1e-6),
+ with_cp=False,
+ upsample_cfg=dict(mode='bilinear', align_corners=False)):
+
+ self.transformer_norm_cfg = transformer_norm_cfg
+ self.drop_paths = drop_paths
+ self.num_heads = num_heads
+ self.num_window_sizes = num_window_sizes
+ self.num_mlp_ratios = num_mlp_ratios
+ self.with_rpe = with_rpe
+ self.with_pad_mask = with_pad_mask
+
+ super().__init__(num_branches, block, num_blocks, num_inchannels,
+ num_channels, multiscale_output, with_cp, conv_cfg,
+ norm_cfg, upsample_cfg)
+
+ def _make_one_branch(self,
+ branch_index,
+ block,
+ num_blocks,
+ num_channels,
+ stride=1):
+ """Build one branch."""
+ # HRFormerBlock does not support down sample layer yet.
+ assert stride == 1 and self.in_channels[branch_index] == num_channels[
+ branch_index]
+ layers = []
+ layers.append(
+ block(
+ self.in_channels[branch_index],
+ num_channels[branch_index],
+ num_heads=self.num_heads[branch_index],
+ window_size=self.num_window_sizes[branch_index],
+ mlp_ratio=self.num_mlp_ratios[branch_index],
+ drop_path=self.drop_paths[0],
+ norm_cfg=self.norm_cfg,
+ transformer_norm_cfg=self.transformer_norm_cfg,
+ init_cfg=None,
+ with_rpe=self.with_rpe,
+ with_pad_mask=self.with_pad_mask))
+
+ self.in_channels[
+ branch_index] = self.in_channels[branch_index] * block.expansion
+ for i in range(1, num_blocks[branch_index]):
+ layers.append(
+ block(
+ self.in_channels[branch_index],
+ num_channels[branch_index],
+ num_heads=self.num_heads[branch_index],
+ window_size=self.num_window_sizes[branch_index],
+ mlp_ratio=self.num_mlp_ratios[branch_index],
+ drop_path=self.drop_paths[i],
+ norm_cfg=self.norm_cfg,
+ transformer_norm_cfg=self.transformer_norm_cfg,
+ init_cfg=None,
+ with_rpe=self.with_rpe,
+ with_pad_mask=self.with_pad_mask))
+ return nn.Sequential(*layers)
+
+ def _make_fuse_layers(self):
+ """Build fuse layers."""
+ if self.num_branches == 1:
+ return None
+ num_branches = self.num_branches
+ num_inchannels = self.in_channels
+ fuse_layers = []
+ for i in range(num_branches if self.multiscale_output else 1):
+ fuse_layer = []
+ for j in range(num_branches):
+ if j > i:
+ fuse_layer.append(
+ nn.Sequential(
+ build_conv_layer(
+ self.conv_cfg,
+ num_inchannels[j],
+ num_inchannels[i],
+ kernel_size=1,
+ stride=1,
+ bias=False),
+ build_norm_layer(self.norm_cfg,
+ num_inchannels[i])[1],
+ nn.Upsample(
+ scale_factor=2**(j - i),
+ mode=self.upsample_cfg['mode'],
+ align_corners=self.
+ upsample_cfg['align_corners'])))
+ elif j == i:
+ fuse_layer.append(None)
+ else:
+ conv3x3s = []
+ for k in range(i - j):
+ if k == i - j - 1:
+ num_outchannels_conv3x3 = num_inchannels[i]
+ with_out_act = False
+ else:
+ num_outchannels_conv3x3 = num_inchannels[j]
+ with_out_act = True
+ sub_modules = [
+ build_conv_layer(
+ self.conv_cfg,
+ num_inchannels[j],
+ num_inchannels[j],
+ kernel_size=3,
+ stride=2,
+ padding=1,
+ groups=num_inchannels[j],
+ bias=False,
+ ),
+ build_norm_layer(self.norm_cfg,
+ num_inchannels[j])[1],
+ build_conv_layer(
+ self.conv_cfg,
+ num_inchannels[j],
+ num_outchannels_conv3x3,
+ kernel_size=1,
+ stride=1,
+ bias=False,
+ ),
+ build_norm_layer(self.norm_cfg,
+ num_outchannels_conv3x3)[1]
+ ]
+ if with_out_act:
+ sub_modules.append(nn.ReLU(False))
+ conv3x3s.append(nn.Sequential(*sub_modules))
+ fuse_layer.append(nn.Sequential(*conv3x3s))
+ fuse_layers.append(nn.ModuleList(fuse_layer))
+
+ return nn.ModuleList(fuse_layers)
+
+ def get_num_inchannels(self):
+ """Return the number of input channels."""
+ return self.in_channels
+
+
+@BACKBONES.register_module()
+class HRFormer(HRNet):
+ """HRFormer backbone.
+
+ This backbone is the implementation of `HRFormer: High-Resolution
+ Transformer for Dense Prediction `_.
+
+ Args:
+ extra (dict): Detailed configuration for each stage of HRNet.
+ There must be 4 stages, the configuration for each stage must have
+ 5 keys:
+
+ - num_modules (int): The number of HRModule in this stage.
+ - num_branches (int): The number of branches in the HRModule.
+ - block (str): The type of block.
+ - num_blocks (tuple): The number of blocks in each branch.
+ The length must be equal to num_branches.
+ - num_channels (tuple): The number of channels in each branch.
+ The length must be equal to num_branches.
+ in_channels (int): Number of input image channels. Normally 3.
+ conv_cfg (dict): Dictionary to construct and config conv layer.
+ Default: None.
+ norm_cfg (dict): Config of norm layer.
+ Use `SyncBN` by default.
+ transformer_norm_cfg (dict): Config of transformer norm layer.
+ Use `LN` by default.
+ norm_eval (bool): Whether to set norm layers to eval mode, namely,
+ freeze running stats (mean and var). Note: Effect on Batch Norm
+ and its variants only. Default: False.
+ zero_init_residual (bool): Whether to use zero init for last norm layer
+ in resblocks to let them behave as identity. Default: False.
+ frozen_stages (int): Stages to be frozen (stop grad and set eval mode).
+ -1 means not freezing any parameters. Default: -1.
+ Example:
+ >>> from mmpose.models import HRFormer
+ >>> import torch
+ >>> extra = dict(
+ >>> stage1=dict(
+ >>> num_modules=1,
+ >>> num_branches=1,
+ >>> block='BOTTLENECK',
+ >>> num_blocks=(2, ),
+ >>> num_channels=(64, )),
+ >>> stage2=dict(
+ >>> num_modules=1,
+ >>> num_branches=2,
+ >>> block='HRFORMER',
+ >>> window_sizes=(7, 7),
+ >>> num_heads=(1, 2),
+ >>> mlp_ratios=(4, 4),
+ >>> num_blocks=(2, 2),
+ >>> num_channels=(32, 64)),
+ >>> stage3=dict(
+ >>> num_modules=4,
+ >>> num_branches=3,
+ >>> block='HRFORMER',
+ >>> window_sizes=(7, 7, 7),
+ >>> num_heads=(1, 2, 4),
+ >>> mlp_ratios=(4, 4, 4),
+ >>> num_blocks=(2, 2, 2),
+ >>> num_channels=(32, 64, 128)),
+ >>> stage4=dict(
+ >>> num_modules=2,
+ >>> num_branches=4,
+ >>> block='HRFORMER',
+ >>> window_sizes=(7, 7, 7, 7),
+ >>> num_heads=(1, 2, 4, 8),
+ >>> mlp_ratios=(4, 4, 4, 4),
+ >>> num_blocks=(2, 2, 2, 2),
+ >>> num_channels=(32, 64, 128, 256)))
+ >>> self = HRFormer(extra, in_channels=1)
+ >>> self.eval()
+ >>> inputs = torch.rand(1, 1, 32, 32)
+ >>> level_outputs = self.forward(inputs)
+ >>> for level_out in level_outputs:
+ ... print(tuple(level_out.shape))
+ (1, 32, 8, 8)
+ (1, 64, 4, 4)
+ (1, 128, 2, 2)
+ (1, 256, 1, 1)
+ """
+
+ blocks_dict = {'BOTTLENECK': Bottleneck, 'HRFORMERBLOCK': HRFormerBlock}
+
+ def __init__(self,
+ extra,
+ in_channels=3,
+ conv_cfg=None,
+ norm_cfg=dict(type='BN', requires_grad=True),
+ transformer_norm_cfg=dict(type='LN', eps=1e-6),
+ norm_eval=False,
+ with_cp=False,
+ zero_init_residual=False,
+ frozen_stages=-1):
+
+ # stochastic depth
+ depths = [
+ extra[stage]['num_blocks'][0] * extra[stage]['num_modules']
+ for stage in ['stage2', 'stage3', 'stage4']
+ ]
+ depth_s2, depth_s3, _ = depths
+ drop_path_rate = extra['drop_path_rate']
+ dpr = [
+ x.item() for x in torch.linspace(0, drop_path_rate, sum(depths))
+ ]
+ extra['stage2']['drop_path_rates'] = dpr[0:depth_s2]
+ extra['stage3']['drop_path_rates'] = dpr[depth_s2:depth_s2 + depth_s3]
+ extra['stage4']['drop_path_rates'] = dpr[depth_s2 + depth_s3:]
+
+ # HRFormer use bilinear upsample as default
+ upsample_cfg = extra.get('upsample', {
+ 'mode': 'bilinear',
+ 'align_corners': False
+ })
+ extra['upsample'] = upsample_cfg
+ self.transformer_norm_cfg = transformer_norm_cfg
+ self.with_rpe = extra.get('with_rpe', True)
+ self.with_pad_mask = extra.get('with_pad_mask', False)
+
+ super().__init__(extra, in_channels, conv_cfg, norm_cfg, norm_eval,
+ with_cp, zero_init_residual, frozen_stages)
+
+ def _make_stage(self,
+ layer_config,
+ num_inchannels,
+ multiscale_output=True):
+ """Make each stage."""
+ num_modules = layer_config['num_modules']
+ num_branches = layer_config['num_branches']
+ num_blocks = layer_config['num_blocks']
+ num_channels = layer_config['num_channels']
+ block = self.blocks_dict[layer_config['block']]
+ num_heads = layer_config['num_heads']
+ num_window_sizes = layer_config['window_sizes']
+ num_mlp_ratios = layer_config['mlp_ratios']
+ drop_path_rates = layer_config['drop_path_rates']
+
+ modules = []
+ for i in range(num_modules):
+ # multiscale_output is only used at the last module
+ if not multiscale_output and i == num_modules - 1:
+ reset_multiscale_output = False
+ else:
+ reset_multiscale_output = True
+
+ modules.append(
+ HRFomerModule(
+ num_branches,
+ block,
+ num_blocks,
+ num_inchannels,
+ num_channels,
+ num_heads,
+ num_window_sizes,
+ num_mlp_ratios,
+ reset_multiscale_output,
+ drop_paths=drop_path_rates[num_blocks[0] *
+ i:num_blocks[0] * (i + 1)],
+ with_rpe=self.with_rpe,
+ with_pad_mask=self.with_pad_mask,
+ conv_cfg=self.conv_cfg,
+ norm_cfg=self.norm_cfg,
+ transformer_norm_cfg=self.transformer_norm_cfg,
+ with_cp=self.with_cp,
+ upsample_cfg=self.upsample_cfg))
+ num_inchannels = modules[-1].get_num_inchannels()
+
+ return nn.Sequential(*modules), num_inchannels
diff --git a/grounded-sam-osx/transformer_utils/mmpose/models/backbones/hrnet.py b/grounded-sam-osx/transformer_utils/mmpose/models/backbones/hrnet.py
new file mode 100644
index 0000000000000000000000000000000000000000..87dc8cef555b5e8d78fcc69293047b0cbe2ea8a6
--- /dev/null
+++ b/grounded-sam-osx/transformer_utils/mmpose/models/backbones/hrnet.py
@@ -0,0 +1,604 @@
+# Copyright (c) OpenMMLab. All rights reserved.
+import copy
+
+import torch.nn as nn
+from mmcv.cnn import (build_conv_layer, build_norm_layer, constant_init,
+ normal_init)
+from torch.nn.modules.batchnorm import _BatchNorm
+
+from mmpose.utils import get_root_logger
+from ..builder import BACKBONES
+from .resnet import BasicBlock, Bottleneck, get_expansion
+from .utils import load_checkpoint
+
+
+class HRModule(nn.Module):
+ """High-Resolution Module for HRNet.
+
+ In this module, every branch has 4 BasicBlocks/Bottlenecks. Fusion/Exchange
+ is in this module.
+ """
+
+ def __init__(self,
+ num_branches,
+ blocks,
+ num_blocks,
+ in_channels,
+ num_channels,
+ multiscale_output=False,
+ with_cp=False,
+ conv_cfg=None,
+ norm_cfg=dict(type='BN'),
+ upsample_cfg=dict(mode='nearest', align_corners=None)):
+
+ # Protect mutable default arguments
+ norm_cfg = copy.deepcopy(norm_cfg)
+ super().__init__()
+ self._check_branches(num_branches, num_blocks, in_channels,
+ num_channels)
+
+ self.in_channels = in_channels
+ self.num_branches = num_branches
+
+ self.multiscale_output = multiscale_output
+ self.norm_cfg = norm_cfg
+ self.conv_cfg = conv_cfg
+ self.upsample_cfg = upsample_cfg
+ self.with_cp = with_cp
+ self.branches = self._make_branches(num_branches, blocks, num_blocks,
+ num_channels)
+ self.fuse_layers = self._make_fuse_layers()
+ self.relu = nn.ReLU(inplace=True)
+
+ @staticmethod
+ def _check_branches(num_branches, num_blocks, in_channels, num_channels):
+ """Check input to avoid ValueError."""
+ if num_branches != len(num_blocks):
+ error_msg = f'NUM_BRANCHES({num_branches}) ' \
+ f'!= NUM_BLOCKS({len(num_blocks)})'
+ raise ValueError(error_msg)
+
+ if num_branches != len(num_channels):
+ error_msg = f'NUM_BRANCHES({num_branches}) ' \
+ f'!= NUM_CHANNELS({len(num_channels)})'
+ raise ValueError(error_msg)
+
+ if num_branches != len(in_channels):
+ error_msg = f'NUM_BRANCHES({num_branches}) ' \
+ f'!= NUM_INCHANNELS({len(in_channels)})'
+ raise ValueError(error_msg)
+
+ def _make_one_branch(self,
+ branch_index,
+ block,
+ num_blocks,
+ num_channels,
+ stride=1):
+ """Make one branch."""
+ downsample = None
+ if stride != 1 or \
+ self.in_channels[branch_index] != \
+ num_channels[branch_index] * get_expansion(block):
+ downsample = nn.Sequential(
+ build_conv_layer(
+ self.conv_cfg,
+ self.in_channels[branch_index],
+ num_channels[branch_index] * get_expansion(block),
+ kernel_size=1,
+ stride=stride,
+ bias=False),
+ build_norm_layer(
+ self.norm_cfg,
+ num_channels[branch_index] * get_expansion(block))[1])
+
+ layers = []
+ layers.append(
+ block(
+ self.in_channels[branch_index],
+ num_channels[branch_index] * get_expansion(block),
+ stride=stride,
+ downsample=downsample,
+ with_cp=self.with_cp,
+ norm_cfg=self.norm_cfg,
+ conv_cfg=self.conv_cfg))
+ self.in_channels[branch_index] = \
+ num_channels[branch_index] * get_expansion(block)
+ for _ in range(1, num_blocks[branch_index]):
+ layers.append(
+ block(
+ self.in_channels[branch_index],
+ num_channels[branch_index] * get_expansion(block),
+ with_cp=self.with_cp,
+ norm_cfg=self.norm_cfg,
+ conv_cfg=self.conv_cfg))
+
+ return nn.Sequential(*layers)
+
+ def _make_branches(self, num_branches, block, num_blocks, num_channels):
+ """Make branches."""
+ branches = []
+
+ for i in range(num_branches):
+ branches.append(
+ self._make_one_branch(i, block, num_blocks, num_channels))
+
+ return nn.ModuleList(branches)
+
+ def _make_fuse_layers(self):
+ """Make fuse layer."""
+ if self.num_branches == 1:
+ return None
+
+ num_branches = self.num_branches
+ in_channels = self.in_channels
+ fuse_layers = []
+ num_out_branches = num_branches if self.multiscale_output else 1
+
+ for i in range(num_out_branches):
+ fuse_layer = []
+ for j in range(num_branches):
+ if j > i:
+ fuse_layer.append(
+ nn.Sequential(
+ build_conv_layer(
+ self.conv_cfg,
+ in_channels[j],
+ in_channels[i],
+ kernel_size=1,
+ stride=1,
+ padding=0,
+ bias=False),
+ build_norm_layer(self.norm_cfg, in_channels[i])[1],
+ nn.Upsample(
+ scale_factor=2**(j - i),
+ mode=self.upsample_cfg['mode'],
+ align_corners=self.
+ upsample_cfg['align_corners'])))
+ elif j == i:
+ fuse_layer.append(None)
+ else:
+ conv_downsamples = []
+ for k in range(i - j):
+ if k == i - j - 1:
+ conv_downsamples.append(
+ nn.Sequential(
+ build_conv_layer(
+ self.conv_cfg,
+ in_channels[j],
+ in_channels[i],
+ kernel_size=3,
+ stride=2,
+ padding=1,
+ bias=False),
+ build_norm_layer(self.norm_cfg,
+ in_channels[i])[1]))
+ else:
+ conv_downsamples.append(
+ nn.Sequential(
+ build_conv_layer(
+ self.conv_cfg,
+ in_channels[j],
+ in_channels[j],
+ kernel_size=3,
+ stride=2,
+ padding=1,
+ bias=False),
+ build_norm_layer(self.norm_cfg,
+ in_channels[j])[1],
+ nn.ReLU(inplace=True)))
+ fuse_layer.append(nn.Sequential(*conv_downsamples))
+ fuse_layers.append(nn.ModuleList(fuse_layer))
+
+ return nn.ModuleList(fuse_layers)
+
+ def forward(self, x):
+ """Forward function."""
+ if self.num_branches == 1:
+ return [self.branches[0](x[0])]
+
+ for i in range(self.num_branches):
+ x[i] = self.branches[i](x[i])
+
+ x_fuse = []
+ for i in range(len(self.fuse_layers)):
+ y = 0
+ for j in range(self.num_branches):
+ if i == j:
+ y += x[j]
+ else:
+ y += self.fuse_layers[i][j](x[j])
+ x_fuse.append(self.relu(y))
+ return x_fuse
+
+
+@BACKBONES.register_module()
+class HRNet(nn.Module):
+ """HRNet backbone.
+
+ `High-Resolution Representations for Labeling Pixels and Regions
+ `__
+
+ Args:
+ extra (dict): detailed configuration for each stage of HRNet.
+ in_channels (int): Number of input image channels. Default: 3.
+ conv_cfg (dict): dictionary to construct and config conv layer.
+ norm_cfg (dict): dictionary to construct and config norm layer.
+ norm_eval (bool): Whether to set norm layers to eval mode, namely,
+ freeze running stats (mean and var). Note: Effect on Batch Norm
+ and its variants only. Default: False
+ with_cp (bool): Use checkpoint or not. Using checkpoint will save some
+ memory while slowing down the training speed.
+ zero_init_residual (bool): whether to use zero init for last norm layer
+ in resblocks to let them behave as identity.
+ frozen_stages (int): Stages to be frozen (stop grad and set eval mode).
+ -1 means not freezing any parameters. Default: -1.
+
+ Example:
+ >>> from mmpose.models import HRNet
+ >>> import torch
+ >>> extra = dict(
+ >>> stage1=dict(
+ >>> num_modules=1,
+ >>> num_branches=1,
+ >>> block='BOTTLENECK',
+ >>> num_blocks=(4, ),
+ >>> num_channels=(64, )),
+ >>> stage2=dict(
+ >>> num_modules=1,
+ >>> num_branches=2,
+ >>> block='BASIC',
+ >>> num_blocks=(4, 4),
+ >>> num_channels=(32, 64)),
+ >>> stage3=dict(
+ >>> num_modules=4,
+ >>> num_branches=3,
+ >>> block='BASIC',
+ >>> num_blocks=(4, 4, 4),
+ >>> num_channels=(32, 64, 128)),
+ >>> stage4=dict(
+ >>> num_modules=3,
+ >>> num_branches=4,
+ >>> block='BASIC',
+ >>> num_blocks=(4, 4, 4, 4),
+ >>> num_channels=(32, 64, 128, 256)))
+ >>> self = HRNet(extra, in_channels=1)
+ >>> self.eval()
+ >>> inputs = torch.rand(1, 1, 32, 32)
+ >>> level_outputs = self.forward(inputs)
+ >>> for level_out in level_outputs:
+ ... print(tuple(level_out.shape))
+ (1, 32, 8, 8)
+ """
+
+ blocks_dict = {'BASIC': BasicBlock, 'BOTTLENECK': Bottleneck}
+
+ def __init__(self,
+ extra,
+ in_channels=3,
+ conv_cfg=None,
+ norm_cfg=dict(type='BN'),
+ norm_eval=False,
+ with_cp=False,
+ zero_init_residual=False,
+ frozen_stages=-1):
+ # Protect mutable default arguments
+ norm_cfg = copy.deepcopy(norm_cfg)
+ super().__init__()
+ self.extra = extra
+ self.conv_cfg = conv_cfg
+ self.norm_cfg = norm_cfg
+ self.norm_eval = norm_eval
+ self.with_cp = with_cp
+ self.zero_init_residual = zero_init_residual
+ self.frozen_stages = frozen_stages
+
+ # stem net
+ self.norm1_name, norm1 = build_norm_layer(self.norm_cfg, 64, postfix=1)
+ self.norm2_name, norm2 = build_norm_layer(self.norm_cfg, 64, postfix=2)
+
+ self.conv1 = build_conv_layer(
+ self.conv_cfg,
+ in_channels,
+ 64,
+ kernel_size=3,
+ stride=2,
+ padding=1,
+ bias=False)
+
+ self.add_module(self.norm1_name, norm1)
+ self.conv2 = build_conv_layer(
+ self.conv_cfg,
+ 64,
+ 64,
+ kernel_size=3,
+ stride=2,
+ padding=1,
+ bias=False)
+
+ self.add_module(self.norm2_name, norm2)
+ self.relu = nn.ReLU(inplace=True)
+
+ self.upsample_cfg = self.extra.get('upsample', {
+ 'mode': 'nearest',
+ 'align_corners': None
+ })
+
+ # stage 1
+ self.stage1_cfg = self.extra['stage1']
+ num_channels = self.stage1_cfg['num_channels'][0]
+ block_type = self.stage1_cfg['block']
+ num_blocks = self.stage1_cfg['num_blocks'][0]
+
+ block = self.blocks_dict[block_type]
+ stage1_out_channels = num_channels * get_expansion(block)
+ self.layer1 = self._make_layer(block, 64, stage1_out_channels,
+ num_blocks)
+
+ # stage 2
+ self.stage2_cfg = self.extra['stage2']
+ num_channels = self.stage2_cfg['num_channels']
+ block_type = self.stage2_cfg['block']
+
+ block = self.blocks_dict[block_type]
+ num_channels = [
+ channel * get_expansion(block) for channel in num_channels
+ ]
+ self.transition1 = self._make_transition_layer([stage1_out_channels],
+ num_channels)
+ self.stage2, pre_stage_channels = self._make_stage(
+ self.stage2_cfg, num_channels)
+
+ # stage 3
+ self.stage3_cfg = self.extra['stage3']
+ num_channels = self.stage3_cfg['num_channels']
+ block_type = self.stage3_cfg['block']
+
+ block = self.blocks_dict[block_type]
+ num_channels = [
+ channel * get_expansion(block) for channel in num_channels
+ ]
+ self.transition2 = self._make_transition_layer(pre_stage_channels,
+ num_channels)
+ self.stage3, pre_stage_channels = self._make_stage(
+ self.stage3_cfg, num_channels)
+
+ # stage 4
+ self.stage4_cfg = self.extra['stage4']
+ num_channels = self.stage4_cfg['num_channels']
+ block_type = self.stage4_cfg['block']
+
+ block = self.blocks_dict[block_type]
+ num_channels = [
+ channel * get_expansion(block) for channel in num_channels
+ ]
+ self.transition3 = self._make_transition_layer(pre_stage_channels,
+ num_channels)
+
+ self.stage4, pre_stage_channels = self._make_stage(
+ self.stage4_cfg,
+ num_channels,
+ multiscale_output=self.stage4_cfg.get('multiscale_output', False))
+
+ self._freeze_stages()
+
+ @property
+ def norm1(self):
+ """nn.Module: the normalization layer named "norm1" """
+ return getattr(self, self.norm1_name)
+
+ @property
+ def norm2(self):
+ """nn.Module: the normalization layer named "norm2" """
+ return getattr(self, self.norm2_name)
+
+ def _make_transition_layer(self, num_channels_pre_layer,
+ num_channels_cur_layer):
+ """Make transition layer."""
+ num_branches_cur = len(num_channels_cur_layer)
+ num_branches_pre = len(num_channels_pre_layer)
+
+ transition_layers = []
+ for i in range(num_branches_cur):
+ if i < num_branches_pre:
+ if num_channels_cur_layer[i] != num_channels_pre_layer[i]:
+ transition_layers.append(
+ nn.Sequential(
+ build_conv_layer(
+ self.conv_cfg,
+ num_channels_pre_layer[i],
+ num_channels_cur_layer[i],
+ kernel_size=3,
+ stride=1,
+ padding=1,
+ bias=False),
+ build_norm_layer(self.norm_cfg,
+ num_channels_cur_layer[i])[1],
+ nn.ReLU(inplace=True)))
+ else:
+ transition_layers.append(None)
+ else:
+ conv_downsamples = []
+ for j in range(i + 1 - num_branches_pre):
+ in_channels = num_channels_pre_layer[-1]
+ out_channels = num_channels_cur_layer[i] \
+ if j == i - num_branches_pre else in_channels
+ conv_downsamples.append(
+ nn.Sequential(
+ build_conv_layer(
+ self.conv_cfg,
+ in_channels,
+ out_channels,
+ kernel_size=3,
+ stride=2,
+ padding=1,
+ bias=False),
+ build_norm_layer(self.norm_cfg, out_channels)[1],
+ nn.ReLU(inplace=True)))
+ transition_layers.append(nn.Sequential(*conv_downsamples))
+
+ return nn.ModuleList(transition_layers)
+
+ def _make_layer(self, block, in_channels, out_channels, blocks, stride=1):
+ """Make layer."""
+ downsample = None
+ if stride != 1 or in_channels != out_channels:
+ downsample = nn.Sequential(
+ build_conv_layer(
+ self.conv_cfg,
+ in_channels,
+ out_channels,
+ kernel_size=1,
+ stride=stride,
+ bias=False),
+ build_norm_layer(self.norm_cfg, out_channels)[1])
+
+ layers = []
+ layers.append(
+ block(
+ in_channels,
+ out_channels,
+ stride=stride,
+ downsample=downsample,
+ with_cp=self.with_cp,
+ norm_cfg=self.norm_cfg,
+ conv_cfg=self.conv_cfg))
+ for _ in range(1, blocks):
+ layers.append(
+ block(
+ out_channels,
+ out_channels,
+ with_cp=self.with_cp,
+ norm_cfg=self.norm_cfg,
+ conv_cfg=self.conv_cfg))
+
+ return nn.Sequential(*layers)
+
+ def _make_stage(self, layer_config, in_channels, multiscale_output=True):
+ """Make stage."""
+ num_modules = layer_config['num_modules']
+ num_branches = layer_config['num_branches']
+ num_blocks = layer_config['num_blocks']
+ num_channels = layer_config['num_channels']
+ block = self.blocks_dict[layer_config['block']]
+
+ hr_modules = []
+ for i in range(num_modules):
+ # multi_scale_output is only used for the last module
+ if not multiscale_output and i == num_modules - 1:
+ reset_multiscale_output = False
+ else:
+ reset_multiscale_output = True
+
+ hr_modules.append(
+ HRModule(
+ num_branches,
+ block,
+ num_blocks,
+ in_channels,
+ num_channels,
+ reset_multiscale_output,
+ with_cp=self.with_cp,
+ norm_cfg=self.norm_cfg,
+ conv_cfg=self.conv_cfg,
+ upsample_cfg=self.upsample_cfg))
+
+ in_channels = hr_modules[-1].in_channels
+
+ return nn.Sequential(*hr_modules), in_channels
+
+ def _freeze_stages(self):
+ """Freeze parameters."""
+ if self.frozen_stages >= 0:
+ self.norm1.eval()
+ self.norm2.eval()
+
+ for m in [self.conv1, self.norm1, self.conv2, self.norm2]:
+ for param in m.parameters():
+ param.requires_grad = False
+
+ for i in range(1, self.frozen_stages + 1):
+ if i == 1:
+ m = getattr(self, 'layer1')
+ else:
+ m = getattr(self, f'stage{i}')
+
+ m.eval()
+ for param in m.parameters():
+ param.requires_grad = False
+
+ if i < 4:
+ m = getattr(self, f'transition{i}')
+ m.eval()
+ for param in m.parameters():
+ param.requires_grad = False
+
+ def init_weights(self, pretrained=None):
+ """Initialize the weights in backbone.
+
+ Args:
+ pretrained (str, optional): Path to pre-trained weights.
+ Defaults to None.
+ """
+ if isinstance(pretrained, str):
+ logger = get_root_logger()
+ load_checkpoint(self, pretrained, strict=False, logger=logger)
+ elif pretrained is None:
+ for m in self.modules():
+ if isinstance(m, nn.Conv2d):
+ normal_init(m, std=0.001)
+ elif isinstance(m, (_BatchNorm, nn.GroupNorm)):
+ constant_init(m, 1)
+
+ if self.zero_init_residual:
+ for m in self.modules():
+ if isinstance(m, Bottleneck):
+ constant_init(m.norm3, 0)
+ elif isinstance(m, BasicBlock):
+ constant_init(m.norm2, 0)
+ else:
+ raise TypeError('pretrained must be a str or None')
+
+ def forward(self, x):
+ """Forward function."""
+ x = self.conv1(x)
+ x = self.norm1(x)
+ x = self.relu(x)
+ x = self.conv2(x)
+ x = self.norm2(x)
+ x = self.relu(x)
+ x = self.layer1(x)
+
+ x_list = []
+ for i in range(self.stage2_cfg['num_branches']):
+ if self.transition1[i] is not None:
+ x_list.append(self.transition1[i](x))
+ else:
+ x_list.append(x)
+ y_list = self.stage2(x_list)
+
+ x_list = []
+ for i in range(self.stage3_cfg['num_branches']):
+ if self.transition2[i] is not None:
+ x_list.append(self.transition2[i](y_list[-1]))
+ else:
+ x_list.append(y_list[i])
+ y_list = self.stage3(x_list)
+
+ x_list = []
+ for i in range(self.stage4_cfg['num_branches']):
+ if self.transition3[i] is not None:
+ x_list.append(self.transition3[i](y_list[-1]))
+ else:
+ x_list.append(y_list[i])
+ y_list = self.stage4(x_list)
+
+ return y_list
+
+ def train(self, mode=True):
+ """Convert the model into training mode."""
+ super().train(mode)
+ self._freeze_stages()
+ if mode and self.norm_eval:
+ for m in self.modules():
+ if isinstance(m, _BatchNorm):
+ m.eval()
diff --git a/grounded-sam-osx/transformer_utils/mmpose/models/backbones/hrt.py b/grounded-sam-osx/transformer_utils/mmpose/models/backbones/hrt.py
new file mode 100644
index 0000000000000000000000000000000000000000..67be3d4429d03360698701b7cd6e67e7c7a0b4ad
--- /dev/null
+++ b/grounded-sam-osx/transformer_utils/mmpose/models/backbones/hrt.py
@@ -0,0 +1,676 @@
+# --------------------------------------------------------
+# High Resolution Transformer
+# Copyright (c) 2021 Microsoft
+# Licensed under The MIT License [see LICENSE for details]
+# Written by Rao Fu, RainbowSecret
+# --------------------------------------------------------
+
+import pdb
+import torch
+import torch.nn as nn
+from mmcv.cnn import (
+ build_conv_layer,
+ build_norm_layer,
+ constant_init,
+ kaiming_init,
+ normal_init,
+)
+# from mmcv.runner import load_checkpoint
+from .hrt_checkpoint import load_checkpoint
+from mmcv.runner.checkpoint import load_state_dict
+from mmcv.utils.parrots_wrapper import _BatchNorm
+
+from mmpose.models.utils.ops import resize
+from mmpose.utils import get_root_logger
+from ..builder import BACKBONES
+from .modules.bottleneck_block import Bottleneck
+from .modules.transformer_block import GeneralTransformerBlock
+
+
+class HighResolutionTransformerModule(nn.Module):
+ def __init__(
+ self,
+ num_branches,
+ blocks,
+ num_blocks,
+ in_channels,
+ num_channels,
+ multiscale_output,
+ with_cp=False,
+ conv_cfg=None,
+ norm_cfg=dict(type="BN", requires_grad=True),
+ num_heads=None,
+ num_window_sizes=None,
+ num_mlp_ratios=None,
+ drop_paths=0.0,
+ ):
+ super(HighResolutionTransformerModule, self).__init__()
+ self._check_branches(num_branches, num_blocks, in_channels, num_channels)
+
+ self.in_channels = in_channels
+ self.num_branches = num_branches
+
+ self.multiscale_output = multiscale_output
+ self.norm_cfg = norm_cfg
+ self.conv_cfg = conv_cfg
+ self.with_cp = with_cp
+ self.branches = self._make_branches(
+ num_branches,
+ blocks,
+ num_blocks,
+ num_channels,
+ num_heads,
+ num_window_sizes,
+ num_mlp_ratios,
+ drop_paths,
+ )
+ self.fuse_layers = self._make_fuse_layers()
+ self.relu = nn.ReLU(inplace=True)
+
+ # MHSA parameters
+ self.num_heads = num_heads
+ self.num_window_sizes = num_window_sizes
+ self.num_mlp_ratios = num_mlp_ratios
+
+ def _check_branches(self, num_branches, num_blocks, in_channels, num_channels):
+ logger = get_root_logger()
+ if num_branches != len(num_blocks):
+ error_msg = "NUM_BRANCHES({}) <> NUM_BLOCKS({})".format(
+ num_branches, len(num_blocks)
+ )
+ logger.error(error_msg)
+ raise ValueError(error_msg)
+
+ if num_branches != len(num_channels):
+ error_msg = "NUM_BRANCHES({}) <> NUM_CHANNELS({})".format(
+ num_branches, len(num_channels)
+ )
+ logger.error(error_msg)
+ raise ValueError(error_msg)
+
+ if num_branches != len(in_channels):
+ error_msg = "NUM_BRANCHES({}) <> IN_CHANNELS({})".format(
+ num_branches, len(in_channels)
+ )
+ logger.error(error_msg)
+ raise ValueError(error_msg)
+
+ def _make_one_branch(
+ self,
+ branch_index,
+ block,
+ num_blocks,
+ num_channels,
+ num_heads,
+ num_window_sizes,
+ num_mlp_ratios,
+ drop_paths,
+ stride=1,
+ ):
+ """Make one branch."""
+ downsample = None
+ if (
+ stride != 1
+ or self.in_channels[branch_index]
+ != num_channels[branch_index] * block.expansion
+ ):
+ downsample = nn.Sequential(
+ build_conv_layer(
+ self.conv_cfg,
+ self.in_channels[branch_index],
+ num_channels[branch_index] * block.expansion,
+ kernel_size=1,
+ stride=stride,
+ bias=False,
+ ),
+ build_norm_layer(
+ self.norm_cfg, num_channels[branch_index] * block.expansion
+ )[1],
+ )
+
+ layers = []
+
+ layers.append(
+ block(
+ self.in_channels[branch_index],
+ num_channels[branch_index],
+ num_heads=num_heads[branch_index],
+ window_size=num_window_sizes[branch_index],
+ mlp_ratio=num_mlp_ratios[branch_index],
+ drop_path=drop_paths[0],
+ norm_cfg=self.norm_cfg,
+ conv_cfg=self.conv_cfg,
+ )
+ )
+ self.in_channels[branch_index] = num_channels[branch_index] * block.expansion
+ for i in range(1, num_blocks[branch_index]):
+ layers.append(
+ block(
+ self.in_channels[branch_index],
+ num_channels[branch_index],
+ num_heads=num_heads[branch_index],
+ window_size=num_window_sizes[branch_index],
+ mlp_ratio=num_mlp_ratios[branch_index],
+ drop_path=drop_paths[i],
+ norm_cfg=self.norm_cfg,
+ conv_cfg=self.conv_cfg,
+ )
+ )
+
+ return nn.Sequential(*layers)
+
+ def _make_branches(
+ self,
+ num_branches,
+ block,
+ num_blocks,
+ num_channels,
+ num_heads,
+ num_window_sizes,
+ num_mlp_ratios,
+ drop_paths,
+ ):
+ """Make branches."""
+ branches = []
+
+ for i in range(num_branches):
+ branches.append(
+ self._make_one_branch(
+ i,
+ block,
+ num_blocks,
+ num_channels,
+ num_heads,
+ num_window_sizes,
+ num_mlp_ratios,
+ drop_paths,
+ )
+ )
+
+ return nn.ModuleList(branches)
+
+ def _make_fuse_layers(self):
+ """Build fuse layer."""
+ if self.num_branches == 1:
+ return None
+
+ num_branches = self.num_branches
+ in_channels = self.in_channels
+ fuse_layers = []
+ num_out_branches = num_branches if self.multiscale_output else 1
+ for i in range(num_out_branches):
+ fuse_layer = []
+ for j in range(num_branches):
+ if j > i:
+ fuse_layer.append(
+ nn.Sequential(
+ build_conv_layer(
+ self.conv_cfg,
+ in_channels[j],
+ in_channels[i],
+ kernel_size=1,
+ stride=1,
+ padding=0,
+ bias=False,
+ ),
+ build_norm_layer(self.norm_cfg, in_channels[i])[1],
+ nn.Upsample(
+ scale_factor=2 ** (j - i),
+ mode="bilinear",
+ align_corners=False,
+ ),
+ )
+ )
+ elif j == i:
+ fuse_layer.append(None)
+ else:
+ conv_downsamples = []
+ for k in range(i - j):
+ if k == i - j - 1:
+ conv_downsamples.append(
+ nn.Sequential(
+ build_conv_layer(
+ self.conv_cfg,
+ in_channels[j],
+ in_channels[j],
+ kernel_size=3,
+ stride=2,
+ padding=1,
+ groups=in_channels[j],
+ bias=False,
+ ),
+ build_norm_layer(self.norm_cfg, in_channels[j])[1],
+ build_conv_layer(
+ self.conv_cfg,
+ in_channels[j],
+ in_channels[i],
+ kernel_size=1,
+ stride=1,
+ bias=False,
+ ),
+ build_norm_layer(self.norm_cfg, in_channels[i])[1],
+ )
+ )
+ else:
+ conv_downsamples.append(
+ nn.Sequential(
+ build_conv_layer(
+ self.conv_cfg,
+ in_channels[j],
+ in_channels[j],
+ kernel_size=3,
+ stride=2,
+ padding=1,
+ groups=in_channels[j],
+ bias=False,
+ ),
+ build_norm_layer(self.norm_cfg, in_channels[j])[1],
+ build_conv_layer(
+ self.conv_cfg,
+ in_channels[j],
+ in_channels[j],
+ kernel_size=1,
+ stride=1,
+ bias=False,
+ ),
+ build_norm_layer(self.norm_cfg, in_channels[j])[1],
+ nn.ReLU(inplace=True),
+ )
+ )
+ fuse_layer.append(nn.Sequential(*conv_downsamples))
+ fuse_layers.append(nn.ModuleList(fuse_layer))
+ return nn.ModuleList(fuse_layers)
+
+ def forward(self, x):
+ """Forward function."""
+ if self.num_branches == 1:
+ return [self.branches[0](x[0])]
+
+ for i in range(self.num_branches):
+ x[i] = self.branches[i](x[i])
+
+ x_fuse = []
+ for i in range(len(self.fuse_layers)):
+ y = x[0] if i == 0 else self.fuse_layers[i][0](x[0])
+ for j in range(1, self.num_branches):
+ if i == j:
+ y += x[j]
+ elif j > i:
+ y = y + resize(
+ self.fuse_layers[i][j](x[j]),
+ size=x[i].shape[2:],
+ mode="bilinear",
+ align_corners=False,
+ )
+ else:
+ y += self.fuse_layers[i][j](x[j])
+ x_fuse.append(self.relu(y))
+ return x_fuse
+
+
+@BACKBONES.register_module()
+class HRT(nn.Module):
+ """HRT backbone.
+ High Resolution Transformer Backbone
+ """
+
+ blocks_dict = {
+ "BOTTLENECK": Bottleneck,
+ "TRANSFORMER_BLOCK": GeneralTransformerBlock,
+ }
+
+ def __init__(
+ self,
+ extra,
+ in_channels=3,
+ conv_cfg=None,
+ norm_cfg=dict(type="BN", requires_grad=True),
+ norm_eval=False,
+ with_cp=False,
+ zero_init_residual=False,
+ ):
+ super(HRT, self).__init__()
+ self.extra = extra
+ self.conv_cfg = conv_cfg
+ self.norm_cfg = norm_cfg
+ self.norm_eval = norm_eval
+ self.with_cp = with_cp
+ self.zero_init_residual = zero_init_residual
+
+ # stem net
+ self.norm1_name, norm1 = build_norm_layer(self.norm_cfg, 64, postfix=1)
+ self.norm2_name, norm2 = build_norm_layer(self.norm_cfg, 64, postfix=2)
+
+ self.conv1 = build_conv_layer(
+ self.conv_cfg,
+ in_channels,
+ 64,
+ kernel_size=3,
+ stride=2,
+ padding=1,
+ bias=False,
+ )
+ self.add_module(self.norm1_name, norm1)
+
+ self.conv2 = build_conv_layer(
+ self.conv_cfg, 64, 64, kernel_size=3, stride=2, padding=1, bias=False
+ )
+ self.add_module(self.norm2_name, norm2)
+ self.relu = nn.ReLU(inplace=True)
+
+ # generat drop path rate list
+ depth_s2 = (
+ self.extra["stage2"]["num_blocks"][0] * self.extra["stage2"]["num_modules"]
+ )
+ depth_s3 = (
+ self.extra["stage3"]["num_blocks"][0] * self.extra["stage3"]["num_modules"]
+ )
+ depth_s4 = (
+ self.extra["stage4"]["num_blocks"][0] * self.extra["stage4"]["num_modules"]
+ )
+ depths = [depth_s2, depth_s3, depth_s4]
+ drop_path_rate = self.extra["drop_path_rate"]
+ dpr = [x.item() for x in torch.linspace(0, drop_path_rate, sum(depths))]
+
+ logger = get_root_logger()
+ logger.info(dpr)
+
+ # stage 1
+ self.stage1_cfg = self.extra["stage1"]
+ num_channels = self.stage1_cfg["num_channels"][0]
+ block_type = self.stage1_cfg["block"]
+ num_blocks = self.stage1_cfg["num_blocks"][0]
+
+ block = self.blocks_dict[block_type]
+ stage1_out_channels = num_channels * block.expansion
+ self.layer1 = self._make_layer(block, 64, num_channels, num_blocks)
+
+ # stage 2
+ self.stage2_cfg = self.extra["stage2"]
+ num_channels = self.stage2_cfg["num_channels"]
+ block_type = self.stage2_cfg["block"]
+
+ block = self.blocks_dict[block_type]
+ num_channels = [channel * block.expansion for channel in num_channels]
+ self.transition1 = self._make_transition_layer(
+ [stage1_out_channels], num_channels
+ )
+ self.stage2, pre_stage_channels = self._make_stage(
+ self.stage2_cfg, num_channels, drop_paths=dpr[0:depth_s2]
+ )
+
+ # stage 3
+ self.stage3_cfg = self.extra["stage3"]
+ num_channels = self.stage3_cfg["num_channels"]
+ block_type = self.stage3_cfg["block"]
+
+ block = self.blocks_dict[block_type]
+ num_channels = [channel * block.expansion for channel in num_channels]
+ self.transition2 = self._make_transition_layer(pre_stage_channels, num_channels)
+ self.stage3, pre_stage_channels = self._make_stage(
+ self.stage3_cfg,
+ num_channels,
+ drop_paths=dpr[depth_s2 : depth_s2 + depth_s3],
+ )
+
+ # stage 4
+ self.stage4_cfg = self.extra["stage4"]
+ num_channels = self.stage4_cfg["num_channels"]
+ block_type = self.stage4_cfg["block"]
+
+ block = self.blocks_dict[block_type]
+ num_channels = [channel * block.expansion for channel in num_channels]
+ self.transition3 = self._make_transition_layer(pre_stage_channels, num_channels)
+ self.stage4, pre_stage_channels = self._make_stage(
+ self.stage4_cfg,
+ num_channels,
+ multiscale_output=self.stage4_cfg.get("multiscale_output", True),
+ drop_paths=dpr[depth_s2 + depth_s3 :],
+ )
+
+ @property
+ def norm1(self):
+ """nn.Module: the normalization layer named "norm1" """
+ return getattr(self, self.norm1_name)
+
+ @property
+ def norm2(self):
+ """nn.Module: the normalization layer named "norm2" """
+ return getattr(self, self.norm2_name)
+
+ def _make_transition_layer(self, num_channels_pre_layer, num_channels_cur_layer):
+ """Make transition layer."""
+ num_branches_cur = len(num_channels_cur_layer)
+ num_branches_pre = len(num_channels_pre_layer)
+
+ transition_layers = []
+ for i in range(num_branches_cur):
+ if i < num_branches_pre:
+ if num_channels_cur_layer[i] != num_channels_pre_layer[i]:
+ transition_layers.append(
+ nn.Sequential(
+ build_conv_layer(
+ self.conv_cfg,
+ num_channels_pre_layer[i],
+ num_channels_cur_layer[i],
+ kernel_size=3,
+ stride=1,
+ padding=1,
+ bias=False,
+ ),
+ build_norm_layer(self.norm_cfg, num_channels_cur_layer[i])[
+ 1
+ ],
+ nn.ReLU(inplace=True),
+ )
+ )
+ else:
+ transition_layers.append(None)
+ else:
+ conv_downsamples = []
+ for j in range(i + 1 - num_branches_pre):
+ in_channels = num_channels_pre_layer[-1]
+ out_channels = (
+ num_channels_cur_layer[i]
+ if j == i - num_branches_pre
+ else in_channels
+ )
+ conv_downsamples.append(
+ nn.Sequential(
+ build_conv_layer(
+ self.conv_cfg,
+ in_channels,
+ out_channels,
+ kernel_size=3,
+ stride=2,
+ padding=1,
+ bias=False,
+ ),
+ build_norm_layer(self.norm_cfg, out_channels)[1],
+ nn.ReLU(inplace=True),
+ )
+ )
+ transition_layers.append(nn.Sequential(*conv_downsamples))
+
+ return nn.ModuleList(transition_layers)
+
+ def _make_layer(
+ self,
+ block,
+ inplanes,
+ planes,
+ blocks,
+ stride=1,
+ num_heads=1,
+ window_size=7,
+ mlp_ratio=4.0,
+ ):
+ """Make each layer."""
+ downsample = None
+ if stride != 1 or inplanes != planes * block.expansion:
+ downsample = nn.Sequential(
+ build_conv_layer(
+ self.conv_cfg,
+ inplanes,
+ planes * block.expansion,
+ kernel_size=1,
+ stride=stride,
+ bias=False,
+ ),
+ build_norm_layer(self.norm_cfg, planes * block.expansion)[1],
+ )
+
+ layers = []
+ if isinstance(block, GeneralTransformerBlock):
+ layers.append(
+ block(
+ inplanes,
+ planes,
+ num_heads=num_heads,
+ window_size=window_size,
+ mlp_ratio=mlp_ratio,
+ norm_cfg=self.norm_cfg,
+ conv_cfg=self.conv_cfg,
+ )
+ )
+ else:
+ layers.append(
+ block(
+ inplanes,
+ planes,
+ stride,
+ downsample=downsample,
+ with_cp=self.with_cp,
+ norm_cfg=self.norm_cfg,
+ conv_cfg=self.conv_cfg,
+ )
+ )
+ inplanes = planes * block.expansion
+ for i in range(1, blocks):
+ layers.append(
+ block(
+ inplanes,
+ planes,
+ with_cp=self.with_cp,
+ norm_cfg=self.norm_cfg,
+ conv_cfg=self.conv_cfg,
+ )
+ )
+
+ return nn.Sequential(*layers)
+
+ def _make_stage(
+ self, layer_config, in_channels, multiscale_output=True, drop_paths=0.0
+ ):
+ """Make each stage."""
+ num_modules = layer_config["num_modules"]
+ num_branches = layer_config["num_branches"]
+ num_blocks = layer_config["num_blocks"]
+ num_channels = layer_config["num_channels"]
+ block = self.blocks_dict[layer_config["block"]]
+
+ num_heads = layer_config["num_heads"]
+ num_window_sizes = layer_config["num_window_sizes"]
+ num_mlp_ratios = layer_config["num_mlp_ratios"]
+
+ hr_modules = []
+ for i in range(num_modules):
+ # multi_scale_output is only used for the last module
+ if not multiscale_output and i == num_modules - 1:
+ reset_multiscale_output = False
+ else:
+ reset_multiscale_output = True
+
+ hr_modules.append(
+ HighResolutionTransformerModule(
+ num_branches,
+ block,
+ num_blocks,
+ in_channels,
+ num_channels,
+ reset_multiscale_output,
+ with_cp=self.with_cp,
+ norm_cfg=self.norm_cfg,
+ conv_cfg=self.conv_cfg,
+ num_heads=num_heads,
+ num_window_sizes=num_window_sizes,
+ num_mlp_ratios=num_mlp_ratios,
+ drop_paths=drop_paths[num_blocks[0] * i : num_blocks[0] * (i + 1)],
+ )
+ )
+
+ return nn.Sequential(*hr_modules), in_channels
+
+ def init_weights(self, pretrained=None):
+ """Initialize the weights in backbone.
+
+ Args:
+ pretrained (str, optional): Path to pre-trained weights.
+ Defaults to None.
+ """
+ if isinstance(pretrained, str):
+ logger = get_root_logger()
+ ckpt = load_checkpoint(self, pretrained, strict=False)
+ if "model" in ckpt:
+ msg = self.load_state_dict(ckpt["model"], strict=False)
+ logger.info(msg)
+ elif pretrained is None:
+ for m in self.modules():
+ if isinstance(m, nn.Conv2d):
+ """mmseg: kaiming_init(m)"""
+ normal_init(m, std=0.001)
+ elif isinstance(m, (_BatchNorm, nn.GroupNorm)):
+ constant_init(m, 1)
+
+ if self.zero_init_residual:
+ for m in self.modules():
+ if isinstance(m, Bottleneck):
+ constant_init(m.norm3, 0)
+ elif isinstance(m, BasicBlock):
+ constant_init(m.norm2, 0)
+ else:
+ raise TypeError("pretrained must be a str or None")
+
+ def forward(self, x):
+ """Forward function."""
+ x = self.conv1(x)
+ x = self.norm1(x)
+ x = self.relu(x)
+ x = self.conv2(x)
+ x = self.norm2(x)
+ x = self.relu(x)
+ x = self.layer1(x)
+
+ x_list = []
+ for i in range(self.stage2_cfg["num_branches"]):
+ if self.transition1[i] is not None:
+ x_list.append(self.transition1[i](x))
+ else:
+ x_list.append(x)
+ y_list = self.stage2(x_list)
+
+ x_list = []
+ for i in range(self.stage3_cfg["num_branches"]):
+ if self.transition2[i] is not None:
+ x_list.append(self.transition2[i](y_list[-1]))
+ else:
+ x_list.append(y_list[i])
+ y_list = self.stage3(x_list)
+
+ x_list = []
+ for i in range(self.stage4_cfg["num_branches"]):
+ if self.transition3[i] is not None:
+ x_list.append(self.transition3[i](y_list[-1]))
+ else:
+ x_list.append(y_list[i])
+ y_list = self.stage4(x_list)
+
+ return y_list
+
+ def train(self, mode=True):
+ """Convert the model into training mode."""
+ super(HRT, self).train(mode)
+ if mode and self.norm_eval:
+ for m in self.modules():
+ if isinstance(m, _BatchNorm):
+ m.eval()
diff --git a/grounded-sam-osx/transformer_utils/mmpose/models/backbones/hrt_checkpoint.py b/grounded-sam-osx/transformer_utils/mmpose/models/backbones/hrt_checkpoint.py
new file mode 100644
index 0000000000000000000000000000000000000000..e27749d45ad2e1b24e50de8b85af90b4464e91ba
--- /dev/null
+++ b/grounded-sam-osx/transformer_utils/mmpose/models/backbones/hrt_checkpoint.py
@@ -0,0 +1,500 @@
+# Copyright (c) Open-MMLab. All rights reserved.
+import io
+import os
+import os.path as osp
+import pkgutil
+import time
+import warnings
+from collections import OrderedDict
+from importlib import import_module
+from tempfile import TemporaryDirectory
+
+import torch
+import torchvision
+from torch.optim import Optimizer
+from torch.utils import model_zoo
+from torch.nn import functional as F
+
+import mmcv
+from mmcv.fileio import FileClient
+from mmcv.fileio import load as load_file
+from mmcv.parallel import is_module_wrapper
+from mmcv.utils import mkdir_or_exist
+from mmcv.runner import get_dist_info
+
+ENV_MMCV_HOME = 'MMCV_HOME'
+ENV_XDG_CACHE_HOME = 'XDG_CACHE_HOME'
+DEFAULT_CACHE_DIR = '~/.cache'
+
+
+def _get_mmcv_home():
+ mmcv_home = os.path.expanduser(
+ os.getenv(
+ ENV_MMCV_HOME,
+ os.path.join(
+ os.getenv(ENV_XDG_CACHE_HOME, DEFAULT_CACHE_DIR), 'mmcv')))
+
+ mkdir_or_exist(mmcv_home)
+ return mmcv_home
+
+
+def load_state_dict(module, state_dict, strict=False, logger=None):
+ """Load state_dict to a module.
+
+ This method is modified from :meth:`torch.nn.Module.load_state_dict`.
+ Default value for ``strict`` is set to ``False`` and the message for
+ param mismatch will be shown even if strict is False.
+
+ Args:
+ module (Module): Module that receives the state_dict.
+ state_dict (OrderedDict): Weights.
+ strict (bool): whether to strictly enforce that the keys
+ in :attr:`state_dict` match the keys returned by this module's
+ :meth:`~torch.nn.Module.state_dict` function. Default: ``False``.
+ logger (:obj:`logging.Logger`, optional): Logger to log the error
+ message. If not specified, print function will be used.
+ """
+ unexpected_keys = []
+ all_missing_keys = []
+ err_msg = []
+
+ metadata = getattr(state_dict, '_metadata', None)
+ state_dict = state_dict.copy()
+ if metadata is not None:
+ state_dict._metadata = metadata
+
+ # use _load_from_state_dict to enable checkpoint version control
+ def load(module, prefix=''):
+ # recursively check parallel module in case that the model has a
+ # complicated structure, e.g., nn.Module(nn.Module(DDP))
+ if is_module_wrapper(module):
+ module = module.module
+ local_metadata = {} if metadata is None else metadata.get(
+ prefix[:-1], {})
+ module._load_from_state_dict(state_dict, prefix, local_metadata, True,
+ all_missing_keys, unexpected_keys,
+ err_msg)
+ for name, child in module._modules.items():
+ if child is not None:
+ load(child, prefix + name + '.')
+
+ load(module)
+ load = None # break load->load reference cycle
+
+ # ignore "num_batches_tracked" of BN layers
+ missing_keys = [
+ key for key in all_missing_keys if 'num_batches_tracked' not in key
+ ]
+
+ if unexpected_keys:
+ err_msg.append('unexpected key in source '
+ f'state_dict: {", ".join(unexpected_keys)}\n')
+ if missing_keys:
+ err_msg.append(
+ f'missing keys in source state_dict: {", ".join(missing_keys)}\n')
+
+ rank, _ = get_dist_info()
+ if len(err_msg) > 0 and rank == 0:
+ err_msg.insert(
+ 0, 'The model and loaded state dict do not match exactly\n')
+ err_msg = '\n'.join(err_msg)
+ if strict:
+ raise RuntimeError(err_msg)
+ elif logger is not None:
+ logger.warning(err_msg)
+ else:
+ print(err_msg)
+
+
+def load_url_dist(url, model_dir=None):
+ """In distributed setting, this function only download checkpoint at local
+ rank 0."""
+ rank, world_size = get_dist_info()
+ rank = int(os.environ.get('LOCAL_RANK', rank))
+ if rank == 0:
+ checkpoint = model_zoo.load_url(url, model_dir=model_dir)
+ if world_size > 1:
+ torch.distributed.barrier()
+ if rank > 0:
+ checkpoint = model_zoo.load_url(url, model_dir=model_dir)
+ return checkpoint
+
+
+def load_pavimodel_dist(model_path, map_location=None):
+ """In distributed setting, this function only download checkpoint at local
+ rank 0."""
+ try:
+ from pavi import modelcloud
+ except ImportError:
+ raise ImportError(
+ 'Please install pavi to load checkpoint from modelcloud.')
+ rank, world_size = get_dist_info()
+ rank = int(os.environ.get('LOCAL_RANK', rank))
+ if rank == 0:
+ model = modelcloud.get(model_path)
+ with TemporaryDirectory() as tmp_dir:
+ downloaded_file = osp.join(tmp_dir, model.name)
+ model.download(downloaded_file)
+ checkpoint = torch.load(downloaded_file, map_location=map_location)
+ if world_size > 1:
+ torch.distributed.barrier()
+ if rank > 0:
+ model = modelcloud.get(model_path)
+ with TemporaryDirectory() as tmp_dir:
+ downloaded_file = osp.join(tmp_dir, model.name)
+ model.download(downloaded_file)
+ checkpoint = torch.load(
+ downloaded_file, map_location=map_location)
+ return checkpoint
+
+
+def load_fileclient_dist(filename, backend, map_location):
+ """In distributed setting, this function only download checkpoint at local
+ rank 0."""
+ rank, world_size = get_dist_info()
+ rank = int(os.environ.get('LOCAL_RANK', rank))
+ allowed_backends = ['ceph']
+ if backend not in allowed_backends:
+ raise ValueError(f'Load from Backend {backend} is not supported.')
+ if rank == 0:
+ fileclient = FileClient(backend=backend)
+ buffer = io.BytesIO(fileclient.get(filename))
+ checkpoint = torch.load(buffer, map_location=map_location)
+ if world_size > 1:
+ torch.distributed.barrier()
+ if rank > 0:
+ fileclient = FileClient(backend=backend)
+ buffer = io.BytesIO(fileclient.get(filename))
+ checkpoint = torch.load(buffer, map_location=map_location)
+ return checkpoint
+
+
+def get_torchvision_models():
+ model_urls = dict()
+ for _, name, ispkg in pkgutil.walk_packages(torchvision.models.__path__):
+ if ispkg:
+ continue
+ _zoo = import_module(f'torchvision.models.{name}')
+ if hasattr(_zoo, 'model_urls'):
+ _urls = getattr(_zoo, 'model_urls')
+ model_urls.update(_urls)
+ return model_urls
+
+
+def get_external_models():
+ mmcv_home = _get_mmcv_home()
+ default_json_path = osp.join(mmcv.__path__[0], 'model_zoo/open_mmlab.json')
+ default_urls = load_file(default_json_path)
+ assert isinstance(default_urls, dict)
+ external_json_path = osp.join(mmcv_home, 'open_mmlab.json')
+ if osp.exists(external_json_path):
+ external_urls = load_file(external_json_path)
+ assert isinstance(external_urls, dict)
+ default_urls.update(external_urls)
+
+ return default_urls
+
+
+def get_mmcls_models():
+ mmcls_json_path = osp.join(mmcv.__path__[0], 'model_zoo/mmcls.json')
+ mmcls_urls = load_file(mmcls_json_path)
+
+ return mmcls_urls
+
+
+def get_deprecated_model_names():
+ deprecate_json_path = osp.join(mmcv.__path__[0],
+ 'model_zoo/deprecated.json')
+ deprecate_urls = load_file(deprecate_json_path)
+ assert isinstance(deprecate_urls, dict)
+
+ return deprecate_urls
+
+
+def _process_mmcls_checkpoint(checkpoint):
+ state_dict = checkpoint['state_dict']
+ new_state_dict = OrderedDict()
+ for k, v in state_dict.items():
+ if k.startswith('backbone.'):
+ new_state_dict[k[9:]] = v
+ new_checkpoint = dict(state_dict=new_state_dict)
+
+ return new_checkpoint
+
+
+def _load_checkpoint(filename, map_location=None):
+ """Load checkpoint from somewhere (modelzoo, file, url).
+
+ Args:
+ filename (str): Accept local filepath, URL, ``torchvision://xxx``,
+ ``open-mmlab://xxx``. Please refer to ``docs/model_zoo.md`` for
+ details.
+ map_location (str | None): Same as :func:`torch.load`. Default: None.
+
+ Returns:
+ dict | OrderedDict: The loaded checkpoint. It can be either an
+ OrderedDict storing model weights or a dict containing other
+ information, which depends on the checkpoint.
+ """
+ if filename.startswith('modelzoo://'):
+ warnings.warn('The URL scheme of "modelzoo://" is deprecated, please '
+ 'use "torchvision://" instead')
+ model_urls = get_torchvision_models()
+ model_name = filename[11:]
+ checkpoint = load_url_dist(model_urls[model_name])
+ elif filename.startswith('torchvision://'):
+ model_urls = get_torchvision_models()
+ model_name = filename[14:]
+ checkpoint = load_url_dist(model_urls[model_name])
+ elif filename.startswith('open-mmlab://'):
+ model_urls = get_external_models()
+ model_name = filename[13:]
+ deprecated_urls = get_deprecated_model_names()
+ if model_name in deprecated_urls:
+ warnings.warn(f'open-mmlab://{model_name} is deprecated in favor '
+ f'of open-mmlab://{deprecated_urls[model_name]}')
+ model_name = deprecated_urls[model_name]
+ model_url = model_urls[model_name]
+ # check if is url
+ if model_url.startswith(('http://', 'https://')):
+ checkpoint = load_url_dist(model_url)
+ else:
+ filename = osp.join(_get_mmcv_home(), model_url)
+ if not osp.isfile(filename):
+ raise IOError(f'{filename} is not a checkpoint file')
+ checkpoint = torch.load(filename, map_location=map_location)
+ elif filename.startswith('mmcls://'):
+ model_urls = get_mmcls_models()
+ model_name = filename[8:]
+ checkpoint = load_url_dist(model_urls[model_name])
+ checkpoint = _process_mmcls_checkpoint(checkpoint)
+ elif filename.startswith(('http://', 'https://')):
+ checkpoint = load_url_dist(filename)
+ elif filename.startswith('pavi://'):
+ model_path = filename[7:]
+ checkpoint = load_pavimodel_dist(model_path, map_location=map_location)
+ elif filename.startswith('s3://'):
+ checkpoint = load_fileclient_dist(
+ filename, backend='ceph', map_location=map_location)
+ else:
+ if not osp.isfile(filename):
+ raise IOError(f'{filename} is not a checkpoint file')
+ checkpoint = torch.load(filename, map_location=map_location)
+ return checkpoint
+
+
+def load_checkpoint(model,
+ filename,
+ map_location='cpu',
+ strict=False,
+ logger=None):
+ """Load checkpoint from a file or URI.
+
+ Args:
+ model (Module): Module to load checkpoint.
+ filename (str): Accept local filepath, URL, ``torchvision://xxx``,
+ ``open-mmlab://xxx``. Please refer to ``docs/model_zoo.md`` for
+ details.
+ map_location (str): Same as :func:`torch.load`.
+ strict (bool): Whether to allow different params for the model and
+ checkpoint.
+ logger (:mod:`logging.Logger` or None): The logger for error message.
+
+ Returns:
+ dict or OrderedDict: The loaded checkpoint.
+ """
+ checkpoint = _load_checkpoint(filename, map_location)
+ # OrderedDict is a subclass of dict
+ if not isinstance(checkpoint, dict):
+ raise RuntimeError(
+ f'No state_dict found in checkpoint file {filename}')
+ # get state_dict from checkpoint
+ if 'state_dict' in checkpoint:
+ state_dict = checkpoint['state_dict']
+ elif 'model' in checkpoint:
+ state_dict = checkpoint['model']
+ else:
+ state_dict = checkpoint
+ # strip prefix of state_dict
+ if list(state_dict.keys())[0].startswith('module.'):
+ state_dict = {k[7:]: v for k, v in state_dict.items()}
+
+ # for MoBY, load model of online branch
+ if sorted(list(state_dict.keys()))[0].startswith('encoder'):
+ state_dict = {k.replace('encoder.', ''): v for k, v in state_dict.items() if k.startswith('encoder.')}
+
+ # reshape absolute position embedding
+ if state_dict.get('absolute_pos_embed') is not None:
+ absolute_pos_embed = state_dict['absolute_pos_embed']
+ N1, L, C1 = absolute_pos_embed.size()
+ N2, C2, H, W = model.absolute_pos_embed.size()
+ if N1 != N2 or C1 != C2 or L != H*W:
+ logger.warning("Error in loading absolute_pos_embed, pass")
+ else:
+ state_dict['absolute_pos_embed'] = absolute_pos_embed.view(N2, H, W, C2).permute(0, 3, 1, 2)
+
+ # interpolate position bias table if needed
+ # relative_position_bias_table_keys = [k for k in state_dict.keys() if "relative_position_bias_table" in k]
+ # for table_key in relative_position_bias_table_keys:
+ # table_pretrained = state_dict[table_key]
+ # table_current = model.state_dict()[table_key]
+ # L1, nH1 = table_pretrained.size()
+ # L2, nH2 = table_current.size()
+ # if nH1 != nH2:
+ # logger.warning(f"Error in loading {table_key}, pass")
+ # else:
+ # if L1 != L2:
+ # S1 = int(L1 ** 0.5)
+ # S2 = int(L2 ** 0.5)
+ # table_pretrained_resized = F.interpolate(
+ # table_pretrained.permute(1, 0).view(1, nH1, S1, S1),
+ # size=(S2, S2), mode='bicubic')
+ # state_dict[table_key] = table_pretrained_resized.view(nH2, L2).permute(1, 0)
+
+ # load state_dict
+ load_state_dict(model, state_dict, strict, logger)
+ return checkpoint
+
+
+def weights_to_cpu(state_dict):
+ """Copy a model state_dict to cpu.
+
+ Args:
+ state_dict (OrderedDict): Model weights on GPU.
+
+ Returns:
+ OrderedDict: Model weights on GPU.
+ """
+ state_dict_cpu = OrderedDict()
+ for key, val in state_dict.items():
+ state_dict_cpu[key] = val.cpu()
+ return state_dict_cpu
+
+
+def _save_to_state_dict(module, destination, prefix, keep_vars):
+ """Saves module state to `destination` dictionary.
+
+ This method is modified from :meth:`torch.nn.Module._save_to_state_dict`.
+
+ Args:
+ module (nn.Module): The module to generate state_dict.
+ destination (dict): A dict where state will be stored.
+ prefix (str): The prefix for parameters and buffers used in this
+ module.
+ """
+ for name, param in module._parameters.items():
+ if param is not None:
+ destination[prefix + name] = param if keep_vars else param.detach()
+ for name, buf in module._buffers.items():
+ # remove check of _non_persistent_buffers_set to allow nn.BatchNorm2d
+ if buf is not None:
+ destination[prefix + name] = buf if keep_vars else buf.detach()
+
+
+def get_state_dict(module, destination=None, prefix='', keep_vars=False):
+ """Returns a dictionary containing a whole state of the module.
+
+ Both parameters and persistent buffers (e.g. running averages) are
+ included. Keys are corresponding parameter and buffer names.
+
+ This method is modified from :meth:`torch.nn.Module.state_dict` to
+ recursively check parallel module in case that the model has a complicated
+ structure, e.g., nn.Module(nn.Module(DDP)).
+
+ Args:
+ module (nn.Module): The module to generate state_dict.
+ destination (OrderedDict): Returned dict for the state of the
+ module.
+ prefix (str): Prefix of the key.
+ keep_vars (bool): Whether to keep the variable property of the
+ parameters. Default: False.
+
+ Returns:
+ dict: A dictionary containing a whole state of the module.
+ """
+ # recursively check parallel module in case that the model has a
+ # complicated structure, e.g., nn.Module(nn.Module(DDP))
+ if is_module_wrapper(module):
+ module = module.module
+
+ # below is the same as torch.nn.Module.state_dict()
+ if destination is None:
+ destination = OrderedDict()
+ destination._metadata = OrderedDict()
+ destination._metadata[prefix[:-1]] = local_metadata = dict(
+ version=module._version)
+ _save_to_state_dict(module, destination, prefix, keep_vars)
+ for name, child in module._modules.items():
+ if child is not None:
+ get_state_dict(
+ child, destination, prefix + name + '.', keep_vars=keep_vars)
+ for hook in module._state_dict_hooks.values():
+ hook_result = hook(module, destination, prefix, local_metadata)
+ if hook_result is not None:
+ destination = hook_result
+ return destination
+
+
+def save_checkpoint(model, filename, optimizer=None, meta=None):
+ """Save checkpoint to file.
+
+ The checkpoint will have 3 fields: ``meta``, ``state_dict`` and
+ ``optimizer``. By default ``meta`` will contain version and time info.
+
+ Args:
+ model (Module): Module whose params are to be saved.
+ filename (str): Checkpoint filename.
+ optimizer (:obj:`Optimizer`, optional): Optimizer to be saved.
+ meta (dict, optional): Metadata to be saved in checkpoint.
+ """
+ if meta is None:
+ meta = {}
+ elif not isinstance(meta, dict):
+ raise TypeError(f'meta must be a dict or None, but got {type(meta)}')
+ meta.update(mmcv_version=mmcv.__version__, time=time.asctime())
+
+ if is_module_wrapper(model):
+ model = model.module
+
+ if hasattr(model, 'CLASSES') and model.CLASSES is not None:
+ # save class name to the meta
+ meta.update(CLASSES=model.CLASSES)
+
+ checkpoint = {
+ 'meta': meta,
+ 'state_dict': weights_to_cpu(get_state_dict(model))
+ }
+ # save optimizer state dict in the checkpoint
+ if isinstance(optimizer, Optimizer):
+ checkpoint['optimizer'] = optimizer.state_dict()
+ elif isinstance(optimizer, dict):
+ checkpoint['optimizer'] = {}
+ for name, optim in optimizer.items():
+ checkpoint['optimizer'][name] = optim.state_dict()
+
+ if filename.startswith('pavi://'):
+ try:
+ from pavi import modelcloud
+ from pavi.exception import NodeNotFoundError
+ except ImportError:
+ raise ImportError(
+ 'Please install pavi to load checkpoint from modelcloud.')
+ model_path = filename[7:]
+ root = modelcloud.Folder()
+ model_dir, model_name = osp.split(model_path)
+ try:
+ model = modelcloud.get(model_dir)
+ except NodeNotFoundError:
+ model = root.create_training_model(model_dir)
+ with TemporaryDirectory() as tmp_dir:
+ checkpoint_file = osp.join(tmp_dir, model_name)
+ with open(checkpoint_file, 'wb') as f:
+ torch.save(checkpoint, f)
+ f.flush()
+ model.create_file(checkpoint_file, name=model_name)
+ else:
+ mmcv.mkdir_or_exist(osp.dirname(filename))
+ # immediately flush buffer
+ with open(filename, 'wb') as f:
+ torch.save(checkpoint, f)
+ f.flush()
\ No newline at end of file
diff --git a/grounded-sam-osx/transformer_utils/mmpose/models/backbones/i3d.py b/grounded-sam-osx/transformer_utils/mmpose/models/backbones/i3d.py
new file mode 100644
index 0000000000000000000000000000000000000000..64f330abac1facc16db743ef3ffbcd23248d6865
--- /dev/null
+++ b/grounded-sam-osx/transformer_utils/mmpose/models/backbones/i3d.py
@@ -0,0 +1,215 @@
+# Copyright (c) OpenMMLab. All rights reserved.
+# Code is modified from `Third-party pytorch implementation of i3d
+# `.
+
+import torch
+import torch.nn as nn
+
+from ..builder import BACKBONES
+from .base_backbone import BaseBackbone
+
+
+class Conv3dBlock(nn.Module):
+ """Basic 3d convolution block for I3D.
+
+ Args:
+ in_channels (int): Input channels of this block.
+ out_channels (int): Output channels of this block.
+ expansion (float): The multiplier of in_channels and out_channels.
+ Default: 1.
+ kernel_size (tuple[int]): kernel size of the 3d convolution layer.
+ Default: (1, 1, 1).
+ stride (tuple[int]): stride of the block. Default: (1, 1, 1)
+ padding (tuple[int]): padding of the input tensor. Default: (0, 0, 0)
+ use_bias (bool): whether to enable bias in 3d convolution layer.
+ Default: False
+ use_bn (bool): whether to use Batch Normalization after 3d convolution
+ layer. Default: True
+ use_relu (bool): whether to use ReLU after Batch Normalization layer.
+ Default: True
+ """
+
+ def __init__(self,
+ in_channels,
+ out_channels,
+ expansion=1.0,
+ kernel_size=(1, 1, 1),
+ stride=(1, 1, 1),
+ padding=(0, 0, 0),
+ use_bias=False,
+ use_bn=True,
+ use_relu=True):
+ super().__init__()
+
+ in_channels = int(in_channels * expansion)
+ out_channels = int(out_channels * expansion)
+
+ self.conv3d = nn.Conv3d(
+ in_channels,
+ out_channels,
+ kernel_size,
+ padding=padding,
+ stride=stride,
+ bias=use_bias)
+
+ self.use_bn = use_bn
+ self.use_relu = use_relu
+
+ if self.use_bn:
+ self.batch3d = nn.BatchNorm3d(out_channels)
+
+ if self.use_relu:
+ self.activation = nn.ReLU(inplace=True)
+
+ def forward(self, x):
+ """Forward function."""
+ out = self.conv3d(x)
+ if self.use_bn:
+ out = self.batch3d(out)
+ if self.use_relu:
+ out = self.activation(out)
+ return out
+
+
+class Mixed(nn.Module):
+ """Inception block for I3D.
+
+ Args:
+ in_channels (int): Input channels of this block.
+ out_channels (int): Output channels of this block.
+ expansion (float): The multiplier of in_channels and out_channels.
+ Default: 1.
+ """
+
+ def __init__(self, in_channels, out_channels, expansion=1.0):
+ super(Mixed, self).__init__()
+ # Branch 0
+ self.branch_0 = Conv3dBlock(
+ in_channels, out_channels[0], expansion, kernel_size=(1, 1, 1))
+
+ # Branch 1
+ branch_1_conv1 = Conv3dBlock(
+ in_channels, out_channels[1], expansion, kernel_size=(1, 1, 1))
+ branch_1_conv2 = Conv3dBlock(
+ out_channels[1],
+ out_channels[2],
+ expansion,
+ kernel_size=(3, 3, 3),
+ padding=(1, 1, 1))
+ self.branch_1 = nn.Sequential(branch_1_conv1, branch_1_conv2)
+
+ # Branch 2
+ branch_2_conv1 = Conv3dBlock(
+ in_channels, out_channels[3], expansion, kernel_size=(1, 1, 1))
+ branch_2_conv2 = Conv3dBlock(
+ out_channels[3],
+ out_channels[4],
+ expansion,
+ kernel_size=(3, 3, 3),
+ padding=(1, 1, 1))
+ self.branch_2 = nn.Sequential(branch_2_conv1, branch_2_conv2)
+
+ # Branch3
+ branch_3_pool = nn.MaxPool3d(
+ kernel_size=(3, 3, 3),
+ stride=(1, 1, 1),
+ padding=(1, 1, 1),
+ ceil_mode=True)
+ branch_3_conv2 = Conv3dBlock(
+ in_channels, out_channels[5], expansion, kernel_size=(1, 1, 1))
+ self.branch_3 = nn.Sequential(branch_3_pool, branch_3_conv2)
+
+ def forward(self, x):
+ """Forward function."""
+ out_0 = self.branch_0(x)
+ out_1 = self.branch_1(x)
+ out_2 = self.branch_2(x)
+ out_3 = self.branch_3(x)
+ out = torch.cat((out_0, out_1, out_2, out_3), 1)
+ return out
+
+
+@BACKBONES.register_module()
+class I3D(BaseBackbone):
+ """I3D backbone.
+
+ Please refer to the `paper `__ for
+ details.
+
+ Args:
+ in_channels (int): Input channels of the backbone, which is decided
+ on the input modality.
+ expansion (float): The multiplier of in_channels and out_channels.
+ Default: 1.
+ """
+
+ def __init__(self, in_channels=3, expansion=1.0):
+ super(I3D, self).__init__()
+
+ # expansion must be an integer multiple of 1/8
+ expansion = round(8 * expansion) / 8.0
+
+ # xut Layer
+ self.conv3d_1a_7x7 = Conv3dBlock(
+ out_channels=64,
+ in_channels=in_channels / expansion,
+ expansion=expansion,
+ kernel_size=(7, 7, 7),
+ stride=(2, 2, 2),
+ padding=(2, 3, 3))
+ self.maxPool3d_2a_3x3 = nn.MaxPool3d(
+ kernel_size=(1, 3, 3), stride=(1, 2, 2), padding=(0, 1, 1))
+
+ # Layer 2
+ self.conv3d_2b_1x1 = Conv3dBlock(
+ out_channels=64,
+ in_channels=64,
+ expansion=expansion,
+ kernel_size=(1, 1, 1))
+ self.conv3d_2c_3x3 = Conv3dBlock(
+ out_channels=192,
+ in_channels=64,
+ expansion=expansion,
+ kernel_size=(3, 3, 3),
+ padding=(1, 1, 1))
+ self.maxPool3d_3a_3x3 = nn.MaxPool3d(
+ kernel_size=(1, 3, 3), stride=(1, 2, 2), padding=(0, 1, 1))
+
+ # Mixed_3b
+ self.mixed_3b = Mixed(192, [64, 96, 128, 16, 32, 32], expansion)
+ self.mixed_3c = Mixed(256, [128, 128, 192, 32, 96, 64], expansion)
+ self.maxPool3d_4a_3x3 = nn.MaxPool3d(
+ kernel_size=(3, 3, 3), stride=(2, 2, 2), padding=(1, 1, 1))
+
+ # Mixed 4
+ self.mixed_4b = Mixed(480, [192, 96, 208, 16, 48, 64], expansion)
+ self.mixed_4c = Mixed(512, [160, 112, 224, 24, 64, 64], expansion)
+ self.mixed_4d = Mixed(512, [128, 128, 256, 24, 64, 64], expansion)
+ self.mixed_4e = Mixed(512, [112, 144, 288, 32, 64, 64], expansion)
+ self.mixed_4f = Mixed(528, [256, 160, 320, 32, 128, 128], expansion)
+
+ self.maxPool3d_5a_2x2 = nn.MaxPool3d(
+ kernel_size=(2, 2, 2), stride=(2, 2, 2), padding=(0, 0, 0))
+
+ # Mixed 5
+ self.mixed_5b = Mixed(832, [256, 160, 320, 32, 128, 128], expansion)
+ self.mixed_5c = Mixed(832, [384, 192, 384, 48, 128, 128], expansion)
+
+ def forward(self, x):
+ out = self.conv3d_1a_7x7(x)
+ out = self.maxPool3d_2a_3x3(out)
+ out = self.conv3d_2b_1x1(out)
+ out = self.conv3d_2c_3x3(out)
+ out = self.maxPool3d_3a_3x3(out)
+ out = self.mixed_3b(out)
+ out = self.mixed_3c(out)
+ out = self.maxPool3d_4a_3x3(out)
+ out = self.mixed_4b(out)
+ out = self.mixed_4c(out)
+ out = self.mixed_4d(out)
+ out = self.mixed_4e(out)
+ out = self.mixed_4f(out)
+ out = self.maxPool3d_5a_2x2(out)
+ out = self.mixed_5b(out)
+ out = self.mixed_5c(out)
+ return out
diff --git a/grounded-sam-osx/transformer_utils/mmpose/models/backbones/litehrnet.py b/grounded-sam-osx/transformer_utils/mmpose/models/backbones/litehrnet.py
new file mode 100644
index 0000000000000000000000000000000000000000..954368841eb631e3dc6c77e9810f6980f3739bf3
--- /dev/null
+++ b/grounded-sam-osx/transformer_utils/mmpose/models/backbones/litehrnet.py
@@ -0,0 +1,984 @@
+# ------------------------------------------------------------------------------
+# Adapted from https://github.com/HRNet/Lite-HRNet
+# Original licence: Apache License 2.0.
+# ------------------------------------------------------------------------------
+
+import mmcv
+import torch
+import torch.nn as nn
+import torch.nn.functional as F
+import torch.utils.checkpoint as cp
+from mmcv.cnn import (ConvModule, DepthwiseSeparableConvModule,
+ build_conv_layer, build_norm_layer, constant_init,
+ normal_init)
+from torch.nn.modules.batchnorm import _BatchNorm
+
+from mmpose.utils import get_root_logger
+from ..builder import BACKBONES
+from .utils import channel_shuffle, load_checkpoint
+
+
+class SpatialWeighting(nn.Module):
+ """Spatial weighting module.
+
+ Args:
+ channels (int): The channels of the module.
+ ratio (int): channel reduction ratio.
+ conv_cfg (dict): Config dict for convolution layer.
+ Default: None, which means using conv2d.
+ norm_cfg (dict): Config dict for normalization layer.
+ Default: None.
+ act_cfg (dict): Config dict for activation layer.
+ Default: (dict(type='ReLU'), dict(type='Sigmoid')).
+ The last ConvModule uses Sigmoid by default.
+ """
+
+ def __init__(self,
+ channels,
+ ratio=16,
+ conv_cfg=None,
+ norm_cfg=None,
+ act_cfg=(dict(type='ReLU'), dict(type='Sigmoid'))):
+ super().__init__()
+ if isinstance(act_cfg, dict):
+ act_cfg = (act_cfg, act_cfg)
+ assert len(act_cfg) == 2
+ assert mmcv.is_tuple_of(act_cfg, dict)
+ self.global_avgpool = nn.AdaptiveAvgPool2d(1)
+ self.conv1 = ConvModule(
+ in_channels=channels,
+ out_channels=int(channels / ratio),
+ kernel_size=1,
+ stride=1,
+ conv_cfg=conv_cfg,
+ norm_cfg=norm_cfg,
+ act_cfg=act_cfg[0])
+ self.conv2 = ConvModule(
+ in_channels=int(channels / ratio),
+ out_channels=channels,
+ kernel_size=1,
+ stride=1,
+ conv_cfg=conv_cfg,
+ norm_cfg=norm_cfg,
+ act_cfg=act_cfg[1])
+
+ def forward(self, x):
+ out = self.global_avgpool(x)
+ out = self.conv1(out)
+ out = self.conv2(out)
+ return x * out
+
+
+class CrossResolutionWeighting(nn.Module):
+ """Cross-resolution channel weighting module.
+
+ Args:
+ channels (int): The channels of the module.
+ ratio (int): channel reduction ratio.
+ conv_cfg (dict): Config dict for convolution layer.
+ Default: None, which means using conv2d.
+ norm_cfg (dict): Config dict for normalization layer.
+ Default: None.
+ act_cfg (dict): Config dict for activation layer.
+ Default: (dict(type='ReLU'), dict(type='Sigmoid')).
+ The last ConvModule uses Sigmoid by default.
+ """
+
+ def __init__(self,
+ channels,
+ ratio=16,
+ conv_cfg=None,
+ norm_cfg=None,
+ act_cfg=(dict(type='ReLU'), dict(type='Sigmoid'))):
+ super().__init__()
+ if isinstance(act_cfg, dict):
+ act_cfg = (act_cfg, act_cfg)
+ assert len(act_cfg) == 2
+ assert mmcv.is_tuple_of(act_cfg, dict)
+ self.channels = channels
+ total_channel = sum(channels)
+ self.conv1 = ConvModule(
+ in_channels=total_channel,
+ out_channels=int(total_channel / ratio),
+ kernel_size=1,
+ stride=1,
+ conv_cfg=conv_cfg,
+ norm_cfg=norm_cfg,
+ act_cfg=act_cfg[0])
+ self.conv2 = ConvModule(
+ in_channels=int(total_channel / ratio),
+ out_channels=total_channel,
+ kernel_size=1,
+ stride=1,
+ conv_cfg=conv_cfg,
+ norm_cfg=norm_cfg,
+ act_cfg=act_cfg[1])
+
+ def forward(self, x):
+ mini_size = x[-1].size()[-2:]
+ out = [F.adaptive_avg_pool2d(s, mini_size) for s in x[:-1]] + [x[-1]]
+ out = torch.cat(out, dim=1)
+ out = self.conv1(out)
+ out = self.conv2(out)
+ out = torch.split(out, self.channels, dim=1)
+ out = [
+ s * F.interpolate(a, size=s.size()[-2:], mode='nearest')
+ for s, a in zip(x, out)
+ ]
+ return out
+
+
+class ConditionalChannelWeighting(nn.Module):
+ """Conditional channel weighting block.
+
+ Args:
+ in_channels (int): The input channels of the block.
+ stride (int): Stride of the 3x3 convolution layer.
+ reduce_ratio (int): channel reduction ratio.
+ conv_cfg (dict): Config dict for convolution layer.
+ Default: None, which means using conv2d.
+ norm_cfg (dict): Config dict for normalization layer.
+ Default: dict(type='BN').
+ with_cp (bool): Use checkpoint or not. Using checkpoint will save some
+ memory while slowing down the training speed. Default: False.
+ """
+
+ def __init__(self,
+ in_channels,
+ stride,
+ reduce_ratio,
+ conv_cfg=None,
+ norm_cfg=dict(type='BN'),
+ with_cp=False):
+ super().__init__()
+ self.with_cp = with_cp
+ self.stride = stride
+ assert stride in [1, 2]
+
+ branch_channels = [channel // 2 for channel in in_channels]
+
+ self.cross_resolution_weighting = CrossResolutionWeighting(
+ branch_channels,
+ ratio=reduce_ratio,
+ conv_cfg=conv_cfg,
+ norm_cfg=norm_cfg)
+
+ self.depthwise_convs = nn.ModuleList([
+ ConvModule(
+ channel,
+ channel,
+ kernel_size=3,
+ stride=self.stride,
+ padding=1,
+ groups=channel,
+ conv_cfg=conv_cfg,
+ norm_cfg=norm_cfg,
+ act_cfg=None) for channel in branch_channels
+ ])
+
+ self.spatial_weighting = nn.ModuleList([
+ SpatialWeighting(channels=channel, ratio=4)
+ for channel in branch_channels
+ ])
+
+ def forward(self, x):
+
+ def _inner_forward(x):
+ x = [s.chunk(2, dim=1) for s in x]
+ x1 = [s[0] for s in x]
+ x2 = [s[1] for s in x]
+
+ x2 = self.cross_resolution_weighting(x2)
+ x2 = [dw(s) for s, dw in zip(x2, self.depthwise_convs)]
+ x2 = [sw(s) for s, sw in zip(x2, self.spatial_weighting)]
+
+ out = [torch.cat([s1, s2], dim=1) for s1, s2 in zip(x1, x2)]
+ out = [channel_shuffle(s, 2) for s in out]
+
+ return out
+
+ if self.with_cp and x.requires_grad:
+ out = cp.checkpoint(_inner_forward, x)
+ else:
+ out = _inner_forward(x)
+
+ return out
+
+
+class Stem(nn.Module):
+ """Stem network block.
+
+ Args:
+ in_channels (int): The input channels of the block.
+ stem_channels (int): Output channels of the stem layer.
+ out_channels (int): The output channels of the block.
+ expand_ratio (int): adjusts number of channels of the hidden layer
+ in InvertedResidual by this amount.
+ conv_cfg (dict): Config dict for convolution layer.
+ Default: None, which means using conv2d.
+ norm_cfg (dict): Config dict for normalization layer.
+ Default: dict(type='BN').
+ with_cp (bool): Use checkpoint or not. Using checkpoint will save some
+ memory while slowing down the training speed. Default: False.
+ """
+
+ def __init__(self,
+ in_channels,
+ stem_channels,
+ out_channels,
+ expand_ratio,
+ conv_cfg=None,
+ norm_cfg=dict(type='BN'),
+ with_cp=False):
+ super().__init__()
+ self.in_channels = in_channels
+ self.out_channels = out_channels
+ self.conv_cfg = conv_cfg
+ self.norm_cfg = norm_cfg
+ self.with_cp = with_cp
+
+ self.conv1 = ConvModule(
+ in_channels=in_channels,
+ out_channels=stem_channels,
+ kernel_size=3,
+ stride=2,
+ padding=1,
+ conv_cfg=self.conv_cfg,
+ norm_cfg=self.norm_cfg,
+ act_cfg=dict(type='ReLU'))
+
+ mid_channels = int(round(stem_channels * expand_ratio))
+ branch_channels = stem_channels // 2
+ if stem_channels == self.out_channels:
+ inc_channels = self.out_channels - branch_channels
+ else:
+ inc_channels = self.out_channels - stem_channels
+
+ self.branch1 = nn.Sequential(
+ ConvModule(
+ branch_channels,
+ branch_channels,
+ kernel_size=3,
+ stride=2,
+ padding=1,
+ groups=branch_channels,
+ conv_cfg=conv_cfg,
+ norm_cfg=norm_cfg,
+ act_cfg=None),
+ ConvModule(
+ branch_channels,
+ inc_channels,
+ kernel_size=1,
+ stride=1,
+ padding=0,
+ conv_cfg=conv_cfg,
+ norm_cfg=norm_cfg,
+ act_cfg=dict(type='ReLU')),
+ )
+
+ self.expand_conv = ConvModule(
+ branch_channels,
+ mid_channels,
+ kernel_size=1,
+ stride=1,
+ padding=0,
+ conv_cfg=conv_cfg,
+ norm_cfg=norm_cfg,
+ act_cfg=dict(type='ReLU'))
+ self.depthwise_conv = ConvModule(
+ mid_channels,
+ mid_channels,
+ kernel_size=3,
+ stride=2,
+ padding=1,
+ groups=mid_channels,
+ conv_cfg=conv_cfg,
+ norm_cfg=norm_cfg,
+ act_cfg=None)
+ self.linear_conv = ConvModule(
+ mid_channels,
+ branch_channels
+ if stem_channels == self.out_channels else stem_channels,
+ kernel_size=1,
+ stride=1,
+ padding=0,
+ conv_cfg=conv_cfg,
+ norm_cfg=norm_cfg,
+ act_cfg=dict(type='ReLU'))
+
+ def forward(self, x):
+
+ def _inner_forward(x):
+ x = self.conv1(x)
+ x1, x2 = x.chunk(2, dim=1)
+
+ x2 = self.expand_conv(x2)
+ x2 = self.depthwise_conv(x2)
+ x2 = self.linear_conv(x2)
+
+ out = torch.cat((self.branch1(x1), x2), dim=1)
+
+ out = channel_shuffle(out, 2)
+
+ return out
+
+ if self.with_cp and x.requires_grad:
+ out = cp.checkpoint(_inner_forward, x)
+ else:
+ out = _inner_forward(x)
+
+ return out
+
+
+class IterativeHead(nn.Module):
+ """Extra iterative head for feature learning.
+
+ Args:
+ in_channels (int): The input channels of the block.
+ norm_cfg (dict): Config dict for normalization layer.
+ Default: dict(type='BN').
+ """
+
+ def __init__(self, in_channels, norm_cfg=dict(type='BN')):
+ super().__init__()
+ projects = []
+ num_branchs = len(in_channels)
+ self.in_channels = in_channels[::-1]
+
+ for i in range(num_branchs):
+ if i != num_branchs - 1:
+ projects.append(
+ DepthwiseSeparableConvModule(
+ in_channels=self.in_channels[i],
+ out_channels=self.in_channels[i + 1],
+ kernel_size=3,
+ stride=1,
+ padding=1,
+ norm_cfg=norm_cfg,
+ act_cfg=dict(type='ReLU'),
+ dw_act_cfg=None,
+ pw_act_cfg=dict(type='ReLU')))
+ else:
+ projects.append(
+ DepthwiseSeparableConvModule(
+ in_channels=self.in_channels[i],
+ out_channels=self.in_channels[i],
+ kernel_size=3,
+ stride=1,
+ padding=1,
+ norm_cfg=norm_cfg,
+ act_cfg=dict(type='ReLU'),
+ dw_act_cfg=None,
+ pw_act_cfg=dict(type='ReLU')))
+ self.projects = nn.ModuleList(projects)
+
+ def forward(self, x):
+ x = x[::-1]
+
+ y = []
+ last_x = None
+ for i, s in enumerate(x):
+ if last_x is not None:
+ last_x = F.interpolate(
+ last_x,
+ size=s.size()[-2:],
+ mode='bilinear',
+ align_corners=True)
+ s = s + last_x
+ s = self.projects[i](s)
+ y.append(s)
+ last_x = s
+
+ return y[::-1]
+
+
+class ShuffleUnit(nn.Module):
+ """InvertedResidual block for ShuffleNetV2 backbone.
+
+ Args:
+ in_channels (int): The input channels of the block.
+ out_channels (int): The output channels of the block.
+ stride (int): Stride of the 3x3 convolution layer. Default: 1
+ conv_cfg (dict): Config dict for convolution layer.
+ Default: None, which means using conv2d.
+ norm_cfg (dict): Config dict for normalization layer.
+ Default: dict(type='BN').
+ act_cfg (dict): Config dict for activation layer.
+ Default: dict(type='ReLU').
+ with_cp (bool): Use checkpoint or not. Using checkpoint will save some
+ memory while slowing down the training speed. Default: False.
+ """
+
+ def __init__(self,
+ in_channels,
+ out_channels,
+ stride=1,
+ conv_cfg=None,
+ norm_cfg=dict(type='BN'),
+ act_cfg=dict(type='ReLU'),
+ with_cp=False):
+ super().__init__()
+ self.stride = stride
+ self.with_cp = with_cp
+
+ branch_features = out_channels // 2
+ if self.stride == 1:
+ assert in_channels == branch_features * 2, (
+ f'in_channels ({in_channels}) should equal to '
+ f'branch_features * 2 ({branch_features * 2}) '
+ 'when stride is 1')
+
+ if in_channels != branch_features * 2:
+ assert self.stride != 1, (
+ f'stride ({self.stride}) should not equal 1 when '
+ f'in_channels != branch_features * 2')
+
+ if self.stride > 1:
+ self.branch1 = nn.Sequential(
+ ConvModule(
+ in_channels,
+ in_channels,
+ kernel_size=3,
+ stride=self.stride,
+ padding=1,
+ groups=in_channels,
+ conv_cfg=conv_cfg,
+ norm_cfg=norm_cfg,
+ act_cfg=None),
+ ConvModule(
+ in_channels,
+ branch_features,
+ kernel_size=1,
+ stride=1,
+ padding=0,
+ conv_cfg=conv_cfg,
+ norm_cfg=norm_cfg,
+ act_cfg=act_cfg),
+ )
+
+ self.branch2 = nn.Sequential(
+ ConvModule(
+ in_channels if (self.stride > 1) else branch_features,
+ branch_features,
+ kernel_size=1,
+ stride=1,
+ padding=0,
+ conv_cfg=conv_cfg,
+ norm_cfg=norm_cfg,
+ act_cfg=act_cfg),
+ ConvModule(
+ branch_features,
+ branch_features,
+ kernel_size=3,
+ stride=self.stride,
+ padding=1,
+ groups=branch_features,
+ conv_cfg=conv_cfg,
+ norm_cfg=norm_cfg,
+ act_cfg=None),
+ ConvModule(
+ branch_features,
+ branch_features,
+ kernel_size=1,
+ stride=1,
+ padding=0,
+ conv_cfg=conv_cfg,
+ norm_cfg=norm_cfg,
+ act_cfg=act_cfg))
+
+ def forward(self, x):
+
+ def _inner_forward(x):
+ if self.stride > 1:
+ out = torch.cat((self.branch1(x), self.branch2(x)), dim=1)
+ else:
+ x1, x2 = x.chunk(2, dim=1)
+ out = torch.cat((x1, self.branch2(x2)), dim=1)
+
+ out = channel_shuffle(out, 2)
+
+ return out
+
+ if self.with_cp and x.requires_grad:
+ out = cp.checkpoint(_inner_forward, x)
+ else:
+ out = _inner_forward(x)
+
+ return out
+
+
+class LiteHRModule(nn.Module):
+ """High-Resolution Module for LiteHRNet.
+
+ It contains conditional channel weighting blocks and
+ shuffle blocks.
+
+
+ Args:
+ num_branches (int): Number of branches in the module.
+ num_blocks (int): Number of blocks in the module.
+ in_channels (list(int)): Number of input image channels.
+ reduce_ratio (int): Channel reduction ratio.
+ module_type (str): 'LITE' or 'NAIVE'
+ multiscale_output (bool): Whether to output multi-scale features.
+ with_fuse (bool): Whether to use fuse layers.
+ conv_cfg (dict): dictionary to construct and config conv layer.
+ norm_cfg (dict): dictionary to construct and config norm layer.
+ with_cp (bool): Use checkpoint or not. Using checkpoint will save some
+ memory while slowing down the training speed.
+ """
+
+ def __init__(
+ self,
+ num_branches,
+ num_blocks,
+ in_channels,
+ reduce_ratio,
+ module_type,
+ multiscale_output=False,
+ with_fuse=True,
+ conv_cfg=None,
+ norm_cfg=dict(type='BN'),
+ with_cp=False,
+ ):
+ super().__init__()
+ self._check_branches(num_branches, in_channels)
+
+ self.in_channels = in_channels
+ self.num_branches = num_branches
+
+ self.module_type = module_type
+ self.multiscale_output = multiscale_output
+ self.with_fuse = with_fuse
+ self.norm_cfg = norm_cfg
+ self.conv_cfg = conv_cfg
+ self.with_cp = with_cp
+
+ if self.module_type.upper() == 'LITE':
+ self.layers = self._make_weighting_blocks(num_blocks, reduce_ratio)
+ elif self.module_type.upper() == 'NAIVE':
+ self.layers = self._make_naive_branches(num_branches, num_blocks)
+ else:
+ raise ValueError("module_type should be either 'LITE' or 'NAIVE'.")
+ if self.with_fuse:
+ self.fuse_layers = self._make_fuse_layers()
+ self.relu = nn.ReLU()
+
+ def _check_branches(self, num_branches, in_channels):
+ """Check input to avoid ValueError."""
+ if num_branches != len(in_channels):
+ error_msg = f'NUM_BRANCHES({num_branches}) ' \
+ f'!= NUM_INCHANNELS({len(in_channels)})'
+ raise ValueError(error_msg)
+
+ def _make_weighting_blocks(self, num_blocks, reduce_ratio, stride=1):
+ """Make channel weighting blocks."""
+ layers = []
+ for i in range(num_blocks):
+ layers.append(
+ ConditionalChannelWeighting(
+ self.in_channels,
+ stride=stride,
+ reduce_ratio=reduce_ratio,
+ conv_cfg=self.conv_cfg,
+ norm_cfg=self.norm_cfg,
+ with_cp=self.with_cp))
+
+ return nn.Sequential(*layers)
+
+ def _make_one_branch(self, branch_index, num_blocks, stride=1):
+ """Make one branch."""
+ layers = []
+ layers.append(
+ ShuffleUnit(
+ self.in_channels[branch_index],
+ self.in_channels[branch_index],
+ stride=stride,
+ conv_cfg=self.conv_cfg,
+ norm_cfg=self.norm_cfg,
+ act_cfg=dict(type='ReLU'),
+ with_cp=self.with_cp))
+ for i in range(1, num_blocks):
+ layers.append(
+ ShuffleUnit(
+ self.in_channels[branch_index],
+ self.in_channels[branch_index],
+ stride=1,
+ conv_cfg=self.conv_cfg,
+ norm_cfg=self.norm_cfg,
+ act_cfg=dict(type='ReLU'),
+ with_cp=self.with_cp))
+
+ return nn.Sequential(*layers)
+
+ def _make_naive_branches(self, num_branches, num_blocks):
+ """Make branches."""
+ branches = []
+
+ for i in range(num_branches):
+ branches.append(self._make_one_branch(i, num_blocks))
+
+ return nn.ModuleList(branches)
+
+ def _make_fuse_layers(self):
+ """Make fuse layer."""
+ if self.num_branches == 1:
+ return None
+
+ num_branches = self.num_branches
+ in_channels = self.in_channels
+ fuse_layers = []
+ num_out_branches = num_branches if self.multiscale_output else 1
+ for i in range(num_out_branches):
+ fuse_layer = []
+ for j in range(num_branches):
+ if j > i:
+ fuse_layer.append(
+ nn.Sequential(
+ build_conv_layer(
+ self.conv_cfg,
+ in_channels[j],
+ in_channels[i],
+ kernel_size=1,
+ stride=1,
+ padding=0,
+ bias=False),
+ build_norm_layer(self.norm_cfg, in_channels[i])[1],
+ nn.Upsample(
+ scale_factor=2**(j - i), mode='nearest')))
+ elif j == i:
+ fuse_layer.append(None)
+ else:
+ conv_downsamples = []
+ for k in range(i - j):
+ if k == i - j - 1:
+ conv_downsamples.append(
+ nn.Sequential(
+ build_conv_layer(
+ self.conv_cfg,
+ in_channels[j],
+ in_channels[j],
+ kernel_size=3,
+ stride=2,
+ padding=1,
+ groups=in_channels[j],
+ bias=False),
+ build_norm_layer(self.norm_cfg,
+ in_channels[j])[1],
+ build_conv_layer(
+ self.conv_cfg,
+ in_channels[j],
+ in_channels[i],
+ kernel_size=1,
+ stride=1,
+ padding=0,
+ bias=False),
+ build_norm_layer(self.norm_cfg,
+ in_channels[i])[1]))
+ else:
+ conv_downsamples.append(
+ nn.Sequential(
+ build_conv_layer(
+ self.conv_cfg,
+ in_channels[j],
+ in_channels[j],
+ kernel_size=3,
+ stride=2,
+ padding=1,
+ groups=in_channels[j],
+ bias=False),
+ build_norm_layer(self.norm_cfg,
+ in_channels[j])[1],
+ build_conv_layer(
+ self.conv_cfg,
+ in_channels[j],
+ in_channels[j],
+ kernel_size=1,
+ stride=1,
+ padding=0,
+ bias=False),
+ build_norm_layer(self.norm_cfg,
+ in_channels[j])[1],
+ nn.ReLU(inplace=True)))
+ fuse_layer.append(nn.Sequential(*conv_downsamples))
+ fuse_layers.append(nn.ModuleList(fuse_layer))
+
+ return nn.ModuleList(fuse_layers)
+
+ def forward(self, x):
+ """Forward function."""
+ if self.num_branches == 1:
+ return [self.layers[0](x[0])]
+
+ if self.module_type.upper() == 'LITE':
+ out = self.layers(x)
+ elif self.module_type.upper() == 'NAIVE':
+ for i in range(self.num_branches):
+ x[i] = self.layers[i](x[i])
+ out = x
+
+ if self.with_fuse:
+ out_fuse = []
+ for i in range(len(self.fuse_layers)):
+ # `y = 0` will lead to decreased accuracy (0.5~1 mAP)
+ y = out[0] if i == 0 else self.fuse_layers[i][0](out[0])
+ for j in range(self.num_branches):
+ if i == j:
+ y += out[j]
+ else:
+ y += self.fuse_layers[i][j](out[j])
+ out_fuse.append(self.relu(y))
+ out = out_fuse
+ if not self.multiscale_output:
+ out = [out[0]]
+ return out
+
+
+@BACKBONES.register_module()
+class LiteHRNet(nn.Module):
+ """Lite-HRNet backbone.
+
+ `Lite-HRNet: A Lightweight High-Resolution Network
+ `_.
+
+ Code adapted from 'https://github.com/HRNet/Lite-HRNet'.
+
+ Args:
+ extra (dict): detailed configuration for each stage of HRNet.
+ in_channels (int): Number of input image channels. Default: 3.
+ conv_cfg (dict): dictionary to construct and config conv layer.
+ norm_cfg (dict): dictionary to construct and config norm layer.
+ norm_eval (bool): Whether to set norm layers to eval mode, namely,
+ freeze running stats (mean and var). Note: Effect on Batch Norm
+ and its variants only. Default: False
+ with_cp (bool): Use checkpoint or not. Using checkpoint will save some
+ memory while slowing down the training speed.
+
+ Example:
+ >>> from mmpose.models import LiteHRNet
+ >>> import torch
+ >>> extra=dict(
+ >>> stem=dict(stem_channels=32, out_channels=32, expand_ratio=1),
+ >>> num_stages=3,
+ >>> stages_spec=dict(
+ >>> num_modules=(2, 4, 2),
+ >>> num_branches=(2, 3, 4),
+ >>> num_blocks=(2, 2, 2),
+ >>> module_type=('LITE', 'LITE', 'LITE'),
+ >>> with_fuse=(True, True, True),
+ >>> reduce_ratios=(8, 8, 8),
+ >>> num_channels=(
+ >>> (40, 80),
+ >>> (40, 80, 160),
+ >>> (40, 80, 160, 320),
+ >>> )),
+ >>> with_head=False)
+ >>> self = LiteHRNet(extra, in_channels=1)
+ >>> self.eval()
+ >>> inputs = torch.rand(1, 1, 32, 32)
+ >>> level_outputs = self.forward(inputs)
+ >>> for level_out in level_outputs:
+ ... print(tuple(level_out.shape))
+ (1, 40, 8, 8)
+ """
+
+ def __init__(self,
+ extra,
+ in_channels=3,
+ conv_cfg=None,
+ norm_cfg=dict(type='BN'),
+ norm_eval=False,
+ with_cp=False):
+ super().__init__()
+ self.extra = extra
+ self.conv_cfg = conv_cfg
+ self.norm_cfg = norm_cfg
+ self.norm_eval = norm_eval
+ self.with_cp = with_cp
+
+ self.stem = Stem(
+ in_channels,
+ stem_channels=self.extra['stem']['stem_channels'],
+ out_channels=self.extra['stem']['out_channels'],
+ expand_ratio=self.extra['stem']['expand_ratio'],
+ conv_cfg=self.conv_cfg,
+ norm_cfg=self.norm_cfg)
+
+ self.num_stages = self.extra['num_stages']
+ self.stages_spec = self.extra['stages_spec']
+
+ num_channels_last = [
+ self.stem.out_channels,
+ ]
+ for i in range(self.num_stages):
+ num_channels = self.stages_spec['num_channels'][i]
+ num_channels = [num_channels[i] for i in range(len(num_channels))]
+ setattr(
+ self, f'transition{i}',
+ self._make_transition_layer(num_channels_last, num_channels))
+
+ stage, num_channels_last = self._make_stage(
+ self.stages_spec, i, num_channels, multiscale_output=True)
+ setattr(self, f'stage{i}', stage)
+
+ self.with_head = self.extra['with_head']
+ if self.with_head:
+ self.head_layer = IterativeHead(
+ in_channels=num_channels_last,
+ norm_cfg=self.norm_cfg,
+ )
+
+ def _make_transition_layer(self, num_channels_pre_layer,
+ num_channels_cur_layer):
+ """Make transition layer."""
+ num_branches_cur = len(num_channels_cur_layer)
+ num_branches_pre = len(num_channels_pre_layer)
+
+ transition_layers = []
+ for i in range(num_branches_cur):
+ if i < num_branches_pre:
+ if num_channels_cur_layer[i] != num_channels_pre_layer[i]:
+ transition_layers.append(
+ nn.Sequential(
+ build_conv_layer(
+ self.conv_cfg,
+ num_channels_pre_layer[i],
+ num_channels_pre_layer[i],
+ kernel_size=3,
+ stride=1,
+ padding=1,
+ groups=num_channels_pre_layer[i],
+ bias=False),
+ build_norm_layer(self.norm_cfg,
+ num_channels_pre_layer[i])[1],
+ build_conv_layer(
+ self.conv_cfg,
+ num_channels_pre_layer[i],
+ num_channels_cur_layer[i],
+ kernel_size=1,
+ stride=1,
+ padding=0,
+ bias=False),
+ build_norm_layer(self.norm_cfg,
+ num_channels_cur_layer[i])[1],
+ nn.ReLU()))
+ else:
+ transition_layers.append(None)
+ else:
+ conv_downsamples = []
+ for j in range(i + 1 - num_branches_pre):
+ in_channels = num_channels_pre_layer[-1]
+ out_channels = num_channels_cur_layer[i] \
+ if j == i - num_branches_pre else in_channels
+ conv_downsamples.append(
+ nn.Sequential(
+ build_conv_layer(
+ self.conv_cfg,
+ in_channels,
+ in_channels,
+ kernel_size=3,
+ stride=2,
+ padding=1,
+ groups=in_channels,
+ bias=False),
+ build_norm_layer(self.norm_cfg, in_channels)[1],
+ build_conv_layer(
+ self.conv_cfg,
+ in_channels,
+ out_channels,
+ kernel_size=1,
+ stride=1,
+ padding=0,
+ bias=False),
+ build_norm_layer(self.norm_cfg, out_channels)[1],
+ nn.ReLU()))
+ transition_layers.append(nn.Sequential(*conv_downsamples))
+
+ return nn.ModuleList(transition_layers)
+
+ def _make_stage(self,
+ stages_spec,
+ stage_index,
+ in_channels,
+ multiscale_output=True):
+ num_modules = stages_spec['num_modules'][stage_index]
+ num_branches = stages_spec['num_branches'][stage_index]
+ num_blocks = stages_spec['num_blocks'][stage_index]
+ reduce_ratio = stages_spec['reduce_ratios'][stage_index]
+ with_fuse = stages_spec['with_fuse'][stage_index]
+ module_type = stages_spec['module_type'][stage_index]
+
+ modules = []
+ for i in range(num_modules):
+ # multi_scale_output is only used last module
+ if not multiscale_output and i == num_modules - 1:
+ reset_multiscale_output = False
+ else:
+ reset_multiscale_output = True
+
+ modules.append(
+ LiteHRModule(
+ num_branches,
+ num_blocks,
+ in_channels,
+ reduce_ratio,
+ module_type,
+ multiscale_output=reset_multiscale_output,
+ with_fuse=with_fuse,
+ conv_cfg=self.conv_cfg,
+ norm_cfg=self.norm_cfg,
+ with_cp=self.with_cp))
+ in_channels = modules[-1].in_channels
+
+ return nn.Sequential(*modules), in_channels
+
+ def init_weights(self, pretrained=None):
+ """Initialize the weights in backbone.
+
+ Args:
+ pretrained (str, optional): Path to pre-trained weights.
+ Defaults to None.
+ """
+ if isinstance(pretrained, str):
+ logger = get_root_logger()
+ load_checkpoint(self, pretrained, strict=False, logger=logger)
+ elif pretrained is None:
+ for m in self.modules():
+ if isinstance(m, nn.Conv2d):
+ normal_init(m, std=0.001)
+ elif isinstance(m, (_BatchNorm, nn.GroupNorm)):
+ constant_init(m, 1)
+ else:
+ raise TypeError('pretrained must be a str or None')
+
+ def forward(self, x):
+ """Forward function."""
+ x = self.stem(x)
+
+ y_list = [x]
+ for i in range(self.num_stages):
+ x_list = []
+ transition = getattr(self, f'transition{i}')
+ for j in range(self.stages_spec['num_branches'][i]):
+ if transition[j]:
+ if j >= len(y_list):
+ x_list.append(transition[j](y_list[-1]))
+ else:
+ x_list.append(transition[j](y_list[j]))
+ else:
+ x_list.append(y_list[j])
+ y_list = getattr(self, f'stage{i}')(x_list)
+
+ x = y_list
+ if self.with_head:
+ x = self.head_layer(x)
+
+ return [x[0]]
+
+ def train(self, mode=True):
+ """Convert the model into training mode."""
+ super().train(mode)
+ if mode and self.norm_eval:
+ for m in self.modules():
+ if isinstance(m, _BatchNorm):
+ m.eval()
diff --git a/grounded-sam-osx/transformer_utils/mmpose/models/backbones/mobilenet_v2.py b/grounded-sam-osx/transformer_utils/mmpose/models/backbones/mobilenet_v2.py
new file mode 100644
index 0000000000000000000000000000000000000000..5dc0cd1b7dfdec2aa751861e39fc1c1a45ec488e
--- /dev/null
+++ b/grounded-sam-osx/transformer_utils/mmpose/models/backbones/mobilenet_v2.py
@@ -0,0 +1,275 @@
+# Copyright (c) OpenMMLab. All rights reserved.
+import copy
+import logging
+
+import torch.nn as nn
+import torch.utils.checkpoint as cp
+from mmcv.cnn import ConvModule, constant_init, kaiming_init
+from torch.nn.modules.batchnorm import _BatchNorm
+
+from ..builder import BACKBONES
+from .base_backbone import BaseBackbone
+from .utils import load_checkpoint, make_divisible
+
+
+class InvertedResidual(nn.Module):
+ """InvertedResidual block for MobileNetV2.
+
+ Args:
+ in_channels (int): The input channels of the InvertedResidual block.
+ out_channels (int): The output channels of the InvertedResidual block.
+ stride (int): Stride of the middle (first) 3x3 convolution.
+ expand_ratio (int): adjusts number of channels of the hidden layer
+ in InvertedResidual by this amount.
+ conv_cfg (dict): Config dict for convolution layer.
+ Default: None, which means using conv2d.
+ norm_cfg (dict): Config dict for normalization layer.
+ Default: dict(type='BN').
+ act_cfg (dict): Config dict for activation layer.
+ Default: dict(type='ReLU6').
+ with_cp (bool): Use checkpoint or not. Using checkpoint will save some
+ memory while slowing down the training speed. Default: False.
+ """
+
+ def __init__(self,
+ in_channels,
+ out_channels,
+ stride,
+ expand_ratio,
+ conv_cfg=None,
+ norm_cfg=dict(type='BN'),
+ act_cfg=dict(type='ReLU6'),
+ with_cp=False):
+ # Protect mutable default arguments
+ norm_cfg = copy.deepcopy(norm_cfg)
+ act_cfg = copy.deepcopy(act_cfg)
+ super().__init__()
+ self.stride = stride
+ assert stride in [1, 2], f'stride must in [1, 2]. ' \
+ f'But received {stride}.'
+ self.with_cp = with_cp
+ self.use_res_connect = self.stride == 1 and in_channels == out_channels
+ hidden_dim = int(round(in_channels * expand_ratio))
+
+ layers = []
+ if expand_ratio != 1:
+ layers.append(
+ ConvModule(
+ in_channels=in_channels,
+ out_channels=hidden_dim,
+ kernel_size=1,
+ conv_cfg=conv_cfg,
+ norm_cfg=norm_cfg,
+ act_cfg=act_cfg))
+ layers.extend([
+ ConvModule(
+ in_channels=hidden_dim,
+ out_channels=hidden_dim,
+ kernel_size=3,
+ stride=stride,
+ padding=1,
+ groups=hidden_dim,
+ conv_cfg=conv_cfg,
+ norm_cfg=norm_cfg,
+ act_cfg=act_cfg),
+ ConvModule(
+ in_channels=hidden_dim,
+ out_channels=out_channels,
+ kernel_size=1,
+ conv_cfg=conv_cfg,
+ norm_cfg=norm_cfg,
+ act_cfg=None)
+ ])
+ self.conv = nn.Sequential(*layers)
+
+ def forward(self, x):
+
+ def _inner_forward(x):
+ if self.use_res_connect:
+ return x + self.conv(x)
+ return self.conv(x)
+
+ if self.with_cp and x.requires_grad:
+ out = cp.checkpoint(_inner_forward, x)
+ else:
+ out = _inner_forward(x)
+
+ return out
+
+
+@BACKBONES.register_module()
+class MobileNetV2(BaseBackbone):
+ """MobileNetV2 backbone.
+
+ Args:
+ widen_factor (float): Width multiplier, multiply number of
+ channels in each layer by this amount. Default: 1.0.
+ out_indices (None or Sequence[int]): Output from which stages.
+ Default: (7, ).
+ frozen_stages (int): Stages to be frozen (all param fixed).
+ Default: -1, which means not freezing any parameters.
+ conv_cfg (dict): Config dict for convolution layer.
+ Default: None, which means using conv2d.
+ norm_cfg (dict): Config dict for normalization layer.
+ Default: dict(type='BN').
+ act_cfg (dict): Config dict for activation layer.
+ Default: dict(type='ReLU6').
+ norm_eval (bool): Whether to set norm layers to eval mode, namely,
+ freeze running stats (mean and var). Note: Effect on Batch Norm
+ and its variants only. Default: False.
+ with_cp (bool): Use checkpoint or not. Using checkpoint will save some
+ memory while slowing down the training speed. Default: False.
+ """
+
+ # Parameters to build layers. 4 parameters are needed to construct a
+ # layer, from left to right: expand_ratio, channel, num_blocks, stride.
+ arch_settings = [[1, 16, 1, 1], [6, 24, 2, 2], [6, 32, 3, 2],
+ [6, 64, 4, 2], [6, 96, 3, 1], [6, 160, 3, 2],
+ [6, 320, 1, 1]]
+
+ def __init__(self,
+ widen_factor=1.,
+ out_indices=(7, ),
+ frozen_stages=-1,
+ conv_cfg=None,
+ norm_cfg=dict(type='BN'),
+ act_cfg=dict(type='ReLU6'),
+ norm_eval=False,
+ with_cp=False):
+ # Protect mutable default arguments
+ norm_cfg = copy.deepcopy(norm_cfg)
+ act_cfg = copy.deepcopy(act_cfg)
+ super().__init__()
+ self.widen_factor = widen_factor
+ self.out_indices = out_indices
+ for index in out_indices:
+ if index not in range(0, 8):
+ raise ValueError('the item in out_indices must in '
+ f'range(0, 8). But received {index}')
+
+ if frozen_stages not in range(-1, 8):
+ raise ValueError('frozen_stages must be in range(-1, 8). '
+ f'But received {frozen_stages}')
+ self.out_indices = out_indices
+ self.frozen_stages = frozen_stages
+ self.conv_cfg = conv_cfg
+ self.norm_cfg = norm_cfg
+ self.act_cfg = act_cfg
+ self.norm_eval = norm_eval
+ self.with_cp = with_cp
+
+ self.in_channels = make_divisible(32 * widen_factor, 8)
+
+ self.conv1 = ConvModule(
+ in_channels=3,
+ out_channels=self.in_channels,
+ kernel_size=3,
+ stride=2,
+ padding=1,
+ conv_cfg=self.conv_cfg,
+ norm_cfg=self.norm_cfg,
+ act_cfg=self.act_cfg)
+
+ self.layers = []
+
+ for i, layer_cfg in enumerate(self.arch_settings):
+ expand_ratio, channel, num_blocks, stride = layer_cfg
+ out_channels = make_divisible(channel * widen_factor, 8)
+ inverted_res_layer = self.make_layer(
+ out_channels=out_channels,
+ num_blocks=num_blocks,
+ stride=stride,
+ expand_ratio=expand_ratio)
+ layer_name = f'layer{i + 1}'
+ self.add_module(layer_name, inverted_res_layer)
+ self.layers.append(layer_name)
+
+ if widen_factor > 1.0:
+ self.out_channel = int(1280 * widen_factor)
+ else:
+ self.out_channel = 1280
+
+ layer = ConvModule(
+ in_channels=self.in_channels,
+ out_channels=self.out_channel,
+ kernel_size=1,
+ stride=1,
+ padding=0,
+ conv_cfg=self.conv_cfg,
+ norm_cfg=self.norm_cfg,
+ act_cfg=self.act_cfg)
+ self.add_module('conv2', layer)
+ self.layers.append('conv2')
+
+ def make_layer(self, out_channels, num_blocks, stride, expand_ratio):
+ """Stack InvertedResidual blocks to build a layer for MobileNetV2.
+
+ Args:
+ out_channels (int): out_channels of block.
+ num_blocks (int): number of blocks.
+ stride (int): stride of the first block. Default: 1
+ expand_ratio (int): Expand the number of channels of the
+ hidden layer in InvertedResidual by this ratio. Default: 6.
+ """
+ layers = []
+ for i in range(num_blocks):
+ if i >= 1:
+ stride = 1
+ layers.append(
+ InvertedResidual(
+ self.in_channels,
+ out_channels,
+ stride,
+ expand_ratio=expand_ratio,
+ conv_cfg=self.conv_cfg,
+ norm_cfg=self.norm_cfg,
+ act_cfg=self.act_cfg,
+ with_cp=self.with_cp))
+ self.in_channels = out_channels
+
+ return nn.Sequential(*layers)
+
+ def init_weights(self, pretrained=None):
+ if isinstance(pretrained, str):
+ logger = logging.getLogger()
+ load_checkpoint(self, pretrained, strict=False, logger=logger)
+ elif pretrained is None:
+ for m in self.modules():
+ if isinstance(m, nn.Conv2d):
+ kaiming_init(m)
+ elif isinstance(m, (_BatchNorm, nn.GroupNorm)):
+ constant_init(m, 1)
+ else:
+ raise TypeError('pretrained must be a str or None')
+
+ def forward(self, x):
+ x = self.conv1(x)
+
+ outs = []
+ for i, layer_name in enumerate(self.layers):
+ layer = getattr(self, layer_name)
+ x = layer(x)
+ if i in self.out_indices:
+ outs.append(x)
+
+ if len(outs) == 1:
+ return outs[0]
+ return tuple(outs)
+
+ def _freeze_stages(self):
+ if self.frozen_stages >= 0:
+ for param in self.conv1.parameters():
+ param.requires_grad = False
+ for i in range(1, self.frozen_stages + 1):
+ layer = getattr(self, f'layer{i}')
+ layer.eval()
+ for param in layer.parameters():
+ param.requires_grad = False
+
+ def train(self, mode=True):
+ super().train(mode)
+ self._freeze_stages()
+ if mode and self.norm_eval:
+ for m in self.modules():
+ if isinstance(m, _BatchNorm):
+ m.eval()
diff --git a/grounded-sam-osx/transformer_utils/mmpose/models/backbones/mobilenet_v3.py b/grounded-sam-osx/transformer_utils/mmpose/models/backbones/mobilenet_v3.py
new file mode 100644
index 0000000000000000000000000000000000000000..d640abec79f06d689f2d4bc1e92999946bc07261
--- /dev/null
+++ b/grounded-sam-osx/transformer_utils/mmpose/models/backbones/mobilenet_v3.py
@@ -0,0 +1,188 @@
+# Copyright (c) OpenMMLab. All rights reserved.
+import copy
+import logging
+
+import torch.nn as nn
+from mmcv.cnn import ConvModule, constant_init, kaiming_init
+from torch.nn.modules.batchnorm import _BatchNorm
+
+from ..builder import BACKBONES
+from .base_backbone import BaseBackbone
+from .utils import InvertedResidual, load_checkpoint
+
+
+@BACKBONES.register_module()
+class MobileNetV3(BaseBackbone):
+ """MobileNetV3 backbone.
+
+ Args:
+ arch (str): Architecture of mobilnetv3, from {small, big}.
+ Default: small.
+ conv_cfg (dict): Config dict for convolution layer.
+ Default: None, which means using conv2d.
+ norm_cfg (dict): Config dict for normalization layer.
+ Default: dict(type='BN').
+ out_indices (None or Sequence[int]): Output from which stages.
+ Default: (-1, ), which means output tensors from final stage.
+ frozen_stages (int): Stages to be frozen (all param fixed).
+ Default: -1, which means not freezing any parameters.
+ norm_eval (bool): Whether to set norm layers to eval mode, namely,
+ freeze running stats (mean and var). Note: Effect on Batch Norm
+ and its variants only. Default: False.
+ with_cp (bool): Use checkpoint or not. Using checkpoint will save
+ some memory while slowing down the training speed.
+ Default: False.
+ """
+ # Parameters to build each block:
+ # [kernel size, mid channels, out channels, with_se, act type, stride]
+ arch_settings = {
+ 'small': [[3, 16, 16, True, 'ReLU', 2],
+ [3, 72, 24, False, 'ReLU', 2],
+ [3, 88, 24, False, 'ReLU', 1],
+ [5, 96, 40, True, 'HSwish', 2],
+ [5, 240, 40, True, 'HSwish', 1],
+ [5, 240, 40, True, 'HSwish', 1],
+ [5, 120, 48, True, 'HSwish', 1],
+ [5, 144, 48, True, 'HSwish', 1],
+ [5, 288, 96, True, 'HSwish', 2],
+ [5, 576, 96, True, 'HSwish', 1],
+ [5, 576, 96, True, 'HSwish', 1]],
+ 'big': [[3, 16, 16, False, 'ReLU', 1],
+ [3, 64, 24, False, 'ReLU', 2],
+ [3, 72, 24, False, 'ReLU', 1],
+ [5, 72, 40, True, 'ReLU', 2],
+ [5, 120, 40, True, 'ReLU', 1],
+ [5, 120, 40, True, 'ReLU', 1],
+ [3, 240, 80, False, 'HSwish', 2],
+ [3, 200, 80, False, 'HSwish', 1],
+ [3, 184, 80, False, 'HSwish', 1],
+ [3, 184, 80, False, 'HSwish', 1],
+ [3, 480, 112, True, 'HSwish', 1],
+ [3, 672, 112, True, 'HSwish', 1],
+ [5, 672, 160, True, 'HSwish', 1],
+ [5, 672, 160, True, 'HSwish', 2],
+ [5, 960, 160, True, 'HSwish', 1]]
+ } # yapf: disable
+
+ def __init__(self,
+ arch='small',
+ conv_cfg=None,
+ norm_cfg=dict(type='BN'),
+ out_indices=(-1, ),
+ frozen_stages=-1,
+ norm_eval=False,
+ with_cp=False):
+ # Protect mutable default arguments
+ norm_cfg = copy.deepcopy(norm_cfg)
+ super().__init__()
+ assert arch in self.arch_settings
+ for index in out_indices:
+ if index not in range(-len(self.arch_settings[arch]),
+ len(self.arch_settings[arch])):
+ raise ValueError('the item in out_indices must in '
+ f'range(0, {len(self.arch_settings[arch])}). '
+ f'But received {index}')
+
+ if frozen_stages not in range(-1, len(self.arch_settings[arch])):
+ raise ValueError('frozen_stages must be in range(-1, '
+ f'{len(self.arch_settings[arch])}). '
+ f'But received {frozen_stages}')
+ self.arch = arch
+ self.conv_cfg = conv_cfg
+ self.norm_cfg = norm_cfg
+ self.out_indices = out_indices
+ self.frozen_stages = frozen_stages
+ self.norm_eval = norm_eval
+ self.with_cp = with_cp
+
+ self.in_channels = 16
+ self.conv1 = ConvModule(
+ in_channels=3,
+ out_channels=self.in_channels,
+ kernel_size=3,
+ stride=2,
+ padding=1,
+ conv_cfg=conv_cfg,
+ norm_cfg=norm_cfg,
+ act_cfg=dict(type='HSwish'))
+
+ self.layers = self._make_layer()
+ self.feat_dim = self.arch_settings[arch][-1][2]
+
+ def _make_layer(self):
+ layers = []
+ layer_setting = self.arch_settings[self.arch]
+ for i, params in enumerate(layer_setting):
+ (kernel_size, mid_channels, out_channels, with_se, act,
+ stride) = params
+ if with_se:
+ se_cfg = dict(
+ channels=mid_channels,
+ ratio=4,
+ act_cfg=(dict(type='ReLU'), dict(type='HSigmoid')))
+ else:
+ se_cfg = None
+
+ layer = InvertedResidual(
+ in_channels=self.in_channels,
+ out_channels=out_channels,
+ mid_channels=mid_channels,
+ kernel_size=kernel_size,
+ stride=stride,
+ se_cfg=se_cfg,
+ with_expand_conv=True,
+ conv_cfg=self.conv_cfg,
+ norm_cfg=self.norm_cfg,
+ act_cfg=dict(type=act),
+ with_cp=self.with_cp)
+ self.in_channels = out_channels
+ layer_name = f'layer{i + 1}'
+ self.add_module(layer_name, layer)
+ layers.append(layer_name)
+ return layers
+
+ def init_weights(self, pretrained=None):
+ if isinstance(pretrained, str):
+ logger = logging.getLogger()
+ load_checkpoint(self, pretrained, strict=False, logger=logger)
+ elif pretrained is None:
+ for m in self.modules():
+ if isinstance(m, nn.Conv2d):
+ kaiming_init(m)
+ elif isinstance(m, nn.BatchNorm2d):
+ constant_init(m, 1)
+ else:
+ raise TypeError('pretrained must be a str or None')
+
+ def forward(self, x):
+ x = self.conv1(x)
+
+ outs = []
+ for i, layer_name in enumerate(self.layers):
+ layer = getattr(self, layer_name)
+ x = layer(x)
+ if i in self.out_indices or \
+ i - len(self.layers) in self.out_indices:
+ outs.append(x)
+
+ if len(outs) == 1:
+ return outs[0]
+ return tuple(outs)
+
+ def _freeze_stages(self):
+ if self.frozen_stages >= 0:
+ for param in self.conv1.parameters():
+ param.requires_grad = False
+ for i in range(1, self.frozen_stages + 1):
+ layer = getattr(self, f'layer{i}')
+ layer.eval()
+ for param in layer.parameters():
+ param.requires_grad = False
+
+ def train(self, mode=True):
+ super().train(mode)
+ self._freeze_stages()
+ if mode and self.norm_eval:
+ for m in self.modules():
+ if isinstance(m, _BatchNorm):
+ m.eval()
diff --git a/grounded-sam-osx/transformer_utils/mmpose/models/backbones/modules/__init__.py b/grounded-sam-osx/transformer_utils/mmpose/models/backbones/modules/__init__.py
new file mode 100644
index 0000000000000000000000000000000000000000..e69de29bb2d1d6434b8b29ae775ad8c2e48c5391
diff --git a/grounded-sam-osx/transformer_utils/mmpose/models/backbones/modules/basic_block.py b/grounded-sam-osx/transformer_utils/mmpose/models/backbones/modules/basic_block.py
new file mode 100644
index 0000000000000000000000000000000000000000..44feef44dfc43a7b40b82752d9a82df35f1108ba
--- /dev/null
+++ b/grounded-sam-osx/transformer_utils/mmpose/models/backbones/modules/basic_block.py
@@ -0,0 +1,126 @@
+# --------------------------------------------------------
+# High Resolution Transformer
+# Copyright (c) 2021 Microsoft
+# Licensed under The MIT License [see LICENSE for details]
+# Written by Rao Fu, RainbowSecret
+# --------------------------------------------------------
+
+import os
+import copy
+import logging
+import torch.nn as nn
+import torch.nn.functional as F
+import torch.utils.checkpoint as cp
+from .transformer_block import TransformerBlock
+
+from mmcv.cnn import (
+ build_conv_layer,
+ build_norm_layer,
+ build_plugin_layer,
+ constant_init,
+ kaiming_init,
+)
+
+
+class BasicBlock(nn.Module):
+ """Only replce the second 3x3 Conv with the TransformerBlocker"""
+
+ expansion = 1
+
+ def __init__(
+ self,
+ inplanes,
+ planes,
+ stride=1,
+ downsample=None,
+ with_cp=False,
+ conv_cfg=None,
+ norm_cfg=dict(type="BN"),
+ mhsa_flag=False,
+ num_heads=1,
+ num_halo_block=1,
+ num_mlp_ratio=4,
+ num_sr_ratio=1,
+ with_rpe=False,
+ with_ffn=True,
+ ):
+ super(BasicBlock, self).__init__()
+ norm_cfg = copy.deepcopy(norm_cfg)
+
+ self.in_channels = inplanes
+ self.out_channels = planes
+ self.stride = stride
+ self.with_cp = with_cp
+ self.downsample = downsample
+
+ self.norm1_name, norm1 = build_norm_layer(norm_cfg, planes, postfix=1)
+ self.norm2_name, norm2 = build_norm_layer(norm_cfg, planes, postfix=2)
+
+ self.conv1 = build_conv_layer(
+ conv_cfg,
+ inplanes,
+ planes,
+ 3,
+ stride=stride,
+ padding=1,
+ dilation=1,
+ bias=False,
+ )
+ self.add_module(self.norm1_name, norm1)
+
+ if not mhsa_flag:
+ self.conv2 = build_conv_layer(
+ conv_cfg, planes, planes, 3, padding=1, bias=False
+ )
+ self.add_module(self.norm2_name, norm2)
+ else:
+ self.conv2 = TransformerBlock(
+ planes,
+ num_heads=num_heads,
+ mlp_ratio=num_mlp_ratio,
+ sr_ratio=num_sr_ratio,
+ input_resolution=num_resolution,
+ with_rpe=with_rpe,
+ with_ffn=with_ffn,
+ )
+
+ self.relu = nn.ReLU(inplace=True)
+
+ @property
+ def norm1(self):
+ """nn.Module: normalization layer after the first convolution layer"""
+ return getattr(self, self.norm1_name)
+
+ @property
+ def norm2(self):
+ """nn.Module: normalization layer after the second convolution layer"""
+ return getattr(self, self.norm2_name)
+
+ def forward(self, x):
+ """Forward function."""
+
+ def _inner_forward(x):
+ identity = x
+
+ out = self.conv1(x)
+ out = self.norm1(out)
+ out = self.relu(out)
+
+ out = self.conv2(out)
+ out = self.norm2(out)
+
+ if self.downsample is not None:
+ identity = self.downsample(x)
+
+ out += identity
+
+ return out
+
+ if self.with_cp and x.requires_grad:
+ out = cp.checkpoint(_inner_forward, x)
+ else:
+ out = _inner_forward(x)
+
+ out = self.relu(out)
+
+ return out
diff --git a/grounded-sam-osx/transformer_utils/mmpose/models/backbones/modules/bottleneck_block.py b/grounded-sam-osx/transformer_utils/mmpose/models/backbones/modules/bottleneck_block.py
new file mode 100644
index 0000000000000000000000000000000000000000..9ccd11c24b3e10391fd751ca8a7b7e571acd7aee
--- /dev/null
+++ b/grounded-sam-osx/transformer_utils/mmpose/models/backbones/modules/bottleneck_block.py
@@ -0,0 +1,122 @@
+# --------------------------------------------------------
+# High Resolution Transformer
+# Copyright (c) 2021 Microsoft
+# Licensed under The MIT License [see LICENSE for details]
+# Written by Rao Fu, RainbowSecret
+# --------------------------------------------------------
+
+import os
+import copy
+import logging
+import torch.nn as nn
+import torch.nn.functional as F
+import torch.utils.checkpoint as cp
+
+from mmcv.cnn import build_conv_layer, build_norm_layer
+
+
+class Bottleneck(nn.Module):
+ expansion = 4
+
+ def __init__(
+ self,
+ inplanes,
+ planes,
+ stride=1,
+ downsample=None,
+ with_cp=None,
+ norm_cfg=dict(type="BN"),
+ conv_cfg=None,
+ ):
+ super(Bottleneck, self).__init__()
+ norm_cfg = copy.deepcopy(norm_cfg)
+
+ self.in_channels = inplanes
+ self.out_channels = planes
+ self.stride = stride
+ self.with_cp = with_cp
+ self.downsample = downsample
+
+ self.conv1_stride = 1
+ self.conv2_stride = stride
+
+ self.norm1_name, norm1 = build_norm_layer(norm_cfg, planes, postfix=1)
+ self.norm2_name, norm2 = build_norm_layer(norm_cfg, planes, postfix=2)
+ self.norm3_name, norm3 = build_norm_layer(
+ norm_cfg, planes * self.expansion, postfix=3
+ )
+
+ self.conv1 = build_conv_layer(
+ conv_cfg,
+ inplanes,
+ planes,
+ kernel_size=1,
+ stride=self.conv1_stride,
+ bias=False,
+ )
+ self.add_module(self.norm1_name, norm1)
+
+ self.conv2 = build_conv_layer(
+ conv_cfg,
+ planes,
+ planes,
+ kernel_size=3,
+ stride=self.conv2_stride,
+ padding=1,
+ bias=False,
+ )
+ self.add_module(self.norm2_name, norm2)
+
+ self.conv3 = build_conv_layer(
+ conv_cfg, planes, planes * self.expansion, kernel_size=1, bias=False
+ )
+ self.add_module(self.norm3_name, norm3)
+ self.relu = nn.ReLU(inplace=True)
+
+ @property
+ def norm1(self):
+ """nn.Module: normalization layer after the first convolution layer"""
+ return getattr(self, self.norm1_name)
+
+ @property
+ def norm2(self):
+ """nn.Module: normalization layer after the second convolution layer"""
+ return getattr(self, self.norm2_name)
+
+ @property
+ def norm3(self):
+ """nn.Module: normalization layer after the third convolution layer"""
+ return getattr(self, self.norm3_name)
+
+ def forward(self, x):
+ """Forward function."""
+
+ def _inner_forward(x):
+ identity = x
+
+ out = self.conv1(x)
+ out = self.norm1(out)
+ out = self.relu(out)
+
+ out = self.conv2(out)
+ out = self.norm2(out)
+ out = self.relu(out)
+
+ out = self.conv3(out)
+ out = self.norm3(out)
+
+ if self.downsample is not None:
+ identity = self.downsample(x)
+
+ out += identity
+
+ return out
+
+ if self.with_cp and x.requires_grad:
+ out = cp.checkpoint(_inner_forward, x)
+ else:
+ out = _inner_forward(x)
+
+ out = self.relu(out)
+
+ return out
diff --git a/grounded-sam-osx/transformer_utils/mmpose/models/backbones/modules/ffn_block.py b/grounded-sam-osx/transformer_utils/mmpose/models/backbones/modules/ffn_block.py
new file mode 100644
index 0000000000000000000000000000000000000000..00ef023334a3eb2ff4eb7172b4b75131d7c08262
--- /dev/null
+++ b/grounded-sam-osx/transformer_utils/mmpose/models/backbones/modules/ffn_block.py
@@ -0,0 +1,195 @@
+# --------------------------------------------------------
+# High Resolution Transformer
+# Copyright (c) 2021 Microsoft
+# Licensed under The MIT License [see LICENSE for details]
+# Written by Rao Fu, RainbowSecret
+# --------------------------------------------------------
+
+import torch
+import torch.nn as nn
+
+
+class Mlp(nn.Module):
+ def __init__(
+ self,
+ in_features,
+ hidden_features=None,
+ out_features=None,
+ act_layer=nn.GELU,
+ drop=0.0,
+ ):
+ super().__init__()
+ out_features = out_features or in_features
+ hidden_features = hidden_features or in_features
+ self.fc1 = nn.Linear(in_features, hidden_features)
+ self.act = act_layer()
+ self.fc2 = nn.Linear(hidden_features, out_features)
+ self.drop = nn.Dropout(drop)
+
+ def forward(self, x, H, W):
+ x = self.fc1(x)
+ x = self.act(x)
+ x = self.drop(x)
+ x = self.fc2(x)
+ x = self.drop(x)
+ return x
+
+
+class MlpDW(nn.Module):
+ def __init__(
+ self,
+ in_features,
+ hidden_features=None,
+ out_features=None,
+ act_layer=nn.GELU,
+ dw_act_layer=nn.GELU,
+ drop=0.0,
+ ):
+ super().__init__()
+ out_features = out_features or in_features
+ hidden_features = hidden_features or in_features
+ self.fc1 = nn.Conv2d(in_features, hidden_features, kernel_size=1)
+ self.act1 = act_layer()
+ self.dw3x3 = nn.Conv2d(
+ hidden_features,
+ hidden_features,
+ kernel_size=3,
+ stride=1,
+ groups=hidden_features,
+ padding=1,
+ )
+ self.act2 = dw_act_layer()
+ self.fc2 = nn.Conv2d(hidden_features, out_features, kernel_size=1)
+ self.drop = nn.Dropout(drop)
+
+ def forward(self, x, H, W):
+ B, N, C = x.shape
+
+ if N == (H * W + 1):
+ cls_tokens = x[:, 0, :]
+ x_ = x[:, 1:, :].permute(0, 2, 1).contiguous().reshape(B, C, H, W)
+ else:
+ x_ = x.permute(0, 2, 1).contiguous().reshape(B, C, H, W)
+
+ x_ = self.fc1(x_)
+ x_ = self.act1(x_)
+ x_ = self.dw3x3(x_)
+ x_ = self.act2(x_)
+ x_ = self.drop(x_)
+ x_ = self.fc2(x_)
+ x_ = self.drop(x_)
+ x_ = x_.reshape(B, C, -1).permute(0, 2, 1).contiguous()
+
+ if N == (H * W + 1):
+ x = torch.cat((cls_tokens.unsqueeze(1), x_), dim=1)
+ else:
+ x = x_
+
+ return x
+
+
+class MlpDWBN(nn.Module):
+ def __init__(
+ self,
+ in_features,
+ hidden_features=None,
+ out_features=None,
+ act_layer=nn.GELU,
+ dw_act_layer=nn.GELU,
+ drop=0.0,
+ ):
+ super().__init__()
+ out_features = out_features or in_features
+ hidden_features = hidden_features or in_features
+ self.fc1 = nn.Conv2d(in_features, hidden_features, kernel_size=1)
+ self.act1 = act_layer()
+ self.norm1 = nn.BatchNorm2d(hidden_features)
+ self.dw3x3 = nn.Conv2d(
+ hidden_features,
+ hidden_features,
+ kernel_size=3,
+ stride=1,
+ groups=hidden_features,
+ padding=1,
+ )
+ self.act2 = dw_act_layer()
+ self.norm2 = nn.BatchNorm2d(hidden_features)
+ self.fc2 = nn.Conv2d(hidden_features, out_features, kernel_size=1)
+ self.act3 = act_layer()
+ self.norm3 = nn.BatchNorm2d(out_features)
+ self.drop = nn.Dropout(drop)
+
+ def forward(self, x, H, W):
+ B, N, C = x.shape
+
+ if N == (H * W + 1):
+ cls_tokens = x[:, 0, :]
+ x_ = x[:, 1:, :].permute(0, 2, 1).contiguous().reshape(B, C, H, W)
+ else:
+ x_ = x.permute(0, 2, 1).contiguous().reshape(B, C, H, W)
+
+ x_ = self.fc1(x_)
+ x_ = self.norm1(x_)
+ x_ = self.act1(x_)
+ x_ = self.dw3x3(x_)
+ x_ = self.norm2(x_)
+ x_ = self.act2(x_)
+ x_ = self.drop(x_)
+ x_ = self.fc2(x_)
+ x_ = self.norm3(x_)
+ x_ = self.act3(x_)
+ x_ = self.drop(x_)
+ x_ = x_.reshape(B, C, -1).permute(0, 2, 1).contiguous()
+
+ if N == (H * W + 1):
+ x = torch.cat((cls_tokens.unsqueeze(1), x_), dim=1)
+ else:
+ x = x_
+
+ return x
+
+
+class MlpDWBN2D(nn.Module):
+ def __init__(
+ self,
+ in_features,
+ hidden_features=None,
+ out_features=None,
+ act_layer=nn.GELU,
+ dw_act_layer=nn.GELU,
+ drop=0.0,
+ ):
+ super().__init__()
+ out_features = out_features or in_features
+ hidden_features = hidden_features or in_features
+ self.fc1 = nn.Conv2d(in_features, hidden_features, kernel_size=1)
+ self.act1 = act_layer()
+ self.norm1 = nn.BatchNorm2d(hidden_features)
+ self.dw3x3 = nn.Conv2d(
+ hidden_features,
+ hidden_features,
+ kernel_size=3,
+ stride=1,
+ groups=hidden_features,
+ padding=1,
+ )
+ self.act2 = dw_act_layer()
+ self.norm2 = nn.BatchNorm2d(hidden_features)
+ self.fc2 = nn.Conv2d(hidden_features, out_features, kernel_size=1)
+ self.act3 = act_layer()
+ self.norm3 = nn.BatchNorm2d(out_features)
+ self.drop = nn.Dropout(drop)
+
+ def forward(self, x):
+ x = self.fc1(x)
+ x = self.norm1(x)
+ x = self.act1(x)
+ x = self.dw3x3(x)
+ x = self.norm2(x)
+ x = self.act2(x)
+ x = self.drop(x)
+ x = self.fc2(x)
+ x = self.norm3(x)
+ x = self.act3(x)
+ x = self.drop(x)
+ return x
diff --git a/grounded-sam-osx/transformer_utils/mmpose/models/backbones/modules/multihead_attention.py b/grounded-sam-osx/transformer_utils/mmpose/models/backbones/modules/multihead_attention.py
new file mode 100644
index 0000000000000000000000000000000000000000..d726ea377a407bdb4e8cf5d0bc44a371a1e3545b
--- /dev/null
+++ b/grounded-sam-osx/transformer_utils/mmpose/models/backbones/modules/multihead_attention.py
@@ -0,0 +1,348 @@
+# --------------------------------------------------------
+# Copyright (c) 2021 Microsoft
+# Licensed under The MIT License [see LICENSE for details]
+# Modified by RainbowSecret from:
+# https://github.com/pytorch/pytorch/blob/master/torch/nn/modules/activation.py#L852
+# --------------------------------------------------------
+
+import copy
+import math
+import warnings
+import torch
+import torch.nn.functional as F
+from torch import nn, Tensor
+from torch.nn.modules.module import Module
+from torch._jit_internal import Optional, Tuple
+from torch.overrides import has_torch_function, handle_torch_function
+from torch.nn.functional import linear, pad, softmax, dropout
+
+
+class MultiheadAttention(Module):
+ bias_k: Optional[torch.Tensor]
+ bias_v: Optional[torch.Tensor]
+
+ def __init__(
+ self,
+ embed_dim,
+ num_heads,
+ dropout=0.0,
+ bias=True,
+ add_bias_kv=False,
+ add_zero_attn=False,
+ kdim=None,
+ vdim=None,
+ ):
+ super(MultiheadAttention, self).__init__()
+ self.embed_dim = embed_dim
+ self.kdim = kdim if kdim is not None else embed_dim
+ self.vdim = vdim if vdim is not None else embed_dim
+ self._qkv_same_embed_dim = self.kdim == embed_dim and self.vdim == embed_dim
+
+ self.num_heads = num_heads
+ self.dropout = dropout
+ self.head_dim = embed_dim // num_heads
+ assert (
+ self.head_dim * num_heads == self.embed_dim
+ ), "embed_dim must be divisible by num_heads"
+
+ self.k_proj = nn.Linear(self.kdim, embed_dim, bias=bias)
+ self.v_proj = nn.Linear(self.vdim, embed_dim, bias=bias)
+ self.q_proj = nn.Linear(embed_dim, embed_dim, bias=bias)
+ self.out_proj = nn.Linear(embed_dim, embed_dim)
+
+ self.in_proj_bias = None
+ self.in_proj_weight = None
+ self.bias_k = self.bias_v = None
+ self.q_proj_weight = None
+ self.k_proj_weight = None
+ self.v_proj_weight = None
+ self.add_zero_attn = add_zero_attn
+
+ def __setstate__(self, state):
+ # Support loading old MultiheadAttention checkpoints generated by v1.1.0
+ if "_qkv_same_embed_dim" not in state:
+ state["_qkv_same_embed_dim"] = True
+
+ super(MultiheadAttention, self).__setstate__(state)
+
+ def forward(
+ self,
+ query,
+ key,
+ value,
+ key_padding_mask=None,
+ need_weights=False,
+ attn_mask=None,
+ residual_attn=None,
+ ):
+ if not self._qkv_same_embed_dim:
+ return self.multi_head_attention_forward(
+ query,
+ key,
+ value,
+ self.embed_dim,
+ self.num_heads,
+ self.in_proj_weight,
+ self.in_proj_bias,
+ self.bias_k,
+ self.bias_v,
+ self.add_zero_attn,
+ self.dropout,
+ self.out_proj.weight,
+ self.out_proj.bias,
+ training=self.training,
+ key_padding_mask=key_padding_mask,
+ need_weights=need_weights,
+ attn_mask=attn_mask,
+ use_separate_proj_weight=True,
+ q_proj_weight=self.q_proj_weight,
+ k_proj_weight=self.k_proj_weight,
+ v_proj_weight=self.v_proj_weight,
+ out_dim=self.vdim,
+ residual_attn=residual_attn,
+ )
+ else:
+ return self.multi_head_attention_forward(
+ query,
+ key,
+ value,
+ self.embed_dim,
+ self.num_heads,
+ self.in_proj_weight,
+ self.in_proj_bias,
+ self.bias_k,
+ self.bias_v,
+ self.add_zero_attn,
+ self.dropout,
+ self.out_proj.weight,
+ self.out_proj.bias,
+ training=self.training,
+ key_padding_mask=key_padding_mask,
+ need_weights=need_weights,
+ attn_mask=attn_mask,
+ out_dim=self.vdim,
+ residual_attn=residual_attn,
+ )
+
+ def multi_head_attention_forward(
+ self,
+ query: Tensor,
+ key: Tensor,
+ value: Tensor,
+ embed_dim_to_check: int,
+ num_heads: int,
+ in_proj_weight: Tensor,
+ in_proj_bias: Tensor,
+ bias_k: Optional[Tensor],
+ bias_v: Optional[Tensor],
+ add_zero_attn: bool,
+ dropout_p: float,
+ out_proj_weight: Tensor,
+ out_proj_bias: Tensor,
+ training: bool = True,
+ key_padding_mask: Optional[Tensor] = None,
+ need_weights: bool = False,
+ attn_mask: Optional[Tensor] = None,
+ use_separate_proj_weight: bool = False,
+ q_proj_weight: Optional[Tensor] = None,
+ k_proj_weight: Optional[Tensor] = None,
+ v_proj_weight: Optional[Tensor] = None,
+ static_k: Optional[Tensor] = None,
+ static_v: Optional[Tensor] = None,
+ out_dim: Optional[Tensor] = None,
+ residual_attn: Optional[Tensor] = None,
+ ) -> Tuple[Tensor, Optional[Tensor]]:
+ if not torch.jit.is_scripting():
+ tens_ops = (
+ query,
+ key,
+ value,
+ in_proj_weight,
+ in_proj_bias,
+ bias_k,
+ bias_v,
+ out_proj_weight,
+ out_proj_bias,
+ )
+ if any([type(t) is not Tensor for t in tens_ops]) and has_torch_function(
+ tens_ops
+ ):
+ return handle_torch_function(
+ multi_head_attention_forward,
+ tens_ops,
+ query,
+ key,
+ value,
+ embed_dim_to_check,
+ num_heads,
+ in_proj_weight,
+ in_proj_bias,
+ bias_k,
+ bias_v,
+ add_zero_attn,
+ dropout_p,
+ out_proj_weight,
+ out_proj_bias,
+ training=training,
+ key_padding_mask=key_padding_mask,
+ need_weights=need_weights,
+ attn_mask=attn_mask,
+ use_separate_proj_weight=use_separate_proj_weight,
+ q_proj_weight=q_proj_weight,
+ k_proj_weight=k_proj_weight,
+ v_proj_weight=v_proj_weight,
+ static_k=static_k,
+ static_v=static_v,
+ )
+ tgt_len, bsz, embed_dim = query.size()
+ key = query if key is None else key
+ value = query if value is None else value
+
+ assert embed_dim == embed_dim_to_check
+ # allow MHA to have different sizes for the feature dimension
+ assert key.size(0) == value.size(0) and key.size(1) == value.size(1)
+
+ head_dim = embed_dim // num_heads
+ v_head_dim = out_dim // num_heads
+ assert (
+ head_dim * num_heads == embed_dim
+ ), "embed_dim must be divisible by num_heads"
+ scaling = float(head_dim) ** -0.5
+
+ q = self.q_proj(query) * scaling
+ k = self.k_proj(key)
+ v = self.v_proj(value)
+
+ if attn_mask is not None:
+ assert (
+ attn_mask.dtype == torch.float32
+ or attn_mask.dtype == torch.float64
+ or attn_mask.dtype == torch.float16
+ or attn_mask.dtype == torch.uint8
+ or attn_mask.dtype == torch.bool
+ ), "Only float, byte, and bool types are supported for attn_mask, not {}".format(
+ attn_mask.dtype
+ )
+ if attn_mask.dtype == torch.uint8:
+ warnings.warn(
+ "Byte tensor for attn_mask in nn.MultiheadAttention is deprecated. Use bool tensor instead."
+ )
+ attn_mask = attn_mask.to(torch.bool)
+
+ if attn_mask.dim() == 2:
+ attn_mask = attn_mask.unsqueeze(0)
+ if list(attn_mask.size()) != [1, query.size(0), key.size(0)]:
+ raise RuntimeError("The size of the 2D attn_mask is not correct.")
+ elif attn_mask.dim() == 3:
+ if list(attn_mask.size()) != [
+ bsz * num_heads,
+ query.size(0),
+ key.size(0),
+ ]:
+ raise RuntimeError("The size of the 3D attn_mask is not correct.")
+ else:
+ raise RuntimeError(
+ "attn_mask's dimension {} is not supported".format(attn_mask.dim())
+ )
+
+ # convert ByteTensor key_padding_mask to bool
+ if key_padding_mask is not None and key_padding_mask.dtype == torch.uint8:
+ warnings.warn(
+ "Byte tensor for key_padding_mask in nn.MultiheadAttention is deprecated. Use bool tensor instead."
+ )
+ key_padding_mask = key_padding_mask.to(torch.bool)
+
+ q = q.contiguous().view(tgt_len, bsz * num_heads, head_dim).transpose(0, 1)
+ if k is not None:
+ k = k.contiguous().view(-1, bsz * num_heads, head_dim).transpose(0, 1)
+ if v is not None:
+ v = v.contiguous().view(-1, bsz * num_heads, v_head_dim).transpose(0, 1)
+
+ src_len = k.size(1)
+
+ if key_padding_mask is not None:
+ assert key_padding_mask.size(0) == bsz
+ assert key_padding_mask.size(1) == src_len
+
+ if add_zero_attn:
+ src_len += 1
+ k = torch.cat(
+ [
+ k,
+ torch.zeros(
+ (k.size(0), 1) + k.size()[2:], dtype=k.dtype, device=k.device
+ ),
+ ],
+ dim=1,
+ )
+ v = torch.cat(
+ [
+ v,
+ torch.zeros(
+ (v.size(0), 1) + v.size()[2:], dtype=v.dtype, device=v.device
+ ),
+ ],
+ dim=1,
+ )
+ if attn_mask is not None:
+ attn_mask = pad(attn_mask, (0, 1))
+ if key_padding_mask is not None:
+ key_padding_mask = pad(key_padding_mask, (0, 1))
+
+ attn_output_weights = torch.bmm(q, k.transpose(1, 2))
+ assert list(attn_output_weights.size()) == [bsz * num_heads, tgt_len, src_len]
+
+ """
+ Attention weight for the invalid region is -inf
+ """
+ if attn_mask is not None:
+ if attn_mask.dtype == torch.bool:
+ attn_output_weights.masked_fill_(attn_mask, float("-inf"))
+ else:
+ attn_output_weights += attn_mask
+
+ if key_padding_mask is not None:
+ attn_output_weights = attn_output_weights.view(
+ bsz, num_heads, tgt_len, src_len
+ )
+ attn_output_weights = attn_output_weights.masked_fill(
+ key_padding_mask.unsqueeze(1).unsqueeze(2),
+ float("-inf"),
+ )
+ attn_output_weights = attn_output_weights.view(
+ bsz * num_heads, tgt_len, src_len
+ )
+
+ if residual_attn is not None:
+ attn_output_weights = attn_output_weights.view(
+ bsz, num_heads, tgt_len, src_len
+ )
+ attn_output_weights += residual_attn.unsqueeze(0)
+ attn_output_weights = attn_output_weights.view(
+ bsz * num_heads, tgt_len, src_len
+ )
+
+ """
+ Reweight the attention map before softmax().
+ attn_output_weights: (b*n_head, n, hw)
+ """
+ attn_output_weights = softmax(attn_output_weights, dim=-1)
+ attn_output_weights = dropout(
+ attn_output_weights, p=dropout_p, training=training
+ )
+
+ attn_output = torch.bmm(attn_output_weights, v)
+ assert list(attn_output.size()) == [bsz * num_heads, tgt_len, v_head_dim]
+ attn_output = (
+ attn_output.transpose(0, 1).contiguous().view(tgt_len, bsz, out_dim)
+ )
+ attn_output = linear(attn_output, out_proj_weight, out_proj_bias)
+
+ if need_weights:
+ # average attention weights over heads
+ attn_output_weights = attn_output_weights.view(
+ bsz, num_heads, tgt_len, src_len
+ )
+ return attn_output, attn_output_weights.sum(dim=1) / num_heads
+ else:
+ return attn_output
diff --git a/grounded-sam-osx/transformer_utils/mmpose/models/backbones/modules/multihead_isa_attention.py b/grounded-sam-osx/transformer_utils/mmpose/models/backbones/modules/multihead_isa_attention.py
new file mode 100644
index 0000000000000000000000000000000000000000..deb25dfa96cc592cc58c825dc0eccd726c1592ed
--- /dev/null
+++ b/grounded-sam-osx/transformer_utils/mmpose/models/backbones/modules/multihead_isa_attention.py
@@ -0,0 +1,435 @@
+# --------------------------------------------------------
+# Copyright (c) 2021 Microsoft
+# Licensed under The MIT License [see LICENSE for details]
+# Modified by Lang Huang, RainbowSecret from:
+# https://github.com/openseg-group/openseg.pytorch/blob/master/lib/models/modules/isa_block.py
+# --------------------------------------------------------
+
+
+import copy
+import math
+import warnings
+import torch
+from torch import nn, Tensor
+from torch.nn import functional as F
+from torch._jit_internal import Optional, Tuple
+from torch.overrides import has_torch_function, handle_torch_function
+from torch.nn.functional import linear, pad, softmax, dropout
+
+from einops import rearrange
+from timm.models.layers import to_2tuple, trunc_normal_
+
+from .multihead_attention import MultiheadAttention
+
+
+class MHA_(MultiheadAttention):
+ """ "Multihead Attention with extra flags on the q/k/v and out projections."""
+
+ bias_k: Optional[torch.Tensor]
+ bias_v: Optional[torch.Tensor]
+
+ def __init__(self, *args, rpe=False, window_size=7, **kwargs):
+ super(MHA_, self).__init__(*args, **kwargs)
+
+ self.rpe = rpe
+ if rpe:
+ self.window_size = [window_size] * 2
+ # define a parameter table of relative position bias
+ # self.relative_position_bias_table = nn.Parameter(
+ # torch.zeros(
+ # (2 * self.window_size[0] - 1) * (2 * self.window_size[1] - 1),
+ # self.num_heads,
+ # )
+ # ) # 2*Wh-1 * 2*Ww-1, nH
+ # get pair-wise relative position index for each token inside the window
+ coords_h = torch.arange(self.window_size[0])
+ coords_w = torch.arange(self.window_size[1])
+ coords = torch.stack(torch.meshgrid([coords_h, coords_w])) # 2, Wh, Ww
+ coords_flatten = torch.flatten(coords, 1) # 2, Wh*Ww
+ relative_coords = (
+ coords_flatten[:, :, None] - coords_flatten[:, None, :]
+ ) # 2, Wh*Ww, Wh*Ww
+ relative_coords = relative_coords.permute(
+ 1, 2, 0
+ ).contiguous() # Wh*Ww, Wh*Ww, 2
+ relative_coords[:, :, 0] += self.window_size[0] - 1 # shift to start from 0
+ relative_coords[:, :, 1] += self.window_size[1] - 1
+ relative_coords[:, :, 0] *= 2 * self.window_size[1] - 1
+ relative_position_index = relative_coords.sum(-1) # Wh*Ww, Wh*Ww
+ self.register_buffer("relative_position_index", relative_position_index)
+ # trunc_normal_(self.relative_position_bias_table, std=0.02)
+
+ def forward(
+ self,
+ query,
+ key,
+ value,
+ key_padding_mask=None,
+ need_weights=False,
+ attn_mask=None,
+ do_qkv_proj=True,
+ do_out_proj=True,
+ rpe=True,
+ ):
+ if not self._qkv_same_embed_dim:
+ return self.multi_head_attention_forward(
+ query,
+ key,
+ value,
+ self.embed_dim,
+ self.num_heads,
+ self.in_proj_weight,
+ self.in_proj_bias,
+ self.bias_k,
+ self.bias_v,
+ self.add_zero_attn,
+ self.dropout,
+ self.out_proj.weight,
+ self.out_proj.bias,
+ training=self.training,
+ key_padding_mask=key_padding_mask,
+ need_weights=need_weights,
+ attn_mask=attn_mask,
+ use_separate_proj_weight=True,
+ q_proj_weight=self.q_proj_weight,
+ k_proj_weight=self.k_proj_weight,
+ v_proj_weight=self.v_proj_weight,
+ out_dim=self.vdim,
+ do_qkv_proj=do_qkv_proj,
+ do_out_proj=do_out_proj,
+ rpe=rpe,
+ )
+ else:
+ return self.multi_head_attention_forward(
+ query,
+ key,
+ value,
+ self.embed_dim,
+ self.num_heads,
+ self.in_proj_weight,
+ self.in_proj_bias,
+ self.bias_k,
+ self.bias_v,
+ self.add_zero_attn,
+ self.dropout,
+ self.out_proj.weight,
+ self.out_proj.bias,
+ training=self.training,
+ key_padding_mask=key_padding_mask,
+ need_weights=need_weights,
+ attn_mask=attn_mask,
+ out_dim=self.vdim,
+ do_qkv_proj=do_qkv_proj,
+ do_out_proj=do_out_proj,
+ rpe=rpe,
+ )
+
+ def multi_head_attention_forward(
+ self,
+ query: Tensor,
+ key: Tensor,
+ value: Tensor,
+ embed_dim_to_check: int,
+ num_heads: int,
+ in_proj_weight: Tensor,
+ in_proj_bias: Tensor,
+ bias_k: Optional[Tensor],
+ bias_v: Optional[Tensor],
+ add_zero_attn: bool,
+ dropout_p: float,
+ out_proj_weight: Tensor,
+ out_proj_bias: Tensor,
+ training: bool = True,
+ key_padding_mask: Optional[Tensor] = None,
+ need_weights: bool = False,
+ attn_mask: Optional[Tensor] = None,
+ use_separate_proj_weight: bool = False,
+ q_proj_weight: Optional[Tensor] = None,
+ k_proj_weight: Optional[Tensor] = None,
+ v_proj_weight: Optional[Tensor] = None,
+ static_k: Optional[Tensor] = None,
+ static_v: Optional[Tensor] = None,
+ out_dim: Optional[Tensor] = None,
+ do_qkv_proj: bool = True,
+ do_out_proj: bool = True,
+ rpe=True,
+ ) -> Tuple[Tensor, Optional[Tensor]]:
+ if not torch.jit.is_scripting():
+ tens_ops = (
+ query,
+ key,
+ value,
+ in_proj_weight,
+ in_proj_bias,
+ bias_k,
+ bias_v,
+ out_proj_weight,
+ out_proj_bias,
+ )
+ if any([type(t) is not Tensor for t in tens_ops]) and has_torch_function(
+ tens_ops
+ ):
+ return handle_torch_function(
+ multi_head_attention_forward,
+ tens_ops,
+ query,
+ key,
+ value,
+ embed_dim_to_check,
+ num_heads,
+ in_proj_weight,
+ in_proj_bias,
+ bias_k,
+ bias_v,
+ add_zero_attn,
+ dropout_p,
+ out_proj_weight,
+ out_proj_bias,
+ training=training,
+ key_padding_mask=key_padding_mask,
+ need_weights=need_weights,
+ attn_mask=attn_mask,
+ use_separate_proj_weight=use_separate_proj_weight,
+ q_proj_weight=q_proj_weight,
+ k_proj_weight=k_proj_weight,
+ v_proj_weight=v_proj_weight,
+ static_k=static_k,
+ static_v=static_v,
+ )
+ tgt_len, bsz, embed_dim = query.size()
+ key = query if key is None else key
+ value = query if value is None else value
+
+ assert embed_dim == embed_dim_to_check
+ # allow MHA to have different sizes for the feature dimension
+ assert key.size(0) == value.size(0) and key.size(1) == value.size(1)
+
+ head_dim = embed_dim // num_heads
+ v_head_dim = out_dim // num_heads
+ assert (
+ head_dim * num_heads == embed_dim
+ ), "embed_dim must be divisible by num_heads"
+ scaling = float(head_dim) ** -0.5
+
+ # whether or not use the original query/key/value
+ q = self.q_proj(query) * scaling if do_qkv_proj else query
+ k = self.k_proj(key) if do_qkv_proj else key
+ v = self.v_proj(value) if do_qkv_proj else value
+
+ if attn_mask is not None:
+ assert (
+ attn_mask.dtype == torch.float32
+ or attn_mask.dtype == torch.float64
+ or attn_mask.dtype == torch.float16
+ or attn_mask.dtype == torch.uint8
+ or attn_mask.dtype == torch.bool
+ ), "Only float, byte, and bool types are supported for attn_mask, not {}".format(
+ attn_mask.dtype
+ )
+ if attn_mask.dtype == torch.uint8:
+ warnings.warn(
+ "Byte tensor for attn_mask in nn.MultiheadAttention is deprecated. Use bool tensor instead."
+ )
+ attn_mask = attn_mask.to(torch.bool)
+
+ if attn_mask.dim() == 2:
+ attn_mask = attn_mask.unsqueeze(0)
+ if list(attn_mask.size()) != [1, query.size(0), key.size(0)]:
+ raise RuntimeError("The size of the 2D attn_mask is not correct.")
+ elif attn_mask.dim() == 3:
+ if list(attn_mask.size()) != [
+ bsz * num_heads,
+ query.size(0),
+ key.size(0),
+ ]:
+ raise RuntimeError("The size of the 3D attn_mask is not correct.")
+ else:
+ raise RuntimeError(
+ "attn_mask's dimension {} is not supported".format(attn_mask.dim())
+ )
+
+ # convert ByteTensor key_padding_mask to bool
+ if key_padding_mask is not None and key_padding_mask.dtype == torch.uint8:
+ warnings.warn(
+ "Byte tensor for key_padding_mask in nn.MultiheadAttention is deprecated. Use bool tensor instead."
+ )
+ key_padding_mask = key_padding_mask.to(torch.bool)
+
+ q = q.contiguous().view(tgt_len, bsz * num_heads, head_dim).transpose(0, 1)
+ if k is not None:
+ k = k.contiguous().view(-1, bsz * num_heads, head_dim).transpose(0, 1)
+ if v is not None:
+ v = v.contiguous().view(-1, bsz * num_heads, v_head_dim).transpose(0, 1)
+
+ src_len = k.size(1)
+
+ if key_padding_mask is not None:
+ assert key_padding_mask.size(0) == bsz
+ assert key_padding_mask.size(1) == src_len
+
+ if add_zero_attn:
+ src_len += 1
+ k = torch.cat(
+ [
+ k,
+ torch.zeros(
+ (k.size(0), 1) + k.size()[2:], dtype=k.dtype, device=k.device
+ ),
+ ],
+ dim=1,
+ )
+ v = torch.cat(
+ [
+ v,
+ torch.zeros(
+ (v.size(0), 1) + v.size()[2:], dtype=v.dtype, device=v.device
+ ),
+ ],
+ dim=1,
+ )
+ if attn_mask is not None:
+ attn_mask = pad(attn_mask, (0, 1))
+ if key_padding_mask is not None:
+ key_padding_mask = pad(key_padding_mask, (0, 1))
+
+ attn_output_weights = torch.bmm(q, k.transpose(1, 2))
+ assert list(attn_output_weights.size()) == [bsz * num_heads, tgt_len, src_len]
+
+ """
+ Add relative position embedding
+ """
+ if self.rpe and rpe:
+ # NOTE: for simplicity, we assume the src_len == tgt_len == window_size**2 here
+ # print('src, tar, window', src_len, tgt_len, self.window_size[0], self.window_size[1])
+ # assert src_len == self.window_size[0] * self.window_size[1] \
+ # and tgt_len == self.window_size[0] * self.window_size[1], \
+ # f"src{src_len}, tgt{tgt_len}, window{self.window_size[0]}"
+ # relative_position_bias = self.relative_position_bias_table[
+ # self.relative_position_index.view(-1)
+ # ].view(
+ # self.window_size[0] * self.window_size[1],
+ # self.window_size[0] * self.window_size[1],
+ # -1,
+ # ) # Wh*Ww,Wh*Ww,nH
+ # relative_position_bias = relative_position_bias.permute(
+ # 2, 0, 1
+ # ).contiguous() # nH, Wh*Ww, Wh*Ww
+ # HELLO!!!!!
+ attn_output_weights = attn_output_weights.view(
+ bsz, num_heads, tgt_len, src_len
+ ) # + relative_position_bias.unsqueeze(0)
+ attn_output_weights = attn_output_weights.view(
+ bsz * num_heads, tgt_len, src_len
+ )
+
+ """
+ Attention weight for the invalid region is -inf
+ """
+ if attn_mask is not None:
+ if attn_mask.dtype == torch.bool:
+ attn_output_weights.masked_fill_(attn_mask, float("-inf"))
+ else:
+ attn_output_weights += attn_mask
+
+ if key_padding_mask is not None:
+ attn_output_weights = attn_output_weights.view(
+ bsz, num_heads, tgt_len, src_len
+ )
+ attn_output_weights = attn_output_weights.masked_fill(
+ key_padding_mask.unsqueeze(1).unsqueeze(2),
+ float("-inf"),
+ )
+ attn_output_weights = attn_output_weights.view(
+ bsz * num_heads, tgt_len, src_len
+ )
+
+ """
+ Reweight the attention map before softmax().
+ attn_output_weights: (b*n_head, n, hw)
+ """
+ attn_output_weights = softmax(attn_output_weights, dim=-1)
+ attn_output_weights = dropout(
+ attn_output_weights, p=dropout_p, training=training
+ )
+
+ attn_output = torch.bmm(attn_output_weights, v)
+ assert list(attn_output.size()) == [bsz * num_heads, tgt_len, v_head_dim]
+ attn_output = (
+ attn_output.transpose(0, 1).contiguous().view(tgt_len, bsz, out_dim)
+ )
+ if do_out_proj:
+ attn_output = linear(attn_output, out_proj_weight, out_proj_bias)
+
+ if need_weights:
+ # average attention weights over heads
+ attn_output_weights = attn_output_weights.view(
+ bsz, num_heads, tgt_len, src_len
+ )
+ return attn_output, q, k, attn_output_weights.sum(dim=1) / num_heads
+ else:
+ return attn_output, q, k # additionaly return the query and key
+
+
+class PadBlock(object):
+ """ "Make the size of feature map divisible by local group size."""
+
+ def __init__(self, local_group_size=7):
+ self.lgs = local_group_size
+ if not isinstance(self.lgs, (tuple, list)):
+ self.lgs = to_2tuple(self.lgs)
+ assert len(self.lgs) == 2
+
+ def pad_if_needed(self, x, size):
+ n, h, w, c = size
+ pad_h = math.ceil(h / self.lgs[0]) * self.lgs[0] - h
+ pad_w = math.ceil(w / self.lgs[1]) * self.lgs[1] - w
+ if pad_h > 0 or pad_w > 0: # center-pad the feature on H and W axes
+ return F.pad(
+ x,
+ (0, 0, pad_w // 2, pad_w - pad_w // 2, pad_h // 2, pad_h - pad_h // 2),
+ )
+ return x
+
+ def depad_if_needed(self, x, size):
+ n, h, w, c = size
+ pad_h = math.ceil(h / self.lgs[0]) * self.lgs[0] - h
+ pad_w = math.ceil(w / self.lgs[1]) * self.lgs[1] - w
+ if pad_h > 0 or pad_w > 0: # remove the center-padding on feature
+ return x[:, pad_h // 2 : pad_h // 2 + h, pad_w // 2 : pad_w // 2 + w, :]
+ return x
+
+
+class LocalPermuteModule(object):
+ """ "Permute the feature map to gather pixels in local groups, and the reverse permutation"""
+
+ def __init__(self, local_group_size=7):
+ self.lgs = local_group_size
+ if not isinstance(self.lgs, (tuple, list)):
+ self.lgs = to_2tuple(self.lgs)
+ assert len(self.lgs) == 2
+
+ def permute(self, x, size):
+ n, h, w, c = size
+ return rearrange(
+ x,
+ "n (qh ph) (qw pw) c -> (ph pw) (n qh qw) c",
+ n=n,
+ qh=h // self.lgs[0],
+ ph=self.lgs[0],
+ qw=w // self.lgs[0],
+ pw=self.lgs[0],
+ c=c,
+ )
+
+ def rev_permute(self, x, size):
+ n, h, w, c = size
+ return rearrange(
+ x,
+ "(ph pw) (n qh qw) c -> n (qh ph) (qw pw) c",
+ n=n,
+ qh=h // self.lgs[0],
+ ph=self.lgs[0],
+ qw=w // self.lgs[0],
+ pw=self.lgs[0],
+ c=c,
+ )
diff --git a/grounded-sam-osx/transformer_utils/mmpose/models/backbones/modules/multihead_isa_pool_attention.py b/grounded-sam-osx/transformer_utils/mmpose/models/backbones/modules/multihead_isa_pool_attention.py
new file mode 100644
index 0000000000000000000000000000000000000000..3b039022102a9a26fc1210e24910edd6d9ada560
--- /dev/null
+++ b/grounded-sam-osx/transformer_utils/mmpose/models/backbones/modules/multihead_isa_pool_attention.py
@@ -0,0 +1,59 @@
+# --------------------------------------------------------
+# Copyright (c) 2021 Microsoft
+# Licensed under The MIT License [see LICENSE for details]
+# Modified by Lang Huang, RainbowSecret from:
+# https://github.com/openseg-group/openseg.pytorch/blob/master/lib/models/modules/isa_block.py
+# --------------------------------------------------------
+
+import os
+import pdb
+import math
+import torch
+import torch.nn as nn
+
+from .multihead_isa_attention import MHA_, PadBlock, LocalPermuteModule
+
+
+class InterlacedPoolAttention(nn.Module):
+ r"""interlaced sparse multi-head self attention (ISA) module with relative position bias.
+ Args:
+ dim (int): Number of input channels.
+ window_size (tuple[int]): Window size.
+ num_heads (int): Number of attention heads.
+ qkv_bias (bool, optional): If True, add a learnable bias to query, key, value. Default: True
+ qk_scale (float | None, optional): Override default qk scale of head_dim ** -0.5 if set
+ attn_drop (float, optional): Dropout ratio of attention weight. Default: 0.0
+ proj_drop (float, optional): Dropout ratio of output. Default: 0.0
+ """
+
+ def __init__(self, embed_dim, num_heads, window_size=7, rpe=True, **kwargs):
+ super(InterlacedPoolAttention, self).__init__()
+
+ self.dim = embed_dim
+ self.num_heads = num_heads
+ self.window_size = window_size
+ self.with_rpe = rpe
+
+ self.attn = MHA_(
+ embed_dim, num_heads, rpe=rpe, window_size=window_size, **kwargs
+ )
+ self.pad_helper = PadBlock(window_size)
+ self.permute_helper = LocalPermuteModule(window_size)
+
+ def forward(self, x, H, W, **kwargs):
+ B, N, C = x.shape
+ x = x.view(B, H, W, C)
+ # attention
+ # pad
+ x_pad = self.pad_helper.pad_if_needed(x, x.size())
+ # permute
+ x_permute = self.permute_helper.permute(x_pad, x_pad.size())
+ # attention
+ out, _, _ = self.attn(
+ x_permute, x_permute, x_permute, rpe=self.with_rpe, **kwargs
+ )
+ # reverse permutation
+ out = self.permute_helper.rev_permute(out, x_pad.size())
+ # de-pad, pooling with `ceil_mode=True` will do implicit padding, so we need to remove it, too
+ out = self.pad_helper.depad_if_needed(out, x.size())
+ return out.reshape(B, N, C)
diff --git a/grounded-sam-osx/transformer_utils/mmpose/models/backbones/modules/transformer_block.py b/grounded-sam-osx/transformer_utils/mmpose/models/backbones/modules/transformer_block.py
new file mode 100644
index 0000000000000000000000000000000000000000..9571e8c70843662d466d3903acc5d54eab27bd4c
--- /dev/null
+++ b/grounded-sam-osx/transformer_utils/mmpose/models/backbones/modules/transformer_block.py
@@ -0,0 +1,211 @@
+# --------------------------------------------------------
+# High Resolution Transformer
+# Copyright (c) 2021 Microsoft
+# Licensed under The MIT License [see LICENSE for details]
+# Written by Rao Fu, RainbowSecret
+# --------------------------------------------------------
+
+import os
+import math
+import logging
+import torch
+import torch.nn as nn
+from functools import partial
+
+from .multihead_isa_pool_attention import InterlacedPoolAttention
+
+from mmcv.cnn import build_conv_layer, build_norm_layer
+
+BN_MOMENTUM = 0.1
+
+
+def drop_path(x, drop_prob: float = 0.0, training: bool = False):
+ """Drop paths (Stochastic Depth) per sample (when applied in main path of residual blocks).
+ This is the same as the DropConnect impl I created for EfficientNet, etc networks, however,
+ the original name is misleading as 'Drop Connect' is a different form of dropout in a separate paper...
+ See discussion: https://github.com/tensorflow/tpu/issues/494#issuecomment-532968956 ... I've opted for
+ changing the layer and argument names to 'drop path' rather than mix DropConnect as a layer name and use
+ 'survival rate' as the argument.
+ """
+ if drop_prob == 0.0 or not training:
+ return x
+ keep_prob = 1 - drop_prob
+ shape = (x.shape[0],) + (1,) * (
+ x.ndim - 1
+ ) # work with diff dim tensors, not just 2D ConvNets
+ random_tensor = keep_prob + torch.rand(shape, dtype=x.dtype, device=x.device)
+ random_tensor.floor_() # binarize
+ output = x.div(keep_prob) * random_tensor
+ return output
+
+
+class DropPath(nn.Module):
+ """Drop paths (Stochastic Depth) per sample (when applied in main path of residual blocks)."""
+
+ def __init__(self, drop_prob=None):
+ super(DropPath, self).__init__()
+ self.drop_prob = drop_prob
+
+ def forward(self, x):
+ return drop_path(x, self.drop_prob, self.training)
+
+ def extra_repr(self):
+ # (Optional)Set the extra information about this module. You can test
+ # it by printing an object of this class.
+ return "drop_prob={}".format(self.drop_prob)
+
+
+class MlpDWBN(nn.Module):
+ def __init__(
+ self,
+ in_features,
+ hidden_features=None,
+ out_features=None,
+ act_layer=nn.GELU,
+ dw_act_layer=nn.GELU,
+ drop=0.0,
+ conv_cfg=None,
+ norm_cfg=dict(type="BN", requires_grad=True),
+ ):
+ super().__init__()
+ out_features = out_features or in_features
+ hidden_features = hidden_features or in_features
+ self.fc1 = build_conv_layer(
+ conv_cfg,
+ in_features,
+ hidden_features,
+ kernel_size=1,
+ stride=1,
+ padding=0,
+ bias=True,
+ )
+ self.act1 = act_layer()
+ self.norm1 = build_norm_layer(norm_cfg, hidden_features)[1]
+ self.dw3x3 = build_conv_layer(
+ conv_cfg,
+ hidden_features,
+ hidden_features,
+ kernel_size=3,
+ stride=1,
+ padding=1,
+ groups=hidden_features,
+ )
+ self.act2 = dw_act_layer()
+ self.norm2 = build_norm_layer(norm_cfg, hidden_features)[1]
+ self.fc2 = build_conv_layer(
+ conv_cfg,
+ hidden_features,
+ out_features,
+ kernel_size=1,
+ stride=1,
+ padding=0,
+ bias=True,
+ )
+ self.act3 = act_layer()
+ self.norm3 = build_norm_layer(norm_cfg, out_features)[1]
+ # self.drop = nn.Dropout(drop, inplace=True)
+
+ def forward(self, x, H, W):
+ if len(x.shape) == 3:
+ B, N, C = x.shape
+ if N == (H * W + 1):
+ cls_tokens = x[:, 0, :]
+ x_ = x[:, 1:, :].permute(0, 2, 1).contiguous().reshape(B, C, H, W)
+ else:
+ x_ = x.permute(0, 2, 1).contiguous().reshape(B, C, H, W)
+
+ x_ = self.fc1(x_)
+ x_ = self.norm1(x_)
+ x_ = self.act1(x_)
+ x_ = self.dw3x3(x_)
+ x_ = self.norm2(x_)
+ x_ = self.act2(x_)
+ # x_ = self.drop(x_)
+ x_ = self.fc2(x_)
+ x_ = self.norm3(x_)
+ x_ = self.act3(x_)
+ # x_ = self.drop(x_)
+ x_ = x_.reshape(B, C, -1).permute(0, 2, 1).contiguous()
+ if N == (H * W + 1):
+ x = torch.cat((cls_tokens.unsqueeze(1), x_), dim=1)
+ else:
+ x = x_
+ return x
+
+ elif len(x.shape) == 4:
+ x = self.fc1(x)
+ x = self.norm1(x)
+ x = self.act1(x)
+ x = self.dw3x3(x)
+ x = self.norm2(x)
+ x = self.act2(x)
+ x = self.drop(x)
+ x = self.fc2(x)
+ x = self.norm3(x)
+ x = self.act3(x)
+ x = self.drop(x)
+ return x
+
+ else:
+ raise RuntimeError("Unsupported input shape: {}".format(x.shape))
+
+
+class GeneralTransformerBlock(nn.Module):
+ expansion = 1
+
+ def __init__(
+ self,
+ inplanes,
+ planes,
+ num_heads,
+ window_size=7,
+ mlp_ratio=4.0,
+ qkv_bias=True,
+ qk_scale=None,
+ drop=0.0,
+ attn_drop=0.0,
+ drop_path=0.0,
+ act_layer=nn.GELU,
+ norm_layer=partial(nn.LayerNorm, eps=1e-6),
+ conv_cfg=None,
+ norm_cfg=dict(type="BN", requires_grad=True),
+ ):
+ super().__init__()
+ self.dim = inplanes
+ self.out_dim = planes
+ self.num_heads = num_heads
+ self.window_size = window_size
+ self.mlp_ratio = mlp_ratio
+ self.conv_cfg = conv_cfg
+ self.norm_cfg = norm_cfg
+
+ self.attn = InterlacedPoolAttention(
+ self.dim, num_heads=num_heads, window_size=window_size, dropout=attn_drop
+ )
+
+ self.norm1 = norm_layer(self.dim)
+ self.norm2 = norm_layer(self.out_dim)
+ self.drop_path = DropPath(drop_path) if drop_path > 0.0 else nn.Identity()
+ mlp_hidden_dim = int(self.dim * mlp_ratio)
+ self.mlp = MlpDWBN(
+ in_features=self.dim,
+ hidden_features=mlp_hidden_dim,
+ out_features=self.out_dim,
+ act_layer=act_layer,
+ dw_act_layer=act_layer,
+ drop=drop,
+ conv_cfg=conv_cfg,
+ norm_cfg=norm_cfg,
+ )
+
+ def forward(self, x):
+ B, C, H, W = x.size()
+ # reshape
+ x = x.view(B, C, -1).permute(0, 2, 1).contiguous()
+ # Attention
+ x = x + self.drop_path(self.attn(self.norm1(x), H, W))
+ # FFN
+ x = x + self.drop_path(self.mlp(self.norm2(x), H, W))
+ # reshape
+ x = x.permute(0, 2, 1).contiguous().view(B, C, H, W)
+ return x
diff --git a/grounded-sam-osx/transformer_utils/mmpose/models/backbones/mspn.py b/grounded-sam-osx/transformer_utils/mmpose/models/backbones/mspn.py
new file mode 100644
index 0000000000000000000000000000000000000000..71cee34e399780e8b67eac43d862b65a3ce05412
--- /dev/null
+++ b/grounded-sam-osx/transformer_utils/mmpose/models/backbones/mspn.py
@@ -0,0 +1,513 @@
+# Copyright (c) OpenMMLab. All rights reserved.
+import copy as cp
+from collections import OrderedDict
+
+import torch.nn as nn
+import torch.nn.functional as F
+from mmcv.cnn import (ConvModule, MaxPool2d, constant_init, kaiming_init,
+ normal_init)
+from mmcv.runner.checkpoint import load_state_dict
+
+from mmpose.utils import get_root_logger
+from ..builder import BACKBONES
+from .base_backbone import BaseBackbone
+from .resnet import Bottleneck as _Bottleneck
+from .utils.utils import get_state_dict
+
+
+class Bottleneck(_Bottleneck):
+ expansion = 4
+ """Bottleneck block for MSPN.
+
+ Args:
+ in_channels (int): Input channels of this block.
+ out_channels (int): Output channels of this block.
+ stride (int): stride of the block. Default: 1
+ downsample (nn.Module): downsample operation on identity branch.
+ Default: None
+ norm_cfg (dict): dictionary to construct and config norm layer.
+ Default: dict(type='BN')
+ """
+
+ def __init__(self, in_channels, out_channels, **kwargs):
+ super().__init__(in_channels, out_channels * 4, **kwargs)
+
+
+class DownsampleModule(nn.Module):
+ """Downsample module for MSPN.
+
+ Args:
+ block (nn.Module): Downsample block.
+ num_blocks (list): Number of blocks in each downsample unit.
+ num_units (int): Numbers of downsample units. Default: 4
+ has_skip (bool): Have skip connections from prior upsample
+ module or not. Default:False
+ norm_cfg (dict): dictionary to construct and config norm layer.
+ Default: dict(type='BN')
+ in_channels (int): Number of channels of the input feature to
+ downsample module. Default: 64
+ """
+
+ def __init__(self,
+ block,
+ num_blocks,
+ num_units=4,
+ has_skip=False,
+ norm_cfg=dict(type='BN'),
+ in_channels=64):
+ # Protect mutable default arguments
+ norm_cfg = cp.deepcopy(norm_cfg)
+ super().__init__()
+ self.has_skip = has_skip
+ self.in_channels = in_channels
+ assert len(num_blocks) == num_units
+ self.num_blocks = num_blocks
+ self.num_units = num_units
+ self.norm_cfg = norm_cfg
+ self.layer1 = self._make_layer(block, in_channels, num_blocks[0])
+ for i in range(1, num_units):
+ module_name = f'layer{i + 1}'
+ self.add_module(
+ module_name,
+ self._make_layer(
+ block, in_channels * pow(2, i), num_blocks[i], stride=2))
+
+ def _make_layer(self, block, out_channels, blocks, stride=1):
+ downsample = None
+ if stride != 1 or self.in_channels != out_channels * block.expansion:
+ downsample = ConvModule(
+ self.in_channels,
+ out_channels * block.expansion,
+ kernel_size=1,
+ stride=stride,
+ padding=0,
+ norm_cfg=self.norm_cfg,
+ act_cfg=None,
+ inplace=True)
+
+ units = list()
+ units.append(
+ block(
+ self.in_channels,
+ out_channels,
+ stride=stride,
+ downsample=downsample,
+ norm_cfg=self.norm_cfg))
+ self.in_channels = out_channels * block.expansion
+ for _ in range(1, blocks):
+ units.append(block(self.in_channels, out_channels))
+
+ return nn.Sequential(*units)
+
+ def forward(self, x, skip1, skip2):
+ out = list()
+ for i in range(self.num_units):
+ module_name = f'layer{i + 1}'
+ module_i = getattr(self, module_name)
+ x = module_i(x)
+ if self.has_skip:
+ x = x + skip1[i] + skip2[i]
+ out.append(x)
+ out.reverse()
+
+ return tuple(out)
+
+
+class UpsampleUnit(nn.Module):
+ """Upsample unit for upsample module.
+
+ Args:
+ ind (int): Indicates whether to interpolate (>0) and whether to
+ generate feature map for the next hourglass-like module.
+ num_units (int): Number of units that form a upsample module. Along
+ with ind and gen_cross_conv, nm_units is used to decide whether
+ to generate feature map for the next hourglass-like module.
+ in_channels (int): Channel number of the skip-in feature maps from
+ the corresponding downsample unit.
+ unit_channels (int): Channel number in this unit. Default:256.
+ gen_skip: (bool): Whether or not to generate skips for the posterior
+ downsample module. Default:False
+ gen_cross_conv (bool): Whether to generate feature map for the next
+ hourglass-like module. Default:False
+ norm_cfg (dict): dictionary to construct and config norm layer.
+ Default: dict(type='BN')
+ out_channels (int): Number of channels of feature output by upsample
+ module. Must equal to in_channels of downsample module. Default:64
+ """
+
+ def __init__(self,
+ ind,
+ num_units,
+ in_channels,
+ unit_channels=256,
+ gen_skip=False,
+ gen_cross_conv=False,
+ norm_cfg=dict(type='BN'),
+ out_channels=64):
+ # Protect mutable default arguments
+ norm_cfg = cp.deepcopy(norm_cfg)
+ super().__init__()
+ self.num_units = num_units
+ self.norm_cfg = norm_cfg
+ self.in_skip = ConvModule(
+ in_channels,
+ unit_channels,
+ kernel_size=1,
+ stride=1,
+ padding=0,
+ norm_cfg=self.norm_cfg,
+ act_cfg=None,
+ inplace=True)
+ self.relu = nn.ReLU(inplace=True)
+
+ self.ind = ind
+ if self.ind > 0:
+ self.up_conv = ConvModule(
+ unit_channels,
+ unit_channels,
+ kernel_size=1,
+ stride=1,
+ padding=0,
+ norm_cfg=self.norm_cfg,
+ act_cfg=None,
+ inplace=True)
+
+ self.gen_skip = gen_skip
+ if self.gen_skip:
+ self.out_skip1 = ConvModule(
+ in_channels,
+ in_channels,
+ kernel_size=1,
+ stride=1,
+ padding=0,
+ norm_cfg=self.norm_cfg,
+ inplace=True)
+
+ self.out_skip2 = ConvModule(
+ unit_channels,
+ in_channels,
+ kernel_size=1,
+ stride=1,
+ padding=0,
+ norm_cfg=self.norm_cfg,
+ inplace=True)
+
+ self.gen_cross_conv = gen_cross_conv
+ if self.ind == num_units - 1 and self.gen_cross_conv:
+ self.cross_conv = ConvModule(
+ unit_channels,
+ out_channels,
+ kernel_size=1,
+ stride=1,
+ padding=0,
+ norm_cfg=self.norm_cfg,
+ inplace=True)
+
+ def forward(self, x, up_x):
+ out = self.in_skip(x)
+
+ if self.ind > 0:
+ up_x = F.interpolate(
+ up_x,
+ size=(x.size(2), x.size(3)),
+ mode='bilinear',
+ align_corners=True)
+ up_x = self.up_conv(up_x)
+ out = out + up_x
+ out = self.relu(out)
+
+ skip1 = None
+ skip2 = None
+ if self.gen_skip:
+ skip1 = self.out_skip1(x)
+ skip2 = self.out_skip2(out)
+
+ cross_conv = None
+ if self.ind == self.num_units - 1 and self.gen_cross_conv:
+ cross_conv = self.cross_conv(out)
+
+ return out, skip1, skip2, cross_conv
+
+
+class UpsampleModule(nn.Module):
+ """Upsample module for MSPN.
+
+ Args:
+ unit_channels (int): Channel number in the upsample units.
+ Default:256.
+ num_units (int): Numbers of upsample units. Default: 4
+ gen_skip (bool): Whether to generate skip for posterior downsample
+ module or not. Default:False
+ gen_cross_conv (bool): Whether to generate feature map for the next
+ hourglass-like module. Default:False
+ norm_cfg (dict): dictionary to construct and config norm layer.
+ Default: dict(type='BN')
+ out_channels (int): Number of channels of feature output by upsample
+ module. Must equal to in_channels of downsample module. Default:64
+ """
+
+ def __init__(self,
+ unit_channels=256,
+ num_units=4,
+ gen_skip=False,
+ gen_cross_conv=False,
+ norm_cfg=dict(type='BN'),
+ out_channels=64):
+ # Protect mutable default arguments
+ norm_cfg = cp.deepcopy(norm_cfg)
+ super().__init__()
+ self.in_channels = list()
+ for i in range(num_units):
+ self.in_channels.append(Bottleneck.expansion * out_channels *
+ pow(2, i))
+ self.in_channels.reverse()
+ self.num_units = num_units
+ self.gen_skip = gen_skip
+ self.gen_cross_conv = gen_cross_conv
+ self.norm_cfg = norm_cfg
+ for i in range(num_units):
+ module_name = f'up{i + 1}'
+ self.add_module(
+ module_name,
+ UpsampleUnit(
+ i,
+ self.num_units,
+ self.in_channels[i],
+ unit_channels,
+ self.gen_skip,
+ self.gen_cross_conv,
+ norm_cfg=self.norm_cfg,
+ out_channels=64))
+
+ def forward(self, x):
+ out = list()
+ skip1 = list()
+ skip2 = list()
+ cross_conv = None
+ for i in range(self.num_units):
+ module_i = getattr(self, f'up{i + 1}')
+ if i == 0:
+ outi, skip1_i, skip2_i, _ = module_i(x[i], None)
+ elif i == self.num_units - 1:
+ outi, skip1_i, skip2_i, cross_conv = module_i(x[i], out[i - 1])
+ else:
+ outi, skip1_i, skip2_i, _ = module_i(x[i], out[i - 1])
+ out.append(outi)
+ skip1.append(skip1_i)
+ skip2.append(skip2_i)
+ skip1.reverse()
+ skip2.reverse()
+
+ return out, skip1, skip2, cross_conv
+
+
+class SingleStageNetwork(nn.Module):
+ """Single_stage Network.
+
+ Args:
+ unit_channels (int): Channel number in the upsample units. Default:256.
+ num_units (int): Numbers of downsample/upsample units. Default: 4
+ gen_skip (bool): Whether to generate skip for posterior downsample
+ module or not. Default:False
+ gen_cross_conv (bool): Whether to generate feature map for the next
+ hourglass-like module. Default:False
+ has_skip (bool): Have skip connections from prior upsample
+ module or not. Default:False
+ num_blocks (list): Number of blocks in each downsample unit.
+ Default: [2, 2, 2, 2] Note: Make sure num_units==len(num_blocks)
+ norm_cfg (dict): dictionary to construct and config norm layer.
+ Default: dict(type='BN')
+ in_channels (int): Number of channels of the feature from ResNetTop.
+ Default: 64.
+ """
+
+ def __init__(self,
+ has_skip=False,
+ gen_skip=False,
+ gen_cross_conv=False,
+ unit_channels=256,
+ num_units=4,
+ num_blocks=[2, 2, 2, 2],
+ norm_cfg=dict(type='BN'),
+ in_channels=64):
+ # Protect mutable default arguments
+ norm_cfg = cp.deepcopy(norm_cfg)
+ num_blocks = cp.deepcopy(num_blocks)
+ super().__init__()
+ assert len(num_blocks) == num_units
+ self.has_skip = has_skip
+ self.gen_skip = gen_skip
+ self.gen_cross_conv = gen_cross_conv
+ self.num_units = num_units
+ self.unit_channels = unit_channels
+ self.num_blocks = num_blocks
+ self.norm_cfg = norm_cfg
+
+ self.downsample = DownsampleModule(Bottleneck, num_blocks, num_units,
+ has_skip, norm_cfg, in_channels)
+ self.upsample = UpsampleModule(unit_channels, num_units, gen_skip,
+ gen_cross_conv, norm_cfg, in_channels)
+
+ def forward(self, x, skip1, skip2):
+ mid = self.downsample(x, skip1, skip2)
+ out, skip1, skip2, cross_conv = self.upsample(mid)
+
+ return out, skip1, skip2, cross_conv
+
+
+class ResNetTop(nn.Module):
+ """ResNet top for MSPN.
+
+ Args:
+ norm_cfg (dict): dictionary to construct and config norm layer.
+ Default: dict(type='BN')
+ channels (int): Number of channels of the feature output by ResNetTop.
+ """
+
+ def __init__(self, norm_cfg=dict(type='BN'), channels=64):
+ # Protect mutable default arguments
+ norm_cfg = cp.deepcopy(norm_cfg)
+ super().__init__()
+ self.top = nn.Sequential(
+ ConvModule(
+ 3,
+ channels,
+ kernel_size=7,
+ stride=2,
+ padding=3,
+ norm_cfg=norm_cfg,
+ inplace=True), MaxPool2d(kernel_size=3, stride=2, padding=1))
+
+ def forward(self, img):
+ return self.top(img)
+
+
+@BACKBONES.register_module()
+class MSPN(BaseBackbone):
+ """MSPN backbone. Paper ref: Li et al. "Rethinking on Multi-Stage Networks
+ for Human Pose Estimation" (CVPR 2020).
+
+ Args:
+ unit_channels (int): Number of Channels in an upsample unit.
+ Default: 256
+ num_stages (int): Number of stages in a multi-stage MSPN. Default: 4
+ num_units (int): Number of downsample/upsample units in a single-stage
+ network. Default: 4
+ Note: Make sure num_units == len(self.num_blocks)
+ num_blocks (list): Number of bottlenecks in each
+ downsample unit. Default: [2, 2, 2, 2]
+ norm_cfg (dict): dictionary to construct and config norm layer.
+ Default: dict(type='BN')
+ res_top_channels (int): Number of channels of feature from ResNetTop.
+ Default: 64.
+
+ Example:
+ >>> from mmpose.models import MSPN
+ >>> import torch
+ >>> self = MSPN(num_stages=2,num_units=2,num_blocks=[2,2])
+ >>> self.eval()
+ >>> inputs = torch.rand(1, 3, 511, 511)
+ >>> level_outputs = self.forward(inputs)
+ >>> for level_output in level_outputs:
+ ... for feature in level_output:
+ ... print(tuple(feature.shape))
+ ...
+ (1, 256, 64, 64)
+ (1, 256, 128, 128)
+ (1, 256, 64, 64)
+ (1, 256, 128, 128)
+ """
+
+ def __init__(self,
+ unit_channels=256,
+ num_stages=4,
+ num_units=4,
+ num_blocks=[2, 2, 2, 2],
+ norm_cfg=dict(type='BN'),
+ res_top_channels=64):
+ # Protect mutable default arguments
+ norm_cfg = cp.deepcopy(norm_cfg)
+ num_blocks = cp.deepcopy(num_blocks)
+ super().__init__()
+ self.unit_channels = unit_channels
+ self.num_stages = num_stages
+ self.num_units = num_units
+ self.num_blocks = num_blocks
+ self.norm_cfg = norm_cfg
+
+ assert self.num_stages > 0
+ assert self.num_units > 1
+ assert self.num_units == len(self.num_blocks)
+ self.top = ResNetTop(norm_cfg=norm_cfg)
+ self.multi_stage_mspn = nn.ModuleList([])
+ for i in range(self.num_stages):
+ if i == 0:
+ has_skip = False
+ else:
+ has_skip = True
+ if i != self.num_stages - 1:
+ gen_skip = True
+ gen_cross_conv = True
+ else:
+ gen_skip = False
+ gen_cross_conv = False
+ self.multi_stage_mspn.append(
+ SingleStageNetwork(has_skip, gen_skip, gen_cross_conv,
+ unit_channels, num_units, num_blocks,
+ norm_cfg, res_top_channels))
+
+ def forward(self, x):
+ """Model forward function."""
+ out_feats = []
+ skip1 = None
+ skip2 = None
+ x = self.top(x)
+ for i in range(self.num_stages):
+ out, skip1, skip2, x = self.multi_stage_mspn[i](x, skip1, skip2)
+ out_feats.append(out)
+
+ return out_feats
+
+ def init_weights(self, pretrained=None):
+ """Initialize model weights."""
+ if isinstance(pretrained, str):
+ logger = get_root_logger()
+ state_dict_tmp = get_state_dict(pretrained)
+ state_dict = OrderedDict()
+ state_dict['top'] = OrderedDict()
+ state_dict['bottlenecks'] = OrderedDict()
+ for k, v in state_dict_tmp.items():
+ if k.startswith('layer'):
+ if 'downsample.0' in k:
+ state_dict['bottlenecks'][k.replace(
+ 'downsample.0', 'downsample.conv')] = v
+ elif 'downsample.1' in k:
+ state_dict['bottlenecks'][k.replace(
+ 'downsample.1', 'downsample.bn')] = v
+ else:
+ state_dict['bottlenecks'][k] = v
+ elif k.startswith('conv1'):
+ state_dict['top'][k.replace('conv1', 'top.0.conv')] = v
+ elif k.startswith('bn1'):
+ state_dict['top'][k.replace('bn1', 'top.0.bn')] = v
+
+ load_state_dict(
+ self.top, state_dict['top'], strict=False, logger=logger)
+ for i in range(self.num_stages):
+ load_state_dict(
+ self.multi_stage_mspn[i].downsample,
+ state_dict['bottlenecks'],
+ strict=False,
+ logger=logger)
+ else:
+ for m in self.multi_stage_mspn.modules():
+ if isinstance(m, nn.Conv2d):
+ kaiming_init(m)
+ elif isinstance(m, nn.BatchNorm2d):
+ constant_init(m, 1)
+ elif isinstance(m, nn.Linear):
+ normal_init(m, std=0.01)
+
+ for m in self.top.modules():
+ if isinstance(m, nn.Conv2d):
+ kaiming_init(m)
diff --git a/grounded-sam-osx/transformer_utils/mmpose/models/backbones/pvt.py b/grounded-sam-osx/transformer_utils/mmpose/models/backbones/pvt.py
new file mode 100644
index 0000000000000000000000000000000000000000..62527a7dc817513c08f42ccbb166c75cab514873
--- /dev/null
+++ b/grounded-sam-osx/transformer_utils/mmpose/models/backbones/pvt.py
@@ -0,0 +1,592 @@
+# Copyright (c) OpenMMLab. All rights reserved.
+import math
+import warnings
+
+import numpy as np
+import torch
+import torch.nn as nn
+import torch.nn.functional as F
+from mmcv.cnn import (Conv2d, build_activation_layer, build_norm_layer,
+ constant_init, normal_init, trunc_normal_init)
+from mmcv.cnn.bricks.drop import build_dropout
+from mmcv.cnn.bricks.transformer import MultiheadAttention
+from mmcv.cnn.utils.weight_init import trunc_normal_
+from mmcv.runner import (BaseModule, ModuleList, Sequential, _load_checkpoint,
+ load_state_dict)
+from torch.nn.modules.utils import _pair as to_2tuple
+
+from ...utils import get_root_logger
+from ..builder import BACKBONES
+from ..utils import PatchEmbed, nchw_to_nlc, nlc_to_nchw, pvt_convert
+
+
+class MixFFN(BaseModule):
+ """An implementation of MixFFN of PVT.
+
+ The differences between MixFFN & FFN:
+ 1. Use 1X1 Conv to replace Linear layer.
+ 2. Introduce 3X3 Depth-wise Conv to encode positional information.
+
+ Args:
+ embed_dims (int): The feature dimension. Same as
+ `MultiheadAttention`.
+ feedforward_channels (int): The hidden dimension of FFNs.
+ act_cfg (dict, optional): The activation config for FFNs.
+ Default: dict(type='GELU').
+ ffn_drop (float, optional): Probability of an element to be
+ zeroed in FFN. Default 0.0.
+ dropout_layer (obj:`ConfigDict`): The dropout_layer used
+ when adding the shortcut.
+ Default: None.
+ use_conv (bool): If True, add 3x3 DWConv between two Linear layers.
+ Defaults: False.
+ init_cfg (obj:`mmcv.ConfigDict`): The Config for initialization.
+ Default: None.
+ """
+
+ def __init__(self,
+ embed_dims,
+ feedforward_channels,
+ act_cfg=dict(type='GELU'),
+ ffn_drop=0.,
+ dropout_layer=None,
+ use_conv=False,
+ init_cfg=None):
+ super(MixFFN, self).__init__(init_cfg=init_cfg)
+
+ self.embed_dims = embed_dims
+ self.feedforward_channels = feedforward_channels
+ self.act_cfg = act_cfg
+ activate = build_activation_layer(act_cfg)
+
+ in_channels = embed_dims
+ fc1 = Conv2d(
+ in_channels=in_channels,
+ out_channels=feedforward_channels,
+ kernel_size=1,
+ stride=1,
+ bias=True)
+ if use_conv:
+ # 3x3 depth wise conv to provide positional encode information
+ dw_conv = Conv2d(
+ in_channels=feedforward_channels,
+ out_channels=feedforward_channels,
+ kernel_size=3,
+ stride=1,
+ padding=(3 - 1) // 2,
+ bias=True,
+ groups=feedforward_channels)
+ fc2 = Conv2d(
+ in_channels=feedforward_channels,
+ out_channels=in_channels,
+ kernel_size=1,
+ stride=1,
+ bias=True)
+ drop = nn.Dropout(ffn_drop)
+ layers = [fc1, activate, drop, fc2, drop]
+ if use_conv:
+ layers.insert(1, dw_conv)
+ self.layers = Sequential(*layers)
+ self.dropout_layer = build_dropout(
+ dropout_layer) if dropout_layer else torch.nn.Identity()
+
+ def forward(self, x, hw_shape, identity=None):
+ out = nlc_to_nchw(x, hw_shape)
+ out = self.layers(out)
+ out = nchw_to_nlc(out)
+ if identity is None:
+ identity = x
+ return identity + self.dropout_layer(out)
+
+
+class SpatialReductionAttention(MultiheadAttention):
+ """An implementation of Spatial Reduction Attention of PVT.
+
+ This module is modified from MultiheadAttention which is a module from
+ mmcv.cnn.bricks.transformer.
+
+ Args:
+ embed_dims (int): The embedding dimension.
+ num_heads (int): Parallel attention heads.
+ attn_drop (float): A Dropout layer on attn_output_weights.
+ Default: 0.0.
+ proj_drop (float): A Dropout layer after `nn.MultiheadAttention`.
+ Default: 0.0.
+ dropout_layer (obj:`ConfigDict`): The dropout_layer used
+ when adding the shortcut. Default: None.
+ batch_first (bool): Key, Query and Value are shape of
+ (batch, n, embed_dim)
+ or (n, batch, embed_dim). Default: False.
+ qkv_bias (bool): enable bias for qkv if True. Default: True.
+ norm_cfg (dict): Config dict for normalization layer.
+ Default: dict(type='LN').
+ sr_ratio (int): The ratio of spatial reduction of Spatial Reduction
+ Attention of PVT. Default: 1.
+ init_cfg (obj:`mmcv.ConfigDict`): The Config for initialization.
+ Default: None.
+ """
+
+ def __init__(self,
+ embed_dims,
+ num_heads,
+ attn_drop=0.,
+ proj_drop=0.,
+ dropout_layer=None,
+ batch_first=True,
+ qkv_bias=True,
+ norm_cfg=dict(type='LN'),
+ sr_ratio=1,
+ init_cfg=None):
+ super().__init__(
+ embed_dims,
+ num_heads,
+ attn_drop,
+ proj_drop,
+ batch_first=batch_first,
+ dropout_layer=dropout_layer,
+ bias=qkv_bias,
+ init_cfg=init_cfg)
+
+ self.sr_ratio = sr_ratio
+ if sr_ratio > 1:
+ self.sr = Conv2d(
+ in_channels=embed_dims,
+ out_channels=embed_dims,
+ kernel_size=sr_ratio,
+ stride=sr_ratio)
+ # The ret[0] of build_norm_layer is norm name.
+ self.norm = build_norm_layer(norm_cfg, embed_dims)[1]
+
+ # handle the BC-breaking from https://github.com/open-mmlab/mmcv/pull/1418 # noqa
+ from mmpose import digit_version, mmcv_version
+ if mmcv_version < digit_version('1.3.17'):
+ warnings.warn('The legacy version of forward function in'
+ 'SpatialReductionAttention is deprecated in'
+ 'mmcv>=1.3.17 and will no longer support in the'
+ 'future. Please upgrade your mmcv.')
+ self.forward = self.legacy_forward
+
+ def forward(self, x, hw_shape, identity=None):
+
+ x_q = x
+ if self.sr_ratio > 1:
+ x_kv = nlc_to_nchw(x, hw_shape)
+ x_kv = self.sr(x_kv)
+ x_kv = nchw_to_nlc(x_kv)
+ x_kv = self.norm(x_kv)
+ else:
+ x_kv = x
+
+ if identity is None:
+ identity = x_q
+
+ # Because the dataflow('key', 'query', 'value') of
+ # ``torch.nn.MultiheadAttention`` is (num_query, batch,
+ # embed_dims), We should adjust the shape of dataflow from
+ # batch_first (batch, num_query, embed_dims) to num_query_first
+ # (num_query ,batch, embed_dims), and recover ``attn_output``
+ # from num_query_first to batch_first.
+ if self.batch_first:
+ x_q = x_q.transpose(0, 1)
+ x_kv = x_kv.transpose(0, 1)
+
+ out = self.attn(query=x_q, key=x_kv, value=x_kv)[0]
+
+ if self.batch_first:
+ out = out.transpose(0, 1)
+
+ return identity + self.dropout_layer(self.proj_drop(out))
+
+ def legacy_forward(self, x, hw_shape, identity=None):
+ """multi head attention forward in mmcv version < 1.3.17."""
+ x_q = x
+ if self.sr_ratio > 1:
+ x_kv = nlc_to_nchw(x, hw_shape)
+ x_kv = self.sr(x_kv)
+ x_kv = nchw_to_nlc(x_kv)
+ x_kv = self.norm(x_kv)
+ else:
+ x_kv = x
+
+ if identity is None:
+ identity = x_q
+
+ out = self.attn(query=x_q, key=x_kv, value=x_kv)[0]
+
+ return identity + self.dropout_layer(self.proj_drop(out))
+
+
+class PVTEncoderLayer(BaseModule):
+ """Implements one encoder layer in PVT.
+
+ Args:
+ embed_dims (int): The feature dimension.
+ num_heads (int): Parallel attention heads.
+ feedforward_channels (int): The hidden dimension for FFNs.
+ drop_rate (float): Probability of an element to be zeroed.
+ after the feed forward layer. Default: 0.0.
+ attn_drop_rate (float): The drop out rate for attention layer.
+ Default: 0.0.
+ drop_path_rate (float): stochastic depth rate. Default: 0.0.
+ qkv_bias (bool): enable bias for qkv if True.
+ Default: True.
+ act_cfg (dict): The activation config for FFNs.
+ Default: dict(type='GELU').
+ norm_cfg (dict): Config dict for normalization layer.
+ Default: dict(type='LN').
+ sr_ratio (int): The ratio of spatial reduction of Spatial Reduction
+ Attention of PVT. Default: 1.
+ use_conv_ffn (bool): If True, use Convolutional FFN to replace FFN.
+ Default: False.
+ init_cfg (dict, optional): Initialization config dict.
+ Default: None.
+ """
+
+ def __init__(self,
+ embed_dims,
+ num_heads,
+ feedforward_channels,
+ drop_rate=0.,
+ attn_drop_rate=0.,
+ drop_path_rate=0.,
+ qkv_bias=True,
+ act_cfg=dict(type='GELU'),
+ norm_cfg=dict(type='LN'),
+ sr_ratio=1,
+ use_conv_ffn=False,
+ init_cfg=None):
+ super(PVTEncoderLayer, self).__init__(init_cfg=init_cfg)
+
+ # The ret[0] of build_norm_layer is norm name.
+ self.norm1 = build_norm_layer(norm_cfg, embed_dims)[1]
+
+ self.attn = SpatialReductionAttention(
+ embed_dims=embed_dims,
+ num_heads=num_heads,
+ attn_drop=attn_drop_rate,
+ proj_drop=drop_rate,
+ dropout_layer=dict(type='DropPath', drop_prob=drop_path_rate),
+ qkv_bias=qkv_bias,
+ norm_cfg=norm_cfg,
+ sr_ratio=sr_ratio)
+
+ # The ret[0] of build_norm_layer is norm name.
+ self.norm2 = build_norm_layer(norm_cfg, embed_dims)[1]
+
+ self.ffn = MixFFN(
+ embed_dims=embed_dims,
+ feedforward_channels=feedforward_channels,
+ ffn_drop=drop_rate,
+ dropout_layer=dict(type='DropPath', drop_prob=drop_path_rate),
+ use_conv=use_conv_ffn,
+ act_cfg=act_cfg)
+
+ def forward(self, x, hw_shape):
+ x = self.attn(self.norm1(x), hw_shape, identity=x)
+ x = self.ffn(self.norm2(x), hw_shape, identity=x)
+
+ return x
+
+
+class AbsolutePositionEmbedding(BaseModule):
+ """An implementation of the absolute position embedding in PVT.
+
+ Args:
+ pos_shape (int): The shape of the absolute position embedding.
+ pos_dim (int): The dimension of the absolute position embedding.
+ drop_rate (float): Probability of an element to be zeroed.
+ Default: 0.0.
+ """
+
+ def __init__(self, pos_shape, pos_dim, drop_rate=0., init_cfg=None):
+ super().__init__(init_cfg=init_cfg)
+
+ if isinstance(pos_shape, int):
+ pos_shape = to_2tuple(pos_shape)
+ elif isinstance(pos_shape, tuple):
+ if len(pos_shape) == 1:
+ pos_shape = to_2tuple(pos_shape[0])
+ assert len(pos_shape) == 2, \
+ f'The size of image should have length 1 or 2, ' \
+ f'but got {len(pos_shape)}'
+ self.pos_shape = pos_shape
+ self.pos_dim = pos_dim
+
+ self.pos_embed = nn.Parameter(
+ torch.zeros(1, pos_shape[0] * pos_shape[1], pos_dim))
+ self.drop = nn.Dropout(p=drop_rate)
+
+ def init_weights(self):
+ trunc_normal_(self.pos_embed, std=0.02)
+
+ def resize_pos_embed(self, pos_embed, input_shape, mode='bilinear'):
+ """Resize pos_embed weights.
+
+ Resize pos_embed using bilinear interpolate method.
+
+ Args:
+ pos_embed (torch.Tensor): Position embedding weights.
+ input_shape (tuple): Tuple for (downsampled input image height,
+ downsampled input image width).
+ mode (str): Algorithm used for upsampling:
+ ``'nearest'`` | ``'linear'`` | ``'bilinear'`` | ``'bicubic'`` |
+ ``'trilinear'``. Default: ``'bilinear'``.
+
+ Return:
+ torch.Tensor: The resized pos_embed of shape [B, L_new, C].
+ """
+ assert pos_embed.ndim == 3, 'shape of pos_embed must be [B, L, C]'
+ pos_h, pos_w = self.pos_shape
+ pos_embed_weight = pos_embed[:, (-1 * pos_h * pos_w):]
+ pos_embed_weight = pos_embed_weight.reshape(
+ 1, pos_h, pos_w, self.pos_dim).permute(0, 3, 1, 2).contiguous()
+ pos_embed_weight = F.interpolate(
+ pos_embed_weight, size=input_shape, mode=mode)
+ pos_embed_weight = torch.flatten(pos_embed_weight,
+ 2).transpose(1, 2).contiguous()
+ pos_embed = pos_embed_weight
+
+ return pos_embed
+
+ def forward(self, x, hw_shape, mode='bilinear'):
+ pos_embed = self.resize_pos_embed(self.pos_embed, hw_shape, mode)
+ return self.drop(x + pos_embed)
+
+
+@BACKBONES.register_module()
+class PyramidVisionTransformer(BaseModule):
+ """Pyramid Vision Transformer (PVT)
+
+ Implementation of `Pyramid Vision Transformer: A Versatile Backbone for
+ Dense Prediction without Convolutions
+ `_.
+
+ Args:
+ pretrain_img_size (int | tuple[int]): The size of input image when
+ pretrain. Defaults: 224.
+ in_channels (int): Number of input channels. Default: 3.
+ embed_dims (int): Embedding dimension. Default: 64.
+ num_stags (int): The num of stages. Default: 4.
+ num_layers (Sequence[int]): The layer number of each transformer encode
+ layer. Default: [3, 4, 6, 3].
+ num_heads (Sequence[int]): The attention heads of each transformer
+ encode layer. Default: [1, 2, 5, 8].
+ patch_sizes (Sequence[int]): The patch_size of each patch embedding.
+ Default: [4, 2, 2, 2].
+ strides (Sequence[int]): The stride of each patch embedding.
+ Default: [4, 2, 2, 2].
+ paddings (Sequence[int]): The padding of each patch embedding.
+ Default: [0, 0, 0, 0].
+ sr_ratios (Sequence[int]): The spatial reduction rate of each
+ transformer encode layer. Default: [8, 4, 2, 1].
+ out_indices (Sequence[int] | int): Output from which stages.
+ Default: (0, 1, 2, 3).
+ mlp_ratios (Sequence[int]): The ratio of the mlp hidden dim to the
+ embedding dim of each transformer encode layer.
+ Default: [8, 8, 4, 4].
+ qkv_bias (bool): Enable bias for qkv if True. Default: True.
+ drop_rate (float): Probability of an element to be zeroed.
+ Default 0.0.
+ attn_drop_rate (float): The drop out rate for attention layer.
+ Default 0.0.
+ drop_path_rate (float): stochastic depth rate. Default 0.1.
+ use_abs_pos_embed (bool): If True, add absolute position embedding to
+ the patch embedding. Defaults: True.
+ use_conv_ffn (bool): If True, use Convolutional FFN to replace FFN.
+ Default: False.
+ act_cfg (dict): The activation config for FFNs.
+ Default: dict(type='GELU').
+ norm_cfg (dict): Config dict for normalization layer.
+ Default: dict(type='LN').
+ pretrained (str, optional): model pretrained path. Default: None.
+ convert_weights (bool): The flag indicates whether the
+ pre-trained model is from the original repo. We may need
+ to convert some keys to make it compatible.
+ Default: True.
+ init_cfg (dict or list[dict], optional): Initialization config dict.
+ Default: None.
+ """
+
+ def __init__(self,
+ pretrain_img_size=224,
+ in_channels=3,
+ embed_dims=64,
+ num_stages=4,
+ num_layers=[3, 4, 6, 3],
+ num_heads=[1, 2, 5, 8],
+ patch_sizes=[4, 2, 2, 2],
+ strides=[4, 2, 2, 2],
+ paddings=[0, 0, 0, 0],
+ sr_ratios=[8, 4, 2, 1],
+ out_indices=(0, 1, 2, 3),
+ mlp_ratios=[8, 8, 4, 4],
+ qkv_bias=True,
+ drop_rate=0.,
+ attn_drop_rate=0.,
+ drop_path_rate=0.1,
+ use_abs_pos_embed=True,
+ norm_after_stage=False,
+ use_conv_ffn=False,
+ act_cfg=dict(type='GELU'),
+ norm_cfg=dict(type='LN', eps=1e-6),
+ pretrained=None,
+ convert_weights=True,
+ init_cfg=None):
+ super().__init__(init_cfg=init_cfg)
+
+ self.convert_weights = convert_weights
+ if isinstance(pretrain_img_size, int):
+ pretrain_img_size = to_2tuple(pretrain_img_size)
+ elif isinstance(pretrain_img_size, tuple):
+ if len(pretrain_img_size) == 1:
+ pretrain_img_size = to_2tuple(pretrain_img_size[0])
+ assert len(pretrain_img_size) == 2, \
+ f'The size of image should have length 1 or 2, ' \
+ f'but got {len(pretrain_img_size)}'
+
+ assert not (init_cfg and pretrained), \
+ 'init_cfg and pretrained cannot be setting at the same time'
+ if isinstance(pretrained, str):
+ self.init_cfg = dict(type='Pretrained', checkpoint=pretrained)
+ elif pretrained is None:
+ self.init_cfg = init_cfg
+ else:
+ raise TypeError('pretrained must be a str or None')
+
+ self.embed_dims = embed_dims
+
+ self.num_stages = num_stages
+ self.num_layers = num_layers
+ self.num_heads = num_heads
+ self.patch_sizes = patch_sizes
+ self.strides = strides
+ self.sr_ratios = sr_ratios
+ assert num_stages == len(num_layers) == len(num_heads) \
+ == len(patch_sizes) == len(strides) == len(sr_ratios)
+
+ self.out_indices = out_indices
+ assert max(out_indices) < self.num_stages
+ self.pretrained = pretrained
+
+ # transformer encoder
+ dpr = [
+ x.item()
+ for x in torch.linspace(0, drop_path_rate, sum(num_layers))
+ ] # stochastic num_layer decay rule
+
+ cur = 0
+ self.layers = ModuleList()
+ for i, num_layer in enumerate(num_layers):
+ embed_dims_i = embed_dims * num_heads[i]
+ patch_embed = PatchEmbed(
+ in_channels=in_channels,
+ embed_dims=embed_dims_i,
+ kernel_size=patch_sizes[i],
+ stride=strides[i],
+ padding=paddings[i],
+ bias=True,
+ norm_cfg=norm_cfg)
+
+ layers = ModuleList()
+ if use_abs_pos_embed:
+ pos_shape = pretrain_img_size // np.prod(patch_sizes[:i + 1])
+ pos_embed = AbsolutePositionEmbedding(
+ pos_shape=pos_shape,
+ pos_dim=embed_dims_i,
+ drop_rate=drop_rate)
+ layers.append(pos_embed)
+ layers.extend([
+ PVTEncoderLayer(
+ embed_dims=embed_dims_i,
+ num_heads=num_heads[i],
+ feedforward_channels=mlp_ratios[i] * embed_dims_i,
+ drop_rate=drop_rate,
+ attn_drop_rate=attn_drop_rate,
+ drop_path_rate=dpr[cur + idx],
+ qkv_bias=qkv_bias,
+ act_cfg=act_cfg,
+ norm_cfg=norm_cfg,
+ sr_ratio=sr_ratios[i],
+ use_conv_ffn=use_conv_ffn) for idx in range(num_layer)
+ ])
+ in_channels = embed_dims_i
+ # The ret[0] of build_norm_layer is norm name.
+ if norm_after_stage:
+ norm = build_norm_layer(norm_cfg, embed_dims_i)[1]
+ else:
+ norm = nn.Identity()
+ self.layers.append(ModuleList([patch_embed, layers, norm]))
+ cur += num_layer
+
+ def init_weights(self, pretrained=None):
+ if isinstance(pretrained, str):
+ self.init_cfg = dict(type='Pretrained', checkpoint=pretrained)
+
+ logger = get_root_logger()
+ if self.init_cfg is None:
+ logger.warn(f'No pre-trained weights for '
+ f'{self.__class__.__name__}, '
+ f'training start from scratch')
+ for m in self.modules():
+ if isinstance(m, nn.Linear):
+ trunc_normal_init(m, std=.02, bias=0.)
+ elif isinstance(m, nn.LayerNorm):
+ constant_init(m, 1.0)
+ elif isinstance(m, nn.Conv2d):
+ fan_out = m.kernel_size[0] * m.kernel_size[
+ 1] * m.out_channels
+ fan_out //= m.groups
+ normal_init(m, 0, math.sqrt(2.0 / fan_out))
+ elif isinstance(m, AbsolutePositionEmbedding):
+ m.init_weights()
+ else:
+ assert 'checkpoint' in self.init_cfg, f'Only support ' \
+ f'specify `Pretrained` in ' \
+ f'`init_cfg` in ' \
+ f'{self.__class__.__name__} '
+ checkpoint = _load_checkpoint(
+ self.init_cfg['checkpoint'], logger=logger, map_location='cpu')
+ logger.warn(f'Load pre-trained model for '
+ f'{self.__class__.__name__} from original repo')
+ if 'state_dict' in checkpoint:
+ state_dict = checkpoint['state_dict']
+ elif 'model' in checkpoint:
+ state_dict = checkpoint['model']
+ else:
+ state_dict = checkpoint
+ if self.convert_weights:
+ # Because pvt backbones are not supported by mmcls,
+ # so we need to convert pre-trained weights to match this
+ # implementation.
+ state_dict = pvt_convert(state_dict)
+ load_state_dict(self, state_dict, strict=False, logger=logger)
+
+ def forward(self, x):
+ outs = []
+
+ for i, layer in enumerate(self.layers):
+ x, hw_shape = layer[0](x)
+
+ for block in layer[1]:
+ x = block(x, hw_shape)
+ x = layer[2](x)
+ x = nlc_to_nchw(x, hw_shape)
+ if i in self.out_indices:
+ outs.append(x)
+
+ return outs
+
+
+@BACKBONES.register_module()
+class PyramidVisionTransformerV2(PyramidVisionTransformer):
+ """Implementation of `PVTv2: Improved Baselines with Pyramid Vision
+ Transformer `_."""
+
+ def __init__(self, **kwargs):
+ super(PyramidVisionTransformerV2, self).__init__(
+ patch_sizes=[7, 3, 3, 3],
+ paddings=[3, 1, 1, 1],
+ use_abs_pos_embed=False,
+ norm_after_stage=True,
+ use_conv_ffn=True,
+ **kwargs)
diff --git a/grounded-sam-osx/transformer_utils/mmpose/models/backbones/regnet.py b/grounded-sam-osx/transformer_utils/mmpose/models/backbones/regnet.py
new file mode 100644
index 0000000000000000000000000000000000000000..693417c2d61066e4e9a90989ad61700448028e58
--- /dev/null
+++ b/grounded-sam-osx/transformer_utils/mmpose/models/backbones/regnet.py
@@ -0,0 +1,317 @@
+# Copyright (c) OpenMMLab. All rights reserved.
+import copy
+
+import numpy as np
+import torch.nn as nn
+from mmcv.cnn import build_conv_layer, build_norm_layer
+
+from ..builder import BACKBONES
+from .resnet import ResNet
+from .resnext import Bottleneck
+
+
+@BACKBONES.register_module()
+class RegNet(ResNet):
+ """RegNet backbone.
+
+ More details can be found in `paper `__ .
+
+ Args:
+ arch (dict): The parameter of RegNets.
+ - w0 (int): initial width
+ - wa (float): slope of width
+ - wm (float): quantization parameter to quantize the width
+ - depth (int): depth of the backbone
+ - group_w (int): width of group
+ - bot_mul (float): bottleneck ratio, i.e. expansion of bottleneck.
+ strides (Sequence[int]): Strides of the first block of each stage.
+ base_channels (int): Base channels after stem layer.
+ in_channels (int): Number of input image channels. Default: 3.
+ dilations (Sequence[int]): Dilation of each stage.
+ out_indices (Sequence[int]): Output from which stages.
+ style (str): `pytorch` or `caffe`. If set to "pytorch", the stride-two
+ layer is the 3x3 conv layer, otherwise the stride-two layer is
+ the first 1x1 conv layer. Default: "pytorch".
+ frozen_stages (int): Stages to be frozen (all param fixed). -1 means
+ not freezing any parameters. Default: -1.
+ norm_cfg (dict): dictionary to construct and config norm layer.
+ Default: dict(type='BN', requires_grad=True).
+ norm_eval (bool): Whether to set norm layers to eval mode, namely,
+ freeze running stats (mean and var). Note: Effect on Batch Norm
+ and its variants only. Default: False.
+ with_cp (bool): Use checkpoint or not. Using checkpoint will save some
+ memory while slowing down the training speed. Default: False.
+ zero_init_residual (bool): whether to use zero init for last norm layer
+ in resblocks to let them behave as identity. Default: True.
+
+ Example:
+ >>> from mmpose.models import RegNet
+ >>> import torch
+ >>> self = RegNet(
+ arch=dict(
+ w0=88,
+ wa=26.31,
+ wm=2.25,
+ group_w=48,
+ depth=25,
+ bot_mul=1.0),
+ out_indices=(0, 1, 2, 3))
+ >>> self.eval()
+ >>> inputs = torch.rand(1, 3, 32, 32)
+ >>> level_outputs = self.forward(inputs)
+ >>> for level_out in level_outputs:
+ ... print(tuple(level_out.shape))
+ (1, 96, 8, 8)
+ (1, 192, 4, 4)
+ (1, 432, 2, 2)
+ (1, 1008, 1, 1)
+ """
+ arch_settings = {
+ 'regnetx_400mf':
+ dict(w0=24, wa=24.48, wm=2.54, group_w=16, depth=22, bot_mul=1.0),
+ 'regnetx_800mf':
+ dict(w0=56, wa=35.73, wm=2.28, group_w=16, depth=16, bot_mul=1.0),
+ 'regnetx_1.6gf':
+ dict(w0=80, wa=34.01, wm=2.25, group_w=24, depth=18, bot_mul=1.0),
+ 'regnetx_3.2gf':
+ dict(w0=88, wa=26.31, wm=2.25, group_w=48, depth=25, bot_mul=1.0),
+ 'regnetx_4.0gf':
+ dict(w0=96, wa=38.65, wm=2.43, group_w=40, depth=23, bot_mul=1.0),
+ 'regnetx_6.4gf':
+ dict(w0=184, wa=60.83, wm=2.07, group_w=56, depth=17, bot_mul=1.0),
+ 'regnetx_8.0gf':
+ dict(w0=80, wa=49.56, wm=2.88, group_w=120, depth=23, bot_mul=1.0),
+ 'regnetx_12gf':
+ dict(w0=168, wa=73.36, wm=2.37, group_w=112, depth=19, bot_mul=1.0),
+ }
+
+ def __init__(self,
+ arch,
+ in_channels=3,
+ stem_channels=32,
+ base_channels=32,
+ strides=(2, 2, 2, 2),
+ dilations=(1, 1, 1, 1),
+ out_indices=(3, ),
+ style='pytorch',
+ deep_stem=False,
+ avg_down=False,
+ frozen_stages=-1,
+ conv_cfg=None,
+ norm_cfg=dict(type='BN', requires_grad=True),
+ norm_eval=False,
+ with_cp=False,
+ zero_init_residual=True):
+ # Protect mutable default arguments
+ norm_cfg = copy.deepcopy(norm_cfg)
+ super(ResNet, self).__init__()
+
+ # Generate RegNet parameters first
+ if isinstance(arch, str):
+ assert arch in self.arch_settings, \
+ f'"arch": "{arch}" is not one of the' \
+ ' arch_settings'
+ arch = self.arch_settings[arch]
+ elif not isinstance(arch, dict):
+ raise TypeError('Expect "arch" to be either a string '
+ f'or a dict, got {type(arch)}')
+
+ widths, num_stages = self.generate_regnet(
+ arch['w0'],
+ arch['wa'],
+ arch['wm'],
+ arch['depth'],
+ )
+ # Convert to per stage format
+ stage_widths, stage_blocks = self.get_stages_from_blocks(widths)
+ # Generate group widths and bot muls
+ group_widths = [arch['group_w'] for _ in range(num_stages)]
+ self.bottleneck_ratio = [arch['bot_mul'] for _ in range(num_stages)]
+ # Adjust the compatibility of stage_widths and group_widths
+ stage_widths, group_widths = self.adjust_width_group(
+ stage_widths, self.bottleneck_ratio, group_widths)
+
+ # Group params by stage
+ self.stage_widths = stage_widths
+ self.group_widths = group_widths
+ self.depth = sum(stage_blocks)
+ self.stem_channels = stem_channels
+ self.base_channels = base_channels
+ self.num_stages = num_stages
+ assert 1 <= num_stages <= 4
+ self.strides = strides
+ self.dilations = dilations
+ assert len(strides) == len(dilations) == num_stages
+ self.out_indices = out_indices
+ assert max(out_indices) < num_stages
+ self.style = style
+ self.deep_stem = deep_stem
+ if self.deep_stem:
+ raise NotImplementedError(
+ 'deep_stem has not been implemented for RegNet')
+ self.avg_down = avg_down
+ self.frozen_stages = frozen_stages
+ self.conv_cfg = conv_cfg
+ self.norm_cfg = norm_cfg
+ self.with_cp = with_cp
+ self.norm_eval = norm_eval
+ self.zero_init_residual = zero_init_residual
+ self.stage_blocks = stage_blocks[:num_stages]
+
+ self._make_stem_layer(in_channels, stem_channels)
+
+ _in_channels = stem_channels
+ self.res_layers = []
+ for i, num_blocks in enumerate(self.stage_blocks):
+ stride = self.strides[i]
+ dilation = self.dilations[i]
+ group_width = self.group_widths[i]
+ width = int(round(self.stage_widths[i] * self.bottleneck_ratio[i]))
+ stage_groups = width // group_width
+
+ res_layer = self.make_res_layer(
+ block=Bottleneck,
+ num_blocks=num_blocks,
+ in_channels=_in_channels,
+ out_channels=self.stage_widths[i],
+ expansion=1,
+ stride=stride,
+ dilation=dilation,
+ style=self.style,
+ avg_down=self.avg_down,
+ with_cp=self.with_cp,
+ conv_cfg=self.conv_cfg,
+ norm_cfg=self.norm_cfg,
+ base_channels=self.stage_widths[i],
+ groups=stage_groups,
+ width_per_group=group_width)
+ _in_channels = self.stage_widths[i]
+ layer_name = f'layer{i + 1}'
+ self.add_module(layer_name, res_layer)
+ self.res_layers.append(layer_name)
+
+ self._freeze_stages()
+
+ self.feat_dim = stage_widths[-1]
+
+ def _make_stem_layer(self, in_channels, base_channels):
+ self.conv1 = build_conv_layer(
+ self.conv_cfg,
+ in_channels,
+ base_channels,
+ kernel_size=3,
+ stride=2,
+ padding=1,
+ bias=False)
+ self.norm1_name, norm1 = build_norm_layer(
+ self.norm_cfg, base_channels, postfix=1)
+ self.add_module(self.norm1_name, norm1)
+ self.relu = nn.ReLU(inplace=True)
+
+ @staticmethod
+ def generate_regnet(initial_width,
+ width_slope,
+ width_parameter,
+ depth,
+ divisor=8):
+ """Generates per block width from RegNet parameters.
+
+ Args:
+ initial_width ([int]): Initial width of the backbone
+ width_slope ([float]): Slope of the quantized linear function
+ width_parameter ([int]): Parameter used to quantize the width.
+ depth ([int]): Depth of the backbone.
+ divisor (int, optional): The divisor of channels. Defaults to 8.
+
+ Returns:
+ list, int: return a list of widths of each stage and the number of
+ stages
+ """
+ assert width_slope >= 0
+ assert initial_width > 0
+ assert width_parameter > 1
+ assert initial_width % divisor == 0
+ widths_cont = np.arange(depth) * width_slope + initial_width
+ ks = np.round(
+ np.log(widths_cont / initial_width) / np.log(width_parameter))
+ widths = initial_width * np.power(width_parameter, ks)
+ widths = np.round(np.divide(widths, divisor)) * divisor
+ num_stages = len(np.unique(widths))
+ widths, widths_cont = widths.astype(int).tolist(), widths_cont.tolist()
+ return widths, num_stages
+
+ @staticmethod
+ def quantize_float(number, divisor):
+ """Converts a float to closest non-zero int divisible by divior.
+
+ Args:
+ number (int): Original number to be quantized.
+ divisor (int): Divisor used to quantize the number.
+
+ Returns:
+ int: quantized number that is divisible by devisor.
+ """
+ return int(round(number / divisor) * divisor)
+
+ def adjust_width_group(self, widths, bottleneck_ratio, groups):
+ """Adjusts the compatibility of widths and groups.
+
+ Args:
+ widths (list[int]): Width of each stage.
+ bottleneck_ratio (float): Bottleneck ratio.
+ groups (int): number of groups in each stage
+
+ Returns:
+ tuple(list): The adjusted widths and groups of each stage.
+ """
+ bottleneck_width = [
+ int(w * b) for w, b in zip(widths, bottleneck_ratio)
+ ]
+ groups = [min(g, w_bot) for g, w_bot in zip(groups, bottleneck_width)]
+ bottleneck_width = [
+ self.quantize_float(w_bot, g)
+ for w_bot, g in zip(bottleneck_width, groups)
+ ]
+ widths = [
+ int(w_bot / b)
+ for w_bot, b in zip(bottleneck_width, bottleneck_ratio)
+ ]
+ return widths, groups
+
+ def get_stages_from_blocks(self, widths):
+ """Gets widths/stage_blocks of network at each stage.
+
+ Args:
+ widths (list[int]): Width in each stage.
+
+ Returns:
+ tuple(list): width and depth of each stage
+ """
+ width_diff = [
+ width != width_prev
+ for width, width_prev in zip(widths + [0], [0] + widths)
+ ]
+ stage_widths = [
+ width for width, diff in zip(widths, width_diff[:-1]) if diff
+ ]
+ stage_blocks = np.diff([
+ depth for depth, diff in zip(range(len(width_diff)), width_diff)
+ if diff
+ ]).tolist()
+ return stage_widths, stage_blocks
+
+ def forward(self, x):
+ x = self.conv1(x)
+ x = self.norm1(x)
+ x = self.relu(x)
+
+ outs = []
+ for i, layer_name in enumerate(self.res_layers):
+ res_layer = getattr(self, layer_name)
+ x = res_layer(x)
+ if i in self.out_indices:
+ outs.append(x)
+
+ if len(outs) == 1:
+ return outs[0]
+ return tuple(outs)
diff --git a/grounded-sam-osx/transformer_utils/mmpose/models/backbones/resnest.py b/grounded-sam-osx/transformer_utils/mmpose/models/backbones/resnest.py
new file mode 100644
index 0000000000000000000000000000000000000000..0a2d4081df1417155f0626646f5fe3d0dbfc2864
--- /dev/null
+++ b/grounded-sam-osx/transformer_utils/mmpose/models/backbones/resnest.py
@@ -0,0 +1,338 @@
+# Copyright (c) OpenMMLab. All rights reserved.
+import torch
+import torch.nn as nn
+import torch.nn.functional as F
+import torch.utils.checkpoint as cp
+from mmcv.cnn import build_conv_layer, build_norm_layer
+
+from ..builder import BACKBONES
+from .resnet import Bottleneck as _Bottleneck
+from .resnet import ResLayer, ResNetV1d
+
+
+class RSoftmax(nn.Module):
+ """Radix Softmax module in ``SplitAttentionConv2d``.
+
+ Args:
+ radix (int): Radix of input.
+ groups (int): Groups of input.
+ """
+
+ def __init__(self, radix, groups):
+ super().__init__()
+ self.radix = radix
+ self.groups = groups
+
+ def forward(self, x):
+ batch = x.size(0)
+ if self.radix > 1:
+ x = x.view(batch, self.groups, self.radix, -1).transpose(1, 2)
+ x = F.softmax(x, dim=1)
+ x = x.reshape(batch, -1)
+ else:
+ x = torch.sigmoid(x)
+ return x
+
+
+class SplitAttentionConv2d(nn.Module):
+ """Split-Attention Conv2d.
+
+ Args:
+ in_channels (int): Same as nn.Conv2d.
+ out_channels (int): Same as nn.Conv2d.
+ kernel_size (int | tuple[int]): Same as nn.Conv2d.
+ stride (int | tuple[int]): Same as nn.Conv2d.
+ padding (int | tuple[int]): Same as nn.Conv2d.
+ dilation (int | tuple[int]): Same as nn.Conv2d.
+ groups (int): Same as nn.Conv2d.
+ radix (int): Radix of SpltAtConv2d. Default: 2
+ reduction_factor (int): Reduction factor of SplitAttentionConv2d.
+ Default: 4.
+ conv_cfg (dict): Config dict for convolution layer. Default: None,
+ which means using conv2d.
+ norm_cfg (dict): Config dict for normalization layer. Default: None.
+ """
+
+ def __init__(self,
+ in_channels,
+ channels,
+ kernel_size,
+ stride=1,
+ padding=0,
+ dilation=1,
+ groups=1,
+ radix=2,
+ reduction_factor=4,
+ conv_cfg=None,
+ norm_cfg=dict(type='BN')):
+ super().__init__()
+ inter_channels = max(in_channels * radix // reduction_factor, 32)
+ self.radix = radix
+ self.groups = groups
+ self.channels = channels
+ self.conv = build_conv_layer(
+ conv_cfg,
+ in_channels,
+ channels * radix,
+ kernel_size,
+ stride=stride,
+ padding=padding,
+ dilation=dilation,
+ groups=groups * radix,
+ bias=False)
+ self.norm0_name, norm0 = build_norm_layer(
+ norm_cfg, channels * radix, postfix=0)
+ self.add_module(self.norm0_name, norm0)
+ self.relu = nn.ReLU(inplace=True)
+ self.fc1 = build_conv_layer(
+ None, channels, inter_channels, 1, groups=self.groups)
+ self.norm1_name, norm1 = build_norm_layer(
+ norm_cfg, inter_channels, postfix=1)
+ self.add_module(self.norm1_name, norm1)
+ self.fc2 = build_conv_layer(
+ None, inter_channels, channels * radix, 1, groups=self.groups)
+ self.rsoftmax = RSoftmax(radix, groups)
+
+ @property
+ def norm0(self):
+ return getattr(self, self.norm0_name)
+
+ @property
+ def norm1(self):
+ return getattr(self, self.norm1_name)
+
+ def forward(self, x):
+ x = self.conv(x)
+ x = self.norm0(x)
+ x = self.relu(x)
+
+ batch, rchannel = x.shape[:2]
+ if self.radix > 1:
+ splits = x.view(batch, self.radix, -1, *x.shape[2:])
+ gap = splits.sum(dim=1)
+ else:
+ gap = x
+ gap = F.adaptive_avg_pool2d(gap, 1)
+ gap = self.fc1(gap)
+
+ gap = self.norm1(gap)
+ gap = self.relu(gap)
+
+ atten = self.fc2(gap)
+ atten = self.rsoftmax(atten).view(batch, -1, 1, 1)
+
+ if self.radix > 1:
+ attens = atten.view(batch, self.radix, -1, *atten.shape[2:])
+ out = torch.sum(attens * splits, dim=1)
+ else:
+ out = atten * x
+ return out.contiguous()
+
+
+class Bottleneck(_Bottleneck):
+ """Bottleneck block for ResNeSt.
+
+ Args:
+ in_channels (int): Input channels of this block.
+ out_channels (int): Output channels of this block.
+ groups (int): Groups of conv2.
+ width_per_group (int): Width per group of conv2. 64x4d indicates
+ ``groups=64, width_per_group=4`` and 32x8d indicates
+ ``groups=32, width_per_group=8``.
+ radix (int): Radix of SpltAtConv2d. Default: 2
+ reduction_factor (int): Reduction factor of SplitAttentionConv2d.
+ Default: 4.
+ avg_down_stride (bool): Whether to use average pool for stride in
+ Bottleneck. Default: True.
+ stride (int): stride of the block. Default: 1
+ dilation (int): dilation of convolution. Default: 1
+ downsample (nn.Module): downsample operation on identity branch.
+ Default: None
+ style (str): `pytorch` or `caffe`. If set to "pytorch", the stride-two
+ layer is the 3x3 conv layer, otherwise the stride-two layer is
+ the first 1x1 conv layer.
+ conv_cfg (dict): dictionary to construct and config conv layer.
+ Default: None
+ norm_cfg (dict): dictionary to construct and config norm layer.
+ Default: dict(type='BN')
+ with_cp (bool): Use checkpoint or not. Using checkpoint will save some
+ memory while slowing down the training speed.
+ """
+
+ def __init__(self,
+ in_channels,
+ out_channels,
+ groups=1,
+ width_per_group=4,
+ base_channels=64,
+ radix=2,
+ reduction_factor=4,
+ avg_down_stride=True,
+ **kwargs):
+ super().__init__(in_channels, out_channels, **kwargs)
+
+ self.groups = groups
+ self.width_per_group = width_per_group
+
+ # For ResNet bottleneck, middle channels are determined by expansion
+ # and out_channels, but for ResNeXt bottleneck, it is determined by
+ # groups and width_per_group and the stage it is located in.
+ if groups != 1:
+ assert self.mid_channels % base_channels == 0
+ self.mid_channels = (
+ groups * width_per_group * self.mid_channels // base_channels)
+
+ self.avg_down_stride = avg_down_stride and self.conv2_stride > 1
+
+ self.norm1_name, norm1 = build_norm_layer(
+ self.norm_cfg, self.mid_channels, postfix=1)
+ self.norm3_name, norm3 = build_norm_layer(
+ self.norm_cfg, self.out_channels, postfix=3)
+
+ self.conv1 = build_conv_layer(
+ self.conv_cfg,
+ self.in_channels,
+ self.mid_channels,
+ kernel_size=1,
+ stride=self.conv1_stride,
+ bias=False)
+ self.add_module(self.norm1_name, norm1)
+ self.conv2 = SplitAttentionConv2d(
+ self.mid_channels,
+ self.mid_channels,
+ kernel_size=3,
+ stride=1 if self.avg_down_stride else self.conv2_stride,
+ padding=self.dilation,
+ dilation=self.dilation,
+ groups=groups,
+ radix=radix,
+ reduction_factor=reduction_factor,
+ conv_cfg=self.conv_cfg,
+ norm_cfg=self.norm_cfg)
+ delattr(self, self.norm2_name)
+
+ if self.avg_down_stride:
+ self.avd_layer = nn.AvgPool2d(3, self.conv2_stride, padding=1)
+
+ self.conv3 = build_conv_layer(
+ self.conv_cfg,
+ self.mid_channels,
+ self.out_channels,
+ kernel_size=1,
+ bias=False)
+ self.add_module(self.norm3_name, norm3)
+
+ def forward(self, x):
+
+ def _inner_forward(x):
+ identity = x
+
+ out = self.conv1(x)
+ out = self.norm1(out)
+ out = self.relu(out)
+
+ out = self.conv2(out)
+
+ if self.avg_down_stride:
+ out = self.avd_layer(out)
+
+ out = self.conv3(out)
+ out = self.norm3(out)
+
+ if self.downsample is not None:
+ identity = self.downsample(x)
+
+ out += identity
+
+ return out
+
+ if self.with_cp and x.requires_grad:
+ out = cp.checkpoint(_inner_forward, x)
+ else:
+ out = _inner_forward(x)
+
+ out = self.relu(out)
+
+ return out
+
+
+@BACKBONES.register_module()
+class ResNeSt(ResNetV1d):
+ """ResNeSt backbone.
+
+ Please refer to the `paper `__
+ for details.
+
+ Args:
+ depth (int): Network depth, from {50, 101, 152, 200}.
+ groups (int): Groups of conv2 in Bottleneck. Default: 32.
+ width_per_group (int): Width per group of conv2 in Bottleneck.
+ Default: 4.
+ radix (int): Radix of SpltAtConv2d. Default: 2
+ reduction_factor (int): Reduction factor of SplitAttentionConv2d.
+ Default: 4.
+ avg_down_stride (bool): Whether to use average pool for stride in
+ Bottleneck. Default: True.
+ in_channels (int): Number of input image channels. Default: 3.
+ stem_channels (int): Output channels of the stem layer. Default: 64.
+ num_stages (int): Stages of the network. Default: 4.
+ strides (Sequence[int]): Strides of the first block of each stage.
+ Default: ``(1, 2, 2, 2)``.
+ dilations (Sequence[int]): Dilation of each stage.
+ Default: ``(1, 1, 1, 1)``.
+ out_indices (Sequence[int]): Output from which stages. If only one
+ stage is specified, a single tensor (feature map) is returned,
+ otherwise multiple stages are specified, a tuple of tensors will
+ be returned. Default: ``(3, )``.
+ style (str): `pytorch` or `caffe`. If set to "pytorch", the stride-two
+ layer is the 3x3 conv layer, otherwise the stride-two layer is
+ the first 1x1 conv layer.
+ deep_stem (bool): Replace 7x7 conv in input stem with 3 3x3 conv.
+ Default: False.
+ avg_down (bool): Use AvgPool instead of stride conv when
+ downsampling in the bottleneck. Default: False.
+ frozen_stages (int): Stages to be frozen (stop grad and set eval mode).
+ -1 means not freezing any parameters. Default: -1.
+ conv_cfg (dict | None): The config dict for conv layers. Default: None.
+ norm_cfg (dict): The config dict for norm layers.
+ norm_eval (bool): Whether to set norm layers to eval mode, namely,
+ freeze running stats (mean and var). Note: Effect on Batch Norm
+ and its variants only. Default: False.
+ with_cp (bool): Use checkpoint or not. Using checkpoint will save some
+ memory while slowing down the training speed. Default: False.
+ zero_init_residual (bool): Whether to use zero init for last norm layer
+ in resblocks to let them behave as identity. Default: True.
+ """
+
+ arch_settings = {
+ 50: (Bottleneck, (3, 4, 6, 3)),
+ 101: (Bottleneck, (3, 4, 23, 3)),
+ 152: (Bottleneck, (3, 8, 36, 3)),
+ 200: (Bottleneck, (3, 24, 36, 3)),
+ 269: (Bottleneck, (3, 30, 48, 8))
+ }
+
+ def __init__(self,
+ depth,
+ groups=1,
+ width_per_group=4,
+ radix=2,
+ reduction_factor=4,
+ avg_down_stride=True,
+ **kwargs):
+ self.groups = groups
+ self.width_per_group = width_per_group
+ self.radix = radix
+ self.reduction_factor = reduction_factor
+ self.avg_down_stride = avg_down_stride
+ super().__init__(depth=depth, **kwargs)
+
+ def make_res_layer(self, **kwargs):
+ return ResLayer(
+ groups=self.groups,
+ width_per_group=self.width_per_group,
+ base_channels=self.base_channels,
+ radix=self.radix,
+ reduction_factor=self.reduction_factor,
+ avg_down_stride=self.avg_down_stride,
+ **kwargs)
diff --git a/grounded-sam-osx/transformer_utils/mmpose/models/backbones/resnet.py b/grounded-sam-osx/transformer_utils/mmpose/models/backbones/resnet.py
new file mode 100644
index 0000000000000000000000000000000000000000..649496a755020140d94eb32fbe79d1ff135c86ca
--- /dev/null
+++ b/grounded-sam-osx/transformer_utils/mmpose/models/backbones/resnet.py
@@ -0,0 +1,701 @@
+# Copyright (c) OpenMMLab. All rights reserved.
+import copy
+
+import torch.nn as nn
+import torch.utils.checkpoint as cp
+from mmcv.cnn import (ConvModule, build_conv_layer, build_norm_layer,
+ constant_init, kaiming_init)
+from mmcv.utils.parrots_wrapper import _BatchNorm
+
+from ..builder import BACKBONES
+from .base_backbone import BaseBackbone
+
+
+class BasicBlock(nn.Module):
+ """BasicBlock for ResNet.
+
+ Args:
+ in_channels (int): Input channels of this block.
+ out_channels (int): Output channels of this block.
+ expansion (int): The ratio of ``out_channels/mid_channels`` where
+ ``mid_channels`` is the output channels of conv1. This is a
+ reserved argument in BasicBlock and should always be 1. Default: 1.
+ stride (int): stride of the block. Default: 1
+ dilation (int): dilation of convolution. Default: 1
+ downsample (nn.Module): downsample operation on identity branch.
+ Default: None.
+ style (str): `pytorch` or `caffe`. It is unused and reserved for
+ unified API with Bottleneck.
+ with_cp (bool): Use checkpoint or not. Using checkpoint will save some
+ memory while slowing down the training speed.
+ conv_cfg (dict): dictionary to construct and config conv layer.
+ Default: None
+ norm_cfg (dict): dictionary to construct and config norm layer.
+ Default: dict(type='BN')
+ """
+
+ def __init__(self,
+ in_channels,
+ out_channels,
+ expansion=1,
+ stride=1,
+ dilation=1,
+ downsample=None,
+ style='pytorch',
+ with_cp=False,
+ conv_cfg=None,
+ norm_cfg=dict(type='BN')):
+ # Protect mutable default arguments
+ norm_cfg = copy.deepcopy(norm_cfg)
+ super().__init__()
+ self.in_channels = in_channels
+ self.out_channels = out_channels
+ self.expansion = expansion
+ assert self.expansion == 1
+ assert out_channels % expansion == 0
+ self.mid_channels = out_channels // expansion
+ self.stride = stride
+ self.dilation = dilation
+ self.style = style
+ self.with_cp = with_cp
+ self.conv_cfg = conv_cfg
+ self.norm_cfg = norm_cfg
+
+ self.norm1_name, norm1 = build_norm_layer(
+ norm_cfg, self.mid_channels, postfix=1)
+ self.norm2_name, norm2 = build_norm_layer(
+ norm_cfg, out_channels, postfix=2)
+
+ self.conv1 = build_conv_layer(
+ conv_cfg,
+ in_channels,
+ self.mid_channels,
+ 3,
+ stride=stride,
+ padding=dilation,
+ dilation=dilation,
+ bias=False)
+ self.add_module(self.norm1_name, norm1)
+ self.conv2 = build_conv_layer(
+ conv_cfg,
+ self.mid_channels,
+ out_channels,
+ 3,
+ padding=1,
+ bias=False)
+ self.add_module(self.norm2_name, norm2)
+
+ self.relu = nn.ReLU(inplace=True)
+ self.downsample = downsample
+
+ @property
+ def norm1(self):
+ """nn.Module: the normalization layer named "norm1" """
+ return getattr(self, self.norm1_name)
+
+ @property
+ def norm2(self):
+ """nn.Module: the normalization layer named "norm2" """
+ return getattr(self, self.norm2_name)
+
+ def forward(self, x):
+ """Forward function."""
+
+ def _inner_forward(x):
+ identity = x
+
+ out = self.conv1(x)
+ out = self.norm1(out)
+ out = self.relu(out)
+
+ out = self.conv2(out)
+ out = self.norm2(out)
+
+ if self.downsample is not None:
+ identity = self.downsample(x)
+
+ out += identity
+
+ return out
+
+ if self.with_cp and x.requires_grad:
+ out = cp.checkpoint(_inner_forward, x)
+ else:
+ out = _inner_forward(x)
+
+ out = self.relu(out)
+
+ return out
+
+
+class Bottleneck(nn.Module):
+ """Bottleneck block for ResNet.
+
+ Args:
+ in_channels (int): Input channels of this block.
+ out_channels (int): Output channels of this block.
+ expansion (int): The ratio of ``out_channels/mid_channels`` where
+ ``mid_channels`` is the input/output channels of conv2. Default: 4.
+ stride (int): stride of the block. Default: 1
+ dilation (int): dilation of convolution. Default: 1
+ downsample (nn.Module): downsample operation on identity branch.
+ Default: None.
+ style (str): ``"pytorch"`` or ``"caffe"``. If set to "pytorch", the
+ stride-two layer is the 3x3 conv layer, otherwise the stride-two
+ layer is the first 1x1 conv layer. Default: "pytorch".
+ with_cp (bool): Use checkpoint or not. Using checkpoint will save some
+ memory while slowing down the training speed.
+ conv_cfg (dict): dictionary to construct and config conv layer.
+ Default: None
+ norm_cfg (dict): dictionary to construct and config norm layer.
+ Default: dict(type='BN')
+ """
+
+ def __init__(self,
+ in_channels,
+ out_channels,
+ expansion=4,
+ stride=1,
+ dilation=1,
+ downsample=None,
+ style='pytorch',
+ with_cp=False,
+ conv_cfg=None,
+ norm_cfg=dict(type='BN')):
+ # Protect mutable default arguments
+ norm_cfg = copy.deepcopy(norm_cfg)
+ super().__init__()
+ assert style in ['pytorch', 'caffe']
+
+ self.in_channels = in_channels
+ self.out_channels = out_channels
+ self.expansion = expansion
+ assert out_channels % expansion == 0
+ self.mid_channels = out_channels // expansion
+ self.stride = stride
+ self.dilation = dilation
+ self.style = style
+ self.with_cp = with_cp
+ self.conv_cfg = conv_cfg
+ self.norm_cfg = norm_cfg
+
+ if self.style == 'pytorch':
+ self.conv1_stride = 1
+ self.conv2_stride = stride
+ else:
+ self.conv1_stride = stride
+ self.conv2_stride = 1
+
+ self.norm1_name, norm1 = build_norm_layer(
+ norm_cfg, self.mid_channels, postfix=1)
+ self.norm2_name, norm2 = build_norm_layer(
+ norm_cfg, self.mid_channels, postfix=2)
+ self.norm3_name, norm3 = build_norm_layer(
+ norm_cfg, out_channels, postfix=3)
+
+ self.conv1 = build_conv_layer(
+ conv_cfg,
+ in_channels,
+ self.mid_channels,
+ kernel_size=1,
+ stride=self.conv1_stride,
+ bias=False)
+ self.add_module(self.norm1_name, norm1)
+ self.conv2 = build_conv_layer(
+ conv_cfg,
+ self.mid_channels,
+ self.mid_channels,
+ kernel_size=3,
+ stride=self.conv2_stride,
+ padding=dilation,
+ dilation=dilation,
+ bias=False)
+
+ self.add_module(self.norm2_name, norm2)
+ self.conv3 = build_conv_layer(
+ conv_cfg,
+ self.mid_channels,
+ out_channels,
+ kernel_size=1,
+ bias=False)
+ self.add_module(self.norm3_name, norm3)
+
+ self.relu = nn.ReLU(inplace=True)
+ self.downsample = downsample
+
+ @property
+ def norm1(self):
+ """nn.Module: the normalization layer named "norm1" """
+ return getattr(self, self.norm1_name)
+
+ @property
+ def norm2(self):
+ """nn.Module: the normalization layer named "norm2" """
+ return getattr(self, self.norm2_name)
+
+ @property
+ def norm3(self):
+ """nn.Module: the normalization layer named "norm3" """
+ return getattr(self, self.norm3_name)
+
+ def forward(self, x):
+ """Forward function."""
+
+ def _inner_forward(x):
+ identity = x
+
+ out = self.conv1(x)
+ out = self.norm1(out)
+ out = self.relu(out)
+
+ out = self.conv2(out)
+ out = self.norm2(out)
+ out = self.relu(out)
+
+ out = self.conv3(out)
+ out = self.norm3(out)
+
+ if self.downsample is not None:
+ identity = self.downsample(x)
+
+ out += identity
+
+ return out
+
+ if self.with_cp and x.requires_grad:
+ out = cp.checkpoint(_inner_forward, x)
+ else:
+ out = _inner_forward(x)
+
+ out = self.relu(out)
+
+ return out
+
+
+def get_expansion(block, expansion=None):
+ """Get the expansion of a residual block.
+
+ The block expansion will be obtained by the following order:
+
+ 1. If ``expansion`` is given, just return it.
+ 2. If ``block`` has the attribute ``expansion``, then return
+ ``block.expansion``.
+ 3. Return the default value according the the block type:
+ 1 for ``BasicBlock`` and 4 for ``Bottleneck``.
+
+ Args:
+ block (class): The block class.
+ expansion (int | None): The given expansion ratio.
+
+ Returns:
+ int: The expansion of the block.
+ """
+ if isinstance(expansion, int):
+ assert expansion > 0
+ elif expansion is None:
+ if hasattr(block, 'expansion'):
+ expansion = block.expansion
+ elif issubclass(block, BasicBlock):
+ expansion = 1
+ elif issubclass(block, Bottleneck):
+ expansion = 4
+ else:
+ raise TypeError(f'expansion is not specified for {block.__name__}')
+ else:
+ raise TypeError('expansion must be an integer or None')
+
+ return expansion
+
+
+class ResLayer(nn.Sequential):
+ """ResLayer to build ResNet style backbone.
+
+ Args:
+ block (nn.Module): Residual block used to build ResLayer.
+ num_blocks (int): Number of blocks.
+ in_channels (int): Input channels of this block.
+ out_channels (int): Output channels of this block.
+ expansion (int, optional): The expansion for BasicBlock/Bottleneck.
+ If not specified, it will firstly be obtained via
+ ``block.expansion``. If the block has no attribute "expansion",
+ the following default values will be used: 1 for BasicBlock and
+ 4 for Bottleneck. Default: None.
+ stride (int): stride of the first block. Default: 1.
+ avg_down (bool): Use AvgPool instead of stride conv when
+ downsampling in the bottleneck. Default: False
+ conv_cfg (dict): dictionary to construct and config conv layer.
+ Default: None
+ norm_cfg (dict): dictionary to construct and config norm layer.
+ Default: dict(type='BN')
+ downsample_first (bool): Downsample at the first block or last block.
+ False for Hourglass, True for ResNet. Default: True
+ """
+
+ def __init__(self,
+ block,
+ num_blocks,
+ in_channels,
+ out_channels,
+ expansion=None,
+ stride=1,
+ avg_down=False,
+ conv_cfg=None,
+ norm_cfg=dict(type='BN'),
+ downsample_first=True,
+ **kwargs):
+ # Protect mutable default arguments
+ norm_cfg = copy.deepcopy(norm_cfg)
+ self.block = block
+ self.expansion = get_expansion(block, expansion)
+
+ downsample = None
+ if stride != 1 or in_channels != out_channels:
+ downsample = []
+ conv_stride = stride
+ if avg_down and stride != 1:
+ conv_stride = 1
+ downsample.append(
+ nn.AvgPool2d(
+ kernel_size=stride,
+ stride=stride,
+ ceil_mode=True,
+ count_include_pad=False))
+ downsample.extend([
+ build_conv_layer(
+ conv_cfg,
+ in_channels,
+ out_channels,
+ kernel_size=1,
+ stride=conv_stride,
+ bias=False),
+ build_norm_layer(norm_cfg, out_channels)[1]
+ ])
+ downsample = nn.Sequential(*downsample)
+
+ layers = []
+ if downsample_first:
+ layers.append(
+ block(
+ in_channels=in_channels,
+ out_channels=out_channels,
+ expansion=self.expansion,
+ stride=stride,
+ downsample=downsample,
+ conv_cfg=conv_cfg,
+ norm_cfg=norm_cfg,
+ **kwargs))
+ in_channels = out_channels
+ for _ in range(1, num_blocks):
+ layers.append(
+ block(
+ in_channels=in_channels,
+ out_channels=out_channels,
+ expansion=self.expansion,
+ stride=1,
+ conv_cfg=conv_cfg,
+ norm_cfg=norm_cfg,
+ **kwargs))
+ else: # downsample_first=False is for HourglassModule
+ for i in range(0, num_blocks - 1):
+ layers.append(
+ block(
+ in_channels=in_channels,
+ out_channels=in_channels,
+ expansion=self.expansion,
+ stride=1,
+ conv_cfg=conv_cfg,
+ norm_cfg=norm_cfg,
+ **kwargs))
+ layers.append(
+ block(
+ in_channels=in_channels,
+ out_channels=out_channels,
+ expansion=self.expansion,
+ stride=stride,
+ downsample=downsample,
+ conv_cfg=conv_cfg,
+ norm_cfg=norm_cfg,
+ **kwargs))
+
+ super().__init__(*layers)
+
+
+@BACKBONES.register_module()
+class ResNet(BaseBackbone):
+ """ResNet backbone.
+
+ Please refer to the `paper `__ for
+ details.
+
+ Args:
+ depth (int): Network depth, from {18, 34, 50, 101, 152}.
+ in_channels (int): Number of input image channels. Default: 3.
+ stem_channels (int): Output channels of the stem layer. Default: 64.
+ base_channels (int): Middle channels of the first stage. Default: 64.
+ num_stages (int): Stages of the network. Default: 4.
+ strides (Sequence[int]): Strides of the first block of each stage.
+ Default: ``(1, 2, 2, 2)``.
+ dilations (Sequence[int]): Dilation of each stage.
+ Default: ``(1, 1, 1, 1)``.
+ out_indices (Sequence[int]): Output from which stages. If only one
+ stage is specified, a single tensor (feature map) is returned,
+ otherwise multiple stages are specified, a tuple of tensors will
+ be returned. Default: ``(3, )``.
+ style (str): `pytorch` or `caffe`. If set to "pytorch", the stride-two
+ layer is the 3x3 conv layer, otherwise the stride-two layer is
+ the first 1x1 conv layer.
+ deep_stem (bool): Replace 7x7 conv in input stem with 3 3x3 conv.
+ Default: False.
+ avg_down (bool): Use AvgPool instead of stride conv when
+ downsampling in the bottleneck. Default: False.
+ frozen_stages (int): Stages to be frozen (stop grad and set eval mode).
+ -1 means not freezing any parameters. Default: -1.
+ conv_cfg (dict | None): The config dict for conv layers. Default: None.
+ norm_cfg (dict): The config dict for norm layers.
+ norm_eval (bool): Whether to set norm layers to eval mode, namely,
+ freeze running stats (mean and var). Note: Effect on Batch Norm
+ and its variants only. Default: False.
+ with_cp (bool): Use checkpoint or not. Using checkpoint will save some
+ memory while slowing down the training speed. Default: False.
+ zero_init_residual (bool): Whether to use zero init for last norm layer
+ in resblocks to let them behave as identity. Default: True.
+
+ Example:
+ >>> from mmpose.models import ResNet
+ >>> import torch
+ >>> self = ResNet(depth=18, out_indices=(0, 1, 2, 3))
+ >>> self.eval()
+ >>> inputs = torch.rand(1, 3, 32, 32)
+ >>> level_outputs = self.forward(inputs)
+ >>> for level_out in level_outputs:
+ ... print(tuple(level_out.shape))
+ (1, 64, 8, 8)
+ (1, 128, 4, 4)
+ (1, 256, 2, 2)
+ (1, 512, 1, 1)
+ """
+
+ arch_settings = {
+ 18: (BasicBlock, (2, 2, 2, 2)),
+ 34: (BasicBlock, (3, 4, 6, 3)),
+ 50: (Bottleneck, (3, 4, 6, 3)),
+ 101: (Bottleneck, (3, 4, 23, 3)),
+ 152: (Bottleneck, (3, 8, 36, 3))
+ }
+
+ def __init__(self,
+ depth,
+ in_channels=3,
+ stem_channels=64,
+ base_channels=64,
+ expansion=None,
+ num_stages=4,
+ strides=(1, 2, 2, 2),
+ dilations=(1, 1, 1, 1),
+ out_indices=(3, ),
+ style='pytorch',
+ deep_stem=False,
+ avg_down=False,
+ frozen_stages=-1,
+ conv_cfg=None,
+ norm_cfg=dict(type='BN', requires_grad=True),
+ norm_eval=False,
+ with_cp=False,
+ zero_init_residual=True):
+ # Protect mutable default arguments
+ norm_cfg = copy.deepcopy(norm_cfg)
+ super().__init__()
+ if depth not in self.arch_settings:
+ raise KeyError(f'invalid depth {depth} for resnet')
+ self.depth = depth
+ self.stem_channels = stem_channels
+ self.base_channels = base_channels
+ self.num_stages = num_stages
+ assert 1 <= num_stages <= 4
+ self.strides = strides
+ self.dilations = dilations
+ assert len(strides) == len(dilations) == num_stages
+ self.out_indices = out_indices
+ assert max(out_indices) < num_stages
+ self.style = style
+ self.deep_stem = deep_stem
+ self.avg_down = avg_down
+ self.frozen_stages = frozen_stages
+ self.conv_cfg = conv_cfg
+ self.norm_cfg = norm_cfg
+ self.with_cp = with_cp
+ self.norm_eval = norm_eval
+ self.zero_init_residual = zero_init_residual
+ self.block, stage_blocks = self.arch_settings[depth]
+ self.stage_blocks = stage_blocks[:num_stages]
+ self.expansion = get_expansion(self.block, expansion)
+
+ self._make_stem_layer(in_channels, stem_channels)
+
+ self.res_layers = []
+ _in_channels = stem_channels
+ _out_channels = base_channels * self.expansion
+ for i, num_blocks in enumerate(self.stage_blocks):
+ stride = strides[i]
+ dilation = dilations[i]
+ res_layer = self.make_res_layer(
+ block=self.block,
+ num_blocks=num_blocks,
+ in_channels=_in_channels,
+ out_channels=_out_channels,
+ expansion=self.expansion,
+ stride=stride,
+ dilation=dilation,
+ style=self.style,
+ avg_down=self.avg_down,
+ with_cp=with_cp,
+ conv_cfg=conv_cfg,
+ norm_cfg=norm_cfg)
+ _in_channels = _out_channels
+ _out_channels *= 2
+ layer_name = f'layer{i + 1}'
+ self.add_module(layer_name, res_layer)
+ self.res_layers.append(layer_name)
+
+ self._freeze_stages()
+
+ self.feat_dim = res_layer[-1].out_channels
+
+ def make_res_layer(self, **kwargs):
+ """Make a ResLayer."""
+ return ResLayer(**kwargs)
+
+ @property
+ def norm1(self):
+ """nn.Module: the normalization layer named "norm1" """
+ return getattr(self, self.norm1_name)
+
+ def _make_stem_layer(self, in_channels, stem_channels):
+ """Make stem layer."""
+ if self.deep_stem:
+ self.stem = nn.Sequential(
+ ConvModule(
+ in_channels,
+ stem_channels // 2,
+ kernel_size=3,
+ stride=2,
+ padding=1,
+ conv_cfg=self.conv_cfg,
+ norm_cfg=self.norm_cfg,
+ inplace=True),
+ ConvModule(
+ stem_channels // 2,
+ stem_channels // 2,
+ kernel_size=3,
+ stride=1,
+ padding=1,
+ conv_cfg=self.conv_cfg,
+ norm_cfg=self.norm_cfg,
+ inplace=True),
+ ConvModule(
+ stem_channels // 2,
+ stem_channels,
+ kernel_size=3,
+ stride=1,
+ padding=1,
+ conv_cfg=self.conv_cfg,
+ norm_cfg=self.norm_cfg,
+ inplace=True))
+ else:
+ self.conv1 = build_conv_layer(
+ self.conv_cfg,
+ in_channels,
+ stem_channels,
+ kernel_size=7,
+ stride=2,
+ padding=3,
+ bias=False)
+ self.norm1_name, norm1 = build_norm_layer(
+ self.norm_cfg, stem_channels, postfix=1)
+ self.add_module(self.norm1_name, norm1)
+ self.relu = nn.ReLU(inplace=True)
+ self.maxpool = nn.MaxPool2d(kernel_size=3, stride=2, padding=1)
+
+ def _freeze_stages(self):
+ """Freeze parameters."""
+ if self.frozen_stages >= 0:
+ if self.deep_stem:
+ self.stem.eval()
+ for param in self.stem.parameters():
+ param.requires_grad = False
+ else:
+ self.norm1.eval()
+ for m in [self.conv1, self.norm1]:
+ for param in m.parameters():
+ param.requires_grad = False
+
+ for i in range(1, self.frozen_stages + 1):
+ m = getattr(self, f'layer{i}')
+ m.eval()
+ for param in m.parameters():
+ param.requires_grad = False
+
+ def init_weights(self, pretrained=None):
+ """Initialize the weights in backbone.
+
+ Args:
+ pretrained (str, optional): Path to pre-trained weights.
+ Defaults to None.
+ """
+ super().init_weights(pretrained)
+ if pretrained is None:
+ for m in self.modules():
+ if isinstance(m, nn.Conv2d):
+ kaiming_init(m)
+ elif isinstance(m, (_BatchNorm, nn.GroupNorm)):
+ constant_init(m, 1)
+
+ if self.zero_init_residual:
+ for m in self.modules():
+ if isinstance(m, Bottleneck):
+ constant_init(m.norm3, 0)
+ elif isinstance(m, BasicBlock):
+ constant_init(m.norm2, 0)
+
+ def forward(self, x):
+ """Forward function."""
+ if self.deep_stem:
+ x = self.stem(x)
+ else:
+ x = self.conv1(x)
+ x = self.norm1(x)
+ x = self.relu(x)
+ x = self.maxpool(x)
+ outs = []
+ for i, layer_name in enumerate(self.res_layers):
+ res_layer = getattr(self, layer_name)
+ x = res_layer(x)
+ if i in self.out_indices:
+ outs.append(x)
+ if len(outs) == 1:
+ return outs[0]
+ return tuple(outs)
+
+ def train(self, mode=True):
+ """Convert the model into training mode."""
+ super().train(mode)
+ self._freeze_stages()
+ if mode and self.norm_eval:
+ for m in self.modules():
+ # trick: eval have effect on BatchNorm only
+ if isinstance(m, _BatchNorm):
+ m.eval()
+
+
+@BACKBONES.register_module()
+class ResNetV1d(ResNet):
+ r"""ResNetV1d variant described in `Bag of Tricks
+ `__.
+
+ Compared with default ResNet(ResNetV1b), ResNetV1d replaces the 7x7 conv in
+ the input stem with three 3x3 convs. And in the downsampling block, a 2x2
+ avg_pool with stride 2 is added before conv, whose stride is changed to 1.
+ """
+
+ def __init__(self, **kwargs):
+ super().__init__(deep_stem=True, avg_down=True, **kwargs)
diff --git a/grounded-sam-osx/transformer_utils/mmpose/models/backbones/resnext.py b/grounded-sam-osx/transformer_utils/mmpose/models/backbones/resnext.py
new file mode 100644
index 0000000000000000000000000000000000000000..c10dc33f98ac3229c77bf306acf19950c295f904
--- /dev/null
+++ b/grounded-sam-osx/transformer_utils/mmpose/models/backbones/resnext.py
@@ -0,0 +1,162 @@
+# Copyright (c) OpenMMLab. All rights reserved.
+from mmcv.cnn import build_conv_layer, build_norm_layer
+
+from ..builder import BACKBONES
+from .resnet import Bottleneck as _Bottleneck
+from .resnet import ResLayer, ResNet
+
+
+class Bottleneck(_Bottleneck):
+ """Bottleneck block for ResNeXt.
+
+ Args:
+ in_channels (int): Input channels of this block.
+ out_channels (int): Output channels of this block.
+ groups (int): Groups of conv2.
+ width_per_group (int): Width per group of conv2. 64x4d indicates
+ ``groups=64, width_per_group=4`` and 32x8d indicates
+ ``groups=32, width_per_group=8``.
+ stride (int): stride of the block. Default: 1
+ dilation (int): dilation of convolution. Default: 1
+ downsample (nn.Module): downsample operation on identity branch.
+ Default: None
+ style (str): `pytorch` or `caffe`. If set to "pytorch", the stride-two
+ layer is the 3x3 conv layer, otherwise the stride-two layer is
+ the first 1x1 conv layer.
+ conv_cfg (dict): dictionary to construct and config conv layer.
+ Default: None
+ norm_cfg (dict): dictionary to construct and config norm layer.
+ Default: dict(type='BN')
+ with_cp (bool): Use checkpoint or not. Using checkpoint will save some
+ memory while slowing down the training speed.
+ """
+
+ def __init__(self,
+ in_channels,
+ out_channels,
+ base_channels=64,
+ groups=32,
+ width_per_group=4,
+ **kwargs):
+ super().__init__(in_channels, out_channels, **kwargs)
+ self.groups = groups
+ self.width_per_group = width_per_group
+
+ # For ResNet bottleneck, middle channels are determined by expansion
+ # and out_channels, but for ResNeXt bottleneck, it is determined by
+ # groups and width_per_group and the stage it is located in.
+ if groups != 1:
+ assert self.mid_channels % base_channels == 0
+ self.mid_channels = (
+ groups * width_per_group * self.mid_channels // base_channels)
+
+ self.norm1_name, norm1 = build_norm_layer(
+ self.norm_cfg, self.mid_channels, postfix=1)
+ self.norm2_name, norm2 = build_norm_layer(
+ self.norm_cfg, self.mid_channels, postfix=2)
+ self.norm3_name, norm3 = build_norm_layer(
+ self.norm_cfg, self.out_channels, postfix=3)
+
+ self.conv1 = build_conv_layer(
+ self.conv_cfg,
+ self.in_channels,
+ self.mid_channels,
+ kernel_size=1,
+ stride=self.conv1_stride,
+ bias=False)
+ self.add_module(self.norm1_name, norm1)
+ self.conv2 = build_conv_layer(
+ self.conv_cfg,
+ self.mid_channels,
+ self.mid_channels,
+ kernel_size=3,
+ stride=self.conv2_stride,
+ padding=self.dilation,
+ dilation=self.dilation,
+ groups=groups,
+ bias=False)
+
+ self.add_module(self.norm2_name, norm2)
+ self.conv3 = build_conv_layer(
+ self.conv_cfg,
+ self.mid_channels,
+ self.out_channels,
+ kernel_size=1,
+ bias=False)
+ self.add_module(self.norm3_name, norm3)
+
+
+@BACKBONES.register_module()
+class ResNeXt(ResNet):
+ """ResNeXt backbone.
+
+ Please refer to the `paper `__ for
+ details.
+
+ Args:
+ depth (int): Network depth, from {50, 101, 152}.
+ groups (int): Groups of conv2 in Bottleneck. Default: 32.
+ width_per_group (int): Width per group of conv2 in Bottleneck.
+ Default: 4.
+ in_channels (int): Number of input image channels. Default: 3.
+ stem_channels (int): Output channels of the stem layer. Default: 64.
+ num_stages (int): Stages of the network. Default: 4.
+ strides (Sequence[int]): Strides of the first block of each stage.
+ Default: ``(1, 2, 2, 2)``.
+ dilations (Sequence[int]): Dilation of each stage.
+ Default: ``(1, 1, 1, 1)``.
+ out_indices (Sequence[int]): Output from which stages. If only one
+ stage is specified, a single tensor (feature map) is returned,
+ otherwise multiple stages are specified, a tuple of tensors will
+ be returned. Default: ``(3, )``.
+ style (str): `pytorch` or `caffe`. If set to "pytorch", the stride-two
+ layer is the 3x3 conv layer, otherwise the stride-two layer is
+ the first 1x1 conv layer.
+ deep_stem (bool): Replace 7x7 conv in input stem with 3 3x3 conv.
+ Default: False.
+ avg_down (bool): Use AvgPool instead of stride conv when
+ downsampling in the bottleneck. Default: False.
+ frozen_stages (int): Stages to be frozen (stop grad and set eval mode).
+ -1 means not freezing any parameters. Default: -1.
+ conv_cfg (dict | None): The config dict for conv layers. Default: None.
+ norm_cfg (dict): The config dict for norm layers.
+ norm_eval (bool): Whether to set norm layers to eval mode, namely,
+ freeze running stats (mean and var). Note: Effect on Batch Norm
+ and its variants only. Default: False.
+ with_cp (bool): Use checkpoint or not. Using checkpoint will save some
+ memory while slowing down the training speed. Default: False.
+ zero_init_residual (bool): Whether to use zero init for last norm layer
+ in resblocks to let them behave as identity. Default: True.
+
+ Example:
+ >>> from mmpose.models import ResNeXt
+ >>> import torch
+ >>> self = ResNeXt(depth=50, out_indices=(0, 1, 2, 3))
+ >>> self.eval()
+ >>> inputs = torch.rand(1, 3, 32, 32)
+ >>> level_outputs = self.forward(inputs)
+ >>> for level_out in level_outputs:
+ ... print(tuple(level_out.shape))
+ (1, 256, 8, 8)
+ (1, 512, 4, 4)
+ (1, 1024, 2, 2)
+ (1, 2048, 1, 1)
+ """
+
+ arch_settings = {
+ 50: (Bottleneck, (3, 4, 6, 3)),
+ 101: (Bottleneck, (3, 4, 23, 3)),
+ 152: (Bottleneck, (3, 8, 36, 3))
+ }
+
+ def __init__(self, depth, groups=32, width_per_group=4, **kwargs):
+ self.groups = groups
+ self.width_per_group = width_per_group
+ super().__init__(depth, **kwargs)
+
+ def make_res_layer(self, **kwargs):
+ return ResLayer(
+ groups=self.groups,
+ width_per_group=self.width_per_group,
+ base_channels=self.base_channels,
+ **kwargs)
diff --git a/grounded-sam-osx/transformer_utils/mmpose/models/backbones/rsn.py b/grounded-sam-osx/transformer_utils/mmpose/models/backbones/rsn.py
new file mode 100644
index 0000000000000000000000000000000000000000..29038afe2a77dcb3d3b027b1549d478916a50727
--- /dev/null
+++ b/grounded-sam-osx/transformer_utils/mmpose/models/backbones/rsn.py
@@ -0,0 +1,616 @@
+# Copyright (c) OpenMMLab. All rights reserved.
+import copy as cp
+
+import torch
+import torch.nn as nn
+import torch.nn.functional as F
+from mmcv.cnn import (ConvModule, MaxPool2d, constant_init, kaiming_init,
+ normal_init)
+
+from ..builder import BACKBONES
+from .base_backbone import BaseBackbone
+
+
+class RSB(nn.Module):
+ """Residual Steps block for RSN. Paper ref: Cai et al. "Learning Delicate
+ Local Representations for Multi-Person Pose Estimation" (ECCV 2020).
+
+ Args:
+ in_channels (int): Input channels of this block.
+ out_channels (int): Output channels of this block.
+ num_steps (int): Numbers of steps in RSB
+ stride (int): stride of the block. Default: 1
+ downsample (nn.Module): downsample operation on identity branch.
+ Default: None.
+ norm_cfg (dict): dictionary to construct and config norm layer.
+ Default: dict(type='BN')
+ expand_times (int): Times by which the in_channels are expanded.
+ Default:26.
+ res_top_channels (int): Number of channels of feature output by
+ ResNet_top. Default:64.
+ """
+
+ expansion = 1
+
+ def __init__(self,
+ in_channels,
+ out_channels,
+ num_steps=4,
+ stride=1,
+ downsample=None,
+ with_cp=False,
+ norm_cfg=dict(type='BN'),
+ expand_times=26,
+ res_top_channels=64):
+ # Protect mutable default arguments
+ norm_cfg = cp.deepcopy(norm_cfg)
+ super().__init__()
+ assert num_steps > 1
+ self.in_channels = in_channels
+ self.branch_channels = self.in_channels * expand_times
+ self.branch_channels //= res_top_channels
+ self.out_channels = out_channels
+ self.stride = stride
+ self.downsample = downsample
+ self.with_cp = with_cp
+ self.norm_cfg = norm_cfg
+ self.num_steps = num_steps
+ self.conv_bn_relu1 = ConvModule(
+ self.in_channels,
+ self.num_steps * self.branch_channels,
+ kernel_size=1,
+ stride=self.stride,
+ padding=0,
+ norm_cfg=self.norm_cfg,
+ inplace=False)
+ for i in range(self.num_steps):
+ for j in range(i + 1):
+ module_name = f'conv_bn_relu2_{i + 1}_{j + 1}'
+ self.add_module(
+ module_name,
+ ConvModule(
+ self.branch_channels,
+ self.branch_channels,
+ kernel_size=3,
+ stride=1,
+ padding=1,
+ norm_cfg=self.norm_cfg,
+ inplace=False))
+ self.conv_bn3 = ConvModule(
+ self.num_steps * self.branch_channels,
+ self.out_channels * self.expansion,
+ kernel_size=1,
+ stride=1,
+ padding=0,
+ act_cfg=None,
+ norm_cfg=self.norm_cfg,
+ inplace=False)
+ self.relu = nn.ReLU(inplace=False)
+
+ def forward(self, x):
+ """Forward function."""
+
+ identity = x
+ x = self.conv_bn_relu1(x)
+ spx = torch.split(x, self.branch_channels, 1)
+ outputs = list()
+ outs = list()
+ for i in range(self.num_steps):
+ outputs_i = list()
+ outputs.append(outputs_i)
+ for j in range(i + 1):
+ if j == 0:
+ inputs = spx[i]
+ else:
+ inputs = outputs[i][j - 1]
+ if i > j:
+ inputs = inputs + outputs[i - 1][j]
+ module_name = f'conv_bn_relu2_{i + 1}_{j + 1}'
+ module_i_j = getattr(self, module_name)
+ outputs[i].append(module_i_j(inputs))
+
+ outs.append(outputs[i][i])
+ out = torch.cat(tuple(outs), 1)
+ out = self.conv_bn3(out)
+
+ if self.downsample is not None:
+ identity = self.downsample(identity)
+ out = out + identity
+
+ out = self.relu(out)
+
+ return out
+
+
+class Downsample_module(nn.Module):
+ """Downsample module for RSN.
+
+ Args:
+ block (nn.Module): Downsample block.
+ num_blocks (list): Number of blocks in each downsample unit.
+ num_units (int): Numbers of downsample units. Default: 4
+ has_skip (bool): Have skip connections from prior upsample
+ module or not. Default:False
+ num_steps (int): Number of steps in a block. Default:4
+ norm_cfg (dict): dictionary to construct and config norm layer.
+ Default: dict(type='BN')
+ in_channels (int): Number of channels of the input feature to
+ downsample module. Default: 64
+ expand_times (int): Times by which the in_channels are expanded.
+ Default:26.
+ """
+
+ def __init__(self,
+ block,
+ num_blocks,
+ num_steps=4,
+ num_units=4,
+ has_skip=False,
+ norm_cfg=dict(type='BN'),
+ in_channels=64,
+ expand_times=26):
+ # Protect mutable default arguments
+ norm_cfg = cp.deepcopy(norm_cfg)
+ super().__init__()
+ self.has_skip = has_skip
+ self.in_channels = in_channels
+ assert len(num_blocks) == num_units
+ self.num_blocks = num_blocks
+ self.num_units = num_units
+ self.num_steps = num_steps
+ self.norm_cfg = norm_cfg
+ self.layer1 = self._make_layer(
+ block,
+ in_channels,
+ num_blocks[0],
+ expand_times=expand_times,
+ res_top_channels=in_channels)
+ for i in range(1, num_units):
+ module_name = f'layer{i + 1}'
+ self.add_module(
+ module_name,
+ self._make_layer(
+ block,
+ in_channels * pow(2, i),
+ num_blocks[i],
+ stride=2,
+ expand_times=expand_times,
+ res_top_channels=in_channels))
+
+ def _make_layer(self,
+ block,
+ out_channels,
+ blocks,
+ stride=1,
+ expand_times=26,
+ res_top_channels=64):
+ downsample = None
+ if stride != 1 or self.in_channels != out_channels * block.expansion:
+ downsample = ConvModule(
+ self.in_channels,
+ out_channels * block.expansion,
+ kernel_size=1,
+ stride=stride,
+ padding=0,
+ norm_cfg=self.norm_cfg,
+ act_cfg=None,
+ inplace=True)
+
+ units = list()
+ units.append(
+ block(
+ self.in_channels,
+ out_channels,
+ num_steps=self.num_steps,
+ stride=stride,
+ downsample=downsample,
+ norm_cfg=self.norm_cfg,
+ expand_times=expand_times,
+ res_top_channels=res_top_channels))
+ self.in_channels = out_channels * block.expansion
+ for _ in range(1, blocks):
+ units.append(
+ block(
+ self.in_channels,
+ out_channels,
+ num_steps=self.num_steps,
+ expand_times=expand_times,
+ res_top_channels=res_top_channels))
+
+ return nn.Sequential(*units)
+
+ def forward(self, x, skip1, skip2):
+ out = list()
+ for i in range(self.num_units):
+ module_name = f'layer{i + 1}'
+ module_i = getattr(self, module_name)
+ x = module_i(x)
+ if self.has_skip:
+ x = x + skip1[i] + skip2[i]
+ out.append(x)
+ out.reverse()
+
+ return tuple(out)
+
+
+class Upsample_unit(nn.Module):
+ """Upsample unit for upsample module.
+
+ Args:
+ ind (int): Indicates whether to interpolate (>0) and whether to
+ generate feature map for the next hourglass-like module.
+ num_units (int): Number of units that form a upsample module. Along
+ with ind and gen_cross_conv, nm_units is used to decide whether
+ to generate feature map for the next hourglass-like module.
+ in_channels (int): Channel number of the skip-in feature maps from
+ the corresponding downsample unit.
+ unit_channels (int): Channel number in this unit. Default:256.
+ gen_skip: (bool): Whether or not to generate skips for the posterior
+ downsample module. Default:False
+ gen_cross_conv (bool): Whether to generate feature map for the next
+ hourglass-like module. Default:False
+ norm_cfg (dict): dictionary to construct and config norm layer.
+ Default: dict(type='BN')
+ out_channels (in): Number of channels of feature output by upsample
+ module. Must equal to in_channels of downsample module. Default:64
+ """
+
+ def __init__(self,
+ ind,
+ num_units,
+ in_channels,
+ unit_channels=256,
+ gen_skip=False,
+ gen_cross_conv=False,
+ norm_cfg=dict(type='BN'),
+ out_channels=64):
+ # Protect mutable default arguments
+ norm_cfg = cp.deepcopy(norm_cfg)
+ super().__init__()
+ self.num_units = num_units
+ self.norm_cfg = norm_cfg
+ self.in_skip = ConvModule(
+ in_channels,
+ unit_channels,
+ kernel_size=1,
+ stride=1,
+ padding=0,
+ norm_cfg=self.norm_cfg,
+ act_cfg=None,
+ inplace=True)
+ self.relu = nn.ReLU(inplace=True)
+
+ self.ind = ind
+ if self.ind > 0:
+ self.up_conv = ConvModule(
+ unit_channels,
+ unit_channels,
+ kernel_size=1,
+ stride=1,
+ padding=0,
+ norm_cfg=self.norm_cfg,
+ act_cfg=None,
+ inplace=True)
+
+ self.gen_skip = gen_skip
+ if self.gen_skip:
+ self.out_skip1 = ConvModule(
+ in_channels,
+ in_channels,
+ kernel_size=1,
+ stride=1,
+ padding=0,
+ norm_cfg=self.norm_cfg,
+ inplace=True)
+
+ self.out_skip2 = ConvModule(
+ unit_channels,
+ in_channels,
+ kernel_size=1,
+ stride=1,
+ padding=0,
+ norm_cfg=self.norm_cfg,
+ inplace=True)
+
+ self.gen_cross_conv = gen_cross_conv
+ if self.ind == num_units - 1 and self.gen_cross_conv:
+ self.cross_conv = ConvModule(
+ unit_channels,
+ out_channels,
+ kernel_size=1,
+ stride=1,
+ padding=0,
+ norm_cfg=self.norm_cfg,
+ inplace=True)
+
+ def forward(self, x, up_x):
+ out = self.in_skip(x)
+
+ if self.ind > 0:
+ up_x = F.interpolate(
+ up_x,
+ size=(x.size(2), x.size(3)),
+ mode='bilinear',
+ align_corners=True)
+ up_x = self.up_conv(up_x)
+ out = out + up_x
+ out = self.relu(out)
+
+ skip1 = None
+ skip2 = None
+ if self.gen_skip:
+ skip1 = self.out_skip1(x)
+ skip2 = self.out_skip2(out)
+
+ cross_conv = None
+ if self.ind == self.num_units - 1 and self.gen_cross_conv:
+ cross_conv = self.cross_conv(out)
+
+ return out, skip1, skip2, cross_conv
+
+
+class Upsample_module(nn.Module):
+ """Upsample module for RSN.
+
+ Args:
+ unit_channels (int): Channel number in the upsample units.
+ Default:256.
+ num_units (int): Numbers of upsample units. Default: 4
+ gen_skip (bool): Whether to generate skip for posterior downsample
+ module or not. Default:False
+ gen_cross_conv (bool): Whether to generate feature map for the next
+ hourglass-like module. Default:False
+ norm_cfg (dict): dictionary to construct and config norm layer.
+ Default: dict(type='BN')
+ out_channels (int): Number of channels of feature output by upsample
+ module. Must equal to in_channels of downsample module. Default:64
+ """
+
+ def __init__(self,
+ unit_channels=256,
+ num_units=4,
+ gen_skip=False,
+ gen_cross_conv=False,
+ norm_cfg=dict(type='BN'),
+ out_channels=64):
+ # Protect mutable default arguments
+ norm_cfg = cp.deepcopy(norm_cfg)
+ super().__init__()
+ self.in_channels = list()
+ for i in range(num_units):
+ self.in_channels.append(RSB.expansion * out_channels * pow(2, i))
+ self.in_channels.reverse()
+ self.num_units = num_units
+ self.gen_skip = gen_skip
+ self.gen_cross_conv = gen_cross_conv
+ self.norm_cfg = norm_cfg
+ for i in range(num_units):
+ module_name = f'up{i + 1}'
+ self.add_module(
+ module_name,
+ Upsample_unit(
+ i,
+ self.num_units,
+ self.in_channels[i],
+ unit_channels,
+ self.gen_skip,
+ self.gen_cross_conv,
+ norm_cfg=self.norm_cfg,
+ out_channels=64))
+
+ def forward(self, x):
+ out = list()
+ skip1 = list()
+ skip2 = list()
+ cross_conv = None
+ for i in range(self.num_units):
+ module_i = getattr(self, f'up{i + 1}')
+ if i == 0:
+ outi, skip1_i, skip2_i, _ = module_i(x[i], None)
+ elif i == self.num_units - 1:
+ outi, skip1_i, skip2_i, cross_conv = module_i(x[i], out[i - 1])
+ else:
+ outi, skip1_i, skip2_i, _ = module_i(x[i], out[i - 1])
+ out.append(outi)
+ skip1.append(skip1_i)
+ skip2.append(skip2_i)
+ skip1.reverse()
+ skip2.reverse()
+
+ return out, skip1, skip2, cross_conv
+
+
+class Single_stage_RSN(nn.Module):
+ """Single_stage Residual Steps Network.
+
+ Args:
+ unit_channels (int): Channel number in the upsample units. Default:256.
+ num_units (int): Numbers of downsample/upsample units. Default: 4
+ gen_skip (bool): Whether to generate skip for posterior downsample
+ module or not. Default:False
+ gen_cross_conv (bool): Whether to generate feature map for the next
+ hourglass-like module. Default:False
+ has_skip (bool): Have skip connections from prior upsample
+ module or not. Default:False
+ num_steps (int): Number of steps in RSB. Default: 4
+ num_blocks (list): Number of blocks in each downsample unit.
+ Default: [2, 2, 2, 2] Note: Make sure num_units==len(num_blocks)
+ norm_cfg (dict): dictionary to construct and config norm layer.
+ Default: dict(type='BN')
+ in_channels (int): Number of channels of the feature from ResNet_Top.
+ Default: 64.
+ expand_times (int): Times by which the in_channels are expanded in RSB.
+ Default:26.
+ """
+
+ def __init__(self,
+ has_skip=False,
+ gen_skip=False,
+ gen_cross_conv=False,
+ unit_channels=256,
+ num_units=4,
+ num_steps=4,
+ num_blocks=[2, 2, 2, 2],
+ norm_cfg=dict(type='BN'),
+ in_channels=64,
+ expand_times=26):
+ # Protect mutable default arguments
+ norm_cfg = cp.deepcopy(norm_cfg)
+ num_blocks = cp.deepcopy(num_blocks)
+ super().__init__()
+ assert len(num_blocks) == num_units
+ self.has_skip = has_skip
+ self.gen_skip = gen_skip
+ self.gen_cross_conv = gen_cross_conv
+ self.num_units = num_units
+ self.num_steps = num_steps
+ self.unit_channels = unit_channels
+ self.num_blocks = num_blocks
+ self.norm_cfg = norm_cfg
+
+ self.downsample = Downsample_module(RSB, num_blocks, num_steps,
+ num_units, has_skip, norm_cfg,
+ in_channels, expand_times)
+ self.upsample = Upsample_module(unit_channels, num_units, gen_skip,
+ gen_cross_conv, norm_cfg, in_channels)
+
+ def forward(self, x, skip1, skip2):
+ mid = self.downsample(x, skip1, skip2)
+ out, skip1, skip2, cross_conv = self.upsample(mid)
+
+ return out, skip1, skip2, cross_conv
+
+
+class ResNet_top(nn.Module):
+ """ResNet top for RSN.
+
+ Args:
+ norm_cfg (dict): dictionary to construct and config norm layer.
+ Default: dict(type='BN')
+ channels (int): Number of channels of the feature output by ResNet_top.
+ """
+
+ def __init__(self, norm_cfg=dict(type='BN'), channels=64):
+ # Protect mutable default arguments
+ norm_cfg = cp.deepcopy(norm_cfg)
+ super().__init__()
+ self.top = nn.Sequential(
+ ConvModule(
+ 3,
+ channels,
+ kernel_size=7,
+ stride=2,
+ padding=3,
+ norm_cfg=norm_cfg,
+ inplace=True), MaxPool2d(kernel_size=3, stride=2, padding=1))
+
+ def forward(self, img):
+ return self.top(img)
+
+
+@BACKBONES.register_module()
+class RSN(BaseBackbone):
+ """Residual Steps Network backbone. Paper ref: Cai et al. "Learning
+ Delicate Local Representations for Multi-Person Pose Estimation" (ECCV
+ 2020).
+
+ Args:
+ unit_channels (int): Number of Channels in an upsample unit.
+ Default: 256
+ num_stages (int): Number of stages in a multi-stage RSN. Default: 4
+ num_units (int): NUmber of downsample/upsample units in a single-stage
+ RSN. Default: 4 Note: Make sure num_units == len(self.num_blocks)
+ num_blocks (list): Number of RSBs (Residual Steps Block) in each
+ downsample unit. Default: [2, 2, 2, 2]
+ num_steps (int): Number of steps in a RSB. Default:4
+ norm_cfg (dict): dictionary to construct and config norm layer.
+ Default: dict(type='BN')
+ res_top_channels (int): Number of channels of feature from ResNet_top.
+ Default: 64.
+ expand_times (int): Times by which the in_channels are expanded in RSB.
+ Default:26.
+ Example:
+ >>> from mmpose.models import RSN
+ >>> import torch
+ >>> self = RSN(num_stages=2,num_units=2,num_blocks=[2,2])
+ >>> self.eval()
+ >>> inputs = torch.rand(1, 3, 511, 511)
+ >>> level_outputs = self.forward(inputs)
+ >>> for level_output in level_outputs:
+ ... for feature in level_output:
+ ... print(tuple(feature.shape))
+ ...
+ (1, 256, 64, 64)
+ (1, 256, 128, 128)
+ (1, 256, 64, 64)
+ (1, 256, 128, 128)
+ """
+
+ def __init__(self,
+ unit_channels=256,
+ num_stages=4,
+ num_units=4,
+ num_blocks=[2, 2, 2, 2],
+ num_steps=4,
+ norm_cfg=dict(type='BN'),
+ res_top_channels=64,
+ expand_times=26):
+ # Protect mutable default arguments
+ norm_cfg = cp.deepcopy(norm_cfg)
+ num_blocks = cp.deepcopy(num_blocks)
+ super().__init__()
+ self.unit_channels = unit_channels
+ self.num_stages = num_stages
+ self.num_units = num_units
+ self.num_blocks = num_blocks
+ self.num_steps = num_steps
+ self.norm_cfg = norm_cfg
+
+ assert self.num_stages > 0
+ assert self.num_steps > 1
+ assert self.num_units > 1
+ assert self.num_units == len(self.num_blocks)
+ self.top = ResNet_top(norm_cfg=norm_cfg)
+ self.multi_stage_rsn = nn.ModuleList([])
+ for i in range(self.num_stages):
+ if i == 0:
+ has_skip = False
+ else:
+ has_skip = True
+ if i != self.num_stages - 1:
+ gen_skip = True
+ gen_cross_conv = True
+ else:
+ gen_skip = False
+ gen_cross_conv = False
+ self.multi_stage_rsn.append(
+ Single_stage_RSN(has_skip, gen_skip, gen_cross_conv,
+ unit_channels, num_units, num_steps,
+ num_blocks, norm_cfg, res_top_channels,
+ expand_times))
+
+ def forward(self, x):
+ """Model forward function."""
+ out_feats = []
+ skip1 = None
+ skip2 = None
+ x = self.top(x)
+ for i in range(self.num_stages):
+ out, skip1, skip2, x = self.multi_stage_rsn[i](x, skip1, skip2)
+ out_feats.append(out)
+
+ return out_feats
+
+ def init_weights(self, pretrained=None):
+ """Initialize model weights."""
+ for m in self.multi_stage_rsn.modules():
+ if isinstance(m, nn.Conv2d):
+ kaiming_init(m)
+ elif isinstance(m, nn.BatchNorm2d):
+ constant_init(m, 1)
+ elif isinstance(m, nn.Linear):
+ normal_init(m, std=0.01)
+
+ for m in self.top.modules():
+ if isinstance(m, nn.Conv2d):
+ kaiming_init(m)
diff --git a/grounded-sam-osx/transformer_utils/mmpose/models/backbones/scnet.py b/grounded-sam-osx/transformer_utils/mmpose/models/backbones/scnet.py
new file mode 100644
index 0000000000000000000000000000000000000000..3786c5731d685638cfa64a83e5d4a5e2eee545de
--- /dev/null
+++ b/grounded-sam-osx/transformer_utils/mmpose/models/backbones/scnet.py
@@ -0,0 +1,248 @@
+# Copyright (c) OpenMMLab. All rights reserved.
+import copy
+
+import torch
+import torch.nn as nn
+import torch.nn.functional as F
+import torch.utils.checkpoint as cp
+from mmcv.cnn import build_conv_layer, build_norm_layer
+
+from ..builder import BACKBONES
+from .resnet import Bottleneck, ResNet
+
+
+class SCConv(nn.Module):
+ """SCConv (Self-calibrated Convolution)
+
+ Args:
+ in_channels (int): The input channels of the SCConv.
+ out_channels (int): The output channel of the SCConv.
+ stride (int): stride of SCConv.
+ pooling_r (int): size of pooling for scconv.
+ conv_cfg (dict): dictionary to construct and config conv layer.
+ Default: None
+ norm_cfg (dict): dictionary to construct and config norm layer.
+ Default: dict(type='BN')
+ """
+
+ def __init__(self,
+ in_channels,
+ out_channels,
+ stride,
+ pooling_r,
+ conv_cfg=None,
+ norm_cfg=dict(type='BN', momentum=0.1)):
+ # Protect mutable default arguments
+ norm_cfg = copy.deepcopy(norm_cfg)
+ super().__init__()
+
+ assert in_channels == out_channels
+
+ self.k2 = nn.Sequential(
+ nn.AvgPool2d(kernel_size=pooling_r, stride=pooling_r),
+ build_conv_layer(
+ conv_cfg,
+ in_channels,
+ in_channels,
+ kernel_size=3,
+ stride=1,
+ padding=1,
+ bias=False),
+ build_norm_layer(norm_cfg, in_channels)[1],
+ )
+ self.k3 = nn.Sequential(
+ build_conv_layer(
+ conv_cfg,
+ in_channels,
+ in_channels,
+ kernel_size=3,
+ stride=1,
+ padding=1,
+ bias=False),
+ build_norm_layer(norm_cfg, in_channels)[1],
+ )
+ self.k4 = nn.Sequential(
+ build_conv_layer(
+ conv_cfg,
+ in_channels,
+ in_channels,
+ kernel_size=3,
+ stride=stride,
+ padding=1,
+ bias=False),
+ build_norm_layer(norm_cfg, out_channels)[1],
+ nn.ReLU(inplace=True),
+ )
+
+ def forward(self, x):
+ """Forward function."""
+ identity = x
+
+ out = torch.sigmoid(
+ torch.add(identity, F.interpolate(self.k2(x),
+ identity.size()[2:])))
+ out = torch.mul(self.k3(x), out)
+ out = self.k4(out)
+
+ return out
+
+
+class SCBottleneck(Bottleneck):
+ """SC(Self-calibrated) Bottleneck.
+
+ Args:
+ in_channels (int): The input channels of the SCBottleneck block.
+ out_channels (int): The output channel of the SCBottleneck block.
+ """
+
+ pooling_r = 4
+
+ def __init__(self, in_channels, out_channels, **kwargs):
+ super().__init__(in_channels, out_channels, **kwargs)
+ self.mid_channels = out_channels // self.expansion // 2
+
+ self.norm1_name, norm1 = build_norm_layer(
+ self.norm_cfg, self.mid_channels, postfix=1)
+ self.norm2_name, norm2 = build_norm_layer(
+ self.norm_cfg, self.mid_channels, postfix=2)
+ self.norm3_name, norm3 = build_norm_layer(
+ self.norm_cfg, out_channels, postfix=3)
+
+ self.conv1 = build_conv_layer(
+ self.conv_cfg,
+ in_channels,
+ self.mid_channels,
+ kernel_size=1,
+ stride=1,
+ bias=False)
+ self.add_module(self.norm1_name, norm1)
+
+ self.k1 = nn.Sequential(
+ build_conv_layer(
+ self.conv_cfg,
+ self.mid_channels,
+ self.mid_channels,
+ kernel_size=3,
+ stride=self.stride,
+ padding=1,
+ bias=False),
+ build_norm_layer(self.norm_cfg, self.mid_channels)[1],
+ nn.ReLU(inplace=True))
+
+ self.conv2 = build_conv_layer(
+ self.conv_cfg,
+ in_channels,
+ self.mid_channels,
+ kernel_size=1,
+ stride=1,
+ bias=False)
+ self.add_module(self.norm2_name, norm2)
+
+ self.scconv = SCConv(self.mid_channels, self.mid_channels, self.stride,
+ self.pooling_r, self.conv_cfg, self.norm_cfg)
+
+ self.conv3 = build_conv_layer(
+ self.conv_cfg,
+ self.mid_channels * 2,
+ out_channels,
+ kernel_size=1,
+ stride=1,
+ bias=False)
+ self.add_module(self.norm3_name, norm3)
+
+ def forward(self, x):
+ """Forward function."""
+
+ def _inner_forward(x):
+ identity = x
+
+ out_a = self.conv1(x)
+ out_a = self.norm1(out_a)
+ out_a = self.relu(out_a)
+
+ out_a = self.k1(out_a)
+
+ out_b = self.conv2(x)
+ out_b = self.norm2(out_b)
+ out_b = self.relu(out_b)
+
+ out_b = self.scconv(out_b)
+
+ out = self.conv3(torch.cat([out_a, out_b], dim=1))
+ out = self.norm3(out)
+
+ if self.downsample is not None:
+ identity = self.downsample(x)
+
+ out += identity
+
+ return out
+
+ if self.with_cp and x.requires_grad:
+ out = cp.checkpoint(_inner_forward, x)
+ else:
+ out = _inner_forward(x)
+
+ out = self.relu(out)
+
+ return out
+
+
+@BACKBONES.register_module()
+class SCNet(ResNet):
+ """SCNet backbone.
+
+ Improving Convolutional Networks with Self-Calibrated Convolutions,
+ Jiang-Jiang Liu, Qibin Hou, Ming-Ming Cheng, Changhu Wang, Jiashi Feng,
+ IEEE CVPR, 2020.
+ http://mftp.mmcheng.net/Papers/20cvprSCNet.pdf
+
+ Args:
+ depth (int): Depth of scnet, from {50, 101}.
+ in_channels (int): Number of input image channels. Normally 3.
+ base_channels (int): Number of base channels of hidden layer.
+ num_stages (int): SCNet stages, normally 4.
+ strides (Sequence[int]): Strides of the first block of each stage.
+ dilations (Sequence[int]): Dilation of each stage.
+ out_indices (Sequence[int]): Output from which stages.
+ style (str): `pytorch` or `caffe`. If set to "pytorch", the stride-two
+ layer is the 3x3 conv layer, otherwise the stride-two layer is
+ the first 1x1 conv layer.
+ deep_stem (bool): Replace 7x7 conv in input stem with 3 3x3 conv
+ avg_down (bool): Use AvgPool instead of stride conv when
+ downsampling in the bottleneck.
+ frozen_stages (int): Stages to be frozen (stop grad and set eval mode).
+ -1 means not freezing any parameters.
+ norm_cfg (dict): Dictionary to construct and config norm layer.
+ norm_eval (bool): Whether to set norm layers to eval mode, namely,
+ freeze running stats (mean and var). Note: Effect on Batch Norm
+ and its variants only.
+ with_cp (bool): Use checkpoint or not. Using checkpoint will save some
+ memory while slowing down the training speed.
+ zero_init_residual (bool): Whether to use zero init for last norm layer
+ in resblocks to let them behave as identity.
+
+ Example:
+ >>> from mmpose.models import SCNet
+ >>> import torch
+ >>> self = SCNet(depth=50, out_indices=(0, 1, 2, 3))
+ >>> self.eval()
+ >>> inputs = torch.rand(1, 3, 224, 224)
+ >>> level_outputs = self.forward(inputs)
+ >>> for level_out in level_outputs:
+ ... print(tuple(level_out.shape))
+ (1, 256, 56, 56)
+ (1, 512, 28, 28)
+ (1, 1024, 14, 14)
+ (1, 2048, 7, 7)
+ """
+
+ arch_settings = {
+ 50: (SCBottleneck, [3, 4, 6, 3]),
+ 101: (SCBottleneck, [3, 4, 23, 3])
+ }
+
+ def __init__(self, depth, **kwargs):
+ if depth not in self.arch_settings:
+ raise KeyError(f'invalid depth {depth} for SCNet')
+ super().__init__(depth, **kwargs)
diff --git a/grounded-sam-osx/transformer_utils/mmpose/models/backbones/seresnet.py b/grounded-sam-osx/transformer_utils/mmpose/models/backbones/seresnet.py
new file mode 100644
index 0000000000000000000000000000000000000000..ac2d53b40a4593bce96d5c7c3bb4e06d38353d0b
--- /dev/null
+++ b/grounded-sam-osx/transformer_utils/mmpose/models/backbones/seresnet.py
@@ -0,0 +1,125 @@
+# Copyright (c) OpenMMLab. All rights reserved.
+import torch.utils.checkpoint as cp
+
+from ..builder import BACKBONES
+from .resnet import Bottleneck, ResLayer, ResNet
+from .utils.se_layer import SELayer
+
+
+class SEBottleneck(Bottleneck):
+ """SEBottleneck block for SEResNet.
+
+ Args:
+ in_channels (int): The input channels of the SEBottleneck block.
+ out_channels (int): The output channel of the SEBottleneck block.
+ se_ratio (int): Squeeze ratio in SELayer. Default: 16
+ """
+
+ def __init__(self, in_channels, out_channels, se_ratio=16, **kwargs):
+ super().__init__(in_channels, out_channels, **kwargs)
+ self.se_layer = SELayer(out_channels, ratio=se_ratio)
+
+ def forward(self, x):
+
+ def _inner_forward(x):
+ identity = x
+
+ out = self.conv1(x)
+ out = self.norm1(out)
+ out = self.relu(out)
+
+ out = self.conv2(out)
+ out = self.norm2(out)
+ out = self.relu(out)
+
+ out = self.conv3(out)
+ out = self.norm3(out)
+
+ out = self.se_layer(out)
+
+ if self.downsample is not None:
+ identity = self.downsample(x)
+
+ out += identity
+
+ return out
+
+ if self.with_cp and x.requires_grad:
+ out = cp.checkpoint(_inner_forward, x)
+ else:
+ out = _inner_forward(x)
+
+ out = self.relu(out)
+
+ return out
+
+
+@BACKBONES.register_module()
+class SEResNet(ResNet):
+ """SEResNet backbone.
+
+ Please refer to the `paper `__ for
+ details.
+
+ Args:
+ depth (int): Network depth, from {50, 101, 152}.
+ se_ratio (int): Squeeze ratio in SELayer. Default: 16.
+ in_channels (int): Number of input image channels. Default: 3.
+ stem_channels (int): Output channels of the stem layer. Default: 64.
+ num_stages (int): Stages of the network. Default: 4.
+ strides (Sequence[int]): Strides of the first block of each stage.
+ Default: ``(1, 2, 2, 2)``.
+ dilations (Sequence[int]): Dilation of each stage.
+ Default: ``(1, 1, 1, 1)``.
+ out_indices (Sequence[int]): Output from which stages. If only one
+ stage is specified, a single tensor (feature map) is returned,
+ otherwise multiple stages are specified, a tuple of tensors will
+ be returned. Default: ``(3, )``.
+ style (str): `pytorch` or `caffe`. If set to "pytorch", the stride-two
+ layer is the 3x3 conv layer, otherwise the stride-two layer is
+ the first 1x1 conv layer.
+ deep_stem (bool): Replace 7x7 conv in input stem with 3 3x3 conv.
+ Default: False.
+ avg_down (bool): Use AvgPool instead of stride conv when
+ downsampling in the bottleneck. Default: False.
+ frozen_stages (int): Stages to be frozen (stop grad and set eval mode).
+ -1 means not freezing any parameters. Default: -1.
+ conv_cfg (dict | None): The config dict for conv layers. Default: None.
+ norm_cfg (dict): The config dict for norm layers.
+ norm_eval (bool): Whether to set norm layers to eval mode, namely,
+ freeze running stats (mean and var). Note: Effect on Batch Norm
+ and its variants only. Default: False.
+ with_cp (bool): Use checkpoint or not. Using checkpoint will save some
+ memory while slowing down the training speed. Default: False.
+ zero_init_residual (bool): Whether to use zero init for last norm layer
+ in resblocks to let them behave as identity. Default: True.
+
+ Example:
+ >>> from mmpose.models import SEResNet
+ >>> import torch
+ >>> self = SEResNet(depth=50, out_indices=(0, 1, 2, 3))
+ >>> self.eval()
+ >>> inputs = torch.rand(1, 3, 224, 224)
+ >>> level_outputs = self.forward(inputs)
+ >>> for level_out in level_outputs:
+ ... print(tuple(level_out.shape))
+ (1, 256, 56, 56)
+ (1, 512, 28, 28)
+ (1, 1024, 14, 14)
+ (1, 2048, 7, 7)
+ """
+
+ arch_settings = {
+ 50: (SEBottleneck, (3, 4, 6, 3)),
+ 101: (SEBottleneck, (3, 4, 23, 3)),
+ 152: (SEBottleneck, (3, 8, 36, 3))
+ }
+
+ def __init__(self, depth, se_ratio=16, **kwargs):
+ if depth not in self.arch_settings:
+ raise KeyError(f'invalid depth {depth} for SEResNet')
+ self.se_ratio = se_ratio
+ super().__init__(depth, **kwargs)
+
+ def make_res_layer(self, **kwargs):
+ return ResLayer(se_ratio=self.se_ratio, **kwargs)
diff --git a/grounded-sam-osx/transformer_utils/mmpose/models/backbones/seresnext.py b/grounded-sam-osx/transformer_utils/mmpose/models/backbones/seresnext.py
new file mode 100644
index 0000000000000000000000000000000000000000..c5c4e4ce03684f8a9bd0c6166969c01bace54bd2
--- /dev/null
+++ b/grounded-sam-osx/transformer_utils/mmpose/models/backbones/seresnext.py
@@ -0,0 +1,168 @@
+# Copyright (c) OpenMMLab. All rights reserved.
+from mmcv.cnn import build_conv_layer, build_norm_layer
+
+from ..builder import BACKBONES
+from .resnet import ResLayer
+from .seresnet import SEBottleneck as _SEBottleneck
+from .seresnet import SEResNet
+
+
+class SEBottleneck(_SEBottleneck):
+ """SEBottleneck block for SEResNeXt.
+
+ Args:
+ in_channels (int): Input channels of this block.
+ out_channels (int): Output channels of this block.
+ base_channels (int): Middle channels of the first stage. Default: 64.
+ groups (int): Groups of conv2.
+ width_per_group (int): Width per group of conv2. 64x4d indicates
+ ``groups=64, width_per_group=4`` and 32x8d indicates
+ ``groups=32, width_per_group=8``.
+ stride (int): stride of the block. Default: 1
+ dilation (int): dilation of convolution. Default: 1
+ downsample (nn.Module): downsample operation on identity branch.
+ Default: None
+ se_ratio (int): Squeeze ratio in SELayer. Default: 16
+ style (str): `pytorch` or `caffe`. If set to "pytorch", the stride-two
+ layer is the 3x3 conv layer, otherwise the stride-two layer is
+ the first 1x1 conv layer.
+ conv_cfg (dict): dictionary to construct and config conv layer.
+ Default: None
+ norm_cfg (dict): dictionary to construct and config norm layer.
+ Default: dict(type='BN')
+ with_cp (bool): Use checkpoint or not. Using checkpoint will save some
+ memory while slowing down the training speed.
+ """
+
+ def __init__(self,
+ in_channels,
+ out_channels,
+ base_channels=64,
+ groups=32,
+ width_per_group=4,
+ se_ratio=16,
+ **kwargs):
+ super().__init__(in_channels, out_channels, se_ratio, **kwargs)
+ self.groups = groups
+ self.width_per_group = width_per_group
+
+ # We follow the same rational of ResNext to compute mid_channels.
+ # For SEResNet bottleneck, middle channels are determined by expansion
+ # and out_channels, but for SEResNeXt bottleneck, it is determined by
+ # groups and width_per_group and the stage it is located in.
+ if groups != 1:
+ assert self.mid_channels % base_channels == 0
+ self.mid_channels = (
+ groups * width_per_group * self.mid_channels // base_channels)
+
+ self.norm1_name, norm1 = build_norm_layer(
+ self.norm_cfg, self.mid_channels, postfix=1)
+ self.norm2_name, norm2 = build_norm_layer(
+ self.norm_cfg, self.mid_channels, postfix=2)
+ self.norm3_name, norm3 = build_norm_layer(
+ self.norm_cfg, self.out_channels, postfix=3)
+
+ self.conv1 = build_conv_layer(
+ self.conv_cfg,
+ self.in_channels,
+ self.mid_channels,
+ kernel_size=1,
+ stride=self.conv1_stride,
+ bias=False)
+ self.add_module(self.norm1_name, norm1)
+ self.conv2 = build_conv_layer(
+ self.conv_cfg,
+ self.mid_channels,
+ self.mid_channels,
+ kernel_size=3,
+ stride=self.conv2_stride,
+ padding=self.dilation,
+ dilation=self.dilation,
+ groups=groups,
+ bias=False)
+
+ self.add_module(self.norm2_name, norm2)
+ self.conv3 = build_conv_layer(
+ self.conv_cfg,
+ self.mid_channels,
+ self.out_channels,
+ kernel_size=1,
+ bias=False)
+ self.add_module(self.norm3_name, norm3)
+
+
+@BACKBONES.register_module()
+class SEResNeXt(SEResNet):
+ """SEResNeXt backbone.
+
+ Please refer to the `paper `__ for
+ details.
+
+ Args:
+ depth (int): Network depth, from {50, 101, 152}.
+ groups (int): Groups of conv2 in Bottleneck. Default: 32.
+ width_per_group (int): Width per group of conv2 in Bottleneck.
+ Default: 4.
+ se_ratio (int): Squeeze ratio in SELayer. Default: 16.
+ in_channels (int): Number of input image channels. Default: 3.
+ stem_channels (int): Output channels of the stem layer. Default: 64.
+ num_stages (int): Stages of the network. Default: 4.
+ strides (Sequence[int]): Strides of the first block of each stage.
+ Default: ``(1, 2, 2, 2)``.
+ dilations (Sequence[int]): Dilation of each stage.
+ Default: ``(1, 1, 1, 1)``.
+ out_indices (Sequence[int]): Output from which stages. If only one
+ stage is specified, a single tensor (feature map) is returned,
+ otherwise multiple stages are specified, a tuple of tensors will
+ be returned. Default: ``(3, )``.
+ style (str): `pytorch` or `caffe`. If set to "pytorch", the stride-two
+ layer is the 3x3 conv layer, otherwise the stride-two layer is
+ the first 1x1 conv layer.
+ deep_stem (bool): Replace 7x7 conv in input stem with 3 3x3 conv.
+ Default: False.
+ avg_down (bool): Use AvgPool instead of stride conv when
+ downsampling in the bottleneck. Default: False.
+ frozen_stages (int): Stages to be frozen (stop grad and set eval mode).
+ -1 means not freezing any parameters. Default: -1.
+ conv_cfg (dict | None): The config dict for conv layers. Default: None.
+ norm_cfg (dict): The config dict for norm layers.
+ norm_eval (bool): Whether to set norm layers to eval mode, namely,
+ freeze running stats (mean and var). Note: Effect on Batch Norm
+ and its variants only. Default: False.
+ with_cp (bool): Use checkpoint or not. Using checkpoint will save some
+ memory while slowing down the training speed. Default: False.
+ zero_init_residual (bool): Whether to use zero init for last norm layer
+ in resblocks to let them behave as identity. Default: True.
+
+ Example:
+ >>> from mmpose.models import SEResNeXt
+ >>> import torch
+ >>> self = SEResNet(depth=50, out_indices=(0, 1, 2, 3))
+ >>> self.eval()
+ >>> inputs = torch.rand(1, 3, 224, 224)
+ >>> level_outputs = self.forward(inputs)
+ >>> for level_out in level_outputs:
+ ... print(tuple(level_out.shape))
+ (1, 256, 56, 56)
+ (1, 512, 28, 28)
+ (1, 1024, 14, 14)
+ (1, 2048, 7, 7)
+ """
+
+ arch_settings = {
+ 50: (SEBottleneck, (3, 4, 6, 3)),
+ 101: (SEBottleneck, (3, 4, 23, 3)),
+ 152: (SEBottleneck, (3, 8, 36, 3))
+ }
+
+ def __init__(self, depth, groups=32, width_per_group=4, **kwargs):
+ self.groups = groups
+ self.width_per_group = width_per_group
+ super().__init__(depth, **kwargs)
+
+ def make_res_layer(self, **kwargs):
+ return ResLayer(
+ groups=self.groups,
+ width_per_group=self.width_per_group,
+ base_channels=self.base_channels,
+ **kwargs)
diff --git a/grounded-sam-osx/transformer_utils/mmpose/models/backbones/shufflenet_v1.py b/grounded-sam-osx/transformer_utils/mmpose/models/backbones/shufflenet_v1.py
new file mode 100644
index 0000000000000000000000000000000000000000..9f98cbd2132250ec13adcce6e642c966b0dbd7cc
--- /dev/null
+++ b/grounded-sam-osx/transformer_utils/mmpose/models/backbones/shufflenet_v1.py
@@ -0,0 +1,329 @@
+# Copyright (c) OpenMMLab. All rights reserved.
+import copy
+import logging
+
+import torch
+import torch.nn as nn
+import torch.utils.checkpoint as cp
+from mmcv.cnn import (ConvModule, build_activation_layer, constant_init,
+ normal_init)
+from torch.nn.modules.batchnorm import _BatchNorm
+
+from ..builder import BACKBONES
+from .base_backbone import BaseBackbone
+from .utils import channel_shuffle, load_checkpoint, make_divisible
+
+
+class ShuffleUnit(nn.Module):
+ """ShuffleUnit block.
+
+ ShuffleNet unit with pointwise group convolution (GConv) and channel
+ shuffle.
+
+ Args:
+ in_channels (int): The input channels of the ShuffleUnit.
+ out_channels (int): The output channels of the ShuffleUnit.
+ groups (int, optional): The number of groups to be used in grouped 1x1
+ convolutions in each ShuffleUnit. Default: 3
+ first_block (bool, optional): Whether it is the first ShuffleUnit of a
+ sequential ShuffleUnits. Default: True, which means not using the
+ grouped 1x1 convolution.
+ combine (str, optional): The ways to combine the input and output
+ branches. Default: 'add'.
+ conv_cfg (dict): Config dict for convolution layer. Default: None,
+ which means using conv2d.
+ norm_cfg (dict): Config dict for normalization layer.
+ Default: dict(type='BN').
+ act_cfg (dict): Config dict for activation layer.
+ Default: dict(type='ReLU').
+ with_cp (bool, optional): Use checkpoint or not. Using checkpoint
+ will save some memory while slowing down the training speed.
+ Default: False.
+
+ Returns:
+ Tensor: The output tensor.
+ """
+
+ def __init__(self,
+ in_channels,
+ out_channels,
+ groups=3,
+ first_block=True,
+ combine='add',
+ conv_cfg=None,
+ norm_cfg=dict(type='BN'),
+ act_cfg=dict(type='ReLU'),
+ with_cp=False):
+ # Protect mutable default arguments
+ norm_cfg = copy.deepcopy(norm_cfg)
+ act_cfg = copy.deepcopy(act_cfg)
+ super().__init__()
+ self.in_channels = in_channels
+ self.out_channels = out_channels
+ self.first_block = first_block
+ self.combine = combine
+ self.groups = groups
+ self.bottleneck_channels = self.out_channels // 4
+ self.with_cp = with_cp
+
+ if self.combine == 'add':
+ self.depthwise_stride = 1
+ self._combine_func = self._add
+ assert in_channels == out_channels, (
+ 'in_channels must be equal to out_channels when combine '
+ 'is add')
+ elif self.combine == 'concat':
+ self.depthwise_stride = 2
+ self._combine_func = self._concat
+ self.out_channels -= self.in_channels
+ self.avgpool = nn.AvgPool2d(kernel_size=3, stride=2, padding=1)
+ else:
+ raise ValueError(f'Cannot combine tensors with {self.combine}. '
+ 'Only "add" and "concat" are supported')
+
+ self.first_1x1_groups = 1 if first_block else self.groups
+ self.g_conv_1x1_compress = ConvModule(
+ in_channels=self.in_channels,
+ out_channels=self.bottleneck_channels,
+ kernel_size=1,
+ groups=self.first_1x1_groups,
+ conv_cfg=conv_cfg,
+ norm_cfg=norm_cfg,
+ act_cfg=act_cfg)
+
+ self.depthwise_conv3x3_bn = ConvModule(
+ in_channels=self.bottleneck_channels,
+ out_channels=self.bottleneck_channels,
+ kernel_size=3,
+ stride=self.depthwise_stride,
+ padding=1,
+ groups=self.bottleneck_channels,
+ conv_cfg=conv_cfg,
+ norm_cfg=norm_cfg,
+ act_cfg=None)
+
+ self.g_conv_1x1_expand = ConvModule(
+ in_channels=self.bottleneck_channels,
+ out_channels=self.out_channels,
+ kernel_size=1,
+ groups=self.groups,
+ conv_cfg=conv_cfg,
+ norm_cfg=norm_cfg,
+ act_cfg=None)
+
+ self.act = build_activation_layer(act_cfg)
+
+ @staticmethod
+ def _add(x, out):
+ # residual connection
+ return x + out
+
+ @staticmethod
+ def _concat(x, out):
+ # concatenate along channel axis
+ return torch.cat((x, out), 1)
+
+ def forward(self, x):
+
+ def _inner_forward(x):
+ residual = x
+
+ out = self.g_conv_1x1_compress(x)
+ out = self.depthwise_conv3x3_bn(out)
+
+ if self.groups > 1:
+ out = channel_shuffle(out, self.groups)
+
+ out = self.g_conv_1x1_expand(out)
+
+ if self.combine == 'concat':
+ residual = self.avgpool(residual)
+ out = self.act(out)
+ out = self._combine_func(residual, out)
+ else:
+ out = self._combine_func(residual, out)
+ out = self.act(out)
+ return out
+
+ if self.with_cp and x.requires_grad:
+ out = cp.checkpoint(_inner_forward, x)
+ else:
+ out = _inner_forward(x)
+
+ return out
+
+
+@BACKBONES.register_module()
+class ShuffleNetV1(BaseBackbone):
+ """ShuffleNetV1 backbone.
+
+ Args:
+ groups (int, optional): The number of groups to be used in grouped 1x1
+ convolutions in each ShuffleUnit. Default: 3.
+ widen_factor (float, optional): Width multiplier - adjusts the number
+ of channels in each layer by this amount. Default: 1.0.
+ out_indices (Sequence[int]): Output from which stages.
+ Default: (2, )
+ frozen_stages (int): Stages to be frozen (all param fixed).
+ Default: -1, which means not freezing any parameters.
+ conv_cfg (dict): Config dict for convolution layer. Default: None,
+ which means using conv2d.
+ norm_cfg (dict): Config dict for normalization layer.
+ Default: dict(type='BN').
+ act_cfg (dict): Config dict for activation layer.
+ Default: dict(type='ReLU').
+ norm_eval (bool): Whether to set norm layers to eval mode, namely,
+ freeze running stats (mean and var). Note: Effect on Batch Norm
+ and its variants only. Default: False.
+ with_cp (bool): Use checkpoint or not. Using checkpoint will save some
+ memory while slowing down the training speed. Default: False.
+ """
+
+ def __init__(self,
+ groups=3,
+ widen_factor=1.0,
+ out_indices=(2, ),
+ frozen_stages=-1,
+ conv_cfg=None,
+ norm_cfg=dict(type='BN'),
+ act_cfg=dict(type='ReLU'),
+ norm_eval=False,
+ with_cp=False):
+ # Protect mutable default arguments
+ norm_cfg = copy.deepcopy(norm_cfg)
+ act_cfg = copy.deepcopy(act_cfg)
+ super().__init__()
+ self.stage_blocks = [4, 8, 4]
+ self.groups = groups
+
+ for index in out_indices:
+ if index not in range(0, 3):
+ raise ValueError('the item in out_indices must in '
+ f'range(0, 3). But received {index}')
+
+ if frozen_stages not in range(-1, 3):
+ raise ValueError('frozen_stages must be in range(-1, 3). '
+ f'But received {frozen_stages}')
+ self.out_indices = out_indices
+ self.frozen_stages = frozen_stages
+ self.conv_cfg = conv_cfg
+ self.norm_cfg = norm_cfg
+ self.act_cfg = act_cfg
+ self.norm_eval = norm_eval
+ self.with_cp = with_cp
+
+ if groups == 1:
+ channels = (144, 288, 576)
+ elif groups == 2:
+ channels = (200, 400, 800)
+ elif groups == 3:
+ channels = (240, 480, 960)
+ elif groups == 4:
+ channels = (272, 544, 1088)
+ elif groups == 8:
+ channels = (384, 768, 1536)
+ else:
+ raise ValueError(f'{groups} groups is not supported for 1x1 '
+ 'Grouped Convolutions')
+
+ channels = [make_divisible(ch * widen_factor, 8) for ch in channels]
+
+ self.in_channels = int(24 * widen_factor)
+
+ self.conv1 = ConvModule(
+ in_channels=3,
+ out_channels=self.in_channels,
+ kernel_size=3,
+ stride=2,
+ padding=1,
+ conv_cfg=conv_cfg,
+ norm_cfg=norm_cfg,
+ act_cfg=act_cfg)
+ self.maxpool = nn.MaxPool2d(kernel_size=3, stride=2, padding=1)
+
+ self.layers = nn.ModuleList()
+ for i, num_blocks in enumerate(self.stage_blocks):
+ first_block = (i == 0)
+ layer = self.make_layer(channels[i], num_blocks, first_block)
+ self.layers.append(layer)
+
+ def _freeze_stages(self):
+ if self.frozen_stages >= 0:
+ for param in self.conv1.parameters():
+ param.requires_grad = False
+ for i in range(self.frozen_stages):
+ layer = self.layers[i]
+ layer.eval()
+ for param in layer.parameters():
+ param.requires_grad = False
+
+ def init_weights(self, pretrained=None):
+ if isinstance(pretrained, str):
+ logger = logging.getLogger()
+ load_checkpoint(self, pretrained, strict=False, logger=logger)
+ elif pretrained is None:
+ for name, m in self.named_modules():
+ if isinstance(m, nn.Conv2d):
+ if 'conv1' in name:
+ normal_init(m, mean=0, std=0.01)
+ else:
+ normal_init(m, mean=0, std=1.0 / m.weight.shape[1])
+ elif isinstance(m, (_BatchNorm, nn.GroupNorm)):
+ constant_init(m, val=1, bias=0.0001)
+ if isinstance(m, _BatchNorm):
+ if m.running_mean is not None:
+ nn.init.constant_(m.running_mean, 0)
+ else:
+ raise TypeError('pretrained must be a str or None. But received '
+ f'{type(pretrained)}')
+
+ def make_layer(self, out_channels, num_blocks, first_block=False):
+ """Stack ShuffleUnit blocks to make a layer.
+
+ Args:
+ out_channels (int): out_channels of the block.
+ num_blocks (int): Number of blocks.
+ first_block (bool, optional): Whether is the first ShuffleUnit of a
+ sequential ShuffleUnits. Default: False, which means using
+ the grouped 1x1 convolution.
+ """
+ layers = []
+ for i in range(num_blocks):
+ first_block = first_block if i == 0 else False
+ combine_mode = 'concat' if i == 0 else 'add'
+ layers.append(
+ ShuffleUnit(
+ self.in_channels,
+ out_channels,
+ groups=self.groups,
+ first_block=first_block,
+ combine=combine_mode,
+ conv_cfg=self.conv_cfg,
+ norm_cfg=self.norm_cfg,
+ act_cfg=self.act_cfg,
+ with_cp=self.with_cp))
+ self.in_channels = out_channels
+
+ return nn.Sequential(*layers)
+
+ def forward(self, x):
+ x = self.conv1(x)
+ x = self.maxpool(x)
+
+ outs = []
+ for i, layer in enumerate(self.layers):
+ x = layer(x)
+ if i in self.out_indices:
+ outs.append(x)
+
+ if len(outs) == 1:
+ return outs[0]
+ return tuple(outs)
+
+ def train(self, mode=True):
+ super().train(mode)
+ self._freeze_stages()
+ if mode and self.norm_eval:
+ for m in self.modules():
+ if isinstance(m, _BatchNorm):
+ m.eval()
diff --git a/grounded-sam-osx/transformer_utils/mmpose/models/backbones/shufflenet_v2.py b/grounded-sam-osx/transformer_utils/mmpose/models/backbones/shufflenet_v2.py
new file mode 100644
index 0000000000000000000000000000000000000000..e93533367afe4efa01fa67d14cafcca006c990e8
--- /dev/null
+++ b/grounded-sam-osx/transformer_utils/mmpose/models/backbones/shufflenet_v2.py
@@ -0,0 +1,302 @@
+# Copyright (c) OpenMMLab. All rights reserved.
+import copy
+import logging
+
+import torch
+import torch.nn as nn
+import torch.utils.checkpoint as cp
+from mmcv.cnn import ConvModule, constant_init, normal_init
+from torch.nn.modules.batchnorm import _BatchNorm
+
+from ..builder import BACKBONES
+from .base_backbone import BaseBackbone
+from .utils import channel_shuffle, load_checkpoint
+
+
+class InvertedResidual(nn.Module):
+ """InvertedResidual block for ShuffleNetV2 backbone.
+
+ Args:
+ in_channels (int): The input channels of the block.
+ out_channels (int): The output channels of the block.
+ stride (int): Stride of the 3x3 convolution layer. Default: 1
+ conv_cfg (dict): Config dict for convolution layer.
+ Default: None, which means using conv2d.
+ norm_cfg (dict): Config dict for normalization layer.
+ Default: dict(type='BN').
+ act_cfg (dict): Config dict for activation layer.
+ Default: dict(type='ReLU').
+ with_cp (bool): Use checkpoint or not. Using checkpoint will save some
+ memory while slowing down the training speed. Default: False.
+ """
+
+ def __init__(self,
+ in_channels,
+ out_channels,
+ stride=1,
+ conv_cfg=None,
+ norm_cfg=dict(type='BN'),
+ act_cfg=dict(type='ReLU'),
+ with_cp=False):
+ # Protect mutable default arguments
+ norm_cfg = copy.deepcopy(norm_cfg)
+ act_cfg = copy.deepcopy(act_cfg)
+ super().__init__()
+ self.stride = stride
+ self.with_cp = with_cp
+
+ branch_features = out_channels // 2
+ if self.stride == 1:
+ assert in_channels == branch_features * 2, (
+ f'in_channels ({in_channels}) should equal to '
+ f'branch_features * 2 ({branch_features * 2}) '
+ 'when stride is 1')
+
+ if in_channels != branch_features * 2:
+ assert self.stride != 1, (
+ f'stride ({self.stride}) should not equal 1 when '
+ f'in_channels != branch_features * 2')
+
+ if self.stride > 1:
+ self.branch1 = nn.Sequential(
+ ConvModule(
+ in_channels,
+ in_channels,
+ kernel_size=3,
+ stride=self.stride,
+ padding=1,
+ groups=in_channels,
+ conv_cfg=conv_cfg,
+ norm_cfg=norm_cfg,
+ act_cfg=None),
+ ConvModule(
+ in_channels,
+ branch_features,
+ kernel_size=1,
+ stride=1,
+ padding=0,
+ conv_cfg=conv_cfg,
+ norm_cfg=norm_cfg,
+ act_cfg=act_cfg),
+ )
+
+ self.branch2 = nn.Sequential(
+ ConvModule(
+ in_channels if (self.stride > 1) else branch_features,
+ branch_features,
+ kernel_size=1,
+ stride=1,
+ padding=0,
+ conv_cfg=conv_cfg,
+ norm_cfg=norm_cfg,
+ act_cfg=act_cfg),
+ ConvModule(
+ branch_features,
+ branch_features,
+ kernel_size=3,
+ stride=self.stride,
+ padding=1,
+ groups=branch_features,
+ conv_cfg=conv_cfg,
+ norm_cfg=norm_cfg,
+ act_cfg=None),
+ ConvModule(
+ branch_features,
+ branch_features,
+ kernel_size=1,
+ stride=1,
+ padding=0,
+ conv_cfg=conv_cfg,
+ norm_cfg=norm_cfg,
+ act_cfg=act_cfg))
+
+ def forward(self, x):
+
+ def _inner_forward(x):
+ if self.stride > 1:
+ out = torch.cat((self.branch1(x), self.branch2(x)), dim=1)
+ else:
+ x1, x2 = x.chunk(2, dim=1)
+ out = torch.cat((x1, self.branch2(x2)), dim=1)
+
+ out = channel_shuffle(out, 2)
+
+ return out
+
+ if self.with_cp and x.requires_grad:
+ out = cp.checkpoint(_inner_forward, x)
+ else:
+ out = _inner_forward(x)
+
+ return out
+
+
+@BACKBONES.register_module()
+class ShuffleNetV2(BaseBackbone):
+ """ShuffleNetV2 backbone.
+
+ Args:
+ widen_factor (float): Width multiplier - adjusts the number of
+ channels in each layer by this amount. Default: 1.0.
+ out_indices (Sequence[int]): Output from which stages.
+ Default: (0, 1, 2, 3).
+ frozen_stages (int): Stages to be frozen (all param fixed).
+ Default: -1, which means not freezing any parameters.
+ conv_cfg (dict): Config dict for convolution layer.
+ Default: None, which means using conv2d.
+ norm_cfg (dict): Config dict for normalization layer.
+ Default: dict(type='BN').
+ act_cfg (dict): Config dict for activation layer.
+ Default: dict(type='ReLU').
+ norm_eval (bool): Whether to set norm layers to eval mode, namely,
+ freeze running stats (mean and var). Note: Effect on Batch Norm
+ and its variants only. Default: False.
+ with_cp (bool): Use checkpoint or not. Using checkpoint will save some
+ memory while slowing down the training speed. Default: False.
+ """
+
+ def __init__(self,
+ widen_factor=1.0,
+ out_indices=(3, ),
+ frozen_stages=-1,
+ conv_cfg=None,
+ norm_cfg=dict(type='BN'),
+ act_cfg=dict(type='ReLU'),
+ norm_eval=False,
+ with_cp=False):
+ # Protect mutable default arguments
+ norm_cfg = copy.deepcopy(norm_cfg)
+ act_cfg = copy.deepcopy(act_cfg)
+ super().__init__()
+ self.stage_blocks = [4, 8, 4]
+ for index in out_indices:
+ if index not in range(0, 4):
+ raise ValueError('the item in out_indices must in '
+ f'range(0, 4). But received {index}')
+
+ if frozen_stages not in range(-1, 4):
+ raise ValueError('frozen_stages must be in range(-1, 4). '
+ f'But received {frozen_stages}')
+ self.out_indices = out_indices
+ self.frozen_stages = frozen_stages
+ self.conv_cfg = conv_cfg
+ self.norm_cfg = norm_cfg
+ self.act_cfg = act_cfg
+ self.norm_eval = norm_eval
+ self.with_cp = with_cp
+
+ if widen_factor == 0.5:
+ channels = [48, 96, 192, 1024]
+ elif widen_factor == 1.0:
+ channels = [116, 232, 464, 1024]
+ elif widen_factor == 1.5:
+ channels = [176, 352, 704, 1024]
+ elif widen_factor == 2.0:
+ channels = [244, 488, 976, 2048]
+ else:
+ raise ValueError('widen_factor must be in [0.5, 1.0, 1.5, 2.0]. '
+ f'But received {widen_factor}')
+
+ self.in_channels = 24
+ self.conv1 = ConvModule(
+ in_channels=3,
+ out_channels=self.in_channels,
+ kernel_size=3,
+ stride=2,
+ padding=1,
+ conv_cfg=conv_cfg,
+ norm_cfg=norm_cfg,
+ act_cfg=act_cfg)
+
+ self.maxpool = nn.MaxPool2d(kernel_size=3, stride=2, padding=1)
+
+ self.layers = nn.ModuleList()
+ for i, num_blocks in enumerate(self.stage_blocks):
+ layer = self._make_layer(channels[i], num_blocks)
+ self.layers.append(layer)
+
+ output_channels = channels[-1]
+ self.layers.append(
+ ConvModule(
+ in_channels=self.in_channels,
+ out_channels=output_channels,
+ kernel_size=1,
+ conv_cfg=conv_cfg,
+ norm_cfg=norm_cfg,
+ act_cfg=act_cfg))
+
+ def _make_layer(self, out_channels, num_blocks):
+ """Stack blocks to make a layer.
+
+ Args:
+ out_channels (int): out_channels of the block.
+ num_blocks (int): number of blocks.
+ """
+ layers = []
+ for i in range(num_blocks):
+ stride = 2 if i == 0 else 1
+ layers.append(
+ InvertedResidual(
+ in_channels=self.in_channels,
+ out_channels=out_channels,
+ stride=stride,
+ conv_cfg=self.conv_cfg,
+ norm_cfg=self.norm_cfg,
+ act_cfg=self.act_cfg,
+ with_cp=self.with_cp))
+ self.in_channels = out_channels
+
+ return nn.Sequential(*layers)
+
+ def _freeze_stages(self):
+ if self.frozen_stages >= 0:
+ for param in self.conv1.parameters():
+ param.requires_grad = False
+
+ for i in range(self.frozen_stages):
+ m = self.layers[i]
+ m.eval()
+ for param in m.parameters():
+ param.requires_grad = False
+
+ def init_weights(self, pretrained=None):
+ if isinstance(pretrained, str):
+ logger = logging.getLogger()
+ load_checkpoint(self, pretrained, strict=False, logger=logger)
+ elif pretrained is None:
+ for name, m in self.named_modules():
+ if isinstance(m, nn.Conv2d):
+ if 'conv1' in name:
+ normal_init(m, mean=0, std=0.01)
+ else:
+ normal_init(m, mean=0, std=1.0 / m.weight.shape[1])
+ elif isinstance(m, (_BatchNorm, nn.GroupNorm)):
+ constant_init(m.weight, val=1, bias=0.0001)
+ if isinstance(m, _BatchNorm):
+ if m.running_mean is not None:
+ nn.init.constant_(m.running_mean, 0)
+ else:
+ raise TypeError('pretrained must be a str or None. But received '
+ f'{type(pretrained)}')
+
+ def forward(self, x):
+ x = self.conv1(x)
+ x = self.maxpool(x)
+
+ outs = []
+ for i, layer in enumerate(self.layers):
+ x = layer(x)
+ if i in self.out_indices:
+ outs.append(x)
+
+ if len(outs) == 1:
+ return outs[0]
+ return tuple(outs)
+
+ def train(self, mode=True):
+ super().train(mode)
+ self._freeze_stages()
+ if mode and self.norm_eval:
+ for m in self.modules():
+ if isinstance(m, nn.BatchNorm2d):
+ m.eval()
diff --git a/grounded-sam-osx/transformer_utils/mmpose/models/backbones/swin.py b/grounded-sam-osx/transformer_utils/mmpose/models/backbones/swin.py
new file mode 100644
index 0000000000000000000000000000000000000000..2449cdca591bc0bbf601295bde11efe834b49f8a
--- /dev/null
+++ b/grounded-sam-osx/transformer_utils/mmpose/models/backbones/swin.py
@@ -0,0 +1,733 @@
+# Copyright (c) OpenMMLab. All rights reserved.
+from collections import OrderedDict
+from copy import deepcopy
+
+import torch
+import torch.nn as nn
+import torch.nn.functional as F
+import torch.utils.checkpoint as cp
+from mmcv.cnn import build_norm_layer, constant_init, trunc_normal_init
+from mmcv.cnn.bricks.transformer import FFN, build_dropout
+from mmcv.cnn.utils.weight_init import trunc_normal_
+from mmcv.runner import _load_checkpoint
+from mmcv.utils import to_2tuple
+
+from ...utils import get_root_logger
+from ..builder import BACKBONES
+from ..utils.transformer import PatchEmbed, PatchMerging
+from .base_backbone import BaseBackbone
+from .utils.ckpt_convert import swin_converter
+
+
+class WindowMSA(nn.Module):
+ """Window based multi-head self-attention (W-MSA) module with relative
+ position bias.
+
+ Args:
+ embed_dims (int): Number of input channels.
+ num_heads (int): Number of attention heads.
+ window_size (tuple[int]): The height and width of the window.
+ qkv_bias (bool, optional): If True, add a learnable bias to q, k, v.
+ Default: True.
+ qk_scale (float | None, optional): Override default qk scale of
+ head_dim ** -0.5 if set. Default: None.
+ attn_drop_rate (float, optional): Dropout ratio of attention weight.
+ Default: 0.0
+ proj_drop_rate (float, optional): Dropout ratio of output. Default: 0.
+ """
+
+ def __init__(self,
+ embed_dims,
+ num_heads,
+ window_size,
+ qkv_bias=True,
+ qk_scale=None,
+ attn_drop_rate=0.,
+ proj_drop_rate=0.):
+
+ super().__init__()
+ self.embed_dims = embed_dims
+ self.window_size = window_size # Wh, Ww
+ self.num_heads = num_heads
+ head_embed_dims = embed_dims // num_heads
+ self.scale = qk_scale or head_embed_dims**-0.5
+
+ # define a parameter table of relative position bias
+ self.relative_position_bias_table = nn.Parameter(
+ torch.zeros((2 * window_size[0] - 1) * (2 * window_size[1] - 1),
+ num_heads)) # 2*Wh-1 * 2*Ww-1, nH
+
+ # About 2x faster than original impl
+ Wh, Ww = self.window_size
+ rel_index_coords = self.double_step_seq(2 * Ww - 1, Wh, 1, Ww)
+ rel_position_index = rel_index_coords + rel_index_coords.T
+ rel_position_index = rel_position_index.flip(1).contiguous()
+ self.register_buffer('relative_position_index', rel_position_index)
+
+ self.qkv = nn.Linear(embed_dims, embed_dims * 3, bias=qkv_bias)
+ self.attn_drop = nn.Dropout(attn_drop_rate)
+ self.proj = nn.Linear(embed_dims, embed_dims)
+ self.proj_drop = nn.Dropout(proj_drop_rate)
+
+ self.softmax = nn.Softmax(dim=-1)
+
+ def init_weights(self):
+ trunc_normal_(self.relative_position_bias_table, std=0.02)
+
+ def forward(self, x, mask=None):
+ """
+ Args:
+
+ x (tensor): input features with shape of (num_windows*B, N, C)
+ mask (tensor | None, Optional): mask with shape of (num_windows,
+ Wh*Ww, Wh*Ww), value should be between (-inf, 0].
+ """
+ B, N, C = x.shape
+ qkv = self.qkv(x).reshape(B, N, 3, self.num_heads,
+ C // self.num_heads).permute(2, 0, 3, 1, 4)
+ # make torchscript happy (cannot use tensor as tuple)
+ q, k, v = qkv[0], qkv[1], qkv[2]
+
+ q = q * self.scale
+ attn = (q @ k.transpose(-2, -1))
+
+ relative_position_bias = self.relative_position_bias_table[
+ self.relative_position_index.view(-1)].view(
+ self.window_size[0] * self.window_size[1],
+ self.window_size[0] * self.window_size[1],
+ -1) # Wh*Ww,Wh*Ww,nH
+ relative_position_bias = relative_position_bias.permute(
+ 2, 0, 1).contiguous() # nH, Wh*Ww, Wh*Ww
+ attn = attn + relative_position_bias.unsqueeze(0)
+
+ if mask is not None:
+ nW = mask.shape[0]
+ attn = attn.view(B // nW, nW, self.num_heads, N,
+ N) + mask.unsqueeze(1).unsqueeze(0)
+ attn = attn.view(-1, self.num_heads, N, N)
+ attn = self.softmax(attn)
+
+ attn = self.attn_drop(attn)
+
+ x = (attn @ v).transpose(1, 2).reshape(B, N, C)
+ x = self.proj(x)
+ x = self.proj_drop(x)
+ return x
+
+ @staticmethod
+ def double_step_seq(step1, len1, step2, len2):
+ seq1 = torch.arange(0, step1 * len1, step1)
+ seq2 = torch.arange(0, step2 * len2, step2)
+ return (seq1[:, None] + seq2[None, :]).reshape(1, -1)
+
+
+class ShiftWindowMSA(nn.Module):
+ """Shifted Window Multihead Self-Attention Module.
+
+ Args:
+ embed_dims (int): Number of input channels.
+ num_heads (int): Number of attention heads.
+ window_size (int): The height and width of the window.
+ shift_size (int, optional): The shift step of each window towards
+ right-bottom. If zero, act as regular window-msa. Defaults to 0.
+ qkv_bias (bool, optional): If True, add a learnable bias to q, k, v.
+ Default: True
+ qk_scale (float | None, optional): Override default qk scale of
+ head_dim ** -0.5 if set. Defaults: None.
+ attn_drop_rate (float, optional): Dropout ratio of attention weight.
+ Defaults: 0.
+ proj_drop_rate (float, optional): Dropout ratio of output.
+ Defaults: 0.
+ dropout_layer (dict, optional): The dropout_layer used before output.
+ Defaults: dict(type='DropPath', drop_prob=0.).
+ """
+
+ def __init__(self,
+ embed_dims,
+ num_heads,
+ window_size,
+ shift_size=0,
+ qkv_bias=True,
+ qk_scale=None,
+ attn_drop_rate=0,
+ proj_drop_rate=0,
+ dropout_layer=dict(type='DropPath', drop_prob=0.)):
+ super().__init__()
+
+ self.window_size = window_size
+ self.shift_size = shift_size
+ assert 0 <= self.shift_size < self.window_size
+
+ self.w_msa = WindowMSA(
+ embed_dims=embed_dims,
+ num_heads=num_heads,
+ window_size=to_2tuple(window_size),
+ qkv_bias=qkv_bias,
+ qk_scale=qk_scale,
+ attn_drop_rate=attn_drop_rate,
+ proj_drop_rate=proj_drop_rate)
+
+ self.drop = build_dropout(dropout_layer)
+
+ def forward(self, query, hw_shape):
+ B, L, C = query.shape
+ H, W = hw_shape
+ assert L == H * W, 'input feature has wrong size'
+ query = query.view(B, H, W, C)
+
+ # pad feature maps to multiples of window size
+ pad_r = (self.window_size - W % self.window_size) % self.window_size
+ pad_b = (self.window_size - H % self.window_size) % self.window_size
+ query = F.pad(query, (0, 0, 0, pad_r, 0, pad_b))
+ H_pad, W_pad = query.shape[1], query.shape[2]
+
+ # cyclic shift
+ if self.shift_size > 0:
+ shifted_query = torch.roll(
+ query,
+ shifts=(-self.shift_size, -self.shift_size),
+ dims=(1, 2))
+
+ # calculate attention mask for SW-MSA
+ img_mask = torch.zeros((1, H_pad, W_pad, 1), device=query.device)
+ h_slices = (slice(0, -self.window_size),
+ slice(-self.window_size,
+ -self.shift_size), slice(-self.shift_size, None))
+ w_slices = (slice(0, -self.window_size),
+ slice(-self.window_size,
+ -self.shift_size), slice(-self.shift_size, None))
+ cnt = 0
+ for h in h_slices:
+ for w in w_slices:
+ img_mask[:, h, w, :] = cnt
+ cnt += 1
+
+ # nW, window_size, window_size, 1
+ mask_windows = self.window_partition(img_mask)
+ mask_windows = mask_windows.view(
+ -1, self.window_size * self.window_size)
+ attn_mask = mask_windows.unsqueeze(1) - mask_windows.unsqueeze(2)
+ attn_mask = attn_mask.masked_fill(attn_mask != 0,
+ float(-100.0)).masked_fill(
+ attn_mask == 0, float(0.0))
+ else:
+ shifted_query = query
+ attn_mask = None
+
+ # nW*B, window_size, window_size, C
+ query_windows = self.window_partition(shifted_query)
+ # nW*B, window_size*window_size, C
+ query_windows = query_windows.view(-1, self.window_size**2, C)
+
+ # W-MSA/SW-MSA (nW*B, window_size*window_size, C)
+ attn_windows = self.w_msa(query_windows, mask=attn_mask)
+
+ # merge windows
+ attn_windows = attn_windows.view(-1, self.window_size,
+ self.window_size, C)
+
+ # B H' W' C
+ shifted_x = self.window_reverse(attn_windows, H_pad, W_pad)
+ # reverse cyclic shift
+ if self.shift_size > 0:
+ x = torch.roll(
+ shifted_x,
+ shifts=(self.shift_size, self.shift_size),
+ dims=(1, 2))
+ else:
+ x = shifted_x
+
+ if pad_r > 0 or pad_b:
+ x = x[:, :H, :W, :].contiguous()
+
+ x = x.view(B, H * W, C)
+
+ x = self.drop(x)
+ return x
+
+ def window_reverse(self, windows, H, W):
+ """
+ Args:
+ windows: (num_windows*B, window_size, window_size, C)
+ H (int): Height of image
+ W (int): Width of image
+ Returns:
+ x: (B, H, W, C)
+ """
+ window_size = self.window_size
+ B = int(windows.shape[0] / (H * W / window_size / window_size))
+ x = windows.view(B, H // window_size, W // window_size, window_size,
+ window_size, -1)
+ x = x.permute(0, 1, 3, 2, 4, 5).contiguous().view(B, H, W, -1)
+ return x
+
+ def window_partition(self, x):
+ """
+ Args:
+ x: (B, H, W, C)
+ Returns:
+ windows: (num_windows*B, window_size, window_size, C)
+ """
+ B, H, W, C = x.shape
+ window_size = self.window_size
+ x = x.view(B, H // window_size, window_size, W // window_size,
+ window_size, C)
+ windows = x.permute(0, 1, 3, 2, 4, 5).contiguous()
+ windows = windows.view(-1, window_size, window_size, C)
+ return windows
+
+
+class SwinBlock(nn.Module):
+ """"
+ Args:
+ embed_dims (int): The feature dimension.
+ num_heads (int): Parallel attention heads.
+ feedforward_channels (int): The hidden dimension for FFNs.
+ window_size (int, optional): The local window scale. Default: 7.
+ shift (bool, optional): whether to shift window or not. Default False.
+ qkv_bias (bool, optional): enable bias for qkv if True. Default: True.
+ qk_scale (float | None, optional): Override default qk scale of
+ head_dim ** -0.5 if set. Default: None.
+ drop_rate (float, optional): Dropout rate. Default: 0.
+ attn_drop_rate (float, optional): Attention dropout rate. Default: 0.
+ drop_path_rate (float, optional): Stochastic depth rate. Default: 0.
+ act_cfg (dict, optional): The config dict of activation function.
+ Default: dict(type='GELU').
+ norm_cfg (dict, optional): The config dict of normalization.
+ Default: dict(type='LN').
+ with_cp (bool, optional): Use checkpoint or not. Using checkpoint
+ will save some memory while slowing down the training speed.
+ Default: False.
+ """
+
+ def __init__(self,
+ embed_dims,
+ num_heads,
+ feedforward_channels,
+ window_size=7,
+ shift=False,
+ qkv_bias=True,
+ qk_scale=None,
+ drop_rate=0.,
+ attn_drop_rate=0.,
+ drop_path_rate=0.,
+ act_cfg=dict(type='GELU'),
+ norm_cfg=dict(type='LN'),
+ with_cp=False):
+
+ super(SwinBlock, self).__init__()
+
+ self.with_cp = with_cp
+
+ self.norm1 = build_norm_layer(norm_cfg, embed_dims)[1]
+ self.attn = ShiftWindowMSA(
+ embed_dims=embed_dims,
+ num_heads=num_heads,
+ window_size=window_size,
+ shift_size=window_size // 2 if shift else 0,
+ qkv_bias=qkv_bias,
+ qk_scale=qk_scale,
+ attn_drop_rate=attn_drop_rate,
+ proj_drop_rate=drop_rate,
+ dropout_layer=dict(type='DropPath', drop_prob=drop_path_rate))
+
+ self.norm2 = build_norm_layer(norm_cfg, embed_dims)[1]
+ self.ffn = FFN(
+ embed_dims=embed_dims,
+ feedforward_channels=feedforward_channels,
+ num_fcs=2,
+ ffn_drop=drop_rate,
+ dropout_layer=dict(type='DropPath', drop_prob=drop_path_rate),
+ act_cfg=act_cfg,
+ add_identity=True,
+ init_cfg=None)
+
+ def forward(self, x, hw_shape):
+
+ def _inner_forward(x):
+ identity = x
+ x = self.norm1(x)
+ x = self.attn(x, hw_shape)
+
+ x = x + identity
+
+ identity = x
+ x = self.norm2(x)
+ x = self.ffn(x, identity=identity)
+
+ return x
+
+ if self.with_cp and x.requires_grad:
+ x = cp.checkpoint(_inner_forward, x)
+ else:
+ x = _inner_forward(x)
+
+ return x
+
+
+class SwinBlockSequence(nn.Module):
+ """Implements one stage in Swin Transformer.
+
+ Args:
+ embed_dims (int): The feature dimension.
+ num_heads (int): Parallel attention heads.
+ feedforward_channels (int): The hidden dimension for FFNs.
+ depth (int): The number of blocks in this stage.
+ window_size (int, optional): The local window scale. Default: 7.
+ qkv_bias (bool, optional): enable bias for qkv if True. Default: True.
+ qk_scale (float | None, optional): Override default qk scale of
+ head_dim ** -0.5 if set. Default: None.
+ drop_rate (float, optional): Dropout rate. Default: 0.
+ attn_drop_rate (float, optional): Attention dropout rate. Default: 0.
+ drop_path_rate (float | list[float], optional): Stochastic depth
+ rate. Default: 0.
+ downsample (nn.Module | None, optional): The downsample operation
+ module. Default: None.
+ act_cfg (dict, optional): The config dict of activation function.
+ Default: dict(type='GELU').
+ norm_cfg (dict, optional): The config dict of normalization.
+ Default: dict(type='LN').
+ with_cp (bool, optional): Use checkpoint or not. Using checkpoint
+ will save some memory while slowing down the training speed.
+ Default: False.
+ """
+
+ def __init__(self,
+ embed_dims,
+ num_heads,
+ feedforward_channels,
+ depth,
+ window_size=7,
+ qkv_bias=True,
+ qk_scale=None,
+ drop_rate=0.,
+ attn_drop_rate=0.,
+ drop_path_rate=0.,
+ downsample=None,
+ act_cfg=dict(type='GELU'),
+ norm_cfg=dict(type='LN'),
+ with_cp=False):
+ super().__init__()
+
+ if isinstance(drop_path_rate, list):
+ drop_path_rates = drop_path_rate
+ assert len(drop_path_rates) == depth
+ else:
+ drop_path_rates = [deepcopy(drop_path_rate) for _ in range(depth)]
+
+ self.blocks = nn.ModuleList()
+ for i in range(depth):
+ block = SwinBlock(
+ embed_dims=embed_dims,
+ num_heads=num_heads,
+ feedforward_channels=feedforward_channels,
+ window_size=window_size,
+ shift=False if i % 2 == 0 else True,
+ qkv_bias=qkv_bias,
+ qk_scale=qk_scale,
+ drop_rate=drop_rate,
+ attn_drop_rate=attn_drop_rate,
+ drop_path_rate=drop_path_rates[i],
+ act_cfg=act_cfg,
+ norm_cfg=norm_cfg,
+ with_cp=with_cp)
+ self.blocks.append(block)
+
+ self.downsample = downsample
+
+ def forward(self, x, hw_shape):
+ for block in self.blocks:
+ x = block(x, hw_shape)
+
+ if self.downsample:
+ x_down, down_hw_shape = self.downsample(x, hw_shape)
+ return x_down, down_hw_shape, x, hw_shape
+ else:
+ return x, hw_shape, x, hw_shape
+
+
+@BACKBONES.register_module()
+class SwinTransformer(BaseBackbone):
+ """ Swin Transformer
+ A PyTorch implement of : `Swin Transformer:
+ Hierarchical Vision Transformer using Shifted Windows` -
+ https://arxiv.org/abs/2103.14030
+
+ Inspiration from
+ https://github.com/microsoft/Swin-Transformer
+
+ Args:
+ pretrain_img_size (int | tuple[int]): The size of input image when
+ pretrain. Defaults: 224.
+ in_channels (int): The num of input channels.
+ Defaults: 3.
+ embed_dims (int): The feature dimension. Default: 96.
+ patch_size (int | tuple[int]): Patch size. Default: 4.
+ window_size (int): Window size. Default: 7.
+ mlp_ratio (int): Ratio of mlp hidden dim to embedding dim.
+ Default: 4.
+ depths (tuple[int]): Depths of each Swin Transformer stage.
+ Default: (2, 2, 6, 2).
+ num_heads (tuple[int]): Parallel attention heads of each Swin
+ Transformer stage. Default: (3, 6, 12, 24).
+ strides (tuple[int]): The patch merging or patch embedding stride of
+ each Swin Transformer stage. (In swin, we set kernel size equal to
+ stride.) Default: (4, 2, 2, 2).
+ out_indices (tuple[int]): Output from which stages.
+ Default: (0, 1, 2, 3).
+ qkv_bias (bool, optional): If True, add a learnable bias to query, key,
+ value. Default: True
+ qk_scale (float | None, optional): Override default qk scale of
+ head_dim ** -0.5 if set. Default: None.
+ patch_norm (bool): If add a norm layer for patch embed and patch
+ merging. Default: True.
+ drop_rate (float): Dropout rate. Defaults: 0.
+ attn_drop_rate (float): Attention dropout rate. Default: 0.
+ drop_path_rate (float): Stochastic depth rate. Defaults: 0.1.
+ use_abs_pos_embed (bool): If True, add absolute position embedding to
+ the patch embedding. Defaults: False.
+ act_cfg (dict): Config dict for activation layer.
+ Default: dict(type='LN').
+ norm_cfg (dict): Config dict for normalization layer at
+ output of backone. Defaults: dict(type='LN').
+ with_cp (bool, optional): Use checkpoint or not. Using checkpoint
+ will save some memory while slowing down the training speed.
+ Default: False.
+ pretrained (str, optional): model pretrained path. Default: None.
+ convert_weights (bool): The flag indicates whether the
+ pre-trained model is from the original repo. We may need
+ to convert some keys to make it compatible.
+ Default: False.
+ frozen_stages (int): Stages to be frozen (stop grad and set eval mode).
+ Default: -1 (-1 means not freezing any parameters).
+ """
+
+ def __init__(
+ self,
+ pretrain_img_size=224,
+ in_channels=3,
+ embed_dims=96,
+ patch_size=4,
+ window_size=7,
+ mlp_ratio=4,
+ depths=(2, 2, 6, 2),
+ num_heads=(3, 6, 12, 24),
+ strides=(4, 2, 2, 2),
+ out_indices=(0, 1, 2, 3),
+ qkv_bias=True,
+ qk_scale=None,
+ patch_norm=True,
+ drop_rate=0.,
+ attn_drop_rate=0.,
+ drop_path_rate=0.1,
+ use_abs_pos_embed=False,
+ act_cfg=dict(type='GELU'),
+ norm_cfg=dict(type='LN'),
+ with_cp=False,
+ convert_weights=False,
+ frozen_stages=-1,
+ ):
+ self.convert_weights = convert_weights
+ self.frozen_stages = frozen_stages
+ if isinstance(pretrain_img_size, int):
+ pretrain_img_size = to_2tuple(pretrain_img_size)
+ elif isinstance(pretrain_img_size, tuple):
+ if len(pretrain_img_size) == 1:
+ pretrain_img_size = to_2tuple(pretrain_img_size[0])
+ assert len(pretrain_img_size) == 2, \
+ f'The size of image should have length 1 or 2, ' \
+ f'but got {len(pretrain_img_size)}'
+
+ super(SwinTransformer, self).__init__()
+
+ num_layers = len(depths)
+ self.out_indices = out_indices
+ self.use_abs_pos_embed = use_abs_pos_embed
+
+ assert strides[0] == patch_size, 'Use non-overlapping patch embed.'
+
+ self.patch_embed = PatchEmbed(
+ in_channels=in_channels,
+ embed_dims=embed_dims,
+ conv_type='Conv2d',
+ kernel_size=patch_size,
+ stride=strides[0],
+ norm_cfg=norm_cfg if patch_norm else None,
+ init_cfg=None)
+
+ if self.use_abs_pos_embed:
+ patch_row = pretrain_img_size[0] // patch_size
+ patch_col = pretrain_img_size[1] // patch_size
+ num_patches = patch_row * patch_col
+ self.absolute_pos_embed = nn.Parameter(
+ torch.zeros((1, num_patches, embed_dims)))
+
+ self.drop_after_pos = nn.Dropout(p=drop_rate)
+
+ # set stochastic depth decay rule
+ total_depth = sum(depths)
+ dpr = [
+ x.item() for x in torch.linspace(0, drop_path_rate, total_depth)
+ ]
+
+ self.stages = nn.ModuleList()
+ in_channels = embed_dims
+ for i in range(num_layers):
+ if i < num_layers - 1:
+ downsample = PatchMerging(
+ in_channels=in_channels,
+ out_channels=2 * in_channels,
+ stride=strides[i + 1],
+ norm_cfg=norm_cfg if patch_norm else None,
+ init_cfg=None)
+ else:
+ downsample = None
+
+ stage = SwinBlockSequence(
+ embed_dims=in_channels,
+ num_heads=num_heads[i],
+ feedforward_channels=mlp_ratio * in_channels,
+ depth=depths[i],
+ window_size=window_size,
+ qkv_bias=qkv_bias,
+ qk_scale=qk_scale,
+ drop_rate=drop_rate,
+ attn_drop_rate=attn_drop_rate,
+ drop_path_rate=dpr[sum(depths[:i]):sum(depths[:i + 1])],
+ downsample=downsample,
+ act_cfg=act_cfg,
+ norm_cfg=norm_cfg,
+ with_cp=with_cp)
+ self.stages.append(stage)
+ if downsample:
+ in_channels = downsample.out_channels
+
+ self.num_features = [int(embed_dims * 2**i) for i in range(num_layers)]
+ # Add a norm layer for each output
+ for i in out_indices:
+ layer = build_norm_layer(norm_cfg, self.num_features[i])[1]
+ layer_name = f'norm{i}'
+ self.add_module(layer_name, layer)
+
+ def train(self, mode=True):
+ """Convert the model into training mode while keep layers freezed."""
+ super(SwinTransformer, self).train(mode)
+ self._freeze_stages()
+
+ def _freeze_stages(self):
+ if self.frozen_stages >= 0:
+ self.patch_embed.eval()
+ for param in self.patch_embed.parameters():
+ param.requires_grad = False
+ if self.use_abs_pos_embed:
+ self.absolute_pos_embed.requires_grad = False
+ self.drop_after_pos.eval()
+
+ for i in range(1, self.frozen_stages + 1):
+
+ if (i - 1) in self.out_indices:
+ norm_layer = getattr(self, f'norm{i-1}')
+ norm_layer.eval()
+ for param in norm_layer.parameters():
+ param.requires_grad = False
+
+ m = self.stages[i - 1]
+ m.eval()
+ for param in m.parameters():
+ param.requires_grad = False
+
+ def init_weights(self, pretrained=None):
+ """Initialize the weights in backbone.
+
+ Args:
+ pretrained (str, optional): Path to pre-trained weights.
+ Defaults to None.
+ """
+ if isinstance(pretrained, str):
+ logger = get_root_logger()
+ ckpt = _load_checkpoint(
+ pretrained, logger=logger, map_location='cpu')
+ if 'state_dict' in ckpt:
+ _state_dict = ckpt['state_dict']
+ elif 'model' in ckpt:
+ _state_dict = ckpt['model']
+ else:
+ _state_dict = ckpt
+ if self.convert_weights:
+ # supported loading weight from original repo,
+ _state_dict = swin_converter(_state_dict)
+
+ state_dict = OrderedDict()
+ for k, v in _state_dict.items():
+ if k.startswith('backbone.'):
+ state_dict[k[9:]] = v
+
+ # strip prefix of state_dict
+ if list(state_dict.keys())[0].startswith('module.'):
+ state_dict = {k[7:]: v for k, v in state_dict.items()}
+
+ # reshape absolute position embedding
+ if state_dict.get('absolute_pos_embed') is not None:
+ absolute_pos_embed = state_dict['absolute_pos_embed']
+ N1, L, C1 = absolute_pos_embed.size()
+ N2, C2, H, W = self.absolute_pos_embed.size()
+ if N1 != N2 or C1 != C2 or L != H * W:
+ logger.warning('Error in loading absolute_pos_embed, pass')
+ else:
+ state_dict['absolute_pos_embed'] = absolute_pos_embed.view(
+ N2, H, W, C2).permute(0, 3, 1, 2).contiguous()
+
+ # interpolate position bias table if needed
+ relative_position_bias_table_keys = [
+ k for k in state_dict.keys()
+ if 'relative_position_bias_table' in k
+ ]
+ for table_key in relative_position_bias_table_keys:
+ table_pretrained = state_dict[table_key]
+ table_current = self.state_dict()[table_key]
+ L1, nH1 = table_pretrained.size()
+ L2, nH2 = table_current.size()
+ if nH1 != nH2:
+ logger.warning(f'Error in loading {table_key}, pass')
+ elif L1 != L2:
+ S1 = int(L1**0.5)
+ S2 = int(L2**0.5)
+ table_pretrained_resized = F.interpolate(
+ table_pretrained.permute(1, 0).reshape(1, nH1, S1, S1),
+ size=(S2, S2),
+ mode='bicubic')
+ state_dict[table_key] = table_pretrained_resized.view(
+ nH2, L2).permute(1, 0).contiguous()
+
+ # load state_dict
+ self.load_state_dict(state_dict, False)
+ elif pretrained is None:
+ if self.use_abs_pos_embed:
+ trunc_normal_(self.absolute_pos_embed, std=0.02)
+ for m in self.modules():
+ if isinstance(m, nn.Linear):
+ trunc_normal_init(m, std=.02, bias=0.)
+ elif isinstance(m, nn.LayerNorm):
+ constant_init(m, 1.0)
+ else:
+ raise TypeError('pretrained must be a str or None')
+
+ def forward(self, x):
+ x, hw_shape = self.patch_embed(x)
+
+ if self.use_abs_pos_embed:
+ x = x + self.absolute_pos_embed
+ x = self.drop_after_pos(x)
+
+ outs = []
+ for i, stage in enumerate(self.stages):
+ x, hw_shape, out, out_hw_shape = stage(x, hw_shape)
+ if i in self.out_indices:
+ norm_layer = getattr(self, f'norm{i}')
+ out = norm_layer(out)
+ out = out.view(-1, *out_hw_shape,
+ self.num_features[i]).permute(0, 3, 1,
+ 2).contiguous()
+ outs.append(out)
+
+ return outs
diff --git a/grounded-sam-osx/transformer_utils/mmpose/models/backbones/tcformer.py b/grounded-sam-osx/transformer_utils/mmpose/models/backbones/tcformer.py
new file mode 100644
index 0000000000000000000000000000000000000000..a0805cdddd17bbba50bf203e2bc9012efd86ba03
--- /dev/null
+++ b/grounded-sam-osx/transformer_utils/mmpose/models/backbones/tcformer.py
@@ -0,0 +1,283 @@
+# Copyright (c) OpenMMLab. All rights reserved.
+import math
+
+import torch
+import torch.nn as nn
+from mmcv.cnn import (build_norm_layer, constant_init, normal_init,
+ trunc_normal_init)
+from mmcv.runner import _load_checkpoint, load_state_dict
+
+from ...utils import get_root_logger
+from ..builder import BACKBONES
+from ..utils import (PatchEmbed, TCFormerDynamicBlock, TCFormerRegularBlock,
+ TokenConv, cluster_dpc_knn, merge_tokens,
+ tcformer_convert, token2map)
+
+
+class CTM(nn.Module):
+ """Clustering-based Token Merging module in TCFormer.
+
+ Args:
+ sample_ratio (float): The sample ratio of tokens.
+ embed_dim (int): Input token feature dimension.
+ dim_out (int): Output token feature dimension.
+ k (int): number of the nearest neighbor used i DPC-knn algorithm.
+ """
+
+ def __init__(self, sample_ratio, embed_dim, dim_out, k=5):
+ super().__init__()
+ self.sample_ratio = sample_ratio
+ self.dim_out = dim_out
+ self.conv = TokenConv(
+ in_channels=embed_dim,
+ out_channels=dim_out,
+ kernel_size=3,
+ stride=2,
+ padding=1)
+ self.norm = nn.LayerNorm(self.dim_out)
+ self.score = nn.Linear(self.dim_out, 1)
+ self.k = k
+
+ def forward(self, token_dict):
+ token_dict = token_dict.copy()
+ x = self.conv(token_dict)
+ x = self.norm(x)
+ token_score = self.score(x)
+ token_weight = token_score.exp()
+
+ token_dict['x'] = x
+ B, N, C = x.shape
+ token_dict['token_score'] = token_score
+
+ cluster_num = max(math.ceil(N * self.sample_ratio), 1)
+ idx_cluster, cluster_num = cluster_dpc_knn(token_dict, cluster_num,
+ self.k)
+ down_dict = merge_tokens(token_dict, idx_cluster, cluster_num,
+ token_weight)
+
+ H, W = token_dict['map_size']
+ H = math.floor((H - 1) / 2 + 1)
+ W = math.floor((W - 1) / 2 + 1)
+ down_dict['map_size'] = [H, W]
+
+ return down_dict, token_dict
+
+
+@BACKBONES.register_module()
+class TCFormer(nn.Module):
+ """Token Clustering Transformer (TCFormer)
+
+ Implementation of `Not All Tokens Are Equal: Human-centric Visual
+ Analysis via Token Clustering Transformer
+ `
+
+ Args:
+ in_channels (int): Number of input channels. Default: 3.
+ embed_dims (list[int]): Embedding dimension. Default:
+ [64, 128, 256, 512].
+ num_heads (Sequence[int]): The attention heads of each transformer
+ encode layer. Default: [1, 2, 5, 8].
+ mlp_ratios (Sequence[int]): The ratio of the mlp hidden dim to the
+ embedding dim of each transformer block.
+ qkv_bias (bool): Enable bias for qkv if True. Default: True.
+ qk_scale (float | None, optional): Override default qk scale of
+ head_dim ** -0.5 if set. Default: None.
+ drop_rate (float): Probability of an element to be zeroed.
+ Default 0.0.
+ attn_drop_rate (float): The drop out rate for attention layer.
+ Default 0.0.
+ drop_path_rate (float): stochastic depth rate. Default 0.
+ norm_cfg (dict): Config dict for normalization layer.
+ Default: dict(type='LN', eps=1e-6).
+ num_layers (Sequence[int]): The layer number of each transformer encode
+ layer. Default: [3, 4, 6, 3].
+ sr_ratios (Sequence[int]): The spatial reduction rate of each
+ transformer block. Default: [8, 4, 2, 1].
+ num_stages (int): The num of stages. Default: 4.
+ pretrained (str, optional): model pretrained path. Default: None.
+ k (int): number of the nearest neighbor used for local density.
+ sample_ratios (list[float]): The sample ratios of CTM modules.
+ Default: [0.25, 0.25, 0.25]
+ return_map (bool): If True, transfer dynamic tokens to feature map at
+ last. Default: False
+ convert_weights (bool): The flag indicates whether the
+ pre-trained model is from the original repo. We may need
+ to convert some keys to make it compatible.
+ Default: True.
+ """
+
+ def __init__(self,
+ in_channels=3,
+ embed_dims=[64, 128, 256, 512],
+ num_heads=[1, 2, 4, 8],
+ mlp_ratios=[4, 4, 4, 4],
+ qkv_bias=True,
+ qk_scale=None,
+ drop_rate=0.,
+ attn_drop_rate=0.,
+ drop_path_rate=0.,
+ norm_cfg=dict(type='LN', eps=1e-6),
+ num_layers=[3, 4, 6, 3],
+ sr_ratios=[8, 4, 2, 1],
+ num_stages=4,
+ pretrained=None,
+ k=5,
+ sample_ratios=[0.25, 0.25, 0.25],
+ return_map=False,
+ convert_weights=True):
+ super().__init__()
+
+ self.num_layers = num_layers
+ self.num_stages = num_stages
+ self.grid_stride = sr_ratios[0]
+ self.embed_dims = embed_dims
+ self.sr_ratios = sr_ratios
+ self.mlp_ratios = mlp_ratios
+ self.sample_ratios = sample_ratios
+ self.return_map = return_map
+ self.convert_weights = convert_weights
+
+ # stochastic depth decay rule
+ dpr = [
+ x.item()
+ for x in torch.linspace(0, drop_path_rate, sum(num_layers))
+ ]
+ cur = 0
+
+ # In stage 1, use the standard transformer blocks
+ for i in range(1):
+ patch_embed = PatchEmbed(
+ in_channels=in_channels if i == 0 else embed_dims[i - 1],
+ embed_dims=embed_dims[i],
+ kernel_size=7,
+ stride=4,
+ padding=3,
+ bias=True,
+ norm_cfg=dict(type='LN', eps=1e-6))
+
+ block = nn.ModuleList([
+ TCFormerRegularBlock(
+ dim=embed_dims[i],
+ num_heads=num_heads[i],
+ mlp_ratio=mlp_ratios[i],
+ qkv_bias=qkv_bias,
+ qk_scale=qk_scale,
+ drop=drop_rate,
+ attn_drop=attn_drop_rate,
+ drop_path=dpr[cur + j],
+ norm_cfg=norm_cfg,
+ sr_ratio=sr_ratios[i]) for j in range(num_layers[i])
+ ])
+ norm = build_norm_layer(norm_cfg, embed_dims[i])[1]
+
+ cur += num_layers[i]
+
+ setattr(self, f'patch_embed{i + 1}', patch_embed)
+ setattr(self, f'block{i + 1}', block)
+ setattr(self, f'norm{i + 1}', norm)
+
+ # In stage 2~4, use TCFormerDynamicBlock for dynamic tokens
+ for i in range(1, num_stages):
+ ctm = CTM(sample_ratios[i - 1], embed_dims[i - 1], embed_dims[i],
+ k)
+
+ block = nn.ModuleList([
+ TCFormerDynamicBlock(
+ dim=embed_dims[i],
+ num_heads=num_heads[i],
+ mlp_ratio=mlp_ratios[i],
+ qkv_bias=qkv_bias,
+ qk_scale=qk_scale,
+ drop=drop_rate,
+ attn_drop=attn_drop_rate,
+ drop_path=dpr[cur + j],
+ norm_cfg=norm_cfg,
+ sr_ratio=sr_ratios[i]) for j in range(num_layers[i])
+ ])
+ norm = build_norm_layer(norm_cfg, embed_dims[i])[1]
+ cur += num_layers[i]
+
+ setattr(self, f'ctm{i}', ctm)
+ setattr(self, f'block{i + 1}', block)
+ setattr(self, f'norm{i + 1}', norm)
+
+ self.init_weights(pretrained)
+
+ def init_weights(self, pretrained=None):
+ if isinstance(pretrained, str):
+ logger = get_root_logger()
+
+ checkpoint = _load_checkpoint(
+ pretrained, logger=logger, map_location='cpu')
+ logger.warning(f'Load pre-trained model for '
+ f'{self.__class__.__name__} from original repo')
+ if 'state_dict' in checkpoint:
+ state_dict = checkpoint['state_dict']
+ elif 'model' in checkpoint:
+ state_dict = checkpoint['model']
+ else:
+ state_dict = checkpoint
+
+ if self.convert_weights:
+ # We need to convert pre-trained weights to match this
+ # implementation.
+ state_dict = tcformer_convert(state_dict)
+ load_state_dict(self, state_dict, strict=False, logger=logger)
+
+ elif pretrained is None:
+ for m in self.modules():
+ if isinstance(m, nn.Linear):
+ trunc_normal_init(m, std=.02, bias=0.)
+ elif isinstance(m, nn.LayerNorm):
+ constant_init(m, 1.0)
+ elif isinstance(m, nn.Conv2d):
+ fan_out = m.kernel_size[0] * m.kernel_size[
+ 1] * m.out_channels
+ fan_out //= m.groups
+ normal_init(m, 0, math.sqrt(2.0 / fan_out))
+ else:
+ raise TypeError('pretrained must be a str or None')
+
+ def forward(self, x):
+ outs = []
+
+ i = 0
+ patch_embed = getattr(self, f'patch_embed{i + 1}')
+ block = getattr(self, f'block{i + 1}')
+ norm = getattr(self, f'norm{i + 1}')
+ x, (H, W) = patch_embed(x)
+ for blk in block:
+ x = blk(x, H, W)
+ x = norm(x)
+
+ # init token dict
+ B, N, _ = x.shape
+ device = x.device
+ idx_token = torch.arange(N)[None, :].repeat(B, 1).to(device)
+ agg_weight = x.new_ones(B, N, 1)
+ token_dict = {
+ 'x': x,
+ 'token_num': N,
+ 'map_size': [H, W],
+ 'init_grid_size': [H, W],
+ 'idx_token': idx_token,
+ 'agg_weight': agg_weight
+ }
+ outs.append(token_dict.copy())
+
+ # stage 2~4
+ for i in range(1, self.num_stages):
+ ctm = getattr(self, f'ctm{i}')
+ block = getattr(self, f'block{i + 1}')
+ norm = getattr(self, f'norm{i + 1}')
+
+ token_dict = ctm(token_dict) # down sample
+ for j, blk in enumerate(block):
+ token_dict = blk(token_dict)
+
+ token_dict['x'] = norm(token_dict['x'])
+ outs.append(token_dict)
+
+ if self.return_map:
+ outs = [token2map(token_dict) for token_dict in outs]
+ return outs
diff --git a/grounded-sam-osx/transformer_utils/mmpose/models/backbones/tcn.py b/grounded-sam-osx/transformer_utils/mmpose/models/backbones/tcn.py
new file mode 100644
index 0000000000000000000000000000000000000000..deca2290aeb1830bc3e241b819157369371aaf27
--- /dev/null
+++ b/grounded-sam-osx/transformer_utils/mmpose/models/backbones/tcn.py
@@ -0,0 +1,267 @@
+# Copyright (c) OpenMMLab. All rights reserved.
+import copy
+
+import torch.nn as nn
+from mmcv.cnn import ConvModule, build_conv_layer, constant_init, kaiming_init
+from mmcv.utils.parrots_wrapper import _BatchNorm
+
+from mmpose.core import WeightNormClipHook
+from ..builder import BACKBONES
+from .base_backbone import BaseBackbone
+
+
+class BasicTemporalBlock(nn.Module):
+ """Basic block for VideoPose3D.
+
+ Args:
+ in_channels (int): Input channels of this block.
+ out_channels (int): Output channels of this block.
+ mid_channels (int): The output channels of conv1. Default: 1024.
+ kernel_size (int): Size of the convolving kernel. Default: 3.
+ dilation (int): Spacing between kernel elements. Default: 3.
+ dropout (float): Dropout rate. Default: 0.25.
+ causal (bool): Use causal convolutions instead of symmetric
+ convolutions (for real-time applications). Default: False.
+ residual (bool): Use residual connection. Default: True.
+ use_stride_conv (bool): Use optimized TCN that designed
+ specifically for single-frame batching, i.e. where batches have
+ input length = receptive field, and output length = 1. This
+ implementation replaces dilated convolutions with strided
+ convolutions to avoid generating unused intermediate results.
+ Default: False.
+ conv_cfg (dict): dictionary to construct and config conv layer.
+ Default: dict(type='Conv1d').
+ norm_cfg (dict): dictionary to construct and config norm layer.
+ Default: dict(type='BN1d').
+ """
+
+ def __init__(self,
+ in_channels,
+ out_channels,
+ mid_channels=1024,
+ kernel_size=3,
+ dilation=3,
+ dropout=0.25,
+ causal=False,
+ residual=True,
+ use_stride_conv=False,
+ conv_cfg=dict(type='Conv1d'),
+ norm_cfg=dict(type='BN1d')):
+ # Protect mutable default arguments
+ conv_cfg = copy.deepcopy(conv_cfg)
+ norm_cfg = copy.deepcopy(norm_cfg)
+ super().__init__()
+ self.in_channels = in_channels
+ self.out_channels = out_channels
+ self.mid_channels = mid_channels
+ self.kernel_size = kernel_size
+ self.dilation = dilation
+ self.dropout = dropout
+ self.causal = causal
+ self.residual = residual
+ self.use_stride_conv = use_stride_conv
+
+ self.pad = (kernel_size - 1) * dilation // 2
+ if use_stride_conv:
+ self.stride = kernel_size
+ self.causal_shift = kernel_size // 2 if causal else 0
+ self.dilation = 1
+ else:
+ self.stride = 1
+ self.causal_shift = kernel_size // 2 * dilation if causal else 0
+
+ self.conv1 = nn.Sequential(
+ ConvModule(
+ in_channels,
+ mid_channels,
+ kernel_size=kernel_size,
+ stride=self.stride,
+ dilation=self.dilation,
+ bias='auto',
+ conv_cfg=conv_cfg,
+ norm_cfg=norm_cfg))
+ self.conv2 = nn.Sequential(
+ ConvModule(
+ mid_channels,
+ out_channels,
+ kernel_size=1,
+ bias='auto',
+ conv_cfg=conv_cfg,
+ norm_cfg=norm_cfg))
+
+ if residual and in_channels != out_channels:
+ self.short_cut = build_conv_layer(conv_cfg, in_channels,
+ out_channels, 1)
+ else:
+ self.short_cut = None
+
+ self.dropout = nn.Dropout(dropout) if dropout > 0 else None
+
+ def forward(self, x):
+ """Forward function."""
+ if self.use_stride_conv:
+ assert self.causal_shift + self.kernel_size // 2 < x.shape[2]
+ else:
+ assert 0 <= self.pad + self.causal_shift < x.shape[2] - \
+ self.pad + self.causal_shift <= x.shape[2]
+
+ out = self.conv1(x)
+ if self.dropout is not None:
+ out = self.dropout(out)
+
+ out = self.conv2(out)
+ if self.dropout is not None:
+ out = self.dropout(out)
+
+ if self.residual:
+ if self.use_stride_conv:
+ res = x[:, :, self.causal_shift +
+ self.kernel_size // 2::self.kernel_size]
+ else:
+ res = x[:, :,
+ (self.pad + self.causal_shift):(x.shape[2] - self.pad +
+ self.causal_shift)]
+
+ if self.short_cut is not None:
+ res = self.short_cut(res)
+ out = out + res
+
+ return out
+
+
+@BACKBONES.register_module()
+class TCN(BaseBackbone):
+ """TCN backbone.
+
+ Temporal Convolutional Networks.
+ More details can be found in the
+ `paper `__ .
+
+ Args:
+ in_channels (int): Number of input channels, which equals to
+ num_keypoints * num_features.
+ stem_channels (int): Number of feature channels. Default: 1024.
+ num_blocks (int): NUmber of basic temporal convolutional blocks.
+ Default: 2.
+ kernel_sizes (Sequence[int]): Sizes of the convolving kernel of
+ each basic block. Default: ``(3, 3, 3)``.
+ dropout (float): Dropout rate. Default: 0.25.
+ causal (bool): Use causal convolutions instead of symmetric
+ convolutions (for real-time applications).
+ Default: False.
+ residual (bool): Use residual connection. Default: True.
+ use_stride_conv (bool): Use TCN backbone optimized for
+ single-frame batching, i.e. where batches have input length =
+ receptive field, and output length = 1. This implementation
+ replaces dilated convolutions with strided convolutions to avoid
+ generating unused intermediate results. The weights are
+ interchangeable with the reference implementation. Default: False
+ conv_cfg (dict): dictionary to construct and config conv layer.
+ Default: dict(type='Conv1d').
+ norm_cfg (dict): dictionary to construct and config norm layer.
+ Default: dict(type='BN1d').
+ max_norm (float|None): if not None, the weight of convolution layers
+ will be clipped to have a maximum norm of max_norm.
+
+ Example:
+ >>> from mmpose.models import TCN
+ >>> import torch
+ >>> self = TCN(in_channels=34)
+ >>> self.eval()
+ >>> inputs = torch.rand(1, 34, 243)
+ >>> level_outputs = self.forward(inputs)
+ >>> for level_out in level_outputs:
+ ... print(tuple(level_out.shape))
+ (1, 1024, 235)
+ (1, 1024, 217)
+ """
+
+ def __init__(self,
+ in_channels,
+ stem_channels=1024,
+ num_blocks=2,
+ kernel_sizes=(3, 3, 3),
+ dropout=0.25,
+ causal=False,
+ residual=True,
+ use_stride_conv=False,
+ conv_cfg=dict(type='Conv1d'),
+ norm_cfg=dict(type='BN1d'),
+ max_norm=None):
+ # Protect mutable default arguments
+ conv_cfg = copy.deepcopy(conv_cfg)
+ norm_cfg = copy.deepcopy(norm_cfg)
+ super().__init__()
+ self.in_channels = in_channels
+ self.stem_channels = stem_channels
+ self.num_blocks = num_blocks
+ self.kernel_sizes = kernel_sizes
+ self.dropout = dropout
+ self.causal = causal
+ self.residual = residual
+ self.use_stride_conv = use_stride_conv
+ self.max_norm = max_norm
+
+ assert num_blocks == len(kernel_sizes) - 1
+ for ks in kernel_sizes:
+ assert ks % 2 == 1, 'Only odd filter widths are supported.'
+
+ self.expand_conv = ConvModule(
+ in_channels,
+ stem_channels,
+ kernel_size=kernel_sizes[0],
+ stride=kernel_sizes[0] if use_stride_conv else 1,
+ bias='auto',
+ conv_cfg=conv_cfg,
+ norm_cfg=norm_cfg)
+
+ dilation = kernel_sizes[0]
+ self.tcn_blocks = nn.ModuleList()
+ for i in range(1, num_blocks + 1):
+ self.tcn_blocks.append(
+ BasicTemporalBlock(
+ in_channels=stem_channels,
+ out_channels=stem_channels,
+ mid_channels=stem_channels,
+ kernel_size=kernel_sizes[i],
+ dilation=dilation,
+ dropout=dropout,
+ causal=causal,
+ residual=residual,
+ use_stride_conv=use_stride_conv,
+ conv_cfg=conv_cfg,
+ norm_cfg=norm_cfg))
+ dilation *= kernel_sizes[i]
+
+ if self.max_norm is not None:
+ # Apply weight norm clip to conv layers
+ weight_clip = WeightNormClipHook(self.max_norm)
+ for module in self.modules():
+ if isinstance(module, nn.modules.conv._ConvNd):
+ weight_clip.register(module)
+
+ self.dropout = nn.Dropout(dropout) if dropout > 0 else None
+
+ def forward(self, x):
+ """Forward function."""
+ x = self.expand_conv(x)
+
+ if self.dropout is not None:
+ x = self.dropout(x)
+
+ outs = []
+ for i in range(self.num_blocks):
+ x = self.tcn_blocks[i](x)
+ outs.append(x)
+
+ return tuple(outs)
+
+ def init_weights(self, pretrained=None):
+ """Initialize the weights."""
+ super().init_weights(pretrained)
+ if pretrained is None:
+ for m in self.modules():
+ if isinstance(m, nn.modules.conv._ConvNd):
+ kaiming_init(m, mode='fan_in', nonlinearity='relu')
+ elif isinstance(m, _BatchNorm):
+ constant_init(m, 1)
diff --git a/grounded-sam-osx/transformer_utils/mmpose/models/backbones/utils/__init__.py b/grounded-sam-osx/transformer_utils/mmpose/models/backbones/utils/__init__.py
new file mode 100644
index 0000000000000000000000000000000000000000..52a30ca9f7c8e90b6c6fa2fd8a9705ca0403b259
--- /dev/null
+++ b/grounded-sam-osx/transformer_utils/mmpose/models/backbones/utils/__init__.py
@@ -0,0 +1,11 @@
+# Copyright (c) OpenMMLab. All rights reserved.
+from .channel_shuffle import channel_shuffle
+from .inverted_residual import InvertedResidual
+from .make_divisible import make_divisible
+from .se_layer import SELayer
+from .utils import load_checkpoint
+
+__all__ = [
+ 'channel_shuffle', 'make_divisible', 'InvertedResidual', 'SELayer',
+ 'load_checkpoint'
+]
diff --git a/grounded-sam-osx/transformer_utils/mmpose/models/backbones/utils/channel_shuffle.py b/grounded-sam-osx/transformer_utils/mmpose/models/backbones/utils/channel_shuffle.py
new file mode 100644
index 0000000000000000000000000000000000000000..aedd826bee690d42d92ed8a7f538b221e5b069e2
--- /dev/null
+++ b/grounded-sam-osx/transformer_utils/mmpose/models/backbones/utils/channel_shuffle.py
@@ -0,0 +1,29 @@
+# Copyright (c) OpenMMLab. All rights reserved.
+import torch
+
+
+def channel_shuffle(x, groups):
+ """Channel Shuffle operation.
+
+ This function enables cross-group information flow for multiple groups
+ convolution layers.
+
+ Args:
+ x (Tensor): The input tensor.
+ groups (int): The number of groups to divide the input tensor
+ in the channel dimension.
+
+ Returns:
+ Tensor: The output tensor after channel shuffle operation.
+ """
+
+ batch_size, num_channels, height, width = x.size()
+ assert (num_channels % groups == 0), ('num_channels should be '
+ 'divisible by groups')
+ channels_per_group = num_channels // groups
+
+ x = x.view(batch_size, groups, channels_per_group, height, width)
+ x = torch.transpose(x, 1, 2).contiguous()
+ x = x.view(batch_size, groups * channels_per_group, height, width)
+
+ return x
diff --git a/grounded-sam-osx/transformer_utils/mmpose/models/backbones/utils/ckpt_convert.py b/grounded-sam-osx/transformer_utils/mmpose/models/backbones/utils/ckpt_convert.py
new file mode 100644
index 0000000000000000000000000000000000000000..14a43892c6630be31e915ed1f8b9164ba250e8bd
--- /dev/null
+++ b/grounded-sam-osx/transformer_utils/mmpose/models/backbones/utils/ckpt_convert.py
@@ -0,0 +1,62 @@
+# Copyright (c) OpenMMLab. All rights reserved.
+
+# This script consists of several convert functions which
+# can modify the weights of model in original repo to be
+# pre-trained weights.
+
+from collections import OrderedDict
+
+
+def swin_converter(ckpt):
+
+ new_ckpt = OrderedDict()
+
+ def correct_unfold_reduction_order(x):
+ out_channel, in_channel = x.shape
+ x = x.reshape(out_channel, 4, in_channel // 4)
+ x = x[:, [0, 2, 1, 3], :].transpose(1,
+ 2).reshape(out_channel, in_channel)
+ return x
+
+ def correct_unfold_norm_order(x):
+ in_channel = x.shape[0]
+ x = x.reshape(4, in_channel // 4)
+ x = x[[0, 2, 1, 3], :].transpose(0, 1).reshape(in_channel)
+ return x
+
+ for k, v in ckpt.items():
+ if k.startswith('head'):
+ continue
+ elif k.startswith('layers'):
+ new_v = v
+ if 'attn.' in k:
+ new_k = k.replace('attn.', 'attn.w_msa.')
+ elif 'mlp.' in k:
+ if 'mlp.fc1.' in k:
+ new_k = k.replace('mlp.fc1.', 'ffn.layers.0.0.')
+ elif 'mlp.fc2.' in k:
+ new_k = k.replace('mlp.fc2.', 'ffn.layers.1.')
+ else:
+ new_k = k.replace('mlp.', 'ffn.')
+ elif 'downsample' in k:
+ new_k = k
+ if 'reduction.' in k:
+ new_v = correct_unfold_reduction_order(v)
+ elif 'norm.' in k:
+ new_v = correct_unfold_norm_order(v)
+ else:
+ new_k = k
+ new_k = new_k.replace('layers', 'stages', 1)
+ elif k.startswith('patch_embed'):
+ new_v = v
+ if 'proj' in k:
+ new_k = k.replace('proj', 'projection')
+ else:
+ new_k = k
+ else:
+ new_v = v
+ new_k = k
+
+ new_ckpt['backbone.' + new_k] = new_v
+
+ return new_ckpt
diff --git a/grounded-sam-osx/transformer_utils/mmpose/models/backbones/utils/inverted_residual.py b/grounded-sam-osx/transformer_utils/mmpose/models/backbones/utils/inverted_residual.py
new file mode 100644
index 0000000000000000000000000000000000000000..dff762c570550e4a738ae1833a4c82c18777115d
--- /dev/null
+++ b/grounded-sam-osx/transformer_utils/mmpose/models/backbones/utils/inverted_residual.py
@@ -0,0 +1,128 @@
+# Copyright (c) OpenMMLab. All rights reserved.
+import copy
+
+import torch.nn as nn
+import torch.utils.checkpoint as cp
+from mmcv.cnn import ConvModule
+
+from .se_layer import SELayer
+
+
+class InvertedResidual(nn.Module):
+ """Inverted Residual Block.
+
+ Args:
+ in_channels (int): The input channels of this Module.
+ out_channels (int): The output channels of this Module.
+ mid_channels (int): The input channels of the depthwise convolution.
+ kernel_size (int): The kernel size of the depthwise convolution.
+ Default: 3.
+ groups (None or int): The group number of the depthwise convolution.
+ Default: None, which means group number = mid_channels.
+ stride (int): The stride of the depthwise convolution. Default: 1.
+ se_cfg (dict): Config dict for se layer. Default: None, which means no
+ se layer.
+ with_expand_conv (bool): Use expand conv or not. If set False,
+ mid_channels must be the same with in_channels.
+ Default: True.
+ conv_cfg (dict): Config dict for convolution layer. Default: None,
+ which means using conv2d.
+ norm_cfg (dict): Config dict for normalization layer.
+ Default: dict(type='BN').
+ act_cfg (dict): Config dict for activation layer.
+ Default: dict(type='ReLU').
+ with_cp (bool): Use checkpoint or not. Using checkpoint will save some
+ memory while slowing down the training speed. Default: False.
+
+ Returns:
+ Tensor: The output tensor.
+ """
+
+ def __init__(self,
+ in_channels,
+ out_channels,
+ mid_channels,
+ kernel_size=3,
+ groups=None,
+ stride=1,
+ se_cfg=None,
+ with_expand_conv=True,
+ conv_cfg=None,
+ norm_cfg=dict(type='BN'),
+ act_cfg=dict(type='ReLU'),
+ with_cp=False):
+ # Protect mutable default arguments
+ norm_cfg = copy.deepcopy(norm_cfg)
+ act_cfg = copy.deepcopy(act_cfg)
+ super().__init__()
+ self.with_res_shortcut = (stride == 1 and in_channels == out_channels)
+ assert stride in [1, 2]
+ self.with_cp = with_cp
+ self.with_se = se_cfg is not None
+ self.with_expand_conv = with_expand_conv
+
+ if groups is None:
+ groups = mid_channels
+
+ if self.with_se:
+ assert isinstance(se_cfg, dict)
+ if not self.with_expand_conv:
+ assert mid_channels == in_channels
+
+ if self.with_expand_conv:
+ self.expand_conv = ConvModule(
+ in_channels=in_channels,
+ out_channels=mid_channels,
+ kernel_size=1,
+ stride=1,
+ padding=0,
+ conv_cfg=conv_cfg,
+ norm_cfg=norm_cfg,
+ act_cfg=act_cfg)
+ self.depthwise_conv = ConvModule(
+ in_channels=mid_channels,
+ out_channels=mid_channels,
+ kernel_size=kernel_size,
+ stride=stride,
+ padding=kernel_size // 2,
+ groups=groups,
+ conv_cfg=conv_cfg,
+ norm_cfg=norm_cfg,
+ act_cfg=act_cfg)
+ if self.with_se:
+ self.se = SELayer(**se_cfg)
+ self.linear_conv = ConvModule(
+ in_channels=mid_channels,
+ out_channels=out_channels,
+ kernel_size=1,
+ stride=1,
+ padding=0,
+ conv_cfg=conv_cfg,
+ norm_cfg=norm_cfg,
+ act_cfg=None)
+
+ def forward(self, x):
+
+ def _inner_forward(x):
+ out = x
+
+ if self.with_expand_conv:
+ out = self.expand_conv(out)
+
+ out = self.depthwise_conv(out)
+
+ if self.with_se:
+ out = self.se(out)
+
+ out = self.linear_conv(out)
+
+ if self.with_res_shortcut:
+ return x + out
+ return out
+
+ if self.with_cp and x.requires_grad:
+ out = cp.checkpoint(_inner_forward, x)
+ else:
+ out = _inner_forward(x)
+
+ return out
diff --git a/grounded-sam-osx/transformer_utils/mmpose/models/backbones/utils/make_divisible.py b/grounded-sam-osx/transformer_utils/mmpose/models/backbones/utils/make_divisible.py
new file mode 100644
index 0000000000000000000000000000000000000000..b7666be65939d5c76057e73927c230029cb1871d
--- /dev/null
+++ b/grounded-sam-osx/transformer_utils/mmpose/models/backbones/utils/make_divisible.py
@@ -0,0 +1,25 @@
+# Copyright (c) OpenMMLab. All rights reserved.
+def make_divisible(value, divisor, min_value=None, min_ratio=0.9):
+ """Make divisible function.
+
+ This function rounds the channel number down to the nearest value that can
+ be divisible by the divisor.
+
+ Args:
+ value (int): The original channel number.
+ divisor (int): The divisor to fully divide the channel number.
+ min_value (int, optional): The minimum value of the output channel.
+ Default: None, means that the minimum value equal to the divisor.
+ min_ratio (float, optional): The minimum ratio of the rounded channel
+ number to the original channel number. Default: 0.9.
+ Returns:
+ int: The modified output channel number
+ """
+
+ if min_value is None:
+ min_value = divisor
+ new_value = max(min_value, int(value + divisor / 2) // divisor * divisor)
+ # Make sure that round down does not go down by more than (1-min_ratio).
+ if new_value < min_ratio * value:
+ new_value += divisor
+ return new_value
diff --git a/grounded-sam-osx/transformer_utils/mmpose/models/backbones/utils/se_layer.py b/grounded-sam-osx/transformer_utils/mmpose/models/backbones/utils/se_layer.py
new file mode 100644
index 0000000000000000000000000000000000000000..07f70802eb1b98b1f22516ba62b1533557f428ed
--- /dev/null
+++ b/grounded-sam-osx/transformer_utils/mmpose/models/backbones/utils/se_layer.py
@@ -0,0 +1,54 @@
+# Copyright (c) OpenMMLab. All rights reserved.
+import mmcv
+import torch.nn as nn
+from mmcv.cnn import ConvModule
+
+
+class SELayer(nn.Module):
+ """Squeeze-and-Excitation Module.
+
+ Args:
+ channels (int): The input (and output) channels of the SE layer.
+ ratio (int): Squeeze ratio in SELayer, the intermediate channel will be
+ ``int(channels/ratio)``. Default: 16.
+ conv_cfg (None or dict): Config dict for convolution layer.
+ Default: None, which means using conv2d.
+ act_cfg (dict or Sequence[dict]): Config dict for activation layer.
+ If act_cfg is a dict, two activation layers will be configurated
+ by this dict. If act_cfg is a sequence of dicts, the first
+ activation layer will be configurated by the first dict and the
+ second activation layer will be configurated by the second dict.
+ Default: (dict(type='ReLU'), dict(type='Sigmoid'))
+ """
+
+ def __init__(self,
+ channels,
+ ratio=16,
+ conv_cfg=None,
+ act_cfg=(dict(type='ReLU'), dict(type='Sigmoid'))):
+ super().__init__()
+ if isinstance(act_cfg, dict):
+ act_cfg = (act_cfg, act_cfg)
+ assert len(act_cfg) == 2
+ assert mmcv.is_tuple_of(act_cfg, dict)
+ self.global_avgpool = nn.AdaptiveAvgPool2d(1)
+ self.conv1 = ConvModule(
+ in_channels=channels,
+ out_channels=int(channels / ratio),
+ kernel_size=1,
+ stride=1,
+ conv_cfg=conv_cfg,
+ act_cfg=act_cfg[0])
+ self.conv2 = ConvModule(
+ in_channels=int(channels / ratio),
+ out_channels=channels,
+ kernel_size=1,
+ stride=1,
+ conv_cfg=conv_cfg,
+ act_cfg=act_cfg[1])
+
+ def forward(self, x):
+ out = self.global_avgpool(x)
+ out = self.conv1(out)
+ out = self.conv2(out)
+ return x * out
diff --git a/grounded-sam-osx/transformer_utils/mmpose/models/backbones/utils/utils.py b/grounded-sam-osx/transformer_utils/mmpose/models/backbones/utils/utils.py
new file mode 100644
index 0000000000000000000000000000000000000000..2a53c94a90a1802cc0c4dcfceba241711c989640
--- /dev/null
+++ b/grounded-sam-osx/transformer_utils/mmpose/models/backbones/utils/utils.py
@@ -0,0 +1,612 @@
+# Copyright (c) OpenMMLab. All rights reserved.
+from collections import OrderedDict
+
+from mmcv.runner.checkpoint import _load_checkpoint, load_state_dict
+
+
+# Copyright (c) Open-MMLab. All rights reserved.
+import io
+import os
+import os.path as osp
+import pkgutil
+import time
+import warnings
+from collections import OrderedDict
+from importlib import import_module
+from tempfile import TemporaryDirectory
+
+import torch
+import torchvision
+from torch.optim import Optimizer
+from torch.utils import model_zoo
+from torch.nn import functional as F
+
+import mmcv
+from mmcv.fileio import FileClient
+from mmcv.fileio import load as load_file
+from mmcv.parallel import is_module_wrapper
+from mmcv.utils import mkdir_or_exist
+from mmcv.runner import get_dist_info
+
+from scipy import interpolate
+import numpy as np
+import math
+
+ENV_MMCV_HOME = 'MMCV_HOME'
+ENV_XDG_CACHE_HOME = 'XDG_CACHE_HOME'
+DEFAULT_CACHE_DIR = '~/.cache'
+
+
+def _get_mmcv_home():
+ mmcv_home = os.path.expanduser(
+ os.getenv(
+ ENV_MMCV_HOME,
+ os.path.join(
+ os.getenv(ENV_XDG_CACHE_HOME, DEFAULT_CACHE_DIR), 'mmcv')))
+
+ mkdir_or_exist(mmcv_home)
+ return mmcv_home
+
+
+def load_state_dict(module, state_dict, strict=False, logger=None):
+ """Load state_dict to a module.
+ This method is modified from :meth:`torch.nn.Module.load_state_dict`.
+ Default value for ``strict`` is set to ``False`` and the message for
+ param mismatch will be shown even if strict is False.
+ Args:
+ module (Module): Module that receives the state_dict.
+ state_dict (OrderedDict): Weights.
+ strict (bool): whether to strictly enforce that the keys
+ in :attr:`state_dict` match the keys returned by this module's
+ :meth:`~torch.nn.Module.state_dict` function. Default: ``False``.
+ logger (:obj:`logging.Logger`, optional): Logger to log the error
+ message. If not specified, print function will be used.
+ """
+ unexpected_keys = []
+ all_missing_keys = []
+ err_msg = []
+
+ metadata = getattr(state_dict, '_metadata', None)
+ state_dict = state_dict.copy()
+ if metadata is not None:
+ state_dict._metadata = metadata
+
+ # use _load_from_state_dict to enable checkpoint version control
+ def load(module, prefix=''):
+ # recursively check parallel module in case that the model has a
+ # complicated structure, e.g., nn.Module(nn.Module(DDP))
+ if is_module_wrapper(module):
+ module = module.module
+ local_metadata = {} if metadata is None else metadata.get(
+ prefix[:-1], {})
+ module._load_from_state_dict(state_dict, prefix, local_metadata, True,
+ all_missing_keys, unexpected_keys,
+ err_msg)
+ for name, child in module._modules.items():
+ if child is not None:
+ load(child, prefix + name + '.')
+
+ load(module)
+ load = None # break load->load reference cycle
+
+ # ignore "num_batches_tracked" of BN layers
+ missing_keys = [
+ key for key in all_missing_keys if 'num_batches_tracked' not in key
+ ]
+
+ if unexpected_keys:
+ err_msg.append('unexpected key in source '
+ f'state_dict: {", ".join(unexpected_keys)}\n')
+ if missing_keys:
+ err_msg.append(
+ f'missing keys in source state_dict: {", ".join(missing_keys)}\n')
+
+ rank, _ = get_dist_info()
+ if len(err_msg) > 0 and rank == 0:
+ err_msg.insert(
+ 0, 'The model and loaded state dict do not match exactly\n')
+ err_msg = '\n'.join(err_msg)
+ if strict:
+ raise RuntimeError(err_msg)
+ elif logger is not None:
+ logger.warning(err_msg)
+ else:
+ print(err_msg)
+
+
+def load_url_dist(url, model_dir=None, map_location="cpu"):
+ """In distributed setting, this function only download checkpoint at local
+ rank 0."""
+ rank, world_size = get_dist_info()
+ rank = int(os.environ.get('LOCAL_RANK', rank))
+ if rank == 0:
+ checkpoint = model_zoo.load_url(url, model_dir=model_dir, map_location=map_location)
+ if world_size > 1:
+ torch.distributed.barrier()
+ if rank > 0:
+ checkpoint = model_zoo.load_url(url, model_dir=model_dir, map_location=map_location)
+ return checkpoint
+
+
+def load_pavimodel_dist(model_path, map_location=None):
+ """In distributed setting, this function only download checkpoint at local
+ rank 0."""
+ try:
+ from pavi import modelcloud
+ except ImportError:
+ raise ImportError(
+ 'Please install pavi to load checkpoint from modelcloud.')
+ rank, world_size = get_dist_info()
+ rank = int(os.environ.get('LOCAL_RANK', rank))
+ if rank == 0:
+ model = modelcloud.get(model_path)
+ with TemporaryDirectory() as tmp_dir:
+ downloaded_file = osp.join(tmp_dir, model.name)
+ model.download(downloaded_file)
+ checkpoint = torch.load(downloaded_file, map_location=map_location)
+ if world_size > 1:
+ torch.distributed.barrier()
+ if rank > 0:
+ model = modelcloud.get(model_path)
+ with TemporaryDirectory() as tmp_dir:
+ downloaded_file = osp.join(tmp_dir, model.name)
+ model.download(downloaded_file)
+ checkpoint = torch.load(
+ downloaded_file, map_location=map_location)
+ return checkpoint
+
+
+def load_fileclient_dist(filename, backend, map_location):
+ """In distributed setting, this function only download checkpoint at local
+ rank 0."""
+ rank, world_size = get_dist_info()
+ rank = int(os.environ.get('LOCAL_RANK', rank))
+ allowed_backends = ['ceph']
+ if backend not in allowed_backends:
+ raise ValueError(f'Load from Backend {backend} is not supported.')
+ if rank == 0:
+ fileclient = FileClient(backend=backend)
+ buffer = io.BytesIO(fileclient.get(filename))
+ checkpoint = torch.load(buffer, map_location=map_location)
+ if world_size > 1:
+ torch.distributed.barrier()
+ if rank > 0:
+ fileclient = FileClient(backend=backend)
+ buffer = io.BytesIO(fileclient.get(filename))
+ checkpoint = torch.load(buffer, map_location=map_location)
+ return checkpoint
+
+
+def get_torchvision_models():
+ model_urls = dict()
+ for _, name, ispkg in pkgutil.walk_packages(torchvision.models.__path__):
+ if ispkg:
+ continue
+ _zoo = import_module(f'torchvision.models.{name}')
+ if hasattr(_zoo, 'model_urls'):
+ _urls = getattr(_zoo, 'model_urls')
+ model_urls.update(_urls)
+ return model_urls
+
+
+def get_external_models():
+ mmcv_home = _get_mmcv_home()
+ default_json_path = osp.join(mmcv.__path__[0], 'model_zoo/open_mmlab.json')
+ default_urls = load_file(default_json_path)
+ assert isinstance(default_urls, dict)
+ external_json_path = osp.join(mmcv_home, 'open_mmlab.json')
+ if osp.exists(external_json_path):
+ external_urls = load_file(external_json_path)
+ assert isinstance(external_urls, dict)
+ default_urls.update(external_urls)
+
+ return default_urls
+
+
+def get_mmcls_models():
+ mmcls_json_path = osp.join(mmcv.__path__[0], 'model_zoo/mmcls.json')
+ mmcls_urls = load_file(mmcls_json_path)
+
+ return mmcls_urls
+
+
+def get_deprecated_model_names():
+ deprecate_json_path = osp.join(mmcv.__path__[0],
+ 'model_zoo/deprecated.json')
+ deprecate_urls = load_file(deprecate_json_path)
+ assert isinstance(deprecate_urls, dict)
+
+ return deprecate_urls
+
+
+def _process_mmcls_checkpoint(checkpoint):
+ state_dict = checkpoint['state_dict']
+ new_state_dict = OrderedDict()
+ for k, v in state_dict.items():
+ if k.startswith('backbone.'):
+ new_state_dict[k[9:]] = v
+ new_checkpoint = dict(state_dict=new_state_dict)
+
+ return new_checkpoint
+
+
+def _load_checkpoint(filename, map_location=None):
+ """Load checkpoint from somewhere (modelzoo, file, url).
+ Args:
+ filename (str): Accept local filepath, URL, ``torchvision://xxx``,
+ ``open-mmlab://xxx``. Please refer to ``docs/model_zoo.md`` for
+ details.
+ map_location (str | None): Same as :func:`torch.load`. Default: None.
+ Returns:
+ dict | OrderedDict: The loaded checkpoint. It can be either an
+ OrderedDict storing model weights or a dict containing other
+ information, which depends on the checkpoint.
+ """
+ if filename.startswith('modelzoo://'):
+ warnings.warn('The URL scheme of "modelzoo://" is deprecated, please '
+ 'use "torchvision://" instead')
+ model_urls = get_torchvision_models()
+ model_name = filename[11:]
+ checkpoint = load_url_dist(model_urls[model_name])
+ elif filename.startswith('torchvision://'):
+ model_urls = get_torchvision_models()
+ model_name = filename[14:]
+ checkpoint = load_url_dist(model_urls[model_name])
+ elif filename.startswith('open-mmlab://'):
+ model_urls = get_external_models()
+ model_name = filename[13:]
+ deprecated_urls = get_deprecated_model_names()
+ if model_name in deprecated_urls:
+ warnings.warn(f'open-mmlab://{model_name} is deprecated in favor '
+ f'of open-mmlab://{deprecated_urls[model_name]}')
+ model_name = deprecated_urls[model_name]
+ model_url = model_urls[model_name]
+ # check if is url
+ if model_url.startswith(('http://', 'https://')):
+ checkpoint = load_url_dist(model_url)
+ else:
+ filename = osp.join(_get_mmcv_home(), model_url)
+ if not osp.isfile(filename):
+ raise IOError(f'{filename} is not a checkpoint file')
+ checkpoint = torch.load(filename, map_location=map_location)
+ elif filename.startswith('mmcls://'):
+ model_urls = get_mmcls_models()
+ model_name = filename[8:]
+ checkpoint = load_url_dist(model_urls[model_name])
+ checkpoint = _process_mmcls_checkpoint(checkpoint)
+ elif filename.startswith(('http://', 'https://')):
+ checkpoint = load_url_dist(filename)
+ elif filename.startswith('pavi://'):
+ model_path = filename[7:]
+ checkpoint = load_pavimodel_dist(model_path, map_location=map_location)
+ elif filename.startswith('s3://'):
+ checkpoint = load_fileclient_dist(
+ filename, backend='ceph', map_location=map_location)
+ else:
+ if not osp.isfile(filename):
+ raise IOError(f'{filename} is not a checkpoint file')
+ checkpoint = torch.load(filename, map_location=map_location)
+ return checkpoint
+
+
+def cosine_scheduler(base_value, final_value, epochs, niter_per_ep, warmup_epochs=0,
+ start_warmup_value=0, warmup_steps=-1):
+ warmup_schedule = np.array([])
+ warmup_iters = warmup_epochs * niter_per_ep
+ if warmup_steps > 0:
+ warmup_iters = warmup_steps
+ print("Set warmup steps = %d" % warmup_iters)
+ if warmup_epochs > 0:
+ warmup_schedule = np.linspace(start_warmup_value, base_value, warmup_iters)
+
+ iters = np.arange(epochs * niter_per_ep - warmup_iters)
+ schedule = np.array(
+ [final_value + 0.5 * (base_value - final_value) * (1 + math.cos(math.pi * i / (len(iters)))) for i in iters])
+
+ schedule = np.concatenate((warmup_schedule, schedule))
+
+ assert len(schedule) == epochs * niter_per_ep
+ return schedule
+
+
+def load_checkpoint(model,
+ filename,
+ map_location='cpu',
+ strict=False,
+ logger=None,
+ patch_padding='pad',
+ ):
+ """Load checkpoint from a file or URI.
+ Args:
+ model (Module): Module to load checkpoint.
+ filename (str): Accept local filepath, URL, ``torchvision://xxx``,
+ ``open-mmlab://xxx``. Please refer to ``docs/model_zoo.md`` for
+ details.
+ map_location (str): Same as :func:`torch.load`.
+ strict (bool): Whether to allow different params for the model and
+ checkpoint.
+ logger (:mod:`logging.Logger` or None): The logger for error message.
+ patch_padding (str): 'pad' or 'bilinear' or 'bicubic', used for interpolate patch embed from 14x14 to 16x16
+ Returns:
+ dict or OrderedDict: The loaded checkpoint.
+ """
+ checkpoint = _load_checkpoint(filename, map_location)
+ # OrderedDict is a subclass of dict
+ if not isinstance(checkpoint, dict):
+ raise RuntimeError(
+ f'No state_dict found in checkpoint file {filename}')
+ # get state_dict from checkpoint
+ if 'state_dict' in checkpoint:
+ state_dict = checkpoint['state_dict']
+ elif 'model' in checkpoint:
+ state_dict = checkpoint['model']
+ elif 'module' in checkpoint:
+ state_dict = checkpoint['module']
+ else:
+ state_dict = checkpoint
+ # strip prefix of state_dict
+ if list(state_dict.keys())[0].startswith('module.'):
+ state_dict = {k[7:]: v for k, v in state_dict.items()}
+
+ # for MoBY, load model of online branch
+ if sorted(list(state_dict.keys()))[0].startswith('encoder'):
+ state_dict = {k.replace('encoder.', ''): v for k, v in state_dict.items() if k.startswith('encoder.')}
+
+ rank, _ = get_dist_info()
+
+ if 'patch_embed.proj.weight' in state_dict:
+ proj_weight = state_dict['patch_embed.proj.weight']
+ orig_size = proj_weight.shape[2:]
+ current_size = model.patch_embed.proj.weight.shape[2:]
+ padding_size = current_size[0] - orig_size[0]
+ padding_l = padding_size // 2
+ padding_r = padding_size - padding_l
+ if orig_size != current_size:
+ if 'pad' in patch_padding:
+ proj_weight = torch.nn.functional.pad(proj_weight, (padding_l, padding_r, padding_l, padding_r))
+ elif 'bilinear' in patch_padding:
+ proj_weight = torch.nn.functional.interpolate(proj_weight, size=current_size, mode='bilinear', align_corners=False)
+ elif 'bicubic' in patch_padding:
+ proj_weight = torch.nn.functional.interpolate(proj_weight, size=current_size, mode='bicubic', align_corners=False)
+ state_dict['patch_embed.proj.weight'] = proj_weight
+
+ if 'pos_embed' in state_dict:
+ pos_embed_checkpoint = state_dict['pos_embed']
+ embedding_size = pos_embed_checkpoint.shape[-1]
+ H, W = model.patch_embed.patch_shape
+ num_patches = model.patch_embed.num_patches
+ num_extra_tokens = model.pos_embed.shape[-2] - num_patches
+ # height (== width) for the checkpoint position embedding
+ orig_size = int((pos_embed_checkpoint.shape[-2] - num_extra_tokens) ** 0.5)
+ if rank == 0:
+ print("Position interpolate from %dx%d to %dx%d" % (orig_size, orig_size, H, W))
+ extra_tokens = pos_embed_checkpoint[:, :num_extra_tokens]
+ # only the position tokens are interpolated
+ pos_tokens = pos_embed_checkpoint[:, num_extra_tokens:]
+ pos_tokens = pos_tokens.reshape(-1, orig_size, orig_size, embedding_size).permute(0, 3, 1, 2)
+ pos_tokens = torch.nn.functional.interpolate(
+ pos_tokens, size=(H, W), mode='bicubic', align_corners=False)
+ pos_tokens = pos_tokens.permute(0, 2, 3, 1).flatten(1, 2)
+ new_pos_embed = torch.cat((extra_tokens, pos_tokens), dim=1)
+ state_dict['pos_embed'] = new_pos_embed
+
+ # load state_dict
+ load_state_dict(model, state_dict, strict, logger)
+ return checkpoint
+
+
+def weights_to_cpu(state_dict):
+ """Copy a model state_dict to cpu.
+ Args:
+ state_dict (OrderedDict): Model weights on GPU.
+ Returns:
+ OrderedDict: Model weights on GPU.
+ """
+ state_dict_cpu = OrderedDict()
+ for key, val in state_dict.items():
+ state_dict_cpu[key] = val.cpu()
+ return state_dict_cpu
+
+
+def _save_to_state_dict(module, destination, prefix, keep_vars):
+ """Saves module state to `destination` dictionary.
+ This method is modified from :meth:`torch.nn.Module._save_to_state_dict`.
+ Args:
+ module (nn.Module): The module to generate state_dict.
+ destination (dict): A dict where state will be stored.
+ prefix (str): The prefix for parameters and buffers used in this
+ module.
+ """
+ for name, param in module._parameters.items():
+ if param is not None:
+ destination[prefix + name] = param if keep_vars else param.detach()
+ for name, buf in module._buffers.items():
+ # remove check of _non_persistent_buffers_set to allow nn.BatchNorm2d
+ if buf is not None:
+ destination[prefix + name] = buf if keep_vars else buf.detach()
+
+
+def get_state_dict(module, destination=None, prefix='', keep_vars=False):
+ """Returns a dictionary containing a whole state of the module.
+ Both parameters and persistent buffers (e.g. running averages) are
+ included. Keys are corresponding parameter and buffer names.
+ This method is modified from :meth:`torch.nn.Module.state_dict` to
+ recursively check parallel module in case that the model has a complicated
+ structure, e.g., nn.Module(nn.Module(DDP)).
+ Args:
+ module (nn.Module): The module to generate state_dict.
+ destination (OrderedDict): Returned dict for the state of the
+ module.
+ prefix (str): Prefix of the key.
+ keep_vars (bool): Whether to keep the variable property of the
+ parameters. Default: False.
+ Returns:
+ dict: A dictionary containing a whole state of the module.
+ """
+ # recursively check parallel module in case that the model has a
+ # complicated structure, e.g., nn.Module(nn.Module(DDP))
+ if is_module_wrapper(module):
+ module = module.module
+
+ # below is the same as torch.nn.Module.state_dict()
+ if destination is None:
+ destination = OrderedDict()
+ destination._metadata = OrderedDict()
+ destination._metadata[prefix[:-1]] = local_metadata = dict(
+ version=module._version)
+ _save_to_state_dict(module, destination, prefix, keep_vars)
+ for name, child in module._modules.items():
+ if child is not None:
+ get_state_dict(
+ child, destination, prefix + name + '.', keep_vars=keep_vars)
+ for hook in module._state_dict_hooks.values():
+ hook_result = hook(module, destination, prefix, local_metadata)
+ if hook_result is not None:
+ destination = hook_result
+ return destination
+
+
+def save_checkpoint(model, filename, optimizer=None, meta=None):
+ """Save checkpoint to file.
+ The checkpoint will have 3 fields: ``meta``, ``state_dict`` and
+ ``optimizer``. By default ``meta`` will contain version and time info.
+ Args:
+ model (Module): Module whose params are to be saved.
+ filename (str): Checkpoint filename.
+ optimizer (:obj:`Optimizer`, optional): Optimizer to be saved.
+ meta (dict, optional): Metadata to be saved in checkpoint.
+ """
+ if meta is None:
+ meta = {}
+ elif not isinstance(meta, dict):
+ raise TypeError(f'meta must be a dict or None, but got {type(meta)}')
+ meta.update(mmcv_version=mmcv.__version__, time=time.asctime())
+
+ if is_module_wrapper(model):
+ model = model.module
+
+ if hasattr(model, 'CLASSES') and model.CLASSES is not None:
+ # save class name to the meta
+ meta.update(CLASSES=model.CLASSES)
+
+ checkpoint = {
+ 'meta': meta,
+ 'state_dict': weights_to_cpu(get_state_dict(model))
+ }
+ # save optimizer state dict in the checkpoint
+ if isinstance(optimizer, Optimizer):
+ checkpoint['optimizer'] = optimizer.state_dict()
+ elif isinstance(optimizer, dict):
+ checkpoint['optimizer'] = {}
+ for name, optim in optimizer.items():
+ checkpoint['optimizer'][name] = optim.state_dict()
+
+ if filename.startswith('pavi://'):
+ try:
+ from pavi import modelcloud
+ from pavi.exception import NodeNotFoundError
+ except ImportError:
+ raise ImportError(
+ 'Please install pavi to load checkpoint from modelcloud.')
+ model_path = filename[7:]
+ root = modelcloud.Folder()
+ model_dir, model_name = osp.split(model_path)
+ try:
+ model = modelcloud.get(model_dir)
+ except NodeNotFoundError:
+ model = root.create_training_model(model_dir)
+ with TemporaryDirectory() as tmp_dir:
+ checkpoint_file = osp.join(tmp_dir, model_name)
+ with open(checkpoint_file, 'wb') as f:
+ torch.save(checkpoint, f)
+ f.flush()
+ model.create_file(checkpoint_file, name=model_name)
+ else:
+ mmcv.mkdir_or_exist(osp.dirname(filename))
+ # immediately flush buffer
+ with open(filename, 'wb') as f:
+ torch.save(checkpoint, f)
+ f.flush()
+
+
+# def load_checkpoint(model,
+# filename,
+# map_location='cpu',
+# strict=False,
+# logger=None):
+# """Load checkpoint from a file or URI.
+#
+# Args:
+# model (Module): Module to load checkpoint.
+# filename (str): Accept local filepath, URL, ``torchvision://xxx``,
+# ``open-mmlab://xxx``.
+# map_location (str): Same as :func:`torch.load`.
+# strict (bool): Whether to allow different params for the model and
+# checkpoint.
+# logger (:mod:`logging.Logger` or None): The logger for error message.
+#
+# Returns:
+# dict or OrderedDict: The loaded checkpoint.
+# """
+# checkpoint = _load_checkpoint(filename, map_location)
+# # OrderedDict is a subclass of dict
+# if not isinstance(checkpoint, dict):
+# raise RuntimeError(
+# f'No state_dict found in checkpoint file {filename}')
+# # get state_dict from checkpoint
+# if 'state_dict' in checkpoint:
+# state_dict_tmp = checkpoint['state_dict']
+# else:
+# state_dict_tmp = checkpoint
+#
+# state_dict = OrderedDict()
+# # strip prefix of state_dict
+# for k, v in state_dict_tmp.items():
+# if k.startswith('module.backbone.'):
+# state_dict[k[16:]] = v
+# elif k.startswith('module.'):
+# state_dict[k[7:]] = v
+# elif k.startswith('backbone.'):
+# state_dict[k[9:]] = v
+# else:
+# state_dict[k] = v
+# # load state_dict
+# load_state_dict(model, state_dict, strict, logger)
+# return checkpoint
+#
+#
+# def get_state_dict(filename, map_location='cpu'):
+# """Get state_dict from a file or URI.
+#
+# Args:
+# filename (str): Accept local filepath, URL, ``torchvision://xxx``,
+# ``open-mmlab://xxx``.
+# map_location (str): Same as :func:`torch.load`.
+#
+# Returns:
+# OrderedDict: The state_dict.
+# """
+# checkpoint = _load_checkpoint(filename, map_location)
+# # OrderedDict is a subclass of dict
+# if not isinstance(checkpoint, dict):
+# raise RuntimeError(
+# f'No state_dict found in checkpoint file {filename}')
+# # get state_dict from checkpoint
+# if 'state_dict' in checkpoint:
+# state_dict_tmp = checkpoint['state_dict']
+# else:
+# state_dict_tmp = checkpoint
+#
+# state_dict = OrderedDict()
+# # strip prefix of state_dict
+# for k, v in state_dict_tmp.items():
+# if k.startswith('module.backbone.'):
+# state_dict[k[16:]] = v
+# elif k.startswith('module.'):
+# state_dict[k[7:]] = v
+# elif k.startswith('backbone.'):
+# state_dict[k[9:]] = v
+# else:
+# state_dict[k] = v
+#
+# return state_dict
diff --git a/grounded-sam-osx/transformer_utils/mmpose/models/backbones/v2v_net.py b/grounded-sam-osx/transformer_utils/mmpose/models/backbones/v2v_net.py
new file mode 100644
index 0000000000000000000000000000000000000000..99462af711069a34c13628364e2c466163507861
--- /dev/null
+++ b/grounded-sam-osx/transformer_utils/mmpose/models/backbones/v2v_net.py
@@ -0,0 +1,257 @@
+# ------------------------------------------------------------------------------
+# Copyright and License Information
+# Adapted from
+# https://github.com/microsoft/voxelpose-pytorch/blob/main/lib/models/v2v_net.py
+# Original Licence: MIT License
+# ------------------------------------------------------------------------------
+
+import torch.nn as nn
+import torch.nn.functional as F
+from mmcv.cnn import ConvModule
+
+from ..builder import BACKBONES
+from .base_backbone import BaseBackbone
+
+
+class Basic3DBlock(nn.Module):
+ """A basic 3D convolutional block.
+
+ Args:
+ in_channels (int): Input channels of this block.
+ out_channels (int): Output channels of this block.
+ kernel_size (int): Kernel size of the convolution operation
+ conv_cfg (dict): Dictionary to construct and config conv layer.
+ Default: dict(type='Conv3d')
+ norm_cfg (dict): Dictionary to construct and config norm layer.
+ Default: dict(type='BN3d')
+ """
+
+ def __init__(self,
+ in_channels,
+ out_channels,
+ kernel_size,
+ conv_cfg=dict(type='Conv3d'),
+ norm_cfg=dict(type='BN3d')):
+ super(Basic3DBlock, self).__init__()
+ self.block = ConvModule(
+ in_channels,
+ out_channels,
+ kernel_size,
+ stride=1,
+ padding=((kernel_size - 1) // 2),
+ conv_cfg=conv_cfg,
+ norm_cfg=norm_cfg,
+ bias=True)
+
+ def forward(self, x):
+ """Forward function."""
+ return self.block(x)
+
+
+class Res3DBlock(nn.Module):
+ """A residual 3D convolutional block.
+
+ Args:
+ in_channels (int): Input channels of this block.
+ out_channels (int): Output channels of this block.
+ kernel_size (int): Kernel size of the convolution operation
+ Default: 3
+ conv_cfg (dict): Dictionary to construct and config conv layer.
+ Default: dict(type='Conv3d')
+ norm_cfg (dict): Dictionary to construct and config norm layer.
+ Default: dict(type='BN3d')
+ """
+
+ def __init__(self,
+ in_channels,
+ out_channels,
+ kernel_size=3,
+ conv_cfg=dict(type='Conv3d'),
+ norm_cfg=dict(type='BN3d')):
+ super(Res3DBlock, self).__init__()
+ self.res_branch = nn.Sequential(
+ ConvModule(
+ in_channels,
+ out_channels,
+ kernel_size,
+ stride=1,
+ padding=((kernel_size - 1) // 2),
+ conv_cfg=conv_cfg,
+ norm_cfg=norm_cfg,
+ bias=True),
+ ConvModule(
+ out_channels,
+ out_channels,
+ kernel_size,
+ stride=1,
+ padding=((kernel_size - 1) // 2),
+ conv_cfg=conv_cfg,
+ norm_cfg=norm_cfg,
+ act_cfg=None,
+ bias=True))
+
+ if in_channels == out_channels:
+ self.skip_con = nn.Sequential()
+ else:
+ self.skip_con = ConvModule(
+ in_channels,
+ out_channels,
+ 1,
+ stride=1,
+ padding=0,
+ conv_cfg=conv_cfg,
+ norm_cfg=norm_cfg,
+ act_cfg=None,
+ bias=True)
+
+ def forward(self, x):
+ """Forward function."""
+ res = self.res_branch(x)
+ skip = self.skip_con(x)
+ return F.relu(res + skip, True)
+
+
+class Pool3DBlock(nn.Module):
+ """A 3D max-pool block.
+
+ Args:
+ pool_size (int): Pool size of the 3D max-pool layer
+ """
+
+ def __init__(self, pool_size):
+ super(Pool3DBlock, self).__init__()
+ self.pool_size = pool_size
+
+ def forward(self, x):
+ """Forward function."""
+ return F.max_pool3d(
+ x, kernel_size=self.pool_size, stride=self.pool_size)
+
+
+class Upsample3DBlock(nn.Module):
+ """A 3D upsample block.
+
+ Args:
+ in_channels (int): Input channels of this block.
+ out_channels (int): Output channels of this block.
+ kernel_size (int): Kernel size of the transposed convolution operation.
+ Default: 2
+ stride (int): Kernel size of the transposed convolution operation.
+ Default: 2
+ """
+
+ def __init__(self, in_channels, out_channels, kernel_size=2, stride=2):
+ super(Upsample3DBlock, self).__init__()
+ assert kernel_size == 2
+ assert stride == 2
+ self.block = nn.Sequential(
+ nn.ConvTranspose3d(
+ in_channels,
+ out_channels,
+ kernel_size=kernel_size,
+ stride=stride,
+ padding=0,
+ output_padding=0), nn.BatchNorm3d(out_channels), nn.ReLU(True))
+
+ def forward(self, x):
+ """Forward function."""
+ return self.block(x)
+
+
+class EncoderDecorder(nn.Module):
+ """An encoder-decoder block.
+
+ Args:
+ in_channels (int): Input channels of this block
+ """
+
+ def __init__(self, in_channels=32):
+ super(EncoderDecorder, self).__init__()
+
+ self.encoder_pool1 = Pool3DBlock(2)
+ self.encoder_res1 = Res3DBlock(in_channels, in_channels * 2)
+ self.encoder_pool2 = Pool3DBlock(2)
+ self.encoder_res2 = Res3DBlock(in_channels * 2, in_channels * 4)
+
+ self.mid_res = Res3DBlock(in_channels * 4, in_channels * 4)
+
+ self.decoder_res2 = Res3DBlock(in_channels * 4, in_channels * 4)
+ self.decoder_upsample2 = Upsample3DBlock(in_channels * 4,
+ in_channels * 2, 2, 2)
+ self.decoder_res1 = Res3DBlock(in_channels * 2, in_channels * 2)
+ self.decoder_upsample1 = Upsample3DBlock(in_channels * 2, in_channels,
+ 2, 2)
+
+ self.skip_res1 = Res3DBlock(in_channels, in_channels)
+ self.skip_res2 = Res3DBlock(in_channels * 2, in_channels * 2)
+
+ def forward(self, x):
+ """Forward function."""
+ skip_x1 = self.skip_res1(x)
+ x = self.encoder_pool1(x)
+ x = self.encoder_res1(x)
+
+ skip_x2 = self.skip_res2(x)
+ x = self.encoder_pool2(x)
+ x = self.encoder_res2(x)
+
+ x = self.mid_res(x)
+
+ x = self.decoder_res2(x)
+ x = self.decoder_upsample2(x)
+ x = x + skip_x2
+
+ x = self.decoder_res1(x)
+ x = self.decoder_upsample1(x)
+ x = x + skip_x1
+
+ return x
+
+
+@BACKBONES.register_module()
+class V2VNet(BaseBackbone):
+ """V2VNet.
+
+ Please refer to the `paper `
+ for details.
+
+ Args:
+ input_channels (int):
+ Number of channels of the input feature volume.
+ output_channels (int):
+ Number of channels of the output volume.
+ mid_channels (int):
+ Input and output channels of the encoder-decoder block.
+ """
+
+ def __init__(self, input_channels, output_channels, mid_channels=32):
+ super(V2VNet, self).__init__()
+
+ self.front_layers = nn.Sequential(
+ Basic3DBlock(input_channels, mid_channels // 2, 7),
+ Res3DBlock(mid_channels // 2, mid_channels),
+ )
+
+ self.encoder_decoder = EncoderDecorder(in_channels=mid_channels)
+
+ self.output_layer = nn.Conv3d(
+ mid_channels, output_channels, kernel_size=1, stride=1, padding=0)
+
+ self._initialize_weights()
+
+ def forward(self, x):
+ """Forward function."""
+ x = self.front_layers(x)
+ x = self.encoder_decoder(x)
+ x = self.output_layer(x)
+
+ return x
+
+ def _initialize_weights(self):
+ for m in self.modules():
+ if isinstance(m, nn.Conv3d):
+ nn.init.normal_(m.weight, 0, 0.001)
+ nn.init.constant_(m.bias, 0)
+ elif isinstance(m, nn.ConvTranspose3d):
+ nn.init.normal_(m.weight, 0, 0.001)
+ nn.init.constant_(m.bias, 0)
diff --git a/grounded-sam-osx/transformer_utils/mmpose/models/backbones/vgg.py b/grounded-sam-osx/transformer_utils/mmpose/models/backbones/vgg.py
new file mode 100644
index 0000000000000000000000000000000000000000..f7d467017a5520f399c84b1235ec64c99b805b42
--- /dev/null
+++ b/grounded-sam-osx/transformer_utils/mmpose/models/backbones/vgg.py
@@ -0,0 +1,193 @@
+# Copyright (c) OpenMMLab. All rights reserved.
+import torch.nn as nn
+from mmcv.cnn import ConvModule, constant_init, kaiming_init, normal_init
+from mmcv.utils.parrots_wrapper import _BatchNorm
+
+from ..builder import BACKBONES
+from .base_backbone import BaseBackbone
+
+
+def make_vgg_layer(in_channels,
+ out_channels,
+ num_blocks,
+ conv_cfg=None,
+ norm_cfg=None,
+ act_cfg=dict(type='ReLU'),
+ dilation=1,
+ with_norm=False,
+ ceil_mode=False):
+ layers = []
+ for _ in range(num_blocks):
+ layer = ConvModule(
+ in_channels=in_channels,
+ out_channels=out_channels,
+ kernel_size=3,
+ dilation=dilation,
+ padding=dilation,
+ bias=True,
+ conv_cfg=conv_cfg,
+ norm_cfg=norm_cfg,
+ act_cfg=act_cfg)
+ layers.append(layer)
+ in_channels = out_channels
+ layers.append(nn.MaxPool2d(kernel_size=2, stride=2, ceil_mode=ceil_mode))
+
+ return layers
+
+
+@BACKBONES.register_module()
+class VGG(BaseBackbone):
+ """VGG backbone.
+
+ Args:
+ depth (int): Depth of vgg, from {11, 13, 16, 19}.
+ with_norm (bool): Use BatchNorm or not.
+ num_classes (int): number of classes for classification.
+ num_stages (int): VGG stages, normally 5.
+ dilations (Sequence[int]): Dilation of each stage.
+ out_indices (Sequence[int]): Output from which stages. If only one
+ stage is specified, a single tensor (feature map) is returned,
+ otherwise multiple stages are specified, a tuple of tensors will
+ be returned. When it is None, the default behavior depends on
+ whether num_classes is specified. If num_classes <= 0, the default
+ value is (4, ), outputting the last feature map before classifier.
+ If num_classes > 0, the default value is (5, ), outputting the
+ classification score. Default: None.
+ frozen_stages (int): Stages to be frozen (all param fixed). -1 means
+ not freezing any parameters.
+ norm_eval (bool): Whether to set norm layers to eval mode, namely,
+ freeze running stats (mean and var). Note: Effect on Batch Norm
+ and its variants only. Default: False.
+ ceil_mode (bool): Whether to use ceil_mode of MaxPool. Default: False.
+ with_last_pool (bool): Whether to keep the last pooling before
+ classifier. Default: True.
+ """
+
+ # Parameters to build layers. Each element specifies the number of conv in
+ # each stage. For example, VGG11 contains 11 layers with learnable
+ # parameters. 11 is computed as 11 = (1 + 1 + 2 + 2 + 2) + 3,
+ # where 3 indicates the last three fully-connected layers.
+ arch_settings = {
+ 11: (1, 1, 2, 2, 2),
+ 13: (2, 2, 2, 2, 2),
+ 16: (2, 2, 3, 3, 3),
+ 19: (2, 2, 4, 4, 4)
+ }
+
+ def __init__(self,
+ depth,
+ num_classes=-1,
+ num_stages=5,
+ dilations=(1, 1, 1, 1, 1),
+ out_indices=None,
+ frozen_stages=-1,
+ conv_cfg=None,
+ norm_cfg=None,
+ act_cfg=dict(type='ReLU'),
+ norm_eval=False,
+ ceil_mode=False,
+ with_last_pool=True):
+ super().__init__()
+ if depth not in self.arch_settings:
+ raise KeyError(f'invalid depth {depth} for vgg')
+ assert num_stages >= 1 and num_stages <= 5
+ stage_blocks = self.arch_settings[depth]
+ self.stage_blocks = stage_blocks[:num_stages]
+ assert len(dilations) == num_stages
+
+ self.num_classes = num_classes
+ self.frozen_stages = frozen_stages
+ self.norm_eval = norm_eval
+ with_norm = norm_cfg is not None
+
+ if out_indices is None:
+ out_indices = (5, ) if num_classes > 0 else (4, )
+ assert max(out_indices) <= num_stages
+ self.out_indices = out_indices
+
+ self.in_channels = 3
+ start_idx = 0
+ vgg_layers = []
+ self.range_sub_modules = []
+ for i, num_blocks in enumerate(self.stage_blocks):
+ num_modules = num_blocks + 1
+ end_idx = start_idx + num_modules
+ dilation = dilations[i]
+ out_channels = 64 * 2**i if i < 4 else 512
+ vgg_layer = make_vgg_layer(
+ self.in_channels,
+ out_channels,
+ num_blocks,
+ conv_cfg=conv_cfg,
+ norm_cfg=norm_cfg,
+ act_cfg=act_cfg,
+ dilation=dilation,
+ with_norm=with_norm,
+ ceil_mode=ceil_mode)
+ vgg_layers.extend(vgg_layer)
+ self.in_channels = out_channels
+ self.range_sub_modules.append([start_idx, end_idx])
+ start_idx = end_idx
+ if not with_last_pool:
+ vgg_layers.pop(-1)
+ self.range_sub_modules[-1][1] -= 1
+ self.module_name = 'features'
+ self.add_module(self.module_name, nn.Sequential(*vgg_layers))
+
+ if self.num_classes > 0:
+ self.classifier = nn.Sequential(
+ nn.Linear(512 * 7 * 7, 4096),
+ nn.ReLU(True),
+ nn.Dropout(),
+ nn.Linear(4096, 4096),
+ nn.ReLU(True),
+ nn.Dropout(),
+ nn.Linear(4096, num_classes),
+ )
+
+ def init_weights(self, pretrained=None):
+ super().init_weights(pretrained)
+ if pretrained is None:
+ for m in self.modules():
+ if isinstance(m, nn.Conv2d):
+ kaiming_init(m)
+ elif isinstance(m, _BatchNorm):
+ constant_init(m, 1)
+ elif isinstance(m, nn.Linear):
+ normal_init(m, std=0.01)
+
+ def forward(self, x):
+ outs = []
+ vgg_layers = getattr(self, self.module_name)
+ for i in range(len(self.stage_blocks)):
+ for j in range(*self.range_sub_modules[i]):
+ vgg_layer = vgg_layers[j]
+ x = vgg_layer(x)
+ if i in self.out_indices:
+ outs.append(x)
+ if self.num_classes > 0:
+ x = x.view(x.size(0), -1)
+ x = self.classifier(x)
+ outs.append(x)
+ if len(outs) == 1:
+ return outs[0]
+ else:
+ return tuple(outs)
+
+ def _freeze_stages(self):
+ vgg_layers = getattr(self, self.module_name)
+ for i in range(self.frozen_stages):
+ for j in range(*self.range_sub_modules[i]):
+ m = vgg_layers[j]
+ m.eval()
+ for param in m.parameters():
+ param.requires_grad = False
+
+ def train(self, mode=True):
+ super().train(mode)
+ self._freeze_stages()
+ if mode and self.norm_eval:
+ for m in self.modules():
+ # trick: eval have effect on BatchNorm only
+ if isinstance(m, _BatchNorm):
+ m.eval()
diff --git a/grounded-sam-osx/transformer_utils/mmpose/models/backbones/vipnas_mbv3.py b/grounded-sam-osx/transformer_utils/mmpose/models/backbones/vipnas_mbv3.py
new file mode 100644
index 0000000000000000000000000000000000000000..ed990e3966b27301dbaf081e3ec0e908704dfc8b
--- /dev/null
+++ b/grounded-sam-osx/transformer_utils/mmpose/models/backbones/vipnas_mbv3.py
@@ -0,0 +1,179 @@
+# Copyright (c) OpenMMLab. All rights reserved.
+import copy
+import logging
+
+import torch.nn as nn
+from mmcv.cnn import ConvModule
+from torch.nn.modules.batchnorm import _BatchNorm
+
+from ..builder import BACKBONES
+from .base_backbone import BaseBackbone
+from .utils import InvertedResidual, load_checkpoint
+
+
+@BACKBONES.register_module()
+class ViPNAS_MobileNetV3(BaseBackbone):
+ """ViPNAS_MobileNetV3 backbone.
+
+ "ViPNAS: Efficient Video Pose Estimation via Neural Architecture Search"
+ More details can be found in the `paper
+ `__ .
+
+ Args:
+ wid (list(int)): Searched width config for each stage.
+ expan (list(int)): Searched expansion ratio config for each stage.
+ dep (list(int)): Searched depth config for each stage.
+ ks (list(int)): Searched kernel size config for each stage.
+ group (list(int)): Searched group number config for each stage.
+ att (list(bool)): Searched attention config for each stage.
+ stride (list(int)): Stride config for each stage.
+ act (list(dict)): Activation config for each stage.
+ conv_cfg (dict): Config dict for convolution layer.
+ Default: None, which means using conv2d.
+ norm_cfg (dict): Config dict for normalization layer.
+ Default: dict(type='BN').
+ frozen_stages (int): Stages to be frozen (all param fixed).
+ Default: -1, which means not freezing any parameters.
+ norm_eval (bool): Whether to set norm layers to eval mode, namely,
+ freeze running stats (mean and var). Note: Effect on Batch Norm
+ and its variants only. Default: False.
+ with_cp (bool): Use checkpoint or not. Using checkpoint will save
+ some memory while slowing down the training speed.
+ Default: False.
+ """
+
+ def __init__(self,
+ wid=[16, 16, 24, 40, 80, 112, 160],
+ expan=[None, 1, 5, 4, 5, 5, 6],
+ dep=[None, 1, 4, 4, 4, 4, 4],
+ ks=[3, 3, 7, 7, 5, 7, 5],
+ group=[None, 8, 120, 20, 100, 280, 240],
+ att=[None, True, True, False, True, True, True],
+ stride=[2, 1, 2, 2, 2, 1, 2],
+ act=[
+ 'HSwish', 'ReLU', 'ReLU', 'ReLU', 'HSwish', 'HSwish',
+ 'HSwish'
+ ],
+ conv_cfg=None,
+ norm_cfg=dict(type='BN'),
+ frozen_stages=-1,
+ norm_eval=False,
+ with_cp=False):
+ # Protect mutable default arguments
+ norm_cfg = copy.deepcopy(norm_cfg)
+ super().__init__()
+ self.wid = wid
+ self.expan = expan
+ self.dep = dep
+ self.ks = ks
+ self.group = group
+ self.att = att
+ self.stride = stride
+ self.act = act
+ self.conv_cfg = conv_cfg
+ self.norm_cfg = norm_cfg
+ self.frozen_stages = frozen_stages
+ self.norm_eval = norm_eval
+ self.with_cp = with_cp
+
+ self.conv1 = ConvModule(
+ in_channels=3,
+ out_channels=self.wid[0],
+ kernel_size=self.ks[0],
+ stride=self.stride[0],
+ padding=self.ks[0] // 2,
+ conv_cfg=conv_cfg,
+ norm_cfg=norm_cfg,
+ act_cfg=dict(type=self.act[0]))
+
+ self.layers = self._make_layer()
+
+ def _make_layer(self):
+ layers = []
+ layer_index = 0
+ for i, dep in enumerate(self.dep[1:]):
+ mid_channels = self.wid[i + 1] * self.expan[i + 1]
+
+ if self.att[i + 1]:
+ se_cfg = dict(
+ channels=mid_channels,
+ ratio=4,
+ act_cfg=(dict(type='ReLU'), dict(type='HSigmoid')))
+ else:
+ se_cfg = None
+
+ if self.expan[i + 1] == 1:
+ with_expand_conv = False
+ else:
+ with_expand_conv = True
+
+ for j in range(dep):
+ if j == 0:
+ stride = self.stride[i + 1]
+ in_channels = self.wid[i]
+ else:
+ stride = 1
+ in_channels = self.wid[i + 1]
+
+ layer = InvertedResidual(
+ in_channels=in_channels,
+ out_channels=self.wid[i + 1],
+ mid_channels=mid_channels,
+ kernel_size=self.ks[i + 1],
+ groups=self.group[i + 1],
+ stride=stride,
+ se_cfg=se_cfg,
+ with_expand_conv=with_expand_conv,
+ conv_cfg=self.conv_cfg,
+ norm_cfg=self.norm_cfg,
+ act_cfg=dict(type=self.act[i + 1]),
+ with_cp=self.with_cp)
+ layer_index += 1
+ layer_name = f'layer{layer_index}'
+ self.add_module(layer_name, layer)
+ layers.append(layer_name)
+ return layers
+
+ def init_weights(self, pretrained=None):
+ if isinstance(pretrained, str):
+ logger = logging.getLogger()
+ load_checkpoint(self, pretrained, strict=False, logger=logger)
+ elif pretrained is None:
+ for m in self.modules():
+ if isinstance(m, nn.Conv2d):
+ nn.init.normal_(m.weight, std=0.001)
+ for name, _ in m.named_parameters():
+ if name in ['bias']:
+ nn.init.constant_(m.bias, 0)
+ elif isinstance(m, nn.BatchNorm2d):
+ nn.init.constant_(m.weight, 1)
+ nn.init.constant_(m.bias, 0)
+ else:
+ raise TypeError('pretrained must be a str or None')
+
+ def forward(self, x):
+ x = self.conv1(x)
+
+ for i, layer_name in enumerate(self.layers):
+ layer = getattr(self, layer_name)
+ x = layer(x)
+
+ return x
+
+ def _freeze_stages(self):
+ if self.frozen_stages >= 0:
+ for param in self.conv1.parameters():
+ param.requires_grad = False
+ for i in range(1, self.frozen_stages + 1):
+ layer = getattr(self, f'layer{i}')
+ layer.eval()
+ for param in layer.parameters():
+ param.requires_grad = False
+
+ def train(self, mode=True):
+ super().train(mode)
+ self._freeze_stages()
+ if mode and self.norm_eval:
+ for m in self.modules():
+ if isinstance(m, _BatchNorm):
+ m.eval()
diff --git a/grounded-sam-osx/transformer_utils/mmpose/models/backbones/vipnas_resnet.py b/grounded-sam-osx/transformer_utils/mmpose/models/backbones/vipnas_resnet.py
new file mode 100644
index 0000000000000000000000000000000000000000..81b028ed5f5caad5f59c68b7f82c1a4661cf4d6f
--- /dev/null
+++ b/grounded-sam-osx/transformer_utils/mmpose/models/backbones/vipnas_resnet.py
@@ -0,0 +1,589 @@
+# Copyright (c) OpenMMLab. All rights reserved.
+import copy
+
+import torch.nn as nn
+import torch.utils.checkpoint as cp
+from mmcv.cnn import ConvModule, build_conv_layer, build_norm_layer
+from mmcv.cnn.bricks import ContextBlock
+from mmcv.utils.parrots_wrapper import _BatchNorm
+
+from ..builder import BACKBONES
+from .base_backbone import BaseBackbone
+
+
+class ViPNAS_Bottleneck(nn.Module):
+ """Bottleneck block for ViPNAS_ResNet.
+
+ Args:
+ in_channels (int): Input channels of this block.
+ out_channels (int): Output channels of this block.
+ expansion (int): The ratio of ``out_channels/mid_channels`` where
+ ``mid_channels`` is the input/output channels of conv2. Default: 4.
+ stride (int): stride of the block. Default: 1
+ dilation (int): dilation of convolution. Default: 1
+ downsample (nn.Module): downsample operation on identity branch.
+ Default: None.
+ style (str): ``"pytorch"`` or ``"caffe"``. If set to "pytorch", the
+ stride-two layer is the 3x3 conv layer, otherwise the stride-two
+ layer is the first 1x1 conv layer. Default: "pytorch".
+ with_cp (bool): Use checkpoint or not. Using checkpoint will save some
+ memory while slowing down the training speed.
+ conv_cfg (dict): dictionary to construct and config conv layer.
+ Default: None
+ norm_cfg (dict): dictionary to construct and config norm layer.
+ Default: dict(type='BN')
+ kernel_size (int): kernel size of conv2 searched in ViPANS.
+ groups (int): group number of conv2 searched in ViPNAS.
+ attention (bool): whether to use attention module in the end of
+ the block.
+ """
+
+ def __init__(self,
+ in_channels,
+ out_channels,
+ expansion=4,
+ stride=1,
+ dilation=1,
+ downsample=None,
+ style='pytorch',
+ with_cp=False,
+ conv_cfg=None,
+ norm_cfg=dict(type='BN'),
+ kernel_size=3,
+ groups=1,
+ attention=False):
+ # Protect mutable default arguments
+ norm_cfg = copy.deepcopy(norm_cfg)
+ super().__init__()
+ assert style in ['pytorch', 'caffe']
+
+ self.in_channels = in_channels
+ self.out_channels = out_channels
+ self.expansion = expansion
+ assert out_channels % expansion == 0
+ self.mid_channels = out_channels // expansion
+ self.stride = stride
+ self.dilation = dilation
+ self.style = style
+ self.with_cp = with_cp
+ self.conv_cfg = conv_cfg
+ self.norm_cfg = norm_cfg
+
+ if self.style == 'pytorch':
+ self.conv1_stride = 1
+ self.conv2_stride = stride
+ else:
+ self.conv1_stride = stride
+ self.conv2_stride = 1
+
+ self.norm1_name, norm1 = build_norm_layer(
+ norm_cfg, self.mid_channels, postfix=1)
+ self.norm2_name, norm2 = build_norm_layer(
+ norm_cfg, self.mid_channels, postfix=2)
+ self.norm3_name, norm3 = build_norm_layer(
+ norm_cfg, out_channels, postfix=3)
+
+ self.conv1 = build_conv_layer(
+ conv_cfg,
+ in_channels,
+ self.mid_channels,
+ kernel_size=1,
+ stride=self.conv1_stride,
+ bias=False)
+ self.add_module(self.norm1_name, norm1)
+ self.conv2 = build_conv_layer(
+ conv_cfg,
+ self.mid_channels,
+ self.mid_channels,
+ kernel_size=kernel_size,
+ stride=self.conv2_stride,
+ padding=kernel_size // 2,
+ groups=groups,
+ dilation=dilation,
+ bias=False)
+
+ self.add_module(self.norm2_name, norm2)
+ self.conv3 = build_conv_layer(
+ conv_cfg,
+ self.mid_channels,
+ out_channels,
+ kernel_size=1,
+ bias=False)
+ self.add_module(self.norm3_name, norm3)
+
+ if attention:
+ self.attention = ContextBlock(out_channels,
+ max(1.0 / 16, 16.0 / out_channels))
+ else:
+ self.attention = None
+
+ self.relu = nn.ReLU(inplace=True)
+ self.downsample = downsample
+
+ @property
+ def norm1(self):
+ """nn.Module: the normalization layer named "norm1" """
+ return getattr(self, self.norm1_name)
+
+ @property
+ def norm2(self):
+ """nn.Module: the normalization layer named "norm2" """
+ return getattr(self, self.norm2_name)
+
+ @property
+ def norm3(self):
+ """nn.Module: the normalization layer named "norm3" """
+ return getattr(self, self.norm3_name)
+
+ def forward(self, x):
+ """Forward function."""
+
+ def _inner_forward(x):
+ identity = x
+
+ out = self.conv1(x)
+ out = self.norm1(out)
+ out = self.relu(out)
+
+ out = self.conv2(out)
+ out = self.norm2(out)
+ out = self.relu(out)
+
+ out = self.conv3(out)
+ out = self.norm3(out)
+
+ if self.attention is not None:
+ out = self.attention(out)
+
+ if self.downsample is not None:
+ identity = self.downsample(x)
+
+ out += identity
+
+ return out
+
+ if self.with_cp and x.requires_grad:
+ out = cp.checkpoint(_inner_forward, x)
+ else:
+ out = _inner_forward(x)
+
+ out = self.relu(out)
+
+ return out
+
+
+def get_expansion(block, expansion=None):
+ """Get the expansion of a residual block.
+
+ The block expansion will be obtained by the following order:
+
+ 1. If ``expansion`` is given, just return it.
+ 2. If ``block`` has the attribute ``expansion``, then return
+ ``block.expansion``.
+ 3. Return the default value according the the block type:
+ 4 for ``ViPNAS_Bottleneck``.
+
+ Args:
+ block (class): The block class.
+ expansion (int | None): The given expansion ratio.
+
+ Returns:
+ int: The expansion of the block.
+ """
+ if isinstance(expansion, int):
+ assert expansion > 0
+ elif expansion is None:
+ if hasattr(block, 'expansion'):
+ expansion = block.expansion
+ elif issubclass(block, ViPNAS_Bottleneck):
+ expansion = 1
+ else:
+ raise TypeError(f'expansion is not specified for {block.__name__}')
+ else:
+ raise TypeError('expansion must be an integer or None')
+
+ return expansion
+
+
+class ViPNAS_ResLayer(nn.Sequential):
+ """ViPNAS_ResLayer to build ResNet style backbone.
+
+ Args:
+ block (nn.Module): Residual block used to build ViPNAS ResLayer.
+ num_blocks (int): Number of blocks.
+ in_channels (int): Input channels of this block.
+ out_channels (int): Output channels of this block.
+ expansion (int, optional): The expansion for BasicBlock/Bottleneck.
+ If not specified, it will firstly be obtained via
+ ``block.expansion``. If the block has no attribute "expansion",
+ the following default values will be used: 1 for BasicBlock and
+ 4 for Bottleneck. Default: None.
+ stride (int): stride of the first block. Default: 1.
+ avg_down (bool): Use AvgPool instead of stride conv when
+ downsampling in the bottleneck. Default: False
+ conv_cfg (dict): dictionary to construct and config conv layer.
+ Default: None
+ norm_cfg (dict): dictionary to construct and config norm layer.
+ Default: dict(type='BN')
+ downsample_first (bool): Downsample at the first block or last block.
+ False for Hourglass, True for ResNet. Default: True
+ kernel_size (int): Kernel Size of the corresponding convolution layer
+ searched in the block.
+ groups (int): Group number of the corresponding convolution layer
+ searched in the block.
+ attention (bool): Whether to use attention module in the end of the
+ block.
+ """
+
+ def __init__(self,
+ block,
+ num_blocks,
+ in_channels,
+ out_channels,
+ expansion=None,
+ stride=1,
+ avg_down=False,
+ conv_cfg=None,
+ norm_cfg=dict(type='BN'),
+ downsample_first=True,
+ kernel_size=3,
+ groups=1,
+ attention=False,
+ **kwargs):
+ # Protect mutable default arguments
+ norm_cfg = copy.deepcopy(norm_cfg)
+ self.block = block
+ self.expansion = get_expansion(block, expansion)
+
+ downsample = None
+ if stride != 1 or in_channels != out_channels:
+ downsample = []
+ conv_stride = stride
+ if avg_down and stride != 1:
+ conv_stride = 1
+ downsample.append(
+ nn.AvgPool2d(
+ kernel_size=stride,
+ stride=stride,
+ ceil_mode=True,
+ count_include_pad=False))
+ downsample.extend([
+ build_conv_layer(
+ conv_cfg,
+ in_channels,
+ out_channels,
+ kernel_size=1,
+ stride=conv_stride,
+ bias=False),
+ build_norm_layer(norm_cfg, out_channels)[1]
+ ])
+ downsample = nn.Sequential(*downsample)
+
+ layers = []
+ if downsample_first:
+ layers.append(
+ block(
+ in_channels=in_channels,
+ out_channels=out_channels,
+ expansion=self.expansion,
+ stride=stride,
+ downsample=downsample,
+ conv_cfg=conv_cfg,
+ norm_cfg=norm_cfg,
+ kernel_size=kernel_size,
+ groups=groups,
+ attention=attention,
+ **kwargs))
+ in_channels = out_channels
+ for _ in range(1, num_blocks):
+ layers.append(
+ block(
+ in_channels=in_channels,
+ out_channels=out_channels,
+ expansion=self.expansion,
+ stride=1,
+ conv_cfg=conv_cfg,
+ norm_cfg=norm_cfg,
+ kernel_size=kernel_size,
+ groups=groups,
+ attention=attention,
+ **kwargs))
+ else: # downsample_first=False is for HourglassModule
+ for i in range(0, num_blocks - 1):
+ layers.append(
+ block(
+ in_channels=in_channels,
+ out_channels=in_channels,
+ expansion=self.expansion,
+ stride=1,
+ conv_cfg=conv_cfg,
+ norm_cfg=norm_cfg,
+ kernel_size=kernel_size,
+ groups=groups,
+ attention=attention,
+ **kwargs))
+ layers.append(
+ block(
+ in_channels=in_channels,
+ out_channels=out_channels,
+ expansion=self.expansion,
+ stride=stride,
+ downsample=downsample,
+ conv_cfg=conv_cfg,
+ norm_cfg=norm_cfg,
+ kernel_size=kernel_size,
+ groups=groups,
+ attention=attention,
+ **kwargs))
+
+ super().__init__(*layers)
+
+
+@BACKBONES.register_module()
+class ViPNAS_ResNet(BaseBackbone):
+ """ViPNAS_ResNet backbone.
+
+ "ViPNAS: Efficient Video Pose Estimation via Neural Architecture Search"
+ More details can be found in the `paper
+ `__ .
+
+ Args:
+ depth (int): Network depth, from {18, 34, 50, 101, 152}.
+ in_channels (int): Number of input image channels. Default: 3.
+ num_stages (int): Stages of the network. Default: 4.
+ strides (Sequence[int]): Strides of the first block of each stage.
+ Default: ``(1, 2, 2, 2)``.
+ dilations (Sequence[int]): Dilation of each stage.
+ Default: ``(1, 1, 1, 1)``.
+ out_indices (Sequence[int]): Output from which stages. If only one
+ stage is specified, a single tensor (feature map) is returned,
+ otherwise multiple stages are specified, a tuple of tensors will
+ be returned. Default: ``(3, )``.
+ style (str): `pytorch` or `caffe`. If set to "pytorch", the stride-two
+ layer is the 3x3 conv layer, otherwise the stride-two layer is
+ the first 1x1 conv layer.
+ deep_stem (bool): Replace 7x7 conv in input stem with 3 3x3 conv.
+ Default: False.
+ avg_down (bool): Use AvgPool instead of stride conv when
+ downsampling in the bottleneck. Default: False.
+ frozen_stages (int): Stages to be frozen (stop grad and set eval mode).
+ -1 means not freezing any parameters. Default: -1.
+ conv_cfg (dict | None): The config dict for conv layers. Default: None.
+ norm_cfg (dict): The config dict for norm layers.
+ norm_eval (bool): Whether to set norm layers to eval mode, namely,
+ freeze running stats (mean and var). Note: Effect on Batch Norm
+ and its variants only. Default: False.
+ with_cp (bool): Use checkpoint or not. Using checkpoint will save some
+ memory while slowing down the training speed. Default: False.
+ zero_init_residual (bool): Whether to use zero init for last norm layer
+ in resblocks to let them behave as identity. Default: True.
+ wid (list(int)): Searched width config for each stage.
+ expan (list(int)): Searched expansion ratio config for each stage.
+ dep (list(int)): Searched depth config for each stage.
+ ks (list(int)): Searched kernel size config for each stage.
+ group (list(int)): Searched group number config for each stage.
+ att (list(bool)): Searched attention config for each stage.
+ """
+
+ arch_settings = {
+ 50: ViPNAS_Bottleneck,
+ }
+
+ def __init__(self,
+ depth,
+ in_channels=3,
+ num_stages=4,
+ strides=(1, 2, 2, 2),
+ dilations=(1, 1, 1, 1),
+ out_indices=(3, ),
+ style='pytorch',
+ deep_stem=False,
+ avg_down=False,
+ frozen_stages=-1,
+ conv_cfg=None,
+ norm_cfg=dict(type='BN', requires_grad=True),
+ norm_eval=False,
+ with_cp=False,
+ zero_init_residual=True,
+ wid=[48, 80, 160, 304, 608],
+ expan=[None, 1, 1, 1, 1],
+ dep=[None, 4, 6, 7, 3],
+ ks=[7, 3, 5, 5, 5],
+ group=[None, 16, 16, 16, 16],
+ att=[None, True, False, True, True]):
+ # Protect mutable default arguments
+ norm_cfg = copy.deepcopy(norm_cfg)
+ super().__init__()
+ if depth not in self.arch_settings:
+ raise KeyError(f'invalid depth {depth} for resnet')
+ self.depth = depth
+ self.stem_channels = dep[0]
+ self.num_stages = num_stages
+ assert 1 <= num_stages <= 4
+ self.strides = strides
+ self.dilations = dilations
+ assert len(strides) == len(dilations) == num_stages
+ self.out_indices = out_indices
+ assert max(out_indices) < num_stages
+ self.style = style
+ self.deep_stem = deep_stem
+ self.avg_down = avg_down
+ self.frozen_stages = frozen_stages
+ self.conv_cfg = conv_cfg
+ self.norm_cfg = norm_cfg
+ self.with_cp = with_cp
+ self.norm_eval = norm_eval
+ self.zero_init_residual = zero_init_residual
+ self.block = self.arch_settings[depth]
+ self.stage_blocks = dep[1:1 + num_stages]
+
+ self._make_stem_layer(in_channels, wid[0], ks[0])
+
+ self.res_layers = []
+ _in_channels = wid[0]
+ for i, num_blocks in enumerate(self.stage_blocks):
+ expansion = get_expansion(self.block, expan[i + 1])
+ _out_channels = wid[i + 1] * expansion
+ stride = strides[i]
+ dilation = dilations[i]
+ res_layer = self.make_res_layer(
+ block=self.block,
+ num_blocks=num_blocks,
+ in_channels=_in_channels,
+ out_channels=_out_channels,
+ expansion=expansion,
+ stride=stride,
+ dilation=dilation,
+ style=self.style,
+ avg_down=self.avg_down,
+ with_cp=with_cp,
+ conv_cfg=conv_cfg,
+ norm_cfg=norm_cfg,
+ kernel_size=ks[i + 1],
+ groups=group[i + 1],
+ attention=att[i + 1])
+ _in_channels = _out_channels
+ layer_name = f'layer{i + 1}'
+ self.add_module(layer_name, res_layer)
+ self.res_layers.append(layer_name)
+
+ self._freeze_stages()
+
+ self.feat_dim = res_layer[-1].out_channels
+
+ def make_res_layer(self, **kwargs):
+ """Make a ViPNAS ResLayer."""
+ return ViPNAS_ResLayer(**kwargs)
+
+ @property
+ def norm1(self):
+ """nn.Module: the normalization layer named "norm1" """
+ return getattr(self, self.norm1_name)
+
+ def _make_stem_layer(self, in_channels, stem_channels, kernel_size):
+ """Make stem layer."""
+ if self.deep_stem:
+ self.stem = nn.Sequential(
+ ConvModule(
+ in_channels,
+ stem_channels // 2,
+ kernel_size=3,
+ stride=2,
+ padding=1,
+ conv_cfg=self.conv_cfg,
+ norm_cfg=self.norm_cfg,
+ inplace=True),
+ ConvModule(
+ stem_channels // 2,
+ stem_channels // 2,
+ kernel_size=3,
+ stride=1,
+ padding=1,
+ conv_cfg=self.conv_cfg,
+ norm_cfg=self.norm_cfg,
+ inplace=True),
+ ConvModule(
+ stem_channels // 2,
+ stem_channels,
+ kernel_size=3,
+ stride=1,
+ padding=1,
+ conv_cfg=self.conv_cfg,
+ norm_cfg=self.norm_cfg,
+ inplace=True))
+ else:
+ self.conv1 = build_conv_layer(
+ self.conv_cfg,
+ in_channels,
+ stem_channels,
+ kernel_size=kernel_size,
+ stride=2,
+ padding=kernel_size // 2,
+ bias=False)
+ self.norm1_name, norm1 = build_norm_layer(
+ self.norm_cfg, stem_channels, postfix=1)
+ self.add_module(self.norm1_name, norm1)
+ self.relu = nn.ReLU(inplace=True)
+ self.maxpool = nn.MaxPool2d(kernel_size=3, stride=2, padding=1)
+
+ def _freeze_stages(self):
+ """Freeze parameters."""
+ if self.frozen_stages >= 0:
+ if self.deep_stem:
+ self.stem.eval()
+ for param in self.stem.parameters():
+ param.requires_grad = False
+ else:
+ self.norm1.eval()
+ for m in [self.conv1, self.norm1]:
+ for param in m.parameters():
+ param.requires_grad = False
+
+ for i in range(1, self.frozen_stages + 1):
+ m = getattr(self, f'layer{i}')
+ m.eval()
+ for param in m.parameters():
+ param.requires_grad = False
+
+ def init_weights(self, pretrained=None):
+ """Initialize model weights."""
+ super().init_weights(pretrained)
+ if pretrained is None:
+ for m in self.modules():
+ if isinstance(m, nn.Conv2d):
+ nn.init.normal_(m.weight, std=0.001)
+ for name, _ in m.named_parameters():
+ if name in ['bias']:
+ nn.init.constant_(m.bias, 0)
+ elif isinstance(m, nn.BatchNorm2d):
+ nn.init.constant_(m.weight, 1)
+ nn.init.constant_(m.bias, 0)
+
+ def forward(self, x):
+ """Forward function."""
+ if self.deep_stem:
+ x = self.stem(x)
+ else:
+ x = self.conv1(x)
+ x = self.norm1(x)
+ x = self.relu(x)
+ x = self.maxpool(x)
+ outs = []
+ for i, layer_name in enumerate(self.res_layers):
+ res_layer = getattr(self, layer_name)
+ x = res_layer(x)
+ if i in self.out_indices:
+ outs.append(x)
+ if len(outs) == 1:
+ return outs[0]
+ return tuple(outs)
+
+ def train(self, mode=True):
+ """Convert the model into training mode."""
+ super().train(mode)
+ self._freeze_stages()
+ if mode and self.norm_eval:
+ for m in self.modules():
+ # trick: eval have effect on BatchNorm only
+ if isinstance(m, _BatchNorm):
+ m.eval()
diff --git a/grounded-sam-osx/transformer_utils/mmpose/models/backbones/vit.py b/grounded-sam-osx/transformer_utils/mmpose/models/backbones/vit.py
new file mode 100644
index 0000000000000000000000000000000000000000..8306e35624837301ef3376eae143f4f728746a1e
--- /dev/null
+++ b/grounded-sam-osx/transformer_utils/mmpose/models/backbones/vit.py
@@ -0,0 +1,327 @@
+# Copyright (c) OpenMMLab. All rights reserved.
+import math
+
+import torch
+from functools import partial
+import torch.nn as nn
+import torch.nn.functional as F
+import torch.utils.checkpoint as checkpoint
+
+from timm.models.layers import drop_path, to_2tuple, trunc_normal_
+
+from ..builder import BACKBONES
+from .base_backbone import BaseBackbone
+from einops import repeat
+
+class DropPath(nn.Module):
+ """Drop paths (Stochastic Depth) per sample (when applied in main path of residual blocks).
+ """
+
+ def __init__(self, drop_prob=None):
+ super(DropPath, self).__init__()
+ self.drop_prob = drop_prob
+
+ def forward(self, x):
+ return drop_path(x, self.drop_prob, self.training)
+
+ def extra_repr(self):
+ return 'p={}'.format(self.drop_prob)
+
+
+class Mlp(nn.Module):
+ def __init__(self, in_features, hidden_features=None, out_features=None, act_layer=nn.GELU, drop=0.):
+ super().__init__()
+ out_features = out_features or in_features
+ hidden_features = hidden_features or in_features
+ self.fc1 = nn.Linear(in_features, hidden_features)
+ self.act = act_layer()
+ self.fc2 = nn.Linear(hidden_features, out_features)
+ self.drop = nn.Dropout(drop)
+
+ def forward(self, x):
+ x = self.fc1(x)
+ x = self.act(x)
+ x = self.fc2(x)
+ x = self.drop(x)
+ return x
+
+
+class Attention(nn.Module):
+ def __init__(
+ self, dim, num_heads=8, qkv_bias=False, qk_scale=None, attn_drop=0.,
+ proj_drop=0., attn_head_dim=None, ):
+ super().__init__()
+ self.num_heads = num_heads
+ head_dim = dim // num_heads
+ self.dim = dim
+
+ if attn_head_dim is not None:
+ head_dim = attn_head_dim
+ all_head_dim = head_dim * self.num_heads
+
+ self.scale = qk_scale or head_dim ** -0.5
+
+ self.qkv = nn.Linear(dim, all_head_dim * 3, bias=qkv_bias)
+
+ self.attn_drop = nn.Dropout(attn_drop)
+ self.proj = nn.Linear(all_head_dim, dim)
+ self.proj_drop = nn.Dropout(proj_drop)
+
+ def forward(self, x):
+ B, N, C = x.shape
+ qkv = self.qkv(x)
+ qkv = qkv.reshape(B, N, 3, self.num_heads, -1).permute(2, 0, 3, 1, 4)
+ q, k, v = qkv[0], qkv[1], qkv[2] # make torchscript happy (cannot use tensor as tuple)
+
+ q = q * self.scale
+ attn = (q @ k.transpose(-2, -1))
+
+ attn = attn.softmax(dim=-1)
+ attn = self.attn_drop(attn)
+
+ x = (attn @ v).transpose(1, 2).reshape(B, N, -1)
+ x = self.proj(x)
+ x = self.proj_drop(x)
+
+ return x
+
+
+class Block(nn.Module):
+
+ def __init__(self, dim, num_heads, mlp_ratio=4., qkv_bias=False, qk_scale=None,
+ drop=0., attn_drop=0., drop_path=0., act_layer=nn.GELU,
+ norm_layer=nn.LayerNorm, attn_head_dim=None
+ ):
+ super().__init__()
+
+ self.norm1 = norm_layer(dim)
+ self.attn = Attention(
+ dim, num_heads=num_heads, qkv_bias=qkv_bias, qk_scale=qk_scale,
+ attn_drop=attn_drop, proj_drop=drop, attn_head_dim=attn_head_dim
+ )
+
+ # NOTE: drop path for stochastic depth, we shall see if this is better than dropout here
+ self.drop_path = DropPath(drop_path) if drop_path > 0. else nn.Identity()
+ self.norm2 = norm_layer(dim)
+ mlp_hidden_dim = int(dim * mlp_ratio)
+ self.mlp = Mlp(in_features=dim, hidden_features=mlp_hidden_dim, act_layer=act_layer, drop=drop)
+
+ def forward(self, x):
+ x = x + self.drop_path(self.attn(self.norm1(x)))
+ x = x + self.drop_path(self.mlp(self.norm2(x)))
+ return x
+
+
+class PatchEmbed(nn.Module):
+ """ Image to Patch Embedding
+ """
+
+ def __init__(self, img_size=224, patch_size=16, in_chans=3, embed_dim=768, ratio=1):
+ super().__init__()
+ img_size = to_2tuple(img_size)
+ patch_size = to_2tuple(patch_size)
+ num_patches = (img_size[1] // patch_size[1]) * (img_size[0] // patch_size[0]) * (ratio ** 2)
+ self.patch_shape = (int(img_size[0] // patch_size[0] * ratio), int(img_size[1] // patch_size[1] * ratio))
+ self.origin_patch_shape = (int(img_size[0] // patch_size[0]), int(img_size[1] // patch_size[1]))
+ self.img_size = img_size
+ self.patch_size = patch_size
+ self.num_patches = num_patches
+
+ self.proj = nn.Conv2d(in_chans, embed_dim, kernel_size=patch_size, stride=(patch_size[0] // ratio),
+ padding=4 + 2 * (ratio // 2 - 1))
+
+ def forward(self, x, **kwargs):
+ B, C, H, W = x.shape
+ x = self.proj(x)
+ Hp, Wp = x.shape[2], x.shape[3]
+
+ x = x.flatten(2).transpose(1, 2)
+ return x, (Hp, Wp)
+
+
+class HybridEmbed(nn.Module):
+ """ CNN Feature Map Embedding
+ Extract feature map from CNN, flatten, project to embedding dim.
+ """
+
+ def __init__(self, backbone, img_size=224, feature_size=None, in_chans=3, embed_dim=768):
+ super().__init__()
+ assert isinstance(backbone, nn.Module)
+ img_size = to_2tuple(img_size)
+ self.img_size = img_size
+ self.backbone = backbone
+ if feature_size is None:
+ with torch.no_grad():
+ training = backbone.training
+ if training:
+ backbone.eval()
+ o = self.backbone(torch.zeros(1, in_chans, img_size[0], img_size[1]))[-1]
+ feature_size = o.shape[-2:]
+ feature_dim = o.shape[1]
+ backbone.train(training)
+ else:
+ feature_size = to_2tuple(feature_size)
+ feature_dim = self.backbone.feature_info.channels()[-1]
+ self.num_patches = feature_size[0] * feature_size[1]
+ self.proj = nn.Linear(feature_dim, embed_dim)
+
+ def forward(self, x):
+ x = self.backbone(x)[-1]
+ x = x.flatten(2).transpose(1, 2)
+ x = self.proj(x)
+ return x
+
+
+@BACKBONES.register_module()
+class ViT(BaseBackbone):
+
+ def __init__(self,
+ img_size=(256, 192), patch_size=16, in_chans=3, num_classes=80, embed_dim=1024, depth=24,
+ num_heads=16, mlp_ratio=4., qkv_bias=True, qk_scale=None, drop_rate=0., attn_drop_rate=0.,
+ drop_path_rate=0.5, hybrid_backbone=None, norm_layer=nn.LayerNorm, use_checkpoint=False,
+ frozen_stages=-1, ratio=1, last_norm=True,
+ patch_padding='pad', freeze_attn=False, freeze_ffn=False, task_tokens_num=1+1+2+2+25
+ ):
+ # Protect mutable default arguments
+ super(ViT, self).__init__()
+ norm_layer = norm_layer or partial(nn.LayerNorm, eps=1e-6)
+ self.num_classes = num_classes
+ self.num_features = self.embed_dim = embed_dim # num_features for consistency with other models
+ self.frozen_stages = frozen_stages
+ self.use_checkpoint = use_checkpoint
+ self.patch_padding = patch_padding
+ self.freeze_attn = freeze_attn
+ self.freeze_ffn = freeze_ffn
+ self.depth = depth
+ self.task_tokens_num = task_tokens_num
+
+ if hybrid_backbone is not None:
+ self.patch_embed = HybridEmbed(
+ hybrid_backbone, img_size=img_size, in_chans=in_chans, embed_dim=embed_dim)
+ else:
+ self.patch_embed = PatchEmbed(
+ img_size=img_size, patch_size=patch_size, in_chans=in_chans, embed_dim=embed_dim, ratio=ratio)
+ num_patches = self.patch_embed.num_patches
+
+ # task tokens for HPS estimation
+ self.task_tokens = nn.Parameter(torch.zeros(1, task_tokens_num, embed_dim))
+ trunc_normal_(self.task_tokens, std=.02)
+
+ # since the pretraining model has class token
+ self.pos_embed = nn.Parameter(torch.zeros(1, num_patches + 1, embed_dim))
+
+ dpr = [x.item() for x in torch.linspace(0, drop_path_rate, depth)] # stochastic depth decay rule
+
+ self.blocks = nn.ModuleList([
+ Block(
+ dim=embed_dim, num_heads=num_heads, mlp_ratio=mlp_ratio, qkv_bias=qkv_bias, qk_scale=qk_scale,
+ drop=drop_rate, attn_drop=attn_drop_rate, drop_path=dpr[i], norm_layer=norm_layer,
+ )
+ for i in range(depth)])
+
+ self.last_norm = norm_layer(embed_dim) if last_norm else nn.Identity()
+
+ if self.pos_embed is not None:
+ trunc_normal_(self.pos_embed, std=.02)
+
+ self._freeze_stages()
+
+ def _freeze_stages(self):
+ """Freeze parameters."""
+ if self.frozen_stages >= 0:
+ self.patch_embed.eval()
+ for param in self.patch_embed.parameters():
+ param.requires_grad = False
+
+ for i in range(1, self.frozen_stages + 1):
+ m = self.blocks[i]
+ m.eval()
+ for param in m.parameters():
+ param.requires_grad = False
+
+ if self.freeze_attn:
+ for i in range(0, self.depth):
+ m = self.blocks[i]
+ m.attn.eval()
+ m.norm1.eval()
+ for param in m.attn.parameters():
+ param.requires_grad = False
+ for param in m.norm1.parameters():
+ param.requires_grad = False
+
+ if self.freeze_ffn:
+ self.pos_embed.requires_grad = False
+ self.patch_embed.eval()
+ for param in self.patch_embed.parameters():
+ param.requires_grad = False
+ for i in range(0, self.depth):
+ m = self.blocks[i]
+ m.mlp.eval()
+ m.norm2.eval()
+ for param in m.mlp.parameters():
+ param.requires_grad = False
+ for param in m.norm2.parameters():
+ param.requires_grad = False
+
+ def init_weights(self, pretrained=None):
+ """Initialize the weights in backbone.
+ Args:
+ pretrained (str, optional): Path to pre-trained weights.
+ Defaults to None.
+ """
+ super().init_weights(pretrained, patch_padding=self.patch_padding)
+
+ if pretrained is None:
+ def _init_weights(m):
+ if isinstance(m, nn.Linear):
+ trunc_normal_(m.weight, std=.02)
+ if isinstance(m, nn.Linear) and m.bias is not None:
+ nn.init.constant_(m.bias, 0)
+ elif isinstance(m, nn.LayerNorm):
+ nn.init.constant_(m.bias, 0)
+ nn.init.constant_(m.weight, 1.0)
+
+ self.apply(_init_weights)
+
+ def get_num_layers(self):
+ return len(self.blocks)
+
+ @torch.jit.ignore
+ def no_weight_decay(self):
+ return {'pos_embed', 'cls_token'}
+
+ def forward_features(self, x):
+ B, C, H, W = x.shape
+ x, (Hp, Wp) = self.patch_embed(x)
+ task_tokens = repeat(self.task_tokens, '() n d -> b n d', b=B)
+ if self.pos_embed is not None:
+ # fit for multiple GPU training
+ # since the first element for pos embed (sin-cos manner) is zero, it will cause no difference
+ x = x + self.pos_embed[:, 1:] + self.pos_embed[:, :1]
+
+ x = torch.cat((task_tokens, x), dim=1)
+
+ for blk in self.blocks:
+ if self.use_checkpoint:
+ x = checkpoint.checkpoint(blk, x)
+ else:
+ x = blk(x)
+
+ x = self.last_norm(x)
+
+ task_tokens = x[:, :self.task_tokens_num] # [N,J,C]
+ # task_tokens = torch.cat(task_tokens_, dim=-1)
+ xp = x[:, self.task_tokens_num:] # [N,Hp*Wp,C]
+
+ xp = xp.permute(0, 2, 1).reshape(B, -1, Hp, Wp).contiguous()
+
+ return xp, task_tokens
+
+ def forward(self, x):
+ x = self.forward_features(x)
+ return x
+
+ def train(self, mode=True):
+ """Convert the model into training mode."""
+ super().train(mode)
+ self._freeze_stages()
\ No newline at end of file
diff --git a/grounded-sam-osx/transformer_utils/mmpose/models/builder.py b/grounded-sam-osx/transformer_utils/mmpose/models/builder.py
new file mode 100644
index 0000000000000000000000000000000000000000..47f0a53121633fb6185a4d514c05a5862a9d74cf
--- /dev/null
+++ b/grounded-sam-osx/transformer_utils/mmpose/models/builder.py
@@ -0,0 +1,49 @@
+# Copyright (c) OpenMMLab. All rights reserved.
+from mmcv.cnn import MODELS as MMCV_MODELS
+from mmcv.cnn import build_model_from_cfg
+from mmcv.utils import Registry, build_from_cfg
+
+MODELS = Registry(
+ 'models', build_func=build_model_from_cfg, parent=MMCV_MODELS)
+
+BACKBONES = MODELS
+NECKS = MODELS
+HEADS = MODELS
+LOSSES = MODELS
+POSENETS = MODELS
+MESH_MODELS = MODELS
+TRANSFORMER = Registry('Transformer')
+
+
+def build_backbone(cfg):
+ """Build backbone."""
+ return BACKBONES.build(cfg)
+
+
+def build_neck(cfg):
+ """Build neck."""
+ return NECKS.build(cfg)
+
+
+def build_head(cfg):
+ """Build head."""
+ return HEADS.build(cfg)
+
+
+def build_loss(cfg):
+ """Build loss."""
+ return LOSSES.build(cfg)
+
+
+def build_posenet(cfg):
+ """Build posenet."""
+ return POSENETS.build(cfg)
+
+
+def build_mesh_model(cfg):
+ """Build mesh model."""
+ return MESH_MODELS.build(cfg)
+
+def build_transformer(cfg, default_args=None):
+ """Builder for Transformer."""
+ return build_from_cfg(cfg, TRANSFORMER, default_args)
\ No newline at end of file
diff --git a/grounded-sam-osx/transformer_utils/mmpose/models/detectors/__init__.py b/grounded-sam-osx/transformer_utils/mmpose/models/detectors/__init__.py
new file mode 100644
index 0000000000000000000000000000000000000000..823cd5d52c2723c6a537765a7f083a444016e8f7
--- /dev/null
+++ b/grounded-sam-osx/transformer_utils/mmpose/models/detectors/__init__.py
@@ -0,0 +1,7 @@
+# Copyright (c) OpenMMLab. All rights reserved.
+from .top_down import TopDown
+from .poseur import Poseur
+
+__all__ = [
+ 'TopDown', 'Poseur'
+]
diff --git a/grounded-sam-osx/transformer_utils/mmpose/models/detectors/base.py b/grounded-sam-osx/transformer_utils/mmpose/models/detectors/base.py
new file mode 100644
index 0000000000000000000000000000000000000000..5d459b42de66012c88ff37d7d845265d06efebc7
--- /dev/null
+++ b/grounded-sam-osx/transformer_utils/mmpose/models/detectors/base.py
@@ -0,0 +1,131 @@
+# Copyright (c) OpenMMLab. All rights reserved.
+from abc import ABCMeta, abstractmethod
+from collections import OrderedDict
+
+import torch
+import torch.distributed as dist
+import torch.nn as nn
+
+
+class BasePose(nn.Module, metaclass=ABCMeta):
+ """Base class for pose detectors.
+
+ All recognizers should subclass it.
+ All subclass should overwrite:
+ Methods:`forward_train`, supporting to forward when training.
+ Methods:`forward_test`, supporting to forward when testing.
+
+ Args:
+ backbone (dict): Backbone modules to extract feature.
+ head (dict): Head modules to give output.
+ train_cfg (dict): Config for training. Default: None.
+ test_cfg (dict): Config for testing. Default: None.
+ """
+
+ @abstractmethod
+ def forward_train(self, img, img_metas, **kwargs):
+ """Defines the computation performed at training."""
+
+ @abstractmethod
+ def forward_test(self, img, img_metas, **kwargs):
+ """Defines the computation performed at testing."""
+
+ @abstractmethod
+ def forward(self, img, img_metas, return_loss=True, **kwargs):
+ """Forward function."""
+
+ @staticmethod
+ def _parse_losses(losses):
+ """Parse the raw outputs (losses) of the network.
+
+ Args:
+ losses (dict): Raw output of the network, which usually contain
+ losses and other necessary information.
+
+ Returns:
+ tuple[Tensor, dict]: (loss, log_vars), loss is the loss tensor \
+ which may be a weighted sum of all losses, log_vars \
+ contains all the variables to be sent to the logger.
+ """
+ log_vars = OrderedDict()
+ for loss_name, loss_value in losses.items():
+ if isinstance(loss_value, torch.Tensor):
+ log_vars[loss_name] = loss_value.mean()
+ elif isinstance(loss_value, float):
+ log_vars[loss_name] = loss_value
+ elif isinstance(loss_value, list):
+ log_vars[loss_name] = sum(_loss.mean() for _loss in loss_value)
+ else:
+ raise TypeError(
+ f'{loss_name} is not a tensor or list of tensors or float')
+
+ loss = sum(_value for _key, _value in log_vars.items()
+ if 'loss' in _key)
+
+ log_vars['loss'] = loss
+ for loss_name, loss_value in log_vars.items():
+ # reduce loss when distributed training
+ if not isinstance(loss_value, float):
+ if dist.is_available() and dist.is_initialized():
+ loss_value = loss_value.data.clone()
+ dist.all_reduce(loss_value.div_(dist.get_world_size()))
+ log_vars[loss_name] = loss_value.item()
+ else:
+ log_vars[loss_name] = loss_value
+
+ return loss, log_vars
+
+ def train_step(self, data_batch, optimizer, **kwargs):
+ """The iteration step during training.
+
+ This method defines an iteration step during training, except for the
+ back propagation and optimizer updating, which are done in an optimizer
+ hook. Note that in some complicated cases or models, the whole process
+ including back propagation and optimizer updating is also defined in
+ this method, such as GAN.
+
+ Args:
+ data_batch (dict): The output of dataloader.
+ optimizer (:obj:`torch.optim.Optimizer` | dict): The optimizer of
+ runner is passed to ``train_step()``. This argument is unused
+ and reserved.
+
+ Returns:
+ dict: It should contain at least 3 keys: ``loss``, ``log_vars``,
+ ``num_samples``.
+ ``loss`` is a tensor for back propagation, which can be a
+ weighted sum of multiple losses.
+ ``log_vars`` contains all the variables to be sent to the
+ logger.
+ ``num_samples`` indicates the batch size (when the model is
+ DDP, it means the batch size on each GPU), which is used for
+ averaging the logs.
+ """
+ losses = self.forward(**data_batch)
+
+ loss, log_vars = self._parse_losses(losses)
+
+ outputs = dict(
+ loss=loss,
+ log_vars=log_vars,
+ num_samples=len(next(iter(data_batch.values()))))
+
+ return outputs
+
+ def val_step(self, data_batch, optimizer, **kwargs):
+ """The iteration step during validation.
+
+ This method shares the same signature as :func:`train_step`, but used
+ during val epochs. Note that the evaluation after training epochs is
+ not implemented with this method, but an evaluation hook.
+ """
+ results = self.forward(return_loss=False, **data_batch)
+
+ outputs = dict(results=results)
+
+ return outputs
+
+ @abstractmethod
+ def show_result(self, **kwargs):
+ """Visualize the results."""
+ raise NotImplementedError
diff --git a/grounded-sam-osx/transformer_utils/mmpose/models/detectors/poseur.py b/grounded-sam-osx/transformer_utils/mmpose/models/detectors/poseur.py
new file mode 100644
index 0000000000000000000000000000000000000000..b5c98ea95af4ee114e2dc731bf1b3e83489b8563
--- /dev/null
+++ b/grounded-sam-osx/transformer_utils/mmpose/models/detectors/poseur.py
@@ -0,0 +1,278 @@
+import warnings
+
+import mmcv
+import numpy as np
+from mmcv.image import imwrite
+from mmcv.visualization.image import imshow
+
+from mmpose.core import imshow_keypoints
+from .. import builder
+from ..builder import POSENETS
+from .base import BasePose
+import torch
+from config import cfg
+
+try:
+ from mmcv.runner import auto_fp16
+except ImportError:
+ warnings.warn('auto_fp16 from mmpose will be deprecated from v0.15.0'
+ 'Please install mmcv>=1.1.4')
+ from mmpose.core import auto_fp16
+
+from .top_down import TopDown
+
+
+@POSENETS.register_module()
+class Poseur(TopDown):
+ def __init__(self, *args, **kwargs):
+ if 'filp_fuse_type' in kwargs:
+ self.filp_fuse_type = kwargs.pop('filp_fuse_type')
+ else:
+ self.filp_fuse_type = 'default'
+ super().__init__(*args, **kwargs)
+
+ def init_weights(self, pretrained=None):
+ """Weight initialization for model."""
+ self.backbone.init_weights(pretrained)
+ if self.with_neck:
+ self.neck.init_weights()
+ if self.with_keypoint:
+ self.keypoint_head.init_weights()
+
+ @auto_fp16(apply_to=('img',))
+ def forward(self,
+ img,
+ coord_target=None,
+ coord_target_weight=None,
+ bbox_target=None,
+ bbox_target_weight=None,
+ hp_target=None,
+ hp_target_weight=None,
+ img_metas=None,
+ return_loss=True,
+ return_heatmap=False,
+ coord_init=None,
+ query_init=None,
+ **kwargs):
+ """Calls either forward_train or forward_test depending on whether
+ return_loss=True. Note this setting will change the expected inputs.
+ When `return_loss=True`, img and img_meta are single-nested (i.e.
+ Tensor and List[dict]), and when `resturn_loss=False`, img and img_meta
+ should be double nested (i.e. List[Tensor], List[List[dict]]), with
+ the outer list indicating test time augmentations.
+
+ Note:
+ batch_size: N
+ num_keypoints: K
+ num_img_channel: C (Default: 3)
+ img height: imgH
+ img weight: imgW
+ heatmaps height: H
+ heatmaps weight: W
+
+ Args:
+ img (torch.Tensor[NxCximgHximgW]): Input images.
+ target (torch.Tensor[NxKxHxW]): Target heatmaps.
+ target_weight (torch.Tensor[NxKx1]): Weights across
+ different joint types.
+ img_metas (list(dict)): Information about data augmentation
+ By default this includes:
+ - "image_file: path to the image file
+ - "center": center of the bbox
+ - "scale": scale of the bbox
+ - "rotation": rotation of the bbox
+ - "bbox_score": score of bbox
+ return_loss (bool): Option to `return loss`. `return loss=True`
+ for training, `return loss=False` for validation & test.
+ return_heatmap (bool) : Option to return heatmap.
+
+ Returns:
+ dict|tuple: if `return loss` is true, then return losses.
+ Otherwise, return predicted poses, boxes, image paths
+ and heatmaps.
+ """
+ return self.forward_mesh_recovery(img, coord_init=coord_init, query_init=query_init,
+ **kwargs)
+ # if return_loss:
+ # return self.forward_train(img,
+ # coord_target, coord_target_weight,
+ # hp_target, hp_target_weight, img_metas,
+ # **kwargs)
+ # return self.forward_test(
+ # img, img_metas, return_heatmap=return_heatmap, **kwargs)
+
+ def forward_train(self, img, coord_target, coord_target_weight,
+ hp_target, hp_target_weight, img_metas, **kwargs):
+ """
+ :param img:
+ :param coord_target: [2, 17, 2]
+ :param coord_target_weight: [2, 17, 2]
+ :param hp_target: [2, 4, 17, 64, 48]
+ :param hp_target_weight: [2, 4, 17, 1]
+ :param img_metas:
+ :param kwargs:
+ :return:
+ """
+ """Defines the computation performed at every call when training."""
+ output = self.backbone(img)
+ img_feat = output[-1]
+ if self.with_neck:
+ output = self.neck(output)
+ if self.with_keypoint:
+ # output = self.keypoint_head(output, img_metas)
+ enc_output, dec_output = self.keypoint_head(output)
+
+ return img_feat, enc_output, dec_output, None
+
+ def seperate_sigma_from_score(self, score):
+ if score.shape[2] == 3:
+ sigma = score[:, :, [1, 2]]
+ score = score[:, :, [0]]
+ return score, sigma
+ elif score.shape[2] == 1:
+ return score, None
+ else:
+ raise
+
+ def forward_mesh_recovery(self, output, coord_init=None, query_init=None, **kwargs):
+ """
+ :param img:
+ :param coord_target: [2, 17, 2]
+ :param coord_target_weight: [2, 17, 2]
+ :param hp_target: [2, 4, 17, 64, 48]
+ :param hp_target_weight: [2, 4, 17, 1]
+ :param img_metas:
+ :param kwargs:
+ :return:
+ """
+ """Defines the computation performed at every call when training."""
+ # output = self.backbone(img)
+ img_feat = output[-1]
+ # print(len(output))
+ if self.with_neck:
+ output = self.neck(output)
+ if self.with_keypoint:
+ # output = self.keypoint_head(output, img_metas)
+ enc_output, dec_output = self.keypoint_head(output, coord_init=coord_init, query_init=query_init)
+
+ return dec_output.feat[-1]
+
+ def forward_test(self, img, img_metas, return_heatmap=False, **kwargs):
+ """Defines the computation performed at every call when testing."""
+ assert img.size(0) == len(img_metas)
+ batch_size, _, img_height, img_width = img.shape
+ if batch_size > 1:
+ assert 'bbox_id' in img_metas[0]
+
+ result = {}
+
+ features = self.backbone(img)
+ if self.with_neck:
+ features = self.neck(features)
+ if self.with_keypoint:
+ output_regression, output_regression_score = self.keypoint_head.inference_model(
+ features, flip_pairs=None)
+ output_regression_score, output_regression_sigma = self.seperate_sigma_from_score(output_regression_score)
+
+ if self.test_cfg['flip_test']:
+ img_flipped = img.flip(3)
+ features_flipped = self.backbone(img_flipped)
+ if self.with_neck:
+ features_flipped = self.neck(features_flipped)
+ if self.with_keypoint:
+ output_regression_flipped, output_regression_score_flipped = self.keypoint_head.inference_model(
+ features_flipped, img_metas[0]['flip_pairs'])
+ output_regression_score_flipped, output_regression_sigma_flipped = \
+ self.seperate_sigma_from_score(output_regression_score_flipped)
+ if self.filp_fuse_type == 'default':
+ output_regression = (output_regression +
+ output_regression_flipped) * 0.5
+
+ output_regression_score = (output_regression_score +
+ output_regression_score_flipped) * 0.5
+ elif self.filp_fuse_type == 'type1':
+ # output_regression = (output_regression * output_regression_score + output_regression_flipped * output_regression_score_flipped)\
+ # /(output_regression_score + output_regression_score_flipped+1e-9)
+ output_regression, output_regression_flipped = \
+ torch.from_numpy(output_regression), torch.from_numpy(output_regression_flipped)
+
+ output_regression_score, output_regression_score_flipped = \
+ torch.from_numpy(output_regression_score), torch.from_numpy(output_regression_score_flipped)
+
+ output_regression = (
+ output_regression * output_regression_score + output_regression_flipped * output_regression_score_flipped) \
+ / (output_regression_score + output_regression_score_flipped + 1e-9)
+
+ diff = 1 - (output_regression_score - output_regression_score_flipped).abs()
+ output_regression_score = (output_regression_score * output_regression_score_flipped * diff) ** 2
+
+ output_regression = output_regression.numpy()
+ output_regression_score = output_regression_score.numpy()
+ elif self.filp_fuse_type == 'type2':
+ # output_regression = (output_regression * output_regression_score + output_regression_flipped * output_regression_score_flipped)\
+ # /(output_regression_score + output_regression_score_flipped+1e-9)
+ output_regression, output_regression_flipped = \
+ torch.from_numpy(output_regression), torch.from_numpy(output_regression_flipped)
+
+ output_regression_sigma, output_regression_sigma_flipped = \
+ torch.from_numpy(output_regression_sigma), torch.from_numpy(output_regression_sigma_flipped)
+
+ output_regression_p, output_regression_p_flipped = \
+ self.get_p(output_regression_sigma), self.get_p(output_regression_sigma_flipped)
+
+ p_to_coord_index = 5
+ output_regression = (
+ output_regression * output_regression_p ** p_to_coord_index + output_regression_flipped * output_regression_p_flipped ** p_to_coord_index) \
+ / (
+ output_regression_p ** p_to_coord_index + output_regression_p_flipped ** p_to_coord_index + 1e-10)
+
+ output_regression_score = (output_regression_p + output_regression_p_flipped) * 0.5
+
+ output_regression = output_regression.numpy()
+ output_regression_score = output_regression_score.numpy()
+ else:
+ NotImplementedError
+
+ if self.with_keypoint:
+ keypoint_result = self.keypoint_head.decode_keypoints(
+ img_metas, output_regression, output_regression_score, [img_width, img_height])
+ result.update(keypoint_result)
+
+ if not return_heatmap:
+ output_heatmap = None
+
+ result['output_heatmap'] = output_heatmap
+
+ return result
+
+ def get_p(self, output_regression_sigma, p_x=0.2):
+ output_regression_p = (1 - np.exp(-(p_x / output_regression_sigma)))
+ output_regression_p = output_regression_p[:, :, 0] * output_regression_p[:, :, 1]
+ output_regression_p = output_regression_p[:, :, None]
+ return output_regression_p * 0.7
+ # 0.2 0.7 7421
+ # 0.2 0.7 7610
+ # 0.17 0.7
+
+ def forward_dummy(self, img):
+ """Used for computing network FLOPs.
+
+ See ``tools/get_flops.py``.
+
+ Args:
+ img (torch.Tensor): Input image.
+
+ Returns:
+ Tensor: Output heatmaps.
+ """
+ output = self.backbone(img)
+ if self.with_neck:
+ output = self.neck(output)
+ if self.with_keypoint:
+ img_h, img_w = 256, 192
+ img_metas = [{}]
+ img_metas[0]['batch_input_shape'] = (img_h, img_w)
+ img_metas[0]['img_shape'] = (img_h, img_w, 3)
+ # output = self.keypoint_head(output, img_metas)
+ output = self.keypoint_head(output)
+ return output
diff --git a/grounded-sam-osx/transformer_utils/mmpose/models/detectors/top_down.py b/grounded-sam-osx/transformer_utils/mmpose/models/detectors/top_down.py
new file mode 100644
index 0000000000000000000000000000000000000000..99215ec70b2381fbc01be6e448e30a09f83cda2b
--- /dev/null
+++ b/grounded-sam-osx/transformer_utils/mmpose/models/detectors/top_down.py
@@ -0,0 +1,311 @@
+# Copyright (c) OpenMMLab. All rights reserved.
+import warnings
+
+import mmcv
+import numpy as np
+from mmcv.image import imwrite
+from mmcv.utils.misc import deprecated_api_warning
+from mmcv.visualization.image import imshow
+
+from mmpose.core import imshow_bboxes, imshow_keypoints
+from .. import builder
+from ..builder import POSENETS
+from .base import BasePose
+
+try:
+ from mmcv.runner import auto_fp16
+except ImportError:
+ warnings.warn('auto_fp16 from mmpose will be deprecated from v0.15.0'
+ 'Please install mmcv>=1.1.4')
+ from mmpose.core import auto_fp16
+
+
+@POSENETS.register_module()
+class TopDown(BasePose):
+ """Top-down pose detectors.
+
+ Args:
+ backbone (dict): Backbone modules to extract feature.
+ keypoint_head (dict): Keypoint head to process feature.
+ train_cfg (dict): Config for training. Default: None.
+ test_cfg (dict): Config for testing. Default: None.
+ pretrained (str): Path to the pretrained models.
+ loss_pose (None): Deprecated arguments. Please use
+ `loss_keypoint` for heads instead.
+ """
+
+ def __init__(self,
+ backbone,
+ neck=None,
+ keypoint_head=None,
+ train_cfg=None,
+ test_cfg=None,
+ pretrained=None,
+ loss_pose=None):
+ super().__init__()
+ self.fp16_enabled = False
+
+ self.backbone = builder.build_backbone(backbone)
+
+ self.train_cfg = train_cfg
+ self.test_cfg = test_cfg
+
+ if neck is not None:
+ self.neck = builder.build_neck(neck)
+
+ if keypoint_head is not None:
+ keypoint_head['train_cfg'] = train_cfg
+ keypoint_head['test_cfg'] = test_cfg
+
+ if 'loss_keypoint' not in keypoint_head and loss_pose is not None:
+ warnings.warn(
+ '`loss_pose` for TopDown is deprecated, '
+ 'use `loss_keypoint` for heads instead. See '
+ 'https://github.com/open-mmlab/mmpose/pull/382'
+ ' for more information.', DeprecationWarning)
+ keypoint_head['loss_keypoint'] = loss_pose
+
+ self.keypoint_head = builder.build_head(keypoint_head)
+ self.pretrained = pretrained
+ self.init_weights()
+
+ @property
+ def with_neck(self):
+ """Check if has neck."""
+ return hasattr(self, 'neck')
+
+ @property
+ def with_keypoint(self):
+ """Check if has keypoint_head."""
+ return hasattr(self, 'keypoint_head')
+
+ def init_weights(self, pretrained=None):
+ """Weight initialization for model."""
+ if pretrained is not None:
+ self.pretrained = pretrained
+ self.backbone.init_weights(self.pretrained)
+ if self.with_neck:
+ self.neck.init_weights()
+ if self.with_keypoint:
+ self.keypoint_head.init_weights()
+
+ @auto_fp16(apply_to=('img', ))
+ def forward(self,
+ img,
+ target=None,
+ target_weight=None,
+ img_metas=None,
+ return_loss=True,
+ return_heatmap=False,
+ **kwargs):
+ """Calls either forward_train or forward_test depending on whether
+ return_loss=True. Note this setting will change the expected inputs.
+ When `return_loss=True`, img and img_meta are single-nested (i.e.
+ Tensor and List[dict]), and when `resturn_loss=False`, img and img_meta
+ should be double nested (i.e. List[Tensor], List[List[dict]]), with
+ the outer list indicating test time augmentations.
+
+ Note:
+ - batch_size: N
+ - num_keypoints: K
+ - num_img_channel: C (Default: 3)
+ - img height: imgH
+ - img width: imgW
+ - heatmaps height: H
+ - heatmaps weight: W
+
+ Args:
+ img (torch.Tensor[NxCximgHximgW]): Input images.
+ target (torch.Tensor[NxKxHxW]): Target heatmaps.
+ target_weight (torch.Tensor[NxKx1]): Weights across
+ different joint types.
+ img_metas (list(dict)): Information about data augmentation
+ By default this includes:
+
+ - "image_file: path to the image file
+ - "center": center of the bbox
+ - "scale": scale of the bbox
+ - "rotation": rotation of the bbox
+ - "bbox_score": score of bbox
+ return_loss (bool): Option to `return loss`. `return loss=True`
+ for training, `return loss=False` for validation & test.
+ return_heatmap (bool) : Option to return heatmap.
+
+ Returns:
+ dict|tuple: if `return loss` is true, then return losses. \
+ Otherwise, return predicted poses, boxes, image paths \
+ and heatmaps.
+ """
+ if return_loss:
+ return self.forward_train(img, target, target_weight, img_metas,
+ **kwargs)
+ return self.forward_test(
+ img, img_metas, return_heatmap=return_heatmap, **kwargs)
+
+ def forward_train(self, img, target, target_weight, img_metas, **kwargs):
+ """Defines the computation performed at every call when training."""
+ output = self.backbone(img)
+ if self.with_neck:
+ output = self.neck(output)
+ if self.with_keypoint:
+ output = self.keypoint_head(output)
+
+ # if return loss
+ losses = dict()
+ if self.with_keypoint:
+ keypoint_losses = self.keypoint_head.get_loss(
+ output, target, target_weight)
+ losses.update(keypoint_losses)
+ keypoint_accuracy = self.keypoint_head.get_accuracy(
+ output, target, target_weight)
+ losses.update(keypoint_accuracy)
+
+ return losses
+
+ def forward_test(self, img, img_metas, return_heatmap=False, **kwargs):
+ """Defines the computation performed at every call when testing."""
+ assert img.size(0) == len(img_metas)
+ batch_size, _, img_height, img_width = img.shape
+ if batch_size > 1:
+ assert 'bbox_id' in img_metas[0]
+
+ result = {}
+
+ features = self.backbone(img)
+ if self.with_neck:
+ features = self.neck(features)
+ if self.with_keypoint:
+ output_heatmap = self.keypoint_head.inference_model(
+ features, flip_pairs=None)
+
+ if self.test_cfg.get('flip_test', True):
+ img_flipped = img.flip(3)
+ features_flipped = self.backbone(img_flipped)
+ if self.with_neck:
+ features_flipped = self.neck(features_flipped)
+ if self.with_keypoint:
+ output_flipped_heatmap = self.keypoint_head.inference_model(
+ features_flipped, img_metas[0]['flip_pairs'])
+ output_heatmap = (output_heatmap + output_flipped_heatmap)
+ if self.test_cfg.get('regression_flip_shift', False):
+ output_heatmap[..., 0] -= 1.0 / img_width
+ output_heatmap = output_heatmap / 2
+
+ if self.with_keypoint:
+ keypoint_result = self.keypoint_head.decode(
+ img_metas, output_heatmap, img_size=[img_width, img_height])
+ result.update(keypoint_result)
+
+ if not return_heatmap:
+ output_heatmap = None
+
+ result['output_heatmap'] = output_heatmap
+
+ return result
+
+ def forward_dummy(self, img):
+ """Used for computing network FLOPs.
+
+ See ``tools/get_flops.py``.
+
+ Args:
+ img (torch.Tensor): Input image.
+
+ Returns:
+ Tensor: Output heatmaps.
+ """
+ output = self.backbone(img)
+ if self.with_neck:
+ output = self.neck(output)
+ if self.with_keypoint:
+ output = self.keypoint_head(output)
+ return output
+
+ @deprecated_api_warning({'pose_limb_color': 'pose_link_color'},
+ cls_name='TopDown')
+ def show_result(self,
+ img,
+ result,
+ skeleton=None,
+ kpt_score_thr=0.3,
+ bbox_color='green',
+ pose_kpt_color=None,
+ pose_link_color=None,
+ text_color='white',
+ radius=4,
+ thickness=1,
+ font_scale=0.5,
+ bbox_thickness=1,
+ win_name='',
+ show=False,
+ show_keypoint_weight=False,
+ wait_time=0,
+ out_file=None):
+ """Draw `result` over `img`.
+
+ Args:
+ img (str or Tensor): The image to be displayed.
+ result (list[dict]): The results to draw over `img`
+ (bbox_result, pose_result).
+ skeleton (list[list]): The connection of keypoints.
+ skeleton is 0-based indexing.
+ kpt_score_thr (float, optional): Minimum score of keypoints
+ to be shown. Default: 0.3.
+ bbox_color (str or tuple or :obj:`Color`): Color of bbox lines.
+ pose_kpt_color (np.array[Nx3]`): Color of N keypoints.
+ If None, do not draw keypoints.
+ pose_link_color (np.array[Mx3]): Color of M links.
+ If None, do not draw links.
+ text_color (str or tuple or :obj:`Color`): Color of texts.
+ radius (int): Radius of circles.
+ thickness (int): Thickness of lines.
+ font_scale (float): Font scales of texts.
+ win_name (str): The window name.
+ show (bool): Whether to show the image. Default: False.
+ show_keypoint_weight (bool): Whether to change the transparency
+ using the predicted confidence scores of keypoints.
+ wait_time (int): Value of waitKey param.
+ Default: 0.
+ out_file (str or None): The filename to write the image.
+ Default: None.
+
+ Returns:
+ Tensor: Visualized img, only if not `show` or `out_file`.
+ """
+ img = mmcv.imread(img)
+ img = img.copy()
+
+ bbox_result = []
+ bbox_labels = []
+ pose_result = []
+ for res in result:
+ if 'bbox' in res:
+ bbox_result.append(res['bbox'])
+ bbox_labels.append(res.get('label', None))
+ pose_result.append(res['keypoints'])
+
+ if bbox_result:
+ bboxes = np.vstack(bbox_result)
+ # draw bounding boxes
+ imshow_bboxes(
+ img,
+ bboxes,
+ labels=bbox_labels,
+ colors=bbox_color,
+ text_color=text_color,
+ thickness=bbox_thickness,
+ font_scale=font_scale,
+ show=False)
+
+ if pose_result:
+ imshow_keypoints(img, pose_result, skeleton, kpt_score_thr,
+ pose_kpt_color, pose_link_color, radius,
+ thickness)
+
+ if show:
+ imshow(img, win_name, wait_time)
+
+ if out_file is not None:
+ imwrite(img, out_file)
+
+ return img
diff --git a/grounded-sam-osx/transformer_utils/mmpose/models/heads/__init__.py b/grounded-sam-osx/transformer_utils/mmpose/models/heads/__init__.py
new file mode 100644
index 0000000000000000000000000000000000000000..80c1be50a9bb91eb9e0f97c6bbcca70cf1478a87
--- /dev/null
+++ b/grounded-sam-osx/transformer_utils/mmpose/models/heads/__init__.py
@@ -0,0 +1,11 @@
+# Copyright (c) OpenMMLab. All rights reserved.
+from .topdown_heatmap_base_head import TopdownHeatmapBaseHead
+from .topdown_heatmap_multi_stage_head import (TopdownHeatmapMSMUHead,
+ TopdownHeatmapMultiStageHead)
+from .topdown_heatmap_simple_head import TopdownHeatmapSimpleHead
+from .poseur_head import Poseur_noise_sample
+
+__all__ = [
+ 'TopdownHeatmapSimpleHead', 'TopdownHeatmapMultiStageHead',
+ 'TopdownHeatmapMSMUHead', 'TopdownHeatmapBaseHead',
+]
diff --git a/grounded-sam-osx/transformer_utils/mmpose/models/heads/poseur_head.py b/grounded-sam-osx/transformer_utils/mmpose/models/heads/poseur_head.py
new file mode 100644
index 0000000000000000000000000000000000000000..d01232247db1d687144d8fff2a3b226dd66fdcf5
--- /dev/null
+++ b/grounded-sam-osx/transformer_utils/mmpose/models/heads/poseur_head.py
@@ -0,0 +1,759 @@
+import numpy as np
+import torch
+import torch.nn as nn
+import copy
+import math
+import warnings
+from mmcv.cnn import build_upsample_layer, Linear, bias_init_with_prob, constant_init, normal_init
+import torch.nn.functional as F
+from mmcv.cnn import normal_init
+
+from mmpose.core.evaluation import (keypoint_pck_accuracy,
+ keypoints_from_regression)
+from mmpose.core.post_processing import fliplr_regression
+from mmpose.models.builder import build_loss, HEADS, build_transformer
+from mmpose.core.evaluation import pose_pck_accuracy
+from mmpose.models.utils.transformer import inverse_sigmoid
+from mmcv.cnn import Conv2d, build_activation_layer
+from mmcv.cnn.bricks.transformer import Linear, FFN, build_positional_encoding
+from mmcv.cnn import ConvModule
+import torch.distributions as distributions
+from .rle_regression_head import nets, nett, RealNVP, nets3d, nett3d
+from easydict import EasyDict
+from mmpose.models.losses.regression_loss import L1Loss
+from mmpose.models.losses.rle_loss import RLELoss_poseur, RLEOHKMLoss
+from config import cfg
+from utils.human_models import smpl_x
+from torch.distributions.utils import lazy_property
+
+from torch.distributions import MultivariateNormal
+
+
+def fliplr_rle_regression(regression,
+ regression_score,
+ flip_pairs,
+ center_mode='static',
+ center_x=0.5,
+ center_index=0):
+ """Flip human joints horizontally.
+
+ Note:
+ batch_size: N
+ num_keypoint: K
+ Args:
+ regression (np.ndarray([..., K, C])): Coordinates of keypoints, where K
+ is the joint number and C is the dimension. Example shapes are:
+ - [N, K, C]: a batch of keypoints where N is the batch size.
+ - [N, T, K, C]: a batch of pose sequences, where T is the frame
+ number.
+ flip_pairs (list[tuple()]): Pairs of keypoints which are mirrored
+ (for example, left ear -- right ear).
+ center_mode (str): The mode to set the center location on the x-axis
+ to flip around. Options are:
+ - static: use a static x value (see center_x also)
+ - root: use a root joint (see center_index also)
+ center_x (float): Set the x-axis location of the flip center. Only used
+ when center_mode=static.
+ center_index (int): Set the index of the root joint, whose x location
+ will be used as the flip center. Only used when center_mode=root.
+
+ Returns:
+ tuple: Flipped human joints.
+
+ - regression_flipped (np.ndarray([..., K, C])): Flipped joints.
+ """
+ assert regression.ndim >= 2, f'Invalid pose shape {regression.shape}'
+
+ allowed_center_mode = {'static', 'root'}
+ assert center_mode in allowed_center_mode, 'Get invalid center_mode ' \
+ f'{center_mode}, allowed choices are {allowed_center_mode}'
+
+ if center_mode == 'static':
+ x_c = center_x
+ elif center_mode == 'root':
+ assert regression.shape[-2] > center_index
+ x_c = regression[..., center_index:center_index + 1, 0]
+
+ regression_flipped = regression.copy()
+ regression_score_flipped = regression_score.copy()
+
+ # Swap left-right parts
+ for left, right in flip_pairs:
+ regression_flipped[..., left, :] = regression[..., right, :]
+ regression_flipped[..., right, :] = regression[..., left, :]
+ regression_score_flipped[..., left, :] = regression_score[..., right, :]
+ regression_score_flipped[..., right, :] = regression_score[..., left, :]
+
+ # Flip horizontally
+ regression_flipped[..., 0] = x_c * 2 - regression_flipped[..., 0]
+ return regression_flipped, regression_score_flipped
+
+
+class Linear_with_norm(nn.Module):
+ def __init__(self, in_channel, out_channel, bias=True, norm=True):
+ super(Linear_with_norm, self).__init__()
+ self.bias = bias
+ self.norm = norm
+ self.linear = nn.Linear(in_channel, out_channel, bias)
+ nn.init.xavier_uniform_(self.linear.weight, gain=0.01)
+
+ def forward(self, x):
+ y = x.matmul(self.linear.weight.t())
+
+ if self.norm:
+ x_norm = torch.norm(x, dim=-1, keepdim=True)
+ y = y / x_norm
+
+ if self.bias:
+ y = y + self.linear.bias
+ return y
+
+def deepapply(obj, fn):
+ r"""Applies `fn` to all tensors referenced in `obj`"""
+
+ if torch.is_tensor(obj):
+ obj = fn(obj)
+ elif isinstance(obj, dict):
+ for key, value in obj.items():
+ obj[key] = deepapply(value, fn)
+ elif isinstance(obj, list):
+ for i, value in enumerate(obj):
+ obj[i] = deepapply(value, fn)
+ elif isinstance(obj, tuple):
+ obj = tuple(
+ deepapply(value, fn)
+ for value in obj
+ )
+ elif hasattr(obj, '__dict__'):
+ deepapply(obj.__dict__, fn)
+
+ return obj
+
+
+__init__ = MultivariateNormal.__init__
+
+
+def init(self, *args, **kwargs):
+ __init__(self, *args, **kwargs)
+
+ self.__class__ = type(
+ self.__class__.__name__,
+ (self.__class__, nn.Module),
+ {},
+ )
+
+ nn.Module.__init__(self)
+
+
+MultivariateNormal.__init__ = init
+MultivariateNormal._apply = deepapply
+
+
+@HEADS.register_module()
+class Poseur_noise_sample(nn.Module):
+ """
+ rle loss for transformer_utils
+ """
+
+ def __init__(self,
+ in_channels,
+ num_queries=17,
+ num_reg_fcs=2,
+ positional_encoding=dict(
+ type='SinePositionalEncoding',
+ num_feats=128,
+ normalize=True),
+ transformer=None,
+ with_box_refine=False,
+ as_two_stage=False,
+ heatmap_size=[64, 48],
+ num_joints=17,
+ loss_coord_enc=None,
+ loss_coord_dec=None,
+ loss_hp_keypoint=None,
+ use_heatmap_loss=True,
+ train_cfg=None,
+ test_cfg=None,
+ use_udp=False,
+ ):
+ super().__init__()
+ self.use_udp = use_udp
+ self.num_queries = num_queries
+ self.num_reg_fcs = num_reg_fcs
+ self.in_channels = in_channels
+ self.act_cfg = transformer.get('act_cfg', dict(type='ReLU', inplace=True))
+ self.activate = build_activation_layer(self.act_cfg)
+ self.positional_encoding = build_positional_encoding(positional_encoding)
+ self.with_box_refine = with_box_refine
+ self.as_two_stage = as_two_stage
+ if self.as_two_stage:
+ transformer['as_two_stage'] = self.as_two_stage
+ self.transformer = build_transformer(transformer)
+ self.embed_dims = self.transformer.embed_dims
+ assert 'num_feats' in positional_encoding
+ num_feats = positional_encoding['num_feats']
+ assert num_feats * 2 == self.embed_dims, 'embed_dims should' \
+ f' be exactly 2 times of num_feats. Found {self.embed_dims}' \
+ f' and {num_feats}.'
+
+ self.num_joints = num_joints
+ # self.num_joints = len(smpl_x.pos_joint_part['rhand'])
+ self.heatmap_size = heatmap_size
+ self.loss_coord_enc = build_loss(loss_coord_enc)
+ self.loss_coord_dec = build_loss(loss_coord_dec)
+
+ self.use_dec_rle_loss = isinstance(self.loss_coord_dec, RLELoss_poseur) or isinstance(self.loss_coord_dec,
+ RLEOHKMLoss)
+ self.use_heatmap_loss = use_heatmap_loss
+ if self.use_heatmap_loss:
+ self.loss_hp = build_loss(loss_hp_keypoint)
+
+ self.train_cfg = {} if train_cfg is None else train_cfg
+ self.test_cfg = {} if test_cfg is None else test_cfg
+
+ enc_prior = MultivariateNormal(torch.zeros(2), torch.eye(2))
+ dec_prior = MultivariateNormal(torch.zeros(2), torch.eye(2))
+ masks = torch.from_numpy(np.array([[0, 1], [1, 0]] * 3).astype(np.float32))
+
+ enc_prior3d = MultivariateNormal(torch.zeros(3), torch.eye(3))
+ dec_prior3d = MultivariateNormal(torch.zeros(3), torch.eye(3))
+ masks3d = torch.from_numpy(np.array([[0, 0, 1], [1, 1, 0]] * 3).astype(np.float32))
+
+ self.enc_flow2d = RealNVP(nets, nett, masks, enc_prior)
+ self.enc_flow3d = RealNVP(nets3d, nett3d, masks3d, enc_prior3d)
+
+ if self.use_dec_rle_loss:
+ self.dec_flow2d = RealNVP(nets, nett, masks, dec_prior)
+ self.dec_flow3d = RealNVP(nets3d, nett3d, masks3d, dec_prior3d)
+
+ self._init_layers()
+
+ def _init_layers(self):
+ """Initialize classification branch and regression branch of head."""
+
+ fc_coord_branch = []
+ for _ in range(self.num_reg_fcs):
+ fc_coord_branch.append(Linear(self.embed_dims, self.embed_dims))
+ fc_coord_branch.append(nn.ReLU())
+ fc_coord_branch.append(Linear(self.embed_dims, 3))
+ fc_coord_branch = nn.Sequential(*fc_coord_branch)
+
+ if self.use_dec_rle_loss:
+ fc_sigma_branch = []
+ for _ in range(self.num_reg_fcs):
+ fc_sigma_branch.append(Linear(self.embed_dims, self.embed_dims))
+ fc_sigma_branch.append(Linear_with_norm(self.embed_dims, 3, norm=False))
+ fc_sigma_branch = nn.Sequential(*fc_sigma_branch)
+
+ def _get_clones(module, N):
+ return nn.ModuleList([copy.deepcopy(module) for i in range(N)])
+
+ num_pred = self.transformer.decoder.num_layers
+
+ if self.with_box_refine:
+ self.fc_coord_branches = _get_clones(fc_coord_branch, num_pred)
+ self.fc_coord_output_branches = _get_clones(fc_coord_branch, num_pred)
+ if self.use_dec_rle_loss:
+ self.fc_sigma_branches = _get_clones(fc_sigma_branch, num_pred)
+ else:
+ self.fc_coord_branches = nn.ModuleList(
+ [fc_coord_branch for _ in range(num_pred)])
+ if isinstance(self.loss_coord_dec, RLELoss) or isinstance(self.loss_coord_dec, RLEOHKMLoss):
+ self.fc_sigma_branches = nn.ModuleList([fc_sigma_branch for _ in range(1)])
+
+ if self.as_two_stage:
+ self.query_embedding = None
+ else:
+ self.query_embedding = nn.Embedding(self.num_queries,
+ self.embed_dims * 2)
+
+ if self.use_heatmap_loss:
+ from mmcv.cnn import build_upsample_layer
+ # simplebaseline style
+ num_layers = 3
+ num_kernels = [4, 4, 4]
+ num_filters = [256, 256, 256]
+
+ layers = []
+ for i in range(num_layers):
+ kernel, padding, output_padding = \
+ self._get_deconv_cfg(num_kernels[i])
+
+ planes = num_filters[i]
+ if i == 0:
+ layers.append(
+ build_upsample_layer(
+ dict(type='deconv'),
+ in_channels=self.embed_dims,
+ out_channels=planes,
+ kernel_size=kernel,
+ stride=2,
+ padding=padding,
+ output_padding=output_padding,
+ bias=False))
+ else:
+ layers.append(
+ build_upsample_layer(
+ dict(type='deconv'),
+ in_channels=planes,
+ out_channels=planes,
+ kernel_size=kernel,
+ stride=2,
+ padding=padding,
+ output_padding=output_padding,
+ bias=False))
+
+ layers.append(nn.BatchNorm2d(planes))
+ layers.append(nn.ReLU(inplace=True))
+ self.in_channels = planes
+
+ self.deconv_layer = nn.Sequential(*layers)
+ self.final_layer = nn.Sequential(
+ ConvModule(
+ self.embed_dims,
+ self.num_joints,
+ kernel_size=1,
+ stride=1,
+ padding=0,
+ norm_cfg=None,
+ act_cfg=None,
+ inplace=False)
+ )
+
+ @staticmethod
+ def _get_deconv_cfg(deconv_kernel):
+ """Get configurations for deconv layers."""
+ if deconv_kernel == 4:
+ padding = 1
+ output_padding = 0
+ elif deconv_kernel == 3:
+ padding = 1
+ output_padding = 1
+ elif deconv_kernel == 2:
+ padding = 0
+ output_padding = 0
+ else:
+ raise ValueError(f'Not supported num_kernels ({deconv_kernel}).')
+
+ return deconv_kernel, padding, output_padding
+
+ def init_weights(self):
+ """Initialize weights of the DeformDETR head."""
+ self.transformer.init_weights()
+
+ # for m in [self.fc_coord_branches, self.fc_sigma_branches]:
+ for m in [self.fc_coord_branches]:
+ for mm in m:
+ if isinstance(mm, nn.Linear):
+ nn.init.xavier_uniform_(mm.weight, gain=0.01)
+
+ for m in [self.fc_coord_output_branches]:
+ for mm in m:
+ if isinstance(mm, nn.Linear):
+ nn.init.xavier_uniform_(mm.weight, gain=0.01)
+
+ if self.use_heatmap_loss:
+ for _, m in self.deconv_layer.named_modules():
+ if isinstance(m, nn.ConvTranspose2d):
+ normal_init(m, std=0.001)
+ elif isinstance(m, nn.BatchNorm2d):
+ constant_init(m, 1)
+ for m in self.final_layer.modules():
+ if isinstance(m, nn.Conv2d):
+ normal_init(m, std=0.001, bias=0)
+ elif isinstance(m, nn.BatchNorm2d):
+ constant_init(m, 1)
+
+ def forward(self, mlvl_feats, coord_init=None, query_init=None):
+
+ batch_size = mlvl_feats[0].size(0)
+ img_w, img_h = self.train_cfg['image_size']
+ img_masks = mlvl_feats[0].new_ones(
+ (batch_size, img_h, img_w))
+ for img_id in range(batch_size):
+ img_masks[img_id, :img_h, :img_w] = 0
+
+ mlvl_masks = []
+ mlvl_positional_encodings = []
+ for feat in mlvl_feats:
+ mlvl_masks.append(F.interpolate(img_masks[None], size=feat.shape[-2:]).to(torch.bool).squeeze(0))
+ mlvl_positional_encodings.append(
+ self.positional_encoding(mlvl_masks[-1]))
+
+ query_embeds = None
+ if not self.as_two_stage:
+ query_embeds = self.query_embedding.weight
+
+ memory, spatial_shapes, level_start_index, hs, init_reference, inter_references, \
+ enc_outputs = self.transformer(
+ mlvl_feats,
+ mlvl_masks,
+ query_embeds,
+ mlvl_positional_encodings,
+ reg_branches=self.fc_coord_branches if self.with_box_refine else None, # noqa:E501
+ cls_branches=None, # noqa:E501
+ coord_init=coord_init,
+ query_init=query_init,
+ )
+ hs = hs.permute(0, 2, 1, 3)
+ outputs_coords = []
+
+ dec_outputs = EasyDict(pred_jts=outputs_coords, feat=hs)
+
+ return enc_outputs, dec_outputs
+
+ def get_loss(self, enc_output, dec_output, coord_target, coord_target_weight, hp_target, hp_target_weight):
+ losses = dict()
+ if self.as_two_stage and enc_output is not None:
+ enc_rle_loss = self.get_enc_rle_loss(enc_output, coord_target, coord_target_weight)
+ losses.update(enc_rle_loss)
+
+ dec_rle_loss = self.get_dec_rle_loss(dec_output, coord_target, coord_target_weight)
+ losses.update(dec_rle_loss)
+
+ return losses
+
+ def get_enc_rle_loss(self, output, target, target_weight):
+ """Calculate top-down keypoint loss.
+ Note:
+ batch_size: N
+ num_keypoints: K
+ Args:
+ output (torch.Tensor[N, K, 2]): Output keypoints.
+ target (torch.Tensor[N, K, 2]): Target keypoints.
+ target_weight (torch.Tensor[N, K, 2]):
+ Weights across different joint types.
+ """
+
+ losses = dict()
+ assert not isinstance(self.loss_coord_enc, nn.Sequential)
+ assert target.dim() == 3 and target_weight.dim() == 3
+
+ BATCH_SIZE = output.sigma.size(0)
+ gt_uvd = target.reshape(output.pred_jts.shape)
+ gt_uvd_weight = target_weight.reshape(output.pred_jts.shape)
+ gt_3d_mask = gt_uvd_weight[:, :, 2].reshape(-1)
+
+ assert output.pred_jts.shape == output.sigma.shape, (output.pred_jts.shape, output.sigma.shape)
+ bar_mu = (output.pred_jts - gt_uvd) / output.sigma
+ bar_mu = bar_mu.reshape(-1, 3)
+ bar_mu_3d = bar_mu[gt_3d_mask > 0]
+ bar_mu_2d = bar_mu[gt_3d_mask < 1][:, :2]
+ # (B, K, 3)
+ log_phi_3d = self.enc_flow3d.log_prob(bar_mu_3d)
+ log_phi_2d = self.enc_flow2d.log_prob(bar_mu_2d)
+ log_phi = torch.zeros_like(bar_mu[:, 0])
+ # print(gt_3d_mask)
+ log_phi[gt_3d_mask > 0] = log_phi_3d
+ log_phi[gt_3d_mask < 1] = log_phi_2d
+ log_phi = log_phi.reshape(BATCH_SIZE, self.num_joints, 1)
+
+ output.nf_loss = torch.log(output.sigma) - log_phi
+ losses['enc_rle_loss'] = self.loss_coord_enc(output, target, target_weight)
+
+ return losses
+
+ def get_enc_rle_loss_old(self, output, target, target_weight):
+ """Calculate top-down keypoint loss.
+ Note:
+ batch_size: N
+ num_keypoints: K
+ Args:
+ output (torch.Tensor[N, K, 2]): Output keypoints.
+ target (torch.Tensor[N, K, 2]): Target keypoints.
+ target_weight (torch.Tensor[N, K, 2]):
+ Weights across different joint types.
+ """
+
+ losses = dict()
+ assert not isinstance(self.loss_coord_enc, nn.Sequential)
+ assert target.dim() == 3 and target_weight.dim() == 3
+
+ BATCH_SIZE = output.sigma.size(0)
+ gt_uv = target.reshape(output.pred_jts.shape)
+ bar_mu = (output.pred_jts - gt_uv) / output.sigma
+ # (B, K, 1)
+ log_phi = self.enc_flow.log_prob(bar_mu.reshape(-1, 2)).reshape(BATCH_SIZE, self.num_joints, 1)
+ output.nf_loss = torch.log(output.sigma) - log_phi
+ losses['enc_rle_loss'] = self.loss_coord_enc(output, target, target_weight)
+
+ return losses
+
+ def get_dec_rle_loss(self, output, target, target_weight):
+ """Calculate top-down keypoint loss.
+
+ Note:
+ batch_size: N
+ num_keypoints: K
+
+ Args:
+ output (torch.Tensor[N, K, 2]): Output keypoints.
+ target (torch.Tensor[N, K, 2]): Target keypoints.
+ target_weight (torch.Tensor[N, K, 2]):
+ Weights across different joint types.
+ """
+
+ losses = dict()
+ assert not isinstance(self.loss_coord_dec, nn.Sequential)
+ assert target.dim() == 3 and target_weight.dim() == 3
+ target = target.repeat(1, self.transformer.num_noise_sample + 1, 1)
+ target_weight = target_weight.repeat(1, self.transformer.num_noise_sample + 1, 1)
+
+ if self.with_box_refine:
+ if self.use_dec_rle_loss:
+ for i in range(len(output.pred_jts)):
+ pred_jts, sigma = output.pred_jts[i], output.sigma[i]
+ output_i = EasyDict(
+ pred_jts=pred_jts,
+ sigma=sigma
+ )
+ BATCH_SIZE = output_i.sigma.size(0)
+ gt_uvd = target.reshape(output_i.pred_jts.shape)
+ gt_uvd_weight = target_weight.reshape(pred_jts.shape)
+ gt_3d_mask = gt_uvd_weight[:, :, 2].reshape(-1)
+
+ assert pred_jts.shape == sigma.shape, (pred_jts.shape, sigma.shape)
+ bar_mu = (output_i.pred_jts - gt_uvd) / output_i.sigma
+ bar_mu = bar_mu.reshape(-1, 3)
+ bar_mu_3d = bar_mu[gt_3d_mask > 0]
+ bar_mu_2d = bar_mu[gt_3d_mask < 1][:, :2]
+ # (B, K, 3)
+ log_phi_3d = self.dec_flow3d.log_prob(bar_mu_3d)
+ log_phi_2d = self.dec_flow2d.log_prob(bar_mu_2d)
+ log_phi = torch.zeros_like(bar_mu[:, 0])
+ log_phi[gt_3d_mask > 0] = log_phi_3d
+ log_phi[gt_3d_mask < 1] = log_phi_2d
+ log_phi = log_phi.reshape(BATCH_SIZE, self.num_joints * (self.transformer.num_noise_sample + 1), 1)
+ output_i.nf_loss = torch.log(output_i.sigma) - log_phi
+ losses['dec_rle_loss_{}'.format(i)] = self.loss_coord_dec(output_i, target, target_weight)
+ else:
+ for i, pred_jts in enumerate(output.pred_jts):
+ losses['dec_rle_loss_{}'.format(i)] = self.loss_coord_dec(pred_jts, target, target_weight)
+ else:
+ if self.use_dec_rle_loss:
+ BATCH_SIZE = output.sigma.size(0)
+ gt_uv = target.reshape(output.pred_jts.shape)
+ bar_mu = (output.pred_jts - gt_uv) / output.sigma
+ # (B, K, 1)
+ log_phi = self.dec_flow.log_prob(bar_mu.reshape(-1, 2)).reshape(BATCH_SIZE, self.num_joints, 1)
+ output.nf_loss = torch.log(output.sigma) - log_phi
+ losses['dec_rle_loss'] = self.loss_coord_dec(output, target, target_weight) * 0
+ else:
+ losses['dec_rle_loss'] = self.loss_coord_dec(output.pred_jts, target + 0.5, target_weight) * 0
+
+ return losses
+
+ def get_hp_loss(self, output, target, target_weight):
+ """Calculate top-down keypoint loss.
+
+ Note:
+ batch_size: N
+ num_keypoints: K
+ heatmaps height: H
+ heatmaps weight: W
+
+ Args:
+ output (torch.Tensor[NxKxHxW]): Output heatmaps.
+ target (torch.Tensor[NxKxHxW]): Target heatmaps.
+ target_weight (torch.Tensor[NxKx1]):
+ Weights across different joint types.
+ """
+
+ losses = dict()
+
+ if isinstance(self.loss_hp, nn.Sequential):
+ if not isinstance(output, dict):
+ assert len(self.loss_hp) == output.size(0)
+ assert target.dim() == 5 and target_weight.dim() == 4
+ num_hp_layers = output.size(0)
+ for i in range(num_hp_layers):
+ target_i = target[:, i, :, :, :]
+ target_weight_i = target_weight[:, i, :, :]
+ losses['mse_loss_{}'.format(i)] = self.loss_hp[i](output[i], target_i, target_weight_i)
+ else:
+ out_hp_backbone = output['backbone']
+ num_hp_layers = out_hp_backbone.size(0)
+ for i in range(num_hp_layers):
+ target_i = target[:, i, :, :, :]
+ target_weight_i = target_weight[:, i, :, :]
+ losses['mse_loss_backbone_{}'.format(i)] = self.loss_hp[i](out_hp_backbone[i], target_i,
+ target_weight_i)
+
+ out_hp_enc = output['enc']
+ for lvl in range(len(out_hp_enc)):
+ if lvl == 2 or lvl == 5:
+ # if lvl == 5:
+ for i in range(3):
+ target_i = target[:, i + 1, :, :, :]
+ target_weight_i = target_weight[:, i + 1, :, :]
+ # losses['reg_loss'] += self.loss(output[i], target, target_weight).sum()
+ if lvl == 2:
+ loss_weight = 0.1
+ elif lvl == 5:
+ loss_weight = 1.0
+
+ losses['mse_loss_enc_layer{}_c{}'.format(lvl, i + 3)] = loss_weight * self.loss_hp[i + 1](
+ out_hp_enc[lvl][i], target_i, target_weight_i)
+ else:
+
+ assert target.dim() == 4 and target_weight.dim() == 3
+ losses['mse_loss'] = self.loss_hp(output, target, target_weight)
+
+ return losses
+
+ def get_accuracy(self, enc_output, dec_output, coord_target, coord_target_weight, hp_target, hp_target_weight):
+ """Calculate accuracy for top-down keypoint loss.
+
+ Note:
+ batch_size: N
+ num_keypoints: K
+
+ Args:
+ output (torch.Tensor[N, K, 2]): Output keypoints.
+ target (torch.Tensor[N, K, 2]): Target keypoints.
+ target_weight (torch.Tensor[N, K, 2]):
+ Weights across different joint types.
+ """
+
+ accuracy = dict()
+ # coord_output = output["coord"]
+ if self.as_two_stage and enc_output is not None:
+ coord_output = enc_output.pred_jts
+ N = coord_output.shape[0]
+
+ _, avg_acc, cnt = keypoint_pck_accuracy(
+ coord_output.detach().cpu().numpy(),
+ coord_target.detach().cpu().numpy(),
+ coord_target_weight[:, :, 0].detach().cpu().numpy() > 0,
+ thr=0.05,
+ normalize=np.ones((N, 2), dtype=np.float32))
+ accuracy['enc_coord_acc'] = avg_acc
+
+ coord_output = dec_output.pred_jts
+ if coord_output.dim() == 4:
+ coord_output = coord_output[-1]
+ N = coord_output.shape[0]
+
+ if not self.use_dec_rle_loss:
+ coord_target += 0.5
+ # self.num_joints
+ _, avg_acc, cnt = keypoint_pck_accuracy(
+ coord_output[:, :self.num_joints].detach().cpu().numpy(),
+ coord_target.detach().cpu().numpy(),
+ coord_target_weight[:, :, 0].detach().cpu().numpy() > 0,
+ thr=0.05,
+ normalize=np.ones((N, 2), dtype=np.float32))
+ accuracy['dec_coord_acc'] = avg_acc
+
+ # if self.use_heatmap_loss and self.use_multi_stage_memory:
+ # assert hp_target.dim() == 5 and hp_target_weight.dim() == 4
+ # _, avg_acc, _ = pose_pck_accuracy(
+ # hp_output_backbone[0].detach().cpu().numpy(),
+ # hp_target[:, 0, ...].detach().cpu().numpy(),
+ # hp_target_weight[:, 0,
+ # ...].detach().cpu().numpy().squeeze(-1) > 0)
+ # accuracy['hp_acc_backbone'] = float(avg_acc)
+
+ # _, avg_acc, _ = pose_pck_accuracy(
+ # hp_output_enc[-1][0].detach().cpu().numpy(),
+ # hp_target[:, 1, ...].detach().cpu().numpy(),
+ # hp_target_weight[:, 1,
+ # ...].detach().cpu().numpy().squeeze(-1) > 0)
+ # accuracy['hp_acc_enc'] = float(avg_acc)
+
+ # else:
+ if self.use_heatmap_loss:
+ hp_output = dec_output["hp"]
+ _, avg_acc, _ = pose_pck_accuracy(
+ hp_output.detach().cpu().numpy(),
+ hp_target.detach().cpu().numpy(),
+ hp_target_weight.detach().cpu().numpy().squeeze(-1) > 0)
+ accuracy['hp_acc'] = float(avg_acc)
+
+ return accuracy
+
+ def inference_model(self, x, flip_pairs=None):
+ """Inference function.
+
+ Returns:
+ output_regression (np.ndarray): Output regression.
+
+ Args:
+ x (torch.Tensor[N, K, 2]): Input features.
+ flip_pairs (None | list[tuple()):
+ Pairs of keypoints which are mirrored.
+ """
+ output_enc, output_dec = self.forward(x)
+ output_regression, output_regression_score = output_dec.pred_jts.detach().cpu().numpy(), output_dec.maxvals.detach().cpu().numpy()
+ output_sigma = output_dec.sigma.detach().cpu().numpy()
+ output_sigma = output_sigma[-1]
+ output_regression_score = np.concatenate([output_regression_score, output_sigma], axis=2)
+
+ if output_regression.ndim == 4:
+ output_regression = output_regression[-1]
+
+ if flip_pairs is not None:
+
+ output_regression, output_regression_score = fliplr_rle_regression(
+ output_regression, output_regression_score, flip_pairs)
+
+ return output_regression, output_regression_score
+
+ def decode_keypoints(self, img_metas, output_regression, output_regression_score, img_size):
+ """Decode keypoints from output regression.
+
+ Args:
+ img_metas (list(dict)): Information about data augmentation
+ By default this includes:
+ - "image_file: path to the image file
+ - "center": center of the bbox
+ - "scale": scale of the bbox
+ - "rotation": rotation of the bbox
+ - "bbox_score": score of bbox
+ output_regression (np.ndarray[N, K, 2]): model
+ predicted regression vector.
+ img_size (tuple(img_width, img_height)): model input image size.
+ """
+ batch_size = len(img_metas)
+
+ if 'bbox_id' in img_metas[0]:
+ bbox_ids = []
+ else:
+ bbox_ids = None
+
+ c = np.zeros((batch_size, 2), dtype=np.float32)
+ s = np.zeros((batch_size, 2), dtype=np.float32)
+ image_paths = []
+ score = np.ones(batch_size)
+ for i in range(batch_size):
+ c[i, :] = img_metas[i]['center']
+ s[i, :] = img_metas[i]['scale']
+ image_paths.append(img_metas[i]['image_file'])
+
+ if 'bbox_score' in img_metas[i]:
+ score[i] = np.array(img_metas[i]['bbox_score']).reshape(-1)
+
+ if bbox_ids is not None:
+ bbox_ids.append(img_metas[i]['bbox_id'])
+
+ preds, maxvals = keypoints_from_regression(output_regression, c, s,
+ img_size)
+
+ all_preds = np.zeros((batch_size, preds.shape[1], 3), dtype=np.float32)
+ all_boxes = np.zeros((batch_size, 6), dtype=np.float32)
+ all_preds[:, :, 0:2] = preds[:, :, 0:2]
+ # all_preds[:, :, 2:3] = maxvals
+ all_preds[:, :, 2:3] = output_regression_score
+ all_boxes[:, 0:2] = c[:, 0:2]
+ all_boxes[:, 2:4] = s[:, 0:2]
+ all_boxes[:, 4] = np.prod(s * 200.0, axis=1)
+ all_boxes[:, 5] = score
+
+ result = {}
+
+ result['preds'] = all_preds
+ result['boxes'] = all_boxes
+ result['image_paths'] = image_paths
+ result['bbox_ids'] = bbox_ids
+
+ return result
diff --git a/grounded-sam-osx/transformer_utils/mmpose/models/heads/rle_regression_head.py b/grounded-sam-osx/transformer_utils/mmpose/models/heads/rle_regression_head.py
new file mode 100644
index 0000000000000000000000000000000000000000..b96a19155f6ec13f86e069d75d15ea4b70f133fa
--- /dev/null
+++ b/grounded-sam-osx/transformer_utils/mmpose/models/heads/rle_regression_head.py
@@ -0,0 +1,426 @@
+import numpy as np
+import torch.nn as nn
+from mmcv.cnn import normal_init
+
+from mmpose.core.evaluation import (keypoint_pck_accuracy,
+ keypoints_from_regression)
+from mmpose.core.post_processing import fliplr_regression
+from mmpose.models.builder import HEADS, build_loss
+
+import torch
+import torch.nn as nn
+import torch.distributions as distributions
+from easydict import EasyDict
+
+def rle_fliplr_regression(regression,
+ regression_score,
+ flip_pairs,
+ center_mode='static',
+ center_x=0.5,
+ center_index=0,
+ shift=True):
+ """Flip human joints horizontally.
+
+ Note:
+ batch_size: N
+ num_keypoint: K
+ Args:
+ regression (np.ndarray([..., K, C])): Coordinates of keypoints, where K
+ is the joint number and C is the dimension. Example shapes are:
+ - [N, K, C]: a batch of keypoints where N is the batch size.
+ - [N, T, K, C]: a batch of pose sequences, where T is the frame
+ number.
+ flip_pairs (list[tuple()]): Pairs of keypoints which are mirrored
+ (for example, left ear -- right ear).
+ center_mode (str): The mode to set the center location on the x-axis
+ to flip around. Options are:
+ - static: use a static x value (see center_x also)
+ - root: use a root joint (see center_index also)
+ center_x (float): Set the x-axis location of the flip center. Only used
+ when center_mode=static.
+ center_index (int): Set the index of the root joint, whose x location
+ will be used as the flip center. Only used when center_mode=root.
+
+ Returns:
+ tuple: Flipped human joints.
+
+ - regression_flipped (np.ndarray([..., K, C])): Flipped joints.
+ """
+ assert regression.ndim >= 2, f'Invalid pose shape {regression.shape}'
+
+ # flip
+ # width_dim = 48
+ # if shift:
+ # regression[:, :, 0] = - regression[:, :, 0] - 1 / (width_dim * 4)
+ # else:
+ # regression[:, :, 0] = -1 / width_dim - regression[:, :, 0]
+
+ allowed_center_mode = {'static', 'root'}
+ assert center_mode in allowed_center_mode, 'Get invalid center_mode ' \
+ f'{center_mode}, allowed choices are {allowed_center_mode}'
+
+ if center_mode == 'static':
+ x_c = center_x
+ elif center_mode == 'root':
+ assert regression.shape[-2] > center_index
+ x_c = regression[..., center_index:center_index + 1, 0]
+
+ regression_flipped = regression.copy()
+ regression_score_flipped = regression_score.copy()
+
+ # Swap left-right parts
+ for left, right in flip_pairs:
+ regression_flipped[..., left, :] = regression[..., right, :]
+ regression_flipped[..., right, :] = regression[..., left, :]
+ regression_score_flipped[..., left, :] = regression_score[..., right, :]
+ regression_score_flipped[..., right, :] = regression_score[..., left, :]
+
+ # Flip horizontally
+ regression_flipped[..., 0] = x_c * 2 - regression_flipped[..., 0]
+ return regression_flipped, regression_score_flipped
+
+
+def nets():
+ return nn.Sequential(nn.Linear(2, 64), nn.LeakyReLU(), nn.Linear(64, 64), nn.LeakyReLU(), nn.Linear(64, 2), nn.Tanh())
+
+def nets3d():
+ return nn.Sequential(nn.Linear(3, 64), nn.LeakyReLU(), nn.Linear(64, 64), nn.LeakyReLU(), nn.Linear(64, 3), nn.Tanh())
+ # return nn.Sequential(nn.Linear(3, 256), nn.LeakyReLU(), nn.Linear(256, 2), nn.Tanh())
+
+def nett():
+ return nn.Sequential(nn.Linear(2, 64), nn.LeakyReLU(), nn.Linear(64, 64), nn.LeakyReLU(), nn.Linear(64, 2))
+
+def nett3d():
+ return nn.Sequential(nn.Linear(3, 64), nn.LeakyReLU(), nn.Linear(64, 64), nn.LeakyReLU(), nn.Linear(64, 3))
+ # return nn.Sequential(nn.Linear(3, 256), nn.LeakyReLU(), nn.Linear(256, 2))
+
+
+class Linear(nn.Module):
+ def __init__(self, in_channel, out_channel, bias=True, norm=True):
+ super(Linear, self).__init__()
+ self.bias = bias
+ self.norm = norm
+ self.linear = nn.Linear(in_channel, out_channel, bias)
+ nn.init.xavier_uniform_(self.linear.weight, gain=0.01)
+
+ def forward(self, x):
+ y = x.matmul(self.linear.weight.t())
+
+ if self.norm:
+ x_norm = torch.norm(x, dim=1, keepdim=True)
+ y = y / x_norm
+
+ if self.bias:
+ y = y + self.linear.bias
+ return y
+
+
+class RealNVP(nn.Module):
+ def __init__(self, nets, nett, mask, prior):
+ super(RealNVP, self).__init__()
+
+ self.prior = prior
+ self.register_buffer('mask', mask)
+ self.t = torch.nn.ModuleList([nett() for _ in range(len(mask))])
+ self.s = torch.nn.ModuleList([nets() for _ in range(len(mask))])
+
+ def _init(self):
+ for m in self.t:
+ for mm in m.modules():
+ if isinstance(mm, nn.Linear):
+ nn.init.xavier_uniform_(mm.weight, gain=0.01)
+ for m in self.s:
+ for mm in m.modules():
+ if isinstance(mm, nn.Linear):
+ nn.init.xavier_uniform_(mm.weight, gain=0.01)
+
+ def forward_p(self, z):
+ x = z
+ for i in range(len(self.t)):
+ x_ = x * self.mask[i]
+ s = self.s[i](x_) * (1 - self.mask[i])
+ t = self.t[i](x_) * (1 - self.mask[i])
+ x = x_ + (1 - self.mask[i]) * (x * torch.exp(s) + t)
+ return x
+
+ def backward_p(self, x):
+ log_det_J, z = x.new_zeros(x.shape[0]), x
+ for i in reversed(range(len(self.t))):
+ z_ = self.mask[i] * z
+ s = self.s[i](z_) * (1 - self.mask[i])
+ t = self.t[i](z_) * (1 - self.mask[i])
+ z = (1 - self.mask[i]) * (z - t) * torch.exp(-s) + z_
+ log_det_J -= s.sum(dim=1)
+ return z, log_det_J
+
+ def log_prob(self, x):
+ DEVICE = x.device
+ if self.prior.loc.device != DEVICE:
+ self.prior.loc = self.prior.loc.to(DEVICE)
+ self.prior.scale_tril = self.prior.scale_tril.to(DEVICE)
+ self.prior._unbroadcasted_scale_tril = self.prior._unbroadcasted_scale_tril.to(DEVICE)
+ self.prior.covariance_matrix = self.prior.covariance_matrix.to(DEVICE)
+ self.prior.precision_matrix = self.prior.precision_matrix.to(DEVICE)
+
+ z, logp = self.backward_p(x)
+ return self.prior.log_prob(z) + logp
+
+ def sample(self, batchSize):
+ z = self.prior.sample((batchSize, 1))
+ x = self.forward_p(z)
+ return x
+
+ def forward(self, x):
+ return self.log_prob(x)
+
+
+@HEADS.register_module()
+class RLERegressionHead(nn.Module):
+ """Deeppose regression head with fully connected layers.
+
+ paper ref: Alexander Toshev and Christian Szegedy,
+ ``DeepPose: Human Pose Estimation via Deep Neural Networks.''.
+
+ Args:
+ in_channels (int): Number of input channels
+ num_joints (int): Number of joints
+ loss_keypoint (dict): Config for keypoint loss. Default: None.
+ """
+
+ def __init__(self,
+ in_channels,
+ num_joints,
+ loss_keypoint=None,
+ train_cfg=None,
+ test_cfg=None):
+ super().__init__()
+
+ self.in_channels = in_channels
+ self.num_joints = num_joints
+
+ self.loss = build_loss(loss_keypoint)
+
+ self.train_cfg = {} if train_cfg is None else train_cfg
+ self.test_cfg = {} if test_cfg is None else test_cfg
+
+ # self.fc = nn.Linear(self.in_channels, self.num_joints * 2)
+ # self.avg_pool = nn.AdaptiveAvgPool2d(1)
+ # self.fcs, out_channel = self._make_fc_layer()
+
+ # self.fc_coord = Linear(self.in_channels, self.num_joints * 2)
+ # self.fc_sigma = Linear(self.in_channels, self.num_joints * 2, norm=False)
+ self.fc_coord = Linear(self.in_channels, self.num_joints * 3)
+ self.fc_sigma = Linear(self.in_channels, self.num_joints * 3, norm=False)
+
+ self.fc_layers = [self.fc_coord, self.fc_sigma]
+
+ self.share_flow = True
+
+ prior = distributions.MultivariateNormal(torch.zeros(2), torch.eye(2))
+ masks = torch.from_numpy(np.array([[0, 1], [1, 0]] * 3).astype(np.float32))
+
+ prior3d = distributions.MultivariateNormal(torch.zeros(3), torch.eye(3))
+ masks3d = torch.from_numpy(np.array([[0, 0, 1], [1, 1, 0]] * 3).astype(np.float32))
+
+ self.flow2d = RealNVP(nets, nett, masks, prior)
+ self.flow3d = RealNVP(nets3d, nett3d, masks3d, prior3d)
+
+
+ # def _make_fc_layer(self):
+ # fc_layers = []
+ # num_deconv = len(self.fc_dim)
+ # input_channel = self.feature_channel
+ # for i in range(num_deconv):
+ # if self.fc_dim[i] > 0:
+ # fc = nn.Linear(input_channel, self.fc_dim[i])
+ # bn = nn.BatchNorm1d(self.fc_dim[i])
+ # fc_layers.append(fc)
+ # fc_layers.append(bn)
+ # fc_layers.append(nn.ReLU(inplace=True))
+ # input_channel = self.fc_dim[i]
+ # else:
+ # fc_layers.append(nn.Identity())
+ #
+ # return nn.Sequential(*fc_layers), input_channel
+
+
+ def forward(self, x):
+ """Forward function."""
+ # output = self.fc(x)
+ # N, C = output.shape
+ # return output.reshape([N, C // 2, 2])
+ BATCH_SIZE = x.shape[0]
+ out_coord = self.fc_coord(x).reshape(BATCH_SIZE, self.num_joints, 3)
+ assert out_coord.shape[2] == 3
+
+ out_sigma = self.fc_sigma(x).reshape(BATCH_SIZE, self.num_joints, -1)
+
+ # (B, N, 3)
+ pred_jts = out_coord.reshape(BATCH_SIZE, self.num_joints, 3)
+ sigma = out_sigma.reshape(BATCH_SIZE, self.num_joints, -1).sigmoid() + 1e-9
+ scores = 1 - sigma
+ # (B, N, 1)
+ scores = torch.mean(scores, dim=2, keepdim=True)
+
+ output = EasyDict(
+ pred_jts=pred_jts,
+ sigma=sigma,
+ maxvals=scores.float(),
+ )
+ return output
+
+ def get_loss(self, output, target, target_weight):
+ """Calculate top-down keypoint loss.
+
+ Note:
+ batch_size: N
+ num_keypoints: K
+
+ Args:
+ output (torch.Tensor[N, K, 2]): Output keypoints.
+ target (torch.Tensor[N, K, 2]): Target keypoints.
+ target_weight (torch.Tensor[N, K, 2]):
+ Weights across different joint types.
+ """
+
+ losses = dict()
+ assert not isinstance(self.loss, nn.Sequential)
+ assert target.dim() == 3 and target_weight.dim() == 3
+
+ BATCH_SIZE = output.sigma.size(0)
+ gt_uvd = target.reshape(output.pred_jts.shape)
+ bar_mu = (output.pred_jts - gt_uvd) / output.sigma
+ # (B, K, 1)
+ log_phi = self.flow.log_prob(bar_mu.reshape(-1, 2)).reshape(BATCH_SIZE, self.num_joints, 1)
+ output.nf_loss = torch.log(output.sigma) - log_phi
+ losses['reg_loss'] = self.loss(output, target, target_weight)
+
+ return losses
+
+ def get_accuracy(self, output, target, target_weight):
+ """Calculate accuracy for top-down keypoint loss.
+
+ Note:
+ batch_size: N
+ num_keypoints: K
+
+ Args:
+ output (torch.Tensor[N, K, 2]): Output keypoints.
+ target (torch.Tensor[N, K, 2]): Target keypoints.
+ target_weight (torch.Tensor[N, K, 2]):
+ Weights across different joint types.
+ """
+
+ accuracy = dict()
+
+ N = output.pred_jts.shape[0]
+
+ _, avg_acc, cnt = keypoint_pck_accuracy(
+ output.pred_jts.detach().cpu().numpy(),
+ target.detach().cpu().numpy(),
+ target_weight[:, :, 0].detach().cpu().numpy() > 0,
+ thr=0.05,
+ normalize=np.ones((N, 2), dtype=np.float32))
+ accuracy['acc_pose'] = avg_acc
+
+ return accuracy
+
+ def inference_model(self, x, flip_pairs=None):
+ """Inference function.
+
+ Returns:
+ output_regression (np.ndarray): Output regression.
+
+ Args:
+ x (torch.Tensor[N, K, 2]): Input features.
+ flip_pairs (None | list[tuple()):
+ Pairs of keypoints which are mirrored.
+ """
+ output = self.forward(x)
+
+ if flip_pairs is not None:
+ output_regression, output_regression_score = rle_fliplr_regression(
+ output.pred_jts.detach().cpu().numpy(), output.maxvals.detach().cpu().numpy(), flip_pairs, center_x=0.0)
+ else:
+ output_regression = output.pred_jts.detach().cpu().numpy()
+ output_regression_score = output.maxvals.detach().cpu().numpy()
+
+ output_regression += 0.5
+ # output = EasyDict(
+ # preds=output_regression,
+ # maxvals=output_regression_score,
+ # )
+ return output_regression
+
+ def decode(self, img_metas, output, pixel_std=200.0, **kwargs):
+ """Decode the keypoints from output regression.
+
+ Args:
+ img_metas (list(dict)): Information about data augmentation
+ By default this includes:
+ - "image_file: path to the image file
+ - "center": center of the bbox
+ - "scale": scale of the bbox
+ - "rotation": rotation of the bbox
+ - "bbox_score": score of bbox
+ output (np.ndarray[N, K, 2]): predicted regression vector.
+ kwargs: dict contains 'img_size'.
+ img_size (tuple(img_width, img_height)): input image size.
+ """
+ batch_size = len(img_metas)
+
+ if 'bbox_id' in img_metas[0]:
+ bbox_ids = []
+ else:
+ bbox_ids = None
+
+ c = np.zeros((batch_size, 2), dtype=np.float32)
+ s = np.zeros((batch_size, 2), dtype=np.float32)
+ image_paths = []
+ score = np.ones(batch_size)
+ for i in range(batch_size):
+ c[i, :] = img_metas[i]['center']
+ s[i, :] = img_metas[i]['scale']
+ image_paths.append(img_metas[i]['image_file'])
+
+ if 'bbox_score' in img_metas[i]:
+ score[i] = np.array(img_metas[i]['bbox_score']).reshape(-1)
+ if bbox_ids is not None:
+ bbox_ids.append(img_metas[i]['bbox_id'])
+
+ preds, maxvals = keypoints_from_regression(output, c, s, kwargs['img_size'], pixel_std)
+ # maxvals = output.maxvals
+
+ all_preds = np.zeros((batch_size, preds.shape[1], 3), dtype=np.float32)
+ all_boxes = np.zeros((batch_size, 6), dtype=np.float32)
+ all_preds[:, :, 0:2] = preds[:, :, 0:2]
+ all_preds[:, :, 2:3] = maxvals
+ all_boxes[:, 0:2] = c[:, 0:2]
+ all_boxes[:, 2:4] = s[:, 0:2]
+ all_boxes[:, 4] = np.prod(s * pixel_std, axis=1)
+ all_boxes[:, 5] = score
+
+ result = {}
+ result['preds'] = all_preds
+ result['boxes'] = all_boxes
+ result['image_paths'] = image_paths
+ result['bbox_ids'] = bbox_ids
+
+ return result
+
+ def init_weights(self):
+ for m in self.fc_layers:
+ if isinstance(m, nn.Linear):
+ nn.init.xavier_uniform_(m.weight, gain=0.01)
+
+
+ # for m in self.flow.t:
+ # for mm in m.modules():
+ # if isinstance(mm, nn.Linear):
+ # nn.init.xavier_uniform_(mm.weight, gain=0.01)
+
+ # for m in self.flow.s:
+ # for mm in m.modules():
+ # if isinstance(mm, nn.Linear):
+ # nn.init.xavier_uniform_(mm.weight, gain=0.01)
+ # normal_init(self.fc, mean=0, std=0.01, bias=0)
diff --git a/grounded-sam-osx/transformer_utils/mmpose/models/heads/topdown_heatmap_base_head.py b/grounded-sam-osx/transformer_utils/mmpose/models/heads/topdown_heatmap_base_head.py
new file mode 100644
index 0000000000000000000000000000000000000000..09646ead353fb054f066b9fc6816748a43287e2c
--- /dev/null
+++ b/grounded-sam-osx/transformer_utils/mmpose/models/heads/topdown_heatmap_base_head.py
@@ -0,0 +1,120 @@
+# Copyright (c) OpenMMLab. All rights reserved.
+from abc import ABCMeta, abstractmethod
+
+import numpy as np
+import torch.nn as nn
+
+from mmpose.core.evaluation.top_down_eval import keypoints_from_heatmaps
+
+
+class TopdownHeatmapBaseHead(nn.Module):
+ """Base class for top-down heatmap heads.
+
+ All top-down heatmap heads should subclass it.
+ All subclass should overwrite:
+
+ Methods:`get_loss`, supporting to calculate loss.
+ Methods:`get_accuracy`, supporting to calculate accuracy.
+ Methods:`forward`, supporting to forward model.
+ Methods:`inference_model`, supporting to inference model.
+ """
+
+ __metaclass__ = ABCMeta
+
+ @abstractmethod
+ def get_loss(self, **kwargs):
+ """Gets the loss."""
+
+ @abstractmethod
+ def get_accuracy(self, **kwargs):
+ """Gets the accuracy."""
+
+ @abstractmethod
+ def forward(self, **kwargs):
+ """Forward function."""
+
+ @abstractmethod
+ def inference_model(self, **kwargs):
+ """Inference function."""
+
+ def decode(self, img_metas, output, **kwargs):
+ """Decode keypoints from heatmaps.
+
+ Args:
+ img_metas (list(dict)): Information about data augmentation
+ By default this includes:
+
+ - "image_file: path to the image file
+ - "center": center of the bbox
+ - "scale": scale of the bbox
+ - "rotation": rotation of the bbox
+ - "bbox_score": score of bbox
+ output (np.ndarray[N, K, H, W]): model predicted heatmaps.
+ """
+ batch_size = len(img_metas)
+
+ if 'bbox_id' in img_metas[0]:
+ bbox_ids = []
+ else:
+ bbox_ids = None
+
+ c = np.zeros((batch_size, 2), dtype=np.float32)
+ s = np.zeros((batch_size, 2), dtype=np.float32)
+ image_paths = []
+ score = np.ones(batch_size)
+ for i in range(batch_size):
+ c[i, :] = img_metas[i]['center']
+ s[i, :] = img_metas[i]['scale']
+ image_paths.append(img_metas[i]['image_file'])
+
+ if 'bbox_score' in img_metas[i]:
+ score[i] = np.array(img_metas[i]['bbox_score']).reshape(-1)
+ if bbox_ids is not None:
+ bbox_ids.append(img_metas[i]['bbox_id'])
+
+ preds, maxvals = keypoints_from_heatmaps(
+ output,
+ c,
+ s,
+ unbiased=self.test_cfg.get('unbiased_decoding', False),
+ post_process=self.test_cfg.get('post_process', 'default'),
+ kernel=self.test_cfg.get('modulate_kernel', 11),
+ valid_radius_factor=self.test_cfg.get('valid_radius_factor',
+ 0.0546875),
+ use_udp=self.test_cfg.get('use_udp', False),
+ target_type=self.test_cfg.get('target_type', 'GaussianHeatmap'))
+
+ all_preds = np.zeros((batch_size, preds.shape[1], 3), dtype=np.float32)
+ all_boxes = np.zeros((batch_size, 6), dtype=np.float32)
+ all_preds[:, :, 0:2] = preds[:, :, 0:2]
+ all_preds[:, :, 2:3] = maxvals
+ all_boxes[:, 0:2] = c[:, 0:2]
+ all_boxes[:, 2:4] = s[:, 0:2]
+ all_boxes[:, 4] = np.prod(s * 200.0, axis=1)
+ all_boxes[:, 5] = score
+
+ result = {}
+
+ result['preds'] = all_preds
+ result['boxes'] = all_boxes
+ result['image_paths'] = image_paths
+ result['bbox_ids'] = bbox_ids
+
+ return result
+
+ @staticmethod
+ def _get_deconv_cfg(deconv_kernel):
+ """Get configurations for deconv layers."""
+ if deconv_kernel == 4:
+ padding = 1
+ output_padding = 0
+ elif deconv_kernel == 3:
+ padding = 1
+ output_padding = 1
+ elif deconv_kernel == 2:
+ padding = 0
+ output_padding = 0
+ else:
+ raise ValueError(f'Not supported num_kernels ({deconv_kernel}).')
+
+ return deconv_kernel, padding, output_padding
diff --git a/grounded-sam-osx/transformer_utils/mmpose/models/heads/topdown_heatmap_multi_stage_head.py b/grounded-sam-osx/transformer_utils/mmpose/models/heads/topdown_heatmap_multi_stage_head.py
new file mode 100644
index 0000000000000000000000000000000000000000..c439f5b6332d72a66db75bf599035411c4e1e0d1
--- /dev/null
+++ b/grounded-sam-osx/transformer_utils/mmpose/models/heads/topdown_heatmap_multi_stage_head.py
@@ -0,0 +1,572 @@
+# Copyright (c) OpenMMLab. All rights reserved.
+import copy as cp
+
+import torch.nn as nn
+from mmcv.cnn import (ConvModule, DepthwiseSeparableConvModule, Linear,
+ build_activation_layer, build_conv_layer,
+ build_norm_layer, build_upsample_layer, constant_init,
+ kaiming_init, normal_init)
+
+from mmpose.core.evaluation import pose_pck_accuracy
+from mmpose.core.post_processing import flip_back
+from mmpose.models.builder import build_loss
+from ..builder import HEADS
+from .topdown_heatmap_base_head import TopdownHeatmapBaseHead
+
+
+@HEADS.register_module()
+class TopdownHeatmapMultiStageHead(TopdownHeatmapBaseHead):
+ """Top-down heatmap multi-stage head.
+
+ TopdownHeatmapMultiStageHead is consisted of multiple branches,
+ each of which has num_deconv_layers(>=0) number of deconv layers
+ and a simple conv2d layer.
+
+ Args:
+ in_channels (int): Number of input channels.
+ out_channels (int): Number of output channels.
+ num_stages (int): Number of stages.
+ num_deconv_layers (int): Number of deconv layers.
+ num_deconv_layers should >= 0. Note that 0 means
+ no deconv layers.
+ num_deconv_filters (list|tuple): Number of filters.
+ If num_deconv_layers > 0, the length of
+ num_deconv_kernels (list|tuple): Kernel sizes.
+ loss_keypoint (dict): Config for keypoint loss. Default: None.
+ """
+
+ def __init__(self,
+ in_channels=512,
+ out_channels=17,
+ num_stages=1,
+ num_deconv_layers=3,
+ num_deconv_filters=(256, 256, 256),
+ num_deconv_kernels=(4, 4, 4),
+ extra=None,
+ loss_keypoint=None,
+ train_cfg=None,
+ test_cfg=None):
+ super().__init__()
+
+ self.in_channels = in_channels
+ self.num_stages = num_stages
+ self.loss = build_loss(loss_keypoint)
+
+ self.train_cfg = {} if train_cfg is None else train_cfg
+ self.test_cfg = {} if test_cfg is None else test_cfg
+ self.target_type = self.test_cfg.get('target_type', 'GaussianHeatmap')
+
+ if extra is not None and not isinstance(extra, dict):
+ raise TypeError('extra should be dict or None.')
+
+ # build multi-stage deconv layers
+ self.multi_deconv_layers = nn.ModuleList([])
+ for _ in range(self.num_stages):
+ if num_deconv_layers > 0:
+ deconv_layers = self._make_deconv_layer(
+ num_deconv_layers,
+ num_deconv_filters,
+ num_deconv_kernels,
+ )
+ elif num_deconv_layers == 0:
+ deconv_layers = nn.Identity()
+ else:
+ raise ValueError(
+ f'num_deconv_layers ({num_deconv_layers}) should >= 0.')
+ self.multi_deconv_layers.append(deconv_layers)
+
+ identity_final_layer = False
+ if extra is not None and 'final_conv_kernel' in extra:
+ assert extra['final_conv_kernel'] in [0, 1, 3]
+ if extra['final_conv_kernel'] == 3:
+ padding = 1
+ elif extra['final_conv_kernel'] == 1:
+ padding = 0
+ else:
+ # 0 for Identity mapping.
+ identity_final_layer = True
+ kernel_size = extra['final_conv_kernel']
+ else:
+ kernel_size = 1
+ padding = 0
+
+ # build multi-stage final layers
+ self.multi_final_layers = nn.ModuleList([])
+ for i in range(self.num_stages):
+ if identity_final_layer:
+ final_layer = nn.Identity()
+ else:
+ final_layer = build_conv_layer(
+ cfg=dict(type='Conv2d'),
+ in_channels=num_deconv_filters[-1]
+ if num_deconv_layers > 0 else in_channels,
+ out_channels=out_channels,
+ kernel_size=kernel_size,
+ stride=1,
+ padding=padding)
+ self.multi_final_layers.append(final_layer)
+
+ def get_loss(self, output, target, target_weight):
+ """Calculate top-down keypoint loss.
+
+ Note:
+ - batch_size: N
+ - num_keypoints: K
+ - num_outputs: O
+ - heatmaps height: H
+ - heatmaps weight: W
+
+ Args:
+ output (torch.Tensor[N,K,H,W]):
+ Output heatmaps.
+ target (torch.Tensor[N,K,H,W]):
+ Target heatmaps.
+ target_weight (torch.Tensor[N,K,1]):
+ Weights across different joint types.
+ """
+
+ losses = dict()
+
+ assert isinstance(output, list)
+ assert target.dim() == 4 and target_weight.dim() == 3
+
+ if isinstance(self.loss, nn.Sequential):
+ assert len(self.loss) == len(output)
+ for i in range(len(output)):
+ target_i = target
+ target_weight_i = target_weight
+ if isinstance(self.loss, nn.Sequential):
+ loss_func = self.loss[i]
+ else:
+ loss_func = self.loss
+ loss_i = loss_func(output[i], target_i, target_weight_i)
+ if 'heatmap_loss' not in losses:
+ losses['heatmap_loss'] = loss_i
+ else:
+ losses['heatmap_loss'] += loss_i
+
+ return losses
+
+ def get_accuracy(self, output, target, target_weight):
+ """Calculate accuracy for top-down keypoint loss.
+
+ Note:
+ - batch_size: N
+ - num_keypoints: K
+ - heatmaps height: H
+ - heatmaps weight: W
+
+ Args:
+ output (torch.Tensor[N,K,H,W]): Output heatmaps.
+ target (torch.Tensor[N,K,H,W]): Target heatmaps.
+ target_weight (torch.Tensor[N,K,1]):
+ Weights across different joint types.
+ """
+
+ accuracy = dict()
+
+ if self.target_type == 'GaussianHeatmap':
+ _, avg_acc, _ = pose_pck_accuracy(
+ output[-1].detach().cpu().numpy(),
+ target.detach().cpu().numpy(),
+ target_weight.detach().cpu().numpy().squeeze(-1) > 0)
+ accuracy['acc_pose'] = float(avg_acc)
+
+ return accuracy
+
+ def forward(self, x):
+ """Forward function.
+
+ Returns:
+ out (list[Tensor]): a list of heatmaps from multiple stages.
+ """
+ out = []
+ assert isinstance(x, list)
+ for i in range(self.num_stages):
+ y = self.multi_deconv_layers[i](x[i])
+ y = self.multi_final_layers[i](y)
+ out.append(y)
+ return out
+
+ def inference_model(self, x, flip_pairs=None):
+ """Inference function.
+
+ Returns:
+ output_heatmap (np.ndarray): Output heatmaps.
+
+ Args:
+ x (List[torch.Tensor[NxKxHxW]]): Input features.
+ flip_pairs (None | list[tuple()):
+ Pairs of keypoints which are mirrored.
+ """
+ output = self.forward(x)
+ assert isinstance(output, list)
+ output = output[-1]
+
+ if flip_pairs is not None:
+ # perform flip
+ output_heatmap = flip_back(
+ output.detach().cpu().numpy(),
+ flip_pairs,
+ target_type=self.target_type)
+ # feature is not aligned, shift flipped heatmap for higher accuracy
+ if self.test_cfg.get('shift_heatmap', False):
+ output_heatmap[:, :, :, 1:] = output_heatmap[:, :, :, :-1]
+ else:
+ output_heatmap = output.detach().cpu().numpy()
+
+ return output_heatmap
+
+ def _make_deconv_layer(self, num_layers, num_filters, num_kernels):
+ """Make deconv layers."""
+ if num_layers != len(num_filters):
+ error_msg = f'num_layers({num_layers}) ' \
+ f'!= length of num_filters({len(num_filters)})'
+ raise ValueError(error_msg)
+ if num_layers != len(num_kernels):
+ error_msg = f'num_layers({num_layers}) ' \
+ f'!= length of num_kernels({len(num_kernels)})'
+ raise ValueError(error_msg)
+
+ layers = []
+ for i in range(num_layers):
+ kernel, padding, output_padding = \
+ self._get_deconv_cfg(num_kernels[i])
+
+ planes = num_filters[i]
+ layers.append(
+ build_upsample_layer(
+ dict(type='deconv'),
+ in_channels=self.in_channels,
+ out_channels=planes,
+ kernel_size=kernel,
+ stride=2,
+ padding=padding,
+ output_padding=output_padding,
+ bias=False))
+ layers.append(nn.BatchNorm2d(planes))
+ layers.append(nn.ReLU(inplace=True))
+ self.in_channels = planes
+
+ return nn.Sequential(*layers)
+
+ def init_weights(self):
+ """Initialize model weights."""
+ for _, m in self.multi_deconv_layers.named_modules():
+ if isinstance(m, nn.ConvTranspose2d):
+ normal_init(m, std=0.001)
+ elif isinstance(m, nn.BatchNorm2d):
+ constant_init(m, 1)
+ for m in self.multi_final_layers.modules():
+ if isinstance(m, nn.Conv2d):
+ normal_init(m, std=0.001, bias=0)
+
+
+class PredictHeatmap(nn.Module):
+ """Predict the heat map for an input feature.
+
+ Args:
+ unit_channels (int): Number of input channels.
+ out_channels (int): Number of output channels.
+ out_shape (tuple): Shape of the output heatmap.
+ use_prm (bool): Whether to use pose refine machine. Default: False.
+ norm_cfg (dict): dictionary to construct and config norm layer.
+ Default: dict(type='BN')
+ """
+
+ def __init__(self,
+ unit_channels,
+ out_channels,
+ out_shape,
+ use_prm=False,
+ norm_cfg=dict(type='BN')):
+ # Protect mutable default arguments
+ norm_cfg = cp.deepcopy(norm_cfg)
+ super().__init__()
+ self.unit_channels = unit_channels
+ self.out_channels = out_channels
+ self.out_shape = out_shape
+ self.use_prm = use_prm
+ if use_prm:
+ self.prm = PRM(out_channels, norm_cfg=norm_cfg)
+ self.conv_layers = nn.Sequential(
+ ConvModule(
+ unit_channels,
+ unit_channels,
+ kernel_size=1,
+ stride=1,
+ padding=0,
+ norm_cfg=norm_cfg,
+ inplace=False),
+ ConvModule(
+ unit_channels,
+ out_channels,
+ kernel_size=3,
+ stride=1,
+ padding=1,
+ norm_cfg=norm_cfg,
+ act_cfg=None,
+ inplace=False))
+
+ def forward(self, feature):
+ feature = self.conv_layers(feature)
+ output = nn.functional.interpolate(
+ feature, size=self.out_shape, mode='bilinear', align_corners=True)
+ if self.use_prm:
+ output = self.prm(output)
+ return output
+
+
+class PRM(nn.Module):
+ """Pose Refine Machine.
+
+ Please refer to "Learning Delicate Local Representations
+ for Multi-Person Pose Estimation" (ECCV 2020).
+
+ Args:
+ out_channels (int): Channel number of the output. Equals to
+ the number of key points.
+ norm_cfg (dict): dictionary to construct and config norm layer.
+ Default: dict(type='BN')
+ """
+
+ def __init__(self, out_channels, norm_cfg=dict(type='BN')):
+ # Protect mutable default arguments
+ norm_cfg = cp.deepcopy(norm_cfg)
+ super().__init__()
+ self.out_channels = out_channels
+ self.global_pooling = nn.AdaptiveAvgPool2d((1, 1))
+ self.middle_path = nn.Sequential(
+ Linear(self.out_channels, self.out_channels),
+ build_norm_layer(dict(type='BN1d'), out_channels)[1],
+ build_activation_layer(dict(type='ReLU')),
+ Linear(self.out_channels, self.out_channels),
+ build_norm_layer(dict(type='BN1d'), out_channels)[1],
+ build_activation_layer(dict(type='ReLU')),
+ build_activation_layer(dict(type='Sigmoid')))
+
+ self.bottom_path = nn.Sequential(
+ ConvModule(
+ self.out_channels,
+ self.out_channels,
+ kernel_size=1,
+ stride=1,
+ padding=0,
+ norm_cfg=norm_cfg,
+ inplace=False),
+ DepthwiseSeparableConvModule(
+ self.out_channels,
+ 1,
+ kernel_size=9,
+ stride=1,
+ padding=4,
+ norm_cfg=norm_cfg,
+ inplace=False), build_activation_layer(dict(type='Sigmoid')))
+ self.conv_bn_relu_prm_1 = ConvModule(
+ self.out_channels,
+ self.out_channels,
+ kernel_size=3,
+ stride=1,
+ padding=1,
+ norm_cfg=norm_cfg,
+ inplace=False)
+
+ def forward(self, x):
+ out = self.conv_bn_relu_prm_1(x)
+ out_1 = out
+
+ out_2 = self.global_pooling(out_1)
+ out_2 = out_2.view(out_2.size(0), -1)
+ out_2 = self.middle_path(out_2)
+ out_2 = out_2.unsqueeze(2)
+ out_2 = out_2.unsqueeze(3)
+
+ out_3 = self.bottom_path(out_1)
+ out = out_1 * (1 + out_2 * out_3)
+
+ return out
+
+
+@HEADS.register_module()
+class TopdownHeatmapMSMUHead(TopdownHeatmapBaseHead):
+ """Heads for multi-stage multi-unit heads used in Multi-Stage Pose
+ estimation Network (MSPN), and Residual Steps Networks (RSN).
+
+ Args:
+ unit_channels (int): Number of input channels.
+ out_channels (int): Number of output channels.
+ out_shape (tuple): Shape of the output heatmap.
+ num_stages (int): Number of stages.
+ num_units (int): Number of units in each stage.
+ use_prm (bool): Whether to use pose refine machine (PRM).
+ Default: False.
+ norm_cfg (dict): dictionary to construct and config norm layer.
+ Default: dict(type='BN')
+ loss_keypoint (dict): Config for keypoint loss. Default: None.
+ """
+
+ def __init__(self,
+ out_shape,
+ unit_channels=256,
+ out_channels=17,
+ num_stages=4,
+ num_units=4,
+ use_prm=False,
+ norm_cfg=dict(type='BN'),
+ loss_keypoint=None,
+ train_cfg=None,
+ test_cfg=None):
+ # Protect mutable default arguments
+ norm_cfg = cp.deepcopy(norm_cfg)
+ super().__init__()
+
+ self.train_cfg = {} if train_cfg is None else train_cfg
+ self.test_cfg = {} if test_cfg is None else test_cfg
+ self.target_type = self.test_cfg.get('target_type', 'GaussianHeatmap')
+
+ self.out_shape = out_shape
+ self.unit_channels = unit_channels
+ self.out_channels = out_channels
+ self.num_stages = num_stages
+ self.num_units = num_units
+
+ self.loss = build_loss(loss_keypoint)
+
+ self.predict_layers = nn.ModuleList([])
+ for i in range(self.num_stages):
+ for j in range(self.num_units):
+ self.predict_layers.append(
+ PredictHeatmap(
+ unit_channels,
+ out_channels,
+ out_shape,
+ use_prm,
+ norm_cfg=norm_cfg))
+
+ def get_loss(self, output, target, target_weight):
+ """Calculate top-down keypoint loss.
+
+ Note:
+ - batch_size: N
+ - num_keypoints: K
+ - num_outputs: O
+ - heatmaps height: H
+ - heatmaps weight: W
+
+ Args:
+ output (torch.Tensor[N,O,K,H,W]): Output heatmaps.
+ target (torch.Tensor[N,O,K,H,W]): Target heatmaps.
+ target_weight (torch.Tensor[N,O,K,1]):
+ Weights across different joint types.
+ """
+
+ losses = dict()
+
+ assert isinstance(output, list)
+ assert target.dim() == 5 and target_weight.dim() == 4
+ assert target.size(1) == len(output)
+
+ if isinstance(self.loss, nn.Sequential):
+ assert len(self.loss) == len(output)
+ for i in range(len(output)):
+ target_i = target[:, i, :, :, :]
+ target_weight_i = target_weight[:, i, :, :]
+
+ if isinstance(self.loss, nn.Sequential):
+ loss_func = self.loss[i]
+ else:
+ loss_func = self.loss
+
+ loss_i = loss_func(output[i], target_i, target_weight_i)
+ if 'heatmap_loss' not in losses:
+ losses['heatmap_loss'] = loss_i
+ else:
+ losses['heatmap_loss'] += loss_i
+
+ return losses
+
+ def get_accuracy(self, output, target, target_weight):
+ """Calculate accuracy for top-down keypoint loss.
+
+ Note:
+ - batch_size: N
+ - num_keypoints: K
+ - heatmaps height: H
+ - heatmaps weight: W
+
+ Args:
+ output (torch.Tensor[N,K,H,W]): Output heatmaps.
+ target (torch.Tensor[N,K,H,W]): Target heatmaps.
+ target_weight (torch.Tensor[N,K,1]):
+ Weights across different joint types.
+ """
+
+ accuracy = dict()
+
+ if self.target_type == 'GaussianHeatmap':
+ assert isinstance(output, list)
+ assert target.dim() == 5 and target_weight.dim() == 4
+ _, avg_acc, _ = pose_pck_accuracy(
+ output[-1].detach().cpu().numpy(),
+ target[:, -1, ...].detach().cpu().numpy(),
+ target_weight[:, -1,
+ ...].detach().cpu().numpy().squeeze(-1) > 0)
+ accuracy['acc_pose'] = float(avg_acc)
+
+ return accuracy
+
+ def forward(self, x):
+ """Forward function.
+
+ Returns:
+ out (list[Tensor]): a list of heatmaps from multiple stages
+ and units.
+ """
+ out = []
+ assert isinstance(x, list)
+ assert len(x) == self.num_stages
+ assert isinstance(x[0], list)
+ assert len(x[0]) == self.num_units
+ assert x[0][0].shape[1] == self.unit_channels
+ for i in range(self.num_stages):
+ for j in range(self.num_units):
+ y = self.predict_layers[i * self.num_units + j](x[i][j])
+ out.append(y)
+
+ return out
+
+ def inference_model(self, x, flip_pairs=None):
+ """Inference function.
+
+ Returns:
+ output_heatmap (np.ndarray): Output heatmaps.
+
+ Args:
+ x (list[torch.Tensor[N,K,H,W]]): Input features.
+ flip_pairs (None | list[tuple]):
+ Pairs of keypoints which are mirrored.
+ """
+ output = self.forward(x)
+ assert isinstance(output, list)
+ output = output[-1]
+ if flip_pairs is not None:
+ output_heatmap = flip_back(
+ output.detach().cpu().numpy(),
+ flip_pairs,
+ target_type=self.target_type)
+ # feature is not aligned, shift flipped heatmap for higher accuracy
+ if self.test_cfg.get('shift_heatmap', False):
+ output_heatmap[:, :, :, 1:] = output_heatmap[:, :, :, :-1]
+ else:
+ output_heatmap = output.detach().cpu().numpy()
+ return output_heatmap
+
+ def init_weights(self):
+ """Initialize model weights."""
+ for m in self.predict_layers.modules():
+ if isinstance(m, nn.Conv2d):
+ kaiming_init(m)
+ elif isinstance(m, nn.BatchNorm2d):
+ constant_init(m, 1)
+ elif isinstance(m, nn.Linear):
+ normal_init(m, std=0.01)
diff --git a/grounded-sam-osx/transformer_utils/mmpose/models/heads/topdown_heatmap_simple_head.py b/grounded-sam-osx/transformer_utils/mmpose/models/heads/topdown_heatmap_simple_head.py
new file mode 100644
index 0000000000000000000000000000000000000000..5ddc058d5634a5c63970a1efb8eaa66b158da1ec
--- /dev/null
+++ b/grounded-sam-osx/transformer_utils/mmpose/models/heads/topdown_heatmap_simple_head.py
@@ -0,0 +1,339 @@
+# Copyright (c) OpenMMLab. All rights reserved.
+import torch
+import torch.nn as nn
+from mmcv.cnn import (build_conv_layer, build_norm_layer, build_upsample_layer,
+ constant_init, normal_init)
+
+from mmpose.core.evaluation import pose_pck_accuracy
+from mmpose.core.post_processing import flip_back
+from mmpose.models.builder import build_loss
+from mmpose.models.utils.ops import resize
+from ..builder import HEADS
+from .topdown_heatmap_base_head import TopdownHeatmapBaseHead
+
+
+@HEADS.register_module()
+class TopdownHeatmapSimpleHead(TopdownHeatmapBaseHead):
+ """Top-down heatmap simple head. paper ref: Bin Xiao et al. ``Simple
+ Baselines for Human Pose Estimation and Tracking``.
+
+ TopdownHeatmapSimpleHead is consisted of (>=0) number of deconv layers
+ and a simple conv2d layer.
+
+ Args:
+ in_channels (int): Number of input channels
+ out_channels (int): Number of output channels
+ num_deconv_layers (int): Number of deconv layers.
+ num_deconv_layers should >= 0. Note that 0 means
+ no deconv layers.
+ num_deconv_filters (list|tuple): Number of filters.
+ If num_deconv_layers > 0, the length of
+ num_deconv_kernels (list|tuple): Kernel sizes.
+ in_index (int|Sequence[int]): Input feature index. Default: 0
+ input_transform (str|None): Transformation type of input features.
+ Options: 'resize_concat', 'multiple_select', None.
+ Default: None.
+
+ - 'resize_concat': Multiple feature maps will be resized to the
+ same size as the first one and then concat together.
+ Usually used in FCN head of HRNet.
+ - 'multiple_select': Multiple feature maps will be bundle into
+ a list and passed into decode head.
+ - None: Only one select feature map is allowed.
+ align_corners (bool): align_corners argument of F.interpolate.
+ Default: False.
+ loss_keypoint (dict): Config for keypoint loss. Default: None.
+ """
+
+ def __init__(self,
+ in_channels,
+ out_channels,
+ num_deconv_layers=3,
+ num_deconv_filters=(256, 256, 256),
+ num_deconv_kernels=(4, 4, 4),
+ extra=None,
+ in_index=0,
+ input_transform=None,
+ align_corners=False,
+ loss_keypoint=None,
+ train_cfg=None,
+ test_cfg=None):
+ super().__init__()
+
+ self.in_channels = in_channels
+ self.loss = build_loss(loss_keypoint)
+
+ self.train_cfg = {} if train_cfg is None else train_cfg
+ self.test_cfg = {} if test_cfg is None else test_cfg
+ self.target_type = self.test_cfg.get('target_type', 'GaussianHeatmap')
+
+ self._init_inputs(in_channels, in_index, input_transform)
+ self.in_index = in_index
+ self.align_corners = align_corners
+
+ if extra is not None and not isinstance(extra, dict):
+ raise TypeError('extra should be dict or None.')
+
+ if num_deconv_layers > 0:
+ self.deconv_layers = self._make_deconv_layer(
+ num_deconv_layers,
+ num_deconv_filters,
+ num_deconv_kernels,
+ )
+ elif num_deconv_layers == 0:
+ self.deconv_layers = nn.Identity()
+ else:
+ raise ValueError(
+ f'num_deconv_layers ({num_deconv_layers}) should >= 0.')
+
+ identity_final_layer = False
+ if extra is not None and 'final_conv_kernel' in extra:
+ assert extra['final_conv_kernel'] in [0, 1, 3]
+ if extra['final_conv_kernel'] == 3:
+ padding = 1
+ elif extra['final_conv_kernel'] == 1:
+ padding = 0
+ else:
+ # 0 for Identity mapping.
+ identity_final_layer = True
+ kernel_size = extra['final_conv_kernel']
+ else:
+ kernel_size = 1
+ padding = 0
+
+ if identity_final_layer:
+ self.final_layer = nn.Identity()
+ else:
+ conv_channels = num_deconv_filters[
+ -1] if num_deconv_layers > 0 else self.in_channels
+
+ layers = []
+ if extra is not None:
+ num_conv_layers = extra.get('num_conv_layers', 0)
+ num_conv_kernels = extra.get('num_conv_kernels',
+ [1] * num_conv_layers)
+
+ for i in range(num_conv_layers):
+ layers.append(
+ build_conv_layer(
+ dict(type='Conv2d'),
+ in_channels=conv_channels,
+ out_channels=conv_channels,
+ kernel_size=num_conv_kernels[i],
+ stride=1,
+ padding=(num_conv_kernels[i] - 1) // 2))
+ layers.append(
+ build_norm_layer(dict(type='BN'), conv_channels)[1])
+ layers.append(nn.ReLU(inplace=True))
+
+ layers.append(
+ build_conv_layer(
+ cfg=dict(type='Conv2d'),
+ in_channels=conv_channels,
+ out_channels=out_channels,
+ kernel_size=kernel_size,
+ stride=1,
+ padding=padding))
+
+ if len(layers) > 1:
+ self.final_layer = nn.Sequential(*layers)
+ else:
+ self.final_layer = layers[0]
+
+ def get_loss(self, output, target, target_weight):
+ """Calculate top-down keypoint loss.
+
+ Note:
+ - batch_size: N
+ - num_keypoints: K
+ - heatmaps height: H
+ - heatmaps weight: W
+
+ Args:
+ output (torch.Tensor[N,K,H,W]): Output heatmaps.
+ target (torch.Tensor[N,K,H,W]): Target heatmaps.
+ target_weight (torch.Tensor[N,K,1]):
+ Weights across different joint types.
+ """
+
+ losses = dict()
+
+ assert not isinstance(self.loss, nn.Sequential)
+ assert target.dim() == 4 and target_weight.dim() == 3
+ losses['heatmap_loss'] = self.loss(output, target, target_weight)
+
+ return losses
+
+ def get_accuracy(self, output, target, target_weight):
+ """Calculate accuracy for top-down keypoint loss.
+
+ Note:
+ - batch_size: N
+ - num_keypoints: K
+ - heatmaps height: H
+ - heatmaps weight: W
+
+ Args:
+ output (torch.Tensor[N,K,H,W]): Output heatmaps.
+ target (torch.Tensor[N,K,H,W]): Target heatmaps.
+ target_weight (torch.Tensor[N,K,1]):
+ Weights across different joint types.
+ """
+
+ accuracy = dict()
+
+ if self.target_type == 'GaussianHeatmap':
+ _, avg_acc, _ = pose_pck_accuracy(
+ output.detach().cpu().numpy(),
+ target.detach().cpu().numpy(),
+ target_weight.detach().cpu().numpy().squeeze(-1) > 0)
+ accuracy['acc_pose'] = float(avg_acc)
+
+ return accuracy
+
+ def forward(self, x):
+ """Forward function."""
+ x = self._transform_inputs(x)
+ x = self.deconv_layers(x)
+ x = self.final_layer(x)
+ return x
+
+ def inference_model(self, x, flip_pairs=None):
+ """Inference function.
+
+ Returns:
+ output_heatmap (np.ndarray): Output heatmaps.
+
+ Args:
+ x (torch.Tensor[N,K,H,W]): Input features.
+ flip_pairs (None | list[tuple]):
+ Pairs of keypoints which are mirrored.
+ """
+ output = self.forward(x)
+
+ if flip_pairs is not None:
+ output_heatmap = flip_back(
+ output.detach().cpu().numpy(),
+ flip_pairs,
+ target_type=self.target_type)
+ # feature is not aligned, shift flipped heatmap for higher accuracy
+ if self.test_cfg.get('shift_heatmap', False):
+ output_heatmap[:, :, :, 1:] = output_heatmap[:, :, :, :-1]
+ else:
+ output_heatmap = output.detach().cpu().numpy()
+ return output_heatmap
+
+ def _init_inputs(self, in_channels, in_index, input_transform):
+ """Check and initialize input transforms.
+
+ The in_channels, in_index and input_transform must match.
+ Specifically, when input_transform is None, only single feature map
+ will be selected. So in_channels and in_index must be of type int.
+ When input_transform is not None, in_channels and in_index must be
+ list or tuple, with the same length.
+
+ Args:
+ in_channels (int|Sequence[int]): Input channels.
+ in_index (int|Sequence[int]): Input feature index.
+ input_transform (str|None): Transformation type of input features.
+ Options: 'resize_concat', 'multiple_select', None.
+
+ - 'resize_concat': Multiple feature maps will be resize to the
+ same size as first one and than concat together.
+ Usually used in FCN head of HRNet.
+ - 'multiple_select': Multiple feature maps will be bundle into
+ a list and passed into decode head.
+ - None: Only one select feature map is allowed.
+ """
+
+ if input_transform is not None:
+ assert input_transform in ['resize_concat', 'multiple_select']
+ self.input_transform = input_transform
+ self.in_index = in_index
+ if input_transform is not None:
+ assert isinstance(in_channels, (list, tuple))
+ assert isinstance(in_index, (list, tuple))
+ assert len(in_channels) == len(in_index)
+ if input_transform == 'resize_concat':
+ self.in_channels = sum(in_channels)
+ else:
+ self.in_channels = in_channels
+ else:
+ assert isinstance(in_channels, int)
+ assert isinstance(in_index, int)
+ self.in_channels = in_channels
+
+ def _transform_inputs(self, inputs):
+ """Transform inputs for decoder.
+
+ Args:
+ inputs (list[Tensor] | Tensor): multi-level img features.
+
+ Returns:
+ Tensor: The transformed inputs
+ """
+ if not isinstance(inputs, list):
+ return inputs
+
+ if self.input_transform == 'resize_concat':
+ inputs = [inputs[i] for i in self.in_index]
+ upsampled_inputs = [
+ resize(
+ input=x,
+ size=inputs[0].shape[2:],
+ mode='bilinear',
+ align_corners=self.align_corners) for x in inputs
+ ]
+ inputs = torch.cat(upsampled_inputs, dim=1)
+ elif self.input_transform == 'multiple_select':
+ inputs = [inputs[i] for i in self.in_index]
+ else:
+ inputs = inputs[self.in_index]
+
+ return inputs
+
+ def _make_deconv_layer(self, num_layers, num_filters, num_kernels):
+ """Make deconv layers."""
+ if num_layers != len(num_filters):
+ error_msg = f'num_layers({num_layers}) ' \
+ f'!= length of num_filters({len(num_filters)})'
+ raise ValueError(error_msg)
+ if num_layers != len(num_kernels):
+ error_msg = f'num_layers({num_layers}) ' \
+ f'!= length of num_kernels({len(num_kernels)})'
+ raise ValueError(error_msg)
+
+ layers = []
+ for i in range(num_layers):
+ kernel, padding, output_padding = \
+ self._get_deconv_cfg(num_kernels[i])
+
+ planes = num_filters[i]
+ layers.append(
+ build_upsample_layer(
+ dict(type='deconv'),
+ in_channels=self.in_channels,
+ out_channels=planes,
+ kernel_size=kernel,
+ stride=2,
+ padding=padding,
+ output_padding=output_padding,
+ bias=False))
+ layers.append(nn.BatchNorm2d(planes))
+ layers.append(nn.ReLU(inplace=True))
+ self.in_channels = planes
+
+ return nn.Sequential(*layers)
+
+ def init_weights(self):
+ """Initialize model weights."""
+ for _, m in self.deconv_layers.named_modules():
+ if isinstance(m, nn.ConvTranspose2d):
+ normal_init(m, std=0.001)
+ elif isinstance(m, nn.BatchNorm2d):
+ constant_init(m, 1)
+ for m in self.final_layer.modules():
+ if isinstance(m, nn.Conv2d):
+ normal_init(m, std=0.001, bias=0)
+ elif isinstance(m, nn.BatchNorm2d):
+ constant_init(m, 1)
diff --git a/grounded-sam-osx/transformer_utils/mmpose/models/losses/__init__.py b/grounded-sam-osx/transformer_utils/mmpose/models/losses/__init__.py
new file mode 100644
index 0000000000000000000000000000000000000000..6502f7b19e8ab71cbdca028cd8b14bffde24cf20
--- /dev/null
+++ b/grounded-sam-osx/transformer_utils/mmpose/models/losses/__init__.py
@@ -0,0 +1,17 @@
+# Copyright (c) OpenMMLab. All rights reserved.
+from .classfication_loss import BCELoss
+from .heatmap_loss import AdaptiveWingLoss
+from .mesh_loss import GANLoss, MeshLoss
+from .mse_loss import JointsMSELoss, JointsOHKMMSELoss
+from .multi_loss_factory import AELoss, HeatmapLoss, MultiLossFactory
+from .regression_loss import (BoneLoss, L1Loss, MPJPELoss, MSELoss, RLELoss,
+ SemiSupervisionLoss, SmoothL1Loss, SoftWingLoss,
+ WingLoss)
+from .rle_loss import RLELoss_poseur
+
+__all__ = [
+ 'JointsMSELoss', 'JointsOHKMMSELoss', 'HeatmapLoss', 'AELoss',
+ 'MultiLossFactory', 'MeshLoss', 'GANLoss', 'SmoothL1Loss', 'WingLoss',
+ 'MPJPELoss', 'MSELoss', 'L1Loss', 'BCELoss', 'BoneLoss',
+ 'SemiSupervisionLoss', 'SoftWingLoss', 'AdaptiveWingLoss', 'RLELoss'
+]
diff --git a/grounded-sam-osx/transformer_utils/mmpose/models/losses/classfication_loss.py b/grounded-sam-osx/transformer_utils/mmpose/models/losses/classfication_loss.py
new file mode 100644
index 0000000000000000000000000000000000000000..b79b69d035611f75f10e8722aaea4362659509e2
--- /dev/null
+++ b/grounded-sam-osx/transformer_utils/mmpose/models/losses/classfication_loss.py
@@ -0,0 +1,41 @@
+# Copyright (c) OpenMMLab. All rights reserved.
+import torch.nn as nn
+import torch.nn.functional as F
+
+from ..builder import LOSSES
+
+
+@LOSSES.register_module()
+class BCELoss(nn.Module):
+ """Binary Cross Entropy loss."""
+
+ def __init__(self, use_target_weight=False, loss_weight=1.):
+ super().__init__()
+ self.criterion = F.binary_cross_entropy
+ self.use_target_weight = use_target_weight
+ self.loss_weight = loss_weight
+
+ def forward(self, output, target, target_weight=None):
+ """Forward function.
+
+ Note:
+ - batch_size: N
+ - num_labels: K
+
+ Args:
+ output (torch.Tensor[N, K]): Output classification.
+ target (torch.Tensor[N, K]): Target classification.
+ target_weight (torch.Tensor[N, K] or torch.Tensor[N]):
+ Weights across different labels.
+ """
+
+ if self.use_target_weight:
+ assert target_weight is not None
+ loss = self.criterion(output, target, reduction='none')
+ if target_weight.dim() == 1:
+ target_weight = target_weight[:, None]
+ loss = (loss * target_weight).mean()
+ else:
+ loss = self.criterion(output, target)
+
+ return loss * self.loss_weight
diff --git a/grounded-sam-osx/transformer_utils/mmpose/models/losses/heatmap_loss.py b/grounded-sam-osx/transformer_utils/mmpose/models/losses/heatmap_loss.py
new file mode 100644
index 0000000000000000000000000000000000000000..9471457ca0da2d43441da1d394bc45b3e8ca3ee7
--- /dev/null
+++ b/grounded-sam-osx/transformer_utils/mmpose/models/losses/heatmap_loss.py
@@ -0,0 +1,86 @@
+# Copyright (c) OpenMMLab. All rights reserved.
+import torch
+import torch.nn as nn
+
+from ..builder import LOSSES
+
+
+@LOSSES.register_module()
+class AdaptiveWingLoss(nn.Module):
+ """Adaptive wing loss. paper ref: 'Adaptive Wing Loss for Robust Face
+ Alignment via Heatmap Regression' Wang et al. ICCV'2019.
+
+ Args:
+ alpha (float), omega (float), epsilon (float), theta (float)
+ are hyper-parameters.
+ use_target_weight (bool): Option to use weighted MSE loss.
+ Different joint types may have different target weights.
+ loss_weight (float): Weight of the loss. Default: 1.0.
+ """
+
+ def __init__(self,
+ alpha=2.1,
+ omega=14,
+ epsilon=1,
+ theta=0.5,
+ use_target_weight=False,
+ loss_weight=1.):
+ super().__init__()
+ self.alpha = float(alpha)
+ self.omega = float(omega)
+ self.epsilon = float(epsilon)
+ self.theta = float(theta)
+ self.use_target_weight = use_target_weight
+ self.loss_weight = loss_weight
+
+ def criterion(self, pred, target):
+ """Criterion of wingloss.
+
+ Note:
+ batch_size: N
+ num_keypoints: K
+
+ Args:
+ pred (torch.Tensor[NxKxHxW]): Predicted heatmaps.
+ target (torch.Tensor[NxKxHxW]): Target heatmaps.
+ """
+ H, W = pred.shape[2:4]
+ delta = (target - pred).abs()
+
+ A = self.omega * (
+ 1 / (1 + torch.pow(self.theta / self.epsilon, self.alpha - target))
+ ) * (self.alpha - target) * (torch.pow(
+ self.theta / self.epsilon,
+ self.alpha - target - 1)) * (1 / self.epsilon)
+ C = self.theta * A - self.omega * torch.log(
+ 1 + torch.pow(self.theta / self.epsilon, self.alpha - target))
+
+ losses = torch.where(
+ delta < self.theta,
+ self.omega *
+ torch.log(1 +
+ torch.pow(delta / self.epsilon, self.alpha - target)),
+ A * delta - C)
+
+ return torch.mean(losses)
+
+ def forward(self, output, target, target_weight):
+ """Forward function.
+
+ Note:
+ batch_size: N
+ num_keypoints: K
+
+ Args:
+ output (torch.Tensor[NxKxHxW]): Output heatmaps.
+ target (torch.Tensor[NxKxHxW]): Target heatmaps.
+ target_weight (torch.Tensor[NxKx1]):
+ Weights across different joint types.
+ """
+ if self.use_target_weight:
+ loss = self.criterion(output * target_weight.unsqueeze(-1),
+ target * target_weight.unsqueeze(-1))
+ else:
+ loss = self.criterion(output, target)
+
+ return loss * self.loss_weight
diff --git a/grounded-sam-osx/transformer_utils/mmpose/models/losses/mesh_loss.py b/grounded-sam-osx/transformer_utils/mmpose/models/losses/mesh_loss.py
new file mode 100644
index 0000000000000000000000000000000000000000..f9d18bd7296a189ec2f24c422cc05a19035d3224
--- /dev/null
+++ b/grounded-sam-osx/transformer_utils/mmpose/models/losses/mesh_loss.py
@@ -0,0 +1,340 @@
+# Copyright (c) OpenMMLab. All rights reserved.
+import torch
+import torch.nn as nn
+
+from ..builder import LOSSES
+from ..utils.geometry import batch_rodrigues
+
+
+def perspective_projection(points, rotation, translation, focal_length,
+ camera_center):
+ """This function computes the perspective projection of a set of 3D points.
+
+ Note:
+ - batch size: B
+ - point number: N
+
+ Args:
+ points (Tensor([B, N, 3])): A set of 3D points
+ rotation (Tensor([B, 3, 3])): Camera rotation matrix
+ translation (Tensor([B, 3])): Camera translation
+ focal_length (Tensor([B,])): Focal length
+ camera_center (Tensor([B, 2])): Camera center
+
+ Returns:
+ projected_points (Tensor([B, N, 2])): Projected 2D
+ points in image space.
+ """
+
+ batch_size = points.shape[0]
+ K = torch.zeros([batch_size, 3, 3], device=points.device)
+ K[:, 0, 0] = focal_length
+ K[:, 1, 1] = focal_length
+ K[:, 2, 2] = 1.
+ K[:, :-1, -1] = camera_center
+
+ # Transform points
+ points = torch.einsum('bij,bkj->bki', rotation, points)
+ points = points + translation.unsqueeze(1)
+
+ # Apply perspective distortion
+ projected_points = points / points[:, :, -1].unsqueeze(-1)
+
+ # Apply camera intrinsics
+ projected_points = torch.einsum('bij,bkj->bki', K, projected_points)
+ projected_points = projected_points[:, :, :-1]
+ return projected_points
+
+
+@LOSSES.register_module()
+class MeshLoss(nn.Module):
+ """Mix loss for 3D human mesh. It is composed of loss on 2D joints, 3D
+ joints, mesh vertices and smpl parameters (if any).
+
+ Args:
+ joints_2d_loss_weight (float): Weight for loss on 2D joints.
+ joints_3d_loss_weight (float): Weight for loss on 3D joints.
+ vertex_loss_weight (float): Weight for loss on 3D verteices.
+ smpl_pose_loss_weight (float): Weight for loss on SMPL
+ pose parameters.
+ smpl_beta_loss_weight (float): Weight for loss on SMPL
+ shape parameters.
+ img_res (int): Input image resolution.
+ focal_length (float): Focal length of camera model. Default=5000.
+ """
+
+ def __init__(self,
+ joints_2d_loss_weight,
+ joints_3d_loss_weight,
+ vertex_loss_weight,
+ smpl_pose_loss_weight,
+ smpl_beta_loss_weight,
+ img_res,
+ focal_length=5000):
+
+ super().__init__()
+ # Per-vertex loss on the mesh
+ self.criterion_vertex = nn.L1Loss(reduction='none')
+
+ # Joints (2D and 3D) loss
+ self.criterion_joints_2d = nn.SmoothL1Loss(reduction='none')
+ self.criterion_joints_3d = nn.SmoothL1Loss(reduction='none')
+
+ # Loss for SMPL parameter regression
+ self.criterion_regr = nn.MSELoss(reduction='none')
+
+ self.joints_2d_loss_weight = joints_2d_loss_weight
+ self.joints_3d_loss_weight = joints_3d_loss_weight
+ self.vertex_loss_weight = vertex_loss_weight
+ self.smpl_pose_loss_weight = smpl_pose_loss_weight
+ self.smpl_beta_loss_weight = smpl_beta_loss_weight
+ self.focal_length = focal_length
+ self.img_res = img_res
+
+ def joints_2d_loss(self, pred_joints_2d, gt_joints_2d, joints_2d_visible):
+ """Compute 2D reprojection loss on the joints.
+
+ The loss is weighted by joints_2d_visible.
+ """
+ conf = joints_2d_visible.float()
+ loss = (conf *
+ self.criterion_joints_2d(pred_joints_2d, gt_joints_2d)).mean()
+ return loss
+
+ def joints_3d_loss(self, pred_joints_3d, gt_joints_3d, joints_3d_visible):
+ """Compute 3D joints loss for the examples that 3D joint annotations
+ are available.
+
+ The loss is weighted by joints_3d_visible.
+ """
+ conf = joints_3d_visible.float()
+ if len(gt_joints_3d) > 0:
+ gt_pelvis = (gt_joints_3d[:, 2, :] + gt_joints_3d[:, 3, :]) / 2
+ gt_joints_3d = gt_joints_3d - gt_pelvis[:, None, :]
+ pred_pelvis = (pred_joints_3d[:, 2, :] +
+ pred_joints_3d[:, 3, :]) / 2
+ pred_joints_3d = pred_joints_3d - pred_pelvis[:, None, :]
+ return (
+ conf *
+ self.criterion_joints_3d(pred_joints_3d, gt_joints_3d)).mean()
+ return pred_joints_3d.sum() * 0
+
+ def vertex_loss(self, pred_vertices, gt_vertices, has_smpl):
+ """Compute 3D vertex loss for the examples that 3D human mesh
+ annotations are available.
+
+ The loss is weighted by the has_smpl.
+ """
+ conf = has_smpl.float()
+ loss_vertex = self.criterion_vertex(pred_vertices, gt_vertices)
+ loss_vertex = (conf[:, None, None] * loss_vertex).mean()
+ return loss_vertex
+
+ def smpl_losses(self, pred_rotmat, pred_betas, gt_pose, gt_betas,
+ has_smpl):
+ """Compute SMPL parameters loss for the examples that SMPL parameter
+ annotations are available.
+
+ The loss is weighted by has_smpl.
+ """
+ conf = has_smpl.float()
+ gt_rotmat = batch_rodrigues(gt_pose.view(-1, 3)).view(-1, 24, 3, 3)
+ loss_regr_pose = self.criterion_regr(pred_rotmat, gt_rotmat)
+ loss_regr_betas = self.criterion_regr(pred_betas, gt_betas)
+ loss_regr_pose = (conf[:, None, None, None] * loss_regr_pose).mean()
+ loss_regr_betas = (conf[:, None] * loss_regr_betas).mean()
+ return loss_regr_pose, loss_regr_betas
+
+ def project_points(self, points_3d, camera):
+ """Perform orthographic projection of 3D points using the camera
+ parameters, return projected 2D points in image plane.
+
+ Note:
+ - batch size: B
+ - point number: N
+
+ Args:
+ points_3d (Tensor([B, N, 3])): 3D points.
+ camera (Tensor([B, 3])): camera parameters with the
+ 3 channel as (scale, translation_x, translation_y)
+
+ Returns:
+ Tensor([B, N, 2]): projected 2D points \
+ in image space.
+ """
+ batch_size = points_3d.shape[0]
+ device = points_3d.device
+ cam_t = torch.stack([
+ camera[:, 1], camera[:, 2], 2 * self.focal_length /
+ (self.img_res * camera[:, 0] + 1e-9)
+ ],
+ dim=-1)
+ camera_center = camera.new_zeros([batch_size, 2])
+ rot_t = torch.eye(
+ 3, device=device,
+ dtype=points_3d.dtype).unsqueeze(0).expand(batch_size, -1, -1)
+ joints_2d = perspective_projection(
+ points_3d,
+ rotation=rot_t,
+ translation=cam_t,
+ focal_length=self.focal_length,
+ camera_center=camera_center)
+ return joints_2d
+
+ def forward(self, output, target):
+ """Forward function.
+
+ Args:
+ output (dict): dict of network predicted results.
+ Keys: 'vertices', 'joints_3d', 'camera',
+ 'pose'(optional), 'beta'(optional)
+ target (dict): dict of ground-truth labels.
+ Keys: 'vertices', 'joints_3d', 'joints_3d_visible',
+ 'joints_2d', 'joints_2d_visible', 'pose', 'beta',
+ 'has_smpl'
+
+ Returns:
+ dict: dict of losses.
+ """
+ losses = {}
+
+ # Per-vertex loss for the shape
+ pred_vertices = output['vertices']
+
+ gt_vertices = target['vertices']
+ has_smpl = target['has_smpl']
+ loss_vertex = self.vertex_loss(pred_vertices, gt_vertices, has_smpl)
+ losses['vertex_loss'] = loss_vertex * self.vertex_loss_weight
+
+ # Compute loss on SMPL parameters, if available
+ if 'pose' in output.keys() and 'beta' in output.keys():
+ pred_rotmat = output['pose']
+ pred_betas = output['beta']
+ gt_pose = target['pose']
+ gt_betas = target['beta']
+ loss_regr_pose, loss_regr_betas = self.smpl_losses(
+ pred_rotmat, pred_betas, gt_pose, gt_betas, has_smpl)
+ losses['smpl_pose_loss'] = \
+ loss_regr_pose * self.smpl_pose_loss_weight
+ losses['smpl_beta_loss'] = \
+ loss_regr_betas * self.smpl_beta_loss_weight
+
+ # Compute 3D joints loss
+ pred_joints_3d = output['joints_3d']
+ gt_joints_3d = target['joints_3d']
+ joints_3d_visible = target['joints_3d_visible']
+ loss_joints_3d = self.joints_3d_loss(pred_joints_3d, gt_joints_3d,
+ joints_3d_visible)
+ losses['joints_3d_loss'] = loss_joints_3d * self.joints_3d_loss_weight
+
+ # Compute 2D reprojection loss for the 2D joints
+ pred_camera = output['camera']
+ gt_joints_2d = target['joints_2d']
+ joints_2d_visible = target['joints_2d_visible']
+ pred_joints_2d = self.project_points(pred_joints_3d, pred_camera)
+
+ # Normalize keypoints to [-1,1]
+ # The coordinate origin of pred_joints_2d is
+ # the center of the input image.
+ pred_joints_2d = 2 * pred_joints_2d / (self.img_res - 1)
+ # The coordinate origin of gt_joints_2d is
+ # the top left corner of the input image.
+ gt_joints_2d = 2 * gt_joints_2d / (self.img_res - 1) - 1
+ loss_joints_2d = self.joints_2d_loss(pred_joints_2d, gt_joints_2d,
+ joints_2d_visible)
+ losses['joints_2d_loss'] = loss_joints_2d * self.joints_2d_loss_weight
+
+ return losses
+
+
+@LOSSES.register_module()
+class GANLoss(nn.Module):
+ """Define GAN loss.
+
+ Args:
+ gan_type (str): Support 'vanilla', 'lsgan', 'wgan', 'hinge'.
+ real_label_val (float): The value for real label. Default: 1.0.
+ fake_label_val (float): The value for fake label. Default: 0.0.
+ loss_weight (float): Loss weight. Default: 1.0.
+ Note that loss_weight is only for generators; and it is always 1.0
+ for discriminators.
+ """
+
+ def __init__(self,
+ gan_type,
+ real_label_val=1.0,
+ fake_label_val=0.0,
+ loss_weight=1.0):
+ super().__init__()
+ self.gan_type = gan_type
+ self.loss_weight = loss_weight
+ self.real_label_val = real_label_val
+ self.fake_label_val = fake_label_val
+
+ if self.gan_type == 'vanilla':
+ self.loss = nn.BCEWithLogitsLoss()
+ elif self.gan_type == 'lsgan':
+ self.loss = nn.MSELoss()
+ elif self.gan_type == 'wgan':
+ self.loss = self._wgan_loss
+ elif self.gan_type == 'hinge':
+ self.loss = nn.ReLU()
+ else:
+ raise NotImplementedError(
+ f'GAN type {self.gan_type} is not implemented.')
+
+ @staticmethod
+ def _wgan_loss(input, target):
+ """wgan loss.
+
+ Args:
+ input (Tensor): Input tensor.
+ target (bool): Target label.
+
+ Returns:
+ Tensor: wgan loss.
+ """
+ return -input.mean() if target else input.mean()
+
+ def get_target_label(self, input, target_is_real):
+ """Get target label.
+
+ Args:
+ input (Tensor): Input tensor.
+ target_is_real (bool): Whether the target is real or fake.
+
+ Returns:
+ (bool | Tensor): Target tensor. Return bool for wgan, \
+ otherwise, return Tensor.
+ """
+
+ if self.gan_type == 'wgan':
+ return target_is_real
+ target_val = (
+ self.real_label_val if target_is_real else self.fake_label_val)
+ return input.new_ones(input.size()) * target_val
+
+ def forward(self, input, target_is_real, is_disc=False):
+ """
+ Args:
+ input (Tensor): The input for the loss module, i.e., the network
+ prediction.
+ target_is_real (bool): Whether the targe is real or fake.
+ is_disc (bool): Whether the loss for discriminators or not.
+ Default: False.
+
+ Returns:
+ Tensor: GAN loss value.
+ """
+ target_label = self.get_target_label(input, target_is_real)
+ if self.gan_type == 'hinge':
+ if is_disc: # for discriminators in hinge-gan
+ input = -input if target_is_real else input
+ loss = self.loss(1 + input).mean()
+ else: # for generators in hinge-gan
+ loss = -input.mean()
+ else: # other gan types
+ loss = self.loss(input, target_label)
+
+ # loss_weight is always 1.0 for discriminators
+ return loss if is_disc else loss * self.loss_weight
diff --git a/grounded-sam-osx/transformer_utils/mmpose/models/losses/mse_loss.py b/grounded-sam-osx/transformer_utils/mmpose/models/losses/mse_loss.py
new file mode 100644
index 0000000000000000000000000000000000000000..f972efadfdfe0093c9ae1b308c6f82a9ccd72f73
--- /dev/null
+++ b/grounded-sam-osx/transformer_utils/mmpose/models/losses/mse_loss.py
@@ -0,0 +1,153 @@
+# Copyright (c) OpenMMLab. All rights reserved.
+import torch
+import torch.nn as nn
+
+from ..builder import LOSSES
+
+
+@LOSSES.register_module()
+class JointsMSELoss(nn.Module):
+ """MSE loss for heatmaps.
+
+ Args:
+ use_target_weight (bool): Option to use weighted MSE loss.
+ Different joint types may have different target weights.
+ loss_weight (float): Weight of the loss. Default: 1.0.
+ """
+
+ def __init__(self, use_target_weight=False, loss_weight=1.):
+ super().__init__()
+ self.criterion = nn.MSELoss()
+ self.use_target_weight = use_target_weight
+ self.loss_weight = loss_weight
+
+ def forward(self, output, target, target_weight):
+ """Forward function."""
+ batch_size = output.size(0)
+ num_joints = output.size(1)
+
+ heatmaps_pred = output.reshape(
+ (batch_size, num_joints, -1)).split(1, 1)
+ heatmaps_gt = target.reshape((batch_size, num_joints, -1)).split(1, 1)
+
+ loss = 0.
+
+ for idx in range(num_joints):
+ heatmap_pred = heatmaps_pred[idx].squeeze(1)
+ heatmap_gt = heatmaps_gt[idx].squeeze(1)
+ if self.use_target_weight:
+ loss += self.criterion(heatmap_pred * target_weight[:, idx],
+ heatmap_gt * target_weight[:, idx])
+ else:
+ loss += self.criterion(heatmap_pred, heatmap_gt)
+
+ return loss / num_joints * self.loss_weight
+
+
+@LOSSES.register_module()
+class CombinedTargetMSELoss(nn.Module):
+ """MSE loss for combined target.
+ CombinedTarget: The combination of classification target
+ (response map) and regression target (offset map).
+ Paper ref: Huang et al. The Devil is in the Details: Delving into
+ Unbiased Data Processing for Human Pose Estimation (CVPR 2020).
+
+ Args:
+ use_target_weight (bool): Option to use weighted MSE loss.
+ Different joint types may have different target weights.
+ loss_weight (float): Weight of the loss. Default: 1.0.
+ """
+
+ def __init__(self, use_target_weight, loss_weight=1.):
+ super().__init__()
+ self.criterion = nn.MSELoss(reduction='mean')
+ self.use_target_weight = use_target_weight
+ self.loss_weight = loss_weight
+
+ def forward(self, output, target, target_weight):
+ batch_size = output.size(0)
+ num_channels = output.size(1)
+ heatmaps_pred = output.reshape(
+ (batch_size, num_channels, -1)).split(1, 1)
+ heatmaps_gt = target.reshape(
+ (batch_size, num_channels, -1)).split(1, 1)
+ loss = 0.
+ num_joints = num_channels // 3
+ for idx in range(num_joints):
+ heatmap_pred = heatmaps_pred[idx * 3].squeeze()
+ heatmap_gt = heatmaps_gt[idx * 3].squeeze()
+ offset_x_pred = heatmaps_pred[idx * 3 + 1].squeeze()
+ offset_x_gt = heatmaps_gt[idx * 3 + 1].squeeze()
+ offset_y_pred = heatmaps_pred[idx * 3 + 2].squeeze()
+ offset_y_gt = heatmaps_gt[idx * 3 + 2].squeeze()
+ if self.use_target_weight:
+ heatmap_pred = heatmap_pred * target_weight[:, idx]
+ heatmap_gt = heatmap_gt * target_weight[:, idx]
+ # classification loss
+ loss += 0.5 * self.criterion(heatmap_pred, heatmap_gt)
+ # regression loss
+ loss += 0.5 * self.criterion(heatmap_gt * offset_x_pred,
+ heatmap_gt * offset_x_gt)
+ loss += 0.5 * self.criterion(heatmap_gt * offset_y_pred,
+ heatmap_gt * offset_y_gt)
+ return loss / num_joints * self.loss_weight
+
+
+@LOSSES.register_module()
+class JointsOHKMMSELoss(nn.Module):
+ """MSE loss with online hard keypoint mining.
+
+ Args:
+ use_target_weight (bool): Option to use weighted MSE loss.
+ Different joint types may have different target weights.
+ topk (int): Only top k joint losses are kept.
+ loss_weight (float): Weight of the loss. Default: 1.0.
+ """
+
+ def __init__(self, use_target_weight=False, topk=8, loss_weight=1.):
+ super().__init__()
+ assert topk > 0
+ self.criterion = nn.MSELoss(reduction='none')
+ self.use_target_weight = use_target_weight
+ self.topk = topk
+ self.loss_weight = loss_weight
+
+ def _ohkm(self, loss):
+ """Online hard keypoint mining."""
+ ohkm_loss = 0.
+ N = len(loss)
+ for i in range(N):
+ sub_loss = loss[i]
+ _, topk_idx = torch.topk(
+ sub_loss, k=self.topk, dim=0, sorted=False)
+ tmp_loss = torch.gather(sub_loss, 0, topk_idx)
+ ohkm_loss += torch.sum(tmp_loss) / self.topk
+ ohkm_loss /= N
+ return ohkm_loss
+
+ def forward(self, output, target, target_weight):
+ """Forward function."""
+ batch_size = output.size(0)
+ num_joints = output.size(1)
+ if num_joints < self.topk:
+ raise ValueError(f'topk ({self.topk}) should not '
+ f'larger than num_joints ({num_joints}).')
+ heatmaps_pred = output.reshape(
+ (batch_size, num_joints, -1)).split(1, 1)
+ heatmaps_gt = target.reshape((batch_size, num_joints, -1)).split(1, 1)
+
+ losses = []
+ for idx in range(num_joints):
+ heatmap_pred = heatmaps_pred[idx].squeeze(1)
+ heatmap_gt = heatmaps_gt[idx].squeeze(1)
+ if self.use_target_weight:
+ losses.append(
+ self.criterion(heatmap_pred * target_weight[:, idx],
+ heatmap_gt * target_weight[:, idx]))
+ else:
+ losses.append(self.criterion(heatmap_pred, heatmap_gt))
+
+ losses = [loss.mean(dim=1).unsqueeze(dim=1) for loss in losses]
+ losses = torch.cat(losses, dim=1)
+
+ return self._ohkm(losses) * self.loss_weight
diff --git a/grounded-sam-osx/transformer_utils/mmpose/models/losses/multi_loss_factory.py b/grounded-sam-osx/transformer_utils/mmpose/models/losses/multi_loss_factory.py
new file mode 100644
index 0000000000000000000000000000000000000000..65f90a761d0e5f94309023288f0d3ec848ec82dd
--- /dev/null
+++ b/grounded-sam-osx/transformer_utils/mmpose/models/losses/multi_loss_factory.py
@@ -0,0 +1,281 @@
+# ------------------------------------------------------------------------------
+# Adapted from https://github.com/HRNet/HigherHRNet-Human-Pose-Estimation
+# Original licence: Copyright (c) Microsoft, under the MIT License.
+# ------------------------------------------------------------------------------
+
+import torch
+import torch.nn as nn
+
+from ..builder import LOSSES
+
+
+def _make_input(t, requires_grad=False, device=torch.device('cpu')):
+ """Make zero inputs for AE loss.
+
+ Args:
+ t (torch.Tensor): input
+ requires_grad (bool): Option to use requires_grad.
+ device: torch device
+
+ Returns:
+ torch.Tensor: zero input.
+ """
+ inp = torch.autograd.Variable(t, requires_grad=requires_grad)
+ inp = inp.sum()
+ inp = inp.to(device)
+ return inp
+
+
+@LOSSES.register_module()
+class HeatmapLoss(nn.Module):
+ """Accumulate the heatmap loss for each image in the batch.
+
+ Args:
+ supervise_empty (bool): Whether to supervise empty channels.
+ """
+
+ def __init__(self, supervise_empty=True):
+ super().__init__()
+ self.supervise_empty = supervise_empty
+
+ def forward(self, pred, gt, mask):
+ """Forward function.
+
+ Note:
+ - batch_size: N
+ - heatmaps weight: W
+ - heatmaps height: H
+ - max_num_people: M
+ - num_keypoints: K
+
+ Args:
+ pred (torch.Tensor[N,K,H,W]):heatmap of output.
+ gt (torch.Tensor[N,K,H,W]): target heatmap.
+ mask (torch.Tensor[N,H,W]): mask of target.
+ """
+ assert pred.size() == gt.size(
+ ), f'pred.size() is {pred.size()}, gt.size() is {gt.size()}'
+
+ if not self.supervise_empty:
+ empty_mask = (gt.sum(dim=[2, 3], keepdim=True) > 0).float()
+ loss = ((pred - gt)**2) * empty_mask.expand_as(
+ pred) * mask[:, None, :, :].expand_as(pred)
+ else:
+ loss = ((pred - gt)**2) * mask[:, None, :, :].expand_as(pred)
+ loss = loss.mean(dim=3).mean(dim=2).mean(dim=1)
+ return loss
+
+
+@LOSSES.register_module()
+class AELoss(nn.Module):
+ """Associative Embedding loss.
+
+ `Associative Embedding: End-to-End Learning for Joint Detection and
+ Grouping `_.
+ """
+
+ def __init__(self, loss_type):
+ super().__init__()
+ self.loss_type = loss_type
+
+ def singleTagLoss(self, pred_tag, joints):
+ """Associative embedding loss for one image.
+
+ Note:
+ - heatmaps weight: W
+ - heatmaps height: H
+ - max_num_people: M
+ - num_keypoints: K
+
+ Args:
+ pred_tag (torch.Tensor[KxHxW,1]): tag of output for one image.
+ joints (torch.Tensor[M,K,2]): joints information for one image.
+ """
+ tags = []
+ pull = 0
+ for joints_per_person in joints:
+ tmp = []
+ for joint in joints_per_person:
+ if joint[1] > 0:
+ tmp.append(pred_tag[joint[0]])
+ if len(tmp) == 0:
+ continue
+ tmp = torch.stack(tmp)
+ tags.append(torch.mean(tmp, dim=0))
+ pull = pull + torch.mean((tmp - tags[-1].expand_as(tmp))**2)
+
+ num_tags = len(tags)
+ if num_tags == 0:
+ return (
+ _make_input(torch.zeros(1).float(), device=pred_tag.device),
+ _make_input(torch.zeros(1).float(), device=pred_tag.device))
+ elif num_tags == 1:
+ return (_make_input(
+ torch.zeros(1).float(), device=pred_tag.device), pull)
+
+ tags = torch.stack(tags)
+
+ size = (num_tags, num_tags)
+ A = tags.expand(*size)
+ B = A.permute(1, 0)
+
+ diff = A - B
+
+ if self.loss_type == 'exp':
+ diff = torch.pow(diff, 2)
+ push = torch.exp(-diff)
+ push = torch.sum(push) - num_tags
+ elif self.loss_type == 'max':
+ diff = 1 - torch.abs(diff)
+ push = torch.clamp(diff, min=0).sum() - num_tags
+ else:
+ raise ValueError('Unknown ae loss type')
+
+ push_loss = push / ((num_tags - 1) * num_tags) * 0.5
+ pull_loss = pull / (num_tags)
+
+ return push_loss, pull_loss
+
+ def forward(self, tags, joints):
+ """Accumulate the tag loss for each image in the batch.
+
+ Note:
+ - batch_size: N
+ - heatmaps weight: W
+ - heatmaps height: H
+ - max_num_people: M
+ - num_keypoints: K
+
+ Args:
+ tags (torch.Tensor[N,KxHxW,1]): tag channels of output.
+ joints (torch.Tensor[N,M,K,2]): joints information.
+ """
+ pushes, pulls = [], []
+ joints = joints.cpu().data.numpy()
+ batch_size = tags.size(0)
+ for i in range(batch_size):
+ push, pull = self.singleTagLoss(tags[i], joints[i])
+ pushes.append(push)
+ pulls.append(pull)
+ return torch.stack(pushes), torch.stack(pulls)
+
+
+@LOSSES.register_module()
+class MultiLossFactory(nn.Module):
+ """Loss for bottom-up models.
+
+ Args:
+ num_joints (int): Number of keypoints.
+ num_stages (int): Number of stages.
+ ae_loss_type (str): Type of ae loss.
+ with_ae_loss (list[bool]): Use ae loss or not in multi-heatmap.
+ push_loss_factor (list[float]):
+ Parameter of push loss in multi-heatmap.
+ pull_loss_factor (list[float]):
+ Parameter of pull loss in multi-heatmap.
+ with_heatmap_loss (list[bool]):
+ Use heatmap loss or not in multi-heatmap.
+ heatmaps_loss_factor (list[float]):
+ Parameter of heatmap loss in multi-heatmap.
+ supervise_empty (bool): Whether to supervise empty channels.
+ """
+
+ def __init__(self,
+ num_joints,
+ num_stages,
+ ae_loss_type,
+ with_ae_loss,
+ push_loss_factor,
+ pull_loss_factor,
+ with_heatmaps_loss,
+ heatmaps_loss_factor,
+ supervise_empty=True):
+ super().__init__()
+
+ assert isinstance(with_heatmaps_loss, (list, tuple)), \
+ 'with_heatmaps_loss should be a list or tuple'
+ assert isinstance(heatmaps_loss_factor, (list, tuple)), \
+ 'heatmaps_loss_factor should be a list or tuple'
+ assert isinstance(with_ae_loss, (list, tuple)), \
+ 'with_ae_loss should be a list or tuple'
+ assert isinstance(push_loss_factor, (list, tuple)), \
+ 'push_loss_factor should be a list or tuple'
+ assert isinstance(pull_loss_factor, (list, tuple)), \
+ 'pull_loss_factor should be a list or tuple'
+
+ self.num_joints = num_joints
+ self.num_stages = num_stages
+ self.ae_loss_type = ae_loss_type
+ self.with_ae_loss = with_ae_loss
+ self.push_loss_factor = push_loss_factor
+ self.pull_loss_factor = pull_loss_factor
+ self.with_heatmaps_loss = with_heatmaps_loss
+ self.heatmaps_loss_factor = heatmaps_loss_factor
+
+ self.heatmaps_loss = \
+ nn.ModuleList(
+ [
+ HeatmapLoss(supervise_empty)
+ if with_heatmaps_loss else None
+ for with_heatmaps_loss in self.with_heatmaps_loss
+ ]
+ )
+
+ self.ae_loss = \
+ nn.ModuleList(
+ [
+ AELoss(self.ae_loss_type) if with_ae_loss else None
+ for with_ae_loss in self.with_ae_loss
+ ]
+ )
+
+ def forward(self, outputs, heatmaps, masks, joints):
+ """Forward function to calculate losses.
+
+ Note:
+ - batch_size: N
+ - heatmaps weight: W
+ - heatmaps height: H
+ - max_num_people: M
+ - num_keypoints: K
+ - output_channel: C C=2K if use ae loss else K
+
+ Args:
+ outputs (list(torch.Tensor[N,C,H,W])): outputs of stages.
+ heatmaps (list(torch.Tensor[N,K,H,W])): target of heatmaps.
+ masks (list(torch.Tensor[N,H,W])): masks of heatmaps.
+ joints (list(torch.Tensor[N,M,K,2])): joints of ae loss.
+ """
+ heatmaps_losses = []
+ push_losses = []
+ pull_losses = []
+ for idx in range(len(outputs)):
+ offset_feat = 0
+ if self.heatmaps_loss[idx]:
+ heatmaps_pred = outputs[idx][:, :self.num_joints]
+ offset_feat = self.num_joints
+ heatmaps_loss = self.heatmaps_loss[idx](heatmaps_pred,
+ heatmaps[idx],
+ masks[idx])
+ heatmaps_loss = heatmaps_loss * self.heatmaps_loss_factor[idx]
+ heatmaps_losses.append(heatmaps_loss)
+ else:
+ heatmaps_losses.append(None)
+
+ if self.ae_loss[idx]:
+ tags_pred = outputs[idx][:, offset_feat:]
+ batch_size = tags_pred.size()[0]
+ tags_pred = tags_pred.contiguous().view(batch_size, -1, 1)
+
+ push_loss, pull_loss = self.ae_loss[idx](tags_pred,
+ joints[idx])
+ push_loss = push_loss * self.push_loss_factor[idx]
+ pull_loss = pull_loss * self.pull_loss_factor[idx]
+
+ push_losses.append(push_loss)
+ pull_losses.append(pull_loss)
+ else:
+ push_losses.append(None)
+ pull_losses.append(None)
+
+ return heatmaps_losses, push_losses, pull_losses
diff --git a/grounded-sam-osx/transformer_utils/mmpose/models/losses/regression_loss.py b/grounded-sam-osx/transformer_utils/mmpose/models/losses/regression_loss.py
new file mode 100644
index 0000000000000000000000000000000000000000..fc7aa33847d8fdc8c6e096b7e3467759024af053
--- /dev/null
+++ b/grounded-sam-osx/transformer_utils/mmpose/models/losses/regression_loss.py
@@ -0,0 +1,530 @@
+# Copyright (c) OpenMMLab. All rights reserved.
+import math
+
+import torch
+import torch.nn as nn
+import torch.nn.functional as F
+
+from ..builder import LOSSES
+from ..utils.realnvp import RealNVP
+
+
+@LOSSES.register_module()
+class RLELoss(nn.Module):
+ """RLE Loss.
+
+ `Human Pose Regression With Residual Log-Likelihood Estimation
+ arXiv: `_.
+
+ Code is modified from `the official implementation
+ `_.
+
+ Args:
+ use_target_weight (bool): Option to use weighted MSE loss.
+ Different joint types may have different target weights.
+ size_average (bool): Option to average the loss by the batch_size.
+ residual (bool): Option to add L1 loss and let the flow
+ learn the residual error distribution.
+ q_dis (string): Option for the identity Q(error) distribution,
+ Options: "laplace" or "gaussian"
+ """
+
+ def __init__(self,
+ use_target_weight=False,
+ size_average=True,
+ residual=True,
+ q_dis='laplace'):
+ super(RLELoss, self).__init__()
+ self.size_average = size_average
+ self.use_target_weight = use_target_weight
+ self.residual = residual
+ self.q_dis = q_dis
+
+ self.flow_model = RealNVP()
+
+ def forward(self, output, target, target_weight=None):
+ """Forward function.
+
+ Note:
+ - batch_size: N
+ - num_keypoints: K
+ - dimension of keypoints: D (D=2 or D=3)
+
+ Args:
+ output (torch.Tensor[N, K, D*2]): Output regression,
+ including coords and sigmas.
+ target (torch.Tensor[N, K, D]): Target regression.
+ target_weight (torch.Tensor[N, K, D]):
+ Weights across different joint types.
+ """
+ pred = output[:, :, :2]
+ sigma = output[:, :, 2:4].sigmoid()
+
+ error = (pred - target) / (sigma + 1e-9)
+ # (B, K, 2)
+ log_phi = self.flow_model.log_prob(error.reshape(-1, 2))
+ log_phi = log_phi.reshape(target.shape[0], target.shape[1], 1)
+ log_sigma = torch.log(sigma).reshape(target.shape[0], target.shape[1],
+ 2)
+ nf_loss = log_sigma - log_phi
+
+ if self.residual:
+ assert self.q_dis in ['laplace', 'gaussian', 'strict']
+ if self.q_dis == 'laplace':
+ loss_q = torch.log(sigma * 2) + torch.abs(error)
+ else:
+ loss_q = torch.log(
+ sigma * math.sqrt(2 * math.pi)) + 0.5 * error**2
+
+ loss = nf_loss + loss_q
+ else:
+ loss = nf_loss
+
+ if self.use_target_weight:
+ assert target_weight is not None
+ loss *= target_weight
+
+ if self.size_average:
+ loss /= len(loss)
+
+ return loss.sum()
+
+
+@LOSSES.register_module()
+class SmoothL1Loss(nn.Module):
+ """SmoothL1Loss loss.
+
+ Args:
+ use_target_weight (bool): Option to use weighted MSE loss.
+ Different joint types may have different target weights.
+ loss_weight (float): Weight of the loss. Default: 1.0.
+ """
+
+ def __init__(self, use_target_weight=False, loss_weight=1.):
+ super().__init__()
+ self.criterion = F.smooth_l1_loss
+ self.use_target_weight = use_target_weight
+ self.loss_weight = loss_weight
+
+ def forward(self, output, target, target_weight=None):
+ """Forward function.
+
+ Note:
+ - batch_size: N
+ - num_keypoints: K
+ - dimension of keypoints: D (D=2 or D=3)
+
+ Args:
+ output (torch.Tensor[N, K, D]): Output regression.
+ target (torch.Tensor[N, K, D]): Target regression.
+ target_weight (torch.Tensor[N, K, D]):
+ Weights across different joint types.
+ """
+ if self.use_target_weight:
+ assert target_weight is not None
+ loss = self.criterion(output * target_weight,
+ target * target_weight)
+ else:
+ loss = self.criterion(output, target)
+
+ return loss * self.loss_weight
+
+
+@LOSSES.register_module()
+class WingLoss(nn.Module):
+ """Wing Loss. paper ref: 'Wing Loss for Robust Facial Landmark Localisation
+ with Convolutional Neural Networks' Feng et al. CVPR'2018.
+
+ Args:
+ omega (float): Also referred to as width.
+ epsilon (float): Also referred to as curvature.
+ use_target_weight (bool): Option to use weighted MSE loss.
+ Different joint types may have different target weights.
+ loss_weight (float): Weight of the loss. Default: 1.0.
+ """
+
+ def __init__(self,
+ omega=10.0,
+ epsilon=2.0,
+ use_target_weight=False,
+ loss_weight=1.):
+ super().__init__()
+ self.omega = omega
+ self.epsilon = epsilon
+ self.use_target_weight = use_target_weight
+ self.loss_weight = loss_weight
+
+ # constant that smoothly links the piecewise-defined linear
+ # and nonlinear parts
+ self.C = self.omega * (1.0 - math.log(1.0 + self.omega / self.epsilon))
+
+ def criterion(self, pred, target):
+ """Criterion of wingloss.
+
+ Note:
+ - batch_size: N
+ - num_keypoints: K
+ - dimension of keypoints: D (D=2 or D=3)
+
+ Args:
+ pred (torch.Tensor[N, K, D]): Output regression.
+ target (torch.Tensor[N, K, D]): Target regression.
+ """
+ delta = (target - pred).abs()
+ losses = torch.where(
+ delta < self.omega,
+ self.omega * torch.log(1.0 + delta / self.epsilon), delta - self.C)
+ return torch.mean(torch.sum(losses, dim=[1, 2]), dim=0)
+
+ def forward(self, output, target, target_weight=None):
+ """Forward function.
+
+ Note:
+ - batch_size: N
+ - num_keypoints: K
+ - dimension of keypoints: D (D=2 or D=3)
+
+ Args:
+ output (torch.Tensor[N, K, D]): Output regression.
+ target (torch.Tensor[N, K, D]): Target regression.
+ target_weight (torch.Tensor[N,K,D]):
+ Weights across different joint types.
+ """
+ if self.use_target_weight:
+ assert target_weight is not None
+ loss = self.criterion(output * target_weight,
+ target * target_weight)
+ else:
+ loss = self.criterion(output, target)
+
+ return loss * self.loss_weight
+
+
+@LOSSES.register_module()
+class SoftWingLoss(nn.Module):
+ """Soft Wing Loss 'Structure-Coherent Deep Feature Learning for Robust Face
+ Alignment' Lin et al. TIP'2021.
+
+ loss =
+ 1. |x| , if |x| < omega1
+ 2. omega2*ln(1+|x|/epsilon) + B, if |x| >= omega1
+
+ Args:
+ omega1 (float): The first threshold.
+ omega2 (float): The second threshold.
+ epsilon (float): Also referred to as curvature.
+ use_target_weight (bool): Option to use weighted MSE loss.
+ Different joint types may have different target weights.
+ loss_weight (float): Weight of the loss. Default: 1.0.
+ """
+
+ def __init__(self,
+ omega1=2.0,
+ omega2=20.0,
+ epsilon=0.5,
+ use_target_weight=False,
+ loss_weight=1.):
+ super().__init__()
+ self.omega1 = omega1
+ self.omega2 = omega2
+ self.epsilon = epsilon
+ self.use_target_weight = use_target_weight
+ self.loss_weight = loss_weight
+
+ # constant that smoothly links the piecewise-defined linear
+ # and nonlinear parts
+ self.B = self.omega1 - self.omega2 * math.log(1.0 + self.omega1 /
+ self.epsilon)
+
+ def criterion(self, pred, target):
+ """Criterion of wingloss.
+
+ Note:
+ batch_size: N
+ num_keypoints: K
+ dimension of keypoints: D (D=2 or D=3)
+
+ Args:
+ pred (torch.Tensor[N, K, D]): Output regression.
+ target (torch.Tensor[N, K, D]): Target regression.
+ """
+ delta = (target - pred).abs()
+ losses = torch.where(
+ delta < self.omega1, delta,
+ self.omega2 * torch.log(1.0 + delta / self.epsilon) + self.B)
+ return torch.mean(torch.sum(losses, dim=[1, 2]), dim=0)
+
+ def forward(self, output, target, target_weight=None):
+ """Forward function.
+
+ Note:
+ batch_size: N
+ num_keypoints: K
+ dimension of keypoints: D (D=2 or D=3)
+
+ Args:
+ output (torch.Tensor[N, K, D]): Output regression.
+ target (torch.Tensor[N, K, D]): Target regression.
+ target_weight (torch.Tensor[N, K, D]):
+ Weights across different joint types.
+ """
+ if self.use_target_weight:
+ assert target_weight is not None
+ loss = self.criterion(output * target_weight,
+ target * target_weight)
+ else:
+ loss = self.criterion(output, target)
+
+ return loss * self.loss_weight
+
+
+@LOSSES.register_module()
+class MPJPELoss(nn.Module):
+ """MPJPE (Mean Per Joint Position Error) loss.
+
+ Args:
+ use_target_weight (bool): Option to use weighted MSE loss.
+ Different joint types may have different target weights.
+ loss_weight (float): Weight of the loss. Default: 1.0.
+ """
+
+ def __init__(self, use_target_weight=False, loss_weight=1.):
+ super().__init__()
+ self.use_target_weight = use_target_weight
+ self.loss_weight = loss_weight
+
+ def forward(self, output, target, target_weight=None):
+ """Forward function.
+
+ Note:
+ - batch_size: N
+ - num_keypoints: K
+ - dimension of keypoints: D (D=2 or D=3)
+
+ Args:
+ output (torch.Tensor[N, K, D]): Output regression.
+ target (torch.Tensor[N, K, D]): Target regression.
+ target_weight (torch.Tensor[N,K,D]):
+ Weights across different joint types.
+ """
+
+ if self.use_target_weight:
+ assert target_weight is not None
+ loss = torch.mean(
+ torch.norm((output - target) * target_weight, dim=-1))
+ else:
+ loss = torch.mean(torch.norm(output - target, dim=-1))
+
+ return loss * self.loss_weight
+
+
+@LOSSES.register_module()
+class L1Loss(nn.Module):
+ """L1Loss loss ."""
+
+ def __init__(self, use_target_weight=False, loss_weight=1.):
+ super().__init__()
+ self.criterion = F.l1_loss
+ self.use_target_weight = use_target_weight
+ self.loss_weight = loss_weight
+
+ def forward(self, output, target, target_weight=None):
+ """Forward function.
+
+ Note:
+ - batch_size: N
+ - num_keypoints: K
+
+ Args:
+ output (torch.Tensor[N, K, 2]): Output regression.
+ target (torch.Tensor[N, K, 2]): Target regression.
+ target_weight (torch.Tensor[N, K, 2]):
+ Weights across different joint types.
+ """
+ if self.use_target_weight:
+ assert target_weight is not None
+ loss = self.criterion(output * target_weight,
+ target * target_weight)
+ else:
+ loss = self.criterion(output, target)
+
+ return loss * self.loss_weight
+
+
+@LOSSES.register_module()
+class MSELoss(nn.Module):
+ """MSE loss for coordinate regression."""
+
+ def __init__(self, use_target_weight=False, loss_weight=1.):
+ super().__init__()
+ self.criterion = F.mse_loss
+ self.use_target_weight = use_target_weight
+ self.loss_weight = loss_weight
+
+ def forward(self, output, target, target_weight=None):
+ """Forward function.
+
+ Note:
+ - batch_size: N
+ - num_keypoints: K
+
+ Args:
+ output (torch.Tensor[N, K, 2]): Output regression.
+ target (torch.Tensor[N, K, 2]): Target regression.
+ target_weight (torch.Tensor[N, K, 2]):
+ Weights across different joint types.
+ """
+ if self.use_target_weight:
+ assert target_weight is not None
+ loss = self.criterion(output * target_weight,
+ target * target_weight)
+ else:
+ loss = self.criterion(output, target)
+
+ return loss * self.loss_weight
+
+
+@LOSSES.register_module()
+class BoneLoss(nn.Module):
+ """Bone length loss.
+
+ Args:
+ joint_parents (list): Indices of each joint's parent joint.
+ use_target_weight (bool): Option to use weighted bone loss.
+ Different bone types may have different target weights.
+ loss_weight (float): Weight of the loss. Default: 1.0.
+ """
+
+ def __init__(self, joint_parents, use_target_weight=False, loss_weight=1.):
+ super().__init__()
+ self.joint_parents = joint_parents
+ self.use_target_weight = use_target_weight
+ self.loss_weight = loss_weight
+
+ self.non_root_indices = []
+ for i in range(len(self.joint_parents)):
+ if i != self.joint_parents[i]:
+ self.non_root_indices.append(i)
+
+ def forward(self, output, target, target_weight=None):
+ """Forward function.
+
+ Note:
+ - batch_size: N
+ - num_keypoints: K
+ - dimension of keypoints: D (D=2 or D=3)
+
+ Args:
+ output (torch.Tensor[N, K, D]): Output regression.
+ target (torch.Tensor[N, K, D]): Target regression.
+ target_weight (torch.Tensor[N, K-1]):
+ Weights across different bone types.
+ """
+ output_bone = torch.norm(
+ output - output[:, self.joint_parents, :],
+ dim=-1)[:, self.non_root_indices]
+ target_bone = torch.norm(
+ target - target[:, self.joint_parents, :],
+ dim=-1)[:, self.non_root_indices]
+ if self.use_target_weight:
+ assert target_weight is not None
+ loss = torch.mean(
+ torch.abs((output_bone * target_weight).mean(dim=0) -
+ (target_bone * target_weight).mean(dim=0)))
+ else:
+ loss = torch.mean(
+ torch.abs(output_bone.mean(dim=0) - target_bone.mean(dim=0)))
+
+ return loss * self.loss_weight
+
+
+@LOSSES.register_module()
+class SemiSupervisionLoss(nn.Module):
+ """Semi-supervision loss for unlabeled data. It is composed of projection
+ loss and bone loss.
+
+ Paper ref: `3D human pose estimation in video with temporal convolutions
+ and semi-supervised training` Dario Pavllo et al. CVPR'2019.
+
+ Args:
+ joint_parents (list): Indices of each joint's parent joint.
+ projection_loss_weight (float): Weight for projection loss.
+ bone_loss_weight (float): Weight for bone loss.
+ warmup_iterations (int): Number of warmup iterations. In the first
+ `warmup_iterations` iterations, the model is trained only on
+ labeled data, and semi-supervision loss will be 0.
+ This is a workaround since currently we cannot access
+ epoch number in loss functions. Note that the iteration number in
+ an epoch can be changed due to different GPU numbers in multi-GPU
+ settings. So please set this parameter carefully.
+ warmup_iterations = dataset_size // samples_per_gpu // gpu_num
+ * warmup_epochs
+ """
+
+ def __init__(self,
+ joint_parents,
+ projection_loss_weight=1.,
+ bone_loss_weight=1.,
+ warmup_iterations=0):
+ super().__init__()
+ self.criterion_projection = MPJPELoss(
+ loss_weight=projection_loss_weight)
+ self.criterion_bone = BoneLoss(
+ joint_parents, loss_weight=bone_loss_weight)
+ self.warmup_iterations = warmup_iterations
+ self.num_iterations = 0
+
+ @staticmethod
+ def project_joints(x, intrinsics):
+ """Project 3D joint coordinates to 2D image plane using camera
+ intrinsic parameters.
+
+ Args:
+ x (torch.Tensor[N, K, 3]): 3D joint coordinates.
+ intrinsics (torch.Tensor[N, 4] | torch.Tensor[N, 9]): Camera
+ intrinsics: f (2), c (2), k (3), p (2).
+ """
+ while intrinsics.dim() < x.dim():
+ intrinsics.unsqueeze_(1)
+ f = intrinsics[..., :2]
+ c = intrinsics[..., 2:4]
+ _x = torch.clamp(x[:, :, :2] / x[:, :, 2:], -1, 1)
+ if intrinsics.shape[-1] == 9:
+ k = intrinsics[..., 4:7]
+ p = intrinsics[..., 7:9]
+
+ r2 = torch.sum(_x[:, :, :2]**2, dim=-1, keepdim=True)
+ radial = 1 + torch.sum(
+ k * torch.cat((r2, r2**2, r2**3), dim=-1),
+ dim=-1,
+ keepdim=True)
+ tan = torch.sum(p * _x, dim=-1, keepdim=True)
+ _x = _x * (radial + tan) + p * r2
+ _x = f * _x + c
+ return _x
+
+ def forward(self, output, target):
+ losses = dict()
+
+ self.num_iterations += 1
+ if self.num_iterations <= self.warmup_iterations:
+ return losses
+
+ labeled_pose = output['labeled_pose']
+ unlabeled_pose = output['unlabeled_pose']
+ unlabeled_traj = output['unlabeled_traj']
+ unlabeled_target_2d = target['unlabeled_target_2d']
+ intrinsics = target['intrinsics']
+
+ # projection loss
+ unlabeled_output = unlabeled_pose + unlabeled_traj
+ unlabeled_output_2d = self.project_joints(unlabeled_output, intrinsics)
+ loss_proj = self.criterion_projection(unlabeled_output_2d,
+ unlabeled_target_2d, None)
+ losses['proj_loss'] = loss_proj
+
+ # bone loss
+ loss_bone = self.criterion_bone(unlabeled_pose, labeled_pose, None)
+ losses['bone_loss'] = loss_bone
+
+ return losses
diff --git a/grounded-sam-osx/transformer_utils/mmpose/models/losses/rle_loss.py b/grounded-sam-osx/transformer_utils/mmpose/models/losses/rle_loss.py
new file mode 100644
index 0000000000000000000000000000000000000000..5973da8df59dd4804af746bd7fb83a23fbb78c35
--- /dev/null
+++ b/grounded-sam-osx/transformer_utils/mmpose/models/losses/rle_loss.py
@@ -0,0 +1,180 @@
+import math
+import mmcv
+import torch
+import torch.nn as nn
+import torch.nn.functional as F
+
+from ..builder import LOSSES
+
+
+@LOSSES.register_module()
+class RLELoss_poseur_old(nn.Module):
+ ''' RLE Regression Loss
+ '''
+
+ def __init__(self, OUTPUT_3D=False, use_target_weight=True, size_average=True):
+ super(RLELoss_poseur_old, self).__init__()
+ self.size_average = size_average
+ self.amp = 1 / math.sqrt(2 * math.pi)
+
+ def logQ(self, gt_uv, pred_jts, sigma):
+ return torch.log(sigma / self.amp) + torch.abs(gt_uv - pred_jts) / (math.sqrt(2) * sigma + 1e-9)
+
+ def forward(self, output, target_uv, target_uv_weight):
+
+ pred_jts = output.pred_jts
+ sigma = output.sigma
+ gt_uv = target_uv.reshape(pred_jts.shape)
+ gt_uv_weight = target_uv_weight.reshape(pred_jts.shape)
+
+
+
+ nf_loss = output.nf_loss * gt_uv_weight[:, :, :1]
+ # print(gt_uv.min(), gt_uv.max())
+
+ residual = True
+ if residual:
+ Q_logprob = self.logQ(gt_uv, pred_jts, sigma) * gt_uv_weight
+ loss = nf_loss + Q_logprob
+
+ if self.size_average and gt_uv_weight.sum() > 0:
+ return loss.sum() / len(loss)
+ else:
+ return loss.sum()
+
+@LOSSES.register_module()
+class RLELoss_poseur(nn.Module):
+ ''' RLE Regression Loss
+ '''
+
+ def __init__(self, OUTPUT_3D=False, use_target_weight=True, size_average=True):
+ super(RLELoss_poseur, self).__init__()
+ self.size_average = size_average
+ self.amp = 1 / math.sqrt(2 * math.pi)
+
+ def logQ(self, gt_uv, pred_jts, sigma):
+ return torch.log(sigma / self.amp) + torch.abs(gt_uv - pred_jts) / (math.sqrt(2) * sigma + 1e-9)
+
+ def forward(self, output, target_uvd, target_uvd_weight):
+
+ pred_jts = output.pred_jts
+ sigma = output.sigma
+ gt_uv = target_uvd.reshape(pred_jts.shape)
+ gt_uv_weight = target_uvd_weight.reshape(pred_jts.shape)
+
+ # nf_loss = output.nf_loss * gt_uv_weight[:, :, :1]
+ nf_loss = output.nf_loss * gt_uv_weight
+
+ residual = True
+ if residual:
+ Q_logprob = self.logQ(gt_uv, pred_jts, sigma) * gt_uv_weight
+ loss = nf_loss + Q_logprob
+
+ if self.size_average and gt_uv_weight.sum() > 0:
+ return loss.sum() / len(loss)
+ else:
+ return loss.sum()
+
+@LOSSES.register_module()
+class RLEOHKMLoss(nn.Module):
+ ''' RLE Regression Loss
+ '''
+
+ def __init__(self, OUTPUT_3D=False, use_target_weight=True, size_average=True, topk=8,
+ ori_weight = 1.0, ohkm_weight = 0.0):
+ super(RLEOHKMLoss, self).__init__()
+ self.size_average = size_average
+ self.amp = 1 / math.sqrt(2 * math.pi)
+ self.topk = topk
+ self.ori_weight = ori_weight
+ self.ohkm_weight = ohkm_weight
+ self.neg_inf = -float("Inf")
+
+ def logQ(self, gt_uv, pred_jts, sigma):
+ return torch.log(sigma / self.amp) + torch.abs(gt_uv - pred_jts) / (math.sqrt(2) * sigma + 1e-9)
+
+ def ohkm(self, loss, weight):
+ # mask = weight == 0
+ loss_value = loss.clone().detach()
+ loss_value[weight == 0] = self.neg_inf
+ _, topk_idx = torch.topk(
+ loss_value, k=self.topk, dim=1, sorted=False)
+ tmp_loss = torch.gather(loss, 1, topk_idx)
+ tmp_weight = torch.gather(weight, 1, topk_idx)
+ # tmp_loss[tmp_loss==-float("Inf")] = 0
+ tmp_loss = tmp_loss * tmp_weight
+ tmp_loss = tmp_loss.flatten(start_dim=1).sum(dim = 1)
+ # tmp_weight = tmp_weight.flatten(start_dim=1).sum(dim = 1)
+ # tmp_loss = tmp_loss / tmp_weight
+
+ return tmp_loss.mean()
+
+ def ori(self, loss, weight):
+ # mask = weight == 0
+ loss = loss * weight
+ loss = loss.flatten(start_dim=1).sum(dim = 1)
+ # weight = weight.flatten(start_dim=1).sum(dim = 1)
+
+ return loss.mean()
+
+ def forward(self, output, target_uv, target_uv_weight):
+
+ pred_jts = output.pred_jts
+ sigma = output.sigma
+ gt_uv = target_uv.reshape(pred_jts.shape)
+ gt_uv_weight = target_uv_weight.reshape(pred_jts.shape)
+
+ # gt_uv_weight = gt_uv_weight[:, :, :1]
+ nf_loss = output.nf_loss
+ q_loss = self.logQ(gt_uv, pred_jts, sigma)
+
+ # nf_loss_ohkm = self.ohkm(nf_loss, gt_uv_weight)
+ # q_loss_ohkm = self.ohkm(q_loss, gt_uv_weight)
+
+ ori_loss = nf_loss + q_loss
+ ohkm_loss = self.ohkm(ori_loss, gt_uv_weight)
+ ori_loss = self.ori(ori_loss, gt_uv_weight)
+
+ loss = self.ori_weight * ori_loss + self.ohkm_weight * ohkm_loss
+ return loss #TODO mean?
+
+
+ # nf_loss = output.nf_loss * gt_uv_weight
+
+
+ # Q_logprob = self.logQ(gt_uv, pred_jts, sigma) * gt_uv_weight
+ # loss = nf_loss + Q_logprob
+
+ # return loss.sum() / len(loss)
+
+
+@LOSSES.register_module()
+class RLELoss3D(nn.Module):
+ ''' RLE Regression Loss 3D
+ '''
+
+ def __init__(self, OUTPUT_3D=False, size_average=True):
+ super(RLELoss3D, self).__init__()
+ self.size_average = size_average
+ self.amp = 1 / math.sqrt(2 * math.pi)
+
+ def logQ(self, gt_uv, pred_jts, sigma):
+ return torch.log(sigma / self.amp) + torch.abs(gt_uv - pred_jts) / (math.sqrt(2) * sigma + 1e-9)
+
+ def forward(self, output, labels):
+ nf_loss = output.nf_loss
+ pred_jts = output.pred_jts
+ sigma = output.sigma
+ gt_uv = labels['target_uvd'].reshape(pred_jts.shape)
+ gt_uv_weight = labels['target_uvd_weight'].reshape(pred_jts.shape)
+ nf_loss = nf_loss * gt_uv_weight
+
+ residual = True
+ if residual:
+ Q_logprob = self.logQ(gt_uv, pred_jts, sigma) * gt_uv_weight
+ loss = nf_loss + Q_logprob
+
+ if self.size_average and gt_uv_weight.sum() > 0:
+ return loss.sum() / len(loss)
+ else:
+ return loss.sum()
\ No newline at end of file
diff --git a/grounded-sam-osx/transformer_utils/mmpose/models/misc/__init__.py b/grounded-sam-osx/transformer_utils/mmpose/models/misc/__init__.py
new file mode 100644
index 0000000000000000000000000000000000000000..ef101fec61e72abc0eb90266d453b5b22331378d
--- /dev/null
+++ b/grounded-sam-osx/transformer_utils/mmpose/models/misc/__init__.py
@@ -0,0 +1 @@
+# Copyright (c) OpenMMLab. All rights reserved.
diff --git a/grounded-sam-osx/transformer_utils/mmpose/models/misc/discriminator.py b/grounded-sam-osx/transformer_utils/mmpose/models/misc/discriminator.py
new file mode 100644
index 0000000000000000000000000000000000000000..712f0a8b566e3dcbc0cd13206610d3c750b942ab
--- /dev/null
+++ b/grounded-sam-osx/transformer_utils/mmpose/models/misc/discriminator.py
@@ -0,0 +1,307 @@
+# ------------------------------------------------------------------------------
+# Adapted from https://github.com/akanazawa/hmr
+# Original licence: Copyright (c) 2018 akanazawa, under the MIT License.
+# ------------------------------------------------------------------------------
+
+from abc import abstractmethod
+
+import torch
+import torch.nn as nn
+from mmcv.cnn import normal_init, xavier_init
+
+from mmpose.models.utils.geometry import batch_rodrigues
+
+
+class BaseDiscriminator(nn.Module):
+ """Base linear module for SMPL parameter discriminator.
+
+ Args:
+ fc_layers (Tuple): Tuple of neuron count,
+ such as (9, 32, 32, 1)
+ use_dropout (Tuple): Tuple of bool define use dropout or not
+ for each layer, such as (True, True, False)
+ drop_prob (Tuple): Tuple of float defined the drop prob,
+ such as (0.5, 0.5, 0)
+ use_activation(Tuple): Tuple of bool define use active function
+ or not, such as (True, True, False)
+ """
+
+ def __init__(self, fc_layers, use_dropout, drop_prob, use_activation):
+ super().__init__()
+ self.fc_layers = fc_layers
+ self.use_dropout = use_dropout
+ self.drop_prob = drop_prob
+ self.use_activation = use_activation
+ self._check()
+ self.create_layers()
+
+ def _check(self):
+ """Check input to avoid ValueError."""
+ if not isinstance(self.fc_layers, tuple):
+ raise TypeError(f'fc_layers require tuple, '
+ f'get {type(self.fc_layers)}')
+
+ if not isinstance(self.use_dropout, tuple):
+ raise TypeError(f'use_dropout require tuple, '
+ f'get {type(self.use_dropout)}')
+
+ if not isinstance(self.drop_prob, tuple):
+ raise TypeError(f'drop_prob require tuple, '
+ f'get {type(self.drop_prob)}')
+
+ if not isinstance(self.use_activation, tuple):
+ raise TypeError(f'use_activation require tuple, '
+ f'get {type(self.use_activation)}')
+
+ l_fc_layer = len(self.fc_layers)
+ l_use_drop = len(self.use_dropout)
+ l_drop_prob = len(self.drop_prob)
+ l_use_activation = len(self.use_activation)
+
+ pass_check = (
+ l_fc_layer >= 2 and l_use_drop < l_fc_layer
+ and l_drop_prob < l_fc_layer and l_use_activation < l_fc_layer
+ and l_drop_prob == l_use_drop)
+
+ if not pass_check:
+ msg = 'Wrong BaseDiscriminator parameters!'
+ raise ValueError(msg)
+
+ def create_layers(self):
+ """Create layers."""
+ l_fc_layer = len(self.fc_layers)
+ l_use_drop = len(self.use_dropout)
+ l_use_activation = len(self.use_activation)
+
+ self.fc_blocks = nn.Sequential()
+
+ for i in range(l_fc_layer - 1):
+ self.fc_blocks.add_module(
+ name=f'regressor_fc_{i}',
+ module=nn.Linear(
+ in_features=self.fc_layers[i],
+ out_features=self.fc_layers[i + 1]))
+
+ if i < l_use_activation and self.use_activation[i]:
+ self.fc_blocks.add_module(
+ name=f'regressor_af_{i}', module=nn.ReLU())
+
+ if i < l_use_drop and self.use_dropout[i]:
+ self.fc_blocks.add_module(
+ name=f'regressor_fc_dropout_{i}',
+ module=nn.Dropout(p=self.drop_prob[i]))
+
+ @abstractmethod
+ def forward(self, inputs):
+ """Forward function."""
+ msg = 'the base class [BaseDiscriminator] is not callable!'
+ raise NotImplementedError(msg)
+
+ def init_weights(self):
+ """Initialize model weights."""
+ for m in self.fc_blocks.named_modules():
+ if isinstance(m, nn.Linear):
+ xavier_init(m, gain=0.01)
+
+
+class ShapeDiscriminator(BaseDiscriminator):
+ """Discriminator for SMPL shape parameters, the inputs is (batch_size x 10)
+
+ Args:
+ fc_layers (Tuple): Tuple of neuron count, such as (10, 5, 1)
+ use_dropout (Tuple): Tuple of bool define use dropout or
+ not for each layer, such as (True, True, False)
+ drop_prob (Tuple): Tuple of float defined the drop prob,
+ such as (0.5, 0)
+ use_activation(Tuple): Tuple of bool define use active
+ function or not, such as (True, False)
+ """
+
+ def __init__(self, fc_layers, use_dropout, drop_prob, use_activation):
+ if fc_layers[-1] != 1:
+ msg = f'the neuron count of the last layer ' \
+ f'must be 1, but got {fc_layers[-1]}'
+ raise ValueError(msg)
+
+ super().__init__(fc_layers, use_dropout, drop_prob, use_activation)
+
+ def forward(self, inputs):
+ """Forward function."""
+ return self.fc_blocks(inputs)
+
+
+class PoseDiscriminator(nn.Module):
+ """Discriminator for SMPL pose parameters of each joint. It is composed of
+ discriminators for each joints. The inputs is (batch_size x joint_count x
+ 9)
+
+ Args:
+ channels (Tuple): Tuple of channel number,
+ such as (9, 32, 32, 1)
+ joint_count (int): Joint number, such as 23
+ """
+
+ def __init__(self, channels, joint_count):
+ super().__init__()
+ if channels[-1] != 1:
+ msg = f'the neuron count of the last layer ' \
+ f'must be 1, but got {channels[-1]}'
+ raise ValueError(msg)
+ self.joint_count = joint_count
+
+ self.conv_blocks = nn.Sequential()
+ len_channels = len(channels)
+ for idx in range(len_channels - 2):
+ self.conv_blocks.add_module(
+ name=f'conv_{idx}',
+ module=nn.Conv2d(
+ in_channels=channels[idx],
+ out_channels=channels[idx + 1],
+ kernel_size=1,
+ stride=1))
+
+ self.fc_layer = nn.ModuleList()
+ for idx in range(joint_count):
+ self.fc_layer.append(
+ nn.Linear(
+ in_features=channels[len_channels - 2], out_features=1))
+
+ def forward(self, inputs):
+ """Forward function.
+
+ The input is (batch_size x joint_count x 9).
+ """
+ # shape: batch_size x 9 x 1 x joint_count
+ inputs = inputs.transpose(1, 2).unsqueeze(2).contiguous()
+ # shape: batch_size x c x 1 x joint_count
+ internal_outputs = self.conv_blocks(inputs)
+ outputs = []
+ for idx in range(self.joint_count):
+ outputs.append(self.fc_layer[idx](internal_outputs[:, :, 0, idx]))
+
+ return torch.cat(outputs, 1), internal_outputs
+
+ def init_weights(self):
+ """Initialize model weights."""
+ for m in self.conv_blocks:
+ if isinstance(m, nn.Conv2d):
+ normal_init(m, std=0.001, bias=0)
+ for m in self.fc_layer.named_modules():
+ if isinstance(m, nn.Linear):
+ xavier_init(m, gain=0.01)
+
+
+class FullPoseDiscriminator(BaseDiscriminator):
+ """Discriminator for SMPL pose parameters of all joints.
+
+ Args:
+ fc_layers (Tuple): Tuple of neuron count,
+ such as (736, 1024, 1024, 1)
+ use_dropout (Tuple): Tuple of bool define use dropout or not
+ for each layer, such as (True, True, False)
+ drop_prob (Tuple): Tuple of float defined the drop prob,
+ such as (0.5, 0.5, 0)
+ use_activation(Tuple): Tuple of bool define use active
+ function or not, such as (True, True, False)
+ """
+
+ def __init__(self, fc_layers, use_dropout, drop_prob, use_activation):
+ if fc_layers[-1] != 1:
+ msg = f'the neuron count of the last layer must be 1,' \
+ f' but got {fc_layers[-1]}'
+ raise ValueError(msg)
+
+ super().__init__(fc_layers, use_dropout, drop_prob, use_activation)
+
+ def forward(self, inputs):
+ """Forward function."""
+ return self.fc_blocks(inputs)
+
+
+class SMPLDiscriminator(nn.Module):
+ """Discriminator for SMPL pose and shape parameters. It is composed of a
+ discriminator for SMPL shape parameters, a discriminator for SMPL pose
+ parameters of all joints and a discriminator for SMPL pose parameters of
+ each joint.
+
+ Args:
+ beta_channel (tuple of int): Tuple of neuron count of the
+ discriminator of shape parameters. Defaults to (10, 5, 1)
+ per_joint_channel (tuple of int): Tuple of neuron count of the
+ discriminator of each joint. Defaults to (9, 32, 32, 1)
+ full_pose_channel (tuple of int): Tuple of neuron count of the
+ discriminator of full pose. Defaults to (23*32, 1024, 1024, 1)
+ """
+
+ def __init__(self,
+ beta_channel=(10, 5, 1),
+ per_joint_channel=(9, 32, 32, 1),
+ full_pose_channel=(23 * 32, 1024, 1024, 1)):
+ super().__init__()
+ self.joint_count = 23
+ # The count of SMPL shape parameter is 10.
+ assert beta_channel[0] == 10
+ # Use 3 x 3 rotation matrix as the pose parameters
+ # of each joint, so the input channel is 9.
+ assert per_joint_channel[0] == 9
+ assert self.joint_count * per_joint_channel[-2] \
+ == full_pose_channel[0]
+
+ self.beta_channel = beta_channel
+ self.per_joint_channel = per_joint_channel
+ self.full_pose_channel = full_pose_channel
+ self._create_sub_modules()
+
+ def _create_sub_modules(self):
+ """Create sub discriminators."""
+
+ # create theta discriminator for each joint
+ self.pose_discriminator = PoseDiscriminator(self.per_joint_channel,
+ self.joint_count)
+
+ # create full pose discriminator for total joints
+ fc_layers = self.full_pose_channel
+ use_dropout = tuple([False] * (len(fc_layers) - 1))
+ drop_prob = tuple([0.5] * (len(fc_layers) - 1))
+ use_activation = tuple([True] * (len(fc_layers) - 2) + [False])
+
+ self.full_pose_discriminator = FullPoseDiscriminator(
+ fc_layers, use_dropout, drop_prob, use_activation)
+
+ # create shape discriminator for betas
+ fc_layers = self.beta_channel
+ use_dropout = tuple([False] * (len(fc_layers) - 1))
+ drop_prob = tuple([0.5] * (len(fc_layers) - 1))
+ use_activation = tuple([True] * (len(fc_layers) - 2) + [False])
+ self.shape_discriminator = ShapeDiscriminator(fc_layers, use_dropout,
+ drop_prob,
+ use_activation)
+
+ def forward(self, thetas):
+ """Forward function."""
+ _, poses, shapes = thetas
+
+ batch_size = poses.shape[0]
+ shape_disc_value = self.shape_discriminator(shapes)
+
+ # The first rotation matrix is global rotation
+ # and is NOT used in discriminator.
+ if poses.dim() == 2:
+ rotate_matrixs = \
+ batch_rodrigues(poses.contiguous().view(-1, 3)
+ ).view(batch_size, 24, 9)[:, 1:, :]
+ else:
+ rotate_matrixs = poses.contiguous().view(batch_size, 24,
+ 9)[:, 1:, :].contiguous()
+ pose_disc_value, pose_inter_disc_value \
+ = self.pose_discriminator(rotate_matrixs)
+ full_pose_disc_value = self.full_pose_discriminator(
+ pose_inter_disc_value.contiguous().view(batch_size, -1))
+ return torch.cat(
+ (pose_disc_value, full_pose_disc_value, shape_disc_value), 1)
+
+ def init_weights(self):
+ """Initialize model weights."""
+ self.full_pose_discriminator.init_weights()
+ self.pose_discriminator.init_weights()
+ self.shape_discriminator.init_weights()
diff --git a/grounded-sam-osx/transformer_utils/mmpose/models/necks/__init__.py b/grounded-sam-osx/transformer_utils/mmpose/models/necks/__init__.py
new file mode 100644
index 0000000000000000000000000000000000000000..0593f61c01fa9968260b939f7ccd50311c058595
--- /dev/null
+++ b/grounded-sam-osx/transformer_utils/mmpose/models/necks/__init__.py
@@ -0,0 +1,8 @@
+# Copyright (c) OpenMMLab. All rights reserved.
+from .fpn import FPN
+from .gap_neck import GlobalAveragePooling
+from .posewarper_neck import PoseWarperNeck
+from .tcformer_mta_neck import MTA
+from .channel_mapper import ChannelMapper
+
+__all__ = ['GlobalAveragePooling', 'PoseWarperNeck', 'FPN', 'MTA']
diff --git a/grounded-sam-osx/transformer_utils/mmpose/models/necks/channel_mapper.py b/grounded-sam-osx/transformer_utils/mmpose/models/necks/channel_mapper.py
new file mode 100644
index 0000000000000000000000000000000000000000..113d170e9d55b9e2d3984c6838a86e4c659fa75c
--- /dev/null
+++ b/grounded-sam-osx/transformer_utils/mmpose/models/necks/channel_mapper.py
@@ -0,0 +1,76 @@
+import torch.nn as nn
+from mmcv.cnn import ConvModule, xavier_init
+
+from ..builder import NECKS
+
+
+@NECKS.register_module()
+class ChannelMapper(nn.Module):
+ r"""Channel Mapper to reduce/increase channels of backbone features.
+
+ This is used to reduce/increase channels of backbone features.
+
+ Args:
+ in_channels (List[int]): Number of input channels per scale.
+ out_channels (int): Number of output channels (used at each scale).
+ kernel_size (int, optional): kernel_size for reducing channels (used
+ at each scale). Default: 3.
+ conv_cfg (dict, optional): Config dict for convolution layer.
+ Default: None.
+ norm_cfg (dict, optional): Config dict for normalization layer.
+ Default: None.
+ act_cfg (dict, optional): Config dict for activation layer in
+ ConvModule. Default: dict(type='ReLU').
+
+ Example:
+ >>> import torch
+ >>> in_channels = [2, 3, 5, 7]
+ >>> scales = [340, 170, 84, 43]
+ >>> inputs = [torch.rand(1, c, s, s)
+ ... for c, s in zip(in_channels, scales)]
+ >>> self = ChannelMapper(in_channels, 11, 3).eval()
+ >>> outputs = self.forward(inputs)
+ >>> for i in range(len(outputs)):
+ ... print(f'outputs[{i}].shape = {outputs[i].shape}')
+ outputs[0].shape = torch.Size([1, 11, 340, 340])
+ outputs[1].shape = torch.Size([1, 11, 170, 170])
+ outputs[2].shape = torch.Size([1, 11, 84, 84])
+ outputs[3].shape = torch.Size([1, 11, 43, 43])
+ """
+
+ def __init__(self,
+ in_channels,
+ out_channels,
+ kernel_size=3,
+ conv_cfg=None,
+ norm_cfg=None,
+ act_cfg=dict(type='ReLU')):
+ super(ChannelMapper, self).__init__()
+ assert isinstance(in_channels, list)
+
+ self.convs = nn.ModuleList()
+ for in_channel in in_channels:
+ self.convs.append(
+ ConvModule(
+ in_channel,
+ out_channels,
+ kernel_size,
+ padding=(kernel_size - 1) // 2,
+ conv_cfg=conv_cfg,
+ norm_cfg=norm_cfg,
+ act_cfg=act_cfg))
+
+ # default init_weights for conv(msra) and norm in ConvModule
+ def init_weights(self):
+ """Initialize the weights of ChannelMapper module."""
+ for m in self.modules():
+ if isinstance(m, nn.Conv2d):
+ xavier_init(m, distribution='uniform')
+
+ def forward(self, inputs):
+ """Forward function."""
+
+
+ assert len(inputs) == len(self.convs)
+ outs = [self.convs[i](inputs[i]) for i in range(len(inputs))]
+ return tuple(outs)
diff --git a/grounded-sam-osx/transformer_utils/mmpose/models/necks/fpn.py b/grounded-sam-osx/transformer_utils/mmpose/models/necks/fpn.py
new file mode 100644
index 0000000000000000000000000000000000000000..795a8af0b6904153a9b4e1a41d7b803381874162
--- /dev/null
+++ b/grounded-sam-osx/transformer_utils/mmpose/models/necks/fpn.py
@@ -0,0 +1,207 @@
+# Copyright (c) OpenMMLab. All rights reserved.
+import torch.nn as nn
+import torch.nn.functional as F
+from mmcv.cnn import ConvModule, xavier_init
+from mmcv.runner import auto_fp16
+
+from ..builder import NECKS
+
+
+@NECKS.register_module()
+class FPN(nn.Module):
+ r"""Feature Pyramid Network.
+
+ This is an implementation of paper `Feature Pyramid Networks for Object
+ Detection `_.
+
+ Args:
+ in_channels (list[int]): Number of input channels per scale.
+ out_channels (int): Number of output channels (used at each scale).
+ num_outs (int): Number of output scales.
+ start_level (int): Index of the start input backbone level used to
+ build the feature pyramid. Default: 0.
+ end_level (int): Index of the end input backbone level (exclusive) to
+ build the feature pyramid. Default: -1, which means the last level.
+ add_extra_convs (bool | str): If bool, it decides whether to add conv
+ layers on top of the original feature maps. Default to False.
+ If True, it is equivalent to `add_extra_convs='on_input'`.
+ If str, it specifies the source feature map of the extra convs.
+ Only the following options are allowed
+
+ - 'on_input': Last feat map of neck inputs (i.e. backbone feature).
+ - 'on_lateral': Last feature map after lateral convs.
+ - 'on_output': The last output feature map after fpn convs.
+ relu_before_extra_convs (bool): Whether to apply relu before the extra
+ conv. Default: False.
+ no_norm_on_lateral (bool): Whether to apply norm on lateral.
+ Default: False.
+ conv_cfg (dict): Config dict for convolution layer. Default: None.
+ norm_cfg (dict): Config dict for normalization layer. Default: None.
+ act_cfg (dict): Config dict for activation layer in ConvModule.
+ Default: None.
+ upsample_cfg (dict): Config dict for interpolate layer.
+ Default: dict(mode='nearest').
+
+ Example:
+ >>> import torch
+ >>> in_channels = [2, 3, 5, 7]
+ >>> scales = [340, 170, 84, 43]
+ >>> inputs = [torch.rand(1, c, s, s)
+ ... for c, s in zip(in_channels, scales)]
+ >>> self = FPN(in_channels, 11, len(in_channels)).eval()
+ >>> outputs = self.forward(inputs)
+ >>> for i in range(len(outputs)):
+ ... print(f'outputs[{i}].shape = {outputs[i].shape}')
+ outputs[0].shape = torch.Size([1, 11, 340, 340])
+ outputs[1].shape = torch.Size([1, 11, 170, 170])
+ outputs[2].shape = torch.Size([1, 11, 84, 84])
+ outputs[3].shape = torch.Size([1, 11, 43, 43])
+ """
+
+ def __init__(self,
+ in_channels,
+ out_channels,
+ num_outs,
+ start_level=0,
+ end_level=-1,
+ add_extra_convs=False,
+ relu_before_extra_convs=False,
+ no_norm_on_lateral=False,
+ conv_cfg=None,
+ norm_cfg=None,
+ act_cfg=None,
+ upsample_cfg=dict(mode='nearest')):
+ super().__init__()
+ assert isinstance(in_channels, list)
+ self.in_channels = in_channels
+ self.out_channels = out_channels
+ self.num_ins = len(in_channels)
+ self.num_outs = num_outs
+ self.relu_before_extra_convs = relu_before_extra_convs
+ self.no_norm_on_lateral = no_norm_on_lateral
+ self.fp16_enabled = False
+ self.upsample_cfg = upsample_cfg.copy()
+
+ if end_level == -1 or end_level == self.num_ins - 1:
+ self.backbone_end_level = self.num_ins
+ assert num_outs >= self.num_ins - start_level
+ else:
+ # if end_level is not the last level, no extra level is allowed
+ self.backbone_end_level = end_level + 1
+ assert end_level < self.num_ins
+ assert num_outs == end_level - start_level + 1
+ self.start_level = start_level
+ self.end_level = end_level
+ self.add_extra_convs = add_extra_convs
+ assert isinstance(add_extra_convs, (str, bool))
+ if isinstance(add_extra_convs, str):
+ # Extra_convs_source choices: 'on_input', 'on_lateral', 'on_output'
+ assert add_extra_convs in ('on_input', 'on_lateral', 'on_output')
+ elif add_extra_convs: # True
+ self.add_extra_convs = 'on_input'
+
+ self.lateral_convs = nn.ModuleList()
+ self.fpn_convs = nn.ModuleList()
+
+ for i in range(self.start_level, self.backbone_end_level):
+ l_conv = ConvModule(
+ in_channels[i],
+ out_channels,
+ 1,
+ conv_cfg=conv_cfg,
+ norm_cfg=norm_cfg if not self.no_norm_on_lateral else None,
+ act_cfg=act_cfg,
+ inplace=False)
+ fpn_conv = ConvModule(
+ out_channels,
+ out_channels,
+ 3,
+ padding=1,
+ conv_cfg=conv_cfg,
+ norm_cfg=norm_cfg,
+ act_cfg=act_cfg,
+ inplace=False)
+
+ self.lateral_convs.append(l_conv)
+ self.fpn_convs.append(fpn_conv)
+
+ # add extra conv layers (e.g., RetinaNet)
+ extra_levels = num_outs - self.backbone_end_level + self.start_level
+ if self.add_extra_convs and extra_levels >= 1:
+ for i in range(extra_levels):
+ if i == 0 and self.add_extra_convs == 'on_input':
+ in_channels = self.in_channels[self.backbone_end_level - 1]
+ else:
+ in_channels = out_channels
+ extra_fpn_conv = ConvModule(
+ in_channels,
+ out_channels,
+ 3,
+ stride=2,
+ padding=1,
+ conv_cfg=conv_cfg,
+ norm_cfg=norm_cfg,
+ act_cfg=act_cfg,
+ inplace=False)
+ self.fpn_convs.append(extra_fpn_conv)
+
+ def init_weights(self):
+ """Initialize model weights."""
+ for m in self.modules():
+ if isinstance(m, nn.Conv2d):
+ xavier_init(m, distribution='uniform')
+
+ @auto_fp16()
+ def forward(self, inputs):
+ """Forward function."""
+ assert len(inputs) == len(self.in_channels)
+
+ # build laterals
+ laterals = [
+ lateral_conv(inputs[i + self.start_level])
+ for i, lateral_conv in enumerate(self.lateral_convs)
+ ]
+
+ # build top-down path
+ used_backbone_levels = len(laterals)
+ for i in range(used_backbone_levels - 1, 0, -1):
+ # In some cases, fixing `scale factor` (e.g. 2) is preferred, but
+ # it cannot co-exist with `size` in `F.interpolate`.
+ if 'scale_factor' in self.upsample_cfg:
+ # fix runtime error of "+=" inplace operation in PyTorch 1.10
+ laterals[i - 1] = laterals[i - 1] + F.interpolate(
+ laterals[i], **self.upsample_cfg)
+ else:
+ prev_shape = laterals[i - 1].shape[2:]
+ laterals[i - 1] = laterals[i - 1] + F.interpolate(
+ laterals[i], size=prev_shape, **self.upsample_cfg)
+
+ # build outputs
+ # part 1: from original levels
+ outs = [
+ self.fpn_convs[i](laterals[i]) for i in range(used_backbone_levels)
+ ]
+ # part 2: add extra levels
+ if self.num_outs > len(outs):
+ # use max pool to get more levels on top of outputs
+ # (e.g., Faster R-CNN, Mask R-CNN)
+ if not self.add_extra_convs:
+ for i in range(self.num_outs - used_backbone_levels):
+ outs.append(F.max_pool2d(outs[-1], 1, stride=2))
+ # add conv layers on top of original feature maps (RetinaNet)
+ else:
+ if self.add_extra_convs == 'on_input':
+ extra_source = inputs[self.backbone_end_level - 1]
+ elif self.add_extra_convs == 'on_lateral':
+ extra_source = laterals[-1]
+ elif self.add_extra_convs == 'on_output':
+ extra_source = outs[-1]
+ else:
+ raise NotImplementedError
+ outs.append(self.fpn_convs[used_backbone_levels](extra_source))
+ for i in range(used_backbone_levels + 1, self.num_outs):
+ if self.relu_before_extra_convs:
+ outs.append(self.fpn_convs[i](F.relu(outs[-1])))
+ else:
+ outs.append(self.fpn_convs[i](outs[-1]))
+ return outs
diff --git a/grounded-sam-osx/transformer_utils/mmpose/models/necks/gap_neck.py b/grounded-sam-osx/transformer_utils/mmpose/models/necks/gap_neck.py
new file mode 100644
index 0000000000000000000000000000000000000000..5e6ad68ec11110daaad3a66e09d67efb355c4b93
--- /dev/null
+++ b/grounded-sam-osx/transformer_utils/mmpose/models/necks/gap_neck.py
@@ -0,0 +1,37 @@
+# Copyright (c) OpenMMLab. All rights reserved.
+import torch
+import torch.nn as nn
+
+from ..builder import NECKS
+
+
+@NECKS.register_module()
+class GlobalAveragePooling(nn.Module):
+ """Global Average Pooling neck.
+
+ Note that we use `view` to remove extra channel after pooling. We do not
+ use `squeeze` as it will also remove the batch dimension when the tensor
+ has a batch dimension of size 1, which can lead to unexpected errors.
+ """
+
+ def __init__(self):
+ super().__init__()
+ self.gap = nn.AdaptiveAvgPool2d((1, 1))
+
+ def init_weights(self):
+ pass
+
+ def forward(self, inputs):
+ if isinstance(inputs, tuple):
+ outs = tuple([self.gap(x) for x in inputs])
+ outs = tuple(
+ [out.view(x.size(0), -1) for out, x in zip(outs, inputs)])
+ elif isinstance(inputs, list):
+ outs = [self.gap(x) for x in inputs]
+ outs = [out.view(x.size(0), -1) for out, x in zip(outs, inputs)]
+ elif isinstance(inputs, torch.Tensor):
+ outs = self.gap(inputs)
+ outs = outs.view(inputs.size(0), -1)
+ else:
+ raise TypeError('neck inputs should be tuple or torch.tensor')
+ return outs
diff --git a/grounded-sam-osx/transformer_utils/mmpose/models/necks/posewarper_neck.py b/grounded-sam-osx/transformer_utils/mmpose/models/necks/posewarper_neck.py
new file mode 100644
index 0000000000000000000000000000000000000000..dd4ddfbf8984857a6110f19b0a7d703b53f1c433
--- /dev/null
+++ b/grounded-sam-osx/transformer_utils/mmpose/models/necks/posewarper_neck.py
@@ -0,0 +1,329 @@
+# Copyright (c) OpenMMLab. All rights reserved.
+import mmcv
+import torch
+import torch.nn as nn
+from mmcv.cnn import (build_conv_layer, build_norm_layer, constant_init,
+ normal_init)
+from mmcv.utils import digit_version
+from torch.nn.modules.batchnorm import _BatchNorm
+
+from mmpose.models.utils.ops import resize
+from ..backbones.resnet import BasicBlock, Bottleneck
+from ..builder import NECKS
+
+try:
+ from mmcv.ops import DeformConv2d
+ has_mmcv_full = True
+except (ImportError, ModuleNotFoundError):
+ has_mmcv_full = False
+
+
+@NECKS.register_module()
+class PoseWarperNeck(nn.Module):
+ """PoseWarper neck.
+
+ `"Learning temporal pose estimation from sparsely-labeled videos"
+ `_.
+
+ Args:
+ in_channels (int): Number of input channels from backbone
+ out_channels (int): Number of output channels
+ inner_channels (int): Number of intermediate channels of the res block
+ deform_groups (int): Number of groups in the deformable conv
+ dilations (list|tuple): different dilations of the offset conv layers
+ trans_conv_kernel (int): the kernel of the trans conv layer, which is
+ used to get heatmap from the output of backbone. Default: 1
+ res_blocks_cfg (dict|None): config of residual blocks. If None,
+ use the default values. If not None, it should contain the
+ following keys:
+
+ - block (str): the type of residual block, Default: 'BASIC'.
+ - num_blocks (int): the number of blocks, Default: 20.
+
+ offsets_kernel (int): the kernel of offset conv layer.
+ deform_conv_kernel (int): the kernel of defomrable conv layer.
+ in_index (int|Sequence[int]): Input feature index. Default: 0
+ input_transform (str|None): Transformation type of input features.
+ Options: 'resize_concat', 'multiple_select', None.
+ Default: None.
+
+ - 'resize_concat': Multiple feature maps will be resize to \
+ the same size as first one and than concat together. \
+ Usually used in FCN head of HRNet.
+ - 'multiple_select': Multiple feature maps will be bundle into \
+ a list and passed into decode head.
+ - None: Only one select feature map is allowed.
+
+ freeze_trans_layer (bool): Whether to freeze the transition layer
+ (stop grad and set eval mode). Default: True.
+ norm_eval (bool): Whether to set norm layers to eval mode, namely,
+ freeze running stats (mean and var). Note: Effect on Batch Norm
+ and its variants only. Default: False.
+ im2col_step (int): the argument `im2col_step` in deformable conv,
+ Default: 80.
+ """
+ blocks_dict = {'BASIC': BasicBlock, 'BOTTLENECK': Bottleneck}
+ minimum_mmcv_version = '1.3.17'
+
+ def __init__(self,
+ in_channels,
+ out_channels,
+ inner_channels,
+ deform_groups=17,
+ dilations=(3, 6, 12, 18, 24),
+ trans_conv_kernel=1,
+ res_blocks_cfg=None,
+ offsets_kernel=3,
+ deform_conv_kernel=3,
+ in_index=0,
+ input_transform=None,
+ freeze_trans_layer=True,
+ norm_eval=False,
+ im2col_step=80):
+ super().__init__()
+ self.in_channels = in_channels
+ self.out_channels = out_channels
+ self.inner_channels = inner_channels
+ self.deform_groups = deform_groups
+ self.dilations = dilations
+ self.trans_conv_kernel = trans_conv_kernel
+ self.res_blocks_cfg = res_blocks_cfg
+ self.offsets_kernel = offsets_kernel
+ self.deform_conv_kernel = deform_conv_kernel
+ self.in_index = in_index
+ self.input_transform = input_transform
+ self.freeze_trans_layer = freeze_trans_layer
+ self.norm_eval = norm_eval
+ self.im2col_step = im2col_step
+
+ identity_trans_layer = False
+
+ assert trans_conv_kernel in [0, 1, 3]
+ kernel_size = trans_conv_kernel
+ if kernel_size == 3:
+ padding = 1
+ elif kernel_size == 1:
+ padding = 0
+ else:
+ # 0 for Identity mapping.
+ identity_trans_layer = True
+
+ if identity_trans_layer:
+ self.trans_layer = nn.Identity()
+ else:
+ self.trans_layer = build_conv_layer(
+ cfg=dict(type='Conv2d'),
+ in_channels=in_channels,
+ out_channels=out_channels,
+ kernel_size=kernel_size,
+ stride=1,
+ padding=padding)
+
+ # build chain of residual blocks
+ if res_blocks_cfg is not None and not isinstance(res_blocks_cfg, dict):
+ raise TypeError('res_blocks_cfg should be dict or None.')
+
+ if res_blocks_cfg is None:
+ block_type = 'BASIC'
+ num_blocks = 20
+ else:
+ block_type = res_blocks_cfg.get('block', 'BASIC')
+ num_blocks = res_blocks_cfg.get('num_blocks', 20)
+
+ block = self.blocks_dict[block_type]
+
+ res_layers = []
+ downsample = nn.Sequential(
+ build_conv_layer(
+ cfg=dict(type='Conv2d'),
+ in_channels=out_channels,
+ out_channels=inner_channels,
+ kernel_size=1,
+ stride=1,
+ bias=False),
+ build_norm_layer(dict(type='BN'), inner_channels)[1])
+ res_layers.append(
+ block(
+ in_channels=out_channels,
+ out_channels=inner_channels,
+ downsample=downsample))
+
+ for _ in range(1, num_blocks):
+ res_layers.append(block(inner_channels, inner_channels))
+ self.offset_feats = nn.Sequential(*res_layers)
+
+ # build offset layers
+ self.num_offset_layers = len(dilations)
+ assert self.num_offset_layers > 0, 'Number of offset layers ' \
+ 'should be larger than 0.'
+
+ target_offset_channels = 2 * offsets_kernel**2 * deform_groups
+
+ offset_layers = [
+ build_conv_layer(
+ cfg=dict(type='Conv2d'),
+ in_channels=inner_channels,
+ out_channels=target_offset_channels,
+ kernel_size=offsets_kernel,
+ stride=1,
+ dilation=dilations[i],
+ padding=dilations[i],
+ bias=False,
+ ) for i in range(self.num_offset_layers)
+ ]
+ self.offset_layers = nn.ModuleList(offset_layers)
+
+ # build deformable conv layers
+ assert digit_version(mmcv.__version__) >= \
+ digit_version(self.minimum_mmcv_version), \
+ f'Current MMCV version: {mmcv.__version__}, ' \
+ f'but MMCV >= {self.minimum_mmcv_version} is required, see ' \
+ f'https://github.com/open-mmlab/mmcv/issues/1440, ' \
+ f'Please install the latest MMCV.'
+
+ if has_mmcv_full:
+ deform_conv_layers = [
+ DeformConv2d(
+ in_channels=out_channels,
+ out_channels=out_channels,
+ kernel_size=deform_conv_kernel,
+ stride=1,
+ padding=int(deform_conv_kernel / 2) * dilations[i],
+ dilation=dilations[i],
+ deform_groups=deform_groups,
+ im2col_step=self.im2col_step,
+ ) for i in range(self.num_offset_layers)
+ ]
+ else:
+ raise ImportError('Please install the full version of mmcv '
+ 'to use `DeformConv2d`.')
+
+ self.deform_conv_layers = nn.ModuleList(deform_conv_layers)
+
+ self.freeze_layers()
+
+ def freeze_layers(self):
+ if self.freeze_trans_layer:
+ self.trans_layer.eval()
+
+ for param in self.trans_layer.parameters():
+ param.requires_grad = False
+
+ def init_weights(self):
+ for m in self.modules():
+ if isinstance(m, nn.Conv2d):
+ normal_init(m, std=0.001)
+ elif isinstance(m, (_BatchNorm, nn.GroupNorm)):
+ constant_init(m, 1)
+ elif isinstance(m, DeformConv2d):
+ filler = torch.zeros([
+ m.weight.size(0),
+ m.weight.size(1),
+ m.weight.size(2),
+ m.weight.size(3)
+ ],
+ dtype=torch.float32,
+ device=m.weight.device)
+ for k in range(m.weight.size(0)):
+ filler[k, k,
+ int(m.weight.size(2) / 2),
+ int(m.weight.size(3) / 2)] = 1.0
+ m.weight = torch.nn.Parameter(filler)
+ m.weight.requires_grad = True
+
+ # posewarper offset layer weight initialization
+ for m in self.offset_layers.modules():
+ constant_init(m, 0)
+
+ def _transform_inputs(self, inputs):
+ """Transform inputs for decoder.
+
+ Args:
+ inputs (list[Tensor] | Tensor): multi-level img features.
+
+ Returns:
+ Tensor: The transformed inputs
+ """
+ if not isinstance(inputs, list):
+ return inputs
+
+ if self.input_transform == 'resize_concat':
+ inputs = [inputs[i] for i in self.in_index]
+ upsampled_inputs = [
+ resize(
+ input=x,
+ size=inputs[0].shape[2:],
+ mode='bilinear',
+ align_corners=self.align_corners) for x in inputs
+ ]
+ inputs = torch.cat(upsampled_inputs, dim=1)
+ elif self.input_transform == 'multiple_select':
+ inputs = [inputs[i] for i in self.in_index]
+ else:
+ inputs = inputs[self.in_index]
+
+ return inputs
+
+ def forward(self, inputs, frame_weight):
+ assert isinstance(inputs, (list, tuple)), 'PoseWarperNeck inputs ' \
+ 'should be list or tuple, even though the length is 1, ' \
+ 'for unified processing.'
+
+ output_heatmap = 0
+ if len(inputs) > 1:
+ inputs = [self._transform_inputs(input) for input in inputs]
+ inputs = [self.trans_layer(input) for input in inputs]
+
+ # calculate difference features
+ diff_features = [
+ self.offset_feats(inputs[0] - input) for input in inputs
+ ]
+
+ for i in range(len(inputs)):
+ if frame_weight[i] == 0:
+ continue
+ warped_heatmap = 0
+ for j in range(self.num_offset_layers):
+ offset = (self.offset_layers[j](diff_features[i]))
+ warped_heatmap_tmp = self.deform_conv_layers[j](inputs[i],
+ offset)
+ warped_heatmap += warped_heatmap_tmp / \
+ self.num_offset_layers
+
+ output_heatmap += warped_heatmap * frame_weight[i]
+
+ else:
+ inputs = inputs[0]
+ inputs = self._transform_inputs(inputs)
+ inputs = self.trans_layer(inputs)
+
+ num_frames = len(frame_weight)
+ batch_size = inputs.size(0) // num_frames
+ ref_x = inputs[:batch_size]
+ ref_x_tiled = ref_x.repeat(num_frames, 1, 1, 1)
+
+ offset_features = self.offset_feats(ref_x_tiled - inputs)
+
+ warped_heatmap = 0
+ for j in range(self.num_offset_layers):
+ offset = self.offset_layers[j](offset_features)
+
+ warped_heatmap_tmp = self.deform_conv_layers[j](inputs, offset)
+ warped_heatmap += warped_heatmap_tmp / self.num_offset_layers
+
+ for i in range(num_frames):
+ if frame_weight[i] == 0:
+ continue
+ output_heatmap += warped_heatmap[i * batch_size:(i + 1) *
+ batch_size] * frame_weight[i]
+
+ return output_heatmap
+
+ def train(self, mode=True):
+ """Convert the model into training mode."""
+ super().train(mode)
+ self.freeze_layers()
+ if mode and self.norm_eval:
+ for m in self.modules():
+ if isinstance(m, _BatchNorm):
+ m.eval()
diff --git a/grounded-sam-osx/transformer_utils/mmpose/models/necks/tcformer_mta_neck.py b/grounded-sam-osx/transformer_utils/mmpose/models/necks/tcformer_mta_neck.py
new file mode 100644
index 0000000000000000000000000000000000000000..6723fb018e7799c1c0104868b1ca87c56cd28351
--- /dev/null
+++ b/grounded-sam-osx/transformer_utils/mmpose/models/necks/tcformer_mta_neck.py
@@ -0,0 +1,224 @@
+# Copyright (c) OpenMMLab. All rights reserved.
+import math
+
+import torch.nn as nn
+import torch.nn.functional as F
+from mmcv.cnn import ConvModule, constant_init, normal_init, trunc_normal_init
+from mmcv.runner import BaseModule
+
+from ..builder import NECKS
+from ..utils import TCFormerDynamicBlock, token2map, token_interp
+
+
+@NECKS.register_module()
+class MTA(BaseModule):
+ """Multi-stage Token feature Aggregation (MTA) module in TCFormer.
+
+ Args:
+ in_channels (list[int]): Number of input channels per stage.
+ Default: [64, 128, 256, 512].
+ out_channels (int): Number of output channels (used at each scale).
+ num_outs (int): Number of output scales. Default: 4.
+ start_level (int): Index of the start input backbone level used to
+ build the feature pyramid. Default: 0.
+ end_level (int): Index of the end input backbone level (exclusive) to
+ build the feature pyramid. Default: -1, which means the last level.
+ add_extra_convs (bool | str): If bool, it decides whether to add conv
+ layers on top of the original feature maps. Default to False.
+ If True, it is equivalent to `add_extra_convs='on_input'`.
+ If str, it specifies the source feature map of the extra convs.
+ Only the following options are allowed
+ - 'on_input': Last feat map of neck inputs (i.e. backbone feature).
+ - 'on_output': The last output feature map after fpn convs.
+ relu_before_extra_convs (bool): Whether to apply relu before the extra
+ conv. Default: False.
+ no_norm_on_lateral (bool): Whether to apply norm on lateral.
+ Default: False.
+ conv_cfg (dict): Config dict for convolution layer. Default: None.
+ norm_cfg (dict): Config dict for normalization layer. Default: None.
+ act_cfg (dict): Config dict for activation layer in ConvModule.
+ num_heads (Sequence[int]): The attention heads of each transformer
+ block. Default: [2, 2, 2, 2].
+ mlp_ratios (Sequence[int]): The ratio of the mlp hidden dim to the
+ embedding dim of each transformer block.
+ sr_ratios (Sequence[int]): The spatial reduction rate of each
+ transformer block. Default: [8, 4, 2, 1].
+ qkv_bias (bool): Enable bias for qkv if True. Default: True.
+ qk_scale (float | None, optional): Override default qk scale of
+ head_dim ** -0.5 if set. Default: None.
+ drop_rate (float): Probability of an element to be zeroed.
+ Default 0.0.
+ attn_drop_rate (float): The drop out rate for attention layer.
+ Default 0.0.
+ drop_path_rate (float): stochastic depth rate. Default 0.
+ transformer_norm_cfg (dict): Config dict for normalization layer
+ in transformer blocks. Default: dict(type='LN').
+ use_sr_conv (bool): If True, use a conv layer for spatial reduction.
+ If False, use a pooling process for spatial reduction. Defaults:
+ False.
+ """
+
+ def __init__(
+ self,
+ in_channels=[64, 128, 256, 512],
+ out_channels=128,
+ num_outs=4,
+ start_level=0,
+ end_level=-1,
+ add_extra_convs=False,
+ relu_before_extra_convs=False,
+ no_norm_on_lateral=False,
+ conv_cfg=None,
+ norm_cfg=None,
+ act_cfg=None,
+ num_heads=[2, 2, 2, 2],
+ mlp_ratios=[4, 4, 4, 4],
+ sr_ratios=[8, 4, 2, 1],
+ qkv_bias=True,
+ qk_scale=None,
+ drop_rate=0.,
+ attn_drop_rate=0.,
+ drop_path_rate=0.,
+ transformer_norm_cfg=dict(type='LN'),
+ use_sr_conv=False,
+ ):
+ super().__init__()
+ assert isinstance(in_channels, list)
+ self.in_channels = in_channels
+ self.out_channels = out_channels
+ self.num_ins = len(in_channels)
+ self.num_outs = num_outs
+ self.no_norm_on_lateral = no_norm_on_lateral
+ self.fp16_enabled = False
+ self.norm_cfg = norm_cfg
+ self.conv_cfg = conv_cfg
+ self.act_cfg = act_cfg
+ self.mlp_ratios = mlp_ratios
+
+ if end_level == -1 or end_level == self.num_ins - 1:
+ self.backbone_end_level = self.num_ins
+ assert num_outs >= self.num_ins - start_level
+ else:
+ # if end_level is not the last level, no extra level is allowed
+ self.backbone_end_level = end_level + 1
+ assert end_level < self.num_ins
+ assert num_outs == end_level - start_level + 1
+ self.start_level = start_level
+ self.end_level = end_level
+
+ self.lateral_convs = nn.ModuleList()
+ self.merge_blocks = nn.ModuleList()
+
+ for i in range(self.start_level, self.backbone_end_level):
+ l_conv = ConvModule(
+ in_channels[i],
+ out_channels,
+ 1,
+ conv_cfg=conv_cfg,
+ norm_cfg=norm_cfg if not self.no_norm_on_lateral else None,
+ act_cfg=act_cfg,
+ inplace=False)
+ self.lateral_convs.append(l_conv)
+
+ for i in range(self.start_level, self.backbone_end_level - 1):
+ merge_block = TCFormerDynamicBlock(
+ dim=out_channels,
+ num_heads=num_heads[i],
+ mlp_ratio=mlp_ratios[i],
+ qkv_bias=qkv_bias,
+ qk_scale=qk_scale,
+ drop=drop_rate,
+ attn_drop=attn_drop_rate,
+ drop_path=drop_path_rate,
+ norm_cfg=transformer_norm_cfg,
+ sr_ratio=sr_ratios[i],
+ use_sr_conv=use_sr_conv)
+ self.merge_blocks.append(merge_block)
+
+ # add extra conv layers (e.g., RetinaNet)
+ self.relu_before_extra_convs = relu_before_extra_convs
+
+ self.add_extra_convs = add_extra_convs
+ assert isinstance(add_extra_convs, (str, bool))
+ if isinstance(add_extra_convs, str):
+ # Extra_convs_source choices: 'on_input', 'on_output'
+ assert add_extra_convs in ('on_input', 'on_output')
+ elif add_extra_convs: # True
+ self.add_extra_convs = 'on_input'
+
+ self.extra_convs = nn.ModuleList()
+ extra_levels = num_outs - (self.end_level + 1 - self.start_level)
+ if self.add_extra_convs and extra_levels >= 1:
+ for i in range(extra_levels):
+ if i == 0 and self.add_extra_convs == 'on_input':
+ in_channels = self.in_channels[self.end_level]
+ else:
+ in_channels = out_channels
+ extra_fpn_conv = ConvModule(
+ in_channels,
+ out_channels,
+ 3,
+ stride=2,
+ padding=1,
+ conv_cfg=conv_cfg,
+ norm_cfg=norm_cfg,
+ act_cfg=act_cfg,
+ inplace=False)
+ self.extra_convs.append(extra_fpn_conv)
+
+ def init_weights(self):
+ for m in self.modules():
+ if isinstance(m, nn.Linear):
+ trunc_normal_init(m, std=.02, bias=0.)
+ elif isinstance(m, nn.LayerNorm):
+ constant_init(m, 1.0)
+ elif isinstance(m, nn.Conv2d):
+ fan_out = m.kernel_size[0] * m.kernel_size[1] * m.out_channels
+ fan_out //= m.groups
+ normal_init(m, 0, math.sqrt(2.0 / fan_out))
+
+ def forward(self, inputs):
+ """Forward function."""
+ assert len(inputs) == len(self.in_channels)
+
+ # build lateral tokens
+ input_dicts = []
+ for i, lateral_conv in enumerate(self.lateral_convs):
+ tmp = inputs[i + self.start_level].copy()
+ tmp['x'] = lateral_conv(tmp['x'].unsqueeze(2).permute(
+ 0, 3, 1, 2)).permute(0, 2, 3, 1).squeeze(2)
+ input_dicts.append(tmp)
+
+ # merge from high level to low level
+ for i in range(len(input_dicts) - 2, -1, -1):
+ input_dicts[i]['x'] = input_dicts[i]['x'] + token_interp(
+ input_dicts[i], input_dicts[i + 1])
+ input_dicts[i] = self.merge_blocks[i](input_dicts[i])
+
+ # transform to feature map
+ outs = [token2map(token_dict) for token_dict in input_dicts]
+
+ # part 2: add extra levels
+ used_backbone_levels = len(outs)
+ if self.num_outs > len(outs):
+ # use max pool to get more levels on top of outputs
+ if not self.add_extra_convs:
+ for i in range(self.num_outs - used_backbone_levels):
+ outs.append(F.max_pool2d(outs[-1], 1, stride=2))
+ # add conv layers on top of original feature maps
+ else:
+ if self.add_extra_convs == 'on_input':
+ tmp = inputs[self.backbone_end_level - 1]
+ extra_source = token2map(tmp)
+ elif self.add_extra_convs == 'on_output':
+ extra_source = outs[-1]
+ else:
+ raise NotImplementedError
+
+ outs.append(self.extra_convs[0](extra_source))
+ for i in range(1, self.num_outs - used_backbone_levels):
+ if self.relu_before_extra_convs:
+ outs.append(self.extra_convs[i](F.relu(outs[-1])))
+ else:
+ outs.append(self.extra_convs[i](outs[-1]))
+ return outs
diff --git a/grounded-sam-osx/transformer_utils/mmpose/models/registry.py b/grounded-sam-osx/transformer_utils/mmpose/models/registry.py
new file mode 100644
index 0000000000000000000000000000000000000000..f354ae9e137262e2f375a64aef74c3af20baae63
--- /dev/null
+++ b/grounded-sam-osx/transformer_utils/mmpose/models/registry.py
@@ -0,0 +1,13 @@
+# Copyright (c) OpenMMLab. All rights reserved.
+import warnings
+
+from .builder import BACKBONES, HEADS, LOSSES, NECKS, POSENETS
+
+__all__ = ['BACKBONES', 'HEADS', 'LOSSES', 'NECKS', 'POSENETS']
+
+warnings.simplefilter('once', DeprecationWarning)
+warnings.warn(
+ 'Registries (BACKBONES, NECKS, HEADS, LOSSES, POSENETS) have '
+ 'been moved to mmpose.models.builder. Importing from '
+ 'mmpose.models.registry will be deprecated in the future.',
+ DeprecationWarning)
diff --git a/grounded-sam-osx/transformer_utils/mmpose/models/utils/__init__.py b/grounded-sam-osx/transformer_utils/mmpose/models/utils/__init__.py
new file mode 100644
index 0000000000000000000000000000000000000000..1d7e8f6482ce3e2c06229a578f22536bd75e5260
--- /dev/null
+++ b/grounded-sam-osx/transformer_utils/mmpose/models/utils/__init__.py
@@ -0,0 +1,24 @@
+# Copyright (c) OpenMMLab. All rights reserved.
+from .ckpt_convert import pvt_convert, tcformer_convert
+from .geometry import batch_rodrigues, quat_to_rotmat, rot6d_to_rotmat
+from .misc import torch_meshgrid_ij
+from .ops import resize
+from .realnvp import RealNVP
+from .smpl import SMPL
+from .tcformer_utils import (TCFormerDynamicBlock, TCFormerRegularBlock,
+ TokenConv, cluster_dpc_knn, merge_tokens,
+ token2map, token_interp)
+from .transformer import (PatchEmbed, PatchMerging, nchw_to_nlc, nlc_to_nchw,
+ PoseurTransformer_v3, DetrTransformerEncoder_zero_layer,
+ DeformableDetrTransformerDecoder, DetrTransformerDecoderLayer_grouped)
+
+from .positional_encoding import (LearnedPositionalEncoding,
+ SinePositionalEncoding)
+
+__all__ = [
+ 'SMPL', 'PatchEmbed', 'nchw_to_nlc', 'nlc_to_nchw', 'pvt_convert',
+ 'PatchMerging', 'batch_rodrigues', 'quat_to_rotmat', 'rot6d_to_rotmat',
+ 'resize', 'RealNVP', 'torch_meshgrid_ij', 'token2map', 'TokenConv',
+ 'TCFormerRegularBlock', 'TCFormerDynamicBlock', 'cluster_dpc_knn',
+ 'merge_tokens', 'token_interp', 'tcformer_convert'
+]
diff --git a/grounded-sam-osx/transformer_utils/mmpose/models/utils/ckpt_convert.py b/grounded-sam-osx/transformer_utils/mmpose/models/utils/ckpt_convert.py
new file mode 100644
index 0000000000000000000000000000000000000000..f5213937db3641bf7300156a2be3f2225326f02b
--- /dev/null
+++ b/grounded-sam-osx/transformer_utils/mmpose/models/utils/ckpt_convert.py
@@ -0,0 +1,94 @@
+# Copyright (c) OpenMMLab. All rights reserved.
+
+# This script consists of several convert functions which
+# can modify the weights of model in original repo to be
+# pre-trained weights.
+
+from collections import OrderedDict
+
+import torch
+
+
+def pvt_convert(ckpt):
+ new_ckpt = OrderedDict()
+ # Process the concat between q linear weights and kv linear weights
+ use_abs_pos_embed = False
+ use_conv_ffn = False
+ for k in ckpt.keys():
+ if k.startswith('pos_embed'):
+ use_abs_pos_embed = True
+ if k.find('dwconv') >= 0:
+ use_conv_ffn = True
+ for k, v in ckpt.items():
+ if k.startswith('head'):
+ continue
+ if k.startswith('norm.'):
+ continue
+ if k.startswith('cls_token'):
+ continue
+ if k.startswith('pos_embed'):
+ stage_i = int(k.replace('pos_embed', ''))
+ new_k = k.replace(f'pos_embed{stage_i}',
+ f'layers.{stage_i - 1}.1.0.pos_embed')
+ if stage_i == 4 and v.size(1) == 50: # 1 (cls token) + 7 * 7
+ new_v = v[:, 1:, :] # remove cls token
+ else:
+ new_v = v
+ elif k.startswith('patch_embed'):
+ stage_i = int(k.split('.')[0].replace('patch_embed', ''))
+ new_k = k.replace(f'patch_embed{stage_i}',
+ f'layers.{stage_i - 1}.0')
+ new_v = v
+ if 'proj.' in new_k:
+ new_k = new_k.replace('proj.', 'projection.')
+ elif k.startswith('block'):
+ stage_i = int(k.split('.')[0].replace('block', ''))
+ layer_i = int(k.split('.')[1])
+ new_layer_i = layer_i + use_abs_pos_embed
+ new_k = k.replace(f'block{stage_i}.{layer_i}',
+ f'layers.{stage_i - 1}.1.{new_layer_i}')
+ new_v = v
+ if 'attn.q.' in new_k:
+ sub_item_k = k.replace('q.', 'kv.')
+ new_k = new_k.replace('q.', 'attn.in_proj_')
+ new_v = torch.cat([v, ckpt[sub_item_k]], dim=0)
+ elif 'attn.kv.' in new_k:
+ continue
+ elif 'attn.proj.' in new_k:
+ new_k = new_k.replace('proj.', 'attn.out_proj.')
+ elif 'attn.sr.' in new_k:
+ new_k = new_k.replace('sr.', 'sr.')
+ elif 'mlp.' in new_k:
+ string = f'{new_k}-'
+ new_k = new_k.replace('mlp.', 'ffn.layers.')
+ if 'fc1.weight' in new_k or 'fc2.weight' in new_k:
+ new_v = v.reshape((*v.shape, 1, 1))
+ new_k = new_k.replace('fc1.', '0.')
+ new_k = new_k.replace('dwconv.dwconv.', '1.')
+ if use_conv_ffn:
+ new_k = new_k.replace('fc2.', '4.')
+ else:
+ new_k = new_k.replace('fc2.', '3.')
+ string += f'{new_k} {v.shape}-{new_v.shape}'
+ elif k.startswith('norm'):
+ stage_i = int(k[4])
+ new_k = k.replace(f'norm{stage_i}', f'layers.{stage_i - 1}.2')
+ new_v = v
+ else:
+ new_k = k
+ new_v = v
+ new_ckpt[new_k] = new_v
+
+ return new_ckpt
+
+
+def tcformer_convert(ckpt):
+ new_ckpt = OrderedDict()
+ # Process the concat between q linear weights and kv linear weights
+ for k, v in ckpt.items():
+ if 'patch_embed' in k:
+ new_k = k.replace('.proj.', '.projection.')
+ else:
+ new_k = k
+ new_ckpt[new_k] = v
+ return new_ckpt
diff --git a/grounded-sam-osx/transformer_utils/mmpose/models/utils/geometry.py b/grounded-sam-osx/transformer_utils/mmpose/models/utils/geometry.py
new file mode 100644
index 0000000000000000000000000000000000000000..0ceadaec30cd2c9bb3fbada132e1ea674f2e8754
--- /dev/null
+++ b/grounded-sam-osx/transformer_utils/mmpose/models/utils/geometry.py
@@ -0,0 +1,68 @@
+# Copyright (c) OpenMMLab. All rights reserved.
+import torch
+from torch.nn import functional as F
+
+
+def rot6d_to_rotmat(x):
+ """Convert 6D rotation representation to 3x3 rotation matrix.
+
+ Based on Zhou et al., "On the Continuity of Rotation
+ Representations in Neural Networks", CVPR 2019
+ Input:
+ (B,6) Batch of 6-D rotation representations
+ Output:
+ (B,3,3) Batch of corresponding rotation matrices
+ """
+ x = x.view(-1, 3, 2)
+ a1 = x[:, :, 0]
+ a2 = x[:, :, 1]
+ b1 = F.normalize(a1)
+ b2 = F.normalize(a2 - torch.einsum('bi,bi->b', b1, a2).unsqueeze(-1) * b1)
+ b3 = torch.cross(b1, b2)
+ return torch.stack((b1, b2, b3), dim=-1)
+
+
+def batch_rodrigues(theta):
+ """Convert axis-angle representation to rotation matrix.
+ Args:
+ theta: size = [B, 3]
+ Returns:
+ Rotation matrix corresponding to the quaternion
+ -- size = [B, 3, 3]
+ """
+ l2norm = torch.norm(theta + 1e-8, p=2, dim=1)
+ angle = torch.unsqueeze(l2norm, -1)
+ normalized = torch.div(theta, angle)
+ angle = angle * 0.5
+ v_cos = torch.cos(angle)
+ v_sin = torch.sin(angle)
+ quat = torch.cat([v_cos, v_sin * normalized], dim=1)
+ return quat_to_rotmat(quat)
+
+
+def quat_to_rotmat(quat):
+ """Convert quaternion coefficients to rotation matrix.
+ Args:
+ quat: size = [B, 4] 4 <===>(w, x, y, z)
+ Returns:
+ Rotation matrix corresponding to the quaternion
+ -- size = [B, 3, 3]
+ """
+ norm_quat = quat
+ norm_quat = norm_quat / norm_quat.norm(p=2, dim=1, keepdim=True)
+ w, x, y, z = norm_quat[:, 0], norm_quat[:, 1],\
+ norm_quat[:, 2], norm_quat[:, 3]
+
+ B = quat.size(0)
+
+ w2, x2, y2, z2 = w.pow(2), x.pow(2), y.pow(2), z.pow(2)
+ wx, wy, wz = w * x, w * y, w * z
+ xy, xz, yz = x * y, x * z, y * z
+
+ rotMat = torch.stack([
+ w2 + x2 - y2 - z2, 2 * xy - 2 * wz, 2 * wy + 2 * xz, 2 * wz + 2 * xy,
+ w2 - x2 + y2 - z2, 2 * yz - 2 * wx, 2 * xz - 2 * wy, 2 * wx + 2 * yz,
+ w2 - x2 - y2 + z2
+ ],
+ dim=1).view(B, 3, 3)
+ return rotMat
diff --git a/grounded-sam-osx/transformer_utils/mmpose/models/utils/misc.py b/grounded-sam-osx/transformer_utils/mmpose/models/utils/misc.py
new file mode 100644
index 0000000000000000000000000000000000000000..8c784588ef0c0ef58badf5c68d0a9602e14d6079
--- /dev/null
+++ b/grounded-sam-osx/transformer_utils/mmpose/models/utils/misc.py
@@ -0,0 +1,13 @@
+# Copyright (c) OpenMMLab. All rights reserved.
+import torch
+from packaging import version
+
+_torch_version_meshgrid_indexing = version.parse(
+ torch.__version__) >= version.parse('1.10.0a0')
+
+
+def torch_meshgrid_ij(*tensors):
+ if _torch_version_meshgrid_indexing:
+ return torch.meshgrid(*tensors, indexing='ij')
+ else:
+ return torch.meshgrid(*tensors) # Uses indexing='ij' by default
diff --git a/grounded-sam-osx/transformer_utils/mmpose/models/utils/ops.py b/grounded-sam-osx/transformer_utils/mmpose/models/utils/ops.py
new file mode 100644
index 0000000000000000000000000000000000000000..858d0a92148a591d235e58bfce8990207632fb39
--- /dev/null
+++ b/grounded-sam-osx/transformer_utils/mmpose/models/utils/ops.py
@@ -0,0 +1,29 @@
+# Copyright (c) OpenMMLab. All rights reserved.
+import warnings
+
+import torch
+import torch.nn.functional as F
+
+
+def resize(input,
+ size=None,
+ scale_factor=None,
+ mode='nearest',
+ align_corners=None,
+ warning=True):
+ if warning:
+ if size is not None and align_corners:
+ input_h, input_w = tuple(int(x) for x in input.shape[2:])
+ output_h, output_w = tuple(int(x) for x in size)
+ if output_h > input_h or output_w > output_h:
+ if ((output_h > 1 and output_w > 1 and input_h > 1
+ and input_w > 1) and (output_h - 1) % (input_h - 1)
+ and (output_w - 1) % (input_w - 1)):
+ warnings.warn(
+ f'When align_corners={align_corners}, '
+ 'the output would more aligned if '
+ f'input size {(input_h, input_w)} is `x+1` and '
+ f'out size {(output_h, output_w)} is `nx+1`')
+ if isinstance(size, torch.Size):
+ size = tuple(int(x) for x in size)
+ return F.interpolate(input, size, scale_factor, mode, align_corners)
diff --git a/grounded-sam-osx/transformer_utils/mmpose/models/utils/positional_encoding.py b/grounded-sam-osx/transformer_utils/mmpose/models/utils/positional_encoding.py
new file mode 100644
index 0000000000000000000000000000000000000000..4d3882cd515884794caeab3e06a40b22b6635b66
--- /dev/null
+++ b/grounded-sam-osx/transformer_utils/mmpose/models/utils/positional_encoding.py
@@ -0,0 +1,155 @@
+import math
+
+import torch
+import torch.nn as nn
+from mmcv.cnn.bricks.transformer import POSITIONAL_ENCODING
+from mmcv.runner import BaseModule
+
+
+@POSITIONAL_ENCODING.register_module()
+class SinePositionalEncoding(BaseModule):
+ """Position encoding with sine and cosine functions.
+ See `End-to-End Object Detection with Transformers
+ `_ for details.
+ Args:
+ num_feats (int): The feature dimension for each position
+ along x-axis or y-axis. Note the final returned dimension
+ for each position is 2 times of this value.
+ temperature (int, optional): The temperature used for scaling
+ the position embedding. Defaults to 10000.
+ normalize (bool, optional): Whether to normalize the position
+ embedding. Defaults to False.
+ scale (float, optional): A scale factor that scales the position
+ embedding. The scale will be used only when `normalize` is True.
+ Defaults to 2*pi.
+ eps (float, optional): A value added to the denominator for
+ numerical stability. Defaults to 1e-6.
+ offset (float): offset add to embed when do the normalization.
+ Defaults to 0.
+ init_cfg (dict or list[dict], optional): Initialization config dict.
+ Default: None
+ """
+
+ def __init__(self,
+ num_feats,
+ temperature=10000,
+ normalize=False,
+ scale=2 * math.pi,
+ eps=1e-6,
+ offset=0.,
+ init_cfg=None):
+ super(SinePositionalEncoding, self).__init__(init_cfg)
+ if normalize:
+ assert isinstance(scale, (float, int)), 'when normalize is set,' \
+ 'scale should be provided and in float or int type, ' \
+ f'found {type(scale)}'
+ self.num_feats = num_feats
+ self.temperature = temperature
+ self.normalize = normalize
+ self.scale = scale
+ self.eps = eps
+ self.offset = offset
+
+ def forward(self, mask):
+ """Forward function for `SinePositionalEncoding`.
+ Args:
+ mask (Tensor): ByteTensor mask. Non-zero values representing
+ ignored positions, while zero values means valid positions
+ for this image. Shape [bs, h, w].
+ Returns:
+ pos (Tensor): Returned position embedding with shape
+ [bs, num_feats*2, h, w].
+ """
+ # For convenience of exporting to ONNX, it's required to convert
+ # `masks` from bool to int.
+ mask = mask.to(torch.int)
+ not_mask = 1 - mask # logical_not
+ y_embed = not_mask.cumsum(1, dtype=torch.float32)
+ x_embed = not_mask.cumsum(2, dtype=torch.float32)
+ if self.normalize:
+ y_embed = (y_embed + self.offset) / \
+ (y_embed[:, -1:, :] + self.eps) * self.scale
+ x_embed = (x_embed + self.offset) / \
+ (x_embed[:, :, -1:] + self.eps) * self.scale
+ dim_t = torch.arange(
+ self.num_feats, dtype=torch.float32, device=mask.device)
+ dim_t = self.temperature**(2 * (dim_t // 2) / self.num_feats)
+ pos_x = x_embed[:, :, :, None] / dim_t
+ pos_y = y_embed[:, :, :, None] / dim_t
+ # use `view` instead of `flatten` for dynamically exporting to ONNX
+ B, H, W = mask.size()
+ pos_x = torch.stack(
+ (pos_x[:, :, :, 0::2].sin(), pos_x[:, :, :, 1::2].cos()),
+ dim=4).view(B, H, W, -1)
+ pos_y = torch.stack(
+ (pos_y[:, :, :, 0::2].sin(), pos_y[:, :, :, 1::2].cos()),
+ dim=4).view(B, H, W, -1)
+ pos = torch.cat((pos_y, pos_x), dim=3).permute(0, 3, 1, 2)
+ return pos
+
+ def __repr__(self):
+ """str: a string that describes the module"""
+ repr_str = self.__class__.__name__
+ repr_str += f'(num_feats={self.num_feats}, '
+ repr_str += f'temperature={self.temperature}, '
+ repr_str += f'normalize={self.normalize}, '
+ repr_str += f'scale={self.scale}, '
+ repr_str += f'eps={self.eps})'
+ return repr_str
+
+
+@POSITIONAL_ENCODING.register_module()
+class LearnedPositionalEncoding(BaseModule):
+ """Position embedding with learnable embedding weights.
+ Args:
+ num_feats (int): The feature dimension for each position
+ along x-axis or y-axis. The final returned dimension for
+ each position is 2 times of this value.
+ row_num_embed (int, optional): The dictionary size of row embeddings.
+ Default 50.
+ col_num_embed (int, optional): The dictionary size of col embeddings.
+ Default 50.
+ init_cfg (dict or list[dict], optional): Initialization config dict.
+ """
+
+ def __init__(self,
+ num_feats,
+ row_num_embed=50,
+ col_num_embed=50,
+ init_cfg=dict(type='Uniform', layer='Embedding')):
+ super(LearnedPositionalEncoding, self).__init__(init_cfg)
+ self.row_embed = nn.Embedding(row_num_embed, num_feats)
+ self.col_embed = nn.Embedding(col_num_embed, num_feats)
+ self.num_feats = num_feats
+ self.row_num_embed = row_num_embed
+ self.col_num_embed = col_num_embed
+
+ def forward(self, mask):
+ """Forward function for `LearnedPositionalEncoding`.
+ Args:
+ mask (Tensor): ByteTensor mask. Non-zero values representing
+ ignored positions, while zero values means valid positions
+ for this image. Shape [bs, h, w].
+ Returns:
+ pos (Tensor): Returned position embedding with shape
+ [bs, num_feats*2, h, w].
+ """
+ h, w = mask.shape[-2:]
+ x = torch.arange(w, device=mask.device)
+ y = torch.arange(h, device=mask.device)
+ x_embed = self.col_embed(x)
+ y_embed = self.row_embed(y)
+ pos = torch.cat(
+ (x_embed.unsqueeze(0).repeat(h, 1, 1), y_embed.unsqueeze(1).repeat(
+ 1, w, 1)),
+ dim=-1).permute(2, 0,
+ 1).unsqueeze(0).repeat(mask.shape[0], 1, 1, 1)
+ return pos
+
+ def __repr__(self):
+ """str: a string that describes the module"""
+ repr_str = self.__class__.__name__
+ repr_str += f'(num_feats={self.num_feats}, '
+ repr_str += f'row_num_embed={self.row_num_embed}, '
+ repr_str += f'col_num_embed={self.col_num_embed})'
+ return repr_str
\ No newline at end of file
diff --git a/grounded-sam-osx/transformer_utils/mmpose/models/utils/realnvp.py b/grounded-sam-osx/transformer_utils/mmpose/models/utils/realnvp.py
new file mode 100644
index 0000000000000000000000000000000000000000..911953e8f9d1056d44a2d3538d750e89b9bd6a7a
--- /dev/null
+++ b/grounded-sam-osx/transformer_utils/mmpose/models/utils/realnvp.py
@@ -0,0 +1,76 @@
+# Copyright (c) OpenMMLab. All rights reserved.
+import torch
+import torch.nn as nn
+from torch import distributions
+
+
+class RealNVP(nn.Module):
+ """RealNVP: a flow-based generative model
+
+ `Density estimation using Real NVP
+ arXiv: `_.
+
+ Code is modified from `the official implementation of RLE
+ `_.
+
+ See also `real-nvp-pytorch
+ `_.
+ """
+
+ @staticmethod
+ def get_scale_net():
+ """Get the scale model in a single invertable mapping."""
+ return nn.Sequential(
+ nn.Linear(2, 64), nn.LeakyReLU(), nn.Linear(64, 64),
+ nn.LeakyReLU(), nn.Linear(64, 2), nn.Tanh())
+
+ @staticmethod
+ def get_trans_net():
+ """Get the translation model in a single invertable mapping."""
+ return nn.Sequential(
+ nn.Linear(2, 64), nn.LeakyReLU(), nn.Linear(64, 64),
+ nn.LeakyReLU(), nn.Linear(64, 2))
+
+ @property
+ def prior(self):
+ """The prior distribution."""
+ return distributions.MultivariateNormal(self.loc, self.cov)
+
+ def __init__(self):
+ super(RealNVP, self).__init__()
+
+ self.register_buffer('loc', torch.zeros(2))
+ self.register_buffer('cov', torch.eye(2))
+ self.register_buffer(
+ 'mask', torch.tensor([[0, 1], [1, 0]] * 3, dtype=torch.float32))
+
+ self.s = torch.nn.ModuleList(
+ [self.get_scale_net() for _ in range(len(self.mask))])
+ self.t = torch.nn.ModuleList(
+ [self.get_trans_net() for _ in range(len(self.mask))])
+ self.init_weights()
+
+ def init_weights(self):
+ """Initialization model weights."""
+ for m in self.modules():
+ if isinstance(m, nn.Linear):
+ nn.init.xavier_uniform_(m.weight, gain=0.01)
+
+ def backward_p(self, x):
+ """Apply mapping form the data space to the latent space and calculate
+ the log determinant of the Jacobian matrix."""
+
+ log_det_jacob, z = x.new_zeros(x.shape[0]), x
+ for i in reversed(range(len(self.t))):
+ z_ = self.mask[i] * z
+ s = self.s[i](z_) * (1 - self.mask[i]) # torch.exp(s): betas
+ t = self.t[i](z_) * (1 - self.mask[i]) # gammas
+ z = (1 - self.mask[i]) * (z - t) * torch.exp(-s) + z_
+ log_det_jacob -= s.sum(dim=1)
+ return z, log_det_jacob
+
+ def log_prob(self, x):
+ """Calculate the log probability of given sample in data space."""
+
+ z, log_det = self.backward_p(x)
+ return self.prior.log_prob(z) + log_det
diff --git a/grounded-sam-osx/transformer_utils/mmpose/models/utils/smpl.py b/grounded-sam-osx/transformer_utils/mmpose/models/utils/smpl.py
new file mode 100644
index 0000000000000000000000000000000000000000..fe723d483aadb7ce7e0e9f50ef8da7b10e7529e5
--- /dev/null
+++ b/grounded-sam-osx/transformer_utils/mmpose/models/utils/smpl.py
@@ -0,0 +1,184 @@
+# Copyright (c) OpenMMLab. All rights reserved.
+import numpy as np
+import torch
+import torch.nn as nn
+
+from ..builder import MESH_MODELS
+
+try:
+ from smplx import SMPL as SMPL_
+ has_smpl = True
+except (ImportError, ModuleNotFoundError):
+ has_smpl = False
+
+
+@MESH_MODELS.register_module()
+class SMPL(nn.Module):
+ """SMPL 3d human mesh model of paper ref: Matthew Loper. ``SMPL: A skinned
+ multi-person linear model''. This module is based on the smplx project
+ (https://github.com/vchoutas/smplx).
+
+ Args:
+ smpl_path (str): The path to the folder where the model weights are
+ stored.
+ joints_regressor (str): The path to the file where the joints
+ regressor weight are stored.
+ """
+
+ def __init__(self, smpl_path, joints_regressor):
+ super().__init__()
+
+ assert has_smpl, 'Please install smplx to use SMPL.'
+
+ self.smpl_neutral = SMPL_(
+ model_path=smpl_path,
+ create_global_orient=False,
+ create_body_pose=False,
+ create_transl=False,
+ gender='neutral')
+
+ self.smpl_male = SMPL_(
+ model_path=smpl_path,
+ create_betas=False,
+ create_global_orient=False,
+ create_body_pose=False,
+ create_transl=False,
+ gender='male')
+
+ self.smpl_female = SMPL_(
+ model_path=smpl_path,
+ create_betas=False,
+ create_global_orient=False,
+ create_body_pose=False,
+ create_transl=False,
+ gender='female')
+
+ joints_regressor = torch.tensor(
+ np.load(joints_regressor), dtype=torch.float)[None, ...]
+ self.register_buffer('joints_regressor', joints_regressor)
+
+ self.num_verts = self.smpl_neutral.get_num_verts()
+ self.num_joints = self.joints_regressor.shape[1]
+
+ def smpl_forward(self, model, **kwargs):
+ """Apply a specific SMPL model with given model parameters.
+
+ Note:
+ B: batch size
+ V: number of vertices
+ K: number of joints
+
+ Returns:
+ outputs (dict): Dict with mesh vertices and joints.
+ - vertices: Tensor([B, V, 3]), mesh vertices
+ - joints: Tensor([B, K, 3]), 3d joints regressed
+ from mesh vertices.
+ """
+
+ betas = kwargs['betas']
+ batch_size = betas.shape[0]
+ device = betas.device
+ output = {}
+ if batch_size == 0:
+ output['vertices'] = betas.new_zeros([0, self.num_verts, 3])
+ output['joints'] = betas.new_zeros([0, self.num_joints, 3])
+ else:
+ smpl_out = model(**kwargs)
+ output['vertices'] = smpl_out.vertices
+ output['joints'] = torch.matmul(
+ self.joints_regressor.to(device), output['vertices'])
+ return output
+
+ def get_faces(self):
+ """Return mesh faces.
+
+ Note:
+ F: number of faces
+
+ Returns:
+ faces: np.ndarray([F, 3]), mesh faces
+ """
+ return self.smpl_neutral.faces
+
+ def forward(self,
+ betas,
+ body_pose,
+ global_orient,
+ transl=None,
+ gender=None):
+ """Forward function.
+
+ Note:
+ B: batch size
+ J: number of controllable joints of model, for smpl model J=23
+ K: number of joints
+
+ Args:
+ betas: Tensor([B, 10]), human body shape parameters of SMPL model.
+ body_pose: Tensor([B, J*3] or [B, J, 3, 3]), human body pose
+ parameters of SMPL model. It should be axis-angle vector
+ ([B, J*3]) or rotation matrix ([B, J, 3, 3)].
+ global_orient: Tensor([B, 3] or [B, 1, 3, 3]), global orientation
+ of human body. It should be axis-angle vector ([B, 3]) or
+ rotation matrix ([B, 1, 3, 3)].
+ transl: Tensor([B, 3]), global translation of human body.
+ gender: Tensor([B]), gender parameters of human body. -1 for
+ neutral, 0 for male , 1 for female.
+
+ Returns:
+ outputs (dict): Dict with mesh vertices and joints.
+ - vertices: Tensor([B, V, 3]), mesh vertices
+ - joints: Tensor([B, K, 3]), 3d joints regressed from
+ mesh vertices.
+ """
+
+ batch_size = betas.shape[0]
+ pose2rot = True if body_pose.dim() == 2 else False
+ if batch_size > 0 and gender is not None:
+ output = {
+ 'vertices': betas.new_zeros([batch_size, self.num_verts, 3]),
+ 'joints': betas.new_zeros([batch_size, self.num_joints, 3])
+ }
+
+ mask = gender < 0
+ _out = self.smpl_forward(
+ self.smpl_neutral,
+ betas=betas[mask],
+ body_pose=body_pose[mask],
+ global_orient=global_orient[mask],
+ transl=transl[mask] if transl is not None else None,
+ pose2rot=pose2rot)
+ output['vertices'][mask] = _out['vertices']
+ output['joints'][mask] = _out['joints']
+
+ mask = gender == 0
+ _out = self.smpl_forward(
+ self.smpl_male,
+ betas=betas[mask],
+ body_pose=body_pose[mask],
+ global_orient=global_orient[mask],
+ transl=transl[mask] if transl is not None else None,
+ pose2rot=pose2rot)
+ output['vertices'][mask] = _out['vertices']
+ output['joints'][mask] = _out['joints']
+
+ mask = gender == 1
+ _out = self.smpl_forward(
+ self.smpl_male,
+ betas=betas[mask],
+ body_pose=body_pose[mask],
+ global_orient=global_orient[mask],
+ transl=transl[mask] if transl is not None else None,
+ pose2rot=pose2rot)
+ output['vertices'][mask] = _out['vertices']
+ output['joints'][mask] = _out['joints']
+ else:
+ return self.smpl_forward(
+ self.smpl_neutral,
+ betas=betas,
+ body_pose=body_pose,
+ global_orient=global_orient,
+ transl=transl,
+ pose2rot=pose2rot)
+
+ return output
diff --git a/grounded-sam-osx/transformer_utils/mmpose/models/utils/tcformer_utils.py b/grounded-sam-osx/transformer_utils/mmpose/models/utils/tcformer_utils.py
new file mode 100644
index 0000000000000000000000000000000000000000..8d3a28534c83d60e52ed0382f54a4d9f4902e018
--- /dev/null
+++ b/grounded-sam-osx/transformer_utils/mmpose/models/utils/tcformer_utils.py
@@ -0,0 +1,995 @@
+# Copyright (c) OpenMMLab. All rights reserved.
+import math
+
+import torch
+import torch.nn as nn
+import torch.nn.functional as F
+from mmcv.cnn import build_norm_layer, trunc_normal_init
+from mmcv.cnn.bricks.transformer import build_dropout
+
+try:
+ from torch.cuda.amp import autocast
+ WITH_AUTOCAST = True
+except ImportError:
+ WITH_AUTOCAST = False
+
+
+def get_grid_index(init_grid_size, map_size, device):
+ """For every initial grid, get its index in the feature map.
+ Note:
+ [H_init, W_init]: shape of initial grid
+ [H, W]: shape of feature map
+ N_init: numbers of initial token
+
+ Args:
+ init_grid_size (list[int] or tuple[int]): initial grid resolution in
+ format [H_init, W_init].
+ map_size (list[int] or tuple[int]): feature map resolution in format
+ [H, W].
+ device: the device of output
+
+ Returns:
+ idx (torch.LongTensor[B, N_init]): index in flattened feature map.
+ """
+ H_init, W_init = init_grid_size
+ H, W = map_size
+ idx = torch.arange(H * W, device=device).reshape(1, 1, H, W)
+ idx = F.interpolate(idx.float(), [H_init, W_init], mode='nearest').long()
+ return idx.flatten()
+
+
+def index_points(points, idx):
+ """Sample features following the index.
+ Note:
+ B: batch size
+ N: point number
+ C: channel number of each point
+ Ns: sampled point number
+
+ Args:
+ points (torch.Tensor[B, N, C]): input points data
+ idx (torch.LongTensor[B, S]): sample index
+
+ Returns:
+ new_points (torch.Tensor[B, Ns, C]):, indexed points data
+ """
+ device = points.device
+ B = points.shape[0]
+ view_shape = list(idx.shape)
+ view_shape[1:] = [1] * (len(view_shape) - 1)
+ repeat_shape = list(idx.shape)
+ repeat_shape[0] = 1
+ batch_indices = torch.arange(
+ B, dtype=torch.long).to(device).view(view_shape).repeat(repeat_shape)
+ new_points = points[batch_indices, idx, :]
+ return new_points
+
+
+def token2map(token_dict):
+ """Transform vision tokens to feature map. This function only works when
+ the resolution of the feature map is not higher than the initial grid
+ structure.
+
+ Note:
+ B: batch size
+ C: channel number of each token
+ [H, W]: shape of feature map
+ N_init: numbers of initial token
+
+ Args:
+ token_dict (dict): dict for token information.
+
+ Returns:
+ x_out (Tensor[B, C, H, W]): feature map.
+ """
+
+ x = token_dict['x']
+ H, W = token_dict['map_size']
+ H_init, W_init = token_dict['init_grid_size']
+ idx_token = token_dict['idx_token']
+ B, N, C = x.shape
+ N_init = H_init * W_init
+ device = x.device
+
+ if N_init == N and N == H * W:
+ # for the initial tokens with grid structure, just reshape
+ return x.reshape(B, H, W, C).permute(0, 3, 1, 2).contiguous()
+
+ # for each initial grid, get the corresponding index in
+ # the flattened feature map.
+ idx_hw = get_grid_index([H_init, W_init], [H, W],
+ device=device)[None, :].expand(B, -1)
+ idx_batch = torch.arange(B, device=device)[:, None].expand(B, N_init)
+ value = x.new_ones(B * N_init)
+
+ # choose the way with fewer flops.
+ if N_init < N * H * W:
+ # use sparse matrix multiplication
+ # Flops: B * N_init * (C+2)
+ idx_hw = idx_hw + idx_batch * H * W
+ idx_tokens = idx_token + idx_batch * N
+ coor = torch.stack([idx_hw, idx_tokens], dim=0).reshape(2, B * N_init)
+
+ # torch.sparse do not support gradient for
+ # sparse tensor, so we detach it
+ value = value.detach().to(torch.float32)
+
+ # build a sparse matrix with the shape [B * H * W, B * N]
+ A = torch.sparse.FloatTensor(coor, value,
+ torch.Size([B * H * W, B * N]))
+
+ # normalize the weight for each row
+ if WITH_AUTOCAST:
+ with autocast(enabled=False):
+ all_weight = A @ x.new_ones(B * N, 1).type(
+ torch.float32) + 1e-6
+ else:
+ all_weight = A @ x.new_ones(B * N, 1).type(torch.float32) + 1e-6
+ value = value / all_weight[idx_hw.reshape(-1), 0]
+
+ # update the matrix with normalize weight
+ A = torch.sparse.FloatTensor(coor, value,
+ torch.Size([B * H * W, B * N]))
+
+ # sparse matrix multiplication
+ if WITH_AUTOCAST:
+ with autocast(enabled=False):
+ x_out = A @ x.reshape(B * N, C).to(torch.float32) # [B*H*W, C]
+ else:
+ x_out = A @ x.reshape(B * N, C).to(torch.float32) # [B*H*W, C]
+
+ else:
+ # use dense matrix multiplication
+ # Flops: B * N * H * W * (C+2)
+ coor = torch.stack([idx_batch, idx_hw, idx_token],
+ dim=0).reshape(3, B * N_init)
+
+ # build a matrix with shape [B, H*W, N]
+ A = torch.sparse.FloatTensor(coor, value, torch.Size([B, H * W,
+ N])).to_dense()
+ # normalize the weight
+ A = A / (A.sum(dim=-1, keepdim=True) + 1e-6)
+
+ x_out = A @ x # [B, H*W, C]
+
+ x_out = x_out.type(x.dtype)
+ x_out = x_out.reshape(B, H, W, C).permute(0, 3, 1, 2).contiguous()
+ return x_out
+
+
+def map2token(feature_map, token_dict):
+ """Transform feature map to vision tokens. This function only works when
+ the resolution of the feature map is not higher than the initial grid
+ structure.
+
+ Note:
+ B: batch size
+ C: channel number
+ [H, W]: shape of feature map
+ N_init: numbers of initial token
+
+ Args:
+ feature_map (Tensor[B, C, H, W]): feature map.
+ token_dict (dict): dict for token information.
+
+ Returns:
+ out (Tensor[B, N, C]): token features.
+ """
+ idx_token = token_dict['idx_token']
+ N = token_dict['token_num']
+ H_init, W_init = token_dict['init_grid_size']
+ N_init = H_init * W_init
+
+ B, C, H, W = feature_map.shape
+ device = feature_map.device
+
+ if N_init == N and N == H * W:
+ # for the initial tokens with grid structure, just reshape
+ return feature_map.flatten(2).permute(0, 2, 1).contiguous()
+
+ idx_hw = get_grid_index([H_init, W_init], [H, W],
+ device=device)[None, :].expand(B, -1)
+
+ idx_batch = torch.arange(B, device=device)[:, None].expand(B, N_init)
+ value = feature_map.new_ones(B * N_init)
+
+ # choose the way with fewer flops.
+ if N_init < N * H * W:
+ # use sparse matrix multiplication
+ # Flops: B * N_init * (C+2)
+ idx_token = idx_token + idx_batch * N
+ idx_hw = idx_hw + idx_batch * H * W
+ indices = torch.stack([idx_token, idx_hw], dim=0).reshape(2, -1)
+
+ # sparse mm do not support gradient for sparse matrix
+ value = value.detach().to(torch.float32)
+ # build a sparse matrix with shape [B*N, B*H*W]
+ A = torch.sparse_coo_tensor(indices, value, (B * N, B * H * W))
+ # normalize the matrix
+ if WITH_AUTOCAST:
+ with autocast(enabled=False):
+ all_weight = A @ torch.ones(
+ [B * H * W, 1], device=device, dtype=torch.float32) + 1e-6
+ else:
+ all_weight = A @ torch.ones(
+ [B * H * W, 1], device=device, dtype=torch.float32) + 1e-6
+ value = value / all_weight[idx_token.reshape(-1), 0]
+
+ A = torch.sparse_coo_tensor(indices, value, (B * N, B * H * W))
+ # out: [B*N, C]
+ if WITH_AUTOCAST:
+ with autocast(enabled=False):
+ out = A @ feature_map.permute(0, 2, 3, 1).contiguous().reshape(
+ B * H * W, C).float()
+ else:
+ out = A @ feature_map.permute(0, 2, 3, 1).contiguous().reshape(
+ B * H * W, C).float()
+ else:
+ # use dense matrix multiplication
+ # Flops: B * N * H * W * (C+2)
+ indices = torch.stack([idx_batch, idx_token, idx_hw],
+ dim=0).reshape(3, -1)
+ value = value.detach() # To reduce the training time, we detach here.
+ A = torch.sparse_coo_tensor(indices, value, (B, N, H * W)).to_dense()
+ # normalize the matrix
+ A = A / (A.sum(dim=-1, keepdim=True) + 1e-6)
+
+ out = A @ feature_map.permute(0, 2, 3, 1).reshape(B, H * W,
+ C).contiguous()
+
+ out = out.type(feature_map.dtype)
+ out = out.reshape(B, N, C)
+ return out
+
+
+def token_interp(target_dict, source_dict):
+ """Transform token features between different distribution.
+
+ Note:
+ B: batch size
+ N: token number
+ C: channel number
+
+ Args:
+ target_dict (dict): dict for target token information
+ source_dict (dict): dict for source token information.
+
+ Returns:
+ x_out (Tensor[B, N, C]): token features.
+ """
+
+ x_s = source_dict['x']
+ idx_token_s = source_dict['idx_token']
+ idx_token_t = target_dict['idx_token']
+ T = target_dict['token_num']
+ B, S, C = x_s.shape
+ N_init = idx_token_s.shape[1]
+
+ weight = target_dict['agg_weight'] if 'agg_weight' in target_dict.keys(
+ ) else None
+ if weight is None:
+ weight = x_s.new_ones(B, N_init, 1)
+ weight = weight.reshape(-1)
+
+ # choose the way with fewer flops.
+ if N_init < T * S:
+ # use sparse matrix multiplication
+ # Flops: B * N_init * (C+2)
+ idx_token_t = idx_token_t + torch.arange(
+ B, device=x_s.device)[:, None] * T
+ idx_token_s = idx_token_s + torch.arange(
+ B, device=x_s.device)[:, None] * S
+ coor = torch.stack([idx_token_t, idx_token_s],
+ dim=0).reshape(2, B * N_init)
+
+ # torch.sparse does not support grad for sparse matrix
+ weight = weight.float().detach().to(torch.float32)
+ # build a matrix with shape [B*T, B*S]
+ A = torch.sparse.FloatTensor(coor, weight, torch.Size([B * T, B * S]))
+ # normalize the matrix
+ if WITH_AUTOCAST:
+ with autocast(enabled=False):
+ all_weight = A.type(torch.float32) @ x_s.new_ones(
+ B * S, 1).type(torch.float32) + 1e-6
+ else:
+ all_weight = A.type(torch.float32) @ x_s.new_ones(B * S, 1).type(
+ torch.float32) + 1e-6
+ weight = weight / all_weight[idx_token_t.reshape(-1), 0]
+ A = torch.sparse.FloatTensor(coor, weight, torch.Size([B * T, B * S]))
+ # sparse matmul
+ if WITH_AUTOCAST:
+ with autocast(enabled=False):
+ x_out = A.type(torch.float32) @ x_s.reshape(B * S, C).type(
+ torch.float32)
+ else:
+ x_out = A.type(torch.float32) @ x_s.reshape(B * S, C).type(
+ torch.float32)
+ else:
+ # use dense matrix multiplication
+ # Flops: B * T * S * (C+2)
+ idx_batch = torch.arange(
+ B, device=x_s.device)[:, None].expand(B, N_init)
+ coor = torch.stack([idx_batch, idx_token_t, idx_token_s],
+ dim=0).reshape(3, B * N_init)
+ weight = weight.detach() # detach to reduce training time
+ # build a matrix with shape [B, T, S]
+ A = torch.sparse.FloatTensor(coor, weight, torch.Size([B, T,
+ S])).to_dense()
+ # normalize the matrix
+ A = A / (A.sum(dim=-1, keepdim=True) + 1e-6)
+ # dense matmul
+ x_out = A @ x_s
+
+ x_out = x_out.reshape(B, T, C).type(x_s.dtype)
+ return x_out
+
+
+def cluster_dpc_knn(token_dict, cluster_num, k=5, token_mask=None):
+ """Cluster tokens with DPC-KNN algorithm.
+
+ Note:
+ B: batch size
+ N: token number
+ C: channel number
+
+ Args:
+ token_dict (dict): dict for token information
+ cluster_num (int): cluster number
+ k (int): number of the nearest neighbor used for local density.
+ token_mask (Tensor[B, N]): mask indicating which token is the
+ padded empty token. Non-zero value means the token is meaningful,
+ zero value means the token is an empty token. If set to None, all
+ tokens are regarded as meaningful.
+
+ Return:
+ idx_cluster (Tensor[B, N]): cluster index of each token.
+ cluster_num (int): actual cluster number. In this function, it equals
+ to the input cluster number.
+ """
+
+ with torch.no_grad():
+ x = token_dict['x']
+ B, N, C = x.shape
+
+ dist_matrix = torch.cdist(x, x) / (C**0.5)
+
+ if token_mask is not None:
+ token_mask = token_mask > 0
+ # in order to not affect the local density, the
+ # distance between empty tokens and any other
+ # tokens should be the maximal distance.
+ dist_matrix = \
+ dist_matrix * token_mask[:, None, :] +\
+ (dist_matrix.max() + 1) * (~token_mask[:, None, :])
+
+ # get local density
+ dist_nearest, index_nearest = torch.topk(
+ dist_matrix, k=k, dim=-1, largest=False)
+
+ density = (-(dist_nearest**2).mean(dim=-1)).exp()
+ # add a little noise to ensure no tokens have the same density.
+ density = density + torch.rand(
+ density.shape, device=density.device, dtype=density.dtype) * 1e-6
+
+ if token_mask is not None:
+ # the density of empty token should be 0
+ density = density * token_mask
+
+ # get distance indicator
+ mask = density[:, None, :] > density[:, :, None]
+ mask = mask.type(x.dtype)
+ dist_max = dist_matrix.flatten(1).max(dim=-1)[0][:, None, None]
+ dist, index_parent = (dist_matrix * mask + dist_max *
+ (1 - mask)).min(dim=-1)
+
+ # select clustering center according to score
+ score = dist * density
+ _, index_down = torch.topk(score, k=cluster_num, dim=-1)
+
+ # assign tokens to the nearest center
+ dist_matrix = index_points(dist_matrix, index_down)
+
+ idx_cluster = dist_matrix.argmin(dim=1)
+
+ # make sure cluster center merge to itself
+ idx_batch = torch.arange(
+ B, device=x.device)[:, None].expand(B, cluster_num)
+ idx_tmp = torch.arange(
+ cluster_num, device=x.device)[None, :].expand(B, cluster_num)
+ idx_cluster[idx_batch.reshape(-1),
+ index_down.reshape(-1)] = idx_tmp.reshape(-1)
+
+ return idx_cluster, cluster_num
+
+
+def merge_tokens(token_dict, idx_cluster, cluster_num, token_weight=None):
+ """Merge tokens in the same cluster to a single cluster. Implemented by
+ torch.index_add(). Flops: B*N*(C+2)
+
+ Note:
+ B: batch size
+ N: token number
+ C: channel number
+
+ Args:
+ token_dict (dict): dict for input token information
+ idx_cluster (Tensor[B, N]): cluster index of each token.
+ cluster_num (int): cluster number
+ token_weight (Tensor[B, N, 1]): weight for each token.
+
+ Return:
+ out_dict (dict): dict for output token information
+ """
+
+ x = token_dict['x']
+ idx_token = token_dict['idx_token']
+ agg_weight = token_dict['agg_weight']
+
+ B, N, C = x.shape
+ if token_weight is None:
+ token_weight = x.new_ones(B, N, 1)
+
+ idx_batch = torch.arange(B, device=x.device)[:, None]
+ idx = idx_cluster + idx_batch * cluster_num
+
+ all_weight = token_weight.new_zeros(B * cluster_num, 1)
+ all_weight.index_add_(
+ dim=0, index=idx.reshape(B * N), source=token_weight.reshape(B * N, 1))
+ all_weight = all_weight + 1e-6
+ norm_weight = token_weight / all_weight[idx]
+
+ # average token features
+ x_merged = x.new_zeros(B * cluster_num, C)
+ source = x * norm_weight
+ x_merged.index_add_(
+ dim=0,
+ index=idx.reshape(B * N),
+ source=source.reshape(B * N, C).type(x.dtype))
+ x_merged = x_merged.reshape(B, cluster_num, C)
+
+ idx_token_new = index_points(idx_cluster[..., None], idx_token).squeeze(-1)
+ weight_t = index_points(norm_weight, idx_token)
+ agg_weight_new = agg_weight * weight_t
+ agg_weight_new / agg_weight_new.max(dim=1, keepdim=True)[0]
+
+ out_dict = {}
+ out_dict['x'] = x_merged
+ out_dict['token_num'] = cluster_num
+ out_dict['map_size'] = token_dict['map_size']
+ out_dict['init_grid_size'] = token_dict['init_grid_size']
+ out_dict['idx_token'] = idx_token_new
+ out_dict['agg_weight'] = agg_weight_new
+ return out_dict
+
+
+class MLP(nn.Module):
+ """FFN with Depthwise Conv of TCFormer.
+
+ Args:
+ in_features (int): The feature dimension.
+ hidden_features (int, optional): The hidden dimension of FFNs.
+ Defaults: The same as in_features.
+ out_features (int, optional): The output feature dimension.
+ Defaults: The same as in_features.
+ act_layer (nn.Module, optional): The activation config for FFNs.
+ Default: nn.GELU.
+ drop (float, optional): drop out rate. Default: 0.
+ """
+
+ def __init__(self,
+ in_features,
+ hidden_features=None,
+ out_features=None,
+ act_layer=nn.GELU,
+ drop=0.):
+ super().__init__()
+ out_features = out_features or in_features
+ hidden_features = hidden_features or in_features
+ self.fc1 = nn.Linear(in_features, hidden_features)
+ self.dwconv = DWConv(hidden_features)
+ self.act = act_layer()
+ self.fc2 = nn.Linear(hidden_features, out_features)
+ self.drop = nn.Dropout(drop)
+
+ def init_weights(self):
+ """init weights."""
+ for m in self.modules():
+ if isinstance(m, nn.Linear):
+ trunc_normal_init(m, std=.02, bias=0.)
+ elif isinstance(m, nn.LayerNorm):
+ nn.init.constant_(m.bias, 0)
+ nn.init.constant_(m.weight, 1.0)
+ elif isinstance(m, nn.Conv2d):
+ fan_out = m.kernel_size[0] * m.kernel_size[1] * m.out_channels
+ fan_out //= m.groups
+ m.weight.data.normal_(0, math.sqrt(2.0 / fan_out))
+ if m.bias is not None:
+ m.bias.data.zero_()
+
+ def forward(self, x, H, W):
+ x = self.fc1(x)
+ x = self.dwconv(x, H, W)
+ x = self.act(x)
+ x = self.drop(x)
+ x = self.fc2(x)
+ x = self.drop(x)
+ return x
+
+
+class DWConv(nn.Module):
+ """Depthwise Conv for regular grid-based tokens.
+
+ Args:
+ dim (int): The feature dimension.
+ """
+
+ def __init__(self, dim=768):
+ super(DWConv, self).__init__()
+ self.dwconv = nn.Conv2d(dim, dim, 3, 1, 1, bias=True, groups=dim)
+
+ def forward(self, x, H, W):
+ B, N, C = x.shape
+ x = x.transpose(1, 2).view(B, C, H, W)
+ x = self.dwconv(x)
+ x = x.flatten(2).transpose(1, 2)
+ return x
+
+
+class TCFormerRegularAttention(nn.Module):
+ """Spatial Reduction Attention for regular grid-based tokens.
+
+ Args:
+ dim (int): The feature dimension of tokens,
+ num_heads (int): Parallel attention heads.
+ qkv_bias (bool): enable bias for qkv if True. Default: False.
+ qk_scale (float | None, optional): Override default qk scale of
+ head_dim ** -0.5 if set. Default: None.
+ attn_drop (float): A Dropout layer on attn_output_weights.
+ Default: 0.0.
+ proj_drop (float): A Dropout layer after attention process.
+ Default: 0.0.
+ sr_ratio (int): The ratio of spatial reduction of Spatial Reduction
+ Attention. Default: 1.
+ use_sr_conv (bool): If True, use a conv layer for spatial reduction.
+ If False, use a pooling process for spatial reduction. Defaults:
+ True.
+ """
+
+ def __init__(
+ self,
+ dim,
+ num_heads=8,
+ qkv_bias=False,
+ qk_scale=None,
+ attn_drop=0.,
+ proj_drop=0.,
+ sr_ratio=1,
+ use_sr_conv=True,
+ ):
+ super().__init__()
+ assert dim % num_heads == 0, \
+ f'dim {dim} should be divided by num_heads {num_heads}.'
+
+ self.dim = dim
+ self.num_heads = num_heads
+ head_dim = dim // num_heads
+ self.scale = qk_scale or head_dim**-0.5
+
+ self.q = nn.Linear(dim, dim, bias=qkv_bias)
+ self.kv = nn.Linear(dim, dim * 2, bias=qkv_bias)
+ self.attn_drop = nn.Dropout(attn_drop)
+ self.proj = nn.Linear(dim, dim)
+ self.proj_drop = nn.Dropout(proj_drop)
+
+ self.sr_ratio = sr_ratio
+ self.use_sr_conv = use_sr_conv
+ if sr_ratio > 1 and self.use_sr_conv:
+ self.sr = nn.Conv2d(
+ dim, dim, kernel_size=sr_ratio, stride=sr_ratio)
+ self.norm = nn.LayerNorm(dim)
+
+ def init_weights(self):
+ for m in self.modules():
+ if isinstance(m, nn.Linear):
+ trunc_normal_init(m, std=.02, bias=0.)
+ elif isinstance(m, nn.LayerNorm):
+ nn.init.constant_(m.bias, 0)
+ nn.init.constant_(m.weight, 1.0)
+ elif isinstance(m, nn.Conv2d):
+ fan_out = m.kernel_size[0] * m.kernel_size[1] * m.out_channels
+ fan_out //= m.groups
+ m.weight.data.normal_(0, math.sqrt(2.0 / fan_out))
+ if m.bias is not None:
+ m.bias.data.zero_()
+
+ def forward(self, x, H, W):
+ B, N, C = x.shape
+ q = self.q(x).reshape(B, N, self.num_heads,
+ C // self.num_heads).permute(0, 2, 1, 3)
+
+ if self.sr_ratio > 1:
+ kv = x.permute(0, 2, 1).reshape(B, C, H, W)
+ if self.use_sr_conv:
+ kv = self.sr(kv).reshape(B, C, -1).permute(0, 2,
+ 1).contiguous()
+ kv = self.norm(kv)
+ else:
+ kv = F.avg_pool2d(
+ kv, kernel_size=self.sr_ratio, stride=self.sr_ratio)
+ kv = kv.reshape(B, C, -1).permute(0, 2, 1).contiguous()
+ else:
+ kv = x
+
+ kv = self.kv(kv).reshape(B, -1, 2, self.num_heads,
+ C // self.num_heads).permute(2, 0, 3, 1,
+ 4).contiguous()
+ k, v = kv[0], kv[1]
+
+ attn = (q * self.scale) @ k.transpose(-2, -1)
+ attn = attn.softmax(dim=-1)
+ attn = self.attn_drop(attn)
+
+ x = (attn @ v).transpose(1, 2).reshape(B, N, C)
+ x = self.proj(x)
+ x = self.proj_drop(x)
+
+ return x
+
+
+class TCFormerRegularBlock(nn.Module):
+ """Transformer block for regular grid-based tokens.
+
+ Args:
+ dim (int): The feature dimension.
+ num_heads (int): Parallel attention heads.
+ mlp_ratio (int): The expansion ratio for the FFNs.
+ qkv_bias (bool): enable bias for qkv if True. Default: False.
+ qk_scale (float | None, optional): Override default qk scale of
+ head_dim ** -0.5 if set. Default: None.
+ drop (float): Dropout layers after attention process and in FFN.
+ Default: 0.0.
+ attn_drop (float): A Dropout layer on attn_output_weights.
+ Default: 0.0.
+ drop_path (int, optional): The drop path rate of transformer block.
+ Default: 0.0
+ act_layer (nn.Module, optional): The activation config for FFNs.
+ Default: nn.GELU.
+ norm_cfg (dict): Config dict for normalization layer.
+ Default: dict(type='LN').
+ sr_ratio (int): The ratio of spatial reduction of Spatial Reduction
+ Attention. Default: 1.
+ use_sr_conv (bool): If True, use a conv layer for spatial reduction.
+ If False, use a pooling process for spatial reduction. Defaults:
+ True.
+ """
+
+ def __init__(self,
+ dim,
+ num_heads,
+ mlp_ratio=4.,
+ qkv_bias=False,
+ qk_scale=None,
+ drop=0.,
+ attn_drop=0.,
+ drop_path=0.,
+ act_layer=nn.GELU,
+ norm_cfg=dict(type='LN'),
+ sr_ratio=1,
+ use_sr_conv=True):
+ super().__init__()
+ self.norm1 = build_norm_layer(norm_cfg, dim)[1]
+
+ self.attn = TCFormerRegularAttention(
+ dim,
+ num_heads=num_heads,
+ qkv_bias=qkv_bias,
+ qk_scale=qk_scale,
+ attn_drop=attn_drop,
+ proj_drop=drop,
+ sr_ratio=sr_ratio,
+ use_sr_conv=use_sr_conv)
+ self.drop_path = build_dropout(
+ dict(type='DropPath', drop_prob=drop_path))
+
+ self.norm2 = build_norm_layer(norm_cfg, dim)[1]
+ mlp_hidden_dim = int(dim * mlp_ratio)
+ self.mlp = MLP(
+ in_features=dim,
+ hidden_features=mlp_hidden_dim,
+ act_layer=act_layer,
+ drop=drop)
+
+ def init_weights(self):
+ for m in self.modules():
+ if isinstance(m, nn.Linear):
+ trunc_normal_init(m, std=.02, bias=0.)
+ elif isinstance(m, nn.LayerNorm):
+ nn.init.constant_(m.bias, 0)
+ nn.init.constant_(m.weight, 1.0)
+ elif isinstance(m, nn.Conv2d):
+ fan_out = m.kernel_size[0] * m.kernel_size[1] * m.out_channels
+ fan_out //= m.groups
+ m.weight.data.normal_(0, math.sqrt(2.0 / fan_out))
+ if m.bias is not None:
+ m.bias.data.zero_()
+
+ def forward(self, x, H, W):
+ x = x + self.drop_path(self.attn(self.norm1(x), H, W))
+ x = x + self.drop_path(self.mlp(self.norm2(x), H, W))
+ return x
+
+
+class TokenConv(nn.Conv2d):
+ """Conv layer for dynamic tokens.
+
+ A skip link is added between the input and output tokens to reserve detail
+ tokens.
+ """
+
+ def __init__(self, **kwargs):
+ super().__init__(**kwargs)
+ groups = kwargs['groups'] if 'groups' in kwargs.keys() else 1
+ self.skip = nn.Conv1d(
+ in_channels=kwargs['in_channels'],
+ out_channels=kwargs['out_channels'],
+ kernel_size=1,
+ bias=False,
+ groups=groups)
+
+ def forward(self, token_dict):
+ x = token_dict['x']
+ x = self.skip(x.permute(0, 2, 1)).permute(0, 2, 1)
+ x_map = token2map(token_dict)
+ x_map = super().forward(x_map)
+ x = x + map2token(x_map, token_dict)
+ return x
+
+
+class TCMLP(nn.Module):
+ """FFN with Depthwise Conv for dynamic tokens.
+
+ Args:
+ in_features (int): The feature dimension.
+ hidden_features (int, optional): The hidden dimension of FFNs.
+ Defaults: The same as in_features.
+ out_features (int, optional): The output feature dimension.
+ Defaults: The same as in_features.
+ act_layer (nn.Module, optional): The activation config for FFNs.
+ Default: nn.GELU.
+ drop (float, optional): drop out rate. Default: 0.
+ """
+
+ def __init__(self,
+ in_features,
+ hidden_features=None,
+ out_features=None,
+ act_layer=nn.GELU,
+ drop=0.):
+ super().__init__()
+ out_features = out_features or in_features
+ hidden_features = hidden_features or in_features
+ self.fc1 = nn.Linear(in_features, hidden_features)
+ self.dwconv = TokenConv(
+ in_channels=hidden_features,
+ out_channels=hidden_features,
+ kernel_size=3,
+ padding=1,
+ stride=1,
+ bias=True,
+ groups=hidden_features)
+ self.act = act_layer()
+ self.fc2 = nn.Linear(hidden_features, out_features)
+ self.drop = nn.Dropout(drop)
+
+ def init_weights(self):
+ """init weights."""
+ for m in self.modules():
+ if isinstance(m, nn.Linear):
+ trunc_normal_init(m, std=.02, bias=0.)
+ elif isinstance(m, nn.LayerNorm):
+ nn.init.constant_(m.bias, 0)
+ nn.init.constant_(m.weight, 1.0)
+ elif isinstance(m, nn.Conv2d):
+ fan_out = m.kernel_size[0] * m.kernel_size[1] * m.out_channels
+ fan_out //= m.groups
+ m.weight.data.normal_(0, math.sqrt(2.0 / fan_out))
+ if m.bias is not None:
+ m.bias.data.zero_()
+
+ def forward(self, token_dict):
+ token_dict['x'] = self.fc1(token_dict['x'])
+ x = self.dwconv(token_dict)
+ x = self.act(x)
+ x = self.drop(x)
+ x = self.fc2(x)
+ x = self.drop(x)
+ return x
+
+
+class TCFormerDynamicAttention(TCFormerRegularAttention):
+ """Spatial Reduction Attention for dynamic tokens."""
+
+ def forward(self, q_dict, kv_dict):
+ """Attention process for dynamic tokens.
+ Dynamic tokens are represented by a dict with the following keys:
+ x (torch.Tensor[B, N, C]): token features.
+ token_num(int): token number.
+ map_size(list[int] or tuple[int]): feature map resolution in
+ format [H, W].
+ init_grid_size(list[int] or tuple[int]): initial grid resolution
+ in format [H_init, W_init].
+ idx_token(torch.LongTensor[B, N_init]): indicates which token
+ the initial grid belongs to.
+ agg_weight(torch.LongTensor[B, N_init] or None): weight for
+ aggregation. Indicates the weight of each token in its
+ cluster. If set to None, uniform weight is used.
+
+ Note:
+ B: batch size
+ N: token number
+ C: channel number
+ Ns: sampled point number
+ [H_init, W_init]: shape of initial grid
+ [H, W]: shape of feature map
+ N_init: numbers of initial token
+
+ Args:
+ q_dict (dict): dict for query token information
+ kv_dict (dict): dict for key and value token information
+
+ Return:
+ x (torch.Tensor[B, N, C]): output token features.
+ """
+
+ q = q_dict['x']
+ kv = kv_dict['x']
+ B, Nq, C = q.shape
+ Nkv = kv.shape[1]
+ conf_kv = kv_dict['token_score'] if 'token_score' in kv_dict.keys(
+ ) else kv.new_zeros(B, Nkv, 1)
+
+ q = self.q(q).reshape(B, Nq, self.num_heads,
+ C // self.num_heads).permute(0, 2, 1,
+ 3).contiguous()
+
+ if self.sr_ratio > 1:
+ tmp = torch.cat([kv, conf_kv], dim=-1)
+ tmp_dict = kv_dict.copy()
+ tmp_dict['x'] = tmp
+ tmp_dict['map_size'] = q_dict['map_size']
+ tmp = token2map(tmp_dict)
+
+ kv = tmp[:, :C]
+ conf_kv = tmp[:, C:]
+
+ if self.use_sr_conv:
+ kv = self.sr(kv)
+ _, _, h, w = kv.shape
+ kv = kv.reshape(B, C, -1).permute(0, 2, 1).contiguous()
+ kv = self.norm(kv)
+ else:
+ kv = F.avg_pool2d(
+ kv, kernel_size=self.sr_ratio, stride=self.sr_ratio)
+ kv = kv.reshape(B, C, -1).permute(0, 2, 1).contiguous()
+
+ conf_kv = F.avg_pool2d(
+ conf_kv, kernel_size=self.sr_ratio, stride=self.sr_ratio)
+ conf_kv = conf_kv.reshape(B, 1, -1).permute(0, 2, 1).contiguous()
+
+ kv = self.kv(kv).reshape(B, -1, 2, self.num_heads,
+ C // self.num_heads).permute(2, 0, 3, 1,
+ 4).contiguous()
+ k, v = kv[0], kv[1]
+
+ attn = (q * self.scale) @ k.transpose(-2, -1)
+
+ conf_kv = conf_kv.squeeze(-1)[:, None, None, :]
+ attn = attn + conf_kv
+ attn = attn.softmax(dim=-1)
+ attn = self.attn_drop(attn)
+
+ x = (attn @ v).transpose(1, 2).reshape(B, Nq, C)
+ x = self.proj(x)
+ x = self.proj_drop(x)
+ return x
+
+
+# Transformer block for dynamic tokens
+class TCFormerDynamicBlock(TCFormerRegularBlock):
+ """Transformer block for dynamic tokens.
+
+ Args:
+ dim (int): The feature dimension.
+ num_heads (int): Parallel attention heads.
+ mlp_ratio (int): The expansion ratio for the FFNs.
+ qkv_bias (bool): enable bias for qkv if True. Default: False.
+ qk_scale (float | None, optional): Override default qk scale of
+ head_dim ** -0.5 if set. Default: None.
+ drop (float): Dropout layers after attention process and in FFN.
+ Default: 0.0.
+ attn_drop (float): A Dropout layer on attn_output_weights.
+ Default: 0.0.
+ drop_path (int, optional): The drop path rate of transformer block.
+ Default: 0.0
+ act_layer (nn.Module, optional): The activation config for FFNs.
+ Default: nn.GELU.
+ norm_cfg (dict): Config dict for normalization layer.
+ Default: dict(type='LN').
+ sr_ratio (int): The ratio of spatial reduction of Spatial Reduction
+ Attention. Default: 1.
+ use_sr_conv (bool): If True, use a conv layer for spatial reduction.
+ If False, use a pooling process for spatial reduction. Defaults:
+ True.
+ """
+
+ def __init__(self,
+ dim,
+ num_heads,
+ mlp_ratio=4.,
+ qkv_bias=False,
+ qk_scale=None,
+ drop=0.,
+ attn_drop=0.,
+ drop_path=0.,
+ act_layer=nn.GELU,
+ norm_cfg=dict(type='LN'),
+ sr_ratio=1,
+ use_sr_conv=True):
+ super(TCFormerRegularBlock, self).__init__()
+ self.norm1 = build_norm_layer(norm_cfg, dim)[1]
+
+ self.attn = TCFormerDynamicAttention(
+ dim,
+ num_heads=num_heads,
+ qkv_bias=qkv_bias,
+ qk_scale=qk_scale,
+ attn_drop=attn_drop,
+ proj_drop=drop,
+ sr_ratio=sr_ratio,
+ use_sr_conv=use_sr_conv)
+ self.drop_path = build_dropout(
+ dict(type='DropPath', drop_prob=drop_path))
+
+ self.norm2 = build_norm_layer(norm_cfg, dim)[1]
+ mlp_hidden_dim = int(dim * mlp_ratio)
+ self.mlp = TCMLP(
+ in_features=dim,
+ hidden_features=mlp_hidden_dim,
+ act_layer=act_layer,
+ drop=drop)
+
+ def forward(self, inputs):
+ """Forward function.
+
+ Args:
+ inputs (dict or tuple[dict] or list[dict]): input dynamic
+ token information. If a single dict is provided, it's
+ regraded as query and key, value. If a tuple or list
+ of dict is provided, the first one is regarded as key
+ and the second one is regarded as key, value.
+
+ Return:
+ q_dict (dict): dict for output token information
+ """
+ if isinstance(inputs, tuple) or isinstance(inputs, list):
+ q_dict, kv_dict = inputs
+ else:
+ q_dict, kv_dict = inputs, None
+
+ x = q_dict['x']
+ # norm1
+ q_dict['x'] = self.norm1(q_dict['x'])
+ if kv_dict is None:
+ kv_dict = q_dict
+ else:
+ kv_dict['x'] = self.norm1(kv_dict['x'])
+
+ # attn
+ x = x + self.drop_path(self.attn(q_dict, kv_dict))
+
+ # mlp
+ q_dict['x'] = self.norm2(x)
+ x = x + self.drop_path(self.mlp(q_dict))
+ q_dict['x'] = x
+
+ return q_dict
diff --git a/grounded-sam-osx/transformer_utils/mmpose/models/utils/transformer.py b/grounded-sam-osx/transformer_utils/mmpose/models/utils/transformer.py
new file mode 100644
index 0000000000000000000000000000000000000000..ce8a7bb1b7b6bebb9c17c7483c5c052ec049518e
--- /dev/null
+++ b/grounded-sam-osx/transformer_utils/mmpose/models/utils/transformer.py
@@ -0,0 +1,1138 @@
+# Copyright (c) OpenMMLab. All rights reserved.
+import math
+from typing import Sequence
+
+import torch
+import torch.nn as nn
+import torch.nn.functional as F
+from mmcv.cnn import build_conv_layer, build_norm_layer
+from mmcv.runner.base_module import BaseModule
+from mmcv.utils import to_2tuple
+from mmpose.models.builder import TRANSFORMER
+
+from easydict import EasyDict
+from einops import rearrange, repeat
+from mmcv.runner import force_fp32
+from mmcv.cnn.bricks.transformer import (BaseTransformerLayer,
+ TransformerLayerSequence,
+ build_transformer_layer_sequence)
+from mmcv.cnn.bricks.registry import (TRANSFORMER_LAYER,
+ TRANSFORMER_LAYER_SEQUENCE)
+import torch.distributions as distributions
+from mmcv.ops.multi_scale_deform_attn import MultiScaleDeformableAttention
+from torch.nn.init import normal_
+import copy
+import warnings
+from mmcv.cnn import build_activation_layer, build_norm_layer, xavier_init
+
+from utils.human_models import smpl_x
+
+from config import cfg
+
+
+def point_sample(input, point_coords, **kwargs):
+ """
+ A wrapper around :function:`torch.nn.functional.grid_sample` to support 3D point_coords tensors.
+ Unlike :function:`torch.nn.functional.grid_sample` it assumes `point_coords` to lie inside
+ [0, 1] x [0, 1] square.
+ Args:
+ input (Tensor): A tensor of shape (N, C, H, W) that contains features map on a H x W grid.
+ point_coords (Tensor): A tensor of shape (N, P, 2) or (N, Hgrid, Wgrid, 2) that contains
+ [0, 1] x [0, 1] normalized point coordinates.
+ Returns:
+ output (Tensor): A tensor of shape (N, C, P) or (N, C, Hgrid, Wgrid) that contains
+ features for points in `point_coords`. The features are obtained via bilinear
+ interplation from `input` the same way as :function:`torch.nn.functional.grid_sample`.
+ """
+ add_dim = False
+ if point_coords.dim() == 3:
+ add_dim = True
+ point_coords = point_coords.unsqueeze(2)
+ output = F.grid_sample(input, 2.0 * point_coords - 1.0, **kwargs)
+ if add_dim:
+ output = output.squeeze(3)
+ return output
+
+
+def nlc_to_nchw(x, hw_shape):
+ """Convert [N, L, C] shape tensor to [N, C, H, W] shape tensor.
+
+ Args:
+ x (Tensor): The input tensor of shape [N, L, C] before conversion.
+ hw_shape (Sequence[int]): The height and width of output feature map.
+
+ Returns:
+ Tensor: The output tensor of shape [N, C, H, W] after conversion.
+ """
+ H, W = hw_shape
+ assert len(x.shape) == 3
+ B, L, C = x.shape
+ assert L == H * W, 'The seq_len does not match H, W'
+ return x.transpose(1, 2).reshape(B, C, H, W).contiguous()
+
+
+def nchw_to_nlc(x):
+ """Flatten [N, C, H, W] shape tensor to [N, L, C] shape tensor.
+
+ Args:
+ x (Tensor): The input tensor of shape [N, C, H, W] before conversion.
+
+ Returns:
+ Tensor: The output tensor of shape [N, L, C] after conversion.
+ """
+ assert len(x.shape) == 4
+ return x.flatten(2).transpose(1, 2).contiguous()
+
+
+class AdaptivePadding(nn.Module):
+ """Applies padding to input (if needed) so that input can get fully covered
+ by filter you specified. It support two modes "same" and "corner". The
+ "same" mode is same with "SAME" padding mode in TensorFlow, pad zero around
+ input. The "corner" mode would pad zero to bottom right.
+
+ Args:
+ kernel_size (int | tuple): Size of the kernel:
+ stride (int | tuple): Stride of the filter. Default: 1:
+ dilation (int | tuple): Spacing between kernel elements.
+ Default: 1
+ padding (str): Support "same" and "corner", "corner" mode
+ would pad zero to bottom right, and "same" mode would
+ pad zero around input. Default: "corner".
+ Example:
+ >>> kernel_size = 16
+ >>> stride = 16
+ >>> dilation = 1
+ >>> input = torch.rand(1, 1, 15, 17)
+ >>> adap_pad = AdaptivePadding(
+ >>> kernel_size=kernel_size,
+ >>> stride=stride,
+ >>> dilation=dilation,
+ >>> padding="corner")
+ >>> out = adap_pad(input)
+ >>> assert (out.shape[2], out.shape[3]) == (16, 32)
+ >>> input = torch.rand(1, 1, 16, 17)
+ >>> out = adap_pad(input)
+ >>> assert (out.shape[2], out.shape[3]) == (16, 32)
+ """
+
+ def __init__(self, kernel_size=1, stride=1, dilation=1, padding='corner'):
+
+ super(AdaptivePadding, self).__init__()
+
+ assert padding in ('same', 'corner')
+
+ kernel_size = to_2tuple(kernel_size)
+ stride = to_2tuple(stride)
+ padding = to_2tuple(padding)
+ dilation = to_2tuple(dilation)
+
+ self.padding = padding
+ self.kernel_size = kernel_size
+ self.stride = stride
+ self.dilation = dilation
+
+ def get_pad_shape(self, input_shape):
+ input_h, input_w = input_shape
+ kernel_h, kernel_w = self.kernel_size
+ stride_h, stride_w = self.stride
+ output_h = math.ceil(input_h / stride_h)
+ output_w = math.ceil(input_w / stride_w)
+ pad_h = max((output_h - 1) * stride_h +
+ (kernel_h - 1) * self.dilation[0] + 1 - input_h, 0)
+ pad_w = max((output_w - 1) * stride_w +
+ (kernel_w - 1) * self.dilation[1] + 1 - input_w, 0)
+ return pad_h, pad_w
+
+ def forward(self, x):
+ pad_h, pad_w = self.get_pad_shape(x.size()[-2:])
+ if pad_h > 0 or pad_w > 0:
+ if self.padding == 'corner':
+ x = F.pad(x, [0, pad_w, 0, pad_h])
+ elif self.padding == 'same':
+ x = F.pad(x, [
+ pad_w // 2, pad_w - pad_w // 2, pad_h // 2,
+ pad_h - pad_h // 2
+ ])
+ return x
+
+
+class PatchEmbed(BaseModule):
+ """Image to Patch Embedding.
+
+ We use a conv layer to implement PatchEmbed.
+
+ Args:
+ in_channels (int): The num of input channels. Default: 3
+ embed_dims (int): The dimensions of embedding. Default: 768
+ conv_type (str): The config dict for embedding
+ conv layer type selection. Default: "Conv2d.
+ kernel_size (int): The kernel_size of embedding conv. Default: 16.
+ stride (int): The slide stride of embedding conv.
+ Default: None (Would be set as `kernel_size`).
+ padding (int | tuple | string ): The padding length of
+ embedding conv. When it is a string, it means the mode
+ of adaptive padding, support "same" and "corner" now.
+ Default: "corner".
+ dilation (int): The dilation rate of embedding conv. Default: 1.
+ bias (bool): Bias of embed conv. Default: True.
+ norm_cfg (dict, optional): Config dict for normalization layer.
+ Default: None.
+ input_size (int | tuple | None): The size of input, which will be
+ used to calculate the out size. Only work when `dynamic_size`
+ is False. Default: None.
+ init_cfg (`mmcv.ConfigDict`, optional): The Config for initialization.
+ Default: None.
+ """
+
+ def __init__(
+ self,
+ in_channels=3,
+ embed_dims=768,
+ conv_type='Conv2d',
+ kernel_size=16,
+ stride=16,
+ padding='corner',
+ dilation=1,
+ bias=True,
+ norm_cfg=None,
+ input_size=None,
+ init_cfg=None,
+ ):
+ super(PatchEmbed, self).__init__(init_cfg=init_cfg)
+
+ self.embed_dims = embed_dims
+ if stride is None:
+ stride = kernel_size
+
+ kernel_size = to_2tuple(kernel_size)
+ stride = to_2tuple(stride)
+ dilation = to_2tuple(dilation)
+
+ if isinstance(padding, str):
+ self.adap_padding = AdaptivePadding(
+ kernel_size=kernel_size,
+ stride=stride,
+ dilation=dilation,
+ padding=padding)
+ # disable the padding of conv
+ padding = 0
+ else:
+ self.adap_padding = None
+ padding = to_2tuple(padding)
+
+ self.projection = build_conv_layer(
+ dict(type=conv_type),
+ in_channels=in_channels,
+ out_channels=embed_dims,
+ kernel_size=kernel_size,
+ stride=stride,
+ padding=padding,
+ dilation=dilation,
+ bias=bias)
+
+ if norm_cfg is not None:
+ self.norm = build_norm_layer(norm_cfg, embed_dims)[1]
+ else:
+ self.norm = None
+
+ if input_size:
+ input_size = to_2tuple(input_size)
+ # `init_out_size` would be used outside to
+ # calculate the num_patches
+ # when `use_abs_pos_embed` outside
+ self.init_input_size = input_size
+ if self.adap_padding:
+ pad_h, pad_w = self.adap_padding.get_pad_shape(input_size)
+ input_h, input_w = input_size
+ input_h = input_h + pad_h
+ input_w = input_w + pad_w
+ input_size = (input_h, input_w)
+
+ # https://pytorch.org/docs/stable/generated/torch.nn.Conv2d.html
+ h_out = (input_size[0] + 2 * padding[0] - dilation[0] *
+ (kernel_size[0] - 1) - 1) // stride[0] + 1
+ w_out = (input_size[1] + 2 * padding[1] - dilation[1] *
+ (kernel_size[1] - 1) - 1) // stride[1] + 1
+ self.init_out_size = (h_out, w_out)
+ else:
+ self.init_input_size = None
+ self.init_out_size = None
+
+ def forward(self, x):
+ """
+ Args:
+ x (Tensor): Has shape (B, C, H, W). In most case, C is 3.
+
+ Returns:
+ tuple: Contains merged results and its spatial shape.
+
+ - x (Tensor): Has shape (B, out_h * out_w, embed_dims)
+ - out_size (tuple[int]): Spatial shape of x, arrange as
+ (out_h, out_w).
+ """
+
+ if self.adap_padding:
+ x = self.adap_padding(x)
+
+ x = self.projection(x)
+ out_size = (x.shape[2], x.shape[3])
+ x = x.flatten(2).transpose(1, 2)
+ if self.norm is not None:
+ x = self.norm(x)
+ return x, out_size
+
+
+class PatchMerging(BaseModule):
+ """Merge patch feature map.
+
+ This layer groups feature map by kernel_size, and applies norm and linear
+ layers to the grouped feature map. Our implementation uses `nn.Unfold` to
+ merge patch, which is about 25% faster than original implementation.
+ Instead, we need to modify pretrained models for compatibility.
+
+ Args:
+ in_channels (int): The num of input channels.
+ to gets fully covered by filter and stride you specified..
+ Default: True.
+ out_channels (int): The num of output channels.
+ kernel_size (int | tuple, optional): the kernel size in the unfold
+ layer. Defaults to 2.
+ stride (int | tuple, optional): the stride of the sliding blocks in the
+ unfold layer. Default: None. (Would be set as `kernel_size`)
+ padding (int | tuple | string ): The padding length of
+ embedding conv. When it is a string, it means the mode
+ of adaptive padding, support "same" and "corner" now.
+ Default: "corner".
+ dilation (int | tuple, optional): dilation parameter in the unfold
+ layer. Default: 1.
+ bias (bool, optional): Whether to add bias in linear layer or not.
+ Defaults: False.
+ norm_cfg (dict, optional): Config dict for normalization layer.
+ Default: dict(type='LN').
+ init_cfg (dict, optional): The extra config for initialization.
+ Default: None.
+ """
+
+ def __init__(self,
+ in_channels,
+ out_channels,
+ kernel_size=2,
+ stride=None,
+ padding='corner',
+ dilation=1,
+ bias=False,
+ norm_cfg=dict(type='LN'),
+ init_cfg=None):
+ super().__init__(init_cfg=init_cfg)
+ self.in_channels = in_channels
+ self.out_channels = out_channels
+ if stride:
+ stride = stride
+ else:
+ stride = kernel_size
+
+ kernel_size = to_2tuple(kernel_size)
+ stride = to_2tuple(stride)
+ dilation = to_2tuple(dilation)
+
+ if isinstance(padding, str):
+ self.adap_padding = AdaptivePadding(
+ kernel_size=kernel_size,
+ stride=stride,
+ dilation=dilation,
+ padding=padding)
+ # disable the padding of unfold
+ padding = 0
+ else:
+ self.adap_padding = None
+
+ padding = to_2tuple(padding)
+ self.sampler = nn.Unfold(
+ kernel_size=kernel_size,
+ dilation=dilation,
+ padding=padding,
+ stride=stride)
+
+ sample_dim = kernel_size[0] * kernel_size[1] * in_channels
+
+ if norm_cfg is not None:
+ self.norm = build_norm_layer(norm_cfg, sample_dim)[1]
+ else:
+ self.norm = None
+
+ self.reduction = nn.Linear(sample_dim, out_channels, bias=bias)
+
+ def forward(self, x, input_size):
+ """
+ Args:
+ x (Tensor): Has shape (B, H*W, C_in).
+ input_size (tuple[int]): The spatial shape of x, arrange as (H, W).
+ Default: None.
+
+ Returns:
+ tuple: Contains merged results and its spatial shape.
+
+ - x (Tensor): Has shape (B, Merged_H * Merged_W, C_out)
+ - out_size (tuple[int]): Spatial shape of x, arrange as
+ (Merged_H, Merged_W).
+ """
+ B, L, C = x.shape
+ assert isinstance(input_size, Sequence), f'Expect ' \
+ f'input_size is ' \
+ f'`Sequence` ' \
+ f'but get {input_size}'
+
+ H, W = input_size
+ assert L == H * W, 'input feature has wrong size'
+
+ x = x.view(B, H, W, C).permute([0, 3, 1, 2]) # B, C, H, W
+ # Use nn.Unfold to merge patch. About 25% faster than original method,
+ # but need to modify pretrained model for compatibility
+
+ if self.adap_padding:
+ x = self.adap_padding(x)
+ H, W = x.shape[-2:]
+
+ x = self.sampler(x)
+ # if kernel_size=2 and stride=2, x should has shape (B, 4*C, H/2*W/2)
+
+ out_h = (H + 2 * self.sampler.padding[0] - self.sampler.dilation[0] *
+ (self.sampler.kernel_size[0] - 1) -
+ 1) // self.sampler.stride[0] + 1
+ out_w = (W + 2 * self.sampler.padding[1] - self.sampler.dilation[1] *
+ (self.sampler.kernel_size[1] - 1) -
+ 1) // self.sampler.stride[1] + 1
+
+ output_size = (out_h, out_w)
+ x = x.transpose(1, 2) # B, H/2*W/2, 4*C
+ x = self.norm(x) if self.norm else x
+ x = self.reduction(x)
+ return x, output_size
+
+
+def inverse_sigmoid(x, eps=1e-5):
+ """Inverse function of sigmoid.
+ Args:
+ x (Tensor): The tensor to do the
+ inverse.
+ eps (float): EPS avoid numerical
+ overflow. Defaults 1e-5.
+ Returns:
+ Tensor: The x has passed the inverse
+ function of sigmoid, has same
+ shape with input.
+ """
+ x = x.clamp(min=0, max=1)
+ x1 = x.clamp(min=eps)
+ x2 = (1 - x).clamp(min=eps)
+ return torch.log(x1 / x2)
+
+
+@TRANSFORMER_LAYER_SEQUENCE.register_module()
+class DetrTransformerEncoder_zero_layer():
+ def __init__(self, *args, post_norm_cfg=dict(type='LN'), **kwargs):
+ pass
+
+ def __call__(self,
+ query,
+ key,
+ value,
+ query_pos=None,
+ key_pos=None,
+ attn_masks=None,
+ query_key_padding_mask=None,
+ key_padding_mask=None,
+ **kwargs):
+ query = query + query_pos
+ return query
+
+
+@TRANSFORMER_LAYER.register_module()
+class DetrTransformerDecoderLayer_grouped(BaseTransformerLayer):
+ def __init__(self,
+ attn_cfgs,
+ feedforward_channels,
+ ffn_dropout=0.0,
+ operation_order=None,
+ act_cfg=dict(type='ReLU', inplace=True),
+ norm_cfg=dict(type='LN'),
+ ffn_num_fcs=2,
+ num_joints=17,
+ **kwargs):
+ super(DetrTransformerDecoderLayer_grouped, self).__init__(
+ attn_cfgs=attn_cfgs,
+ feedforward_channels=feedforward_channels,
+ ffn_dropout=ffn_dropout,
+ operation_order=operation_order,
+ act_cfg=act_cfg,
+ norm_cfg=norm_cfg,
+ ffn_num_fcs=ffn_num_fcs,
+ **kwargs)
+ # assert len(operation_order) == 6
+ # assert set(operation_order) == set(
+ # ['self_attn', 'norm', 'cross_attn', 'ffn'])
+ self.num_joints = num_joints
+ # self.num_joints = len(smpl_x.pos_joint_part['rhand'])
+ # self.num_joints = len(smpl_x.pos_joint_part['body']) + len(smpl_x.pos_joint_part['rhand']) + len(smpl_x.pos_joint_part['lhand'])
+
+ def forward(self,
+ query,
+ key=None,
+ value=None,
+ query_pos=None,
+ key_pos=None,
+ attn_masks=None,
+ query_key_padding_mask=None,
+ key_padding_mask=None,
+ **kwargs):
+
+ norm_index = 0
+ attn_index = 0
+ ffn_index = 0
+ identity = query
+ if attn_masks is None:
+ attn_masks = [None for _ in range(self.num_attn)]
+ elif isinstance(attn_masks, torch.Tensor):
+ attn_masks = [
+ copy.deepcopy(attn_masks) for _ in range(self.num_attn)
+ ]
+ warnings.warn(f'Use same attn_mask in all attentions in '
+ f'{self.__class__.__name__} ')
+ else:
+ assert len(attn_masks) == self.num_attn, f'The length of ' \
+ f'attn_masks {len(attn_masks)} must be equal ' \
+ f'to the number of attention in ' \
+ f'operation_order {self.num_attn}'
+
+ for layer in self.operation_order:
+ if layer == 'self_attn':
+ # print(query.shape)
+ assert query.size(0) % self.num_joints == 0, f'query.shape: {query.shape}, num_joints: {self.num_joints}'
+ num_group = query.size(0) // self.num_joints
+ bs = query.size(1)
+
+ temp_query = rearrange(query, '(g k) b c -> k (g b) c',
+ g=num_group, k=self.num_joints)
+ temp_identity = rearrange(identity, '(g k) b c -> k (g b) c',
+ g=num_group, k=self.num_joints)
+ temp_query_pos = rearrange(query_pos, '(g k) b c -> k (g b) c',
+ g=num_group, k=self.num_joints)
+
+ temp_key = temp_value = temp_query
+ query = self.attentions[attn_index](
+ temp_query,
+ temp_key,
+ temp_value,
+ temp_identity if self.pre_norm else None,
+ query_pos=temp_query_pos,
+ key_pos=temp_query_pos,
+ attn_mask=attn_masks[attn_index],
+ key_padding_mask=query_key_padding_mask,
+ **kwargs)
+
+ query = rearrange(query, 'k (g b) c -> (g k) b c',
+ g=num_group, b=bs)
+
+ attn_index += 1
+ identity = query
+
+ elif layer == 'norm':
+ query = self.norms[norm_index](query)
+ norm_index += 1
+
+ elif layer == 'cross_attn':
+ query = self.attentions[attn_index](
+ query,
+ key,
+ value,
+ identity if self.pre_norm else None,
+ query_pos=query_pos,
+ key_pos=key_pos,
+ attn_mask=attn_masks[attn_index],
+ key_padding_mask=key_padding_mask,
+ **kwargs)
+ attn_index += 1
+ identity = query
+
+ elif layer == 'ffn':
+ query = self.ffns[ffn_index](
+ query, identity if self.pre_norm else None)
+ ffn_index += 1
+ if 'cross_attn' not in self.operation_order:
+ query = query + value.sum() * 0
+
+ return query
+
+
+@TRANSFORMER_LAYER_SEQUENCE.register_module()
+class DeformableDetrTransformerDecoder(TransformerLayerSequence):
+ """Implements the decoder in DETR transformer.
+ Args:
+ return_intermediate (bool): Whether to return intermediate outputs.
+ coder_norm_cfg (dict): Config of last normalization layer. Default:
+ `LN`.
+ """
+
+ def __init__(self, *args, return_intermediate=False, **kwargs):
+
+ super(DeformableDetrTransformerDecoder, self).__init__(*args, **kwargs)
+ self.return_intermediate = return_intermediate
+
+ def forward(self,
+ query,
+ *args,
+ reference_points=None,
+ valid_ratios=None,
+ reg_branches=None,
+ fc_coord=None,
+ **kwargs):
+ output = query
+ intermediate = []
+ intermediate_reference_points = []
+
+ for lid, layer in enumerate(self.layers):
+ if reference_points.shape[-1] == 4:
+ reference_points_input = reference_points[:, :, None] * \
+ torch.cat([valid_ratios, valid_ratios], -1)[:, None]
+ else:
+ assert reference_points.shape[-1] == 3
+ # print(reference_points.shape, valid_ratios.shape) # [48,65,3], [48,4,3]
+ reference_points_input = reference_points[:, :, None, :2] * \
+ valid_ratios[:, None]
+ # assert reference_points.shape[-1] == 2
+ # reference_points_input = reference_points[:, :, None] * \
+ # valid_ratios[:, None]
+ # print(output.shape, reference_points_input.shape)
+ output = layer(
+ output,
+ *args,
+ reference_points=reference_points_input,
+ **kwargs)
+ output = output.permute(1, 0, 2)
+
+ # if reg_branches is not None:
+ # tmp = reg_branches[lid](output)
+ #
+ # if fc_coord is not None:
+ # tmp = fc_coord(tmp)
+ #
+ # if reference_points.shape[-1] == 4:
+ # new_reference_points = tmp + inverse_sigmoid(
+ # reference_points)
+ # new_reference_points = new_reference_points.sigmoid()
+ # else:
+ # assert reference_points.shape[-1] == 3
+ # new_reference_points = tmp
+ # new_reference_points[..., :3] = tmp[
+ # ..., :3] + inverse_sigmoid(reference_points)
+ # new_reference_points = new_reference_points.sigmoid()
+ # # else:
+ # # assert reference_points.shape[-1] == 2
+ # # new_reference_points = tmp
+ # # new_reference_points[..., :2] = tmp[
+ # # ..., :2] + inverse_sigmoid(reference_points)
+ # # new_reference_points = new_reference_points.sigmoid()
+ # # # reference_points = new_reference_points.detach()
+ # # reference_points = new_reference_points
+ # reference_points = new_reference_points
+ output = output.permute(1, 0, 2)
+ if self.return_intermediate:
+ intermediate.append(output)
+ intermediate_reference_points.append(reference_points)
+
+ if self.return_intermediate:
+ return torch.stack(intermediate), torch.stack(
+ intermediate_reference_points)
+
+ return output, reference_points
+
+
+class Linear_with_norm(nn.Module):
+ def __init__(self, in_channel, out_channel, bias=True, norm=True):
+ super(Linear_with_norm, self).__init__()
+ self.bias = bias
+ self.norm = norm
+ self.linear = nn.Linear(in_channel, out_channel, bias)
+ nn.init.xavier_uniform_(self.linear.weight, gain=0.01)
+
+ def forward(self, x):
+ y = x.matmul(self.linear.weight.t())
+
+ if self.norm:
+ x_norm = torch.norm(x, dim=1, keepdim=True)
+ y = y / x_norm
+
+ if self.bias:
+ y = y + self.linear.bias
+ return y
+
+
+@TRANSFORMER.register_module()
+class Transformer(BaseModule):
+ """Implements the DETR transformer.
+ Following the official DETR implementation, this module copy-paste
+ from torch.nn.Transformer with modifications:
+ * positional encodings are passed in MultiheadAttention
+ * extra LN at the end of encoder is removed
+ * decoder returns a stack of activations from all decoding layers
+ See `paper: End-to-End Object Detection with Transformers
+ `_ for details.
+ Args:
+ encoder (`mmcv.ConfigDict` | Dict): Config of
+ TransformerEncoder. Defaults to None.
+ decoder ((`mmcv.ConfigDict` | Dict)): Config of
+ TransformerDecoder. Defaults to None
+ init_cfg (obj:`mmcv.ConfigDict`): The Config for initialization.
+ Defaults to None.
+ """
+
+ def __init__(self, encoder=None, decoder=None, init_cfg=None):
+ super(Transformer, self).__init__(init_cfg=init_cfg)
+ self.encoder = build_transformer_layer_sequence(encoder)
+ self.decoder = build_transformer_layer_sequence(decoder)
+ # self.embed_dims = self.encoder.embed_dims
+
+ def init_weights(self):
+ # follow the official DETR to init parameters
+ for m in self.modules():
+ if hasattr(m, 'weight') and m.weight.dim() > 1:
+ xavier_init(m, distribution='uniform')
+ self._is_init = True
+
+ def forward(self, x, mask, query_embed, pos_embed):
+ """Forward function for `Transformer`.
+ Args:
+ x (Tensor): Input query with shape [bs, c, h, w] where
+ c = embed_dims.
+ mask (Tensor): The key_padding_mask used for encoder and decoder,
+ with shape [bs, h, w].
+ query_embed (Tensor): The query embedding for decoder, with shape
+ [num_query, c].
+ pos_embed (Tensor): The positional encoding for encoder and
+ decoder, with the same shape as `x`.
+ Returns:
+ tuple[Tensor]: results of decoder containing the following tensor.
+ - out_dec: Output from decoder. If return_intermediate_dec \
+ is True output has shape [num_dec_layers, bs,
+ num_query, embed_dims], else has shape [1, bs, \
+ num_query, embed_dims].
+ - memory: Output results from encoder, with shape \
+ [bs, embed_dims, h, w].
+ """
+ bs, c, h, w = x.shape
+ # use `view` instead of `flatten` for dynamically exporting to ONNX
+ x = x.view(bs, c, -1).permute(2, 0, 1) # [bs, c, h, w] -> [h*w, bs, c]
+ pos_embed = pos_embed.view(bs, c, -1).permute(2, 0, 1)
+ query_embed = query_embed.unsqueeze(1).repeat(
+ 1, bs, 1) # [num_query, dim] -> [num_query, bs, dim]
+ mask = mask.view(bs, -1) # [bs, h, w] -> [bs, h*w]
+ memory = self.encoder(
+ query=x,
+ key=None,
+ value=None,
+ query_pos=pos_embed,
+ query_key_padding_mask=mask)
+ target = torch.zeros_like(query_embed)
+ # out_dec: [num_layers, num_query, bs, dim]
+ out_dec = self.decoder(
+ query=target,
+ key=memory,
+ value=memory,
+ key_pos=pos_embed,
+ query_pos=query_embed,
+ key_padding_mask=mask)
+ out_dec = out_dec.transpose(1, 2)
+ memory = memory.permute(1, 2, 0).reshape(bs, c, h, w)
+ return out_dec, memory
+
+
+@TRANSFORMER.register_module()
+class PoseurTransformer_v3(Transformer):
+ """ add noise training """
+
+ def __init__(self,
+ as_two_stage=False,
+ num_feature_levels=4,
+ two_stage_num_proposals=300,
+ num_joints=17,
+ use_soft_argmax=False,
+ use_soft_argmax_def=False,
+ proposal_feature='backbone_s', # or encoder_memory
+ image_size=[192, 256],
+ init_q_sigmoid=False,
+ soft_arg_stride=4,
+ add_feat_2_query=False,
+ query_pose_emb=True,
+ num_noise_sample=3,
+ num_noise_point=4,
+ noise_sigma=0.2,
+ embed_dims=256,
+ **kwargs):
+ super(PoseurTransformer_v3, self).__init__(**kwargs)
+ assert query_pose_emb == True
+ # self.num_noise_sample = num_noise_sample
+ self.num_noise_sample = num_noise_sample
+ self.num_noise_point = num_noise_point
+ self.noise_sigma = noise_sigma
+ self.add_feat_2_query = add_feat_2_query
+ self.as_two_stage = as_two_stage
+ self.num_feature_levels = num_feature_levels
+ self.two_stage_num_proposals = two_stage_num_proposals
+ try:
+ self.embed_dims = self.encoder.embed_dims
+ except:
+ self.embed_dims = embed_dims
+ self.num_joints = num_joints
+ # self.num_joints = 17
+ # self.num_joints = len(smpl_x.pos_joint_part['rhand']) # body_joints+bboxes
+ # self.num_joints = len(smpl_x.pos_joint_part['body']) + len(smpl_x.pos_joint_part['rhand']) + len(smpl_x.pos_joint_part['lhand'])
+ self.use_soft_argmax = use_soft_argmax
+ self.use_soft_argmax_def = use_soft_argmax_def
+ assert not (self.use_soft_argmax & self.use_soft_argmax_def)
+ self.init_q_sigmoid = init_q_sigmoid
+ self.image_size = image_size
+ self.soft_arg_stride = soft_arg_stride
+ self.proposal_feature = proposal_feature
+ self.query_pose_emb = query_pose_emb
+ self.prior = distributions.MultivariateNormal(torch.zeros(2), torch.eye(2) * self.noise_sigma)
+ self.init_layers()
+
+ def init_layers(self):
+ """Initialize layers of the DeformableDetrTransformer."""
+ self.level_embeds = nn.Parameter(
+ torch.Tensor(self.num_feature_levels, self.embed_dims))
+
+ if self.as_two_stage:
+ self.avg_pool = nn.AdaptiveAvgPool2d(1)
+ # self.fc_sigma = Linear_with_norm(self.embed_dims, self.num_joints * 2, norm=False)
+ self.fc_sigma = Linear_with_norm(self.embed_dims, self.num_joints * 3, norm=False)
+ if self.use_soft_argmax:
+ self.soft_argmax_coord = Heatmap1DHead(in_channels=self.embed_dims, expand_ratio=2, hidden_dims=(512,),
+ image_size=self.image_size, stride=self.soft_arg_stride)
+ self.fc_layers = [self.fc_sigma]
+ elif self.use_soft_argmax_def:
+ self.soft_argmax_coord = Heatmap2DHead(in_channels=self.embed_dims,
+ image_size=self.image_size, stride=self.soft_arg_stride)
+ self.fc_layers = [self.fc_sigma]
+ else:
+ # self.fc_coord = Linear_with_norm(self.embed_dims, self.num_joints * 2)
+ self.fc_coord = Linear_with_norm(self.embed_dims, self.num_joints * 3)
+ self.fc_layers = [self.fc_coord, self.fc_sigma]
+
+ if self.query_pose_emb:
+ self.pos_trans = nn.Linear(self.embed_dims * 2,
+ self.embed_dims)
+ self.pos_trans_norm = nn.LayerNorm(self.embed_dims)
+ # self.pos_embed = nn.Embedding(17,self.embed_dims)
+ self.pos_embed = nn.Embedding(self.num_joints, self.embed_dims)
+ else:
+ self.pos_trans = nn.Linear(self.embed_dims * 2,
+ self.embed_dims * 2)
+ self.pos_trans_norm = nn.LayerNorm(self.embed_dims * 2)
+ else:
+ self.reference_points = nn.Linear(self.embed_dims, 2)
+ self.fp16_enabled = False
+
+ def init_weights(self):
+ """Initialize the transformer weights."""
+ for p in self.parameters():
+ if p.dim() > 1:
+ nn.init.xavier_uniform_(p)
+ for m in self.modules():
+ if isinstance(m, MultiScaleDeformableAttention):
+ m.init_weights()
+ if not self.as_two_stage:
+ xavier_init(self.reference_points, distribution='uniform', bias=0.)
+ normal_(self.level_embeds)
+ if self.use_soft_argmax:
+ self.soft_argmax_coord.init_weights()
+
+ if self.as_two_stage:
+ for m in self.fc_layers:
+ if isinstance(m, nn.Linear):
+ nn.init.xavier_uniform_(m.weight, gain=0.01)
+
+ def gen_encoder_output_proposals(self, memory, memory_padding_mask,
+ spatial_shapes):
+ """Generate proposals from encoded memory.
+ Args:
+ memory (Tensor) : The output of encoder,
+ has shape (bs, num_key, embed_dim). num_key is
+ equal the number of points on feature map from
+ all level.
+ memory_padding_mask (Tensor): Padding mask for memory.
+ has shape (bs, num_key).
+ spatial_shapes (Tensor): The shape of all feature maps.
+ has shape (num_level, 2).
+ Returns:
+ tuple: A tuple of feature map and bbox prediction.
+ - output_memory (Tensor): The input of decoder, \
+ has shape (bs, num_key, embed_dim). num_key is \
+ equal the number of points on feature map from \
+ all levels.
+ - output_proposals (Tensor): The normalized proposal \
+ after a inverse sigmoid, has shape \
+ (bs, num_keys, 4).
+ """
+
+ N, S, C = memory.shape
+ proposals = []
+ _cur = 0
+ for lvl, (H, W) in enumerate(spatial_shapes):
+ mask_flatten_ = memory_padding_mask[:, _cur:(_cur + H * W)].view(
+ N, H, W, 1)
+ valid_H = torch.sum(~mask_flatten_[:, :, 0, 0], 1)
+ valid_W = torch.sum(~mask_flatten_[:, 0, :, 0], 1)
+
+ grid_y, grid_x = torch.meshgrid(
+ torch.linspace(
+ 0, H - 1, H, dtype=torch.float32, device=memory.device),
+ torch.linspace(
+ 0, W - 1, W, dtype=torch.float32, device=memory.device))
+ grid = torch.cat([grid_x.unsqueeze(-1), grid_y.unsqueeze(-1)], -1)
+
+ scale = torch.cat([valid_W.unsqueeze(-1),
+ valid_H.unsqueeze(-1)], 1).view(N, 1, 1, 2)
+ grid = (grid.unsqueeze(0).expand(N, -1, -1, -1) + 0.5) / scale
+ wh = torch.ones_like(grid) * 0.05 * (2.0 ** lvl)
+ # proposal = torch.cat((grid, wh), -1).view(N, -1, 4)
+ proposal = grid.view(N, -1, 2)
+ proposals.append(proposal)
+ _cur += (H * W)
+ output_proposals = torch.cat(proposals, 1)
+ output_proposals_valid = ((output_proposals > 0.01) &
+ (output_proposals < 0.99)).all(
+ -1, keepdim=True)
+ output_proposals = torch.log(output_proposals / (1 - output_proposals))
+ output_proposals = output_proposals.masked_fill(
+ memory_padding_mask.unsqueeze(-1), float('inf'))
+ output_proposals = output_proposals.masked_fill(
+ ~output_proposals_valid, float('inf'))
+
+ output_memory = memory
+ output_memory = output_memory.masked_fill(
+ memory_padding_mask.unsqueeze(-1), float(0))
+ output_memory = output_memory.masked_fill(~output_proposals_valid,
+ float(0))
+ output_memory = self.enc_output_norm(self.enc_output(output_memory))
+ return output_memory, output_proposals
+
+ @staticmethod
+ def get_reference_points(spatial_shapes, valid_ratios, device):
+ """Get the reference points used in decoder.
+ Args:
+ spatial_shapes (Tensor): The shape of all
+ feature maps, has shape (num_level, 2).
+ valid_ratios (Tensor): The radios of valid
+ points on the feature map, has shape
+ (bs, num_levels, 2)
+ device (obj:`device`): The device where
+ reference_points should be.
+ Returns:
+ Tensor: reference points used in decoder, has \
+ shape (bs, num_keys, num_levels, 2).
+ """
+ # print(spatial_shapes)
+ reference_points_list = []
+ for lvl, (H, W) in enumerate(spatial_shapes):
+ # TODO check this 0.5
+ ref_y, ref_x = torch.meshgrid(
+ torch.linspace(
+ 0.5, H - 0.5, H, dtype=torch.float32, device=device),
+ torch.linspace(
+ 0.5, W - 0.5, W, dtype=torch.float32, device=device))
+ ref_y = ref_y.reshape(-1)[None] / (
+ valid_ratios[:, None, lvl, 1] * H)
+ ref_x = ref_x.reshape(-1)[None] / (
+ valid_ratios[:, None, lvl, 0] * W)
+ ref = torch.stack((ref_x, ref_y), -1)
+ reference_points_list.append(ref)
+ # print(reference_points_list[-1]) # range:(0,1)
+ # print(H, W) [8,6]
+ reference_points = torch.cat(reference_points_list, 1)
+ reference_points = reference_points[:, :, None] * valid_ratios[:, None]
+ return reference_points
+
+ def get_valid_ratio(self, mask):
+ """Get the valid radios of feature maps of all level."""
+ _, H, W = mask.shape
+ valid_H = torch.sum(~mask[:, :, 0], 1)
+ valid_W = torch.sum(~mask[:, 0, :], 1)
+ valid_ratio_h = valid_H.float() / H
+ valid_ratio_w = valid_W.float() / W
+ valid_ratio = torch.stack([valid_ratio_w, valid_ratio_h], -1)
+ return valid_ratio
+
+ def get_proposal_pos_embed(self,
+ proposals,
+ num_pos_feats=128,
+ temperature=10000):
+ """Get the position embedding of proposal."""
+ num_pos_feats = self.embed_dims // 3 + 1
+ scale = 2 * math.pi
+ dim_t = torch.arange(
+ num_pos_feats, dtype=torch.float32, device=proposals.device)
+ dim_t = temperature ** (2 * (dim_t // 2) / num_pos_feats)
+ # N, L, 2
+ if self.init_q_sigmoid:
+ proposals = proposals.sigmoid() * scale
+ else:
+ proposals = proposals * scale
+
+ # N, L, 3, 86
+ pos = proposals[:, :, :, None] / dim_t
+ # N, L, 3, 43, 2
+ pos = torch.stack((pos[:, :, :, 0::2].sin(), pos[:, :, :, 1::2].cos()), dim=4).flatten(2)
+ return pos[:, :, :self.embed_dims]
+
+ @force_fp32(apply_to=('mlvl_feats', 'query_embed', 'mlvl_pos_embeds'))
+ def forward(self,
+ mlvl_feats,
+ mlvl_masks,
+ query_embed,
+ mlvl_pos_embeds,
+ reg_branches=None,
+ fc_coord=None,
+ cls_branches=None,
+ coord_init=None,
+ query_init=None,
+ **kwargs):
+ assert self.as_two_stage or query_embed is not None
+
+ feat_flatten = []
+ mask_flatten = []
+ lvl_pos_embed_flatten = []
+ spatial_shapes = []
+ for lvl, (feat, mask, pos_embed) in enumerate(
+ zip(mlvl_feats, mlvl_masks, mlvl_pos_embeds)):
+ bs, c, h, w = feat.shape
+ spatial_shape = (h, w)
+ spatial_shapes.append(spatial_shape)
+ feat = feat.flatten(2).transpose(1, 2)
+ mask = mask.flatten(1)
+ pos_embed = pos_embed.flatten(2).transpose(1, 2)
+ lvl_pos_embed = pos_embed + self.level_embeds[lvl].view(1, 1, -1)
+ lvl_pos_embed_flatten.append(lvl_pos_embed)
+ feat_flatten.append(feat)
+ mask_flatten.append(mask)
+ feat_flatten = torch.cat(feat_flatten, 1)
+ mask_flatten = torch.cat(mask_flatten, 1)
+ lvl_pos_embed_flatten = torch.cat(lvl_pos_embed_flatten, 1)
+ spatial_shapes = torch.as_tensor(
+ spatial_shapes, dtype=torch.long, device=feat_flatten.device)
+ level_start_index = torch.cat((spatial_shapes.new_zeros(
+ (1,)), spatial_shapes.prod(1).cumsum(0)[:-1]))
+ valid_ratios = torch.stack(
+ [self.get_valid_ratio(m) for m in mlvl_masks], 1)
+ # [bs, H*W, num_lvls, 2]
+ # print(spatial_shape)
+ reference_points = \
+ self.get_reference_points(spatial_shapes,
+ valid_ratios,
+ device=feat.device)
+ # print(reference_points.shape, valid_ratios.shape) # [bs, 4080, 4, 2]; [bs, 4, 2]
+ feat_flatten = feat_flatten.permute(1, 0, 2) # (H*W, bs, embed_dims)
+ lvl_pos_embed_flatten = lvl_pos_embed_flatten.permute(
+ 1, 0, 2) # (H*W, bs, embed_dims)
+
+ memory = self.encoder(
+ query=feat_flatten,
+ key=None,
+ value=None,
+ query_pos=lvl_pos_embed_flatten,
+ query_key_padding_mask=mask_flatten,
+ spatial_shapes=spatial_shapes,
+ reference_points=reference_points,
+ level_start_index=level_start_index,
+ valid_ratios=valid_ratios,
+ **kwargs)
+
+ memory = memory.permute(1, 0, 2)
+ bs, _, c = memory.shape
+
+ if self.proposal_feature == 'backbone_l':
+ x = mlvl_feats[0]
+ elif self.proposal_feature == 'backbone_s':
+ x = mlvl_feats[-1]
+ point_sample_feat = mlvl_feats[-1]
+ elif self.proposal_feature == 'encoder_memory_l':
+ x = memory.permute(0, 2, 1)[:, :, :int(level_start_index[1])].view_as(mlvl_feats[0])
+ point_sample_feat = memory.permute(0, 2, 1)[:, :, :int(level_start_index[1])].view_as(mlvl_feats[0])
+ elif self.proposal_feature == 'encoder_memory_s':
+ x = memory.permute(0, 2, 1)[:, :, int(level_start_index[-1]):].view_as(mlvl_feats[-1])
+ else:
+ raise NotImplementedError
+
+ BATCH_SIZE = x.shape[0]
+
+ if coord_init is not None:
+ pred_jts = coord_init
+ enc_outputs = None
+ else:
+ if self.use_soft_argmax:
+ out_coord = self.soft_argmax_coord(x) # bs, 17, 2
+ assert out_coord.shape[2] == 2
+ x = self.avg_pool(x).reshape(BATCH_SIZE, -1)
+ out_sigma = self.fc_sigma(x).reshape(BATCH_SIZE, self.num_joints, -1)
+ elif self.use_soft_argmax_def:
+ out_coord = self.soft_argmax_coord(x) # bs, 17, 2
+ assert out_coord.shape[2] == 2
+ x = self.avg_pool(x).reshape(BATCH_SIZE, -1)
+ out_sigma = self.fc_sigma(x).reshape(BATCH_SIZE, self.num_joints, -1)
+ else:
+ x = self.avg_pool(x).reshape(BATCH_SIZE, -1)
+ out_coord = self.fc_coord(x).reshape(BATCH_SIZE, self.num_joints, 3)
+ assert out_coord.shape[2] == 3
+ out_sigma = self.fc_sigma(x).reshape(BATCH_SIZE, self.num_joints, -1)
+
+ # (B, N, 3)
+ pred_jts = out_coord.reshape(BATCH_SIZE, self.num_joints, 3)
+ sigma = out_sigma.reshape(BATCH_SIZE, self.num_joints, -1).sigmoid()
+ scores = 1 - sigma
+
+ scores = torch.mean(scores, dim=2, keepdim=True)
+ enc_outputs = EasyDict(
+ pred_jts=pred_jts,
+ sigma=sigma,
+ maxvals=scores.float(),
+ )
+
+ reference_points = pred_jts.detach()
+ reference_points_cliped = reference_points.clip(0, 1)
+
+ init_reference_out = reference_points_cliped
+ if query_init is not None:
+ query = query_init
+ else:
+ pred_jts_pos_embed = self.get_proposal_pos_embed(reference_points.detach())
+ reference_points_pos_embed = self.get_proposal_pos_embed(reference_points_cliped.detach()) # query init here
+ if self.add_feat_2_query:
+ query_feat = point_sample(point_sample_feat, init_reference_out, align_corners=False).permute(0, 2, 1)
+ reference_points_pos_embed = reference_points_pos_embed + query_feat
+ query_pos_emb = torch.cat([pred_jts_pos_embed, reference_points_pos_embed], dim=2)
+ pos_trans_out = self.pos_trans_norm(self.pos_trans(query_pos_emb))
+
+ query = pos_trans_out
+
+ query_pos = self.pos_embed.weight.clone().repeat(bs, 1, 1).contiguous()
+
+ # decoder
+ query = query.permute(1, 0, 2)
+ memory = memory.permute(1, 0, 2)
+ query_pos = query_pos.permute(1, 0, 2)
+ inter_states, inter_references = self.decoder(
+ query=query,
+ key=None,
+ value=memory,
+ query_pos=query_pos,
+ key_padding_mask=mask_flatten,
+ reference_points=reference_points,
+ spatial_shapes=spatial_shapes,
+ level_start_index=level_start_index,
+ valid_ratios=valid_ratios,
+ reg_branches=reg_branches,
+ fc_coord=fc_coord,
+ **kwargs)
+ inter_references_out = inter_references
+ return memory.permute(1, 0, 2), spatial_shapes, level_start_index, inter_states, init_reference_out, \
+ inter_references_out, enc_outputs
diff --git a/grounded-sam-osx/transformer_utils/mmpose/ops/__init__.py b/grounded-sam-osx/transformer_utils/mmpose/ops/__init__.py
new file mode 100644
index 0000000000000000000000000000000000000000..d6af823310ad59c2d1e52274f8af9a0fc0f14a72
--- /dev/null
+++ b/grounded-sam-osx/transformer_utils/mmpose/ops/__init__.py
@@ -0,0 +1,9 @@
+from .multi_scale_deform_attn import (MultiScaleDeformableAttention_share_value,
+ MultiScaleDeformableAttention_bottle_neck_v,
+ MultiScaleDeformableAttention_post_value,
+ MultiScaleDeformableAttention_post_v_stirct,
+ )
+
+__all__ = [
+ 'MultiScaleDeformableAttention',
+]
\ No newline at end of file
diff --git a/grounded-sam-osx/transformer_utils/mmpose/ops/csrc/pytorch/info.cpp b/grounded-sam-osx/transformer_utils/mmpose/ops/csrc/pytorch/info.cpp
new file mode 100644
index 0000000000000000000000000000000000000000..d252ba2edf71649c976923f9836da801fd71b48b
--- /dev/null
+++ b/grounded-sam-osx/transformer_utils/mmpose/ops/csrc/pytorch/info.cpp
@@ -0,0 +1,55 @@
+// modified from
+// https://github.com/facebookresearch/detectron2/blob/master/detectron2/layers/csrc/vision.cpp
+#include "pytorch_cpp_helper.hpp"
+
+#ifdef MMCV_WITH_CUDA
+#ifndef HIP_DIFF
+#include
+int get_cudart_version() { return CUDART_VERSION; }
+#endif
+#endif
+
+std::string get_compiling_cuda_version() {
+#ifdef MMCV_WITH_CUDA
+#ifndef HIP_DIFF
+ std::ostringstream oss;
+ // copied from
+ // https://github.com/pytorch/pytorch/blob/master/aten/src/ATen/cuda/detail/CUDAHooks.cpp#L231
+ auto printCudaStyleVersion = [&](int v) {
+ oss << (v / 1000) << "." << (v / 10 % 100);
+ if (v % 10 != 0) {
+ oss << "." << (v % 10);
+ }
+ };
+ printCudaStyleVersion(get_cudart_version());
+ return oss.str();
+#else
+ return std::string("rocm not vailable");
+#endif
+#else
+ return std::string("not available");
+#endif
+}
+
+// similar to
+// https://github.com/pytorch/pytorch/blob/master/aten/src/ATen/Version.cpp
+std::string get_compiler_version() {
+ std::ostringstream ss;
+#if defined(__GNUC__)
+#ifndef __clang__
+ { ss << "GCC " << __GNUC__ << "." << __GNUC_MINOR__; }
+#endif
+#endif
+
+#if defined(__clang_major__)
+ {
+ ss << "clang " << __clang_major__ << "." << __clang_minor__ << "."
+ << __clang_patchlevel__;
+ }
+#endif
+
+#if defined(_MSC_VER)
+ { ss << "MSVC " << _MSC_FULL_VER; }
+#endif
+ return ss.str();
+}
\ No newline at end of file
diff --git a/grounded-sam-osx/transformer_utils/mmpose/ops/csrc/pytorch/ms_deform_attn.cpp b/grounded-sam-osx/transformer_utils/mmpose/ops/csrc/pytorch/ms_deform_attn.cpp
new file mode 100644
index 0000000000000000000000000000000000000000..1fda9aeba25b8fd87fd8b9e2d7e27d646271d7b3
--- /dev/null
+++ b/grounded-sam-osx/transformer_utils/mmpose/ops/csrc/pytorch/ms_deform_attn.cpp
@@ -0,0 +1,79 @@
+/*!
+**************************************************************************************************
+* Deformable DETR
+* Copyright (c) 2020 SenseTime. All Rights Reserved.
+* Licensed under the Apache License, Version 2.0 [see LICENSE for details]
+**************************************************************************************************
+* Modified from
+*https://github.com/chengdazhi/Deformable-Convolution-V2-PyTorch/tree/pytorch_1.0.0
+**************************************************************************************************
+*/
+
+#include "pytorch_cpp_helper.hpp"
+
+#ifdef MMCV_WITH_CUDA
+Tensor ms_deform_attn_cuda_forward(const Tensor &value,
+ const Tensor &spatial_shapes,
+ const Tensor &level_start_index,
+ const Tensor &sampling_loc,
+ const Tensor &attn_weight,
+ const int im2col_step);
+
+void ms_deform_attn_cuda_backward(
+ const Tensor &value, const Tensor &spatial_shapes,
+ const Tensor &level_start_index, const Tensor &sampling_loc,
+ const Tensor &attn_weight, const Tensor &grad_output, Tensor &grad_value,
+ Tensor &grad_sampling_loc, Tensor &grad_attn_weight, const int im2col_step);
+
+#endif
+
+Tensor ms_deform_attn_forward(const Tensor &value, const Tensor &spatial_shapes,
+ const Tensor &level_start_index,
+ const Tensor &sampling_loc,
+ const Tensor &attn_weight,
+ const int im2col_step) {
+ if (value.type().is_cuda()) {
+#ifdef MMCV_WITH_CUDA
+ CHECK_CUDA_INPUT(value)
+ CHECK_CUDA_INPUT(spatial_shapes)
+ CHECK_CUDA_INPUT(level_start_index)
+ CHECK_CUDA_INPUT(sampling_loc)
+ CHECK_CUDA_INPUT(attn_weight)
+ return ms_deform_attn_cuda_forward(value, spatial_shapes, level_start_index,
+ sampling_loc, attn_weight, im2col_step);
+#else
+ AT_ERROR("Not compiled with GPU support");
+#endif
+ }
+ AT_ERROR("Not implemented on the CPU");
+}
+
+void ms_deform_attn_backward(const Tensor &value, const Tensor &spatial_shapes,
+ const Tensor &level_start_index,
+ const Tensor &sampling_loc,
+ const Tensor &attn_weight,
+ const Tensor &grad_output, Tensor &grad_value,
+ Tensor &grad_sampling_loc,
+ Tensor &grad_attn_weight, const int im2col_step) {
+ if (value.type().is_cuda()) {
+#ifdef MMCV_WITH_CUDA
+ CHECK_CUDA_INPUT(value)
+ CHECK_CUDA_INPUT(spatial_shapes)
+ CHECK_CUDA_INPUT(level_start_index)
+ CHECK_CUDA_INPUT(sampling_loc)
+ CHECK_CUDA_INPUT(attn_weight)
+ CHECK_CUDA_INPUT(grad_output)
+ CHECK_CUDA_INPUT(grad_value)
+ CHECK_CUDA_INPUT(grad_sampling_loc)
+ CHECK_CUDA_INPUT(grad_attn_weight)
+ ms_deform_attn_cuda_backward(value, spatial_shapes, level_start_index,
+ sampling_loc, attn_weight, grad_output,
+ grad_value, grad_sampling_loc,
+ grad_attn_weight, im2col_step);
+#else
+ AT_ERROR("Not compiled with GPU support");
+#endif
+ } else {
+ AT_ERROR("Not implemented on the CPU");
+ }
+}
\ No newline at end of file
diff --git a/grounded-sam-osx/transformer_utils/mmpose/ops/csrc/pytorch/ms_deform_attn_cuda.cu b/grounded-sam-osx/transformer_utils/mmpose/ops/csrc/pytorch/ms_deform_attn_cuda.cu
new file mode 100644
index 0000000000000000000000000000000000000000..4c2ad396cf68ae470431e2cba362506bc068cc7d
--- /dev/null
+++ b/grounded-sam-osx/transformer_utils/mmpose/ops/csrc/pytorch/ms_deform_attn_cuda.cu
@@ -0,0 +1,360 @@
+/*!
+**************************************************************************************************
+* Deformable DETR
+* Copyright (c) 2020 SenseTime. All Rights Reserved.
+* Licensed under the Apache License, Version 2.0 [see LICENSE for details]
+**************************************************************************************************
+* Modified from
+*https://github.com/chengdazhi/Deformable-Convolution-V2-PyTorch/tree/pytorch_1.0.0
+**************************************************************************************************
+*/
+
+#include
+#include
+#include
+#include
+
+#include
+#include
+#include
+
+template
+void ms_deformable_im2col_cuda(cudaStream_t stream, const scalar_t *data_value,
+ const int64_t *data_spatial_shapes,
+ const int64_t *data_level_start_index,
+ const scalar_t *data_sampling_loc,
+ const scalar_t *data_attn_weight,
+ const int batch_size, const int spatial_size,
+ const int num_heads, const int channels,
+ const int num_levels, const int num_query,
+ const int num_point, scalar_t *data_col) {
+ const int num_kernels = batch_size * num_query * num_heads * channels;
+ const int num_actual_kernels = batch_size * num_query * num_heads * channels;
+ const int num_threads = CUDA_NUM_THREADS;
+ ms_deformable_im2col_gpu_kernel
+ <<>>(
+ num_kernels, data_value, data_spatial_shapes, data_level_start_index,
+ data_sampling_loc, data_attn_weight, batch_size, spatial_size,
+ num_heads, channels, num_levels, num_query, num_point, data_col);
+
+ cudaError_t err = cudaGetLastError();
+ if (err != cudaSuccess) {
+ printf("error in ms_deformable_im2col_cuda: %s\n", cudaGetErrorString(err));
+ }
+}
+
+template
+void ms_deformable_col2im_cuda(
+ cudaStream_t stream, const scalar_t *grad_col, const scalar_t *data_value,
+ const int64_t *data_spatial_shapes, const int64_t *data_level_start_index,
+ const scalar_t *data_sampling_loc, const scalar_t *data_attn_weight,
+ const int batch_size, const int spatial_size, const int num_heads,
+ const int channels, const int num_levels, const int num_query,
+ const int num_point, scalar_t *grad_value, scalar_t *grad_sampling_loc,
+ scalar_t *grad_attn_weight) {
+ const int num_threads =
+ (channels > CUDA_NUM_THREADS) ? CUDA_NUM_THREADS : channels;
+ const int num_kernels = batch_size * num_query * num_heads * channels;
+ const int num_actual_kernels = batch_size * num_query * num_heads * channels;
+ if (channels > 1024) {
+ if ((channels & 1023) == 0) {
+ ms_deformable_col2im_gpu_kernel_shm_reduce_v2_multi_blocks
+ <<>>(
+ num_kernels, grad_col, data_value, data_spatial_shapes,
+ data_level_start_index, data_sampling_loc, data_attn_weight,
+ batch_size, spatial_size, num_heads, channels, num_levels,
+ num_query, num_point, grad_value, grad_sampling_loc,
+ grad_attn_weight);
+ } else {
+ ms_deformable_col2im_gpu_kernel_gm
+ <<